Конвертер DBF файлов онлайн, бесплатное преобразование документов в DBF
| Расширение файла | .dbf |
| Категория файла | documents |
| Программы | Microsoft Access 2016 Microsoft Excel 2016 Microsoft Visual FoxPro Corel Quattro Pro X7 Apache OpenOffice HiBase Group DBF Viewer 2000 Astersoft DBF Manager DBF Viewer Plus DBFView Swiftpage Act! Alpha Software Alpha Anywhere Planamesa NeoOffice (Mac) GTK DBF Editor (Mac & Linux) multisoft FlagShip (Linux) |
| Основная программа | dBase |
| Разработчик | dBASE |
| MIME type | application/dbase application/x-dbase application/dbf application/x-dbf zz-application/zz-winassoc-dbf |
onlineconvertfree.com
Как открыть файл DBF в Excel

Одним из самых популярных форматов хранения структурируемых данных является DBF. Этот формат отличается универсальностью, то есть, его поддерживают множество систем СУБД и других программ. Его используют не только как элемент для хранения данных, но и как средство для обмена ими между приложениями. Поэтому довольно актуальным становится вопрос открытия файлов с данным расширением в табличном процессоре Excel.
Способы открытия файлов DBF в Excel
Следует знать, что и в самом формате DBF существует несколько модификаций:
- dBase II;
- dBase III;
- dBase IV;
- FoxPro и др.
Тип документа тоже влияет на корректность его открытия программами. Но нужно отметить, что Excel поддерживает корректную работу практически со всеми типами файлов DBF.
Следует сказать, что в большинстве случаев Excel справляется с открытием данного формата вполне успешно, то есть, открывает этот документ так же, как данная программа открывала бы, например, свой «родной» формат xls. А вот сохранять файлы в формате DBF стандартными средствами Эксель перестал после версии Excel 2007. Впрочем, это уже тема для отдельного урока.
Урок: Как перевести Excel в DBF
Способ 1: запуск через окно открытия файлов
Одним из самых простых и интуитивно понятных вариантов открытия документов с расширением DBF в Excel является запуск их через окно открытия файлов.
- Запускаем программу Excel и переходим во вкладку «Файл».
- После попадания в вышеуказанную вкладку щелкаем по пункту «Открыть» в меню, расположенном в левой части окна.
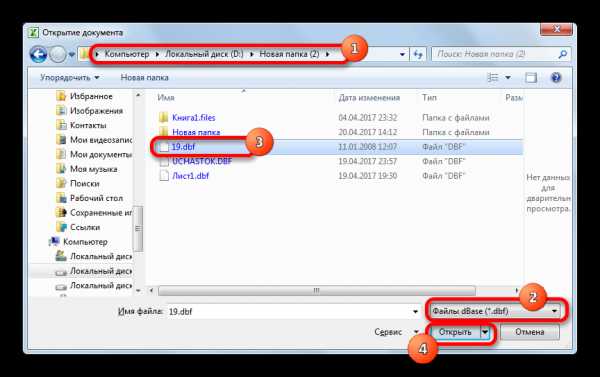
- Открывается стандартное окно открытия документов. Перемещаемся в тот каталог на жестком диске или сменном носителе, где расположен документ, который нужно открыть. В правой нижней части окна в поле переключения расширений файлов выставляем переключатель в позицию «Файлы dBase (*.dbf)» или «Все файлы (*.*)». Это очень важный момент. Многие пользователи не могут открыть файл просто потому, что не выполняют данное требование и элемент с указанным расширением им не виден. После этого документы в формате DBF должны отобразиться в окне, если они присутствуют в данном каталоге. Выделяем документ, который следует запустить, и щелкаем по кнопке «Открыть» в нижнем правом углу окна.
- После последнего действия выбранный документ DBF будет запущен в программе Excel на листе.
Способ 2: открытие двойным щелчком по файлу
Также популярным способом открытия документов является запуск путем двойного щелчка левой кнопкой мыши по соответствующему файлу. Но дело в том, что по умолчанию, если специально не прописывать в системных настройках, программа Эксель не связана с расширением DBF. Поэтому без дополнительных манипуляций таким способом файл открыть не получится. Посмотрим, как это можно сделать.
- Итак, делаем двойной щелчок левой кнопкой мыши по тому файлу формата DBF, который желаем открыть.
- Если на данном компьютере в системных настройках формат DBF не связан ни с одной программой, то запустится окошко, которое сообщит, что не удалось открыть файл. В нем будут предложены варианты действий:
- Поиск соответствий в Интернете;
- Выбор программы из списка установленных программ.
Так как подразумевается, что табличный процессор Microsoft Excel у нас уже установлен, то переставляем переключатель во вторую позицию и щелкаем по клавише «OK» в нижней части окна.

Если же данное расширение уже связано с другой программой, но мы хотим запустить его именно в Excel, то поступаем несколько иначе. Кликаем по наименованию документа правой кнопкой мыши. Запускается контекстное меню. Выбираем в нем позицию «Открыть с помощью». Открывается ещё один список. Если в нем имеется наименование «Microsoft Excel», то кликаем по нему, если же вы такое название не найдете, то переходим по пункту «Выбрать программу…».

Есть ещё один вариант. Кликаем по наименованию документа правой кнопкой мыши. В списке, открывшемся после последнего действия, выбираем позицию «Свойства».

В запустившемся окошке «Свойства» перемещаемся во вкладку «Общие», если запуск произошел в какой-то другой вкладке. Около параметра «Приложение» жмем на кнопку «Изменить…».
- При выборе любого из трех данных вариантов запускается окно открытия файла. Опять же, если в списке рекомендуемых программ в верхней части окна присутствует наименование «Microsoft Excel», то щелкаем по нему, а в обратном случае жмем на кнопку «Обзор…» в нижней части окна.
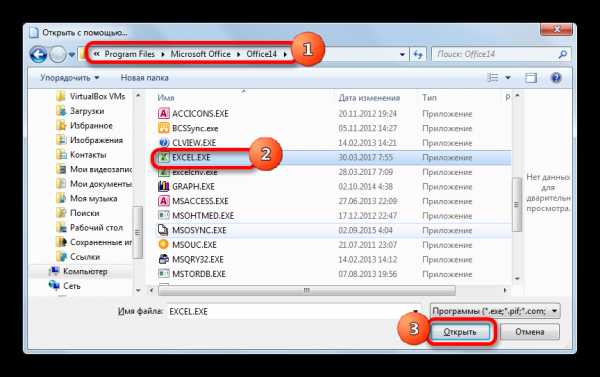
- В случае последнего действия в директории расположения программ на компьютере открывается окошко «Открыть с помощью…» в виде Проводника. В нем нужно перейти в папку, которая содержит файл запуска программы Эксель. Точный адрес пути к этой папки зависит от версии Excel, которая у вас установлена, а точнее от версии пакета Microsoft Office. Общий шаблон пути будет выглядеть следующим образом:
C:\Program Files\Microsoft Office\Office#Вместо символа «#» требуется подставить номер версии вашего офисного продукта. Так для Excel 2010 это будет номер «14», а точный путь к папке будет соответственно выглядеть так:
C:\Program Files\Microsoft Office\Office14Для Excel 2007 номер будет «12», для Excel 2013 – «15», для Excel 2016 – «16».
Итак, перемещаемся в указанную выше директорию и ищем файл с наименованием «EXCEL.EXE». Если у вас в системе не запущено отображение расширений, то его название будет выглядеть просто как «EXCEL». Выделяем данное наименование и жмем на кнопку «Открыть».
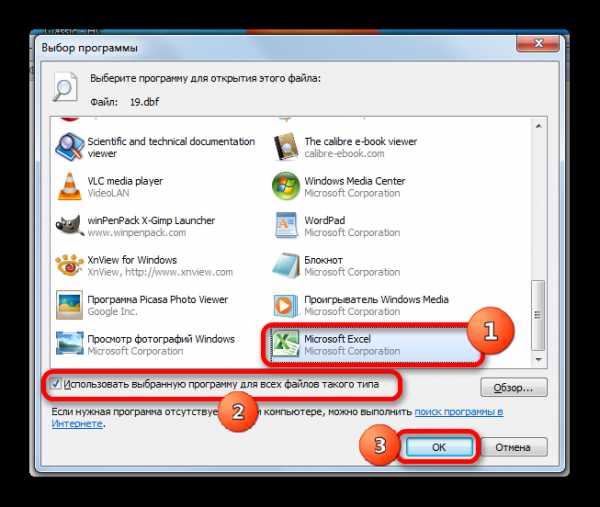
- После этого мы автоматически переносимся опять в окно выбора программы. На этот раз наименование «Microsoft Office» тут точно будет отображаться. Если пользователь желает, чтобы данное приложение всегда по умолчанию открывало документы DBF двойным кликом мышки по ним, то нужно удостовериться, что около параметра «Использовать выбранную программу для всех файлов такого типа» стоит галочка. Если же вы планируете только одиночное открытие документа DBF в Excel, а далее собираетесь открывать данный тип файлов в другой программе, то, наоборот, данную галочку следует снять. После того, как все указанные настройки выполнены, жмем на кнопку «OK».
- После этого документ DBF будет запущен в программе Excel, и если пользователь выставил галочку в соответствующем месте в окне выбора программы, то теперь файлы данного расширения будут открываться в Экселе автоматически после двойного клика по ним левой кнопкой мыши.
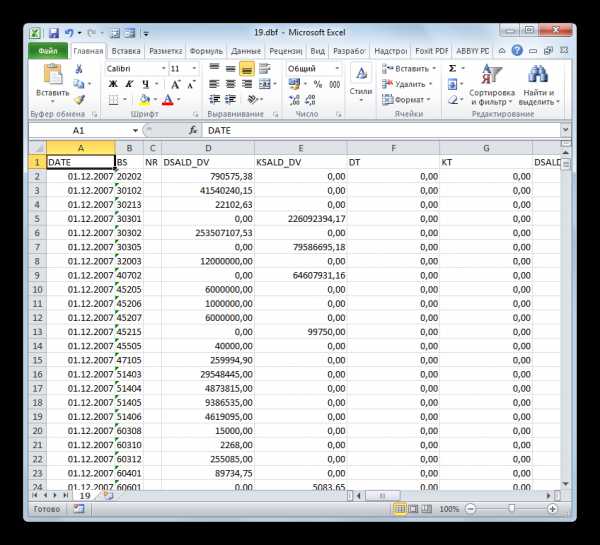
Как видим, открыть файлы DBF в Эксель довольно просто. Но, к сожалению, многие начинающие пользователи путаются и не знают, как это сделать. Например, они не догадываются выставить соответствующий формат в окне открытия документа через интерфейс Эксель. Ещё большую сложность для некоторых юзеров составляет открытие документов DBF двойным щелчком левой кнопки мыши, так как для этого нужно изменить некоторые системные установки через окно выбора программы.
Мы рады, что смогли помочь Вам в решении проблемы.Опишите, что у вас не получилось. Наши специалисты постараются ответить максимально быстро.
Помогла ли вам эта статья?
ДА НЕТlumpics.ru
Файл формата dbf: чем открыть, описание, особенности
Формат DBF применяется к текстовым и числовым файлам Системы Управления Базой Данных (СУБД). В статье рассмотрим особенности формата и чем открыть DBF файл.

Общее описание формата DBF
DBF расшифровывается как DataBase File. Файлы DBF первоначально использовались в dBase II вплоть до dBase Version IV.
Внутри DBF-файл состоит из заголовка с порядковым номером формата и непосредственно информации в виде таблицы установленного размера.
История возникновения
В 1978 году Уэйн Рэтлифф запустил проект формата для СУБД Vulcan. В следующем году программа Вулкан в составе с первой сборкой формата DBF поступила в продажу.
Затем в 1980 году Вулкан получил другое название – dBase II. В программе стала применяться вторая ревизия формата. Право продажи получила фирма Ashton−Tate.
Далее последовали сборки dBase III и dBase III+, использовавшие третью версию DBF. Программы оказались несовместимы по размеру.
Последний (седьмой) вариант формата появился вместе с dBase 7 for Windows.
Как и чем открыть файл DBF расширения
Мы подготовили список инструментов, чем открыть DBF в программе Excel или просмотреть онлайн.
Как открыть формат DBF в Excel
Начнем с электронных таблиц Excel. Программа входит в офисный пакет Microsoft и в ней присутствует функция чтения формата DBF.

Если на компьютере не установлен пакет Office, то скачайте дистрибутив с сайта Microsoft и установите нужные программы.
Чтобы открыть файл DBF в таблице Excel:
- нажмите на документ правой кнопкой мыши, чтобы вызвать контекстное меню;
- наведите курсор мыши на «Открыть» с помощью и переходите в пункт Выбрать программу;
- выберите Microsoft Office Excel, нажмите «Ок»;
- нужный файл откроется в виде таблицы Excel.
Открываем расширение DBF онлайн
Открывается файл формата DBF и на веб-сайте Jobtools. Правда, без редактирования.
Чтобы попасть на страницу просмотрщика:
- в URL-строке браузера введите адрес http://jobtools.ru
- в окне кликните кнопку Файл, затем «Открыть»;
- в поле DBF нажмите «Выбрать файл»;
- найдите нужный документ и щелкните «Загрузить».
Файл отобразится в окне браузера.
Интерфейс простой, нет опций кроме просмотра и постраничной прокрутки.
Чтобы открыть другой файл, нажмите кнопку «Reset» и повторите загрузку.
Чем открыть DBF на компьютере
Кроме стандартного Офиса открываются и правятся файлы DBF через сторонние программы.
Приложение DBF Commander предоставляет распространенные операции с файлами DBF: просмотр, редактура и распечатка файлов. Поддерживается экспорт в форматы CSV, XML, HTML и Excel. Файл кодируется и декодируется алгоритмом AES-256 (Rijndael). Записи удаляются и восстанавливаются, доступна сборка таблицы.
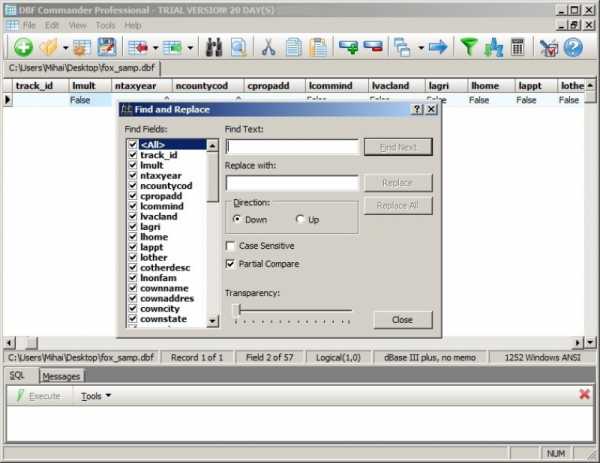
Какие могут быть проблемы с DBF файлом
Случается, что при попытке открыть файл с расширением DBF программа выбивает ошибку File not found (Файл не найден).
В этом случае откройте файл в другой программе. Подойдет Advantage Data Base. Создайте таблицу, импортируйте исходный файл и поменяйте компоненты.
Другой выход – конвертируйте в текстовый формат doc, docx или exl и откройте в офисной программе.
Следующий тип ошибки – file or table does not exist. Это значит, что файл оказался в папке с временной копией. Откройте папку и задайте значение TSession. для переменной Session.PrivateDir.

Если программа выбивает ошибку Table Level Changed,значит,несовместимы компоненты. Установите компоненты TTable. Проверьте, правильно ли связаны файл DBF и хранилище pft.
Если не открывается файл при подключении к базе, откройте соединение и задайте новое имя OleDbCommand cmd = new OleDbCommand («SELECT * FROM Employees») с расширением DBF.
freesoft.ru
DBF чем открыть
Сегодня мы рассмотрим:

DBF – формат файлов, применяемых для баз данных, которые используются для хранения и передачи информации. Если вам необходимо открыть файл с расширением .dbf, то существует несколько программ, позволяющих осуществить эту задачу.
Как открыть файл DBF
Прежде всего, на компьютер должна быть установлено специальное ПО, которое будет поддерживать файлы DBF. Сегодня существует масса программ, справляющихся с этой задачей:
Так как файл DBF – это, по сути, организованная таблица, содержащая в себе текстовую информацию, то ее можно открыть через известную программу для просмотра и редактирования таблиц.
Скачать Microsoft Excel бесплатно
Загрузить программу
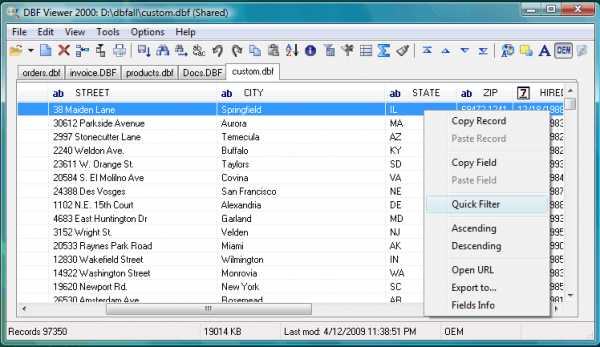
DBF Viewer 2000.
Прекрасная программа, осуществляющая работу с DBF-файлами, которая при достаточно простом интерфейсе имеет множество настроек. Программа имеет статус условно-бесплатной – вам будет предоставлен тестовый период, в течение которого вы сможете понять, подходит вам такая программа или нет.
Скачать DBF Viewer 2000 бесплатно
Загрузить программу
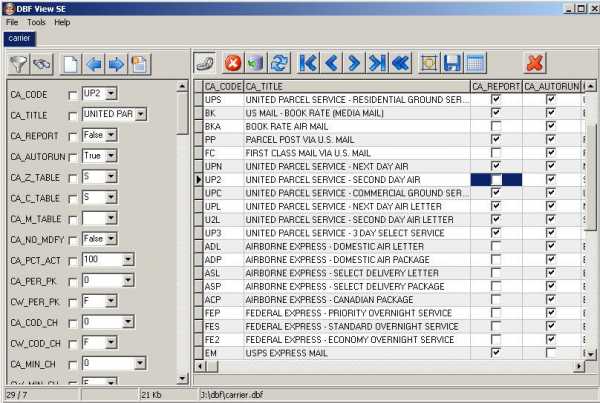
DBF View
Миниатюрная, простая и, главное, бесплатная программа для просмотра и редактирования файлов DBF. Может похвастаться высокой скоростью работы, а также русскоязычным интерфейсом.
Скачать DBF View бесплатно
Загрузить программу
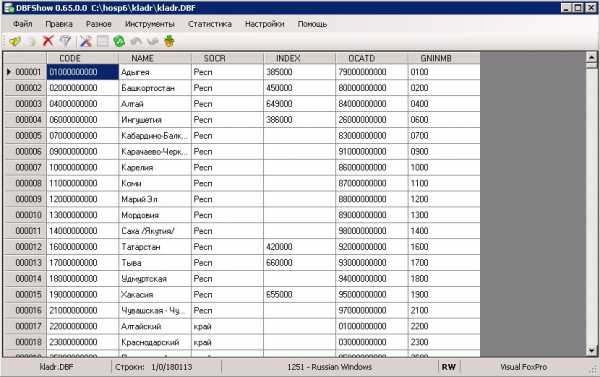
DBFShow
Программа от российского разработчика для просмотра и редактирования DBF-файлов. Имеет весь необходимый набор функций для работы с DBF, но в то же время распространяется бесплатно с официального сайта разработчика.
Скачать DBFShow бесплатно
Загрузить программу
chopen.net
Чем открыть DBF

DBF – файловый формат, созданный для работы с базами данных, отчетами и электронными таблицами. Его структура состоит из заголовка, в котором описывается содержимое, и основной части, где находится весь контент в табличном виде. Отличительная черта этого расширения – возможность взаимодействия с большинством систем управления баз данных.
Программы для открытия
Рассмотрим софт поддерживающий просмотр данного формата.
Читайте также: Конвертирование данных из Microsoft Excel в формат DBF
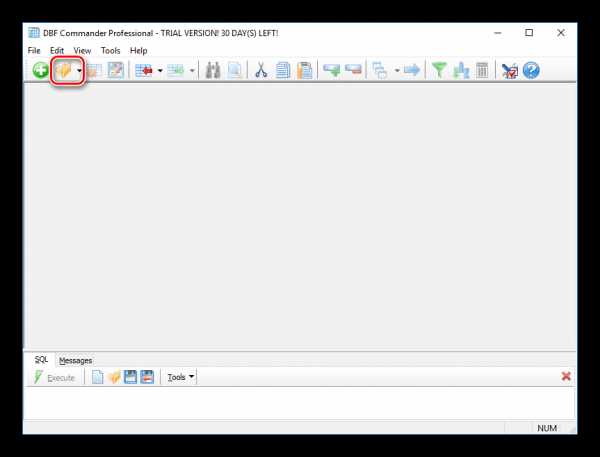
Способ 1: DBF Commander
DBF Commander — многофункциональное приложение для обработки DBF файлов различных кодировок, позволяет производить базовые манипуляции с документами. Распространяется платно, но имеет пробный период.
Скачать DBF Commander с официального сайта
Для открытия:
- Нажмите на вторую пиктограмму или воспользуйтесь сочетанием клавиш Ctrl + O.
- Выделите необходимый документ и кликните «Открыть».
- Пример открытой таблицы:
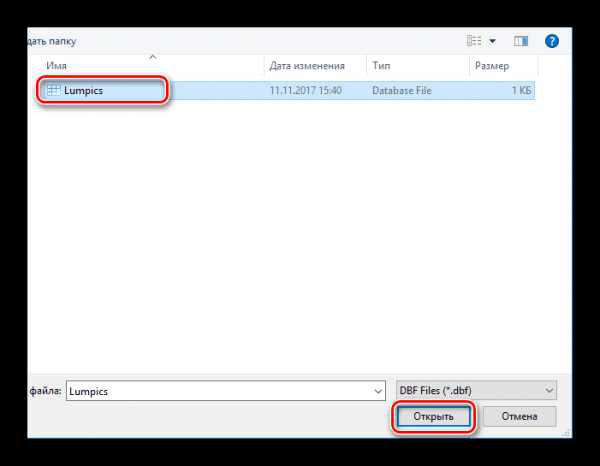
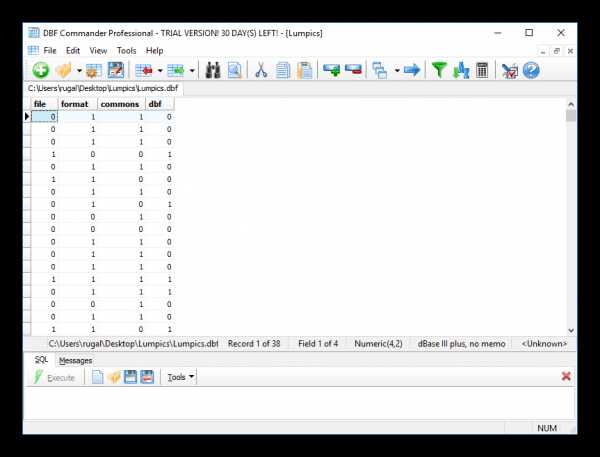
Способ 2: DBF Viewer Plus
DBF Viewer Plus – бесплатный инструмент для просмотра и редактирования DBF, простой и удобный интерфейс представлен на английском языке. Имеет функцию создания собственных таблиц, не требует инсталляции.
Скачать DBF Viewer Plus с официального сайта
Для просмотра:
- Выберите первую пиктограмму «Open».
- Выделите нужный файл и кликните «Открыть».
- Так будет выглядеть результат проделанных манипуляций:
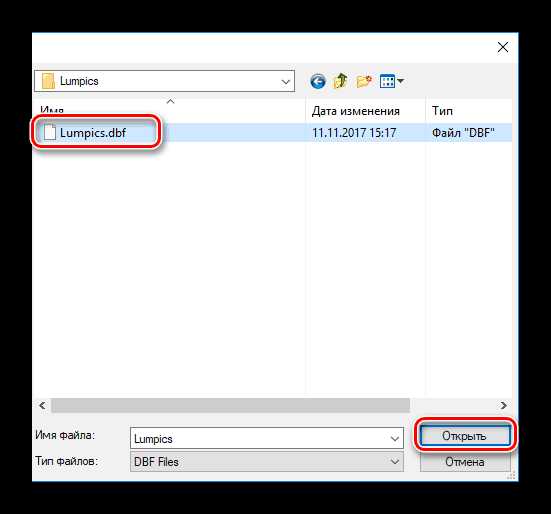
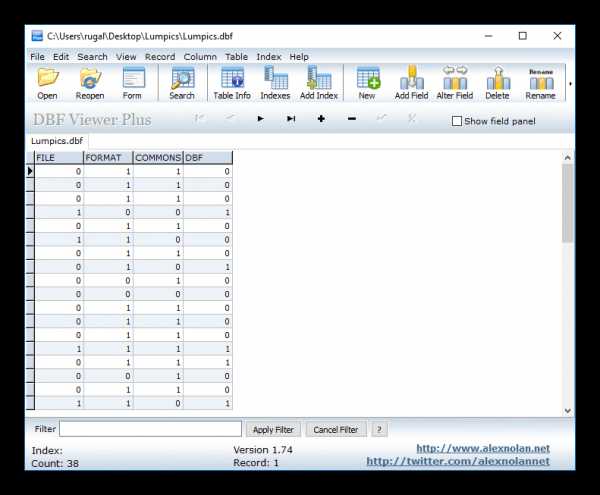
Способ 3: DBF Viewer 2000
DBF Viewer 2000 — программа с довольно упрощённым интерфейсом, позволяет работать с файлами объёмом более 2 ГБ. Имеет русский язык и пробный период использования.
Скачать DBF Viewer 2000 с официального сайта
Чтобы открыть:
- В меню кликните на первую пиктограмму или воспользуйтесь вышеупомянутым сочетанием Ctrl + O.
- Отметьте нужный файл, воспользуйтесь кнопкой «Открыть».
- Так будет выглядеть открытый документ:
Способ 4: CDBF
CDBF — мощный способ редактирования и просмотра баз данных, также позволяет создавать отчеты. Расширить функционал можно, используя дополнительные плагины. Присутствует русский язык, распространяется платно, однако имеет триал версию.
Скачать CDBF с официального сайта
Для просмотра:
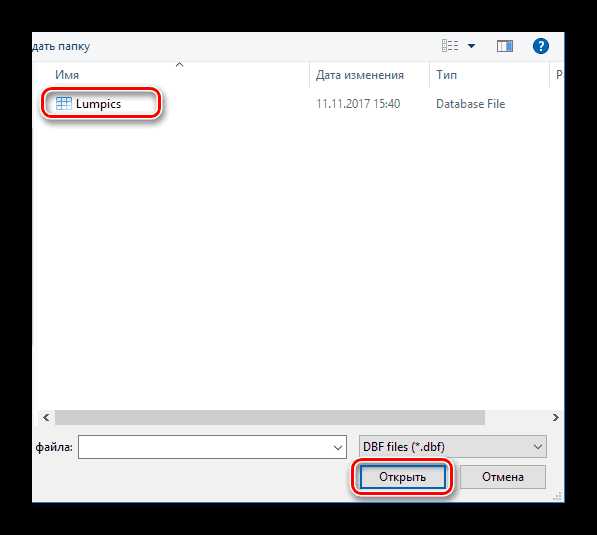
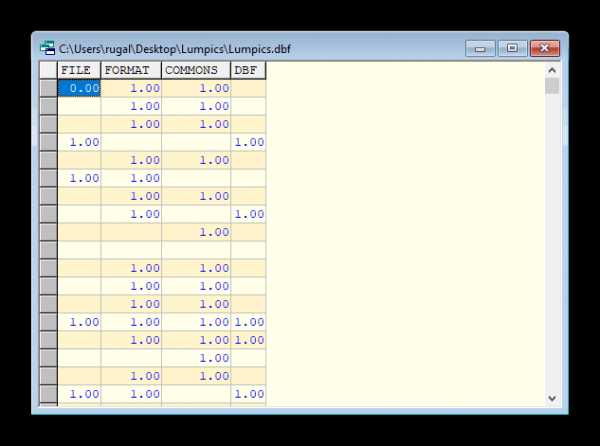
- Нажмите на первую иконку под надписью «File».
- Выделите документ соответствующего расширения, затем кликните «Открыть».
- В рабочей области откроется дочернее окно с результатом.
Способ 5: Microsoft Excel
Excel — один из компонентов пакета программ Microsoft Office, хорошо известного большинству пользователей.
Чтобы открыть:
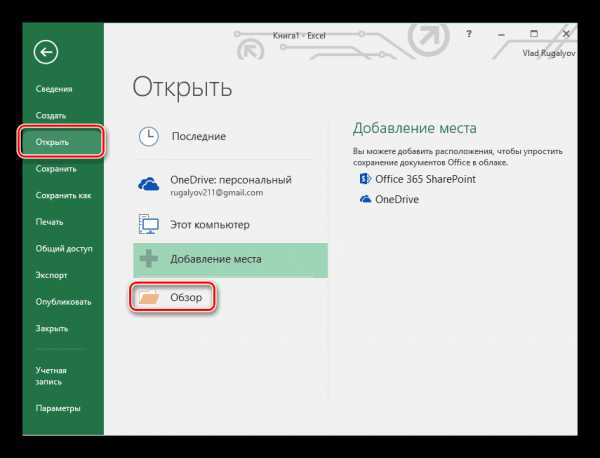
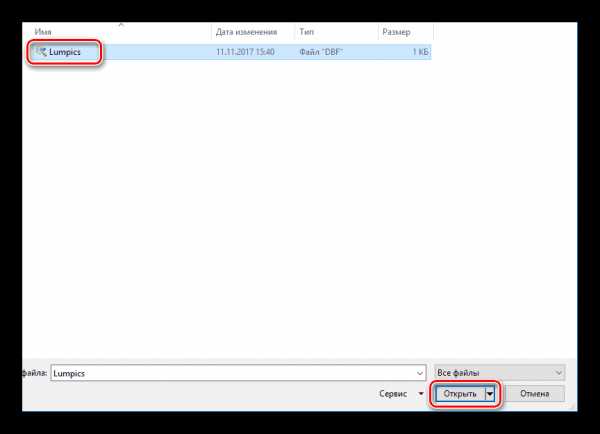
- В левом меню перейдите во вкладку «Открыть», нажмите «Обзор».
- Выделите необходимый файл, кликните «Открыть».
- Сразу же откроется таблица подобного вида:
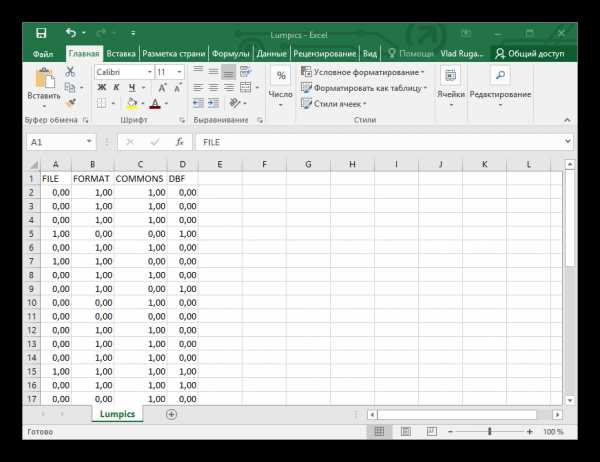
Заключение
Мы рассмотрели основные способы открытия DBF документов. Из подборки выделяется лишь DBF Viewer Plus — полностью бесплатное ПО, в отличие от остальных, которые распространяются на платной основе и имеют только пробный период.
Мы рады, что смогли помочь Вам в решении проблемы.Опишите, что у вас не получилось. Наши специалисты постараются ответить максимально быстро.
Помогла ли вам эта статья?
ДА НЕТlumpics.ru
Конвертировать DBF в TXT онлайн, бесплатно преобразовать .dbf в .txt
| Расширение файла | .dbf |
| Категория файла | documents |
| Программы | Microsoft Access 2016 Microsoft Excel 2016 Microsoft Visual FoxPro Corel Quattro Pro X7 Apache OpenOffice HiBase Group DBF Viewer 2000 Astersoft DBF Manager DBF Viewer Plus DBFView Swiftpage Act! Alpha Software Alpha Anywhere Planamesa NeoOffice (Mac) GTK DBF Editor (Mac & Linux) multisoft FlagShip (Linux) |
| Основная программа | dBase |
| Разработчик | dBASE |
| MIME type | application/dbase application/x-dbase application/dbf application/x-dbf zz-application/zz-winassoc-dbf |
onlineconvertfree.com
формат DBF dBASE
Все конвертеры
Формат файлов DBF Database
Программное обеспечение для управления базами данных dBASE использовало расширение DBF для сохранения стандартных файлов базы данных. Благодаря популярности этого формата dBASE — не единственная программа для работы с базами данных, которая поддерживает формат DBF. Другие приложения «xBASE» также поддерживают этот формат. Популярность этого формата основана на простоте его структуры и том факте, что формат DBF был одним из самых ранних форматов этого типа, адаптированным сообществом специалистов по базами данных.
Технические сведения о файлах DBF
Содержимое файла DBF состоит из нескольких наборов данных, которые организованы и хранятся в массивах. В качестве формата DBF был внедрен в dBASE II. Он использовался и в последующих версиях dBASE — III, III + и IV. DBF-файлы были одним из первых файлов баз данных с заголовком, который позволяет программам, изначально не владеющим информацией о структуре данных в определенном файле, читать такие файлы. Таким образом, их можно открыть в Microsoft Excel, OpenOffice Calc и многих других приложениях.
Дополнительная информация о формате DBF
| Расширение файла | .dbf |
| Категория файлов | Database |
| Связанные программы | dBase Microsoft Access 2016 Microsoft Excel 2016 Microsoft Visual FoxPro Corel Quattro Pro X7 Apache OpenOffice HiBase Group DBF Viewer 2000 Astersoft DBF Manager DBF Viewer Plus DBFView Swiftpage Act! Alpha Software Alpha Anywhere Planamesa NeoOffice (Mac) GTK DBF Editor (Mac & Linux) multisoft FlagShip (Linux) |
| Полезные ссылки | Более подробную информацию о DBF можно найти здесь |
| Разработчики | dBASE |
www.online-convert.com

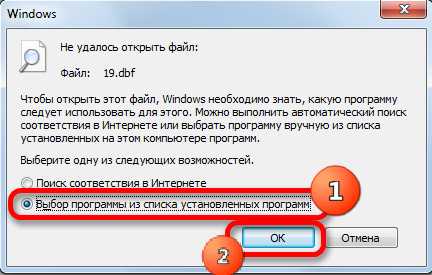
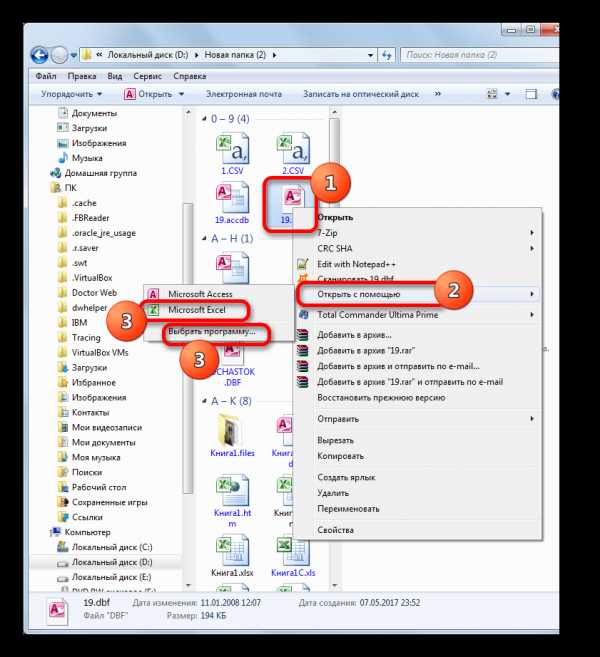
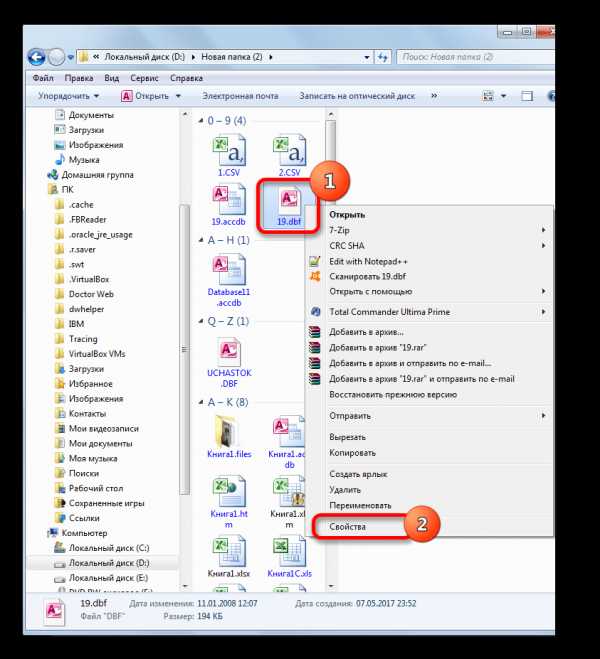








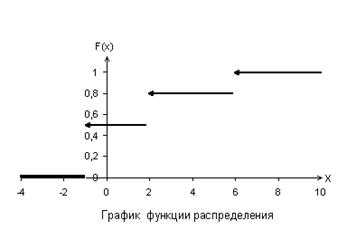
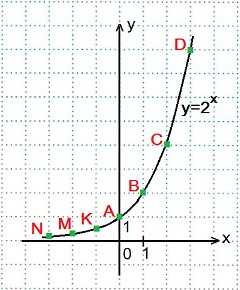 при х=0, х=±1, х=±2, х=±3.
при х=0, х=±1, х=±2, х=±3.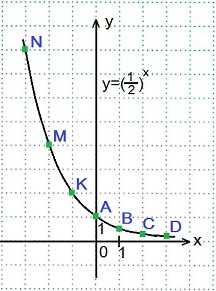 x=0, y=(½)0=1; Точка A.
x=0, y=(½)0=1; Точка A.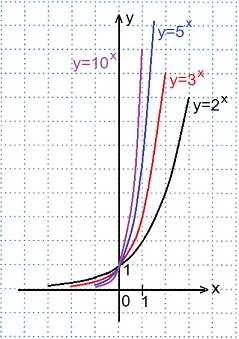 Переменная х может принимать любое значение (D (y)=R), при этом значение у всегда будет больше нуля (E (y)=R+).
Переменная х может принимать любое значение (D (y)=R), при этом значение у всегда будет больше нуля (E (y)=R+).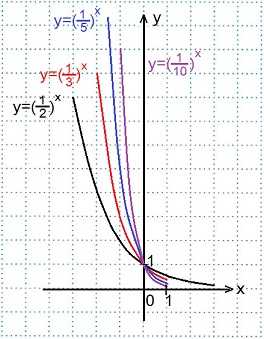 Переменная х может принимать любое значение: D (y)=R, при этом область значений функции: E (y)=R+.
Переменная х может принимать любое значение: D (y)=R, при этом область значений функции: E (y)=R+.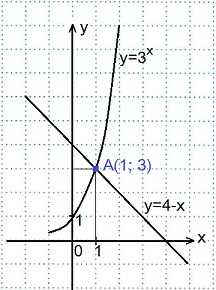 В одной координатной плоскости построим графики функций: у=3х и у=4-х.
В одной координатной плоскости построим графики функций: у=3х и у=4-х.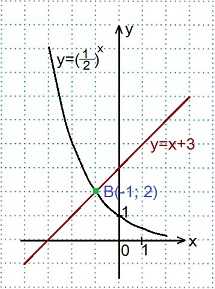


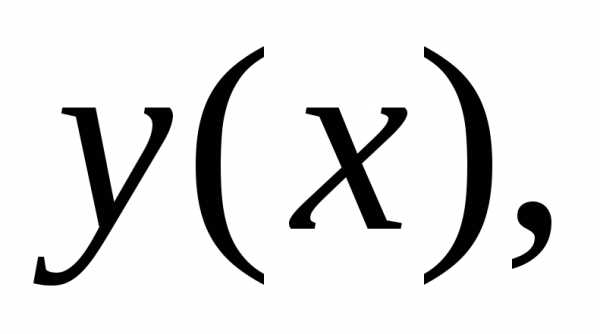 удовлетворяющей начальному условию:.
(1.2)
удовлетворяющей начальному условию:.
(1.2)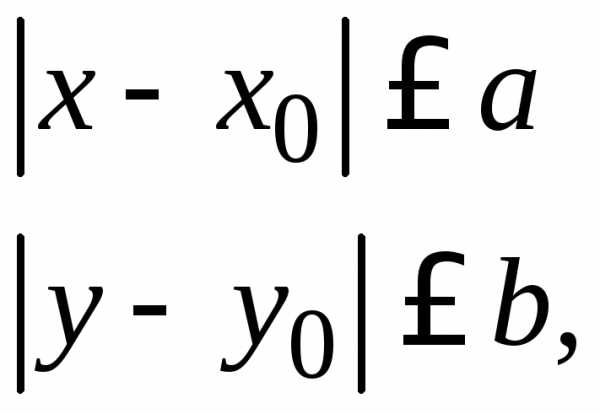 (1.3)
(1.3)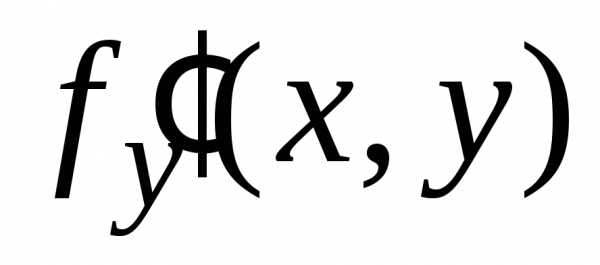 ,
то приможно принять.
,
то приможно принять. [х0,
х00+Н]
найти решение уравнения (1.1) при начальном
условии (1.2).
[х0,
х00+Н]
найти решение уравнения (1.1) при начальном
условии (1.2). вычисляется
в каждой точке
вычисляется
в каждой точке 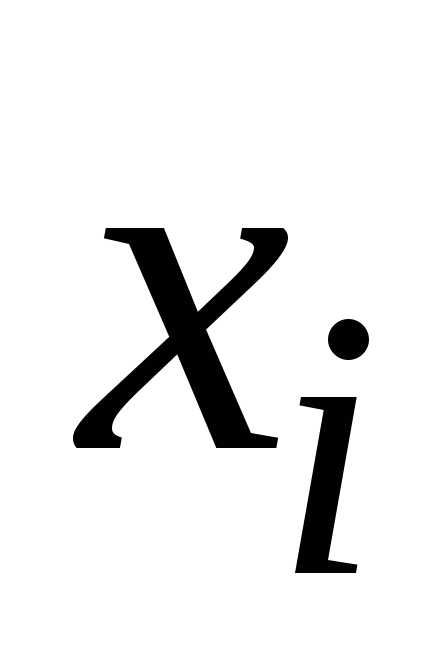 .
При этом, как правило, для вычисления
значения
.
При этом, как правило, для вычисления
значения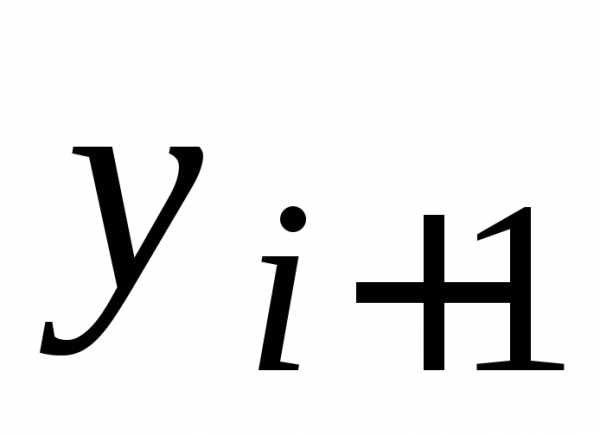 используется уже вычисленное значение
используется уже вычисленное значение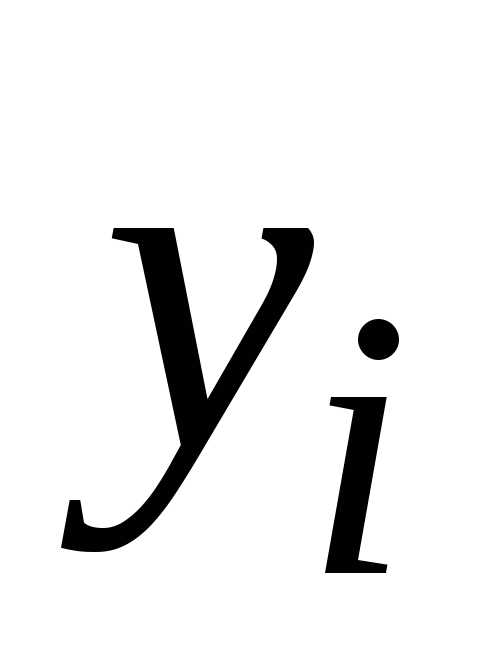 .
.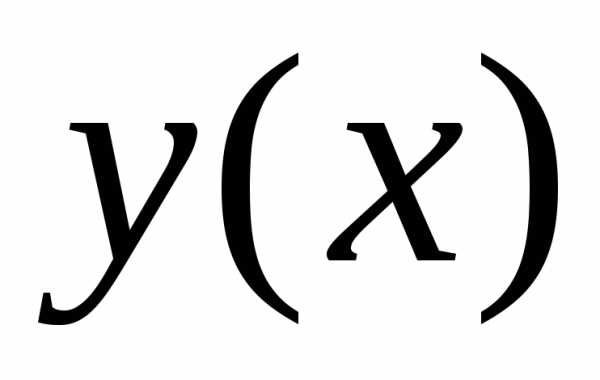 ,
получают как предел последовательности
функций
,
получают как предел последовательности
функций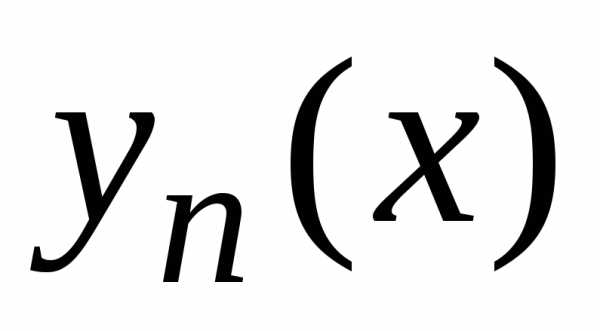 ,
которые находятся по рекурсивной формуле
,
которые находятся по рекурсивной формуле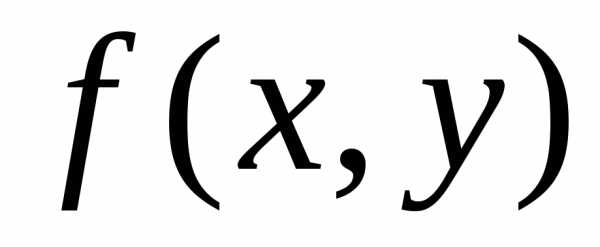 в некотором замкнутом прямоугольнике
в некотором замкнутом прямоугольнике ,
содержащем множество точек
,
содержащем множество точек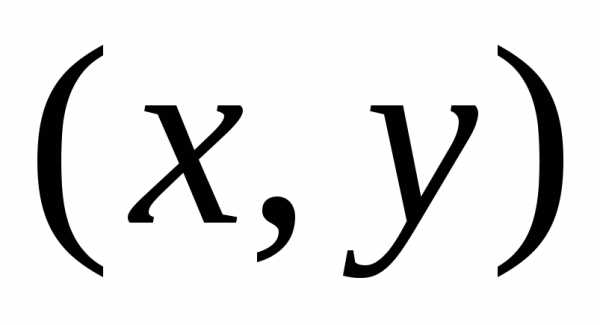 ,
для которых выполняются условияудовлетворяет условию Липшица по
,
для которых выполняются условияудовлетворяет условию Липшица по :
: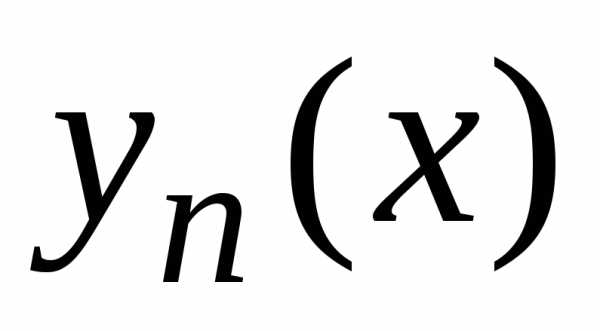 сходятся на некотором отрезкек точному решению задачи Коши.
сходятся на некотором отрезкек точному решению задачи Коши.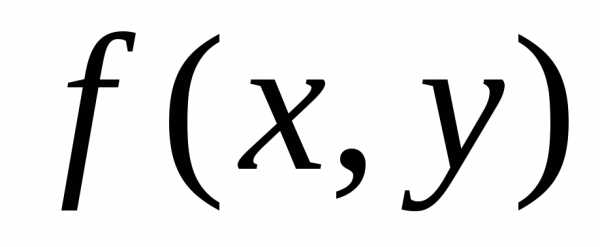 непрерывна в области
непрерывна в области ,
то оценка погрешности приближенного
решения
,
то оценка погрешности приближенного
решения 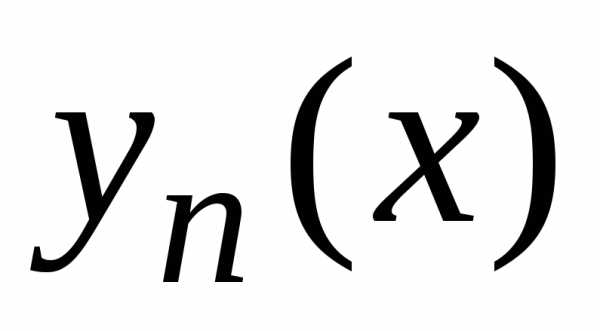 на отрезке дается неравенством:
на отрезке дается неравенством: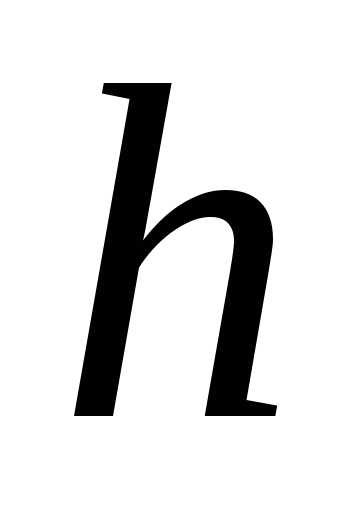 определяется из условия:
определяется из условия: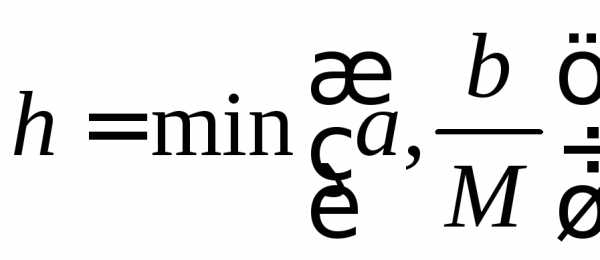 .
.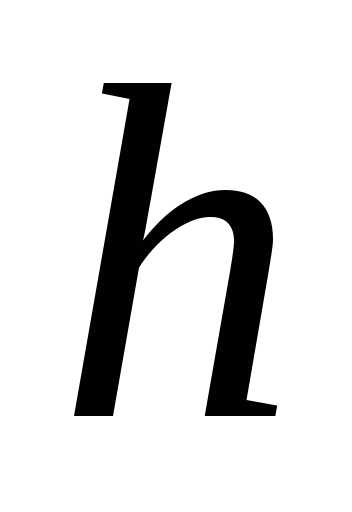 ,
построим систему равноотстоящих узлов,
().
,
построим систему равноотстоящих узлов,
().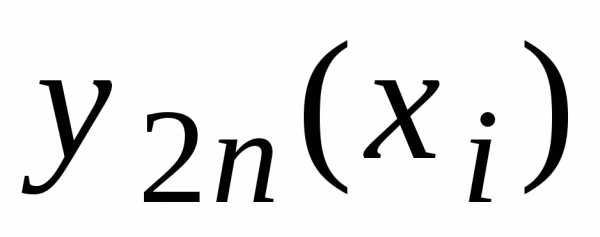 – вычисленное значение
– вычисленное значение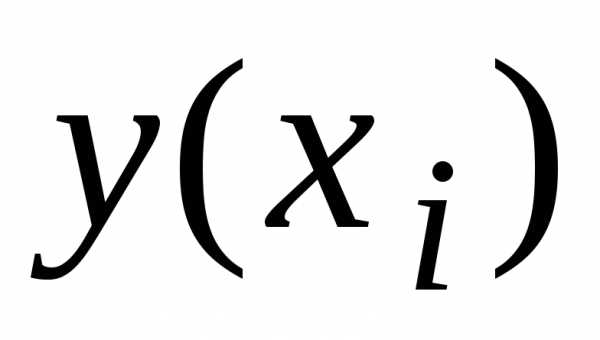 с шагом
с шагом ,
а
,
а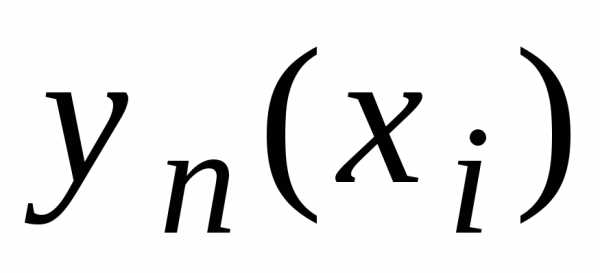 – соответствующее узловое значение,
полученное с шагомh,
то для ориентировочной оценки погрешности
последнего значения можно использовать
формулу:
– соответствующее узловое значение,
полученное с шагомh,
то для ориентировочной оценки погрешности
последнего значения можно использовать
формулу: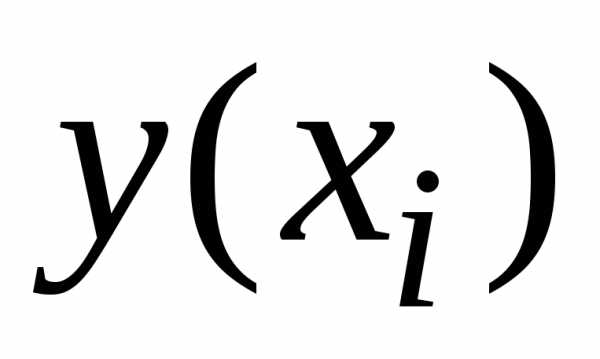 – точное
значение решения в узле
– точное
значение решения в узле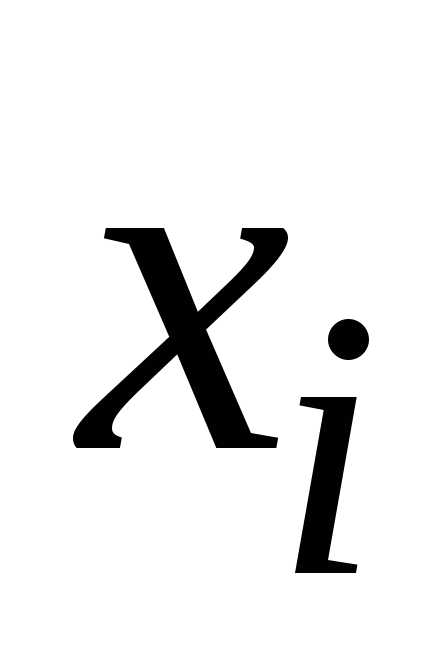 ,
,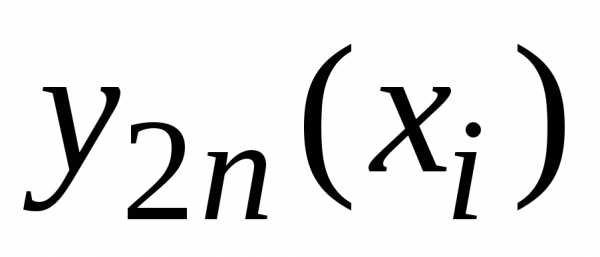 ,
,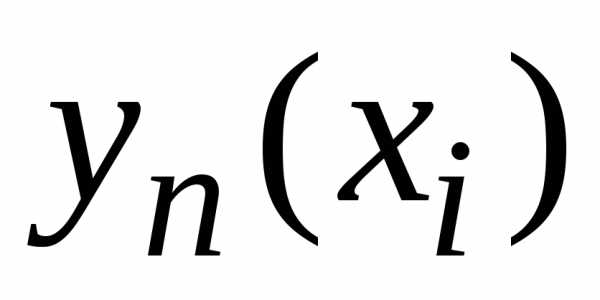 –
приближенные значения решения в узле
–
приближенные значения решения в узле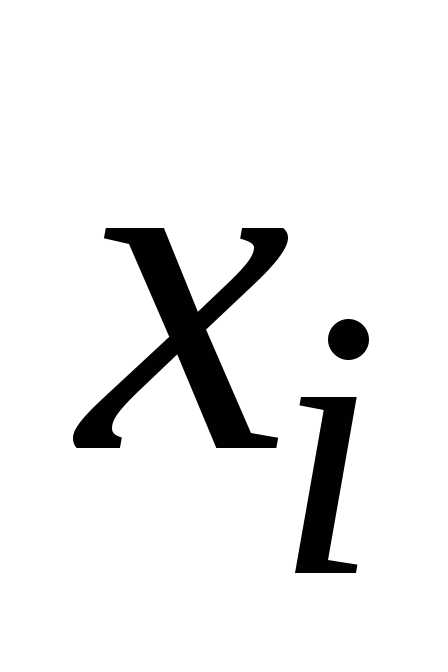 с шагом
с шагом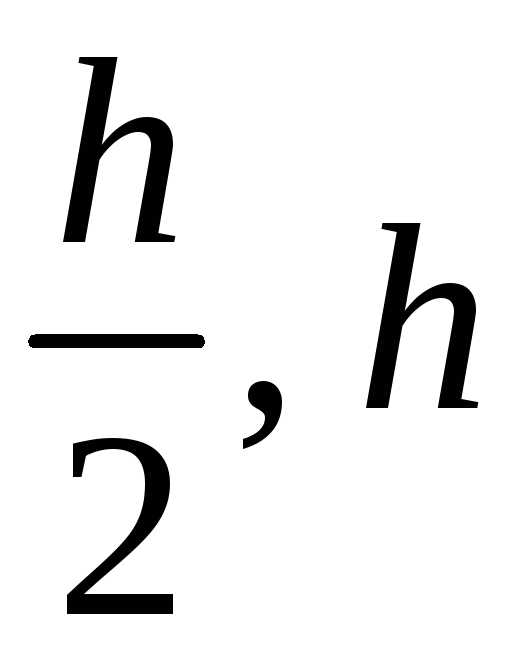 – соответственно.
– соответственно.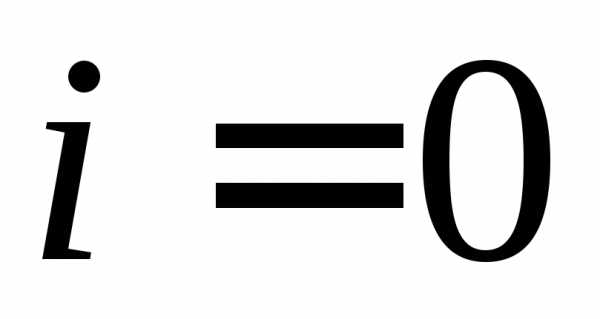 ),
либо получено как результат предыдущего
шага. Для получения следующего значения
),
либо получено как результат предыдущего
шага. Для получения следующего значения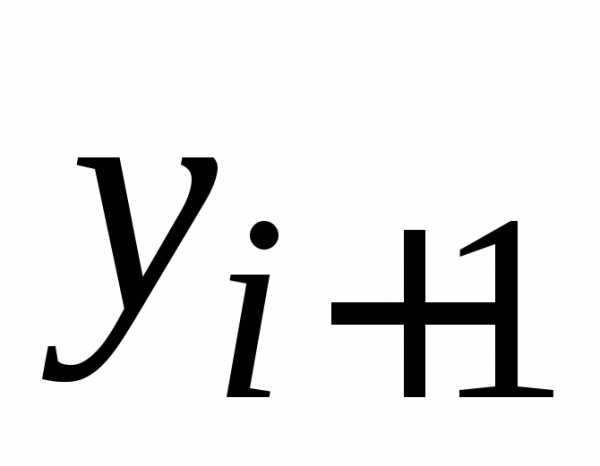 вначале вычисляются числа:
вначале вычисляются числа: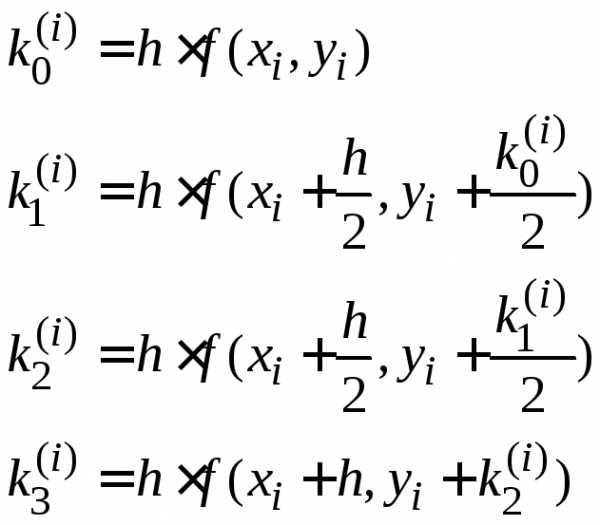 ,
(1.6)
,
(1.6) –
вычисленное значение
–
вычисленное значение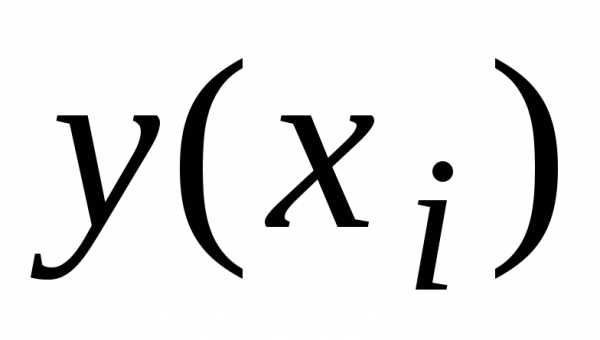 с
шагом
с
шагом ,
а
,
а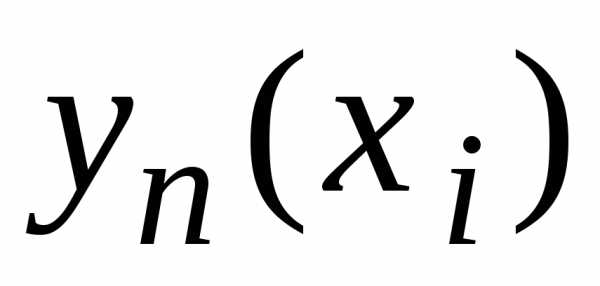 –
соответствующее узловое значение,
полученное с шагомh,
–
соответствующее узловое значение,
полученное с шагомh,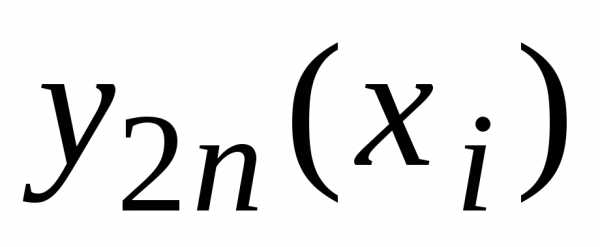 можно использовать формулу:
можно использовать формулу: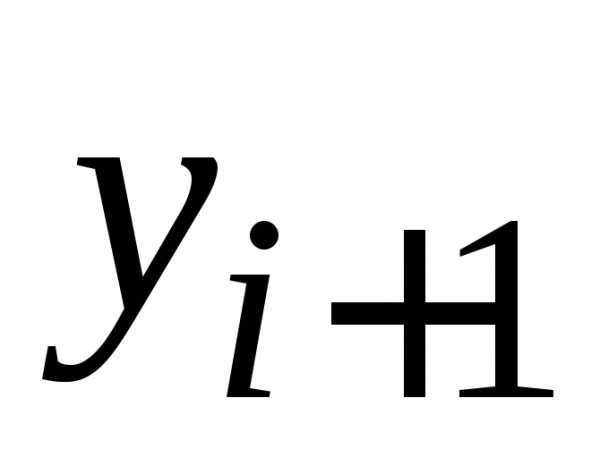 требуется не одно предыдущее значение
требуется не одно предыдущее значение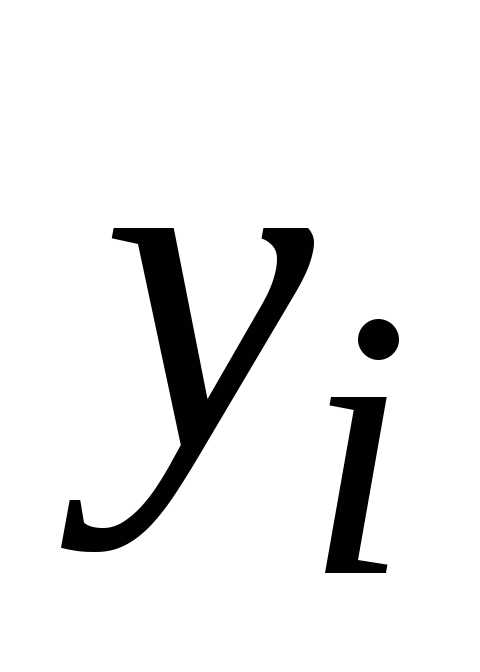 ,
а несколько. Так, дляk-шагового
метода требуются значения:
.
,
а несколько. Так, дляk-шагового
метода требуются значения:
.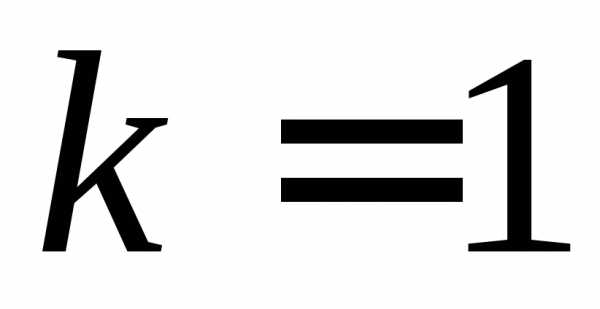 и совпадает с рассмотренным ранее
методом Эйлера первого порядка. В
практических расчетах чаще используется
метод Адамса, имеющий четвертый порядок
точности и использующий на каждом шаге
результаты предыдущих четырех значений
приближенного решения. Именно этот
метод называют обычно методом Адамса.
Рассмотрим расчетные формулы для данного
метода.
и совпадает с рассмотренным ранее
методом Эйлера первого порядка. В
практических расчетах чаще используется
метод Адамса, имеющий четвертый порядок
точности и использующий на каждом шаге
результаты предыдущих четырех значений
приближенного решения. Именно этот
метод называют обычно методом Адамса.
Рассмотрим расчетные формулы для данного
метода.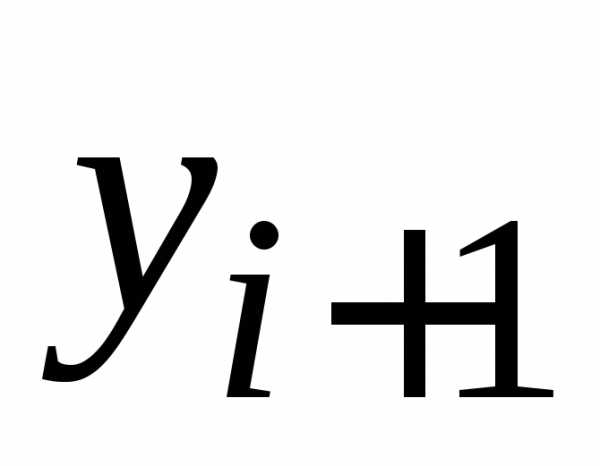 по методу Адамса имеет вид:
по методу Адамса имеет вид: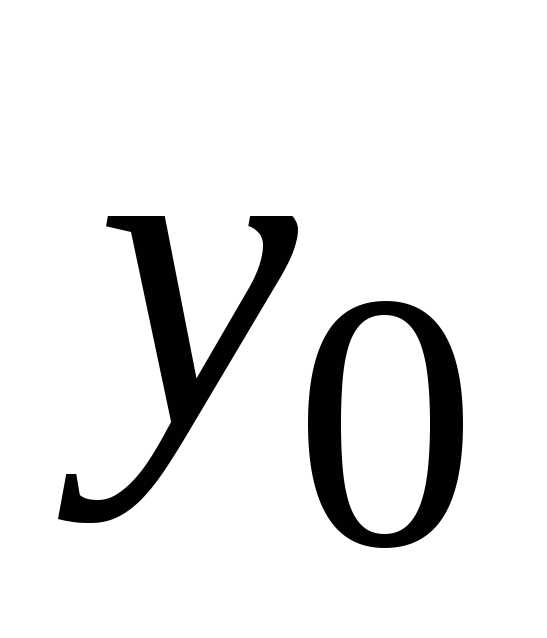 ,
надо вычислить еще
,
надо вычислить еще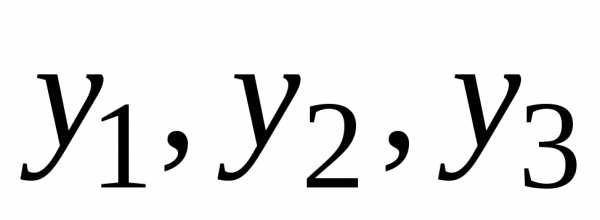 каким-либо другим способом (например,
методом Рунге–Кутта), что существенно
усложняет алгоритм. Кроме того, метод
Адамса не позволяет (без усложнения
формул) изменить шагh в процессе
счета.
каким-либо другим способом (например,
методом Рунге–Кутта), что существенно
усложняет алгоритм. Кроме того, метод
Адамса не позволяет (без усложнения
формул) изменить шагh в процессе
счета.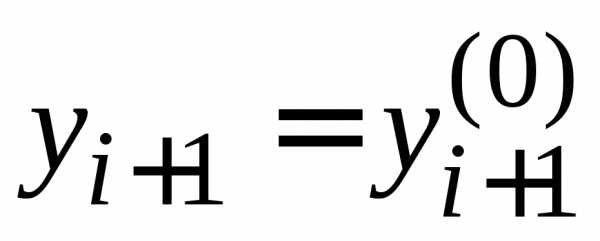 в новом узле;
в новом узле;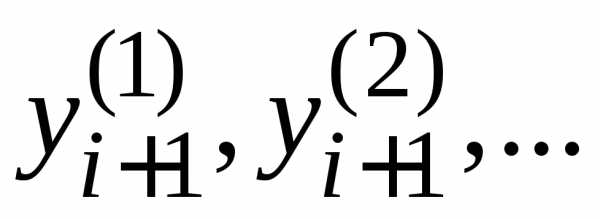
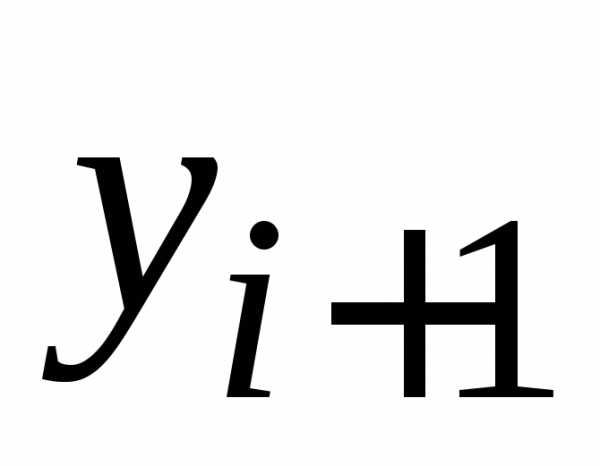 .
.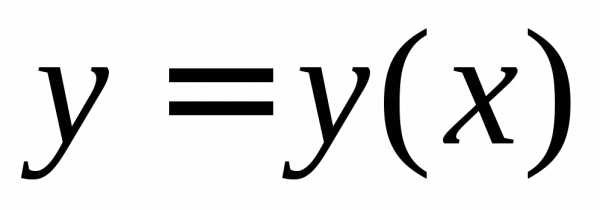 ,
которая внутри отрезка
,
которая внутри отрезка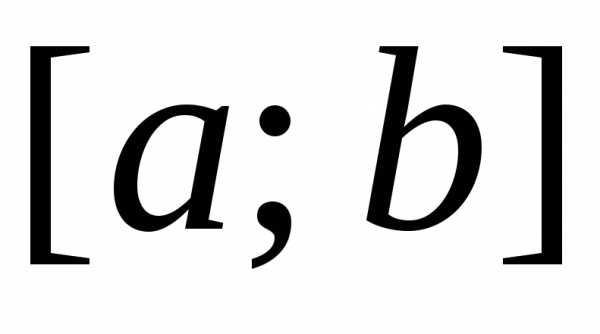 удовлетворяет
уравнению (110), а на концах отрезка —
краевым условиям
удовлетворяет
уравнению (110), а на концах отрезка —
краевым условиям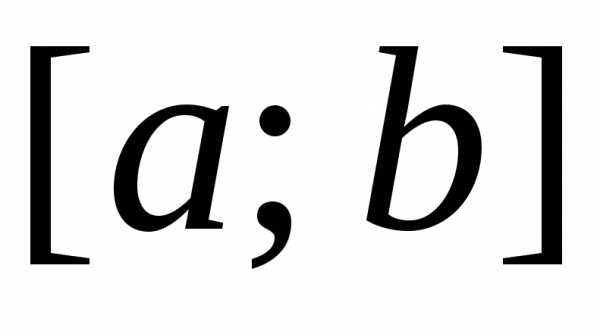 функции,–
заданные постоянные, причеми.
функции,–
заданные постоянные, причеми.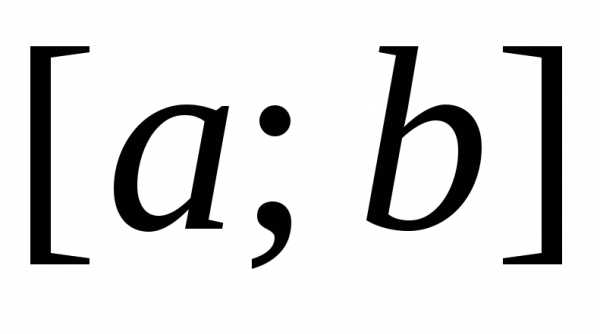 наn равных частей с шагом
наn равных частей с шагом 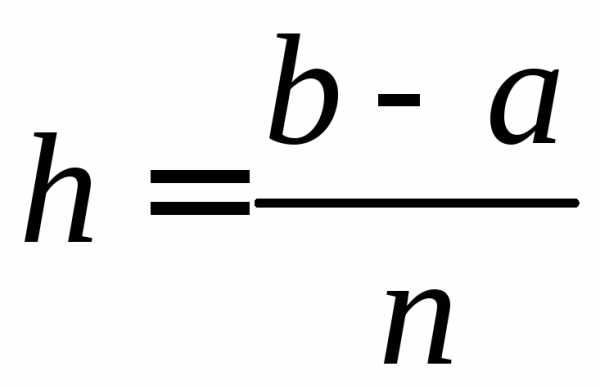 и получаем точки,
в которых требуется найти искомые
значения.
и получаем точки,
в которых требуется найти искомые
значения.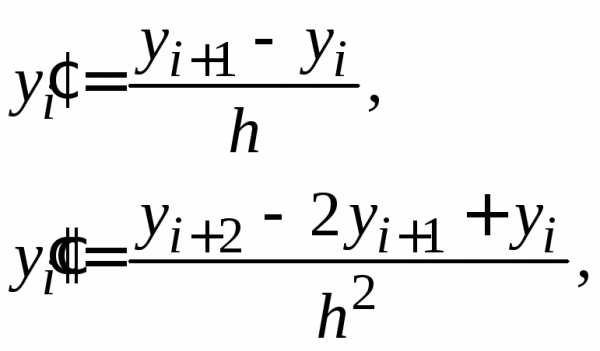
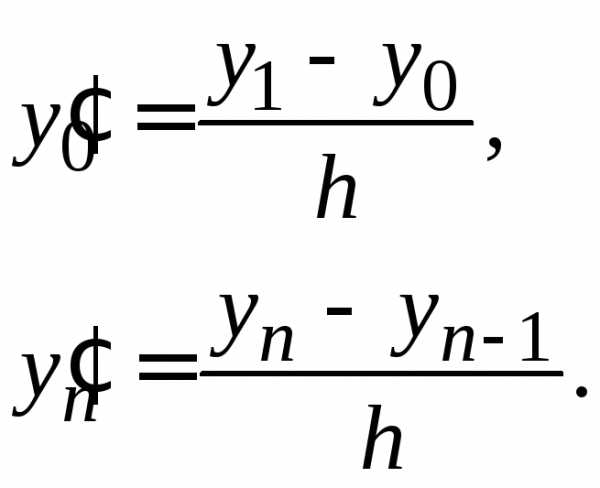
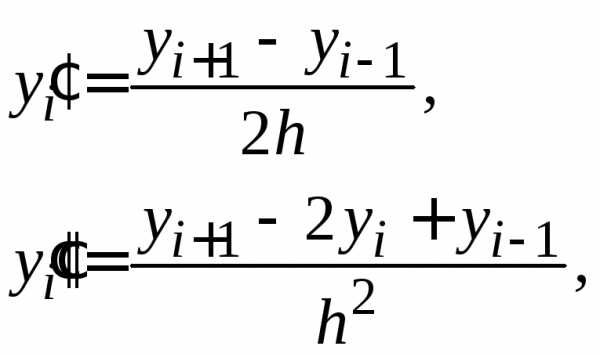
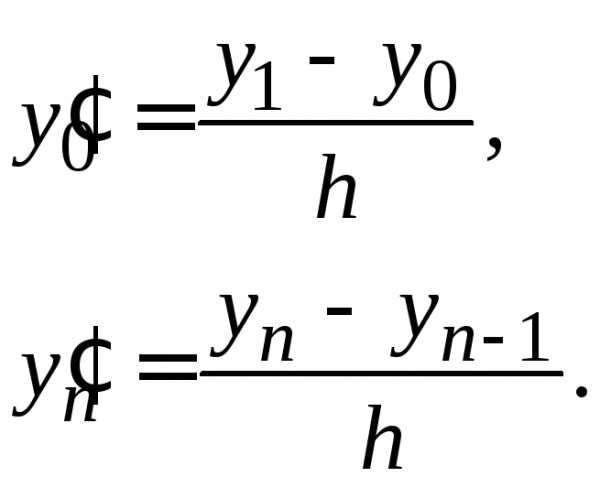
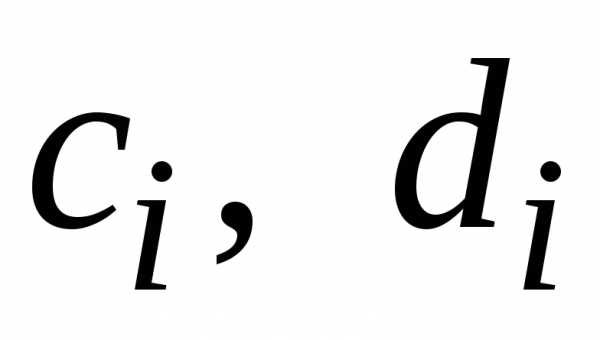 последовательно вычисляются по формулам:
последовательно вычисляются по формулам: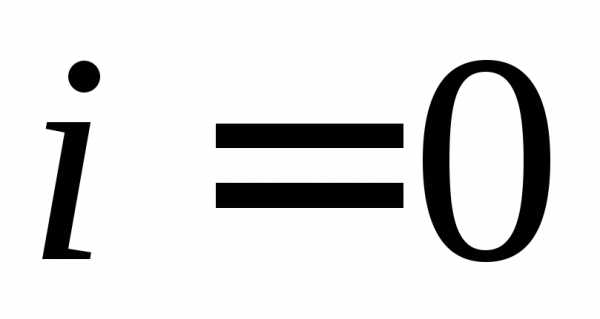
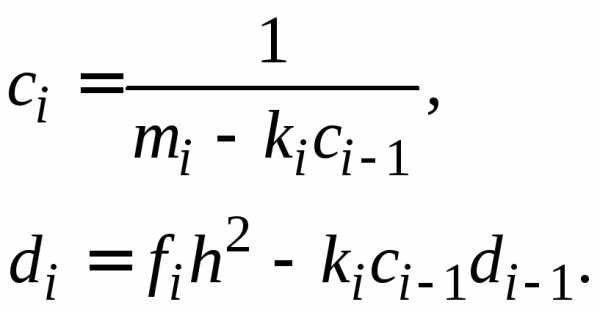
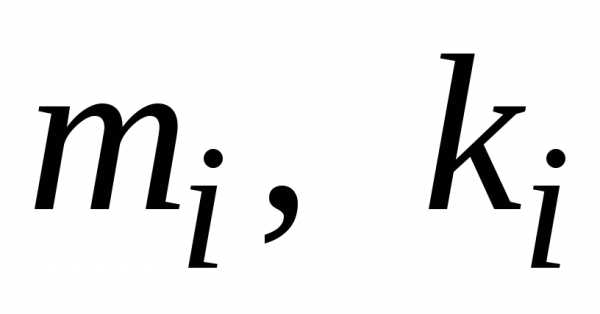 .
Находим
.
Находим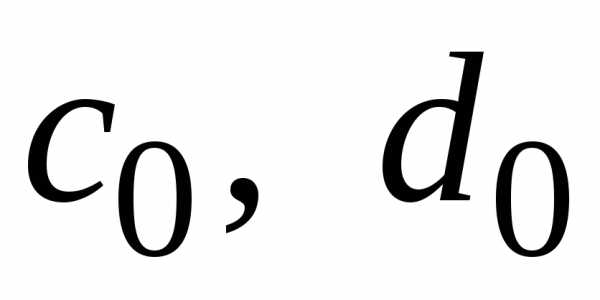 по формулам (1.25). Затем вычисляем
по формулам (1.25). Затем вычисляем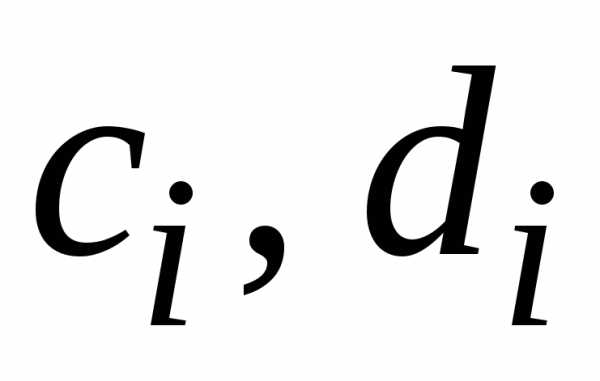 по формулам (1.26) для
по формулам (1.26) для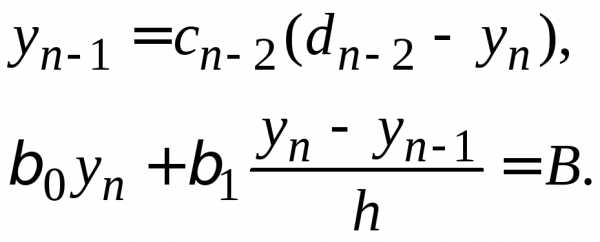
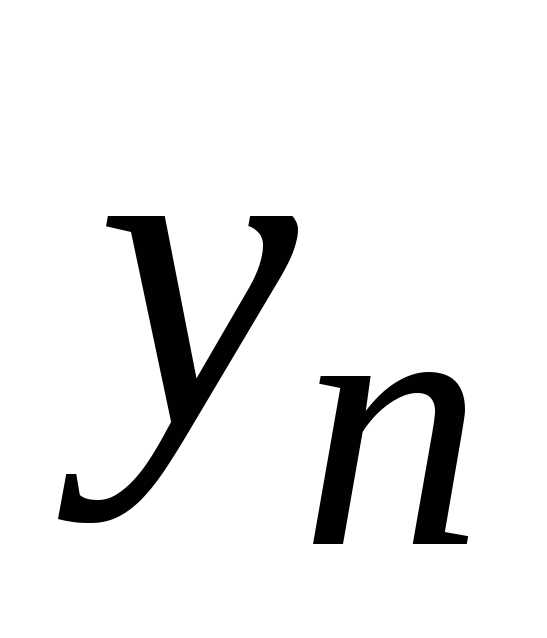 ,
будем иметь
,
будем иметь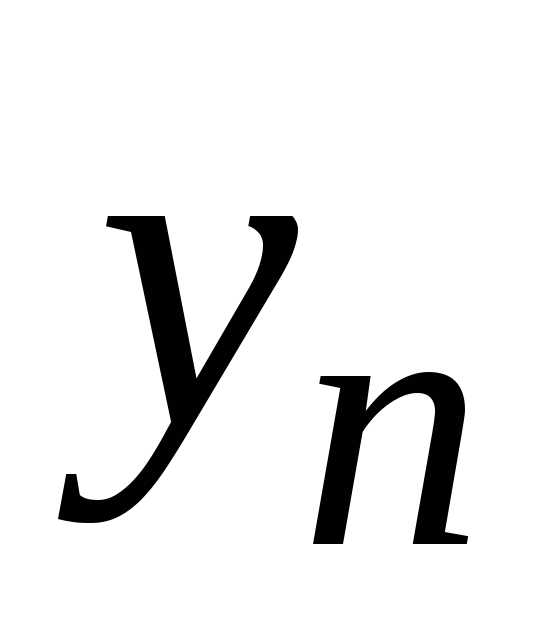 .
Затем вычисляем значения,
последовательно применяя рекуррентные
формулы (1.22):
.
Затем вычисляем значения,
последовательно применяя рекуррентные
формулы (1.22):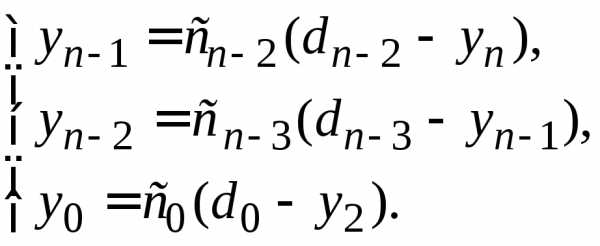
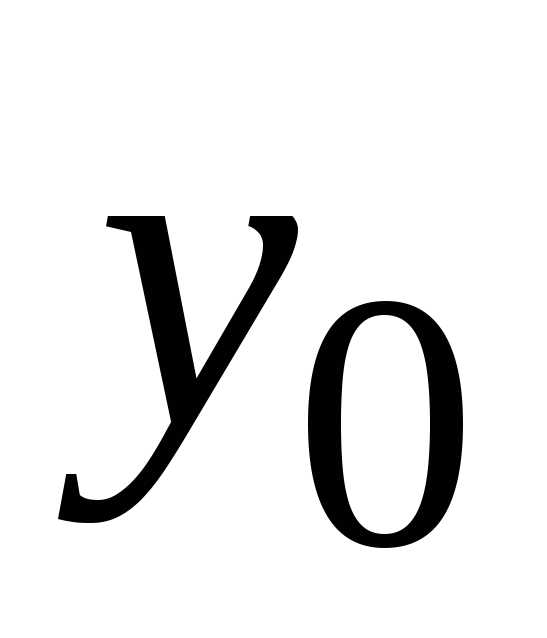 находим из предпоследнего уравнения
системы (1.16):
находим из предпоследнего уравнения
системы (1.16):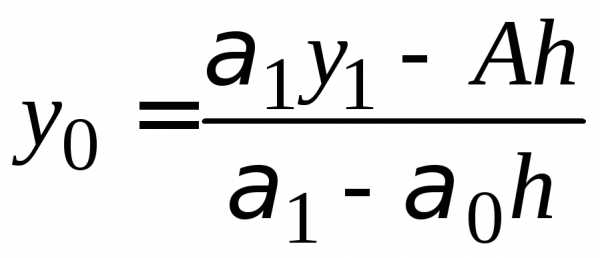
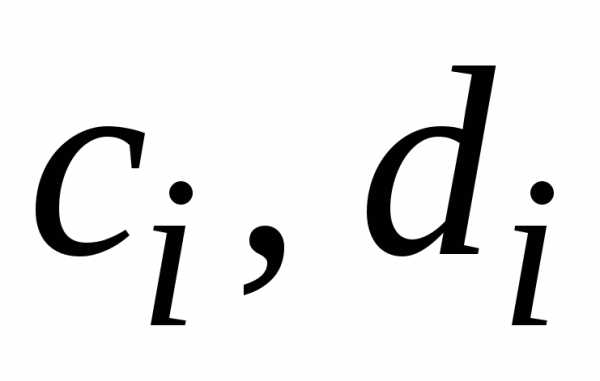 в порядке возрастания индекса
в порядке возрастания индекса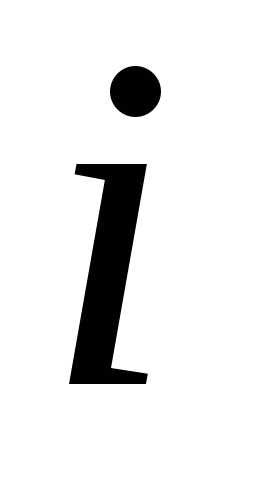 .
При этом для вычисления значений
.
При этом для вычисления значений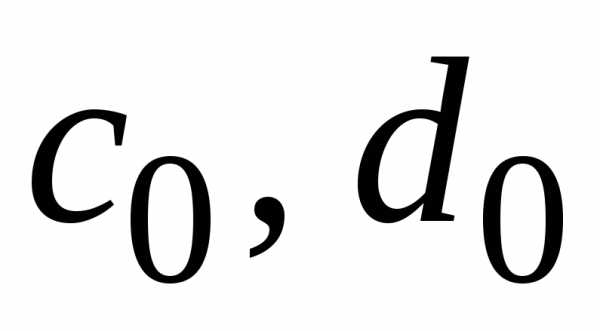 используется краевое условие на левом
конце отрезка интегрирования. Затем на
первом шаге обратного хода происходит
согласование полученных чиселс краевым условием на правом конце
отрезка интегрирования, после чего
последовательно получаются значения
искомой функции
используется краевое условие на левом
конце отрезка интегрирования. Затем на
первом шаге обратного хода происходит
согласование полученных чиселс краевым условием на правом конце
отрезка интегрирования, после чего
последовательно получаются значения
искомой функции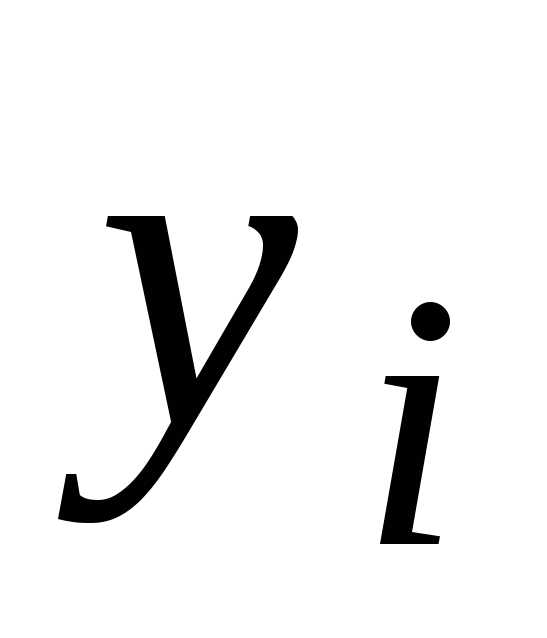 в порядке убывания индекса
в порядке убывания индекса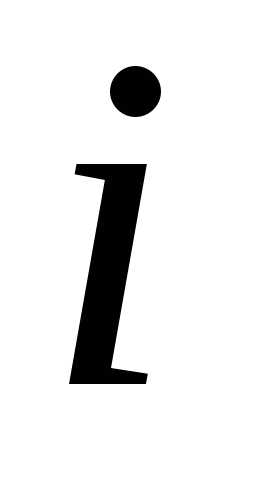 .
.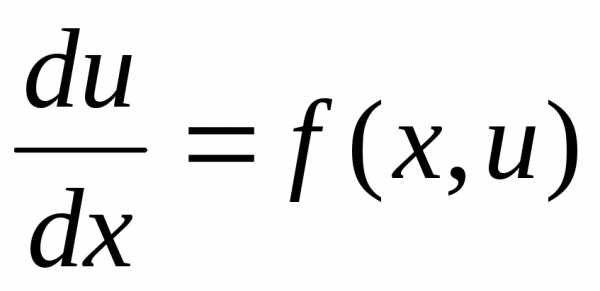 и начальное
условие:
.
и начальное
условие:
. находятся приближенно в виде дискретной
числовой последовательности {yi}, где
находятся приближенно в виде дискретной
числовой последовательности {yi}, где 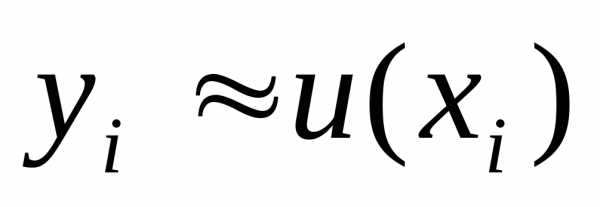 .
.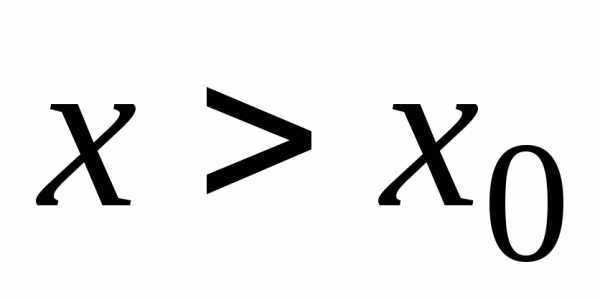 ,,
тогда,
,,
тогда,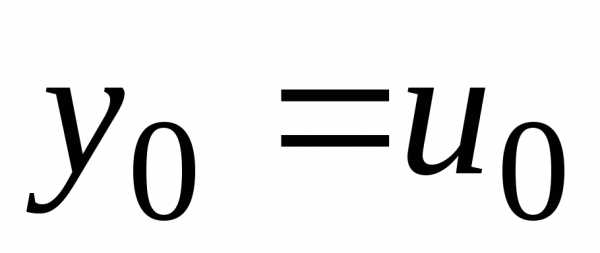 ,,.
,,.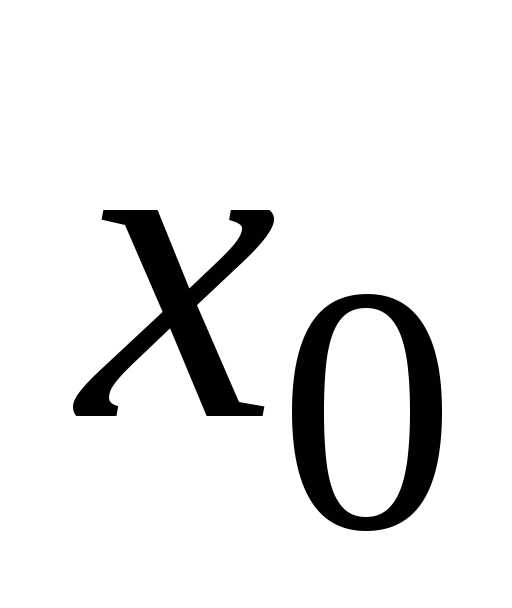 .
Метод Эйлера является методом Рунге-Кутта
первого порядка.
.
Метод Эйлера является методом Рунге-Кутта
первого порядка.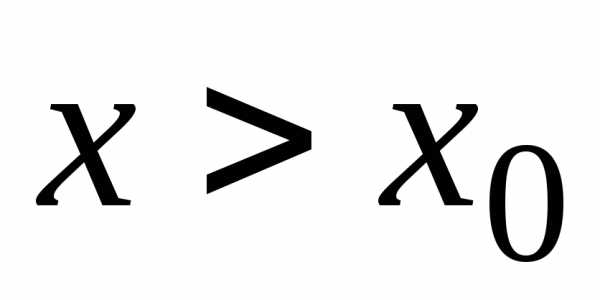 )
записывается с помощью формулы:
)
записывается с помощью формулы: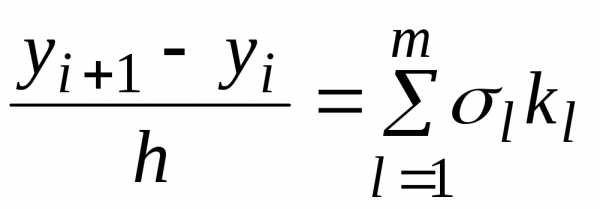 ,
где
порядок метода,
,
где
порядок метода, 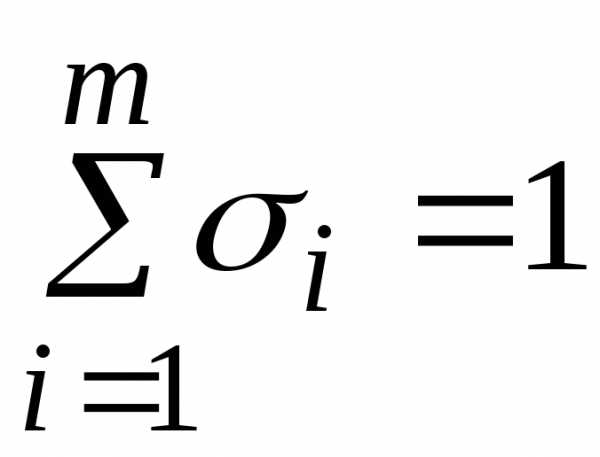 ,
, ,
,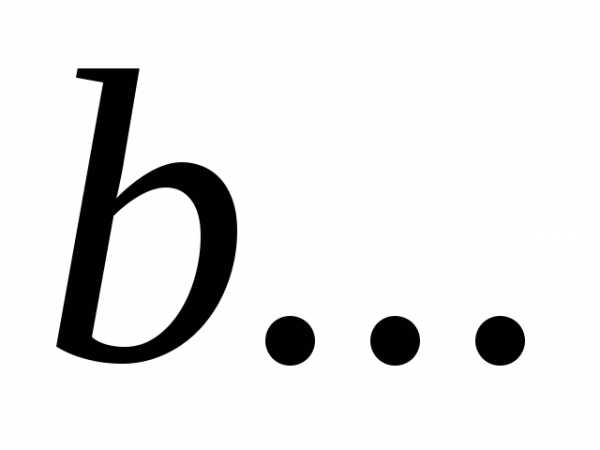 ,
, выбираются из соображений точности.
выбираются из соображений точности.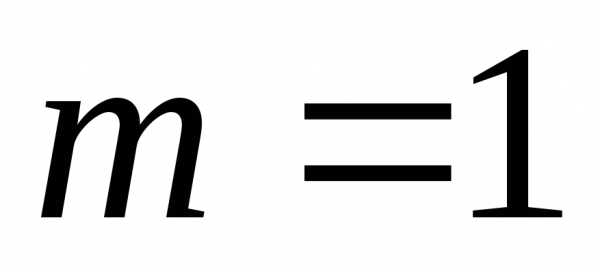 .
.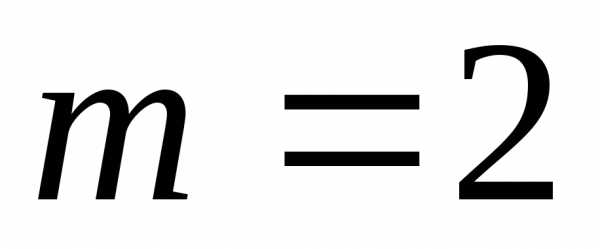 имеется уже семейство методов Рунге-Кутта
второго порядка, для которых должно
выполнятся условие.
имеется уже семейство методов Рунге-Кутта
второго порядка, для которых должно
выполнятся условие.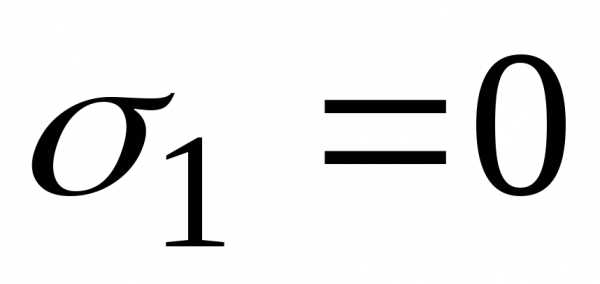 ,
,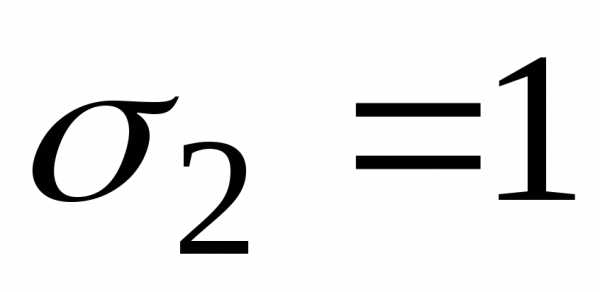 ,
получаетсямодифицированный
метод Эйлера:
,
получаетсямодифицированный
метод Эйлера: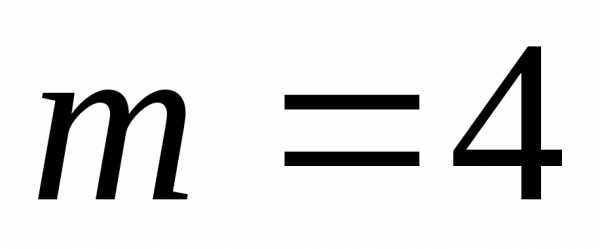 )
порядка точности. Ниже приведены примеры
методов четвертого порядка:
)
порядка точности. Ниже приведены примеры
методов четвертого порядка: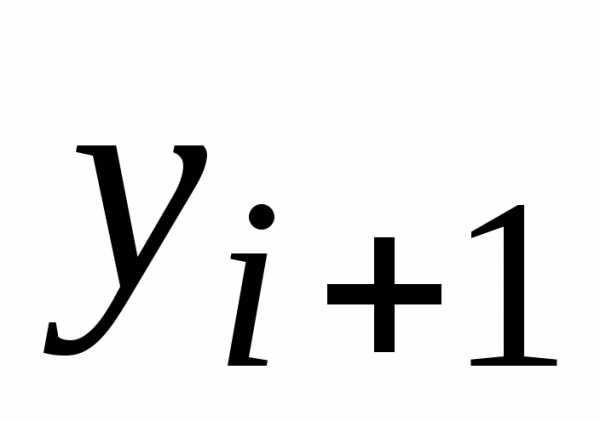 вычисляется с помощью последовательных
приближений. Например, для метода Эйлера
за начальное приближение берется,
найденное значение уточняется по формуле,
где
вычисляется с помощью последовательных
приближений. Например, для метода Эйлера
за начальное приближение берется,
найденное значение уточняется по формуле,
где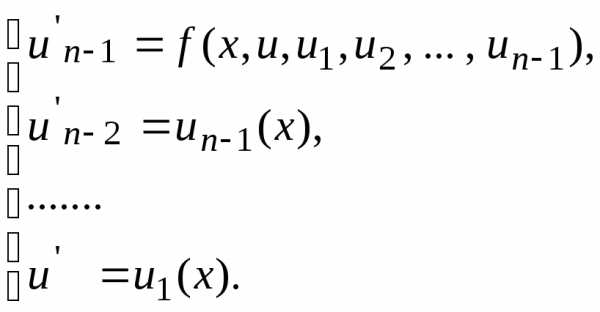
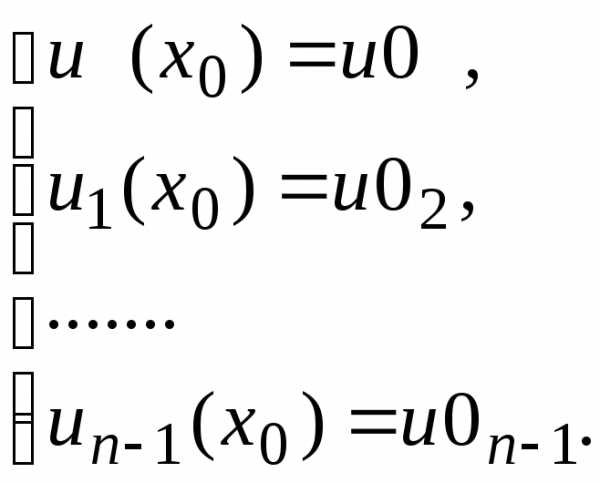
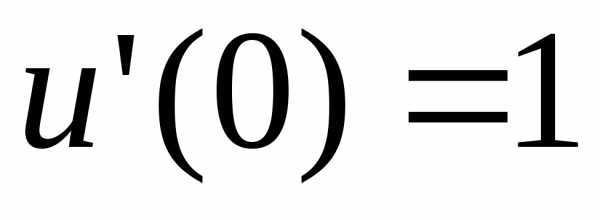 .
Введение дополнительной функциисводит задачу к эквивалентной системе
двух уравнений с начальными условиями
.
Введение дополнительной функциисводит задачу к эквивалентной системе
двух уравнений с начальными условиями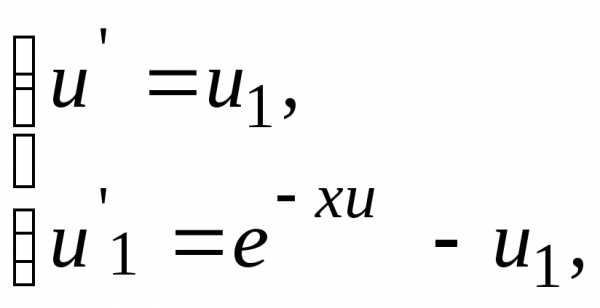
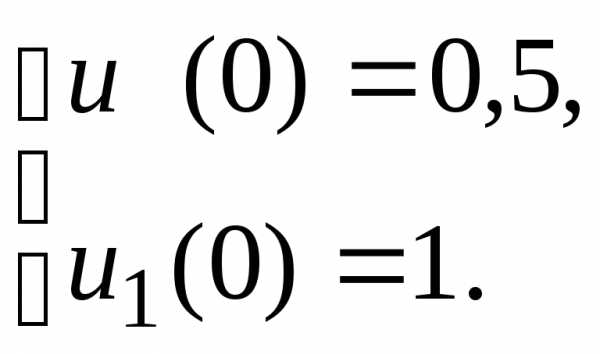
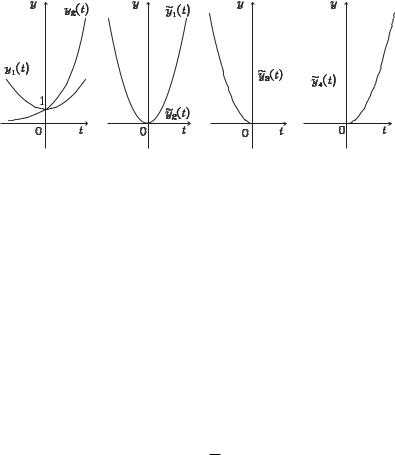
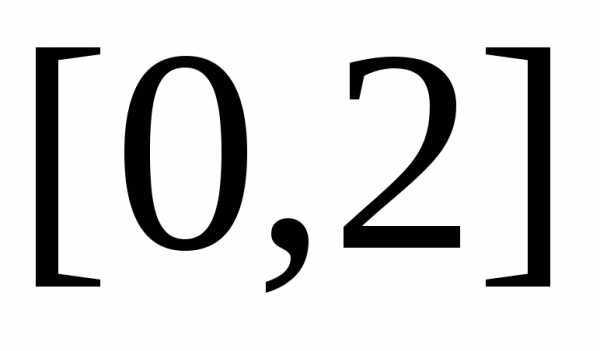 ,
на сетке с 15-ю равноотстоящими узлами
получается:
,
на сетке с 15-ю равноотстоящими узлами
получается:

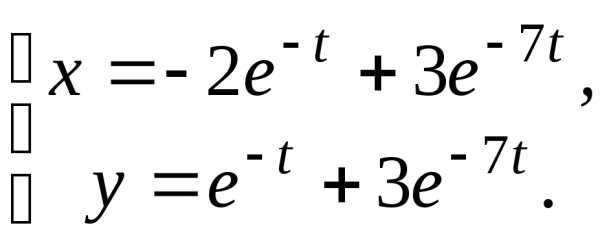 2.
2.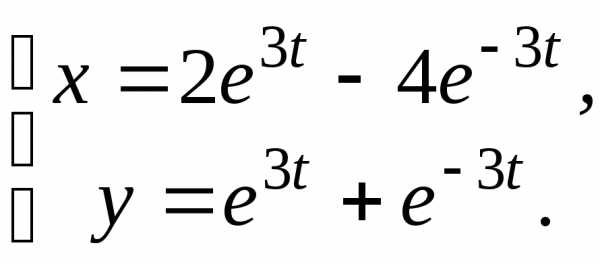 3.
3.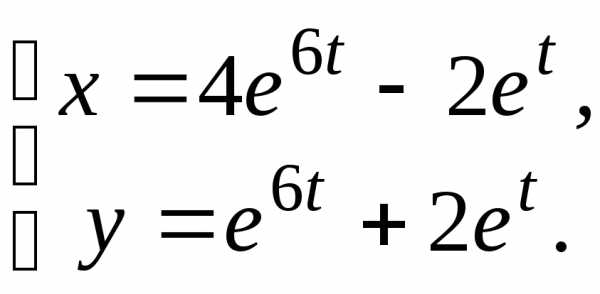
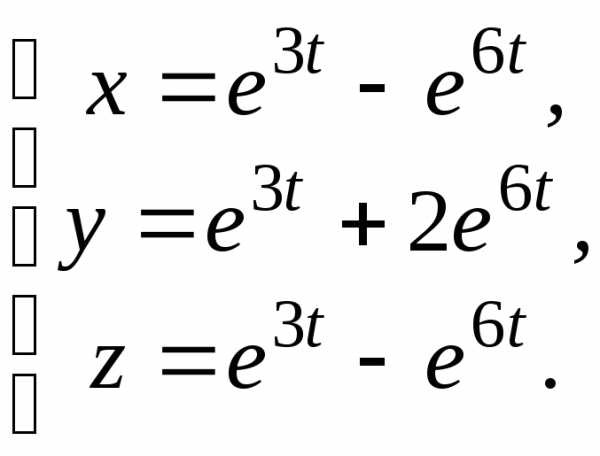 5.
5.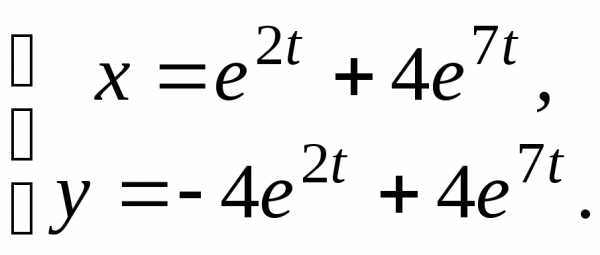 6.
6.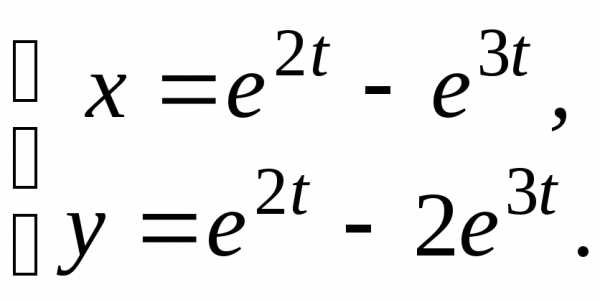
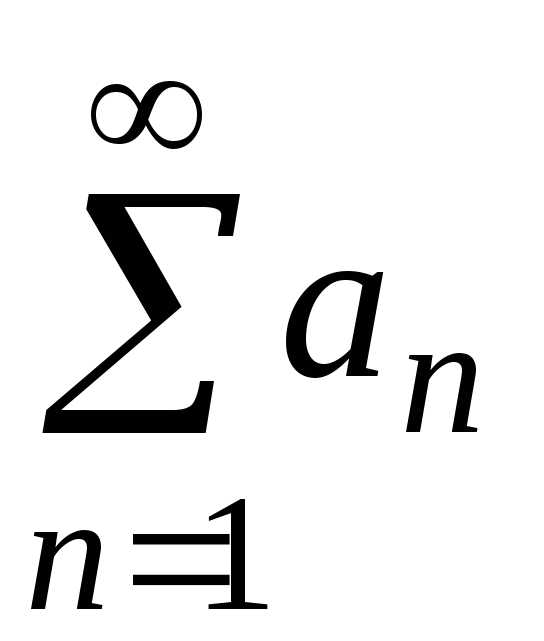 .
.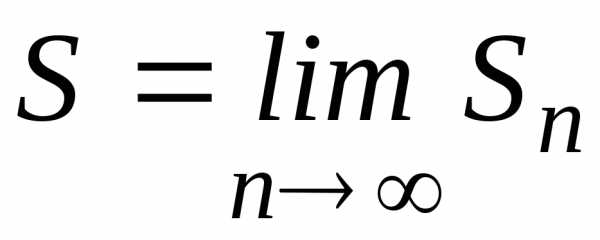 ,
в противном случае ряд называется
расходящимся.
,
в противном случае ряд называется
расходящимся.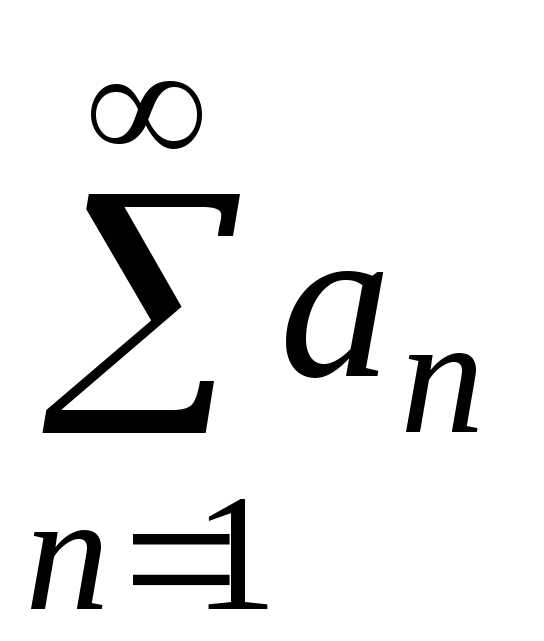 сходится,
то общий член рядаn
стремится к нулю, т.е.
сходится,
то общий член рядаn
стремится к нулю, т.е. 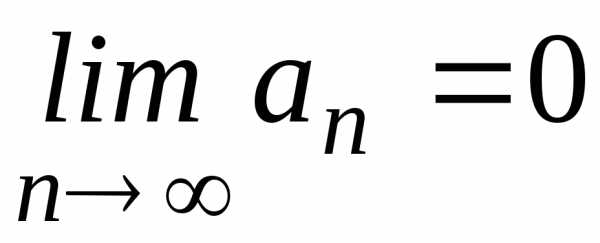 .
.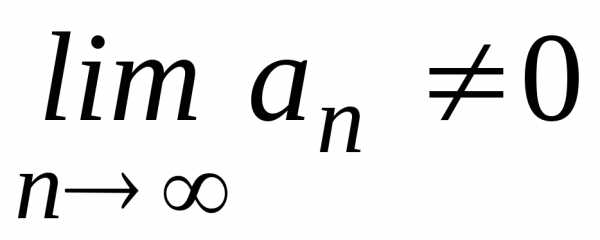 ,
то ряд расходится.
,
то ряд расходится.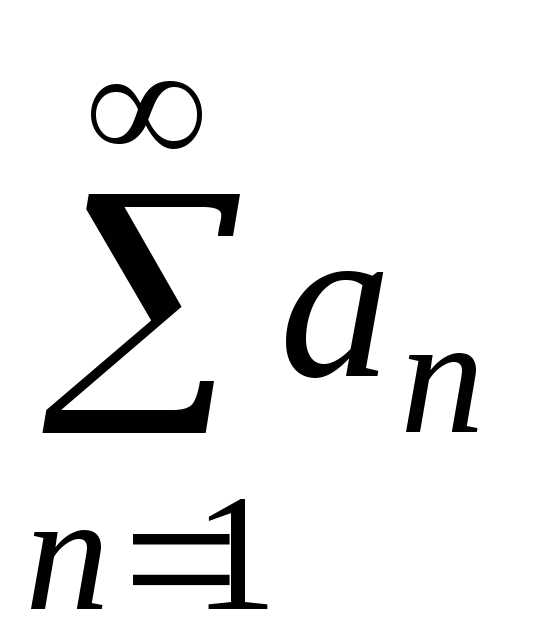 и
и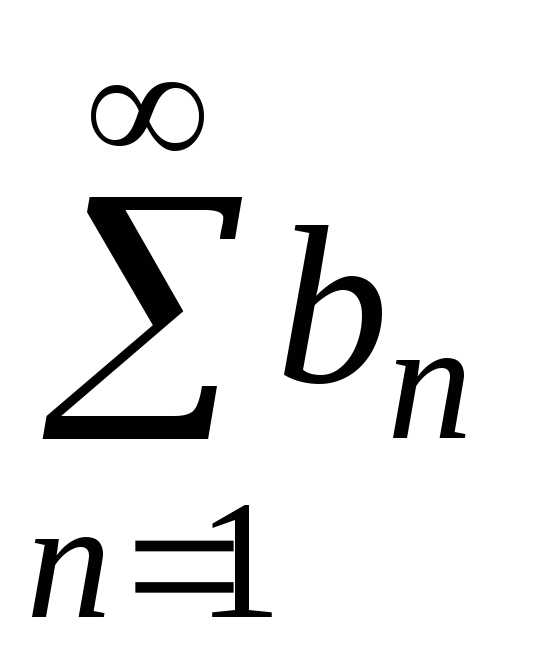 — ряды с положительными членами, причемanbn для всех номеров, начиная с некоторого n=k.
Тогда
— ряды с положительными членами, причемanbn для всех номеров, начиная с некоторого n=k.
Тогда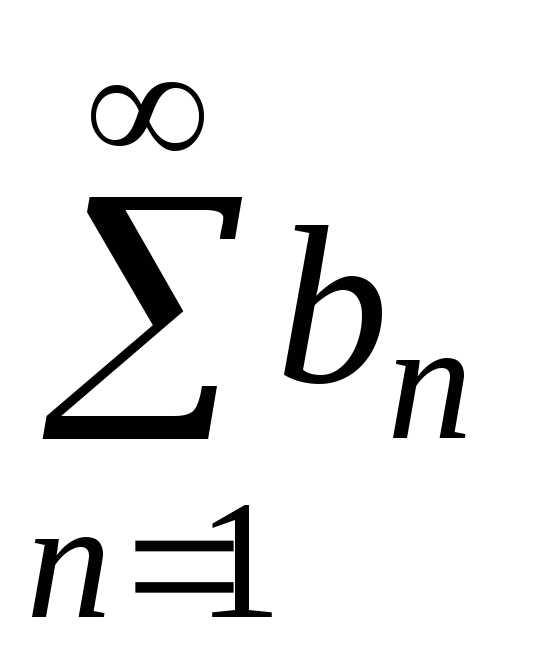 сходится,
то сходится и ряд
сходится,
то сходится и ряд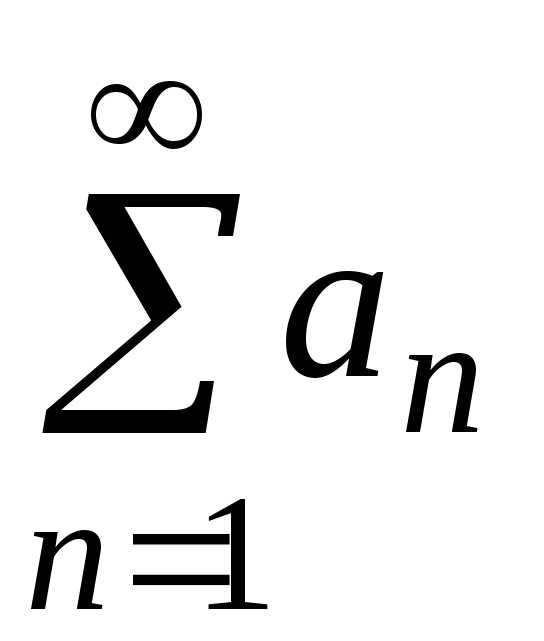 ;
;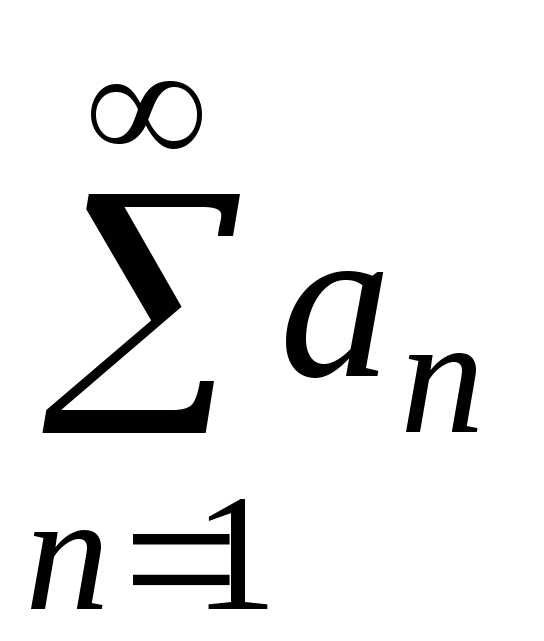 расходится, то расходится и ряд
расходится, то расходится и ряд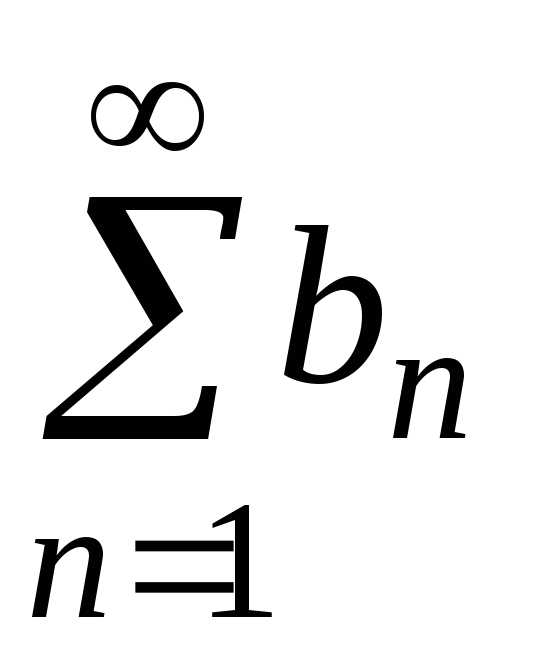 .
.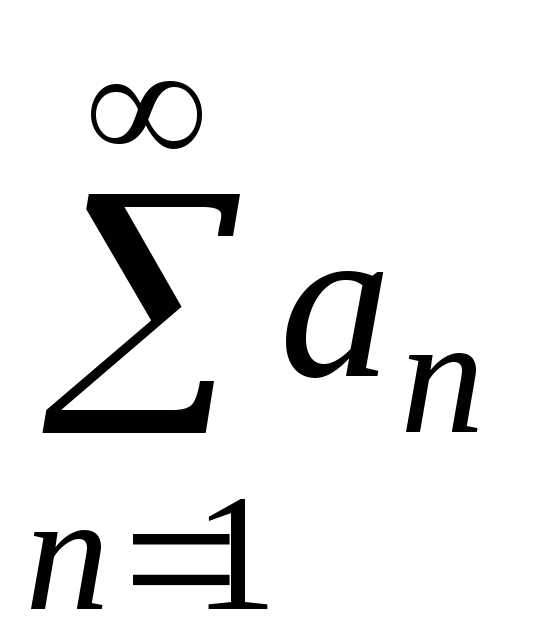 и
и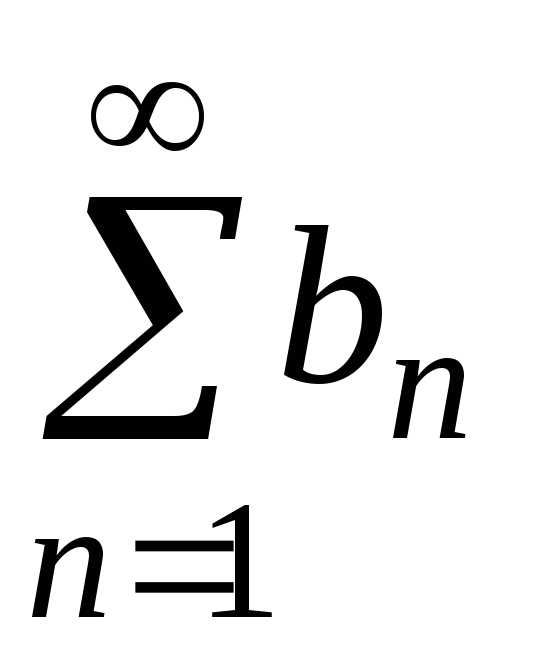 —
ряды с положительными членами и пусть
существует конечный, отличный от нуля
предел
—
ряды с положительными членами и пусть
существует конечный, отличный от нуля
предел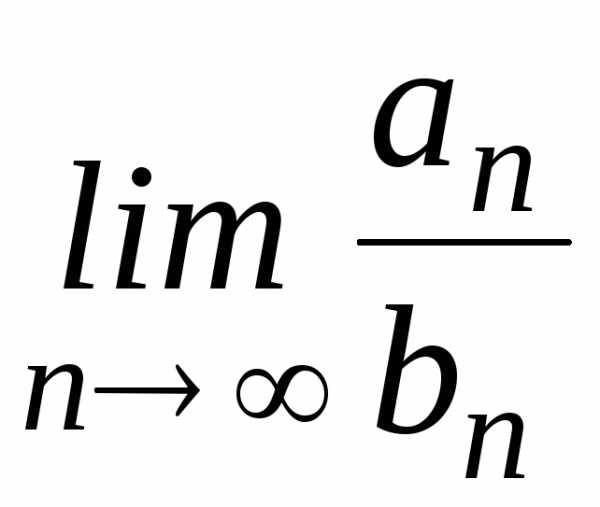 .
Тогда оба ряда ведут себя одинаково,
т.е. сходятся или расходятся одновременно.
.
Тогда оба ряда ведут себя одинаково,
т.е. сходятся или расходятся одновременно.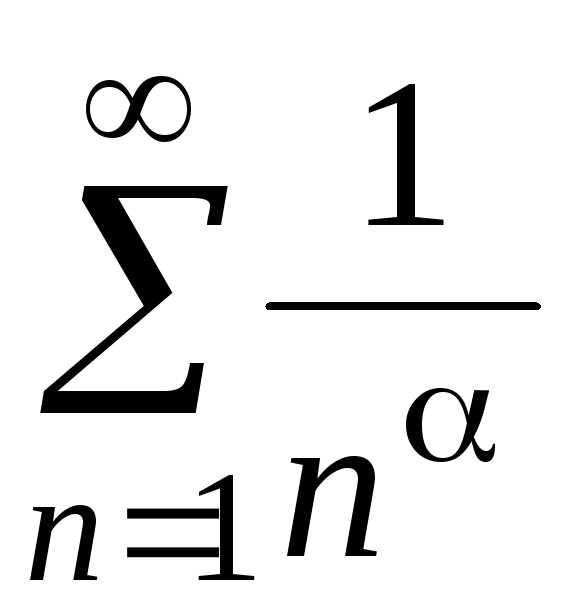 ,
при этом, если1,
то ряд сходится, если 1,
то ряд расходится;
,
при этом, если1,
то ряд сходится, если 1,
то ряд расходится;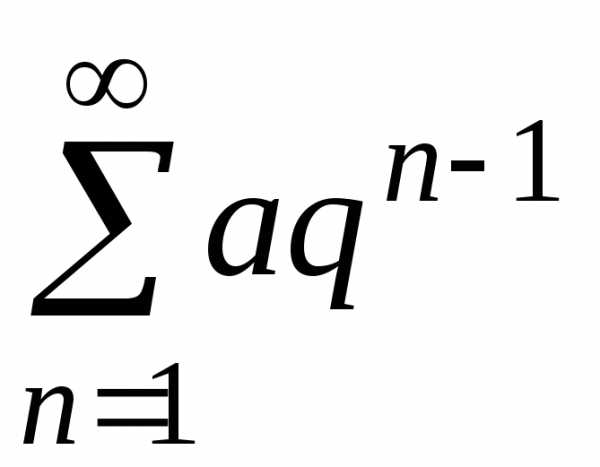 ,
если |q|<1,
то ряд сходится; в противном случае –
расходится.
,
если |q|<1,
то ряд сходится; в противном случае –
расходится.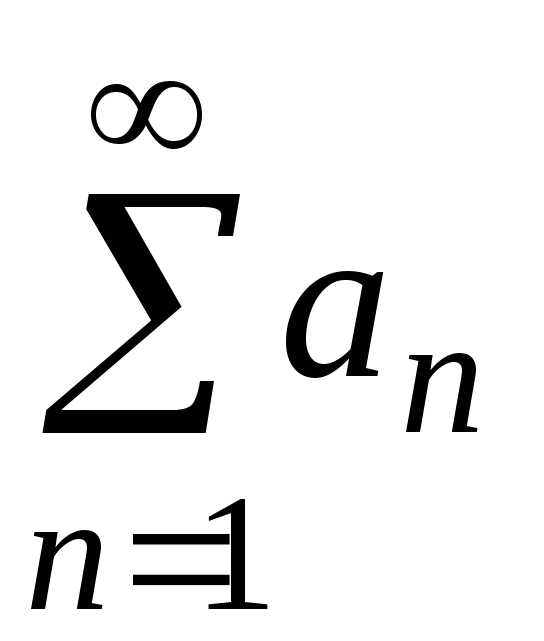 — ряд с положительными членами, и
существует конечный предел.
— ряд с положительными членами, и
существует конечный предел.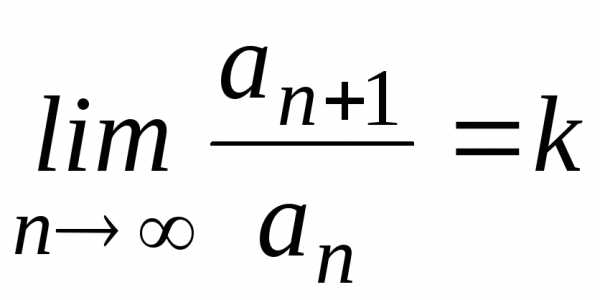 ,
тогда если k<1,
то ряд сходится, если k>1,
то ряд расходится. Если k=1,
то ряд может как сходиться, так и
расходиться; в этом случае требуется
исследовать ряд другими методами.
,
тогда если k<1,
то ряд сходится, если k>1,
то ряд расходится. Если k=1,
то ряд может как сходиться, так и
расходиться; в этом случае требуется
исследовать ряд другими методами.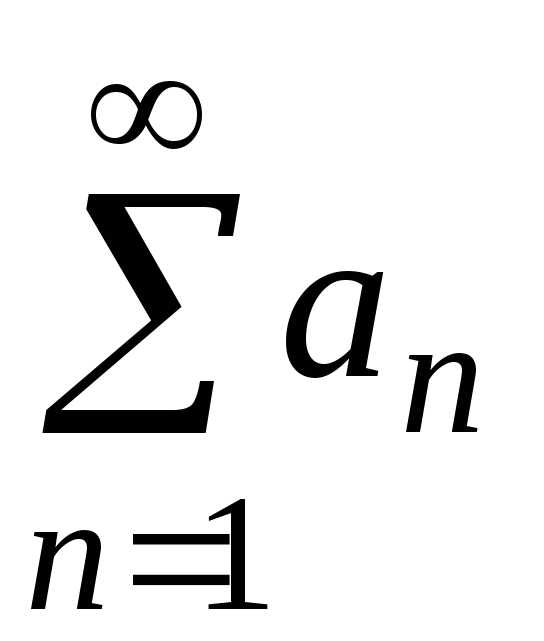 — ряд с положительными членами и существует
конечный предел:
— ряд с положительными членами и существует
конечный предел: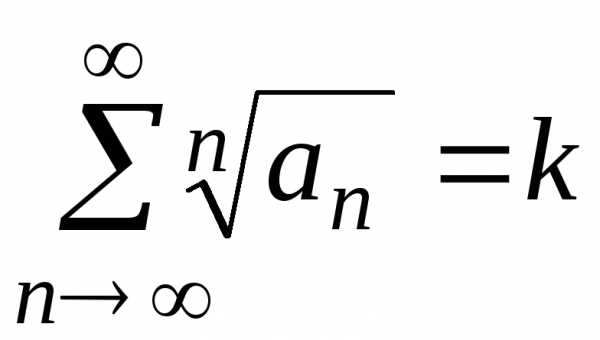 ,
тогда если k<1,
то ряд сходится, если k>1,
то ряд расходится, если k=1,
то ряд может как сходиться, так и
расходиться; в этом случае требуется
исследовать ряд другими методами.
,
тогда если k<1,
то ряд сходится, если k>1,
то ряд расходится, если k=1,
то ряд может как сходиться, так и
расходиться; в этом случае требуется
исследовать ряд другими методами.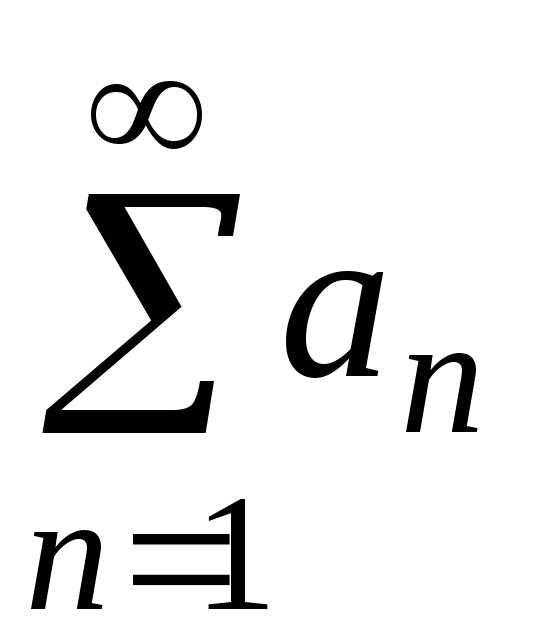 — ряд с положительными членами, для
которого существует положительная,
непрерывная и монотонно убывающая на
промежутке [1;)
функция f(x) такая, что f(n)=an, n=1;2;….
Тогда ряд
— ряд с положительными членами, для
которого существует положительная,
непрерывная и монотонно убывающая на
промежутке [1;)
функция f(x) такая, что f(n)=an, n=1;2;….
Тогда ряд 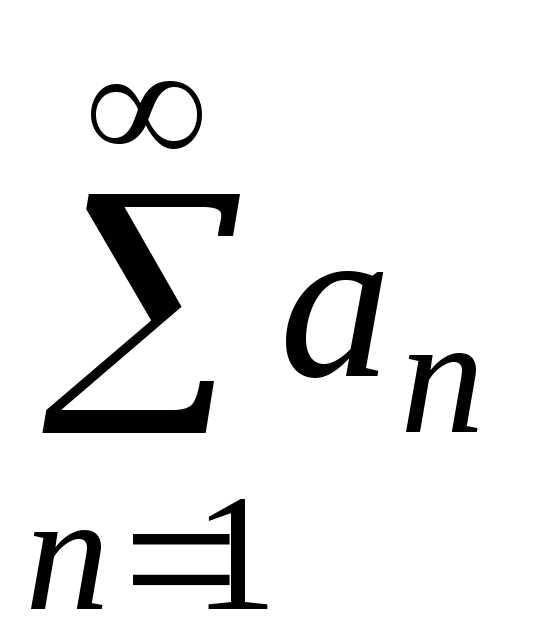 и несобственный интеграл
и несобственный интеграл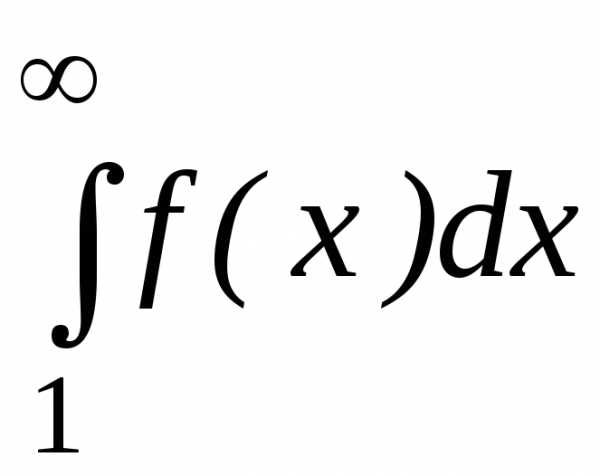 сходятся или расходятся одновременно.
сходятся или расходятся одновременно.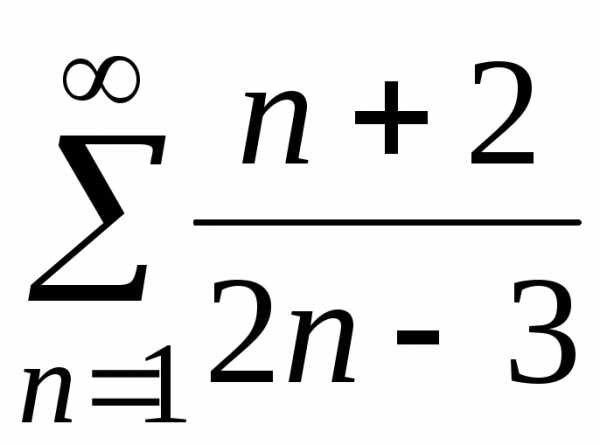 ;
б)
;
б)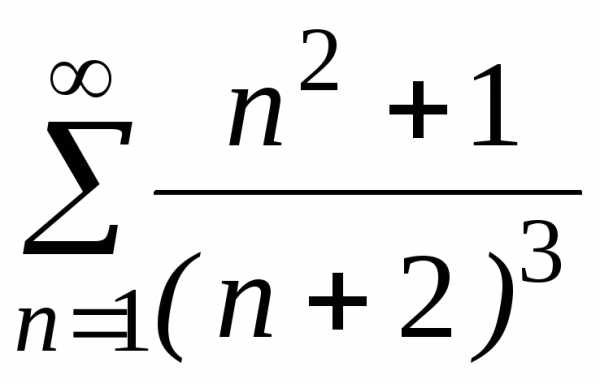 ;
в)
;
в)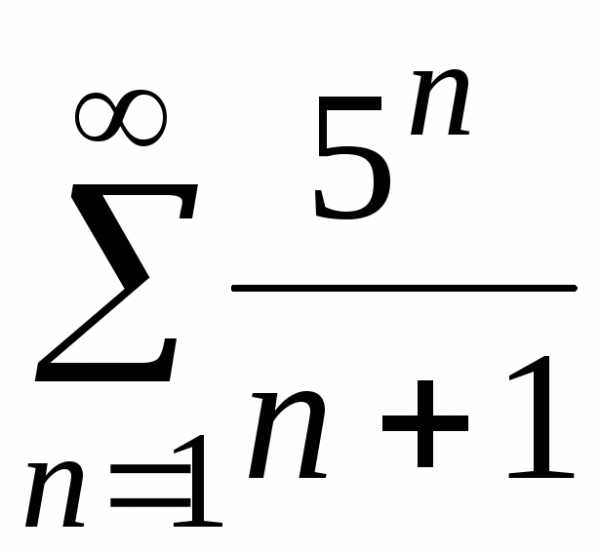 ;
г)
;
г)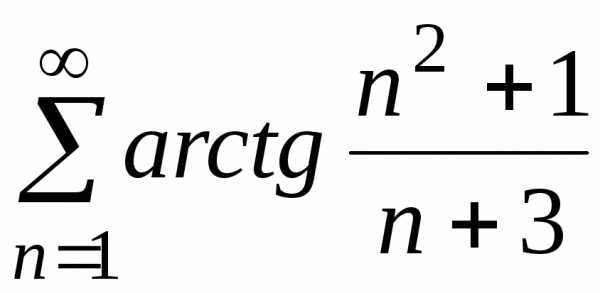 ;
;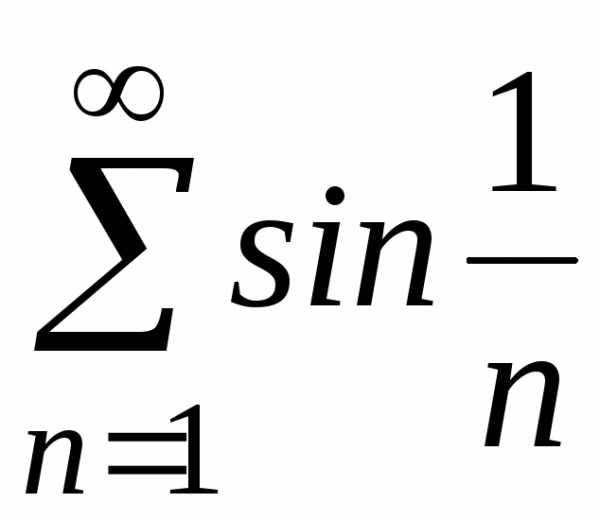 ;
е)
;
е)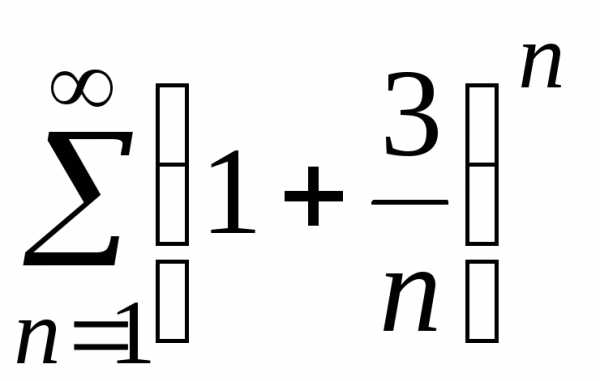 .
.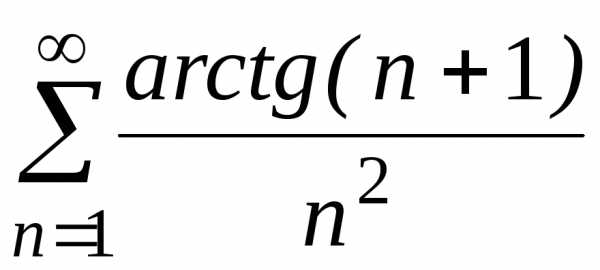 ;
б)
;
б)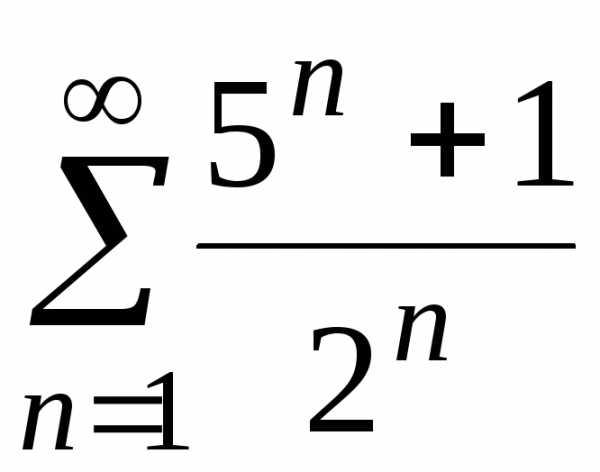 ;
в)
;
в)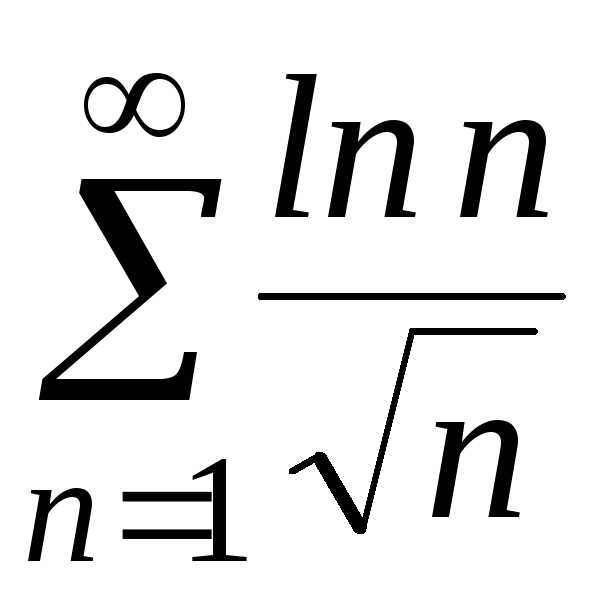 ;
г)
;
г)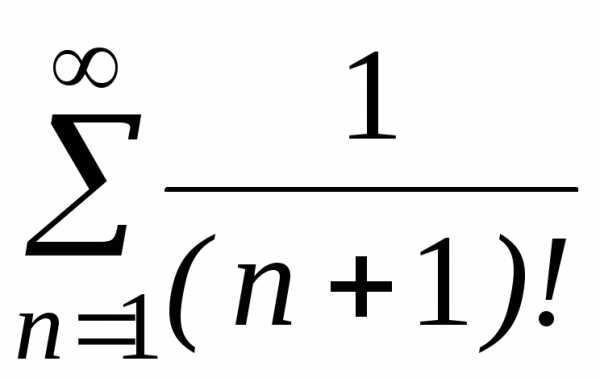 ;
;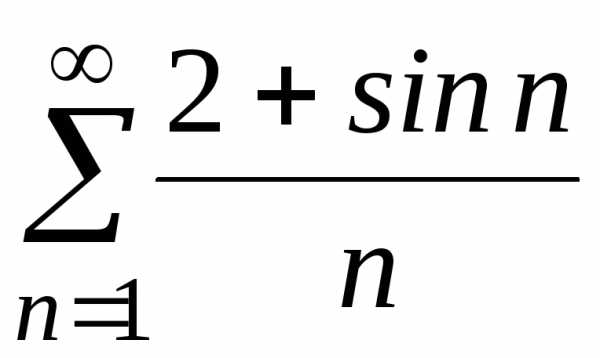 .
.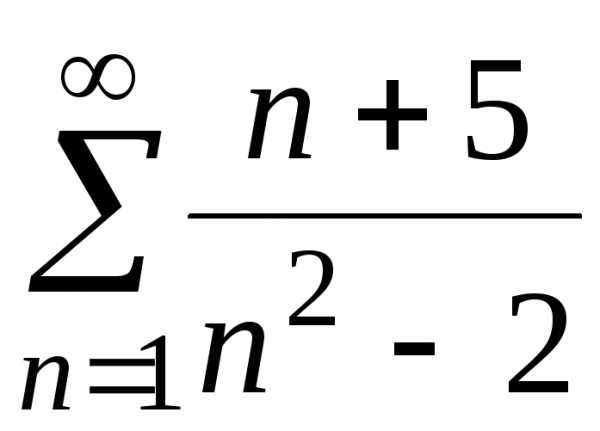 ;
б)
;
б)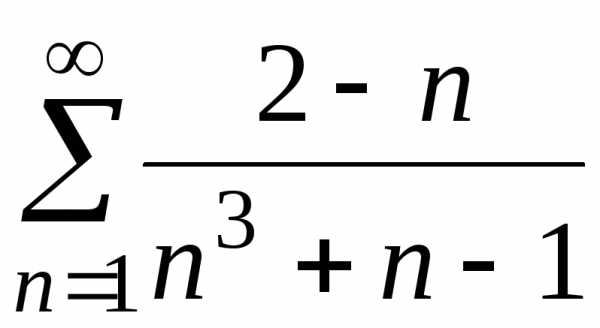 ;
в)
;
в)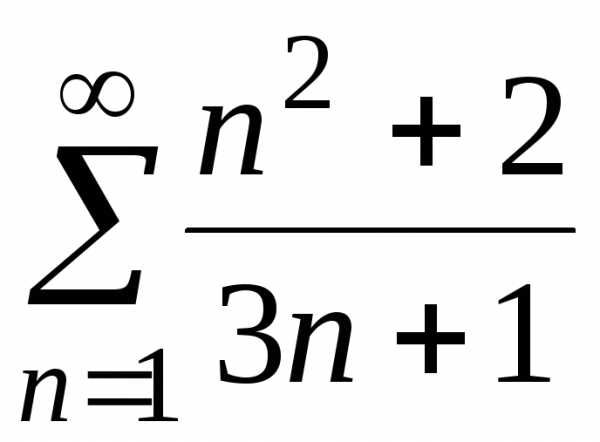 ;
г)
;
г)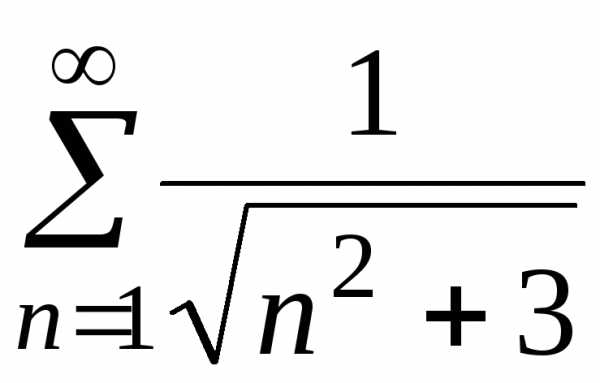 ;
;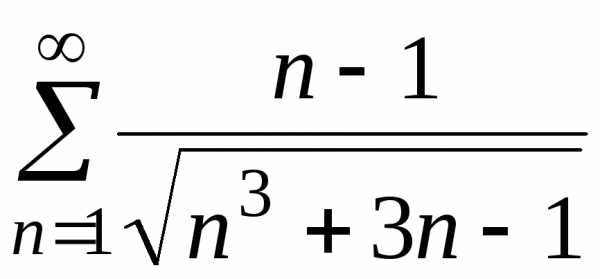 ;
е)
;
е)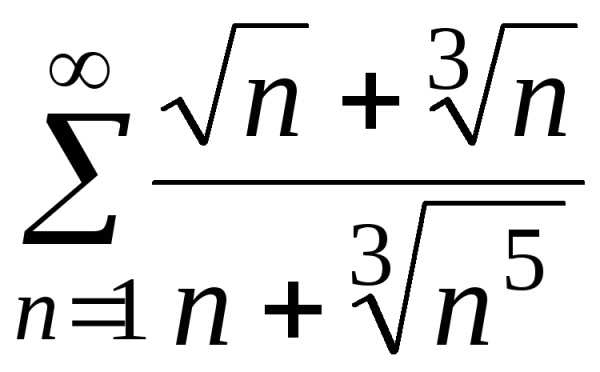 ;
ж)
;
ж)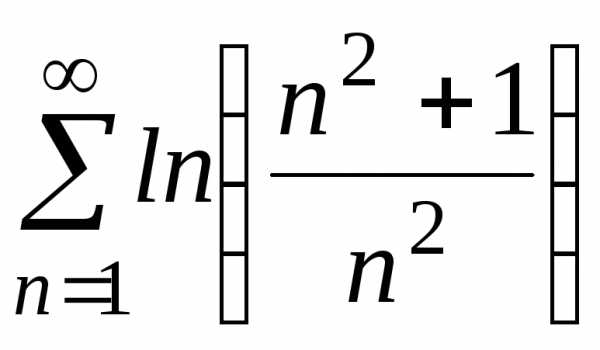 ;
з)
;
з)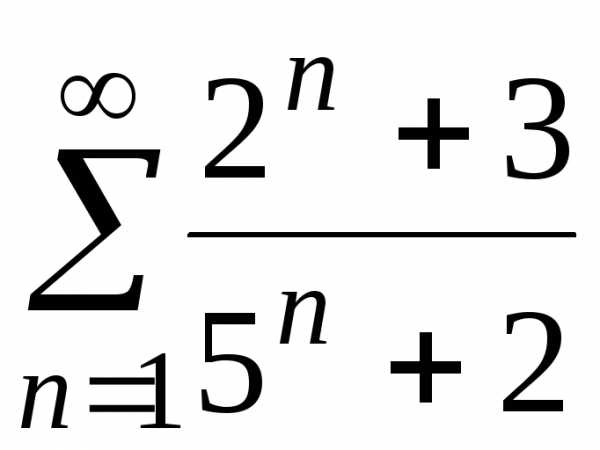 .
.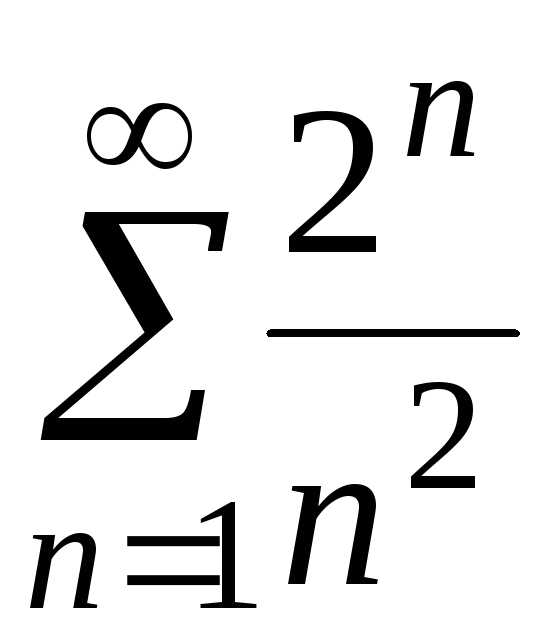 ;
б)
;
б)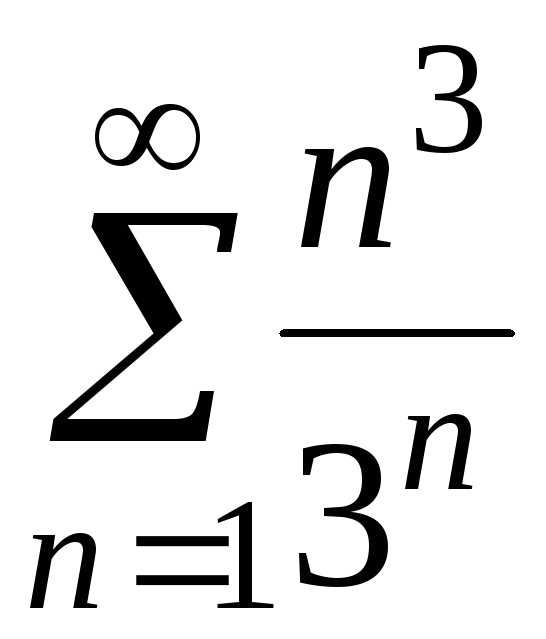 ;
в)
;
в)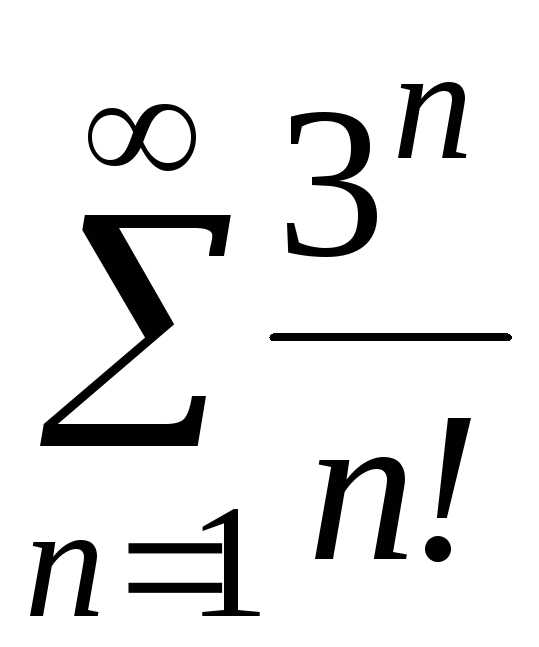 ;
г)
;
г)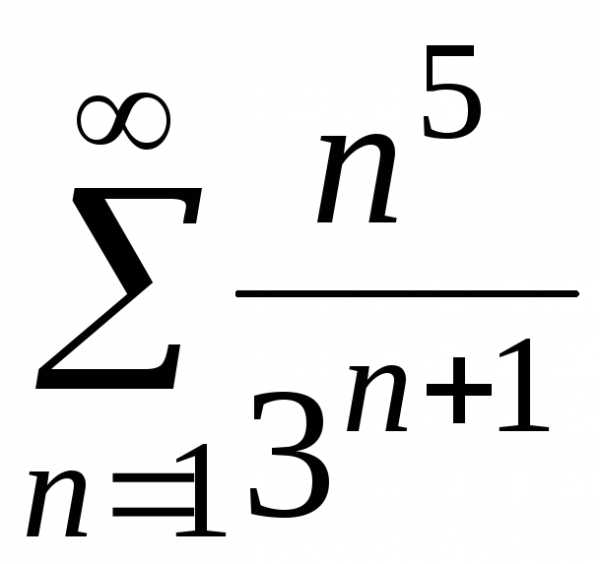 ;
д)
;
д)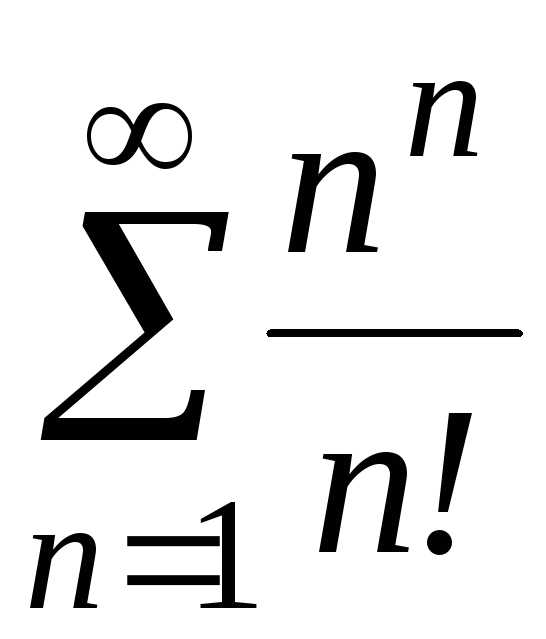 ;
е)
;
е)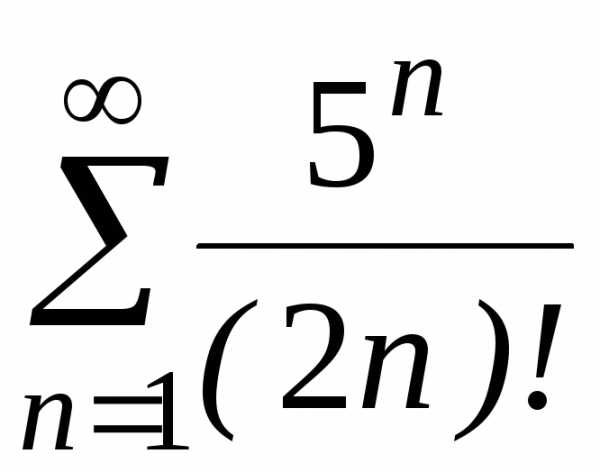 .
.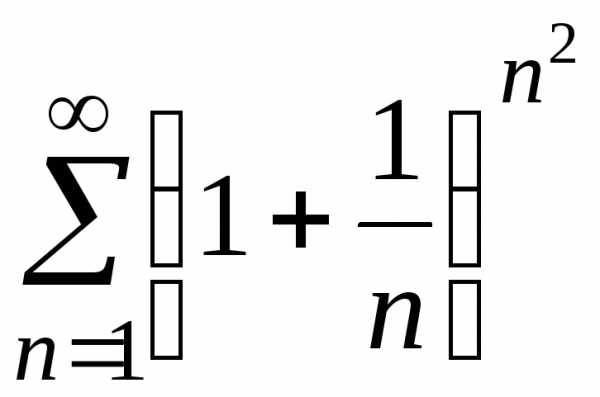 ;
б)
;
б)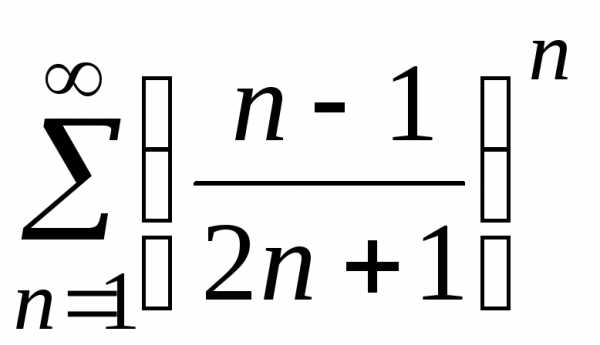 ;
в)
;
в)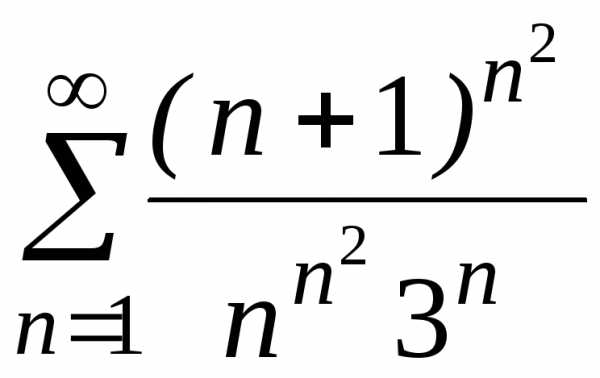 .
.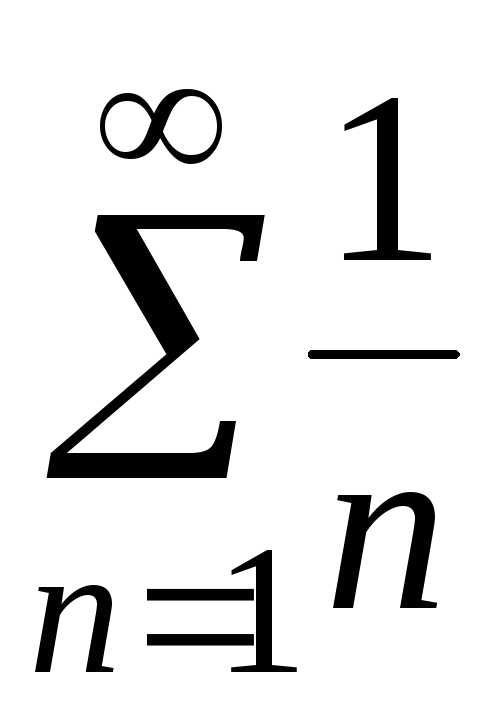 ;
б)
;
б)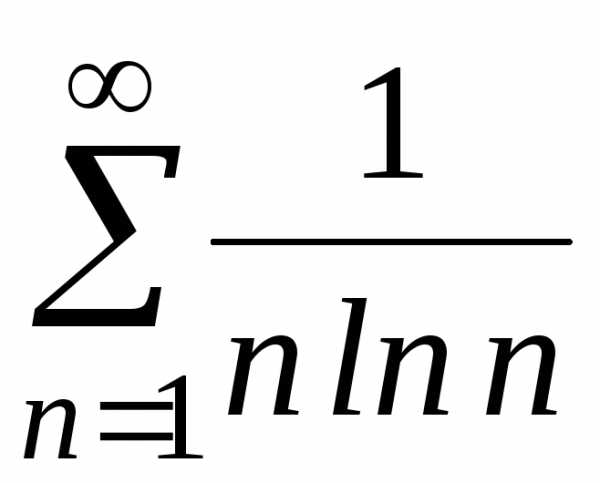 ;
в)
;
в)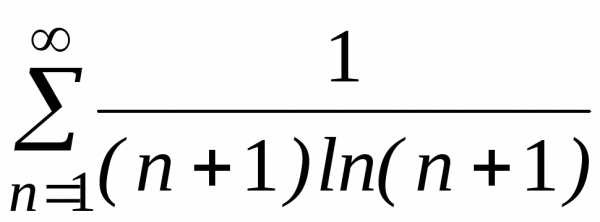 .
.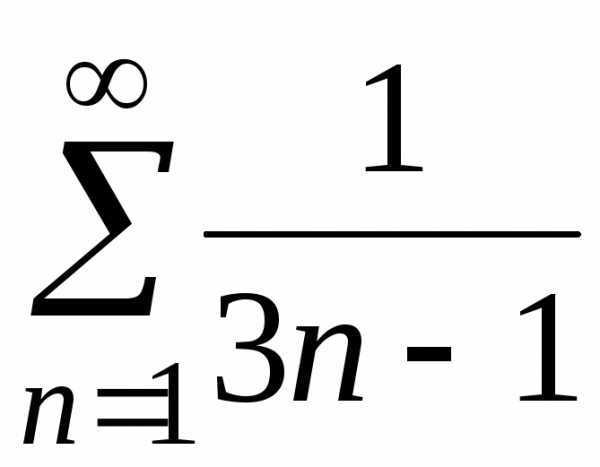 ;
б)
;
б)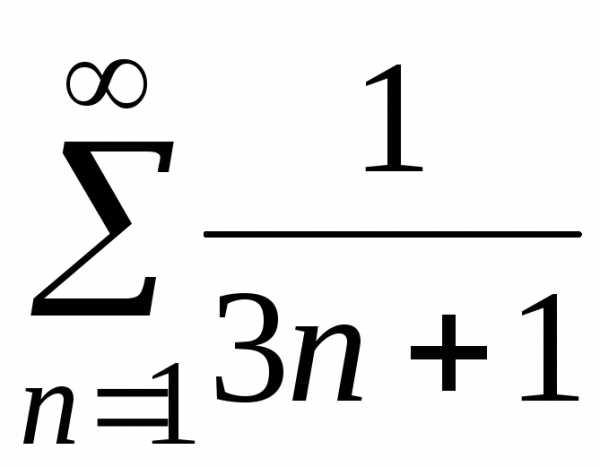 ;
в)
;
в)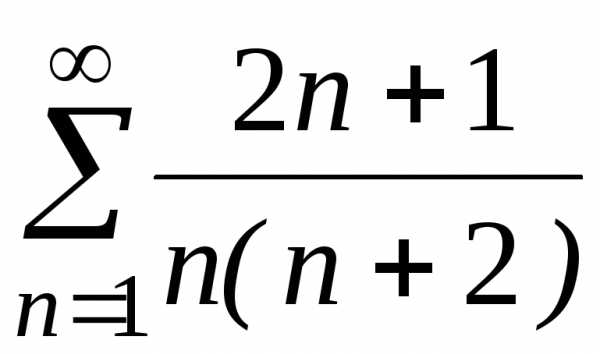 ;
г)
;
г)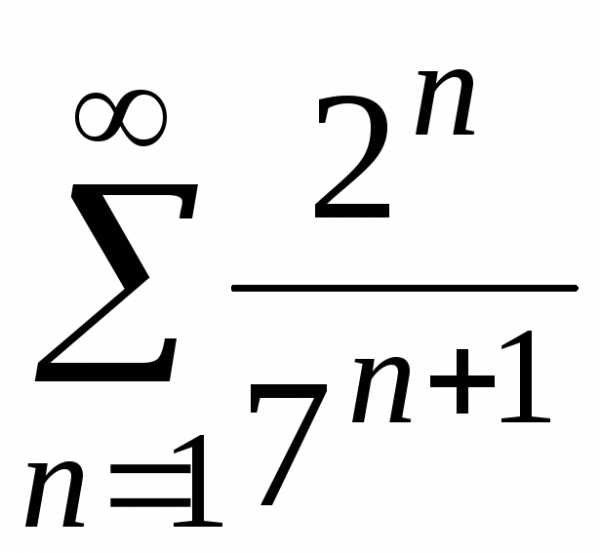 ;
д)
;
д)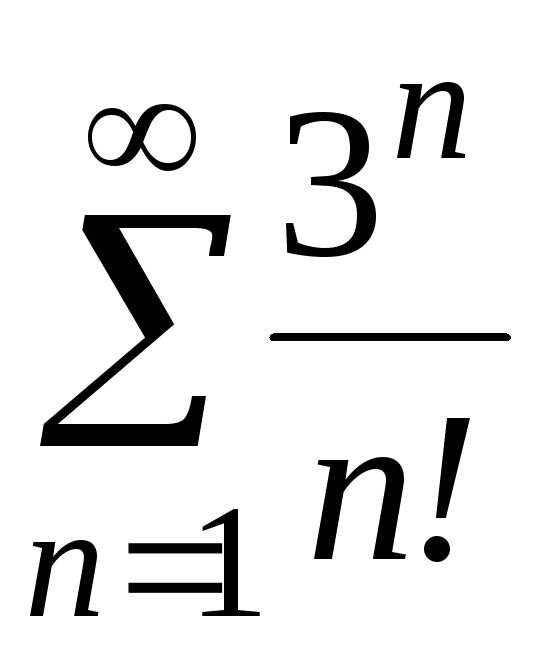 ;
;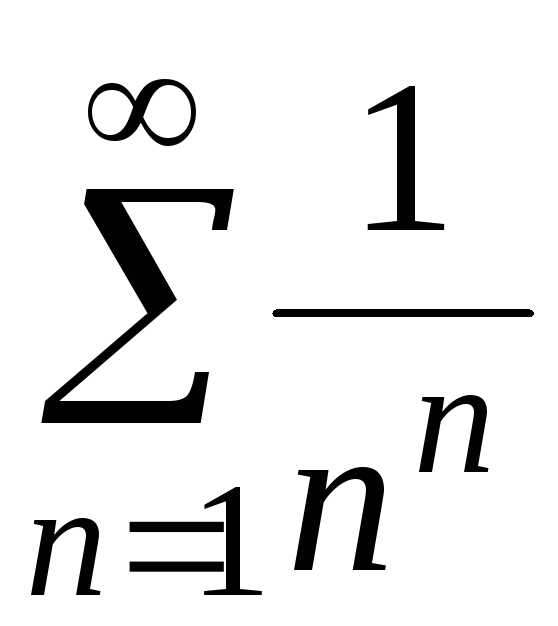 ;
ж)
;
ж)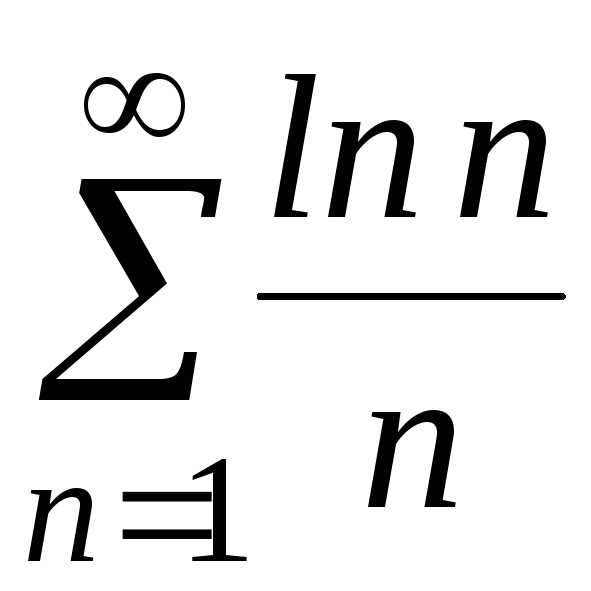 ;
з)
;
з)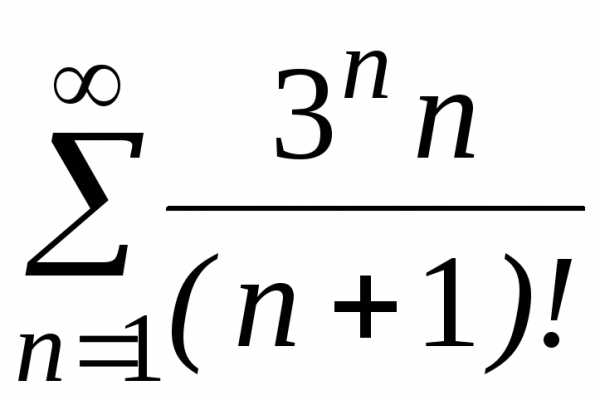 ;
и)
;
и)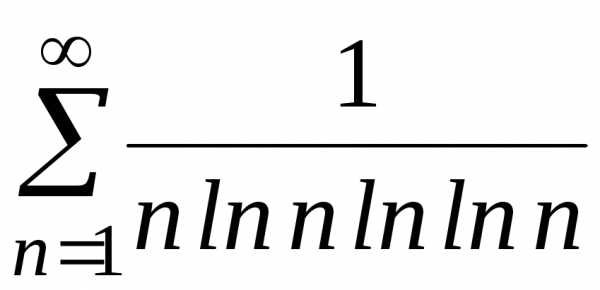 .
.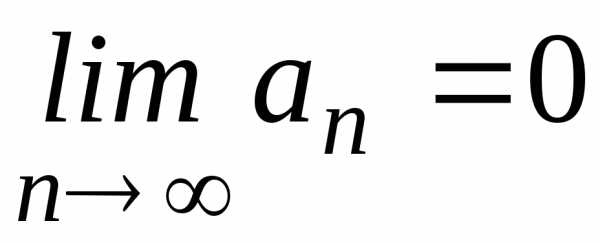 ;
в) расходится; г) расходится;
;
в) расходится; г) расходится;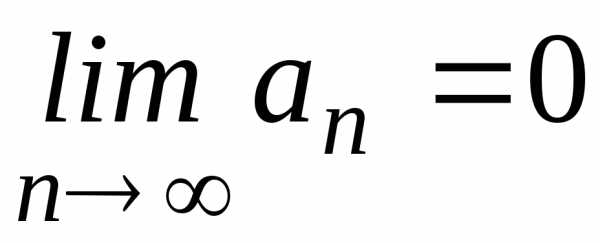 ;
е) расходится.
;
е) расходится.


























