Формула естественного прироста населения — GeographyWeb.ru
Естественный прирост — формула для расчетов
Итак, разбираем вопрос «Естественный прирост населения», расчетные формулы и что означает размерность в промилле:
- Естественный прирост Еп базируется на разнице между рождаемостью и смертностью населения. Значение Еп может быть отрицательным, когда рождаемость Р людей меньше смертности С населения страны (региона или района) за год (месяц). Например: родилось Р = 2500 человек за определенный период, а умерло С = 2800, в этом случае по формуле естественный прирост населения составит Еп=Р-С=2500-2800= -300. Это значит, что смертность превышает рождаемость людей на 300 человек за выбранный период времени: год, квартал, месяц в стране, регионе или области. Если результат положительный, это означает, что рождается людей больше, чем умирает за указанное время.
- Формула для расчета естественного прироста населения: Еп=Р-С
- Из рисунка определяем, что естественный прирост населения Еп=-440, -3944, -6708, -2535 отрицательный, каждое число означает превышение смертности людей над их рождаемостью в отношении местности (страна, регион, область) за указанный период времени. В этом случает, говорят о естественной убыли населения.
- Еп=440, 3944, 6708, 2535 положительный, это означает, что количество родившихся людей больше чем умерших за конкретный временной период.
Промилле естественный прирост населения
- Промилле — прежде всего, это одна тысячная доля в целом или одна десятая процента (1 / 10 %), с латыни переводится как — на тысячу. Символ обозначающий промилле похож на проценты %, но отличается одним добавлением «нуля» — ‰ .
- 100% = 1000‰ ; 10%=100‰ ; 1%=10‰ ; 0,1%=1‰.
- В промилле измеряют показатели — коэффициенты естественного прироста населения, показатели рождаемости и смертности. В этом случае необходимо иметь количественный данные о численности N населения страны или региона, области, города. Показатели или коэффициенты естественного прироста рассчитываются по формулам: Кеп=Еп/(N:1000) ‰, Кр=Р/(N:1000) ‰, Кс=С/(N:1000) ‰ — размерность «промилле», т.е. расчет показателя естественного прироста по указанным формулам достаточно прост, если вы имеете справочные данные по N.
- Как ввести символ ‰ на компьютере в операционной системе Windows? Удерживаем Alt последовательно набираем 0137 при включённом «Num Lock», т.е., это комбинированное сочетание клавиш Alt-0137.
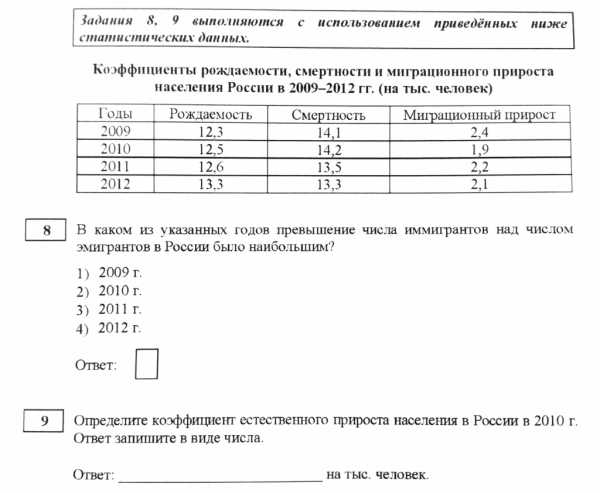 Пример — 1 (Ответ 8: 2009, 9: -1,7‰)
Пример — 1 (Ответ 8: 2009, 9: -1,7‰)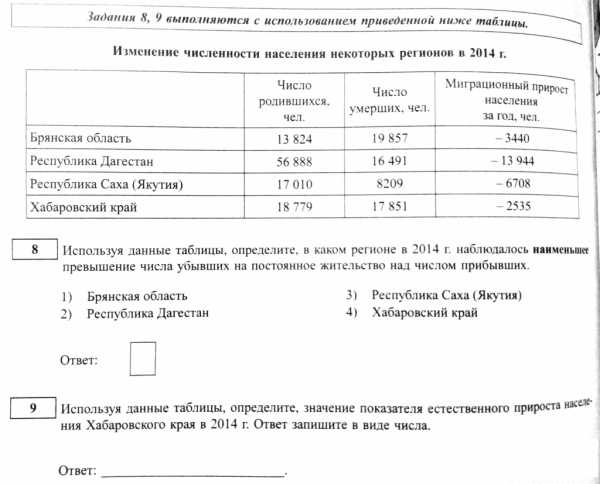 Пример — 2 (Ответ 8: 4, 9: 982)
Раздел: Прирост населения, естественный и миграционный, расчетные формулы, коэффициенты прироста
Пример — 2 (Ответ 8: 4, 9: 982)
Раздел: Прирост населения, естественный и миграционный, расчетные формулы, коэффициенты прироста
geographyweb.ru
Естественный прирост населения — Мегаэнциклопедия Кирилла и Мефодия — статья
| Белгородская область | 2, 9 | 1, 8 | — | -5, 4 | -7, 5 | -7, 1 | -5, 8 | -4, 5 | -3, 7 | -3, 4 | -3, 5 |
| Брянская область | 5, 5 | 2, 5 | 0, 1 | -6, 7 | -10, 4 | -10, 8 | -9, 5 | -7, 6 | -6, 8 | -5, 8 | -6, 3 |
| Владимирская область | 4, 2 | 3, 0 | -0, 4 | -8, 9 | -11, 5 | -11, 1 | -9, 8 | -8, 5 | -8, 0 | -7, 6 | -7, 3 |
| Воронежская область | 3, 1 | 0, 4 | -2, 4 | -8, 4 | -10, 3 | -10, 4 | -9, 7 | -8, 7 | -7, 9 | -6, 6 | -6, 8 |
| Ивановская область | 2, 6 | 0, 8 | -2, 4 | -11, 2 | -13, 6 | -13, 3 | -11, 0 | -9, 0 | -9, 0 | -8, 0 | -8, 0 |
| Калужская область | 3, 2 | 1, 4 | -0, 5 | -8, 6 | -10, 7 | -10, 3 | -8, 4 | -7, 3 | -6, 9 | -6, 2 | -5, 5 |
| Костромская область | 1, 5 | 1, 2 | -0, 8 | -9, 2 | -10, 8 | -11, 3 | -8, 9 | -7, 1 | -6, 7 | -5, 4 | -5, 6 |
| Курская область | 2, 5 | -0, 4 | -2, 0 | -8, 3 | -10, 4 | -11, 1 | -10, 1 | -7, 9 | -7, 6 | -6, 8 | -6, 4 |
| Липецкая область | 5, 0 | 1, 5 | -0, 7 | -7, 8 | -8, 7 | -8, 6 | -7, 8 | -6, 8 | -6, 3 | -5, 6 | -5, 8 |
| Московская область | 4, 0 | 2, 0 | -2, 0 | -10, 3 | -9, 8 | -8, 5 | -7, 9 | -7, 0 | -6, 1 | -4, 9 | -4, 5 |
| Орловская область | 2, 4 | 0, 5 | -0, 7 | -7, 4 | -9, 8 | -10 | -8, 9 | -7, 9 | -7, 0 | -6, 2 | -6, 4 |
| Рязанская область | 2, 5 | -0, 4 | -2, 4 | -10, 2 | -12, 3 | -11, 9 | -10, 7 | -9, 6 | -8, 5 | -7, 7 | -7, 9 |
| Смоленская область | 1, 3 | 1, 0 | -1, 4 | -9, 1 | -13, 0 | -13, 0 | -12, 0 | -10, 0 | -9, 6 | -9, 4 | -8, 0 |
| Тамбовская область | 2, 2 | -1, 4 | -3, 2 | -9, 0 | -11, 0 | -10, 9 | -10, 1 | -8, 7 | -8, 6 | -8, 0 | -8, 0 |
| Тверская область | -1, 0 | -2, 3 | -3, 4 | -12, 3 | -14, 1 | -13, 8 | -12, 3 | -10, 4 | -10, 0 | -8, 9 | -9, 1 |
| Тульская область | 3, 1 | -0, 5 | -4, 3 | -12, 1 | -14, 2 | -14, 2 | -12, 9 | -12, 0 | -11, 4 | -9, 9 | -9, 8 |
| Ярославская область | 2, 3 | 1, 0 | -1, 9 | -9, 8 | -10, 7 | -10, 7 | -8, 9 | -7, 6 | -7, 0 | -5, 7 | -5, 9 |
| г. Москва | 2, 3 | 1, 9 | -2, 2 | -8, 5 | -5, 8 | -3, 4 | -3, 2 | -2, 2 | -1, 5 | -0, 4 | -0, 2 |
| Республика Карелия | 8, 4 | 6, 6 | 3, 1 | -7, 9 | -7, 8 | -8, 2 | -6, 8 | -5, 3 | -5, 1 | -4, 0 | -4, 1 |
| Республика Коми | 10, 5 | 10, 1 | 6, 1 | -3, 5 | -3, 5 | -4, 1 | -2, 7 | -0, 8 | -0, 5 | -0, 4 | -0, 2 |
| Архангельская область (в т. ч. Ненецкий автономный округ) | 6, 8 | 7, 5 | 3, 7 | -6, 1 | -7, 5 | -6, 3 | -4, 9 | -2, 8 | -2, 6 | -2, 1 | -2, 0 |
| Вологодская область | 2, 5 | 4, 1 | 1, 4 | -7, 7 | -7, 2 | -8, 3 | -6, 2 | -4, 3 | -4, 3 | -3, 8 | -4, 3 |
| Калининградская область | 9, 4 | 6, 6 | 2, 8 | -5, 0 | -7, 3 | -9, 2 | -7, 2 | -4, 5 | -4, 0 | -3, 1 | -2, 8 |
| Ленинградская область | 2, 6 | 2, 4 | -1, 5 | -10, 9 | -12, 1 | -12, 5 | -11, 4 | -9, 9 | -9, 2 | -7, 8 | -7, 0 |
| Мурманская область | 10, 6 | 9, 7 | 5, 4 | -3, 2 | -3, 0 | -3, 6 | -2, 9 | -1, 4 | -1, 3 | -1, 2 | -0, 2 |
| Новгородская область | 0, 6 | 0, 2 | -1, 8 | -11, 9 | -12, 6 | -13, 2 | -11, 7 | -9, 4 | -10, 3 | -9, 2 | -8, 8 |
| Псковская область | -1, 6 | -2, 6 | -3, 2 | -13, 1 | -14, 9 | -15, 7 | -14, 4 | -11, 2 | -11, 7 | -10, 5 | -10, 7 |
| г. Санкт-Петербург | 3, 5 | 2, 1 | -1, 4 | -8, 9 | -9, 4 | -7, 4 | -6, 5 | -5, 3 | -4, 2 | -2, 8 | -2, 0 |
| Республика Адыгея | 6, 1 | 4, 4 | 1, 9 | -3, 7 | -5, 9 | -4, 9 | -4, 7 | -2, 8 | -2, 1 | -1, 6 | -1, 2 |
| Республика Калмыкия | 11, 7 | 14, 6 | 12, 7 | 3, 1 | 0, 1 | 1, 5 | 2, 2 | 3, 5 | 4, 8 | 4, 1 | 4, 3 |
| Краснодарский край | 4, 9 | 2, 8 | -0, 1 | -5, 3 | -6, 3 | -5, 3 | -4, 4 | -3, 1 | -2, 0 | -1, 3 | -1, 4 |
| Астраханская область | 5, 7 | 5, 8 | 4, 7 | -3, 4 | -4, 4 | -3, 3 | -2, 3 | -0, 6 | 0, 6 | 0, 8 | 0, 7 |
| Волгоградская область | 6, 1 | 4, 3 | 1, 3 | -5, 5 | -7, 0 | -6, 3 | -5, 5 | -3, 9 | -3, 2 | -3, 1 | -3, 3 |
| Ростовская область | 4, 4 | 3, 4 | — | -6, 5 | -6, 2 | -6, 7 | -6, 0 | -4, 8 | -4, 2 | -3, 8 | -3, 8 |
| Республика Дагестан | 22, 1 | 19, 9 | 19, 9 | 13, 6 | 9, 0 | 9, 6 | 9, 3 | 11, 3 | 12, 4 | 12, 4 | 11, 8 |
| Республика Ингушетия | 15, 4 | 14, 3 | 15, 8 | 18, 5 | 16, 1 | 10, 2 | 11, 4 | 13, 4 | 15, 2 | 15, 0 | 22, 8 |
| Кабардино-Балкарская Республика | 13, 1 | 12, 6 | 11, 5 | 3, 2 | 0, 4 | -0, 1 | 0, 6 | 3, 3 | 4, 4 | 4, 2 | 5, 2 |
| Карачаево-Черкесская Республика | 11, 2 | 11, 5 | 8, 8 | 2, 6 | -0, 7 | 0, 1 | 0, 3 | 3, 4 | 3, 8 | 3, 5 | 2, 9 |
| Республика Северная Осетия | 10, 4 | 7, 2 | 7, 4 | 0, 3 | -2, 0 | -1, 1 | 0, 2 | 2, 5 | 2, 8 | 2, 9 | 3, 6 |
| Чеченская Республика | 15, 4 | 14, 3 | 15, 8 | — | — | 19, 8 | 18, 9 | 22, 4 | 24, 8 | 23, 8 | 24, 4 |
| Ставропольский край | 5, 2 | 4, 7 | 3, 2 | -2, 9 | -4, 6 | -4, 4 | -4, 1 | -2, 1 | -1, 2 | -1, 1 | -0, 5 |
| Республика Башкортостан | 9, 3 | 8, 2 | 6, 5 | -1, 5 | -2, 9 | -3, 4 | -2, 5 | -0, 9 | -0, 3 | 0, 6 | 0, 6 |
| Республика Марий Эл | 6, 2 | 7, 2 | 5, 5 | -3, 5 | -5, 8 | -6, 7 | -5, 3 | -3, 4 | -2, 9 | -2, 2 | -2, 5 |
| Республика Мордовия | 6, 2 | 4, 1 | 2, 0 | -5, 1 | -8, 4 | -8, 6 | -7, 8 | -6, 6 | -5, 9 | -5, 9 | -6, 2 |
| Республика Татарстан | 7, 1 | 6, 3 | 5, 5 | -2, 5 | -3, 7 | -4, 0 | -3, 2 | -2, 1 | -1, 2 | -0, 3 | -0, 2 |
| Удмуртская Республика | 7, 1 | 7, 1 | 5, 3 | -4, 3 | -3, 5 | -4, 4 | -3, 0 | -1, 4 | -0, 7 | 0, 6 | -0, 3 |
| Чувашская Республика | 9, 4 | 6, 6 | 5, 7 | -2, 9 | -4, 7 | -5, 1 | -4, 4 | -2, 9 | -2, 7 | -1, 1 | -1, 6 |
| Пермский край | 6, 3 | 4, 3 | 2, 8 | -6, 7 | -6, 5 | -7, 0 | -5, 5 | -3, 6 | -2, 5 | -1, 7 | -1, 2 |
| Кировская область | 2, 2 | 2, 9 | 0, 9 | -8, 3 | -8, 7 | -9, 7 | -8, 0 | -6, 2 | -5, 8 | -5, 2 | -5, 0 |
| Нижегородская область | 3, 9 | 1, 4 | -1, 6 | -9, 6 | -10, 4 | -11, 1 | -9, 9 | -8, 4 | -7, 6 | -6, 6 | -7, 0 |
| Оренбургская область | 7, 7 | 7, 8 | 5, 8 | -3, 3 | -4, 7 | -5, 0 | -3, 9 | -2, 5 | -1, 9 | -0, 5 | -0, 4 |
| Пензенская область | 4, 9 | 3, 1 | 0, 1 | -6, 8 | -9, 5 | -9, 8 | -8, 5 | -6, 4 | -6, 1 | -5, 5 | -5, 7 |
| Самарская область | 7, 0 | 4, 8 | 1, 2 | -6, 2 | -8, 5 | -6, 5 | -5, 6 | -4, 6 | -3, 9 | -3, 3 | -3, 6 |
| Саратовская область | 5, 1 | 3, 1 | 1, 6 | -5, 7 | -8, 3 | -7, 8 | -6, 5 | -5, 1 | -4, 6 | -4, 3 | -4, 9 |
| Ульяновская область | 5, 4 | 4, 1 | 2, 8 | -4, 6 | -7, 5 | -8, 3 | -7, 7 | -6, 5 | -5, 0 | -4, 4 | -5, 2 |
| Курганская область | 6, 3 | 4, 9 | 3, 1 | -5, 7 | -6, 7 | -7, 2 | -5, 8 | -4, 3 | -3, 8 | -3, 1 | -3, 0 |
| Свердловская область | 6, 1 | 4, 7 | 1, 0 | -7, 0 | -8, 2 | -6, 2 | -4, 6 | -3, 2 | -2, 3 | -1, 5 | -0, 9 |
| Тюменская область (в том числе Ханты-Мансийский автономный округ, Ямало-Ненецкий атономный округ) | 9, 1 | 10, 3 | 9, 6 | 0, 8 | 1, 3 | 3, 2 | 3, 9 | 5, 3 | 6, 0 | 6, 7 | 7, 1 |
| Челябинская область | 7, 5 | 6, 1 | 2, 7 | -5, 9 | -6, 6 | -5, 9 | -4, 6 | -3, 1 | -2, 2 | -1, 3 | -1, 0 |
| Республика Алтай | 10, 4 | 10, 0 | 8, 4 | 1, 1 | 1, 3 | 1, 7 | 2, 8 | 7, 2 | 9, 1 | 8, 4 | 8, 3 |
| Республика Бурятия | 10, 4 | 12, 1 | 9, 2 | -0, 3 | -1, 5 | -1, 7 | 0, 3 | 2, 8 | 3, 5 | 4, 4 | 4, 3 |
| Республика Тыва | 19, 6 | 16, 4 | 17, 7 | 7, 1 | 2, 3 | 5, 4 | 7, 0 | 12, 5 | 13, 9 | 14, 5 | 15, 3 |
| Республика Хакасия | 8, 1 | 9, 2 | 4, 7 | -4, 1 | -4, 5 | -5, 9 | -2, 8 | 0, 2 | 1, 0 | 1, 5 | 1, 2 |
| Алтайский край | 6, 6 | 6, 6 | 1, 8 | -6, 0 | -5, 0 | -6, 4 | -5, 1 | -3, 6 | -2, 7 | -1, 9 | -2, 3 |
| Забайкальский край | 10, 6 | 11, 8 | 8, 4 | -0, 6 | -2, 7 | -3, 7 | -1, 6 | 0, 5 | 1, 6 | 2, 2 | 2, 1 |
| Красноярский край | 8, 7 | 8, 6 | 4, 5 | -4, 2 | -5, 5 | -4, 9 | -2, 9 | -1, 5 | -0, 7 | 0, 2 | 0, 1 |
| Иркутская область | 9, 8 | 9, 6 | 6, 2 | -4, 1 | -4, 8 | -5, 1 | -2, 8 | -0, 2 | 0, 9 | 1, 3 | 0, 8 |
| Кемеровская область | 6, 4 | 5, 8 | 1, 6 | -7, 8 | -7, 7 | -7, 9 | -6, 0 | -4, 5 | -3, 3 | -2, 6 | -2, 9 |
| Новосибирская область | 6, 4 | 6, 6 | 2, 4 | -5, 6 | -5, 7 | -5, 5 | -4, 7 | -3, 3 | -2, 0 | -1, 2 | -0, 7 |
| Омская область | 8, 2 | 9, 3 | 5, 6 | -2, 1 | -4, 9 | -5, 1 | -4, 3 | -2, 9 | -1, 9 | -0, 9 | -0, 7 |
| Томская область | 7, 7 | 8, 4 | 3, 9 | -3, 8 | -3, 7 | -3, 8 | -2, 4 | -0, 8 | -0, 1 | 0, 3 | 0, 5 |
| Республика Саха (Якутия) | 12, 3 | 12, 2 | 12, 7 | 5, 5 | 4, 0 | 4, 1 | 4, 7 | 6, 4 | 6, 1 | 7, 0 | 7, 0 |
| Камчатский край | 10, 8 | 9, 8 | 6, 2 | -2, 0 | -1, 7 | -1, 6 | -0, 3 | 0, 1 | 0, 3 | 0, 1 | -0, 5 |
| Приморский край | 10, 6 | 8, 7 | 5, 5 | -3, 7 | -5, 3 | -5, 8 | -4, 5 | -3, 4 | -3, 2 | -2, 0 | -2, 5 |
| Хабаровский край | 10, 1 | 9, 6 | 5, 9 | -3, 9 | -5, 6 | -5, 4 | -3, 9 | -2, 6 | -1, 8 | -1, 1 | -1, 7 |
| Амурская область | 10, 4 | 10, 0 | 7, 6 | -1, 9 | -4, 4 | -4, 8 | -3, 7 | -1, 7 | -2, 2 | 1, 4 | 1, 5 |
| Магаданская область | 10, 7 | 10, 5 | 8, 0 | -2, 7 | -2, 1 | -2, 6 | -2, 5 | -2, 3 | -2, 9 | -1, 2 | -1, 5 |
| Сахалинская область | 10, 2 | 8, 1 | 6, 1 | -8, 3 | -4, 2 | -6, 0 | -3, 8 | -2, 4 | -2, 2 | -2, 4 | -2, 8 |
| Еврейская автономная область | 11, 0 | 10, 9 | 8, 2 | -2, 7 | -4, 8 | -6, 3 | -3, 9 | -2, 1 | -1, 4 | -1, 6 | -1, 9 |
| Чукотский автономный округ | 11, 1 | 11, 4 | 10, 1 | 1, 3 | 1, 9 | 3, 9 | 3, 7 | 4, 1 | 2, 7 | 1, 2 | 0, 9 |
megabook.ru
ОБЩИЙ ПРИРОСТ НАСЕЛЕНИЯ — это… Что такое ОБЩИЙ ПРИРОСТ НАСЕЛЕНИЯ?
- ОБЩИЙ ПРИРОСТ НАСЕЛЕНИЯ
OБЩИЙ ПРИРОСТ НАСЕЛЕНИЯ, разность численностей нас. на начало и конец определ. временного интервала (ΔPобщ = P1 — P0). Выражается в абсолютных числах, может быть положит. и отрицат. Для терр. с неизменными границами О. п. н. равен сумме естественного прироста населения и миграционного прироста населения. Для терр. с меняющимися границами О. п. н. включает также прирост нас., обусловленный изменениями границ. Определение ежегодного О. п. н., абсолютного или относительного (см. Коэффициент прироста населения), — наиболее простой способ наблюдения за динамикой численности населения.
Демографический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор Д.И. Валентей. 1985.
- ОБЩЕСТВО
- ОБЪЕДИНЁННЫЕ АРАБСКИЕ ЭМИРАТЫ
Смотреть что такое «ОБЩИЙ ПРИРОСТ НАСЕЛЕНИЯ» в других словарях:
ПРИРОСТ НАСЕЛЕНИЯ — разность между численностью населения на конец и на начало периода. Общий прирост населения включает естественный и миграционный прирост населения … Словарь терминов по социальной статистике
ПРИРОСТ НАСЕЛЕНИЯ — разность между численностью населения на конец и на начало периода. Общий прирост населения включает естественный и миграционный прирост населения … Социальная статистика. Словарь
ПОКАЗАТЕЛИ РOСТА НАСЕЛЕНИЯ — ПОКАЗАТЕЛИ РOСТА НАСЕЛЕНИЯ, величины, характеризующие изменение числ. нас. во времени. В зависимости от того, растёт, убывает или остаётся неизменной числ. нас., П. р. н. могут быть положительными, отрицательными или равными 0. Различают… … Демографический энциклопедический словарь
Исторические типы воспроизводства населения — стадиальные особенности воспроизводства населения, закономерно присущие определенной стадии или фазе исторического развития общности людей. Исторические типы воспроизводства населения адекватны исторически определенным экономическим, социальным… … Экология человека
Иммиграция населения — Запрос «Иммигрант» перенаправляется сюда; см. также другие значения … Википедия
Список стран по уровню смертности населения — Уровень смертности по странам на 1000 чел. (по данным CIA World Factbook на 2009 год) Эта статья включает в себя две версии списка стран по общему коэф … Википедия
МИГРАЦИЯ НАСЕЛЕНИЯ — (от лат. migratio переселение), перемещения людей (мигрантов) через границы тех или иных терр. с переменой места жительства навсегда или на более или менее длительное время. Поскольку М. н. складывается из миграционных потоков, понятие миграция… … Демографический энциклопедический словарь
Россия. Население: Статистика населения — I А. Статистика населения. Источники сведений о населении Р. До 1897 г. данные о числе жителей в Р. не отличались точностью. Главным способом для исчисления народонаселения служили ревизии, цель которых почти исключительно состояла в счете… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Франция* — (France, Frankreich). Расположение, границы, пространство. С севера Ф. омывает Немецкое море и Ла Манш, с запада Атлантический океан, с юго востока Средиземное море; на северо востоке она граничит с Бельгией, Люксембургом и Германией, на востоке… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Франция — I (France, Frankreich). Расположение, границы, пространство. С севера Ф. омывает Немецкое море и Ла Манш, с запада Атлантический океан, с юго востока Средиземное море; на северо востоке она граничит с Бельгией, Люксембургом и Германией, на… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
demography.academic.ru
Рассчитайте величину годового естественного прироста населения в промилле, если в стране за год родилось 18 500 человек,
Моя племянница попросила помочь решить задачу. С точными науками у меня было всё хорошо и в школе, и в университете, поэтому я согласилась. В голове закрутились формулы по физике, геометрии, химии… Однако, через минуту передо мной лежал лист с заданием по географии. Такого я не ожидала, но я же уже согласилась помочь.
Расчёт годового естественного прироста населения
Под данным параметром подразумевается разница в количестве рождённых детей и умерших людей, в этом случае, за год. Рассчитывается он, как и показатели рождаемости, смертности, на 1000 человек населения, поэтому выражается в промилле.
Итак, надо высчитать естественный прирост. В учебнике я нашла подходящую формулу: ЕП = ((Р – С)/ЧН) х 1000, где ЕП — величина годового естественного прироста, Р — число родившихся за этот же период, С — количество умерших на протяжении года, ЧН — показатель среднегодовой численности населения. В условии есть все необходимые цифры, чтобы в один приём решить задачу:
- Р = 18 500 чел;
- С = 13 200 чел;
- ЧН = 1 596 000 чел;
- 1000 — множитель для преобразования десятичной дроби в промилле.
Отсюда, ЕП = ((18 500 – 13 200)/1 596 000) х 1000 = 3,32 ‰.
Стоит отметить, что положительное значение указывает, что прирост всё же происходит. В случае отрицательной величины наблюдалась бы убыль населения.
Демографические показатели мира
В наше время 90 % прироста населения приходится на африканские, латиноамериканские и азиатские развивающиеся страны. Европа же отличается уменьшением абсолютной численности.
На планете средний уровень рождаемости ныне составляет 22,6%. В государствах Европы, Австралии и Северной Америке этот показатель весьма скромен — 11,4%. Высоким уровнем рождаемости отличаются развивающиеся страны, где он равен 25,4%.
Мировая смертность населения в конце ХХ в. равна 8,9%. В экономически развитых странах уровень смертность выше, чем в развивающихся. Однако, максимально высокий он в самых бедных странах — Эфиопии, Анголе, Сьерра-Леоне, Мали — 20–30%. Низкий уровень в арабских нефтедобывающих странах.
travelask.ru
Как рассчитать прирост населения | Сделай все сам
Прогнозирование прироста населения – дюже значимый инструмент для долгосрочного планирования экономического и общественного становления социума. Это расчет величины его трудовых источников и объема надобностей.

Инструкция
1. Приход населения является суммой величин 2-х показателей – натурального и миграционного прироста . Это разность между нынешним ярусом демографической обстановки и ярусом больше раннего периода. Временной интервал, за тот, что производится расчет, именуется расчетным и может быть краткосрочным (от месяца до нескольких лет) и долгосрочным (5, 10, 15, 25, 100 лет).
2. Натуральный приход – правильная разница между числом родившихся и усопших (число родившихся огромнее числа усопших). Скажем, в России по данным за август 2009 года родилось 151,7 тысячи человек, скончалось 150,7 тысячи человек, значит натуральный приход населения составил 1000 человек. Считается, что если рождаемость превышает смертность, то воспроизведение населения расширенное. Если эти числа приблизительно равны, то воспроизведение примитивное. Если же смертность превышает рождаемость, то воспроизведение суженное, отслеживается мощный демографический спад.
3. Миграционный (либо механический) приход – правильная разница между числом прибывших в страну людей из других стран и числом выбывших из нее граждан.
4. Для определения всеобщей картины демографических изменений в стране применяются показатели прироста населения . Показатель обычного прироста – это разница между числом родившихся и усопших за определенный период, поделенная на всеобщую количество населения . Показатель миграционного прироста населения – это разница между числом прибывших в страну граждан и числом выбывших, поделенная на всеобщую количество. Соответственно, всеобщий показатель прироста населения является суммой этих показателей.
Оценка демографической обстановки в стране является основой для прогнозирования надобностей и трудовых источников социума и, как следствие, объемов производства для удовлетворения нужд населения. Для полноты обзора нужно определить обычный и миграционный прирост и просуммировать эти величины.

Инструкция
1. Для обзора демографической обстановки в стране применяются безусловные и относительные величины 2-х видов прирост а: механического (миграционного) и натурального. 2-й показатель характеризует разницу между числом родившихся и усопших граждан за определенный период времени.
2. Для того, дабы данные были максимально правильными, используются статистические способы, разрешающие отслеживать малейшие метаморфозы. Эти способы включают в себя контроль рождаемости и смертности, осуществляемый особыми органами. Данные для этого поступают из роддомов и клиник и имеют документальную основу.
3. Если число родившихся за определенный период превышает число усопших, то говорят о расширенном воспроизводстве населения. Если они приблизительно идентичны, это примитивное воспроизведение. Если же разность между ними негативна, то оно суженое, что свидетельствует о демографическом спаде и требует вступления экстренных мер по стимулированию рождаемости.
4. Безусловная оценка обычного прирост а заключается в вычислении арифметической разности между объемом воспроизводства на конец и предисловие периода, тот, что может быть любым календарным интервалом, от месяца до 5 лет (краткосрочный обзор) до десятилетий: от 5 до 100 лет (долгосрочный обзор).
5. Скажем, пускай за месяц число родившихся составило 155 000 человек, а число усопших – 153 000. Тогда налицо обычный прирост в 2 000 обитателей. Это дозволено считать простым воспроизводством, от того что разница невелика по сопоставлению с обеими величинами.
6. Относительная оценка натурального прирост а осуществляется путем вычисления показателей. При этом безусловную величину относят к всеобщему числу обитателей. Таким образом, получается некая величина, которая может быть выражена в процентах. Скажем: на предисловие года население страны составляет 50 млн людей. За год родилось 1 млн человек, а скончалось 850 000 обитателей. Безусловный показатель обычного прирост а в этом случае равен 150 000, а относительный – (150 000/50 000 000)•100% = 0,3 %.
Видео по теме
Для определения интенсивности изменений каких-нибудь показателей за определенный период времени применяется комплект колляций, которые получаются способом сопоставления нескольких ярусов показателей, измеренных на различных отметках временной шкалы. В зависимости от того, каким образом сравниваются измеренные показатели между собой, полученные колляции именуются показателем роста, темпом роста, темпом прихода, безусловным приходом либо безусловным значением 1% прихода.
Инструкция
1. Определите, какие именно показатели и каким образом нужно сопоставлять между собой, дабы получить желанное значение безусловного прихода. Исходите из того, что эта колляция должна показывать безусловную скорость метаморфозы исследуемого показателя и рассчитываться как разность между нынешним ярусом и ярусом, принимаемым за базовый.
2. Вычтите из нынешнего значения исследуемого показателя его значение, измеренное в той точке временной шкалы, которая принимается за базовую. Скажем, возможен, что число рабочих, занятых на производстве на предисловие нынешнего месяца составляет 1549 человек, а на предисловие года, которое считается базисным периодом, оно было равно 1200 работникам. В этом случае безусловный приход за период с начала года по предисловие нынешнего месяца составил 349 единиц, потому что 1549-1200=349.
3. Если требуется не только рассчитать данный показатель за один конечный период, но и определить среднее значение безусловного прихода за несколько периодов, то нужно вычислить это значение для всей временной отметки по отношению к предыдущей, после этого сложить полученные величины и поделить их на число периодов. Скажем, возможен, что необходимо вычислить среднее значение безусловного прихода числа занятого на производстве персонала по месяцам нынешнего года. В этом случае отнимите от значения показателя по состоянию на предисловие февраля, соответствующее значение для начала января, после этого проделайте схожие операции для пар март/февраль, апрель/март и т.д. Завершив с этим, сложите полученные значения и поделите итог на порядковый номер последнего из участвовавших в расчете месяцев нынешнего года.
Обратите внимание!
Приход населения принято измерять в процентах, следственно полученный показатель надобно умножить на 100. Всеобщая количество населения берется на предисловие расчетного периода.
Полезный совет
На основе полученных данных и обзоре темпа роста населения дозволено предсказывать становление обстановки на ближайшие периоды.
jprosto.ru
География (тема население) что такое естественный прирост?))
ЕСТЕСТВЕННЫЙ ПРИРОСТ НАСЕЛЕНИЯ — разница между числом родившихся и умерших людей за определенный период времени. определенный период времени. Служит наиболее общей характеристикой интенсивности роста населения, измеряется обычно коэффициентом естественного прироста населения на 1000 жителей в год. Может быть как положительным (например, в Лаосе естественный прирост населения сейчас 24,6), так и отрицательным (например, на Украине — −6,2). Отрицательный естественный прирост населения означает, что в стране умирает больше человек, чем рождается. Формула: ЕП=((Р-С) /Н) *1000, где ЕП — естественный прирост, Р — рождаемость, С — смертность, Н — население. Естественный прирост измеряется в промилле.
Это превышение рождаемости над смертностью
это когда детей делают естественным\традиционным\способом… не естественный прирост это когда китайцы в россии делают детей…
Рождаемость (за опред. время) — Смертность (за опред. время) = Естественный Прирост (за опред. время)
превышенную рождаемость вычесть смертность
разница между числом родившихся и умерших людей за определенный период времени.
Аварцы (маг1арулал) у аварок нет таких»папхах»скорее эта осетинка! <a rel=»nofollow» href=»https://thebiggest.ru/lyudi-i-zhivotnye/mnogochislennye-narody-rossii.html» target=»_blank»>https://thebiggest.ru/lyudi-i-zhivotnye/mnogochislennye-narody-rossii.html</a>
touch.otvet.mail.ru
50. Естественный прирост населения. Метод расчета.
В России в последнее десятилетие численность населения ежегодно уменьшалась и к 1996 г. составила около 147 млн. человек. Показатель естественного прироста, (разница между уровнем рождаемости и уровнем смертности) отрицательный (–6 на 1000 жителей). Отмечается постарение населения. Так, доля населения старших возрастных групп в Санкт-Петербурге составляет около 23%. Снижается доля детского населения (до 20%).
Показатель естественного прироста населения = (число родившихся – число умерших / среднегодовая численность населения) х 1000.
Сам естественный прирост населения не всегда отражает демографическую обстановку в обществе, т.к. одни и те же размеры прироста могут быть получены при разных показателях рождаемости и смертности. Поэтому естественный прирост необходимо оценивать только в соотношении с показателями рождаемости и смертности.
К одному из наиболее неблагоприятных демографических явлений относятся наличие отрицательного естественного прироста, свидетельствующего о явном неблагополучии в обществе.
51. Заболеваемость населения. Факторы риска. Система учета.
Заболеваемость является одним из критериев оценки состояния здоровья населения. Материалы о заболеваемости населения в практической деятельности врача необходимы для: оперативного руководства работой учреждений здравоохранения; оценки эффективности проводимых лечебно-оздоровительных мероприятий, в том числе диспансеризации; оценки здоровья населения и выявления факторов риска, способствующих снижению заболеваемости; планирования объема профилактических осмотров; определения контингента для диспансерного наблюдения, госпитализации, санаторно-курортного лечения, трудоустройства определенного контингента больных и т. д.; текущего и перспективного планирования кадров, сети различных служб и подразделений здравоохранения; прогноза заболеваемости.
В статистике заболеваемости существуют следующие показатели.
Заболеваемость — это совокупность вновь возникших заболеваний за календарный год; рассчитывается как отношение числа вновь возникших заболеваний к средней численности населения, умноженное на 1000.
Болезненность — это распространенность зарегистрированных заболеваний, как вновь возникших, так и ранее существовавших, при первичном обращении в календарном году; статистически выражается как отношение числа всех заболеваний населения за год к средней численности населения, умноженное на 1000.
Патологическая пораженность — совокупность болезней и патологических состояний, выявленных врачами путем активных медицинских осмотров населения; статистически выражается как отношение числа заболеваний, имеющихся на данный момент, к средней численности населения, умноженное на 1000. В основном это хронические заболевания, но могут быть учтены и острые заболевания, имеющиеся на данный момент. В практическом здравоохранении этим термином могут быть определены результаты медицинских осмотров населения. Рассчитывают как отношение числа заболеваний, выявленных при медицинском осмотре, к числу осмотренных лиц, умноженное на 1000.
В зависимости от цели исследования используют различные статистические материалы и учетные документы (медицинские карты, экстренные извещения, листки нетрудоспособности, карты выбывших из стационара, врачебные свидетельства о смерти, другие специальные бланки и анкеты). При изучении заболеваемости и смертности населения пользуются “Международной статистической классификацией болезней и проблем, связанных со здоровьем” (10-й пересмотр, 1995 г., ВОЗ), включающей 21 класс заболеваний, которые разделены на блок рубрик, термины и диагностические формулировки.
studfiles.net

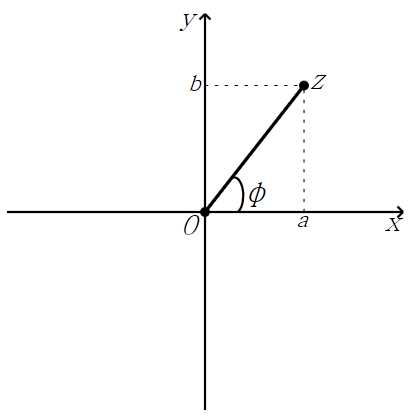
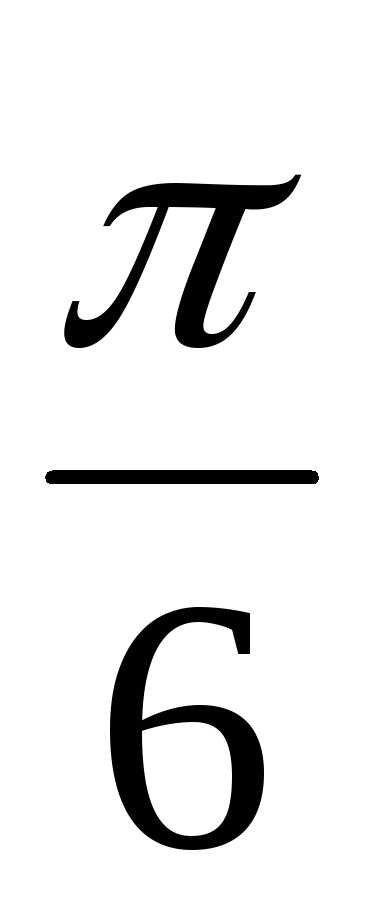 + isin
+ isin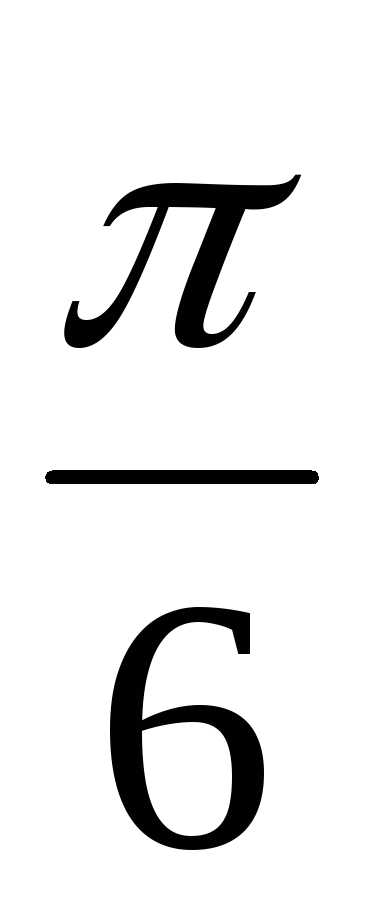 )
и z2 = 3(cos
)
и z2 = 3(cos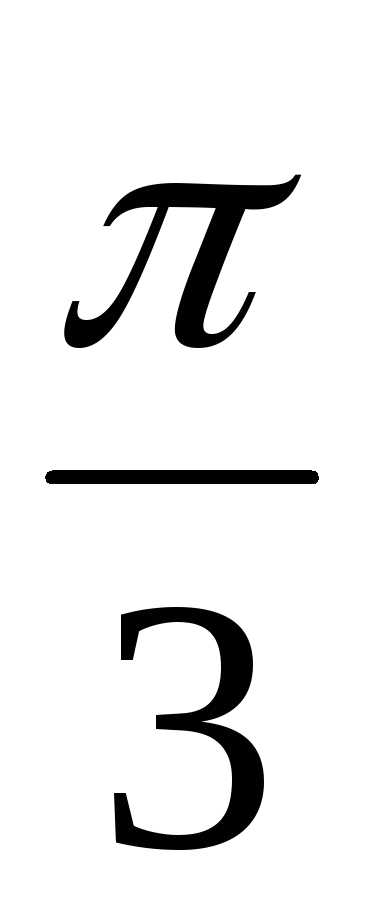 + isin
+ isin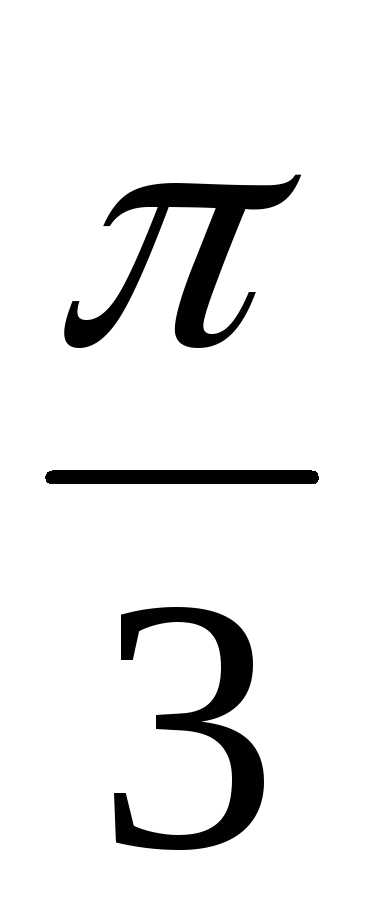 )
найти их произведение z1z2.
)
найти их произведение z1z2. +
+ 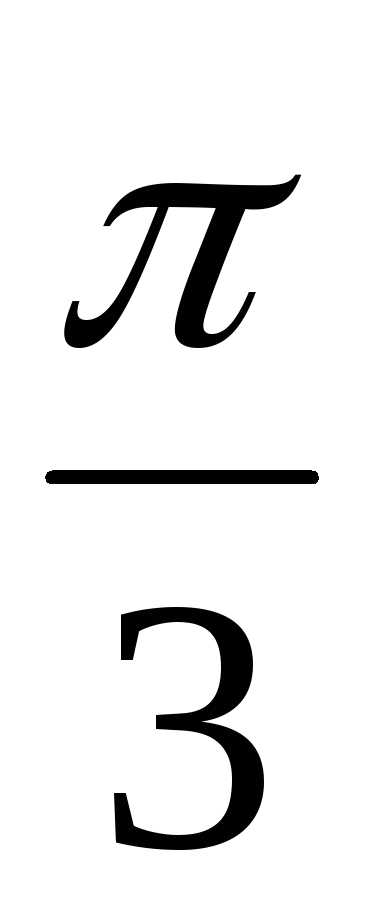 ) + isin(
) + isin(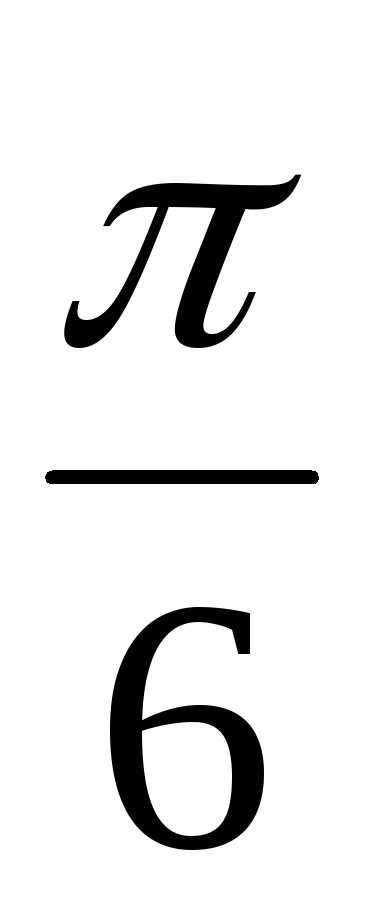 +
+ 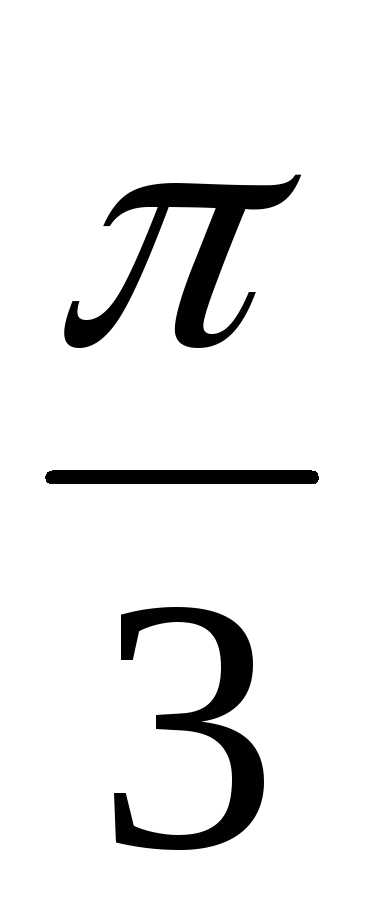 )) = 6(cos
)) = 6(cos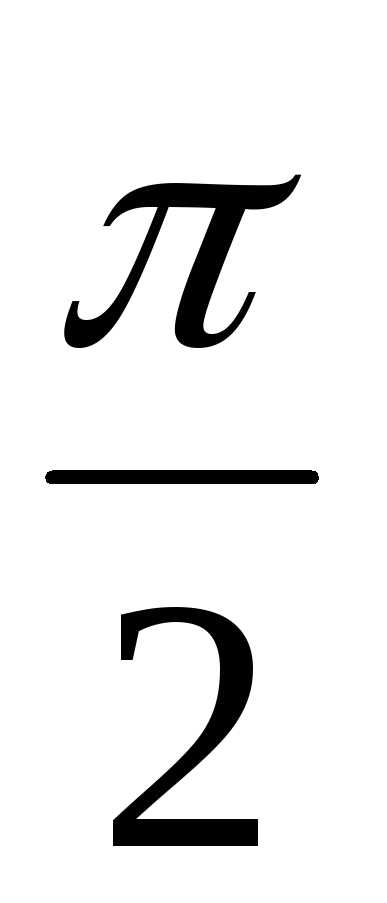 + isin
+ isin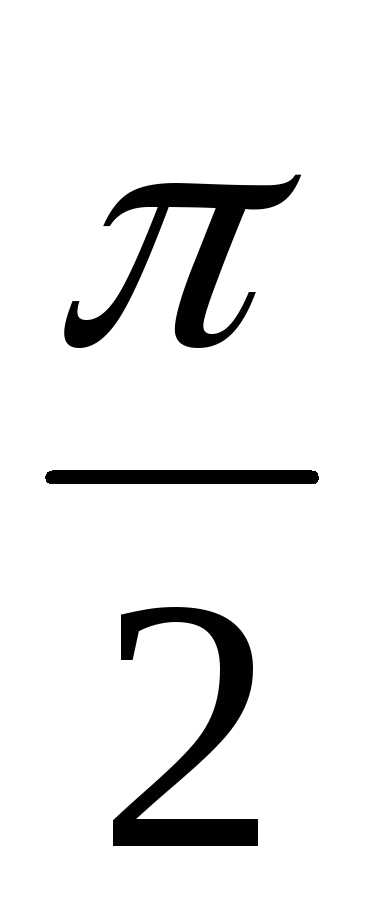 )
– тригонометрическая форма произведения
чисел z1 и z2 или в алгебраической форме z1z2 = 6i.
)
– тригонометрическая форма произведения
чисел z1 и z2 или в алгебраической форме z1z2 = 6i.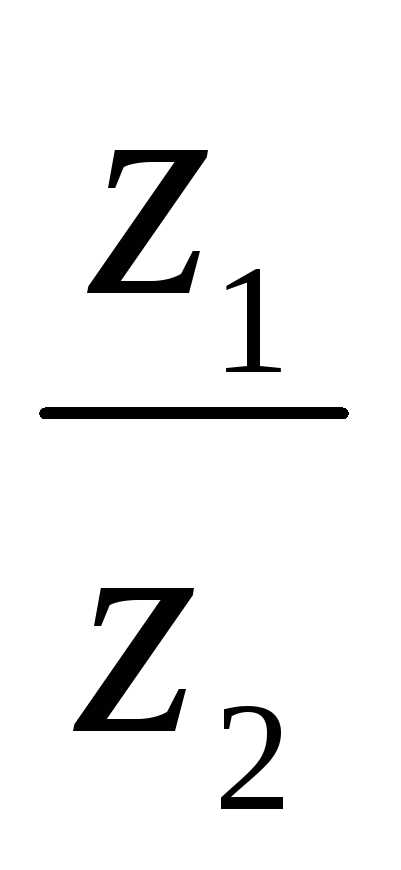 =
=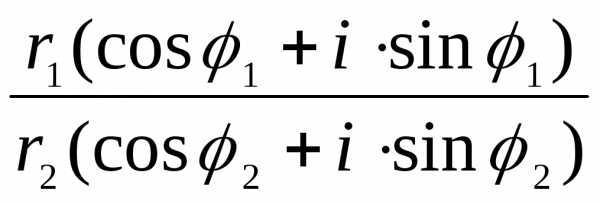 =
= =
=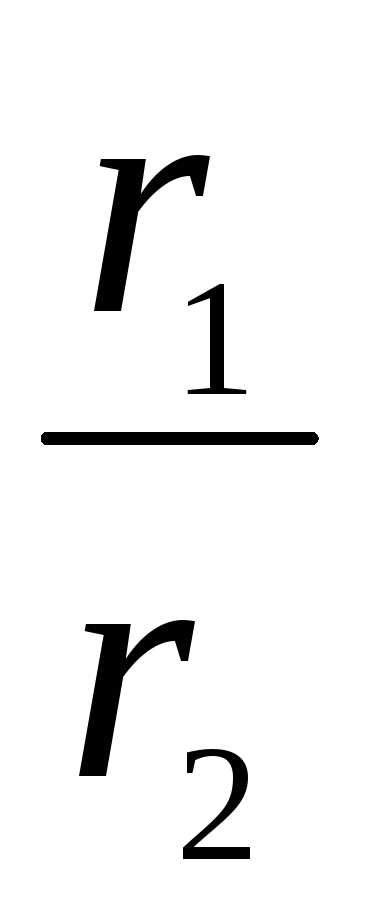 =
=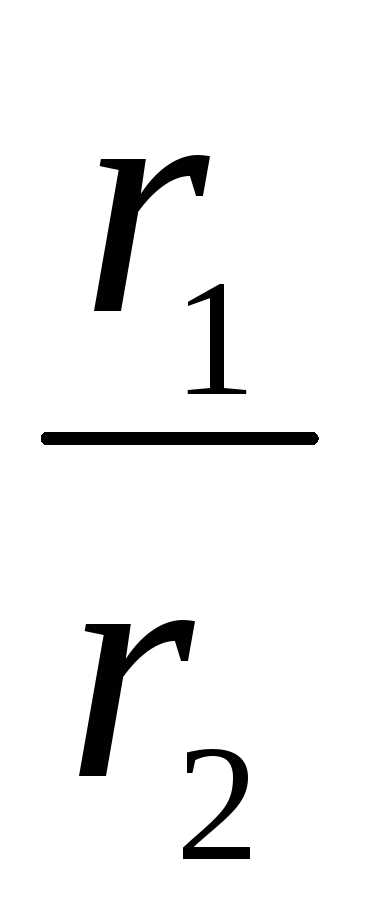 ( cos(1 – 2) + isin(1 – 2))
( cos(1 – 2) + isin(1 – 2))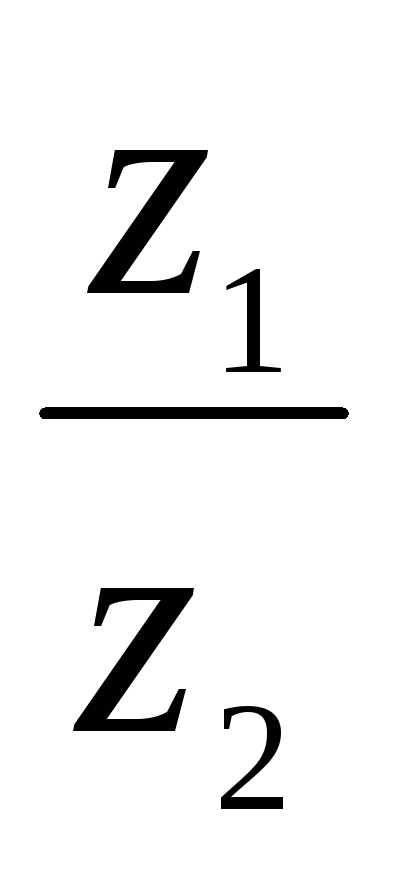 | =
| = 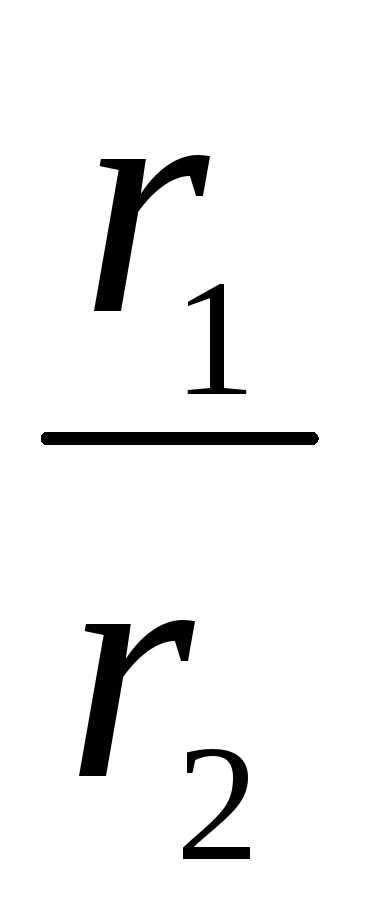 ,
аргумент arg(
,
аргумент arg(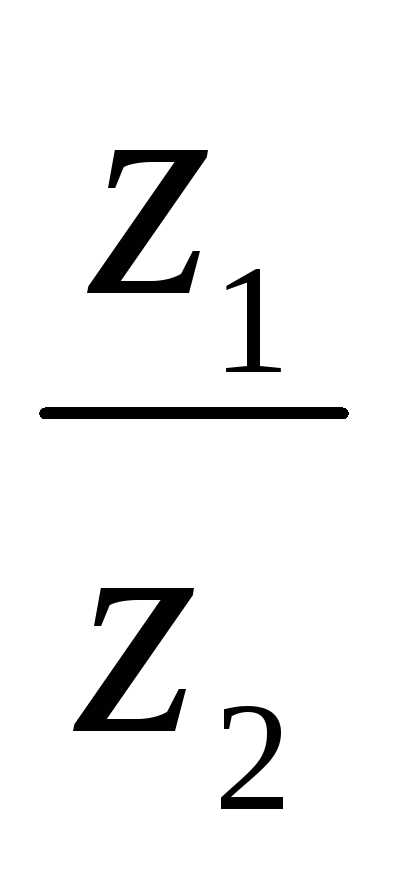 ) = arg z1 – arg z2.
) = arg z1 – arg z2.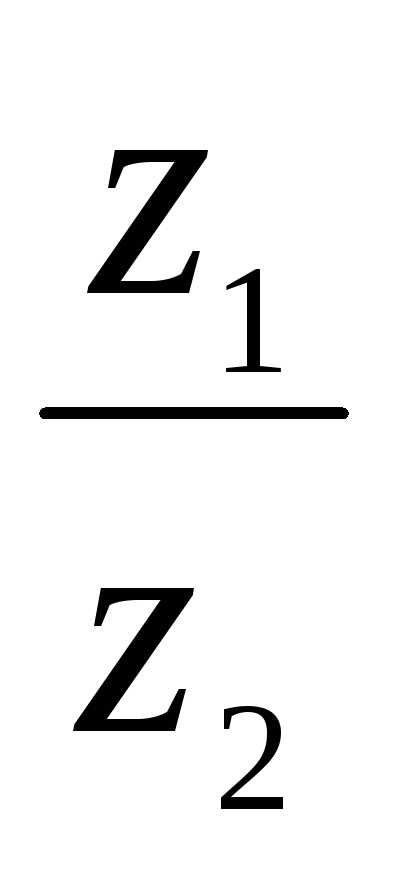 .
.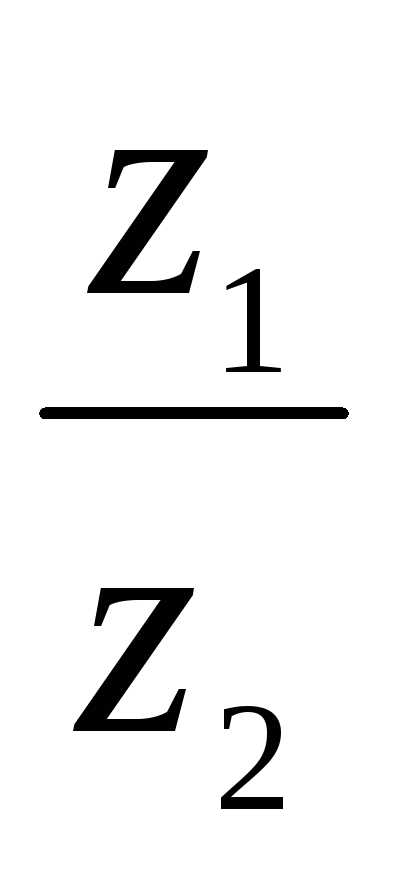 =
= 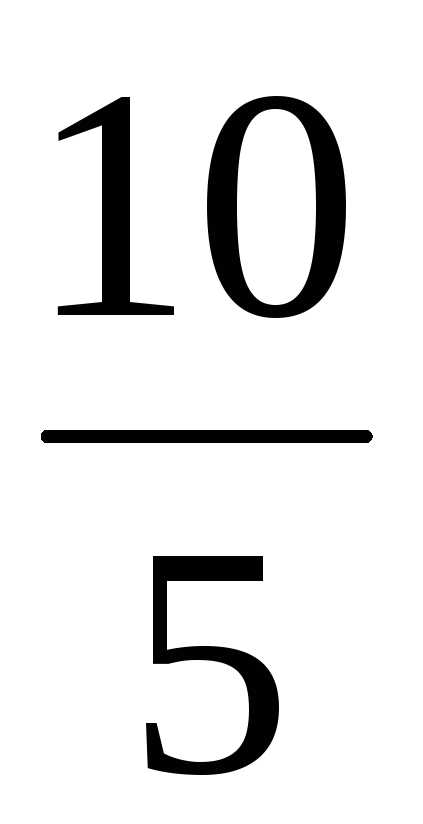 (cos(45 – 60) + isin(45 – 60)) = 2(cos(–15) + isin(–15))
– тригонометрическая форма частного
чисел z1 и z2.
Заметим, что если данное выражение
записать в виде равносильного выражения 2(cos15 – isin15),
то это не будет уже тригонометрической
формой записи комплексного числа.
(cos(45 – 60) + isin(45 – 60)) = 2(cos(–15) + isin(–15))
– тригонометрическая форма частного
чисел z1 и z2.
Заметим, что если данное выражение
записать в виде равносильного выражения 2(cos15 – isin15),
то это не будет уже тригонометрической
формой записи комплексного числа.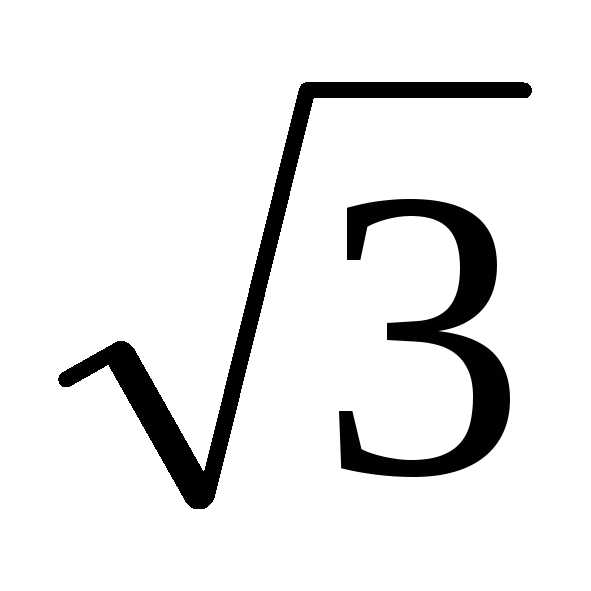 – i,
найти z4.
– i,
найти z4.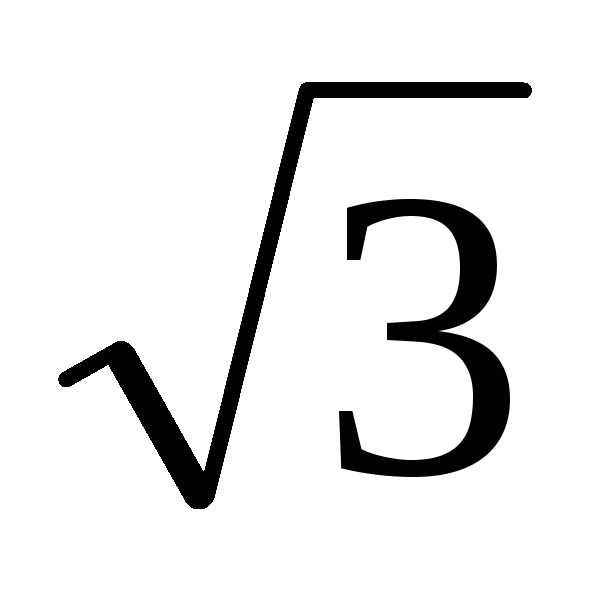 – i = 2(cos
– i = 2(cos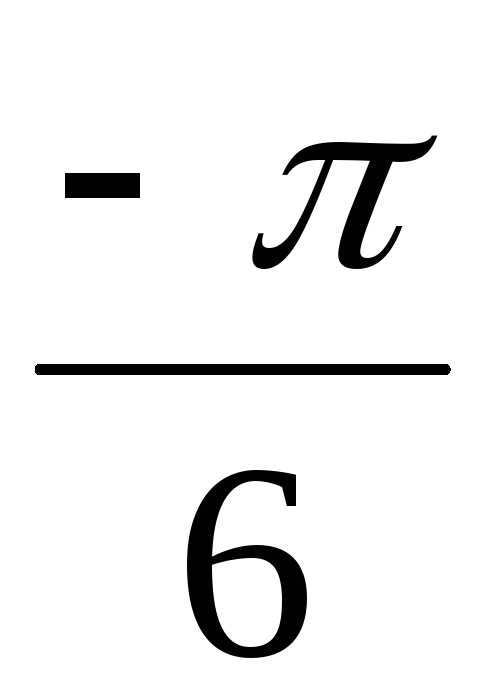 + isin
+ isin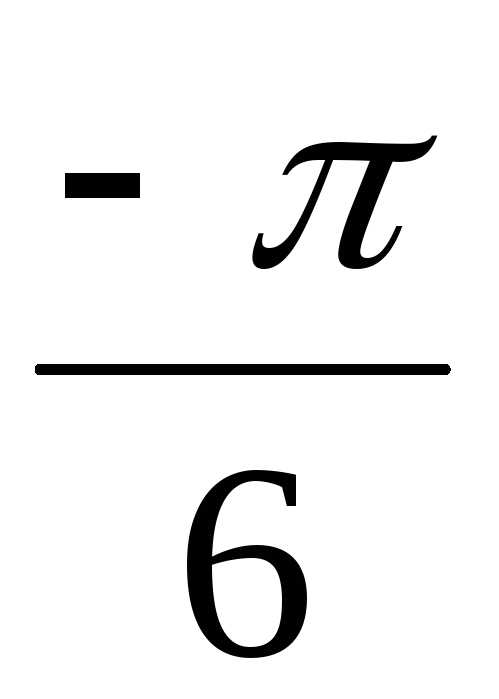 ).
Тогда z4 = (
).
Тогда z4 = (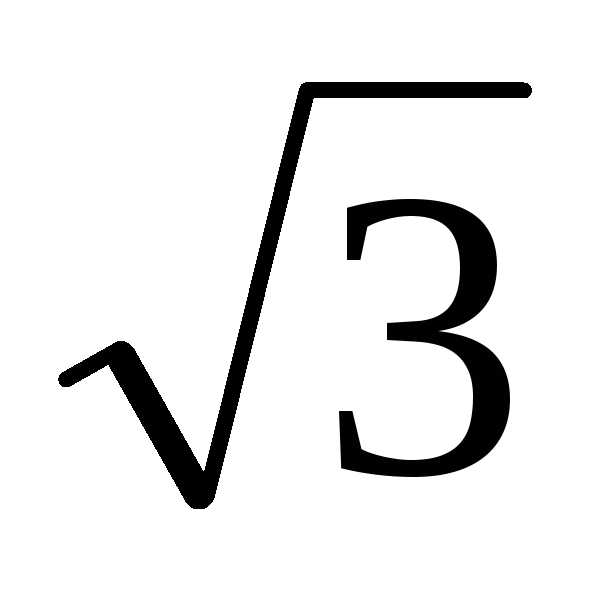 – i)4 = (2(cos
– i)4 = (2(cos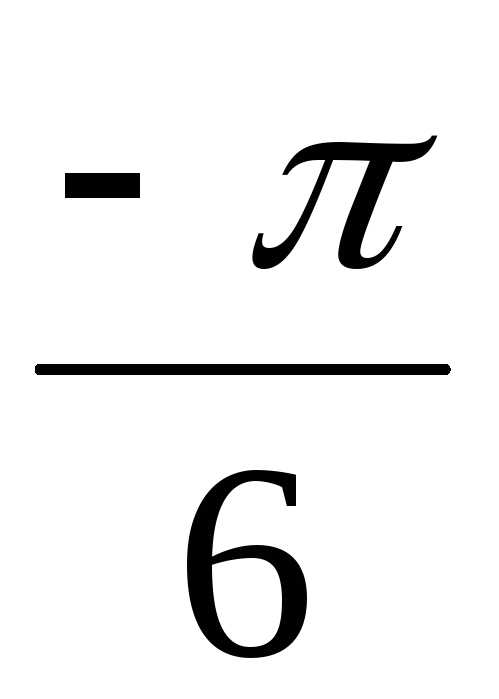 + isin
+ isin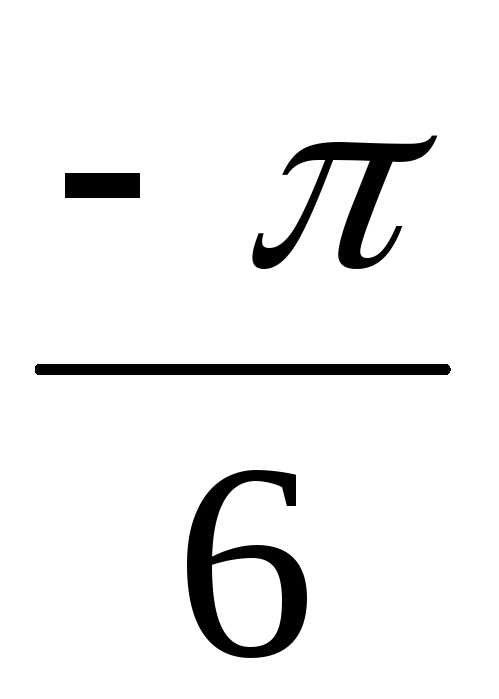 ))4 = 24(cos
))4 = 24(cos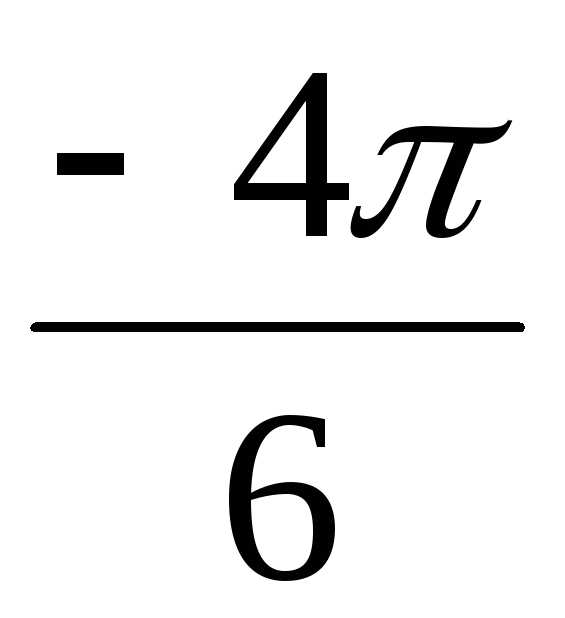 + isin
+ isin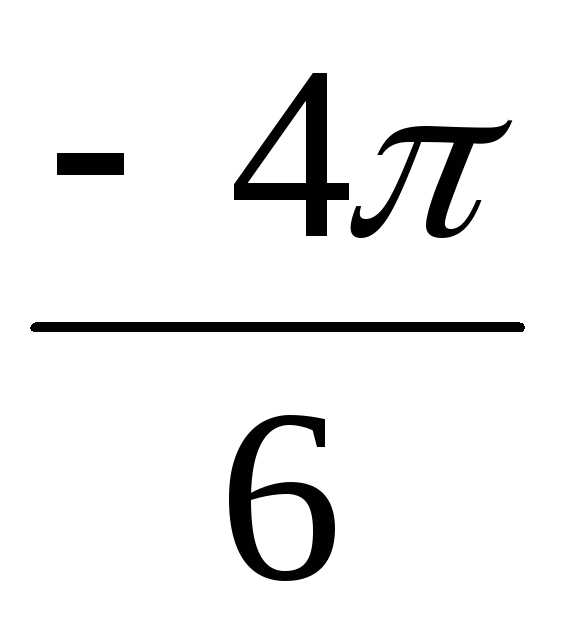 ) =
= 16(cos
) =
= 16(cos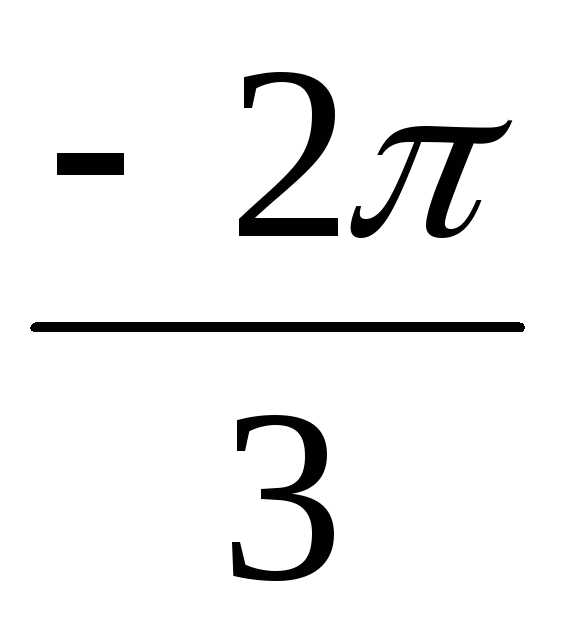 + isin
+ isin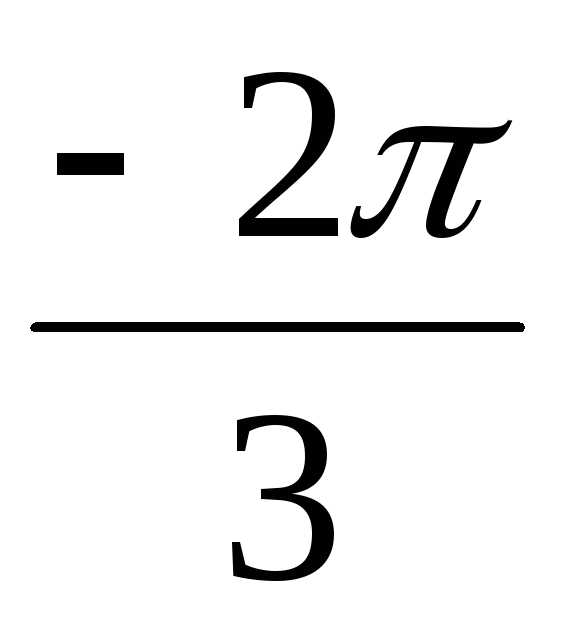 )
– тригонометрическая форма результата
возведения в четвертую степень данного
комплексного числа. Найдем также и
алгебраическую форму записи числа z4. z4 = 16(cos
)
– тригонометрическая форма результата
возведения в четвертую степень данного
комплексного числа. Найдем также и
алгебраическую форму записи числа z4. z4 = 16(cos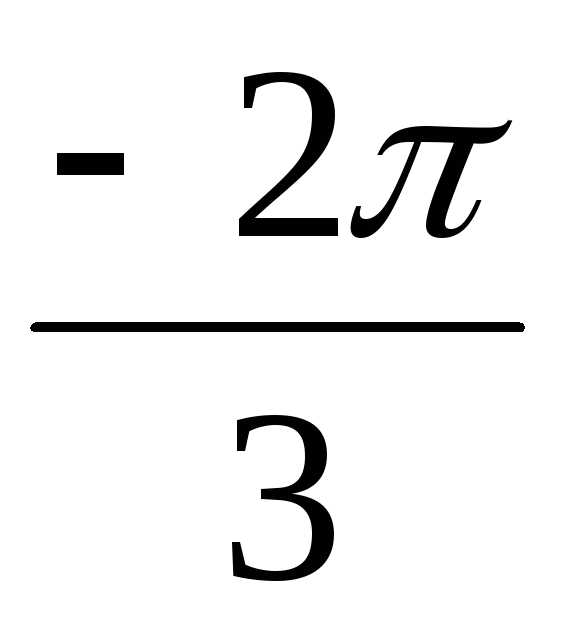 + isin
+ isin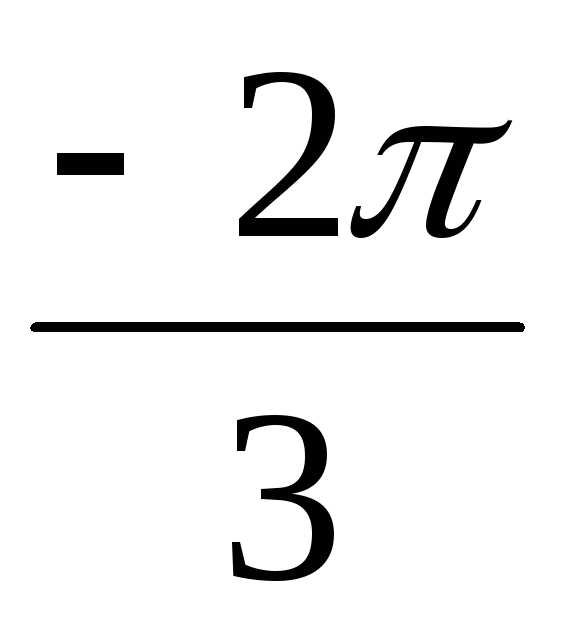 ) = 16(cos
) = 16(cos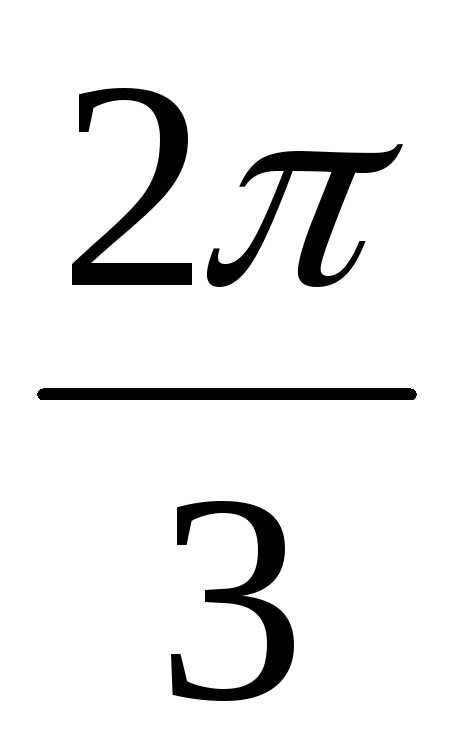 – isin
– isin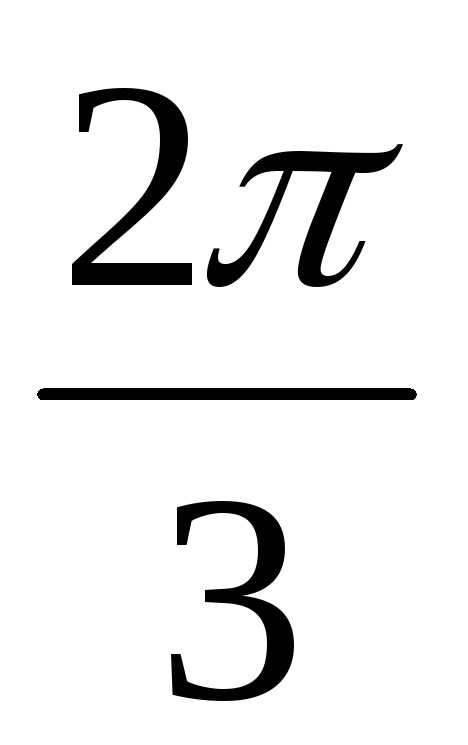 ) = 16(
) = 16(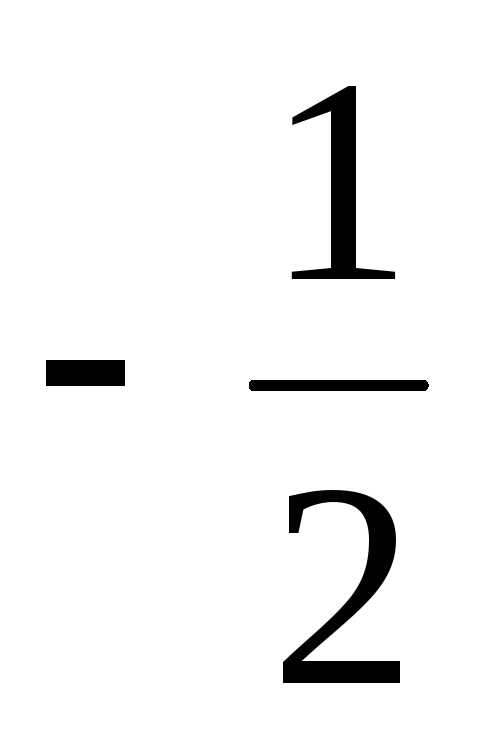 – i
– i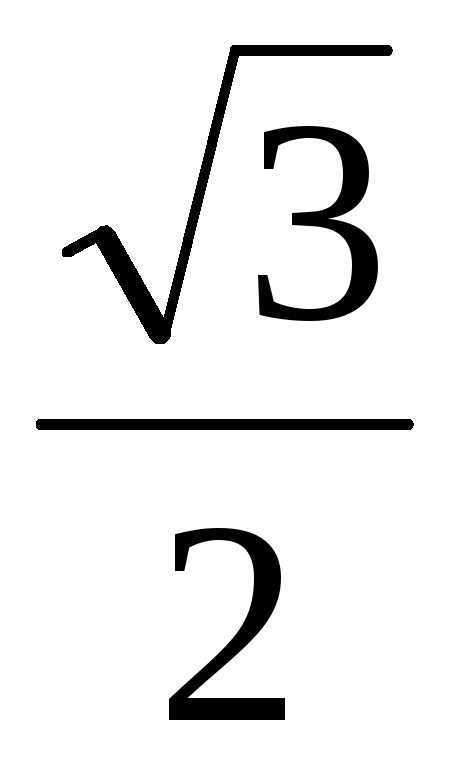 ) =
= –8 – 8
) =
= –8 – 8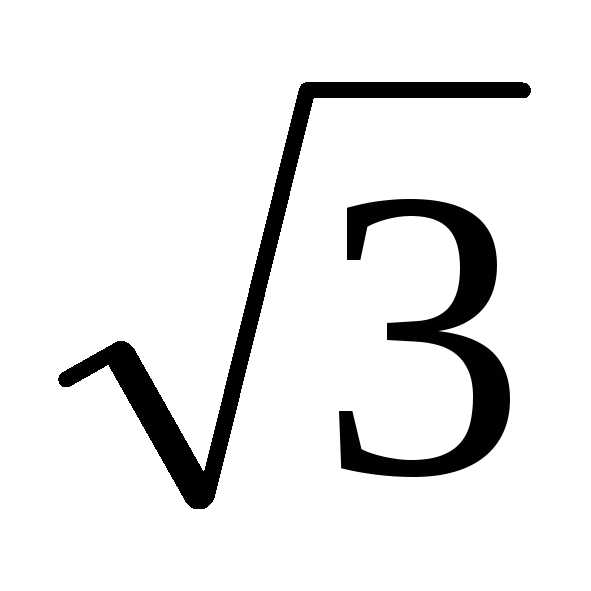 i.
i.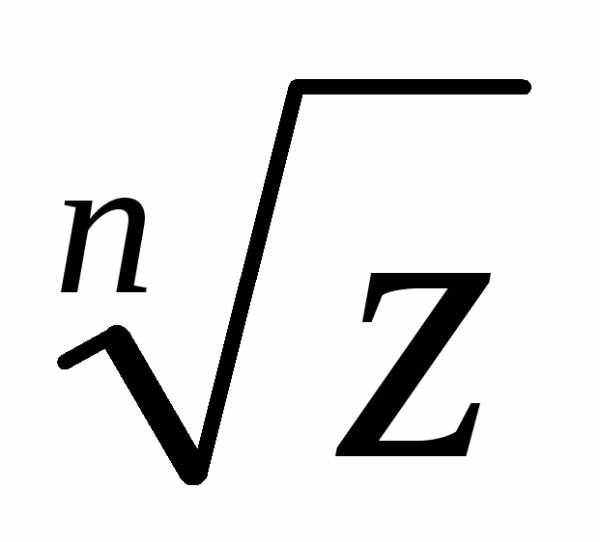 = =
= =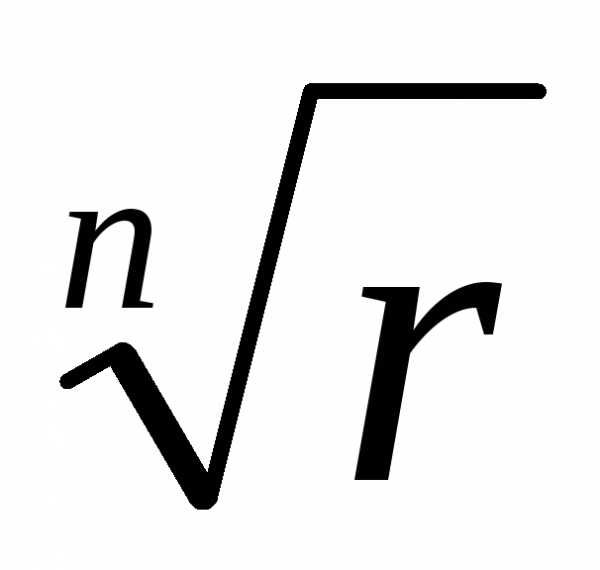 (cos
(cos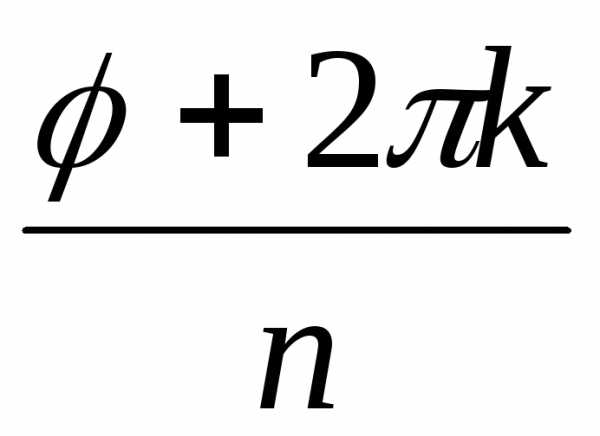 + isin
+ isin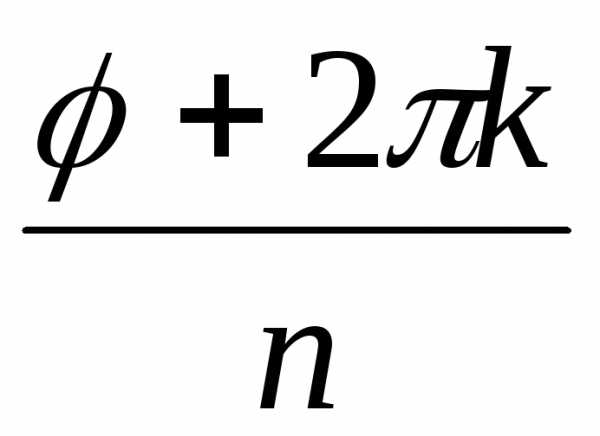 ),
гдеk = 0,
1, …, n – 1.
),
гдеk = 0,
1, …, n – 1.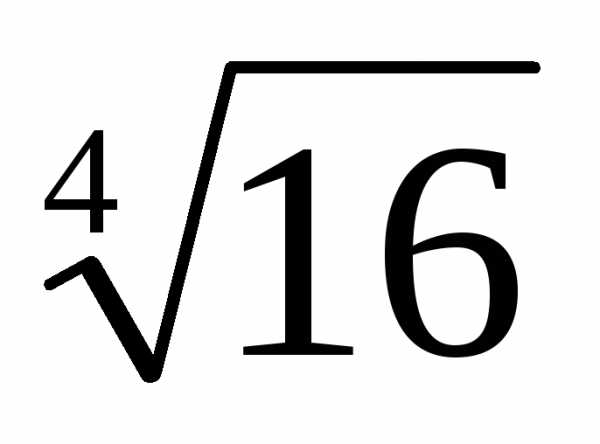 .
.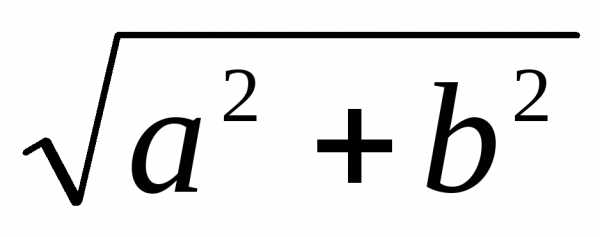 =
=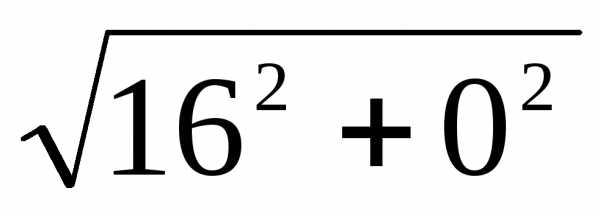 = 16;т. к. a = 16 > 0,
то
=
= 16;т. к. a = 16 > 0,
то
= 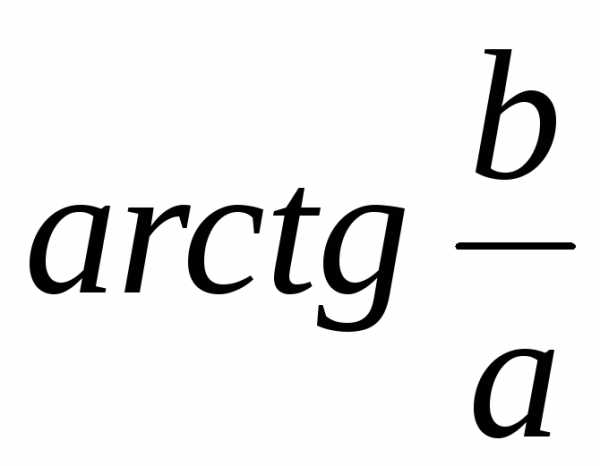 =
= 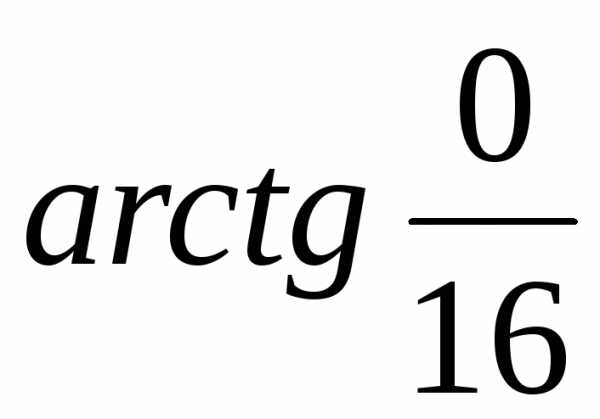 =
=
=
=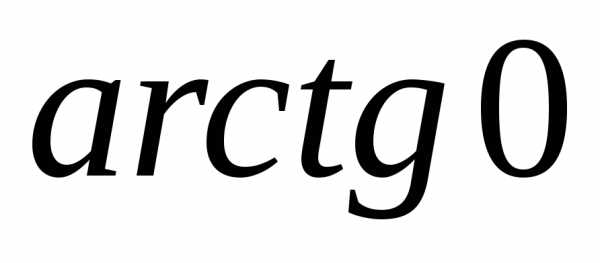 = 0.Тогда z = 16 = r(cos + isin) = 16(cos0 + isin0).
= 0.Тогда z = 16 = r(cos + isin) = 16(cos0 + isin0).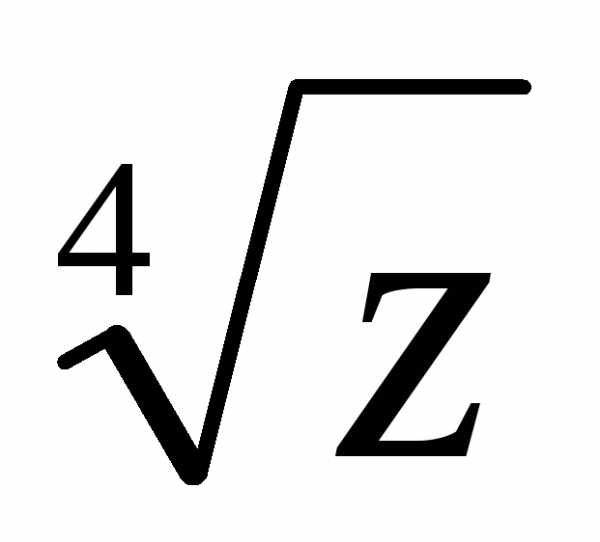 =
= 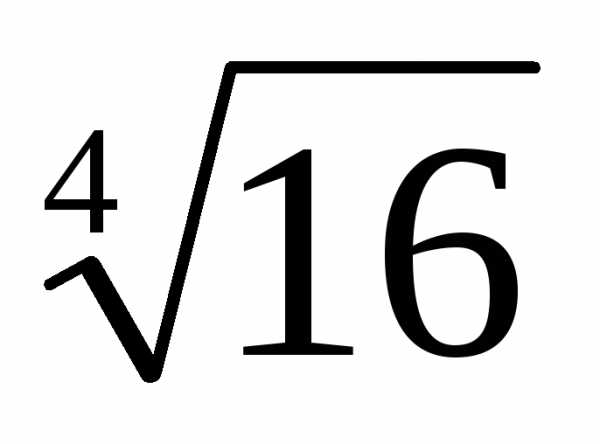 ==
==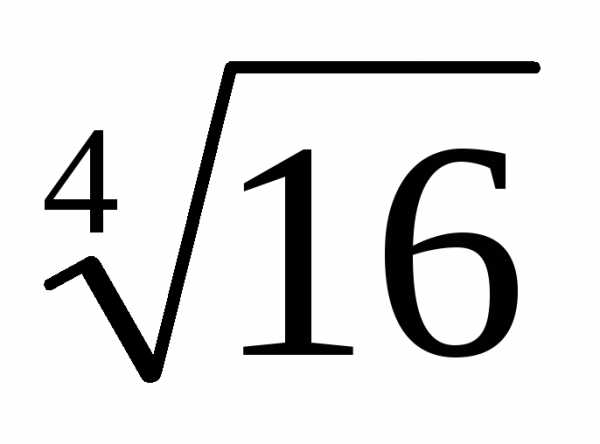 (cos
(cos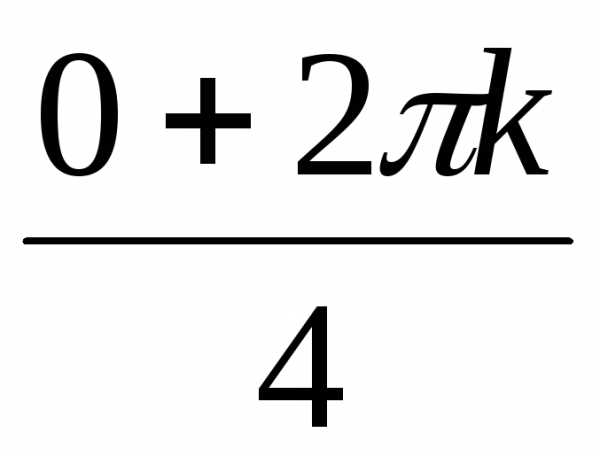 + isin
+ isin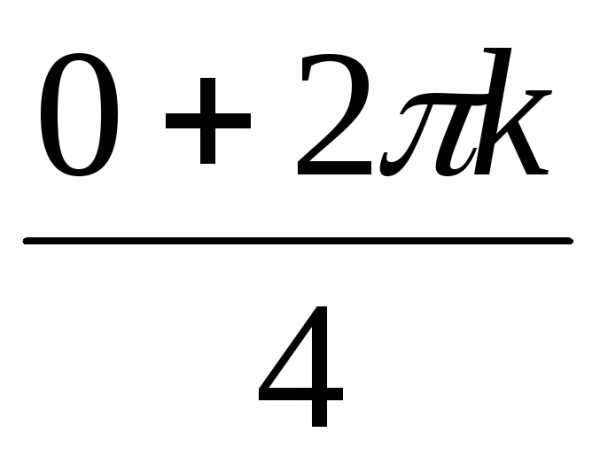 ) =
) =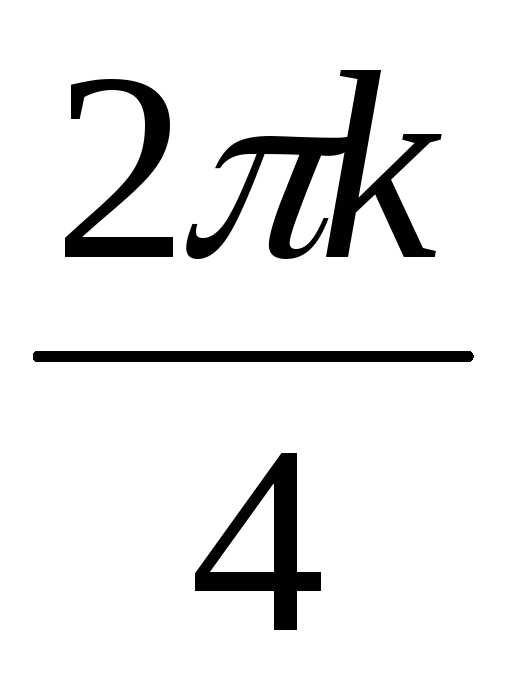 + isin
+ isin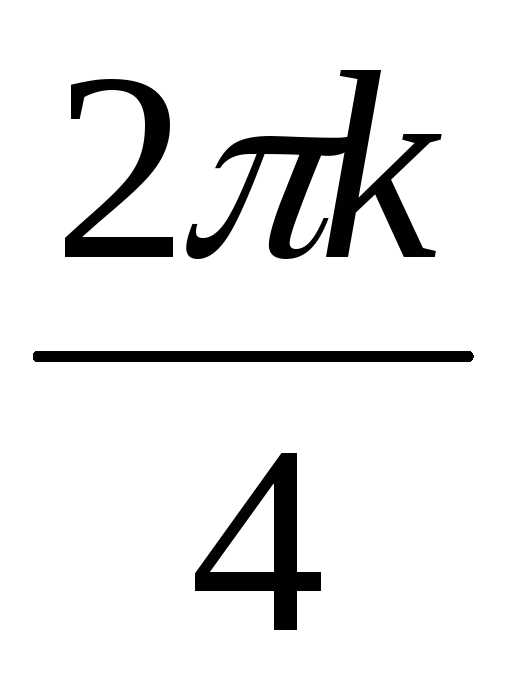 ) ,где k = 0,
1, 2, 3. Найдем
все четыре корня:
) ,где k = 0,
1, 2, 3. Найдем
все четыре корня: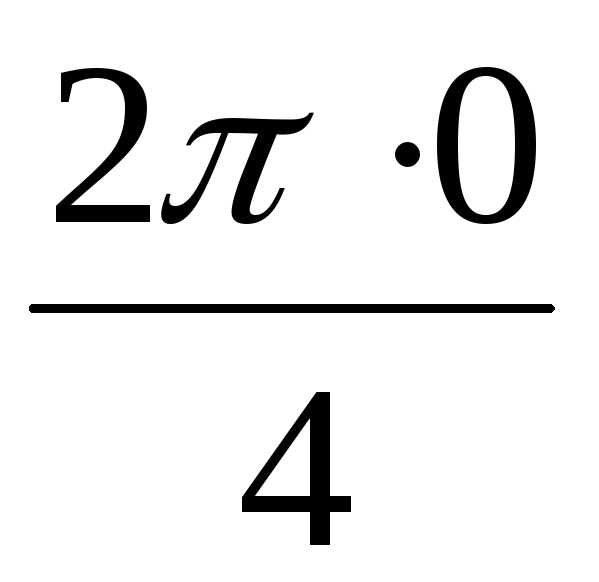 + isin
+ isin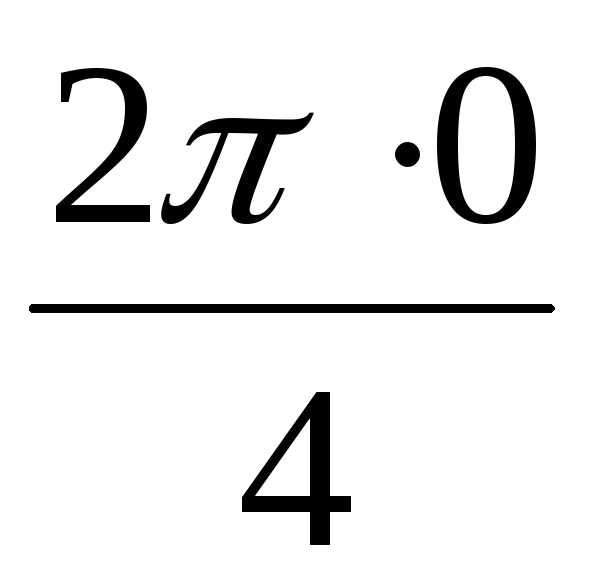 ) = 2
(cos0 + isin0) = 2,
) = 2
(cos0 + isin0) = 2,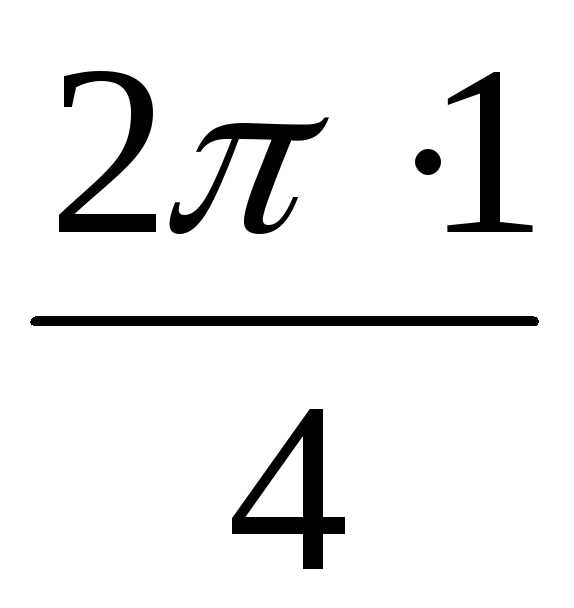 + isin
+ isin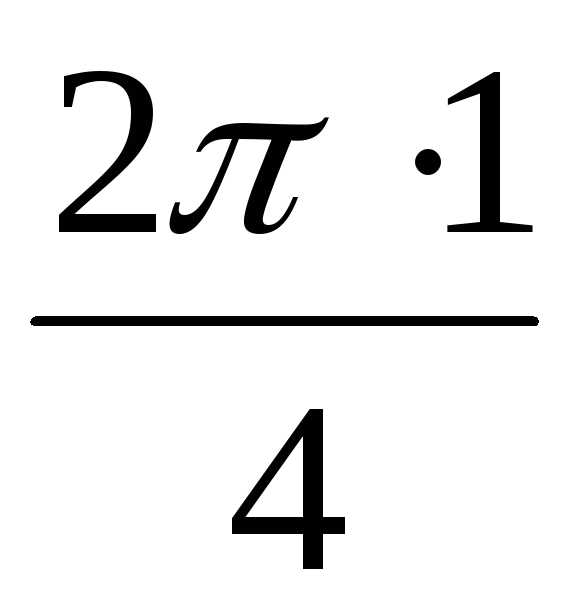 ) = 2(cos
) = 2(cos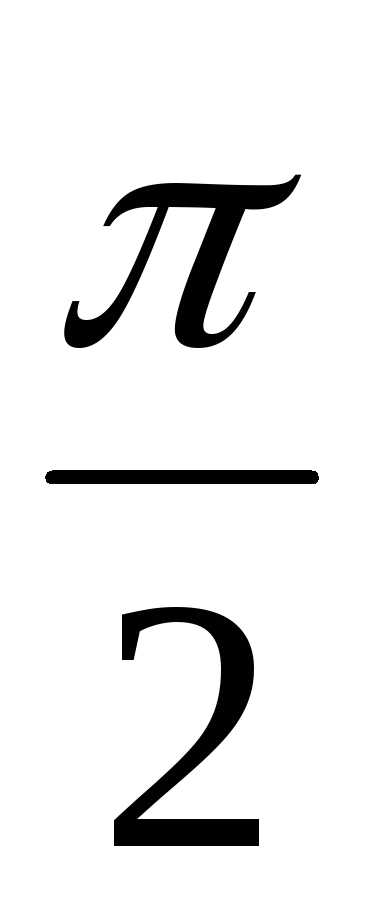 + isin
+ isin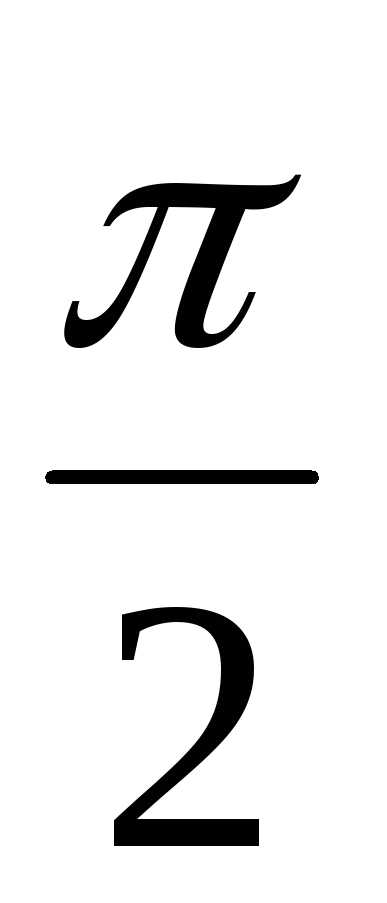 ) = 2(0 +i1) = 2i,
) = 2(0 +i1) = 2i,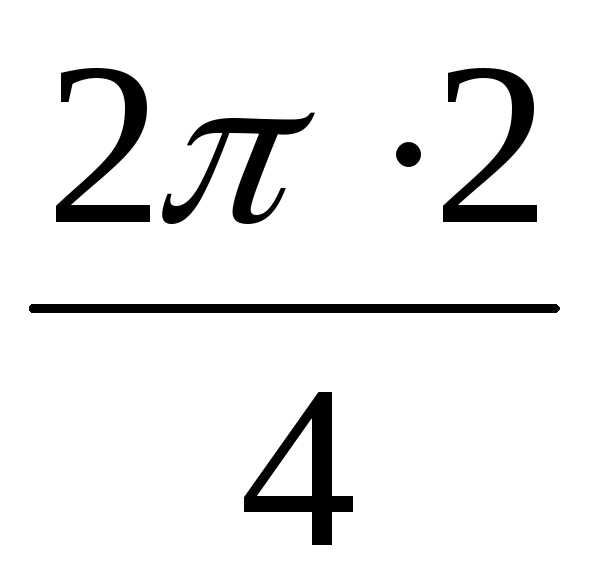 + isin
+ isin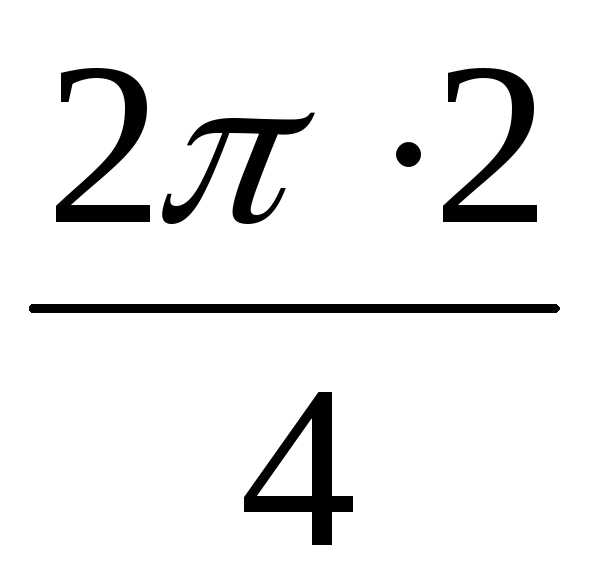 ) = 2(cos + isin) = 2(–1 + i0) = –2,
) = 2(cos + isin) = 2(–1 + i0) = –2,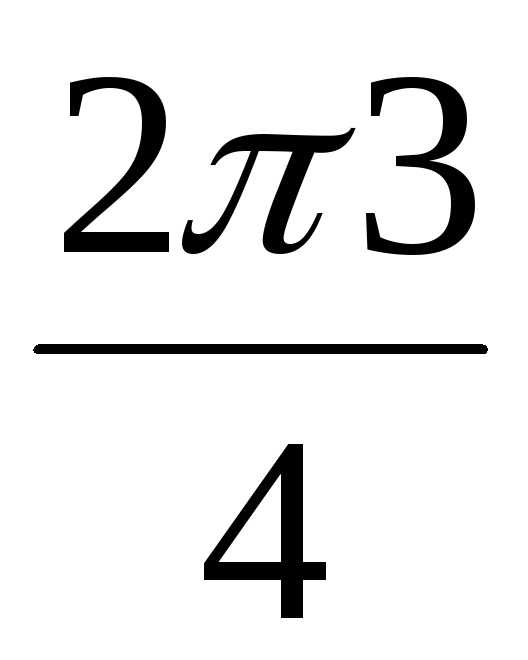 + isin
+ isin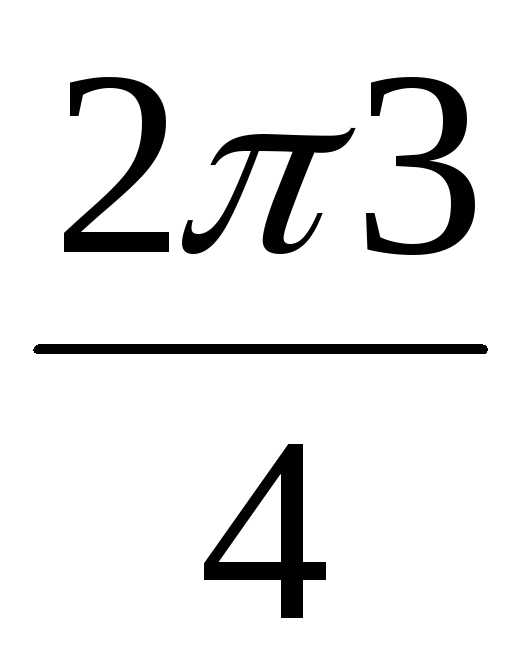 ) = 2(cos
) = 2(cos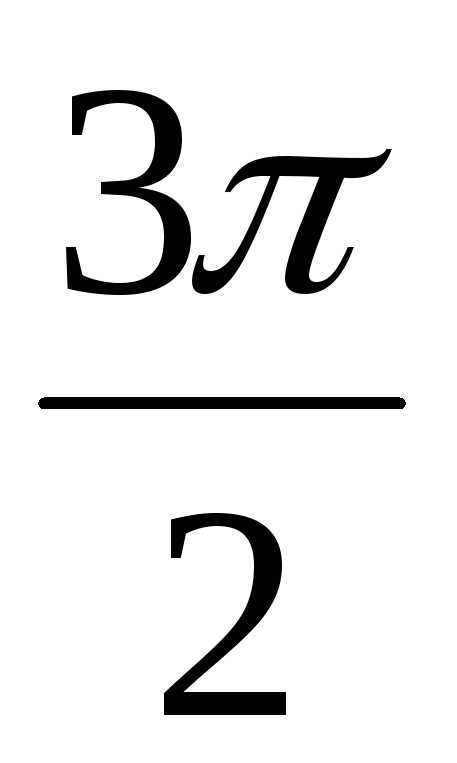 + isin
+ isin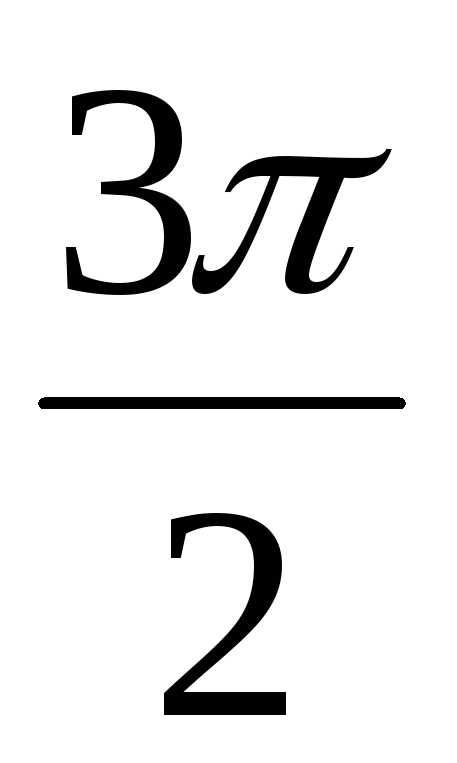 ) = 2(0 –i)) = –2i.
) = 2(0 –i)) = –2i.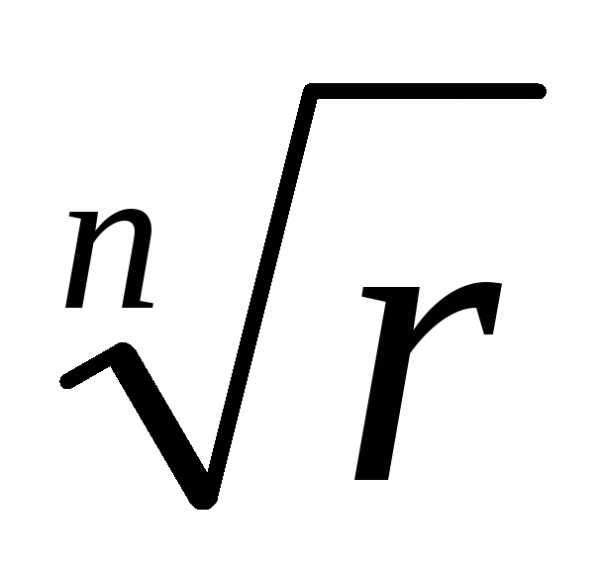 .
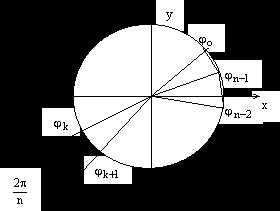
Если эти точки соединить, то в результате
получится правильный n-угольник.
.
Если эти точки соединить, то в результате
получится правильный n-угольник.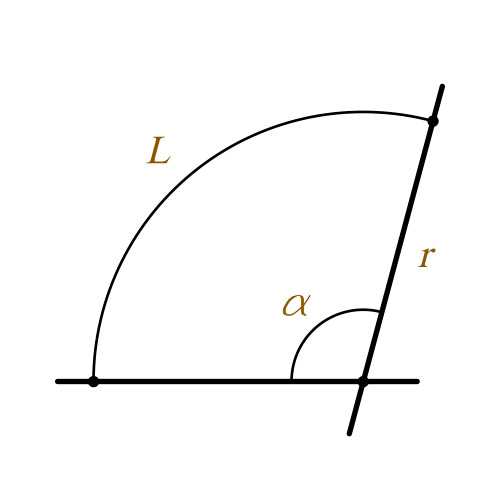


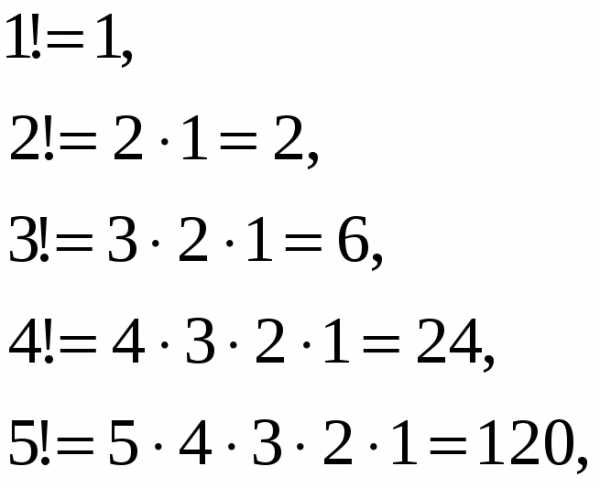
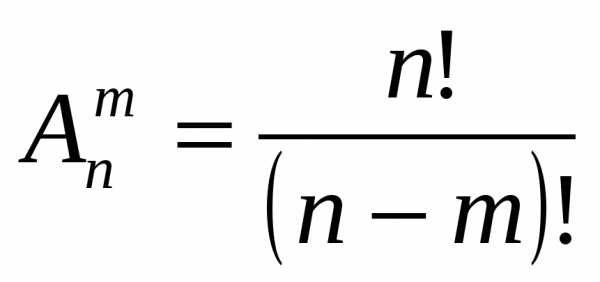
 По формуле получаем номеров.
По формуле получаем номеров.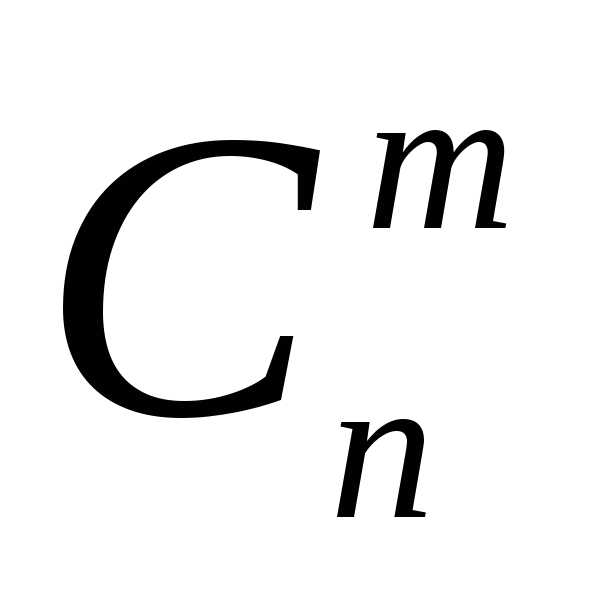 и вычисляется по формуле:
и вычисляется по формуле: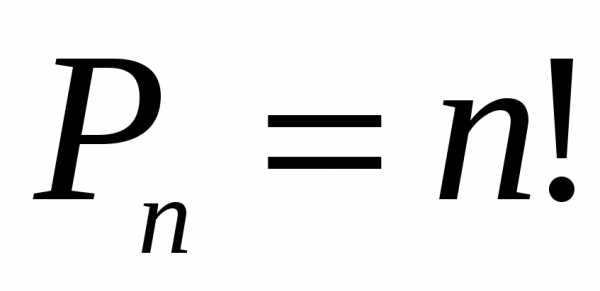


 Добавить
Добавить

