Порядок выполнения действий в формулах Excel
Excel для Microsoft 365 Excel 2021 Excel 2019 Excel 2016 Excel 2013 Excel 2010 Excel 2007 Еще…Меньше
В некоторых случаях порядок вычисления может повлиять на возвращаемое формулой значение, поэтому для получения нужных результатов важно понимать стандартный порядок вычислений и знать, как можно его изменить.
-
Порядок вычислений
Формулы вычисляют значения в определенном порядке. Формула в Excel всегда начинается со знака равно (=). Excel интерпретирует символы после знака равно как формулу. После знака равно вычисляются элементы (операнды), например константы или ссылки на ячейки. Они разделены операторами вычислений. Excel вычисляет формулу слева направо в соответствии с определенным порядком для каждого оператора в формуле.

-
Приоритет операторов в формулах Excel
Если в одной формуле используется несколько операторов, Microsoft Excel выполняет операции в порядке, указанном в приведенной ниже таблице. Если формула содержит операторы с одинаковым приоритетом ( например, если формула содержит операторы умножения и деления), Excel оценивает операторы слева направо.
Оператор
Описание
: (двоеточие)
(один пробел)
, (запятая)
Операторы ссылок
–
Знак «минус»
%
Процент
^
Возведение в степень
* и /
Умножение и деление
+ и —
Сложение и вычитание
&
Объединение двух текстовых строк в одну
=
< >
<=
>=
<>Операторы сравнения
org/ListItem»>
Использование скобок в Excel формулах
Чтобы изменить порядок выполнения формулы, заключите ее часть, которая должна быть выполнена первой, в скобки. Например, результатом приведенной ниже формулы будет число 11, поскольку в Microsoft Excel умножение выполняется раньше сложения. В данной формуле число 2 умножается на 3, а затем к результату добавляется число 5.
=5+2*3
Если же с помощью скобок изменить синтаксис, Microsoft Excel сложит 5 и 2, а затем умножит результат на 3; результатом этих действий будет число 21.
=(5+2)*3
В приведенном ниже примере скобки, в которые заключена первая часть формулы, задают следующий порядок вычислений: определяется значение B4+25, после чего полученный результат делится на сумму значений в ячейках D5, E5 и F5.
=(B4+25)/СУММ(D5:F5)
Калькулятор дробей
Этот калькулятор дробей выполняет базовые и расширенные операции с дробями, выражения с дробями в сочетании с целыми, десятичными и смешанными числами. Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении.
Правила выражения с дробями:
Дроби — используйте косую черту для деления числителя на знаменатель, т.е. для пятисотых введите 5/100 . Если вы используете смешанные числа, оставьте пробел между целой и дробной частями.
Смешанные числа (смешанные числа или дроби) сохраняют один пробел между целым числом и дробью
и используют косую черту для ввода дробей, например, 1 2/3 . Пример отрицательной смешанной дроби: -5 1/2 .
Пример отрицательной смешанной дроби: -5 1/2 .
Поскольку косая черта одновременно является знаком дробной строки и деления, используйте двоеточие (:) в качестве оператора деления дробей, т. е. 1/2 : 1/3 .
Decimals (десятичные числа) вводятся с десятичной точкой . и они автоматически преобразуются в дроби — т.е. 1,45 .
Математические символы
| Символ | Название символа | Значение символа | Пример | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| + | плюс | дополнение | 1/2 + 1/3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| — | знак минус | вычитание | 1 1/2 — 2/3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| * | звездочка | умножение | 2/3 * 3/4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| × | знак умножения | умножение | 2 /3 × 5/6 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| : | знак деления | деление | 1/2 : 3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| / | деление косая черта | деление | 1/3 / 5 1/2 • сложение дробей и смешанных чисел: 8/5 + 6 2/7 • деление целых чисел и дробей: 5 ÷ 1/2 • сложные дроби: 5/8 : 2 2/3 • десятичная дробь: 0,625 • Преобразование дроби в десятичную: 1/4 • Преобразование дроби в процент: 1/8 % • сравнение дробей: 1/4 2/3 • умножение дроби на целое число: 6 * 3/4 • квадратный корень дроби: sqrt(1/16) • уменьшение или упрощение дроби (упрощение) — деление числителя и знаменателя дроби на одно и то же ненулевое число — эквивалентная дробь: 4/22 • выражение со скобками: 1/3 * (1/2 — 3 3/8) • составная дробь: 3/4 от 5/7 • кратные дроби: 2/3 от 3/5 • разделить, чтобы найти частное: 3/5 ÷ 2/3 Калькулятор следует известным правилам для порядка операций .
другие математические задачи »
Видео: Решение простых уравнений с помощью Неизвестно в показателеСтенограмма видео Это вопросы типа экспоненты семейства, которые требуют от вас вспомнить и применить правила экспоненты. 𝑥 в 𝑎 умножить 𝑥 на 𝑏 равно 𝑥 на 𝑎 плюс 𝑏; это правило сложения. 𝑥 на 𝑎 разделить на 𝑥 на 𝑏 равно 𝑥 на 𝑎 минус 𝑏; это правило вычитания. Теперь у нас есть другие видеоролики, в которых более подробно рассказывается об этих правилах, если вы в них не уверены. Но в этом видео мы собираемся использовать эти правила в сочетании с нашими знаниями о различных степенях двойки, тройки, пятерки и десятки для решения некоторых задач. Итак, первый вопрос: найдите значение 𝑥, если два в степени 𝑥 равно восьми в степени 𝑥 плюс три. Ну, на первый взгляд это выглядит сложно. Но, надеюсь, мы сможем вспомнить, что дважды два раза два, два в кубе, равно восьми. Так что я могу повторно выразить восемь как степень двойки. Итак, переписав это уравнение с двумя в кубе вместо восьми, мы получили два в степени 𝑥 равно двум в кубе все в степени 𝑥 плюс три. Теперь у нас есть нечто в степени чего-то в степени чего-то еще, поэтому мы можем использовать правило умножения. Таким образом, два в степени трех, все в степени 𝑥 плюс три просто означает, что два в степени три, умноженные на 𝑥 плюс три, в скобках. Теперь я могу использовать распределительный закон, чтобы перемножить скобки так, чтобы я знал, что 𝑥 равно трем 𝑥 плюс девять. Теперь, если я уберу 𝑥 из обеих частей моего уравнения, у меня будут все 𝑥 с одной стороны. Итак, в левой части 𝑥 убери 𝑥 ничего. А в правой части три 𝑥 отнять 𝑥 будет два 𝑥, а у меня еще останется плюс девять. Так что теперь я пытаюсь получить 𝑥 самостоятельно; уберите девять с обеих сторон. И в левой части ноль за вычетом девяти будет минус девять. А справа у меня есть два 𝑥 плюс девять минус девять, так что эти два сокращаются, поэтому у меня только два 𝑥. Теперь мы все еще хотим знать, что такое единица 𝑥, поэтому мне нужно разделить обе части на два. А два разделить на два — это всего лишь один, поэтому один 𝑥 равен минус девять больше двух. Итак, при решении этого уравнения было несколько ключевых приемов. Во-первых, мы должны были знать, что восемь — это то же самое, что два в кубе, поэтому вам нужно знать свои показатели степени простых чисел, таких как два, три, четыре, пять, десять, те немногие. А затем нам нужно было знать правило умножения, поэтому нам нужно было знать, что два в степени трех все в степени 𝑥 плюс три равно двум в степени трех лотов или трижды 𝑥 плюс три. Затем мы заметили, что это два в степени 𝑥 и два в степени, умноженной на три 𝑥 плюс три, поэтому эти два показателя степени должны быть равны. Остальное было просто, решение линейной алгебры. И мы пришли к нашему окончательному ответу, 𝑥 минус четыре с половиной. Следующий вопрос, решите для 𝑥: девять в степени 𝑥 плюс пять равно двадцати семи в степени 𝑥 минус один. Итак, девять и двадцать семь кратны трем, поэтому трижды три дают нам девять, а трижды трижды три дают двадцать семь. Итак, первая строка равна трем в квадрате в степени 𝑥 плюс пять равно трем в кубе в степени 𝑥 минус один. А теперь снова воспользуемся правилом умножения. Таким образом, мы можем переписать это как три в степени умноженной на два 𝑥 плюс пять равно трем в степени умноженной на три 𝑥 минус один. Итак, теперь у нас есть то же самое основание для наших показателей, три в степени чего-то равно трем в степени чего-то. Теперь, если это так, эти вещи должны быть равны, поэтому два раза 𝑥 плюс пять должны равняться трем умноженным на 𝑥 минус один. И теперь мы можем использовать распределительный закон умножения, чтобы умножить скобки. И мы видим, что два 𝑥 плюс десять равно трем 𝑥 минус пять. Теперь у меня две 𝑥 слева и три 𝑥 справа. Если я уберу две 𝑥 с обеих сторон, у меня все еще будет положительное число 𝑥 с правой стороны, а у меня не будет ни одной 𝑥 с левой стороны. Итак, в левой части у меня есть два 𝑥 плюс десять, уберите два 𝑥, так что два 𝑥 сократятся, и у меня останется только десять. А в правой части у меня три 𝑥 убери два 𝑥 всего один 𝑥 и тогда у меня все еще есть минус три. Итак, теперь я могу добавить три к обеим частям уравнения, что даст мне тринадцать в левой части. А справа у меня три минус три, и у меня есть 𝑥, так что у меня останется 𝑥. Итак, мой ответ: 𝑥 равно тринадцати. Итак, снова в этом вопросе мы должны были подумать об основаниях наших показателей. И в первом случае мы смогли определить, что это три в квадрате. А во втором случае было три в кубе. Таким образом, если мы сможем использовать правило умножения для получения одинаковых оснований в каждом случае, мы сможем просто сравнить показатели напрямую, и это превратит его в часть простой линейной алгебры. Теперь для числа три найдите значение 𝑥, если единица больше ста двадцати пяти в степени 𝑥 равна пяти в степени двойки 𝑥 минус три. Итак, наша первая подсказка здесь заключается в том, что сто двадцать пять — это просто пять в кубе, поэтому я собираюсь повторно выразить сто двадцать пять как пять в кубе. А теперь я воспользуюсь тем фактом, что я знаю об отрицательных показателях, так что пять в отрицательной степени три 𝑥 будет таким же, как один больше пяти в тройке 𝑥, поэтому я собираюсь переформулировать это слева- сторона руки. Так что вместо того, чтобы писать как один на пять в степени три 𝑥, я буду писать как пять в степени минус три 𝑥, так что мы действительно проверяем здесь ваше знание показателей степени. А это равно пяти в степени двойки 𝑥 минус три. Итак, мы пришли к ситуации, когда у нас есть одно и то же основание, пять в каждом случае, и пять в степени минус три 𝑥 равно пяти в степени двойки 𝑥 плюс два 𝑥 минус три. Таким образом, эти два показателя степени должны быть равны; минус три 𝑥 должен быть равен двум 𝑥 минус три. Теперь нам нужно решить линейную алгебру, поэтому я добавлю три 𝑥 к обеим частям, чтобы получить положительное число 𝑥 с одной стороны уравнения. А у меня еще минус три, так что пять 𝑥 минус три. Итак, теперь, если я добавлю три к обеим частям уравнения, в левой части у меня будет ноль плюс три, что равно трем, а в правой части у меня будет минус три плюс три. Таким образом, эти два сокращаются, что оставляет мне пять 𝑥, поэтому три равно пяти 𝑥. Итак, теперь просто разделите обе части моего уравнения на пять. А справа у меня 𝑥 умножить на пять, разделить на пять, так что эти две пятерки сокращаются, поэтому я только что получил 𝑥. А это равно трем пятым. Поэтому я делаю свой ответ красивым и ясным: 𝑥 равно трем пятым. Таким образом, ключевым шагом к решению этой задачи было определение того факта, что сто двадцать пять — это пять в степени три, чтобы мы могли получить тот же базовый показатель степени, с которым мы работаем. Затем мы используем правило умножения, и нам нужно было немного знать об отрицательных показателях, чтобы получить это в том же формате. Теперь для нашего последнего примера, номер четыре, найдите значение 𝑥, если тысяча в степени двух третей равна сотне в степени два 𝑥 плюс пять. Теперь у нас есть несколько основных подходов, которые мы могли бы использовать здесь. Мы могли бы заметить тот факт, что тысяча — это десять в кубе, а сотня — это десять в квадрате, чтобы мы могли произвести эти замены, а затем использовать наши степенные правила и попытаться приравнять показатели степени, или мы могли бы использовать наше знание показателей степени, чтобы сказать, что это означает, что кубический корень из чего-то возведенного в квадрат, поэтому кубический корень из тысячи равен десяти, а затем возводим его в квадрат, и мы получаем сотню. И тогда мы видим, что у нас будут одинаковые базы с каждой стороны, так что на самом деле я думаю, что это будет более быстрый способ добраться сюда; так я и пойду. Итак, я проверю левую сторону. Итак, мы просто повторно выражаем, что вместо сотни в степени двух третей мы знаем, что это кубический корень из тысячи, а затем все это возводится в квадрат. Итак, кубический корень из тысячи равен десяти, поэтому левая часть равна десяти в квадрате, то есть всего лишь сотне. Итак, у нас есть сотня равна сотне в степени два 𝑥 плюс пять. Ну, сто это то же самое, что сто в степени один. Итак, теперь у меня есть сотня в степени один равна сотне в степени два 𝑥 плюс пять. Итак, у меня есть та же самая база для моих показателей, поэтому я могу приравнять эти показатели. Ну, это просто оставляет меня с одним равным двум 𝑥 плюс пять, так что просто вычтите пять с обеих сторон. А справа у меня пять минус пять — это ничто, так что отрицательное число четыре равно двум 𝑥. Теперь я могу разделить обе части на два, что означает, что двойки будут сокращаться слева и справа, а минус четыре на два будет просто минус два. Последний пример очень похож на предыдущие. Пример 1. Целое числовое значение равное 2 может выражаться как в дробь \[\frac{2}{1}\] Следовательно, число 2, будет относиться к категории, не только целых чисел, но рациональных. Пример 2. Смешанное значение равное \[2 \frac{1}{2}\] можно преобразовать в дробь равную \[\frac{5}{2}\] Данное значение получается переводом смешанного значения в обычную неправильную дробь: \[
2 \frac{1}{2}=\frac{(2 \times 2)+1}{2}=\frac{4+1}{2}=\frac{5}{2}
\] Следовательно число: Смешанное число \[2 \frac{1}{2}\] можно отнести к рациональному числу. Пример 3. Значение десятичной дроби, у которой значение равно 0,2 можно преобразовать и выразить, как \[\frac{2}{10}\]. Данное значение получилась переводом десятичного значения равного 0,2 в обычную обыкновенную дробь. Данную дробь 0,2 можно записать как значение в виде \[\frac{2}{10}\] из этого следует, что тогда она будет относиться к категории рациональных значений. Пример 4. Периодическую бесконечную дробь, со значением равным 0, (3) можно представить как дробь вида: \[\frac{3}{9}\] Значение дроби получается при помощи перевода дроби периодического вида в дробь обыкновенного типа. Заданную бесконечную периодическую дробь 0, (3) можно выразить как \[\frac{3}{9}\] и тем самым отнести к категории рациональных чисел. Нет времени решать самому? Наши эксперты помогут! Контрольная | от 300 ₽ | Реферат | от 500 ₽ | Курсовая | от 1 000 ₽ | Координатная прямая — это некая линия на плоскости, на которой расположено множество числовых значений. Имеет она следующий вид: На вышеприведенном рисунке приведен фрагмент координатной прямой от значений −5 до 5. Немного иначе обстоят дела с остальными категориями значений: Данные значения расположены между целыми числами и данных значений множество. Пример 1. Нужно определить на координатной прямой рациональное числовое значение . Число располагается между значениями 1 и 2 Дробное значение равное \[\frac{3}{2}\] можно записать как десятичную дробь равную 1,5.
При увеличении участка координатной прямой от 1 до 2, можно увидеть следующую ситуацию: Между целыми значениями 1 и 2 находятся уже другие значения, которые являются десятичными дробями. Здесь же расположена дробь , которая находится там же, где и дробь равная 1,5. Увеличивая указанные отрезки на координатной прямой, можно увидеть остальные значения, которые лежат на данном отрезке. В результате, можно обнаружить десятичные дроби, которые расположены после знака запятой одно значение. Между значениями десятичных дробей, у которых после знака запятой имеют одну цифру, могут находится и другие десятичные дроби. В свою очередь они имеют после запятой два значения. Иными словами, сотые значения на отрезке. Определим числа, которые находятся между десятичными значениями равными 0,1 и 0,2. Пример 2. Необходимо определить на координатной прямой рациональное числовое значение. Данное значение будет находиться ближе к нулевому значению. Числовое значение дроби \[\frac{1}{50}\] равно десятичной дроби 0,02 При увеличении отрезка от 0 до 0,1 можно определить, где расположено рациональное значение равное \[\frac{1}{50}\] Пользуясь рисунком координатной прямой, можно сделать вывод: Пользуясь рисунком координатной прямой, можно сделать вывод: \[\frac{1}{50}\] расположено, там же , где и десятичная дробь равная 0,02. Пример 3. Обозначим на прямой рациональное значение равное 0, (3). Рациональное значение равное 0, (3) будет являться бесконечной периодической дробью. Так как его дробное значение не заканчивается, оно бесконечное 0,33333….. У значения периодической дроби 0,(3) дробная часть будет бесконечной, это значит, что: определить ее точное месторасположение на координатной прямой не представляется возможным. Данное место можно указать лишь частично. Значение десятичной дроби равное 0,33333… будет расположено ближе к простой десятичной дроби значения 0,3. На рисунке, нельзя точно увидеть месторасположение значения 0,(3). Рассмотрим простой пример: (−6) : 2 = −3 В данном примере делимое равно (−6) и является отрицательным значением. Далее можно рассмотреть иной пример. Составим и запишем выражение: 6 : (−2) = −3 В данном примере отрицательным является делитель равный (−2). Однако в двух случаях, при решении примеров, получается одинаковый ответ, который равен (−3). Данные примеры, также, можно записать в виде дробных значений. Вид данных значений следующий \[\frac{-6}{2}=-3,-\frac{6}{-2}=-3\]. Так как в обоих случаях ответ, полученный при вычислении дробей, будет равным, то отрицательный знак, стоящий в числителе или в знаменателе можно вынести как общий. И тем самым, поставить его перед дробью: \[
\frac{-6}{2}=-\frac{6}{2}=-3,\frac{6}{-2}=-\frac{6}{2}=-3
\] Следовательно между дробями и \[\frac{6}{-2}\] и \[-\frac{6}{2}\] есть возможность поставить равенство, так как они имеют одинаковое значение \[\frac{-6}{2}=\frac{6}{-2}=-\frac{6}{2}\] По аналогии с простыми действительными числами, рациональное также может быть противоположным числом. Например: для рационального дробного значения равного \[\frac{1}{2}\] противоположным числом будет значение дроби \[-\frac{1}{2}\]. Данная дробь будет располагаться на координатной прямой в асимметричном расположении относительно дроби \[\frac{1}{2}\] и начала координат. На нижеприведенном рисунке это можно увидеть досконально. Для того чтобы осуществить перевод из смешанного числа в неправильную дробь, необходимо целую часть дроби перемножить со знаменателем дробной части и сложить полученное значение с числителем дробной части. Вычисленное, будет являться числителем нового дробного значения. Следовательно, знаменатель остается прежним значением. Пример 1. Необходимо перевести смешанное число равное \[2 \frac{1}{2}\] в дробь неправильного вида.
Для этого перемножим целую часть на значение знаменателя дробной части. Затем суммируем полученное значение к числителю дроби. (2 × 2) + 1 Определим значение данного выражения: (2 × 2) + 1 = 4 + 1 = 5 Вычисленное значение, которое равно 5 будет являться числителем нового дробного значения. \[
2 \frac{1}{2}=\frac{(2 \times 2)+1}{2}=\frac{4+1}{2}=\frac{5}{2}
\] Чтобы преобразовать в первоначальный вид, нужно обозначить целую часть дроби \[\frac{5}{2}\] и получим \[\frac{5}{2}=2 \frac{1}{2}\]. Данный способ перевода из смешанного значения в неправильный дробный вид, применяется в ситуациях, когда смешанное число имеет положительное значение. Отрицательному числу данный способ, не подходит. Для этого рассмотрим следующую дробь: \[-\frac{5}{2}\]. Определим и выделим в данной дроби целую часть и получим следующее: \[
-2 \frac{1}{2}. \text { То есть }-\frac{5}{2}=-2 \frac{1}{2} \text {. }
\] Для преобразования дроби в первоначальный вид \[-\frac{5}{2}\] необходимо преобразовать смешанное число равное \[-2 \frac{1}{2}\] в неправильную дробь. Однако, если воспользоваться предыдущим правилом. При вычислении данных получен ответ равный \[-\frac{3}{2}\], а правильный ответ должен быть равен \[-\frac{5}{2}\]. Выходит, что смешанное число значения \[-2 \frac{1}{2}\] в неправильную дробь приведено неверно. Для правильного решения необходимо перевести отрицательное число в неправильную дробь. Для этого необходимо целую часть значения перемножить на числитель дроби. Данное решение будет правильным, и ответ получится верным. Пример 2. Нужно выделить в значении неправильной дроби \[-\frac{27}{5}\] целую часть. Полученное число, смешанного значения преобразовать и перевести в неправильную дробь. Применяя известные методы и правила выделим целую часть в заданном значении дроби \[-\frac{27}{5}\]. Для данной дроби она будет равна: \[-\frac{27}{5}=-5 \frac{2}{5}\] Далее полученный результат смешанного числа \[-5 \frac{2}{5}\], необходимо перевести в дробь неправильного вида. Для этого необходимо перемножить целую часть дроби на знаменатель. Из полученного значения необходимо отнять значение числителя дробной части: \[
-5 \frac{2}{5}=\frac{(-5 \times 5)-2}{5}=\frac{-25-2}{5}=\frac{(-25)+(-2)}{5}=-\frac{27}{5}
\] Для этого можно смешанное число переместить в скобки, отрицательный знак при этом расположить за скобками. Затем можно воспользоваться, уже известным правилом преобразования. А именно: умножить значение целой части на знаменатель данной дроби. Далее к полученному значению прибавить числитель. Выполним расчет данным способом, а именно, перевод смешанного число, которое равно \[-5 \frac{2}{5}\] в неправильную дробь. \[
-5 \frac{2}{5}=-\left(5 \frac{2}{5}\right)=-\left(\frac{5 \times 5+2}{5}\right)=-\left(\frac{25+2}{5}\right)=-\left(\frac{27}{5}\right)=-\frac{27}{5}
\] числа » Тут почти все утверждения верны кроме рациональным, ведь мы видим что это число целое. Является, т. к 0 — целое число, целые числа рациональны 123 4 >
>> Цифры или числа — это арифметические значения, используемые для счета, измерения или распознавания времени и для многих других действий. Числа могут быть выражены как цифрами, так и словами соответственно по мере необходимости. Система счисления включает в себя различные типы чисел, например действительные числа, комплексные числа, четные числа, рациональные числа, целые числа и т. д. Числа — это математические или арифметические цифры, используемые для счета, измерения и других арифметических вычислений. Некоторыми примерами чисел являются целые числа, целые числа, натуральные числа, рациональные и иррациональные числа и т. д. Система счисления — это система представления чисел, которая включает такие категории, как ноль, отрицательные числа, рациональные числа, иррациональные числа и комплексные числа. Значение числа определяется: Существуют различные типы чисел, которые подразделяются на наборы по системе счисления. Рациональное число определяется как действительное число в форме A/B, где B не равно нулю. Проще говоря, можно сказать, что любая дробь с ненулевым знаменателем является рациональным числом. Рациональные числа включают в себя все положительные и отрицательные целые числа. Даже 0 является рациональным, поскольку имеет ненулевой знаменатель. Математическое представление рациональных чисел в виде A/B Где, B не равно нулю(0) Рациональные числа представляют собой дробные или десятичные значения. Некоторые из примеров рациональных чисел: Теперь давайте перейдем к вопросу. Рациональными числами называются числа, которые могут быть выражены в виде дробей или отношений двух целых чисел, а также могут быть записаны в виде положительного числа, отрицательного числа, простого числа и даже нуля. Это может быть выражено как p/q, где q ≠ 0 Например, 5/3 — это рациональное число, выражающее деление 5 целых чисел на 3 целых числа. Иррациональные числа — это числа, которые не могут быть выражены в дробях или отношениях целых чисел. Он может быть записан десятичными знаками и иметь бесконечные неповторяющиеся цифры после запятой. Например: √15 =3,8729…….. Ответ: Да, 0 — рациональное число, потому что у него ненулевой знаменатель. Так как число 0 также может быть записано как 0/1. Взгляните на доказательство ниже. Доказательство: Число 0 можно представить следующим образом: ⇒ 0 = 0/1 Из приведенного выше выражения можно сделать вывод, что число 0 можно представить в виде p/q где q не равно нулю. Вопрос 1: Образует ли отношение любых двух целых чисел рациональное число? Ответ: Нет, число называется рациональным, только если оно имеет ненулевой знаменатель. Вопрос 2. Является ли 2,5 рациональным числом? Ответ: Да, 2,5 является рациональным числом, потому что это число также может быть выражено как 25/10, что является отношением целых чисел. Система счисления включает в себя различные типы чисел, например, простые числа, нечетные числа, четные числа, рациональные числа, целые числа и т. A Система счисления или Система счисления определяется как элементарная система для выражения чисел и цифр. Это единственный способ представления чисел в арифметической и алгебраической структуре. Числа используются в различных арифметических значениях, применимых для выполнения различных арифметических операций, таких как сложение, вычитание, умножение и т. д., которые применяются в повседневной жизни для целей вычислений. Значение числа определяется цифрой, ее разрядностью в числе и основанием системы счисления. Числа обычно также известны как цифры и представляют собой математические значения, используемые для счета, измерений, маркировки и измерения основных величин. Числа — это математические значения или цифры, используемые для измерения или вычисления величин. Существуют различные типы чисел на множества по действительной системе счисления. Типы описаны ниже: Ответ: Рациональное число: Рациональные числа имеют форму p/q, где p и q — целые числа, а q ≠ 0. Из-за лежащей в основе структуры чисел, формы p/q, большинство людей находят трудно отличить дроби от рациональных чисел. Когда рациональное число делится, вывод находится в десятичной форме, которая может быть как оканчивающейся, так и повторяющейся. 3, 4, 5 и т. д. — некоторые примеры рациональных чисел, поскольку они могут быть выражены дробью как 3/1, 4/1 и 5/1. Рациональное число — это разновидность действительного числа, имеющая форму p/q, где q≠0. Здесь 0 — целое число и может быть записано в виде p/q, т. е. 0/1, 0/2 и т. д. Следовательно, 0 — рациональное число. Вопрос 1: Определите, является ли 5.153153…. является рациональным числом. Ответ: Рациональное число — это действительное число, имеющее форму p/q, где q≠0. Когда рациональное число разбивается, результатом является десятичное число, которое может быть как завершающим, так и повторяющимся десятичным числом. Здесь заданное число 5.153153…. имеет повторяющиеся цифры. Следовательно, 5,153153…. является рациональным числом. Вопрос 2: Является ли √17 рациональным или иррациональным числом? Ответ: Рациональное число — это действительное число, имеющее форму p/q, где q≠0.
Например: VIN XW8AN2NE3JH035743 или FRAME KZN185-9023353 Поиск по марке автомобиля илипоиск по типоразмеру 01 Марка автомобиля 02 Модель 03 Год выпуска 04 Комплектация 05 Найдите подходящие шины для вашего автомобиля Выбор шин для вашей Infiniti FX VETTEL EDITION 5.0 V8 420 должен быть сделан внимательно, учитывая разные показатели, которые включают тип автомобиля, размер и способы использования транспортного средства в отношении маршрутов преодолеваемых ежедневно. Чтобы помочь вам в этом деликатном поиске, Pirelli создал полный каталог шин для Infiniti, предназначенных для обеспечения отличной эффективности вождения в любых условиях и полную безопасность. В обширном каталоге Pirelli найдете широкий ассортимент шин для Infiniti, разработанные для высоких эксплуатационных характеристик: зимние шины, летние и All Season специально для городских автомобилей, внедорожников, седанов и спортивных автомобилей. Благодаря поиску шин по марке автомобиля вы можете легко и быстро найти оптимальное решение для ваших потребностей: укажите марку, модель, год выпуска и версию вашего автомобиля, и вы узнаете, какой тип шин Pirelli лучше всего подходит для конкретного авто, на основании технических характеристик и критериев стандартизации. Далее вы сможете ознакомиться со списком размеров шин, которые можно установить на данный автомобиль вместо шин, установленных ранее. Положения и условия Благодаря поиску шин по марке автомобиля вы можете легко и быстро найти оптимальное решение для ваших потребностей: укажите марку, модель, год выпуска и версию вашего автомобиля, и вы узнаете, какой тип шин Pirelli лучше всего подходит для конкретного авто, на основании технических характеристик и критериев стандартизации. Далее вы сможете ознакомиться со списком размеров шин, которые можно установить на данный автомобиль вместо шин, установленных ранее. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 9 | Оценить | квадратный корень из 12 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 10 | Оценить | квадратный корень из 20 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 11 | Оценить | квадратный корень из 50 | 94 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 18 | Оценить | квадратный корень из 45 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 19 | Оценить | квадратный корень из 32 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 20 | Оценить | квадратный корень из 18 | 92 |
Сравнительные курсы WM/Refinitiv FX | Рефинитив
Тесты WM/Refinitiv FX
Самые своевременные, прозрачные и надежные форвардные и спот-курсы, охватывающие более 150 валют.
Детали запроса
Детали запроса
- Обзор 909:20 Объявление Item»> Особенности и преимущества
- Ставки
- Как это работает Item»> Блоги
- Узнать больше
Более 20 лет валютные курсы WM/Refinitiv служат полностью независимыми, объективными и непредвзятыми источниками валютных данных. Мы обязуемся обеспечить, чтобы контрольные показатели оставались надежными и фундаментальными компонентами рыночной инфраструктуры и постоянно совершенствовались по мере изменения потребностей рынка.
Наша опубликованная и прозрачная методология расчета полностью соответствует Принципам IOSCO для финансовых показателей. Контрольные ставки WM/Refinitiv Spot, Forward и NDF (включая лондонские спотовые ставки закрытия на 16:00) управляются компанией Refinitiv Benchmark Services Limited, уполномоченной в качестве администратора эталонной оценки в соответствии с EU BMR.
Предназначенные для обеспечения большей прозрачности ценообразования на валютном рынке, курсы WM/Refinitiv строятся на основе данных, полученных непосредственно из рыночных транзакций, с применением нескольких методов проверки зафиксированных и рассчитанных курсов, чтобы получить точные спотовые курсы для каждого исправления в течение дня.
Мы являемся администратором более 30 ключевых ставок и агентом по расчету более 40 основных национальных и региональных процентных ставок и эталонных валютных курсов в 12 разных странах, таких как Сингапур, Гонконг и Россия.
Получите доступ к бесплатным тарифам или запросите информацию о вариантах подписки.
WM/Refinitiv Spot Rates (WMR) «Запрос обратной связи» по ключевым аспектам методологии WMR и требованиям пользователей | Апрель 2022 г.
WMR — это один из наиболее широко используемых наборов бенчмарков FX, и Refinitiv понимает, насколько важны эти курсы для всех пользователей во всем мире. Основные принципы разработки WMR позволяют создавать независимые и прозрачные бенчмарки FX, которые являются надежными и отражают на определенный момент времени широкий спектр валютных рынков в течение всего дня. С момента запуска в 1994, WMR продолжает реагировать на рыночные изменения и предоставлять решения для меняющихся требований пользователей, а Refinitiv по-прежнему стремится к тому, чтобы WMR оставался наиболее подходящим эталоном FX для пользователей. Refinitiv надеется на взаимодействие со всеми участниками рынка и призывает всех использовать эту возможность для предоставления отзывов и участия в непрерывном развитии WMR.
WM/Refinitiv обеспечивает самое широкое покрытие в отрасли, включая внутридневные и спотовые курсы закрытия, форвардные курсы и NDF.
Приверженец нормативных требованийПолностью прозрачная методология, согласованная с IOSCO, и тарифы на 16:00 соответствуют стандартам EU/BMR.
Надежный отраслевой стандартБолее 1000 финансовых учреждений полагаются на курсы WM/Refinitiv для большей ясности при оценке мировых рынков.
Эталонный курс валютной пары USD/BRL в 15:00 (по британскому времени) доступен ежедневно (с задержкой в 24 часа) бесплатно и дает вам надежный курс, ориентированный на транзакции, для оценки рынка.
Эталонный курс валютной пары USD/BRL в 16:00 (по британскому времени) доступен ежедневно (с задержкой в 24 часа) бесплатно и дает вам надежный курс, ориентированный на транзакции, для оценки рынка.
Курсы по 32 валютам по отношению к евро доступны ежедневно (с 30-минутной задержкой) бесплатно. В качестве альтернативы ставки для всех 150+ валют следовали по отношению к евро, фунтам стерлингов и долларам США.
Просмотр последних ставок (под управлением RBSL)Бенчмарк WM/Refinitiv 12:00 EST FX дает вам надежный, ориентированный на транзакции курс, который позволяет вам более четко оценивать рынки.
Просмотр последних ставок (под управлением RBSL) Фиксированный ежедневно с понедельника по пятницу в 16:00 по лондонскому времени, с охватом более 150 валют по отношению к евро, фунтам стерлингов и долларам США. под управлением RBSL.
Фиксировано ежедневно с понедельника по пятницу в 16:00 по лондонскому времени, включая 80 форвардных валют и 11 валют NDF. под управлением RBSL.
под управлением RBSL.
Производится ежедневно с 6:00 до 21:00 по лондонскому времени; 10:00 и 16:00 по сиднейскому времени; 14:00 по новозеландскому времени; 11:00 по сингапурскому времени; 17:00 по нью-йоркскому времени; 11:00 по бангкокскому времени и 10:00 по токийскому времени. под управлением RBSL.
Все тарифы архивируются ежедневно и доступны непосредственно у нас и у других поставщиков.
Производится каждый час с понедельника, 6:00 по гонконгскому/сингапурскому времени, до пятницы, 22:00 по лондонскому времени, включая более 150 валют по отношению к евро, фунтам стерлингов и долларам США. под управлением RBSL.
Пользователи тестов, которые мы администрируем, заключают лицензионные соглашения с Refinitiv, чтобы получить своевременный доступ к данным или использовать тест для финансовых продуктов. Лицензирование и соответствующие сборы варьируются в зависимости от предполагаемого использования данных, механизма доставки, а также времени доставки (доступ в режиме реального времени или доступ с задержкой).
Сравнительные данные доступны на Eikon через наши потоки финансовых данных, а также через сторонних поставщиков рыночных данных и других распространителей.
WM/Refinitiv 2PM CET FX BenchmarkWM/Refinitiv 2PM CET FX Benchmark — независимые, объективные, непредвзятые источники валютных данных. Зарегистрируйтесь здесь для 32 валют по отношению к евро, доступных с 30-минутной задержкой.
Нормативные документы и услуги BenchmarkПросмотрите тесты Refinitiv Refinitiv, узнайте о нашем наборе данных, индексов и тестов. Наш каталог данных предлагает непревзойденные данные и механизмы доставки.
Индексы FX Создавайте свои торговые и инвестиционные продукты, используя ведущую площадку по межбанковской ликвидности, чтобы создавать свои контрольные показатели, отслеживая эффективность глобальных стратегических валют.


 Наиболее распространенные мнемоники для запоминания этого порядка операций:
Наиболее распространенные мнемоники для запоминания этого порядка операций:  Какая десятичная дробь представляет долю выстрелов, которые делает Деа?
Какая десятичная дробь представляет долю выстрелов, которые делает Деа? Есть четыре курицы. Какую часть животных составляют куры? Выразите ответ дробью в простейшей форме.
Есть четыре курицы. Какую часть животных составляют куры? Выразите ответ дробью в простейшей форме. И 𝑥 в степени 𝑎 все в степени 𝑏 равно 𝑥 в степени 𝑎 умножить на 𝑏; это правило умножения.
И 𝑥 в степени 𝑎 все в степени 𝑏 равно 𝑥 в степени 𝑎 умножить на 𝑏; это правило умножения. Итак, теперь у меня есть два в степени 𝑥 равно двум в степени трех лотов 𝑥 плюс три, поэтому эти две вещи должны быть равны. Два в степени чего-то равно двум в степени чего-то; эти две вещи должны быть равны.
Итак, теперь у меня есть два в степени 𝑥 равно двум в степени трех лотов 𝑥 плюс три, поэтому эти две вещи должны быть равны. Два в степени чего-то равно двум в степени чего-то; эти две вещи должны быть равны. Или как смешанное число, 𝑥 равно минус четырем с половиной.
Или как смешанное число, 𝑥 равно минус четырем с половиной. Итак, три в кубе — это двадцать семь. Таким образом, мы можем заменить девять и двадцать семь числами, у которых одинаковые основания для их степеней, то есть три в квадрате и три в кубе.
Итак, три в кубе — это двадцать семь. Таким образом, мы можем заменить девять и двадцать семь числами, у которых одинаковые основания для их степеней, то есть три в квадрате и три в кубе.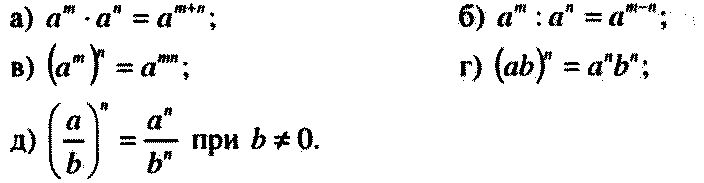
 И тогда я могу использовать правило умножения пять в степени три в степени 𝑥 это просто пять в степени три 𝑥.
И тогда я могу использовать правило умножения пять в степени три в степени 𝑥 это просто пять в степени три 𝑥. И тогда в левой части минус три 𝑥 плюс три 𝑥 равно нулю, а в правой части два 𝑥 плюс три 𝑥 равно пяти 𝑥.
И тогда в левой части минус три 𝑥 плюс три 𝑥 равно нулю, а в правой части два 𝑥 плюс три 𝑥 равно пяти 𝑥. Затем мы взяли наши показатели степени, которые были равны, отрицательные три 𝑥 и два 𝑥 минус три, сделали немного линейной алгебры, а затем придумали наш ответ.
Затем мы взяли наши показатели степени, которые были равны, отрицательные три 𝑥 и два 𝑥 минус три, сделали немного линейной алгебры, а затем придумали наш ответ.





 Иными словами, оба дробных значения удалены от нулевого значения (начала координат) на одинаковом расстоянии.
Иными словами, оба дробных значения удалены от нулевого значения (начала координат) на одинаковом расстоянии. Значение знаменателя останется прежним \[\frac{5}{2}\] Весь процесс проведения расчета можно записать в следующем виде, при помощи выражения:
Значение знаменателя останется прежним \[\frac{5}{2}\] Весь процесс проведения расчета можно записать в следующем виде, при помощи выражения: Которое подразумевает умножение целой части на цифру знаменателя дроби и к полученному значению прибавить числитель дроби, то получается противоречие:
Которое подразумевает умножение целой части на цифру знаменателя дроби и к полученному значению прибавить числитель дроби, то получается противоречие:
 Ответ: абвг
Ответ: абвг

 {2}} = 19 $$
{2}} = 19 $$ Числительные обычно называют числами. Числительные используются в различных арифметических операциях, таких как сложение, вычитание, умножение и т. д., которые применимы в повседневном бизнесе и торговой деятельности.
Числительные обычно называют числами. Числительные используются в различных арифметических операциях, таких как сложение, вычитание, умножение и т. д., которые применимы в повседневном бизнесе и торговой деятельности. Типы описаны ниже:
Типы описаны ниже: -4,-3,-2,-1,0,1,2,3,4,5,………….
-4,-3,-2,-1,0,1,2,3,4,5,…………. Он может быть записан десятичными знаками и иметь бесконечные неповторяющиеся цифры после запятой. Обозначается буквой «П».
Он может быть записан десятичными знаками и иметь бесконечные неповторяющиеся цифры после запятой. Обозначается буквой «П».

 д. Эти числа могут быть выражены в виде цифр или слов соответственно. Например, такие числа, как 40 и 65, выраженные в виде цифр, также могут быть записаны как сорок и шестьдесят пять.
д. Эти числа могут быть выражены в виде цифр или слов соответственно. Например, такие числа, как 40 и 65, выраженные в виде цифр, также могут быть записаны как сорок и шестьдесят пять. Оно представлено цифрами как 2,4,7 и т. д. Примерами чисел являются целые числа, целые числа, натуральные числа, рациональные и иррациональные числа и т. д.
Оно представлено цифрами как 2,4,7 и т. д. Примерами чисел являются целые числа, целые числа, натуральные числа, рациональные и иррациональные числа и т. д. В наборе нет дробей и десятичных знаков. Набор целых чисел обозначается «Z». Набор целых чисел может быть представлен как Z = …..,-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5,…
В наборе нет дробей и десятичных знаков. Набор целых чисел обозначается «Z». Набор целых чисел может быть представлен как Z = …..,-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5,… Обозначается ‘Q’.
Обозначается ‘Q’.  Когда рациональное число разбивается, результатом является десятичное число, которое может быть как завершающим, так и повторяющимся десятичным числом.
Когда рациональное число разбивается, результатом является десятичное число, которое может быть как завершающим, так и повторяющимся десятичным числом.
 Шины Pirelli для Infiniti FX VETTEL EDITION 5.0 V8 420 являются идеальной связью технологии и инновации, выполненые с особым протектором, способным противостоять любым погодным условиям без всякого сомнения. Рисунок протектора шин разработан для обеспечения максимального сцепления по прямой и на повороте, одновременно снижая эффект аквапланирования на мокрой дороге, тормозной путь и расход топлива. Обращаясь к описанию каждого типа шин для Infiniti FX VETTEL EDITION 5.0 V8 420, сможете проверить технические характеристики, сравнивая различные возможности. Выбрав шины для Infiniti FX VETTEL EDITION 5.0 V8 420, которые наиболее подходят вашим требованиям, обратитесь к авторизованному дистрибьютору Pirelli для более подробной информации о технических аспектах и для совершения покупки в полной безопасности. Когда приближается момент смены шин для вашего автомобиля Infiniti FX VETTEL EDITION 5.
Шины Pirelli для Infiniti FX VETTEL EDITION 5.0 V8 420 являются идеальной связью технологии и инновации, выполненые с особым протектором, способным противостоять любым погодным условиям без всякого сомнения. Рисунок протектора шин разработан для обеспечения максимального сцепления по прямой и на повороте, одновременно снижая эффект аквапланирования на мокрой дороге, тормозной путь и расход топлива. Обращаясь к описанию каждого типа шин для Infiniti FX VETTEL EDITION 5.0 V8 420, сможете проверить технические характеристики, сравнивая различные возможности. Выбрав шины для Infiniti FX VETTEL EDITION 5.0 V8 420, которые наиболее подходят вашим требованиям, обратитесь к авторизованному дистрибьютору Pirelli для более подробной информации о технических аспектах и для совершения покупки в полной безопасности. Когда приближается момент смены шин для вашего автомобиля Infiniti FX VETTEL EDITION 5. 0 V8 420, выберите качество и безопасность от Pirelli.
0 V8 420, выберите качество и безопасность от Pirelli.
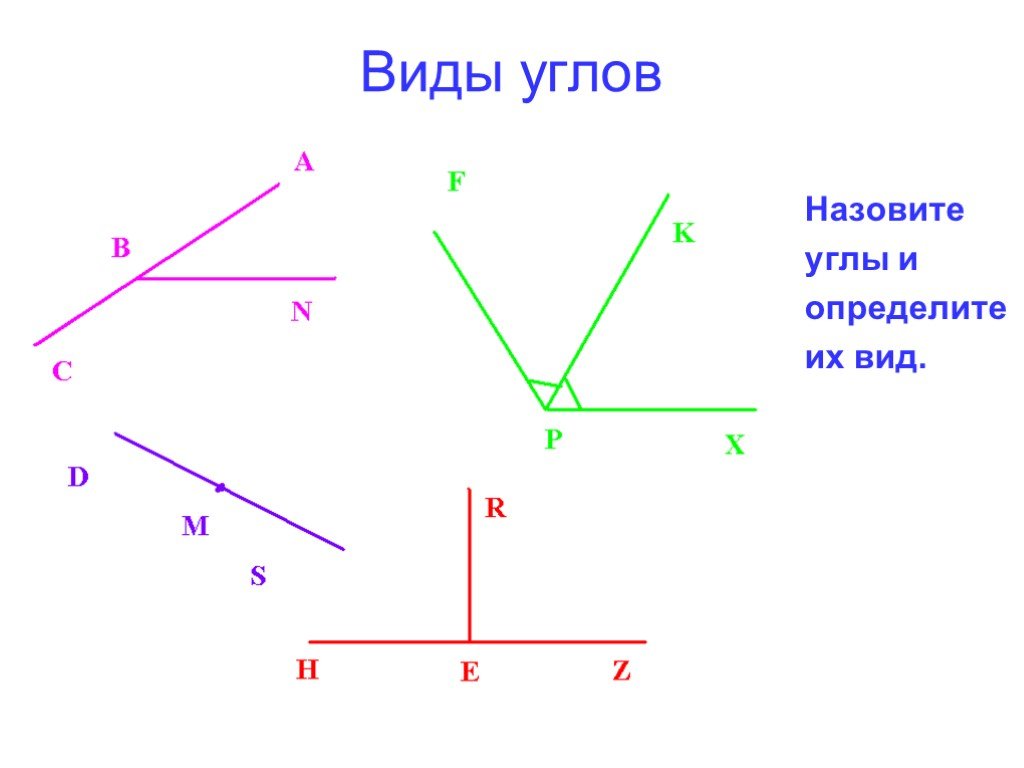
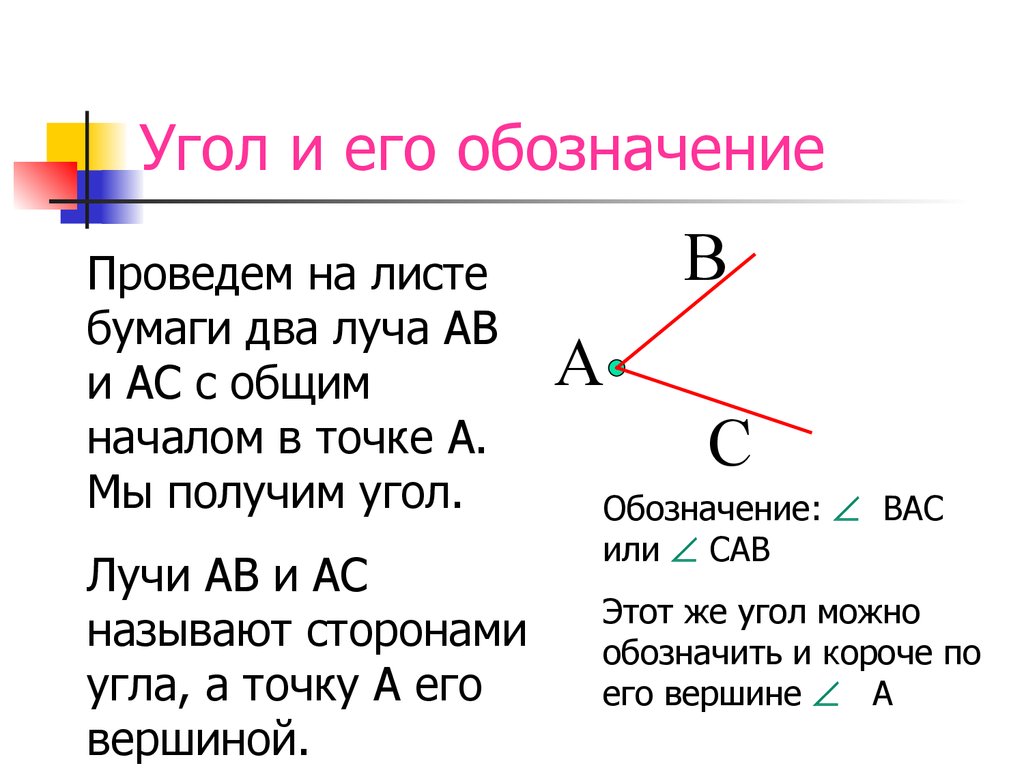
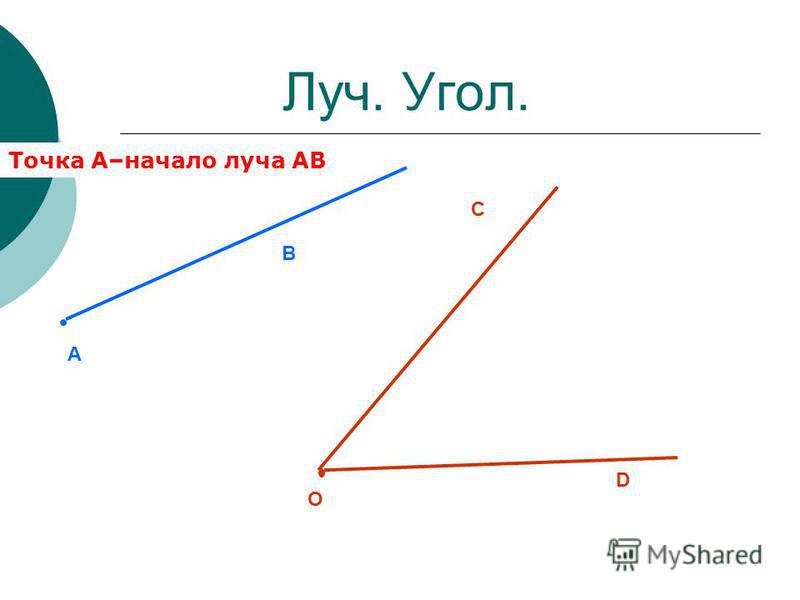 Ваша задача изобразить любой угол используя эти предметы. 3 ряд: ваша задача найти углы в окружающем нас пространстве и указать их. Для этого можете встать и походить по классу. Время на выполнение -20 сек. Покажите итог вашей работы.(хвалю,)
Ваша задача изобразить любой угол используя эти предметы. 3 ряд: ваша задача найти углы в окружающем нас пространстве и указать их. Для этого можете встать и походить по классу. Время на выполнение -20 сек. Покажите итог вашей работы.(хвалю,)
 Он так же состоит из 2 лучей исходящих из одной точки, только эти лучи имеют свое название и называются дополнительными, потому что находятся они на(одной прямой)но направленны в противоположные стороны. (Вешаю определение на доску)Ваня прочитай пожалуйста.
Он так же состоит из 2 лучей исходящих из одной точки, только эти лучи имеют свое название и называются дополнительными, потому что находятся они на(одной прямой)но направленны в противоположные стороны. (Вешаю определение на доску)Ваня прочитай пожалуйста. 2.написать углы а они должны их выписать.( и к тем углам которые составили ученики прикрепить буквы)
2.написать углы а они должны их выписать.( и к тем углам которые составили ученики прикрепить буквы) 136 и найдем там упр.507.Семен прочитай.(читает). Занесем решение этого упражнения в свою тетрадь. Время выполнения 1 минута, (проверяем, ответы с рисунком на слайд.).Если есть ошибки исправьте, у кого нет поставьте себе плюс около задания.
136 и найдем там упр.507.Семен прочитай.(читает). Занесем решение этого упражнения в свою тетрадь. Время выполнения 1 минута, (проверяем, ответы с рисунком на слайд.).Если есть ошибки исправьте, у кого нет поставьте себе плюс около задания.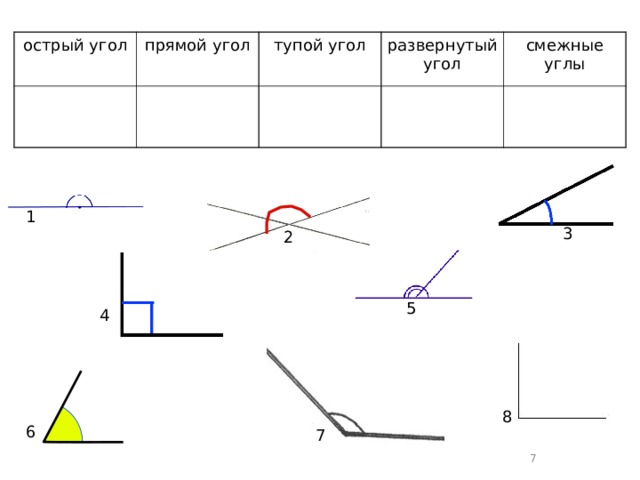 Для ответа используйте шаблон. (выходят к доске и прикрепляют)
Для ответа используйте шаблон. (выходят к доске и прикрепляют)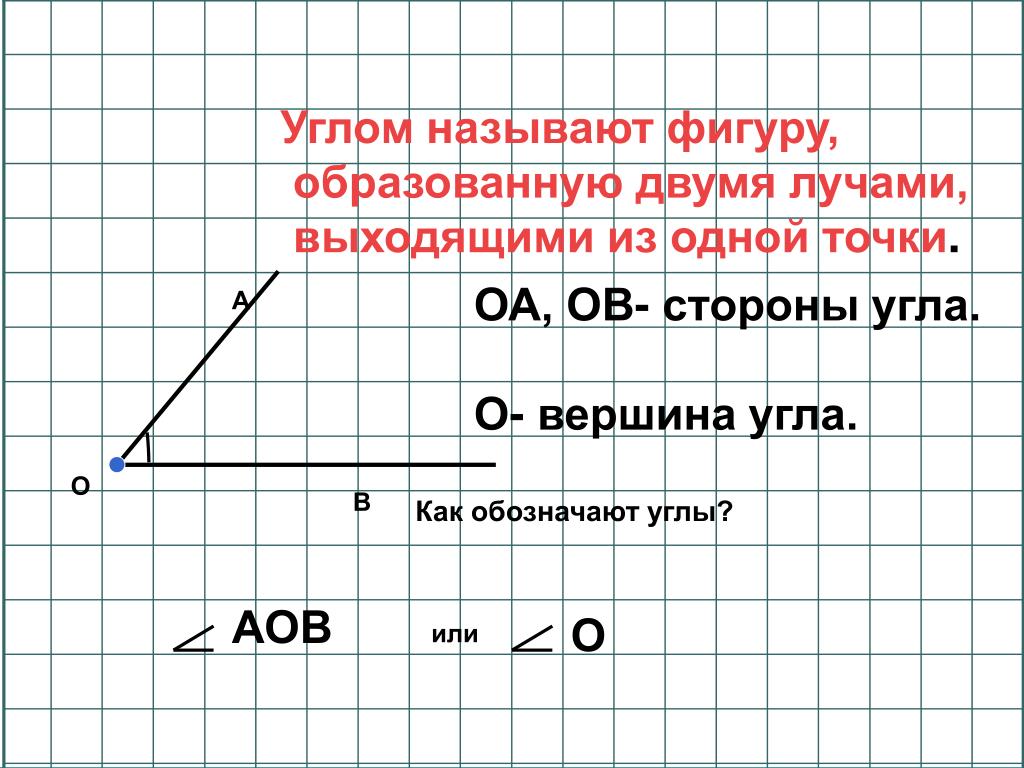 ч развернутый).
ч развернутый).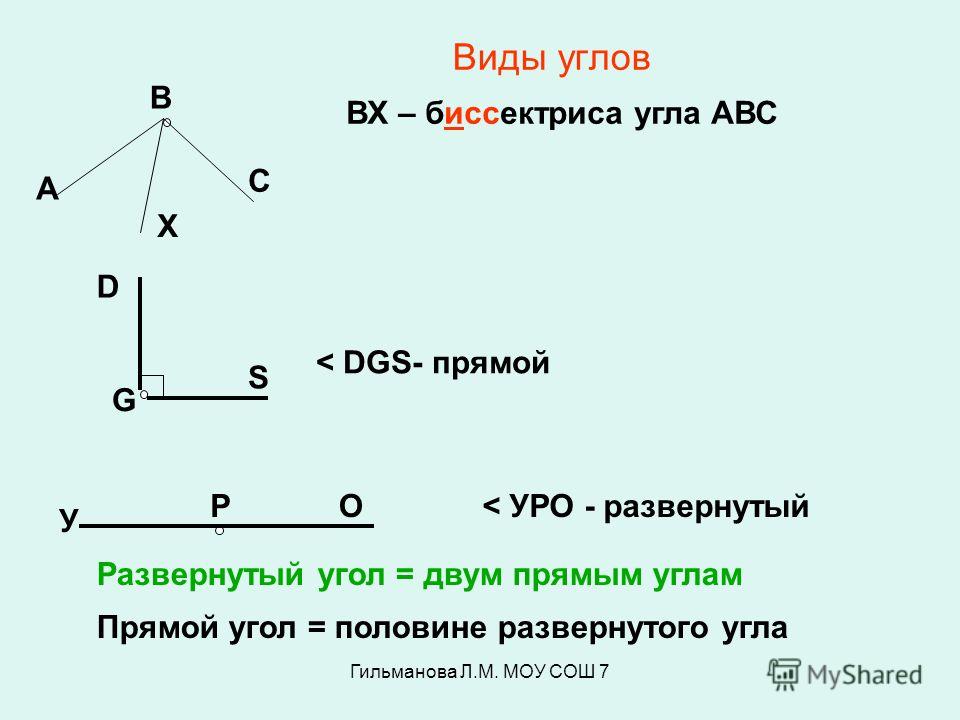
 Планирование – цель и задачи урока ставят учащиеся на основе проблемности. (5 мин.)
Планирование – цель и задачи урока ставят учащиеся на основе проблемности. (5 мин.)



 84 и проверим себя.
84 и проверим себя.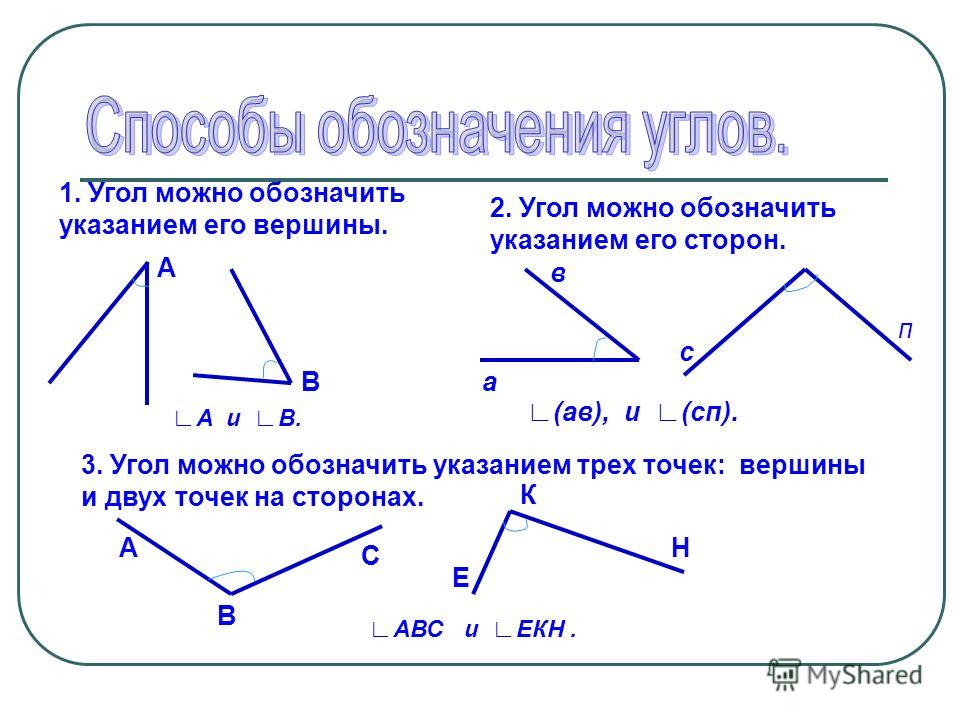




 2.
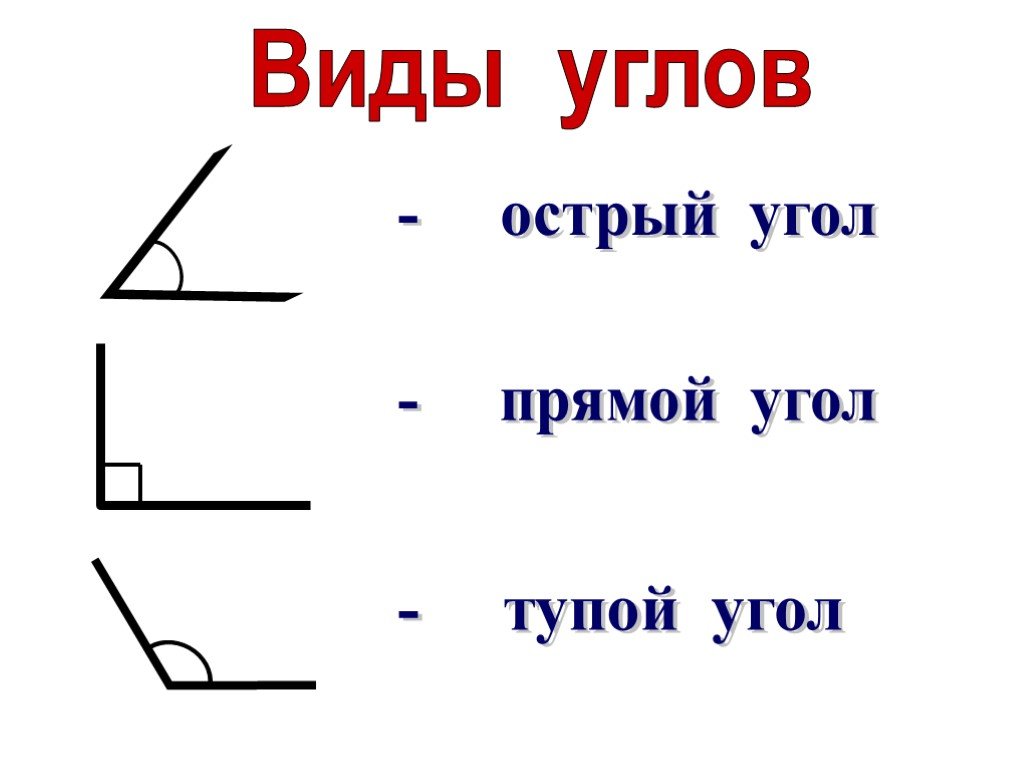
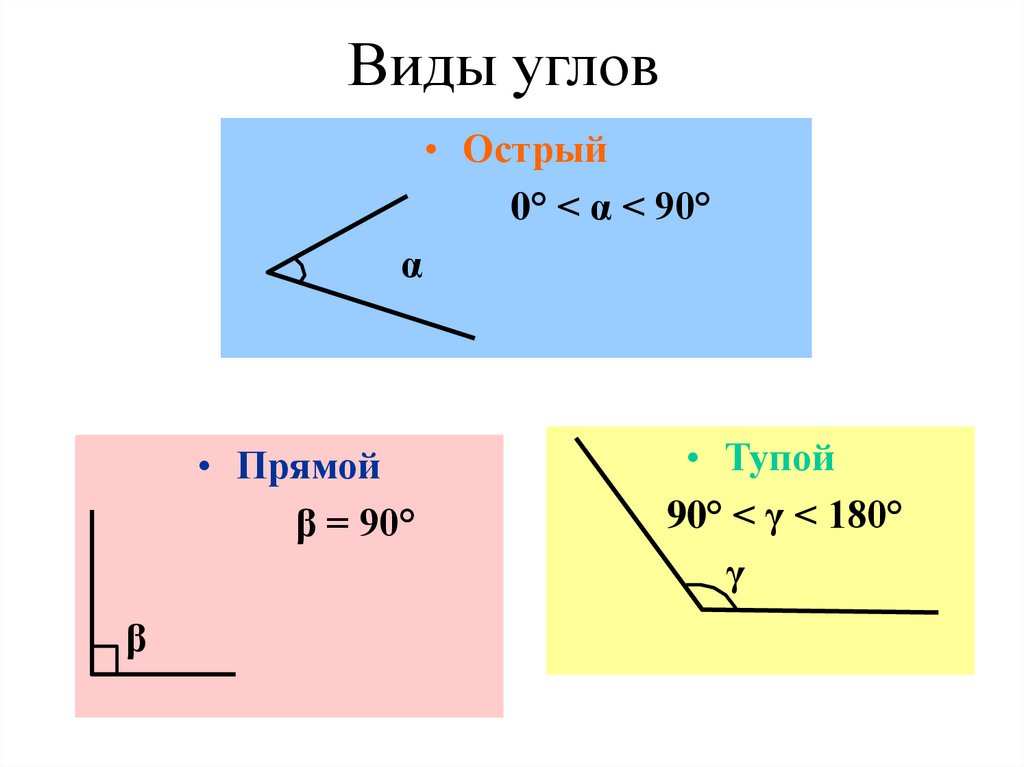
2. Основываясь на измерении, различных типов углов в геометрии
Основываясь на измерении, различных типов углов в геометрии
 Каждое название указывает на определенный диапазон градусных измерений. Равные углы имеют эквивалентные меры. Смежные углы имеют общую вершину и общую сторону.
Каждое название указывает на определенный диапазон градусных измерений. Равные углы имеют эквивалентные меры. Смежные углы имеют общую вершину и общую сторону.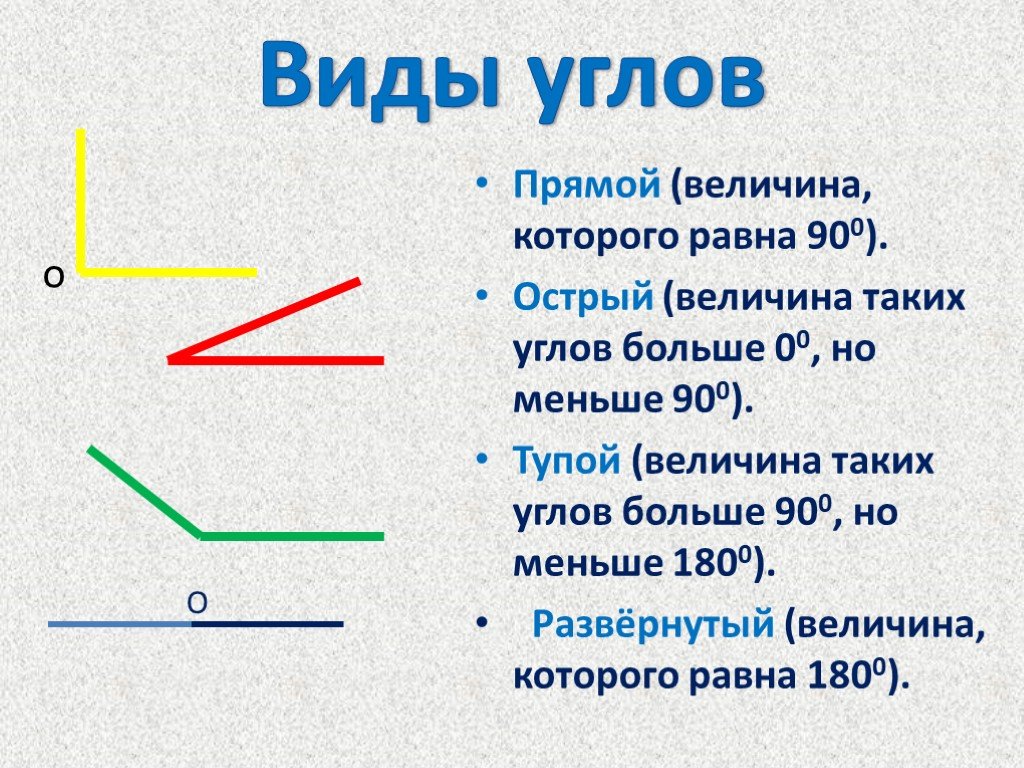 Вы можете записать это как угол abc или, поскольку нет других смежных углов, смежный угол будет выглядеть примерно так, где он будет иметь общую вершину с общей конечной точкой. Поскольку других смежных углов нет, вы также можете просто пометить это на основе вершины, которая равна b.
Вы можете записать это как угол abc или, поскольку нет других смежных углов, смежный угол будет выглядеть примерно так, где он будет иметь общую вершину с общей конечной точкой. Поскольку других смежных углов нет, вы также можете просто пометить это на основе вершины, которая равна b. 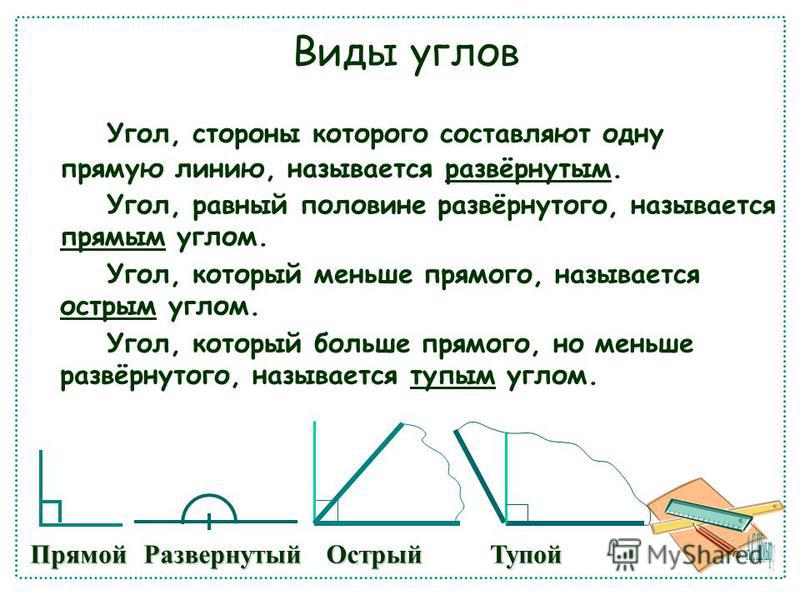

 com. Если вы еще не знакомы с ним, Zapier — это бесплатное приложение, которое позволяет пользователям подключаться и отправлять данные между тысячами различных приложений, включая Calconic.
com. Если вы еще не знакомы с ним, Zapier — это бесплатное приложение, которое позволяет пользователям подключаться и отправлять данные между тысячами различных приложений, включая Calconic. Это идентификатор вашего калькулятора.
Это идентификатор вашего калькулятора.
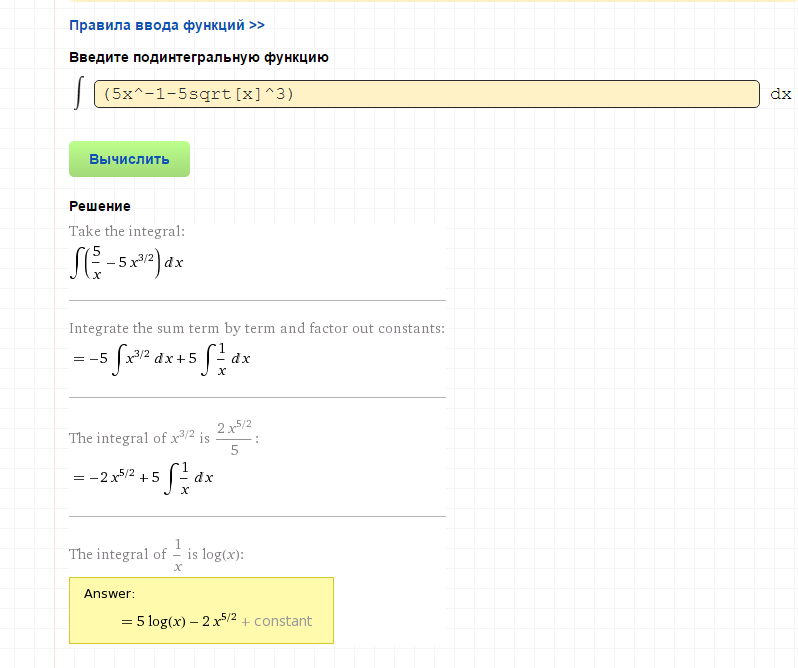 В сегодняшней статье мы узнаем о калькуляторе неопределенного интеграла с шагами и формуле для этого. Прочитав эту статью, вы сможете вычислять неопределенные интегралы вручную и с помощью калькулятора неопределённых интегралов.
В сегодняшней статье мы узнаем о калькуляторе неопределенного интеграла с шагами и формуле для этого. Прочитав эту статью, вы сможете вычислять неопределенные интегралы вручную и с помощью калькулятора неопределённых интегралов. 





 : mille milĭtes propĕrant — идет тысяча воинов; video mille milĭtes — вижу тысячу воинов; зато множественное число milia — тысячи изменяется по падежам:
: mille milĭtes propĕrant — идет тысяча воинов; video mille milĭtes — вижу тысячу воинов; зато множественное число milia — тысячи изменяется по падежам: д.), образуются путем вычитания из него единицы — unus (в сокращенной форме un-) или двойки — duo; напр.: 19 — undeviginti, 18 — duodeviginti, 58 — duodesexaginta, 79 — undeoctoginta. Это же правило действует и для порядковых числительных.
д.), образуются путем вычитания из него единицы — unus (в сокращенной форме un-) или двойки — duo; напр.: 19 — undeviginti, 18 — duodeviginti, 58 — duodesexaginta, 79 — undeoctoginta. Это же правило действует и для порядковых числительных.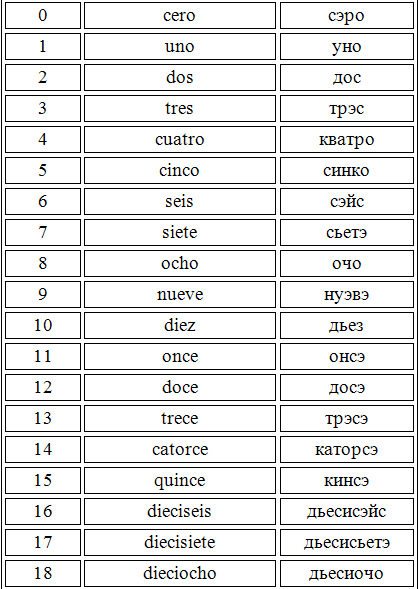 д.; напр.: ter millesĭmus — трехтысячный.
д.; напр.: ter millesĭmus — трехтысячный. д.
д.
 Советы на каждый день
Советы на каждый день года
года Уже 85 лет наша академия готовит кадры для фармотрасли. Подробно рассказываем где это происходит сейчас
Уже 85 лет наша академия готовит кадры для фармотрасли. Подробно рассказываем где это происходит сейчас Знание латинских чисел важно для любого говорящего на латыни, будь вы новичком или продвинутым, поэтому для вашего удобства я включил таблицу ниже. Если вы знаете свои числа от 1 до 100, я обещаю, что вы произведете впечатление на своих друзей, и вы удивите многих Суперкубков своим знанием римских цифр. Удачного подсчета!
Знание латинских чисел важно для любого говорящего на латыни, будь вы новичком или продвинутым, поэтому для вашего удобства я включил таблицу ниже. Если вы знаете свои числа от 1 до 100, я обещаю, что вы произведете впечатление на своих друзей, и вы удивите многих Суперкубков своим знанием римских цифр. Удачного подсчета! Доступно в любое время, в любом месте, на любом устройстве.
Доступно в любое время, в любом месте, на любом устройстве. 0002
Римские числа состоят из семи букв или символов: I [1], V [5], X [10], L [50], C [100], D [500] и M [1000]. Используемые в Древнем Риме и в Средние века, они позволяют считать до 4999 с помощью как аддитивной, так и вычитательной системы. Чтобы сформировать число, мы складываем символы слева направо, пока не получим три одинаковых символа (это аддитивная часть: I, II, III, XXII), затем мы помещаем слева от большего символа число, которое нужно вычесть. (это вычитательная часть: IV, IX, XC). Один и тот же символ нельзя использовать более трех раз подряд, за исключением М (ММММ — это 4000). В отличие от десятичной системы, это аддитивная система, в которой каждый символ имеет свое значение, независимо от того, где он расположен.
0002
Римские числа состоят из семи букв или символов: I [1], V [5], X [10], L [50], C [100], D [500] и M [1000]. Используемые в Древнем Риме и в Средние века, они позволяют считать до 4999 с помощью как аддитивной, так и вычитательной системы. Чтобы сформировать число, мы складываем символы слева направо, пока не получим три одинаковых символа (это аддитивная часть: I, II, III, XXII), затем мы помещаем слева от большего символа число, которое нужно вычесть. (это вычитательная часть: IV, IX, XC). Один и тот же символ нельзя использовать более трех раз подряд, за исключением М (ММММ — это 4000). В отличие от десятичной системы, это аддитивная система, в которой каждый символ имеет свое значение, независимо от того, где он расположен.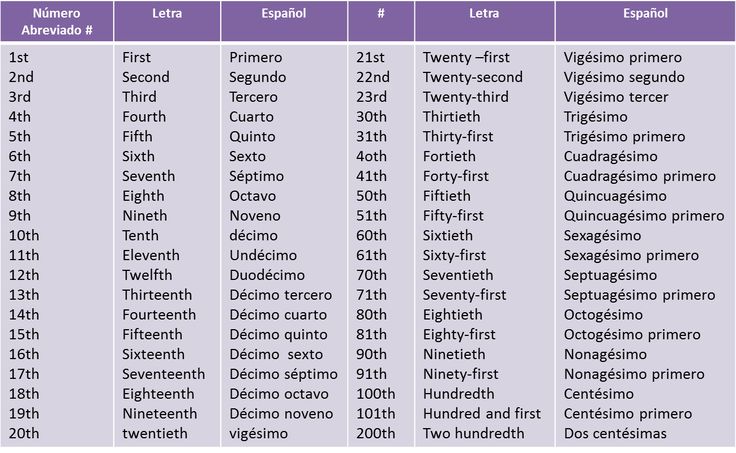



 ru/data/moduleImages/QRCodes/495/e410cf89e76e68fde4d1e58ae3fada99.png
ru/data/moduleImages/QRCodes/495/e410cf89e76e68fde4d1e58ae3fada99.png 248595461287
248595461287
 96000 прописью записывается как Девяносто шесть тысяч.
96000 прописью записывается как Девяносто шесть тысяч.
 Легко
двигаться вперед или назад, чтобы добраться до идеального места. Он доступен на
сети, а также на Android и iOS.
Легко
двигаться вперед или назад, чтобы добраться до идеального места. Он доступен на
сети, а также на Android и iOS. io/yarn-clip/c0fd7ebb-0269-4162-8a08-e3759aba32fa
io/yarn-clip/c0fd7ebb-0269-4162-8a08-e3759aba32fa
 После этого нужно умножить 5 на 6 (множитель у корня) и получить 302.
После этого нужно умножить 5 на 6 (множитель у корня) и получить 302.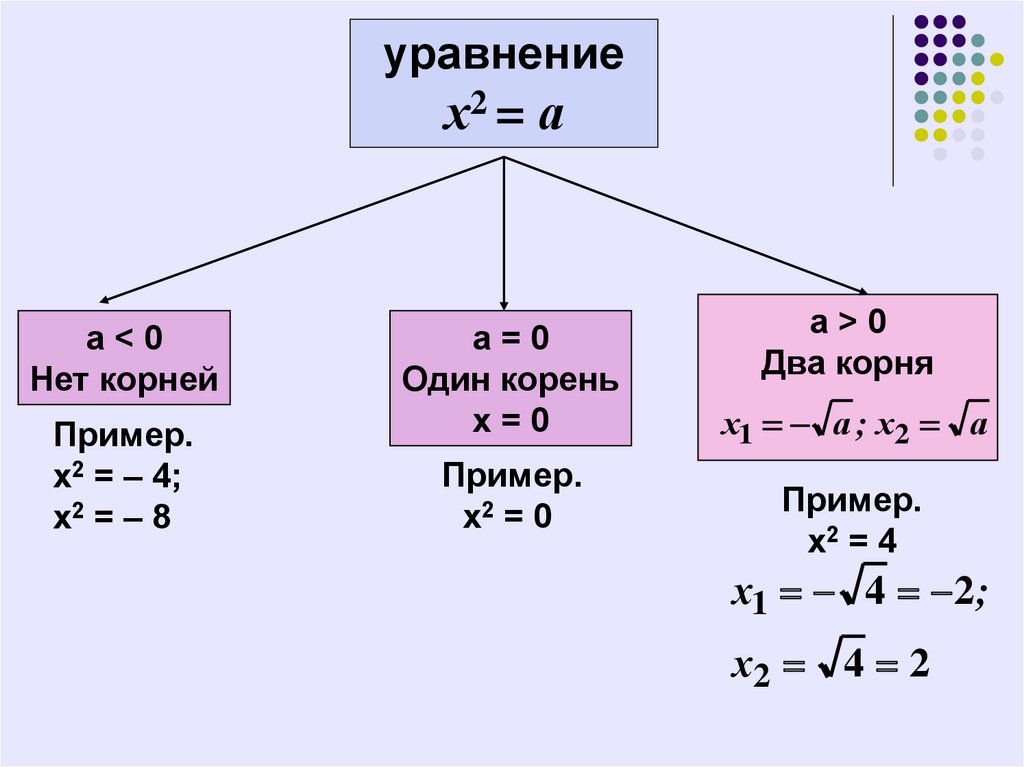
 Кафедра бизнес-информатики Российского университета транспорта
Кафедра бизнес-информатики Российского университета транспорта



 е. a*a = b.
е. a*a = b. В частности, можно сложить или вычесть один из другого 2√7 и 5√7, а вот такие же действия с 2√7 и 5√8 или с 2√2 и 5√7 провести уже не получится. В частности, невозможно вычисление суммы или разности типа 5 + √X или 5 — √X. Если число целое, значит подкоренным числом является 1. Фактически любое число можно записать как N или как N √1.
В частности, можно сложить или вычесть один из другого 2√7 и 5√7, а вот такие же действия с 2√7 и 5√8 или с 2√2 и 5√7 провести уже не получится. В частности, невозможно вычисление суммы или разности типа 5 + √X или 5 — √X. Если число целое, значит подкоренным числом является 1. Фактически любое число можно записать как N или как N √1. Упрощение полученного коэффициента происходит по общим правилам математики.
Упрощение полученного коэффициента происходит по общим правилам математики.
 Нам дано выражение N/(√X +√Y). Умножаем обе части дроби (числитель и знаменатель) на √X -√Y. Вспомните формулу сокращённого умножения. (a+b)*(a-b) = a2 – b2. Применительно к нашему случаю это будет (√X +√Y)*(√X -√Y) = X-Y.
Нам дано выражение N/(√X +√Y). Умножаем обе части дроби (числитель и знаменатель) на √X -√Y. Вспомните формулу сокращённого умножения. (a+b)*(a-b) = a2 – b2. Применительно к нашему случаю это будет (√X +√Y)*(√X -√Y) = X-Y.
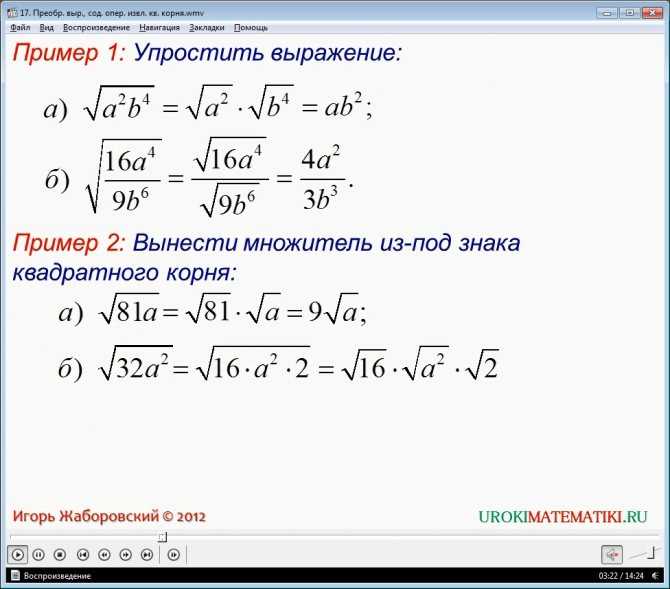
 Теперь нам остаётся сложить лишь числители, знаменатель остаётся прежним. В итоге получаем (√2)/4 + (2√2)/4 = (3√2)/4.
Теперь нам остаётся сложить лишь числители, знаменатель остаётся прежним. В итоге получаем (√2)/4 + (2√2)/4 = (3√2)/4. Мы имеем (√2-√3)*(√2 +√3), по известной формуле (a+b)*(a-b) = a2 – b2 в результате мы получаем (√2-√3)*(√2 +√3) = 2 – 3 = -1.
Мы имеем (√2-√3)*(√2 +√3), по известной формуле (a+b)*(a-b) = a2 – b2 в результате мы получаем (√2-√3)*(√2 +√3) = 2 – 3 = -1.
 Таким образом, все выражение равно нулю, когда хотя бы один из множителей равен нулю.
Таким образом, все выражение равно нулю, когда хотя бы один из множителей равен нулю.
 Первый и наиболее интуитивно понятный метод — стандартный факторинг.
Первый и наиболее интуитивно понятный метод — стандартный факторинг. Числа 2 и 3 работают. (2 * 3 = 6 и 2 + 3 = 5)
Числа 2 и 3 работают. (2 * 3 = 6 и 2 + 3 = 5) Вы можете вычесть справа налево. Затем вы можете добавить 6 справа налево:
Вы можете вычесть справа налево. Затем вы можете добавить 6 справа налево: Эти цифры составляют -6 и -4:
Эти цифры составляют -6 и -4: Мы также установим связи с другими понятиями, которые вам понадобятся в математике более высокого уровня. Давайте начнем!
Мы также установим связи с другими понятиями, которые вам понадобятся в математике более высокого уровня. Давайте начнем! Кубический корень из 64 равен 4, потому что 4 умножить на себя трижды равно 8. Четыре раза по четыре равно 16, 16 умножить на 4 равно 64.
Кубический корень из 64 равен 4, потому что 4 умножить на себя трижды равно 8. Четыре раза по четыре равно 16, 16 умножить на 4 равно 64.

 Если мы посмотрим повнимательнее, то увидим, что множители также можно записать как \(8\times8\):
Если мы посмотрим повнимательнее, то увидим, что множители также можно записать как \(8\times8\):  Самый простой способ найти кубический корень числа — начать с поиска множителей и посмотреть, есть ли в множителях \(3\) одинаковые числа. Например, чтобы найти кубический корень из \(125\), мы начнем с поиска множителей, которые равны \(5\times5\times5\). Поскольку \(5\) трижды умножается на себя, чтобы получить \(125\), мы можем сказать, что \(5\) является кубическим корнем из \(125\).
Самый простой способ найти кубический корень числа — начать с поиска множителей и посмотреть, есть ли в множителях \(3\) одинаковые числа. Например, чтобы найти кубический корень из \(125\), мы начнем с поиска множителей, которые равны \(5\times5\times5\). Поскольку \(5\) трижды умножается на себя, чтобы получить \(125\), мы можем сказать, что \(5\) является кубическим корнем из \(125\).


 Например, в выражении \(\sqrt{50}\) символ является подкоренным, а \(50\), который находится под радикальным символом, называется подкоренным символом.
Например, в выражении \(\sqrt{50}\) символ является подкоренным, а \(50\), который находится под радикальным символом, называется подкоренным символом.
 io/ru/number/decimal-as-a-fraction/8.5″>8.5 в виде обыкновенной дроби — Calculatio</a>
io/ru/number/decimal-as-a-fraction/8.5″>8.5 в виде обыкновенной дроби — Calculatio</a> Кроме того, конечная дробь будет упрощена до простейшей формы, используя наибольший общий делитель (НОД).
Кроме того, конечная дробь будет упрощена до простейшей формы, используя наибольший общий делитель (НОД). Читай дальше!
Читай дальше!

 VisualFractions.com . По состоянию на 3 мая 2023 г. http://visualfractions.com/calculator/improper-to-mixed/what-is-8-5-as-a-mixed-number/.
VisualFractions.com . По состоянию на 3 мая 2023 г. http://visualfractions.com/calculator/improper-to-mixed/what-is-8-5-as-a-mixed-number/. Калькулятор помогает найти значение из операций с несколькими дробями. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении.
Калькулятор помогает найти значение из операций с несколькими дробями. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении. Наиболее распространенные мнемоники для запоминания этого порядка операций:
Наиболее распространенные мнемоники для запоминания этого порядка операций: 
 10.17
10.17