n = 100 count = 0 for i в диапазоне ( 2 , n, 2 ): count + = 1 for i in range ( 3 , n, 3 ): count + = 1 for i in range ( 5 , n, 5 ): count + = 1 for i in range ( 6 , n, 6 ): count - = 1 for i in range ( 10 , n, 10 ): count - = 1 for i in range ( 15 , n, 15 ): count - = 1 for i in range ( 30 , n, 30 ): count + = 1 print (f «Количество положительных целых чисел меньше {n}, которые делятся на 2, 3 или 5, равно {count}». Определение предела функции по Гейне11.1Определения предела по Коши и по Гейне Определение предела функции, которое мы дали в предыдущей главе, называется
также определением «по Коши». Напомним его: Определение 1. (Предел функции по Коши)
Пусть функция f(x) определена в некоторой проколотой
окрестности точки x0. Говорят, что предел функции f(x)
в точке x=x0 равен числу b, если для всякого ε>0 найдётся такое
δ>0, что для всех x из проколотой δ-окрестности точки x0
значения функции лежат в ε-окрестности точки b. Формально: утверждение limx→x0f(x)=b по определению означает, что ∀ε>0 ∃δ>0 ∀x∈˚Uδ(x0):f(x)∈Uε(b), или (см. замечание 3 из предедыщей
лекции 10): ∀ε>0 ∃δ>0 ∀x∈R:0<|x−x0|<δ⇒|f(x)−b|<ε. ∀ε>0 ∃δ>0 ∀x∈R:0<|x−x0|<δ⇒|f(x)−b|<ε. Для некоторых целей нам будет удобно использовать другое определение, известное
как определение предела функции «по Гейне». Оно основано на понятии предела
последовательности. Определение 2. (Определение предела функции по Гейне.)
Пусть снова функция f(x) определена в некоторой проколотой
окрестности точки x0. Говорят, что предел функции f(x)
в точке x=x0 равен числу b, если для любой последовательности
{xn}, стремящейся к x0, все члены которой не равны x0,
выполняется утверждение: последовательность значений функции f(x) в точках
xn стремится к b: f(xn)→b при n→∞. Формально: ∀{xn}:((∀n:xn≠x0)∧(limn→∞xn=x0))⇒limn→∞f(xn)=b. ∀{xn}:((∀n:xn≠x0)∧(limn→∞xn=x0))⇒⇒limn→∞f(xn)=b. Это определение эквивалентно предыдущему (это мы чуть позже докажем) и хорошо
согласуется с интуицией: например, на картинках в разделе примеры и
мотивировка предыдущей лекции мы рисовали
как раз последовательности значений x, и показывали (чисто визуально), что
последовательность соответствующих значений функции стремится к нужному нам
числу. Нужно сказать про несколько тонкостей определения по Гейне: - Вообще говоря, не все значения f(xn) обязаны быть определены:
возможно, какие-то из начальных членов последовательности {xn}
лежат вне области определения функции f(x). Однако, мы знаем, что
функция определена в некоторой проколотой окрестности точки x0, а
последовательность xn стремится к x0, и значит, начиная с
некоторого члена, обязательно окажется внутри той окрестности, где
функция определена. Вместе с дополнительным условием о том, что члены
последовательности не равны x0, это гарантирует, что по крайней мере
начиная с некоторого n=N, все члены последовательности {f(xn)}
определены. А поскольку начальные члены последовательности не влияют на
предел, их можно просто отбросить.
- Условие о том, что все члены последовательности {xn}, не равны
x0, очень важно. Рассмотрим функцию
f(x)={1,x≠2;3,x=2. из примера 12 с предыдущей лекции.
Последовательностьxn={2,n=2k2+1n,n=2k+1 стремится к x0, при этом последовательность значений функции
{f(xn)} имеет вид:f(xn)={3,n=2k,1,n=2k+1, и не имеет предела. Таким образом, если бы мы не требовали от
последовательности {xn} никогда не посещать x0, нам пришлось
бы сказать, что данная функция не имеет предела в точке 2, хотя
согласно определению по Коши оно его имеет. Таким образом, если бы мы не требовали от
последовательности {xn} никогда не посещать x0, нам пришлось
бы сказать, что данная функция не имеет предела в точке 2, хотя
согласно определению по Коши оно его имеет. Требование xn≠x0 соответствует выбору проколотой окрестности для
x0 в определении по Коши вместо обычной окрестности. Заметим, что его также можно ослабить, и требовать, чтобы xn≠x0
не для всех n, а для всех, начиная с некоторого. - Тот факт, что в определении используется квантор всеобщности (для
любой последовательности {xn}…), а не существования, также очень
важен. Рассмотрим функцию
f(x)={x+1,x≤1;x−2,x>1. из примера 13 с предыдущей лекции. У неё нет предела (по
Коши) в точке x=1, поскольку при приближении по x к точке 1 справа
или слева, значение функции f(x) приближается к разным числам (−1 и
2 соответственно). Однако, если мы рассмотрим последовательность xn=1+1/n, она
удовлетворяет всем условиям определения по Гейне, и при этом f(xn)→−1. Если бы достаточно было проверить лишь одну последовательность, мы
могли бы сказать, что предел равен −1. Что не так: выбирая другую
последовательность (например, xn=1−1/n), мы бы получили другой предел
f(xn). Если бы достаточно было проверить лишь одну последовательность, мы
могли бы сказать, что предел равен −1. Что не так: выбирая другую
последовательность (например, xn=1−1/n), мы бы получили другой предел
f(xn).
11.2Эквивалентность определенийТеорема 1. Определения предела по Коши и по Гейне эквивалентны. Доказательство. Из Коши следует Гейне.
Пусть предел функции f при x→x0 равен b по Коши. Докажем, что
тогда он равен b также и по Гейне. Идея доказательства такая. Из определения по Коши следует, что если x
близок к x0 (но при этом не равен x0), f(x) близко к b. Пусть
последовательность xn стремится к x0 и никогда не посещает x0.
Тогда если подождать достаточно долго, xn начнут быть близкими к x0 (и
не равными x0). В этом случае, согласно определению по Коши, f(xn)
окажутся близкими к b. Значит, f(xn) стремится к b. Осталось чётко сформулировать, что значит в каждом случае означают слова
«близко» и «достаточно долго». Утверждение «предел функции f(x) при x→x0 равен b по Коши»
формализуется так: ∀ε1>0 ∃δ1=δ1(ε1)>0 ∀x∈R:0<|x−x0|<δ1⇒|f(x)−b|<ε1.(11.1) ∀ε1>0 ∃δ1=δ1(ε1)>0 ∀x∈R:0<|x−x0|<δ1⇒|f(x)−b|<ε1.(11.1) Докажем, что в этом случае определение по Гейне тоже выполняется. Пусть
xn — произвольная последовательность, стремящаяся к x0 и никогда не
посещающая x0. Тогда для всякого ε2>0 найдётся такое
N2=N2(ε2), что для всех n>N2, выполняется неравенство
|xn−x0|<ε2. Дополнительно известно, что для всех натуральных n,
xn≠x0. Таким образом, для всех n>N2, выполняется неравенство 0<|xn−x0|<ε2. Иными словами, все члены последовательности, начиная с номера N2+1, лежат
в проколотой ε2-окрестности точки x0. Формально: ∀ε2>0 ∃N2=N2(ε) ∀n>N2:0<|xn−x0|<ε2.(11.2) ∀ε2>0 ∃N2=N2(ε) ∀n>N2:0<|xn−x0|<ε2.(11.2) Мы хотим доказать, что в этом случае f(xn)→b. Иными словами, нам
нужно доказать, что для всякого ε>0 найдётся такое N=N(ε), что для
всех n>N выполняется неравенство |f(xn)−b|<ε. Иными словами, нам
нужно доказать, что для всякого ε>0 найдётся такое N=N(ε), что для
всех n>N выполняется неравенство |f(xn)−b|<ε. Сравним утверждения (11.1) и (11.2). Утверждение
(11.1) говорит, что если мы хотим сделать f(x) близким к
b, то нужно потребовать, чтобы x был близок к x0 и не равнялся x0.
Утверждение (11.2) говорит, что если мы хотим, чтобы xn был
близок к x0, то нужно выбрать достаточно большое значение n. Осталось
соединить эти два утверждения. Пусть мы хотим сделать так, чтобы f(xn) был ε-близок к b. Согласно
(11.1), для этого нужно сделать так, чтобы xn был
δ1(ε)-близок к x0. Согласно (11.2), для этого нужно
сделать так, чтобы n был больше, чем N2(δ1(ε)). Иными словами,
мы в утверждении (11.2) в качестве ε2 должны использовать
значение δ1(ε). Действительно, положим N(ε):=N2(δ1(ε)). Тогда согласно
(11.2) для всех n>N(ε), выполняется неравенство 0<|xn−x0|<δ1(ε). Согласно (11.1), для всех значений x, для которых верно
неравенство 0<|x−x0|<δ1(ε), верно неравенство
|f(x)−b|<ε. Значит, для всех xn это неравенство также верно. Значит, для всех xn это неравенство также верно. Итак, для всякого ε>0 мы построили такое N, что для всех n>N
выполняется неравенство |f(xn)−b|<ε. Таким образом, f(xn)→b. Это построение работает для любой последовательности {xn},
удовлетворяющей условиям xn→x0 и xn≠x0 для всех n. Значит,
утверждение определения по Гейне доказано. Из Гейне следует Коши.
Будем доказывать от противного. Пусть есть такая функция f(x), что для неё
выполняется утверждение limx→x0f(x)=b по Гейне, но не выполняется
такое же утверждение по Коши. Запишем формально, что значит «не выполняется такое же утверждение по Коши».
Для этого нужно навесить отрицание на формулу (11.1).
Получится такая штука: ∃ε1>0 ∀δ1>0 ∃x=x(δ1):(0<|x−x0|<δ1)∧|f(x)−b|≥ε1. ∃ε1>0 ∀δ1>0 ∃x=x(δ1):(0<|x−x0|<δ1)∧|f(x)−b|≥ε1. В этой формуле δ1>0 произвольна, а x зависит от этой δ1.
Чтобы прийти к противоречию, мы построим последовательность {xn},
для которой утверждение в определении предела по Гейне будет нарушаться: а
именно, xn будет стремиться к x0, но f(xn) не будет стремиться к
b. Для этого возьмём последовательность δn:=1n. (Как обычно в
таких случаях, подойдёт любая последовательность положительных чисел,
стремящаяся к нулю.) Положим также xn:=x(δn)=x(1n). Для
всякого натурального n, x0−1n<xn<x0+1n. Левая и правая границы стремятся к x0, следовательно, по теореме о
двух милиционерах, xn→x0. Дополнительно верно, что
для всех n, xn≠x0. Таким образом, последовательность {xn}
удовлетворяет условию в определении предела по Гейне. Однако, |f(xn)−b|≥ε1>0. Это значит, что последовательность
{f(xn)} отделена от b, и следовательно не может иметь b
своим пределом (см. упражнение 1 из
лекции 6). Противоречие с определением предела по Гейне: мы построили последовательность
{xn}, стремящуюся к x0 и не посещающую x0, для которой
f(xn)↛b. Это доказывает теорему.∎ 11.3Применение предела по ГейнеДоказывать, что предел чему-то равен, пользуясь определением по Гейне, довольно
тяжело — нужно рассмотреть все возможные последовательности. Зато с ним гораздо
проще доказывать утверждение, что предел не существует или чему-то не равен
— достаточно предъявить одну последовательность. Также с помощью предела по
Гейне можно легко переносить результаты, доказанные для последовательностей, на
функции. Например, докажем теорему о пределе суммы: Зато с ним гораздо
проще доказывать утверждение, что предел не существует или чему-то не равен
— достаточно предъявить одну последовательность. Также с помощью предела по
Гейне можно легко переносить результаты, доказанные для последовательностей, на
функции. Например, докажем теорему о пределе суммы: Утверждение 1. Пусть f(x)→a и g(x)→b при x→x0. Рассмотрим функцию
h(x)=f(x)+g(x). Докажем, что h(x)→a+b при x→x0. Доказательство. Докажем, что для функции h(x) выполняется опрделение
предела по Гейне. Пусть {xn} произвольная последовательность,
удовлетворяющая условиям xn→x0 и xn≠x0 для всех n. Тогда
согласно определению предела по Гейне, примененному к функциям f(x) и
g(x): f(xn)→a,g(xn)→b. По теореме о пределе суммы для
последовательностей, отсюда следует, что h(xn)=f(xn)+g(xn)→a+b. Значит, условие определения по Гейне действительно выполняется: если xn→x0 и xn≠x0 для всех n, то h(xn)→a+b. Утверждение
доказано.∎ Утверждение
доказано.∎ Упражнение 1. Докажите аналогично теоремы о пределе произведения и частного. Кстати, до сих пор мы не доказывали, что предел функции определён однозначно.
Это несложно сделать явно (хорошее упражнение!), но теперь мы получим этот факт
совсем бесплатно.
У нас есть аналогичное утверждение для последовательностей (см. соответствующую
теорему в лекции 4), и с
помощью определения по Гейне он автоматически переносится на предел функции: в
определении по Гейне требуется, чтобы предел f(xn) был одним и тем же для
всех подходящих последовательностей {xn}, и значит если бы нашлось два
разных числа b, удовлетворяющих определению по Гейне, мы бы пришли к
противоречию с единственностью предела последовательности. 11.4Заключение Мы показали, что определения по Коши и по Гейне эквивалентны друг другу, и теперь
в случае необходимости будем пользоваться тем или другим. Как правило, если нам
нужно доказать, что предел чему-то равен, мы будем пользоваться определением по
Коши. Определение по Гейне удобно там, где нужно доказывать противоположное
утверждение (что предел чему-то не равен, или вообще не существует), а также в
некоторых теоретических построениях. Дополнительный бонус определения по Гейне —
оно позволяет переносить на пределы функций ряд свойств, доказанных для пределов
последовательностей, практически «бесплатно». Определение по Гейне удобно там, где нужно доказывать противоположное
утверждение (что предел чему-то не равен, или вообще не существует), а также в
некоторых теоретических построениях. Дополнительный бонус определения по Гейне —
оно позволяет переносить на пределы функций ряд свойств, доказанных для пределов
последовательностей, практически «бесплатно».
← Предыдущая глава
Следующая глава → Предел функции в точкеСегодня рассмотрим подборку новых задач на нахождение предела в точке. Начнем с простых примеров на подстановку значения, чаще всего рассматривают в 11 классе школьной программы по математике.
Далее остановимся и проанализируем пределы с неопределенностями, методы раскрытия неопределенностей, применением первой и второй важных границ и их последствий.
Приведенные примеры полностью не охватят всей темы, но на многие вопросы внесут ясность. Пример 46. Предел функции в точке определяем подстановкой
Так как знаменатель дроби не превращается в ноль то такую задача под силу решить каждому выпускнику школы. Пример 47. Имеем долю полиномов, кроме того знаменатель не содержит особенности (не равен нулю).
Еще одна задача, фактически за 11 класс.
Пример 48. Методом подстановки определяем предел функции
Из условия следует, что граница функции равна двум, если переменная стремится к бесконечности. Пример 49.Прямая подстановка x=2 показывает, что граница в точке имеет особенность {0/0}. Это означает, что и числитель и знаменатель скрыто содержат (x-2).
Выполняем разложение полиномов на простые множители, а потом сокращаем дробь на указанный множитель (x-2).
Предел дроби, которая останется, находим методом подстановки.
Пример 50.Предел функции в точке имеет особенность типа {0/0}.
Избавляемся разницы корней методом умножения на сумму корней (сопряженное выражение), полином раскладываем.
Далее, упростив функцию, находим значение предела в единице. Пример 51.Рассмотрим задачу на сложные пределы.
До сих пор от иррациональности избавлялись методом умножения на сопряженное выражение.
Здесь же, в знаменателе, имеем корень кубический, поэтому нужно использовать формулу разности кубов.
Все остальные преобразования повторяются от условия к условию.
Полином раскладываем на простые множители,
далее сокращаем на множитель, который вносит особенность (0)
и подстановкой x=-3 находим предел функции в точке Пример 52.Особенность вида {0/0} раскрываем с помощью первого замечательного предела и его последствий.
Сначала разницу синусов распишем согласно тригонометрической формуле
sin(7x)-sin(3x)=2sin(2x)cos(5x).
Далее числитель и знаменатель дроби дополняем выражениями, которые необходимы для выделения важных пределов.
Переходим к произведению пределов и оцениваем вложение каждого множителя.
Здесь использовали первый замечательный предел:
и следствия из него
где a и b – произвольные числа. Пример 53. Чтобы раскрыть неопределенность при переменной стремящейся к нулю, используем второй замечательный предел. Чтобы раскрыть неопределенность при переменной стремящейся к нулю, используем второй замечательный предел.
Чтобы выделить экспоненту, приводим показатель к 2-му замечательному пределу, а все остальное, что останется в предельном переходе, даст степень експоненты.
Здесь использовали следствие из второго замечатеьного предела:
Вычислить предел функции в точке:Пример 54. Нужно найти предел функции в точке. Простая подстановка значения показывает, что имеем деление нулей.
Для ее раскрытия разложим на простые множители полиномы и выполним сокращение на множитель, который вносит особенность (х+2).
Однако числитель дальше содержит (x+2), а это значит, что при x=-2 граница равна нулю.
Пример 55.Имеем дробную функцию — в числителе разница корней, в знаменателе — поленом.
Прямая подстановка дает особенность вида {0/0}.
Переменная стремится к минус единице, а это значит, что следует искать и избавляться особенности вида (x+1).
Для этого избавляемся иррациональности умножением на сумму корней, а квадратичную функцию раскладываем на простые множители.
После всех сокращений методом подстановки определяем предел функции в точке
Пример 56.С виду подлимитной функции можно ошибочно заключить, что нужно применить первый предел, но вычисления показали, что все гораздо проще.
Сначала распишем сумму синусов в знаменателе sin(2x)+sin(6x)=2sin(4x)*cos(2x).
Далее расписываем tg(2x), и синус двойного угла sin(4x)=2sin(2x)cos (2x).
Синусы упрощаем и методом подстановки вычисляем предел дроби
Пример 57.Задача на умение использовать вторую замечательный предел:
суть заключается в том, что следует выделить ту часть, которая дает экспоненту.
Остальное, что останется в показателе в предельном переходе даст степень экспоненты.
На этом разбор задач на пределы функций и последовательностей не заканчивается.
В настоящее время подготовлено более 150 готовых ответов к пределам функций, поэтому изучайте и делитесь ссылками на материалы с однокласниками. Ограничения функций | Brilliant Math & Science Wiki Тадеуш Абий,
Патрик Корн,
Мэй Ли,
и способствовал Содержимое- Формальное определение
- Свойства пределов
- Односторонние ограничения
- Двусторонние ограничения
- Бесконечные пределы
- Пределы в бесконечности
- Лимиты по факторингу
- Ограничения по замене
- Правило Лопиталя
- Ограничения функций — решение проблем
- Рекомендации
Основная статья: Определение предела эпсилон-дельта
Точное определение лимита обсуждается в wiki Epsilon-Delta Definition of a Limit. Формальное определение предела функции: Предел \(f(x)\) при приближении \(x\) к \(x_0\) равен \(L\), т.е. \[\lim _{ х \к х_{0} }{f(x)} = L\] , если для каждого \(\epsilon > 0 \) существует \(\delta >0 \) такое, что для всех \(x\) \[ 0 <\влево| x - x_{0} \right |<\delta \textrm{ } \ подразумевает \textrm{ } \left |f(x) - L \right| <\эпсилон. \]
На практике это определение используется только в относительно необычных ситуациях. Для многих приложений проще использовать это определение, чтобы доказать некоторые основные свойства пределов и использовать эти свойства для ответа на простые вопросы, связанные с ограничениями. Наиболее важными свойствами пределов являются алгебраические свойства, которые, по существу, говорят о том, что пределы учитывают алгебраические операции: Предположим, что \( \lim\limits_{x\to a} f(x) = M\) и \(\lim\limits_{x\to a} g(x) = N.\) Тогда \[
\начать{выравнивать}
\lim\limits_{x\to a} \big(f(x)+g(x)\big) &= M+N \\\\
\lim\limits_{x\to a} \big(f(x)-g(x)\big) &= M-N \\\\
\lim\limits_{x\to a} \big(f(x)g(x)\big) &= MN \\\\
\lim\limits_{x\to a} \left(\frac{f(x)}{g(x)}\right) &= \frac MN \ \ \text{ (если } N\ne 0) \\ \\
\lim\limits_{x\to a} f(x)^k &= M^k \ \\text{ (если } M,k > 0). \end{выравнивание}
\] \end{выравнивание}
\]
Все это можно доказать с помощью определения эпсилон-дельта. Обратите внимание, что результаты верны только в том случае, если существуют пределы отдельных функций: если \( \lim\limits_{x\to a} f(x) \) и \( \lim\limits_{x\to a} g( х)\) не существуют, предел их суммы (или разности, произведения или частного) тем не менее может существовать. В сочетании с основными пределами \( \lim_{x\to a} c = c,\), где \( c\) — константа, а \( \lim_{x\to a} x = a,\) свойства можно использовать для вывода пределов, включающих рациональные функции: Пусть \(f(x)\) и \(g(x)\) — полиномы, и предположим, что \(g(a) \ne 0.\) Тогда \[ \lim_{x\to a} \frac{f(x)}{g(x)} = \frac{f(a)}{g(a)}. \]
Это пример непрерывности или того, что иногда называют ограничениями замещения. Обратите внимание, что \(g(a)=0\) — более сложный случай; см. вики Indeterminate Forms для дальнейшего обсуждения. Пусть \(m\) и \(n\) — натуральные числа. n-1}.
\] 9+,\)» мы рассматриваем только значения больше \(a\). Односторонние пределы важны при оценке пределов, содержащих абсолютные значения \(|x|\), знак \(\text{sign}(x)\) , функции пола \(\lfloor x \rfloor\) и другие кусочные функции n-1}.
\] 9+,\)» мы рассматриваем только значения больше \(a\). Односторонние пределы важны при оценке пределов, содержащих абсолютные значения \(|x|\), знак \(\text{sign}(x)\) , функции пола \(\lfloor x \rfloor\) и другие кусочные функции На изображении выше показаны левосторонний и правосторонний пределы непрерывной функции \(f(x).\) Найдите левый и правый пределы сигнум-функции \(\text{signum}(x)\) как \(x \to 0:\) 9-} \frac{|x-1|}{-|x — 1|} = -1 . \] Таким образом, двусторонний предел \( \lim\limits_{x \to 1} \frac{|x — 1|}{x — 1}\) не существует. \(_\квадрат\)
Изображение ниже представляет собой график функции \(f(x)\). Как показано, он непрерывен для всех точек, кроме \(x = -1\) и \(x=2\), которые являются его асимптотами. Найдите все целые точки \(-4 изображение
Поскольку граф непрерывен во всех точках, кроме \(x=-1\) и \(x=2\), двусторонний предел существует в точках \(x=-3\), \(x=-2 \), \(х=0\), \(х=1,\) и \(х=3\). В точке \(x=2,\) нет конечного значения ни для одного из двусторонних пределов, поскольку функция неограниченно возрастает по мере приближения координаты \(x\) к \(2\) (но см. следующий раздел для дальнейшего обсуждения). Ситуация аналогична для \(x=-1.\). Таким образом, точки \(x=-3\), \(x=-2\), \(x=0\), \(x=1,\ ) и \(x=3\) — все целые числа, на которых определены двусторонние пределы. \(_\квадрат\) В точке \(x=2,\) нет конечного значения ни для одного из двусторонних пределов, поскольку функция неограниченно возрастает по мере приближения координаты \(x\) к \(2\) (но см. следующий раздел для дальнейшего обсуждения). Ситуация аналогична для \(x=-1.\). Таким образом, точки \(x=-3\), \(x=-2\), \(x=0\), \(x=1,\ ) и \(x=3\) — все целые числа, на которых определены двусторонние пределы. \(_\квадрат\)
Как было показано в предыдущем разделе, один из способов несуществования предела — это несоответствие односторонних пределов. Другой распространенный способ отсутствия предела в точке \(a\) состоит в том, что функция «взрывается» вблизи \(a,\), т. е. функция неограниченно возрастает. Это происходит в приведенном выше примере при \(x=2,\), где есть вертикальная асимптота. Эта общая ситуация приводит к следующему обозначению: Учитывая функцию \(f(x)\) и действительное число \(a,\), мы говорим \[\lim_{x\to a} f(x) = \infty.\] Если функцию можно сделать произвольно большой, переместив \(x\) достаточно близко к \(a,\) \[\text{для всех } N>0, \text{ существует } \delta>0 \text{ такое, что } 0<|x-a|<\delta \подразумевает f(x)>N. \] \]
Аналогичные определения существуют для односторонних пределов, а также пределов «приближающихся к \(-\infty\)». Предупреждение: Если \(\lim\limits_{x\to a} f(x) = \infty,\), то заманчиво сказать, что предел в \(a\) существует и равен \(\infty .\) Это неверно. Если \(\lim\limits_{x\to a} f(x) = \infty,\) предел равен 9-} \frac{1}{x} = -\infty. \] Чтобы доказать первое утверждение, для любого \(N>0\) в формальном определении можно взять \(\delta = \frac1N,\), и доказательство второго утверждения аналогично. Таким образом, функция неограниченно возрастает с правой стороны и неограниченно убывает с левой стороны. Мы ничего не можем сказать о двустороннем пределе \(\lim\limits_{x\to a} \frac1{x} \ne \infty\) или \(-\infty.\). Сравните это со следующим примером. \(_\квадрат\)
9{n+l}},\] где \(a_0 \neq 0, b_0 \neq 0,\) и \(m,n \in \mathbb N.\) Тогда дано (A), (B ), (C) или (D), \(\displaystyle\lim_{x\rightarrow 0}f(x)\) равно какому из (1), (2), (3) и (4)? Соответствие столбцам: | Столбец-I | Столбец-II | | (A), если \(m>n\) 90 244 | (1) \(\infty\) | | (B) если \(m=n\) | (2) \(-\infty\) | | (C) если \(m0\) \(\hspace{10mm}\) | (3) \(\frac{a_0}{b_0}\) | (D) если \(m| (4) \(0\) | |
Примечание: Например, если (A) правильно соответствует (1), (B ) с (2), (C) с (3) и (D) с (4), тогда ответьте как 1234. \(\infty\)», то есть при неограниченном увеличении \(x\). \(\infty\)», то есть при неограниченном увеличении \(x\). Уравнение \( \lim\limits_{x\to\infty} f(x) = L\) означает, что значения \(f\) можно сделать сколь угодно близкими к \(L\), взяв \(x\ ) достаточно большой. То есть \[\text{для всех } \epsilon > 0, \text{ существует } N>0 \text{ такое, что } x>N \ подразумевает |f(x)-L|<\epsilon.\]
Существуют аналогичные определения для \(\lim\limits_{x\to\infty} f(x) = L,\), а также \(\lim\limits_{x\to\infty} f(x ) = \infty,\) и так далее. Графически \(\lim\limits_{x\to\a} f(x) = \infty\) соответствует вертикальной асимптоте в точке \(a,\), а \( \lim\limits_{x\to\infty } f(x) = L \) соответствует горизонтальной асимптоте в \(L.\) Основная статья: Лимиты по факторингу
Пределы с помощью факторинга относится к методу оценки пределов, который требует нахождения и устранения общих факторов. Основная статья: Ограничения по замене
Оценка пределов путем подстановки относится к идее, что при определенных обстоятельствах (а именно, если исследуемая функция непрерывна) мы можем оценить предел, просто вычислив функцию в интересующей нас точке. {11}} \справа) = \, ?\] {11}} \справа) = \, ?\] - Александров, О. Разрыв .
Получено
12 сентября 2005 г.,
от
https://commons.wikimedia.org/wiki/Файл:Discontinuity_removable.eps.png
Процитировать как: Пределы функций. Brilliant.org .
Извлекаются из
https://brilliant.org/wiki/limits-of-functions/ Исчисление I — Предел Показать мобильное уведомление Показать все примечания Скрыть все примечания Уведомление для мобильных устройств Похоже, вы используете устройство с «узкой» шириной экрана ( т. е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана. Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана. Раздел 2.2: Предел В предыдущем разделе мы рассмотрели пару задач, и в обеих задачах у нас была функция (наклон в случае касательной задачи и средняя скорость изменения в задаче о скорости изменения), и мы хотели чтобы узнать, как эта функция вела себя в какой-то момент \(x = a\). На данном этапе игры нас больше не волнует, откуда взялись функции, и нас больше не волнует, увидим ли мы их снова в будущем или нет. Все, что нам нужно знать или беспокоиться, это то, что у нас есть эти функции, и мы хотим что-то о них знать. Чтобы ответить на вопросы в последнем разделе, мы выбираем значения \(x\), которые все ближе и ближе к \(x = a\), и подставляем их в функцию. Мы также убедились, что рассмотрели значения \(x\), которые были как слева, так и справа от \(x = a\). Сделав это, мы посмотрели на нашу таблицу значений функции и увидели, к чему приближаются значения функции по мере того, как \(x\) становилось все ближе и ближе к \(x = a\), и использовали это, чтобы угадать значение, которое нам нужно. Мы также убедились, что рассмотрели значения \(x\), которые были как слева, так и справа от \(x = a\). Сделав это, мы посмотрели на нашу таблицу значений функции и увидели, к чему приближаются значения функции по мере того, как \(x\) становилось все ближе и ближе к \(x = a\), и использовали это, чтобы угадать значение, которое нам нужно. Этот процесс называется 92} + 25}}{{т — 5}} = 15\] В этих обозначениях мы заметим, что мы всегда даем функцию, с которой работаем, а также значение \(x\) (или \(t\)), к которому мы движемся. В этом разделе мы собираемся применить интуитивный подход к ограничениям и попытаться понять, что они из себя представляют и что они могут рассказать нам о функции. Имея в виду эту цель, мы пока не собираемся вдаваться в то, как мы на самом деле вычисляем лимиты. Вместо этого мы будем полагаться на то, что мы сделали в предыдущем разделе, а также на другой подход, чтобы угадать значение пределов. Оба подхода, которые мы собираемся использовать в этом разделе, разработаны, чтобы помочь нам понять, что такое пределы. Как правило, мы обычно не используем методы, описанные в этом разделе, для вычисления лимитов, и во многих случаях их может быть очень сложно использовать даже для оценки значения лимита, и/или иногда мы будем давать неправильное значение. Мы рассмотрим фактические вычисления пределов в нескольких разделах. Как правило, мы обычно не используем методы, описанные в этом разделе, для вычисления лимитов, и во многих случаях их может быть очень сложно использовать даже для оценки значения лимита, и/или иногда мы будем давать неправильное значение. Мы рассмотрим фактические вычисления пределов в нескольких разделах. Начнем со следующего «определения» лимита. Определение Мы говорим, что предел \(f(x)\) равен \(L\), когда \(x\) приближается к \(a\), и записываем это как \[\ mathop {\lim}\limits_{x \to a} f\left(x \right) = L\] при условии, что мы можем сделать \(f(x)\) настолько близким к \(L\), насколько мы хотим, для всех \(x\), достаточно близких к \(a\), с обеих сторон, фактически не позволяя \( х\) быть \(а\). Это не совсем точное определение предела. Если вы хотите увидеть более точное и математическое определение лимита, вам следует обратиться к разделу «Определение лимита» в конце этой главы. Приведенное выше определение является скорее «рабочим». Это определение помогает нам понять, что такое пределы и что они могут рассказать нам о функциях. Приведенное выше определение является скорее «рабочим». Это определение помогает нам понять, что такое пределы и что они могут рассказать нам о функциях. Так что же означает это определение? Что ж, давайте предположим, что мы знаем, что предел действительно существует. В соответствии с нашим «рабочим» определением мы можем решить, насколько близко к \(L\) мы хотим сделать \(f(x)\). В качестве аргумента предположим, что мы хотим сделать \(f(x)\) не более чем на 0,001 от \(L\). Это означает, что нам нужен один из следующих \[\ begin{array}{lcl}f\left(x\right) — L <0,001 & \hspace{0,25in} & {\mbox{if}}f\left(x\right){\mbox{ is больше, чем L}}\\ L - f\left( x \right) < 0,001& \hspace{0,25in} & {\mbox{if}}f\left( x \right){\mbox{ меньше L }}\конец{массив}\] Теперь согласно «рабочему» определению это означает, что если мы получим \(x\) достаточно близко к \(a\), мы можем сделать одно из приведенных выше истинным. Однако на самом деле это говорит немного больше. В нем говорится, что где-то в мире есть значение \(x\), скажем, \(X\), так что для всех \(x\), которые ближе к \(a\), чем \(X \), то одно из приведенных выше утверждений будет верным. В нем говорится, что где-то в мире есть значение \(x\), скажем, \(X\), так что для всех \(x\), которые ближе к \(a\), чем \(X \), то одно из приведенных выше утверждений будет верным. Это довольно важная идея. В мире существует множество функций, которые мы можем сделать максимально близкими к \(L\) для конкретных значений \(x\), близких к \(a\), но будут и другие значения \(x \) ближе к \(a\), которые дают значения функций, далекие от \(L\). Чтобы предел существовал, как только мы получим \(f(x)\) настолько близко к \(L\), насколько мы хотим для некоторого \(x\), тогда он должен будет оставаться в этом близком к \(L\ ) (или приблизиться) для всех значений \(x\), которые ближе к \(a\). Мы увидим пример этого позже в этом разделе. Проще говоря, определение говорит, что по мере того, как \(x\) становится все ближе и ближе к \(x=a\) (конечно, с обеих сторон…), тогда \(f(x)\) должно приближаться все ближе и ближе к \(L\). Или, когда мы движемся к \(x=a\), тогда \(f(x)\) должно двигаться к \(L\). Важно еще раз отметить, что мы должны смотреть на значения \(x\), которые находятся по обе стороны от \(x=a\). Мы также должны отметить, что нам не разрешено использовать \(x=a\) в определении. Мы будем часто использовать информацию, которую дают нам ограничения, чтобы получить некоторую информацию о том, что происходит прямо в точке \(x=a\), но сам предел не связан с тем, что на самом деле происходит в точке \(x=a\). . Предел связан только с тем, что происходит вокруг точки \(x=a\). Это важное понятие об ограничениях, которые мы должны иметь в виду. Альтернативное обозначение, которое мы иногда будем использовать для обозначения пределов, это .
\[f(x) \to L\hspace{0,25 дюйма}{\rm{as}}\hspace{0,25in}x \to a\] Как мы можем использовать это определение, чтобы оценить пределы? Мы делаем именно то, что делали в предыдущем разделе. Мы берем \(x\) по обе стороны от \(x=a\), которые приближаются все ближе и ближе к \(a\), и подставляем их в нашу функцию. Затем мы смотрим, можем ли мы определить, к какому числу приближаются значения функции, и используем это как нашу оценку. 92} — 2x}}\] Затем мы смотрим, можем ли мы определить, к какому числу приближаются значения функции, и используем это как нашу оценку. 92} — 2x}}\] Показать решение Обратите внимание, что мы сказали оценить значение лимита. Опять же, в этом разделе мы не собираемся напрямую вычислять ограничения. Цель этого раздела — дать нам лучшее представление о том, как работают ограничения и что они могут рассказать нам о функции. Итак, помня об этом, мы собираемся работать почти так же, как в предыдущем разделе. Мы выберем значения \(x\), которые все ближе и ближе к \(x=2\), и подставим эти значения в функцию. Это дает следующую таблицу значений. | \(х\) | \(f(x)\) | \(х\) | \(f(x)\) |
|---|
| 2,5 | 3,4 | 1,5 | 5,0 | 2. 1 1 | 3,857142857 | 1,9 | 4.157894737 | | 2,01 | 3,985074627 | 1,99 | 4.015075377 | | 2,001 | 3,998500750 | 1,999 | 4.001500750 | | 2,0001 | 3,999850007 | 1,9999 | 4.000150008 | | 2.00001 | 3,999985000 | 1,99999 | 4.000015000 |
Обратите внимание, что мы удостоверились и выбрали значения \(x\), которые были по обе стороны от \(x = 2\), и что мы подошли очень близко к \(x = 2\), чтобы убедиться, что любые тенденции, которые мы можем наблюдать, на самом деле верны. 92} — 2x}} = 4\] 92} — 2x}} = 4\] Давайте еще немного подумаем о том, что здесь происходит. Построим график функции из последнего примера. Ниже показан график функции в интересующем диапазоне \(x\). Во-первых, обратите внимание на довольно большую открытую точку \(x = 2\). Это должно напомнить нам, что функция (и, следовательно, график) не существует в точке \(x = 2\). Поскольку мы подставляли значения \(x\) в функцию, мы в действительности двигаемся по графику к точке как \(x = 2\). Это показано на графике двумя стрелками на графике, которые движутся к точке. Когда мы вычисляем пределы, вопрос, который мы на самом деле задаем, заключается в том, к какому значению \(y\) приближается наш график, когда мы приближаемся к \(x = a\) на нашем графике. Мы НЕ спрашиваем, какое значение \(y\) принимает график в рассматриваемой точке. Другими словами, мы спрашиваем, что делает график вокруг точки \(x = a\). В нашем случае мы можем видеть, что по мере того, как \(x\) приближается к 2 (с обеих сторон), функция приближается к \(y = 4\), хотя сама функция даже не существует в \(x = 2\). 2} — 2x}} & {\mbox{if} }x \ne 2\\ 6 & {\mbox{if}}x = 2\end{массив} \right.\] 2} — 2x}} & {\mbox{if} }x \ne 2\\ 6 & {\mbox{if}}x = 2\end{массив} \right.\] Показать решение Прежде всего следует отметить, что это точно такая же функция, как и в первом примере, за исключением того, что мы присвоили ей значение \(x = 2\). Итак, сначала отметим, что \[г\влево( 2 \вправо) = 6\] Что касается оценки значения этого лимита, то по сравнению с первым примером ничего не изменилось. Мы могли бы построить таблицу значений, как в первом примере, или быстро взглянуть на график функции. Любой метод даст нам значение предела. Давайте сначала посмотрим на таблицу значений и посмотрим, что она нам говорит. Обратите внимание, что наличие значения функции в \(x = 2\) не изменит наш выбор для \(x\). Мы выбираем только те значения \(x\), которые приближаются к \(x = 2\), но никогда не берем \(x = 2\). Другими словами, таблица значений, которую мы использовали в первом примере, будет точно такой же таблицей, которую мы будем использовать здесь. Итак, поскольку мы уже сделали это один раз, нет причин переделывать это здесь. Итак, поскольку мы уже сделали это один раз, нет причин переделывать это здесь. Из этой таблицы снова видно, что ограничение равно \[\ mathop {\lim}\limits_{x \to 2} g\left(x\right) = 4\] Предел НЕ 6! Помните из обсуждения после первого примера, что пределы не заботятся о том, что на самом деле делает функция в рассматриваемый момент. Ограничения касаются только того, что происходит на вокруг точки. Поскольку единственное, что мы фактически изменили в функции, это ее поведение при \(x = 2\), это не изменит предел. Давайте также взглянем на график этой функции, чтобы увидеть, говорит ли он о том же самом. Опять же, мы можем видеть, что по мере того, как мы приближаемся к \(x = 2\) на нашем графике, функция все еще приближается к значению \(y\), равному 4. Помните, что мы только спрашиваем, что делает функция около \(x = 2\), и нам все равно, что на самом деле делает функция в \(x = 2\). Затем график также поддерживает вывод о том, что предел равен Затем график также поддерживает вывод о том, что предел равен .
\[\ mathop {\lim}\limits_{x \to 2} g\left(x\right) = 4\] Давайте еще раз остановимся на этом, просто чтобы убедиться, что мы его поняли. Пределы , а не связаны с тем, что происходит в точке \(x = a\). Пределы касаются только того, что происходит вокруг \(x = a\). Мы продолжаем говорить об этом, но это очень важная концепция ограничений, которую мы всегда должны помнить. Поэтому мы будем использовать любую возможность, чтобы напомнить себе об этой идее. Поскольку пределы не связаны с тем, что на самом деле происходит в \(x = a\), мы будем иногда сталкиваться с ситуациями, подобными предыдущему примеру, когда предел в точке и значение функции в точке различны. Это не всегда будет происходить, конечно. Бывают случаи, когда значение функции и предел в точке совпадают, и мы в конечном итоге увидим несколько таких примеров. Однако важно не волноваться по поводу вещей, когда функция и предел не принимают одно и то же значение в какой-то точке. Это случается иногда, поэтому нам нужно будет иметь дело с такими случаями, когда они возникают. Однако важно не волноваться по поводу вещей, когда функция и предел не принимают одно и то же значение в какой-то точке. Это случается иногда, поэтому нам нужно будет иметь дело с такими случаями, когда они возникают. Давайте рассмотрим еще один пример, чтобы попытаться воплотить эту идею в жизнь. Пример 3. Оцените значение следующего предела.
\[\ mathop {\lim}\limits_{\theta\to 0} \,\frac{{1 — \cos\left(\theta\right)}}{\theta}\] Показать решение Во-первых, не волнуйтесь о \(\theta\) в функции. Это просто буква, точно так же, как \(х\) — это буква! Это греческая буква, но это буква, и иногда вам будет предложено иметь дело с греческими буквами, поэтому неплохо начать привыкать к ним на этом этапе. Теперь также обратите внимание, что если мы подставим \(\theta =0\), то получим деление на ноль, поэтому на данный момент функция не существует. На самом деле в этой точке мы получаем 0/0, но из-за деления на ноль эта функция не существует в точке \(\theta=0\). Итак, как и в первом примере, давайте получим таблицу значений и посмотрим, что если мы сможем угадать, к какому значению движется функция. | \(\ тета \) | \(f\влево(\тета\вправо)\) | \(\тета\) | \(f\влево(\тета\вправо)\) |
|---|
| 1 | 0,45969769 | -1 | -0,45969769 | | 0,1 | 0,04995835 | -0,1 | -0,04995835 | | 0,01 | 0,00499996 | -0,01 | -0,00499996 | | 0,001 | 0,00049999 | -0,001 | -0,00049999 |
Хорошо, похоже, что функция приближается к нулевому значению, когда \(\theta\) приближается к 0, конечно, с обеих сторон. Следовательно, мы предполагаем, что предел имеет значение \[\ mathop {\lim}\limits_{\theta\to 0} \,\frac{{1 — \cos\left(\theta\right)}}{\theta} = 0\] Итак, еще раз, предел имел значение, несмотря на то, что функция не существовала в интересующей нас точке. что мы собираемся обсудить. Пример 4. Оцените значение следующего предела.
\[\ mathop {\lim}\limits_{t \to 0} \cos\left({\frac{\pi}}{t}} \right)\] Показать решение Давайте создадим таблицу значений и посмотрим, что происходит с нашей функцией в этом случае. | \(т\) | \(ф(т)\) | \(т\) | \(ф(т)\) |
|---|
| 1 | -1 | -1 | -1 | | 0,1 | 1 | -0,1 | 1 | | 0,01 | 1 | -0,01 | 1 | | 0,001 | 1 | -0,001 | 1 |
Теперь, если бы нам нужно было угадать предел из этой таблицы, мы бы предположили, что предел равен 1. Однако, если бы мы сделали это предположение, мы бы ошиблись. Рассмотрим любую из следующих оценок функции. Однако, если бы мы сделали это предположение, мы бы ошиблись. Рассмотрим любую из следующих оценок функции. \[f\left( {\frac{1}{{2001}}} \right) = — 1\hspace{0,55in}f\left({\frac{2}{{2001}}} \right) = 0 \ hspace {0,5 дюйма} f \ слева ( {\ гидроразрыва {4} {{4001}}} \ справа) = \ гидроразрыва {{\ sqrt 2}} {2} \] Во всех трех вычислениях функции мы оценивали функцию по числу меньше 0,001 и получили три совершенно разных числа. Напомним, что определение предела, с которым мы работаем, требует, чтобы функция приближалась к единственному значению (нашему предположению) по мере того, как \(t\) становится все ближе и ближе к рассматриваемой точке. Это не говорит о том, что только некоторые значения функции должны приближаться к догадке. В нем говорится, что все значения функции должны быть все ближе и ближе к нашему предположению. Чтобы увидеть, что здесь происходит, был бы удобен график функции. Из этого графика видно, что по мере приближения к \(t = 0\) функция начинает сильно колебаться, и чем ближе к \(t = 0\), тем больше скорость колебаний. Напомним из нашего определения предела, что для того, чтобы предел существовал, функция должна стремиться к одному значению по мере того, как мы приближаемся к рассматриваемой точке. Эта функция явно не подходит для одного номера, поэтому этот предел не существует ! Последний пример указывает на недостаток простого выбора значений переменной и использования таблицы значений функции для оценки значения предела. Значения переменной, которые мы выбрали в предыдущем примере, были действительными и фактически были значениями, которые выбрали бы многие. На самом деле, это были точно такие же значения, которые мы использовали в предыдущей задаче, и они работали в этой задаче! При использовании таблицы значений всегда существует вероятность того, что мы выбираем неправильные значения и неправильно угадываем наш лимит. Это то, что мы всегда должны помнить, когда делаем это, чтобы угадать значение ограничений. На самом деле это такая проблема, что после этого раздела мы больше никогда не будем использовать таблицу значений, чтобы угадать значение лимита. Это то, что мы всегда должны помнить, когда делаем это, чтобы угадать значение ограничений. На самом деле это такая проблема, что после этого раздела мы больше никогда не будем использовать таблицу значений, чтобы угадать значение лимита. Этот последний пример также показал нам, что ограничения не обязательно должны существовать. До этого момента мы видели только существующие ограничения, но это не всегда так. Давайте рассмотрим еще один пример в этом разделе. Пример 5. Оцените значение следующего предела.
\[\ mathop {\ lim } \ limit_ {t \ to 0} H \ left ( t \ right) \ hspace {0,25 дюйма} {\ mbox {где}} \ hspace {0,25 дюйма} H \ left ( t \ справа) = \left\{ \begin{array}{ll}0 & {\mbox{if}}t < 0\\ 1 & {\mbox{if}}t \ge 0\end{массив} \right. \] Показать решение Эту функцию часто называют функцией Heaviside или step . Мы могли бы использовать таблицу значений для оценки предела, но, вероятно, в этом случае будет так же быстро использовать график, так что давайте сделаем это. Ниже представлен график этой функции. Мы могли бы использовать таблицу значений для оценки предела, но, вероятно, в этом случае будет так же быстро использовать график, так что давайте сделаем это. Ниже представлен график этой функции. На графике видно, что если мы приближаемся к \(t = 0\) справа, функция приближается к значению \(y\), равному 1. На самом деле она просто остается на уровне 1, но в терминология, которую мы использовали в этом разделе, приближается к 1… Кроме того, если мы движемся к \(t = 0\) слева, функция движется к значению \(y\), равному 0. Согласно нашему определению предела, функция должна двигаться в к одному значению по мере продвижения к \(t = a\) (с обеих сторон). В данном случае этого не происходит, поэтому в этом примере мы также будем говорить, что предела не существует. Обратите внимание, что предел в этом примере немного отличается от предыдущего примера. В предыдущем примере функция не остановилась на одном числе, когда мы приблизились к \(t = 0\). Однако в этом примере функция сводится к одному числу как \(t = 0\) с обеих сторон. Проблема в том, что число на каждой стороне \(t = 0\) разное. Это идея, которую мы рассмотрим более подробно в следующем разделе. Проблема в том, что число на каждой стороне \(t = 0\) разное. Это идея, которую мы рассмотрим более подробно в следующем разделе. Давайте обобщим то, что мы (надеюсь) узнали в этом разделе. В первых трех примерах мы видели, что пределы не заботятся о том, что на самом деле делает функция в рассматриваемой точке. Их интересует только то, что происходит вокруг точки. На самом деле у нас могут быть пределы в \(x = a\), даже если самой функции в этой точке не существует. Точно так же, даже если функция существует в какой-то точке, нет оснований (на данный момент) думать, что предел будет иметь то же значение, что и функция в этой точке. Иногда предел и функция будут иметь одно и то же значение в точке, а иногда они не будут иметь одинакового значения. Далее, в третьем и четвертом примерах мы увидели основную причину отказа от использования таблицы значений для угадывания значения лимита. В этих примерах мы использовали точно такой же набор значений, однако они работали только в одном из примеров. Использование таблиц значений для угадывания значений лимитов — просто не лучший способ получить значение лимита. Это единственный раздел, в котором мы будем это делать. Таблицы значений всегда должны быть вашим последним выбором при поиске значений пределов. Использование таблиц значений для угадывания значений лимитов — просто не лучший способ получить значение лимита. Это единственный раздел, в котором мы будем это делать. Таблицы значений всегда должны быть вашим последним выбором при поиске значений пределов. Последние два примера показали нам, что на самом деле существуют не все ограничения. Мы не должны зацикливаться на идее, что ограничения всегда будут существовать. В большинстве курсов по математическому анализу мы работаем с ограничениями, которые почти всегда существуют, поэтому легко начать думать, что ограничения существуют всегда. Ограничения не всегда существуют, поэтому не привыкайте предполагать, что они будут. Наконец, в четвертом примере мы увидели, что единственный способ справиться с пределом — построить график функции. Иногда это единственный способ, однако этот пример также иллюстрирует недостатки использования графиков. Чтобы использовать график, чтобы угадать значение предела, вы должны иметь возможность набросать график. Для многих функций это не так просто сделать. Для многих функций это не так просто сделать. Есть еще один недостаток в использовании графиков. Даже если у вас есть график, он будет полезен только в том случае, если значение \(y\) приближается к целому числу. Если значение \(y\) приближается, скажем, к \(\frac{{ — 15}}{{123}}\), вы никак не сможете угадать это значение по графику, и мы обычно потребуются точные значения для наших пределов. Таким образом, хотя графики функций иногда могут облегчить вашу жизнь при угадывании значений пределов, они опять же, вероятно, не лучший способ получить значения пределов. Они будут полезны только в том случае, если вы можете получить их в свои руки, а значение лимита является «хорошим» числом. Тогда возникает естественный вопрос: почему мы вообще говорим об использовании таблиц и/или графиков для оценки пределов, если это не лучший способ? Было несколько причин. Во-первых, они могут помочь нам лучше понять, что такое ограничения и что они могут нам сказать. заказ решений на аукционе за минимальную цену с максимальным качествомПредлагаю идею сайта-аукциона по выполнению домашних заданий. Он будет включать: - решение задач по математике (сейчас доступен решебник Филиппова), физике, химии, экономике
- написание лабораторных, рефератов и курсовых
- выполнение заданий по литературе, русскому или иностранному языку.
Основное отличие от большинства сайтов, предлагающих выполнение работ на заказ – сайт рассчитан на две категории пользователей: заказчиков и решающих задания. Причем, по желанию (чтобы заработать, увеличить свой рейтинг, получить решение сложной задачи) пользователи могут играть любую из этих ролей. Объединение сервисов в одну системуОсновой для идеи послужили несколько работающих систем, объединение которых позволит сделать сервис для решения задач на заказ. Эти системы: - Форум, где посетители обмениваются идеями и помогают друг другу
- Система bugtracking, где обнаруженные проблемы проходят путь от публикации до принятия в исполнение и решения
- Аукцион, где цена за товар или услугу определяется в результате торгов
- Система рейтингов, где участники могут оценивать ответы друг друга.
 Причем, чем больше рейтинг пользователя, тем более значимым становится его голос Причем, чем больше рейтинг пользователя, тем более значимым становится его голос
Принцип работыДля удобства и проведения аналогий с реальной жизнью назовем заказчиков студентами, а решающих задания – репетиторами. Итак, студенту необходимо решить несколько задач. Он заходит на сайт, выбирает раздел с соответствующей дисциплиной и создает новую тему (аналогия с форумом). Но при создании темы он также указывает стартовую (максимальную) цену, которую он готов заплатить за решение задач и крайний срок исполнения задания. Можно будет назначить и нулевую цену – если студенту нужно только бесплатное решение. Как только тема создана, все пожелавшие подписаться на раздел репетиторы получают уведомление. Причем, условие получения уведомлений можно настроить. Например, уведомлять только о заказах со стартовой ценой более 500 р. и сроком решения не менее недели. Заинтересовавшиеся репетиторы делают ставки. Причем студент (автор темы) видит ставки и может посмотреть информацию по каждому репетитору (его решения, рейтинг, дату начала участия в проекте). Когда студент посчитает нужным, он может остановить аукцион и назначить задание одному из репетиторов, сделавшему ставку (не обязательно самую низкую, т.к. можно учитывать и другие факторы – см. выше). Когда студент посчитает нужным, он может остановить аукцион и назначить задание одному из репетиторов, сделавшему ставку (не обязательно самую низкую, т.к. можно учитывать и другие факторы – см. выше). Деньги блокируются на счете студента, и репетитор начинает решать задание. Он должен представить его к сроку, заданному изначально. Выполненное решение публикуется в свободном доступе и его может оценить как заказчик, так и другие репетиторы. На этих оценках и строится рейтинг. Если к решению нет претензий – деньги окончательно переводятся со счета студента на счет репетитора. За счет чего будет развиваться сервисПервое – положительная обратная связь. Чем больше условий задач и решений будет опубликовано на сайте, тем чаще его будут находить пользователи через поисковики, будет больше ссылок на готовые решения. Именно поэтому важно размещать решенные задачи в свободном доступе. Знаю это по опыту своего сайта exir.ru (ex irodov.nm.ru) – большая ссылочная база получена исключительно за счет благодарных пользователей. Второе – удобный сервис для заказчиков и для желающих заработать на решениях. Преимущества для заказчиковСтудентам и школьникам не нужно перебирать десятки сайтов для сравнения цен, а потом надеяться, что после оплаты они получат качественное решение (и, вообще, все не закончится перечислением денег). Заказчики создают аукцион на понижение цены и могут смотреть на рейтинги желающих решить задачи и ранее выполненные ими решения. Кроме того, деньги окончательно перечисляются исполнителю только после полного решения. Преимущества для решающих заданияНе нужно создавать и продвигать свой сайт, размещать множество объявлений во всех доступных источниках информации. Заказчики сами придут к вам. Не нужно решать все присланные задания с целью поддержания репутации – можно выбирать те, которые будут интересны по уровню сложности, цене и срокам решения. Преимущества для владельца сервисаЕсли вы не понимаете, какую выгоду получит делающий вам какое-нибудь предложение – будьте осторожны! 🙂 У меня уже есть большой опыт работы с сайтом, предоставляющим бесплатные решения по физике. И вариант с получением прибыли от размещения рекламы подходит и для нового сервиса. Кроме того, мне нравится помогать людям и довольно тяжело смотреть, как множество вопросов по задачам остаются на форуме без ответа. Предложенный аукцион решений сможет значительно сократить число вопросов без ответов. И вариант с получением прибыли от размещения рекламы подходит и для нового сервиса. Кроме того, мне нравится помогать людям и довольно тяжело смотреть, как множество вопросов по задачам остаются на форуме без ответа. Предложенный аукцион решений сможет значительно сократить число вопросов без ответов. В будущем возможен вариант и с получением некоторого небольшого процента от оплаты заказов. Но процент этот должен быть минимален и на начальном этапе он взиматься точно не будет. Что необходимо для создания сервиса- Самым важное сейчас – собрать команду, готовую принять участие в выполнении заданий. Если покупатели заходят в пустой магазин – они надолго забывают в него дорогу.
Поэтому я собираю предварительные заявки от посетителей, готовых заниматься решениями. Не нужно подписания никаких договоров о намерениях. Просто сообщите, на какие темы вы готовы решать задания, какой у вас опыт подобной работы (e-mail: [email protected]). Когда сервис заработает – я пришлю приглашение на регистрацию. - Выбрать платежную систему.
- Сделать подходящий движок для сайта. Нужно решить – создавать его с нуля или изменить какой-нибудь существующий движок (например, форумный) с открытой лицензией.
- Привлечь посетителей. Учитывая посещаемость exir.ru и число публикуемых на форуме вопросов, думаю, это не будет большой проблемой.
Desertai be cukraus Vilniuje: tortai, pyragaičiai, saldainiai Решение линейных дифференциальных уравнений онлайн
Назначение сервиса. Данный онлайн-калькулятор служит для решения линейного дифференциального уравнения с постоянными коэффициентами вида ay(n)+by+c=R(x). Например, y''-2y=0, 2y''+y'-2y=x2. Решение оформляется в формате Word. Для решения уравнений вида y'+x*y=x2 используйте этот калькулятор.
- Шаг №1
- Шаг №2
- Видеоинструкция
- Оформление Word
Инструкция. Для получения онлайн решения введите максимальную степень производной n. Например, для дифференциального уравнения Для получения онлайн решения введите максимальную степень производной n. Например, для дифференциального уравнения y''-2y=0 максимальная степень равна двум, поэтому n=2, для y'''-2y''-y=0 степень равна трем (n=3).
Максимальная степень производной
23456
Пример 1. Общее решение дифференциального уравнения с правой частью:
y» + py’ + qy = R(x)
получается с помощью квадратур из общего решения соответствующего уравнения без правой части
y» + py’ + qy = 0
где R(x) = e αx[P 1(x)cos(βx) + P 2sin(βx)]
1. Для уравнения y»’ — 4y» + 5y’ – 2y = 2x+3 корнями характеристического уравнения r3 – 4r2 + 5r – 2 = 0 являются r=2 кратности 1 и r=1 кратности 2. Следовательно α+β i=0 и не является корнем характеристического уравнения.
Поэтому k=0 и частное решение ищем в виде y = cx + d. Так как y’ = 0, y’’ = 0, y’’’ = 0, то, подставляя в уравнение, получаем 5c — 2cx — 2d = 2x + 3. Приравнивая коэффициенты при одинаковых степенях x, получаем -2c = 2.
-5c – 2d = 3. Следовательно, c=-1, d= -4 и y = -x-4 — частное, а y = -x-4+C1ex + C2e2x — общее решения уравнения. Так как y’ = 0, y’’ = 0, y’’’ = 0, то, подставляя в уравнение, получаем 5c — 2cx — 2d = 2x + 3. Приравнивая коэффициенты при одинаковых степенях x, получаем -2c = 2.
-5c – 2d = 3. Следовательно, c=-1, d= -4 и y = -x-4 — частное, а y = -x-4+C1ex + C2e2x — общее решения уравнения.
2. Для уравнения y»’ — 4y» + 5y’ – 2y = (2x+3)e2x число α+β i=2 является корнем характеристического уравнения кратности 1. Поэтому частное решение ищем в виде y = x(cx + d)e2x.
3. Для уравнения y’’ + y = cos(x) корнями характеристического полинома r2+1 являются числа r = ±i кратности 1. Поэтому частное решение ищем в виде y=x(a1cosx + a2 sinx). Тогда
y’ = (a1 + a2x)cosx + (a2 – a1x)sinx,
y’’ = (2a2 – a1x)cosx + (-2a1-a2x)sinx
Подставляя в исходное уравнение и приводя подобные, получаем 2a2 cosx – 2a1sinx = cosx, откуда a1 = 0;a2=0,5.
4. Найти общее решение уравнения:
y» — 3y’ + 2y = x2 + 3x
Находим решение однородного уравнения y» — 3y’ + 2y = 0.
Характеристическое уравнение: r2-3r+2=0 имеет корни r 1= 1, r 2= 2.
Общее решение уравнения без правой части равно: yОбщ = C1ex + C2e2x
Правая часть уравнения имеет вид R(x) = P(x)e αx, причем P(x) = x 2 + 3x и число α = 0 не является корнем характеристического уравнения. Ищем решение вида:
y* = Ax2 + Bx + C
Находим y»,y’, которые подставляем в равенство:
2Ax 2 + (2B — 6A)x + 2C — 3B + 2A = x 2 + 3x
Приравнивая коэффициенты при одинаковых степенях х, получаем систему:
2A = 1; 2B — 6A = 3; 2C — 3B + 2A = 0,
из которых находим: A = 1/2, B = 3, C = 4, так что
y * = x 2/2 + 3x + 4
Общее решение дифференциального уравнения есть:
y = yОбщ + y*= C1ex + C2e2x + x2/2 + 3x + 4
5. Найти общее решение уравнения: Найти общее решение уравнения: y'' - 3y' = x2 + 3x
Характеристическое уравнение: r2 - 3r = 0 имеет корни r1= 3, r2= 0.
Общее решение уравнения без правой части равно:
yОбщ = C1e3x + C2e0 = C1e3x + C2
Правая часть уравнения имеет вид R(x) = P(x)e αx, причем P(x) = x 2 + 3x и число α = 0 является однократным корнем характеристического уравнения. Ищем решение вида:
y* = x(Ax2 + Bx + C)
Находим y»,y’, которые подставляем в равенство y» — 3y’ = x 2 + 3x.
Приравнивая коэффициенты при одинаковых степенях х, получаем систему:
-9A = 1, -6B + 6A = 3, -3C + 2B = 0,
из которых находим: A = -1/9, B = -11/18, C = -11/27, так что
y * = x 2/9 — 11x/18 -11/27
Общее решение дифференциального уравнения есть:
y = yОбщ + y*= C1e3x + C2 + x2/9 — 11x/18 -11/27
Пример 2. Решить дифференциальное уравнение 8y» +2y’ — 3y = 0. Решить дифференциальное уравнение 8y» +2y’ — 3y = 0.
Решение. Данное дифференциальное уравнение относится к линейным дифференциальным уравнениям с постоянными коэффициентами.
Решение уравнения будем искать в виде y = erx. Для этого составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами:
8r2 +2r — 3 = 0
D = 22 — 4·8·(-3) = 100
,
Корни характеристического уравнения: r1 = 1/2, r2 = -3/4
Следовательно, фундаментальную систему решений составляют функции: y1 = e1/2x, y2 = e-3/4x
Общее решение однородного уравнения имеет вид:
Найдем частное решение при условии: y(0) = -6, y'(0) = 7
Поскольку y(0) = c1+c2, то получаем первое уравнение:
c1+c2 = -6
Находим первую производную:
y’ = 1/2•c1•e1/2•x—3/4•c2•e-3/4•x
Поскольку y'(0) = 1/2•c1—3/4•c2, то получаем второе уравнение:
1/2•c1—3/4•c2 = 7
В итоге получаем систему из двух уравнений:
c1+c2 = -6
1/2•c1—3/4•c2 = 7
которую решаем или методом матриц или методом исключения переменных.
c1 = 2, c2 = -8
Тогда частное решение при заданных начальных условиях можно записать в виде: см. также Дифференциальные уравнения. Пример решения.
Если правая часть уравнения отлична от нуля, то решение ищется по формуле: R(x)=eαx(P1cos(βx)+P2sin(βx))
| R(x) |
Форма записи решения |
| 10•x•e2x |
(Ax + B)e2x |
| x•e-x•cos(3x) |
e-x((Ax+B)cos(3x)+(Cx+D)sin(3x)) |
| (x3-x2+3)cos(x)-x•sin(x) |
(Ax3+Bx2+Cx+D)cos(x)+(Ex3+Fx2+Gx+H)sin(x) |
| cos(x) |
Acos(x) + Bsinx(x) |
| x•sin(x) |
(Ax + B)cos(x) + (Cx + D)sinx(x) |
| x3-x2+3 |
Ax3+Bx2+Cx+D |
Мэтуэй | Популярные задачи| 1 | Найти производную — d/dx | бревно натуральное х | | | 2 | Оценить интеграл | интеграл натурального логарифма x относительно x | | | 3 | Найти производную — d/dx | 92) | | 21 | Оценить интеграл | интеграл от 0 до 1 кубического корня из 1+7x относительно x | | | 22 | Найти производную — d/dx | грех(2x) | | | 23 | Найти производную — d/dx | 9(3x) по отношению к x | | 41 | Оценить интеграл | интеграл от cos(2x) относительно x | | | 42 | Найти производную — d/dx | 1/(корень квадратный из х) | | | 43 | Оценка интеграла 9бесконечность | | | 45 | Найти производную — d/dx | х/2 | | | 46 | Найти производную — d/dx | -cos(x) | | | 47 | Найти производную — d/dx | грех(3x) | 92+1 | | 68 | Оценить интеграл | интеграл от sin(x) по x | | | 69 | Найти производную — d/dx | угловой синус(х) | | | 70 | Оценить предел | ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х | | | 85 | Найти производную — d/dx | лог х | | | 86 | Найти производную — d/dx | арктан(х) | | | 87 | Найти производную — d/dx | бревно натуральное 5х92 | |
Примеры Wolfram|Alpha: пошаговые дифференциальные уравнения Примеры Wolfram|Alpha: пошаговые дифференциальные уравнения Ого! Wolfram|Alpha не работает без JavaScript. converter.org — Конвертер для единиц , какВремя Секунда, Минута, Час, Сутки, Неделя, Месяц (31 день), Год в системе СИ, Миллисекунда, … Давление Паскаль, Бар, Торр, Миллиметр ртутного столба, Миллиметр водяного столба, Дюйм ртутного столба, Дюйм водяного столба, … Длина Метр, Километр, Ангстрем, Ярд, Миля, Дюйм, Астрономическая единица, Световой год, … Индуктивность Генри, Микрогенри, Миллигенри, Килогенри, Вебер на ампер, Абгенри, … Количество информации Бит, Килобит, Байт, Килобайт, Мегабайт, Гигабайт, . .. .. Магнитная индукция Тесла, Пикотесла, Нанотесла, Вебер на квадратный сантиметр, Гаусс, Гамма, Максвелл на квадратный метр, … Магнитный поток Вебер, Максвелл, Квант магнитного потока, Тесла-квадратный метр, Гаусс-квадратный сантиметр, … Масса/вес Килограмм, Метрическая тонна, Унция, Фунт, Стоун, Карат, Фунт, Фун, Момме, Хиакуме, Фынь (кандарин), Лян (таэль), … Массовый расход Килограмм в секунду, Метрическая тонна в час, Длинная тонна в час, Фунт в секунду, Короткая тонна в час, … Момент силы Ньютон-метр, Килоньютон-метр, Миллиньютон-метр, Килограмм-сила-метр, Унция-сила-дюйм, Дина-метр, . .. .. Мощность Ватт, Киловатт, Метрическая лошадиная сила, Британская тепловая единица в час, Фут-фунт-сила в секунду, … Напряжённость магнитного поля Ампер на метр, Микроампер на метр, Миллиампер на метр, Эрстед, Гильберт на метр, … Объём Кубический метр, Литр, Миллилитр, Кубический дюйм, Кубический фут, Галлон, Пинта, Миним, Сяку, Ложка для соли, Стакан, … Объёмный расход Кубический метр в секунду, Литр в минуту, Галлон (США) в минуту, … Плотность Килограмм на кубический метр, Миллиграмм на кубический метр, Грамм на кубический сантиметр, Унция на кубический дюйм, Фунт на кубический фут, . .. .. Площадь Квадратный метр, Гектар, Ар, Квадратный фут, Акр, Квадратный дюйм, … Радиоактивность Беккерель, Кюри, Резерфорд, Распад в секунду, … Сила Ньютон, Дина, Килограмм-сила (килопонд), Фунт-сила, Паундаль, Килоньютон, Деканьютон, Грамм-сила, … Скорость Метр в секунду, Километр в час, Миля в час, Фут в секунду, Узел, … Скорость передачи данных Бит в секунду, Килобит в минуту, Мегабайт в секунду, Гигабайт в секунду, Килобайт в минуту, … Температура Градус Цельсия, Кельвин, Градус Фаренгейта, Градус Реомюра, Градус Ранкина, Градус Рёмера, Градус Делиля, . .. .. Угол Градус, Радиан, Минута дуги, Секунда дуги, Град (гон), Тысячная (НАТО), Румб, Квадрант, … Эквивалентная доза излучения Зиверт, Нанозиверт, Микрозиверт, Джоуль на килограмм, Бэр, Микробэр, Миллибэр, … Электрическая ёмкость Фарад, Микрофарад, Нанофарад, Пикофарад, Интфарад, Абфарад, Статфарад, … Электрическая проводимость Сименс, Мо, Ампер на вольт, … Электрический заряд Кулон, Франклин, Абкулон, Статкулон, Элементарный заряд, Ампер-час, … Электрический ток Ампер, Пикоампер, Наноампер, Микроампер, Абампер, Кулон в секунду, . .. .. Электрическое сопротивление Ом, Пикоом, Наноом, Микроом, Абом, Вольт на ампер, … Энергия Джоуль, Электронвольт, Калория, Британская тепловая единица, Киловатт-час, …
Свойства документа — Единицы изменения — 2016Укажите свойства единиц измерения на уровне документа. Доступно для всех типов документов. Чтобы открыть эту страницу, выполните следующие действия. Откройте документ и выполните одно из следующих действий. - В строке состояния выберите Система единиц измерения, а затем — Редактировать единицы измерения документа.
- Нажмите Параметры
(панель инструментов «Стандартная»). На вкладке Свойства документа выберите Единицы измерения.
При использовании малых единиц измерения, таких как ангстремы, нанометры, микроны, милы или микродюймы, полезно создать шаблоны в качестве основы для документов, использующих эти единицы измерения. Шаблоны могут содержать такие настройки, как: Шаблоны могут содержать такие настройки, как: - Шаг между линиями масштабной сетки
- Зазор между выносными линиями размеров и длина выноски
- Сместить расстояния размеров
- Длина выноски с полкой для заметки
- Длина выноски с полкой для позиции
- Размер стрелки
- Масштаб текста и отображение текста всегда одинакового размера
- Плотность материала
Чтобы сохранить документ как шаблон, выполните следующие действия. - Выберите Файл > Сохранить как.
- Перейдите к расположению шаблонов SOLIDWORKS.
Расположение по умолчанию: C:\ProgramData\SOLIDWORKS\SOLIDWORKS версия\templates\.
- Для пункта Сохранить как тип выберите соответствующий тип шаблона документа.
Например, для детали выберите Шаблоны детали (*.prtdot).
- Нажмите Сохранить.
Система единиц измерения Задает на уровне документа единицы измерения и точность в стандартной системе или позволяет изменить единицы измерения. Стандартные системы: - МКС (метр, килограмм, секунда)
- СГС (сантиметр, грамм, секунда)
- ММГС (миллиметр, грамм, секунда)
- ДФС (дюйм, фунт, секунда)
Выберите Настройка пользователя, чтобы изменить единицы измерения в таблице. Систему единиц измерения можно изменить, не открывая диалоговое окно Свойства документа — Единицы изменения. В строке состояния щелкните Система единиц измерения, а затем выберите систему единиц измерения. Базовые единицы измеренияОтображает единицы измерения размеров на уровне документа. -
Длина
| Единицы измерения |
Десятичные дроби |
Дроби |
Еще |
|---|
|
Определяется выбором Системы единиц измерения.
|
В зависимости от выбора отображает от двух до восьми десятичных разрядов. Нет — не отображает десятичные разряды.
|
Целое число для знаменателя, между 2 и 256.
Только для дюймов, милов, микродюймов или футов и дюймов.
|
|
Округлить до ближайшего разряда
|
Корректирует десятичное округление для разрядов.
|
|
Преобразовать формат из 2’4″ в 2′-4″
|
Отображает футы — дюймы при выполнении импорта из формата футы дюймы.
|
|
-
Длина двойного размера
| Единицы измерения |
Десятичные дроби |
Дроби |
Еще |
|---|
| Нажмите на список, чтобы его изменить. |
В зависимости от выбора отображает от двух до восьми десятичных разрядов. Нет — не отображает десятичные разряды.
|
Целое число для знаменателя, между 2 и 256.
Только для дюймов, милов, микродюймов или футов и дюймов.
|
|
Округлить до ближайшего разряда
|
Корректирует десятичное округление для разрядов.
|
|
Преобразовать формат из 2’4″ в 2′-4″
|
Отображает футы — дюймы при выполнении импорта из формата футы дюймы.
|
|
-
Угол
| Единицы измерения |
Десятичные дроби |
Дроби |
Еще |
|---|
Нажмите на список, чтобы его изменить. |
Только для градусов и радианов.
В зависимости от выбора отображает от двух до восьми десятичных разрядов. Нет — не отображает десятичные разряды.
|
|
|
Примеры базовых единиц измерения| Дюймы в десятичном виде
|
|
| Дюймы в виде дроби |
|
|
Преобразовать формат из 2’4″ в 2′-4″
|
|
|
Длина двойного размера
|
|
|
Градусы Минуты Секунды
|
|
|
Радианов
|
|
Параметры массовых характеристик/сеченияОтображает длину, массу и плотность на уровне документа, которые отображаются в PropertyManager Массовые характеристики или Свойства сечения, что определяется выбором Системы единиц измерения. Также эти свойства определяют единицы измерения, используемые в SimulationXpress. Также эти свойства определяют единицы измерения, используемые в SimulationXpress. Чтобы изменить единицы, в разделе Система единиц измерения выберите параметр Настройка пользователя. | Тип |
Единицы измерения |
Десятичные дроби |
|---|
|
Длина
|
Единицы длины, используемые для объема, площади поверхности, центра массы и других свойств массы или сечения, которые зависят от длины. Например, если Длина в дюймах, единицы измерения площади поверхности — квадратные дюймы. |
В зависимости от выбора отображает от двух до восьми десятичных разрядов. Нет — не отображает десятичные разряды.
|
|
Массу
|
Единицы измерения массы, используемые для плотности и других свойств массы или сечения, которые зависят от массы. |
|
На единицу объема
|
Единицы измерения объема, используемые для плотности. Например, для Массы в граммах и На единицу объема в кубических сантиметрах, единицы измерения плотности — граммы на кубический сантиметр.
|
Единицы измерения движения (Только для сборок)Отображает единицы измерения времени, силы, мощности и энергии для результатов исследований движений и элементов на уровне документа, в зависимости от выбора Системы единиц измерения. |
Десятичные дроби
|
В зависимости от выбора отображает от двух до восьми десятичных разрядов. Нет — не отображает десятичные разряды.
|
Округление десятичных дробейПозволяет контролировать округление десятичных дробей в размерах. Три параметра округления: |
Округлить до половины от нуля
|
Метод округления, при котором 5 округляется с увеличением предыдущего знака. Например, при округлении до одного знака после запятой 46,15 округляется до 46,2.
|
|
Округлить до половины к нулю
|
Метод округления, при котором 5 округляется с сохранением предыдущего знака. Например, 46,15 округляется до 46,1. Например, 46,15 округляется до 46,1.
|
|
Округлить до половины к целому
|
Метод округления, при котором 5 отбрасывается. Если предыдущая цифра четная, она не изменяется. Например, при округлении до одного знака после запятой 46,25 округляется до 46,2. Если предыдущая цифра нечетная, она округляется вверх до следующего четного числа. Данный метод также называется статистическим округлением. Например, при округлении до одного знака после запятой 46,15 округляется до 46,2.
|
|
Усечение без округления
|
Метод, при котором знаки отбрасываются без округления. Например, при округлении до одного знака после запятой 46,19 округляется до 46,1.
|
|
Применять методы округления только к размерам
|
(только детали и сборки). При выборе этого параметра это применяется к правилу округления для измерений и их допусков, включая измерения, значения которых получены из уравнений. Если этот параметр не выбран, это применяется к правилу округления для любого отображения цифр с выполнением округления, включая диалоговые окна, например Массовые характеристики. Если этот параметр не выбран, это применяется к правилу округления для любого отображения цифр с выполнением округления, включая диалоговые окна, например Массовые характеристики.
|
1 Градусов в Миллиметры | 1 градус в мм Конвертируйте 1 градус в миллиметры (градус в мм) с помощью нашего калькулятора перевода и таблиц перевода. Чтобы преобразовать 1 градус в миллиметры, используйте приведенную ниже формулу прямого преобразования.
1 град = 1000 мм.
Вы также можете преобразовать 1 градус в другие угловые (популярные) единицы измерения.
1 ГРАДУС = 1000 МИЛЛИМЕТРОВ Конвертерный калькулятор Количество: От:
ACR — AcresCMK — Квадратные сантиметрыFTK — Квадратные футыHAR — ГектарыINK — Квадратные дюймыKMK — Квадратные километрыMIK — Квадратные милиMTK — Квадратные метрыYDK — Квадратные ярдыANN — YearsDAY — DaysHUR — HoursMCS — MicrosecondsMIN — MinutesMLS — MillisecondsMON — MonthsSEC — SecondsWEE — WeeksBIT — BitsBYT — BytesEBI — ExabitsEBY — ExabytesGBI — GigabitsGBY — GigabytesKBI — KilobitsKBY — KilobytesMBI — MegabitsMBY — MegabytesPBI — PetabitsPBY — PetabytesTBI — TerabitsTBY — TerabytesBLL — Баррели (нефть)CMQ — Кубические сантиметрыFTQ — Кубические футыGLI — Галлоны (Великобритания)GLL — Галлоны (США, жидкость)LTR — ЛитрыMLT — МиллилитрыMTQ — Кубические метрыOZI — Унции UKBTU — BTUCAL — КалорииERG — ErgEVL — Электрон ВольтFPD — Фут-фунтHPH — Лошадиные силы-часIPD — Дюйм-фунтJOU — ДжоулиCMT — СантиметрDMT — ДециметрыFOT — ФутыINH — ДюймыKMT — КилометрыMMT — МиллиметрыMTR — МетрыSMI — МилиYRD — ДворCTM — КаратыGRM — граммыKGM — килограммыLBR — фунтыMGM — миллиграммыONZ — унции TNE — тонны (метрические)DEG — градусыGRD — градыRAD - радианыFPM — футы/минутыFPS — футы/секундыKMH — километры/часKMS — километры/секундыKNT — узлыMPH — мили/часMTS — метры/секундыGCC — Граммы/кубический сантиметрKCC — килограммы/кубический сантиметрKLI — килограммы/литрKMC — килограммы/кубический метрOCI — унции/кубический дюймOGL — унции/галлонPCF — фунты/кубический футPCI — фунты/кубический дюймPGL — фунты/галлонJCM — джоули/сантиметрKGF — килограмм силыNWN — ньютоныPFC — Фунт-силаA0 — Бор, атомная единица длиныAST — АнгстремAU — Астрономическая единицаCBL — длина кабеля (имперская)CBL(US) — Длина кабеля USCH — ЦепиF — Французский charriereFM — FermiFNG — FingerFNG(CLOTH) — Палец (ткань)FTM — FathomFUR — FurlongHH — HandLD — Световой деньLEA — лига (земля)LH — Световой часLM — Световая минутаLN — ЛинияLNK (G. S.) — Ссылка (Gunter’s; Геодезист) LNK (RE) — Link (Ramsden’s; Engineer’s) LS — Световой-секундный — Световой годM — Метр (базовая единица СИ)MIL — Мил (Швеция и Норвегия)MILE DATA — Мили (тактические или данные)MK — MickeyNAIL — Гвоздь (ткань)NL — Морская лигаNM — НанометрNMI — Морские милиNMI I — Морская миляP — PalmPC — ParsecPICA — PicaPM — Пикометр (бикрон, клеймо)POINT — точка (американский, английский)PT — PaceQUART — QuarterSHAKU — Shaku (Japan)SPT — SpatTH — Мил (тыс.) TWP — TwipUM — Микрометр (стар. микрон) XU — X единица измерения; siegbahnABA — Электромагнитная единица AbampereAMP — Ампер (базовая единица Si)ESU — Esu в секунду Статампер (CgsABC — Абкулон Электромагнитная единицаATU — Атомная единица зарядаCLM — КулонFRD — ФарадейMAH — Миллиампер-часSTT — Статкулон Франклин ЭлектростABV — Абвольт (единица Cgs)STV — Статвольт ( Cgs Unit)VLT — Вольт (Si Unit)ACF — Акр-футыACI — Акры-дюймыBIB — Баррели (нефтяные)BII — Баррели (британские)BIU — Баррели (Us Dry)BKT — Ведра (британские)BRO — Галлоны (пивные)BUD — Бушели (Us Dry Level)BUI — Бушели (Imperial)BUU — Бушели (Us Dry Heaped)CMB — CoombsCMI — Cubic MilesCP — CupsCRF — Cord-FootsCRW — Cords (Дрова)CUF — Cubic FathomsCUI — Cubic InchsCUT — Cubic FootsCUY — Cubic ЯрдыDSI — тире (имперские фунты)DSS — десертные ложки (имперские фунты)DSU — тире (США)FBM — борд-футыFFT — пятые FID — жидкие драхмы (имперские)FIS — жидкие скрукле (имперские)FLB — бочки (США, жидкие)FLU — жидкие драмы ( Us) Us FluidramFRK — FirkinsGAI — галлоны (имперские единицы)GAU — галлоны (Us Dry)GAW — галлоны (Us Fluid Wine)GLU — Teacups (gills)GTT — DropsHDI — Hogsheads (Imperial)HHU — Hogsheads (Us)JGR — Jiggers ( Bartending)KLD — KilderkinsLMD — LambdasLOD — LoadsLST — LastsM3 — Кубические метры (Si Unit)MII — Minims (Imperial)MIU — Minims (Us)OZF — Унции (Fluid Us Food NutritioPER — PerchsPKI — Pecks (Imperial)PKU — Pecks (Us) Сухой)PNI — пинчи (британские)PNU — пинчи (американские)PON — PonysPOT — Pottle QuartersPP — стыковые трубыPTI — пинты (британские)PUD — пинты (Us Dry)PUF — пинты (Us Fluid)QRF — Quart S (Us Fluid) QRT — Кварталы QTI — Кварты (британские)QTU — Кварты (Us Dry)RGS — Реестр TonsSCI — Мешки (британские) BagsSCU — Мешки(Us)SHT — Shots (Us)SM — SeamsSTK — Забастовки (Imperial)STU — Забастовки (Us) )TBC — столовые ложки (канадские)TBF — столовые ложки (обычные в США)TBM — столовые ложки (метрические)TBS — столовые ложки (в австралийских единицах измеренияTCA — чайные ложки (канадские) TFD — столовые ложки (Us Food NutritionTIM — чайные ложки (британские)TMF — Timber FootsTMT — чайные ложки ( Метрическая система)TND – тонны (водоизмещение)TNT – тонны (воды)TNW – тонны (фрахт)TSC – чайные ложки (стандарт США)TSF – чайные ложки (США Food Nutrition) WEY — Wey (Us)ACM — Атмосфера-кубический фут в минутуACS — Атмосфера-кубический фут в секунду SecoATC — Атмосфера-кубический сантиметр PeATH — Атмосфера-кубический фут в часBTJ — BTU (Международная таблица) В расчете на BTN — BTU (Международная таблица) В расчете на BTS — БТЕ (международная таблица) по CAS — Калория (международная таблица) ERS — Эрг в секундуFMF — Фут-фунт-сила в минутуFT — Фут-фунт-сила в часFTO — Фут-фунт-сила в секундуHPS — Лошадиная силаLAM — Литр-атмосфера в час MinuteLSC — LusecLTS — Литр атмосферы в секундуPNC — PonceletSQL — Прямой эквивалент квадратного фута TC — Тонна кондиционирования воздухаTMS — Атмосфера-кубический сантиметр PeTRM — Тонна охлаждения (ImperialTRR — Тонна охлаждения (It)AMU — Единица атомной массы UnifiedAT — Анализ тонны (Короткий)ATS — Ton Assay (Длинный)BAC — Bag (Coffee)BDM — Bag (Portland Cement)BRG — BargeCLV — CloveCRT — CrithCT — Carat (Metric)DA — DaltonDRT — Dram (Apothecary Troy)DWT — PennyweightGAM — GammaGR — GrainGV — GraveKIP — KipLB — Фунт (метрический)LBA — ФунтLBT — Фунт (тройской)LBV — Фунт (Avoirdupois)ME — Атомная единица массы Электрон RMRK — MarkMTE — MiteMTM — Клещ (метрический)OZ — Унция (Us Food Nutrition LabelOZT — Унция (аптечная тройка)OZZ — унция (Avoirdupois)PNN — PointQ — квинтал (метрическая система)QR — четверть (неформальная)QRI — четверть (имперская)QRL — четверть длинная (неформальная)SAP — Scruple (аптекарь)SH — тонна короткаяSLG — слаг Geepound HylSLH — SheetST — StoneSWT — Вес в сотни (центум) oTON — Тонна LongWY — WeyZTR — ZentnerARE — AresBD — BoardsBHE — Эквивалент мощности котла DBR — BarnsBRN — BaronysCDA — Cuerda Pr SurveysCRD — CordsCRI — Circular InchsCRM — Circular MilsDNM — DunamsGNT — GunthasHD — HidesRO — RoodsSCT — SectionsSHD — СараиSII — Square Link Gunters InternatiSLR — Square Link RamsdensSQC — Square Chains InternationalSQM — Square Mil Square ThousSQR — Square Rod/Pole/PerchsSRR — Square RoofingsSTR — StremmasTWN — TownshipsYLN — YardlandsARM — Arcminute MoaARS — ArcsecondCNS — Centesimal Second Of ArcCNT — Столетняя минута ArcDOA — Градус (дуги)GRA — Град Градиан GonOCT — OctantQRD — QuadrantSGN - SignSXT — Секстантµ — Угловой MilATA — Атмосфера (техническая)ATM — Атмосфера (стандартная)BAR — BarBRY — Бари (единица Cgs)CMH — Сантиметр Of MercuryCMW – сантиметр водяного столба (4 °C)FTH – фут ртутного столба (условный)FTW – фут водяного столба (392 °F)IMC — Дюйм ртутного столба (условный)INW — Дюйм водяного столба (392 °F)KM — Килограмм-сила на квадратный дюймKSI — Кип на квадратный дюймLTP — Длинная тонна на квадратный футMHG — Микрометр ртутного столбаMMH — Миллиметр ртутного столбаMMW — Миллиметр воды (398 °C)PA — Паскаль (единица Si)PD — фунт на квадратный футPSF — фунт на квадратный футPSI — фунт на квадратный дюймPZ — пьеза (единица Mts)STP — короткая тонна на квадратный футTOR — ТоррATN — атомная единица ForceDYN — Dyne (Cgs Unit)KFF — Килограмм-сила Kilopond Grave-KI — Kip Kip-ForceMGF — Milligrave-Force Gravet-ForceOZC — Унция-силаPDL — PoundalSN — Sthene (единица Mts)TNF — Long Ton-ForceTNL — Short Ton- ForceAUC — атомная единица времениCTN — CenturyCYC — каллипический циклDEC — DecadeFN — FortnightHEL — HelekHIP — гиппархический циклJFF — JiffyKEH — Ke (четверть часа) LSR — Luster LustrumMD — MillidayMLL — MillenniumMMN — MomentMOF — Month (Full)MOG — Month (Greg) Av)MOH — месяц (полый)MOS — месяц (синодический)MTN — метонический цикл EnneadecaeterisOC — OctaeterisPLN — планковское времяSGM — SigmaSHK — ShakeSTH — сотический циклSVD — SvedbergYR — год (общий)YRG — год (григорианский)YRJ — год (юлианский) YRL – год (високосный)YRM – год (среднетропический)B39- Британская термальная единица (39 °F)B59 — Британская термальная единица (59 °F)B60 — Британская термальная единица (60 °F)B63 — Британская термальная единица (63 °F)BOE — эквивалент барреля нефтиBRT — Британская термальная единица ( Iso)BTI — Британская термальная единица (InternatBTM — Британская термальная единица (средняя)BTT — Британская термальная единица (ThermochC15 — Калория (15 °C)C20 — Калория (20 °C)C98 — Калория (398 °C)CAM — Калория ( Среднее значение)CFT — Кубический фут атмосферы CHU — Тепловая единица ЦельсияCL — Калория (Us Fda)CLTH — Калория (термохимическая)CN — Кубический фут природного газаCTA — Кубический сантиметр атмосферыCYD — Кубический ярд атмосферы StandEH — Атомная единица энергии ХартриFTD — Foot-PoundalIMG — Галлон-атмосфераKCA — Большая килокалорияKWH — Киловатт-час Board Of Trade ULTM — Литр-атмосфераQD — QuadRDB — Therm (Ec)RY — RydbergTCE — Тонна угольного эквивалентаTHR — Therm (Us)THU — ThermieTN — Тонна TntTOE — Тонна нефтяного эквивалентаBAN — Ban HartleyBSH — Bit ShannonCD — Candela (Si Base Unit) CandleCPD — Candlepower (New)JK — Si UnitNAT — Nat Nip NepitNBL — NibbleBQ — Беккерель (Si Unit)CI — CurieRD — Rutherford (H)C — Скорость света в вакуумеFPF — фарлонг в две неделиFPH — фут в часIPH — дюйм в часIPM — дюйм в минутуIPS — дюйм в секундуMCH — число МахаMPM — миля в минутуMPS — миля в секундуMS — метр в секунду (единица Си)SPS — скорость звука в AirCDF — Кандела на квадратный футCDI — Кандела на квадратный дюймCDM — Кандела на квадратный метр (Si UFL — FootlambertLMB — LambertSB — Stilb (Cgs Unit)CEL — ЦельсийDDE — Градус DelisleDNE — Градус НьютонаFAN — ФаренгейтGMR — Регулятор газа MarkKEL — Kelvin’sRAN — RankineREA — ReaumurRME — Градус RømerCFM — Кубический фут в минутуFTS — Кубический фут в секундуGPD — Галлон (жидкость США) в суткиGPH — Галлон (жидкость США) в часGPM — Галлон (жидкость США) в минутуINM — Кубический дюйм в минутуINS — Кубический дюйм в секундуLPM — Литр в минутуMQS — кубический метр в секунду (Si UniCM — кулон-метрDB — DebyeEA0 — атомная единица электрического диполяFC — фут-канделя люмен на квадрат FoLMN — люмен на квадратный дюймLX — люкс (единица Si)PH — Phot (единица Cgs)FHP — фут в секунду Час в секундуFMS — фут в минуту в секундуFP — фут в секунду в квадратеG — стандартная гравитацияGAL — галлон GalileoIP — дюйм в минуту в секунду в секундуIP2 — дюйм в секунду в квадратеKNS — узел в секундуMM — миля в минуту в секундуMP — миля в час в секундуMP2 — миля в секунду Секунда в квадратеMSA — метр на секунду в квадрате (Si UFT2 — квадратный фут в секундуM2S — квадратный метр в секунду (Si UnSTX — Стокс (единица Cgs)FTP — фут-фунт)MKG — метр-килограмм-силаNEM — ньютон-метр (единица Si)GML — грамм на секунду MillilitreLAB — фунт (эквивалентный) на галлонLBF — фунт (эквивалентный) на кубический LBI — фунт (экспериментальный) на кубический LBL — фунт (экспериментальный) на галлонOFT — унция (экспериментальный) на кубический OG — унция (эвердупуа) на галлон ) Per GallonOIN — Унция (Avoirdupois) на кубический SFT — Slug на кубический футGSS — Gauss (Cgs Unit)TSL — Tesla (Si Unit)GY — Grey (Si Unit)RDD — RadLBH — Pound Per Foot HourLBS — Фунт на фут в секундуLFT — Фунт-сила-секунда на квадрат LIN — Фунт-сила-секунда на квадрат PAS — Паскаль-секунда (единица Si)PSU — Пуаз (единица Cgs)MX — Максвелл (единица Cgs)WB — Вебер (единица Si)REM — Рентген-эквивалент ManSV — Sievert (Единица Си) S.) — Ссылка (Gunter’s; Геодезист) LNK (RE) — Link (Ramsden’s; Engineer’s) LS — Световой-секундный — Световой годM — Метр (базовая единица СИ)MIL — Мил (Швеция и Норвегия)MILE DATA — Мили (тактические или данные)MK — MickeyNAIL — Гвоздь (ткань)NL — Морская лигаNM — НанометрNMI — Морские милиNMI I — Морская миляP — PalmPC — ParsecPICA — PicaPM — Пикометр (бикрон, клеймо)POINT — точка (американский, английский)PT — PaceQUART — QuarterSHAKU — Shaku (Japan)SPT — SpatTH — Мил (тыс.) TWP — TwipUM — Микрометр (стар. микрон) XU — X единица измерения; siegbahnABA — Электромагнитная единица AbampereAMP — Ампер (базовая единица Si)ESU — Esu в секунду Статампер (CgsABC — Абкулон Электромагнитная единицаATU — Атомная единица зарядаCLM — КулонFRD — ФарадейMAH — Миллиампер-часSTT — Статкулон Франклин ЭлектростABV — Абвольт (единица Cgs)STV — Статвольт ( Cgs Unit)VLT — Вольт (Si Unit)ACF — Акр-футыACI — Акры-дюймыBIB — Баррели (нефтяные)BII — Баррели (британские)BIU — Баррели (Us Dry)BKT — Ведра (британские)BRO — Галлоны (пивные)BUD — Бушели (Us Dry Level)BUI — Бушели (Imperial)BUU — Бушели (Us Dry Heaped)CMB — CoombsCMI — Cubic MilesCP — CupsCRF — Cord-FootsCRW — Cords (Дрова)CUF — Cubic FathomsCUI — Cubic InchsCUT — Cubic FootsCUY — Cubic ЯрдыDSI — тире (имперские фунты)DSS — десертные ложки (имперские фунты)DSU — тире (США)FBM — борд-футыFFT — пятые FID — жидкие драхмы (имперские)FIS — жидкие скрукле (имперские)FLB — бочки (США, жидкие)FLU — жидкие драмы ( Us) Us FluidramFRK — FirkinsGAI — галлоны (имперские единицы)GAU — галлоны (Us Dry)GAW — галлоны (Us Fluid Wine)GLU — Teacups (gills)GTT — DropsHDI — Hogsheads (Imperial)HHU — Hogsheads (Us)JGR — Jiggers ( Bartending)KLD — KilderkinsLMD — LambdasLOD — LoadsLST — LastsM3 — Кубические метры (Si Unit)MII — Minims (Imperial)MIU — Minims (Us)OZF — Унции (Fluid Us Food NutritioPER — PerchsPKI — Pecks (Imperial)PKU — Pecks (Us) Сухой)PNI — пинчи (британские)PNU — пинчи (американские)PON — PonysPOT — Pottle QuartersPP — стыковые трубыPTI — пинты (британские)PUD — пинты (Us Dry)PUF — пинты (Us Fluid)QRF — Quart S (Us Fluid) QRT — Кварталы QTI — Кварты (британские)QTU — Кварты (Us Dry)RGS — Реестр TonsSCI — Мешки (британские) BagsSCU — Мешки(Us)SHT — Shots (Us)SM — SeamsSTK — Забастовки (Imperial)STU — Забастовки (Us) )TBC — столовые ложки (канадские)TBF — столовые ложки (обычные в США)TBM — столовые ложки (метрические)TBS — столовые ложки (в австралийских единицах измеренияTCA — чайные ложки (канадские) TFD — столовые ложки (Us Food NutritionTIM — чайные ложки (британские)TMF — Timber FootsTMT — чайные ложки ( Метрическая система)TND – тонны (водоизмещение)TNT – тонны (воды)TNW – тонны (фрахт)TSC – чайные ложки (стандарт США)TSF – чайные ложки (США Food Nutrition) WEY — Wey (Us)ACM — Атмосфера-кубический фут в минутуACS — Атмосфера-кубический фут в секунду SecoATC — Атмосфера-кубический сантиметр PeATH — Атмосфера-кубический фут в часBTJ — BTU (Международная таблица) В расчете на BTN — BTU (Международная таблица) В расчете на BTS — БТЕ (международная таблица) по CAS — Калория (международная таблица) ERS — Эрг в секундуFMF — Фут-фунт-сила в минутуFT — Фут-фунт-сила в часFTO — Фут-фунт-сила в секундуHPS — Лошадиная силаLAM — Литр-атмосфера в час MinuteLSC — LusecLTS — Литр атмосферы в секундуPNC — PonceletSQL — Прямой эквивалент квадратного фута TC — Тонна кондиционирования воздухаTMS — Атмосфера-кубический сантиметр PeTRM — Тонна охлаждения (ImperialTRR — Тонна охлаждения (It)AMU — Единица атомной массы UnifiedAT — Анализ тонны (Короткий)ATS — Ton Assay (Длинный)BAC — Bag (Coffee)BDM — Bag (Portland Cement)BRG — BargeCLV — CloveCRT — CrithCT — Carat (Metric)DA — DaltonDRT — Dram (Apothecary Troy)DWT — PennyweightGAM — GammaGR — GrainGV — GraveKIP — KipLB — Фунт (метрический)LBA — ФунтLBT — Фунт (тройской)LBV — Фунт (Avoirdupois)ME — Атомная единица массы Электрон RMRK — MarkMTE — MiteMTM — Клещ (метрический)OZ — Унция (Us Food Nutrition LabelOZT — Унция (аптечная тройка)OZZ — унция (Avoirdupois)PNN — PointQ — квинтал (метрическая система)QR — четверть (неформальная)QRI — четверть (имперская)QRL — четверть длинная (неформальная)SAP — Scruple (аптекарь)SH — тонна короткаяSLG — слаг Geepound HylSLH — SheetST — StoneSWT — Вес в сотни (центум) oTON — Тонна LongWY — WeyZTR — ZentnerARE — AresBD — BoardsBHE — Эквивалент мощности котла DBR — BarnsBRN — BaronysCDA — Cuerda Pr SurveysCRD — CordsCRI — Circular InchsCRM — Circular MilsDNM — DunamsGNT — GunthasHD — HidesRO — RoodsSCT — SectionsSHD — СараиSII — Square Link Gunters InternatiSLR — Square Link RamsdensSQC — Square Chains InternationalSQM — Square Mil Square ThousSQR — Square Rod/Pole/PerchsSRR — Square RoofingsSTR — StremmasTWN — TownshipsYLN — YardlandsARM — Arcminute MoaARS — ArcsecondCNS — Centesimal Second Of ArcCNT — Столетняя минута ArcDOA — Градус (дуги)GRA — Град Градиан GonOCT — OctantQRD — QuadrantSGN - SignSXT — Секстантµ — Угловой MilATA — Атмосфера (техническая)ATM — Атмосфера (стандартная)BAR — BarBRY — Бари (единица Cgs)CMH — Сантиметр Of MercuryCMW – сантиметр водяного столба (4 °C)FTH – фут ртутного столба (условный)FTW – фут водяного столба (392 °F)IMC — Дюйм ртутного столба (условный)INW — Дюйм водяного столба (392 °F)KM — Килограмм-сила на квадратный дюймKSI — Кип на квадратный дюймLTP — Длинная тонна на квадратный футMHG — Микрометр ртутного столбаMMH — Миллиметр ртутного столбаMMW — Миллиметр воды (398 °C)PA — Паскаль (единица Si)PD — фунт на квадратный футPSF — фунт на квадратный футPSI — фунт на квадратный дюймPZ — пьеза (единица Mts)STP — короткая тонна на квадратный футTOR — ТоррATN — атомная единица ForceDYN — Dyne (Cgs Unit)KFF — Килограмм-сила Kilopond Grave-KI — Kip Kip-ForceMGF — Milligrave-Force Gravet-ForceOZC — Унция-силаPDL — PoundalSN — Sthene (единица Mts)TNF — Long Ton-ForceTNL — Short Ton- ForceAUC — атомная единица времениCTN — CenturyCYC — каллипический циклDEC — DecadeFN — FortnightHEL — HelekHIP — гиппархический циклJFF — JiffyKEH — Ke (четверть часа) LSR — Luster LustrumMD — MillidayMLL — MillenniumMMN — MomentMOF — Month (Full)MOG — Month (Greg) Av)MOH — месяц (полый)MOS — месяц (синодический)MTN — метонический цикл EnneadecaeterisOC — OctaeterisPLN — планковское времяSGM — SigmaSHK — ShakeSTH — сотический циклSVD — SvedbergYR — год (общий)YRG — год (григорианский)YRJ — год (юлианский) YRL – год (високосный)YRM – год (среднетропический)B39- Британская термальная единица (39 °F)B59 — Британская термальная единица (59 °F)B60 — Британская термальная единица (60 °F)B63 — Британская термальная единица (63 °F)BOE — эквивалент барреля нефтиBRT — Британская термальная единица ( Iso)BTI — Британская термальная единица (InternatBTM — Британская термальная единица (средняя)BTT — Британская термальная единица (ThermochC15 — Калория (15 °C)C20 — Калория (20 °C)C98 — Калория (398 °C)CAM — Калория ( Среднее значение)CFT — Кубический фут атмосферы CHU — Тепловая единица ЦельсияCL — Калория (Us Fda)CLTH — Калория (термохимическая)CN — Кубический фут природного газаCTA — Кубический сантиметр атмосферыCYD — Кубический ярд атмосферы StandEH — Атомная единица энергии ХартриFTD — Foot-PoundalIMG — Галлон-атмосфераKCA — Большая килокалорияKWH — Киловатт-час Board Of Trade ULTM — Литр-атмосфераQD — QuadRDB — Therm (Ec)RY — RydbergTCE — Тонна угольного эквивалентаTHR — Therm (Us)THU — ThermieTN — Тонна TntTOE — Тонна нефтяного эквивалентаBAN — Ban HartleyBSH — Bit ShannonCD — Candela (Si Base Unit) CandleCPD — Candlepower (New)JK — Si UnitNAT — Nat Nip NepitNBL — NibbleBQ — Беккерель (Si Unit)CI — CurieRD — Rutherford (H)C — Скорость света в вакуумеFPF — фарлонг в две неделиFPH — фут в часIPH — дюйм в часIPM — дюйм в минутуIPS — дюйм в секундуMCH — число МахаMPM — миля в минутуMPS — миля в секундуMS — метр в секунду (единица Си)SPS — скорость звука в AirCDF — Кандела на квадратный футCDI — Кандела на квадратный дюймCDM — Кандела на квадратный метр (Si UFL — FootlambertLMB — LambertSB — Stilb (Cgs Unit)CEL — ЦельсийDDE — Градус DelisleDNE — Градус НьютонаFAN — ФаренгейтGMR — Регулятор газа MarkKEL — Kelvin’sRAN — RankineREA — ReaumurRME — Градус RømerCFM — Кубический фут в минутуFTS — Кубический фут в секундуGPD — Галлон (жидкость США) в суткиGPH — Галлон (жидкость США) в часGPM — Галлон (жидкость США) в минутуINM — Кубический дюйм в минутуINS — Кубический дюйм в секундуLPM — Литр в минутуMQS — кубический метр в секунду (Si UniCM — кулон-метрDB — DebyeEA0 — атомная единица электрического диполяFC — фут-канделя люмен на квадрат FoLMN — люмен на квадратный дюймLX — люкс (единица Si)PH — Phot (единица Cgs)FHP — фут в секунду Час в секундуFMS — фут в минуту в секундуFP — фут в секунду в квадратеG — стандартная гравитацияGAL — галлон GalileoIP — дюйм в минуту в секунду в секундуIP2 — дюйм в секунду в квадратеKNS — узел в секундуMM — миля в минуту в секундуMP — миля в час в секундуMP2 — миля в секунду Секунда в квадратеMSA — метр на секунду в квадрате (Si UFT2 — квадратный фут в секундуM2S — квадратный метр в секунду (Si UnSTX — Стокс (единица Cgs)FTP — фут-фунт)MKG — метр-килограмм-силаNEM — ньютон-метр (единица Si)GML — грамм на секунду MillilitreLAB — фунт (эквивалентный) на галлонLBF — фунт (эквивалентный) на кубический LBI — фунт (экспериментальный) на кубический LBL — фунт (экспериментальный) на галлонOFT — унция (экспериментальный) на кубический OG — унция (эвердупуа) на галлон ) Per GallonOIN — Унция (Avoirdupois) на кубический SFT — Slug на кубический футGSS — Gauss (Cgs Unit)TSL — Tesla (Si Unit)GY — Grey (Si Unit)RDD — RadLBH — Pound Per Foot HourLBS — Фунт на фут в секундуLFT — Фунт-сила-секунда на квадрат LIN — Фунт-сила-секунда на квадрат PAS — Паскаль-секунда (единица Si)PSU — Пуаз (единица Cgs)MX — Максвелл (единица Cgs)WB — Вебер (единица Si)REM — Рентген-эквивалент ManSV — Sievert (Единица Си) Кому:
A0 — Бор, атомная единица длиныAST — АнгстремAU — Астрономическая единицаCBL — Длина кабеля (имперская)CBL(US) — Длина кабеля USCH — ЦепиF — Французский charriereFM — ФермиFNG — FingerFNG(CLOTH) — Палец (ткань)FTM — FathomFUR — FurlongHH — HandLD — Световой деньLEA — лига (земля)LH — Световой часLM — Световая минутаLN — ЛинияLNK (G. S.) — Ссылка (Гюнтера; Сюрвейерская)LNK (RE) — Ссылка (Рамсденская; Инженерная)LS — Световая секундаLY — Световая- yearM — метр (базовая единица СИ)MIL — мил (Швеция и Норвегия)MILE DATA — мили (тактические или данные)MK — MickeyNAIL — гвоздь (ткань)NL — морская лигаNM — нанометрNMI — морская миляNMI I — морская миляP — PalmPC — ParsecPICA — PicaPM — пикометр (бикрон, клеймо) POINT — точка (американский, английский) PT — PaceQUART — QuarterSHAKU — Shaku (японский) SPT — SpatTH — Mil (тыс.)TWP — TwipUM — микрометр (стар.: микрон)XU — единица X; siegbahnABA — Электромагнитная единица AbampereAMP — Ампер (базовая единица Si)ESU — Esu в секунду Статампер (CgsABC — Абкулон Электромагнитная единицаATU — Атомная единица зарядаCLM — КулонFRD — ФарадейMAH — Миллиампер-часSTT — Статкулон Франклин ЭлектростABV — Абвольт (единица Cgs)STV — Статвольт ( Cgs Unit)VLT — Вольт (Si Unit)ACF — Акр-футыACI — Акры-дюймыBIB — Баррели (нефтяные)BII — Баррели (британские)BIU — Баррели (Us Dry)BKT — Ведра (британские)BRO — Галлоны (пивные)BUD — Бушели (Us Dry Level)BUI — Бушели (Imperial)BUU — Бушели (Us Dry Heaped)CMB — CoombsCMI — Cubic MilesCP — CupsCRF — Cord-FootsCRW — Cords (Дрова)CUF — Cubic FathomsCUI — Cubic InchsCUT — Cubic FootsCUY — Cubic ЯрдыDSI — тире (имперские фунты)DSS — десертные ложки (имперские фунты)DSU — тире (США)FBM — борд-футыFFT — пятые FID — жидкие драхмы (имперские)FIS — жидкие скрукле (имперские)FLB — бочки (США, жидкие)FLU — жидкие драмы ( Us) Us FluidramFRK — FirkinsGAI — галлоны (имперские единицы)GAU — галлоны (Us Dry)GAW — галлоны (Us Fluid Wine)GLU — Teacups (gills)GTT — DropsHDI — Hogsheads (Imperial)HHU — Hogsheads (Us)JGR — Jiggers ( Bartending)KLD — KilderkinsLMD — LambdasLOD — LoadsLST — LastsM3 — Кубические метры (Si Unit)MII — Minims (Imperial)MIU — Minims (Us)OZF — Унции (Fluid Us Food NutritioPER — PerchsPKI — Pecks (Imperial)PKU — Pecks (Us) Сухой)PNI — пинчи (британские)PNU — пинчи (американские)PON — PonysPOT — Pottle QuartersPP — стыковые трубыPTI — пинты (британские)PUD — пинты (Us Dry)PUF — пинты (Us Fluid)QRF — Quart S (Us Fluid) QRT — Кварталы QTI — Кварты (британские)QTU — Кварты (Us Dry)RGS — Реестр TonsSCI — Мешки (британские) BagsSCU — Мешки(Us)SHT — Shots (Us)SM — SeamsSTK — Забастовки (Imperial)STU — Забастовки (Us) )TBC — столовые ложки (канадские)TBF — столовые ложки (обычные в США)TBM — столовые ложки (метрические)TBS — столовые ложки (в австралийских единицах измеренияTCA — чайные ложки (канадские) TFD — столовые ложки (Us Food NutritionTIM — чайные ложки (британские)TMF — Timber FootsTMT — чайные ложки ( Метрическая система)TND – тонны (водоизмещение)TNT – тонны (воды)TNW – тонны (фрахт)TSC – чайные ложки (стандарт США)TSF – чайные ложки (США Food Nutrition) WEY — Wey (Us)ACM — Атмосфера-кубический фут в минутуACS — Атмосфера-кубический фут в секунду SecoATC — Атмосфера-кубический сантиметр PeATH — Атмосфера-кубический фут в часBTJ — BTU (Международная таблица) В расчете на BTN — BTU (Международная таблица) В расчете на BTS — БТЕ (международная таблица) по CAS — Калория (международная таблица) ERS — Эрг в секундуFMF — Фут-фунт-сила в минутуFT — Фут-фунт-сила в часFTO — Фут-фунт-сила в секундуHPS — Лошадиная силаLAM — Литр-атмосфера в час MinuteLSC — LusecLTS — Литр атмосферы в секундуPNC — PonceletSQL — Прямой эквивалент квадратного фута TC — Тонна кондиционирования воздухаTMS — Атмосфера-кубический сантиметр PeTRM — Тонна охлаждения (ImperialTRR — Тонна охлаждения (It)ACR — AcresCMK — Квадратные сантиметрыFTK — Квадратные футыHAR — ГектарыINK — Квадратные дюймыKMK — Квадратные километрыMIK — Квадратные милиMTK — Квадратные метрыYDK — Квадратные ярдыAMU — Унифицированная атомная единица массыAT — Тонна анализа (краткая)ATS — Тонна анализа (длинная)BAC — Мешок (Кофе)BDM — Мешок (портландцемент)BRG — BargeCLV — CloveCRT — CrithCT — Carat (Metric)DA — DaltonDRT — Dram (Apothecary Troy)DWT — PennyweightGAM — GammaGR — GrainGV — GraveKIP — KipLB — Pound (Metric)LBA — PoundLBT — Pound (Troy)LBV — Pound (Avoirdupois)ME — Атомная единица массы Электрон RMRK — MarkMTE — MiteMTM — Клещ (метрический) OZ — Унция (этикетка питания США OZT — Унция (аптечная Троя) OZZ — Унция (Avoirdupois) PNN — PointQ — Квинтал (метрический) QR — Квартал (неофициальный) QRI — Quarter (Imperial)QRL — Quarter Long (Informal)SAP — Scruple (Apothecary)SH — Ton ShortSLG — Slug Geepound HylSLH — SheetST — StoneSWT — Hundredweight (центум веса oTON — Ton LongWY — WeyZTR — ZentnerANN — YearsDAY — DaysHUR — HoursMCS — MicrosecondsMIN — MinutesMLS — MillisecondsMON — MonthsSEC — SecondsWEE — WeeksARE — AresBD — BoardsBHE — эквивалент мощности котла DBR — BarnsBRN — BaronysCDA — Cuerda Pr SurveysCRD — CordsCRI — Circular InchsCRM — Circular MilsDNM — DunamsGNT — GunthasHD — HidesRO — RoodsSCT — SectionsSHD — ShedsSs — Square Link Gunters InternatiSLR — Square Link RamsdensSQC — Square Chains InternationalSQM — Square Mil Square ThousSQR — Square Rod/Pole/PerchsSRR — Square RoofingsSTR — StremmasTWN — TownshipsYLN — YardlandsARM — Arcminute MoaARS — ArcsecondCNS — Centesimal Second Of ArcCNT — Centesimal Minute Of ArcDOA — Degree (Дуги)GRA — Grad Gradian GonOCT — OctantQRD — QuadrantSGN - SignSXT — Sextantµ — Угловой MilATA — Атмосфера (Техническая)ATM — Атмосфера (Стандартная)BAR — BarBRY — Бари (единица Cgs)CMH — Сантиметр ртутного столбаCMW — Сантиметр водяного столба ( 4 °C)FTH — фут ртутного столба (условный)FTW — фут водяного столба (392 °F)IMC — Дюйм ртутного столба (условный)INW — Дюйм водяного столба (392 °F)KM — Килограмм-сила на квадратный дюймKSI — Кип на квадратный дюймLTP — Длинная тонна на квадратный футMHG — Микрометр ртутного столбаMMH — Миллиметр ртутного столбаMMW — Миллиметр воды (398 °C)PA — Паскаль (единица Si)PD — фунт на квадратный футPSF — фунт на квадратный футPSI — фунт на квадратный дюймPZ — пьеза (единица Mts)STP — короткая тонна на квадратный футTOR — ТоррATN — атомная единица ForceDYN — Dyne (Cgs Unit)KFF — Килограмм-сила Kilopond Grave-KI — Kip Kip-ForceMGF — Milligrave-Force Gravet-ForceOZC — Унция-силаPDL — PoundalSN — Sthene (единица Mts)TNF — Long Ton-ForceTNL — Short Ton- ForceAUC — атомная единица времениCTN — CenturyCYC — каллипический циклDEC — DecadeFN — FortnightHEL — HelekHIP — гиппархический циклJFF — JiffyKEH — Ke (четверть часа) LSR — Luster LustrumMD — MillidayMLL — MillenniumMMN — MomentMOF — Month (Full)MOG — Month (Greg) Av)MOH — месяц (полый)MOS — месяц (синодический)MTN — метонический цикл EnneadecaeterisOC — OctaeterisPLN — планковское времяSGM — SigmaSHK — ShakeSTH — сотический циклSVD — SvedbergYR — год (общий)YRG — год (григорианский)YRJ — год (юлианский) YRL – год (високосный)YRM – год (среднетропический)B39- Британская термальная единица (39 °F)B59 — Британская термальная единица (59 °F)B60 — Британская термальная единица (60 °F)B63 — Британская термальная единица (63 °F)BOE — эквивалент барреля нефтиBRT — Британская термальная единица ( Iso)BTI — Британская термальная единица (InternatBTM — Британская термальная единица (средняя)BTT — Британская термальная единица (ThermochC15 — Калория (15 °C)C20 — Калория (20 °C)C98 — Калория (398 °C)CAM — Калория ( Среднее значение)CFT — Кубический фут атмосферы CHU — Тепловая единица ЦельсияCL — Калория (Us Fda)CLTH — Калория (термохимическая)CN — Кубический фут природного газаCTA — Кубический сантиметр атмосферыCYD — Кубический ярд атмосферы StandEH — Атомная единица энергии ХартриFTD — Foot-PoundalIMG — Галлон-атмосфераKCA — Большая килокалорияKWH — Киловатт-час Board Of Trade ULTM — Литр-атмосфераQD — QuadRDB — Therm (Ec)RY — RydbergTCE — Тонна угольного эквивалентаTHR — Therm (Us)THU — ThermieTN — Тонна TntTOE — Tone Of Oil EquivalentBAN — Ban HartleyBSH — Bit ShannonCD — Candela (Si Base Unit) CandleCPD — Candlepower (New)JK — Si UnitNAT — Nat Nip NepitNBL — NibbleBIT — BitsBYT — BytesEBI — ExabitsEBY — ExabytesGBI — GigabitsGBY — GigabytesKBI — KilobitsKBY — KilobytesMBI — МегабитыMBY — МегабайтыPBI — ПетабитыPBY — ПетабайтыTBI — ТерабитыTBY — ТерабайтыBLL — Баррели (нефть)CMQ — Кубические сантиметрыFTQ — Кубические футыGLI — Галлоны (Великобритания)GLL — Галлоны (жидкости США)LTR — ЛитрыMLT — МиллилитрыMTQ — Кубические метрыOZI — Унции UKBQ — Беккерели ( Si Unit)CI — КюриRD — Резерфорд (H)BTU — BTUCAL — КалорииERG — ErgEVL — Электрон ВольтFPD — Фут-фунтHPH — Лошадиная сила-часIPD — Дюйм-фунтJOU — ДжоульC — Скорость света в вакуумеFPF — Фарлонг в две неделиFPH — Фут в часIPH — Inch Per HourIPM — Inch Per MinuteIPS — Inch Per SecondMCH — Mach NumberMPM — Mile Per MinuteMPS — Mile Per SecondMS — Метр в секунду (Si Unit)SPS — Скорость звука в AirCDF — Candela Per Square FootCDI — Candela Per Square InchCDM — Candela Per Квадратный метр (Si UFL — FootlambertLMB — LambertSB — Stilb (Cgs Unit)CEL — ЦельсийDDE — Градус DelisleDNE — Градус НьютонаFAN — ФаренгейтGMR — Регулирующий газ MarkKEL — Kelvin’sRAN — RankineREA — ReaumurRME — Градус RømerCFM — Кубический фут в минутуFTS — Кубический фут в минуту SecondGPD — галлон (жидкость США) в суткиGPH — галлон (жидкость США) в часGPM — галлон (жидкость США) в минутуINM — кубический дюйм в минутуINS — кубический дюйм в секундуLPM — литр в минутуMQS — кубический метр в секунду (Si UniCM — кулоновый метрDB — DebyeEA0 — атомная единица электрического диполя CMT — сантиметр DMT — дециметрыFOT — футыINH — дюймыKMT — километрыMMT — миллиметрыMTR — метрыSMI — милиYRD — ярдыCTM — каратыGRM — граммыKGM — килограммыLBR — фунтыMGM — миллиграммыONZ — унции TNE — тонны (метрические)DEG — градусыGRD — градыRAD - RadiansFC — Фут-канд Люмен на квадрат FoLMN — Люмен на квадратный дюймLX — Люкс (Единица Si)PH — Фот (Единица Cgs)FHP — Фут в час в секундуFMS — Фут в минуту в секундуFP — Фут в секунду в квадратеdG — Стандартная сила тяжестиGAL — Gal GalileoIP — Дюйм в минуту в секундуIP2 — дюйм в секунду в квадратеKNS — узел в секундуMM — миля в минуту в секундуMP — миля в час в секундуMP2 — миля в секунду в квадратеMSA — метр в секунду в квадрате (Si UFPM — футы/минутыFPS — футы/секундыKMH — километры/ ЧасKMS — Километры/секундыKNT — УзлыMPH — Мили/часMTS — Метры/секундыFT2 — Квадратный фут в секундуM2S — Квадратный метр в секунду (Si UnSTX — Стокс (единица Cgs)FTP — Foot-PoundalMKG — Метр Килограмм-силаNEM — Ньютон-метр (Единица Si )GCC — граммы/кубический сантиметрKCC — килограммы/кубический сантиметрKLI — килограммы/литрKMC — килограммы/кубический метрOCI — унции/кубический дюймOGL — унции/галлонPCF — фунты/кубический футPCI — фунты/кубический дюймPGL — фунты/галлонGML — грамм на миллилитрLAB — фунт (Avoirdupois) Per GallonLBF — фунт (Avoirdupois) на кубический LBI — фунт (Avoirdupois) на кубический LBL — фунт (Avoirdupois) на галлонOFT — унция (Avoirdupois) на кубический OG — унция (Avoirdupois) на галлонOGA — унция (Avoirdupois) на галлонOIN — Унция (Avoirdupois) на кубический SFT — Слаг на кубический футGSS — Гаусс (единица Cgs)TSL — Тесла (единица Si)GY — Грей (единица Si)RDD — RadJCM — Джоули/сантиметрKGF — Килограмм-силаNWN — НьютоныPFC — Фунт силыLBH — Фунт Per Foot HourLBS — Фунт на фут-секундуLFT — Фунт-сила-секунда на квадрат LIN — Фунт-сила-секунда на квадрат PAS — Паскаль-секунда (единица Si)PSU — Пуаз (единица Cgs)MX — Максвелл (единица Cgs)WB — Вебер (Si) Единица)REM — Рентген-эквивалент ManSV — Зиверт (Единица Si) S.) — Ссылка (Гюнтера; Сюрвейерская)LNK (RE) — Ссылка (Рамсденская; Инженерная)LS — Световая секундаLY — Световая- yearM — метр (базовая единица СИ)MIL — мил (Швеция и Норвегия)MILE DATA — мили (тактические или данные)MK — MickeyNAIL — гвоздь (ткань)NL — морская лигаNM — нанометрNMI — морская миляNMI I — морская миляP — PalmPC — ParsecPICA — PicaPM — пикометр (бикрон, клеймо) POINT — точка (американский, английский) PT — PaceQUART — QuarterSHAKU — Shaku (японский) SPT — SpatTH — Mil (тыс.)TWP — TwipUM — микрометр (стар.: микрон)XU — единица X; siegbahnABA — Электромагнитная единица AbampereAMP — Ампер (базовая единица Si)ESU — Esu в секунду Статампер (CgsABC — Абкулон Электромагнитная единицаATU — Атомная единица зарядаCLM — КулонFRD — ФарадейMAH — Миллиампер-часSTT — Статкулон Франклин ЭлектростABV — Абвольт (единица Cgs)STV — Статвольт ( Cgs Unit)VLT — Вольт (Si Unit)ACF — Акр-футыACI — Акры-дюймыBIB — Баррели (нефтяные)BII — Баррели (британские)BIU — Баррели (Us Dry)BKT — Ведра (британские)BRO — Галлоны (пивные)BUD — Бушели (Us Dry Level)BUI — Бушели (Imperial)BUU — Бушели (Us Dry Heaped)CMB — CoombsCMI — Cubic MilesCP — CupsCRF — Cord-FootsCRW — Cords (Дрова)CUF — Cubic FathomsCUI — Cubic InchsCUT — Cubic FootsCUY — Cubic ЯрдыDSI — тире (имперские фунты)DSS — десертные ложки (имперские фунты)DSU — тире (США)FBM — борд-футыFFT — пятые FID — жидкие драхмы (имперские)FIS — жидкие скрукле (имперские)FLB — бочки (США, жидкие)FLU — жидкие драмы ( Us) Us FluidramFRK — FirkinsGAI — галлоны (имперские единицы)GAU — галлоны (Us Dry)GAW — галлоны (Us Fluid Wine)GLU — Teacups (gills)GTT — DropsHDI — Hogsheads (Imperial)HHU — Hogsheads (Us)JGR — Jiggers ( Bartending)KLD — KilderkinsLMD — LambdasLOD — LoadsLST — LastsM3 — Кубические метры (Si Unit)MII — Minims (Imperial)MIU — Minims (Us)OZF — Унции (Fluid Us Food NutritioPER — PerchsPKI — Pecks (Imperial)PKU — Pecks (Us) Сухой)PNI — пинчи (британские)PNU — пинчи (американские)PON — PonysPOT — Pottle QuartersPP — стыковые трубыPTI — пинты (британские)PUD — пинты (Us Dry)PUF — пинты (Us Fluid)QRF — Quart S (Us Fluid) QRT — Кварталы QTI — Кварты (британские)QTU — Кварты (Us Dry)RGS — Реестр TonsSCI — Мешки (британские) BagsSCU — Мешки(Us)SHT — Shots (Us)SM — SeamsSTK — Забастовки (Imperial)STU — Забастовки (Us) )TBC — столовые ложки (канадские)TBF — столовые ложки (обычные в США)TBM — столовые ложки (метрические)TBS — столовые ложки (в австралийских единицах измеренияTCA — чайные ложки (канадские) TFD — столовые ложки (Us Food NutritionTIM — чайные ложки (британские)TMF — Timber FootsTMT — чайные ложки ( Метрическая система)TND – тонны (водоизмещение)TNT – тонны (воды)TNW – тонны (фрахт)TSC – чайные ложки (стандарт США)TSF – чайные ложки (США Food Nutrition) WEY — Wey (Us)ACM — Атмосфера-кубический фут в минутуACS — Атмосфера-кубический фут в секунду SecoATC — Атмосфера-кубический сантиметр PeATH — Атмосфера-кубический фут в часBTJ — BTU (Международная таблица) В расчете на BTN — BTU (Международная таблица) В расчете на BTS — БТЕ (международная таблица) по CAS — Калория (международная таблица) ERS — Эрг в секундуFMF — Фут-фунт-сила в минутуFT — Фут-фунт-сила в часFTO — Фут-фунт-сила в секундуHPS — Лошадиная силаLAM — Литр-атмосфера в час MinuteLSC — LusecLTS — Литр атмосферы в секундуPNC — PonceletSQL — Прямой эквивалент квадратного фута TC — Тонна кондиционирования воздухаTMS — Атмосфера-кубический сантиметр PeTRM — Тонна охлаждения (ImperialTRR — Тонна охлаждения (It)ACR — AcresCMK — Квадратные сантиметрыFTK — Квадратные футыHAR — ГектарыINK — Квадратные дюймыKMK — Квадратные километрыMIK — Квадратные милиMTK — Квадратные метрыYDK — Квадратные ярдыAMU — Унифицированная атомная единица массыAT — Тонна анализа (краткая)ATS — Тонна анализа (длинная)BAC — Мешок (Кофе)BDM — Мешок (портландцемент)BRG — BargeCLV — CloveCRT — CrithCT — Carat (Metric)DA — DaltonDRT — Dram (Apothecary Troy)DWT — PennyweightGAM — GammaGR — GrainGV — GraveKIP — KipLB — Pound (Metric)LBA — PoundLBT — Pound (Troy)LBV — Pound (Avoirdupois)ME — Атомная единица массы Электрон RMRK — MarkMTE — MiteMTM — Клещ (метрический) OZ — Унция (этикетка питания США OZT — Унция (аптечная Троя) OZZ — Унция (Avoirdupois) PNN — PointQ — Квинтал (метрический) QR — Квартал (неофициальный) QRI — Quarter (Imperial)QRL — Quarter Long (Informal)SAP — Scruple (Apothecary)SH — Ton ShortSLG — Slug Geepound HylSLH — SheetST — StoneSWT — Hundredweight (центум веса oTON — Ton LongWY — WeyZTR — ZentnerANN — YearsDAY — DaysHUR — HoursMCS — MicrosecondsMIN — MinutesMLS — MillisecondsMON — MonthsSEC — SecondsWEE — WeeksARE — AresBD — BoardsBHE — эквивалент мощности котла DBR — BarnsBRN — BaronysCDA — Cuerda Pr SurveysCRD — CordsCRI — Circular InchsCRM — Circular MilsDNM — DunamsGNT — GunthasHD — HidesRO — RoodsSCT — SectionsSHD — ShedsSs — Square Link Gunters InternatiSLR — Square Link RamsdensSQC — Square Chains InternationalSQM — Square Mil Square ThousSQR — Square Rod/Pole/PerchsSRR — Square RoofingsSTR — StremmasTWN — TownshipsYLN — YardlandsARM — Arcminute MoaARS — ArcsecondCNS — Centesimal Second Of ArcCNT — Centesimal Minute Of ArcDOA — Degree (Дуги)GRA — Grad Gradian GonOCT — OctantQRD — QuadrantSGN - SignSXT — Sextantµ — Угловой MilATA — Атмосфера (Техническая)ATM — Атмосфера (Стандартная)BAR — BarBRY — Бари (единица Cgs)CMH — Сантиметр ртутного столбаCMW — Сантиметр водяного столба ( 4 °C)FTH — фут ртутного столба (условный)FTW — фут водяного столба (392 °F)IMC — Дюйм ртутного столба (условный)INW — Дюйм водяного столба (392 °F)KM — Килограмм-сила на квадратный дюймKSI — Кип на квадратный дюймLTP — Длинная тонна на квадратный футMHG — Микрометр ртутного столбаMMH — Миллиметр ртутного столбаMMW — Миллиметр воды (398 °C)PA — Паскаль (единица Si)PD — фунт на квадратный футPSF — фунт на квадратный футPSI — фунт на квадратный дюймPZ — пьеза (единица Mts)STP — короткая тонна на квадратный футTOR — ТоррATN — атомная единица ForceDYN — Dyne (Cgs Unit)KFF — Килограмм-сила Kilopond Grave-KI — Kip Kip-ForceMGF — Milligrave-Force Gravet-ForceOZC — Унция-силаPDL — PoundalSN — Sthene (единица Mts)TNF — Long Ton-ForceTNL — Short Ton- ForceAUC — атомная единица времениCTN — CenturyCYC — каллипический циклDEC — DecadeFN — FortnightHEL — HelekHIP — гиппархический циклJFF — JiffyKEH — Ke (четверть часа) LSR — Luster LustrumMD — MillidayMLL — MillenniumMMN — MomentMOF — Month (Full)MOG — Month (Greg) Av)MOH — месяц (полый)MOS — месяц (синодический)MTN — метонический цикл EnneadecaeterisOC — OctaeterisPLN — планковское времяSGM — SigmaSHK — ShakeSTH — сотический циклSVD — SvedbergYR — год (общий)YRG — год (григорианский)YRJ — год (юлианский) YRL – год (високосный)YRM – год (среднетропический)B39- Британская термальная единица (39 °F)B59 — Британская термальная единица (59 °F)B60 — Британская термальная единица (60 °F)B63 — Британская термальная единица (63 °F)BOE — эквивалент барреля нефтиBRT — Британская термальная единица ( Iso)BTI — Британская термальная единица (InternatBTM — Британская термальная единица (средняя)BTT — Британская термальная единица (ThermochC15 — Калория (15 °C)C20 — Калория (20 °C)C98 — Калория (398 °C)CAM — Калория ( Среднее значение)CFT — Кубический фут атмосферы CHU — Тепловая единица ЦельсияCL — Калория (Us Fda)CLTH — Калория (термохимическая)CN — Кубический фут природного газаCTA — Кубический сантиметр атмосферыCYD — Кубический ярд атмосферы StandEH — Атомная единица энергии ХартриFTD — Foot-PoundalIMG — Галлон-атмосфераKCA — Большая килокалорияKWH — Киловатт-час Board Of Trade ULTM — Литр-атмосфераQD — QuadRDB — Therm (Ec)RY — RydbergTCE — Тонна угольного эквивалентаTHR — Therm (Us)THU — ThermieTN — Тонна TntTOE — Tone Of Oil EquivalentBAN — Ban HartleyBSH — Bit ShannonCD — Candela (Si Base Unit) CandleCPD — Candlepower (New)JK — Si UnitNAT — Nat Nip NepitNBL — NibbleBIT — BitsBYT — BytesEBI — ExabitsEBY — ExabytesGBI — GigabitsGBY — GigabytesKBI — KilobitsKBY — KilobytesMBI — МегабитыMBY — МегабайтыPBI — ПетабитыPBY — ПетабайтыTBI — ТерабитыTBY — ТерабайтыBLL — Баррели (нефть)CMQ — Кубические сантиметрыFTQ — Кубические футыGLI — Галлоны (Великобритания)GLL — Галлоны (жидкости США)LTR — ЛитрыMLT — МиллилитрыMTQ — Кубические метрыOZI — Унции UKBQ — Беккерели ( Si Unit)CI — КюриRD — Резерфорд (H)BTU — BTUCAL — КалорииERG — ErgEVL — Электрон ВольтFPD — Фут-фунтHPH — Лошадиная сила-часIPD — Дюйм-фунтJOU — ДжоульC — Скорость света в вакуумеFPF — Фарлонг в две неделиFPH — Фут в часIPH — Inch Per HourIPM — Inch Per MinuteIPS — Inch Per SecondMCH — Mach NumberMPM — Mile Per MinuteMPS — Mile Per SecondMS — Метр в секунду (Si Unit)SPS — Скорость звука в AirCDF — Candela Per Square FootCDI — Candela Per Square InchCDM — Candela Per Квадратный метр (Si UFL — FootlambertLMB — LambertSB — Stilb (Cgs Unit)CEL — ЦельсийDDE — Градус DelisleDNE — Градус НьютонаFAN — ФаренгейтGMR — Регулирующий газ MarkKEL — Kelvin’sRAN — RankineREA — ReaumurRME — Градус RømerCFM — Кубический фут в минутуFTS — Кубический фут в минуту SecondGPD — галлон (жидкость США) в суткиGPH — галлон (жидкость США) в часGPM — галлон (жидкость США) в минутуINM — кубический дюйм в минутуINS — кубический дюйм в секундуLPM — литр в минутуMQS — кубический метр в секунду (Si UniCM — кулоновый метрDB — DebyeEA0 — атомная единица электрического диполя CMT — сантиметр DMT — дециметрыFOT — футыINH — дюймыKMT — километрыMMT — миллиметрыMTR — метрыSMI — милиYRD — ярдыCTM — каратыGRM — граммыKGM — килограммыLBR — фунтыMGM — миллиграммыONZ — унции TNE — тонны (метрические)DEG — градусыGRD — градыRAD - RadiansFC — Фут-канд Люмен на квадрат FoLMN — Люмен на квадратный дюймLX — Люкс (Единица Si)PH — Фот (Единица Cgs)FHP — Фут в час в секундуFMS — Фут в минуту в секундуFP — Фут в секунду в квадратеdG — Стандартная сила тяжестиGAL — Gal GalileoIP — Дюйм в минуту в секундуIP2 — дюйм в секунду в квадратеKNS — узел в секундуMM — миля в минуту в секундуMP — миля в час в секундуMP2 — миля в секунду в квадратеMSA — метр в секунду в квадрате (Si UFPM — футы/минутыFPS — футы/секундыKMH — километры/ ЧасKMS — Километры/секундыKNT — УзлыMPH — Мили/часMTS — Метры/секундыFT2 — Квадратный фут в секундуM2S — Квадратный метр в секунду (Si UnSTX — Стокс (единица Cgs)FTP — Foot-PoundalMKG — Метр Килограмм-силаNEM — Ньютон-метр (Единица Si )GCC — граммы/кубический сантиметрKCC — килограммы/кубический сантиметрKLI — килограммы/литрKMC — килограммы/кубический метрOCI — унции/кубический дюймOGL — унции/галлонPCF — фунты/кубический футPCI — фунты/кубический дюймPGL — фунты/галлонGML — грамм на миллилитрLAB — фунт (Avoirdupois) Per GallonLBF — фунт (Avoirdupois) на кубический LBI — фунт (Avoirdupois) на кубический LBL — фунт (Avoirdupois) на галлонOFT — унция (Avoirdupois) на кубический OG — унция (Avoirdupois) на галлонOGA — унция (Avoirdupois) на галлонOIN — Унция (Avoirdupois) на кубический SFT — Слаг на кубический футGSS — Гаусс (единица Cgs)TSL — Тесла (единица Si)GY — Грей (единица Si)RDD — RadJCM — Джоули/сантиметрKGF — Килограмм-силаNWN — НьютоныPFC — Фунт силыLBH — Фунт Per Foot HourLBS — Фунт на фут-секундуLFT — Фунт-сила-секунда на квадрат LIN — Фунт-сила-секунда на квадрат PAS — Паскаль-секунда (единица Si)PSU — Пуаз (единица Cgs)MX — Максвелл (единица Cgs)WB — Вебер (Si) Единица)REM — Рентген-эквивалент ManSV — Зиверт (Единица Si) Таблица преобразования: градусы в миллиметры| ГРАДУСЫ | | МИЛЛИМЕТРОВ |
|---|
| 1 | = | 1000 | | 2 | = | 2000 | | 3 | = | 3000 | | 4 | = | 4000 | | 5 | = | 5000 | | 7 | = | 7000 | | 8 | = | 8000 | | 9 | = | 9000 | | 10 | = | 10000 |
| МИЛЛИМЕТРОВ | | ГРАДУСОВ |
|---|
| 1 | = | 0,001 | | 2 | = | 0,002 | | 3 | = | 0,003 | | 4 | = | 0,004 | | 5 | = | 0,005 | | 7 | = | 0,007 | | 8 | = | 0,008 | | 9 | = | 0,009 | | 10 | = | 0,01 |
Ближайшие числа для 1 градуса Последние преобразования Градусов в
Миллиметры python — Преобразование hddd° mm. mm′ в десятичные градусы спросил Изменено
2 года, 8 месяцев назад Просмотрено
130 раз Я получаю данные через HTML-документ, прикрепленный к электронному письму (не спрашивайте, почему…). Мне нужно прочитать GPS-координаты из этого файла и создать маршрут с помощью OSM. У меня нет проблем с получением GPS-координат в виде строки, но я действительно изо всех сил пытаюсь сформировать их во что-то, что может использовать OSM. GPS-координаты выглядят так: N53°09.20 E009°11.82, разбиение не проблема, но мне нужно сформировать их в нормальные широту и долготу типа (53.119897, 7.944012). У кого-нибудь была такая же проблема или есть ли библиотека, которую я могу использовать? - python
- карты
- gis
- openstreetmap
- широта-долгота
3 Приведенный ниже код можно использовать для преобразования градусов, минут и секунд в указанном вами формате в десятичные значения долготы и широты: import re
координаты = "N53°09. Теория вероятностей | ЕГЭ по математике (профиль)Вероятностью события $А$ называется отношение числа благоприятных для $А$ исходов к числу всех
равновозможных исходов $P(A)={m}/{n}$, где $n$ – общее количество возможных исходов, а $m$ – количество исходов, благоприятствующих событию
$А$. Вероятность события — это число из отрезка $[0; 1]$ В фирме такси в наличии $50$ легковых автомобилей. $35$ из них чёрные, остальные — жёлтые.
Найдите вероятность того, что на случайный вызов приедет машина жёлтого цвета. Решение: Найдем количество желтых автомобилей: $50-35=15$ Всего имеется $50$ автомобилей, то есть на вызов приедет одна из пятидесяти. Желтых автомобилей $15$,
следовательно, вероятность приезда именно желтого автомобиля равна ${15}/{50}={3}/{10}=0,3$ Ответ:$0,3$ Противоположные событияДва события называются противоположными, если в данном испытании они несовместимы и одно из них обязательно
происходит. Вероятности противоположных событий в сумме дают 1.Событие, противоположное событию $А$, записывают
${(А)}↖{-}$. Вероятности противоположных событий в сумме дают 1.Событие, противоположное событию $А$, записывают
${(А)}↖{-}$. $Р(А)+Р{(А)}↖{-}=1$ Независимые событияДва события $А$ и $В$ называются независимыми, если вероятность появления каждого из них не зависит от того,
появилось другое событие или нет. В противном случае события называются зависимыми. Вероятность произведения двух независимых событий $A$ и $B$ равна произведению этих
вероятностей: $Р(А·В)=Р(А)·Р(В)$ Иван Иванович купил два различных лотерейных билета. Вероятность того, что выиграет первый
лотерейный билет, равна $0,15$. Вероятность того, что выиграет второй лотерейный билет, равна $0,12$. Иван Иванович
участвует в обоих розыгрышах. Считая, что розыгрыши проводятся независимо друг от друга, найдите вероятность того,
что Иван Иванович выиграет в обоих розыгрышах. Решения: Вероятность $Р(А)$ — выиграет первый билет. Вероятность $Р(В)$ — выиграет второй билет. События $А$ и $В$ – это независимые события. То есть, чтобы найти вероятность того, что они произойдут оба
события, нужно найти произведение вероятностей $Р(А·В)=Р(А)·Р(В)$ $Р=0,15·0,12=0,018$ Ответ: $0,018$ Несовместные событияДва события $А$ и $В$ называют несовместными, если отсутствуют исходы, благоприятствующие одновременно как событию
$А$, так и событию $В$. (События, которые не могут произойти одновременно) Вероятность суммы двух несовместных событий $A$ и $B$ равна сумме вероятностей этих
событий: $Р(А+В)=Р(А)+Р(В)$ На экзамене по алгебре школьнику достается один вопрос их всех экзаменационных. Вероятность
того, что это вопрос на тему «Квадратные уравнения», равна $0,3$. Вероятность того, что это вопрос на тему
«Иррациональные уравнения», равна $0,18$. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите
вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем. Решение: Данные события называются несовместные, так как школьнику достанется вопрос ЛИБО по теме «Квадратные уравнения»,
ЛИБО по теме «Иррациональные уравнения». Одновременно темы не могут попасться. Вероятность суммы двух
несовместных событий $A$ и $B$ равна сумме вероятностей этих событий: $Р(А+В)=Р(А)+Р(В)$ $Р = 0,3+0,18=0,48$ Ответ: $0,48$ Совместные событияДва события называются совместными, если появление одного из них не исключает появление другого в одном и том же
испытании. В противном случае события называются несовместными. Вероятность суммы двух совместных событий $A$ и $B$ равна сумме вероятностей этих событий минус
вероятность их произведения: $Р(А+В)=Р(А)+Р(В)-Р(А·В)$ В холле кинотеатра два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится
кофе, равна $0,6$. Вероятность того, что кофе закончится в обоих автоматах, равна $0,32$. Найдите вероятность того,
что к концу дня кофе закончится хотя бы в одном из автоматов. Решение: Обозначим события, пусть: $А$ = кофе закончится в первом автомате, $В$ = кофе закончится во втором автомате. Тогда, $A·B =$ кофе закончится в обоих автоматах, $A + B =$ кофе закончится хотя бы в одном автомате. По условию, $P(A) = P(B) = 0,6; P(A·B) = 0,32$. События $A$ и $B$ совместные, вероятность суммы двух совместных событий равна сумме вероятностей этих событий,
уменьшенной на вероятность их произведения: $P(A + B) = P(A) + P(B) − P(A·B) = 0,6 + 0,6 − 0,32 = 0,88$ Ответ: $0,88$ Часть 5. Теория вероятностей на ЕГЭ. Трудные задачи. – МАТЕМАТИКАЕще одна статья по теории вероятностей. В ней собраны задачи на проценты, вероятности зависимых событий, а также задачи, требующие последовательного подсчёта разных вероятностей. Эти задачи относятся к категории «трудные задачи», однако разобрав их с нами, они таковыми вам уже не покажутся. Теоретическая частьЕсли имеются события А и В, то Эти формулы следуют применять, когда А и В – зависимые совместные события (более простые случаи рассмотрены в предыдущих статьях (часть1, часть 2, часть 3, часть 4). Задачи о зависимых событияхЗадача 5.1 В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,4. Вероятность того, что кофе закончится в обоих автоматах, равна 0,22. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.
Решение.
1-й способ. Так как 0,4 ·0,4 ≠ 0,22, то события «кофе закончился в 1-ом автомате» и «кофе закончился во 2-ом автомате» зависимые. Обозначим через А событие «кофе остался в первом автомате», через В – «кофе остался во втором автомате». Тогда . Событие «кофе остался хотя бы в одном автомате» – это А U В, его вероятность равна Р(А U В) = 1 — 0,22 = 0,78, так как оно противоположно событию «кофе закончился в обоих автоматах». По формуле для пересечения событий: P(A ∩ B) = P(A) + P(B) — P(A ∪ B)= 0,6 + 0,6 — 0,78 = 0,42 2-й способ
Обозначим через Х событие «кофе закончился в первом автомате», через Y – «кофе закончился во втором автомате».
Тогда по условию Р(X) = Р(Y) = 0,4, P(X ∩ Y) = 0,22. Так как P(X ∩ Y) ≠ P(X) · P(Y), то события Х и Y зависимые. По формуле для объединения событий: P(X∪Y)=P(X)+P(Y)-P(X∩Y) = 0,4 + 0,4 – 0,22 = 0,58. Мы нашли вероятность события Х U Y «кофе закончился хотя бы в одном автомате». Противоположным событием будет «кофе остался в обоих автоматах», его вероятность равна = 1 –P(X ∪ Y) = 1 –0,58 = 0,42. 3-й способ.
Составим таблицу вероятностей возможных результатов в конце дня. | Второй автомат | | кофе закончился | кофе остался | | Первый автомат | кофе закончился | 0,22 | | | кофе остался | | |
По условию вероятность события «кофе закончился в обоих автоматах» равна 0,22. Это число мы сразу записали в соответствующую ячейку таблицы. В первом автомате кофе закончится с вероятностью 0,4, поэтому сумма чисел в верхних ячейках таблицы должна быть равна 0,4. Значит, в правой верхней ячейке должно быть число 0,4 – 0,22 = 0,18. Значит, в правой верхней ячейке должно быть число 0,4 – 0,22 = 0,18. | Второй автомат | | кофе закончился | кофе остался | | Первый автомат | кофе закончился | 0,22 | 0,18 | | кофе остался | | |
Во втором автомате кофе закончится с вероятностью 0,4, поэтому сумма чисел в левых ячейках таблицы также должна быть равна 0,4. Значит, в левой нижней ячейке должно быть число 0,4 – 0,22 = 0,18. | Второй автомат | | кофе закончился | кофе остался | | Первый автомат | кофе закончился | 0,22 | 0,18 | | кофе остался | 0,18 | |
Так как сумма чисел во всех четырёх ячейках должна быть равна 1, то искомое число в правой нижней ячейке равно 1 – 0,22 – 0,18 – 0,18 = 0,42. | Второй автомат | | кофе закончился | кофе остался | | Первый автомат | кофе закончился | 0,22 | 0,18 | | кофе остался | 0,18 | 0,42 |
Ответ: 0,42. Задачи на процентыЗадача 5.2 Агрофирма закупает куриные яйца в двух домашних хозяйствах. 60% яиц из первого хозяйства – яйца высшей категории, а из второго хозяйства – 40% яиц высшей категории. Всего высшую категорию получает 48% яиц. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства.
Решение.
Пусть х – искомая вероятность. Пусть всего закуплено n яиц. Тогда в первом хозяйстве закуплено x · n яиц, из них 0,6х·n высшей категории. Во втором хозяйстве закуплено (1- x) · n яиц, из них 0,4 • (1- x) • n высшей категории. Всего высшую категорию имеют 0,48n яиц. Всего высшую категорию имеют 0,48n яиц. Отсюда Ответ: 0,4 Задача 5.3 На фабрике керамической посуды 20% произведённых тарелок имеют дефект. При контроле качества продукции выявляется 70% дефектных тарелок. Остальные тарелки поступают в продажу. Найдите вероятность того, что случайно выбранная при покупке тарелка не имеет дефектов. Ответ округлите до сотых.
Решение.
Пусть всего произведено х тарелок. Качественных тарелок 0,8х (80% от общего числа), они поступают в продажу. Дефектных тарелок 0,2х, из них в продажу поступает 30%, то есть 0,3 • 0,2х = 0,06x.
Всего в продажу поступило 0,8х + 0,06x = 0,86x тарелок.
Вероятность купить тарелку без дефектов равна ≈ 0,93 Ответ: 0,93. Разные задачиЗадача 5.4 На рок-фестивале выступают группы – по одной от каждой из заявленных стран. Порядок выступления определяется жребием. Какова вероятность того, что группа из Финляндии будет выступать после группы из Бельгии, но перед группой из Греции? Результат округлите до сотых.
Решение.
1-й способ.
Будем считать исходом порядок выступления групп на фестивале. Разобьём множество исходов на подмножества следующим образом: в одно подмножество будем включать исходы, полученные перестановками рок-групп из Финляндии, Бельгии и Греции (с сохранением мест всех остальных рок-групп). Тогда в каждом подмножестве будет 6 исходов: ФБГ, ФГБ, БГФ, БФГ, ГБФ, ГФБ. Из этих шести исходов благоприятным будет только БФГ. Следовательно, благоприятными являются 1/6 всех исходов. Искомая вероятность равна 1\6 ≈ 0,17 2-й способ (этот способ не является математически верным, но при решении на экзамене может помочь, если первый способ непонятен) Так как в условии не указано общее число рок-групп, будем считать, что их всего три: из Финляндии, Бельгии и Греции. Будем считать исходом порядок выступлений, всего 6 исходов: ФБГ, ФГБ, БГФ, БФГ, ГБФ, ГФБ. Благоприятным является только исход БФГ. Искомая вероятность равна 1\6 ≈ 0,17. Ответ: 0,17. Задача 5.5 При артиллерийской стрельбе автоматическая система делает выстрел по цели. Если цель не уничтожена, то система делает повторный выстрел. Выстрелы повторяются до тех пор, пока цель не будет уничтожена. Вероятность уничтожения некоторой цели при первом выстреле равна 0,2, а при каждом последующем 0,7. Сколько выстрелов потребуется для того, чтобы вероятность уничтожения цели была не менее 0,98?
Решение.
1-й способ
Вероятность промаха при первом выстреле равна 1 – 0,2 = 0,8. Вероятность промаха при каждом последующем равна 0,3. Подсчитаем число выстрелов, при котором цель остаётся непоражённой с вероятностью менее 1 – 0,98 = 0,02. Вероятность непоражения
после второго выстрела равна 0,8 • 0,3 = 0,24;
после третьего 0,24 • 0,3 = 0,072;
после четвёртого 0,072 • 0,3 = 0,0216;
после пятого 0,0216 • 0,3 = 0,00648. Следовательно, необходимо 5 выстрелов. 2-й способ (этот способ имеет математическое значение, но непригоден на экзамене из-за необходимости приближённого вычисления логарифма) Вероятность непоражения после n выстрелов равна , так как при первом выстреле вероятность промаха 0,8, а при каждом последующем 0,3. По условию необходимо, чтобы
Ответ: 5.
Задача 5.6 Чтобы поступить в институт на специальность «Архитектура», абитуриент должен набрать на ЕГЭ не менее 60 баллов по каждому из трёх предметов – математике, русскому языку и истории. Чтобы поступить на специальность «Живопись», нужно набрать не менее 60 баллов по каждому из трёх предметов – русскому языку, истории и литературе.
Вероятность того, что абитуриент Н. получит не менее 60 баллов по истории, равна 0,8, по русскому языку 0, 5, по литературе 0,6 и по математике 0,9.
Найдите вероятность того, что Н. сможет поступить хотя бы на одну из двух упомянутых специальностей.
Решение. Вероятность того, что Н. не сможет набрать 60 баллов ни по литературе, ни по математике равна (1 – 0,6) • (1 –0,9) = 0,4 • 0,1 = 0,04. Следовательно, хотя бы по одному из этих двух предметов он получит 60 баллов с вероятностью 1 – 0,04 = 0,96.
Для поступления нужно набрать требуемый балл по русскому языку, истории и хотя бы по одному предмету из литературы и математики. Вероятность поступления равна 0,5 • 0,8 • 0,96 = 0,384. Ответ: 0,384. Задача 5.7 В Волшебной стране бывает два типа погоды: хорошая и отличная, причём погода, установившись утром, держится неизменной весь день. Известно, что с вероятностью 0,9 погода завтра будет такой же, как и сегодня. Сегодня 11 марта, погода в Волшебной стране хорошая. Найдите вероятность того, что 14 марта в Волшебной стране будет отличная погода.
Решение. Составим таблицу вероятностей для погоды в Волшебной стране. | 11 марта | 12 марта | 13 марта | 14 марта | хорошая | 1 | | | | | отличная | 0 | | | |
Погода 12 марта с вероятностью 0,9 останется хорошей, с вероятностью 0,1 станет отличной. Занесём эти данные в таблицу. Занесём эти данные в таблицу. | 11 марта | 12 марта | 13 марта | 14 марта | | хорошая | 1 | 0,9 | | | | отличная | 0 | 0,1 | | |
Хорошая погода 13 марта может быть в двух случаях.
1) Погода 12 марта была хорошей и не изменилась. Вероятность этого равна 0,9 • 0,9 = 0,81.
2) Погода 12 марта была отличной и изменилась. Вероятность этого равна 0,1 • 0,1 = 0,01. Таким образом, вероятность хорошей погоды 13 марта равна 0,81 + 0,01 = 0,82. Вероятность отличной погоды 13 марта равна 1 – 0,82 = 0,18. Заносим эти данные в таблицу. | 11 марта | 12 марта | 13 марта | 14 марта | | хорошая | 1 | 0,9 | 0,82 | | | отличная | 0 | 0,1 | 0,18 | |
Отличная погода 14 марта может быть в двух случаях.
1) Погода 13 марта была хорошей и изменилась. Вероятность этого равна 0,82 • 0,1 = 0,082.
2) Погода 13 марта была отличной и не изменилась. Вероятность этого равна 0,18 • 0,9 = 0,162. Таким образом, вероятность отличной погоды 14 марта равна 0,082 + 0,162 = 0,244. | 11 марта | 12 марта | 13 марта | 14 марта | | хорошая | 1 | 0,9 | 0,82 | | | отличная | 0 | 0,1 | 0,18 | 0,244 |
Ответ: 0,244. Подведем итогЭто последняя часть материала по началам теории вероятностей, знание которого необходимо для успешной сдачи ЕГЭ по математике профильного уровня. Для закрепления изученного предлагаю вам задачи для самостоятельного решения. Вы также можете проверить правильность их выполнения, внеся свои ответы в предлагаемую форму. Также рекомендую изучить «Задачи с параметром» и другие уроки по решению заданий ЕГЭ по математике, которые представлены на нашем канале Youtube. Спасибо, что поделились статьей в социальных сетях
Источник «Подготовка к ЕГЭ. Математика. Теория вероятностей». Под редакцией Ф.Ф. Лысенко, С.Ю. Кулабухова
Хитрости для решения вопросов вероятности Применение или использование вероятности можно увидеть в количественных способностях, а также в повседневной жизни. Необходимо изучить основное понятие вероятности. Мы рассмотрим основы, а также проблемы сложного уровня для всех уровней студентов для всех конкурсных экзаменов, особенно SBI PO, SBI CLERK, IBPS PO, IBPS CLERK, RRB PO, NICL AO, LIC AAO, SNAP, MAT, SSC CGL и т. д.
Определение: Вероятность означает возможность или вероятность того, что событие произойдет или произойдет.
Например, когда подбрасывается монета, мы либо выиграем, либо выиграем. Это состояние вероятности. Вероятность наступления события равна отношению благоприятных исходов к общему количеству возможных исходов.
Представляется как Число благоприятных исходов
= __________________________________________________
Общее количество возможных исходов Пространство выборки:- Это набор всех возможных исходов. Обозначается S.
Например,
Образцовое пространство игральной кости, S = [1, 2, 3, 4, 5, 6]
Образцовое пространство монеты, S= [орел, решка] Типы задаваемых вопросов на конкурсном экзамене: 1) На основе монет 2) На основе игральных костей 3) На основе игральных карт 4)900 шары 5 ) Разное Важные вопросы: 1. Вопрос
Монета подбрасывается два раза. Какова вероятность того, что выпадет хотя бы одна решка? A) 3/4
B) 1/4
C) 1/3
D) 2/3
E) Ни один из этих TT, TH, HT,HH]
Общее количество способов = 2 × 2 = 4.
Любимые случаи = 3
P (A) = 3/4 Уловки:-
P (получить хотя бы одну решку )
= 1 – P (без головы)⇒ 1 – 1/4 = 3/4 2. Вопрос
Какова вероятность получить номерную карту при взятии из колоды 52 карт? A) 1/13
B) 1/9
C) 9/13
D) 13/11
E) Ничего из этого Ответ :- C
Сол:
11 Всего карточек.
Пронумерованные карты = 9 (2,3,4,5,6,7,8,9,10) каждой масти
Пронумерованные карты четырех мастей = 4 × 9 = 36
P (E) = 36/52 = 9 /13 3.Вопрос
Есть 7 фиолетовых зажимов и 5 коричневых зажимов. Два клипа выбираются один за другим без замены. Найти вероятность того, что первый будет коричневым, а второй фиолетовым. A) 1/35
B) 35/132
C) 1/132
D) 35/144
E) Ничего из перечисленного × P (P) = (5/12) x (7/11) = 35/132 4.Вопрос
Найдите вероятность выпадения суммы 8 при бросании двух игральных костей? A) 1/8
B) 1/5
C) 1/4
D) 5/36
E) 1/3 Ответ 😀
Sol:
Общее количество способов =
6 = 36 способов.
Благоприятные случаи = (2 , 6) (6, 2) (3, 5) (5, 3) (4, 4) — 5 способов.
P (A) = 5/36 = 5/36 5.Вопрос
Найдите вероятность того, что карта чести будет вытащена случайным образом из колоды из 52 карт. A) 4/13
B) 1/3
C) 5/12
D) 7/52
E) Ничего из перечисленного Ответ:-A
Sol:
Карты чести = 4 (A, J, Q, K) в каждой масти
Карты чести в 4 масти = 4 × 4 = 16
P (карта чести) = 16 /52 = 4/13 6. Вопрос
Какова вероятность того, что выпадет лицевая карта, если карта вытащена наугад из колоды из 52 карт? A) 1/13
B) 2/13
C) 3/13
D) 4/13
E) 5/13 Ответ:-C
Решение: лицевые карты = ( J,Q,K) в каждой масти
Лицевые карты 4 мастей = 3 × 4 = 12 карт.
P (лицевая карта) = 12/52 = 3/13 7.Вопрос
Если два игральных кубика брошены вместе, то какова вероятность того, что выпадет хотя бы одна «тройка»? A) 11/36
B) 1/12
C) 1/36
D) 13/25
E) 13/36 Ответ :- A
Sol:8 6 × 6 = 36.
Вероятность выпадения числа 3 хотя бы один раз
= 1 – (Вероятность не выпадения числа 4)
= 1 – (5/6) x (5/6)
= 1 – 25/36
= 11/36 либо 3, либо 4. A) 1/2
B) 1/3
C) 1/4
D) 2/3
E) 1/6 Ответ:- B
Решение:-
Всего результатов = 6
Вероятность выпадения одного числа при броске игральной кости = 1/6
Итак, P(3) = 1/6 и P(4) = 1/6 4
= P(3)+P(4)
= 1/6 + 1/6
= 1/3 9. Вопрос
Контейнер содержит 1 красный, 3 черных, 2 розовых и 4 фиолетовых камня. Если из контейнера наугад выбран один драгоценный камень, то какова вероятность того, что он будет фиолетовым или черным? A) 1/10
B) 3/10
C) 7/10
D) 9/10
E) Ничего из этого 1 + 3 + 2 + 4 ) = 10
вероятность получить фиолетовый драгоценный камень = 4/10
Вероятность получить черный драгоценный камень = 3/10
Теперь P (фиолетовый или черный) = P(фиолетовый) + P(черный)
= 7/10 10. Вопрос Вопрос
В банке 63 мяча ( 1,2,3,……., 63). Из банки наугад вынимают два шара один за другим без замены. какова вероятность того, что сумма вытащенных шаров четная? А) 5/21
Б) 3/23
В) 5/63
D) 19/63
E) Ни один из этих Ответ:- A
Sol.
Всего шаров = 63
Всего четных шаров = 31 ( 2 , 4 , 6,……., 62)
Теперь требуемая вероятность
= ³¹C₂/63C₂ = (31!/2!29!)/(63! /2!61!)
= (31×30/1×2)/(63×62/1×2)
= (31×30)/(63×62)
= 30/63×2
= 5 /21 11.Вопрос
В классе 30 учеников, 15 мальчиков и 15 девочек. На итоговом экзамене 5 мальчиков и 4 девочки получили пятерку. Если ученица выбрана случайным образом из класса, какова вероятность того, что она выберет девочку или отличницу? A) 1/4
B) 3/10
C) 1/3
D) 2/3
E) Ничего из этого количество мальчиков = 15 и общее количество девочек = 15 Кроме того, девочки, получившие пятерку = 4, и мальчики, получившие пятерку = 5
Вероятность выбора девочки = 15/30 Вероятность выбора отличницы= 9/30 Теперь отличницей может быть девушка.
Значит, вероятность его выбора = 4/30 Требуемая вероятность выбора девушки или отличницы
= 15/30 + 9/30 – 4/30
= 1/2 + 3/10 – 2/15
= 2/3 Вопрос
Какова вероятность того, что из колоды из 52 карт наугад вытащена карта туз или трефа? A) 2/13
B) 3/13
C) 4/13
D) 5/23
E) Ни один из этих
в колоде 13 клубных карт и 1 туз клубной карты. Теперь вероятность получения туза = 4/52 Вероятность получения трефы = 13/52 Вероятность получения туза трефы = 1/52 Требуемая вероятность получения туза или трефы = 4/52 + 13/52 – 1/52
= 16/52
= 4/13 13. Вопрос
Из колоды из 52 карт вынимается одна карта, хорошо перетасованная. Подсчитайте вероятность того, что карта не будет королем. А) 13/12
Б) 13/3
В) 13/7
D) 5/23
E) Ни один из этих Ответ:- A Решение: Хорошо перетасовка обеспечивает равновероятные результаты.
Общее количество королей колоды = 4 Количество благоприятных исходов F= 52 – 4 = 48 Количество возможных исходов = 52 Следовательно, искомая вероятность = 48/52 = 12/13 14.Вопрос
Если P(A) = 7/13, P(B) = 9/13 и P(A∩B) = 4/13, найдите значение P(A|B). A) 1/9
B) 2/9
C) 3/9
D) 4/9
E) Ничего из этого Ответ :- D
Решение: P(A| Б) = Р(А∩В)/Р(В) = (4/13)/(9/13) = 4/9. 15. Вопрос
Монета в одну рупию и монета в две рупии подбрасываются по одному разу, затем вычисляется выборочное пространство. A) [HH, HT, TH, TT] B) [HH, TT] C) [TH, HT] D) [HH, TH, TT] E) Ни один из этих Ответ:- А Решение: Результатом является либо Орел (H), либо Решка (T). Теперь решка на обеих монетах = (H,H) = HH Решка на обеих монетах = ( T, T) = TT Вероятность выпадения орла на монете в одну рупию и решки на монете в две рупии = (H, T) = HT И решка на монете в одну рупию и решка на монете в две рупии = (T, H) = TH Таким образом, выборочное пространство ,S = [HH, HT, TH, TT] 16 Вопрос
Есть 20 билетов с номерами от 1 до 20. Эти билеты перемешиваются, а затем случайным образом вытягивается билет. Найти вероятность того, что номер вытянутого билета кратен 4 или 5? Эти билеты перемешиваются, а затем случайным образом вытягивается билет. Найти вероятность того, что номер вытянутого билета кратен 4 или 5? A) 1/4
B) 2/13
C) 8/15
D) 9/20
E) Ничего из этого {1, 2, 3, 4, …., 19, 20} = 20 Кратность 4: 4, 8, 12, 16, 20 (5 билетов)
Кратность 5: 5, 10, 15, 20 (4 билета) Обратите внимание, что номер билета 20 кратен как 4, так и 5, поэтому мы посчитали его дважды. Следовательно, нам нужно вычесть единицу из общего количества. Общее количество билетов с номерами, кратными 4 или 5: 5 + 4 – 1 = 8 Общее количество билетов равно 20, поэтому вероятность выпадения билета с номером, кратным 4 или 5 равно: P = 8/20 = 2/5 = 0,4 Следовательно, вероятность того, что номер вытянутого билета кратен 4 или 5, составляет 0,4 или 40%. Направление ( 17 – 19):-
В школе общее количество учеников 300, 95 учеников любят только курицу, 120 учеников любят только рыбу, 80 учеников любят только баранину и 5 учеников не любят ничего вышеперечисленного. Если случайно выбран один ученик, найти вероятность того, что Если случайно выбран один ученик, найти вероятность того, что 17) Студент любит баранину. 18 ) он любит курицу или баранину 19 ) он не любит ни рыбу, ни баранину. Решение( 17-19):- Общее количество благоприятных исходов = 300 (Так как всего 300 учеников). Количество раз, когда выбирали любителя курицы = 95 (Поскольку 95 студентов любят курицу). Количество раз, когда выбирался любитель рыбы = 120. Количество раз, когда выбирался любитель баранины = 80. Сколько раз выбирался ученик, которому не нравится ни один из этих продуктов = 5. 17. Вопрос
Найдите вероятность того, что ученик любит баранину? A) 3/10
B) 4/15
C) 1/10
D) 1/15
E) Ни один из этих Ответ:- B
Решение:- 4 90 вероятность того, что учащийся любит баранину = 80/300
= 4/15 18. Вопрос
Какова вероятность того, что учащийся любит курицу или баранину? A) 7/12
B) 5/12
C) 3/4
D) 1/12
E) Ничего из этого Ответ:- A
найти учащегося, который любит курицу или баранину
= (95+80)/300
= 175/300
= 7/12 19. Вопрос Вопрос
Найдите вероятность того, что учащийся не любит ни рыбу, ни баранину. A) 1/2
B) 1/5
C) 1/3
D) 1/4
E) 1/6 Ответ:- C
Решение:-
Вероятность получить ученика, который не любит ни рыбу, ни баранину
= (300–120−80)/300
= 100/300
= 1/3 Направление ( 20-22) :-
В коробке 90 номерных знаков, пронумерованных от 1 до 90. Если из коробки наугад вынуть один номерной знак, то найти вероятность того, что 20) Это двузначное число 21) Число является полным квадратом 22) Число кратно 5 20. Вопрос
Найдите вероятность того, что это двузначное число. A) 1/9
B) 1/10
C) 9/10
D) 7/10
E) Ничего из этого Ответ:-C
Решение: 0 (Поскольку номера пронумерованы от 1 до 90). Количество благоприятных исходов
= 90 – 9 = 81 (здесь, кроме 1 до 9, остальные числа двузначные числа. ) ) Таким образом искомая вероятность
= количество благоприятных исходов/общее количество возможных исходов
= 81/90
= 9/10. 21. Вопрос
Какова вероятность того, что число является полным квадратом? A) 1/9
B) 1/10
C) 9/10
D) 1/7
E) Ни один из этих Ответ:- B
Решение:-
90.
Количество благоприятных исходов = 9 [здесь 1, 4, 9, 16, 25, 36, 49, 64 и 81 — правильные квадраты]
Таким образом, искомая вероятность = 9/90 =1/10 22.Вопрос
Найдите вероятность того, что число кратно 5. 0011 В) 1 /10
D) 1/8
E) 9/10 Ответ:- A
Решение:-
Всего возможных исходов = 90.
Число благоприятных исходов = 18 (здесь 5 × 1, 5 × 2, 5 × 3, …., 5 × 18 кратны 5). Таким образом, искомая вероятность = 18/90 =1/5
Как решать вероятностные задачи? (+ БЕСПЛАТНЫЙ рабочий лист!) Хотите знать, как решать задачи на вероятности? Здесь вы научитесь решать вероятностные словесные задачи. См. также- Как интерпретировать гистограмму
- Как интерпретировать круговые диаграммы
- Как решать перестановки и комбинации
- Как найти среднее, медиану, моду и диапазон заданных данных
Пошаговое руководство по решению вероятностных задач- Вероятность — это вероятность того, что что-то произойдет в будущем. Он выражается как число от нуля (никогда не может произойти) до \(1\) (всегда произойдет).
- Вероятность может быть выражена дробью, десятичной дробью или процентом.
- Чтобы решить вероятностную задачу, определите событие, найдите количество исходов события, затем используйте закон вероятности: )
Вероятностные задачи – пример 1: Если в корзине есть \(8\) красных и \(12\) синих шаров, какова вероятность того, что Джон выберет из корзины красный шар? Решение: Есть \(8\) красных шаров и \(20\) общее количество шаров. Следовательно, вероятность того, что Джон вытащит из корзины красный шар, равна \(8\) из \(20\) или \(\frac{8}{8+12}=\frac{8}{20} =\фракция{2}{5}\). Вероятностные задачи – Пример 2: В мешке находится \(18\) шаров: два зеленых, пять черных, восемь синих, коричневый, красный и один белый. Если из мешка наугад вынуть \(17\) шаров, какова вероятность того, что был удален коричневый шар? Решение: Если из мешка наугад вынуть \(17\) шаров, то в мешке останется один шар.
Вероятность выбора коричневого шара равна \(1\) из \(18\). Следовательно, вероятность не выбрать коричневый шар равна \(17\) из \(18\), а вероятность не выбрать коричневый шар после удаления \(17\) шаров такая же. Упражнения для решения вероятностных задач Решить.- Случайным образом выбирается число от \(1\) до \(10\). Найдите вероятность выбора \(4\) или меньше.
- Случайным образом выбирается число от \(1\) до \(50\). Найдите вероятность выбора кратных \(10\).
- Случайным образом выбирается число от \(1\) до \(10\).
 Найти вероятность выбора \(4\) и множителей \(6\). Найти вероятность выбора \(4\) и множителей \(6\). - Случайным образом выбирается число от \(1\) до \(10\). Найдите вероятность выбора числа, кратного \(3\).
- Случайным образом выбирается число от \(1\) до \(50\). Найдите вероятность выбора простых чисел.
- Случайным образом выбирается число от \(1\) до \(25\). Найти вероятность того, что не будет выбрано составное число.
Загрузить таблицу вероятностных задач- \(\color{blue}{\frac{2}{5}}\)
- \(\color{blue}{\frac{1}{10}}\)
- \(\color{blue}{\frac{1}{2}}\)
- \(\color{blue}{\frac{3}{10}}\)
- \(\color{blue }{\frac{3}{10}}\)
- \(\color{blue}{\frac{9}{25}}\)
Реза Реза — опытный преподаватель математики и эксперт по подготовке к экзаменам, который обучает студентов с 2008 года. помогла многим учащимся поднять свои баллы по стандартизированным тестам и поступить в колледжи своей мечты. Он работает со студентами индивидуально и в группах, ведет как живые, так и онлайн-курсы по математике, а также математическую часть стандартизированных тестов. 10 класс. Алгебра. Решение уравнений в целых числах. Делимость чисел. Задачи | Учебно-методический материал по алгебре (10 класс):Опубликовано 20.04.2019 — 23:54 — Прокофьева Тамара Александровна Задачи по теме Делимость чисел для домашнего задания или для тренировочной работы в группах Скачать:Предварительный просмотр:Делимость чисел №1. Решение уравнений в целых числах - Доказать, что на прямой нет ни одной точки с целочисленными координатами.
- Найти все целочисленные решения уравнения .
- Доказать, что уравнение не имеет решений в целых числах.
- Решить в целых числах уравнение -х+5ху-5у=7.
№2. Свойства делимости - Число а + 1 делится на 3. Доказать, что 4 + 7а делится на 3.
- Числа 2 + а и 35 – в делятся на 11. Доказать, что а + в делится на 11.
- Доказать, что при любом целом п значение выражения кратно 6.
- Доказать что число делится на 3 при любом натуральном п.

………………………………………………………………………………………………… Делимость чисел №1. Решение уравнений в целых числах - Доказать, что на прямой нет ни одной точки с целочисленными координатами.
- Найти все целочисленные решения уравнения .
- Доказать, что уравнение не имеет решений в целых числах.
- Решить в целых числах уравнение -х+5ху-5у=7.
№2. Свойства делимости - Число а + 1 делится на 3. Доказать, что 4 + 7а делится на 3.
- Числа 2 + а и 35 – в делятся на 11. Доказать, что а + в делится на 11.
- Доказать, что при любом целом п значение выражения кратно 6.
- Доказать что число делится на 3 при любом натуральном п.
………………………………………………………………………………………………… Делимость чисел №1. Решение уравнений в целых числах - Доказать, что на прямой нет ни одной точки с целочисленными координатами.
- Найти все целочисленные решения уравнения .
 - Доказать, что уравнение не имеет решений в целых числах.
- Решить в целых числах уравнение -х+5ху-5у=7.
№2. Свойства делимости - Число а + 1 делится на 3. Доказать, что 4 + 7а делится на 3.
- Числа 2 + а и 35 – в делятся на 11. Доказать, что а + в делится на 11.
- Доказать, что при любом целом п значение выражения кратно 6.
- Доказать что число делится на 3 при любом натуральном п.
По теме: методические разработки, презентации и конспектыМетодическая разработка элективного курса «Решение уравнений в целых числах»Публикация содержит методическую разработку элективного курса «Решение уравнений в целых числах» — теоретический, практический материал, историческую справку, список литературы. Предложенная презентац… Натуральные и целые числа. Делимость целых чисел. НОД и НОК натуральных чиселурок алгебры в 10 классе… Конспект урока по теме «Решение уравнений в целых числах»В ходе урока рассмотрены следующие методы решения уравнений в целых числах: разложение на множители; решение уравнения как квадратного относительно одной из переменных; графический. … … Организация учащихся к учебно-исследовательской деятельности по теме «Решение уравнений в целых числах»Актуальность исследования:В школьном курсе математики диофантовы уравнения практически не изучаются, эта тема затрагивается вскользь в восьмом классе, хотя задачи, основанные на решении уравнени… Олимпиадные задания. Решение уравнений в целых числахВ данной работе представлены различные способы решения уравнений в целых числах. Работа может быть использована при подготовке к олимпиадам, на кружковых и факультативных занятиях…. Решение уравнений в целых числахПодготовка к профильному ЕГЭ по математике… решение уравнений в целых числахПредставлена презентация, которая поможет на уроках алгебры, начиная с 7 класса, объяснить решение уравнений в целых числах. Уравнения постепенно усложняются, и их можно использовать для подготовки к … Поделиться: Решение простейших тригонометрических уравнений. 10 класс Похожие презентации: Элементы комбинаторики ( 9-11 классы) Применение производной в науке и в жизни Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде» Знакомство детей с математическими знаками и монетами Тренажёр по математике «Собираем урожай». Счет в пределах 10 Методы обработки экспериментальных данных Лекция 6. Корреляционный и регрессионный анализ Решение задач обязательной части ОГЭ по геометрии Дифференциальные уравнения Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи 1. Решение простейших тригонометрических уравнений.ДевизРешение : « Не делай никогда того, простейших чего не знаешь уравнений. , но научись тригонометрических всему, что следует знать» Пифагор 1 Арксинус у 1 а 0 -а arcsin а х -arcsin а -1 arcsin (-a)=-arcsin a 2 Арккосинус у П-arccos a 1 arccos а х -а 0 а 0 -1 arccos (-a) = П — arccos a 3 Арктангенс у 1 arctg a а х 0 -arctg a -а -1 arctg (-a)=-arctg a 4 Арккотангенс у -а 1 П-arcctg a а arcctg a х 0 0 arcctg (-a)=П-arcсtg a 5 Тест Значение обратных тригонометрических функций 6 Уравнения ПРОСТЕЙШИЕ тригонометрические 7 8. Решение простейших тригонометрических уравненийТема урока Решение простейших тригонометрических уравнений 8 Решение уравнения cosx=a cos x = a y 1 Частые случаи: cos x = 1 cos x = 0 cos x = -1 1 1 0x 0 1 9 Решение уравнения sinx=a sin x = a y y=1 2 1 Частые случаи: sin x = 1 sin x = 0 sin x = -1 y=0 1 1 1 x y = -1 2 10 Решение уравнения tgx=a y tg x = a a – любое число а 2 arctg a x 0 Частных случаев нет 18.07.2019 2 11 Решение уравнения ctgx=a y arcctg x = a a – любое число а arcctg a 0 Частных случаев нет 18.07.2019 12 x Формулы для решения простейших тригонометрических уравнений cos x = a sin x = a cos x = 1 sin x = 1 cos x = 0 sin x = 0 cos x = -1 sin x = -1 tg x = a ctg x = a 13 14 Домашнее задание 1.  Теория: Учебник — п.15, 16, 17 (опорный конспект) – прочитать, проанализировать, выучить формулы 2. Практика: Тест «Простейшие тригонометрические уравнения» – на сайте uztest.ru или Задачник – п.15,16, 17 № 5- 7 3. Творческое: Найти и рассмотреть способы решения тригонометрических уравнений 15 Вы молодцы! Каждый из вас «научился тому, что следует знать» Спасибо за урок ! 16 English
Русский
Правила NCERT Solutions for Class 10 Math Chapter 4 Страница № 81: Вопрос 1: Заполните последний столбец таблицы. С. № | Уравнение | Значение | Скажите, выполняется ли уравнение.
(Да/Нет) | (и) | х + 3 = 0 | х = 3 | — | (ii) | х + 3 = 0 | х = 0 | — | (iii) | х + 3 = 0 | х = — 3 | — | (iv) | х — 7 = 1 | х = 7 | — | (в) | х — 7 = 1 | х = 8 | — | (ви) | 5 х = 25 | х = 0 | — | (vii) | 5 х = 25 | х = 5 | — | (viii) | 5 х = 25 | х = — 5 | — | (икс) | | м = − 6 | — | (х) | | м = 0 | — | (xi) | | м = 6 | — |
Ответ: (i) x + 3 = 0 L. H.S. = x + 3 H.S. = x + 3 Положив x = 3, L.H.S. = 3 + 3 = 6 ≠ RHS ∴ Нет, уравнение не выполняется. (ii) х + 3 = 0 Л.Х.С. = x + 3 Положив x = 0, L.H.S. = 0 + 3 = 3 ≠ R.H.S. ∴ Нет, уравнение не выполняется. (iii) x + 3 = 0 Л.В.С. = x + 3 Положив x = −3, LHS = — 3 + 3 = 0 = RHS ∴ Да, уравнение выполнено. (iv) x − 7 = 1 L.H.S. = x − 7 Поставив x = 7, L.H.S. = 7 — 7 = 0 ≠ RHS ∴ Нет, уравнение не выполняется. (v) x − 7 = 1 L.H.S. = x − 7 Положив x = 8, LHS = 8 — 7 = 1 = RHS ∴ Да, уравнение выполнено. (vi) 5 x = 25 Л.В.С. = 5 x Положив x = 0, L.H.S. = 5 × 0 = 0 ≠ RHS ∴ Нет, уравнение не выполняется. (vii) 5 x = 25 Л. В.С. = 5 x В.С. = 5 x Положив x = 5, L.H.S. = 5 × 5 = 25 = правая сторона ∴ Да, уравнение выполнено. (viii) 5 x = 25 Л.В.С. = 5 x Положив x = −5, L.H.S. = 5 × (−5) = −25 ≠ RHS ∴ Нет, уравнение не выполняется. (икс)
«=»
2 Л.Х.С. «=» Поставив м = −6, Д. В. С. = ≠ Р.Х.С. ∴Нет, уравнение не выполняется. (х)
«=»
2 Л.Х.С. «=» Поставив м = 0, L.H.S. «=» ≠ Р.Х.С. ∴Нет, уравнение не выполняется. (xi)
«=»
2 Л.Х.С. «=» Положив м = 6, Л.В.С. «=» = R.H.S. ∴ Да, уравнение выполнено. Страница № 81: Вопрос 2: Проверить, является ли значение, указанное в скобках, решением данного уравнения: (a) n + 5 = 19 ( n = 1) (b) 7 n + 5 = 19 ( n = − 2) (c) 7 n + 5 = 19 ( n = 2) (d) 4 p − 3 = 13 ( p = 1) 6 (7 9) 4 p − 3 = 13 ( p = − 4) (f) 4 p − 3 = 13 ( p = 0) Ответ: (a) n + 9( n = 1) Ввод n = 1 в левую сторону, n + 5 = 1 + 5 = 6 ≠ 19 As L. H.S. ≠ R.H.S., H.S. ≠ R.H.S., Следовательно, n = 1 не является решением данного уравнения, n + 5 = 19. Помещение n = −2 в LHS, 7 n + 5 = 7 × (−2) + 5 = −14 + 5 = −9 ≠ 19 As L.H.S. ≠ RHS, Следовательно, n = −2 не является решением данного уравнения, 7 n + 5 = 19. (c) 7 n + 5 = 19 ( n = 2) Положив 3n 4 = 2 слева, 7 n + 5 = 7 × (2) + 5 = 14 + 5 = 19 = справа Как L.H.S. = R.H.S., Следовательно, n = 2 является решением данного уравнения, 7 n + 5 = 19. (d) 4 p − 3 = 13 ( p = 1) Положение p = 1 в левой плоскости, 4 p − 3 = (4 × 1) − 3 = 1 ≠ 13 Поскольку левая сторона ≠ правая сторона, данное уравнение, 4 p − 3 = 13. (e) 4 p − 3 = 13 ( p = −4) Помещение p = −4 в L.H.S., 4 9 — 3 = 4 × (-4) — 3 = — 16 — 3 = -19 ≠ 13 Как Л. Х.С. ≠ RHS, Х.С. ≠ RHS, Следовательно, p = −4 не является решением данного уравнения, 4 p − 3 = 13. (f) 4 p − 3 = 13 ( p = 0) Помещение p = 0 в Л.С., − 3 p 4 × 0) − 3 = −3 ≠ 13 Как L.H.S. ≠ R.H.S., Следовательно, p = 0 не является решением данного уравнения, 4 p − 3 = 13. Стр. метод ошибки: (i) 5 p + 2 = 17 (ii) 3 м − 14 = 4 Ответ: (i) 5 p + 2 = 17 Положив p = 1 в Л.С., (5 × 1) + .2 = .7 Вставка p = 2 в левой стороне, (5 × 2) + 2 = 10 + 2 = 12 ≠ в правой стороне. Ввод p = 3 в Л.С.С., (5 × 3) + 2 = 17 = П.С. Следовательно, p = 3 является решением данного уравнения. (ii) 3 м − 14 = 4 Укладка м = 4, (3 × 4) — 14 = -2 ≠ П.С. Укладка м = 5, (3 × 5) − 14 = 1 ≠ П. С. С. Укладка м = 6, (3 × 6) − 14 = 18 − 14 = 4 = R.H.S. Следовательно, м = 6 является решением данного уравнения. Страница № 81: Вопрос 4: Напишите уравнения для следующих утверждений: (i) Сумма чисел x и 4 равна 9. (ii) 2 вычесть из y равно 8. (iii) Десять раз a равно 70. (iv) Число b , разделенное на 5, дает 6. (v) Три четверти t 1 3 равно (vi) Семь раз m плюс 7 дает 77. (vii) Четвертая часть числа x минус 4 дает 4. (viii) Если из 6 умножить на 6 , вы получите 60. (ix) Если вы прибавите 3 к одной трети z , вы получите 30. Ответ: (I) x + 4 = (ii) y — 2 = 8 (iii) 10 A = 70 (iv) (v) 666 (vi) Семь раз по м равно 7 м . 7 м + 7 = 77 (vii) Четвертая часть числа x равна . (viii) Шесть раз y равно 6 y . 6 y − 6 = 60
(ix) Одна треть от z есть . Видео Решение простых уравнений (Страница: 81 , Q.No.: 4) NCERT Решение для 10 класса по математике — простые уравнения 81 , Вопрос 4 Страница № 81: Вопрос 5: Написать следующие уравнения в формулярных формах: (i) p + 4 = 15 (ii) m − 7 = 3 (iii) 2 m = 7 (iv) (v) (vi ) 3 p + 4 = 25 (vii) 4 p − 2 = 18 (viii) Ответ: (i) Сумма p и 4 равна 15. (ii) 7 вычитается из m равно 3. (iii) Удвоенное число m равно 7. (iv) Одна пятая от м равна 3. (v) Три пятых от м равна 6. (vi) Три раза числа p , при добавлении к 4 дает 25 (vii) Когда 2 вычитается из четырех раз числа p , получается 18. (viii) Когда 2 прибавляется к половине числа p , это дает 8. Страница № 82: Вопрос 6: Составьте уравнение для следующих случаев: (i) Ирфан говорит, что у него 7 шариков больше, чем в пять раз больше, чем у Пармита. . У Ирфана 37 шариков. (Возьмем м за число шариков Пармита.) (ii) Отцу Лакшми 49 лет. Он на 4 года старше, чем в три раза старше Лакшми. (Примите возраст Лакшми равным х лет.) (iii) Учитель сообщает классу, что самая высокая оценка, полученная ученицей в ее классе, равна удвоенной самой низкой отметке плюс 7. Наивысшая оценка равна 87. (Возьмите самый низкий балл должен быть l .) (iv) В равнобедренном треугольнике угол при вершине вдвое больше угла при основании. (Пусть угол при основании равен b в градусах. Помните, что сумма углов треугольника равна 180 градусам.) Ответ: (i) Пусть у Пармита м шариков. 5 × Количество шариков у Пармита + 7 = Количество шариков у Ирфана старый. 3 × возраст Лакшми + 4 = возраст отца Лакшми 2 × Самые низкие баллы + 7 = Высшие баллы 2 × l + 7 = 87 2 l + 7 = 87 (iv) Два угла равнобедренного треугольника равны. Пусть угол основания равен b . Угол вершины = 2 × угол основания = 2 B Сумма всех внутренних углов A Δ = 180 ° B + B + 2 B = 180 ° 4 B = 180 °
. Простые и уравнения. Район. Простые имущества. (Страница: 82 , Q.No.: 6) NCERT Решение для класса 10 по математике — простые уравнения 82 , Вопрос 6 Номер страницы 86: Вопрос 1: Дайте сначала
шаг, который вы будете использовать для разделения переменной, а затем решить
уравнение: (а) х + 1 = 0 (б) х + 1 = 0 (в) х — 1 = 5 (г) х + 6 = 2 (д) у — 4 = — 7 (е) у — 4 =
4 (ж) у + 4 = 4 (h) y + 4 = − 4 Ответ: (a) x − 1 = 0 Прибавив 1 к обеим частям данного уравнения, мы получим х — 1 + 1 = 0 + 1 х = 1 (б) х + 1 = 0 Вычитая 1 из обеих частей данного уравнения, мы получаем х + 1 — 1 = 0 — 1 х = -1 (в) х —
1 = 5 Прибавив 1 к обеим частям данного уравнения, мы получим х — 1 + 1 = 5 + 1 х = 6 (г) х + 6 = 2 Вычитая 6 из обеих частей данного уравнения, мы получаем х + 6 — 6 = 2 — 6 х = −4 (д) у − 4 = −7 Прибавив 4 к обеим частям данного уравнения, мы получим г — 4 + 4 = — 7 + 4 г = −3 (е) г − 4 = 4 Прибавив 4 к обеим частям данного уравнения, мы получим у — 4 + 4 = 4 + 4 у = 8 (г) у + 4 = 4 Вычитая 4 из обеих частей данного уравнения, мы получаем г + 4 — 4 = 4 — 4 г = 0 (ч) г + 4 = −4 Вычитая 4 из обеих частей данного уравнения, мы получаем г + 4 — 4 = — 4 — 4 y = −8 Номер страницы 86: Вопрос 2: Дайте сначала
шаг, который вы будете использовать для разделения переменной, а затем решить
уравнение: (а) 3 л = 42 (б) (в) (г) 4 х = 25 (д) 8 у = 36 (е) (ж)
(ч) 20 т = − 10 Ответ: (а) 3 l = 42 Разделив обе части данного уравнения на 3, получим л = 14 (б) Умножая обе части данного уравнения на 2, получаем б = 12 (в) Умножив обе части данного уравнения на 7, получим р = 28 (г) 4 х = 25 Разделив обе части данного уравнения на 4, получим х = (д) 8 у = 36 Разделив обе части данного уравнения на 8, получим г = (ф) Умножая обе части данного уравнения на 3, получаем (г) Умножая обе части данного уравнения на 5, получаем
(ч) 20 т = −10 Разделив обе части данного уравнения на 20, получим Страница № 86: Вопрос 3: Укажите шаги, которые вы будете использовать для разделения переменной, а затем решите уравнение: 7 = 17 (в) (г) Ответ: (a) 3 n − 2 = 46 Прибавив 2 к обеим частям данного уравнения, получим Разделив обе части данного уравнения на 3, получим n = 16 (b) 5 m + 7 = 17 Вычтя 7 из обеих частей данного уравнения, получим 9000 5 м + 7 — 7 = 17 — 7 5 м = 10 Разделив обе части данного уравнения на 5, получим (в) Умножив обе части данного уравнения на 3, получим Разделив обе части данного уравнения на 20, получим получаем (d) Умножив обе части данного уравнения на 10, получим Разделив обе части данного уравнения на 3, получим | p = 220420007 Страница № 86: Вопрос 4: Решите
следующие уравнения: (а) 10 р = 100 (б) 10 р + 10 = 100 (в) (г) (д) (е) 3 с = − 9 (г) 3 с + 12 = 0 (h) 3 с = 0 (i) 2 q = 6 (j) 2 q − 6 = 0 (k) 2 q + 6 = 0 (l) 2 q + 6 = 12 Ответ: (a) 10 p = 100 (б) 10 р + 10 = 100 10 р + 10 — 10 = 100 — 10 10 р = 90 (в) (г) (д) (е) 3 с = −9 (г) 3 с + 12 = 0 3 с + 12 − 12= 0 − 12 3 с = −12 (ч) 3 с = 0 (i) 2 q = 6 (к) 2 q − 6 = 0 2 q − 6 + 6 = 0 + 6 2 q = 6 (к) 2 кв + 6 = 0 2 q + 6 — 6 = 0 — 6 2 q = −6 (левый) 2 q + 6 = 12 2 q + 6 — 6 = 12 — 6 2 q = 6 Страница № 89: Вопрос 1: Решите
следующие уравнения. (а) (б) 5 т + 28 = 10 (в) (г) (д) (е) (ж) (з) 6 z + 10 = − 2 (i) (j) Ответ: (a) (Транспонирование
к
R.H.S.) Разделив обе части на 2, (б) 5 т + 28 = 10 5 t = 10 − 28 = −18 (перенос 28 в правую сторону) Разделив обе части на 5, (в) (Транспонирование
3 по правой стороне) Умножение обеих сторон на 5, a = −1 × 5 = −5 (г) (Транспонирование
7 по правой стороне) Умножение обеих сторон на 4, q = −8 (д) Умножение обеих сторон на 2, 5 х = -10 х 2 = -20 Разделив обе части на 5, (ф) Умножение обеих сторон на 2, Разделив обе части на 5, (г) (Транспонирование справа) Разделив обе части на 7, (ч) 6 z + 10 = −2 6 z = − 2 − 10 = −12 (перенос 10 в
R. H.S.) H.S.) Разделив обе части на 6, (и) Умножение обеих сторон на 2, Разделив обе части на 3, (к) (Транспонирование
−5 до правой стороны) Умножение обеих сторон на 3, 2 б = 8 × 3 = 24 Разделив обе части на 2, б =
«=»
12 Страница № 89: Вопрос 2: Решите
следующие уравнения. (а) 2 ( х + 4) = 12 (б) 3 ( н — 5) = 21 (в) 3 ( н − 5) = − 21 (d) −4 (2 + x ) = 8 (e) 4(2 − х ) = 8 Ответ: (а) 2 ( х + 4) = 12 Разделив обе части на 2, x = 6 − 4 = 2 (перенос 4 в правую сторону) (b) 3 ( n − 5) = 21 Разделив обе части на 3, n = 7 + 5 = 12 (перенос −5 в правую сторону) (c) 3 ( n − 5) = −21 Разделив обе части на 3, n = − 7 + 5 = −2 (перенос −5 в
П. С.С.) С.С.) (г) −4
(2 + х ) = 8 Разделив обе стороны на −4, x = − 2 − 2 = −4 (перенос 2 в правую сторону) (e) 4 (2 − х ) = 8 Разделив обе части на 4, 2 − х = 2 − x = 2 − 2 (Транспонирование 2 в правую сторону) − х = 0 х = 0 Страница № 89: Вопрос 3: Решите
следующие уравнения. (а) 4 = 5
( р — 2) (б) — 4 = 5 ( р — 2) (в) 16 = 4
+ 3 ( t + 2) (г) 4 + 5 ( р — 1) = 34 (д) 0 = 16
+ 4 ( м − 6) Ответ: (а) 4 = 5
( стр − 2) Разделив обе части на 5, (б) −
4 = 5 ( р — 2) Разделив обе части на 5, (в) 16 = 4
+ 3 ( т + 2) 16 − 4 = 3 ( t + 2) (Перенос 4 в левую сторону) 12 = 3 ( т + 2) Разделив обе части на 3, 4 = т + 2 4 − 2 = t (Транспонирование 2 в левую сторону) 2 = т (г) 4 + 5
( п — 1) = 34 5 ( p — 1) = 34 — 4 = 30 (перенос 4 в правую сторону) Разделив обе части на 5, p = 6 + 1 = 7 (перенос −1 в правую сторону) (e) 0 = 16
+ 4 ( м − 6) 0 = 16 + 4 м − 24 0 = −8 + 4 м 4 м = 8 (перенос −8 в левую сторону) Разделив обе части на 4, м = 2 Страница № 89: Вопрос 4: (a) Конструкция 3
уравнения начинающиеся с х = 2 (б) Конструкция 3
уравнения, начинающиеся с x = − 2 Ответ: (a) x = 2 Умножение
с обеих сторон на 5, 5 x = 10 (i) Вычитание
3 с обеих сторон, 5 x − 3 = 10 − 3 5 х − 3 = 7 (ii) Разделение
обе стороны на 2, (b) x = −2 Вычитание
2 с обеих сторон, х − 2 = − 2 − 2 x − 2 = −4 (i) Опять же, x = −2 Умножение
на 6, 6 × х = -2 х 6 6 х = −12 Вычитание
12 с обеих сторон, 6 x − 12 = − 12 − 12 6 x − 12 = −24 (ii) Добавление
24 на обе стороны, 6 x − 12 + 24 = − 24 + 24 6 x + 12 = 0 (iii) Страница № 91: Вопрос 1: Составьте уравнения и решите их, чтобы найти неизвестные числа в таблице. следующие случаи: следующие случаи: а) прибавьте число от 4 до 8 раз; вы получаете 60. (b) Одна пятая числа минус 4 дает 3. в) Если я возьму три четверти числа и прибавлю к нему 3, то получу 21. (d) Когда я вычел 11 из удвоенного числа, в результате получилось 15. д) Мунна вычитает из 50 тетрадей в три раза больше, чем у него.
находит результат равным 8. (f) Ибенхаль загадывает число. Если она прибавит к нему 19 и поделит
суммируй на 5, она получит 8. (ж) Анвар загадывает число. Если он отнимет 7 у
из
число, результат 23. Ответ: (a) Пусть число будет х . 8
умноженное на это число = 8 x 8 x + 4 = 60 8 х = 60 − 4 (Транспонирование 4 в правую сторону) 8 x = 56 Разделение
обе стороны на 8, (б) Пусть число будет х . Одна пятая
этого числа = (Транспонирование
от −4 до правой) Умножение
с обеих сторон на 5, (c) Пусть число будет х . Три четверти
этого числа = (Транспонирование
3 до R.H.S.) Умножение
с обеих сторон по 4,
Разделение
с обеих сторон на 3, (d) Пусть число будет х . Дважды
этого числа = 2 x 2 x − 11 = 15 2 x = 15 + 11 (преобразование −11 в правую сторону) 2 x = 26 Разделение
с обеих сторон по 2, x = 13 (e) Пусть число
книги должны быть x . Трижды
количество книг = 3 x 50
− 3 х = 8 −
3 x = 8 −50 (перенос 50 в правую сторону) −3 х = −42 Разделение
с обеих сторон на −3, (f) Пусть число будет х . Умножение
с обеих сторон по 5, x + 19 = 40 х = 40 − 19 (перенос 19 в правую сторону) x = 21 (г) Пусть число будет х . этого числа = Умножение
обе стороны на 2, Разделение
с обеих сторон на 5, Страница № 91: Вопрос 2: Решите следующее: (a) Учитель сообщает классу, что самая высокая оценка, полученная учеником в ее классе, в два раза выше самой низкой оценки плюс 7. Самый высокий балл 87. Какой самый низкий балл? (б) В равнобедренном треугольнике углы при основании равны. Угол при вершине равен 40°. Чему равны углы при основании треугольника? (Помните, сумма трех углов треугольника равна 180°). (c) Сачин набрал в два раза больше очков, чем Рахул. Вместе их пробеги не дотянули до двух столетий. Сколько пробежек сделал каждый? Ответ: (a) Пусть наименьший результат будет l . 2 × самые низкие оценки + 7 = самые высокие оценки 2 L + 7 = 87 2 L = 87 — 7 (транспозирование 7 к R.H.S. на 2, Таким образом, наименьший балл равен 40.
(b) Пусть углы при основании равны b . Сумма всех внутренних углов треугольника равна 180°. B + B + 40 ° = 180 ° 2 B + 40 ° = 180 ° 2 B = 180º — 40º = 140º (перевод 40 ° до R.H.S.). на 2, Следовательно, углы при основании треугольника равны 70º.
(c) Пусть счет Рахула будет x . Следовательно, оценка Сачина = 2 x Оценка Рахула + Оценка Сачина = 200 — 2 2 x + x = 198 3 x = 198 Dividing Dividing Scies Siste SIDE -SIDS 3, 3, 3, 3, 3, 3, 3, 3 x = 198 . x = 66 Оценка Рахула = 66 Оценка Сачина = 2 × 66 = 132 10 математика — простые уравнения 91 , Вопрос 2 Страница № 91: Вопрос 3: Решите следующее: (i) Ирфан говорит, что у него на 7 шариков больше, чем в пять раз больше, чем у Пармита. У Ирфана 37 шариков. Сколько шариков у Пармита? У Ирфана 37 шариков. Сколько шариков у Пармита? (ii) Отцу Лакшми 49 лет. Он на 4 года старше, чем в три раза старше Лакшми. Сколько лет Лакшми? (iii) Жители Сундарграма посадили деревья в деревенском саду. Некоторые из деревьев были плодовыми деревьями. Количество неплодовых деревьев в два и более раза превышало количество плодовых деревьев. Сколько плодовых деревьев было посажено, если неплодовых было посажено 77? Ответ: (i) Пусть шарики Пармита равны x . 5 умноженное на количество шариков у Пармита = 5 x 5 x + 7 = 37 5 x = 37 − 7 = 30 , Следовательно, у Пармита 6 шариков.
(ii) Пусть возраст Лакшми будет х года. 3 × возраст Лакшми + 4 = возраст ее отца 3 x + 4 = 49 3 x = 49 — 4 (транспонирование от 4 до R.H.S.) 3 x = 45 Разделение обеих сторон на 3, x = 15 x = 15 x = 15 , поэтому Лакшми 15 лет. (iii) Пусть количество фруктовых деревьев равно x . 3 × количество фруктовых деревьев + 2 = количество неплодовых деревьев 3 x + 2 = 77 3 x = 77 − 2 (перенос 2 в правую сторону) 3 x = 75 Разделив обе части уравнения на 3, x = 25 Следовательно, количество фруктовых деревьев равно 25. , Q.No.: 3) NCERT Решение для класса 10 по математике — простые уравнения 91 , Вопрос 3 Номер страницы 92: Вопрос 4: Решите следующую загадку: Я число, Скажи мою личность! Возьми меня семь раз больше И добавь пятьдесят! Чтобы достичь тройного века Вам нужно еще сорок! Ответ: Пусть число будет х . (7 x + 50) + 40 = 300 7 x + 90 = 300 7 x = 300 — 90 (транспозирование с 90 до R.H. Разделив обе части на 7, x = 30 Следовательно, число равно 30. Решения NCERT для главы 3, класс 10, математика Вы учитесь… Получите решения NCERT для главы 3, класс 10 — Пара линейных уравнений с двумя переменными в Teachoo. Ответы на все упражнения, примеры и дополнительные вопросы были предоставлены с видео каждого вопроса Мы изучали линейные уравнения с двумя переменными в классе 9, мы будем изучать пары из линейных уравнений в этой главе. В этой главе мы узнаем - Что такое Линейные уравнения с двумя переменными
- Преобразование утверждений в уравнения и построение графика этих линейных уравнений
- Возможный тип графиков для пары линейных уравнений с двумя переменными — две пересекающиеся линии, две параллельные линии, совпадающие прямые
- Нахождение решение уравнений по графикам
- Непротиворечивость уравнений путем нахождения отношения числа 1 /a 2 , b 1 /b 2 , c 1 /c 2
- и проверка того, являются ли линии
- Совпадающие линии (Бесконечное множество решений)
- Параллельные линии ( Нет решений)
Решение пары линейных уравнений- Замена Метод
- Ликвидация Метод
- Перекрестное умножение Метод
Решение сложных уравнений типа 2/x + 3/y = 4 путем замены переменных (например, подстановка p = 1/x, q = 1/y и решение) Решение вопросов-утверждений путем сначала составления уравнений, а затем решения Щелкните ссылку на упражнение или тему ниже, чтобы начать выполнение главы Примечание. При нажатии на ссылку открывается первый вопрос. Чтобы открыть любой другой вопрос упражнения, перейдите в конец страницы. Есть список со стрелками, в котором есть все вопросы (с важных вопроса также отмечено) При нажатии на ссылку открывается первый вопрос. Чтобы открыть любой другой вопрос упражнения, перейдите в конец страницы. Есть список со стрелками, в котором есть все вопросы (с важных вопроса также отмечено)
Последовательный порядок Пример 3.1 Пример 3.2 Пример 3.3 Пример 3.4 Пример 3.5 Пример 3.6 Примеры Пример 3.7 (необязательно) Вопросы по делу (MCQ) MCQ от NCERT Exemplar
Концепция Составление уравнений графически и алгебраически Нахождение соотношений (согласованность) Графическое решение уравнений Замена Ликвидация Метод перекрестного умножения Смешанные вопросы — Уравнение Смешанные вопросы — Составим уравнение
Что в нем? Получите решения NCERT для главы 3, класс 10 — Пара линейных уравнений с двумя переменными в Teachoo. Ответы на все упражнения, примеры и необязательные вопросы были предоставлены с видео каждого вопроса Ответы на все упражнения, примеры и необязательные вопросы были предоставлены с видео каждого вопроса Мы изучали линейные уравнения с двумя переменными в классе 9, в этой главе мы изучим пары из линейных уравнений. В этой главе мы узнаем - Что такое Линейные уравнения с двумя переменными
- Преобразование утверждений в уравнения и построение графика этих линейных уравнений
- Возможный тип графиков для пары линейных уравнений с двумя переменными — две пересекающиеся линии, две параллельные линии, совпадающие прямые
- Нахождение решение уравнений по графикам
- Непротиворечивость уравнений путем нахождения отношения a 1 /a 2 , b 1 /b 2 , c 1 /c 2 2 2262
- и проверка того, являются ли линии
- Совпадающие линии (Бесконечное множество решений)
- Параллельные линии ( Нет решений)
Решение пары линейных уравнений- Замена Метод
- Исключение Метод
- Перекрестное умножение Метод
Решение сложных уравнений типа 2/x + 3/y = 4 путем замены переменных (например, подстановка p = 1/x, q = 1/y и решение) Решение вопросов-утверждений путем сначала составления уравнений, а затем решения Щелкните ссылку на упражнение или тему ниже, чтобы начать выполнение главы Примечание. Значения функции и точки максимума и минимума Назад к списку Значения функции и точки максимума и минимумаНаибольшее значение функции Наменьшее значение функции Точки max Точки min
Как говорил крестный отец: «Ничего личного». Только производные! Статью Как посчитать производные? надеюсь, ты изучил, без этого дальше будет проблематично. 12 задание по статистике считается достаточно трудным, а все потому, что ребята не прочитали эту статью (joke). В большинстве случаев виной всему невнимательность. 12 задание бывает двух видов: - Найти точку максимума / минимума (просят найти значения «x»).
- Найти наибольшее / наименьшее значение функции (просят найти значения «y»).
Как же действовать в этих случаях? Найти точку максимума / минимума- Взять производную от предложенной функции.
- Приравнять ее к нулю.
 - Найденный или найденные «х» и будут являться точками минимума или максимума.
- Определить с помощью метода интервалов знаки и выбрать, какая точка нужна в задании.
Задания с ЕГЭ: Найдите точку максимума функции - Приравняем ее к нулю:
- Получили одно значение икса, для нахождения знаков подставим −20 слева от корня и 0 справа от корня в преобразованную производную (последняя строчка с преобразованием):
Все верно, сначала функция возрастает, затем убывает — это точка максимума!
Ответ: −15 Найдите точку минимума функции - Преобразуем и возьмем производную:
- Получается один корень «−2», однако не стоит забывать о «−3», она тоже будет влиять на изменение знака.
- Отлично! Сначала функция убывает, затем возрасает — это точка минимума!
Ответ: −2 Найти наибольшее / наименьшее значение функции- Взять производную от предложенной функции.

- Приравнять ее к нулю.
- Найденный «х» и будет являться точкой минимума или максимума.
- Определить с помощью метода интервала знаки и выбрать, какая точка нужна в задании.
- В таких заданиях всегда задается промежуток: иксы, найденные в пункте 3, должны входить в данный промежуток.
- Подставить в первоначальное уравнение полученную точку максимума или минимума, получаем наибольшее или наименьшее значение функции.
Задания с ЕГЭ: Найдите наибольшее значение функции на отрезке [−4; −1]
- Преобразуем и возьмем производную:
- «3» не вдходит в промежуток [−4; −1]. Значит, остается проверить «−3» — это точка максимума?
- Подходит, сначала функция возрастает, затем убывает — это точка максимума, и в ней будет наибольшее значение функции. Остается только подставить в первоначальную функцию:
Ответ: −6 Найдите наибольшее значение функции на отрезке [0; 1,5π] - Берем производную:
- Находим, чему равняется sin(x):
- Но такое невозможно! Sin(x).
 .. .. - Получается, что уравнение не имеет решения, и в таких ситуациях нужно подставлять крайние значения промежутка в первоначальное уравнение:
- Наибольшее значение функции равно «11» при точке максимума (на этом отрезке) «0».
Ответ: 11 Выводы: - 70% ошибок заключается в том, что ребята не запоминают, что в ответ на наибольшее/наименьшее значение функции нужно написать «y», а на точку максимума/минимума написать «х».
- Нет решения у производной при нахождении значений функции? Не беда, подставляй крайние точки промежутка!
- Ответ всегда может быть записан в виде числа или десятичной дроби. Нет? Тогда перерешивай пример.
- В большинстве заданий будет получаться одна точка и наша лень проверять максимум или минимум будет оправдана. Получили одну точку — можно смело писать в ответ.
- А вот с поиском значения функции так поступать не стоит! Проверяйте, что это нужная точка, иначе крайние значения промежутка могут оказаться больше или меньше.

Будь в курсе новых статеек, видео и легкого математического юмора.
Как найти точки минимума и максимума функции, анализируя функцию, её производную и область определенияПоиск точки максимума и минимума функции — довольно распространенная задача в математическом анализе. Иногда требуется экстремум. Многие думают, что под словом «экстремум» подразумевают наибольшее или наименьшее значение функции. Это не совсем верно. Значение может быть наибольшим или минимальным, но не являться экстремумом. Содержание: - Глобальный и локальный максимум
- Исследование
- Область допустимых аргументов
- Асимптоты
- Производная и экстремумы
- Концы интервала и сравнение результатов
- Видео
Глобальный и локальный максимумМаксимум бывает локальным или глобальным. Точка локального максимума — это аргумент, который при подстановке в f(x) даёт значение не меньше, чем в других точках из области около этого аргумента. Для глобального максимума эта область расширяется до всей области допустимых аргументов. Для минимума всё наоборот. Экстремум — это локальное экстремальное — минимальное или максимальное — значение. Для глобального максимума эта область расширяется до всей области допустимых аргументов. Для минимума всё наоборот. Экстремум — это локальное экстремальное — минимальное или максимальное — значение. Как правило, если математиков интересует глобально самое большое значение f(x), то в интервале, не на всей оси аргументов. Подобные задачи обычно сформулированы фразой «найдите точку максимума функции на отрезке». Здесь подразумевается, что надо выявить аргумент, при котором она не меньше, чем на всём остальном указанном отрезке. Поиск локального экстремума является одним из шагов решения такой задачи. Дано y = f(x). Требуется определить пик функции на указанном отрезке. f(x) может достигать его в точке: - экстремума, если она попадает в указанный отрезок,
- разрыва,
- ограничивающей заданный отрезок.
ИсследованиеПик f(x) на отрезке или в интервале находится путём исследования данной функции. План исследования для нахождения максимума на отрезке (или интервале): - Найти область допустимых аргументов и пересечения этой области с областью исследования.
 2 определена на всей оси аргументов. А y = 1/x определена для всех аргументов, кроме x = 0. 2 определена на всей оси аргументов. А y = 1/x определена для всех аргументов, кроме x = 0.Найти пересечение области допустимых аргументов и исследуемого отрезка (интервала) требуется для того, чтобы исключить из рассмотрения ту часть интервала, где функция не определена. Например, требуется найти минимум y = 1/x на отрезке от -2 до 2. На самом деле требуется исследовать два полуинтервала от -2 до 0 и от 0 до 2, так как уравнение у = 1/0 не имеет решения. АсимптотыАсимптота — это такая прямая, к которой функция тянется, но не дотягивается. Если f(x) существует на всей числовой прямой и неразрывна на ней, то вертикальной асимптоты у неё нет. Если же она разрывна, то точка разрыва является вертикальной асимптотой. Для y = 1/x асимптота задаётся уравнением x = 0. Эта функция тянется к нулю по оси аргументов, но дотянется до него, только устремившись в бесконечность. Если на исследуемом отрезке имеется вертикальная асимптота, около которой функция стремится в бесконечность с плюсом, то пик f(x) на здесь не определяется. 3. У неё не может быть экстремумов, она убывает на всей оси аргументов. 3. У неё не может быть экстремумов, она убывает на всей оси аргументов. 2) Достаточно, чтобы при пересечении точки экстремума у производной менялся знак. То есть, до максимума f(x) растёт, а после максимума она убывает — производная была положительной, а стала отрицательной. После того как аргументы для локального максимума были найдены их надо подставить в исходное уравнение и получить максимальное значение f(x). Концы интервала и сравнение результатовПри поиске максимума на отрезке необходимо проверить значение на концах отрезка. Например, для y = 1/x на отрезке [1; 7] максимум будет в точке x = 1. Даже если внутри отрезка есть локальный максимум, нет никакой гарантии, что значение на одном из концов отрезка не будет больше этого максимума. Теперь необходимо сравнить значения в точках разрыва (если f(x) здесь не стремится в бесконечность), на концах исследуемого интервала и экстремум функции. Наибольшее из этих значений и будет максимумом функции на заданном участке прямой. Для задачи с формулировкой «Найдите точку минимума функции» необходимо выбрать наименьшее из локальных минимумов и значений на концах интервала и в точках разрыва. Видео Максимальные и минимальные значения — Подход к исчислению Подход к C A L C U L U S Содержание | Дом 10 МЫ ГОВОРИМ, ЧТО ФУНКЦИЯ f ( x ) имеет относительное максимальное значение при x = a ,
, если f ( a ) равно 90 017 больше , чем любое значение, непосредственно предшествующее или следующее за ним. Мы называем это «относительным» максимумом, потому что другие значения функции на самом деле могут быть больше. Мы говорим, что функция f ( x ) имеет относительное минимальное значение при x = b ,
, если f ( b ) на меньше 90 018, чем любое значение, непосредственно предшествующее или следующее за ним. Опять же, другие значения функции на самом деле могут быть меньше. При таком понимании мы отбросим термин «относительный». Значение функции, значение y , максимальное или минимальное, называется экстремальным значением. Теперь, что характеризует график при экстремальном значении? Касательная к кривой горизонтальна . Мы видим это в точках A и B . Наклон каждой касательной линии — производная при оценке a или b — это 0, f ‘ ( x ) = 0, Более того, в точках непосредственно от слева от максимума — в точке C — наклон касательной положителен: f ‘ ( x ) > 0. справа — в точке D — наклон отрицательный: f ‘ ( x ) Другими словами, максимум f ‘ ( x ) меняет знак с + на — . Как минимум, f ‘ ( x ) меняет знак с − на + . Мы видим, что в точках E и F . Мы видим, что в точках E и F . Также можно заметить, что в максимуме при A график вогнут вниз. (Тема 14 Precalculus.) Хотя, как минимум, на B он вогнут вверх. Значение x , при котором функция имеет либо максимум, либо минимум, называется критическим значением. На рисунке — — критические значения x = a и x = b . Критические значения определяют точки поворота, в которых касательная параллельна оси x . Критические значения — если они есть — будут решений от до f ‘ ( x ) = 0, Пример 1. Пусть f ( x ) = x 2 − 6 х + 5. Есть ли критические значения — поворотные точки? Если да, то определяют ли они максимум или минимум? И каковы координаты на графике этого максимума или минимума? Решение . f ‘ ( x ) = 2 x − 6 = 0 означает x = 3. (Урок 9 алгебры.) (Урок 9 алгебры.) x = 3 — единственное критическое значение. Это х -координата точки поворота. Чтобы определить координату y , оцените f при этом критическом значении — оцените f (3): | ф ( х ) | = | x 2 − 6 x + 5 | | | | f (3) | = | 3 2 − 6 · 3 + 5 | | | | | = | −4. |
Крайнее значение равно −4. Чтобы увидеть, является ли это максимумом или минимумом, в этом случае мы можем просто посмотреть на график. f ( x ) — это парабола, и мы видим, что точка поворота является минимумом. Найдя значение x , где производная равна 0, то мы обнаружили, что вершина параболы находится в точке (3, −4). Но не всегда мы сможем посмотреть на график. Алгебраическое условие минимума состоит в том, что f ‘ ( x ) меняет знак с − на + . Это мы видим в точках E , B , F выше. Значение наклона увеличивается. Теперь сказать, что наклон увеличивается, значит сказать, что при критическом значении вторая производная (Урок 9) — скорость изменения наклона — плюс . Опять же, вот f ( x ): | ф ( х ) | = | x 2 − 6 x + 5. | | | | f ‘ ( x ) | = | 2 х − 6, | | | | f » ( x ) | = | 2. |
f » оценивается при критическом значении 3 — f» (3) = 2 — положительный. Это говорит нам алгебраически, что критическое значение 3 определяет минимум. Это говорит нам алгебраически, что критическое значение 3 определяет минимум. Достаточные условия Теперь мы можем сформулировать эти достаточные условия для экстремальных значений функции при критическом значении и : Функция имеет минимальное значение при x = a if f ‘ ( a ) = 0
и f » ( a ) = a положительное число. Функция имеет максимальное значение при x = a if f ‘ ( a ) = 0
и f » ( a ) = a отрицательное число. В случае максимума наклон касательной равен уменьшается — идет от положительного к отрицательному. Мы видим, что в точках C , A , D . Пример 2. Пусть f ( х ) = 2 х 3 — 9 х 2 + 12 х — 3. Есть ли экстремальные значения? Во-первых, существуют ли какие-либо критические значения — решения для f ‘ ( x ) = 0 — и определяют ли они максимум или минимум? И каковы координаты на графике этого максимума или минимума? Где поворотные моменты? Решение . f’ ( х ) = 6 х 2 — 18 х + 12 f’ ( х ) = 6 х 2 — 18 х + 12 | = | 6( х 2 − 3 х + 2) | | | | | = | 6( х — 1)( х — 2) | | | | | = | 0 |
подразумевает: x = 1 или x = 2. (Урок 37 Алгебры.) Это критические значения. Каждый из них определяет максимум или он определяет минимум? Чтобы ответить, мы должны оценить вторую производную при каждом значении. | ф’ ( х ) | = | 6 x 2 − 18 x + 12. | | | | f » ( x ) | = | 12 x − 18. | | | | ж» (1) | = | 12 — 18 = -6. |
Вторая производная отрицательна. Таким образом, функция имеет максимум при разрешении x = 1, . Чтобы найти y -координату — экстремальное значение — в этом максимуме мы оцениваем f (1): | ф ( х ) | = | 2 x 3 − 9 x 2 + 12 x − 3 | | | | f (1) | = | 2 − 9 + 12 − 3 | | | | | = | 2. |
Максимум приходится на точку (1, 2). Далее, определяет ли x = 2 максимум или минимум? | ф» ( х ) | = | 12 x − 18. | | | | ф» (2) | = | 24 — 18 = 6. |
Вторая производная положительна. Таким образом, функция имеет минимум при x = 2, . Чтобы найти y -координату — экстремальное значение — при этом минимуме, мы оцениваем ф (2): | ф ( х ) | = | 2 x 3 − 9 x 2 + 12 x − 3. | | | | f (2) | = | 16 − 36 + 24 − 3 | | | | | = | 1. |
Минимум приходится на точку (2, 1). Вот собственно график f ( x ): Решения f » ( x ) = 0 указывают точку перегиба в этих решениях, а не максимум или минимум. Пример: y = x 3 . г» = 6 x = 0 подразумевает x = 0. Но x = 0 является точкой перегиба на графике y = x 3 , а не максимумом или минимумом. Пример: y = x 3 . г» = 6 x = 0 подразумевает x = 0. Но x = 0 является точкой перегиба на графике y = x 3 , а не максимумом или минимумом. Другой пример: y = sin x . Решения y » = 0 — это произведения π, которые являются точками перегиба. Задача 1. Найти координаты вершины параболы г = х 2 — 8 х + 1. Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы снова закрыть ответ, нажмите «Обновить» («Reload»).
Сначала решай задачу сам! у’ = 2 х — 8 = 0, Отсюда следует, что x = 4. Это x -координата вершины. Чтобы найти координату y , оцените г в х = 4: y = 4 2 − 8 · 4 + 1 = −15. Вершина находится в точке (4, −15). Задача 2. Исследуйте каждую функцию на наличие максимумов и минимумов. а) y = x 3 − 3 x 2 + 2, у’ = 3 х 2 — 6 x = 3 x ( x — 2) = 0 подразумевает x = 0 или x = 2. у» ( х ) = 6 х — 6, г» (0) = -6. Вторая производная отрицательна. Это означает, что максимальное значение составляет x = 0. Это максимальное значение равно . г (0) = 2. Далее, г» (2) = 12 — 6 = 6. Вторая производная положительна. Это означает, что минимальное значение составляет x = 2. Это минимальное значение равно . y (2) = 2 3 − 3 · 2 2 + 2 = 8 − 12 + 2 = −2. б) y = −2 x 3 − 3 х 2 + 12 х + 10. При x = 1 максимум y = 17. При x = -2 есть минимум y = -10. c) y = 2 x 3 + 3 x 2 + 12 x − 4, Так как f ‘ ( х ) = 0 не имеет действительных решений, экстремальных значений нет. d) y = 3 x 4 − 4 x 3 − 12 x 2 + 2, 9 0003 При x = 0 максимум y = 2. При x = -1 есть минимум y = -3. При x = 2 минимум г = -30. Следующий урок: Применение максимальных и минимальных значений Содержание | Дом
Пожалуйста, сделайте пожертвование, чтобы TheMathPage оставался онлайн.
Даже 1 доллар поможет.
Copyright © 2021 Лоуренс Спектор Вопросы или комментарии? Электронная почта: teacher@themathpage. com com
исчисление — Чтобы найти максимальное значение функции Поскольку мы имеем дело с абсолютным значением функции, мы можем интерпретировать абсолютное значение как расстояние от функции до оси $x$ независимо от направления. Другими словами, мы просто хотим найти точку, наиболее удаленную от оси $x$, независимо от того, находится ли она выше или ниже оси, поскольку расстояние (абсолютное значение) — это все, что нам нужно максимизировать. Имея это в виду, становится ясно, что максимум $\lvert f(x) \rvert$ должен быть либо максимумом, либо минимумом $f(x)$. 92 + 16 х + 6
$$
К сожалению, это последнее выражение больше нельзя разложить на множители, и, поскольку не существует формулы пятой степени для нахождения корней, лучшее, что мы можем сделать, — это найти корни с помощью численных методов. Сделав это, вы обнаружите, что действительные корни даются
\начать{выравнивать}
x_1 &\приблизительно -0,24569\\
x_2 & \приблизительно 0,687122\\
x_3 & \приблизительно 3,44225
\end{выравнивание}
Однако, если мы на самом деле подставим $x_2$ в уравнение $(1)$, мы увидим, что мы не получаем $0$ (на самом деле это приблизительно равно $-3,18$).
Mathway | Популярные задачи| 1 | Найти точное значение | sin(30) | | | 2 | Найти точное значение | sin(45) | | | 3 | Найти точное значение | sin(30 град. ) | | | 4 | Найти точное значение | sin(60 град. ) | | | 5 | Найти точное значение | tan(30 град. ) | | | 6 | Найти точное значение | arcsin(-1) | | | 7 | Найти точное значение | sin(pi/6) | | | 8 | Найти точное значение | cos(pi/4) | | | 9 | Найти точное значение | sin(45 град. ) ) | | | 10 | Найти точное значение | sin(pi/3) | | | 11 | Найти точное значение | arctan(-1) | | | 12 | Найти точное значение | cos(45 град. ) | | | 13 | Найти точное значение | cos(30 град. ) | | | 14 | Найти точное значение | tan(60) | | | 15 | Найти точное значение | csc(45 град. ) | | | 16 | Найти точное значение | tan(60 град. ) | | | 17 | Найти точное значение | sec(30 град. ) ) | | | 18 | Найти точное значение | cos(60 град. ) | | | 19 | Найти точное значение | cos(150) | | | 20 | Найти точное значение | sin(60) | | | 21 | Найти точное значение | cos(pi/2) | | | 22 | Найти точное значение | tan(45 град. ) | | | 23 | Найти точное значение | arctan(- квадратный корень из 3) | | | 24 | Найти точное значение | csc(60 град. ) | | | 25 | Найти точное значение | sec(45 град. ) ) | | | 26 | Найти точное значение | csc(30 град. ) | | | 27 | Найти точное значение | sin(0) | | | 28 | Найти точное значение | sin(120) | | | 29 | Найти точное значение | cos(90) | | | 30 | Преобразовать из радианов в градусы | pi/3 | | | 31 | Найти точное значение | tan(30) | | | 32 | Преобразовать из градусов в радианы | 45 | | | 33 | Найти точное значение | cos(45) | | | 34 | Упростить | sin(theta)^2+cos(theta)^2 | | | 35 | Преобразовать из радианов в градусы | pi/6 | | | 36 | Найти точное значение | cot(30 град. ) ) | | | 37 | Найти точное значение | arccos(-1) | | | 38 | Найти точное значение | arctan(0) | | | 39 | Найти точное значение | cot(60 град. ) | | | 40 | Преобразовать из градусов в радианы | 30 | | | 41 | Преобразовать из радианов в градусы | (2pi)/3 | | | 42 | Найти точное значение | sin((5pi)/3) | | | 43 | Найти точное значение | sin((3pi)/4) | | | 44 | Найти точное значение | tan(pi/2) | | | 45 | Найти точное значение | sin(300) | | | 46 | Найти точное значение | cos(30) | | | 47 | Найти точное значение | cos(60) | | | 48 | Найти точное значение | cos(0) | | | 49 | Найти точное значение | cos(135) | | | 50 | Найти точное значение | cos((5pi)/3) | | | 51 | Найти точное значение | cos(210) | | | 52 | Найти точное значение | sec(60 град. ) ) | | | 53 | Найти точное значение | sin(300 град. ) | | | 54 | Преобразовать из градусов в радианы | 135 | | | 55 | Преобразовать из градусов в радианы | 150 | | | 56 | Преобразовать из радианов в градусы | (5pi)/6 | | | 57 | Преобразовать из радианов в градусы | (5pi)/3 | | | 58 | Преобразовать из градусов в радианы | 89 град. | | | 59 | Преобразовать из градусов в радианы | 60 | | | 60 | Найти точное значение | sin(135 град. ) ) | | | 61 | Найти точное значение | sin(150) | | | 62 | Найти точное значение | sin(240 град. ) | | | 63 | Найти точное значение | cot(45 град. ) | | | 64 | Преобразовать из радианов в градусы | (5pi)/4 | | | 65 | Найти точное значение | sin(225) | | | 66 | Найти точное значение | sin(240) | | | 67 | Найти точное значение | cos(150 град. ) | | | 68 | Найти точное значение | tan(45) | | | 69 | Вычислить | sin(30 град. ) ) | | | 70 | Найти точное значение | sec(0) | | | 71 | Найти точное значение | cos((5pi)/6) | | | 72 | Найти точное значение | csc(30) | | | 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | | | 74 | Найти точное значение | tan((5pi)/3) | | | 75 | Найти точное значение | tan(0) | | | 76 | Вычислить | sin(60 град. ) | | | 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | | | 78 | Преобразовать из радианов в градусы | (3pi)/4 | | | 79 | Найти точное значение | sin((7pi)/4) | | | 80 | Найти точное значение | arcsin(-1/2) | | | 81 | Найти точное значение | sin((4pi)/3) | | | 82 | Найти точное значение | csc(45) | | | 83 | Упростить | arctan( квадратный корень из 3) | | | 84 | Найти точное значение | sin(135) | | | 85 | Найти точное значение | sin(105) | | | 86 | Найти точное значение | sin(150 град. ) ) | | | 87 | Найти точное значение | sin((2pi)/3) | | | 88 | Найти точное значение | tan((2pi)/3) | | | 89 | Преобразовать из радианов в градусы | pi/4 | | | 90 | Найти точное значение | sin(pi/2) | | | 91 | Найти точное значение | sec(45) | | | 92 | Найти точное значение | cos((5pi)/4) | | | 93 | Найти точное значение | cos((7pi)/6) | | | 94 | Найти точное значение | arcsin(0) | | | 95 | Найти точное значение | sin(120 град. ) ) | | | 96 | Найти точное значение | tan((7pi)/6) | | | 97 | Найти точное значение | cos(270) | | | 98 | Найти точное значение | sin((7pi)/6) | | | 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | | | 100 | Преобразовать из градусов в радианы | 88 град. | |
представить число в показательной форме z=-корень из 3+i — вопрос №2265728 — Учеба и наука | | | | Ответы | |
|
| | | | | 29. 12.16 12.16 | |
| |
| |
|
|
Михаил Александров
|
|
|
|
|
|
|
Читать ответы
|
|
|
|
Андрей Андреевич
|
|
|
|
|
|
|
Читать ответы
|
|
|
|
Eleonora Gabrielyan
|
|
|
|
|
|
|
Читать ответы
|
|
| Посмотреть всех экспертов из раздела Учеба и наука > Математика | | Данный пример использовался на экзамене upsc в декабре 2013 и лишь один человек смог решить его . .. 1,3,5,7,9,11,13,15 нужно взять 3 числа и только сложением получить 30. .. 1,3,5,7,9,11,13,15 нужно взять 3 числа и только сложением получить 30. Сколько существует таких натуральных чисел AA, что среди чисел AA, A+15A+15 и A+30A+30 ровно два четырехзначных? Имеется два сосуда, содержащие 30 кг и 20 кг раствора кислоты различной концентрации. Если их слить вместе, то получим раствор, содержащий 81% Мост длиной 90 метров поезд проезжает за минуту, а мимо телеграфного столба (двигаясь с той же скоростью) проезжает за 4040 секунд. Какова длина поезда? даны неразвернутый угол и отрезок… Пользуйтесь нашим приложением
Мэтуэй | Популярные задачи| 1 | Найти точное значение | грех(30) | | | 2 | Найти точное значение | грех(45) | | | 3 | Найти точное значение | грех(30 градусов) | | | 4 | Найти точное значение | грех(60 градусов) | | | 5 | Найти точное значение | загар (30 градусов) | | | 6 | Найти точное значение | угловой синус(-1) | | | 7 | Найти точное значение | грех(пи/6) | | | 8 | Найти точное значение | cos(pi/4) | | | 9 | Найти точное значение | грех(45 градусов) | | | 10 | Найти точное значение | грех(пи/3) | | | 11 | Найти точное значение | арктан(-1) | | | 12 | Найти точное значение | cos(45 градусов) | | | 13 | Найти точное значение | cos(30 градусов) | | | 14 | Найти точное значение | желтовато-коричневый(60) | | | 15 | Найти точное значение | csc(45 градусов) | | | 16 | Найти точное значение | загар (60 градусов) | | | 17 | Найти точное значение | сек(30 градусов) | | | 18 | Найти точное значение | cos(60 градусов) | | | 19 | Найти точное значение | cos(150) | | | 20 | Найти точное значение | грех(60) | | | 21 | Найти точное значение | cos(pi/2) | | | 22 | Найти точное значение | загар (45 градусов) | | | 23 | Найти точное значение | arctan(- квадратный корень из 3) | | | 24 | Найти точное значение | csc(60 градусов) | | | 25 | Найти точное значение | сек(45 градусов) | | | 26 | Найти точное значение | csc(30 градусов) | | | 27 | Найти точное значение | грех(0) | | | 28 | Найти точное значение | грех(120) | | | 29 | Найти точное значение | соз(90) | | | 30 | Преобразовать из радианов в градусы | пи/3 | | | 31 | Найти точное значение | желтовато-коричневый(30) | | | 32 | 92 | | 35 | Преобразовать из радианов в градусы | пи/6 | | | 36 | Найти точное значение | детская кроватка(30 градусов) | | | 37 | Найти точное значение | арккос(-1) | | | 38 | Найти точное значение | арктический(0) | | | 39 | Найти точное значение | детская кроватка(60 градусов) | | | 40 | Преобразование градусов в радианы | 30 | | | 41 | Преобразовать из радианов в градусы | (2 шт. )/3 )/3 | | | 42 | Найти точное значение | sin((5pi)/3) | | | 43 | Найти точное значение | sin((3pi)/4) | | | 44 | Найти точное значение | тан(пи/2) | | | 45 | Найти точное значение | грех(300) | | | 46 | Найти точное значение | соз(30) | | | 47 | Найти точное значение | соз(60) | | | 48 | Найти точное значение | соз(0) | | | 49 | Найти точное значение | соз(135) | | | 50 | Найти точное значение | cos((5pi)/3) | | | 51 | Найти точное значение | cos(210) | | | 52 | Найти точное значение | сек(60 градусов) | | | 53 | Найти точное значение | грех(300 градусов) | | | 54 | Преобразование градусов в радианы | 135 | | | 55 | Преобразование градусов в радианы | 150 | | | 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | | | 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | | | 58 | Преобразование градусов в радианы | 89 градусов | | | 59 | Преобразование градусов в радианы | 60 | | | 60 | Найти точное значение | грех(135 градусов) | | | 61 | Найти точное значение | грех(150) | | | 62 | Найти точное значение | грех(240 градусов) | | | 63 | Найти точное значение | детская кроватка(45 градусов) | | | 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | | | 65 | Найти точное значение | грех(225) | | | 66 | Найти точное значение | грех(240) | | | 67 | Найти точное значение | cos(150 градусов) | | | 68 | Найти точное значение | желтовато-коричневый(45) | | | 69 | Оценить | грех(30 градусов) | | | 70 | Найти точное значение | сек(0) | | | 71 | Найти точное значение | cos((5pi)/6) | | | 72 | Найти точное значение | КСК(30) | | | 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | | | 74 | Найти точное значение | загар((5pi)/3) | | | 75 | Найти точное значение | желтовато-коричневый(0) | | | 76 | Оценить | грех(60 градусов) | | | 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | | | 78 | Преобразовать из радианов в градусы | (3 пи)/4 | | | 79 | Найти точное значение | sin((7pi)/4) | | | 80 | Найти точное значение | угловой синус(-1/2) | | | 81 | Найти точное значение | sin((4pi)/3) | | | 82 | Найти точное значение | КСК(45) | | | 83 | Упростить | арктан(квадратный корень из 3) | | | 84 | Найти точное значение | грех(135) | | | 85 | Найти точное значение | грех(105) | | | 86 | Найти точное значение | грех(150 градусов) | | | 87 | Найти точное значение | sin((2pi)/3) | | | 88 | Найти точное значение | загар((2pi)/3) | | | 89 | Преобразовать из радианов в градусы | пи/4 | | | 90 | Найти точное значение | грех(пи/2) | | | 91 | Найти точное значение | сек(45) | | | 92 | Найти точное значение | cos((5pi)/4) | | | 93 | Найти точное значение | cos((7pi)/6) | | | 94 | Найти точное значение | угловой синус(0) | | | 95 | Найти точное значение | грех(120 градусов) | | | 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | | | 97 | Найти точное значение | соз(270) | | | 98 | Найти точное значение | sin((7pi)/6) | | | 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | | | 100 | Преобразование градусов в радианы | 88 градусов | |
Мэтуэй | Популярные задачи| 1 | Найти точное значение | грех(30) | | | 2 | Найти точное значение | грех(45) | | | 3 | Найти точное значение | грех(30 градусов) | | | 4 | Найти точное значение | грех(60 градусов) | | | 5 | Найти точное значение | загар (30 градусов) | | | 6 | Найти точное значение | угловой синус(-1) | | | 7 | Найти точное значение | грех(пи/6) | | | 8 | Найти точное значение | cos(pi/4) | | | 9 | Найти точное значение | грех(45 градусов) | | | 10 | Найти точное значение | грех(пи/3) | | | 11 | Найти точное значение | арктан(-1) | | | 12 | Найти точное значение | cos(45 градусов) | | | 13 | Найти точное значение | cos(30 градусов) | | | 14 | Найти точное значение | желтовато-коричневый(60) | | | 15 | Найти точное значение | csc(45 градусов) | | | 16 | Найти точное значение | загар (60 градусов) | | | 17 | Найти точное значение | сек(30 градусов) | | | 18 | Найти точное значение | cos(60 градусов) | | | 19 | Найти точное значение | соз(150) | | | 20 | Найти точное значение | грех(60) | | | 21 | Найти точное значение | cos(pi/2) | | | 22 | Найти точное значение | загар (45 градусов) | | | 23 | Найти точное значение | arctan(- квадратный корень из 3) | | | 24 | Найти точное значение | csc(60 градусов) | | | 25 | Найти точное значение | сек(45 градусов) | | | 26 | Найти точное значение | csc(30 градусов) | | | 27 | Найти точное значение | грех(0) | | | 28 | Найти точное значение | грех(120) | | | 29 | Найти точное значение | соз(90) | | | 30 | Преобразовать из радианов в градусы | пи/3 | | | 31 | Найти точное значение | желтовато-коричневый(30) | | | 32 | Преобразование градусов в радианы 92 | | | 35 | Преобразовать из радианов в градусы | пи/6 | | | 36 | Найти точное значение | детская кроватка(30 градусов) | | | 37 | Найти точное значение | арккос(-1) | | | 38 | Найти точное значение | арктический(0) | | | 39 | Найти точное значение | детская кроватка(60 градусов) | | | 40 | Преобразование градусов в радианы | 30 | | | 41 | Преобразовать из радианов в градусы | (2 шт. Линейное Уравнение — Mathcracker.Com Инструкции: Используйте это Калькулятор линейных уравнений вычислить график предоставленного вами линейного уравнения, показав все шаги. Пожалуйста, укажите линейное уравнение (например, \(x + 5y = 2 + \frac{2}{3}x\)) в поле ниже: Подробнее о линейные уравнения Этот калькулятор поможет вам построить график линейного уравнения, которое вы предоставите. Итак, первым шагом является предоставление действительного линейного уравнения, например 2x + 3y = 4, или вы можете предоставить что-то, что не упрощается напрямую, например 2/3 x + y = 4/3 x — 1/2 y + 2. Подойдет любое действительное линейное выражение. . Подойдет любое действительное линейное выражение. . После того, как вы предоставите действительное линейное уравнение, наступает самое легкое время, поскольку все, что вам нужно сделать, это нажать кнопку «Вычислить», и вам будут показаны этапы процесса построения графика линейной функции. Линейные уравнения будут играть важную роль во многих операциях, в том числе для
решить систему линейных уравнений
. Формула линейного уравнения Существуют различные формы, в которых можно записать формулу линейного уравнения. Наиболее распространенными являются
стандартная форма
, который показан ниже Наиболее распространенными являются
стандартная форма
, который показан ниже \[a x + by = c \] Кроме того, существует
форма пересечения наклона
, который показан ниже \[y = mx + n\] Эти две формы могут быть преобразованы из одной в другую, за исключением пары исключений, а именно вертикальной линии, выраженной x = a. Эта линия вертикальна и пересекает ось x в точке (a, 0). Мы имеем, что x = a является стандартной формой линии, но эта линия не имеет наклонного перехвата (по крайней мере, там, где y является зависимой переменной) Мы имеем, что x = a является стандартной формой линии, но эта линия не имеет наклонного перехвата (по крайней мере, там, где y является зависимой переменной) Каковы этапы построения графика линейного уравнения?- Шаг 1: Четко определите имеющееся уравнение
- Шаг 2: Посмотрите коэффициент, который умножает y, если он равен нулю, то у вас есть вертикальная линия
- Шаг 3: Если коэффициент, умножающий y, отличен от нуля, то вы решаете для y, чтобы получить
форма пересечения наклона
- Шаг 4: Используя форму «наклон-пересечение», оцените функцию при x = 0 и x = 1, и тогда у вас будет две точки, через которые проходит прямая
- Шаг 5: Проведите линию, используя две найденные точки в качестве ориентира
Один из самых четких способов провести линию — это иметь две точки, через которые проходит линия, так как часто использование наклона для ориентира может ввести в заблуждение. Решение линейного уравнения в одной переменной Студенты знакомы с системами линейных уравнений, и они более или менее понимают, что нужно сделать. Но затем они задаются вопросом о решении линейного уравнения с одной переменной. Допустим, у вас есть линейное уравнение в форме «наклон-пересечение»: \[y = a + bx \] Как же решить эту проблему? Ну, она уже решена: Для каждого заданного значения x решение y равно y = a + bx. Таким образом, при условии, что \(b \ne 0\), у вас есть бесконечное множество решений линейного уравнения. Ситуация меняется, когда у вас есть два линейных уравнения, в этом случае вам нужно
решить оба уравнения одновременно
. Так ли важны линейные уравнения? Еще бы! Пожалуй, один из самых важных во всей математике. Это объясняется простотой и в то же время широким спектром применения. Пример: калькулятор линейных уравнений Получите график следующего линейного уравнения: \(\frac{1}{3} x + \frac{7}{4} y — \frac{5}{6} = 0\) Решение: Получите уравнение линии в форме наклон-пересечение Нам было дано следующее уравнение. .: .: \[\displaystyle \frac{1}{3}x+\frac{7}{4}y-\frac{5}{6}=0\] Упрощение констант: \[\displaystyle \frac{1}{3}x+\frac{7}{4}y-\frac{5}{6}=0\] Теперь, положив \(y\) в левой части, \(x\) и константу в правой части, получим \[\displaystyle \frac{7}{4}y = -\frac{1}{3}x + \frac{5}{6}\] Теперь, находя \(y\) путем деления обеих частей уравнения на \(\frac{7}{4}\), получается следующее \[\displaystyle y=-\frac{\frac{1}{3}}{\frac{7}{4}}x+\frac{\frac{5}{6}}{\frac{7}{4}}\] и упрощая окончательно получаем следующее \[\displaystyle y=-\frac{4}{21}x+\frac{10}{21}\] Вывод : На основании имеющихся данных мы делаем вывод, что уравнение линии в форме наклонная-пересечение имеет вид: \(\displaystyle y=-\frac{4}{21}x+\frac{10}{21}\), с наклоном \(\displaystyle b = -\frac{4}{21}\) и y-перехватом \(\displaystyle n = \frac{10}{21}\). Учитывая эти данные, представленный линейный график показывает Пример: пример калькулятора линейных уравнений Вычислите следующее: \(\frac{1}{3}x + \frac{5}{4}y = \frac{1}{6}\) Отвечать:
Теперь мы получили следующее уравнение: \[\displaystyle \frac{1}{3}x+\frac{5}{4}y=\frac{1}{6}\] Первый шаг — упрощение констант: \[\displaystyle \frac{1}{3}x+\frac{5}{4}y=\frac{1}{6}\] Поместив \(y\) в левую часть, а \(x\) и постоянный член в правую часть, получим \[\displaystyle \frac{5}{4}y = -\frac{1}{3}x +\frac{1}{6}\] Теперь нам нужно решить \(y\), что достигается делением обеих сторон уравнения на \(\frac{5}{4}\), и получается следующее \[\displaystyle y=-\frac{\frac{1}{3}}{\frac{5}{4}}x+\frac{\frac{1}{6}}{\frac{5}{4}}\] и упрощая окончательно получаем следующее \[\displaystyle y=-\frac{4}{15}x+\frac{2}{15}\] Вывод : Уравнение линии в форме наклон-пересечение, согласно представленной информации, равно \(\displaystyle y=-\frac{4}{15}x+\frac{2}{15}\), с наклоном \(\displaystyle b = -\frac{4}{15}\) и y-пересечением \(\displaystyle n = \frac{2}{15}\). Согласно этим данным, представленный линейный график имеет вид Пример: еще один пример калькулятора линейных уравнений Представляет ли это линию: \( y = 5 \). Если да, то каковы ее характеристики? Отвечать:
Да, это так. Действительно, когда у вас есть выражение типа \( y = 5 \), у вас есть линейное уравнение в форме «наклон-пересечение», с a = 0 и b = 5. Следовательно, мы имеем горизонтальную линию, которая пересекает ось y в точке (0, 5). Больше калькуляторов по алгебре Линии
,
Линейные уравнения
и
линейные функции
всегда будет играть решающую роль в алгебре, представляя также четкую связь с некоторыми основными геометрическими свойствами. С точки зрения применения, возможно
Решение систем линейных уравнений
является одним из самых распространенных применений линий и линейных уравнений. «Линейное уравнение с двумя переменными и его график». Тема: «Линейное уравнение с двумя переменными и его график». Тип урока: изучение нового материала. Вид урока: урок-полилог. Цель: 1. Получить понятие линейного уравнения с двумя переменными, решения уравнения с двумя переменными; познакомиться со свойствами уравнений с двумя переменными; его графиком. 2. Развивать речь, мышление. 3. Воспитывать самостоятельность мышления, любовь к математике. (Цели учителя: формировать у учащихся способы и средства по освоению понятий и содержания темы. Мотивировать изучение алгебры, как науки, создающей математические модели окружающей действительности. Помочь учащимся обогатить свой опыт, взглянув на знакомые понятия с различных точек зрения. Формирование активной, неравнодушной личности.) Оборудование урока: Техническое: компьютер, мультимедиапроектор. Демонстрационное: презентация Microsoft PowerPoint, 3 сосуда. Четыре сосуда: два пустых, два с содержимым и с наклейками «3%» и «30%». Раздаточное: теоретический справочник, тесты, бланки для построения уравнений. Ход урока. 1. Организационный момент. — Добрый день. Меня зовут Елена Евгеньевна. Следующие тридцать минут нам суждено с вами прожить вместе. 2. Вступительное слово учителя: — Какой же язык будет помогать нам в общении на сегодняшнем уроке? (язык математики) — Мне бы хотелось, чтобы у нас сегодня состоялся разговор, ибо как сказал Вовенарг: «Непринужденная беседа — лучшая школа для ума». Хочется еще, чтобы вы помнили слова российского историка Ключевского: «Есть люди, которые умеют говорить, но не умеют ничего сказать. Это ветряные мельницы, которые вечно машут крыльями, но никогда не летают». Надеюсь, что нам сегодня удастся взлететь на вершину новых знаний алгебры. Хочется еще, чтобы вы помнили слова российского историка Ключевского: «Есть люди, которые умеют говорить, но не умеют ничего сказать. Это ветряные мельницы, которые вечно машут крыльями, но никогда не летают». Надеюсь, что нам сегодня удастся взлететь на вершину новых знаний алгебры. — Как вы думаете, может ли алгебра понадобиться, например, в парикмахерской? Оказывается, что такие случаи бывают. Послушаем разговор, который там (довольно давно) однажды состоялся. (Звучит запись разговора): — Ой, здравствуйте, здравствуйте. Мы слышали, что вы математикой увлекаетесь? — обратился к посетителю один из мастеров. — Не поможете ли нам разрешить задачу, с которой мы никак не справимся? — Уж сколько раствора испортили для этого! – добавил другой. — В чем задача? – осведомился посетитель. — У нас имеется два раствора перекиси водорода: 30-процентный и 3-процентный. Нужно их смешать так, чтобы составился 12-процентный раствор. Не можем подыскать правильной пропорции… Учитель: — А вы смогли бы помочь эти мастерам? Задачу можно решить и арифметически. Но язык алгебры приводит здесь к успеху проще и быстрее Но язык алгебры приводит здесь к успеху проще и быстрее Переведем эту задачу с родного языка на язык алгебры: Возьмем 30-процентный раствор перекиси водорода | x граммов | Возьмем 3-процентный раствор перекиси водорода | y граммов | В первой порции содержится чистой перекиси водорода | 0,3x | Во второй порции содержится чистой перекиси водорода | 0,03y | Всего в двух порциях содержится чистой перекиси водорода | 0,3x + 0,03y | Смешаем обе порции | (x + y) граммов | В смеси должно содержаться чистой перекиси водорода | 0,12(x + y) |
0,3x + 0,03y = 0,12(x + y) Что же это за алгебраический объект у нас получился? Попробуем дать ему название. (уравнение) (с двумя переменными) 3. Формулирование темы и целей урока. Это линейное уравнение с двумя переменными. Сформулируем тему урока. (Линейное уравнение с двумя переменными) Чтобы вам хотелось узнать сегодня на уроке? (Что называется линейным уравнением, Что называется решением уравнения с двумя переменными, Свойства линейного уравнения) 4. Актуализация базовых знаний с совместным постижением нового материала Нам ведь уже знакомы похожие объекты? Что это за объекты? (линейные уравнения с одной переменной) Давайте придумаем какое-нибудь линейное уравнение с одной переменной. Пожалуйста, к доске (вызвать 3-4 желающих) -Посмотрите на доску, перед нами действительно линейные уравнения с одной переменной. Вспомним общий вид линейного уравнения с одной переменной. (ax=b, где a и b –некоторые числа, а x-переменная). (ax=b, где a и b –некоторые числа, а x-переменная). Выпишите номера тех уравнений, которые бы вы отнесли к линейным уравнениям с двумя переменными? (1,4,6) (со слайда презентации) 1. 3у+2х=0. 2. 5у – 6 =0. 3. 0,2х2 – у +3=0. 4. х+у=15. 5. 4х – 17 = 0. 6. 5х+2у=12 Выпишите номера тех уравнений, которые бы вы отнесли к линейным уравнениям с двумя переменными? (1,4,6) Определим вид линейного уравнения с двумя переменными: (ax+by=c, где a,b,c некоторые числа, x, y переменные.) Попробуйте сформулировать определение: (Линейным уравнением с двумя переменными называется уравнение вида ax+by=c, где a,b,c некоторые числа, x, y переменные) Откройте теоретический справочник. Прочитайте определение про себя. Не ошиблись ли мы в определении. Есть ли различия? Прочитайте определение про себя. Не ошиблись ли мы в определении. Есть ли различия? Придумайте и запишите в этом справочнике свое линейное уравнение с двумя переменными. Вернемся к линейным уравнениям с одной переменной. Давайте вспомним, как они решаются, и решим какое-нибудь из придуманных уравнений с объяснением, например: 2х+6=10 (Перенесем слагаемое без х в правую часть уравнения, изменив при этом его знак на противоположный: 2х=10-6 , вычислим результат 2х=4. Разделим обе части уравнения на 2, получим х=2). — Ребята , такие уравнения вы хорошо умеете решать. — А какие свойства применяли при решении этих уравнений? (Если в уравнении слагаемое перенести из одной части в другую, изменив его знак, то получится уравнение, равносильное данному.) — А какое еще свойство вы применяли? (Если разделить или умножить обе части уравнения на одно и тоже отличное от нуля число, то получится уравнение равносильное данному. ) ) Линейные уравнения с двумя переменными обладают такими же свойствами. Применяя эти свойства, будем получать равносильные уравнения. Напомните, пожалуйста, какие уравнения называются равносильными? (Уравнения, имеющие одни и те же решения, называют равносильными. Уравнения, не имеющие решений, также считают равносильными.) Для уравнений с двумя переменными все остается в силе. Загляните опять в справочник. Ребята, ведь мы забыли про мастеров из парикмахерской. Это не хорошо. Надо им помочь. Давайте вернемся к той ситуации. Применим свойства уравнений с двумя переменными к полученному нами уравнению, и сведем его к виду, указанному в определении. 0,3x + 0,03y = 0,12(x + y) 0,3x + 0,03y = 0,12x + 0,12y 0,3x – 0,12x = 0,12y – 0,03y 0,18x — 0,09y =0 18x — 9y=0 2x-y=0 При каких значениях x и y наше уравнение обратится в верное равенство? при х=1, у=2 (записываю на доске) (2∙1=2) Что же является решением линейных уравнений с двумя переменными? (Решением уравнения с двумя переменными называется пара значений переменных, обращающая это уравнение в верное равенство. ) ) Прочитайте это определение на странице про себя. Не ошиблись ли мы, давая определение? А какие еще пары чисел будут являться решениями уравнения 2x-y=0? х=2, у=4 х=3, у=6 х=4, у=8 Правильно решениями этого уравнения будут являться числа, одно из которых в два раза больше другого. Т.е 3-процентного раствора надо взять вдвое больше, чем 30-процентного. Как же смешать? (дети показывают на практике) мерить будем мерным стаканчиком. Продолжим знакомство с линейными уравнениями. Присмотритесь, пожалуйста, к этим парам. Может есть у кого предложение, как записать это решение короче, пользуясь символическим языком математики? ( (2, 4), (3,6), (4, 8) и т.д.) -При такой записи необходимо знать, значение какой из переменных стоит на первом месте, а какой – на втором. В записи решений уравнения с переменными х и у на первом месте записывают значения х, а на втором – значение у. В записи решений уравнения с переменными х и у на первом месте записывают значения х, а на втором – значение у. Где-то нам уже встречалась такая запись! Правильно, это координаты точек на координатной плоскости. Отметим на координатной плоскости найденные пары решений. Есть ли еще у нашего уравнения решения? Сколько же у него решений? (бесконечно много) Можем ли мы все его решения нанести на координатную плоскость? (да, они образуют прямую) Все ли решения будут пригодны для ситуации в парикмахерской? Сделаем вывод о количестве решений линейного уравнения с двумя переменными (множество решений уравнения с двумя неизвестными, как правило, бесконечно и его изображение на координатной плоскости — прямая линия, а также может быть и пустым) Всегда ли именно прямая линия? -Рассмотрим уравнения 5х+2у=12. -Для удобства нахождения решений уравнения, воспользовавшись свойствами уравнений, выразим из этого уравнения одну переменную через другую, например у, через х. Для этого перенесем Для этого перенесем слагаемое 5х в правую часть уравнения изменив его знак. 2у= -5х+12. -Разделим обе части этого уравнения на 2: у= -2,5х+6 Уравнения 5х+2у=12 и у= -2,5х+6 – равносильны. -Пользуясь формулой у=-2,5х+6, можно найти сколько угодно решений уравнения 5х+2у=12. Для этого достаточно взять произвольное х и вычислить соответствующее ему значение у. Например: если х=2 , то у= -2,5.2+6=1. если х=0,4 то у= -2,5*0,4+4=5. Пары чисел (2; 1), (0,4; 5) – решение уравнения 5х+2у=12. Это уравнение имеет бесконечно много решений. Этот способ удобен и тогда, когда надо найти не все, а только несколько решений уравнения, причем каждый раз можно выбирать, какую переменную выражать через другую. Рассмотрим уравнение 2x+0y=13 Построим его график: x=6,5 Рассмотрим уравнение 0x+3y=15 Построим его график: y=5 5. Подведение итогов. Спасибо вам за общение. Мне понравился полет ваших мыслей. Понятен ли вам язык алгебры? -Какой вид имеет линейное уравнение с двумя переменными ? (ах+ву=с). -Что называется решением линейного уравнения с двумя переменными ? -Приведите примеры таких уравнений. -Какими свойствами обладают уравнения с двумя переменными? 12.2: Линейные уравнения — Статистика LibreTexts- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 797
Линейная регрессия для двух переменных основана на линейном уравнении с одной независимой переменной. Уравнение имеет вид: Уравнение имеет вид: \[y = a + b\text{x}\номер \] , где \(a\) и \(b\) — постоянные числа. Переменная \(x\) является независимой переменной , и \(y\) является зависимой переменной . Обычно вы выбираете значение для замены независимой переменной, а затем вычисляете зависимую переменную. Пример \(\PageIndex{1}\) Следующие примеры представляют собой линейные уравнения. \[y = 3 + 2\text{x}\nonumber \] \[y = -0,01 + 1,2\text{x}\nonumber \] Упражнение \(\PageIndex{1}\) Является ли следующий пример линейным уравнением? \[y = -0,125 — 3,5\text{x}\номер \] - Ответ
да
График линейного уравнения вида \(y = a + b\text{x}\) представляет собой прямую . Любая линия, которая не является вертикальной, может быть описана этим уравнением. Пример \(\PageIndex{2}\) Нарисуйте уравнение \(y = -1 + 2\text{x}\). Рисунок \(\PageIndex{1}\). Упражнение \(\PageIndex{2}\) Является ли следующий пример линейным уравнением? Почему или почему нет? Рисунок \(\PageIndex{2}\). - Ответить
Нет, график не прямой; следовательно, это не линейное уравнение.
Пример \(\PageIndex{3}\) Служба обработки текстов Аарона (AWPS) выполняет обработку текстов. Стоимость услуг составляет 32 доллара в час плюс единовременная плата в размере 31,50 доллара. Общая стоимость для клиента зависит от количества часов, необходимых для выполнения работы. Найдите уравнение, которое выражает общую стоимость через количество часов , необходимых для выполнения работы. Ответ Пусть \(x =\) количество часов, которое требуется для выполнения работы. Пусть \(y =\) общая стоимость клиента. $31,50 — это фиксированная стоимость. Если выполнение задания занимает \(x\) часов, то \((32)(x)\) — это стоимость только обработки текста. Общая стоимость: \(y = 31,50 + 32\text{x}\) Общая стоимость: \(y = 31,50 + 32\text{x}\) Упражнение \(\PageIndex{3}\) Emma’s Extreme Sports нанимает инструкторов по дельтапланеризму и платит им вознаграждение в размере 50 долларов США за занятие, а также 20 долларов США за каждого ученика в классе. Общая стоимость, которую платит Эмма, зависит от количества учеников в классе. Найдите уравнение, которое выражает общую стоимость через количество учеников в классе. - Ответить
\(у = 50 + 20\текст{х}\)
Наклон и Y-пересечение линейного уравнения Для линейного уравнения \(y = a + b\text{x}\), \(b =\) наклона и \(a = y\)-отрезка. Из алгебры напомним, что наклон — это число, описывающее крутизну линии, а \(у\)-отрезок — это \(у\) координата точки \((0, а)\), где линия пересекает \(y\)-ось. Рисунок \(\PageIndex{3}\):. Три возможных графика \(y = a + b\text{x}\) (a) Если \(b > 0\), линия наклонена вверх вправо. (b) Если \(b = 0\), линия горизонтальна.  (c) Если \(b < 0\), линия наклонена вниз вправо. Пример \(\PageIndex{4}\) Светлана с репетиторами подрабатывает в колледже. За каждое занятие она взимает единовременную плату в размере 25 долларов плюс 15 долларов за час занятий. Линейное уравнение, выражающее общую сумму денег, которую Светлана зарабатывает за каждую сессию, которую она ведет, имеет вид \(y = 25 + 15\text{x}\). Что такое независимые и зависимые переменные? Что такое \(y\)-отрезок и каков наклон? Интерпретируйте их, используя полные предложения. Ответить Независимая переменная (\(x\)) — это количество часов, в течение которых Светлана занимается с репетиторами на каждом занятии. Зависимая переменная (\(y\)) — это сумма в долларах, которую Светлана зарабатывает за каждую сессию. Пересечение \(y\) равно 25 (\(a = 25\)). В начале занятия Светлана взимает единовременную плату в размере 25 долларов США (это когда \(x = 0\)). Наклон равен 15 (\(b = 15\)). За каждое занятие Светлана зарабатывает 15 долларов за каждый час репетиторства. Упражнение \(\PageIndex{4}\) Итан ремонтирует бытовую технику, такую как посудомоечные машины и холодильники. За каждое посещение он берет 25 долларов плюс 20 долларов за час работы. Линейное уравнение, выражающее общую сумму денег, которую Итан зарабатывает за одно посещение, имеет вид \(y = 25 + 20\text{x}\). Что такое независимые и зависимые переменные? Что такое \(y\)-отрезок и каков наклон? Интерпретируйте их, используя полные предложения. - Ответить
Независимая переменная (\(x\)) — это количество часов работы Итана за каждое посещение. Зависимая переменная (\(y\)) — это сумма в долларах, которую Итан зарабатывает за каждое посещение. y -отрезок равен 25 (\(a = 25\)). В начале визита Итан взимает единовременную плату в размере 25 долларов (это когда \(x = 0\)). Наклон равен 20 (\(b = 20\)). За каждое посещение Итан зарабатывает 20 долларов за каждый час работы.
Резюме Самый простой тип ассоциации — это линейная ассоциация. Этот тип взаимосвязи может быть определен алгебраически с помощью используемых уравнений, численно с фактическими или прогнозируемыми значениями данных или графически с помощью построенной кривой. (Линии классифицируются как прямые кривые.) Алгебраически линейное уравнение обычно принимает вид \(y = mx + b\), где \(m\) и \(b\) — константы, \(x\) — независимая переменная, \(y\) — зависимая переменная. В статистическом контексте линейное уравнение записывается в виде \(y = a + bx\), где \(a\) и \(b\) — константы. Эта форма используется, чтобы помочь читателям отличить статистический контекст от алгебраического контекста. В уравнении \(y = a + b\text{x}\) константа b, на которую умножается переменная \(x\) (\(b\) называется коэффициентом), называется склон . Константа а называется \(у\)-перехватом. Этот тип взаимосвязи может быть определен алгебраически с помощью используемых уравнений, численно с фактическими или прогнозируемыми значениями данных или графически с помощью построенной кривой. (Линии классифицируются как прямые кривые.) Алгебраически линейное уравнение обычно принимает вид \(y = mx + b\), где \(m\) и \(b\) — константы, \(x\) — независимая переменная, \(y\) — зависимая переменная. В статистическом контексте линейное уравнение записывается в виде \(y = a + bx\), где \(a\) и \(b\) — константы. Эта форма используется, чтобы помочь читателям отличить статистический контекст от алгебраического контекста. В уравнении \(y = a + b\text{x}\) константа b, на которую умножается переменная \(x\) (\(b\) называется коэффициентом), называется склон . Константа а называется \(у\)-перехватом. Наклон линии — это значение, которое описывает скорость изменения между независимыми и зависимыми переменными. Наклон говорит нам, как зависимая переменная (\(y\)) изменяется в среднем на каждую единицу увеличения независимой (\(x\)) переменной. \(y\) -intercept используется для описания зависимой переменной, когда независимая переменная равна нулю. \(y\) -intercept используется для описания зависимой переменной, когда независимая переменная равна нулю. Обзор формулы \(y = a + b\text{x}\), где a — точка пересечения \(y\), а \(b\) — наклон. Переменная \(x\) является независимой переменной, а \(y\) является зависимой переменной.
Эта страница под названием 12.2: Linear Equations распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax с помощью исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу. - Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- ОпенСтакс
- Лицензия
- СС BY
- Версия лицензии
- 4,0
- Программа OER или Publisher
- ОпенСтакс
- Показать оглавление
- нет
- Теги
- линейные уравнения
- склон
- источник@https://openstax.
 org/details/books/introductory-statistics org/details/books/introductory-statistics - y-перехват
Формулы для линейного уравнения | PrepInsta Формулы и определения для линейных уравнений
- Линейное уравнение — это алгебраическое уравнение, в котором каждый член имеет показатель степени, равный единице, а графическое изображение уравнения представляет собой прямую линию.
- Стандартная форма линейного уравнения: y = mx + b. Где x — переменная, а y, m и b — константы.
Линейные уравнения с одной переменной - Линейное уравнение с одной переменной определяется как ax + b = 0
- Где a и b постоянные, a ≠ 0 , и неизвестно переменная
- Решением уравнения ax + b = 0 является x = – \frac{b}{a} . Мы также можем сказать, что – \frac{b}{a} является корнем линейного уравнения ax + b = 0.

Линейные уравнения с двумя переменными - Линейное уравнение с двумя переменными определяется как ax + by + c = 0
- Где a, b и c являются константами, а также оба a и b ≠ 0
Линейные уравнения с тремя переменными - Линейное уравнение с тремя переменными определяется как ax + by + cz = d
- Где a, b, c и d — константы, а также a, b и c ≠ 0
Формулы и методы для решения линейных уравнений Шаг 1: Решите одно из уравнений относительно x или y. Шаг 2: Подставьте решение из шага 1 в другое уравнение. Шаг 3: Теперь решите это уравнение для второй переменной. Шаг 1: Умножьте оба уравнения с такими числами, чтобы сделать коэффициенты одного из двух неизвестных численно одинаковыми. Шаг 2: Вычтите второе уравнение из первого уравнения. Шаг 3: В любом из двух уравнений подставьте значение неизвестной переменной. Таким образом, путем решения уравнения получается значение другой неизвестной переменной. - Метод перекрестного умножения
Предположим, что есть два уравнения, p_{1}x +q_{1}y = r_{1} ……..(1) p_{2}x +q_{2}y = r_{2} ……..(2) Уравнение умножения (1) на p 2 Уравнение умножения (2) на p1 p_{1}p_{2}x +q_{1}p_{2}y = r_{1}p_{2} p_{1}p_{2}x +p_{1}q_{2}y = p_{1}r_{2} Вычитание,
q_{1}p_{2}y – p_{1}q_ {2}y = r_{1}p_{2} – p_{1}r_{2} или y (q₁ p₂ – q₂p₁) = r₂p₁ – r₁p₂ Следовательно, y = \frac{r_{2} p_{1} – r_{1}p_{2} }{q_{1}p_{2} – q_{2}p_{1} } = \frac{r_{1}p_{2} – r_{ 2}p_{1} }{q_{2}p_{1} – q_{1}p_{2} } где (p₁q₂ – p₂q₁) ≠ 0 Следовательно, \frac{y}{r_{1}p_{2} – r_{2}p_{1} } = \frac{1}{q_{2}p_{ 1} – q_{1}p_{2} } …(3) Умножить уравнение (1) на q 2 Умножить уравнение (2) на q1 p_{1}q_{2}x +q_ {1}q_{2}y = r_{1}q_{2} q_{1}p_{2}x +q_{1}q_{2}y = q_{1}r_{2} Вычитание , p_{1}q_{2}x – p_{2}q_{1}x = r_{1}q_{2} – q_{1}r_{2} или , x(p₁q₂ – p₂q₁) = (q₁r₂ – q₂r₁) или, x = \frac{q_{1}r_{2} – r_{1}q_{2}}{p_{1}q_{2} – p_{2}q_{1 }} Следовательно, \frac{x}{q_{1}r_{2} – r_{1}q_{2}} = \frac{1}{p_{1}q_{2} – p_{2}q_{ 1}} … (4) где (p₁q₂ – p₂q₁) ≠ 0 Из уравнений (3) и (4) получаем, \frac{x}{q_{1}r_{2} – r_ {1}q_{2}} =\frac{y}{r_{1}p_{2} – p_{1}r_{2}} = \frac{1}{p_{1}q_{2} – p_ {2}q_{1}} , где (p₁q₂ – p₂q₁) ≠ 0 r_{1}q_{2}} =\frac{y}{r_{1}p_{2} – r_{2}p_{1} } = \frac{1}{q_{2}p_{1} – q_{1}p_{2} } , что означает x = \frac{q_{1}r_{2} – r_{1}q_{2}}{q_{2}p_{1} – q_{1}p_{2} } y = \frac{r_{1}p_{2} – r_{2}p_{1}}{q_{2}p_{1} – q_{1}p_{2}} Важные формулы линейной Уравнение и ключевые моменты, которые следует запомнить - Предположим, есть два линейных уравнения: a 1 x + b 1 y = c 1 и a 2 x + b 2 y = c 2 y
Теперь, (A) Если \frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}, то будет одно решение , и графики будут иметь пересекающиеся линии. |
|


 ) + SO4-2 (водн.) = BaSO4 (с) + Н2 (Г)
) + SO4-2 (водн.) = BaSO4 (с) + Н2 (Г) 02 кДж/моль.
02 кДж/моль.
 Сульфат бария из-за малой токсичности используется в рентгенографии.
Сульфат бария из-за малой токсичности используется в рентгенографии. Ні, не можна. Прості речовини, окрім кисню, не містять Оксигену. Реакція взаємодії простих речовин з киснем є реакцією окиснення (горіння), в результаті якої утворюються оксиди.
Ні, не можна. Прості речовини, окрім кисню, не містять Оксигену. Реакція взаємодії простих речовин з киснем є реакцією окиснення (горіння), в результаті якої утворюються оксиди.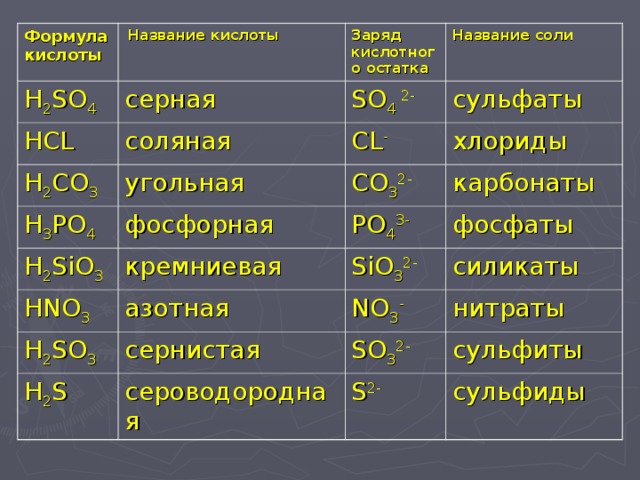

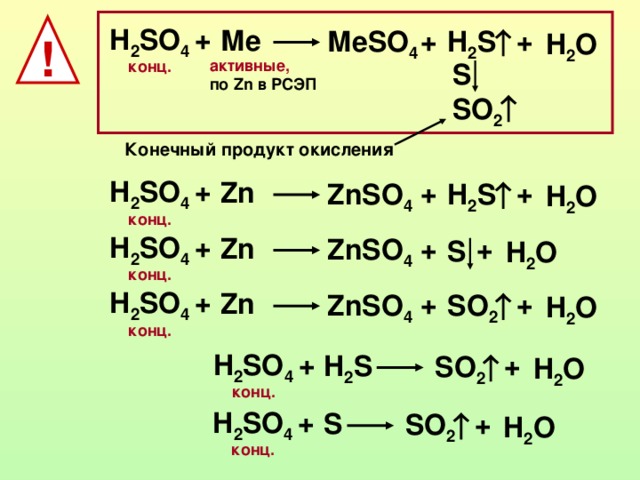



 у.) змішали з достатньою кількістю водню й підірвали. Продукт реакції розчинили у воді масою 200 г. Обчисліть масову частку хлоридної кислоти в отриманому розчині.
у.) змішали з достатньою кількістю водню й підірвали. Продукт реакції розчинили у воді масою 200 г. Обчисліть масову частку хлоридної кислоти в отриманому розчині.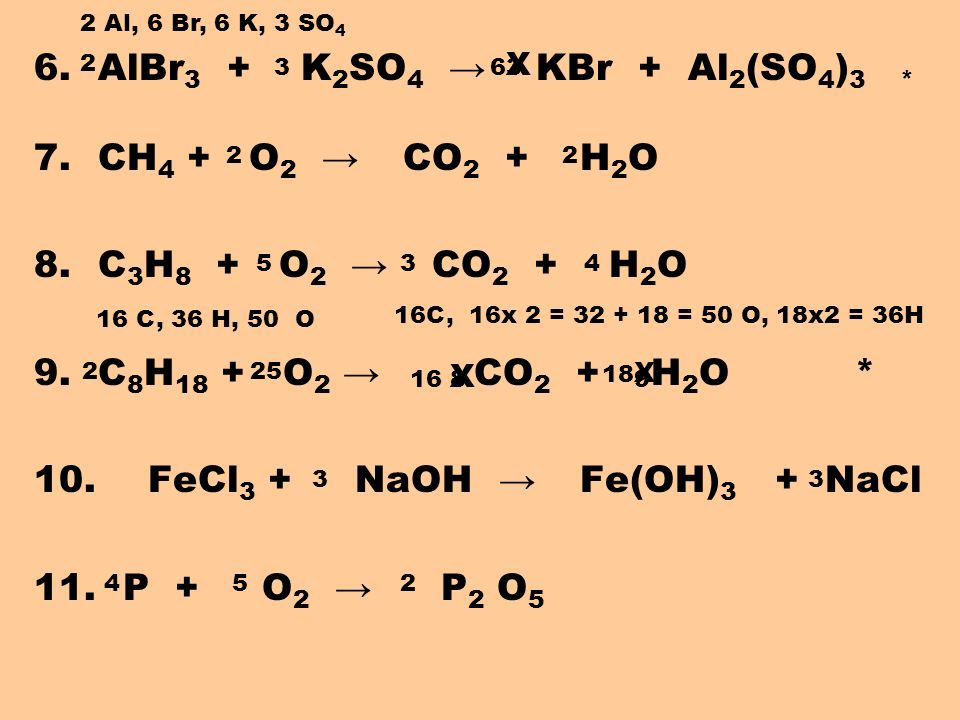 Розраховуємо масу розчину:
Розраховуємо масу розчину: Записуємо рівняння реакції: Na2CO3 + 2HCl=2NaCl + H2O + CO2↑
Записуємо рівняння реакції: Na2CO3 + 2HCl=2NaCl + H2O + CO2↑ Записуємо рівняння реакції:
Записуємо рівняння реакції: 
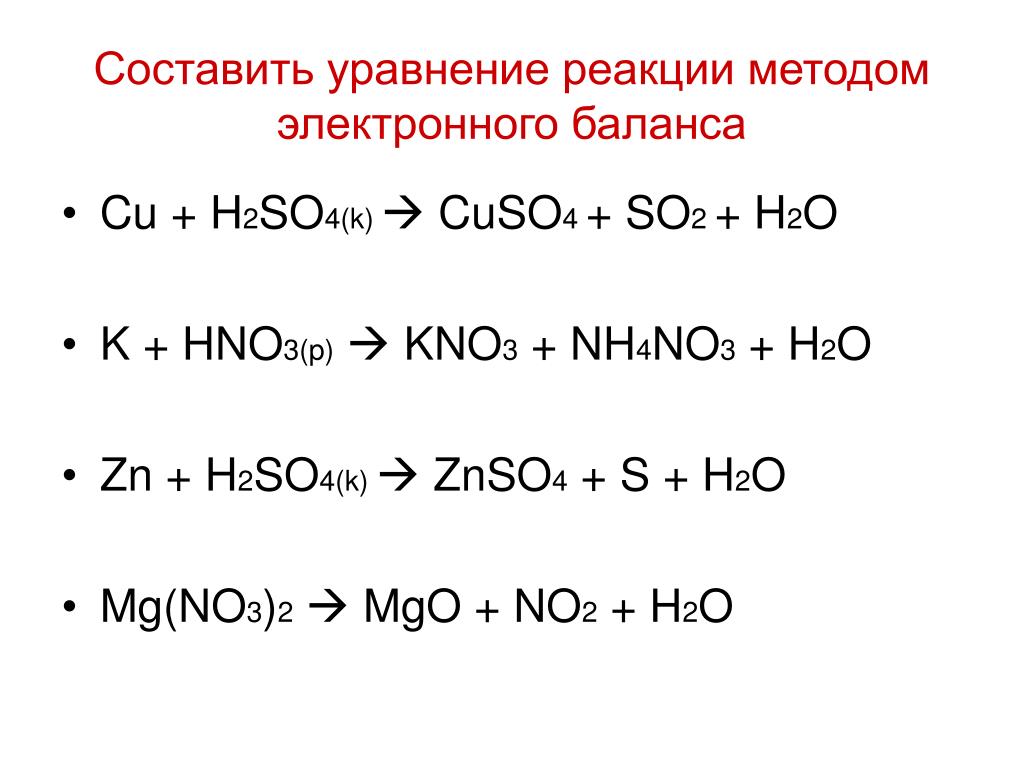 Записуємо рівняння реакції: H2SO4 + 2NaOH = Na2SO4 + 2H2O
Записуємо рівняння реакції: H2SO4 + 2NaOH = Na2SO4 + 2H2O 
 0109 Biochemistry
0109 Biochemistry


 ) + SO4-2 (водн.) = BaSO4 (с) + Н2 (Г)
) + SO4-2 (водн.) = BaSO4 (с) + Н2 (Г) 0109 Biochemistry
0109 Biochemistry По условию задачи , , . Тогда множество есть множество студентов, участвовавших в олимпиадах по математике и физике, множество есть множество студентов, участвовавших в олимпиадах по математике и информатике, множество есть множество студентов, участвовавших в олимпиадах по физике и информатике. По условию задачи , , . Множество есть множество студентов, участвовавших хотя бы в одной олимпиаде. Множество есть множество студентов, участвовавших во всех трёх олимпиадах. По условию задачи . Для ответа на вопрос задачи надо найти . По теореме 1.3
По условию задачи , , . Тогда множество есть множество студентов, участвовавших в олимпиадах по математике и физике, множество есть множество студентов, участвовавших в олимпиадах по математике и информатике, множество есть множество студентов, участвовавших в олимпиадах по физике и информатике. По условию задачи , , . Множество есть множество студентов, участвовавших хотя бы в одной олимпиаде. Множество есть множество студентов, участвовавших во всех трёх олимпиадах. По условию задачи . Для ответа на вопрос задачи надо найти . По теореме 1.3 С английским и французским языками знакомы 8 студентов, с французским и немецким – 10, с английским и немецким – 20. Все три языка изучали 5 первокурсников. Докажите, что в отчёте есть ошибка. Исправьте ошибку, если известно, что при обработке данных произошла потеря информации.
С английским и французским языками знакомы 8 студентов, с французским и немецким – 10, с английским и немецким – 20. Все три языка изучали 5 первокурсников. Докажите, что в отчёте есть ошибка. Исправьте ошибку, если известно, что при обработке данных произошла потеря информации. Шестеро студентов рассказали о посещении одновременно музея, театра и концерта. Сколько студентов участвовали в экскурсионной поездке?
Шестеро студентов рассказали о посещении одновременно музея, театра и концерта. Сколько студентов участвовали в экскурсионной поездке? Отсюда и происходит название формулы.
Отсюда и происходит название формулы. 1 Задача о беспорядках
1 Задача о беспорядках Также через обозначим количество элементов, не обладающих ни одним из свойств . Тогда имеет место формула:
Также через обозначим количество элементов, не обладающих ни одним из свойств . Тогда имеет место формула:
 Он дает по 1 в тех слагаемых суммы , для которых есть подмножество , и 0 для остальных. Число таких подмножеств по определению есть число сочетаний . Следовательно, вклад элемента в правую часть равен
Он дает по 1 в тех слагаемых суммы , для которых есть подмножество , и 0 для остальных. Число таких подмножеств по определению есть число сочетаний . Следовательно, вклад элемента в правую часть равен Оно выражает собой логическое тождество[1] и верно для произвольных множеств . В случае конечных множеств (и, соответственно, в предположении конечности множества ), просуммировав это соотношение по всем и воспользоваться тем, что для произвольного подмножества его мощность равна
Оно выражает собой логическое тождество[1] и верно для произвольных множеств . В случае конечных множеств (и, соответственно, в предположении конечности множества ), просуммировав это соотношение по всем и воспользоваться тем, что для произвольного подмножества его мощность равна Формула включений-исключений дает выражение для числа беспорядков:
Формула включений-исключений дает выражение для числа беспорядков:
 Тогда для произвольных измеримых множеств конечной меры имеет место формула включений-исключений:
Тогда для произвольных измеримых множеств конечной меры имеет место формула включений-исключений: В частном случае, когда мы получаем одну из форм принципа включений-исключений. В самом деле, если положить , где — произвольный элемент из , то получим соотношение для индикаторных функций множеств:
В частном случае, когда мы получаем одну из форм принципа включений-исключений. В самом деле, если положить , где — произвольный элемент из , то получим соотношение для индикаторных функций множеств: Для каждого набора индексов определим как число элементов, входящих только в те множества , для которых . Математически это можно записать так:
Для каждого набора индексов определим как число элементов, входящих только в те множества , для которых . Математически это можно записать так: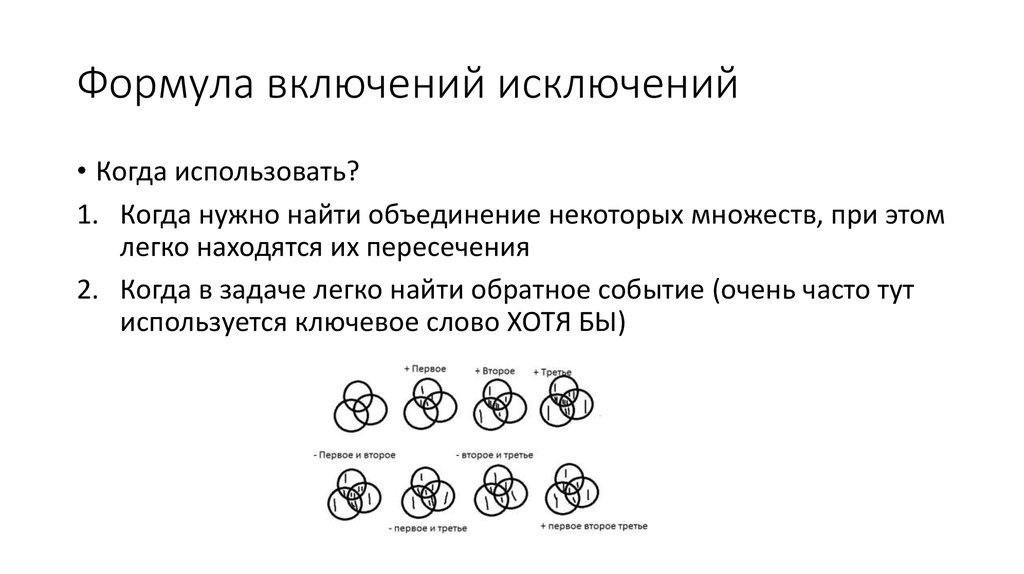 — М.: Изд-во иностранной литературы, 1963. — С. 63-66. — 289 с.
— М.: Изд-во иностранной литературы, 1963. — С. 63-66. — 289 с.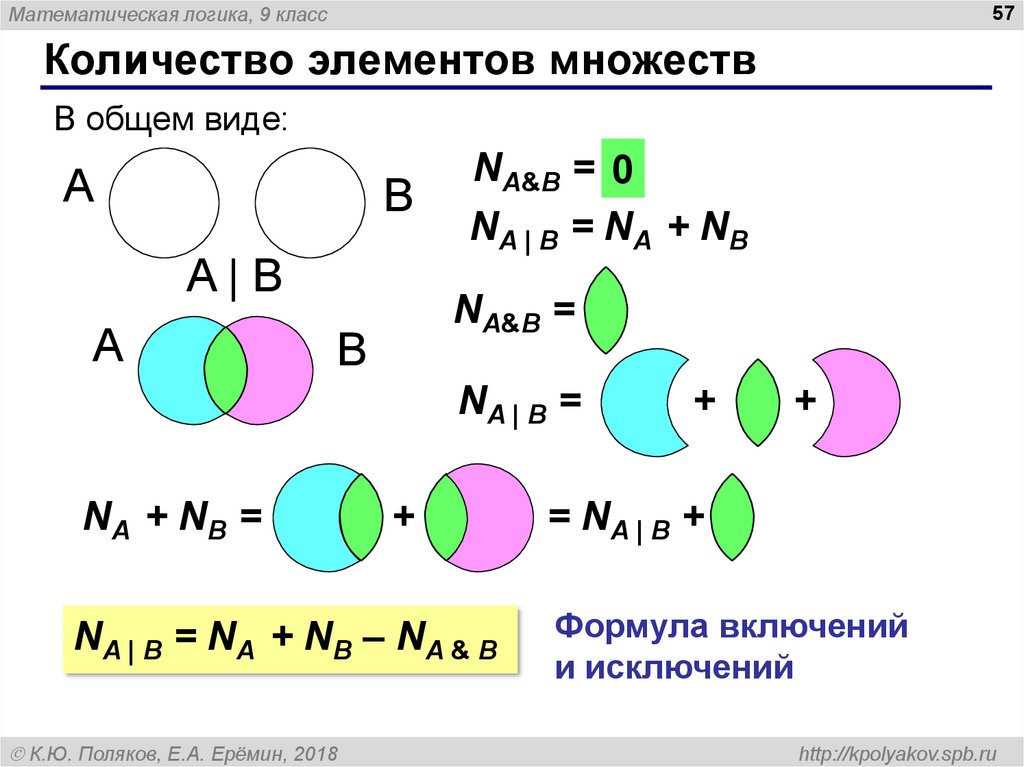 Перечислительная комбинаторика = Enumerative Combinatorics. — М.: «Мир», 1990. — С. 103-107. — 440 с.
Перечислительная комбинаторика = Enumerative Combinatorics. — М.: «Мир», 1990. — С. 103-107. — 440 с.

 \]
\] Тогда по принципу включения и исключения имеем
Тогда по принципу включения и исключения имеем
 \]
\]
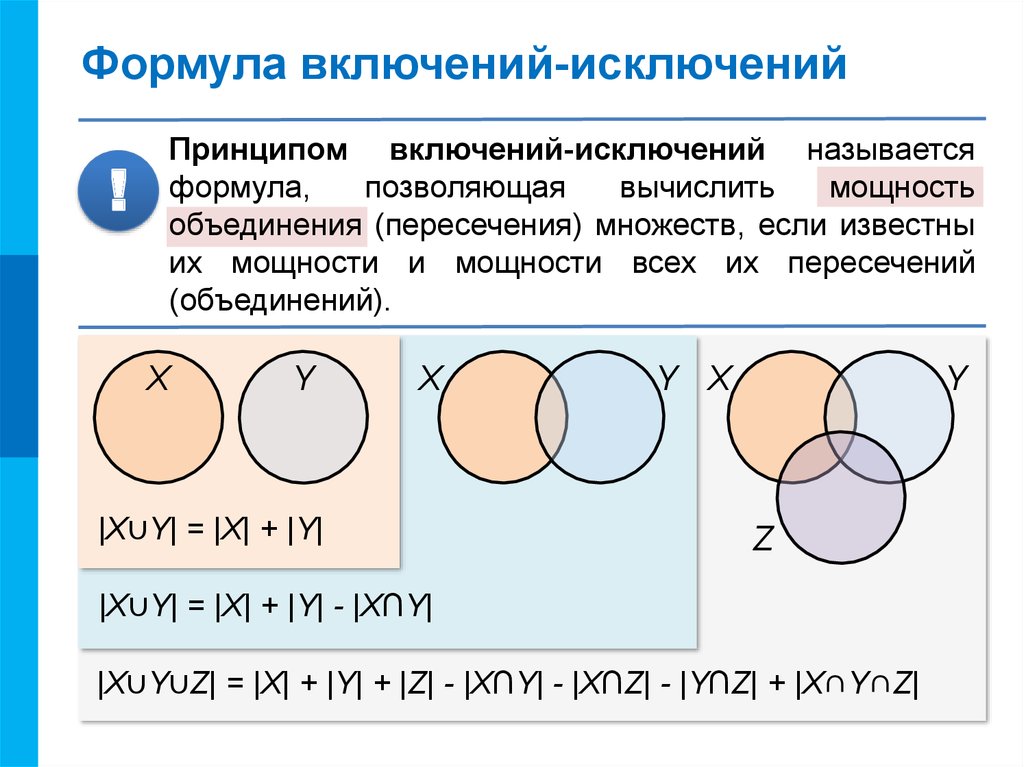 7\). Пусть \(T\) — множество способов, при которых тетраэдр не имеет шаров, \(C\) — множество способов, при которых кубический ящик не имеет шаров, и \(D\) — множество способов, при которых коробка додекаэдра не имеет шаров. Мы хотим найти 97 — 0 = 1806. \ _\квадрат\]
7\). Пусть \(T\) — множество способов, при которых тетраэдр не имеет шаров, \(C\) — множество способов, при которых кубический ящик не имеет шаров, и \(D\) — множество способов, при которых коробка додекаэдра не имеет шаров. Мы хотим найти 97 — 0 = 1806. \ _\квадрат\]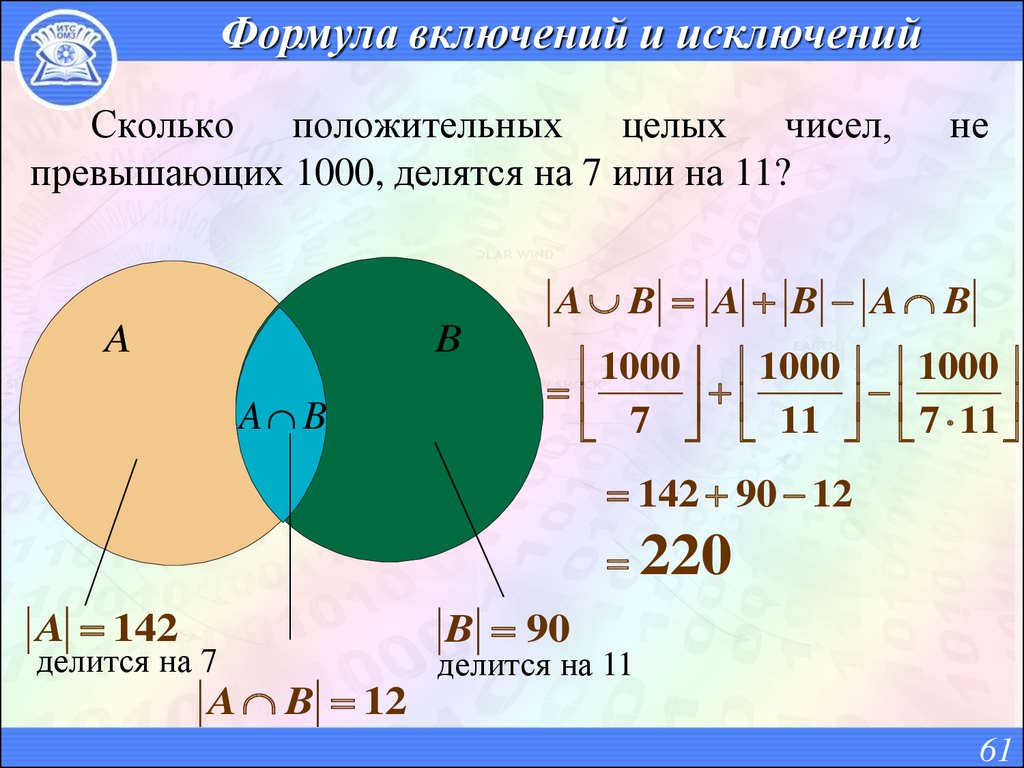
 . + сумма всех пересечений i-го набора.
. + сумма всех пересечений i-го набора. 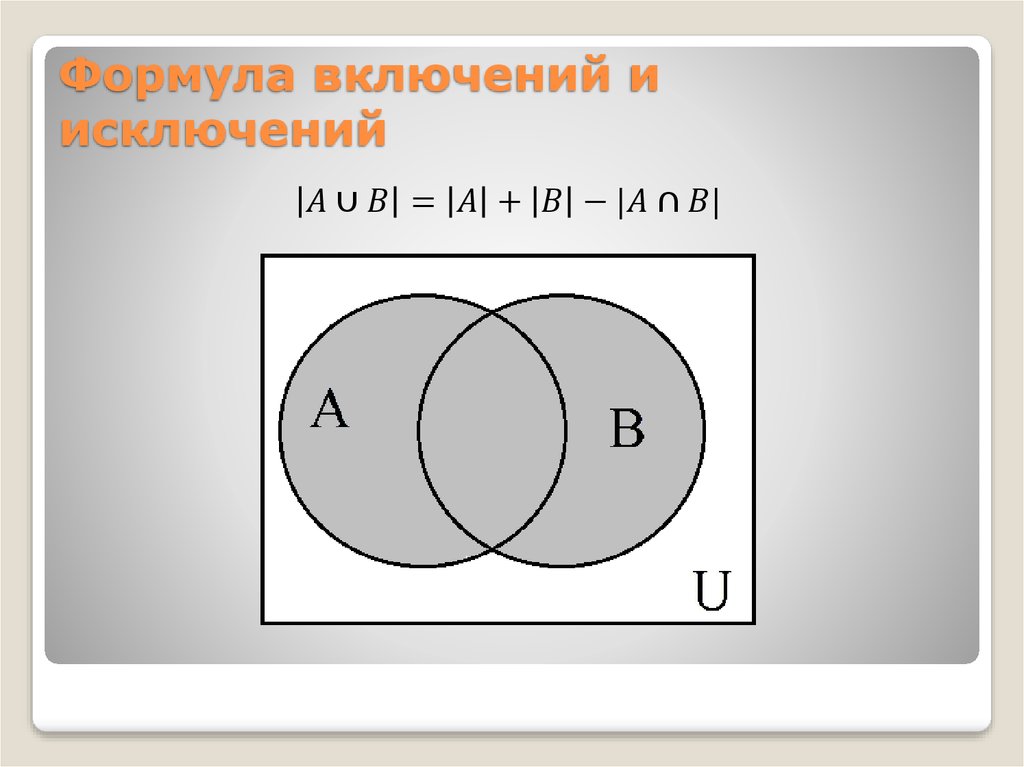 Принцип гласит, что размер объединения двух или более множеств равен сумме их размеров минус размер их пересечения, плюс размер пересечения их попарных пересечений и так далее.
Принцип гласит, что размер объединения двух или более множеств равен сумме их размеров минус размер их пересечения, плюс размер пересечения их попарных пересечений и так далее.
 0327
0327

 Таким образом, если бы мы не требовали от
последовательности {xn} никогда не посещать x0, нам пришлось
бы сказать, что данная функция не имеет предела в точке 2, хотя
согласно определению по Коши оно его имеет.
Таким образом, если бы мы не требовали от
последовательности {xn} никогда не посещать x0, нам пришлось
бы сказать, что данная функция не имеет предела в точке 2, хотя
согласно определению по Коши оно его имеет. Если бы достаточно было проверить лишь одну последовательность, мы
могли бы сказать, что предел равен −1. Что не так: выбирая другую
последовательность (например, xn=1−1/n), мы бы получили другой предел
f(xn).
Если бы достаточно было проверить лишь одну последовательность, мы
могли бы сказать, что предел равен −1. Что не так: выбирая другую
последовательность (например, xn=1−1/n), мы бы получили другой предел
f(xn).
 Иными словами, нам
нужно доказать, что для всякого ε>0 найдётся такое N=N(ε), что для
всех n>N выполняется неравенство |f(xn)−b|<ε.
Иными словами, нам
нужно доказать, что для всякого ε>0 найдётся такое N=N(ε), что для
всех n>N выполняется неравенство |f(xn)−b|<ε. Значит, для всех xn это неравенство также верно.
Значит, для всех xn это неравенство также верно.
 Зато с ним гораздо
проще доказывать утверждение, что предел не существует или чему-то не равен
— достаточно предъявить одну последовательность. Также с помощью предела по
Гейне можно легко переносить результаты, доказанные для последовательностей, на
функции. Например, докажем теорему о пределе суммы:
Зато с ним гораздо
проще доказывать утверждение, что предел не существует или чему-то не равен
— достаточно предъявить одну последовательность. Также с помощью предела по
Гейне можно легко переносить результаты, доказанные для последовательностей, на
функции. Например, докажем теорему о пределе суммы: Утверждение
доказано.∎
Утверждение
доказано.∎ Определение по Гейне удобно там, где нужно доказывать противоположное
утверждение (что предел чему-то не равен, или вообще не существует), а также в
некоторых теоретических построениях. Дополнительный бонус определения по Гейне —
оно позволяет переносить на пределы функций ряд свойств, доказанных для пределов
последовательностей, практически «бесплатно».
Определение по Гейне удобно там, где нужно доказывать противоположное
утверждение (что предел чему-то не равен, или вообще не существует), а также в
некоторых теоретических построениях. Дополнительный бонус определения по Гейне —
оно позволяет переносить на пределы функций ряд свойств, доказанных для пределов
последовательностей, практически «бесплатно».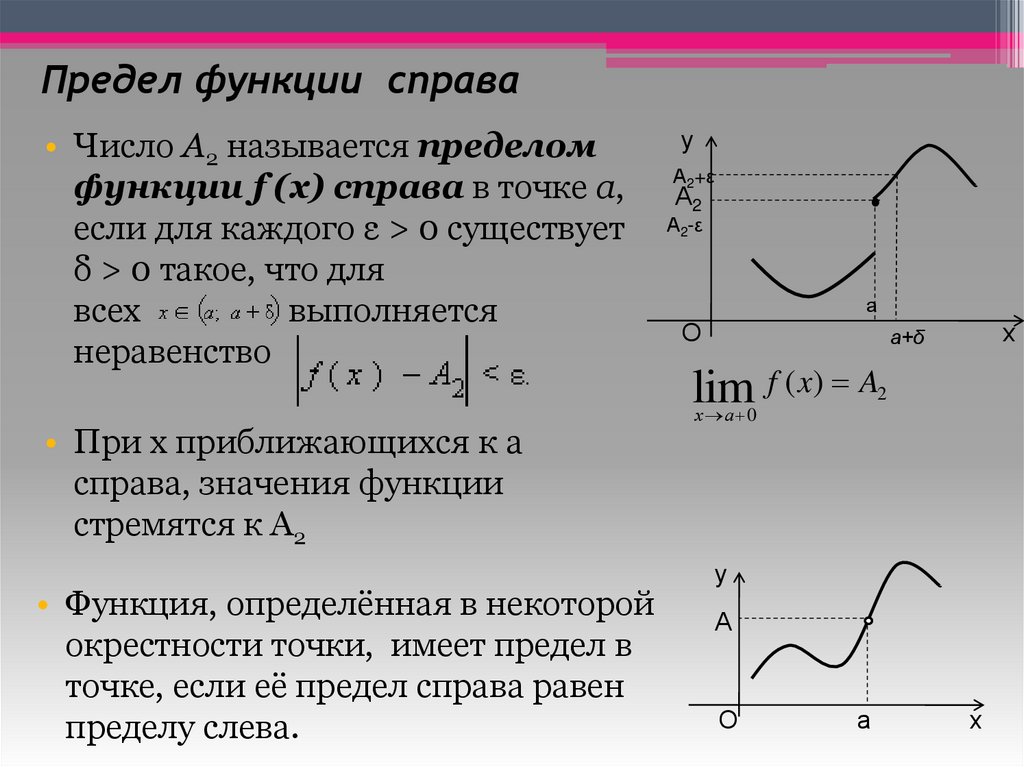

 Чтобы раскрыть неопределенность при переменной стремящейся к нулю, используем второй замечательный предел.
Чтобы раскрыть неопределенность при переменной стремящейся к нулю, используем второй замечательный предел.

 \end{выравнивание}
\]
\end{выравнивание}
\] n-1}.
\] 9+,\)» мы рассматриваем только значения больше \(a\). Односторонние пределы важны при оценке пределов, содержащих абсолютные значения \(|x|\), знак \(\text{sign}(x)\) , функции пола \(\lfloor x \rfloor\) и другие кусочные функции
n-1}.
\] 9+,\)» мы рассматриваем только значения больше \(a\). Односторонние пределы важны при оценке пределов, содержащих абсолютные значения \(|x|\), знак \(\text{sign}(x)\) , функции пола \(\lfloor x \rfloor\) и другие кусочные функции В точке \(x=2,\) нет конечного значения ни для одного из двусторонних пределов, поскольку функция неограниченно возрастает по мере приближения координаты \(x\) к \(2\) (но см. следующий раздел для дальнейшего обсуждения). Ситуация аналогична для \(x=-1.\). Таким образом, точки \(x=-3\), \(x=-2\), \(x=0\), \(x=1,\ ) и \(x=3\) — все целые числа, на которых определены двусторонние пределы. \(_\квадрат\)
В точке \(x=2,\) нет конечного значения ни для одного из двусторонних пределов, поскольку функция неограниченно возрастает по мере приближения координаты \(x\) к \(2\) (но см. следующий раздел для дальнейшего обсуждения). Ситуация аналогична для \(x=-1.\). Таким образом, точки \(x=-3\), \(x=-2\), \(x=0\), \(x=1,\ ) и \(x=3\) — все целые числа, на которых определены двусторонние пределы. \(_\квадрат\) \]
\] \(\infty\)», то есть при неограниченном увеличении \(x\).
\(\infty\)», то есть при неограниченном увеличении \(x\). {11}} \справа) = \, ?\]
{11}} \справа) = \, ?\] Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана. Мы также убедились, что рассмотрели значения \(x\), которые были как слева, так и справа от \(x = a\). Сделав это, мы посмотрели на нашу таблицу значений функции и увидели, к чему приближаются значения функции по мере того, как \(x\) становилось все ближе и ближе к \(x = a\), и использовали это, чтобы угадать значение, которое нам нужно.
Мы также убедились, что рассмотрели значения \(x\), которые были как слева, так и справа от \(x = a\). Сделав это, мы посмотрели на нашу таблицу значений функции и увидели, к чему приближаются значения функции по мере того, как \(x\) становилось все ближе и ближе к \(x = a\), и использовали это, чтобы угадать значение, которое нам нужно. Как правило, мы обычно не используем методы, описанные в этом разделе, для вычисления лимитов, и во многих случаях их может быть очень сложно использовать даже для оценки значения лимита, и/или иногда мы будем давать неправильное значение. Мы рассмотрим фактические вычисления пределов в нескольких разделах.
Как правило, мы обычно не используем методы, описанные в этом разделе, для вычисления лимитов, и во многих случаях их может быть очень сложно использовать даже для оценки значения лимита, и/или иногда мы будем давать неправильное значение. Мы рассмотрим фактические вычисления пределов в нескольких разделах. Приведенное выше определение является скорее «рабочим». Это определение помогает нам понять, что такое пределы и что они могут рассказать нам о функциях.
Приведенное выше определение является скорее «рабочим». Это определение помогает нам понять, что такое пределы и что они могут рассказать нам о функциях. В нем говорится, что где-то в мире есть значение \(x\), скажем, \(X\), так что для всех \(x\), которые ближе к \(a\), чем \(X \), то одно из приведенных выше утверждений будет верным.
В нем говорится, что где-то в мире есть значение \(x\), скажем, \(X\), так что для всех \(x\), которые ближе к \(a\), чем \(X \), то одно из приведенных выше утверждений будет верным.
 Затем мы смотрим, можем ли мы определить, к какому числу приближаются значения функции, и используем это как нашу оценку. 92} — 2x}}\]
Затем мы смотрим, можем ли мы определить, к какому числу приближаются значения функции, и используем это как нашу оценку. 92} — 2x}}\]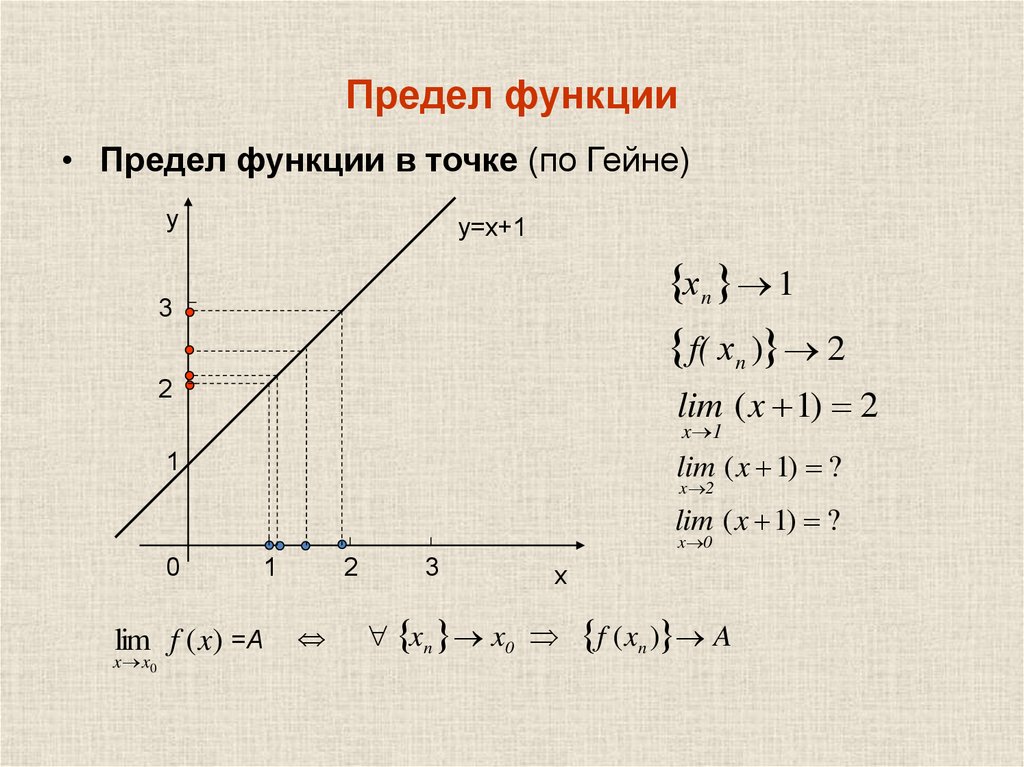 1
1 92} — 2x}} = 4\]
92} — 2x}} = 4\] 2} — 2x}} & {\mbox{if} }x \ne 2\\ 6 & {\mbox{if}}x = 2\end{массив} \right.\]
2} — 2x}} & {\mbox{if} }x \ne 2\\ 6 & {\mbox{if}}x = 2\end{массив} \right.\] Итак, поскольку мы уже сделали это один раз, нет причин переделывать это здесь.
Итак, поскольку мы уже сделали это один раз, нет причин переделывать это здесь. Затем график также поддерживает вывод о том, что предел равен
Затем график также поддерживает вывод о том, что предел равен Однако важно не волноваться по поводу вещей, когда функция и предел не принимают одно и то же значение в какой-то точке. Это случается иногда, поэтому нам нужно будет иметь дело с такими случаями, когда они возникают.
Однако важно не волноваться по поводу вещей, когда функция и предел не принимают одно и то же значение в какой-то точке. Это случается иногда, поэтому нам нужно будет иметь дело с такими случаями, когда они возникают.

 Однако, если бы мы сделали это предположение, мы бы ошиблись. Рассмотрим любую из следующих оценок функции.
Однако, если бы мы сделали это предположение, мы бы ошиблись. Рассмотрим любую из следующих оценок функции.
 Это то, что мы всегда должны помнить, когда делаем это, чтобы угадать значение ограничений. На самом деле это такая проблема, что после этого раздела мы больше никогда не будем использовать таблицу значений, чтобы угадать значение лимита.
Это то, что мы всегда должны помнить, когда делаем это, чтобы угадать значение ограничений. На самом деле это такая проблема, что после этого раздела мы больше никогда не будем использовать таблицу значений, чтобы угадать значение лимита. Мы могли бы использовать таблицу значений для оценки предела, но, вероятно, в этом случае будет так же быстро использовать график, так что давайте сделаем это. Ниже представлен график этой функции.
Мы могли бы использовать таблицу значений для оценки предела, но, вероятно, в этом случае будет так же быстро использовать график, так что давайте сделаем это. Ниже представлен график этой функции. Проблема в том, что число на каждой стороне \(t = 0\) разное. Это идея, которую мы рассмотрим более подробно в следующем разделе.
Проблема в том, что число на каждой стороне \(t = 0\) разное. Это идея, которую мы рассмотрим более подробно в следующем разделе. Использование таблиц значений для угадывания значений лимитов — просто не лучший способ получить значение лимита. Это единственный раздел, в котором мы будем это делать. Таблицы значений всегда должны быть вашим последним выбором при поиске значений пределов.
Использование таблиц значений для угадывания значений лимитов — просто не лучший способ получить значение лимита. Это единственный раздел, в котором мы будем это делать. Таблицы значений всегда должны быть вашим последним выбором при поиске значений пределов. Для многих функций это не так просто сделать.
Для многих функций это не так просто сделать.
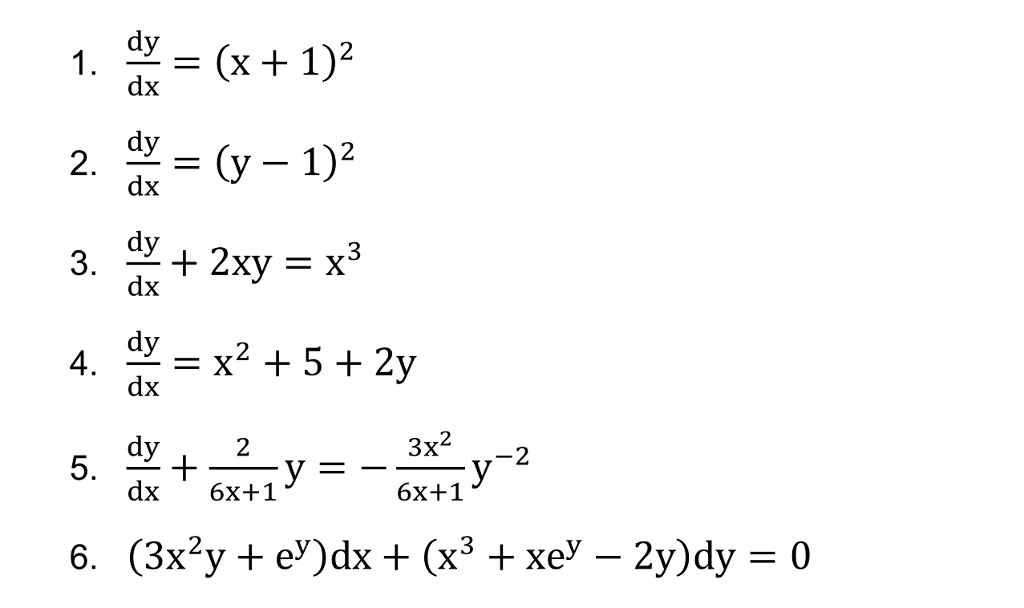 Когда студент посчитает нужным, он может остановить аукцион и назначить задание одному из репетиторов, сделавшему ставку (не обязательно самую низкую, т.к. можно учитывать и другие факторы – см. выше).
Когда студент посчитает нужным, он может остановить аукцион и назначить задание одному из репетиторов, сделавшему ставку (не обязательно самую низкую, т.к. можно учитывать и другие факторы – см. выше).
 И вариант с получением прибыли от размещения рекламы подходит и для нового сервиса. Кроме того, мне нравится помогать людям и довольно тяжело смотреть, как множество вопросов по задачам остаются на форуме без ответа. Предложенный аукцион решений сможет значительно сократить число вопросов без ответов.
И вариант с получением прибыли от размещения рекламы подходит и для нового сервиса. Кроме того, мне нравится помогать людям и довольно тяжело смотреть, как множество вопросов по задачам остаются на форуме без ответа. Предложенный аукцион решений сможет значительно сократить число вопросов без ответов.
 Для получения онлайн решения введите максимальную степень производной n. Например, для дифференциального уравнения
Для получения онлайн решения введите максимальную степень производной n. Например, для дифференциального уравнения  Так как y’ = 0, y’’ = 0, y’’’ = 0, то, подставляя в уравнение, получаем 5c — 2cx — 2d = 2x + 3. Приравнивая коэффициенты при одинаковых степенях x, получаем -2c = 2.
-5c – 2d = 3. Следовательно, c=-1, d= -4 и y = -x-4 — частное, а y = -x-4+C1ex + C2e2x — общее решения уравнения.
Так как y’ = 0, y’’ = 0, y’’’ = 0, то, подставляя в уравнение, получаем 5c — 2cx — 2d = 2x + 3. Приравнивая коэффициенты при одинаковых степенях x, получаем -2c = 2.
-5c – 2d = 3. Следовательно, c=-1, d= -4 и y = -x-4 — частное, а y = -x-4+C1ex + C2e2x — общее решения уравнения.

 Найти общее решение уравнения:
Найти общее решение уравнения:  Решить дифференциальное уравнение 8y» +2y’ — 3y = 0.
Решить дифференциальное уравнение 8y» +2y’ — 3y = 0.


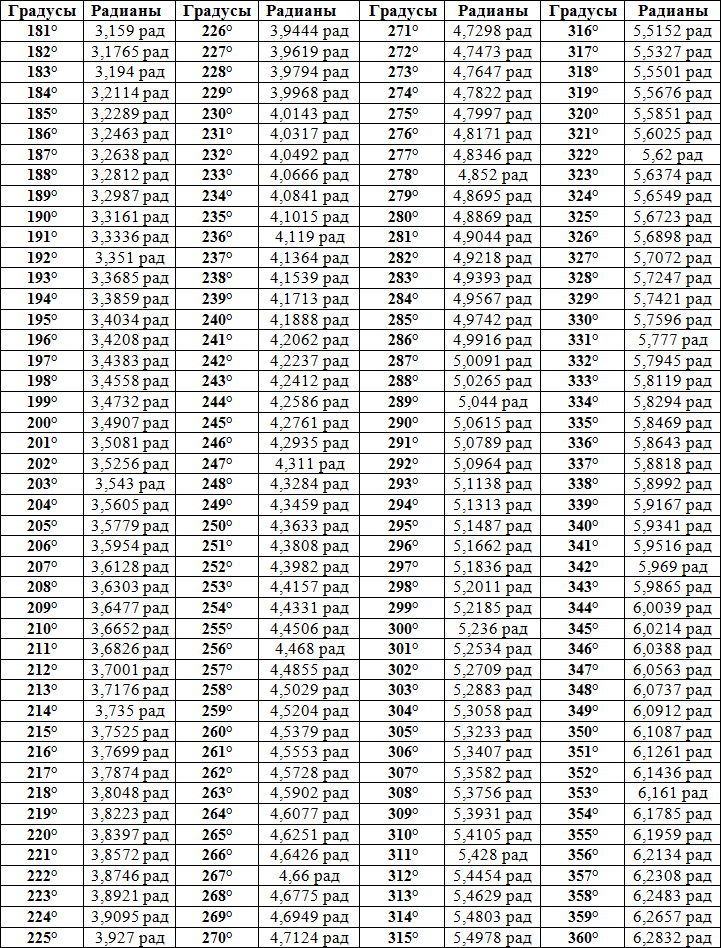 ..
.. ..
.. ..
..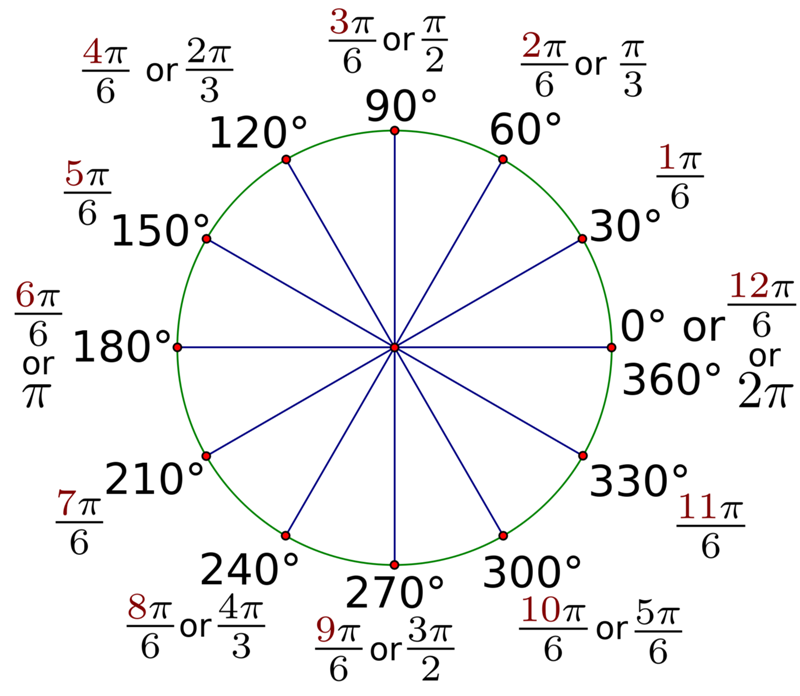 ..
.. Шаблоны могут содержать такие настройки, как:
Шаблоны могут содержать такие настройки, как:




 Также эти свойства определяют единицы измерения, используемые в SimulationXpress.
Также эти свойства определяют единицы измерения, используемые в SimulationXpress.

 Например, 46,15 округляется до 46,1.
Например, 46,15 округляется до 46,1.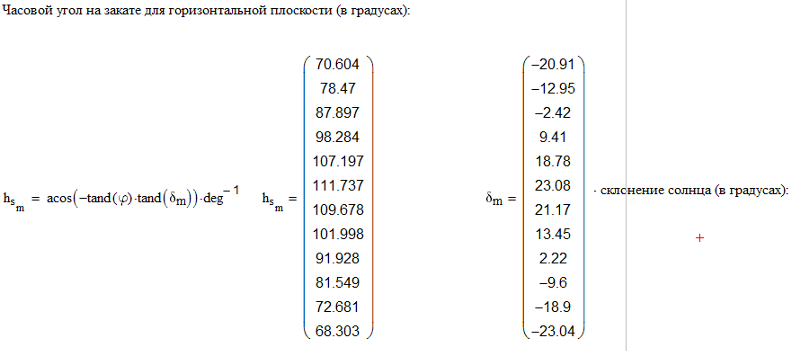 Если этот параметр не выбран, это применяется к правилу округления для любого отображения цифр с выполнением округления, включая диалоговые окна, например Массовые характеристики.
Если этот параметр не выбран, это применяется к правилу округления для любого отображения цифр с выполнением округления, включая диалоговые окна, например Массовые характеристики.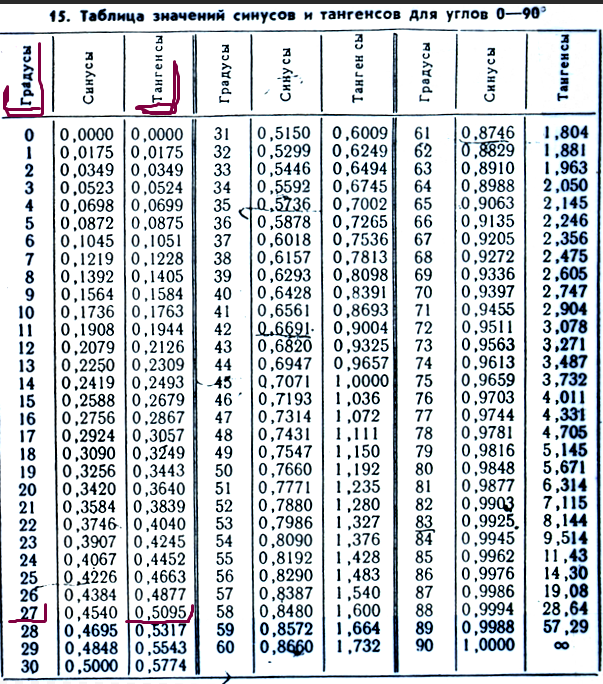 S.) — Ссылка (Gunter’s; Геодезист) LNK (RE) — Link (Ramsden’s; Engineer’s) LS — Световой-секундный — Световой годM — Метр (базовая единица СИ)MIL — Мил (Швеция и Норвегия)MILE DATA — Мили (тактические или данные)MK — MickeyNAIL — Гвоздь (ткань)NL — Морская лигаNM — НанометрNMI — Морские милиNMI I — Морская миляP — PalmPC — ParsecPICA — PicaPM — Пикометр (бикрон, клеймо)POINT — точка (американский, английский)PT — PaceQUART — QuarterSHAKU — Shaku (Japan)SPT — SpatTH — Мил (тыс.) TWP — TwipUM — Микрометр (стар. микрон) XU — X единица измерения; siegbahnABA — Электромагнитная единица AbampereAMP — Ампер (базовая единица Si)ESU — Esu в секунду Статампер (CgsABC — Абкулон Электромагнитная единицаATU — Атомная единица зарядаCLM — КулонFRD — ФарадейMAH — Миллиампер-часSTT — Статкулон Франклин ЭлектростABV — Абвольт (единица Cgs)STV — Статвольт ( Cgs Unit)VLT — Вольт (Si Unit)ACF — Акр-футыACI — Акры-дюймыBIB — Баррели (нефтяные)BII — Баррели (британские)BIU — Баррели (Us Dry)BKT — Ведра (британские)BRO — Галлоны (пивные)BUD — Бушели (Us Dry Level)BUI — Бушели (Imperial)BUU — Бушели (Us Dry Heaped)CMB — CoombsCMI — Cubic MilesCP — CupsCRF — Cord-FootsCRW — Cords (Дрова)CUF — Cubic FathomsCUI — Cubic InchsCUT — Cubic FootsCUY — Cubic ЯрдыDSI — тире (имперские фунты)DSS — десертные ложки (имперские фунты)DSU — тире (США)FBM — борд-футыFFT — пятые FID — жидкие драхмы (имперские)FIS — жидкие скрукле (имперские)FLB — бочки (США, жидкие)FLU — жидкие драмы ( Us) Us FluidramFRK — FirkinsGAI — галлоны (имперские единицы)GAU — галлоны (Us Dry)GAW — галлоны (Us Fluid Wine)GLU — Teacups (gills)GTT — DropsHDI — Hogsheads (Imperial)HHU — Hogsheads (Us)JGR — Jiggers ( Bartending)KLD — KilderkinsLMD — LambdasLOD — LoadsLST — LastsM3 — Кубические метры (Si Unit)MII — Minims (Imperial)MIU — Minims (Us)OZF — Унции (Fluid Us Food NutritioPER — PerchsPKI — Pecks (Imperial)PKU — Pecks (Us) Сухой)PNI — пинчи (британские)PNU — пинчи (американские)PON — PonysPOT — Pottle QuartersPP — стыковые трубыPTI — пинты (британские)PUD — пинты (Us Dry)PUF — пинты (Us Fluid)QRF — Quart S (Us Fluid) QRT — Кварталы QTI — Кварты (британские)QTU — Кварты (Us Dry)RGS — Реестр TonsSCI — Мешки (британские) BagsSCU — Мешки(Us)SHT — Shots (Us)SM — SeamsSTK — Забастовки (Imperial)STU — Забастовки (Us) )TBC — столовые ложки (канадские)TBF — столовые ложки (обычные в США)TBM — столовые ложки (метрические)TBS — столовые ложки (в австралийских единицах измеренияTCA — чайные ложки (канадские) TFD — столовые ложки (Us Food NutritionTIM — чайные ложки (британские)TMF — Timber FootsTMT — чайные ложки ( Метрическая система)TND – тонны (водоизмещение)TNT – тонны (воды)TNW – тонны (фрахт)TSC – чайные ложки (стандарт США)TSF – чайные ложки (США Food Nutrition) WEY — Wey (Us)ACM — Атмосфера-кубический фут в минутуACS — Атмосфера-кубический фут в секунду SecoATC — Атмосфера-кубический сантиметр PeATH — Атмосфера-кубический фут в часBTJ — BTU (Международная таблица) В расчете на BTN — BTU (Международная таблица) В расчете на BTS — БТЕ (международная таблица) по CAS — Калория (международная таблица) ERS — Эрг в секундуFMF — Фут-фунт-сила в минутуFT — Фут-фунт-сила в часFTO — Фут-фунт-сила в секундуHPS — Лошадиная силаLAM — Литр-атмосфера в час MinuteLSC — LusecLTS — Литр атмосферы в секундуPNC — PonceletSQL — Прямой эквивалент квадратного фута TC — Тонна кондиционирования воздухаTMS — Атмосфера-кубический сантиметр PeTRM — Тонна охлаждения (ImperialTRR — Тонна охлаждения (It)AMU — Единица атомной массы UnifiedAT — Анализ тонны (Короткий)ATS — Ton Assay (Длинный)BAC — Bag (Coffee)BDM — Bag (Portland Cement)BRG — BargeCLV — CloveCRT — CrithCT — Carat (Metric)DA — DaltonDRT — Dram (Apothecary Troy)DWT — PennyweightGAM — GammaGR — GrainGV — GraveKIP — KipLB — Фунт (метрический)LBA — ФунтLBT — Фунт (тройской)LBV — Фунт (Avoirdupois)ME — Атомная единица массы Электрон RMRK — MarkMTE — MiteMTM — Клещ (метрический)OZ — Унция (Us Food Nutrition LabelOZT — Унция (аптечная тройка)OZZ — унция (Avoirdupois)PNN — PointQ — квинтал (метрическая система)QR — четверть (неформальная)QRI — четверть (имперская)QRL — четверть длинная (неформальная)SAP — Scruple (аптекарь)SH — тонна короткаяSLG — слаг Geepound HylSLH — SheetST — StoneSWT — Вес в сотни (центум) oTON — Тонна LongWY — WeyZTR — ZentnerARE — AresBD — BoardsBHE — Эквивалент мощности котла DBR — BarnsBRN — BaronysCDA — Cuerda Pr SurveysCRD — CordsCRI — Circular InchsCRM — Circular MilsDNM — DunamsGNT — GunthasHD — HidesRO — RoodsSCT — SectionsSHD — СараиSII — Square Link Gunters InternatiSLR — Square Link RamsdensSQC — Square Chains InternationalSQM — Square Mil Square ThousSQR — Square Rod/Pole/PerchsSRR — Square RoofingsSTR — StremmasTWN — TownshipsYLN — YardlandsARM — Arcminute MoaARS — ArcsecondCNS — Centesimal Second Of ArcCNT — Столетняя минута ArcDOA — Градус (дуги)GRA — Град Градиан GonOCT — OctantQRD — QuadrantSGN - SignSXT — Секстантµ — Угловой MilATA — Атмосфера (техническая)ATM — Атмосфера (стандартная)BAR — BarBRY — Бари (единица Cgs)CMH — Сантиметр Of MercuryCMW – сантиметр водяного столба (4 °C)FTH – фут ртутного столба (условный)FTW – фут водяного столба (392 °F)IMC — Дюйм ртутного столба (условный)INW — Дюйм водяного столба (392 °F)KM — Килограмм-сила на квадратный дюймKSI — Кип на квадратный дюймLTP — Длинная тонна на квадратный футMHG — Микрометр ртутного столбаMMH — Миллиметр ртутного столбаMMW — Миллиметр воды (398 °C)PA — Паскаль (единица Si)PD — фунт на квадратный футPSF — фунт на квадратный футPSI — фунт на квадратный дюймPZ — пьеза (единица Mts)STP — короткая тонна на квадратный футTOR — ТоррATN — атомная единица ForceDYN — Dyne (Cgs Unit)KFF — Килограмм-сила Kilopond Grave-KI — Kip Kip-ForceMGF — Milligrave-Force Gravet-ForceOZC — Унция-силаPDL — PoundalSN — Sthene (единица Mts)TNF — Long Ton-ForceTNL — Short Ton- ForceAUC — атомная единица времениCTN — CenturyCYC — каллипический циклDEC — DecadeFN — FortnightHEL — HelekHIP — гиппархический циклJFF — JiffyKEH — Ke (четверть часа) LSR — Luster LustrumMD — MillidayMLL — MillenniumMMN — MomentMOF — Month (Full)MOG — Month (Greg) Av)MOH — месяц (полый)MOS — месяц (синодический)MTN — метонический цикл EnneadecaeterisOC — OctaeterisPLN — планковское времяSGM — SigmaSHK — ShakeSTH — сотический циклSVD — SvedbergYR — год (общий)YRG — год (григорианский)YRJ — год (юлианский) YRL – год (високосный)YRM – год (среднетропический)B39- Британская термальная единица (39 °F)B59 — Британская термальная единица (59 °F)B60 — Британская термальная единица (60 °F)B63 — Британская термальная единица (63 °F)BOE — эквивалент барреля нефтиBRT — Британская термальная единица ( Iso)BTI — Британская термальная единица (InternatBTM — Британская термальная единица (средняя)BTT — Британская термальная единица (ThermochC15 — Калория (15 °C)C20 — Калория (20 °C)C98 — Калория (398 °C)CAM — Калория ( Среднее значение)CFT — Кубический фут атмосферы CHU — Тепловая единица ЦельсияCL — Калория (Us Fda)CLTH — Калория (термохимическая)CN — Кубический фут природного газаCTA — Кубический сантиметр атмосферыCYD — Кубический ярд атмосферы StandEH — Атомная единица энергии ХартриFTD — Foot-PoundalIMG — Галлон-атмосфераKCA — Большая килокалорияKWH — Киловатт-час Board Of Trade ULTM — Литр-атмосфераQD — QuadRDB — Therm (Ec)RY — RydbergTCE — Тонна угольного эквивалентаTHR — Therm (Us)THU — ThermieTN — Тонна TntTOE — Тонна нефтяного эквивалентаBAN — Ban HartleyBSH — Bit ShannonCD — Candela (Si Base Unit) CandleCPD — Candlepower (New)JK — Si UnitNAT — Nat Nip NepitNBL — NibbleBQ — Беккерель (Si Unit)CI — CurieRD — Rutherford (H)C — Скорость света в вакуумеFPF — фарлонг в две неделиFPH — фут в часIPH — дюйм в часIPM — дюйм в минутуIPS — дюйм в секундуMCH — число МахаMPM — миля в минутуMPS — миля в секундуMS — метр в секунду (единица Си)SPS — скорость звука в AirCDF — Кандела на квадратный футCDI — Кандела на квадратный дюймCDM — Кандела на квадратный метр (Si UFL — FootlambertLMB — LambertSB — Stilb (Cgs Unit)CEL — ЦельсийDDE — Градус DelisleDNE — Градус НьютонаFAN — ФаренгейтGMR — Регулятор газа MarkKEL — Kelvin’sRAN — RankineREA — ReaumurRME — Градус RømerCFM — Кубический фут в минутуFTS — Кубический фут в секундуGPD — Галлон (жидкость США) в суткиGPH — Галлон (жидкость США) в часGPM — Галлон (жидкость США) в минутуINM — Кубический дюйм в минутуINS — Кубический дюйм в секундуLPM — Литр в минутуMQS — кубический метр в секунду (Si UniCM — кулон-метрDB — DebyeEA0 — атомная единица электрического диполяFC — фут-канделя люмен на квадрат FoLMN — люмен на квадратный дюймLX — люкс (единица Si)PH — Phot (единица Cgs)FHP — фут в секунду Час в секундуFMS — фут в минуту в секундуFP — фут в секунду в квадратеG — стандартная гравитацияGAL — галлон GalileoIP — дюйм в минуту в секунду в секундуIP2 — дюйм в секунду в квадратеKNS — узел в секундуMM — миля в минуту в секундуMP — миля в час в секундуMP2 — миля в секунду Секунда в квадратеMSA — метр на секунду в квадрате (Si UFT2 — квадратный фут в секундуM2S — квадратный метр в секунду (Si UnSTX — Стокс (единица Cgs)FTP — фут-фунт)MKG — метр-килограмм-силаNEM — ньютон-метр (единица Si)GML — грамм на секунду MillilitreLAB — фунт (эквивалентный) на галлонLBF — фунт (эквивалентный) на кубический LBI — фунт (экспериментальный) на кубический LBL — фунт (экспериментальный) на галлонOFT — унция (экспериментальный) на кубический OG — унция (эвердупуа) на галлон ) Per GallonOIN — Унция (Avoirdupois) на кубический SFT — Slug на кубический футGSS — Gauss (Cgs Unit)TSL — Tesla (Si Unit)GY — Grey (Si Unit)RDD — RadLBH — Pound Per Foot HourLBS — Фунт на фут в секундуLFT — Фунт-сила-секунда на квадрат LIN — Фунт-сила-секунда на квадрат PAS — Паскаль-секунда (единица Si)PSU — Пуаз (единица Cgs)MX — Максвелл (единица Cgs)WB — Вебер (единица Si)REM — Рентген-эквивалент ManSV — Sievert (Единица Си)
S.) — Ссылка (Gunter’s; Геодезист) LNK (RE) — Link (Ramsden’s; Engineer’s) LS — Световой-секундный — Световой годM — Метр (базовая единица СИ)MIL — Мил (Швеция и Норвегия)MILE DATA — Мили (тактические или данные)MK — MickeyNAIL — Гвоздь (ткань)NL — Морская лигаNM — НанометрNMI — Морские милиNMI I — Морская миляP — PalmPC — ParsecPICA — PicaPM — Пикометр (бикрон, клеймо)POINT — точка (американский, английский)PT — PaceQUART — QuarterSHAKU — Shaku (Japan)SPT — SpatTH — Мил (тыс.) TWP — TwipUM — Микрометр (стар. микрон) XU — X единица измерения; siegbahnABA — Электромагнитная единица AbampereAMP — Ампер (базовая единица Si)ESU — Esu в секунду Статампер (CgsABC — Абкулон Электромагнитная единицаATU — Атомная единица зарядаCLM — КулонFRD — ФарадейMAH — Миллиампер-часSTT — Статкулон Франклин ЭлектростABV — Абвольт (единица Cgs)STV — Статвольт ( Cgs Unit)VLT — Вольт (Si Unit)ACF — Акр-футыACI — Акры-дюймыBIB — Баррели (нефтяные)BII — Баррели (британские)BIU — Баррели (Us Dry)BKT — Ведра (британские)BRO — Галлоны (пивные)BUD — Бушели (Us Dry Level)BUI — Бушели (Imperial)BUU — Бушели (Us Dry Heaped)CMB — CoombsCMI — Cubic MilesCP — CupsCRF — Cord-FootsCRW — Cords (Дрова)CUF — Cubic FathomsCUI — Cubic InchsCUT — Cubic FootsCUY — Cubic ЯрдыDSI — тире (имперские фунты)DSS — десертные ложки (имперские фунты)DSU — тире (США)FBM — борд-футыFFT — пятые FID — жидкие драхмы (имперские)FIS — жидкие скрукле (имперские)FLB — бочки (США, жидкие)FLU — жидкие драмы ( Us) Us FluidramFRK — FirkinsGAI — галлоны (имперские единицы)GAU — галлоны (Us Dry)GAW — галлоны (Us Fluid Wine)GLU — Teacups (gills)GTT — DropsHDI — Hogsheads (Imperial)HHU — Hogsheads (Us)JGR — Jiggers ( Bartending)KLD — KilderkinsLMD — LambdasLOD — LoadsLST — LastsM3 — Кубические метры (Si Unit)MII — Minims (Imperial)MIU — Minims (Us)OZF — Унции (Fluid Us Food NutritioPER — PerchsPKI — Pecks (Imperial)PKU — Pecks (Us) Сухой)PNI — пинчи (британские)PNU — пинчи (американские)PON — PonysPOT — Pottle QuartersPP — стыковые трубыPTI — пинты (британские)PUD — пинты (Us Dry)PUF — пинты (Us Fluid)QRF — Quart S (Us Fluid) QRT — Кварталы QTI — Кварты (британские)QTU — Кварты (Us Dry)RGS — Реестр TonsSCI — Мешки (британские) BagsSCU — Мешки(Us)SHT — Shots (Us)SM — SeamsSTK — Забастовки (Imperial)STU — Забастовки (Us) )TBC — столовые ложки (канадские)TBF — столовые ложки (обычные в США)TBM — столовые ложки (метрические)TBS — столовые ложки (в австралийских единицах измеренияTCA — чайные ложки (канадские) TFD — столовые ложки (Us Food NutritionTIM — чайные ложки (британские)TMF — Timber FootsTMT — чайные ложки ( Метрическая система)TND – тонны (водоизмещение)TNT – тонны (воды)TNW – тонны (фрахт)TSC – чайные ложки (стандарт США)TSF – чайные ложки (США Food Nutrition) WEY — Wey (Us)ACM — Атмосфера-кубический фут в минутуACS — Атмосфера-кубический фут в секунду SecoATC — Атмосфера-кубический сантиметр PeATH — Атмосфера-кубический фут в часBTJ — BTU (Международная таблица) В расчете на BTN — BTU (Международная таблица) В расчете на BTS — БТЕ (международная таблица) по CAS — Калория (международная таблица) ERS — Эрг в секундуFMF — Фут-фунт-сила в минутуFT — Фут-фунт-сила в часFTO — Фут-фунт-сила в секундуHPS — Лошадиная силаLAM — Литр-атмосфера в час MinuteLSC — LusecLTS — Литр атмосферы в секундуPNC — PonceletSQL — Прямой эквивалент квадратного фута TC — Тонна кондиционирования воздухаTMS — Атмосфера-кубический сантиметр PeTRM — Тонна охлаждения (ImperialTRR — Тонна охлаждения (It)AMU — Единица атомной массы UnifiedAT — Анализ тонны (Короткий)ATS — Ton Assay (Длинный)BAC — Bag (Coffee)BDM — Bag (Portland Cement)BRG — BargeCLV — CloveCRT — CrithCT — Carat (Metric)DA — DaltonDRT — Dram (Apothecary Troy)DWT — PennyweightGAM — GammaGR — GrainGV — GraveKIP — KipLB — Фунт (метрический)LBA — ФунтLBT — Фунт (тройской)LBV — Фунт (Avoirdupois)ME — Атомная единица массы Электрон RMRK — MarkMTE — MiteMTM — Клещ (метрический)OZ — Унция (Us Food Nutrition LabelOZT — Унция (аптечная тройка)OZZ — унция (Avoirdupois)PNN — PointQ — квинтал (метрическая система)QR — четверть (неформальная)QRI — четверть (имперская)QRL — четверть длинная (неформальная)SAP — Scruple (аптекарь)SH — тонна короткаяSLG — слаг Geepound HylSLH — SheetST — StoneSWT — Вес в сотни (центум) oTON — Тонна LongWY — WeyZTR — ZentnerARE — AresBD — BoardsBHE — Эквивалент мощности котла DBR — BarnsBRN — BaronysCDA — Cuerda Pr SurveysCRD — CordsCRI — Circular InchsCRM — Circular MilsDNM — DunamsGNT — GunthasHD — HidesRO — RoodsSCT — SectionsSHD — СараиSII — Square Link Gunters InternatiSLR — Square Link RamsdensSQC — Square Chains InternationalSQM — Square Mil Square ThousSQR — Square Rod/Pole/PerchsSRR — Square RoofingsSTR — StremmasTWN — TownshipsYLN — YardlandsARM — Arcminute MoaARS — ArcsecondCNS — Centesimal Second Of ArcCNT — Столетняя минута ArcDOA — Градус (дуги)GRA — Град Градиан GonOCT — OctantQRD — QuadrantSGN - SignSXT — Секстантµ — Угловой MilATA — Атмосфера (техническая)ATM — Атмосфера (стандартная)BAR — BarBRY — Бари (единица Cgs)CMH — Сантиметр Of MercuryCMW – сантиметр водяного столба (4 °C)FTH – фут ртутного столба (условный)FTW – фут водяного столба (392 °F)IMC — Дюйм ртутного столба (условный)INW — Дюйм водяного столба (392 °F)KM — Килограмм-сила на квадратный дюймKSI — Кип на квадратный дюймLTP — Длинная тонна на квадратный футMHG — Микрометр ртутного столбаMMH — Миллиметр ртутного столбаMMW — Миллиметр воды (398 °C)PA — Паскаль (единица Si)PD — фунт на квадратный футPSF — фунт на квадратный футPSI — фунт на квадратный дюймPZ — пьеза (единица Mts)STP — короткая тонна на квадратный футTOR — ТоррATN — атомная единица ForceDYN — Dyne (Cgs Unit)KFF — Килограмм-сила Kilopond Grave-KI — Kip Kip-ForceMGF — Milligrave-Force Gravet-ForceOZC — Унция-силаPDL — PoundalSN — Sthene (единица Mts)TNF — Long Ton-ForceTNL — Short Ton- ForceAUC — атомная единица времениCTN — CenturyCYC — каллипический циклDEC — DecadeFN — FortnightHEL — HelekHIP — гиппархический циклJFF — JiffyKEH — Ke (четверть часа) LSR — Luster LustrumMD — MillidayMLL — MillenniumMMN — MomentMOF — Month (Full)MOG — Month (Greg) Av)MOH — месяц (полый)MOS — месяц (синодический)MTN — метонический цикл EnneadecaeterisOC — OctaeterisPLN — планковское времяSGM — SigmaSHK — ShakeSTH — сотический циклSVD — SvedbergYR — год (общий)YRG — год (григорианский)YRJ — год (юлианский) YRL – год (високосный)YRM – год (среднетропический)B39- Британская термальная единица (39 °F)B59 — Британская термальная единица (59 °F)B60 — Британская термальная единица (60 °F)B63 — Британская термальная единица (63 °F)BOE — эквивалент барреля нефтиBRT — Британская термальная единица ( Iso)BTI — Британская термальная единица (InternatBTM — Британская термальная единица (средняя)BTT — Британская термальная единица (ThermochC15 — Калория (15 °C)C20 — Калория (20 °C)C98 — Калория (398 °C)CAM — Калория ( Среднее значение)CFT — Кубический фут атмосферы CHU — Тепловая единица ЦельсияCL — Калория (Us Fda)CLTH — Калория (термохимическая)CN — Кубический фут природного газаCTA — Кубический сантиметр атмосферыCYD — Кубический ярд атмосферы StandEH — Атомная единица энергии ХартриFTD — Foot-PoundalIMG — Галлон-атмосфераKCA — Большая килокалорияKWH — Киловатт-час Board Of Trade ULTM — Литр-атмосфераQD — QuadRDB — Therm (Ec)RY — RydbergTCE — Тонна угольного эквивалентаTHR — Therm (Us)THU — ThermieTN — Тонна TntTOE — Тонна нефтяного эквивалентаBAN — Ban HartleyBSH — Bit ShannonCD — Candela (Si Base Unit) CandleCPD — Candlepower (New)JK — Si UnitNAT — Nat Nip NepitNBL — NibbleBQ — Беккерель (Si Unit)CI — CurieRD — Rutherford (H)C — Скорость света в вакуумеFPF — фарлонг в две неделиFPH — фут в часIPH — дюйм в часIPM — дюйм в минутуIPS — дюйм в секундуMCH — число МахаMPM — миля в минутуMPS — миля в секундуMS — метр в секунду (единица Си)SPS — скорость звука в AirCDF — Кандела на квадратный футCDI — Кандела на квадратный дюймCDM — Кандела на квадратный метр (Si UFL — FootlambertLMB — LambertSB — Stilb (Cgs Unit)CEL — ЦельсийDDE — Градус DelisleDNE — Градус НьютонаFAN — ФаренгейтGMR — Регулятор газа MarkKEL — Kelvin’sRAN — RankineREA — ReaumurRME — Градус RømerCFM — Кубический фут в минутуFTS — Кубический фут в секундуGPD — Галлон (жидкость США) в суткиGPH — Галлон (жидкость США) в часGPM — Галлон (жидкость США) в минутуINM — Кубический дюйм в минутуINS — Кубический дюйм в секундуLPM — Литр в минутуMQS — кубический метр в секунду (Si UniCM — кулон-метрDB — DebyeEA0 — атомная единица электрического диполяFC — фут-канделя люмен на квадрат FoLMN — люмен на квадратный дюймLX — люкс (единица Si)PH — Phot (единица Cgs)FHP — фут в секунду Час в секундуFMS — фут в минуту в секундуFP — фут в секунду в квадратеG — стандартная гравитацияGAL — галлон GalileoIP — дюйм в минуту в секунду в секундуIP2 — дюйм в секунду в квадратеKNS — узел в секундуMM — миля в минуту в секундуMP — миля в час в секундуMP2 — миля в секунду Секунда в квадратеMSA — метр на секунду в квадрате (Si UFT2 — квадратный фут в секундуM2S — квадратный метр в секунду (Si UnSTX — Стокс (единица Cgs)FTP — фут-фунт)MKG — метр-килограмм-силаNEM — ньютон-метр (единица Si)GML — грамм на секунду MillilitreLAB — фунт (эквивалентный) на галлонLBF — фунт (эквивалентный) на кубический LBI — фунт (экспериментальный) на кубический LBL — фунт (экспериментальный) на галлонOFT — унция (экспериментальный) на кубический OG — унция (эвердупуа) на галлон ) Per GallonOIN — Унция (Avoirdupois) на кубический SFT — Slug на кубический футGSS — Gauss (Cgs Unit)TSL — Tesla (Si Unit)GY — Grey (Si Unit)RDD — RadLBH — Pound Per Foot HourLBS — Фунт на фут в секундуLFT — Фунт-сила-секунда на квадрат LIN — Фунт-сила-секунда на квадрат PAS — Паскаль-секунда (единица Si)PSU — Пуаз (единица Cgs)MX — Максвелл (единица Cgs)WB — Вебер (единица Si)REM — Рентген-эквивалент ManSV — Sievert (Единица Си) S.) — Ссылка (Гюнтера; Сюрвейерская)LNK (RE) — Ссылка (Рамсденская; Инженерная)LS — Световая секундаLY — Световая- yearM — метр (базовая единица СИ)MIL — мил (Швеция и Норвегия)MILE DATA — мили (тактические или данные)MK — MickeyNAIL — гвоздь (ткань)NL — морская лигаNM — нанометрNMI — морская миляNMI I — морская миляP — PalmPC — ParsecPICA — PicaPM — пикометр (бикрон, клеймо) POINT — точка (американский, английский) PT — PaceQUART — QuarterSHAKU — Shaku (японский) SPT — SpatTH — Mil (тыс.)TWP — TwipUM — микрометр (стар.: микрон)XU — единица X; siegbahnABA — Электромагнитная единица AbampereAMP — Ампер (базовая единица Si)ESU — Esu в секунду Статампер (CgsABC — Абкулон Электромагнитная единицаATU — Атомная единица зарядаCLM — КулонFRD — ФарадейMAH — Миллиампер-часSTT — Статкулон Франклин ЭлектростABV — Абвольт (единица Cgs)STV — Статвольт ( Cgs Unit)VLT — Вольт (Si Unit)ACF — Акр-футыACI — Акры-дюймыBIB — Баррели (нефтяные)BII — Баррели (британские)BIU — Баррели (Us Dry)BKT — Ведра (британские)BRO — Галлоны (пивные)BUD — Бушели (Us Dry Level)BUI — Бушели (Imperial)BUU — Бушели (Us Dry Heaped)CMB — CoombsCMI — Cubic MilesCP — CupsCRF — Cord-FootsCRW — Cords (Дрова)CUF — Cubic FathomsCUI — Cubic InchsCUT — Cubic FootsCUY — Cubic ЯрдыDSI — тире (имперские фунты)DSS — десертные ложки (имперские фунты)DSU — тире (США)FBM — борд-футыFFT — пятые FID — жидкие драхмы (имперские)FIS — жидкие скрукле (имперские)FLB — бочки (США, жидкие)FLU — жидкие драмы ( Us) Us FluidramFRK — FirkinsGAI — галлоны (имперские единицы)GAU — галлоны (Us Dry)GAW — галлоны (Us Fluid Wine)GLU — Teacups (gills)GTT — DropsHDI — Hogsheads (Imperial)HHU — Hogsheads (Us)JGR — Jiggers ( Bartending)KLD — KilderkinsLMD — LambdasLOD — LoadsLST — LastsM3 — Кубические метры (Si Unit)MII — Minims (Imperial)MIU — Minims (Us)OZF — Унции (Fluid Us Food NutritioPER — PerchsPKI — Pecks (Imperial)PKU — Pecks (Us) Сухой)PNI — пинчи (британские)PNU — пинчи (американские)PON — PonysPOT — Pottle QuartersPP — стыковые трубыPTI — пинты (британские)PUD — пинты (Us Dry)PUF — пинты (Us Fluid)QRF — Quart S (Us Fluid) QRT — Кварталы QTI — Кварты (британские)QTU — Кварты (Us Dry)RGS — Реестр TonsSCI — Мешки (британские) BagsSCU — Мешки(Us)SHT — Shots (Us)SM — SeamsSTK — Забастовки (Imperial)STU — Забастовки (Us) )TBC — столовые ложки (канадские)TBF — столовые ложки (обычные в США)TBM — столовые ложки (метрические)TBS — столовые ложки (в австралийских единицах измеренияTCA — чайные ложки (канадские) TFD — столовые ложки (Us Food NutritionTIM — чайные ложки (британские)TMF — Timber FootsTMT — чайные ложки ( Метрическая система)TND – тонны (водоизмещение)TNT – тонны (воды)TNW – тонны (фрахт)TSC – чайные ложки (стандарт США)TSF – чайные ложки (США Food Nutrition) WEY — Wey (Us)ACM — Атмосфера-кубический фут в минутуACS — Атмосфера-кубический фут в секунду SecoATC — Атмосфера-кубический сантиметр PeATH — Атмосфера-кубический фут в часBTJ — BTU (Международная таблица) В расчете на BTN — BTU (Международная таблица) В расчете на BTS — БТЕ (международная таблица) по CAS — Калория (международная таблица) ERS — Эрг в секундуFMF — Фут-фунт-сила в минутуFT — Фут-фунт-сила в часFTO — Фут-фунт-сила в секундуHPS — Лошадиная силаLAM — Литр-атмосфера в час MinuteLSC — LusecLTS — Литр атмосферы в секундуPNC — PonceletSQL — Прямой эквивалент квадратного фута TC — Тонна кондиционирования воздухаTMS — Атмосфера-кубический сантиметр PeTRM — Тонна охлаждения (ImperialTRR — Тонна охлаждения (It)ACR — AcresCMK — Квадратные сантиметрыFTK — Квадратные футыHAR — ГектарыINK — Квадратные дюймыKMK — Квадратные километрыMIK — Квадратные милиMTK — Квадратные метрыYDK — Квадратные ярдыAMU — Унифицированная атомная единица массыAT — Тонна анализа (краткая)ATS — Тонна анализа (длинная)BAC — Мешок (Кофе)BDM — Мешок (портландцемент)BRG — BargeCLV — CloveCRT — CrithCT — Carat (Metric)DA — DaltonDRT — Dram (Apothecary Troy)DWT — PennyweightGAM — GammaGR — GrainGV — GraveKIP — KipLB — Pound (Metric)LBA — PoundLBT — Pound (Troy)LBV — Pound (Avoirdupois)ME — Атомная единица массы Электрон RMRK — MarkMTE — MiteMTM — Клещ (метрический) OZ — Унция (этикетка питания США OZT — Унция (аптечная Троя) OZZ — Унция (Avoirdupois) PNN — PointQ — Квинтал (метрический) QR — Квартал (неофициальный) QRI — Quarter (Imperial)QRL — Quarter Long (Informal)SAP — Scruple (Apothecary)SH — Ton ShortSLG — Slug Geepound HylSLH — SheetST — StoneSWT — Hundredweight (центум веса oTON — Ton LongWY — WeyZTR — ZentnerANN — YearsDAY — DaysHUR — HoursMCS — MicrosecondsMIN — MinutesMLS — MillisecondsMON — MonthsSEC — SecondsWEE — WeeksARE — AresBD — BoardsBHE — эквивалент мощности котла DBR — BarnsBRN — BaronysCDA — Cuerda Pr SurveysCRD — CordsCRI — Circular InchsCRM — Circular MilsDNM — DunamsGNT — GunthasHD — HidesRO — RoodsSCT — SectionsSHD — ShedsSs — Square Link Gunters InternatiSLR — Square Link RamsdensSQC — Square Chains InternationalSQM — Square Mil Square ThousSQR — Square Rod/Pole/PerchsSRR — Square RoofingsSTR — StremmasTWN — TownshipsYLN — YardlandsARM — Arcminute MoaARS — ArcsecondCNS — Centesimal Second Of ArcCNT — Centesimal Minute Of ArcDOA — Degree (Дуги)GRA — Grad Gradian GonOCT — OctantQRD — QuadrantSGN - SignSXT — Sextantµ — Угловой MilATA — Атмосфера (Техническая)ATM — Атмосфера (Стандартная)BAR — BarBRY — Бари (единица Cgs)CMH — Сантиметр ртутного столбаCMW — Сантиметр водяного столба ( 4 °C)FTH — фут ртутного столба (условный)FTW — фут водяного столба (392 °F)IMC — Дюйм ртутного столба (условный)INW — Дюйм водяного столба (392 °F)KM — Килограмм-сила на квадратный дюймKSI — Кип на квадратный дюймLTP — Длинная тонна на квадратный футMHG — Микрометр ртутного столбаMMH — Миллиметр ртутного столбаMMW — Миллиметр воды (398 °C)PA — Паскаль (единица Si)PD — фунт на квадратный футPSF — фунт на квадратный футPSI — фунт на квадратный дюймPZ — пьеза (единица Mts)STP — короткая тонна на квадратный футTOR — ТоррATN — атомная единица ForceDYN — Dyne (Cgs Unit)KFF — Килограмм-сила Kilopond Grave-KI — Kip Kip-ForceMGF — Milligrave-Force Gravet-ForceOZC — Унция-силаPDL — PoundalSN — Sthene (единица Mts)TNF — Long Ton-ForceTNL — Short Ton- ForceAUC — атомная единица времениCTN — CenturyCYC — каллипический циклDEC — DecadeFN — FortnightHEL — HelekHIP — гиппархический циклJFF — JiffyKEH — Ke (четверть часа) LSR — Luster LustrumMD — MillidayMLL — MillenniumMMN — MomentMOF — Month (Full)MOG — Month (Greg) Av)MOH — месяц (полый)MOS — месяц (синодический)MTN — метонический цикл EnneadecaeterisOC — OctaeterisPLN — планковское времяSGM — SigmaSHK — ShakeSTH — сотический циклSVD — SvedbergYR — год (общий)YRG — год (григорианский)YRJ — год (юлианский) YRL – год (високосный)YRM – год (среднетропический)B39- Британская термальная единица (39 °F)B59 — Британская термальная единица (59 °F)B60 — Британская термальная единица (60 °F)B63 — Британская термальная единица (63 °F)BOE — эквивалент барреля нефтиBRT — Британская термальная единица ( Iso)BTI — Британская термальная единица (InternatBTM — Британская термальная единица (средняя)BTT — Британская термальная единица (ThermochC15 — Калория (15 °C)C20 — Калория (20 °C)C98 — Калория (398 °C)CAM — Калория ( Среднее значение)CFT — Кубический фут атмосферы CHU — Тепловая единица ЦельсияCL — Калория (Us Fda)CLTH — Калория (термохимическая)CN — Кубический фут природного газаCTA — Кубический сантиметр атмосферыCYD — Кубический ярд атмосферы StandEH — Атомная единица энергии ХартриFTD — Foot-PoundalIMG — Галлон-атмосфераKCA — Большая килокалорияKWH — Киловатт-час Board Of Trade ULTM — Литр-атмосфераQD — QuadRDB — Therm (Ec)RY — RydbergTCE — Тонна угольного эквивалентаTHR — Therm (Us)THU — ThermieTN — Тонна TntTOE — Tone Of Oil EquivalentBAN — Ban HartleyBSH — Bit ShannonCD — Candela (Si Base Unit) CandleCPD — Candlepower (New)JK — Si UnitNAT — Nat Nip NepitNBL — NibbleBIT — BitsBYT — BytesEBI — ExabitsEBY — ExabytesGBI — GigabitsGBY — GigabytesKBI — KilobitsKBY — KilobytesMBI — МегабитыMBY — МегабайтыPBI — ПетабитыPBY — ПетабайтыTBI — ТерабитыTBY — ТерабайтыBLL — Баррели (нефть)CMQ — Кубические сантиметрыFTQ — Кубические футыGLI — Галлоны (Великобритания)GLL — Галлоны (жидкости США)LTR — ЛитрыMLT — МиллилитрыMTQ — Кубические метрыOZI — Унции UKBQ — Беккерели ( Si Unit)CI — КюриRD — Резерфорд (H)BTU — BTUCAL — КалорииERG — ErgEVL — Электрон ВольтFPD — Фут-фунтHPH — Лошадиная сила-часIPD — Дюйм-фунтJOU — ДжоульC — Скорость света в вакуумеFPF — Фарлонг в две неделиFPH — Фут в часIPH — Inch Per HourIPM — Inch Per MinuteIPS — Inch Per SecondMCH — Mach NumberMPM — Mile Per MinuteMPS — Mile Per SecondMS — Метр в секунду (Si Unit)SPS — Скорость звука в AirCDF — Candela Per Square FootCDI — Candela Per Square InchCDM — Candela Per Квадратный метр (Si UFL — FootlambertLMB — LambertSB — Stilb (Cgs Unit)CEL — ЦельсийDDE — Градус DelisleDNE — Градус НьютонаFAN — ФаренгейтGMR — Регулирующий газ MarkKEL — Kelvin’sRAN — RankineREA — ReaumurRME — Градус RømerCFM — Кубический фут в минутуFTS — Кубический фут в минуту SecondGPD — галлон (жидкость США) в суткиGPH — галлон (жидкость США) в часGPM — галлон (жидкость США) в минутуINM — кубический дюйм в минутуINS — кубический дюйм в секундуLPM — литр в минутуMQS — кубический метр в секунду (Si UniCM — кулоновый метрDB — DebyeEA0 — атомная единица электрического диполя CMT — сантиметр DMT — дециметрыFOT — футыINH — дюймыKMT — километрыMMT — миллиметрыMTR — метрыSMI — милиYRD — ярдыCTM — каратыGRM — граммыKGM — килограммыLBR — фунтыMGM — миллиграммыONZ — унции TNE — тонны (метрические)DEG — градусыGRD — градыRAD - RadiansFC — Фут-канд Люмен на квадрат FoLMN — Люмен на квадратный дюймLX — Люкс (Единица Si)PH — Фот (Единица Cgs)FHP — Фут в час в секундуFMS — Фут в минуту в секундуFP — Фут в секунду в квадратеdG — Стандартная сила тяжестиGAL — Gal GalileoIP — Дюйм в минуту в секундуIP2 — дюйм в секунду в квадратеKNS — узел в секундуMM — миля в минуту в секундуMP — миля в час в секундуMP2 — миля в секунду в квадратеMSA — метр в секунду в квадрате (Si UFPM — футы/минутыFPS — футы/секундыKMH — километры/ ЧасKMS — Километры/секундыKNT — УзлыMPH — Мили/часMTS — Метры/секундыFT2 — Квадратный фут в секундуM2S — Квадратный метр в секунду (Si UnSTX — Стокс (единица Cgs)FTP — Foot-PoundalMKG — Метр Килограмм-силаNEM — Ньютон-метр (Единица Si )GCC — граммы/кубический сантиметрKCC — килограммы/кубический сантиметрKLI — килограммы/литрKMC — килограммы/кубический метрOCI — унции/кубический дюймOGL — унции/галлонPCF — фунты/кубический футPCI — фунты/кубический дюймPGL — фунты/галлонGML — грамм на миллилитрLAB — фунт (Avoirdupois) Per GallonLBF — фунт (Avoirdupois) на кубический LBI — фунт (Avoirdupois) на кубический LBL — фунт (Avoirdupois) на галлонOFT — унция (Avoirdupois) на кубический OG — унция (Avoirdupois) на галлонOGA — унция (Avoirdupois) на галлонOIN — Унция (Avoirdupois) на кубический SFT — Слаг на кубический футGSS — Гаусс (единица Cgs)TSL — Тесла (единица Si)GY — Грей (единица Si)RDD — RadJCM — Джоули/сантиметрKGF — Килограмм-силаNWN — НьютоныPFC — Фунт силыLBH — Фунт Per Foot HourLBS — Фунт на фут-секундуLFT — Фунт-сила-секунда на квадрат LIN — Фунт-сила-секунда на квадрат PAS — Паскаль-секунда (единица Si)PSU — Пуаз (единица Cgs)MX — Максвелл (единица Cgs)WB — Вебер (Si) Единица)REM — Рентген-эквивалент ManSV — Зиверт (Единица Si)
S.) — Ссылка (Гюнтера; Сюрвейерская)LNK (RE) — Ссылка (Рамсденская; Инженерная)LS — Световая секундаLY — Световая- yearM — метр (базовая единица СИ)MIL — мил (Швеция и Норвегия)MILE DATA — мили (тактические или данные)MK — MickeyNAIL — гвоздь (ткань)NL — морская лигаNM — нанометрNMI — морская миляNMI I — морская миляP — PalmPC — ParsecPICA — PicaPM — пикометр (бикрон, клеймо) POINT — точка (американский, английский) PT — PaceQUART — QuarterSHAKU — Shaku (японский) SPT — SpatTH — Mil (тыс.)TWP — TwipUM — микрометр (стар.: микрон)XU — единица X; siegbahnABA — Электромагнитная единица AbampereAMP — Ампер (базовая единица Si)ESU — Esu в секунду Статампер (CgsABC — Абкулон Электромагнитная единицаATU — Атомная единица зарядаCLM — КулонFRD — ФарадейMAH — Миллиампер-часSTT — Статкулон Франклин ЭлектростABV — Абвольт (единица Cgs)STV — Статвольт ( Cgs Unit)VLT — Вольт (Si Unit)ACF — Акр-футыACI — Акры-дюймыBIB — Баррели (нефтяные)BII — Баррели (британские)BIU — Баррели (Us Dry)BKT — Ведра (британские)BRO — Галлоны (пивные)BUD — Бушели (Us Dry Level)BUI — Бушели (Imperial)BUU — Бушели (Us Dry Heaped)CMB — CoombsCMI — Cubic MilesCP — CupsCRF — Cord-FootsCRW — Cords (Дрова)CUF — Cubic FathomsCUI — Cubic InchsCUT — Cubic FootsCUY — Cubic ЯрдыDSI — тире (имперские фунты)DSS — десертные ложки (имперские фунты)DSU — тире (США)FBM — борд-футыFFT — пятые FID — жидкие драхмы (имперские)FIS — жидкие скрукле (имперские)FLB — бочки (США, жидкие)FLU — жидкие драмы ( Us) Us FluidramFRK — FirkinsGAI — галлоны (имперские единицы)GAU — галлоны (Us Dry)GAW — галлоны (Us Fluid Wine)GLU — Teacups (gills)GTT — DropsHDI — Hogsheads (Imperial)HHU — Hogsheads (Us)JGR — Jiggers ( Bartending)KLD — KilderkinsLMD — LambdasLOD — LoadsLST — LastsM3 — Кубические метры (Si Unit)MII — Minims (Imperial)MIU — Minims (Us)OZF — Унции (Fluid Us Food NutritioPER — PerchsPKI — Pecks (Imperial)PKU — Pecks (Us) Сухой)PNI — пинчи (британские)PNU — пинчи (американские)PON — PonysPOT — Pottle QuartersPP — стыковые трубыPTI — пинты (британские)PUD — пинты (Us Dry)PUF — пинты (Us Fluid)QRF — Quart S (Us Fluid) QRT — Кварталы QTI — Кварты (британские)QTU — Кварты (Us Dry)RGS — Реестр TonsSCI — Мешки (британские) BagsSCU — Мешки(Us)SHT — Shots (Us)SM — SeamsSTK — Забастовки (Imperial)STU — Забастовки (Us) )TBC — столовые ложки (канадские)TBF — столовые ложки (обычные в США)TBM — столовые ложки (метрические)TBS — столовые ложки (в австралийских единицах измеренияTCA — чайные ложки (канадские) TFD — столовые ложки (Us Food NutritionTIM — чайные ложки (британские)TMF — Timber FootsTMT — чайные ложки ( Метрическая система)TND – тонны (водоизмещение)TNT – тонны (воды)TNW – тонны (фрахт)TSC – чайные ложки (стандарт США)TSF – чайные ложки (США Food Nutrition) WEY — Wey (Us)ACM — Атмосфера-кубический фут в минутуACS — Атмосфера-кубический фут в секунду SecoATC — Атмосфера-кубический сантиметр PeATH — Атмосфера-кубический фут в часBTJ — BTU (Международная таблица) В расчете на BTN — BTU (Международная таблица) В расчете на BTS — БТЕ (международная таблица) по CAS — Калория (международная таблица) ERS — Эрг в секундуFMF — Фут-фунт-сила в минутуFT — Фут-фунт-сила в часFTO — Фут-фунт-сила в секундуHPS — Лошадиная силаLAM — Литр-атмосфера в час MinuteLSC — LusecLTS — Литр атмосферы в секундуPNC — PonceletSQL — Прямой эквивалент квадратного фута TC — Тонна кондиционирования воздухаTMS — Атмосфера-кубический сантиметр PeTRM — Тонна охлаждения (ImperialTRR — Тонна охлаждения (It)ACR — AcresCMK — Квадратные сантиметрыFTK — Квадратные футыHAR — ГектарыINK — Квадратные дюймыKMK — Квадратные километрыMIK — Квадратные милиMTK — Квадратные метрыYDK — Квадратные ярдыAMU — Унифицированная атомная единица массыAT — Тонна анализа (краткая)ATS — Тонна анализа (длинная)BAC — Мешок (Кофе)BDM — Мешок (портландцемент)BRG — BargeCLV — CloveCRT — CrithCT — Carat (Metric)DA — DaltonDRT — Dram (Apothecary Troy)DWT — PennyweightGAM — GammaGR — GrainGV — GraveKIP — KipLB — Pound (Metric)LBA — PoundLBT — Pound (Troy)LBV — Pound (Avoirdupois)ME — Атомная единица массы Электрон RMRK — MarkMTE — MiteMTM — Клещ (метрический) OZ — Унция (этикетка питания США OZT — Унция (аптечная Троя) OZZ — Унция (Avoirdupois) PNN — PointQ — Квинтал (метрический) QR — Квартал (неофициальный) QRI — Quarter (Imperial)QRL — Quarter Long (Informal)SAP — Scruple (Apothecary)SH — Ton ShortSLG — Slug Geepound HylSLH — SheetST — StoneSWT — Hundredweight (центум веса oTON — Ton LongWY — WeyZTR — ZentnerANN — YearsDAY — DaysHUR — HoursMCS — MicrosecondsMIN — MinutesMLS — MillisecondsMON — MonthsSEC — SecondsWEE — WeeksARE — AresBD — BoardsBHE — эквивалент мощности котла DBR — BarnsBRN — BaronysCDA — Cuerda Pr SurveysCRD — CordsCRI — Circular InchsCRM — Circular MilsDNM — DunamsGNT — GunthasHD — HidesRO — RoodsSCT — SectionsSHD — ShedsSs — Square Link Gunters InternatiSLR — Square Link RamsdensSQC — Square Chains InternationalSQM — Square Mil Square ThousSQR — Square Rod/Pole/PerchsSRR — Square RoofingsSTR — StremmasTWN — TownshipsYLN — YardlandsARM — Arcminute MoaARS — ArcsecondCNS — Centesimal Second Of ArcCNT — Centesimal Minute Of ArcDOA — Degree (Дуги)GRA — Grad Gradian GonOCT — OctantQRD — QuadrantSGN - SignSXT — Sextantµ — Угловой MilATA — Атмосфера (Техническая)ATM — Атмосфера (Стандартная)BAR — BarBRY — Бари (единица Cgs)CMH — Сантиметр ртутного столбаCMW — Сантиметр водяного столба ( 4 °C)FTH — фут ртутного столба (условный)FTW — фут водяного столба (392 °F)IMC — Дюйм ртутного столба (условный)INW — Дюйм водяного столба (392 °F)KM — Килограмм-сила на квадратный дюймKSI — Кип на квадратный дюймLTP — Длинная тонна на квадратный футMHG — Микрометр ртутного столбаMMH — Миллиметр ртутного столбаMMW — Миллиметр воды (398 °C)PA — Паскаль (единица Si)PD — фунт на квадратный футPSF — фунт на квадратный футPSI — фунт на квадратный дюймPZ — пьеза (единица Mts)STP — короткая тонна на квадратный футTOR — ТоррATN — атомная единица ForceDYN — Dyne (Cgs Unit)KFF — Килограмм-сила Kilopond Grave-KI — Kip Kip-ForceMGF — Milligrave-Force Gravet-ForceOZC — Унция-силаPDL — PoundalSN — Sthene (единица Mts)TNF — Long Ton-ForceTNL — Short Ton- ForceAUC — атомная единица времениCTN — CenturyCYC — каллипический циклDEC — DecadeFN — FortnightHEL — HelekHIP — гиппархический циклJFF — JiffyKEH — Ke (четверть часа) LSR — Luster LustrumMD — MillidayMLL — MillenniumMMN — MomentMOF — Month (Full)MOG — Month (Greg) Av)MOH — месяц (полый)MOS — месяц (синодический)MTN — метонический цикл EnneadecaeterisOC — OctaeterisPLN — планковское времяSGM — SigmaSHK — ShakeSTH — сотический циклSVD — SvedbergYR — год (общий)YRG — год (григорианский)YRJ — год (юлианский) YRL – год (високосный)YRM – год (среднетропический)B39- Британская термальная единица (39 °F)B59 — Британская термальная единица (59 °F)B60 — Британская термальная единица (60 °F)B63 — Британская термальная единица (63 °F)BOE — эквивалент барреля нефтиBRT — Британская термальная единица ( Iso)BTI — Британская термальная единица (InternatBTM — Британская термальная единица (средняя)BTT — Британская термальная единица (ThermochC15 — Калория (15 °C)C20 — Калория (20 °C)C98 — Калория (398 °C)CAM — Калория ( Среднее значение)CFT — Кубический фут атмосферы CHU — Тепловая единица ЦельсияCL — Калория (Us Fda)CLTH — Калория (термохимическая)CN — Кубический фут природного газаCTA — Кубический сантиметр атмосферыCYD — Кубический ярд атмосферы StandEH — Атомная единица энергии ХартриFTD — Foot-PoundalIMG — Галлон-атмосфераKCA — Большая килокалорияKWH — Киловатт-час Board Of Trade ULTM — Литр-атмосфераQD — QuadRDB — Therm (Ec)RY — RydbergTCE — Тонна угольного эквивалентаTHR — Therm (Us)THU — ThermieTN — Тонна TntTOE — Tone Of Oil EquivalentBAN — Ban HartleyBSH — Bit ShannonCD — Candela (Si Base Unit) CandleCPD — Candlepower (New)JK — Si UnitNAT — Nat Nip NepitNBL — NibbleBIT — BitsBYT — BytesEBI — ExabitsEBY — ExabytesGBI — GigabitsGBY — GigabytesKBI — KilobitsKBY — KilobytesMBI — МегабитыMBY — МегабайтыPBI — ПетабитыPBY — ПетабайтыTBI — ТерабитыTBY — ТерабайтыBLL — Баррели (нефть)CMQ — Кубические сантиметрыFTQ — Кубические футыGLI — Галлоны (Великобритания)GLL — Галлоны (жидкости США)LTR — ЛитрыMLT — МиллилитрыMTQ — Кубические метрыOZI — Унции UKBQ — Беккерели ( Si Unit)CI — КюриRD — Резерфорд (H)BTU — BTUCAL — КалорииERG — ErgEVL — Электрон ВольтFPD — Фут-фунтHPH — Лошадиная сила-часIPD — Дюйм-фунтJOU — ДжоульC — Скорость света в вакуумеFPF — Фарлонг в две неделиFPH — Фут в часIPH — Inch Per HourIPM — Inch Per MinuteIPS — Inch Per SecondMCH — Mach NumberMPM — Mile Per MinuteMPS — Mile Per SecondMS — Метр в секунду (Si Unit)SPS — Скорость звука в AirCDF — Candela Per Square FootCDI — Candela Per Square InchCDM — Candela Per Квадратный метр (Si UFL — FootlambertLMB — LambertSB — Stilb (Cgs Unit)CEL — ЦельсийDDE — Градус DelisleDNE — Градус НьютонаFAN — ФаренгейтGMR — Регулирующий газ MarkKEL — Kelvin’sRAN — RankineREA — ReaumurRME — Градус RømerCFM — Кубический фут в минутуFTS — Кубический фут в минуту SecondGPD — галлон (жидкость США) в суткиGPH — галлон (жидкость США) в часGPM — галлон (жидкость США) в минутуINM — кубический дюйм в минутуINS — кубический дюйм в секундуLPM — литр в минутуMQS — кубический метр в секунду (Si UniCM — кулоновый метрDB — DebyeEA0 — атомная единица электрического диполя CMT — сантиметр DMT — дециметрыFOT — футыINH — дюймыKMT — километрыMMT — миллиметрыMTR — метрыSMI — милиYRD — ярдыCTM — каратыGRM — граммыKGM — килограммыLBR — фунтыMGM — миллиграммыONZ — унции TNE — тонны (метрические)DEG — градусыGRD — градыRAD - RadiansFC — Фут-канд Люмен на квадрат FoLMN — Люмен на квадратный дюймLX — Люкс (Единица Si)PH — Фот (Единица Cgs)FHP — Фут в час в секундуFMS — Фут в минуту в секундуFP — Фут в секунду в квадратеdG — Стандартная сила тяжестиGAL — Gal GalileoIP — Дюйм в минуту в секундуIP2 — дюйм в секунду в квадратеKNS — узел в секундуMM — миля в минуту в секундуMP — миля в час в секундуMP2 — миля в секунду в квадратеMSA — метр в секунду в квадрате (Si UFPM — футы/минутыFPS — футы/секундыKMH — километры/ ЧасKMS — Километры/секундыKNT — УзлыMPH — Мили/часMTS — Метры/секундыFT2 — Квадратный фут в секундуM2S — Квадратный метр в секунду (Si UnSTX — Стокс (единица Cgs)FTP — Foot-PoundalMKG — Метр Килограмм-силаNEM — Ньютон-метр (Единица Si )GCC — граммы/кубический сантиметрKCC — килограммы/кубический сантиметрKLI — килограммы/литрKMC — килограммы/кубический метрOCI — унции/кубический дюймOGL — унции/галлонPCF — фунты/кубический футPCI — фунты/кубический дюймPGL — фунты/галлонGML — грамм на миллилитрLAB — фунт (Avoirdupois) Per GallonLBF — фунт (Avoirdupois) на кубический LBI — фунт (Avoirdupois) на кубический LBL — фунт (Avoirdupois) на галлонOFT — унция (Avoirdupois) на кубический OG — унция (Avoirdupois) на галлонOGA — унция (Avoirdupois) на галлонOIN — Унция (Avoirdupois) на кубический SFT — Слаг на кубический футGSS — Гаусс (единица Cgs)TSL — Тесла (единица Si)GY — Грей (единица Si)RDD — RadJCM — Джоули/сантиметрKGF — Килограмм-силаNWN — НьютоныPFC — Фунт силыLBH — Фунт Per Foot HourLBS — Фунт на фут-секундуLFT — Фунт-сила-секунда на квадрат LIN — Фунт-сила-секунда на квадрат PAS — Паскаль-секунда (единица Si)PSU — Пуаз (единица Cgs)MX — Максвелл (единица Cgs)WB — Вебер (Si) Единица)REM — Рентген-эквивалент ManSV — Зиверт (Единица Si)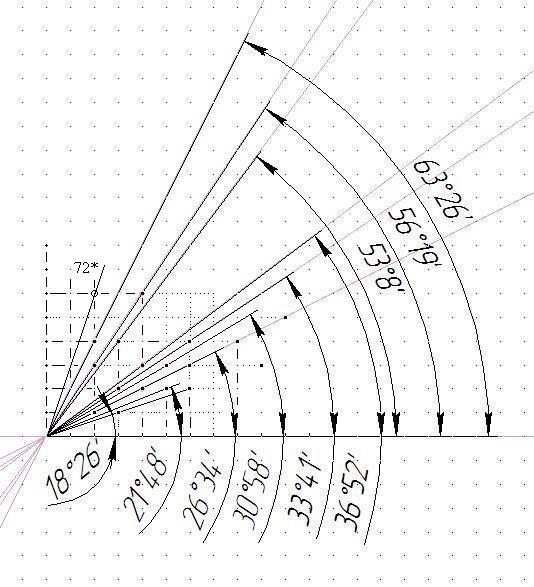 mm′ в десятичные градусы
mm′ в десятичные градусы





 Значит, в правой верхней ячейке должно быть число 0,4 – 0,22 = 0,18.
Значит, в правой верхней ячейке должно быть число 0,4 – 0,22 = 0,18.
 Всего высшую категорию имеют 0,48n яиц.
Всего высшую категорию имеют 0,48n яиц.



 Занесём эти данные в таблицу.
Занесём эти данные в таблицу.





 Вопрос
Вопрос 

 Эти билеты перемешиваются, а затем случайным образом вытягивается билет. Найти вероятность того, что номер вытянутого билета кратен 4 или 5?
Эти билеты перемешиваются, а затем случайным образом вытягивается билет. Найти вероятность того, что номер вытянутого билета кратен 4 или 5? Если случайно выбран один ученик, найти вероятность того, что
Если случайно выбран один ученик, найти вероятность того, что Вопрос
Вопрос  )
)

 Найти вероятность выбора \(4\) и множителей \(6\).
Найти вероятность выбора \(4\) и множителей \(6\).

 …
… 10 класс
10 класс Решение простейших тригонометрических уравненийТема урока
Решение простейших тригонометрических уравненийТема урока Теория: Учебник — п.15, 16, 17 (опорный конспект)
Теория: Учебник — п.15, 16, 17 (опорный конспект) H.S. = x + 3
H.S. = x + 3 В.С. = 5 x
В.С. = 5 x  H.S. ≠ R.H.S.,
H.S. ≠ R.H.S., Х.С. ≠ RHS,
Х.С. ≠ RHS, С.
С.



 H.S.)
H.S.) С.С.)
С.С.) следующие случаи:
следующие случаи:


 У Ирфана 37 шариков. Сколько шариков у Пармита?
У Ирфана 37 шариков. Сколько шариков у Пармита?

 При нажатии на ссылку открывается первый вопрос. Чтобы открыть любой другой вопрос упражнения, перейдите в конец страницы. Есть список со стрелками, в котором есть все вопросы (с важных вопроса также отмечено)
При нажатии на ссылку открывается первый вопрос. Чтобы открыть любой другой вопрос упражнения, перейдите в конец страницы. Есть список со стрелками, в котором есть все вопросы (с важных вопроса также отмечено) Ответы на все упражнения, примеры и необязательные вопросы были предоставлены с видео каждого вопроса
Ответы на все упражнения, примеры и необязательные вопросы были предоставлены с видео каждого вопроса

 ..
..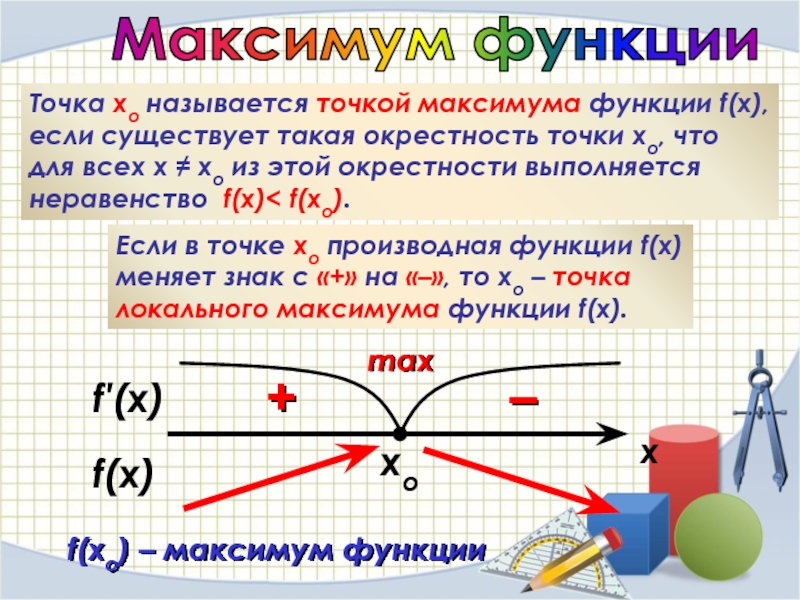
 Для глобального максимума эта область расширяется до всей области допустимых аргументов. Для минимума всё наоборот. Экстремум — это локальное экстремальное — минимальное или максимальное — значение.
Для глобального максимума эта область расширяется до всей области допустимых аргументов. Для минимума всё наоборот. Экстремум — это локальное экстремальное — минимальное или максимальное — значение.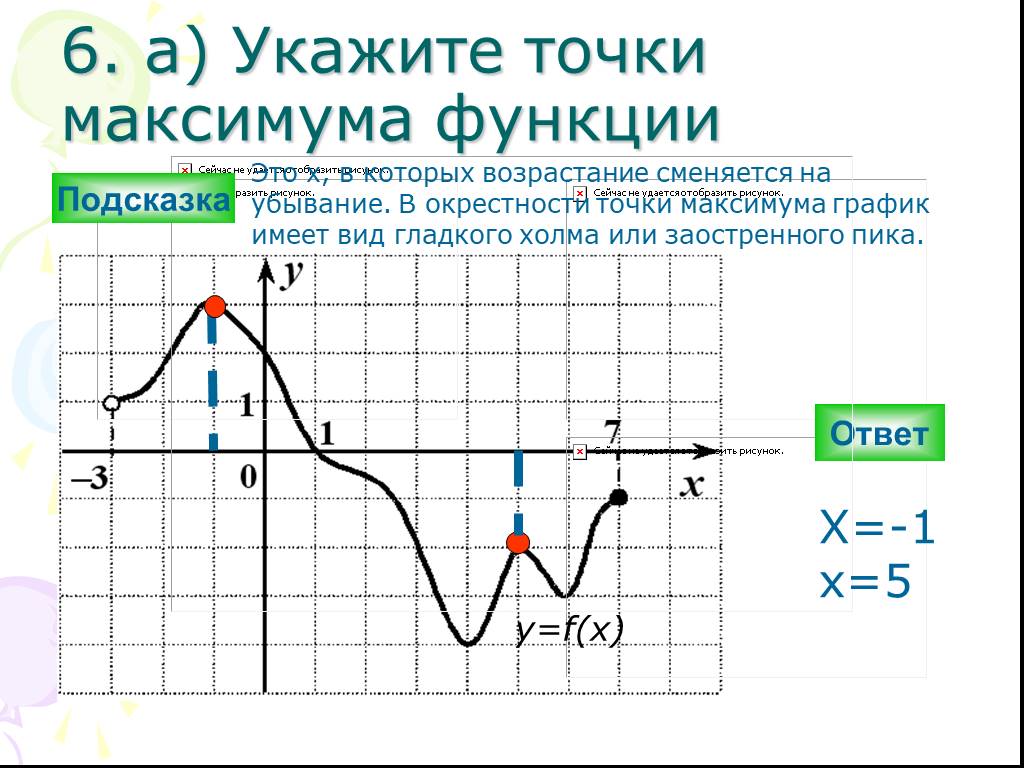 2 определена на всей оси аргументов. А y = 1/x определена для всех аргументов, кроме x = 0.
2 определена на всей оси аргументов. А y = 1/x определена для всех аргументов, кроме x = 0. 3. У неё не может быть экстремумов, она убывает на всей оси аргументов.
3. У неё не может быть экстремумов, она убывает на всей оси аргументов.

 Мы видим, что в точках E и F .
Мы видим, что в точках E и F . (Урок 9 алгебры.)
(Урок 9 алгебры.)
 Это говорит нам алгебраически, что критическое значение 3 определяет минимум.
Это говорит нам алгебраически, что критическое значение 3 определяет минимум. f’ ( х ) = 6 х 2 — 18 х + 12
f’ ( х ) = 6 х 2 — 18 х + 12
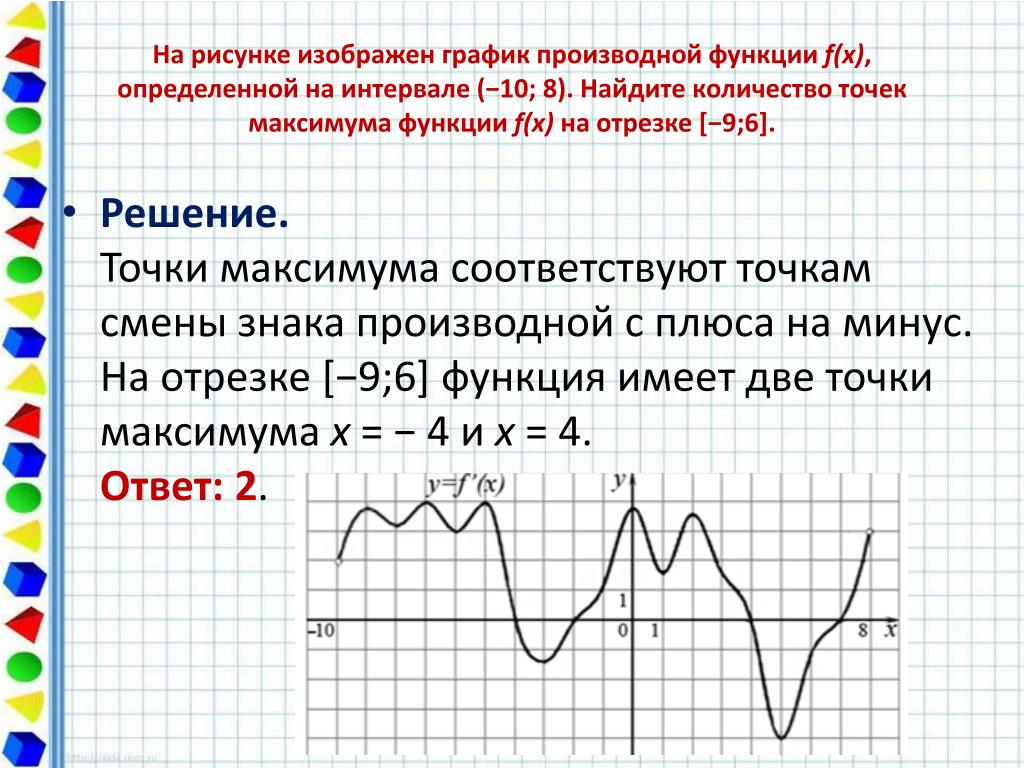
 Пример: y = x 3 . г» = 6 x = 0 подразумевает x = 0. Но x = 0 является точкой перегиба на графике y = x 3 , а не максимумом или минимумом.
Пример: y = x 3 . г» = 6 x = 0 подразумевает x = 0. Но x = 0 является точкой перегиба на графике y = x 3 , а не максимумом или минимумом.

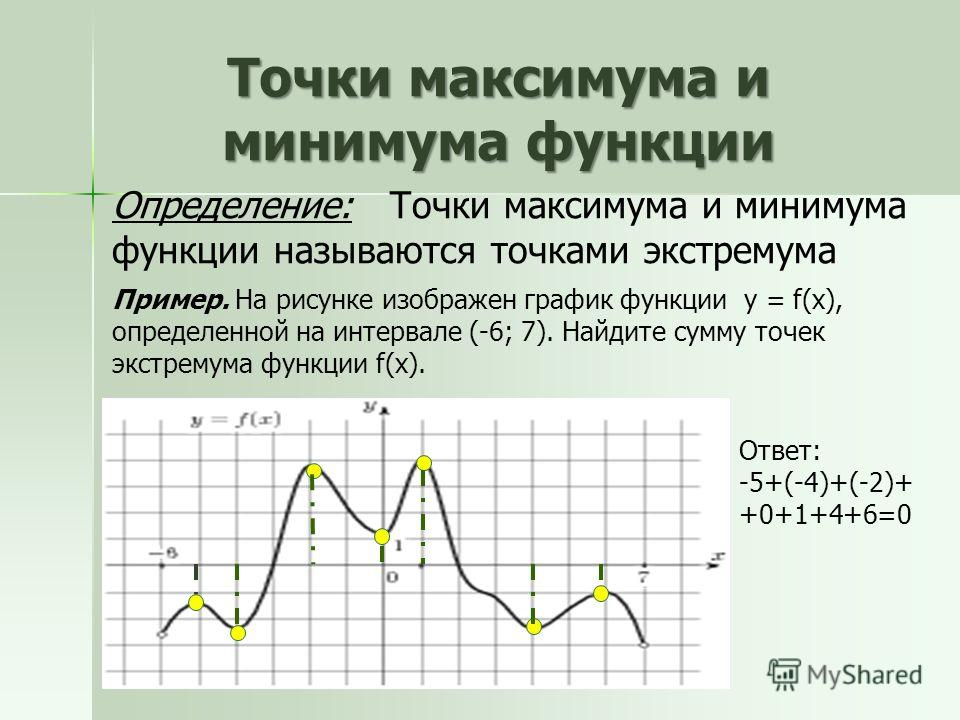 com
com
 )
) )
)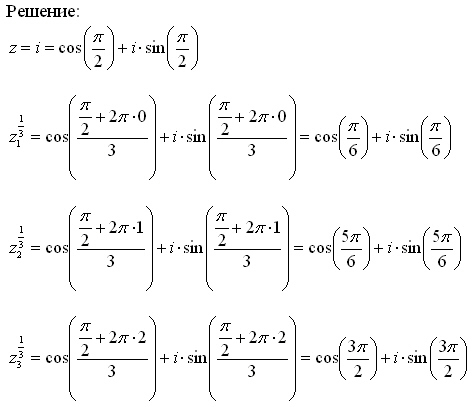 )
)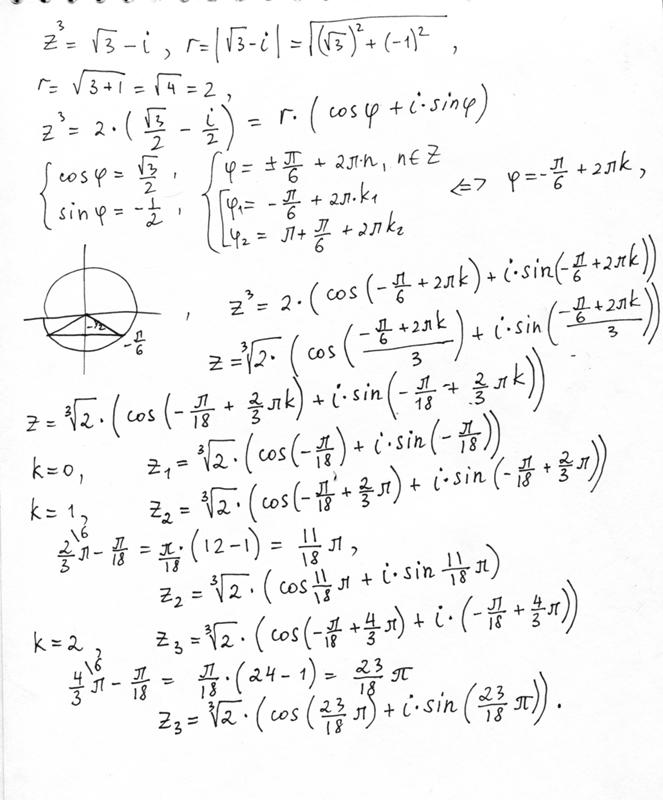 )
) )
)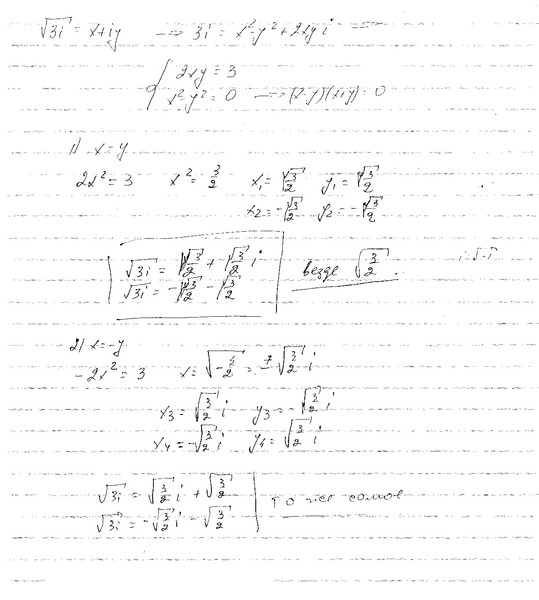 )
) )
) )
) 12.16
12.16 .. 1,3,5,7,9,11,13,15 нужно взять 3 числа и только сложением получить 30.
.. 1,3,5,7,9,11,13,15 нужно взять 3 числа и только сложением получить 30. )/3
)/3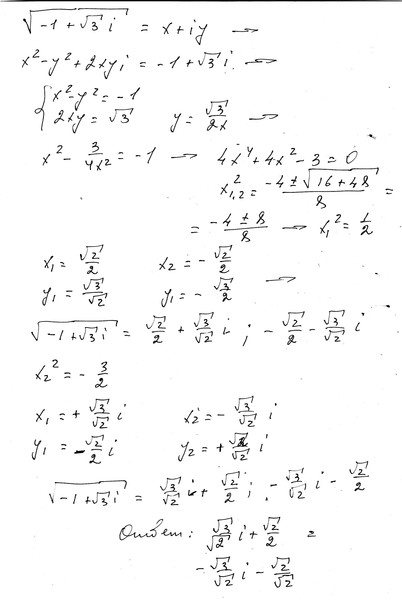
 Наиболее распространенными являются
стандартная форма
, который показан ниже
Наиболее распространенными являются
стандартная форма
, который показан ниже Мы имеем, что x = a является стандартной формой линии, но эта линия не имеет наклонного перехвата (по крайней мере, там, где y является зависимой переменной)
Мы имеем, что x = a является стандартной формой линии, но эта линия не имеет наклонного перехвата (по крайней мере, там, где y является зависимой переменной)

 .:
.:



 Хочется еще, чтобы вы помнили слова российского историка Ключевского: «Есть люди, которые умеют говорить, но не умеют ничего сказать. Это ветряные мельницы, которые вечно машут крыльями, но никогда не летают». Надеюсь, что нам сегодня удастся взлететь на вершину новых знаний алгебры.
Хочется еще, чтобы вы помнили слова российского историка Ключевского: «Есть люди, которые умеют говорить, но не умеют ничего сказать. Это ветряные мельницы, которые вечно машут крыльями, но никогда не летают». Надеюсь, что нам сегодня удастся взлететь на вершину новых знаний алгебры. Но язык алгебры приводит здесь к успеху проще и быстрее
Но язык алгебры приводит здесь к успеху проще и быстрее
 (ax=b, где a и b –некоторые числа, а x-переменная).
(ax=b, где a и b –некоторые числа, а x-переменная). Прочитайте определение про себя. Не ошиблись ли мы в определении. Есть ли различия?
Прочитайте определение про себя. Не ошиблись ли мы в определении. Есть ли различия? )
) )
) В записи решений уравнения с переменными х и у на первом месте записывают значения х, а на втором – значение у.
В записи решений уравнения с переменными х и у на первом месте записывают значения х, а на втором – значение у. Для этого перенесем
Для этого перенесем
 Уравнение имеет вид:
Уравнение имеет вид:
 Общая стоимость: \(y = 31,50 + 32\text{x}\)
Общая стоимость: \(y = 31,50 + 32\text{x}\) (c) Если \(b < 0\), линия наклонена вниз вправо.
(c) Если \(b < 0\), линия наклонена вниз вправо.
 Этот тип взаимосвязи может быть определен алгебраически с помощью используемых уравнений, численно с фактическими или прогнозируемыми значениями данных или графически с помощью построенной кривой. (Линии классифицируются как прямые кривые.) Алгебраически линейное уравнение обычно принимает вид \(y = mx + b\), где \(m\) и \(b\) — константы, \(x\) — независимая переменная, \(y\) — зависимая переменная. В статистическом контексте линейное уравнение записывается в виде \(y = a + bx\), где \(a\) и \(b\) — константы. Эта форма используется, чтобы помочь читателям отличить статистический контекст от алгебраического контекста. В уравнении \(y = a + b\text{x}\) константа b, на которую умножается переменная \(x\) (\(b\) называется коэффициентом), называется склон . Константа а называется \(у\)-перехватом.
Этот тип взаимосвязи может быть определен алгебраически с помощью используемых уравнений, численно с фактическими или прогнозируемыми значениями данных или графически с помощью построенной кривой. (Линии классифицируются как прямые кривые.) Алгебраически линейное уравнение обычно принимает вид \(y = mx + b\), где \(m\) и \(b\) — константы, \(x\) — независимая переменная, \(y\) — зависимая переменная. В статистическом контексте линейное уравнение записывается в виде \(y = a + bx\), где \(a\) и \(b\) — константы. Эта форма используется, чтобы помочь читателям отличить статистический контекст от алгебраического контекста. В уравнении \(y = a + b\text{x}\) константа b, на которую умножается переменная \(x\) (\(b\) называется коэффициентом), называется склон . Константа а называется \(у\)-перехватом. \(y\) -intercept используется для описания зависимой переменной, когда независимая переменная равна нулю.
\(y\) -intercept используется для описания зависимой переменной, когда независимая переменная равна нулю. org/details/books/introductory-statistics
org/details/books/introductory-statistics

