Уравнение по формуле крамера. Линейные уравнения
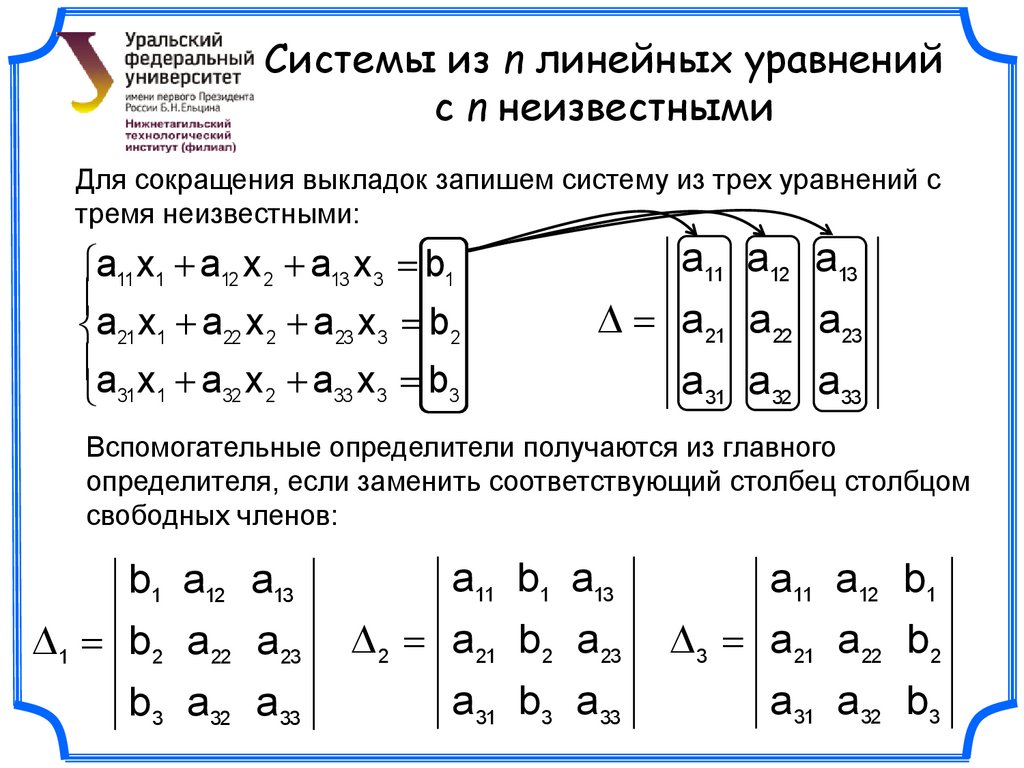
Рассмотрим систему 3-х уравнений с тремя неизвестными
Используя определители 3-го порядка, решение такой системы можно записать в таком же виде, как и для системы двух уравнений, т.е.
(2.4)
если 0. Здесь
Это есть правило Крамера решения системы трех линейных уравнений с тремя неизвестными .
Пример 2.3. Решить систему линейных уравнений при помощи правила Крамера:
Решение . Находим определитель основной матрицы системы
Поскольку 0, то для нахождения решения системы можно применить правило Крамера, но предварительно вычислим еще три определителя:
Проверка:
Следовательно, решение найдено правильно.
Правила Крамера, полученные для линейных систем 2-го и 3-го порядка, наводят на мысль, что такие же правила можно сформулировать и для линейных систем любого порядка. Действительно имеет место
Теорема
Крамера. Квадратная
система линейных уравнений с отличным
от нуля определителем основной матрицы
системы (0) имеет
одно и только одно решение и это решение
вычисляется по формулам
Квадратная
система линейных уравнений с отличным
от нуля определителем основной матрицы
системы (0) имеет
одно и только одно решение и это решение
вычисляется по формулам
(2.5)
где – определитель основной матрицы , i – определитель матрицы , полученной из основной, заменой i -го столбца столбцом свободных членов .
Отметим, что если =0, то правило Крамера не применимо. Это означает, что система либо не имеет вообще решений, либо имеет бесконечно много решений.
Сформулировав теорему Крамера, естественно возникает вопрос о вычислении определителей высших порядков.
2.4. Определители n-го порядка
Дополнительным
минором M ij элемента a ij называется определитель, получаемый
из данного путем вычеркивания i -й
строки и j -го
столбца. Алгебраическим
дополнением A ij элемента a ij называется минор этого элемента, взятого
со знаком (–1) i + j ,
т. е. A ij = (–1) i + j M ij .
е. A ij = (–1) i + j M ij .
Например, найдем миноры и алгебраические дополнения элементов a 23 и a 31 определителя
Получаем
Используя понятие алгебраического дополнения можно сформулировать теорему о разложении определителя n -го порядка по строке или столбцу .
Теорема 2.1. Определитель матрицы A равен сумме произведений всех элементов некоторой строки (или столбца) на их алгебраические дополнения:
(2.6)
Данная теорема лежит в основе одного из основных методов вычисления определителей, т.н. метода понижения порядка . В результате разложения определителя n -го порядка по какой-либо строке или столбцу, получается n определителей (n –1)-го порядка. Чтобы таких определителей было меньше, целесообразно выбирать ту строку или столбец, в которой больше всего нулей. На практике формулу разложения определителя обычно записывают в виде:
т. е.
алгебраические дополнения записывают
в явном виде через миноры.
е.
алгебраические дополнения записывают
в явном виде через миноры.
Примеры 2.4. Вычислить определители, предварительно разложив их по какой-либо строке или столбцу. Обычно в таких случаях выбирают такой столбец или строку, в которой больше всего нулей. Выбранную строку или столбец будем обозначать стрелкой.
2.5. Основные свойства определителей
Разлагая
определитель по какой-либо строке или
столбцу, мы получим n
определителей (n –1)-го
порядка. Затем каждый из этих определителей
(n –1)-го
порядка также можно разложить в сумму
определителей (n –2)-го
порядка. Продолжая этот процесс, можно
дойти до определителей 1-го порядка,
т.е. до элементов матрицы, определитель
которой вычисляется. Так, для вычисления
определителей 2-го порядка придется
вычислить сумму двух слагаемых, для
определителей 3-го порядка – сумму 6
слагаемых, для определителей 4-го порядка
– 24 слагаемых. Число слагаемых будет
резко возрастать по мере увеличения
порядка определителя. Это означает, что
вычисление определителей очень высоких
порядков становится довольно трудоемкой
задачей, непосильной даже для ЭВМ. Однако
вычислять определители можно и по-другому,
используя свойства определителей.
Это означает, что
вычисление определителей очень высоких
порядков становится довольно трудоемкой
задачей, непосильной даже для ЭВМ. Однако
вычислять определители можно и по-другому,
используя свойства определителей.
Свойство 1 . Определитель не изменится, если в нем поменять местами строки и столбцы, т.е. при транспонировании матрицы :
.
Данное свойство свидетельствует о равноправии строк и столбцов определителя. Иначе говоря, любое утверждение о столбцах определителя справедливо и для его строк и наоборот.
Свойство 2 . Определитель меняет знак при перестановке двух строк (столбцов).
Следствие . Если определитель имеет две одинаковые строки (столбца), то он равен нулю.
Свойство 3 . Общий множитель всех элементов в какой-либо строке (столбце) можно вынести за знак определителя .
Например,
Следствие . Если
все элементы некоторой строки (столбца)
определителя равны нулю, то и сам
определитель равен нулю .
Если
все элементы некоторой строки (столбца)
определителя равны нулю, то и сам
определитель равен нулю .
Свойство 4 . Определитель не изменится, если к элементам одной строки (столбца), прибавить элементы другой строки (столбца), умноженной на какое-либо число .
Например,
Свойство 5 . Определитель произведения матриц равен произведению определителей матриц:
Метод Крамера или так называемое правило Крамера – это способ поиска неизвестных величин из систем уравнений. Его можно использовать только если число искомых значений эквивалентно количеству алгебраических уравнений в системе, то есть образуемая из системы основная матрица должна быть квадратной и не содержать нулевых строчек, а также если её детерминант не должен являться нулевым.
Теорема 1
Теорема Крамера Если главный определитель $D$ основной матрицы, составленной на основе коэффициентов уравнений, не равен нулю, то система уравнений совместна, причём решение у неё существует единственное. Решение такой системы вычисляется через так называемые формулы Крамера для решения систем линейных уравнений:
$x_i = \frac{D_i}{D}$
Решение такой системы вычисляется через так называемые формулы Крамера для решения систем линейных уравнений:
$x_i = \frac{D_i}{D}$
В чем заключается метод Крамера
Суть метода Крамера в следующем:
- Чтобы найти решение системы методом Крамера, первым делом вычисляем главный определитель матрицы $D$. Когда вычисленный детерминант основной матрицы при подсчёте методом Крамера оказался равен нулю, то система не имеет ни одного решения или имеет нескончаемое количество решений. В этом случае для нахождения общего или какого-либо базисного ответа для системы рекомендуется применить метод Гаусса.
- Затем нужно заменить крайний столбец главной матрицы на столбец свободных членов и высчитать определитель $D_1$.
- Повторить то же самое для всех столбцов, получив определители от $D_1$ до $D_n$, где $n$ — номер крайнего справа столбца.
- После того как найдены все детерминанты $D_1$…$D_n$, можно высчитать неизвестные переменные по формуле $x_i = \frac{D_i}{D}$.

Приёмы для вычисления определителя матрицы
Для вычисления определителя матрицы с размерностью больше чем 2 на 2, можно использовать несколько способов:
- Правило треугольников, или правило Саррюса, напоминающее это же правило. Суть метода треугольников в том, что при вычислении определителя произведения всех чисел, соединённых на рисунке красной линией справа, записываются со знаком плюс, а все числа, соединённые аналогичным образом на рисунке слева – со знаком минус. B то, и другое правило подходит для матриц размером 3 х 3. В случае же правила Саррюса сначала переписывается сама матрица, а рядом с ней рядом переписываются ещё раз её первый и второй столбец. Через матрицу и эти дополнительные столбцы проводятся диагонали, члены матрицы, лежащие на главной диагонали или на параллельной ей записываются со знаком плюс, а элементы, лежащие на побочной диагонали или параллельно ей — со знаком минус.
Рисунок 1. Правило треугольников для вычисления определителя для метода Крамера
- С помощью метода, известного как метод Гаусса, также иногда этот метод называют понижением порядка определителя.
 В этом случае матрица преобразуется и приводится к треугольному виду, а затем перемножаются все числа, стоящие на главной диагонали. Следует помнить, что при таком поиске определителя нельзя домножать или делить строчки или столбцы на числа без вынесения их как множителя или делителя. В случае поиска определителя возможно только вычитать и складывать строки и столбы между собой, предварительно помножив вычитаемую строку на ненулевой множитель. Также при каждой перестановке строчек или столбцов матрицы местами следует помнить о необходимости смены конечного знака у матрицы.
В этом случае матрица преобразуется и приводится к треугольному виду, а затем перемножаются все числа, стоящие на главной диагонали. Следует помнить, что при таком поиске определителя нельзя домножать или делить строчки или столбцы на числа без вынесения их как множителя или делителя. В случае поиска определителя возможно только вычитать и складывать строки и столбы между собой, предварительно помножив вычитаемую строку на ненулевой множитель. Также при каждой перестановке строчек или столбцов матрицы местами следует помнить о необходимости смены конечного знака у матрицы. - При решении методом Крамера СЛАУ с 4 неизвестными, лучше всего будет применять именно метод Гаусса для поиска и нахождения определителей или опредлять детерминант через поиск миноров.
Решение систем уравнений методом Крамера
Применим метод Крамера для системы из 2 уравнений и двумя искомыми величинами:
$\begin{cases} a_1x_1 + a_2x_2 = b_1 \\ a_3x_1 + a_4x_2 = b_2 \\ \end{cases}$
Отобразим её в расширенной форме для удобства:
$A = \begin{array}{cc|c} a_1 & a_2 & b_1 \\ a_3 & a_4 & b_1 \\ \end{array}$
Найдём определитель основной матрицы, также называемый главным определителем системы:
$D = \begin{array}{|cc|} a_1 & a_2 \\ a_3 & a_4 \\ \end{array} = a_1 \cdot a_4 – a_3 \cdot a_2$
Если главный определитель не равен нулю, то для решения слау методом Крамера необходимо высчитать ещё парочку определителей от двух матриц с заменёнными столбцами основной матрицы на строчку свободных членов:
$D_1 = \begin{array}{|cc|} b_1 & a_2 \\ b_2 & a_4 \\ \end{array} = b_1 \cdot a_4 – b_2 \cdot a_4$
$D_2 = \begin{array}{|cc|} a_1 & b_1 \\ a_3 & b_2 \\ \end{array} = a_1 \cdot b_2 – a_3 \cdot b_1$
Теперь найдём неизвестные $x_1$ и $x_2$:
$x_1 = \frac {D_1}{D}$
$x_2 = \frac {D_2}{D}$
Пример 1
Метод Крамера для решения СЛАУ с основной матрицей 3 порядка (3 x 3) и тремя искомыми.
Решите систему уравнений:
$\begin{cases} 3x_1 – 2x_2 + 4x_3 = 21 \\ 3x_1 +4x_2 + 2x_3 = 9\\ 2x_1 – x_2 — x_3 = 10 \\ \end{cases}$
Сосчитаем главный детерминант матрицы пользуясь вышеизложенным под пунктом номер 1 правилом:
$D = \begin{array}{|ccc|} 3 & -2 & 4 \\3 & 4 & -2 \\ 2 & -1 & 1 \\ \end{array} = 3 \cdot 4 \cdot (-1) + 2 \cdot (-2) \cdot 2 + 4 \cdot 3 \cdot (-1) – 4 \cdot 4 \cdot 2 – 3 \cdot (-2) \cdot (-1) — (-1) \cdot 2 \cdot 3 = — 12 – 8 -12 -32 – 6 + 6 = — 64$
А теперь три других детерминанта:
$D_1 = \begin{array}{|ccc|} 21 & 2 & 4 \\ 9 & 4 & 2 \\ 10 & 1 & 1 \\ \end{array} = 21 \cdot 4 \cdot 1 + (-2) \cdot 2 \cdot 10 + 9 \cdot (-1) \cdot 4 – 4 \cdot 4 \cdot 10 – 9 \cdot (-2) \cdot (-1) — (-1) \cdot 2 \cdot 21 = — 84 – 40 – 36 – 160 – 18 + 42 = — 296$
$D_2 = \begin{array}{|ccc|} 3 & 21 & 4 \\3 & 9 & 2 \\ 2 & 10 & 1 \\ \end{array} = 3 \cdot 9 \cdot (- 1) + 3 \cdot 10 \cdot 4 + 21 \cdot 2 \cdot 2 – 4 \cdot 9 \cdot 2 – 21 \cdot 3 \cdot (-1) – 2 \cdot 10 \cdot 3 = — 27 + 120 + 84 – 72 + 63 – 60 = 108$
$D_3 = \begin{array}{|ccc|} 3 & -2 & 21 \\ 3 & 4 & 9 \\ 2 & 1 & 10 \\ \end{array} = 3 \cdot 4 \cdot 10 + 3 \cdot (-1) \cdot 21 + (-2) \cdot 9 \cdot 2 – 21 \cdot 4 \cdot 2 — (-2) \cdot 3 \cdot 10 — (-1) \cdot 9 \cdot 3 = 120 – 63 – 36 – 168 + 60 + 27 = — 60$
Найдём искомые величины:
$x_1 = \frac{D_1} {D} = \frac{- 296}{-64} = 4 \frac{5}{8}$
$x_2 = \frac{D_1} {D} = \frac{108} {-64} = — 1 \frac {11} {16}$
$x_3 = \frac{D_1} {D} = \frac{-60} {-64} = \frac {15} {16}$
2. Решение систем уравнений матричным методом (при помощи обратной матрицы).
Решение систем уравнений матричным методом (при помощи обратной матрицы).
3. Метод Гаусса решения систем уравнений.
Метод Крамера.
Метод Крамера применяется для решения систем линейных алгебраических уравнений (СЛАУ ).
Формулы на примере системы из двух уравнений с двумя переменными.
Дано: Решить методом Крамера систему
Относительно переменных х и у .
Решение:
Найдем определитель матрицы, составленный из коэффициентов системы Вычисление определителей. :
Применим формулы Крамера и найдем значения переменных:
и .
Пример 1:
Решить систему уравнений:
относительно переменных х и у .
Решение:
Заменим в этом определителе первый столбец столбцом коэффициентов из правой части системы и найдем его значение:
Сделаем аналогичное действие, заменив в первом определителе второй столбец:
Применим формулы Крамера и найдем значения переменных:
и .
Ответ:
Замечание: Этим методом можно решать системы и большей размерности.
Замечание: Если получается, что , а делить на ноль нельзя, то говорят, что система не имеет единственного решения. В этом случае система имеет или бесконечно много решений или не имеет решений вообще.
Пример 2 (бесконечное количество решений):
Решить систему уравнений:
относительно переменных х и у .
Решение:
Найдем определитель матрицы, составленный из коэффициентов системы:
Решение систем методом подстановки.
Первое из уравнений системы — равенство, верное при любых значениях переменных (потому что 4 всегда равно 4). Значит, остается только одно уравнение. Это уравнение связи между переменными .
Получили, решением системы являются любые пары значений переменных, связанных между собой равенством .
Общее решение запишется так:
Частные решения можно определять выбирая произвольное значение у и вычисляя х по этому равенству связи.
и т.д.
Таких решений бесконечно много.
Ответ: общее решение
Частные решения:
Пример 3 (решений нет, система несовместна):
Решить систему уравнений:
Решение:
Найдем определитель матрицы, составленный из коэффициентов системы:
Применять формулы Крамера нельзя. Решим эту систему методом подстановки
Второе уравнение системы — равенство, неверное ни при каких значениях переменных (конечно же, так как -15 не равно 2). Если одно из уравнений системы не верно ни при каких значениях переменных, то и вся системы не имеет решений.
Ответ: решений нет
Методы Крамера и Гаусса – одни из самых популярных методов решения СЛАУ . К тому же, в ряде случаев целесообразно использовать именно конкретные методы. Сессия близка, и сейчас самое время повторить или освоить их с нуля. Сегодня разбираемся с решением методом Крамера. Ведь решение системы линейных уравнений методом Крамера — весьма полезный навык.
Системы линейных алгебраических уравнений
Система линейных алгебраических уравнений – система уравнений вида:
Набор значений x , при котором уравнения системы обращаются в тождества, называется решением системы, a и b – вещественные коэффициенты. Простенькую систему, состоящую из двух уравнений с двумя неизвестными, можно решить в уме либо выразив одну переменную через другую. Но переменных (иксов) в СЛАУ может быть гораздо больше двух, и здесь простыми школьными манипуляциями не обойтись. Что же делать? Например, решать СЛАУ методом Крамера!
Итак, пусть система состоит из n уравнений с n неизвестными.
Такую систему можно переписать в матричном виде
Здесь A – основная матрица системы, X и B , соответственно, матрицы-столбцы неизвестных переменных и свободных членов.
Решение СЛАУ методом Крамера
Если определитель главной матрицы не равен нулю (матрица невырожденная), систему можно решать по методу Крамера.
Согласно методу Крамера, решение находится по формулам:
Здесь дельта – определитель главной матрицы, а дельта x n-ное – определитель, полученный из определителя главной матрицы путем заменой n-ного столбца на столбец свободных членов.
В этом и заключается вся суть метода Крамера. Подставляя найденные по вышеприведенным формулам значения x в искомую систему, убеждаемся в правильности (или наоборот) нашего решения. Чтобы Вы быстрее уловили суть, приведем ниже пример подробного решения СЛАУ методом Крамера:
Даже если у Вас не получится с первого раза, не расстраивайтесь! Немного практики, и Вы начнете щелкать СЛАУ как орешки. Более того, сейчас совершенно необязательно корпеть над тетрадью, решая громоздкие выкладки и исписывая стержень. Можно легко решить СЛАУ методом Крамера в режиме онлайн, лишь подставив в готовую форму коэффициенты. Испробовать онлайн калькулятор решения методом Крамера можно, к примеру, на этом сайте .
А если система оказалась упорной и не сдается, Вы всегда можете обратиться за помощью к нашим авторам, например, чтобы . Будь в системе хоть 100 неизвестных, мы обязательно решим ее верно и точно в срок!
В первой части мы рассмотрели немного теоретического материала, метод подстановки, а также метод почленного сложения уравнений системы. Всем, кто зашел на сайт через эту страницу рекомендую ознакомиться с первой частью. Возможно, некоторым посетителям покажется материал слишком простым, но по ходу решения систем линейных уравнений я сделал ряд очень важных замечаний и выводов, касающихся решения математических задач в целом.
А сейчас мы разберём правило Крамера, а также решение системы линейных уравнений с помощью обратной матрицы (матричный метод). Все материалы изложены просто, подробно и понятно, практически все читатели смогут научиться решать системы вышеуказанными способами.
Сначала мы подробно рассмотрим правило Крамера для системы двух линейных уравнений с двумя неизвестными. Зачем? – Ведь простейшую систему можно решить школьным методом, методом почленного сложения!
Зачем? – Ведь простейшую систему можно решить школьным методом, методом почленного сложения!
Дело в том, что пусть иногда, но встречается такое задание – решить систему двух линейных уравнений с двумя неизвестными по формулам Крамера. Во-вторых, более простой пример поможет понять, как использовать правило Крамера для более сложного случая – системы трех уравнений с тремя неизвестными.
Кроме того, существуют системы линейных уравнений с двумя переменными, которые целесообразно решать именно по правилу Крамера!
Рассмотрим систему уравнений
На первом шаге вычислим определитель , его называют главным определителем системы .
метод Гаусса .
Если , то система имеет единственное решение, и для нахождения корней мы должны вычислить еще два определителя:
и
На практике вышеуказанные определители также могут обозначаться латинской буквой .
Корни уравнения находим по формулам:
,
Пример 7
Решить систему линейных уравнений
Решение : Мы видим, что коэффициенты уравнения достаточно велики, в правой части присутствуют десятичные дроби с запятой. Запятая – довольно редкий гость в практических заданиях по математике, эту систему я взял из эконометрической задачи.
Запятая – довольно редкий гость в практических заданиях по математике, эту систему я взял из эконометрической задачи.
Как решить такую систему? Можно попытаться выразить одну переменную через другую, но в этом случае наверняка получатся страшные навороченные дроби, с которыми крайне неудобно работать, да и оформление решения будет выглядеть просто ужасно. Можно умножить второе уравнение на 6 и провести почленное вычитание, но и здесь возникнут те же самые дроби.
Что делать? В подобных случаях и приходят на помощь формулы Крамера.
;
;
Ответ : ,
Оба корня обладают бесконечными хвостами, и найдены приближенно, что вполне приемлемо (и даже обыденно) для задач эконометрики.
Комментарии здесь не нужны, поскольку задание решается по готовым формулам, однако, есть один нюанс. Когда используете данный метод, обязательным фрагментом оформления задания является следующий фрагмент: «, значит, система имеет единственное решение» . В противном случае рецензент может Вас наказать за неуважение к теореме Крамера.
В противном случае рецензент может Вас наказать за неуважение к теореме Крамера.
Совсем не лишней будет проверка, которую удобно провести на калькуляторе: подставляем приближенные значения в левую часть каждого уравнения системы. В результате с небольшой погрешностью должны получиться числа, которые находятся в правых частях.
Пример 8
Ответ представить в обыкновенных неправильных дробях. Сделать проверку.
Это пример для самостоятельного решения (пример чистового оформления и ответ в конце урока).
Переходим к рассмотрению правила Крамера для системы трех уравнений с тремя неизвестными:
Находим главный определитель системы:
Если , то система имеет бесконечно много решений или несовместна (не имеет решений). В этом случае правило Крамера не поможет, нужно использовать метод Гаусса .
Если , то система имеет единственное решение и для нахождения корней мы должны вычислить еще три определителя:
, ,
И, наконец, ответ рассчитывается по формулам:
Как видите, случай «три на три» принципиально ничем не отличается от случая «два на два», столбец свободных членов последовательно «прогуливается» слева направо по столбцам главного определителя.
Пример 9
Решить систему по формулам Крамера.
Решение : Решим систему по формулам Крамера.
, значит, система имеет единственное решение.
Ответ : .
Собственно, здесь опять комментировать особо нечего, ввиду того, что решение проходит по готовым формулам. Но есть пара замечаний.
Бывает так, что в результате вычислений получаются «плохие» несократимые дроби, например: .
Я рекомендую следующий алгоритм «лечения». Если под рукой нет компьютера, поступаем так:
1) Возможно, допущена ошибка в вычислениях. Как только Вы столкнулись с «плохой» дробью, сразу необходимо проверить, правильно ли переписано условие . Если условие переписано без ошибок, то нужно пересчитать определители, используя разложение по другой строке (столбцу).
2) Если в результате проверки ошибок не выявлено, то вероятнее всего, допущена опечатка в условии задания. В этом случае спокойно и ВНИМАТЕЛЬНО прорешиваем задание до конца, а затем обязательно делаем проверку и оформляем ее на чистовике после решения. Конечно, проверка дробного ответа – занятие неприятное, но зато будет обезоруживающий аргумент для преподавателя, который ну очень любит ставить минус за всякую бяку вроде . Как управляться с дробями, подробно расписано в ответе для Примера 8.
Конечно, проверка дробного ответа – занятие неприятное, но зато будет обезоруживающий аргумент для преподавателя, который ну очень любит ставить минус за всякую бяку вроде . Как управляться с дробями, подробно расписано в ответе для Примера 8.
Если под рукой есть компьютер, то для проверки используйте автоматизированную программу, которую можно бесплатно скачать в самом начале урока. Кстати, выгоднее всего сразу воспользоваться программой (еще до начала решения), Вы сразу будете видеть промежуточный шаг, на котором допустили ошибку! Этот же калькулятор автоматически рассчитывает решение системы матричным методом.
Замечание второе. Время от времени встречаются системы в уравнениях которых отсутствуют некоторые переменные, например:
Здесь в первом уравнении отсутствует переменная , во втором – переменная . В таких случаях очень важно правильно и ВНИМАТЕЛЬНО записать главный определитель:
– на месте отсутствующих переменных ставятся нули.
Кстати определители с нулями рационально раскрывать по той строке (столбцу), в которой находится ноль, так как вычислений получается заметно меньше.
Пример 10
Решить систему по формулам Крамера.
Это пример для самостоятельного решения (образец чистового оформления и ответ в конце урока).
Для случая системы 4 уравнений с 4 неизвестными формулы Крамера записываются по аналогичным принципам. Живой пример можно посмотреть на уроке Свойства определителя. Понижение порядка определителя – пять определителей 4-го порядка вполне решабельны. Хотя задача уже весьма напоминает ботинок профессора на груди у студента-счастливчика.
Решение системы с помощью обратной матрицыМетод обратной матрицы – это, по существу, частный случай матричного уравнения (см. Пример №3 указанного урока).
Для изучения данного параграфа необходимо уметь раскрывать определители, находить обратную матрицу и выполнять матричное умножение. Соответствующие ссылки будут даны по ходу объяснений.
Пример 11
Решить систему с матричным методом
Решение : Запишем систему в матричной форме:
, где
Пожалуйста, посмотрите на систему уравнений и на матрицы. По какому принципу записываем элементы в матрицы, думаю, всем понятно. Единственный комментарий: если бы в уравнениях отсутствовали некоторые переменные, то на соответствующих местах в матрице нужно было бы поставить нули.
По какому принципу записываем элементы в матрицы, думаю, всем понятно. Единственный комментарий: если бы в уравнениях отсутствовали некоторые переменные, то на соответствующих местах в матрице нужно было бы поставить нули.
Обратную матрицу найдем по формуле:
, где – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .
Сначала разбираемся с определителем:
Здесь определитель раскрыт по первой строке.
Внимание! Если , то обратной матрицы не существует, и решить систему матричным методом невозможно. В этом случае система решается методом исключения неизвестных (методом Гаусса) .
Теперь нужно вычислить 9 миноров и записать их в матрицу миноров
Справка: Полезно знать смысл двойных подстрочных индексов в линейной алгебре. Первая цифра – это номер строки, в которой находится данный элемент. Вторая цифра – это номер столбца, в котором находится данный элемент:
То есть, двойной подстрочный индекс указывает, что элемент находится в первой строке, третьем столбце, а, например, элемент находится в 3 строке, 2 столбце
Матрицы метод крамера примеры.
 Метод крамера решения систем линейных уравнений
Метод крамера решения систем линейных уравненийМетоды Крамера и Гаусса – одни из самых популярных методов решения СЛАУ . К тому же, в ряде случаев целесообразно использовать именно конкретные методы. Сессия близка, и сейчас самое время повторить или освоить их с нуля. Сегодня разбираемся с решением методом Крамера. Ведь решение системы линейных уравнений методом Крамера — весьма полезный навык.
Системы линейных алгебраических уравнений
Система линейных алгебраических уравнений – система уравнений вида:
Набор значений x , при котором уравнения системы обращаются в тождества, называется решением системы, a и b – вещественные коэффициенты. Простенькую систему, состоящую из двух уравнений с двумя неизвестными, можно решить в уме либо выразив одну переменную через другую. Но переменных (иксов) в СЛАУ может быть гораздо больше двух, и здесь простыми школьными манипуляциями не обойтись. Что же делать? Например, решать СЛАУ методом Крамера!
Итак, пусть система состоит из n уравнений с n неизвестными.
Такую систему можно переписать в матричном виде
Здесь A – основная матрица системы, X и B , соответственно, матрицы-столбцы неизвестных переменных и свободных членов.
Решение СЛАУ методом Крамера
Если определитель главной матрицы не равен нулю (матрица невырожденная), систему можно решать по методу Крамера.
Согласно методу Крамера, решение находится по формулам:
Здесь дельта – определитель главной матрицы, а дельта x n-ное – определитель, полученный из определителя главной матрицы путем заменой n-ного столбца на столбец свободных членов.
В этом и заключается вся суть метода Крамера. Подставляя найденные по вышеприведенным формулам значения x в искомую систему, убеждаемся в правильности (или наоборот) нашего решения. Чтобы Вы быстрее уловили суть, приведем ниже пример подробного решения СЛАУ методом Крамера:
Даже если у Вас не получится с первого раза, не расстраивайтесь! Немного практики, и Вы начнете щелкать СЛАУ как орешки. Более того, сейчас совершенно необязательно корпеть над тетрадью, решая громоздкие выкладки и исписывая стержень. Можно легко решить СЛАУ методом Крамера в режиме онлайн, лишь подставив в готовую форму коэффициенты. Испробовать онлайн калькулятор решения методом Крамера можно, к примеру, на этом сайте .
Более того, сейчас совершенно необязательно корпеть над тетрадью, решая громоздкие выкладки и исписывая стержень. Можно легко решить СЛАУ методом Крамера в режиме онлайн, лишь подставив в готовую форму коэффициенты. Испробовать онлайн калькулятор решения методом Крамера можно, к примеру, на этом сайте .
А если система оказалась упорной и не сдается, Вы всегда можете обратиться за помощью к нашим авторам, например, чтобы . Будь в системе хоть 100 неизвестных, мы обязательно решим ее верно и точно в срок!
С количеством уравнений одинаковым с количеством неизвестных с главным определителем матрицы, который не равен нулю, коэффициентов системы (для подобных уравнений решение есть и оно только одно).
Теорема Крамера.
Когда определитель матрицы квадратной системы ненулевой, значит, система совместна и у нее есть одно решение и его можно найти по формулам Крамера :
где Δ — определитель матрицы системы ,
Δ i — определитель матрицы системы, в котором вместо i -го столбца находится столбец правых частей.
Когда определитель системы нулевой, значит, система может стать совместной или несовместной.
Этот способ обычно применяют для небольших систем с объемными вычислениями и если когда необходимо определить 1-ну из неизвестных. Сложность метода в том, что нужно вычислять много определителей.
Описание метода Крамера.
Есть система уравнений:
Систему 3-х уравнений можно решить методом Крамера, который рассмотрен выше для системы 2-х уравнений.
Составляем определитель из коэффициентов у неизвестных:
Это будет определитель системы . Когда D≠0 , значит, система совместна. Теперь составим 3 дополнительных определителя:
,,
Решаем систему по формулам Крамера :
Примеры решения систем уравнений методом Крамера.
Пример 1 .
Дана система:
Решим ее методом Крамера.
Сначала нужно вычислить определитель матрицы системы:
Т.к. Δ≠0, значит, из теоремы Крамера система совместна и у нее есть одно решение. Вычисляем дополнительные определители. Определитель Δ 1 получаем из определителя Δ, заменяя его первый столбец столбцом свободных коэффициентов. Получаем:
Вычисляем дополнительные определители. Определитель Δ 1 получаем из определителя Δ, заменяя его первый столбец столбцом свободных коэффициентов. Получаем:
Таким же путем получаем определитель Δ 2 из определителя матрицы системы заменяя второй столбец столбцом свободных коэффициентов:
Рассмотрим систему 3-х уравнений с тремя неизвестными
Используя определители 3-го порядка, решение такой системы можно записать в таком же виде, как и для системы двух уравнений, т.е.
(2.4)
если 0. Здесь
Это есть правило Крамера решения системы трех линейных уравнений с тремя неизвестными .
Пример 2.3. Решить систему линейных уравнений при помощи правила Крамера:
Решение . Находим определитель основной матрицы системы
Поскольку 0, то для нахождения решения системы можно применить правило Крамера, но предварительно вычислим еще три определителя:
Проверка:
Следовательно,
решение найдено правильно.
Правила Крамера, полученные для линейных систем 2-го и 3-го порядка, наводят на мысль, что такие же правила можно сформулировать и для линейных систем любого порядка. Действительно имеет место
Теорема Крамера. Квадратная система линейных уравнений с отличным от нуля определителем основной матрицы системы (0) имеет одно и только одно решение и это решение вычисляется по формулам
(2.5)
где – определитель основной матрицы , i – определитель матрицы , полученной из основной, заменой i -го столбца столбцом свободных членов .
Отметим, что если =0, то правило Крамера не применимо. Это означает, что система либо не имеет вообще решений, либо имеет бесконечно много решений.
Сформулировав теорему Крамера, естественно возникает вопрос о вычислении определителей высших порядков.
2.4. Определители n-го порядка
Дополнительным
минором M ij элемента a ij называется определитель, получаемый
из данного путем вычеркивания i -й
строки и j -го
столбца. Алгебраическим
дополнением A ij элемента a ij называется минор этого элемента, взятого
со знаком (–1) i + j ,
т.е. A ij = (–1) i + j M ij .
Алгебраическим
дополнением A ij элемента a ij называется минор этого элемента, взятого
со знаком (–1) i + j ,
т.е. A ij = (–1) i + j M ij .
Например, найдем миноры и алгебраические дополнения элементов a 23 и a 31 определителя
Получаем
Используя понятие алгебраического дополнения можно сформулировать теорему о разложении определителя n -го порядка по строке или столбцу .
Теорема 2.1. Определитель матрицы A равен сумме произведений всех элементов некоторой строки (или столбца) на их алгебраические дополнения:
(2.6)
Данная
теорема лежит в основе одного из основных
методов вычисления определителей, т.н. метода
понижения порядка .
В результате разложения определителя n -го
порядка по какой-либо строке или столбцу,
получается n
определителей (n –1)-го
порядка. Чтобы таких определителей было
меньше, целесообразно выбирать ту строку
или столбец, в которой больше всего
нулей. На практике формулу разложения
определителя обычно записывают в виде:
Чтобы таких определителей было
меньше, целесообразно выбирать ту строку
или столбец, в которой больше всего
нулей. На практике формулу разложения
определителя обычно записывают в виде:
т.е. алгебраические дополнения записывают в явном виде через миноры.
Примеры 2.4. Вычислить определители, предварительно разложив их по какой-либо строке или столбцу. Обычно в таких случаях выбирают такой столбец или строку, в которой больше всего нулей. Выбранную строку или столбец будем обозначать стрелкой.
2.5. Основные свойства определителей
Разлагая
определитель по какой-либо строке или
столбцу, мы получим n
определителей (n –1)-го
порядка. Затем каждый из этих определителей
(n –1)-го
порядка также можно разложить в сумму
определителей (n –2)-го
порядка. Продолжая этот процесс, можно
дойти до определителей 1-го порядка,
т.е. до элементов матрицы, определитель
которой вычисляется. Так, для вычисления
определителей 2-го порядка придется
вычислить сумму двух слагаемых, для
определителей 3-го порядка – сумму 6
слагаемых, для определителей 4-го порядка
– 24 слагаемых. Число слагаемых будет
резко возрастать по мере увеличения
порядка определителя. Это означает, что
вычисление определителей очень высоких
порядков становится довольно трудоемкой
задачей, непосильной даже для ЭВМ. Однако
вычислять определители можно и по-другому,
используя свойства определителей.
Число слагаемых будет
резко возрастать по мере увеличения
порядка определителя. Это означает, что
вычисление определителей очень высоких
порядков становится довольно трудоемкой
задачей, непосильной даже для ЭВМ. Однако
вычислять определители можно и по-другому,
используя свойства определителей.
Свойство 1 . Определитель не изменится, если в нем поменять местами строки и столбцы, т.е. при транспонировании матрицы :
.
Данное свойство свидетельствует о равноправии строк и столбцов определителя. Иначе говоря, любое утверждение о столбцах определителя справедливо и для его строк и наоборот.
Свойство 2 . Определитель меняет знак при перестановке двух строк (столбцов).
Следствие . Если определитель имеет две одинаковые строки (столбца), то он равен нулю.
Свойство
3 . Общий
множитель всех элементов в какой-либо
строке (столбце) можно вынести за знак
определителя .
Например,
Следствие . Если все элементы некоторой строки (столбца) определителя равны нулю, то и сам определитель равен нулю .
Свойство 4 . Определитель не изменится, если к элементам одной строки (столбца), прибавить элементы другой строки (столбца), умноженной на какое-либо число .
Например,
Свойство 5 . Определитель произведения матриц равен произведению определителей матриц:
Для того чтобы освоить данный параграф Вы должны уметь раскрывать определители «два на два» и «три на три». Если с определителями плохо, пожалуйста, изучите урок Как вычислить определитель?
Сначала мы подробно рассмотрим правило Крамера для системы двух линейных уравнений с двумя неизвестными. Зачем? – Ведь простейшую систему можно решить школьным методом, методом почленного сложения!
Дело в том, что пусть иногда, но встречается такое задание – решить систему двух линейных уравнений с двумя неизвестными по формулам Крамера. Во-вторых, более простой пример поможет понять, как использовать правило Крамера для более сложного случая – системы трех уравнений с тремя неизвестными.
Во-вторых, более простой пример поможет понять, как использовать правило Крамера для более сложного случая – системы трех уравнений с тремя неизвестными.
Кроме того, существуют системы линейных уравнений с двумя переменными, которые целесообразно решать именно по правилу Крамера!
Рассмотрим систему уравнений
На первом шаге вычислим определитель , его называют главным определителем системы .
метод Гаусса .
Если , то система имеет единственное решение, и для нахождения корней мы должны вычислить еще два определителя:
и
На практике вышеуказанные определители также могут обозначаться латинской буквой .
Корни уравнения находим по формулам:
,
Пример 7
Решить систему линейных уравнений
Решение : Мы видим, что коэффициенты уравнения достаточно велики, в правой части присутствуют десятичные дроби с запятой. Запятая – довольно редкий гость в практических заданиях по математике, эту систему я взял из эконометрической задачи.
Как решить такую систему? Можно попытаться выразить одну переменную через другую, но в этом случае наверняка получатся страшные навороченные дроби, с которыми крайне неудобно работать, да и оформление решения будет выглядеть просто ужасно. Можно умножить второе уравнение на 6 и провести почленное вычитание, но и здесь возникнут те же самые дроби.
Что делать? В подобных случаях и приходят на помощь формулы Крамера.
;
;
Ответ : ,
Оба корня обладают бесконечными хвостами, и найдены приближенно, что вполне приемлемо (и даже обыденно) для задач эконометрики.
Комментарии здесь не нужны, поскольку задание решается по готовым формулам, однако, есть один нюанс. Когда используете данный метод, обязательным фрагментом оформления задания является следующий фрагмент: «, значит, система имеет единственное решение» . В противном случае рецензент может Вас наказать за неуважение к теореме Крамера.
Совсем не лишней будет проверка, которую удобно провести на калькуляторе: подставляем приближенные значения в левую часть каждого уравнения системы. В результате с небольшой погрешностью должны получиться числа, которые находятся в правых частях.
В результате с небольшой погрешностью должны получиться числа, которые находятся в правых частях.
Пример 8
Ответ представить в обыкновенных неправильных дробях. Сделать проверку.
Это пример для самостоятельного решения (пример чистового оформления и ответ в конце урока).
Переходим к рассмотрению правила Крамера для системы трех уравнений с тремя неизвестными:
Находим главный определитель системы:
Если , то система имеет бесконечно много решений или несовместна (не имеет решений). В этом случае правило Крамера не поможет, нужно использовать метод Гаусса .
Если , то система имеет единственное решение и для нахождения корней мы должны вычислить еще три определителя:
, ,
И, наконец, ответ рассчитывается по формулам:
Как видите, случай «три на три» принципиально ничем не отличается от случая «два на два», столбец свободных членов последовательно «прогуливается» слева направо по столбцам главного определителя.
Пример 9
Решить систему по формулам Крамера.
Решение : Решим систему по формулам Крамера.
, значит, система имеет единственное решение.
Ответ : .
Собственно, здесь опять комментировать особо нечего, ввиду того, что решение проходит по готовым формулам. Но есть пара замечаний.
Бывает так, что в результате вычислений получаются «плохие» несократимые дроби, например: .
Я рекомендую следующий алгоритм «лечения». Если под рукой нет компьютера, поступаем так:
1) Возможно, допущена ошибка в вычислениях. Как только Вы столкнулись с «плохой» дробью, сразу необходимо проверить, правильно ли переписано условие . Если условие переписано без ошибок, то нужно пересчитать определители, используя разложение по другой строке (столбцу).
2) Если в результате проверки ошибок не выявлено, то вероятнее всего, допущена опечатка в условии задания. В этом случае спокойно и ВНИМАТЕЛЬНО прорешиваем задание до конца, а затем обязательно делаем проверку и оформляем ее на чистовике после решения. Конечно, проверка дробного ответа – занятие неприятное, но зато будет обезоруживающий аргумент для преподавателя, который ну очень любит ставить минус за всякую бяку вроде . Как управляться с дробями, подробно расписано в ответе для Примера 8.
Конечно, проверка дробного ответа – занятие неприятное, но зато будет обезоруживающий аргумент для преподавателя, который ну очень любит ставить минус за всякую бяку вроде . Как управляться с дробями, подробно расписано в ответе для Примера 8.
Если под рукой есть компьютер, то для проверки используйте автоматизированную программу, которую можно бесплатно скачать в самом начале урока. Кстати, выгоднее всего сразу воспользоваться программой (еще до начала решения), Вы сразу будете видеть промежуточный шаг, на котором допустили ошибку! Этот же калькулятор автоматически рассчитывает решение системы матричным методом.
Замечание второе. Время от времени встречаются системы в уравнениях которых отсутствуют некоторые переменные, например:
Здесь в первом уравнении отсутствует переменная , во втором – переменная . В таких случаях очень важно правильно и ВНИМАТЕЛЬНО записать главный определитель:
– на месте отсутствующих переменных ставятся нули.
Кстати определители с нулями рационально раскрывать по той строке (столбцу), в которой находится ноль, так как вычислений получается заметно меньше.
Пример 10
Решить систему по формулам Крамера.
Это пример для самостоятельного решения (образец чистового оформления и ответ в конце урока).
Для случая системы 4 уравнений с 4 неизвестными формулы Крамера записываются по аналогичным принципам. Живой пример можно посмотреть на уроке Свойства определителя. Понижение порядка определителя – пять определителей 4-го порядка вполне решабельны. Хотя задача уже весьма напоминает ботинок профессора на груди у студента-счастливчика.
Решение системы с помощью обратной матрицы
Метод обратной матрицы – это, по существу, частный случай матричного уравнения (см. Пример №3 указанного урока).
Для изучения данного параграфа необходимо уметь раскрывать определители, находить обратную матрицу и выполнять матричное умножение. Соответствующие ссылки будут даны по ходу объяснений.
Пример 11
Решить систему с матричным методом
Решение : Запишем систему в матричной форме:
, где
Пожалуйста, посмотрите на систему уравнений и на матрицы. По какому принципу записываем элементы в матрицы, думаю, всем понятно. Единственный комментарий: если бы в уравнениях отсутствовали некоторые переменные, то на соответствующих местах в матрице нужно было бы поставить нули.
По какому принципу записываем элементы в матрицы, думаю, всем понятно. Единственный комментарий: если бы в уравнениях отсутствовали некоторые переменные, то на соответствующих местах в матрице нужно было бы поставить нули.
Обратную матрицу найдем по формуле:
, где – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .
Сначала разбираемся с определителем:
Здесь определитель раскрыт по первой строке.
Внимание! Если , то обратной матрицы не существует, и решить систему матричным методом невозможно. В этом случае система решается методом исключения неизвестных (методом Гаусса) .
Теперь нужно вычислить 9 миноров и записать их в матрицу миноров
Справка: Полезно знать смысл двойных подстрочных индексов в линейной алгебре. Первая цифра – это номер строки, в которой находится данный элемент. Вторая цифра – это номер столбца, в котором находится данный элемент:
То есть, двойной подстрочный индекс указывает, что элемент находится в первой строке, третьем столбце, а, например, элемент находится в 3 строке, 2 столбце
В ходе решения расчет миноров лучше расписать подробно, хотя, при определенном опыте их можно приноровиться считать с ошибками устно.


 В этом случае матрица преобразуется и приводится к треугольному виду, а затем перемножаются все числа, стоящие на главной диагонали. Следует помнить, что при таком поиске определителя нельзя домножать или делить строчки или столбцы на числа без вынесения их как множителя или делителя. В случае поиска определителя возможно только вычитать и складывать строки и столбы между собой, предварительно помножив вычитаемую строку на ненулевой множитель. Также при каждой перестановке строчек или столбцов матрицы местами следует помнить о необходимости смены конечного знака у матрицы.
В этом случае матрица преобразуется и приводится к треугольному виду, а затем перемножаются все числа, стоящие на главной диагонали. Следует помнить, что при таком поиске определителя нельзя домножать или делить строчки или столбцы на числа без вынесения их как множителя или делителя. В случае поиска определителя возможно только вычитать и складывать строки и столбы между собой, предварительно помножив вычитаемую строку на ненулевой множитель. Также при каждой перестановке строчек или столбцов матрицы местами следует помнить о необходимости смены конечного знака у матрицы. Неравенства
Неравенства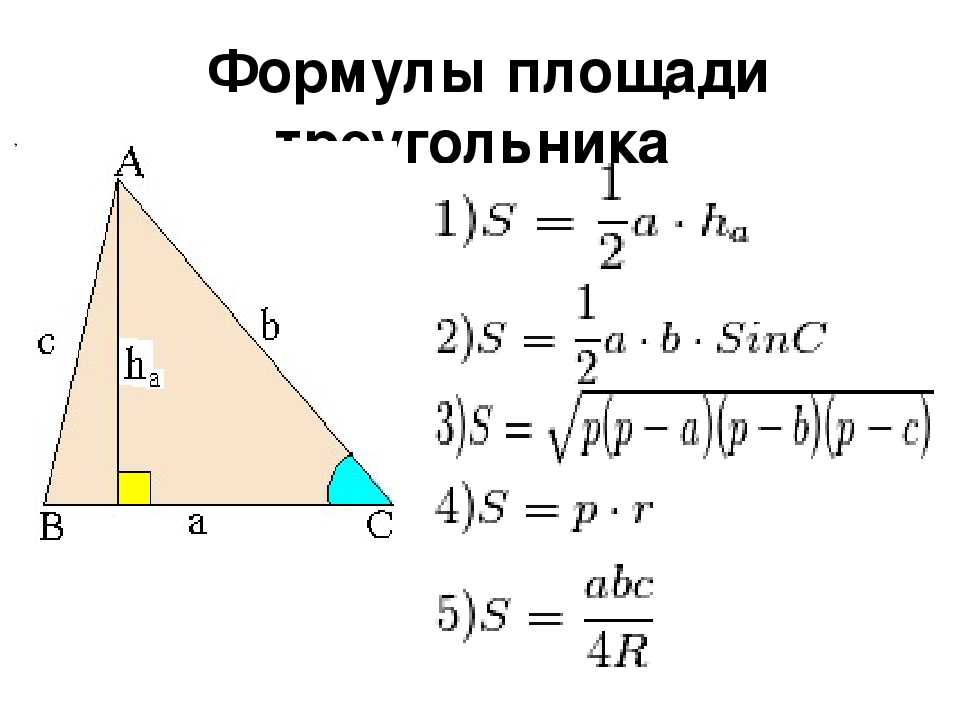 Точки называются вершинами треугольника, а отрезки — его сторонами. В геометрических задачах треугольник обычно изображают специальным симовлом — △, после которго пишут названия вершин треугольника напр. △ABC.
Точки называются вершинами треугольника, а отрезки — его сторонами. В геометрических задачах треугольник обычно изображают специальным симовлом — △, после которго пишут названия вершин треугольника напр. △ABC. Например:
Например:
 Против равных сторон лежат равные углы:
Против равных сторон лежат равные углы:
 Из векторов, образующих медианы, можно составить треугольник.
Из векторов, образующих медианы, можно составить треугольник.

 Важным свойством прямоугольных треугольников является Теорема Пифагора. Он утверждает, что в прямоугольном треугольнике, сумма квадратов основания и перпендикуляра равна квадрату гипотенузы треугольника.
Важным свойством прямоугольных треугольников является Теорема Пифагора. Он утверждает, что в прямоугольном треугольнике, сумма квадратов основания и перпендикуляра равна квадрату гипотенузы треугольника. 
 Например, в ∆ABC, если AC = 3, то AB = 3&redic;3 и BC = 6. Подводя итог, приведенные ниже формулы могут быть применены к вычислить две другие стороны 30°-60°-9Треугольник 0°, когда дана одна из трех сторон.
Например, в ∆ABC, если AC = 3, то AB = 3&redic;3 и BC = 6. Подводя итог, приведенные ниже формулы могут быть применены к вычислить две другие стороны 30°-60°-9Треугольник 0°, когда дана одна из трех сторон.
 Все конгруэнтные треугольники подобны, но не обязательно все подобные треугольники конгруэнтны.
Все конгруэнтные треугольники подобны, но не обязательно все подобные треугольники конгруэнтны. s 1 и s 2 — соответствующие стороны первого и второго треугольника соответственно.
s 1 и s 2 — соответствующие стороны первого и второго треугольника соответственно.
 Следовательно, две конгруэнтные фигуры подобны, но обратное не обязательно верно.
Следовательно, две конгруэнтные фигуры подобны, но обратное не обязательно верно.

 3.
3.


 Неравенства и системы неравенств с двумя переменными.
Неравенства и системы неравенств с двумя переменными. Производная и ее применения
Производная и ее применения Правила вычисления первообразных.
Правила вычисления первообразных. Простейшие задачи на построение.
Простейшие задачи на построение.
 Понятие движения.
Понятие движения. В математике, также как и в физике, механике, электротехнике, помимо действительных чисел используются числа более общей природы, которые называются комплексными числами.
В математике, также как и в физике, механике, электротехнике, помимо действительных чисел используются числа более общей природы, которые называются комплексными числами. 02.15 «Поварское кондитерское дело».
02.15 «Поварское кондитерское дело».
 Уметь применять правила при выполнении практических заданий.
Уметь применять правила при выполнении практических заданий. Прежде чем мы начнем, запомните, что значение i = \sqrt {-1}
Прежде чем мы начнем, запомните, что значение i = \sqrt {-1}
 Для этих очень больших углов значение, которое мы получаем в правиле 3, удалит всю деталь, и мы оставим только десятичные дроби, чтобы найти угол. Посмотрите, если 1\\text{поворот} равен 360°, сколько поворотов v равно 3150°?
Для этих очень больших углов значение, которое мы получаем в правиле 3, удалит всю деталь, и мы оставим только десятичные дроби, чтобы найти угол. Посмотрите, если 1\\text{поворот} равен 360°, сколько поворотов v равно 3150°? рисунок 2:Рисунок 2.
рисунок 2:Рисунок 2. Леманна в разделе «Полномочия и корни».
Леманна в разделе «Полномочия и корни». 9{\frac{1}{5}} \left[ \cos \cfrac{210° + k \cdot 360°}{5} + i \sin \cfrac{210° + k \cdot 360°}{5} \ right]=
9{\frac{1}{5}} \left[ \cos \cfrac{210° + k \cdot 360°}{5} + i \sin \cfrac{210° + k \cdot 360°}{5} \ right]= 40 + 0.91i \right]=
40 + 0.91i \right]= 20 — 0.97i \right]=
20 — 0.97i \right]= Действительное число предшествует мнимому. Комплексные числа отличаются от простых чисел просто тем, что состоят из двух частей и образуют комплекс.
Действительное число предшествует мнимому. Комплексные числа отличаются от простых чисел просто тем, что состоят из двух частей и образуют комплекс. В мнимом числе bi b — ненулевое действительное число, а i называется мнимой единицей, известной как йота. Квадратное значение бита равно -1.
В мнимом числе bi b — ненулевое действительное число, а i называется мнимой единицей, известной как йота. Квадратное значение бита равно -1.
 Тогда свойство вычитания этих чисел выглядит следующим образом:
Тогда свойство вычитания этих чисел выглядит следующим образом:


 Найдите значение выражения:
Найдите значение выражения: Найдите значение выражения:
Найдите значение выражения: Запишите в виде степени с основанием 2 число:
Запишите в виде степени с основанием 2 число: Решите уравнение:
Решите уравнение: Маша купила билет раньше, чем Миша, но позже, чем Наташа. Петя и Наташа не стояли рядом, а Дима не был рядом ни с Наташей, ни с Машей, ни с Петей. Кто за кем стоял в очереди?
Маша купила билет раньше, чем Миша, но позже, чем Наташа. Петя и Наташа не стояли рядом, а Дима не был рядом ни с Наташей, ни с Машей, ни с Петей. Кто за кем стоял в очереди? -256 —
-256 — 0 —
0 — (-3)3>(-4)5 —
(-3)3>(-4)5 — 27 —
27 — 6×43+3 —
6×43+3 —

 (маленький/мало)
(маленький/мало)
 ) Вишал самый умный из 3 братьев.
) Вишал самый умный из 3 братьев. ) смелый как медведь
) смелый как медведь ) Кит — самое большое животное, которое я когда-либо видел.
) Кит — самое большое животное, которое я когда-либо видел. ) Влажнее, влажнее , самый влажный
) Влажнее, влажнее , самый влажный ) Больше
) Больше ) Положительная степень
) Положительная степень Мы разбираем все ключевые элементы, чтобы вы могли получить адекватную помощь по Common Core: 5th Grade Math.
С обязательными концепциями обучения и соответствующими практическими вопросами прямо у вас под рукой, вы получите много помощи Common Core: 5th Grade Math в кратчайшие сроки.
Получите помощь сегодня с нашей обширной коллекцией необходимой информации Common Core: 5th Grade Math.
Мы разбираем все ключевые элементы, чтобы вы могли получить адекватную помощь по Common Core: 5th Grade Math.
С обязательными концепциями обучения и соответствующими практическими вопросами прямо у вас под рукой, вы получите много помощи Common Core: 5th Grade Math в кратчайшие сроки.
Получите помощь сегодня с нашей обширной коллекцией необходимой информации Common Core: 5th Grade Math. Math.Content.5.GB.3
Math.Content.5.GB.3 Math.Content.5.MD.C.3b
Math.Content.5.MD.C.3b Math.Content.5.NBT.A.3b
Math.Content.5.NBT.A.3b Content.5.NBT.A.1
Content.5.NBT.A.1 Math.Content.5.NF.B.4b
Math.Content.5.NF.B.4b Math.Content.5.NF.B.6
Math.Content.5.NF.B.6 Центр передового опыта Национальной ассоциации губернаторов и Совет руководителей школ штата. Все права защищены.
Центр передового опыта Национальной ассоциации губернаторов и Совет руководителей школ штата. Все права защищены.  В разделе «Измерения и данные» ваш ребенок может найти площадь фигуры, изучить линейные графики или найти объем, а числа и операции в категории «десять» помогут вашему ребенку изучить сложение и вычитание чисел со степенями и числовыми отношениями. . Число и операции в категории дробей попросят вашего ребенка складывать и вычитать, используя дроби. Наконец, в разделе «Операции и алгебраическое мышление» вашего ребенка попросят решить уравнения, используя правильный порядок чисел.
В разделе «Измерения и данные» ваш ребенок может найти площадь фигуры, изучить линейные графики или найти объем, а числа и операции в категории «десять» помогут вашему ребенку изучить сложение и вычитание чисел со степенями и числовыми отношениями. . Число и операции в категории дробей попросят вашего ребенка складывать и вычитать, используя дроби. Наконец, в разделе «Операции и алгебраическое мышление» вашего ребенка попросят решить уравнения, используя правильный порядок чисел. Каждый правильный ответ также подробно объясняется, поэтому вы можете быть уверены, что у вашего ребенка есть возможность ознакомиться с соответствующей информацией. Эта справка Common Core 5th Grade Math проста в использовании и является отличным дополнением к любому учебному плану.
Каждый правильный ответ также подробно объясняется, поэтому вы можете быть уверены, что у вашего ребенка есть возможность ознакомиться с соответствующей информацией. Эта справка Common Core 5th Grade Math проста в использовании и является отличным дополнением к любому учебному плану.


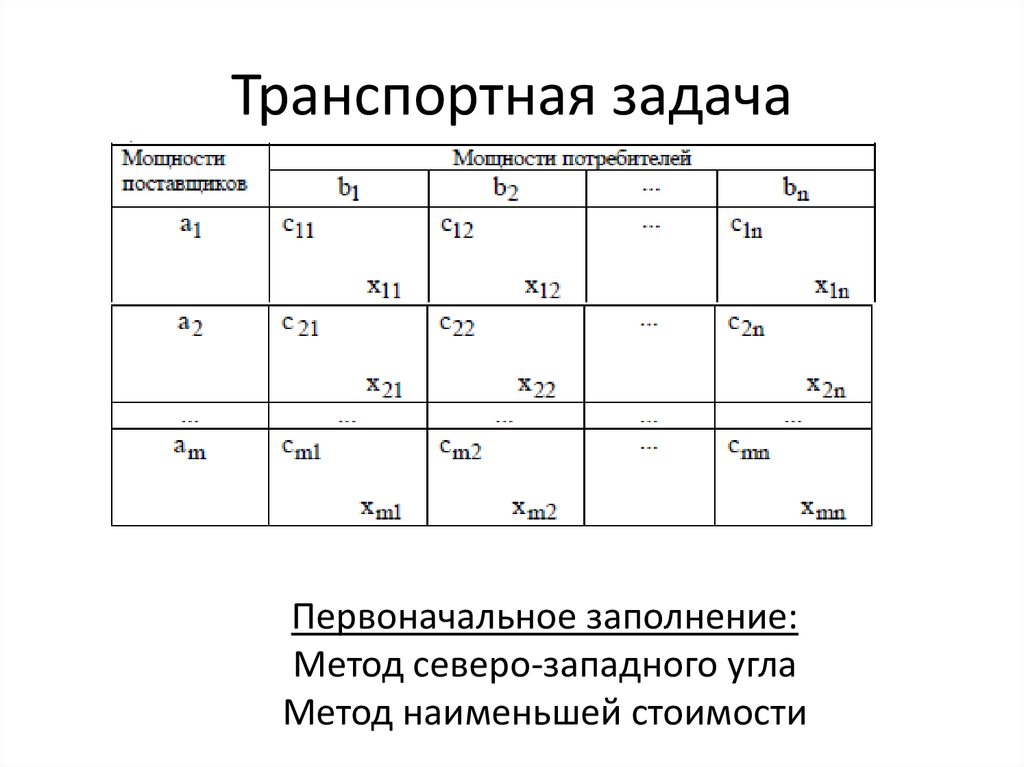
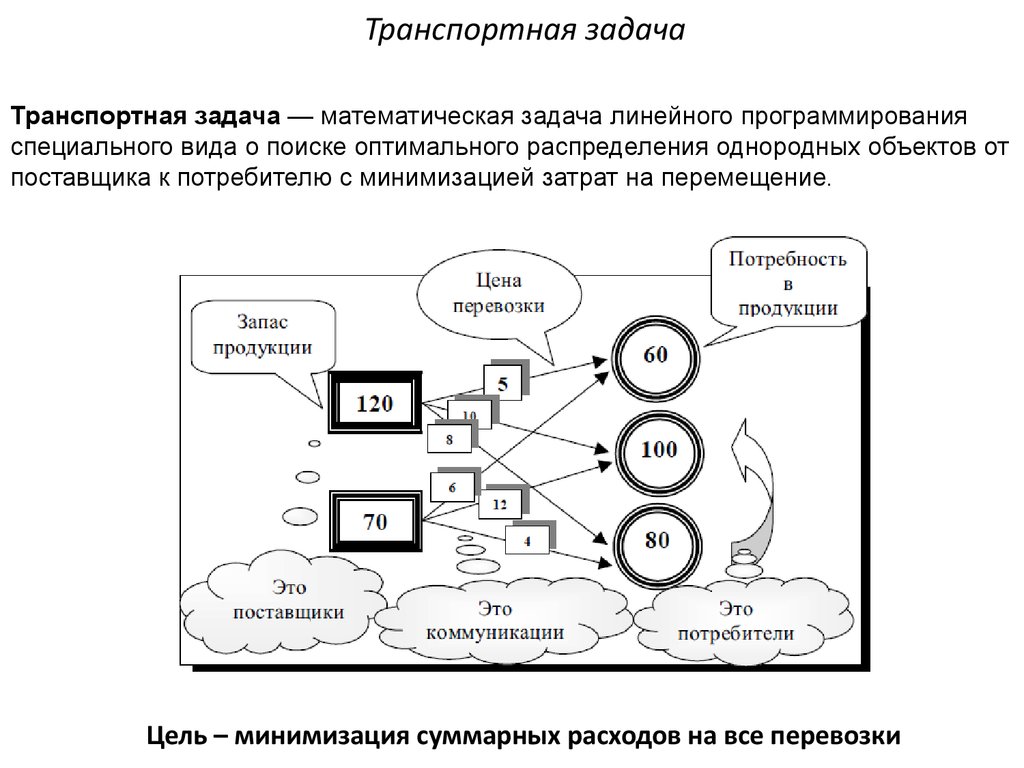 В случае закрытой задачи от поставщиков будут вывезены все запасы груза, и все заявки потребителей будут удовлетворены. В случае открытой задачи для ее решения придется вводить фиктивных поставщиков или потребителей.
В случае закрытой задачи от поставщиков будут вывезены все запасы груза, и все заявки потребителей будут удовлетворены. В случае открытой задачи для ее решения придется вводить фиктивных поставщиков или потребителей. То есть сперва заполняется самая верхняя левая ячейка («северо-западная» ячейка), потом следующая справа и т. д. Затем переходят на новую строку и вновь заполняют ее слева направо. И так пока таблица не будет заполнена полностью.
То есть сперва заполняется самая верхняя левая ячейка («северо-западная» ячейка), потом следующая справа и т. д. Затем переходят на новую строку и вновь заполняют ее слева направо. И так пока таблица не будет заполнена полностью. Затем все эти действия повторяются заново, только при этом уже не учитываются заполненные клетки.
Затем все эти действия повторяются заново, только при этом уже не учитываются заполненные клетки. Если во время решения задачи получился вырожденный план, то его необходимо пополнить, проставив в недостающем числе клеток нулевую перевозку и превратив, тем самым, эти клетки в базисные (общий баланс и суммарная стоимость перевозок плана при этом не изменятся).
Если во время решения задачи получился вырожденный план, то его необходимо пополнить, проставив в недостающем числе клеток нулевую перевозку и превратив, тем самым, эти клетки в базисные (общий баланс и суммарная стоимость перевозок плана при этом не изменятся).


 ед.
ед. 2 // Волшебный форум (@romix). URL: http://kb.mista.ru/article.php?id=859 (дата обращения: 29.10.2013)
2 // Волшебный форум (@romix). URL: http://kb.mista.ru/article.php?id=859 (дата обращения: 29.10.2013)
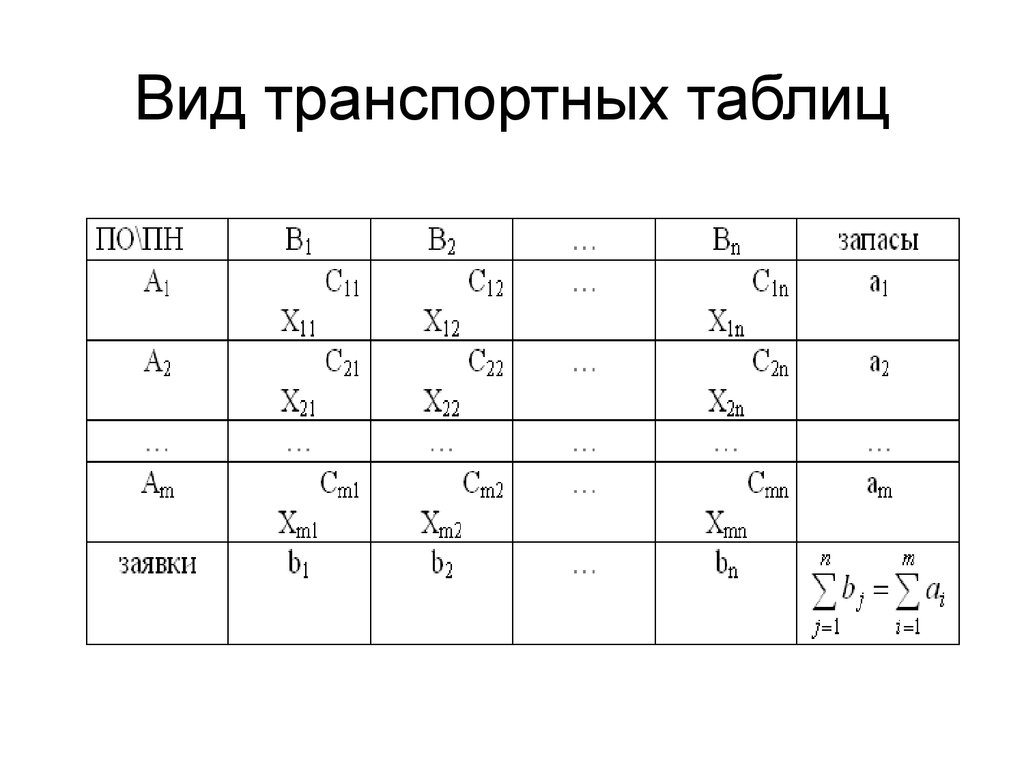 Сейчас мы перейдем к рассмотрению одного вопроса также из области перевозок грузов, который, однако, к решению транспортной задачи уже не сводится.
[c.157]
Сейчас мы перейдем к рассмотрению одного вопроса также из области перевозок грузов, который, однако, к решению транспортной задачи уже не сводится.
[c.157] В приложениях значительный интерес представляет стохастическая постановка транспортной задачи, в которой предполагается, что спрос 6j — bj(ft>) в /-м пункте потребления случайная величина. Допустим вначале, что спрос bj непрерывно распределен с плотностью fpj(bj) [66, 326].
[c.35]
В приложениях значительный интерес представляет стохастическая постановка транспортной задачи, в которой предполагается, что спрос 6j — bj(ft>) в /-м пункте потребления случайная величина. Допустим вначале, что спрос bj непрерывно распределен с плотностью fpj(bj) [66, 326].
[c.35] Частными видами таких задач являются [c.29]
Частными видами таких задач являются [c.29] Алгоритмы решения А-задачи довольно эффективны, но все же с их помощью можно решать задачи меньшей размерности, чем для транспортных моделей. В обобщенной транспортной задаче возможны те же модификации, что и в обычной транспортной задаче.
[c.185]
Алгоритмы решения А-задачи довольно эффективны, но все же с их помощью можно решать задачи меньшей размерности, чем для транспортных моделей. В обобщенной транспортной задаче возможны те же модификации, что и в обычной транспортной задаче.
[c.185] х-ва. К математич. программированию относится теория двойственности, с помощью к-рой изучается связь между нарами т. н. двойственных или сопряжённых задач, характеризующих различные аспекты механизма оптимизации. Выводы теории двойственности позволяют сопоставить оптимальный план нронз-ва с системой оценок производственных факторов. Теория двойственности математич. программирования тесно связана с теорией игр.
[c.403]
х-ва. К математич. программированию относится теория двойственности, с помощью к-рой изучается связь между нарами т. н. двойственных или сопряжённых задач, характеризующих различные аспекты механизма оптимизации. Выводы теории двойственности позволяют сопоставить оптимальный план нронз-ва с системой оценок производственных факторов. Теория двойственности математич. программирования тесно связана с теорией игр.
[c.403]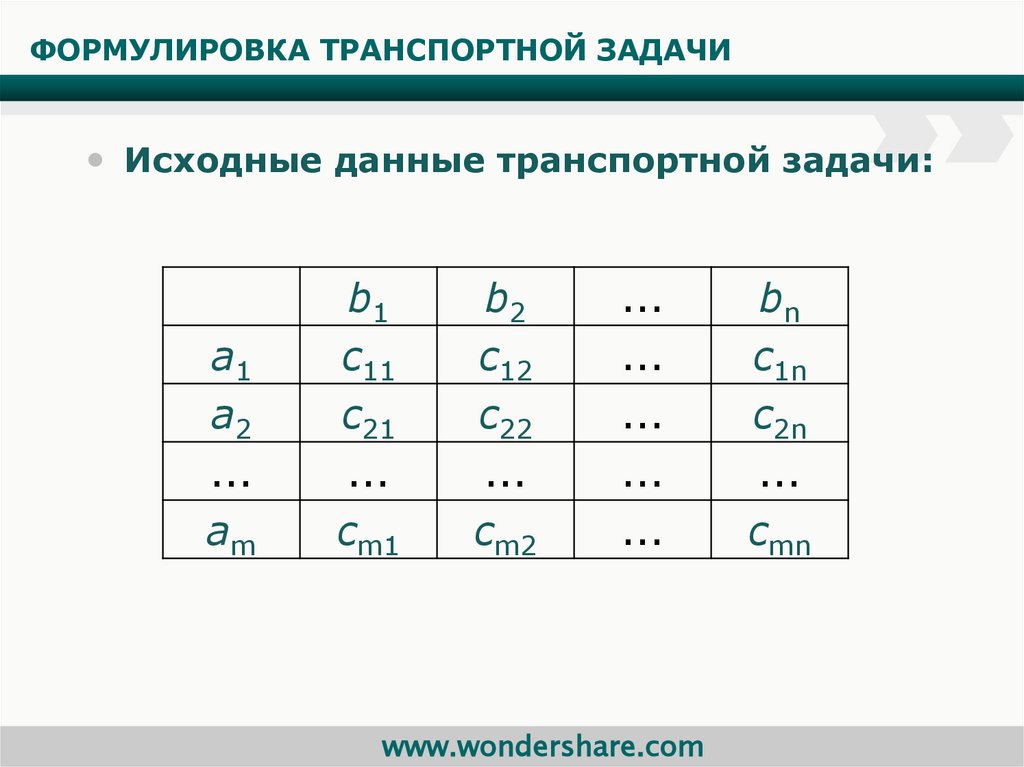 Заметим, что элемент ds( в общем случае может отличаться от элемента d(s в силу, например, одностороннего движения в том или ином направлении. Требуется определить кратчайший маршрут между узлом s и каким-либо другим узлом t. Для решения задачи исходные данные заносят в матрицу. Далее применяют или алгоритм Беллмана динамического программирования, или метод Дейкстры, который является его модификацией. Эти алгоритмы весьма просты, и справку по ним можно найти, например, в справочнике [39].
[c.161]
Заметим, что элемент ds( в общем случае может отличаться от элемента d(s в силу, например, одностороннего движения в том или ином направлении. Требуется определить кратчайший маршрут между узлом s и каким-либо другим узлом t. Для решения задачи исходные данные заносят в матрицу. Далее применяют или алгоритм Беллмана динамического программирования, или метод Дейкстры, который является его модификацией. Эти алгоритмы весьма просты, и справку по ним можно найти, например, в справочнике [39].
[c.161] В статье [12] рассмотрены соответствующие модификации алгоритма К. В. Кима и известного метода декомпозиции. Вычислительные аспекты рассмотренных сетевых задач обсуждаются в статье [16]. В частности, соответствующие графы могут иметь большую размерность вследствие многократного дублирования (по числу продуктов) вершин и дуг исходной транспортной сети, однако на практике существует возможность существенного уменьшения этой размерности. В статье даются сравнительные оценки этих моделей для случая, когда возможно применение их обеих. Результаты весьма огра—ниченного эксперимента показали некоторую предпочтительность более частной модели.
[c.71]
В статье [12] рассмотрены соответствующие модификации алгоритма К. В. Кима и известного метода декомпозиции. Вычислительные аспекты рассмотренных сетевых задач обсуждаются в статье [16]. В частности, соответствующие графы могут иметь большую размерность вследствие многократного дублирования (по числу продуктов) вершин и дуг исходной транспортной сети, однако на практике существует возможность существенного уменьшения этой размерности. В статье даются сравнительные оценки этих моделей для случая, когда возможно применение их обеих. Результаты весьма огра—ниченного эксперимента показали некоторую предпочтительность более частной модели.
[c.71]
 Это понимание должно быть достаточно глубоким, чтобы оно позволяло разрабатывать прогностические модели переноса плазмы, которые можно было бы проверить экспериментально, а затем использовать для моделирования будущих характеристик сжигания плазмы в ИТЭР и термоядерных энергетических реакторах следующего шага. Чтобы добиться успеха в науке о переносе, важно охарактеризовать локальные флуктуации и перенос в термоядерной плазме, понять основные механизмы, ответственные за перенос, и, в конечном итоге, контролировать эти процессы переноса. Эти цели должны преследоваться в нескольких направлениях исследований, и основные темы семинара TTF развиваются, чтобы отражать новые достижения в понимании физики.
Это понимание должно быть достаточно глубоким, чтобы оно позволяло разрабатывать прогностические модели переноса плазмы, которые можно было бы проверить экспериментально, а затем использовать для моделирования будущих характеристик сжигания плазмы в ИТЭР и термоядерных энергетических реакторах следующего шага. Чтобы добиться успеха в науке о переносе, важно охарактеризовать локальные флуктуации и перенос в термоядерной плазме, понять основные механизмы, ответственные за перенос, и, в конечном итоге, контролировать эти процессы переноса. Эти цели должны преследоваться в нескольких направлениях исследований, и основные темы семинара TTF развиваются, чтобы отражать новые достижения в понимании физики.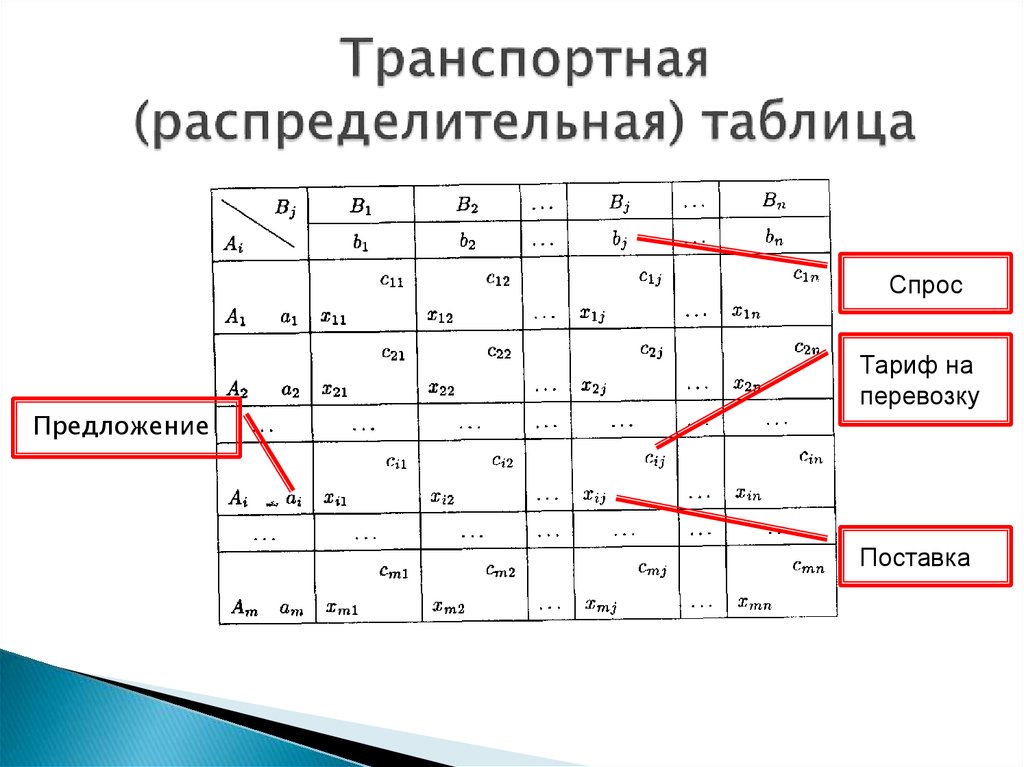 Эта инициатива Predict First повысит эффективность использования экспериментальной среды выполнения в ближайшем будущем и обеспечит более строгие проверочные тесты для теории, делающей следующий шаг к конечной цели TTF по созданию проверенных прогнозирующих транспортных моделей.
Эта инициатива Predict First повысит эффективность использования экспериментальной среды выполнения в ближайшем будущем и обеспечит более строгие проверочные тесты для теории, делающей следующий шаг к конечной цели TTF по созданию проверенных прогнозирующих транспортных моделей. В настоящее время правила не требуют подтверждения вакцинации или ношения маски в помещении (но это настоятельно рекомендуется), и поэтому мы также не будем требовать ни того, ни другого. Однако, учитывая, что это будет совместная встреча США и ЕС, а количество случаев заболевания в некоторых местах снова начинает расти, мы strongly encourage everyone to
В настоящее время правила не требуют подтверждения вакцинации или ношения маски в помещении (но это настоятельно рекомендуется), и поэтому мы также не будем требовать ни того, ни другого. Однако, учитывая, что это будет совместная встреча США и ЕС, а количество случаев заболевания в некоторых местах снова начинает расти, мы strongly encourage everyone to  Успешный семинар потребует особой осторожности и усердия со стороны участников, и мы просим всех быть внимательными и осторожными в отношении COVID. Обратите внимание, что все участники TTF (личные или виртуальные) должны соблюдать правила поведения на собраниях APS, доступные по адресу https://www.aps.org/meetings/policies/code-conduct.cfm. Это включает в себя уважение личного выбора других участников в отношении мер предосторожности COVID, вакцинации и ношения масок.
Успешный семинар потребует особой осторожности и усердия со стороны участников, и мы просим всех быть внимательными и осторожными в отношении COVID. Обратите внимание, что все участники TTF (личные или виртуальные) должны соблюдать правила поведения на собраниях APS, доступные по адресу https://www.aps.org/meetings/policies/code-conduct.cfm. Это включает в себя уважение личного выбора других участников в отношении мер предосторожности COVID, вакцинации и ношения масок. пандемия. Вот почему министр транспорта достопочтенный Омар Альгабра в начале этого года создал Национальную целевую группу по цепочке поставок для изучения ключевых вопросов, влияющих на работу цепочки поставок в Канаде. Задача Целевой группы заключалась в том, чтобы разработать рекомендации о том, как мы можем сделать нашу цепочку транспортных поставок более прочной, а жизнь канадцев — более доступной.
пандемия. Вот почему министр транспорта достопочтенный Омар Альгабра в начале этого года создал Национальную целевую группу по цепочке поставок для изучения ключевых вопросов, влияющих на работу цепочки поставок в Канаде. Задача Целевой группы заключалась в том, чтобы разработать рекомендации о том, как мы можем сделать нашу цепочку транспортных поставок более прочной, а жизнь канадцев — более доступной.

 Мы продолжаем работать над поиском ответов, чтобы цепочка поставок в Канаде оставалась эффективной и надежной. Я также хочу поблагодарить Национальную рабочую группу по цепочке поставок за их усилия в течение последних нескольких месяцев. Заключительный отчет Целевой группы окажется бесценным, поскольку Канада разрабатывает свою Национальную стратегию цепочки поставок» 9.0003
Мы продолжаем работать над поиском ответов, чтобы цепочка поставок в Канаде оставалась эффективной и надежной. Я также хочу поблагодарить Национальную рабочую группу по цепочке поставок за их усилия в течение последних нескольких месяцев. Заключительный отчет Целевой группы окажется бесценным, поскольку Канада разрабатывает свою Национальную стратегию цепочки поставок» 9.0003 По мере того, как наша экономика восстанавливается и растет, мы должны делать инвестиции и вносить изменения, которые не только устранят эти сбои, но и укрепят нашу рабочую силу в долгосрочной перспективе. Заключительный отчет Национальной целевой группы по цепочке поставок и ее рекомендации будут иметь решающее значение для этой работы, помогая нам принимать обоснованные стратегические решения».
По мере того, как наша экономика восстанавливается и растет, мы должны делать инвестиции и вносить изменения, которые не только устранят эти сбои, но и укрепят нашу рабочую силу в долгосрочной перспективе. Заключительный отчет Национальной целевой группы по цепочке поставок и ее рекомендации будут иметь решающее значение для этой работы, помогая нам принимать обоснованные стратегические решения».
 Целевая группа опубликовала свой окончательный отчет 6 октября 2022 г.
Целевая группа опубликовала свой окончательный отчет 6 октября 2022 г.

 Но 12 дес. на 43 не делится. Поэтому делим 129 на 43.
Но 12 дес. на 43 не делится. Поэтому делим 129 на 43.
 Но 50 дес. на 84 не делятся. Поэтому делим 504 на 84.
Но 50 дес. на 84 не делятся. Поэтому делим 504 на 84. 28084.
28084. 24 метра
24 метра 72 метра
72 метра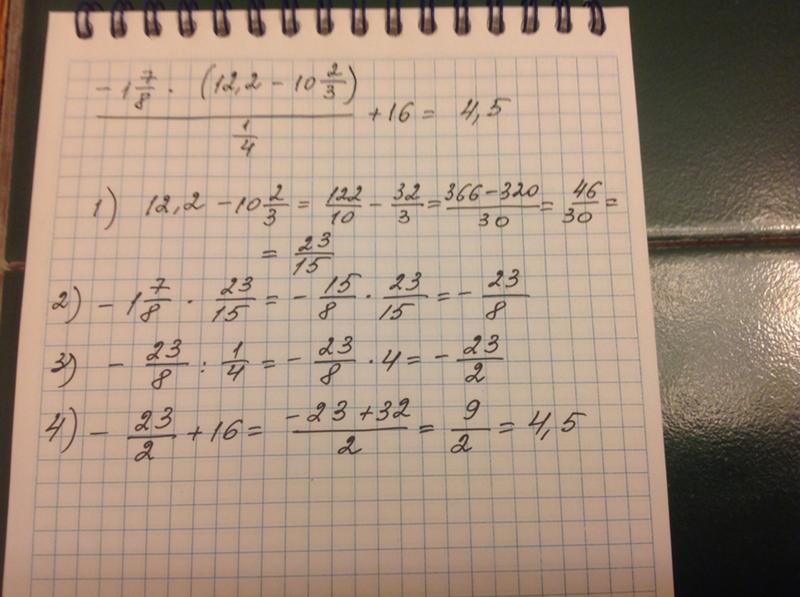
 we can now add that answer below the dividend:
we can now add that answer below the dividend: can now add that answer below the dividend:
can now add that answer below the dividend: 0030
0030 VisualFractions.com . По состоянию на 26 марта 2023 г. http://visualfractions.com/calculator/long-division/what-is-212-divided-by-469-using-long-division /.
VisualFractions.com . По состоянию на 26 марта 2023 г. http://visualfractions.com/calculator/long-division/what-is-212-divided-by-469-using-long-division /.
 Кроме того, мы можем сказать о числе 212, что даже
Кроме того, мы можем сказать о числе 212, что даже  е. остаток от полного деления на 212 равен нулю. Существует бесконечное количество кратных 212. Наименьшие кратные 212:
е. остаток от полного деления на 212 равен нулю. Существует бесконечное количество кратных 212. Наименьшие кратные 212:


 Преобразуем
расширенную матрицу системы:
Преобразуем
расширенную матрицу системы:
 Приведены многочисленные задачи экономического содержания, которые показывают возможности применения математического аппарата в экономических исследова…
Приведены многочисленные задачи экономического содержания, которые показывают возможности применения математического аппарата в экономических исследова…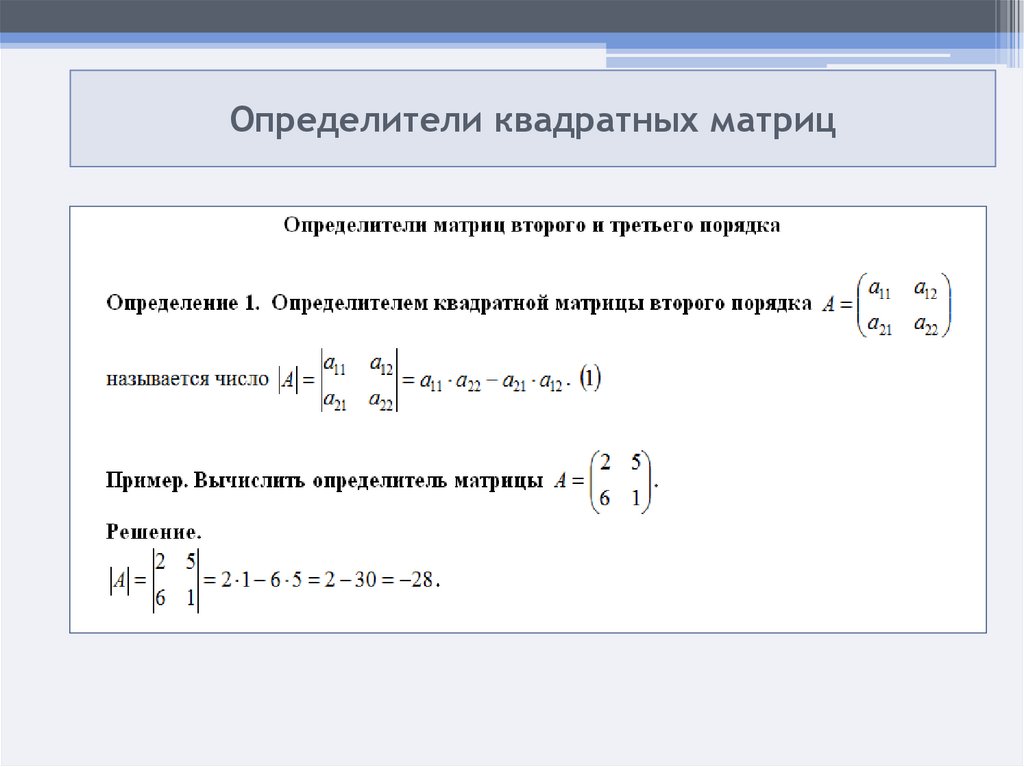
 Во вторую часть работы включены задачи по теме «Линейные операторы в линейных пространствах». Приводятся методические разъяснения и даются практические советы к решению задач…
Во вторую часть работы включены задачи по теме «Линейные операторы в линейных пространствах». Приводятся методические разъяснения и даются практические советы к решению задач…
 К. Пчельник, Е. А. Сетько, И. И. Ревчук. -Гродно. ГрГУ, Матрицы и определители. Аналитическая геометрия на плоскости и в пространстве: пособие. 2007, — 164с. Пособие содержит краткие теоретические сведения по матричной алгебре, аналитической геометрии на плоскости и в пространстве, примеры решения задач, задачи для самостоятельного решения и задания для контрольной работы. Матрицы и определители. Системы линейных уравнений. Собственные вект…
К. Пчельник, Е. А. Сетько, И. И. Ревчук. -Гродно. ГрГУ, Матрицы и определители. Аналитическая геометрия на плоскости и в пространстве: пособие. 2007, — 164с. Пособие содержит краткие теоретические сведения по матричной алгебре, аналитической геометрии на плоскости и в пространстве, примеры решения задач, задачи для самостоятельного решения и задания для контрольной работы. Матрицы и определители. Системы линейных уравнений. Собственные вект…
 б 2 x 4 + a 2 x 4
б 2 x 4 + a 2 x 4 



 В основном они используются в области науки и техники.
В основном они используются в области науки и техники.
 Система уравнений считается непротиворечивой, если она имеет решение.
Система уравнений считается непротиворечивой, если она имеет решение.

 Мы можем написать векторное произведение \(\vec{a} =a_1\hat{i}+a_2\hat{j}+a_3\hat{k}\) и \(\vec{b} =b_1\hat{ i}+b_2\hat{j}+b_3\hat{k}\) в качестве определителя.
Мы можем написать векторное произведение \(\vec{a} =a_1\hat{i}+a_2\hat{j}+a_3\hat{k}\) и \(\vec{b} =b_1\hat{ i}+b_2\hat{j}+b_3\hat{k}\) в качестве определителя. Мы можем написать скалярное тройное произведение \(\vec{a} =a_1\hat{i}+a_2\hat{j}+a_3\hat{k}\)
Мы можем написать скалярное тройное произведение \(\vec{a} =a_1\hat{i}+a_2\hat{j}+a_3\hat{k}\) 





 1 Каковы применения матриц и определителей?
1 Каковы применения матриц и определителей? 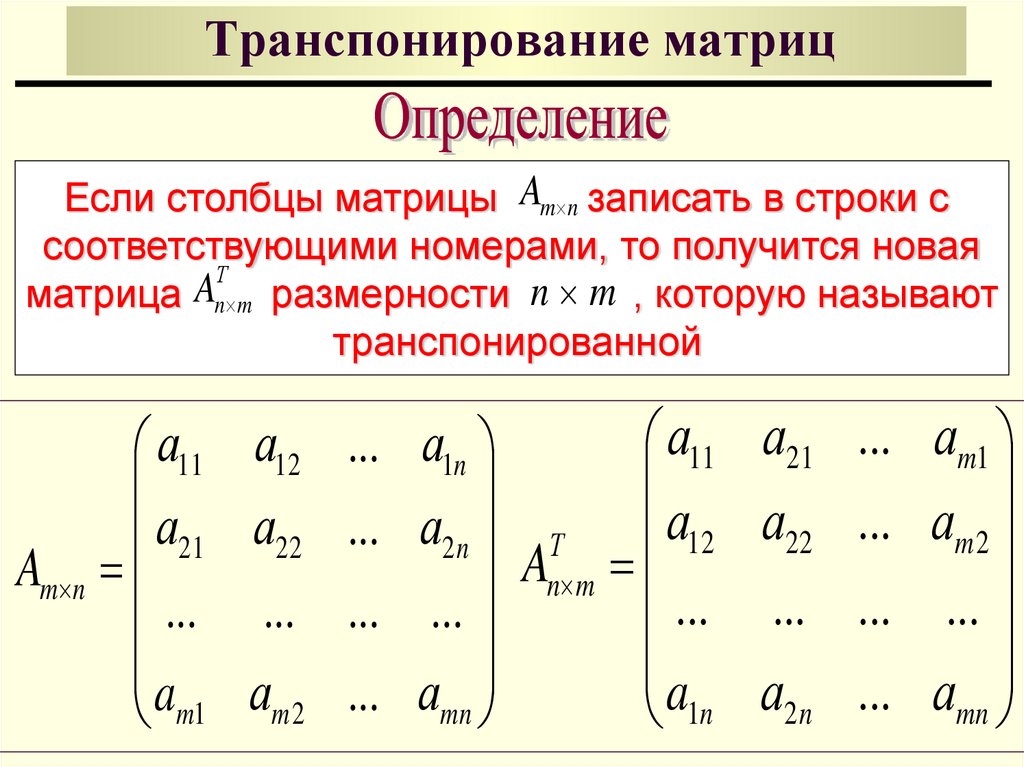

 Но потом говорится, что b не должно быть равным нулю.
Но потом говорится, что b не должно быть равным нулю.


 Например, в записи 4 × 3 множимым является 4, а множителем 3, но эти два числа ещё можно назвать сомножителями. Ошибкой это не будет.
Например, в записи 4 × 3 множимым является 4, а множителем 3, но эти два числа ещё можно назвать сомножителями. Ошибкой это не будет.
 Запишите в тетради, что 7 не равно 8
Запишите в тетради, что 7 не равно 8 Умножьте 2 на 3
Умножьте 2 на 3 Например, следующие выражения являются буквенными:
Например, следующие выражения являются буквенными: Например, запишем следующее выражение:
Например, запишем следующее выражение: Такие задания как раз и требуют, чтобы вместо переменной подставили её значение. Давайте выполним это задание. Значение переменной x равно 5. Подставляем эту пятёрку в исходное выражение x + 10 и получаем 5 + 10 = 15.
Такие задания как раз и требуют, чтобы вместо переменной подставили её значение. Давайте выполним это задание. Значение переменной x равно 5. Подставляем эту пятёрку в исходное выражение x + 10 и получаем 5 + 10 = 15.
 Когда перед нами подобное задание, мы сразу должны понимать, что от нас требуют решить пример. В народе это звучит как «решить пример«, но более правильно надо говорить «найти значение выражения». Решить пример и найти значение выражения это фактически одно и то же.
Когда перед нами подобное задание, мы сразу должны понимать, что от нас требуют решить пример. В народе это звучит как «решить пример«, но более правильно надо говорить «найти значение выражения». Решить пример и найти значение выражения это фактически одно и то же. Найдите значение выражения a + 3 при a = 7
Найдите значение выражения a + 3 при a = 7 долгосрочные цели, чтобы в конечном итоге достичь того, что вначале было только мечтами».
долгосрочные цели, чтобы в конечном итоге достичь того, что вначале было только мечтами». »
»



 Воспользовавшись одной из программ банка, вы оплачиваете уже собственное жилье. Залогом для получения кредитных средств является приобретаемое имущество, предусмотрена система его страхования от порчи, утраты или повреждений. При покупке частного дома оформление залога осуществляется на земельный участок.
Воспользовавшись одной из программ банка, вы оплачиваете уже собственное жилье. Залогом для получения кредитных средств является приобретаемое имущество, предусмотрена система его страхования от порчи, утраты или повреждений. При покупке частного дома оформление залога осуществляется на земельный участок.
 Отзывы клиентов банка Отзывы о кредитах в банке Российский капитал на крупнейших банковских порталах имеют противоречивую окраску.
Отзывы клиентов банка Отзывы о кредитах в банке Российский капитал на крупнейших банковских порталах имеют противоречивую окраску. Больше или меньше 8 дм2 площадь этого прямоугольника? На сколько квадратных сантиметров меньше?
Больше или меньше 8 дм2 площадь этого прямоугольника? На сколько квадратных сантиметров меньше?
 Ср
Ср Вс
Вс Чт
Чт

 Я также установил время фиксированного шага…
Я также установил время фиксированного шага… ..
.. ..
.. Однако я нашел ссылку, которая Общаться …
Однако я нашел ссылку, которая Общаться …
 В некритичных случаях нужно обращаться в walk-in клинику или к семейному доктору. Моя жена поставила бы этот пункт на первое место в этом списке. Она стояла в очереди к гастроэнтерологу в течение 6 месяцев, и так и не попала. Корень проблемы по моему мнению — отсутсвие частных клиник.
В некритичных случаях нужно обращаться в walk-in клинику или к семейному доктору. Моя жена поставила бы этот пункт на первое место в этом списке. Она стояла в очереди к гастроэнтерологу в течение 6 месяцев, и так и не попала. Корень проблемы по моему мнению — отсутсвие частных клиник. Например, в 2 часа езды от города есть курорт, похожий по размерам с Роза Хутор в Сочи. Он также принимал зимнюю олимпиаду в 2010 году. К качеству горнолыжного отдыха претензий нет, все на высшем уровне. Курорт Whistler Blackcomb можно сравнить с «Розой Хутор»: большие горы, много трасс, хорошая инфраструктура. Ехать туда 120 километров.
Например, в 2 часа езды от города есть курорт, похожий по размерам с Роза Хутор в Сочи. Он также принимал зимнюю олимпиаду в 2010 году. К качеству горнолыжного отдыха претензий нет, все на высшем уровне. Курорт Whistler Blackcomb можно сравнить с «Розой Хутор»: большие горы, много трасс, хорошая инфраструктура. Ехать туда 120 километров. То есть если хочешь пойти на хайкинг в субботу, значит, в пятницу в 07:00 нужно караулить свободный слот. Через минуту мест уже нет или сайт ложится. Не успел — никуда в субботу не идешь.
То есть если хочешь пойти на хайкинг в субботу, значит, в пятницу в 07:00 нужно караулить свободный слот. Через минуту мест уже нет или сайт ложится. Не успел — никуда в субботу не идешь. В крупной корпорации платят больше на 20—30% — 7000—8000 CAD (423 242—483 705 Р). Дохода в размере 5000—6000 CAD (302 316—362 779 Р) одному человеку достаточно, чтобы жить сдержанно, без накоплений и особых развлечений: снимать дешевую квартиру или делить ее с кем-то, покупать продукты в супермаркете, особо никуда не ездить, готовить дома. Если вас двое, расходы вырастают в полтора раза.
В крупной корпорации платят больше на 20—30% — 7000—8000 CAD (423 242—483 705 Р). Дохода в размере 5000—6000 CAD (302 316—362 779 Р) одному человеку достаточно, чтобы жить сдержанно, без накоплений и особых развлечений: снимать дешевую квартиру или делить ее с кем-то, покупать продукты в супермаркете, особо никуда не ездить, готовить дома. Если вас двое, расходы вырастают в полтора раза. Как это выглядит, можно посмотреть на «Ютубе».
Как это выглядит, можно посмотреть на «Ютубе». Квартиру сдают абсолютно пустой.
Квартиру сдают абсолютно пустой. пункт про толерантность).
пункт про толерантность).
 ст.гПа
ст.гПа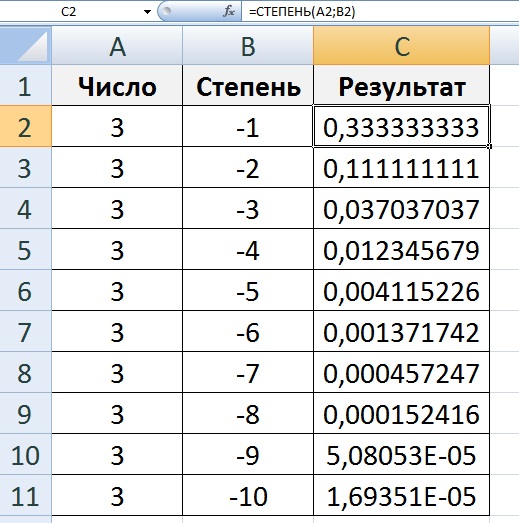 Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении.
Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении. е. 1,45 .
е. 1,45 . Наиболее распространенные мнемоники для запоминания этого порядка операций:
Наиболее распространенные мнемоники для запоминания этого порядка операций:  Какую часть населения составляют младенцы?
Какую часть населения составляют младенцы?