Угол. Виды углов — прямой, острый, тупой
М — Ох, и устали же мы сегодня. Целый день перетаскивали из угла в угол наш волшебный говорящий буфет.
Помните, как выглядит план наших парадных залов? Мы хотели поставить буфет в один из углов золотого зала. Но, сколько не пытались это сделать, у нас толком ничего не получилось. Если мы приставляли его к одной стене, то между буфетом и другой стеной оставалось пространство. Тогда мы попытались поставить буфет в зелёный зал. Там он вообще не входил ни в один из углов.
- Мы так устали. И теперь просто не представляем, что же нам делать, куда можно поставить наш волшебный буфет.
- Плюс, слышишь, наш компьютер включился. Наверное, сейчас нам по скайпу будет звонить царица Математика.
-
Ах, мои дорогие Плюс и Минус! Очень обидно, что прежде чем двигать по всему
замку буфет, вы не познакомились с темой «Виды углов». Придётся
сегодня мне объяснить вам эту тему.
Итак, сегодня мы поговорим о видах углов — прямых, острых и тупых углах.
- Какие странные названия — прямой, острый, тупой.
- Что же такое угол? Если мы поставим точку, а от этой точки проведём прямую, у нас получится прямая, ограниченная с одной стороны точкой. Такая линия называется луч. А если из этой же точки мы проведём ещё один луч, то у нас получится угол. При этом точка, из которой были проведены лучи, называется вершиной угла, а сами лучи в этом случае называются стороны угла.
Посмотрите, какие разнообразные углы можно построить:
Среди них вы можете увидеть и острые, и прямые, и тупые углы.
- А как же мы отличим, какие из углов острые, какие — прямые, а какие — тупые?
-
Начнём мы с прямого угла. Посмотрите на этот лист бумаги. Сейчас мы перегнём
его вдвое, потом ещё раз вдвое. Только сгибать надо аккуратно.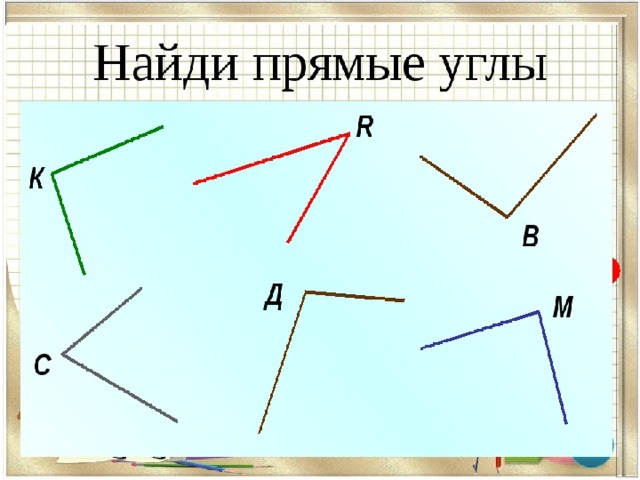 Так, чтобы линии
сгиба совместились и не выглядывали одна из-под другой. Наш лист сложен в 4
раза. И вот получился угол. Такой угол, который образуется аккуратным сгибанием
листа в четыре раза, называется прямым углом.
Так, чтобы линии
сгиба совместились и не выглядывали одна из-под другой. Наш лист сложен в 4
раза. И вот получился угол. Такой угол, который образуется аккуратным сгибанием
листа в четыре раза, называется прямым углом.
А сейчас развернём лист бумаги:
Видите, на нём видны линии сгиба. И у нас видны уже четыре угла с одной общей вершиной. А ещё есть специальная линейка—треугольник. У неё один угол прямой и два острых. Сейчас мы положим такую линейку на наш лист бумаги так, чтобы вершины прямого угла линейки и углов на бумаге совместились. А теперь попытаемся совместить стороны. Получилось?
- Да, стороны прямого угла треугольника точно легли на стороны прямого угла на бумаге.
- Теперь так же положим линейку и на остальные три угла. Как видите, и здесь совмещаются стороны. Значит точно, все эти углы одинаковые. Все они – прямые.
-
С прямыми углами понятно.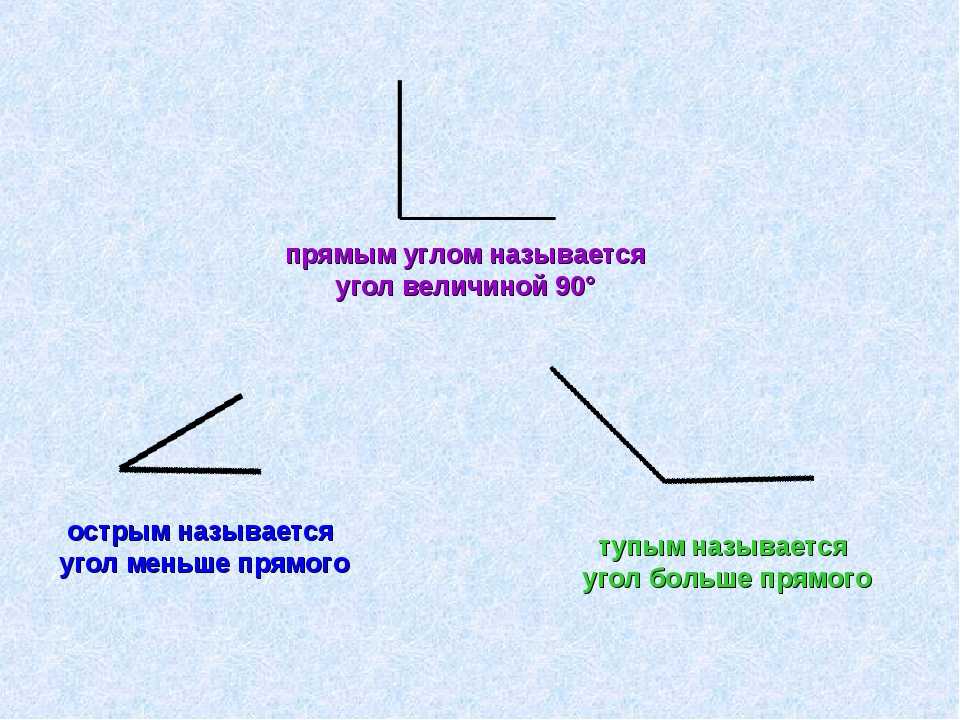 А что же это за углы — острые и тупые.
А что же это за углы — острые и тупые.
- Я хочу вам показать один угол. Видите, он такой острый, что его вершиной даже можно слегка уколоться.
А теперь посмотрите, угол развернулся, раскрылся. Его вершиной уже вряд ли можно уколоться. Теперь угол стал тупым:
А теперь давайте вернёмся к тем углам, которые мы нарисовали. Сейчас на первый угол кладём линейку.
Вершина линейки совмещается с вершиной угла. Одна из сторон линейки совместилась со стороной угла, а вот вторая спряталась под треугольником. Значит, угол раскрыт меньше, чем прямой угол треугольника. Такие углы, которые раскрыты меньше прямого угла, называются острыми углами.
Посмотрите на следующий угол. Он раскрыт значительно шире первого, но, когда мы прикладываем к нему линейку:
Видно, что одна из сторон опять спряталась под линейку. Значит, этот угол тоже острый.
Переходим к следующему углу:
Его
вершина и стороны точно совместились с вершиной и сторонами прямого угла
линейки.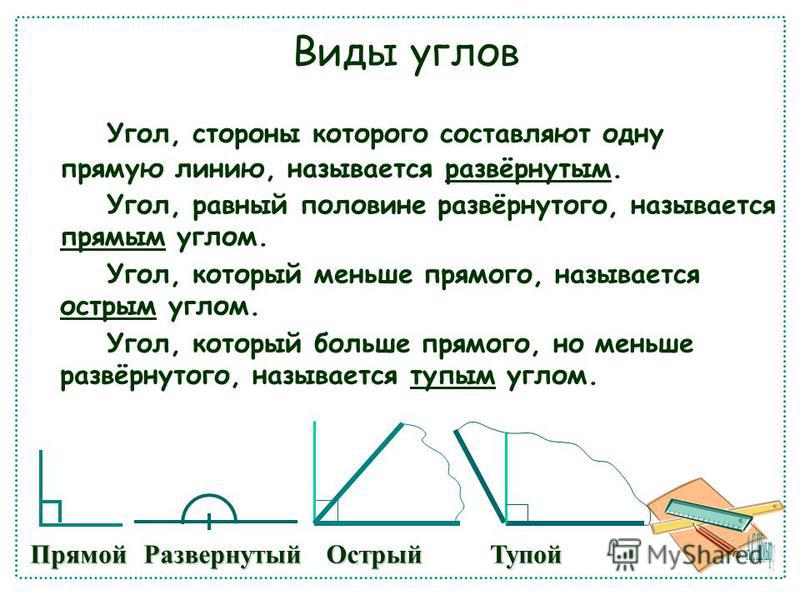 Как вы думаете, какой это угол?
Как вы думаете, какой это угол?
- Конечно, прямой!
- Совершенно верно. Этот угол прямой. А вот этот?
- Наверное, острый. Видите, как он наклонился.
- А если приложить линейку? Ну что, какой угол?
- Я ошибся… Этот угол тоже прямой………….
- Ну что же, продолжим. Рассмотрим следующий угол:
Посмотрите, между второй стороной линейки и стороной нарисованного угла как будто ещё один уголок появился. Значит, этот угол раскрыт немного шире, чем прямой. Такие углы, которые раскрыты больше прямого угла, называются тупыми углами.
- Ну, а если посмотреть на последний угол, то здесь даже без линейки-треугольника понятно, что он тупой.
- Да, это очень хорошо видно. Но мы всё-таки приложим линейку и к нему:
Сейчас очень хорошо видно, что этот угол раскрыт намного шире прямого. Конечно, он - тупой.
Ну что, Плюс и Минус, вы поняли, какие бывают углы?
-
Да, поняли.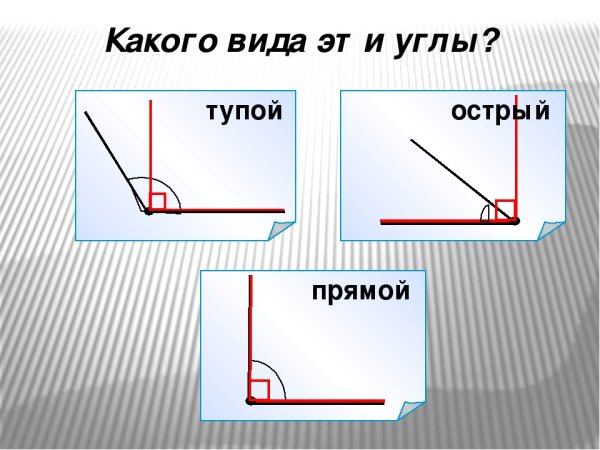 А если присмотреться, то в обычных комнатах все углы — прямые.
А если присмотреться, то в обычных комнатах все углы — прямые.
- А еще прямые углы у учебников и тетрадей.
- У школьных парт и столов.
- И у нашего волшебного буфета тоже все углы прямые.
- Значит, поставить его можно только туда, где стены образуют прямой угол. Посмотрите ещё раз внимательно на план парадных залов.
Ну, где вы можете найти прямой угол?
- По-моему, в золотом зале все углы тупые, в зелёном — все острые. А вот прямой….
- Мне кажется, я вижу два прямых угла в синем зале. Но, всё-таки, проверю-ка я это при помощи линейки:
Урра! Получилось! В синем зале- 2 прямых угла. Вот если бы мы сначала поработали с планом парадных залов, не пришлось бы волшебный буфет таскать по всему дворцу.
- Ну, а теперь повторите, пожалуйста, чему вы сегодня научились.
- Угол образуется двумя лучами, которые выходят из одной точки.
-
Прямой угол можно получить аккуратным сгибанием листа бумаги вчетверо. Но лучше воспользоваться специальной линейкой-треугольником.
Но лучше воспользоваться специальной линейкой-треугольником.
- Углы, которые раскрыты меньше прямого угла, называются острыми углами.
- Углы, которые раскрыты больше прямого угла, называются тупыми углами.
- Хорошо, урок вы усвоили. А теперь за работу — поставьте волшебный буфет туда, куда его можно поставить — в синий зал.
До свидания.
- До свидания, царица. Спасибо за урок!
- До свидания, ребята. Нам пора за работу.
Урок математики по теме «Виды углов». 2-й класс
Цели:
1. Познакомить учащихся с видами углов, понятиями “прямой угол”, “острый
угол”,“тупой угол”;
2. Учить определять прямые, острые и тупые углы с помощью модели прямого угла
(угольника), обучить сравнению углов;
3. Развивать пространственное воображение, навык работы с чертежными
инструментами, мышление, глазомер;
4. Воспитывать у учащихся отношения делового сотрудничества (доброжелательность
друг другу, уважать мнение других, уметь слушать товарищей), аккуратность,
прививать интерес к предмету.
Планируемые результаты: учащиеся научатся различать виды углов; анализировать и делать выводы; использовать полученные знания в учении и повседневной жизни.
Оборудование: угольник, линейка, веер у каждого ученика, карточки, модели углов из картона.
Ход урока
I. Организационный момент.
Урок начинается с приветствия и психологического настроя на работу.
Учитель. Начнем наш урок непременно с улыбки. Пожалуйста, подарите улыбки мне, соседу по парте, гостям
– Проверьте, все ли у вас на рабочем месте. Вы готовы начать урок?
– А с каким настроением вы пришли сегодня на урок, пусть за вас ответит ваш друг
смайлик.
(Учащиеся показывают выбранный ими смайлик, который соответствует их настроению.)
– Я вижу, что у вас хорошее настроение, тогда добро пожаловать на урок математики!
*Чтобы спорилось нужное дело,
*Чтобы в жизни не знать неудач,
*В математики мир отправимся смело,
*В мир примеров и разных задач.
А девизом нашего урока будут такие слова:
*Думать – коллективно!
*Решать – оперативно!
*Отвечать – доказательно!
*Учиться – старательно!
* И открытия – нас ждут обязательно!
II. Актуализация опорных знаний . Повторение изученного.
1. – Решите уравнения. Расставьте буквы в порядке убывания соответствующих корней уравнения и расшифруйте слово.
Х – 365 = 274(Р)
х – 32 = 896 (П)
715 – х = 398(О)
273 + х = 500(Й)
502 – х = 99 (Я)
х + 26 = 401(М)
(Ответ: прямой )
2. – Решите примеры и расшифруйте слово.
1х2х6:12х7х2:1(Г)
159х(0х4) (О)
(804:804)х5 (Л)
9х2х1:18х5х2:1 (У)
Ключ:10, 14, 0, 5.
Ответ: угол (учитель записывает слово “угол” на доске).
– Незнайка летом отправился в деревню Простоквашино. Он всерьез решил
заняться подсчетами. Помогите ему. После каждого правильного ответа я буду
открывать одну букву, из которых потом вы сложите слово.
Помогите ему. После каждого правильного ответа я буду
открывать одну букву, из которых потом вы сложите слово.
*Сколько лапок у 5 цыплят? (С)
*Сколько крыльев у 3 гусят? (Ы)
*Сколько пятачков у 14 поросят? (О)
*Сколько копыт у 7 ягнят? (Й)
*Сколько рогов у 7 козлят? (Р)
*Сколько очков у 8 бабушек? (Т)
– Какое слово получилось? (Острый.) (Учитель записывает слово “острый” на доске.)
3. – Найди значения выражений. Расставьте буквы в порядке убывания.
60 – 12:2= (О)
36 + 7х2 = (Й)
53 + 5х2 = (П)
100 – 10:2 = (У)
8х2 – 16 = 88 + 6х2= (Т)
– Какое слово получилось? (Тупой.) (Учитель записывает слово на доске.)
– Прочитайте слова на доске и подумайте, как они могут быть связаны между собой
и с нашим сегодняшним уроком. (Прямой, острый и тупой – это виды углов.
Сформулируйте тему нашего урока. Тема нашего урока: “Виды углов”.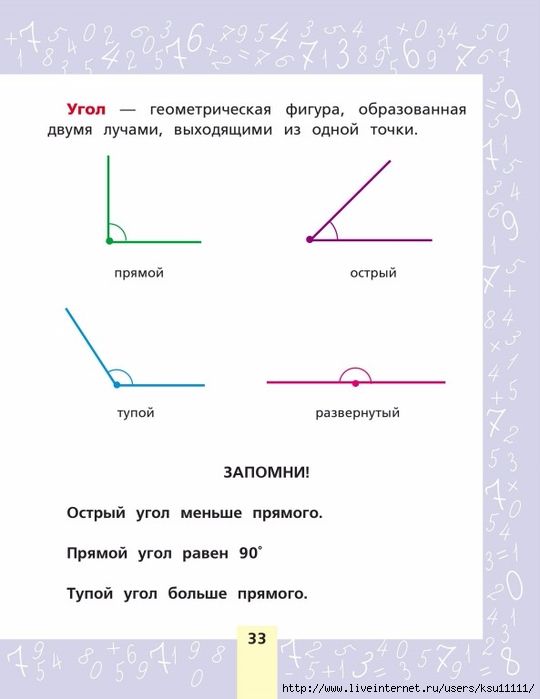 )
)
III. Сообщение темы, целей урока.
– Сегодня на уроке мы узнаем,какие бывают углы, научимся их узнавать, сравнивать,различать и строить. Подумайте, какие инструменты нам понадобятся на уроке? (Линейка, угольник, карандаш.)
– Где можно встретить углы в окружающем нас мире? (Крыши домов, угол доски, угол платочка, книжки, угол стола, полочки, угол в комнате, угол между стрелками часов, компас, веер и т.д.)
IV. Введение новых знаний.
– Что такое угол? Как он получается? (Ответы учащихся.)
Задание 1. – Начертите в тетради два луча с общим началом, которые пересекаются под прямым углом. Можно использовать угольник. (Учащиеся самостоятельно выполняют задание.)
– Сравните угол, начерченный вами, с изображенными на доске углами. (В учебнике.)
(Угол под номером 2 называется прямым.)
А вот как называются угол 1 и 3, узнаете позже.
Задание 2. – Работа в парах. 1. Рассмотрите рисунки.
– Работа в парах. 1. Рассмотрите рисунки.
У кого наконечник копья острый, а у кого тупой? Каким копьем удобнее охотиться?
– Как можно назвать углы, изображенные на рисунке рядом с первобытными охотниками? (Учащиеся называют углы: Острый и тупой. Затем отыскивают на рисунке острый и тупой углы и называют их.)
2. Выполнение задания учебника № 1, с.108.
V. Первичная проверка понимания.
Задание. (На партах у каждого ученика лежит веер. Дети их принесли заранее.) Раскройте веер, изобразите угол. На какой угол раскрыли каждый веер? (Дети по цепочке называют свой угол.)
– Рассмотрите рисунок. На какой угол раскрыт каждый веер на данном рисунке?
– Какой угол вам неизвестен? (Учащиеся получают информацию о развернутом угле.)
Физкультминутка (под музыку)
– Точка – наклоны головы влево – вправо,
– развернутый угол – руки в стороны,
– прямой угол – руки под углом 90*,
– острый угол – руки в стороны – вверх, образуя острый угол;
– тупой угол – руки в стороны, образуя тупой угол.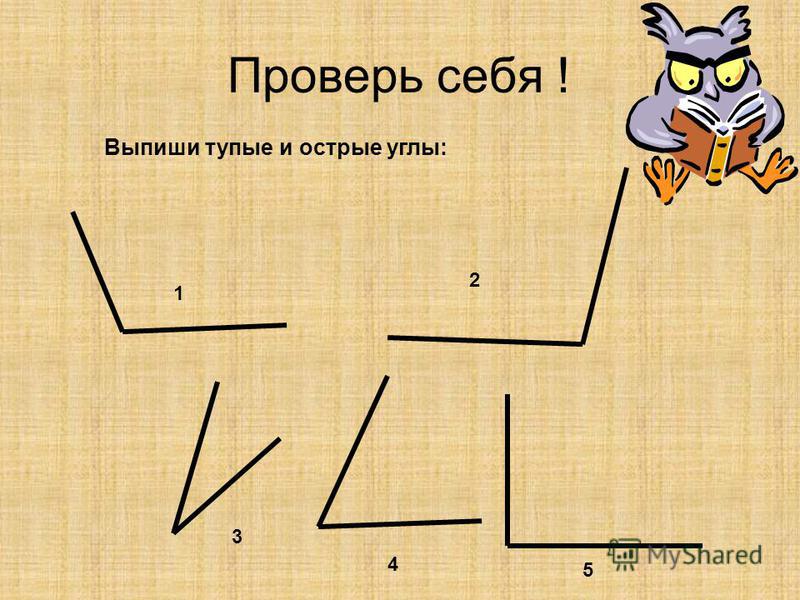
V. Работа по теме урока. Практическая работа.
Задание 1. Начертить прямой и острый углы, расположив их так, как показано на рисунке. (Образец на доске.) – Луч зеленого цвета.
– Какой угол меньше: острый или прямой?
Вывод: Угол острый меньше прямого, потому что он укладывается в прямом.
– Проведите из общей вершины этих углов несколько лучей так, чтобы с лучём
зеленого цвета они образовывали острые углы. (Задание выполняется в парах.)
– Давайте сделаем вывод о величине прямого и острого углов.
Учащиеся делают вывод: Все острые углы меньше прямого.
Задание 2. Начертите тупой и прямой углы, расположив их так, как показано на рисунке. (Уч-ся самостоятельно выполняют задание по образцу.)
– Луч зеленого цвета.
– Какой угол больше :тупой или прямой?
– Проведите из общей вершины этих углов несколько лучей так, чтобы с зеленым
лучом зеленого цвета они образовывали тупые углы.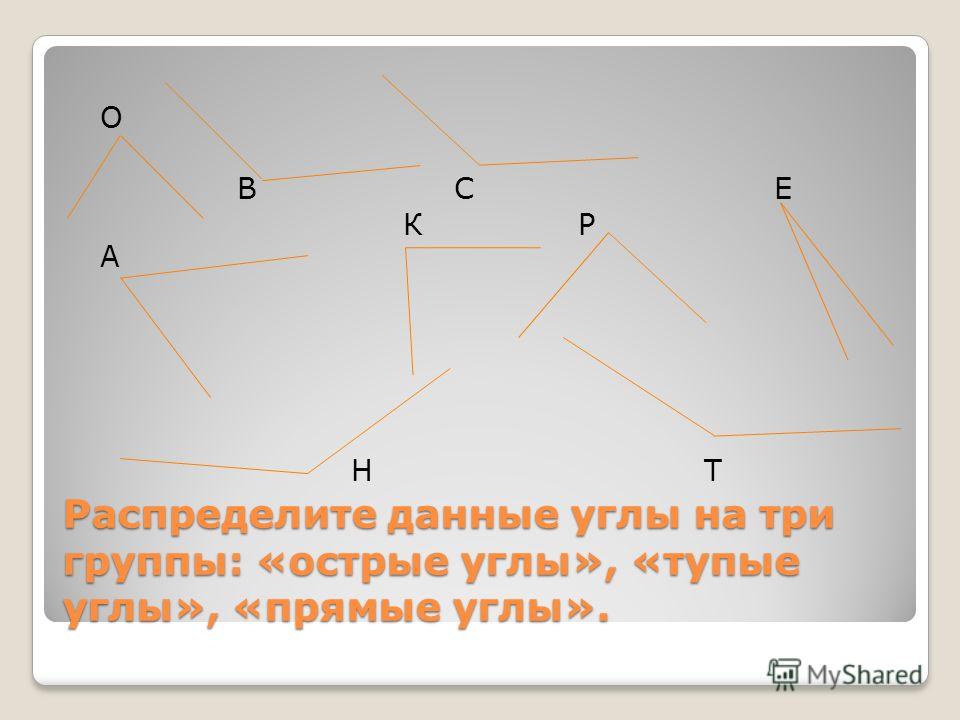
(Один ученик выполняет задание у доски, а остальные – в своих тетрадях.)
– Сравните по величине тупой и прямой углы.
Учащиеся делают вывод: Все тупые углы больше прямого.
VI. Закрепление изученного материала.
Задание 1. На чертеже один угол “лишний”. Найди его.
Задание 2. На схеме изображено пересечение шоссейных дорог.
Выпиши получившиеся углы –
А) Прямые:
Б) Острые:
В) Тупые:
Задание 3. Покажи на чертеже прямые углы – красным цветом, острые углы – зеленым, тупые углы – синим. (Работа в группе.)
VII.Обобщение изучаемого на уроке.
– Впишите пропущенные слова.
1) Прямой угол_______________________тупого угла.
2)Тупой угол________________________острого угла.
(Задание выполняется с комментированием.)
VIII. Рефлексия деятельности.
– С какими видами углов вы сегодня познакомились?
Заранее подготовленные дети читают стихи.
Угол.
1. Мама мой взяла листок,
И загнула уголок,
Угол вот такой у взрослых
Называется прямым
Если угол уже – острым,
Если шире то – тупым.2. Я острый – начертить хочу,
Сейчас возьму и начерчу.
Веду из точки две прямых,
Как будто два луча,
И видим Острый угол мы,
Как острие меча.3. А для угла тупого
Все повторяем снова
Из точки две прямых ведем,
Но их пошире разведем.
На чертеж мой посмотри,
Он, как ножницы внутри,
Если их за два кольца
Мы раздвинем до конца.
– Как узнать, острый угол или тупой?
– Оцените свою работу на уроке?
– Кто хорошо разобрался в новом материале?
– Кому нужна помощь?
Учитель: Отметьте свое настроение после нашего урока.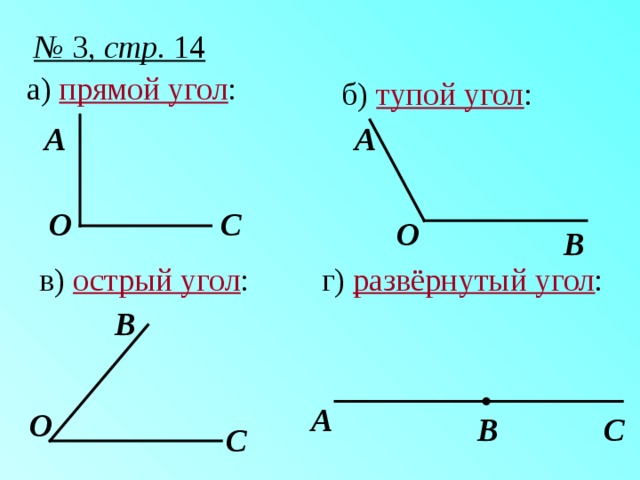
IХ. Домашнее задание:
1. При помощи угольника проверьте углы в окружающих нас предметах (у стола, у
шкафа и т.д.).
2. Начертите в тетради фигуры с прямыми, тупыми и острыми углами.
Что такое прямые, острые, тупые и рефлекторные углы?
Мы объясняем, что такое прямые, острые, тупые и рефлекторные углы и как дети узнают о разных углах с помощью KS1 и KS2.
или Зарегистрируйтесь, чтобы добавить к своим сохраненным ресурсам
Что такое прямые, острые, тупые и рефлекторные углы?
| Прямой угол — это угол, равный 90° (градусов). Он также известен как «четверть оборота», потому что это четверть полного оборота, составляющая 360°. Прямой угол изображается маленьким квадратом внутри угла. | |
| Острый угол — это угол, чей размер МЕНЬШЕ 90˚. | |
Тупой угол — это угол, имеющий размеры от 90˚ до 180˚. | |
| Угол рефлекса — это угол, который измеряется между 180˚ и 360˚. |
Что дети узнают об углах в KS1?
Дети начинают изучать язык направления в Год 1 , когда говорят о четверти, половине и полном обороте. Учителя поощряют детей узнавать об поворотах, заставляя их вставать и делать четверть, половину и полный оборот по классу. Они также могут дать детям небольшую фигурку или куклу, чтобы они поместили их на картинку и потренировались выполнять различные повороты. Очень важно, чтобы дети понимали концепцию этих поворотов, так как это основа для изучения углов.
К концу Год 2 , они должны уметь говорить об этих поворотах и объяснять, в каком направлении они идут: по часовой или против часовой стрелки.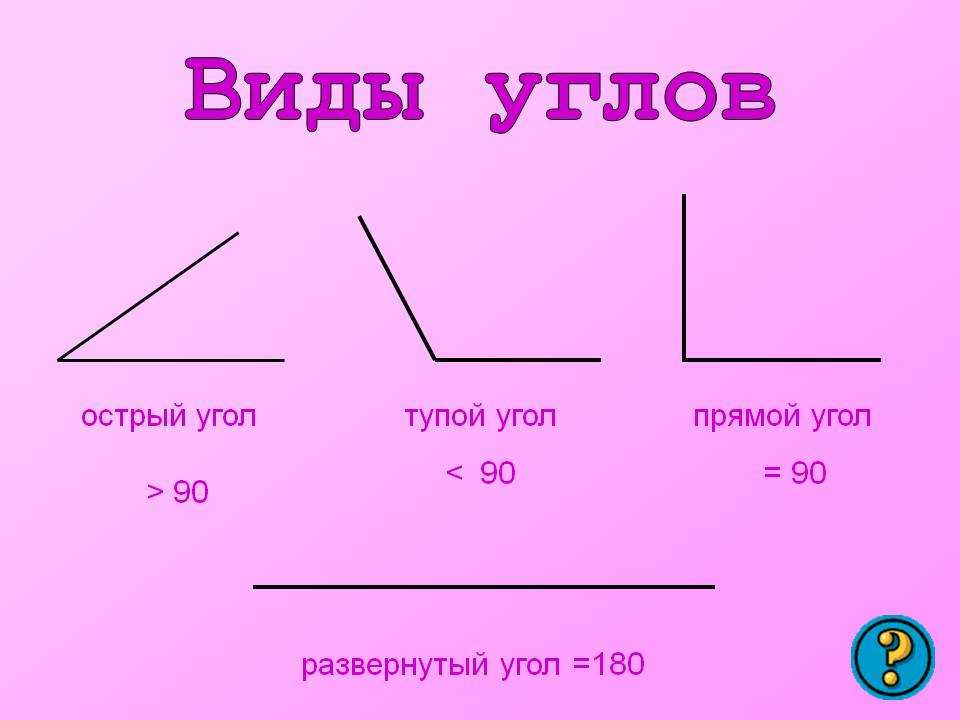 В течение 2-го года дети также учатся определять время с точностью до четверти часа, поэтому они должны знать, в каком направлении движутся стрелки на часах.
В течение 2-го года дети также учатся определять время с точностью до четверти часа, поэтому они должны знать, в каком направлении движутся стрелки на часах.
Что дети узнают об углах в KS3?
В Year 3 дети должны будут распознавать прямые углы и знать, что два прямых угла составляют пол-оборота, три — три четверти оборота и четыре — полный оборот. Им нужно определить, являются ли углы больше или меньше прямого угла.
В 4 классе дети должны знать об острых и тупых углах.
В 5 классе дети начинают использовать транспортир для измерения острых, тупых и рефлекторных углов. Детям также необходимо вычислять углы вокруг точки, по прямой линии и в пределах 90°.
Детям года 6 нужно будет повернуть фигуры на 90° или 180°. Им нужно будет использовать транспортир для измерения и рисования углов и вычисления углов в треугольнике или вокруг точки, а также для нахождения неизвестных углов в треугольниках, четырехугольниках и правильных многоугольниках.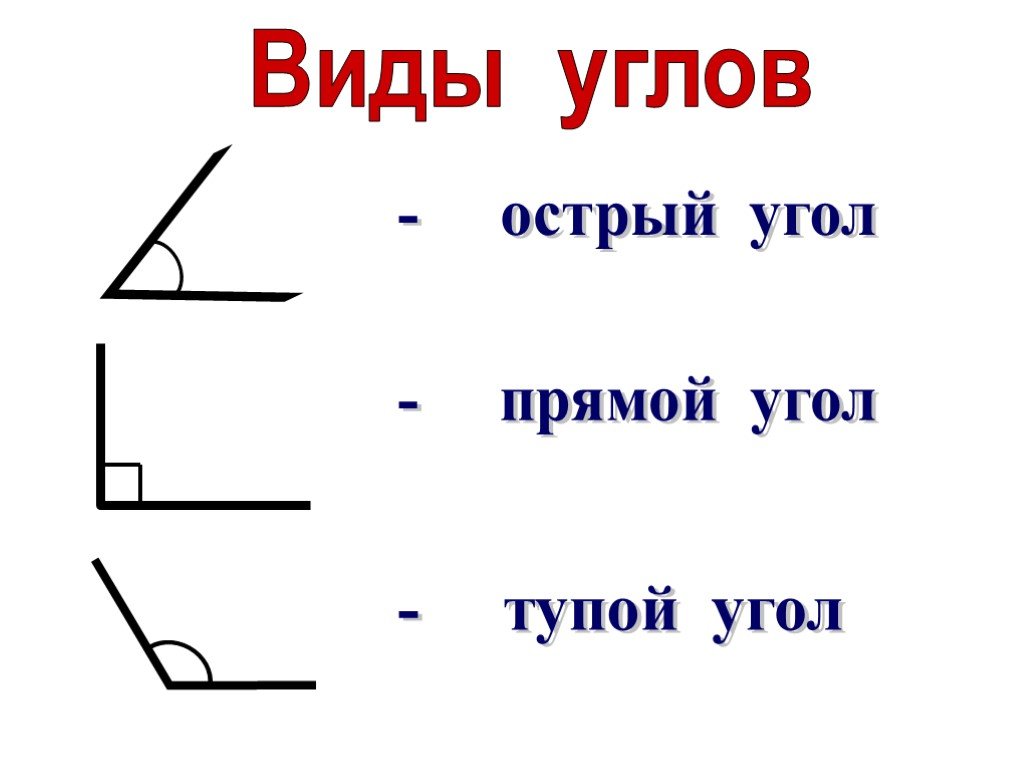
Использование транспортира
Учителя обычно тратят много времени на обучение детей тому, как пользоваться транспортиром, так как им это часто трудно.
Транспортиры размечены от 0˚ до 180˚ слева направо, а также справа налево, к чему нужно привыкнуть! Детям снова показывают, что два прямых угла составляют прямую линию, а поскольку 90˚ x 2 = 180˚, это измерение прямой линии.
Что касается острых и тупых углов, детям можно дать набор углов, которые нужно вырезать, измерить, а затем разделить на две группы. Им также можно задать вопросы, подобные следующим:
Какая из этих фигур имеет один тупой угол и два острых угла?
(Ответ: третья фигура.)
Посмотрите на внутренние углы этой фигуры. Обозначьте острые углы красным цветом, тупые углы синим цветом и рефлекторный угол зеленым цветом.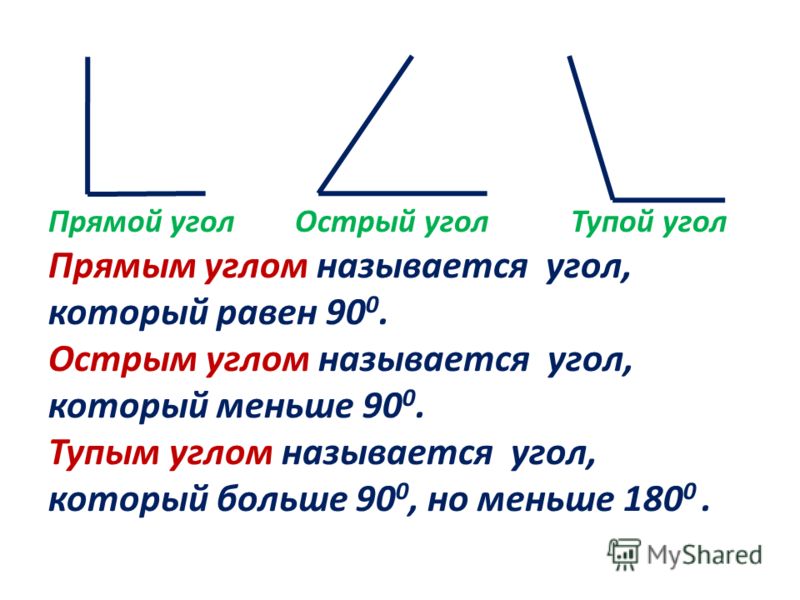
Рабочие листы и задания по углам
Чтобы помочь вашему ребенку применить свои знания о формах и углах на практике, загрузите рабочие листы по углам и другие рабочие листы по геометрии.
Что такое острый угол? Определение, свойства, формулы и примеры
Что такое угол?
В геометрии два луча, имеющие общий конец, образуют угол. Общий конец называется вершиной, а два луча называются плечами угла.
Родственные игры
Определение острого угла
Любой угол, величина которого больше 0° и меньше 90°, называется острым углом.
∠ABC равна 30° и, следовательно, это острый угол.
Связанные листы
Типы углов
Существует три основных типа углов: острый угол, прямой угол и тупой угол.
Острый угол: угол меньше 90°
Прямой угол: угол ровно 90°
Тупой угол: угол больше 90°
Примеры острых углов
Острый угол меньше 90°
Следовательно, 67°, 45°, 23°, 52°, 86°, 14 ° все примеры острых углов.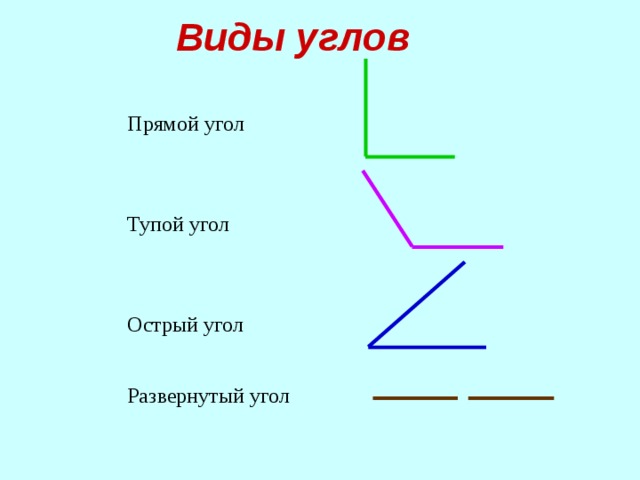
Разделив прямой угол (90˚), мы получим два или более острых угла, так как каждый вновь образованный угол будет меньше 90˚.
- Прямоугольный
Реальные примеры острых углов
Если мы нарежем пиццу на 5 или более кусочков, каждый кусок пиццы будет образовывать острый угол.
Каждый кусочек пиццы образует острый угол.
Другой пример — настенные часы. Стрелки настенных часов в несколько часов дня образуют острые углы. Например, 10 часов.
Часовая и минутная стрелки образуют острый угол в положении «10 часов».
Пара открытых ножниц, открытый рот аллигатора и клюв птиц образуют острые углы.
Остроугольный треугольник
Треугольник, образованный всеми углами меньше 90˚, также известен как остроугольный треугольник. Например, в равностороннем треугольнике все три угла равны 60°, что делает его остроугольным. 9Остроугольный треугольник
2. В угле 180˚, если один угол тупой (больше 90˚), другой угол всегда будет острым (меньше 90˚).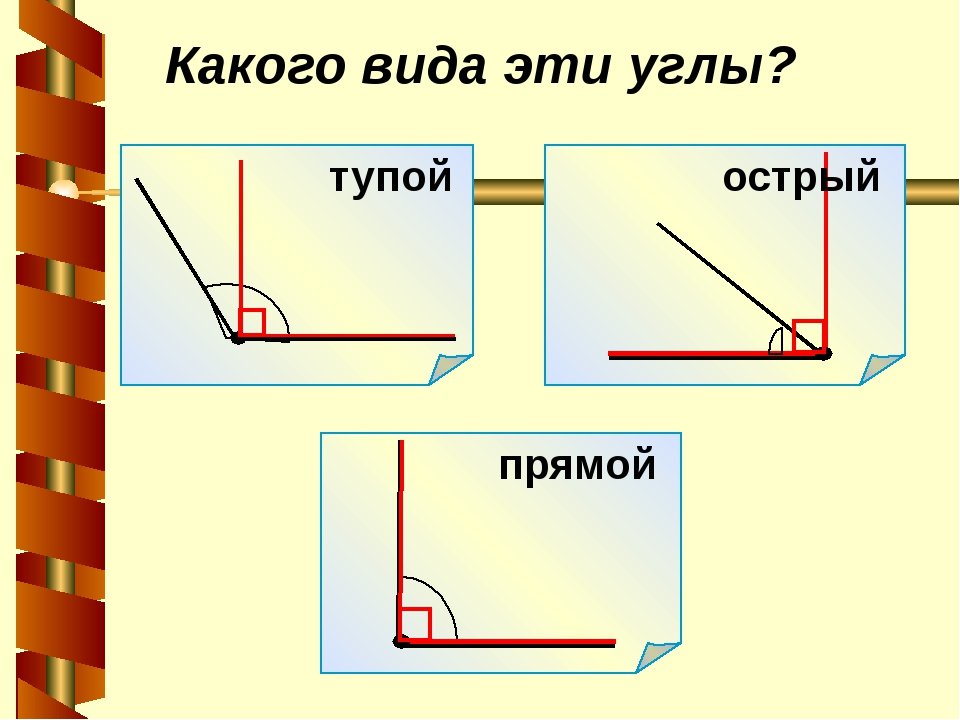
Решенные примеры для острого угла
Вопрос 1: Мера трех углов следующая:
- 75°
- 112°
- 17°
Укажите тип угла в каждом случае.
Ответ:
- Острый угол- так как 75° меньше 90°
- Тупой угол – поскольку 112° больше 90°
- Острый угол — поскольку 17° меньше 90°
Вопрос 2: Меры некоторых углов приведены ниже: D
Найдите все острые углы
Ответ: Острые углы: ∠A , ∠B и ∠E, так как все эти углы меньше 90 °
Вопрос 3: Состояние Верно или Ложно :
- Угол, равный 45°, является прямым.
- Угол, равный 85°, является острым.
- Угол измерения 90° — тупой угол.

- Угол, равный 15°, является острым.
Решение:
- Ложь
- Правда
- Ложь
- Правда
Практические задачи на острый угол
1
Определение острых углов.
I и III
I и II
II и IV
II и III
Правильный ответ: I и II
Первый и второй углы острые, потому что они меньше 90°.
2
Что получится, если два луча имеют общий конец?
луч
прямая
угол
отрезок
Правильный ответ: угол
Угол образуется, когда два луча имеют общий конец.
3
Угол с величиной 0° называется
полным углом
прямым углом
прямым углом
ни одним из этих
правильный ответ: ни одним из этих
Не было бы угла с 0°. Таким образом, ответ будет вариантом d.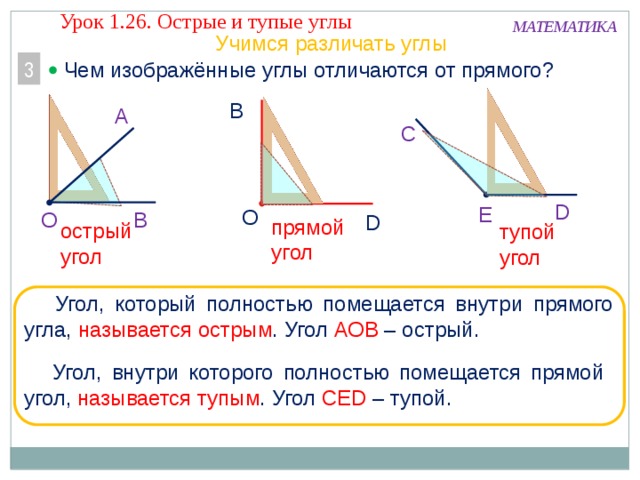




 Приводим стратегию измерения этого показателя по книге «Маркетинг от потребителя».
Приводим стратегию измерения этого показателя по книге «Маркетинг от потребителя». Тогда компания вроде бы может не беспокоиться по поводу своей эффективности и, возможно, не станет стремиться к более высокому уровню потребительской удовлетворенности. К тому же меры по ее повышению требуют времени и денег, и многие менеджеры могут посчитать, что дальнейший рост не оправдывает затрат. Этот аргумент не работает для компании, где удовлетворенность клиентов в приоритете и считается главным показателем эффективности. Чтобы в полной мере понять, что такое удовлетворенность и как усилить ее потенциал для получения прибыли, нужно детальнее изучить вопрос.
Тогда компания вроде бы может не беспокоиться по поводу своей эффективности и, возможно, не станет стремиться к более высокому уровню потребительской удовлетворенности. К тому же меры по ее повышению требуют времени и денег, и многие менеджеры могут посчитать, что дальнейший рост не оправдывает затрат. Этот аргумент не работает для компании, где удовлетворенность клиентов в приоритете и считается главным показателем эффективности. Чтобы в полной мере понять, что такое удовлетворенность и как усилить ее потенциал для получения прибыли, нужно детальнее изучить вопрос.
 И когда они уйдут, продажи и прибыли, скорее всего, снизятся.
И когда они уйдут, продажи и прибыли, скорее всего, снизятся.
 Другой способ интерпретации этого заключается в том, что насыщенная молекула имеет максимально возможное количество атомов водорода, чтобы быть ациклическим алканом. Таким образом, число атомов водорода может быть представлено как 2C+2, что является общим молекулярным представлением алкана. Например, для молекулярной формулы C 3 H 4 количество фактических атомов водорода, необходимых для насыщения соединения, составляет 8 [2C+2=(2×3)+2=8] . Соединению требуется еще 4 атома водорода, чтобы быть полностью насыщенным (ожидаемое количество атомов водорода — наблюдаемое количество атомов водорода = 8-4 = 4) . Степень ненасыщенности равна 2, или половине количества атомов водорода, необходимых для того, чтобы молекула классифицировалась как насыщенная. Следовательно, формула DoB делится на 2. Формула вычитает количество X, потому что галоген (X) заменяет водород в соединении. Например, в хлорэтане C 2 H 5 Cl, на один водород меньше по сравнению с этаном, C 2 H 6 .
Другой способ интерпретации этого заключается в том, что насыщенная молекула имеет максимально возможное количество атомов водорода, чтобы быть ациклическим алканом. Таким образом, число атомов водорода может быть представлено как 2C+2, что является общим молекулярным представлением алкана. Например, для молекулярной формулы C 3 H 4 количество фактических атомов водорода, необходимых для насыщения соединения, составляет 8 [2C+2=(2×3)+2=8] . Соединению требуется еще 4 атома водорода, чтобы быть полностью насыщенным (ожидаемое количество атомов водорода — наблюдаемое количество атомов водорода = 8-4 = 4) . Степень ненасыщенности равна 2, или половине количества атомов водорода, необходимых для того, чтобы молекула классифицировалась как насыщенная. Следовательно, формула DoB делится на 2. Формула вычитает количество X, потому что галоген (X) заменяет водород в соединении. Например, в хлорэтане C 2 H 5 Cl, на один водород меньше по сравнению с этаном, C 2 H 6 .


 ) C 5 H 7 Cl (d.) C 9 H 9 NO 4
) C 5 H 7 Cl (d.) C 9 H 9 NO 4  Таким образом, формула может давать множество возможных структур для данной молекулярной формулы.)
Таким образом, формула может давать множество возможных структур для данной молекулярной формулы.)  3 H 5 BR 90005. 3 H 5 . Следующая молекула – кофеин (C 8 H 10 N 4 O 2 ), определяем степени ненасыщенности (DoU).
3 H 5 BR 90005. 3 H 5 . Следующая молекула – кофеин (C 8 H 10 N 4 O 2 ), определяем степени ненасыщенности (DoU). GradeHub вычисляет средние оценки экзаменов и курсовых работ по модулям. Кредиты для модуля используются в качестве взвешивания для общего среднегодового значения.
GradeHub вычисляет средние оценки экзаменов и курсовых работ по модулям. Кредиты для модуля используются в качестве взвешивания для общего среднегодового значения.

 Такой калькулятор подходит для выпускников старших классов и учащихся ВУЗОВ. Из-за его внешнего сходства с программируемыми моделями калькуляторов, многие считают, что его недопустимо использовать на Едином Государственном Экзамене. Это ошибочное мнение.
Такой калькулятор подходит для выпускников старших классов и учащихся ВУЗОВ. Из-за его внешнего сходства с программируемыми моделями калькуляторов, многие считают, что его недопустимо использовать на Едином Государственном Экзамене. Это ошибочное мнение.




 Скачать или заказать инструкцию можно также на сайте производителя.
Скачать или заказать инструкцию можно также на сайте производителя. Хотя сертификат, подтверждающий пригодность модели для использования на ЕГЭ, — необязательный документ, он станет главным аргументом в споре с комиссией. Следовательно, надёжнее использовать сертифицированные изделия. Пользователи продукции Casio могут принести на экзамен не только сертификат, но и письмо-подтверждение генерального директора компании. Убедитесь, что в документах упомянута серия вашего устройства.
Хотя сертификат, подтверждающий пригодность модели для использования на ЕГЭ, — необязательный документ, он станет главным аргументом в споре с комиссией. Следовательно, надёжнее использовать сертифицированные изделия. Пользователи продукции Casio могут принести на экзамен не только сертификат, но и письмо-подтверждение генерального директора компании. Убедитесь, что в документах упомянута серия вашего устройства. Он работает тремя различными способами, основанными на:
Он работает тремя различными способами, основанными на: Более того, из общей теории относительности мы знаем, что вся Вселенная не только расширяется, но даже является ускоренным расширением! Это означает, что расстояние между двумя точками постоянно становится все больше и больше, но мы не можем чувствовать это каждый день, потому что все масштабы в мире тоже расширяются.
Более того, из общей теории относительности мы знаем, что вся Вселенная не только расширяется, но даже является ускоренным расширением! Это означает, что расстояние между двумя точками постоянно становится все больше и больше, но мы не можем чувствовать это каждый день, потому что все масштабы в мире тоже расширяются. наш калькулятор величины ускорения). Это неверно в ситуации, когда меняется и масса, например, при ракетной тяге, когда сгоревшее топливо выходит из сопла ракеты. См. наш калькулятор тяги ракеты, чтобы узнать больше.
наш калькулятор величины ускорения). Это неверно в ситуации, когда меняется и масса, например, при ракетной тяге, когда сгоревшее топливо выходит из сопла ракеты. См. наш калькулятор тяги ракеты, чтобы узнать больше. Что ж, это ложь. Космос — это вакуум, и звука там не слышно (звуковым волнам для распространения требуется материя). Эти бои должны быть беззвучными! В космосе никто не услышит твой крик.
Что ж, это ложь. Космос — это вакуум, и звука там не слышно (звуковым волнам для распространения требуется материя). Эти бои должны быть беззвучными! В космосе никто не услышит твой крик. наш калькулятор скорости).
наш калькулятор скорости). В ней он сформулировал закон всемирного тяготения, гласящий, что любые два объекта, обладающих массой, будут притягиваться друг к другу с силой, экспоненциально зависящей от расстояния между этими объектами (в частности, она обратно пропорциональна квадрату расстояния). Чем тяжелее объекты, тем больше сила гравитации. Это объясняет, например, почему планеты вращаются вокруг очень плотного Солнца.
В ней он сформулировал закон всемирного тяготения, гласящий, что любые два объекта, обладающих массой, будут притягиваться друг к другу с силой, экспоненциально зависящей от расстояния между этими объектами (в частности, она обратно пропорциональна квадрату расстояния). Чем тяжелее объекты, тем больше сила гравитации. Это объясняет, например, почему планеты вращаются вокруг очень плотного Солнца.
 Когда вы подставите его и уменьшите единицы измерения, вы получите
Когда вы подставите его и уменьшите единицы измерения, вы получите  Обычно у нас есть две части, перпендикулярные друг другу: центростремительная и тангенциальная . Центростремительное ускорение изменяет направление скорости и, следовательно, форму трека, но не влияет на значение скорости. С другой стороны, тангенциальное ускорение всегда перпендикулярно траектории движения. Он изменяет только значение скорости , а не ее направление.
Обычно у нас есть две части, перпендикулярные друг другу: центростремительная и тангенциальная . Центростремительное ускорение изменяет направление скорости и, следовательно, форму трека, но не влияет на значение скорости. С другой стороны, тангенциальное ускорение всегда перпендикулярно траектории движения. Он изменяет только значение скорости , а не ее направление.

 Оба имеют величину и направление, но их единицы измерения — м/с и м/с² соответственно.
Оба имеют величину и направление, но их единицы измерения — м/с и м/с² соответственно.
 Он начинает двигаться вверх и вперед, под некоторым наклоном к земле. Чем дальше он летит, тем медленнее его подъем – и, наконец, он начинает снижаться, то двигаясь то вниз, то вперед и, наконец, снова ударяясь о землю. Если бы вы могли проследить его путь, это была бы кривая, называемая траекторией в форме параболы. Любой объект, движущийся таким образом, находится в движении снаряда. Кстати, у нас есть калькулятор скорости стрелы, который анализирует движение стрелы — попробуйте!
Он начинает двигаться вверх и вперед, под некоторым наклоном к земле. Чем дальше он летит, тем медленнее его подъем – и, наконец, он начинает снижаться, то двигаясь то вниз, то вперед и, наконец, снова ударяясь о землю. Если бы вы могли проследить его путь, это была бы кривая, называемая траекторией в форме параболы. Любой объект, движущийся таким образом, находится в движении снаряда. Кстати, у нас есть калькулятор скорости стрелы, который анализирует движение стрелы — попробуйте! Наш калькулятор движения снаряда выполняет следующие шаги, чтобы найти все остальные параметры:
Наш калькулятор движения снаряда выполняет следующие шаги, чтобы найти все остальные параметры: 2 \sin(2\alpha) / gR=V2sin(2α)/g 92 \! + \! 2 g h}}{g}R=Vxt=VcosαgVsinα+(Vsinα)2+2gh
2 \sin(2\alpha) / gR=V2sin(2α)/g 92 \! + \! 2 g h}}{g}R=Vxt=VcosαgVsinα+(Vsinα)2+2gh Он также может работать «наоборот». Например, введите время полета, расстояние и начальную высоту, и наблюдайте, как он сделает все расчеты за вас!
Он также может работать «наоборот». Например, введите время полета, расстояние и начальную высоту, и наблюдайте, как он сделает все расчеты за вас!
 Сопротивление воздуха также будет иметь значение в реальной жизни, но для большинства теоретических расчетов оно незначительно и поэтому игнорируется. Если у снаряда есть крылья , это также повлияет на его движение, так как он будет скользить.
Сопротивление воздуха также будет иметь значение в реальной жизни, но для большинства теоретических расчетов оно незначительно и поэтому игнорируется. Если у снаряда есть крылья , это также повлияет на его движение, так как он будет скользить.

 Одну и ту же задачу можно решать разными
способами. Какими? Назовите их.
Одну и ту же задачу можно решать разными
способами. Какими? Назовите их.






 Первый автомат
работал 10 минут, а второй – 20 минут. Всего за это
время было упаковано 320 пачек печенья. Сколько
пачек в минуту упаковывает каждый автомат?
Первый автомат
работал 10 минут, а второй – 20 минут. Всего за это
время было упаковано 320 пачек печенья. Сколько
пачек в минуту упаковывает каждый автомат?
 § 3. Решение задач с помощью уравнений. Упражнения №№ 3.1 — 3.53. Мерзляк, Поляков: Алгебра. Углубленный уровень: 7 класс. Учебник — М.: Вентана-Граф (Российский учебник). Электронная ознакомительная версия для покупки пособия. Цитаты из книги использованы в учебных целях.
§ 3. Решение задач с помощью уравнений. Упражнения №№ 3.1 — 3.53. Мерзляк, Поляков: Алгебра. Углубленный уровень: 7 класс. Учебник — М.: Вентана-Граф (Российский учебник). Электронная ознакомительная версия для покупки пособия. Цитаты из книги использованы в учебных целях.


 Углубленный уровень: 7 класс. Учебник — М.: Вентана-Граф, 2019 (Российский учебник). 3. Решение задач с помощью уравнений.
Углубленный уровень: 7 класс. Учебник — М.: Вентана-Граф, 2019 (Российский учебник). 3. Решение задач с помощью уравнений. Кроме того, учащиеся будут решать площадь поверхности и объем трехмерных фигур. Задание на производительность требует, чтобы учащиеся разработали экономичную и компактную коробку для хлопьев.
Кроме того, учащиеся будут решать площадь поверхности и объем трехмерных фигур. Задание на производительность требует, чтобы учащиеся разработали экономичную и компактную коробку для хлопьев. Кроме того, они разработают логические аргументы в отношении фотографий и приведут доказательства в поддержку своих рассуждений.
Кроме того, они разработают логические аргументы в отношении фотографий и приведут доказательства в поддержку своих рассуждений. Кроме того, учащиеся будут использовать вероятности и правдоподобие, чтобы найти и организовать все возможные события для ситуации. Наконец, учащиеся будут делать прогнозы о событиях и разрабатывать логические аргументы о том, как лучше всего играть в игру.
Кроме того, учащиеся будут использовать вероятности и правдоподобие, чтобы найти и организовать все возможные события для ситуации. Наконец, учащиеся будут делать прогнозы о событиях и разрабатывать логические аргументы о том, как лучше всего играть в игру. РП.А.1. Вычислить удельные ставки, связанные с отношениями фракций, включая отношения длин, площадей и других величин, измеренных в одинаковых или разных единицах. Например, если человек проходит $1/2$ мили за каждые $1/4$ часа, рассчитайте удельную норму как комплексную дробь $\frac{1/2}{1/4}$ миль в час, что эквивалентно $2$ миль. в час.
РП.А.1. Вычислить удельные ставки, связанные с отношениями фракций, включая отношения длин, площадей и других величин, измеренных в одинаковых или разных единицах. Например, если человек проходит $1/2$ мили за каждые $1/4$ часа, рассчитайте удельную норму как комплексную дробь $\frac{1/2}{1/4}$ миль в час, что эквивалентно $2$ миль. в час. РП.А.2.а. Определите, находятся ли две величины в пропорциональном соотношении, например, проверив эквивалентные отношения в таблице или нарисовав график на координатной плоскости и наблюдая, является ли график прямой линией, проходящей через начало координат.
РП.А.2.а. Определите, находятся ли две величины в пропорциональном соотношении, например, проверив эквивалентные отношения в таблице или нарисовав график на координатной плоскости и наблюдая, является ли график прямой линией, проходящей через начало координат. РП.А.2.д. Объясните, что означает точка $(x, y)$ на графике пропорциональной зависимости с точки зрения ситуации, обратив особое внимание на точки $(0, 0)$ и $(1, r)$, где $r$ является единичной ставкой.
РП.А.2.д. Объясните, что означает точка $(x, y)$ на графике пропорциональной зависимости с точки зрения ситуации, обратив особое внимание на точки $(0, 0)$ и $(1, r)$, где $r$ является единичной ставкой. НС. 7 класс — Система счисления
НС. 7 класс — Система счисления
 НС.А.2.а. Поймите, что умножение распространяется с дробей на рациональные числа, требуя, чтобы операции продолжали удовлетворять свойствам операций, в частности свойству распределения, что приводит к таким продуктам, как $(-1)(-1) = 1$ и правилам умножения со знаком числа. Интерпретируйте произведения рациональных чисел, описывая контексты реального мира.
НС.А.2.а. Поймите, что умножение распространяется с дробей на рациональные числа, требуя, чтобы операции продолжали удовлетворять свойствам операций, в частности свойству распределения, что приводит к таким продуктам, как $(-1)(-1) = 1$ и правилам умножения со знаком числа. Интерпретируйте произведения рациональных чисел, описывая контексты реального мира.
 EE.A.2. Поймите, что переписывание выражения в разных формах в контексте задачи может пролить свет на проблему и на то, как связаны в ней величины. Например, $a + 0,05a = 1,05a$ означает, что «увеличение на $5\%$» равносильно «умножению на $1,05$».
EE.A.2. Поймите, что переписывание выражения в разных формах в контексте задачи может пролить свет на проблему и на то, как связаны в ней величины. Например, $a + 0,05a = 1,05a$ означает, что «увеличение на $5\%$» равносильно «умножению на $1,05$». 50$. Если вы хотите разместить полотенцесушитель $9\frac34$ дюймов в центре двери шириной $27 \frac12$ дюймов, вам нужно будет разместить планку на расстоянии около $9$ дюймов от каждого края; эту оценку можно использовать в качестве проверки точного вычисления.
50$. Если вы хотите разместить полотенцесушитель $9\frac34$ дюймов в центре двери шириной $27 \frac12$ дюймов, вам нужно будет разместить планку на расстоянии около $9$ дюймов от каждого края; эту оценку можно использовать в качестве проверки точного вычисления. Например, периметр прямоугольника равен $54$ см. Его длина $6$ см. Какова его ширина?
Например, периметр прямоугольника равен $54$ см. Его длина $6$ см. Какова его ширина?


 Например, оцените среднюю длину слова в книге путем случайной выборки слов из книги; предсказать победителя школьных выборов на основе случайно выбранных данных опроса. Оцените, насколько далеко может быть оценка или прогноз.
Например, оцените среднюю длину слова в книге путем случайной выборки слов из книги; предсказать победителя школьных выборов на основе случайно выбранных данных опроса. Оцените, насколько далеко может быть оценка или прогноз. Например, решите, длиннее ли слова в главе учебника по естествознанию для седьмого класса, чем слова в главе из учебника по естествознанию для четвертого класса.
Например, решите, длиннее ли слова в главе учебника по естествознанию для седьмого класса, чем слова в главе из учебника по естествознанию для четвертого класса. Например, подбрасывая числовой куб 600 раз, предскажите, что число 3 или 6 выпадет примерно 200 раз, но, вероятно, не ровно 200 раз.
Например, подбрасывая числовой куб 600 раз, предскажите, что число 3 или 6 выпадет примерно 200 раз, но, вероятно, не ровно 200 раз. Например, найдите приблизительную вероятность того, что крутящийся пенни упадет решкой вверх или что брошенный бумажный стаканчик упадет открытым концом вниз. Судя по наблюдаемым частотам, результаты для крутящегося пенни кажутся равновероятными?
Например, найдите приблизительную вероятность того, что крутящийся пенни упадет решкой вверх или что брошенный бумажный стаканчик упадет открытым концом вниз. Судя по наблюдаемым частотам, результаты для крутящегося пенни кажутся равновероятными?

 Это еще более актуально, когда вы имеете дело с файлом Microsoft Word. Microsoft Office, включая Microsoft Word, в наши дни стал очень дорогим, поэтому вы не можете просто установить его на свой компьютер всякий раз, когда вам нужно просмотреть файл. На самом деле, в таких случаях было бы намного лучше, если бы вы просто преобразовали его в другой тип файла. Free DOC to PDF Converter от Free PDF Solutions позволяет пользователям конвертировать свои файлы DOC в PDF , чтобы они могли просматривать их в программах для чтения PDF.
Это еще более актуально, когда вы имеете дело с файлом Microsoft Word. Microsoft Office, включая Microsoft Word, в наши дни стал очень дорогим, поэтому вы не можете просто установить его на свой компьютер всякий раз, когда вам нужно просмотреть файл. На самом деле, в таких случаях было бы намного лучше, если бы вы просто преобразовали его в другой тип файла. Free DOC to PDF Converter от Free PDF Solutions позволяет пользователям конвертировать свои файлы DOC в PDF , чтобы они могли просматривать их в программах для чтения PDF. Наконец, в нижней части экрана находятся параметры для настройки выходного файла.
Наконец, в нижней части экрана находятся параметры для настройки выходного файла. Излишне говорить, что это невероятно раздражает.
Излишне говорить, что это невероятно раздражает.

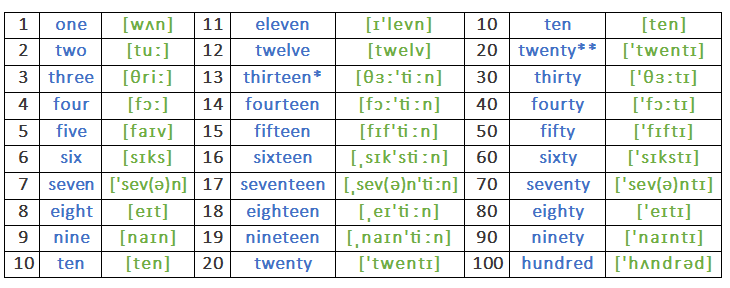
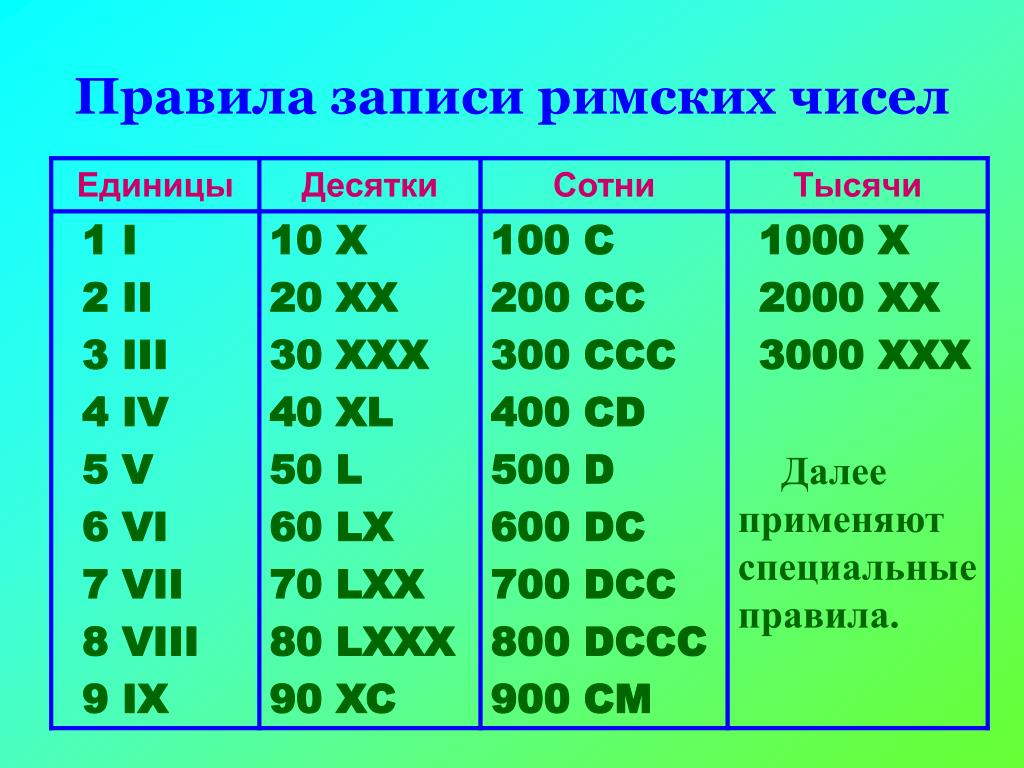 Чтобы выразить 10000 римскими цифрами, мы напишем римскую цифру «X» с винкулумом или чертой над ней. В этой статье мы объясним, как правильно преобразовать 10000 в римские цифры.
Чтобы выразить 10000 римскими цифрами, мы напишем римскую цифру «X» с винкулумом или чертой над ней. В этой статье мы объясним, как правильно преобразовать 10000 в римские цифры.
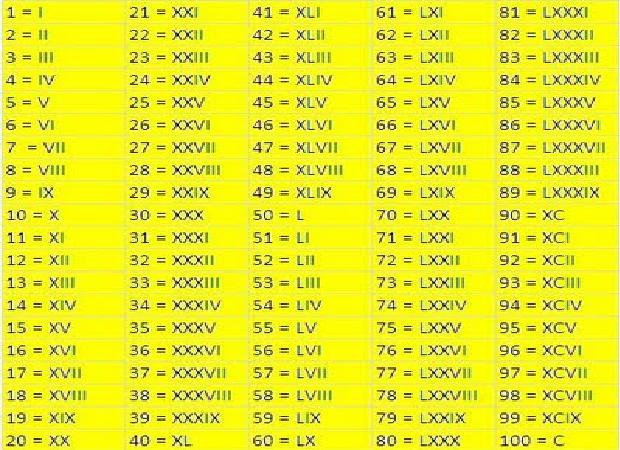 Нуль представляется с помощью слово nulla. Согласно латинскому языку, слово nulla означает отсутствие. До сих пор не существует определенного символа или буквы для обозначения нуля в римской системе счисления.
Нуль представляется с помощью слово nulla. Согласно латинскому языку, слово nulla означает отсутствие. До сих пор не существует определенного символа или буквы для обозначения нуля в римской системе счисления.

 При этом данные услуги должны быть уже оказаны сторонними организациями и индивидуальными предпринимателями.
При этом данные услуги должны быть уже оказаны сторонними организациями и индивидуальными предпринимателями. д.
д. Мы нажимаем «Принять», после чего переходим к опции «Номер страницы» и там определяем местоположение римской цифры:
Мы нажимаем «Принять», после чего переходим к опции «Номер страницы» и там определяем местоположение римской цифры: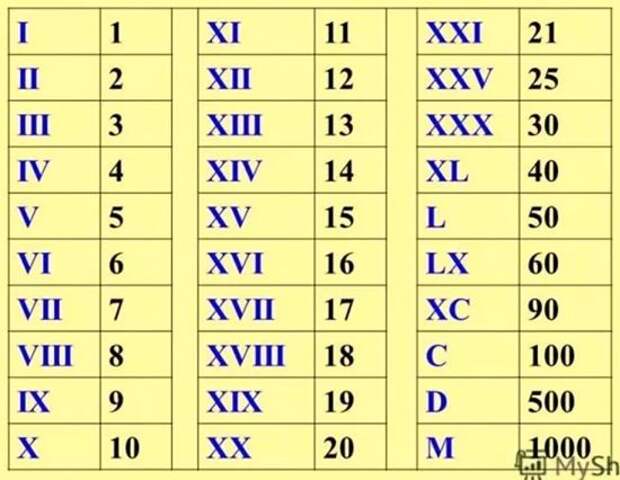 Во всплывающем окне мы выбираем арабские цифры в поле «Числовой формат»:
Во всплывающем окне мы выбираем арабские цифры в поле «Числовой формат»: Для этого мы перейдем в меню «Вставка» и в группе «Верхний и нижний колонтитулы» нажмем «Нижний колонтитул», чтобы выбрать нужный дизайн:
Для этого мы перейдем в меню «Вставка» и в группе «Верхний и нижний колонтитулы» нажмем «Нижний колонтитул», чтобы выбрать нужный дизайн:
 Это потому, что число 4000 не может быть представлено обычными римскими цифрами. связанные калькуляторы конвертер римских цифр позволяет преобразовывать обычные числа в римские цифры или римские цифры в числа. Калькулятор перевода даты в римские цифры. напишите как улучшить эту страницу. Этот простой конвертер римских цифр можно использовать в любое время для преобразования чисел в римские цифры. если вам нужно преобразовать арабские цифры в римские, просто введите число в поле справа и нажмите кнопку «преобразовать в римские». вы получите точное представление числа римскими цифрами. Конвертер римских цифр введите римскую цифру или число и нажмите кнопку конвертировать: расчет римских цифр конвертер даты в римские цифры таблица преобразования римских цифр конвертер даты в римские цифры как конвертировать число в римские цифры отправить отзыв. Конвертировать 2019на римскую цифру что такое 2019 римскими цифрами? как написать 2019 римскими цифрами? введите обычный номер в поле, и он будет преобразован автоматически.
Это потому, что число 4000 не может быть представлено обычными римскими цифрами. связанные калькуляторы конвертер римских цифр позволяет преобразовывать обычные числа в римские цифры или римские цифры в числа. Калькулятор перевода даты в римские цифры. напишите как улучшить эту страницу. Этот простой конвертер римских цифр можно использовать в любое время для преобразования чисел в римские цифры. если вам нужно преобразовать арабские цифры в римские, просто введите число в поле справа и нажмите кнопку «преобразовать в римские». вы получите точное представление числа римскими цифрами. Конвертер римских цифр введите римскую цифру или число и нажмите кнопку конвертировать: расчет римских цифр конвертер даты в римские цифры таблица преобразования римских цифр конвертер даты в римские цифры как конвертировать число в римские цифры отправить отзыв. Конвертировать 2019на римскую цифру что такое 2019 римскими цифрами? как написать 2019 римскими цифрами? введите обычный номер в поле, и он будет преобразован автоматически. римские цифры узнать больше о римских цифрах.
римские цифры узнать больше о римских цифрах. так:.
так:.

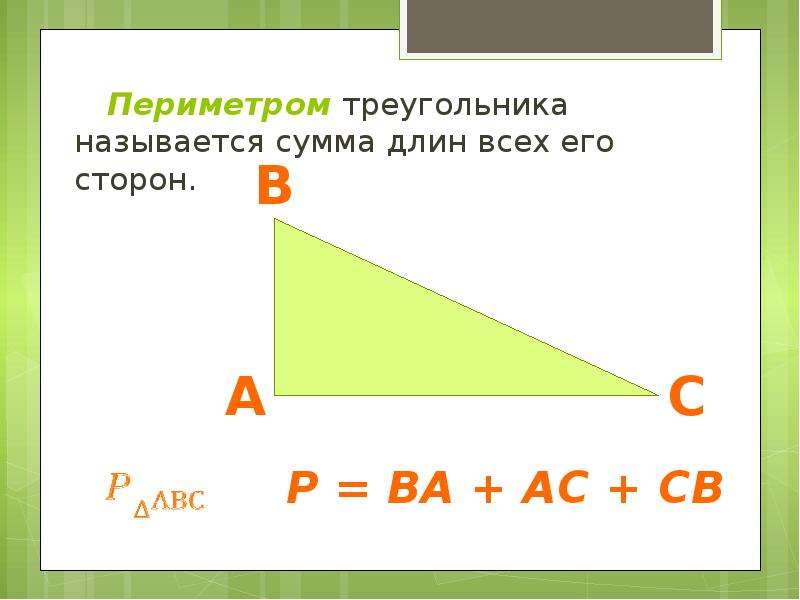
 Найдите периметр треугольника 18 + 10 + 10 ∙ 2 = 48 см – периметр треугольника.
Ответ: 48 см.
Найдите периметр треугольника 18 + 10 + 10 ∙ 2 = 48 см – периметр треугольника.
Ответ: 48 см.
 68
Проверочные работы с.69
68
Проверочные работы с.69
 Multiple-choice
Multiple-choice Найди периметр.
Найди периметр.
 Multiple-choice
Multiple-choice
 Какой ответ показывает взятую часть?
Какой ответ показывает взятую часть? ответил 28.03.13
ответил 28.03.13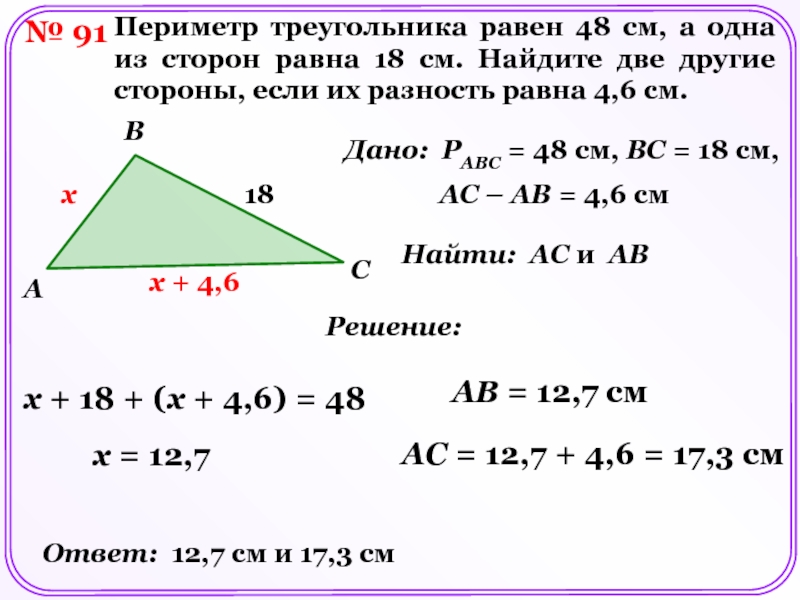 ответил 09.08.13
ответил 09.08.13
 ответил 28.03.13
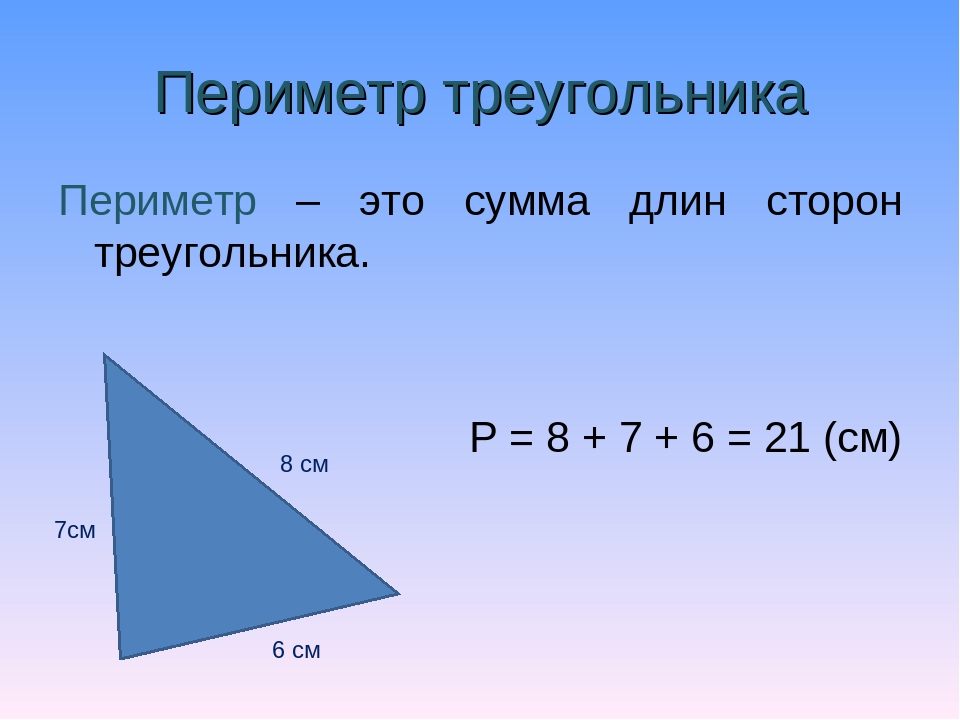
ответил 28.03.13 Используя это и уравнения, которые мы нашли для размеров каждой стороны, мы можем решить для x и использовать это значение, чтобы определить меру каждой стороны.
Используя это и уравнения, которые мы нашли для размеров каждой стороны, мы можем решить для x и использовать это значение, чтобы определить меру каждой стороны. ответил 28.03.13
ответил 28.03.13 е. 47 = [сторона 3] + [сторона 1] + [сторона 2])
е. 47 = [сторона 3] + [сторона 1] + [сторона 2]) Никаких пакетов или подписок, платите только за то время, которое вам нужно.
Никаких пакетов или подписок, платите только за то время, которое вам нужно. ответил 04.10.17
ответил 04.10.17

 Участвуйте в олимпиаде и получите диплом победителя.
Участвуйте в олимпиаде и получите диплом победителя.
 Их изучение начинается с первого класса. Программа второго класса расширяет, пополняет эти…
Их изучение начинается с первого класса. Программа второго класса расширяет, пополняет эти… ..
.. Многие памятники древности указывают на знание геометрических…
Многие памятники древности указывают на знание геометрических… Угол
Угол Даже первобытный человек был знаком с геометрическими фигурами – их он видел в…
Даже первобытный человек был знаком с геометрическими фигурами – их он видел в… Нужно многое запомнить, и если вы не знаете, с чего начать, подготовка к тесту может оказаться сложной задачей. Но хорошая новость в том, что это не обязательно! Мы создали это учебное пособие по математике GED, чтобы помочь.
Нужно многое запомнить, и если вы не знаете, с чего начать, подготовка к тесту может оказаться сложной задачей. Но хорошая новость в том, что это не обязательно! Мы создали это учебное пособие по математике GED, чтобы помочь. Общие темы теста GED по математике: базовая математика, геометрия, базовая алгебра и графики и функции.
Общие темы теста GED по математике: базовая математика, геометрия, базовая алгебра и графики и функции. Для некоторых математических вопросов будет доступен встроенный экранный калькулятор Texas Instruments® TI-30XS. Вопросы по базовым математическим навыкам, таким как умножение десятичных знаков, сложение дробей, использование деления в большую сторону, возведения в степень и другие базовые математические навыки, не будут иметь экранного калькулятора.
Для некоторых математических вопросов будет доступен встроенный экранный калькулятор Texas Instruments® TI-30XS. Вопросы по базовым математическим навыкам, таким как умножение десятичных знаков, сложение дробей, использование деления в большую сторону, возведения в степень и другие базовые математические навыки, не будут иметь экранного калькулятора. Вы можете загрузить лист математических формул и объяснение, к которым у вас будет доступ во время прохождения теста GED по математике.
Вы можете загрузить лист математических формул и объяснение, к которым у вас будет доступ во время прохождения теста GED по математике.
 Некоторые ячейки в таблице будут иметь поле, в которое учащийся вводит число, чтобы таблица была правильной.
Некоторые ячейки в таблице будут иметь поле, в которое учащийся вводит число, чтобы таблица была правильной. Узнайте о кругах, треугольниках, четырехугольниках, кубах, призмах, пирамидах, цилиндрах и конусах. Вам будут задавать вопросы о площади и периметре двухмерных фигур, а также об объеме и поверхности трехмерных фигур.
Узнайте о кругах, треугольниках, четырехугольниках, кубах, призмах, пирамидах, цилиндрах и конусах. Вам будут задавать вопросы о площади и периметре двухмерных фигур, а также об объеме и поверхности трехмерных фигур.
 Делая заметки, вы вовлекаете вас в учебный материал, а не только слушаете, читаете или видите информацию. Когда вы совершаете какое-либо действие, вашему мозгу нужно включить большую часть своего мозга. Вы делаете что-то, поэтому вы больше сосредотачиваетесь.
Делая заметки, вы вовлекаете вас в учебный материал, а не только слушаете, читаете или видите информацию. Когда вы совершаете какое-либо действие, вашему мозгу нужно включить большую часть своего мозга. Вы делаете что-то, поэтому вы больше сосредотачиваетесь. Определите, как вы можете использовать эти новые знания в реальных жизненных ситуациях. Теперь просмотрите материал, который был неясен, и вы, вероятно, обнаружите, что он более понятен.
Определите, как вы можете использовать эти новые знания в реальных жизненных ситуациях. Теперь просмотрите материал, который был неясен, и вы, вероятно, обнаружите, что он более понятен. Подумайте о своей реальности и своем расписании. Что было бы разумным для изучения каждую неделю? Не ставьте цели, которых слишком трудно достичь, но и не делайте их слишком легкими. Подтолкните себя немного, но знайте свои пределы.
Подумайте о своей реальности и своем расписании. Что было бы разумным для изучения каждую неделю? Не ставьте цели, которых слишком трудно достичь, но и не делайте их слишком легкими. Подтолкните себя немного, но знайте свои пределы. «Я собираюсь сдать экзамен GED по математике в июне» трудно контролировать. Вы не знаете, пройдете вы или нет. Вместо этого поставьте перед собой цель: «Я собираюсь сдать GED по математике в июне». Это означает, что вам нужно подготовиться к тесту к июню, чтобы вы могли быть готовы к нему. Не забывайте ставить более мелкие цели, которые помогут вам их достичь!
«Я собираюсь сдать экзамен GED по математике в июне» трудно контролировать. Вы не знаете, пройдете вы или нет. Вместо этого поставьте перед собой цель: «Я собираюсь сдать GED по математике в июне». Это означает, что вам нужно подготовиться к тесту к июню, чтобы вы могли быть готовы к нему. Не забывайте ставить более мелкие цели, которые помогут вам их достичь! Получение неправильного ответа на самом деле поможет вам лучше учиться.
Получение неправильного ответа на самом деле поможет вам лучше учиться. Это уменьшает количество вариантов и повышает ваши шансы на правильное угадывание!
Это уменьшает количество вариантов и повышает ваши шансы на правильное угадывание! Онлайн-обучение — отличный способ подготовиться к GED! Все ваши уроки будут проходить в одном легкодоступном классе с персонализированными материалами, доступными круглосуточно и без выходных. Учитесь на своих условиях в удобном для вас стиле! С онлайн-академией GED вы можете:
Онлайн-обучение — отличный способ подготовиться к GED! Все ваши уроки будут проходить в одном легкодоступном классе с персонализированными материалами, доступными круглосуточно и без выходных. Учитесь на своих условиях в удобном для вас стиле! С онлайн-академией GED вы можете: Приспособьте свое обучение к вашему напряженному дню. Никогда не бывает дедлайнов, и вы сами решаете, когда делать перерывы — никакого давления. Постановка учебных целей всегда поощряется, но вас никогда не наказывают за их невыполнение.
Приспособьте свое обучение к вашему напряженному дню. Никогда не бывает дедлайнов, и вы сами решаете, когда делать перерывы — никакого давления. Постановка учебных целей всегда поощряется, но вас никогда не наказывают за их невыполнение. Оценка того, насколько сложным будет тест, зависит от конкретного экзамена, который вам нужно сдать, а также от знаний и навыков, которые вы приобрели. Чтобы узнать, какой объем подготовки к экзамену NES вам потребуется, начните с прохождения практического теста NES перед тем, как приступить к учебной программе. Результаты помогут вам в определении конкретных концепций, на которые следует обратить внимание.
Оценка того, насколько сложным будет тест, зависит от конкретного экзамена, который вам нужно сдать, а также от знаний и навыков, которые вы приобрели. Чтобы узнать, какой объем подготовки к экзамену NES вам потребуется, начните с прохождения практического теста NES перед тем, как приступить к учебной программе. Результаты помогут вам в определении конкретных концепций, на которые следует обратить внимание. Вы начнете верить в себя и в свою способность заработать хорошие баллы в результате подготовки к NES по математике.
Вы начнете верить в себя и в свою способность заработать хорошие баллы в результате подготовки к NES по математике. Проходной балл на одном или нескольких из этих экзаменов определяет, будет ли выдан сертификат преподавателя. Поскольку ваша преподавательская карьера зависит от того, насколько хорошо вы сдадите этот экзамен, подготовка к экзаменам NES является абсолютной необходимостью. К счастью, вам не нужно довольствоваться учебным пособием по РЭШ в печатной форме, в котором нет объяснений. В Интернете есть много динамических практических курсов NES, которые предлагают полные уроки и пошаговые объяснения.
Проходной балл на одном или нескольких из этих экзаменов определяет, будет ли выдан сертификат преподавателя. Поскольку ваша преподавательская карьера зависит от того, насколько хорошо вы сдадите этот экзамен, подготовка к экзаменам NES является абсолютной необходимостью. К счастью, вам не нужно довольствоваться учебным пособием по РЭШ в печатной форме, в котором нет объяснений. В Интернете есть много динамических практических курсов NES, которые предлагают полные уроки и пошаговые объяснения.
 )
) )
) )
) )
) )
) )
) )
) )
) Как решать нестандартные задачи по обратным тригонометрическим функциям? Как найти синус от арксинуса, косинус от арккосинуса, синус от арккосинуса, косинус от арксинуса? Сегодня мы ответим на эти вопросы. Если Вы не видели наши предыдущие уроки по теме «Функция y=arcsin x, y=arccos x, y=arctg x, y=arcctg x, их графики и свойства», то обязательно посмотрите их, тогда этот урок будет Вам очень понятен. Мы покажем Вам, чему равны синус от арксинуса и косинус от арккосинуса. Научим Вас находить синус от арккосинуса, косинус от арксинуса. Для закрепления материала мы предложим Вам небольшое домашнее задание. Подробный план урока и ссылки на предыдущие уроки Вы можете найти в описании под видео.
00:00 Начало видео.
00:54 Как вычислить sin (arcsin 1/2) и cos (arccos 1/2)?
03:06 Как вычислить sin (arccos 2/7)?
07:09 Как вычислить cos (arcsin (-3/4))?
09:21 Домашнее задание.
Если Вы впервые на нашем канале или не смотрели наши предыдущие уроки, то рекомендуем Вам посмотреть следующие видео:
Чётность и нечётность обратных тригонометрических функций.
Как решать нестандартные задачи по обратным тригонометрическим функциям? Как найти синус от арксинуса, косинус от арккосинуса, синус от арккосинуса, косинус от арксинуса? Сегодня мы ответим на эти вопросы. Если Вы не видели наши предыдущие уроки по теме «Функция y=arcsin x, y=arccos x, y=arctg x, y=arcctg x, их графики и свойства», то обязательно посмотрите их, тогда этот урок будет Вам очень понятен. Мы покажем Вам, чему равны синус от арксинуса и косинус от арккосинуса. Научим Вас находить синус от арккосинуса, косинус от арксинуса. Для закрепления материала мы предложим Вам небольшое домашнее задание. Подробный план урока и ссылки на предыдущие уроки Вы можете найти в описании под видео.
00:00 Начало видео.
00:54 Как вычислить sin (arcsin 1/2) и cos (arccos 1/2)?
03:06 Как вычислить sin (arccos 2/7)?
07:09 Как вычислить cos (arcsin (-3/4))?
09:21 Домашнее задание.
Если Вы впервые на нашем канале или не смотрели наши предыдущие уроки, то рекомендуем Вам посмотреть следующие видео:
Чётность и нечётность обратных тригонометрических функций.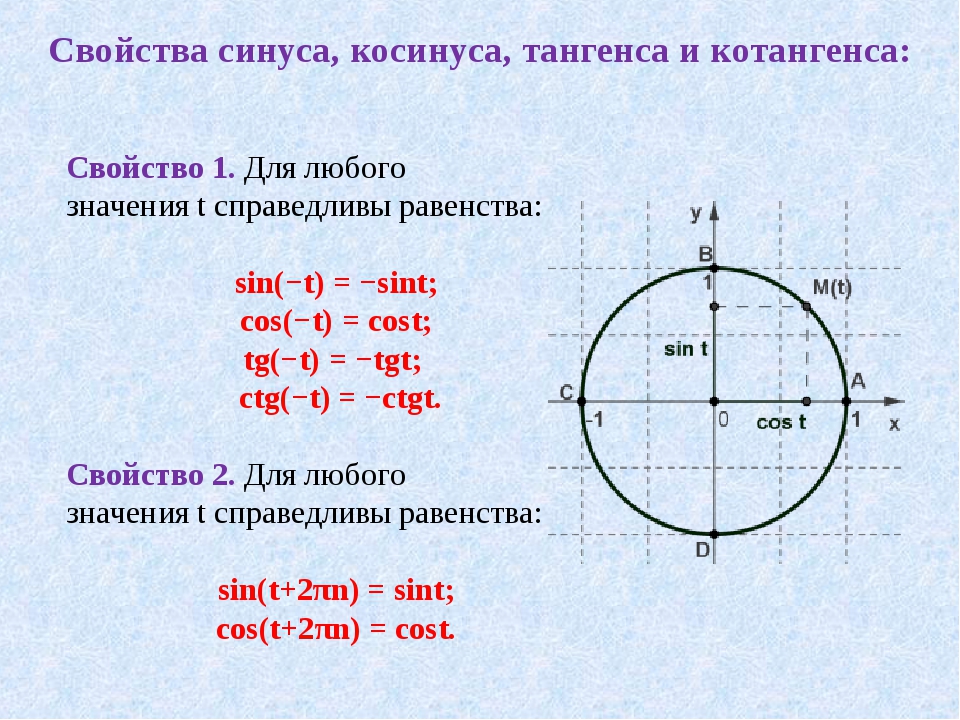 Тригонометрия 8-11 класс. https://rutube.ru/video/d59d2ccaad93dfe5717de935b245d055/
Арккотангенс числа a. Функция y = arcctg x и её график. Как найти арккотангенс числа. Тригонометрия 8-11 класс. https://rutube.ru/video/2373773ffed6926281358929f4fac34a/
Арктангенс числа a. Функция y = arctg x, её свойства и график. Как найти арктангенс числа. Тригонометрия 8-11 класс. https://rutube.ru/video/0f923078705365cbc266f7d1c83c44a5/
Арккосинус числа a. Функция y = arccos x, её свойства и график. Выражения с арккосинусом. Тригонометрия 8-11 класс. https://rutube.ru/video/c930c1e9f935651acbca82b8c4b2a9bd/
Арксинус числа a. Функция y = arcsin x, её свойства и график. Выражения с арксинусом. Тригонометрия 8-11 класс. https://rutube.ru/video/4b7fb1027f7b7a7b2c85c89c3fecec26/
Основное тригонометрическое тождество. Упрощение тригонометрических выражений. Тригонометрия. Геометрия 9 класс. Алгебра 10 класс. Часть 12. https://rutube.ru/video/458402dea2fc63846652e01cf35d69f3/
Все уроки по теме «Функция и её свойства» можно найти в плейлисте: https://rutube.
Тригонометрия 8-11 класс. https://rutube.ru/video/d59d2ccaad93dfe5717de935b245d055/
Арккотангенс числа a. Функция y = arcctg x и её график. Как найти арккотангенс числа. Тригонометрия 8-11 класс. https://rutube.ru/video/2373773ffed6926281358929f4fac34a/
Арктангенс числа a. Функция y = arctg x, её свойства и график. Как найти арктангенс числа. Тригонометрия 8-11 класс. https://rutube.ru/video/0f923078705365cbc266f7d1c83c44a5/
Арккосинус числа a. Функция y = arccos x, её свойства и график. Выражения с арккосинусом. Тригонометрия 8-11 класс. https://rutube.ru/video/c930c1e9f935651acbca82b8c4b2a9bd/
Арксинус числа a. Функция y = arcsin x, её свойства и график. Выражения с арксинусом. Тригонометрия 8-11 класс. https://rutube.ru/video/4b7fb1027f7b7a7b2c85c89c3fecec26/
Основное тригонометрическое тождество. Упрощение тригонометрических выражений. Тригонометрия. Геометрия 9 класс. Алгебра 10 класс. Часть 12. https://rutube.ru/video/458402dea2fc63846652e01cf35d69f3/
Все уроки по теме «Функция и её свойства» можно найти в плейлисте: https://rutube.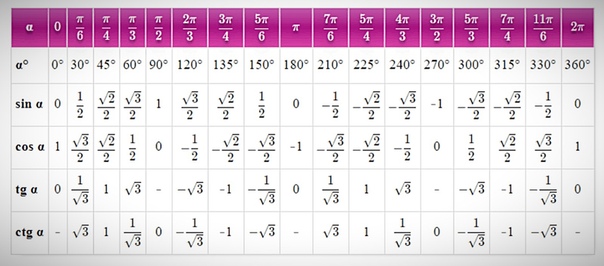 ru/plst/57182
#обратныетригонометрическиефункции #чётностьобратныхтригонометрическихфункций #нечётностьобратныхтригонометрическихфункций #синусотарксинуса #косинусотарккосинуса #тангенсотарктангенса #котангенсотарккотангенса #sinarcsin #cosarccos #tgarctg #ctgarcctg #cosarcsin #sinarccos #тригонометрическиефункцииалгебра10 #МатематикаОтБаканчиковой
тригонометрия, алгебра тригонометрические функции, тригонометрические функции алгебра 10, обратные тригонометрические функции, синус от арксинуса, косинус от арккосинуса, тангенс от арктангенса, котангенс от арккотангенса, sin arcsin, cos arccos, tg arctg, ctg arcctg, cos arcsin, sin arcos
ru/plst/57182
#обратныетригонометрическиефункции #чётностьобратныхтригонометрическихфункций #нечётностьобратныхтригонометрическихфункций #синусотарксинуса #косинусотарккосинуса #тангенсотарктангенса #котангенсотарккотангенса #sinarcsin #cosarccos #tgarctg #ctgarcctg #cosarcsin #sinarccos #тригонометрическиефункцииалгебра10 #МатематикаОтБаканчиковой
тригонометрия, алгебра тригонометрические функции, тригонометрические функции алгебра 10, обратные тригонометрические функции, синус от арксинуса, косинус от арккосинуса, тангенс от арктангенса, котангенс от арккотангенса, sin arcsin, cos arccos, tg arctg, ctg arcctg, cos arcsin, sin arcos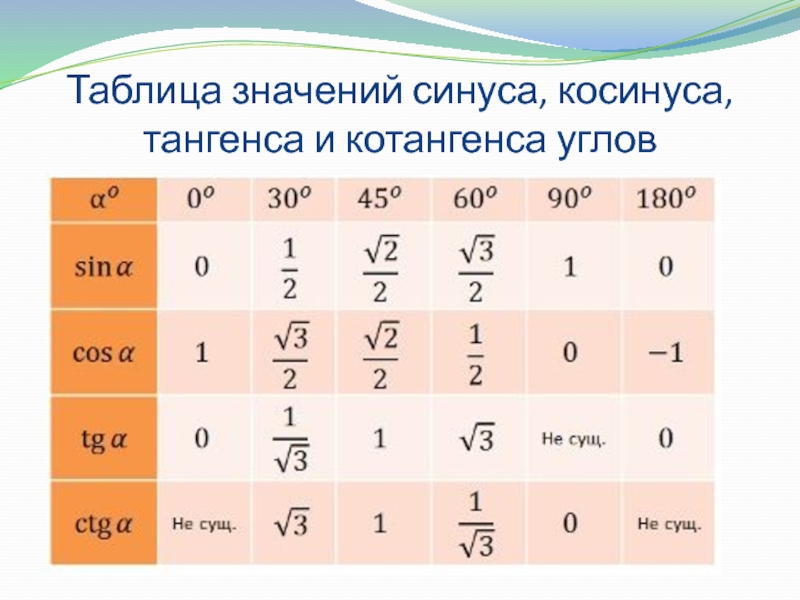 Согласно теореме Пифагора
Согласно теореме Пифагора Итак, чтобы вычислить косинус, вам нужно будет найти гипотенузу по теореме Пифагора:
Итак, чтобы вычислить косинус, вам нужно будет найти гипотенузу по теореме Пифагора: Наша смежная сторона будет другой стороной, имеющей в качестве вершины .
Наша смежная сторона будет другой стороной, имеющей в качестве вершины .

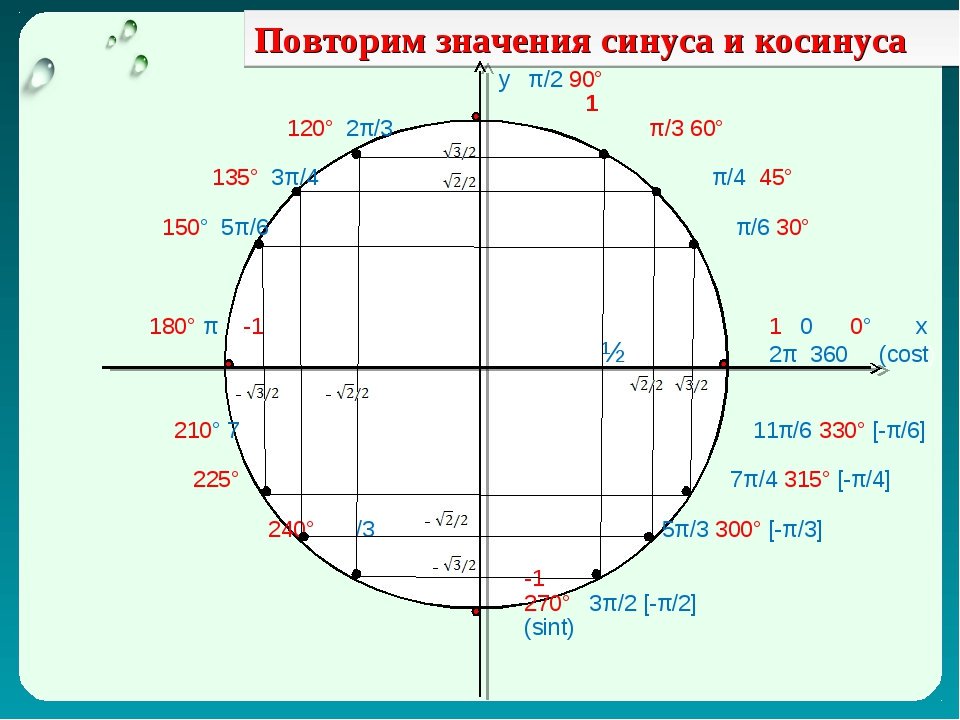

 Итак, получаем x = -4y — 2.
Итак, получаем x = -4y — 2. Давайте поймем разницу между этими двумя методами с помощью приведенной ниже таблицы:
Давайте поймем разницу между этими двумя методами с помощью приведенной ниже таблицы:


 Из этого уравнения найдем значение x через y, то есть x = 5-y. Теперь подставляем это значение в уравнение 2, получаем 3(5-y)+y=11.
Из этого уравнения найдем значение x через y, то есть x = 5-y. Теперь подставляем это значение в уравнение 2, получаем 3(5-y)+y=11. В этом методе мы подставляем значение переменной, найденное одним уравнением, во второе уравнение. Его очень легко использовать, когда у нас есть меньшие числа, но в случае больших чисел или дробных коэффициентов применять метод подстановки становится утомительно.
В этом методе мы подставляем значение переменной, найденное одним уравнением, во второе уравнение. Его очень легко использовать, когда у нас есть меньшие числа, но в случае больших чисел или дробных коэффициентов применять метод подстановки становится утомительно.
 Затем мы подставляем это значение в другое уравнение, чтобы найти значение y. Наконец, мы снова подставляем значение y в любое заданное уравнение, чтобы найти x.
Затем мы подставляем это значение в другое уравнение, чтобы найти значение y. Наконец, мы снова подставляем значение y в любое заданное уравнение, чтобы найти x. (Прямые параллельны.)
(Прямые параллельны.)

