| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | sin(45 град. ) ) |
|
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град.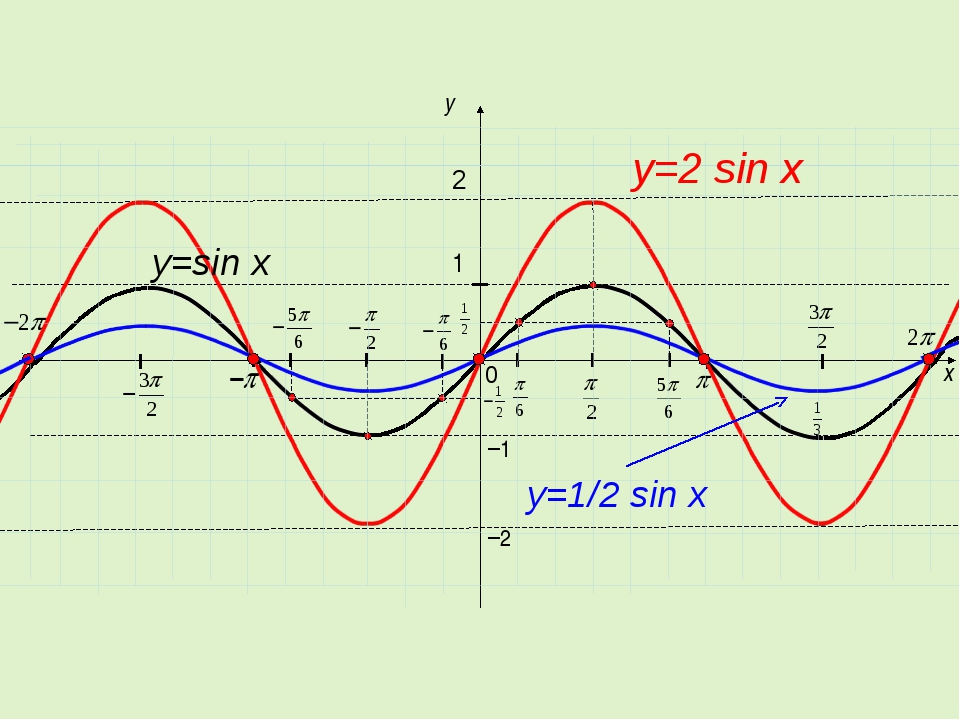 ) ) |
|
| 17 | Найти точное значение | sec(30 град. ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень 3) | |
| 24 | Найти точное значение | csc(60 град.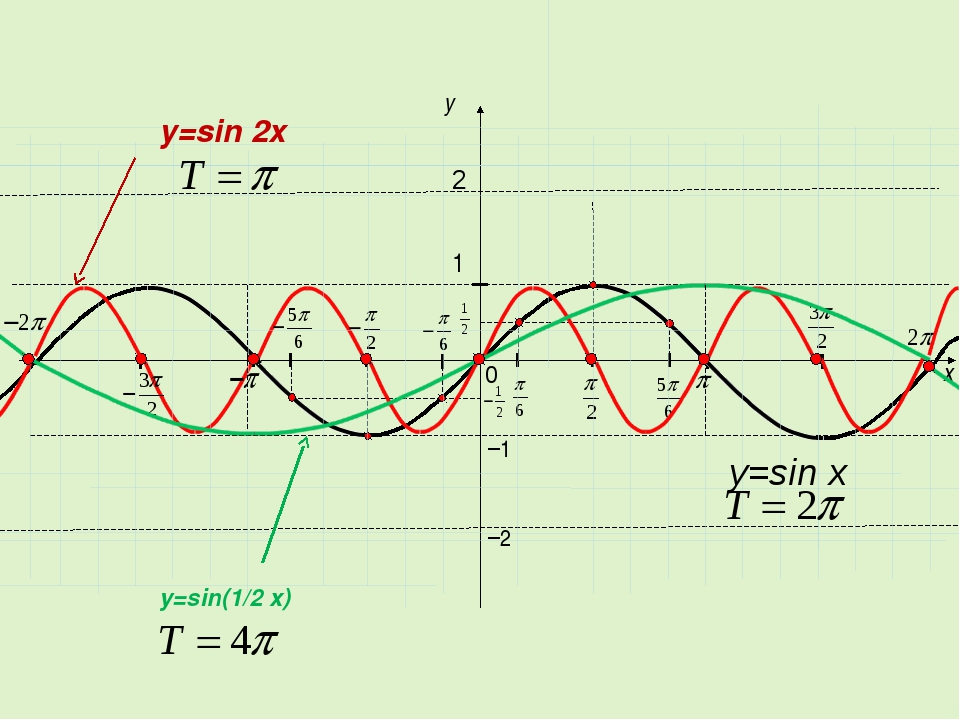 ) ) |
|
| 25 | Найти точное значение | sec(45 град. ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) ) |
|
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) ) |
|
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) ) |
|
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) ) |
|
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) ) |
|
| 77 | Найти точное значение | arctan(-( квадратный корень 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) ) |
|
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град.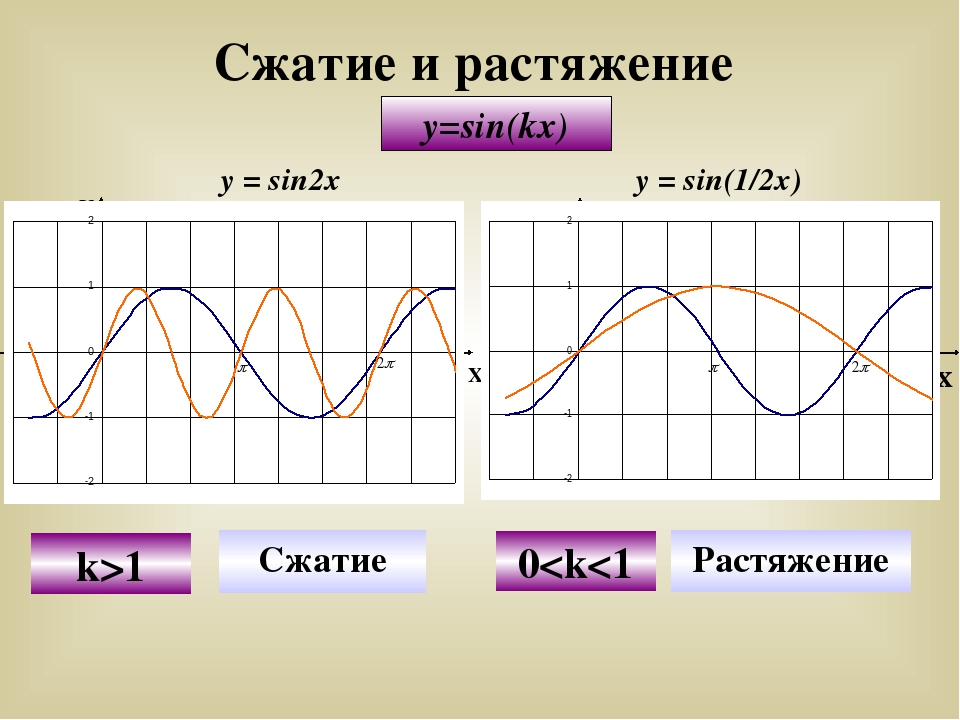 ) ) |
|
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град.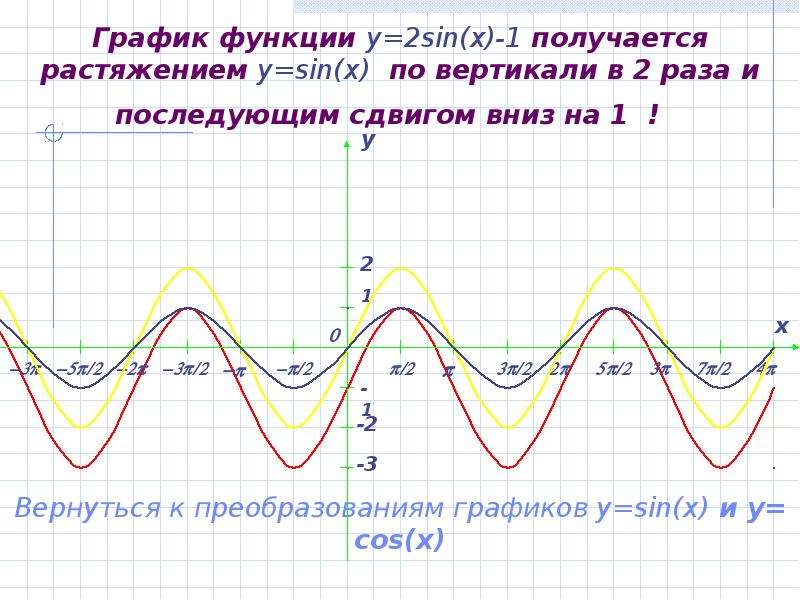 ) ) |
|
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | sin(45 град. ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град.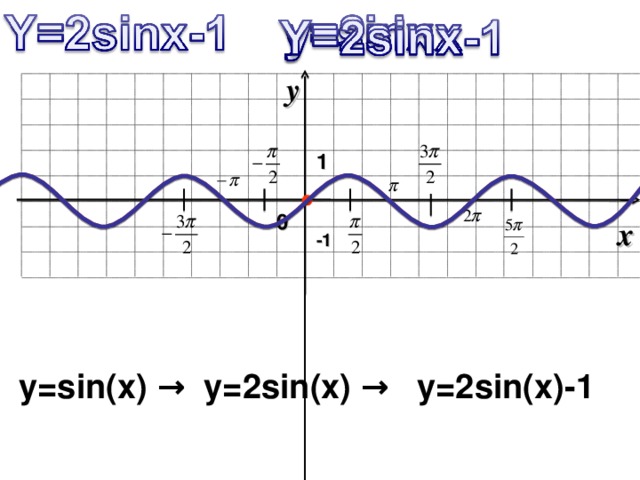 ) ) |
|
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) ) |
|
| 23 | Найти точное значение | arctan(- квадратный корень 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град.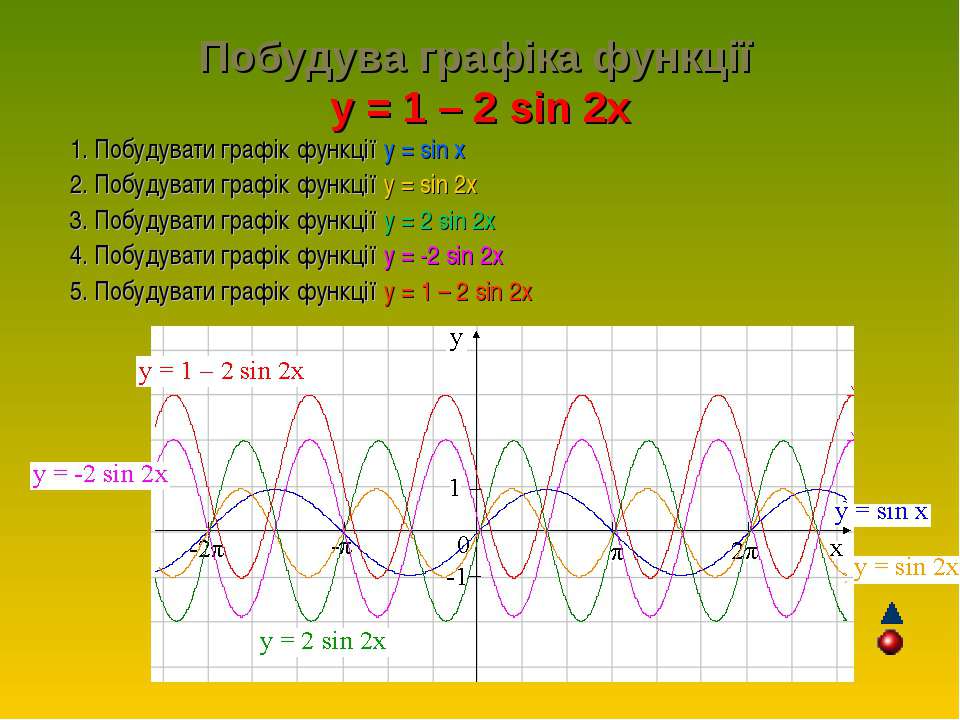 ) ) |
|
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град.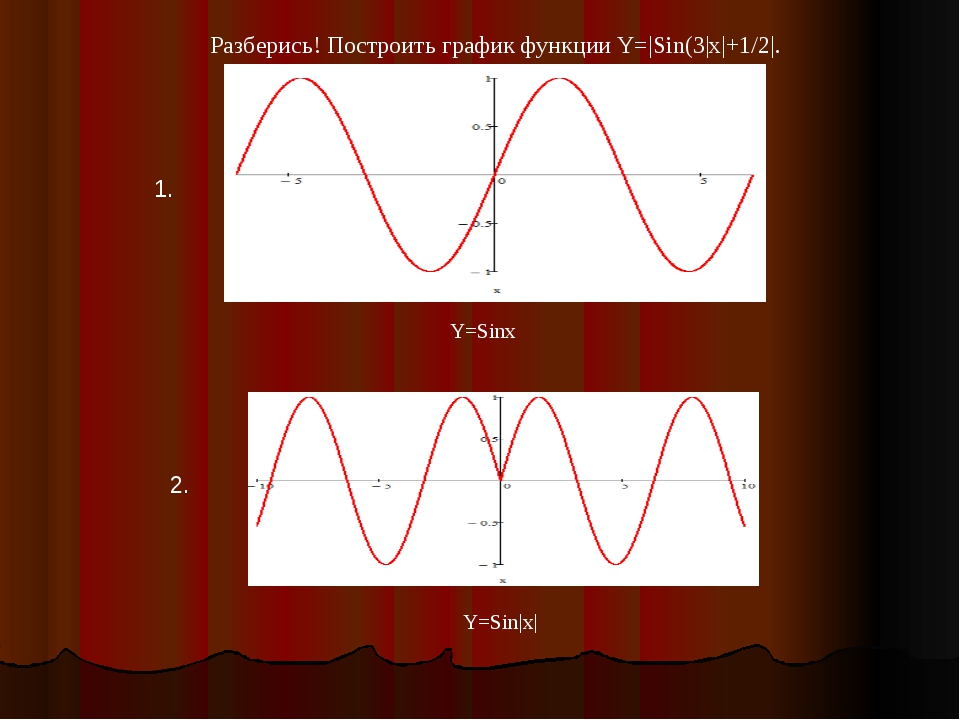 ) ) |
|
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град.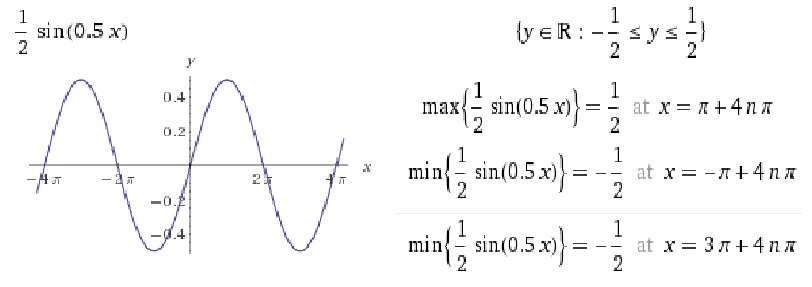 ) ) |
|
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град.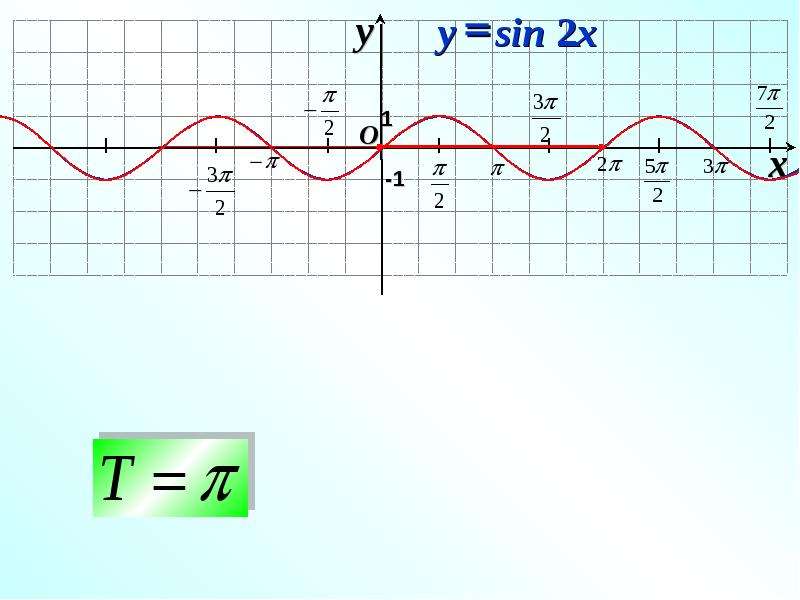 ) ) |
|
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) ) |
|
| 77 | Найти точное значение | arctan(-( квадратный корень 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град.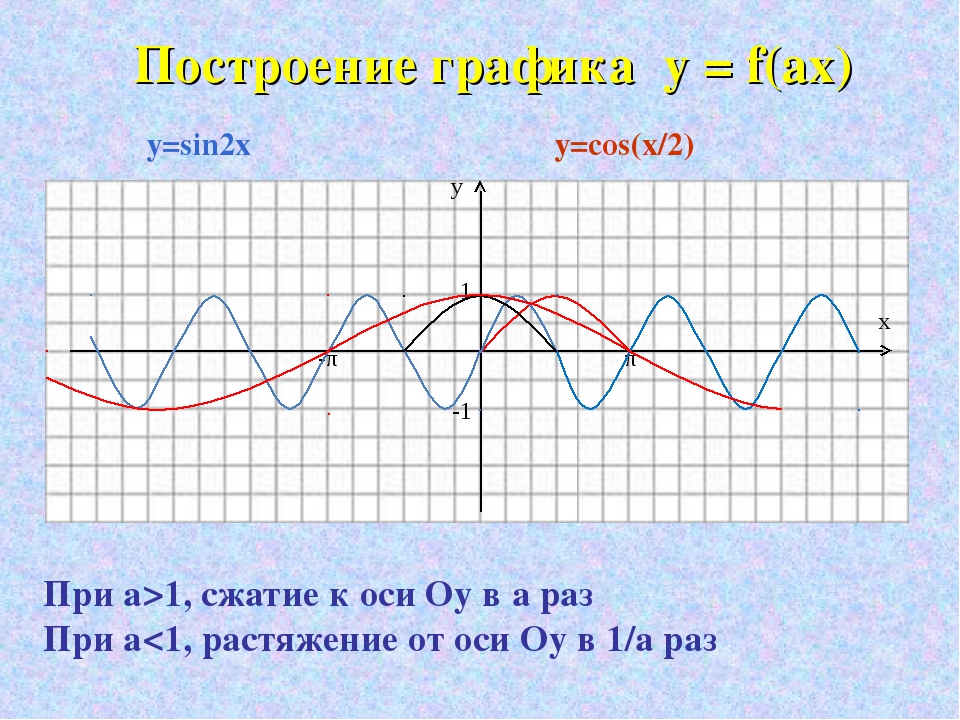 ) ) |
|
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град.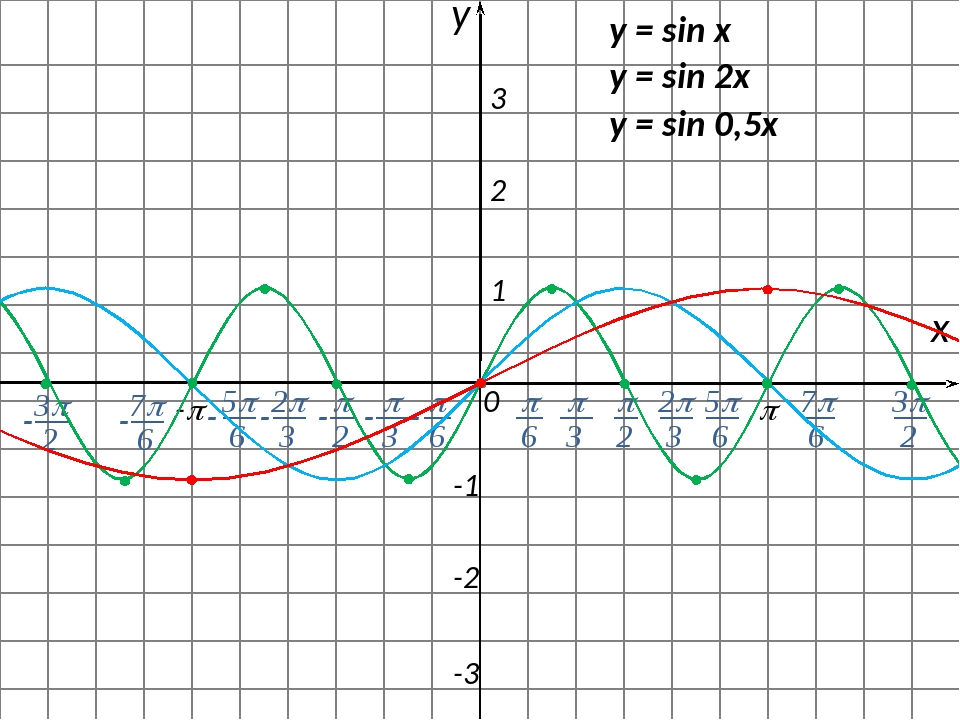 ) ) |
|
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
График функции y=sin x. Построить график функции у=sin2x и у=sin График функции y sin 2x
Построить функцию
Мы предлагаем вашему вниманию сервис по потроению графиков функций онлайн, все права на который принадлежат компании Desmos . 2/16=1)
2/16=1)
С нами легко в режиме онлайн строить графики различной сложности. Построение производится мгновенно. Сервис востребован для нахождения точек пересечения функций, для изображения графиков для дальнейшего их перемещения в Word документ в качестве иллюстраций при решении задач, для анализа поведенческих особенностей графиков функций. Оптимальным браузером для работы с графиками на данной странице сайта является Google Chrome. При использовании других браузеров корректность работы не гарантируется.
Как построить график функции y=sin x? Для начала рассмотрим график синуса на промежутке .
Единичный отрезок берём длиной 2 клеточки тетради. На оси Oy отмечаем единицу.
На оси Oy отмечаем единицу.
Для удобства число π/2 округляем до 1,5 (а не до 1,6, как требуется по правилам округления). В этом случае отрезку длиной π/2 соответствуют 3 клеточки.
На оси Ox отмечаем не единичные отрезки, а отрезки длиной π/2 (через каждые 3 клеточки). Соответственно, отрезку длиной π соответствует 6 клеточек, отрезку длиной π/6 — 1 клеточка.
При таком выборе единичного отрезка график, изображённый на листе тетради в клеточку, максимально соответствует графику функции y=sin x.
Составим таблицу значений синуса на промежутке :
Полученные точки отметим на координатной плоскости:
Так как y=sin x — нечётная функция, график синуса симметричен относительно начала отсчёта — точки O(0;0). С учётом этого факта продолжим построение графика влево, то точки -π:
Функция y=sin x — периодическая с периодом T=2π. Поэтому график функции, взятый на на промежутке [-π;π], повторяется бесконечное число раз вправо и влево.
«Построение графика функции с модулем» — Y = lnx. Закрепили знания на ранее изученных функциях. Построение графиков функций. Вопрос классу. Y = x2 – 2x – 3. Проектная деятельность. Урок обобщения и систематизации знаний. График функции. Актуализация знаний о графиках функций. Обобщение. Попробуйте самостоятельно построить графики. Y = f(x).
Закрепили знания на ранее изученных функциях. Построение графиков функций. Вопрос классу. Y = x2 – 2x – 3. Проектная деятельность. Урок обобщения и систематизации знаний. График функции. Актуализация знаний о графиках функций. Обобщение. Попробуйте самостоятельно построить графики. Y = f(x).
««Графики функций» 9 класс» — Цели урока. Большему значению аргумента соответствует большее значение функции. Нули функции. Определение. Заполните пропуски. Установите соответствие между функцией и вершиной. Тренажер. Выберите уравнение, с помощью которого задана линейная функция. Установите соответствие. Выберите уравнение. Обратная пропорциональность.
«Графики функций с модулями» — Найдём вершину функции. Кубическая функция. Отрицательная сторона. Графики функций. Квадратичная функция. Сложная функция. Функция с модулем. Графики функций надо обязательно уметь строить. Подготовка к ЕГЭ. Графики функций с модулями. Парабола. График функции.
«Уравнение касательной к графику функции» — Производная в точке. Правила дифференцирования. График функции. Алгоритм нахождения уравнения. Ответьте на вопросы. Геометрический смысл производной. Номера из учебника. Уравнение касательной к графику функции. Определение. Касательная к графику функции. Основные формулы дифференцирования. Провести касательную.
Правила дифференцирования. График функции. Алгоритм нахождения уравнения. Ответьте на вопросы. Геометрический смысл производной. Номера из учебника. Уравнение касательной к графику функции. Определение. Касательная к графику функции. Основные формулы дифференцирования. Провести касательную.
«Построение графиков функций» — Построение графика функции y = sinx. Линия тангенсов. Алгебра. Тема: Построение графиков функций. График функции y = sinx. Выполнила: Филиппова Наталья Васильевна учитель математики Белоярская средняя общеобразовательная школа №1. Построить график функции y=sin(x) +cos(x).
«График обратной пропорциональности» — Применение гиперболы. Гипербола. Монотонность функции. Чётность, нечётность. Функция «Обратная пропорциональность». График. Построение графика обратной пропорциональности. Гипербола и космические спутники. Однополостной гиперболоид. Асимптота. Применение гиперболоидов. Определение обратной пропорциональности.
Всего в теме 25 презентаций
Урок и презентация на тему: «Функция y=sin(x).
 Определения и свойства»
Определения и свойства»Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.
Пособия и тренажеры в интернет-магазине «Интеграл» для 10 класса от 1С
Решаем задачи по геометрии. Интерактивные задания на построение для 7-10 классов
Программная среда «1С: Математический конструктор 6.1»
Что будем изучать:
- Свойства функции Y=sin(X).
- График функции.
- Как строить график и его масштаб.
- Примеры.
Свойства синуса. Y=sin(X)
Ребята, мы уже познакомились с тригонометрическими функциями числового аргумента. Вы помните их?
Давайте познакомимся поближе с функцией Y=sin(X)
Запишем некоторые свойства этой функции:
1) Область определения – множество действительных чисел.
2) Функция нечетная. Давайте вспомним определение нечетной функции. Функция называется нечетной если
выполняется равенство: y(-x)=-y(x).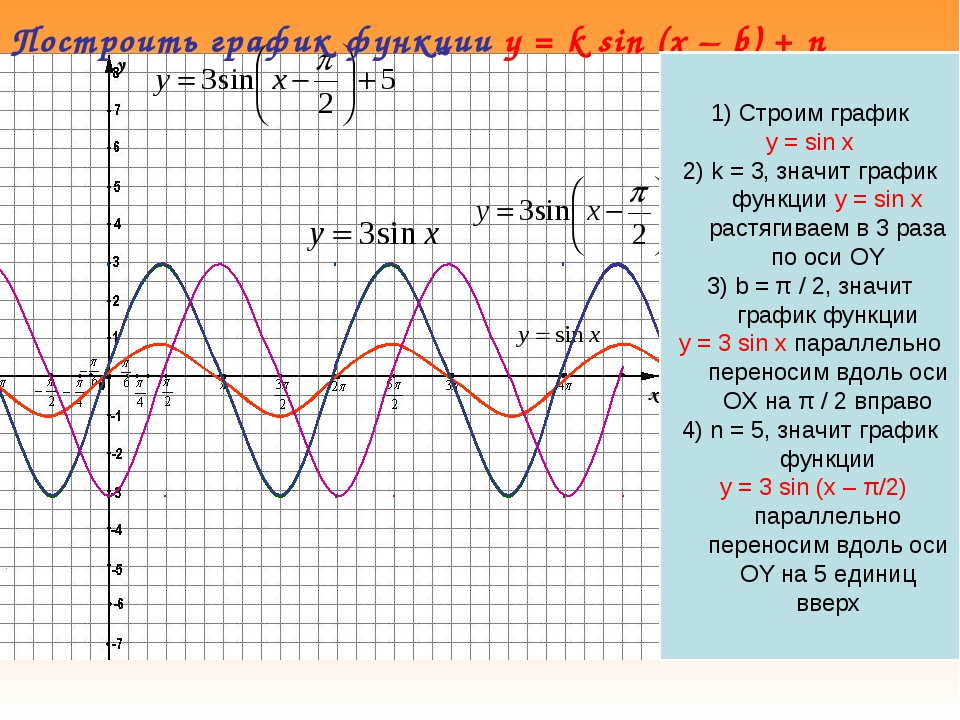 Как мы помним из формул привидения: sin(-x)=-sin(x). Определение выполнилось, значит Y=sin(X) – нечетная функция.
Как мы помним из формул привидения: sin(-x)=-sin(x). Определение выполнилось, значит Y=sin(X) – нечетная функция.
3) Функция Y=sin(X) возрастает на отрезке и убывает на отрезке [π/2; π]. Когда мы движемся по первой четверти (против часовой стрелки), ордината увеличивается, а при движении по второй четверти она уменьшается.
4) Функция Y=sin(X) ограничена снизу и сверху. Данное свойство следует из того, что
-1 ≤ sin(X) ≤ 1
5) Наименьшее значение функции равно -1 (при х = — π/2+ πk). Наибольшее значение функции равно 1 (при х = π/2+ πk).
Давайте, воспользовавшись свойствами 1-5, построим график функции Y=sin(X). Будем строить наш график последовательно, применяя наши свойства. Начнем строить график на отрезке .
Особое внимание стоит обратить на масштаб. На оси ординат удобнее принять единичный отрезок равный 2 клеточкам, а на оси абсцисс — единичный отрезок (две клеточки) принять равным π/3 (смотрите рисунок).
Построение графика функции синус х, y=sin(x)
Посчитаем значения функции на нашем отрезке:
Построим график по нашим точкам, с учетом третьего свойства.
Таблица преобразований для формул привидения
Воспользуемся вторым свойством, которое говорит, что наша функция нечетная, а это значит, что ее можно отразить симметрично относительно начало координат:
Мы знаем, что sin(x+ 2π) = sin(x). Это значит, что на отрезке [- π; π] график выглядит так же, как на отрезке [π; 3π] или или [-3π; — π] и так далее. Нам остается аккуратно перерисовать график на предыдущем рисунке на всю ось абсцисс.
График функции Y=sin(X) называют — синусоидой.
Напишем еще несколько свойств согласно построенному графику:
6) Функция Y=sin(X) возрастает на любом отрезке вида: [- π/2+ 2πk; π/2+ 2πk], k – целое число и убывает на любом отрезке вида: [π/2+ 2πk; 3π/2+ 2πk], k – целое число.
7) Функция Y=sin(X) – непрерывная функция. Посмотрим на график функции и убедимся что у нашей функции нет разрывов, это и означает непрерывность.
8) Область значений: отрезок [- 1; 1]. Это также хорошо видно из графика функции.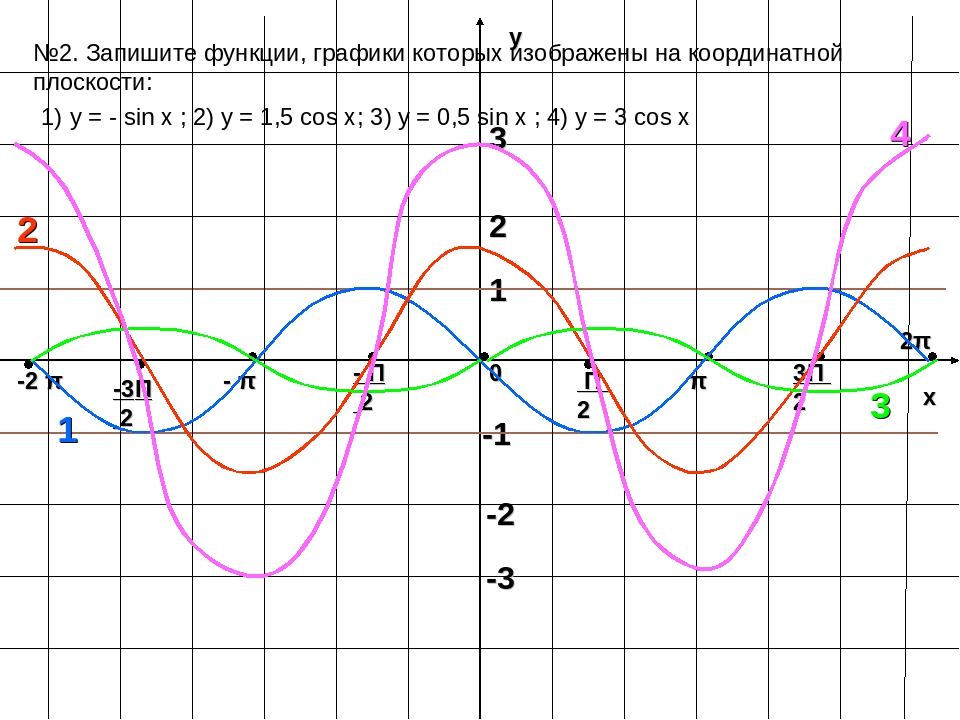
9) Функция Y=sin(X) — периодическая функция. Посмотрим опять на график и увидим, что функция принимает одни и те же значения, через некоторые промежутки.
Примеры задач с синусом
1. Решить уравнение sin(x)= x-π
Решение: Построим 2 графика функции: y=sin(x) и y=x-π (см. рисунок).
Наши графики пересекаются в одной точке А(π;0), это и есть ответ: x = π
2. Построить график функции y=sin(π/6+x)-1
Решение: Искомый график получится путем переноса графика функции y=sin(x) на π/6 единиц влево и 1 единицу вниз.
Решение: Построим график функции и рассмотрим наш отрезок [π/2; 5π/4].
На графике функции видно, что наибольшие и наименьшие значения достигаются на концах отрезка, в точках π/2 и 5π/4 соответственно.
Ответ: sin(π/2) = 1 – наибольшее значение, sin(5π/4) = наименьшее значение.
Задачи на синус для самостоятельного решения
- Решите уравнение: sin(x)= x+3π, sin(x)= x-5π
- Построить график функции y=sin(π/3+x)-2
- Построить график функции y=sin(-2π/3+x)+1
- Найти наибольшее и наименьшее значение функции y=sin(x) на отрезке
- Найти наибольшее и наименьшее значение функции y=sin(x) на отрезке [- π/3; 5π/6]
Преобразование графиков функций.
 Система творческих задач. | Методическая разработка по алгебре (9 класс) по теме:
Система творческих задач. | Методическая разработка по алгебре (9 класс) по теме:Преобразование графиков функций. Системы творческих задач.
Развитие познавательного интереса учащихся к математике должно иметь системный характер. Поэтому для решения этой проблемы можно использовать систему творческих задач. Нами была выбрана тема: «Преобразование графиков функций», т.к. педагогический эксперимент проходил во второй четверти с учащимися 10 класса, которые уже изучили данную тему. Преобразование графиков функций, построение графиков функций позволяет разнообразить виды выполняемых заданий, использовать математические знания при изображении «рисунков», проявить свои творческие способности, использовать в процессе обучение знания по информатике, что делает обучение более интересным и увлекательным.
Данную тему с учащимися изучать на факультативных занятиях. Конечно, можно изучать предложенную тему и на уроках, но для этого не предусмотрено времени. Если только на уроках давать основные правила преобразований функций, а саму систему творческих задач задавать в виде домашнего задания.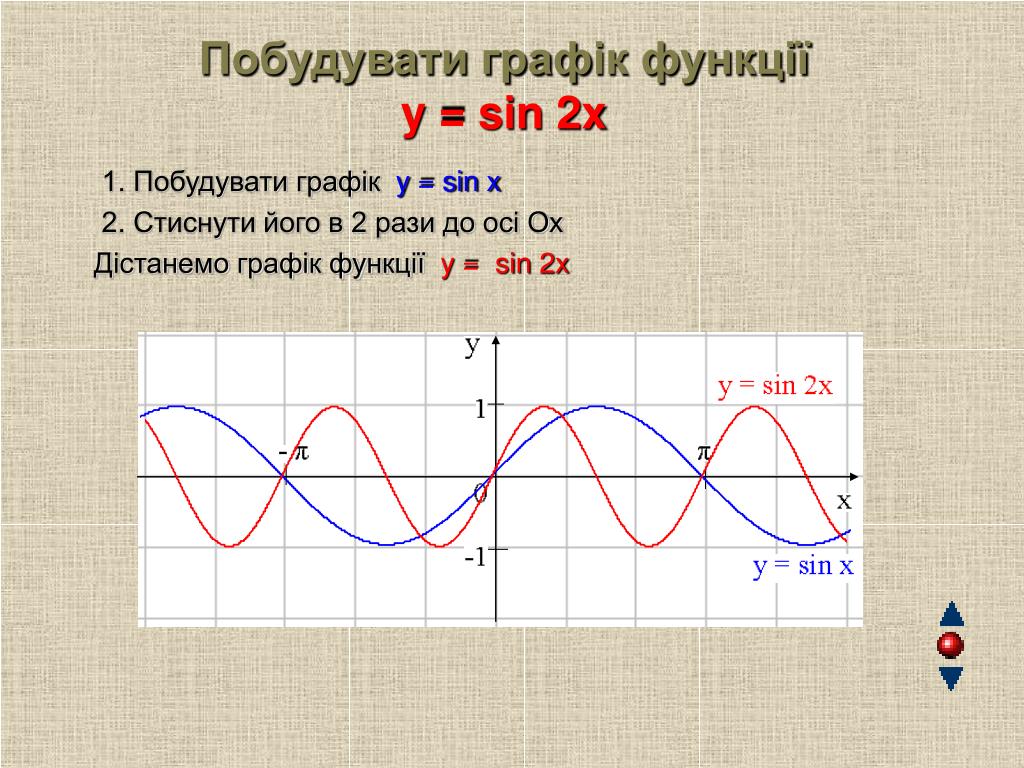
Рассмотрим основные преобразования графиков функций, которые можно вынести для изучения на факультативные занятия:
Построение графиков путем сдвига графиков основных функций
1. Чтобы построить график функции y=f(x)=с, нужно график функции y=f(x) сдвинуть вдоль оси Оу на с единиц в ту сторону, совпадающую со знаком с.
y=x2+2
y=x2
y=x2-4
2. Чтобы построить график функции y=f(x+с), нужно график функции y=f(x) сдвинуть вдоль оси Ох на с единиц в ту сторону, противоположенную знаку с.
y=x2
y=(x+2)2 y=(x-2)2
Преобразование графиков путем симметричного отображения относительно осей координат графика основной функции
- Чтобы построить график функции y=-f(x),нужно построить изображение симметричное графику функции y=f(x) относительно оси Ох.

y=x2-x
y=-(x2-x)
4. Чтобы построить график функции y=f(-x), нужно построить изображение, симметричное графику функции y=f(x), относительно оси Оу.
Y=sin(-x)
Y=sin(x)
Построение графиков функций путем деформации (сжатия или растяжения) графиков основных функций
5.Чтобы построить график функции y=аf(x), при а>0, надо график функции y=f(x) растянуть вдоль оси Оу при а>1 и сжать вдоль оси Оу при 0
Y=4cos(x)
y=1/2cos(x)
Y=cos(x)
6. Чтобы построить график функции у=f(wx) при w>0, нужно график функции у=f(х) сжать вдоль оси Ох, если w>1. И растянуть вдоль оси Ох, если 0
Чтобы построить график функции у=f(wx) при w>0, нужно график функции у=f(х) сжать вдоль оси Ох, если w>1. И растянуть вдоль оси Ох, если 0
y=sin(x) y=sin(2x)
y=sin(1/2x)
Преобразование графиков функций, аналитическое выражение которых содержит знак абсолютной величины
7. у=f(|x|). Функция у=f(х) четная. Чтобы построить ее график, достаточно построить для х≥0 график функции у=f(х), а затем отобразить его относительно оси Оу
Y=1/4×2+|x|-2 Y=1/4×2+x-2
8. у=|f(x)|. Можно данную функцию рассматривать как совокупность двух функций
f(x), где f(x)≥0
y=
-f(x), где f(x)
Чтобы построить график функции у=|f(х)|, достаточно построить график функции у=f(х), и ту часть графика которая расположена в нижней полуплоскости, симметрично отобразить относительно оси Ох.
y=|1/4×2-x-2|
y=1/4×2-x-2
9. Чтобы построить график функции |y|=f(x), у=х/6
Чтобы построить график функции |y|=f(x), у=х/6
достаточно построить график функции у=f(х),
и ту часть графика, которая расположена |y|=x/6
в верхней полуплоскости симметрично
отобразить относительно оси Ох.
10. у=|f(|x|)|. Можно данную функцию рассматривать как совокупность двух функций f(|x|), где f(x)≥0
y=
-f(|x|), где f(x)
Чтобы построить график функции, у=|f(|x|)|, достаточно построить график функции у=f(х), и ту часть графика которая расположена в нижней полуплоскости, симметрично отразить относительно оси Ох. Затем получившийся график симметрично отобразить относительно оси Оу.
y=|1/4×2-|x|-2|
y=1/4×2-x-2
Сложение и вычитание графиков
11. Чтобы построить график функции у=f(x)±w(x).надо построить сначала график одной более простой функции, а затем к нему пристроить график второй более простой функции, ординаты которого откладываются от соответствующих точек первого графика. Разность представляют в виде суммы и строят выше указанным способом.
Чтобы построить график функции у=f(x)±w(x).надо построить сначала график одной более простой функции, а затем к нему пристроить график второй более простой функции, ординаты которого откладываются от соответствующих точек первого графика. Разность представляют в виде суммы и строят выше указанным способом.
Y=x-sin(2x)
Y=x
y=cos(2x)
Умножение и деление графиков
12.Чтобы построить график функции у=f(x)w(x), надо построить графики функций у=f(x) и у=w(x), и перемножить значения ординат, соответствующие одним и тем же значениям аргумента. Деление графиков можно привести к умножению.
y=x
y=xsin(5x)
Система творческих задач в процессе обучения преобразованию графиков функции
- Задачи на первый тип преобразования y=f(x)=c.

1.1. «Лопата»
y=x2-4, [-1.5;1.5];
y=-1.7, [-1.5;1.5];
y=3, [-1;1];
x=0, [-1.7;3].
1.2. «Китаец»
y=x2-1, [-0.5;0.5];
y=2, и y=2.2, [-3;3];
y=1, [-1.5;-0.5] и [0.5;1.5];
y=x2-2, [-2;2].
2. Задачи на второй тип преобразования y=f(x±c).
2.1. «Цветочек»
y=sin(x),
y=sin(x+3), [-3;3];
x=sin(y),
x=sin(y+3),
y=x, [-4;0];
x=-4 и y=-4, [-4;-1];
точка:[0;0].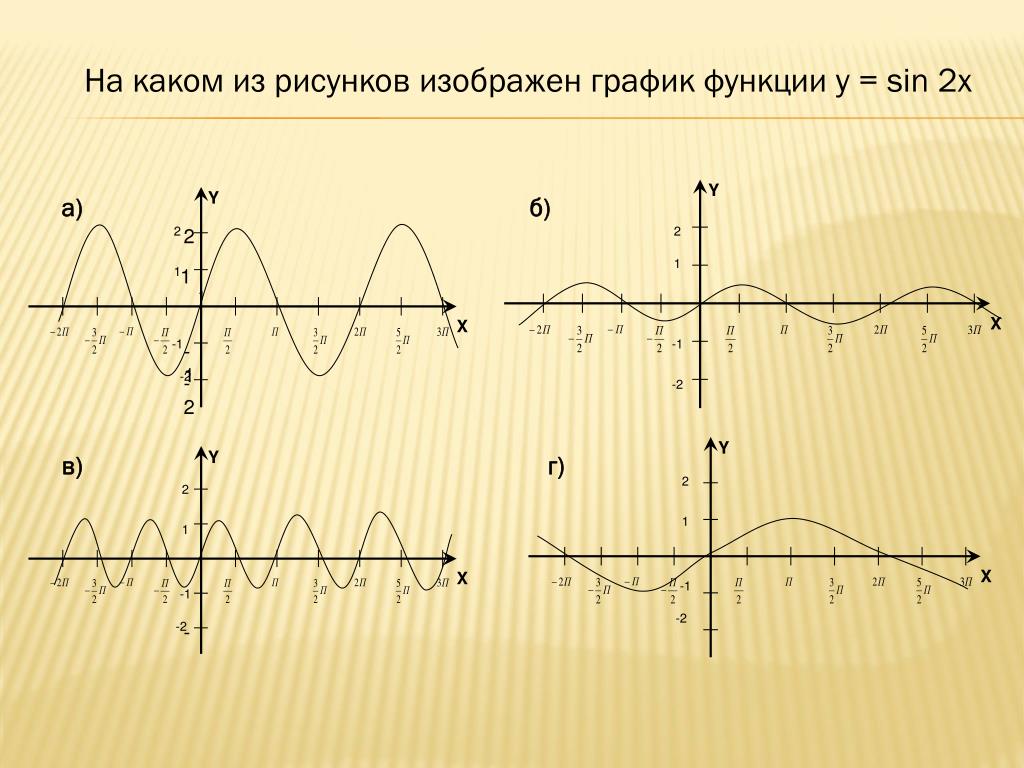
2.2. «Ваза».
x=sin(y+3)+2,
x=sin(y)-2, [-3;3];
y=sin(x)-1.5,
y=sin(x+3)-1.5,
y=3 и y=-3, [-2;2];
y=-0.5 и y=-2.5, [-2.5;2.5];
y=cos (x)-1.5 и cos(x+3)-1.5, [-1.5;1.5]
3. Задачи на третий тип преобразований y=-f(x).
3.1. «Девочка»
y=-2,
y=-x2+2, [-2;2];
y=-x2+4,
y=x2+2, [-1;1];
точки: [-0.5;3];[0.5;3];[0;2.5].
3.2. «Грибок»
y=x2-4, [-1;1];
y=-x2+5, y=1, [-2;2];
x=-1, x=1, [-3;1].
3.3. «Человечек»
y=-x2+5,
[-1;1];
y=x2+3,
y=cos(x),
[-3;3];
y=cos(x)+2 ,
y=x2+1, [-1.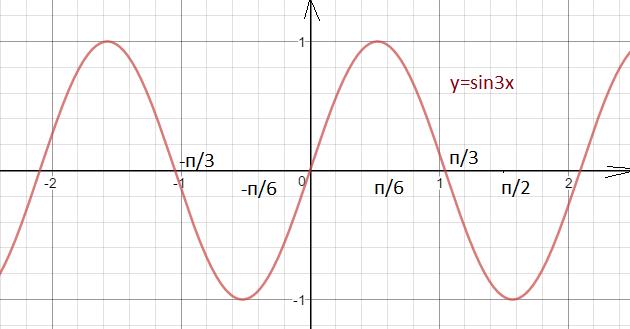 2;1.2];
2;1.2];
точки: [-1.5;4],[1.5;4],[0;4].
4. Задачи на четвертый тип преобразований y=f(-x).
4.1. «Сороконожка»
y=sin(x),
y=sin(x)+0.5, [0;5];
y=sin(x)-0.5,
y=sin(-x),
y=sin(-x)+0.5, [-5;0];
y=sin(-x)-0.5,
y=x2-1,
[-1;1];
y=-x2+1, точки: [-1.5;-1.5], [1.5;-1.5].
4.2. «Очки»
y=sin(x), [-5;3];
y=sin(-x), [-3;5];
4.3. «Бокал»
x=-sin(у),
[-6;0];
x=-sin(у)+0.5,
y=x2,
y=cos(1/2x)+9, [-3;3];
y=-cos(1/2x)+9,
y=-6, [-2;2].
5. Задачи на пятый тип преобразования y=af(x)
5.1. «Восьмерка»
x=2sin(y),
x=2sin(-y), [-3;3].
x=sin(y),
x=sin-(-y),
5.2. «Тройка»
x=2sin(y), [0;3],[-3;-1.5];
x=2sin(-y),[1.5;3],[-3;0];
x=sin(y), [0;3],[-3;-1.5];
x=sin-(y), ),[1.5;3],[-3;0].
5.3. «Пятерка»
x=2sin(y), [-3;-1.5];
x=-2sin(y), [-3;0];
x=sin(y), [-3;-1.5];
x=-sin(y), [-3;0];
y=(x-1)2+1,
[0;2];
y=1/2(x-1)2+1. 5,
5,
x=0.5, x=0, [0;2];
y=0, y=2, [-0.5;0].
6.Задачи на шестой тип преобразований y=f(wx)
6.1. «Улыбка»
y=1/10×2-3, [-4.5;4.5];
y=-1, [-5;5];
y=sin(x), [0;5];
y=sin(-x), [-5;0].
6.2. «Зверь»
y=sin(1/2x),
y=sin(1/2x+3), [-6;6];
y=1/10×2-2, [-3;3];
y=1/3×2+6, [-4;4];
y=x2+1.5, [-1;1];
y=x+6, [0;3];
y=-x+6, [-3;0];
x=1/9(x-6)2-4,
[3;9].
x=-1/9(x-6)2+4,
6.3 «Ведро»
y=1/3×2-9, [-6;-3] и [3;6];
y=cos(1/4x)+3,
y=-cos(1/4x)+3, [-6;6];
y=6cos(1/4x)+3,
y=-6, [-3;3].
7. Задачи на седьмой тип преобразований y=f(|x|).
7.1 «Лягушка» y=-x2+|4x|,
y=-x2+|2x|, [-4;4];
y=1/6×2-4,
y=0, y=1/8×2-6, [-7;7];
y=-x2-1,[0;2];
y=-x2+1, [-2;0].
7.2 «Клещ»
,
[-4;4];
x=|1/4y2-4|,
|y|=|x|, [-4.5;-3] и [3;4.5];
y=2.5, [-2.5; 2.5];
точки: [-1;3], [1;3].
7.3 «Инопланетянин»
y=-1/4×2+7,
[-4;4];
y=x2-4|x|-1,
x=(y+1)2-8,
[-1;3];
x=-(y+1)2+8,
y=|x|+4, [-4;-2], [2;4];
точки: [-1;5], [1;5], [0;4],
[-4;8], [4;8].
8. Задачи на восьмой тип преобразования y=|f(x)|
8.1. «Сердце»
y=|2sin(x)|+3,
[-3;3];
y=|x|,
8.2. «Бабочка» y=|2sin(x/2)|+3,
[-6;6];
y=|1/2x|,
y=-|x|+2,
[-3;3];
y=-2|sin(x)|-1,
y=-x2+5,
[-1;1];
y=|x|+5,
точки: [0.5;4.5],[-0.5;4.5], [0;4].
9. Задачи на девятый тип преобразований |y|=f(x).
9.1. «Жук»
|y|=2sin(1/2x), [0;6];
|y|=x-6, [6;8];
|y|=x-1, [3;4];
|y|=x-3, [4.5;5.5];
|y|=-x-3, [0.5;1.5];
x=4.5, [-1.5;1.5];
точки: [5;0.5], [5;-0.5].
9.2. «Бантик»
|y|=, [-4;4];
x=4, x= -4, [-2;2];
y=-|x|, [-4;4];
y=-|2x|, [-2;2];
y=-4, [-4;-2] и [2;4].
9.3. «Морда»
|y|=|2sin(x)|+3, [-3;3];
|y|=|sin(x)|+3, [-3;3];
y=1/2sin|x|+3,
y=x-1 [-4.5;4.5];
y=|2/9x|-2
y=-x2+2, [-1;1];
точки: [-1.5;3], [1.5;3], [-0.5;1.5], [0.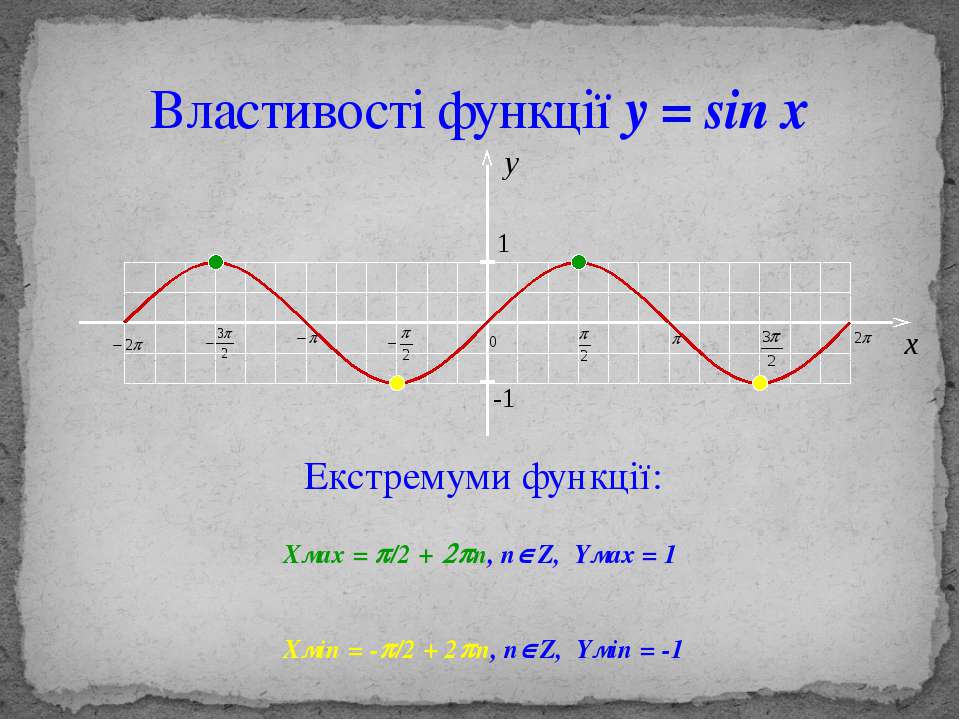 5;1.5].
5;1.5].
10. Задачи на десятый тип преобразований y=|f(|x|)|.
10.1. «Конфетка»
|y|=|log2|x||, [-2;2];
x=|1/2sin(6y)+2|,
[-1;1];
x=|1/2sin(6y)-2|,
y=1, y=-1, [-0.5;0.5].
10.2. «Птица»
|y|=|log2|x||, [-2;2];
x=|1/2sin(6y)+2|,
[-1;1];
x=|1/2sin(6y)-2|,
y=-2×2+1.5, [-0.5;0.5];
y=-cos(x)-2, [-1.5;1.5];
y=-10×2+2, [0.25;0.25];
y=x-0.5, [-1.5;-0.5];
y=-x-0.5,[0.5;1.5].
11. Задачи на одиннадцатый тип преобразований y=f(x)±w(x).
11.1. «Рыба» |y|=-1/8×2+2, [-4;4];
y=-1/8×2+|1/2sin(6x)|+2, [-1;3];
|y|=x+4, [4;6];
x=-2, [-1.5;1.5];
x=1/4(y-5)2;
[-2;2];
x=1/4(y-5)2+|sin(6y)|,
точка: [-3;1.5].
11.2. «Цветок» —
|y|=-1/10×2-1,
|y|=-1/10×2-1+|sin(3x)|
[-3;3];
y=|x|+|sin(x)|-5. 5
5
y=|x|-5.5
x=0, [-4.5;-1].
11.3. «Зонтик»
y=-1/5×2+4, [-5;5];
y=-1/25×2-|sin(3x)|, [-5;5];
y=-1/25×2,
y=6(x+1)2-6, [-1.5;0].
12. Задачи на двенадцатый тип преобразования y=f(x)w(x).
12.1. «Пирамидка»
x=ysin(2y),
[-7.5;0].
x=-ysin(2y),
12.2. «Рыбка»
y=sin(3x)x,
[-3.7;0];
x=sin(3y)y,
y=-x-5, [-3.3;-1.7];
точка: [-3;-2.5].
12.3. «Ёлочка»
x=ysin(3y),
[-10;0];
x=-ysin(3y),
y=10, [-10;10];
y=x2-11, [-1;1].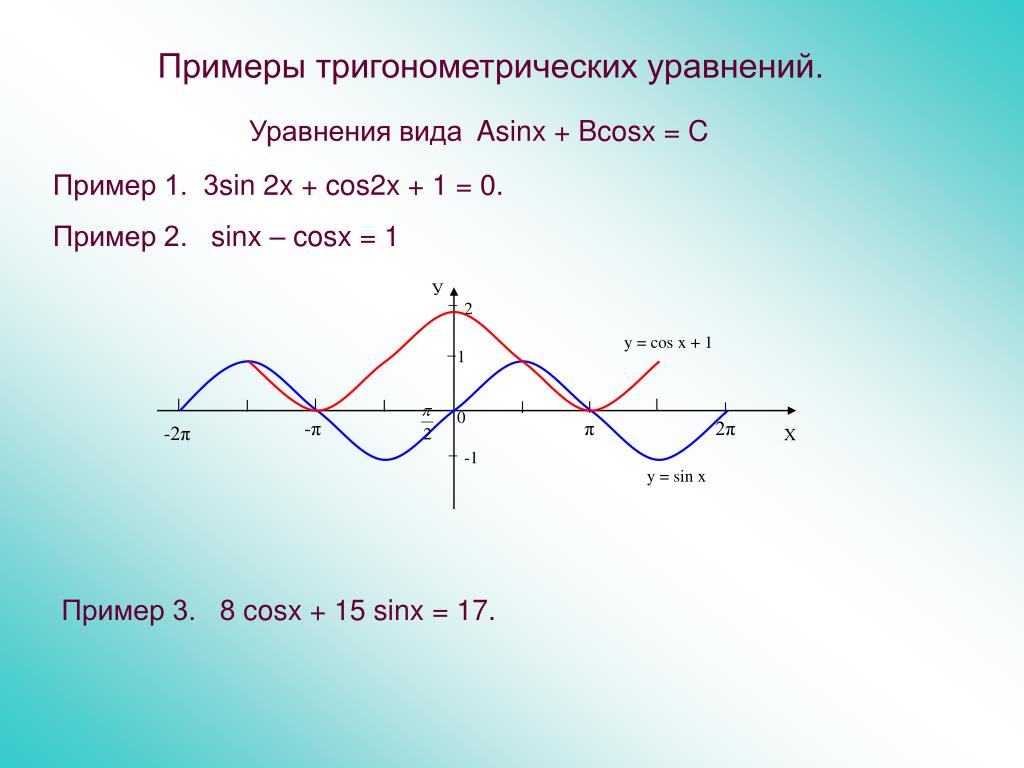
Обучающая часть.
Рассмотрим методику изучения данной темы на примере одного занятия:
1 занятие.
Тема: Преобразование графиков функций путем сдвига основных функций.
Оборудование: цветной мел, шаблоны (парабола), доска с системой координат.
Ход урока:
1.Сообщение темы и цели урока.
Учитель: Сегодня мы начинаем занятия по теме: «Преобразование графиков функций». Мы научимся различным преобразованиям, а главное мы будем с помощью преобразований создавать «картинки». Итак, начинаем первое занятие «Преобразование графиков функций путем сдвига основных функций». Мы будем подходить творчески к выполнению преобразованию графиков функций и будем строить «картинки», поэтому, обратите внимание на то что, на координатной плоскости мы будем строить несколько графиков функций, причем каждая функция будет рассматриваться на отдельном промежутке. Вспомогательные чертежи будем строить тонкой линией, выделяя только «основные» графики функции цветными карандашами (цветным мелом на доске).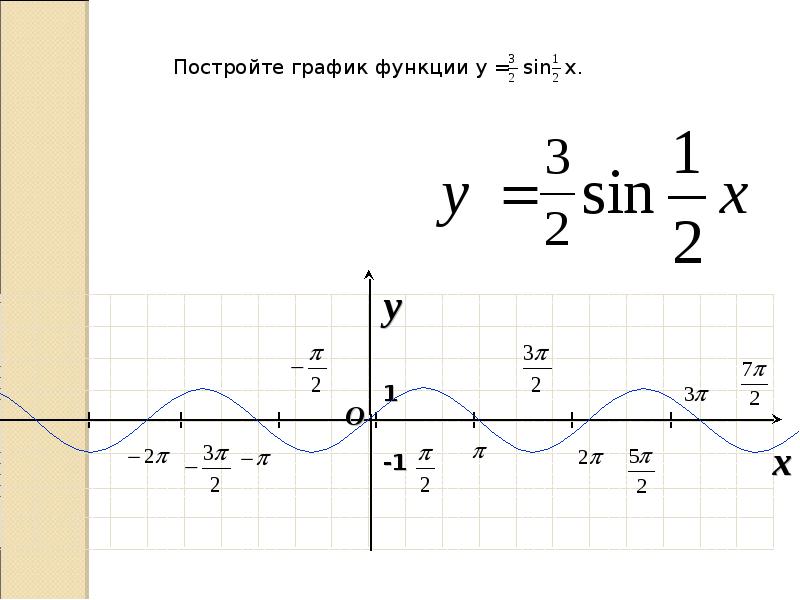
2. Изучение новой темы.
Учитель: Предложенная на сегодняшнем занятии тема не является для вас новой. Но мы еще раз повторим известные вам преобразования. Запишем в тетрадь правила преобразований:
- Чтобы построить график функции y=f(x)=с, нужно
график функции y=f(x) сдвинуть вдоль оси Оу на с единиц в ту сторону, совпадающую со знаком с.
2.Чтобы построить график функции y=f(x+с),
нужно график функции y=f(x) сдвинуть вдоль
оси Ох на с единиц в ту сторону,
противоположенную знаку с.
При написании правил учитель с помощью шаблона параболы демонстрирует учащимся, как совершать записанные преобразования.
После чего учитель выписывает на доску функции:
1) y=x2-1, [-0.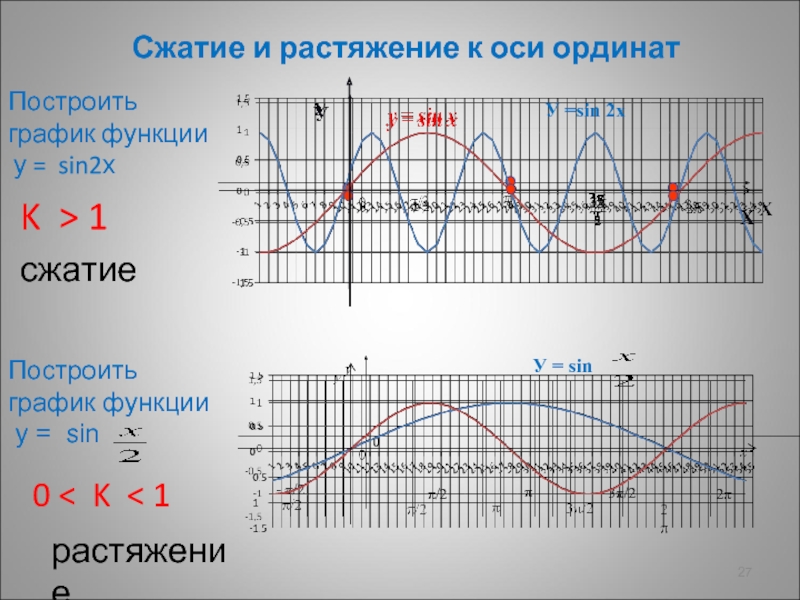 5;0.5]; 2) y=2, [-3;3]; 3) y=2.2, [-3;3]; 4) y=1, [-1.5;-0.5] и [0.5;1.5];
5;0.5]; 2) y=2, [-3;3]; 3) y=2.2, [-3;3]; 4) y=1, [-1.5;-0.5] и [0.5;1.5];
5) y=x2-2, [-2;2].
Работа учащихся с места.
Учитель: Посмотрите внимательно на первую функцию. Что будет являться графиком этой функции?
Ученик: Графиком этой функции будет парабола.
Учитель: С помощью какого преобразования будем строить график этой функции?
Ученик: С помощью параллельного переноса графика функции у=х2 вдоль оси ОУ на 1 единицу вниз.
Учитель: Что будет являться графиком других функций?
Ученик: Это будут прямые параллельные оси ОУ.
Учитель вызывает одного ученика построить графики предложенных функций. Перед выполнением каждого задания следует
обратить внимание учащихся на масштаб.
В данном случае за единичный отрезок удобнее
Принять две клетки.
В результате чего у учащихся должен
получиться следующий рисунок:
После чего учащимся предлагается следующее задание:
Учитель: Сейчас обратное задание по данному рисунку подобрать функции, задающие графики на определенных промежутках, составляющие рисунок:
Каждый у себя в тетради выполняет это задание.
Предполагаем следующую систему вопросов:
1. На каких промежутках рассматриваются графики функций.
2.Элементы графиков каких функций представлены на чертеже.
3. Какие преобразования совершаются.
Учитель вызывает одного
ученика записать полученные функции
затем всем классом проверяем правильность
выполнения задания.
Правильное решение: y=x2-4, [-1.5;1.5]; y=-1.7, [-1.5;1.5]; y=3, [-1;1];
x=0, [-1.7;3].
Аналогично разбираем и второе преобразование.
2.Постановка домашнего задания.
Учитель: Попробуйте самостоятельно придумать по одному рисунку на каждый из изученных типов преобразований и их комбинацию.
Все остальные занятия проводятся аналогично первому, только с нарастающей сложностью.
Рассмотрим примерный план каждого занятия.
1 занятие.
Тема: Преобразование графиков функций путем сдвига основных функций.
На первом занятии учащимся предлагались для повторения знакомые им преобразования y=f(x)=c и y=f(x+c). В начале были записаны правила данных преобразований, а после рассмотрены по одному примеру (1.2. и 2.2.) на каждый из типов преобразований.
В начале были записаны правила данных преобразований, а после рассмотрены по одному примеру (1.2. и 2.2.) на каждый из типов преобразований.
2 занятие.
Тема: Преобразование графиков путем симметричного отображения относительно осей координат графика основной функции.
На втором занятии учащимся были предложены следующие типы преобразований: y=-f(x) и y=f(-x). В начале были записаны правила данных преобразований, а после рассмотрены по одному примеру (3.1. и 4.1.) на каждый из типов преобразований.
3 занятие.
Тема: Построение графиков путем деформации (сжатия или растяжения) графиков основных функций.
На третьем занятии учащимся предлагались для повторения знакомые им преобразования y=аf(x) и y=f(wx). В начале были записаны правила данных преобразований, а после рассмотрены по одному примеру (5.3. и 6.3.) на каждый из типов преобразований.
4 занятие.
Тема: Преобразование графиков функций, аналитическое выражение которых содержит знак абсолютной величины.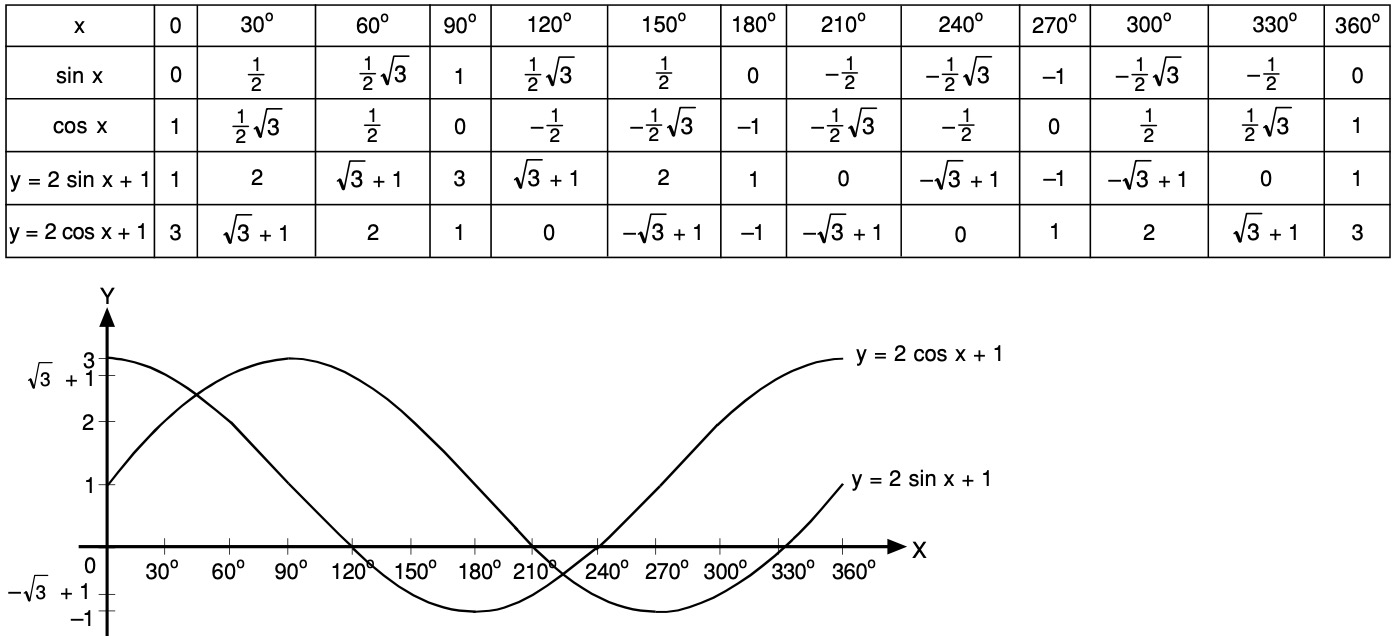
На четвертом занятии учащимся были предложены следующие типы преобразований y=f(|x|) и y=|f(x)|. В начале были записаны правила данных преобразований, а после рассмотрены по одному примеру (7.1. и 8.1.) на каждый из типов преобразований
5 занятие.
Тема: Преобразование графиков функций, аналитическое выражение которых содержит знак абсолютной величины.
На пятом занятии учащимся были предложены следующие типы преобразований |y|=f(x) и y=|f(|x|)|. В начале были записаны правила данных преобразований, а после рассмотрены по одному примеру (9.1. и 10.1.) на каждый из типов преобразований.
6 занятие.
Тема: Сложение и вычитание графиков. Сложение и умножение графиков.
На шестом занятии учащимся были предложены следующие типы преобразований y=f(x)±w(x) и y=f(x)w(x). В начале были записаны правила данных преобразований, а после рассмотрены по одному примеру (11.1. и 12.2.) на каждый из типов преобразований.
Общей целью формирования учебных умений было постепенное повышение в обучении роли продуктивных умений (умение видеть проблему, сформулировать ее, сделать выводы и обобщения и т.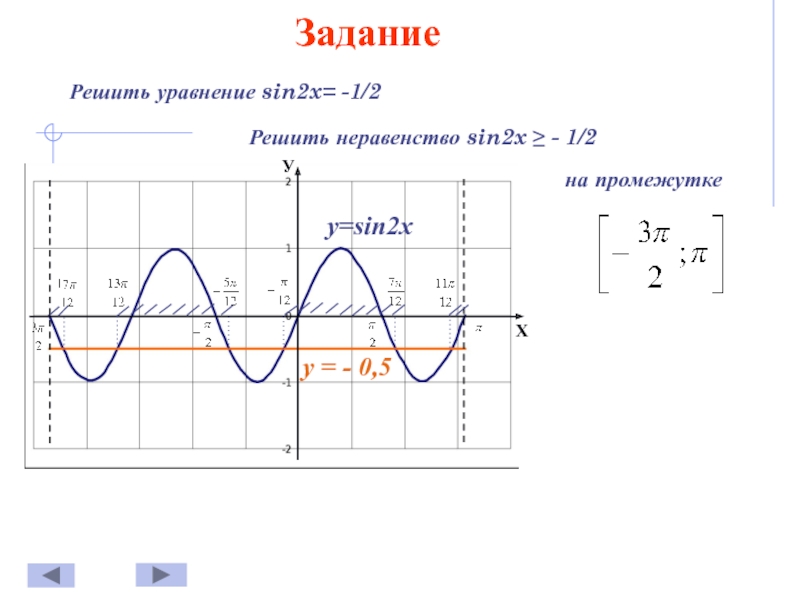 п.)
п.)
В результате наблюдений, были зафиксированы определенные изменения в структуре познавательного интереса к математике, говорящие об его развитии и переходе его у отдельных школьников на более высокий уровень.
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ, ИХ ГРАФИКИ И СВОЙСТВА
Функция y = cos x. Ее свойства и график
Функция y = cos x Ее свойства и график 1 Сегодня мы рассмотрим Построение графика функции y = cos x; Свойства функции y = cos x; Изменение графика функции y = cos x в зависимости от изменения функции и
ПодробнееТема 1.4 Функции, их свойства и графики
Тема. 4 Функции, их свойства и графики Автор: Переверзьева Н.С. Преподаватель математики Лицей 6 Цели урока: Ознакомиться с понятием «функция», закрепить его на примерах Усвоить новые термины Узнать методы
4 Функции, их свойства и графики Автор: Переверзьева Н.С. Преподаватель математики Лицей 6 Цели урока: Ознакомиться с понятием «функция», закрепить его на примерах Усвоить новые термины Узнать методы
Графики тригонометрических функций
Графики тригонометрических функций Функция у = sin x, ее свойства Преобразование графиков тригонометрических функций путем параллельного переноса Преобразование графиков тригонометрических функций путем
ПодробнееМатематика. Алгебра и начала анализа
А.В. Землянко Математика. Алгебра и начала анализа Воронеж СОДЕРЖАНИЕ ТЕМА 1. ОСНОВНЫЕ СВОЙСТВА ФУНКЦИИ… 6 1.1. Числовая функция… 6 1.2. График функции… 9 1.3. Преобразование графиков функции…
ПодробнееКонтрольная работа 2. 1 вариант. 2 вариант. 1). Для функции f (х) = 3х 2 х Найти f (0), f (1), f (-3), f (5).
Контрольная работа 1 вариант 1) Для f (х) = х + х 1 Найти f (), f (1), f (-), f (5) 1) Для f (х) = х х + Найти f (), f (1), f (-), f (5) ) Найти D(у), если: у 5х 5 в) у х х 5х 6 г) 7х 1 у х х у х ) Найти
ПодробнееДифференциальное исчисление
Дифференциальное исчисление Основные понятия и формулы Определение 1 Производной функции в точке называется предел отношения приращения функции к приращению аргумента, при условии, что приращение аргумента
ПодробнееТригонометрические функции
Тригонометрические функции Угол в это угол, составляющий развернутого угла 80 Угол в радиан есть центральный угол, опирающийся на такую дугу окружности, длина которой равна радиусу этой окружности Развернутый
ПодробнееТригонометрические функции
А. Г. Малкова. Подготовка к ЕГЭ по математике. Материалы сайта EGE-Study.ru Тригонометрические функции В школьной программе изучаются четыре тригонометрических функции синус, косинус, тангенс и котангенс.
Г. Малкова. Подготовка к ЕГЭ по математике. Материалы сайта EGE-Study.ru Тригонометрические функции В школьной программе изучаются четыре тригонометрических функции синус, косинус, тангенс и котангенс.
Тема 9 «Функция. Свойства функций»
Тема 9 «Функция. Свойства функций» Пусть X некоторое непустое множество действительных чисел. И пусть указан закон f, по которому каждому числу х ϵ X ставится в соответствие единственное число y ϵ Y, обозначаемое
Подробнее( ) 2 ( ) ( ) ( ) ( ) ( ) ( ) ( )
Ответы к пособию «Математика. Уровень стандарта. Часть. Алгебра и начала анализа. 0 класс. Тетрадь для оценивания результатов обучения» Т. Л. Корниенко, В. И. Фиготина Вариант.. Г.. Г.. В.. САМОСТОЯТЕЛЬНАЯ
ПодробнееТема 39. «Производные функций»
Тема 39.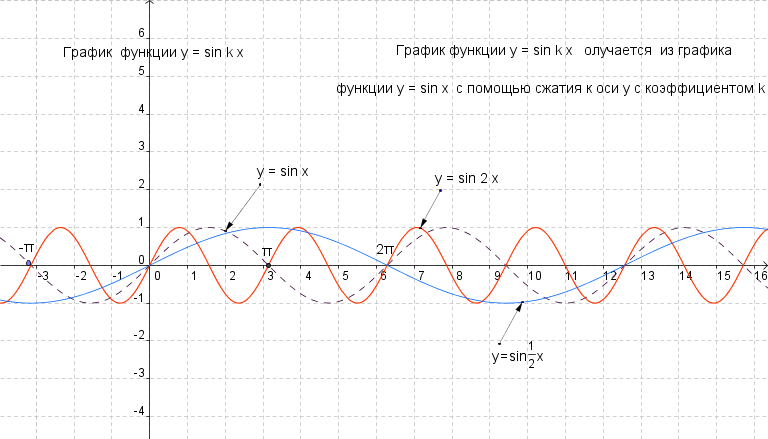 «Производные функций» Функция Производной функции в точке х 0 называется предел отношения приращения функции к приращению переменной, то есть = lim = lim + ( ) Таблица производных: Производная
«Производные функций» Функция Производной функции в точке х 0 называется предел отношения приращения функции к приращению переменной, то есть = lim = lim + ( ) Таблица производных: Производная
Тригонометрические неравенства
Тригонометрические неравенства Неравенства, содержащие переменную только под знаком тригонометрической функции, называются тригонометрическими. При решении тригонометрических неравенств используют свойство
ПодробнееСтепенная функция. Функция вида y=x k, где k>0 постоянная, называется степенной функцией. Если k=1, то y=x линейная функция, ее график прямая линия.
Степенная функция Функция вида y=x k, где k>0 постоянная, называется степенной функцией. Если k=1, то y=x линейная функция, ее график прямая линия. Если k=2, то y=x 2 квадратичная функция, ее график парабола.
ПодробнееФУНКЦИИ в ЕГЭ по математике
ГОУ ВПО «КЕМЕРОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ» КАФЕДРА ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ФУНКЦИИ в ЕГЭ по математике Кемерово 2010 Функции в ЕГЭ по математике/ ГОУ ВПО «Кемеровский государственный университет»;
ПодробнееОпределение 1.
 Функция y = ax + bx + c, где a, b, c — действительные числа, причем a 0, называется квадратичной. 1) Область определения. ( f ) R.
Функция y = ax + bx + c, где a, b, c — действительные числа, причем a 0, называется квадратичной. 1) Область определения. ( f ) R.СВОЙСТВА ФУНКЦИИ И ЕЕ ГРАФИК Определение. Функция, где,, — действительные числа, причем 0, называется квадратичной. Область определения. ( f R, так как выражение определено для любых. Область значений.
Подробнее3. Производная функции
. Производная функции Актуальность темы Понятие производной одно из основных понятий математического анализа. В настоящее время понятия производной находит большое применение в различных областях науки
ПодробнееИССЛЕДОВАНИЕ ФУНКЦИЙ
Министерство образования Российской Федерации Российский государственный университет нефти и газа имени И.М. Губкина В.И. Иванов С.И. Васин Методические указания к изучению темы ИССЛЕДОВАНИЕ ФУНКЦИЙ (для
ПодробнееТЕСТ Запишите координаты точек на координатной прямой, показанной на рисунке.

wwwaleeiivanovcom ДЗ Функции ТЕСТ 0 Запишите координаты точек на координатной прямой, показанной на рисунке ) G(-), C(-), K(-), A(4), J(0), M() ) G(-5), C(-6), K(-), A(9), J(0), M(5) ) G(-9), C(-5), K(-4),
ПодробнееСодержание первой четверти
класс I четверть Тузова Валентина Андреевна учитель математики, e-mail [email protected] Расписание консультаций: Вторник 5:00-7:00, среда 5:00-6:00, четверг 5:00-7:00 Критерии оценивания учащихся
Подробнее«ИССЛЕДОВАНИЕ ФУНКЦИЙ»
Министерство образования Российской Федерации Российский государственный университет нефти и газа имени И.М. Губкина В.И. Иванов С.И. Васин Методические указания к изучению темы «ИССЛЕДОВАНИЕ ФУНКЦИЙ»
ПодробнееВ.И. Иванов С.И. Васин
Министерство образования Российской Федерации Российский государственный университет нефти и газа имени И. М. Губкина В.И. Иванов С.И. Васин Методические указания к изучению темы «ИССЛЕДОВАНИЕ ФУНКЦИЙ»
М. Губкина В.И. Иванов С.И. Васин Методические указания к изучению темы «ИССЛЕДОВАНИЕ ФУНКЦИЙ»
Примерные практические задания:
Банк заданий по теме «ПРОИЗВОДНАЯ» МАТЕМАТИКА 11 класс (база) Учащиеся должны знать/понимать: Понятие производной. Определение производной. Теоремы и правила нахождения производных суммы, разности, произведения
ПодробнееСОДЕРЖАНИЕ Сроки Упражнения для
Тематическое планирование по алгебре и началам анализа (заочное отделение) в 1 классе Учебник: А.Г. Мордкович и др. в двух частях, Мнемозина 1 г Самостоятельные работы. Л.А. Александрова. Алгебра и начала
ПодробнееФункции, их свойства и графики
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «ТЮМЕНСКИЙ ГОСУДАРСТВЕННЫЙ НЕФТЕГАЗОВЫЙ УНИВЕРСИТЕТ»
Подробнее4 Лекция Функция
Функция Понятие функции Способы задания функции Характеристики функции Обратная функция Предел функции Предел функции в точке Односторонние пределы Предел функции при x Бесконечно большая функция 4 Лекция
ПодробнееУД 373: / ISBN ББ 22.
 1я721. в.., 2018 ISBN
1я721. в.., 2018 ISBNУД 373:51.171 64 64 в, я ава.. 10 11 /… : Э, 018. 160. (. ). ISBN 978504093535, 10 11. П ё. П ё,. П 1011,,. УД 373:51 ББ.1я71 ISBN 978504093535 в.., 018. «Иаьв «Э», 018 СОДЕРЖАНИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА,
ПодробнееПРИЛОЖЕНИЯ ПРОИЗВОДНОЙ
М и н и с т е р с т в о о б р а з о в а н и я и н а у к и Р о с с и й с к о й Ф е д е р а ц и и Федеральное государственное автономное образовательное учреждение высшего профессионального образования Национальный
ПодробнееУ 373: ISBN ISBN У К 373:51
У 373:5. 7 3 3 Э. : /.. Р,..,..,… :, 7. 3. (. ). ISBN 978-5-4-4595-,. 36 ( ),, -,. 3.,,.. У К 373:5 К.я7 ISBN 978-5-44595- в в, 7 Оф. ООО «И а ь в «Э», 7 Содержание Предисловие 6 Тренировочный ТесТ алгебра
ПодробнееСинус и косинус угла синусом косинусом
Синус и косинус угла Слово «тригонометрия» впервые встречается в заглавии книги немецкого теолога и математика Питискуса (1505 г.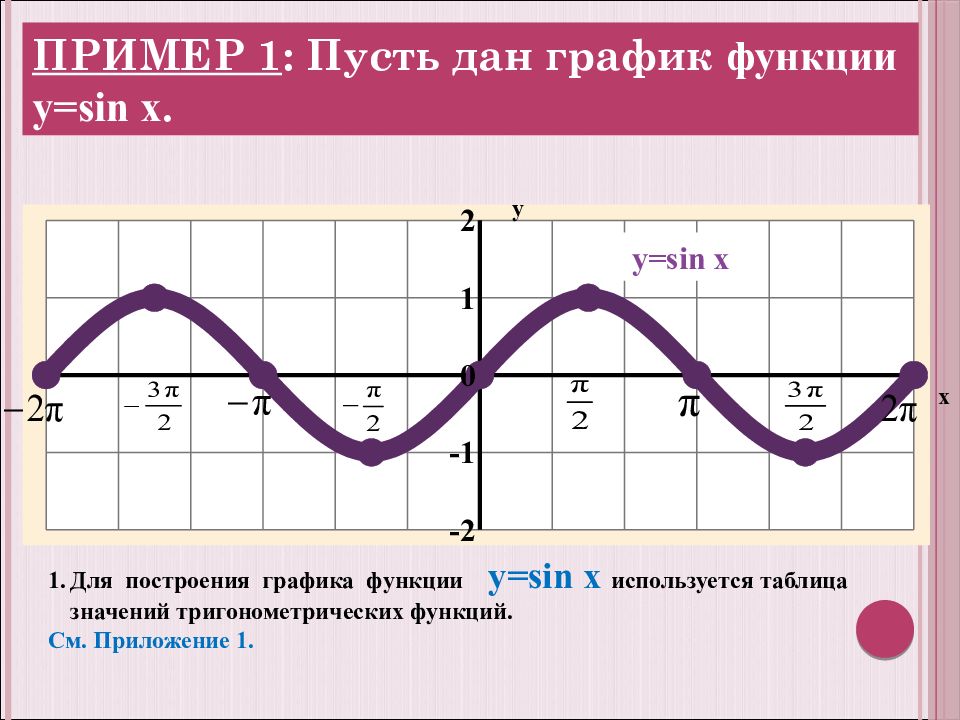 ) и происходит от греческих слов — треугольник и — измерять. Иными словами,
) и происходит от греческих слов — треугольник и — измерять. Иными словами,
Математический анализ
Кафедра математики и информатики Математический анализ Учебно-методический комплекс для студентов ВПО, обучающихся с применением дистанционных технологий Модуль 4 Приложения производной Составитель: доцент
Подробнее3. Дифференцирование функций
lim 3 Дифференцирование функций 3 Производная функции Производной функции f в точке называют следующий предел f f df f ‘ d, где f ‘ и df d условные обозначения производной Операция нахождения производной
ПодробнееАЛГЕБРА И НАЧАЛА АНАЛИЗА
СОДЕРЖАНИЕ АЛГЕБРА И НАЧАЛА АНАЛИЗА ФУНКЦИИ…10 Основные свойства функций…11 Четность и нечетность…11 Периодичность…12 Нули функции…12 Монотонность (возрастание, убывание).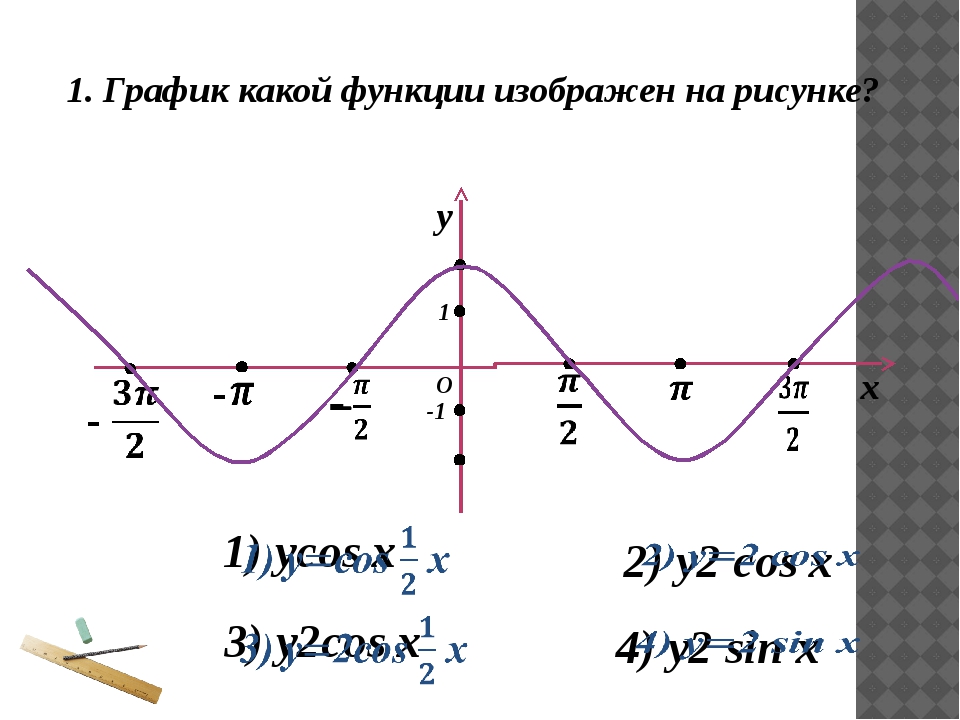 ..13 Экстремумы (максимумы
..13 Экстремумы (максимумы
и построения их графиков
Применение производной для исследования функций и построения их графиков 1. Достаточные признаки монотонности функции. Достаточное условие возрастания функции Если f ( x ) > 0 в каждой точке интервала
Подробнеезаказ решений на аукционе за минимальную цену с максимальным качеством
Предлагаю идею сайта-аукциона по выполнению домашних заданий. Он будет включать:
- решение задач по математике (сейчас доступен решебник Филиппова), физике, химии, экономике
- написание лабораторных, рефератов и курсовых
- выполнение заданий по литературе, русскому или иностранному языку.
Основное отличие от большинства сайтов, предлагающих выполнение работ на заказ – сайт рассчитан на две категории пользователей: заказчиков и решающих задания. Причем, по желанию (чтобы заработать, увеличить свой рейтинг, получить решение сложной задачи) пользователи могут играть любую из этих ролей.
Причем, по желанию (чтобы заработать, увеличить свой рейтинг, получить решение сложной задачи) пользователи могут играть любую из этих ролей.
Объединение сервисов в одну систему
Основой для идеи послужили несколько работающих систем, объединение которых позволит сделать сервис для решения задач на заказ. Эти системы:
- Форум, где посетители обмениваются идеями и помогают друг другу
- Система bugtracking, где обнаруженные проблемы проходят путь от публикации до принятия в исполнение и решения
- Аукцион, где цена за товар или услугу определяется в результате торгов
- Система рейтингов, где участники могут оценивать ответы друг друга. Причем, чем больше рейтинг пользователя, тем более значимым становится его голос
Принцип работы
Для удобства и проведения аналогий с реальной жизнью назовем заказчиков студентами, а решающих задания – репетиторами.
Итак, студенту необходимо решить несколько задач. Он заходит на сайт, выбирает раздел с соответствующей дисциплиной и создает новую тему (аналогия с форумом). Но при создании темы он также указывает стартовую (максимальную) цену, которую он готов заплатить за решение задач и крайний срок исполнения задания. Можно будет назначить и нулевую цену – если студенту нужно только бесплатное решение.
Как только тема создана, все пожелавшие подписаться на раздел репетиторы получают уведомление. Причем, условие получения уведомлений можно настроить. Например, уведомлять только о заказах со стартовой ценой более 500 р. и сроком решения не менее недели.
Заинтересовавшиеся репетиторы делают ставки. Причем студент (автор темы) видит ставки и может посмотреть информацию по каждому репетитору (его решения, рейтинг, дату начала участия в проекте). Когда студент посчитает нужным, он может остановить аукцион и назначить задание одному из репетиторов, сделавшему ставку (не обязательно самую низкую, т. к. можно учитывать и другие факторы – см. выше).
к. можно учитывать и другие факторы – см. выше).
Деньги блокируются на счете студента, и репетитор начинает решать задание. Он должен представить его к сроку, заданному изначально. Выполненное решение публикуется в свободном доступе и его может оценить как заказчик, так и другие репетиторы. На этих оценках и строится рейтинг. Если к решению нет претензий – деньги окончательно переводятся со счета студента на счет репетитора.
За счет чего будет развиваться сервис
Первое – положительная обратная связь. Чем больше условий задач и решений будет опубликовано на сайте, тем чаще его будут находить пользователи через поисковики, будет больше ссылок на готовые решения. Именно поэтому важно размещать решенные задачи в свободном доступе. Знаю это по опыту своего сайта exir.ru (ex irodov.nm.ru) – большая ссылочная база получена исключительно за счет благодарных пользователей.
Второе – удобный сервис для заказчиков и для желающих заработать на решениях.
Преимущества для заказчиков
Студентам и школьникам не нужно перебирать десятки сайтов для сравнения цен, а потом надеяться, что после оплаты они получат качественное решение (и, вообще, все не закончится перечислением денег). Заказчики создают аукцион на понижение цены и могут смотреть на рейтинги желающих решить задачи и ранее выполненные ими решения. Кроме того, деньги окончательно перечисляются исполнителю только после полного решения.
Преимущества для решающих задания
Не нужно создавать и продвигать свой сайт, размещать множество объявлений во всех доступных источниках информации. Заказчики сами придут к вам. Не нужно решать все присланные задания с целью поддержания репутации – можно выбирать те, которые будут интересны по уровню сложности, цене и срокам решения.
Преимущества для владельца сервиса
Если вы не понимаете, какую выгоду получит делающий вам какое-нибудь предложение – будьте осторожны! 🙂 У меня уже есть большой опыт работы с сайтом, предоставляющим бесплатные решения по физике. И вариант с получением прибыли от размещения рекламы подходит и для нового сервиса. Кроме того, мне нравится помогать людям и довольно тяжело смотреть, как множество вопросов по задачам остаются на форуме без ответа. Предложенный аукцион решений сможет значительно сократить число вопросов без ответов.
И вариант с получением прибыли от размещения рекламы подходит и для нового сервиса. Кроме того, мне нравится помогать людям и довольно тяжело смотреть, как множество вопросов по задачам остаются на форуме без ответа. Предложенный аукцион решений сможет значительно сократить число вопросов без ответов.
В будущем возможен вариант и с получением некоторого небольшого процента от оплаты заказов. Но процент этот должен быть минимален и на начальном этапе он взиматься точно не будет.
Что необходимо для создания сервиса
- Самым важное сейчас – собрать команду, готовую принять участие в выполнении заданий. Если покупатели заходят в пустой магазин – они надолго забывают в него дорогу.
Поэтому я собираю предварительные заявки от посетителей, готовых заниматься решениями. Не нужно подписания никаких договоров о намерениях. Просто сообщите, на какие темы вы готовы решать задания, какой у вас опыт подобной работы (e-mail: [email protected]). Когда сервис заработает – я пришлю приглашение на регистрацию.

- Выбрать платежную систему.
- Сделать подходящий движок для сайта. Нужно решить – создавать его с нуля или изменить какой-нибудь существующий движок (например, форумный) с открытой лицензией.
- Привлечь посетителей. Учитывая посещаемость exir.ru и число публикуемых на форуме вопросов, думаю, это не будет большой проблемой.
1 2 cos x 2 график
Вы искали 1 2 cos x 2 график? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и 1 2 x 4 график, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «1 2 cos x 2 график».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как 1 2 cos x 2 график,1 2 x 4 график,1 2 x график,1 2 график,1 2 х график,1 2x график,1 3 x график,1 ln x график,1 x 2 график,1 x 2 график функции,1 x 3 график,1 x 3 график функции,1 x 4 график,1 x в квадрате график,1 x график,1 x график функции,1 y график,1 график,1 корень из х график,1 постройте график функции y,1 х 1 4 построить график функции,1 х 2 график,1 х 3 график,1 х в квадрате график,1 х график,1 х график функции,1 х2 график,2 1 x построить график,2 arctg x график,2 ln x график,2 x 3 график,2 x график,2 x график функции,2 график,2 х 1 график,2x 1 2 график,2x 1 график,2x 2 1 график,2x 2 график,2x 2 график функции,2x 3 график,2x x 2 график,2x x 2 график функции,2x y 2 график,2x y 4 график,2x график,2x график функции,2×2 график,2х график,3 sin x график,3 x график,3 х график,3 х график функции,3d график онлайн,3d графики онлайн,3x 2 график,3x y 2 график,3x график,3д график онлайн,4 2 построить график,4 x 2 график,4 x 2 график функции,4 x график,4 x2 график,4 в степени х график,4 х 2 график,4 х в квадрате график,4 х график,4x x 2 график,4x x 2 график функции,5 x график,6 x график,8 x график,a x график,arctg 2 x график,arctg 2x график,cos x 1 график,cos x 2 график,cos2x 1 график,e x график,e y график,e график,f y 2 x 2,graph online,lgx график,ln x 1 график,online graph,sin 1 x график,sin 2 x график,sin 3 x график,sin x 1 2 график,sin x 1 график,sin x 2 график,sin x 3 график,sin2x график,sinx x график,sqrt x график,tg 2 x график,x 0 y 0 график,x 0 y 0 график функции,x 0 график,x 1 2 график,x 1 2 график построить,x 1 3 график,x 1 x 2x график,x 1 в квадрате график,x 1 график,x 1 график функции,x 2 1 график,x 2 2x 3 график,x 2 2x график,x 2 2x график функции,x 2 3 график,x 2 3x 2 график,x 2 3x 2 график функции,x 2 4 график,x 2 5 график,x 2 a 2 график,x 2 y 1 график,x 2 y 2 0 график,x 2 y 2 1 график,x 2 y 2 2x график,x 2 y 2 4 график,x 2 y 2 5 график,x 2 y 2 a 2 график,x 2 y 2 график,x 2 y 3 график,x 2 график,x 2 график функции,x 2x 2 график,x 3 1 график,x 3 2 график,x 3 2 график функции,x 3 x 1 график функции,x 3 график,x 4 x 1 график функции,x 4 график,x 4 график функции,x 4 функция,x 5 график,x 5 график функции,x 6 график,x 6 график функции,x a 2 y 2 a 2 график,x a график,x arctg x график,x e график,x e график функции,x log x график,x ot y,x sinx график,x sqrt y график,x y 0 график,x y 1 построить график,x y 2 график,x y 3 график,x y 4 график,x y 5 график,x y 6 график,x y ru,x y график,x y построить,x y построить график,x в 2 степени график,x в 4 степени график,x в квадрате график,x в степени 2 график,x в степени 3 график,x в степени 4 график,x график,x график функции,x от y,x у 2 график,x2 4 график,x3 1 график,x3 график,x3 график функции,x4 график,xy график,y 0 5x 2 график,y 0 x 0 график функции,y 0 x график,y 0 x график функции y,y 0 график,y 0 график функции,y 1 2 cos 2 x график,y 1 2 x график,y 1 2 график,y 1 2 график функции,y 1 2x 2 график функции,y 1 2x график функции,y 1 2×2 график функции,y 1 3 x 2 график,y 1 3 x 2 график функции,y 1 3x 2 график,y 1 4 x,y 1 4 x график,y 1 4x,y 1 4x 2 график,y 1 4x график,y 1 5 x график,y 1 5 x график функции,y 1 5x график,y 1 9x,y 1 9x график,y 1 x 1 построить график,y 1 x 2 5,y 1 x 2 график,y 1 x 2 график функции,y 1 x 3 график,y 1 x 4,y 1 x график,y 1 x график функции,y 1 x построить график,y 1 график,y 1 график функции,y 1 х 2,y 10 x график,y 2 1 график,y 2 2x график,y 2 3 в степени x,y 2 3x построить график,y 2 4x график,y 2 5x график функции,y 2 x 1 график функции,y 2 x 3 график,y 2 x 3 график функции,y 2 x график,y 2 x график функции,y 2 в степени x 3,y 2 график,y 2 график функции,y 2 х график,y 2 х график функции,y 2 ч y ч 2,y 2sin3x график,y 2x 1 график функции,y 2x 2 x 1,y 2x 3 x 1,y 2x 3 график функции,y 2x 3 построить график функции,y 2x x,y 2x x 2 график,y 2x график,y 2x график функции,y 2x построить график,y 2×2 2,y 2×2 график функции,y 3 2x график,y 3 sin x график,y 3 x 2 график,y 3 x 2 график функции,y 3 x график,y 3 x график функции,y 3 в степени x 2,y 3 график,y 3sin2x график,y 3x 1 график,y 3x 1 график функции,y 3x 2 график,y 3x 2 график функции,y 3x 2 построить график функции,y 3x 6 график,y 3x x 2,y 4 1 x,y 4 x,y 4 x 1,y 4 x 1 2,y 4 x 1 2 график,y 4 x 2 график,y 4 x 2 график функции,y 4 x график,y 4 x график функции,y 4 x построить график,y 4 x построить график функции,y 4 x2 график,y 4 в степени x,y 4 в степени x график функции,y 4 в степени x график функции y,y 4 график,y 4x,y 4x 1,y 4x 1 2,y 4x 2 график,y 4x 2 график функции,y 4x x 2 график,y 4x график,y 4x график функции,y 5 2x график функции,y 5 x,y 5 x 2 построить график,y 5 x график,y 5 x график функции,y 5 x построить график функции,y 5x график функции,y 6 x график,y 7 x,y 7 x график,y 9 x график,y 9 x график функции,y 9 x график функции y,y a x график,y cos x 1 график,y cos x 2 график,y cos3x 2 график,y e график,y sin3x график,y sinx в квадрате график,y sqrt x график,y sqrt x график функции y,y x 0,y x 0 5,y x 1 2 график,y x 1 2 график функции,y x 1 4,y x 1 в квадрате график функции,y x 1 график функции,y x 1 построить график,y x 10 график,y x 10 построить график функции,y x 2 3 график,y x 2 4 построить график,y x 2 4x 5 построить график данной функции по графику определить,y x 2 x 3 график,y x 2 график,y x 2 график функции,y x 2 построить график,y x 2 построить график функции,y x 2 постройте график,y x 3 2 график,y x 3 4,y x 3 4 график,y x 3 4x,y x 3 5,y x 3 x 0,y x 3 x построить график,y x 3 график построить,y x 3 график функции как построить,y x 3 построить график,y x 4,y x 4 1,y x 4 2 график функции,y x 4 3,y x 4 x,y x 4 x построить график,y x 4 график,y x 4 график функции,y x 4 построить график функции,y x 5,y x 5 0,y x 5 x,y x 5 график,y x 5 график функции,y x 5 построить график функции,y x 6,y x 6 1,y x 6 график,y x 6 построить график,y x 6 постройте график,y x 7,y x 7 график,y x 7 график функции,y x 8 график,y x 9,y x 9 график функции,y x a график,y x r,y x ru,y x sgn x,y x x2,y x y 2 0 график функции,y x в 3 степени график,y x в 6 степени график,y x в квадрате построить график,y x в степени 2,y x в степени 2 3,y x график,y x график функции,y x график функций,y x как построить график,y x как построить график функции,y x построить график,y x постройте график,y x решение,y x2 2 график функции,y x2 3 график функции,y x2 3x график,y x2 график,y x2 график функции,y x2 построить график функции,y x4,y x4 y 1,y x4 график функции,y x5,y x5 график функции,y x6,y x6 график,y x6 график функции,y от x,y х 2 график,y х 2 график функции,y х 2 х 3,y х 4 график,yotx графики онлайн,z x y график,генератор графиков,генератор графиков функций,гипербола онлайн,граф решишь,график,график 1,график 1 2 x,график 1 2 х,график 1 2x,график 1 2x 2,график 1 3 x,график 1 sin x,график 1 x,график 1 x 2,график 1 x 3,график 1 x в квадрате,график 1 корень из х,график 1 х,график 1 х 2,график 1 х 3,график 1 х в квадрате,график 1 х2,график 2 tg x,график 2 x,график 2 x 3,график 2 в степени x,график 2 синус х,график 2 х,график 2cos2x,график 2x,график 2x 1,график 2x 2,график 2x 2 1,график 2x 3,график 2x x 2,график 2×2,график 2х,график 3 2 x,график 3 2x,график 3 x,график 3 x 1,график 3 x 2,график 3 х,график 3x,график 3x 2,график 4 x,график 4 x 2,график 4 в степени х,график 4 х,график 4 х 2,график 4 х в квадрате,график 4x x 2,график 4x y 2,график 5 x,график 6 x,график a x,график arctg 1 x,график arctg 2x,график arctg x 2,график cos 2 x,график e x,график e y,график lgx,график ln 1 x,график sin 1 x,график sin 2 x,график sin x построить график,график sin3x,график sinx x,график sqrt x,график tg 2 x,график x,график x 0,график x 1 2,график x 1 3,график x 2,график x 2 1,график x 2 2x,график x 2 3,график x 2 4,график x 2 y 2 0,график x 3,график x 3 1,график x 3 2,график x 4,график x 4 2,график x 5,график x 6,график x a,график x e,график x e y,график x sqrt y,график x y,график x y 0,график x y 2,график x y 8,график x y a,график x y z,график x в 2 степени,график x в степени 2,график x в степени 3,график x2 4,график x3,график x3 1,график x4,график xy,график y,график y 0,график y 1,график y 1 2,график y 1 2 x,график y 1 2x,график y 1 2×2,график y 1 3 x 2 x,график y 1 3x 2,график y 1 4 x,график y 1 5 x,график y 1 x,график y 1 x 2,график y 1 x 4,график y 10 x,график y 2,график y 2 1,график y 2 2x,график y 2 2x 1,график y 2 3x,график y 2 5 x,график y 2 cos x,график y 2 x 1,график y 2 x 3,график y 2 корень x,график y 2 х,график y 2cos x,график y 2x,график y 2x x 2,график y 2x x2,график y 3 2x,график y 3 x,график y 3 x 2,график y 3 в степени x 2,график y 3 корень x,график y 3sin2x,график y 3x,график y 3x 2,график y 4,график y 4 x,график y 4 x 2,график y 4 x 3,график y 4 x2,график y 4x,график y 4x 1,график y 4x 2,график y 4x x 2,график y 5 2x,график y 5 x,график y 7 x,график y 8 x,график y 9 x,график y e,график y sqrt x,график y tg 2 x,график y tg 2x,график y x,график y x 0,график y x 1 x 5,график y x 1 в квадрате,график y x 10,график y x 2,график y x 2 3,график y x 3 2,график y x 4,график y x 4 и y x 4,график y x 5,график y x 5 2,график y x 6,график y x 7,график y x 8,график y x a,график y x в 3 степени,график y x в 7 степени,график y x в квадрате 1,график y x2,график y х 2,график z x y,график в полярной системе координат онлайн,график в полярных координатах онлайн,график в пространстве онлайн,график в трехмерном пространстве онлайн,график гиперболы онлайн построить,график е,график зависимости онлайн построить,график икс в степени икс,график калькулятор,график квадратичной функции онлайн,график квадратичной функции построить онлайн,график комплексной функции онлайн,график координат,график корень из х 1,график косинус 3х,график кусочной функции онлайн,график логарифма онлайн,график логарифмической функции онлайн,график математика,график нарисовать,график начертить,график неявной функции онлайн,график окружности онлайн,график окружности онлайн построить,график онлайн,график онлайн 3d,график онлайн в полярной системе координат,график онлайн в полярных координатах,график онлайн в пространстве,график онлайн в трехмерном пространстве,график онлайн квадратичной функции,график онлайн неявной функции,график онлайн по точкам,график онлайн по уравнению,график онлайн по формуле,график онлайн по функции,график онлайн построение,график онлайн построить,график онлайн построить x y z,график онлайн построить по точкам,график онлайн построить по уравнению,график онлайн построить с модулем,график онлайн с модулем,график онлайн трехмерный,график онлайн функция,график онлайн чертить,график параболы онлайн,график параметрической функции онлайн,график по точкам онлайн,график по уравнению онлайн,график по формуле онлайн,график по функции,график по функции онлайн,график построение,график построение онлайн,график решить,график с корнем онлайн с,график с модулем онлайн,график с модулем онлайн построить,график сайт,график синус х 2,график системы уравнений онлайн,график степенной функции онлайн,график строить,график строить онлайн,график тригонометрической функции онлайн,график у 1,график у 1 2 х,график у 1 2х,график у 1 2х2,график у 1 x,график у 1 корень из х,график у 1 х,график у 1 х 2,график у 2,график у 2 x,график у 3 x,график у 3 х,график у 3х,график у 4 х,график у x,график у x 2,график у х,график у х 1,график у х 1 х 3,график у х 2 5,график у х 4,график у х 5,график у х 7,график у х 8,график у х в степени 2,график у х2 1,график уравнения y 2 x 2,график уравнения онлайн,график функции,график функции 1 2 x,график функции 1 2 х,график функции 1 cos x 1,график функции 1 x,график функции 1 x 2,график функции 1 x 3,график функции 1 x 4,график функции 1 x в квадрате,график функции 1 корень из х,график функции 1 х,график функции 1 х 2,график функции 1 х 3,график функции 1 х в квадрате,график функции 2 1 х,график функции 2 3 x,график функции 2 x,график функции 2 x 1,график функции 2 x 3,график функции 2 y 1 x,график функции 2 х 1,график функции 2x,график функции 2x 2 x,график функции 3 1 х,график функции 3 x,график функции 3 x 1,график функции 3 x 2,график функции 3 х,график функции 4 x,график функции 4 x 2,график функции 4 в степени х,график функции 4 х,график функции 4 х 2,график функции 5 x,график функции sin 1 x,график функции x,график функции x 1,график функции x 1 2,график функции x 1 3,график функции x 1 в квадрате,график функции x 2,график функции x 2 1,график функции x 2 3,график функции x 2 4x,график функции x 2 y 2,график функции x 2 y 2 4,график функции x 2 y 2 9,график функции x 2 y 2 9 график,график функции x 2x 2,график функции x 3,график функции x 3 1,график функции x 3 2,график функции x 3 sin y,график функции x 3 x 1 x,график функции x 3 x 2 1,график функции x 4,график функции x 4 2,график функции x 5,график функции x 6,график функции x e,график функции x y,график функции x y 0 x,график функции x y 1,график функции x y 5,график функции x y a,график функции x3,график функции y 0,график функции y 0 x 0,график функции y 1,график функции y 1 2,график функции y 1 2x,график функции y 1 3 x 2,график функции y 1 3x в квадрате,график функции y 1 4x в квадрате,график функции y 1 x 4,график функции y 1 x в квадрате,график функции y 2,график функции y 2 1,график функции y 2 3x,график функции y 2 x,график функции y 2 x 1,график функции y 2 x 3,график функции y 2 x2,график функции y 2x,график функции y 2x 2,график функции y 2x 3,график функции y 2×2,график функции y 2×2 1,график функции y 3,график функции y 3 2x,график функции y 3 x,график функции y 3 x 2,график функции y 3x 2,график функции y 4 x,график функции y 4 x 2,график функции y 4 в x степени,график функции y 4x 2,график функции y 5,график функции y 5 2x,график функции y 5 x,график функции y 5 x 2,график функции y 5x,график функции y 5x 2,график функции y 5x 4,график функции y 6 2x,график функции y lg x,график функции y tg 2x,график функции y x,график функции y x 1,график функции y x 1 2,график функции y x 1 4,график функции y x 1 x 2,график функции y x 1 в квадрате,график функции y x 10,график функции y x 2 3,график функции y x 2 3 x 2x,график функции y x 2 5,график функции y x 2 x 0,график функции y x 3 2,график функции y x 3 4,график функции y x 3 как построить,график функции y x 4,график функции y x 4 2,график функции y x 4 3,график функции y x 5,график функции y x 6,график функции y x 7,график функции y x 9,график функции y x sqrt x 2,график функции y x в квадрате 1,график функции y x как построить,график функции y x2,график функции y x2 1,график функции y x2 3,график функции y x4,график функции y x5,график функции y x6,график функции y х,график функции в полярных координатах онлайн,график функции двух переменных онлайн,график функции двух переменных онлайн построить,график функции как выглядит,график функции калькулятор,график функции калькулятор онлайн,график функции нарисовать,график функции одна вторая икс в квадрате,график функции онлайн,график функции онлайн x y z,график функции онлайн двух переменных,график функции онлайн калькулятор,график функции онлайн неявной,график функции онлайн по точкам,график функции онлайн построение,график функции онлайн построить,график функции онлайн построить по точкам,график функции онлайн построить с корнем,график функции онлайн построить с модулем,график функции онлайн построить с решением,график функции онлайн с модулем,график функции онлайн с решением,график функции параметрической онлайн,график функции по,график функции по точкам онлайн,график функции по точкам онлайн построить,график функции построение,график функции построение онлайн,график функции решение,график функции решить онлайн,график функции с модулем онлайн,график функции с решением онлайн,график функции синус 2х,график функции строить онлайн,график функции у,график функции у 1 2 х,график функции у 1 2х,график функции у 1 х 2,график функции у 1 х в квадрате,график функции у 2,график функции у 2 x,график функции у 3,график функции у 3 x,график функции у 4х в квадрате,график функции у x,график функции у x 1,график функции у x 2,график функции х,график функции х 1,график функции х 1 2,график функции х 2 1,график функции х 2 y,график функции х 3 2,график функции х 4,график функции х 4 2,график функции х 4 х 2,график функции х y,график функции х y 2,график функции х в 4 степени,график функции х в квадрате минус х,график функции х в квадрате х,график функции х делить на х,график функции х у,график функций,график функций онлайн,график функция онлайн,график х,график х 0,график х 1,график х 1 2,график х 1 в квадрате,график х 2,график х 2 1,график х 2 3,график х 2 y 2,график х 3,график х 3 1,график х 3 2,график х 4,график х y 2,график х в квадрате,график х в квадрате 1,график х в квадрате 4,график х в степени 2,график х в степени 4,график х е х,график х и у,график х у,график х у 4,график х у z,график х2 1,график х3,график чертить онлайн,график экспоненты в степени минус х,графика онлайн,графика точками,графики,графики x 2 y 2,графики y 2 x,графики в полярной системе координат онлайн,графики в полярных координатах онлайн,графики онлайн,графики онлайн 3d,графики онлайн в полярной системе координат,графики онлайн в полярных координатах,графики онлайн по точкам,графики онлайн полярная система координат,графики онлайн построение,графики онлайн построение по точкам,графики онлайн построение по уравнению,графики онлайн трехмерные,графики по точкам онлайн,графики по точкам онлайн построение,графики построение,графики построение онлайн,графики построить,графики построить онлайн,графики рисовать онлайн,графики строить,графики строить онлайн,графики уравнений онлайн,графики функции онлайн,графики функций x 2 y 2,графики функций калькулятор,графики функций онлайн,графики функций онлайн калькулятор,графики функций онлайн построение,графики функций онлайн с модулем,графики функций онлайн с решением,графики функций построение,графики функций построение онлайн,графики функций построить,графики функций с модулем онлайн,графики функций строить онлайн,графики чертить,графический калькулятор онлайн,графический онлайн калькулятор,графическое решение уравнений онлайн,графік,графік функції y 2 x,графік функції y x 2,графік функції онлайн,графіки,графіки онлайн,графопостроитель онлайн,дослідити функцію та побудувати її графік онлайн,е график,е х график,изобразите график функции,изобразить график функции онлайн,изоклины онлайн построение,икс в степени икс график,инженерная графика онлайн построение,используя график функции y f x постройте график функции,используя график функции построить график функции,исследовать график функции онлайн,исследовать график функции онлайн с решением,исследовать и построить график функции онлайн,исследовать функцию и построить график онлайн решение калькулятор,как выглядит график,как выглядит график x 2 y 2,как выглядит график функции,как начертить график функции,как построить x y,как построить y x,как построить график x y,как построить график x y 2,как построить график y 2 x,как построить график y x,как построить график y x 2,как построить график функции x 2 y,как построить график функции x y,как построить график функции x y 2,как построить график функции x y 3,как построить график функции y,как построить график функции y x,как построить график функции y x 2,как построить график функции по уравнению,калькулятор график,калькулятор график функции,калькулятор графика функции,калькулятор графики функций,калькулятор графиков,калькулятор графиков онлайн,калькулятор графиков функций,калькулятор графиков функций онлайн,калькулятор графиков функций онлайн с решением,калькулятор графический онлайн,калькулятор для построения графиков функций,калькулятор онлайн график функции,калькулятор онлайн графиков,калькулятор онлайн построить график функции,калькулятор построения графиков функций,калькулятор построения графиков функций онлайн,калькулятор построить график функции,калькулятор функции график,калькулятор функции онлайн,калькулятор функций,калькулятор функций графики,калькулятор функций графики онлайн,калькулятор функций онлайн,квадратичная функция онлайн,конструктор графиков,конструктор графиков онлайн,конструктор онлайн функций,конструктор функций онлайн,координатная плоскость онлайн,координатная плоскость онлайн рисовать,координатная прямая онлайн,косинус 3х график,косинус х 2 график,лучший построитель графиков,лучший построитель графиков онлайн,математика график,математикам ру построение графика,найти график функции,нарисовать график,нарисовать график онлайн,нарисовать график онлайн вручную,нарисовать график онлайн по точкам,нарисовать график по точкам онлайн,нарисовать график функции,нарисовать график функции онлайн,нарисовать онлайн функцию,нарисовать функцию онлайн,начертите график,начертить график,начертить график онлайн,начертить график онлайн по точкам,начертить график по точкам онлайн,начертить график функции онлайн,неравенства график онлайн,окружность построить онлайн,онлайн 3d график,онлайн гипербола,онлайн график,онлайн график в полярной системе координат,онлайн график квадратичной функции,онлайн график логарифма,онлайн график логарифмической функции,онлайн график по таблице,онлайн график по точкам,онлайн график по уравнению,онлайн график по формуле,онлайн график построение,онлайн график с модулем,онлайн график функции,онлайн график функции z x y,онлайн график функции с модулем,онлайн графика,онлайн графики,онлайн графики в полярных координатах,онлайн графики в пространстве,онлайн графики по точкам,онлайн графики с модулем,онлайн графики уравнений,онлайн графики функции,онлайн графики функций построить,онлайн графіки,онлайн калькулятор график функции,онлайн калькулятор графики функций,онлайн калькулятор графиков,онлайн калькулятор графиков функций,онлайн калькулятор графиков функций с решением,онлайн калькулятор для функций,онлайн калькулятор построения графиков функций,онлайн калькулятор построить график функции,онлайн калькулятор функции,онлайн калькулятор функций,онлайн квадратичная функция,онлайн конструктор графиков,онлайн конструктор функций,онлайн координатная плоскость,онлайн координатная прямая,онлайн описать функцию,онлайн парабола,онлайн побудова графіків,онлайн побудова графіків функцій,онлайн построение,онлайн построение гиперболы,онлайн построение график функции,онлайн построение графика,онлайн построение графика в полярной системе координат,онлайн построение графика в полярных координатах,онлайн построение графика квадратичной функции,онлайн построение графика функции,онлайн построение графиков,онлайн построение графиков 3d,онлайн построение графиков в полярных координатах,онлайн построение графиков в трехмерной системе координат,онлайн построение графиков зависимости,онлайн построение графиков неравенств,онлайн построение графиков онлайн в полярной системе координат онлайн,онлайн построение графиков по точкам,онлайн построение графиков по уравнению,онлайн построение графиков по физике,онлайн построение графиков с двумя переменными,онлайн построение графиков с корнем,онлайн построение графиков с корнями,онлайн построение графиков с модулем,онлайн построение графиков сложных функций,онлайн построение графиков тригонометрических функций,онлайн построение графиков уравнений,онлайн построение графиков функции,онлайн построение графиков функций,онлайн построение графиков функций x y z,онлайн построение графиков функций по уравнению,онлайн построение графиков функций с модулем,онлайн построение графиков функций с решением,онлайн построение графов,онлайн построение квадратичной функции,онлайн построение кривых,онлайн построение логарифмических графиков,онлайн построение нескольких графиков в одной системе координат,онлайн построение окружности,онлайн построение параболы,онлайн построение синусоиды,онлайн построение тригонометрических графиков,онлайн построение тригонометрических функций,онлайн построение фигур,онлайн построение функций,онлайн построения графиков,онлайн построитель,онлайн построитель графиков,онлайн построитель графиков функций,онлайн построитель функций,онлайн построить график квадратичной функции,онлайн построить графики функций,онлайн постройка графика,онлайн постройка графиков,онлайн постройка графиков функций,онлайн программа для построения графиков,онлайн программа построения графиков,онлайн решение графика функции,онлайн решение графиков,онлайн решение графиков функций,онлайн решение графических уравнений,онлайн решение квадратичной функции,онлайн решение параболы,онлайн решение функций,онлайн решение функция,онлайн решить график функции,онлайн рисование графиков,онлайн система координат,онлайн составить график функции,онлайн составление графика,онлайн составление графиков,онлайн строим график,онлайн строим графики,онлайн строитель графиков,онлайн строитель графиков функций,онлайн строитель функций,онлайн строительство графиков,онлайн строить график функции,онлайн строить графики функций,онлайн трехмерная система координат,онлайн функции,онлайн функция,онлайн функция график,онлайн функция решение,онлайн чертить график,онлайн черчение графиков,описать график функции онлайн,описать функцию онлайн,определить функцию по графику онлайн,парабола онлайн,парабола онлайн построение,парабола построение онлайн,параболы онлайн построение,по графику определить функцию онлайн,по математике графики,по формуле построить график,побудова графіків,побудова графіків онлайн,побудова графіків функцій,побудова графіків функцій онлайн,побудувати графік,побудувати графік онлайн,побудувати графік функції,побудувати графік функції онлайн,побудувати графік функції онлайн розв язок,побудуйте графік функції,полярная система координат графики онлайн,построение 3д графиков онлайн,построение в полярных координатах онлайн,построение график,построение график онлайн,построение график функции,построение график функции онлайн,построение графика,построение графика в полярной системе координат онлайн,построение графика в полярных координатах онлайн,построение графика квадратичной функции онлайн,построение графика онлайн,построение графика онлайн в полярных координатах,построение графика онлайн по точкам,построение графика онлайн по функции,построение графика по точкам,построение графика по точкам онлайн,построение графика по функции онлайн,построение графика функции,построение графика функции онлайн,построение графика функции онлайн с решением,построение графики,построение графики функций,построение графиков,построение графиков xyz онлайн,построение графиков в полярной системе координат онлайн,построение графиков в полярной системе координат онлайн с решением,построение графиков в полярных координатах онлайн,построение графиков в пространстве онлайн,построение графиков в трехмерной системе координат онлайн,построение графиков в трехмерном пространстве онлайн,построение графиков зависимости онлайн,построение графиков на миллиметровке онлайн,построение графиков неравенств онлайн,построение графиков онлайн,построение графиков онлайн 3д,построение графиков онлайн xyz,построение графиков онлайн в полярной системе координат,построение графиков онлайн в полярных координатах,построение графиков онлайн в пространстве,построение графиков онлайн в трехмерной системе координат,построение графиков онлайн на миллиметровке,построение графиков онлайн неравенств,построение графиков онлайн по таблице,построение графиков онлайн по точкам,построение графиков онлайн по точкам на миллиметровке,построение графиков онлайн по уравнению,построение графиков онлайн по физике,построение графиков онлайн с двумя переменными,построение графиков онлайн с корнем,построение графиков онлайн с корнями,построение графиков онлайн с модулем,построение графиков онлайн с параметром,построение графиков онлайн с решением,построение графиков онлайн трехмерных,построение графиков по таблице онлайн,построение графиков по точкам,построение графиков по точкам онлайн,построение графиков по уравнению онлайн,построение графиков по физике онлайн,построение графиков полярных онлайн,построение графиков с двумя переменными онлайн,построение графиков с корнем онлайн,построение графиков с корнями онлайн,построение графиков с модулем онлайн,построение графиков с параметром онлайн,построение графиков сложных функций онлайн,построение графиков тригонометрических онлайн,построение графиков тригонометрических функций онлайн,построение графиков уравнений онлайн,построение графиков функции,построение графиков функции онлайн,построение графиков функции онлайн с решением,построение графиков функции с решением онлайн,построение графиков функций,построение графиков функций онлайн,построение графиков функций онлайн x y z,построение графиков функций онлайн по уравнению,построение графиков функций онлайн с модулем,построение графиков функций онлайн с подробным решением,построение графиков функций онлайн с решением,построение графиков функций по уравнению онлайн,построение графиков функций с модулем онлайн,построение графиков функций с решением онлайн,построение графов онлайн,построение квадратичной функции онлайн,построение кривых онлайн,построение логарифмических графиков онлайн,построение нескольких графиков в одной системе координат онлайн,построение нескольких графиков онлайн,построение обратной функции онлайн,построение окружности онлайн,построение онлайн,построение онлайн кривых,построение параболы онлайн,построение параболы онлайн по квадратному уравнению,построение параболы по квадратному уравнению онлайн,построение параметрических графиков онлайн с решением,построение полярных графиков онлайн,построение пространственных графиков онлайн,построение синусоиды онлайн,построение сложных графиков онлайн,построение сложных графиков функций онлайн,построение точек онлайн по координатам,построение точек по координатам онлайн,построение трехмерных графиков онлайн,построение тригонометрических графиков онлайн,построение тригонометрических функций онлайн,построение уравнений онлайн,построение функции,построение функции онлайн,построение функций,построение функций онлайн,построения графиков онлайн,построитель графиков,построитель графиков онлайн,построитель графиков функций,построитель графиков функций онлайн,построитель онлайн,построитель функций,построитель функций онлайн,построить y x 2 x 1,построить гиперболу онлайн,построить гиперболу онлайн по уравнению,построить гиперболу по уравнению онлайн,построить график,построить график 1 x 2,построить график 3d,построить график x 3 x 2,построить график x f y,построить график x sin x,построить график x y,построить график x y 1,построить график x y z онлайн,построить график x y в квадрате,построить график y,построить график y 1 x,построить график y 2 2x,построить график y 2 x,построить график y 2 x 3,построить график y 2x,построить график y 3 2 x,построить график y 4 x,построить график y cos2x,построить график y x,построить график y x 1,построить график y x 2,построить график y x 3,построить график y x 4,построить график y x 4 2,построить график y x 5,построить график y x 6,построить график в полярной системе координат онлайн,построить график в полярных координатах онлайн,построить график в трехмерном пространстве онлайн,построить график зависимости онлайн,построить график зависимости онлайн по точкам,построить график зависимости по точкам онлайн,построить график квадратичной функции онлайн,построить график квадратичной функции онлайн с решением,построить график логарифмической функции онлайн,построить график неявной функции онлайн,построить график обратной функции онлайн,построить график окружности онлайн,построить график онлайн,построить график онлайн x y z,построить график онлайн в полярной системе координат,построить график онлайн в трехмерном пространстве,построить график онлайн неявной функции,построить график онлайн окружности,построить график онлайн по данным таблицы,построить график онлайн по координатам,построить график онлайн по таблице,построить график онлайн по таблице онлайн,построить график онлайн по точкам,построить график онлайн по точкам x y,построить график онлайн по точкам на миллиметровке,построить график онлайн по точкам онлайн,построить график онлайн по уравнению,построить график онлайн по уравнению онлайн,построить график онлайн по функции,построить график онлайн с модулем,построить график параметрической функции онлайн,построить график по данным таблицы онлайн,построить график по координатам онлайн,построить график по таблице онлайн,построить график по точкам,построить график по точкам онлайн,построить график по уравнению онлайн,построить график по уравнению функции,построить график по функции онлайн,построить график с корнем онлайн с,построить график с модулем онлайн,построить график системы уравнений онлайн,построить график тригонометрической функции онлайн,построить график тригонометрической функции онлайн с решением,построить график у 2 х,построить график у 4 х,построить график у x 2 3 x 2,построить график у х 1 2,построить график у х 2,построить график у х 3,построить график у х 4,построить график уравнения,построить график уравнения онлайн,построить график уравнения онлайн с решением,построить график функции,построить график функции 1 x 1,построить график функции 1 x 2,построить график функции 1 y 2x,построить график функции 1 у 3 х,построить график функции 2 5 x 2,построить график функции 2 5x 2,построить график функции x 1 2,построить график функции x 2 1,построить график функции x 3 2x 2 x 3,построить график функции x f y,построить график функции x y,построить график функции x y 4,построить график функции y,построить график функции y 1 2 x 2,построить график функции y 1 2x 2,построить график функции y 1 2×2,построить график функции y 1 x,построить график функции y 1 x 3,построить график функции y 2 3 x,построить график функции y 2 3x,построить график функции y 2 5x,построить график функции y 2 x 3,построить график функции y 2 x 5,построить график функции y 2x 3,построить график функции y 2x 4 x 2 1 решение,построить график функции y 3 2x,построить график функции y 3 x 2,построить график функции y 3x в квадрате,построить график функции y 4 x,построить график функции y 4 x 1,построить график функции y 5 2x,построить график функции y 5 x 2,построить график функции y 5x 2,построить график функции y 8 x,построить график функции y cos x 1,построить график функции y x,построить график функции y x 1,построить график функции y x 1 2,построить график функции y x 1 2 3,построить график функции y x 1 4,построить график функции y x 1 x 2,построить график функции y x 1 x 3,построить график функции y x 10,построить график функции y x 2,построить график функции y x 2 3,построить график функции y x 3,построить график функции y x 3 2,построить график функции y x 4 2,построить график функции y x 4 x,построить график функции y x 5,построить график функции y x 7,построить график функции y x 8,построить график функции y x cos x,построить график функции y x sin x,построить график функции в полярной системе координат онлайн,построить график функции в трехмерном пространстве онлайн,построить график функции двух переменных онлайн,построить график функции калькулятор,построить график функции онлайн,построить график функции онлайн в полярной системе координат,построить график функции онлайн в трехмерном пространстве,построить график функции онлайн калькулятор,построить график функции онлайн по точкам,построить график функции онлайн по уравнению,построить график функции онлайн по уравнению онлайн,построить график функции онлайн по уравнению с решением,построить график функции онлайн с корнем,построить график функции онлайн с модулем,построить график функции онлайн с подробным решением,построить график функции онлайн с подробным решением 9 класс,построить график функции онлайн с решением,построить график функции онлайн с решением 10 класс,построить график функции онлайн с таблицей точек,построить график функции по модулю онлайн,построить график функции по точкам онлайн,построить график функции по уравнению,построить график функции по уравнению онлайн,построить график функции с корнем онлайн,построить график функции с модулем онлайн,построить график функции с модулем онлайн с подробным решением,построить график функции у,построить график функции у 1 х,построить график функции у 1 х 2,построить график функции у 2 х,построить график функции у х,построить график функции у х в квадрате,построить график функции х в квадрате,построить график функции х у,построить график функции х у 4,построить график функции х у 5,построить график функций,построить график функций онлайн с решением,построить график функций с решением онлайн,построить график х у 2,построить графики,построить графики онлайн,построить графики онлайн по точкам,построить графики по точкам онлайн,построить графики функций,построить графики функций в одной системе координат,построить графики функций онлайн,построить графики функций онлайн с решением,построить и исследовать график функции онлайн,построить и прочитать график функции,построить интегральную кривую онлайн,построить интегральные кривые онлайн,построить калибровочный график онлайн,построить кривую заданную уравнением в полярной системе координат онлайн,построить кривую онлайн,построить кривые по заданным уравнениям онлайн с решением,построить линии уровня функции онлайн,построить несколько графиков на одном онлайн,построить область ограниченную линиями онлайн,построить окружность онлайн,построить онлайн график в полярных координатах,построить онлайн график логарифмической функции,построить онлайн график с модулем,построить онлайн график функции по точкам,построить онлайн график функций,построить онлайн фигуру,построить параболу онлайн,построить параболу онлайн по уравнению,построить параболу по уравнению онлайн,построить по точкам график зависимости онлайн,построить прямую онлайн,построить прямую онлайн по уравнению,построить прямую по уравнению онлайн,построить тригонометрический график онлайн,построить функции онлайн,построить функцию,построить функцию онлайн,построить функцию онлайн с решением,построить функция онлайн,построить эллипс онлайн,построить эскиз графика функции онлайн,построй график функции,постройка графика,постройка графика онлайн,постройка графика онлайн по точкам,постройка графика по точкам онлайн,постройка графика функции,постройка графика функции онлайн,постройка графиков,постройка графиков онлайн,постройка графиков функций онлайн,постройте график,постройте график x y,постройте график y 2 x,постройте график y x,постройте график y x 2,постройте график y x 6,постройте график онлайн,постройте график уравнений,постройте график уравнения 2×2 y 4x 3,постройте график функции,постройте график функции x 3,постройте график функции x y 2 y 0 x,постройте график функции y,постройте график функции y 1 2,постройте график функции y 1 3 x 2,постройте график функции y 1 3x 2,постройте график функции y 1 4x,постройте график функции y 1 6x,постройте график функции y 1 x,постройте график функции y 2,постройте график функции y 2 3 x,постройте график функции y 2 корень 3 степени из x,постройте график функции y 2x,постройте график функции y 3 4 x 1,постройте график функции y 3 х 1,постройте график функции y x,постройте график функции y x 1,постройте график функции y x 1 2,постройте график функции y x 1 x 3 x 4,постройте график функции y x 10,постройте график функции y x 2 x 3 x 1,постройте график функции y x 3,постройте график функции y x 3 2,постройте график функции y x 5,постройте график функции y х 2,постройте график функции игрек равен,постройте график функции игрек равно,постройте график функции онлайн,постройте график функции онлайн с решением,постройте график функции у,постройте график функции у 1 4х2,постройте график функции у 1 x,постройте график функции х у,постройте график функций,постройте график функций y,постройте графики,постройте графики функций,преобразование графиков функций онлайн,преобразование функции онлайн,программа для построения графиков онлайн,программа для построения графиков функций онлайн,программа онлайн для построения графиков,программа онлайн построения графиков,программа построения графиков онлайн,программа построения графиков функций онлайн,прямая у х,прямоугольная система координат онлайн,решение y 1 x,решение график функции,решение графика функции онлайн,решение графиков,решение графиков онлайн,решение графиков функций,решение графиков функций онлайн,решение графиков функций онлайн с решением,решение графических уравнений онлайн,решение квадратичной функции онлайн,решение онлайн графика функции,решение онлайн графиков функций,решение онлайн квадратичной функции,решение онлайн функции,решение параболы онлайн,решение функции онлайн,решение функции онлайн с решением и графиком,решение функций онлайн,решение функций онлайн с решением,решение функций онлайн с решением и графиком,решение функция онлайн,решите графически уравнение онлайн,решите уравнение графически онлайн,решить график,решить график функции онлайн,решить график функции онлайн с решением,решить графически уравнение онлайн,решить графически уравнение онлайн с решением,решить онлайн график функции,решить онлайн функцию,решить уравнение графически онлайн,решить функцию онлайн,решить функцию онлайн с решением и построить график онлайн,рисование графиков онлайн,рисовать графики онлайн,рисовать онлайн графики,сайт для построения графиков,сайт для построения графиков функций,сайт построения графиков функции,свойства функции онлайн,сделать график онлайн,сделать график онлайн по данным,сделать график онлайн по точкам,сделать график по точкам онлайн,синусоида график онлайн,система координат онлайн,создание графиков онлайн,составить график функции онлайн,составить онлайн график функции,составление графика онлайн,составление графиков онлайн,составление онлайн графика,составление онлайн графиков,строение графика функции онлайн,строим график,строим графики онлайн,строим онлайн график,строитель графиков,строитель графиков онлайн,строитель графиков функций онлайн,строитель функций онлайн,строительство графиков онлайн,строить график,строить график онлайн,строить график функции онлайн,строить графики,строить графики онлайн,строить графики функций онлайн,трехмерная система координат онлайн,трехмерная система координат онлайн построение,трехмерная система координат онлайн построение по точкам,трехмерные графики онлайн,трехмерный график онлайн,тригонометрические графики онлайн,у 1 2х график,у 1 2х график функции,у 1 2х2 график,у 1 3х2 график,у 1 x график функции,у 1 график,у 1 график функции,у 1 корень из х график,у 1 х 2 график,у 1 х 2 график функции,у 1 х 3 график,у 1 х в квадрате график функции,у 1 х график,у 1 х2 график функции,у 2 x 2 график,у 2 x 2 график функции,у 2 x график,у 2 график,у 2 график функции,у 2 х 1 график,у 2 х построить график,у 2х 1 построить график,у 3 x график,у 3 x график функции,у 3 в степени х график,у 3 график,у 3 график функции,у 3 х 2 график,у 3 х график,у 3 х построить график функции,у 3х график,у 4 х 2 график функции,у 4 х построить график,у 5 х 2 график,у 5 х график,у x 2 график,у x график,у x график функции,у график функции,у х 1 2,у х 1 2 график,у х 1 график,у х 2 1 график,у х 2 построить график,у х 4,у х 4 2 график,у х 4 3,у х 4 график,у х 5 график функции,у х 6 график,у х в 2 степени график,у х в степени 2 график,у х график,у х построить график функции,у х2 1 график,функции график построение,функции калькулятор,функции онлайн,функции онлайн калькулятор,функции онлайн построить,функции онлайн с решением,функции решение онлайн,функция 1 3x 2,функция 1 x график,функция 2 x,функция 3 x,функция 4 x,функция x 1 график,функция x 2 график,функция x 4,функция x 5,функция y 1 2x в квадрате,функция y 5 x,функция y x 4,функция y x 5,функция график онлайн,функция квадратичная онлайн,функция онлайн,функция онлайн график,функция онлайн построить,функция онлайн решение,функция по точкам онлайн,функция построить онлайн,функция решение онлайн,х 0 график,х 1 в квадрате график,х 1 в квадрате график функции,х 1 график,х 1 х 2 построить график,х 2 1 график,х 2 4 график,х 2 4 график функции,х 2 y 2 1 график,х 2 y 4,х 2 график,х 3 1 график,х 3 график,х 4 график,х 4 график функции,х 4 функция,х y 2 график,х y график,х y график функции,х в квадрате 1 график,х в квадрате 4 график,х в степени 2 график,х график,х и у график,х у z график,х у график,х2 1 график,чертить график онлайн,чертить графики,черчение графиков онлайн.
Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как 1 2 cos x 2 график,1 2 x 4 график,1 2 x график,1 2 график,1 2 х график,1 2x график,1 3 x график,1 ln x график,1 x 2 график,1 x 2 график функции,1 x 3 график,1 x 3 график функции,1 x 4 график,1 x в квадрате график,1 x график,1 x график функции,1 y график,1 график,1 корень из х график,1 постройте график функции y,1 х 1 4 построить график функции,1 х 2 график,1 х 3 график,1 х в квадрате график,1 х график,1 х график функции,1 х2 график,2 1 x построить график,2 arctg x график,2 ln x график,2 x 3 график,2 x график,2 x график функции,2 график,2 х 1 график,2x 1 2 график,2x 1 график,2x 2 1 график,2x 2 график,2x 2 график функции,2x 3 график,2x x 2 график,2x x 2 график функции,2x y 2 график,2x y 4 график,2x график,2x график функции,2×2 график,2х график,3 sin x график,3 x график,3 х график,3 х график функции,3d график онлайн,3d графики онлайн,3x 2 график,3x y 2 график,3x график,3д график онлайн,4 2 построить график,4 x 2 график,4 x 2 график функции,4 x график,4 x2 график,4 в степени х график,4 х 2 график,4 х в квадрате график,4 х график,4x x 2 график,4x x 2 график функции,5 x график,6 x график,8 x график,a x график,arctg 2 x график,arctg 2x график,cos x 1 график,cos x 2 график,cos2x 1 график,e x график,e y график,e график,f y 2 x 2,graph online,lgx график,ln x 1 график,online graph,sin 1 x график,sin 2 x график,sin 3 x график,sin x 1 2 график,sin x 1 график,sin x 2 график,sin x 3 график,sin2x график,sinx x график,sqrt x график,tg 2 x график,x 0 y 0 график,x 0 y 0 график функции,x 0 график,x 1 2 график,x 1 2 график построить,x 1 3 график,x 1 x 2x график,x 1 в квадрате график,x 1 график,x 1 график функции,x 2 1 график,x 2 2x 3 график,x 2 2x график,x 2 2x график функции,x 2 3 график,x 2 3x 2 график,x 2 3x 2 график функции,x 2 4 график,x 2 5 график,x 2 a 2 график,x 2 y 1 график,x 2 y 2 0 график,x 2 y 2 1 график,x 2 y 2 2x график,x 2 y 2 4 график,x 2 y 2 5 график,x 2 y 2 a 2 график,x 2 y 2 график,x 2 y 3 график,x 2 график,x 2 график функции,x 2x 2 график,x 3 1 график,x 3 2 график,x 3 2 график функции,x 3 x 1 график функции,x 3 график,x 4 x 1 график функции,x 4 график,x 4 график функции,x 4 функция,x 5 график,x 5 график функции,x 6 график,x 6 график функции,x a 2 y 2 a 2 график,x a график,x arctg x график,x e график,x e график функции,x log x график,x ot y,x sinx график,x sqrt y график,x y 0 график,x y 1 построить график,x y 2 график,x y 3 график,x y 4 график,x y 5 график,x y 6 график,x y ru,x y график,x y построить,x y построить график,x в 2 степени график,x в 4 степени график,x в квадрате график,x в степени 2 график,x в степени 3 график,x в степени 4 график,x график,x график функции,x от y,x у 2 график,x2 4 график,x3 1 график,x3 график,x3 график функции,x4 график,xy график,y 0 5x 2 график,y 0 x 0 график функции,y 0 x график,y 0 x график функции y,y 0 график,y 0 график функции,y 1 2 cos 2 x график,y 1 2 x график,y 1 2 график,y 1 2 график функции,y 1 2x 2 график функции,y 1 2x график функции,y 1 2×2 график функции,y 1 3 x 2 график,y 1 3 x 2 график функции,y 1 3x 2 график,y 1 4 x,y 1 4 x график,y 1 4x,y 1 4x 2 график,y 1 4x график,y 1 5 x график,y 1 5 x график функции,y 1 5x график,y 1 9x,y 1 9x график,y 1 x 1 построить график,y 1 x 2 5,y 1 x 2 график,y 1 x 2 график функции,y 1 x 3 график,y 1 x 4,y 1 x график,y 1 x график функции,y 1 x построить график,y 1 график,y 1 график функции,y 1 х 2,y 10 x график,y 2 1 график,y 2 2x график,y 2 3 в степени x,y 2 3x построить график,y 2 4x график,y 2 5x график функции,y 2 x 1 график функции,y 2 x 3 график,y 2 x 3 график функции,y 2 x график,y 2 x график функции,y 2 в степени x 3,y 2 график,y 2 график функции,y 2 х график,y 2 х график функции,y 2 ч y ч 2,y 2sin3x график,y 2x 1 график функции,y 2x 2 x 1,y 2x 3 x 1,y 2x 3 график функции,y 2x 3 построить график функции,y 2x x,y 2x x 2 график,y 2x график,y 2x график функции,y 2x построить график,y 2×2 2,y 2×2 график функции,y 3 2x график,y 3 sin x график,y 3 x 2 график,y 3 x 2 график функции,y 3 x график,y 3 x график функции,y 3 в степени x 2,y 3 график,y 3sin2x график,y 3x 1 график,y 3x 1 график функции,y 3x 2 график,y 3x 2 график функции,y 3x 2 построить график функции,y 3x 6 график,y 3x x 2,y 4 1 x,y 4 x,y 4 x 1,y 4 x 1 2,y 4 x 1 2 график,y 4 x 2 график,y 4 x 2 график функции,y 4 x график,y 4 x график функции,y 4 x построить график,y 4 x построить график функции,y 4 x2 график,y 4 в степени x,y 4 в степени x график функции,y 4 в степени x график функции y,y 4 график,y 4x,y 4x 1,y 4x 1 2,y 4x 2 график,y 4x 2 график функции,y 4x x 2 график,y 4x график,y 4x график функции,y 5 2x график функции,y 5 x,y 5 x 2 построить график,y 5 x график,y 5 x график функции,y 5 x построить график функции,y 5x график функции,y 6 x график,y 7 x,y 7 x график,y 9 x график,y 9 x график функции,y 9 x график функции y,y a x график,y cos x 1 график,y cos x 2 график,y cos3x 2 график,y e график,y sin3x график,y sinx в квадрате график,y sqrt x график,y sqrt x график функции y,y x 0,y x 0 5,y x 1 2 график,y x 1 2 график функции,y x 1 4,y x 1 в квадрате график функции,y x 1 график функции,y x 1 построить график,y x 10 график,y x 10 построить график функции,y x 2 3 график,y x 2 4 построить график,y x 2 4x 5 построить график данной функции по графику определить,y x 2 x 3 график,y x 2 график,y x 2 график функции,y x 2 построить график,y x 2 построить график функции,y x 2 постройте график,y x 3 2 график,y x 3 4,y x 3 4 график,y x 3 4x,y x 3 5,y x 3 x 0,y x 3 x построить график,y x 3 график построить,y x 3 график функции как построить,y x 3 построить график,y x 4,y x 4 1,y x 4 2 график функции,y x 4 3,y x 4 x,y x 4 x построить график,y x 4 график,y x 4 график функции,y x 4 построить график функции,y x 5,y x 5 0,y x 5 x,y x 5 график,y x 5 график функции,y x 5 построить график функции,y x 6,y x 6 1,y x 6 график,y x 6 построить график,y x 6 постройте график,y x 7,y x 7 график,y x 7 график функции,y x 8 график,y x 9,y x 9 график функции,y x a график,y x r,y x ru,y x sgn x,y x x2,y x y 2 0 график функции,y x в 3 степени график,y x в 6 степени график,y x в квадрате построить график,y x в степени 2,y x в степени 2 3,y x график,y x график функции,y x график функций,y x как построить график,y x как построить график функции,y x построить график,y x постройте график,y x решение,y x2 2 график функции,y x2 3 график функции,y x2 3x график,y x2 график,y x2 график функции,y x2 построить график функции,y x4,y x4 y 1,y x4 график функции,y x5,y x5 график функции,y x6,y x6 график,y x6 график функции,y от x,y х 2 график,y х 2 график функции,y х 2 х 3,y х 4 график,yotx графики онлайн,z x y график,генератор графиков,генератор графиков функций,гипербола онлайн,граф решишь,график,график 1,график 1 2 x,график 1 2 х,график 1 2x,график 1 2x 2,график 1 3 x,график 1 sin x,график 1 x,график 1 x 2,график 1 x 3,график 1 x в квадрате,график 1 корень из х,график 1 х,график 1 х 2,график 1 х 3,график 1 х в квадрате,график 1 х2,график 2 tg x,график 2 x,график 2 x 3,график 2 в степени x,график 2 синус х,график 2 х,график 2cos2x,график 2x,график 2x 1,график 2x 2,график 2x 2 1,график 2x 3,график 2x x 2,график 2×2,график 2х,график 3 2 x,график 3 2x,график 3 x,график 3 x 1,график 3 x 2,график 3 х,график 3x,график 3x 2,график 4 x,график 4 x 2,график 4 в степени х,график 4 х,график 4 х 2,график 4 х в квадрате,график 4x x 2,график 4x y 2,график 5 x,график 6 x,график a x,график arctg 1 x,график arctg 2x,график arctg x 2,график cos 2 x,график e x,график e y,график lgx,график ln 1 x,график sin 1 x,график sin 2 x,график sin x построить график,график sin3x,график sinx x,график sqrt x,график tg 2 x,график x,график x 0,график x 1 2,график x 1 3,график x 2,график x 2 1,график x 2 2x,график x 2 3,график x 2 4,график x 2 y 2 0,график x 3,график x 3 1,график x 3 2,график x 4,график x 4 2,график x 5,график x 6,график x a,график x e,график x e y,график x sqrt y,график x y,график x y 0,график x y 2,график x y 8,график x y a,график x y z,график x в 2 степени,график x в степени 2,график x в степени 3,график x2 4,график x3,график x3 1,график x4,график xy,график y,график y 0,график y 1,график y 1 2,график y 1 2 x,график y 1 2x,график y 1 2×2,график y 1 3 x 2 x,график y 1 3x 2,график y 1 4 x,график y 1 5 x,график y 1 x,график y 1 x 2,график y 1 x 4,график y 10 x,график y 2,график y 2 1,график y 2 2x,график y 2 2x 1,график y 2 3x,график y 2 5 x,график y 2 cos x,график y 2 x 1,график y 2 x 3,график y 2 корень x,график y 2 х,график y 2cos x,график y 2x,график y 2x x 2,график y 2x x2,график y 3 2x,график y 3 x,график y 3 x 2,график y 3 в степени x 2,график y 3 корень x,график y 3sin2x,график y 3x,график y 3x 2,график y 4,график y 4 x,график y 4 x 2,график y 4 x 3,график y 4 x2,график y 4x,график y 4x 1,график y 4x 2,график y 4x x 2,график y 5 2x,график y 5 x,график y 7 x,график y 8 x,график y 9 x,график y e,график y sqrt x,график y tg 2 x,график y tg 2x,график y x,график y x 0,график y x 1 x 5,график y x 1 в квадрате,график y x 10,график y x 2,график y x 2 3,график y x 3 2,график y x 4,график y x 4 и y x 4,график y x 5,график y x 5 2,график y x 6,график y x 7,график y x 8,график y x a,график y x в 3 степени,график y x в 7 степени,график y x в квадрате 1,график y x2,график y х 2,график z x y,график в полярной системе координат онлайн,график в полярных координатах онлайн,график в пространстве онлайн,график в трехмерном пространстве онлайн,график гиперболы онлайн построить,график е,график зависимости онлайн построить,график икс в степени икс,график калькулятор,график квадратичной функции онлайн,график квадратичной функции построить онлайн,график комплексной функции онлайн,график координат,график корень из х 1,график косинус 3х,график кусочной функции онлайн,график логарифма онлайн,график логарифмической функции онлайн,график математика,график нарисовать,график начертить,график неявной функции онлайн,график окружности онлайн,график окружности онлайн построить,график онлайн,график онлайн 3d,график онлайн в полярной системе координат,график онлайн в полярных координатах,график онлайн в пространстве,график онлайн в трехмерном пространстве,график онлайн квадратичной функции,график онлайн неявной функции,график онлайн по точкам,график онлайн по уравнению,график онлайн по формуле,график онлайн по функции,график онлайн построение,график онлайн построить,график онлайн построить x y z,график онлайн построить по точкам,график онлайн построить по уравнению,график онлайн построить с модулем,график онлайн с модулем,график онлайн трехмерный,график онлайн функция,график онлайн чертить,график параболы онлайн,график параметрической функции онлайн,график по точкам онлайн,график по уравнению онлайн,график по формуле онлайн,график по функции,график по функции онлайн,график построение,график построение онлайн,график решить,график с корнем онлайн с,график с модулем онлайн,график с модулем онлайн построить,график сайт,график синус х 2,график системы уравнений онлайн,график степенной функции онлайн,график строить,график строить онлайн,график тригонометрической функции онлайн,график у 1,график у 1 2 х,график у 1 2х,график у 1 2х2,график у 1 x,график у 1 корень из х,график у 1 х,график у 1 х 2,график у 2,график у 2 x,график у 3 x,график у 3 х,график у 3х,график у 4 х,график у x,график у x 2,график у х,график у х 1,график у х 1 х 3,график у х 2 5,график у х 4,график у х 5,график у х 7,график у х 8,график у х в степени 2,график у х2 1,график уравнения y 2 x 2,график уравнения онлайн,график функции,график функции 1 2 x,график функции 1 2 х,график функции 1 cos x 1,график функции 1 x,график функции 1 x 2,график функции 1 x 3,график функции 1 x 4,график функции 1 x в квадрате,график функции 1 корень из х,график функции 1 х,график функции 1 х 2,график функции 1 х 3,график функции 1 х в квадрате,график функции 2 1 х,график функции 2 3 x,график функции 2 x,график функции 2 x 1,график функции 2 x 3,график функции 2 y 1 x,график функции 2 х 1,график функции 2x,график функции 2x 2 x,график функции 3 1 х,график функции 3 x,график функции 3 x 1,график функции 3 x 2,график функции 3 х,график функции 4 x,график функции 4 x 2,график функции 4 в степени х,график функции 4 х,график функции 4 х 2,график функции 5 x,график функции sin 1 x,график функции x,график функции x 1,график функции x 1 2,график функции x 1 3,график функции x 1 в квадрате,график функции x 2,график функции x 2 1,график функции x 2 3,график функции x 2 4x,график функции x 2 y 2,график функции x 2 y 2 4,график функции x 2 y 2 9,график функции x 2 y 2 9 график,график функции x 2x 2,график функции x 3,график функции x 3 1,график функции x 3 2,график функции x 3 sin y,график функции x 3 x 1 x,график функции x 3 x 2 1,график функции x 4,график функции x 4 2,график функции x 5,график функции x 6,график функции x e,график функции x y,график функции x y 0 x,график функции x y 1,график функции x y 5,график функции x y a,график функции x3,график функции y 0,график функции y 0 x 0,график функции y 1,график функции y 1 2,график функции y 1 2x,график функции y 1 3 x 2,график функции y 1 3x в квадрате,график функции y 1 4x в квадрате,график функции y 1 x 4,график функции y 1 x в квадрате,график функции y 2,график функции y 2 1,график функции y 2 3x,график функции y 2 x,график функции y 2 x 1,график функции y 2 x 3,график функции y 2 x2,график функции y 2x,график функции y 2x 2,график функции y 2x 3,график функции y 2×2,график функции y 2×2 1,график функции y 3,график функции y 3 2x,график функции y 3 x,график функции y 3 x 2,график функции y 3x 2,график функции y 4 x,график функции y 4 x 2,график функции y 4 в x степени,график функции y 4x 2,график функции y 5,график функции y 5 2x,график функции y 5 x,график функции y 5 x 2,график функции y 5x,график функции y 5x 2,график функции y 5x 4,график функции y 6 2x,график функции y lg x,график функции y tg 2x,график функции y x,график функции y x 1,график функции y x 1 2,график функции y x 1 4,график функции y x 1 x 2,график функции y x 1 в квадрате,график функции y x 10,график функции y x 2 3,график функции y x 2 3 x 2x,график функции y x 2 5,график функции y x 2 x 0,график функции y x 3 2,график функции y x 3 4,график функции y x 3 как построить,график функции y x 4,график функции y x 4 2,график функции y x 4 3,график функции y x 5,график функции y x 6,график функции y x 7,график функции y x 9,график функции y x sqrt x 2,график функции y x в квадрате 1,график функции y x как построить,график функции y x2,график функции y x2 1,график функции y x2 3,график функции y x4,график функции y x5,график функции y x6,график функции y х,график функции в полярных координатах онлайн,график функции двух переменных онлайн,график функции двух переменных онлайн построить,график функции как выглядит,график функции калькулятор,график функции калькулятор онлайн,график функции нарисовать,график функции одна вторая икс в квадрате,график функции онлайн,график функции онлайн x y z,график функции онлайн двух переменных,график функции онлайн калькулятор,график функции онлайн неявной,график функции онлайн по точкам,график функции онлайн построение,график функции онлайн построить,график функции онлайн построить по точкам,график функции онлайн построить с корнем,график функции онлайн построить с модулем,график функции онлайн построить с решением,график функции онлайн с модулем,график функции онлайн с решением,график функции параметрической онлайн,график функции по,график функции по точкам онлайн,график функции по точкам онлайн построить,график функции построение,график функции построение онлайн,график функции решение,график функции решить онлайн,график функции с модулем онлайн,график функции с решением онлайн,график функции синус 2х,график функции строить онлайн,график функции у,график функции у 1 2 х,график функции у 1 2х,график функции у 1 х 2,график функции у 1 х в квадрате,график функции у 2,график функции у 2 x,график функции у 3,график функции у 3 x,график функции у 4х в квадрате,график функции у x,график функции у x 1,график функции у x 2,график функции х,график функции х 1,график функции х 1 2,график функции х 2 1,график функции х 2 y,график функции х 3 2,график функции х 4,график функции х 4 2,график функции х 4 х 2,график функции х y,график функции х y 2,график функции х в 4 степени,график функции х в квадрате минус х,график функции х в квадрате х,график функции х делить на х,график функции х у,график функций,график функций онлайн,график функция онлайн,график х,график х 0,график х 1,график х 1 2,график х 1 в квадрате,график х 2,график х 2 1,график х 2 3,график х 2 y 2,график х 3,график х 3 1,график х 3 2,график х 4,график х y 2,график х в квадрате,график х в квадрате 1,график х в квадрате 4,график х в степени 2,график х в степени 4,график х е х,график х и у,график х у,график х у 4,график х у z,график х2 1,график х3,график чертить онлайн,график экспоненты в степени минус х,графика онлайн,графика точками,графики,графики x 2 y 2,графики y 2 x,графики в полярной системе координат онлайн,графики в полярных координатах онлайн,графики онлайн,графики онлайн 3d,графики онлайн в полярной системе координат,графики онлайн в полярных координатах,графики онлайн по точкам,графики онлайн полярная система координат,графики онлайн построение,графики онлайн построение по точкам,графики онлайн построение по уравнению,графики онлайн трехмерные,графики по точкам онлайн,графики по точкам онлайн построение,графики построение,графики построение онлайн,графики построить,графики построить онлайн,графики рисовать онлайн,графики строить,графики строить онлайн,графики уравнений онлайн,графики функции онлайн,графики функций x 2 y 2,графики функций калькулятор,графики функций онлайн,графики функций онлайн калькулятор,графики функций онлайн построение,графики функций онлайн с модулем,графики функций онлайн с решением,графики функций построение,графики функций построение онлайн,графики функций построить,графики функций с модулем онлайн,графики функций строить онлайн,графики чертить,графический калькулятор онлайн,графический онлайн калькулятор,графическое решение уравнений онлайн,графік,графік функції y 2 x,графік функції y x 2,графік функції онлайн,графіки,графіки онлайн,графопостроитель онлайн,дослідити функцію та побудувати її графік онлайн,е график,е х график,изобразите график функции,изобразить график функции онлайн,изоклины онлайн построение,икс в степени икс график,инженерная графика онлайн построение,используя график функции y f x постройте график функции,используя график функции построить график функции,исследовать график функции онлайн,исследовать график функции онлайн с решением,исследовать и построить график функции онлайн,исследовать функцию и построить график онлайн решение калькулятор,как выглядит график,как выглядит график x 2 y 2,как выглядит график функции,как начертить график функции,как построить x y,как построить y x,как построить график x y,как построить график x y 2,как построить график y 2 x,как построить график y x,как построить график y x 2,как построить график функции x 2 y,как построить график функции x y,как построить график функции x y 2,как построить график функции x y 3,как построить график функции y,как построить график функции y x,как построить график функции y x 2,как построить график функции по уравнению,калькулятор график,калькулятор график функции,калькулятор графика функции,калькулятор графики функций,калькулятор графиков,калькулятор графиков онлайн,калькулятор графиков функций,калькулятор графиков функций онлайн,калькулятор графиков функций онлайн с решением,калькулятор графический онлайн,калькулятор для построения графиков функций,калькулятор онлайн график функции,калькулятор онлайн графиков,калькулятор онлайн построить график функции,калькулятор построения графиков функций,калькулятор построения графиков функций онлайн,калькулятор построить график функции,калькулятор функции график,калькулятор функции онлайн,калькулятор функций,калькулятор функций графики,калькулятор функций графики онлайн,калькулятор функций онлайн,квадратичная функция онлайн,конструктор графиков,конструктор графиков онлайн,конструктор онлайн функций,конструктор функций онлайн,координатная плоскость онлайн,координатная плоскость онлайн рисовать,координатная прямая онлайн,косинус 3х график,косинус х 2 график,лучший построитель графиков,лучший построитель графиков онлайн,математика график,математикам ру построение графика,найти график функции,нарисовать график,нарисовать график онлайн,нарисовать график онлайн вручную,нарисовать график онлайн по точкам,нарисовать график по точкам онлайн,нарисовать график функции,нарисовать график функции онлайн,нарисовать онлайн функцию,нарисовать функцию онлайн,начертите график,начертить график,начертить график онлайн,начертить график онлайн по точкам,начертить график по точкам онлайн,начертить график функции онлайн,неравенства график онлайн,окружность построить онлайн,онлайн 3d график,онлайн гипербола,онлайн график,онлайн график в полярной системе координат,онлайн график квадратичной функции,онлайн график логарифма,онлайн график логарифмической функции,онлайн график по таблице,онлайн график по точкам,онлайн график по уравнению,онлайн график по формуле,онлайн график построение,онлайн график с модулем,онлайн график функции,онлайн график функции z x y,онлайн график функции с модулем,онлайн графика,онлайн графики,онлайн графики в полярных координатах,онлайн графики в пространстве,онлайн графики по точкам,онлайн графики с модулем,онлайн графики уравнений,онлайн графики функции,онлайн графики функций построить,онлайн графіки,онлайн калькулятор график функции,онлайн калькулятор графики функций,онлайн калькулятор графиков,онлайн калькулятор графиков функций,онлайн калькулятор графиков функций с решением,онлайн калькулятор для функций,онлайн калькулятор построения графиков функций,онлайн калькулятор построить график функции,онлайн калькулятор функции,онлайн калькулятор функций,онлайн квадратичная функция,онлайн конструктор графиков,онлайн конструктор функций,онлайн координатная плоскость,онлайн координатная прямая,онлайн описать функцию,онлайн парабола,онлайн побудова графіків,онлайн побудова графіків функцій,онлайн построение,онлайн построение гиперболы,онлайн построение график функции,онлайн построение графика,онлайн построение графика в полярной системе координат,онлайн построение графика в полярных координатах,онлайн построение графика квадратичной функции,онлайн построение графика функции,онлайн построение графиков,онлайн построение графиков 3d,онлайн построение графиков в полярных координатах,онлайн построение графиков в трехмерной системе координат,онлайн построение графиков зависимости,онлайн построение графиков неравенств,онлайн построение графиков онлайн в полярной системе координат онлайн,онлайн построение графиков по точкам,онлайн построение графиков по уравнению,онлайн построение графиков по физике,онлайн построение графиков с двумя переменными,онлайн построение графиков с корнем,онлайн построение графиков с корнями,онлайн построение графиков с модулем,онлайн построение графиков сложных функций,онлайн построение графиков тригонометрических функций,онлайн построение графиков уравнений,онлайн построение графиков функции,онлайн построение графиков функций,онлайн построение графиков функций x y z,онлайн построение графиков функций по уравнению,онлайн построение графиков функций с модулем,онлайн построение графиков функций с решением,онлайн построение графов,онлайн построение квадратичной функции,онлайн построение кривых,онлайн построение логарифмических графиков,онлайн построение нескольких графиков в одной системе координат,онлайн построение окружности,онлайн построение параболы,онлайн построение синусоиды,онлайн построение тригонометрических графиков,онлайн построение тригонометрических функций,онлайн построение фигур,онлайн построение функций,онлайн построения графиков,онлайн построитель,онлайн построитель графиков,онлайн построитель графиков функций,онлайн построитель функций,онлайн построить график квадратичной функции,онлайн построить графики функций,онлайн постройка графика,онлайн постройка графиков,онлайн постройка графиков функций,онлайн программа для построения графиков,онлайн программа построения графиков,онлайн решение графика функции,онлайн решение графиков,онлайн решение графиков функций,онлайн решение графических уравнений,онлайн решение квадратичной функции,онлайн решение параболы,онлайн решение функций,онлайн решение функция,онлайн решить график функции,онлайн рисование графиков,онлайн система координат,онлайн составить график функции,онлайн составление графика,онлайн составление графиков,онлайн строим график,онлайн строим графики,онлайн строитель графиков,онлайн строитель графиков функций,онлайн строитель функций,онлайн строительство графиков,онлайн строить график функции,онлайн строить графики функций,онлайн трехмерная система координат,онлайн функции,онлайн функция,онлайн функция график,онлайн функция решение,онлайн чертить график,онлайн черчение графиков,описать график функции онлайн,описать функцию онлайн,определить функцию по графику онлайн,парабола онлайн,парабола онлайн построение,парабола построение онлайн,параболы онлайн построение,по графику определить функцию онлайн,по математике графики,по формуле построить график,побудова графіків,побудова графіків онлайн,побудова графіків функцій,побудова графіків функцій онлайн,побудувати графік,побудувати графік онлайн,побудувати графік функції,побудувати графік функції онлайн,побудувати графік функції онлайн розв язок,побудуйте графік функції,полярная система координат графики онлайн,построение 3д графиков онлайн,построение в полярных координатах онлайн,построение график,построение график онлайн,построение график функции,построение график функции онлайн,построение графика,построение графика в полярной системе координат онлайн,построение графика в полярных координатах онлайн,построение графика квадратичной функции онлайн,построение графика онлайн,построение графика онлайн в полярных координатах,построение графика онлайн по точкам,построение графика онлайн по функции,построение графика по точкам,построение графика по точкам онлайн,построение графика по функции онлайн,построение графика функции,построение графика функции онлайн,построение графика функции онлайн с решением,построение графики,построение графики функций,построение графиков,построение графиков xyz онлайн,построение графиков в полярной системе координат онлайн,построение графиков в полярной системе координат онлайн с решением,построение графиков в полярных координатах онлайн,построение графиков в пространстве онлайн,построение графиков в трехмерной системе координат онлайн,построение графиков в трехмерном пространстве онлайн,построение графиков зависимости онлайн,построение графиков на миллиметровке онлайн,построение графиков неравенств онлайн,построение графиков онлайн,построение графиков онлайн 3д,построение графиков онлайн xyz,построение графиков онлайн в полярной системе координат,построение графиков онлайн в полярных координатах,построение графиков онлайн в пространстве,построение графиков онлайн в трехмерной системе координат,построение графиков онлайн на миллиметровке,построение графиков онлайн неравенств,построение графиков онлайн по таблице,построение графиков онлайн по точкам,построение графиков онлайн по точкам на миллиметровке,построение графиков онлайн по уравнению,построение графиков онлайн по физике,построение графиков онлайн с двумя переменными,построение графиков онлайн с корнем,построение графиков онлайн с корнями,построение графиков онлайн с модулем,построение графиков онлайн с параметром,построение графиков онлайн с решением,построение графиков онлайн трехмерных,построение графиков по таблице онлайн,построение графиков по точкам,построение графиков по точкам онлайн,построение графиков по уравнению онлайн,построение графиков по физике онлайн,построение графиков полярных онлайн,построение графиков с двумя переменными онлайн,построение графиков с корнем онлайн,построение графиков с корнями онлайн,построение графиков с модулем онлайн,построение графиков с параметром онлайн,построение графиков сложных функций онлайн,построение графиков тригонометрических онлайн,построение графиков тригонометрических функций онлайн,построение графиков уравнений онлайн,построение графиков функции,построение графиков функции онлайн,построение графиков функции онлайн с решением,построение графиков функции с решением онлайн,построение графиков функций,построение графиков функций онлайн,построение графиков функций онлайн x y z,построение графиков функций онлайн по уравнению,построение графиков функций онлайн с модулем,построение графиков функций онлайн с подробным решением,построение графиков функций онлайн с решением,построение графиков функций по уравнению онлайн,построение графиков функций с модулем онлайн,построение графиков функций с решением онлайн,построение графов онлайн,построение квадратичной функции онлайн,построение кривых онлайн,построение логарифмических графиков онлайн,построение нескольких графиков в одной системе координат онлайн,построение нескольких графиков онлайн,построение обратной функции онлайн,построение окружности онлайн,построение онлайн,построение онлайн кривых,построение параболы онлайн,построение параболы онлайн по квадратному уравнению,построение параболы по квадратному уравнению онлайн,построение параметрических графиков онлайн с решением,построение полярных графиков онлайн,построение пространственных графиков онлайн,построение синусоиды онлайн,построение сложных графиков онлайн,построение сложных графиков функций онлайн,построение точек онлайн по координатам,построение точек по координатам онлайн,построение трехмерных графиков онлайн,построение тригонометрических графиков онлайн,построение тригонометрических функций онлайн,построение уравнений онлайн,построение функции,построение функции онлайн,построение функций,построение функций онлайн,построения графиков онлайн,построитель графиков,построитель графиков онлайн,построитель графиков функций,построитель графиков функций онлайн,построитель онлайн,построитель функций,построитель функций онлайн,построить y x 2 x 1,построить гиперболу онлайн,построить гиперболу онлайн по уравнению,построить гиперболу по уравнению онлайн,построить график,построить график 1 x 2,построить график 3d,построить график x 3 x 2,построить график x f y,построить график x sin x,построить график x y,построить график x y 1,построить график x y z онлайн,построить график x y в квадрате,построить график y,построить график y 1 x,построить график y 2 2x,построить график y 2 x,построить график y 2 x 3,построить график y 2x,построить график y 3 2 x,построить график y 4 x,построить график y cos2x,построить график y x,построить график y x 1,построить график y x 2,построить график y x 3,построить график y x 4,построить график y x 4 2,построить график y x 5,построить график y x 6,построить график в полярной системе координат онлайн,построить график в полярных координатах онлайн,построить график в трехмерном пространстве онлайн,построить график зависимости онлайн,построить график зависимости онлайн по точкам,построить график зависимости по точкам онлайн,построить график квадратичной функции онлайн,построить график квадратичной функции онлайн с решением,построить график логарифмической функции онлайн,построить график неявной функции онлайн,построить график обратной функции онлайн,построить график окружности онлайн,построить график онлайн,построить график онлайн x y z,построить график онлайн в полярной системе координат,построить график онлайн в трехмерном пространстве,построить график онлайн неявной функции,построить график онлайн окружности,построить график онлайн по данным таблицы,построить график онлайн по координатам,построить график онлайн по таблице,построить график онлайн по таблице онлайн,построить график онлайн по точкам,построить график онлайн по точкам x y,построить график онлайн по точкам на миллиметровке,построить график онлайн по точкам онлайн,построить график онлайн по уравнению,построить график онлайн по уравнению онлайн,построить график онлайн по функции,построить график онлайн с модулем,построить график параметрической функции онлайн,построить график по данным таблицы онлайн,построить график по координатам онлайн,построить график по таблице онлайн,построить график по точкам,построить график по точкам онлайн,построить график по уравнению онлайн,построить график по уравнению функции,построить график по функции онлайн,построить график с корнем онлайн с,построить график с модулем онлайн,построить график системы уравнений онлайн,построить график тригонометрической функции онлайн,построить график тригонометрической функции онлайн с решением,построить график у 2 х,построить график у 4 х,построить график у x 2 3 x 2,построить график у х 1 2,построить график у х 2,построить график у х 3,построить график у х 4,построить график уравнения,построить график уравнения онлайн,построить график уравнения онлайн с решением,построить график функции,построить график функции 1 x 1,построить график функции 1 x 2,построить график функции 1 y 2x,построить график функции 1 у 3 х,построить график функции 2 5 x 2,построить график функции 2 5x 2,построить график функции x 1 2,построить график функции x 2 1,построить график функции x 3 2x 2 x 3,построить график функции x f y,построить график функции x y,построить график функции x y 4,построить график функции y,построить график функции y 1 2 x 2,построить график функции y 1 2x 2,построить график функции y 1 2×2,построить график функции y 1 x,построить график функции y 1 x 3,построить график функции y 2 3 x,построить график функции y 2 3x,построить график функции y 2 5x,построить график функции y 2 x 3,построить график функции y 2 x 5,построить график функции y 2x 3,построить график функции y 2x 4 x 2 1 решение,построить график функции y 3 2x,построить график функции y 3 x 2,построить график функции y 3x в квадрате,построить график функции y 4 x,построить график функции y 4 x 1,построить график функции y 5 2x,построить график функции y 5 x 2,построить график функции y 5x 2,построить график функции y 8 x,построить график функции y cos x 1,построить график функции y x,построить график функции y x 1,построить график функции y x 1 2,построить график функции y x 1 2 3,построить график функции y x 1 4,построить график функции y x 1 x 2,построить график функции y x 1 x 3,построить график функции y x 10,построить график функции y x 2,построить график функции y x 2 3,построить график функции y x 3,построить график функции y x 3 2,построить график функции y x 4 2,построить график функции y x 4 x,построить график функции y x 5,построить график функции y x 7,построить график функции y x 8,построить график функции y x cos x,построить график функции y x sin x,построить график функции в полярной системе координат онлайн,построить график функции в трехмерном пространстве онлайн,построить график функции двух переменных онлайн,построить график функции калькулятор,построить график функции онлайн,построить график функции онлайн в полярной системе координат,построить график функции онлайн в трехмерном пространстве,построить график функции онлайн калькулятор,построить график функции онлайн по точкам,построить график функции онлайн по уравнению,построить график функции онлайн по уравнению онлайн,построить график функции онлайн по уравнению с решением,построить график функции онлайн с корнем,построить график функции онлайн с модулем,построить график функции онлайн с подробным решением,построить график функции онлайн с подробным решением 9 класс,построить график функции онлайн с решением,построить график функции онлайн с решением 10 класс,построить график функции онлайн с таблицей точек,построить график функции по модулю онлайн,построить график функции по точкам онлайн,построить график функции по уравнению,построить график функции по уравнению онлайн,построить график функции с корнем онлайн,построить график функции с модулем онлайн,построить график функции с модулем онлайн с подробным решением,построить график функции у,построить график функции у 1 х,построить график функции у 1 х 2,построить график функции у 2 х,построить график функции у х,построить график функции у х в квадрате,построить график функции х в квадрате,построить график функции х у,построить график функции х у 4,построить график функции х у 5,построить график функций,построить график функций онлайн с решением,построить график функций с решением онлайн,построить график х у 2,построить графики,построить графики онлайн,построить графики онлайн по точкам,построить графики по точкам онлайн,построить графики функций,построить графики функций в одной системе координат,построить графики функций онлайн,построить графики функций онлайн с решением,построить и исследовать график функции онлайн,построить и прочитать график функции,построить интегральную кривую онлайн,построить интегральные кривые онлайн,построить калибровочный график онлайн,построить кривую заданную уравнением в полярной системе координат онлайн,построить кривую онлайн,построить кривые по заданным уравнениям онлайн с решением,построить линии уровня функции онлайн,построить несколько графиков на одном онлайн,построить область ограниченную линиями онлайн,построить окружность онлайн,построить онлайн график в полярных координатах,построить онлайн график логарифмической функции,построить онлайн график с модулем,построить онлайн график функции по точкам,построить онлайн график функций,построить онлайн фигуру,построить параболу онлайн,построить параболу онлайн по уравнению,построить параболу по уравнению онлайн,построить по точкам график зависимости онлайн,построить прямую онлайн,построить прямую онлайн по уравнению,построить прямую по уравнению онлайн,построить тригонометрический график онлайн,построить функции онлайн,построить функцию,построить функцию онлайн,построить функцию онлайн с решением,построить функция онлайн,построить эллипс онлайн,построить эскиз графика функции онлайн,построй график функции,постройка графика,постройка графика онлайн,постройка графика онлайн по точкам,постройка графика по точкам онлайн,постройка графика функции,постройка графика функции онлайн,постройка графиков,постройка графиков онлайн,постройка графиков функций онлайн,постройте график,постройте график x y,постройте график y 2 x,постройте график y x,постройте график y x 2,постройте график y x 6,постройте график онлайн,постройте график уравнений,постройте график уравнения 2×2 y 4x 3,постройте график функции,постройте график функции x 3,постройте график функции x y 2 y 0 x,постройте график функции y,постройте график функции y 1 2,постройте график функции y 1 3 x 2,постройте график функции y 1 3x 2,постройте график функции y 1 4x,постройте график функции y 1 6x,постройте график функции y 1 x,постройте график функции y 2,постройте график функции y 2 3 x,постройте график функции y 2 корень 3 степени из x,постройте график функции y 2x,постройте график функции y 3 4 x 1,постройте график функции y 3 х 1,постройте график функции y x,постройте график функции y x 1,постройте график функции y x 1 2,постройте график функции y x 1 x 3 x 4,постройте график функции y x 10,постройте график функции y x 2 x 3 x 1,постройте график функции y x 3,постройте график функции y x 3 2,постройте график функции y x 5,постройте график функции y х 2,постройте график функции игрек равен,постройте график функции игрек равно,постройте график функции онлайн,постройте график функции онлайн с решением,постройте график функции у,постройте график функции у 1 4х2,постройте график функции у 1 x,постройте график функции х у,постройте график функций,постройте график функций y,постройте графики,постройте графики функций,преобразование графиков функций онлайн,преобразование функции онлайн,программа для построения графиков онлайн,программа для построения графиков функций онлайн,программа онлайн для построения графиков,программа онлайн построения графиков,программа построения графиков онлайн,программа построения графиков функций онлайн,прямая у х,прямоугольная система координат онлайн,решение y 1 x,решение график функции,решение графика функции онлайн,решение графиков,решение графиков онлайн,решение графиков функций,решение графиков функций онлайн,решение графиков функций онлайн с решением,решение графических уравнений онлайн,решение квадратичной функции онлайн,решение онлайн графика функции,решение онлайн графиков функций,решение онлайн квадратичной функции,решение онлайн функции,решение параболы онлайн,решение функции онлайн,решение функции онлайн с решением и графиком,решение функций онлайн,решение функций онлайн с решением,решение функций онлайн с решением и графиком,решение функция онлайн,решите графически уравнение онлайн,решите уравнение графически онлайн,решить график,решить график функции онлайн,решить график функции онлайн с решением,решить графически уравнение онлайн,решить графически уравнение онлайн с решением,решить онлайн график функции,решить онлайн функцию,решить уравнение графически онлайн,решить функцию онлайн,решить функцию онлайн с решением и построить график онлайн,рисование графиков онлайн,рисовать графики онлайн,рисовать онлайн графики,сайт для построения графиков,сайт для построения графиков функций,сайт построения графиков функции,свойства функции онлайн,сделать график онлайн,сделать график онлайн по данным,сделать график онлайн по точкам,сделать график по точкам онлайн,синусоида график онлайн,система координат онлайн,создание графиков онлайн,составить график функции онлайн,составить онлайн график функции,составление графика онлайн,составление графиков онлайн,составление онлайн графика,составление онлайн графиков,строение графика функции онлайн,строим график,строим графики онлайн,строим онлайн график,строитель графиков,строитель графиков онлайн,строитель графиков функций онлайн,строитель функций онлайн,строительство графиков онлайн,строить график,строить график онлайн,строить график функции онлайн,строить графики,строить графики онлайн,строить графики функций онлайн,трехмерная система координат онлайн,трехмерная система координат онлайн построение,трехмерная система координат онлайн построение по точкам,трехмерные графики онлайн,трехмерный график онлайн,тригонометрические графики онлайн,у 1 2х график,у 1 2х график функции,у 1 2х2 график,у 1 3х2 график,у 1 x график функции,у 1 график,у 1 график функции,у 1 корень из х график,у 1 х 2 график,у 1 х 2 график функции,у 1 х 3 график,у 1 х в квадрате график функции,у 1 х график,у 1 х2 график функции,у 2 x 2 график,у 2 x 2 график функции,у 2 x график,у 2 график,у 2 график функции,у 2 х 1 график,у 2 х построить график,у 2х 1 построить график,у 3 x график,у 3 x график функции,у 3 в степени х график,у 3 график,у 3 график функции,у 3 х 2 график,у 3 х график,у 3 х построить график функции,у 3х график,у 4 х 2 график функции,у 4 х построить график,у 5 х 2 график,у 5 х график,у x 2 график,у x график,у x график функции,у график функции,у х 1 2,у х 1 2 график,у х 1 график,у х 2 1 график,у х 2 построить график,у х 4,у х 4 2 график,у х 4 3,у х 4 график,у х 5 график функции,у х 6 график,у х в 2 степени график,у х в степени 2 график,у х график,у х построить график функции,у х2 1 график,функции график построение,функции калькулятор,функции онлайн,функции онлайн калькулятор,функции онлайн построить,функции онлайн с решением,функции решение онлайн,функция 1 3x 2,функция 1 x график,функция 2 x,функция 3 x,функция 4 x,функция x 1 график,функция x 2 график,функция x 4,функция x 5,функция y 1 2x в квадрате,функция y 5 x,функция y x 4,функция y x 5,функция график онлайн,функция квадратичная онлайн,функция онлайн,функция онлайн график,функция онлайн построить,функция онлайн решение,функция по точкам онлайн,функция построить онлайн,функция решение онлайн,х 0 график,х 1 в квадрате график,х 1 в квадрате график функции,х 1 график,х 1 х 2 построить график,х 2 1 график,х 2 4 график,х 2 4 график функции,х 2 y 2 1 график,х 2 y 4,х 2 график,х 3 1 график,х 3 график,х 4 график,х 4 график функции,х 4 функция,х y 2 график,х y график,х y график функции,х в квадрате 1 график,х в квадрате 4 график,х в степени 2 график,х график,х и у график,х у z график,х у график,х2 1 график,чертить график онлайн,чертить графики,черчение графиков онлайн.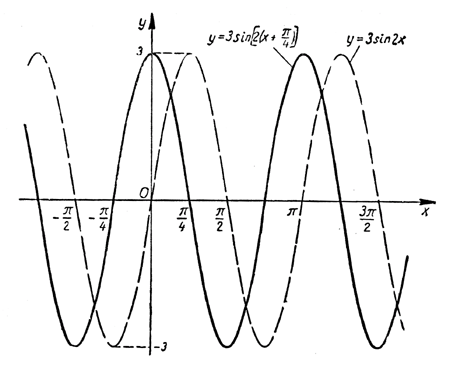 На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и 1 2 cos x 2 график. Просто введите задачу в окошко и нажмите
«решить» здесь (например, 1 2 x график).
На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и 1 2 cos x 2 график. Просто введите задачу в окошко и нажмите
«решить» здесь (например, 1 2 x график).
Где можно решить любую задачу по математике, а так же 1 2 cos x 2 график Онлайн?
Решить задачу 1 2 cos x 2 график вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Функция обратной синусоиды
Функция обратной синусоидыФункция y = sin -1 x = arcsin x и ее график:
Поскольку y = sin -1 x является обратной функцией y = sin x, функция y = sin -1 x тогда и только тогда, когда sin y = x . Чтобы получить график y = sin -1 x, начните с графика y = sin x. | |
Ограничить область определения функции однозначным region — обычно используется (выделено красным справа) для sin -1 x. Это оставляет диапазон ограниченной функции неизменным как [-1, 1]. | |
Отразите этот график поперек линии y = x, чтобы получить график y = sin -1 x (y = arcsin x), черная кривая справа. Обратите внимание, что y = sin -1 x имеет домен [-1, 1] и диапазон. Он строго увеличивается на всей своей территории. | |
Итак, когда вы попросите калькулятор построить график y = sin -1 x, вы получите график, показанный справа. (Окно просмотра составляет [-2, 2] x [-2, 2].) (Окно просмотра составляет [-2, 2] x [-2, 2].) |
Вычисление y = sin
-1 x:Пример 1: Вычислить sin
-1 (1/2)Большинство людей знакомы (и более комфортно) с тригонометрическими функциями, чем с их обратными.Следовательно, первый шаг в оценке этого выражения — сказать, что если y = sin -1 (1/2), то sin y = 1/2. Эта простая тригонометрическая функция имеет бесконечное количество решений:
Пять из этих решений обозначены вертикальными линиями на графике y = sin x ниже.
Итак, значение sin -1 (1/2) определяется приведенными выше выражениями? Нет! Жизненно важно помнить, что функция обратной синусоиды является однозначной и однозначной функцией.Только одно из бесконечного числа решений, приведенных выше, является желаемым результатом. Который из? Помните, что диапазон sin -1 x равен, что показано синим цветом на рисунке выше.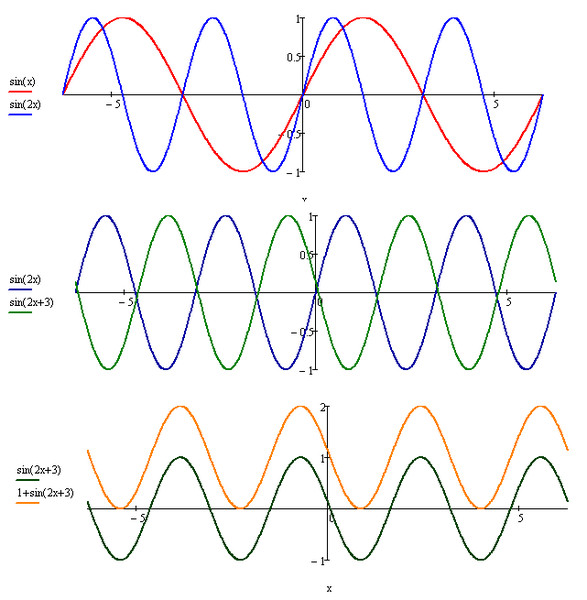 Это действительно важно знать область и диапазон обратных тригонометрических функций! (Почему этот синий интервал отмечен на оси x, если он представляет диапазон sin -1 x? Потому что диапазон обратной функции равен области главной функции.) Единственное решение y = sin x, которое попадает в требуемый диапазон, — это (сплошная красная линия на рисунке выше). Следовательно,
Это действительно важно знать область и диапазон обратных тригонометрических функций! (Почему этот синий интервал отмечен на оси x, если он представляет диапазон sin -1 x? Потому что диапазон обратной функции равен области главной функции.) Единственное решение y = sin x, которое попадает в требуемый диапазон, — это (сплошная красная линия на рисунке выше). Следовательно,
Пример 2: Что такое
Справа показана единичная круговая диаграмма. Обратите внимание, что кандидатами на решение являются:
Однако только одно из этих значений находится в диапазоне sin -1 x (), поэтому:
Производная y = sin -1 x:
Производная y = sin -1 x: (Щелкните здесь, чтобы получить вывод. )
)
Графики y = sin -1 x и его производной показаны справа. Область y ‘равна (-1,1). Поскольку y = sin -1 x всегда увеличивается, y ‘> 0 для всех x в своей области.
Интегралы, включающие функцию обратной синусоиды
Так как,. Это означает, что функция арксинуса возникает при обсуждении интегралов (и площадей) «относительно нормально выглядящих» алгебраических функций.Например:
Это заштрихованная область, показанная на снимке экрана TI-89 справа. (Окно [-0,5, 1,1] x [0, 3].)
последнее обновление 16 января 2009 г., Джерри Л. Стэнбро
3. Графики y = asin (bx + c) и y = acos (bx + c)
М. Борна
В этом разделе мы встречаем следующие 2 типа графиков:
y = a sin ( bx + c )
и
y = a cos ( bx + c )
И b , и c на этих графиках влияют на фазовый сдвиг (или смещение ), определяемый как:
`текст (Фазовый сдвиг) = (- c) / b`
Сдвиг фазы — это величина смещения кривой
в горизонтальном направлении от нормального положения.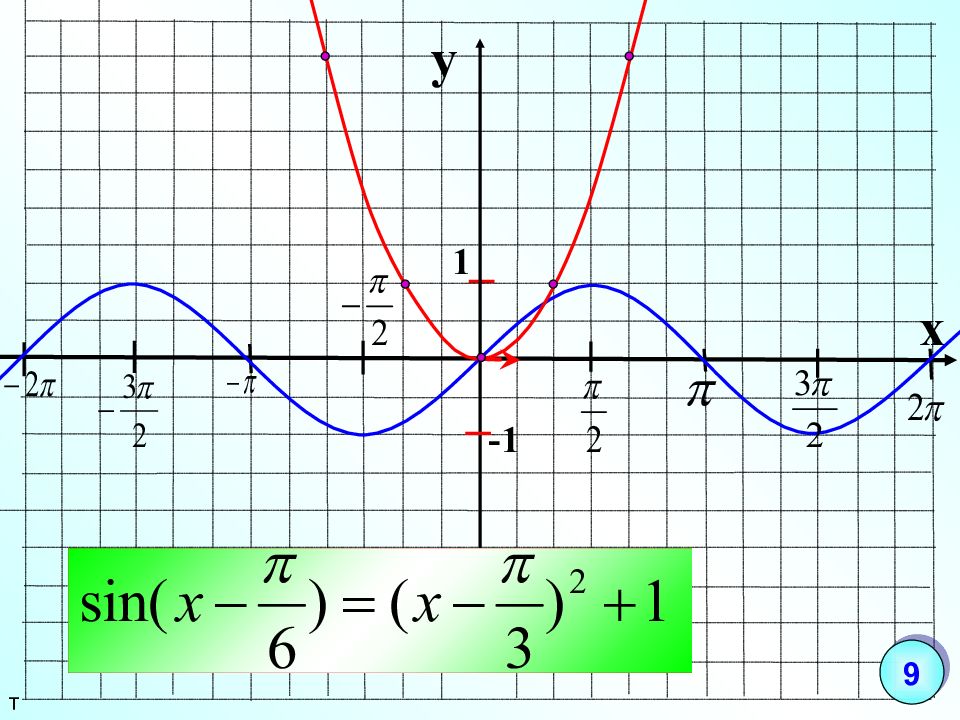 Смещение будет к влево, , если фазовый сдвиг отрицательный, и к вправо, , если фазовый сдвиг положительный.
Смещение будет к влево, , если фазовый сдвиг отрицательный, и к вправо, , если фазовый сдвиг положительный.
В этой формуле нет ничего волшебного. Мы просто решаем выражение в скобках для нуля; `bx + c = 0`.
Пример 1
Нарисуйте кривую
y = грех (2 x + 1)
Ответ
Давайте сначала посмотрим на график `y = sin 2x` (без« + 1 »), чтобы понять, что означает фазовый сдвиг.
Амплитуда равна 1, а период равен `(2π) / 2 = π.`
Я нарисовал чуть больше 2-х циклов, начиная с `x = 0`.
Теперь рассмотрим фазовый сдвиг. Используя приведенную выше формулу, нам нужно будет сместить нашу кривую на:
Фазовый сдвиг `= -c / b = -1 / 2 = -0,5`
Это означает, что нам нужно сместить кривую влево (поскольку фазовый сдвиг отрицательный) на «0,5».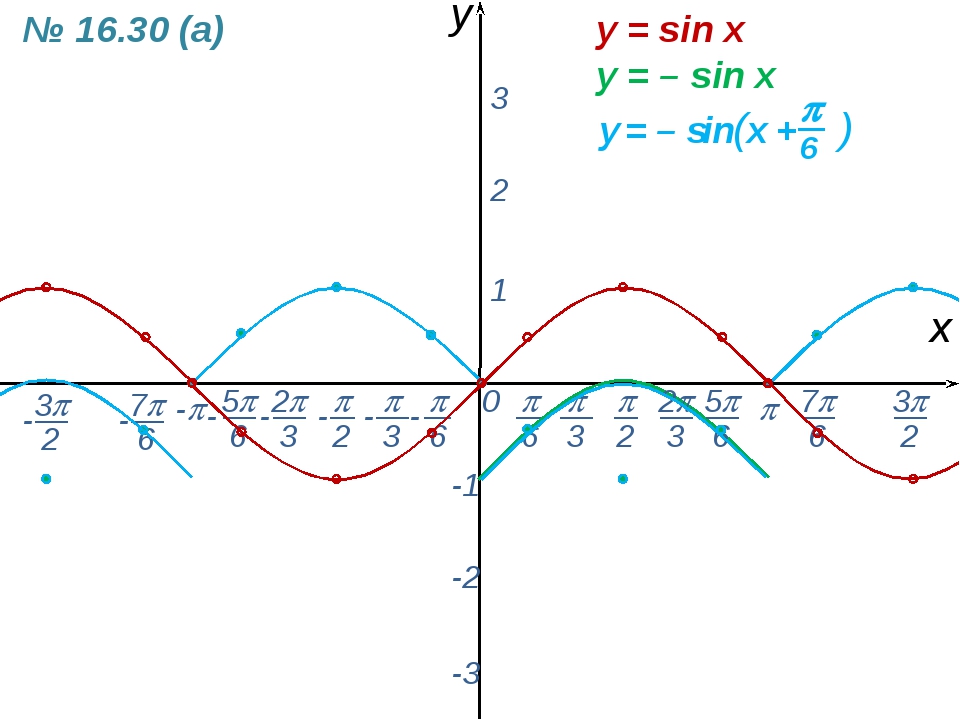 Вот ответ (выделен зеленым). Я сохранил исходное значение y = sin 2 x (выделено серым пунктиром), чтобы вы могли видеть, что происходит.
Вот ответ (выделен зеленым). Я сохранил исходное значение y = sin 2 x (выделено серым пунктиром), чтобы вы могли видеть, что происходит.
Обратите внимание, что кривая проходит через:
- (-0,5, 0) по оси x (потому что мы смещали кривую влево на 0,5) и
- sin 1 = 0,84 по оси y . Это число получается заменой x = 0 на y = sin (2 x + 1); (в радианах, конечно).
Пример 2
Эскиз
`y = 12cos (2x-pi / 8)`
Ответ
В этом примере
амплитуда `a = 12` и
`b = 2`, поэтому период =` (2π) / b = (2π) / 2 = π`, и
`c = -pi / 8`
, поэтому сдвиг фазы равен
`-c / b = — (- pi» / «8) / 2 = pi / 16`
Это означает, что нам нужно переместить график косинусов в справа от его нормального положения (так как смещение
положительный в этом примере) на `pi / 16`.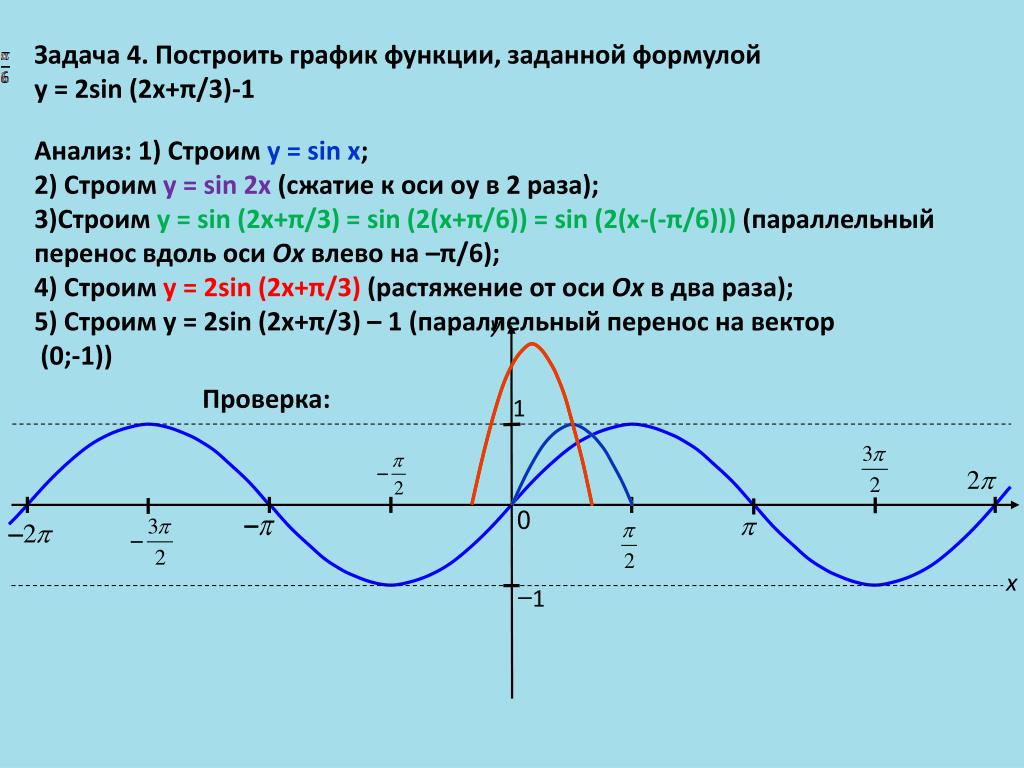
Без фазового сдвига косинусоидальная кривая будет иметь вид y = 12 cos 2 x , а ее график будет следующим:
Теперь сдвинем вправо на π /16 ≈ 0,1963:
Вы можете увидеть исходную кривую косинуса (выделена серым пунктиром), и мы сместили ее на `pi / 16` вправо, чтобы получить требуемый график` y = 12 cos (2x — π / 8) `зеленым цветом.
Фазовый сдвиг Интерактивный
В следующем интерактиве используйте ползунок, чтобы изменить значение c , которое смещает кривую.Соблюдайте Значения « c » и «смещение» и как они меняются, когда вы переместите кривую влево и вправо.
Вы видите пример `y = sin (pi t)`. Это имеет период , определяемый как `(2 pi) / b = (2π) / π = 2`.
Вы также можете увидеть корпус с косинусом , выбрав его вверху.
График: `y = sin (pi t — 0)`
Смещение = `(-c) / b = 0 / pi = 0`
Авторские права © www.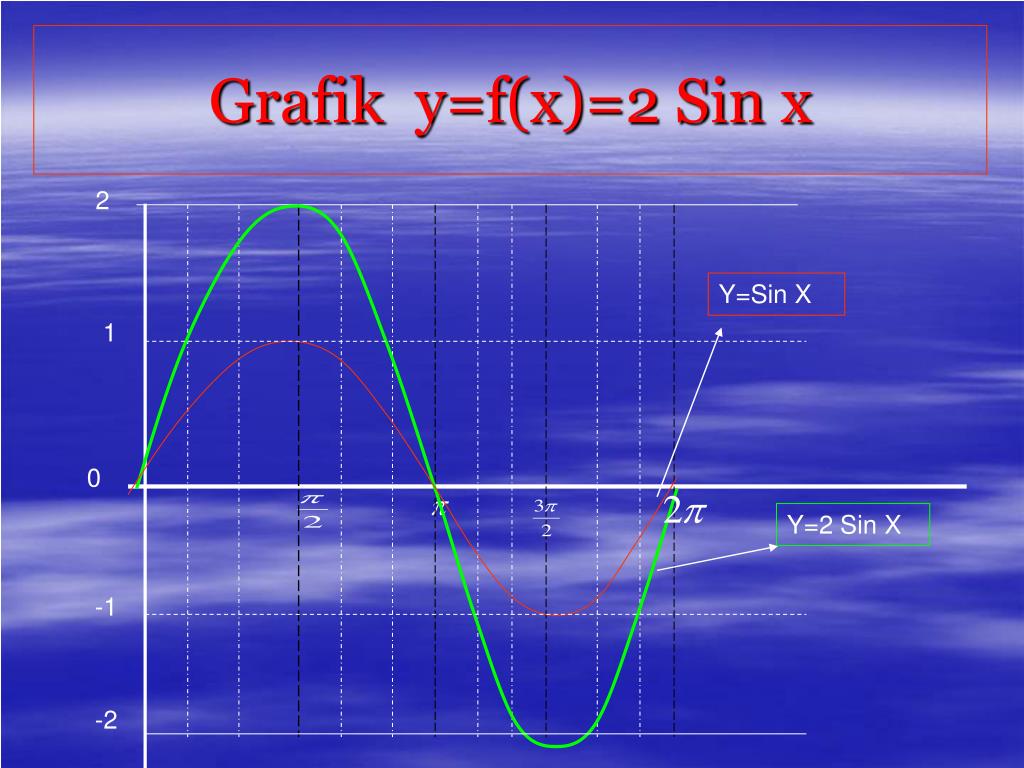 intmath.com
intmath.com
Фазовый угол или фазовый сдвиг?
Фазовый угол не всегда определяется так же, как фаза Сдвиг .
Угол фазы для синусоиды y = a sin ( bx + c ) обычно принимается равным c , а сдвиг фазы обычно задается как `- c / b`, как мы видели выше.
Напоминание: В последнем разделе мы увидели, как выразить синусоидальные кривые в терминах частоты.
Пример: Инженеры-электронщики разделяют термины «фазовый угол» и «фазовый сдвиг» и используют сочетание радианов и градусов.У нас может быть ток, выраженный следующим образом:
I = 50 sin (2 π (100) t + 30 °)
Это означает, что амплитуда равна 50 A, частота 100 Гц и фазовый угол 30 °.
См. Приложение фазового угла на
Применение в цепях переменного тока
в главе о комплексных числах.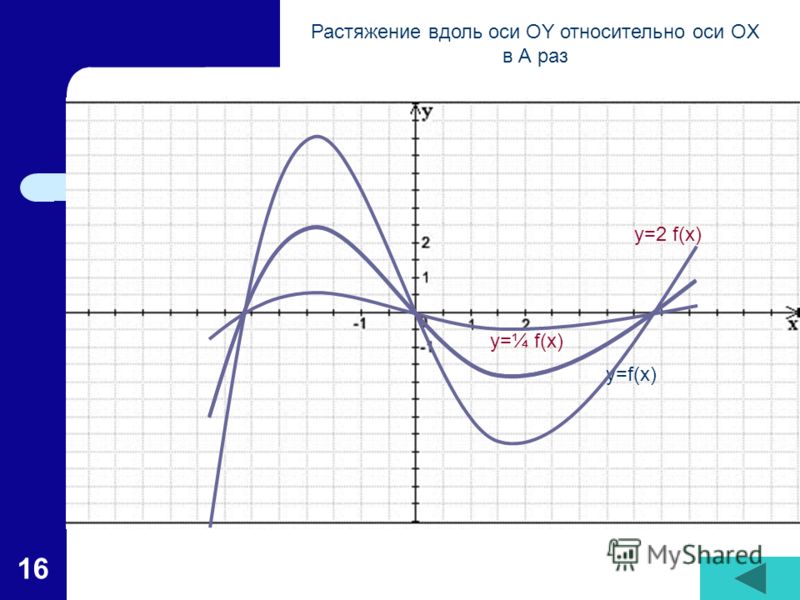
Также см. Обсуждение этого вопроса в разделе «Фазовый сдвиг или фазовый угол?». в математическом блоге.
Для простоты мы будем в основном использовать термин сдвиг фазы в этой главе.
Аплет графика амплитуды, периода и фазового сдвига
Следующий интерактив поможет вам изучить три ключевых понятия при построении тригонометрических графиков — амплитуду, период и фазовый сдвиг.
Используйте ползунки под графиком для изменения каждой из амплитуды , периода и сдвига фазы графика.
Ось «x» имеет целочисленный масштаб (конечно, в радианах), а кратные «пи» обозначены красной линией.
Вы также можете изменить функцию на косинус. Надеюсь, вы увидите, что концепции работают одинаково как для синусоидальных, так и для косинусоидальных кривых.
График: `y = a sin (bx + c) =` `sin (x)`
Период = `(2pi) / b = 6,28 / 1 = 6,28`
Смещение = `(-c) / b = 0/1 = 0`
Авторские права © www.intmath.com
Упражнения
Нарисуйте следующий график.
1. `y = sin (2x + π / 6)`
Ответ
`а = 1;`
`» период «= (2π) / 2 = π`
`» смещение «= -c / b = — (π / 6) / 2 = -π / 12`
Итак, нам нужно переместить синусоидальный график на влево на (потому что у нас есть отрицательное число) его нормального положения на `pi / 12`.
0,25π0,5π0,75ππ1-1xy`-pi / 12`
График `y = sin (2x + pi / 6)` для `0 ≤ x ≤ pi`
Кривая `y = sin (2x)` показана серым пунктиром, а ответ, сдвинутый на `pi / 12` влево, показан темно-зеленым.
2. `y = 3 sin (x + π / 4)`
Ответ
`a = 3`;
`» период «= 2π`;
`» смещение «= -c / b = — (π / 4) / 1 = -π / 4`
0,5ππ1,5π2π123-1-2-3xy`-pi / 4`
График `y = 3sin (x + pi / 4)` для `0 ≤ x ≤ 2pi`
Кривая `y = 3sin (x)` показана серым пунктиром, а ответ, смещенный на `pi / 4` влево, показан темно-зеленым.
3. `y = 2 cos (x — π / 8)`
Ответ
`a = 2`;
`» период «= 2π`;
`» смещение «= -c / b = — (- π / 8) / 1 = π / 8`
Это означает, что нам нужно переместить y = 2 cos x в точку справа через `π / 8.`
0.5ππ1.5π2π12-1-2xy`pi / 8`
График `y = 2 cos (x-pi / 8)` для `0 ≤ x ≤ 2pi`
Кривая `y = 2cos (x)` показана серым пунктиром, а ответ после сдвига на `pi / 8` вправо — темно-зеленым.
4. `y = -cos (2x — π)`
Ответ
Давайте рассмотрим это по очереди.
Начнем с простого рисования графика y = cos \ 2x.
`a = 1`; `» период «= (2π) / 2 = π.`
Теперь давайте сместим кривую (сейчас мы рассматриваем «минус π» часть вопроса.
`» смещение «= -c / b = — (- π) / 2 = π / 2`
Таким образом, мы должны сдвинуть каждую точку кривой вправо (поскольку сдвиг фазы — положительное число) на «пи / 2».Это дает нам y = cos (2 x — π ), синяя пунктирная кривая.
Теперь нам нужно рассмотреть минус перед выражением y = −cos (2 x — π ). Минус просто даст нам зеркальное отображение по оси x , поскольку каждое положительное значение становится отрицательным, а каждое отрицательное значение становится положительным. Другими словами, минус переворачивает все с ног на голову.
Ответ для графика y = −cos (2 x — π ) — это зеленая кривая:
Но подождите, это то, с чего мы начали! Выглядит так же, как `y = cos \ 2x`.
Этот пример показывает интересную вещь о фазовом сдвиге и периодических функциях. Если вы сдвинете достаточно далеко, вы можете легко получить эквивалентные синусоидальные или косинусные выражения.
Вы лучше поймете, почему это работает, в разделе «Суммы и разности углов», с которым мы познакомимся позже.
Обратные тригонометрические функции | Precalculus II
Понимание и использование функций обратного синуса, косинуса и тангенса
Чтобы использовать обратные тригонометрические функции, мы должны понимать, что обратная тригонометрическая функция «отменяет» то, что «делает» исходная тригонометрическая функция, как и в случае с любой другой функцией и ее обратной.{−1} (б) = а [/ латекс].
Имейте в виду, что функции синуса, косинуса и тангенса не взаимно однозначны. График каждой функции не прошел бы тест горизонтальной линии. Фактически, никакая периодическая функция не может быть взаимно однозначной, потому что каждый выход в ее диапазоне соответствует по крайней мере одному входу в каждом периоде, а количество периодов бесконечно. Как и в случае с другими функциями, которые не являются взаимно однозначными, нам нужно будет ограничить область каждой функции, чтобы получить новую функцию, которая является взаимно однозначной.Мы выбираем область для каждой функции, которая включает число 0. На рисунке 2 показан график синусоидальной функции, ограниченной [latex] \ left [\ frac {- \ pi} {2} \ text {,} \ frac {\ pi } {2} \ right] [/ latex] и график функции косинуса, ограниченной [0, π].
Рис. 2. (a) Синусоидальная функция в ограниченной области [latex] \ left [- \ frac {\ pi} {2} \ text {,} \ frac {\ pi} {2} \ right] [ /латекс]; (b) Косинусная функция в ограниченной области [0, π]
На рисунке 3 показан график касательной функции, ограниченной [latex] \ left (- \ frac {\ pi} {2} \ text {,} \ frac {\ pi} {2} \ right) [/ latex].
Рисунок 3. Функция касания в ограниченной области [latex] \ left (- \ frac {\ pi} {2} \ text {,} \ frac {\ pi} {2} \ right) [/ latex]
Эти обычные варианты выбора для ограниченной области в некоторой степени произвольны, но они имеют важные полезные характеристики. Каждый домен включает начало координат и некоторые положительные значения, и, что наиболее важно, каждый результат дает взаимно однозначную обратимую функцию. Обычный выбор для ограниченной области касательной функции также имеет то полезное свойство, что он простирается от одной вертикальной асимптоты к следующей вместо того, чтобы быть разделенным на две части асимптотой.{−1} x [/ latex] имеет домен всех действительных чисел и диапазон [latex] \ left (- \ frac {\ pi} {2} \ text {,} \ frac {\ pi} {2} \ right) [/латекс]. Чтобы найти область , и диапазон , обратных тригонометрических функций, переключите область и диапазон исходных функций. Каждый график обратной тригонометрической функции является отражением графика исходной функции относительно линии [латекс] y = x [/ latex].
Рисунок 4. Функция синуса и функция обратного синуса (или арксинуса)
Рисунок 5.{−1} (0,96593) \ приблизительно \ frac {5 \ pi} {12} [/ латекс]
Попробуйте 1
Учитывая [латекс] \ cos (0,5) \ приблизительно 0,8776 [/ латекс], напишите соотношение, включающее обратный косинус.
Решение
Нахождение точного значения выражений, содержащих функции обратного синуса, косинуса и тангенса
Теперь, когда мы можем идентифицировать обратные функции, мы научимся их оценивать. Для большинства значений в их областях мы должны оценивать обратные тригонометрические функции с помощью калькулятора, интерполяции из таблицы или других численных методов.\ circ) [/ latex], и их отражения в другие квадранты.
Как: при наличии «особого» входного значения вычислить обратную тригонометрическую функцию.
- Найдите угол x , для которого исходная тригонометрическая функция имеет выход, равный заданному входу для обратной тригонометрической функции.
- Если x не входит в заданный диапазон обратного преобразования, найдите другой угол y , который находится в заданном диапазоне и имеет тот же синус, косинус или тангенс, что и x , в зависимости от того, который соответствует заданному обратному. функция.{−1} (\ frac {1} {2}) [/ латекс]
Решение
Использование калькулятора для вычисления обратных тригонометрических функций
Чтобы оценить обратные тригонометрические функции , которые не используют специальные углы, обсуждавшиеся ранее, нам понадобится калькулятор или другой тип технологии. Большинство научных калькуляторов и приложений-эмуляторов калькуляторов имеют специальные клавиши или кнопки для функций обратного синуса, косинуса и тангенса. Они могут быть помечены, например, как SIN-1, ARCSIN или ASIN.
В предыдущей главе мы работали с тригонометрией на прямоугольном треугольнике, чтобы найти стороны треугольника с учетом одной стороны и дополнительного угла. Используя обратные тригонометрические функции, мы можем найти углы прямоугольного треугольника с двумя сторонами, и мы можем использовать калькулятор, чтобы найти значения с точностью до нескольких десятичных знаков.
В этих примерах и упражнениях ответы будут интерпретироваться как углы, и мы будем использовать θ в качестве независимой переменной. Значение, отображаемое на калькуляторе, может быть в градусах или радианах, поэтому обязательно установите режим, соответствующий приложению.{\ circ} \ hfill & \ text {Оценить.} \ end {array} [/ latex]
Попробовать 4
Решите треугольник на рисунке 9 относительно угла θ.
Рисунок 9
Решение
Нахождение точных значений составных функций с обратными тригонометрическими функциями
Бывают случаи, когда нам нужно составить тригонометрическую функцию с обратной тригонометрической функцией. {- 1} (\ cos \ theta) = \ frac {\ pi} {2} — \ theta \ text {if} 0 \ leq \ theta \ leq \ pi \\ [/ latex].{−1} (\ cos (\ frac {13 \ pi} {6})) \\ [/ latex]
- путем прямой оценки.
- способом, описанным ранее.
Решение
- Здесь мы можем непосредственно оценить внутреннюю часть композиции.
[латекс] \ begin {array} \ cos \ left (\ frac {13 \ pi} {6} \ right) = \ cos \ left (\ frac {\ pi} {6} +2 \ pi \ right) \ \ \ hfill = \ cos \ left (\ frac {\ pi} {6} \ right) \\ \ hfill = \ frac {\ sqrt {3}} {2} \ end {array} \\ [/ latex]
Теперь мы можем вычислить обратную функцию, как делали раньше.{−1} (\ frac {4} {5}) \\ [/ latex] находится в квадранте I, [latex] \ sin {\ theta} \\ [/ latex] должно быть положительным, поэтому решением будет [latex ] \ frac {3} {5} \\ [/ latex]. См. Рисунок 11.
Рис. 11. Прямой треугольник, иллюстрирующий, что если [latex] \ cos \ theta = \ frac {4} {5} [/ latex], то [latex] \ sin \ theta = \ frac {3} {5} \ \ [/ латекс]
Мы знаем, что обратный косинус всегда дает угол в интервале [0, π], поэтому мы знаем, что синус этого угла должен быть положительным; поэтому [латекс] \ sin \ left (\ cos ^ {- 1} \ left (\ frac {4} {5} \ right) \ right) = \ sin \ theta = \ frac {3} {5} \\ [ /латекс].{−1} \ left (\ frac {7} {4} \ right) \ right) \\ [/ latex].
Решение
Хотя мы могли бы использовать ту же технику, что и в Примере 6, мы продемонстрируем здесь другую технику. Изнутри мы знаем, что существует такой угол, что [latex] \ tan \ theta = \ frac {7} {4} \\ [/ latex]. Мы можем представить это как противоположные и смежные стороны прямоугольного треугольника, как показано на рисунке 12.
Рис. 12. Прямоугольный треугольник с двумя известными сторонами
Используя теорему Пифагора, мы можем найти гипотенузу этого треугольника.{−1} \ left (4x \ right) \ right) \\ [/ latex] для [латекса] — \ frac {1} {4} \ leq x \ leq \ frac {1} {4} \\ [/ латекс].
Решение
Ключевые концепции
- Обратная функция — это функция, которая «отменяет» другую функцию. Область определения обратной функции — это диапазон исходной функции, а диапазон обратной функции — это область определения исходной функции.
- Поскольку тригонометрические функции не взаимно однозначны в своих естественных областях, обратные тригонометрические функции определены для ограниченных областей.{−1} \ left (\ sin x \ right) = \ frac {\ pi} {2} −x [/ latex] если [латекс] — \ frac {\ pi} {2} \ leq x \ leq \ frac {\ pi} {2} [/ латекс].
- При оценке состава тригонометрической функции с обратной тригонометрической функцией нарисуйте контрольный треугольник, чтобы помочь определить соотношение сторон, представляющее выходные данные тригонометрической функции.
- При оценке состава тригонометрической функции с обратной тригонометрической функцией вы можете использовать тригонометрические тождества, чтобы помочь в определении соотношения сторон.{−1} (2) [/ латекс]. Объясните, как это можно сделать, используя функцию косинуса или функцию обратного косинуса.
5. Почему область синусоидальной функции [latex] \ sin x [/ latex] должна быть ограничена [latex] \ left [- \ frac {\ pi} {2} \ text {,} \ frac { \ pi} {2} \ right] [/ latex] для существования функции обратного синуса?
6. Обсудите, почему это утверждение неверно: [latex] \ arccos (\ cos x) = x [/ latex] для всех x .
7. Определите, является ли следующее утверждение истинным или ложным, и объясните свой ответ: [latex] \ arccos (−x) = \ pi− \ arccos x [/ latex].{−1} х [/ латекс]? Используйте графический калькулятор, чтобы приблизиться к ответу.
53. Предположим, что к зданию прислонена 13-футовая лестница, достигающая дна окна второго этажа на высоте 12 футов над землей. Какой угол в радианах образует лестница со зданием?
54. Предположим, вы проезжаете 0,6 мили по дороге, так что вертикальное расстояние изменяется от 0 до 150 футов. Какой угол подъема дороги?
55. Равнобедренный треугольник имеет две равные стороны длиной 9 дюймов.Оставшаяся сторона имеет длину 8 дюймов. Найдите угол между стороной 9 дюймов и стороной 8 дюймов.
56. Без использования калькулятора приблизительно определите значение [латекс] \ арктан (10,000) [/ латекс]. Объясните, почему ваш ответ разумен.
57. Ферма крыши дома состоит из двух одинаковых прямоугольных треугольников. У каждого есть основание 12 футов и высота 4 фута. Найдите величину острого угла, примыкающего к 4-футовой стороне.
58. Линия [latex] y = \ frac {3} {5} x [/ latex] проходит через начало координат в плоскости x , y .Каков угол между линией и положительной осью x ?
59. Линия [latex] y = — \ frac {3} {7} x [/ latex] проходит через начало координат в плоскости x , y . Какова мера угла, который образует линия с отрицательной осью x ?
60. Какой процентный уклон должен иметь дорога, если угол наклона дороги составляет 4 градуса? (Процентный уклон определяется как изменение высоты дороги на 100-футовом горизонтальном расстоянии.Например, уклон 5% означает, что дорога поднимается на 5 футов на каждые 100 футов горизонтального расстояния.)
61. 20-футовая лестница прислоняется к стене здания так, чтобы ее основание находилось на расстоянии 10 футов от основания здания. Если согласно спецификациям угол подъема лестницы должен составлять от 35 до 45 градусов, соответствует ли размещение этой лестницы требованиям безопасности?
62. Предположим, 15-футовая лестница прислонена к стене дома так, что угол подъема лестницы составляет 42 градуса.Как далеко от дома находится подножие лестницы?
Тригонометрия: синусоида
Covid-19 привел мир к феноменальному переходу.
Электронное обучение — это будущее уже сегодня.
Оставайтесь дома, оставайтесь в безопасности и продолжайте учиться !!!
Синусоидальный график: Тригонометрическая функция sinx является периодической функцией.
Функция синуса имеет максимальное значение как +1 и минимальное значение как -1.Поскольку sin (-x) = -sinx, sinx — нечетная функция.
Значение функции sin x повторяется через каждые 2π единиц «x». Следовательно, эта функция периодическая с периодом 2π Функция, график которой представляет собой форму синусоиды, называется синусоидальной функцией, а такие графики называются синусоидальным графиком.Некоторые определения, используемые в синусоиде:
Амплитуда: Это половина расстояния между максимальным и минимальным значениями.
Термин «а» в общей форме синусоидальной функции представляет амплитуду этой функции.
Амплитуда является постоянной для синусоидальных функций.
Период: Это наименьшее время, необходимое функции для выполнения одного полного цикла.
Из общего вида синусоидальной функции период T может быть записан как `T = 2π / b
Теперь вернемся к простейшей синусоидальной функции.
y = a sin bx
, где a = амплитуда.
Period = 2π / b
Sin (0) = 0, поэтому синусоидальный график всегда начинается с нуля.
По мере увеличения b период уменьшается.Фазовый сдвиг синусоидальной функции
y = a sin (bx + c) + d
Оба b и c влияют на фазовый сдвиг или движение графикаЕсли c —— ——> Положительный ————> сдвиг вправо
Если c ————> Отрицательный ———- -> сдвиг влево.
Если d ————> Положительно ————> график сдвинут вверх на d единиц.
Если d ————> Отрицательно ————> график сдвинут вниз на d единиц.
Фазовый сдвиг = — c / b
Период = 2π / b
Фазовый сдвиг — это величина, на которую кривая смещается в горизонтальном направлении от своего нормального положения.
Фазовый сдвиг, отрицательный ————> Левое смещение
Фазовое смещение, положительное ————> Правое смещение
Чтобы найти фазовый сдвиг, просто сделайте
bx + c = 0 и решаем.
Пример:
y = 2 sin (2x +1)
Здесь амплитуда = a = 2
2x + 1 = 0 ⇒ x = -1/2, поэтому фазовый сдвиг = -1/2.
Период = 2π / b
Период = 2π / b = 2π / 2 = π
Синусоидальный графикГрафический словарь
Домашняя страница
Covid-19 повлиял на физическое взаимодействие между людьми.
Не позволяйте этому влиять на ваше обучение.
Графики: синус и косинус
Чтобы увидеть, как изображены функции синуса и косинуса, воспользуйтесь калькулятором, компьютером или набором тригонометрических таблиц, чтобы определить значения функций синуса и косинуса для ряда различных градусы (или радианы) меры (см. Таблицу 1).
Затем постройте эти значения и получите основные графики функции синуса и косинуса (рисунок 1).
Рисунок 1
Один период а) синусоидальной функции и б) косинусной функции.Синус-функция и косинус-функция имеют периоды 2π; поэтому образцы, показанные на рисунке, непрерывно повторяются слева и справа (рисунок 2).
Несколько периодов функции синуса а) и функции косинуса б).К функциям синуса и косинуса можно добавить несколько дополнительных членов и множителей, которые изменяют их форму.
Дополнительный член A в функции y = A + sin x учитывает вертикальный сдвиг в графике синусоидальных функций. Это также верно для функции косинуса (рисунок 3).
Рисунок 3
Примеры нескольких вертикальных сдвигов синусоидальной функции.Дополнительный коэффициент B в функции y = B sin x допускает изменение амплитуды синусоидальной функции. Амплитуда, | B | — максимальное отклонение от оси x , то есть половина разницы между максимальным и минимальным значениями графика. Это также верно для функции косинуса (рисунок 4).
Рисунок 4
Примеры нескольких амплитуд синусоидальной функции.Объединение этих цифр дает функции y = A + B sin x , а также y = A + B cos x . Эти две функции имеют минимальные и максимальные значения , как определено следующими формулами. Максимальное значение функции — M = A + | B |. Это максимальное значение возникает всякий раз, когда sin x = 1 или cos x = 1. Минимальное значение функции составляет m = A — | B |.Этот минимум возникает всякий раз, когда sin x = -1 или cos x = -1.
Пример 1: Постройте график функции y = 1 + 2 sin x . Какие максимальные и минимальные значения функции?
Максимальное значение — 1 + 2 = 3. Минимальное значение — 1 −2 = -1 (Рисунок 5).
Рисунок 5
Чертеж для примера 1.Пример 2: Постройте график функции y = 4 + 3 sin x . Какие максимальные и минимальные значения функции?
Максимальное значение 4 + 3 = 7. Минимальное значение 4 — 3 = 1 (Рисунок 6).
Рисунок 6
Рисунок для примера 2.Дополнительный коэффициент C в функции y = sin Cx допускает изменение периода (длительность цикла) синусоидальной функции.(Это также верно для функции косинуса.) Период функции y = sin Cx равен 2π / | C |. Таким образом, функция y = sin 5 x имеет период 2π / 5. На рисунке 7 показаны дополнительные примеры.
Рисунок 7
Примеры нескольких частот а) синусоидальной функции и б) косинусной функции.Дополнительный член D в функции y = sin ( x + D ) учитывает сдвиг фазы (перемещение графика влево или вправо) на графике синусоидальных функций.(Это также верно для функции косинуса.) Сдвиг фазы равен | D |. Это положительное число. Не имеет значения, будет ли сдвиг влево (если D положительный) или вправо (если D отрицательный). Функция синуса нечетная, а функция косинуса четная. Функция косинуса выглядит точно так же, как функция синуса, за исключением того, что она сдвинута на π / 2 единицы влево (рисунок 8). Другими словами,
Рисунок 8
Примеры нескольких фазовых сдвигов синусоидальной функции.Пример 3: Каковы амплитуда, период, фазовый сдвиг, максимальное и минимальное значения
y = 3 + 2 sin (3 x ‐2)
y = 4 cos2π x
Пример 4: Нарисуйте график y = cosπ x .
Поскольку cos x имеет период 2π, cos π x имеет период 2 (рисунок 9).
Рисунок 9
Чертеж для примера 4.Пример 5: Нарисуйте график y = 3 cos (2x + π / 2).
Поскольку cos x имеет период 2π, cos 2x имеет период π (рисунок 10).
Рисунок 10
Рисунок для примера 5.График функции y = — f ( x ) находится путем отражения графика функции y = f ( x ) относительно оси x . Таким образом, рисунок может также представлять график y = −3 sin 2 x . В частности,
Важно понимать отношения между функциями синуса и косинуса и то, как сдвиги фазы могут изменять их графики.
Тригонометрия: тригонометрические функции
Амплитуда: Максимальное значение ординаты (y) на графике называется его « амплитудой ».
Период: «Период» тригонометрической функции — это наименьшее положительное число, которое при добавлении к исходной круговой мере угла дает такое же значение функции.
На рисунке показан график y = sin x для одного полного периода.
Общие графики синусоидальной функции:
Для синусоидальной функции вида: y = a sin bx
Амплитуда = | а |
Период = `(2 \ pi) / b`
Пример 1
Найти амплитуду и период функции y = `2 sin (x / 3)`
Решение: Для данной функции y = 2 sin `(x / 3)` = 2 sin `(1 / 3x)`
Амплитуда = | а | = 2
Период = `(2 \ pi) / b` =` (2 \ pi) / ((1) / 3) `= 6` \ pi`
График y = cos x (x измеряется в радианах)
Из графика функции косинуса, показанного выше,
Для y = cos x:
Амплитуда = 1
Период = 2` \ pi`
Домен: -` \ infty`
Диапазон: -1 `\ leq` y` \ leq` +1
На рисунке справа показан график y = cos x для одного полного периода.
График y = cos x (x измеряется в градусах)
Общие графики функции косинуса:
Для функции косинуса вида:
y = a cos bx
Амплитуда = | а |
Период = `(2 \ pi) / b`
Пример 2:
Найти амплитуду и период функции y = `(1) / 2` cos 3x
Решение: Для данной функции y = `(1) / 2` cos 3x
Амплитуда = | а | = `(1) / 2`
Период = `(2 \ pi) / b` =` (2pi) / 3`
График y = tan x (x измеряется в радианах)
График y = tan x = (sin x) / cos x был показан выше.Из определения функции видно, что значение касательной функции не определено для всех значений x, для которых `cos x = 0` (деление на ноль не определено). Следовательно, область определения касательной функции исключает нечетное целое число, кратное `(\ pi) / 2`. Вертикальные асимптоты можно наблюдать на всех этих значениях x.
Примечание:
Как видно из графика, касательная функция имеет период пи (`\ pi`).Это загар (`\ pi` +` \ theta`) = `tan (\ theta)`
Из графика, приведенного выше,
Для y = tan x:
Амплитуда = нет; нет максимального значения для функции касательной.
Period = `\ pi` (функция касания завершает один цикл от` (- \ pi) / 2 до (\ pi) / 2) `
Домен: -` \ infty`
Диапазон: -` \ infty`
На рисунке справа показан график y = tan x для одного полного периода.
График y = tan x (x измеряется в градусах)
Общие графики касательной функции:
Для касательной функции вида:
y = загар bx
Период = `\ pi / b`
Пример 3:
График y = `(1) / 2` tan 3x
Решение: Для данной функции y = `(1) / 2` tan 3x
Период = `\ pi / 3`
Пунктирными линиями показаны вертикальные асимптоты, которые встречаются в
x = `\ pi / 6 \ pm (n \ pi) / 3`, где n — целое число.
График y = cosec x (x измеряется в радианах)
График y = cosec x = `(1) / sin x` был показан выше. Из определения функции видно, что значение cosec функция не определена для всех значений x, для которых sin x = 0 (деление на ноль не определено).Следовательно, область определения функции cosec исключает целые числа, кратные `\ pi`. Вертикальные асимптоты существуют для всех этих значений x.
Из графика, приведенного выше,
Для y = cosec x:
Амплитуда = нет; нет максимального значения для функции cosec.
Период = `2 \ pi`
Домен: -` \ infty`
Диапазон: y `\ le` -1 или y` \ ge` 1
На рисунке справа показан график y = cosec x для одного полного периода.
График y = cosec x (x измеряется в градусах)
Общие графики функции Cosec:
Для функции cosec вида:
y = cosec bx
Период = `(2 \ pi) / b`
Пример 4
График y = cosec 2x
Решение: Для данной функции y = cosec 2x
Период = `(2 \ pi) / 2` =` \ pi`
Пунктирными линиями показаны вертикальные асимптоты, которые
встречаются при x = `(n \ pi) / 2`, где n — целое число.
График y = sec x (x измеряется в радианах)
График y = sec x = `(1) / cos x` показан выше красным цветом. Из определения функции видно, что значение y = sec x не определен для всех значений x, для которых cos x = 0 (деление на ноль не определено).Следовательно, область определения secx исключает нечетный интеграл кратные `(\ pi) / 2`. Вертикальные асимптоты существуют для всех этих значений x.
Из графика, приведенного выше,
Для y = sec x:
Амплитуда = нет; нет максимального значения для функции sec.
Период = 2` \ pi`
Домен: -` \ infty`
Диапазон: y `\ le` -1 или y` \ ge` 1
На рисунке справа показан график y = sec x для одного полного периода.
График y = sec x (x измеряется в градусах)
Общие графики сек Функция:
Для секущей функции вида:
y = сек bx
Период = `(2 \ pi) / b`
Пример 5:
График y = sec 3x
Решение: Для данной функции y = sec 3x
Период = `(2 \ pi) / 3`
Пунктирными линиями показаны вертикальные асимптоты, которые встречаются в
x = `\ pi / 6 \ pm (n \ pi) / 3`, где n — целое число.
График y = cot x (x измеряется в радианах)
График y = cot x = `(cos x) / sin x` был показан выше. Из определения функции мы видим, что значение (y = cot x) функция не определена для всех значений x, для которых `sin x = 0` (деление на ноль не определено).Следовательно, область касательной функция исключает целые числа, кратные `\ pi`. Вертикальные асимптоты можно наблюдать на всех этих значениях x.
Примечание:
Функция Cot имеет период `пи` (` \ pi`). Это cot (`\ pi` +` \ theta`) = cot (`\ theta`), что также видно из графика.
Для y = детская кроватка x:
Амплитуда = нет; не существует максимального значения для функции детской кроватки.
Period = `\ pi` (функция касания завершает один цикл от` (- \ pi) / 2 до (\ pi) / 2) `
Домен: -` \ infty`
Диапазон: -` \ infty`
На рисунке справа показан график y = cot x для одного полного периода.
График y = детская кроватка x (x измеряется в градусах)
Общие графики функции котангенса:
Для функции котангенса вида:
y = детская кроватка bx
Период = `\ pi / b`
Пример 6:
График y = детская кроватка `(x) / 2`
Решение: Для данной функции y = cot` (x) / 2`
Период = `(\ pi) / ((1) / 2)` = `2 \ pi`
Математическая сцена — Функции 2 — Урок 6
Математическая сцена — Функции 2 — Урок 6 — Обратные функции2009 Rasmus ehf и Джанн Сак
Урок 6
.Обратный функции
ср уже видели некоторые функции, противоположные друг другу.В функции f (x) = x 2 и g (x) = √x являются обратные друг другу, если мы ограничим значения x до
неотрицательные числа. Эти функции компенсируют друг друга в том смысле, что если мы применим сначала одну функцию, а затем другую к числу, то это как если бы ничего не произошло, номер такой же, как был изначально. смотреть на следующий пример:f (x) = x 2 и g (x) =
f (2) = 2 2 = 4 и g (4) = √4 = 2
f (g (a)) = = a
g (f (a)) = = а
Это не так независимо от того, какую из двух функций f (x) или g (x) мы применяем первой, результат та же.Диапазон одной функции становится областью другой.
Функция имеет инверсию, только если она взаимно однозначна и далее. В этом случае мы ограничиваем наши значения x неотрицательными числами так, чтобы функция f (x) = x 2 удовлетворяет это условие. Другими словами, функция имеет инверсию, если она увеличивается или уменьшается на это домен. Функция g (x) = √x возрастает и может только возьмите неотрицательные числа, что снова означает, что f (x) = x 2 ограничено неотрицательными числами.
Мы можем найти уравнение обратной функции алгебраически, решив уравнение функции для x. Посмотрите на следующий пример:
Пример 1
Найдите обратное значение для следующих функций:
а) f (x) = 2x + 4
у = 2х + 4 поставьте y вместо f (x)
2x = 4 года
x = 2 + y Мы разделили на 2
Это уравнение, в котором x является функцией y.Имя переменной не имеет значение, поэтому мы можем поменять местами x и y. Если мы назовем эту функцию g, мы получим уравнение обратной функции f (x).
г (х) = у = х 2 .
Мы можем проверить наш результат, введя число.
f (1) = 21 + 4 = 6 и g (6) = 6 2 = 3 2 = 1
Если мы используем общее значение a, получаем
f (a) = 2a + 4 и g (2a + 4) = (2a + 4) 2 = а + 2 2 = а
б) f (x) = sin 2x, D f = [/ 4, / 4 , f (x) возрастает на этом интервале и следовательно, имеет обратную функцию.
у = грех 2x
2x = sin 1 y
х = грех 1 у
Обратная функция: g (x) = sin 1 x.
В большинстве книг инверсия функции записывается с использованием индекса 1 так что f (x) имеет обратную функцию f 1 (x).Это не означает 1 / f, это просто обозначение обратной функции.
В приведенном выше примере f 1 (х) = грех 1 х.
Проверять.
f (/ 12) = грех 2/12 =
f 1 () = sin 1 = / 6 = / 12
в) f (x) = e 2x
y = e 2x
ln y = ln e 2x = 2x
x = ln y
Обратный функция f (x), следовательно, f 1 (x) = ln x.
г) f (x) = x 2 1, Д ф = рэнд +
г = х 2 1
х 2 = у + 1
Обратная функция: д)
Выбираем D f = R + и кубы обе части уравнения
Тогда извлеките квадратный корень
Обратная функция:
Если функция f (x) либо всегда увеличивается, либо всегда убывая, он имеет обратную функцию f 1 (x).
Диапазон f (x) становится областью f . 1 (х).
Находим уравнение обратного уравнения: решение уравнения y = f (x) относительно x.
Пример 2
Как нам нужно ограничить область определения функции f (x) = sin x, чтобы она имеет обратную функцию? Мы знаем, что непрерывная функция, которая всегда увеличение (или уменьшение) имеет обратное.
Итак, смотрим на производная функции f (x) = sin x, f (x) = cos x.
Используя единичный круг, мы можем видеть, что cos x положителен из / 2 к / 2 и отрицательный на остальной части круга.
Посмотрите на график е (х) = грех х.
Мы видим, что график растет на / 2 <х < / 2 поэтому f (x) = sin x имеет обратное значение, если мы ограничиваем область этим интервалом.
Мы могли бы выбрать другой интервал, например / 2 <х <3/2 где функция убывает, но обычно интервал / 2 <х < / 2 выбран.Пример 3
Найдите интервал, на котором функция f (x) = x 2 4x + 3 возрастает, ограничьте область этим интервалом, а затем найдите формулу для обратная функция. Наконец, нарисуйте график как f (x), так и f 1 (x) в той же системе координат.
Начнем с поиска вершины параболы, дифференцируя и находя, где производная равна нулю. ( Касательная к f (x) в вершине горизонтальна, поэтому производная равна ноль)
f (x) = x 2 4x + 3
f (x) = 2x 4 = 0
2x = 4
х = 2
Вершина — это то место, где x = 2, и после этого функция возрастает.Поэтому мы выберите домен
D f = . Чтобы найти уравнение обратное нам нужно решить уравнение у = х 2 4x + 3 для x.
у = х 2 4х + 3
у 3 = х 2 4х
y 3 + 4 знак равно х 2 4х + 4
у + 1 = (х 2) 2
Завершите квадрат, добавив половину коэффициента при x (2) в квадрате (4) к обеим сторонам уравнения и используя правило
а 2 2ab + б 2 = (а б) 2 .ср выберите +, поскольку x находится на интервале
Вставить x вместо y
Теперь рисуем график, предварительно составив таблицу значений.
Расчет f (2) сообщает нам что f (x) = y принимает значения от 1 вверх (функция возрастает). Поэтому нам нужно начать с нахождения f 1 (1).
Два графики показаны ниже.
Отметим, что два графика являются зеркальным отображением друг друга на линии y = x. (в линия, разделяющая угол между осями x и y пополам). Мы также можем видеть это из таблица значений. Каждая точка на f (x) является зеркальным отображением точки на
f 1 (х). Например, (2, 1) находится на f (x) и (1, 2) находится на f 1 (x). (3, 0) находится на f (x) и (0, 3) на f 1 (x).В общем случае, если (a, b) находится на одном графе, то (b, a) находится на графике обратной функции.График функции и ее обратная функция всегда являются зеркалом изображение друг друга в строке y = x.
Пример 4
Посмотрите на функцию f (x) = e x и ее обратную функция g (x) = ln x.
Функция f (x) = e x может принимать любое значение x, поэтому его домен все действительные числа R.
р.
Ценности, которые f (x) = e x дубль всегда положительна, поэтому его диапазон равен интервал .
Функция g (x) = ln x может принимать только положительные значения x, поэтому это домен.
С другой стороны, функция g (x) = ln x дает все значения действительных чисел, поэтому она диапазон составляетДиапазон функции то же самое, что и домен его инверсии, а домен функции — это диапазон его обратного.
Графики двух функций показаны ниже. Обратите внимание, что они являются зеркальными отображениями друг друга на линии y = x.
Пример 5
Найдите интервал, на котором функция повышается. Выбирая этот интервал в качестве области, находим уравнение его обратной функции затем нарисуйте оба графика в одной системе координат.
Дифференцируйте, используя цепное правило, чтобы найти, где функция увеличивается, а где уменьшается,
Знаменатель всегда положительный, поэтому его x в числителе говорит нам, где функция увеличение или уменьшение.
Функция возрастает для неотрицательных значений x, поэтому мы выбираем область
D f = Затем мы решаем для x, чтобы найти обратное.
у = 1 + (х 2 + 1)
у 1 = (х 2 + 1)
(y 1) 2 = x 2 + 1
х 2 = (у 1) 2 1
= y 2 2y + 1 1
= y 2 2y
(выбирая положительный значение для x)
Обратная функция:
Графики f (x), f 1 (x) и линия y = x выглядят так.
Пример 6
Найти обратную функцию и нарисуйте графики в одной системе координат.
График имеет вертикальную асимптота x = 1 и горизонтальная асимптота y = 2. Область не содержит x = 1.
Мы дифференцируем, чтобы найти наклон графика.
Знаменатель всегда положительный, а числитель всегда отрицательный, что означает что наклон графика всегда отрицательный.Таким образом, функция убывает на все это домен.
Мы находим обратную функцию, решая относительно x.
Обратное
Сначала избавься от дроби затем переместите все члены с x в левую руку сторона уравнения.
Теперь x можно разложить на множители.
Мы видим, что y не может быть 2.
Эта функция имеет вертикальную асимптота в x = 2 и горизонтальная асимптота по y = 1.Это полная противоположность f (x), который имеет вертикальную асимптоту по x = 1 и горизонтальную асимптоту по y = 2.

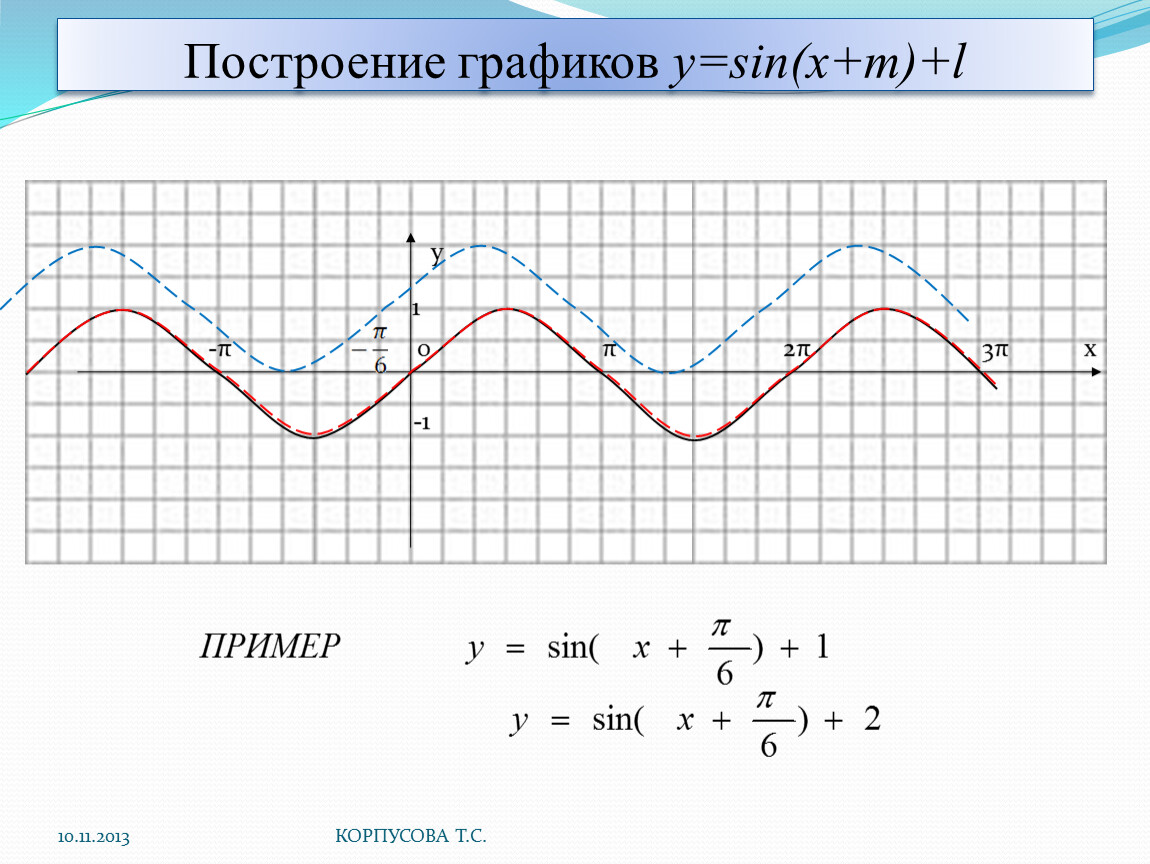
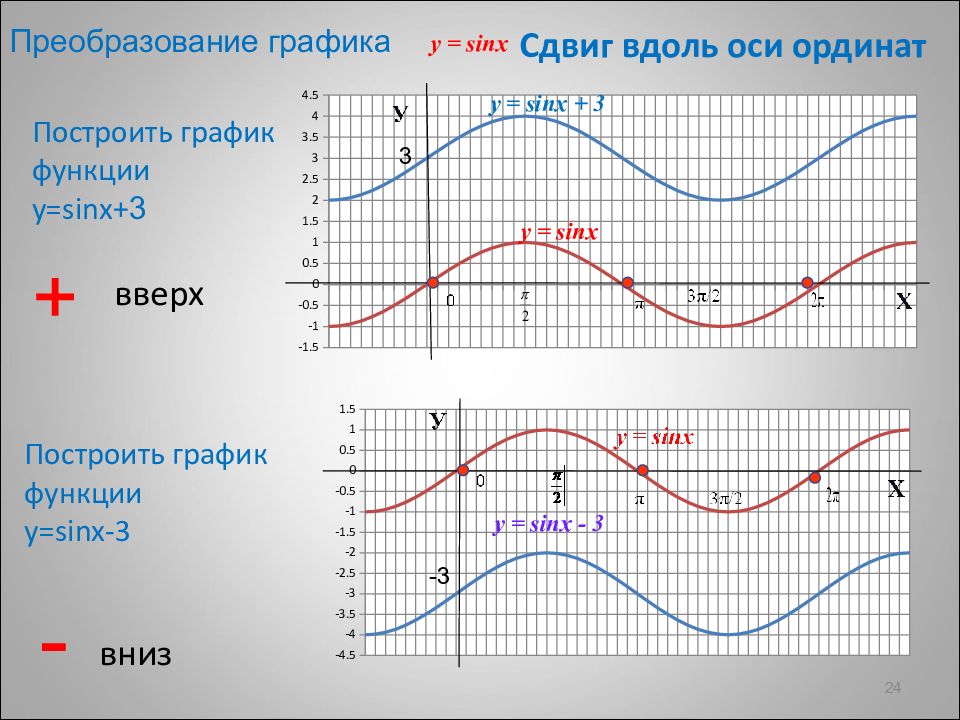

 Но, поскольку y = sin x не взаимно однозначно, его область должна быть ограничена, чтобы y = sin -1 x был функцией.
Но, поскольку y = sin x не взаимно однозначно, его область должна быть ограничена, чтобы y = sin -1 x был функцией. От второй строки отнимаем
первую, от третьей — четыре первых, от четвертой — две первых:
От второй строки отнимаем
первую, от третьей — четыре первых, от четвертой — две первых: $$
$$ В заголовке таблицы выписываются переменные, свободные переменные отмечаются стрелкой. Далее свободным переменным
придаются любые, одновременно не равные нулю значений и из зависимости между свободными и связанными переменными
находятся значения остальных переменных. Для рассматриваемой задачи эта зависимость имеет вид:
В заголовке таблицы выписываются переменные, свободные переменные отмечаются стрелкой. Далее свободным переменным
придаются любые, одновременно не равные нулю значений и из зависимости между свободными и связанными переменными
находятся значения остальных переменных. Для рассматриваемой задачи эта зависимость имеет вид: Частное решение системы:
Частное решение системы:

 Я думаю для читающих это очевидно. (Кто решал систему уравнений методом Крамера, найдут общие черты)
Я думаю для читающих это очевидно. (Кто решал систему уравнений методом Крамера, найдут общие черты)
 Что бы сделать ноль в место элемента $a_{21}$, надо от второй строки вычесть первую, и разность записать во второй строке. Что бы сделать ноль в место элемента $a_{31}$, надо от третьей строки вычесть первую и разность записать в третьей строке. Что бы сделать ноль в место элемента $a_{41}$, надо от четвёртой строки вычесть первую умноженную на 2 и разность записать в четвёртой строке. Что бы сделать ноль в место элемента $a_{31}$, надо от пятой строки вычесть первую умноженную на 2 и разность записать в пятой строке.
Что бы сделать ноль в место элемента $a_{21}$, надо от второй строки вычесть первую, и разность записать во второй строке. Что бы сделать ноль в место элемента $a_{31}$, надо от третьей строки вычесть первую и разность записать в третьей строке. Что бы сделать ноль в место элемента $a_{41}$, надо от четвёртой строки вычесть первую умноженную на 2 и разность записать в четвёртой строке. Что бы сделать ноль в место элемента $a_{31}$, надо от пятой строки вычесть первую умноженную на 2 и разность записать в пятой строке.
 Что бы найти векторы, что входят в ФСР нам надо вместо $x_4$ подставить 1, а вместо $x_5$ подставить 0, найти $x_1$, $x_2$ и $x_3$, а потом наоборот $x_4=0$ и $x_5=1$.
Что бы найти векторы, что входят в ФСР нам надо вместо $x_4$ подставить 1, а вместо $x_5$ подставить 0, найти $x_1$, $x_2$ и $x_3$, а потом наоборот $x_4=0$ и $x_5=1$.




 Это наглядно, красиво и никогда не дает сбоев. Есть только одно но, нужно делать очень много ручной работы и использовать понятия ранга матрицы
Это наглядно, красиво и никогда не дает сбоев. Есть только одно но, нужно делать очень много ручной работы и использовать понятия ранга матрицы
 Это очевидно
Это очевидно Это связано с тем, что мы свободные переменные выбрали как нашей душе угодно, а не самые крайние правые.
Это связано с тем, что мы свободные переменные выбрали как нашей душе угодно, а не самые крайние правые. 
 Труды его признаны и востребованы по сей день во всем мире, несмотря на то что наука не стоит на месте. Особо занимательным является тот факт, что господин Эйлер принял непосредственное участие в становлении российской школы высшей математики, тем более что волею судеб он дважды возвращался в наше государство. Ученый обладал уникальной способностью выстраивать прозрачные в своей логике алгоритмы, отсекая все лишнее и в кратчайшие сроки переходя от общего к частному. Не станем перечислять все его заслуги, так как это займет немалое количество времени, и обратимся непосредственно к теме статьи. Именно он предложил использовать графическое изображение операций над множествами. Круги Эйлера решение любой, даже самой сложно составленной задачи, способны изобразить наглядно.
Труды его признаны и востребованы по сей день во всем мире, несмотря на то что наука не стоит на месте. Особо занимательным является тот факт, что господин Эйлер принял непосредственное участие в становлении российской школы высшей математики, тем более что волею судеб он дважды возвращался в наше государство. Ученый обладал уникальной способностью выстраивать прозрачные в своей логике алгоритмы, отсекая все лишнее и в кратчайшие сроки переходя от общего к частному. Не станем перечислять все его заслуги, так как это займет немалое количество времени, и обратимся непосредственно к теме статьи. Именно он предложил использовать графическое изображение операций над множествами. Круги Эйлера решение любой, даже самой сложно составленной задачи, способны изобразить наглядно.

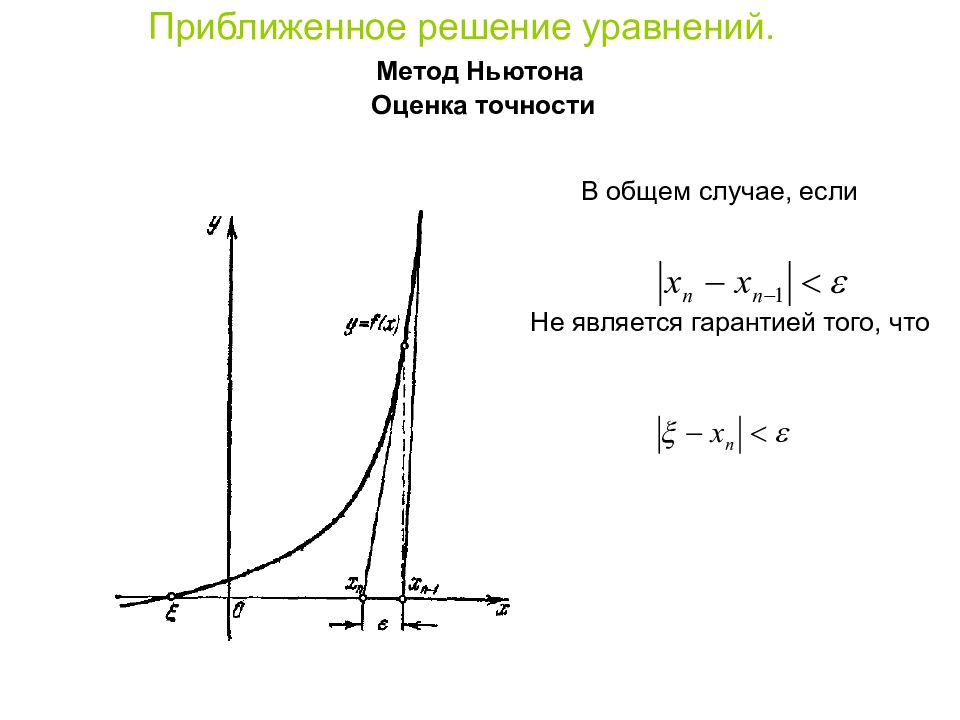 На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и калькулятор онлайн метод ньютона. Просто введите задачу в окошко и нажмите
«решить» здесь (например, онлайн полином ньютона).
На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и калькулятор онлайн метод ньютона. Просто введите задачу в окошко и нажмите
«решить» здесь (например, онлайн полином ньютона).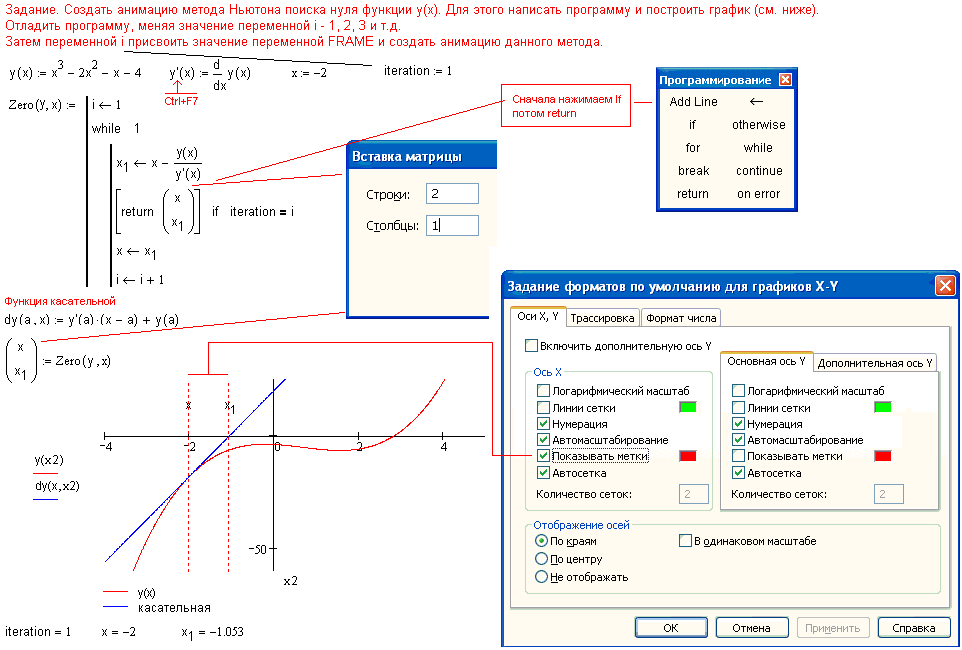
 Выберем две начальные точки C 1 x 1 ; y 1 {\displaystyle C_{1}x_{1};y_{1}} и C 2 x 2 ; y 2 {\displaystyle C_{2}x_{2};y_{2}} и проведем через них прямую. Она пересечет ось абсцисс в точке x 3 ; 0 {\displaystyle x_{3};0}. Теперь найдем значение функции с абсциссой x 3 {\displaystyle x_{3}}. Временно будем считать x 3 {\displaystyle x_{3}} корнем на отрезке }. Пусть точка C 3 {\displaystyle C_{3}} имеет абсциссу x 3 {\displaystyle x_{3}} и лежит на графике. Теперь вместо точек C 1 {\displaystyle C_{1}} и C 2 {\displaystyle C_{2}} мы возьмём точку C 3 {\displaystyle C_{3}} и точку C 2 {\displaystyle C_{2}}. Теперь с этими двумя точками проделаем ту же операцию и так далее, то есть будем получать две точки C n + 1 {\displaystyle C_{n+1}} и C n {\displaystyle C_{n}} и повторять операцию с ними. Отрезок, соединяющий последние две точки, пересекает ось абсцисс в точке, значение абсциссы которой можно приближённо считать корнем. Эти действия нужно повторять до тех пор, пока не получим значение корня с нужным приближением.
Выберем две начальные точки C 1 x 1 ; y 1 {\displaystyle C_{1}x_{1};y_{1}} и C 2 x 2 ; y 2 {\displaystyle C_{2}x_{2};y_{2}} и проведем через них прямую. Она пересечет ось абсцисс в точке x 3 ; 0 {\displaystyle x_{3};0}. Теперь найдем значение функции с абсциссой x 3 {\displaystyle x_{3}}. Временно будем считать x 3 {\displaystyle x_{3}} корнем на отрезке }. Пусть точка C 3 {\displaystyle C_{3}} имеет абсциссу x 3 {\displaystyle x_{3}} и лежит на графике. Теперь вместо точек C 1 {\displaystyle C_{1}} и C 2 {\displaystyle C_{2}} мы возьмём точку C 3 {\displaystyle C_{3}} и точку C 2 {\displaystyle C_{2}}. Теперь с этими двумя точками проделаем ту же операцию и так далее, то есть будем получать две точки C n + 1 {\displaystyle C_{n+1}} и C n {\displaystyle C_{n}} и повторять операцию с ними. Отрезок, соединяющий последние две точки, пересекает ось абсцисс в точке, значение абсциссы которой можно приближённо считать корнем. Эти действия нужно повторять до тех пор, пока не получим значение корня с нужным приближением.
 {3}-18x-83=0} методом секущих. Зададимся точностью ε=0.001 и возьмём в качестве начальных приближений x 0 {\displaystyle x_{0}} и x 1 {\displaystyle x_{1}} концы отрезка, на котором отделён корень: x 0 = 8 {\displaystyle x_{0}=8} и x 1 = 3 {\displaystyle x_{1}=3}, числовые значения x 0 = 8 {\displaystyle x_{0}=8} и x 1 = 3 {\displaystyle x_{1}=3} выбраны произвольно. Вычисления ведутся до тех пор, пока не будет выполнено неравенство | x i + 1 − x i | ε {\displaystyle |x_{i+1}-x_{i}| f ″ b f b 0 {\displaystyle fbfb 0}, то можно доказать, что погрешность приближенного решения стремится к нулю при n → ∞ {\displaystyle n\rightarrow \infty }, то есть метод сходится и сходится со скоростью геометрической прогрессии при этом говорят, что он имеет линейную скорость сходимости.
{3}-18x-83=0} методом секущих. Зададимся точностью ε=0.001 и возьмём в качестве начальных приближений x 0 {\displaystyle x_{0}} и x 1 {\displaystyle x_{1}} концы отрезка, на котором отделён корень: x 0 = 8 {\displaystyle x_{0}=8} и x 1 = 3 {\displaystyle x_{1}=3}, числовые значения x 0 = 8 {\displaystyle x_{0}=8} и x 1 = 3 {\displaystyle x_{1}=3} выбраны произвольно. Вычисления ведутся до тех пор, пока не будет выполнено неравенство | x i + 1 − x i | ε {\displaystyle |x_{i+1}-x_{i}| f ″ b f b 0 {\displaystyle fbfb 0}, то можно доказать, что погрешность приближенного решения стремится к нулю при n → ∞ {\displaystyle n\rightarrow \infty }, то есть метод сходится и сходится со скоростью геометрической прогрессии при этом говорят, что он имеет линейную скорость сходимости.
 Сохранившиеся работы Диофанта сообщают об этом. Однако первым, кто понял его методы, был Ферма в XVII веке, а первым, кто дал объяснение методу хорд, был Ньютон 1670-е годов
Сохранившиеся работы Диофанта сообщают об этом. Однако первым, кто понял его методы, был Ферма в XVII веке, а первым, кто дал объяснение методу хорд, был Ньютон 1670-е годов
 Метод случайных концов наудачу выберем две точки на окружности и проведём через них хорду Чтобы посчитать искомую вероятность
Метод случайных концов наудачу выберем две точки на окружности и проведём через них хорду Чтобы посчитать искомую вероятность При этом значения располагаются по окружности, а связи между ними отображаются в виде хорд
При этом значения располагаются по окружности, а связи между ними отображаются в виде хорд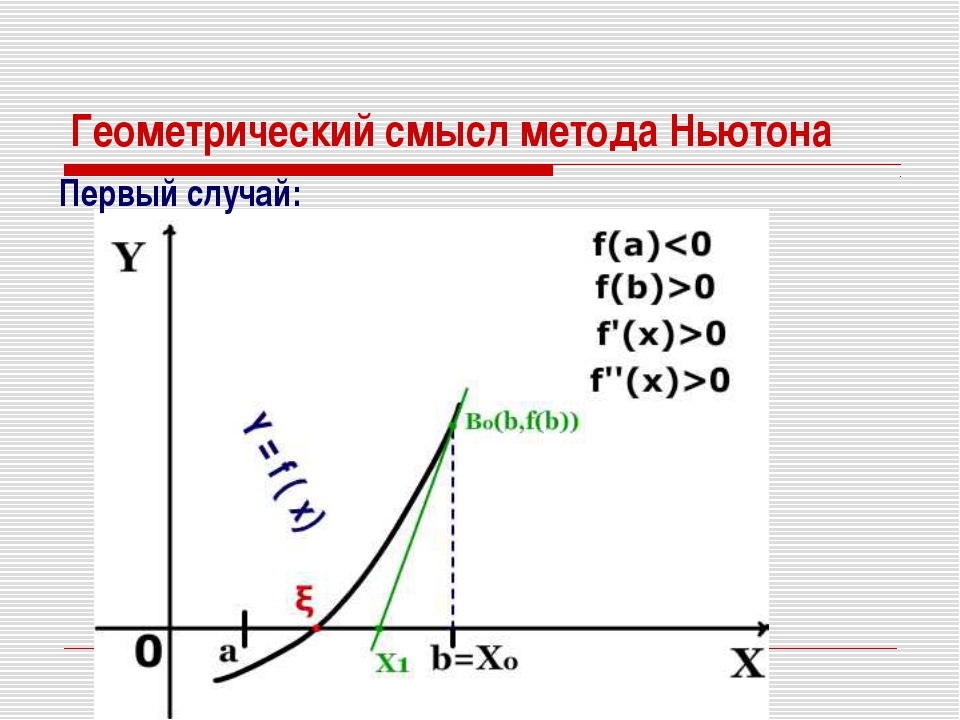 Идея метода состоит
Идея метода состоит По степени развития нервной
По степени развития нервной Составил таблицу хорд соответствующим дугам от 0 до 180 ввёл
Составил таблицу хорд соответствующим дугам от 0 до 180 ввёл Обобщённая теорема Ролля Формула конечных
Обобщённая теорема Ролля Формула конечных
 При решении уравнения методом хорд поводится прямая соединяющая концы отрезка. Из двух точек А и В выбирается х0. Метод хорд Онлайн калькулятор. Решения нелинейных уравнений и основан на последовательном сужении интервала, содержащего единственный корень уравнения. Итерационный процесс выполняется до того момента, пока не будет достигнута заданная точность.
При решении уравнения методом хорд поводится прямая соединяющая концы отрезка. Из двух точек А и В выбирается х0. Метод хорд Онлайн калькулятор. Решения нелинейных уравнений и основан на последовательном сужении интервала, содержащего единственный корень уравнения. Итерационный процесс выполняется до того момента, пока не будет достигнута заданная точность. Методы. Лекция 12. Решение нелинейных уравнений ТОЭ. На языке Pascal реализуются четыре метода: дихотомии, касательных, хорд и простых итераций. Проводится сравнение их эффективности с точки. Модификации метода Ньютона. Метод хорд и касательных. Материал из Википедии свободной энциклопедии. Перенаправление на: Метод хорд. Что такое.moda Вики является. Regula falsi и метод хорд разные алгоритмы? Помогите. Онлайн калькулятор для нахождения корней уравнений алгебраических и трансцендентных методом хорд также известный как метод секущих.
Методы. Лекция 12. Решение нелинейных уравнений ТОЭ. На языке Pascal реализуются четыре метода: дихотомии, касательных, хорд и простых итераций. Проводится сравнение их эффективности с точки. Модификации метода Ньютона. Метод хорд и касательных. Материал из Википедии свободной энциклопедии. Перенаправление на: Метод хорд. Что такое.moda Вики является. Regula falsi и метод хорд разные алгоритмы? Помогите. Онлайн калькулятор для нахождения корней уравнений алгебраических и трансцендентных методом хорд также известный как метод секущих. Метод хорд это Что такое Метод хорд? DIC Academic. Метод хорд. Этот метод при тех же предположениях обеспечивает более быстрое нахождение корня, чем метод половинного деления. Для этого. 4.3 Метод хорд стр.1 Delphi Plus. Презентация на тему Комбинированный метод хорд и касательных, предмет презентации: Математика. Этот материал содержит 10 слайдов. 1.4. Метод хорд. В данной работе рассмотрены такие, как метод деления отрезка пополам, метод простой итерации, метод Ньютона касательных, метод хорд,.
Метод хорд это Что такое Метод хорд? DIC Academic. Метод хорд. Этот метод при тех же предположениях обеспечивает более быстрое нахождение корня, чем метод половинного деления. Для этого. 4.3 Метод хорд стр.1 Delphi Plus. Презентация на тему Комбинированный метод хорд и касательных, предмет презентации: Математика. Этот материал содержит 10 слайдов. 1.4. Метод хорд. В данной работе рассмотрены такие, как метод деления отрезка пополам, метод простой итерации, метод Ньютона касательных, метод хорд,. Используемый метод: метод.
Используемый метод: метод.
 Очередное.
Очередное. В качестве метода был выбран метод хорд, который позволяет приблизить значение равновесной цены к максимально рациональной цене для. Метод хорд или метод секущих. Рассматриваются алгоритмы реализации численных методов. деления отрезка пополам, метод касательных, метод хорд 1. деления отрезка. Метод хорд Программирование на C, C и Java. Метод хорд. Рассматриваемый метод так же, как и метод дихотомии предназначен для уточнения корня на интервале на концах которого левая часть.
В качестве метода был выбран метод хорд, который позволяет приблизить значение равновесной цены к максимально рациональной цене для. Метод хорд или метод секущих. Рассматриваются алгоритмы реализации численных методов. деления отрезка пополам, метод касательных, метод хорд 1. деления отрезка. Метод хорд Программирование на C, C и Java. Метод хорд. Рассматриваемый метод так же, как и метод дихотомии предназначен для уточнения корня на интервале на концах которого левая часть.
 Если требуется анализ процесса или решение задачи, автор сделает задания, чтобы по итогу контрольная работа стала допуском к зачету или основанием для получения высокого промежуточного балла.
Если требуется анализ процесса или решение задачи, автор сделает задания, чтобы по итогу контрольная работа стала допуском к зачету или основанием для получения высокого промежуточного балла.
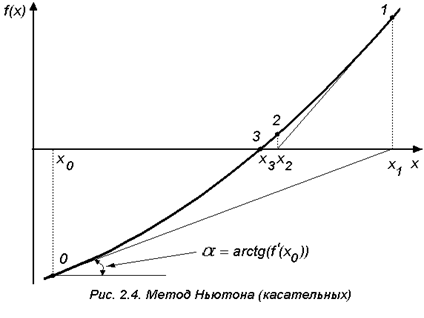 Но на практике удобнее сразу занулять то, что находится и сверху и снизу рассматриваемого элемента. Наш калькулятор использует именно этот подход.
Но на практике удобнее сразу занулять то, что находится и сверху и снизу рассматриваемого элемента. Наш калькулятор использует именно этот подход.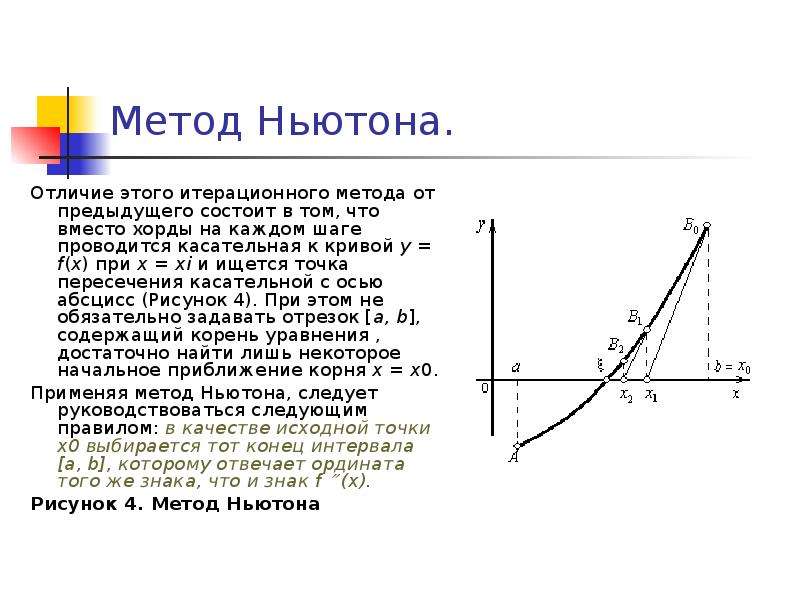

 Нам необходимо сделать нулевыми все элементы матрицы ниже главной диагонали. Сначала мы получаем нули в первом столбце.
Для этого мы последовательно вычитаем первую строку, домноженную на нужное нам число (такое, чтоб при вычитании мы получили ноль в первом элементе строки), из всех ниже лежащих строк.
Затем проделываем то же самое для второй строки, чтобы получить нули во втором столбце ниже главной диагонали матрицы. И так далее пока не доберемся до предпоследней строки.
Нам необходимо сделать нулевыми все элементы матрицы ниже главной диагонали. Сначала мы получаем нули в первом столбце.
Для этого мы последовательно вычитаем первую строку, домноженную на нужное нам число (такое, чтоб при вычитании мы получили ноль в первом элементе строки), из всех ниже лежащих строк.
Затем проделываем то же самое для второй строки, чтобы получить нули во втором столбце ниже главной диагонали матрицы. И так далее пока не доберемся до предпоследней строки.
 т.е. 02+=bc0.
т.е. 02+=bc0. Индексы коэффициентов (aij) системы обозначают номера уравнения (i) и неизвестного (j), при котором стоит этот коэффициент, соответственно.
Индексы коэффициентов (aij) системы обозначают номера уравнения (i) и неизвестного (j), при котором стоит этот коэффициент, соответственно. Если уравнений больше, чем неизвестных, она называется переопределённой.
Если уравнений больше, чем неизвестных, она называется переопределённой. 5) Графики…
5) Графики… 2. Возможности применения метода замены неизвестного при решении алгебраических уравнений В этой главе выявим возможности применения метода замены неизвестного при решении алгебраических уравнений в стандартных и нестандартных…
2. Возможности применения метода замены неизвестного при решении алгебраических уравнений В этой главе выявим возможности применения метода замены неизвестного при решении алгебраических уравнений в стандартных и нестандартных…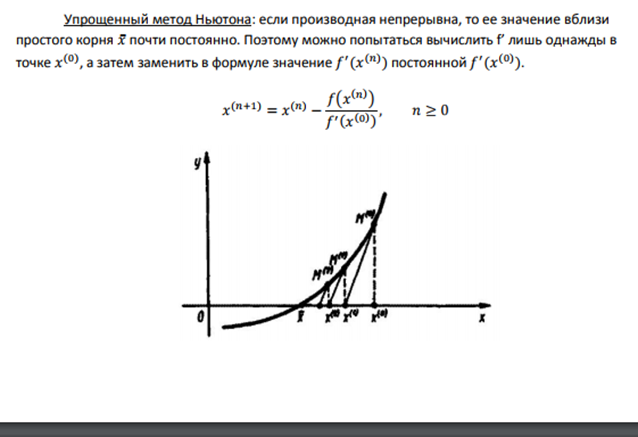 Но всё рано или поздно приедается…. И подумал тогда Жо рдан – а зачем вообще мучиться с обратным ходом гауссовского алгоритма? Не проще ли сразу получить ответ с помощью дополнительных элементарных преобразований?
Но всё рано или поздно приедается…. И подумал тогда Жо рдан – а зачем вообще мучиться с обратным ходом гауссовского алгоритма? Не проще ли сразу получить ответ с помощью дополнительных элементарных преобразований?


 К первой строке прибавили третью строку.
К первой строке прибавили третью строку.
 Образец такого решения есть в Примере №7 статьи об однородных системах линейных уравнений , причём там выбран другой базис .
Образец такого решения есть в Примере №7 статьи об однородных системах линейных уравнений , причём там выбран другой базис .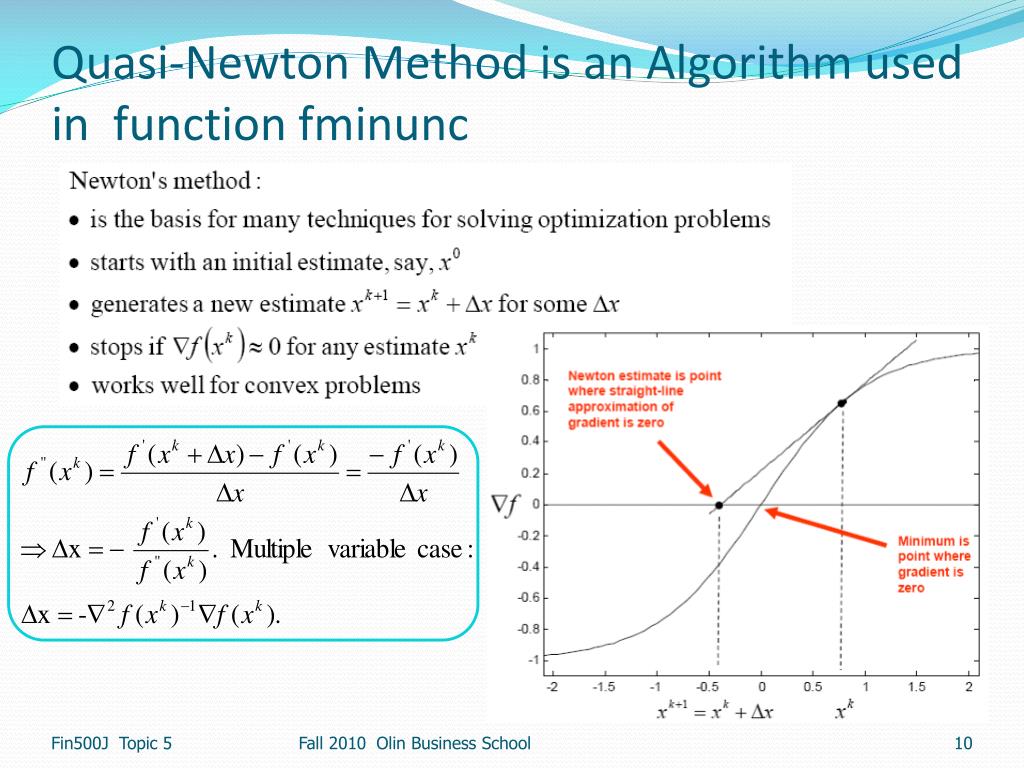 Для этого запишем её в одной упряжке с единичной матрицей, и понеслась «двойка скакунов»:
Для этого запишем её в одной упряжке с единичной матрицей, и понеслась «двойка скакунов»: Обратите внимание, что здесь вместо перестановки можно организовать «шестёрки» в 1-м столбце (наименьшее общее кратное (НОК) чисел 3, 2 и 1) . Решение через НОК особенно удобно, когда в первом столбце отсутствуют «единицы».
Обратите внимание, что здесь вместо перестановки можно организовать «шестёрки» в 1-м столбце (наименьшее общее кратное (НОК) чисел 3, 2 и 1) . Решение через НОК особенно удобно, когда в первом столбце отсутствуют «единицы».




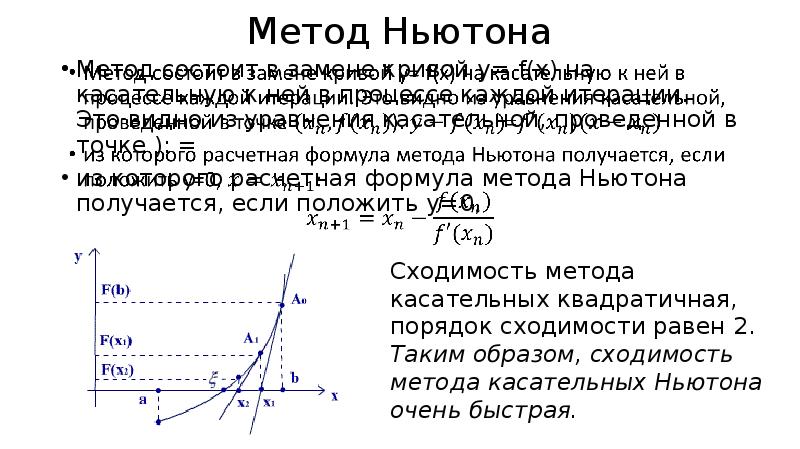


 Вторая Делим ее на 17/3:
Вторая Делим ее на 17/3: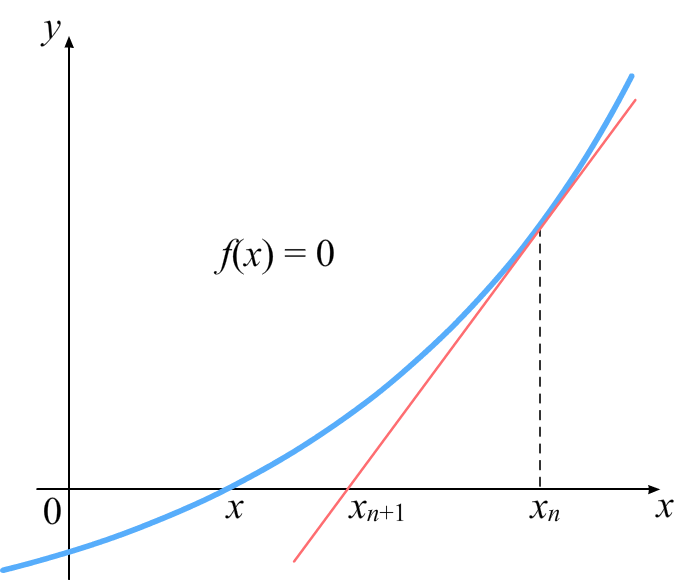 Конвертер единиц измерения количества информацииКурсы валютРазмеры женской одежды и обувиРазмеры мужской одежды и обувиКонвертер угловой скорости и частоты вращенияКонвертер ускоренияКонвертер углового ускоренияКонвертер плотностиКонвертер удельного объемаКонвертер момента инерцииКонвертер момента силыКонвертер вращающего моментаКонвертер удельной теплоты сгорания (по массе)Конвертер плотности энергии и удельной теплоты сгорания топлива (по объему)Конвертер разности температурКонвертер коэффициента теплового расширенияКонвертер термического сопротивленияКонвертер удельной теплопроводностиКонвертер удельной теплоёмкостиКонвертер энергетической экспозиции и мощности теплового излученияКонвертер плотности теплового потокаКонвертер коэффициента теплоотдачиКонвертер объёмного расходаКонвертер массового расходаКонвертер молярного расходаКонвертер плотности потока массыКонвертер молярной концентрацииКонвертер массовой концентрации в раствореКонвертер динамической (абсолютной) вязкостиКонвертер кинематической вязкостиКонвертер поверхностного натяженияКонвертер паропроницаемостиКонвертер плотности потока водяного параКонвертер уровня звукаКонвертер чувствительности микрофоновКонвертер уровня звукового давления (SPL)Конвертер уровня звукового давления с возможностью выбора опорного давленияКонвертер яркостиКонвертер силы светаКонвертер освещённостиКонвертер разрешения в компьютерной графикеКонвертер частоты и длины волныОптическая сила в диоптриях и фокусное расстояниеОптическая сила в диоптриях и увеличение линзы (×)Конвертер электрического зарядаКонвертер линейной плотности зарядаКонвертер поверхностной плотности зарядаКонвертер объемной плотности зарядаКонвертер электрического токаКонвертер линейной плотности токаКонвертер поверхностной плотности токаКонвертер напряжённости электрического поляКонвертер электростатического потенциала и напряженияКонвертер электрического сопротивленияКонвертер удельного электрического сопротивленияКонвертер электрической проводимостиКонвертер удельной электрической проводимостиЭлектрическая емкостьКонвертер индуктивностиКонвертер реактивной мощностиКонвертер Американского калибра проводовУровни в dBm (дБм или дБмВт), dBV (дБВ), ваттах и др.
Конвертер единиц измерения количества информацииКурсы валютРазмеры женской одежды и обувиРазмеры мужской одежды и обувиКонвертер угловой скорости и частоты вращенияКонвертер ускоренияКонвертер углового ускоренияКонвертер плотностиКонвертер удельного объемаКонвертер момента инерцииКонвертер момента силыКонвертер вращающего моментаКонвертер удельной теплоты сгорания (по массе)Конвертер плотности энергии и удельной теплоты сгорания топлива (по объему)Конвертер разности температурКонвертер коэффициента теплового расширенияКонвертер термического сопротивленияКонвертер удельной теплопроводностиКонвертер удельной теплоёмкостиКонвертер энергетической экспозиции и мощности теплового излученияКонвертер плотности теплового потокаКонвертер коэффициента теплоотдачиКонвертер объёмного расходаКонвертер массового расходаКонвертер молярного расходаКонвертер плотности потока массыКонвертер молярной концентрацииКонвертер массовой концентрации в раствореКонвертер динамической (абсолютной) вязкостиКонвертер кинематической вязкостиКонвертер поверхностного натяженияКонвертер паропроницаемостиКонвертер плотности потока водяного параКонвертер уровня звукаКонвертер чувствительности микрофоновКонвертер уровня звукового давления (SPL)Конвертер уровня звукового давления с возможностью выбора опорного давленияКонвертер яркостиКонвертер силы светаКонвертер освещённостиКонвертер разрешения в компьютерной графикеКонвертер частоты и длины волныОптическая сила в диоптриях и фокусное расстояниеОптическая сила в диоптриях и увеличение линзы (×)Конвертер электрического зарядаКонвертер линейной плотности зарядаКонвертер поверхностной плотности зарядаКонвертер объемной плотности зарядаКонвертер электрического токаКонвертер линейной плотности токаКонвертер поверхностной плотности токаКонвертер напряжённости электрического поляКонвертер электростатического потенциала и напряженияКонвертер электрического сопротивленияКонвертер удельного электрического сопротивленияКонвертер электрической проводимостиКонвертер удельной электрической проводимостиЭлектрическая емкостьКонвертер индуктивностиКонвертер реактивной мощностиКонвертер Американского калибра проводовУровни в dBm (дБм или дБмВт), dBV (дБВ), ваттах и др. единицахКонвертер магнитодвижущей силыКонвертер напряженности магнитного поляКонвертер магнитного потокаКонвертер магнитной индукцииРадиация. Конвертер мощности поглощенной дозы ионизирующего излученияРадиоактивность. Конвертер радиоактивного распадаРадиация. Конвертер экспозиционной дозыРадиация. Конвертер поглощённой дозыКонвертер десятичных приставокПередача данныхКонвертер единиц типографики и обработки изображенийКонвертер единиц измерения объема лесоматериаловВычисление молярной массыПериодическая система химических элементов Д. И. Менделеева
единицахКонвертер магнитодвижущей силыКонвертер напряженности магнитного поляКонвертер магнитного потокаКонвертер магнитной индукцииРадиация. Конвертер мощности поглощенной дозы ионизирующего излученияРадиоактивность. Конвертер радиоактивного распадаРадиация. Конвертер экспозиционной дозыРадиация. Конвертер поглощённой дозыКонвертер десятичных приставокПередача данныхКонвертер единиц типографики и обработки изображенийКонвертер единиц измерения объема лесоматериаловВычисление молярной массыПериодическая система химических элементов Д. И. Менделеева Например, если надавить лезвием острого ножа на помидор или морковь, овощ будет разрезан пополам. Площадь поверхности лезвия, соприкасающаяся с овощем, мала, поэтому давление достаточно велико, чтобы разрезать этот овощ. Если же надавить с той же силой на помидор или морковь тупым ножом, то, скорее всего, овощ не разрежется, так как площадь поверхности ножа теперь больше, а значит давление — меньше.
Например, если надавить лезвием острого ножа на помидор или морковь, овощ будет разрезан пополам. Площадь поверхности лезвия, соприкасающаяся с овощем, мала, поэтому давление достаточно велико, чтобы разрезать этот овощ. Если же надавить с той же силой на помидор или морковь тупым ножом, то, скорее всего, овощ не разрежется, так как площадь поверхности ножа теперь больше, а значит давление — меньше. Люди и животные страдают от сильных перепадов давления. Пониженное давление вызывает у людей и животных проблемы разной степени тяжести, от психического и физического дискомфорта до заболеваний с летальным исходом. По этой причине, в кабинах самолетов поддерживается давление выше атмосферного на данной высоте, потому что атмосферное давление на крейсерской высоте полета слишком низкое.
Люди и животные страдают от сильных перепадов давления. Пониженное давление вызывает у людей и животных проблемы разной степени тяжести, от психического и физического дискомфорта до заболеваний с летальным исходом. По этой причине, в кабинах самолетов поддерживается давление выше атмосферного на данной высоте, потому что атмосферное давление на крейсерской высоте полета слишком низкое. Обозначается факториал восклицательным знаком после числа — «n!».
Обозначается факториал восклицательным знаком после числа — «n!». 28803779534. Факториал числа Эйлера, другого трансцендентного числа, Γ(e) ~ 1.567468255 (упрощенно, факториал числа e).
28803779534. Факториал числа Эйлера, другого трансцендентного числа, Γ(e) ~ 1.567468255 (упрощенно, факториал числа e). Да и вообще, код занимает больше места, чем мог бы. Чтобы избежать повторного написания одной и той же логики, в языках программирования существуют функции.
Да и вообще, код занимает больше места, чем мог бы. Чтобы избежать повторного написания одной и той же логики, в языках программирования существуют функции. Первая строчка этого примера является описанием нашей функции. factorial — идентификатор, то есть имя нашей функции. После идентификатора в круглых скобках идет список параметров, которые получает наша функция. Список состоит из перечисленных через запятую идентификаторов параметров. В нашем случае список состоит из одной величины n. В конце строки ставится двоеточие.
Первая строчка этого примера является описанием нашей функции. factorial — идентификатор, то есть имя нашей функции. После идентификатора в круглых скобках идет список параметров, которые получает наша функция. Список состоит из перечисленных через запятую идентификаторов параметров. В нашем случае список состоит из одной величины n. В конце строки ставится двоеточие.

 Эти переменные становятся недоступными после выхода из функции.
Эти переменные становятся недоступными после выхода из функции.
 Поэтому вывод переменной
Поэтому вывод переменной  Вот как это не стоит делать:
Вот как это не стоит делать: Рекурсия
Рекурсия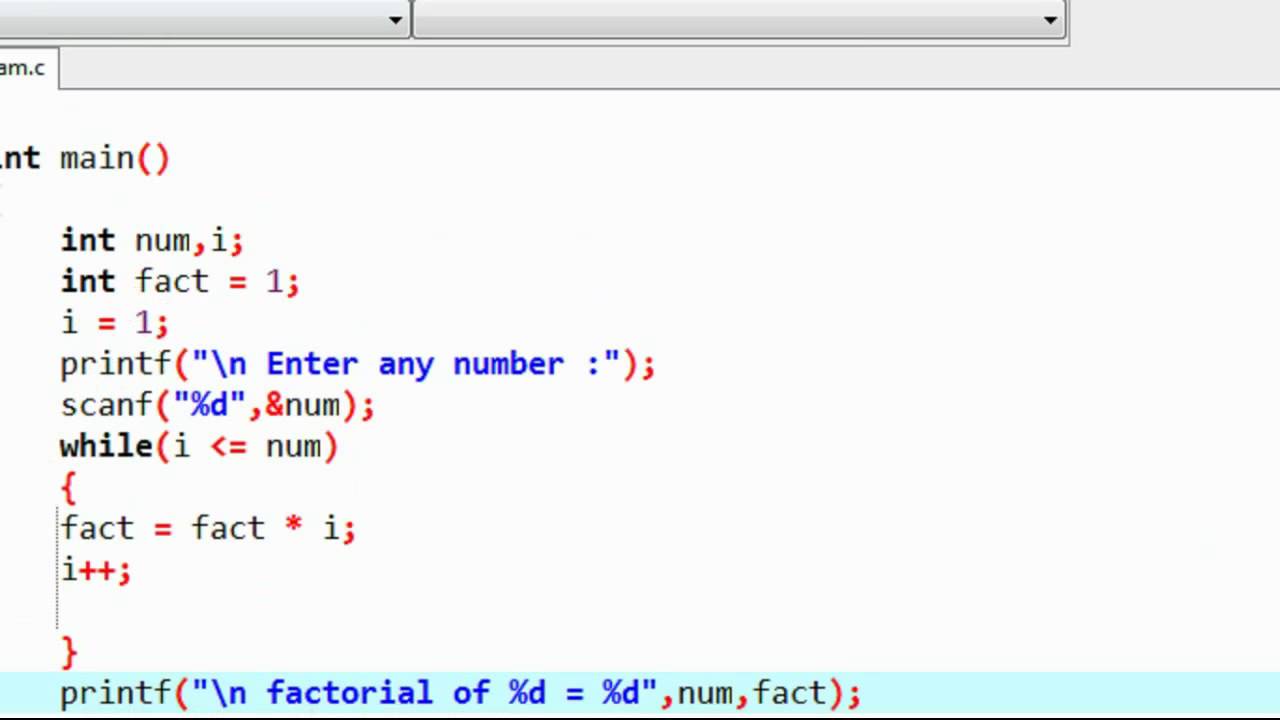

 Например, факториал числа 7 выглядит так:
Например, факториал числа 7 выглядит так:  Тем не менее у начинающих программистов остаётся вопрос: «Как вычислить факториал в «Паскале»?»
Тем не менее у начинающих программистов остаётся вопрос: «Как вычислить факториал в «Паскале»?»

 Я делаю это, чтобы изучить и быть знакомым со Swift, поэтому я хочу понять это самостоятельно.
Я делаю это, чтобы изучить и быть знакомым со Swift, поэтому я хочу понять это самостоятельно. Добавьте
Добавьте  append(digit)
}
return result.reversed()
}
func factorial(_ n: Int) -> String {
var result = [1]
for i in 2...n {
result = result.map { $0 * i }
result = carryAll(result)
}
return result.map(String.init).joined()
}
print(factorial(1000))
append(digit)
}
return result.reversed()
}
func factorial(_ n: Int) -> String {
var result = [1]
for i in 2...n {
result = result.map { $0 * i }
result = carryAll(result)
}
return result.map(String.init).joined()
}
print(factorial(1000))
 В этом примере вычисляются факториал из шести. В общем, с помощью факториала можно подсчитать количество способов у организовать группу отдельных элементов (перемитации). Чтобы вычислить факториал числа, используйте функцию ФАКТС.
В этом примере вычисляются факториал из шести. В общем, с помощью факториала можно подсчитать количество способов у организовать группу отдельных элементов (перемитации). Чтобы вычислить факториал числа, используйте функцию ФАКТС.
 С примером реализации вы наверняка сталкивались и не раз, но для полноты картины, я просто обязан его описать. :))
С примером реализации вы наверняка сталкивались и не раз, но для полноты картины, я просто обязан его описать. :))
 377 CPU seconds
377 CPU seconds Обозначим, через T(n) — время выполнения программы.
Обозначим, через T(n) — время выполнения программы. в «Моделирование трехместного оператора» в «Справочном руководстве по Python»).
в «Моделирование трехместного оператора» в «Справочном руководстве по Python»). Теперь вспомним, каково определение факториала. В школьном учебнике математики определение факториала звучит так: факториал есть произведение натуральных чисел от 1 до заданного числа. Это не совсем точное определение, потому что, строго говоря, факториал нуля тоже определен, и он равен 1, это во-первых. А во-вторых, мы с вами понимаем, что в математике произведение включает в себя как минимум два числа, а для единицы у нас получится произведение из одного числа, что как-то странно. Рассмотрим другое определение факториала. n факториал мы с вами будем вычислять по формуле, которая включает в себя два случая: n! = 1, когда n = 0, и вычисляется как факториал числа на единицу меньшего, умноженного на само это число, если n — это натуральное число. И рассмотрим постановку задачи. Нам с вами даны два целых числа, n и k. Результатом является A — число размещений. n должно быть положительным или равным нулю. k должно быть больше или равно n, и оба эти числа должны принадлежать множеству целых чисел.
Теперь вспомним, каково определение факториала. В школьном учебнике математики определение факториала звучит так: факториал есть произведение натуральных чисел от 1 до заданного числа. Это не совсем точное определение, потому что, строго говоря, факториал нуля тоже определен, и он равен 1, это во-первых. А во-вторых, мы с вами понимаем, что в математике произведение включает в себя как минимум два числа, а для единицы у нас получится произведение из одного числа, что как-то странно. Рассмотрим другое определение факториала. n факториал мы с вами будем вычислять по формуле, которая включает в себя два случая: n! = 1, когда n = 0, и вычисляется как факториал числа на единицу меньшего, умноженного на само это число, если n — это натуральное число. И рассмотрим постановку задачи. Нам с вами даны два целых числа, n и k. Результатом является A — число размещений. n должно быть положительным или равным нулю. k должно быть больше или равно n, и оба эти числа должны принадлежать множеству целых чисел. Мы с вами проверим при вводе, что это действительно так. Связью в данном случае является наша формула. И теперь рассмотрим программу, которая решает нашу задачу. Здесь у нас две переменных целого типа, это n и k. Кроме того, у нас есть три переменных вещественного типа: это n1 и k1, которые мы будем использовать для организации надежного ввода данных, и переменная a, которая является результатом. Так как результатом является частное, то переменная a, конечно же, имеет вещественный тип. Далее рассмотрим функцию, которая называется f. На входе у нее целое число, а на выходе — значение вещественного типа, причем эта функция будет рекурсивной, так как эта функция будет вычислять значение по второй формуле, где значение факториала вычисляется через факториал числа, на единицу меньшего. И посмотрите, как интересно. Наши исходные данные имеют целый тип, а результат — вещественный, хотя вроде бы у нас результатом является произведение целых чисел. Почему же мы выбрали вещественный тип для результата? Дело в том, что у целого типа гораздо более узкий диапазон, чем у вещественного.
Мы с вами проверим при вводе, что это действительно так. Связью в данном случае является наша формула. И теперь рассмотрим программу, которая решает нашу задачу. Здесь у нас две переменных целого типа, это n и k. Кроме того, у нас есть три переменных вещественного типа: это n1 и k1, которые мы будем использовать для организации надежного ввода данных, и переменная a, которая является результатом. Так как результатом является частное, то переменная a, конечно же, имеет вещественный тип. Далее рассмотрим функцию, которая называется f. На входе у нее целое число, а на выходе — значение вещественного типа, причем эта функция будет рекурсивной, так как эта функция будет вычислять значение по второй формуле, где значение факториала вычисляется через факториал числа, на единицу меньшего. И посмотрите, как интересно. Наши исходные данные имеют целый тип, а результат — вещественный, хотя вроде бы у нас результатом является произведение целых чисел. Почему же мы выбрали вещественный тип для результата? Дело в том, что у целого типа гораздо более узкий диапазон, чем у вещественного. То есть мы выбрали вещественный тип для результата, чтобы просто можно было вычислять значения факториалов больших чисел. И теперь записываем тело функции, используя вторую формулу. Если n = 0, то результатом будет 1, а в противном случае мы делаем рекурсивный вызов нашей функции, то есть вычисляем факториал числа, на единицу меньшего, и домножаем его на очередное n. Далее рассмотрим основную программу. Мы вводим два целых числа, на которые накладываются ограничения, соответствующие пункту три в постановке задачи. При этом, чтобы при вводе нецелых чисел наша программа не завершалась аварийно, мы используем переменные n1 и k1 вещественного типа, читаем в них значения, и будем повторять наш ввод до тех пор, пока n1 не будет больше или равно нулю, k1 не будет больше или равно n1, и, кроме того, на переменную k1 еще наложено ограничение сверху, то есть ее значение не может превышать числа 170. Это самое большое число, факториал которого мы сможем вычислить. И кроме того, n1 и k1 должны быть целого типа, то есть результат округления равен самому этому числу, как для первого, так и для второго числа.
То есть мы выбрали вещественный тип для результата, чтобы просто можно было вычислять значения факториалов больших чисел. И теперь записываем тело функции, используя вторую формулу. Если n = 0, то результатом будет 1, а в противном случае мы делаем рекурсивный вызов нашей функции, то есть вычисляем факториал числа, на единицу меньшего, и домножаем его на очередное n. Далее рассмотрим основную программу. Мы вводим два целых числа, на которые накладываются ограничения, соответствующие пункту три в постановке задачи. При этом, чтобы при вводе нецелых чисел наша программа не завершалась аварийно, мы используем переменные n1 и k1 вещественного типа, читаем в них значения, и будем повторять наш ввод до тех пор, пока n1 не будет больше или равно нулю, k1 не будет больше или равно n1, и, кроме того, на переменную k1 еще наложено ограничение сверху, то есть ее значение не может превышать числа 170. Это самое большое число, факториал которого мы сможем вычислить. И кроме того, n1 и k1 должны быть целого типа, то есть результат округления равен самому этому числу, как для первого, так и для второго числа. Затем мы, для того чтобы передать наше значение в функцию, чтобы оно приобрело целый тип, мы переменной n присваиваем результат округления n1 до целого, а переменной k — результат округления k1 до целого. Вычисляем значения переменной a, вызывая нашу функцию два раза, и выводим на экран полученный результат. Затем наша программа завершается. Рассмотрим программу с использованием рекурсивной функции для вычисления количества размещений по заданной формуле. Вначале у нас объявлены все глобальные переменные: это n и k — два значения, для которых мы будем считать количество размещений; это две переменных n1 и k1 типа real, для того чтобы проверить правильность ввода исходных данных; и это величина a, которая является результатом. Так как по формуле значение a является частным, то есть одна величина делится на другую, здесь нужно использовать переменную типа real, несмотря на то, что результат будет целым числом. Далее у нас следует тело функции, которое использует рекурсивную формулу.
Затем мы, для того чтобы передать наше значение в функцию, чтобы оно приобрело целый тип, мы переменной n присваиваем результат округления n1 до целого, а переменной k — результат округления k1 до целого. Вычисляем значения переменной a, вызывая нашу функцию два раза, и выводим на экран полученный результат. Затем наша программа завершается. Рассмотрим программу с использованием рекурсивной функции для вычисления количества размещений по заданной формуле. Вначале у нас объявлены все глобальные переменные: это n и k — два значения, для которых мы будем считать количество размещений; это две переменных n1 и k1 типа real, для того чтобы проверить правильность ввода исходных данных; и это величина a, которая является результатом. Так как по формуле значение a является частным, то есть одна величина делится на другую, здесь нужно использовать переменную типа real, несмотря на то, что результат будет целым числом. Далее у нас следует тело функции, которое использует рекурсивную формулу. При n = 0, результат будет равен 1, а во всех остальных случаях он будет считаться по формуле: факториал предыдущего числа, умноженный на текущее число. Далее мы рассматриваем основную программу, которая всегда располагается после всех процедур и функций. В основной программе вводятся значения n и k, причем пользователю сообщается, какие ограничения наложены на эти значения. У нас n должно быть больше или равно нулю, k должно быть больше или равно n, и оба значения должны быть целыми числами. Мы читаем данные в переменной n1 и k1, для того чтобы можно было проверить, что эти данные принадлежат к целому типу. Если это не так, то есть какое-нибудь из чисел не равно своей целой части, то будет повторный ввод данных. Далее, мы с вами приводим n и k к целому типу, чтобы можно было передать их в качестве аргументов в функцию, потому что параметр, который мы передаем в функцию, имеет целый тип. Дальше мы считаем значение a, вызывая функцию два раза, и выводим на экран полученный результат.
При n = 0, результат будет равен 1, а во всех остальных случаях он будет считаться по формуле: факториал предыдущего числа, умноженный на текущее число. Далее мы рассматриваем основную программу, которая всегда располагается после всех процедур и функций. В основной программе вводятся значения n и k, причем пользователю сообщается, какие ограничения наложены на эти значения. У нас n должно быть больше или равно нулю, k должно быть больше или равно n, и оба значения должны быть целыми числами. Мы читаем данные в переменной n1 и k1, для того чтобы можно было проверить, что эти данные принадлежат к целому типу. Если это не так, то есть какое-нибудь из чисел не равно своей целой части, то будет повторный ввод данных. Далее, мы с вами приводим n и k к целому типу, чтобы можно было передать их в качестве аргументов в функцию, потому что параметр, который мы передаем в функцию, имеет целый тип. Дальше мы считаем значение a, вызывая функцию два раза, и выводим на экран полученный результат. Давайте попробуем запустить программу и введем исходные данные. Если я дам, например, значения, равные 3 и 8, то я получу результат, который мы с вами получали, когда рассматривали саму формулу. Теперь попробуем, что будет, если я введу данные, например, наоборот. Программа не восприняла эти данные, нужно вести их заново, допустим, то есть первым должно стоять число, которое меньше. Теперь посмотрим, что будет получаться, если я введу, например, нецелые числа. [БЕЗ_ЗВУКА] В данном случае результат у нас не достигнут, данные не введены, и нам нужно повторить ввод. Если я ввожу числа в правильном порядке, то я получаю правильный результат. Обращаю ваше внимание, что если я ошибусь второй раз, то есть задам сначала большее число, а потом меньшее, то снова будет повторный ввод, как в данном случае. Если я даю правильную пару, то получаю результат. То же самое происходит, если я ввожу не только нецелые числа, но и, например, отрицательные. − 1,5 и 4,3 — это неправильная пара значений.
Давайте попробуем запустить программу и введем исходные данные. Если я дам, например, значения, равные 3 и 8, то я получу результат, который мы с вами получали, когда рассматривали саму формулу. Теперь попробуем, что будет, если я введу данные, например, наоборот. Программа не восприняла эти данные, нужно вести их заново, допустим, то есть первым должно стоять число, которое меньше. Теперь посмотрим, что будет получаться, если я введу, например, нецелые числа. [БЕЗ_ЗВУКА] В данном случае результат у нас не достигнут, данные не введены, и нам нужно повторить ввод. Если я ввожу числа в правильном порядке, то я получаю правильный результат. Обращаю ваше внимание, что если я ошибусь второй раз, то есть задам сначала большее число, а потом меньшее, то снова будет повторный ввод, как в данном случае. Если я даю правильную пару, то получаю результат. То же самое происходит, если я ввожу не только нецелые числа, но и, например, отрицательные. − 1,5 и 4,3 — это неправильная пара значений. Если я введу правильную пару, первое число должно быть меньше, а второе — больше, и оба должны быть целыми, то тогда получается результат. Таким образом, эта программа работает правильно и проверяет исходные данные на допустимость, то есть проверяет, что числа у нас принадлежат к расширенному натуральному ряду. Они являются либо натуральным числом, либо допустимо значение, равное нулю. И также проверяется, что у нас с вами k больше или равно n. При вводе неправильных данных происходит повторный ввод, и так, пока пользователь не даст нам правильную пару чисел. Только в этом случае мы с вами получим результат. [ЗВУК] [ЗВУК] [ЗВУК]
Если я введу правильную пару, первое число должно быть меньше, а второе — больше, и оба должны быть целыми, то тогда получается результат. Таким образом, эта программа работает правильно и проверяет исходные данные на допустимость, то есть проверяет, что числа у нас принадлежат к расширенному натуральному ряду. Они являются либо натуральным числом, либо допустимо значение, равное нулю. И также проверяется, что у нас с вами k больше или равно n. При вводе неправильных данных происходит повторный ввод, и так, пока пользователь не даст нам правильную пару чисел. Только в этом случае мы с вами получим результат. [ЗВУК] [ЗВУК] [ЗВУК] Эта программа находит произведение всех чисел от 1 до указанного пользователем числа.
Эта программа находит произведение всех чисел от 1 до указанного пользователем числа. Если условие истинно, оно выполнит оператор и присвоит значение переменной «fact» как единицу. В противном случае, если условие ложно, выполняется инструкция else. Используя цикл for, умножьте все числа от 1 до n и отобразите факториал данного числа в качестве вывода.
Если условие истинно, оно выполнит оператор и присвоит значение переменной «fact» как единицу. В противном случае, если условие ложно, выполняется инструкция else. Используя цикл for, умножьте все числа от 1 до n и отобразите факториал данного числа в качестве вывода.


 Он используется для написания сложных и вложенных циклов. Если вы не понимаете цикл for, вам следует изучить его в нашем другом блоге или на курсах.
Он используется для написания сложных и вложенных циклов. Если вы не понимаете цикл for, вам следует изучить его в нашем другом блоге или на курсах.



 Свод оборотов и сальдо по всем синтетическим счетам, который предназначен для контроля учётных записей
Свод оборотов и сальдо по всем синтетическим счетам, который предназначен для контроля учётных записей 4. Лицо, получившее чек – чекодержатель
4. Лицо, получившее чек – чекодержатель  Документ, применяемый при выдаче материалов со склада и при перемещении материалов внутри учреждения
Документ, применяемый при выдаче материалов со склада и при перемещении материалов внутри учреждения  налоги
налоги Запасы отражаются в Балансе в составе…
Запасы отражаются в Балансе в составе… Какие из затрат по приобретению основных средств не относятся на увеличение их балансовой стоимости
Какие из затрат по приобретению основных средств не относятся на увеличение их балансовой стоимости
 В каком размере ему следует выплатить суточные?
В каком размере ему следует выплатить суточные?
 Дт151 Кт 66
Дт151 Кт 66 Начислена амортизация на ДБА.
Начислена амортизация на ДБА. Дт83 Кт 134
Дт83 Кт 134 Дт 97 Кт 66
Дт 97 Кт 66 Часть активов предприятия, которая остается после вычета его обязательств – это
Часть активов предприятия, которая остается после вычета его обязательств – это систематическое распределение стоимости необоротных активов которые амортизируются в течении срока полезного ископаемого.
систематическое распределение стоимости необоротных активов которые амортизируются в течении срока полезного ископаемого. в
в

 -х.;
-х.;





 Смит
Смит




 Правая сторона …
Правая сторона … Для того чтобы узнать правильные ответы на тест, нужно нажать на надпись «показать правильные ответы» внизу страницы со списком вопросов. Правильный ответ будет подчеркнут снизу цветной линией.
Для того чтобы узнать правильные ответы на тест, нужно нажать на надпись «показать правильные ответы» внизу страницы со списком вопросов. Правильный ответ будет подчеркнут снизу цветной линией.
 Амортизация основных средств начисляется в течение
Амортизация основных средств начисляется в течение Бухгалтерская отчетность составляется на основе данных учета
Бухгалтерская отчетность составляется на основе данных учета Бухгалтерский баланс представляет собой таблицу, состоящую из
Бухгалтерский баланс представляет собой таблицу, состоящую из В активе баланса сгруппированы
В активе баланса сгруппированы В состав годовой бухгалтерской отчетности обязательно включаются
В состав годовой бухгалтерской отчетности обязательно включаются П.Рудановским
П.Рудановским Главный бухгалтер назначается (освобождается) на должность
Главный бухгалтер назначается (освобождается) на должность Для следующих случаев проведение инвентаризации обязательно
Для следующих случаев проведение инвентаризации обязательно
 В связи с этим тест по бухгалтерским проводкам онлайн приобретает всё большую популярность.
В связи с этим тест по бухгалтерским проводкам онлайн приобретает всё большую популярность. В 2019 году оценивать результаты тестирования имеет право не только сам работодатель, но и специальные независимые центры по оценке квалификации».
В 2019 году оценивать результаты тестирования имеет право не только сам работодатель, но и специальные независимые центры по оценке квалификации». В связи с этим вопросы по проводкам могут составляться с учетом специфики компании. Поэтому при подготовке к тестированию в определенную фирму рекомендуется заранее изучить основное направление деятельности компании. И на основе полученных сведений провести профильную подготовку.
В связи с этим вопросы по проводкам могут составляться с учетом специфики компании. Поэтому при подготовке к тестированию в определенную фирму рекомендуется заранее изучить основное направление деятельности компании. И на основе полученных сведений провести профильную подготовку.
 Знания соискателя оцениваются в процентном соотношении верных и неверных ответов либо в установленных баллах.
Знания соискателя оцениваются в процентном соотношении верных и неверных ответов либо в установленных баллах. Прежде чем записаться на платные курсы повышения квалификации следует обязательно пройти такую предварительную проверку знаний. Также подборка тренировочных задач поможет подготовиться к более серьёзным вопросам, которые будут в тестах при сдаче экзамена на аттестат профессионального бухгалтера.
Прежде чем записаться на платные курсы повышения квалификации следует обязательно пройти такую предварительную проверку знаний. Также подборка тренировочных задач поможет подготовиться к более серьёзным вопросам, которые будут в тестах при сдаче экзамена на аттестат профессионального бухгалтера. ru
ru ru
ru ru
ru Освоили два способа: вынесение общего множителя за скобки и группировку. В этом уроке — следующий мощный способ: формулы сокращённого умножения . В краткой записи — ФСУ.
Освоили два способа: вынесение общего множителя за скобки и группировку. В этом уроке — следующий мощный способ: формулы сокращённого умножения . В краткой записи — ФСУ. Просто перемножаем скобки и приводим подобные. Так получаются все формулы сокращённого умножения. Сокращённое умножение — это потому, что в самих формулах нет перемножения скобок и приведения подобных. Сокращены.) Сразу дан результат.
Просто перемножаем скобки и приводим подобные. Так получаются все формулы сокращённого умножения. Сокращённое умножение — это потому, что в самих формулах нет перемножения скобок и приведения подобных. Сокращены.) Сразу дан результат. Их не так уж и много и они легко запоминаются, а запомнить их нужно. Обозначения которые используются в формулах, могут принимать любой вид (число или многочлен).
Их не так уж и много и они легко запоминаются, а запомнить их нужно. Обозначения которые используются в формулах, могут принимать любой вид (число или многочлен).
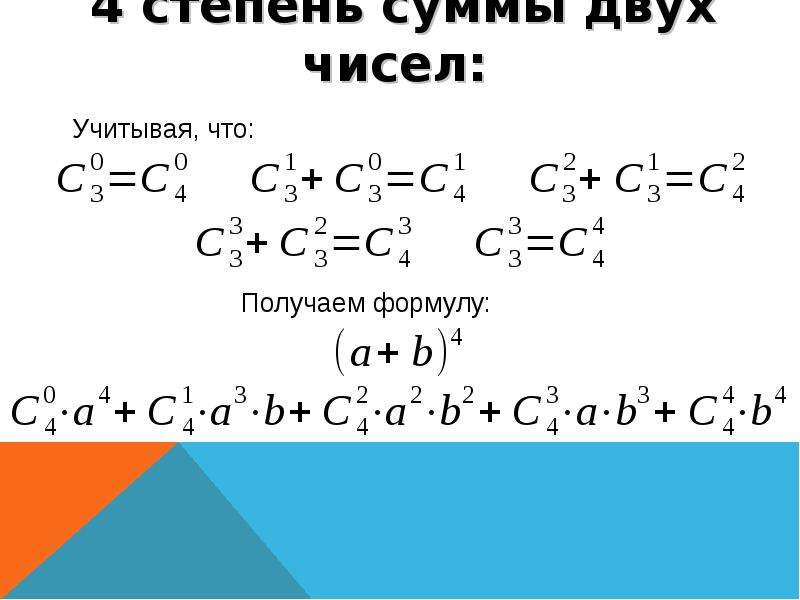





 Однако сфера применения ФСУ намного шире, и не ограничивается кратким умножением. Перечислим основные направления.
Однако сфера применения ФСУ намного шире, и не ограничивается кратким умножением. Перечислим основные направления. 7.
7.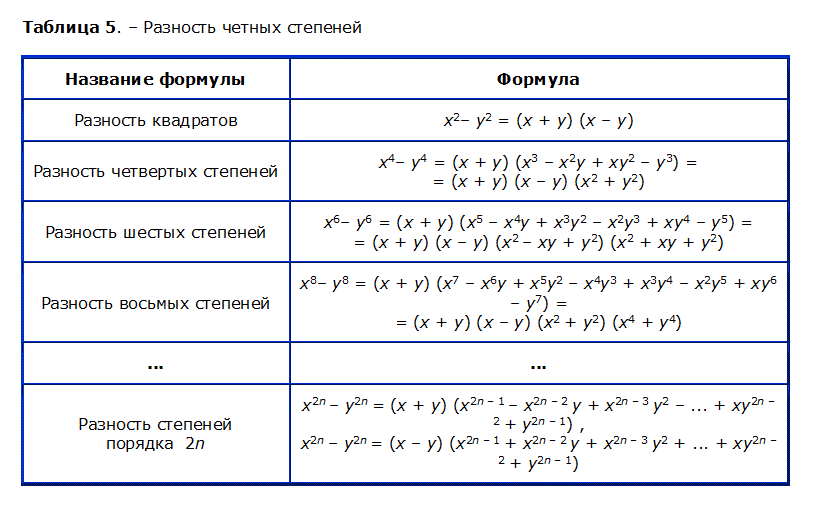
 Например,
Например,








 a * (a — b) + b * (a — b) = (a — b) * (a + b)
a * (a — b) + b * (a — b) = (a — b) * (a + b)


 Большинство формул сокращенного умножения можно получить из бинома Ньютона — в этом Вы скоро убедитесь.
Большинство формул сокращенного умножения можно получить из бинома Ньютона — в этом Вы скоро убедитесь. 7.
7. Равенства, выражающие эти случаи, называются формулами сокращённого умножения.
Равенства, выражающие эти случаи, называются формулами сокращённого умножения.





 {2}}\)
{2}}\) 5 $ в свою конфигурацию.
5 $ в свою конфигурацию. Запасной 3
для п. Получаем, что сумма равна 180 градусам. Это важный факт, о котором следует помнить.
Запасной 3
для п. Получаем, что сумма равна 180 градусам. Это важный факт, о котором следует помнить. Вы видите, где «н —
2 «происходит от? Это дает нам количество треугольников в многоугольнике.Как
Как вы думаете, много ли треугольников будет у 5-стороннего многоугольника?
Вы видите, где «н —
2 «происходит от? Это дает нам количество треугольников в многоугольнике.Как
Как вы думаете, много ли треугольников будет у 5-стороннего многоугольника? Давайте посмотрим на K 3 , полный граф (со всеми возможными ребрами) с 3 вершинами.
Давайте посмотрим на K 3 , полный граф (со всеми возможными ребрами) с 3 вершинами. В формуле суммы степеней мы суммируем степень, количество ребер, инцидентных каждой вершине.Степень — это свойство, связанное с ребрами. Ребра — это соединения между двумя вершинами. Суммирование степеней каждой вершины неизбежно приведет к пересчету ребер.
В формуле суммы степеней мы суммируем степень, количество ребер, инцидентных каждой вершине.Степень — это свойство, связанное с ребрами. Ребра — это соединения между двумя вершинами. Суммирование степеней каждой вершины неизбежно приведет к пересчету ребер.
 com
com Правильный многоугольник с наименьшим количеством сторон — тремя — и есть равносторонний треугольник. Правильный многоугольник с большинством сторон, обычно используемый в классах геометрии, вероятно, двенадцатигранник, или 12-угольник, с 12 сторонами и 12 внутренними углами:
Правильный многоугольник с наименьшим количеством сторон — тремя — и есть равносторонний треугольник. Правильный многоугольник с большинством сторон, обычно используемый в классах геометрии, вероятно, двенадцатигранник, или 12-угольник, с 12 сторонами и 12 внутренними углами:

 Это , а не угол отражения (более 180 °), создаваемый вращением от внешней стороны одной стороны к другой. Это распространенное заблуждение. Например, в равностороннем треугольнике внешний угол равен , а не 360 ° — 60 ° = 300 °, как если бы мы вращались от одной стороны до конца вокруг вершины к другой стороне.
Это , а не угол отражения (более 180 °), создаваемый вращением от внешней стороны одной стороны к другой. Это распространенное заблуждение. Например, в равностороннем треугольнике внешний угол равен , а не 360 ° — 60 ° = 300 °, как если бы мы вращались от одной стороны до конца вокруг вершины к другой стороне.
 {\ circ} $$
{\ circ} $$ {\ circ}
{\ circ}
 Хотя вы знаете, что сумма внешних углов равна 360, вы можете использовать формулу, чтобы найти единственный внешний угол, только если многоугольник правильный!
Хотя вы знаете, что сумма внешних углов равна 360, вы можете использовать формулу, чтобы найти единственный внешний угол, только если многоугольник правильный!

 Это подводит нас к важной теореме в геометрии, известной как теорема о сумме углов треугольника.
Это подводит нас к важной теореме в геометрии, известной как теорема о сумме углов треугольника.




 Теперь мы можем сказать, что 5x и 9x = градусы остальных углов треугольника.Мы просто складываем 4x + 5x + 9x, приравниваем сумму к 180 градусам и решаем относительно x. Найдя x, мы подставляем значение x в 4x и упрощаем, чтобы найти меру наименьшего угла треугольника.
Теперь мы можем сказать, что 5x и 9x = градусы остальных углов треугольника.Мы просто складываем 4x + 5x + 9x, приравниваем сумму к 180 градусам и решаем относительно x. Найдя x, мы подставляем значение x в 4x и упрощаем, чтобы найти меру наименьшего угла треугольника.