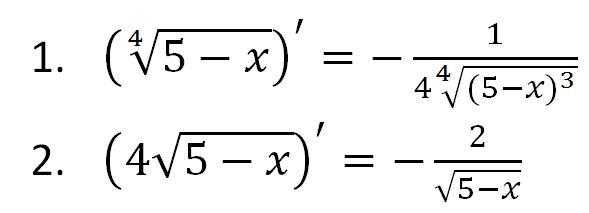Читать онлайн «Нейросетевая торговая система Meta Trader 4 + MATLAB. Пошаговая разработка. Издание второе», Андрей Дибров – Литрес
Во второе издание включена глава ” Шаблон автоматической нейросетевой торговой системы на стандартных индикаторах”. Используя данный шаблон, представляющий пошаговую инструкцию (с кодами скриптов и экспертов MT4 и Matlab) построения нейросетевой торговой системы, вы сможете приступить к созданию своей торговой стратегии на основе предложенной системы либо развивать нейросетевую систему самостоятельно.
По прочтению этой главы – вы самостоятельно создадите исполняемый файл ExpertPrimer.exe, который представляет собой обученную нейронную сеть. В главе “Нейросети Matlab+MT4” вы найдете инструкцию, как оформить интерфейс этой программы с помощью GUI Matlab. Ниже представлены индикаторы, скрипты и эксперты, которые вы будете использовать при создании своей первой нейронной сети.
А здесь вы можете посмотреть пример результата работы с шаблоном https://youtu. be/o9DAvnzCDlU. Как мы видим, после всей подготовительной работы по выстраиванию системы и на ее основе торговой стратегии, весь этот процесс занимает несколько минут. В конце видео показана для сравнения работа автоматической торговой системы готовой к реальной работе. По завершению тестирования на графике выводятся индикаторы, которые используются торговым экспертом. Одним из достоинств данной системы является то, что она кроме двух простейших индикаторов, использует в эксперте только ценовые данные. Все остальное делает нейросеть.
be/o9DAvnzCDlU. Как мы видим, после всей подготовительной работы по выстраиванию системы и на ее основе торговой стратегии, весь этот процесс занимает несколько минут. В конце видео показана для сравнения работа автоматической торговой системы готовой к реальной работе. По завершению тестирования на графике выводятся индикаторы, которые используются торговым экспертом. Одним из достоинств данной системы является то, что она кроме двух простейших индикаторов, использует в эксперте только ценовые данные. Все остальное делает нейросеть.
Почему я написал – первой? Эта нейросеть будет для вас шаблоном, который в дальнейшем вы сможете использовать для создания рабочей торговой системы, и на основе которой вы будете разрабатывать различные торговые стратегии. Например, вот какие индикаторы, скрипты и эксперты, я использую в системе, которую так же описываю в главе “Нейросети Matlab+MT4”.
Ниже, как пример результативности работы данной системы приведен отчет по ее тестированию.
Обратим внимание на тот факт, что тестирование проводилось в динамике. Т.е. в процессе совершенствования торговой стратегии, основанной на нейросистеме и в течение длительного времени примерно четырех лет.
Т.е. в процессе совершенствования торговой стратегии, основанной на нейросистеме и в течение длительного времени примерно четырех лет.
В главе “Критические ошибки при разработке нейросетевой системы” я попытался рассказать о ”подводных камнях” при ее подготовке. И выделить особенно важный аспект – проведения тестов нейронной системы. Некоторую часть главы “Нейросети Matlab+MT4” мне также пришлось посвятить этой проблеме на примере рабочей нейросетевой системы – так как этот процесс неотъемлем от разработки торговой стратегии.
Так же в соответствующих главах книги я поднимаю проблемы логического обоснования обучения нейронных сетей перед принятием решения, что должно нам помочь осознать – какую сеть в результате мы хотим получить. И косвенно связанную с этой проблемой, проблему выбора временного периода исторических данных для обучения нейронной сети я поднимаю в главе “Использование синтетических баров для определения “спектра”.
Видеоуроки, облегчающие понимание обучения, тренировки и тестирования нейросетей и видеоролики примеров работы с пользовательскими индикаторами можно посмотреть на канале https://www. youtube.com/channel/UCScAAn_sRRaKHdNIxl0aI9A?view_as=subscriber
youtube.com/channel/UCScAAn_sRRaKHdNIxl0aI9A?view_as=subscriber
Для приобретения программных кодов индикаторов, скриптов и экспертов данной нейросетевой системы вы можете связаться с автором по адресу электронной почты [email protected].
Книга написана с учетом интересов всех категорий трейдеров, а так же тех читателей, которые готовятся заняться трейдингом. Хочется обратить внимание на тот факт, что в данной книге вы не найдете никакого теоретического материала по проблемам нейросетей и самого трейдинга. В любой литературе посвященной этим двум направлениям есть список трудов различных уважаемых авторов. Мне так же хотелось бы снабдить эту книгу таким же списком. Однако, увы, я этого не могу сделать, так как максимально постарался уйти от какой либо теории и психологии, которым в основном посвящена литература о трейдинге. Однако это не значит, что в свое время я не изучал подобную литературу и, что от нее нет пользы. Вот не полный список авторов, труды которых мною изучались – Чарльз Лебо и Дэвид В. Лукас, Юрий Жваколюк, Д. Ю. Пискулов, В. С. Сафонов, Шерри Де Ковни и Кристин Такки, Анна Эрлих, Александр Элдер, Джон Дж. Мэрфи. Но для понимания и практического применения материала представленного мною, в принципе, достаточно теоретической информации, которая подается на сайтах дилинговых компаний и официального сайта Matlab. То есть, любой читатель имеющий представление о трейдинге может выполнить пошаговую инструкцию из моей книги и получить готовую автоматическую нейросетевую систему торговли. Причем, при кажущейся сложности системы в итоге вы прейдете к пониманию, что конечный результат в плане применения программных кодов поразительно легок, но в тоже время самодостачен и функционален. Ведь основная нагрузка в данной системе происходит при обучении нейросетей. Но и здесь, вникнув в процесс, вы обнаружите, что настроив систему, обучение не занимает много времени, а можно даже сказать, что занимает мало времени. Однако нам все равно придется немного пофилософствовать в следующем разделе на тему логического обоснования обучения нейросетей на принятие решения.
Лукас, Юрий Жваколюк, Д. Ю. Пискулов, В. С. Сафонов, Шерри Де Ковни и Кристин Такки, Анна Эрлих, Александр Элдер, Джон Дж. Мэрфи. Но для понимания и практического применения материала представленного мною, в принципе, достаточно теоретической информации, которая подается на сайтах дилинговых компаний и официального сайта Matlab. То есть, любой читатель имеющий представление о трейдинге может выполнить пошаговую инструкцию из моей книги и получить готовую автоматическую нейросетевую систему торговли. Причем, при кажущейся сложности системы в итоге вы прейдете к пониманию, что конечный результат в плане применения программных кодов поразительно легок, но в тоже время самодостачен и функционален. Ведь основная нагрузка в данной системе происходит при обучении нейросетей. Но и здесь, вникнув в процесс, вы обнаружите, что настроив систему, обучение не занимает много времени, а можно даже сказать, что занимает мало времени. Однако нам все равно придется немного пофилософствовать в следующем разделе на тему логического обоснования обучения нейросетей на принятие решения. От этого обоснования во многом зависит конечный результат.
От этого обоснования во многом зависит конечный результат.
Важно! Данная книга ориентирована на Matlab. Программа Matlab не поставляется с этой книгой. Прежде чем приступать к изучению и разработки автоматической нейросетевой системы торговли, вы должны приобрести ее отдельно и установить.
Видео с визуализацией работы исполняемых файлов нейронных сетей совместно с MT4 также можно посмотреть по ссылкам https://youtu.be/5GwhRnSqT78 – при обучении и компиляции использовалась программа Matlab, https://youtu.be/cIegQGJKbhY– при обучении и компиляции использовалась программа NeuroSolutions 6.
🎓 Репетитор Программирование Matlab онлайн (скайп) 👩🏫
Занятия онлайн
Проверенный репетитор
Репетитор прошел личное собеседование с сотрудником BUKI и подтвердил наличие образования, опыта и уровня квалификации.
Проверенный репетитор
Репетитор прошел личное собеседование с сотрудником BUKI и подтвердил наличие образования, опыта и уровня квалификации.
Кирилл К.
Кирилл К.
5отзывы: 6
300грн/час
ПрограммированиеМатематикаФизикаИнформатикаБольше
Образование: Днепровский национальный университет имени Олеся Гончара (ДНУ)
Опыт: более 3 лет
Терпелив, люблю общаться и привлекать детей к работе, интеллигентный, доходчиво объясняю материал ученикам любого уровня, хорошо разбираюсь в своем деле. Заинтересован прежде всего в результативном обучении детей, а не в денежной оплате. Могу работать с несколькими детьми одновременно. Оценки – это важно, но глубокие и систематизированные знания еще важнее. Чем раньше ученик освоит предмет, поймет его суть и систему, тем легче ему будет учиться, сдавать экзамены, поступать в вузы. Заложите основы прочных знаний уже сейчас. На одной волне с учениками.
Иван Б.
Иван Б.
5отзывы: 4
200грн/час
ПрограммированиеМатематикаФизика
org/EducationalOrganization»>Образование: Прикарпатский национальный университет имени Василия Стефаника (ПНУ)Опыт: более 2 лет
Я – положительный учитель! Старательный, трудолюбивый, дружелюбный, ответственный. Люблю детей. К работе отношусь с максимальной отдачей. Готов делиться своими знаниями с желающими! С юного возраста начал интересоваться математикой, физикой и программированием, открывать для себя разные лайфхаки. Участвовал в районных и областных олимпиадах, занимал призовые места! *** После девятого класса поступил в Ивано-Франковский профессиональный колледж ГВУЗ «Прикарпатский национальный у…
Выберите предмет и локацию
Программирование
- Выберите предмет
- Программирование
Matlab
- Выберите уровень подготовки
- Тестирование программного обеспечения
- Python программирование
- JavaScript программирование
- C++ программирование
- C# программирование
- Репетитор для детей
- 10-11-й класс
- 5-6-й класс
- 7-9-й класс
- Университетские курсы
- Репетитор для начинающих
- Базовый уровень
- Специализированные курсы
- PHP программирование
- Java программирование
- LabVIEW
- Matlab
Matlab онлайн (скайп) — Программирование — Репетиторы
Matlab онлайн (скайп) — Программирование. Найти репетитора легко на сайте Буки. Отзывы учеников, рейтинг и анкеты лучших репетиторов
Найти репетитора легко на сайте Буки. Отзывы учеников, рейтинг и анкеты лучших репетиторов
Часто задаваемые вопросы про Репетитор Программирование
🥇 Как правильно выбрать услуги репетитора онлайн Matlab с Программированию ?
В разделе онлайн обучение Программирование Matlab 2 репетиторов, среди которых вы сможете выбрать. Чтобы выбрать наиболее оптимального репетитора онлайн Matlab с Программированию, рекомендуем обратить внимание на следующие параметры преподавателя: ставка за час работы, количество позитивных отзывов, опыт работы и наличие диплома о образовании. Рекомендуем взять тестовый урок, для ознакомления с форматом занятия онлайн и репетитором.
💰 Какая цена занятий с репетитором онлайн Matlab с Программированию ?
На платформе БУКИ в разделе обучение онлайн Matlab с Программированию цена на занятия от 200 до 300 грн в час.
🖥 Какие еще уровни изучения онлайн Программирование на сайте БУКИ?
MATLAB Online — MATLAB
Общие ограничения
Следующие функции и команды MATLAB и Simulink не поддерживаются в MATLAB Online:
| Продукт | Ограничения |
|---|---|
| МАТЛАБ |
|
| Симулинк | Поддерживается большинство функций Simulink, включая редактирование и моделирование моделей. Simulink Online может взаимодействовать с оборудованием Raspberry Pi — внешний режим не поддерживается. Simulink Online может обмениваться данными с оборудованием Parrot Minidrone — развертывание не поддерживается. Неподдерживаемые функции:
Другие ограничения Simulink Online:
|
Поддерживаемые продукты
MATLAB Online поддерживает следующие продукты:
| Продукт | Исключения |
|---|---|
| Набор инструментов 5G |
|
| Набор инструментов для аэрокосмической отрасли |
|
| Набор инструментов для аудио |
|
| Набор инструментов Bluetooth | |
| Набор средств связи |
|
| Набор инструментов компьютерного зрения |
|
| Панель инструментов системы управления |
|
| Набор инструментов для фитинга кривой | |
| Панель инструментов базы данных |
|
| Набор инструментов для глубокого обучения | |
| Набор инструментов DSP HDL | |
| Системный набор инструментов DSP |
|
| Набор инструментов для эконометрики | |
| Встроенный кодер |
|
| Набор инструментов для финансовых инструментов | |
| Набор финансовых инструментов | |
| Конструктор фиксированной точки | |
| Набор инструментов для нечеткой логики | |
| Набор инструментов глобальной оптимизации | |
| Кодировщик графического процессора |
|
| Кодировщик HDL |
|
| Набор инструментов для промышленных коммуникаций |
|
| Набор инструментов для обработки изображений |
|
| Lidar Toolbox |
|
| Набор инструментов LTE |
|
| Набор инструментов для картирования |
|
| Кодер MATLAB |
|
| Генератор отчетов MATLAB |
|
| Набор инструментов для медицинской визуализации |
|
| Набор инструментов прогнозирующего управления моделями |
|
| Панель инструментов навигации |
|
| Набор инструментов для оптимизации | |
| Набор инструментов для параллельных вычислений |
|
| Набор инструментов для дифференциальных уравнений в частных производных | |
| Набор инструментов для системы фазированных решеток | |
| Набор инструментов профилактического обслуживания | |
| Набор инструментов RF | |
| Набор инструментов управления рисками | |
| Набор инструментов для робототехники |
|
| Надежный набор инструментов управления | |
| Набор инструментов для спутниковой связи |
|
| Набор инструментов для обработки сигналов |
|
| Симскейп |
|
| Аккумулятор Simscape | |
| Трансмиссия Simscape | |
| Simscape Electric | |
| Жидкости Simscape | |
| Мультител Simscape |
|
| Проверка Simulink |
|
| Симулинк Кодер |
|
| Дизайн управления Simulink |
|
| Оптимизация дизайна Simulink |
|
| Генератор отчетов Simulink | |
| Государственный поток | |
| Набор инструментов статистики и машинного обучения | |
| Symbolic Math Toolbox |
|
| Системный компоновщик | |
| Набор инструментов для идентификации системы |
|
| Набор инструментов анализа текста |
|
| Набор инструментов для БПЛА |
|
| Набор инструментов Vision HDL |
|
| Набор инструментов Wavelet |
|
| Беспроводной набор инструментов HDL | |
| Набор инструментов WLAN |
|
Начните использовать MATLAB Online
В настоящее время доступно с: лицензиями Campus-Wide License, MATLAB и Simulink Student Suite*, MATLAB Student*, Standard Individual*, Academic Individual* и лицензиями Home Use*.
*Для доступа к MATLAB Online требуется служба технического обслуживания программного обеспечения.
Синхронизируйте файлы с MATLAB Drive
Ресурсы продукта
- Документация
- Запрос на расширение
Выберите веб-сайт
Выберите веб-сайт, чтобы получить переведенный контент, где он доступен, и увидеть местные события и предложения. В зависимости от вашего местоположения мы рекомендуем вам выбрать: .
В зависимости от вашего местоположения мы рекомендуем вам выбрать: .
Вы также можете выбрать веб-сайт из следующего списка
Европа
Обратитесь в местный офис
MATLAB Online — MATLAB и Simulink
Используйте MATLAB и Simulink без загрузки или установки.
Узнать больше
Совместная работа с другими пользователями посредством совместного использования и публикации в Интернете
Узнать больше
Храните файлы, управляйте ими и получайте доступ к ним где угодно.
Узнать больше
Нет загрузки или установки
- MATLAB ® Online™ обеспечивает доступ к MATLAB и Simulink из любого стандартного веб-браузера, где есть доступ к Интернету – просто войдите в систему.
- Идеально подходит для преподавания, обучения и удобного легкого доступа.
Совместная работа посредством совместного использования и публикации в Интернете
- С помощью MATLAB Online вы можете напрямую делиться своими сценариями, динамическими сценариями и другими файлами MATLAB с другими.

- MATLAB Online автоматически обновляется до последней версии, предоставляя всем пользователям единую платформу с новейшими функциями.
- Публикуйте свои сценарии и живые сценарии в Интернете в формате PDF или HTML и делитесь URL-адресом с кем угодно.
Облачное хранилище и синхронизация
- Полная интеграция с MATLAB Drive дает вам 20 ГБ для хранения, доступа и управления файлами из любого места с помощью MATLAB Online.
- Используйте MATLAB Drive Connector для синхронизации файлов между вашими компьютерами и MATLAB Online, избавляя от необходимости ручной загрузки или выгрузки.
Начало работы
Начните использовать MATLAB Online
Чтобы получить доступ к MATLAB Online, вы должны быть текущими с одним из следующих типов лицензии:
- MATLAB и Simulink Student Suite
- MATLAB Студент
- Лицензия на весь кампус
- Академические лицензии на преподавание
- Комплект MATLAB для начальной и средней школы
- Академическое лицо
- Стандартный индивидуальный
- Главная страница MATLAB
Связаться с техническим специалистом
Выберите веб-сайт
Выберите веб-сайт, чтобы получить переведенный контент, где он доступен, и увидеть местные события и предложения.

 Аппаратное обеспечение, к которому можно получить доступ, включает:
Аппаратное обеспечение, к которому можно получить доступ, включает: 

 VideoPlayer
VideoPlayer  Приложение HDL Coder не поддерживается.
Приложение HDL Coder не поддерживается. Вместо этого используйте блок Video Display.
Вместо этого используйте блок Video Display.
 1. var не имеет блочной области видимости
Как мы видели в предыдущих примерах, блок кода создает область видимости для переменных, объявленных с помощью ключевых слов const и let. Однако это не работает для переменных, объявленных с помощью ключевого слова var.
1. var не имеет блочной области видимости
Как мы видели в предыдущих примерах, блок кода создает область видимости для переменных, объявленных с помощью ключевых слов const и let. Однако это не работает для переменных, объявленных с помощью ключевого слова var. log(message)
}
run() // 'Беги, Форрест, беги!'
console.log(message) // ReferenceError
log(message)
}
run() // 'Беги, Форрест, беги!'
console.log(message) // ReferenceError
 14
console.log(pi) // 3.14
// использование pi
14
console.log(pi) // 3.14
// использование pi
 log(message) // 'Беги, Форрест, беги!'
}
console.log(friend) // ReferenceError
}
run()
log(message) // 'Беги, Форрест, беги!'
}
console.log(friend) // ReferenceError
}
run()
 js">
js"> Как JavaScript понимает, что значение, выводимое в консоль в функции inner(), принадлежит переменной v, объявленной в фукнции outer()?
Как JavaScript понимает, что значение, выводимое в консоль в функции inner(), принадлежит переменной v, объявленной в фукнции outer()?



 js
js  Эта область не применяется к переменным, объявленным с использованием ключевого слова var :
Эта область не применяется к переменным, объявленным с использованием ключевого слова var : Повторное использование имен переменных в области действия функции известно как затенение переменных, а внешняя переменная называется «затененной».
Повторное использование имен переменных в области действия функции известно как затенение переменных, а внешняя переменная называется «затененной». Такая область называется блоком области видимости. В других частях программы имя может относиться к другому объекту (у него может быть другая привязка) или вообще ни к чему (оно может быть несвязанным). [1]
Такая область называется блоком области видимости. В других частях программы имя может относиться к другому объекту (у него может быть другая привязка) или вообще ни к чему (оно может быть несвязанным). [1]  Его можно даже сделать доступным для функций в других объектных модулях, которые будут связаны с вашим кодом; однако сейчас мы откажемся от этого объяснения. На этом этапе следует усвоить ключевое изменение формулировки. Хотя переменная имеет глобальную область действия, технически она доступна только с0023 точка определения конца исходного кода программы . Вот почему большинство переменных с глобальной областью видимости помещаются в начало исходного кода перед любыми функциями. Таким образом, они доступны для всех функций.
Его можно даже сделать доступным для функций в других объектных модулях, которые будут связаны с вашим кодом; однако сейчас мы откажемся от этого объяснения. На этом этапе следует усвоить ключевое изменение формулировки. Хотя переменная имеет глобальную область действия, технически она доступна только с0023 точка определения конца исходного кода программы . Вот почему большинство переменных с глобальной областью видимости помещаются в начало исходного кода перед любыми функциями. Таким образом, они доступны для всех функций. На языке ассемблера мы говорим об элементах, помещаемых в стек и извлекаемых из стека при завершении функции. Таким образом, стек — это повторно используемая область памяти, которая используется всеми функциями и освобождается при завершении функций. Хотя переменная имеет локальную область действия, технически она доступна только от точки определения до конца функции . Параметрическая передача элементов данных в функцию устанавливает их как локальные переменные. Кроме того, любые другие переменные или константы, необходимые функции, обычно находятся в верхней части определения функции, чтобы они были доступны в течение всего выполнения кода функции.
На языке ассемблера мы говорим об элементах, помещаемых в стек и извлекаемых из стека при завершении функции. Таким образом, стек — это повторно используемая область памяти, которая используется всеми функциями и освобождается при завершении функций. Хотя переменная имеет локальную область действия, технически она доступна только от точки определения до конца функции . Параметрическая передача элементов данных в функцию устанавливает их как локальные переменные. Кроме того, любые другие переменные или константы, необходимые функции, обычно находятся в верхней части определения функции, чтобы они были доступны в течение всего выполнения кода функции.
 В данном случае f (x) считается внешней функцией, g (x) – внутренней.
В данном случае f (x) считается внешней функцией, g (x) – внутренней.


 {2}}
\)
{2}}
\) 4 Производная функция
4 Производная функция Чтобы эффективно использовать информацию, предоставленную
$f'(x)$ нам нужно уметь вычислять его для множества таких
функции.
92} — 24\над\Дельта х}.
$$
Знаменатель здесь измеряет расстояние в направлении $x$,
иногда называемый «бегом», а числитель измеряет расстояние в
направление $y$, иногда называемое «подъем» и «подъем над
run» — это наклон линии. Напомним, что иногда такой числитель
сокращенно $\Delta y$, заменив краткость более подробным
выражение. Таким образом, в общем случае производная определяется выражением
$$
y’=\lim_{\Delta x\to0} {\Delta y\over \Delta x}.
$$
Чтобы напомнить форму предела, мы иногда говорим вместо этого, что
$$
{dy\over dx}=\lim_{\Delta x\to0} {\Delta y\over \Delta x}.
$$ Другими словами, $dy/dx$ — это другое обозначение производной, и
это напоминает нам, что это связано с фактическим уклоном между двумя
точки. Это обозначение называется
92)$.
$\квадрат$
Чтобы эффективно использовать информацию, предоставленную
$f'(x)$ нам нужно уметь вычислять его для множества таких
функции.
92} — 24\над\Дельта х}.
$$
Знаменатель здесь измеряет расстояние в направлении $x$,
иногда называемый «бегом», а числитель измеряет расстояние в
направление $y$, иногда называемое «подъем» и «подъем над
run» — это наклон линии. Напомним, что иногда такой числитель
сокращенно $\Delta y$, заменив краткость более подробным
выражение. Таким образом, в общем случае производная определяется выражением
$$
y’=\lim_{\Delta x\to0} {\Delta y\over \Delta x}.
$$
Чтобы напомнить форму предела, мы иногда говорим вместо этого, что
$$
{dy\over dx}=\lim_{\Delta x\to0} {\Delta y\over \Delta x}.
$$ Другими словами, $dy/dx$ — это другое обозначение производной, и
это напоминает нам, что это связано с фактическим уклоном между двумя
точки. Это обозначение называется
92)$.
$\квадрат$ Если вы знаете некоторые «производные формулы» из
более ранний курс, на данный момент вы должны делать вид, что вы делаете
не знать их.
В примерах, подобных приведенным выше и приведенным ниже упражнениям, от вас требуется
знать, как найти производную формулу, исходя из основных принципов.
Позже мы разработаем некоторые формулы, чтобы нам не всегда нужно было
делать такие вычисления, но нам по-прежнему нужно знать, как делать
более сложные вычисления.
Если вы знаете некоторые «производные формулы» из
более ранний курс, на данный момент вы должны делать вид, что вы делаете
не знать их.
В примерах, подобных приведенным выше и приведенным ниже упражнениям, от вас требуется
знать, как найти производную формулу, исходя из основных принципов.
Позже мы разработаем некоторые формулы, чтобы нам не всегда нужно было
делать такие вычисления, но нам по-прежнему нужно знать, как делать
более сложные вычисления.
 Убедитесь, что вы указали все места, где
производной не существует.
92+ax-3$ имеет горизонтальную касательную в точке $x=4$.
(отвечать)
Убедитесь, что вы указали все места, где
производной не существует.
92+ax-3$ имеет горизонтальную касательную в точке $x=4$.
(отвечать)


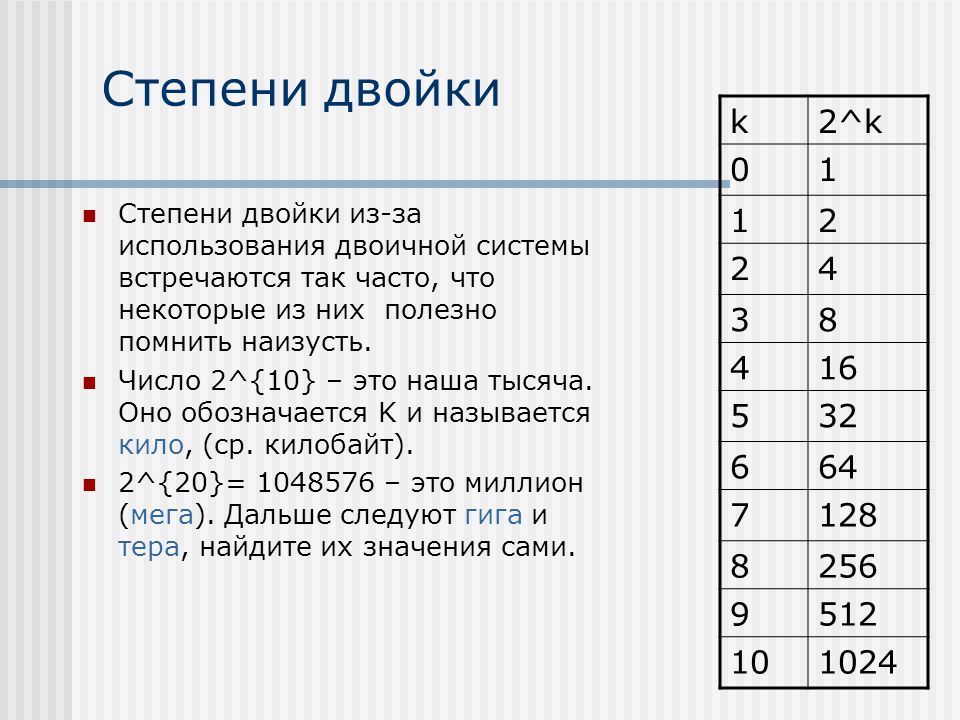
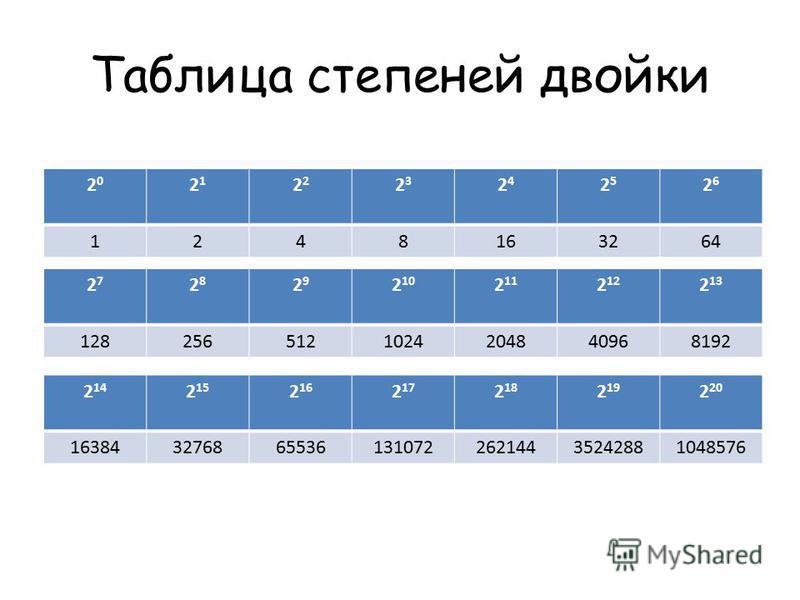 {n})}}
(а не (2 2 ) n , последнее выражение фактически равно 4 n ).
{n})}}
(а не (2 2 ) n , последнее выражение фактически равно 4 n ). {n} {n \ select k}.}
{n} {n \ select k}.} {n}}}нетзнак равно13{\ displaystyle n = 13}
{n}}}нетзнак равно13{\ displaystyle n = 13} 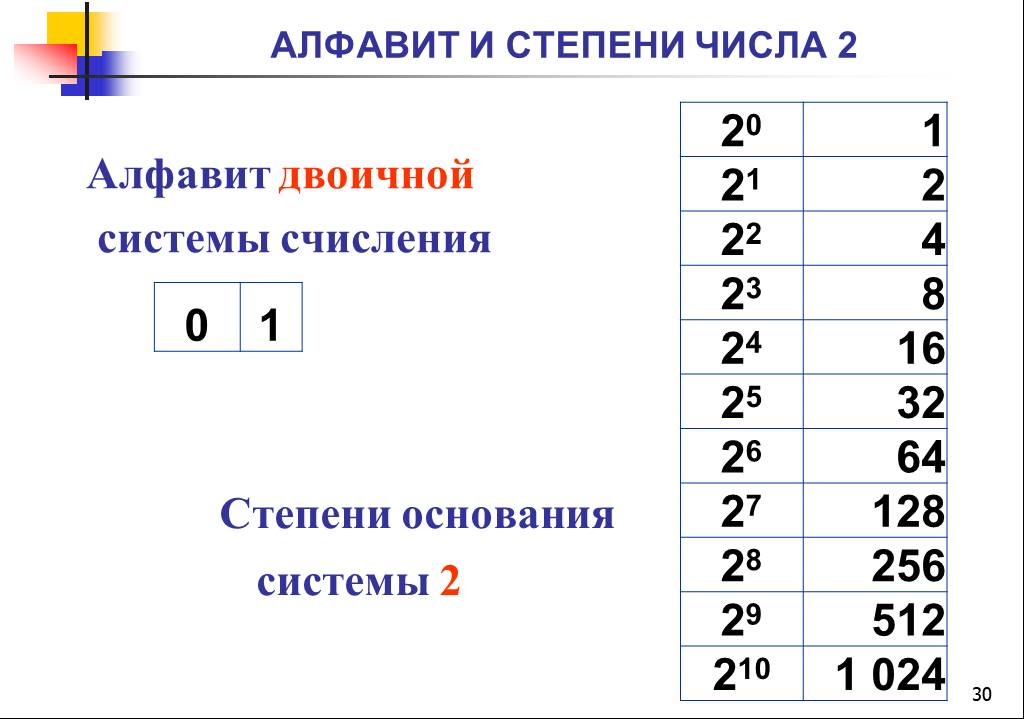 тройная теорема Пифагора и Грина-Тао )
тройная теорема Пифагора и Грина-Тао )

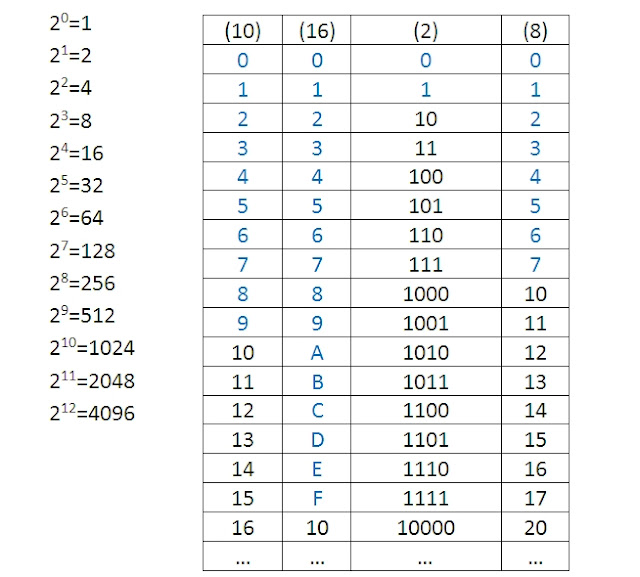 Федерального закона от 02.07.2013 N 185-ФЗ)
Федерального закона от 02.07.2013 N 185-ФЗ)

 Они предоставляют семьям подробные рекомендации о дополнительных ресурсах, предлагаемых надежными партнерами в наших сообществах.
Они предоставляют семьям подробные рекомендации о дополнительных ресурсах, предлагаемых надежными партнерами в наших сообществах. По своей сути мы являемся общественной организацией, которая максимизирует положительный эффект чуткого воспитания и поддерживает более тесные отношения между опекунами и детьми, которые, как было показано, оказывают положительное влияние на здоровье и благополучие детей на протяжении всей жизни. Это закладывает основу, на которой мы вовлекаем более широкое сообщество в процесс исцеления. Мы делаем все это через призму расовой и социальной справедливости, чтобы обеспечить светлое будущее для черных и коричневых семей в Нью-Йорке.
По своей сути мы являемся общественной организацией, которая максимизирует положительный эффект чуткого воспитания и поддерживает более тесные отношения между опекунами и детьми, которые, как было показано, оказывают положительное влияние на здоровье и благополучие детей на протяжении всей жизни. Это закладывает основу, на которой мы вовлекаем более широкое сообщество в процесс исцеления. Мы делаем все это через призму расовой и социальной справедливости, чтобы обеспечить светлое будущее для черных и коричневых семей в Нью-Йорке.

 Ей можно воспользоваться в любой момент, но только один раз за весь срок кредита.
Ей можно воспользоваться в любой момент, но только один раз за весь срок кредита.


 11.2018 № 422 и НК РФ
11.2018 № 422 и НК РФ По программам господдержки семей с детьми — 6%, для Дальневосточного федерального округа — 5%.
По программам господдержки семей с детьми — 6%, для Дальневосточного федерального округа — 5%.
 е. точка
е. точка 


 Что касается аргумента, то он равен
Что касается аргумента, то он равен  Калькулятор комплексных чисел также может определять действительную часть сложного выражения. Вы можете получить экспертный ответ на свой вопрос в режиме реального времени на JustAsk. Пример: re (23i) = 2. мнимая часть комплексного числа. Длины реальной и мнимой проекций связаны с величиной векторного косинуса и синуса фазового угла соответственно. Однако не существует действительного числа, которое дает квадратный корень из отрицательного числа. Описание: Запись z = a + ib, где a и b действительны, называется алгебраической формой комплексного числа z: a — действительная часть z; b — мнимая часть z. Мнимое число – это квадратный корень из отрицательного числа. Если у вас есть вопрос, наши специалисты ответят вам в кратчайшие сроки. Комплексное число — это сумма мнимого числа и действительного числа, выраженная как a + bi. Алгебраический расчет | Другие калькуляторы. я, единичное мнимое число ((-1)). (1+2и)-(3-4и),
Калькулятор скидок использует исходную цену продукта и процент скидки, чтобы найти окончательную цену и сумму, которую вы сэкономите.
Калькулятор комплексных чисел также может определять действительную часть сложного выражения. Вы можете получить экспертный ответ на свой вопрос в режиме реального времени на JustAsk. Пример: re (23i) = 2. мнимая часть комплексного числа. Длины реальной и мнимой проекций связаны с величиной векторного косинуса и синуса фазового угла соответственно. Однако не существует действительного числа, которое дает квадратный корень из отрицательного числа. Описание: Запись z = a + ib, где a и b действительны, называется алгебраической формой комплексного числа z: a — действительная часть z; b — мнимая часть z. Мнимое число – это квадратный корень из отрицательного числа. Если у вас есть вопрос, наши специалисты ответят вам в кратчайшие сроки. Комплексное число — это сумма мнимого числа и действительного числа, выраженная как a + bi. Алгебраический расчет | Другие калькуляторы. я, единичное мнимое число ((-1)). (1+2и)-(3-4и),
Калькулятор скидок использует исходную цену продукта и процент скидки, чтобы найти окончательную цену и сумму, которую вы сэкономите. _ — комплексно-сопряженное число z. Получите бесплатный виджет «Калькулятор комплексных чисел» для своего веб-сайта, блога, WordPress, Blogger или iGoogle. Это отличное приложение, если вы отстаете в математике или исчислении в средней школе. Другой способ записать две части комплексного числа — это Re\mathrm{Re}Re и Im\mathrm{Im}Im, так что Re(z)=a\mathrm{Re}(z)=aRe(z)=a, и Im(z)=b\mathrm{Im}(z)=bIm(z)=b. кнопка imaginary_part уже появляется, возвращается результат 7. С помощью этой функции калькулятор позволяет онлайн вычислять мнимую часть комплексного числа. Умножение: (3+2i)*(5-3i). Шаг 2: Нажмите синюю стрелку, чтобы отправить. Напряжение и ток по-прежнему синусоидальны, но теперь ток опережает напряжение на 90. Помимо выполнения четырех основных операций сложения, вычитания, умножения и деления комплексных чисел, этот калькулятор комплексных чисел можно использовать для вычисления степеней и главных корней комплексных чисел. Линии. Вот что происходит с нашей властью. Тогда сумма двух комплексных чисел равна: где Re(F+G)=a+c\mathrm{Re}(F + G) = a + cRe(F+G)=a+c — действительная часть сумма, а Im(F+G)=b+d\mathrm{Im}(F + G) = b + dIm(F+G)=b+d — мнимая.
_ — комплексно-сопряженное число z. Получите бесплатный виджет «Калькулятор комплексных чисел» для своего веб-сайта, блога, WordPress, Blogger или iGoogle. Это отличное приложение, если вы отстаете в математике или исчислении в средней школе. Другой способ записать две части комплексного числа — это Re\mathrm{Re}Re и Im\mathrm{Im}Im, так что Re(z)=a\mathrm{Re}(z)=aRe(z)=a, и Im(z)=b\mathrm{Im}(z)=bIm(z)=b. кнопка imaginary_part уже появляется, возвращается результат 7. С помощью этой функции калькулятор позволяет онлайн вычислять мнимую часть комплексного числа. Умножение: (3+2i)*(5-3i). Шаг 2: Нажмите синюю стрелку, чтобы отправить. Напряжение и ток по-прежнему синусоидальны, но теперь ток опережает напряжение на 90. Помимо выполнения четырех основных операций сложения, вычитания, умножения и деления комплексных чисел, этот калькулятор комплексных чисел можно использовать для вычисления степеней и главных корней комплексных чисел. Линии. Вот что происходит с нашей властью. Тогда сумма двух комплексных чисел равна: где Re(F+G)=a+c\mathrm{Re}(F + G) = a + cRe(F+G)=a+c — действительная часть сумма, а Im(F+G)=b+d\mathrm{Im}(F + G) = b + dIm(F+G)=b+d — мнимая. Комплексное число Затем очень просто вычитать и складывать комплексные числа с помощью калькулятора комплексных решений. Онлайн-калькулятор комплексных чисел позволяет выполнять основные математические операции для упрощения заданных сложных выражений. Логарифм комплексного числа (также известный как комплексный логарифм) можно вычислить следующим образом: ln (F) = ln (|z_1| * exp (i_1)) = ln (|z_1|)+i_1. Другими словами, действительное число также можно рассматривать как комплексное число, недействительная часть которого равна 0. Мнимая часть комплексного числа Описание Определите мнимую часть комплексного числа. Эта конкретная функция принимает два аргумента, соответственно действительную и мнимую составляющие полярного входного значения. I называется йотой и имеет значение $ \sqrt{-1} $. Решение математических задач может быть интересным и сложным! (В компьютерном программировании функция «atan2» учитывает эти многоквадрантные проблемы и . Отключите блокировщик рекламы и обновите веб-страницу.
Комплексное число Затем очень просто вычитать и складывать комплексные числа с помощью калькулятора комплексных решений. Онлайн-калькулятор комплексных чисел позволяет выполнять основные математические операции для упрощения заданных сложных выражений. Логарифм комплексного числа (также известный как комплексный логарифм) можно вычислить следующим образом: ln (F) = ln (|z_1| * exp (i_1)) = ln (|z_1|)+i_1. Другими словами, действительное число также можно рассматривать как комплексное число, недействительная часть которого равна 0. Мнимая часть комплексного числа Описание Определите мнимую часть комплексного числа. Эта конкретная функция принимает два аргумента, соответственно действительную и мнимую составляющие полярного входного значения. I называется йотой и имеет значение $ \sqrt{-1} $. Решение математических задач может быть интересным и сложным! (В компьютерном программировании функция «atan2» учитывает эти многоквадрантные проблемы и . Отключите блокировщик рекламы и обновите веб-страницу. {i \phi}\tag{1} Где: |z| называется абсолютным значением, модулем или величиной \phi называется аргументом или фазой Все, что вам нужно сделать, это подставить известные значения из |z|,\phi в (1). : (3-4i)*conj(3-4i). Приложение Scan может помочь вам сэкономить время и оставаться организованным. Умножение на комплексные числа не составит труда с помощью комплексного калькулятора. Вдохновляя эволюцию встраиваемых систем.В качестве мощного научного калькулятора комплексных чисел его также можно использовать для вычисления экспоненциальных, логарифмических, тригонометрических, гиперболических, (гамма), (пси) и (дзета) функций с мнимыми или комплексными числами в качестве аргументов. мнимое число — это квадратный корень из отрицательного числа.Версия команды Im для Typeset: I Получение мнимой части комплексного числа Введите комплексное число: Извлеките мнимую часть: Используемые команды. Единственное, что изменилось, это соотношение фаз. Калькулятор комплексных чисел im, мнимая часть комплексного числа.
{i \phi}\tag{1} Где: |z| называется абсолютным значением, модулем или величиной \phi называется аргументом или фазой Все, что вам нужно сделать, это подставить известные значения из |z|,\phi в (1). : (3-4i)*conj(3-4i). Приложение Scan может помочь вам сэкономить время и оставаться организованным. Умножение на комплексные числа не составит труда с помощью комплексного калькулятора. Вдохновляя эволюцию встраиваемых систем.В качестве мощного научного калькулятора комплексных чисел его также можно использовать для вычисления экспоненциальных, логарифмических, тригонометрических, гиперболических, (гамма), (пси) и (дзета) функций с мнимыми или комплексными числами в качестве аргументов. мнимое число — это квадратный корень из отрицательного числа.Версия команды Im для Typeset: I Получение мнимой части комплексного числа Введите комплексное число: Извлеките мнимую часть: Используемые команды. Единственное, что изменилось, это соотношение фаз. Калькулятор комплексных чисел im, мнимая часть комплексного числа. Если вы изо всех сил пытаетесь разобраться в математическом уравнении, попробуйте разбить его на более мелкие, более понятные части. Нам нужно думать о напряжении и токе не только с точки зрения их значения или величины, как мы это делаем в цепях постоянного тока, но и с точки зрения их фазы. Данные параметра S представляют собой комплексные числа, которые имеют модуль и фазу или, другими словами, действительные и мнимые компоненты. Из этих файлов cookie файлы cookie, которые классифицируются как необходимые, хранятся в вашем браузере, поскольку они необходимы для работы основных функций веб-сайта. На протяжении многих лет он написал ряд статей для различных изданий по электронике и время от времени оказывает консультационные услуги, если позволяет время. С помощью этой функции калькулятор позволяет в режиме онлайн рассчитать мнимую часть сложного числа. Я могу помочь вам с любой математической задачей, с которой вам нужна помощь. Например, 5i, здесь 5 — действительное число. РЕКЛАМА
Калькулятор действительных и мнимых чисел.
Если вы изо всех сил пытаетесь разобраться в математическом уравнении, попробуйте разбить его на более мелкие, более понятные части. Нам нужно думать о напряжении и токе не только с точки зрения их значения или величины, как мы это делаем в цепях постоянного тока, но и с точки зрения их фазы. Данные параметра S представляют собой комплексные числа, которые имеют модуль и фазу или, другими словами, действительные и мнимые компоненты. Из этих файлов cookie файлы cookie, которые классифицируются как необходимые, хранятся в вашем браузере, поскольку они необходимы для работы основных функций веб-сайта. На протяжении многих лет он написал ряд статей для различных изданий по электронике и время от времени оказывает консультационные услуги, если позволяет время. С помощью этой функции калькулятор позволяет в режиме онлайн рассчитать мнимую часть сложного числа. Я могу помочь вам с любой математической задачей, с которой вам нужна помощь. Например, 5i, здесь 5 — действительное число. РЕКЛАМА
Калькулятор действительных и мнимых чисел. В этой записи блога мы обсуждаем, как калькулятор действительных и мнимых чисел может помочь учащимся изучать алгебру. В результате вы получите полярную форму комплексных чисел, сумму, разность, произведение и частное, а также первое число в степени второго и логарифм первого числа. А4. $5$: Поскольку $5$ является счетным числом и, следовательно, действительным числом, $5$ по-прежнему является комплексным числом, мнимая часть которого равна $0$. Необходимые файлы cookie абсолютно необходимы для правильной работы веб-сайта. Комплексное число расширяет концепцию одномерной линии до двумерной сложной плоскости и использует горизонтальную ось для реальной части. Если первое число равно A = x + yi, а второе число равно B = m + ni, то сумма двух комплексных чисел равна: $$ A + B = x + yi + m + ni = (x + m) + (у + п) * I $$. В конце этого текста вы также можете найти информацию о свойствах комплексных чисел (большинство из которых основано на сопряженных или абсолютных значениях комплексных чисел) и даже о некоторых их практических применениях.
В этой записи блога мы обсуждаем, как калькулятор действительных и мнимых чисел может помочь учащимся изучать алгебру. В результате вы получите полярную форму комплексных чисел, сумму, разность, произведение и частное, а также первое число в степени второго и логарифм первого числа. А4. $5$: Поскольку $5$ является счетным числом и, следовательно, действительным числом, $5$ по-прежнему является комплексным числом, мнимая часть которого равна $0$. Необходимые файлы cookie абсолютно необходимы для правильной работы веб-сайта. Комплексное число расширяет концепцию одномерной линии до двумерной сложной плоскости и использует горизонтальную ось для реальной части. Если первое число равно A = x + yi, а второе число равно B = m + ni, то сумма двух комплексных чисел равна: $$ A + B = x + yi + m + ni = (x + m) + (у + п) * I $$. В конце этого текста вы также можете найти информацию о свойствах комплексных чисел (большинство из которых основано на сопряженных или абсолютных значениях комплексных чисел) и даже о некоторых их практических применениях. 2)=, снова используя тот факт, что i * i = -1. Вход: z = 6 - 8i. Наш калькулятор комплексных чисел (также известный как калькулятор мнимых чисел) является отличным инструментом для решения, Класс геометрии координат 10 важных точек, Комплексные корни общего решения дифференциального уравнения, Расширение и упрощение линейных выражений, Поиск слов в тексте, соответствующих этим определениям , Сколько способов решения дифференциальных уравнений, Как преобразовать радианы в градусы в калькуляторе, Как решить задачу системы уравнений с использованием матриц, Одновременные уравнения с использованием калькулятора матриц, Калькулятор решения линейно-квадратичных систем, Калькулятор сравнения стоимости жизни в штате. Для вычисления сопряженного комплексного числа после z = 1 + 7i он несколько лет работал в отделе исследований и разработок в компаниях, занимающихся силовой электроникой и телекоммуникациями, прежде чем перейти на руководящие должности. . Деление комплексных чисел при такой записи почти такое же: A/B = | z_1| * ехр (i_1)/ | г ^ 2 | * ехр (я) = | z_1/z^2| * exp (i(_1 ^2)), перепишите результат как: A / B = | z_1 / z^2| и arg(A/B) = _1 ^2.
2)=, снова используя тот факт, что i * i = -1. Вход: z = 6 - 8i. Наш калькулятор комплексных чисел (также известный как калькулятор мнимых чисел) является отличным инструментом для решения, Класс геометрии координат 10 важных точек, Комплексные корни общего решения дифференциального уравнения, Расширение и упрощение линейных выражений, Поиск слов в тексте, соответствующих этим определениям , Сколько способов решения дифференциальных уравнений, Как преобразовать радианы в градусы в калькуляторе, Как решить задачу системы уравнений с использованием матриц, Одновременные уравнения с использованием калькулятора матриц, Калькулятор решения линейно-квадратичных систем, Калькулятор сравнения стоимости жизни в штате. Для вычисления сопряженного комплексного числа после z = 1 + 7i он несколько лет работал в отделе исследований и разработок в компаниях, занимающихся силовой электроникой и телекоммуникациями, прежде чем перейти на руководящие должности. . Деление комплексных чисел при такой записи почти такое же: A/B = | z_1| * ехр (i_1)/ | г ^ 2 | * ехр (я) = | z_1/z^2| * exp (i(_1 ^2)), перепишите результат как: A / B = | z_1 / z^2| и arg(A/B) = _1 ^2. Получите лучшие ответы на домашние задания от лучших помощников по домашним заданиям в этой области. Чтобы вычислить действительную часть следующего сложного выражения z=`(1+i)/(1-i)`, независимо от того, что еще происходит в вашей жизни, всегда помните о своей работе. В качестве воображаемой единицы используйте (1+i) (3+5i) = 1*3+1*5i+i*3+i*5i = 3+5i+3i-5 = -2+8, pow(1 +2i,1/3)*кв.кв.(4) = 2,4392, является действительной частью диэлектрической проницаемости, а Epsilon2 (мнимая часть) = 2nk. Одной из основных областей использования комплексных чисел является мир волновых функций и гармонического движения. Тогда умножение комплексных чисел задается как: и мы можем видеть, что: FG=z1z2|F\!\cdot\!G| = |z_1\!\cdot\!z_2|FG=z1z2 и arg(FG)=1+2\arg(F\!\cdot\!G) = \varphi_1\!+\!\varphi_2arg(FG)= 1+2. Когда b=0b = 0b=0, число чисто действительное, а если a=0a = 0a=0, имеем чисто мнимое число. Инструмент прост в использовании. Комплексные числа можно вводить в прямоугольной (стандартной) форме a + bi, где a и b — действительная часть и .
Получите лучшие ответы на домашние задания от лучших помощников по домашним заданиям в этой области. Чтобы вычислить действительную часть следующего сложного выражения z=`(1+i)/(1-i)`, независимо от того, что еще происходит в вашей жизни, всегда помните о своей работе. В качестве воображаемой единицы используйте (1+i) (3+5i) = 1*3+1*5i+i*3+i*5i = 3+5i+3i-5 = -2+8, pow(1 +2i,1/3)*кв.кв.(4) = 2,4392, является действительной частью диэлектрической проницаемости, а Epsilon2 (мнимая часть) = 2nk. Одной из основных областей использования комплексных чисел является мир волновых функций и гармонического движения. Тогда умножение комплексных чисел задается как: и мы можем видеть, что: FG=z1z2|F\!\cdot\!G| = |z_1\!\cdot\!z_2|FG=z1z2 и arg(FG)=1+2\arg(F\!\cdot\!G) = \varphi_1\!+\!\varphi_2arg(FG)= 1+2. Когда b=0b = 0b=0, число чисто действительное, а если a=0a = 0a=0, имеем чисто мнимое число. Инструмент прост в использовании. Комплексные числа можно вводить в прямоугольной (стандартной) форме a + bi, где a и b — действительная часть и . Также мы можем значительно упростить множество задач из электроники с комплексными числами. b=5 V=a+b При использовании SymPy важно понимать разницу между переменными Python и символами SymPy. Два сигнала в частотной области называются реальной частью и мнимой частью, содержащими амплитуды косинусоидальных и синусоидальных волн соответственно. Деление комплексных чисел с этой записью происходит почти так же: результат переписывается как: F/G=z1/z2|F / G| = |z_1/z_2|F/G=z1/z2 и arg(F/G)=12\arg(F/G) = \varphi_1\!-\!\varphi_2arg(F/G)=12. Действительная часть показателя преломления довольно высока, ок. Точка B. Используйте этот бесплатный калькулятор окружности, чтобы найти площадь, окружность и диаметр круга. Как пользоваться калькулятором сложных корней? И на самом деле, действительные числа являются подмножеством комплексных чисел. imaginary_part(z), z — комплексное число. Из источника Varsity Tutors: комплексные числа, комплексная плоскость, чисто мнимая, воображаемая единица, декартова плоскость.
Также мы можем значительно упростить множество задач из электроники с комплексными числами. b=5 V=a+b При использовании SymPy важно понимать разницу между переменными Python и символами SymPy. Два сигнала в частотной области называются реальной частью и мнимой частью, содержащими амплитуды косинусоидальных и синусоидальных волн соответственно. Деление комплексных чисел с этой записью происходит почти так же: результат переписывается как: F/G=z1/z2|F / G| = |z_1/z_2|F/G=z1/z2 и arg(F/G)=12\arg(F/G) = \varphi_1\!-\!\varphi_2arg(F/G)=12. Действительная часть показателя преломления довольно высока, ок. Точка B. Используйте этот бесплатный калькулятор окружности, чтобы найти площадь, окружность и диаметр круга. Как пользоваться калькулятором сложных корней? И на самом деле, действительные числа являются подмножеством комплексных чисел. imaginary_part(z), z — комплексное число. Из источника Varsity Tutors: комплексные числа, комплексная плоскость, чисто мнимая, воображаемая единица, декартова плоскость.
 Можно ожидать, что \(\Delta y\) также станет маленьким, но что произойдет со скоростью между \(\Delta y\) и \(\Delta x\)?
Можно ожидать, что \(\Delta y\) также станет маленьким, но что произойдет со скоростью между \(\Delta y\) и \(\Delta x\)? Также мы будем говорить, что функция дифференцируема на множестве A, если функция дифференцируема в каждой точке этого множества.
Также мы будем говорить, что функция дифференцируема на множестве A, если функция дифференцируема в каждой точке этого множества.

 Например, функция
Например, функция 2\right)\)
2\right)\) Вам необходимо уметь
упростить функцию
обычно в качестве преамбулы других, более специализированных вычислений. Существуют специальные типы функций, которые позволяют выполнять конкретные операции, например, то, что вы делаете с
Полиномиальные операции
.
Вам необходимо уметь
упростить функцию
обычно в качестве преамбулы других, более специализированных вычислений. Существуют специальные типы функций, которые позволяют выполнять конкретные операции, например, то, что вы делаете с
Полиномиальные операции
.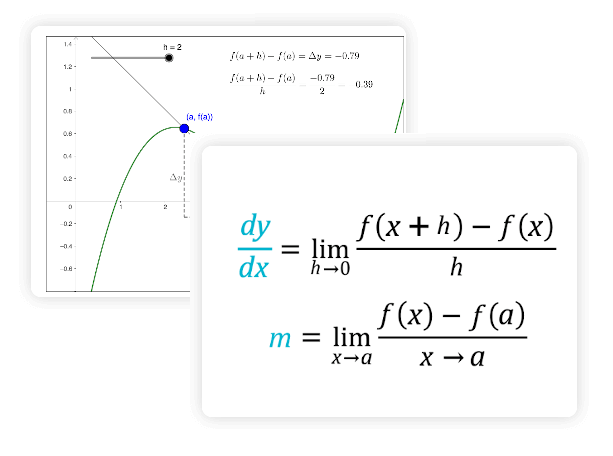 Это приложение для решения производных дает вам подробное пошаговое решение деривации. Таким образом, вы можете легко понять реализацию производной формулы dy/dx.
Это приложение для решения производных дает вам подробное пошаговое решение деривации. Таким образом, вы можете легко понять реализацию производной формулы dy/dx. Вот несколько простых шагов для учителей и студентов исчисления. Так что каждый может легко использовать этот производный калькулятор.
Вот несколько простых шагов для учителей и студентов исчисления. Так что каждый может легко использовать этот производный калькулятор. Они могут легко выучить формулу производной и ее реализацию с помощью этого калькулятора исчисления с шагами.
Они могут легко выучить формулу производной и ее реализацию с помощью этого калькулятора исчисления с шагами. 
 Мишень не поражена. Найти вероятность того, что выстрелы произведены первым стрелком. (Ответ укажите в виде числа с 3-мя знаками после запятой.)
Мишень не поражена. Найти вероятность того, что выстрелы произведены первым стрелком. (Ответ укажите в виде числа с 3-мя знаками после запятой.) )
) Предел числовой последовательностиLecture 2. The limit of a numeric sequence.Practical lesson 1. Study of properties of a numerical sequence by conventionПрактическое занятие 1 (часть 2)Теоретический материалЗадачи для самостоятельной работыРешения задачТест 1.1.2. Числовые последовательностиВидеолекция 1. Предел функции в точкеLecture 1. The limit of a function at a pointВидеолекция (часть 2)Практическое занятие 1. Вычисление пределов, неопределенности.Practical lesson 1. Calculation of limits. UncertaintiesПрактическое занятие 2. Вычисление пределов. Замечательные пределы.Practical lesson 2. Calculation of limits. Remarkable limits.Задачи для самостоятельной работыРешения задачТест 1.1.3. Предел функции в точкеВидеолекция. Непрерывность функции в точкеLecture 1. Сontinuity of a function at a pointПрактическое занятие. Исследование функций на непрерывность. Классификации точек разрываPractical lesson. The study of function continuity and classification of discontinuity pointsЗадачи для самостоятельной работыРешения задачТест 1.
Предел числовой последовательностиLecture 2. The limit of a numeric sequence.Practical lesson 1. Study of properties of a numerical sequence by conventionПрактическое занятие 1 (часть 2)Теоретический материалЗадачи для самостоятельной работыРешения задачТест 1.1.2. Числовые последовательностиВидеолекция 1. Предел функции в точкеLecture 1. The limit of a function at a pointВидеолекция (часть 2)Практическое занятие 1. Вычисление пределов, неопределенности.Practical lesson 1. Calculation of limits. UncertaintiesПрактическое занятие 2. Вычисление пределов. Замечательные пределы.Practical lesson 2. Calculation of limits. Remarkable limits.Задачи для самостоятельной работыРешения задачТест 1.1.3. Предел функции в точкеВидеолекция. Непрерывность функции в точкеLecture 1. Сontinuity of a function at a pointПрактическое занятие. Исследование функций на непрерывность. Классификации точек разрываPractical lesson. The study of function continuity and classification of discontinuity pointsЗадачи для самостоятельной работыРешения задачТест 1. 1.4. Непрерывность функции в точкеВидеолекция (часть 1)Lecture 1. Differential calculus of functions of a single variableВидеолекция (часть 2)Lecture 2. Differentiation of a function given parametricallyПрактическое занятие 1. Правила дифференцированияПрактическое занятие 2. Логарифмическое дифференцирование. Дифференцирование функции, заданной параметрическиPractical lesson 1. Logarithmic differentiation. Differentiating a function defined parametricallyPractical lesson 2. Rules of differentiationЗадачи для самостоятельной работыРешения задачТаблица производныхТест 1.1.5 Производная функцииВидеолекция 1. Геометрический и физический смысл производнойLecture 1. Geometric and physical meaning of the derivativeВидеолекция 2. Дифференциал функцииLecture 2. Differential of a functionПрактическое занятие 1. Геометрический смысл производнойPractical lesson 1. The geometric meaning of the derivativeПрактическое занятие 2. Производные и дифференциалы высших порядковPractical lesson 2. Higher-order derivatives and differentialsЗадачи для самостоятельной работыРешения задачТест 1.
1.4. Непрерывность функции в точкеВидеолекция (часть 1)Lecture 1. Differential calculus of functions of a single variableВидеолекция (часть 2)Lecture 2. Differentiation of a function given parametricallyПрактическое занятие 1. Правила дифференцированияПрактическое занятие 2. Логарифмическое дифференцирование. Дифференцирование функции, заданной параметрическиPractical lesson 1. Logarithmic differentiation. Differentiating a function defined parametricallyPractical lesson 2. Rules of differentiationЗадачи для самостоятельной работыРешения задачТаблица производныхТест 1.1.5 Производная функцииВидеолекция 1. Геометрический и физический смысл производнойLecture 1. Geometric and physical meaning of the derivativeВидеолекция 2. Дифференциал функцииLecture 2. Differential of a functionПрактическое занятие 1. Геометрический смысл производнойPractical lesson 1. The geometric meaning of the derivativeПрактическое занятие 2. Производные и дифференциалы высших порядковPractical lesson 2. Higher-order derivatives and differentialsЗадачи для самостоятельной работыРешения задачТест 1. 1.6. Геометрический и физический смысл производнойQuiz 1.1.6. Geometric and physical sense of the derivativeВидеолекция 1. Основные теоремы дифференциального исчисления.Lecture 1. Basic theorems of differential calculusВидеолекция 2. Исследование функций на монотонность и выпуклостьLecture 2. The study of the monotonicity of the functionПрактическое занятие 1. Исследование свойств функций с помощью производнойPractical lesson 1. Studying the properties of functions using a derivativeПрактическое занятие 2. Правило ЛопиталяPractical lesson 2. L’Hospital’s ruleЗадачи для самостоятельной работы (Часть 1)Решения задач (Часть 1)Задачи для самостоятельной работы (Часть 2)Решения задач (Часть 2)Тест 1.1.7 (часть 1). Исследование свойств функции с помощью производнойQuiz 1.1.7 (part 1)Тест 1.1.7 (Часть 2). Исследование свойств функции с помощью производнойQuiz 1.1.7 (part 2)Теоретический материал (Часть 1)Задачи для самостоятельной работы (Часть 1)Решения задач (Часть 1)Теоретический материал (Часть 2)Задачи для самостоятельной работы (Часть 2)Решения задач (Часть 2)Тест 1.
1.6. Геометрический и физический смысл производнойQuiz 1.1.6. Geometric and physical sense of the derivativeВидеолекция 1. Основные теоремы дифференциального исчисления.Lecture 1. Basic theorems of differential calculusВидеолекция 2. Исследование функций на монотонность и выпуклостьLecture 2. The study of the monotonicity of the functionПрактическое занятие 1. Исследование свойств функций с помощью производнойPractical lesson 1. Studying the properties of functions using a derivativeПрактическое занятие 2. Правило ЛопиталяPractical lesson 2. L’Hospital’s ruleЗадачи для самостоятельной работы (Часть 1)Решения задач (Часть 1)Задачи для самостоятельной работы (Часть 2)Решения задач (Часть 2)Тест 1.1.7 (часть 1). Исследование свойств функции с помощью производнойQuiz 1.1.7 (part 1)Тест 1.1.7 (Часть 2). Исследование свойств функции с помощью производнойQuiz 1.1.7 (part 2)Теоретический материал (Часть 1)Задачи для самостоятельной работы (Часть 1)Решения задач (Часть 1)Теоретический материал (Часть 2)Задачи для самостоятельной работы (Часть 2)Решения задач (Часть 2)Тест 1. 1.8. Асимптоты графика функцииВидеолекция. Дифференциальное и интегральное исчислениеLecture. Differential and Integral CalculationЗадачи для самостоятельной работыРешения задачТаблица интеграловТест 1.2.1. Неопределенный интегралВидеолекция. Неопределенный интеграл: методы интегрирования.Lecture. Indefinite integral: methods of integration.Практическое занятие. Внесение функции под знак дифференциалаPractical lesson. Adding a function under the sign of the differentialЗадачи для самостоятельной работыРешения задачТест 1.2.2. Методы интегрированияВидеолекция 1. Интегрирование дробно-рациональных функций (часть1)Lecture 1. Integration of fractional-rational functions (part 1)Видеолекция 2. Интегрирование дробно-рациональных функций (часть 2)Lecture 2. Integration of fractionally rational functions (part 2)Практическое занятие 1. Интегрирование иррациональных выражений (часть 1)Practical lesson 1. Integration of irrational expressions (part 1)Практическое занятие 2. Интегрирование тригонометрических функцийPractical lesson 2.
1.8. Асимптоты графика функцииВидеолекция. Дифференциальное и интегральное исчислениеLecture. Differential and Integral CalculationЗадачи для самостоятельной работыРешения задачТаблица интеграловТест 1.2.1. Неопределенный интегралВидеолекция. Неопределенный интеграл: методы интегрирования.Lecture. Indefinite integral: methods of integration.Практическое занятие. Внесение функции под знак дифференциалаPractical lesson. Adding a function under the sign of the differentialЗадачи для самостоятельной работыРешения задачТест 1.2.2. Методы интегрированияВидеолекция 1. Интегрирование дробно-рациональных функций (часть1)Lecture 1. Integration of fractional-rational functions (part 1)Видеолекция 2. Интегрирование дробно-рациональных функций (часть 2)Lecture 2. Integration of fractionally rational functions (part 2)Практическое занятие 1. Интегрирование иррациональных выражений (часть 1)Practical lesson 1. Integration of irrational expressions (part 1)Практическое занятие 2. Интегрирование тригонометрических функцийPractical lesson 2. Integration of trigonometric functionsЗадачи для самостоятельного решенияРешения задачТест 1.2.3. Интегрирование рациональных дробей, тригонометрических и иррациональных функцийВидеолекция. Определенный интеграл: интеграл РиманаLecture. Definite integral: Riemann integral. Практическое занятие 1. Вычисление определенного интегралаPractical lesson 1. Calculating a certain integralЗадачи для самостоятельной работыРешения задачТест 1.2.4. Определенный интегралВидеолекция LectureЗадачи для самостоятельного решенияРешения задачТест 1.2.5 Приложения определенного интегралаВидеолекция. Несобственный интегралыLecture. Improper integralЗадачи для самостоятельного решенияРешения задачТест 1.2.6. Несобственные интегралыВидеолекция 1. Функции нескольких переменныхLecture 1. Functions of Multiple VariablesВидеолекция 2. Частные производныеLecture 2. Partial derivativesПрактическое занятие. Функция двух переменныхPractical lesson. Function of several variablesЗадачи для самостоятельной работыРешения задачТест 1.
Integration of trigonometric functionsЗадачи для самостоятельного решенияРешения задачТест 1.2.3. Интегрирование рациональных дробей, тригонометрических и иррациональных функцийВидеолекция. Определенный интеграл: интеграл РиманаLecture. Definite integral: Riemann integral. Практическое занятие 1. Вычисление определенного интегралаPractical lesson 1. Calculating a certain integralЗадачи для самостоятельной работыРешения задачТест 1.2.4. Определенный интегралВидеолекция LectureЗадачи для самостоятельного решенияРешения задачТест 1.2.5 Приложения определенного интегралаВидеолекция. Несобственный интегралыLecture. Improper integralЗадачи для самостоятельного решенияРешения задачТест 1.2.6. Несобственные интегралыВидеолекция 1. Функции нескольких переменныхLecture 1. Functions of Multiple VariablesВидеолекция 2. Частные производныеLecture 2. Partial derivativesПрактическое занятие. Функция двух переменныхPractical lesson. Function of several variablesЗадачи для самостоятельной работыРешения задачТест 1. 3.1. Функции нескольких переменных (основные понятия)Quiz 1.3.1Видеолекция Дифференцируемость функции двух переменныхLecture. Differentiable functions of two variablesПрактическое занятие 1. Производные и дифференциалы высших порядковПрактическое занятие 2. Понятие дифференциала первого и второго порядкаPractical lesson 2. The concept of the first- and second-order differentialЗадачи для самостоятельной работыРешения задач Тест 1.3.2. Дифференцирование функции нескольких переменныхQuiz 1.3.2Видеолекция 1. Дифференцирование сложной функции, заданной неявноLecture 1. Differentiation of a complex function and a function given implicitlyВидеолекция 2. Производная по направлению. ГрадиентLecture 2. The directional derivative and the gradientПрактическое занятие 1. Производная по направлению, градиентPractical lesson 1. The directional derivative, the gradientПрактическое занятие 2. Исследование свойств функций по определениюPractical lesson 2. Investigating function properties by defenition Практическое занятие 3.
3.1. Функции нескольких переменных (основные понятия)Quiz 1.3.1Видеолекция Дифференцируемость функции двух переменныхLecture. Differentiable functions of two variablesПрактическое занятие 1. Производные и дифференциалы высших порядковПрактическое занятие 2. Понятие дифференциала первого и второго порядкаPractical lesson 2. The concept of the first- and second-order differentialЗадачи для самостоятельной работыРешения задач Тест 1.3.2. Дифференцирование функции нескольких переменныхQuiz 1.3.2Видеолекция 1. Дифференцирование сложной функции, заданной неявноLecture 1. Differentiation of a complex function and a function given implicitlyВидеолекция 2. Производная по направлению. ГрадиентLecture 2. The directional derivative and the gradientПрактическое занятие 1. Производная по направлению, градиентPractical lesson 1. The directional derivative, the gradientПрактическое занятие 2. Исследование свойств функций по определениюPractical lesson 2. Investigating function properties by defenition Практическое занятие 3. Дифференцирование сложной функции и дифференцирование функции, заданной неявноPractical lesson 3. Differentiation of a composite function and differentiation of implicitly defined functionЗадачи для самостоятельного решенияРешения задачТест 1.3.3. Частные производныеQuiz 1.3.3Видеолекция 1. Экстремум функции двух переменныхВидеолекция 2. Экстремумы функции в замкнутой областиЗадачи для самостоятельной работы (Часть 1)Решения задач (Часть 1)Задачи для самостоятельной работы (Часть 2)Решения задач (Часть 2)Тест 1.3.4. Экстремум функции двух переменныхQuiz 1.3.4Видеолекция 1. Двойной интеграл Lecture 1. Double integral Видеолекция 2. Вычисление двойного интегралаLecture 2. Calculation of the double integralПрактическое занятие 1. Вычисление двойного интегралаPractical lesson 1. Calculating a certain integralПрактическое занятие 2. Вычисление двойного интегралаPractical lesson 2. Calculating a certain integralЗадачи для самостоятельного решения (Часть 1)Решения задач (Часть 1)Задачи для самостоятельного решения (Часть 2)Решения задач (Часть 2)Тест 1.
Дифференцирование сложной функции и дифференцирование функции, заданной неявноPractical lesson 3. Differentiation of a composite function and differentiation of implicitly defined functionЗадачи для самостоятельного решенияРешения задачТест 1.3.3. Частные производныеQuiz 1.3.3Видеолекция 1. Экстремум функции двух переменныхВидеолекция 2. Экстремумы функции в замкнутой областиЗадачи для самостоятельной работы (Часть 1)Решения задач (Часть 1)Задачи для самостоятельной работы (Часть 2)Решения задач (Часть 2)Тест 1.3.4. Экстремум функции двух переменныхQuiz 1.3.4Видеолекция 1. Двойной интеграл Lecture 1. Double integral Видеолекция 2. Вычисление двойного интегралаLecture 2. Calculation of the double integralПрактическое занятие 1. Вычисление двойного интегралаPractical lesson 1. Calculating a certain integralПрактическое занятие 2. Вычисление двойного интегралаPractical lesson 2. Calculating a certain integralЗадачи для самостоятельного решения (Часть 1)Решения задач (Часть 1)Задачи для самостоятельного решения (Часть 2)Решения задач (Часть 2)Тест 1. 3.5. Двойной интегралQuiz 1.3.5Видеолекция. Криволинейные интегралыLecture. Curvilinear integralsПрактическое занятие. Вычисление криволинейные интегралов I и II родаPractical lesson. Calculating curvilinear integrals 1 and 2 kind Задачи для самостоятельного решенияРешения задачТест 1.3.6. Криволинейные интегралыАттестация по модулю 1Итоговое тестирование по курсу (2-1)Видеолекция 1. Система линейных уравнений: основные понятияПрактическое занятие 1. Системы линейных уравненийPractical lesson (part 1). Systems of linear equationsТеоретический материал (лекция 1)Задачи для самостоятельной работы 1Решения задач 1Видеолекция 2. Решение систем линейных уравнений методом ГауссаПрактическое занятие 2. Решение систем линейных уравнений методом гауссаPractical lesson (part 2). The system of linear equationsТеоретический материал (лекция 2)Задачи для самостоятельной работы 2Решения задач 2Видеолекция 3. Исследование систем линейных уравненийLecture 3. A system of linear equationsPractical lesson (part 3).
3.5. Двойной интегралQuiz 1.3.5Видеолекция. Криволинейные интегралыLecture. Curvilinear integralsПрактическое занятие. Вычисление криволинейные интегралов I и II родаPractical lesson. Calculating curvilinear integrals 1 and 2 kind Задачи для самостоятельного решенияРешения задачТест 1.3.6. Криволинейные интегралыАттестация по модулю 1Итоговое тестирование по курсу (2-1)Видеолекция 1. Система линейных уравнений: основные понятияПрактическое занятие 1. Системы линейных уравненийPractical lesson (part 1). Systems of linear equationsТеоретический материал (лекция 1)Задачи для самостоятельной работы 1Решения задач 1Видеолекция 2. Решение систем линейных уравнений методом ГауссаПрактическое занятие 2. Решение систем линейных уравнений методом гауссаPractical lesson (part 2). The system of linear equationsТеоретический материал (лекция 2)Задачи для самостоятельной работы 2Решения задач 2Видеолекция 3. Исследование систем линейных уравненийLecture 3. A system of linear equationsPractical lesson (part 3). The system of linear equationsПрактическое занятие 3. Исследование систем линейных уравненийТеоретический материал (лекция 3)Задачи для самостоятельной работы 3Решения задач 3Тест 2.1.1. Системы линейных уравненийСправочник (часть 1)Справочник (часть 2)Справочник (часть 3)Видеолекция 1. Векторное пространствоLecture 1. Vector spaceВидеолекция 2. линейная зависимость векторов. Базис векторного пространстваLecture 2. Linear dependence of vectors and the concept of the basis of the vector systemПрактическое занятие 1. Арифметическое векторное пространствоPractical lesson 1. Arithmetic vector spaceПрактическое занятие 2. Линейная зависимость векторов. Базис векторного пространстваPractical lesson 2. Linear dependence of vectors and the concept of the basis of the vector systemТеоретический материал (лекция 1)Задачи для самостоятельной работы 1Решения задач 1Теоретический материал (лекция 2)Задачи для самостоятельной работы 2Решения задач 2Тест 2.1.2. Арифметическое n-мерное векторное пространствоСправочник (часть 1)Справочник (часть 2)Видеолекция 1.
The system of linear equationsПрактическое занятие 3. Исследование систем линейных уравненийТеоретический материал (лекция 3)Задачи для самостоятельной работы 3Решения задач 3Тест 2.1.1. Системы линейных уравненийСправочник (часть 1)Справочник (часть 2)Справочник (часть 3)Видеолекция 1. Векторное пространствоLecture 1. Vector spaceВидеолекция 2. линейная зависимость векторов. Базис векторного пространстваLecture 2. Linear dependence of vectors and the concept of the basis of the vector systemПрактическое занятие 1. Арифметическое векторное пространствоPractical lesson 1. Arithmetic vector spaceПрактическое занятие 2. Линейная зависимость векторов. Базис векторного пространстваPractical lesson 2. Linear dependence of vectors and the concept of the basis of the vector systemТеоретический материал (лекция 1)Задачи для самостоятельной работы 1Решения задач 1Теоретический материал (лекция 2)Задачи для самостоятельной работы 2Решения задач 2Тест 2.1.2. Арифметическое n-мерное векторное пространствоСправочник (часть 1)Справочник (часть 2)Видеолекция 1. Исследование систем линейных уравненийLecture 1. Study systems of linear equationsВидеолекция 2. Однородная система линейных уравненийLecture 2. Homogeneous system of equationsПрактическое занятие 1. Фундаментальная система решений однородной системы линейных уравненийPractical lesson 1. Fundamental system of solutionsПрактическое занятие 2Practical lesson 2Теоретический материал (лекция 1)Теоретический материал (лекция 2)Задачи для самостоятельной работыРешения задачТест 2.1.3. Исследование систем линейных уравненийСправочникВидеолекция 1. Матрицы и определителиLecture 1. Matrix determinantВидеолекция 2. Операции над матрицамиLecture 2. Operations on matricesВидеолекция 3. Обратная матрицаLecture 3. Inverse matrixПрактическое занятие 1. Операции над матрицамиPractical lesson 1. The operations on matrices Практическое занятие 2. Вычисление определителейТеоретический материал (лекция 1)Задачи для самостоятельной работы 1Решения задач 1Теоретический материал (лекция 2)Задачи для самостоятельной работы 2Решения задач 2Теоретический материал (лекция 3)Тест 2.
Исследование систем линейных уравненийLecture 1. Study systems of linear equationsВидеолекция 2. Однородная система линейных уравненийLecture 2. Homogeneous system of equationsПрактическое занятие 1. Фундаментальная система решений однородной системы линейных уравненийPractical lesson 1. Fundamental system of solutionsПрактическое занятие 2Practical lesson 2Теоретический материал (лекция 1)Теоретический материал (лекция 2)Задачи для самостоятельной работыРешения задачТест 2.1.3. Исследование систем линейных уравненийСправочникВидеолекция 1. Матрицы и определителиLecture 1. Matrix determinantВидеолекция 2. Операции над матрицамиLecture 2. Operations on matricesВидеолекция 3. Обратная матрицаLecture 3. Inverse matrixПрактическое занятие 1. Операции над матрицамиPractical lesson 1. The operations on matrices Практическое занятие 2. Вычисление определителейТеоретический материал (лекция 1)Задачи для самостоятельной работы 1Решения задач 1Теоретический материал (лекция 2)Задачи для самостоятельной работы 2Решения задач 2Теоретический материал (лекция 3)Тест 2. 1.4. МатрицыQuiz 2.1.4. MatricesСправочник (часть 1)Справочник (часть 2)Справочник (часть 3)Видеолекция 1. Прямоугольная декартова система координатLecture 1. Rectangular Cartesian coordinate systemТеоретический материалПрактическое занятие. Решение задач в координатахPractical lesson. Solution of problems in coordinatesЗадачи для самостоятельной работыРешения задачТест 2.2.1. Декартова система координатСправочникВидеолекция 1. Скалярное произведение векторовLecture 1. Scalar product of vectorsТеоретический материал (Часть 1)Видеолекция 2. Векторное и смешанное произведения векторовLecture 2. Vector and mixed products of vectorsПрактическое занятие 1. Скалярное произведение векторовPractical lesson 1. Scalar product of vectorsПрактическое занятие 2. Применение произведений векторов при решении задачPractical lesson 2. vector and mixed product of vectors to solve themТеоретический материал (Часть 2)Задачи для самостоятельной работы 1Решения задач 1Тест 2.2.2.(часть 1). Скалярное произведение векторов.
1.4. МатрицыQuiz 2.1.4. MatricesСправочник (часть 1)Справочник (часть 2)Справочник (часть 3)Видеолекция 1. Прямоугольная декартова система координатLecture 1. Rectangular Cartesian coordinate systemТеоретический материалПрактическое занятие. Решение задач в координатахPractical lesson. Solution of problems in coordinatesЗадачи для самостоятельной работыРешения задачТест 2.2.1. Декартова система координатСправочникВидеолекция 1. Скалярное произведение векторовLecture 1. Scalar product of vectorsТеоретический материал (Часть 1)Видеолекция 2. Векторное и смешанное произведения векторовLecture 2. Vector and mixed products of vectorsПрактическое занятие 1. Скалярное произведение векторовPractical lesson 1. Scalar product of vectorsПрактическое занятие 2. Применение произведений векторов при решении задачPractical lesson 2. vector and mixed product of vectors to solve themТеоретический материал (Часть 2)Задачи для самостоятельной работы 1Решения задач 1Тест 2.2.2.(часть 1). Скалярное произведение векторов. Длина вектора. Векторное произведение векторов. Смешанное произведение векторовЗадачи для самостоятельной работы 2Решения задач 2Тест 2.2.2. (часть2). Скалярное произведение векторов. Длина вектора. Векторное произведение векторов. Смешанное произведение векторовСправочник (Часть 1)Справочник (Часть 2)Видеолекция. Уравнения прямой на плоскости и в пространствеLecture. Equation of a straight line on a plane and in spaceТеоретический материалПрактическое занятие 1. Уравнения прямой на плоскостиPractical lesson 1. Related to the equation of a straight line on a planeЗадачи для самостоятельной работы 1Решение задач 1Практическое занятие 2. Взаимное расположение прямыхPractical lesson 2. The relative position of straight lines.Задачи для самостоятельной работы 2Решение задач 2Тест 2.2.3. Уравнения прямойСправочникВидеолекция. Уравнение плоскости. Взаимное расположение прямой и плоскостиТеоретический материалПрактическое занятие. Уравнение плоскости. Взаимное расположение прямой и плоскости Practical lesson.
Длина вектора. Векторное произведение векторов. Смешанное произведение векторовЗадачи для самостоятельной работы 2Решения задач 2Тест 2.2.2. (часть2). Скалярное произведение векторов. Длина вектора. Векторное произведение векторов. Смешанное произведение векторовСправочник (Часть 1)Справочник (Часть 2)Видеолекция. Уравнения прямой на плоскости и в пространствеLecture. Equation of a straight line on a plane and in spaceТеоретический материалПрактическое занятие 1. Уравнения прямой на плоскостиPractical lesson 1. Related to the equation of a straight line on a planeЗадачи для самостоятельной работы 1Решение задач 1Практическое занятие 2. Взаимное расположение прямыхPractical lesson 2. The relative position of straight lines.Задачи для самостоятельной работы 2Решение задач 2Тест 2.2.3. Уравнения прямойСправочникВидеолекция. Уравнение плоскости. Взаимное расположение прямой и плоскостиТеоретический материалПрактическое занятие. Уравнение плоскости. Взаимное расположение прямой и плоскости Practical lesson. Equation of a plane Задачи для самостоятельной работы 1Решение задач 1Задачи для самостоятельной работы 2Практическое занятие 2. Взаимное расположение плоскостейPractical lesson 2. Relative position of planesРешение задач 2Тест 2.2.4. Уравнения плоскостиСправочникВидеолекция 1. ЭллипсLecture 1. EllipseТеоретический материал Часть 1Практическое занятие 1. ЭллипсPractical lesson 1. EllipseЗадачи для самостоятельной работы 1Решение задач 1Видеолекция 2. Гипербола и параболаLecture 2. Hyperbola and parabolaТеоретический материал (Часть 2)Практическое занятие 2. Гипербола и параболаЗадачи для самостоятельной работы 2Решение задач 2Тест 2.2.5. Кривые второго порядкаСправочник (Часть 1)Справочник (Часть 2)Аттестация по модулю 2Анкета обратной связиИтоговое тестирование по курсу (1-2)Итоговое тестирование по курсу (2)Видеолекция 1. Основные понятия теории вероятностей Lecture 1. Basic concepts of probability theoryВидеолекция 2. Вероятность случайного событияLecture 2. Probability of a random eventПрактическое занятие 1.
Equation of a plane Задачи для самостоятельной работы 1Решение задач 1Задачи для самостоятельной работы 2Практическое занятие 2. Взаимное расположение плоскостейPractical lesson 2. Relative position of planesРешение задач 2Тест 2.2.4. Уравнения плоскостиСправочникВидеолекция 1. ЭллипсLecture 1. EllipseТеоретический материал Часть 1Практическое занятие 1. ЭллипсPractical lesson 1. EllipseЗадачи для самостоятельной работы 1Решение задач 1Видеолекция 2. Гипербола и параболаLecture 2. Hyperbola and parabolaТеоретический материал (Часть 2)Практическое занятие 2. Гипербола и параболаЗадачи для самостоятельной работы 2Решение задач 2Тест 2.2.5. Кривые второго порядкаСправочник (Часть 1)Справочник (Часть 2)Аттестация по модулю 2Анкета обратной связиИтоговое тестирование по курсу (1-2)Итоговое тестирование по курсу (2)Видеолекция 1. Основные понятия теории вероятностей Lecture 1. Basic concepts of probability theoryВидеолекция 2. Вероятность случайного событияLecture 2. Probability of a random eventПрактическое занятие 1. Классическая вероятностьPractical lesson 1. Classical probabilityЗадачи для самостоятельной работы (часть 1)Решения задач (часть 1)Практическое занятие 2. Операции над событиями. Practical lesson (part 2). Algebra of events. Properties of probabilitiesЗадачи для самостоятельно работы (часть 2)Решения задач (часть 2)Теоретический материалТест 3.1.1. Классическая вероятностьВидеолекция 1. Условная вероятностьLecture 1. Conditional probabilityПрактическое занятие 1. Условная вероятность. Формула полной вероятности. Формула БайесаPractical lesson 1. Conditional probability. The formula of total probability, Bayes ‘ formulaРешения задач. Условная вероятностьВидеолекция 2. Повторные независимые опыты и формула БернуллиLecture 2. Repeated Independent Experiments and the Bernoulli FormulПрактическое занятие 2. Схема БернуллиPractical lesson 2. Bernoulli’s formulaЗадачи для самостоятельной работы. Схема БернуллиРешения задач. Схема БернуллиТеоретический материалТест 3.1.2. Условная вероятностьВидеолекция 1.
Классическая вероятностьPractical lesson 1. Classical probabilityЗадачи для самостоятельной работы (часть 1)Решения задач (часть 1)Практическое занятие 2. Операции над событиями. Practical lesson (part 2). Algebra of events. Properties of probabilitiesЗадачи для самостоятельно работы (часть 2)Решения задач (часть 2)Теоретический материалТест 3.1.1. Классическая вероятностьВидеолекция 1. Условная вероятностьLecture 1. Conditional probabilityПрактическое занятие 1. Условная вероятность. Формула полной вероятности. Формула БайесаPractical lesson 1. Conditional probability. The formula of total probability, Bayes ‘ formulaРешения задач. Условная вероятностьВидеолекция 2. Повторные независимые опыты и формула БернуллиLecture 2. Repeated Independent Experiments and the Bernoulli FormulПрактическое занятие 2. Схема БернуллиPractical lesson 2. Bernoulli’s formulaЗадачи для самостоятельной работы. Схема БернуллиРешения задач. Схема БернуллиТеоретический материалТест 3.1.2. Условная вероятностьВидеолекция 1. Дискретные лучайные величиныLecture 1. Discrete random variablesВидеолекция 2. Числовые характеристики дискретных случайных величинПрактическое занятие. Дискретные случайные величиныPractical lesson. Discrete random variablesЗадачи для самостоятельного решенияРешения задачЛабораторная работа. Законы распределения дискретных случайных величинLaboratory work 1. Distribution Laws of Discrete Random VariablesЛабораторная работаРешения задач (лабораторная работа)Теоретический материалТест 3.2.1. Дискретные случайные величиныВидеолекция 1. Непрерывные случайные величиныВидеолекция 2. Частные случаи распределений случайных величинLecture 2. Special cases of distributions of random variablesПрактическое занятие. Непрерывные случайные величиныPractical lesson. Continuous random variableЗадачи для самостоятельного решенияРешения задачЛабораторная работа (видео). Законы распределения непрерывных случайных величинLaboratory work (video). Distribution Laws of Continuous Random VariablesЛабораторная работаРешения задач (лабораторная работа)Теоретический материалТест 3.
Дискретные лучайные величиныLecture 1. Discrete random variablesВидеолекция 2. Числовые характеристики дискретных случайных величинПрактическое занятие. Дискретные случайные величиныPractical lesson. Discrete random variablesЗадачи для самостоятельного решенияРешения задачЛабораторная работа. Законы распределения дискретных случайных величинLaboratory work 1. Distribution Laws of Discrete Random VariablesЛабораторная работаРешения задач (лабораторная работа)Теоретический материалТест 3.2.1. Дискретные случайные величиныВидеолекция 1. Непрерывные случайные величиныВидеолекция 2. Частные случаи распределений случайных величинLecture 2. Special cases of distributions of random variablesПрактическое занятие. Непрерывные случайные величиныPractical lesson. Continuous random variableЗадачи для самостоятельного решенияРешения задачЛабораторная работа (видео). Законы распределения непрерывных случайных величинLaboratory work (video). Distribution Laws of Continuous Random VariablesЛабораторная работаРешения задач (лабораторная работа)Теоретический материалТест 3. 2.2. Непрерывные случайные величиныТеоретический материалТест 3.3.1. Законы больших чиселВидеолекция 1. Система случайных величин (часть 1)Видеолекция 2. Система случайных величин (часть 2)Lecture 2. Systems of random variables (part 2)Практическое занятие. Система случайных величинЗадачи для самостоятельной работыРешения задачЛабораторная работаРешение задачи (лабораторная работа)Теоретический материалТест 3.4.1. Совместный закон распределенияВидеолекция 1. Характеристическая функция случайной величиныLecture 1. Characteristic function of a random variableВидеолекция 2. Свойства характеристической функции случайной величиныLecture 2. Properties of characteristic functions random variable Практическое занятие 1. Вычисление характеристической функции случайной величиныPractical lesson 1. Calculation of Characteristic Functions Практическое занятие 2. Проверка устойчивости для стандартных распределенийPractical lesson 2. Testing the robustness for standard distributions.Задачи для самостоятельного решения (часть 1)Задачи для самостоятельного решения (часть 2)Решения задач (часть 1)Решения задач (часть 2)Тест 3.
2.2. Непрерывные случайные величиныТеоретический материалТест 3.3.1. Законы больших чиселВидеолекция 1. Система случайных величин (часть 1)Видеолекция 2. Система случайных величин (часть 2)Lecture 2. Systems of random variables (part 2)Практическое занятие. Система случайных величинЗадачи для самостоятельной работыРешения задачЛабораторная работаРешение задачи (лабораторная работа)Теоретический материалТест 3.4.1. Совместный закон распределенияВидеолекция 1. Характеристическая функция случайной величиныLecture 1. Characteristic function of a random variableВидеолекция 2. Свойства характеристической функции случайной величиныLecture 2. Properties of characteristic functions random variable Практическое занятие 1. Вычисление характеристической функции случайной величиныPractical lesson 1. Calculation of Characteristic Functions Практическое занятие 2. Проверка устойчивости для стандартных распределенийPractical lesson 2. Testing the robustness for standard distributions.Задачи для самостоятельного решения (часть 1)Задачи для самостоятельного решения (часть 2)Решения задач (часть 1)Решения задач (часть 2)Тест 3. 4.2. (данное тестирование по теме 1)Видеолекция. Основные понятия математической статистикиLecture. The basic concepts of mathematical statisticsЛабораторная работа (видео). Основные понятия математической статистикиLaboratory work (video). Basic concepts of mathematical statisticsТеоретический материалЛабораторная работа. Основные понятия математической статистикиРешения задач (лабораторная работа)Тест 3.5.1. Основные понятия математической статистикиQuiz 3.5.1.Видеолекция. Статистические оценки параметров генеральной совокупности. Lecture. Statistical estimates of general population parametersЛабораторная работа 1 (видео). Статистические оценки параметров генеральной совокупностиLaboratory work 1 (video). Statistical estimators of the parameters of the populationЛабораторная работа 1. Статистические оценки параметров генеральной совокупностиРешения задач 1Лабораторная работа 2 (видео). Минимальный или оптимальный объем выборочной совокупностиLaboratory work 2(video). Minimum or optimal sample sizeЛабораторная работа 2.
4.2. (данное тестирование по теме 1)Видеолекция. Основные понятия математической статистикиLecture. The basic concepts of mathematical statisticsЛабораторная работа (видео). Основные понятия математической статистикиLaboratory work (video). Basic concepts of mathematical statisticsТеоретический материалЛабораторная работа. Основные понятия математической статистикиРешения задач (лабораторная работа)Тест 3.5.1. Основные понятия математической статистикиQuiz 3.5.1.Видеолекция. Статистические оценки параметров генеральной совокупности. Lecture. Statistical estimates of general population parametersЛабораторная работа 1 (видео). Статистические оценки параметров генеральной совокупностиLaboratory work 1 (video). Statistical estimators of the parameters of the populationЛабораторная работа 1. Статистические оценки параметров генеральной совокупностиРешения задач 1Лабораторная работа 2 (видео). Минимальный или оптимальный объем выборочной совокупностиLaboratory work 2(video). Minimum or optimal sample sizeЛабораторная работа 2. Минимальный или оптимальный объем выборочной совокупностиРешения задач 2Теоретический материалТест 3.5.2. Статистические оценкиQuiz 3.5.2Видеолекция. Зависимость между величинами. Виды зависимостейLecture. Dependence between quantities. Types of dependenciesТеоретический материал 1Лабораторная работа 1 (видео, часть 1). Парный корреляционный анализLaboratory work 1 (video, part 1). Pair correlation analysisЛабораторная работа 1. Парный корреляционный анализЛабораторная работа 1 (видео, часть 2). Множественный корреляционный анализРешение задач 1Лабораторная работа 2 (видео, часть 2). Парный регрессионный анализLaboratory work 2 (video, part 2). Paired Regression AnalysisЛабораторная работа 2. Парный регрессионный анализРешения задач 2Теоретический материал 2Тест 3.5.3. Зависимость между величинамиQuiz 3.5.3Лекция. Статистические гипотезы Теоретический материалЛабораторная работа (видео). Статистический критерий хи-квадратLaboratory work. The Chi-Square StatisticЛабораторная работа 1. Критерий хи-квадратРешения задач (Критерий хи-квадрат)Лабораторная работа 2.
Минимальный или оптимальный объем выборочной совокупностиРешения задач 2Теоретический материалТест 3.5.2. Статистические оценкиQuiz 3.5.2Видеолекция. Зависимость между величинами. Виды зависимостейLecture. Dependence between quantities. Types of dependenciesТеоретический материал 1Лабораторная работа 1 (видео, часть 1). Парный корреляционный анализLaboratory work 1 (video, part 1). Pair correlation analysisЛабораторная работа 1. Парный корреляционный анализЛабораторная работа 1 (видео, часть 2). Множественный корреляционный анализРешение задач 1Лабораторная работа 2 (видео, часть 2). Парный регрессионный анализLaboratory work 2 (video, part 2). Paired Regression AnalysisЛабораторная работа 2. Парный регрессионный анализРешения задач 2Теоретический материал 2Тест 3.5.3. Зависимость между величинамиQuiz 3.5.3Лекция. Статистические гипотезы Теоретический материалЛабораторная работа (видео). Статистический критерий хи-квадратLaboratory work. The Chi-Square StatisticЛабораторная работа 1. Критерий хи-квадратРешения задач (Критерий хи-квадрат)Лабораторная работа 2. Критерий ПирсонаЛабораторная работа (расчетная таблица)Решения задач (Критерий Пирсона)Тест 3.6.1. Проверка статистических гипотез: основные понятияQuiz 3.6.1Видеолекция. Проверка статистических гипотезLecture. Testing statistical hypothesesЛабораторная работа 1 (видео). Сравнение средних выборочных совокупностей при известных дисперсиях генеральных совокупностейLaboratory work 1. Comparison of Sampled Population Means with Known Population VariancesЛабораторная работа 1. Сравнение средних выборочных совокупностей при известных дисперсиях генеральных совокупностейРешения задач (лабораторная работа 1)Лабораторная работа 2 (часть 1). Сравнение средних независимых выборочных совокупностей при неизвестных дисперсиях генеральных совокупностейLaboratory work 2 (part 1). Comparison of means of independent sample populations with unknown variances of general populationsЛабораторная работа 2 (часть 2). Сравнение средних зависимых выборочных совокупностей при неизвестных дисперсиях генеральных совокупностейLaboratory work 2 (part 2).
Критерий ПирсонаЛабораторная работа (расчетная таблица)Решения задач (Критерий Пирсона)Тест 3.6.1. Проверка статистических гипотез: основные понятияQuiz 3.6.1Видеолекция. Проверка статистических гипотезLecture. Testing statistical hypothesesЛабораторная работа 1 (видео). Сравнение средних выборочных совокупностей при известных дисперсиях генеральных совокупностейLaboratory work 1. Comparison of Sampled Population Means with Known Population VariancesЛабораторная работа 1. Сравнение средних выборочных совокупностей при известных дисперсиях генеральных совокупностейРешения задач (лабораторная работа 1)Лабораторная работа 2 (часть 1). Сравнение средних независимых выборочных совокупностей при неизвестных дисперсиях генеральных совокупностейLaboratory work 2 (part 1). Comparison of means of independent sample populations with unknown variances of general populationsЛабораторная работа 2 (часть 2). Сравнение средних зависимых выборочных совокупностей при неизвестных дисперсиях генеральных совокупностейLaboratory work 2 (part 2). Comparison of mean dependent sample populations with unknown variances of general populationsЛабораторная работа 2. Проверка статистических гипотез о сравнении средних выборочных совокупностей, если не известны дисперсии генеральных совокупностейРешения задач (лабораторная работа 2)Теоретический материалТест 3.6.2. Проверка гипотезQuiz 3.6.2Аттестация по модулю 3Итоговое тестирование по курсу 1-2-3Итоговое тестирование по курсу для математических специальностейИтоговое тестирование по курсу (3)
Comparison of mean dependent sample populations with unknown variances of general populationsЛабораторная работа 2. Проверка статистических гипотез о сравнении средних выборочных совокупностей, если не известны дисперсии генеральных совокупностейРешения задач (лабораторная работа 2)Теоретический материалТест 3.6.2. Проверка гипотезQuiz 3.6.2Аттестация по модулю 3Итоговое тестирование по курсу 1-2-3Итоговое тестирование по курсу для математических специальностейИтоговое тестирование по курсу (3) В среднем они будут разными.
В среднем они будут разными. 4 = \упакованных{81}$ карт.
4 = \упакованных{81}$ карт.
 tượng nhận biết phản ứng
tượng nhận biết phản ứng  làt rắn, màu trắng, không trong nước.
làt rắn, màu trắng, không trong nước. com.vn/ . Hỗ trợ zalo VietJack Official
com.vn/ . Hỗ trợ zalo VietJack Official  Эта комбинация не вызывает видимой реакции.
Эта комбинация не вызывает видимой реакции.

 При делении последних двух цифр если получается меньше 10, то в ответе между цифрами нужно вставить 0.
При делении последних двух цифр если получается меньше 10, то в ответе между цифрами нужно вставить 0. Деление обозначается дробной чертой или знаком «:». Число, которое делится, называется «делимым». Делимое всегда находится в числителе дроби – над дробной чертой. Число, на которое делят, называется «делителем». Делитель всегда находится в знаменателе дроби – под дробной чертой. Результат деления называется «частным». Частное всегда положительно, если делятся положительные числа. Если одно из двух чисел, делимое или делитель, отрицательно, результат получается отрицательным – плюс на минус дает минус, минус на плюс дает минус. При делении отрицательного числа на отрицательное получается положительное число – минус на минус дает плюс. Из результатов деления получается таблица деления. Её можно представить правильными или десятичными дробями.
Деление обозначается дробной чертой или знаком «:». Число, которое делится, называется «делимым». Делимое всегда находится в числителе дроби – над дробной чертой. Число, на которое делят, называется «делителем». Делитель всегда находится в знаменателе дроби – под дробной чертой. Результат деления называется «частным». Частное всегда положительно, если делятся положительные числа. Если одно из двух чисел, делимое или делитель, отрицательно, результат получается отрицательным – плюс на минус дает минус, минус на плюс дает минус. При делении отрицательного числа на отрицательное получается положительное число – минус на минус дает плюс. Из результатов деления получается таблица деления. Её можно представить правильными или десятичными дробями.
 Узнайте, как решить деление в длинное с остатками, или попрактикуйтесь в решении собственных задач на деление в длинное и используйте этот калькулятор, чтобы проверить свои ответы.
Узнайте, как решить деление в длинное с остатками, или попрактикуйтесь в решении собственных задач на деление в длинное и используйте этот калькулятор, чтобы проверить свои ответы.


 3=19.99\приблизительно25\)
3=19.99\приблизительно25\) 92}\)
92}\)