Спальный гарнитур Афина «корень крем», 1,6
Скидка
35%
Наведите на картинку для увеличения
- Описание
- Характеристики
- Скидки
Спальный гарнитур Афина в цвете «крем» (есть в цвете «орех»). Это модульная спальня, можно собрать свой гарнитур из необходимых элементов.
Цена указана за комплект:
— Кровать (160х200) — Ш 2070*Г 2100*В 1530 (Есть кровать (180х200) — Ш 2270*Г 2100*В 1530 Дороже)
— Тумбочка — Ш 495*Г 500*В 500
— Комод 4х ств. — Ш 950*Г 500*В 890
— Ш 950*Г 500*В 890
— Зеркало рамочное — Ш 820*В 820
— Шкаф 3-х ств — Ш 1445*Г 600*В 2285, (Есть 4-х, 5-ти, 6-ти дверные Дороже). ВНИМАНИЕ — в комплект НЕ входят внутренние полки шкафа и докупаются отдельно!
В кровать можно установить ящик с подъемным механизмом.
- Цвет — крем корень
- Фасады — МДФ с фрезеровкой и шелкографией.
- Корпус — ЛДСП
- На изголовье находится мягкое основание
- Декоративные элементы и накладки — ППУ и ПУ, класс экологичности Е1 (полностью безопасна)
- Декоративные элементы, фасады, накладки покрыты темной патиной и матовым лаком на водной основе
- Фурнитура — итальянская фирма Salice: ручка «кнопка» и «скоба» (металл — бронза)
- На зеркале — прямой или криволинейный фацет
- спальные гарнитуры
- белый/ваниль/молочный
- Классика
- ЛДСП
- МДФ
- МДФ
- ППУ
- ПУ
Кровать с подъемным механизмом имеет ящик для постельного белья, находящийся в основании кровати под ортопедической решёткой. Доступ к бельевому ящику обеспечивает подъемный механизм.
Доступ к бельевому ящику обеспечивает подъемный механизм.
- можно укомплектовать (опция)
Эра
Коллекция:Афина (Эра)
Страна производства:- Россия
Хотите получить дополнительные скидки?
- Зарегистрируйтесь на сайте. На многие товары действуют дополни тельные скидки, доступные только зарегистрированным пользователям. Не забудьте отметить подписку на новости!
- Вступите в нашу группа https://vk.com/stulstolcom. Мы регулярно освещаем акции и спецпредложения на нашей страничке.
Если у Вас возникли вопросы — обращайтесь к нашим сотрудникам.
- Дополнительные скидки на многие товары
- Льготная доставка на ряд позиций
- Подписка на акции и промокоды
- Отслеживание заказов на персональной странице
- Возможность настроить магазин под себя для более удобных покупок
- Ускоренное оформление последующих заказов
Цвет изображения на мониторе может отличаться от реального!
Производитель оставляет за собой право вносить конструктивные изменения, без отображения их в каталоге. Оттенки цвета изделия могут не совпадать с имеющимися в каталоге.
Оттенки цвета изделия могут не совпадать с имеющимися в каталоге.
Товары в коллекции
- Вы просматривали ранее
- Похожие товары
Наша компания производит доставку по всей России и ближнему зарубежью: Казахстан, Беларусь.
Гарантия качества и сервисное обслуживаниеМы предлагаем только те товары, в качестве которых мы уверены.
Возврат товара в течение 14 днейУ вас есть 14 дней, для того чтобы протестировать вашу покупку
3-8- Курс
- NCERT
- Класс 12
- Класс 11
- Класс 10
- Класс 9
- Класс 8
- Класс 7
- Класс 6
- IIT JEE
- NCERT
- Exam
- JEE MAINS
- JEE ADVANCED
- X BOARDS
- XII BOARDS
- NEET
- Предыдущий год (по годам)
- Физика Предыдущий год
- Химия Предыдущий год
- Биология Предыдущий год
- Новый Все образцы работ
- Образцы работ по биологии
- Образцы работ по физике
- Образцы работ по химии
- Загрузить PDF-файлы
- Класс 12
- Класс 11
- Класс 10
- Класс 9
- Класс 8
- Класс 7
- Класс 6
- Экзаменационный уголок
- Онлайн-класс 9 0925
- Викторина
- Задать вопрос в Whatsapp
- Поиск Doubtnut
- Английский словарь
- Блог
- Скачать
- Получить приложение
-
Создание документа
Статья -
Сохранение документа в OneDrive
Статья -
Создание макета и редактирование
Статья -
Совместная работа
Статья -
Настройка мобильных приложений
Статья -
Дополнительные сведения
Статья -
Добавлять текст, изображения, картинки и видео.
-
Искать материалы по теме среди надежных источников.
-
Получать доступ к документам с компьютера, планшета и телефона с помощью OneDrive.
-
Делиться документами и работать над ними совместно.
-
Отслеживать и просматривать изменения.

-
На вкладке Файл нажмите кнопку Создать.
-
В поле Поиск шаблонов в сети введите тип создаваемого документа и нажмите ВВОД.
-
Установите курсор и введите текст.
-
Чтобы изменить форматирование, выделите текст и выберите одну из команд: Полужирный, Курсив, Маркеры, Нумерация и т. д.
-
Выберите вкладку Вставка.
org/ListItem»>
-
Таблицы — нажмите Таблицы, наведите указатель на нужный размер и выберите его.
-
Рисунки — нажмите Рисунки, найдите изображение на компьютере, выберите стоковое изображение или выполните поиск в Bing.
Примечание: В более старых версиях Word Изображения из Интернета могут располагаться на ленте рядом с элементом Рисунки.
org/ListItem»>
-
Значки — нажмите Значки, выберите нужный значок и щелкните Вставить.
-
Трехмерные модели — нажмите Трехмерные модели, выберите источник (из файла или из Интернета), перейдите к нужному изображению и нажмите кнопку Вставить.
-
Графические элементы SmartArt — нажмите SmartArt, выберите рисунок SmartArtи нажмите ОК.

-
Диаграмма — нажмите Диаграммы, выделите диаграмму и нажмите ОК.
-
Снимок экрана — нажмите Снимок и выберите один из вариантов в раскрывающемся меню.
- Все темы
- Бизнес
- Программное обеспечение и инструменты для бизнеса
- Обработка текстов
- Microsoft Word
Демонстрация в вашем профиле LinkedIn в разделе «Лицензии и сертификаты»
Загрузите или распечатайте в формате PDF, чтобы поделиться с другими
Поделитесь изображением в Интернете, чтобы продемонстрировать свое мастерство
Дэвид Риверс
- 5 звезд Текущее значение: 883 77%
- 4 звезды Текущее значение: 214 18%
- 3 звезды Текущее значение: 39 3%
- 2 звезды Текущее значение: 3 <1%
- 1 звезда Текущее значение: 6 <1%
- Индикаторная корзина упрощает визуальное распознавание необходимости пополнения запасов.

- Являясь частью серии BinTelligence, индикаторная корзина представляет собой инновационную недорогую альтернативу высокотехнологичным системам управления запасами.
- Складируйте, выбирайте, переворачивайте и пополняйте!
- ЗАПАС Индикаторная корзина, используя разделитель, чтобы обозначить объем для инвентарного резерва.
- ПОДБИРАЙТЕ с синей стороны мусорного ведра, пока не дойдете до разделителя.
- ПЕРЕВЕРНИТЕ корзину на оранжевый резерв, чтобы указать, что уровень запасов низкий.
- ПОПОЛНИТЕ корзину и повторите!
- Ярко-оранжевый триггерный цвет, используемый в программах Lean и 5S.
- Простая организация поставок и незавершенного производства.
- Контейнер с двойным бункером можно наполнять или собирать с обеих сторон.
- Большая площадь для маркировки с обеих сторон.
- Свернутый гребень обеспечивает дополнительную прочность при заполнении до максимальной емкости.

- Работает с 14-дюймовыми проволочными стеллажами, 12-дюймовыми стальными стеллажами и стеллажными системами.
- Контейнеры доступны в 2 размерах.
- Передаточное отношение 1:90, расцепление для прямого деления, ручное вращение патрона на 360°
- Маховик со шкалой
- Нониус деление 10 дюймов
- 6 масок для прямого деления на 2, 3, 4, 6, 8 , 12, 24 части
- Закаленные и отшлифованные зубья с 3-х кулачковым патроном, 6,5″ или 7,75″
- 0 Вращение патрона на 360°
- Маховик со шкалой
- Нониус деление 10»
- 6 масок для прямого деления на 2, 3, 4, 6, 8, 12, 24 части
- Закаленные и отшлифованные зубья с 3- кулачковый патрон, 6,5″ или 7,75″
- 9 0907 Toppers Talk
Вопрос
Обновлено:26/04/2023 ПУБЛИКАЦИЯ СУРЫ-АЛГЕБРА-ИСПОЛНЕНИЕ 3.
Краткое руководство по началу работы с Word
Краткое руководство по началу работы с Word
Краткое руководство по началу работы с Word
Создание документа
Далее:
Знакомство с Word
Word для Windows, Mac OS или мобильных устройств позволяет: Создавать документы с нуля или с помощью готового шаблона.
Создание документа
Совет: Чтобы начать с нуля, выберите Новый документ. Чтобы попрактиковаться в использовании функций Word, воспользуйтесь учебным руководством, например Добро пожаловать в Word, Вставка первого оглавления и т. д.
Добавление и форматирование текста
Добавление рисунков, фигур, диаграмм, графических элементов SmartArt и т. д.
Выберите нужный элемент:
Фигуры — нажмите Фигуры и выберите фигуру из раскрывающегося списка.
Далее:
Сохранение документа в OneDrive в Word
Практическая работа «Работа с фрагментами текста» 1. скоро у нас каникулы. Я поеду вместе с папой в сочи. митя с братом поедут в город иркутск, на озеро байкал. а таня будет отдыхать в деревне у тети зои. Эта деревня стоит на берегу оки. У тети в доме живет кот мурзик. 2. Переместите каждую фразу, начинающуюся с прописной буквы на новую строку, чтобы получилось стихотворение. Затем удалите «лишние» слова из стихотворения. У лукоморья дуб очень старый, но еще зеленый; Златая тяжелая цепь на дубе том: И днем и ночью, утром и вечером кот ученый Всё ходит по цепи круг за кругом; Идет направо песнь тоскливую заводит, Налево страшную сказку говорит. Там чудеса чудесные: там добрый леший бродит, Русалка распрекрасная там на ветвях сидит… 3. Отредактируйте текст таким образом, чтобы каждая пословица начиналась с новой строки. Шило в мешке не утаишь. Не все коту масленица. Кончил дело, гуляй смело. Готовь сани летом, а телегу — зимой. Пар кости не ломит. Без труда не выловишь рыбку из пруда. Не все золото, что блестит. Слово — серебро, молчанье — золото. Раньше встанешь — раньше работу кончишь. Цыплят по осени считают. Делу — время, потехе — час. Сначала подумай, потом начинай. Семь раз примерь, один раз отрежь. Работа страшна не рукам, а глазам. Дело мастера боится. От добра добра не ищут. 4. Удалите в каждой строке лишнее слово: а) Витебск, Минск, Москва, Гомель, Могилёв. б) Школа, гимназия, лицей, цирк, институт. в) Сентябрь, октябрь, ноябрь, зима, март, апрель. 5. Добавьте антонимы к словам (день — ночь) Белый – Теплый – Веселый – Храбрый – Умный – 6. Вставьте в слова пропущенные буквы. Старй могучий дуб, болшое яблоко, маленкий рыжий лиснок, бабушкн дом, теплая медвежья шба. 7. Удалите лишнее слово из каждой строки. Приставка, предлог, суффикс, окончание, корень; 8. Теперьяподнимитетоже. 9. Исправьте алгоритм, чтобы саженец был посажен. Засыпь ямку. Поставь лопату и лейку на место. Выкопай ямку. Возьми лейку и полей саженец. Возьми лопату и саженец. Посади саженец в ямку. 10. Добавьте слог «НА», чтобы восстановить слова. (Используйте копирование или перемещение, а не простой набор текста) КАРЕЙКА, КАВА, KОMTA, КАТОХОДЕЦ, ЗНИЕ НА 11. Замените числительные и восстановите стихотворение с помощью встроенной функции «Найти-Заменить». У про100го 100рожа Непро100рный дом: Часто в нем 100ножка Бродит под 100лом. Дорожит 100ножка Чи100тою ног И 100личной ваксой Чистит 100 сапог. Microsoft Word и Outlook имеют функцию под названием «Быстрые части». Вы можете сохранить выбранный текст в библиотеку и вставить его в электронные письма и документы. Он хорошо работает с шаблонами MS Word в качестве библиотеки предложений для выбора и повторного использования текста и изображений. Quick Parts являются мощными и могут сэкономить много времени. Однако есть некоторые проблемы с Quick Parts. Вы не можете легко поделиться ими между несколькими пользователями, и они хранятся на отдельных устройствах. Хорошая новость заключается в том, что есть жизнеспособные альтернативы, которые стоит рассмотреть. На вкладке «Вставка» в MS Word и MS Outlook в группе «Текст» вы найдете кнопку «Быстрые части». Если вы нажмете «Быстрые части», вы увидите, что вы можете добавить автотекст, поля свойств документа, коды полей и организатор стандартных блоков. Чтобы добавить текст или изображение в экспресс-блоки, просто выделите текст, перейдите на вкладку «Вставка» и в группе «Текст» нажмите «Экспресс-блоки». Выберите «Сохранить выделение в быстрых частях». Вы увидите следующие варианты: Имя — присвойте быстрой части легко запоминающееся имя. Галерея. Хотя вы можете добавить экспресс-часть в другую галерею, лучше оставить ее по умолчанию. Категория — Категория по умолчанию — «Общая». Если у вас много быстрых частей, вы можете создать несколько категорий, например «Недвижимость», «Завещания», «Закрытие» и т. д. Эти категории облегчат поиск быстрой части, которую вы хотите вставить. Описание — добавьте описание, чтобы напомнить себе о намерении пункта или изображения. Сохранить в — настройка по умолчанию сохраняет выбранные вами элементы в Building Blocks. Параметры. Управляет тем, как текст или изображения вставляются в документ или сообщение электронной почты. Выберите вставку выделения вместе с содержимым («Вставить только содержимое»), как отдельный абзац или как отдельную страницу. Когда вы вводите имя быстрой части в электронное письмо или документ и нажимаете F3, быстрая часть будет вставлена автоматически. Или щелкните Quick Parts (СОВЕТ: щелкните правой кнопкой мыши, чтобы добавить кнопку Quick Parts на панель быстрого доступа, чтобы вам не приходилось искать ее) и выберите из раскрывающегося меню. Имейте в виду, что Quick Parts не являются общими между MS Word и MS Outlook. Ваша галерея строительных блоков уникальна для каждого приложения. Хотя вы можете щелкнуть «Быстрые части» и выбрать «Организатор строительных блоков» и отредактировать имя и расположение быстрой части, вы не можете редактировать текст. Вам нужно будет вставить экспресс-часть, внести в нее изменения и повторно сохранить. Хотя они чрезвычайно полезны, Quick Parts имеют некоторые существенные недостатки для юридических фирм, которые хотят использовать общую библиотеку статей. Их необходимо создать резервную копию и перенести, если вы переходите на другую версию MS Word или Outlook или переходите на новый компьютер. Стандартные блоки в быстрых частях недоступны в MS Word для Mac 2019. Они также недоступны в браузерных или мобильных версиях MS Word или Outlook. Если вы сохраните экспресс-блоки в определенном шаблоне (. Конечно, если вы ищете простую в использовании и совместно используемую библиотеку предложений, это зависит от вашего варианта использования. Многие, если не большинство продуктов для сборки документов, таких как Lawyaw, Documate, AfterPattern, HotDocs, Pathagorus, Form Tool Pro, ActiveDocs и другие, могут автоматизировать и повторно использовать разделы содержимого в документах. Многие инструменты автоматизации контрактов имеют схожие функции. Если вы ищете что-то, что требует немного меньше времени для запуска и запуска, такие продукты, как TextExpander, теперь имеют версию Team. Существует также множество продуктов, которые не только позволяют хранить и вставлять фрагменты вашего собственного контента, но также предоставляют стандартные библиотеки предложений. Продукты по подписке, такие как ElderDocs и LawGood, предоставляют инструменты для составления чертежей с контентом для интеграции контента для конкретной практики. Сборка документа Afterpattern имеет пункты и подписки от Bloomberg, Lexis и Westlaw, предоставляющие опции. Для пунктов для MS Outlook в команде, надстройка Ablebits, общие шаблоны электронной почты, имеет множество отличных функций для фирм и начинается с 3 долларов США на пользователя после 60-дневной бесплатной пробной версии. Еще один набор надстроек для продуктов Microsoft поступает от OfficeatWork. QuickParts — отличный способ добавлять форматированный текст (например, таблицы), изображения и фрагменты в документы MS Word и электронные письма Outlook. Однако для большей гибкости и контроля рассмотрите другие инструменты, специально созданные для многопользовательской стандартизации и администрирования, чтобы по-настоящему использовать ноу-хау вашей компании. С Дэвидом Риверсом
Нравится 3404 пользователям Продолжительность: 2ч 31м
Уровень мастерства: начальный + средний
Выпущено: 9/24/2018 Начать бесплатную пробную версию на 1 месяц Узнайте, как с легкостью создавать, редактировать, форматировать и обмениваться документами с помощью Microsoft Word 2019. Следуйте вместе с Дэвидом Риверсом, который покажет все основные функции этого мощного инструмента. Поделитесь тем, что вы узнали, и станьте выдающимся профессионалом в желаемой отрасли с сертификатом, демонстрирующим ваши знания, полученные на курсе. Обучение
LinkedIn Обучение 1 145 оценок Общий рейтинг рассчитывается на основе среднего значения представленных оценок. 5/5
26 июля 2022 г.
Укажите число, чтобы получить всю информацию о нем:
Случайное число
Число 130 является четным. Составное число
Целое положительное число 130
является трехзначным.
Укажите число, чтобы получить всю информацию о нем:
Случайное число
Число 252 является четным. Составное число
Натуральное число 252
является трехзначным. Нажмите на изображение, чтобы увеличить Технические характеристики
Подробности
Отзывы Многие продукты для металлообработки содержат металлы, на которые распространяется последнее предупреждение в соответствии с Предложением 65. Воздействие элементов может быть вредным. Может вызвать рак и нанести вред репродуктивной системе. Детали Краткий обзор эффективного управления запасами: двухцветная индикаторная корзина Akro-Mils имеет оранжевую резервную секцию для предотвращения нехватки товара и остановки сборочной линии Высота центра 5 дюймов Токарный патрон Ø 6 дюймов Высота центра 5 дюймов Токарный патрон Ø 6 дюймов Мы будем рады помочь вам принять правильное решение для достижения ваших бизнес-целей Все машины время от времени нуждаются в пит-стопе. Посмотреть услуги Получите личное впечатление на одном из наших объектов! Многие машины в нашем портфолио всегда есть на складе и доступны для демонстрации. Заказать демонстрацию Приветствие* Миссис Миссис Доктор Функция работы*Финансовый управляющий управляющему управляющему управляющему.0003 State*AlaskaAlabamaArkansasAmerican SamoaArizonaCaliforniaColoradoConnecticutDistrict of ColumbiaDelawareFloridaFederated MicronesiaGeorgiaGuamHawaiiIowaIdahoIllinoisIndianaKansasKentuckyLouisianaMassachusettsMarylandMaineMarshall IslandsMichiganMinnesotaMissouriNorthern Mariana IslandsMississippiMontanaNorth CarolinaNorth DakotaNebraskaNew HampshireNew JerseyNew MexicoNevadaNew YorkOhioOklahomaOregonPennsylvaniaPuerto RicoPalauRhode IslandSouth CarolinaSouth DakotaTennesseeTexasUnited States Minor Outlying IslandsUtahVirginiaUS Virgin IslandsVermontWashingtonWisconsinWest VirginiaWyoming ПромышленностьГорнодобывающая промышленностьПрофессиональное образование и высшие учебные заведенияХимияЭлектропромышленность, в т. Запрошенная дата доставки*В кратчайшие срокиВ течение 3-6 месяцевВ течение 6-12 месяцев Подпишитесь на рассылку новостей Этот сайт защищен reCAPTCHA, к нему применяются Политика конфиденциальности и Условия обслуживания Google. Спасибо! Мы получили ваш запрос и ценим ваш интерес! Наш торговый представитель свяжется с вами в течение 1 рабочего дня. Твердый карбонат кальция разлагается
при нагревании с образованием углекислого газа и твердого оксида кальция. Какой из перечисленных символических
уравнения с символами состояния описывает эту химическую реакцию? (A) Газ CaCO3 вступает в реакцию с образованием CaO
газ плюс CO2 твердый. (B) Твердое вещество CaCO3 реагирует с образованием CaO
твердое вещество плюс газ CO2. (C) Твердое вещество Ca2CO3 реагирует с образованием CaO
газ плюс угарный газ. (D) Реакция твердого вещества CaCO3 и газообразного O2
с образованием твердого CaO и газообразного CO2. (E) Реакция твердого CaCO3 и газообразного CO2
с образованием твердого CaO. Первое предложение в этом вопросе
является химическим утверждением. Химические формулы в символах
за уравнениями также могут следовать символы состояния. Буква s, l или g пишется
в круглых скобках, чтобы сказать, является ли вещество в реакции твердой жидкостью или
газ. При изучении вариантов ответа (D) и
(E), мы видим, что в левой части каждого уравнения используется знак плюс. Это говорит нам о том, что есть два
реагенты. Правильное символьное уравнение может
содержат только один реагент. Таким образом, мы можем устранить эти два
варианты ответов, потому что они содержат слишком много реагентов. Продолжим читать
химическое заявление. Давайте создадим базовое уравнение слова
используя названия реагентов и продуктов. Слева от стрелки реакции,
напишем карбонат кальция. И справа от реакции
стрелка, напишем углекислый газ плюс оксид кальция. Химическое утверждение говорит нам о
состояния двух видов, участвующих в реакции. И карбонат кальция, и кальций
оксид – это твердое вещество. И хотя он не включен
в химическом утверждении мы ожидаем, что углекислый газ будет газом. Перепишем наше основное слово
уравнение, используя правильные символы состояния. Наконец-то мы сможем
узнайте, что химическая формула углекислого газа – CO2. Давайте продолжим и заменим
слова «углекислый газ» с CO2 в нашем уравнении. Мы можем исключить выбор (A)
потому что символ штата рядом с карбонатом кальция и оксидом кальция должен быть
«s» для твердого тела. Кроме того, государственный символ рядом с CO2
должно быть «g» для газа. Вариант (А) не является правильным ответом
выбор, потому что символьное уравнение содержит неправильные символы состояния. Мы также можем исключить выбор ответа
(C) потому что символ состояния рядом с оксидом кальция должен быть «s» для твердого вещества, а не «g»
для газа. В дополнение к этому неправильному состоянию
означает, что химическая формула углекислого газа неверна. Остается только выбор ответа (B),
что является нашим правильным выбором ответа. Вариант ответа (В) правильный
символьное уравнение с символами состояния, которое соответствует химическому утверждению, представленному в
вопрос. Вопрос Обновлено: 26.04.2023 видео РЕКЛАМА লিখিত জবাব Подтверждено экспертами CaCO3(s)тепло−−→ CaO(s)+ CO2(g)Карбонат кальция Оксид кальцияДвуокись углерода 1 молекула 1 молекула 1 молекула 1 моль 1 моль 1 моль40+12+ 48=100г 40+ 16=56g 12+32=44g Был ли этот ответ полезен? 698 Аб Падхаи каро бина адс ке Khareedo DN Про и дехо сари видео бина киси объявление ки рукаават ке! সংশ্লিষ্ট ভিডিও Для реакции : CaCO_(3) (s) hArr CaO (s) + CO_(2) (g) 3070 7541 Карбонат кальция разлагается при нагревании по следующим уравнениям: CaCO_(3 )(s) Leftrightarrow CaO(s)+CO_(2)(g) Сколько молей CO_(2) получится при разложении 50 г CaCO_(3) ? 34507031 75 ग्राम CaCO3 को ग्राम करने पर उत्पन्न CO2 का Н.Т.П. पर आयतन व मात्रा ज्ञात करो । 142060462 Какая масса CaO получится при нагревании 3 молей CaCO3? [Атомная масса Ca=40] 203078763 CaCO3 реагирует с HCl с образованием CaCl2, CO2 и h3O. 233092353 Что такое количество тепла, необходимое для получения 128 г CaCO3 с использованием CaCO3 и последующим восстановлением углеродом. Реакции 328699379 Предсказать знак ΔS для реакции : 435647894 Напишите значение Kp и уравнение KC для CaCO3(s)⇔CaO(s)+CO2 (g) 508091020 Text Solution Назовите тип химической реакции, представленный следующими уравнениями: CaCO_(3)(s)overset(«Heat»)(to)CaO(s)+CO_(2)( ж) 571116073 Text Solution Назовите тип химической реакции, представленной следующими уравнениями: 571116167 Text Solution At 1000 K in 0,654 Сосуд L CaCO3(s) берется.
Работа с текстом в ворде 2019 практическая работа: Лабораторно-практическая работа «Выполнение работ в текстовом редакторе WORD»
Создание документа в Word — Служба поддержки Майкрософт
org/ListItem»>
org/ItemList»>
Практическая работа по информатике по теме «Работа с фрагментами текста»
 Отредактируйте предложенный текст. Расставьте пропущенные знаки препинания и замените, где требуется строчные буквы на прописные.
Отредактируйте предложенный текст. Расставьте пропущенные знаки препинания и замените, где требуется строчные буквы на прописные.  (Используйте клавиши Delete, Enter и Backspace).
(Используйте клавиши Delete, Enter и Backspace). 
Треугольник, отрезок, длина, квадрат, круг;
Дождь, снег, осадки, иней, град;
Запятая, точка, двоеточие, тире, союз;
Сложение, умножение, деление, слагаемое, вычитание;
Дуб, дерево, ольха, тополь, ясень;
Секунда, час, год, вечер, неделя;
Горький, горячий, кислый, соленый, сладкий;
Футбол, волейбол, хоккей, плавание, баскетбол. Измените фразу по указанию преподавателя: расставьте пробелы и знаки препинания таким образом, чтобы получилось как можно больше различных фраз.
Измените фразу по указанию преподавателя: расставьте пробелы и знаки препинания таким образом, чтобы получилось как можно больше различных фраз. 
Быстрые части: хорошие, плохие и альтернативные
Основы быстрых частей MS
 Для юристов организатор строительных блоков может быть настроен для хранения текста — предложений или даже абзаца — с неповрежденным форматированием и изображениями.
Для юристов организатор строительных блоков может быть настроен для хранения текста — предложений или даже абзаца — с неповрежденным форматированием и изображениями. dotx. Если вы хотите, чтобы текст или изображение были доступны для любого из ваших документов, сохраните его в Building Blocks.dotx. Если вы хотите, чтобы быстрые части сохранялись с определенным шаблоном, при сохранении быстрой части в файл шаблона (.dotx) вы заметите, что можете сохранить быстрые части только с этим шаблоном. Или вы можете сохранить Quick Parts в Normal.dotm. Быстрые части будут доступны только этому пользователю. Эти опции есть только в MS Word, единственная опция в MS Outlook — это «normalemail.dotm».
dotx. Если вы хотите, чтобы текст или изображение были доступны для любого из ваших документов, сохраните его в Building Blocks.dotx. Если вы хотите, чтобы быстрые части сохранялись с определенным шаблоном, при сохранении быстрой части в файл шаблона (.dotx) вы заметите, что можете сохранить быстрые части только с этим шаблоном. Или вы можете сохранить Quick Parts в Normal.dotm. Быстрые части будут доступны только этому пользователю. Эти опции есть только в MS Word, единственная опция в MS Outlook — это «normalemail.dotm». Вставка быстрой части в документ или сообщение электронной почты

Для редактирования существующей быстрой части
Ограничения Quick Parts
 dotx), то экспресс-блоки для этого шаблона станут доступны другим пользователям в MS Word. Полезно для общих шаблонов вашей команды на сервере или общем облачном диске. Однако имейте в виду, что если вы случайно поделитесь шаблоном (.dotx) с любым по электронной почте, они смогут увидеть все связанные быстрые части, независимо от того, откроют ли они его как шаблон или как документ. Вы не можете поделиться галереей стандартных блоков в MS Outlook без некоторых существенных настроек.
dotx), то экспресс-блоки для этого шаблона станут доступны другим пользователям в MS Word. Полезно для общих шаблонов вашей команды на сервере или общем облачном диске. Однако имейте в виду, что если вы случайно поделитесь шаблоном (.dotx) с любым по электронной почте, они смогут увидеть все связанные быстрые части, независимо от того, откроют ли они его как шаблон или как документ. Вы не можете поделиться галереей стандартных блоков в MS Outlook без некоторых существенных настроек. Альтернативы Quick Parts
 Litera Content Companion позволяет создать общую библиотеку содержимого для добавления в Word и другие документы. Content Companion также анонимизирует содержимое из предыдущих документов, чтобы вы случайно не получили конфиденциальную информацию
Litera Content Companion позволяет создать общую библиотеку содержимого для добавления в Word и другие документы. Content Companion также анонимизирует содержимое из предыдущих документов, чтобы вы случайно не получили конфиденциальную информацию Созданные для Microsoft 365, они имеют приложения для создания шаблонов, библиотеки предложений для MS Word и многое другое. Фирмы, вложившие средства в создание сложных шаблонов MS Word и желающие более эффективно создавать общие библиотеки контента и управлять ими, могут получить два инструмента — Uploader, который позволяет фирмам создавать (или выбирать) повторно используемый контент и делиться им в MS SharePoint, чтобы контент доступен в разных местах, на разных устройствах и платформах. С помощью средства выбора содержимого вы можете вставлять содержимое из общей библиотеки предложений в любом месте. По цене $ 1,69за пользователя в месяц и 2,69 долл. США за пользователя в месяц соответственно, эти сложные, но легкие инструменты улучшают и расширяют возможности пакета Microsoft.
Созданные для Microsoft 365, они имеют приложения для создания шаблонов, библиотеки предложений для MS Word и многое другое. Фирмы, вложившие средства в создание сложных шаблонов MS Word и желающие более эффективно создавать общие библиотеки контента и управлять ими, могут получить два инструмента — Uploader, который позволяет фирмам создавать (или выбирать) повторно используемый контент и делиться им в MS SharePoint, чтобы контент доступен в разных местах, на разных устройствах и платформах. С помощью средства выбора содержимого вы можете вставлять содержимое из общей библиотеки предложений в любом месте. По цене $ 1,69за пользователя в месяц и 2,69 долл. США за пользователя в месяц соответственно, эти сложные, но легкие инструменты улучшают и расширяют возможности пакета Microsoft. Заключение

Ворд 2019Онлайн-класс Essential Training
Предварительный просмотр Детали курса
 Этот курс охватывает множество тем, включая использование шаблонов и стандартных блоков для создания стильного документа с мгновенной целью; создание нумерованных и маркированных списков; работа со столбцами и таблицами; добавление изображений и фигур в ваши документы; совместная работа над документами с вашей командой; и обмен документами через OneDrive, электронную почту и другие средства. Кроме того, узнайте, как использовать средства проверки правописания в Word для проверки орфографии и грамматики, подсчета слов и т. д.
Этот курс охватывает множество тем, включая использование шаблонов и стандартных блоков для создания стильного документа с мгновенной целью; создание нумерованных и маркированных списков; работа со столбцами и таблицами; добавление изображений и фигур в ваши документы; совместная работа над документами с вашей командой; и обмен документами через OneDrive, электронную почту и другие средства. Кроме того, узнайте, как использовать средства проверки правописания в Word для проверки орфографии и грамматики, подсчета слов и т. д. Навыки, которые вы приобретете
Получите общий сертификат

Познакомьтесь с инструктором
Отзывы учащихся
 Оценки и обзоры могут быть отправлены только тогда, когда неанонимные учащиеся завершат не менее 40% курса. Это помогает нам избежать поддельных отзывов и спама.
Оценки и обзоры могут быть отправлены только тогда, когда неанонимные учащиеся завершат не менее 40% курса. Это помогает нам избежать поддельных отзывов и спама.
Эжил Арасан BE, C. Eng, PMP, RMP, CCMp
Eng, PMP, RMP, CCMp Эжил Арасан BE, C.Eng, PMP, RMP, CCMp
Специалист по управлению проектами ищет сложные проекты
Панкадж Кумар Ядав Панкадж Кумар Ядав
Стажер в AlmaBetter | 🌟 Студент | Эксель | Питон | SQL | Таблица | PowerBI | Машинное обучение | Специалист по данным
Карен Гивенс Карен Гивенс
Старший зарегистрированный консультант по виртуальным отделениям

Делители 130: Запишите все делители числа 130 и 189
делители, простота, двоичный вид, куб, квадрат
Четность:
Сумма цифр:
4
Произведение цифр:
0
Количество цифр:
3
Все делители числа
1
2
5
10
13
26
65
130
Количество делителей
8
Сумма делителей
252
Простое число
Квадратный корень
11,4017542509914
Кубический корень
5,06579701910089
Квадрат
16900
Куб
2197000
Обратное число
0,00769230769230769
Предыдущее число:
129
Следующее число:
131
 Оно записывается 3 цифрами.
Сумма цифр, из которых состоит число 130, равна 4, а их произведение равно 0.
Число 130 является четным.
Всего число 130 имеет 8 делителей:
1,
2,
5,
10,
13,
26,
65,
130,
. Сумма делителей равна 252. Куб числа 130 равен 16900, а квадрат составляет 2197000.
Квадратный корень рассматриваемого числа равен 11,4017542509914. Кубический корень равен 5,06579701910089.
Число, которое является обратным к числу 130, выглядит как 0,00769230769230769.
Оно записывается 3 цифрами.
Сумма цифр, из которых состоит число 130, равна 4, а их произведение равно 0.
Число 130 является четным.
Всего число 130 имеет 8 делителей:
1,
2,
5,
10,
13,
26,
65,
130,
. Сумма делителей равна 252. Куб числа 130 равен 16900, а квадрат составляет 2197000.
Квадратный корень рассматриваемого числа равен 11,4017542509914. Кубический корень равен 5,06579701910089.
Число, которое является обратным к числу 130, выглядит как 0,00769230769230769.
делители, простота, двоичный вид, куб, квадрат
Четность:

Сумма цифр:
9
Произведение цифр:
20
Количество цифр:
3
Все делители числа
1
2
3
4
6
7
9
12
14
18
21
28
36
42
63
84
126
252
Количество делителей
18
Сумма делителей
728
Простое число
Квадратный корень
15,8745078663875
Кубический корень
6,31635959765638
Квадрат
63504
Куб
16003008
Обратное число
0,00396825396825397
Предыдущее число:
251
Следующее число:
253
 Оно записывается 3 цифрами.
Сумма цифр, из которых состоит число 252, равна 9, а их произведение равно 20.
Число 252 является четным.
Всего число 252 имеет 18 делителей:
1,
2,
3,
4,
6,
7,
9,
12,
14,
18,
21,
28,
36,
42,
63,
84,
126,
252,
. Сумма делителей равна 728. Куб числа 252 равен 63504, а квадрат составляет 16003008.
Квадратный корень рассматриваемого числа равен 15,8745078663875. Кубический корень равен 6,31635959765638.
Число, которое является обратным к числу 252, выглядит как 0,00396825396825397.
Оно записывается 3 цифрами.
Сумма цифр, из которых состоит число 252, равна 9, а их произведение равно 20.
Число 252 является четным.
Всего число 252 имеет 18 делителей:
1,
2,
3,
4,
6,
7,
9,
12,
14,
18,
21,
28,
36,
42,
63,
84,
126,
252,
. Сумма делителей равна 728. Куб числа 252 равен 63504, а квадрат составляет 16003008.
Квадратный корень рассматриваемого числа равен 15,8745078663875. Кубический корень равен 6,31635959765638.
Число, которое является обратным к числу 252, выглядит как 0,00396825396825397.
AKRO-MILS 40-130 — Разделитель типа Разделитель бункера для хранения
Торговая марка АКРО-МИЛС Тип Разделители Ширина 6-2/25″ Глубина 4/25″ Высота 2-91/100″ Цвет Черный Материал Полимеры промышленного класса Для использования с 36462 Индикаторная ячейка Размеры 11-5/8″ Ш x 6-5/8″ Г x 4″ В Модель № 40-130 Количество штук в упаковке of Pieces in Pack»> 24 Кол-во в упаковке 24 Стойка 65 Да Вес 0,08 фунта. Страна происхождения СОЕДИНЕННЫЕ ШТАТЫ АМЕРИКИ Преимущества
Особенности
Делитель ST 130 — Делительные головки
Делитель ST 130 — Делительные головки — KNUTH Нужна помощь в поиске машины?
Сервис KNUTH
 Благодаря нашим комплексным планам обслуживания, обучения и установки вы всегда будете получать максимально возможную производительность от своих машин KNUTH.
Благодаря нашим комплексным планам обслуживания, обучения и установки вы всегда будете получать максимально возможную производительность от своих машин KNUTH. Посмотреть машины KNUTH в действии
 ч. полупроводники и системы хранения энергииЭнергетика и коммунальные услуги, такие как коммунальные услуги, электростанции и т.д. производство грузовиков и мотоцикловПищевая промышленностьАэрокосмическая промышленностьМашиностроениеМеталлостроительство и слесарное делоМеталлургия — производство и переработка сталиВоенная промышленностьЖелезнодорожное строительствоСудостроениеТехнологии резки и субподрядСтроительство спецтехники, в т.ч. машины для сельского и лесного хозяйстваГосударственные, общественные и религиозные учрежденияКамнеобработкаИнструментальное производствоМеханизация и субподрядДругоеРазмер станочного хозяйствадо 5 станков>5 станков>10 станков
ч. полупроводники и системы хранения энергииЭнергетика и коммунальные услуги, такие как коммунальные услуги, электростанции и т.д. производство грузовиков и мотоцикловПищевая промышленностьАэрокосмическая промышленностьМашиностроениеМеталлостроительство и слесарное делоМеталлургия — производство и переработка сталиВоенная промышленностьЖелезнодорожное строительствоСудостроениеТехнологии резки и субподрядСтроительство спецтехники, в т.ч. машины для сельского и лесного хозяйстваГосударственные, общественные и религиозные учрежденияКамнеобработкаИнструментальное производствоМеханизация и субподрядДругоеРазмер станочного хозяйствадо 5 станков>5 станков>10 станков
Co2 cao уравнение: ионные уравнения CaO + CO2 = CaCO3
Видео с вопросами: Определение химического уравнения с символами состояний, которое соответствует химическому утверждению
Стенограмма видео
 Химическое утверждение описывает
химическая реакция словами. С другой стороны, ответ
выборы являются символическими уравнениями. Символьные уравнения, также известные как
химические уравнения, используйте химические символы для обозначения реакции. Например, мы видим CaCO3 в
несколько вариантов ответа. Ca — это химический символ,
представляет собой элемент кальция. C — химический символ, который
представляет собой углерод. А О — это химический символ, который
представляет собой кислород. Три — это индекс, который говорит
нам, сколько определенного типа атома присутствует. В целом, CaCO3 является химическим
формула.
Химическое утверждение описывает
химическая реакция словами. С другой стороны, ответ
выборы являются символическими уравнениями. Символьные уравнения, также известные как
химические уравнения, используйте химические символы для обозначения реакции. Например, мы видим CaCO3 в
несколько вариантов ответа. Ca — это химический символ,
представляет собой элемент кальция. C — химический символ, который
представляет собой углерод. А О — это химический символ, который
представляет собой кислород. Три — это индекс, который говорит
нам, сколько определенного типа атома присутствует. В целом, CaCO3 является химическим
формула.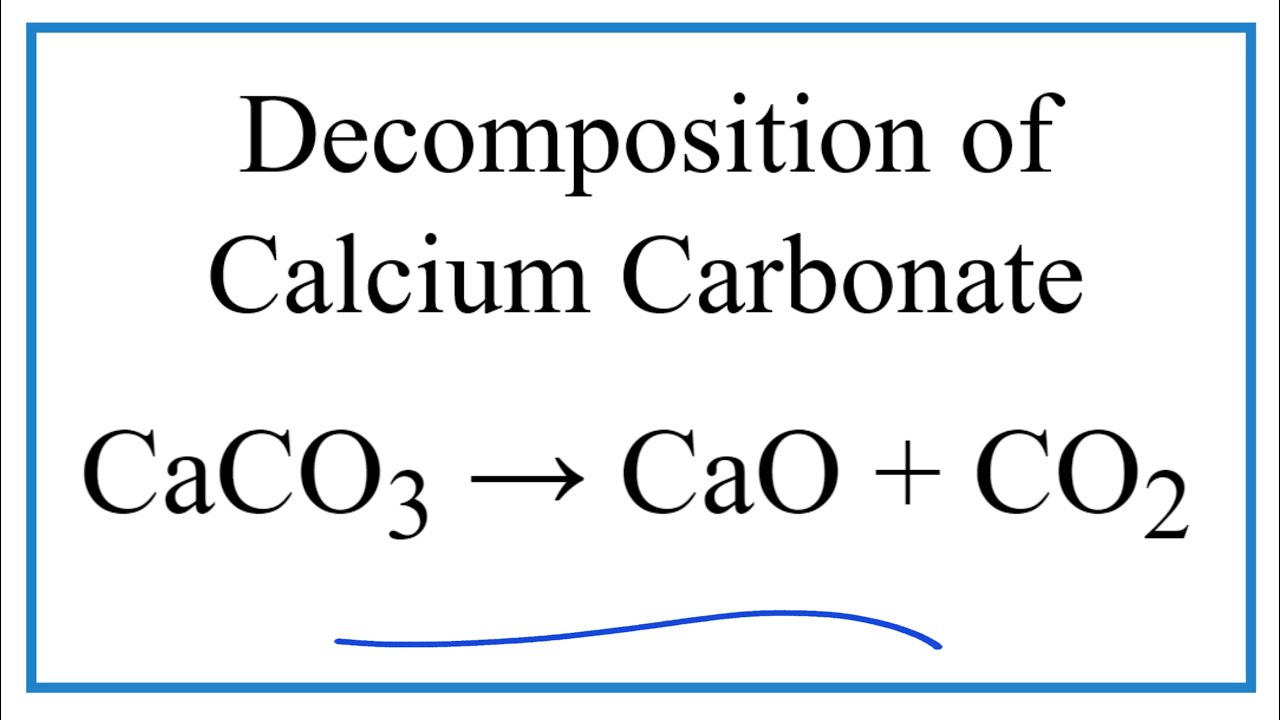 Наша задача ответить на этот вопрос
состоит в том, чтобы взять представленную химическую формулировку и перевести ее в правильную символическую форму.
уравнение. В предоставленном химическом заявлении,
мы можем определить слово «разлагает» как ключевое слово. Химические виды, появляющиеся на
слева от ключевого слова находятся реагенты химической реакции. Только один вид, кальций
карбонат, появляется слева от ключевого слова. Это означает, что химический
реакция имеет только один реагент.
Наша задача ответить на этот вопрос
состоит в том, чтобы взять представленную химическую формулировку и перевести ее в правильную символическую форму.
уравнение. В предоставленном химическом заявлении,
мы можем определить слово «разлагает» как ключевое слово. Химические виды, появляющиеся на
слева от ключевого слова находятся реагенты химической реакции. Только один вид, кальций
карбонат, появляется слева от ключевого слова. Это означает, что химический
реакция имеет только один реагент. «Производство» — еще одно ключевое слово.
что свидетельствует о том, что реагент образует продукты. Справа от этого ключевого слова мы
может найти слова, которые представляют продукты. Углекислый газ и твердый кальций
оксида разделены словом «и», что означает наличие двух разных
продукты, образующиеся в результате реакции.
«Производство» — еще одно ключевое слово.
что свидетельствует о том, что реагент образует продукты. Справа от этого ключевого слова мы
может найти слова, которые представляют продукты. Углекислый газ и твердый кальций
оксида разделены словом «и», что означает наличие двух разных
продукты, образующиеся в результате реакции. После карбоната кальция и кальция
оксид, мы напишем «s» внутри скобок. И после углекислого газа мы
напишите букву «г» внутри скобок.
После карбоната кальция и кальция
оксид, мы напишем «s» внутри скобок. И после углекислого газа мы
напишите букву «г» внутри скобок. В этом уравнении записывается как
CO — химическая формула угарного газа.
В этом уравнении записывается как
CO — химическая формула угарного газа. атомная масса Ca = 40, C = 12, O = 16)
Информация, собранная из приведенных данных, может быть резюмирована следующим образом:
(i) Карбонат кальция, также называемый известняком, при нагревании разлагается с образованием оксида кальция и диоксида углерода.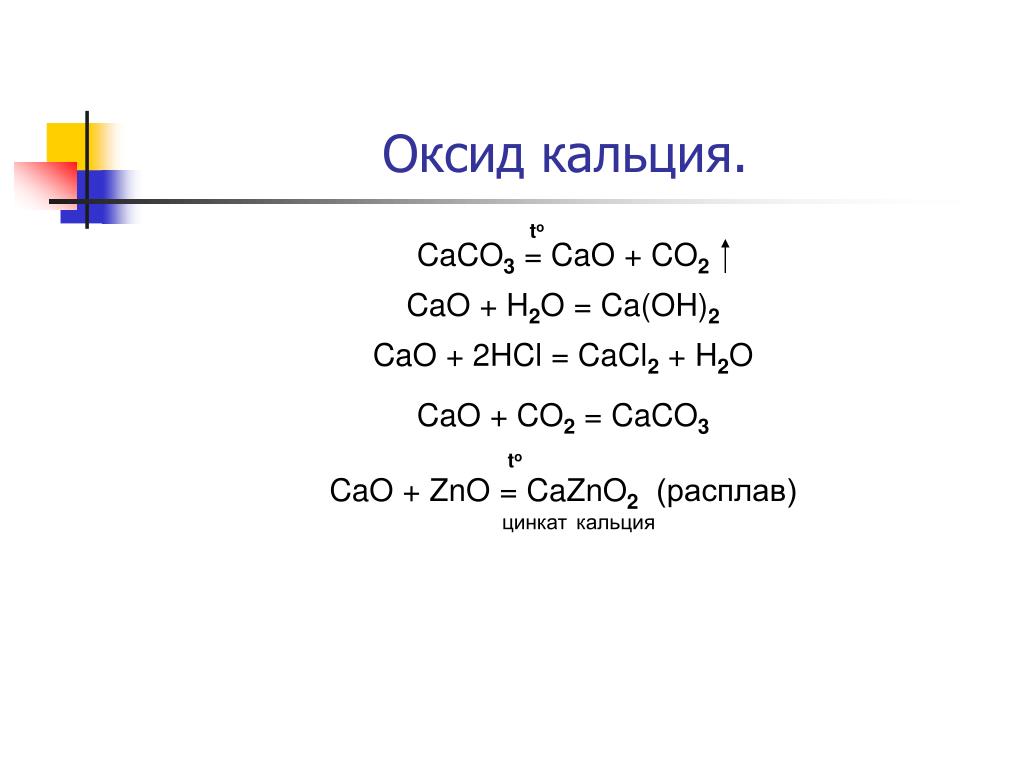
(ii) С точки зрения символьного уравнения, CaCO3(s) разлагается с образованием CaO(s) и CO2g.
(iii) 1 молекула CaCO3 распадается на 1 молекулу CaO и 1 молекулу CO2.
(iv) 1 моль CaCO3 разлагается на 1 моль CaO и 1 моль CO2.
(v) 100 г CaCO3 разлагаются на 56 г CaO и 44 г CO2.
(दिया है : Ca=40,C=12,O=16) Приблизительная масса (в г) CaCO3, необходимая для полной реакции с 25 мл 0,75 М HCl, составляет (атомная масса Ca=40, C=12O=16, Cl=35,5 и H=1)
Приблизительная масса (в г) CaCO3, необходимая для полной реакции с 25 мл 0,75 М HCl, составляет (атомная масса Ca=40, C=12O=16, Cl=35,5 и H=1)
CaCO3(т)=CaO(т)+CO2(г),ΔH∘=42,8 ккал
CaO(т)+3C(т)=CaC2+CO(г),ΔH∘=111 ккал
CaCO3(s)Δ−−→CaO(s)+CO2(g)
CaCO3(s)Heat—→CaO(s)+CO2(g)
Минус синус пи на 2: Mathway | Популярные задачи
| 1 | Найти производную — d/dx | бревно натуральное х | |
| 2 | Оценить интеграл | интеграл натурального логарифма x относительно x | |
| 3 | Найти производную — d/dx | 92)||
| 21 | Оценить интеграл | интеграл от 0 до 1 кубического корня из 1+7x относительно x | |
| 22 | Найти производную — d/dx | грех(2x) | |
| 23 | Найти производную — d/dx | 9(3x) по отношению к x||
| 41 | Оценить интеграл | интеграл от cos(2x) относительно x | |
| 42 | Найти производную — d/dx | 1/(корень квадратный из х) | |
| 43 | Оценка интеграла 9бесконечность | ||
| 45 | Найти производную — d/dx | х/2 | |
| 46 | Найти производную — d/dx | -cos(x) | |
| 47 | Найти производную — d/dx | грех(3x) | 92+1|
| 68 | Оценить интеграл | интеграл от sin(x) по x | |
| 69 | Найти производную — d/dx | угловой синус(х) | |
| 70 | Оценить предел | ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х | |
| 85 | Найти производную — d/dx | лог х | |
| 86 | Найти производную — d/dx | арктан(х) | |
| 87 | Найти производную — d/dx | бревно натуральное 5х92 |
я правда не понимаю помогите пожалуйста
Предварительное исчисление
Эшли Г.
Найдите точное значение арктангенса (sin (PI/2)). Для полной оценки объясните свои рассуждения.
Подписаться І 1
Подробнее
Отчет
2 ответа от опытных наставников
Лучший Новейшие Самый старыйАвтор: ЛучшиеНовыеСамыеСтарые
Шервуд П. ответил 18.09.20
Репетитор
4.9 (83)
Наставник пациента и Clear Precalculus Tutor
Об этом репетиторе ›
Об этом репетиторе ›
Постановка задачи: найти точное значение arctan(sin(PI/2)).
Во-первых, обратите внимание, что угол Pi/2 выражен в единицах радиан , а не в градусах. 2*пи радиан = 360 градусов.
Пи/2 радиан = 90 градусов.
Во-вторых, просмотрите определение функций f(u) = sin(u) и g(v) = arctan(v). Я использую u и v в качестве имен переменных, чтобы их не путали с координатами x и y в декартовой системе координат.
sin(u) = длина стороны прямоугольного треугольника, противоположной углу u, где 1 — длина гипотенузы этого прямоугольного треугольника. Для углов u > 90 градусов, но менее 270 градусов, sin(u) будет отрицательным. Для углов u > 270 градусов, но меньше 360 градусов, u будет положительным.
Это связано с тем, что гипотенуза прямоугольного треугольника, используемая для вычисления sin(u), описывает единичную окружность, идущую против часовой стрелки вокруг начала декартовой системы координат. Точки (x,y) на этой единичной окружности = (cos(u),sin(u)). Угол u измеряется против часовой стрелки, начиная с 0 для положительной оси x.
Когда u = Pi/2, точка (x,y) на единичной окружности = (0,1). Итак, sin(Pi/2) = sin(90 градусов) = 1,
arctan(v) = размер угла g в прямоугольном треугольнике, где отношение длины стороны, противоположной углу g (эта длина = координата y точки на единице окружность для угла g) разделить на длину стороны, примыкающей к углу g (= координата x этой точки на единичной окружности) = v. Поскольку на единичной окружности есть две точки, которые могут иметь одинаковое отношение y/x диапазон функции arctan(v) ограничен значением -Pi/2 < arctan(v) < Pi/2.
Поскольку на единичной окружности есть две точки, которые могут иметь одинаковое отношение y/x диапазон функции arctan(v) ограничен значением -Pi/2 < arctan(v) < Pi/2.
Когда v =1, это означает, что y/x = 1 для координат (x,y) на единичной окружности. Это происходит в точке (sqrt(2)/2,sqrt(2)/2) . Обратите внимание, что (- sqrt(2)/2,-sqrt(2)/2) выходит за допустимые пределы.
Угол g(1) = arctg(1) = arctg(sin(Pi/2)) = 45 градусов = Pi/4
Голосовать за 0 Понизить
Подробнее
Отчет
Дуг В. ответил 09/18/20
Репетитор
Новое в Византе
Репетитор по математике в старших классах
Смотрите таких репетиторов
Смотрите таких репетиторов
Привет, Эшли.
Чтобы найти значение arctan(sin(pi/2)), необходимо вычислить две функции: сначала найти значение sin(pi/2), а затем найти значение arctan(x), где x значение sin(pi/2).
Я не уверен, насколько хорошо вы изучили тригонометрию до этого момента, но я буду основывать свое объяснение на использовании углов вращения и единичной окружности. Когда конечная сторона угла пересекает единичную окружность в точке (x, y), то x — косинус угла, а y — синус угла. (Кроме того, отношение y/x является тангенсом угла.) Поскольку pi/2 представляет собой угол поворота, конечная сторона которого проходит через точку (0, 1) на единичной окружности, координата y этой точки равна значение греха (пи/2). Итак, sin(pi/2) = 1,
Теперь вам нужно определить, что такое arctan(1). «Arctan» — это слово, используемое для описания функции арктангенса. Функция arctan принимает действительное число в качестве входных данных и выводит угол поворота, для которого тангенс этого угла является действительным числом.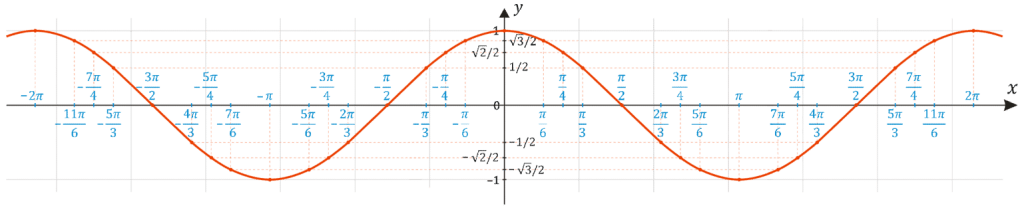 (Обратите внимание, что поскольку функция тангенса является периодической, существует бесконечно много углов, имеющих одно и то же значение тангенса. Однако, если мы ограничимся углами между -pi/2 и pi/2, будет только один угол, который имеет конкретное значение тангенса .) В этом случае вы находите угол поворота между -pi/2 и pi/2 со значением касательной, равным 1. Это происходит в точке на единичной окружности, где координаты x и y равны. . Это точка в первом квадранте, где прямая y = x пересекает единичный круг, и координаты этой точки равны (sqrt(2)/2, sqrt(2)/2). Угол поворота между -pi/2 и pi/2, связанный с этой точкой, равен pi/4.
(Обратите внимание, что поскольку функция тангенса является периодической, существует бесконечно много углов, имеющих одно и то же значение тангенса. Однако, если мы ограничимся углами между -pi/2 и pi/2, будет только один угол, который имеет конкретное значение тангенса .) В этом случае вы находите угол поворота между -pi/2 и pi/2 со значением касательной, равным 1. Это происходит в точке на единичной окружности, где координаты x и y равны. . Это точка в первом квадранте, где прямая y = x пересекает единичный круг, и координаты этой точки равны (sqrt(2)/2, sqrt(2)/2). Угол поворота между -pi/2 и pi/2, связанный с этой точкой, равен pi/4.
Итак, arctan(sin(pi/2)) = pi/4.
Дуг
Голосовать за 0 Понизить
Подробнее
Отчет
Все еще ищете помощи? Получите правильный ответ, быстро.
Задайте вопрос бесплатно
Получите бесплатный ответ на быстрый вопрос.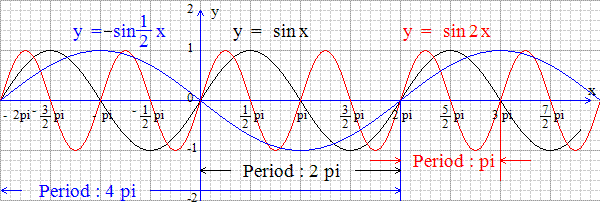






 5),
5),




 Геометрические формы определяются с использованием системы координат и алгебраических принципов. Некоторый
считать введение аналитической геометрии, также называемой координатной или декартовой геометрией, началом
современной математики.
Геометрические формы определяются с использованием системы координат и алгебраических принципов. Некоторый
считать введение аналитической геометрии, также называемой координатной или декартовой геометрией, началом
современной математики. Например, точка \((\text{5,5},5)\) неоднозначна. Это
Значение \(x\) \(\text{5,5}\) или значение \(y\) \(\text{5,5}\)?
Например, точка \((\text{5,5},5)\) неоднозначна. Это
Значение \(x\) \(\text{5,5}\) или значение \(y\) \(\text{5,5}\)?
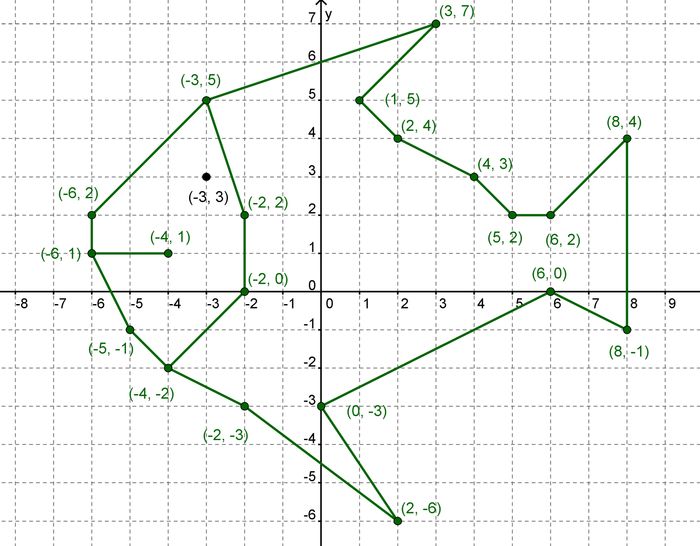

 Кратчайшее расстояние между двумя точками равно
старая добрая линия, и здесь мы начнем с двух
точек на этой миллиметровке.
Кратчайшее расстояние между двумя точками равно
старая добрая линия, и здесь мы начнем с двух
точек на этой миллиметровке. Кроме того, мы уточняем
некоторые аргументы в пользу того, как должна быть проведена эта линия из точки А
(1,0) в точку B (4,5). Если вы думаете об этой строке кода как о
предложение, функция — это глагол, а аргументы — это
объекты предложения. Кодовое предложение также заканчивается
точка с запятой вместо точки.
Кроме того, мы уточняем
некоторые аргументы в пользу того, как должна быть проведена эта линия из точки А
(1,0) в точку B (4,5). Если вы думаете об этой строке кода как о
предложение, функция — это глагол, а аргументы — это
объекты предложения. Кодовое предложение также заканчивается
точка с запятой вместо точки.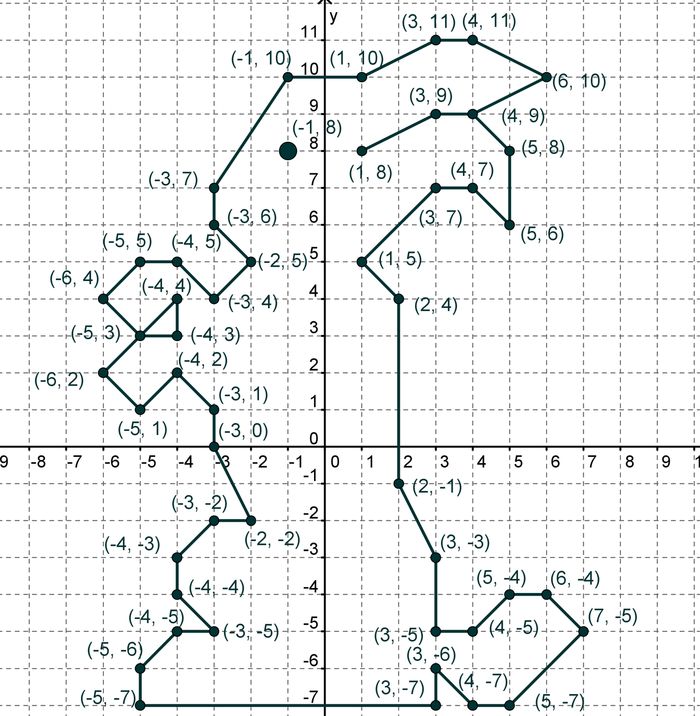 (0,0) можно найти в левом верхнем углу
с положительным направлением вправо по горизонтали и вниз
вертикально.
(0,0) можно найти в левом верхнем углу
с положительным направлением вправо по горизонтали и вниз
вертикально.
 Фактически он идентичен rect() с той разницей, что эллипс рисуется там, где
ограничивающая рамка прямоугольника будет. Режим по умолчанию для ellipse() — это «ЦЕНТР», а не «УГОЛ».
Фактически он идентичен rect() с той разницей, что эллипс рисуется там, где
ограничивающая рамка прямоугольника будет. Режим по умолчанию для ellipse() — это «ЦЕНТР», а не «УГОЛ».


 Даля 166
Даля 166 Дегтярева 174
Дегтярева 174 Макарова 543
Макарова 543 Герцена 123
Герцена 123 Гагарина 114
Гагарина 114 Каразина 305
Каразина 305 Примеры вычисления определителей.
Примеры вычисления определителей. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса.
Free xml sitemap generator
Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса.
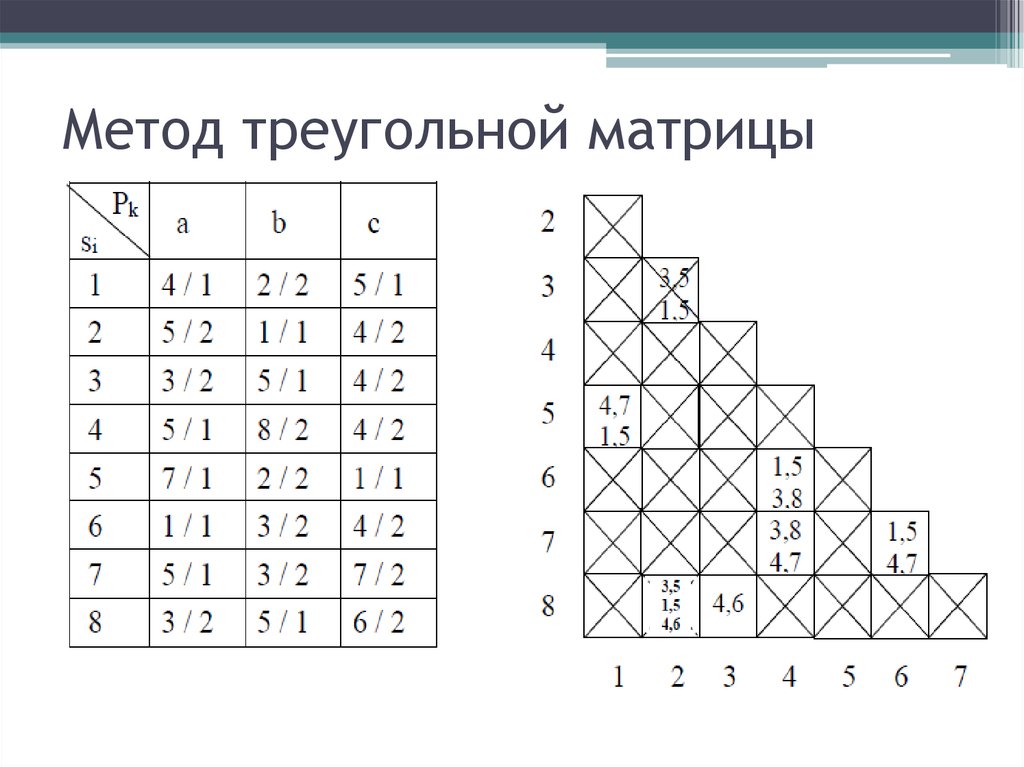
Free xml sitemap generator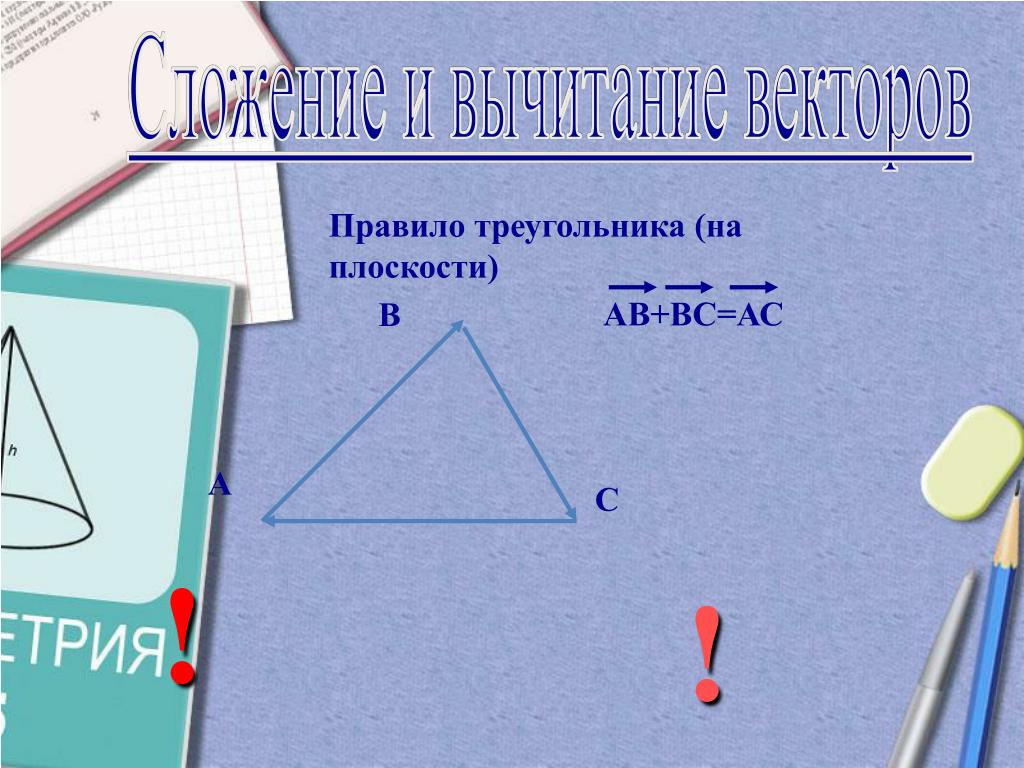 Верхняя треугольная матрица — это квадратная матрица, все элементы которой ниже главной диагонали равны нулю. Нижняя треугольная матрица — это квадратная матрица, все элементы которой выше главной диагонали равны нулю. Матрицы на изображении, приведенном ниже, являются верхней треугольной и нижней треугольной матрицами порядка «4 × 4».
Верхняя треугольная матрица — это квадратная матрица, все элементы которой ниже главной диагонали равны нулю. Нижняя треугольная матрица — это квадратная матрица, все элементы которой выше главной диагонали равны нулю. Матрицы на изображении, приведенном ниже, являются верхней треугольной и нижней треугольной матрицами порядка «4 × 4».

 Квадратная матрица «A = [a ij ]» называется нижней треугольной матрицей, если a ij = 0 для всех i < j.
Квадратная матрица «A = [a ij ]» называется нижней треугольной матрицей, если a ij = 0 для всех i < j. , а транспонированием нижней треугольной матрицы является верхняя треугольная матрица, т. е. L T = U.
, а транспонированием нижней треугольной матрицы является верхняя треугольная матрица, т. е. L T = U.
 Докажите, что транспонирование верхней треугольной матрицы является нижней треугольной матрицей.
Докажите, что транспонирование верхней треугольной матрицы является нижней треугольной матрицей. 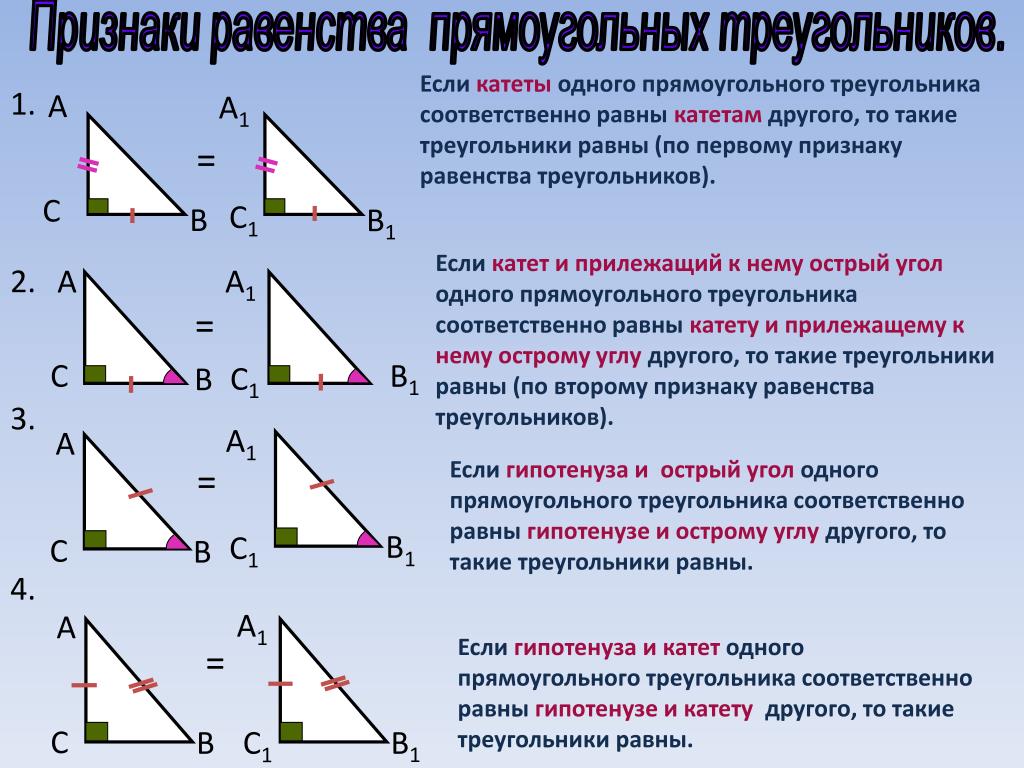

 Предположим, что есть две матрицы, отображающие оценки, выставленные двумя судьями двум участникам конкурса пения и рисунка.
Предположим, что есть две матрицы, отображающие оценки, выставленные двумя судьями двум участникам конкурса пения и рисунка.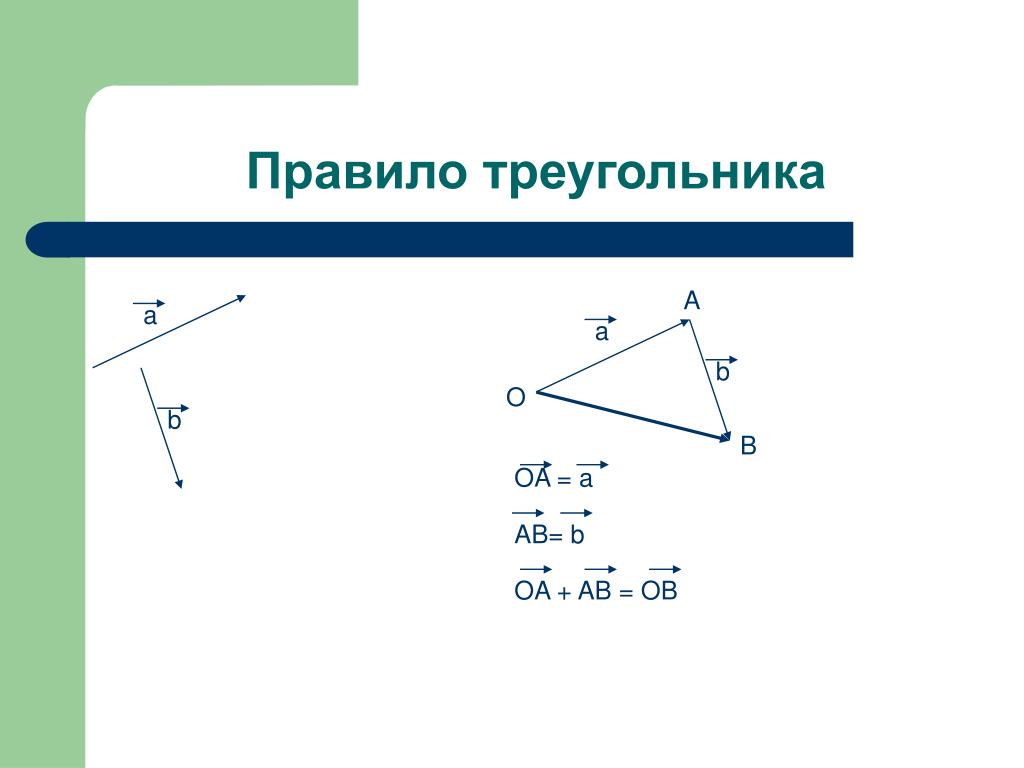 Чтобы сложить соответствующие элементы двух матриц, мы сразу видим, что порядки матриц должны совпадать. Например, мы не можем сложить матрицу порядка 2×3 с другой матрицей порядка 3×2.
Чтобы сложить соответствующие элементы двух матриц, мы сразу видим, что порядки матриц должны совпадать. Например, мы не можем сложить матрицу порядка 2×3 с другой матрицей порядка 3×2. Под этим понимается C(1, 1) = A(1, 1) + B(1, 1) = a + e, C(1, 2) = A(1, 2) + B(1, 2) = б + ж и так далее. Поэтому у нас
Под этим понимается C(1, 1) = A(1, 1) + B(1, 1) = a + e, C(1, 2) = A(1, 2) + B(1, 2) = б + ж и так далее. Поэтому у нас Вычитание этих матриц C = A – B дает матрицу порядка 2×2. Его элементы можно получить, вычитая соответствующие элементы этих двух матриц. Под этим понимается C(1, 1) = A(1, 1) – B(1, 1) = i – m, C(1, 2) = A(1, 2) – B(1, 2) = j-n и так далее.
Вычитание этих матриц C = A – B дает матрицу порядка 2×2. Его элементы можно получить, вычитая соответствующие элементы этих двух матриц. Под этим понимается C(1, 1) = A(1, 1) – B(1, 1) = i – m, C(1, 2) = A(1, 2) – B(1, 2) = j-n и так далее.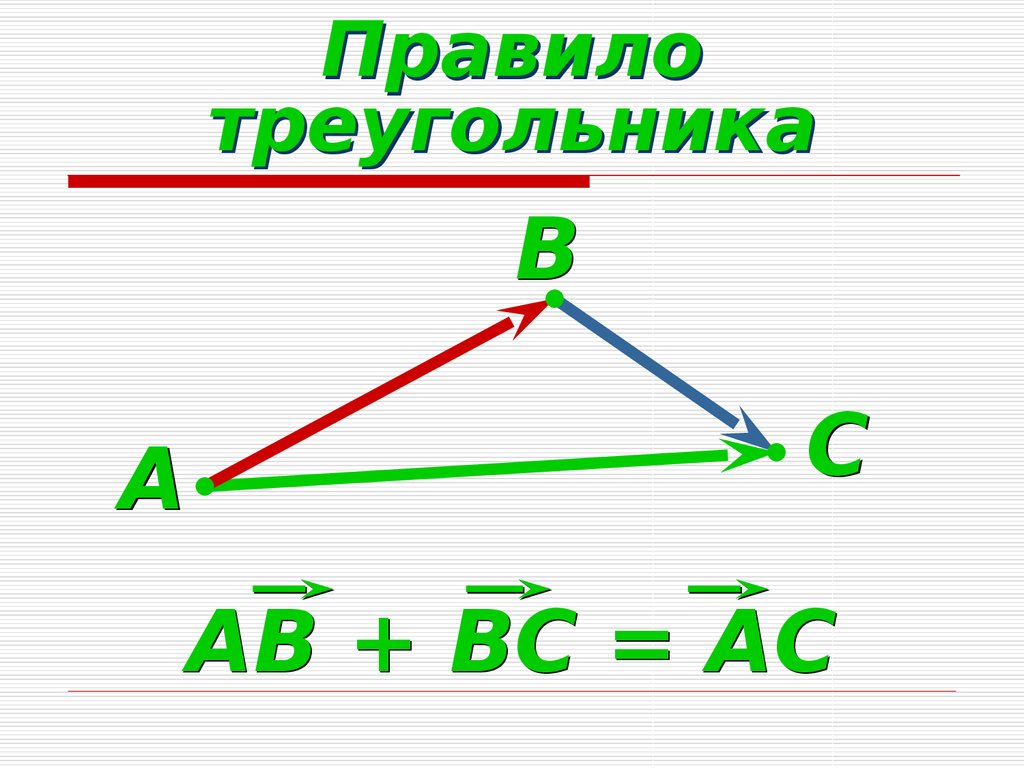 Вычитание двух матриц не является коммутативным, то есть A-B≠B-A.
Вычитание двух матриц не является коммутативным, то есть A-B≠B-A. Следовательно, мы видим A-(B-C)≠(A-B)-C.
Следовательно, мы видим A-(B-C)≠(A-B)-C.
 Если ты всё сделал правильно, то получил в результате 7. Скобок в этом примере нет, но всё равно можно было запутаться в порядке выполнения. Умножение, деление и остальные действия по порядку — так нужно было считать.
Если ты всё сделал правильно, то получил в результате 7. Скобок в этом примере нет, но всё равно можно было запутаться в порядке выполнения. Умножение, деление и остальные действия по порядку — так нужно было считать. Являясь мощнейшим средством успешного разрешения практически любых задач научно-прикладного характера, математика одновременно представляет собой универсальный язык науки, а значит, и важнейшую составляющую общемировой культуры. Вот почему одна из важнейших целей ее изучения заключается в повышении общего кругозора, культуры мышления, формировании естественнонаучного мировоззрения.
Являясь мощнейшим средством успешного разрешения практически любых задач научно-прикладного характера, математика одновременно представляет собой универсальный язык науки, а значит, и важнейшую составляющую общемировой культуры. Вот почему одна из важнейших целей ее изучения заключается в повышении общего кругозора, культуры мышления, формировании естественнонаучного мировоззрения. Она не терпит спекуляций и произвола в толковании различных закономерностей, их логическом обосновании. Она – само воплощение жесткой логики и упорядоченности, взаимозависимости происходящих в окружающем мире событий и явлений. Помогая людям в постижении мира, она позволяет им все больше узнавать о законах его развития, поскольку абсолютно все законы имеют математическое выражение, подчиняясь царящему в математике порядку.
Она не терпит спекуляций и произвола в толковании различных закономерностей, их логическом обосновании. Она – само воплощение жесткой логики и упорядоченности, взаимозависимости происходящих в окружающем мире событий и явлений. Помогая людям в постижении мира, она позволяет им все больше узнавать о законах его развития, поскольку абсолютно все законы имеют математическое выражение, подчиняясь царящему в математике порядку. За примерами здесь далеко ходить не надо: давайте вспомним хотя бы о том, что на протяжении всей жизни, с младенчества и до глубокой старости мы постоянно осуществляем подсчет тех или иных величин, планируя, например, дату получения подарка от родителей, семейный бюджет или рассчитывая протяжённость пути в сопоставлении со временем и скоростью передвижения, площадь жилых объектов, объём полезного пространства – этот перечень при желании можно было бы продолжить до бесконечности.
За примерами здесь далеко ходить не надо: давайте вспомним хотя бы о том, что на протяжении всей жизни, с младенчества и до глубокой старости мы постоянно осуществляем подсчет тех или иных величин, планируя, например, дату получения подарка от родителей, семейный бюджет или рассчитывая протяжённость пути в сопоставлении со временем и скоростью передвижения, площадь жилых объектов, объём полезного пространства – этот перечень при желании можно было бы продолжить до бесконечности. Прогресс в различных сферах научного познания и практической деятельности был бы попросту невозможен без использования достижений современной математики, ее развитого вычислительного и логического аппарата.
Прогресс в различных сферах научного познания и практической деятельности был бы попросту невозможен без использования достижений современной математики, ее развитого вычислительного и логического аппарата. К счастью, эти легко запоминающиеся математические трюки станут вашими лучшими друзьями в следующий раз, когда вы столкнетесь с непростым уравнением, а калькулятора под рукой нет. Кроме того, не пропустите эти уроки математики, которые вы действительно будете использовать в реальной жизни.
К счастью, эти легко запоминающиеся математические трюки станут вашими лучшими друзьями в следующий раз, когда вы столкнетесь с непростым уравнением, а калькулятора под рукой нет. Кроме того, не пропустите эти уроки математики, которые вы действительно будете использовать в реальной жизни. hmc.edu очень просто. Просто сложите две цифры вместе и поместите сумму в середину. Например, если вы умножаете 25 на 11, сложите два и пять вместе, чтобы получить семь, и поместите семерку между этими двумя числами, чтобы получить окончательный ответ, который равен 275.
hmc.edu очень просто. Просто сложите две цифры вместе и поместите сумму в середину. Например, если вы умножаете 25 на 11, сложите два и пять вместе, чтобы получить семь, и поместите семерку между этими двумя числами, чтобы получить окончательный ответ, который равен 275.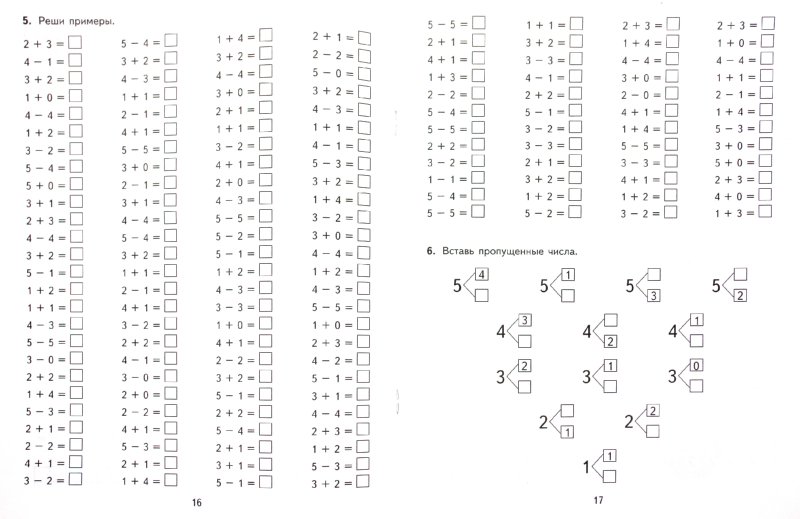 В соответствии с education.cu-portland.edu, просто исключите нули из уравнения, а затем добавьте их обратно. Например, если вы умножаете 600 на 400, исключите нули и решите шесть раз по четыре, что равно 24. После этого подсчитайте общее количество нулей, которые были в исходном уравнении, и прикрепите их к числу, которое вы решили, чтобы найти свой окончательный ответ. Поскольку в исходном уравнении было четыре нуля, ваш окончательный ответ для этого примера — 240 000. Так работает ментальная арифметика.
В соответствии с education.cu-portland.edu, просто исключите нули из уравнения, а затем добавьте их обратно. Например, если вы умножаете 600 на 400, исключите нули и решите шесть раз по четыре, что равно 24. После этого подсчитайте общее количество нулей, которые были в исходном уравнении, и прикрепите их к числу, которое вы решили, чтобы найти свой окончательный ответ. Поскольку в исходном уравнении было четыре нуля, ваш окончательный ответ для этого примера — 240 000. Так работает ментальная арифметика.
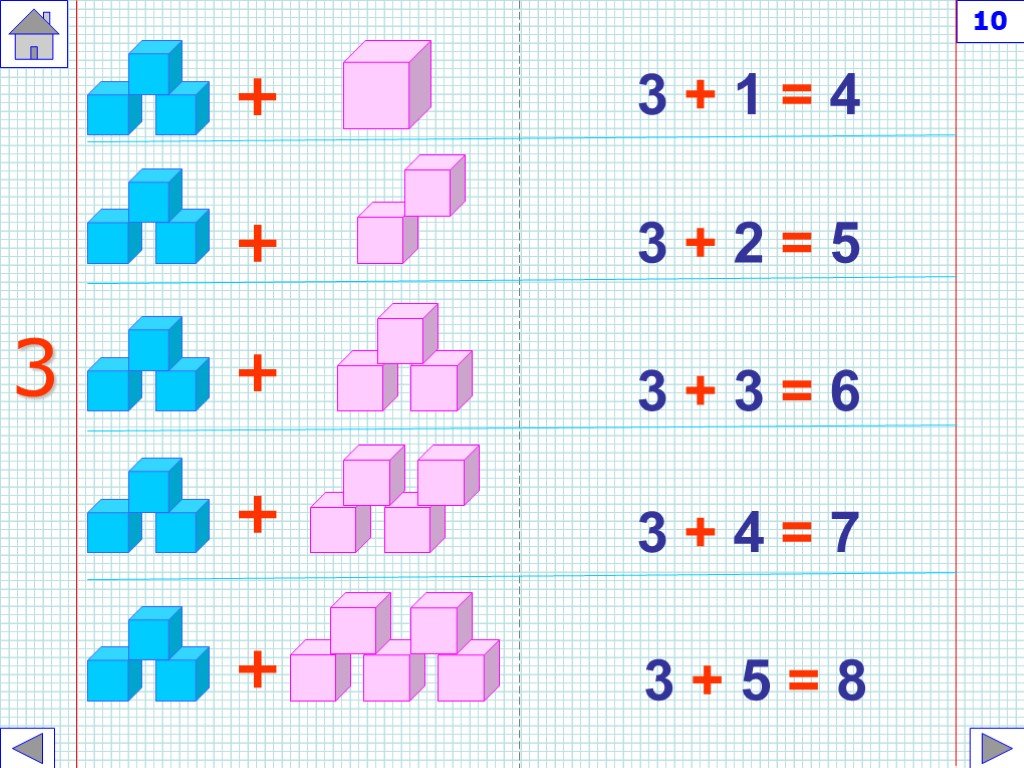 Чтобы умножить число на 1000, переместите запятую на три знака вправо. Например, если вам нужно умножить 366,78 на 100, сдвиньте запятую на два знака вправо, чтобы получить окончательный результат 36 678. Кстати, если вы сможете решить эту математическую задачу с первого раза, возможно, вы гений.
Чтобы умножить число на 1000, переместите запятую на три знака вправо. Например, если вам нужно умножить 366,78 на 100, сдвиньте запятую на два знака вправо, чтобы получить окончательный результат 36 678. Кстати, если вы сможете решить эту математическую задачу с первого раза, возможно, вы гений. «Если бы у вас было 17 кварталов, сколько бы у вас было денег? Каждые четыре четверти составляют доллар, поэтому 16 четвертей равняются четырем долларам или 400 центам. Дополнительная четверть добавляет 25 центов, итого 425 центов», — объясняет Сноу.
«Если бы у вас было 17 кварталов, сколько бы у вас было денег? Каждые четыре четверти составляют доллар, поэтому 16 четвертей равняются четырем долларам или 400 центам. Дополнительная четверть добавляет 25 центов, итого 425 центов», — объясняет Сноу. com
com
 Если вы продолжите, вы в конечном итоге окажетесь на 1. Каждый раз.
Если вы продолжите, вы в конечном итоге окажетесь на 1. Каждый раз.
 Давайте расширим эту идею до трех измерений. В трех измерениях есть четыре числа. На изображении выше это A, B, C и G. Первые три — это размеры коробки, а G — диагональ, идущая от одного из верхних углов к противоположному нижнему углу.
Давайте расширим эту идею до трех измерений. В трех измерениях есть четыре числа. На изображении выше это A, B, C и G. Первые три — это размеры коробки, а G — диагональ, идущая от одного из верхних углов к противоположному нижнему углу. Но они также не смогли доказать, что такого ящика не существует, поэтому идет охота за идеальным прямоугольным параллелепипедом.
Но они также не смогли доказать, что такого ящика не существует, поэтому идет охота за идеальным прямоугольным параллелепипедом.  По сути, проблема работает следующим образом:
По сути, проблема работает следующим образом:
 Определяем среду реакции. У нас один из реагентов — серная кислота, значит, среда у нас однозначно кислая.
Определяем среду реакции. У нас один из реагентов — серная кислота, значит, среда у нас однозначно кислая. Теперь надо уравнять реакции восстановления и окисления между собой ( чтобы “количество принятых электронов было равно количеству отданных”)
Теперь надо уравнять реакции восстановления и окисления между собой ( чтобы “количество принятых электронов было равно количеству отданных”) Сокращаем одинаковые молекулы слева и справа:
Сокращаем одинаковые молекулы слева и справа: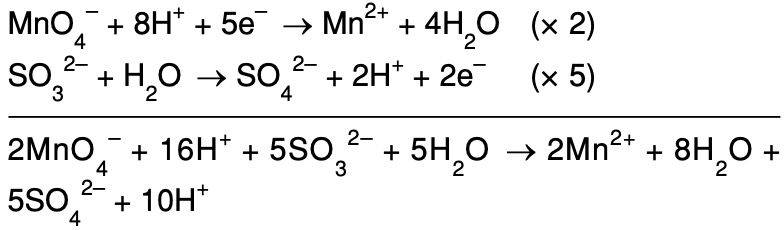
 Ph4 + HMnO4 → MnO2 + … + …
Ph4 + HMnO4 → MnO2 + … + …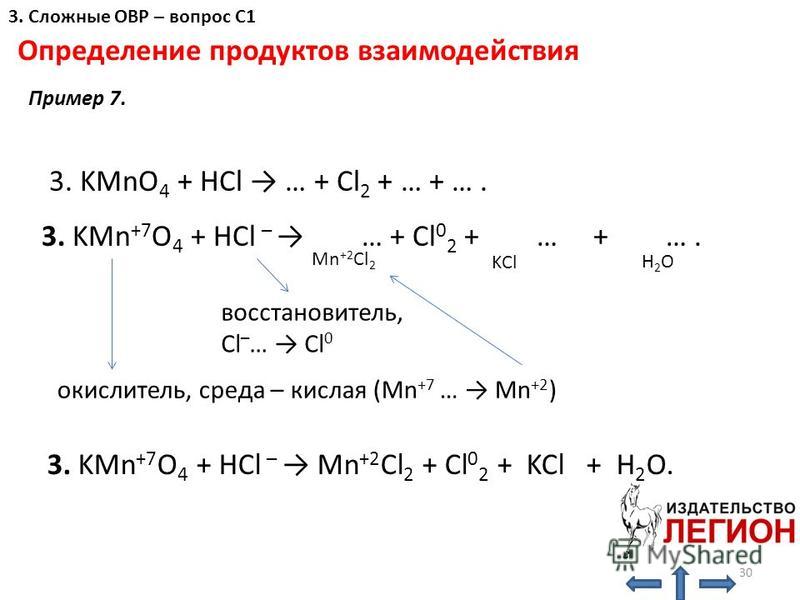 K2Cr2O7 + 6KI + 7h3SO4 = 3I2 + Cr2(SO4)3 + 4K2SO4 + 7h3Cr+6 + 3ē → Cr+3
K2Cr2O7 + 6KI + 7h3SO4 = 3I2 + Cr2(SO4)3 + 4K2SO4 + 7h3Cr+6 + 3ē → Cr+3  2KMnO4 + 16HCl = 5Cl2 + 2MnCl2 + 2KCl + 8h3OMn+7 + 5ē → Mn+2
2KMnO4 + 16HCl = 5Cl2 + 2MnCl2 + 2KCl + 8h3OMn+7 + 5ē → Mn+2  2NO + 3KClO + 2KOH = 2KNO3 + 3KCl + h3ON+2 — 3ē → N+5
2NO + 3KClO + 2KOH = 2KNO3 + 3KCl + h3ON+2 — 3ē → N+5 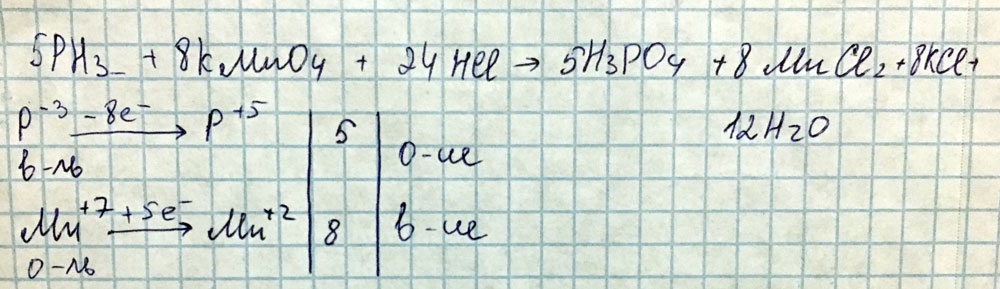 5Zn + 2KMnO4 + 8h3SO4 = 5ZnSO4 + 2MnSO4 + K2SO4 + 8h3OMn+7 + 5ē → Mn+2
5Zn + 2KMnO4 + 8h3SO4 = 5ZnSO4 + 2MnSO4 + K2SO4 + 8h3OMn+7 + 5ē → Mn+2 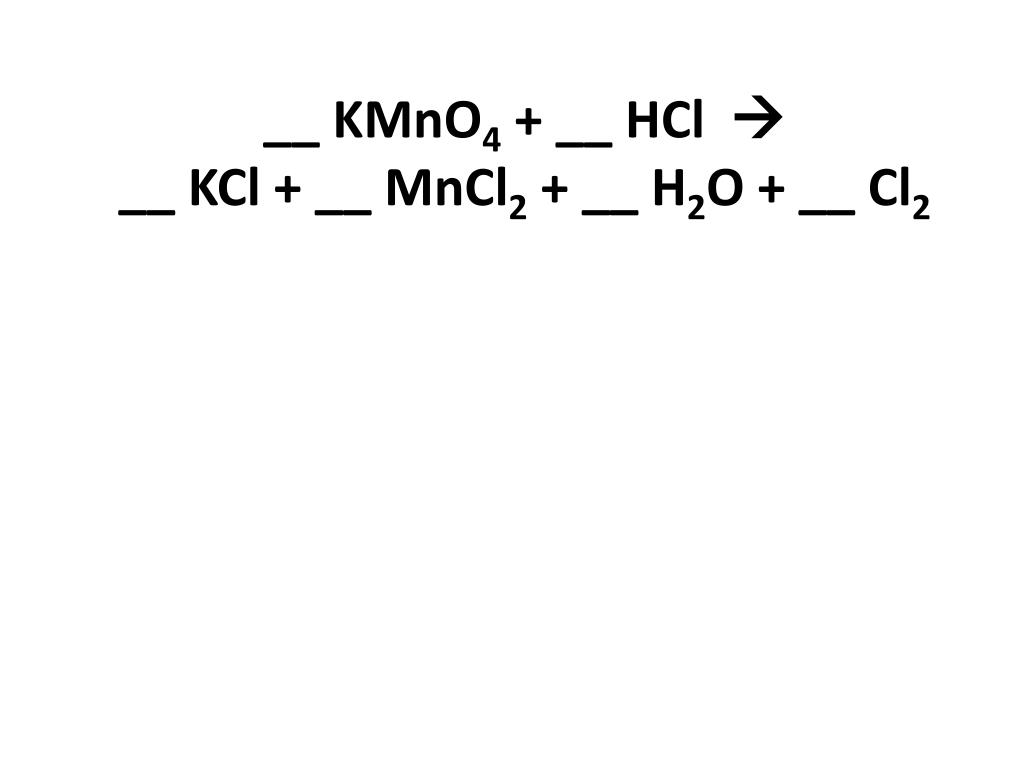
 Напишите уравнения четырех возможных реакций.
Напишите уравнения четырех возможных реакций. 4Ca + 10HNO3(конц) = 4Сa(NO3)2 + N2O + 5h3O
4Ca + 10HNO3(конц) = 4Сa(NO3)2 + N2O + 5h3O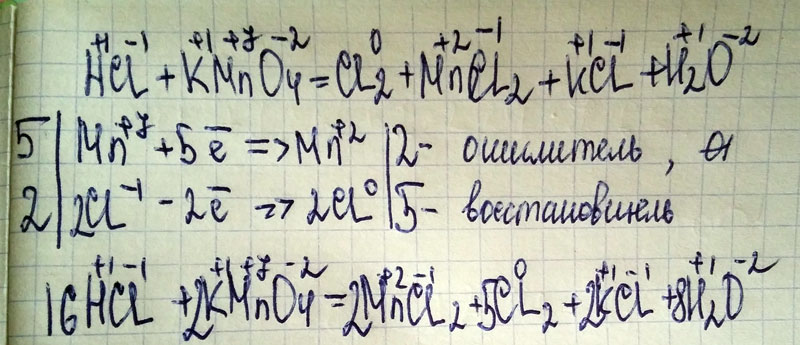 C + 2h3SO4(конц)= CO2 + 2SO2 + 2h3O
C + 2h3SO4(конц)= CO2 + 2SO2 + 2h3O 5NaNO3 + 2P = 5NaNO2 + P2O5
5NaNO3 + 2P = 5NaNO2 + P2O5 С2Н2 → Х1 → СН3СООН → Х2 → Х3 → уксусная кислота
С2Н2 → Х1 → СН3СООН → Х2 → Х3 → уксусная кислота 1) 2K + 2C2H5OH → 2C2H5OK + h3
1) 2K + 2C2H5OH → 2C2H5OK + h3 ) → Ch4-CH=C(Ch4)-Ch4 + h3O + KBr
) → Ch4-CH=C(Ch4)-Ch4 + h3O + KBr ) → C6H5-CH=Ch3+KBr + h3O
) → C6H5-CH=Ch3+KBr + h3O 1) Ch4СОOH + NaOH → Ch4СОONa + h3O
1) Ch4СОOH + NaOH → Ch4СОONa + h3O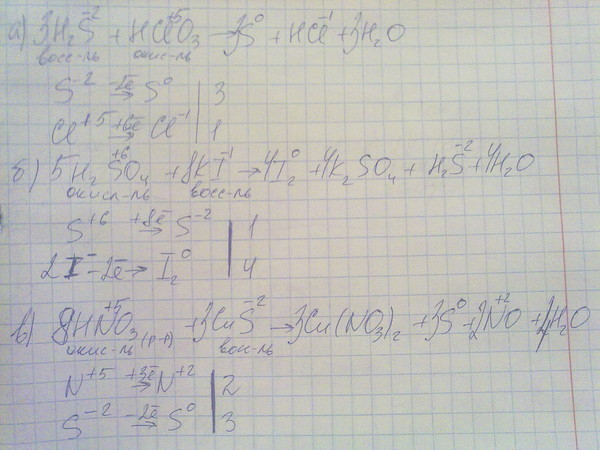
 Относительная плотность паров этого вещества по водороду равна 16. Объем необходимого на сжигание кислорода равен объему выделившегося азота. Определите молекулярную формулу соединения.
Относительная плотность паров этого вещества по водороду равна 16. Объем необходимого на сжигание кислорода равен объему выделившегося азота. Определите молекулярную формулу соединения. у.). Определите молекулярную формулу амина, приведите его название.
у.). Определите молекулярную формулу амина, приведите его название.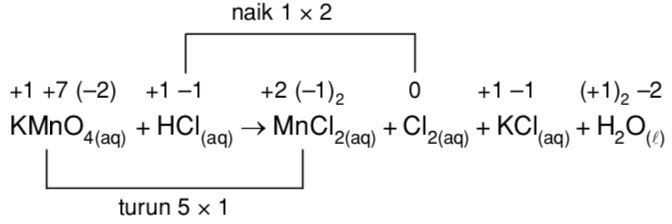
 Cnh3n + Cl2 = Cnh3nCl2
Cnh3n + Cl2 = Cnh3nCl2 Сnh3n+ HCl → Cnh3n+1Cl
Сnh3n+ HCl → Cnh3n+1Cl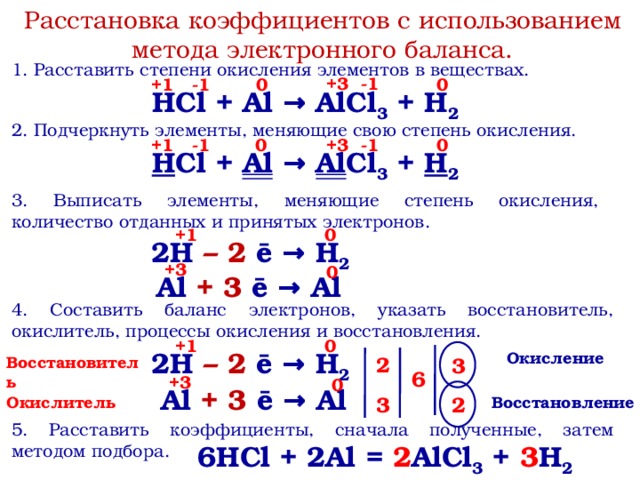 Туба для обучения
Химическая реакция
0
Туба для обучения
Химическая реакция
0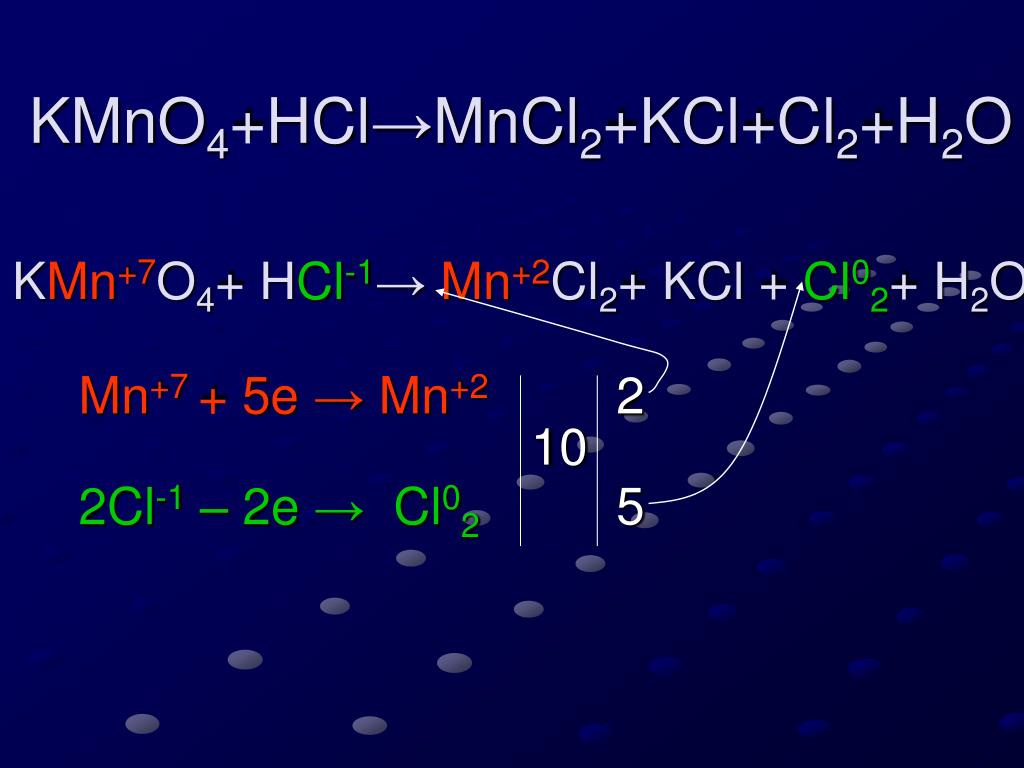 Реакция представляет собой реакцию электронного обмена, е.и. это окислительно-восстановительная реакция (окислительно-восстановительная реакция). Этот тип реакции очень легко уравновешивается ионно-электронным методом. Теперь мы узнаем, как использовать ионно-электронный метод для балансировки реакции.
Реакция представляет собой реакцию электронного обмена, е.и. это окислительно-восстановительная реакция (окислительно-восстановительная реакция). Этот тип реакции очень легко уравновешивается ионно-электронным методом. Теперь мы узнаем, как использовать ионно-электронный метод для балансировки реакции. Отдача электрона химическим веществом называется реакцией окисления. Таким образом, полуреакция окисления для приведенной выше реакции должна быть следующей:0007
Отдача электрона химическим веществом называется реакцией окисления. Таким образом, полуреакция окисления для приведенной выше реакции должна быть следующей:0007 Это означает уравнение (1)x5.
Это означает уравнение (1)x5.  Обсудим некоторые интересные факты о реакциях HCl и KMnO 4 .
Обсудим некоторые интересные факты о реакциях HCl и KMnO 4 . Потому что в этой реакции KMnO 4 является окислителем , который окисляет HCl до Cl 2 , восстанавливаясь до MnCl 2 . Степень окисления Mn снижается с +7 до +2.
Потому что в этой реакции KMnO 4 является окислителем , который окисляет HCl до Cl 2 , восстанавливаясь до MnCl 2 . Степень окисления Mn снижается с +7 до +2.  Кроме того, Cl 2 будет мешать титрованию .
Кроме того, Cl 2 будет мешать титрованию . 
