Интегральные функции:
- Si(x)
- Интегральный синус от x
- Ci(x)
- Интегральный косинус от x
- Shi(x)
- Интегральный гиперболический синус от x
- Chi(x)
- Интегральный гиперболический косинус от x
В выражениях можно применять следующие операции:
- Действительные числа
- вводить в виде 7.
 3
3- — возведение в степень
- x + 7
- — сложение
- x — 6
- — вычитание
- 15/7
- — дробь
Другие функции:
- asec(x)
- Функция — арксеканс от x
- acsc(x)
- Функция — арккосеканс от x
- sec(x)
- Функция — секанс от x
- csc(x)
- Функция — косеканс от x
- floor(x)
- Функция — округление x в меньшую сторону (пример floor(4.5)==4.0)
- ceiling(x)
- Функция — округление x в большую сторону (пример ceiling(4.5)==5.0)
- sign(x)
- Функция — Знак x
- erf(x)
- Функция ошибок (или интеграл вероятности)
- laplace(x)
- Функция Лапласа
- asech(x)
- Функция — гиперболический арксеканс от x
- csch(x)
- Функция — гиперболический косеканс от x
- sech(x)
- Функция — гиперболический секанс от x
- acsch(x)
- Функция — гиперболический арккосеканс от x
Постоянные:
- pi
- Число «Пи», которое примерно равно ~3.
 14159..
14159.. - e
- Число e — основание натурального логарифма, примерно равно ~2,7183..
- i
- Комплексная единица
- oo
- Символ бесконечности — знак для бесконечности
Решение уравнений с неизвестным в 4 степени. Степенные или показательные уравнения
На канал на youtube нашего сайта сайт, чтобы быть в курсе всех новых видео уроков.
Для начала вспомним основные формулы степеней и их свойства.
Произведение числа a само на себя происходит n раз, это выражение мы можем записать как a a … a=a n
1. a 0 = 1 (a ≠ 0)
3. a n a m = a n + m
4. (a n) m = a nm
5. a n b n = (ab) n
7. a n /a m = a n — m
Степенные или показательные уравнения – это уравнения в которых переменные находятся в степенях (или показателях), а основанием является число.
Примеры показательных уравнений:
В данном примере число 6 является основанием оно всегда стоит внизу, а переменная x степенью или показателем.
Приведем еще примеры показательных уравнений.
2 x *5=10
16 x — 4 x — 6=0
Теперь разберем как решаются показательные уравнения?
Возьмем простое уравнение:
2 х = 2 3
Такой пример можно решить даже в уме. Видно, что x=3. Ведь чтобы левая и правая часть были равны нужно вместо x поставить число 3.
А теперь посмотрим как нужно это решение оформить:
2 х = 2 3
х = 3
Для того, чтобы решить такое уравнение, мы убрали одинаковые основания (то есть двойки) и записали то что осталось, это степени. Получили искомый ответ.
Теперь подведем итоги нашего решения.
Алгоритм решения показательного уравнения:
1. Нужно проверить одинаковые ли основания у уравнения справа и слева. Если основания не одинаковые ищем варианты для решения данного примера.
2. После того как основания станут одинаковыми, приравниваем степени и решаем полученное новое уравнение.
Теперь прорешаем несколько примеров:
Начнем с простого.
Основания в левой и правой части равны числу 2, значит мы можем основание отбросить и приравнять их степени.
x+2=4 Получилось простейшее уравнение.
x=4 — 2
x=2
Ответ: x=2
В следующем примере видно, что основания разные это 3 и 9.
3 3х — 9 х+8 = 0
Для начала переносим девятку в правую сторону, получаем:
Теперь нужно сделать одинаковые основания. Мы знаем что 9=3 2 . Воспользуемся формулой степеней (a n) m = a nm .
3 3х = (3 2) х+8
Получим 9 х+8 =(3 2) х+8 =3 2х+16
3 3х = 3 2х+16 теперь видно что в левой и правой стороне основания одинаковые и равные тройке, значит мы их можем отбросить и приравнять степени.
3x=2x+16 получили простейшее уравнение
3x — 2x=16
x=16
Ответ: x=16.
Смотрим следующий пример:
2 2х+4 — 10 4 х = 2 4
В первую очередь смотрим на основания, основания разные два и четыре. А нам нужно, чтобы были — одинаковые. Преобразовываем четверку по формуле (a n) m = a nm .
4 х = (2 2) х = 2 2х
И еще используем одну формулу a n a m = a n + m:
2 2х+4 = 2 2х 2 4
Добавляем в уравнение:
2 2х 2 4 — 10 2 2х = 24
Мы привели пример к одинаковым основаниям. Но нам мешают другие числа 10 и 24. Что с ними делать? Если приглядеться видно, что в левой части у нас повторяется 2 2х,вот и ответ — 2 2х мы можем вынести за скобки:
2 2х (2 4 — 10) = 24
Посчитаем выражение в скобках:
2 4 — 10 = 16 — 10 = 6
Все уравнение делим на 6:
Представим 4=2 2:
2 2х = 2 2 основания одинаковые, отбрасываем их и приравниваем степени.
2х = 2 получилось простейшее уравнение. Делим его на 2 получаем
х = 1
Ответ: х = 1.
Решим уравнение:
9 х – 12*3 х +27= 0
Преобразуем:
9 х = (3 2) х = 3 2х
Получаем уравнение:
3 2х — 12 3 х +27 = 0
Основания у нас одинаковы равны трем.В данном примере видно, что у первой тройки степень в два раза (2x) больше, чем у второй (просто x). В таком случаем можно решить методом замены . Число с наименьшей степенью заменяем:
В таком случаем можно решить методом замены . Число с наименьшей степенью заменяем:
Тогда 3 2х = (3 х) 2 = t 2
Заменяем в уравнении все степени с иксами на t:
t 2 — 12t+27 = 0
Получаем квадратное уравнение. Решаем через дискриминант, получаем:
D=144-108=36
t 1 = 9
t 2 = 3
Возвращаемся к переменной x .
Берем t 1:
t 1 = 9 = 3 х
Стало быть,
3 х = 9
3 х = 3 2
х 1 = 2
Один корень нашли. Ищем второй, из t 2:
t 2 = 3 = 3 х
3 х = 3 1
х 2 = 1
Ответ: х 1 = 2; х 2 = 1.
На сайте Вы можете в разделе ПОМОГИТЕ РЕШИТЬ задавать интересующие вопросы мы Вам обязательно ответим.
Вступайте в группу
Решение Декарта — Эйлера
Сделав подстановку , получим уравнение в следующем виде (он называется «неполным»):
y 4 + p y 2 + q y + r = 0 .
Корни y 1 , y 2 , y 3 , y 4 такого уравнения равны одному из следующих выражений:
в которых сочетания знаков выбираются таким образом, чтобы выполнялось следующее соотношение:
,
причём z 1 , z 2 и z 3 — это корни кубического уравнения
Решение Феррари
Основная статья : Метод Феррари
Представим уравнение четвёртой степени в виде:
A x 4 + B x 3 + C x 2 + D x + E = 0,
Его решение может быть найдено из следующих выражений:
если β = 0
, решив u 4 + αu 2 + γ = 0
и, сделав подстановку , найдём корни:
. , (любой знак квадратного корня подойдёт)
, (три комплексных корня, один из которых подойдёт)
Два ± s должны иметь одинаковый знак, ± t — независимы. Для того, чтобы найти все корни, надо найти x для знаковых комбинаций ± s ,± t = +,+ для +,− для −,+ для −,−. Двойные корни появятся два раза, тройные корни — три раза и корни четвёртого порядка — четыре раза. Порядок корней зависит от того, какой из кубических корней U выбран.
, (любой знак квадратного корня подойдёт)
, (три комплексных корня, один из которых подойдёт)
Два ± s должны иметь одинаковый знак, ± t — независимы. Для того, чтобы найти все корни, надо найти x для знаковых комбинаций ± s ,± t = +,+ для +,− для −,+ для −,−. Двойные корни появятся два раза, тройные корни — три раза и корни четвёртого порядка — четыре раза. Порядок корней зависит от того, какой из кубических корней U выбран.
См. также
- Легко решаемые типы уравнений 4 степени: Биквадратное уравнение , возвратное уравнение четвёртой степени
Литература
- Корн Г., Корн Т. (1974) Справочник по математике.
Ссылки
- Решение Феррари (англ.)
Wikimedia Foundation . 2010 .
Смотреть что такое «Уравнение четвертой степени» в других словарях:
- Expression
- Equation
- Inequality
- Contact us
- Simplify
- Factor
- Expand
- GCF
- LCM
- Solve
- Graph
- System
- Solve
- Graph
- Система
- Математический решатель на вашем сайте
уравнение четвертой степени — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN quartic equation … Справочник технического переводчика
График многочлена 4 ой степени с четырьмя корнями и тремя критическими точками. Уравнение четвёртой степени в математике алгебраическое уравнение вида: Четвёртая степень для алгебраических уравнений является наивысшей, при которой… … Википедия
Уравнение четвёртой степени в математике алгебраическое уравнение вида: Четвёртая степень для алгебраических уравнений является наивысшей, при которой… … Википедия
Уравнение вида: anxn + an − 1xn − 1 + … + a1x + a0 = 0 называется возвратным, если его коэффициенты, стоящие на симметричных позициях, равны, то есть если an − k = ak, при k = 0, 1, …, n. Содержание 1 Уравнение четвёртой степени … Википедия
В котором неизвестный член в четвертой степени. Полный словарь иностранных слов, вошедших в употребление в русском языке. Попов М., 1907. БИКВАДРАТНОЕ УРАВНЕНИЕ от лат. bis, дважды, и quadratum, квадрат. Уравнение, в котором наибольшая степень… … Словарь иностранных слов русского языка
Вместе с арифметикой есть наука о числах и через посредство чисел о величинах вообще. Не занимаясь изучением свойств каких нибудь определенных, конкретных величин, обе эти науки исследуют свойства отвлеченных величин как таковых, независимо от… … Энциклопедический словарь Ф.А. Брокгауза и И. А. Ефрона
А. Ефрона
Совокупность прикладных знаний, позволяющих авиационным инженерам на занятий в области аэродинамики, проблем прочности, двигателестроения и динамики полета летательных аппаратов (т.е. теории) создать новый летательный аппарат или улучшить… … Энциклопедия Кольера
Самой древней математической деятельностью был счет. Счет был необходим, чтобы следить за поголовьем скота и вести торговлю. Некоторые первобытные племена подсчитывали количество предметов, сопоставляя им различные части тела, главным образом… … Энциклопедия Кольера
История технологий По периодам и регионам: Неолитическая революция Древние технологии Египта Наука и технологии древней Индии Наука и технологии древнего Китая Технологии Древней Греции Технологии Древнего Рима Технологии исламского мира… … Википедия
Уравнением называется математическое соотношение, выражающее равенство двух алгебраических выражений. Если равенство справедливо для любых допустимых значений входящих в него неизвестных, то оно называется тождеством; например, соотношение вида… … Энциклопедия Кольера
Теорема Абеля Руффини утверждает, что общее уравнение степени при неразрешимо в радикалах. 4+b=0$
4+b=0$
Корни уравнения такой разновидности находятся с помощью применения формул сокращённого умножения.
Вскоре после того, как Кардано опубликовал способ решения кубических уравнений, его ученики и последователи нашли способы сведения общего уравнения четвертой степени к кубическому уравнению. Изложим наиболее простой способ, принадлежащий Л. Феррари.
При изложении способа нужно будет воспользоваться следующей элементарной леммой.
Лемма. Для того чтобы квадратный трехчлен был квадратом линейного двучлена, необходимо и достаточно, чтобы его дискриминант равнялся нулю.
Доказательство. Необходимость. Пусть . Тогда Достаточность. Пусть Тогда
Идея излагаемого способа состоит в том, чтобы представить левую часть уравнения в виде разности двух квадратов. Тогда ее можно будет разложить на два множителя второй степени, и решение уравнения приведется к решению двух квадратных уравнений. Для достижения цели левую часть представим в виде:
Здесь у — вспомогательная неизвестная, которую нужно подобрать так, чтобы выражение в квадратных скобках оказалось квадратом линейного двучлена. В силу леммы для этого необходимо и достаточно выполнения условия
В силу леммы для этого необходимо и достаточно выполнения условия
Это условие есть уравнение третьей степени относительно у. После раскрытия скобок оно преобразуется к виду
Пусть — один из корней этого уравнения. Тогда при условие будет выполнено, так что имеет место
при некоторых k и I. Исходное уравнение примет вид
Приравнивая нулю каждый из сомножителей, мы найдем четыре корня исходного уравнения.
Сделаем еще одно замечание. Пусть — корни первого сомножителя, и — корни второго. Тогда Сложив эти равенства, получим, что
Таким образом, мы получили выражение корня вспомогательного кубического уравнения через корни исходного уравнения четвертой степени.
Пример. Решить уравнение . Согласно изложенному выше методу преобразуем левую часть:
Теперь положим . После образований получим уравнение
Легко видеть, что одним из корней этого уравнения является число . Подставив его в преобразованную левую часть исходного уравнения, получим:
Приравнивая сомножители нулю, получим
Что касается уравнений выше четвертой степени, то здесь были известны некоторые классы уравнений сравнительно частного вида, допускающих алгебраические решения в радикалах, т. е. в виде результатов арифметических действий и действия извлечения корня. Однако попытки дать решение общих уравнений пятой степени и выше были безуспешны, пока, наконец, в начале 19 в. Руффини и Абель не доказали, что решение такого рода для общих уравнений выше четвертой степени невозможно. Наконец, в 1830 г. гениальному французскому математику Э. Галуа удалось найти необходимые и достаточные условия (проверяемые довольно сложно) для разрешимости в радикалах конкретно заданного уравнения. При этом Галуа создал и использовал новую для своего времени теорию групп подстановок.
е. в виде результатов арифметических действий и действия извлечения корня. Однако попытки дать решение общих уравнений пятой степени и выше были безуспешны, пока, наконец, в начале 19 в. Руффини и Абель не доказали, что решение такого рода для общих уравнений выше четвертой степени невозможно. Наконец, в 1830 г. гениальному французскому математику Э. Галуа удалось найти необходимые и достаточные условия (проверяемые довольно сложно) для разрешимости в радикалах конкретно заданного уравнения. При этом Галуа создал и использовал новую для своего времени теорию групп подстановок.
2x 4 + 5x 3 — 11x 2 — 20x + 12 = 0
Для начала нужно методом подбора найти один корень. Обычно он является делителем свободного члена. В данном случае делителями числа 12 являются ±1, ±2, ±3, ±4, ±6, ±12. Начнем их подставлять по-очереди:
1: 2 + 5 — 11 — 20 + 12 = -12 ⇒ число 1
-1: 2 — 5 — 11 + 20 + 12 = 18 ⇒ число -1 не является корнем многочлена
2: 2 ∙ 16 + 5 ∙ 8 — 11 ∙ 4 — 20 ∙ 2 + 12 = 0 ⇒ число 2 является корнем многочлена
Мы нашли 1 из корней многочлена. Корнем многочлена является 2, а значит исходный многочлен должен делиться на x — 2 . Для того, чтобы выполнить деление многочленов, воспользуемся схемой Горнера:
Корнем многочлена является 2, а значит исходный многочлен должен делиться на x — 2 . Для того, чтобы выполнить деление многочленов, воспользуемся схемой Горнера:
| 2 | 5 | -11 | -20 | 12 | |
| 2 |
В верхней строке выставляются коэффициенты исходного многочлена. В первой ячейке второй строки ставится найденный нами корень 2. Во второй строке пишутся коэффициенты многочлена, который получится в результате деления. Они считаются так:
| Во вторую ячейку второй строки запишем число 2, просто перенеся его из соответствующей ячейки первой строки. | ||||||||||||
| 2 ∙ 2 + 5 = 9 | ||||||||||||
| 2 ∙ 9 — 11 = 7 | ||||||||||||
| 2 ∙ 7 — 20 = -6 | ||||||||||||
| 2 ∙ (-6) + 12 = 0 |
Последнее число — это остаток от деления. Если он равен 0, значит мы все верно посчитали.
Если он равен 0, значит мы все верно посчитали.
2x 4 + 5x 3 — 11x 2 — 20x + 12 = (x — 2)(2x 3 + 9x 2 + 7x — 6)
Но это еще не конец. Можно попробовать разложить таким же способом многочлен 2x 3 + 9x 2 + 7x — 6.
Опять ищем корень среди делителей свободного члена. Делителями числа -6 являются ±1, ±2, ±3, ±6.
1: 2 + 9 + 7 — 6 = 12 ⇒ число 1 не является корнем многочлена
-1: -2 + 9 — 7 — 6 = -6 ⇒ число -1 не является корнем многочлена
2: 2 ∙ 8 + 9 ∙ 4 + 7 ∙ 2 — 6 = 60 ⇒ число 2 не является корнем многочлена
-2: 2 ∙ (-8) + 9 ∙ 4 + 7 ∙ (-2) — 6 = 0 ⇒ число -2 является корнем многочлена
Напишем найденный корень в нашу схему Горнера и начнем заполнять пустые ячейки:
| Во вторую ячейку третьей строки запишем число 2, просто перенеся его из соответствующей ячейки второй строки. | ||||||||||||||||||
| -2 ∙ 2 + 9 = 5 | ||||||||||||||||||
| -2 ∙ 5 + 7 = -3 | ||||||||||||||||||
| -2 ∙ (-3) — 6 = 0 |
Таким образом мы исходный многочлен разложили на множители:
2x 4 + 5x 3 — 11x 2 — 20x + 12 = (x — 2)(x + 2)(2x 2 + 5x — 3)
Многочлен 2x 2 + 5x — 3 тоже можно разложить на множители. Для этого можно решить квадратное уравнение через дискриминант , а можно поискать корень среди делителей числа -3. Так или иначе, мы придем к выводу, что корнем этого многочлена является число -3
Для этого можно решить квадратное уравнение через дискриминант , а можно поискать корень среди делителей числа -3. Так или иначе, мы придем к выводу, что корнем этого многочлена является число -3
| Во вторую ячейку четвертой строки запишем число 2, просто перенеся его из соответствующей ячейки третьей строки. | ||||||||||||||||||||||||
| -3 ∙ 2 + 5 = -1 | ||||||||||||||||||||||||
| -3 ∙ (-1) — 3 = 0 |
Таким образом мы исходный многочлен разложили на линейные множители.
Решение уравнений n-й степени
| решение уравнений в n-й степени
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Симметрия и решения полиномиальных уравнений
ОбзорПоиски решений полиномиальных уравнений продолжались на протяжении восемнадцатого века. Примерно в 1770 году в течение пары лет математики ряда стран почти одновременно добились успехов, которые привели к новым подходам к решению проблемы. Было разочарование в том, что ни одно из достижений не привело к общему решению уравнений высших степеней, но некоторые конкретные уравнения удалось решить после этой работы. Что еще более важно, новые подходы предоставили средства для ответа на вопрос о разрешимости полиномиальных уравнений вообще в начале следующего столетия.
Исходная информация Уравнение — это просто выражение, в котором утверждается, что две стороны равны, и в нем не может быть ничего, кроме чисел. На раннем этапе развития алгебры наибольший интерес представляли уравнения, в которых какой-либо символ использовался для обозначения неизвестной величины, значение которой должно было быть определено на основе информации, предоставленной уравнением. Линейные уравнения (те, которые включают только переменную в первой степени) можно было решить без особых обозначений, и впечатляло, что вавилонская математика уже достигла уровня решения квадратных уравнений (которые также включают вторую степень переменной). Описание решения обычно выражалось словами, а не символами.
На раннем этапе развития алгебры наибольший интерес представляли уравнения, в которых какой-либо символ использовался для обозначения неизвестной величины, значение которой должно было быть определено на основе информации, предоставленной уравнением. Линейные уравнения (те, которые включают только переменную в первой степени) можно было решить без особых обозначений, и впечатляло, что вавилонская математика уже достигла уровня решения квадратных уравнений (которые также включают вторую степень переменной). Описание решения обычно выражалось словами, а не символами.
Тот же самый подход продолжался даже в шестнадцатом веке с решением кубических уравнений (включая третьи степени переменной) и уравнений четвертой степени (с учетом четвертых степеней переменной).
переменная). Они были решены усилиями итальянских математиков, и решения были представлены словами. Методы не подвергались тщательной проверке до тех пор, пока полученные ответы работали в исходном уравнении. Только в работах Франсуа Виета (1540–1603) была предпринята некоторая попытка применить строгость геометрии к методам алгебры.
Однако, несмотря на усилия Виета, в общем вопросе о решении уравнений пятой степени (с пятыми степенями переменной) не было достигнуто никакого прогресса. К концу восемнадцатого века Александр-Теофиль Вандермонд (1735-1796) прочитал доклад перед Академией наук в Париже о новом подходе к решению уравнений пятой степени и полиномиальных уравнений в целом. Он утверждал, что каждое уравнение, в котором степень переменной равна единице, может быть решена стандартными средствами. Его работа по этому вопросу была бы более известна, если бы он был членом Академии во время родов (1770 г.), потому что это облегчило бы ему публикацию своих утверждений. Как бы то ни было, его статья не публиковалась до 1774 года, а тем временем Жозеф-Луи Лагранж (1736–1813), один из величайших математиков века, опубликовал пару статей по этому вопросу. Возможно, разочарованный, зная, что первая публикация в научном мире имеет решающее значение, Вандермонде не продолжил свои исследования по решению полиномиальных уравнений.
Другим математиком, чьи работы предвосхитили работы Лагранжа, был Эдвард Варинг (1736-1798). В его случае недостатком, мешавшим его дальнейшему прогрессу, было отсталое состояние математики в Англии при его жизни. В результате сознательного решения английских математиков следовать практике сэра Исаака Ньютона (1642–1727), а не ведущим ученым Европы, английская математика отошла от достижений остального мира. Работа Варинга получила высокую оценку Лагранжа и других, но он не был в среде, где прогресс был легким.
Лагранж, напротив, провел время в математических центрах Европы, в результате чего его работа могла получить быстрое распространение. Его подход к полиномиальным уравнениям был отчасти историческим, поскольку он отступил назад, чтобы изучить, как итальянским математикам удавалось находить решения для уравнений кубической и четвертой степени. На основе этого анализа ему удалось сформулировать исследовательскую программу для
как решать уравнения пятой степени (и более высокой степени). Как оказалось, хотя он и не смог ничего придумать в качестве общего решения уравнения пятой степени, его переоценка своих предшественников предоставила существенные элементы для вывода, к которому пришел Эварист Галуа (1811-1832), а именно: что уравнение пятой степени не может быть решено традиционными средствами.
Как оказалось, хотя он и не смог ничего придумать в качестве общего решения уравнения пятой степени, его переоценка своих предшественников предоставила существенные элементы для вывода, к которому пришел Эварист Галуа (1811-1832), а именно: что уравнение пятой степени не может быть решено традиционными средствами.
Идея, которую Лагранж привнес в решение полиномиальных уравнений, была идеей симметрии. Вместо того, чтобы просто искать решения исходного уравнения, он искал другие соотношения, которым должны удовлетворять решения, в надежде, что они будут проще, чем исходное уравнение. Пока еще можно было восстановить исходные решения из решений новых вспомогательных уравнений, метод будет работать для получения этих исходных решений.
Если посмотреть на квадратное уравнение (с коэффициентом при квадрате члена, равным единице), то сумма решений уравнения равна минусу коэффициента при члене первого порядка. Произведение решений равно постоянному члену. Этот подход мог бы стать альтернативой квадратной формуле для решения квадратного уравнения. Подобные стратегии дают вспомогательные уравнения для решения кубических
и уравнения четвертой степени, поскольку кубическое уравнение можно свести к вспомогательному квадратному, а уравнение четвертой степени — к вспомогательному кубическому.
Этот подход мог бы стать альтернативой квадратной формуле для решения квадратного уравнения. Подобные стратегии дают вспомогательные уравнения для решения кубических
и уравнения четвертой степени, поскольку кубическое уравнение можно свести к вспомогательному квадратному, а уравнение четвертой степени — к вспомогательному кубическому.
Проблема применения стратегии Лагранжа к уравнениям пятой степени стала очевидной в работе Джан Франческо Мальфатти (1731-1807). В статье 1770 года он показал, что если попытаться найти вспомогательное уравнение для квинтики, результат будет шестой степени. Поскольку показатель степени переменной в этом вспомогательном методе выше, чем в оригинале, это только усугубило проблему. Когда при решении кубического уравнения обнаруживались уравнения шестой степени, их можно было рассматривать как квадратичные уравнения. Те, которые возникли в результате работы с квинтикой, не могли быть сокращены таким образом.
Работа Лагранжа послужила основой для новой дисциплины математики, называемой теорией групп. Это можно рассматривать как изучение симметрии, возникшее в результате попыток Лагранжа найти симметричные функции решений уравнения. Функция симметрична, если некоторая замена значений переменных, представляющих решения, не меняет значения функции. Например, x + y сохраняет то же значение, если x и y поменять местами.
Это можно рассматривать как изучение симметрии, возникшее в результате попыток Лагранжа найти симметричные функции решений уравнения. Функция симметрична, если некоторая замена значений переменных, представляющих решения, не меняет значения функции. Например, x + y сохраняет то же значение, если x и y поменять местами.
Теория групп оказалась основой для доказательства того, что не существует формулы для решения всех уравнений пятой степени, как это было для младших степеней переменной. Это не означало, что отдельные уравнения пятой степени не могли быть решены, поскольку некоторые из них решались веками ранее. Что доказательство действительно гарантировало, так это то, что любой метод решения, претендующий на решение всех уравнений пятой степени, должен был выйти за рамки стандартных алгебраических операций, которым раньше уделялось внимание. Целый раздел математики, известный как теория Галуа, посвящен применению теории групп (основанной на симметрии) к изучению полиномиальных уравнений и их решений.

 14159..
14159.. 05.2006
05.2006  03.2005
03.2005 
 Работать тоже было без проблем. Это вело меня шаг за шагом к решению, а не просто давало решение. Таким образом, я тоже научился объяснять проблемы. К тому времени, когда я закончил, я научился решать проблемы. Я нашел их функциональными для промежуточной алгебры, базовой математики и исправительной алгебры, которые помогли мне в моих математических классах. Может быть, это как раз то, что вам нужно. Почему бы не попробовать это?
Работать тоже было без проблем. Это вело меня шаг за шагом к решению, а не просто давало решение. Таким образом, я тоже научился объяснять проблемы. К тому времени, когда я закончил, я научился решать проблемы. Я нашел их функциональными для промежуточной алгебры, базовой математики и исправительной алгебры, которые помогли мне в моих математических классах. Может быть, это как раз то, что вам нужно. Почему бы не попробовать это?
 Поэтому расположение цветов не совпадает, но сама последовательность четко сохраняется. Затем нужно посчитать, сколько пар цветов, сколько пар лепестков в каждом цветке?
Поэтому расположение цветов не совпадает, но сама последовательность четко сохраняется. Затем нужно посчитать, сколько пар цветов, сколько пар лепестков в каждом цветке? В конце выполнения задания ребенка нужно спросить, на что он обратил внимание, считая героев (все картинки с героями расположены по порядку счета).
В конце выполнения задания ребенка нужно спросить, на что он обратил внимание, считая героев (все картинки с героями расположены по порядку счета). Когда ребенок объединит точки, то увидит, что могло бы помочь туристу в этой ситуации.
Когда ребенок объединит точки, то увидит, что могло бы помочь туристу в этой ситуации.
 Затем ребенок должен выполнить все указанные в задании действия — сначала сравнить число, является ли оно меньше 5, как указано в ромбе со знаком вопроса. Если да — то следующее действие будет по стрелке «Да», если нет, то по стрелке «Нет». Дальше выполняется сложение или вычитание, и в нижний кружок вписывается ответ. Выполнять задание можно множество раз, меняя только число в верхнем кружке.
Затем ребенок должен выполнить все указанные в задании действия — сначала сравнить число, является ли оно меньше 5, как указано в ромбе со знаком вопроса. Если да — то следующее действие будет по стрелке «Да», если нет, то по стрелке «Нет». Дальше выполняется сложение или вычитание, и в нижний кружок вписывается ответ. Выполнять задание можно множество раз, меняя только число в верхнем кружке. Столбики-цепочки. Все темы. Быстрый устный счёт. 1 класс — О. В. Узорова
Столбики-цепочки. Все темы. Быстрый устный счёт. 1 класс — О. В. Узорова Полезные и увлекательные задания. 1 класс — О. В. Узорова
Полезные и увлекательные задания. 1 класс — О. В. Узорова Нескучные задачи и нелегкие примеры. С ответами и пояснениями. 1 класс — О. В. Узорова
Нескучные задачи и нелегкие примеры. С ответами и пояснениями. 1 класс — О. В. Узорова Разрядный состав чисел до 10. 1 класс — Группа авторов
Разрядный состав чисел до 10. 1 класс — Группа авторов 1 класс — И. Соловьева
1 класс — И. Соловьева Числа и фигуры. 1 класс — С. В. Бахтина
Числа и фигуры. 1 класс — С. В. Бахтина Геометрические задания. 1 класс — О. В. Узорова
Геометрические задания. 1 класс — О. В. Узорова 1 класс — Д. В. Овчаров
1 класс — Д. В. Овчаров Все примеры на все темы школьной программы. 1 класс — Т. С. Позднева
Все примеры на все темы школьной программы. 1 класс — Т. С. Позднева 1 класс — И. О. Родин
1 класс — И. О. Родин 1 класс — О. В. Узорова
1 класс — О. В. Узорова Вот семь уникальных идей для увлекательных математических занятий в соответствии с CCSS для первого класса, которые помогут вам начать работу:
Вот семь уникальных идей для увлекательных математических занятий в соответствии с CCSS для первого класса, которые помогут вам начать работу: Затем попросите учеников перевернуть поезд и написать новую последовательность. Это поможет им понять, что независимо от порядка чисел общая сумма одинакова.
Затем попросите учеников перевернуть поезд и написать новую последовательность. Это поможет им понять, что независимо от порядка чисел общая сумма одинакова. Затем вы можете использовать разноцветные яблоки, чтобы продемонстрировать задачу со словами. Например, показаны все различные комбинации красных и желтых яблок, которые можно использовать для создания коробки из 10 штук.
Затем вы можете использовать разноцветные яблоки, чтобы продемонстрировать задачу со словами. Например, показаны все различные комбинации красных и желтых яблок, которые можно использовать для создания коробки из 10 штук. Затем каждый игрок по очереди бросает кубик и прибавляет один (или вычитает один, в зависимости от игры) и ставит свою фишку на соответствующее число. Игра заканчивается, когда учащиеся используют все свои фишки.
Затем каждый игрок по очереди бросает кубик и прибавляет один (или вычитает один, в зависимости от игры) и ставит свою фишку на соответствующее число. Игра заканчивается, когда учащиеся используют все свои фишки. Существуют сотни игр и приложений, которые рекламируют развлечение и увлекательность, но как узнать, какое из них лучше всего подходит для ваших учеников?
Существуют сотни игр и приложений, которые рекламируют развлечение и увлекательность, но как узнать, какое из них лучше всего подходит для ваших учеников? Когда вы ищете приложение, есть несколько особенностей, которые вы можете проверить, чтобы убедиться, что они соответствуют вашим потребностям.
Когда вы ищете приложение, есть несколько особенностей, которые вы можете проверить, чтобы убедиться, что они соответствуют вашим потребностям. развиваем математические способности!
развиваем математические способности! Этот продукт доступен учителям и школам, требует наличия учетной записи Office 365 и доступен для платформ Android и iOS.
Этот продукт доступен учителям и школам, требует наличия учетной записи Office 365 и доступен для платформ Android и iOS. Игры на стратегии сложения и вычитания, разрядность, определение времени и многое другое доступны в категории первого класса. В то время как в веселых играх со счетом используются числовые линии и диаграммы сотен, группировка по десяткам использует наборы разноцветных объектов. Кроме того, SplashLearn охватывает принципы математики и чтения для разных классов, чтобы дети могли продолжать играть в новые игры по мере их взросления.
Игры на стратегии сложения и вычитания, разрядность, определение времени и многое другое доступны в категории первого класса. В то время как в веселых играх со счетом используются числовые линии и диаграммы сотен, группировка по десяткам использует наборы разноцветных объектов. Кроме того, SplashLearn охватывает принципы математики и чтения для разных классов, чтобы дети могли продолжать играть в новые игры по мере их взросления. Игры могут быть адаптированы к потребностям учащихся и предлагают практику с более чем 40 математическими навыками в сочетании с математическими занятиями в автономном режиме в виде печатных форм.
Игры могут быть адаптированы к потребностям учащихся и предлагают практику с более чем 40 математическими навыками в сочетании с математическими занятиями в автономном режиме в виде печатных форм. Создайте несколько учетных записей и адаптируйте игры к потребностям каждого игрока.
Создайте несколько учетных записей и адаптируйте игры к потребностям каждого игрока.
 Игры по-разному помогают детям в освоении основ математики. Также доступны Kahoot Algebra и Geometry, чтобы охватить все основные математические концепции 1-го класса.
Игры по-разному помогают детям в освоении основ математики. Также доступны Kahoot Algebra и Geometry, чтобы охватить все основные математические концепции 1-го класса.
 Г. Помогите доказать, используя параллельный перенос
Г. Помогите доказать, используя параллельный перенос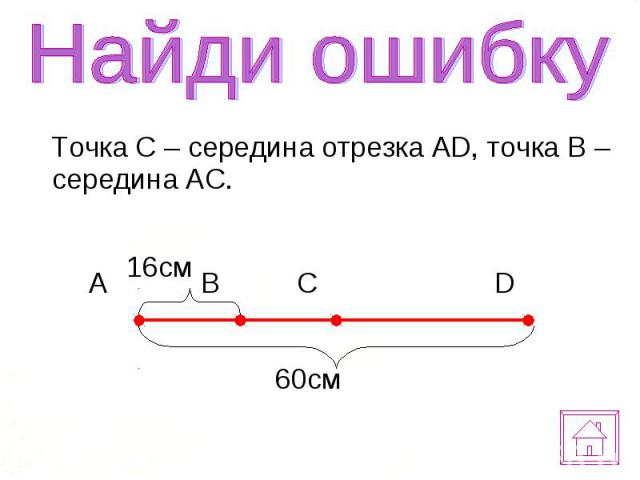 П. ГДЗ. Вариант 12.
П. ГДЗ. Вариант 12. Следовательно:
Следовательно:
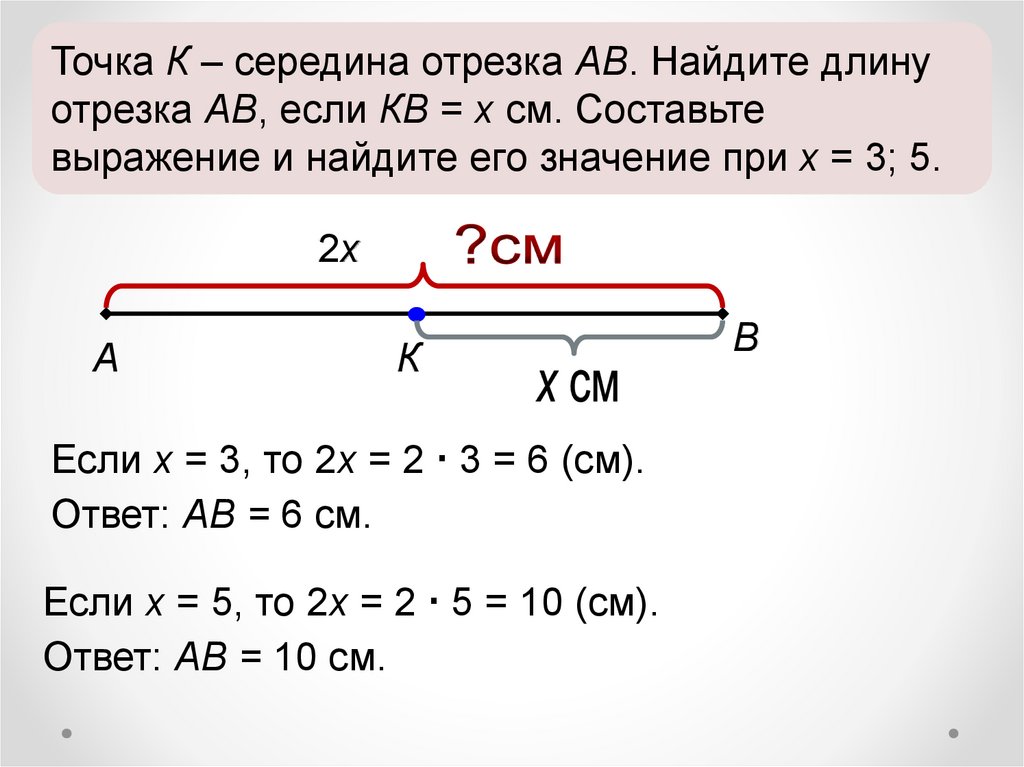
 Чтобы найти другую точку, мы проходим ту же величину в противоположном направлении от средней точки, 9 единиц по оси x и – 7 единиц по оси y до точки (21, – 10).
Чтобы найти другую точку, мы проходим ту же величину в противоположном направлении от средней точки, 9 единиц по оси x и – 7 единиц по оси y до точки (21, – 10). 
 Таким образом, если мы назовем другую точку, мы знаем, что:
Таким образом, если мы назовем другую точку, мы знаем, что: Сложите значения x вместе и разделите их на 2, и сделайте то же самое для значений y.
Сложите значения x вместе и разделите их на 2, и сделайте то же самое для значений y. Если вы получили (10,14), возможно, вы забыли разделить свои координаты x и y на 2. Если вы получили (6,6), возможно, вы нашли среднее значение x 1 и y 2 и x 2 и y 1 вместо того, чтобы хранить вместе координаты x и координаты y. Если вы получили (7, 5), возможно, вы поменяли местами координаты x и y.
Если вы получили (10,14), возможно, вы забыли разделить свои координаты x и y на 2. Если вы получили (6,6), возможно, вы нашли среднее значение x 1 и y 2 и x 2 и y 1 вместо того, чтобы хранить вместе координаты x и координаты y. Если вы получили (7, 5), возможно, вы поменяли местами координаты x и y.

 См. mid-, point
См. mid-, point Шнайдер, Лаура Воззелла|4 февраля 2021 г.|Washington Post
Шнайдер, Лаура Воззелла|4 февраля 2021 г.|Washington Post

 1. Вычислите. а) б) ; в)
1. Вычислите. а) б) ; в) 1 Вычислите. а) б) ; в)
1 Вычислите. а) б) ; в) 1. Вычислите. а) б) ; в)
1. Вычислите. а) б) ; в) 1 Вычислите. а) б) ; в)
1 Вычислите. а) б) ; в) ..
.. 852 просмотра 3 месяца назад. Тамбувалский математический класс. Тамбувал …
852 просмотра 3 месяца назад. Тамбувалский математический класс. Тамбувал …  ..
..
 * h * 40 / ∆T
* h * 40 / ∆T  Она представляет собой расшифровку свойств стеклопакета и описывает характеристики основных материалов, используемых при изготовлении.
Она представляет собой расшифровку свойств стеклопакета и описывает характеристики основных материалов, используемых при изготовлении. Марка качества М1 – гарантия того, что в окне будет наименьшее количество оптических искажений, пузырьков и других дефектов.
Марка качества М1 – гарантия того, что в окне будет наименьшее количество оптических искажений, пузырьков и других дефектов. 3.1 (4.4.1) и Optilam Clear 3.3.1 (4.4.1).
3.1 (4.4.1) и Optilam Clear 3.3.1 (4.4.1).



 Запишите разницу между текущей доступной памятью и изначально доступной памятью. Пример: Перед запуском теста доступная память составляла 51440 МБ памяти. Доступная память уменьшилась до 51428 МБ во время теста. Таким образом, значение First VUser Memory составляет 12 МБ (= 51440-51428).
Запишите разницу между текущей доступной памятью и изначально доступной памятью. Пример: Перед запуском теста доступная память составляла 51440 МБ памяти. Доступная память уменьшилась до 51428 МБ во время теста. Таким образом, значение First VUser Memory составляет 12 МБ (= 51440-51428). Пример: 131059 МБ
Пример: 131059 МБ Заявление:
Заявление:
 /макс. проекционное отношение
/макс. проекционное отношение на клавиатуре или перемещайте ползунок Throw Distance вперед и назад, пока не найдете число в поле значения, которое представляет
расстояние между объективом проектора и поверхностью экрана. На графическом изображении экрана в середине
калькулятор, вы увидите размерные линии, которые сообщат вам размеры высоты, ширины и диагонали вашего изображения.
на клавиатуре или перемещайте ползунок Throw Distance вперед и назад, пока не найдете число в поле значения, которое представляет
расстояние между объективом проектора и поверхностью экрана. На графическом изображении экрана в середине
калькулятор, вы увидите размерные линии, которые сообщат вам размеры высоты, ширины и диагонали вашего изображения.
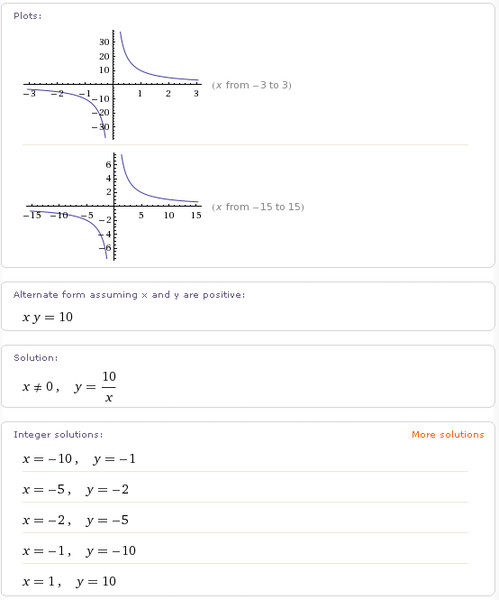 Рассмотрим построение графиков на примерах.
Рассмотрим построение графиков на примерах.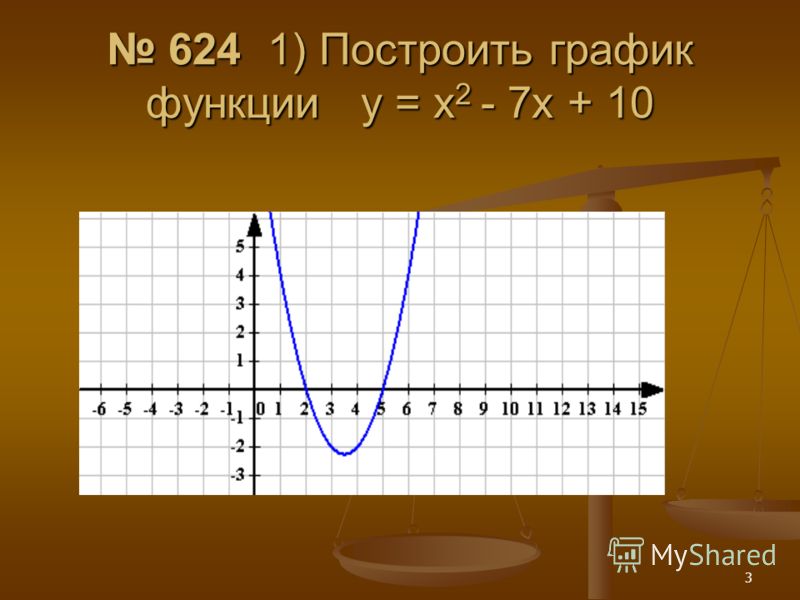
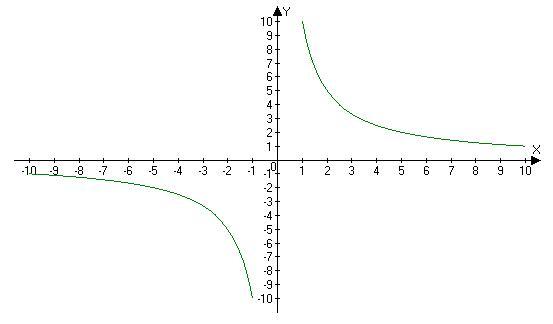
 Я рекомендую решать задачу общими соображениями, а проверять подстановкой.
Я рекомендую решать задачу общими соображениями, а проверять подстановкой.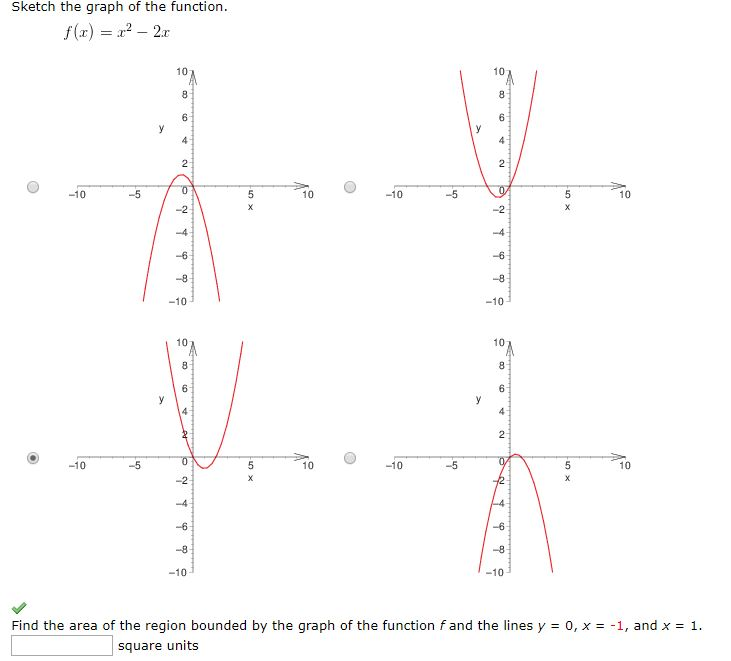



 Качество сборки на высоком уровне. Толщиномер получил компактный корпус, выполненный из высокопрочного пластика, который выдерживает неблагоприятные условия и механические воздействия. Динамический датчик плотно прилегает к исследуемой поверхности, что упрощает процесс измерения.
Качество сборки на высоком уровне. Толщиномер получил компактный корпус, выполненный из высокопрочного пластика, который выдерживает неблагоприятные условия и механические воздействия. Динамический датчик плотно прилегает к исследуемой поверхности, что упрощает процесс измерения. Позвонить
Позвонить  Позвонить
Позвонить 
 Через секунду раздастся звуковой сигнал, а результаты измерения отобразятся на экране с определенной подсветкой индикации замера
Через секунду раздастся звуковой сигнал, а результаты измерения отобразятся на экране с определенной подсветкой индикации замера Все заказы отправляются день в день, если заказ оформлен до 17:00 с ПН-СБ, (Воскресенье выходной)
Все заказы отправляются день в день, если заказ оформлен до 17:00 с ПН-СБ, (Воскресенье выходной) Оплата наличными возможна только при покупке самовывозом из головного офиса, либо у наших представителей/магазинов вашего города.
Оплата наличными возможна только при покупке самовывозом из головного офиса, либо у наших представителей/магазинов вашего города.
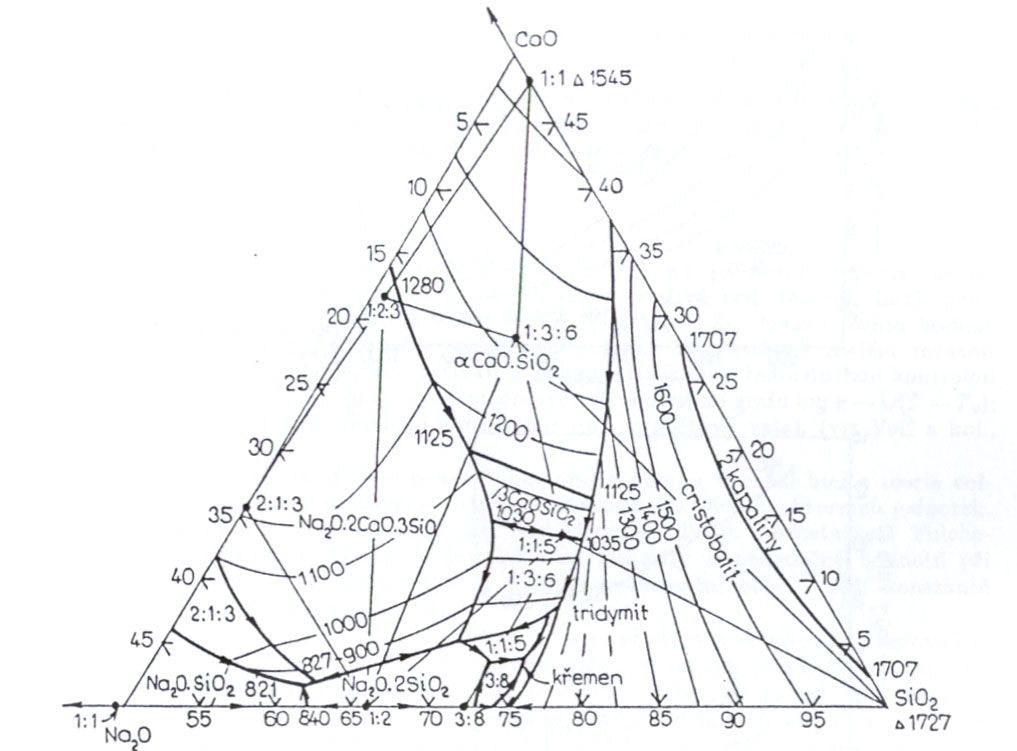

 В обзоре представлены изотермические разрезы при 1500, 1380, 1280, 900 и 700 °С, а также гипотетическая проекция ликвидуса и схема реакции. Недавно [2004Han] и [2009Rha] исследовали псевдодвойной разрез в воздухе вдоль стыка Fe 2 O 3 -Al 2 O 3 .
В обзоре представлены изотермические разрезы при 1500, 1380, 1280, 900 и 700 °С, а также гипотетическая проекция ликвидуса и схема реакции. Недавно [2004Han] и [2009Rha] исследовали псевдодвойной разрез в воздухе вдоль стыка Fe 2 O 3 -Al 2 O 3 .
 56Муа]. Результаты [Han, 2004] и [Rha, 2009] указывают на большую растворимость Al 2 O 3 в гематите, чем найденная [1956Mua].
56Муа]. Результаты [Han, 2004] и [Rha, 2009] указывают на большую растворимость Al 2 O 3 в гематите, чем найденная [1956Mua]. 10-28
10-28
 д.) и модель мира подходит для ваш проблемный домен. Мир лучше аппроксимируется эллипсоидом (сплющенной сферой), чем сферой, но проще выполнять вычисления, предполагая, что Земля является сферой, и вносимая ошибка может быть минимальной. Особенно, если ваша программа просто ищет «грубые» ответы, которые не будут использоваться, скажем, в инженерных проектах.
д.) и модель мира подходит для ваш проблемный домен. Мир лучше аппроксимируется эллипсоидом (сплющенной сферой), чем сферой, но проще выполнять вычисления, предполагая, что Земля является сферой, и вносимая ошибка может быть минимальной. Особенно, если ваша программа просто ищет «грубые» ответы, которые не будут использоваться, скажем, в инженерных проектах.
 Градус берет свое начало в Вавилоне, чья система счисления была основана на шестидесяти. В то время считалось, что Солнце вращается вокруг Земли. Расчеты показывают, что Солнцу потребовалось ровно 360 дней, чтобы совершить полный оборот. Итак, с каждым днем Солнце проходило часть этого пути. Эта дуга, соответствующая пути Солнца по своей орбите в течение одних суток, равнялась углу, вершиной которого был центр нашей планеты. Этот угол стал единицей измерения и получил название градуса или угла градуса. Хотя позже было показано, что именно Земля вращалась вокруг Солнца, а не наоборот, этот способ измерения углов сохранился до наших дней. Еще одним наследием вавилонян является деление времени на часы, минуты и секунды, что также сделано по аналогичной шкале
Градус берет свое начало в Вавилоне, чья система счисления была основана на шестидесяти. В то время считалось, что Солнце вращается вокруг Земли. Расчеты показывают, что Солнцу потребовалось ровно 360 дней, чтобы совершить полный оборот. Итак, с каждым днем Солнце проходило часть этого пути. Эта дуга, соответствующая пути Солнца по своей орбите в течение одних суток, равнялась углу, вершиной которого был центр нашей планеты. Этот угол стал единицей измерения и получил название градуса или угла градуса. Хотя позже было показано, что именно Земля вращалась вокруг Солнца, а не наоборот, этот способ измерения углов сохранился до наших дней. Еще одним наследием вавилонян является деление времени на часы, минуты и секунды, что также сделано по аналогичной шкале

 Чему равняется b в уравнении 2x2 + 12x — 36 = 0?
Чему равняется b в уравнении 2x2 + 12x — 36 = 0? 1 —
1 — В квадратном уравнении 6x2 — x + 4 = 0 второй коэффициент равен …
В квадратном уравнении 6x2 — x + 4 = 0 второй коэффициент равен … √6400 = …
√6400 = … Решите задачу Найти длины сторон прямоугольника, если его периметр равен 18 см, а площадь 20 см2
Решите задачу Найти длины сторон прямоугольника, если его периметр равен 18 см, а площадь 20 см2 4х2+4х+1=0
4х2+4х+1=0 4х2 – 3х – 4=0
4х2 – 3х – 4=0 -49/24
-49/24 средним
средним 19/7
19/7 № 73:
№ 73: No.: 1)
No.: 1)
 No.: 2)
No.: 2) Выясните, сколько шариков у них было в начале.
Выясните, сколько шариков у них было в начале.
 квадратные уравнения 76 , Вопрос 3
квадратные уравнения 76 , Вопрос 3

 NO.: 2)
NO.: 2) Если бы она получила на 2 балла больше по математике и на 3 балла меньше по английскому языку, произведение их оценок было бы 210. Найдите ее отметки по двум предметам.
Если бы она получила на 2 балла больше по математике и на 3 балла меньше по английскому языку, произведение их оценок было бы 210. Найдите ее отметки по двум предметам. Следовательно, длина меньшей стороны будет
Следовательно, длина меньшей стороны будет Если бы скорость была на 5 км/ч больше, то то же самое путешествие заняло бы на 1 час меньше. Найдите скорость поезда.
Если бы скорость была на 5 км/ч больше, то то же самое путешествие заняло бы на 1 час меньше. Найдите скорость поезда.

 5454545454 + c = 0, получаем
5454545454 + c = 0, получаем No.: 2)
No.: 2) И, следовательно, можно спроектировать желаемую прямоугольную манговую рощу.
И, следовательно, можно спроектировать желаемую прямоугольную манговую рощу. Уравнение с AX 2 + BX + C = 0, мы получаем
Уравнение с AX 2 + BX + C = 0, мы получаем = л (40 − л ) = 40 л − л 2
= л (40 − л ) = 40 л − л 2 
 2, где (h, k) — центр, r — радиус.
2, где (h, k) — центр, r — радиус.


 То есть площадь прямоугольника — это длина, умноженная на ширину. В качестве особого случая, поскольку l = w в случае квадрата, площадь квадрата со стороной s определяется по формуле: A = s2 (площадь).
То есть площадь прямоугольника — это длина, умноженная на ширину. В качестве особого случая, поскольку l = w в случае квадрата, площадь квадрата со стороной s определяется по формуле: A = s2 (площадь).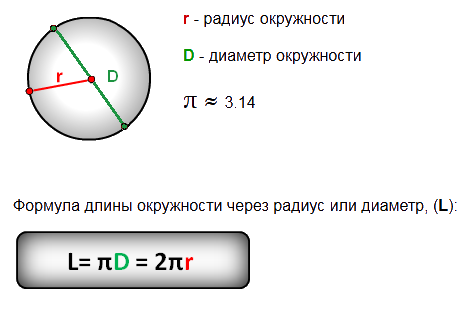 Используйте раскрывающийся список, чтобы выбрать тип расчета, например, Вычислить площадь из диаметра
Используйте раскрывающийся список, чтобы выбрать тип расчета, например, Вычислить площадь из диаметра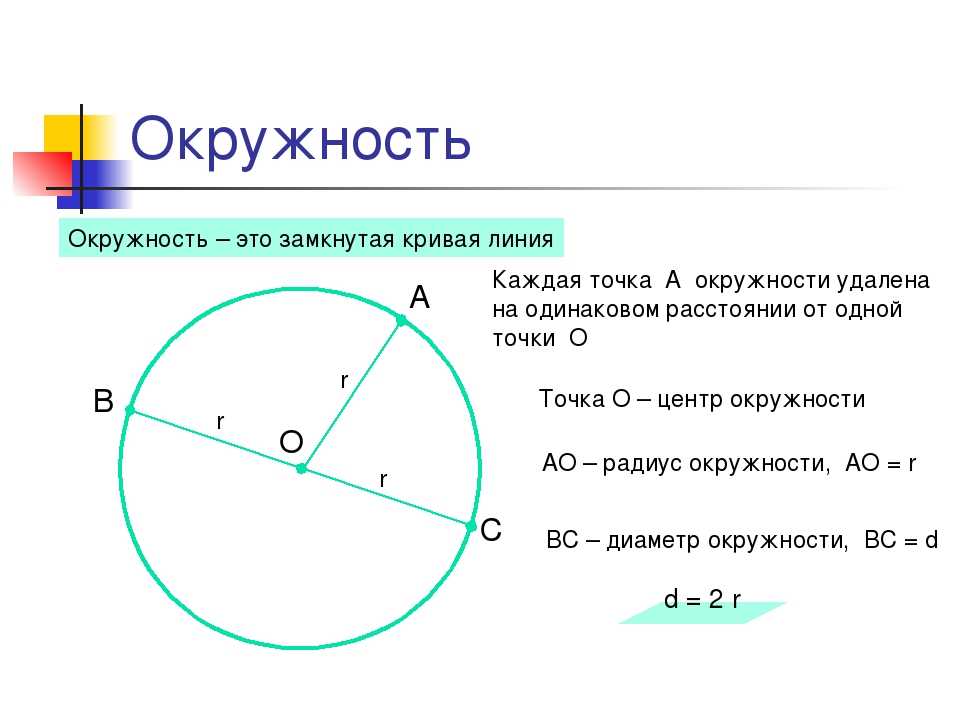 Площадь круга — это мера единичных квадратов, которые могут поместиться внутри фигуры. Чтобы вычислить площадь круга, мы используем формулу площади круга, используя радиус или диаметр. 92
Площадь круга — это мера единичных квадратов, которые могут поместиться внутри фигуры. Чтобы вычислить площадь круга, мы используем формулу площади круга, используя радиус или диаметр. 92 2
92
2
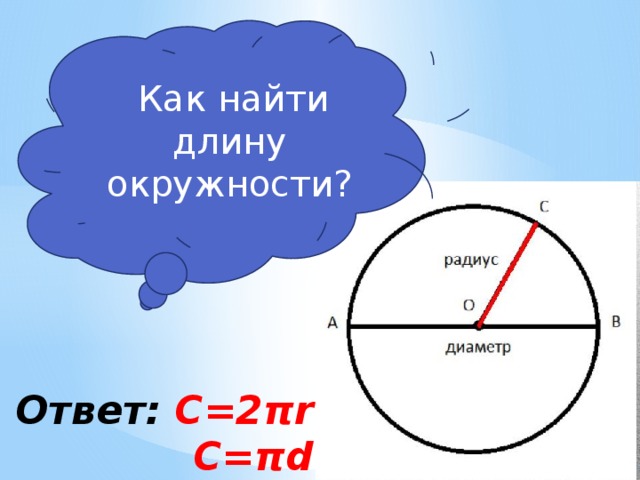
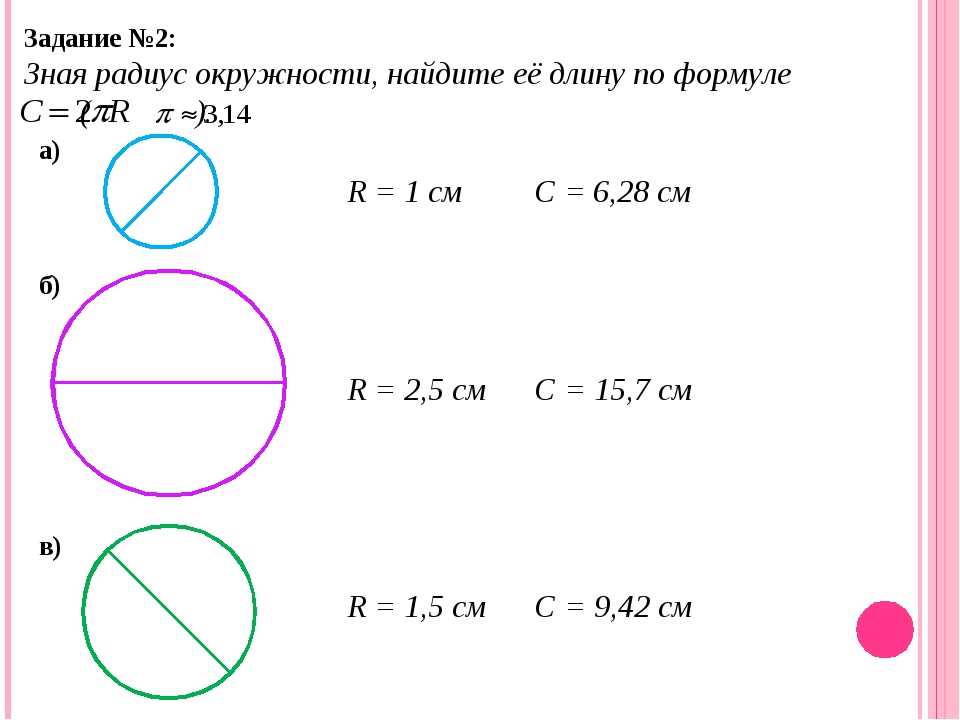
92 Зная радиус круга, мы можем найти его длину окружности по формуле
Зная радиус круга, мы можем найти его длину окружности по формуле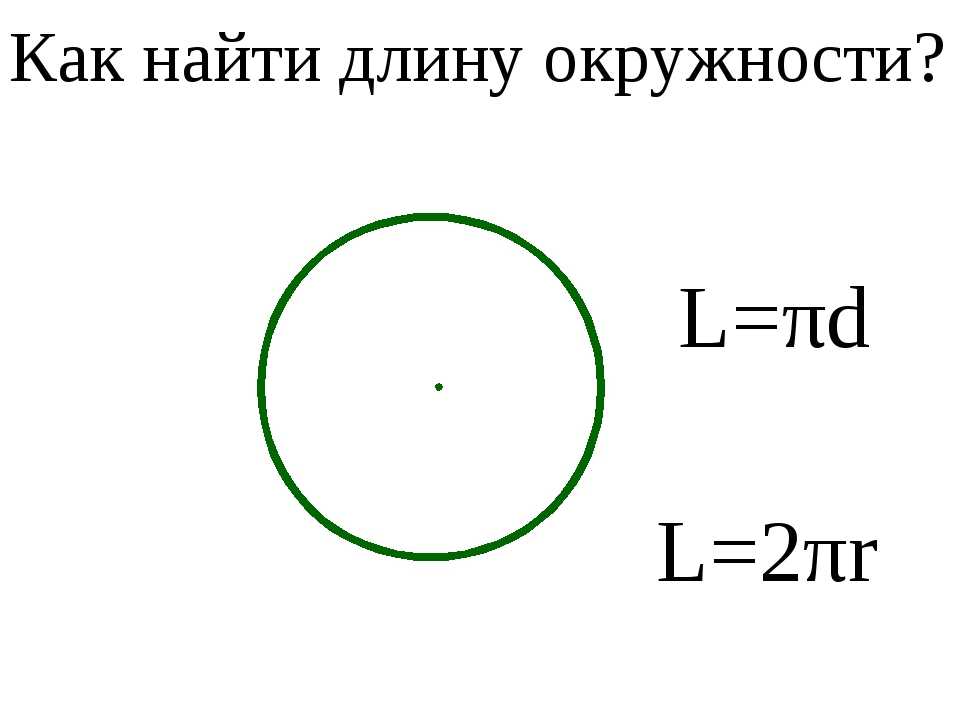 1
1 3
>
Вопрос 2
3
>
Вопрос 2 Найдите площадь тени…
Найдите площадь тени…