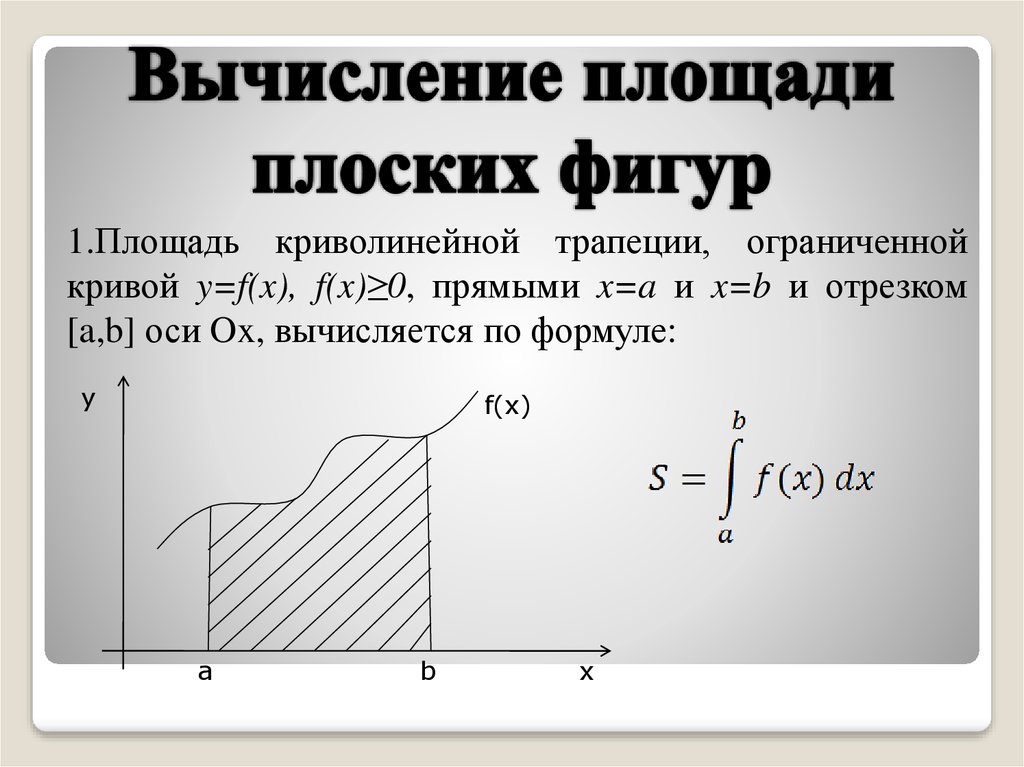
Cайт учителя химии Малютиной Галины Ильиничны
Тривиальные названия веществ
Тривиальные названия органических и неорганических веществ
Химическая номенклатура — совокупность названий индивидуальных химических веществ, их групп и классов, а также правила составления этих названий.
Система наименований химических соединений длительное время развивалась хаотично, наименования давались в основном первооткрывателями каких-либо соединений. Многие вещества известны настолько давно, что происхождение их наименований носит легендарный характер. Исторически сложившиеся «собственные имена» выделяют как тривиальные названия. Такие названия не выражают строения соединения и чрезвычайно разнообразны.
| Тривиальное название | Формула вещества | Современная номенклатура |
А | ||
| Алебастр | 2CaSO4 . H2O H2O | Гидрат сульфат кальция (2/1) |
| Ангидрит | CaSO4 | Сульфат кальция |
| Ангидрид | SO3 | Оксид серы (VI) |
| Антихлор | Na2S2O3 | Тиосульфат натрия |
| Английская соль(горькая соль) | MgSO4. 7 H2O | Гептагидрат сульфата магния |
Б | ||
| Барит | BaSO4 | Сульфат бария |
| Баритовая вода | Ba(OH)2 | Гидроксид бария |
| Белила титановые | TiO2 | Оксид титана (IV) |
| Белила цинковые | ZnO | Оксид цинка |
| Берлинская лазурь | KFe[Fe(CN)6] | Гексацианоферрат(II) железа (III) калия |
| Бертоллетова соль | KСlO3 | Хлорат калия |
| Благородные (инертные) газы | He, Ne, Ar, Kr, Xe, Rn. | Неметаллы VIII группы главной подгруппы |
| Болотный (рудничный) газ | СН4 | Метан |
| Бура | Na2B4O7. 10 H2O | Декагидрат тетрабората натрия |
| Бурый газ («лисий хвост») | NO2 | Оксид азота (IV) |
В | ||
| Веселящий газ | N2O | Оксид азота (I) |
| Водяной газ | Смесь СО и Н2 | Смесь оксида углерода (II) и водорода |
Г | ||
| Гашеная известь | Са(ОН)2 | Гидроксид кальция |
| Гипосульфит (фото) | Na2S2O3 . 5 H2O | Пентагидрат тиосульфата натрия |
| Глауберова соль | Na2SO4 . 10 H2O | Декагидрат сульфата натрия |
| Глёт свинцовый | PbO | Оксид свинца (II) |
| Глинозём | Al2O3 | Оксид алюминия |
Е | ||
| Едкий натр (каустик) | NaOH | Гидроксид натрия |
| Едкое кали | KOH | Гидроксид калия |
Ж | ||
| Желтая кровяная соль | K4Fe(CN)6. 3H2O 3H2O | Тригидрат гексацианоферрата (III) калия |
| Жженая магнезия | MgO | Оксид магния |
| Жидкое стекло | Na2SiO3 | Силикат натрия |
И | ||
| Известь жженая (негашеная, кипелка) | CaO | Оксид кальция |
| Известь гашеная (пушонка) | Ca(OH)2 | Гидроксид кальция |
| Известняк (мел и мрамор) | СаСО3 | Карбонат кальция |
К | ||
| Киноварь | HgS | Сульфид ртути (II) |
| Каменная (поваренная, пищевая, кухонная, галит (прир. Минерал) | NaCl | Хлорид натрия |
| Киноварь | HgS | Сульфид ртути (II) |
| Красная кровяная соль | K3Fe(CN)6 | Гексацианоферрат(II) калия |
| Кремнезём (также пе-сок, кварц, сажа белая) | SiO2 | Оксид кремния (IV) |
| Купоросное масло (ак-кумуляторная кислота) | H2SO4 | Серная кислота |
| Купоросы | MIISO4. nH2O nH2O | Кристаллогидраты сульфатов некоторых двухвалентных металлов |
Л | ||
| Ляпис | AgNO3 | Нитрат серебра |
М | ||
| Магнезит (белая магнезия) | MgCO3 | Карбонат магния |
| Мирабилит (глауберова соль) | Na2SO4.10 H2O | Декагидрат сульфата натрия |
| Мочевина | CO(NH2)2 | Карбамид |
Н | ||
| Нашатырный спирт | NH3. xH2O | Водный раствор аммиака |
| Нашатырь | NH4Cl | Хлорид аммония |
О | ||
| Олеум | Р-р SO3 в конц. H2SO4 | Раствор оксида серы (VI) в серной кислоте |
| Оловянный камень | SnO2 | Оксид олова (IV) |
П | ||
| Пергидроль | 30% водный р-рH2O2 | Пероксид водорода (30%) |
| Пирит | FeS2 | Железный колчедан |
| Плавиковая кислота | HF | Фтороводородная кислота |
| Поташ | K2CO3 | Карбонат калия |
С | ||
| Сажа (угол, кокс) | С | Углерод |
| Селитра | MNO3 | Нитраты щелочных (I гр. гл. подгр.) и щелочно-земельных (II гр. гл. подгр.) металлов гл. подгр.) и щелочно-земельных (II гр. гл. подгр.) металлов |
| Серная печень | Na2Sx | Полисульфиды натрия |
| Серный цвет | S | Сера (порошок) |
| Сода кристаллическая | Na2CO3 .10 H2O | Декагидрат карбоната натрия |
| Сода питьевая | NaHCO3 | Гидрокарбонат натрия |
| Сода кальцинированная | Na2CO3 | Карбонат натрия |
| Соляная кислота | HCl | Хлороводородная кислота |
| Сухой лёд (углекислый газ) | CO2 | Оксид углерода (IV) |
| Сусальное золото | SnS2, Au | Металлическое золото; сульфид олова (IV) |
| Станиоль | Sn | Оловянная фольга |
Х | ||
| Хлорная известь | Ca(OCl)Cl | Смешанный хлорид-гипохлорид кальция |
| Хромпик (калиевый) | K2Cr2O7 | Дихромат калия |
У | ||
| Угарный газ | CO | Оксид углерода (II) |
Ц | ||
| Царская водка | HNO3 (1V) и HCl (3V) | Смесь концентрированных кислот азотной и соляной |
Презентация к Блиц — турниру по химии «Юные любители химии» 8-А,8-В классы
Перегляд файлу
Попередній слайд 1 / 98 Наступний слайд
Зміст слайдів
Номер слайду 1
«Юные любители химии»по теме «Основные классы неорганической химии»Блиц-турнир между 8-А и 8-В кл. Разработала: уч. химии ЗГ №11 Иванисова Валентина Михайловна
Разработала: уч. химии ЗГ №11 Иванисова Валентина Михайловна
Номер слайду 2
Нетрадиционное определение химии. Химия – это наука, умеющая творить чудеса, требующая к себе самогосерьезного отношения
Номер слайду 3
Конкурсы. Представление команд. Терминологический бой.«Отгадай-ка!».«Шиворот-навыворот».«Определи меня».«Созвездие талантов»
Номер слайду 4
Приветствие команд. Команда №2 Команда №1
Номер слайду 5
Терминологический бой. Дать определение терминам: кислотаоксидсоль основание.
Номер слайду 6
Конкурс « Отгадай-ка »Нахожусь, друзья, везде: В минералах и в воде. Без меня вы как без рук: Нет меня — огонь потух.
Номер слайду 7
« Отгадай-ка » Первый слог — предлог известный. Слог второй трудней найти: Часть его ищите в цифрах, К ней добавьте букву Й. Чтобы целое узнать, Нужно вам металл назвать.
Номер слайду 8
« Отгадай-ка »Внутри меня — сухая трава. С обоих концов — согласные. В целом я — газ, дорогие друзья, И название, думаю, ясно вам.
Номер слайду 9
« Отгадай-ка »Первый мой слог означает крушение. Крохотен слог мой второй. Рождаюсь я только в зеленых растениях. Отгадайте-ка, кто я такой.
Номер слайду 10
« Отгадай-ка »Слог мой первый — предлог. Слог второй — сообщение. Чтобы назвать меня смог, Вспомни кальция соединение.
Номер слайду 11
« Отгадай-ка »Первый слог мой — повозка большая. Моральная сила — вот слог мой второй. В целом, важнейшую роль выполняя, Хотя и невидим, всегда я с тобой.
Номер слайду 12
« Отгадай-ка »С КА — активный я металл, С ГЕ — я очень легкий газ. Чтобы ты нас разгадал, Глянь в систему еще раз.
Номер слайду 13
« Отгадай-ка »с М — единица; с Б — я в больнице; с Р — я на сцене; с С — на столе. Кто мы такие? Скажите-ка мне!
Номер слайду 14
« Отгадай-ка »Я укрощаю рек теченье, Моря при этом создаю. Запаситесь-ка терпеньем, Узнать себя я помогу. Вы подумайте немного, Вместо О поставьте А, И потечет вода свободно, Ведь металлом стала я.
Номер слайду 15
« Отгадай-ка »Я светоносный элемент. Я спички вам зажгу в момент. Сожгут меня — и под водой Оксид мой станет кислотой.
Номер слайду 16
«Шиворот-навыворот»Не все то аурум, что блестит. Недонатрий хлорид на столе, перенатрий хлорид на голове. За купрумный грош удавился. Феррумный характер. С тех пор много аш-два-о утекло. Уходит, как аш-два-о в кремний (IY) оксид.
Номер слайду 17
ВЫ готовы к ИССЛЕДОВАТЕЛЬСКОЙ работе ?
Номер слайду 18
Жизнь моя в опасности без правил безопасности
Номер слайду 19
«Определи меня»В пробирках №1,2,3,4,5 находятся вещества Na. Cl, Ba. Cl2, Na. OH, HCl, h3 SO4. C помощью выданных реактивов определите в какой пробирке находится каждое из этих веществ.
Номер слайду 20
«Искусственная кровь»Уравнение реакции: Fe. Cl3 + 3 KCNS = Fe(CNS)3 + 3 KCl. Проведение опыта: намочить одну ватку раствором Феррум (III) хлорида и протереть ей руку одного из ведущих. Другую ватку намочить раствором Калий роданида и протереть ей лезвие ножа. Провести ножом по руке ведущего – появится так называемая «искусственная кровь».
Провести ножом по руке ведущего – появится так называемая «искусственная кровь».
Номер слайду 21
Созвездие талантов. Каждая команда по очереди выбирает 3 вопроса из любой темы знаний (оксиды, основания, кислоты, соли, формулы, генетическая связь) для своей команды и отвечает любой член команды, который знает ответ. За каждый правильный ответ команда получает 1 балл. Каждая команда выбирает 3 вопроса для команды соперника. За каждый правильный ответ команда получает 1 балл. Личный зачет (по 3 вопроса) Каждая команда выбирает одного участника. Участники по очереди открывают вопросы и отвечают на них самостоятельно. Выбирается лучший из лучших.
Номер слайду 22
— оксиды- основания- кислоты- формулы- соли- генетическая связь. Темы заданий:
Номер слайду 23
123456789101112131415161718192021222324252627282930313233343536ppt_xxshearxshearppt_x
Номер слайду 24
Наша встреча – лишь игра,И расставаться нам пора. Будете с улыбкой вспоминать. Как пытались баллы добывать. Но не важен в баллах результат,Дружба побеждает – это факт. А находчивость по жизни вас ведет,Знатокам всегда, везде везет!
Но не важен в баллах результат,Дружба побеждает – это факт. А находчивость по жизни вас ведет,Знатокам всегда, везде везет!
Номер слайду 25
1?К какой группе оксидов относятся вещества ?Na2 O, К2 О, Ca. O
Номер слайду 26
1!Ответ:к группе основных оксидов.
Номер слайду 27
2?К какой группе оксидов относятся вещества ?Н2 O, СО2, SO3
Номер слайду 28
2!Ответ:к группе кислотных оксидов.
Номер слайду 29
3?Найдите лишнюю формулу и дайте название этому веществу ?Н2 SO4, h3 СО3, SO3, HCl
Номер слайду 30
3!SO3- Сульфур (VI) оксид
Номер слайду 31
4?Fе2 O3 Ca. OAl2 O3 Zn. OAg2 OCO2 SO3 Ba. OK2 OНайдите выигрышный путь, который составляют оксиды, взаимодействующие с водой ?
Номер слайду 32
4!Fе2 O3 Ca. OAl2 O3 Zn. OAg2 OCO2 SO3 Ba. OK2 O
Номер слайду 33
5?В какой реакции из простых веществ образуются оксиды ?реакция соединения;реакция разложения;реакция замещения;
Номер слайду 34
5!Реакция соединения2 Н2 + О2 = 2 Н2 О
Номер слайду 35
6?Чтоб появиться я сумел,Прокаливают белый мел,Меня дает огонь в печи,И пламя маленькой свечи,И стоит только сделать вдох,Чтоб я на свет явиться смог. Я в газированной воде,Я в хлебе, в соде, я – везде!Думаю узнали нас. Это — ….
Я в газированной воде,Я в хлебе, в соде, я – везде!Думаю узнали нас. Это — ….
Номер слайду 36
6!Углекислый газ. CO2
Номер слайду 37
7?Мы провели опрос простой. Он высветил состав такой: Оксиген с Гидрогеном вместе – «о» и «аш»Образуют дружную группу ОН (о-аш). Что за вещества с группой этой,И есть ли у них главная примета?
Номер слайду 38
7!Основания Me(OH)n
Номер слайду 39
8?Найдите лишнюю формулу и дайте название этому веществу ?Na. OH, KCl, Na2 SO3, Ba. Cl2
Номер слайду 40
8!Na. OH- Натрий гидроксид, щелочь
Номер слайду 41
9?Свойства оснований. Основания. Na. OHFe(OH)3 Ca(OH)2 Cu(OH)2 Взаимодействие с кислотамикисл. Разъедающее действиеомра. Раствор фенолфталеина окрашивается в красный цветомдс. Выберите для каждого основания характерные свойства. Буквы, соответствующие правильному ответу, дают название химического вещества, без которого невозможна жизнь на Земле.
Номер слайду 42
9!КИСЛОРОД
Номер слайду 43
10?Раствор гидроксида калия вступает в химические реакции с веществами, формулы которых а) СО2 б) h3 S в) Са(ОН)2г) Cu д) Na. NO3 e) Mg
NO3 e) Mg
Номер слайду 44
10!Ответ: а, б
Номер слайду 45
11?Выберите ряд формул, в котором все вещества являются основаниямиа) Fe2 O3, Zn. O, Cu(OH)2 б) Ba(NO3)2, Ba(OН)2, Н2 SО4 в) КОН, Fe(OH)3, Na. ОН г) Zn(OН)2, НCl, h3 O
Номер слайду 46
11!Ответ: в
Номер слайду 47
12?Установите соответствие. Растворимое основание А. КОННерастворимое основание B. Сu(OH)2 C. Na. OH D. Ni(OH)2
Номер слайду 48
12!Ответ: 1-А,С 2- B,D
Номер слайду 49
13?Образуйте из слогов:ме-нит-ний- ще-рат-маг-ная-за-ния. Металл, при взаимодействии с кислотой выделяется водород. Кислота, при взаимодействии которой с металлами не образуется водород. Тип реакции между кислотой и металлом.
Номер слайду 50
13!Магний. Нитратная. Замещения
Номер слайду 51
14?Укажите кислоту, которая не соответствует признаку, объединяющему их в ряд: Слабая кислота среди сильных: HNO3, h3 SO4, HCl, h3 CO32) Двухосновная кислота среди одноосновных: HI, HBr, HF ,h3 S
Номер слайду 52
14!Карбонатная кислота h3 CO3 Сульфидная кислота h3 S
Номер слайду 53
15?Кислоты, входящие в состав «царской» водки
Номер слайду 54
15!Ца́рская во́дка — смесь концентрированных нитратной (1 объём) и хлоридной (3 объёма) кислот. 1 HCl : 3 HNO3
1 HCl : 3 HNO3
Номер слайду 55
16? Число формул кислот в следующем списке: h3 CO3, KOH, h3 SO4, Na. NO3, HNO3, Ca. CO3
Номер слайду 56
16!Ответ:3
Номер слайду 57
17?сульфиднаясиликатнаянитратнаясульфитнаяортофосфатнаякарбонатная. h3 SO3 h3 Sh3 CO3 Соотнесите название кислотfillcolorfill.typefill.onfillcolorfill.typefill.onfillcolorfill.typefill.on
Номер слайду 58
17!сульфитнаясульфиднаякарбонатная. h3 SO3 h3 Sh3 CO3fillcolorfill.typefill.onfillcolorfill.typefill.onfillcolorfill.typefill.on
Номер слайду 59
18?сульфиднаясиликатнаянитратнаясульфитнаяортофосфатнаякарбонатная. h3 Si. O3 h4 PO4 HNO3 Соотнесите название кислотfillcolorfill.typefill.onfillcolorfill.typefill.onfillcolorfill.typefill.on
Номер слайду 60
18!силикатнаяортофосфатнаянитратная. h3 Si. O3 h4 PO4 HNO3fillcolorfill.typefill.onfillcolorfill.typefill.onfillcolorfill.typefill.on
Номер слайду 61
19?Формулы только солей приведены в ряду 1) НСl, Na.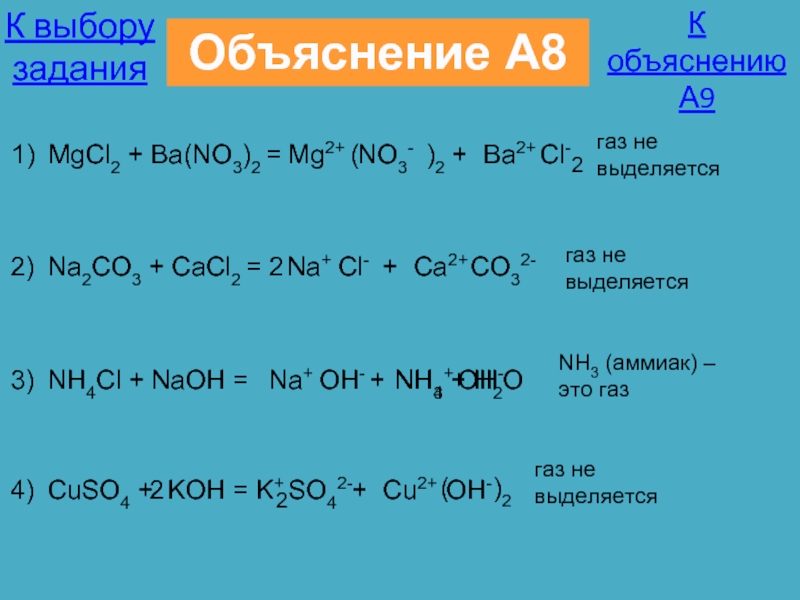 Cl, HNO3 2) h3 SO3, К2 SO4, h3 S 3) Ca(OH)2, h4 PO4, Ca3(PO4)2 4) Na2 SO4, Na. NO3, КNO3
Cl, HNO3 2) h3 SO3, К2 SO4, h3 S 3) Ca(OH)2, h4 PO4, Ca3(PO4)2 4) Na2 SO4, Na. NO3, КNO3
Номер слайду 62
19!Ответ: 4
Номер слайду 63
20?Определите вещество, которое является лишним в каждой строчке. А. Na. Cl KNO3 Li3 PO4 Ca. CO3 В. Cu. S K2 SO4 Ba. SO4 Mg. CO3
Номер слайду 64
20!А. Ca. CO3 – нерастворимая соль. В. K2 SO4 – растворимая соль
Номер слайду 65
21?Я, конечно, очень нужен,Без меня не сваришь ужин,Не засолишь огурца,Не заправишь холодца,Но не только лишь в еде,Я живу в морской воде. Если льется слеза из глаза,Вкус припомните вы сразу. Кто догадлив, говорит –Это….
Номер слайду 66
21!Ответ: натрия хлорид
Номер слайду 67
22?Fе. Cl2 Ca. NO3 Al. Cl3 Zn. SO4 Ag. NO3 Ba. CO3 Ba. SO3 Ba. SO4 KNO3 Найдите выигрышный путь, который составляют соли, растворимые в воде ?
Номер слайду 68
22!Fе. Cl2 Ca(NO3)2 Al. Cl3 Zn. SO4 Ag. NO3 Ba. CO3 Ba. SO3 Ba. SO4 KNO3
Номер слайду 69
23?Дать названия веществам: Ca(NO3)2, K2 SO3, Li2 CO3, Cu. SO4.
SO4.
Номер слайду 70
23!Ответ: кальций нитрат, калий сульфит, литий карбонат, купрум (II) сульфат
Номер слайду 71
24?Хотя я соль, но под водой. Вас удивлю своей средой. Посуду мыть, стирать белье. Могу (и это не вранье). Есть у меня одна сестра. Она. Изжогу вылечить должна,Кто знает свойств моих природу,Ответит сразу, кто я — ….
Номер слайду 72
24!Ответ : сода
Номер слайду 73
25?Составьте формулы солей: Калий сульфид. Купрум (II) сульфат Алюминий фосфат Натрий хлорид
Номер слайду 74
25!Ответ: K2 S, Cu. SO4, Al. PO4, Na. Cl
Номер слайду 75
26?OHCl. SO4 KNa. Ca. Назовите образовавшиеся вещества
Номер слайду 76
26!OHCl. SO4 KКалий гидроксид. Калий хлорид. Калий сульфат. Na. Натрий гидроксид. Натрий хлорид Натрий сульфат. Ca. Кальций гидроксид. Кальций хлорид. Кальций сульфат
Номер слайду 77
27?Назовите формулы кислот соответствующих оксидов: Сульфур (VI) оксид, Нитроген (V) оксид, Карбон (IV) оксид, Фосфор (V) оксид
Номер слайду 78
27!Ответ: h3 SO4, HNO3, h3 CO3, h4 PO4
Номер слайду 79
28?Назовите общую формулу высших оксидов следующих химических элементов: нитроген, фосфор, арсен
Номер слайду 80
28!Ответ: R2 O5
Номер слайду 81
29?Назовите формулы оснований соответствующих оксидов: Купрум (II) оксид, Калий оксид, Барий оксид, Алюминий оксид
Номер слайду 82
29!Ответ: Cu(OH)2, KOH, Ba(OH)2, Al(OH)3
Номер слайду 83
30? Зная классификацию неорганических соединений, распределите вещества по основным классам:1)Na. Cl, 2)Na. OH, 3)CO2, 4)Ba(OH)2, 5)h3 SO4, 6)Cu(OH)2, 7)HF, 8)SO3, 9)Mg. O, 10)Li2 O, 11)Mg. Cl2, 12)Mg(OH)2, 13)HNO3, 14)Na2 CO3, 15)K3 PO4, 16)h3 S.
Cl, 2)Na. OH, 3)CO2, 4)Ba(OH)2, 5)h3 SO4, 6)Cu(OH)2, 7)HF, 8)SO3, 9)Mg. O, 10)Li2 O, 11)Mg. Cl2, 12)Mg(OH)2, 13)HNO3, 14)Na2 CO3, 15)K3 PO4, 16)h3 S.
Номер слайду 84
30!Ответ: оксиды (3,8,9,10), основания (2,4,6,12), кислоты (5,7,13,16) соли (1,11,14,15)
Номер слайду 85
31? Металл Основный оксид Основание Соль (Na) Na2 SO4 Неметалл Кислотный оксид Кислота Соль (S)
Номер слайду 86
31!Na – Na2 O – Na. OH – Na2 SO4 S – SO3 – h3 SO4 — Na2 SO4
Номер слайду 87
32?Установите соответствие между химической формулой вещества и классом неорганических соединений, к которому оно принадлежит.1) Mg. O 2) Н3 РО4 3) Аl(ОН)3 4) Na. OH А. кислоты. Б. щелочи. В. оксиды. Г. нерастворимые основания
Номер слайду 88
32!Ответ: 1-В, 2-А, 3-Г, 4-Б
Номер слайду 89
33?Найдите вещество -Х
Номер слайду 90
33!Ответ: Р2 О5
Номер слайду 91
34?Пришла телеграмма: «Пропали вещества А и В, вместо них появилось неизвестное вещество С». Вам надо разыскать эти вещества. Итак, вы отправляетесь на поиски: SО3 + h3 O —> А; Mg. О + h3 O —> В (при нагревании)А + В —> С.
Вам надо разыскать эти вещества. Итак, вы отправляетесь на поиски: SО3 + h3 O —> А; Mg. О + h3 O —> В (при нагревании)А + В —> С.
Номер слайду 92
34!Ответ: Mg. SО4 магний сульфат
Номер слайду 93
35?XYНайдите X и Y?
Номер слайду 94
35!Ответы: Х – Ca(OH)2 Y – Ca. SO4
Номер слайду 95
36?Х?Найдите вещества
Номер слайду 96
36!Ответ: SO2, Ca. O (или Ca(OH)2)
Номер слайду 97
Наша встреча – лишь игра,И расставаться нам пора. Будете с улыбкой вспоминать. Как пытались баллы добывать. Но не важен в баллах результат,Дружба побеждает – это факт. А находчивость по жизни вас ведет,Знатокам всегда, везде везет!
Номер слайду 98
Использованные материалы: Игра-зачет «Созвездие талантов» — учитель химии МОУ Хворостянской СОШ Рязкова Н. А.;Викторина «Занимательная химия» — учитель химии Шмыкова И. А., МБОУ СОШИ№29, г. Георгиевск, Ставропольский край;Картинки «эксперименты» http://s3.timetoast.com/public/uploads/photos/3654368/Image.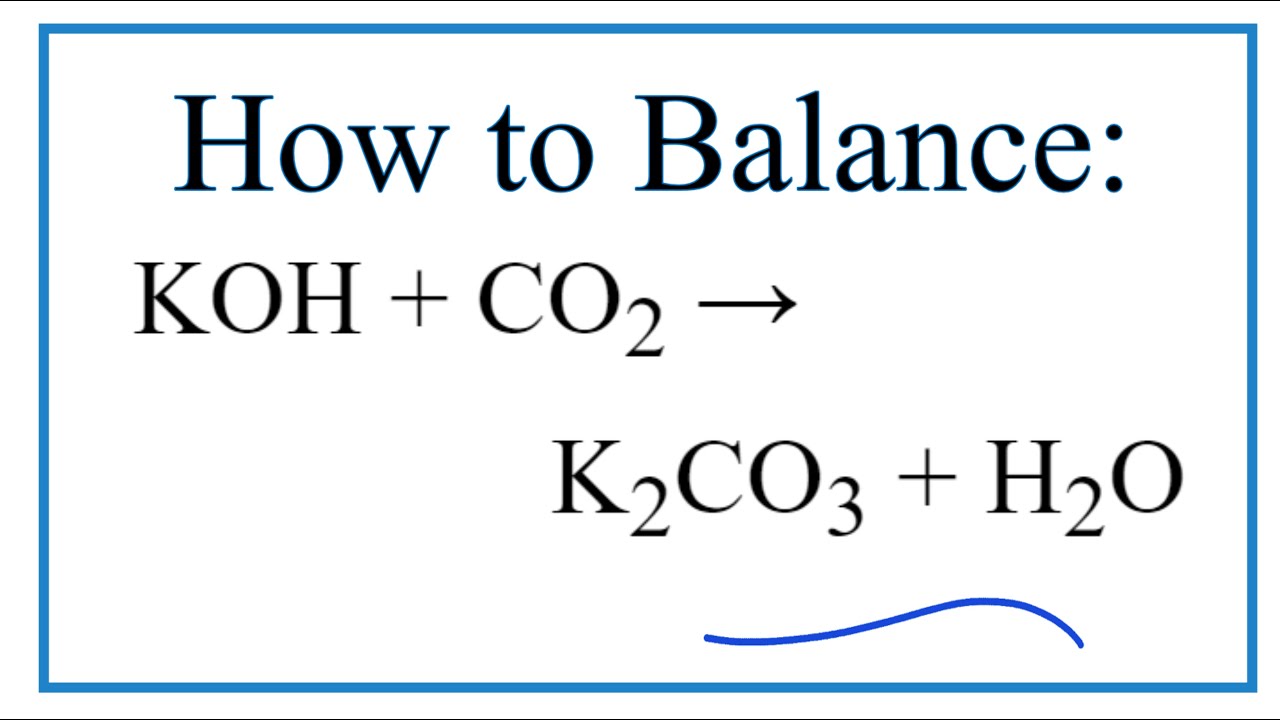 Gen.jpg?1362932222; Картинки «колбы»http://www.freetorg.com.ua/_data/lead/1359/696272i.jpg
Gen.jpg?1362932222; Картинки «колбы»http://www.freetorg.com.ua/_data/lead/1359/696272i.jpg
Вызванное карбонатами растворение урансодержащих осадков в условиях выщелачивания цемента
. 1999 г., апрель; 1(2):177-82. doi: 10.1039/a809262a.М Саттон 1 , P Warwick, A Hall, C Jones
принадлежность
- 1 Химический факультет Университета Лафборо, Лестершир, Великобритания LE11 3TU.
- PMID: 11529097
- DOI: 10.1039/а809262а
М. Sutton et al.
J Мониторинг окружающей среды. 1999 апрель
1999 апрель
Авторы
М Саттон 1 , П. Уорвик, А. Холл, К. Джонс
принадлежность
- 1 Химический факультет Университета Лафборо, Лестершир, Великобритания LE11 3TU.
- PMID: 11529097
- DOI: 10.1039/а809262а
Абстрактный
Исследовано влияние карбоната на растворимость урана (VI) в аэробных и цементирующих условиях. Эта информация имеет отношение к захоронению низкоактивных ядерных отходов. К раствору нитрата уранила добавляли водный раствор NaOH, KOH, Ca(OH)2 и раствор цементного выщелачивания. Затем добавляли увеличивающиеся количества карбоната аммония для повторного растворения осадков. Осадки были охарактеризованы с помощью измерений порошковой рентгеновской дифракции (XRPD) и модельных исследований. Расчеты модели проводились с использованием кода спецификации MINTEQA2 с расширенной базой данных, включающей константы стабильности урана, взятые из базы данных HATCHES. Сравнивали измеренное и предсказанное количество CO3(2-), необходимое для растворения осадков. Знания, полученные в «чистых» системах, были использованы для объяснения процессов осаждения и повторного растворения, наблюдаемых в системе фильтрата. Недостаточная растворимость урана при низких уровнях содержания карбонатов поставила под вопрос литературные константы образования UO2(OH)3- и UO2(OH)4(2-). Приблизительное значение log K, равное 26,8, для образования K2U2O7 было рассчитано по результатам KOH при pH 12.
К раствору нитрата уранила добавляли водный раствор NaOH, KOH, Ca(OH)2 и раствор цементного выщелачивания. Затем добавляли увеличивающиеся количества карбоната аммония для повторного растворения осадков. Осадки были охарактеризованы с помощью измерений порошковой рентгеновской дифракции (XRPD) и модельных исследований. Расчеты модели проводились с использованием кода спецификации MINTEQA2 с расширенной базой данных, включающей константы стабильности урана, взятые из базы данных HATCHES. Сравнивали измеренное и предсказанное количество CO3(2-), необходимое для растворения осадков. Знания, полученные в «чистых» системах, были использованы для объяснения процессов осаждения и повторного растворения, наблюдаемых в системе фильтрата. Недостаточная растворимость урана при низких уровнях содержания карбонатов поставила под вопрос литературные константы образования UO2(OH)3- и UO2(OH)4(2-). Приблизительное значение log K, равное 26,8, для образования K2U2O7 было рассчитано по результатам KOH при pH 12. В целом ожидается, что растворимость урана будет незначительной на полигонах ядерных отходов с низким уровнем активности, поскольку должны сохраняться анаэробные условия. Однако это исследование показало, что растворимость в фильтрате может повышаться при высоком уровне pH и высоком уровне карбоната, если будут развиваться аэробные условия. Образуются растворимые формы U(VI). Новая часть исследования заключалась в том, чтобы воспроизвести эффекты и сопоставить повышенную растворимость с предсказаниями модели. Следовательно, исследование вновь подчеркнуло необходимость надлежащего экологического мониторинга таких участков.
В целом ожидается, что растворимость урана будет незначительной на полигонах ядерных отходов с низким уровнем активности, поскольку должны сохраняться анаэробные условия. Однако это исследование показало, что растворимость в фильтрате может повышаться при высоком уровне pH и высоком уровне карбоната, если будут развиваться аэробные условия. Образуются растворимые формы U(VI). Новая часть исследования заключалась в том, чтобы воспроизвести эффекты и сопоставить повышенную растворимость с предсказаниями модели. Следовательно, исследование вновь подчеркнуло необходимость надлежащего экологического мониторинга таких участков.
Похожие статьи
- Характеристики осаждения ионов уранила при различных значениях pH в зависимости от присутствия карбонат-ионов и перекиси водорода.
Ким К.В., Ким Й.Х., Ли С.И., Ли Дж.В., Джо К.С., Ли Э.Х., Ким Дж.С., Сонг К., Сонг К.С. Ким К.
 В. и др.
Технологии экологических наук. 2009 1 апреля; 43 (7): 2355-61. дои: 10.1021/es802951b.
Технологии экологических наук. 2009.
PMID: 19452886
В. и др.
Технологии экологических наук. 2009 1 апреля; 43 (7): 2355-61. дои: 10.1021/es802951b.
Технологии экологических наук. 2009.
PMID: 19452886 - Торможение урана и тория цементной закладкой, разработанной для захоронения радиоактивных отходов.
Фелипе-Сотело М., Хинчлифф Дж., Филд Л.П., Милодовски А.Е., Приди О., Рид Д. Фелипе-Сотело М. и др. Хемосфера. 2017 июль; 179: 127-138. doi: 10.1016/j.chemosphere.2017.03.109. Epub 2017 26 марта. Хемосфера. 2017. PMID: 28364648
- Стабильность геля гидрата силиката кальция, легированного U(VI), в рассолах, относящихся к хранилищу, изучали с помощью экспериментов по выщелачиванию и спектроскопии.
Вольтер Дж.М., Шмейде К., Вайс С., Бок Ф., Брендлер В., Штумпф Т. Уолтер Дж. М. и соавт.
 Хемосфера. 2019 март; 218: 241-251. doi: 10.1016/j.chemosphere.2018.11.074. Epub 2018 14 ноября.
Хемосфера. 2019.
PMID: 30471505
Хемосфера. 2019 март; 218: 241-251. doi: 10.1016/j.chemosphere.2018.11.074. Epub 2018 14 ноября.
Хемосфера. 2019.
PMID: 30471505 - Видообразование и биодоступность урана в водных системах: обзор.
Маркич С.Ю. Маркич СЯ. Журнал «Научный мир». 2002 15 марта; 2: 707-29. doi: 10.1100/tsw.2002.130. Журнал «Научный мир». 2002. PMID: 12805996 Бесплатная статья ЧВК. Обзор.
- Взгляд на взаимодействие цианобактерий с ураном.
Acharya C, Apte SK. Ачарья С. и др. Фотосинтез рез. 2013 ноябрь; 118 (1-2): 83-94. doi: 10.1007/s11120-013-9928-9. Epub 2013 8 октября. Фотосинтез Рез. 2013. PMID: 24101170 Обзор.
Посмотреть все похожие статьи
Цитируется
- Поперечный биомониторинг металлов у взрослого населения в послевоенной восточной Хорватии: различия между районами умеренного и тяжелого боя.

Ергович М., Мискулин М., Пунтарич Д., Гмайнич Р., Милас Дж., Сипос Л. Ергович М. и соавт. Croat Med J. 2010 Oct;51(5):451-60. doi: 10.3325/cmj.2010.51.451. Хорватский мед J. 2010. PMID: 20960595 Бесплатная статья ЧВК.
Типы публикаций
термины MeSH
вещества
Каково итоговое ионное уравнение для h3CO3 + 2 KOH => K2(CO3) + 2 h3O, сбалансируйте уравнение, если оно не равно
Выберите область веб-сайта для поискаИскать на этом сайте
Цитата страницы Начать эссе значок-вопрос Задайте вопрос Начать бесплатную пробную версию Скачать PDF PDF Цитата страницы Цитировать Поделиться ссылкой ДелитьсяСсылайтесь на эту страницу следующим образом:
«Что такое чистое ионное уравнение для
h3CO3 + 2 KOH => K2(CO3) + 2 h3O
пожалуйста, сбалансируйте уравнение, если это не так».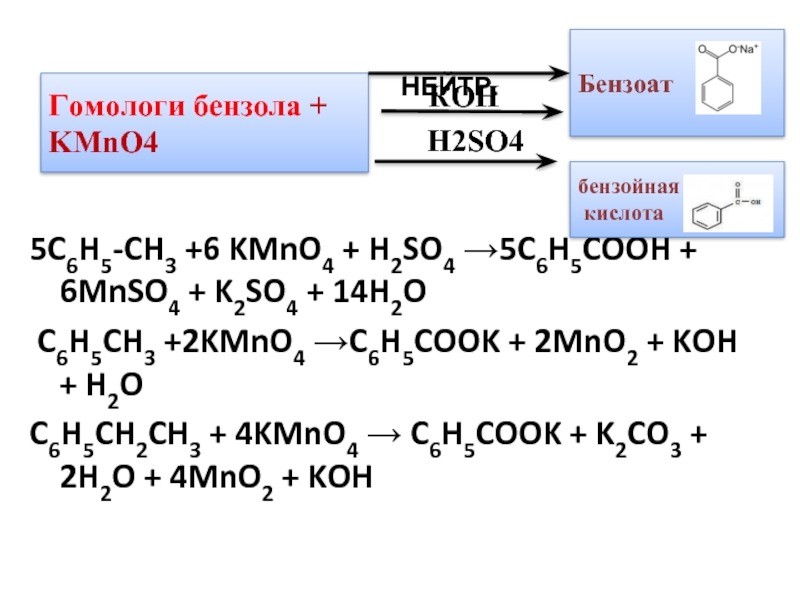 -co3-2-360707.
Доступ 19(-)_(aq) rarr 2H_2O_((l))`
-co3-2-360707.
Доступ 19(-)_(aq) rarr 2H_2O_((l))`
См. eNotes без рекламы
Начните с 48-часовой бесплатной пробной версией , чтобы получить доступ к более чем 30 000 дополнительных руководств и более чем 350 000 вопросов помощи при выполнении домашних заданий, на которые наши эксперты ответили.
Получите 48 часов бесплатного доступаУже зарегистрированы? Войдите здесь.
Утверждено редакцией eNotes Задайте вопросПохожие вопросы
Просмотреть всеНаука
Последний ответ опубликован 09 февраля 2016 г. в 1:09:35.
Если аминокислотная последовательность двух организмов одинакова, будет ли похожа и их ДНК? почему ?
1 Ответ преподавателя
Наука
Последний ответ опубликован 17 июля 2012 г.

 В. и др.
Технологии экологических наук. 2009 1 апреля; 43 (7): 2355-61. дои: 10.1021/es802951b.
Технологии экологических наук. 2009.
PMID: 19452886
В. и др.
Технологии экологических наук. 2009 1 апреля; 43 (7): 2355-61. дои: 10.1021/es802951b.
Технологии экологических наук. 2009.
PMID: 19452886 Хемосфера. 2019 март; 218: 241-251. doi: 10.1016/j.chemosphere.2018.11.074. Epub 2018 14 ноября.
Хемосфера. 2019.
PMID: 30471505
Хемосфера. 2019 март; 218: 241-251. doi: 10.1016/j.chemosphere.2018.11.074. Epub 2018 14 ноября.
Хемосфера. 2019.
PMID: 30471505
 Можно ли начертить план здания (прямоугольной формы в основании) длиной 50 м и шириной 20 м на странице тетради, если использовать масштаб 1 : 50? Какой масштаб следует использовать, чтобы план поместился на странице тетради?
Можно ли начертить план здания (прямоугольной формы в основании) длиной 50 м и шириной 20 м на странице тетради, если использовать масштаб 1 : 50? Какой масштаб следует использовать, чтобы план поместился на странице тетради?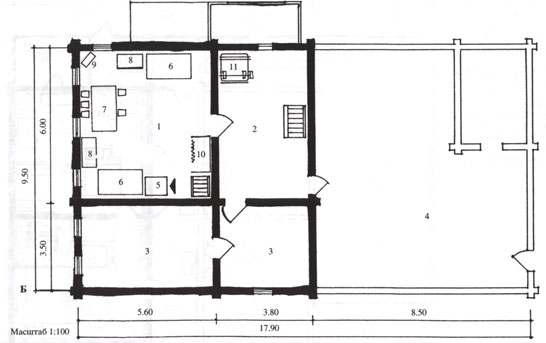 Тогда длина здания на плане будет 20 см, а ширина здания на плане будет 2000 см • 1/250 = 2000/250 см = 8 см.
Тогда длина здания на плане будет 20 см, а ширина здания на плане будет 2000 см • 1/250 = 2000/250 см = 8 см. На материале других школьных предметов придумайте две задачи с использованием масштаба и решите их.
На материале других школьных предметов придумайте две задачи с использованием масштаба и решите их.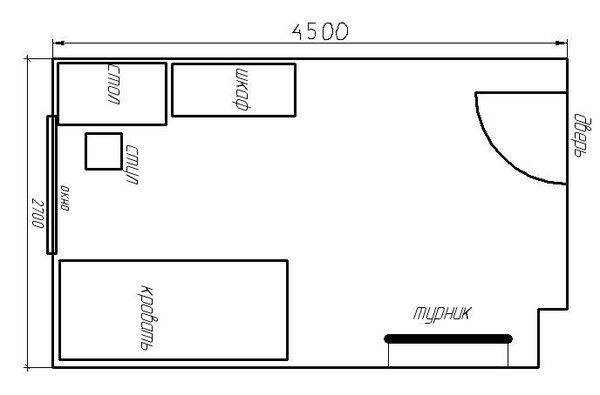

 В. Рудницкой для 4 класса, тетради на печатной основе «Математика» Н.В. Рудницкой, «Дружим с математикой» Е.Э. Кочуровой, линейка, транспортир, карандаш, треугольник, рулетка.
В. Рудницкой для 4 класса, тетради на печатной основе «Математика» Н.В. Рудницкой, «Дружим с математикой» Е.Э. Кочуровой, линейка, транспортир, карандаш, треугольник, рулетка. Сравнение своих выводов с правилом.
Сравнение своих выводов с правилом.
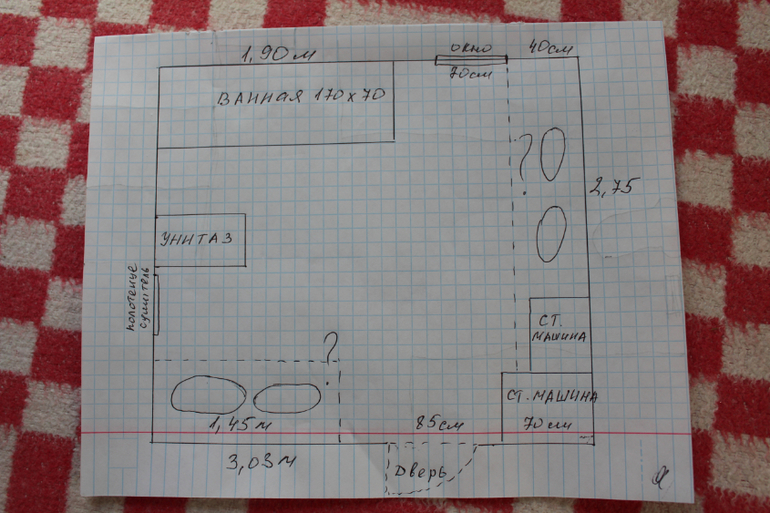
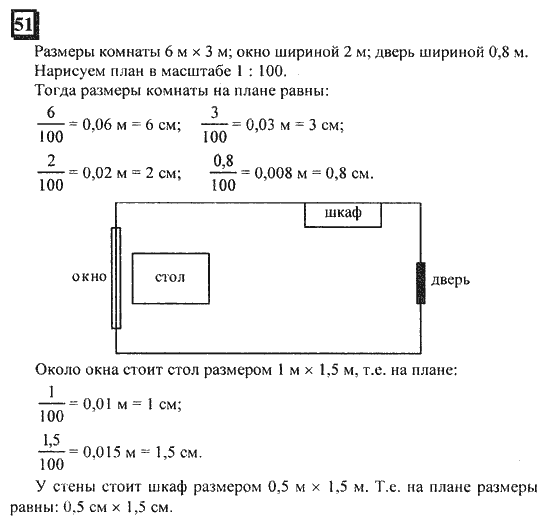 2=8см).
2=8см).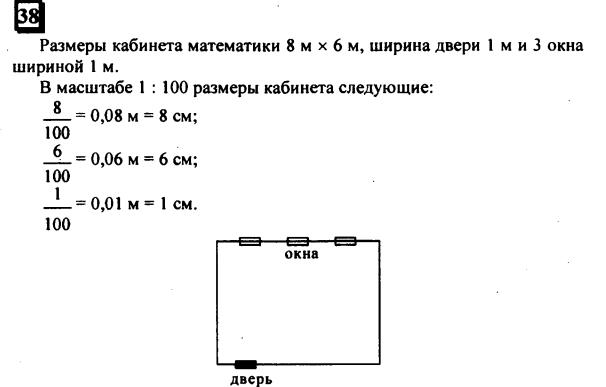 Дети измеряют длину класса ширину, выбирают масштаб, вычисляют размеры на плане, вычерчивают прямоугольник, углы строят с помощью транспортира или треугольника, записывают масштаб.
Дети измеряют длину класса ширину, выбирают масштаб, вычисляют размеры на плане, вычерчивают прямоугольник, углы строят с помощью транспортира или треугольника, записывают масштаб.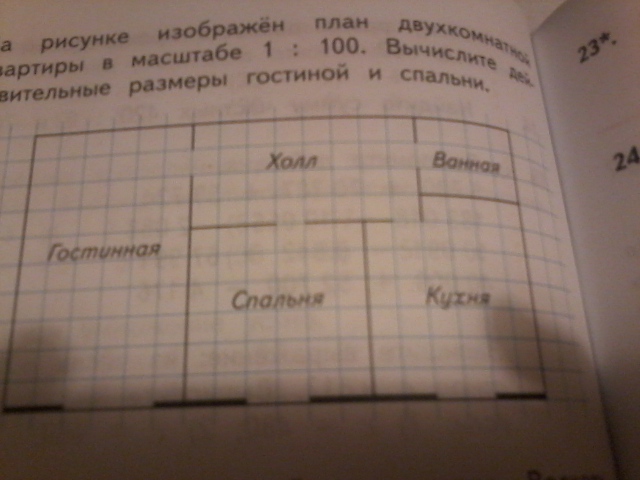 з.
з. Здание фактически разделено на три уровня, чтобы показать предлагаемую внутреннюю планировку помещений. На участке есть два дома, главный дом и гостевой дом, и оба имеют съемные слои, чтобы показать внутренний вид. Для облегчения транспортировки модель также состоит из двух секций, причем стык проходит между двумя домами.
Здание фактически разделено на три уровня, чтобы показать предлагаемую внутреннюю планировку помещений. На участке есть два дома, главный дом и гостевой дом, и оба имеют съемные слои, чтобы показать внутренний вид. Для облегчения транспортировки модель также состоит из двух секций, причем стык проходит между двумя домами.
 Клиент также хотел показать многоярусные многоярусные автостоянки в задней части зданий, так как дополнительные парковочные места были очень привлекательными. Эта модель также включает светодиодное освещение, которое вы можете увидеть, если щелкнете раздел «Подсветка» выше.
Клиент также хотел показать многоярусные многоярусные автостоянки в задней части зданий, так как дополнительные парковочные места были очень привлекательными. Эта модель также включает светодиодное освещение, которое вы можете увидеть, если щелкнете раздел «Подсветка» выше. Нашим решением стало это стилизованное трехмерное изображение здания с напольными панелями из прозрачного акрила, позволяющее зрителю с первого взгляда оценить вертикальное и горизонтальное расположение всех основных промышленных компонентов, задействованных в процессе. Создание модели включало в себя расшифровку и рационализацию огромного объема технических чертежей, чтобы мы могли разработать упрощенное представление основного производственного оборудования. Важнейшей частью этого процесса было поддержание постоянного диалога с клиентом, чтобы убедиться, что мы правильно интерпретируем информацию. Модель длиной чуть более 2,4 метра может легко рассмотреть группа людей, что делает ее идеальной отправной точкой для экскурсии по зданию.
Нашим решением стало это стилизованное трехмерное изображение здания с напольными панелями из прозрачного акрила, позволяющее зрителю с первого взгляда оценить вертикальное и горизонтальное расположение всех основных промышленных компонентов, задействованных в процессе. Создание модели включало в себя расшифровку и рационализацию огромного объема технических чертежей, чтобы мы могли разработать упрощенное представление основного производственного оборудования. Важнейшей частью этого процесса было поддержание постоянного диалога с клиентом, чтобы убедиться, что мы правильно интерпретируем информацию. Модель длиной чуть более 2,4 метра может легко рассмотреть группа людей, что делает ее идеальной отправной точкой для экскурсии по зданию. Это было нашим решением. Из первоначального концептуального наброска мы спроектировали и построили модель всего за 6 рабочих дней, включая съемные крыши, взаимозаменяемые планировки пола и покрытие из плексигласа. Все это измерялось всего 350 x 290 мм и помещается в небольшой мягкий чемодан, который соответствует ограничениям на провоз ручной клади в полете.
Это было нашим решением. Из первоначального концептуального наброска мы спроектировали и построили модель всего за 6 рабочих дней, включая съемные крыши, взаимозаменяемые планировки пола и покрытие из плексигласа. Все это измерялось всего 350 x 290 мм и помещается в небольшой мягкий чемодан, который соответствует ограничениям на провоз ручной клади в полете. Главное прибрежное место должно было быть точно сформировано на суше, чтобы отразить драматические контуры на месте.
Главное прибрежное место должно было быть точно сформировано на суше, чтобы отразить драматические контуры на месте. ..
Посмотреть нашу галерею >
..
Посмотреть нашу галерею > В качестве практики мы обязательно будем иметь вас в виду, если нам когда-либо потребуются встроенные модели. будущее.» Кельвин Найду
В качестве практики мы обязательно будем иметь вас в виду, если нам когда-либо потребуются встроенные модели. будущее.» Кельвин Найду 
 Канада немного смешанная, но обычно метрическая.
Канада немного смешанная, но обычно метрическая. 




 Является ли ваш ответ примерно таким, каким вы его ожидали?
Является ли ваш ответ примерно таким, каким вы его ожидали? 


 Суть данного термина состоит в том, что мы находим значение любой тригонометрической функции (sin α, cos α, tg α, ctg α) через формулу тангенса половинного угла. Этот вариант намного проще и рациональнее, так как выполнять дальнейшие вычисления легче без корней, а с целыми числами.
Суть данного термина состоит в том, что мы находим значение любой тригонометрической функции (sin α, cos α, tg α, ctg α) через формулу тангенса половинного угла. Этот вариант намного проще и рациональнее, так как выполнять дальнейшие вычисления легче без корней, а с целыми числами. Для работы в задаче должен быть определен входящие тангенсы и котангенсы.
Для работы в задаче должен быть определен входящие тангенсы и котангенсы.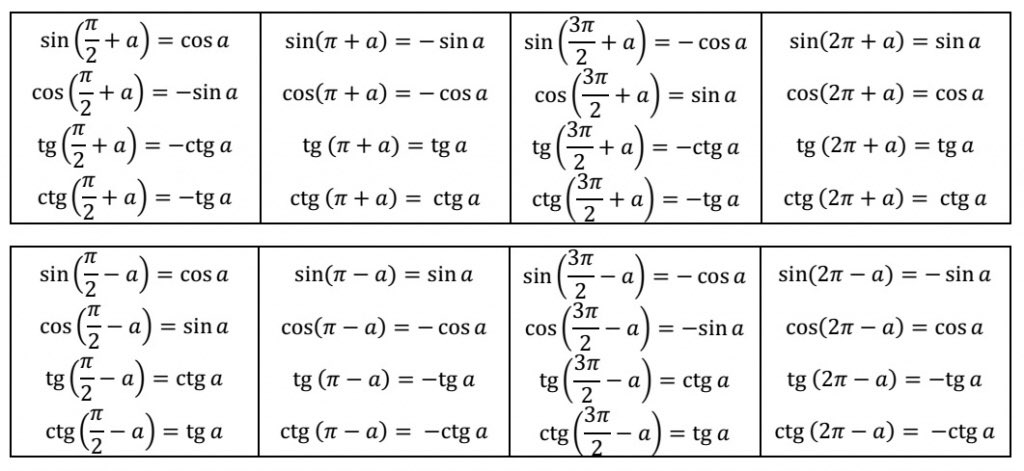 Воспользуемся основным тождеством из тригонометрии и заменим единицы в знаменателе на сумму квадратов sin и cos, после чего получаем 2·sinα2·cosα2sin2α2+cos2α2 и cos2α2-sin2α2sin2α2+cos2α2
Воспользуемся основным тождеством из тригонометрии и заменим единицы в знаменателе на сумму квадратов sin и cos, после чего получаем 2·sinα2·cosα2sin2α2+cos2α2 и cos2α2-sin2α2sin2α2+cos2α2
 Это намного проще и понятнее. Мы выражаем все формулы через tg половинного угла. Данное преобразование обязательно пригодится при решении разнообразных уравнений и задач, интегрировании основных функций sin α, cos α, tg α, ctg α.
Это намного проще и понятнее. Мы выражаем все формулы через tg половинного угла. Данное преобразование обязательно пригодится при решении разнообразных уравнений и задач, интегрировании основных функций sin α, cos α, tg α, ctg α.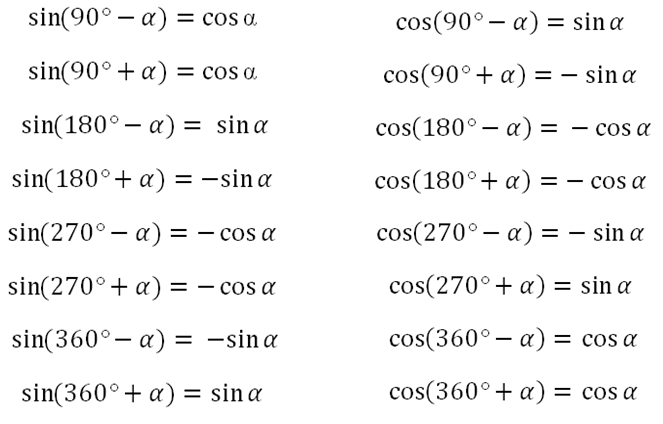 Упрощенная версия выглядит как
Упрощенная версия выглядит как д., как было задано в списке пожеланий:
д., как было задано в списке пожеланий: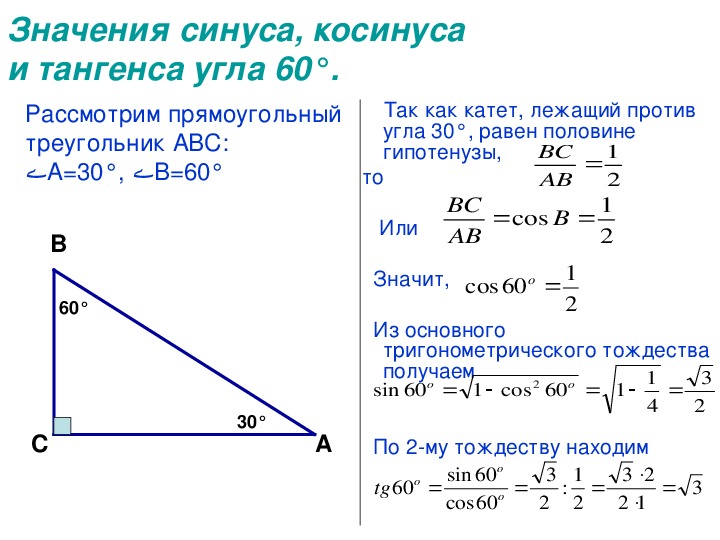 04.2023 9 0003
04.2023 9 0003
 Обязательно наличие открытой скобки
Обязательно наличие открытой скобки
 Cпасибо за то,
Cпасибо за то, Например то, что от перемены мест множителей произведение не меняется: 4×6 = 6×4. Отметьте такие «зеркальные» ответы определенным цветом — это поможет запомнить и не запутаться при повторении.
Например то, что от перемены мест множителей произведение не меняется: 4×6 = 6×4. Отметьте такие «зеркальные» ответы определенным цветом — это поможет запомнить и не запутаться при повторении.

 Итак, квадратный корень из -16 равен 4i.
Итак, квадратный корень из -16 равен 4i.  Умножение начинает становиться немного сложнее. Учтите:
Умножение начинает становиться немного сложнее. Учтите:  054054054054054 & -0.32432432432432434 i
054054054054054 & -0.32432432432432434 i
 Не совсем уверен, почему, но по какой-то причине мы не можем, и когда мы это делаем, нам нужно умножить на что-то, чтобы избавиться от квадратного корня.
Не совсем уверен, почему, но по какой-то причине мы не можем, и когда мы это делаем, нам нужно умножить на что-то, чтобы избавиться от квадратного корня.  Не надо, не надо этого делать. Корень 2 — единственное, что создает проблему, поэтому вы можете оставить 2 прямо там, как есть. Хорошо?
Не надо, не надо этого делать. Корень 2 — единственное, что создает проблему, поэтому вы можете оставить 2 прямо там, как есть. Хорошо? 

 р.
р. 24
24 Мы полагаем, что каждый из перечисленных типов вопросов потребует включения у студента определенных мыслительных операций, описанных Б. Блумом.
Мы полагаем, что каждый из перечисленных типов вопросов потребует включения у студента определенных мыслительных операций, описанных Б. Блумом.
 docx
docx 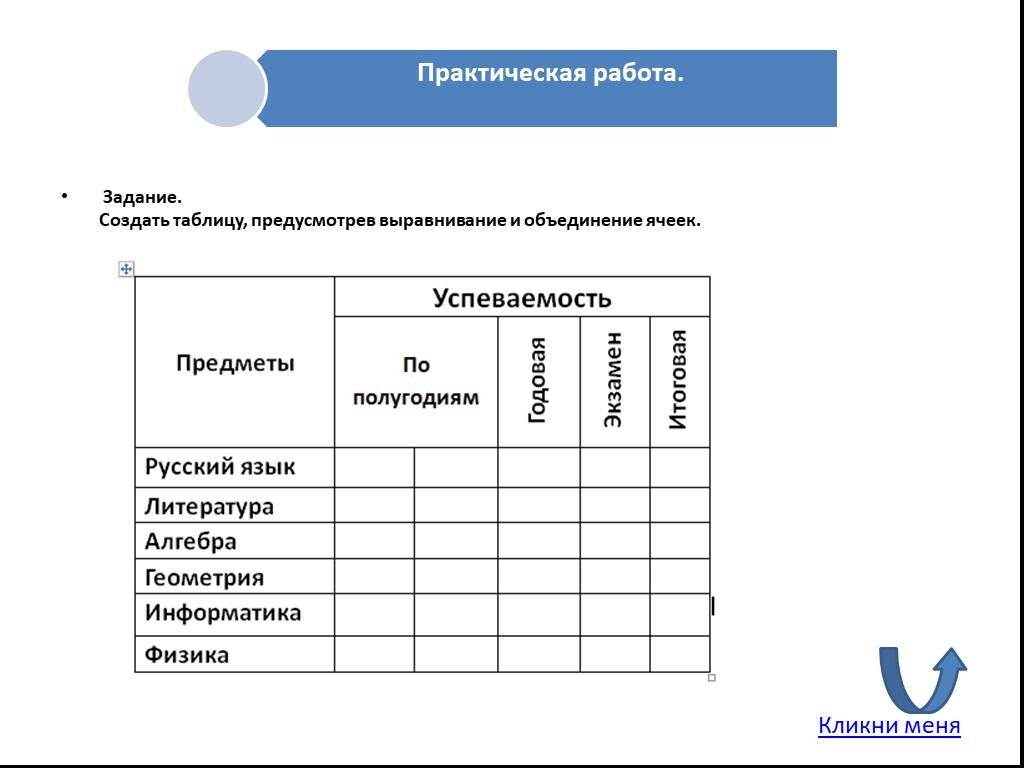 Microsoft Word помогает развивать и развивать эти навыки различными способами.
Microsoft Word помогает развивать и развивать эти навыки различными способами. Студенты могут использовать жирный шрифт, курсив, цвета и тени, чтобы выразить свою индивидуальность. Это веселое и простое занятие, которое учащиеся могут выполнить в первый день в школе, так как вы можете демонстрировать их в течение всего года!
Студенты могут использовать жирный шрифт, курсив, цвета и тени, чтобы выразить свою индивидуальность. Это веселое и простое занятие, которое учащиеся могут выполнить в первый день в школе, так как вы можете демонстрировать их в течение всего года! Учащиеся могут совместно работать над сочинением со своими одноклассниками, поделившись документом, а затем воспользовавшись функцией отслеживания изменений. Это позволяет одному учащемуся оставлять отзывы и вносить изменения в сочинение другого учащегося, в то же время позволяя первоначальному владельцу письма сохранить исходный документ и просмотреть предложения по написанию.
Учащиеся могут совместно работать над сочинением со своими одноклассниками, поделившись документом, а затем воспользовавшись функцией отслеживания изменений. Это позволяет одному учащемуся оставлять отзывы и вносить изменения в сочинение другого учащегося, в то же время позволяя первоначальному владельцу письма сохранить исходный документ и просмотреть предложения по написанию.
 Эти карточки можно сохранить в OneDrive, и учащиеся могут получить к ним доступ в любое время.
Эти карточки можно сохранить в OneDrive, и учащиеся могут получить к ним доступ в любое время.
 Учащиеся могут нарисовать животное, используя формы и изображения в Microsoft Word. Нарисовав свое собственное животное, учащиеся могут использовать текст, чтобы описать свое животное и установить связи с другими областями обучения.
Учащиеся могут нарисовать животное, используя формы и изображения в Microsoft Word. Нарисовав свое собственное животное, учащиеся могут использовать текст, чтобы описать свое животное и установить связи с другими областями обучения. Одним из способов использования Microsoft Word учителями является отслеживание успеваемости учащихся. Используя функцию «активность», учителя могут просматривать прогресс учащихся, включая дату и время выполнения каждой активности.
Одним из способов использования Microsoft Word учителями является отслеживание успеваемости учащихся. Используя функцию «активность», учителя могут просматривать прогресс учащихся, включая дату и время выполнения каждой активности. Документы можно переносить на страницы, предоставляя неограниченный доступ к ресурсам для любого школьного проекта.
Документы можно переносить на страницы, предоставляя неограниченный доступ к ресурсам для любого школьного проекта. Выберите навык, над которым вы работали в классе, или навык, который, как вы знаете, должен повторить ваш ученик. Например, пусть учащиеся запишут:
Выберите навык, над которым вы работали в классе, или навык, который, как вы знаете, должен повторить ваш ученик. Например, пусть учащиеся запишут: Каждое задание отправляет учащихся на поиски различных типов слов.
Каждое задание отправляет учащихся на поиски различных типов слов. Все, что вам нужно, это слова на вашей стене, четкие ожидания и навык, который вы хотите, чтобы студенты практиковали.
Все, что вам нужно, это слова на вашей стене, четкие ожидания и навык, который вы хотите, чтобы студенты практиковали.

 Как вычислить площадь фигуры.
Это китайское напоминание, и на данном
моменте я больше не останавливаюсь.
Как вычислить площадь фигуры.
Это китайское напоминание, и на данном
моменте я больше не останавливаюсь.
 n при n целом и положительном
n при n целом и положительном x, sin x, cos x
x, sin x, cos x Радиус и круг кривизны. Центр кривизны. Эволюта и эвольвента
Радиус и круг кривизны. Центр кривизны. Эволюта и эвольвента Геометрическое изображение функции двух переменных
Геометрическое изображение функции двух переменных Получение функции на основании экспериментальных данных по методу наименьших квадратов
Получение функции на основании экспериментальных данных по методу наименьших квадратов Интегрирование по частям
Интегрирование по частям Формула Чебышева
Формула Чебышева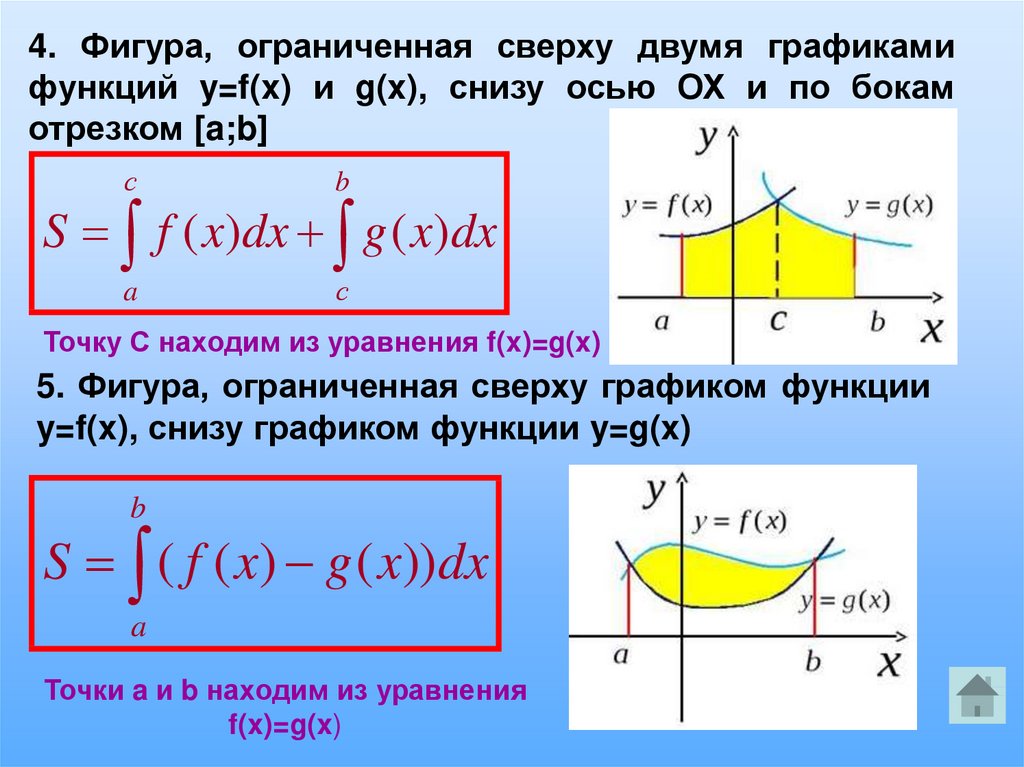 Но знаете ли вы, что интеграция
можно также использовать для нахождения длины кривой? В этом видео мы выведем
формула для длины дуги с использованием интегрирования, а затем посмотрите на некоторые ключевые
применения этой формулы.
Но знаете ли вы, что интеграция
можно также использовать для нахождения длины кривой? В этом видео мы выведем
формула для длины дуги с использованием интегрирования, а затем посмотрите на некоторые ключевые
применения этой формулы. Итак, мы собираемся определить длину
кривой 𝐿 с уравнением 𝑦 равно 𝑓 кривой 𝑥 как предел длины
эти вписанные многоугольники, предполагая, что предел существует.
Итак, мы собираемся определить длину
кривой 𝐿 с уравнением 𝑦 равно 𝑓 кривой 𝑥 как предел длины
эти вписанные многоугольники, предполагая, что предел существует.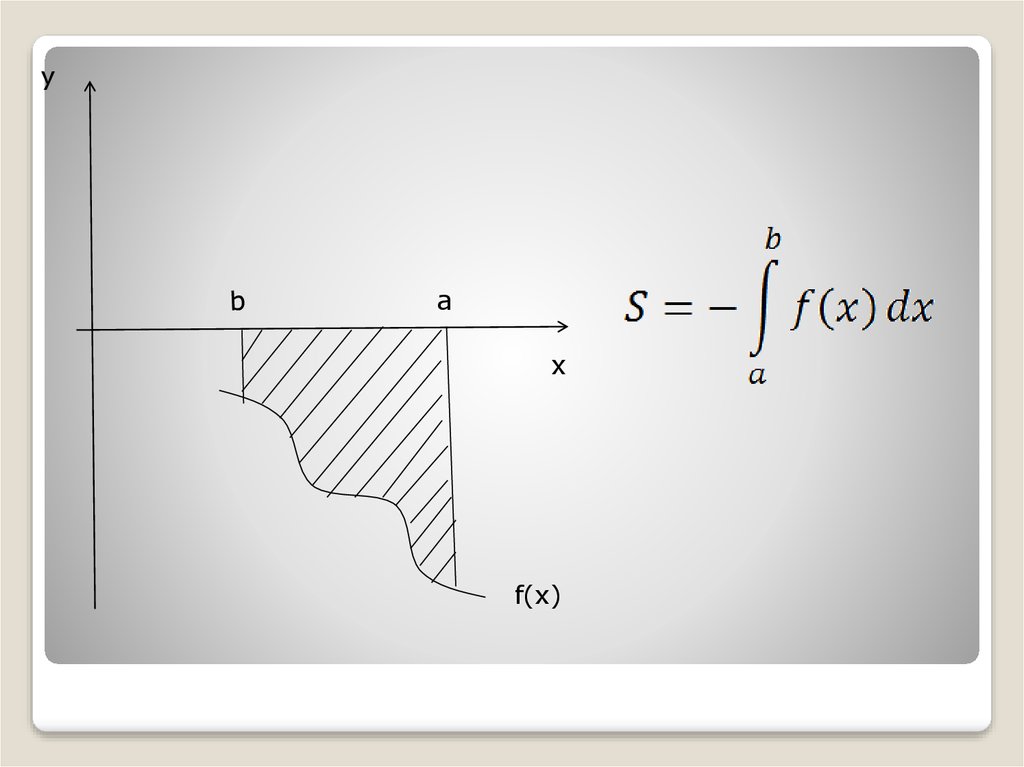
 По определению можно сказать, что это
равен интегралу между 𝑎 и 𝑏 квадратного корня из одного из 𝑓 простых чисел
𝑥 в квадрате относительно 𝑥. И мы получили окончательный
формула.
По определению можно сказать, что это
равен интегралу между 𝑎 и 𝑏 квадратного корня из одного из 𝑓 простых чисел
𝑥 в квадрате относительно 𝑥. И мы получили окончательный
формула.
 И это довольно упрощает
мило. Подынтегральная функция становится квадратом
корень из единицы плюс 𝑥 в квадрате из четырех минус 𝑥 в квадрате. Мы можем упростить выражение
внутри квадратного корня путем умножения числителя и знаменателя
число один на четыре минус 𝑥 в квадрате. И когда мы добавляем это, мы получаем четыре
минус 𝑥 в квадрате плюс 𝑥 в квадрате на четыре минус 𝑥 в квадрате. Минус 𝑥 в квадрате плюс 𝑥 в квадрате
равен нулю. Таким образом, наша подынтегральная функция становится
квадратный корень из четырех на четыре минус 𝑥 в квадрате.
И это довольно упрощает
мило. Подынтегральная функция становится квадратом
корень из единицы плюс 𝑥 в квадрате из четырех минус 𝑥 в квадрате. Мы можем упростить выражение
внутри квадратного корня путем умножения числителя и знаменателя
число один на четыре минус 𝑥 в квадрате. И когда мы добавляем это, мы получаем четыре
минус 𝑥 в квадрате плюс 𝑥 в квадрате на четыре минус 𝑥 в квадрате. Минус 𝑥 в квадрате плюс 𝑥 в квадрате
равен нулю. Таким образом, наша подынтегральная функция становится
квадратный корень из четырех на четыре минус 𝑥 в квадрате. Итак, мы имеем, что 𝐿 равно двум
умножить на определенный интеграл, вычисленный между нулем и двумя единицами по квадрату
четыре минус 𝑥 в квадрате. Теперь это может выглядеть действительно
противный. Но мы можем вычислить этот интеграл
с помощью замены. Напомним, что производная от
арксинус 𝑥 равен единице, превышающей квадратный корень из одного минус 𝑥 в квадрате. Итак, мы перепишем наше подынтегральное выражение
медленно.
Итак, мы имеем, что 𝐿 равно двум
умножить на определенный интеграл, вычисленный между нулем и двумя единицами по квадрату
четыре минус 𝑥 в квадрате. Теперь это может выглядеть действительно
противный. Но мы можем вычислить этот интеграл
с помощью замены. Напомним, что производная от
арксинус 𝑥 равен единице, превышающей квадратный корень из одного минус 𝑥 в квадрате. Итак, мы перепишем наше подынтегральное выражение
медленно. Когда 𝑥 равно двум, 𝑢 равно
равно двум разделить на два, что равно единице. А когда 𝑥 равно нулю, 𝑢 равно
ноль разделить на два, что равно нулю.
Когда 𝑥 равно двум, 𝑢 равно
равно двум разделить на два, что равно единице. А когда 𝑥 равно нулю, 𝑢 равно
ноль разделить на два, что равно нулю. Применение этой формулы
точно так же, как применение предыдущей формулы, которую мы использовали. Посмотрим, как это может выглядеть
нравиться.
Применение этой формулы
точно так же, как применение предыдущей формулы, которую мы использовали. Посмотрим, как это может выглядеть
нравиться. Итак, мы собираемся сказать, что 𝑐
равно нулю, а 𝑑 равно четырем. Замена всего, что мы знаем
в эту формулу, и мы получаем, что 𝐿 равно определенному интегралу между нулем
и четыре из квадратного корня из одного плюс два 𝑦 в квадрате, оцененные по отношению к
𝑦. Ну, два 𝑦 в квадрате — это
то же, что четыре 𝑦 в квадрате. Итак, чтобы найти длину дуги
нас интересует, нам нужно вычислить определенный интеграл квадратного корня из
один плюс четыре 𝑦 в квадрате между нулем и четырьмя. Мы собираемся использовать наш графический
калькулятор для этого. И когда мы это делаем, мы получаем, что
длина дуги равна 16,81863, что равно 16,8 единицы с точностью до трех
значимые фигуры.
Итак, мы собираемся сказать, что 𝑐
равно нулю, а 𝑑 равно четырем. Замена всего, что мы знаем
в эту формулу, и мы получаем, что 𝐿 равно определенному интегралу между нулем
и четыре из квадратного корня из одного плюс два 𝑦 в квадрате, оцененные по отношению к
𝑦. Ну, два 𝑦 в квадрате — это
то же, что четыре 𝑦 в квадрате. Итак, чтобы найти длину дуги
нас интересует, нам нужно вычислить определенный интеграл квадратного корня из
один плюс четыре 𝑦 в квадрате между нулем и четырьмя. Мы собираемся использовать наш графический
калькулятор для этого. И когда мы это делаем, мы получаем, что
длина дуги равна 16,81863, что равно 16,8 единицы с точностью до трех
значимые фигуры.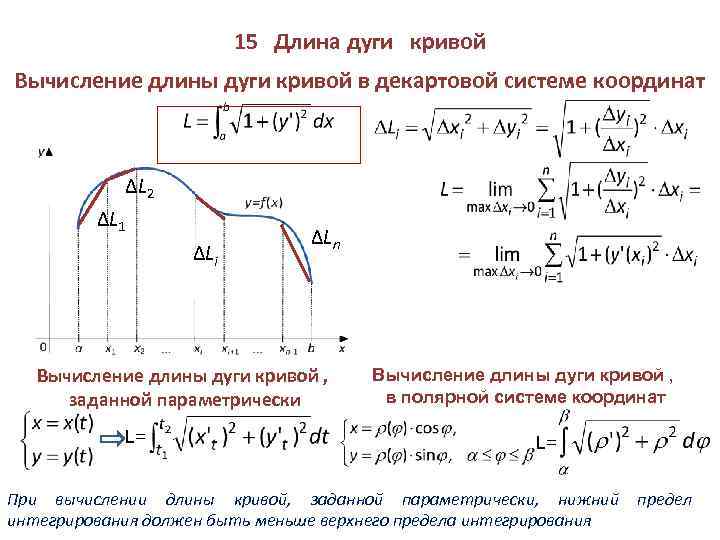 Итак, у нас есть единая формула. Длина дуги определяется как 𝐿 равно
интеграл d𝑠, где d𝑠 равен квадратному корню из единицы плюс d𝑦 на d𝑥
в квадрате d𝑥, если 𝑦 равно 𝑓 из 𝑥 на некотором замкнутом интервале от 𝑎 до 𝑏. А d𝑠 равно квадратному корню из
один плюс d𝑥 на d𝑦 в квадрате d𝑦, если 𝑥 равно 𝑔 числа 𝑦 для некоторого замкнутого интервала
𝑐 к 𝑑. В нашем последнем примере мы собираемся
посмотреть, как определить функцию длины дуги 𝑠 из 𝑥 из заданной точки.
Итак, у нас есть единая формула. Длина дуги определяется как 𝐿 равно
интеграл d𝑠, где d𝑠 равен квадратному корню из единицы плюс d𝑦 на d𝑥
в квадрате d𝑥, если 𝑦 равно 𝑓 из 𝑥 на некотором замкнутом интервале от 𝑎 до 𝑏. А d𝑠 равно квадратному корню из
один плюс d𝑥 на d𝑦 в квадрате d𝑦, если 𝑥 равно 𝑔 числа 𝑦 для некоторого замкнутого интервала
𝑐 к 𝑑. В нашем последнем примере мы собираемся
посмотреть, как определить функцию длины дуги 𝑠 из 𝑥 из заданной точки. Итак, мы начнем с простой работы
узнать, что такое d𝑦 by d𝑥. Не забудьте дифференцировать
функции такого рода, мы умножаем на мощность, а затем уменьшаем эту мощность на
один. Таким образом, d𝑦 на d𝑥 равно трем
более двух раз по четыре 𝑥 в половинной степени. Четыре разделить на два равно два. Итак, мы видим, что d𝑦 на d𝑥 равно
до шести 𝑥 в половинной степени. А это значит, что мы можем заменить
то, что мы знаем до сих пор в нашей формуле для d𝑠. Получаем квадратный корень из одного плюса
шесть 𝑥 в степени половины квадрата d𝑥.
Итак, мы начнем с простой работы
узнать, что такое d𝑦 by d𝑥. Не забудьте дифференцировать
функции такого рода, мы умножаем на мощность, а затем уменьшаем эту мощность на
один. Таким образом, d𝑦 на d𝑥 равно трем
более двух раз по четыре 𝑥 в половинной степени. Четыре разделить на два равно два. Итак, мы видим, что d𝑦 на d𝑥 равно
до шести 𝑥 в половинной степени. А это значит, что мы можем заменить
то, что мы знаем до сих пор в нашей формуле для d𝑠. Получаем квадратный корень из одного плюса
шесть 𝑥 в степени половины квадрата d𝑥. Так это нижняя граница. Мы ищем генерала
функция, поэтому верхний предел будет просто 𝑥. И мы видим, что аргумент
функция будет задана интегралом между единицей и 𝑥 квадрата
корень из единицы плюс 36𝑥d𝑥. Итак, как мы оцениваем это
Интеграл? Мы не можем полагаться на калькулятор, и,
на самом деле, нам нужно будет использовать замену.
Так это нижняя граница. Мы ищем генерала
функция, поэтому верхний предел будет просто 𝑥. И мы видим, что аргумент
функция будет задана интегралом между единицей и 𝑥 квадрата
корень из единицы плюс 36𝑥d𝑥. Итак, как мы оцениваем это
Интеграл? Мы не можем полагаться на калькулятор, и,
на самом деле, нам нужно будет использовать замену. Теперь мы заменим единицу плюс 36 на
𝑢. Я изменил квадратный корень на
сила половины. И заменяем d𝑥 на 36 d𝑢. Так что осталось только оценить
этот интеграл между заданными пределами.
Теперь мы заменим единицу плюс 36 на
𝑢. Я изменил квадратный корень на
сила половины. И заменяем d𝑥 на 36 d𝑢. Так что осталось только оценить
этот интеграл между заданными пределами.
 Мы также увидели, что мы можем использовать это
формула для нахождения общего уравнения длины дуги для функции из заданного
отправную точку, изменив верхний предел нашего интеграла на 𝑥 или 𝑦, в зависимости от
контекст.
Мы также увидели, что мы можем использовать это
формула для нахождения общего уравнения длины дуги для функции из заданного
отправную точку, изменив верхний предел нашего интеграла на 𝑥 или 𝑦, в зависимости от
контекст.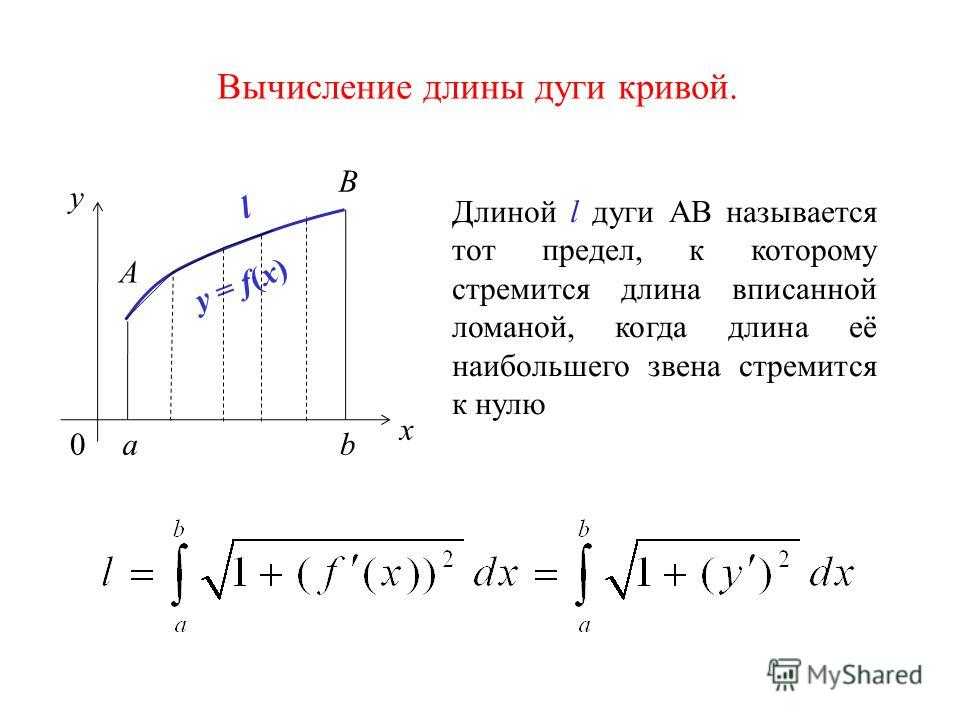 Давайте посмотрим, как производные и интегралы соединяются вместе, чтобы найти длину кривой!
Давайте посмотрим, как производные и интегралы соединяются вместе, чтобы найти длину кривой! На этот раз вам не нужно иметь дело с правыми или левыми конечными точками, поскольку оба значения используются для поиска сегментов. Длину каждого отдельного отрезка можно найти с помощью теоремы Пифагора.
На этот раз вам не нужно иметь дело с правыми или левыми конечными точками, поскольку оба значения используются для поиска сегментов. Длину каждого отдельного отрезка можно найти с помощью теоремы Пифагора. $$
$$ Однако также можно найти длину дуги кривых, которые описываются с помощью уравнений, таких как уравнение окружности 92.$$
Однако также можно найти длину дуги кривых, которые описываются с помощью уравнений, таких как уравнение окружности 92.$$
 С помощью этих измерений могут быть рассчитаны расстояния. И это далеко не все возможные измерения, а лишь наиболее распространенные из них.
В случаях измерений площади (квадратный метр, квадратный километр, ар, гектар, морган, акр и другие), температуры
(в градусах по Цельсию, по Кельвину, по Фаренгейту), скорости (м/с, км/час, миль/ч, узлы, мах), веса
(центнер, килограмм, метрическая тонна, американская тонна, стандартная тонна, фунт и другие) и объема
(кубический метр, гектолитр, английский галлон жидкости, американский жидкий галлон, американский сухой галлон, баррель и другие)
ситуация не намного лучше. А если всего этого вам показалось мало — большинство из этих единиц также имеют подразделения и высшие единицы
(например, милли-, санти-, деци-). Короче говоря, хаос, в котором так трудно разобраться без помощи справочника или других средств.
Данный калькулятор единиц измерения идеально подходит для перевода данных единиц.
С помощью этих измерений могут быть рассчитаны расстояния. И это далеко не все возможные измерения, а лишь наиболее распространенные из них.
В случаях измерений площади (квадратный метр, квадратный километр, ар, гектар, морган, акр и другие), температуры
(в градусах по Цельсию, по Кельвину, по Фаренгейту), скорости (м/с, км/час, миль/ч, узлы, мах), веса
(центнер, килограмм, метрическая тонна, американская тонна, стандартная тонна, фунт и другие) и объема
(кубический метр, гектолитр, английский галлон жидкости, американский жидкий галлон, американский сухой галлон, баррель и другие)
ситуация не намного лучше. А если всего этого вам показалось мало — большинство из этих единиц также имеют подразделения и высшие единицы
(например, милли-, санти-, деци-). Короче говоря, хаос, в котором так трудно разобраться без помощи справочника или других средств.
Данный калькулятор единиц измерения идеально подходит для перевода данных единиц.
 Как видно из данных примеров, все достаточно просто. Нужно только знать правила выполнения элементарных арифметических действий.
Как видно из данных примеров, все достаточно просто. Нужно только знать правила выполнения элементарных арифметических действий. Например, слово «миллиметр» состоит из приставки «милли» и слова «метр». «Милли» означает «тысячная доля». Так, дословно слово «миллиметр» можно перевести как «тысячная доля метра».
Например, слово «миллиметр» состоит из приставки «милли» и слова «метр». «Милли» означает «тысячная доля». Так, дословно слово «миллиметр» можно перевести как «тысячная доля метра». Так что, иногда лучше просто выучить что-то наизусть и никогда не забывать.
Так что, иногда лучше просто выучить что-то наизусть и никогда не забывать.

 9406
9406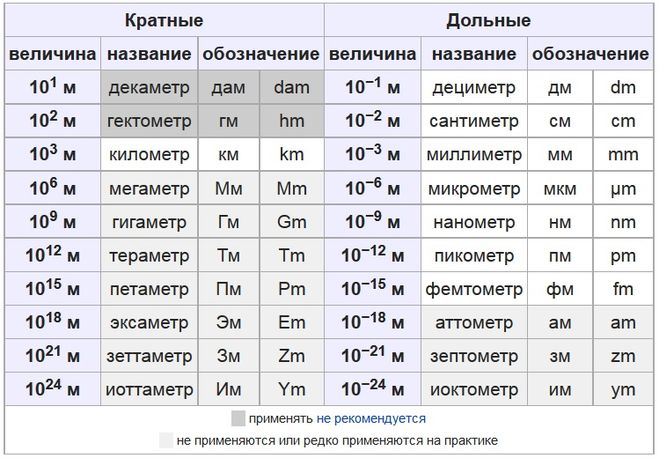 43
43 9661
9661 ..
..


 То есть предел (1) можно рассматривать как функцию от x.
То есть предел (1) можно рассматривать как функцию от x. «Определение функции»). Так, в выражении
«Определение функции»). Так, в выражении При этом знак штриха может быть опущен. Например, следующие два обозначения эквивалентны: . Здесь подразумевается, что переменные и мы считаем постоянными. Тогда в данном контексте, является функцией от одной переменной . К зависимой переменной производной также добавляют нижний индекс переменной, по которой выполняется дифференцирование:
При этом знак штриха может быть опущен. Например, следующие два обозначения эквивалентны: . Здесь подразумевается, что переменные и мы считаем постоянными. Тогда в данном контексте, является функцией от одной переменной . К зависимой переменной производной также добавляют нижний индекс переменной, по которой выполняется дифференцирование: Обычно время обозначают буквой t. Тогда
Обычно время обозначают буквой t. Тогда


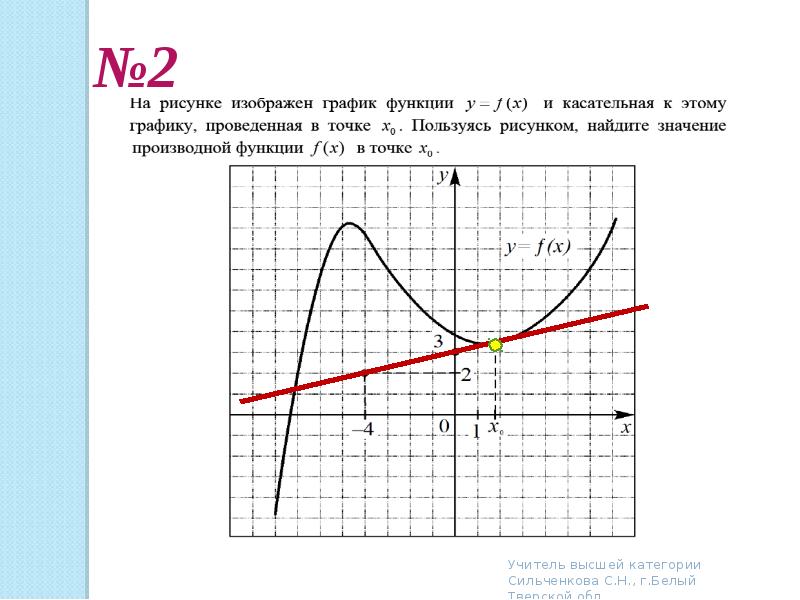
 Найдем отношение приращения функции к приращению ее аргумента в точке x:
Найдем отношение приращения функции к приращению ее аргумента в точке x: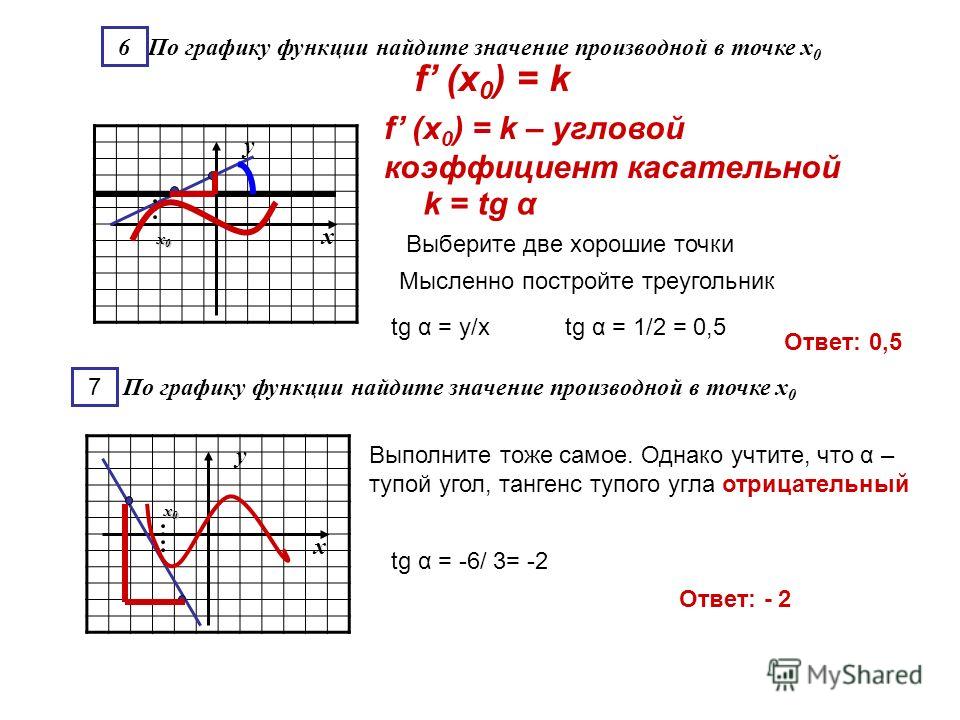
 Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «вычислить значение производной на каждом из участков графика».
Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «вычислить значение производной на каждом из участков графика». На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и вычислить значение производной на каждом из участков графика. Просто введите задачу в окошко и нажмите
«решить» здесь (например, геометрический смысл производной примеры решения задач).
На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и вычислить значение производной на каждом из участков графика. Просто введите задачу в окошко и нажмите
«решить» здесь (например, геометрический смысл производной примеры решения задач).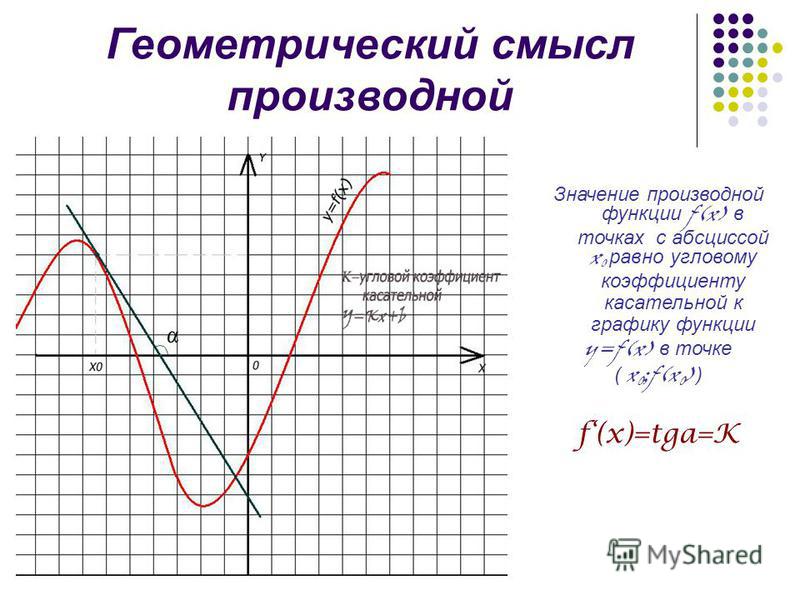
 Выполните следующие шаги, чтобы использовать этот инструмент:
Выполните следующие шаги, чтобы использовать этот инструмент:
 Это потому, что это может позволить вам улучшить свои навыки решения проблем за короткое время. Точно так же наш инструмент лучше всего поможет вам в расчете производных в точке. Есть и другие преимущества калькулятора формулы производной в точке. Это:
Это потому, что это может позволить вам улучшить свои навыки решения проблем за короткое время. Точно так же наш инструмент лучше всего поможет вам в расчете производных в точке. Есть и другие преимущества калькулятора формулы производной в точке. Это:
 При этом дифференцировании мы сначала находим производную функции, а затем подставляем в нее точку.
При этом дифференцировании мы сначала находим производную функции, а затем подставляем в нее точку.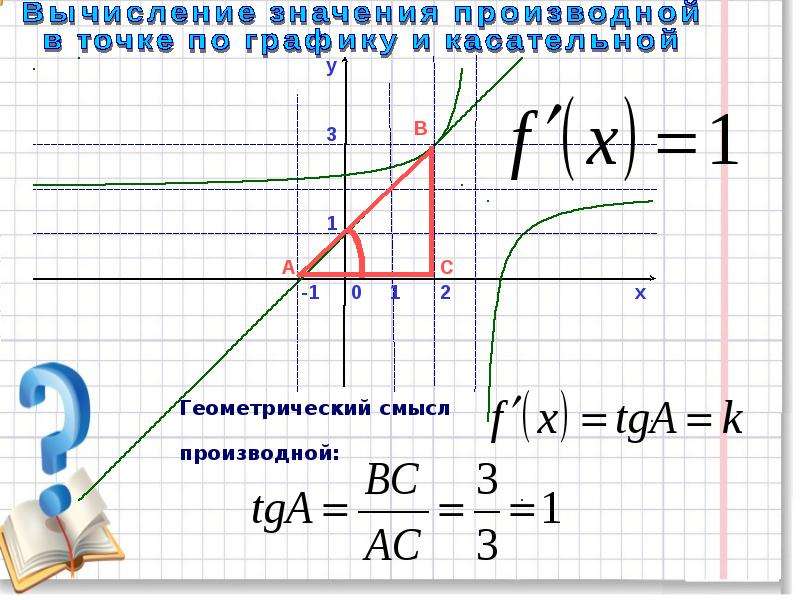 Вы также можете просто использовать URL-адрес нашего веб-сайта для доступа к веб-сайту.
Вы также можете просто использовать URL-адрес нашего веб-сайта для доступа к веб-сайту. Например, нахождение наклона в определенной точке выполняется путем нахождения производной в этой точке.
Например, нахождение наклона в определенной точке выполняется путем нахождения производной в этой точке.