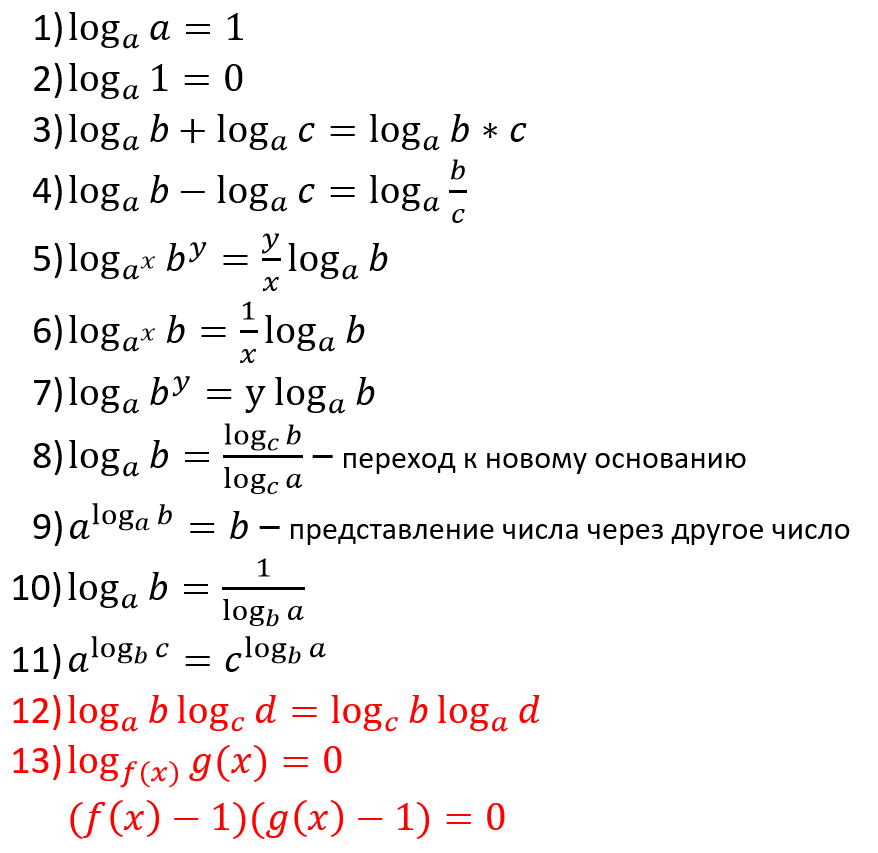Второй замечательный предел, следствия, примеры
Второй замечательный (особый) предел часто вызывает трудности у студентов, хотя сам предел довольно прост и понятен на практике. Он позволяет раскрывать неопределенности вида единица в степени бесконечность . Замечательный предел имеет следующий вид
где «е»-экспонента.
1)
2)
3)
4)
5)
6)
На практике следствия второго предела реже встречаются на практике чем он сам, однако без них некоторые задачи в простой способ не решить.
Примеры на замечательный пределРассмотрим некоторые примеры из сборника А.В. Тевяшев, А.Г. Литвин, Г.М. Кривошеева и др.»Высшая математика в примерах и задачах. Ч.5 Тесты» (Харьков, 2007, ст. 99).
Пример 6.1. Найти предел функции
а)
Решение.
Преобразуем функцию к виду при котором возможно применить формулу замечательного предела
В результате можем применить правило замечательного предела
б)
Решение.
Подобно предыдущему примеру превращаем функцию в скобках чтобы применить замечательный предел
Нужно отметить, что в этом примере и во многих подобных константы в степенях, как правило вклада не несут. Функцию можно расписать следующим образом
Предел умышленно расписан в виде произведения двух множителей чтобы Вы убедились что константы в степенях вклада не несут. Их цель запутать Вас, если плохо знаете теоретический материал или сомневаетесь в правильности решения. Во всех последующих примерах мы не будем расписывать примеры на произведение двух границ, однако помните, что они не меняют конечного результата (вклад — множитель единица).
————————————
в)
Решение.
Выполняем преобразование заданной функции
Запись в таком виде сделана специально, потому что степень нужно свести к подобному виду
В такой простой способ получили искомый предел функции. В дальнейшем необходимые замены или подсказки будут выделены цветом из общего решения.
г)
Решение.
Выполним замену переменных в пределе
и определенные преобразования для нахождения предела
Бывают случаи, когда прямо применить правило второго замечательного предела довольно сложно, в таких ситуациях используйте простые замены которые Вам понятны и позволяют в быстрый способ найти предел.
Пример 6. 2 Вычислить предел функции
а)
Решение.
Сводим функцию к правилу замечательного предела
Подставляем и вычисляем, выполняя нужные манипуляции с показателями
в)
Решение.
За известным уже алгоритмом преобразуем функцию
Применяя определение второго важного предела находим
Пример 6. 3 Определить предел функции
б)
Решение.
Сведем функцию для применения замечательного предела
Подставляем в границу и упрощаем
г)
Решение.
«Как найти предел ? — скажете Вы, ведь переменная равна минус бесконечности.
В этом примере видим что аргумент стремится к минус бесконечности, кроме того функция в скобках следует не до единицы, а до 2 при больших аргументах.
Учитывая что степень отрицательный получим следующее значение предела
Во всех примерах второго замечательного предела следует сначала проверять условие что выражение в скобках стремится к единице. Если нет, то предел функции в зависимости от степени будет равен или нулю или бесконечности. Те из Вас кто часто решает примеры такие проверки осуществляет автоматически. Остальные сводят границу в экспоненте в определенном степени, но все равно вылезает множителем или ноль или бесконечность. В конечном варианте правы все, однако в первом случае тратится гораздо меньше времени, которое так необходима на контрольных работах, тестах, ВНО. Поэтому выбирайте для себя простой путь и делайте в обучении правильные выводы.
Пример 6. 5 Найти предел функции
а)
Решение.
Заданный пример на вид отличается от предыдущих, однако решение получаем по такой же схеме. Выполняем преобразования функции в скобках под правило замечательного предела
Выполняем преобразования функции в скобках под правило замечательного предела
Осталось в степени выделить обратный множитель
и подставить в границу
По такой схеме вычисляйте все подобные пределы, она проста и не требует дополнительных пояснений.
————————————
в)
Решение.
К рассматриваемому примеру великих преобразований делать не нужно. Он имеет достаточно простую запись и решение осуществляем в одну строку
Практикуйте с подобными пределами, используйте удобные для себя схемы сведения задач под необходимое правило. Не бойтесь делать ошибки — без них обучение не обходится!
Второй замечательный предел
Вторым замечательным пределом называется предел
,
где
— иррациональное число.
Непосредственная подстановка бесконечности в выражение приводит к бесконечности вида .
Значит, если при непосредственном вычислении предела у вас получилась неопределённость
такого вида, то решать задачу следует путём приведения ко второму замечательному пределу. Во всех этих задачах
для получения второго замечательного предела требуется производить замену сложной функции более простой.
Во всех этих задачах
для получения второго замечательного предела требуется производить замену сложной функции более простой.
Второй замечательный предел может быть записан в другом виде, если положить тогда .
Из условия
получим
(Alt)
Пример 1. Найти предел .
Решение. Подстановка вместо x бесконечности приводит к неопределённости:
.
Значит, нужно привести выражение ко второму замечательному пределу. Облегчим себе жизнь перед заменой сложной функции более простой, представив степень :
.
Заменяем функцию 6x переменной n, которая также стремится к бесконечности:
.
Это второй замечательный предел, индивидуальна только степень числа е:
.
А проверить решение задачи на пределы можно на калькуляторе пределов онлайн.
Пример 2. Найти предел .
Решение. Непосредственная подстановка приводит к неопределённости «бесконечность делить на бесконечность в степени бесконечность»:
.
Бесконечность в показателе степени — признак того, что выражение можно привести к отношению двух вторых замечательных пределов. В самом деле, если числитель и знаменатель поделить почленно на x, то слева и в числителе и в знаменателе будет уже по единице:
.
Почти второй замечательный предел. А чтобы это было не почти, а вторым замечательным пределом, нужно, чтобы во вторых слагаемых и в числителе, и в знаменателе были единицы. Для этого произведём замены функций:
.
.
Подставляем и получаем:
.
Это уже отношение вторых замечательных пределов, а степени выражений в числителе и знаменателе — индивидуальны:
.
Пример 3. Найти предел
Решение. Применяем разновидность (Alt) второго замечательного предела:
Проверить решение задачи на пределы можно на калькуляторе пределов онлайн.
Второй замечательный предел служит средством решения многих задач физики, биологии, социальных наук. Показательная функция с основанием e возникает при выводе количественного закона, которому подчиняются многие естественные процессы: рост народонаселения, рост количества древесины на лесных массивах, радиоактивный распад и т.д.
Для вывода этого закона используется формула сложных процентов
,
где —
сумма, наращенная через t лет, —
начальная сумма, p — процентная такса, t — время роста в годах.
При этом предполагается, что проценты присоединяются к начальной сумме в конце каждого года. Если же ввести условие присоединения процентов по отдельным частям года, равным 1/n доле его, а процентная такса p по-прежнему пусть относится к целому году, то по истечении каждой такой части года наращенные суммы соответственно составят
По прошествии одного года начальная сумма обратится в , по прошествии двух лет — в , по прошествии t лет — в .
Если же предположить, что прирост процентов происходит непрерывно, т. е. число промежутков, на которые делится год, неограниченно возрастает (), а каждый из них стремится к нулю, то величина наращенной суммы выразится следующей формулой:
,
очень напоминающей второй замечательный предел.
Чтобы выразить этот предел через e, положим , тогда . Из условия следует, что , поэтому
Используя формулу альтернативного представления второго замечательного предела (Alt), приведённую в начале статьи, получим показательный закон роста:
.
Заменив p на -p, получим показательный закон убывания:
.
Например, если население страны возрастает на 2% в год, то по формуле показательного закона роста можно с неплохим приближением рассчитать численность населения страны через t лет: , где — численность населения в начале отсчёта.
| Назад | Листать | Вперёд>>> |
Нет времени вникать в решение? Можно заказать работу!
К началу страницы
Пройти тест по теме Предел
Начало темы «Предел»
Что такое предел функции и как его найти
Первый замечательный предел
Продолжение темы «Предел»
Бесконечно малые
Исчисление I. Пределы в бесконечности, часть II
Показать мобильное уведомление Показать все примечания Скрыть все примечания
Мобильное уведомление
Похоже, вы находитесь на устройстве с «узкой» шириной экрана ( т. е. вы, вероятно, на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
е. вы, вероятно, на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Раздел 2.8: Пределы на бесконечности, Часть II
В предыдущем разделе мы рассмотрели пределы на бесконечность многочленов и/или рациональные выражения, включающие многочлены. В этом разделе мы хотим взглянуть на некоторые другие типы функций, которые часто проявляются в пределах бесконечности. Функции, которые мы будем здесь рассматривать, — это экспоненты, натуральные логарифмы и арктангенсы. 9{-x}} = \infty\]
Суть этого примера заключалась в том, чтобы показать, что если показатель экспоненты стремится к бесконечности в пределе, то экспоненциальная функция также стремится к бесконечности в пределе. Точно так же, если экспонента стремится к минус бесконечности в пределе, тогда экспонента в пределе стремится к нулю.
Точно так же, если экспонента стремится к минус бесконечности в пределе, тогда экспонента в пределе стремится к нулю.
Заметим также, что в последнем разделе значение предела не зависело от того, ушли ли мы в плюс или минус бесконечность. В приведенном выше примере мы уже видели, что изменение знака бесконечности может изменить ответ, поэтому не замыкайтесь на каких-либо предположениях, которые вы могли сделать из работы в предыдущем разделе! 9{ — 15x}}} \справа)\)
Показать все решения Скрыть все решения
Итак, единственная разница между этими двумя пределами заключается в том, что в первом мы берем предел, когда мы идем к плюс бесконечности, а во втором мы идем к минус бесконечности. К этому моменту мы смогли «повторно использовать» работу из первого ограничения, по крайней мере, в части второго ограничения. С экспонентами, которые часто не будут иметь место, мы собираемся рассматривать каждую из них как отдельные проблемы. 9{ — 15x}}} \right) = \infty — \infty + \infty + 0 — 0\]
9{ — 15x}}} \right) = \infty — \infty + \infty + 0 — 0\]
Последние два термина не проблема (однако они будут в следующей части, понимаете?). Однако первые три представляют собой проблему, поскольку они представляют нам еще одну неопределенную форму.
При работе с многочленами мы выносим на множитель член с наибольшим показателем в нем. Давайте сделаем то же самое здесь. Однако теперь нам приходится иметь дело как с положительными, так и с отрицательными показателями, а также с тем, что мы подразумеваем под «самым большим» показателем. Имея дело с ними здесь, мы смотрим на термины, вызывающие проблемы, и спрашиваем: «Каков наибольший показатель степени в этих терминах?». Итак, поскольку проблемы вызывают только первые три члена ( 9{ — 25x}}} \справа)} \справа]\]
Обратите внимание, что при этом факторинге все оставшиеся экспоненты теперь имеют отрицательные показатели, и мы знаем, что для этого предела (, т.е. , уходящего в положительную бесконечность) все они будут равны нулю в пределе, и поэтому больше не будут вызывать проблем.
Теперь мы можем взять предел двух факторов. Первое — это явно бесконечность, а второе — конечное число (в данном случае — единица), поэтому раздел «Факты из бесконечных пределов» дает нам следующий предел: 9{ — 15x}}} \right)\) Показать решение
Давайте начнем так же, как и в первой части. Возьмем предел каждой из частей. На этот раз обратите внимание, что, поскольку наш предел стремится к отрицательной бесконечности, первые три экспоненты фактически устремляются к нулю (потому что их показатели степени стремятся к минус бесконечности в пределе). Последние две экспоненты в пределе уйдут в бесконечность (потому что их показатели в пределе уйдут в плюс бесконечность).
Получение пределов дает, 9{ — 15x}}} \right) = 0 — 0 + 0 + \infty — \infty \]
Таким образом, последние два члена являются здесь проблемой, поскольку они снова оставляют нас с неопределенной формой. Как и в первом примере, мы собираемся исключить «наибольшую» экспоненту в последних двух терминах. { — 15x}}\). 9{ — 15x}}} \справа) = — \infty \]
{ — 15x}}\). 9{ — 15x}}} \справа) = — \infty \]
Итак, при работе с суммами и/или разностями показательных функций мы ищем экспоненту с «наибольшей» степенью и помним здесь, что «наибольшая» означает степень, наиболее далекую от нуля. Также помните, что если мы смотрим на предел плюс бесконечность, только экспоненты с положительными показателями будут вызывать проблемы, поэтому это единственные условия, на которые мы обращаем внимание при определении наибольшего показателя. Точно так же, если мы смотрим на предел минус бесконечность, то только экспоненты с отрицательными показателями будут вызывать проблемы, и поэтому только они рассматриваются при определении наибольшего показателя.
Наконец, как вы могли догадаться из предыдущего примера, при работе с суммой и/или разностью экспонент все, что нам нужно сделать, это посмотреть на наибольшую экспоненту, чтобы определить поведение всего выражения. Опять же, помня, что если предел равен плюс бесконечности, мы рассматриваем экспоненты только с положительными показателями, а если мы смотрим на предел минус бесконечность, мы рассматриваем только экспоненты с отрицательными показателями.
Давайте теперь рассмотрим некоторые рациональные функции, включающие экспоненты. 9{ — x}}}}\) Показать решение
Основная концепция, связанная с решением этой задачи, такая же, как и с рациональными выражениями в предыдущем разделе. Мы смотрим на знаменатель и определяем экспоненциальную функцию с «наибольшей» степенью, которую мы затем выносим как из числителя, так и из знаменателя. Мы будем использовать те же рассуждения, что и в предыдущем примере, чтобы определить «наибольшую» экспоненту. В случае, когда мы рассматриваем предел плюс бесконечность, мы рассматриваем экспоненты только с положительными показателями. 9{ — x}}}}\) Показать решение
В этом случае мы собираемся минус бесконечность в пределе, поэтому мы будем смотреть на экспоненты в знаменателе с отрицательными показателями при определении «наибольшего» показателя. Однако в этой задаче есть только один, поэтому мы будем использовать его.
Опять же, не забывайте смотреть только на знаменатель. НЕ используйте экспоненту из числителя, даже если она «больше», чем экспонента в знаменателе. Мы всегда смотрим только на знаменатель, когда определяем, какой член вынести за скобки, независимо от того, что происходит в числителе. 9+ }} \ln x = — \infty \hspace{0,5 дюйма}\hspace{0,25 дюйма}\mathop {\lim }\limits_{x \to \infty} \ln x = \infty \]
НЕ используйте экспоненту из числителя, даже если она «больше», чем экспонента в знаменателе. Мы всегда смотрим только на знаменатель, когда определяем, какой член вынести за скобки, независимо от того, что происходит в числителе. 9+ }} \ln x = — \infty \hspace{0,5 дюйма}\hspace{0,25 дюйма}\mathop {\lim }\limits_{x \to \infty} \ln x = \infty \]
Обратите внимание, что нам пришлось сделать правый предел для первого, так как мы не можем подставить отрицательные \(x\) в логарифм. Это означает, что нормального предела не будет, поскольку мы должны смотреть на \(x\) с обеих сторон рассматриваемой точки, а \(x\) слева от нуля отрицательны.
Из предыдущего примера видно, что если аргумент журнала (то, что мы берем из журнала) стремится к нулю справа ( , т.е. всегда положительное), тогда журнал достигает отрицательной бесконечности в пределе, а если аргумент достигает бесконечности, то журнал также достигает бесконечности в пределе.
Обратите также внимание, что мы не можем смотреть на предел логарифма, когда \(x\) приближается к минус бесконечности, поскольку мы не можем подставлять отрицательные числа в логарифм. { — 1}}x\) Показать решение
9{ — 1}} \ влево ( {\ гидроразрыва {1} {x}} \ справа) = — \ гидроразрыва {\ пи {2} \]
{ — 1}}x\) Показать решение
9{ — 1}} \ влево ( {\ гидроразрыва {1} {x}} \ справа) = — \ гидроразрыва {\ пи {2} \]
Чтобы увидеть точное и математическое определение этого типа предела, см. раздел «Определение предела» в конце этой главы.
Объяснение урока: Число Эйлера (𝑒) как предел
В этом объяснении мы узнаем, как использовать определение 𝑒 (число Эйлера) для оценки некоторых специальные лимиты.
Число Эйлера (𝑒=2,71828…) очень полезно и возникает во многих различных областях науки. математика, включая расчет сложных процентов, задачи оптимизации, исчисление и определение функция, представляющая стандартное нормальное распределение вероятностей.
Число могло быть изначально найдено при поиске экспоненциальной функции, которая дифференцируется сама в себя. Однако мы также можем найти число Эйлера, используя пределы, и это то, что мы рассмотрим в этом объяснении.
Мы можем определить число Эйлера, используя следующий предел:
𝑒=1+1𝑥.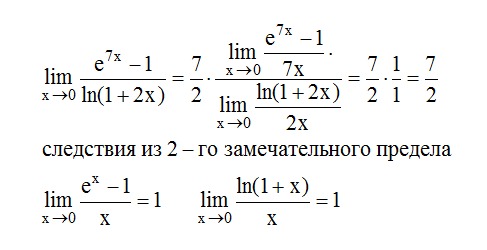 lim→∞
lim→∞
Используя таблицу значений, мы можем увидеть, как этот предел приближается к числу Эйлера по мере увеличения 𝑥.
| 𝑥 | 1+1 𝑥 |
|---|---|
| 1 | 1+11=2 |
| 10 | 1+110=2,59374… | 100 | 1+1100=2,70481… |
| 1 000 | 1+11000=2,71692… |
| 10 000 | 903 20 1+110000=2,71814…|
| 100 000 | 1+1100000=2,71826… |
Мы можем использовать этот предел, чтобы помочь оценить пределы и решить проблемы, связанные с пределами этой формы. Прежде чем мы посмотрим на любой примеров, давайте рассмотрим другой предел, который также приводит к числу Эйлера.
Попробуем подставить 𝑥=1𝑦 в наш предыдущий предел. Поскольку мы рассматриваем предел как
𝑥→∞ и 𝑥=1𝑦, мы можем сказать, что при 𝑥→∞,
𝑦→0. Подставляя их в 𝑒=1+1𝑥lim→∞,
мы получим
𝑒=(1+𝑦). lim→
lim→
Теперь мы знаем два предела, которые дают число Эйлера. Подведем итоги только что показанных результатов.
Определение: число Эйлера как предел оценить пределы, которые мы не могли раньше.
Пример 1: вычисление предела с использованием константы Эйлера
Определить lim→∞1+1𝑥.
Ответ
Мы могли бы сначала попытаться вычислить этот предел напрямую. В нашем пределе 𝑥 приближается к бесконечности, что означает, что знаменатель 1𝑥 неограниченно растет, а числитель остается постоянным, поэтому 1𝑥 приближается к 0. Это означает, что выражение в наших скобках приближается к 1. Однако наш показатель степени (4𝑥) равен приближается к бесконечности, когда 𝑥 приближается к бесконечности.
Итак, мы получаем lim→∞∞1+1𝑥=1, что является неопределенной формой. Это означает, что нам нужно будет попробовать какой-то другой метод для оценки нашего предела.
Заметим, что заданный нами предел очень похож на тот, который выражает значение числа Эйлера: 𝑒=1+1𝑥. lim→∞
lim→∞
нам дали показатель степени 4𝑥, а не 𝑥. Мы можем использовать законы экспонент, чтобы перевыразить это следующим образом:
Прежде чем мы сможем подставить число Эйлера в предельное выражение, нам нужно вывести показатель степени 4 за предел. При условии, что новый предел существует, мы можем использовать правило степени для пределов, чтобы добиться этого:
Предел внутри нашей экспоненты существует, потому что это просто наш предельный результат для числа Эйлера 𝑒. Итак, мы используем наш предельный результат и заменяем предел в скобках на 𝑒, что дает нам limlim→∞→∞1+1𝑥=1+1𝑥=𝑒.
Наш следующий пример показывает, как мы можем использовать наш другой предельный результат, чтобы помочь нам оценить предел.
Пример 2. Нахождение пределов путем их преобразования в формы пределов в натуральной степени
Определить lim→(𝑥+1).
Ответ
Поскольку нас просят оценить предел, мы могли бы начать с попытки сделать это напрямую. Когда 𝑥 приближается к 0, выражение в скобках приближается к 1, а величина нашего показателя степени неограниченно растет. Это неопределенная форма, а именно 1∞, поэтому нам нужно будет попробовать другой метод.
Когда 𝑥 приближается к 0, выражение в скобках приближается к 1, а величина нашего показателя степени неограниченно растет. Это неопределенная форма, а именно 1∞, поэтому нам нужно будет попробовать другой метод.
Мы видим, что наш предел аналогичен одному из наших предельных результатов, включающих число Эйлера, которое равно lim→(1+𝑥)=𝑒.
Итак, мы можем попробовать использовать этот результат, чтобы оценить наш предел.
Для этого мы хотим, чтобы наш показатель степени 1110𝑥 был таким же, как у предельного результата, который равен 1𝑥. Чтобы сделать это, мы начнем с использования наших законов показателей степени, чтобы переписать наш предел: где мы переставляем члены в скобках и используем тот факт, что 1110𝑥=1𝑥⋅1110.
На данный момент мы хотим использовать наш предельный результат, включающий число Эйлера; однако сначала нам нужно вывести нашу экспоненту за пределы нашего предела, а для этого нам нужно использовать правило степени для пределов.
Это говорит нам, что мы можем вывести экспоненту за пределы предела при условии, что наш новый предел существует.
В нашем случае имеем limlim→→(1+𝑥)=(1+𝑥), и мы знаем, что это верно потому что предел в наших скобках точно такой же, как предельный результат, включающий число Эйлера. Подставляя этот предел равным 𝑒, получаем (1+𝑥)=𝑒.lim→
Не всегда возможно напрямую использовать наши предельные результаты для числа Эйлера 𝑒. Возможно, нам придется использовать другие инструменты, такие как полиномиальное деление, факторинг или замену. Однако основная предпосылка та же самая: мы берем предел, который мы не можем оценить, и записываем его в форме для 𝑒, которую мы затем можем использовать для оценки наших предельных результатов.
Пример 3. Оценка предела путем преобразования его в форму предела в натуральной степени
Определить lim→∞1−7𝑥.
Ответ
Нас просят оценить предел, который мы могли бы попытаться оценить напрямую. Таким образом, когда 𝑥 приближается к ∞, выражение в скобках приближается к 1, а показатель степени неограниченно растет. Следовательно, имеем lim→∞∞1−7𝑥=1.
Следовательно, имеем lim→∞∞1−7𝑥=1.
Это неопределенная форма, поэтому нам нужно будет попробовать другой метод для оценки этого предела.
Этот предел подобен одному из предельных результатов, связанных с числом Эйлера, поэтому мы можем попробовать использовать этот результат, чтобы помочь нам оценить наш предел. У нас есть много вариантов, как это сделать.
Мы попытаемся записать этот предел в форме, где мы можем использовать 𝑒=(1+𝑛).lim→
Однако также можно использовать 𝑒=1+1𝑛. lim→∞
Обычно один из предельных результатов оказывается проще, чем другой, и может быть очень сложно определить, какой предельный результат использовать, просто взглянув на вопрос, поэтому, если мы застряли, используя один результат, мы всегда можем попробовать использовать другой предел, который находится в форме с показателем степени 1𝑛.
Чтобы записать наш предел в этой форме, мы будем использовать замену. Мы хотели бы 1+𝑛 в наших скобках, поэтому мы используем замену 𝑛=−7𝑥.
Мы можем изменить эту замену, чтобы найти 𝑥 через 𝑛 так, чтобы 𝑥=−7𝑛.
Умножая это на 5, мы получаем 5𝑥=−35𝑛.
Используя эту замену, мы можем переписать наш предел как и мы хотим знать, что происходит с точки зрения 𝑛, поэтому нам нужно посмотреть на нашу замену. Поскольку 𝑥 приближается к бесконечности, −7𝑥 приближается к 0, а поскольку 𝑛=−7𝑥, мы также должны иметь то, что 𝑛 приближается к 0,9.0003
Это дает нам limlim→∞→(1+𝑛)=(1+𝑛).
Теперь воспользуемся одним из законов экспонент: limlim→ →(1+𝑛)=(1+𝑛).
Наконец, применим степенное правило для пределов: limlim→→ (1+𝑛)=(1+𝑛),, что, как мы знаем, мы можем сделать в этом случае, потому что полученный предел является нашим предельным результатом, включающим число Эйлера.
Все, что нам нужно сделать сейчас, это заменить этот предел на 𝑒 и переставить так, чтобы в итоге мы получили (1+𝑛)=𝑒=1𝑒.lim→
В нашем следующем примере мы рассмотрим предел рациональной функции, возведенной в линейный показатель.
Пример 4. Решение пределов путем преобразования их в формы пределов в натуральном показателе
Определить lim→∞𝑥+4𝑥−4.
Ответ
Мы могли бы попробовать вычислить этот предел напрямую. В наших скобках у нас есть рациональная функция, и мы знаем, что по мере того, как 𝑥 приближается к ∞, мы можем увидеть, что происходит, посмотрев на частное старших членов в нашей рациональной функции. Поскольку это равно 1, предел нашей рациональной функции также равен 1. Однако наш показатель степени неограниченно растет, поэтому мы имеем lim→∞∞𝑥+4𝑥−4=1, что является неопределенная форма. Поэтому нам нужно будет попробовать другой метод для оценки этого предела.
Вместо этого попробуем оценить это, используя предельный результат, включающий число Эйлера: →∞→∞𝑥+4𝑥−4=𝑥−4+8𝑥−4=1+8𝑥−4.
Если мы сравним два предела, мы увидим, что нам нужно использовать замену. Мы хотим, чтобы в скобках было 1+1𝑛, поэтому мы используем замену 1𝑛=8𝑥−4.
Когда 𝑥 приближается к бесконечности, мы видим, что 8𝑥−4 приближается к 0, поэтому 𝑛 также должно стремиться к бесконечности.
Прежде чем использовать эту замену, нам также нужно переставить 𝑥 через 𝑛, что мы можем сделать следующим образом.
Возьмем обратное значение обеих частей нашей подстановки, что даст нам 𝑛=𝑥−48.
Затем умножаем на 8 и прибавляем по 4 к обеим сторонам: 𝑥=8𝑛+4.
Теперь мы можем использовать эту замену, чтобы переписать наш предел: 1+1𝑛.
Мы хотим использовать наш предельный результат, но сначала нам нужно, чтобы показатель степени был равен 𝑛. Для этого нам сначала потребуется использовать законы экспонент в сочетании с правилом произведения для пределов, так что 1𝑛⋅1+1𝑛.
Чтобы использовать правило произведения для пределов, нам нужно, чтобы существовал предел обоих факторов. Мы покажем в нашей работе, что оба этих предела существуют.
Мы можем вычислить один из этих пределов напрямую: lim→∞1+1𝑛=1.
Затем, чтобы вычислить наш другой предел, мы используем законы экспонент и правило степени для пределов, истинно при условии, что этот предел существует, а мы знаем, что он существует, потому что это наш предыдущий предельный результат. Это означает, что мы можем заменить этот предел константой Эйлера 𝑒: 1+1𝑛=𝑒.lim→∞
Следовательно, мы показали lim→∞𝑥+4𝑥−4=𝑒.
Мы также можем использовать эти результаты для решения пределов, включающих более сложные функции.
Пример 5. Оценка пределов путем преобразования их в формы пределов в натуральной степени
Определить limtan→−4𝑥+1cot.
Ответ
Мы могли бы попробовать вычислить этот предел напрямую. Внутри скобок у нас непрерывная функция, поэтому мы можем просто подставить 𝑥=0. Однако наш показатель степени неограниченно растет, поэтому мы имеем limtanlimtan→→∞∞−4𝑥+1=−40+1=1,cot, что является неопределенной формой, поэтому мы нужно будет попробовать другой метод, чтобы оценить этот предел.
Вместо этого попробуем оценить это, используя предельный результат, включающий число Эйлера, то есть 𝑒=(1+𝑛).lim→
Чтобы сравнить это с пределом, нас просят find нам нужно будет преобразовать выражение в скобках в форму 1+𝑛. Для этого мы начнем с подстановки 𝑛=−4𝑥.tan
. Мы знаем, что когда 𝑥 приближается к 0, −4𝑥tan будет приближаться к 0 путем прямой подстановки, поэтому 𝑛 также должно стремиться к 0. Кроме того, взяв обратную величину обоих стороны нашей замены и перестановки, мы имеем −4𝑛=1𝑥=𝑥.tancot
Используя все это, мы можем переписать наш предел в виде законы показателей и правило степени для пределов для получения требуемого показателя степени 1𝑛: 𝑛).
Конечно, это при условии, что предел внутри наших скобок существует, что, как мы знаем, существует, поскольку lim→(1+𝑛)=𝑒.
Наконец, мы можем использовать наш предельный результат, чтобы вычислить предел в скобках как константу Эйлера:0003
Следовательно, мы смогли показать limtan→−4𝑥+1=1𝑒. cot
cot
До сих пор мы исследовали пределы, которые приводят к числу Эйлера. Рассмотрим теперь некоторые ограничения, приводящие к обратная функция 𝑓(𝑥)=𝑒. Когда мы рассматриваем любую экспоненциальную функцию, 𝑝(𝑥)=𝑎, мы знаем, что его обратная функция является логарифмической функцией с основанием 𝑎, 𝑞(𝑥)=𝑥log. Поэтому, когда мы рассматриваем обратную функцию 𝑓(𝑥)=𝑒, мы знаем, что это будет логарифмическая функция с основанием 𝑒, 𝑔(𝑥)=𝑥log, натуральный логарифм. Натуральный логарифм функция может быть записана как 𝑔(𝑥)=(𝑥)ln. Вот график, показывающий экспоненциальную функцию и функция натурального логарифма. Мы можем видеть, как они являются отражением друг друга в строке 𝑦=𝑥.
Прежде чем мы определим натуральный логарифм как предел, напомним некоторые полезные свойства:
- 𝑦=𝑥ln эквивалентно 𝑒=𝑥,
- 𝑒=𝑥ln,
- ln 𝑒=1,
- ln1 =0,
- loglnln𝑥=𝑥𝑎.
Для каждого 𝑥,𝑦∈ℝ и 𝑛∈ℝ, - lnlnln𝑥𝑦=𝑥+𝑦,
- lnlnln𝑥𝑦=𝑥−𝑦,
- lnln𝑥=𝑛𝑥,
- lnlog𝑥×𝑒=1.

Мы начнем с рассмотрения уравнения
| 𝑦=𝑎−1, | (1) |
где 𝑥 и 𝑦 — переменные, а 𝑎 — вещественная константа. Для этого уравнение, мы можем видеть, что когда 𝑥→0, 𝑎→1 и, следовательно, 𝑦→0 тоже. Мы можем переместить 1 в другую часть уравнения и взять натуральный логарифм обеих частей этого уравнения, чтобы получить lnln𝑎=(𝑦+1).
Используя свойства логарифмов, мы можем преобразовать это в
| 𝑥𝑎=(𝑦+1)𝑥=(𝑦+1)𝑎.lnlnlnln | (2) |
Теперь рассмотрим следующий предел: lim→𝑎−1𝑥.
Используя (1) и (2), мы можем переписать это как limlimlnln→→𝑎−1𝑥=𝑦𝑎(𝑦+1).
Обратите внимание, что, как упоминалось ранее, когда 𝑥→0, 𝑦→0 также. Мы можем изменить правую часть этого уравнения, используя свойства логарифмов и пределов, следующим образом:
limlimlnlnlimlnlnlimlnlnlnlimlnlnlnlim→→→→→→𝑎−1𝑥=𝑦𝑎(𝑦+1)=𝑎(𝑦+1)= 𝑎(𝑦+1)=𝑎(𝑦 +1)=𝑎(𝑦+1).
Теперь можно заметить, что предел в знаменателе дроби — это предел, равный числу Эйлера. Следовательно, мы можем сказать, что limlnlnln→𝑎−1𝑥=𝑎𝑒=𝑎.
Мы можем использовать это предельное определение натурального логарифма для решения задач. Еще пара определений пределов которые также могут помочь нам решить проблемы limloglogandlimln→→(𝑥+1)𝑥=𝑒(𝑥+1)𝑥=1.
Ниже мы можем обобщить пределы, полученные в виде логарифмов.
Определение: логарифмы как ограничения
LimlnlimlogliMln → → → 𝑎 — 1𝑥 = 𝑎, (𝑥+1) 𝑥 = 𝑒, (𝑥+1) 𝑥 = 1.
Давайте теперь рассмотрим несколько примеров того, как мы можем использовать эти ограничения для решения задач.
Пример 6. Вычисление предела с помощью натурального логарифма
Определить lim→7−12𝑥.
Ответ
Нам дали ограничение на оценку, поэтому мы можем сначала попытаться сделать это напрямую. Если мы подставим 0 в наш предел,
мы получим 00, который не определен. Следовательно, нам нужно будет использовать какой-то другой метод для определения
этот предел.
Следовательно, нам нужно будет использовать какой-то другой метод для определения
этот предел.
Когда мы смотрим на этот предел, мы можем заметить, что он очень похож на предел, вычисляемый с помощью натурального логарифма. Позволять сравним его с этим пределом: limln→𝑎−1𝑥=𝑎.
Мы заметили, что это очень похоже на предел, который нас попросили оценить. Константа 𝑎 равна до 7. У нас также есть небольшие различия в показателе степени и знаменателе дроби. Мощность 3𝑥 вместо 𝑥, а в знаменателе 2𝑥 вместо 𝑥. Чтобы оценить предел, нам нужно попытаться манипулировать им, чтобы он был более похож на предел, который нам дали.
Начнем с изменения показателя степени. Мы можем сделать это, используя замену. Мы хотим сделать так, чтобы экспонента была просто переменная, а не переменная, умноженная на константу. Мы можем использовать замену 3𝑥=𝑢, что эквивалентно к 𝑥=𝑢3.
Перед тем, как мы сделаем эту замену, мы должны рассмотреть, что произойдет с пределом. В пределе, указанном в вопросе, мы
рассматривают, когда 𝑥→0. Мы используем замену 𝑥=𝑢3, поэтому мы можем видеть
что когда 𝑥 стремится к 0, то же самое будет и 𝑢. Следовательно, когда 𝑥→0,
𝑢→0 также. Теперь мы можем выполнить нашу замену следующим образом:
limlim→→7−12𝑥=7−1.
В пределе, указанном в вопросе, мы
рассматривают, когда 𝑥→0. Мы используем замену 𝑥=𝑢3, поэтому мы можем видеть
что когда 𝑥 стремится к 0, то же самое будет и 𝑢. Следовательно, когда 𝑥→0,
𝑢→0 также. Теперь мы можем выполнить нашу замену следующим образом:
limlim→→7−12𝑥=7−1.
Теперь мы можем видеть, что показатель степени равен просто 𝑢. Мы убрали коэффициент с помощью подстановки. Теперь это выглядит очень похоже на форму, которая нам нужна для ее оценки. Осталось разобраться с коэффициентом 𝑢 в знаменателе дроби. Мы можем начать с перемещения константы перед дробью: limlim→→7−1=327−1𝑢.
Теперь, используя предельные законы, мы можем переместить постоянный коэффициент перед пределом: limlim→→327−1𝑢=327−1𝑢.
Теперь мы можем видеть, что наш предел имеет форму limln→𝑎−1𝑥=𝑎, поэтому мы можем оценить
чтобы получить наше решение:
limlimln→→7−12𝑥=327−1𝑢=327.
Теперь мы рассмотрим последний пример в этом объяснении.
Пример 7. Вычисление предела с помощью натурального логарифма
Определить limln→(𝑥−1)𝑥−2.
Ответ
Мы могли бы попытаться решить этот вопрос с помощью прямой замены. Однако, если мы попытаемся подставить 𝑥=2 в пределе мы получим 00, что не определено. Нам нужно будет использовать другой метод в чтобы оценить этот предел. Заметим, что он похож на предел, который мы умеем вычислять, а именно limln→(𝑥+1)𝑥=1.
Мы заметили, что между этими двумя ограничениями есть несколько различий. Это значение, при котором лимит оценивается и с добавлением некоторых постоянных членов как в числителе, так и в знаменателе. Мы можем выполнить замену в нашем исходном пределе, чтобы попытаться заставить его выглядеть как предел, который мы знаем, как оценивать. мы заменим 𝑥−2=𝑢, что эквивалентно 𝑥=𝑢+2.
Прежде чем мы выполним эту замену, нам нужно рассмотреть, что произойдет с предельным значением 𝑥→2. Поскольку у нас есть 𝑢=𝑥−2, мы можем сказать, что при 𝑥→2, 𝑢→0. Мы
теперь готов заменить:
limlnlimln→→(𝑥−1)𝑥−2=(𝑢+1)𝑢.
Поскольку у нас есть 𝑢=𝑥−2, мы можем сказать, что при 𝑥→2, 𝑢→0. Мы
теперь готов заменить:
limlnlimln→→(𝑥−1)𝑥−2=(𝑢+1)𝑢.
После этой подстановки мы видим, что предел в точности имеет вид limln→(𝑥+1)𝑥=1. Следовательно, мы можем сказать, что limln→(𝑥−1)𝑥−2=1.
Давайте закончим повторением некоторых основных моментов этого объяснения.
Ключевые моменты
- Мы нашли и доказали два полезных предельных результата, связанных с числом Эйлера: 𝑒=(1+𝑥)𝑒=1+1𝑛.limandlim→→∞
- Мы нашли и доказали три полезных предельных результата, связанных с натуральным логарифмом: limlnlimlogloglimln→→→𝑎−1𝑥=𝑎,(𝑥+1)𝑥=𝑒,(𝑥+1)𝑥=1.
- Мы можем использовать эти результаты для оценки пределов, которые дают неопределенные формы путем прямой замены или оценки.
- Чтобы использовать эти результаты, иногда нам может понадобиться манипулировать нашим пределом, используя такие методы, как полиномиальное деление,
замещение или факторинг.




 Выбрав полку, к примеру, перемещаете ее мышкой на свободное место на стене и все необходимые элементы для ее установки и монтажа будут автоматически подобраны программой. Все элементы легко перемещаются или заменяются на другие, рабочую область возможно уменьшать или увеличивать в масштабе с помощью колесика мыши. Две смежные секции можно объединить, соединив их смежными стойками.
Выбрав полку, к примеру, перемещаете ее мышкой на свободное место на стене и все необходимые элементы для ее установки и монтажа будут автоматически подобраны программой. Все элементы легко перемещаются или заменяются на другие, рабочую область возможно уменьшать или увеличивать в масштабе с помощью колесика мыши. Две смежные секции можно объединить, соединив их смежными стойками. 00-19.00
00-19.00 За 2 месяца вы с нуля научитесь создавать фотореалистичные интерьеры.
За 2 месяца вы с нуля научитесь создавать фотореалистичные интерьеры.

 И может добавить уроки по Unreal Engine 4 – сейчас, как мне кажется, этот движок набирает популярность.
И может добавить уроки по Unreal Engine 4 – сейчас, как мне кажется, этот движок набирает популярность.  С 3Ds MAX знаком еще с 2004 года, но серьезно заняться изучением всё как-то стимула не хватало. Ознакомившись с бесплатным курсом, мне понравилась подача материала и финальные работы конкурсантов, они выглядят прекрасно, особенно для начинающего 3D специалиста. Оперативные и четкие ответы помогли без труда записаться на курс и пройти его с хорошим результатом на выходе, в итоге первая и красивая картинка в своей работе в 3D.
С 3Ds MAX знаком еще с 2004 года, но серьезно заняться изучением всё как-то стимула не хватало. Ознакомившись с бесплатным курсом, мне понравилась подача материала и финальные работы конкурсантов, они выглядят прекрасно, особенно для начинающего 3D специалиста. Оперативные и четкие ответы помогли без труда записаться на курс и пройти его с хорошим результатом на выходе, в итоге первая и красивая картинка в своей работе в 3D.  Проверка заданий проходит достаточно быстро, есть хорошая обратная связь как на сайте ученика так и в группе в VK где помогают кураторы, учителя и ученики.
Проверка заданий проходит достаточно быстро, есть хорошая обратная связь как на сайте ученика так и в группе в VK где помогают кураторы, учителя и ученики. 



 Я использовал это со времен Алгебры I, и мне всегда было интересно, в чем смысл трехмерного графика и как его использовать. Сейчас я изучаю многомерное исчисление в колледже и регулярно использую трехмерные графики. Это помогло мне визуализировать и понять касательные плоскости и трехмерные функции. Я бы хотел, чтобы он мог показывать точки пересечения на трехмерном графике (может быть, он и делает, но я еще не разобрался с этим), но он делает больше, чем многие другие калькуляторы, и делает это более элегантно. Мне нравится это приложение, и я рекомендую его всем, кто занимается математикой, инженерным делом или даже старшекласснику, который ищет быстрый, дешевый и простой графический калькулятор
Я использовал это со времен Алгебры I, и мне всегда было интересно, в чем смысл трехмерного графика и как его использовать. Сейчас я изучаю многомерное исчисление в колледже и регулярно использую трехмерные графики. Это помогло мне визуализировать и понять касательные плоскости и трехмерные функции. Я бы хотел, чтобы он мог показывать точки пересечения на трехмерном графике (может быть, он и делает, но я еще не разобрался с этим), но он делает больше, чем многие другие калькуляторы, и делает это более элегантно. Мне нравится это приложение, и я рекомендую его всем, кто занимается математикой, инженерным делом или даже старшекласснику, который ищет быстрый, дешевый и простой графический калькулятор Возможность визуализировать поверхности с различными уровнями контрастности помогает с относительной ориентацией и определением их пересечений. Трехмерная перспектива под любым углом является точной. Это приложение было создано высокопрофессиональными поклонниками математики. Сообщество в долгу!
Возможность визуализировать поверхности с различными уровнями контрастности помогает с относительной ориентацией и определением их пересечений. Трехмерная перспектива под любым углом является точной. Это приложение было создано высокопрофессиональными поклонниками математики. Сообщество в долгу!
 п.
п.

 Ответ: (-11; -3).
Ответ: (-11; -3). Узоры и орнаменты на посуде»
Узоры и орнаменты на посуде»
 Модуль положительного числа равен самому числу. Модуль нуля равен нулю.А(7)
Модуль положительного числа равен самому числу. Модуль нуля равен нулю.А(7) Решение уравнений│х — а│ — расстояние от а до х
Решение уравнений│х — а│ — расстояние от а до х 9 = | -9 | = | 9 |;
9 = | -9 | = | 9 |;



 После умножения числителя и знаменателя
на сопряженное числителю выражение
,
имеем:
После умножения числителя и знаменателя
на сопряженное числителю выражение
,
имеем:

 Для этого числитель и знаменатель
умножаем на число 4:
Для этого числитель и знаменатель
умножаем на число 4: Найти предел функции
.
Найти предел функции
.

 Просто действительная часть – составная: . Для наглядности ответ можно переписать так: .
Просто действительная часть – составная: . Для наглядности ответ можно переписать так: . В знаменателе уже есть , поэтому сопряженным выражением в данном случае является , то есть
В знаменателе уже есть , поэтому сопряженным выражением в данном случае является , то есть 
 3).
3).
 Теперь мы знаем, что для любого
невырожденная матрица 𝑛 на 𝑛, 𝐴, умноженная на ее обратную, является тождеством
матрица. Итак, теперь с левой стороны мы
имеют единичную матрицу 𝑛-by-𝑛. А теперь, поскольку определитель
матрица 𝐴 является скалярной, на нее можно умножить. И это дает нам определитель
𝐴, умноженное на единичную матрицу, равно 𝐴, умноженному на ее сопряженное. И это показывает, что наш первый
утверждение 𝐴 сопряженное 𝐴 действительно равно определителю 𝐴, умноженному на 𝐼
для невырожденной матрицы 𝐴.
Теперь мы знаем, что для любого
невырожденная матрица 𝑛 на 𝑛, 𝐴, умноженная на ее обратную, является тождеством
матрица. Итак, теперь с левой стороны мы
имеют единичную матрицу 𝑛-by-𝑛. А теперь, поскольку определитель
матрица 𝐴 является скалярной, на нее можно умножить. И это дает нам определитель
𝐴, умноженное на единичную матрицу, равно 𝐴, умноженному на ее сопряженное. И это показывает, что наш первый
утверждение 𝐴 сопряженное 𝐴 действительно равно определителю 𝐴, умноженному на 𝐼
для невырожденной матрицы 𝐴. И поэтому можно сказать, что наш второй
выражение верно и для невырожденной матрицы. Все данное выражение
поэтому верно для невырожденной матрицы 𝐴.
И поэтому можно сказать, что наш второй
выражение верно и для невырожденной матрицы. Все данное выражение
поэтому верно для невырожденной матрицы 𝐴. Тогда в наших первых двух выражениях
мы умножаем на ноль. И все, что умножается на ноль,
равен нулю. С правой стороны мы
умножение единичной матрицы на ноль, что дает нам нулевую матрицу. И определитель нуля
матрица равна нулю. И так левая рука, середина
член, а правый член равны нулю. Это означает, что для единичного
матрица, где определитель равен нулю, то данное утверждение также
истинный. Следовательно, 𝐴, умноженное на сопряженное 𝐴
равен присоединенному 𝐴, умноженному на 𝐴 равен определителю 𝐴, умноженному
на 𝐼 верно для любой квадратной матрицы 𝐴 порядка 𝑛.
Тогда в наших первых двух выражениях
мы умножаем на ноль. И все, что умножается на ноль,
равен нулю. С правой стороны мы
умножение единичной матрицы на ноль, что дает нам нулевую матрицу. И определитель нуля
матрица равна нулю. И так левая рука, середина
член, а правый член равны нулю. Это означает, что для единичного
матрица, где определитель равен нулю, то данное утверждение также
истинный. Следовательно, 𝐴, умноженное на сопряженное 𝐴
равен присоединенному 𝐴, умноженному на 𝐴 равен определителю 𝐴, умноженному
на 𝐼 верно для любой квадратной матрицы 𝐴 порядка 𝑛.
 \ast$ единственна, или, другими словами, $\ast$ является инволюцией. Каждая H*-алгебра есть прямая сумма собственной алгебры и алгебры, в которой $a \circ b=0$ для всех $a$ и $b$.
\ast$ единственна, или, другими словами, $\ast$ является инволюцией. Каждая H*-алгебра есть прямая сумма собственной алгебры и алгебры, в которой $a \circ b=0$ для всех $a$ и $b$.
 14159..
14159..
 Сколько килограммов картофеля собрали с каждого участка, если с каждого квадратного метра собирали поровну?
Сколько килограммов картофеля собрали с каждого участка, если с каждого квадратного метра собирали поровну? 1) Первый множитель 127, он на 27 больше второго множителя. Найди произведение этих чисел.
1) Первый множитель 127, он на 27 больше второго множителя. Найди произведение этих чисел. Найди лишнее уравнение.
Найди лишнее уравнение. Именно поэтому он может назначить дополнительные анализы и исследования.
Именно поэтому он может назначить дополнительные анализы и исследования. 5-2 часа до и после интенсивной тренировки.
5-2 часа до и после интенсивной тренировки. При этом жиры – полиненасыщенные, углеводы – сложные. Минимум 3 приема пищи, потребление углеводов относительно тренировок – за 1.5-2 часа до и после.
При этом жиры – полиненасыщенные, углеводы – сложные. Минимум 3 приема пищи, потребление углеводов относительно тренировок – за 1.5-2 часа до и после. И наоборот, ошибки при формировании рациона не дают атлету прийти к цели. Если вы правильно питаетесь, то мышцы будут расти быстрее, тело всегда будет находиться в тонусе. Вы также сможете увеличивать нагрузки и организовывать разнообразный тренировочный процесс со сменой планов.
И наоборот, ошибки при формировании рациона не дают атлету прийти к цели. Если вы правильно питаетесь, то мышцы будут расти быстрее, тело всегда будет находиться в тонусе. Вы также сможете увеличивать нагрузки и организовывать разнообразный тренировочный процесс со сменой планов. Сложнее с их качеством, но об этом далее. Объем потребляемых калорий проще всего рассчитать по формуле Лайла Макдональда, также можно использовать калькуляторы из интернета (как правило, они базируются на этой же формуле).
Сложнее с их качеством, но об этом далее. Объем потребляемых калорий проще всего рассчитать по формуле Лайла Макдональда, также можно использовать калькуляторы из интернета (как правило, они базируются на этой же формуле). 2, так как вы хотите набрать массу. Значит, потреблять придется 3360 ккал в сутки. Тогда вы сможете рассчитывать на наращивание до 2-2.5 кг мышечной массы за месяц.
2, так как вы хотите набрать массу. Значит, потреблять придется 3360 ккал в сутки. Тогда вы сможете рассчитывать на наращивание до 2-2.5 кг мышечной массы за месяц. Поэтому питание для набора массы основывается именно на нем. При регулярных силовых тренировках важно потреблять до 2 г белка на каждый килограмм веса. Но каждую ситуацию стоит рассматривать индивидуально. Нередки случаи, когда оптимальным будет потребление 2.5 г белка на каждый килограмм веса и даже его увеличение до 3 г. Однако повышать его долю в рационе стоит только в ситуациях, когда набора массы не происходит и все прочие факторы вы исключили.
Поэтому питание для набора массы основывается именно на нем. При регулярных силовых тренировках важно потреблять до 2 г белка на каждый килограмм веса. Но каждую ситуацию стоит рассматривать индивидуально. Нередки случаи, когда оптимальным будет потребление 2.5 г белка на каждый килограмм веса и даже его увеличение до 3 г. Однако повышать его долю в рационе стоит только в ситуациях, когда набора массы не происходит и все прочие факторы вы исключили. Также старайтесь сочетать разные протеины. Оптимальный вариант – сделать ставку на белок животного происхождения, но регулярно добавлять к нему растительный.
Также старайтесь сочетать разные протеины. Оптимальный вариант – сделать ставку на белок животного происхождения, но регулярно добавлять к нему растительный. В них много Омега-9 жирных кислот, которые нормализуют уровень сахара, укрепляют сердечно-сосудистую систему, помогают избегать скачков артериального давления и стабилизируют обмен веществ. Не забудьте и об Омега-3,6 жирных кислотах – ими богат рыбий жир, подсолнечное и соевое масла, многие орехи и другие продукты. А вот от снеков, красного мяса, кондитерских изделий и других источников вредных насыщенных жиров лучше отказаться.
В них много Омега-9 жирных кислот, которые нормализуют уровень сахара, укрепляют сердечно-сосудистую систему, помогают избегать скачков артериального давления и стабилизируют обмен веществ. Не забудьте и об Омега-3,6 жирных кислотах – ими богат рыбий жир, подсолнечное и соевое масла, многие орехи и другие продукты. А вот от снеков, красного мяса, кондитерских изделий и других источников вредных насыщенных жиров лучше отказаться.
 )
)

 В дальнейшем его будет крайне проблематично сбросить. Поэтому сделайте ставку на полезные продукты сразу, чтобы добиться скорейших результатов и не навредить здоровью.
В дальнейшем его будет крайне проблематично сбросить. Поэтому сделайте ставку на полезные продукты сразу, чтобы добиться скорейших результатов и не навредить здоровью. Упражнение 7А.
Упражнение 7А. Линейные уравнения с одной переменной
>
Линейные уравнения с одной переменной. Упражнение 7Б.
>
Вопрос 5
Линейные уравнения с одной переменной
>
Линейные уравнения с одной переменной. Упражнение 7Б.
>
Вопрос 5 Найдите число.
Найдите число.
 Прочтите приведенную ниже статистику удержания и привлечения клиентов, чтобы увидеть разницу между ними.
Прочтите приведенную ниже статистику удержания и привлечения клиентов, чтобы увидеть разницу между ними.
 Вот где на помощь приходит цифровой маркетинг.
Вот где на помощь приходит цифровой маркетинг.





 Если, в частности, a = 0, то вместо символа 0+0 пишут +0. Аналогично если x→a и при этом x и называются соответственно предел справа и предел слева функции f(x) в точке а . Чтобы существовал предел функции f(x) при x→
a необходимо и достаточно, чтобы . Функция f(x) называется непрерывной в точке x 0 , если предел
Если, в частности, a = 0, то вместо символа 0+0 пишут +0. Аналогично если x→a и при этом x и называются соответственно предел справа и предел слева функции f(x) в точке а . Чтобы существовал предел функции f(x) при x→
a необходимо и достаточно, чтобы . Функция f(x) называется непрерывной в точке x 0 , если предел
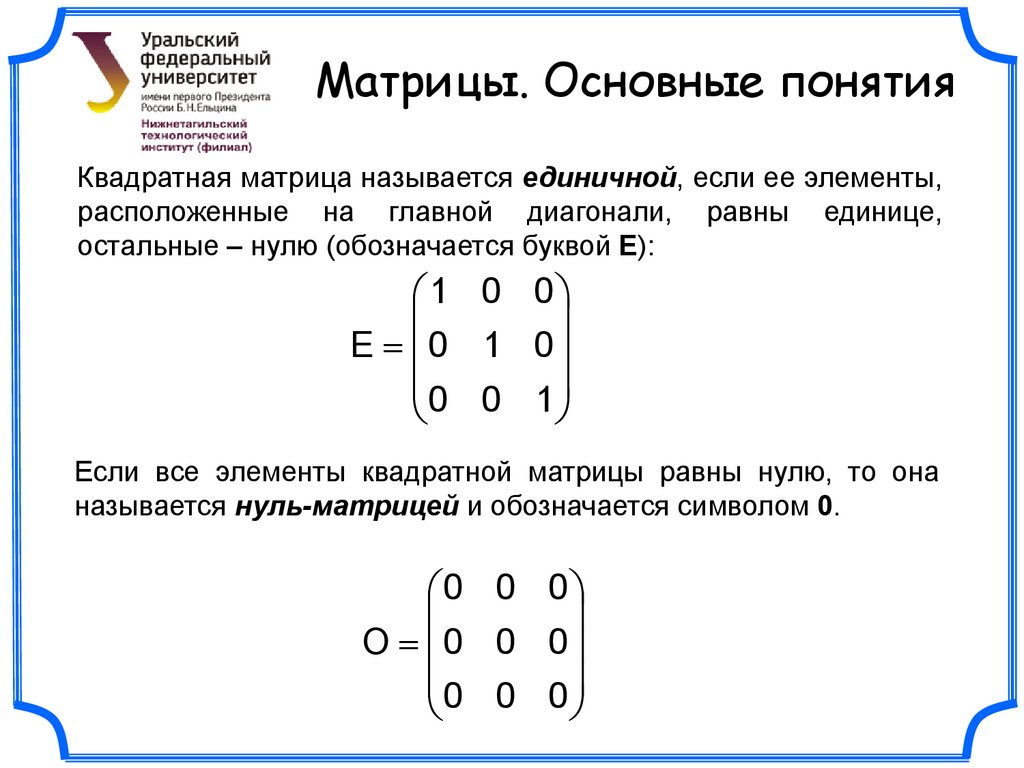
 Функция y = E(x) (целая часть от x ) в точках с целыми абсциссами имеет разрывы первого рода, или скачки.
Функция y = E(x) (целая часть от x ) в точках с целыми абсциссами имеет разрывы первого рода, или скачки. ед. превратятся в 200 ден.ед. Посмотрим теперь, во что превратятся 100 ден. ед., если процентные деньги присоединять к основному капиталу каждые полгода. По истечении полугодия 100 ден. ед. вырастут в 100 ×1,5 = 150, а еще через полгода — в 150× 1,5 = 225 (ден. ед.). Если присоединение делать каждые 1/3 года, то по истечении года 100 ден. ед. превратятся в 100 ×
(1 +1/3) 3 ≈ 237 (ден. ед.). Будем учащать сроки присоединения процентных денег до 0,1 года, до 0,01 года, до 0,001 года и т.д. Тогда из 100 ден. ед. спустя год получится:
ед. превратятся в 200 ден.ед. Посмотрим теперь, во что превратятся 100 ден. ед., если процентные деньги присоединять к основному капиталу каждые полгода. По истечении полугодия 100 ден. ед. вырастут в 100 ×1,5 = 150, а еще через полгода — в 150× 1,5 = 225 (ден. ед.). Если присоединение делать каждые 1/3 года, то по истечении года 100 ден. ед. превратятся в 100 ×
(1 +1/3) 3 ≈ 237 (ден. ед.). Будем учащать сроки присоединения процентных денег до 0,1 года, до 0,01 года, до 0,001 года и т.д. Тогда из 100 ден. ед. спустя год получится: 1 .
Пользуясь определением предела числовой последовательности, доказать, что последовательность x n =(n-1)/n имеет предел, равный 1.
1 .
Пользуясь определением предела числовой последовательности, доказать, что последовательность x n =(n-1)/n имеет предел, равный 1. Затем, применяя теорему предел частного и предел суммы, найдем:
Затем, применяя теорему предел частного и предел суммы, найдем:
 Нас интересует понятие предела функции, так как именно с ними чаще всего сталкиваются студенты. Но сначала — самое общее определение предела:
Нас интересует понятие предела функции, так как именно с ними чаще всего сталкиваются студенты. Но сначала — самое общее определение предела:
 Вообще стоит сказать, что в разрешении таких неопределенностей есть определенный элемент искусства: нужно заметить, как можно преобразовать функцию таким образом, чтобы неопределенность ушла. В нашем случае разделим числитель и знаменатель на х в старшей степени. Что получится?
Вообще стоит сказать, что в разрешении таких неопределенностей есть определенный элемент искусства: нужно заметить, как можно преобразовать функцию таким образом, чтобы неопределенность ушла. В нашем случае разделим числитель и знаменатель на х в старшей степени. Что получится?
 2 стремится к нулю.
2 стремится к нулю. Так как функция sin x всегда стремится к единице, когда приближается к нулю, для нее справедливо тождество:
Так как функция sin x всегда стремится к единице, когда приближается к нулю, для нее справедливо тождество: (n-1)
(n-1)
 В итоге мы получили ∆ A = 26, следовательно обратная матрица существует.
В итоге мы получили ∆ A = 26, следовательно обратная матрица существует.
 (2+1) = -1.
(2+1) = -1. Он также используется для изучения электрических цепей, квантовой механики и оптики. Эти матрицы имеют решающее значение для измерения выходной мощности батареи и преобразования электрической энергии в другую полезную энергию с помощью резисторов. При применении законов Кирхгофа для напряжения и тока для решения задач обратные матрицы чрезвычайно важны. Продолжайте читать, чтобы узнать больше.
Он также используется для изучения электрических цепей, квантовой механики и оптики. Эти матрицы имеют решающее значение для измерения выходной мощности батареи и преобразования электрической энергии в другую полезную энергию с помощью резисторов. При применении законов Кирхгофа для напряжения и тока для решения задач обратные матрицы чрезвычайно важны. Продолжайте читать, чтобы узнать больше.
 9{ – 1}} = \frac{{adjA}}{{|A|}}\) где \(|A| \ne 0\)
9{ – 1}} = \frac{{adjA}}{{|A|}}\) где \(|A| \ne 0\) { – 1}}} \right| = \frac{1}{{|A|}}\). 9{ – 1}}\)
{ – 1}}} \right| = \frac{1}{{|A|}}\). 9{ – 1}}\) Это также говорит нам о последовательном или непоследовательном поведении решения уравнений.
Это также говорит нам о последовательном или непоследовательном поведении решения уравнений. { – 1}}\) не будет существовать. 9{ – 1}}\) не будет существовать.
{ – 1}}\) не будет существовать. 9{ – 1}}\) не будет существовать.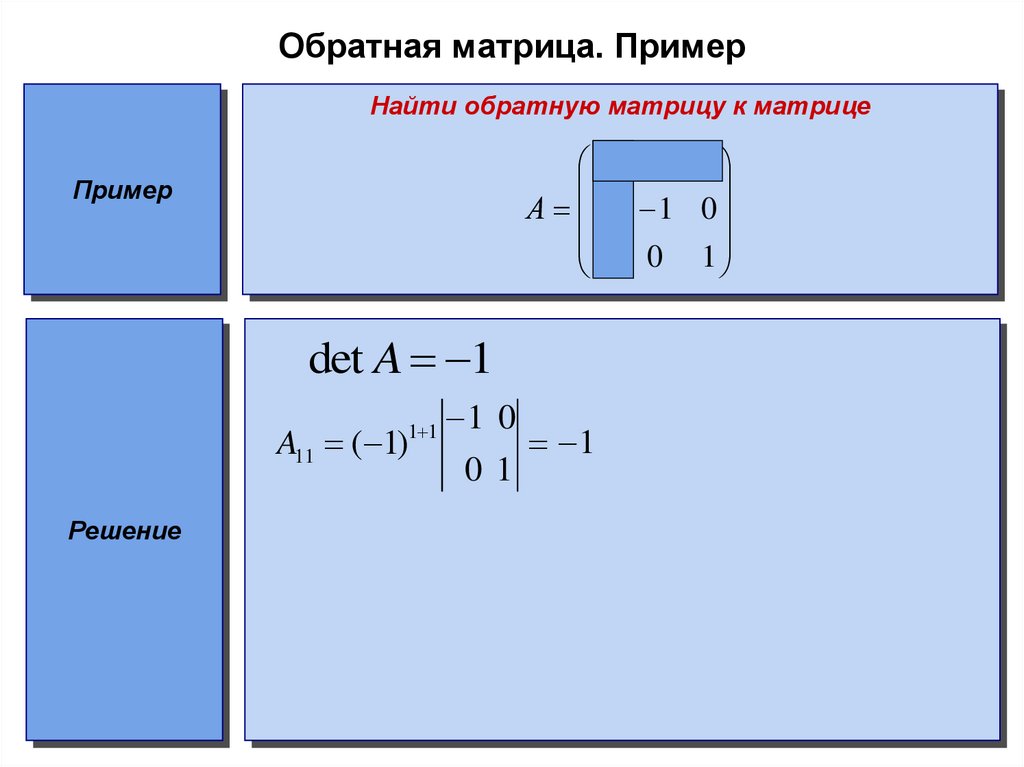 3. Найдите обратную матрицу \(\left[ {\begin{array}{*{20}{c}} 0&1&2\\ 1&2&3\\ 3&1&1 \end{array}} \right]\), используя элементарные операции
3. Найдите обратную матрицу \(\left[ {\begin{array}{*{20}{c}} 0&1&2\\ 1&2&3\\ 3&1&1 \end{array}} \right]\), используя элементарные операции  4. Решите следующую систему линейных уравнений методом обращения матриц: \(5x + 2y = 3,\,3x + 2y = 5\)
4. Решите следующую систему линейных уравнений методом обращения матриц: \(5x + 2y = 3,\,3x + 2y = 5\)  \)
\) Мы узнали об обратной матрице, ее свойствах и примерах. С его помощью можно решить массу сложных задач. Он используется для решения линейных уравнений и других математических функций, таких как исчисление, оптика и квантовая физика. Он имеет широкий спектр реальных приложений, что привело к тому, что он играет решающую роль в математике.
Мы узнали об обратной матрице, ее свойствах и примерах. С его помощью можно решить массу сложных задач. Он используется для решения линейных уравнений и других математических функций, таких как исчисление, оптика и квантовая физика. Он имеет широкий спектр реальных приложений, что привело к тому, что он играет решающую роль в математике. Обратная матрица единственна. Это будет доказано с помощью метода от противного.
Обратная матрица единственна. Это будет доказано с помощью метода от противного.
 Определение эквивалентного выражения для матриц с использованием свойств обратных матриц
Определение эквивалентного выражения для матриц с использованием свойств обратных матриц



 Когда мы перемножили матрицы 𝐴 и 𝐵, результирующая матрица была единичной матрицей. Напомним, что любая квадратная матрица (с ненулевым определителем) имеет обратную такую, что 𝐴𝐴=𝐼. Поскольку произведение матрицы 𝐴 и матрицы 𝐵 было единичной матрицей, матрица 𝐵 должна быть обратной матрице 𝐴.
Когда мы перемножили матрицы 𝐴 и 𝐵, результирующая матрица была единичной матрицей. Напомним, что любая квадратная матрица (с ненулевым определителем) имеет обратную такую, что 𝐴𝐴=𝐼. Поскольку произведение матрицы 𝐴 и матрицы 𝐵 было единичной матрицей, матрица 𝐵 должна быть обратной матрице 𝐴.


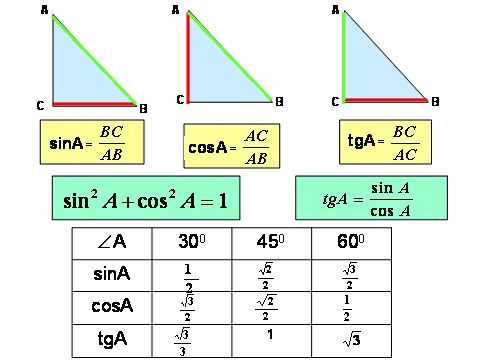
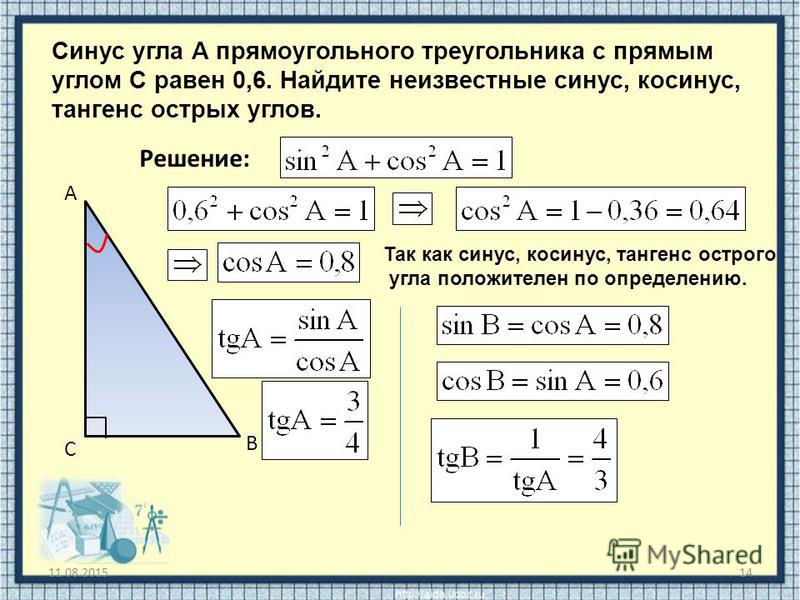
 5 Соотношения синуса, косинуса и тангенса и приложения тригонометрии – Fanshawe Pre-Health Sciences Mathematics 1
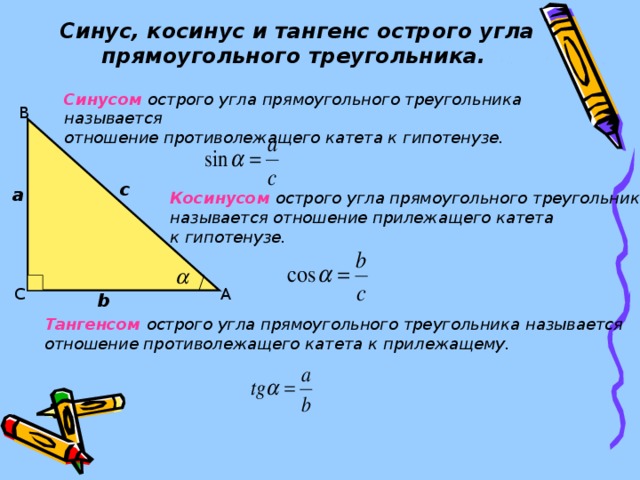
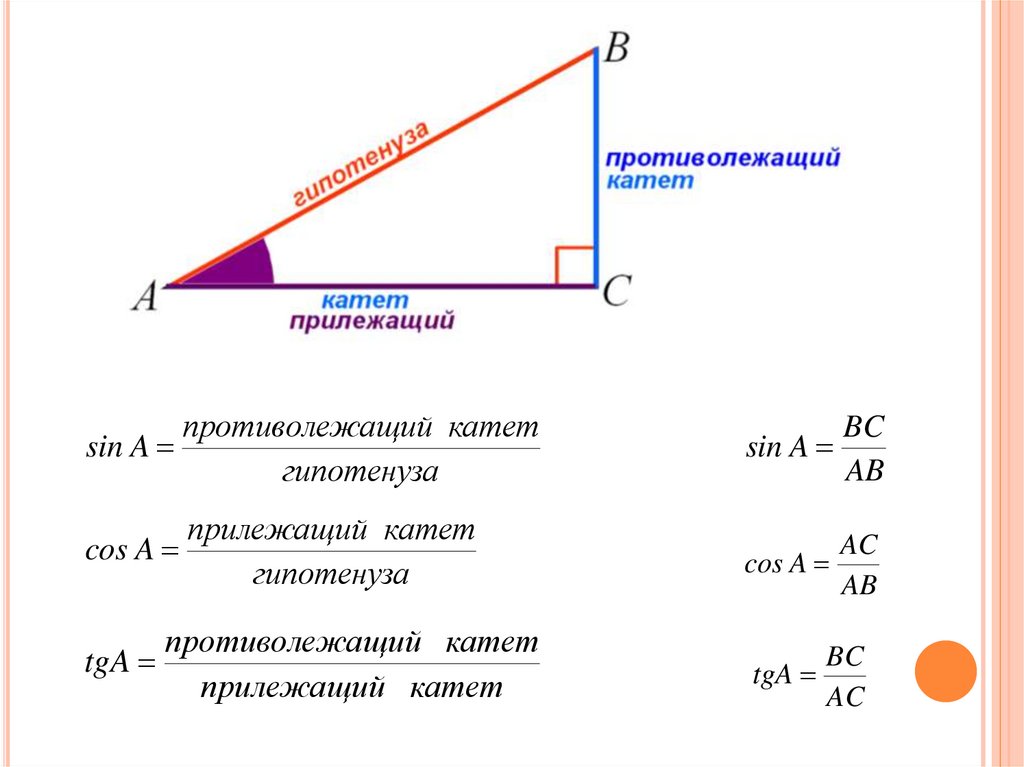
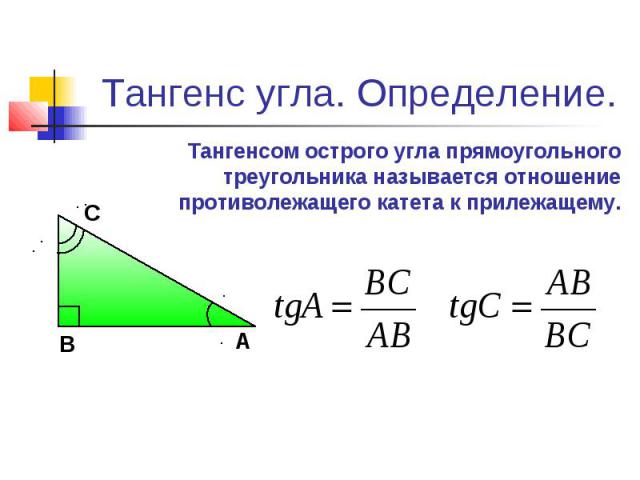
5 Соотношения синуса, косинуса и тангенса и приложения тригонометрии – Fanshawe Pre-Health Sciences Mathematics 1 Два других угла прямоугольного треугольника — острые углы (с мерой меньше [латекс]90[/латекс] градусов). Один из этих углов мы называем опорным углом и используем [латекс]θ[/латекс] (тета) для его представления.
Два других угла прямоугольного треугольника — острые углы (с мерой меньше [латекс]90[/латекс] градусов). Один из этих углов мы называем опорным углом и используем [латекс]θ[/латекс] (тета) для его представления. 5.3
5.3
 5.2 опорными углами могут быть угол [латекс]Е[/латекс] или угол [латекс]F[/латекс]. Используя определение тригонометрических отношений, мы можем написать [latex]sin(E)=\frac{e}{d}[/latex], [latex]cos(E)=\frac{f}{d}[/latex ] и [латекс]тан(Е)=\фрак{е}{е}[/латекс].
5.2 опорными углами могут быть угол [латекс]Е[/латекс] или угол [латекс]F[/латекс]. Используя определение тригонометрических отношений, мы можем написать [latex]sin(E)=\frac{e}{d}[/latex], [latex]cos(E)=\frac{f}{d}[/latex ] и [латекс]тан(Е)=\фрак{е}{е}[/латекс]. При необходимости округлить до четырех знаков после запятой.
При необходимости округлить до четырех знаков после запятой. Мы адаптируем нашу стратегию решения задач для приложений тригонометрии. Кроме того, поскольку в этих задачах будет задействован прямоугольный треугольник, полезно нарисовать его (если рисунок не предоставлен) и пометить его с помощью данной информации. Мы включим это в первый шаг стратегии решения проблем для тригонометрических приложений.
Мы адаптируем нашу стратегию решения задач для приложений тригонометрии. Кроме того, поскольку в этих задачах будет задействован прямоугольный треугольник, полезно нарисовать его (если рисунок не предоставлен) и пометить его с помощью данной информации. Мы включим это в первый шаг стратегии решения проблем для тригонометрических приложений.
 }\;0,57&\overset?=8,03 \div14\\ 0,57&=0,57\checkmark\\[3ex] \text{b.}\;0,82& \overset?=11,47 \div14\\ 0,82&=0,82 \checkmark \end{align*}[/latex]
}\;0,57&\overset?=8,03 \div14\\ 0,57&=0,57\checkmark\\[3ex] \text{b.}\;0,82& \overset?=11,47 \div14\\ 0,82&=0,82 \checkmark \end{align*}[/latex]
 {-1}[/latex] находятся на вашем научном калькуляторе. . 9\circ[/латекс]
{-1}[/latex] находятся на вашем научном калькуляторе. . 9\circ[/латекс]

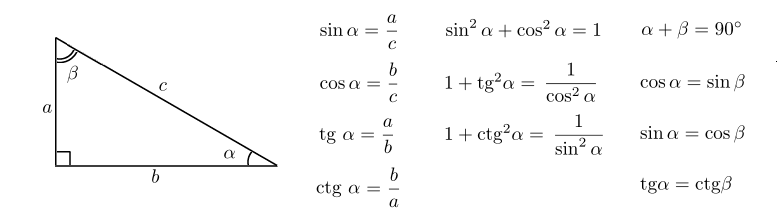
 Нарисуйте прямоугольный треугольник и обозначьте указанные части.
Нарисуйте прямоугольный треугольник и обозначьте указанные части.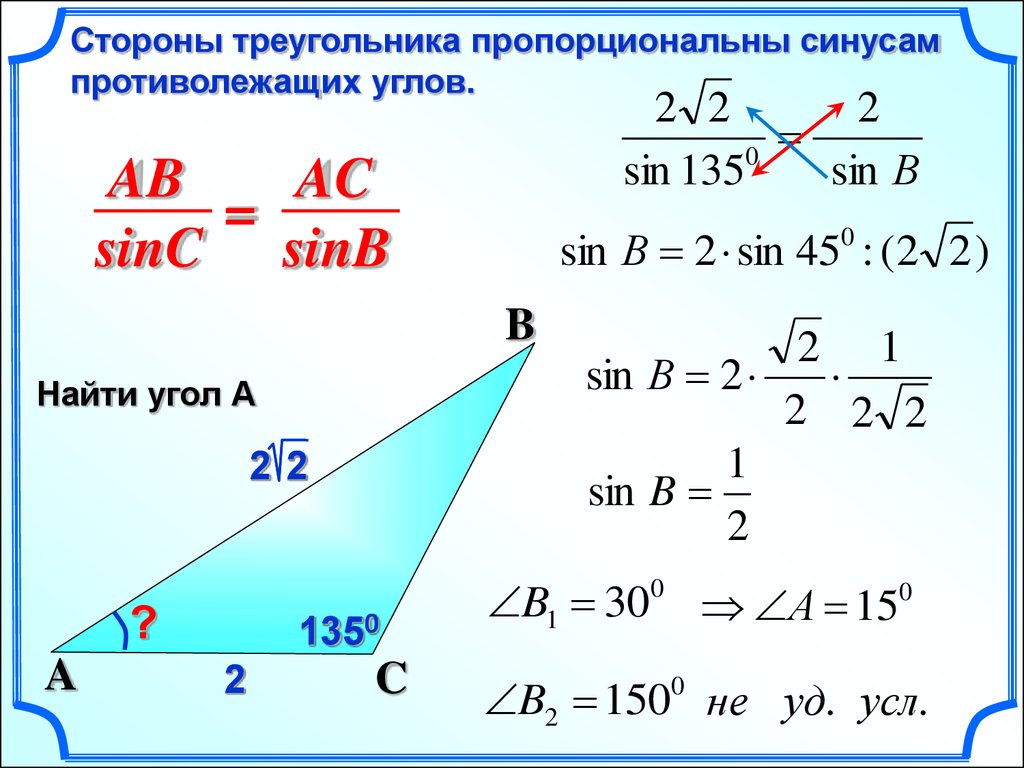 0 International License, если не указано иное.
0 International License, если не указано иное. В нашем примере θ = 60°, а прилежащее равно 4 см.
В нашем примере θ = 60°, а прилежащее равно 4 см. Это напоминает нам уравнение:
Это напоминает нам уравнение: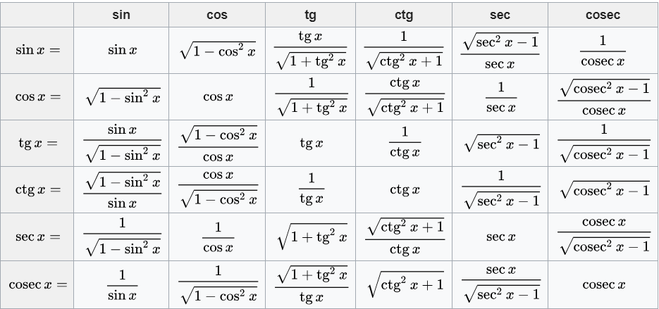
 Так как второй аргумент (основание) опущен, предполагается, что он равен 10. Результат (1) — степень, в которую необходимо возвести основание, чтобы получить число 10.
Так как второй аргумент (основание) опущен, предполагается, что он равен 10. Результат (1) — степень, в которую необходимо возвести основание, чтобы получить число 10. Логарифмом числа b по основанию a называют такую степень, в которую надо возвести число a, чтобы получить число b.
Логарифмом числа b по основанию a называют такую степень, в которую надо возвести число a, чтобы получить число b.



 Когда мы не можем решить задачу с помощью показателей, мы используем логарифмы. Существуют различные формулы логарифмов, которые выводятся с использованием законов показателей. Давайте изучим их, используя несколько решенных примеров.
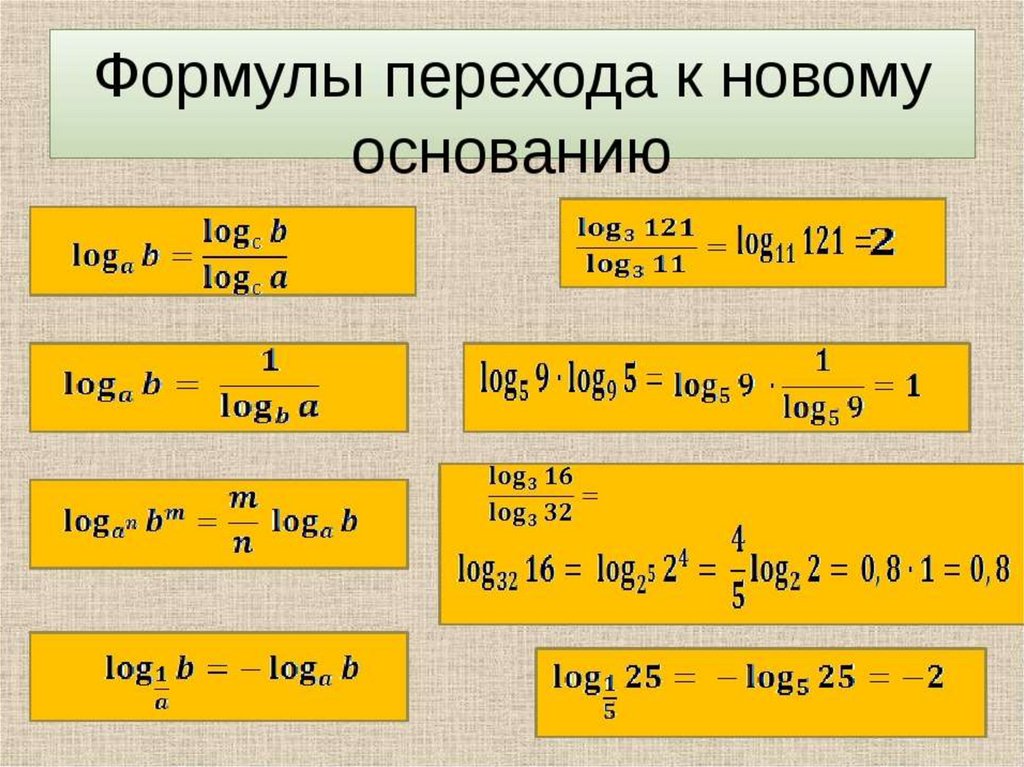
Когда мы не можем решить задачу с помощью показателей, мы используем логарифмы. Существуют различные формулы логарифмов, которые выводятся с использованием законов показателей. Давайте изучим их, используя несколько решенных примеров. 0014 b (xy) = log b x + log b y называется формулой произведения бревен. Точно так же все свойства вместе с их именами указаны в таблице ниже.
0014 b (xy) = log b x + log b y называется формулой произведения бревен. Точно так же все свойства вместе с их именами указаны в таблице ниже.
 а) 5 3 = 125 б) 3 -3 = 1/27.
а) 5 3 = 125 б) 3 -3 = 1/27.
 Мы также используем определение логарифма при выводе логарифмических формул. т. е. мы преобразуем логарифмическую форму в экспоненциальную форму и наоборот при выводе. Подробный вывод формул журнала можно найти в разделе «Что такое формулы журнала?» раздел этой страницы.
Мы также используем определение логарифма при выводе логарифмических формул. т. е. мы преобразуем логарифмическую форму в экспоненциальную форму и наоборот при выводе. Подробный вывод формул журнала можно найти в разделе «Что такое формулы журнала?» раздел этой страницы. Обычно в калькуляторах есть опции для вычисления логарифмов чисел с основанием 10 и с основанием «e». Чтобы найти логарифмы чисел с другим основанием, кроме 10 и «е», мы используем формулу замены основания. Например лог 2 3 = (лог. 3) / (лог. 2).
Обычно в калькуляторах есть опции для вычисления логарифмов чисел с основанием 10 и с основанием «e». Чтобы найти логарифмы чисел с другим основанием, кроме 10 и «е», мы используем формулу замены основания. Например лог 2 3 = (лог. 3) / (лог. 2). Например, 43 = 64; следовательно, 3 — это логарифм 64 по основанию 4, или 3 = log464. Точно так же мы знаем, что 103 = 1000, тогда 3 = log101000. Логарифмы с основанием 10 обычно известны как обычные или бриггсовские логарифмы и просто записываются как log n. В этой статье мы обсудим, что такое логарифм, формулы логарифмов, основные формулы логарифмов, правило изменения основания, правила и формулы логарифмов, для чего используется логарифм и т. д.
Например, 43 = 64; следовательно, 3 — это логарифм 64 по основанию 4, или 3 = log464. Точно так же мы знаем, что 103 = 1000, тогда 3 = log101000. Логарифмы с основанием 10 обычно известны как обычные или бриггсовские логарифмы и просто записываются как log n. В этой статье мы обсудим, что такое логарифм, формулы логарифмов, основные формулы логарифмов, правило изменения основания, правила и формулы логарифмов, для чего используется логарифм и т. д.

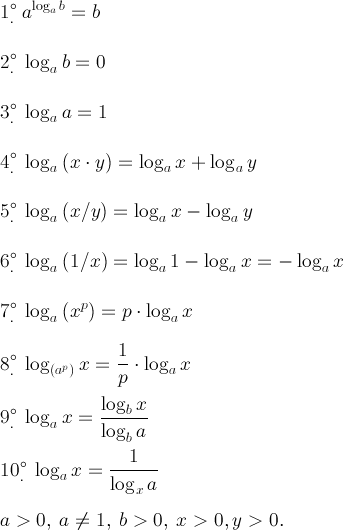 0003
0003
 Если число меньше единицы, характеристика отрицательна, и число на единицу больше числа нулей справа от запятой.
Если число меньше единицы, характеристика отрицательна, и число на единицу больше числа нулей справа от запятой. Например, чтобы получить значение log1015,27, сначала разделите характеристику и часть мантиссы.
Например, чтобы получить значение log1015,27, сначала разделите характеристику и часть мантиссы.