почему эти примеры невозможно решить
На протяжении веков лучшие умы человечества решали одну математическую задачу за другой, однако есть несколько, не поддавшихся до сих пор никому. За нахождение алгоритма их решения некоторые фонды и компании готовы заплатить большие деньги. Представляем вашему вниманию подборку из 10 нерешенных математических задач, которые до сих пор остаются неподвластными даже лучшим умам.
Василий Парфенов
Гипотеза Коллатца
Небольшой прогресс в решении этой задачи почти вековой давности наметился буквально в прошлом месяце. Однако знаменитый американской математик Терренс Тао лишь ближе всех подошел к нему, но ответа все равно пока не нашел. Гипотеза Коллатца является фундаментом такой математической дисциплины, как «Динамические системы», которая, в свою очередь, важна для множества других прикладных наук, например, химии и биологии. Сиракузская проблема выглядит, как простой безобидный вопрос, но именно это делает ее особенной. Несмотря на все попытки, эта проблема до сих пор остается самой известной нерешенной математической задачей.
Несмотря на все попытки, эта проблема до сих пор остается самой известной нерешенной математической задачей.
Проблема Гольдбаха (бинарная)
Проблема была сформулирована Кристианом Гольдбахом в его переписке с другим величайшим светилом математики Леонардом Эйлером в 1742 году. Сам Кристиан ставил вопрос несколько проще: «каждое нечетное число, больше 5, можно представить в виде суммы трех простых чисел». В 2013 году перуанский математик Харальд Хельфготт нашел окончательное решение этого варианта. Однако предложенное Эйлером следствие этого утверждения, которое и назвали «бинарной проблемой Гольдбаха», до сих пор не поддается никому. Это одна из самых древних нерешенных математических задач человечества.
Гипотеза о числах-близнецах
Как и всегда в математике, если проблема не решается «в лоб», к ней подходят с другого конца. Например, в 2013 году было доказано, что количество простых чисел, отличающихся на 70 миллионов, бесконечно. Тогда же, с разницей менее чем в месяц, значение разницы было улучшено до 59 470 640, а затем и вовсе на порядок — до 4 982 086. На данный момент существуют теоретические обоснования бесконечности пар простых чисел с разницей в 12 и 6, однако доказанной является лишь разность в 246. Как и прочие проблемы такого рода, гипотеза о числах-близнецах особенно важна для криптографии. Однако, до сих пор она остается нерешенной математической проблемой, над которой бьются лучшие умы.
Тогда же, с разницей менее чем в месяц, значение разницы было улучшено до 59 470 640, а затем и вовсе на порядок — до 4 982 086. На данный момент существуют теоретические обоснования бесконечности пар простых чисел с разницей в 12 и 6, однако доказанной является лишь разность в 246. Как и прочие проблемы такого рода, гипотеза о числах-близнецах особенно важна для криптографии. Однако, до сих пор она остается нерешенной математической проблемой, над которой бьются лучшие умы.
Гипотеза Римана
Одна из «проблем тысячелетия», за решение которой назначен приз в миллион долларов, а также вхождение в пантеон «богов» современной математики. На деле, доказательство этой гипотезы настолько сильно толкнет вперед теорию чисел, что это событие по праву будет называться историческим. Многие вычисления и утверждения в математике строятся на предположении о том, что «гипотеза Римана» верна, и до сих пор никого не подводили. Немецкий математик сформулировал знаменитую задачу 160 лет назад, и с тех пор к ее решению подступались неисчислимое количество раз, однако до сих пор она остается, пожалуй, самой неприступной нерешенной задачей современной математики.
Гипотеза Берча и Суиннертон-Дайера
Эллиптическими кривыми называются такие линии на графике, которые описываются, на первый взгляд, безобидными уравнениями вида y²=x³+ax+b. Некоторые их свойства чрезвычайно важны для алгебры и теории чисел, а решение данной задачи может серьезно продвинуть науку вперед. Наибольший прогресс в нахождении ответа на эту нерешенную математическую задачу был достигнут в 1977 году коллективом математиков из Англии и США, которые смогли найти доказательство гипотезы Берча и Суиннертон-Дайера для одного из частных случаев.
Проблема плотной упаковки равных сфер
Под размерностью или измерением понимается количество линий, вдоль которых размещаются шары. В реальной жизни больше третьей размерности не встречается, однако математика оперирует и гипотетическими значениями. Решение этой задачи может серьезно продвинуть не только теорию чисел и геометрию вперед, но также поможет в химии, информатике и физике. Пожалуй, это одна из немногих нерешенных математических задач, которая имеет четкое практическое применение.
Пожалуй, это одна из немногих нерешенных математических задач, которая имеет четкое практическое применение.
Проблема развязывания
Первые шаги на пути решения этой задачи были сделаны в 2011 году американским математиком Грегом Купербергом. В его работе развязывание узла из 139 вершин было сокращено со 108 часов до 10 минут. Результат впечатляющий, но это лишь частный случай. На данный момент существует несколько десятков алгоритмов разной степени эффективности, однако ни один из них не является универсальным. Среди применений этой области математики — биология, в частности, процессы сворачивания белков.
Самый большой кардинал
Мощность множества характеризуется его кардинальным числом или просто кардиналом. Существует целая онлайн-энциклопедия бесконечностей и примечательных «конечностей», названная в честь Георга Кантора. Этот немецкий математик первым обнаружил, что неисчислимые множества могут быть больше или меньше друг друга. Более того, он смог доказать разницу в мощностях различных бесконечностей. Проблема тут заключается в доказательстве того, что существует кардинал (или, возможно, кардиналы) с некоторым заданным большим кардинальным свойством. До сих пор эта задача остается нерешенной.
Более того, он смог доказать разницу в мощностях различных бесконечностей. Проблема тут заключается в доказательстве того, что существует кардинал (или, возможно, кардиналы) с некоторым заданным большим кардинальным свойством. До сих пор эта задача остается нерешенной.
Что не так с суммой числа π и e?
Если от предыдущего абзаца у читателя не заболела голова, то вот продолжение загадки — а что с πe, π/e и π-e? Также неизвестно, а знать это наверняка довольно важно для теории чисел. Трансцедентность числа доказал в конце XIX века Фердинанд фон Линдеман вместе с невозможностью решения задачи квадратуры круга. С тех пор значимых подвижек в решении вопроса не было.
Является ли γ рациональной?
Значение γ было вычислено до нескольких тысяч знаков после запятой, первые четыре из которых — 0,5772. Она достаточно широко используется в математике, в том числе вместе с другим числом Эйлера — e. Согласно теории цепных дробей, если постоянная Эйлера-Маскерони является рациональной дробью, то ее знаменатель должен быть больше 10 в 242 080 степени. Но пока доказать ее рациональность не удалось — для этого нам и нашим компьютерам нужно больше времени. До этих пор рациональность постоянной γ остается нерешенной математической проблемой.
Согласно теории цепных дробей, если постоянная Эйлера-Маскерони является рациональной дробью, то ее знаменатель должен быть больше 10 в 242 080 степени. Но пока доказать ее рациональность не удалось — для этого нам и нашим компьютерам нужно больше времени. До этих пор рациональность постоянной γ остается нерешенной математической проблемой.
примеры и способы решения математических задач для родителей
На протяжении всего обучения школьникам приходится решать задачи — в начальной школе по математике, а затем по алгебре, геометрии, физике и химии. И хотя условия задач в разных науках отличаются, способы решения основаны на одних и тех же логических принципах. Понимание того, как устроена простая задача по математике, поможет ребёнку разработать алгоритмы для решения задач из других областей науки. Поэтому учить ребёнка решать задачи необходимо уже с первого класса.
Нередки случаи, когда точные науки вызывают у детей сопротивление. Видя это, учителя и родители записывают таких детей в «гуманитарии», из-за чего они только укрепляются во мнении, что точные науки — это не для них.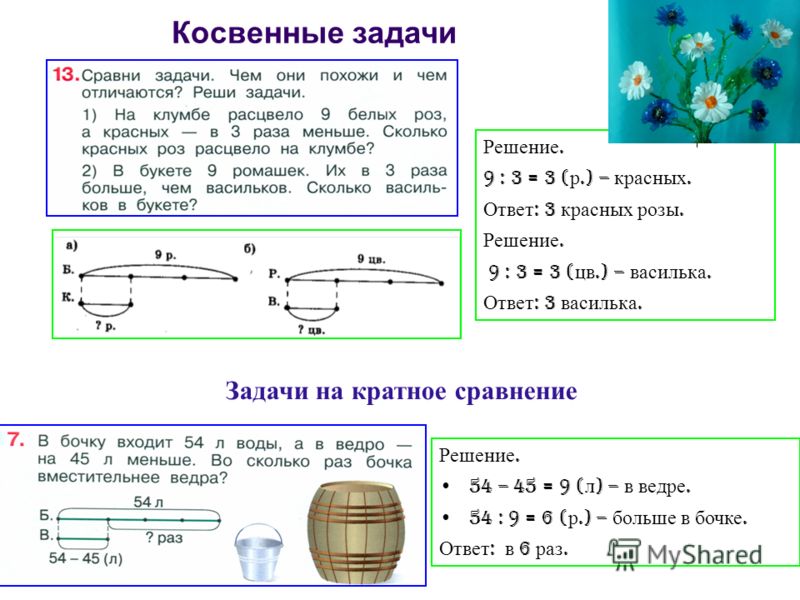 Преподаватель математики Анна Эккерман уверена, что проблемы с математикой часто имеют исключительно психологический характер:
Преподаватель математики Анна Эккерман уверена, что проблемы с математикой часто имеют исключительно психологический характер:
Детям вбивают в голову, что математика — это сложно. К длинным нудным параграфам в учебнике сложно подступиться. Учитель ставит на ребёнке клеймо «троечника» или «двоечника». Если не внушать детям, что они глупые и у них ничего не получится, у них получится ровно всё.
Чтобы ребёнку было интересно учить математику, он должен понимать, как эти знания пригодятся ему, даже если он не собирается становиться программистом или инженером.
Математика ежедневно помогает нам считать деньги, без умения вычислять периметр и площадь невозможно сделать ремонт, а навык составления пропорций незаменим в кулинарии — используйте это. Превращайте ежедневные бытовые вопросы в математические задачи для ребёнка: пусть польза математики станет для него очевидна.
Конечно, найти в быту применение иррациональным числам или квадратным уравнениям не так просто. И если польза этих знаний вызывает у подростка вопросы, объясните ему, что с их помощью мы тренируем память, развиваем логическое мышление и остроту ума — навыки, в равной степени необходимые как «технарям», так и «гуманитариям».
И если польза этих знаний вызывает у подростка вопросы, объясните ему, что с их помощью мы тренируем память, развиваем логическое мышление и остроту ума — навыки, в равной степени необходимые как «технарям», так и «гуманитариям».
<<Форма демодоступа>>
Как правильно научить ребёнка решать задачи
Если ребёнок только начинает осваивать навык решения задач, приучите его придерживаться определённого алгоритма.
1. Внимательно читаем условия
Лучше вслух и несколько раз. После того как ребёнок прочитал задачу, задайте ему вопросы по тексту и убедитесь, что ему понятно, что вычислять нужно количество грибов, а не огурцов. Старайтесь не нервничать, если ребёнок упустил что-то из вида. Дайте ему разобраться самостоятельно. Если в условиях упоминаются неизвестные ребёнку реалии — объясните, о чём идёт речь.
Особую сложность представляют задачи с косвенным вопросом, например:
«Один динозавр съел 16 деревьев, это на 3 меньше, чем съел второй динозавр. Сколько деревьев съел второй динозавр?». Невнимательно прочитав условия, ребёнок посчитает 16−3, и получит неправильный ответ, ведь эта задача на самом деле требует не вычитания, а сложения.
Сколько деревьев съел второй динозавр?». Невнимательно прочитав условия, ребёнок посчитает 16−3, и получит неправильный ответ, ведь эта задача на самом деле требует не вычитания, а сложения.
2. Делаем описание задачи
В решении некоторых задач поможет представление данных в виде схемы, графика или рисунка. Чем ярче сложится образ, тем проще будет его осмыслить. Наглядная запись позволит ребёнку не только быстро разобраться в условиях задачи, но и поможет увидеть связь между ними. Часто план решения возникает уже на этом этапе.
Ребёнок должен чётко понимать значения словесных формул и знать, какие математические действия им соответствуют.
Формы краткой записи условий задач / shkola4nm.ru
3. Выбор способа решения
Наглядно записанное условие должно подтолкнуть ребёнка к нахождению решения. Если этого не произошло, попробуйте задать наводящие вопросы, проиллюстрировать задачу при помощи окружающих предметов или разыграть сценку. Если один из способов объяснения не сработал — придумайте другой. Многократное повторение одного и того же вопроса неэффективно.
Многократное повторение одного и того же вопроса неэффективно.
Все, даже самые сложные, математические задачи сводятся к принципу «из двух известных получаем неизвестное». Но для нахождения этой пары чисел часто требуется выполнить несколько действий, то есть разложить задачу на несколько более простых.
Ребёнок должен знать способы получения неизвестных данных из двух известных:
- слагаемое = сумма − слагаемое
- вычитаемое = уменьшаемое − разность
- уменьшаемое = вычитаемое + разность
- множитель = произведение ÷ множитель
- делитель = делимое ÷ частное
- делимое = делитель × частное
После того как план действий найден, подробно запишите решение. Оно должно отражать всю последовательность действий — так ребёнок сможет запомнить принцип и пользоваться им в дальнейшем.
4. Формулировка ответа
Ответ должен быть полным и точным. Это не просто формальность: обдумывая ответ, ребёнок привыкает серьёзно относиться к результатам своего труда.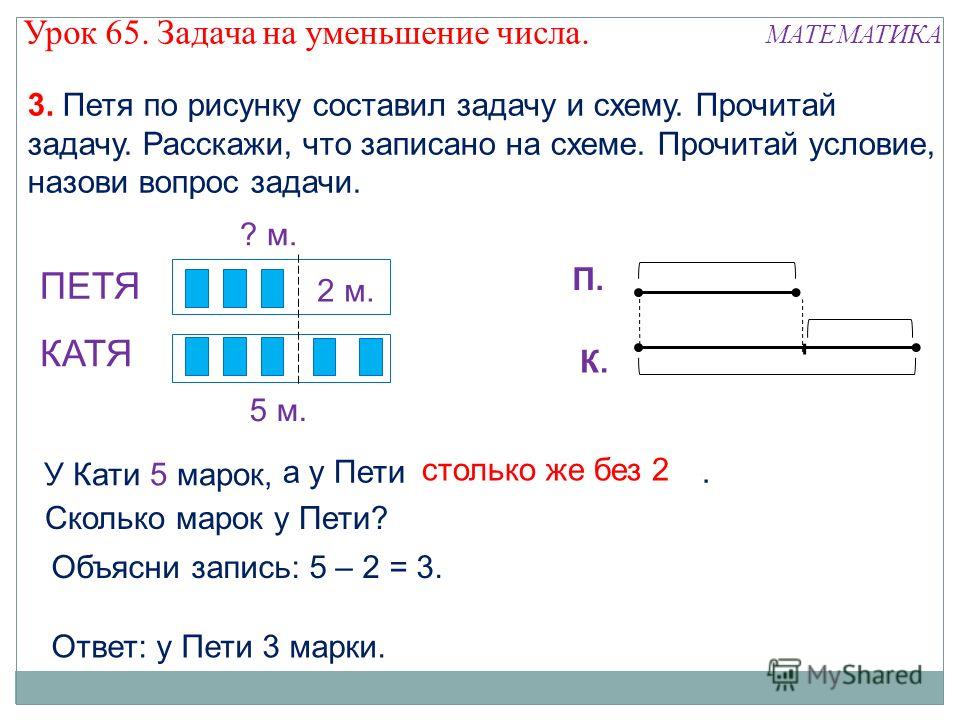 А главное — из описания должна быть понятна логика решения.
А главное — из описания должна быть понятна логика решения.
Одна из самых распространённых ошибок — представление в ответе не тех данных, о которых спрашивалось изначально. Если такая проблема возникает, нужно вернуться к первому пункту.
5. Закрепление результата
Не стоит думать, что выполнив задание один раз, ребёнок сразу научится решать задачи. Полученный результат нужно зафиксировать. Для этого подумайте над решённой задачей ещё немного: предложите ребёнку поискать другой способ решения или спросите, как изменится ответ при изменении того или иного параметра в условии.
Важно, чтобы у ребёнка сложился чёткий алгоритм рассуждений и действий в каждом из вариантов.
В нашей онлайн-школе, помимо уроков, ученики могут закреплять свои знания на консультациях в формате открытых часов, где учителя разбирают темы, вызвавшие затруднения, показывают необычные задачи и различные способы их решения.
<<Форма курс 5-11>>
Что поможет ребёнку решать задачи
В заключение расскажем о том, как сделать процесс решения задач проще и интереснее:
- Для того чтобы решать задачи, необходимо уметь считать. Следует выучить с ребёнком таблицу умножения, освоить примеры с дробями и простые уравнения.
- Чтобы решение задач не превратилось для ребёнка в рутину, проявите фантазию. Меняйте текст задания в соответствии с интересами ребёнка. Например, решать задачи на движение будет куда интереснее, если заменить банальные поезда трансформерами, летящими навстречу друг другу в эпической схватке.
- Дети с развитой логикой учатся решать задачи быстрее. Советуем разбавлять чисто математические задания логическими. Задачи «с подвохом» избавят ребёнка от шаблонного мышления, а задания с большим количеством лишних данных научат выделять главное из большого количества условий.
<<Блок перелинковки>>
После того как ребёнок решит достаточно задач одного типа, предложите ему самому придумать задачу. Это позволит ему не только закрепить материал, но и проявить творческие способности.
Это позволит ему не только закрепить материал, но и проявить творческие способности.
Константинов. Как решить задачу (и) научить детей математике
В начале июля от ковида умер НН (Николай Николаевич) Константинов, один из создателей углубленного преподавания математики в СССР. Через математические олимпиады, кружки, матклассы в московских школах прошли тысячи детей, обнаруживших склонность к точным наукам, – и после многие из них составили цвет науки. Это был чарующий мир: помимо углубленного изучения математики школьники ходили в походы, летом отправлялись в матлагерь, организованный на хуторе в Эстонии, или в составе строительного отряда на Беломорскую биологическую станцию, а затем собирались в подмосковных лесах на слеты ББС с палатками, кострами и пением бардовских песен.
Многое из этого организовал Константинов. Он был в прямом смысле легендарной личностью – про него рассказывали невероятные легенды: что, например, его видели одновременно в разных местах. Пересказывали историю, как люди ехали на велосипедах по шоссе, и Константинов несколько раз их обгонял, ни разу при этом не проехав навстречу.
Про себя Константинов рассказывал, что интересовался в детстве биологией, занимался в кружке юных натуралистов, но потом грянуло «разоблачение» генетики академиком Лысенко, и идти учиться биологии в СССР стало бессмысленно. Константинов увлекся физикой и математикой, окончил физфак МГУ. Преподаватели университета традиционно устраивали математические кружки для школьников, Константинов постепенно втянулся в эту деятельность и разработал знаменитую впоследствии среди московских матклассов систему «листков»: каждый листок был посвящен отдельной теме, в нем коротко излагались основы теории и содержались задачи – решая их, школьник постепенно разбирался и усваивал теорию.
Это было ключевым методом обучения, решение все усложнявшихся задач, – и Константинов (конечно, не он один) эти задачи придумывал. Одной из его задач открывался знаменитый учебник Владимира Арнольда «Обыкновенные дифференциальные уравнения» – Арнольд использовал задачу Константинова, чтобы проиллюстрировать понятие фазового пространства:
Из города A в город B ведут две не пересекающиеся дороги. Известно, что две машины, выезжающие по разным дорогам из A в B и связанные веревкой некоторой длины, меньшей 2l, смогли проехать из A в B, не порвав веревки. Могут ли разминуться, не коснувшись, два круглых воза радиуса l, центры которых движутся по этим дорогам навстречу друг другу? (Ответ: нет).
Известно, что две машины, выезжающие по разным дорогам из A в B и связанные веревкой некоторой длины, меньшей 2l, смогли проехать из A в B, не порвав веревки. Могут ли разминуться, не коснувшись, два круглых воза радиуса l, центры которых движутся по этим дорогам навстречу друг другу? (Ответ: нет).
«Листочки» эти (ужасного качества, отпечатанные на пишущей машинке под множество копирок) помнят все, кто учился в московских матклассах и посещал, соответственно, еженедельные дополнительные занятия по математике. Матклассы появились под шумок школьной реформы, вводившей профобразование. По воспоминаниям Константинова, математик Александр Кронрод, у которого он был аспирантом, создал маткласс в одной из московских школ и привлек его к преподаванию.
«Листочек» с задачамиМатематик Александр Шень, много лет развивавший эту систему углубленного обучения математике, вспоминает статью Константинова, в которой тот объяснял, почему важно, чтобы школьники самостоятельно решали задачи:
– Он говорил, что вкус к решению простых задач оригинальным способом сейчас утрачен. Если человек читает, то он вполне может быть кандидатом наук, но может быть не в состоянии придумывать что-то простое. Вот задача: есть баллон на 100 литров, в котором имеется газ под высоким давлением. И есть два пустых баллона по 50 литров, нужно газ разлить по этим двум баллоном, но каким-нибудь простым способом, домашними средствами. Константинов пишет, что он давал эту задачу многим кандидатам наук, и большинство так ничего и не придумали, а на самом деле способ очень простой и широко применяется – правда, в чем состоит способ, Константинов не написал. Я думаю, надо в пустой баллон налить воду, соединить с большим баллоном шлангом с краном, открыть кран, баллон с водой поместить наверх, тогда вода перетечет вниз, займет половину места в большом, после чего надо закрыть кран и то же повторить со вторым 50-литровым баллоном. Еще один пример Константинова – разрыв теории с практикой. У них был школьник, отличник по всем предметам. Они приехали на Белое море, он поставил рюкзак и пошел гулять.
Если человек читает, то он вполне может быть кандидатом наук, но может быть не в состоянии придумывать что-то простое. Вот задача: есть баллон на 100 литров, в котором имеется газ под высоким давлением. И есть два пустых баллона по 50 литров, нужно газ разлить по этим двум баллоном, но каким-нибудь простым способом, домашними средствами. Константинов пишет, что он давал эту задачу многим кандидатам наук, и большинство так ничего и не придумали, а на самом деле способ очень простой и широко применяется – правда, в чем состоит способ, Константинов не написал. Я думаю, надо в пустой баллон налить воду, соединить с большим баллоном шлангом с краном, открыть кран, баллон с водой поместить наверх, тогда вода перетечет вниз, займет половину места в большом, после чего надо закрыть кран и то же повторить со вторым 50-литровым баллоном. Еще один пример Константинова – разрыв теории с практикой. У них был школьник, отличник по всем предметам. Они приехали на Белое море, он поставил рюкзак и пошел гулять. Приходит – рюкзака нет. Выяснилось, что, хотя он изучал географию, идея, что бывают приливы, ему в голову не пришла. Другой школьник в том же походе, видя, что вода в море очень чистая, набрал ее для чая, не подумавши, что в море вода соленая, хотя наверняка учился этому на географии.
Приходит – рюкзака нет. Выяснилось, что, хотя он изучал географию, идея, что бывают приливы, ему в голову не пришла. Другой школьник в том же походе, видя, что вода в море очень чистая, набрал ее для чая, не подумавши, что в море вода соленая, хотя наверняка учился этому на географии.
Шень говорит, что Константинов «с 60-х годов не то что незаметно для советской власти, но ниже радара построил вполне развитую систему математического образования. Она начиналась с кружков, потом – математические классы, дальше – для тех, кто мог поступить, – мехмат. В 90-е появился Независимый университет – это тоже в значительной степени заслуга Константинова».
Шень описывает эту систему, вспоминая собственный опыт преподавания в школе:
С точки зрения советской власти, ВМШ почти не существовала. А матклассы советская власть терпела
– По средам, вечером, с 4 до 6, любой московский школьник (6–7-го класса) мог прийти на занятие математического кружка, который назывался «Вечерняя математическая школа» – не надо записываться, просто можно было прийти в любую среду с 16. 00 (в других кружках Москвы день занятий, конечно, мог отличаться. – Прим.). Для школьников было общее задание, которое мы готовили, листочек с, допустим, шестью задачами. В каждой аудитории – три преподавателя, среди них часто студенты. Школьники решают задачи, когда думают, что решили, поднимают руку, подходит преподаватель, выслушивает решение. Мы старались, чтобы никто не ушел совсем обиженный, то есть было желательно, чтобы большинство людей решили по крайней мере две задачи. Если человек все решил, ему давались дополнительные задачи. Важно, что занятия тематически были более-менее независимыми: школьник не смог прийти в этот раз – придет в следующий (и ему должна быть понятна тема несмотря на пропуск. – Прим.). Смысл кружков состоял в том, чтобы люди поняли, интересно им решать задачи или нет. Так продолжалось в течение учебного года, а в его конце происходило собеседование для желающих попасть в матклассы (которые обычно охватывали последние три года школы, 8–10-й классы).
00 (в других кружках Москвы день занятий, конечно, мог отличаться. – Прим.). Для школьников было общее задание, которое мы готовили, листочек с, допустим, шестью задачами. В каждой аудитории – три преподавателя, среди них часто студенты. Школьники решают задачи, когда думают, что решили, поднимают руку, подходит преподаватель, выслушивает решение. Мы старались, чтобы никто не ушел совсем обиженный, то есть было желательно, чтобы большинство людей решили по крайней мере две задачи. Если человек все решил, ему давались дополнительные задачи. Важно, что занятия тематически были более-менее независимыми: школьник не смог прийти в этот раз – придет в следующий (и ему должна быть понятна тема несмотря на пропуск. – Прим.). Смысл кружков состоял в том, чтобы люди поняли, интересно им решать задачи или нет. Так продолжалось в течение учебного года, а в его конце происходило собеседование для желающих попасть в матклассы (которые обычно охватывали последние три года школы, 8–10-й классы). Школьники приходили на собеседование так же, как на кружок, но тут уже регистрировалось четко, что кто решил, выяснялось, у кого результаты лучше. В конце концов объявлялся список, кто попал в маткласс следующего года (и дети переводились из своих прежних школ в школы, где набирались матклассы. – Прим.). При этом с точки зрения советской власти и органов образования, ВМШ почти не существовала. По вечерам какие-то кружки по математике в школе – это нормально, кто туда приходит – никого не волнует. А матклассы советская власть терпела. Это был сложный политической момент, директора школ как-то договаривались, уговаривали, чтобы матклассы открыли. Райком иногда не разрешал открывать, то есть все всегда было в подвешенном состоянии, но в основном разрешали, они даже не мешали набирать школьников по конкурсу, в это дело не лезли. В школе происходило то же самое, что на кружках, но уже с помощью задач изучалась в целом некоторая теория. Это было параллельно с обычными уроками алгебры и геометрии: обычные уроки – четыре часа в неделю, и еще четыре урока дополнительных.
Школьники приходили на собеседование так же, как на кружок, но тут уже регистрировалось четко, что кто решил, выяснялось, у кого результаты лучше. В конце концов объявлялся список, кто попал в маткласс следующего года (и дети переводились из своих прежних школ в школы, где набирались матклассы. – Прим.). При этом с точки зрения советской власти и органов образования, ВМШ почти не существовала. По вечерам какие-то кружки по математике в школе – это нормально, кто туда приходит – никого не волнует. А матклассы советская власть терпела. Это был сложный политической момент, директора школ как-то договаривались, уговаривали, чтобы матклассы открыли. Райком иногда не разрешал открывать, то есть все всегда было в подвешенном состоянии, но в основном разрешали, они даже не мешали набирать школьников по конкурсу, в это дело не лезли. В школе происходило то же самое, что на кружках, но уже с помощью задач изучалась в целом некоторая теория. Это было параллельно с обычными уроками алгебры и геометрии: обычные уроки – четыре часа в неделю, и еще четыре урока дополнительных.
Районная олимпиада по математике – это был первый уровень сети
– Константинов был известен как один из ключевых деятелей олимпиадного движения, он организовал многопредметную олимпиаду Турнир Ломоносова, затем – Турнир городов. Это было важно?
– Олимпиады были и до Константинова – московская, всесоюзная, они проводились официально. Олимпиады были важны, поскольку это был способ привлечь детей на кружки: о проведении олимпиад объявлялось по школам, после можно было пригласить победителей на математический кружок. Константинов каким-то образом договорился с гороно, что к обычным школьным задачам районной олимпиады в конце добавят задачу посложнее, более интересную, и для проверки этой задачи Константинов пришлет специальных помощников, студентов. Вообще учителям было все это трудно проверять, даже обычные задачи, а уж эту дополнительную особенно сложно, но студенты приезжали и старались деликатно договориться и проверить эти последние задачи, смотрели, какие школьники хорошо выступили, переписывали их данные, и им посылалось предложение прийти уже на городскую олимпиаду, а также в вечернюю математическую школу. То есть районная олимпиада по математике – это был первый уровень сети. После этого школьник попадал в математические кружки, в математические классы. Но официально этого не существовало. До 80-го года Константинов был официальным членом оргкомитета Всесоюзной олимпиады, но эта роль его не была, как теперь говорят, институционализирована. В 80-м его выгнали.
То есть районная олимпиада по математике – это был первый уровень сети. После этого школьник попадал в математические кружки, в математические классы. Но официально этого не существовало. До 80-го года Константинов был официальным членом оргкомитета Всесоюзной олимпиады, но эта роль его не была, как теперь говорят, институционализирована. В 80-м его выгнали.
– Почему выгнали?
– Мне кажется, я даже видел текст доноса, который написал профессор МГУ. У меня, к сожалению, нет этого документа, поэтому я не могу твердо утверждать, но кажется, донос был несколько антисемитского характера, что какой-то школьник Гинзбург как-то нарушал правила олимпиады, в общем, какой-то бред. После этого Константинова выгнали. Мне показывали этот текст на бумаге, но откуда этот текст был, было ли это заверенной копией или какие-то доброжелатели списали где-нибудь, я не берусь сказать.
Идея была привлечь школьников в кружки
– А Турнир городов и Турнир Ломоносова?
– Турнир городов как раз связан с тем, что Константинова выгнали. Когда его выгнали, другие люди тоже, по-моему, ушли в знак протеста. И Толпыго в Киеве, Анджанс в Риге и Константинов в Москве решили: давайте мы вместо олимпиады сами составим трудные задачи, а все желающие эти задачи придут решать. Советская власть не препятствовала, было разрешено провести турнир в каком-то вузе или в школе. Соответственно, в Москве Константинов потом забрал все работы на проверку, а в Риге и Киеве проверяли тамошние люди. После этого сверили критерии, результаты по всем городам, и школьники могли сравнить свои успехи. Но в отличие от олимпиады, никакой официальной пользы от этого не было. Человек решил задачу, у него есть бумажка, что он решил задачу, но ее особенно предъявлять никуда нельзя было, никаких преимуществ она не давала, бумажка и бумажка. А Турнир Ломоносова был устроен для более младших школьников. Идея была в том, что он – вместо районной олимпиады – привлечет школьников в кружки, и не только по математике, там были физика, химия, биология, астрономия, лингвистика в какой-то момент образовалась.
Когда его выгнали, другие люди тоже, по-моему, ушли в знак протеста. И Толпыго в Киеве, Анджанс в Риге и Константинов в Москве решили: давайте мы вместо олимпиады сами составим трудные задачи, а все желающие эти задачи придут решать. Советская власть не препятствовала, было разрешено провести турнир в каком-то вузе или в школе. Соответственно, в Москве Константинов потом забрал все работы на проверку, а в Риге и Киеве проверяли тамошние люди. После этого сверили критерии, результаты по всем городам, и школьники могли сравнить свои успехи. Но в отличие от олимпиады, никакой официальной пользы от этого не было. Человек решил задачу, у него есть бумажка, что он решил задачу, но ее особенно предъявлять никуда нельзя было, никаких преимуществ она не давала, бумажка и бумажка. А Турнир Ломоносова был устроен для более младших школьников. Идея была в том, что он – вместо районной олимпиады – привлечет школьников в кружки, и не только по математике, там были физика, химия, биология, астрономия, лингвистика в какой-то момент образовалась. Разные люди приходили, говорили: «А давайте мы еще сделаем конкурс по лингвистике». Константинов спрашивал: «А есть ли у вас для этого люди?» – «Человек 15–20 соберем, пришлем своих представителей, потом соберем работы и проверим».
Разные люди приходили, говорили: «А давайте мы еще сделаем конкурс по лингвистике». Константинов спрашивал: «А есть ли у вас для этого люди?» – «Человек 15–20 соберем, пришлем своих представителей, потом соберем работы и проверим».
– Все московские вечерние кружки были как-то связаны с Константиновым? Это все были просто группы энтузиастов?
– Не то что был какой-то список, надо было зарегистрироваться и аккредитоваться у Константинова. Если человек хотел вести кружок, он мог его вести совершенно произвольно. Посмотрев, что его приятели ведут кружок где-то, он мог договориться о кружке в своей школе, например. Кружки были разные, все составляли свои задачи. Там не было такого, что прислали задачи из центра.
Вы набрали тут класс, слишком много евреев
– Считается, что советская власть, которой нужны были светлые математические, физические и прочие головы для производства оружия или чего-то подобного, закрывали глаза на то, чем еще занимаются ученые, если это не сопровождалось слишком большой крамолой. Такое ощущение, что “константиновская”, условно назовем ее, система развилась в этой слепой зоне, куда советская власть не смотрела.
Такое ощущение, что “константиновская”, условно назовем ее, система развилась в этой слепой зоне, куда советская власть не смотрела.
– Благодаря всем этим оружейным программам академики типа Курчатова, Королева были уважаемыми людьми в советской системе. Поэтому, когда они говорили, что нам нужно организовать физико-математические интернаты, объясняли, как это будет полезно для военно-промышленного комплекса, то на уровне ЦК это могли разрешить. После этого все спускалось на какие-то нижние уровни, там могли ставить палки в колеса, но было общее благословение за счет влияния военных, ВПК и соответствующих академиков. Когда Ершов (Андрей Ершов, крупный советский теоретик программирования. – Прим.) пробивал курс информатики в 1984 или 1985 году и писал письма в политбюро, он упирал именно на то, что это важно для обороны. Видимо, его поддерживали члены военно-промышленной комиссии. Отдельно была идеологическая проблема, когда школьники матклассов вели себя неправильно с точки зрения советской власти, она, конечно, была недовольна. Но если из Ленинского райкома объясняли: вы набрали тут класс, слишком много евреев, – невозможно было позвонить какому-то академику, чтобы он перезвонил в ЦК и сказал: что вы делаете? Надо было отвечать: мы в этом году не будем набирать, или вписать каких-нибудь несуществующих школьников, чтобы уменьшить процент евреев, в другой школе набирать класс, другие предпринимать хитрости. По-моему, Гриша Гальперин рассказывал, как Константинов объяснял устойчивость системы математического образования: система действительно требовала сотрудничества с советскими органами образования, чтобы разрешили занятия в школе, кружок в помещении вуза. Но она требовала на таком низком уровне, что это не выглядело вопиющим. Весь размах системы был в каждом отдельном месте неясен. Как якобы говорил Константинов, бывают отдельные понятливые чиновники, которые видят всю угрозу, но не в состоянии объяснить на языке, понятном их начальству.
Но если из Ленинского райкома объясняли: вы набрали тут класс, слишком много евреев, – невозможно было позвонить какому-то академику, чтобы он перезвонил в ЦК и сказал: что вы делаете? Надо было отвечать: мы в этом году не будем набирать, или вписать каких-нибудь несуществующих школьников, чтобы уменьшить процент евреев, в другой школе набирать класс, другие предпринимать хитрости. По-моему, Гриша Гальперин рассказывал, как Константинов объяснял устойчивость системы математического образования: система действительно требовала сотрудничества с советскими органами образования, чтобы разрешили занятия в школе, кружок в помещении вуза. Но она требовала на таком низком уровне, что это не выглядело вопиющим. Весь размах системы был в каждом отдельном месте неясен. Как якобы говорил Константинов, бывают отдельные понятливые чиновники, которые видят всю угрозу, но не в состоянии объяснить на языке, понятном их начальству.
– Константинов занимался информатикой?
– Нет. Он был учеником Кронрода, его диссертация по топологии плоскости. Он преподавал какое-то время, его из университета выгнали, кажется, в связи с «письмом девяноста девяти» в защиту Есенина-Вольпина (в 1968 году 99 ученых подписали письмо против принудительной госпитализации математика и диссидента Александра Есенина-Вольпина в психбольницу. – Прим.). Потом Константинов попал в Институт экономики, математическая экономика. Лаборатория Кронрода изначально была лабораторией для расчетов по бомбе, поэтому у них были численные методы, технология программирования, а потом уже не по бомбе, а вообще. У Константинова из работ по информатике – знаменитый фильм с кошкой, но это просто школьный проект. Просто школьникам было интересно, он вместе с ними это делал, получился такой исторический первый мультфильм компьютерный.
Он был учеником Кронрода, его диссертация по топологии плоскости. Он преподавал какое-то время, его из университета выгнали, кажется, в связи с «письмом девяноста девяти» в защиту Есенина-Вольпина (в 1968 году 99 ученых подписали письмо против принудительной госпитализации математика и диссидента Александра Есенина-Вольпина в психбольницу. – Прим.). Потом Константинов попал в Институт экономики, математическая экономика. Лаборатория Кронрода изначально была лабораторией для расчетов по бомбе, поэтому у них были численные методы, технология программирования, а потом уже не по бомбе, а вообще. У Константинова из работ по информатике – знаменитый фильм с кошкой, но это просто школьный проект. Просто школьникам было интересно, он вместе с ними это делал, получился такой исторический первый мультфильм компьютерный.
– Константинов был связан с колмогоровской реформой школьного математического образования? (Андрей Колмогоров, крупнейший математик 20-го века, в конце 60-х участвовал в подготовке новых учебников по математике. – Прим.)
– Прим.)
– Абсолютно нет. Константинов с этим вообще никак не связан.
Хотели как лучше, а получилось как у Черномырдина
– Часто можно встретить людей, которые говорят: восхищаюсь теми, кто разбирается в математике, я после 4–5-го класса уже ничего не понимал. Мне кажется, колмогоровская реформа ввела в школах очень формальный курс математики, и в результате детей, способных к математике, было сразу видно, но для остальных это было точкой отсечения, они быстро переставали понимать и интересоваться.
– Я бы не сказал, что тут есть именно элемент отбора. Безусловно, Колмогоров хотел как лучше, а получилось плохо. Не то что для математических школьников это замечательно, а для нематематических это плохо, – для всех получилось неудачно. Тому много причин. Были сначала учебники, еще восходящие к учебникам Киселева (конца 19-го – начала 20-го века. – Прим.), их постепенно упрощали, но все это было, конечно, тоскливо: что-то школьники еще понимали, но с некоторого момента переставали, когда начинались тригонометрические уравнения – совершенно ни к селу ни к городу, зачем их решать, почему их решать? Так что то, что было раньше, тоже было некачественным. Были разные математики, которые хотели это по-разному исправить, у них были совершенно завиральные идеи. Колмогоров помимо интерната (школа-интернат при МГУ для одаренных детей, созданный при участии Колмогорова. – Прим.), где он как следует работал, вроде еще пробовал свои идеи в обычной школе, но несерьезно. Конечно, у них не было представления, что учителя могут понять. Они составили программу, и когда составляли программу, говорили: ну нельзя же вот этого не знать. Потом по этой программе начали писать учебники. Потом выяснилось, что никто ничего по программе не успевает, не понимает, поэтому все содержательное постепенно выбрасывалось, оставались только упражнения, которые было легко выполнить, ничего не понимая. Упражнения можно было выполнить, но понимание не совершенствовалось, и в следующем классе проблемы повторялись. Была идея, причем с самыми лучшими побуждениями, что в старых гимназиях решали слишком много задач арифметическими способами: большой бидон, маленький бидон, если бы маленький бидон был как большой, то сколько бы тогда… Зачем это все, мы научим решать уравнения – общий метод, это гораздо проще.
Были разные математики, которые хотели это по-разному исправить, у них были совершенно завиральные идеи. Колмогоров помимо интерната (школа-интернат при МГУ для одаренных детей, созданный при участии Колмогорова. – Прим.), где он как следует работал, вроде еще пробовал свои идеи в обычной школе, но несерьезно. Конечно, у них не было представления, что учителя могут понять. Они составили программу, и когда составляли программу, говорили: ну нельзя же вот этого не знать. Потом по этой программе начали писать учебники. Потом выяснилось, что никто ничего по программе не успевает, не понимает, поэтому все содержательное постепенно выбрасывалось, оставались только упражнения, которые было легко выполнить, ничего не понимая. Упражнения можно было выполнить, но понимание не совершенствовалось, и в следующем классе проблемы повторялись. Была идея, причем с самыми лучшими побуждениями, что в старых гимназиях решали слишком много задач арифметическими способами: большой бидон, маленький бидон, если бы маленький бидон был как большой, то сколько бы тогда… Зачем это все, мы научим решать уравнения – общий метод, это гораздо проще. Но выяснилось, что школьники не понимают, что означает буква «икс» в уравнении, и учителя не в состоянии им это объяснить. Как-то вместо этой скучной, но понятной деятельности с бидонами стало нужно переписывать формулы, писать загадочную ОДЗ – «область допустимых значений», непонятную, но писать ее обязательно надо. Можно было даже поступить в технический вуз, так ничего и не поняв, просто научившись решать по правилам. Хорошие репетиторы тем и славились, что могут плохого школьника научить сдать экзамены по математике без того, чтобы он разобрался, – просто какой-то тип задач будет уметь решать, и хорошо. Тогда это было со вступительными экзаменами, так же сейчас с ЕГЭ происходит. С реформой матобразования получилось плохо, наверное, если бы ее не было, было бы лучше. Но никакого злого умысла, естественно, не было. Хотели как лучше, а получилось как у Черномырдина.
Но выяснилось, что школьники не понимают, что означает буква «икс» в уравнении, и учителя не в состоянии им это объяснить. Как-то вместо этой скучной, но понятной деятельности с бидонами стало нужно переписывать формулы, писать загадочную ОДЗ – «область допустимых значений», непонятную, но писать ее обязательно надо. Можно было даже поступить в технический вуз, так ничего и не поняв, просто научившись решать по правилам. Хорошие репетиторы тем и славились, что могут плохого школьника научить сдать экзамены по математике без того, чтобы он разобрался, – просто какой-то тип задач будет уметь решать, и хорошо. Тогда это было со вступительными экзаменами, так же сейчас с ЕГЭ происходит. С реформой матобразования получилось плохо, наверное, если бы ее не было, было бы лучше. Но никакого злого умысла, естественно, не было. Хотели как лучше, а получилось как у Черномырдина.
В классе, который я набирал, был школьник с приводом в милицию, потому что он взорвал лифт
– К 80-м вокруг матклассов сформировался круг позднесоветской творческой и научной интеллигенции. Их дети шли в эти классы, становились студентами, потом сами преподавали, ну и впоследствии их дети шли в школу. Вы много работали с детьми в кружках и матклассах. Появлялись самородки-Ломоносовы, непонятно откуда вынырнувшие?
Их дети шли в эти классы, становились студентами, потом сами преподавали, ну и впоследствии их дети шли в школу. Вы много работали с детьми в кружках и матклассах. Появлялись самородки-Ломоносовы, непонятно откуда вынырнувшие?
– Детей, у которых родители были классифицированными математиками и их с детства дрессировали, чтобы они решали задачи, – вот их как раз было малое количество. Какие-то люди детям читают книжки на ночь, потом говорят, что можно попробовать сходить в кружок, – не то что их с детства готовили к кружку. Можно поставить вопрос так: если бы детей не приняли в математический класс, у скольких родители были бы озабочены тем, чтобы найти репетиторов для поступления на мехмат или в физтех. Думаю, половина на половину. Были родители, которые волновались за поступление, а были родители, которые радовались, что школьник, вместо того чтобы со шпаной сжигать телефонные будки, шел в математический класс. Допустим, в школы присылали приглашение – примите участие в олимпиаде. Явно школьник должен быть на общем фоне способным, проявлять себя. Учитель или учительница, видя, что есть хороший школьник, говорит: сходи на олимпиаду. Или приятель школьника идет на олимпиаду, и он за компанию решил сходить. В классе, который я набирал в 57-й школе, как-то был школьник с приводом в милицию, потому что он взорвал лифт. Не то что он взорвал лифт в целях теракта, он просто интересовался химическими опытами. Это был чисто научный начальный толчок.
Явно школьник должен быть на общем фоне способным, проявлять себя. Учитель или учительница, видя, что есть хороший школьник, говорит: сходи на олимпиаду. Или приятель школьника идет на олимпиаду, и он за компанию решил сходить. В классе, который я набирал в 57-й школе, как-то был школьник с приводом в милицию, потому что он взорвал лифт. Не то что он взорвал лифт в целях теракта, он просто интересовался химическими опытами. Это был чисто научный начальный толчок.
– Этот мир математических классов, кружков, олимпиад, походов, эстонского хутора, стройотрядов на ББС – был замкнутым? Прекрасный замкнутый мир?
– Естественно, люди друг друга знали, была некоторая компания, но абсолютно не закрытая. Я учился во 2-й школе, мало кого знал. Потом участвовал в проведении олимпиад, Константинов предложил помочь набирать детей в 91-ю школу. Первый раз, когда я пришел на слет ББС, где выпускники и ученики математических классов разных школ собираются в одном месте, поют песни и жгут костры, то был поражен, что там какой-то праздник жизни, а я абсолютно на нем чужой, никого не знаю, а они все знают друг друга очень хорошо. Естественно, со временем я более-менее тоже всех узнал. Никакого оттенка элитного клуба в этом не было.
Естественно, со временем я более-менее тоже всех узнал. Никакого оттенка элитного клуба в этом не было.
Сравнивать сферического единорога в вакууме с реально существующим
– Нужно ли создание такой среды для того, чтобы происходил бурный рост математики?
– Смысл такой среды – если говорить прагматически: для подобной системы преподавания, когда со школьниками много разговаривают при решении задачи, нужно, чтобы на 20 школьников приходилось три преподавателя. Это возможно, только если людям интересно этим заниматься, если студенты приходят в школу в качестве преподавателей, водят школьников в походы.
– Но в результате в Советском Союзе сложилась двухуровневая система, где большинство школьников математики не знали, но при этом появлялся отдельный мир для математиков, ну и, возможно, в других дисциплинах. Система, которая ищет среди множества школьников самых одаренных, учит их дополнительно и поставляет для университетов. Советская система математического образования устроилась, как устроилась, в той ситуации, в которой была. Если бы можно было устраивать по-другому, может, какая-то другая система была бы более эффективной?
Если бы можно было устраивать по-другому, может, какая-то другая система была бы более эффективной?
– Невозможно сравнивать сферического единорога в вакууме с реально существующим. Можно спросить: какие простые действия могли бы улучшить сейчас положение с математическим или физическим образованием. Когда есть некоторая ситуация, можно попытаться понять, как ее можно улучшить. Сейчас одно действие очевидно – перестать давать каждый год на ЕГЭ одни и те же задачи, начать честно проверять тот ужасно низкий уровень, который есть у школьников. Разделить выпускной статус ЕГЭ и вступительный, проводить два разных экзамена. Это было бы организационно возможное и полезное решение.
Константинов на уроке, 2000-е.Лучше, если бы человек занимался в школе тем, чем ему интересно, не пытаясь соревноваться
– Вы заговорили о современной России, сейчас в школах больше детей понимают математику, чем понимали в Советском Союзе?
– Происходит странная вещь. Сейчас есть система олимпиад, но совершенно не такая, как в Советском Союзе. Олимпиады были, но зарплата директора или статус школы зависел от того, сколько в школе победителей олимпиад. Олимпиады, кроме международных, не учитывались при поступлении. Олимпиады были ради удовольствия. Сейчас вокруг олимпиад возникла какая-то параллельная система, довольно неплохо финансируемая, всякие «Сириусы» (Образовательный центр в Сочи по выявлению одаренных детей, созданный по инициативе Путина. – Прим.), сборы такие, сборы сякие. В результате школьники вместо того, чтобы учиться в школе, все время ездят на сборы, и там их тренируют. Появилась дикая идея, что целью и критерием обучения математике в школе является победа на каких-то олимпиадах. Возникли репетиторы, готовящие к олимпиадам. В советское время было бы совершенно невозможно себе представить, кому придет в голову нанимать репетитора для подготовки к олимпиадам, которые ничего не дают. Может, некоторые из репетиторов – квалифицированные преподаватели, хотя, конечно, не очень хорошо, что это зависит от наличия у школьников и их родителей денег.
Сейчас есть система олимпиад, но совершенно не такая, как в Советском Союзе. Олимпиады были, но зарплата директора или статус школы зависел от того, сколько в школе победителей олимпиад. Олимпиады, кроме международных, не учитывались при поступлении. Олимпиады были ради удовольствия. Сейчас вокруг олимпиад возникла какая-то параллельная система, довольно неплохо финансируемая, всякие «Сириусы» (Образовательный центр в Сочи по выявлению одаренных детей, созданный по инициативе Путина. – Прим.), сборы такие, сборы сякие. В результате школьники вместо того, чтобы учиться в школе, все время ездят на сборы, и там их тренируют. Появилась дикая идея, что целью и критерием обучения математике в школе является победа на каких-то олимпиадах. Возникли репетиторы, готовящие к олимпиадам. В советское время было бы совершенно невозможно себе представить, кому придет в голову нанимать репетитора для подготовки к олимпиадам, которые ничего не дают. Может, некоторые из репетиторов – квалифицированные преподаватели, хотя, конечно, не очень хорошо, что это зависит от наличия у школьников и их родителей денег. Благодаря этим олимпиадам в разных местах, где вообще ничего никогда не было, образовались достаточно высокого уровня занятия по математике, но по немного странной и дикой программе вокруг этих олимпиад: если что-то в олимпиаде не встречается, то мы изучать этого не будем, потому что зачем? Средний уровень участников Всероссийской олимпиады от этого стал лучше, но на фоне этого по результатам ЕГЭ, наверное, стало хуже. Хотя все качественное обучение программированию, которое сейчас в России есть, – это результат именно олимпиад. Можно ли было представить в советское время, что вдруг в Петрозаводском университете появится команда студентов, которые знают базовые алгоритмы и умеют их быстро реализовывать. Никогда такого бы не было. А сейчас в совершенно неожиданных городах появляются центры олимпиад. Для программирования это как раз хорошо, потому что они после этого идут работать – это точно пригодится. А для математики это не так хорошо. Лучше, если бы человек занимался в школе тем, что ему интересно, не пытаясь соревноваться, – просто читал бы книжки, разбирался в чем-то.
Благодаря этим олимпиадам в разных местах, где вообще ничего никогда не было, образовались достаточно высокого уровня занятия по математике, но по немного странной и дикой программе вокруг этих олимпиад: если что-то в олимпиаде не встречается, то мы изучать этого не будем, потому что зачем? Средний уровень участников Всероссийской олимпиады от этого стал лучше, но на фоне этого по результатам ЕГЭ, наверное, стало хуже. Хотя все качественное обучение программированию, которое сейчас в России есть, – это результат именно олимпиад. Можно ли было представить в советское время, что вдруг в Петрозаводском университете появится команда студентов, которые знают базовые алгоритмы и умеют их быстро реализовывать. Никогда такого бы не было. А сейчас в совершенно неожиданных городах появляются центры олимпиад. Для программирования это как раз хорошо, потому что они после этого идут работать – это точно пригодится. А для математики это не так хорошо. Лучше, если бы человек занимался в школе тем, что ему интересно, не пытаясь соревноваться, – просто читал бы книжки, разбирался в чем-то. А когда олимпиады вдруг кончаются, то совершенно непонятно, что делать дальше. Это как если бы человек всю жизнь занимался теннисом, стал чемпионом мира среди юниоров, а потом узнал, что соревнования для более старших если и проводятся, то никого не интересуют. В смысле умений – олимпиадная подготовка, безусловно, им способствует, – но в смысле интересов после окончания олимпиад происходит ломка.
А когда олимпиады вдруг кончаются, то совершенно непонятно, что делать дальше. Это как если бы человек всю жизнь занимался теннисом, стал чемпионом мира среди юниоров, а потом узнал, что соревнования для более старших если и проводятся, то никого не интересуют. В смысле умений – олимпиадная подготовка, безусловно, им способствует, – но в смысле интересов после окончания олимпиад происходит ломка.
В материальном смысле поддержка сейчас гораздо больше. Другое дело, что она связана с политическими играми
– После того как советская власть закончилась, система математического образования нашла новые точки опоры в России без советской власти?
– Ведущие ученые не перестали меньше интересоваться образованием школьников, они просто уехали.
– ЦК партии должен интересоваться.
– Поскольку от советской власти ничего не нужно было, кроме разрешения, было важно, чтобы ЦК партии как раз не интересовался. Постсоветская власть – наоборот. Например, Независимый университет и Московский центр непрерывного математического образования были очень обязаны префекту Центрального округа Москвы Музыкантскому, который организовал для них здание. Боря Музыкантский, его сын, учился в 57-й школе. Мы с ним ходили в поход даже в Карелию, он брал с собой своего отца Александра Ильича, которого я тогда тоже хорошо знал, мы были в походе неделю. Когда потом Константинов пришел к нему, было ясно, что это не жулики. Позже стали финансироваться Турниры городов. В материальном смысле поддержка сейчас гораздо больше. Другое дело, что она связана с политическими играми, с ЕГЭ, с «Сириусом», который вроде как хорош, но там Ролдугин. Все сложно.
Например, Независимый университет и Московский центр непрерывного математического образования были очень обязаны префекту Центрального округа Москвы Музыкантскому, который организовал для них здание. Боря Музыкантский, его сын, учился в 57-й школе. Мы с ним ходили в поход даже в Карелию, он брал с собой своего отца Александра Ильича, которого я тогда тоже хорошо знал, мы были в походе неделю. Когда потом Константинов пришел к нему, было ясно, что это не жулики. Позже стали финансироваться Турниры городов. В материальном смысле поддержка сейчас гораздо больше. Другое дело, что она связана с политическими играми, с ЕГЭ, с «Сириусом», который вроде как хорош, но там Ролдугин. Все сложно.
Обратные задачи / Задачи / Справочник по математике для начальной школы
- Главная
- Справочники
- Справочник по математике для начальной школы
- Задачи
- Обратные задачи
В обратной задаче одна из искомых величин становится известной, а одна из данных величин становится неизвестной.
Прямая задача:
У Тани было 3 зелёных шарика и 2 красных. Сколько всего шариков было у Тани?
Первая обратная задача:
У Тани было 5 шариков, 3 шарика были зелёными, а остальные красные. Сколько красных шариков было у Тани?
Ты видишь, что известная величина — красные шарики — стала неизвестной.
А неизвестная величина — общее количество шариков — стало известной.
Вторая обратная задача:
У Тани было 5 шариков, 2 шарика были красными, а остальные зелёные. Сколько зелёных шариков было у Тани?
Ты видишь, что известная величина — зелёные шарики — стала неизвестной.
А неизвестная величина — общее количество шариков — стало известной.
ТАКИЕ ЗАДАЧИ НАЗЫВАЮТСЯ ОБРАТНЫМИ.
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Образцы оформления задачи
Цена. Количество. Стоимость
Количество. Стоимость
Скорость, время, расстояние
Задачи
Правило встречается в следующих упражнениях:
1 класс
Страница 48. Урок 25, Петерсон, Учебник, часть 2
Страница 50. Урок 26, Петерсон, Учебник, часть 2
Страница 53. Урок 27, Петерсон, Учебник, часть 2
Страница 60. Урок 31, Петерсон, Учебник, часть 2
Страница 63. Урок 32, Петерсон, Учебник, часть 2
Страница 8. Урок 5, Петерсон, Учебник, часть 3
Страница 25. Урок 13, Петерсон, Учебник, часть 3
Страница 33. Урок 17,
Петерсон, Учебник, часть 3
Урок 17,
Петерсон, Учебник, часть 3
Страница 65. Урок 33, Петерсон, Учебник, часть 3
Страница 91. Повторение, Петерсон, Учебник, часть 3
2 класс
Страница 64, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 72, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 83, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 88, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 45, Моро, Волкова, Рабочая тетрадь, часть 1
Страница 16. Вариант 1. № 1,
Моро, Волкова, Проверочные работы
Вариант 1. № 1,
Моро, Волкова, Проверочные работы
Страница 81, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 84, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 89, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 106, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
3 класс
Страница 27, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 36, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 32, Моро, Волкова, Рабочая тетрадь, часть 1
Страница 10, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 71, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 101, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 21, Моро, Волкова, Рабочая тетрадь, часть 2
Страница 35. Урок 13,
Петерсон, Учебник, часть 1
Урок 13,
Петерсон, Учебник, часть 1
Страница 38. Урок 14, Петерсон, Учебник, часть 1
Страница 40. Урок 15, Петерсон, Учебник, часть 1
4 класс
Страница 5, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 11, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 76, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 87, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 68, Моро, Волкова, Рабочая тетрадь, часть 1
Страница 28, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 32, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 66, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 99, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 29, Моро, Волкова, Рабочая тетрадь, часть 2
«Красивые» задачи в математике
- Авторы
- Руководители
- Файлы работы
- Наградные документы
Бузарова А. А. 1
А. 1
1МБОУ СОШ №30
Караева Д.А. 1
1МБОУ СОШ №30 г. Владикавказ
Автор работы награжден дипломом победителя II степени
Диплом школьникаСвидетельство руководителя
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
Введение
Мaтемaтикa – один из интереснейших школьных предметoв. Ее принято считать наукой строгой, определенной. Тем более удивительно, что именнo нa уроках математики мы столкнулись с выражением «красивые задачи». Очевидным стало возникновение вопроса: «красивыe» задачи в мaтeматике – какие они?»
Четких формулировок и определений «красивой» математической задачи в изученной литературе не оказалось, поэтому возник определенный исследовательский интерес – какие математические задачи считать «красивыми», как определить грань между «красивой» задачей и задачей обычной?
Актуальность выбранной темы была подтверждена в ходе обсуждения ее с руководителем, который одобрил выбор темы исследования. Действительно, дать определение «красивой» задачи, подобрать такие задачи, классифицировать их определенным образом весьма интересно и полезно.
Действительно, дать определение «красивой» задачи, подобрать такие задачи, классифицировать их определенным образом весьма интересно и полезно.
Были определены:
Объектная область исследования — учебный предмет «математика».
Объект исследования – решение математических задач.
Предмет исследования – математические задачи определенного типа.
Цель нашего исследования — из множества математических задач выбрать определенные («красивые») задачи и классифицировать их по некоторым признакам, что позволит использовать их в качестве материала для математического саморазвития.
Задачи:
изучить научную литературу, научные публикации по данной теме.
Определить понятие «красивая» задача в математике.
Классифицировать найденные задачи.
Методы исследования: теоретические, эмпирические, математические.
Ожидаемые результаты: Исследование сущности и классификация «красивых» математических задач.
Глава I. «Красота» в математике
Математику принято считать строгой наукой, при изучении которой нет места эмоциям, хотя очень многие заинтересованы этим предметом.
Известно, что решение задачи – одно из основных средств математического обучения. Основная цель математической задачи – развитие творческого и математического мышления, и, вместе с тем – эстетического восприятия, вкуса. Существует широко распространенное мнение, что математика движима почти исключительно эстетическими мотивами, а попытки раскрыть содержание понятий «чувство красоты», «красивая задача» предпринимаются многими математиками. Например, Г. Биркгоф дал интересную характеристику эстетической привлекательности математического объекта:
,
где М – мера красоты,
О – мера порядка,
С – мера усилий, затрачиваемых для понимания сущности объекта1.
Из этой формулы следует, что для ученика красивыми математическими объектами будут те, восприятие которых сопряжено с наименьшими усилиями с его стороны. Эстетическая мера объекта будет увеличиваться с упорядочиванием структуры.
Многие планиметрические задачи напрямую связаны с понятием «красивая», то есть «доставляющая наслаждение, приятная внешним видом, гармоничностью, стройностью». Восприятие эстетической стороны такой задачи начинается с условия и чертежа.
Например, задача построения с помощью циркуля фигуры, изображенной на рисунке (рис. 1), привлекает внимание, прежде всего, условием — красивым узором. Но затем возникают фантазии на данную тему, и получаются оригинальные узоры, построение которых возможно лишь с помощью циркуля.
Решение «красивых» задач должно быть наглядно, неожиданно, просто. Задачи, удовлетворяющие такому требованию неизменно вызывают интерес, побуждают к поиску более коротких и простых путей решения, что способствует развитию творческого начала.
Как отмечают некоторые авторы, «красивая» математическая задача должна отвечать определенным требованиям:
1) условие задачи должно быть интересным; если задача геометрическая, то чертеж к ней – красивым;
2) задача должна содержать нестандартный элемент, отличающий ее от большинства задач по данной теме, предлагаемых в учебниках. При этом нестандартность может проявляться как в самом условии, так и в методах решения. Особый интерес в этом смысле представляют задачи, имеющие несколько различных методов решения, и многовариантные задачи, имеющие несколько ответов;
3) задача должна быть доступна как по формулировке условия, так и по сложности и объему используемого в решении материала;
4) в решении красивой задачи не должны использоваться не всем известные приемы и способы решения;
5) в решении задачи должна быть спрятана «изюминка», чтобы оно было наглядно и удивительно просто.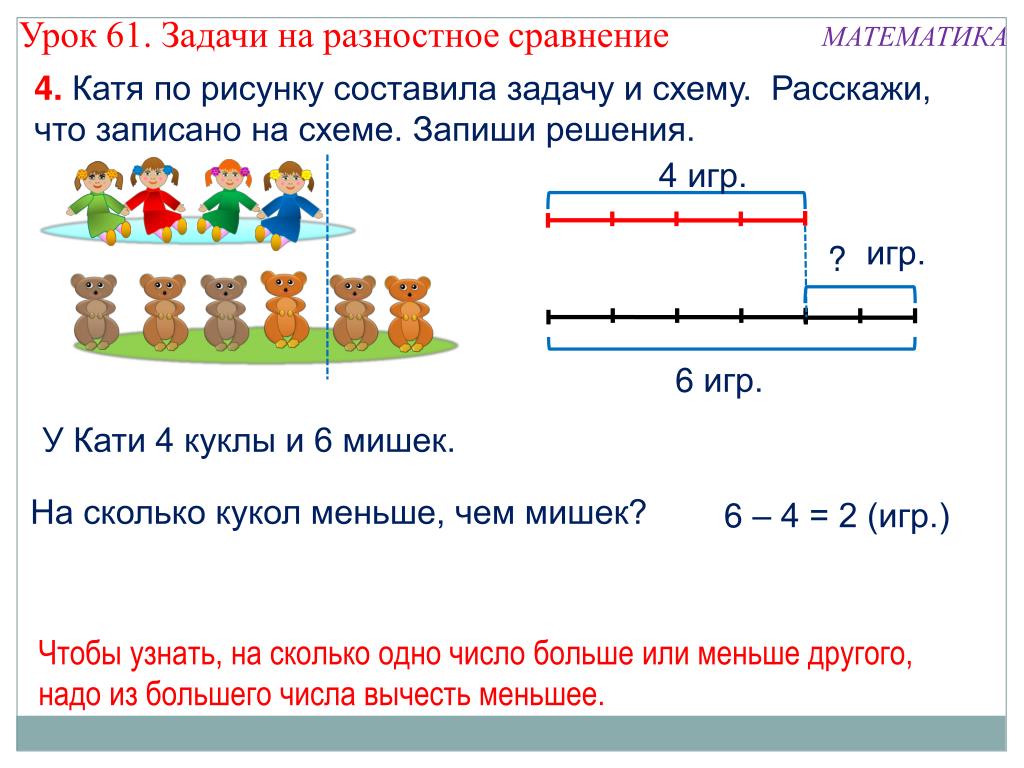
Обучаясь в среднем звене и готовясь к математическим олимпиадам, сталкиваешься со множеством «красивых» задач, отвечающих указанным признакам; становится понятным, что их можно классифицировать на несколько групп:
1) «красивые» задачи по решению;
2) «красивые» задачи по чертежу;
3) «красивые» задачи по содержанию;
4) «красивые» олимпиадные задачи.
Содержание данной классификации раскроем далее.
Глава II. Классификация красивых задач
2.1 «Красивые» задачи по содержанию
Некоторые «красивые» задачи привлекают учеников примечательной особенностью, находящейся в содержании поставленной задачи. Приведем пример:
Маленький Петя подпилил все ножки у квадратного табурета и четыре отпиленных кусочка потерял (рис. 2). Оказалось, что длины всех кусочков различны и что табурет после этого стоит на полу, пусть наклонно, но по-прежнему касаясь, пола всеми четырьмя концами ножек. Дедушка решил починить табурет, однако нашел только три кусочка с длинами 8, 9 и 10 см. Какой длины может быть четвертый кусочек?
2). Оказалось, что длины всех кусочков различны и что табурет после этого стоит на полу, пусть наклонно, но по-прежнему касаясь, пола всеми четырьмя концами ножек. Дедушка решил починить табурет, однако нашел только три кусочка с длинами 8, 9 и 10 см. Какой длины может быть четвертый кусочек?
Решение. Пусть А, В, С, D – концы исходных ножек табуретки, а А1, В1, С1, D1 – подпиленных. А1А + В1В = С1С + D1D. Поскольку табуретка стоит, касаясь пола четырьмя ножками, то точки А1, В1, С1 и D1 лежат в одной плоскости. Табуретка квадратная, значит, плоскости АВА1В1 и СDС1D1 параллельны. Следовательно, А1В1 // С1D1. Аналогично, В1С1 // А1D1. таким образом, четырехугольник А1В1С1D1 – параллелограмм, и его диагонали пересекаются в точке О1. Пусть О – центр квадрата АВСD. Заметим, что отрезок ОО1 – средняя линия как в трапеции АСС1А1, так и в трапеции ВDD1В1, а значит , А1А+ С1С= 2ОО1= В1В+ D1D.
Теперь переберем возможные длины отпиленной части, расположенной по диагонали от потерянной. При этом получим, что длина отпиленной части удовлетворяет одному из равенств:
При этом получим, что длина отпиленной части удовлетворяет одному из равенств:
8+x=9+10, 9+x=8+10, 10+x=8+9, x=7, x=9,x=11.
Поскольку длины всех кусков различны, одна из них равна 9, то остаются только варианты 7 и 11.
Ответ: 7,11.
2.2 «Красивые» задачи по чертежу
Задачи на построение чертежей, вызывают интерес именно условием — красивый чертеж. Возникает возможность фантазировать на данную тему, в результате получаются оригинальные чертежи.
Задача
Зигзаг разделил правильный девятиугольник на треугольники, как показано на рисунке (рис. 3). Какая часть площади больше: закрашенная или незакрашенная?
Решение. Проведем в девятиугольнике еще несколько диагоналей (рис. 4).
Девятиугольник разбился на 13 треугольников. На рисунке образовалось много параллелограммов и трапеций с диагоналями. Расставим номера треугольников, причем одинаковым номером отметим равные треугольники разных цветов. 12 из них разбились на пары, а тринадцатому, который оказался закрашенным, пары не хватило. Значит, закрашенная часть площади девятиугольника больше его незакрашенной части.
На рисунке образовалось много параллелограммов и трапеций с диагоналями. Расставим номера треугольников, причем одинаковым номером отметим равные треугольники разных цветов. 12 из них разбились на пары, а тринадцатому, который оказался закрашенным, пары не хватило. Значит, закрашенная часть площади девятиугольника больше его незакрашенной части.
Ответ: закрашенная.
2.3 «Красивые» задачи по решению
Нестандартность решения может проявляться и в методах решения. Особый интерес в этом смысле представляют задачи, имеющие несколько различных методов решения, и многовариантные задачи, имеющие несколько ответов.
Задача
Дан острый угол А, вершина которого недоступна (находится за пределами чертежа). Постройте биссектрису данного угла.
Эту задачу можно решить, как минимум, двумя способами, каждый из которых по-своему красив.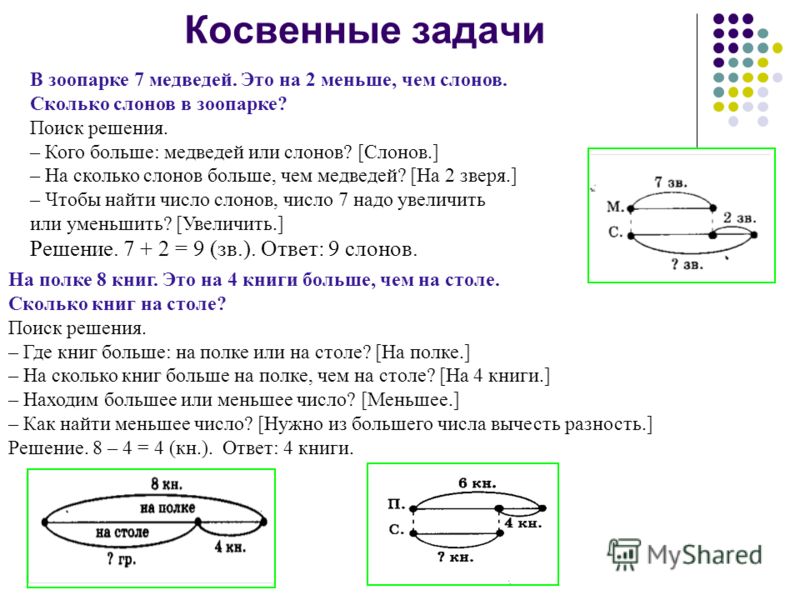
Способ 1 опирается на тот факт, что три биссектрисы треугольника пересекаются в одной точке. Взяв две произвольные точки В и С на сторонах данного угла, получим треугольник АВС (с одной недоступной вершиной), две биссектрисы которого можно построить. Точка пересечения этих биссектрис лежит на искомой биссектрисе. Аналогично можно найти и вторую точку (рис. 5).
Способ 2 использует свойство углов с соответственно параллельными сторонами: проведя на равных расстояниях от сторон данного угла прямые А1В1и А1С1, параллельные соответственно сторонам АВ и АС, так чтобы точка их пересечения лежала внутри угла, получим угол В1А1С1, равный данному. Очевидно, что биссектриса В1А1С1 лежит на искомой биссектрисе угла ВАС (рис. 6).
2.4 «Красивые» олимпиадные задачи
Приведем пример «красивой» олимпиадной задачи.
Задача
Дана белая доска размером 100*100 клеток (рис. 7). Двое по очереди красят ее клетки в черный цвет, причем первый всегда закрашивает квадрат 2*2, а второй—три клетки, образующие «уголок». Уже покрашенную клетку второй раз красить нельзя. Проигрывает тот, кто не может сделать очередной ход. Кто выигрывает при правильной игре: первый или второй?
7). Двое по очереди красят ее клетки в черный цвет, причем первый всегда закрашивает квадрат 2*2, а второй—три клетки, образующие «уголок». Уже покрашенную клетку второй раз красить нельзя. Проигрывает тот, кто не может сделать очередной ход. Кто выигрывает при правильной игре: первый или второй?
Ответ: второй
Решение. В одном из углов доски второй игрок своим первым ходом закрашивает три клетки в прямоугольнике 2×3, а три оставшиеся клетки из этого прямоугольника объявляет резервом. В дальнейшем второй игрок делает все возможные ходы, не затрагивая резерва. Если такой ход становится невозможным, то закрашиваются клетки резерва. Ясно, что ответного хода у первого игрока нет.
Заключение
Работа по выбранной теме осуществлялась в соответствии с планом исследования, а именно: были определены объектная область, объект и предмет исследования, сформулирована гипотеза, поставлены цели и задачи, а также определены ожидаемые результаты. Были указаны используемые методы исследования, определена проблема, обоснована актуальность.
Были указаны используемые методы исследования, определена проблема, обоснована актуальность.
Анализируя выполнение поставленных задач, можно сказать следующее:
В ходе исследования дано определение «красивой» математической задачи, проведена классификация таких задач по определенным признакам, а именно:
— задачи, «красивые» по решению;
-задачи, «красивые» по содержанию;
-задачи, «красивые» по чертежу;
-«красивые» олимпиадные задачи.
Изучена литература по вопросу исследования, всего изучено 10 научных публикаций и других источников.
В ходе данного исследования были использованы заявленные методы (теоретические, эмпирические, математические).
Анализируя планируемые ожидаемые результаты исследования, можно отметить, что как основной результат работы проведена классификация «красивых» математических задач.
Список литературы
Бахтина, Т.П. Раз задачка, два задачка…-М.:Аскар,2001.
Биркгоф Г. Математика и психология. — М., 1977.
Ковалёва, С.П. Олимпиадные задания по математике 9 класс – В.: Учитель 2005.
Леман, И. Увлекательная математика/ Пер. с нем. Ю.А. Данилова. М., 1985.
Лихтарников, Л.М. Задачи мудрецов: Кн. для учащихся. – М.: Просвещение: АО «Учебная литература», 1996.
Прасолов, В.В. Задачи по планиметрии. – М.: Наука, 1986.
Фарков, А.В. Математические олимпиады в школе – М.: Айрис пресс, 2002.
Фарков, А.В. Математические олимпиады в школе 5-11 класс – М.:Айрис пресс, 2005.
Фарков, А.В. Готовимся к олимпиадам по математике – М.: Экзамен, 2006.
Математические олимпиады и олимпиадные задачи – http://www.zaba.ru.
Международный математический конкурс «Кенгуру» — http://.Kenguru.sp.ru.-
Московская математическая олимпиада школьников -http://olympiadas.mccme.ru/m
Прилоджения
Рис. 1
Рис. 2
Рис. 3
Рис. 4
Рис. 5
Рис. 6
Р ис. 7
1Биркгоф Г. Математика и психология. — М., 1977.
Просмотров работы: 1612
интервью с автором проекта Николаем Андреевым
Уже 15 лет все желающие углубиться в математику и понять, как научные принципы работают в реальной жизни, заходят на сайт «Математические Этюды». Мы поговорили с автором проекта, заведующим лаборатории популяризации и пропаганды математики Математического института им. В. А. Стеклова Николаем Андреевым о том, в чем преимущества 3D-графики при иллюстрации задач, реально ли сделать популярное приложение про математику и что нового появилось в «Этюдах» в последнее время.
В. А. Стеклова Николаем Андреевым о том, в чем преимущества 3D-графики при иллюстрации задач, реально ли сделать популярное приложение про математику и что нового появилось в «Этюдах» в последнее время.
В этом году вашему проекту исполнилось 15 лет, но, как я понимаю, это не единственная круглая дата в ближайшие месяцы?
Действительно, этой осенью круглых дат у нас много! Если идти в обратном порядке, то в ноябре 2015 года наша книга «Математическая составляющая» стала лауреатом премии «Просветитель», в 2010 году нашему проекту была присуждена Премия Президента РФ в области науки и инноваций для молодых ученых – причем впервые не за научные достижения, а за популяризацию науки. 15 лет назад открылся сайт «Математические этюды», а в декабре 2002 года появился наш первый математический фильм.
Николай Андреев на Международном конгрессе математиков в Рио-де-Жанейро, 2018
То есть, сам проект начался еще в 2002 году, а сайт появился три года спустя?
Да, так и есть.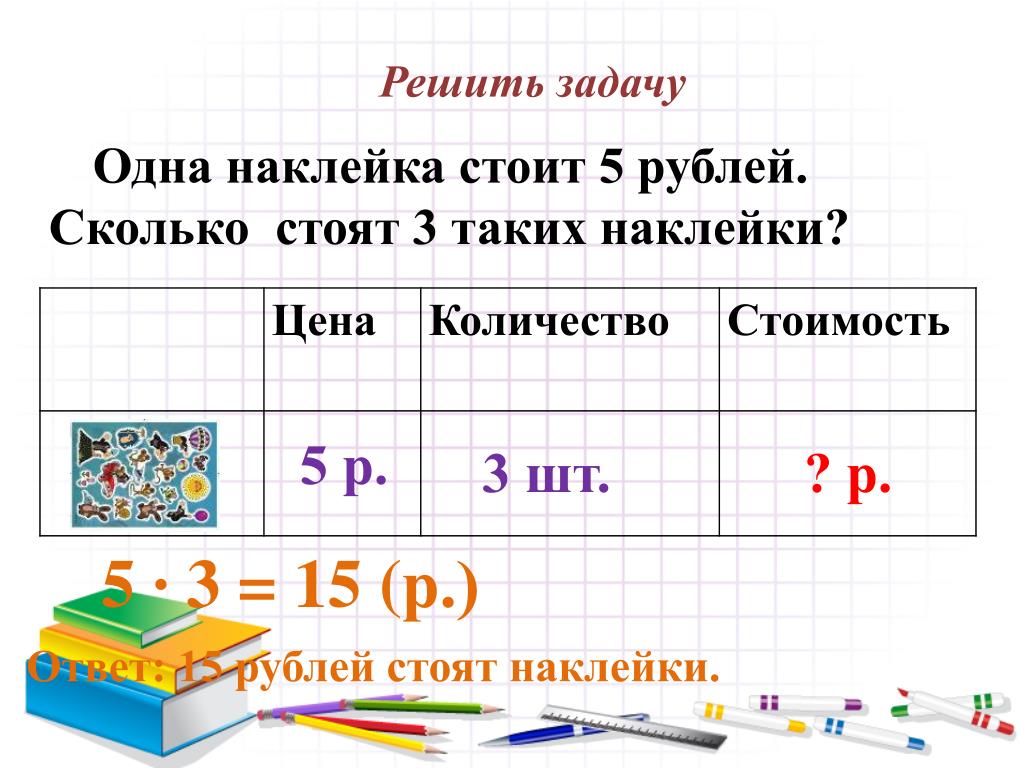 В какой-то момент мне показалось, что о задачах, которыми я занимался в науке, можно красиво и понятно рассказать с использованием 3D-графики. Представления о 3D-графике у меня тогда были только примерные, но было понятно, что это отдельная наука и изучать ее я не готов. Поэтому я кинул клич на интернет-форумах, где обитали специалисты по 3D-графике. Так мы познакомились с мультипликатором Михаилом Калиниченко, с ним мы начали что-то пробовать и, собственно говоря, работаем вместе по сей день. Правда, первые два фильма – про задачу Томсона и про контактное число шаров – я теперь показываю редко, сегодня они кажутся не такими захватывающими. Но в начале 2000-х они очень понравились и учителям, и научному сообществу. Поэтому мы продолжили создавать фильмы, математические расчеты для создания фильма стал делать Никита Панюнин, а в 2005 году совершенно уникальный человек Роман Кокшаров создал нашу полянку с мальчишкой у доски – сайт в интернете.
В какой-то момент мне показалось, что о задачах, которыми я занимался в науке, можно красиво и понятно рассказать с использованием 3D-графики. Представления о 3D-графике у меня тогда были только примерные, но было понятно, что это отдельная наука и изучать ее я не готов. Поэтому я кинул клич на интернет-форумах, где обитали специалисты по 3D-графике. Так мы познакомились с мультипликатором Михаилом Калиниченко, с ним мы начали что-то пробовать и, собственно говоря, работаем вместе по сей день. Правда, первые два фильма – про задачу Томсона и про контактное число шаров – я теперь показываю редко, сегодня они кажутся не такими захватывающими. Но в начале 2000-х они очень понравились и учителям, и научному сообществу. Поэтому мы продолжили создавать фильмы, математические расчеты для создания фильма стал делать Никита Панюнин, а в 2005 году совершенно уникальный человек Роман Кокшаров создал нашу полянку с мальчишкой у доски – сайт в интернете.
А где вы показывали этюды, пока у вас не было сайта?
Были лекции, в том числе в школах, на них и демонстрировались фильмы. Это направление очень важно по сей день, сегодня у нас в копилке больше тысячи лекций – вполне себе немаленькая цифра.
Это направление очень важно по сей день, сегодня у нас в копилке больше тысячи лекций – вполне себе немаленькая цифра.
Из крупных событий я бы выделил Конгресс по математическому образованию в Копенгагене 2004 года: на нем впервые состоялась национальная презентация России. Туда приехало много российских учителей математики, проходила огромная выставка, читались доклады, в том числе наш про «Математические этюды».
Сегодня для нас 3D-графика – это привычное дело, но в начале 2000-х была совсем другая картина. Почему вам показалось, что именно такая форма будет удачной? Было ли это на тот момент новаторством в России?
И не только в России, но и в международных масштабах. 3D-графика в популяризации науки, действительно, была совершенно уникальной историей, это давало огромный приток посетителей на сайт. Любителей математических этюдов тоже стало больше, потому что таким образом математику еще не объяснял никто. Причем оценили такой подход не только наши пользователи, но и трехмерщики. В России ежегодно проходит крупнейшее мероприятие по 3D-графике – CG Event. И на первом CG Event представили несколько пленарных докладов, среди выступающих был сотрудник студии Pixar, представитель «Базелевса» – компании Тимура Бекмамбетова, который как раз тогда снял «Дозоры», и были мы с докладом по «Математическим этюдам». И даже на трехмерщиков они тогда произвели огромное впечатление.
В России ежегодно проходит крупнейшее мероприятие по 3D-графике – CG Event. И на первом CG Event представили несколько пленарных докладов, среди выступающих был сотрудник студии Pixar, представитель «Базелевса» – компании Тимура Бекмамбетова, который как раз тогда снял «Дозоры», и были мы с докладом по «Математическим этюдам». И даже на трехмерщиков они тогда произвели огромное впечатление.
Сейчас, конечно, 3D-графика стала более привычной, но главное ее преимущество для нас осталось неизменным – с ее помощью можно нарисовать математические картинки по-честному: с нужным соотношением сторон, чтобы развертка правильно разворачивалась и так далее. Сделать это каким-либо еще способом практически невозможно. А в математике честность и правильность нужна во всем, включая рисунки. Например, мы в книжке «Математическая составляющая» убили массу сил на то, чтобы рисунки были действительно честными, и это отдельная наша гордость. В фильмах происходит точно так же.
Вы упомянули, что в проекте собрано более тысячи лекций.
 А что в принципе сегодня представляют собой «Математические этюды» с точки зрения цифр: сколько заданий, сколько посетителей?
А что в принципе сегодня представляют собой «Математические этюды» с точки зрения цифр: сколько заданий, сколько посетителей?Сейчас на сайте представлено более 60 фильмов, более 30 миниатюр и 30 моделей.
Что касается посещений, в лучшие времена у нас было по 15 000 уникальных посетителей в день, для России и для математического сайта это очень неплохо, сейчас – поменьше. Последние несколько лет мы много работали над книгой и мало обновляли сайт, но надеемся, что новый материал и более активное присутствие в соцсетях не только восстановят, но и прибавят нам посетителей, а самое главное – людей, интересующихся математикой.
Лекция
Вы можете коротко охарактеризовать каждый из основных разделов? Что попадает в «Этюды», что – в «Модели» или «Миниатюры»?
«Этюды» – это фильмы о различных математических задачах, решенных и нерешенных, а также о приложениях математики, например, в технике. Один из таких культовых фильмов – о том, как поворачивают поезда метро и железнодорожные составы. Все мы пользуемся транспортом, но далеко не все задумывались, что при повороте радиус внешнего рельса больше, чем радиус внутреннего. Соответственно, путь, которое проходит внешнее колесо, больше, чем путь, которое проходит внутреннее. А между тем колеса вращаются с одной и той же скоростью, они сидят на единой оси! Оказывается, что проблему помогает решить геометрия.
Все мы пользуемся транспортом, но далеко не все задумывались, что при повороте радиус внешнего рельса больше, чем радиус внутреннего. Соответственно, путь, которое проходит внешнее колесо, больше, чем путь, которое проходит внутреннее. А между тем колеса вращаются с одной и той же скоростью, они сидят на единой оси! Оказывается, что проблему помогает решить геометрия.
«Миниатюры» – это совсем маленькие зарисовки, тем не менее они ничуть не менее интересны. Обычно они посвящены какому-то конкретному математическому факту. Например, у нас много миниатюр про используемые в школе понятия вроде параболы, гиперболы, они полезны для учителей, которые показывают их на уроках математики. При этом среди миниатюр есть сюжеты, которые по-новому раскрывают даже такие привычные понятия, как та же парабола: например, сюжет про параболическое решето.
В разделе «Модели» мы хотим собрать электронную энциклопедию всех идей, которые иллюстрируют математические факты и теоремы в реальном физическом мире. Мне это кажется ценным, потому что у нас пока нет хороших музеев науки, и даже в имеющихся математические отделы очень маленькие: сложно придумать модель, в которой как-то показывается математический факт. Сейчас на рабочей версии сайта собрано больше 400 таких моделей, постепенно мы будем выкладывать их в открытый доступ.
Мне это кажется ценным, потому что у нас пока нет хороших музеев науки, и даже в имеющихся математические отделы очень маленькие: сложно придумать модель, в которой как-то показывается математический факт. Сейчас на рабочей версии сайта собрано больше 400 таких моделей, постепенно мы будем выкладывать их в открытый доступ.
По какому принципу сегодня отбирается материал, который попадает на сайт?
На самом деле, не так много нетривиальных математических сюжетов, о которых еще не шла речь в классических книгах. Одна из наших целей – находить и представлять такие сюжеты. И если возникает идея, что какой-то из них можно представить и он будет интересен, то мы начинаем над ним работать. Когда первый вариант фильма готов, мы его показываем на лекциях, обкатываем, смотрим на реакцию, иногда чуть-чуть поправляем, и потом уже он появляется на сайте. Наша лаборатория популяризации и пропаганды математики существует в центральном математическом месте нашей страны – в Математическом институте им.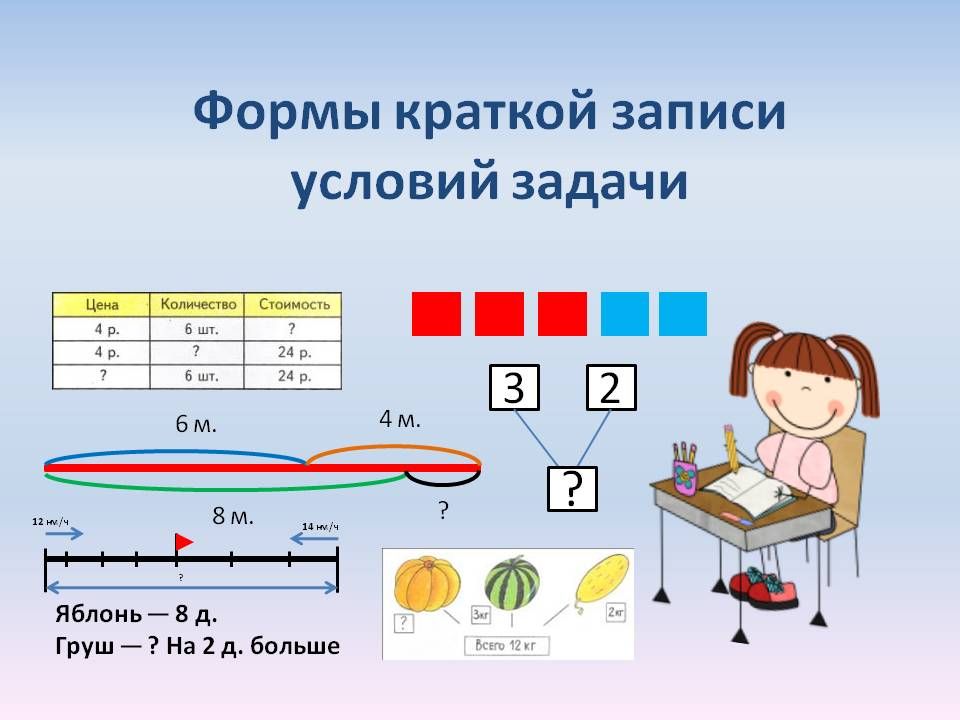 В. А. Стеклова РАН. К нам заходит почти весь институт, все понимают, что наша деятельность важна, делятся своими мыслями. Соответственно, мы можем черпать идеи с переднего края науки, получать их из первых рук, от людей, которые занимаются данной темой. Благодаря этому получается интересно, качественно и неизбито.
В. А. Стеклова РАН. К нам заходит почти весь институт, все понимают, что наша деятельность важна, делятся своими мыслями. Соответственно, мы можем черпать идеи с переднего края науки, получать их из первых рук, от людей, которые занимаются данной темой. Благодаря этому получается интересно, качественно и неизбито.
Вы говорите, что у вас в «Этюдах» представлены как решенные, так и нерешенные задачи. Бывало ли такое, что вы публиковали задачу, а потом ее кто-то решал?
Пока нет, но некоторые продвижения в решении подобных задач были. Мы не стесняемся дописывать опубликованные тексты, дополнять их комментариями. Но случая, чтобы приходилось прямо переделывать фильм, не было.
При этом мы выбираем задачи, формулировки которых понятны школьникам и широкой общественности. Интересно, что даже среди них есть такие, которые математики не умеют решать! И тут важно демонстрировать школьникам, что на их век еще что-то осталось, потому что многие воспринимают математику как науку времен Пифагора, в которой ничего нового уже не найдешь. Задача «Математических этюдов» – изменить их мнение, помочь полюбить математику. Потому что, конечно, научить математике никакой сайт не может, он может только вдохновить школьника: возможно, после он в книжках пороется, а главное, поработает сам – в математике это основное. Вторая важная задача – это дать учителям хороший по качеству материал для работы с детьми.
Задача «Математических этюдов» – изменить их мнение, помочь полюбить математику. Потому что, конечно, научить математике никакой сайт не может, он может только вдохновить школьника: возможно, после он в книжках пороется, а главное, поработает сам – в математике это основное. Вторая важная задача – это дать учителям хороший по качеству материал для работы с детьми.
Как бы вы посоветовали выстроить свою работу с сайтом школьнику, который готовится к олимпиаде?
Мы не различаем школьников, которые готовятся к олимпиаде, к ЕГЭ и так далее. Наш подход в том, что человек должен обладать математическими знаниями и общей математической культурой. И если это будет, то дальше уже приложится и участие в олимпиадах, и большие баллы на ЕГЭ. Но все-таки, например, международные олимпиады – это сейчас некий спорт, а мы скорее рассчитаны на широкую аудиторию, для которой важнее общее знание математики, а не конкретных олимпиадных приемов. При этом мы стараемся делать фильмы многослойными, чтобы посетитель любого уровня в любом случае узнал что-то новое и интересное.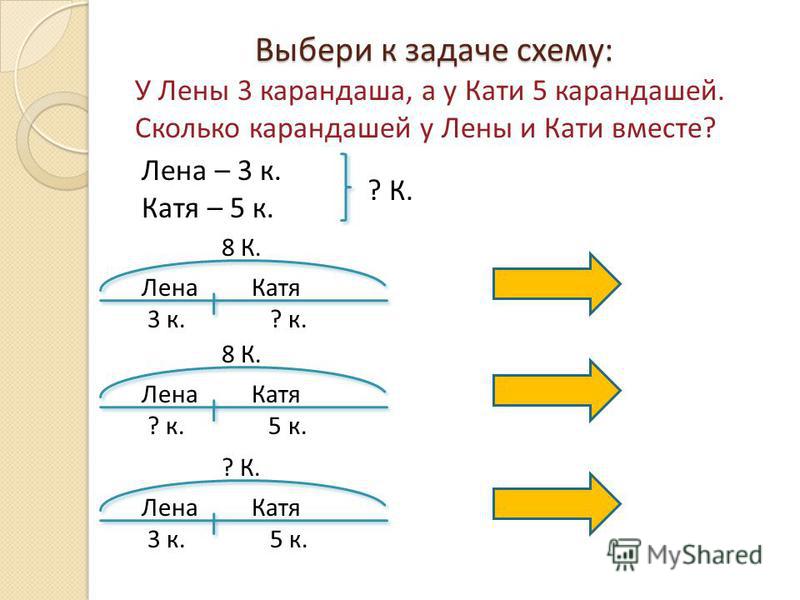 Кто-то просто картинку посмотрит, а кто-то поймет, какая теорема за ней стоит.
Кто-то просто картинку посмотрит, а кто-то поймет, какая теорема за ней стоит.
Полвека международных олимпиад: задания и решения →
И как я понимаю, у вас в каждом разделе есть ссылки на книги, чтобы можно было не только посмотреть, но и дополнительно почитать.
Сегодня далеко не все дети открывали книжку, например, «Прямые и кривые» Васильева и Гутенмахера, а это одна из лучших книг про конические сечения, про параболу, гиперболу, эллипс. С одной стороны, это достаточно стандартная рекомендация, с другой – ссылка не помешает: кто-то о ней узнает и прочитает. Это еще одна цель нашего проекта – стать проводником между современным обществом и тем пластом потрясающей литературы, которая была опубликована в советское время: рассказать про книжку, показать из нее какой-нибудь красивый сюжет, чтобы человек обратил на нее внимание. А в книге «Математическая составляющая» мы даже сделали раздел «Книжная полка».
У проекта есть версии на английском, французском, итальянском.
 Насколько он популярен среди ваших заграничных коллег? Может быть, у вас есть планы дальнейшего расширения?
Насколько он популярен среди ваших заграничных коллег? Может быть, у вас есть планы дальнейшего расширения?Планы есть, правда, пока с переводами была большая проблема, и сайты на других языках содержат существенно меньше материала, чем русская версия. Но показательно, что на последнем международном математическом конгрессе в Рио-де-Жанейро в 2018 году нам дали приглашенный доклад на секции по популяризации математики, мы показывали там свои фильмы, то есть в мире сайт известен. По статистике мы тоже видим, что посетители приходят из разных стран, но их пока не так много. Мы будем исправлять положение: сейчас почти весь наш материал перевела на английский Татьяна Блинкова, и мы постепенно будем выкладывать его на сайте. Надеемся, что после этого пользователей по всему миру будет еще больше.
Николай Андреев на Международном конгрессе математиков в Рио-де-Жанейро, 2018
Помимо этюдов, моделей и миниатюр у вас еще есть раздел iMath
Чтение и понимание письменных математических задач
Словесные задачи по математике часто представляют собой проблему, поскольку они требуют, чтобы учащиеся прочитали и поняли текст задачи, определили вопрос, на который нужно ответить, и, наконец, составили и решили числовое уравнение.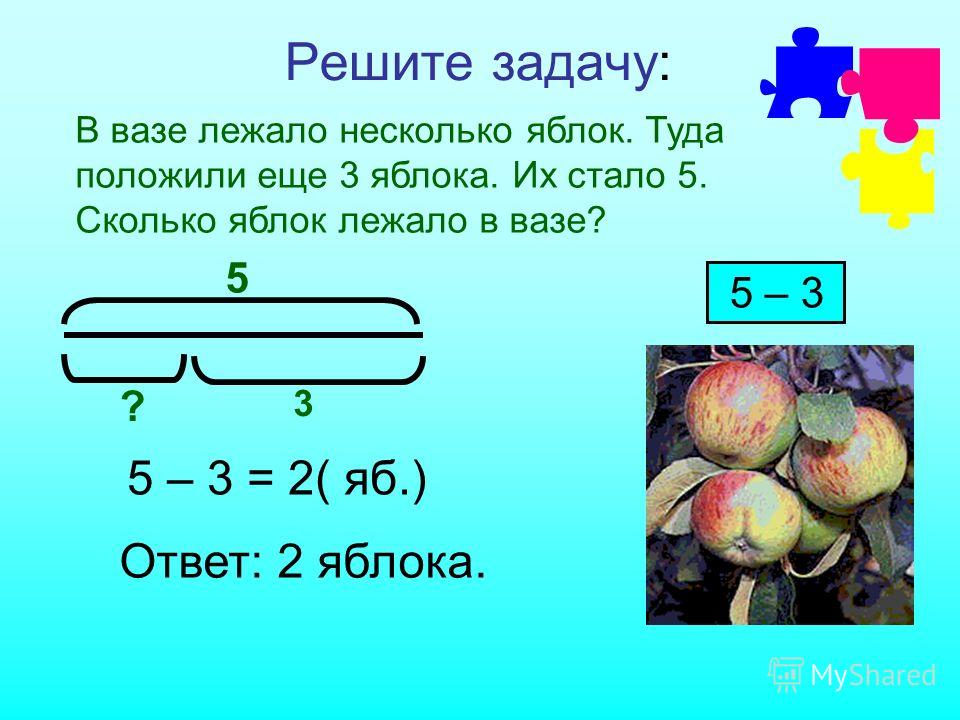 У многих ELL могут возникнуть трудности с чтением и пониманием письменного содержания словесной задачи. Если учащийся изучает английский как второй язык, он может еще не знать ключевую терминологию, необходимую для решения уравнения. Другими словами, ELL, получившие формальное образование в своих странах, как правило, не испытывают математических трудностей; следовательно, их борьба начинается, когда они сталкиваются с проблемами слов на втором языке, который они еще не освоили (Бернардо, 2005). По этой причине рекомендуется, чтобы учащиеся изучили ключевую терминологию, прежде чем пытаться решать математические текстовые задачи.
У многих ELL могут возникнуть трудности с чтением и пониманием письменного содержания словесной задачи. Если учащийся изучает английский как второй язык, он может еще не знать ключевую терминологию, необходимую для решения уравнения. Другими словами, ELL, получившие формальное образование в своих странах, как правило, не испытывают математических трудностей; следовательно, их борьба начинается, когда они сталкиваются с проблемами слов на втором языке, который они еще не освоили (Бернардо, 2005). По этой причине рекомендуется, чтобы учащиеся изучили ключевую терминологию, прежде чем пытаться решать математические текстовые задачи.
Ключевые преимущества
Как только изучающие английский язык узнают ключевую терминологию, используемую в математических задачах, им будет легче научиться писать числовые уравнения. Для учителей важно предоставить ELL возможность изучать и практиковать ключевые словарные слова.
Хотя ключевые слова очень важны, они являются лишь частью процесса.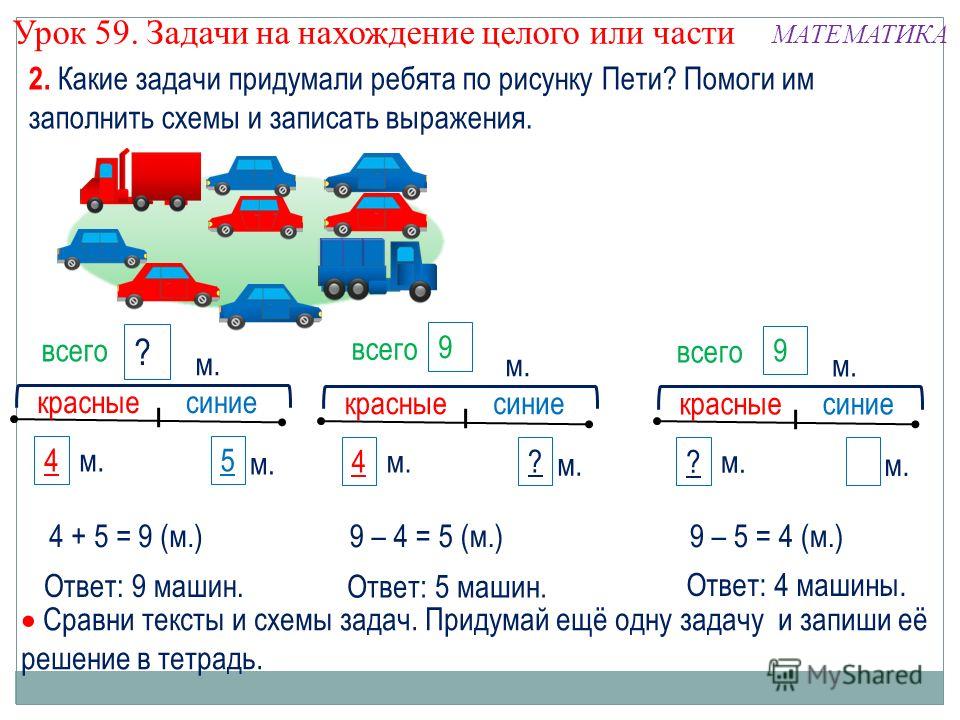 Понимание языка в текстовых задачах имеет решающее значение для всех учащихся. Им нужно знать значение слов. Но поскольку слова часто используются по-разному и проблемы ставятся по-разному, есть некоторые предостерегающие сообщения. Вот пример задачи, в которой используется «меньше чем» для составления уравнения на вычитание.
Понимание языка в текстовых задачах имеет решающее значение для всех учащихся. Им нужно знать значение слов. Но поскольку слова часто используются по-разному и проблемы ставятся по-разному, есть некоторые предостерегающие сообщения. Вот пример задачи, в которой используется «меньше чем» для составления уравнения на вычитание.
У Марии 24 шарика, что на 8 меньше, чем у Паоло. Сколько шариков у Паоло? Если бы мы сосредоточились только на использовании ключевых слов, «меньше чем» было бы сигналом для выбора чисел и вычитания. Ученик может сразу сделать вывод, что ответ равен 16, но задача заключается не в этом, и ребенок будет неправ. (Правильный ответ, кстати, 32).
Исследования показали, что если мы попросим учащихся полагаться только на знание того, что определенные ключевые слова сигнализируют о конкретных операциях, мы можем фактически увести их от попыток понять проблемы. Они будут склонны искать только те слова и числа, которые есть в задаче, даже если они не имеют отношения к ответу. Это не поможет им впоследствии стать математическими специалистами, даже если они хорошо владеют английским языком.
Это не поможет им впоследствии стать математическими специалистами, даже если они хорошо владеют английским языком.
Несмотря на то, что определение ключевых слов проводилось с обычными учащимися, последствия использования этих слов для учащихся ELL одинаковы. Они не смогли бы решить проблему выше. Однако, если учителя будут следовать предложенному процессу чтения задачи несколько раз (как в младших, так и в старших классах) и обсуждать ее значение, учащиеся поймут. Еще один хороший инструмент — научить их рисовать или моделировать задачи. Чтобы проиллюстрировать описанную выше проблему, вы можете сказать: «Вот Марии 24 года». Затем нарисуйте 24 единицы, фигуры, формы и т. д., чтобы представить 24. «Вот у Паоло; у него больше, потому что у Марии меньше, чем у него». Нарисуйте 24 единицы, фигуры, формы и т. д., чтобы представить 24, и добавьте еще 8. «Значит, у Паоло должно быть больше 24. Сколько еще? 8. Итак, сколько всего у Паоло?»
Разница между знанием значения слов «меньше чем» и использованием «меньше чем» в качестве ключа к операции. Мы хотим, чтобы учащиеся знали значение слов, а также видели их в контексте всей проблемы.
Мы хотим, чтобы учащиеся знали значение слов, а также видели их в контексте всей проблемы.
Предлагаемые занятия
Младшие классы
Ежедневно тренируйтесь решать проблемы, просто задавая больше вопросов. Например:
- Сколько учеников сегодня принесли домашнее задание?
- Сколько еще детей вчера принесли домашнее задание?
- У нас было 8 маркеров на доске, а теперь осталось только 3. Сколько мы убрали?
- Сколько животных в этом журнале? Сколько млекопитающих? Сколько птиц? (введение в дроби и проценты)
Продолжайте ежедневно использовать ключевую терминологию и помещать ее в контекст (например, меньше, больше, разница, время, каждый и т. д.). Покажите учащимся, как легко можно неправильно понять проблему.
Старшие классы
- Медленно и внимательно читать текстовые задачи несколько раз, чтобы все ученики поняли.
- Если возможно, разбейте проблему на более мелкие сегменты.
- Позвольте учащимся разыграть словесные задачи, чтобы лучше понять, что их просят решить.

- Обеспечьте манипуляторы, чтобы помочь учащимся визуализировать проблему.
- Совершайте полевые или пешие прогулки, чтобы определить расстояние, скорость, площадь покрытия и т. д.
- Попросите учащихся провести опросы, интервью, практические исследования в реальных ситуациях, чтобы вычислить проценты, различия и математические вычисления более высокого порядка. навыки и умения.
- Позвольте учащимся делать рисунки или диаграммы, чтобы помочь им понять проблемы.
Key terminology
Addition + | Subtraction — |
|---|---|
combined | minus |
Multiplication x | Division ÷ |
multiplied | divided by |
Дополнительные идеи, которые можно использовать для поддержки обучения математике в классе ELL, см. в Учебнике по математике для изучающих английский язык.
в Учебнике по математике для изучающих английский язык.
Математика как комплексное решение задач
Джейкоб Клерляйн и Шина Херви, Generation Ready
К тому времени, когда маленькие дети поступают в школу, они уже на пути к тому, чтобы научиться решать задачи. С самого рождения дети учатся учиться: они реагируют на свое окружение и реакцию окружающих. Это осмысление опыта является непрерывным, рекурсивным процессом. Мы давно знаем, что чтение — это сложная деятельность по решению проблем. Совсем недавно учителя пришли к пониманию того, что повышение математической грамотности — это также сложная деятельность по решению проблем, которая становится более мощной и гибкой, если практиковаться чаще. Проблема в математике — это любая ситуация, которая должна быть решена с помощью математических инструментов, но для которой нет очевидной стратегии. Если путь вперед очевиден, это не проблема — это простое приложение.
Математики всегда понимали, что решение задач занимает центральное место в их дисциплине, потому что без задачи нет математики.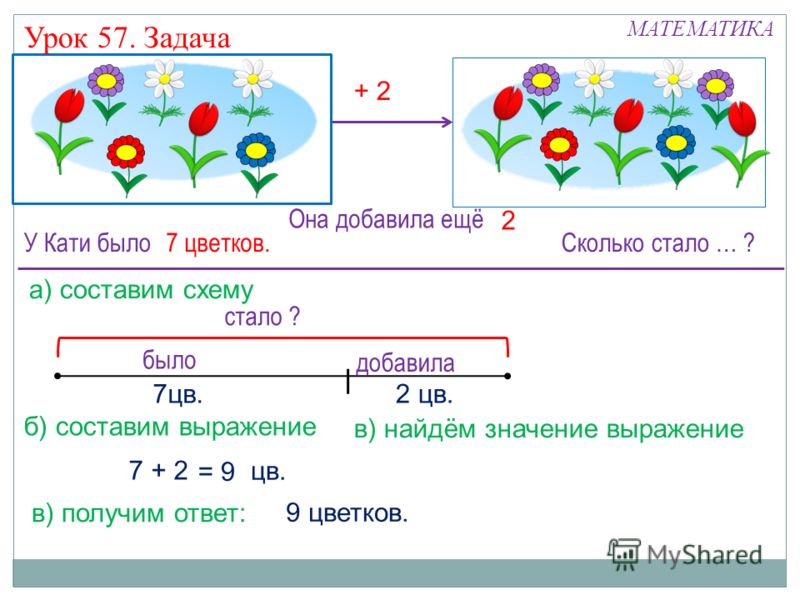 Решение проблем играет центральную роль в мышлении педагогов-теоретиков с момента публикации книги Полиа «Как это решить» в 1945 году. Национальный совет учителей математики (NCTM) последовательно выступает за решение проблем для почти 40 лет, в то время как международные тенденции в преподавании математики показали повышенное внимание к решению задач и математическому моделированию, начиная с начала 19 века.90-е. По мере того, как преподаватели во всем мире все больше осознавали, что предоставление опыта решения задач имеет решающее значение для того, чтобы учащиеся могли осмысленно использовать и применять математические знания (Wu and Zhang, 2006), мало что изменилось на школьном уровне в Соединенных Штатах.
Решение проблем играет центральную роль в мышлении педагогов-теоретиков с момента публикации книги Полиа «Как это решить» в 1945 году. Национальный совет учителей математики (NCTM) последовательно выступает за решение проблем для почти 40 лет, в то время как международные тенденции в преподавании математики показали повышенное внимание к решению задач и математическому моделированию, начиная с начала 19 века.90-е. По мере того, как преподаватели во всем мире все больше осознавали, что предоставление опыта решения задач имеет решающее значение для того, чтобы учащиеся могли осмысленно использовать и применять математические знания (Wu and Zhang, 2006), мало что изменилось на школьном уровне в Соединенных Штатах.
«Решение задач — это не только цель изучения математики, но и основное средство для этого».
(NCTM, 2000, стр. 52)
В 2011 году Стандарты Common Core State включили Стандарты процессов NCTM по решению задач, рассуждению и доказательству, общению, представлению и связям в Стандарты математической практики. Для многих учителей математики это был первый раз, когда они должны были объединить сотрудничество учащихся и обсуждение с решением проблем. Эта практика требует обучения совершенно по-другому, поскольку школы перешли от ориентированного на учителя к более диалогическому подходу к преподаванию и обучению. Задача учителей состоит в том, чтобы научить учащихся не только решать задачи, но и изучать математику посредством решения задач. Хотя многие учащиеся могут развить беглость процедур, им часто не хватает глубокого концептуального понимания, необходимого для решения новых задач или установления связей между математическими идеями.
Для многих учителей математики это был первый раз, когда они должны были объединить сотрудничество учащихся и обсуждение с решением проблем. Эта практика требует обучения совершенно по-другому, поскольку школы перешли от ориентированного на учителя к более диалогическому подходу к преподаванию и обучению. Задача учителей состоит в том, чтобы научить учащихся не только решать задачи, но и изучать математику посредством решения задач. Хотя многие учащиеся могут развить беглость процедур, им часто не хватает глубокого концептуального понимания, необходимого для решения новых задач или установления связей между математическими идеями.
«Однако учебная программа по решению задач требует от учителя другой роли. Вместо того, чтобы руководить уроком, учитель должен предоставить ученикам время для решения проблем, самостоятельного поиска стратегий и решений и научиться оценивать свои собственные результаты. Несмотря на то, что учитель должен присутствовать очень активно, главное внимание в классе должно быть сосредоточено на мыслительных процессах учащихся».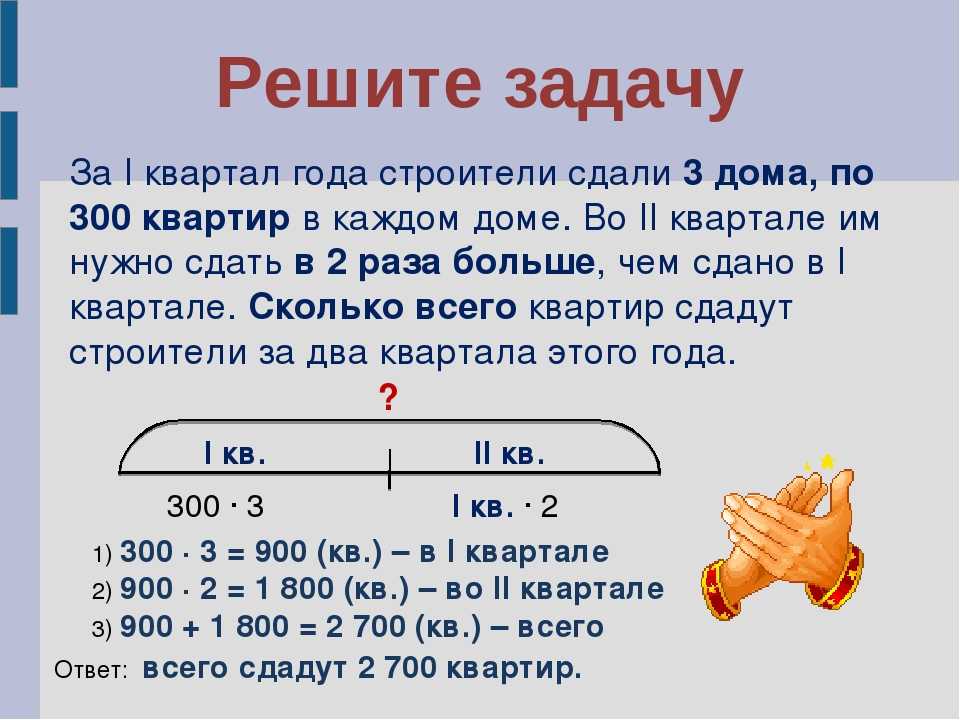
(Burns, 2000, стр. 29)
Обучение решению проблем
Чтобы понять, как учащиеся становятся способными решать задачи, нам нужно взглянуть на теории, лежащие в основе обучения математике. К ним относятся признание аспектов обучения, связанных с развитием, и тот важный факт, что учащиеся активно участвуют в изучении математики посредством «действий, разговоров, размышлений, обсуждений, наблюдений, исследований, слушания и рассуждений» (Copley, 2000, стр. 29). . Концепция совместного конструирования обучения является основой теории. Более того, мы знаем, что каждый студент находится на своем уникальном пути развития.
Убеждения, лежащие в основе эффективного преподавания математики
- Самобытность, язык и культура каждого учащегося должны уважаться и цениться.
- Каждый учащийся имеет право на доступ к эффективному математическому образованию.
- Каждый ученик может стать успешным учеником по математике.
Дети приходят в школу с интуитивным пониманием математики. Учителю необходимо установить связь и опираться на это понимание через опыт, который позволяет учащимся изучать математику и делиться своими идеями в содержательном диалоге с учителем и своими сверстниками.
Учителю необходимо установить связь и опираться на это понимание через опыт, который позволяет учащимся изучать математику и делиться своими идеями в содержательном диалоге с учителем и своими сверстниками.
Обучение происходит в социальных условиях (Выготский, 1978). Учащиеся строят понимание посредством участия в решении проблем и взаимодействия с другими в этих действиях. Благодаря этим социальным взаимодействиям учащиеся чувствуют, что они могут рисковать, пробовать новые стратегии, а также давать и получать обратную связь. Они учатся совместно, когда делятся разными точками зрения или обсуждают способы решения проблемы. Именно через разговоры о проблемах и обсуждение своих идей дети строят знания и осваивают язык, чтобы осмысливать опыт.
Учащиеся приобретают понимание математики и развивают навыки решения задач в результате решения задач, а не непосредственного обучения (Hiebert1997). Роль учителя состоит в том, чтобы создавать проблемы и представлять ситуации, которые обеспечивают форум, на котором может происходить решение проблем.
Почему важно решать проблемы?
Наши учащиеся живут в обществе, основанном на информации и технологиях, где им необходимо уметь критически мыслить о сложных проблемах, а также «анализировать и логически мыслить о новых ситуациях, разрабатывать неопределенные процедуры решения и ясно и убедительно сообщать свое решение другим». (Баруди, 1998). Математическое образование важно не только из-за «роли контролера, которую математика играет в доступе учащихся к образовательным и экономическим возможностям», но и потому, что процессы решения задач и приобретение стратегий решения задач готовят учащихся к жизни после школы (Кобб). и Ходж, 2002).
Важность решения задач при изучении математики исходит из убеждения, что математика в первую очередь связана с рассуждениями, а не с запоминанием. Решение проблем позволяет учащимся развивать понимание и объяснять процессы, используемые для достижения решений, а не запоминать и применять набор процедур. Именно благодаря решению задач учащиеся развивают более глубокое понимание математических концепций, становятся более вовлеченными и ценят актуальность и полезность математики (Wu and Zhang, 2006). Решение задач по математике способствует развитию:
Решение задач по математике способствует развитию:
- Способность мыслить творчески, критически и логически
- Способность структурировать и организовывать
- Способность обрабатывать информацию
- Удовольствие от интеллектуальной задачи
- Навыки решения проблем, которые помогают им исследовать и понимать мир
Решение задач должно лежать в основе всех аспектов преподавания математики, чтобы учащиеся могли ощутить силу математики в окружающем их мире. Этот метод позволяет учащимся рассматривать решение задач как средство построения, оценки и уточнения своих математических теорий и теорий других.
Проблемы, которые являются «проблемными»
Требования учителя к ученикам очень важны. Учащиеся учатся справляться со сложными проблемами, только столкнувшись с ними. Учащиеся должны иметь возможность работать над сложными задачами, а не над серией простых задач, вытекающих из сложной задачи. Это важно для стимулирования математических рассуждений учащихся и формирования прочных математических знаний 90–160 (Энтони и Уолшоу, 2007). Задача учителей заключается в обеспечении того, чтобы задачи, которые они ставят, были разработаны для поддержки обучения математике и были подходящими и сложными для всех учащихся. Задачи должны быть достаточно сложными, чтобы вызвать затруднения , но не настолько сложными, чтобы учащиеся не смогли добиться успеха. Учителя, которые понимают это правильно, создают устойчивых решателей проблем, которые знают, что при настойчивости они могут добиться успеха. Задачи должны находиться в «зоне ближайшего развития» учащихся (Выготский 19).68). Эти типы сложных проблем предоставят возможности для обсуждения и обучения.
Задача учителей заключается в обеспечении того, чтобы задачи, которые они ставят, были разработаны для поддержки обучения математике и были подходящими и сложными для всех учащихся. Задачи должны быть достаточно сложными, чтобы вызвать затруднения , но не настолько сложными, чтобы учащиеся не смогли добиться успеха. Учителя, которые понимают это правильно, создают устойчивых решателей проблем, которые знают, что при настойчивости они могут добиться успеха. Задачи должны находиться в «зоне ближайшего развития» учащихся (Выготский 19).68). Эти типы сложных проблем предоставят возможности для обсуждения и обучения.
Учащиеся будут иметь возможность объяснить свои идеи, ответить на идеи других и бросить вызов своему мышлению. Те ученики, которые думают, что математика — это все о «правильном» ответе, нуждаются в поддержке и поощрении, чтобы пойти на риск. Терпимость к трудностям необходима для решения проблем, потому что «застревание» — это неизбежный этап решения практически любой проблемы. Выход из тупика обычно требует времени и включает в себя использование различных подходов. Студенты должны научиться этому на опыте. Эффективных задач:
Выход из тупика обычно требует времени и включает в себя использование различных подходов. Студенты должны научиться этому на опыте. Эффективных задач:
- Доступны и расширяемы
- Разрешить отдельным лицам принимать решения
- Способствовать обсуждению и общению
- Поощряйте оригинальность и изобретательность
- Поощряйте «что, если?» и «а что, если нет?» вопросы
- Содержит элемент неожиданности (адаптировано из Ahmed, 1987)
«Студенты учатся решать задачи по математике в первую очередь путем «действия, разговора, размышления, обсуждения, наблюдения, исследования, слушания и рассуждений».
(Copley, 2000, стр. 29)
«…когда учащиеся проводят совместное исследование. Оно становится мини-обществом – сообществом учащихся, занятых математической деятельностью, дискурсом и размышлениями. Учащимся должна быть предоставлена возможность действовать как математики, позволяя, поддерживая и бросая вызов их «математизации» конкретных ситуаций. Сообщество обеспечивает среду, в которой отдельные математические идеи могут быть выражены и проверены на соответствие идеям других… Это позволяет учащимся стать более ясными и уверенными в том, что они знают и понимают».
Сообщество обеспечивает среду, в которой отдельные математические идеи могут быть выражены и проверены на соответствие идеям других… Это позволяет учащимся стать более ясными и уверенными в том, что они знают и понимают».
(Fosnot, 2005, стр. 10)
Исследования показывают, что «классы, в которых ориентация последовательно определяет результаты задач с точки зрения ответов, а не мыслительных процессов, связанных с получением ответов, отрицательно влияет на мыслительные процессы и математические тождества. учащихся 90 160 (Энтони и Уолшоу, 2007 г., стр. 122).
Эффективные учителя формируют у своих учеников хорошие привычки решать проблемы. Их вопросы разработаны, чтобы помочь детям использовать различные стратегии и материалы для решения проблем. Студенты часто хотят начать без плана в виду. Посредством соответствующих вопросов учитель дает учащимся некоторую структуру для начала решения проблемы, не говоря им, что именно делать. В 1945 Полиа опубликовал следующие четыре принципа решения проблем, чтобы помочь учителям помочь своим ученикам.
- Понять и изучить проблему
- Найти стратегию
- Используйте стратегию для решения проблемы
- Оглянитесь назад и подумайте над решением
Решение проблем — это не линейный, а сложный интерактивный процесс. Учащиеся перемещаются вперед и назад между фазами Pólya и между ними. Стандарты Common Core State описывают этот процесс следующим образом:
«Подкованные в математике учащиеся начинают с того, что объясняют себе смысл задачи и ищут точки входа в ее решение. Они анализируют данные, ограничения, отношения и цели. Они строят предположения о форме и значении решения и планируют путь решения, а не просто пытаются найти решение. Они рассматривают аналогичные проблемы и пробуют частные случаи и более простые формы исходной задачи, чтобы получить представление о ее решении. Они отслеживают и оценивают свой прогресс и при необходимости меняют курс». (Стандарты обучения математике нового поколения штата Нью-Йорк, 2017 г.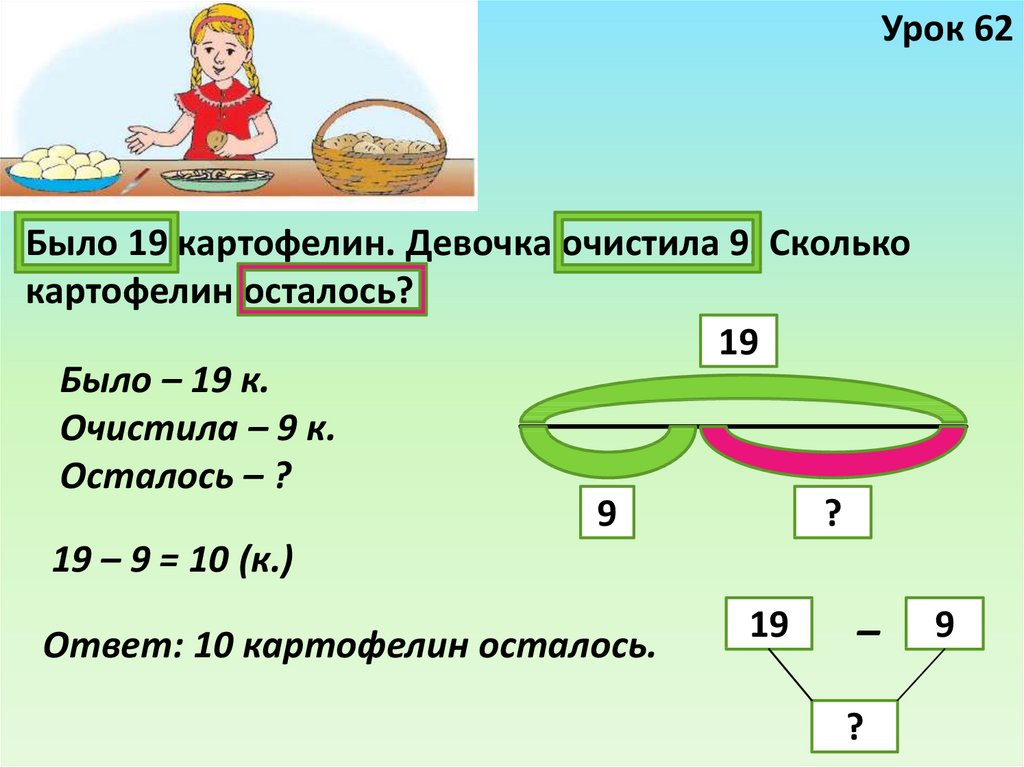 ).
).
Принципы решения проблем Полиа
- Понять и изучить проблему
- Найти стратегию
- Используйте стратегию для решения проблемы
- Оглянитесь назад и подумайте над решением
Учащиеся перемещаются вперед и назад по ходу решения задач.
Цель состоит в том, чтобы учащиеся имели ряд стратегий, которые они используют для решения проблем, и понимали, что может быть более одного решения. Важно понимать, что процесс столь же важен, если не более важен, чем получение решения, поскольку именно в процессе решения учащиеся раскрывают математику. Получение ответа — это не конец процесса. Размышление о стратегиях, используемых для решения проблемы, дает дополнительный опыт обучения. Изучение подхода, используемого для решения одной проблемы, помогает учащимся более комфортно использовать эту стратегию в различных других ситуациях.
При осмыслении идей учащиеся должны иметь возможность работать как самостоятельно, так и совместно. Будут времена, когда учащиеся должны иметь возможность работать самостоятельно, а иногда им нужно будет иметь возможность работать в небольших группах, чтобы они могли делиться идеями и учиться с другими и у них.
Будут времена, когда учащиеся должны иметь возможность работать самостоятельно, а иногда им нужно будет иметь возможность работать в небольших группах, чтобы они могли делиться идеями и учиться с другими и у них.
Реальность
Эффективные учителя математики создают для учащихся целенаправленный учебный опыт, решая задачи в релевантных и осмысленных контекстах. Хотя текстовые задачи — это способ поместить математику в контекст, он не делает ее автоматически реальной. Задача учителей состоит в том, чтобы давать учащимся задачи, основанные на их опыте реальности, а не просить их приостановить его. Реалистичность не означает, что задачи обязательно связаны с реальным контекстом, скорее они заставляют учащихся думать «настоящим» образом.
Планирование беседы
Планируя и продвигая беседу, учителя могут активно вовлекать учащихся в математическое мышление. На уроках математики, насыщенных дискурсом, учащиеся объясняют и обсуждают стратегии и процессы, которые они используют при решении математических задач, тем самым связывая свой повседневный язык со специальной лексикой математики.
Учащиеся должны понимать, как общаться математически, давать разумные математические объяснения и обосновывать свои решения. Эффективные учителя поощряют своих учеников сообщать свои идеи устно, письменно и с использованием различных представлений. Слушая учеников, учителя могут лучше понять, что знают их ученики, и неправильные представления, которые у них могут быть. Именно заблуждения открывают окно в процесс обучения студентов. Эффективные учителя рассматривают мышление как «процесс понимания», они могут использовать мышление своих учеников как ресурс для дальнейшего обучения. Такие учителя отзывчивы как к своим ученикам, так и к дисциплине математики.
«Сегодня математика требует не только вычислительных навыков, но и способности мыслить и рассуждать математически, чтобы решать новые задачи и изучать новые идеи, с которыми учащиеся столкнутся в будущем. Обучение улучшается в классах, где учащиеся должны оценивать свои собственные идеи и идеи других, им предлагается делать математические предположения и проверять их, а также им помогают развивать свои навыки рассуждения».
(Джон Ван де Валле)
«Капитал. Превосходство в математическом образовании требует справедливости — высоких ожиданий и сильной поддержки для всех учащихся».
(NTCM)
Заключение
То, как учителя организуют обучение в классе, во многом зависит от того, что они знают и думают о математике, а также от того, что они понимают в преподавании и изучении математики. Учителя должны признать, что процессы решения проблем развиваются с течением времени и значительно улучшаются за счет эффективных методов обучения. Роль учителя начинается с выбора подробных задач по решению задач, которые сосредоточены на математике, которую учитель хочет, чтобы их ученики изучали. Подход к решению проблем – это не только способ развития мышления учащихся, но и создание контекста для изучения математических понятий. Решение проблем позволяет учащимся перенести то, что они уже узнали, в незнакомые ситуации. Подход к решению проблем позволяет учащимся активно формировать свои представления о математике и брать на себя ответственность за свое обучение. Задача учителей математики состоит в том, чтобы развивать у учащихся процесс математического мышления наряду со знаниями и создавать возможности для представления даже рутинных математических задач в контексте решения проблем.
Задача учителей математики состоит в том, чтобы развивать у учащихся процесс математического мышления наряду со знаниями и создавать возможности для представления даже рутинных математических задач в контексте решения проблем.
Учитывая усилия, предпринятые на сегодняшний день для включения решения задач в качестве неотъемлемой части учебного плана по математике, и ограниченную реализацию в классах, для достижения этой цели потребуется нечто большее, чем риторика. Хотя ценное профессиональное обучение, ресурсы и дополнительное время являются важными шагами, возможно, что решение задач по математике будет цениться только тогда, когда оценка с высокими ставками будет отражать важность решения учащимися сложных задач.
Что делает математическую задачу ХОРОШЕЙ? – Двухминутное руководство для учителя
Мы часто узнаем хорошую математическую задачу, когда видим ее — или, может быть, поработав над ней какое-то время — но трудно сказать, что именно делает задачу такой хорошей, и под «хорошей» мы подразумеваем математически стоящую задачу и . . Мы пришли к оценке следующих особенностей, которые, по нашему мнению, являются важными компонентами хорошей задачи :
. Мы пришли к оценке следующих особенностей, которые, по нашему мнению, являются важными компонентами хорошей задачи :
Как и в случае с хорошей историей, людей нужно с самого начала вовлекать в интересную проблему. Если требуется слишком много времени, чтобы понять, о чем проблема, или если она разбита на слишком много маленьких кусочков, становится трудно понять, какова цель или почему вы вообще изучаете проблему.
Четкое и краткое изложение проблемы и быстрая «зацепка» — лучший способ вовлечь людей в проблему, и сделать задачу (т. доступным для всех учащихся.
Вот несколько примеров задач с четкими и краткими целями. (Они не обязательно соответствуют более поздним критериям, но они определенно соответствуют критерию № 1.) Они требуют некоторых базовых знаний, но если у вас есть эти базовые знания, вы можете довольно быстро попасться на крючок:
Можно ли любую трапецию разрезать и превратить в прямоугольник?
Почему каждая сумма 5 последовательных чисел делится на 5?
Выходит ли кривая для y= 1,01 x выше кривой для y= 100 x 2 + 1 ?
Что больше, красная область или синяя область?
Обратите внимание, что основная цель может быть общей или частной по своей природе, а зацепка может быть основана на шаблоне, ключевом вопросе или визуальном сигнале. Существует широкий спектр возможностей для изготовления крючка. что мы не здесь проблемы, которые начинаются с полутора страниц настройки и нескольких подвопросов, прежде чем мы когда-либо доберемся до конечной точки всего этого. Чтобы было ясно, мы не говорим, что большие объемы информации или контекстуальный фон несовместимы с хорошими математическими задачами. Действительно, многие хорошие математические задачи будут включать в себя глубокое погружение в соответствующие контексты и просеивание потенциально полезной информации, чтобы решить, что нужно включить в решение, но наша точка зрения заключается в том, что с хорошими задачами мы уже заранее понимаем цель. on, а не только в конце (или вообще не).
Существует широкий спектр возможностей для изготовления крючка. что мы не здесь проблемы, которые начинаются с полутора страниц настройки и нескольких подвопросов, прежде чем мы когда-либо доберемся до конечной точки всего этого. Чтобы было ясно, мы не говорим, что большие объемы информации или контекстуальный фон несовместимы с хорошими математическими задачами. Действительно, многие хорошие математические задачи будут включать в себя глубокое погружение в соответствующие контексты и просеивание потенциально полезной информации, чтобы решить, что нужно включить в решение, но наша точка зрения заключается в том, что с хорошими задачами мы уже заранее понимаем цель. on, а не только в конце (или вообще не).
Итак, в хорошей задаче вам не нужно слишком много работать над выяснением вопроса, но…
2. Путь решения не очевиден сразу . Если ответ или путь к этому ответу действительно очевиден, то это вообще не проблема, не так ли? Другими словами, если первое, что пытается сделать человек, сразу же срабатывает, то это скорее процедурное упражнение, чем проблема.
В хорошей задаче нет однозначного пути, который ведет прямо к ответу. Может быть несколько путей, которые кажутся правдоподобными, и мы не узнаем, сработают ли они, пока не попытаемся следовать им и не посмотрим, как далеко мы продвинемся — может быть, они все сработают, что было бы хорошо, но мы не можем сказать, Начало. А может есть нет сначала чистый путь, и нам придется немного исследовать его в темноте, прежде чем мы найдем многообещающий первый шаг. (Исследование в темноте — не всегда положительный опыт, но именно поэтому так важно иметь четкую цель — по крайней мере, вы знаете, что исследуете в темноте за .)
Следствием этой функции является то, что хорошо проблемы обязательно потребуют по крайней мере пару минут, чтобы решить (или добраться до удовлетворительной точки остановки). Если вы сможете решить ее за 30 секунд, мы не будем считать это хорошей задачей. Важно потратить хотя бы немного осмысленного времени на работу над проблемой, потому что это дает вам возможность подумать о том, что вы делаете и куда направляетесь, дает вам опыт, которым вы можете поделиться с другими людьми, и позволяет вам инвестировать время и усилия в проблему, чтобы она действительно окупилась, когда вы найдете решение.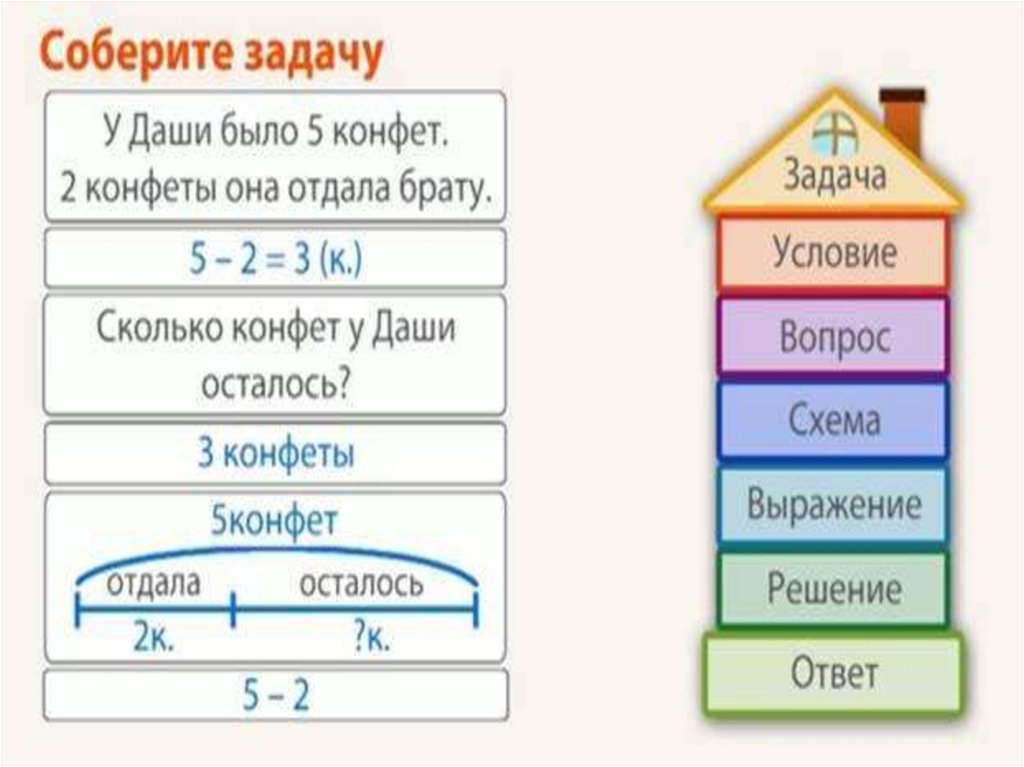
Работа над хорошими задачами иногда может занять 2-3 минуты (но это были значимые и полезные 2-3 минуты), а может занять час или даже несколько недель. Эти временные рамки не гарантируют, что это хорошая задача (к сожалению, люди могут тратить часы на решение плохих задач, например, на деление в длинное число 12 389 010 270, деленное на 112, или на попытку найти форму случайной матрицы 5 × 5 с уменьшенным числом строк). ), но мы думаем, что хорошие проблемы требуют усилий и времени, чтобы их раскрыть.
Итак, если большая часть наших усилий уходит на поиск работающего решения, важно, чтобы…
3.
Проблема допускает несколько плодотворных путей .Иногда проблема удовлетворяет признаку № 1 (четкая цель) и признаку № 2 (требует определенных усилий, чтобы найти решение), но, в конце концов, есть только один способ прорваться и решить ее. Возьмем в качестве примера следующую задачу:
Проблема из ежедневной головоломки Вы, скорее всего, будете пробовать много вещей, которые вообще не работают, пока вам, наконец, не повезет найти ключ для ее разблокировки (подсказка: обратите внимание, что первое «дополнение» — это делитель «суммы»), и в ретроспективе кажется, что проблема явно вводила в заблуждение (символ сложения на самом деле не представляет сложение).
Этими задачами может быть интересно поделиться, и после того, как вы прорветесь, часто возникает чувство выполненного долга, но обычно они могут служить «трюком» или головоломкой. Люди, которые их разгадывают, образуют эксклюзивный клуб тех, кто разгадал трюк. (Некоторым людям нравится делиться этими проблемами просто для того, чтобы посмотреть, столь же «умны» другие, как они. Например, вот задача с подвохом, где люди действительно могут получить членские билеты, если разберутся в этом трюке.) Но, если вам случится, думать о вещах по-другому или не иметь опыта, позволяющего прорваться, то вы, вероятно, надолго останетесь в тупике и в конце концов просто сломаетесь до «Хорошо, скажите мне, как это решить».
Вместо этого мы предпочитаем такие задачи:
Определим бинарный оператор § таким образом, что 1 § 1 = 1 и 2 § 4 = 16 . Каковы другие примеры вашего бинарного оператора в действии?
Эта проблема допускает несколько плодотворных путей. Один человек может подумать о показателях и определить a § b как a b . Но другие люди могут думать иначе, например, § b = a 4 или
Один человек может подумать о показателях и определить a § b как a b . Но другие люди могут думать иначе, например, § b = a 4 или
a § b = ab , когда оба нечетны, и a § b = 2 ab четно, когда хотя бы одно. Все эти идеи на самом деле соответствуют требованиям задачи и могут привести к интересным идеям о свойствах операций (например, одна из вышеперечисленных является коммутативной) и четкости (например, два экземпляра не определяют операцию однозначно). .
Эти типы проблем с несколькими плодотворными путями позволяют разнообразить мысли и делают проблему более интересной для обсуждения с другими, потому что мы можем искренне интересоваться тем, что думают о ней другие люди.
До сих пор критерии, которые мы изложили, могли привести к хорошей задаче в любой предметной области, поэтому давайте уточним, что…
4.
Хорошая математическая задача включает в себя полезные математические идеи .
То, что делает проблему стоящей, зависит от человека. Что-то полезное для четвероклассника может быть не столь ценным для студента, изучающего математику. Дело не только в том, на каком уровне математики находится человек, но и в том, какие аспекты математики он ценит. Например, люди, приверженные использованию математики в качестве инструмента для обеспечения социальной справедливости, могут рассматривать математические представления, количественно оценивающие неравенство, как полезные. Людям, которые надеются стать инженерами, могут пригодиться дифференциальные уравнения. (А для других полезная математика может просто зависеть от критерия № 5; см. ниже).
Математика в хорошей задаче не слишком перегружена математическими мелочами и не слишком потеряна в контексте «реального мира». Например, задача Daily Brain Teaser из № 3 в конечном итоге зависит от довольно запутанной экспоненциальной функции, которая, вероятно, не имеет смысла для большинства людей. А задача сравнения между y= 1,01 x и y= 100 x 2 + 1, хотя и имеет четкую цель, сама по себе, вероятно, не очень стоящая.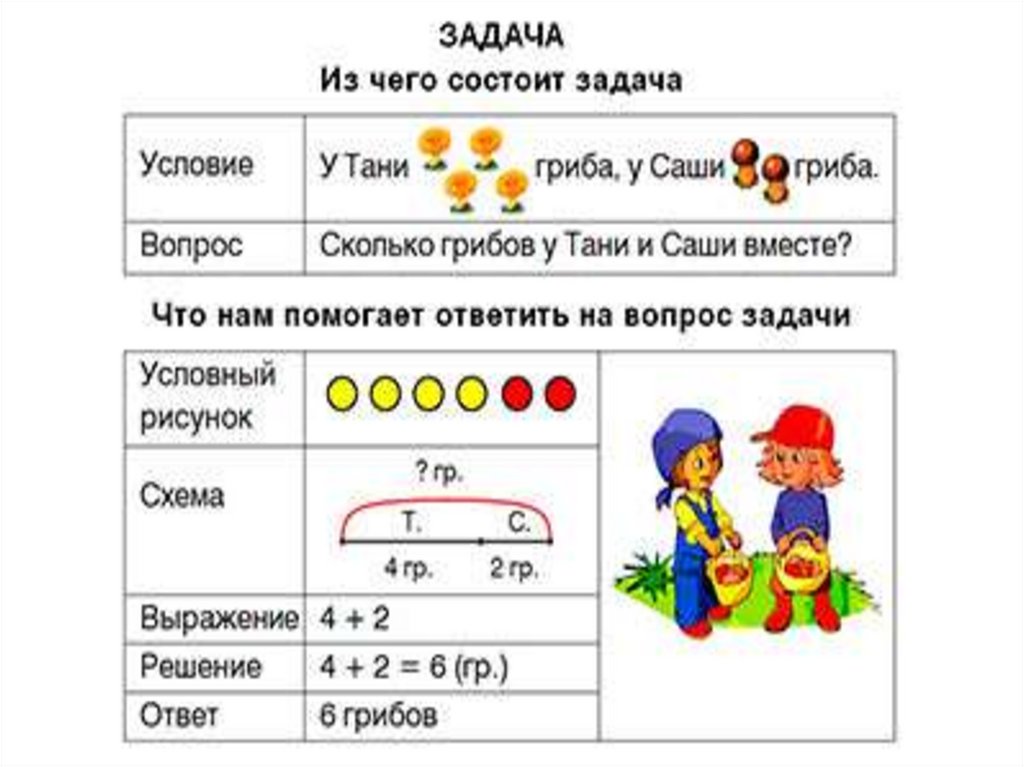 Но, возможно, было бы целесообразно расширить его до более широкой идеи об экспоненциальном росте по сравнению с полиномиальным ростом в целом. Пример задачи равно , вероятно, полезной для многих школьников, изучающих математику, является проблема Красной/Синей области, описанная выше, потому что она может показаться эзотерической на первый взгляд, но на самом деле приводит к важным идеям о связи между треугольной площадью и площадью параллелограмма, а также об инвариантности сравнения площадей. хотя ситуация постоянно меняется.
Но, возможно, было бы целесообразно расширить его до более широкой идеи об экспоненциальном росте по сравнению с полиномиальным ростом в целом. Пример задачи равно , вероятно, полезной для многих школьников, изучающих математику, является проблема Красной/Синей области, описанная выше, потому что она может показаться эзотерической на первый взгляд, но на самом деле приводит к важным идеям о связи между треугольной площадью и площадью параллелограмма, а также об инвариантности сравнения площадей. хотя ситуация постоянно меняется.
Проблемы, соответствующие критерию №4, находятся в зоне Златовласки. Они включают соответствующие и достижимые математические идеи и практики. В целом, эта функция помогает четко указать, что хорошая проблема не обязательно является хорошей проблемой 9.0159 везде и в любое время — это хорошая задача для конкретных целей и с конкретными людьми.
И, наконец, немного субъективно…
5. Над хорошей математической задачей весело работать над .
Могут быть проблемы, которые удовлетворяют требованиям пунктов с 1 по 4, но над которыми сложно работать или которые не соответствуют индивидуальным предпочтениям. А некоторые проблемы могут доставлять удовольствие одному человеку, но не находить отклика у других. Так что, в конечном счете, здесь есть доля личной субъективности, но, надеюсь, если вы ищете хорошие задачи, ваш вкус в хороших задачах, по крайней мере, в чем-то похож на вкус ваших сверстников, ваших студентов или кого-то еще, кто может решать задачи с ними. ты.
Заключение и ресурсы
Одно важное предостережение заключается в том, что эти функции, как мы обнаружили, важны для хороших математических задач, но это не распространяется непосредственно на учебный план по математике . Учебная программа — это гораздо больше, чем набор хороших задач, поэтому мы не хотим, чтобы кто-то ошибочно принял это за одобрение определенного типа учебной программы или подхода к обучению. Мы думаем, что хорошие задачи являются необходимой частью хорошей учебной программы по математике, но учебная программа также должна включать хорошо продуманную разработку концепции наряду с процедурной практикой. Он должен иметь отношение к жизни учащихся и, в идеале, должен быть направлен на улучшение мира, в котором мы все живем.
Он должен иметь отношение к жизни учащихся и, в идеале, должен быть направлен на улучшение мира, в котором мы все живем.
Но что касается конкретно хороших математических задач, вот несколько мест, где вы можете их найти:
https://www.openmiddle.com/
http://mathpractices.edc.org/
https://gfletchy .com/3-act-lessons/
https://www.illustrativemathematics.org/
https://www.youcubed.org/
https://wodb.ca/
Подробнее см. на http:// bit.ly/GoToMathTasks
Поделитесь своими хорошими задачами (или задачами, которые могут быть «хорошими», но вы не уверены) в комментариях ниже.
Самуэль Оттен ([email protected]) с Зандрой де Араужо и Джепилом Ханом
Нравится:
Нравится Загрузка…
Как решать сложные математические задачи
Родитель одного из наших учеников написал сегодня о периодическом расстройстве своей дочери из-за сложности некоторых задач на наших курсах. Она отлично работает на наших курсах и легко входит в число самых лучших учеников в классе, который она брала со мной, и все же иногда она сталкивается с проблемами, которые не может решить.
Кроме того, у нее есть доступ к отличному учителю математики в ее школе, который иногда тоже не может помочь ей решить эти проблемы. (Это не мелочь для него — у меня есть ученики, которые тоже приносят мне задачи, которые я не могу решить!) Ее вопрос: «Почему это должно быть так сложно?»
Дело в том, что нужно делать трудные вещи
Мы задаем трудные вопросы, потому что многие проблемы, которые стоит решить в жизни, сложны. Если бы они были легкими, кто-то другой решил бы их до того, как вы до них доберетесь. Вот почему на занятиях в ведущих университетах есть тесты, по которым почти никто не набирает 70%, не говоря уже о том, чтобы получить высший балл. Они обучают будущих исследователей, и весь смысл исследования заключается в том, чтобы найти и ответить на вопросы, которые никогда не были решены. Вы не можете научиться этому, не сталкиваясь с проблемами, которые не можете решить. Если вы последовательно решаете каждую задачу в классе правильно, вы не должны слишком радоваться — это означает, что вы учитесь недостаточно эффективно. Вам нужно найти класс посложнее.
Вам нужно найти класс посложнее.
Проблема недостаточной сложности выходит далеко за рамки того, что вы не изучаете математику (или что-то еще) так быстро, как только можете. Я думаю, что многое из того, что мы делаем в AoPS, готовит учащихся к задачам, выходящим далеко за рамки математики. Те же самые стратегии, которые используются при решении очень сложных математических задач, могут быть использованы для решения очень многих задач. Я считаю, что мы учим студентов, как думать, как решать сложные проблемы, и что математика оказывается лучшим способом сделать это для многих людей.
Первый шаг в решении сложных проблем — принять и понять их важность. Не уклоняйтесь от них. Они научат вас гораздо большему, чем рабочий лист с простыми задачами. Блестящий «Ага!» 90–160 мгновений почти всегда рождаются в умах, взращенных долгими периодами разочарований. Но без этого разочарования эти блестящие идеи никогда не возникнут.
Стратегии решения сложных математических задач и не только
Вот несколько стратегий решения сложных задач и разочарования, которое они вызывают:
Сделай что-нибудь . Да, проблема сложная. Да вы понятия не имеете, что делать, чтобы решить эту проблему. В какой-то момент вы должны перестать пялиться и начать пробовать что-то новое. Большая часть не будет работать. Примите тот факт, что многие ваши усилия будут потрачены впустую. Но есть шанс, что один из ваших ударов во что-то попадет, и даже если нет, усилия могут подготовить ваш разум к победной идее, когда придет время.
Да, проблема сложная. Да вы понятия не имеете, что делать, чтобы решить эту проблему. В какой-то момент вы должны перестать пялиться и начать пробовать что-то новое. Большая часть не будет работать. Примите тот факт, что многие ваши усилия будут потрачены впустую. Но есть шанс, что один из ваших ударов во что-то попадет, и даже если нет, усилия могут подготовить ваш разум к победной идее, когда придет время.
Мы начали разрабатывать программу начальной школы за несколько месяцев до того, как у нас появилась идея создать Академию Зверей. Наш ведущий разработчик учебной программы написал 100–200 страниц контента, придумав множество различных стилей и подходов, которые мы могли бы использовать. Ни одна из этих страниц не войдет в окончательную работу, но они породили множество идей для контента, который мы будем использовать. Возможно, что еще более важно, это подготовило нас к тому, что, когда мы, наконец, пришли к идее Академии Зверей, мы были достаточно уверены, чтобы следовать ей.
Упростите задачу . Попробуйте меньшие числа и особые случаи. Снять ограничения. Или добавить ограничения. Настройте свои цели немного ниже, а затем поднимите их, как только вы решите более простую проблему.
Подумай об успехах . Вы решили много проблем. Некоторые из них были даже трудными задачами! Как ты сделал это? Начните с проблем, похожих на ту, с которой вы столкнулись, но подумайте и о других, которые не имеют ничего общего с вашей текущей проблемой. Подумайте о стратегиях, которые вы использовали для решения этих проблем, и вы можете просто наткнуться на решение.
Несколько месяцев назад я играл с некоторыми задачами Project Euler и наткнулся на задачу, которая (в конце концов) сводилась к генерации целочисленных решений для c ² = a ² + b ² + ab эффективным образом. Теория чисел не моя сильная сторона, но мой путь к решению заключался в том, чтобы сначала вспомнить метод построения пифагорейских троек. Затем я подумал о том, как сгенерировать этот метод, и путь к решению стал ясен. (Я предполагаю, что некоторые из наших математически продвинутых читателей настолько усвоили процесс решения этого типа диофантова уравнения, что вам не нужно путешествовать с Пифагором, чтобы добраться до него!)
Затем я подумал о том, как сгенерировать этот метод, и путь к решению стал ясен. (Я предполагаю, что некоторые из наших математически продвинутых читателей настолько усвоили процесс решения этого типа диофантова уравнения, что вам не нужно путешествовать с Пифагором, чтобы добраться до него!)
Сосредоточьтесь на том, что вы еще не использовали . Многие задачи (особенно задачи геометрии) имеют много движущихся частей. Оглянитесь на проблему и открытия, которые вы сделали до сих пор, и спросите себя: «Что я еще не использовал конструктивным образом?» Ответ на этот вопрос часто является ключом к вашему следующему шагу.
Работа в обратном направлении . Это особенно полезно при поиске доказательств. Вместо того, чтобы начинать с того, что вы знаете, и двигаться к тому, чего вы хотите, начните с того, чего вы хотите, и спросите себя, что вам нужно для этого.
Просить о помощи . Это тяжело для многих отличников. Вы так привыкли все делать правильно, быть тем, о ком все спрашивают, что вам трудно признать, что вам нужна помощь. Когда я впервые попал в программу математической олимпиады (MOP) на втором курсе, я был выше головы. Я мало что понимал из того, что происходило в классе. Однажды я обратился за помощью к профессору — очень трудно было набраться смелости сделать это. Я ничего не понял из того, что он сказал мне в течение 15 минут, когда он работал со мной наедине. Я просто не мог признать это и просить о дополнительной помощи, поэтому перестал просить. Я мог бы многому, гораздо большему научиться, если бы был более готов признаться людям, которых я просто не понимаю. (Отчасти поэтому в наших классах теперь есть функция, позволяющая учащимся задавать вопросы анонимно.) Преодолей это. Вы застрянете. Вам понадобится помощь. И если вы попросите об этом, вы добьетесь гораздо большего, чем если бы вы этого не сделали.
Когда я впервые попал в программу математической олимпиады (MOP) на втором курсе, я был выше головы. Я мало что понимал из того, что происходило в классе. Однажды я обратился за помощью к профессору — очень трудно было набраться смелости сделать это. Я ничего не понял из того, что он сказал мне в течение 15 минут, когда он работал со мной наедине. Я просто не мог признать это и просить о дополнительной помощи, поэтому перестал просить. Я мог бы многому, гораздо большему научиться, если бы был более готов признаться людям, которых я просто не понимаю. (Отчасти поэтому в наших классах теперь есть функция, позволяющая учащимся задавать вопросы анонимно.) Преодолей это. Вы застрянете. Вам понадобится помощь. И если вы попросите об этом, вы добьетесь гораздо большего, чем если бы вы этого не сделали.
Начать раньше . Это не очень помогает в тестах на время, но в случае более сложных заданий, которые являются частью учебы в колледже и жизни, это необходимо. Не ждите до последней минуты — сложные задачи достаточно сложны и без необходимости сталкиваться с нехваткой времени. Более того, для полного понимания сложных идей требуется много времени. Люди, которых вы знаете, которые кажутся чертовски умными и которые, кажется, придумывают идеи намного быстрее, чем вы могли бы, часто являются людьми, которые просто думали о проблемах гораздо дольше, чем вы. Я использовал эту стратегию в колледже с большим успехом — в первые несколько недель каждого семестра я продвигался вперед во всех своих классах. Поэтому к концу семестра я обдумывал ключевые идеи гораздо дольше, чем большинство моих одноклассников, что значительно облегчало экзамены и тому подобное в конце курса.
Более того, для полного понимания сложных идей требуется много времени. Люди, которых вы знаете, которые кажутся чертовски умными и которые, кажется, придумывают идеи намного быстрее, чем вы могли бы, часто являются людьми, которые просто думали о проблемах гораздо дольше, чем вы. Я использовал эту стратегию в колледже с большим успехом — в первые несколько недель каждого семестра я продвигался вперед во всех своих классах. Поэтому к концу семестра я обдумывал ключевые идеи гораздо дольше, чем большинство моих одноклассников, что значительно облегчало экзамены и тому подобное в конце курса.
Сделай перерыв . Отвлекитесь на некоторое время от проблемы. Когда вы вернетесь к этому, вы можете обнаружить, что не полностью избавились от проблемы — фоновые процессы вашего мозга продолжают отключаться, и вы окажетесь намного ближе к решению. Конечно, намного легче сделать перерыв, если вы начнете рано.
Начать сначала . Отложите всю предыдущую работу, возьмите свежий лист бумаги и попробуйте начать с нуля. Ваша другая работа все еще будет там, если вы захотите извлечь из нее позже, и, возможно, она подготовила вас к тому, чтобы извлечь выгоду из идей, которые вы сделаете во время второго раунда.
Ваша другая работа все еще будет там, если вы захотите извлечь из нее позже, и, возможно, она подготовила вас к тому, чтобы извлечь выгоду из идей, которые вы сделаете во время второго раунда.
Сдаться . Всех не решишь. В какой-то момент пришло время сократить свои потери и двигаться дальше. Это особенно верно, когда вы тренируетесь и пытаетесь узнать что-то новое. Одна-единственная трудная задача обычно научит вас большему за первый или два часа, чем за следующие шесть, а есть еще много проблем, на которых можно учиться. Итак, установите себе ограничение по времени, и если вы все еще безнадежно застряли в его конце, то прочитайте решения и двигайтесь дальше.
Будьте самоанализом . Если вы сдаетесь и читаете решение, то читайте его активно, а не пассивно. Читая его, подумайте, какие подсказки в задаче могли привести вас к этому решению. Подумайте, что вы сделали не так в своем расследовании. Если в решении есть математические факты, которые вы не понимаете, идите исследовать. Я был совершенно сбит с толку, когда впервые увидел кучу материала о «модах» в олимпиадном решении — у нас тогда не было интернета, поэтому я не мог легко узнать, насколько проста модульная арифметика! Теперь у вас есть интернет, так что у вас нет оправдания. Если вы решили проблему, не хлопайте себя по спине. Подумайте о ключевых шагах, которые вы сделали, и о том, каковы были признаки того, что вы должны их попробовать. Подумайте о тупиках, которые вы исследовали на пути к решению, и о том, как вы могли их избежать. Эти уроки пригодятся вам позже.
Я был совершенно сбит с толку, когда впервые увидел кучу материала о «модах» в олимпиадном решении — у нас тогда не было интернета, поэтому я не мог легко узнать, насколько проста модульная арифметика! Теперь у вас есть интернет, так что у вас нет оправдания. Если вы решили проблему, не хлопайте себя по спине. Подумайте о ключевых шагах, которые вы сделали, и о том, каковы были признаки того, что вы должны их попробовать. Подумайте о тупиках, которые вы исследовали на пути к решению, и о том, как вы могли их избежать. Эти уроки пригодятся вам позже.
Вернись . Если вы сдались и посмотрели на решения, то вернитесь и повторите попытку через несколько недель. Если у вас нет никаких решений, на которые можно было бы обратить внимание, сохраняйте проблему актуальной. Сохраните это на бумаге или в уме.
Ричард Фейнман однажды написал, что держит в уме четыре или пять проблем. Всякий раз, когда он слышал о новой стратегии или технике, он быстро просматривал свои проблемы и смотрел, сможет ли он использовать их для решения одной из своих проблем. Он приписывает этой практике некоторые анекдоты, которые дали Фейнману такую репутацию гения. Это еще одно доказательство того, что быть гением — это очень много усилий, подготовки и способности справляться с трудностями.
Он приписывает этой практике некоторые анекдоты, которые дали Фейнману такую репутацию гения. Это еще одно доказательство того, что быть гением — это очень много усилий, подготовки и способности справляться с трудностями.
Что такое проблема? | NZ Maths
Мы обсуждаем «Что такое проблема» под тремя заголовками: определение, примеры и задачи, которые интересуют учащихся.
ОпределениеПроблема есть проблема, потому что вы не знаете сразу, как это сделать.
Самое странное в проблемах то, что то, что является проблемой для одного человека, не обязательно является проблемой для кого-то другого. Это потому, что нет двух людей с одинаковым набором переживаний. Следовательно, один человек может понять формулировку проблемы быстрее, чем один из его друзей. Скорее всего, вы сможете решить больше задач, чем ваши ученики, просто потому, что вы более опытны и обладаете большим словарным запасом.
Теперь не все математические вопросы являются задачами. Для начала, вопрос, относящийся к последней математике, которую вы преподавали в классе, не является проблемой в том смысле, в каком мы будем использовать это слово. Ваши ученики уже знают стратегию, которую можно использовать в таких вопросах.
Для начала, вопрос, относящийся к последней математике, которую вы преподавали в классе, не является проблемой в том смысле, в каком мы будем использовать это слово. Ваши ученики уже знают стратегию, которую можно использовать в таких вопросах.
Более того, хотя многие задачи являются задачами со словами, не все вопросы со словами являются задачами. Точно так же вопрос без слов или с несколькими словами все еще может быть проблемой.
Проблемы должны быть представлены на соответствующем уровне. Они должны стать вызовом для учащихся. В то же время они не должны быть слишком сложными. Студенты должны чувствовать, что у них есть разумный шанс решить проблему самостоятельно или в группе.
Вам нужно просмотреть задачи, которые собираетесь использовать, и убедиться, что они подходят для вашего класса. Вы должны проверить, что все члены класса могут что-то получить от задачи. Есть ли момент, когда более слабые ученики могут остановиться, но все равно выиграют от решения проблемы? Есть ли что-то, чтобы расширить более способных студентов? Существует ли метод, который все учащиеся могут использовать для решения задачи? Есть ли более сложный метод, который бросит вызов некоторым из ваших учеников?
Так что же может помешать вам или одному из ваших учеников решить математическую задачу? Ну, во-первых, в формулировке может быть что-то, чего вы не понимаете. Во-вторых, вы можете не увидеть, как начать работу . У вас может не быть очевидной стратегии , которую вы могли бы использовать. В-третьих, вы можете не знать правильный кусок математики для использования. И в-четвертых, вы можете знать правильную стратегию и правильную математику, но вам может не быть , используя их правильно , иначе вы не сможете понять, как сложить их вместе, чтобы найти решение.
Во-вторых, вы можете не увидеть, как начать работу . У вас может не быть очевидной стратегии , которую вы могли бы использовать. В-третьих, вы можете не знать правильный кусок математики для использования. И в-четвертых, вы можете знать правильную стратегию и правильную математику, но вам может не быть , используя их правильно , иначе вы не сможете понять, как сложить их вместе, чтобы найти решение.
Чтобы помочь вам лучше понять, что такое проблема и для кого она является проблемой, вот несколько примеров проблем. Мы считаем, что Задача 1 подходит для Уровня 1, Задача 2 — для Уровня 2, Задача 3 — для Уровня 3 и так далее.
Проблема 1: Коревые пятна (Уровень 1)
У бедной Пэм корь. У нее по одному пятну на подбородке, по одному пятну на каждой ноге, по одному пятну на каждой руке и по одному пятну на животе. Сколько пятен от кори у Пэм?
На следующее утро Пэм просыпается с еще большим количеством пятен! Теперь у нее два на подбородке, по два на каждой руке и каждой ноге и два на животе. Сколько мест у нее сейчас?
Сколько мест у нее сейчас?
Проблема 2: Записи (Уровень 2)
Рози и Рату рыскали в семейной машине. Каждый из них собрал вместе все кассеты, которые смог найти. Той ночью Рози и Рату рассортировали и пересчитали кассеты. Они обнаружили, что
- , когда они считали четверками, у них оставалось три из 9.0030
- когда они считали пятерками, у них не осталось больше
- , когда они считали по три, у них не оставалось лишнего.
Их отец знал, что у них меньше 18 кассет. Сколько лент они собрали?
Задача 3: телепрограммы (уровень 3)
У животных в сарае всего 26 ног и 10 голов.
Если в амбаре только овцы и куры, сколько их там?
Задача 4: Башни (Уровень 4)
Том любит строить башни. У него есть коллекция черных кубиков и белых кубиков. Если поставить разные кубики друг на друга, получится башня. Если высота башни равна количеству кубов, используемых в этой башне,
- , сколько различных башен, имеющих высоту один, можно построить?
- сколько различных башен высотой два можно построить?
- сколько различных башен высотой три можно построить?
- сколько разных башен можно построить за 9 башен0012 любая конкретная высота?
Задача 5: Теннис (уровень 5)
В круговом чемпионате по теннису 20 человек должны играть друг с другом. Сколько игр нужно сыграть?
Сколько игр нужно сыграть?
Организаторы решают, что игр слишком много, и вместо этого проводят соревнование на выбывание. Сколько игр проводится по этой системе?
Задача 6. Числа (уровень 6)
Различные целые числа складываются вместе, чтобы получить 2001. Каково наибольшее возможное произведение этих целых чисел?
Другим аспектом проблем является их внутренний интерес. В классе проблема должна быть чем-то, что интересует учащихся и что они определенно хотят или должны решить. Вы можете сделать задачи более привлекательными для учащихся, помещая их в интересующий их контекст и используя их имена для персонажей задачи.
Вероятно, вы знаете, как сделать шесть вышеперечисленных задач более подходящими для вашего класса. Например, если в вашем классе 1-го уровня есть что-то о больших кошках, вы можете заменить пятна кори пятнами на леопарде. Задачу 2 очень легко изменить, изменив имена на имена учащихся вашего класса. Что вы могли бы сделать с другими задачами, чтобы приблизить их к интересам ваших учеников?
Что вы могли бы сделать с другими задачами, чтобы приблизить их к интересам ваших учеников?
Целью этого веб-сайта является помочь вам предоставить своим ученикам опыт обучения, чтобы они были готовы уверенно решать любые проблемы, возникающие на их пути. Для этого им нужно будет увидеть, как интерпретировать вопрос; выбирать и использовать подходящие стратегии; и использовать стратегии и математику, которые они знают, для решения проблем.
Математические задачи от Good Will Hunting, с решениями | Йорген Вейсдал
Фото : © 1997 Miramax PicturesЦель этой статьи — рассказать вам о решениях двух математических задач, решенных вымышленным персонажем Уиллом в фильме 1997 года, удостоенном премии «Оскар», «Умница Уилл Хантинг». Повествование в значительной степени основано на отличной статье «Математика в охоте за доброй волей II: проблемы с точки зрения студентов » Хорвата, Коранди и Сабо (2010).
Музыка для настроения Spotify. Приятного чтения!
Краткое изложение Умница Уилл Хантинг рассказывает историю вымышленного персонажа Уилла Хантинга, который, несмотря на свой исключительный интеллект, работает уборщиком в Массачусетском технологическом институте в Бостоне. Там он однажды замечает задачу на доске в коридоре, поставленную профессором Джеральдом Ламбо, обладателем медали Филдса. Обладая эйдетической памятью, Уилл запоминает задачу и решает ее перед зеркалом в своей ванной дома в Южном Бостоне. Вернувшись на следующий день в Массачусетский технологический институт, он не может ничего с собой поделать, но анонимно представляет свое решение на доске.
Там он однажды замечает задачу на доске в коридоре, поставленную профессором Джеральдом Ламбо, обладателем медали Филдса. Обладая эйдетической памятью, Уилл запоминает задачу и решает ее перед зеркалом в своей ванной дома в Южном Бостоне. Вернувшись на следующий день в Массачусетский технологический институт, он не может ничего с собой поделать, но анонимно представляет свое решение на доске.
Когда на следующий день ни один из студентов Ламбо не претендует на зачет, профессор ставит другую, более сложную задачу. Уилл снова решает ее, но профессор ловит его в момент написания своего решения, который потрясен, узнав, что самый блестящий молодой математик в Массачусетском технологическом институте — необразованный уборщик.
Профессор Джеральд Ламбо (в исполнении Стеллана Скарсгарда) просматривает предложенное Уиллом решение. Фото : © 1997 Miramax PicturesЗадача 1: По графу G найти 1. Матрица смежности, AРисунок 1: График G
2. Матрица, задающая количество 3-шаговых блужданий
3.Производящая функция для блужданий от i → j
4. Производящая функция для блужданий от 1 → 3
Первая задача теории графов требует количества обходов от вершины i до вершины j в графе G. Для этого пусть G — граф с множеством вершин V = {1, 2 , 3, 4} и множество ребер E = {(1,2), (1,4), (2,4), (2,3),(2,3)}, где (2,3) — обоюдоострый.
Решения задачи 1
Задача 1.1
Для заданного графа G найдите матрицу смежности A
Матрица смежности — это квадратная матрица, используемая для представления конечного графа. Элементы матрицы смежности L указывают, являются ли пары вершин в графе смежными или нет. Для простого графа с набором вершин V матрица смежности представляет собой квадрат |L| × |Л| матрица такая, что ее элемент L ᵢⱼ равен 1, когда есть одно ребро из вершины i до вершины j , 2, если их два, и ноль, если нет ребер из вершины i в вершину j. Все диагональные элементы матрицы равны нулю, поскольку ребра из вершины i в саму себя (петли) не допускаются в простых графах. Для всех ступенчатых обходов длины 1 вдоль множества ребер E это дает нам следующую матрицу смежности для графа G:
Все диагональные элементы матрицы равны нулю, поскольку ребра из вершины i в саму себя (петли) не допускаются в простых графах. Для всех ступенчатых обходов длины 1 вдоль множества ребер E это дает нам следующую матрицу смежности для графа G:
Задача 1.2
Найдите матрицу, определяющую количество трехшаговых прогулок
Во второй задаче задачи 1 нужно найти матрицу, которая кодирует все возможные прогулки длины 3 (Knill, 2003). То есть найти количество различных последовательностей ребер, соединяющих каждую отдельную последовательность вершин.
n + 1 шаг от i до j состоит из n шагов от i до k и затем 1 шаг от к до j . То есть запись ij L ⁿ⁺¹ задается суммой:
Equation 1 Которое на английском языке для этой задачи гласит, что «количество обходов длины 3 из вершины i в j» равно сумма «количества прогулок длины 2 от вершины i до k» , умноженная на «количество прогулок длины 1 от вершины k до j» для k = 1,2. Путем матричного умножения, для всех ступенчатых обходов длины 3 от i до j это дает следующую матрицу:
Путем матричного умножения, для всех ступенчатых обходов длины 3 от i до j это дает следующую матрицу:
Задача 1.3
Найти производящую функцию для обходов из i → j
Третья задача в задаче 1 запрашивает производящую функцию из вершины i от до j . Чтобы ответить на этот вопрос, Хорват и др. (2010) рассматривают аналитическую производящую функцию, определяемую степенным рядом
Уравнение 2Где коэффициент zⁿ обозначает число n шаговая прогулка от i до j . Из задачи 1.3 мы нашли, что ω_n(i → j) является ij элементом матрицы Lⁿ . В задаче требуется производящая функция, которая дает все элементы одновременно, поэтому имеет смысл рассмотреть матрицу L , заданную знакомым степенным рядом (Horváth et al, 2010):
Уравнение 3 Где Lⁿ — это матрица, содержащая количество ступенчатых обходов от каждой вершины i до j (общий случай решения задачи 1. 2). Сумма может быть рассчитана с использованием известного тождества для геометрического степенного ряда, а именно: Согласно Horváth et al (2010) для матрицы M пусть Mᵢⱼ обозначает матрицу, полученную из M удалением i -го столбца и j -й строки. Если мы это сделаем, мы получим матрицу N, ij запись равна
2). Сумма может быть рассчитана с использованием известного тождества для геометрического степенного ряда, а именно: Согласно Horváth et al (2010) для матрицы M пусть Mᵢⱼ обозначает матрицу, полученную из M удалением i -го столбца и j -й строки. Если мы это сделаем, мы получим матрицу N, ij запись равна
По правилу Крамера, если M обратима (существует некоторая n×n матрица N такая, что M × N = N × M = 00159 I_n 901), то 3 6 60159 I_n Уравнение 6
То есть запись ij обратной матрицы M: 8
Замена M:
Решение 1.3. 9(i+j) (вероятно, из-за обозначений), и он обозначает единичную матрицу с 1 вместо более распространенного I .Задача 1.4
Найти производящую функцию для блужданий от 1 → 3
Для решения задачи 1.4 просто применим общую формулу для блужданий от i к j (из задачи 1.3) к случаю блужданий от 1 → 3 :
Уравнение 9.
Определители которого легко найти:
Уравнения 10 и 11. Определители ( I − zL ) и его младший/приведенный определитель ( I ₁₃ − zL ₁₃)Задав следующие выражения, получим, используя определение определителя:
Уравнение 12. Формула для определения производящей функции для обходов из вершины 1 в вершину 3. Уравнение 13. Формула для определения значений производящей функции для блужданий из вершины 1 в вершину 3, решеннаяДля получения коэффициентов этого степенного ряда вычисляется ряд Тейлора функции:
Уравнение 14. f(z) — ряд Маклорена, где fⁿ(0) — n-я производная от f при 0,Для нашего выражения f(z) мы можем использовать правило частных, где g(z) = 2z² и h(z) = 4z³− 6z² −z +1. В фильме Уилл приводит значения первых шести производных разложения f(z):
Решение 1.4. Разложение Тейлора для определения значений производящей функции для блужданий из вершины 1 в вершину 3В шоке профессор Ламбо смотрит на правильное решение второй задачи, данное анонимным уборщиком, которого он только что прогнал. Фото : © 1997 Miramax Pictures
Фото : © 1997 Miramax PicturesПоскольку Уилл не расписался на доске за решение первой задачи, профессор Ламбо поставил вторую задачу, о которой он сообщает своему классу , что «нам потребовалось более двух лет, чтобы доказать» . Задача снова касается древовидных структур:
Задача 2
a. Сколько существует деревьев с n помеченными вершинами?
б. Нарисуйте все гомоморфно неприводимые деревья с n = 10
Решения задачи 2
Как указывают Horváth et al (2010), задача 2a на самом деле просто запрашивает формулу Кэли, которая для каждого положительного целого числа n количество деревьев на n -помеченных вершинах равно nⁿ⁻². Формула названа в честь Артура Кэли, но известна с тех пор, как была открыта Карлом Вильгельмом Борхардтом в 1860 году. учитывайте степени вершин, и поэтому с тех пор он носит его имя. Есть несколько известных доказательств результата.
Заключительное задание, задача 2б требует рисунков все гомоморфно неприводимых деревьев с n = 10. Гомоморфно неприводимое дерево — это дерево, не имеющее точек степени 2. Проблема, вероятно, была навеяна статьей Число гомоморфно неприводимых деревьев и других видов Харари и Принса ( 1959).
Гомоморфно неприводимое дерево — это дерево, не имеющее точек степени 2. Проблема, вероятно, была навеяна статьей Число гомоморфно неприводимых деревьев и других видов Харари и Принса ( 1959).
Мы можем сгруппировать гомоморфно неприводимые деревья, пометив их вершины цифрами 1,…., 10 и степени их вершин цифрами d₁, …,d₁₀ (Horváth et al, 2010). Поскольку у деревьев 10 вершин, мы знаем, что у них 9края. Мы можем классифицировать эти различные деревья по количеству их листьев (узлов/вершин степени вершины 1):
- Если есть 9 листьев и 1 нелист, то мы получаем «звезду», единственную вершину, соединенную с каждым листом. :
- Если 8 листьев и 2 нелиста, то d₁ + d₂ = 10 и d₁ ≥ d₂ ≥ 3, поэтому либо: a) d₁ =7 и d₂ = 3 (одно дерево), или b ) d₁ = 6 и d₂ = 4 (одно дерево), или c) d₁ = d₂ = 5 (одно дерево).
- Если листьев 7 , то d₁ + d₂ + d₃ = 11 и d₁ ≥ d₂ ≥d₃ ≥ 3, поэтому либо a) d₁ = d₂ = 5 и d₃ = 3 (два дерева), либо b) d₁ = 5 и d₂ = d₃ = 3 (три дерева).



 Производящая функция для блужданий от i → j
Производящая функция для блужданий от i → j 
 Какие величины должны стоять в пустых клетках таблицы? 20 м ? 5 с ? 5 м/с ?
Какие величины должны стоять в пустых клетках таблицы? 20 м ? 5 с ? 5 м/с ? Тогда скорость лодки по течению, складывается из ее собственной скорости и скорости течения : 7 + 2 = 9 (км/ч) А скорость лодки против течения реки получается вычитанием из собственной скорости лодки скорости течения реки: 7 – 2 = 5 км/ч.
Тогда скорость лодки по течению, складывается из ее собственной скорости и скорости течения : 7 + 2 = 9 (км/ч) А скорость лодки против течения реки получается вычитанием из собственной скорости лодки скорости течения реки: 7 – 2 = 5 км/ч. Какое расстояние проплыл катер за это время, если скорость течения реки 2 км/ч ? УЧЕБНИК № 294 (15 + 2) ∙ 2 + (15 – 2 ) ∙ 3 = 73 (км) решение
Какое расстояние проплыл катер за это время, если скорость течения реки 2 км/ч ? УЧЕБНИК № 294 (15 + 2) ∙ 2 + (15 – 2 ) ∙ 3 = 73 (км) решение Значит через 15 мин после падения шляпы расстояние между лодкой и шляпой будет равно 150 ∙ 15 = 2250 (м). При изменении скорости реки ответ не изменится. решение
Значит через 15 мин после падения шляпы расстояние между лодкой и шляпой будет равно 150 ∙ 15 = 2250 (м). При изменении скорости реки ответ не изменится. решение 05.2017
66541
05.2017
66541
 Удачи в прохождении!
Удачи в прохождении! 05.2017
16628
05.2017
16628
 02.2021
1133
02.2021
1133



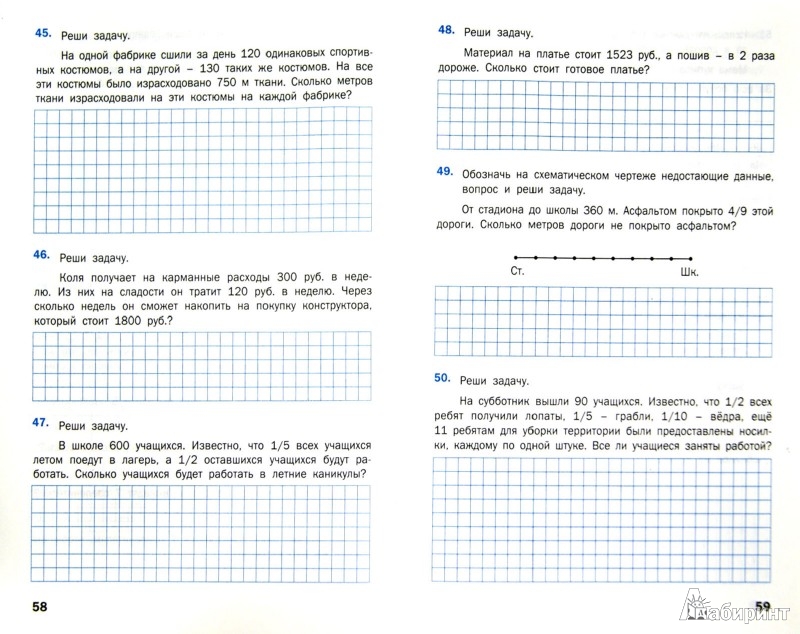
 01.2016
17943
01.2016
17943
 09.2018
4258
09.2018
4258
 Задания составлены с учетом типичных ошибок, которые допускают учащиеся.
Задания составлены с учетом типичных ошибок, которые допускают учащиеся.
 04.2020
1199
0
04.2020
1199
0
 11.2013
11047
11.2013
11047
 02.2021
799
02.2021
799




 Данная разработка представляет собой работу по математике в 5 классе на тему: » Среднее арифметическое». Эта тема кажется ребятам достаточно простой, но на самом деле является очень важной и требует тщательной отработки. Необходимо научиться выражать любой элемент из определения среднего арифметического.
Данная разработка представляет собой работу по математике в 5 классе на тему: » Среднее арифметическое». Эта тема кажется ребятам достаточно простой, но на самом деле является очень важной и требует тщательной отработки. Необходимо научиться выражать любой элемент из определения среднего арифметического. 05.2021
436
0
05.2021
436
0
 Я. Виленкина и др. «Математика. 5 класс»
Я. Виленкина и др. «Математика. 5 класс» 04.2017
9482
04.2017
9482
 Тест проверяет умение применять изученные правила при сравнении обыкновенных дробей.
Тест проверяет умение применять изученные правила при сравнении обыкновенных дробей. 03.2021
336
03.2021
336
 08.2015
2379
08.2015
2379
 Для того, чтобы выполнить задание, нужно использовать ответ предыдущего задания. Об этом нужно сообщить учащимся до выполнения теста.
Для того, чтобы выполнить задание, нужно использовать ответ предыдущего задания. Об этом нужно сообщить учащимся до выполнения теста.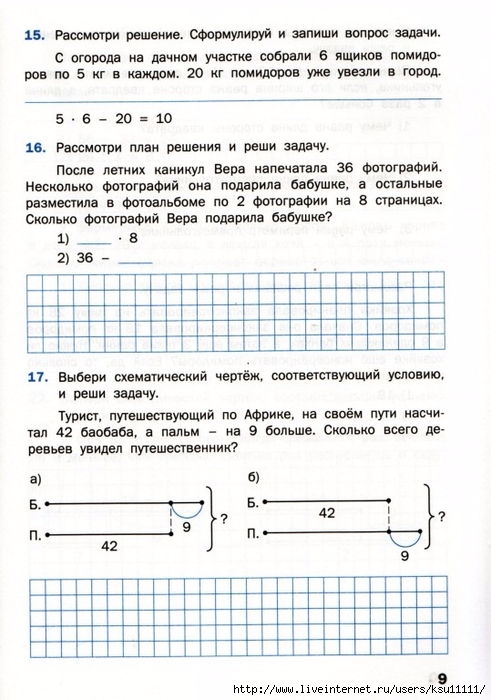 Сюжетные задачи на все арифметические действия (10 вопросов)
Сюжетные задачи на все арифметические действия (10 вопросов)
 04.2020
8107
0
04.2020
8107
0
 04.2022
117
0
04.2022
117
0
 Вновь открытый тест содержит другие вопросы из банка вопросов.
Вновь открытый тест содержит другие вопросы из банка вопросов.
 = Vсоб. + Vтеч.= 15 + 2 = 17 (км/ч.)
= Vсоб. + Vтеч.= 15 + 2 = 17 (км/ч.)
 теч, км/ч
теч, км/ч
 теч, км/ч
теч, км/ч
 Во-вторых, многие из них однотипны — это задачи на движение или на работу. Главное — знать к ним подход.
Во-вторых, многие из них однотипны — это задачи на движение или на работу. Главное — знать к ним подход. Из года в год мы, репетиторы, наблюдаем парадоксальную картину: ученики одиннадцатого класса долго думают, как записать, что « на больше ». А в школе в этот момент они «проходят» первообразные и интегралы 🙂
Из года в год мы, репетиторы, наблюдаем парадоксальную картину: ученики одиннадцатого класса долго думают, как записать, что « на больше ». А в школе в этот момент они «проходят» первообразные и интегралы 🙂
 В нее сразу можно внести расстояние — и велосипедист, и автомобилист проехали по км. Можно внести скорость — она равна и для велосипедиста и автомобилиста соответственно. Осталось заполнить графу «время».
В нее сразу можно внести расстояние — и велосипедист, и автомобилист проехали по км. Можно внести скорость — она равна и для велосипедиста и автомобилиста соответственно. Осталось заполнить графу «время». Получим:
Получим: Расстояние в обеих строчках таблицы пишем одинаковое — километров. Осталось записать время. Поскольку , на путь из в велосипедист затратит время , а на обратный путь время .
Расстояние в обеих строчках таблицы пишем одинаковое — километров. Осталось записать время. Поскольку , на путь из в велосипедист затратит время , а на обратный путь время .
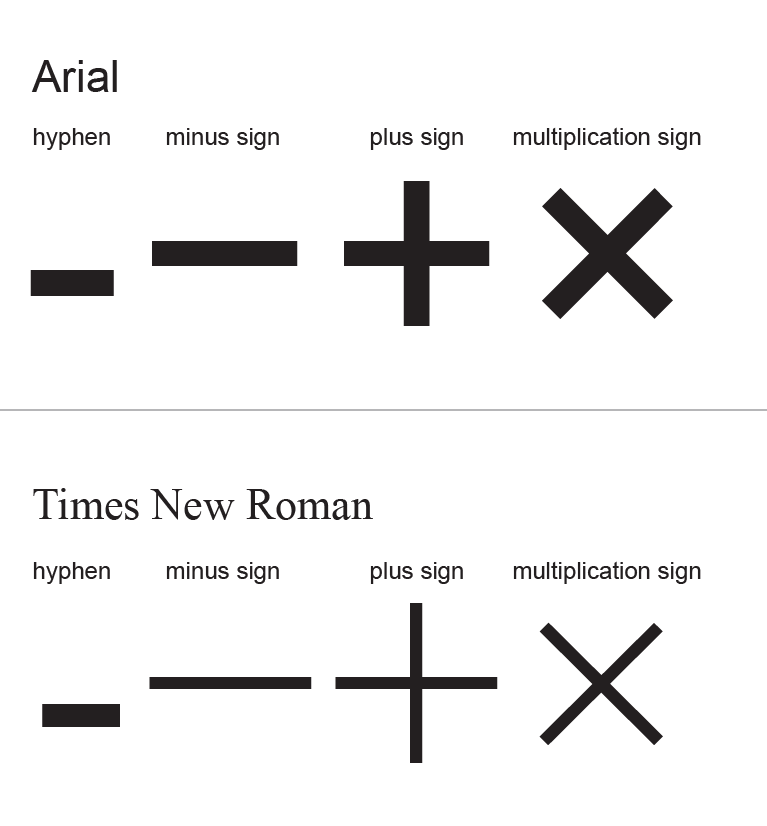
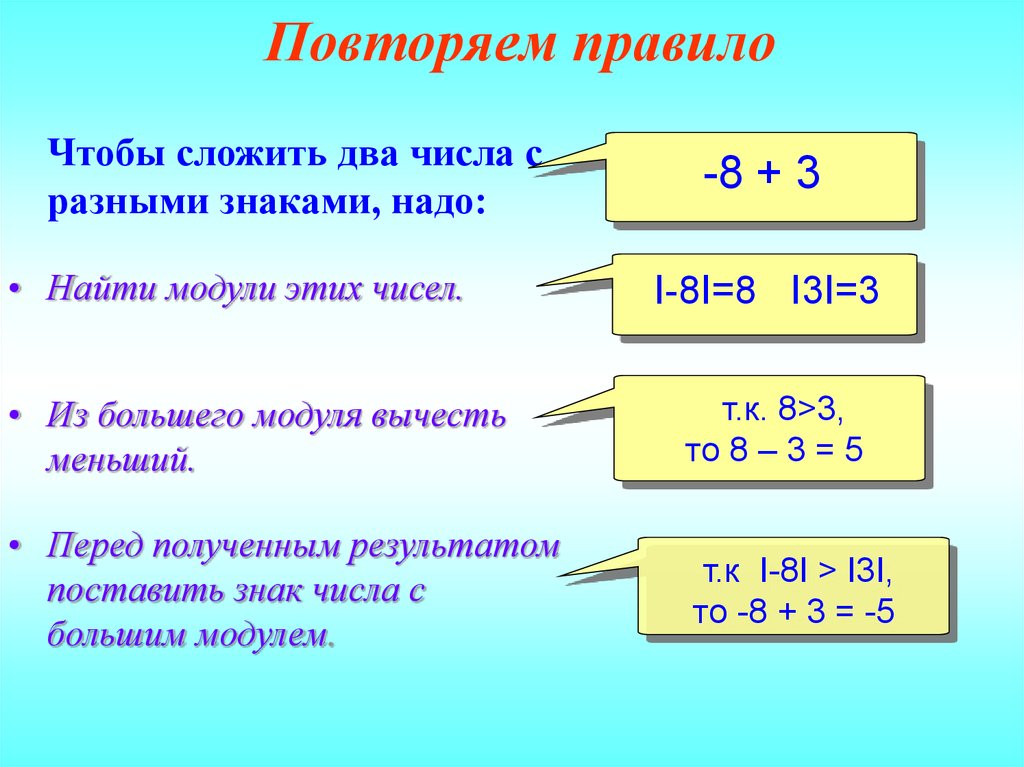
 Правда, в младшем школьном возрасте дети не особо стараются вникать во все математические нюансы.
Правда, в младшем школьном возрасте дети не особо стараются вникать во все математические нюансы. Читается как: минус один, минус два, минус три.
Читается как: минус один, минус два, минус три.

 При каждом шаге влево число будет уменьшаться в меньшую сторону. И при каждом шаге вправо число будет увеличиваться. Стрелка, направленная вправо, указывает на положительное направление отсчёта.
При каждом шаге влево число будет уменьшаться в меньшую сторону. И при каждом шаге вправо число будет увеличиваться. Стрелка, направленная вправо, указывает на положительное направление отсчёта.
 Ноль меньше любого положительного числа.
Ноль меньше любого положительного числа. Сравните числа 5 и 7
Сравните числа 5 и 7



 У. 1
У. 1 Цель расширения: обеспечить выполнение операции вычитания для любых чисел. В результате расширения получается множество (кольцо) целых чисел, состоящее из положительных (натуральных) чисел, отрицательных чисел и нуля.
Цель расширения: обеспечить выполнение операции вычитания для любых чисел. В результате расширения получается множество (кольцо) целых чисел, состоящее из положительных (натуральных) чисел, отрицательных чисел и нуля.

 ..». Вот как индийский математик Брахмагупта излагал правила сложения и вычитания: «имущество и имущество есть имущество, сумма двух долгов есть долг; сумма имущества и нуля есть имущество; сумма двух нулей есть нуль… Долг, который отнимают от нуля, становится имуществом, а имущество – долгом. Если нужно отнять имущество от долга, а долг от имущества, то берут их сумму». «Сумма двух имуществ есть имущество».
..». Вот как индийский математик Брахмагупта излагал правила сложения и вычитания: «имущество и имущество есть имущество, сумма двух долгов есть долг; сумма имущества и нуля есть имущество; сумма двух нулей есть нуль… Долг, который отнимают от нуля, становится имуществом, а имущество – долгом. Если нужно отнять имущество от долга, а долг от имущества, то берут их сумму». «Сумма двух имуществ есть имущество».
 и закупает товара на 3000 р., у него остается 5000 — 3000 = 2000, р. Если же он имеет 3000 р., а закупает на 5000 р., то он остается в долгу на 2000 р. В соответствии с этим считали, что здесь совершается вычитание 3000 — 5000, результатом же является число 2000 с точкой наверху, означающее «две тысячи долга». Толкование это носило искусственный характер, купец никогда не находил сумму долга вычитанием 3000 — 5000, а всегда выполнял вычитание 5000 — 3000.
и закупает товара на 3000 р., у него остается 5000 — 3000 = 2000, р. Если же он имеет 3000 р., а закупает на 5000 р., то он остается в долгу на 2000 р. В соответствии с этим считали, что здесь совершается вычитание 3000 — 5000, результатом же является число 2000 с точкой наверху, означающее «две тысячи долга». Толкование это носило искусственный характер, купец никогда не находил сумму долга вычитанием 3000 — 5000, а всегда выполнял вычитание 5000 — 3000.

 На состязании в решении задач с придворными математиками Фридриха II Леонардо Пизанскому было предложено решить задачу: требовалось найти капитал нескольких лиц. Фибоначчи получил отрицательное значение. «Этот случай, — сказал Фибоначчи, — невозможен, разве только принять, что один имел не капитал, а долг». Однако в явном виде отрицательные числа применил впервые в конце XV столетия французский математик Шюке. Автор рукописного трактата по арифметике и алгебре «Наука о числах в трёх частях». Символика Шюке приближается к современной.
На состязании в решении задач с придворными математиками Фридриха II Леонардо Пизанскому было предложено решить задачу: требовалось найти капитал нескольких лиц. Фибоначчи получил отрицательное значение. «Этот случай, — сказал Фибоначчи, — невозможен, разве только принять, что один имел не капитал, а долг». Однако в явном виде отрицательные числа применил впервые в конце XV столетия французский математик Шюке. Автор рукописного трактата по арифметике и алгебре «Наука о числах в трёх частях». Символика Шюке приближается к современной.

 (Например: термометр, шкала глубин и высот)
(Например: термометр, шкала глубин и высот)



 ). Чех Ян Видман уже писал «+» и «–» для сложения и вычитания.
). Чех Ян Видман уже писал «+» и «–» для сложения и вычитания.
 Но в то же время Диофант употребляет такие обороты речи, как «Прибавим к обеим сторонам отрицательное», и даже формулирует правило знаков: «Отрицательное, умноженное на отрицательное, дает положительное, тогда как отрицательное, умноженное на положительное, дает отрицательное» (то, что сейчас обычно формулируют: «Минус на минус дает плюс, минус на плюс дает минус»).
Но в то же время Диофант употребляет такие обороты речи, как «Прибавим к обеим сторонам отрицательное», и даже формулирует правило знаков: «Отрицательное, умноженное на отрицательное, дает положительное, тогда как отрицательное, умноженное на положительное, дает отрицательное» (то, что сейчас обычно формулируют: «Минус на минус дает плюс, минус на плюс дает минус»).

 Индийские математики используют отрицательные числа с VII в. н. э.: Брахмагупта сформулировал правила арифметических действий с ними. В его произведении мы читаем: « имущество и имущество есть имущество, сумма двух долгов есть долг; сумма имущества и нуля есть имущество; сумма двух нулей есть нуль… Долг, который отнимают от нуля, становится имуществом, а имущество – долгом. Если нужно отнять имущество от долга, а долг от имущества, то берут их сумму».
Индийские математики используют отрицательные числа с VII в. н. э.: Брахмагупта сформулировал правила арифметических действий с ними. В его произведении мы читаем: « имущество и имущество есть имущество, сумма двух долгов есть долг; сумма имущества и нуля есть имущество; сумма двух нулей есть нуль… Долг, который отнимают от нуля, становится имуществом, а имущество – долгом. Если нужно отнять имущество от долга, а долг от имущества, то берут их сумму».
 И. Глейзер, История математики в школе IV-VI классы. Москва, Просвещение, 1981)
И. Глейзер, История математики в школе IV-VI классы. Москва, Просвещение, 1981)
 Сам Штифель писал: «Нуль находится между истинными и абсурдными числами…» (Г.И. Глейзер, История математики в школе IV-VI классы. Москва, Просвещение, 1981)
Сам Штифель писал: «Нуль находится между истинными и абсурдными числами…» (Г.И. Глейзер, История математики в школе IV-VI классы. Москва, Просвещение, 1981)
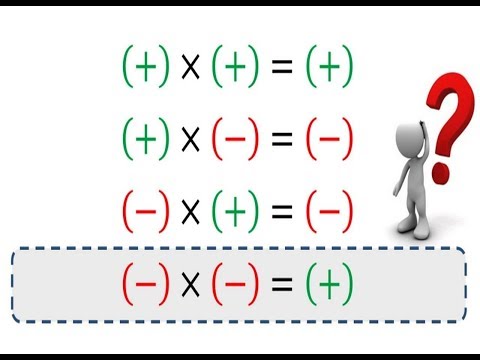


 Кольман.
Кольман.
 Г. «Положительные и отрицательные числа», учебное пособие по математике для 6-го класса, 2001.
Г. «Положительные и отрицательные числа», учебное пособие по математике для 6-го класса, 2001.

 Дело в том, что оно, по сути дела, означает «ничто», «пустоту», однако его значение действительно трудно переоценить. Для этого достаточно вспомнить хотя бы то, что именно с нулевой отметки начинается отсчет координат положения точки в любой системе координат.
Дело в том, что оно, по сути дела, означает «ничто», «пустоту», однако его значение действительно трудно переоценить. Для этого достаточно вспомнить хотя бы то, что именно с нулевой отметки начинается отсчет координат положения точки в любой системе координат. Приведем примеры их осуществления и некоторые пояснения к ним.
Приведем примеры их осуществления и некоторые пояснения к ним.

 Таким образом, теоретически оно может представлять собой абсолютно любое число.
Таким образом, теоретически оно может представлять собой абсолютно любое число. От того, насколько быстро и правильно ребенок научится выполнять арифметические действия, будет зависеть скорость выполнения им логических (смысловых) операции в старших класах и уровень понимания предмета в целом. Репетитор по математике довольно часто сталкивается с вычислительными проблемами учащихся, мешающими добиваться высоких результатов.
От того, насколько быстро и правильно ребенок научится выполнять арифметические действия, будет зависеть скорость выполнения им логических (смысловых) операции в старших класах и уровень понимания предмета в целом. Репетитор по математике довольно часто сталкивается с вычислительными проблемами учащихся, мешающими добиваться высоких результатов.
 А на это потребуется время. Учитывая еще и тот факт, что ученик думает и пишет одновременно, задача репетитора по математике еще большет усложняется. Хорошей зрительной, смысловой и двигательной памятью слабый ученик не обладает, а поэтому лучше предложить альтернативный текст правила:
А на это потребуется время. Учитывая еще и тот факт, что ученик думает и пишет одновременно, задача репетитора по математике еще большет усложняется. Хорошей зрительной, смысловой и двигательной памятью слабый ученик не обладает, а поэтому лучше предложить альтернативный текст правила: Навести порядок в этом хаосе репетитору по математике нужно как можно быстрее. В процессе решения примеров применяются опорные подсказки (словесные и визуальные), которые в сочетании аккуратным и подробным офофрмлением делают свое дело. Нужно помнить, что каждое слово, произнесенное репетитором по математике в момент решения любой задачи несет или подсказку или помеху. Каждая фраза анализируется ребенком на предмет установления связи с теми или иным математическим объектом (явлением) и его образом на бумаге.
Навести порядок в этом хаосе репетитору по математике нужно как можно быстрее. В процессе решения примеров применяются опорные подсказки (словесные и визуальные), которые в сочетании аккуратным и подробным офофрмлением делают свое дело. Нужно помнить, что каждое слово, произнесенное репетитором по математике в момент решения любой задачи несет или подсказку или помеху. Каждая фраза анализируется ребенком на предмет установления связи с теми или иным математическим объектом (явлением) и его образом на бумаге.
 После этого записывается тождество a-b=a+(-b)
После этого записывается тождество a-b=a+(-b) Для улучшения устойчиваости запоминания можно призвать на помощь визуальные подсказки — фишечки. Например, интересный способ перевовода вычитания отрицательного числа в сложение. Репетитор по математике соединяет два минуса одной линией (как показано на рисунке), и взору ученика открывается знак «плюс» (в пересечении со скобкой).
Для улучшения устойчиваости запоминания можно призвать на помощь визуальные подсказки — фишечки. Например, интересный способ перевовода вычитания отрицательного числа в сложение. Репетитор по математике соединяет два минуса одной линией (как показано на рисунке), и взору ученика открывается знак «плюс» (в пересечении со скобкой). Однако, практика показывает, что этот путь не всегда приносит хорошие дивиденды. Потребность в осознании того, что человек делает, чаще всего появляется после запоминания этапов применяемого алгоритма и практического закрепления вычислительных операций.
Однако, практика показывает, что этот путь не всегда приносит хорошие дивиденды. Потребность в осознании того, что человек делает, чаще всего появляется после запоминания этапов применяемого алгоритма и практического закрепления вычислительных операций.





