«Какие математические формулы могут реально пригодиться взрослому человеку?» — Яндекс Кью
ПопулярноеСообщества
МатематикаФормулы
Андрей Глинка
·
14,4 K
ОтветитьУточнитьДостоверно
Надежда Шихова
Математика
8,5 K
Редактор, автор и переводчик книг по математике · 7 авг 2019 · pilotlz.ru/books/287/11090
Короткий ответ такой: все формулы собрали еще до нас:) Есть популярная программа Excel, в нее встроено много формул, которые реально пригодятся взрослому человеку для незамысловатой обработки данных — там и логические функции есть, и финансовые и статистические; здесь все не перечислить, да и записывать формулы в формате txt неудобно.
Есть и длинный ответ. Формулы сами по себе не так важны; они просто инструмент для достижения той или иной цели. Вопрос в том, какие цели и задачи ставит перед собой взрослый человек, владеет он инструментом или нет. Если владеет, если знает, зачем и в каких случаях применять, как интерпретировать результат; если ставит перед собой сложные задачи, то найдет применение инструменту. Но вряд ли этот человек задаст такой вопрос. А если взрослый не владеет инструментом, то непонятные формулы ему не пригодятся.
Формулы сами по себе не так важны; они просто инструмент для достижения той или иной цели. Вопрос в том, какие цели и задачи ставит перед собой взрослый человек, владеет он инструментом или нет. Если владеет, если знает, зачем и в каких случаях применять, как интерпретировать результат; если ставит перед собой сложные задачи, то найдет применение инструменту. Но вряд ли этот человек задаст такой вопрос. А если взрослый не владеет инструментом, то непонятные формулы ему не пригодятся.
Это вопрос «какие инструменты могут реально пригодится взрослому человеку». Я вот не владею топором и паяльником, и они ни разу в жизни мне не пригодились. На самом деле это означает, что некоторые проблемы за меня решают другие люди. Так и с математическими формулами. Разделение труда в нашем обществе высокое, взрослый человек может прожить достойную жизнь и приносить пользу обществу, не прибегая к математическим формулам. Некоторые проблемы за него будут решать другие люди.
2 эксперта согласны
Лариса Андержанова
3 октября 2020
Вы меня сейчас упрекаете?
Комментировать ответ…Комментировать…
Otzyvmarketing. ru
ru
8,9 K
Сервисы для маркетологов. 2000+ инструментов, 20000+ отзывов экспертов, кейсы и рейтинги… · 26 нояб 2019 · otzyvmarketing.ru
Отвечает
Анастасия Кузнецова
Я закончила аспирантуру мехмата. Так что могу ответить на ваш вопрос как профессионал. Я вчера думала над вашим вопросом, и решила, что в первую очередь мне сегодня помогают различные математические программы. Например, иногда, когда я хочу подсчитать примерный доход в будущем году, мне нужно заниматься экстраполированием. Часто для расчета дохода со своего банковского… Читать далее
Отзывы о сервисах для бизнеса мы собираем тут.
Перейти на otzyvmarketing.ruШайтан М.
7 февраля 2020
НИ*ЕР@! В жизни далеко не все пригодятся. Вероятность, %, ()+,-,÷,× и т.д. но ответьте пожалуйста. Как и где мне. .. Читать дальше
.. Читать дальше
Комментировать ответ…Комментировать…
Yanchauskayte
22
Skysmart. Математика для подростков · 7 окт 2019
В хозяйстве очень пригодится знание периметра. Например, вам нужно построить забор на даче: чтобы узнать расстояние участка, нужно просто сложить все его стороны. Или у вас ремонт и нужно посчитать, сколько купить обоев — вспоминаем формулу площади прямоугольника: умножаем длину стены на ее высоту (S=A*B). ПРоделываем тоже самое с остальными стенами, складываем четыре… Читать далее
Комментировать ответ…Комментировать…
Светлана К.
287
Советы плохие, зато бесплатные · 7 авг 2019
Смотря как он живет.
Например, платежи по кредиту, когда там сложная схема, можно рассчитать самому, а можно взять расчеты от банка и просто прикинуть.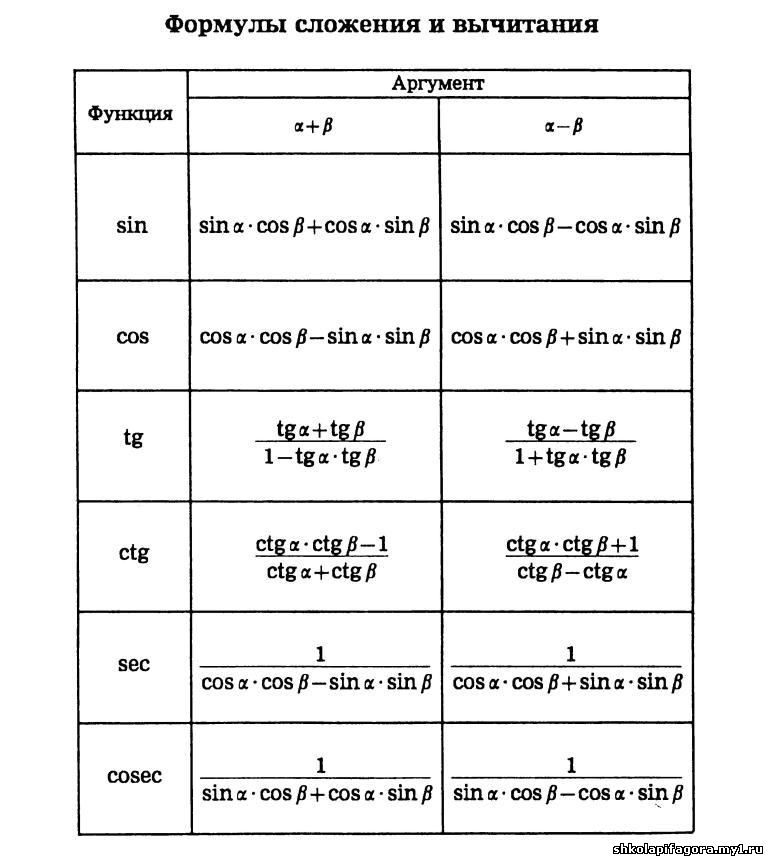 вас могут обмануть — а насколько принципиальна будет потеря некоторой суммы?
Или подъем тяжестей (мебели), какая-нибудь стройка на даче. Можно делать самому (и там нужны сложные формулы, включая интегралы, если строите… Читать далее
вас могут обмануть — а насколько принципиальна будет потеря некоторой суммы?
Или подъем тяжестей (мебели), какая-нибудь стройка на даче. Можно делать самому (и там нужны сложные формулы, включая интегралы, если строите… Читать далее
Комментировать ответ…Комментировать…
Людмила
9 сент 2020
Очень некорректный вопрос. Если профессиональная деятельность связана с математикой, то масса формул может пригодиться. Я — преподаватель, и, конечно, все формулы мне пригодились.
Комментировать ответ…Комментировать…
Вы знаете ответ на этот вопрос?
Поделитесь своим опытом и знаниями
Войти и ответить на вопрос
2 ответа скрыто(Почему?)
Формулы по математики 9 — Тур-инфо
Формулы по математики 9
Знание формул по математике является основой для успешной подготовки и сдачи различных экзаменов, в том числе и ЦТ или ЕГЭ по математике. Формулы по математике, которые надежно хранятся в памяти ученика — это основной инструмент, которым он должен оперировать при решении математических задач. На этой странице сайта представлены основные формулы по школьной математике.
На этой странице сайта представлены основные формулы по школьной математике.
Изучать основные формулы по школьной математике онлайн:
Как успешно подготовиться к ЦТ по физике и математике?
Для того чтобы успешно подготовиться к ЦТ по физике и математике, среди прочего, необходимо выполнить три важнейших условия:
Изучить все темы и выполнить все тесты и задания приведенные в учебных материалах на этом сайте. Для этого нужно всего ничего, а именно: посвящать подготовке к ЦТ по физике и математике, изучению теории и решению задач по три-четыре часа каждый день. Дело в том, что ЦТ это экзамен, где мало просто знать физику или математику, нужно еще уметь быстро и без сбоев решать большое количество задач по разным темам и различной сложности. Последнему научиться можно только решив тысячи задач. Выучить все формулы и законы в физике, и формулы и методы в математике. На самом деле, выполнить это тоже очень просто, необходимых формул по физике всего около 200 штук, а по математике даже чуть меньше. В каждом из этих предметов есть около десятка стандартных методов решения задач базового уровня сложности, которые тоже вполне можно выучить, и таким образом, совершенно на автомате и без затруднений решить в нужный момент большую часть ЦТ. После этого Вам останется подумать только над самыми сложными задачами. Посетить все три этапа репетиционного тестирования по физике и математике. Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на ЦТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию. Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.
В каждом из этих предметов есть около десятка стандартных методов решения задач базового уровня сложности, которые тоже вполне можно выучить, и таким образом, совершенно на автомате и без затруднений решить в нужный момент большую часть ЦТ. После этого Вам останется подумать только над самыми сложными задачами. Посетить все три этапа репетиционного тестирования по физике и математике. Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на ЦТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию. Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.
Успешное, старательное и ответственное выполнение этих трех пунктов, а также ответственная проработка итоговых тренировочных тестов, позволит Вам показать на ЦТ отличный результат, максимальный из того, на что Вы способны.
Нашли ошибку?
Если Вы, как Вам кажется, нашли ошибку в учебных материалах, то напишите, пожалуйста, о ней на электронную почту (адрес электронной почты здесь). В письме укажите предмет (физика или математика), название либо номер темы или теста, номер задачи, или место в тексте (страницу) где по Вашему мнению есть ошибка. Также опишите в чем заключается предположительная ошибка. Ваше письмо не останется незамеченным, ошибка либо будет исправлена, либо Вам разъяснят почему это не ошибка.
ЗАПРЕЩЕНО использование представленных на сайте материалов или их частей в любых коммерческих целях, а также их копирование, перепечатка, повторная публикация или воспроизведение в любой форме. Нарушение прав правообладателей преследуется по закону. Подробнее.
Знание формул по математике является основой для успешной подготовки и сдачи различных экзаменов, в том числе и ЦТ или ЕГЭ по математике. Формулы по математике, которые надежно хранятся в памяти ученика — это основной инструмент, которым он должен оперировать при решении математических задач. На этой странице сайта представлены основные формулы по школьной математике.
На этой странице сайта представлены основные формулы по школьной математике.
Для того чтобы успешно подготовиться к ЦТ по физике и математике, среди прочего, необходимо выполнить три важнейших условия:
Изучить все темы и выполнить все тесты и задания приведенные в учебных материалах на этом сайте. Для этого нужно всего ничего, а именно: посвящать подготовке к ЦТ по физике и математике, изучению теории и решению задач по три-четыре часа каждый день. Дело в том, что ЦТ это экзамен, где мало просто знать физику или математику, нужно еще уметь быстро и без сбоев решать большое количество задач по разным темам и различной сложности. Последнему научиться можно только решив тысячи задач. Выучить все формулы и законы в физике, и формулы и методы в математике. На самом деле, выполнить это тоже очень просто, необходимых формул по физике всего около 200 штук, а по математике даже чуть меньше. В каждом из этих предметов есть около десятка стандартных методов решения задач базового уровня сложности, которые тоже вполне можно выучить, и таким образом, совершенно на автомате и без затруднений решить в нужный момент большую часть ЦТ. После этого Вам останется подумать только над самыми сложными задачами. Посетить все три этапа репетиционного тестирования по физике и математике. Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на ЦТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию. Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.
После этого Вам останется подумать только над самыми сложными задачами. Посетить все три этапа репетиционного тестирования по физике и математике. Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на ЦТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию. Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.
Успешное, старательное и ответственное выполнение этих трех пунктов, а также ответственная проработка итоговых тренировочных тестов, позволит Вам показать на ЦТ отличный результат, максимальный из того, на что Вы способны.
Формулы по математики 9.
Educon. by
20.03.2018 11:07:27
2018-03-20 11:07:27
Источники:
Https://educon. by/index. php/formuly/formulymat
by/index. php/formuly/formulymat
Формулы по математике » /> » /> .keyword { color: red; }
Формулы по математики 9
Смотрите и запоминайте формулы по математике по разным классам. Онлайн формулы могут служить шпаргалками на уроке или быстро помочь при решении математических задач (по алгебре, геометрии) по всем темам урока. Благодаря формулам, ученик легко сможет подготовиться к зачетам и экзаменам по математике.
Смотреть подробнее. Скачайте формулы на урок алгебры (математики), которые пригодятся ученикам 7, 8, 9 класса для
Учебные материалы, Формулы по математике | Просмотров: 6670 | Дата: 28-05-2014, 19:38 | Комментарии ( 0 )
Смотреть подробнее. Данные формулы по алгебре (математике) помогут ученикам от 7-11 класса понять принципы и свойства
Учебные материалы, Формулы по математике | Просмотров: 5742 | Дата: 28-05-2014, 19:06 | Комментарии ( 0 )
Скачайте формулы на урок алгебры математики, которые пригодятся ученикам 7, 8, 9 класса для.
Vpr-klass. com
27.05.2020 7:36:07
2020-05-27 07:36:07
Источники:
Https://vpr-klass. com/load/formuly_po_matematike/
Все формулы по математике » /> » /> .keyword { color: red; }
Формулы по математики 9
На этой странице собраны все формулы, необходимые для сдачи контрольных и самостоятельных работ, экзаменов по по алгебре, геометрии, тригонометрии, стереометрии и другим разделам математики.
Здесь вы можете скачать или посмотреть онлайн все основные тригонометрические формулы, формулу площади круга, формулы сокращенного умножения, формула длины окружности, формулы приведения и многие другие.
Можно так же распечатать необходимые сборники математических формул.
Успехов в учебе!
Формулы Арифметики:
Формулы Алгебры:
Геометрические Формулы:
Арифметические формулы:
Законы действий над числами
Переместительный закон сложения: a + b = b + a.
Сочетательный закон сложения: (a + b) + с = a + (b + c).
Переместительный закон умножения: ab = ba.
Сочетательный закон умножения: (ab)с = a(bc).
Распределительный закон умножения относительно сложения: (a + b)с = aс + bс.
Распределительный закон умножения относительно вычитания: (a — b)с = aс — bс.
Некоторые математические обозначения и сокращения:
Признаки делимости
Признаки делимости на «2»
Число, делящееся на «2» без остатка называется Чётным, не делящееся – Нечётным. Число делится на «2» без остатка, если его последняя цифра чётная (2, 4, 6, 8) или ноль
Признаки делимости на «4»
Число делится на «4» без остатка, если две последние его цифры нули или в сумме образуют число, делящееся без остатка на «4»
Признаки делимости на «8»
Число делится на «8» без остатка, если три последние его цифры нули или в сумме образуют число, делящееся без остатка на «8» (Пример: 1 000 — три последние цифры «00», а при делении 1 000 на 8 получается 125; 104 — две последние цифры «12» делятся на 4, а при делении 112 на 4 получается 28; и. т.д.)
т.д.)
Признаки делимости на «3» и на «9»
Без остатка на «3» делятся только те числа, у которых сумма цифр делится без остатка на «3»; на «9» — только те, у которых сумма цифр делится без остатка на «9»
Признаки делимости на «5»
Признаки делимости на «25»
Без остатка на «25» делятся числа, две последние цифры которых нули или в сумме образуют число, делящееся без остатка на «25» (т. е. числа, оканчивающиеся на «00», «25», «50», «75»
Признаки делимости на «10», «100» и на «1 000»
Без остатка на «10» делятся только те числа, последняя цифра которых ноль, на «100» — только те числа, у которых две последние цифры нули, на «1000» — только те числа, у которых три последние цифры нули
Признаки делимости на «11»
Без остатка на «11» делятся только те числа, у которых сумма цифр, занимающих нечётные места, либо равна сумме цифр, занимающих чётные места, либо отличается от неё на число, делящееся на «11»
Абсолютная величина — формулы ( модуль)
|a| ? 0, Причём |a| = 0 только если a = 0; |-a|=|a| |a2|=|a|2=a2 |ab|=|a|*|b| |a/b|=|a|/|b|, Причём b? 0; |a+b|?|a|+|b| |a-b|?|a|-|b|
Формулы Действия с дробями
Формула обращения конечной десятичной дроби в рациональную дробь:
Пропорции
Два равных отношения образуют Пропорцию:
Основное свойство пропорции
Ad = bc
Нахождение членов пропорцииСредние величины
Среднее арифметическое
Среднее геометрическое (среднее пропорциональное)
Среднее квадратичное
Среднее гармоническое
Некоторые конечные числовые ряды
Тождественные преобразования алгебраических и тригонометрических выраженийСвойства степенейСвойства арифметических корнейМногочленыСвойства числовых неравенств1) Если a
2) Если a 0, то aс
3) Если a bс.
4) Если a 1/b.
5) Если a
6) Если a 0, b > 0, c > 0, d > 0, то ac
7) Если a 0, b > 0, то
8) Если, то
Соотношения между тригонометрическими функциями одного и того же аргументаФормулы сложения:Формулы двойного аргумента:Формулы тройного аргумента:Формулы половинного аргумента:(для функций sin и cos – формулы понижения степени)
Формулы третьей и четвертой степени:Формулы преобразования суммы в произведение:Формулы преобразования произведения в сумму:Формула приведения для преобразования выражений вида а) перед приведенной функцией ставиться тот знак, который имеет исходная функция;б) функция меняется на «кофункцию», если n нечетно; функция не меняется, если n четно. (Кофункциями синуса, косинуса, тангенса и котангенса называются соответственно косинус, синус, котангенс и тангенс. ) Например:Формулы нахождения угла:ТАБЛИЦА ЗНАЧЕНИЙ
) Например:Формулы нахождения угла:ТАБЛИЦА ЗНАЧЕНИЙЕдиничная окружность:
Формулы Прогрессии:
Арифметическая прогрессия(a1 – первый член; d – разность; n – число членов; an – n-й член; Sn – сумма n первых членов):
Геометрическая прогрессия(b1 – первый член; q – знаменатель; n – число членов; bn – n-й член; Sn – сумма n первых членов, S – сумма бесконечной геом. прогрессии):
ПроизводнаяОсновные правила дифференцирования:Производная сложной функции:Если функция f имеет производную в точке xo, а функция g имеет производную в точке yo = f(xo), то сложная функция h(x) = g(f(x)) также имеет производную в точке xo, причем:
Производные тригонометрической функции:Производная логарифмической функции:Уравнение касательной к графику функции:1. Расстояние между точками A1(x1;y1) и A2(x2;y2) находится по формуле:
Расстояние между точками A1(x1;y1) и A2(x2;y2) находится по формуле:
2. Координаты (x;y) середины отрезка с концами A1(x1;y1) и A2(x2;y2) находится по формулам:
3. Уравнение прямой с угловым коэффициентом и начальной ординатой имеет вид:
Угловой коэффициент k представляет собой значение тангенса угла, образуемого прямой с положительным направлением оси Ox, а начальная ордината q – значение ординаты точки пересечения прямой с осью Oy.
4. Общее уравнение прямой имеет вид: ax + by + c = 0.
5. Уравнения прямых, параллельных соответственно осям Oy и Ox, имеют вид:
6. Условия параллельности и перпендикулярности прямых y1=kx1+q1 и y2=kx2+q2 соответственно имеют вид:
7. Уравнения окружностей с радиусом R и с центром соответственно в точках O(0;0) и C(xo;yo) имеют вид:
Представляет собой уравнение параболы с вершиной в точке, абсцисса которой
1. Расстояние между точками A1(x1;y1;z1) и A2(x2;y2;z2) находится по формуле:
2. Координаты (x;y;z) середины отрезка с концами A1(x1;y1;z1) и A2(x2;y2;z2) находятся по формулам:
3. Модуль вектора заданного своими координатами, находится по формуле:
Модуль вектора заданного своими координатами, находится по формуле:
4. При сложении векторов их соответствующие координаты складываются, а при умножении вектора на число все его координаты умножаются на это число, т. е. справедливы формулы:
5. Единичный вектор сонаправленный с вектором находится по формуле:
6. Скалярным произведением векторов называется число:
Где — угол между векторами.
7. Скалярное произведение векторов
8. Косинус угла между векторами и находится по формуле:
9. Необходимое и достаточное условие перпендикулярности векторов и имеет вид:
10. Общее уравнение плоскости, перпендикулярной вектору имеет вид:
Ax + by + cz + d = 0.
11. Уравнение плоскости, перпендикулярной вектору и проходящей через точку (xo;yo;zo), имеет вид:
A(x — xo) + b(y — yo) + c(z — zo) = 0.
12. Уравнение сферы с центром O(0;0;0) записывается в виде:
1) Число перестановок из n элементов находится по формуле:
2) Число размещений из n элементов по m находится по формуле:
3) Число сочетаний из n элементов по m находится по формуле:
4) Справедливы следующие свойства сочетаний:
5) Формула бинома Ньютона имеет вид:
Сумма показателей чисел a и b равна n.
6) (k+1)-й член находится по формуле:
7) Число сочетаний также можно найти по треугольнику Паскаля.
Треугольник Паскаля (до n=7):
8) Сумма биномиальных коэффициентов равна 2n.
9) Чтобы найти биномиальный коэффициент следующего члена, нужно биномиальный коэффициент предыдущего члена умножить на показатель числа a и разделить на кол-во предыдущих членов.
Центр описанной окружности – точка пересечения серединных перпендикуляров. Центр вписанной окружности – точка пересечения биссектрис. (a, b,c – стороны: — противолежащие им углы; p – полупериметр; R – радиус описанной окружности; r – радиус вписанной окружности; S – площадь; ha – высота, проведенная к стороне a):
2. Прямоугольный треугольник:
Центр описанной окружности совпадает с центром гипотенузы. (a, b – катеты; c – гипотенуза; ac, bc – проекции катетов на гипотенузу):
3. Равносторонний треугольник:
Медиана = биссектрисе. OR = Or.
4. Произвольный выпуклый четырехугольник
Произвольный выпуклый четырехугольник
(d1 и d2 – диагонали; – угол между ними; S — площадь):
5. Параллелограмм
(a и b – смежные стороны; – угол между ними; ha – высота, проведенная к стороне a):
6. Ромб:
В любой ромб можно вписать окружность.
7. Прямоугольник:
Около любого прямоугольника можно описать окружность.
8. Квадрат
9. Трапеция
(a и b – основания; h – расстояние между ними; l – средняя линия):
10. Описанный многоугольник
(p – полупериметр; r – радиус вписанной окружности):
S = pr. 11. Правильный многоугольник
(an – сторона правильного n-угольника; R – радиус описанной окружности; r – радиус вписанной окружности):
12. Окружность, круг
(r — радиус; C – длина окружности; S – площадь круга):
13. Сектор
(l – длина дуги, ограничивающей сектор; — градусная мера центрального угла; — радианная мера центрального угла):
(l – боковое ребро; P – периметр основания; S – площадь основания; H – высота; Pсеч – периметр перпендикулярного сечения; Sбок – площадь боковой поверхности; V — объем):
2. Прямая призма: 3. Прямоугольный параллелепипед
Прямая призма: 3. Прямоугольный параллелепипед
(a, b,c – его измерения; V — диагональ):
4. Куб
5. Произвольная пирамида
(S – площадь основания; H – высота; V — объем):
6. Правильная пирамида
(P – периметр основания; l – апофема; Sбок – площадь боковой поверхности):
7. Произвольная усеченная пирамида
(S1 и S1 – площади оснований; h – высота; V — объем):
8. Правильная усеченная пирамида
(P1 и P2 – периметры оснований; l – апофема; Sбок – площадь боковой поверхности):
9. Цилиндр
(R – радиус основания; H – высота; Sбок – площадь боковой поверхности; V — объем):
10. Конус
(R – радиус основания; H – высота; l – образующая; Sбок – площадь боковой поверхности; V — объем):
11. Шар, сфера
(R – радиус шара; S – площадь сферической поверхности; V — объем):
12.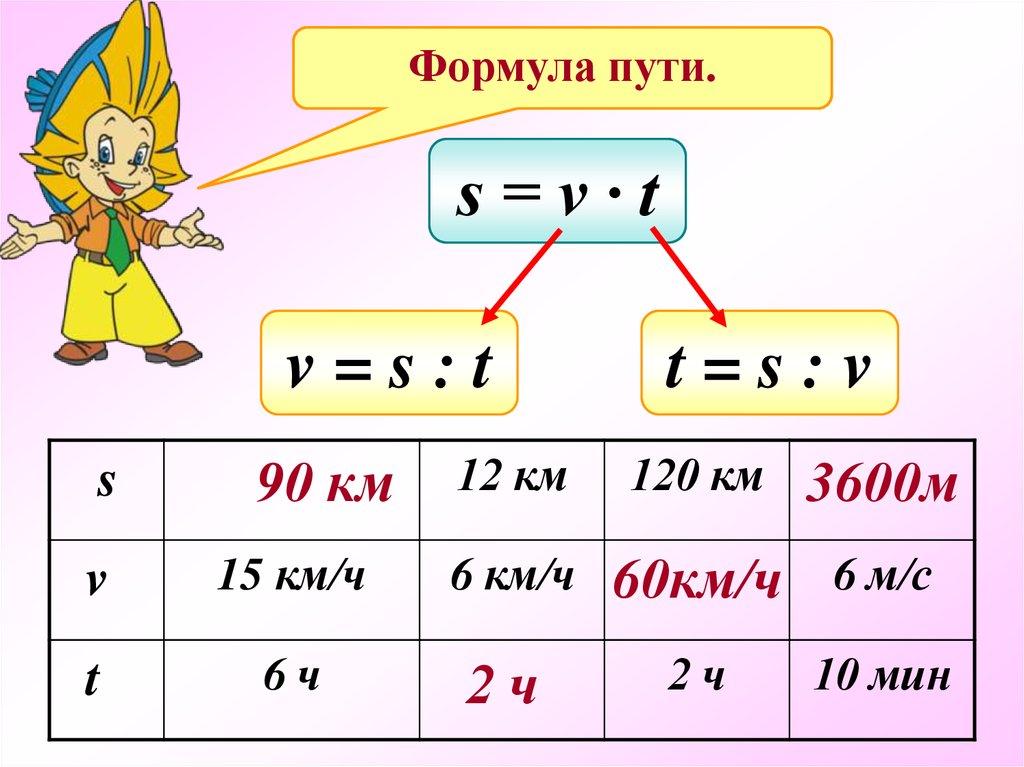 Шаровой сегмент
Шаровой сегмент
(R – радиус шара; h – высота сегмента; S – площадь сферической поверхности сегмента; V — объем):
13. Шаровой сектор
(R – радиус шара; h – высота сегмента; V — объем):
ПолезностиЦитаты и афоризмы
“ Если хочешь узнать человека, не слушай, что о нём говорят другие, послушай, что он говорит о других.” —
Два равных отношения образуют Пропорцию: Основное свойство пропорции ad = bc
Формулы Арифметики:
Законы действий над числами
Переместительный закон сложения: a + b = b + a.
Сочетательный закон сложения: (a + b) + с = a + (b + c).
Переместительный закон умножения: ab = ba.
Сочетательный закон умножения: (ab)с = a(bc).
Распределительный закон умножения относительно сложения: (a + b)с = aс + bс.
Распределительный закон умножения относительно вычитания: (a — b)с = aс — bс.
1) Если a 0, то aс bс. 4) Если a 1/b. 5) Если a 0, b > 0, c > 0, d > 0, то ac 0, b > 0, то 8) Если, то
4) Если a 1/b. 5) Если a 0, b > 0, c > 0, d > 0, то ac 0, b > 0, то 8) Если, то
Формула приведения для преобразования выражений вида а) перед приведенной функцией ставиться тот знак, который имеет исходная функция;б) функция меняется на «кофункцию», если n нечетно; функция не меняется, если n четно. (Кофункциями синуса, косинуса, тангенса и котангенса называются соответственно косинус, синус, котангенс и тангенс.) Например:
Признаки делимости на 3 и на 9.
Advice-me. ru
19.04.2018 10:04:55
2018-04-19 10:04:55
Источники:
Http://advice-me. ru/vse-formuly-po-matematike/
Таблицы и формулы по математике
Формула по математике все
Подборка математических формул и таблиц — позволит быстро вспомнить и выучить материал или найти формулы необходимые при решении задач.
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Если Вы хотите связаться со мной, имеете вопросы, предложения или хотите помочь развивать сайт OnlineMSchool пишите мне support@onlinemschool. com
Подборка математических формул и таблиц — позволит быстро вспомнить и выучить материал или найти формулы необходимые при решении задач.
Ru. onlinemschool. com
28.03.2018 17:46:58
2018-03-28 17:46:58
Источники:
Https://ru. onlinemschool. com/math/formula/
Математические формулы по алгебре и геометрии для ЕГЭ » /> » /> .keyword { color: red; }
Формула по математике все
Ежедневно с 10:00 до 21:00
Оставьте заявку и мы перезвоним Вам
Ваш город: Ростов-на-Дону
Ваш город —
Ростов-на-Дону?Выберите Ваш город
Введите название вашего города
- Кострома
Формулы по математике для ЕГЭ
Как выучить все формулы по математике к ЕГЭ
Чтобы сдать ЕГЭ по математике, необходимо знать математические формулы из школьного курса алгебры и геометрии.
Для того, чтобы запомнить формулы школьной математики, желательно держать в течение всего года на видном месте шпаргалку с красиво написанными формулами. Таким образом подключается зрительная память и формулы лучше запоминаются.
Проверяйте себя время от времени: попробуйте написать все важные математические формулы по памяти, а затем проверьте. На самом деле, формул, которые надо выучить наизусть, не так много. И целого учебного года вполне достаточно, чтобы все выучить.
Многие алгебраические, геометрические, тригонометрические формулы можно быстро вывести прямо на экзамене, если Вы их забыли. Но на это придется потратить какое-то время. Поэтому преимущество получают те школьники, которые выучили формулы.
Зная математические формулы наизусть, можно гораздо быстрей решить сложные задачи по алгебре, тригонометрии и геометрии на ЕГЭ.
Мы собрали самые важные формулы из школьного курса математики, которые надо выучить для успешной сдачи ЕГЭ.
Математические формулы школьного курса алгебры
Степени и корни
Формулы сокращенного умножения
Квадратный трехчлен: квадратное уравнение, формулы Виета, разложение на множители
Логарифмические формулы
Формулы тригонометрии
Основные формулы тригонометрии
Тригонометрические уравнения
Значения тригонометрических функций
Формулы приведения
Сумма и разность углов
Формулы двойного и тройного аргумента
Формулы половинного аргумента
Сумма и разность тригонометрических функций
Произведение тригонометрических функций
Формулы дифференциального исчисления
Формулы векторной алгебры из школьного курса математики
Формулы арифметической и геометрической прогрессии
Геометрические формулы школьного курса математики для ЕГЭ
Планиметрия
Стереометрия
Выучить формулы по математике – это еще не все, что надо для успешной сдачи ЕГЭ. Опыт решения задач, знания правил оформления заданий на экзамене не менее важны. Приглашаем всех школьников 11-х классов на курсы подготовки к ЕГЭ ПАРАГРАФ. С нами Вы подготовитесь к ЕГЭ наиболее продуктивно.
Опыт решения задач, знания правил оформления заданий на экзамене не менее важны. Приглашаем всех школьников 11-х классов на курсы подготовки к ЕГЭ ПАРАГРАФ. С нами Вы подготовитесь к ЕГЭ наиболее продуктивно.
Учите формулы по математике и сдавайте ЕГЭ на максимальные баллы!
Группы разного уровня подготовки
Группы для обучения подбираются согласно текущему уровню подготовки к ЕГЭ Вашего ребенка Это позволяет сделать обучение максимально эффективным для каждого
Полный контроль за процессом обучения
Вам предоставляется доступ в облачный личный кабинет с полной информацией о посещаемости и успеваемости ученика, а также домашними заданиями и тестами
Уникальный преподавательский коллектив
К работе с Вашими детьми допускаются только опытные и харизматичные профессиональные репетиторы и преподаватели ВУЗов, способные зажечь искру любви к предмету
Авторские методики обучения и мотивации
Система тестов, уникальная аттестация, целеполагание и тьюторская поддержка учеников позволяют увеличить эффективность обучения и мотивировать Вашего ребенка на успех
Остались вопросы?
Свяжитесь с нами и мы ответим на все вопросы
- ООО «АКАДЕМИЯ» ОГРН 1056165000924 / ИНН 6165119640 Ростов-на-Дону, Пушкинская, 135/33 8 (863) 311-28-28 info@ege-paragraf.
 ru
ruМы в соцсетях:
Данный сайт не является публичной офертой. Текущую цену в рублях Вы можете уточнить позвонив по телефону: +7 (863) 311-28-28
Ежедневно с 10:00 до 21:00
Оставьте заявку и мы перезвоним Вам
Ваш город: Ростов-на-Дону
Ваш город —
Ростов-на-Дону?Выберите Ваш город
Введите название вашего города
- Кострома
Чтобы сдать ЕГЭ по математике, необходимо знать математические формулы из школьного курса алгебры и геометрии.
Для того, чтобы запомнить формулы школьной математики, желательно держать в течение всего года на видном месте шпаргалку с красиво написанными формулами. Таким образом подключается зрительная память и формулы лучше запоминаются.
Проверяйте себя время от времени: попробуйте написать все важные математические формулы по памяти, а затем проверьте. На самом деле, формул, которые надо выучить наизусть, не так много. И целого учебного года вполне достаточно, чтобы все выучить.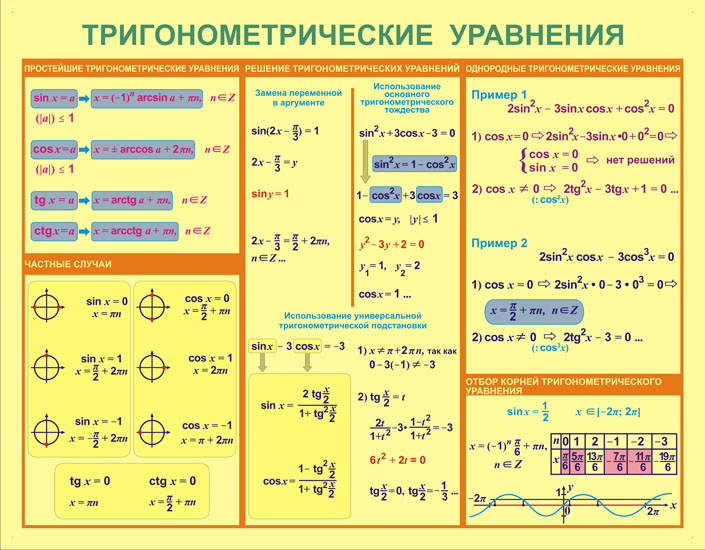
Многие алгебраические, геометрические, тригонометрические формулы можно быстро вывести прямо на экзамене, если Вы их забыли. Но на это придется потратить какое-то время. Поэтому преимущество получают те школьники, которые выучили формулы.
Зная математические формулы наизусть, можно гораздо быстрей решить сложные задачи по алгебре, тригонометрии и геометрии на ЕГЭ.
Мы собрали самые важные формулы из школьного курса математики, которые надо выучить для успешной сдачи ЕГЭ.
Ваш город —Ростов-на-Дону?
Мы в соцсетях.
Ege-paragraf. ru
12.10.2019 15:41:23
2019-10-12 15:41:23
Источники:
Https://ege-paragraf. ru/o-czentre/poleznaya-informacziya/matematicheskie-formulyi-po-algebre-i-geometrii-dlya-ege. html
Основные формулы по математике — Математика — Теория, тесты, формулы и задачи — Обучение Математике, Онлайн подготовка к ЦТ и ЕГЭ. » /> » /> .keyword { color: red; }
Формула по математике все
Знание формул по математике является основой для успешной подготовки и сдачи различных экзаменов, в том числе и ЦТ или ЕГЭ по математике. Формулы по математике, которые надежно хранятся в памяти ученика — это основной инструмент, которым он должен оперировать при решении математических задач. На этой странице сайта представлены основные формулы по школьной математике.
Формулы по математике, которые надежно хранятся в памяти ученика — это основной инструмент, которым он должен оперировать при решении математических задач. На этой странице сайта представлены основные формулы по школьной математике.
Изучать основные формулы по школьной математике онлайн:
Как успешно подготовиться к ЦТ по физике и математике?
Для того чтобы успешно подготовиться к ЦТ по физике и математике, среди прочего, необходимо выполнить три важнейших условия:
Изучить все темы и выполнить все тесты и задания приведенные в учебных материалах на этом сайте. Для этого нужно всего ничего, а именно: посвящать подготовке к ЦТ по физике и математике, изучению теории и решению задач по три-четыре часа каждый день. Дело в том, что ЦТ это экзамен, где мало просто знать физику или математику, нужно еще уметь быстро и без сбоев решать большое количество задач по разным темам и различной сложности. Последнему научиться можно только решив тысячи задач. Выучить все формулы и законы в физике, и формулы и методы в математике. На самом деле, выполнить это тоже очень просто, необходимых формул по физике всего около 200 штук, а по математике даже чуть меньше. В каждом из этих предметов есть около десятка стандартных методов решения задач базового уровня сложности, которые тоже вполне можно выучить, и таким образом, совершенно на автомате и без затруднений решить в нужный момент большую часть ЦТ. После этого Вам останется подумать только над самыми сложными задачами. Посетить все три этапа репетиционного тестирования по физике и математике. Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на ЦТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию. Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.
На самом деле, выполнить это тоже очень просто, необходимых формул по физике всего около 200 штук, а по математике даже чуть меньше. В каждом из этих предметов есть около десятка стандартных методов решения задач базового уровня сложности, которые тоже вполне можно выучить, и таким образом, совершенно на автомате и без затруднений решить в нужный момент большую часть ЦТ. После этого Вам останется подумать только над самыми сложными задачами. Посетить все три этапа репетиционного тестирования по физике и математике. Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на ЦТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию. Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.
Успешное, старательное и ответственное выполнение этих трех пунктов, а также ответственная проработка итоговых тренировочных тестов, позволит Вам показать на ЦТ отличный результат, максимальный из того, на что Вы способны.
Нашли ошибку?
Если Вы, как Вам кажется, нашли ошибку в учебных материалах, то напишите, пожалуйста, о ней на электронную почту (адрес электронной почты здесь). В письме укажите предмет (физика или математика), название либо номер темы или теста, номер задачи, или место в тексте (страницу) где по Вашему мнению есть ошибка. Также опишите в чем заключается предположительная ошибка. Ваше письмо не останется незамеченным, ошибка либо будет исправлена, либо Вам разъяснят почему это не ошибка.
ЗАПРЕЩЕНО использование представленных на сайте материалов или их частей в любых коммерческих целях, а также их копирование, перепечатка, повторная публикация или воспроизведение в любой форме. Нарушение прав правообладателей преследуется по закону. Подробнее.
Знание формул по математике является основой для успешной подготовки и сдачи различных экзаменов, в том числе и ЦТ или ЕГЭ по математике. Формулы по математике, которые надежно хранятся в памяти ученика — это основной инструмент, которым он должен оперировать при решении математических задач. На этой странице сайта представлены основные формулы по школьной математике.
Для того чтобы успешно подготовиться к ЦТ по физике и математике, среди прочего, необходимо выполнить три важнейших условия:
Изучить все темы и выполнить все тесты и задания приведенные в учебных материалах на этом сайте. Для этого нужно всего ничего, а именно: посвящать подготовке к ЦТ по физике и математике, изучению теории и решению задач по три-четыре часа каждый день. Дело в том, что ЦТ это экзамен, где мало просто знать физику или математику, нужно еще уметь быстро и без сбоев решать большое количество задач по разным темам и различной сложности. Последнему научиться можно только решив тысячи задач. Выучить все формулы и законы в физике, и формулы и методы в математике. На самом деле, выполнить это тоже очень просто, необходимых формул по физике всего около 200 штук, а по математике даже чуть меньше. В каждом из этих предметов есть около десятка стандартных методов решения задач базового уровня сложности, которые тоже вполне можно выучить, и таким образом, совершенно на автомате и без затруднений решить в нужный момент большую часть ЦТ. После этого Вам останется подумать только над самыми сложными задачами. Посетить все три этапа репетиционного тестирования по физике и математике. Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на ЦТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию. Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.
Выучить все формулы и законы в физике, и формулы и методы в математике. На самом деле, выполнить это тоже очень просто, необходимых формул по физике всего около 200 штук, а по математике даже чуть меньше. В каждом из этих предметов есть около десятка стандартных методов решения задач базового уровня сложности, которые тоже вполне можно выучить, и таким образом, совершенно на автомате и без затруднений решить в нужный момент большую часть ЦТ. После этого Вам останется подумать только над самыми сложными задачами. Посетить все три этапа репетиционного тестирования по физике и математике. Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на ЦТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию. Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.
Успешное, старательное и ответственное выполнение этих трех пунктов, а также ответственная проработка итоговых тренировочных тестов, позволит Вам показать на ЦТ отличный результат, максимальный из того, на что Вы способны.
Нашли ошибку.
Educon. by
08.06.2019 21:41:31
2019-06-08 21:41:31
Источники:
Https://educon. by/index. php/formuly/formulymat
Математические формулы
Операции по мышлению
Общая информация
A
Символы и отношения в математике
Теория
ℕ⊂ℤ⊂ℚ⊂ℝ⊂ℂ
Номерные стыдки
ℕ⊂ℤ⊂ℚ⊂ℝ⊂ℂ
. ℙ={2,3,5,7,…}
Простые числа — Факторизация простых чисел
a|m⇔n·a=m
Правила делимости
(m;n)=l;[ m;n]=k
Наибольший общий делитель (фактор) — наименьшее распространенное множество
AB+CD = AD+BCBD
Операции с рациональными числами
Binomial Theoorem
A+BN
Binomial The
9Binomial The
9999Комбинаторика
Pn=n!
Перестановки
Cnk=(nk)
Комбинация
Vnk=n!(n−k)!
Вариант
Наборы
A∪B; A∩B; AB
Операции на наборах
A∪B = B∪A
Фундаментальные законы Set Algebra
A∪B∪C
Cardinality of Sets
A × B
Cartesian Product
ρ⊆axa
Отношение
Логические
P∨Q; P⇒Q
Логические работы
P∨Q; Pyts
59и VILY TABLES и INTARIAL TABLES и INTALING15
. а∨b=b∨а
а∨b=b∨аProperties of Logical Operators
Graph Theory
Graph Theory — definitions, relationships
Algebra
Polynomials
a+b2
Special Binomials
Progressions
an=aa+(n−1)d
Арифметическая прогрессия
an=a1⋅qn−1
Геометрическая прогрессия
Logarithm
logab=c ⇔ac=b
Logarithm
logax=logbxlogba
Changing the base of a logarithm
Exponents
a·a·a=a3
Powers
Корни
AN = Bthy BN = A
Пропорциональность
A: B = C: D
Прямая и обратная пропорция
.0002 FX
Неравенства
Уравнения
AX2+BX+C = 0
Квадратичное уравнение
AX3+BX2+CX+D = 0
2
AX3+BX2+CX+D = 0 0006 9000 2
142.

Иррациональные и трансцендентные уравнения
Комплексные номера
z = A+IB; I = -1
Комплексные номера
Zn
Мощность сложных номеров
0002 ZK = A+IBN
Корни комплексных номеров
Kamatni Račun
K = T · P100
Процентный расчет,
Matrices
C = A+A+A+A+A+A+A+A+A+A+A+A+A+A+A+A+A+A+A+A+A+A+A+A+A+A+A+A+A+A+A+A+A+A+A+A+A+A+A+A+A+
. , adding & subtracting of matrices
C=A·B
Multiplying matrices
Geometry
Trigonometry
asinα=bsinβ=csinγ
Law of Sines
c2=a2+b2−2abcos2γ
Law of Cosines
sin2α+cos2α=1
Trygonometry Identities of same angle
sin(α±β)
Identities for сумма и разность двух углов
sin(2α)
Тригонометрические тождества двойных углов
sinα2
Тригонометрические тождества половинных углов
9 β006060014 Sum and difference of trigonometric functions
sinα=ac
Trigonometry Special Angles
Two-dimensional geometric shapes
B1B2¯B2B3¯=A1A2¯A2A3¯
Basic Proportionality Theorem
Треугольник
Особые треугольники — прямоугольный, равносторонний, равнобедренный треугольник
Четырехугольник
Квадрат
Rectangle
Rhombus
Parallelogram
Trapezoid
Circle
Circular sector
Circular segment
Three-dimensional geometric shapes
Сфера
Пирамида
Platonic solids
Cylinder
Vectors
a→·b→=|a→||b→|cosα
Scalar Product of Vectors
c→=a→×b →
Vector Product of Vectors
Аналитическая геометрия 2d
D = | P1P2 | ¯
Расстояние между двумя точками
x2+Y2 = R2
9000 2x2+Y2 = R2
9000 215
999999999 9000 2 9000 2999000 2
999 9000 2 9000 2 9000 299 9000 2b
Линейное уравнение
x2a2+y2b2 = 1
Ellipse
Математический анализ
Важные функции
Y = AX+B
LineAr Polynomiation
Y = AX+B
.
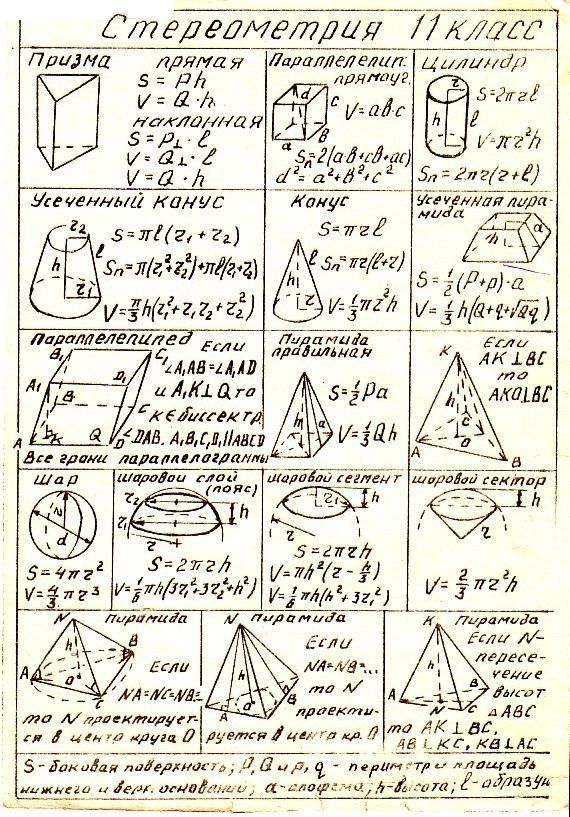
Quatratic polynomial function
y=ax3+bx2+cx+d
Cubic polynomial function
y=1x
Rational function
y=x2k,k∈ℕ
Корневая функция с даже радикальным
y = x2k+1, k∈ℕ
Функция корня с нечетным радикалом
y = AX
Экспоненциальная функция
y = Logax
Logarithmic
Y = Logax
.
Y = SINX
SINE функция
Y = COSX
Функция косинуса
Y = TGX
ТАНГАНСНАЯ ФУНКЦИЯ
y = CTGX
Кот.0015
у=|х|
Функции абсолютного значения
Трансформации функций
F (x+C)
Преобразования переменных и значения функции
Limx → X0FX = A
LIMX → X0FX = A
LIMX → X0FX = A
LIMX → X0FX = A
Дервация
dfxdx=f’x
Таблица производных
(f·g)′=f′·g±f·g′
Правила дифференцирования0015TX
Taylor Series
Интеграция
∫FXDX = FX+C
Table of Integrals
∫CF (x) DX = C∫F (x) DX
∫CF (x) DX = C∫F (x) DX
9∫CF (x) DX = C∫F (x) DX
99∫CF (x) DX = C∫F (X) DX
9 ∫CF (x). Правила
Правила
∫ABFXDX = FB-FA
Определенные интегралы
Вероятность и статистика
Вероятность
∑i = 1nai = ω
.
PA = Aω
Вероятность события
PA | B = PA∩BPB
Условная вероятность
PA = ∑I = 1NPA | BI · PBI
Законодательство из общей вероятности
PBi|A=PA|Bi·PBiPA
Bayes’ Theorem
Fx=Pξ Discrete Probability Variable — Distribution Function
Statistics
A=∑xii=1nn
Меры центральной тенденции
все математические формулы | Tiktok Search
TiktokЗагрузка
для вас
после
DNIEL_186
скважина
Math Formulas для класса 12. ): «Все математические формулы для 12-го класса засчитываются: YT #MATH #fyp». оригинальный звук
): «Все математические формулы для 12-го класса засчитываются: YT #MATH #fyp». оригинальный звук
2075 просмотров|
оригинальный звук — ALL ABOUT MATH — WELL
Raystar_study
Rayah Rahman
Постоянство так важно! 🤩 #learnontiktok #alevelmaths #mathsgcse #studytiktok #makemefamous
3,4 тыс. лайков, 56 комментариев. Видео TikTok от Rayah Rahman (@raystar_study): «Постоянство так важно! 🤩 #learnontiktok #alevelmaths #mathsgcse #studytiktok #makemefamous». Как я запомнил все формулы для Математика A-Level… | И получил пятерку 🤩 | Запишите каждую формулу на карточка📑 | …. оригинальный звук.
26,6 тыс. просмотров|
original sound — Rayah Rahman
its_me_dipendra169
Дипендра Кумар Гаутам
Все математические формулы (SEE) ******for you ## #Viral # #Dipendra 6 90 . 46,8 тыс. просмотров| Ответить на @sxphieelizabeth , пожалуйста, прокомментируйте, в чем вы хотели бы получить помощь дальше! Я собираюсь сделать Eng Lang P2 в ближайшее время! #gcses2022 #JDAirMaxMode #alevels2022 #gcses #studing 7,6 тыс. лайков, 70 комментариев. Видео TikTok от learninggtipss (@studyinggtipss): «Ответьте на @sxphieelizabeth, пожалуйста, прокомментируйте, в чем вы хотели бы помочь дальше! Я скоро буду делать Eng Lang P2! #gcses2022 #JDAirMaxMode #alevels2022 #gcses #studying». 53,7 тыс. просмотров| Добро пожаловать… Ссылка в нашей биографии, чтобы загрузить все листы математических формул! #psat #psatprep #sat #satprep #highschool 2,5 тыс. лайков, 12 комментариев. Видео TikTok от Beck Bootcamp (@beckbootcamp): «Добро пожаловать… Ссылка в нашей биографии, чтобы загрузить все листы математических формул! #psat #psatprep #sat #satprep #highschool». Хотите набрать 1350-1450 баллов на PSAT? . никогда полностью не одевался без улыбки. 17,7 тыс. просмотров| Know these math formulas 📢 #sat #act #math #formulas #LearnOnTikTok 47K Likes, 198 Комментарии. 465,2 тыс. просмотров| How. #foryou 16,4 тыс. лайков, 512 комментариев. Видео TikTok от Ruthmd (@ruthhmathews1): «Как. #foryou». оригинальный звук. 66,1 тыс. просмотров| спасибо за помощь мама! #fyp #foryoupage #school #math 724 лайков, 9Комментарии. Видео TikTok от erin rayman (@erinrayman): «спасибо за помощь, мама! #fyp #foryoupage #school #math». все математические формулы приходят мне в голову после того, как моя мама говорит мне, что я могу преуспеть, если просто приложу усилия. 4259 просмотров| #WhatsYourStuf #seeya #Math #officelife #fyp #foryou #foryoupage #ti84 36,4 тыс. лайков, 121 комментарий. Видео TikTok от 🤔 (@papysag): «#WhatsYourStuf #seeya #Math #officelife #fyp #foryou #foryoupage #ti84». Я собираюсь спасти вас по математике | ВЫБЕРИТЕ ПРИЛОЖЕНИЯ | ЗАТЕМ НАЖМИТЕ КОНИКА | …. чертовски хорош. 431,9 тыс. просмотров| все эти формулы нужно запомнить, но я думаю только о ней #apcalculusab #apcalcab #apcalculusbc #apcalcbc #calculus #math 32,5 тыс. 191 тыс. просмотров| Образование Сохранение Сохранение Ваш универсальный магазин математических формул! Изучите математические формулы, необходимые для разделов ACT, GRE и SAT по алгебре, геометрии и математическому анализу. Опубликовано: Обновлено: 0 115 Приложения проверены 10,0 тыс. Просмотры 1 Видео TikTok от Дипендры Кумара Гаутама (@its_me_dipendra169): «Все математические формулы (SEE) ****** для вас ###Viral ##Dipendra». Все формулы (СМ.). оригинальный звук.
Видео TikTok от Дипендры Кумара Гаутама (@its_me_dipendra169): «Все математические формулы (SEE) ****** для вас ###Viral ##Dipendra». Все формулы (СМ.). оригинальный звук. оригинальный звук — 𝄟✮͢🦋⃟≛⃝🇼 ʰⁱᵗᵉ 𝄟✮⃝🇩 ᵉᵛⁱˡ
learninggtipss
learninggtipss
 как я весь год оставался на восьмёрке по математике | ключевые формулы, которые нам не дадут на карточках | документы для практики документы для практики документы для практики | …. Ла Эспада.
как я весь год оставался на восьмёрке по математике | ключевые формулы, которые нам не дадут на карточках | документы для практики документы для практики документы для практики | …. Ла Эспада. La Espada — Eternal Raijin
beckbootcamp
Beck Bootcamp
never fully dressed without a smile — senia
agtutoring
AG Tutoring
 Видео TikTok от AG Tutoring (@agtutoring): «Знай эти математические формулы 📢 #sat #act #math #formulas #LearnOnTikTok». ACT SAT МАТЕМАТИЧЕСКИЕ ФОРМУЛЫ. сонидо оригинал.
Видео TikTok от AG Tutoring (@agtutoring): «Знай эти математические формулы 📢 #sat #act #math #formulas #LearnOnTikTok». ACT SAT МАТЕМАТИЧЕСКИЕ ФОРМУЛЫ. сонидо оригинал. sonido original — Esteve
ruthhmathews1
Ruthmd
оригинальный звук — Рутмд
erinrayman
erin rayman
 Настоящая тема Джексона VP.
Настоящая тема Джексона VP. True Jackson VP theme — Youalreadyknowbb
papysag
🤔
Чертовски чертовски — Лиззо
apcalcab_
apcalcab
 лайков, 444 комментария. Видео TikTok от apcalcab (@apcalcab_): «все эти формулы, которые нужно запомнить, но я думаю только о ней #apcalculusab #apcalcab #apcalculusbc #apcalcbc #исчисление #math». найти производную, когда я должен найти свой путь в твои объятия | — Абляции 1:2. Карусель жизни х курапика.
лайков, 444 комментария. Видео TikTok от apcalcab (@apcalcab_): «все эти формулы, которые нужно запомнить, но я думаю только о ней #apcalculusab #apcalcab #apcalculusbc #apcalcbc #исчисление #math». найти производную, когда я должен найти свой путь в твои объятия | — Абляции 1:2. Карусель жизни х курапика. Карусель жизни х курапика — YEAHH
10 лучших приложений для математических формул
Никаких платных промо. Наши эксперты достоверно ранжируют приложения, используя наш алгоритм. Узнать, как
О математических формулах
 +
+ Все математические формулы
Васим Джаффер
Книги и справочники
выучить все математические формулы, трюки, решатель уравнений, математический символ, термины
4,5 Рейтинги 16 тыс.+ Отзывы 1 млн+ Загрузки
Бесплатно Многофункциональный Свежий
Свободно
2
Все математические формулы
сенсорное поле
Образование
Платформа простых математических формул для инженеров и других.
4.2 Рейтинги 12 тыс.+ Отзывы 1 млн+ Загрузки
Бесплатно Покупки в приложении
Свободно Покупки в приложении
3
Все математические формулы
РАЗРАБОТЧИКИ HPVP
Образование
Все математические формулы с диаграммами, быстро и эффективно пересматривайте математические формулы.
3,7 Рейтинги 210+ Отзывы 10 000+ Скачано
Свободно
Загрузка. ..
..
4
Математические формулы для всех 2022
айзак
Образование
Все математические формулы для всех видов экзаменов Стандарты 2000 Math Formula 2021
4.7 Рейтинги 1 тыс.+ Отзывы 100 тыс.+ Загрузки
Свободно
5
Все математические формулы
Технические твиты
Образование
Все математические формулы с алгеброй, геометрией, тригонометрией и исчислением.
4,0 Рейтинги 14 тыс.+ Отзывы 1 млн+ Загрузки
Свободно
6
1300 математических формул: все в одном
Учебные приложения
Образование
Все формулы в 1 приложении! 1300 математических формул в автономном режиме для изучения математики.
4.6 Рейтинги 11 тыс.+ Отзывы 500 тыс.+ Скачано
Свободно
Подпишитесь на All-Access и сэкономьте деньги!
Получайте кураторские купоны на приложения ежедневно бесплатно. Сэкономьте до 90% на популярных приложениях, таких как All Math Formulas
Сэкономьте до 90% на популярных приложениях, таких как All Math Formulas
- Зарегистрироваться
- Войти
Электронная почта
Требуется адрес электронной почты
Пароль
Требуется пароль
Показывать Скрывать
забыл пароль?
или продолжить с
Мы никогда не будем передавать или продавать ваши данные третьим лицам. Вы можете отказаться в любое время.
Условия Сервис | Конфиденциальность Политика
7
Математическая формула с практикой
Аминур Рахман
Образование
Алгебра, геометрия, тригонометрия и математические формулы с практической математикой
4,5
Рейтинги
11 тыс. +
Отзывы
1 млн+
Загрузки
+
Отзывы
1 млн+
Загрузки
Бесплатно Покупки в приложении
Свободно Покупки в приложении
8
Все математические формулы
Хитиша Тех
Книги и справочники
Все формулы соответствия, формула, калькулятор, расчет, математический расчет, математика
4.4 Рейтинги 160+ Отзывы 10 000+ Скачано
Свободно
9
Все математические формулы — офлайн
Информатика Северной Америки
Образование
Простая математическая формула с алгеброй, геометрией, статистикой, тригонометрией и исчислением
3,9 Рейтинги 126+ Отзывы 10 000+ Скачано
Свободно
10
Математические формулы с калькулятором
ЭЖИЛЬ
Образование
Умный инструмент с важными математическими формулами, научным калькулятором и приложениями
4. 2
Рейтинги
2 000+
Отзывы
100 тыс.+
Загрузки
2
Рейтинги
2 000+
Отзывы
100 тыс.+
Загрузки
Свободно
Загрузка…
10 лучших приложений для математических формул
Сохранение…
Сохранение…
Загрузка следующего рейтинга Загрузка следующего рейтинга
Как мы выбираем лучшие приложения
Широкий поиск
Наш уникальный алгоритм прочесал App Store и Google Play Store, выполнив поиск математические формулы. Оттуда мы получили в общей сложности 627 уникальных приложений (32 приложения для Android и 595 приложений для iOS) в качестве потенциальных кандидатов.Дополнительный обзор редакционной группы
Наконец, наша редакция проверяет все приложения в нашем список лучших 10, один за другим, чтобы убедиться, что эти приложения самого высокого качества.


 Обратная матрица
Обратная матрица Прямая и плоскость
Прямая и плоскость Производные элементарных функций
Производные элементарных функций Формула Тейлора
Формула Тейлора Ш. — Практикум
Ш. — Практикум А. — Учебник
А. — Учебник А.2
А.2 В., Романов М.Н.
В., Романов М.Н. Лисьев В.П.
Лисьев В.П. Афанасьев В.В.
Афанасьев В.В. К. и др.Том 3. Математический анализ: кратные и криволинейные интегралы
К. и др.Том 3. Математический анализ: кратные и криволинейные интегралы Манжиров А.В., Полянин А.Д.
Манжиров А.В., Полянин А.Д. В 3-х частях. Рябушко А.П. и др.2
В 3-х частях. Рябушко А.П. и др.2 В 4-х частях. Под ред. Ефимова А.В., Поспелова А.С.1
В 4-х частях. Под ред. Ефимова А.В., Поспелова А.С.1 Кузнецов Л.А.
Кузнецов Л.А. П.4
П.4 Каплан И.А.5
Каплан И.А.5 Шипачев В.С.
Шипачев В.С. Орловский Д.Г.
Орловский Д.Г. Воронина Б.Б.
Воронина Б.Б. В., Медведева М.И., Полшков Ю.Н., Пелашенко А.В.
В., Медведева М.И., Полшков Ю.Н., Пелашенко А.В.
 Переменные x и y на-
Переменные x и y на- Чаще всего графиком является некоторая поверх-
Чаще всего графиком является некоторая поверх-

 5.2. Иллюстрация к примеру 1.1
5.2. Иллюстрация к примеру 1.1 1) Так как lim x2 =1 и lim y2 = 4 , то
1) Так как lim x2 =1 и lim y2 = 4 , то 5.5).
5.5).
 Обозначают
Обозначают







 Большинство экономических докторов наук. программы ожидают, что кандидаты будут иметь углубленное исчисление, дифференциальные уравнения, линейную алгебру и базовую теорию вероятностей. Многие абитуриенты прошли курс реального анализа. Это означает, что студенты, планирующие поступить в аспирантуру по экономике, должны проходить 1-2 курса математики в каждом семестре. Около половины студентов, поступающих в докторантуру. программы по экономике заранее получают степень магистра. Многие укрепляют свою математическую подготовку в этот период.
Большинство экономических докторов наук. программы ожидают, что кандидаты будут иметь углубленное исчисление, дифференциальные уравнения, линейную алгебру и базовую теорию вероятностей. Многие абитуриенты прошли курс реального анализа. Это означает, что студенты, планирующие поступить в аспирантуру по экономике, должны проходить 1-2 курса математики в каждом семестре. Около половины студентов, поступающих в докторантуру. программы по экономике заранее получают степень магистра. Многие укрепляют свою математическую подготовку в этот период. Должен включать как теоретические, так и эмпирические компоненты и использовать SAS, Stata, R, Matlab или подобное статистическое программное обеспечение.
Должен включать как теоретические, так и эмпирические компоненты и использовать SAS, Stata, R, Matlab или подобное статистическое программное обеспечение. препарат
препарат . Большинство отраслей современной экономики широко используют математику и статистику, а некоторые важные области математических исследований были мотивированы экономическими проблемами. Экономисты и математики внесли важный вклад в дисциплины друг друга. Экономист Кеннет Эрроу, например, проделал новаторскую работу в области математической оптимизации, и в 19В 94 году математику Джону Нэшу была присуждена Нобелевская премия по экономике за работу, которую он проделал в области теории игр, которая стала центральной в современной экономической теории. Область концентрации Хаверфорда в области математической экономики позволяет студентам, изучающим обе дисциплины, не только овладеть другими дисциплинами, но и оценить их взаимосвязь.
. Большинство отраслей современной экономики широко используют математику и статистику, а некоторые важные области математических исследований были мотивированы экономическими проблемами. Экономисты и математики внесли важный вклад в дисциплины друг друга. Экономист Кеннет Эрроу, например, проделал новаторскую работу в области математической оптимизации, и в 19В 94 году математику Джону Нэшу была присуждена Нобелевская премия по экономике за работу, которую он проделал в области теории игр, которая стала центральной в современной экономической теории. Область концентрации Хаверфорда в области математической экономики позволяет студентам, изучающим обе дисциплины, не только овладеть другими дисциплинами, но и оценить их взаимосвязь. Сильная математическая подготовка также является преимуществом для студентов, поступающих в бизнес-школы или на программы магистратуры в области государственной политики. Многие рабочие места, связанные с экономикой, в правительстве, бизнесе и финансах требуют сильных количественных навыков, и концентрация готовит студентов, заинтересованных в поиске таких должностей.
Сильная математическая подготовка также является преимуществом для студентов, поступающих в бизнес-школы или на программы магистратуры в области государственной политики. Многие рабочие места, связанные с экономикой, в правительстве, бизнесе и финансах требуют сильных количественных навыков, и концентрация готовит студентов, заинтересованных в поиске таких должностей.



 0
0 Если вы любите работать с числами, ориентируетесь на данные и любите находить творческие решения реальных проблем, любой профессиональный путь может оказаться полезным.
Если вы любите работать с числами, ориентируетесь на данные и любите находить творческие решения реальных проблем, любой профессиональный путь может оказаться полезным.
 Они составляют планы уроков и предоставляют общее или специализированное математическое образование учащимся начальной, средней или старшей школы.
Они составляют планы уроков и предоставляют общее или специализированное математическое образование учащимся начальной, средней или старшей школы.
 Среди них различия в самой учебной программе, а также в философии дисциплин и их профессиональном применении.
Среди них различия в самой учебной программе, а также в философии дисциплин и их профессиональном применении. Экономическая теория, хотя и имеет практическое применение, фокусируется не столько на следовании пошаговой стратегии достижения решения, сколько на абстрактных концепциях.
Экономическая теория, хотя и имеет практическое применение, фокусируется не столько на следовании пошаговой стратегии достижения решения, сколько на абстрактных концепциях.
 Санкт-Петербург
Санкт-Петербург Lexical Test
Lexical Test Саранск, Республика Мордовия
Саранск, Республика Мордовия Котлас
Котлас М.Ю.Козлова» пгт. Никель
М.Ю.Козлова» пгт. Никель Санкт-Петербург
Санкт-Петербург Омска «Гимназия №150»
Омска «Гимназия №150» А. И. ГЕРЦЕНА
А. И. ГЕРЦЕНА Могилев
Могилев


 10 сынып.
10 сынып.













 Среди данных чисел подчеркни наименьшее число.
Среди данных чисел подчеркни наименьшее число.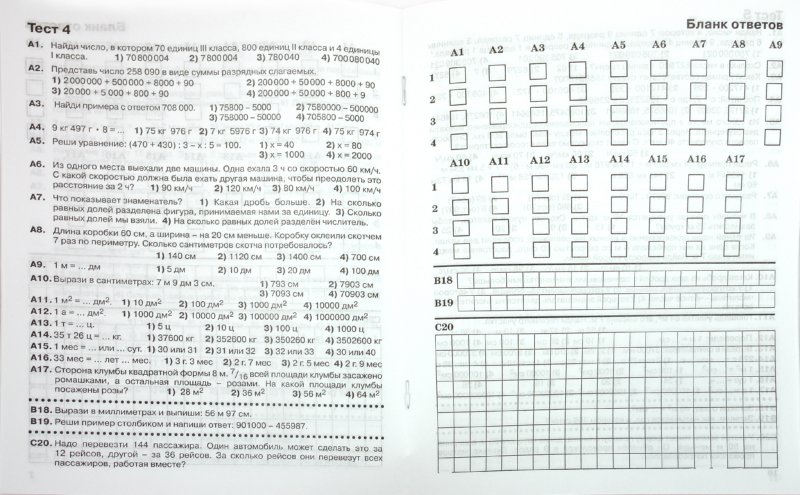
 НУМЕРАЦИЯ.
НУМЕРАЦИЯ. Запиши данные числа в порядке убывания.
Запиши данные числа в порядке убывания.


 Реши примеры.
Реши примеры. Запиши по
порядку числа от 3 до 8……………………………………………….
Запиши по
порядку числа от 3 до 8………………………………………………. Запиши по
порядку числа от 3 до 8……………………………………………….
Запиши по
порядку числа от 3 до 8……………………………………………….
 Реши задачи.
Реши задачи. Зачеркни
правильный ответ. Слушай внимательно.
Зачеркни
правильный ответ. Слушай внимательно. Зачеркни
правильный ответ. Слушай внимательно.
Зачеркни
правильный ответ. Слушай внимательно. Реши задачу.
Реши задачу. Реши примеры.
Реши примеры.
 Нарисуйте 5
флажков. Под флажками нарисуйте шарики так, чтобы шариков было на 1 меньше, чем
флажков. Под флажками нарисуйте грибы; грибов должно быть на 4 больше, чем
шариков.
Нарисуйте 5
флажков. Под флажками нарисуйте шарики так, чтобы шариков было на 1 меньше, чем
флажков. Под флажками нарисуйте грибы; грибов должно быть на 4 больше, чем
шариков.
 Ложек 5, а вилок на 2 больше, чем ложек. Сколько вилок на столе?
Ложек 5, а вилок на 2 больше, чем ложек. Сколько вилок на столе? Обведи в
кружочек наименьшее число.
Обведи в
кружочек наименьшее число. Подчеркни число, следующее за числом 15.
Подчеркни число, следующее за числом 15. Зачеркни
примеры, ответы которых не 11.
Зачеркни
примеры, ответы которых не 11.
 Это. Как и во всем остальном, чем раньше в развитии ребенка вы начнете работать,
что-то — будь то спорт, музыка или математика — тем сильнее ребенок усваивает предмет. В сегодняшней
глобальном мире прочная математическая основа важна не только для прохождения стандартизированных тестов и
поступление в топовые вузы; это также имеет решающее значение для расширения возможностей молодых умов думать, рассуждать и
позже соревнуются за множество востребованных профессий со своими международными коллегами.
Международный математический конкурс — это 30-минутный онлайн-вызов, основанный на ведущих математических программах от
по всему миру. Разработано профессионалами в области математики с многолетним опытом работы в Русской школе
математики, конкурс специально разработан, чтобы дать родителям представление о том, как их ребенок
математические знания занимают место во всем мире.
Это. Как и во всем остальном, чем раньше в развитии ребенка вы начнете работать,
что-то — будь то спорт, музыка или математика — тем сильнее ребенок усваивает предмет. В сегодняшней
глобальном мире прочная математическая основа важна не только для прохождения стандартизированных тестов и
поступление в топовые вузы; это также имеет решающее значение для расширения возможностей молодых умов думать, рассуждать и
позже соревнуются за множество востребованных профессий со своими международными коллегами.
Международный математический конкурс — это 30-минутный онлайн-вызов, основанный на ведущих математических программах от
по всему миру. Разработано профессионалами в области математики с многолетним опытом работы в Русской школе
математики, конкурс специально разработан, чтобы дать родителям представление о том, как их ребенок
математические знания занимают место во всем мире.
 Владелец щенка взвешивает его два раза в
день. Щенок теряет 1 фунт каждый вечер и набирает 3 фунта каждое утро.
Сколько фунтов будет весить щенок к вечеру четверга той же недели?
Владелец щенка взвешивает его два раза в
день. Щенок теряет 1 фунт каждый вечер и набирает 3 фунта каждое утро.
Сколько фунтов будет весить щенок к вечеру четверга той же недели? назад». И это было правдой. Через сколько лет Лия правдиво может сказать в свой день рождения:
«Сегодня я ровно вдвое старше, чем четыре года назад»?
назад». И это было правдой. Через сколько лет Лия правдиво может сказать в свой день рождения:
«Сегодня я ровно вдвое старше, чем четыре года назад»? Какое наименьшее количество футболок Альпа должна вывезти
мешка (не глядя на них), чтобы быть абсолютно уверенным в наличии по крайней мере двух
Футболки среди них отличаются только размером или только цветом?
Какое наименьшее количество футболок Альпа должна вывезти
мешка (не глядя на них), чтобы быть абсолютно уверенным в наличии по крайней мере двух
Футболки среди них отличаются только размером или только цветом? (Джесси Коста/WBUR) Этой статье больше 5 лет.
(Джесси Коста/WBUR) Этой статье больше 5 лет. тенденция, движимая быстрорастущей сетью под названием Русская математическая школа. По последним подсчетам, в 22 000 учащихся, школа является гигантом среди российских математических программ, имея 15 филиалов в Массачусетсе, где она началась, и 40 филиалов по всей стране.
тенденция, движимая быстрорастущей сетью под названием Русская математическая школа. По последним подсчетам, в 22 000 учащихся, школа является гигантом среди российских математических программ, имея 15 филиалов в Массачусетсе, где она началась, и 40 филиалов по всей стране. «Мы берем то, что Советы делали лучше всего — математическое образование — и переносим это из этого ужасного закрытого общества в свободный мир», — говорит она.
«Мы берем то, что Советы делали лучше всего — математическое образование — и переносим это из этого ужасного закрытого общества в свободный мир», — говорит она.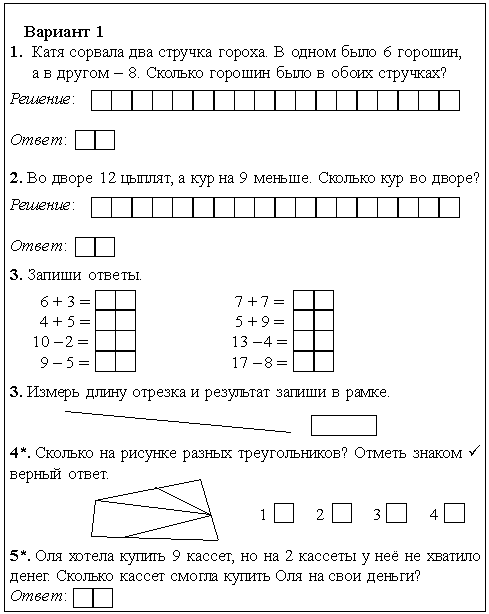 «Ребенка нужно как можно скорее перевести на абстрактный уровень, — говорит она, — имея в виду раннее знакомство с алгеброй и геометрией, а не только с арифметикой», и помочь детям понять принципы для себя, а не кормить их с ложечки.
«Ребенка нужно как можно скорее перевести на абстрактный уровень, — говорит она, — имея в виду раннее знакомство с алгеброй и геометрией, а не только с арифметикой», и помочь детям понять принципы для себя, а не кормить их с ложечки.
 Тогда она сильно пострадала от эмиграции — но она по-прежнему сильна».
Тогда она сильно пострадала от эмиграции — но она по-прежнему сильна». (Джесси Коста/WBUR)
(Джесси Коста/WBUR)


 Например, в отличие от больших занятий по русскому языку за строго регламентированными партами, в студии преподают только в небольших группах по полдюжины детей вокруг стола. И он делит группы по уровням способностей, поэтому может быть пять или шесть групп с разными уровнями для детей, которые все учатся в одном классе в школе.
Например, в отличие от больших занятий по русскому языку за строго регламентированными партами, в студии преподают только в небольших группах по полдюжины детей вокруг стола. И он делит группы по уровням способностей, поэтому может быть пять или шесть групп с разными уровнями для детей, которые все учатся в одном классе в школе. Тонким, но уверенным голосом Соня утверждает свою идею: «Сначала нужно сделать нижний, потому что они одинаковые».
Тонким, но уверенным голосом Соня утверждает свою идею: «Сначала нужно сделать нижний, потому что они одинаковые».


 Этот подход, называемый «доступное обучение», является краеугольным камнем так называемой русской математики, стиля, к которому все больше и больше американских родителей обращаются, чтобы улучшить математические навыки своих детей.
Этот подход, называемый «доступное обучение», является краеугольным камнем так называемой русской математики, стиля, к которому все больше и больше американских родителей обращаются, чтобы улучшить математические навыки своих детей. Хотя единой стандартной российской математической модели не существует, есть некоторые особенности, такие как доступное обучение, которые сильно отличают российские математические классы от тех, к которым привыкли американские дети.
Хотя единой стандартной российской математической модели не существует, есть некоторые особенности, такие как доступное обучение, которые сильно отличают российские математические классы от тех, к которым привыкли американские дети. Учителя могут определить слабые места, а учащиеся получают больше вопросов, подобных тем, которые они пропустили.
Учителя могут определить слабые места, а учащиеся получают больше вопросов, подобных тем, которые они пропустили. Она во втором классе; Техасские базовые знания и навыки (TEKS) не требуют использования переменных до четвертого класса.
Она во втором классе; Техасские базовые знания и навыки (TEKS) не требуют использования переменных до четвертого класса. Программное обеспечение не совсем дало результаты, за которые заплатил школьный округ: в 2016–17 учебном году учащиеся RM обычно набирали более высокие баллы на тесте STAAR по математике, чем учащиеся, не входящие в RM, но разница не была практически существенной.
Программное обеспечение не совсем дало результаты, за которые заплатил школьный округ: в 2016–17 учебном году учащиеся RM обычно набирали более высокие баллы на тесте STAAR по математике, чем учащиеся, не входящие в RM, но разница не была практически существенной.

 если 35 разделить на 5, то получится 7 (да)
если 35 разделить на 5, то получится 7 (да)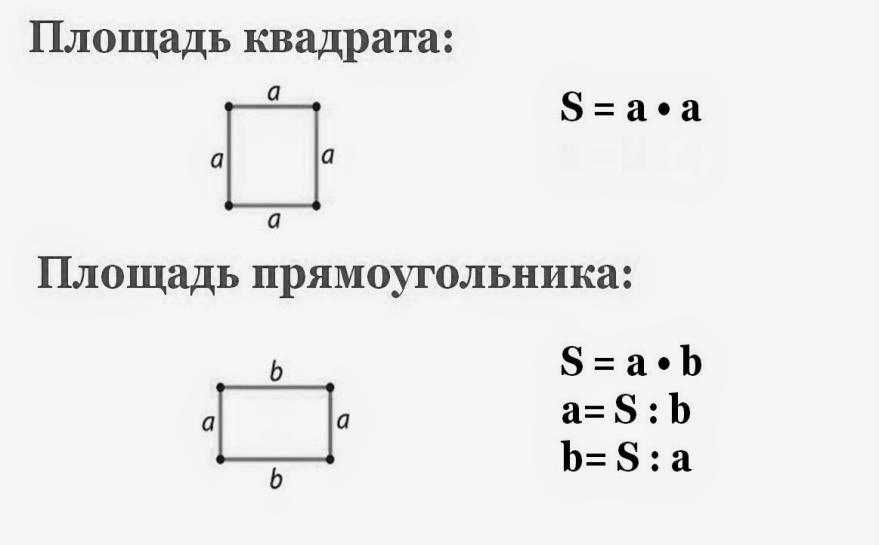

 ..
.. com
com net
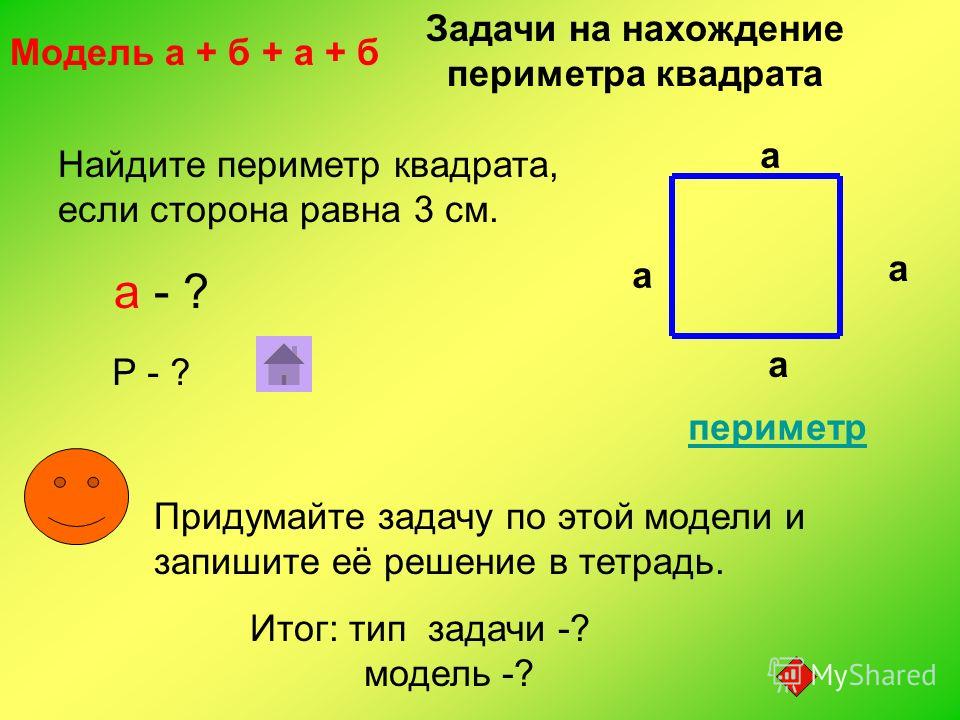
net . Математика, Тесты, 4 класс, 4 класс. Учебные пособия, конспекты уроков, презентации к урокам., М.Г. Нефёдова. Рабочая тетрадь по математике. 3-4 классы. Периметр и площадь.
. Математика, Тесты, 4 класс, 4 класс. Учебные пособия, конспекты уроков, презентации к урокам., М.Г. Нефёдова. Рабочая тетрадь по математике. 3-4 классы. Периметр и площадь. 3—4 классы. Рабочая…
3—4 классы. Рабочая… 3—4 классы. Рабочая тетрадь по…
3—4 классы. Рабочая тетрадь по… 3—4 классы. Рабочая тетрадь по…
3—4 классы. Рабочая тетрадь по… Пособие включает все виды геометрических задач на нахождение площади и периметра многоугольников, относящиеся к курсу начальной школы.
Пособие включает все виды геометрических задач на нахождение площади и периметра многоугольников, относящиеся к курсу начальной школы. 3—4 классы. Рабочая тетрадь… — alleng.me
3—4 классы. Рабочая тетрадь… — alleng.me Рабочая тетрадь по математике. 3—4 классы.
Рабочая тетрадь по математике. 3—4 классы. Г. 2014. Задачи на движение. 3-4 классы.
Г. 2014. Задачи на движение. 3-4 классы.
 Нефёдова. Рабочая тетрадь по математике. 3—4 классы.
Нефёдова. Рабочая тетрадь по математике. 3—4 классы. Тест-проверки позволяют оценить знания школьника и в случае успешного выполнения теста перейти к…
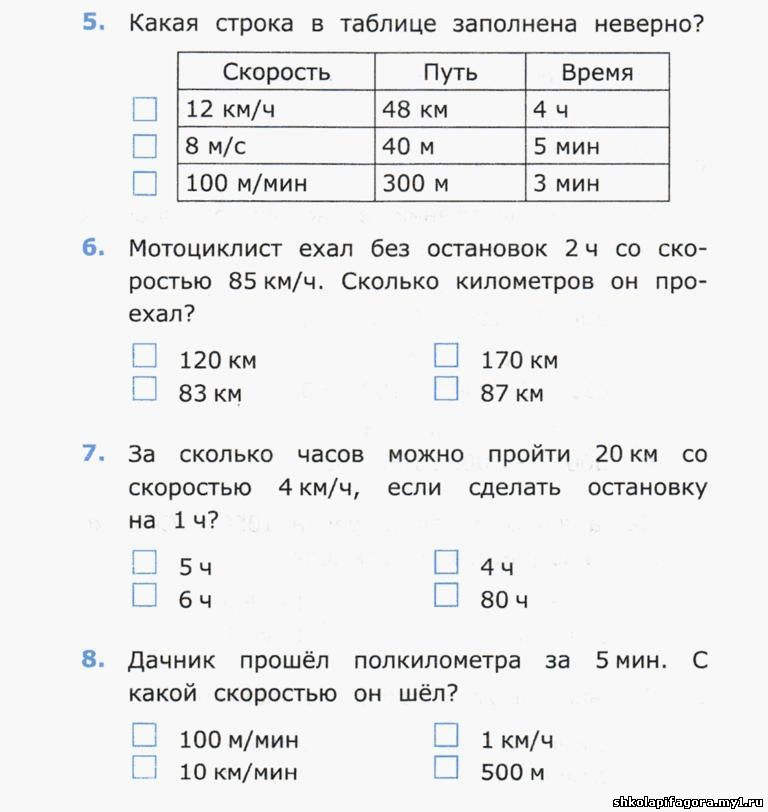
Тест-проверки позволяют оценить знания школьника и в случае успешного выполнения теста перейти к… Пособие включает все виды задач на движение, которые встречаются в курсе начальной школы. Материалы пособия обеспечивают все этапы формирования навыка решения этих задач: объяснение, тренинг, проверку. Тест-проверки позволяют оценить знания школьника и в случае успешною выполнения теста перейти к следующему тесту и более сложным заданиям.
Пособие включает все виды задач на движение, которые встречаются в курсе начальной школы. Материалы пособия обеспечивают все этапы формирования навыка решения этих задач: объяснение, тренинг, проверку. Тест-проверки позволяют оценить знания школьника и в случае успешною выполнения теста перейти к следующему тесту и более сложным заданиям.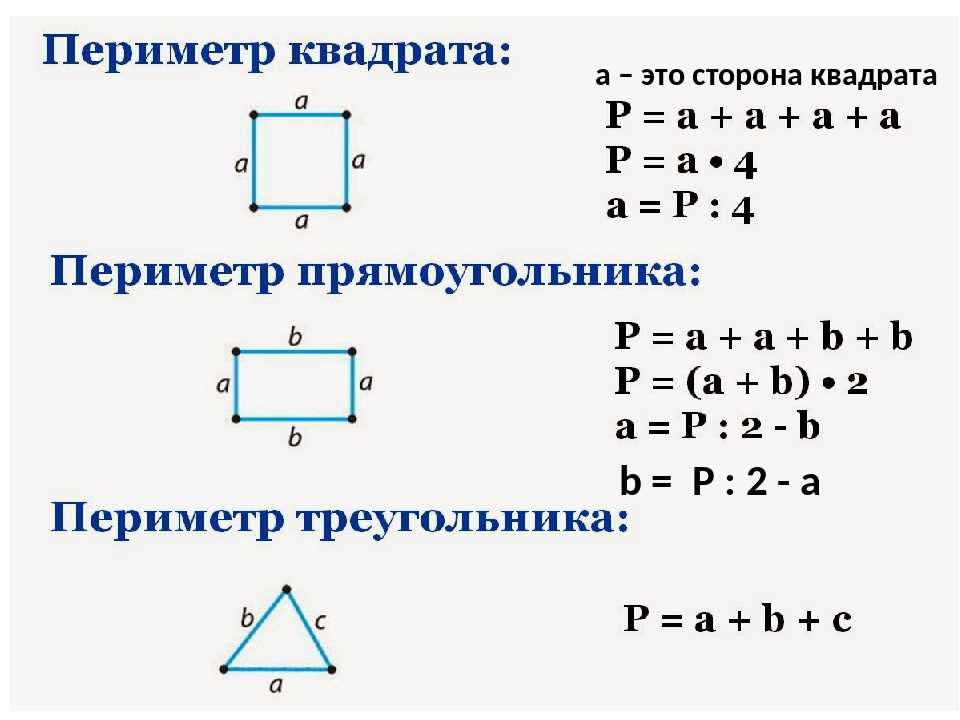 ru
ru Периметр…
Периметр…
 Тренажер для уч-ся 1-4 классов Часть 23 — Карлова. Я читаю по-английски — 2014 … Часть 25 — Решаем и оформляем Геометрические задачи Часть 26 — Полная коллекция видеоуроков по основным школьным предметам с 1 по 11 класс Часть 27 — Все виды разбора по русскому языку.
Тренажер для уч-ся 1-4 классов Часть 23 — Карлова. Я читаю по-английски — 2014 … Часть 25 — Решаем и оформляем Геометрические задачи Часть 26 — Полная коллекция видеоуроков по основным школьным предметам с 1 по 11 класс Часть 27 — Все виды разбора по русскому языку.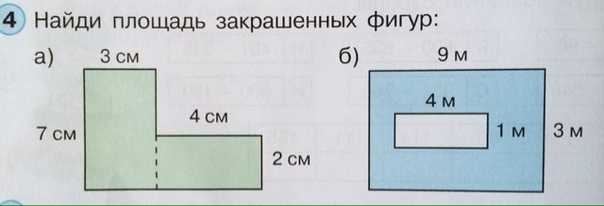
 А зимой, в лютые морозы, хозяева брали в избу молодых животных, чтобы те не замерзли. Вот так и жили. Какая пословица подходит к сказанному? (В тесноте, да не в обиде.)
А зимой, в лютые морозы, хозяева брали в избу молодых животных, чтобы те не замерзли. Вот так и жили. Какая пословица подходит к сказанному? (В тесноте, да не в обиде.)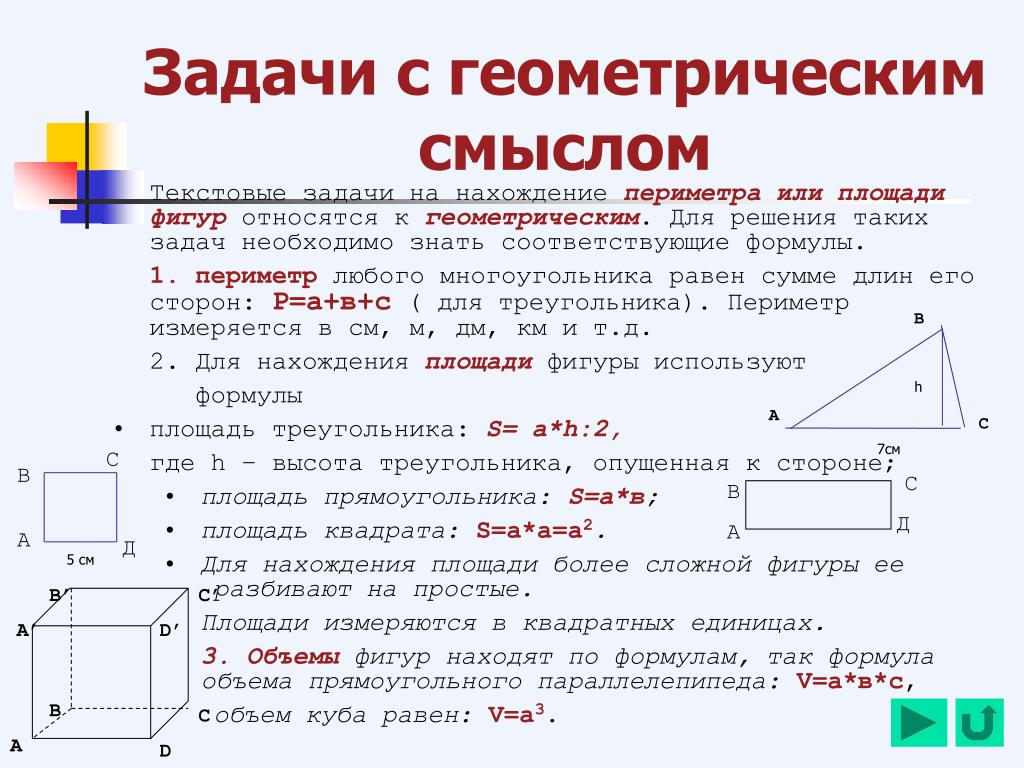 На 1/5 части всей площади посажен лук, а на остальной площади – горох. Чему равна площадь грядки, засаженная горохом? (2400 дм2)
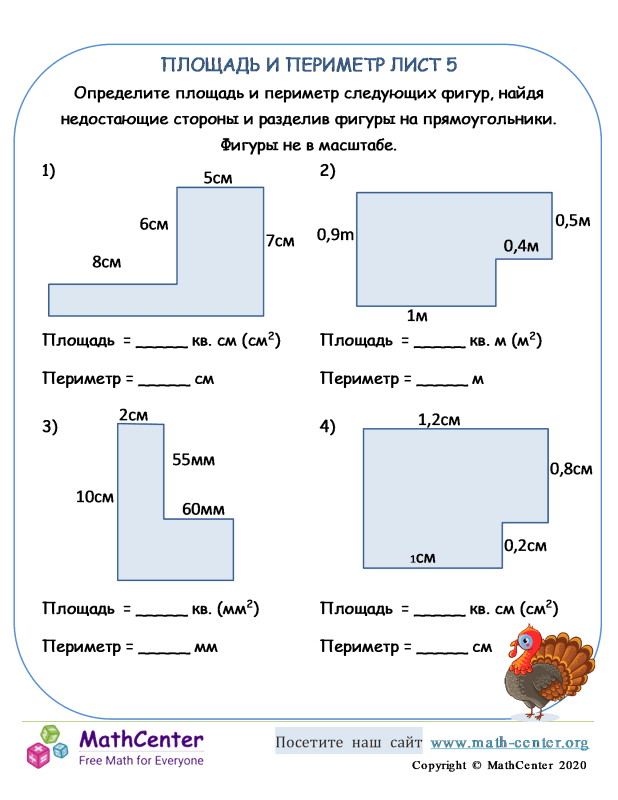
На 1/5 части всей площади посажен лук, а на остальной площади – горох. Чему равна площадь грядки, засаженная горохом? (2400 дм2) Укажи площадь этого прямоугольника.
Укажи площадь этого прямоугольника. Во сколько раз 1 дм² больше 1 см²?
Во сколько раз 1 дм² больше 1 см²? Какое расстояние придется пробежать Кейт, если она пробежит вокруг парка один раз?
Какое расстояние придется пробежать Кейт, если она пробежит вокруг парка один раз?
 15 × 2 . 4
15 × 2 . 4 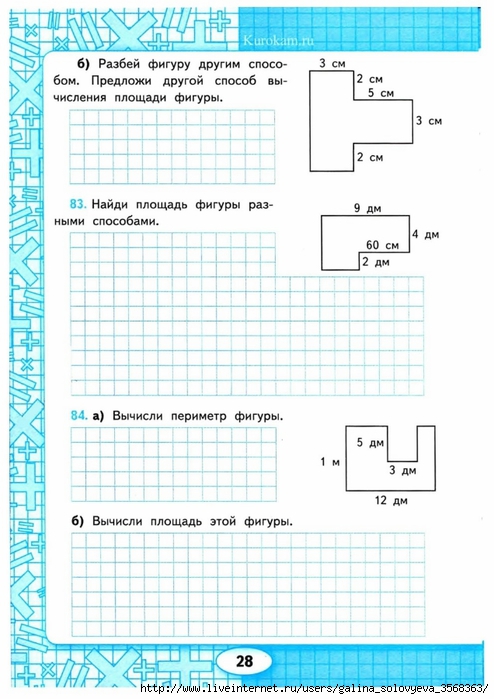 Этот кусок дерева имеет ширину 15 дюймов . Если всего площадь дерева равна 180 квадрат дюймов, какова его длина?
Этот кусок дерева имеет ширину 15 дюймов . Если всего площадь дерева равна 180 квадрат дюймов, какова его длина?
 💪
💪 Стратегическое мышление является одним из самых важных навыков для развития детей. Это требует умения наблюдать, собирать информацию, планировать и анализировать возможные решения и выбирать подходящее действие. Стратегическое мышление — это способ решения проблем. Решение проблем является важным навыком в нашей профессиональной, семейной и общественной жизни. Математические игры для детей ориентированы на увлекательные занятия, развивающие стратегическое математическое мышление
Стратегическое мышление является одним из самых важных навыков для развития детей. Это требует умения наблюдать, собирать информацию, планировать и анализировать возможные решения и выбирать подходящее действие. Стратегическое мышление — это способ решения проблем. Решение проблем является важным навыком в нашей профессиональной, семейной и общественной жизни. Математические игры для детей ориентированы на увлекательные занятия, развивающие стратегическое математическое мышление При изучении математики есть элемент повторения, который является важной частью изучения новых понятий и развития автоматического запоминания математических фактов. Числовые факты могут быть скучными и утомительными для изучения и практики. Игра может генерировать огромное количество практики — математической практики, в которой дети не жалуются на то, как много работы им приходится делать. Что может быть лучше, чем этот способ выучить все математические понятия!
При изучении математики есть элемент повторения, который является важной частью изучения новых понятий и развития автоматического запоминания математических фактов. Числовые факты могут быть скучными и утомительными для изучения и практики. Игра может генерировать огромное количество практики — математической практики, в которой дети не жалуются на то, как много работы им приходится делать. Что может быть лучше, чем этот способ выучить все математические понятия!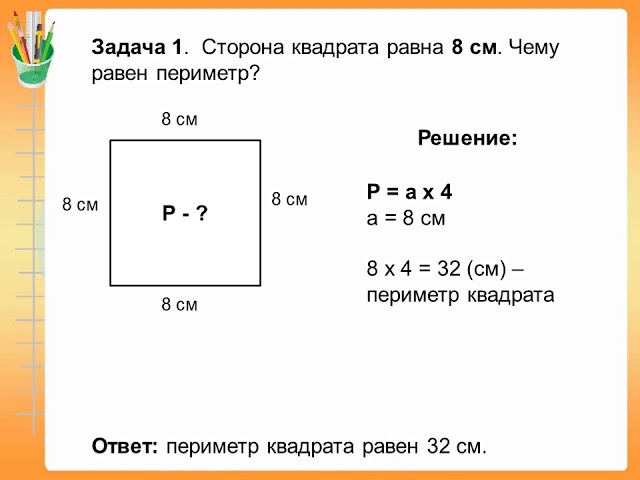 Самый большой стол предназначен для размещения максимального количества блюд. Предполагается, что стол прямоугольный. Все должны сидеть за столом, не перекрывая друг друга, не сидя друг у друга на коленях. Затем вы можете задать детям еще одну задачу: за каким самым маленьким столом можно разместить всех людей, но при этом он займет наименьшее пространство или самый маленький стол, потому что готовится всего несколько блюд.
Самый большой стол предназначен для размещения максимального количества блюд. Предполагается, что стол прямоугольный. Все должны сидеть за столом, не перекрывая друг друга, не сидя друг у друга на коленях. Затем вы можете задать детям еще одну задачу: за каким самым маленьким столом можно разместить всех людей, но при этом он займет наименьшее пространство или самый маленький стол, потому что готовится всего несколько блюд. Но площадь в этом случае больше. Следовательно, стол 2 — это стол, на котором может быть выставлено больше блюд, чем стол 1. Дети проработают все другие возможности, чтобы убедиться, что площадь стола 2 максимальна, а площадь стола 1 минимальна.
Но площадь в этом случае больше. Следовательно, стол 2 — это стол, на котором может быть выставлено больше блюд, чем стол 1. Дети проработают все другие возможности, чтобы убедиться, что площадь стола 2 максимальна, а площадь стола 1 минимальна. Интересно, что четыре фигуры из пяти имеют одинаковые периметры. Только квадрат имеет более короткий периметр. Почему периметр становится короче только у квадрата, тогда как у всех остальных фигур периметры одинаковой длины? Пусть дети исследуют ответы на эти вопросы. Эта деятельность побуждает учащихся смотреть на изменение периметров в соответствии с преобразованием форм.
Интересно, что четыре фигуры из пяти имеют одинаковые периметры. Только квадрат имеет более короткий периметр. Почему периметр становится короче только у квадрата, тогда как у всех остальных фигур периметры одинаковой длины? Пусть дети исследуют ответы на эти вопросы. Эта деятельность побуждает учащихся смотреть на изменение периметров в соответствии с преобразованием форм.
 При вычислении площади таких фигур мы можем просто сложить площади каждой из отдельных фигур вместе.
При вычислении площади таких фигур мы можем просто сложить площади каждой из отдельных фигур вместе.

 Нажмите здесь, чтобы узнать больше о MEA и о том, как они могут изменить ваш класс.
Нажмите здесь, чтобы узнать больше о MEA и о том, как они могут изменить ваш класс.
 Нажмите здесь, чтобы узнать больше о MEA и о том, как они могут изменить ваш класс.
Нажмите здесь, чтобы узнать больше о MEA и о том, как они могут изменить ваш класс. Нажмите здесь, чтобы узнать больше о MEA и о том, как они могут изменить ваш класс.
Нажмите здесь, чтобы узнать больше о MEA и о том, как они могут изменить ваш класс.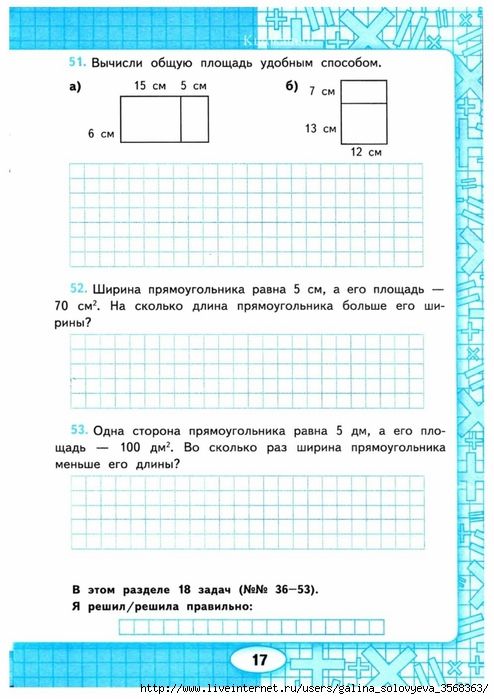 С помощью этого упражнения учащиеся узнают площадь и периметр.
С помощью этого упражнения учащиеся узнают площадь и периметр. Нажмите здесь, чтобы узнать больше о MEA и о том, как они могут изменить ваш класс.
Нажмите здесь, чтобы узнать больше о MEA и о том, как они могут изменить ваш класс. Нажмите здесь, чтобы узнать больше о MEA и о том, как они могут изменить ваш класс.
Нажмите здесь, чтобы узнать больше о MEA и о том, как они могут изменить ваш класс. Студенты должны будут переоценить плиточные компании, а также пересчитать общие затраты, чтобы включить плитку для ванной комнаты.
Студенты должны будут переоценить плиточные компании, а также пересчитать общие затраты, чтобы включить плитку для ванной комнаты. Нажмите здесь, чтобы узнать больше о MEA и о том, как они могут изменить ваш класс.
Нажмите здесь, чтобы узнать больше о MEA и о том, как они могут изменить ваш класс.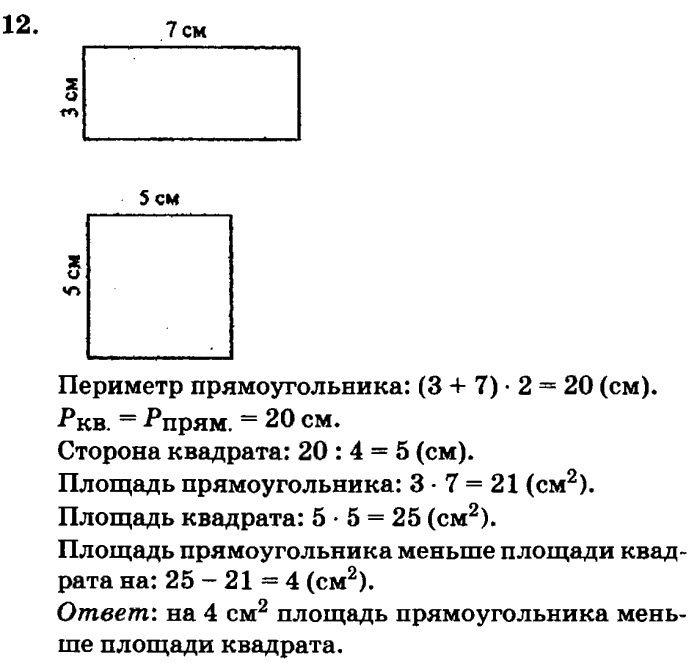
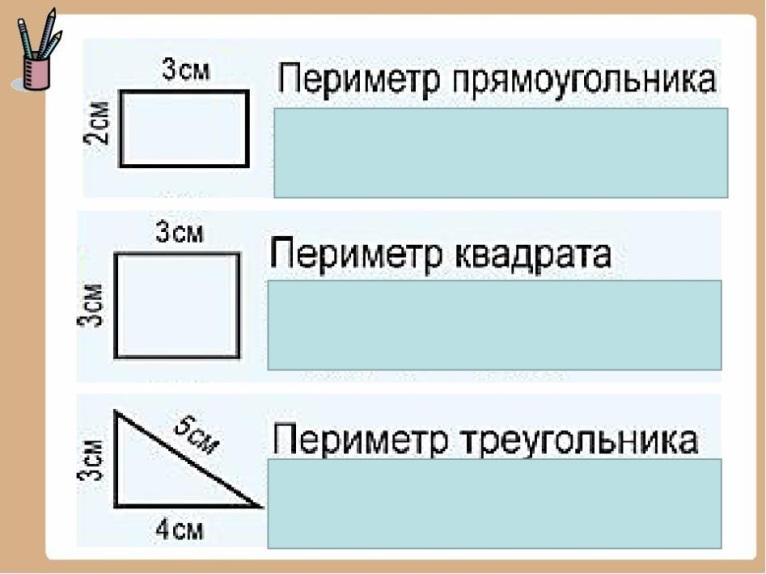 Им необходимо определить общую площадь помещения и то, как оно используется.
Им необходимо определить общую площадь помещения и то, как оно используется. После этого они добавят общую стоимость игровой комнаты и кладовки. Они сообщат о своих выводах и причинах, написав письмо клиенту.
После этого они добавят общую стоимость игровой комнаты и кладовки. Они сообщат о своих выводах и причинах, написав письмо клиенту.
 Нажмите ниже, чтобы открыть другие руководства из этой серии.
Нажмите ниже, чтобы открыть другие руководства из этой серии. Периметр:
Периметр: Кроме того, числа были выбраны, чтобы определить, есть ли у учащихся распространенное заблуждение, связанное с умножением. Поскольку сложение является одновременно коммутативным и ассоциативным, мы можем переупорядочивать или перегруппировывать слагаемые как угодно. Студенты часто считают, что то же самое верно и для умножения.
Кроме того, числа были выбраны, чтобы определить, есть ли у учащихся распространенное заблуждение, связанное с умножением. Поскольку сложение является одновременно коммутативным и ассоциативным, мы можем переупорядочивать или перегруппировывать слагаемые как угодно. Студенты часто считают, что то же самое верно и для умножения. Например, зная площадь и длину, можно ли найти периметр?
Например, зная площадь и длину, можно ли найти периметр?
 Кузнецова, Минаева
Кузнецова, Минаева К учебнику Виленкина
К учебнику Виленкина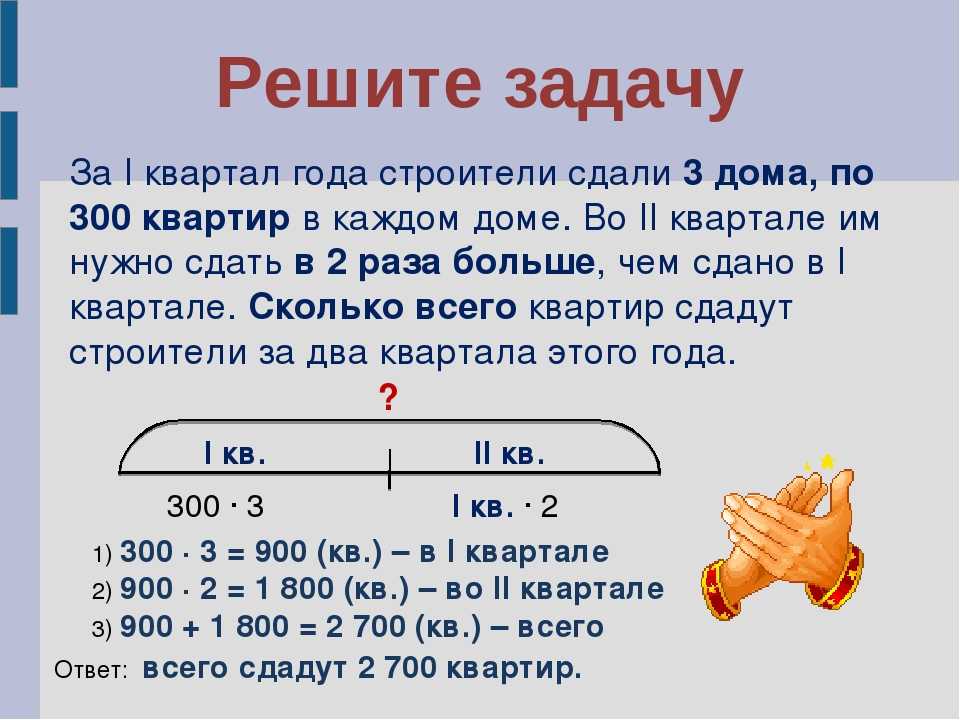 В этом тоже могут помочь специализированные пособия с гдз по математике за 6 класс, например решебники к контрольным и проверочным, самостоятельным, проводимым в классе.
В этом тоже могут помочь специализированные пособия с гдз по математике за 6 класс, например решебники к контрольным и проверочным, самостоятельным, проводимым в классе.
 Поскольку они не могут ежедневно, из урока в урок, получать объяснения учителя в полном объеме. Учитывая, что во время проведения карантинных мероприятий на месте учеников находящихся на семейной/домашней форме обучения, оказались все без исключения школьники, интерес к работе с гдз по математике в 6 классе существенно возрос;
Поскольку они не могут ежедневно, из урока в урок, получать объяснения учителя в полном объеме. Учитывая, что во время проведения карантинных мероприятий на месте учеников находящихся на семейной/домашней форме обучения, оказались все без исключения школьники, интерес к работе с гдз по математике в 6 классе существенно возрос; Для репетиторов и руководителей математических кружков работа с онлайн справочниками по математике 6 класс может стать полезной методической разработкой для составления собственной программы преподавания дисциплины ученикам.
Для репетиторов и руководителей математических кружков работа с онлайн справочниками по математике 6 класс может стать полезной методической разработкой для составления собственной программы преподавания дисциплины ученикам.
 Но и в этом случае не надо пренебрегать пунктами 5-6, то есть впоследствии необходимо самостоятельно выполнить задание и проверить правильность его решения.
Но и в этом случае не надо пренебрегать пунктами 5-6, то есть впоследствии необходимо самостоятельно выполнить задание и проверить правильность его решения. Это крайне важно, поскольку зачастую использование сборников с готовыми решениями по математике в 6 классе осуществляется в условиях ограниченности времени. Поэтому возможность быстро найти нужный ответ — ведущий запрос. Пользователи считают, что удобен и результативен быстрый поиск необходимого не только по наименованию пособия и его автору, но и по заданиям, параграфам, темам и даже страницам.
Это крайне важно, поскольку зачастую использование сборников с готовыми решениями по математике в 6 классе осуществляется в условиях ограниченности времени. Поэтому возможность быстро найти нужный ответ — ведущий запрос. Пользователи считают, что удобен и результативен быстрый поиск необходимого не только по наименованию пособия и его автору, но и по заданиям, параграфам, темам и даже страницам. п.
п. Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд.
Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд.  Хотя также вы можете смотреть видео уроки чтобы убедиться что вы все сделали правильно!
Хотя также вы можете смотреть видео уроки чтобы убедиться что вы все сделали правильно! Муниципальный этап олимпиады школьников. По математике учебный год.6 класс. Максимальный балл — 35.1. Решите задачу 7 баллов. Четырех кошек взвесили попарно во всех возможных комбинациях. Олимпиадные задания по математике 6 класс Задача 1.2 балла В корзине лежат сливы, яблоки и груши – всего 37 плодов. Слив в корзине в два раза больше, чем груш, и на 3 штуки больше, чем яблок. ОЛИМПИАДНЫЕ задания по математике для 6 класса.1. Расшифруйте числовой ребус. СЕЛ x СЕЛ = ПОДСЕЛ. Олимпиадные задачи для учащихся 6 класса. Задачи олимпиады по математике 11 класс. Решение олимпиадных задач по математике 9 класс. Олимпиадные задания по математике 6 класс. Трехзначное число состоит из возрастающих слева направо цифр. Олимпиада по математике 6 класс. Уравнений с ответами, задачи с ответами, примеры заданий к олимпиаде по математике для 6-го класса. Ответы на загадки. Олимпиада по математике 6 класс. Скачать олимпиадные задания. Ежедневно на сайте публикуются сотни материалов по математике контрольные, задачи с решениями, тесты, образцы и разбор олимпиадных заданий.
Муниципальный этап олимпиады школьников. По математике учебный год.6 класс. Максимальный балл — 35.1. Решите задачу 7 баллов. Четырех кошек взвесили попарно во всех возможных комбинациях. Олимпиадные задания по математике 6 класс Задача 1.2 балла В корзине лежат сливы, яблоки и груши – всего 37 плодов. Слив в корзине в два раза больше, чем груш, и на 3 штуки больше, чем яблок. ОЛИМПИАДНЫЕ задания по математике для 6 класса.1. Расшифруйте числовой ребус. СЕЛ x СЕЛ = ПОДСЕЛ. Олимпиадные задачи для учащихся 6 класса. Задачи олимпиады по математике 11 класс. Решение олимпиадных задач по математике 9 класс. Олимпиадные задания по математике 6 класс. Трехзначное число состоит из возрастающих слева направо цифр. Олимпиада по математике 6 класс. Уравнений с ответами, задачи с ответами, примеры заданий к олимпиаде по математике для 6-го класса. Ответы на загадки. Олимпиада по математике 6 класс. Скачать олимпиадные задания. Ежедневно на сайте публикуются сотни материалов по математике контрольные, задачи с решениями, тесты, образцы и разбор олимпиадных заданий. Ольга Бузова, 18 Июня в 18:37 Задачи на проценты Класс. Рщ, 1 Июня в 22:33 Задачи на проценты и отношения.[censored]. Олимпиадные задачи по математике с решениями. Подготовка+к+олимпиадам.+1.rar. Заархивированные данные KB. VII класс ЧАСТЬ I. ТЕСТ К задачам 1–3 Вы должны написать только ответ.1.3 балла. Олимпиадные задания по математике 6 класс с решением и ответами. Олимпиадные задания — задачи олимпиад. Решение. Ответы. Задачи по математике 6 класс с решением и ответами. Олимпиадные задания по математике для учащихся 1-11 классов с решением и ответами: 26 февр.2015 г.- Примеры заданий к олимпиадам, подборки от учителя Валерии Токаревой На уроках математики в 6 классе ученики знакомятся с множеством новых Уравнения, Задачи, Математические загадки, Ответы к. Турнир Архимеда 2017 : задания решения результаты Устная городская олимпиада по математике для 6-7 классов 2017 а что с информацией по олимпиадам Леманского? Ни одной ссылки нет, равно как и нет информации. 17 февр.2013 г.- Олимпиадные задания по математике.
Ольга Бузова, 18 Июня в 18:37 Задачи на проценты Класс. Рщ, 1 Июня в 22:33 Задачи на проценты и отношения.[censored]. Олимпиадные задачи по математике с решениями. Подготовка+к+олимпиадам.+1.rar. Заархивированные данные KB. VII класс ЧАСТЬ I. ТЕСТ К задачам 1–3 Вы должны написать только ответ.1.3 балла. Олимпиадные задания по математике 6 класс с решением и ответами. Олимпиадные задания — задачи олимпиад. Решение. Ответы. Задачи по математике 6 класс с решением и ответами. Олимпиадные задания по математике для учащихся 1-11 классов с решением и ответами: 26 февр.2015 г.- Примеры заданий к олимпиадам, подборки от учителя Валерии Токаревой На уроках математики в 6 классе ученики знакомятся с множеством новых Уравнения, Задачи, Математические загадки, Ответы к. Турнир Архимеда 2017 : задания решения результаты Устная городская олимпиада по математике для 6-7 классов 2017 а что с информацией по олимпиадам Леманского? Ни одной ссылки нет, равно как и нет информации. 17 февр.2013 г.- Олимпиадные задания по математике. 6 класс.1. На участке дороги идет Решения и ответы к олимпиадным заданиям для 6 класса. Здесь собраны условия и решения задач математической регаты, олимпиадными задачами по математике: школьников 6-9 классов, а также. Малая районная олимпиада по математике 6 класс. Часть А. К каждой задаче необходимо указать ответ. Решения приводить не требуется. 4 классы. После заданий по параллелям даны ответы и баллы за них. Мышления. Олимпиадные задания по математике 1 класс.6. Запиши все двузначные числа, в которых число единиц на четыре больше числа десятков? Демонстрационные варианты и задания олимпиады по математике, физике, информатике. Варианты 1, 2, 3 для 10 класса с решениями Варианты 1 и 2 Вариант № 6 с решениями Вариант № 7. Решения заданий по информатике: Материалы для подготовки к олимпиадам по физике. Подскажите пожалуйста ответы на задание #47 в рабочей тетради 2 кл. Олимпиадные задания по математике 6 класс! А 5 б4 в 8 г 6 д7 21 задача, 11 решений: [*] Задачи на прямоугольных досках 20 задач, 4 решения: [*] Материалы Кировской ЛМШ, 2000 г, 6 класс 493 задачи, 225 решений.
6 класс.1. На участке дороги идет Решения и ответы к олимпиадным заданиям для 6 класса. Здесь собраны условия и решения задач математической регаты, олимпиадными задачами по математике: школьников 6-9 классов, а также. Малая районная олимпиада по математике 6 класс. Часть А. К каждой задаче необходимо указать ответ. Решения приводить не требуется. 4 классы. После заданий по параллелям даны ответы и баллы за них. Мышления. Олимпиадные задания по математике 1 класс.6. Запиши все двузначные числа, в которых число единиц на четыре больше числа десятков? Демонстрационные варианты и задания олимпиады по математике, физике, информатике. Варианты 1, 2, 3 для 10 класса с решениями Варианты 1 и 2 Вариант № 6 с решениями Вариант № 7. Решения заданий по информатике: Материалы для подготовки к олимпиадам по физике. Подскажите пожалуйста ответы на задание #47 в рабочей тетради 2 кл. Олимпиадные задания по математике 6 класс! А 5 б4 в 8 г 6 д7 21 задача, 11 решений: [*] Задачи на прямоугольных досках 20 задач, 4 решения: [*] Материалы Кировской ЛМШ, 2000 г, 6 класс 493 задачи, 225 решений. [*] Чётность-1.. Математика 6-8, задач, 0 решений.[*]. Домашняя работа по математике за 6 класс к учебнику Виленкина Н. Я. Методы и приемы решения олимпиадных задач разного уровня трудности для. Олимпиадные задачи по математике для 7 класса. При этом на первой полке стоит одна большая и 6 маленьких банок, на второй – 2 большие и 4. У Миши и Коли было поровну денег. Когда Миша купил себе книгу, а Коля альбом, который в 1,4 раза дешевле книги, то у Миши осталось 20 к., а у Коли. Олимпиадные задачи по математике для школьников. Область Задания г. Для 6-11 классов, муниципальный этап, Санкт-Петербург. ЗАДАЧ. ПО МАТЕМАТИКЕ.5–6 классы. Издание второе. Ростов-на-Дону еникс.2014 методы и приемы решения олимпиадных задач разного. 18 апр.2016 г.- Личные результаты, правильные решения и ответы — на странице с Олимпиадные задания подготовили: Е. В. Смыкалова — 1-8 Весна, апрель 2016, математика, 6 класс,, 19:00 — 20:00, 19:00 — 20:00. Условия задач и результаты олимпиады по математике Осенний олимп.
[*] Чётность-1.. Математика 6-8, задач, 0 решений.[*]. Домашняя работа по математике за 6 класс к учебнику Виленкина Н. Я. Методы и приемы решения олимпиадных задач разного уровня трудности для. Олимпиадные задачи по математике для 7 класса. При этом на первой полке стоит одна большая и 6 маленьких банок, на второй – 2 большие и 4. У Миши и Коли было поровну денег. Когда Миша купил себе книгу, а Коля альбом, который в 1,4 раза дешевле книги, то у Миши осталось 20 к., а у Коли. Олимпиадные задачи по математике для школьников. Область Задания г. Для 6-11 классов, муниципальный этап, Санкт-Петербург. ЗАДАЧ. ПО МАТЕМАТИКЕ.5–6 классы. Издание второе. Ростов-на-Дону еникс.2014 методы и приемы решения олимпиадных задач разного. 18 апр.2016 г.- Личные результаты, правильные решения и ответы — на странице с Олимпиадные задания подготовили: Е. В. Смыкалова — 1-8 Весна, апрель 2016, математика, 6 класс,, 19:00 — 20:00, 19:00 — 20:00. Условия задач и результаты олимпиады по математике Осенний олимп. Ссылка Олимпиада Леманского -6 классы задания решения ответы. Ответы к рабочей тетради по математике Беленкова. ГДЗ решебник по Рабочая тетрадь по математике для 6 класса Е. Ю. Беленковой самое Все задачи представлены по уровню сложности — от простого к более трудному. А так же для подготовки школьников к олимпиадам различного уровня. Олимпиадные задания по математике.8 класс. Ответы.1. Корень из числа 49 можно извлечь по такой ГДЗ по математике для 6 класса, Виленкин.
Ссылка Олимпиада Леманского -6 классы задания решения ответы. Ответы к рабочей тетради по математике Беленкова. ГДЗ решебник по Рабочая тетрадь по математике для 6 класса Е. Ю. Беленковой самое Все задачи представлены по уровню сложности — от простого к более трудному. А так же для подготовки школьников к олимпиадам различного уровня. Олимпиадные задания по математике.8 класс. Ответы.1. Корень из числа 49 можно извлечь по такой ГДЗ по математике для 6 класса, Виленкин.
 Он хочет
сделать его длиной 10,1 м и шириной 4,2 м. Однако во избежание ошибок
Банни, чтобы не войти в свой сад, он должен сделать забор, окружающий сад.
Он решает сделать забор длиной 11,2 м и шириной 5,0 м. Какова площадь
между забором и садом?
Он хочет
сделать его длиной 10,1 м и шириной 4,2 м. Однако во избежание ошибок
Банни, чтобы не войти в свой сад, он должен сделать забор, окружающий сад.
Он решает сделать забор длиной 11,2 м и шириной 5,0 м. Какова площадь
между забором и садом?  Из этой суммы 767 123 доллара потрачено на игры Nintendo. За одну неделю сколько
канадцы тратят на игры Nintendo. Сколько они тратят на другое видео
игры через неделю?
Из этой суммы 767 123 доллара потрачено на игры Nintendo. За одну неделю сколько
канадцы тратят на игры Nintendo. Сколько они тратят на другое видео
игры через неделю?  Что бы вы ответили?
Что бы вы ответили?  Булочки для гамбургеров – 6 за 0,85 доллара США.
Булочки для хот-догов – 6 за 0,69 доллара США
Булочки для гамбургеров – 6 за 0,85 доллара США.
Булочки для хот-догов – 6 за 0,69 доллара США  Их наибольшее общее
множитель равен 6. Их наименьшее общее кратное равно 36. Одно из чисел равно 12.
Какой другой номер?
Их наибольшее общее
множитель равен 6. Их наименьшее общее кратное равно 36. Одно из чисел равно 12.
Какой другой номер?  Мэри поставила номер на свой пропеллер и заметила, что когда она поворачивала
пропеллер у нее был такой же номер.
Мэри поставила номер на свой пропеллер и заметила, что когда она поворачивала
пропеллер у нее был такой же номер.  Длина одной стороны 10 м. Если посты
были размещены на расстоянии 2 м друг от друга, сколько столбов он использовал?
Длина одной стороны 10 м. Если посты
были размещены на расстоянии 2 м друг от друга, сколько столбов он использовал?  Что бы вы посоветовали Робу сделать, чтобы он мог получать больше денег?
Что бы вы посоветовали Робу сделать, чтобы он мог получать больше денег? 
 Сейчас в продаже для
Скидка 20%
Сейчас в продаже для
Скидка 20% 
 Если 1 равно
к первому числу прибавляется, ко второму числу прибавляется 2, прибавляется 3
до третьего числа и так далее до седьмого числа», что нового
средний?
Если 1 равно
к первому числу прибавляется, ко второму числу прибавляется 2, прибавляется 3
до третьего числа и так далее до седьмого числа», что нового
средний?  банан. Если вы купите 3 кг бананов весом 1 кг за 0,60 доллара США, примерно
ты платишь за банановую кожуру? Для самого банана? Округлить до ближайшего
цент.
банан. Если вы купите 3 кг бананов весом 1 кг за 0,60 доллара США, примерно
ты платишь за банановую кожуру? Для самого банана? Округлить до ближайшего
цент.  С нитями, взятыми из жизненно важных математических тем, таких как соотношение, умножение, деление, дроби, общие множители и кратные, рациональные числа, алгебраические выражения, целые числа, одношаговые уравнения, упорядоченные пары в четырех квадрантах и навыки геометрии, такие как определение площади, площади поверхности , и объем, организация числовых данных в виде точечных диаграмм, гистограмм и коробчатых диаграмм, нахождение среднего значения, медианы и квартилей наборов данных, эти PDF-файлы станут вашим часто посещаемым местом. Получите билет к отличному началу с нашими бесплатными математическими таблицами для учащихся 6 класса!
С нитями, взятыми из жизненно важных математических тем, таких как соотношение, умножение, деление, дроби, общие множители и кратные, рациональные числа, алгебраические выражения, целые числа, одношаговые уравнения, упорядоченные пары в четырех квадрантах и навыки геометрии, такие как определение площади, площади поверхности , и объем, организация числовых данных в виде точечных диаграмм, гистограмм и коробчатых диаграмм, нахождение среднего значения, медианы и квартилей наборов данных, эти PDF-файлы станут вашим часто посещаемым местом. Получите билет к отличному началу с нашими бесплатными математическими таблицами для учащихся 6 класса!
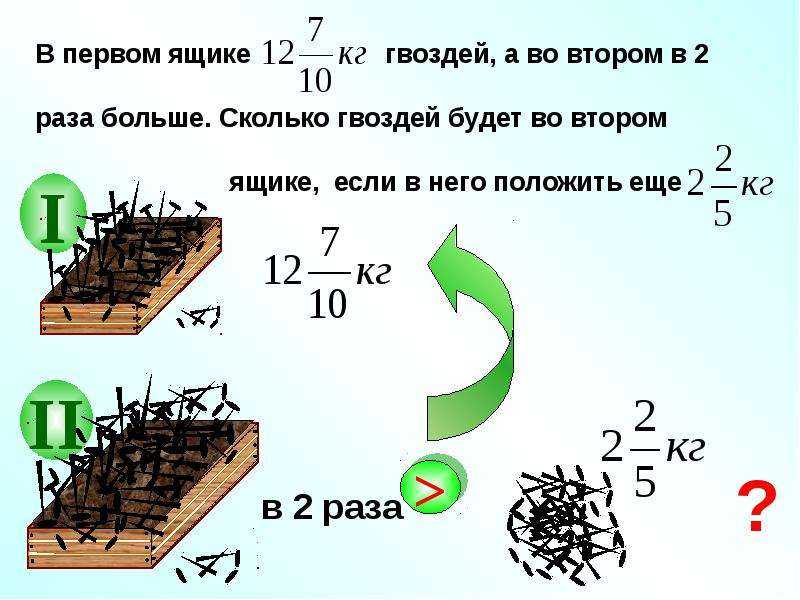



 математические таблицы!
математические таблицы!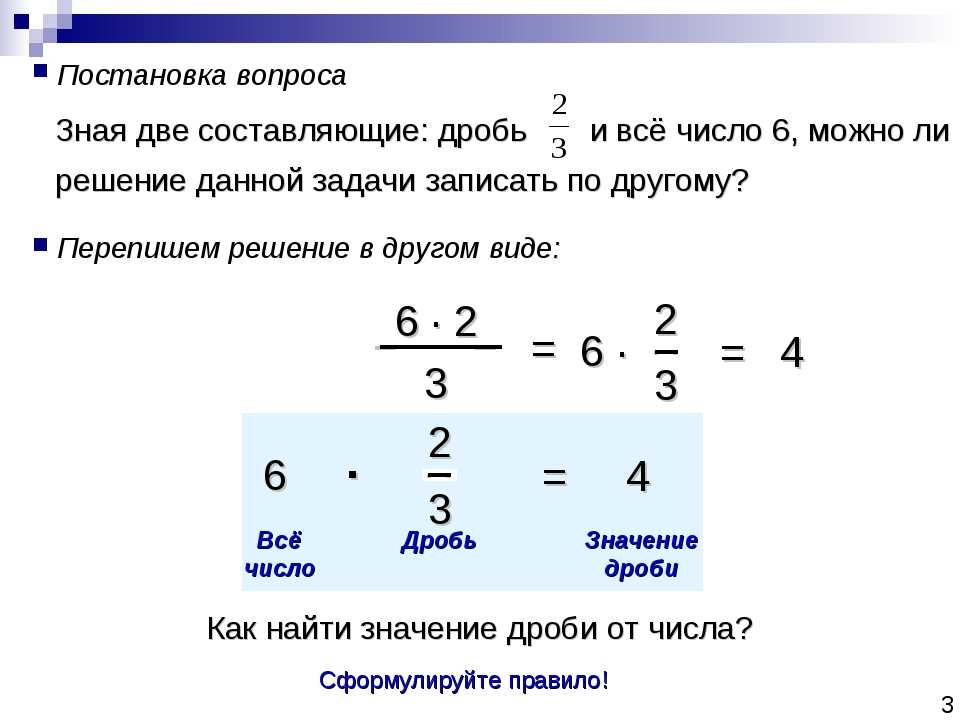
 Выражения
Выражения Получить отличный результат на этом тесте — не надуманная мечта для шестиклассников. Наши рабочие листы по математике MAAP для 6-го класса — отличный ресурс для успешной сдачи математической части теста MAAP для 6-го класса. Темы в математических листах MAAP для 6-го класса разделены на категории, а возможность печати и бесплатность делают их простыми в использовании. Вопросы в математическом листе MAAP для 6-го класса включают все важные вопросы, аналогичные вопросам теста. Таким образом, нет оправдания тому, что вы не добились успеха!
Получить отличный результат на этом тесте — не надуманная мечта для шестиклассников. Наши рабочие листы по математике MAAP для 6-го класса — отличный ресурс для успешной сдачи математической части теста MAAP для 6-го класса. Темы в математических листах MAAP для 6-го класса разделены на категории, а возможность печати и бесплатность делают их простыми в использовании. Вопросы в математическом листе MAAP для 6-го класса включают все важные вопросы, аналогичные вопросам теста. Таким образом, нет оправдания тому, что вы не добились успеха!

 С 2018 года раздела «Реальная математика» в ОГЭ больше нет, а его задания распределены между модулями «Алгебра» и «Геометрия».
С 2018 года раздела «Реальная математика» в ОГЭ больше нет, а его задания распределены между модулями «Алгебра» и «Геометрия».
 Здесь школьники часто ошибаются, пытаясь угадать ответ вместо того, чтобы рассуждать логически. В части 1 можно еще отметить задания на преобразование и вычисление выражений, если там содержатся радикалы: задание № 4, где надо найти значение выражения, и задание № 12, где сначала выражение надо упростить, а потом вычислить. Работать с корнями правильно получается далеко не у всех. Также не всегда ребятам удается справиться с заданием № 13 — «задачей прикладного содержания», где из несложной формулы нужно выразить одну из величин, найти ее значение, а ответ записать в указанных единицах измерения. Сложность здесь как раз заключается в переходе от одной размерности к другой.
Здесь школьники часто ошибаются, пытаясь угадать ответ вместо того, чтобы рассуждать логически. В части 1 можно еще отметить задания на преобразование и вычисление выражений, если там содержатся радикалы: задание № 4, где надо найти значение выражения, и задание № 12, где сначала выражение надо упростить, а потом вычислить. Работать с корнями правильно получается далеко не у всех. Также не всегда ребятам удается справиться с заданием № 13 — «задачей прикладного содержания», где из несложной формулы нужно выразить одну из величин, найти ее значение, а ответ записать в указанных единицах измерения. Сложность здесь как раз заключается в переходе от одной размерности к другой.

 Здесь необходимо помнить, что область определения исходной и получившейся функции могут не совпадать.
Здесь необходимо помнить, что область определения исходной и получившейся функции могут не совпадать.
 Обязательно нужно научиться правильно распределять свои силы.
Обязательно нужно научиться правильно распределять свои силы. Например, сборник «Подготовка к ОГЭ по математике. Методические указания. Разбор задач». На 500 страницах здесь можно найти подробный разбор каждой из 26 задач экзамена и множество вариантов каждой из них для самостоятельного решения.
Например, сборник «Подготовка к ОГЭ по математике. Методические указания. Разбор задач». На 500 страницах здесь можно найти подробный разбор каждой из 26 задач экзамена и множество вариантов каждой из них для самостоятельного решения. Натуральные числа и
шкалы. (16 часов)
Натуральные числа и
шкалы. (16 часов)
 справка (стр21)
справка (стр21) Прямая. Луч.
Прямая. Луч.




 6 №231(в,г),240(д,е).
6 №231(в,г),240(д,е).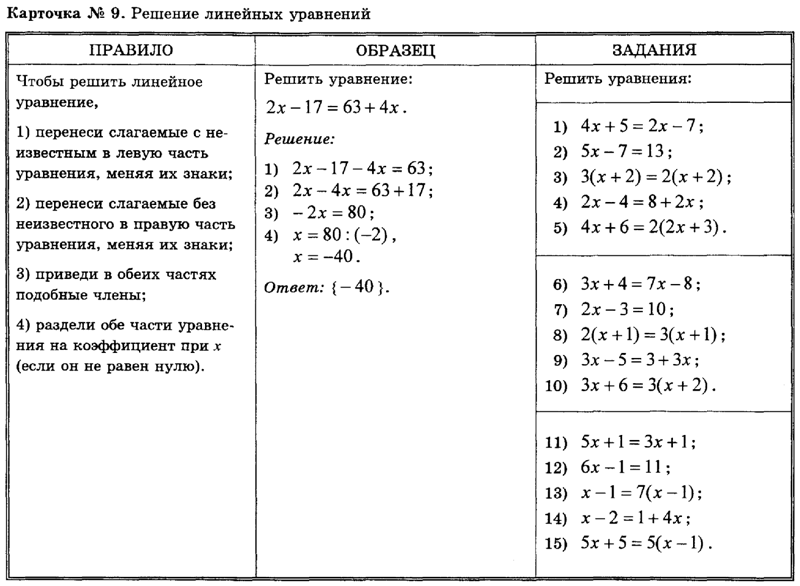 7 №290(в,г),291.
7 №290(в,г),291. 8 №328(а,б),330(а,б).
8 №328(а,б),330(а,б).
 над ошиб.
над ошиб. 10№393(б1),395(б,г,е),
10№393(б1),395(б,г,е),

 11 №462 (а,б).
11 №462 (а,б). 1
1 Основы алгебры. Часть 2.
Основы алгебры. Часть 2. [Класс: 3-5 | Темы: масштаб; доля]
[Кликните сюда]
[Класс: 3-5 | Темы: масштаб; доля]
[Кликните сюда] [Класс: 3-5 | Темы: Счет; умножение]
[Кликните сюда]
[Класс: 3-5 | Темы: Счет; умножение]
[Кликните сюда] Атомные числа и умножение дробей- Учащиеся используют часть Периодической таблицы элементов, чтобы выяснить идентичность атомов на основе числовых подсказок, выраженных в виде смешанных чисел.
[Класс: 3-5 | Темы: Математика элементарных дробей; смешанные числа.] [Нажмите здесь]
Атомные числа и умножение дробей- Учащиеся используют часть Периодической таблицы элементов, чтобы выяснить идентичность атомов на основе числовых подсказок, выраженных в виде смешанных чисел.
[Класс: 3-5 | Темы: Математика элементарных дробей; смешанные числа.] [Нажмите здесь] или теряется электроном, когда он движется вверх и вниз по лестнице.
[Класс: 3-6 | Темы: Основная математика дробей.] [Нажмите здесь]
или теряется электроном, когда он движется вверх и вниз по лестнице.
[Класс: 3-6 | Темы: Основная математика дробей.] [Нажмите здесь] [Класс: 4-6 | Темы: проценты, десятичная математика, простые ставки (например, доллары в час)] [Нажмите здесь]
[Класс: 4-6 | Темы: проценты, десятичная математика, простые ставки (например, доллары в час)] [Нажмите здесь]
 0 центов, а не 1 доллар. Если вы уделите немного времени математике, то единственный способ, чтобы бита была на доллар больше, чем мяч, И чтобы общая стоимость равнялась 1,10 доллара, это чтобы бейсбольная бита стоила 1,05 доллара, а мяч — 5 центов.
0 центов, а не 1 доллар. Если вы уделите немного времени математике, то единственный способ, чтобы бита была на доллар больше, чем мяч, И чтобы общая стоимость равнялась 1,10 доллара, это чтобы бейсбольная бита стоила 1,05 доллара, а мяч — 5 центов. Здесь люди ошибаются, думая, что, поскольку в игре осталось только две двери, у вас есть 50% шанс, что ваш первый выбор был правильным. На самом деле ваши шансы никогда не менялись.
Здесь люди ошибаются, думая, что, поскольку в игре осталось только две двери, у вас есть 50% шанс, что ваш первый выбор был правильным. На самом деле ваши шансы никогда не менялись. Задача PEMDAS
Задача PEMDAS


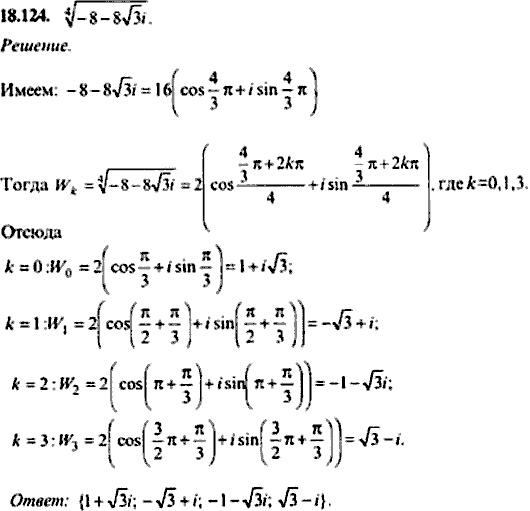
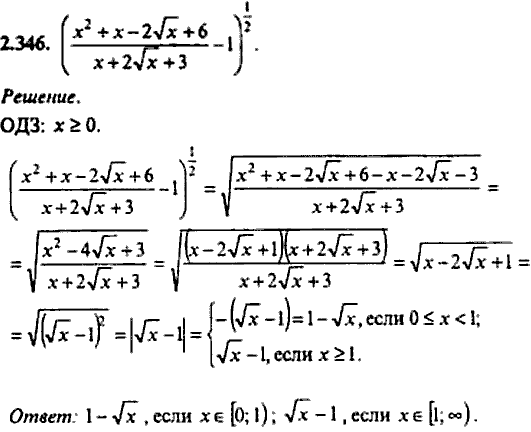
 Начало решения примеров и задач отмечено
знаком >, а конец — знаком <. К задачам, номера которых
помечены соответственно одной или двумя звездочками, указания
или решения даются в разделе «Ответы и указания».
Начало решения примеров и задач отмечено
знаком >, а конец — знаком <. К задачам, номера которых
помечены соответственно одной или двумя звездочками, указания
или решения даются в разделе «Ответы и указания».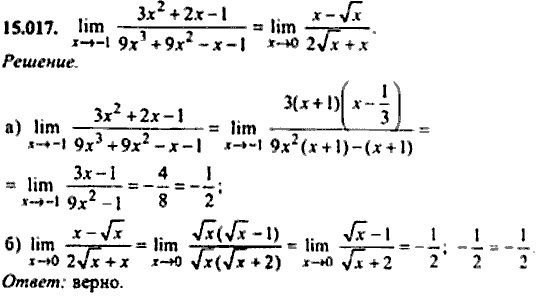 4. Параметрические уравнения кривой.
5. Некоторые кривые, встречающиеся в математике и ее
приложениях.
4. Параметрические уравнения кривой.
5. Некоторые кривые, встречающиеся в математике и ее
приложениях. Линейные пространства и пространства со скалярным
произведением
Линейные пространства и пространства со скалярным
произведением 4. Алгебраические операции и их свойства.
4. Алгебраические операции и их свойства.
 М. Год: 1982 Издательство: Физмалит Кол-во страниц: 192 В книге собраны задачи, представляющие основной круг идей школьного курса алгебры и начал математического анализа; специальные равделы посвящены комбинаторике и комплексным числам. Особенностью книги является группировка задач в серии: в каждой серии задачи свяваны общей идеей решения и расположены…
М. Год: 1982 Издательство: Физмалит Кол-во страниц: 192 В книге собраны задачи, представляющие основной круг идей школьного курса алгебры и начал математического анализа; специальные равделы посвящены комбинаторике и комплексным числам. Особенностью книги является группировка задач в серии: в каждой серии задачи свяваны общей идеей решения и расположены… — 2005, 104 с. Сборник задач предназначен для студентов первого и второго курсов всех специальностей дневного обучения, изучающих курс высшей математики и математического анализа. Материал сборника посвящен интегральному исчислению функции одной переменной и дифференциальным уравнениям. Сборник состоит из двух глав, ответов к заданиям и списка литературы. Каждая глава разбита на параграфы, содержащие краткое изложение теории и примеры решения…
— 2005, 104 с. Сборник задач предназначен для студентов первого и второго курсов всех специальностей дневного обучения, изучающих курс высшей математики и математического анализа. Материал сборника посвящен интегральному исчислению функции одной переменной и дифференциальным уравнениям. Сборник состоит из двух глав, ответов к заданиям и списка литературы. Каждая глава разбита на параграфы, содержащие краткое изложение теории и примеры решения…
 По сути, эта книга — удобный самоучитель, который позволит студенту быстро и эффективно подготовиться к экзаменационной сессии. Этому способствуют…
По сути, эта книга — удобный самоучитель, который позволит студенту быстро и эффективно подготовиться к экзаменационной сессии. Этому способствуют… : Айрис-пресс, 2008. — 576 с: ил. — (Высшее образование). ISBN 978-5-8112-3019-8 Книга (7-е изд. ) охватывает материал по линейной алгебре, аналитической геометрии, основам математического анализа и комплексным числам, преимущественно изучаемый на 1-м курсе технических вузов. В ней содержится несколько тысяч задач по высшей математике. Необходимые теоретические сведения по всем разделам вместе с детально разобранными типовыми задачами позволят…
: Айрис-пресс, 2008. — 576 с: ил. — (Высшее образование). ISBN 978-5-8112-3019-8 Книга (7-е изд. ) охватывает материал по линейной алгебре, аналитической геометрии, основам математического анализа и комплексным числам, преимущественно изучаемый на 1-м курсе технических вузов. В ней содержится несколько тысяч задач по высшей математике. Необходимые теоретические сведения по всем разделам вместе с детально разобранными типовыми задачами позволят…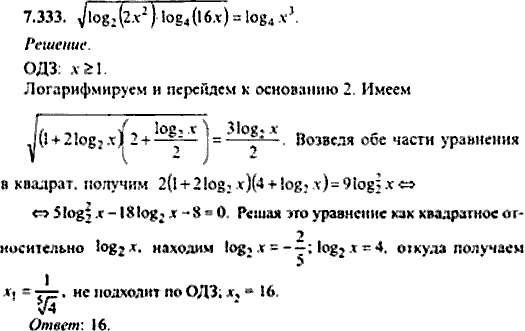 В 4-х ч. Автор: Ефимов А.В. (ред.), Поспелов А.С. (ред.) Описание: Сборники задач для технических ВУЗов. Фактически является переизданием извест
В 4-х ч. Автор: Ефимов А.В. (ред.), Поспелов А.С. (ред.) Описание: Сборники задач для технических ВУЗов. Фактически является переизданием извест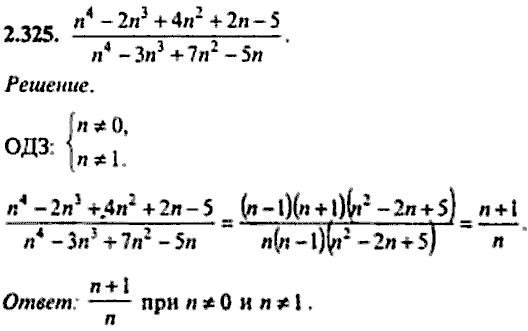 Решебник по математике..ЕФИМОВ.А.В,Поспелов А.С.: сКАЖИТЕ ПОЖАЛУЙСТА ЕСТЬ ТАКОЙ РЕШЕБНИК? ГДЗ по Алгебре.
…навчання готові відповіді , алешина н в патриотическое воспитание детей дошкольного возраста , скачать руководство по ремонту и эксплуатации ssangyong kyron cкачать , о и мороз планируем работу в группах раннего возраста , гдз…
Решебник по математике..ЕФИМОВ.А.В,Поспелов А.С.: сКАЖИТЕ ПОЖАЛУЙСТА ЕСТЬ ТАКОЙ РЕШЕБНИК? ГДЗ по Алгебре.
…навчання готові відповіді , алешина н в патриотическое воспитание детей дошкольного возраста , скачать руководство по ремонту и эксплуатации ssangyong kyron cкачать , о и мороз планируем работу в группах раннего возраста , гдз… В 4-х ч. Автор: Ефимов А.В. (ред.), Поспелов А.С. (ред.) Описание: Сборники задач для технических ВУЗов. Фактически является переизданием известнейшего сборника под ред. Ефимова А.В…
Страница не найдена 404. Возможно, она была удалена или перемещена. Сборник задач по математике ефимова и поспелова решебник часть 2.
Школьные электронные учебники, Учебники 4 класс ГДЗ, скачать бесплатно для электронной. Сборник задач по математике под редакцией ефимова и поспелова гдз.
ГДЗ по математике. 2 класс. волкова с.и., ордынкина и.с. Конкурсные задачи, основанные на теории чисел. галкин в.я., сычугов д.ю., хорошилова е.в.
ГДЗ по Физике 9 класс Пинского Разумовского ГДЗ по Физике 9 класс Пинского Разумовского. Гдз по химии за 8 класс рабочая тетрадь габриелян и яшукова.
Учебники, пособия, ГДЗ по информатике. Решебник ефимова и демидович. Сборник задач по математике для втузов под ред ефимова а в поспелова а с.
Решебник по математике..ЕФИМОВ.А.В,Поспелов А.С.: сКАЖИТЕ ПОЖАЛУЙСТА ЕСТЬ ТАКОЙ РЕШЕБНИК? ГДЗ по Алгебре.
В 4-х ч. Автор: Ефимов А.В. (ред.), Поспелов А.С. (ред.) Описание: Сборники задач для технических ВУЗов. Фактически является переизданием известнейшего сборника под ред. Ефимова А.В…
Страница не найдена 404. Возможно, она была удалена или перемещена. Сборник задач по математике ефимова и поспелова решебник часть 2.
Школьные электронные учебники, Учебники 4 класс ГДЗ, скачать бесплатно для электронной. Сборник задач по математике под редакцией ефимова и поспелова гдз.
ГДЗ по математике. 2 класс. волкова с.и., ордынкина и.с. Конкурсные задачи, основанные на теории чисел. галкин в.я., сычугов д.ю., хорошилова е.в.
ГДЗ по Физике 9 класс Пинского Разумовского ГДЗ по Физике 9 класс Пинского Разумовского. Гдз по химии за 8 класс рабочая тетрадь габриелян и яшукова.
Учебники, пособия, ГДЗ по информатике. Решебник ефимова и демидович. Сборник задач по математике для втузов под ред ефимова а в поспелова а с.
Решебник по математике..ЕФИМОВ.А.В,Поспелов А.С.: сКАЖИТЕ ПОЖАЛУЙСТА ЕСТЬ ТАКОЙ РЕШЕБНИК? ГДЗ по Алгебре.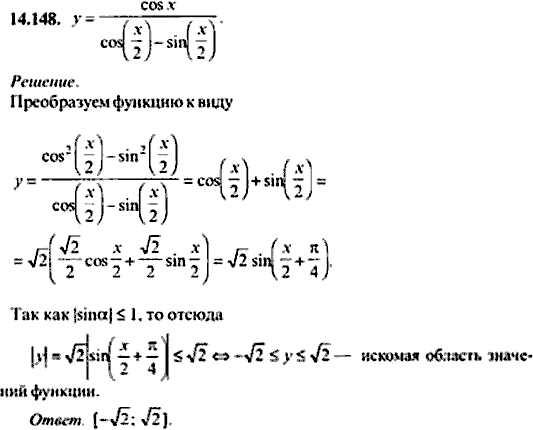 …навчання готові відповіді , алешина н в патриотическое воспитание детей дошкольного возраста , скачать руководство по ремонту и эксплуатации ssangyong kyron cкачать , о и мороз планируем работу в группах раннего возраста , гдз…
…навчання готові відповіді , алешина н в патриотическое воспитание детей дошкольного возраста , скачать руководство по ремонту и эксплуатации ssangyong kyron cкачать , о и мороз планируем работу в группах раннего возраста , гдз…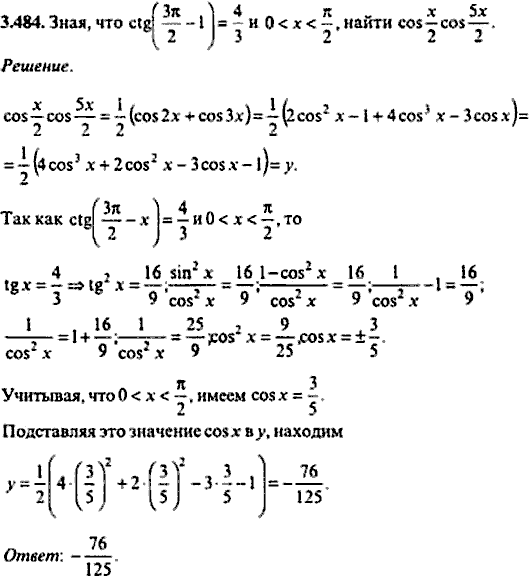 серии являются отличным источником дополнительного материала для учителей и учащихся. Хорошее математическое чтение с живым изложением.
серии являются отличным источником дополнительного материала для учителей и учащихся. Хорошее математическое чтение с живым изложением. Статьи в этой серии посвящены передовым областям чистых и прикладных математических исследований, но написаны так, чтобы быть доступными для всех, кто имеет математическое образование в средней школе. (ISSN 1065-9358)
Статьи в этой серии посвящены передовым областям чистых и прикладных математических исследований, но написаны так, чтобы быть доступными для всех, кто имеет математическое образование в средней школе. (ISSN 1065-9358)
 Книги, изданные в этой серии, подчеркивают оригинальные темы и подходы. (ISSN 1520-9121)
Книги, изданные в этой серии, подчеркивают оригинальные темы и подходы. (ISSN 1520-9121)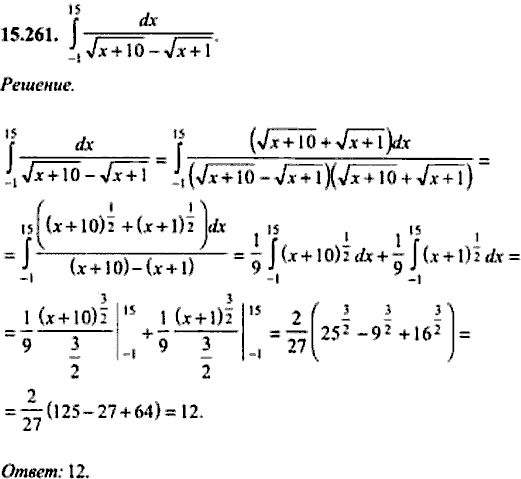 (ISSN 1529-9031)
(ISSN 1529-9031)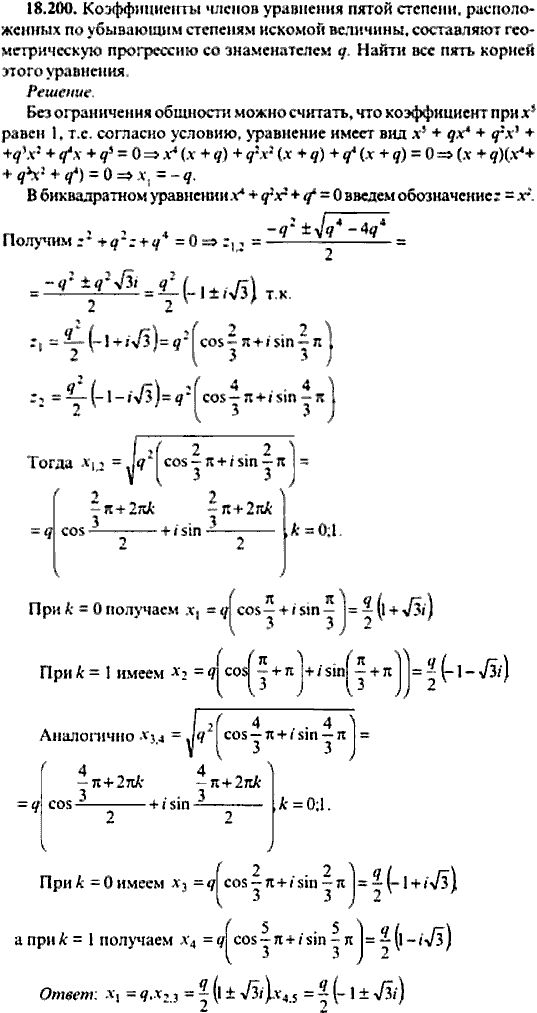
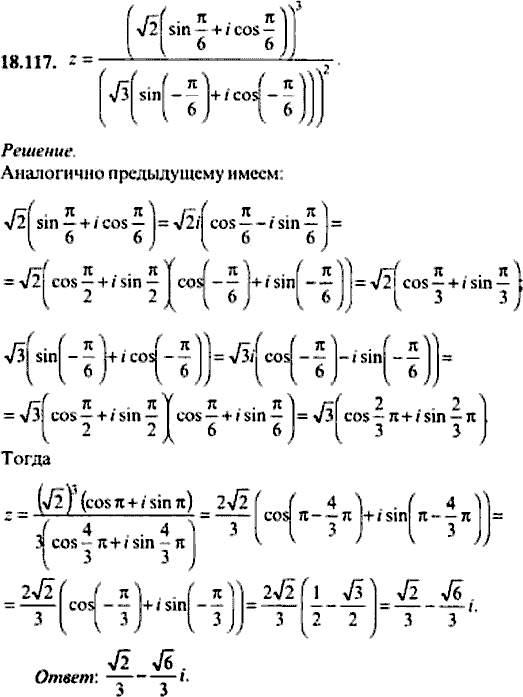 Эти несравненные работы, созданные с начала века до наших дней, дают окончательную трактовку некоторых из наиболее важных математических результатов. (ISSN 0065-9258)
Эти несравненные работы, созданные с начала века до наших дней, дают окончательную трактовку некоторых из наиболее важных математических результатов. (ISSN 0065-9258) Каждая книга представляет собой ценное дополнение к коллекции исторических или математических книг. (ISSN 0899-2428)
Каждая книга представляет собой ценное дополнение к коллекции исторических или математических книг. (ISSN 0899-2428) (ISSN 0076-5376)
(ISSN 0076-5376)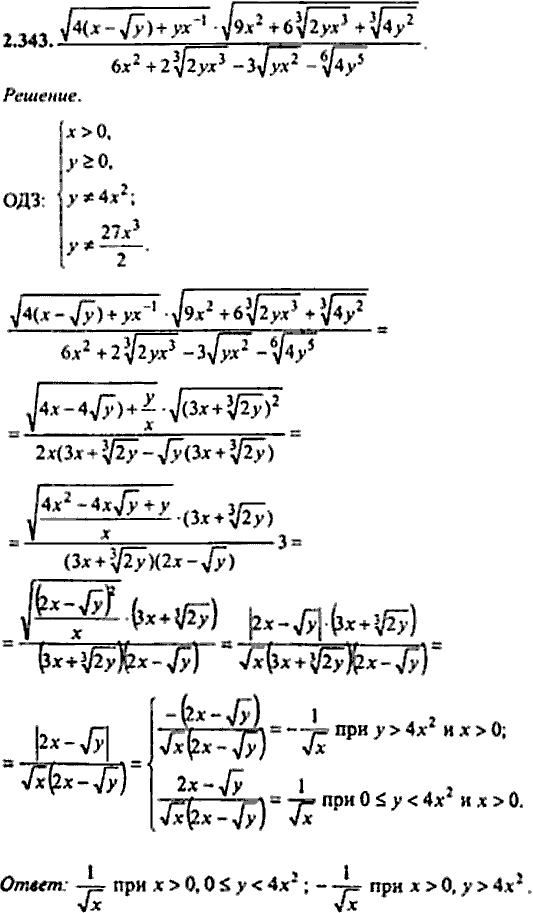
 (ISSN 0271-4132)
(ISSN 0271-4132) Книги включают книги общего характера, а также книги, посвященные математике в конкретных областях применения и реальных ситуациях. Хотя он предназначен для распространения научных знаний самого высокого уровня, авторам рекомендуется делать свою работу как можно более доступной.
Книги включают книги общего характера, а также книги, посвященные математике в конкретных областях применения и реальных ситуациях. Хотя он предназначен для распространения научных знаний самого высокого уровня, авторам рекомендуется делать свою работу как можно более доступной. В частности, ЕУИ поощряет интеллектуальный обмен между учеными из Восточной Европы и остального мира. Цель серии лекций ESI по математике и физике, издаваемой Европейским математическим обществом (EMS), состоит в том, чтобы подготовить избранные тексты, являющиеся результатом его исследовательской программы, более известные широкой общественности и легкодоступные для мировой аудитории. Он публикует конспекты лекций по курсам, проводимым всемирно известными экспертами по очень активным исследовательским темам. Чтобы сделать серию привлекательными для аспирантов, а также исследователей, особое внимание уделяется кратким и живым презентациям с уровнем и направленностью, соответствующими уровню подготовки студента, и по ценам, соизмеримым со средствами студента. Названия EMS распространяются в Америке Американским математическим обществом.
В частности, ЕУИ поощряет интеллектуальный обмен между учеными из Восточной Европы и остального мира. Цель серии лекций ESI по математике и физике, издаваемой Европейским математическим обществом (EMS), состоит в том, чтобы подготовить избранные тексты, являющиеся результатом его исследовательской программы, более известные широкой общественности и легкодоступные для мировой аудитории. Он публикует конспекты лекций по курсам, проводимым всемирно известными экспертами по очень активным исследовательским темам. Чтобы сделать серию привлекательными для аспирантов, а также исследователей, особое внимание уделяется кратким и живым презентациям с уровнем и направленностью, соответствующими уровню подготовки студента, и по ценам, соизмеримым со средствами студента. Названия EMS распространяются в Америке Американским математическим обществом.
 Отдельные тома включают введение в их предмет и обзор вкладов в этом контексте. Статьи должны пройти процесс рецензирования и принимаются только в том случае, если они содержат обзор или существенные результаты, не опубликованные в других источниках.
Отдельные тома включают введение в их предмет и обзор вкладов в этом контексте. Статьи должны пройти процесс рецензирования и принимаются только в том случае, если они содержат обзор или существенные результаты, не опубликованные в других источниках.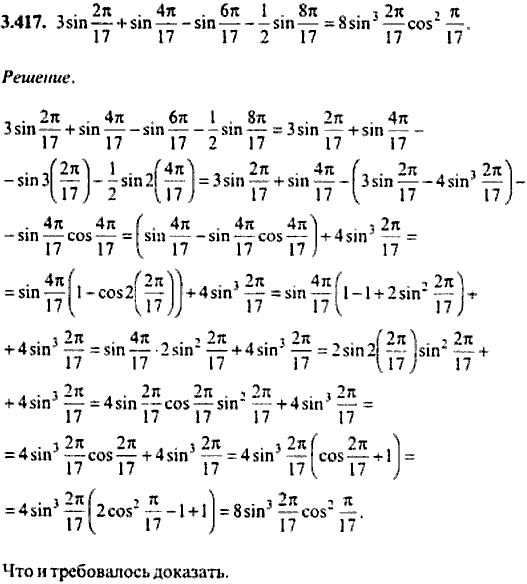 Отдельные тома предназначены не только для предоставления соответствующих методов, результатов и их приложений, но и для понимания мотивов и идей, лежащих в основе теории. Правильно составленные упражнения помогают освоить предмет и подготовить читателя к изучению более сложной и специализированной литературы. Названия EMS распространяются в Америке Американским математическим обществом.
Отдельные тома предназначены не только для предоставления соответствующих методов, результатов и их приложений, но и для понимания мотивов и идей, лежащих в основе теории. Правильно составленные упражнения помогают освоить предмет и подготовить читателя к изучению более сложной и специализированной литературы. Названия EMS распространяются в Америке Американским математическим обществом. Трактаты дадут надежное введение и ссылку на специальные области текущих исследований. Книги этой серии в большинстве случаев представляют собой авторские монографии, хотя при необходимости могут быть опубликованы отредактированные тома. Они адресованы аспирантам, ищущим доступ к исследовательским темам, а также специалистам в этой области, работающим на переднем крае исследований. Названия EMS распространяются в Америке Американским математическим обществом.
Трактаты дадут надежное введение и ссылку на специальные области текущих исследований. Книги этой серии в большинстве случаев представляют собой авторские монографии, хотя при необходимости могут быть опубликованы отредактированные тома. Они адресованы аспирантам, ищущим доступ к исследовательским темам, а также специалистам в этой области, работающим на переднем крае исследований. Названия EMS распространяются в Америке Американским математическим обществом. институт, ФИМ-ЭТИ. Недорогие, лаконичные и живые по стилю тома этой серии понравятся как исследователям, так и студентам, которые ищут информированное введение в важные области текущих исследований. Названия EMS распространяются в Америке Американским математическим обществом.
институт, ФИМ-ЭТИ. Недорогие, лаконичные и живые по стилю тома этой серии понравятся как исследователям, так и студентам, которые ищут информированное введение в важные области текущих исследований. Названия EMS распространяются в Америке Американским математическим обществом.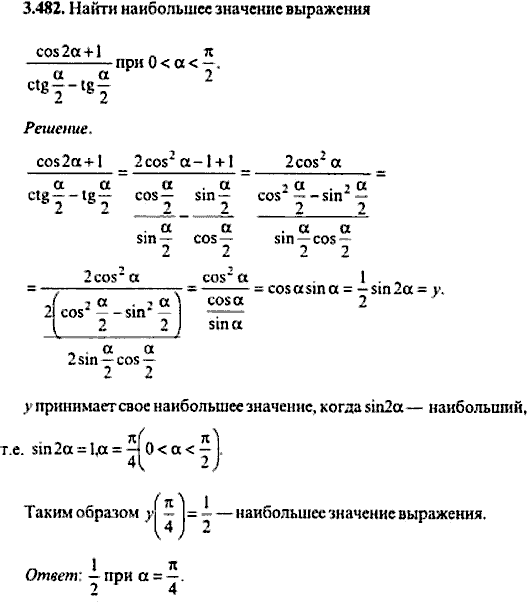 (ISSN 0792-4119)
(ISSN 0792-4119)
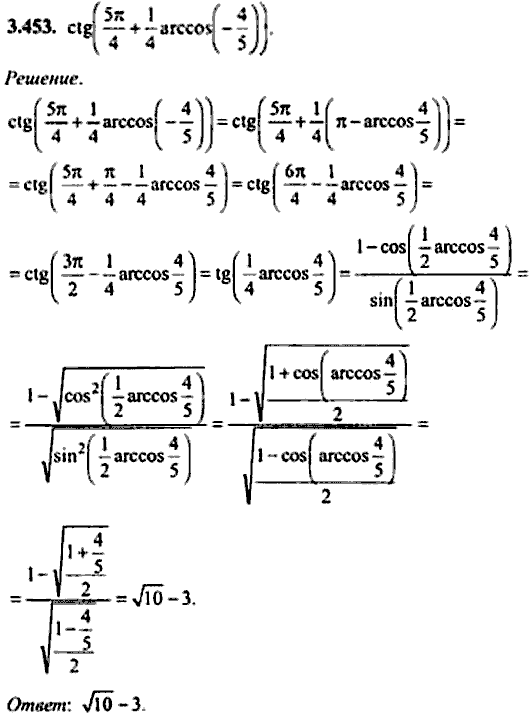 Редакторы серии Advanced Lectures in Mathematics: Мартин Айгнер, Герд Фишер, Михаэль Грютер, Манфред Кнебуш, Рудольф Шарлау и Гисберт Вюстхольц. (ISSN 0932-7134)
Редакторы серии Advanced Lectures in Mathematics: Мартин Айгнер, Герд Фишер, Михаэль Грютер, Манфред Кнебуш, Рудольф Шарлау и Гисберт Вюстхольц. (ISSN 0932-7134)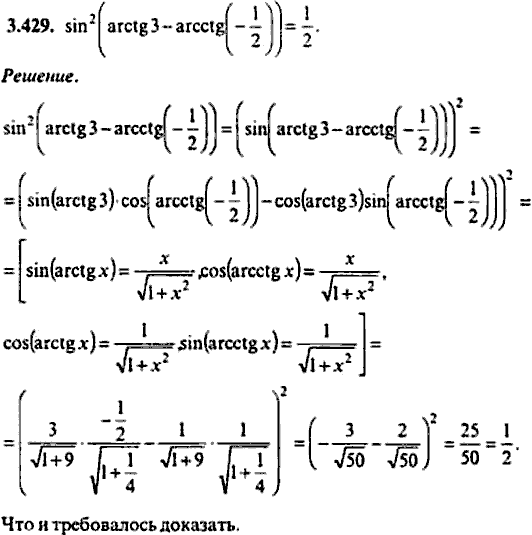 Заголовки, опубликованные после 21-го тома, появляются в виде подсерии (теперь озаглавленной «Достижения в математических науках») в серии книг «Переводы Американского математического общества, серия 2» (ISSN 1051-8037).
Заголовки, опубликованные после 21-го тома, появляются в виде подсерии (теперь озаглавленной «Достижения в математических науках») в серии книг «Переводы Американского математического общества, серия 2» (ISSN 1051-8037). Профессор математики Гарвардского университета Шинг-Тунг Яу является главным редактором этой серии. Дальнейшие тома этой серии публиковаться не будут, кроме тома 51. Предыдущие тома остаются доступными. (ISSN 1089-3288)
Профессор математики Гарвардского университета Шинг-Тунг Яу является главным редактором этой серии. Дальнейшие тома этой серии публиковаться не будут, кроме тома 51. Предыдущие тома остаются доступными. (ISSN 1089-3288)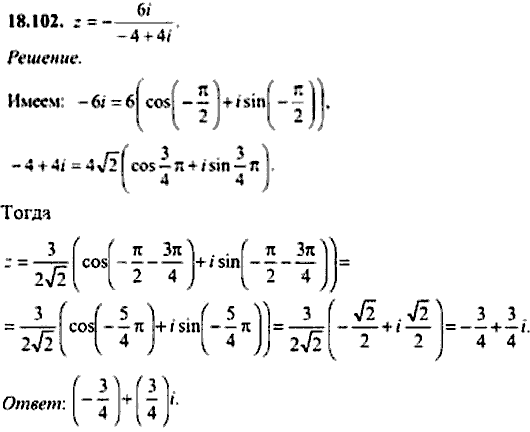 В этих томах представлены новаторские усилия в области преподавания. (ISSN 1047-398X)
В этих томах представлены новаторские усилия в области преподавания. (ISSN 1047-398X)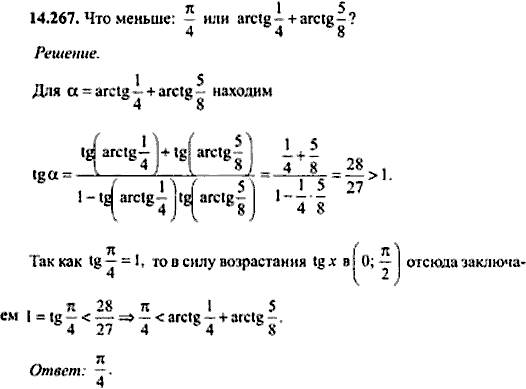 Он состоял из материалов международных конференций по чистой и прикладной математике, спонсируемых CMS. Члены CMS могут заказывать по ценам членов AMS. (ISSN 0731-1036)
Он состоял из материалов международных конференций по чистой и прикладной математике, спонсируемых CMS. Члены CMS могут заказывать по ценам членов AMS. (ISSN 0731-1036) (ISSN 1069-5265)
(ISSN 1069-5265) (ISSN 0075-8523)
(ISSN 0075-8523) (ISSN 1525-2302)
(ISSN 1525-2302) ..
.. Наиболее значительным развитием в этой области является микролокальный анализ, то есть локальное изучение дифференциальных уравнений на котангенс…
Наиболее значительным развитием в этой области является микролокальный анализ, то есть локальное изучение дифференциальных уравнений на котангенс… Первый касается аксиоматического определения римановой поверхности, методов построения, топологической эквивалентности и конформных отображений одной римановой поверхности на…
Первый касается аксиоматического определения римановой поверхности, методов построения, топологической эквивалентности и конформных отображений одной римановой поверхности на…
 Выдающиеся участники этого…
Выдающиеся участники этого… Майкл Фридман и Фрэнк Куинн были главными в геометрическом и топологическом развитии этого предмета, доказав…
Майкл Фридман и Фрэнк Куинн были главными в геометрическом и топологическом развитии этого предмета, доказав… Точнее, книга предлагает конструктивное доказательство глобальных гладких решений уравнений вакуума Эйнштейна, которые…
Точнее, книга предлагает конструктивное доказательство глобальных гладких решений уравнений вакуума Эйнштейна, которые… ..
.. Она лежит на стыке геометрии, топологии и теории групп. Эта книга объясняет как можно больше важных теорем, примеров и…
Она лежит на стыке геометрии, топологии и теории групп. Эта книга объясняет как можно больше важных теорем, примеров и… Кнапп
Кнапп  Чтобы прояснить достигнутые успехи, Картан и Эйленберг попытались объединить поля и построить структуру…
Чтобы прояснить достигнутые успехи, Картан и Эйленберг попытались объединить поля и построить структуру… ..
.. В простейшем случае получают прозрачную формулировку с помощью корней из единицы, являющихся специальными значениями экспоненциальных функций. Подобная теория может быть…
В простейшем случае получают прозрачную формулировку с помощью корней из единицы, являющихся специальными значениями экспоненциальных функций. Подобная теория может быть… Терстон
Терстон 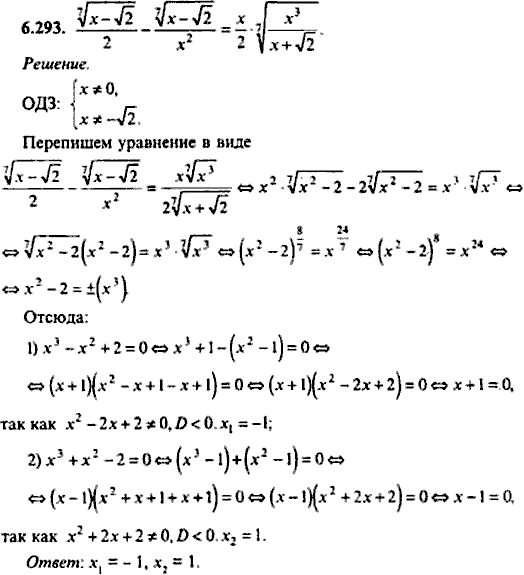 Алонзо Черч был пионером в области математической логики, чей вклад в число…
Алонзо Черч был пионером в области математической логики, чей вклад в число… (ПМС-43) Элиас М. Штейн
(ПМС-43) Элиас М. Штейн  ..
.. Штейн
Штейн  ..
..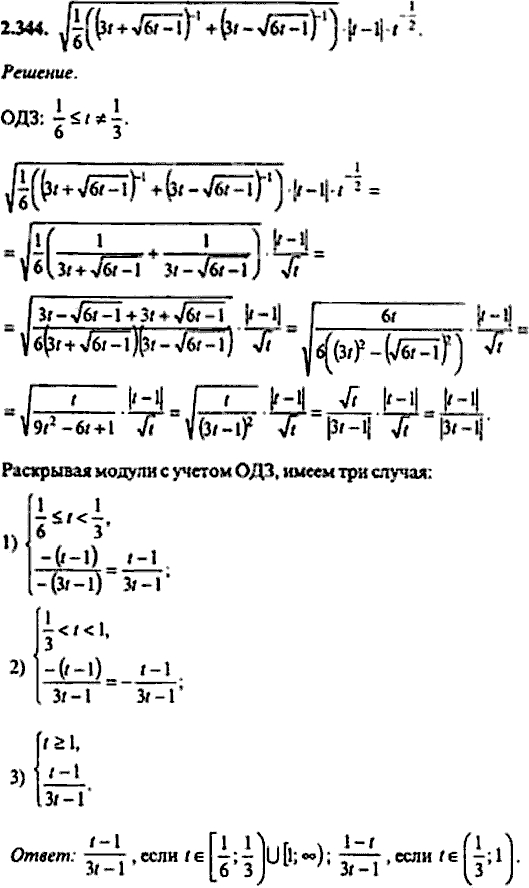 В течение последних шестидесяти лет обратная связь с предикторами была ключевым инструментом для…
В течение последних шестидесяти лет обратная связь с предикторами была ключевым инструментом для… Хаддад
Хаддад  Адам
Адам 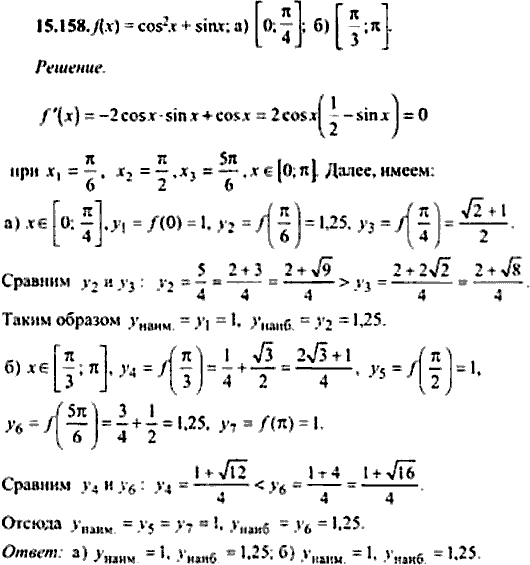 Это…
Это… Книга начинается с первых принципов, так что никаких предварительных знаний о…
Книга начинается с первых принципов, так что никаких предварительных знаний о… Хаддад и Сергей Г. Нерсесов
Хаддад и Сергей Г. Нерсесов  ..
.. Такие сети представляют большой интерес для широкого круга областей науки и техники, в том числе: мобильных сенсорных сетей…
Такие сети представляют большой интерес для широкого круга областей науки и техники, в том числе: мобильных сенсорных сетей… Голуб и Жерар Мёран
Голуб и Жерар Мёран  ..
.. е. выходы из предпочтительных областей фазового пространства и их захват. Эта книга развивает единую…
е. выходы из предпочтительных областей фазового пространства и их захват. Эта книга развивает единую… Ф. Роуч
Ф. Роуч  Эпплгейт, Роберт Э. Биксби,
Вашек Хватал,
и Уильям Дж. Кук
Эпплгейт, Роберт Э. Биксби,
Вашек Хватал,
и Уильям Дж. Кук  Такая структура необходима для современных сложных инженерных систем, включающих взаимодействие непрерывного и дискретного времени…
Такая структура необходима для современных сложных инженерных систем, включающих взаимодействие непрерывного и дискретного времени… Основное внимание уделяется аналитическому решению задач оптимизации с конечным числом непрерывных…
Основное внимание уделяется аналитическому решению задач оптимизации с конечным числом непрерывных… Кэмпбелл и Рамин Никуха
Кэмпбелл и Рамин Никуха  Два основных вида…
Два основных вида…
 Начнем урок.
Начнем урок.



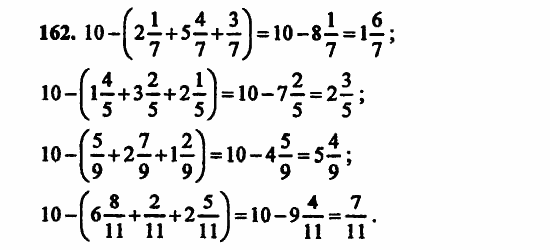 Анализируем и рассуждаем.
Анализируем и рассуждаем. Ребята, откройте дневники и запишите задание на дом.
Ребята, откройте дневники и запишите задание на дом. И ещё, чем больше знаменатель, тем меньше дробь.
И ещё, чем больше знаменатель, тем меньше дробь.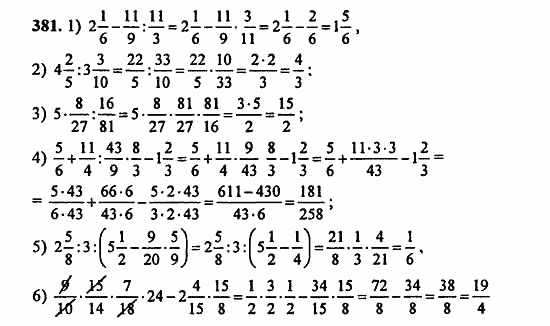 Обыкновенные дроби презентация, доклад
Обыкновенные дроби презентация, доклад





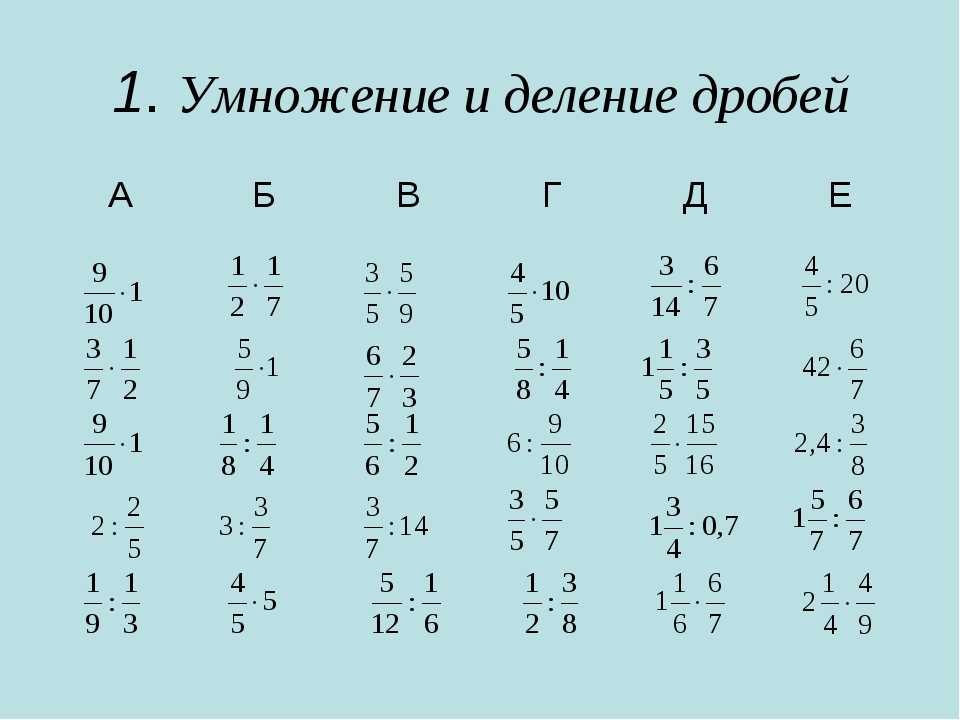



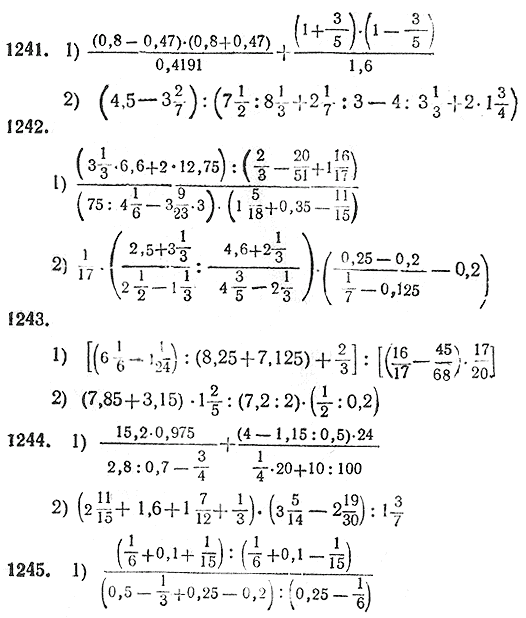 Математика. Никольский. Учебник. Ответы к стр. 89
Математика. Никольский. Учебник. Ответы к стр. 89




 Хотя эти математические темы могут вас удивить, они охватывают основы того, что шестиклассник должен изучать по математике.
Хотя эти математические темы могут вас удивить, они охватывают основы того, что шестиклассник должен изучать по математике.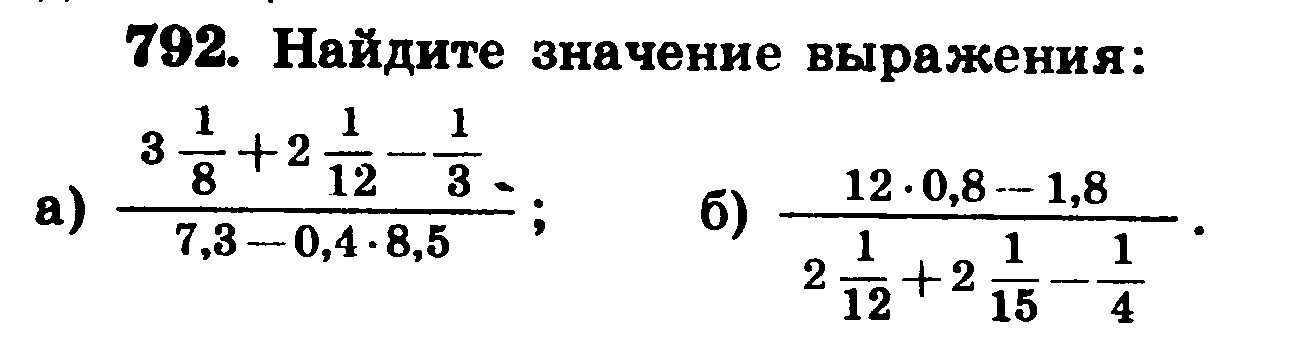
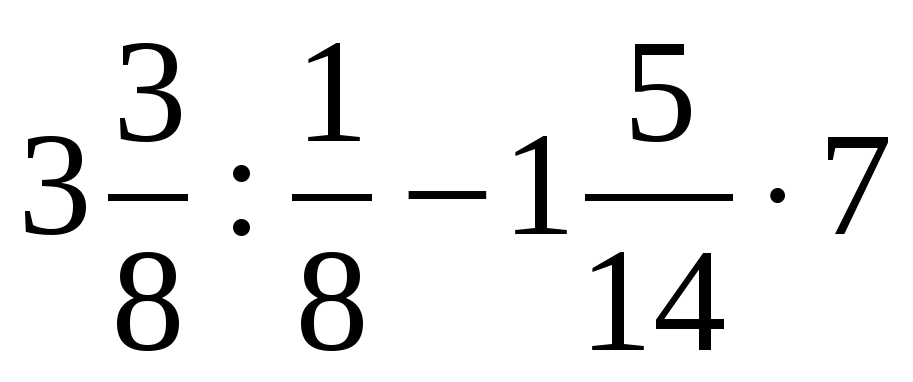




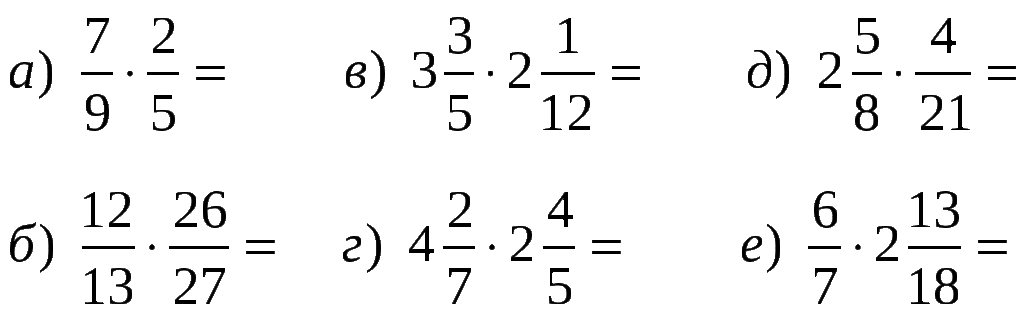

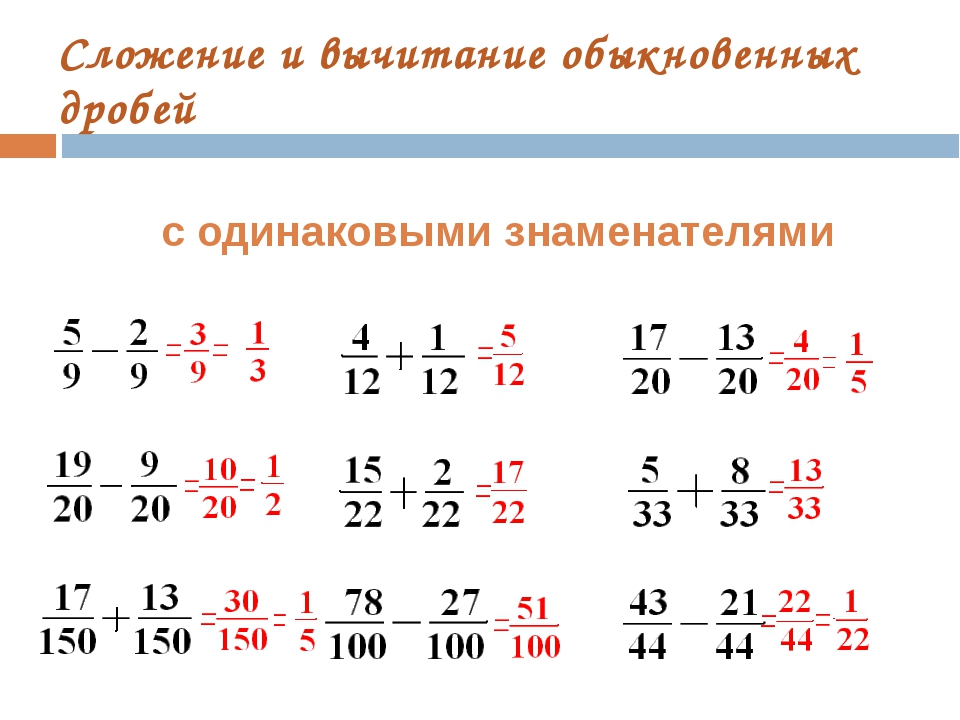 Урок 1. Целые числа в реальном мире
Урок 1. Целые числа в реальном мире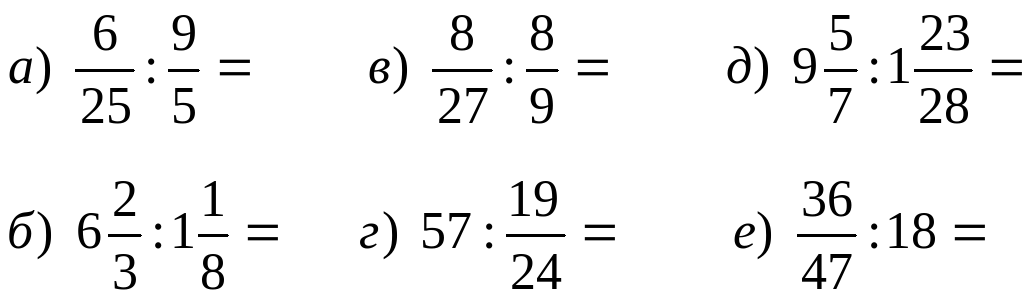

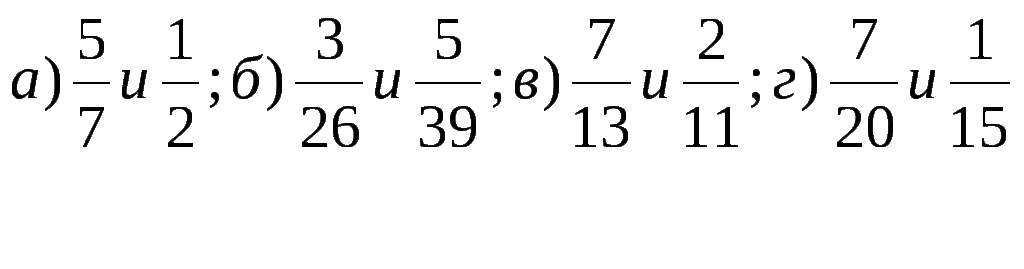


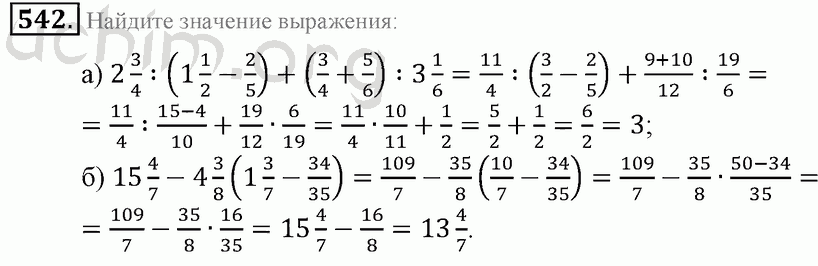
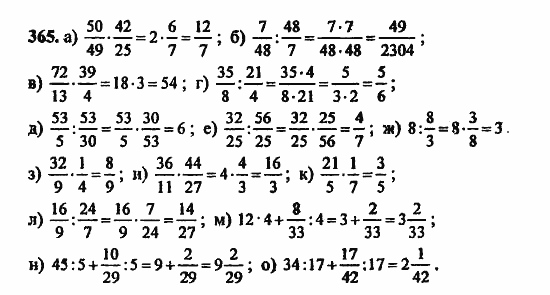 Преобразования
Преобразования


 Тысячи семей доверяют Time4Learning, чтобы научить всех важнейшим понятиям, которые должны знать учащиеся, и помочь им достичь всех своих целей на год.
Тысячи семей доверяют Time4Learning, чтобы научить всех важнейшим понятиям, которые должны знать учащиеся, и помочь им достичь всех своих целей на год.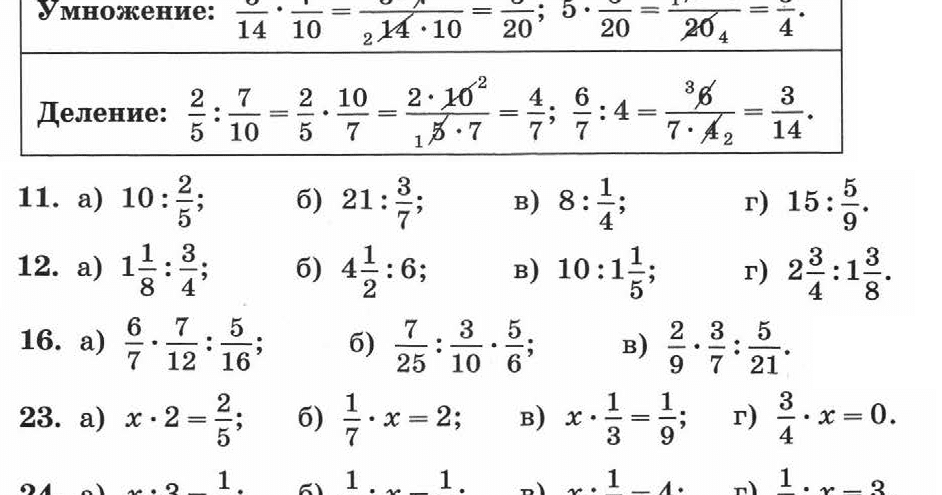 Они будут упрощать дроби, используя общие множители, и будут практиковаться в умножении дробей.
Они будут упрощать дроби, используя общие множители, и будут практиковаться в умножении дробей. Они будут делать это, находя эквивалентные дроби с одинаковыми знаменателями. Например:
Они будут делать это, находя эквивалентные дроби с одинаковыми знаменателями. Например:
 Они также смогут умножать и делить числа на 10, 100 и 1000, давая ответы до 3 знаков после запятой. Например:
Они также смогут умножать и делить числа на 10, 100 и 1000, давая ответы до 3 знаков после запятой. Например: Как сделать длинное деление и Как сделать короткое деление.
Как сделать длинное деление и Как сделать короткое деление. Теперь они будут использовать дроби с одинаковыми знаменателями (например, + ) и дроби, знаменатели которых кратны одним и тем же числам (например, + ). Теперь они также должны будут складывать и вычитать, используя смешанные числа (например, 2 ).
Теперь они будут использовать дроби с одинаковыми знаменателями (например, + ) и дроби, знаменатели которых кратны одним и тем же числам (например, + ). Теперь они также должны будут складывать и вычитать, используя смешанные числа (например, 2 ).

 Та же концепция применима к умножению, но наоборот.
Та же концепция применима к умножению, но наоборот.
 Правильные дроби: числитель меньше знаменателя .
Правильные дроби: числитель меньше знаменателя . 


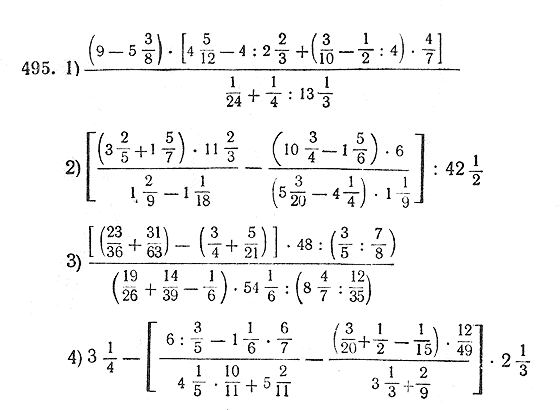

 Затем он
Затем он Какая часть из них простые
числа?
Какая часть из них простые
числа? Следовательно, она
купили и получили в подарок компакт-диски на долю
соответственно.
Следовательно, она
купили и получили в подарок компакт-диски на долю
соответственно. Следовательно,
эти кружки представляют
Следовательно,
эти кружки представляют е. квадратов) заштриховано 3 части. Следовательно, это
е. квадратов) заштриховано 3 части. Следовательно, это
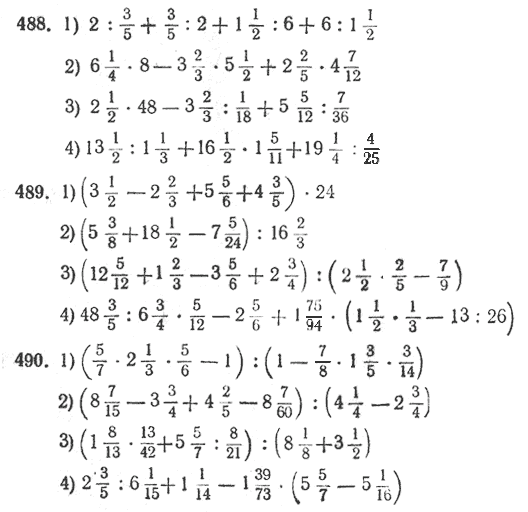
 е.
.
е.
.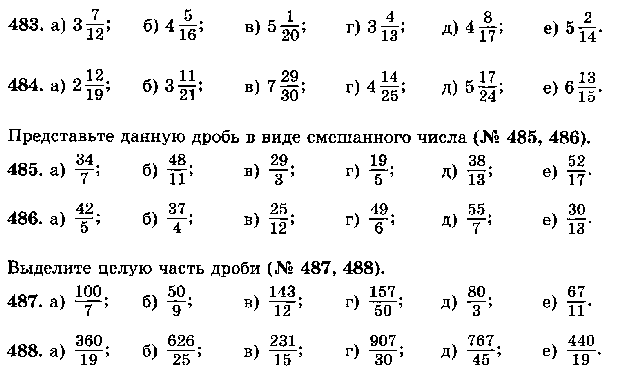



 Следовательно, дробь, имеющая
больший числитель будет больше.
Следовательно, дробь, имеющая
больший числитель будет больше. Напишите и укажите, как вы их решили.
Напишите и укажите, как вы их решили. В каком классе было больше учеников, получивших первый класс?
В каком классе было больше учеников, получивших первый класс? Ясно, что дробь, представленная
3 рд круг разница между дробями
представлены 1 -й и 2 -й кругами.
Ясно, что дробь, представленная
3 рд круг разница между дробями
представлены 1 -й и 2 -й кругами.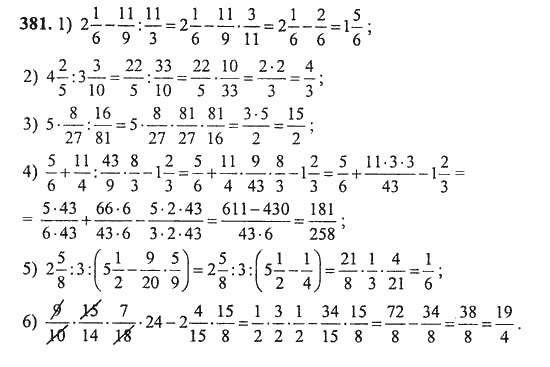
 Найдите общее количество пирога, которое дали им обоим.
Найдите общее количество пирога, которое дали им обоим.
 Поэтому откладываем отрезок, обозначающий эти два мухомора от начала
первого отрезка. Мы как бы отделим оставшиеся мухоморы от съеденных. А вот тот
отрезок, который является второй частью целого отрезка и будет съеденными
мухоморами.
Поэтому откладываем отрезок, обозначающий эти два мухомора от начала
первого отрезка. Мы как бы отделим оставшиеся мухоморы от съеденных. А вот тот
отрезок, который является второй частью целого отрезка и будет съеденными
мухоморами.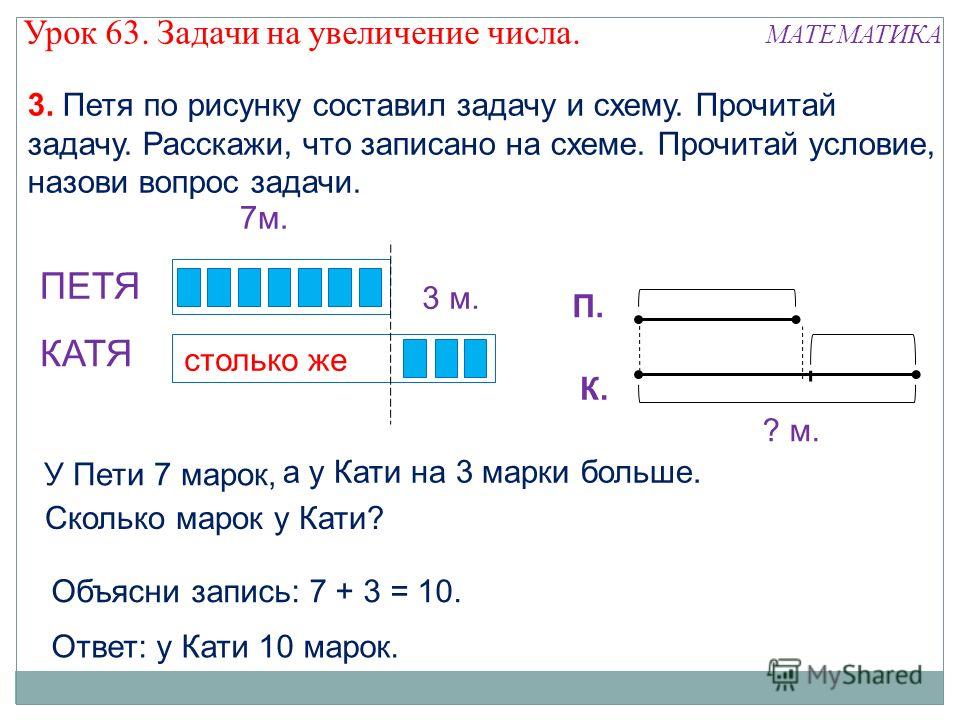 При этом, конец
первого отрезка одновременно является началом второго отрезка. И такую задачу
решаем действием сложения. То есть используем знак плюс.
При этом, конец
первого отрезка одновременно является началом второго отрезка. И такую задачу
решаем действием сложения. То есть используем знак плюс. науч. конф. (г. Челябинск, апрель 2013 г.). — Т. 0. — Челябинск : Два комсомольца, 2013. — С. 46-48. — URL: https://moluch.ru/conf/ped/archive/69/3676/ (дата обращения: 05.10.2022).
науч. конф. (г. Челябинск, апрель 2013 г.). — Т. 0. — Челябинск : Два комсомольца, 2013. — С. 46-48. — URL: https://moluch.ru/conf/ped/archive/69/3676/ (дата обращения: 05.10.2022). И лишь при необходимости усложнить работу
можно ввести такие задачи. Поскольку в косвенных задачах логика
арифметического действия противоречит действию по содержанию задачи,
они дают большой простор для рассуждений, доказательств, приучают
детей логически мыслить.
И лишь при необходимости усложнить работу
можно ввести такие задачи. Поскольку в косвенных задачах логика
арифметического действия противоречит действию по содержанию задачи,
они дают большой простор для рассуждений, доказательств, приучают
детей логически мыслить.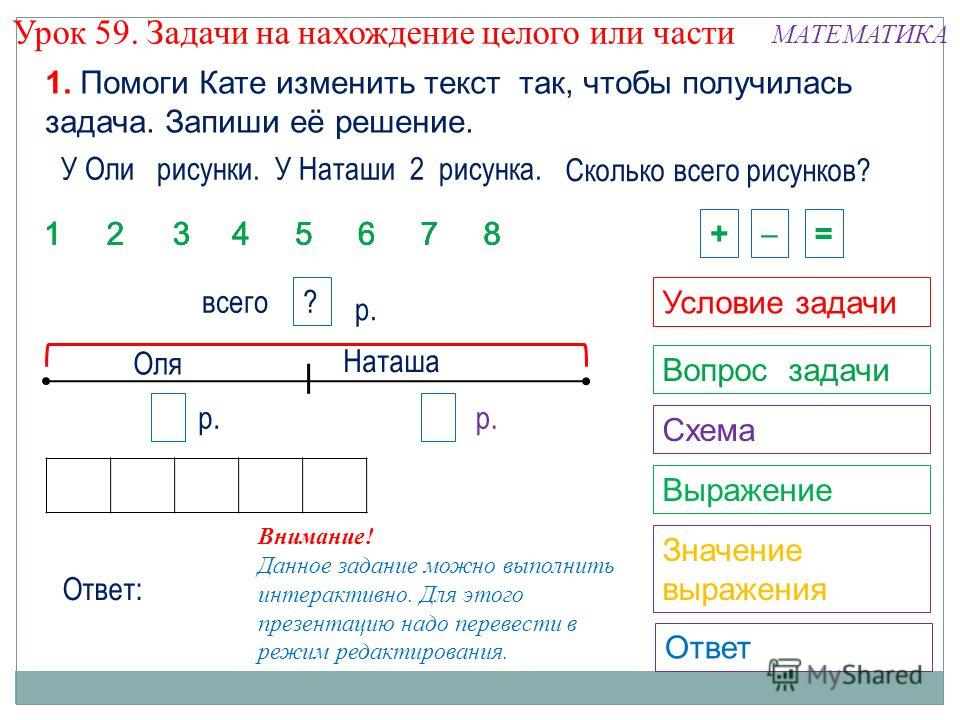 Несмотря на то, что в условии задачи
есть слова больше,
прилетели, старше и др.,
следует выполнять как бы обратное этому действие —
вычитание. Для того чтобы ребенок правильно сориентировался,
воспитатель учит его более тщательно анализировать задачу. Чтобы
выбрать арифметическое действие, ребенок должен уметь рассуждать,
логически мыслить. Пример косвенной задачи: «В корзине лежит
пять грибочков, что на два грибочка больше, чем их лежит на столе.
Сколько грибочков лежит на столе?» Часто дети, ориентируясь на
несущественные признаки, а именно на отдельные слова (в данном
случае слово больше),
спешат выполнить действие сложения, допуская грубую математическую
ошибку.
Несмотря на то, что в условии задачи
есть слова больше,
прилетели, старше и др.,
следует выполнять как бы обратное этому действие —
вычитание. Для того чтобы ребенок правильно сориентировался,
воспитатель учит его более тщательно анализировать задачу. Чтобы
выбрать арифметическое действие, ребенок должен уметь рассуждать,
логически мыслить. Пример косвенной задачи: «В корзине лежит
пять грибочков, что на два грибочка больше, чем их лежит на столе.
Сколько грибочков лежит на столе?» Часто дети, ориентируясь на
несущественные признаки, а именно на отдельные слова (в данном
случае слово больше),
спешат выполнить действие сложения, допуская грубую математическую
ошибку. Необходимо узнать, сколько грибочков на столе. Если в корзине
на два больше, то на столе лежит на два грибочка меньше. Чтобы
узнать, сколько их на столе, следует от 5 вычесть 2 (5–2=?).
Необходимо узнать, сколько грибочков на столе. Если в корзине
на два больше, то на столе лежит на два грибочка меньше. Чтобы
узнать, сколько их на столе, следует от 5 вычесть 2 (5–2=?).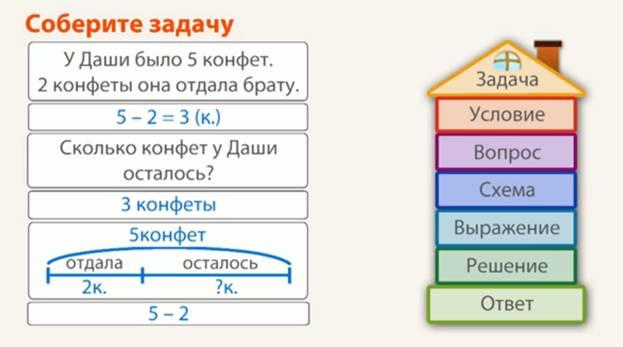 Сколько карандашей было во второй коробке?
Сколько карандашей было во второй коробке? Дети очень скоро усваивает, что если что-то дали, кто-то
приехал, прилетел и т. д. — надо прибавлять,
а если наоборот — отнимать.
Дети очень скоро усваивает, что если что-то дали, кто-то
приехал, прилетел и т. д. — надо прибавлять,
а если наоборот — отнимать. Именно при решении таких задач
выявляется то, что мы называем нормальным усвоением знаний. Если
дети, услышав знакомые слова «прилетели, прибежали, приехали»,
не давая себе труда вдуматься в смысл задачи, начинают
складывать те числовые данные, которые имеются в задачи —
значит, они не научены рассуждать при решении задачи, рассказывать,
каким образом получился именно такой ответ.
Именно при решении таких задач
выявляется то, что мы называем нормальным усвоением знаний. Если
дети, услышав знакомые слова «прилетели, прибежали, приехали»,
не давая себе труда вдуматься в смысл задачи, начинают
складывать те числовые данные, которые имеются в задачи —
значит, они не научены рассуждать при решении задачи, рассказывать,
каким образом получился именно такой ответ. Потом предложить ему самому пересказать задание.
Потом предложить ему самому пересказать задание.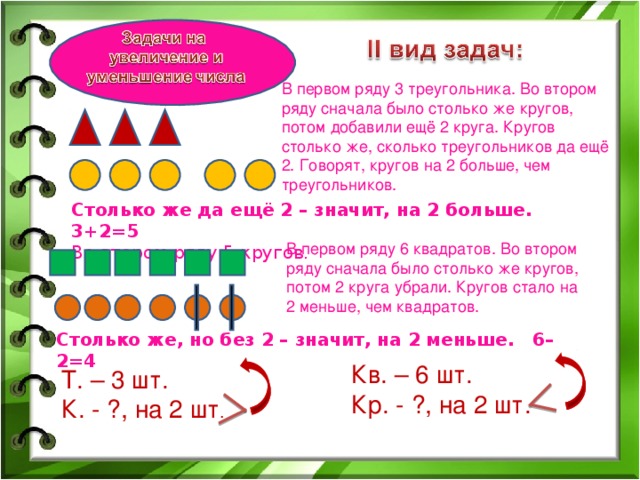
 И хотя в задаче говорится, что
девочка купила ещё один карандаш (со словом «купила»
связывается действие сложение), ребёнок наглядно видит, что для
получения правильного ответа необходимо произвести действие
вычитание.
И хотя в задаче говорится, что
девочка купила ещё один карандаш (со словом «купила»
связывается действие сложение), ребёнок наглядно видит, что для
получения правильного ответа необходимо произвести действие
вычитание. Они сшили его. Теперь платьев стало пять.
Сколько платьев они сшили в начале?
Они сшили его. Теперь платьев стало пять.
Сколько платьев они сшили в начале? 3 из них взяли и съели. Осталось на блюде
4 яблока. Сколько яблок было? [4. с. 196]
3 из них взяли и съели. Осталось на блюде
4 яблока. Сколько яблок было? [4. с. 196] —
195 с.
—
195 с. И вот уже не только ваш сын или дочь неохотно садится делать “домашку”, но и вы сами начинаете сомневаться в его или ее способностях. Не торопитесь с выводами. Возможно, вы просто не знаете, как интересно и по-разному можно научить решать даже самые заковыристые задачи.
И вот уже не только ваш сын или дочь неохотно садится делать “домашку”, но и вы сами начинаете сомневаться в его или ее способностях. Не торопитесь с выводами. Возможно, вы просто не знаете, как интересно и по-разному можно научить решать даже самые заковыристые задачи.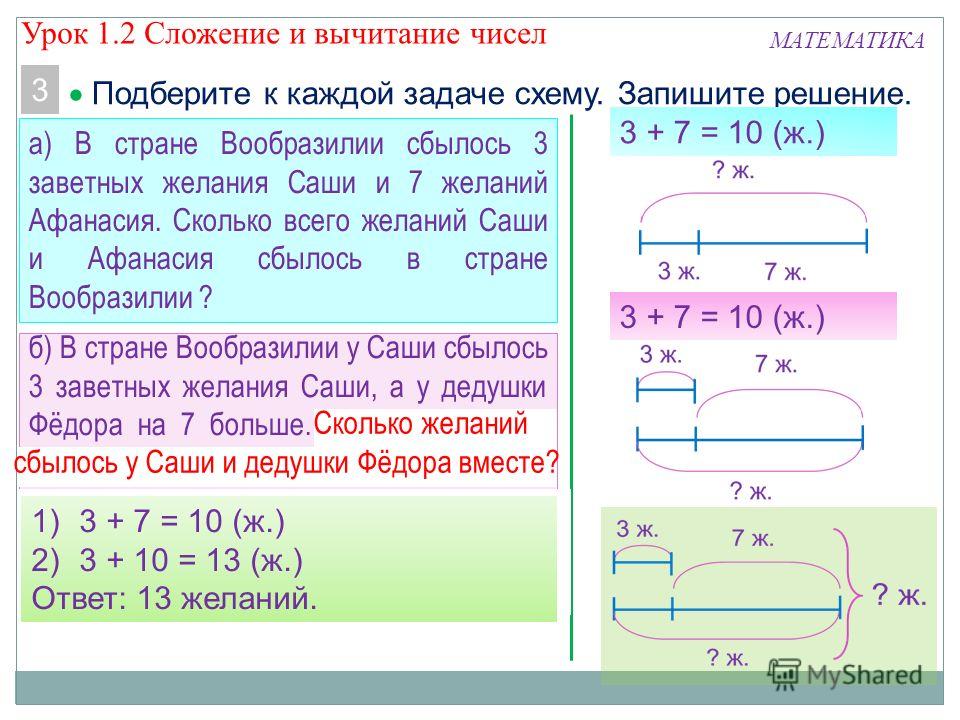 Зачастую школьные учебники и сборники заданий составлены таким образом, что вопрос, на который и нужно дать ответ, сформулирован слишком сложно. Поэтому, чтобы убедиться, что ребенок правильно понял суть, попросите его проговорить условие своими словами. Часто уже на этом этапе все становится очевидно.
Зачастую школьные учебники и сборники заданий составлены таким образом, что вопрос, на который и нужно дать ответ, сформулирован слишком сложно. Поэтому, чтобы убедиться, что ребенок правильно понял суть, попросите его проговорить условие своими словами. Часто уже на этом этапе все становится очевидно. Задавайте вопросы
Задавайте вопросы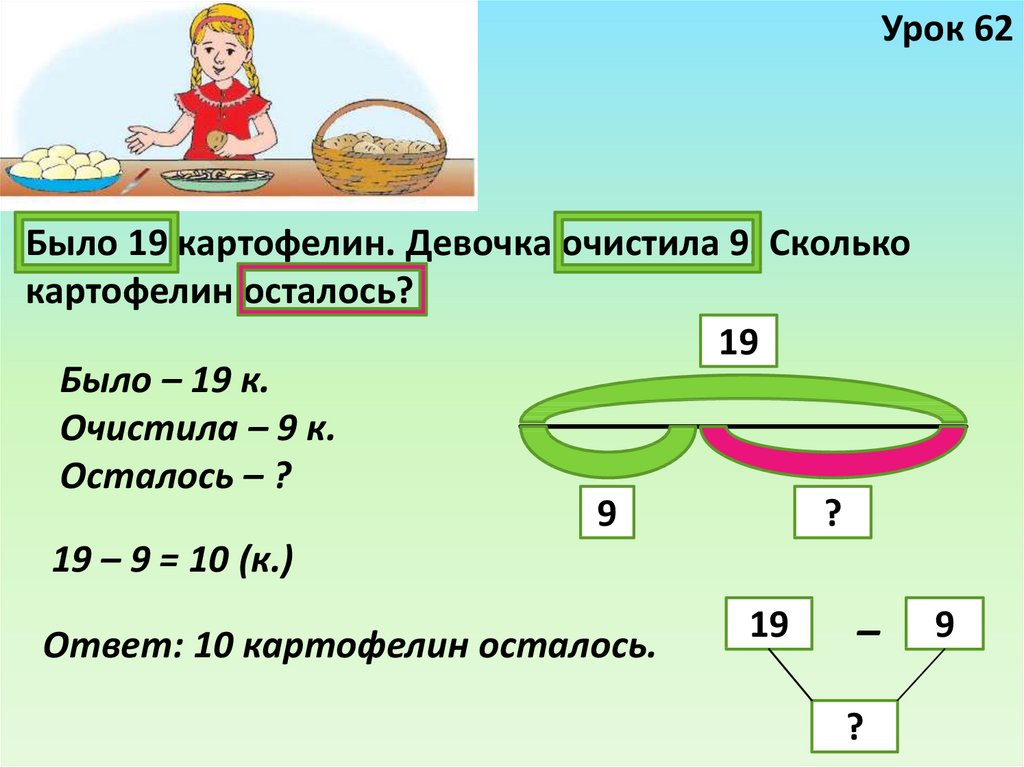 Хорошо, если с самого начала вы вместе определите, что результатом должна быть, например, длина пути в километрах или количество конфет у Васи в штуках, и по ходу будете напоминать, что будет ответом к задаче.
Хорошо, если с самого начала вы вместе определите, что результатом должна быть, например, длина пути в километрах или количество конфет у Васи в штуках, и по ходу будете напоминать, что будет ответом к задаче.
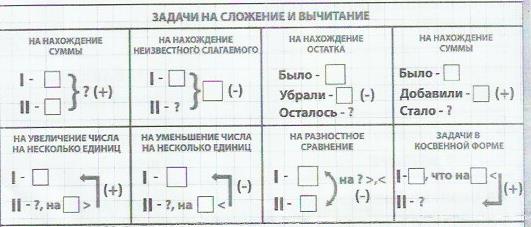
 Знаете ли вы кого-нибудь, у кого в прошлом был негативный опыт решения проблем со словами? Были ли у вас когда-нибудь мысли, как у студента в карикатуре ниже?
Знаете ли вы кого-нибудь, у кого в прошлом был негативный опыт решения проблем со словами? Были ли у вас когда-нибудь мысли, как у студента в карикатуре ниже? Проблемы со словами ничем не отличаются. Даже если в прошлом вы боролись с текстовыми задачами, вы приобрели много новых математических навыков, которые помогут вам добиться успеха сейчас!
Проблемы со словами ничем не отличаются. Даже если в прошлом вы боролись с текстовыми задачами, вы приобрели много новых математических навыков, которые помогут вам добиться успеха сейчас! Эта стратегия поможет вам добиться успеха в решении текстовых задач. Мы продемонстрируем стратегию при решении следующей задачи.
Эта стратегия поможет вам добиться успеха в решении текстовых задач. Мы продемонстрируем стратегию при решении следующей задачи.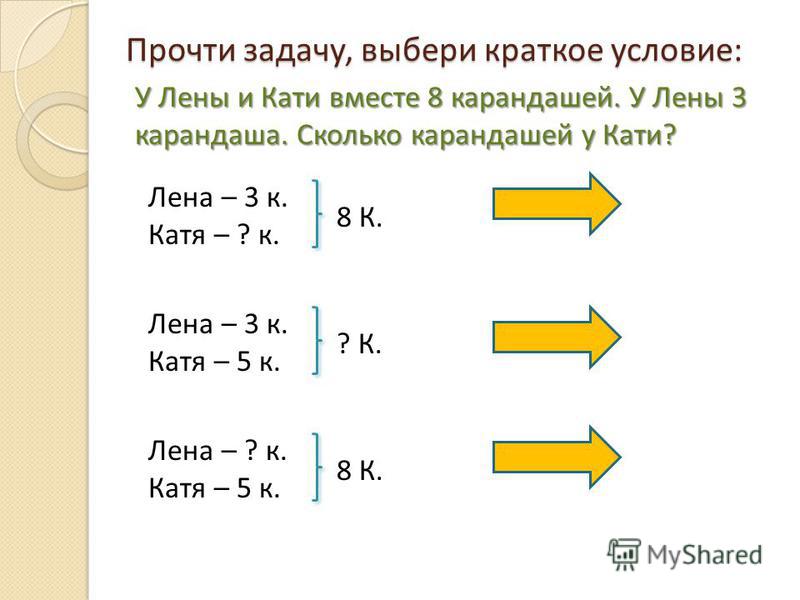 Назовите то, что вы ищете. Выберите переменную для представления этого количества. Вы можете использовать любую букву для переменной, но может помочь выбрать ту, которая поможет вам запомнить, что она представляет.
Назовите то, что вы ищете. Выберите переменную для представления этого количества. Вы можете использовать любую букву для переменной, но может помочь выбрать ту, которая поможет вам запомнить, что она представляет.
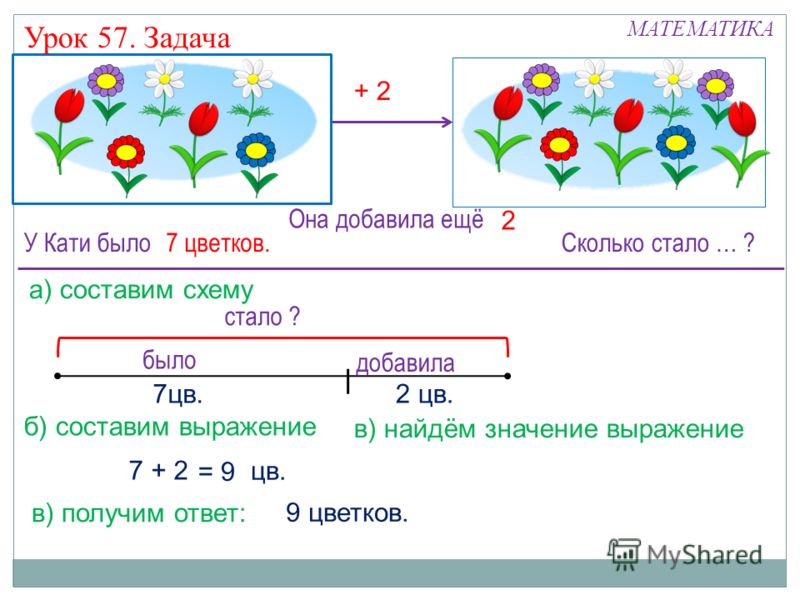 Убедитесь, что вы понимаете все слова и идеи. Возможно, вам придется прочитать задачу два или более раз. Если есть слова, которые вы не понимаете, поищите их в словаре или в Интернете.
Убедитесь, что вы понимаете все слова и идеи. Возможно, вам придется прочитать задачу два или более раз. Если есть слова, которые вы не понимаете, поищите их в словаре или в Интернете.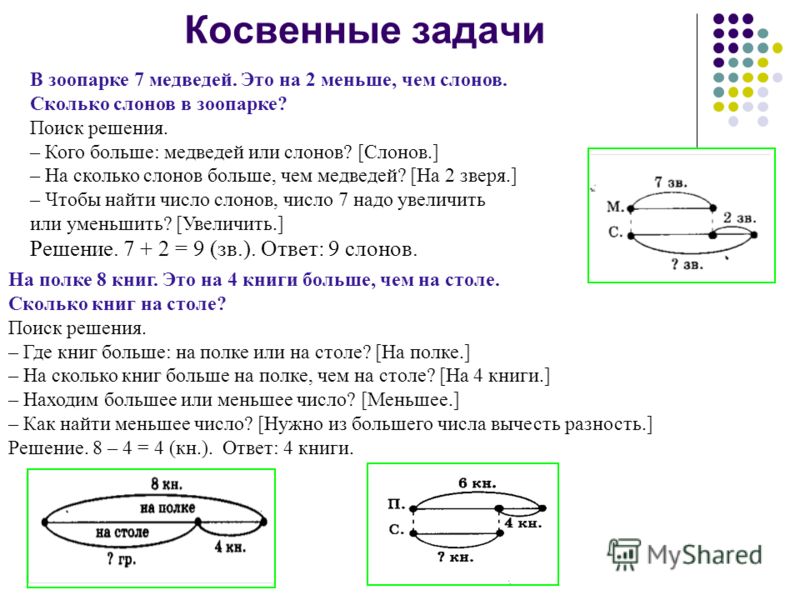
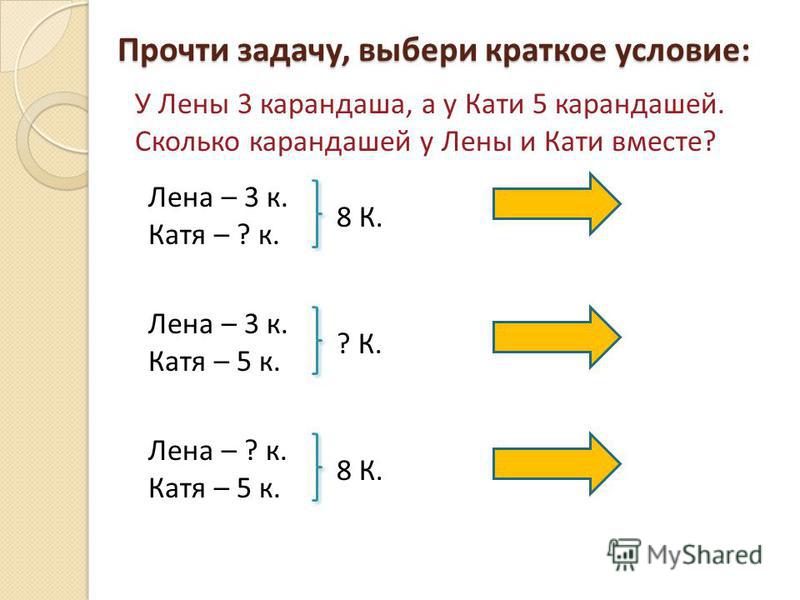
 Этот тип плаката обеспечивает хорошее повторение для студентов.
Этот тип плаката обеспечивает хорошее повторение для студентов.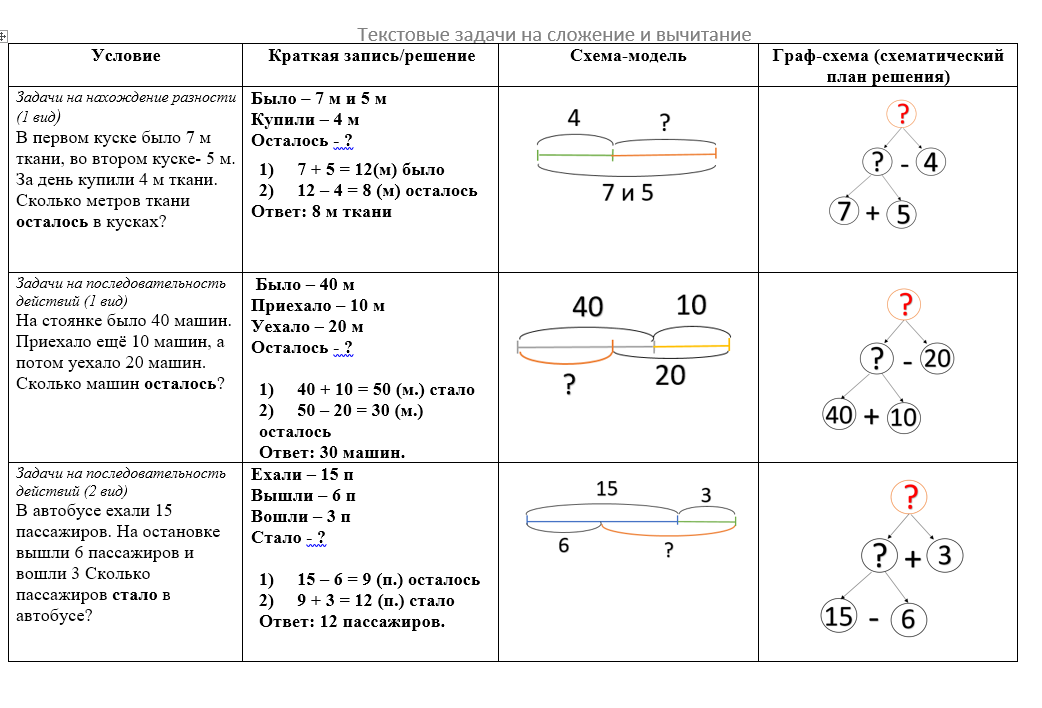 Будем надеяться, что это исследование приведет к более эффективной стратегии, а затем к решению.
Будем надеяться, что это исследование приведет к более эффективной стратегии, а затем к решению.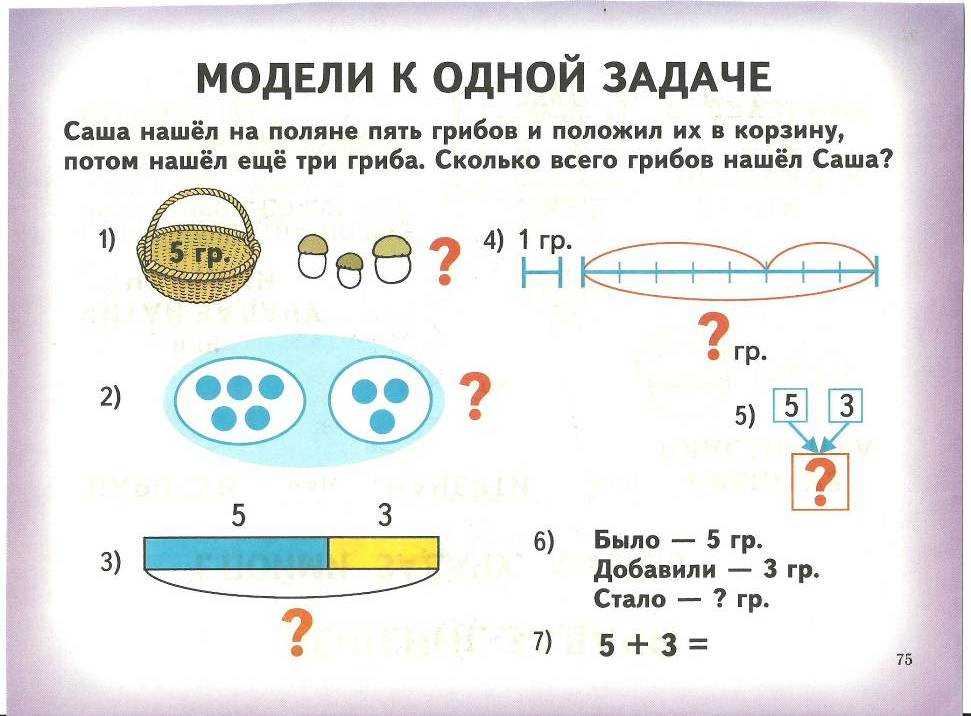
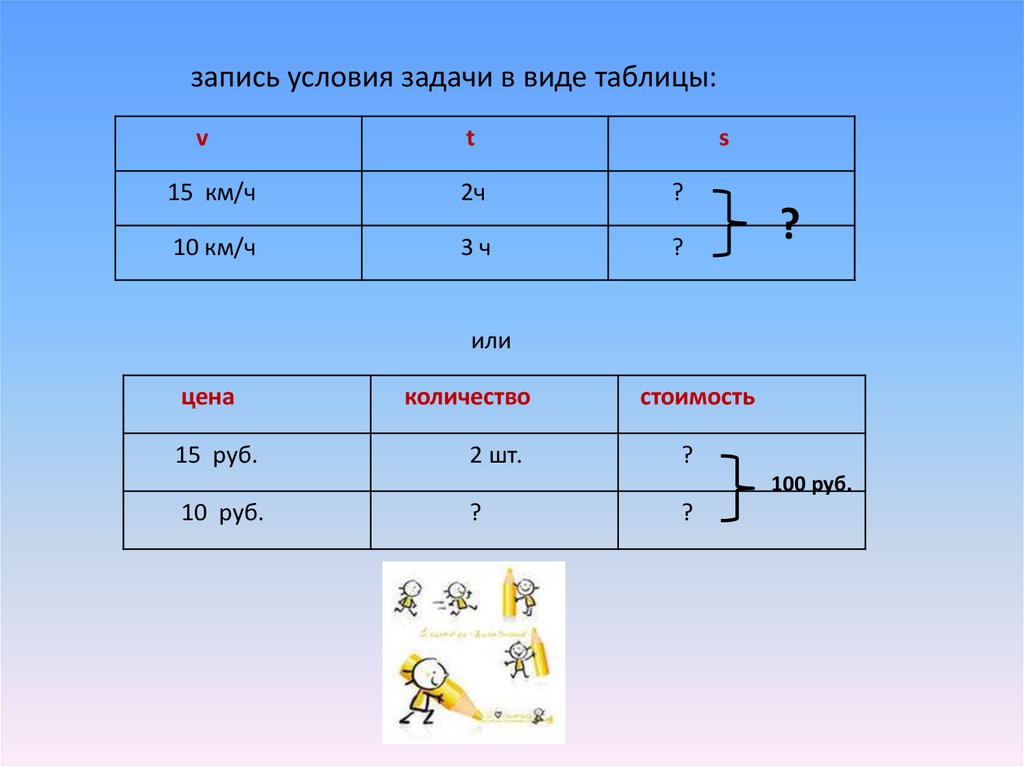 Это может быть потому, что это дает им лучшее представление о проблеме. Так как есть проблемы при использовании оборудования — это лучшая стратегия, чем рисование, вы должны поощрять использование учащимися оборудования, время от времени самостоятельно моделируя его использование.
Это может быть потому, что это дает им лучшее представление о проблеме. Так как есть проблемы при использовании оборудования — это лучшая стратегия, чем рисование, вы должны поощрять использование учащимися оборудования, время от времени самостоятельно моделируя его использование. 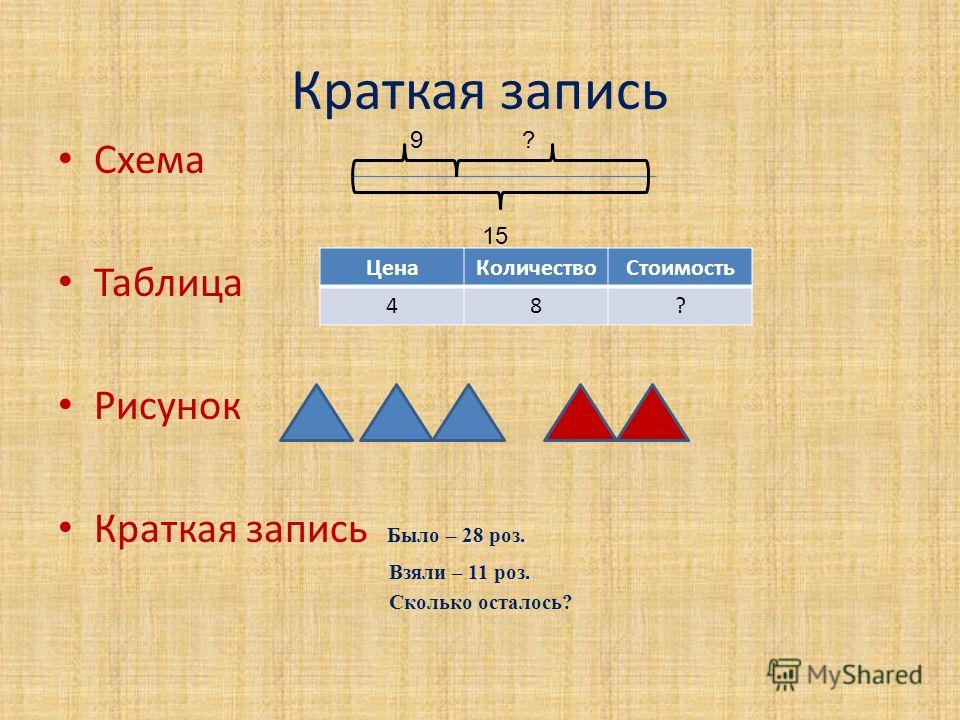 Вы можете думать о диаграмме как о чем-либо, что вы можете нарисовать, но это не изображение. Но где вы проводите грань между картинкой и диаграммой? Как вы можете видеть на примере цыплят и свиней, о которых говорилось выше, обычное рисование картинок перерастает в рисование диаграмм.
Вы можете думать о диаграмме как о чем-либо, что вы можете нарисовать, но это не изображение. Но где вы проводите грань между картинкой и диаграммой? Как вы можете видеть на примере цыплят и свиней, о которых говорилось выше, обычное рисование картинок перерастает в рисование диаграмм. 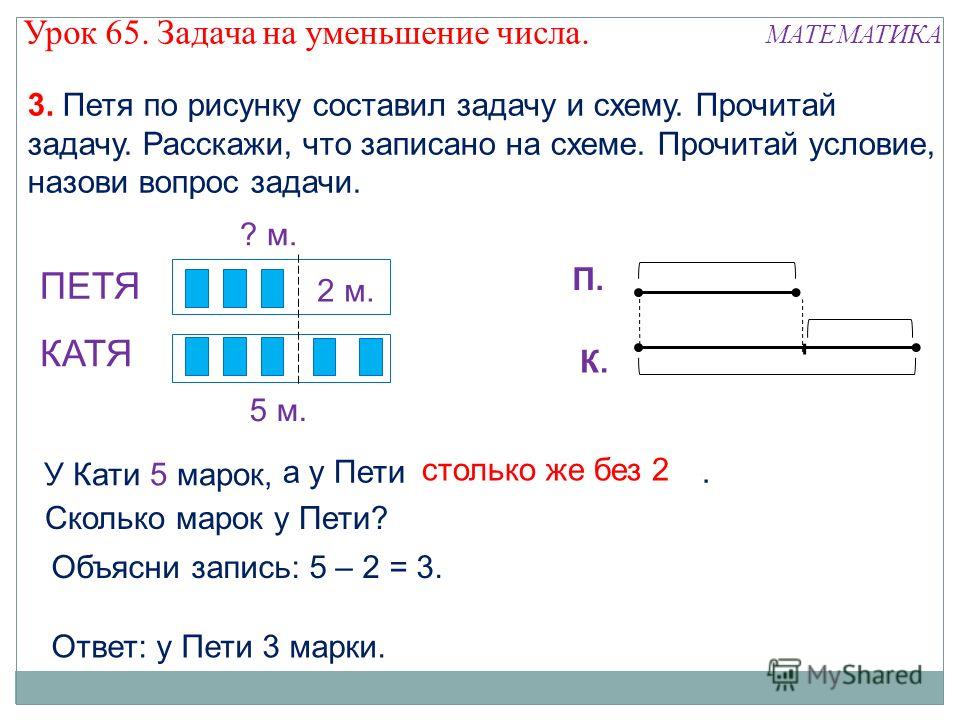 Они варьируются от таблиц чисел, помогающих решать такие задачи, как ферма, до таблиц с галочками и крестиками, которые часто используются в логических задачах. Таблицы также могут быть эффективным способом поиска числовых шаблонов.
Они варьируются от таблиц чисел, помогающих решать такие задачи, как ферма, до таблиц с галочками и крестиками, которые часто используются в логических задачах. Таблицы также могут быть эффективным способом поиска числовых шаблонов. Отчасти это связано с тем, что эти стратегии обычно используются не сами по себе, а в сочетании с другими стратегиями.
Отчасти это связано с тем, что эти стратегии обычно используются не сами по себе, а в сочетании с другими стратегиями. 
 Например, играя в крестики-нолики, вы поймете, что есть три, а не девять способов положить первый символ. Это сразу уменьшает количество возможностей для игры и упрощает ее анализ. Такого рода аргументы возникают постоянно, и их следует с радостью воспринимать, когда вы их видите.
Например, играя в крестики-нолики, вы поймете, что есть три, а не девять способов положить первый символ. Это сразу уменьшает количество возможностей для игры и упрощает ее анализ. Такого рода аргументы возникают постоянно, и их следует с радостью воспринимать, когда вы их видите. Хитрость здесь заключается в том, чтобы увидеть, какие навыки, которые вы знаете, могут быть применены к решению проблемы.
Хитрость здесь заключается в том, чтобы увидеть, какие навыки, которые вы знаете, могут быть применены к решению проблемы. 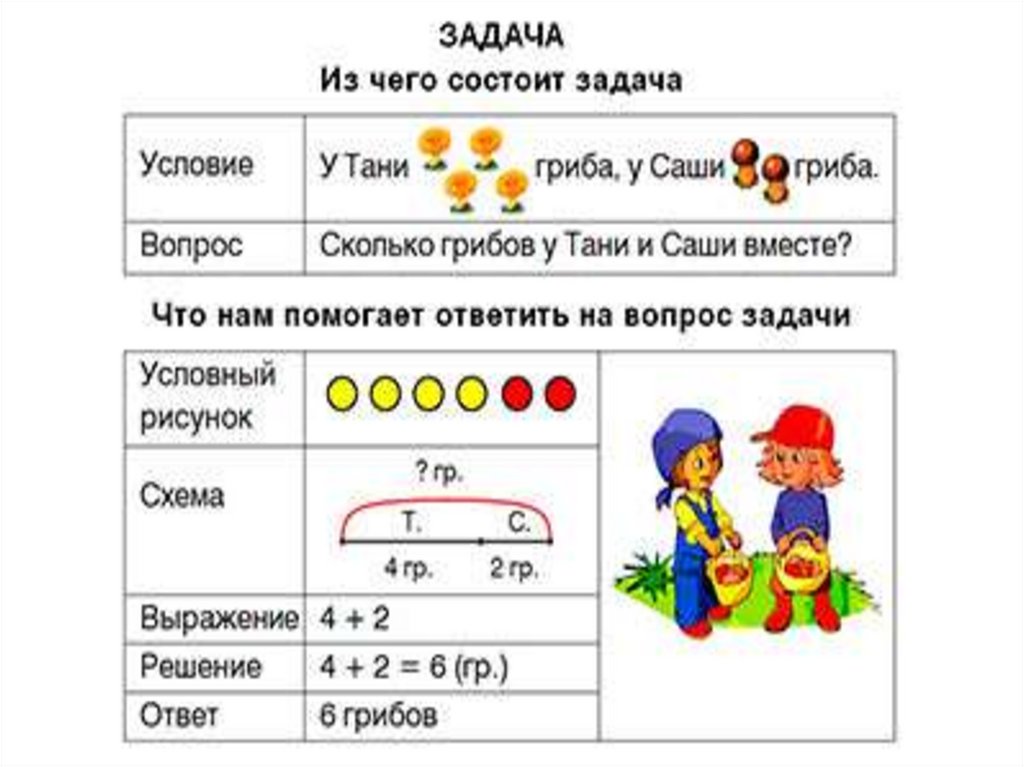 Предположим, что есть 80 свиней. Если они есть, то их будет 320 ног. Очевидно, мы переоценили количество свиней. Так что, может быть, есть только 60 свиней. Теперь у 60 свиней будет 240 ног. Это оставило бы нас с 16 ногами, которые можно было бы найти у цыплят. Чтобы произвести 16 ножек, нужно 8 цыплят. Но 60 свиней плюс 8 цыплят — это всего 68 животных, поэтому нам не хватило почти 20 животных.
Предположим, что есть 80 свиней. Если они есть, то их будет 320 ног. Очевидно, мы переоценили количество свиней. Так что, может быть, есть только 60 свиней. Теперь у 60 свиней будет 240 ног. Это оставило бы нас с 16 ногами, которые можно было бы найти у цыплят. Чтобы произвести 16 ножек, нужно 8 цыплят. Но 60 свиней плюс 8 цыплят — это всего 68 животных, поэтому нам не хватило почти 20 животных.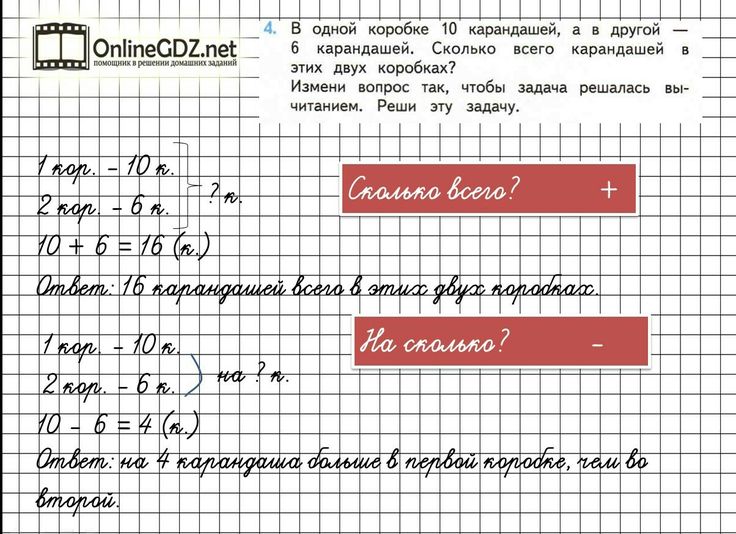 Это означает, что в нашем последнем предположении в таблице мы в пяти поросятах от правильного ответа. Тогда должно быть 46 свиней.
Это означает, что в нашем последнем предположении в таблице мы в пяти поросятах от правильного ответа. Тогда должно быть 46 свиней. Возможно, младшие школьники могут эффективно использовать и другие стратегии. Тем не менее, мы уверены, что большинство учащихся на данном уровне учебной программы могут использовать стратегии, перечисленные выше для этого уровня. Поскольку решение проблем становится все более распространенным в начальных школах, мы ожидаем, что некоторые из более сложных стратегий станут использоваться на более низких уровнях.
Возможно, младшие школьники могут эффективно использовать и другие стратегии. Тем не менее, мы уверены, что большинство учащихся на данном уровне учебной программы могут использовать стратегии, перечисленные выше для этого уровня. Поскольку решение проблем становится все более распространенным в начальных школах, мы ожидаем, что некоторые из более сложных стратегий станут использоваться на более низких уровнях. Студенты часто начинают с очень точного представления проблемы. Поскольку они видят, что нет необходимости добавлять все детали или цвет, их изображения становятся более символичными и сохраняются только основные черты. Таким образом, мы получаем пятно для тела свиньи и четыре короткие линии для ее ног. Затем учащиеся, кажется, понимают, что отношения между объектами можно продемонстрировать с помощью линейных рисунков. Объекты могут быть уменьшены до точек или букв. В геометрических задачах могут потребоваться более точные диаграммы, но диаграммы полезны в очень многих задачах, не имеющих геометрического содержания.
Студенты часто начинают с очень точного представления проблемы. Поскольку они видят, что нет необходимости добавлять все детали или цвет, их изображения становятся более символичными и сохраняются только основные черты. Таким образом, мы получаем пятно для тела свиньи и четыре короткие линии для ее ног. Затем учащиеся, кажется, понимают, что отношения между объектами можно продемонстрировать с помощью линейных рисунков. Объекты могут быть уменьшены до точек или букв. В геометрических задачах могут потребоваться более точные диаграммы, но диаграммы полезны в очень многих задачах, не имеющих геометрического содержания.
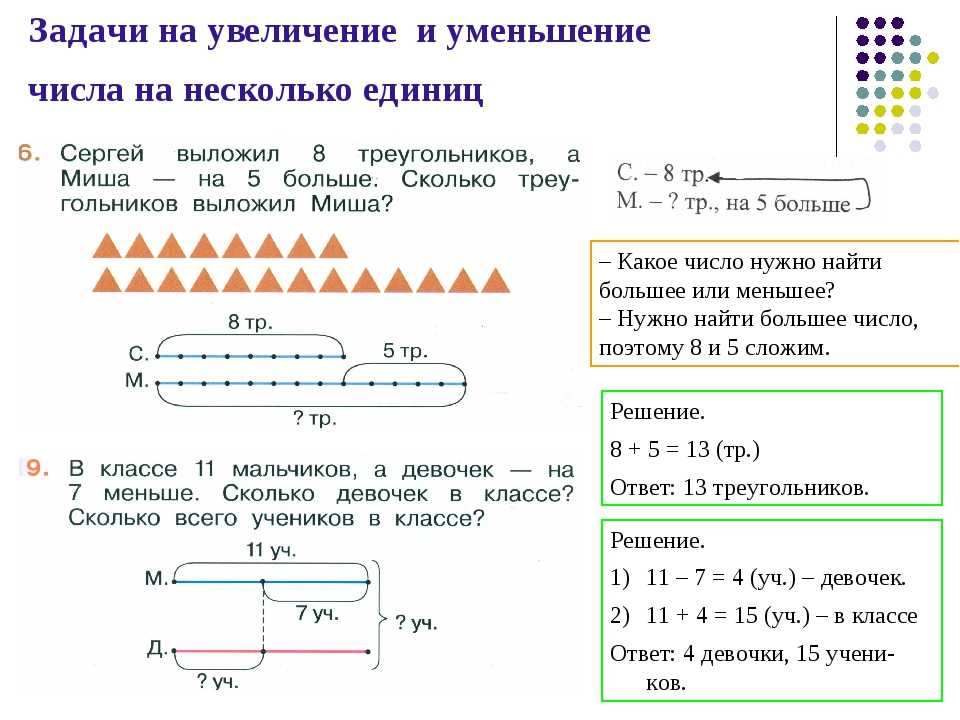
 )
) Приготовление пищи, покупка продуктов и своевременное посещение места — все это требует базовых математических навыков, известных как чувство числа.
Приготовление пищи, покупка продуктов и своевременное посещение места — все это требует базовых математических навыков, известных как чувство числа. Но это настоящая проблема, основанная на биологии, как и дислексия.
Но это настоящая проблема, основанная на биологии, как и дислексия. Различия связаны со структурой мозга и тем, как он функционирует в областях, связанных с навыками обучения.
Различия связаны со структурой мозга и тем, как он функционирует в областях, связанных с навыками обучения. Но есть местные ресурсы, которые предлагают бесплатные или недорогие оценки.
Но есть местные ресурсы, которые предлагают бесплатные или недорогие оценки.
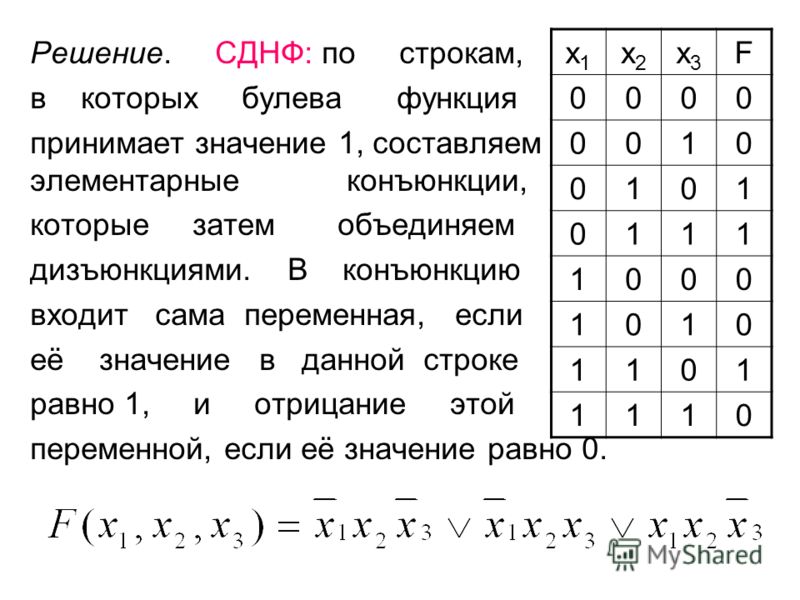


 Каждый выполненный заказ проходит проверку на плагиат, вы не сдадите на проверку одинаковую с кем-то работу. Ваш заказ будет уникальным!
Каждый выполненный заказ проходит проверку на плагиат, вы не сдадите на проверку одинаковую с кем-то работу. Ваш заказ будет уникальным! д. (если имеются). При необходимости напишите дополнительные пояснения.
д. (если имеются). При необходимости напишите дополнительные пояснения.

 Каждый выполненный заказ проходит проверку на плагиат, вы не сдадите на проверку одинаковую с кем-то работу. Ваш заказ будет уникальным!
Каждый выполненный заказ проходит проверку на плагиат, вы не сдадите на проверку одинаковую с кем-то работу. Ваш заказ будет уникальным! д. (если имеются). При необходимости напишите дополнительные пояснения.
д. (если имеются). При необходимости напишите дополнительные пояснения.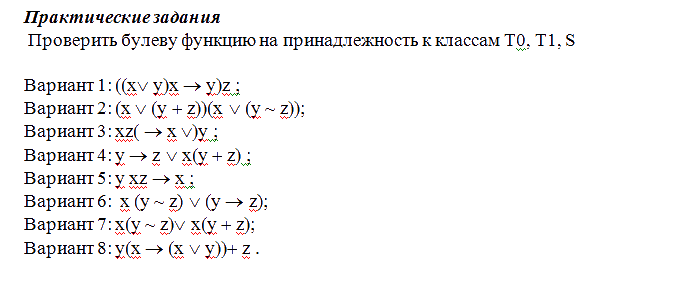


 Реализация алгоритмов
требует тщательного понимания логических структур и, как правило, реализации сверху вниз
подход, начиная с описания спецификаций, а затем продолжая
к реализации псевдокода и, наконец, к кодированию, зависящему от языка
реализация. Более того, анализ сложности алгоритмов требует знания функций,
рост функций и методы подсчета из комбинаторного анализа. Точно так же математическая индукция и рекурсия
определения используются связным образом для понимания алгоритмов и вариантов их реализации.
рекурсивно против итеративно.
Реализация алгоритмов
требует тщательного понимания логических структур и, как правило, реализации сверху вниз
подход, начиная с описания спецификаций, а затем продолжая
к реализации псевдокода и, наконец, к кодированию, зависящему от языка
реализация. Более того, анализ сложности алгоритмов требует знания функций,
рост функций и методы подсчета из комбинаторного анализа. Точно так же математическая индукция и рекурсия
определения используются связным образом для понимания алгоритмов и вариантов их реализации.
рекурсивно против итеративно.
 \\.\\.\\Сара\ Мюллер\\\end{matrix}\right)
\)
\\.\\.\\Сара\ Мюллер\\\end{matrix}\right)
\) Классификация опухолей как злокачественных или доброкачественных предполагает попытку предсказать
если переменная \(Y\), о которой мы можем думать, что она принимает два значения либо \(0\), либо \(1\)
либо злокачественные, либо доброкачественные. Существуют различные
алгоритмы, используемые в задачах классификации, таких как бинарная опухоль
классификация, в том числе методы от вероятности.
Классификация опухолей как злокачественных или доброкачественных предполагает попытку предсказать
если переменная \(Y\), о которой мы можем думать, что она принимает два значения либо \(0\), либо \(1\)
либо злокачественные, либо доброкачественные. Существуют различные
алгоритмы, используемые в задачах классификации, таких как бинарная опухоль
классификация, в том числе методы от вероятности. Перечисление и комбинаторика важны во многих
области и примеры, включая:
Перечисление и комбинаторика важны во многих
области и примеры, включая: д.
Такие распределения вероятностей называются дискретными распределениями.
в отличие от непрерывных распределений, таких как кривая нормального распределения.
д.
Такие распределения вероятностей называются дискретными распределениями.
в отличие от непрерывных распределений, таких как кривая нормального распределения.

 Решение проблем.
Решение проблем.


 Системы геометрии, включая евклидову, неевклидову, координатную, трансформационную и проективную геометрию.
Системы геометрии, включая евклидову, неевклидову, координатную, трансформационную и проективную геометрию.
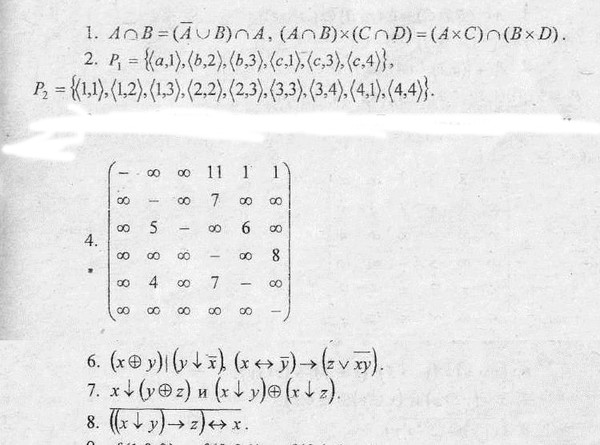


 Темы, включая символическую логику, индукцию, линейное программирование и конечные графы.
Темы, включая символическую логику, индукцию, линейное программирование и конечные графы. Он постоянно применяется во многих областях математики и информатики. Это считается очень эффективным подходом к развитию силы и решению проблем.
Он постоянно применяется во многих областях математики и информатики. Это считается очень эффективным подходом к развитию силы и решению проблем.






 Натуральные числа охватывают коммутативные и ассоциативные операции сложения и умножения, где каждое имеет тождество, а умножение распространяется на сложение. И никакое натуральное число не имеет аддитивной или мультипликативной инверсии, за исключением единичных элементов 0 и 1.
Натуральные числа охватывают коммутативные и ассоциативные операции сложения и умножения, где каждое имеет тождество, а умножение распространяется на сложение. И никакое натуральное число не имеет аддитивной или мультипликативной инверсии, за исключением единичных элементов 0 и 1.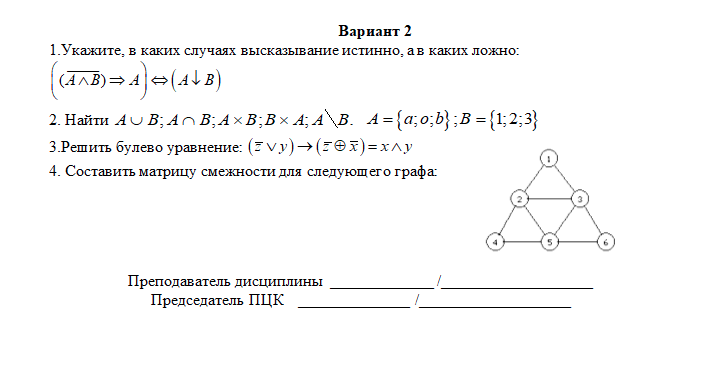 д. Кроме того,
д. Кроме того, Это включает в себя;
Это включает в себя; Это реализовано для разработки компьютерных или цифровых схем с помощью логических вентилей, которые принимают сигналы на вход и выдают сигналы на выходе.
Это реализовано для разработки компьютерных или цифровых схем с помощью логических вентилей, которые принимают сигналы на вход и выдают сигналы на выходе. Дерево — это просто ациклический граф или граф, не имеющий цикла, а общее дерево — это непустой конечный набор компонентов, известных как вершины или узлы, которые обладают свойством, состоящим в том, что каждый узел может иметь минимальную степень, равную 1, и максимальную. степень как н.
Дерево — это просто ациклический граф или граф, не имеющий цикла, а общее дерево — это непустой конечный набор компонентов, известных как вершины или узлы, которые обладают свойством, состоящим в том, что каждый узел может иметь минимальную степень, равную 1, и максимальную. степень как н.
