Лучшие ресурсы и пособия для подготовки к ЕГЭ по профильной математике
Когда до ЕГЭ остаётся немного времени, рассчитывать с помощью теории вероятности свои шансы на успех не стоит. Теперь нужно убедиться в своих знаниях. В этой статье собрали полезные учебники и пособия для повторения теории, а также сборники и сайты для практики.
Пособия и учебники для подготовки к ЕГЭ по математике*
Перед покупкой пособия определитесь со своими целями. Если нужно подтянуть определённое задание, выбирайте пособие, где разбирают конкретно его. Если нужно получить общую и сжатую информацию — берите учебники с самыми важными материалами, формулами и алгоритмами решения.
Обратите внимание также на:
- Репутацию автора и количество отзывов о его учебнике. Покупать лучше проверенные книги известных авторов, чтобы точно быть уверенным в качестве и точности теории.
- Визуальное оформление. Обращайте внимание на наличие иллюстраций и таблиц, а также на качество бумаги.
 Это влияет на эффективность подготовки.
Это влияет на эффективность подготовки.
* Эта подборка подготовлена при участии преподавателя по профильной математике в Вебиуме Эйджея Гаусса.
1️⃣ «ЕГЭ. Математика. Пошаговая подготовка», А.Н. Роганин
+ вся необходимая теория
+ помимо теории есть задания для закрепления пройденного материала
+ сформулирован по схеме «от лёгкого к трудному»
+ подходит для самостоятельной подготовки
— выпущен в 2019 году
Ориентация на ЕГЭ: да
Практика: да
2️⃣ «ЕГЭ 2022 Математика. Профильный уровень. Задачи с параметром», Ю. Садовничий
+ очень подробное объяснение
+ все типы параметров
+ разбит на модули по темам
Ориентация на ЕГЭ: да
Практика: да
Если в ЕГЭ по математике есть проблемы с 17 заданием — параметром, — этот сборник отлично подтянет данную тему. Он полностью посвящён параметрам.
Он полностью посвящён параметрам.
3️⃣ «Математика. Весь школьный курс в таблицах и схемах для подготовки к ЕГЭ», Л.И. Слонимский, И.С. Слонимская
+ вся необходимая теория по блокам
+ удобный формат
Ориентация на ЕГЭ: да
Практика: нет
Информация в таблицах воспринимается легче, что делает это пособие очень удобным в использовании.
4️⃣ «Математика. 7–11 классы. Карманный справочник», Ф.Ф. Лысенко, С.Ю. Кулабухов
+ сжатая теория, которая понятно изложена
+ карманный формат
+ информация собрана по темам
Ориентация на ЕГЭ: да
Практика: нет
Этот справочник поможет в короткие сроки повторить всю теорию. Здесь приводятся все необходимые для ЕГЭ формулы, материал дан кратко и систематизировано.
5️⃣ «Справочник для подготовки к ЕГЭ по математике. Все темы и формулы», Анна Малкова
+ стильный и красивый учебник
+ вся необходимая теория для ЕГЭ
+ новый неизвестный автор
Ориентация на ЕГЭ: да
Практика: нет
Современный справочник с приятным оформлением поможет в подготовке к ЕГЭ. Вся теория подана максимально доступно — можно пройти все темы с нуля.
Вся теория подана максимально доступно — можно пройти все темы с нуля.
6️⃣ «ЕГЭ Математика. Новый полный справочник школьника для подготовки к ЕГЭ», Мордкович, Глизбург, Лаврентьева
+ вся теория
+ по темам
Ориентация на ЕГЭ: да
Практика: нет
7️⃣ «Математика абитуриенту», В. В. Ткачук
+ полный курс математики
+ все уровни сложности
+ показаны уникальные алгоритмы самоподготовки
Ориентация на ЕГЭ: да
Практика: нет
Данный учебник — курс элементарной математики. Он поможет школьнику подготовиться не только к ЕГЭ, но и к вступительным экзаменам в вуз.
Самый доступный для покупки справочник. Разработан при участии авторов учебников для школы.
Сборники и сайты для практики
Любой теоретический материал обязательно нужно закрепить на практике. Поэтому сделали подборку сборников для отработки практической части ЕГЭ и прокачки навыков решения задач.
В связи с изменениями в ЕГЭ 2022 некоторые старые сборники стали неактуальны, однако их всё равно можно решать, особенно вторую часть.
1️⃣ Решу ЕГЭ
+ реальные варианты прошлых лет
+ очень много заданий по всем темам
— объяснение решения к задачам второй части не в формате ЕГЭ
2️⃣ Незнайка
+ деление по типам заданий
+ тесты
+ развёрнутое решение заданий второй части
3️⃣ Открытый банк заданий ФИПИ
+ задания ЕГЭ
+ несколько уровней сложности
— нет ответов
4️⃣ «Типовые экзаменационные варианты», И.В. Ященко
+ создан при участии разработчиков ЕГЭ
+ даны подробные решения
+ соответствует демоверсии
— решения есть не для всех вариантов
5️⃣ «ЕГЭ 2021.
 Математика. Теория вероятностей. Задача 4 и 10»
Математика. Теория вероятностей. Задача 4 и 10»+ разнообразные формулировки
+ помимо тестов, дана небольшая теория
+ много заданий, которые идут от простых к сложным
6️⃣ «ЕГЭ-2022. 40 тренировочных вариантов, математика профильный уровень», Ф.Ф. Лысенко
+ соответствует демоверсии
+ авторские задания
+ задания по темам и целые тесты
— подробное решение не для всех вариантов
7️⃣ «Сборник ЕГЭ 2022 по математике, профильный уровень», Ященко, Семёнов
+ задачи по темам
+ есть решение в формате ЕГЭ
8️⃣ «ЕГЭ 2020. Математика. Профильный уровень. Задания с развернутым ответом», Ю. В. Садовничий
+ только вторая часть
+ задания с разбором
+ присутствует теория
9️⃣ Задачник Вебиума по тригонометрии второй части
В нем задания собраны по уровням, начиная с самых простых и заканчивая заданиями второй части. Все задания структурированы по приемам, которые нужны для успешного решения, и отбора корней.
Все задания структурированы по приемам, которые нужны для успешного решения, и отбора корней.
+ структурированный
+ ориентирован на ЕГЭ 2022
— разборы заданий с подробным оформлением только для студентов курсов Вебиума
1️⃣0️⃣ «Задачи на готовых чертежах. Геометрия 10–11 классы», Э.Н. Балаян
+ подходит для изучения геометрии с нуля
+ есть справочник
— не формат ЕГЭ
1️⃣1️⃣ Резольвента
+ учебные материалы
+ задания
1️⃣2️⃣ Задачи
+ задачи по темам
+ неудобный сайт
1️⃣3️⃣ «Теоремы и задачи школьной геометрии. Базовый и профильный уровни», Р.Н. Гордин
+ теория
+ задачи
Задачники и учебники этого автора представлены в разных вариациях: есть книги по отдельным темам и заданиям ЕГЭ, общие пособия, которые помогут подтянуть весь курс школьной геометрии.
1️⃣4️⃣ «Нестандартные задачи на ЕГЭ по математике», И.В. Яковлев
+ только 18 задание — самая непредсказуемая задача ЕГЭ
+ подробное решение
В нашей онлайн-школе Вебиум тоже очень много полезных материалов для подготовки к ЕГЭ по математике. В группе ВКонтакте каждый день мы делимся разборами различных заданий, теорией, а также проводим интересные интерактивы. На ютуб-канале Эйджей разбирает варианты ЕГЭ и решает задачи прошлых лет. А на сайте Вебиума можно записаться на курс по подготовке!
Чтобы сдать ЕГЭ по профильной математике на высокий балл, необходимо регулярно заниматься и использовать несколько сборников и пособий. Не стоит ограничиваться одним ресурсом. Чем больше заданий получится решить на этапе подготовки, тем выше шансы, что на самом экзамене выпадет задача с известным алгоритмом решения. И тогда 80+ баллов на ЕГЭ обеспечены!
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter. Мы обязательно поправим!
Мы обязательно поправим!
Печатные издания / Межрегиональный центр инновационных технологий в образовании
- Главная
- Издательство МЦИТО
- Библиотека издательства
- Печатные издания
Михайлов В. А., Горев П. М., Утёмов В. В. Научное творчество: Методы конструирования новых идей: Учебное пособие. – Киров: Изд-во МЦИТО, 2014. – 94 с.
ISBN 978-5-906642-01-1
Учебное пособие подготовлено в помощь студентам педагогических направлений подготовки (специальностей), учителям и преподавателям для использования на занятиях по изучению методов и приёмов научного творчества, а именно методов конструирования новых идей – неалгоритмических, частично алгоритмизированных и алгоритмов, в частности алгоритма С. Малкина, с целью формирования творческого мышления и развития творческого воображения учащихся.
Горев П. М., Лунеева О. Л. Межпредметные проекты учащихся средней школы: Математический и естественнонаучный циклы: Учебно-методическое пособие. – Киров: Изд-во МЦИТО, 2014. – 58 с.
– Киров: Изд-во МЦИТО, 2014. – 58 с.
ISBN 978-5-906642-02-8
Пособие знакомит читателя с методическими аспектами подготовки, разработки и проведения межпредметных проектов по математике и естественнонаучным дисциплинам, изучаемым в средней школе. Отдельная глава посвящена описанию возможных проектов учащихся, каждый из которых снабжен списком рекомендуемой для его осуществления литературы. Также приводится разработка рабочей тетради, позволяющей эффективно организовать работу школьников над межпредметными проектами. Описанная в пособии методика многократно апробирована авторами в работе с учащимися 8–10-х классов МОАУ «Лицей № 21» г. Кирова как непосредственно в учебном процессе, так и во внеклассной работе со школьниками в рамках лагерей-тренингов «Математика. Творчество. Интеллект», ведущих историю с 2001 года. Пособие представляет интерес для учителей математики и естественнонаучных дисциплин, студентов педагогических направлений подготовки, учащихся старших классов средних школ и всех тех, кто находится в творческом поиске новых возможностей саморазвития в области математики.
Горев П. М., Утёмов В. В. Уроки развивающей математики. 5–6 классы: Задачи математического кружка: Учебное пособие. – Киров: Изд-во МЦИТО, 2014. – 207 с.
ISBN 978-5-906642-03-5
Учебное пособие представляет собой сборник задач и материалов для проведения дополнительных занятий по математике в 5–6-х классах общеобразовательной школы. В нём содержатся подборки задач как для занятий кружка по математике, так и для самостоятельной работы учащихся во внеурочное время. Книга предназначена в первую очередь для учеников 5–6-х классов, желающих повысить уровень своих знаний по математике, привить себе стойкий интерес к предмету, приобщиться к опыту творческой деятельности, направленной на оригинальное, сильное мышление. Пособие может быть интересно также учителям математики, студентам педагогических направлений подготовки и всем тем, кто находится в творческом поиске новых возможностей педагогической деятельности в области математики.
Горев П. М., Утёмов В. В. Творческие прогулки под звёздами: учебно-методическое пособие. – Киров: Изд-во МЦИТО, 2014. – 123 с., ил.
– Киров: Изд-во МЦИТО, 2014. – 123 с., ил.
ISBN 978-5-906642-04-2
Пособие является седьмым авторским курсом, посвященным отдельным методам, приёмам и идеям диалектического мышления, реализованным на материале, адаптированном для широкого круга читателей. Основная часть пособия оформлена в виде рабочей тетради, что позволяет наиболее оптимально организовать процесс решения предлагаемых ситуаций. Занятия снабжены комментариями для взрослых, в которых раскрывается суть методов и приводятся контрольные решения. Учебное пособие может быть интересно учащимся средней школы, их учителям, воспитателям и родителям, студентам, а также всем тем, кто хочет развить творческую составляющую своего мышления.
Жуйкова И. А., Масютин В. В. По следам первобытного человека: Учебно-методическое пособие. – Киров: Изд-во МЦИТО, 2014. – 49 с.
ISBN 978-5-906642-05-9
Учебное пособие подготовлено в помощь учителям и студентам естественнонаучного и географического направлений. В доступной форме изложены вопросы палеогеографии и палеонтологии. Представленные материалы могут использоваться в дополнительной внеурочной деятельности учителя.
Представленные материалы могут использоваться в дополнительной внеурочной деятельности учителя.
Русских Г. А., Михайлова К. В. Ландшафтоведение в школе: Методические рекомендации. – Киров: Изд-во МЦИТО, 2014. – 29 с.
ISBN 978-5-906642-06-6
В методических рекомендациях раскрываются вопросы теории и методики подготовки школьников к проведению исследовательской работы в процессе изучения ландшафтов родного края. Авторы предлагают оригинальные модели занятий географического кружка в форме выставки и экскурсий в природу, которые разработаны в соответствии с требованиями ФГОС второго поколения. Предлагаемая система занятий по ландшафтоведению состоит из теоретического введения в исследовательскую работу, ряда экскурсий в природу с решением творческих задач, камеральной обработки собранных данных и подведения итогов. Последний этап работы может быть представлен подготовкой выступлений (проектов) школьников, используемых в процессе учебно-практической конференции (урок в форме конференции) и на уроках в качестве сообщений школьников при изучении компонентов ПТК и в целом ПТК разного уровня. Рекомендации представляют интерес для учителей географии, студентов и школьников, которые проявляют интерес к изучению природы.
Рекомендации представляют интерес для учителей географии, студентов и школьников, которые проявляют интерес к изучению природы.
Михайлов В. А., Горев П. М., Утёмов В. В. Научное творчество: Методы конструирования новых идей: Учебное пособие. – Изд. второе, испр. и доп. – Киров: Изд-во МЦИТО, 2014. – 114 с.
ISBN 978-5-906642-07-3
Учебное пособие подготовлено в помощь студентам педагогических направлений подготовки (специальностей), учителям и преподавателям для использования на занятиях по изучению методов и приёмов научного творчества, а именно методов конструирования новых идей – неалгоритмических, частично алгоритмизированных и алгоритмов, в частности алгоритма С. Малкина, с целью формирования творческого мышления и развития творческого воображения учащихся.
Реализация деятельностного подхода в условиях перехода на стандарты второго поколения: Методический сборник / Авт.-сост. Г. А. Русских. – Киров: Изд-во МЦИТО, 2014. – 80 с.
ISBN 978-5-906642-08-0
В сборнике представлены материалы учителей Кировского лицея естественных наук. Материалы из опыта работы и модели уроков учителей-исследователей раскрывают инновационные приемы, которые способствуют реализации в практике работы идей ФГОС второго поколения. Важно, что в сборнике представлены материалы как учителей начальной, так и средней школы. Тематика публикаций свидетельствует о разносторонней направленности исследований по проблемам современной дидактики. Сборник предназначен для творчески работающих учителей и студентов.
Материалы из опыта работы и модели уроков учителей-исследователей раскрывают инновационные приемы, которые способствуют реализации в практике работы идей ФГОС второго поколения. Важно, что в сборнике представлены материалы как учителей начальной, так и средней школы. Тематика публикаций свидетельствует о разносторонней направленности исследований по проблемам современной дидактики. Сборник предназначен для творчески работающих учителей и студентов.
Системно-деятельностный подход в формировании содержания естественнонаучного и географического образования. География: Материалы 41-ой научно-практической конференции педагогических работников в области биологии, географии, химии, экологии образовательных учреждений города Кирова и Кировской области. – Киров: Изд-во МЦИТО, 2014. – 64 с.
ISBN 978-5-906642-09-7
В сборнике представлены материалы докладов 41-ой научно-практической конференции сотрудников кафедры географии Вятского государственного гуманитарного университета. Статьи посвящены методологическим и теоретическим проблемам развития географической науки и методике преподавания географии. Сборник будет полезен педагогическим работникам, преподавателям географических дисциплин высшей школы, учителям географии и студентам.
Сборник будет полезен педагогическим работникам, преподавателям географических дисциплин высшей школы, учителям географии и студентам.
Системно-деятельностный подход в формировании содержания естественнонаучного и географического образования. Биология: Материалы 41-ой научно-практической конференции педагогических работников в области биологии, географии, химии, экологии образовательных учреждений города Кирова и Кировской области. – Киров: Изд-во МЦИТО, 2014. – 47 с.
ISBN 978-5-906642-10-3
В сборнике представлены материалы докладов 41-ой научно-практической конференции, отражающие стратегические направления развития естественнонаучного образования. Статьи посвящены методологическим и теоретическим проблемам развития биологической науки и методики преподавания биологии. Сборник адресован педагогическим работникам, преподавателям биологических дисциплин высшей школы, учителям биологии и студентам.
Книга «Русский язык в математике. Учебное пособие для детей билингвов» Круг Н Г
-
Книги
- Художественная литература
- Нехудожественная литература
- Детская литература
- Литература на иностранных языках
-
Путешествия.
 Хобби. Досуг
Хобби. Досуг
- Книги по искусству
- Биографии. Мемуары. Публицистика
- Комиксы. Манга. Графические романы
- Журналы
- Печать по требованию
- Книги с автографом
- Книги в подарок
- «Москва» рекомендует
-
Авторы • Серии • Издательства • Жанр
-
Электронные книги
- Русская классика
- Детективы
- Экономика
- Журналы
- Пособия
- История
- Политика
- Биографии и мемуары
- Публицистика
-
Aудиокниги
- Электронные аудиокниги
- CD – диски
-
Коллекционные издания
- Зарубежная проза и поэзия
- Русская проза и поэзия
- Детская литература
- История
- Искусство
- Энциклопедии
-
Кулинария.
 Виноделие
Виноделие
- Религия, теология
- Все тематики
-
Антикварные книги
- Детская литература
- Собрания сочинений
- Искусство
- История России до 1917 года
-
Художественная литература.
 Зарубежная
Зарубежная
- Художественная литература. Русская
- Все тематики
- Предварительный заказ
- Прием книг на комиссию
-
Подарки
- Книги в подарок
- Авторские работы
- Бизнес-подарки
- Литературные подарки
- Миниатюрные издания
- Подарки детям
- Подарочные ручки
- Открытки
- Календари
- Все тематики подарков
- Подарочные сертификаты
- Подарочные наборы
- Идеи подарков
-
Канцтовары
- Аксессуары делового человека
- Необычная канцелярия
- Бумажно-беловые принадлежности
- Письменные принадлежности
- Мелкоофисный товар
- Для художников
-
Услуги
- Бонусная программа
- Подарочные сертификаты
- Доставка по всему миру
- Корпоративное обслуживание
- Vip-обслуживание
- Услуги антикварно-букинистического отдела
- Подбор и оформление подарков
- Изготовление эксклюзивных изданий
- Формирование семейной библиотеки
Расширенный поиск
Круг Н. Г.
Г.
Иллюстрации
Рекомендуем посмотреть
Саматова Л. М.
Окружающий мир. Учебное пособие для детей-билингвов. Книга 1
789 ₽
950 ₽ в магазине
Купить
Кожевникова М. Н.
Окружающий мир. Учебное пособие для детей-билингвов. Книга 2
1 071 ₽
1 290 ₽ в магазине
Купить
Бондарь Н. И., Лутин С. А., Кряхтунова О. В.
Учимся жить в России. В1-В2. Учебное пособие
В1-В2. Учебное пособие
1 419 ₽
1 710 ₽ в магазине
Купить
Мозелова И. В.
Русский сувенир. Базовый уровень 2. Учебный комплекс по русскому языку для иностранцев. Учебник
988 ₽
1 190 ₽ в магазине
Купить
Хавронина С. А.
Русский язык в упражнениях. Учебное пособие (для говорящих на английском языке)
996 ₽
1 200 ₽ в магазине
Купить
Гуськова Е.
По русски — легко! Учебное пособие по развитию речи
988 ₽
1 190 ₽ в магазине
Купить
Бабалова Л. Л., Кокорина С. И.
Л., Кокорина С. И.
Практикум по русской грамматике. В 2-х частях. Часть 2. Синтаксис простого и сложного предложения. 5-е издание
722 ₽
870 ₽ в магазине
Купить
Бабалова Л. Л., Кокорина С. И.
Практикум по русской грамматике. В 2-х частях. Часть 1. Корректировочный курс. Падежные формы имен и система глагола. 6-е издание
722 ₽
870 ₽ в магазине
Купить
Мозелова И. В.
Русский сувенир. Базовый уровень 2. Учебный комплекс по русскому языку для иностранцев. Рабочая тетрадь
755 ₽
910 ₽ в магазине
Купить
Губиева И. Г., Яцеленко В. А.
Г., Яцеленко В. А.
50 русских текстов. Книга для чтения на русском языке для иностранцев. 8-е издание
531 ₽
640 ₽ в магазине
Купить
Мозелова И. В.
Русский сувенир. Элементарный уровень. Учебный комплекс по русскому языку для иностранцев. Учебник. (+ 1 CD: Mp3)
1 104 ₽
1 330 ₽ в магазине
Купить
Мозелова И. В.
Русский сувенир. Базовый уровень 2. Учебный комплекс по русскому языку для иностранцев. Учебник (+ CD: Mp3)
1 129 ₽
1 360 ₽ в магазине
Купить
Чернышов С. И., Чернышова А. В.
И., Чернышова А. В.
Поехали! Русский язык для взрослых. Начальный курс. Учебник. Часть 1.2
863 ₽
1 040 ₽ в магазине
Купить
Чернышов С. И., Чернышова А. В.
Поехали! Русский язык для взрослых. Начальный курс. Рабочая тетрадь. Часть 1.1. 6-е издание
1 071 ₽
1 290 ₽ в магазине
Купить
Чернышов С. И., Чернышова А. В.
Поехали! Русский язык для взрослых. Начальный курс. Учебник. Часть 1.1
1 494 ₽
1 800 ₽ в магазине
Купить
Мозелова И. В.
В.
Русский сувенир. Элементарный уровень. Учебный комплекс по русскому языку для иностранцев. Рабочая тетрадь
764 ₽
920 ₽ в магазине
Купить
Чернышов С. И., Чернышова А. В.
Поехали! Русский язык для взрослых. Начальный курс. Рабочая тетрадь. Часть 1.2. 2-е издание
863 ₽
1 040 ₽ в магазине
Купить
Чернышов С. И., Чернышова А. В.
Поехали! Русский язык для взрослых. Базовый курс. Учебник. Часть 2.2. 8-е издание
963 ₽
1 160 ₽ в магазине
Купить
Малышев Г. Г.
Г.
Русская грамматика в картинках для начинающих. 6-е издание
1 062 ₽
1 280 ₽ в магазине
Купить
Долматова О.
Точка Ру. Tochka Ru. Russian course A2. Textbook+Workbook. В 2 книгах
2 556 ₽
3 080 ₽ в магазине
Купить
Загрузить еще
| You are here: Home → Интернет-ресурсы → Интерактивные математические уроки и учебные пособия Для всех марок cK-12 Освещение Math Tools Национальная библиотека
Virtual Manipulatives for Interactive Mathematics Математика Азбука BrainPop Math Topics Математические лакомства Математические занятия Quia Learning Keys Интерактивная онлайн-математика от Teaching Treasures Демонстрационный проект Wolfram В основном элементарные Math ABC KidsCalculate Математическая площадка Визуальное обучение математике Магнит Математика для детей 4—Викторины Математические упражнения для детей Математический словарь для детей Виртуальные манипуляторы от Glencoe Преимущественно средняя школа Shmoop.com Предварительная алгебра MathFlix Числа и операции Учебники по математике мистера Бартона Braining Camp В основном средняя школа Учебники и задачи по математике (с апплетами) Explorelearning Math Gizmos Интерактивная математика Mr. Barton Maths Tutorials Mathematics Illuminated Библиотека и кафе Mathwright Алгебра реального мира Эдвард Заккаро Алгебра часто преподается абстрактно, практически без акцента на том, что такое алгебра или как ее можно использовать для решения реальных задач. Подобно тому, как английский можно перевести на другие языки, текстовые задачи можно «перевести» на математический язык алгебры и легко решить. Real World Algebra объясняет этот процесс в простом для понимания формате с помощью мультфильмов и рисунков. Это облегчает самообучение как ученику, так и любому учителю, который никогда не понимал алгебру в полной мере. => Узнать больше
|
Учебники по конечной математике и прикладному исчислению
| Онлайн-учебники |
| Algebra review | Finite mathematics | Applied calculus | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Copyright © 2007–2016 Stefan Waner App Store: Репетитор по математике и естественным наукамОписаниеБолее 1500 видеоуроков по математике, алгебре, исчислению, физике, химии, технике, статистике. Более 500 часов пошаговых инструкций. Особенности: Курсы Excel в школе. Информация о подписках Math Tutor: — Прочтите наши условия обслуживания (http://www.mathtutordvd.com/public/73.cfm) и политику конфиденциальности (http://www.mathtutordvd.com/public/department12.cfm) для получения дополнительной информации. 000Z» aria-label=»November 15, 2021″> 15 ноября 2021 г. Версия 1.1.2 Обновите базу данных и сетевые библиотеки для повышения производительности. Рейтинги и обзоры785 оценок Спасибо.
Лучшее образовательное приложение
ИСПОЛЬЗУЙТЕ САЙТ ВМЕСТО ПРИЛОЖЕНИЯ
Разработчик Math Tutor DVD, общество с ограниченной ответственностью, указал, что политика конфиденциальности приложения может включать обработку данных, как описано ниже. Для получения дополнительной информации см. политику конфиденциальности разработчика. Данные не собираютсяРазработчик не собирает никаких данных из этого приложения. Методы обеспечения конфиденциальности могут различаться, например, в зависимости от используемых вами функций или вашего возраста. Узнать больше Информация
In что значит в математике: Что означает знак «!» в математике? — Хабр Q&AТаблица математических знаков (символов): значения, распечататьSign in Password recovery Восстановите свой пароль Ваш адрес электронной почты MicroExcel.ru Математика Основные математические знаки и символы Ниже представлена таблица с основными математическими символами и знаками: корень (√), больше (>), меньше (<), равенство (=) и др. Также приведено их краткое описание и примеры для лучшего понимания.
microexcel.ru ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТТаблица знаков зодиака Нахождение площади трапеции: формула и примеры Нахождение длины окружности: формула и задачи Римские цифры: таблицы Таблица синусов Тригонометрическая функция: Тангенс угла (tg) Нахождение площади ромба: формула и примеры Нахождение объема цилиндра: формула и задачи Тригонометрическая функция: Синус угла (sin) Геометрическая фигура: треугольник Нахождение объема шара: формула и задачи Тригонометрическая функция: Косинус угла (cos) Нахождение объема конуса: формула и задачи Таблица сложения чисел Нахождение площади квадрата: формула и примеры Что такое тетраэдр: определение, виды, формулы площади и объема Нахождение объема пирамиды: формула и задачи Признаки подобия треугольников Нахождение периметра прямоугольника: формула и задачи Формула Герона для треугольника Что такое средняя линия треугольника Нахождение площади треугольника: формула и примеры Нахождение площади поверхности конуса: формула и задачи Что такое прямоугольник: определение, свойства, признаки, формулы Разность кубов: формула и примеры Степени натуральных чисел Нахождение площади правильного шестиугольника: формула и примеры Тригонометрические значения углов: sin, cos, tg, ctg Нахождение периметра квадрата: формула и задачи Теорема Фалеса: формулировка и пример решения задачи Сумма кубов: формула и примеры Нахождение объема куба: формула и задачи Куб разности: формула и примеры Нахождение площади шарового сегмента Что такое окружность: определение, свойства, формулы Что такое математика — ИНФОРМАТМатематика — царица всех наук
Как правило, люди думают, что математика — это всего лишь арифметика, то есть изучение чисел и действий с их помощью, например, умножения и деления. На самом деле математика — это намного больше. Это способ описать мир и то, как одна его часть сочетается с другой. Взаимоотношения чисел выражаются в математических символах, которые описывают Вселенную, в которой мы живем. Любой нормальный ребенок может преуспевать в математике, потому что «ощущение числа» — это врожденная способность. Правда, для этого нужно приложить некоторые усилия и затратить немного времени. Умение считать — это еще не все. Ребенку необходимо уметь хорошо выражать свои мысли, чтобы понимать задачи и устанавливать связи между фактами, которые хранятся в памяти. Для того чтобы выучить таблицу умножения, нужны память и речь. Именно поэтому некоторым людям с поврежденным мозгом трудно умножать, хотя другие виды счета не представляют для них сложности. Для того чтобы хорошо знать геометрию и разбираться в форме и пространстве, требуются и другие виды мышления. С помощью математики мы решаем в жизни проблемы, например, делим шоколадку поровну или находим нужный размер ботинок. Благодаря знанию математики ребенок умеет копить карманные деньги и понимает, что можно купить и сколько денег тогда у него останется. Математика — это еще и способность отсчитать нужное количество семян и посеять их в горшочек, отмерять нужное количество муки для пирога или ткани на платье, понять счет футбольной игры и множество других повседневных дел. Везде: в банке, в магазине, дома, на работе — нам необходимо умение понимать числа, формы и меры и обращаться с ними. Числа — это только часть особого математического языка, а лучший способ выучить любой язык — это применять его. И начинать лучше с ранних лет. О математике «умно»Обычно идеализированные свойства исследуемых объектов и процессов формулируются в виде аксиом, затем по строгим правилам логического вывода из них выводятся другие истинные свойства (теоремы). Традиционно математика делится на теоретическую, выполняющую углублённый анализ внутриматематических структур, и прикладную, предоставляющую свои модели другим наукам и инженерным дисциплинам, причём некоторые из них занимают пограничное к математике положение. В частности, формальная логика может рассматриваться и как часть философских наук, и как часть математических наук; механика — и физика, и математика; информатика, компьютерные технологии и алгоритмика относятся как к инженерии, так и к математическим наукам и т. д. В литературе существует много различных определений математики. Разделы математикиЦели и методыМатематика изучает воображаемые, идеальные объекты и соотношения между ними, используя формальный язык. В общем случае математические понятия и теоремы не обязательно имеют соответствие чему-либо в физическом мире. Главная задача прикладного математика — создать математическую модель, достаточно адекватную исследуемому реальному объекту. Задача математика-теоретика — обеспечить достаточный набор удобных средств для достижения этой цели. Содержание математики можно определить как систему математических моделей и инструментов для их создания. Модель объекта учитывает не все его черты, а только самые необходимые для целей изучения (идеализированные). Например, изучая физические свойства апельсина, мы можем абстрагироваться от его цвета и вкуса и представить его (пусть не идеально точно) шаром. Если же нам надо понять, сколько апельсинов получится, если мы сложим вместе два и три, — то можно абстрагироваться и от формы, оставив у модели только одну характеристику — количество. Абстракция и установление связей между объектами в самом общем виде — одно из главных направлений математического творчества. Другое направление, наряду с абстрагированием — обобщение. Например, обобщая понятие «пространство» до пространства n-измерений. Пространство Rn, при n>3 является математической выдумкой. Впрочем, весьма гениальной выдумкой, которая помогает математически разбираться в сложных явлениях. Изучение внутриматематических объектов, как правило, происходит при помощи аксиоматического метода: сначала для исследуемых объектов формулируются список основных понятий и аксиом, а затем из аксиом с помощью правил вывода получают содержательные теоремы, в совокупности образующие математическую модель. Видео-лекция Смирнова С.К. и Ященко И.В. «Что такое математика»: Похожая информация: Алексей Савватеев: зачем нам математика и почему ее должен знать каждыйНаверняка каждый задумывался в школе на уроках алгебры или геометрии, как эти предметы пригодятся нам в жизни. Математик Алексей Савватеев — о пользе науки и о том, почему математика — это не только сложно, но и красиво Об эксперте: Алексей Савватеев — российский математик, популяризатор математики, доктор физико-математических наук, профессор МФТИ, профессор Адыгейского государственного университета, член-корреспондент РАН. Алексей Савватеев | Почему математика может все? Ну, почти… (Видео: РБК Тренды) Математику нужно знать каждому?Эта наука лежит в основе нашего мира, поэтому, я думаю, что положение любого человека в нем прямо пропорционально его пониманию математики. Мое мнение: математика не нужна разве что поэтам, художникам, исполнителям песен — тем, кто имеет дело с вдохновением. Всем остальным людям, особенно если их жизнь связана с чем-то материальным, с окружающим миром и его законами, математические знания точно пригодятся. Дизайнер Артемий Лебедев считал, что математика ему не нужна совсем, но, когда мы с ним побеседовали, я его частично убедил в том, что даже в дизайнерском деле она может быть полезна. Хороший вопрос: нужна ли математика в спорте? Я бы сказал, да. Например, марафонцам в беге на сверхдлинные дистанции или лыжникам важно понимать, укладываются ли они в график. Компьютера и калькулятора, понятно, под рукой нет, но в голове есть простая формула, которая поможет высчитать, укладывается ли спортсмен в отведенное время. Много математики в спортивном ориентировании — чего только стоит вычисление правильного градуса угла. Да и в футболе без базовых знаний математики не обойтись: важно ведь не просто послать мяч, а сделать это с умом, по правильной траектории. Нужна ли сегодня фундаментальная математика?Казалось бы, зачем в наш век современных технологий знать основы, которые закладывали Ферма, Ньютон, Лейбниц, Гаусс, Эйлер, нужно ли сегодня изучать их наследие? Ответ: конечно, нужно. Все современные алгоритмы имеют внутреннюю логику, не понимая которую вы не сможете ими пользоваться. Важно вникать в фундаментальную математику как в основу бытия. А из основы уже можно вытянуть любую ниточку. Алексей Савватеев: «В этом смысле я категорический оппонент тех, кто считает, что в наш век все настолько быстро меняется, что предметные знания отходят на второй план, а важным становится только умение учиться, быстро осваивать новое. Но как вы научитесь учиться, если не знаете таблицу умножения?» (Фото: Unsplash) Чем математика отличается от других наук?Математика — очень сложная для постижения наука. Изучение математики — это когда ты долго поднимаешься по лестнице, хочешь выйти на этаж и понимаешь, что вместо открытого пространства там стены, а на них еще более крутые лестницы, по которым нужно карабкаться. Ты лезешь дальше, с огромным трудом достигаешь следующего этажа и думаешь, что здесь-то ты уже можешь говорить на одном языке с великими учеными — с Пуанкаре, Перельманом, но вокруг опять только стены и лестница. И так этаж за этажом. У тебя нет никакого раздолья, нет награды за твои труды. Что ты получаешь за свое стремление вверх? Пропуск к еще большим трудам. Вот так устроена математика. Из каких уровней состоит математика?Первый этаж математики — это абстракция числа как такового. Это идея о том, что существуют отдельно взятые предметы, и мы можем посчитать, сколько их. Такова первая ступень математики, которую, конечно, проходят все. Хотя, если верить Аурэлю Фоссу — автору книги «Сущность математики», на земле до сих пор остались некие сумеречные народы, которые для счета птиц и чумов, к примеру, используют разные числительные. Они не понимают, как можно считать разные предметы, используя одну систему. Значит, эти народности еще не вышли на первый «этаж математики». А все цивилизованные народы давно на нем стоят. Второй этаж математики обусловлен появлением неизвестных — x, y, z и других. Появляются такие задачи, для решения которых нужно обозначить хоть что-то за x и дальше «выкрутиться» через решение уравнения. В более сложных ситуациях возникают системы уравнений с двумя неизвестными, с тремя и так далее — когда вы занимаетесь большой наукой, будет столько неизвестных, сколько вам нужно. Третий этаж — это исследование операций над цифрами и буквами. Плюс, минус, умножить, разделить, возвести в степень; возникает абстрактное понятие группа, кольцо, поле, модуль и так далее. Этими абстрактными понятиями оперирует вся современная математика. Если вы смогли их освоить, то я вас поздравляю, можно идти на мехмат и пытаться хотя бы первые два года на нем учиться. Так можно продолжать очень долго! Четвертый этаж — это гомологии и когомологии, с которыми я сейчас пытаюсь разобраться. А пятый этаж — это категории. Но в них я ничего не понимаю, и, наверное, еще долго не пойму. Дальше, говорят, возникают этажи, вход на которые открыт только гениальным филдсовским лауреатам. Филдсовская премия (Fields Medal) — самая престижная международная премия и медаль в области математики. Приз и медаль названы в честь Джона Филдса, президента VII международного математического конгресса, проходившего в 1924 году в Торонто. Математики сами надстраивают эти сложнейшие этажи один за другим. Фактически математика — это наука для тех, кто хочет всю жизнь думать и никогда не останавливаться ни на чем. Зашита ли математика в стандарты красоты?Я в это не верю. Мне кажется, что гениальная мелодия или картина — штучная вещь, а стандарта красоты вообще не может быть. Нам обычно все-таки нравится что-то непредсказуемое. То, что построено по каким-то формулам, не привлекает. Наоборот, настоящая красота рождается там, где нарушается конструкция. Любой человек может сказать, что картина идеальна, потому что написана по правилам золотого сечения. Это уловка мозга — мы пытаемся постфактум объяснить то, что нам кажется красивым. Остались ли еще в математике нерешенные задачи?Вы удивитесь, но они есть даже в школьной математике! Вот пример одной из них. Простое число делится только на себя и на единицу: 2, 3, 5, 7, 11, 13, 17, 19. Еще Евклид доказал, что это бесконечный ряд чисел, он никогда не кончится. В этом ряду есть такие пары простых чисел, например, 17 и 19, 101 и 103, 71 и 73 — которые стоят «через одно» друг от друга. Если вы заглянете далеко-далеко в натуральный ряд, то вы будете постоянно обнаруживать, что какие-то два числа, оба простые, стоят вот так — через одно друг за другом. И науке не известно, кончатся ли такие близняшки или их соседство тоже будет бесконечным. Научные модели позволяют делать прогнозы?Если грамотно ввести начальные данные, физические модели предскажут явление довольно точно. Но предсказательная сила уменьшается, если вмешиваются различные факторы — неожиданные или те, что мы и не собирались учитывать. Дальше, в таких науках как химия, биология, медицина с прогнозами все хуже. А к социуму вообще невозможно применить моделирование, потому что если вы ставите людей в некоторые условия, то они начинают себя вести выгодным образом. Прогностические модели в описании социума работают из рук вон плохо, но все равно не надо отчаиваться. Без них еще хуже. Реально предсказать кризисное явление нельзя, и в этом, мне кажется, заключается красота нашего мира. Хотя некоторые говорят, как жаль, мы хотим, чтобы мир был полностью предсказуем. Я, например, этого не хочу, мне не интересно жить в предсказуемом мире. Математика — универсальный язык Вселенной?Я бы сказал так: в широком смысле математика — это язык, на котором Бог общается с нами, передает свои законы посредством такого языка. В узком смысле, конечно, математика остается универсальным языком технической сферы и даже таких наук, как физика, химия и биология. Но то, что это универсальный язык общественных наук, я бы уже не сказал. Определенные закономерности социума математикой описываются, но их надо уметь правильно к социуму прикладывать. Даже знания законов спроса и предложения или теорий аукционов, транспортного моделирования не помогут решить реальные проблемы общества. Вам все равно придется вдумываться в предметную область, читать гуманитарные тексты, написанные в прошлом, и после этого вы сможете принести пользу со своими моделями. То есть, когда речь идет не о законах природы, а о законах общества, математика имеет меньшее значение. И совсем нулевое значение она имеет в законах общения конкретных людей, индивидуальностей друг с другом. Что произойдет в математической сфере в ближайшие годы?Математический прогноз на ближайшие 5–10 лет дать невозможно: наши горизонты планирования — это тысячи лет. Поэтому десятилетие тут играет незначительную роль. За это время можно успеть подкрутить какие-то гипотезы, начать что-то проверять. В чистой математике бывают прорывы — скажем, с 1975 по 2005 годы были сняты чуть ли не пять величайших математических загадок, включая Последнюю Теорему Ферма и гипотезу Пуанкаре. А вот в технической сфере ничего существенного не изобретали уже давно. Сейчас, по сути, допиливаются идеи, которые были высказаны в 50–60-е годы. Мне кажется, технический прогресс приостановился. Сейчас он связан с интернетом, банковскими картами, шифрованием, кодированием — но все это тоже вещи не быстрые, не на ближайшие пять лет. Что прочитать, чтобы вникнуть в основы математики?Чтобы поднатореть в математике, нужно прочесть хотя бы какие-то вводные вещи, например, мою «Математику для гуманитариев» — книга есть в свободном доступе в интернете. Так что умнейте. А дальше — уже вперед, на все этажи забирайтесь, господа альпинисты! Что такое среднее? Определение в математике и формула для расчетаЧто такое среднее значение? Среднее значение — это простое математическое среднее набора из двух или более чисел. Среднее значение для данного набора чисел может быть вычислено более чем одним способом, включая метод среднего арифметического, который использует сумму чисел в ряду, и метод среднего геометрического, который представляет собой среднее значение набора продуктов. Ключевые выводыРасчет среднегоПонимание среднего Среднее значение — это статистический показатель, который можно использовать для оценки производительности с течением времени. Аналитик, который хочет измерить траекторию стоимости акций компании за последние, скажем, 10 дней, подытожит цену закрытия акций в каждый из 10 дней. Затем общая сумма будет разделена на количество дней, чтобы получить среднее арифметическое. Среднее геометрическое будет вычислено путем перемножения всех значений вместе. Затем извлекается корень n-й степени из общего произведения, в данном случае 10 -й корень, чтобы получить среднее значение. Формулы для вычисления среднего арифметического и среднего геометрического Расчеты как для среднего арифметического, так и для среднего геометрического довольно схожи. Расчетная сумма для одного не будет существенно отличаться от другого. Однако между этими двумя подходами есть тонкие различия, которые действительно приводят к разным числам. Среднее арифметическое Формула расчета среднего арифметического состоит в том, чтобы сложить все цифры и разделить на количество использованных цифр. Среднее арифметическоеПлюсы Минусы Среднее геометрическоеСреднее геометрическое более сложно и использует более сложную формулу. Формула для расчета среднего геометрического заключается в перемножении всех значений в наборе данных. Затем возьмите корень суммы, равной количеству значений в этом наборе данных. Например, чтобы вычислить геометрическую величину значений 4 и 9, умножьте два числа вместе, чтобы получить 36. Затем извлеките квадратный корень (поскольку значений два). Среднее геометрическое в этом примере равно 6. Среднее геометрическоеПлюсы Минусы Пример расчета среднего значенияДавайте применим это на практике, изучив цену акции за 10-дневный период. Представьте, что инвестор купил одну акцию за 148,01 доллара. Цена акции в течение следующих 10 дней также включена. Изображение Сабрины Цзян © Investopedia, 2022 Среднее арифметическое составляет 0,67% и представляет собой просто общую сумму доходностей, деленную на 10. Однако среднее арифметическое доходностей является точным только при отсутствии волатильности, что практически невозможно на фондовом рынке. В дополнение к среднему арифметическому и геометрическому среднее гармоническое рассчитывается путем деления числа наблюдений на обратную величину (на единицу больше значения) каждого числа в ряду. Среднее геометрическое влияет на компаундирование и волатильность, что делает его лучшим показателем средней доходности. Поскольку невозможно извлечь корень из отрицательного значения, прибавьте единицу ко всем процентным доходам, чтобы сумма продукта дала положительное число. Возьмите 10 -й -й корень этого числа и не забудьте вычесть из единицы, чтобы получить число в процентах. Среднее геометрическое доходности инвестора за последние пять дней составляет 0,61%. Согласно математическому правилу, среднее геометрическое всегда будет меньше или равно среднему арифметическому. Среднее арифметическое знак равно ( 0,0045 ) + 0,0121 + 0,0726 + . . . + 0,0043 + ( 0,0049 ) + 0,0376 10 знак равно 0,0067 знак равно 0,67 % \begin{align}\text{Среднее арифметическое} &= \tiny{\frac{(0,0045) + 0,0121 + 0,0726 + . Среднее геометрическое знак равно 0,9955 × 1.0121 × 1.0726 × . . . × 1.0043 × 0,9951 × 1.0376 10 − 1 знак равно 0,0061 знак равно 0,61 % \begin{align}\text{Среднее геометрическое} &= \tiny{\sqrt[10]{ 0,9955 \times 1,0121 \times 1,0726 \times … \times 1,0043 \times 0,9951 \times 1,0376 } — 1} \\& = 0,0061 \\&= 0,61\% \\\конец {выровнено}
Среднее геометрическое=100,9955×1,0121×1,0726×…×1,0043×0,9951×1,0376−1=0,0061=0,61% Анализ таблицы показывает, почему среднее геометрическое дает лучшее значение. Когда к каждой цене акций применяется среднее арифметическое 0,67%, конечная стоимость составляет 152,63 доллара. Однако в последний день акции торговались по $157,32. Это означает, что среднее арифметическое доходности занижено. С другой стороны, когда каждая из цен закрытия повышается на среднюю геометрическую доходность 0,61%, рассчитывается точная цена 157,32 доллара. Хотя среднее значение является хорошим инструментом для оценки эффективности компании или портфеля, его также следует использовать с другими фундаментальными и статистическими инструментами, чтобы получить более полную и полную картину исторических и будущих перспектив инвестиций. Примеры случаев, когда средства важны при инвестированииВ бизнесе и инвестициях среднее значение широко используется для анализа производительности. Примеры ситуаций, в которых вы можете столкнуться со средним значением, включают: Что такое среднее значение в математике?В математике и статистике под средним понимается среднее значение набора значений. Среднее значение можно вычислить несколькими способами, включая простое среднее арифметическое (сложите числа и разделите сумму на количество наблюдений), среднее геометрическое и среднее гармоническое. Как найти среднее значение? Среднее значение — это характеристика набора данных, описывающая некоторое среднее значение. В чем разница между средним значением, медианой и модой?Среднее значение — это среднее значение, которое появляется в наборе данных. Вместо этого медиана — это средняя точка выше (ниже), где находится 50% значений в данных. Мода относится к наиболее часто наблюдаемому значению в данных (тот, который встречается чаще всего). Почему важно среднее значение? Среднее значение — это ценный статистический показатель, который сообщает вам, каков ожидаемый результат при сравнении всех точек данных вместе. Хотя это не гарантирует будущих результатов, среднее значение помогает установить ожидания будущих результатов на основе того, что уже произошло. Среднее равно среднему?Среднее значение — это среднее математическое значение набора из двух или более чисел. среднее | Определение, формула и фактыПросмотреть весь связанный контент → означает , в математике количество, имеющее промежуточное значение между значениями крайних членов некоторого множества. Существует несколько видов средних, и метод расчета среднего зависит от известного или предполагаемого отношения, управляющего другими членами. Среднее арифметическое, обозначенное x , из набора N Числа x 1 , x 2 ,…, x N . Среднее арифметическое (обычно синоним среднего) представляет собой точку, относительно которой балансируются числа. Например, если единичные массы размещены на прямой в точках с координатами x 1 , x 2 , …, x n , то среднее арифметическое является координатой центра тяжести системы. Средневзвешенное арифметическое также используется при статистическом анализе сгруппированных данных: каждое число x i является серединой интервала, и каждое соответствующее значение w i — количество точек данных в пределах этого интервала. Для заданного набора данных можно определить множество возможных способов, в зависимости от того, какие характеристики данных представляют интерес. Например, пусть даны пять квадратов со сторонами 1, 1, 2, 5 и 7 см. Средние арифметические и квадратичные средние являются особыми случаями p = 1 и p = 2 p среднего в й степени, M p , определяется по формуле, где p может быть любым действительным числом, кроме нуля. Случай p = −1 также называется гармоническим средним. Взвешенные p x 2 находятся в арифметической прогрессии. Если H — это гармоническое среднее значение x 1 и x 2 , Числа x 1 , H , X 2 H , X 2 . Число G Такое, что x 1 , G , x 2 находятся в геометрическом прогрессе, определяется условием, которое x 1 / G9208 x x x x x x x x x x x / x x / x x / x x / = = x . Все обсуждаемые средства являются частными случаями более общего среднего. Если f есть функция, имеющая обратную f −1 (функция, которая «отменяет» исходную функцию), число называется средним значением x 1 , x 2 , …, x n связанный с f . Когда f ( x ) = x p , обратное значение равно f −1 ( x ) = x 1/ p , а среднее значение равно p th-степенное среднее, M 1 902 Когда f ( x ) = ln x (натуральный логарифм), обратное значение равно f −1 ( x ) = e x , (экспоненциальная функция) а среднее значение является средним геометрическим. Для получения информации о разработке различных определений среднего, см. Вероятность и статистика. Для получения дополнительной технической информации см. статистика и теория вероятностей. Редакторы Британской энциклопедии Эта статья была недавно отредактирована и обновлена Эриком Грегерсеном. Что значит быть успешным в математике?Посетите NAP.edu/10766, чтобы получить дополнительную информацию об этой книге, купить ее в печатном виде или загрузить в виде бесплатного PDF-файла. « Предыдущая: Введение Страница 8 Делиться Цитировать Рекомендуемое цитирование: «Что значит быть успешным в математике?». Национальный исследовательский совет. 2002. Помощь детям в изучении математики . Вашингтон, округ Колумбия: Издательство национальных академий. × Сохранить Отменить Страница 9 Делиться Цитировать Рекомендуемое цитирование: «Что значит быть успешным в математике?». Национальный исследовательский совет. 2002. Помощь детям в изучении математики . Вашингтон, округ Колумбия: Издательство национальных академий. дои: 10.17226/10434. × Сохранить Отменить Наш анализ математики, которую необходимо изучить, наше чтение исследований в области когнитивной психологии и математического образования, наш опыт в качестве учащихся и преподавателей математики, а также наши профессиональные суждения привели нас к принятию комплексного взгляда на успешное изучение математики. Признавая, что ни один термин не охватывает полностью все аспекты опыта, компетентности, знаний и способностей в математике, мы выбрали 9 терминов. Математическое мастерство состоит из пяти направлений: 3 Важнейшей особенностью математических знаний является то, что эти пять нитей переплетены и взаимозависимы. Другие взгляды на изучение математики Страница 10 Делиться Цитировать Рекомендуемое цитирование: «Что значит быть успешным в математике?». Национальный исследовательский совет. 2002. Помощь детям в изучении математики . Вашингтон, округ Колумбия: Издательство национальных академий. дои: 10.17226/10434. × Сохранить Отменить , как правило, подчеркивают только один аспект мастерства, ожидая, что другие аспекты будут развиваться как следствие. Главной идеей этой книги является то, что все учащиеся могут и должны достичь математических знаний. Точно так же, как все учащиеся могут стать опытными читателями, все могут стать опытными в школьной математике. Математические способности — это не то, чего учащиеся достигают только в восьмом или двенадцатом классе; они могут быть профессионалами независимо от их класса. Кроме того, математические способности больше не могут быть ограничены немногими избранными. Все молодые американцы должны научиться мыслить математически, если Соединенные Штаты хотят воспитать образованную рабочую силу и граждан, которых потребует завтрашний мир. (1) Понимание: Понимание математических понятий, операций и отношений — знание того, что означают математические символы, диаграммы, процедуры. Понимание относится к пониманию учащимся фундаментальных математических идей. Студенты с пониманием знают больше, чем отдельные факты и процедуры. Они знают, почему математическая идея важна и в каких контекстах она полезна. Кроме того, они знают о многих связях между математическими идеями. На самом деле степень понимания учащимися связана с богатством и масштабом связей, которые они установили. Например, учащиеся, понимающие деление дробей, могут не только вычислять . Они также могут представить операцию в виде диаграммы и составить задачу для выполнения вычислений. (Если в рецепте требуется чашка сахара, а в наличии имеется 6 чашек сахара, сколько партий по рецепту можно приготовить из имеющегося сахара?) разные ситуации. Если они понимают общий принцип, согласно которому порядок, в котором умножаются два числа, не имеет значения — например, 3 × 5 — это то же самое, что 5 × 3, — им придется выучить вдвое меньше «фактов о числах». Страница 11 Делиться Цитировать Рекомендуемое цитирование: «Что значит быть успешным в математике?». Национальный исследовательский совет. 2002. Помощь детям в изучении математики . Вашингтон, округ Колумбия: Издательство национальных академий. дои: 10.17226/10434. × Сохранить Отменить объема с коэффициентом n 3 , они могут понять многие ситуации, в которых объекты любой формы пропорционально увеличиваются или уменьшаются. (Они могут понять, например, почему чашка на 16 унций, имеющая ту же форму, что и чашка на 8 унций, намного меньше, чем в два раза выше.) Знание, полученное с пониманием, обеспечивает основу для запоминания или реконструкции математических фактов и методы для решения новых и незнакомых проблем и для получения новых знаний. Понимание также помогает учащимся избежать критических ошибок при решении задач, особенно масштабных. Любой ученик с хорошим чувством числа, который умножает 9,83 и 7,65 и получает за ответ 7 519,95, должен сразу увидеть, что что-то не так. Ответ не может быть больше, чем 10 раз по 8 или 80, так как одно число меньше 10, а другое меньше 8. Это рассуждение должно подсказать учащемуся, что десятичная точка поставлена не на место. (2) Информатика: Выполнение математических действий, таких как сложение, вычитание, умножение и деление чисел гибко, точно, эффективно и надлежащим образом. Информатика включает в себя свободное владение процедурами сложения, вычитания, умножения и деления в уме или с помощью бумаги и карандаша, а также знание того, когда и как правильно использовать эти процедуры. Хотя слово , вычисляющее , подразумевает арифметическую процедуру, в этом документе оно также относится к свободному владению процедурами из других разделов математики, таких как измерение (измерение длин), алгебра (решение уравнений), геометрия (построение подобных фигур) и статистика (графические данные). Ученики должны быстро и точно вычислять основные комбинации чисел (6+7, 17−9, 8×4 и т. д.). Они также должны стать точными и эффективными при работе с алгоритмами — пошаговыми процедурами сложения, вычитания, умножения и деления многозначных целых чисел, дробей и десятичных дробей, а также для выполнения других вычислений. Например, у всех учащихся должен быть понятный им алгоритм умножения 64 и 37, достаточно эффективный и достаточно общий, чтобы его можно было использовать с другими двузначными числами, и который можно расширить для использования с большими числами. Использование калькуляторов не должно угрожать развитию вычислительных навыков учащихся. Наоборот, калькуляторы могут улучшить как понимание, так и Page 12 Делиться Цитировать Рекомендуемое цитирование: «Что значит быть успешным в математике?». × Сохранить Отменить
Страница 13 Делиться Цитировать Рекомендуемое цитирование: «Что значит быть успешным в математике?». × Сохранить Отменить и вычисления. 4 Но, как и любое учебное пособие, калькуляторы и компьютеры можно использовать эффективно или не очень эффективно. Учителя должны научиться использовать эти инструменты — и учить студентов использовать их — таким образом, чтобы поддерживать и интегрировать нити мастерства. Точность и эффективность процедур важны, но вычисления также способствуют пониманию. Работая с процедурами, достаточно общими для решения целого класса задач, такими как процедура сложения любых двух дробей, учащиеся получают представление о том, что математика предсказуема, хорошо структурирована и полна шаблонов. Когда учащиеся просто запоминают процедуры, они могут не понять более глубоких идей, которые могут облегчить запоминание и применение того, что они изучают. Дети, которые учатся вычитать с пониманием, редко делают такого рода ошибка. 5 Развитие вычислительных навыков и развитие понимания часто рассматриваются как конкурирующие за внимание в школьной математике. Но противопоставление умения и понимания создает ложную дихотомию. Понимание облегчает усвоение навыков, а процедуры обучения могут укреплять и развивать математическое понимание. (3) Применение: Способность математически формулировать проблемы и разрабатывать стратегии их решения с использованием соответствующих концепций и процедур. Применение предполагает использование концептуальных и процедурных знаний для решения проблем. Понятие или процедура бесполезны, если учащиеся не понимают, когда и где их использовать, а также когда и где они неприменимы. Страница 14 Делиться Цитировать Рекомендуемое цитирование: «Что значит быть успешным в математике?». Национальный исследовательский совет. 2002. Помощь детям в изучении математики . Вашингтон, округ Колумбия: Издательство национальных академий. дои: 10.17226/10434. × Сохранить Отменить Рутинные проблемы всегда можно решить с помощью стандартных процедур. (4) Рассуждение: использование логики для обоснования решения проблемы или расширения от чего-то известного до чего-то еще неизвестного. Рассуждение — это клей, скрепляющий математику. Думая о логических связях между понятиями и ситуациями, учащиеся могут перемещаться по элементам проблемы и видеть, как они сочетаются друг с другом. Один из лучших способов для учащихся улучшить свои рассуждения — объяснить или обосновать свои решения другим. Например, после того, как процедура сложения дробей была разработана, студентов иногда следует просить объяснить и обосновать эту процедуру, а не просто решать практические задачи. В процессе сообщения своих мыслей они оттачивают свои навыки рассуждения. Рассуждения сильно взаимодействуют с другими элементами математических навыков, особенно когда учащиеся решают задачи. Когда учащиеся рассуждают о проблеме, они могут построить свое понимание, выполнить необходимые вычисления, применить свои знания, объяснить свои рассуждения другим и прийти к выводу, что математика разумна и выполнима. (5) Вовлечение: Видеть в математике разумную, полезную и выполнимую задачу — , если вы работаете над ней — и готовность выполнять эту работу. Занятия математикой — ключ к успеху. Наш взгляд на математическое мастерство выходит за рамки способности понимать, вычислять, применять и Page 15 Делиться Цитировать Рекомендуемое цитирование: «Что значит быть успешным в математике?». Национальный исследовательский совет. 2002. Помощь детям в изучении математики . Вашингтон, округ Колумбия: Издательство национальных академий. дои: 10.17226/10434. × Сохранить Отменить
Страница 16 Делиться Цитировать Рекомендуемое цитирование: «Что значит быть успешным в математике?». Национальный исследовательский совет. 2002. Помощь детям в изучении математики . × Сохранить Отменить причина. Это включает в себя взаимодействие с математикой: учащиеся должны иметь личную приверженность идее, что математика имеет смысл и что, приложив разумные усилия, они могут изучить ее и использовать как в школе, так и за ее пределами. Учащиеся, хорошо разбирающиеся в математике, считают ее разумной, полезной и стоящей и считают, что их усилия по ее изучению окупаются; они считают себя эффективными учениками, исполнителями и пользователями математики. Успех в изучении математики требует положительного отношения к предмету. Студенты, занимающиеся математикой, не верят, что есть какой-то таинственный «математический ген», диктующий успех. Они верят, что при достаточном усилии и опыте могут научиться. Если учащиеся должны эффективно изучать, делать и использовать математику, они не должны рассматривать ее как произвольный набор правил и процедур. Занятие математикой требует частых возможностей разобраться в ней, испытать на себе вознаграждение за ее осмысление и осознать преимущества настойчивости. По мере того, как учащиеся совершенствуют свои математические навыки, они становятся более уверенными в своей способности изучать математику и использовать ее. Чем больше математических понятий они понимают, тем более осмысленным становится весь предмет. Напротив, когда они думают, что математику нужно изучать, запоминая, а не осмысливая ее, они начинают терять уверенность в себе как в учениках. Учащиеся, хорошо разбирающиеся в математике, считают, что они могут решать проблемы, развивать понимание и изучать процедуры посредством тяжелой работы, и что получение математических знаний полезно для них. Интеграция навыков Точно так же, как табуретка не может стоять на одной ножке или даже на двух, так и математическое мастерство не может стоять на одной или двух изолированных ветвях. В любой момент урока математики или раздела можно выделить одну или две нити. Но все нити должны в конечном итоге быть рассмотрены, чтобы связи между ними были усилены. Например, урок, основной целью которого является развитие у учащихся понимания математической концепции, может также основываться на решении задач и требовать ряда вычислений. Или студентов могут попросить рассуждать о недавно представленной идее, а не симулировать ее.0005 Страница 17 Делиться Цитировать Рекомендуемое цитирование: «Что значит быть успешным в математике?». Национальный исследовательский совет. 2002. Помощь детям в изучении математики . Вашингтон, округ Колумбия: Издательство национальных академий. дои: 10.17226/10434. × Сохранить Отменить слой представлен с определением и примерами. Кроме того, в течение учебного года учащиеся должны иметь возможность сосредоточиться на различных направлениях в различных сочетаниях. Если учителя регулярно делают акцент только на одном или двух направлениях, игнорируя остальные, математика, которую изучают их ученики, скорее всего, будет неполной и хрупкой. Развивать навыки по отдельности намного сложнее, чем изучать их вместе. На самом деле практически невозможно освоить какое-то одно из направлений в отдельности. Возможно, именно поэтому учащимся так трудно запомнить, например, все правила вычисления с дробями и десятичными знаками, если это все, что они изучают. Обращение ко всем аспектам мастерства делает знания более прочными, долговечными, более адаптируемыми, более полезными и более актуальными. Интеграция навыков математики полностью соответствует типичному подходу учащихся к обучению. Современная школьная математика в США часто предполагает, что дети должны овладеть определенными навыками, прежде чем они смогут понять процедуры и применять их — как будто дети не могут сыграть мелодию, пока не освоят все гаммы. Но учащиеся могут вычислить, что в полосе длиной 5,5 фута находится лента длиной 5,5 фута, прежде чем их научат «переворачивать и умножать». Фактически, решение таких задач может помочь учащимся понять процедуру инвертирования и умножения. Они могли бы, например, заметить, что количество футов длины в 1 футе равно двум. Следовательно, умножение (обратное ) даст общее количество длин в футах в полосе в футах. Точно так же, как симфонию нельзя услышать, последовательно слушая партии каждого инструмента, математических навыков нельзя достичь, изучая каждую из составляющих мастерства по отдельности. При обучении необходимо использовать естественную склонность детей использовать все пять направлений математического мастерства. (Во вставке на страницах 19–20 приведены примеры того, как навыки могут быть интегрированы в изучение решения пропорций.) Таким образом, учащиеся понимают и знают, как применять процедуры, которые от них часто требуется просто запомнить. Страница 18 Делиться Цитировать Рекомендуемое цитирование: «Что значит быть успешным в математике?». Национальный исследовательский совет. 2002. Помощь детям в изучении математики . Вашингтон, округ Колумбия: Издательство национальных академий. дои: 10.17226/10434. × Сохранить Отменить
Страница 19 Делиться Цитировать Рекомендуемое цитирование: «Что значит быть успешным в математике?». Национальный исследовательский совет. 2002. Помощь детям в изучении математики . Вашингтон, округ Колумбия: Издательство национальных академий. дои: 10.17226/10434. × Сохранить Отменить
Страница 20 Делиться Цитировать Рекомендуемое цитирование: «Что значит быть успешным в математике?». Национальный исследовательский совет. 2002. Помощь детям в изучении математики . Вашингтон, округ Колумбия: Издательство национальных академий. дои: 10.17226/10434. × Сохранить Отменить
Страница 21 Делиться Цитировать Рекомендуемое цитирование: «Что значит быть успешным в математике?». Национальный исследовательский совет. × Сохранить Отменить Развитие навыков в начальной и средней школеМатематические навыки нельзя охарактеризовать просто как имеющиеся или отсутствующие. Каждая важная математическая идея может быть понята на многих уровнях и разными способами. Очевидно, что понимание сложения у первоклассника не такое, как у математика или даже у среднего взрослого человека. Но первоклассник все еще может хорошо складывать однозначные числа, если его или ее мышление в этой области включает в себя все пять навыков. Способность к математике развивается со временем. Таким образом, с каждым годом обучения в школе учащиеся должны становиться все более опытными как в старом, так и в новом содержании. Например, третьеклассники должны лучше уметь складывать целые числа, чем в первом классе. Исторически школьная политика в области математики в Соединенных Штатах основывалась на предположении, что только избранная группа учащихся должна овладеть математикой. Это предположение больше несостоятельно. Молодые люди, неспособные мыслить математически, лишены многих лучших возможностей, которые предлагает общество, и общество лишено их потенциального вклада. Многие взрослые предполагают, что различия в успеваемости по математике отражают различия в врожденных способностях, а не различия в индивидуальных усилиях или возможностях учиться. Эти ожидания глубоко недооценивают возможности детей. Основные принципы, понятия и навыки математики доступны всем детям. Когда и родители, и учителя одинаково верят, что тяжелая работа окупается, и когда математика преподается и изучается с использованием всех навыков, успеваемость по математике улучшается для всех учащихся. Тщательные исследования показали, что математическое знание — достижимая цель. В нескольких школах, разбросанных по всей стране, высокий процент учащихся из всех слоев общества добился высоких результатов по математике. Специальные мероприятия в некоторых школах с низкой успеваемостью дали значительный прогресс. Теперь стало известно больше о том, как дети изучают математику, и о том, какие виды обучения способствуют прогрессу. Данные исследований показывают, что все учащиеся, за исключением очень небольшого числа, могут научиться грамотному чтению. Они могут учиться с разной скоростью и могут нуждаться в разном объеме и типах учебной поддержки, чтобы научиться хорошо читать, но все могут научиться читать. 9 То же самое относится к обучению и занятиям математикой. Страница 22 Делиться Цитировать Рекомендуемое цитирование: «Что значит быть успешным в математике?». × Сохранить Отменить
Страница 23 Делиться Цитировать Рекомендуемое цитирование: «Что значит быть успешным в математике?». × Сохранить Отменить
Страница 8 Делиться Цитировать Рекомендуемое цитирование: «Что значит быть успешным в математике?». Национальный исследовательский совет. 2002. Помощь детям в изучении математики . Вашингтон, округ Колумбия: Издательство национальных академий. дои: 10.17226/10434. × Сохранить Отменить Страница 9 Делиться Цитировать Рекомендуемое цитирование: «Что значит быть успешным в математике?». Национальный исследовательский совет. 2002. Помощь детям в изучении математики . Вашингтон, округ Колумбия: Издательство национальных академий. дои: 10. × Сохранить Отменить Страница 10 Делиться Цитировать Рекомендуемое цитирование: «Что значит быть успешным в математике?». Национальный исследовательский совет. 2002. Помощь детям в изучении математики . Вашингтон, округ Колумбия: Издательство национальных академий. дои: 10.17226/10434. × Сохранить Отменить Страница 11 Делиться Цитировать Рекомендуемое цитирование: «Что значит быть успешным в математике?». Национальный исследовательский совет. 2002. Помощь детям в изучении математики . Вашингтон, округ Колумбия: Издательство национальных академий. × Сохранить Отменить Страница 12 Делиться Цитировать Рекомендуемое цитирование: «Что значит быть успешным в математике?». Национальный исследовательский совет. 2002. Помощь детям в изучении математики . Вашингтон, округ Колумбия: Издательство национальных академий. дои: 10.17226/10434. × Сохранить Отменить Страница 13 Делиться Цитировать Рекомендуемое цитирование: «Что значит быть успешным в математике?». Национальный исследовательский совет. 2002. Помощь детям в изучении математики . Вашингтон, округ Колумбия: Издательство национальных академий. × Сохранить Отменить Страница 14 Делиться Цитировать Рекомендуемое цитирование: «Что значит быть успешным в математике?». Национальный исследовательский совет. 2002. Помощь детям в изучении математики . Вашингтон, округ Колумбия: Издательство национальных академий. дои: 10.17226/10434. × Сохранить Отменить Страница 15 Делиться Цитировать Рекомендуемое цитирование: «Что значит быть успешным в математике?». Национальный исследовательский совет. 2002. Помощь детям в изучении математики . Вашингтон, округ Колумбия: Издательство национальных академий. × Сохранить Отменить Страница 16 Делиться Цитировать Рекомендуемое цитирование: «Что значит быть успешным в математике?». Национальный исследовательский совет. 2002. Помощь детям в изучении математики . Вашингтон, округ Колумбия: Издательство национальных академий. дои: 10.17226/10434. × Сохранить Отменить Страница 17 Делиться Цитировать Рекомендуемое цитирование: «Что значит быть успешным в математике?». Национальный исследовательский совет. 2002. Помощь детям в изучении математики . Вашингтон, округ Колумбия: Издательство национальных академий. × Сохранить Отменить Страница 18 Делиться Цитировать Рекомендуемое цитирование: «Что значит быть успешным в математике?». Национальный исследовательский совет. 2002. Помощь детям в изучении математики . Вашингтон, округ Колумбия: Издательство национальных академий. дои: 10.17226/10434. × Сохранить Отменить Страница 19 Делиться Цитировать Рекомендуемое цитирование: «Что значит быть успешным в математике?». Национальный исследовательский совет. 2002. Помощь детям в изучении математики . Вашингтон, округ Колумбия: Издательство национальных академий. × Сохранить Отменить Страница 20 Делиться Цитировать Рекомендуемое цитирование: «Что значит быть успешным в математике?». Национальный исследовательский совет. 2002. Помощь детям в изучении математики . Вашингтон, округ Колумбия: Издательство национальных академий. дои: 10.17226/10434. × Сохранить Отменить Страница 21 Делиться Цитировать Рекомендуемое цитирование: «Что значит быть успешным в математике?». Национальный исследовательский совет. 2002. Помощь детям в изучении математики . Вашингтон, округ Колумбия: Издательство национальных академий. Задачи на логику по математике: Логические задачи по математике для 4 класса с ответамиЛогические задачи для 3 класса с ответами и решениями, задания на логику для детей 9-10 летЗанимательная математика / 3 класс / Задачи на логику Задания на логику для 3 класса от ЛогикЛайк — это более 300 видов занимательных задач и упражнений. Подсказки, решения и пояснения помогут научиться решать любые задачи. Попробуйте развивающий курс ЛогикЛайк! Выберите возраст для старта 3 класс 4+ класс Рекомендуем тематические курсы онлайн для 3 класса Курс логики и мышления Начать Подготовка к олимпиаде Начать Почему дети и родители выбирают ЛогикЛайк? 2 варианта занятий, выбор сложности На LogicLike.com дети учатся рассуждать, развивают логику, способности к математике и познавательный интерес.
У нас есть всё, что вы искали!Попробуйте задания от ЛогикЛайкЛогические задачи Вопросы и загадки на логику Задания на 2D- и 3D‑мышление Простые высказывания Математические ребусы Графические и числовые закономерности Начать курс! Начать курс!
Решение логических задач по математике — один из самых полезных способов тренировки ума,
развития мышления и сообразительности у младших школьников. Задачи на логику 2-3 уровня сложностиПодборка из обучающего курса ЛогикЛайк Для ознакомления предлагаем несколько задач из раздела «Классические логические задачи». У нас ещё очень много (более 3500) интересных задач: логические, математические, пространственные головоломки от простых к сложным.
Задача 1. На разделение предметов
Условие: Для
проведения очередного опыта Профессор купил 9 металлических стержней. Вопрос: Сколько стержней распилил Профессор? Cмотреть решение Ответ: 6 стержней.
Решение Решать задачи онлайн! ВСЯ ЛОГИКА В ИГРОВОЙ ФОРМЕ! Начать занятия!
Задача 2. Разрезание на части
Условие: Юра
разрезал огромную пиццу на 10 кусков. Затем он взял один из кусков и
разрезал его еще на 10. Вопрос: Сколько в результате кусков пиццы у него получилось? Показать решение Ответ: 37 кусков.
Решение Научиться решать задачи!
Задача 3. Сосчитай количество попаданий в цель
Условие: В
компьютерной игре нужно победить монстра. Вопрос: Сколько раз Юра попал в цель, если всего он выстрелил 30 раз, израсходовав все выстрелы? Узнать ответ Ответ: 7.
Комментарий: Начать интерактивные занятия! Взять подсказку Подсказка Решить эту задачу можно методом последовательных рассуждений, а можно еще быстрее и проще. Занятия на ЛогикЛайк помогут научиться с легкостью
решать любые задачи на логику и сообразительность. Решайте 10-15 разных задач в день: математические ребусы, текстовые логические, пространственные, закономерности, алгоритмы и другие. Понравился материал? Поделитесь с друзьями! Научим решать любые логические задачи Более 150 000 детей и родителей со всего мира уже занимаются на сайте ЛогикЛайк. Подключайтесь и развивайте логику и мышление. Начать обучение! Начать обучение
Другие категории заданийпо возрасту и по темам 5-6 лет 6-7 лет 1 класс 2 класс 4 класс Логические задачи Тест: Логические задачи — Математика 3 классАнглийский язык Астрономия Белорусский язык Биология География ИЗО Информатика История Итальянский язык Краеведение Литература Математика Музыка Немецкий язык ОБЖ Обществознание Окружающий мир ОРКСЭ Русский язык Технология Физика Физкультура Химия Черчение Для учителей Дошкольникам VIP — доступ Логические задачи Проверка логического , алгоритмического мышления Математика 3 класс | Автор: Ливанова Ирина Георгиевна | ID: 2153 | Дата: 29. Помещать страницу в закладки могут только зарегистрированные пользователи «;} else {document.getElementById(«torf1″).innerHTML=» «;}; if (answ.charAt(1)==»1») {document.getElementById(«torf2″).innerHTML=» «;} else {document.getElementById(«torf2″).innerHTML=» «;}; if (answ.charAt(2)==»1») {document.getElementById(«torf3″).innerHTML=» «;} else {document.getElementById(«torf3″).innerHTML=» «;}; if (answ.charAt(3)==»1») {document.getElementById(«torf4″).innerHTML=» «;} else {document.getElementById(«torf4″).innerHTML=» «;};
if (answ.charAt(4)==»1») {document.getElementById(«torf5»). «;} else {document.getElementById(«torf5″).innerHTML=» «;}; if (answ.charAt(5)==»1») {document.getElementById(«torf6″).innerHTML=» «;} else {document.getElementById(«torf6″).innerHTML=» «;}; if (answ.charAt(6)==»1») {document.getElementById(«torf7″).innerHTML=» «;} else {document.getElementById(«torf7″).innerHTML=» «;}; if (answ.charAt(7)==»1») {document.getElementById(«torf8″).innerHTML=» «;} else {document.getElementById(«torf8″).innerHTML=» «;}; if (answ.charAt(8)==»1») {document.getElementById(«torf9″).innerHTML=» «;} else {document.getElementById(«torf9″).innerHTML=» «;}; } }
Вопрос №
1
Серёжа покрасил каждую грань кубика разными красками. 4
Вопрос №
2
У Алины несколько кукол. Папа подарил ей не день рождения столько же кукол, сколько у неё было. Теперь у Алины 12 кукол. Сколько кукол подарил ей папа ? 12
Вопрос №
3
Сумма двух чисел равна семи, а их разность равна трём. Найдите эти числа. 3 и 4
Вопрос №
4
Володя, Дима и Петя устроили соревнование. Один из мальчиков решил 12 примеров, второй — 13, а третий — 14. Сколько примеров решил каждый мальчик, если Петя решил примеров меньше, чем Дима, а Дима меньше чем Володя ? Дима -13, Петя — 12, Володя — 14
Вопрос №
5
У Вити сегодня день рождения. 7 лет
Вопрос №
6
Витя, Саша и Андрей смастерили из бумаги кораблик, змея и аиста. Какую игрушку сделал каждый мальчик, если Витя не сделал кораблика и змея, а Саша не делал кораблик? Витя — змея, Саша — кораблик. Андрей — аиста
Вопрос №
7
Маша загадала число. Чтобы его разгадать, возьми число 81, уменьши его в 3 раза, прибавь 6, прибавь 3 сотни. У тебя получилось число, которое задумала Лена. 433
Вопрос №
8
Восьмого марта в кино пришло 100 ребят. 40
Вопрос №
9
На доске нарисованы два круга, внутри которых отмечено несколько точек. Внутри первого из них всего 190 отмеченных точек. Внутри второго — всего 230 отмеченные точки. Внутри обоих кругов одновременно находится ровно 70 точек. А сколько отмеченных точек всего? 300 Показать ответы Получение сертификата Доступно только зарегистрированным пользователям © TestEdu.ru 2013-2022 E-mail администратора: [email protected] Задачи на логику, ответы, 1 класс | Материал по математике (1 класс) по теме:
Задачи на логику. 1 класс А Б 1.Мама купила детям 3 пары варежек. Сколько всего левых варежек и сколько правых варежек? 2. В парке было 7 скамеек. 3скамейки заменили новыми. Сколько скамеек стало в парке? 3.В квартире 2 комнаты. Из одной комнаты сделали две. Сколько комнат стало в квартире? 4. Юра попросил в библиотеке журналы «Нафаня» со второго по шестой номер. 5. В квартире 4 комнаты. Две комнаты соединили вместе и сделали из них одну большую комнату. Сколько комнат стало в квартире? 6. У всех цыплят, которые сидели в корзине, Юля насчитала 10 ног. Сколько цыплят было в корзине? 7. Таня сказала, что у неё кукол больше 4 и меньше 7. Сколько кукол могло быть у Тани? 8. Коля старше Серёжи, а Серёжа старше Миши. Запиши имя мальчика, который моложе всех. 9. На подоконнике лежали 8 зелёных помидоров. Через 3 дня они покраснели. Сколько зелёных помидоров осталось? 10. Кролики сидят в клетке так, что видны их уши. Вова насчитал 5 пар ушей. Сколько кроликов в клетке? 11. Кузнец подковал двух лошадей. Сколько подков ему потребовалось? 12. Алёшу угостили конфетами. Он решил дать своей сестрёнке 4 конфеты, а себе взять 3. Сколько конфет дали Алёше? 13. У Маши и Вани по 9 леденцов. Маша съела 4 леденца, и Ваня сделал тоже самое. Сколько леденцов осталось у Вани? 14. 15. Роме подарили столько значков сколько у него уже было. Рома пересчитал все значки, их оказалось 8. Сколько значков было у Ромы сначала? 16. Чтобы рассадить 7 детей в комнате, не хватает 2 стульев. Сколько стульев в комнате? 17. У паука 4 пары ног, а у жука 3 пары ног. На сколько ног больше у паука, чем у жука? 18. В коробке 6 ячеек. В каждой ячейке умещается только одна ёлочная игрушка. Можно ли в эту коробку положить 4 шарика и 3 шишки? 19. Сестра старше брата на 1 год. На сколько лет сестра будет старше брата через 5 лет? 20. Может ли сумма двух чисел быть равной слагаемому? 21. Может ли разность двух чисел быть равной уменьшаемому? 22. Запиши число меньшее 20, в котором число десятков на 4 меньше числа единиц. 23. На каждую страницу альбома я наклеил 4 переводных картинки. Сколько страниц заняли 8 картинок? 24. 25. Меня зовут Нина Александровна, а моего дедушку(отца моего отца) – Иван Николаевич. Как зовут моего отца? 26. На левой чашке весов стоят пакет с мукой и гиря в 1 кг. На правой чашке весов гиря в 3 кг. Весы в равновесии. Найдите массу пакеты с мукой. 27. в обувном отделе универмага висит указатель: «Обувь 37 – 42 размеров». Можно ли в этом отделе купить обувь 39 размера? 28.Какие двузначные числа можно записать, используя цифры 5 и 6? 29.Сахар-песок продают расфасованным в пакеты по 1 кг, 2кг, 3кг. Мама выбила в кассе чек на покупку 7 кг сахара. Продавщица дала ей 3 пакета с сахаром. Сколько сахара было в каждом из пакетов? Рассмотри возможные случаи. 30. Сравни числа *2 и 95 Сделай запись с помощью одного из знаков . 31. Юля и Марина нашли в лесу поровну грибов. У Юли 4 гриба оказались червивыми, и по дороге домой она их выбросила. А Марина нашла ещё 5 грибов. На сколько грибов у Марины стало больше, чем у Юли? 32. 33.На верхней полке книг столько же, сколько на нижней. На верхнюю полку поставили 3 книги, а с нижней 3 книги сняли. На какой полке стало больше книг и на сколько? 34. В коробке 12 красных и зелёных шаров. Из коробки взяли 3 красных и 4 зелёных шара. После этого в коробке зелёных шаров не осталось. Сколько красных шаров осталось в коробке? 35. В корзине на 5 яблок больше, чем в пакете. Из корзины взяли 7 яблок. Где осталось яблок больше: в корзине или в пакете, и на сколько? 36. К трём замкам волшебник сделал 3 ключа: медный, серебряный и золотой. К каждому замку подходит только один ключ. Медный ключ не подходит к ни к первому, ни ко второму замку. Серебряный ключ не подходит ко второму замку. К какому замку подходит каждый из ключей? 37. У Пети на 4 конфеты меньше, чем у Серёжи. Мама дала Пете ещё 5 конфет. У кого конфет больше и на сколько? 38. 39. У Юры денег ровно столько, чтобы купить 4 вафли или 2 конфеты. Сможет ли он на свои деньги купить 1 конфету и 4 вафли? 40. Запишите 6 чисел по такому правилу: первое 1, второе 2, а каждое следующее равно сумме двух предыдущих. 41. Оля может купить на свои деньги 4 карандаша и 3 тетради. Хватит ли у неё денег, чтобы купить 3 карандаша или 3 тетради? 42. Каждой из трёх внучек дедушка разрешил сорвать с четырёх кустов по одной розе. Сколько роз сорвали все внучки? 43. Запишите 5 чисел по такому правилу: первое 18, второе 10, а каждое следующее равно разности двух предыдущих. 44. Половину числа яблок, лежащих на тарелке, взяли для компота. Сколько яблок осталось на тарелке, если компот сварили из 6 яблок? 45. Купили пакет кефира. Половину всего кефира, который был в пакете, выпили Маша и Даша. В пакете осталось 2 стакана кефира. 46. Дыня тяжелее арбуза и легче тыквы. Что самое тяжелое? 47. На столе лежат овощи: репок на 1 меньше, чем огурцов, а огурцов на 1 меньше, чем помидоров. На сколько репок меньше, чем помидоров? 48. Красная лента короче синей ленты и длиннее зелёной. Какая лента самая короткая? 49. Дима на 1 год старше Серёжи, а Серёжа на 1 год старше Ромы. На сколько лет Дима старше Ромы? 50. За каждую минуту в ванну из крана наливается 10 л воды. За то же время через неплотно прикрытое пробкой отверстие в дне ванны 2 л воды выливается. Увеличивается или уменьшается количество воды в ванне и на сколько литров каждую минуту? 51. Петя взял 3кубика и поставил их один на один так, что получилась «башня». Красный кубик оказался ниже синего, а синий ниже зелёного. Какой кубик Петя поставил выше всех? 52. Из трёх кубиков построили башню. Жёлтый кубик поставили выше синего и ниже красного. Какой кубик оказался выше всех? 53. 54. В коробке лежат пряники и вафли: пряников на 2 меньше, чем вафель. Сколько вафель, если пряников 6? 55. Митя на 2 года старше Гены. Мите 10 лет. Сколько лет Гене? 56. Сумма двух чисел 9. Сумма больше первого слагаемого на 5.Чему равно второе слагаемое? 57. На катке катались на коньках 6 девочек и 2 мальчика. Вскоре троих детей позвали обедать, и они ушли домой. Осталась ли на катке хоть одна девочка? 58. Купили банку виноградного сока. Четверым детям налили из банки по полному стакану сока. После этого в банке осталось ровно столько, сколько выпили дети. Сколько стаканов сока было в банке? 60. Дыня на 3 кг легче арбуза. От дыни отрезали кусок массой 1 кг, а от арбуза – кусок массой 3 кг. Чего осталось больше: дыни или арбуза, и на сколько килограммов?
Лучшие упражнения для логического математического интеллекта — Одним из восьми интеллектов или способностей, определенных Говардом Гарднером в его книге Структуры разума: теория множественного интеллекта , является логический математический интеллект. В традиционной системе образования особое внимание уделяется использованию и развитию логических математических навыков наряду с вербальными навыками. Однако как педагоги и родители, обучающиеся на дому, мы должны осознавать, что все восемь видов интеллекта одинаково важны для продуктивного функционирования в обществе. Таким образом, несмотря на то, что в этом посте в первую очередь будет обсуждаться тема логического математического интеллекта, вы заметите, что эти действия также коснутся нескольких видов интеллекта. Когда говорят, что кто-то «разбирается в математике», что приходит на ум? Этот человек, конечно, хорошо разбирается в цифрах. Но логический математический интеллект означает гораздо больше. Логические математические люди могут легко выявлять и анализировать закономерности, рассуждать дедуктивно, анализировать проблемы логически, критически задавать вопросы и делать выводы, объединяя имеющуюся информацию. Во всех классах и в большинстве семей мы найдем детей, явно предпочитающих логический математический стиль обучения. Как я писал в других статьях о множественном интеллекте, ни у кого нет только одного типа интеллекта. Мы все приходим к пониманию мира благодаря сочетанию 8 видов интеллекта, определенных Гарднером. Это правда, что у людей обычно есть одна или две более сильные способности, которые помогают им легко учиться. Прежде чем мы перейдем к некоторым замечательным занятиям для «умных в математике» детей, давайте сначала рассмотрим некоторые характеристики логического математического интеллекта. Этот пост может содержать партнерские ссылки, и я могу получать небольшую комиссию, когда вы нажимаете на ссылки без каких-либо дополнительных затрат для вас. Являясь партнером Amazon, я зарабатываю на соответствующих покупках. Вы можете прочитать мое полное раскрытие здесь. Существует несколько характеристик логического математического интеллекта, на которые следует обращать внимание при попытке определить доминирующие способности учащихся или детей. Некоторые из этих характеристик включают в себя: Теперь, когда вы знаете наиболее важные характеристики логического математического интеллекта, вы можете начать наблюдать за своими учащимися и определить, сколько из них «сообразительны в математике». Согласно Sage Journals, дети в возрасте 4 или 5 лет могут проявлять предпочтения в отношении того или иного типа интеллекта. В случае с маленькими детьми вы можете просто наблюдать за ними и на основе этого формировать «профиль интеллекта». Для детей старшего возраста, которые умеют читать и писать, помимо наблюдения за ними, вы можете дать им этот тест, который поможет вам определить их сильные и слабые стороны. 1.Загадки и загадкиТе, кто изучает логику и математику, несомненно, полюбят сложные головоломки. Хорошая новость заключается в том, что существует так много вариантов (бесплатных и платных) как для физических, так и для онлайн-материалов. Вот некоторые из наших рекомендаций (для детей от 4 до 8 лет): Рабочие тетради и рабочие тетради для печати : Ознакомьтесь с нашей фантастической тетрадью Numbers Busy. 50 забавных страниц для детей, чтобы попрактиковаться в распознавании чисел, счете и основных математических операциях. Получить сейчас Игры 2. Загадки Загадки Ничто так не тренирует мозг, как хорошая загадка. Не говоря уже о том, что они забавны, особенно для «умного в математике» ребенка. Если вы ищете отличные загадки для маленьких детей, посмотрите здесь. Что мне нравится в этом посте, так это то, что он также дает подсказки к загадкам. 3.Настольные игрыНастольные игры — это фантастические забавные инструменты для обучения. Они развивают навыки сотрудничества, терпение, учатся выигрывать или проигрывать изящно и в зависимости от настольной игры, математические и логические навыки. Вот несколько отличных настольных игр для маленьких детей, которые вы, возможно, захотите попробовать: Знак в математике плюс минус: Знак плюс-минус | это… Что такое Знак плюс-минус?∓ — Минус-плюс: U+2213 mnplusU+2213Нажмите, чтобы скопировать и вставить символТехническая информация
Значение символаИспользуется со знаком и означает, что если там +, то здесь −, и наоборот. Пример: (x ± 1) / (x ∓ 2) будет значить (x + 1) / (x — 2) и (x — 1) / (x + 2) Символ «Минус-плюс» был утвержден как часть Юникода версии 1.1 в 1993 г. Свойства
Кодировка
Наборы с этим символом:Знак плюс минус — no-regime. com com
Знак плюс минус (±) и знак минус плюс (∓) — это символы из математики . ОглавлениетипографияЗнаки плюс, минус и (если есть) минус плюс в шрифтах Arial, Times New Roman, Cambria Math, Linux Libertine, Adobe Garamond, Everson Mono и Andron Mega Corpus вместе с буквами «i» / «I» для обозначения x- соотв. Знак плюс минус в основном состоит из неизменной формы знака плюс того же шрифта со знаком минус под ним, который имеет ту же форму, что и горизонтальная полоса знака плюс. В большинстве случаев между компонентами остается расстояние меньше ширины линии; есть также формы, в которых компоненты соприкасаются. В случае знака минус плюс, знак минус располагается над знаком плюс точно так же. Вертикальное положение символов в системе типографских линий непоследовательно. использоватьТехнологии и коммерцияВ технике знак плюс-минус обозначает неопределенности или допуски . Например, «5 см ± 0,05 см» означает, что фактическая длина может составлять от 4,95 см до 5,05 см. Обозначения относительно межсимвольного интервала непоследовательны; также могут быть выполнены без пробела впоследствии, идентичная единица измерения не должна повторяться, размер и отклонение часто записываются с одним и тем же количеством десятичных знаков (точность): «15,00 ± 0,05 см» или «15,00 ± 0,05 см «. Точно так же может быть выражено в продавце, что вещь с недостатком связана, когда значение измеримого размера (например, вес. Длина) выходит за пределы указанного диапазона, поэтому. математикаКоллекции формулДва символа часто используются в формулах для объединения двух похожих формул для экономии места. Это проиллюстрировано здесь на примере формул из теорем сложения тригонометрии . В компактных обозначениях эти две формулы имеют вид Задачи и примеры для 4 класса по математике решать онлайн: Тест по математике 4 класс — Пройти онлайн тестРешать задачи по математике 4 класс решать онлайн – Тест по математике №4, 4 классМатематика 4 класс задачи решать Математика 4 класс | Онлайн олимпиада. Примите участие бесплатно.Задание по математике для 4 класса (Уравнения)Лимит времени: 0 ИнформацияПримите участие и узнайте свой результат. Вы уже проходили тест ранее. Вы не можете запустить его снова. Вы должны войти или зарегистрироваться для того, чтобы начать тест. Вы должны закончить следующие тесты, чтобы начать этот: Правильных ответов: 0 из 10 Вы набрали 0 из 0 баллов (0) Поздравляем! Поздравляем! Поздравляем! Сделайте работу над ошибками. С ответом С отметкой о просмотре Тест: Решение задач для 4 классаРешение задач с выбором одного ответа на движение, на порпорциональное деление, меру времени. Математика 4 класс | Автор: Степанова Татьяна Николаевна | ID: 1288 | Дата: 14.2.2014 Тесты по Математике для 4 классаТесты по «Математике» для 4 класса Тест применяется на этапе актуализации на уроке «Сложение и вычитание величин» Математика 4 класс | Дата: 13. Вопросы по математике для подготовки к ГКР Математика 4 класс | Дата: 27.3.2019 Цель: проверить сформированность представлений о скорости движения, умение решать задачи на встречное движение. Математика 4 класс | Дата: 22.2.2019 Проверить знания учащихся Математика 4 класс | Дата: 29.1.2019 Тестовая работа с выбором ответа за курс начальной школы Математика 4 класс | Дата: 27.12.2018 Задания для проведения олимпиады по математике в 4 классе Математика 4 класс | Дата: 26.12.2018 Ответь на 5 вопросов теста правильно и получи отметку «5». Математика 4 класс | Дата: 17.10.2018 Проверка владения устными вычислениями, сложение и вычитание многозначных чисел, названия компонентов действий сложения и вычитания Математика 4 класс | Дата: 10.10.2018 Тест содержит основные вопросы за курс математики в начальной школе. Математика 4 класс | Дата: 11.6.2018 Входящий тест по математике, который поможет определить знания полученные в 3 классе. Математика 4 класс | Дата: 20.10.2017 Страница 1 из 12 Тесты по математике (4 класс, по четвертям) с ответами онлайн1. Повторение2. Числа от 1 до 10003. Числа, которые больше 10004. ДругиеОнлайн тесты по математике (4 класс) с ответами составлены в соответствии с действующей программой, утвержденной министерством. Они рассчитаны на учеников выпускного класса младшей школы, которые хотят проверить или закрепить свои знания разделов за каждую четверть, хорошо написать итоговые контрольные работы. Данная подборка заданий – отличный помощник в процессе домашней подготовки к уроку. Ответы можно использовать в качестве подсказок, если возникают трудности при решении какого-либо задания. Вопросы касаются правил, выученных в не только в 4-м, но и предыдущих классах. Они проверяют умение применять элементарные математические действия (сложение, вычитание, умножение и деление) для решения задач и уравнений, работать с дробными числами и разными единицами измерения. Прохождение теста занимает всего 10-15 минут, но его вопросы проверяют все необходимые знание всех разделов. Проверочные задания содержат несколько вариантов ответов, лишь один из которых правильный, поэтому ребенок без труда справиться с тестом. Если с первого раза не получилось добиться идеального результата, значит, нужно ознакомиться с ответами, еще раз повторить проблемные разделы и попробовать пройти тест заново. Вопросы разного уровня сложности, что позволяет объективно оценить знания. Тесты можно просматривать в электронном виде с любого устройства, проходить в удобное время. Итоговые тесты по математике (4 класс) целесообразно использовать в процессе подготовки к итоговым урокам, проверочным работам (в том числе и годовой), так как это один из самых эффективных методов самооценивания. Тест: Развивающие задачи по математике (4 класс)Проверка способности к анализу, обобщению, классификации Математика 4 класс | Автор: Ливанова Ирина Георгиевна | ID: 2202 | Дата: 12. Задание по математике для 4 класса (Уравнения)Лимит времени: 0 ИнформацияПримите участие и узнайте свой результат. Вы уже проходили тест ранее. Вы не можете запустить его снова. Вы должны войти или зарегистрироваться для того, чтобы начать тест. Вы должны закончить следующие тесты, чтобы начать этот: Правильных ответов: 0 из 10 Вы набрали 0 из 0 баллов (0) Поздравляем! Поздравляем! Поздравляем! Сделайте работу над ошибками. С ответом С отметкой о просмотре Вопросы по математике для подготовки к ГКР. Xn—-8sbanwvcjzh9e. xn--p1ai 02.08.2020 23:34:35 2020-08-02 23:34:35 Источники:Https://xn—-8sbanwvcjzh9e. xn--p1ai/matematike/reshat-zadachi-po-matematike-4-klass-reshat-onlajn-test-po-matematike-4-4-klass. html Тесты по математике для 4 класса онлайн | Online Test Pad » /> » /> .keyword { color: red; } Математика 4 класс задачи решать Проверочная работа по МАТЕМАТИКЕ 4 КЛАСС. Постарайся выполнить правильно как можно больше заданий. 1 вариант ВПР 4 класс, математика. При выполнении работы нельзя пользоваться учебниками, рабочими тетрадями, справочниками, калькулятором. Обязательные ответы на все вопросы теста. Таблица умноженияТест предназначен для закрепления изученного материала и его повторения. Удачи в прохождении! Математика решение задачТест для учащихся 3-4 классов по математике задания не простые. Пожелаем удачи. 2 вариант ВПР 4 класс, математикаПри выполнении работы нельзя пользоваться учебниками, рабочими тетрадями, справочниками, калькулятором. Обязательные ответы на все вопросы теста. Таблица умножения от 2 до 1513 заданий. Критерии: «5» — 13 баллов, «4» — 11-12 баллов, «3» — 9-10 баллов. Тест по математике 4 классПроверочная работа по математике за курс начального общего образования На сколько хорошо ты знаешь таблицу умножения?Проверим на сколько хорошо ты знаешь (или недавно выучил) таблицу умножения? Всю таблицу спрашивать не будем. 3 вариант ВПР 4 класс, математикаПри выполнении работы нельзя пользоваться учебниками, рабочими тетрадями, справочниками, калькулятором. Обязательные ответы на все вопросы теста. ВПР 4 класс, математика. 21 вариантПроверочная работа по МАТЕМАТИКЕ 4 КЛАСС. Постарайся выполнить правильно как можно больше заданий. 5 вариант ВПР 4 класс, математикаПри выполнении работы нельзя пользоваться учебниками, рабочими тетрадями, справочниками, калькулятором. Обязательные ответы на все вопросы теста. ВПР 4 класс, математика. 24 вариантПроверочная работа по МАТЕМАТИКЕ 4 КЛАСС. Постарайся выполнить правильно как можно больше заданий. 4 сынып тест №1Қазақ тілі, математика, әдебиеттік оқу пәндері бойынша тестте 30 сұрақ берілген Математика задание 3.8Задание всего одно, но на странице математики по третьему классу вы найдете больше! 4-SINF O’QUVCHILARI UCHUN MATEMATIKA FANIDAN ONLAYN OLIMPIADA4-SINF O’QUVCHILARI UCHUN MATEMATIKA FANIDAN ONLAYN OLIMPIADA. 8 вариант ВПР 4 класс, математикаПри выполнении работы нельзя пользоваться учебниками, рабочими тетрадями, справочниками, калькулятором. Обязательные ответы на все вопросы теста. 4 вариант ВПР 4 класс, математикаПри выполнении работы нельзя пользоваться учебниками, рабочими тетрадями, справочниками, калькулятором. Обязательные ответы на все вопросы теста. Таблица умножения 2Это тест по таблице умножения 2. Тут более все усложненноё и для 3 класса и выше. Удачи в прохождении и надеемся что наш тест вам понравится. Итоговый тест по математике для 4 класса №1.Итоговый тест за курс 4 класса по математике. Содержит 20 заданий. Выполнение теста ограничено по времени. 6 вариант ВПР 4 класс, математикаПри выполнении работы нельзя пользоваться учебниками, рабочими тетрадями, справочниками, калькулятором. Обязательные ответы на все вопросы теста. Перевод единиц измерения величинТест по математике для учащихся 4-5 классов. Чтение и запись многозначных чисел (миллионы, миллиарды)Тест по математике по теме: «Чтение и запись многозначных чисел» 4 класс 13 вариант ВПР 4 класс, математикаПри выполнении работы нельзя пользоваться учебниками, рабочими тетрадями, справочниками, калькулятором. Обязательные ответы на все вопросы теста. Готовимся к ВПР. Задание № 2 «Арифметические действия с числами»Готовимся к ВПР: задание № 2. Тест по теме: «Арифметические действия с числами». Предназначен для проверки знаний обучающихся о порядке действий в выражениях со скобками и без на основе четырех арифметических действий. 10 вариант ВПР 4 класс, математикаПри выполнении работы нельзя пользоваться учебниками, рабочими тетрадями, справочниками, калькулятором. 12 вариант ВПР 4 класс, математикаПри выполнении работы нельзя пользоваться учебниками, рабочими тетрадями, справочниками, калькулятором. Обязательные ответы на все вопросы теста. 7 вариант ВПР 4 класс, математикаПри выполнении работы нельзя пользоваться учебниками, рабочими тетрадями, справочниками, калькулятором. Обязательные ответы на все вопросы теста. ВПР математика 4 клТренировочный тест по математике для подготовки к впр. Включает в себя выражения для вычисления, решение арифметических и геометрических задач. Готовимся к ВПР. Задание № 3 «Арифметический метод».Готовимся к ВПР: задание № 3. Тест по теме: «Арифметический метод». Предназначен для проверки умения решать практико-ориентированные задачи. 11 вариант ВПР 4 класс, математикаПри выполнении работы нельзя пользоваться учебниками, рабочими тетрадями, справочниками, калькулятором. 9 вариант ВПР 4 класс, математикаПри выполнении работы нельзя пользоваться учебниками, рабочими тетрадями, справочниками, калькулятором. Обязательные ответы на все вопросы теста. ВПР по математике 4 класс. 2020Проверочная работа по математике Демоверсии ВПР 2020 года для 4 класса Образец Математика 4 класс ВПР 2020Проверочная работа по математике Демоверсии ВПР 2020 года для 4 класса Образец Математика 4 класс ВПРРешение разных типов заданий заданий из ВПР по математике 4 класса, для проверки своих знанийи закрепления тем. ВПР 4 классС помощью теста вы сможете понять готовы ли вы к ВПР. А также потренероваться перед экзаменом! 31.03.2020 математика ВПРТест ВПР по математике предназначен для учащихся 4 класса. Подготовка к ВПР Таблица умножения 4Это таблица умножения 4, от 1 до 100. Самая усложнённая венрсия на данный момент. Олимпиада для Начальной школы 4 класс МатематикаТест предназначен для учеников 4 классов. Входная контрольная работа по математике 4 классВходная контрольная работа по математике в 4 классе с ответами для УМК «Школа России» (авт: М. И.Моро и др.) Вспомним первый классВспомним первый класс. Такие простые были примеры, но если оно так и есть, тогда сейчас проверим. Начнем? Решение задачДанный тест для учащихся 4 класса поможет провести повторение и закрепление умений решать задачи, поможет привить любовь к математике «Умножение трехзначных чисел»Тема «Умножение трехзначных чисел», встретятся задания на порядок действий и задача Математический диктантТест проводится на этапе устного счёта урока математика в 4 классе. Тема умножение многозначного числа на на круглое число. Математический диктант для учащихся 4 класса. Нумерация многозначных чиселМатематический диктант направлен на формирование устного счета и повторение материала по теме «Нумерация многозначных чисел» Задачи на движение. 5 класс. Вариант 1. 5 класс. Вариант 1.Тесты для учащихся 5 классов состоящие из всех видов задач на движение Тест по теме «Масса и её измерение»Проверочная работа по теме «Масса и её измерение» о средней массе животных представляет собой тест, в который включено 10 вопросов с одним вариантом ответов. Обучающие должны знать единицы измерения массы и их соотношение. Для успешного прохождения необходимо ответить правильно не менее 70% вопросов. Тест для учащихся 3-4 классов по математике задания не простые. Пожелаем удачи. При выполнении работы нельзя пользоваться учебниками, рабочими тетрадями, справочниками, калькулятором. Обязательные ответы на все вопросы теста. Перевод единиц измерения величин Обязательные ответы на все вопросы теста. Onlinetestpad. com 10.08.2018 14:26:20 2018-08-10 14:26:20 Источники:Https://onlinetestpad. com/ru/tests/math/4class Математика для 4 класса: задачи, задания, тесты онлайн. Математика 4 класс задачи решать В четвертом классе вас ждет масса новых интересных задач. Развиваем логику, расширяем восприятие объемных геометрических фигур, плавно начинаем изучение такого важного раздела как «функции», набиваем руку в решении различных видов задач. В разделе содержится много задач, которые помогут понять, где математику можно использовать в жизни, а также понять, как быстрее и легче считать сложные числа. Ученик научится видеть вокруг себя различные математические величины и умело оперировать ими. Задачи и тесты по математике для 4 класса. Learning. ua 22.05.2018 8:49:26 2018-05-22 08:49:26 Источники:Https://learning. ua/matematyka/chetvertyi-klas/ru/ Примеры. Математика 4 класс. Примеры. Математика 4 класс. Задачи по математике 4 класс MAT-ZADACHI. RU RU Математика 4 класс Контрольные работы
Математика 4 класс ->> Примеры Чтобы увидеть решение, наведите на пример курсор мыши.
Простые задачи Составные задачи Школьная математика 4 класс | Систематикадля 4 классов Подтянем математику в школе. от 500 ₽ /занятие Старт сезона. Идёт запись Записаться на кружок Пробное занятие Когда Круглый год Идет набор на лето Продолжительность Для детей 3-7 классов Формат • Мини группы по 4-10 человек Когда Круглый год Идет набор на лето Продолжительность Для детей 3-7 классов Формат • Мини группы по 4-10 человек Что дает курсИнтерес Показываем, что математика бывает не скучной, а интересной. Зажигаем математикой даже гуманитариев. Преодоление страха Снимаем страх перед сложными задачами. Ребенок понимает, что способен решить даже то, что не проходили в классе. Навык решения Размышление над «открытыми» и «нерешаемыми» проблемами развивает логику и воображение. Меньше времени Мы учим думать. Ребенок становится увереннее в своих силах и быстрее справляется с заданиями. Возможность поступить Умение решать олимпиадные и нестандартные задачи ценится при поступлении в сильные школы и вузы. Интересные задачи Интересное объяснение Спортивный интерес У меня получается Интерес к математике у вашего ребенка Я заметил, что даже пятилетние дети решают подобные задачи лучше школьников, испорченных натаскиванием, которым они даются легче, чем студентам, подвергшимся зубрежке в университете, но все же превосходящим своих профессоров. Хуже всех решают эти простые задачи нобелевские и философские лауреаты» Владимир Арнольд Академик, в предисловии к своему сборнику олимпиадных задач Как проходят занятия1 Открываем доступ к материалам за 6 часов до занятия При желании задания можно скачать и распечатать 2 Демонстрируем задачи на экране С помощью графического планшета превращаем экран Zoom в школьную доску 3 Обсуждаем тему в режиме диалога Направляем мысль, но даем детям самим дойти и разобраться 4 Объясняем принцип решения на примере Берем типовую задачу и вместе разбираем решение 5 Решаем задачи от простых к сложным Просим показать ход мысли на экране или написать ответ в чат 6 Уделяем достаточно внимания каждому Даем высказаться всем по очереди, если что-то непонятно — объясняем лично 7 Вызываем спортивный интерес Присваиваем бейджи разного уровня за выполненные домашки Открываем доступ к материалам за 6 часов до занятия При желании задания можно скачать и распечатать Демонстрируем задачи на экране С помощью графического планшета превращаем экран Zoom в школьную доску Обсуждаем тему в режиме диалога Направляем мысль, но даем детям самим дойти и разобраться Объясняем принцип решения на примере Берем типовую задачу и вместе разбираем решение Решаем задачи от простых к сложным Просим показать ход мысли на экране или написать ответ в чат Уделяем достаточно внимания каждому Даем высказаться всем по очереди, если что-то непонятно — объясняем лично Вызываем спортивный интерес Присваиваем бейджи разного уровня за выполненные домашки Продуманная Программа занятий составлена на основе учебников Виленкина, Мерзляка и Никольского. Успеваемость Все пробелы, которые будут выявляться в процессе, мы будем в обязательном порядке закрывать. Вы будете регулярно получать обратную связь об успеваемости и прогрессе вашего ребёнка Домашнее К каждому занятию будет обязательное домашнее задание, которое нужно будет выполнить и сдать, чтобы закрепить тему. Продуманная Программа занятий составлена на основе учебников Виленкина, Мерзляка и Никольского. Наша задача — сделать так чтобы у вашего ребёнка не было проблем с математикой в школе. Для этого мы будем двигаться по школьной программе и разбирать все темы. Успеваемость Все пробелы, которые будут выявляться в процессе, мы будем в обязательном порядке закрывать. Домашнее К каждому занятию будет обязательное домашнее задание, которое нужно будет выполнить и сдать, чтобы закрепить тему. Программа для 4 классов1 модуль 32 занятия 1 модуль 32 занятия 32 занятия Почему стоит учиться онлайнБережем силы Ребенок учится, а не тратит силы на дорогу, поэтому занятия проходят продуктивнее. Сохраняем Занятия в онлайн идут 60 минут — достаточно, чтобы не растерять внимание. Поддерживаем Если ребенок устал и начинает баловаться, отключаем звук, чтобы он не отвлекал остальных детей. Бережем силы Ребенок учится, а не тратит силы на дорогу, поэтому занятия проходят продуктивнее. Сохраняем Занятия в онлайн идут 60 минут — достаточно, чтобы не растерять внимание. Поддерживаем Если ребенок устал и начинает баловаться, отключаем звук, чтобы он не отвлекал остальных детей. У нас онлайн работает Преподаем через интернет больше пяти лет. Знаем тонкости этого формата и обучаем ему всех преподавателей. Преподаватели онлайн-кружкаУ нас преподают замечательные преподаватели. Выпускники (и студенты старших курсов) Мехмата МГУ и МФТИ, ведущие кружков олимпиадной математики с большим опытом, призёры математических олимпиад Опыт с 2017 года Бортников Алексей Образование Институт Робототехника и комплексная автоматизация(РК) МГТУ им. Н.Э. Баумана Места преподавания Год преподавания в школе «КодКласс» 2019г. Места преподавания Работал методистом в ЗФТШ, преподавателем в детской школе программирования «КодКласс», вожатым в лагере «Фоксфорд» Идёт набор Расписание для 4 классовВыберите удобную для вас группу и укажите день недели и время при регистрации Среда: 17:50 — 18:50 Пятница: 16:10 — 17:10 Суббота: 14:00 — 15:00 Воскресенье: 11:10 — 12:10 Стоимость абонементовПо абонементу можно посещать любые кружки и интенсивы Систематики 4 занятия 3200 ₽ 800 ₽ за занятие Записаться 8 занятий 6000 ₽ 750 ₽ за занятие Записаться 16 занятий 11200 ₽ 700 ₽ за занятие Записаться 32 занятия 20800 ₽ 650 ₽ за занятие Записаться 150 человек Прошли курс 50 человек Занимаются сейчас 8 отзывов читать отзывы → Купить абонементВы можете использовать один абонемент для разных онлайн-кружков 150 человек Прошли курс 50 человек Занимаются сейчас читать отзывы → 8 отзывов читать отзывы → Выдаем сертификатКаждый ученик в конце курса получает именной сертификат — он будет доступен по ссылке на нашем сайте. Что понадобится для занятийБумага (лучше завести тетрадь для наших занятий) Карандаша и ластик (желательно) Ученики о насНажмите на имя, чтобы посмотреть пройденные учеником курсы Все отлично. Объясняют материал максимально понятно. Ребенок стал понимать математику лучше, изучены новые темы.
читать полностьюсвернуть Курс интересный, поддерживает ученика в течение учебного года. Есть домашние задания, но делать их необязательно, хотя, на мой взгляд, важно. Достижения: О преподавателе: читать полностьюсвернуть Даниил Попов объяснял всё доступно и сопровождал играми. Дочка очень полюбила преподавателя. читать полностьюсвернуть Отвечаем на частые вопросыДругие занятия по математикеКурс в записи Две задачи на неделю от 9 до 99 лет Видео с теорией, практические задания, проверка преподавателем, видео с разборами заданий Идёт набор Курс в записи Курс олимпиадной математики для 3-4 классов Курс олимпиадной математики для 3-4 классов Видео с теорией, практические задания, проверка преподавателем, видео с разборами заданий Идёт набор Онлайн занятия Олимпиадная математика 3-4 класс продолжающие Олимпиадная математика 3-4 класс продолжающие Видео с теорией, практические задания, проверка преподавателем, видео с разборами заданий Идёт набор Онлайн занятия Олимпиадная математика 3-4 класс начинающие Олимпиадная математика 3-4 класс начинающие Видео с теорией, практические задания, проверка преподавателем, видео с разборами заданий Идёт набор Курс в записи Две задачи на неделю от 9 до 99 лет Две задачи на неделю от 9 до 99 лет Видео с теорией, практические задания, проверка преподавателем, видео с разборами заданий Идёт набор Показать все Другие занятия для 4 классаИдёт запись ТРИЗ и История Цивилизаций Курс по развитию мышления инструментами ТРИЗ. 10 модулей Идёт запись ТРИЗ – интенсив «История Древней Индии» 14 — 26 ноября Модуль 3. История Древней Индии 4 занятия Идёт запись ТРИЗ-интенсив «Месопотамия и Персия» 17-29 октября Модуль 2. История Месопотамии и Персии 4 занятия Идёт запись ТРИЗ – интенсив «История Древней Греции» 15 — 26 августа Модуль 3. История Древней Греции 4 занятия Идёт запись ТРИЗ и История Цивилизаций ТРИЗ и История Цивилизаций Курс по развитию мышления инструментами ТРИЗ. Для тех, кто любит думать, и увлекается историей. 10 модулей Идёт запись ТРИЗ – интенсив «История Древней Индии» ТРИЗ – интенсив «История Древней Индии» Модуль 3. 4 занятия Идёт запись ТРИЗ-интенсив «Месопотамия и Персия» ТРИЗ-интенсив «Месопотамия и Персия» Модуль 2. История Месопотамии и Персии 4 занятия Идёт запись ТРИЗ – интенсив «История Древней Греции» ТРИЗ – интенсив «История Древней Греции» Модуль 3. История Древней Греции 4 занятия Иллюстративная математикаИллюстративная математикаКласс 4 4 класс4.ОА. 4 класс — Операции и алгебраическое мышление4.ОА.А. Используйте четыре операции с целыми числами для решения задач.4. ОА.А.1. Интерпретируйте уравнение умножения как сравнение, например, интерпретируйте $35 = 5 \times 7$ как утверждение, что 35 в 5 раз больше, чем 7, и в 7 раз больше, чем 5. Представьте вербальные утверждения мультипликативных сравнений в виде уравнений умножения. ОА.А.1. Интерпретируйте уравнение умножения как сравнение, например, интерпретируйте $35 = 5 \times 7$ как утверждение, что 35 в 5 раз больше, чем 7, и в 7 раз больше, чем 5. Представьте вербальные утверждения мультипликативных сравнений в виде уравнений умножения.4.ОА.А.2. Умножьте или разделите, чтобы решить текстовые задачи, включающие мультипликативное сравнение, например, используя рисунки и уравнения с символом неизвестного числа для представления проблемы, отличая мультипликативное сравнение от аддитивного сравнения. См. Глоссарий, Таблица 2.4.ОА.А.3. Решите многошаговые словесные задачи, поставленные с целыми числами и имеющие ответы с целыми числами, используя четыре операции, включая задачи, в которых необходимо интерпретировать остатки. Представьте эти проблемы, используя уравнения с буквой, обозначающей неизвестную величину. Оцените обоснованность ответов, используя вычисления в уме и стратегии оценки, включая округление. Оцените обоснованность ответов, используя вычисления в уме и стратегии оценки, включая округление.4.ОА.Б. Знакомство с множителями и множителями.4.ОА.Б.4. Найдите все пары множителей для целого числа в диапазоне от 1 до 100. Признать, что целое число является кратным каждого из его делителей. Определить, является ли заданное целое число в диапазоне от 1 до 100 кратным заданному однозначному числу. Определите, является ли заданное целое число в диапазоне от 1 до 100 простым или составным.4.ОА.С. Создавайте и анализируйте шаблоны.4.ОА.С.5. Создайте шаблон числа или формы, который следует заданному правилу. Определите очевидные особенности шаблона, которые не были явными в самом правиле. Например, учитывая правило «Добавить 3» и начальный номер 1, создайте термины в результирующей последовательности и обратите внимание, что термины чередуются между нечетными и четными числами. Неформально объясните, почему числа будут продолжать чередоваться таким образом. Например, учитывая правило «Добавить 3» и начальный номер 1, создайте термины в результирующей последовательности и обратите внимание, что термины чередуются между нечетными и четными числами. Неформально объясните, почему числа будут продолжать чередоваться таким образом.4.НБТ. 4 класс — Числа и операции с основанием десять4.НБТ.А. Обобщить понимание разряда для многозначных целых чисел.4.НБТ.А.1. Знайте, что в многозначном целом числе цифра на одном месте в десять раз больше, чем на месте справа от нее. Например, поймите, что 700 долларов \дел 70 = 10 долларов, применив концепции разряда и деления.4.НБТ.А.2. Читать и писать многозначные целые числа, используя числа с основанием десять, имена чисел и расширенную форму. Сравните два многозначных числа на основе значений цифр в каждом разряде, используя символы $>$, = и $<$, чтобы записать результаты сравнения. Сравните два многозначных числа на основе значений цифр в каждом разряде, используя символы $>$, = и $<$, чтобы записать результаты сравнения.4.НБТ.А.3. Используйте понимание разрядности для округления многозначных целых чисел до любого места.4.НБТ.Б. Используйте понимание позиционного значения и свойства операций для выполнения многоразрядной арифметики.4.НБТ.Б.5. Умножьте целое число до четырех цифр на однозначное целое число и умножьте два двузначных числа, используя стратегии, основанные на разрядности и свойствах операций. Проиллюстрируйте и объясните расчет, используя уравнения, прямоугольные массивы и/или модели площадей.4. НБТ.Б.6. Находите целые числа в частных и остатках с до четырехзначными делителями и однозначными делителями, используя стратегии, основанные на разрядном значении, свойствах операций и/или взаимосвязи между умножением и делением. Проиллюстрируйте и объясните расчет, используя уравнения, прямоугольные массивы и/или модели площадей. НБТ.Б.6. Находите целые числа в частных и остатках с до четырехзначными делителями и однозначными делителями, используя стратегии, основанные на разрядном значении, свойствах операций и/или взаимосвязи между умножением и делением. Проиллюстрируйте и объясните расчет, используя уравнения, прямоугольные массивы и/или модели площадей.4.НФ. 4 класс — Числа и операции — Дроби4.НФ.А. Расширьте понимание дробной эквивалентности и порядка.4.НФ.А.1. Объясните, почему дробь $a/b$ эквивалентна дроби $(n \times a)/(n \times b)$, используя визуальные модели дробей, обращая внимание на то, как количество и размер частей различаются, даже если сами две фракции имеют одинаковый размер. Используйте этот принцип для распознавания и создания эквивалентных дробей.4. НФ.А.2. Сравните две дроби с разными числителями и разными знаменателями, например, создав общие знаменатели или числители, или сравнив с эталонной дробью, такой как 1/2. Признайте, что сравнения допустимы только тогда, когда две дроби относятся к одному и тому же целому. Запишите результаты сравнений символами $>$, = или $<$ и обоснуйте выводы, например, с помощью визуальной фракционной модели. НФ.А.2. Сравните две дроби с разными числителями и разными знаменателями, например, создав общие знаменатели или числители, или сравнив с эталонной дробью, такой как 1/2. Признайте, что сравнения допустимы только тогда, когда две дроби относятся к одному и тому же целому. Запишите результаты сравнений символами $>$, = или $<$ и обоснуйте выводы, например, с помощью визуальной фракционной модели.4.НФ.Б. Создавайте дроби из единичных дробей, применяя и расширяя предыдущее понимание операций над целыми числами.4.NF.B.3. Под дробью $a/b$, где $a > 1$, понимается сумма дробей $1/b$.4. NF.B.3.а. Понимать сложение и вычитание дробей как соединение и разделение частей, относящихся к одному и тому же целому. NF.B.3.а. Понимать сложение и вычитание дробей как соединение и разделение частей, относящихся к одному и тому же целому.4.NF.B.3.б. Разложите дробь на сумму дробей с одинаковым знаменателем более чем одним способом, записывая каждое разложение уравнением. Обоснуйте разложения, например, с помощью визуальной дробной модели. Примеры: $\frac38 = \frac18 + \frac18 + \frac18$; $\frac38 = \frac18 + \frac28$; $2 \frac18 = 1 + 1 + \frac18 = \frac88 + \frac88 + \frac18.$4.NF.B.3.c. Складывать и вычитать смешанные числа с одинаковыми знаменателями, например, заменяя каждое смешанное число эквивалентной дробью и/или используя свойства операций и отношения между сложением и вычитанием.4. NF.B.3.d. Решайте текстовые задачи, включающие сложение и вычитание дробей, относящихся к одному и тому же целому и имеющих одинаковые знаменатели, например, используя визуальные модели дробей и уравнения для представления задачи. NF.B.3.d. Решайте текстовые задачи, включающие сложение и вычитание дробей, относящихся к одному и тому же целому и имеющих одинаковые знаменатели, например, используя визуальные модели дробей и уравнения для представления задачи.4.NF.B.4. Применяйте и расширяйте прежнее понимание умножения, чтобы умножить дробь на целое число.4.NF.B.4.а. Под дробью $a/b$ следует понимать кратное $1/b$. Например, используйте модель визуальной дроби, чтобы представить $5/4$ как произведение $5 \times (1/4)$, записав вывод уравнением $5/4 = 5 \times (1/4).$4.NF.B.4.b. Понимайте кратное $a/b$ как кратное $1/b$ и используйте это понимание, чтобы умножить дробь на целое число. Например, используйте модель визуальной дроби, чтобы выразить $3 \times (2/5)$ как $6 \times (1/5)$, распознав этот продукт как $6/5$. (Вообще, $n \times (a/b) = (n \times a)/b.$) (Вообще, $n \times (a/b) = (n \times a)/b.$)4.NF.B.4.c. Решайте текстовые задачи, связанные с умножением дроби на целое число, например, используя визуальные модели дробей и уравнения для представления задачи. Например, если каждый человек на вечеринке съест 3/8 фунта ростбифа, а на вечеринке будет 5 человек, сколько фунтов ростбифа потребуется? Между какими двумя целыми числами лежит ваш ответ?4.Н.Ф.К. Понимать десятичную запись дробей и сравнивать десятичные дроби.4.NF.C.5. Выразите дробь со знаменателем 10 в виде эквивалентной дроби со знаменателем 100 и используйте эту технику, чтобы сложить две дроби со знаменателями 10 и 100 соответственно. Но сложение и вычитание с разными знаменателями вообще не обязательны для этого класса. Например, выразите $3/10$ как $30/100$ и добавьте $3/10 + 4/100 = 34/100$. 4.NF.C.6. Используйте десятичную запись для дробей со знаменателем 10 или 100. Например, перепишите $0,62$ как $62/100$; описать длину как $0,62$ метра; найдите $0,62$ на диаграмме с числовыми линиями.4.NF.C.7. Сравните два десятичных знака с сотыми, рассуждая об их размере. Признайте, что сравнения действительны только тогда, когда два десятичных знака относятся к одному и тому же целому. Запишите результаты сравнений символами $>$, = или $<$ и обосновывайте выводы, например, с помощью визуальной модели.4.МД. 4 класс — Измерения и данные4. МД.А. Решайте задачи, связанные с измерением и преобразованием измерений из большей единицы в меньшую. МД.А. Решайте задачи, связанные с измерением и преобразованием измерений из большей единицы в меньшую.4.МД.А.1. Знать относительные размеры единиц измерения в пределах одной системы единиц, в том числе км, м, см; кг, г; фунт, унция; л, мл; ч, мин, сек. В рамках единой системы измерения выражайте измерения в большей единице через меньшую. Запишите эквиваленты измерений в таблицу из двух столбцов. Например, известно, что 1 фут в 12 раз длиннее 1 дюйма. Выразите длину змеи длиной 4 фута как 48 дюймов. Создайте таблицу преобразования для футов и дюймов, перечислив пары чисел $(1, 12)$, $( 2, 24)$, $(3, 36)$, …4.МД.А.2. Используйте четыре операции для решения текстовых задач, связанных с расстояниями, интервалами времени, объемами жидкостей, массами объектов и деньгами, включая задачи с простыми дробями или десятичными знаками, а также задачи, требующие выражения измерений, выраженных в более крупной единице, через меньшую единицу. . Представляйте измеряемые величины с помощью диаграмм, таких как диаграммы с числовыми линиями, которые имеют шкалу измерения. . Представляйте измеряемые величины с помощью диаграмм, таких как диаграммы с числовыми линиями, которые имеют шкалу измерения.4.МД.А.3. Применяйте формулы площади и периметра для прямоугольников в реальных и математических задачах. Например, найдите ширину прямоугольной комнаты, зная площадь пола и длину, рассматривая формулу площади как уравнение умножения с неизвестным коэффициентом.4.МД.Б. Представлять и интерпретировать данные.4.МД.Б.4. Создайте линейный график для отображения набора данных измерений в долях единицы $(1/2, 1/4, 1/8)$. Решайте задачи на сложение и вычитание дробей, используя информацию, представленную в виде линейных графиков. Например, по линейному графику найдите и интерпретируйте разницу в длине между самым длинным и самым коротким экземпляром в коллекции насекомых.4. МД.К. Геометрические измерения: понимать понятия угла и измерять углы. МД.К. Геометрические измерения: понимать понятия угла и измерять углы.4.МД.С.5. Распознавать углы как геометрические фигуры, которые образуются там, где два луча имеют общую конечную точку, и понимать принципы измерения углов:4.MD.C.5.а. Угол измеряется по отношению к окружности с центром в общей конечной точке лучей, принимая во внимание долю дуги окружности между точками, где два луча пересекают окружность. Угол, который проходит через 1/360 окружности, называется «углом в один градус» и может использоваться для измерения углов.4.MD.C.5.b. Угол, который проходит через $n$ углов в один градус, называется угловой мерой, равной $n$ градусам.4.МД. С.6. Измерьте углы в целых числах с помощью транспортира. Эскиз углов заданной меры. С.6. Измерьте углы в целых числах с помощью транспортира. Эскиз углов заданной меры.4.МД.С.7. Признать угловую меру аддитивной. Когда угол разлагается на непересекающиеся части, угловая мера целого равна сумме угловых мер частей. Решите задачи на сложение и вычитание, чтобы найти неизвестные углы на диаграмме в реальном мире, и математические задачи, например, используя уравнение с символом для неизвестной меры угла.4.Г. 4 класс — Геометрия4.Г.А. Рисуйте и идентифицируйте линии и углы, а также классифицируйте фигуры по свойствам их линий и углов.4.Г.А.1. Рисовать точки, прямые, отрезки, лучи, углы (прямые, острые, тупые), перпендикулярные и параллельные прямые. Определите их на двумерных фигурах.4. Г.А.2. Классифицировать двумерные фигуры на основе наличия или отсутствия параллельных или перпендикулярных линий, а также наличия или отсутствия углов заданной величины. Распознавать прямоугольные треугольники как категорию и определять прямоугольные треугольники. Г.А.2. Классифицировать двумерные фигуры на основе наличия или отсутствия параллельных или перпендикулярных линий, а также наличия или отсутствия углов заданной величины. Распознавать прямоугольные треугольники как категорию и определять прямоугольные треугольники.4.Г.А.3. Распознайте линию симметрии двухмерной фигуры как линию, проходящую через фигуру, так что фигуру можно сложить по этой линии на соответствующие части. Определите линейно-симметричные фигуры и нарисуйте линии симметрии.25 фантастических бесплатных математических игр для четвертого класса Математика в четвертом классе приносит много новых задач, таких как деление с остатками и десятичными дробями. 1. Развлекайтесь делением с Remainders WantedУчащиеся четвертого класса учатся делить большие числа, часто с остатком. В этой игре остаток является целью! На каждом ходу учащиеся кладут фишку на число на доске, а затем бросают кубик, чтобы увидеть, на какое число они будут его делить. Остаток — это их счет за этот ход! Узнать больше: Мама-учительница-скаут 2. Предложите им повязки на голову Factor FrenzyДети используют повязки на голову из долларового магазина, чтобы прикладывать ко лбу карточки с произведениями умножения. Их партнеры пытаются заставить их угадать число, рассказывая им факторы, не называя само число. Подробнее: Обучение с видом на горы 3. Разработайте стратегию, чтобы выиграть в игре «Фактор» Напишите числа от 1 до 30, как показано на рисунке. Дополнительная информация: Cognitive Cardio 4. Расскажите о закономерностях, спросив: «Что вы заметили?»Составьте задачу с образцом и попросите учащихся записать то, что они заметили, на стикерах. Соберите и обсудите заметки, чтобы увидеть, какие из них помогут найти правильное число, соответствующее шаблону. Наградные баллы за правильные ответы, если хотите. Подробнее: Семейный вечер математики 5. Угадай, а затем выведи с помощью Решателя числовых шаблонов Нарисуйте круг и задайте диапазон чисел, а затем сообщите учащимся четвертого класса, что вы задумали закономерность. Когда они начнут угадывать числа, запишите их внутри круга, если они соответствуют образцу, и снаружи, если нет. Узнайте больше: Education.com 6. Подбрасывайте кубики LEGO, чтобы попрактиковаться в расстановке значенийКубики LEGO идеально подходят для занятий с расстановкой значений. Бросьте кирпичи на самодельную мишень с кольцами, обозначающими единицы, десятки и так далее. Подсчитайте гвозди каждого кирпича, которые приземляются на кольцо позиционного значения, а затем сложите их, чтобы получить окончательное число. 7. Соберите число, включая десятичные дроби.Дети выбирают несколько карточек с числами, а затем пытаются решить ряд задач, например, составить максимально возможное число. Добавьте десятичную карту, чтобы усложнить игру. Узнайте больше: Mathwire.com 8. Играйте, чтобы выиграть Place Value Yahtzee Эти доски Place Value Yahtzee для бесплатной печати включают различные версии для разных уровней квалификации. Подробнее: Игры 4 Выигрыши/Значение разряда Yahtzee 9. Используйте игральные карты, чтобы попрактиковаться в десятичных разрядахУченики четвертого класса по очереди рисуют карточки, соревнуясь в построении максимально возможного числа до тысячных. Узнайте больше: Игры 4 Gains/Playing Card Decimals 10. Сложите карты, чтобы изучить расширенную формуВозьмите бесплатные распечатанные карты, а затем попросите детей бросить кости и выбрать подходящую карту. Они строят числа на прилагаемом рабочем листе, чтобы получить общее количество. Для дополнительной практики попросите их также написать названия слов. Дополнительная информация: Блог мероприятий для детей 11. Потренируйтесь играть в снежки Готовы к контролируемому хаосу в классе? На каждом листе бумаги напишите по одной цифре, подчеркнув, до какой степени ее нужно округлить. Раздайте каждому ученику по несколько листов и попросите их скомкать их в «снежки». Узнать больше: Tales From a Math Nut четвертого класса 12. Умножайте большие числа, чтобы получить три в рядУчащиеся четвертого класса работают над многозначным умножением, выбирая одно число из поля A и одно из поля B Они перемножают их друг с другом, пока их партнер проверяет их ответ на калькуляторе. Если они понимают это правильно, они помещают маркер на свободную печатную доску. Цель состоит в том, чтобы получить три места подряд. (Сообразительные игроки будут использовать округление, чтобы определить, какие числа выбрать следующими!) Узнайте больше: Учитель в горошек 13. Проведите турнир на частное Задачи на дивизионы соревнуются друг с другом, чтобы определить, у кого частное больше. Учащиеся используют ответ для каждого, чтобы заполнить скобку для следующего раунда. Подробнее: Education.com/Quotient Tournament 14. Дайте ложкам эквивалентную дробьSpoons — это классическая и любимая карточная игра, в которой игроки соревнуются, составляя комбинации из четырех одинаковых карточек, и хватают ложку. каждый раунд. В этой версии они соревнуются, чтобы сопоставить эквивалентные дроби (получите несколько бесплатных печатных карточек по ссылке). Подробнее: Игры 4 Gains/Spoons 15. Расставьте дроби по порядкуУчащиеся вытягивают карточки дробей, меняя их местами, чтобы составить последовательность из четырех карточек в возрастающем порядке. Узнайте, как это работает по ссылке. Подробнее: Math Geek Mama 16. Объявите войну дроби с домино Каждый ученик вытягивает костяшку домино и позиционирует ее как дробь. Затем они сравнивают два, чтобы увидеть, чей больше. Ученик-победитель сохраняет обе костяшки домино. (Больше крутых способов использования домино для дробных игр смотрите по ссылке. Подробнее: Комната Рунде 17. Соединяйте фракции, чтобы учиться и выигрыватьПеределайте набор Connect Four, чтобы играть в игры с дробями! Цель состоит в том, чтобы соответствовать не только вашим цветам, но и самим фракциям. Например, вам нужно четыре четверти подряд, но только три четверти, так что здесь тоже задействована стратегия. Подробнее: Нет времени на карточки 18. Рисуйте дроби без использования чиселМожете ли вы нарисовать дробь без использования чисел? Это задача этой игры фракций. Дети могут рисовать отдельные объекты, разделенные на части, или быть более творческими. Например, они могут нарисовать три яблока и два апельсина, чтобы представить три пятых. Подробнее: Fraction Pictionary/E is for Explore 19. Выстраивайте детей в очередь для практики с десятичной дробью Поднимите и подвигайте учеников четвертого класса, присвоив им числа. Нарисуйте карточку с шестизначным числом и попросите другого учащегося помочь им выстроиться в ряд, сказав что-то вроде: «9 стоит в разряде сотен». Подробнее: Two Sisters Teach 20. Используйте пластиковые яйца, чтобы сопоставлять дроби и десятичные числаВозьмите несколько пластиковых яиц из долларового магазина и напишите дроби на одной половинке с эквивалентными десятичными знаками на другой. Дети работают, чтобы соответствовать им. Узнайте больше: Meg Mac/Pinterest 21. Сразитесь с площадью и периметром, чтобы заполнить страницу графикаБросьте кости, чтобы увидеть размеры вашего следующего прямоугольника, затем отметьте его на доске. Попробуйте заполнить свою страницу полностью раньше, чем это сделает ваш партнер! (Пусть учащиеся напишут площадь и периметр в каждом блоке для практики.) Узнайте больше: Unschooling Conversations 22. Отправляйтесь на поиски мусора с измерениями Вооружите детей измерительными инструментами, а затем отправьте их на поиски объектов, которые соответствуют бесплатным распечатываемым карточкам с заданиями. Подробнее: 123Homeschool4Me 23. Игра в бинго по геометрииУченики четвертого класса изучают такие термины, как прямая, луч и типы углов. Эта бесплатная распечатанная игра в бинго — интересный способ сделать это! Подробнее: You’ve Got This Math 24. Обклейте столы скотчем, чтобы попрактиковаться с транспортиромИспользуйте маркеры и малярную ленту, чтобы дать учащимся множество углов для изучения и измерения! Если вы не можете писать на своих столах, попробуйте вместо этого использовать большой лист плотной бумаги. Подробнее: Курсив и цветные карандаши/Instagram 25. Сложите фигурки, чтобы обнаружить симметрию Разделите учащихся на группы и раздайте бумажные фигурки. Предложите каждой группе поэкспериментировать, складывая свои фигуры, чтобы увидеть, какие из них симметричны и сколько у них линий симметрии. Узнайте больше: Ловушка для учителя Нужны дополнительные идеи для четвертого класса? Ознакомьтесь с лучшими научными экспериментами и занятиями для 4-х классов.Кроме того, подпишитесь на наши бесплатные информационные бюллетени, чтобы получать все последние советы и идеи по обучению!Посмотрите эти 50 задач дня по математике для четвертого классаНачните свой ежедневный урок математики с задачи дня по математике для четвертого класса — это отличный способ подготовить почву для обучения! Включите их в начале своего математического блока, чтобы укрепить уверенность, навыки критического мышления и обучающееся сообщество. Студенты привыкнут читать по смыслу, а также определять ключевую информацию. Предложите учащимся записывать уравнения и рисовать картинки, чтобы объяснить свое мышление, так как это помогает им увидеть свет, когда они застряли! Темы в этих математических задачах для четвертого класса охватывают закономерности и разрядность, сложение/вычитание, умножение, деление, дроби, десятичные дроби, измерения и сравнения. Хотите весь этот набор текстовых задач в одном простом документе? Получите бесплатный пакет PowerPoint, отправив сообщение электронной почты здесь. Все, что вам нужно сделать, это опубликовать одну из задач на доске или экране проектора. Тогда пусть дети взять его оттуда. 1. Джилл написала число 730 918. Она предложила Джейн переставить цифры так, чтобы получилось максимально возможное число. Какое число получилось у Джейн?2. Маркусу дали этот загадочный узор и попросили его заполнить. Какие два числа он должен написать следующими?4, 7, 11, 14, 18, 21, 25, ___, ___ 3. Мистер Математика дал своему классу эти цифры: 1, 5, 7, 9, 2, 8 и 5. Он спросил их, чтобы сделать наименьшее возможное число, используя каждую цифру один раз. Каким будет это число?4. Детективы нашли этот цифровой шаблон как часть кода на клавиатуре для открытия хранилища. 27, 26, 24, 23, 21, __, __. Какие последние две цифры они должны ввести? Детективы нашли этот цифровой шаблон как часть кода на клавиатуре для открытия хранилища. 27, 26, 24, 23, 21, __, __. Какие последние две цифры они должны ввести?5. Велосипед Тома стоит на 50 долларов больше, чем велосипед Боба. Велосипед Боба стоил 180 долларов. Сколько стоил велосипед Тома?6. Рэнди купил 2 бейсболки по $5,25 каждая. Он также купил 2 браслета по 2,50 доллара каждый. Сколько денег он потратил?7. У новой кормушки было замечено много птиц. Было 12 воробьев, 15 ворон, 8 иволг, 3 белки и 9 кардиналов. Сколько птиц было всего?8. Прошлой зимой в музее истории города было много посетителей. В декабре их было 75, в январе — 98, в феврале — 69. Сколько всего посетителей было в музее прошлой зимой?9. Луис обустраивал свой новый офис. Он купил новый компьютер за 350 долларов. Он также купил принтер за 9 долларов.9 и два чернильных картриджа по 37 долларов каждый. Сколько он потратил?10. В обувном магазине Super Duper 3 дня была большая распродажа. Они продали 87 пар обуви в пятницу, 95 пар обуви в субботу и 83 пары обуви в воскресенье. Сколько пар обуви было продано вместе? В обувном магазине Super Duper 3 дня была большая распродажа. Они продали 87 пар обуви в пятницу, 95 пар обуви в субботу и 83 пары обуви в воскресенье. Сколько пар обуви было продано вместе?11. У Пиа была огромная коллекция наклеек. У нее было 280 наклеек. В коллекции ее подруги Джен было 155 наклеек. На сколько больше наклеек у Пии, чем у Джен?12. В этом сезоне Робин набрала 155 очков в баскетболе за Тэрритаун Тайгерс. У нее также было 30 подборов. В прошлом сезоне она набрала 106 очков. На сколько больше очков она набрала в этом сезоне, чем в прошлом?13. Джон пошел пообедать в кафе Cool Cat. Он потратил 1,25 доллара на сокосодержащий напиток и 5,50 доллара на бутерброд. Он также купил брауни за 99 центов. Он дал кассиру 20-долларовую купюру. Сколько сдачи он получил?14. Гоночный автомобиль Ральф проехал 1000 миль в большой автогонке по пересеченной местности. 775 из этих миль он проехал с собакой Спиди в машине. Остаток пути он проехал один. Сколько миль Ральф проехал без Спиди? Остаток пути он проехал один. Сколько миль Ральф проехал без Спиди?15. Пекарня Best Baked испекла 10 250 праздничных печений. Продали почти все. Осталось всего 56 человек. Сколько праздничного печенья они продали?16. На скотном дворе жили 3 кошки и 4 гуся. Сколько всего ног было?17. Донна собирает в саду 5 яблок каждую минуту. Сколько яблок она сорвала за 20 минут?18. Фокусник Моррис вытащил из своей шляпы 2 голубя, кроликов в два раза больше, чем голубей, и мышей в 4 раза больше, чем кроликов. Сколько животных он вытащил из своей шляпы?19. Тина готовит пиццу на 15 гостей. Если предполагается, что каждый человек (включая Тину) съест по 2 кусочка, сколько пицц из 8 кусочков должна приготовить Тина?20. Шеф-повар Чарли украшает праздничный торт кружком ягод. У него 6 ягод клубники, и он хотел бы положить между каждой клубникой по 5 ягод черники. Сколько черники ему нужно?22. Чтобы приготовить рагу на зиму, Джамалу нужно 3 фунта сладкого картофеля. Если они стоят 1,29 доллара за фунт, сколько будет стоить покупка достаточного количества сладкого картофеля? Чтобы приготовить рагу на зиму, Джамалу нужно 3 фунта сладкого картофеля. Если они стоят 1,29 доллара за фунт, сколько будет стоить покупка достаточного количества сладкого картофеля?22. В отеле Swanky 10 этажей. На каждом этаже по 16 номеров. Также есть бальный зал, два конференц-зала и ресторан. Сколько номеров в отеле?23. Миссис Мейсон купила новый книжный шкаф для библиотеки и заполнила его книгами. Было 6 полок. На двух верхних полках было по 50 книг на каждой полке. На нижних четырех полках было по 75 книг на каждой полке. Сколько книг было в новом книжном шкафу?24. Столовая заказала 6 упаковок печенья с шоколадной крошкой и 3 упаковки пирожных. В каждой пачке печенья было по 12 штук. Они продали 45 печенек и 30 пирожных. Сколько печенья осталось?25. В новой начальной школе 30 парт в каждом классе. В каждом классе четыре класса. В школе 5 классов. Сколько парт в школе?26. Джина посадила в своем саду шесть рядов моркови. В каждом ряду было по 30 морковок. Кролики съели половину ее моркови. Сколько морковок у нее осталось? В каждом ряду было по 30 морковок. Кролики съели половину ее моркови. Сколько морковок у нее осталось?27. Джек посадил волшебный боб. Выросшее бобовое растение в первый день было 1 фут высотой. Затем он удваивался в высоту каждый день. Какой высоты было растение на пятый день?28. Университет Большого мозга купил 15 новых суперкомпьютеров и 50 принтеров. Каждый суперкомпьютер стоил 5300 долларов. Принтер стоил 100 долларов. Сколько университет потратил на покупку новых компьютеров?29. В этом году на новом поле для гольфа ежемесячно проводилось 3 турнира. Курс открыт 12 месяцев в году. Каждый турнир был ограничен 101 игроком в гольф и был полным. Сколько гольфистов участвовало в турнирах вместе взятых в этом году?30. Школьный офисный принтер может печатать 200 страниц каждые 10 минут. Если принтер работает час подряд, сколько страниц он может напечатать?31. Люсия делает браслеты из бисера. На каждом браслете по 12 бусин. Для каждой школьной ярмарки она сделала по 55 браслетов. В школе было 3 ярмарки. Сколько браслетов сделала Люсия? На каждом браслете по 12 бусин. Для каждой школьной ярмарки она сделала по 55 браслетов. В школе было 3 ярмарки. Сколько браслетов сделала Люсия?32. Сэмми Спидбол — питчер команды Boogaloo Bearcats. Он практиковал свою подачу в субботу в течение часа утром и часа после обеда. Он бросал 20 передач каждые 30 минут. Сколько тренировочных бросков сделал Сэмми в субботу?33. У Серены было 35 вишен. Она дала по 8 каждой из своих сестер. У нее еще 3 осталось. Сколько сестер у Серены?34. Новая учительница раздавала карандаши своему классу на год. Она хотела раздать их поровну. У нее было 15 упаковок карандашей по 10 карандашей в каждой. У нее было 20 учеников. Сколько карандашей должен получить каждый ученик? Сколько карандашей останется?35. 150 детей записались в летнюю футбольную лигу. Будет десять команд, и Драконы — одна из команд. В каждой команде 3 тренера, и они хотят, чтобы в каждой команде было равное количество игроков. Сколько игроков должно быть на Драконах? Сколько игроков должно быть на Драконах?36. Компания Wonderful Widget ежедневно производит 480 виджетов. Каждый день у них работает 6 машин для изготовления виджетов, причем каждая машина производит одинаковое количество виджетов. Компания работает шесть дней в неделю. Сколько виджетов производит каждая машина?37. У фермера Фрэн 35 кур. Каждая курица несет по дюжине яиц в день. Фрэн упаковывает яйца в пачки по десять штук. Сколько упаковок яиц она упаковывает в день?38. Каждый год в последний день года ReadOn Publishers раздает школам бесплатные книги. У них 900 книг для бесплатной раздачи в этом году. 18 школ подали заявки на бесплатные книги. Сколько должна получить каждая школа, если они распределены равномерно?39. Тренер Синди встречается с каждым игроком для индивидуальной тренировки. Каждый игрок получит 15 минут с тренером. У тренера Синди есть на это 2 часа в субботу. Со сколькими игроками она может встретиться?40. У доктора Беа Велл 120 пациентов. ¼ из них носят очки. Сколько ее пациентов не носят очков? У доктора Беа Велл 120 пациентов. ¼ из них носят очки. Сколько ее пациентов не носят очков?41. У Люси 24 мягкие игрушки. Она любит слонов, и треть ее мягких игрушек — слоны. Половина слонов серые. Сколько у нее слонов?42. Энни собирает ракушки. В ее коллекции 120 ракушек. Они как из Атлантического океана, так и из Тихого океана. ¾ раковин из Атлантического океана. Сколько снарядов из Тихого океана?43. Билл сделал 7/8 своей домашней работы. У Энди 9/10 домашних заданий выполнено. У них одинаковое количество домашних заданий. Кто сделал больше домашних заданий?44. Хосе предложили 2/5 огромной плитки шоколада или 3/6 той же плитки. Он любит шоколад. Что ему выбрать, если он хочет больше всего шоколада?45. У Джанель есть 6 тетрадей для школы. У Донни на 1/3 больше, чем у Джанель. Сколько тетрадей у Джанелл и Донни вместе?46. Тоня нашла два маленьких интересных камня. Черный весит 0,3 унции. Красный весит 0,09.унции. Какой камень весит больше? Черный весит 0,3 унции. Красный весит 0,09.унции. Какой камень весит больше?47. У Лии есть бейсбольная бита длиной 2,5 фута. У Брайсона есть летучая мышь длиной 28 дюймов и еще одна длиной 2 фута 5 дюймов. У кого самая длинная бита?48. Класс мистера Смита собирал монеты в большую банку в течение 6 месяцев. Их монеты весили 2 фунта и 8 унций. Класс мисс Смит сделал то же самое. Их монеты весили 2 ½ фунта. Чьи монеты весили больше?49. Команда по легкой атлетике готовилась к большому соревнованию. Тим бегал по 25 минут каждый день в течение 5 дней. Том бегал по часу каждый день в течение 3 дней. Кто провел больше всего времени в бегах?50. Семья Джонсов уехала в аэропорт в 10:00 на отдых. Их рейс вылетает в 12:30. Они дважды останавливались на 10 минут каждый раз. Они прибыли в аэропорт в 23:30. Сколько времени они провели за рулем?Нравятся математические задачки для четвертого класса? Посетите наш центр четвертого класса, чтобы получить еще больше ресурсов. Ln в математике это: Что означает ln в математике?Что означает ln в математике? – Обзоры ВикиКогда вы видите ln, это означает натуральный логарифм (мы определим натуральные логарифмы ниже). В этом курсе будут использоваться только десятичные и натуральные логарифмы. Аналогично, что такое значение ln? Ln называется натуральным логарифмом. Его также называют логарифмом по основанию e. Здесь константа e обозначает число, являющееся трансцендентным числом и иррациональным, которое приблизительно равно значению 2.71828182845. Натуральный логарифм (ln) может быть представлен как ln x или logex. . Возможен ли журнал 0? журнал 0 не определен. Это ненастоящее число, потому что вы никогда не получите ноль, возведя что-либо в степень чего-либо другого. Вы никогда не сможете достичь нуля, вы можете приблизиться к нему только с помощью бесконечно большой и отрицательной силы. … Это потому, что любое число, увеличенное до 0, равно 1. Может ли ln быть отрицательным? Функция натурального логарифма ln(x) определена только для x>0. Во-вторых, log10 такой же, как ln? Нет, log10(x) не совпадает с ln(x), хотя оба они являются специальными логарифмами, которые чаще встречаются при изучении математики, чем какие-либо… Что такое ln и e в математике?Натуральный бревно, или ln, является обратным e. Буква «e» представляет собой математическую константу, также известную как натуральный показатель степени. Как и π, e является математической константой и имеет заданное значение. Значение e равно примерно 2.71828. … Итак, ln(x) = loge(Икс). Например, ln (5) = loge(5) = 1.609. Каково значение ln 10? Значение журнала от 1 до 10 для базы журнала e
Что такое бесконечность?Это означает, что е увеличивается с очень высокой скоростью, когда е возводится в бесконечную степень, и, таким образом, приводит к очень большому числу, поэтому мы заключаем, что е возводится в бесконечную степень. это бесконечность. Теперь рассмотрим, когда e возводится в степень отрицательной бесконечности. ⇒ е–∞ Существует ли логарифмическая бесконечность? Ложа ∞ = ∞, или ln (∞) = ∞ Мы можем заключить, что как натуральный логарифм, так и значение десятичного логарифма для обратного бесконечности имеют одно и то же значение, т. е. бесконечность. Что такое бесконечность? Ответ на этот вопрос ∞ . Естественная логарифмическая функция строго возрастает, поэтому она всегда растет, хотя и медленно. Как умножить ln? Правило продукта Можете ли вы взять ln нуля?Какой натуральный логарифм нуля? … Функция вещественного натурального логарифма ln (x) определена только для x> 0. Итак, натуральный логарифм нуля не определено. К чему подходит ln of 0? Таким образом, натуральный логарифм нуля равен не определено. ln(0) не определено. Почему мы используем ln? Мы предпочитаем натуральные логарифмы (то есть логарифмы по основанию e), потому что, как описано выше, коэффициенты при натуральном логарифме шкалы непосредственно интерпретируются как приблизительные пропорциональные различия: с коэффициентом 0.06 разница в 1 в x соответствует примерно 6% разнице в y и так далее. Как отписаться от бывшего? Функции f(x) = ln x и g(x) = ex нейтрализуют друг друга, когда одна функция используется для результата другой. Это то же самое, что и с f(x) = log x и g(x) = 10.x или возведения числа в квадрат, а затем извлечения квадратного корня из результата. Как упростить Lnx? Как сокращаются ln и e?Подставьте базовое число e в обе части уравнения. e и ln отменить друг друга оставив нам квадратное уравнение. x = 0 невозможно, так как нет возможности записать 0 как степень. Запишите левую часть как один логарифм. Каково значение логарифма ln 52? Таблицы значений натуральных логарифмов
Что является основанием ln 3? Кроме того, ln3 означает логарифм 3 с e в качестве основания и e = 2.71828, и, следовательно, ln3 =1.0986 (используя научный калькулятор) и, следовательно, ln3≠1 . Что такое лн в математикеНатуральный логарифмНатуральный логарифм — это логарифм по основанию e, где e — иррациональная константа, равная приблизительно 2,718 281 828 . Натуральный логарифм обычно обозначают как ln(x), loge(x) или иногда просто log(x), если основание e подразумевается. [1] Натуральный логарифм числа x (записывается как ln(x)) — это показатель степени, в которую нужно возвести число e, чтобы получить x. Натуральный логарифм может быть определён для любого положительного вещественного числа a как площадь под кривой y = 1/x от 1 до a. Простота этого определения, которое согласуется со многими другими формулами, в которых применяется натуральный логарифм, привела к появлению названия «натуральный». Это определение можно расширить на комплексные числа, о чём будет сказано ниже. Если рассматривать натуральный логарифм как вещественную функцию действительной переменной, то она является обратной функцией к экспоненциальной функции, что приводит к тождествам: Подобно всем логарифмам, натуральный логарифм отображает умножение в сложение: Таким образом, логарифмическая функция представляет собой изоморфизм группы положительных действительных чисел относительно умножения на группу вещественных чисел по сложению, который можно представить в виде функции: Формально ln(a) может быть определён как площадь под кривой графика 1/x от 1 до a, т. Это можно продемонстрировать, допуская следующим образом: Log ln в чем разницаНатуральный логарифм — это логарифм по основанию e, где e — иррациональная константа, равная приблизительно 2,718 281 828 . Натуральный логарифм обычно обозначают как ln(x), loge(x) или иногда просто log(x), если основание e подразумевается. [1] Натуральный логарифм числа x (записывается как ln(x)) — это показатель степени, в которую нужно возвести число e, чтобы получить x. Натуральный логарифм может быть определён для любого положительного вещественного числа a как площадь под кривой y = 1/x от 1 до a. Простота этого определения, которое согласуется со многими другими формулами, в которых применяется натуральный логарифм, привела к появлению названия «натуральный». Это определение можно расширить на комплексные числа, о чём будет сказано ниже. Если рассматривать натуральный логарифм как вещественную функцию действительной переменной, то она является обратной функцией к экспоненциальной функции, что приводит к тождествам: Таким образом, логарифмическая функция представляет собой изоморфизм группы положительных действительных чисел относительно умножения на группу вещественных чисел по сложению, который можно представить в виде функции: Формально ln(a) может быть определён как площадь под кривой графика 1/x от 1 до a, т. Говорящий в этом видео имеет то, что мне кажется австралийским акцентом (приношу свои извинения всем киви, если он на самом деле новозеландец), поэтому мне интересно, отличается ли это от страны к стране — я из Соединенных Штатов. и никогда не слышал, чтобы это произносилось таким образом. Итак, вопрос: как вы произносите $\ln$? Как это произносится другими в вашем регионе? Пожалуйста, включите в свой ответ всю важную региональную информацию ( Редактировать: или профессиональный контекст), что может иметь значение. ОТРЕДАКТИРОВАНО ДОБАВИТЬ: Я прекрасно понимаю, что многие математики предпочитают использовать обозначение «$\log x$» для $\log_e x$, и многие возражают против использования $\log$ для $\log_{ 10}$, также известный как «десятичный логарифм». ВТОРОЕ РЕДАКТИРОВАНИЕ : Я должен был включить это в свой первоначальный пост, но может случиться так, что произношение также зависит от профессионального контекста: то есть, возможно, математики в вашем университете произносят это как «бревно», химики произносят это «элл эн», а школьный учитель в соседнем квартале говорит «ланн». Поэтому, отвечая на вопрос, предоставьте любую соответствующую контекстную информацию, которая может помочь уточнить объем вашего ответа. 92$) Я бы сказал: «элл энн экс в квадрате». $\endgroup$ $\begingroup$ Ванкувер, Канада. $\endgroup$ 6 $\begingroup$ Поскольку английский язык не является родным, и мне приходится довольно часто читать математические выражения, я пользуюсь следующими справочниками: Что касается $\ln$, эти руководства рекомендуют:
из [1] и [2];
из [1], и это совпадает с вашим примером; [2] рекомендует и другие варианты произношения, но я подозреваю, что они встречаются реже. $\endgroup$ 1 $\begingroup$ Я произношу $\ln x$ как «log ex» и обычно пишу его как $\log x,$ или иногда, когда разговариваю с первокурсниками или подобными неопытными людьми, как $\log_e x$ . К сожалению, в учебниках по алгебре для средней школы учащихся учат, что «логарифм» без нижнего индекса всегда означает логарифм с основанием 10$. Поскольку натуральный логарифм действительно представляет собой натуральный логарифм для использования в вычислениях, он записывается как $\log$ без нижнего индекса. Некоторые математики пишут его как $\ln$, но все же понимают, что $\log$, написанное другими, означает логарифм по основанию $e$. Только среди нематематиков этот последний факт неизвестен. Что в нем «естественного» можно увидеть здесь:
\начать{выравнивать}
& \frac d {dx} \log_{10} x = \frac{\text{некоторая постоянная}} x \\[10pt]
& \frac d {dx} \log_6 x = \frac{\text{некоторая другая константа}} x \\[10pt]
& \текст{и т. $\endgroup$ 17 $\begingroup$ Обычно я говорю «журнал», несмотря ни на что, а если используется конкретная база, я говорю «логарифм базы-n». К особым случаям относится «двоичный журнал» для журнала с основанием 2, который я записываю как $\lg$. Вместо $\ln$ я просто произношу буквы «ell-enn» или, вернее, всю эту чертовщину — «натуральное бревно». Иногда я слышал, как ставили ударение на букву «л» и говорили «лин» или «лен», но это случается редко. Я говорю как американский студент — я живу в Техасе, но на самом деле я не уроженец какого-либо другого штата (хотя я жил в Сан-Диего, когда учился в старшей школе). $\endgroup$ $\begingroup$ Когда я учился в школе (в Англии), мы произносили это слово «лонн», но я сижу рядом с учителем математики (английского языка), который говорит «ланн». Теперь я просто произношу это «журнал» FWIW. (Чтобы уточнить, я произношу это «log ex» даже в контекстах, которые требуют от меня писать $\ln x$, с чем мне иногда приходится иметь дело!) $\endgroup$ 4 $\begingroup$ Я израильтянин, учусь в очень международном австралийском университете. В Израиле мы говорим «lan» (произносится близко к английскому слову «gun»). Здесь я столкнулся со столькими вариациями: Все вышеперечисленные были носителями английского языка из разных уголков мира. Что касается твоего «линна», я думаю, что это был новозеландец. Иногда их e звучит как i. $\endgroup$ $\begingroup$ Когда я произносил это вслух, единственный способ, которым я когда-либо говорил или слышал, это как «натуральный логарифм $x$ в квадрате» или «логарифм $x$ в квадрате». У меня также иногда в голове было написано «ell-enn», что значительно экономит время, но может быть неправильным путем, если вы также имеете дело с другими переменными. Я никогда раньше не слышал, чтобы кто-то использовал «linn» или «lunn», хотя это также кажется хорошим способом сэкономить время во время разговора, не путая его с именами переменных. $\endgroup$ 3 $\begingroup$ Отправляясь в среднюю школу в Техасе, я всегда говорил это как аббревиатуру: «el en of ex». «log of ex» = $log(x)$ «лужайка ex» = $ln(x)$ $\endgroup$ $\begingroup$ Однажды я произнес это «лин» перед кучей математических гиков, и все они надо мной смеялись. (Я в США.) На самом деле я никогда раньше не слышал, чтобы это произносилось, и у всех было много раз. Я также слышал «log-en» для естественного журнала, но обычно просто «log», если вы не конкретны. $\endgroup$ $\begingroup$ Я привык: Запомнить $$ \ln(x) =\log_{2,718…}(x) $$ поэтому вполне оправдано называть его журналом . $\begingroup$ Мой преподаватель из Центральной/Восточной Европы, и она произносит $\ln x$ как «Logaritmus x». $\endgroup$ 4 $\begingroup$ Эта тема была причиной многих довольно горячих споров, когда я был 16-17-летним студентом. По крайней мере, в Великобритании «элл-энн» и «лунь» довольно распространены. В университете «бревно» было всем, что имело значение. Это похоже на то, как a/b равно «a на b», «a на b» и «a делится на b»: как только вы достигаете определенного уровня, все понимают, что вы имеете в виду, и вы не чувствуете необходимости спорить. об этом. $\endgroup$ $\begingroup$ Я австралиец, и его акцент кажется мне британским, а не австралийским. $\endgroup$ 1 $\begingroup$ Так как я ежедневно занимаюсь в основном логикой, двусмысленность — это грех. Я всегда говорю «натуральный логарифм» или «логарифмическая база e», чтобы предотвратить неправильное толкование из-за двусмысленности простого слова логарифм. $\endgroup$ 1 $\begingroup$ Исходя из американского опыта компьютерных наук (мы тоже используем журналы!), мы обычно называем его просто «журнал» независимо от того, натуральный это журнал или нет. $\endgroup$ $\begingroup$ По моему опыту, по крайней мере, в области математики, большинство людей называют это просто «бревно». Можно с уверенностью сказать, что когда речь идет о математике, общепризнано, что число ln естественно. Таким образом, когда математики говорят log, они, скорее всего, имеют в виду ln, а не $\log_{10}$. Ваша ситуация, когда «журнал» означает исключительно $\log_{10}$ (о чем вы беспокоитесь), будет редкой. Если кто-то когда-нибудь использует $\log_{10}$, он или она, вероятно, добавит: «Я имею в виду общий журнал с основанием 10». Неспециалисты (я полагаю) редко используют журнал (во всех смыслах), поэтому меня не беспокоит путаница. $\endgroup$ 2 Твой ответЗарегистрируйтесь или войдите в системуЗарегистрируйтесь с помощью Google Зарегистрироваться через Facebook Зарегистрируйтесь, используя адрес электронной почты и пароль Опубликовать как гостьЭлектронная почта Требуется, но никогда не отображается Опубликовать как гостьЭлектронная почта Требуется, но не отображается Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie Алгебра — Логарифмические функции Онлайн-заметки Пола Показать мобильное уведомление Показать все примечания Скрыть все примечания Мобильное уведомление Похоже, вы используете устройство с «узкой» шириной экрана ( т. Раздел 6-2: Логарифмические функцииВ этом разделе нам нужно перейти к функциям логарифмирования. Это может быть сложной функцией для построения графика сразу. Будут некоторые другие обозначения, к которым вы не привыкли, и некоторые свойства могут быть не такими интуитивными. Однако не отчаивайтесь. Как только вы разберетесь с ними, вы обнаружите, что они на самом деле не так уж плохи, и обычно требуется немного поработать с ними, чтобы понять их. Вот определение функции логарифма. 9y} = x\) называется экспоненциальной формой . Обратите внимание, что требование \(x > 0\) на самом деле является результатом того факта, что мы также требуем \(b > 0\). Теперь давайте обратимся к используемым здесь обозначениям, так как обычно это самое большое препятствие, которое ученики должны преодолеть, прежде чем начать понимать логарифмы. Во-первых, «логарифмическая» часть функции — это просто три буквы, которые используются для обозначения того факта, что мы имеем дело с логарифмом. Они не являются переменными и не означают умножения. Они здесь только для того, чтобы сказать нам, что мы имеем дело с логарифмом. 9x}\) в такой форме, но это не так. Просто похоже, что это может быть то, что происходит. Важно соблюдать прямолинейность записи логарифмов, иначе вам будет очень сложно их понять и работать с ними. Теперь давайте кратко рассмотрим, как мы вычисляем логарифмы. Пример 1 Оцените каждый из следующих логарифмов. Показать все решения Скрыть все решения Показать обсуждение Реальность такова, что прямое вычисление логарифмов может быть очень трудным процессом даже для тех, кто действительно в них разбирается. Обычно гораздо проще сначала преобразовать логарифмическую форму в экспоненциальную. В такой форме мы обычно можем получить ответ довольно быстро. 94}\), и т. д. , пока не получите 16. В этом случае нам нужен показатель степени 4. Следовательно, значение этого логарифма равно . \[{\log _2}16 = 4\] Перед тем, как перейти к следующей части, обратите внимание, что основа для них является очень важной частью обозначений. c \({\log _6}216\) Показать решение 93}}} = \frac{{27}}{8}\] Надеюсь, теперь у вас есть представление о том, как вычислять логарифмы, и вы начинаете разбираться в обозначениях. Есть еще несколько оценок, которые мы хотим сделать, однако нам нужно ввести некоторые специальные логарифмы, которые встречаются на очень регулярной основе. Это десятичный логарифм и натуральный логарифм . Вот определения и обозначения, которые мы будем использовать для этих двух логарифмов. \[\ begin{align*}& {\mbox{десятичный логарифм:}}\hspace{0,25 дюйма}\log x = {\log _ {10}}x\\ & {\mbox{натуральный логарифм:}}\ hspace {0,25 дюйма} \ ln x = {\ log _ {\ bf {e}}} x \ end {align *} \] Итак, десятичный логарифм — это просто логарифм по основанию 10, за исключением того, что мы опустили часть обозначения «по основанию 10». Давайте взглянем еще на пару оценок. Пример 2 Оцените каждый из следующих логарифмов. Показать все решения Скрыть все решения Показать обсуждение Чтобы выполнить первые четыре вычисления, нам просто нужно вспомнить, как они обозначаются и какое основание подразумевается этими обозначениями. Последние две оценки должны проиллюстрировать некоторые свойства всех логарифмов, которые мы в конечном итоге рассмотрим. Таким образом, при вычислении логарифмов все, что мы действительно спрашиваем, это какой показатель степени мы положили в основание, чтобы получить число в логарифме. Теперь, прежде чем мы перейдем к некоторым свойствам логарифмов, давайте сначала нарисуем пару быстрых графиков. Пример 3 Нарисуйте график десятичного логарифма и натурального логарифма на одной системе координат. Показать решение Этот пример имеет две точки. Во-первых, он познакомит нас с графиками двух логарифмов, которые мы, скорее всего, увидим в других классах. Кроме того, это даст нам некоторую практику использования нашего калькулятора для оценки этих логарифмов, потому что реальность такова, что именно так нам нужно будет выполнять большинство этих оценок. Вот таблица значений двух логарифмов.
2 часть
Ваше сообщение отправлено! + Гдз по математике Виленкин 6. Принципы эффективной самоподготовки Принципы эффективной самоподготовкиСправочник по математике для 6 класса к Виленкину представляет собой сборник готовых решений и ответов, который составлен на основе учебника математики для шестиклассников, составленного группа российских авторов — Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Решебник на учебник по математике 6 класс от ВиленкинаГДЗ по математике за 6 класс позволяет проверить правильность выполнения домашнего задания учащимися. С его помощью им удается самостоятельно понять алгоритм решения сложных задач. Более того, готовые решения и ответы являются подсказкой для родителей, стремящихся оказать своим детям посильную помощь в подготовке домашних заданий по математике. Решатель позволяет снизить нагрузку на шестиклассников, которые не всегда успевают разобраться в решении примера или задачи на уроке. Интерфейс нашего сайта делает пользование учебником максимально удобным для детей и родителей: Такие опции позволяют сделать процесс выполнения работы по математике максимально эффективным, как с точки зрения результата, так и с точки зрения экономии времени. Учебник по математике для 6 класса от Виленкина, Жохова, Чеснокова и ШварцбургаНа нашем сайте представлены готовые решения и ответы к заданиям учебника для 6 класса от Виленкина Н.Я. В настоящее время в большинстве школ используется 30-е издание, выпущенное в 2013 г. Учебник подробно описывает два основных раздела арифметики: В учебнике также представлена информация о таких арифметических понятиях, как НОК (наименьшее общее кратное) и НОД (наибольший общий делитель), порядке их вычисления, а также особенностях составления пропорций. Книга знакомит шестиклассников с особенностями координат на плоскости, а также с понятием масштаба. Среди школьных предметов особняком стоит математика. Действительно, его изучению посвящено очень много времени. При этом математика начинается уже в первом классе и заканчивается только в конце одиннадцатого. Кроме того, в конце 9-го и 11-го курсов именно по математике предстоит пройти итоговую аттестацию, именуемую ОГЭ и ЕГЭ соответственно. Выпускные экзамены обязательны, т.е. их нельзя избежать ни при каких обстоятельствах. При этом математические способности разных детей сильно отличаются. Не всем предмет дается без труда. В последнем случае будет полезно использовать вспомогательную литературу, например, онлайн-книгу решений Виленкина с содержанием правильных ответов. Учебно-методический комплекс Н.Я. Виленкина, В.И. Жохова, А.С. Чеснокова и С.И. Шварцбурда распространяется издательством «Мнемозина» с 2015 по 2019 год. Используется во многих школах Российской Федерации. За что школьники любят ГДЗ Виленкин по математике?В зависимости от врожденных способностей к точным наукам у разных людей изучение алгебры требует разного уровня усилий и времени. Оснащенный большим количеством полезных прикладных материалов сборник для 6 класса, авторами которого являются Виленкин, Жохов, Чесноков, имеет ряд преимуществ: Ответы, данные в ГДЗ по математике, нельзя просто переписать. Их следует тщательно изучить, найти закономерности и полезные решения. Почему книга решений Виленкина и Жохова для 6 класса может заменить репетитора?Если школьник будет стараться на протяжении всей школьной жизни, то с большой вероятностью он получит высокие баллы на выпускном экзамене и сможет поступить в хороший вуз. При изучении математики особенно важно не допускать пробелов. В шестом классе нужно серьезно подойти к разработке абзацев, решению задач, отработке практических навыков: Достаточная практика в решении примеров и упражнений, а также своевременное устранение пропусков убережет ученика от проблем в старшей школе. Поэтому ГДЗ онлайн можно рекомендовать любому шестикласснику, который сталкивается с непонятными темами на уроках или при выполнении домашних заданий. В шестом классе происходит процесс разделения предмета математики на алгебру и геометрию. Это приводит к тому, что учащимся необходимо осваивать новые сложные понятия и задачи. Однако не каждый студент сможет самостоятельно освоить такой материал, и здесь на помощь придет книга с решениями, созданная автором. Н.Я. Виленкин . Учебник по математике 6 класс станет доступнее, если ГДЗ . Это позволит студенту лучше разобраться с новыми для него темами и задачами, на решенном примере. С помощью данного пособия школьник снижает сложность домашней подготовки к занятиям. Это также позволяет учащимся самостоятельно решать задачи в будущем без каких-либо подсказок. ГДЗ способствует пониманию учащимися языка математики, углубляет их навыки по общим принципам решения математических примеров. ГДЗ за рабочую тетрадь по математике для 6 класса Рудницкая В.Н. можно скачать. ГДЗ к учебнику по математике для 6 класса Виленкин Н. ГДЗ для контрольных работ по математике за 6 класс Жохов В.И. можно скачать. ГДЗ к дидактическим материалам по математике за 6 класс Попов М.А. можно скачать Если ученик действительно хочет разобраться в сложном предмете, ему придется правильно использовать ГДЗ по математике 6 класс Виленкин: Работать необходимо только с теми ГДЗ, которые написаны опытными преподавателями, не содержат опечаток, подробно и понятно объясняют даже самые сложные понятия. ГДЗ по математике за 6 класс Виленкин — онлайн-сборник готовых ответов (из книги решений) на задания одноименного учебника по математике, составленный Виленкиным Н.Я., Жоховым В.И., Чесноковым А.С., Шварцбурд С.И. Позволяет учащимся проверять правильность выполнения домашнего задания и решать сложные задачи, а родителям оказывать своим детям посильную помощь при подготовке домашнего задания по математике. Ассистент по изучению математики в 6 классе — Виленкин Н.Я. 2013Курс математики для 6 класса общеобразовательных школ Российской Федерации включает широкий круг тем, связанных с натуральными и дробными числами. Высокий уровень сложности отдельных заданий часто не позволяет ребенку на занятии разобраться с алгоритмом решения примера. Решением данной задачи может стать Решатель по математике для 6 класса Виленкин Н. Такие варианты позволяют ученикам самостоятельно разобраться в решении той или иной задачи, а родителям адекватно проверить домашнее задание учеников. Кроме того, таким образом можно сэкономить массу времени. Что входит в решение по математике за 6 класс: Виленкин, Жохов, Чесноков, Шварцдурд? Решение, представленное на сайте, составлено на основе учебника по математике для 6 класса под редакцией Виленкина Н.Я. в 30-м издании (2013 г.). Но это вовсе не означает, что здесь нельзя найти решения для более ранних и более поздних редакций: на самом деле нужно ввести в поисковую строку условия примера — и система найдет нужную задачу. Учебник Виленкина Н.Я. включает две основные главы: В первой части учебника подробно описаны понятие и признаки делимости чисел, механизм вычисления наименьшего общего короткого (НОК) и наибольшего общего делителя (НОД), а также алгоритм составления и решения пропорций . Во второй части подробно описаны правила выполнения математических действий с положительными и отрицательными числами, а также порядок решения уравнений с учетом расположения координат на плоскости. Наш сайт готовых домашних заданий – это не только помощь в решении домашних заданий для учащихся 6-х классов и их родителей, но и полноценное практическое пособие, позволяющее самостоятельно постигать азы математики. Гдз Дорофеев и Ф Шарыгин ГДЗ по математике за 5 класс Дорофеев — это онлайн-решение, раскрывающее подробный алгоритм выполнения примеров и задач по одноименному учебнику группы российских ученых — Дорофеева Г. Дорофеев Справочник по математике — важное дополнение к учебному процессу в пятом классеВ пятом классе школьники начинают свой путь со средней ступени общеобразовательной школы, что предполагает увеличение количества предметов и углубление в них. Не всем детям легко удается легко и быстро адаптироваться к новым условиям, возникают трудности с выполнением домашних заданий. Онлайн-решатель по математике Дорофеева для 5 класса позволяет пятиклассникам самостоятельно или с помощью родителей углубиться в предмет, научиться решать примеры и задачи. Сайт ГДЗ Путин предоставляет условия для максимально удобного его использования: Учащиеся и их родители могут найти готовое решение с правильным ответом на основе любого устройства — телефона, компьютера или планшета. Это позволяет детям понять алгоритм решения математических упражнений дома, в спокойной обстановке, а родителям следить за успеваемостью своих детей. ГДЗ по математике за 5 класс от Дорофеева — дроби, многоугольники, рациональные числаВ рамках выполнения домашнего задания учащийся должен закрепить теоретические знания, полученные на занятиях. Что делать, если ребенок выучил формулы, но не успел понять алгоритм решения примеров и задач? Используйте онлайн-сборники готовых домашних заданий, которые являются не основанием для списывания, а образцом для выполнения домашнего задания. Какие упражнения даются в ГДЗ по математике 5 класс Дорофеева? Электронная книга решений составлена на основе 4-го издания учебника Дорофеева Г.В. для 5 класса. Это позволяет родителям помочь пятиклассникам с арифметическими упражнениями. Математика 6 класс Дорофеев, Шарыгин Образование С каждым годом задачи, стоящие перед школьниками, усложняются, как и изучаемые дисциплины. Одним из самых сложных является математика, хорошее знание которой не только очень важно для жизни, но и помогает лучше разбираться в других взаимосвязанных предметах. Постичь мудрость этой науки можно с Решебник к учебнику «Математика 6 класс» Дорофеев, Шарыгин. Что в него входит.Двенадцать глав содержат более тысячи тематических заданий. В конце каждого раздела в ГДЗ по математике 6 класс есть упражнения на повторение и закрепление материала, которые позволят выявить, насколько учащиеся усвоили материал. Вам нужен решатель? Шестиклассникам предстоит постигать основы алгебры и геометрии в этом классе, так как скоро у них будет разделение предмета. «Просвещение», 2017 Математика, как и арифметика как ее важный подраздел, относится к перечню важнейших предметов, изучаемых в общеобразовательной школе. Именно от успешности овладения этой дисциплиной будет зависеть качество и уровень среднего образования, на которое может претендовать ребенок. Ученики с разными входными способностями в математике требуют дифференцированного подхода и разного уровня педагогического внимания. Коллектив опытных авторов-методистов (Дорофеев Г.В., Шарыгин И.Ф., Суворова С.Б. и др.) подготовил учебное пособие для 5 класса. На данной странице сайта представлено содержание V издания, а номера упражнений соответствуют версии 2017-2019 года. Учебное пособие соответствует ФГОС и рекомендовано для всех без исключения образовательных учреждений Российской Федерации. Как решатель Дорофеева для 5 класса помогает лучше понимать школьные задания?Благодаря хорошо подобранным и хорошо отсортированным задачам теперь проще сделать это самостоятельно. Вы можете быстро включить свой компьютер или планшет и подключиться к сайту готовых домашних заданий (DHS). По указателю таблицы легко найти номер нужного упражнения и ознакомиться с его выполнением. После этого нужно закрепить полученные ценные навыки и умения. Готовые ответы помогают: Программа учебника соответствует федеральным образовательным стандартам (ФГОС), обязательным для всех образовательных учреждений. Поэтому готовые решения могут быть адресованы самым широким категориям учащихся. Открытый доступ помогает быстро найти упражнения на сайте. Все номера соответствуют заданиям в учебнике. Какие темы можно пройти самостоятельно на ГДЗ Дорофеева, Шарыгина?Сборник подробно объясняет, как решать отдельные задачи из общеобразовательного курса. Студенту не нужно прилагать больших усилий, чтобы начать учиться. Учебник мотивирует ребенка стать более самостоятельным в контексте обучения. По мере продвижения ученик сам поймет, зачем ему нужно изучать предмет, и будет более осознанно относиться к процессу познания. Правильное отношение к обучению – залог хороших результатов и быстрого прогресса, развития необходимых психических и познавательных качеств, освоения практических приемов работы с числовой информацией. В пятом классе основными темами для учащихся будут следующие: Онлайн-сборник — мощный инструмент, который в умелых руках может одновременно решить большое количество проблем школьников. Однако не следует воспринимать ситуацию слишком упрощенно. ГДЗ по математике 5 класс Доровеев не является источником для простого списывания домашних заданий. Наоборот, это инструмент для развития мышления и более глубокого понимания, а также актуальных требований на уроках. ГДЗ по математике за 5 класс Дорофеев — онлайн-книга решений или сборник готовых ответов, составленный на основе одноименного учебника арифметики известных российских авторов — Дорофеева Г.В., Шарыгина И.Ф., Суворова С.Б. и другие, изданные в 2017 году. На его основе пятиклассникам будет проще разобраться в сложном алгоритме выполнения задач и уравнений, а родителям проверить успеваемость своих детей. Зачем тебе учебник по математике Дорофеева в 5 классе? В пятом классе у школьников закладываются знания по арифметике, которые станут основой для изучения алгебры и геометрии, физики и астрономии в старших классах. На основе практического пособия дети могут дома самостоятельно или со старшими разобрать порядок выполнения сложных примеров и заданий из домашних заданий и сравнить полученные ответы. На основе предложенных решений родители всегда смогут отслеживать успеваемость пятиклассников по предмету. На сайте ВИП-ГДЗ лучше всего использовать готовые домашние задания: достаточно ввести в поисковую строку номер ответа или часть его условия, чтобы получить решение за доли секунды. Кроме такого существенного преимущества, важно отметить: Ученик и родители могут использовать для поиска ответов любой электронный гаджет – будь то телефон, планшет или ноутбук. Что изучают пятиклассники — учебник по математике Дорофеева Г.В.Современная программа изучения арифметики ориентирована на ознакомление школьника с широким кругом тем, важных при дальнейшем изучении алгебры, геометрии, физики и химии. Именно поэтому в ГДЗ по математике для 5 класса Дорофеева можно найти задания и примеры по таким темам, как: Сайт ВИП ГДЗ — это удобная возможность разобраться со сложными примерами и задачами по арифметике в 5 классе без участия репетиторов и дополнительных занятий. Раствор по мату 1 ч 3 кл. Что в инструкцииМатематика 3 класс Моро, Бантова, Бельтюкова Школа России Образование Третьеклассников ждет трудный год. Мало того, что им придется усваивать много новой информации, так еще и постоянная работа по тестированию выбивает из колеи. Именно поэтому систематическое изучение тетрадь ответов к учебнику «Математика 3 класс» Моро, Бантова, Бельтюкова может значительно облегчить жизнь школьников, ведь в этом сборнике все подробно и понятно объяснено. Что в руководстве.Сборник разделен на две части, каждая из которых содержит сто одиннадцать страниц. Также в ГДЗ по математике 3 класс представлены задания базового и высокого уровня сложности. Дополнительные вопросы к параграфам помогут учащимся закрепить изученный материал. Для чего это нужно. Обучение в школах стало настолько сложным, что ученики все чаще начинают страдать истерическими проявлениями и полноценными психозами. Процент суицидальных попыток среди детей достигает критического уровня, и не все они связаны с так называемыми «группами смерти». Просто слишком сильный стресс, который испытывают дети во время учебы, ломает и без того неустойчивую психику. Не менее интересен и тот факт, что, несмотря на усложнение программы, педагоги по каким-то причинам до сих пор не адаптировались к новым условиям, поэтому родителям часто приходится восполнять пробелы в знаниях своих отпрысков, возникающие после уроков. Решебник к учебнику «Математика 3 класс» Моро очень пригодится в данном случае. «Образование», 2012 Издательство: Образование 2015. Интернет дает школьникам массу возможностей для обучения – здесь можно быстро найти решение, чтобы его списать, или получить дополнительные знания. Большинство родителей запрещают своим детям пользоваться электронными источниками информации. Рано или поздно математика вызывает трудности даже у отличника. И если родитель хочет воспитать своего ребенка самостоятельным и независимым от постоянной помощи взрослых, ему придется разрешить ученику использовать любой полезный для него ресурс в обучении, в том числе и готовые домашние задания. Нужен ли ГДЗ ученикам начальных классов?Если дети старшего возраста могут не спрашивать разрешения у мам и пап, а просто скачивать необходимые материалы, то третьеклассники такой привилегии пока лишены. И только родители могут решить, чем пользоваться при выполнении домашнего задания в их ситуации. Онлайн решение по математике для 3 класса (авторы М.И. Моро, М.А.Бантова и Г.В.Бельтюкова) : — не шпаргалка и не возможность списывания при составлении «домашнего задания». Сегодня даже ученики начальной школы сверяются с ними в процессе. самостоятельная работа . Такая книга поможет: Описание пособияПредставлен Решебник для 3 класса М.И. Moreau позволит подготовиться к проверочным и контрольным работам, разобраться с новыми задачами при выполнении домашних заданий. Представленные в публикации правильные ответы соответствуют типовой рабочей программе и будут полезны как ученикам обычных школ, так и тем, кто углубленно изучает математику. Благодаря простой структуре и оформлению в соответствии с требованиями ФГОС данное пособие незаменимо не только для учащихся начальных классов, но и для их учителей. Книга поможет вам быстро подготовить информацию к уроку и станет надежным источником нового для детей. Воспользоваться изданием онлайн можно на нашем сайте – нужно только знать номер нужного упражнения. ГДЗ к рабочей тетради по математике за 3 класс Моро М.И. можно скачать. ГДЗ для проверки работ по математике за 3 класс Волкова С.И. можно скачать. ГДЗ к тетради учебных достижений по математике за 3 класс Волкова С. ГДЗ на контрольно-измерительные материалы по математике за 3 класс Глаголев Ю.И. можно скачать Издательство: Education 2015. Интернет дает школьникам массу возможностей для обучения — здесь можно быстро найти решение, чтобы списать его, или получить дополнительные знания. Большинство родителей запрещают своим детям пользоваться электронными источниками информации. Однако такое знание — не зло, а просто средство, которое можно использовать во благо. Рано или поздно математика вызывает трудности даже у отличника. И если родитель хочет воспитать своего ребенка самостоятельным и независимым от постоянной помощи взрослых, ему придется разрешить ученику использовать любой полезный для него ресурс в обучении, в том числе и готовые домашние задания. Нужен ли ГДЗ ученикам начальных классов? Если дети старшего возраста могут не спрашивать разрешения у мам и пап, а просто скачивать необходимые материалы, то третьеклассники такой привилегии пока лишены. Описание пособия Представлен Решебник для 3 класса М.И. Moreau позволит подготовиться к проверочным и контрольным работам, разобрать новые задания при выполнении домашних заданий. Представленные в публикации правильные ответы соответствуют типовой рабочей программе и будут полезны как ученикам обычных школ, так и тем, кто углубленно изучает математику. Благодаря простой структуре и оформлению в соответствии с требованиями ФГОС данное пособие незаменимо не только для учащихся начальных классов, но и для их учителей. ГДЗ за рабочую тетрадь по математике для 3 класса Моро М.И. можно скачать. ГДЗ для проверки работ по математике за 3 класс Волкова С.И. можно скачать. ГДЗ к тетради учебных достижений по математике за 3 класс Волкова С.И можно скачать. ГДЗ на контрольно-измерительные материалы по математике за 3 класс Глаголев Ю.И. можно скачать Время отводится на изучение арифметики, первый раздел математики начальной школы. Учащимся предстоит освоить таблицу умножения, научиться выполнять действия (сложение, вычитание, деление, поиск целого остатка , умножение) с натуральными числами, решать простые практические задачи трех типов, а также понимать, как работать с цифрами в десятичной системе счисления. Именно от успешности овладения этой дисциплиной будет зависеть качество общеобразовательной подготовки, которую сможет применить ребенок. Моро М.И., Бантова М.А. и Бельтюкова Г.В. являются авторами Решебника для 3 класса. За подготовку к печати и распространение данного пособия в 2019 году отвечает Издательский дом «Просвещение». Онлайн-сборник соответствует ФГОС. Рекомендуется всем без исключения образовательным организациям. Российская Федерация для использования в начальной школе. Почему третьеклассники любят ГДЗ Моро по математике?На самом деле здесь все очень просто. Легко изучить сборник задач с готовыми ответами. Благодаря грамотно подобранным и отсортированным задачам это практически не проблема. Достаточно включить компьютер, телефон или планшет, чтобы подключиться к нашему сайту. С помощью указателя таблицы вы легко сможете найти номер нужного упражнения и ознакомиться с правильным его выполнением. После этого требуется закрепить полученные ценные навыки и умения. Пособие по математике Моро, Бантовой, Бельтюковой на сайте имеет следующие преимущества: Матрица в математике для чего нужна: Математика онлайнМатематика для ИИ: линейная алгебраВ мире IT сейчас часто можно услышать о машинном обучении, нейронных сетях и искусственном интеллекте. И не удивительно — эти отрасли быстро развиваются и используются для решения различного рода задач. Большинство концепций были открыты ещё 50 лет назад, и множество из них основаны на математических принципах. Поэтому у людей, пытающихся войти в данную нишу, часто возникает вопрос: «На каком уровне нужно знать математику?». Эта статья даст представление о некоторых необходимых основах, в частности, о базовых концепциях линейной алгебры. Базовые терминыПо сути, вся линейная алгебра вертится вокруг нескольких понятий: векторы, скаляры, тензоры и матрицы, — всё это очень важно для машинного обучения, ведь благодаря им можно абстрагировать данные и модели. Например, каждая запись в каком-нибудь наборе данных может быть представлена в виде вектора в многомерном пространстве, а параметры нейронных сетей абстрагируются как матрицы. СкалярСкаляр — это просто число, в отличие от вектора или матрицы. Скаляры определены как элементы поля, предназначенные для описания пространства вектора. Несколько скаляров образуют вектор. Скаляры могут быть представлены разными типами чисел: вещественными, действительными или натуральными. Обозначаются скаляры строчными и прописными буквами латинского и греческого алфавита: ВекторВектор — это упорядоченный массив скаляров. Скаляры выступают в роли координат точек в пространстве. Скопление векторов становится так называемым векторным пространством. Векторы можно складывать вместе, перемножать друг на друга и масштабировать. Они обозначаются жирным шрифтом. Каждый элемент вектора имеет индекс. МатрицаМатрица — это двумерный массив скаляров. Обозначается жирным шрифтом в верхнем регистре. Например, если говорить о матрице из вещественных чисел, где m рядов и n столбцов, записывается такая матрица вот так:Поскольку матрица — двумерный массив, элементы матрицы имеют два индекса:Две матрицы могут быть сложены или вычтены одна из другой, только если у матриц одинаковое количество рядов и столбцов. Важно заметить, что матричное произведение дистрибутивно и ассоциативно: Однако, иногда может понадобиться перемножить элементы матриц между собой. Такую операцию называют произведением Адамара (обозначается A ∘ B). Матрицы также можно умножать на векторы и на скаляры. Интересно, что произведением матрицы и вектора будет вектор: ТензорТензор — это многомерный массив чисел. Обычно в нём больше двух измерений, так что он может быть изображён как многомерная сетка, состоящая из чисел. На самом деле, матрицы — те же тензоры, только они двухмерные, вот и все их отличия. ОперацииЕсть несколько операций, которые можно производить с матрицами, и знание которых пригодится для понимания принципов работы ИИ. Транспонирование матрицыВ результате выполнения этой операции появляется так называемая транспонированная матрица. По сути, это зеркальное отображение матрицы по главной диагональной линии, которая начинается в верхнем левом и идёт в правый нижний угол. Транспонированной матрицей от матрицы A будет матрица AT (также A′, Atr, tA или At). Кроме того, транспонированную матрицу можно получить, записав ряды матрицы A как столбцы матрицы AT, а столбцы матрицы A — как ряды матрицы AT. Умножение единичной матрицы на векторСуществует такое понятие как единичная матрица. Перед тем, как вы продолжите, немного информации о диагональной матрице (она очень похожа на единичную). Все элементы матрицы, за исключением тех, что находятся на главной диагонали, равны нулю. Но, в отличие от единичной, на главной диагонали диагональной матрицы элементы имеют значение, не равное 1. Получается, единичная матрица — это вид диагональной матрицы. Они очень полезны для некоторых алгоритмов. Умножение на обратную матрицуОбратная матрица определяется следующим образом: Если умножить матрицу A на обратную ей матрицу A-1, получится единичная матрица. Обратная матрица похожа на обратное число. То есть для a обратным числом будет 1/a. Если обычное число умножить на обратное ему, получится единица: a * 1/a = 1. Здесь то же самое, только с матрицами. Псевдоинверсия Мура-ПенроузаДля неквадратных матриц нужно применять псевдоинверсию Мура-Пенроуза:Где U, D и V — сингулярное разложение матрицы A. Псевдоинверсия D+ матрицы D создаётся путём взятия элементов, обратных элементам матрицы, и её дальнейшим транспонированием. Но будьте осторожны с концепцией обратной матрицы A-1, потому что пока что она больше используется в теории, чем на практике. Это обусловлено тем, что вычислительные способности современных компьютеров позволяют дать лишь приблизительный ответ. Преобразование матрицы в скалярБывает, что нужно преобразовать матрицу в скаляр, для этого нужно найти определитель, он обозначается НормыИногда для работы с вектором нужно знать его размер. Для этого существуют специальные функции, которые называют нормами — Ln. Маленькая буква n обозначает количество измерений, в которых находится вектор. В зависимости от того, сколько измерений в вашем векторном пространстве, нормы будут разными. Наиболее известная норма — норма двумерного пространства (Евклидова норма). Чаще всего она представляет собой Евклидово расстояние от начала вектора до точки в пространстве, находящейся на конце этого вектора. При обобщении пространства на несколько измерений используют глобальную норму:На самом деле, нормой может быть любая функция, удовлетворяющая следующим требованиям: Часто, когда вы создаёте ИИ-приложение, очень важно различать элементы, равные 0, и элементы, имеющие значение, близкое к 0. Для этого используется норма L1. Она проста и растёт с одинаковой скоростью во всех точках векторного пространства. Если любой элемент вектора x движется от 0 к a — эта функция вырастает на a:Как упоминалось выше, в глубоком обучении параметры нейронных сетей абстрагируются как матрицы. Следовательно, нужно знать размер матрицы, и с этим нам поможет норма Фробениуса: ЗаключениеВ этой статье мы затронули основы линейной алгебры, которые пригодятся, чтобы понять, что же происходит в мире нейронных сетей и искусственного интеллекта. Надеемся, эта статья поможет вам начать свой путь в этой сфере. Успехов! Перевод статьи «Mathematics for Artificial Intelligence – Linear Algebra» что это такое в математике, операции и действия, как составить, примерыСпособ КрамераМетод Крамера используют для решения квадратной системы уравнений, представленной в линейном виде, где определитель основной матрицы не равен нулю. Её необходимо заменить равноценным матричным уравнением. Второй столбец вычисляют, а первый уже задан. Есть предположение, что определитель матрицы отличен от нуля. Из этого можно сделать выводы, что существует обратная матрица. Перемножив эквивалентное матричное уравнение на обратного формата матрицу, получим выражение: В итоге получают выражения: Из представленных уравнений выделяют формулы Крамера: Метод Крамера не представляет сложности. Он может быть описан следующим алгоритмом: Высчитывают определитель дельта базовой матрицы. Проверить решение матрицы методом Крамера онлайн позволяет калькулятор автоматического расчёта. Указывается также представление чисел в виде целого числа, обыкновенной или десятичной дроби. После введения всех предусмотренных параметров и нажатия кнопки «Вычислить» получают готовое решение. Предыдущая ПримечанияЛента
Матрица (1999)https://youtube.com/watch?v=ihTvN2iCnhA%3F Томас Андерсон с виду обыкновенный парень. Днём от работает программистом, а в ночное время суток проводит жизнь в необычном формате. Он занимается хакерством. Однажды к нему нагрянули странные люди, они сказали ему, что герой находится в матрице. Объяснить толком, что собой представляет данное явление, гости не могли. Немного позже к Томасу прибыл мужчина, которого власти объявили террористом. Он предложил юноше пойти дальше в изучениях странного понятия. Если же герой боится предпринимать столь глобальные шаги, он должен принять синюю таблетку. В том случае, если любопытство подсказывает двигаться дальше, нужно выпить красную таблетку. Парень решил действовать до конца. С этого мгновения он увидел иное пространство, в которым привычные человеческие каноны бездействуют. Факты о фильме: Кто такой Нео?Первый фильм «Матрица» заставляет нас вспомнить все древние пророчества, начиная с библейских; на каждом шагу нам твердят, что Нео – герой, Избранный, призванный спасти человечество от мира машин. Первая серия трилогии убеждает нас в этом, вторая «Матрица: Перезагрузка» – разочаровывает, третья «Матрица: Революция» – наполняет мессианскую роль Нео особым смыслом. Но кто же он, спаситель человечества эры машин? Молодой человек по имени Томас Андерсон днём работает программистом в солидной компании, а ночью — взламывает компьютеры, орудуя под хакерским ником Нео. Морфеус увлекает Нео за собой, уводит за пределы Матрицы в реальный мир. Символически это означает разрыв с системой, неповиновение властям, открытый переход на сторону террористов-повстанцев. Вот только имя Морфеуса слишком похоже на имя древнегреческого бога сна. Это символ обмана – Нео всё ещё во сне, он не освободился, хотя этого не знает. Нео сначала сопротивляется навязываемой ему роли мессии; но потом принимает на себя ответственность за будущее человечества. Он готов бороться с системой, готов бороться с Матрицей, он верит в то, что спасёт мир. Но вторая и третья части трилогии «Матрица» обрушивают на голову Нео страшную правду: он – такой же винтик в огромной машине мироздания, как и все другие, его действия запрограммированы, предусмотрены, и ему приходится заключать договор с Главным Компьютером, который он хотел уничтожить, и даже действовать с ним заодно. Далее используем свойство степеней Ответ Пример 2 Задание Найдите определитель матрицы А. Решение «Аниматрица»Основная статья: Аниматрица В 2003 году по мотивам вселенной «Матрицы» был выпущен сборник коротких аниме-OVA, связанных между собой общей тематикой и сеттингом. Название является комбинацией двух слов — «аниме» (англ. anime) и «матрица» (англ. matrix). По словам Вачовски, у них изначально были планы создать аниме по мотивам своего нашумевшего фильма, так как японские анимационные фильмы во многом послужили для них вдохновением. Вачовски являются авторами сценария только первого эпизода «Аниматрицы» («Последний полёт „Осириса“»). Для остальных эпизодов лично Вачовски были приглашены другие режиссёры (за исключением эпизода «Мировой рекорд»), которые сами написали сценарии своих работ. Вычисление определителя матрицы при помощи теоремы ЛапласаТеорема Лапласа – это глубокое разложение определителя по элементам. Напомним – минор – это определитель матрицы, который составлен методом вычёркивания – той строки и – того столбца. А алгебраическое дополнение – соответствующий минор, который берётся со знаком минус . Знаки же зависят от места элемента в определителе и определяются по схеме: Приведём пример решения алгебраических дополнений по схеме: Пример Задача Найти алгебраические дополнения элементов определителя: Решение Понятия алгебраического дополнения даёт возможность ещё одного способа определения определителя, который утверждается теоремой Лапласа (про распределение определителя): Теорема Определитель равняется сумме произведения элементов строк (столбца) на их алгебраические дополнения. Например, . – это равенство проверяется непосредственно Заметно, как последнее выражение совпадает с выражением из правила треугольника (правила Саррюса). Пример Задача Вычислить определитель матрицы, разложив его за элементами третьего порядка: Решение Ответ . Аниматрица (2003)https://youtube.com/watch?v=94fPVqJqBGA%3F Аниме сериал про Матрицу. Здесь представлено эпизодических девять частей, полностью открывающие истинность шаткого Мира Матрицы. Благодаря картине можно узнать историю создания иллюзорного пространства, откуда начался создаваться Мир Машин, прокатиться по последним городам человеческого существования, встретиться с последними представителями мира людей, увидеть воочию главные этапы битвы человечества и машин. Цивилизация людей канула в Лету, но вместе с ней появилась новая эпоха, неординарная и автоматизированная. Список эпизодов аниме: Факты о мультфильме: Виды матриц в зависимости от значений их элементов.Если все элементы матрицы $A_{m\times n}$ равны нулю, то такая матрица называется нулевой и обозначается обычно буквой $O$. Например, $\left( \begin{array} {cc} 0 & 0 \\ 0 & 0 \\ 0 & 0 \end{array} \right)$, $\left( \begin{array} {ccc} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{array} \right)$ – нулевые матрицы. Рассмотрим некоторую ненулевую строку матрицы $A$, т.е. такую строку, в которой есть хоть один элемент, отличный от нуля. Ведущим элементом ненулевой строки назовём её первый (считая слева направо) ненулевой элемент. Для примера рассмотрим такую матрицу: Во второй строке ведущим будет четвёртый элемент, т.е. $w_{24}=12$, а в третьей строке ведущим будет второй элемент, т.е. $w_{32}=-9$. Матрица $A_{m\times n}=\left(a_{ij}\right)$ называется ступенчатой, если она удовлетворяет двум условиям: Примеры ступенчатых матриц: Для сравнения: матрица $Q=\left(\begin{array}{ccccc} 2 & -2 & 0 & 1 & 9\\0 & 0 & 0 & 7 & 9\\0 & -5 & 0 & 10 & 6\end{array}\right)$ не является ступенчатой, так как нарушено второе условие в определении ступенчатой матрицы. Ведущие элементы во второй и третьей строках $q_{24}=7$ и $q_{32}=10$ имеют номера $k_2=4$ и $k_3=2$. Для ступенчатой матрицы должно быть выполнено условие $k_2\lt{k_3}$, которое в данном случае нарушено. Отмечу, что если поменять местами вторую и третью строки, то получим ступенчатую матрицу: $\left(\begin{array}{ccccc} 2 & -2 & 0 & 1 & 9\\0 & -5 & 0 & 10 & 6 \\0 & 0 & 0 & 7 & 9\end{array}\right)$. Ступенчатую матрицу называют трапециевидной или трапецеидальной, если для ведущих элементов $a_{1k_1}$, $a_{2k_2}$, …, $a_{rk_r}$ выполнены условия $k_1=1$, $k_2=2$,…, $k_r=r$, т. Примеры трапециевидных матриц: Дадим ещё несколько определений для квадратных матриц. Если все элементы квадратной матрицы, расположенные под главной диагональю, равны нулю, то такую матрицу называют верхней треугольной матрицей. Например, $\left( \begin{array} {cccc} 2 & -2 & 9 & 1 \\ 0 & 9 & 8 & 0 \\ 0 & 0 & 4 & -7 \\ 0 & 0 & 0 & 6 \end{array} \right)$ – верхняя треугольная матрица. Заметьте, что в определении верхней треугольной матрицы ничего не сказано про значения элементов, расположенных над главной диагональю или на главной диагонали. Они могут быть нулевыми или нет, – это несущественно. Например, $\left( \begin{array} {ccc} 0 & 0 & 9 \\ 0 & 0 & 0\\ 0 & 0 & 0 \end{array} \right)$ – тоже верхняя треугольная матрица. Если все элементы квадратной матрицы, расположенные над главной диагональю, равны нулю, то такую матрицу называют нижней треугольной матрицей. Они могут быть нулевыми или нет, – это неважно. Например, $\left( \begin{array} {ccc} -5 & 0 & 0 \\ 0 & 0 & 0\\ 0 & 0 & 9 \end{array} \right)$ и $\left( \begin{array} {ccc} 0 & 0 & 0 \\ 0 & 0 & 0\\ 0 & 0 & 0 \end{array} \right)$ – тоже нижние треугольные матрицы Квадратная матрица называется диагональной, если все элементы этой матрицы, не лежащие на главной диагонали, равны нулю. Пример: $\left( \begin{array} {cccc} 3 & 0 & 0 & 0 \\ 0 & -2 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 6 \end{array} \right)$. Элементы на главной диагонали могут быть любыми (равными нулю или нет), – это несущественно. Диагональная матрица называется единичной, если все элементы этой матрицы, расположенные на главной диагонали, равны 1. Например, $\left(\begin{array} {cccc} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array}\right)$ – единичная матрица четвёртого порядка; $\left(\begin{array} {cc} 1 & 0 \\ 0 & 1 \end{array}\right)$ – единичная матрица второго порядка. Что такое матрицы в математикеМатрица в математике — это абстрактный объект, имеющий вид таблицы чисел или других математических величин. Чаще таблица прямоугольная, но встречаются и другие виды (квадратные, треугольные). Обычно матрица называется заглавной буквой латинского алфавита: матрица A, матрица B. В таблице есть строки (их количество называется m) и столбцы (их количество называется n). Количество строк и столбцов определяет размер матрицы и может называться порядком. Матрицы такого типа называются матрицами строения m×n, или размера m×n, или порядка m×n. Элементы матрицы, т.е. числа или остальные величины, называются строчной буквой. Они имеют 2 нижних индекса, необходимых для определения их положения в матрице. Например, элемент a13 располагается на пересечении 2 строки и 3 столбца. Значения элемента а13 читаются по-отдельности, не как целое число: «а один-три». Откуда они взялись и чем полезныПервые упоминания матрицы появились в Древнем Китае. Это была квадратная таблица, получившая название магического или волшебного квадрата. Самым древним и известным считается квадрат 3×3, датируемый около 2200 г до н.э. Он был высечен на панцире черепахи. В Китае его называют квадрат Ло Шу, а в Западной Европе — «Печать Сатурна». Таким же древним является квадрат, найденный в Кхаджурахо, столице средневекового государства Чандела (IX–XIII вв. В древности матрицы были необходимы преимущественно для решения линейных уравнений. Когда матрицы появились в арабских странах, стали разрабатываться принципы работы с ними, в том числе, принцип сложения. В XVIII веке швейцарский математик, «отец линейной алгебры» Габриэль Крамер опубликовал правило Крамера. Это способ решения систем линейных уравнений с помощью матрицы. Способ Крамера не подходит для решения тех систем линейных уравнений, в которых может быть бесконечное множество решений. В следующем веке появляется метод немецкого математика Карла Фридриха Гаусса. Этот способ решения алгебраических уравнений не является открытием ученого. Впервые о методе Гаусса написали в китайском трактате «Математика в девяти книгах», а сам он только привел способ в удобную форму. Для решения уравнений таким способом необходимо записать расширенную матрицу системы. В отличие от метода Крамера, правило Гаусса можно использовать для решения любых систем линейных уравнений. Детальная разработка теории матриц активно продолжилась с середины XIX века. Наиболее значимые ученые: Уильям Гамильтон, Артур Кэли, Карл Вейерштрасс, Мари Энмон Камиль Жордан, Фердинанд Георг Фробениус. Сам термин «матрица» предложил английский математик Джеймс Сильвестр в 1850 г. В наше время матрицы используются не только для записи и решения систем линейных уравнений. Списки, статистические данные, табеля с информацией — все это в какой-то степени матрица. Их применяют для упрощения подачи и работы с информацией в любой сфере. Например, таблица продаж, где указан год (первый столбец), вид продукции (первая строка), а остальные значения — количество проданных единиц. Нео и Морфеус поменяются ролямиСюжет «Матрицы 4» пока держится в строгом секрете. Между тем, некоторые слухи о содержании фильма все же просочились в Сеть. Они говорят нам о том, что на экранах мы вновь увидим персонажей предыдущих фильмов — Нео, Морфеуса, Тринити, Ниобе и некоторых других. Поговаривают, что это будет приквел, основанный на рассказе Морфеуса в первой части фильма. Напомним, после встречи с Нео он поведал парню о том, что когда-то давно был рожден человек, способный освободить человеческую расу от власти искусственного интеллекта. Этот человек, по его словам умер, но должен был родиться вновь и он родился: Нео — тот освободитель, которого они так ждали. «Матрица» увидит продолжение в мае 2021 года. Кадр из фильма Обладая этими знаниями, мы можем предположить, что теперь увидим прошлое, где герой Киану Ривза был уже взрослым, а Морфеус, напротив — молодым. В том прошлом именно первый Нео будет обучать Морфеуса, а не наоборот. Кроме того, в картине может появиться новый персонаж — девушка, которая должна сыграть важную роль в истории человечества, как было с Нео в первом фильме. Если это приквел, то она вполне может оказаться будущей матерью Нео, если новый сиквел, тот, не сомневаемся, сценаристы придумали для нее не менее захватывающую судьбу. Краткий сюжет трилогии «Матрица»В чём смысл фильма «Матрица», невозможно понять, если пропустить основные вехи развития сюжета. Начинается трилогия со знакомства с главным героем – Томасом Андерсеном (Киану Ривз). Жизнь Томаса протекает обычно, так живут миллионы жителей мегаполисов по всему миру: утром он уходит на работу, весь день кое-как выполняет свои обязанности в офисе. Зато вечером Андерсен увлечён любимым делом: хакерит в интернете под псевдонимом Нео. Однажды на Нео выходит девушка-хакер Тринити. Он встречается с ней в ночном баре, затем разговаривает с её другом Морфеусом и получает подтверждение своим догадкам: есть где-то иная жизнь, не похожая на ту, которой он сейчас живёт. Нео принимает красную капсулу в знак того, что согласен узнать правду. В ответ Морфеус показывает Андерсену истинную реальность. И она, к сожалению, ужасающа. Миром давно уже правят машины. Они поработили людей, заперли их в своеобразные капсулы и подключили к компьютерной матрице, чтобы получать энергию. Нео освободился из-под гнёта машин и присоединился к повстанцам, которые воюют против них и в реальном мире, и в матрице. Молодому человеку пришлось потерять многих друзей и отдать свою жизнь ради того, чтобы в финале Главный компьютер предоставил всем желающим людям возможность покинуть Матрицу. Фильмы«Матрица»Основная статья: Матрица (фильм) Программист одной американской компании Томас Андерсон, также известный в неофициальных кругах как хакер Нео, узнаёт, что наш мир, всё, что есть вокруг, это всего лишь порождение компьютерной программы — Матрицы. На самом же деле на Земле уже давно правят машины, которые выращивают людей на специальных плантациях и используют в качестве источников энергии. Но есть и люди, которые противостоят Машинам, они живут в единственном городе людей, до которого Машины ещё не смогли добраться, и периодически входят в Матрицу. «Матрица: Перезагрузка»Основная статья: Матрица: Перезагрузка Чтобы выполнить свою миссию избранного, Нео необходимо встретиться с Архитектором, с тем, кто создал Матрицу, но найти путь к Архитектору очень непросто. Тем временем Агент Смит нашёл возможность самопроизвольного копирования, и теперь Смит готов сразиться с Нео не в одиночку — Нео придётся сражаться с целой армией Агентов Смитов. Машины всё продолжают искать способы попасть в город людей — Зион, охотники рыщут повсюду. Нео остаётся последней надеждой человечества, если он не справится, мир людей перестанет существовать. «Матрица: Революция»Основная статья: Матрица: Революция Машины начинают последний решающий штурм единственного города людей — Зиона. Сил защитников города не хватит на то, чтобы отразить этот натиск, им остаётся только умереть, защищая свой город. Затраты на фильмы и кассовые сборы
Актёры и персонажи
См. Съёмочная группа
ГонорарыГонорары режиссёров и основных актёров (в долларах США). Расчёт определителяВ линейной алгебре существует понятие определителя или детерминанта. Это число, которое ставят в соответствие каждой квадратной матрице, вычисленное из её элементов по специальной формуле. Определитель или модуль используется для решения большинства задач. Произведения могут отличаться друг от друга составом элементов. Со знаком плюс будут включаться в сумму числа, если их индексы составляют чётную подстановку, в противоположном случае их значение меняется на минус. Определитель обозначается символом det A. Круглые скобки матричной таблицы, обрамляющие её элементы, заменяются на квадратные. Формула определителя: Определитель первого порядка, состоящий из одного элемента, равен самому этому элементу. Детерминант матричной таблицы размером 2*2 второго порядка вычисляется путём перемножения её элементов, расположенных на главной диагонали, и вычитания из них произведения элементов, находящихся в побочной диагонали. Для матрицы также можно найти дискриминант многочлена, отвечающий формуле: Когда у многочлена имеются кратные корни, тогда дискриминант равен нулю. Популярное
Что такое Матрица?Матрица — это замена реальности, виртуальный суррогат. Компьютер дарит людям фальшивую жизнь, доказывая, что очень хорошо узнал характер своих создателей и даже перенял их худшие черты. Искусственный интеллект взял в руки бразды правления расхлябанной человеческой цивилизацией. В сущности, люди сами виноваты: они превратились из личностей в «пользователей», из самостоятельного биологического вида – в батарейки, сырьевой придаток гаджетов, и можно только поражаться гениальному прозрению сценаристов, предвидевших развитие ситуации, которое мы наблюдаем сейчас. Даже Пифия, пророчица, которой так искренне верит Морфеус – одна из программ. Она такая же часть Матрицы, как агенты, преследующие повстанцев, как грозный враг Нео – агент Смит, компьютерный вирус, взбунтовавшийся и против людей, и против машин. Архитектор, автор Матрицы, когда-то пытался создать идеальный мир для человечества, но в итоге вышел далеко не лучший вариант. Библейские оттенки образа Архитектора несомненны: это Бог искусственного интеллекта, действующий сразу в двух мирах: реальном и виртуальном. Именно он объясняет Нео, что нет никакого пророчества, а его задача — перезагрузка Матрицы. Повстанческая группа Морфеуса — это особый механизм саморегуляции Матрицы, который должен найти ошибки в её действующей версии. Уничтожение этого вспомогательного инструмента заранее запрограммировано. Никакого победного исхода не будет. Эта мысль также отражает один из законов социальной и политической истории человечества: очень многие террористы негласно содержались самим государством, его правящими элитами, чтобы выявлять настроения народа и через такие подконтрольные группы находить и разоблачать реальных противников правящего строя. В чём состоит психологическое новаторство трилогии?В трилогии «Матрица» намеренно поставлена с ног на голову главная мечта человечества, ради которой совершалось столько подвигов и преступлений: чаяние светлого будущего. Конец света уже случился, и надо с этим жить. Главный вопрос, который стоит перед героями – нужно ли покидать уютный, убаюкивающий, удобный мир Матрицы ради страшной реальности? Захочет ли человечество отказаться от комфорта ради самостоятельности? Фактически, новый мессия компьютерной эры зовёт людей не вперёд, к вожделенному «светлому будущему», а назад, в прежние времена, когда они не были придатками к компьютерам. Сможет ли человек отвернуться от даров Матрицы, от всего, что создал силами своего интеллекта, попав к своему созданию в добровольное рабство? Новый Морфеус и женский вариант НеоКак мы уже отмечали выше, роль Нео в фильме продолжит играть Киану Ривз (кстати, ему уже 55 лет), роль его протеже Морфеуса, скорее всего, досталась актеру по имени Яхья Абдул Матин II («Рассказ служанки»), чье участие в проекте официально подтверждено. Яхья может сыграть молодого Морфеуса Фото: Instagram / @yahya Женского персонажа, подобного Нео, по некоторым данным, играет 27-летняя Джессика Хенвик («Фортитьюд», «Звездные войны: Пробуждение силы»). Актриса якобы так хорошо показала себя на пробах, что у Ланы Вачовски не было никаких сомнений относительно того, кому доверить столь важную роль. Многих, конечно же, интересует, появится ли в фильме старый добрый агент Смит. Да, возможно, его мы увидим, вот только играть его будет уже не Хьюго Уивинг, также знакомый нам как Элронд из «Властелина колец». Хьюго сам рассказал журналистам о том, что Вачовски звала его сниматься, но расхождения с рабочим графиком вынудили его отказаться и предпочесть четвертой «Матрице» другой проект — театральную постановку «Визит». Роль Тринити, тем временем, продолжит играть Кэрри-Энн Мосс, роль Ниобе — Джада Пинкетт Смит. Кроме них в картине на экране могут появиться Приянка Чопра, Джонатан Грофф, Нил Патрик Харрис, Ламберт Уилсон, Эндрю Колдуэлл, Макс Римельт, Эрендира Ибарра, Тоби Онвумере, Уилльям Барбо. Нахождение определителя матрицыОпределитель матрицы обозначается как $Δ$ или $\det$. Замечание 2 Детерминант возможно найти только для квадратных разновидностей матриц. В простейшем случае, когда матрица состоит из всего одного элемента, её определитель равен этому элементу: Вычислить определитель от матрицы порядка двух можно следуя такому правилу: Определение 1 Определитель матрицы размера 2 равен разности произведений элементов, стоящих на главной диагонали с произведением элементов с побочной диагонали: $\begin{array}{|cc|} a_{11}& a_{12} \\ a_{21} & a_{22} \\ \end{array} = a_{11} \cdot a_{22} – a_{12} \cdot a_{21}$ В случае если определитель матрицы задан размером $3 \times 3$, то найти его можно используя мнемонические правила: Саррюса или треугольников, также можно разложить матрицу по строчке или столбцу или воспользоваться преобразованиями Гаусса. Для определителей большего размера можно использовать преобразования Гаусса и разложение по строчке. ЗаключениеИтак, определитель квадратной матрицы – это число, полученное при помощи заданных чисел, расположенных в виде квадратной таблицы,которое вычисляется по рассмотренным выше формулам. Мы рассмотрели три основных способа вычисления определителя: Также были рассмотрены формулы для решения матрицы второго, третьего и высших порядков. Мы разобрали 10 свойств определителя матриц, благодаря которым можно быстрее и легче найти определитель матрицы. Удобно решать матрицу третьего порядка методом Гаусса, где нужно выполнить элементарные преобразования матрицы и привести её к ступенчатому виду. Определитель матрицы равняется произведению элементов, которые стоят на главной диагонали. Полезная литература Что такое матрицы и что с ними делать? *Первым и, пожалуй, одним из простых понятий, встречающихся в математической науке, является матрица. Что такое матрица?Впервые с этим понятием сталкиваются студенты 1-2 курсов независимо от факультета и выбранной специальности. В общем виде матрица представляет собой прямоугольную таблицу с числами, притом каждое из них занимает определенное место и положение, имеет собственное обозначение. Каждая матрица имеет свое имя. Оно обозначается заглавными буквами латинского алфавита: А, В, С и пр. У каждой матрицы есть свой размер. Одежду подбирать ей не придется, но вот учитывать это параметр при действиях над матрицей нужно обязательно. Размер матрицы определяется, исходя из количества строк и столбцов, которые обозначают m и n соответственно. Пример матрицыВсе числа, образующие таблицу (непосредственно матрицу), называют элементами матрицы. У каждого из них есть свое обозначение с учетом местоположения (строка+столбец). Какие действия можно выполнять над матрицами?Матрицы, как математическая единица, поддаются всем основным действиям: сложение, вычитание, умножение и даже деление. Каждая из операций будет иметь определенный порядок действий и потребует соблюдение конкретных условий. Особенности сложения и вычитания матриц Одним из важнейших требований в данном случае является соразмерность матриц. Оно означает, что размер матриц должен быть одинаковым. В противном случае сложить или вычесть один элемент из другого не удастся. При разном количестве элементов произвести необходимые действия не представляется возможным. Сложение и вычитание соразмерных матриц производится следующим образом: все действия осуществляют над одними и теми же элементами из разных матриц. Как происходит сложение матриц?Вычитание производится аналогично, поэлементно. Особенности умножения матриц Умножение необходимо рассматривать в двух вариантах: Это самый простой вариант развития событий. В данном случае необходимо умножит каждый элемент матрицы на число. Пример умножения матрицыПолучить произведение матриц возможно не во всех случаях. Здесь также необходимо соблюдение определенных условий: число столбцов одной матрицы должно быть равнозначным числу строк другой матрицы. Как умножаются матрицы?Специфика умножения матриц проявляется в следующем: умножение производится не просто поэлементно, но и с учетом строк и столбцов. Элементы новой матрицы получаются в ходе умножения элементов и суммирования двух произведений. То есть фактически нужно умножать строку на столбец. Рассмотрим порядок умножения матриц на примере: Правила умножения матрицыДеление матриц При делении матриц выделяют новое понятие – обратная матрица, которая обозначается А. Произведение матрицы А и А даст единичную матрицу Е. Транспонирование матрицы – это… У матриц есть одно специфическое действие, когда можно поменять местами строки и столбцы. Такая операция называется транспонированием. Если обычная матрица обозначается А, то транспонированная — А. Рассмотрим процесс транспонирования на конкретном примере: Что такое транспортирование матрицы?Определитель матрицы – это… Одним из важнейших элементов матрицы является ее определитель. Данный критерий представляет собой численную характеристику матрицы. Для ее получения нужно, чтобы матрица была квадратной. Расчет определителя производится на основе разности произведений диагоналей: главной и побочной. Понятие определителя в квадратной матрицеДля чего нужны матрицы?Матрицы успешно используются, как в математике, так и иных науках. В экономике использование матричных структур целесообразно при решении некоторых задач. При этом важно чтобы вычисление нужного параметра было можно представить в виде таблицы или системы уравнений. Матрицы также уместны при вычислении в таких науках, как физика, механика, эконометрика и пр. Они упрощают процесс вычисления искомого параметра при грамотной интерпретации известных критериев.
5.1: Что такое матрица? Начнем с того, что матрица — это не что иное, как прямоугольное расположение набора элементов (на самом деле это немного сложнее, но мы вернемся к матрицам больше двух измерений чуть позже). На рис. 5.1 показана матрица размером два на четыре. На рис. 5.2 показана матрица четыре на два. На данный момент игнорируйте содержимое ячеек (например, 1,1). Рисунок 5.1. Пример матрицы «два на четыре»
Рисунок 5.2. Пример матрицы «четыре на два»
Элементы (ячейки) матрицы идентифицируются по их «адресам». Матрицы часто представляются в виде массивов элементов, окруженных вертикальными линиями слева и справа или квадратными скобками слева и справа. На веб-страницах проще использовать «таблицы» для представления матриц. Матрицам можно давать имена; эти имена обычно представляются заглавными жирными буквами. Социологи, использующие матрицы для представления социальных сетей, часто обходятся без математических соглашений и просто отображают свои данные в виде массива помеченных строк и столбцов. Метки на самом деле не являются частью матрицы, а просто для ясности представления. Например, матрица на рис. 5.3 представляет собой матрицу 4 на 4 с дополнительными метками. Рисунок 5.3. Матрица четыре на четыре с дополнительными метками строк и столбцов
Матрицы, используемые в анализе социальных сетей, часто являются «квадратными». Иногда аналитики социальных сетей используют «трехмерную» матрицу. Трехмерная матрица имеет строки, столбцы и «уровни» или «срезы». Каждый «срез» имеет те же строки и столбцы, что и каждый другой срез. UCINET рассматривает эти более сложные трехмерные массивы данных как набор двумерных матриц. Эта страница под названием 5.1: Что такое матрица? распространяется по незаявленной лицензии, автором, ремиксом и/или куратором выступили Роберт Ханнеман и Марк Риддл. Матрица (математика) Факты для детейНа конкретные элементы матрицы часто ссылаются с помощью пар нижних индексов для чисел в каждой из строк и столбцов . В математике матрица (множественное число: матриц ) представляет собой прямоугольник чисел, расположенных в строк и столбцов . Строки представляют собой строки слева направо (горизонтальные), а столбцы идут сверху вниз (вертикально). Верхняя левая ячейка находится в строке 1, столбце 1 (см. диаграмму справа) . Матрицы часто представляются заглавными латинскими буквами, такими как , и , и существуют правила сложения, вычитания и «умножения» матриц вместе, но правила отличаются от правил для чисел. Например, произведение не всегда дает тот же результат, что и умножение обычных чисел. Матрица может иметь более двух измерений, например трехмерная матрица. Кроме того, матрица может быть одномерной, состоящей из одной строки или одного столбца. Многие естественные науки довольно часто используют матрицы. Во многих университетах курсы по матрицам (обычно называемые линейной алгеброй) преподаются очень рано, иногда даже на первом курсе. Матрицы также очень распространены в информатике, технике, физике, экономике и статистике. СодержаниеОпределения и обозначенияГоризонтальные линии в матрице называются строками , а вертикальные линии называются столбцами . Матрица с m 90 264 строк и 90 263 n 90 264 столбцов называется матрицей 90 263 m 90 264 x 90 263 n 90 264 (или матрицей 90 263 m 90 264 × 90 263 n 90 264), а 90 263 m 90 264 и 90 263 n 9 ее измерениями называются Места в матрице, где стоят числа, называются элементами . Мы пишем, чтобы определить m × n матрицу A , где каждый элемент в матрице называется a i,j для всех 1 ≤ 3 ≤ 40263 i j ≤ n . ПримерМатрица — это матрица 4×3. Эта матрица имеет m=4 строки и n=3 столбца. Элемент A [2,3] или a 2,3 равно 7. ОперацииСложениеГлавная страница: Сложение матриц Сумма двух матриц i , j )-й элемент равен сумме ( i , j )-го элемента двух матриц: Две матрицы имеют одинаковые размеры. Здесь верно (и вообще верно для матриц одинаковой размерности). Умножение двух матрицГлавная: Умножение матриц Умножение двух матриц немного сложнее: Итак с номерами: Специальные матрицыСуществуют специальные матрицы. Квадратная матрицаГлавная страница: Квадратная матрица Квадратная матрица имеет столько же строк, сколько и столбцов, поэтому m=n. Пример квадратной матрицы: Эта матрица имеет 3 строки и 3 столбца: m=n=3. ИндивидуальностьГлавная страница: Матрица идентичности У каждой квадратной размерности матрицы есть специальный аналог, называемый «матрицей идентичности», представленный символом . В единичной матрице нет ничего, кроме нулей, за исключением главной диагонали, где все единицы. Например: — единичная матрица. Существует ровно одной единичной матрицы для каждого набора квадратных измерений. Единичная матрица особенная, потому что при умножении любой матрицы на единичную матрицу всегда получается исходная матрица без изменений. Обратная матрицаMain page: Обратимая матрица Обратная матрица — это матрица, которая при умножении на другую матрицу равна единичной матрице. Например: является инверсией . Формула обратной матрицы 2×2: Где определитель матрицы. В матрице 2×2 определитель равен: Матрица с одним столбцом Матрица, которая имеет много строк, но только один столбец, называется вектор-столбцом. ОпределителиГлавная страница: Определитель Определитель берет квадратную матрицу и вычисляет простое число, скаляр. Чтобы понять, что означает это число, возьмите каждый столбец матрицы и нарисуйте его как вектор. Параллелограмм, нарисованный этими векторами, имеет площадь, которая является определителем. Для всех матриц 2×2 формула очень проста: Для матриц 3×3 формула сложнее: Не существует простых формул для определителей больших матриц, и многие программисты изучают, как заставить компьютеры быстро находить большие определители. . Свойства определителейВсе определители следуют трем правилам. Это: Связанные страницыИзображения для детейВсе содержимое статей энциклопедии Kiddle (включая изображения статей и факты) можно свободно использовать по лицензии Attribution-ShareAlike, если не указано иное. Процитируйте эту статью: Матрица (математика) Факты для детей. Энциклопедия Киддла. Математика для глубокого обучения: матрица, сложение матриц и умножение матриц | Мишель Рекса | Фи Навыки
Первоначально я планировал написать синтетическую статью, представляющую наиболее важные математические концепции для Глубокое обучение. Однако, когда я начал, я понял, что для тех, кто не знаком с этими понятиями, эффективнее и быстрее сосредоточиться на одном понятии сразу. Что такое матрица? Я люблю фильмы Матрица. Но мы не будем говорить об этом здесь. Вместо этого я хочу показать вам, что матрицы — это не какое-то эзотерическое заклинание, скрывающее темные секреты, которые могут понять только самые заядлые из нас. Вы когда-нибудь играли в одну из этих карточных игр, где вам нужно табло? Если да, то у меня есть хорошая новость: вы уже знаете, что такое матрица , и вы можете в любой момент вспомнить, как она работает, реконструируя табло.
Согласно Википедии: Как и все в Математика , матрица — это идея , переведенная в определение и представленная с помощью обозначения . Если вы не привыкли к математике нотации , изображение выше может показаться пугающим в Первый взгляд. Давайте разберемся вместе. Символы с зеленым и красным подчеркиванием представляют элементы матрицы: Значение, найденное в первой строке и втором столбце Эта нотация очень удобна, когда мы манипулируем огромными матрицами или когда мы хотим оставаться общими и выражать что-то для каждой матрицы с 90 578 90 613 m 90 614 90 579 строк и 90 578 90 613 n 90 614 90 579 столбцов. Следующие матрица представляет табло, которое мы видели в предыдущем разделе: Матричное представление табло вышеЕсли бы к игре присоединился другой игрок, нам пришлось бы добавить столбец для этого игрока в табло. То же самое произойдет с матрицей : нам потребуется 5 столбцов для представления всей игры. Сложение матрицЧтобы сложить две матрицы вместе, необходимо выполнить обычное сложение по записи, как на изображении ниже. Вы могли заметить, что мы добавляем две матрицы с одинаковыми размерами. Это чрезвычайно важно для матриц. В Mathematics добавление (или любая другая операция) определяется значениями, которые вы добавляете. Вы можете думать об этом как о слове «медведь». В Finance , когда кто-то говорит «медведь», это обычно относится к падению фондового рынка, тогда как в лесу это обычно означает, что кто-то заметил медведя, и вам лучше убраться оттуда как можно быстрее. Давайте рассмотрим простой пример, чтобы убедиться, что мы все на одной волне. Предположим, мы хотим определить дополнение для эмодзи. Вы явно не можете использовать дополнение , которое вы изучаете в школе, но вы всегда можете создать для него правило. Например, мы могли бы сказать следующее: 😃 + 🙁 = 😐 Здесь наше сложение представляет среднюю эмоцию. т.е. счастливое лицо с грустным лицом дает нейтральное лицо. Но вместо этого нас может заинтересовать подсчет количества лиц. 😃 + 🙁 = 2 Здесь добавление двух граней эквивалентно подсчету количества граней. Как видите, это совсем другое. Если вам это интересно, я приглашаю вас ознакомиться с работами Джузеппе Пеано по аксиоматизации. Подводя итог, добавление матрицы представляет собой двухэтапный процесс: Что происходит с умножением? Умножение матрицУмножение матриц — более сложная операция. Вы могли бы ожидать, что это работает как дополнение, но это не так. Если вы когда-нибудь изучали Математику в средней школе, вы, возможно, помните, как решали уравнения с более чем одной переменной, например следующие: уравнения, а затем повторить процесс. Правила умножения матриц гарантируют, что следующее уравнение эквивалентно системе уравнений выше: Как вы можете заметить, мы умножаем матрицу на вектор неизвестных переменных и з . Следовательно, матрица умножение не является коммутативным: вы не можете поменять порядок множителей и ожидать того же результата. Это означает, что вы обычно не может сказать, что a*b = b*a. Вы не можете этого сделать, потому что слева вы переводите с английского на китайский, а справа с китайского на английский. Я почти уверен, что английский и китайский — это не одно и то же. Теперь, когда у вас есть интуиция, я дам вам рецепт умножения матриц. Предположим, что A и B представляют собой две матрицы с размерами соответственно (ma,na) и (mb, nb) и что вы вычисляете A * B. Примеры для 4 класса по математике на сложение и вычитание распечатать: Примеры на сложение. Математика 4 класс.Примеры на сложение. Математика 4 класс. Примеры на сложение. Математика 4 класс. Задачи по математике 4 класс MAT-ZADACHI.RU Математика 4 класс Контрольные работы
Математика 4 класс ->> Примеры Чтобы увидеть решение, наведите на пример курсор мыши.
Простые задачи Составные задачи Примеры на вычитание. Математика 4 класс. Математика 4 класс. Примеры на вычитание. Математика 4 класс. Задачи по математике 4 класс MAT-ZADACHI.RU Математика 4 класс Контрольные работы
Математика 4 класс ->> Примеры Чтобы увидеть решение, наведите на пример курсор мыши.
Простые задачи Составные задачи Сложение и вычитание величин. Видеоурок. Математика 4 Класс — РОСТОВСКИЙ ЦЕНТР ПОМОЩИ ДЕТЯМ № 7 Видеоурок. Математика 4 Класс — РОСТОВСКИЙ ЦЕНТР ПОМОЩИ ДЕТЯМ № 7Содержание Арифметические действия: сложение и вычитание. 4 класс1. Тема урока в 4 –А классе: «Арифметические действия: сложение и вычитание». урок математики 4. задание без ошибок балла задание с ошибкой – 1 балл «5» — 10 баллов «4» — 8 – 9 баллов «3» — 6 – 7 баллов Тема: «Повторение. 5. +309.045 8.244 317.289 Письменное сложение и 6. 1. Решение задачи на нахождение нескольких долей числа. 2. Сложение и вычитание многозначных чисел. 3. Выполнение 2. Сложение и вычитание многозначных чисел. 3. Выполнение Запишите в тетрадь: 9. 3ч 40 мин + 28 мин = 2 ц 30 кг + 64 кг = 105 км 40м + 24 км = Сложение и вычитание величин. Задание 3. 12. В ателье было 240 м ситца. Из него сшили рубашки, платья и простыни. Одну третью часть потратили на пошив рубашек, из 140 м Реши задачу в тетради, записав 14. 1. Решение задачи на нахождение нескольких долей числа. 2. Сложение и вычитание многозначных чисел. 3. Выполнение Примеры 7 (2),(стр.90) 15. Спасибо за работу!
4 класс. Моро. Учебник №2. Ответы к стр. 90 Числа от 1 до 1000 Ответы к стр. 90
1. Составь и реши задачи на сложение и вычитание, используя слова: «Сколько всего …?», «Сколько осталось?», «… больше, чем …», «… меньше, чем …», «На сколько … больше, чем …?». 1) Автобус выехал из деревни и проехал до посёлка 100 км. Затем он проехал 150 км до города. Сколько всего километров проехал автобус? 2) На склад привезли 80 ящиков с яблоками. 3) В первом ящике 20 кг яблок, а во втором – на 2 кг больше, чем в первом. Сколько килограмм яблок во втором ящике? О т в е т: во втором ящике 22 кг яблок. 4) В первом ящике 20 кг яблок, а во втором – на 2 кг меньше, чем в первом. Сколько килограмм яблок во втором ящике? 5) В первом автобусе ехало 35 человек, а во втором – 45. На сколько во втором автобусе ехало человек больше, чем в первом? 2. Вспомни, как называются знаки, которые обозначают сложение и вычитание, и выражения, в которых числа соединены знаком сложения; знаком вычитания. Приведи примеры. Знак сложения: + (плюс), знак вычитания: – (минус). 3. Как называются при сложении и вычитании данные числа и число, которое получается в результате выполнения действия? 3 (первое слагаемое) + 4 (второе слагаемое) = 7 (сумма).
4. Прочитай, используя различные словесные формулировки, следующие равенства: 26 + 8 = 34 72 – 14 = 58 5. Рассмотри примеры и ответь на вопросы: 1) Что получится, если из суммы двух слагаемых вычесть одно из них? 2) Что получится, если к разности прибавить вычитаемое? 3) Что получится, если из уменьшаемого вычесть разность? 1) Получится другое слагаемое. 6. После того как из числа 600 вычли задуманное число, получили 170. Какое число задумали? 600 – х = 170 7. 1) Объясни два способа проверки сложения и вычитания. _867 Проверка: 1) Сложение проверяется вычитанием, а вычитание проверяется сложением и вычитанием. _200100 Проверка: ЗАДАНИЕ НА ПОЛЯХ 306 _ 2507 Ответы по математике. Учебник. 4 класс. Часть 2. Моро М. И., Бантова М. А., Бельтюкова М. А., Волкова С. И., Степанова С. В. Математика. 4 класс 4.6 / 5 ( 30 голосов ) Сложение и вычитание числа 4. Приёмы вычислений.Тема: «Сложение и вычитание числа 4. Приёмы вычислений». Цель: создать условия для открытия способа сложения и вычитания числа 4. Формируемые УУД: личностные: — способность к самооценке на основе критерия успешности учебной деятельности. регулятивные: — уметь определять и формулировать цель на уроке с помощью учителя, проговаривать последовательность действий на уроке; уметь высказывать свое предположение на основе работы с материалом учебника; планировать свое действие в соответствии с поставленной задачей. коммуникативные: — уметь оформлять свои мысли в устной форме; слушать и понимать речь других; учиться работать в паре, формулировать собственное мнение и позицию. познавательные: — уметь ориентироваться в своей системе знаний: отличать новое от уже известного с помощью учителя; добывать новые знания: находить ответы на вопросы, используя учебник, свой жизненный опыт и информацию, полученную на уроке. Тип (вид урока): открытие нового знания. Ход урока. 1.Организационный момент. Звенит звонок! Ты входишь в класс! И БУДЕШЬ МНОГО, МНОГО ЗНАТЬ! — Сегодня на уроке, ребята, мне бы хотелось увидеть , как вы сами умеете добывать знания! А, чтобы урок был удачным — мы будем внимательны, активны и точны! Пожелаем друг другу успеха! II. Актуализация знаний. 1. Минута чистописания. Спишите числа, запишите ещё 2 числа, продолжив закономерность. 2 4 6 … … 1 3 5 … … 2.Устный счёт. — Ребята, приготовьте карточки с числами. Карточки с ответами располагайте слева направо. — Какое число идет при счете перед числом 2? (1) — Какое число называют после числа 8? (9) — 5 уменьши на 3. (2) — К трем прибавь такое же число. (6) -5 без 2. (3) — Первое слагаемое 2, второе слагаемое 3. Сумма? (5) — Найди сумму чисел 4 и 3. (7) — 5 да еще 5. (10) — Какое число находится между числами 3 и 5? (4) — Какое число меньше 9 на 1? (8) — Прочитайте получившийся ряд чисел. — Как можно расположить данные числа? (в порядке возрастания и убывания). — 1 вариант расположите в порядке убывания, 2 вариант – в порядке возрастания. — Проверьте себя. (самопроверка, самооценка) кот. Сколько воробьёв осталось? ( 0) III. Самоопределение к деятельности. На доске: 6+2 5+3 9-2 7+3 8+1 6-3 5-2 5+4 Учитель: — Найдите значения выражений в 1-ом столбике. Игра «Молчанка». (Учитель показывает на выражение, ученики — блок-сигналами показывают ответ.) а) -В 1-ом столбике найдите «лишнее» выражение. Ученики: — 8+1 -лишнее, так как остальные выражения на сложение и вычитание числа 2. Учитель:- Что значит — прибавить 1? (Назвать следующее число) — Что значит — вычесть 1?(Назвать предыдущее число ) — Чем похожи остальные выражения? (Во всех нужно + или — 2 ). — Вспомните, как можно прибавить число 2?(Сначала 1,а затем ещё 1). — Как можно вычесть число 2?(Сначала 1 ,затем ещё 1). б). Учитель:- Найдите значения выражений во 2-ом столбике , комментируя способ решения. (Дети, рассуждая, не могут прокомментировать способ решения в выражении 5+4 ) Учитель: — Чему же будем учиться на уроке? Ученики: — Будем учиться прибавлять и вычитать число 4. Учитель: — Назовите тему урока. Ученики: — Прибавить и вычесть число 4. Научимся сложению с 4 и вычитанию 4. (Идёт целеполагание. Ученики сами называют тему и цель урока) IV.Открытие новых знаний. Учитель: — Подумайте в паре, каким способом можно прибавить число 4? Мы еще не все умеем это делать. Как вы предлагаете облегчить эту работу? — Что вам может помочь сделать это открытие? ( Работа с кружками ) — Положите на стол 5 красных кружков. Возьмите ещё 4 синих кружка. — Поработайте в паре. (Дети работают в паре. Пара, которая готова сигналит о готовности) — Какое открытие сделали? — Как по частям можно прибавить число 4? ( Ученики на доске ставят 5 кружков и практически демонстрируют своё открытие, которое наработали в паре ) Ученики: — К 5 ,прибавим сначала 2 , получится 7 , а затем к 7 прибавим ещё 2 — получится 9. — Можно иначе. Сначала к 5 прибавим 3, получится 8 , а затем к 8 прибавим 1. — Можно, наоборот — к 5 сначала прибавим 1 ,получится 6 ,а к 6 прибавим 3 ,то получится 9. (Учитель на доске фиксирует приёмы прибавления числа 4) 5+4=5+2+2=9 5+4=5+3+1=9 5+4=5+1+3=9 Учитель: -А теперь подумайте, как можно из 7 вычесть 4? Поработайте в паре, используя числовой ряд. (На экране ряд чисел от 1 до 10 .) Учитель: — Кто готов рассказать о своём открытии? (Ученики объясняют самостоятельно с опорой на числовой ряд приёмы вычитания числа 4, делая запись на доске и в тетрадях. Учитель пояснения сопровождает стрелками) Запись на доске: 7-4=7-2-2= 3 7-4=7-3-1=3 7-4=7-1-3=3 — Вы замечательно поработали! V. Физминутка. Мы решали, все решали И немножко подустали. Наш дежурный выходи, И зарядку проведи! (Выходит дежурный, проводит зарядку. ) Раз подняться… VI. Закрепление изученного материала. 1. Работа с учебником. А) Задание №2 стр.-8. (Комментированное упражнение. Ученики объясняют способы сложения и вычитания числа 4 в устной форме) Б) Найдите номер 3. Прочитайте задачу. Вслух прочитает …, остальные поставили пальчики и следим. — Докажите, что это задача (есть условие и вопрос). — Прочитайте только условие задачи. -Прочитайте вопрос задачи. -Как понимаете на 4 года старше? ( Больше лет) -Что означает «больше на 4»? (Столько же и ещё 4.) -Какое выбираете действие? — Вспомните порядок работы над задачей. Что мы выполняем сначала? (схему) — Дальше? (решение, ответ.) Кто желает у доски? -Сделайте схему и запишите решение и ответ к задаче. Самопроверка — У кого так же, как у ….? — Кто по-другому решил задачу? … объясни, как к 6 прибавил 4? (по числовой ленте) – у доски 2. Самостоятельная работа. Задание № 4 стр.8. (Примеры решают по вариантам. Затем учащиеся меняются тетрадями, проводя взаимопроверку). Встаньте, у кого безошибочная работа. Молодцы! Остальные – будьте внимательны! VII. Рефлексия. (Работа по электронному приложению) VIII. Итог урока. Учитель: — Какой была тема урока? Ученик: — Сложение и вычитание числа 4. Учитель: — Как можно прибавить и вычесть число 4? (Ученики повторяют приёмы сложения и вычитания числа 4) Учитель: — Какое задание было для вас интересным? -А какое задание было трудным? (Дети отвечают на вопросы) Рефлексия. Самооценка. Раскрась себе смайлик. Учитель: — Урок окончен! Спасибо! Оценка: 4 — Алгебраическое мышление 1Особенности специального образования Рекомендации по специальному образованию, написанные учителями специального образования штата Индиана, предназначены для повышения вовлеченности и поддержки роста учащихся в рамках специального образования.
% PDF-1. Учебная программа по математике для 4-го класса — Общие основные уроки и оценкиЧто такое математика для 4-го класса? 4 класс фокусируется на трех ключевых достижениях предыдущих лет: (1) развитие понимания с помощью многозначного умножения и деления; (2) развитие понимания эквивалентности дробей и некоторых случаев сложения, вычитания и умножения дробей; и (3) понимание того, что геометрические фигуры можно анализировать и классифицировать на основе их свойств, включая их угловую меру и симметрию. Как мы заказывали агрегаты? Блок 1, Разрядная стоимость, Округление, Сложение и Вычитание , год начинается с основного содержания, на котором основывается большая часть оставшихся единиц — разряда. Учащиеся начинают видеть структуру разрядной системы в контексте мультипликативного сравнения — например, 1 тысяча в 10 раз больше, чем 1 сотня. Затем они используют это понимание места для сравнения, округления, сложения и вычитания чисел до 1 000 000. В , Блок 2, Многозначное умножение , учащиеся используют это понимание разряда, чтобы начать развивать понимание многозначного умножения (включая 2-значное, 3-значное и 4-значное на 1-значное, а также как двузначное умножение на двузначное). Хотя учащиеся познакомились с идеей мультипликативного сравнения в Блоке 1 в контексте структуры нашей системы разметки, они более глубоко вникают в эти типы задач рассказа в этом блоке. Раздел 3, Многозначный Дивизион , аналогично полагается на понимание разряда, чтобы познакомить учащихся с многозначным делением (включая 4-значное, 3-значное и 2-значное на однозначное деление). Студенты продолжают свою работу над многоступенчатыми задачами со словами, работая с остатками, интерпретируя их в контексте задачи. В , Блок 4, Углы , студенты получают формальное введение в углы после многих лет неформальной категоризации форм в соответствии с их углами. В Блок 5, Эквивалентность дробей и упорядочение учащихся работают с эквивалентностью и сравнением дробей, разрабатывая общий метод генерации эквивалентных дробей и исследуя несколько стратегий для сравнения дробей. Это готовит их к Блоку 6, Операциям с дробями , где они начинают изучать операции с дробями (а именно сложение, вычитание и умножение на целое число).Студенты также начинают решать задачи со словами, включающие сложение, вычитание и умножение дробей. Затем это распространяется на блок , блок 7, десятичные дроби , в котором учащиеся изучают десятичные дроби, которые особенно важны, поскольку они являются расширением системы разметки. Они находят эквивалентные десятичные дроби, складывают и вычитают десятичные дроби (включая десятые и сотые, требующие общего знаменателя) и используют десятичную систему счисления. Курс завершается блоком 8 , преобразование единиц , в котором студенты применяют большую часть своего понимания четырех операций, а также дробей и десятичных дробей для решения задач со словами, включающих преобразование большей единицы в меньшую единицу в той же системе. . Этот курс соответствует рамкам учебной программы штата Массачусетс 2017 года, которые включают Общие основные государственные стандарты 2010 года. Кроме того, мы полагаем, что ежедневная беглость речи и практика применения являются важной частью обучения элементарной математике, но не включены в наши математические единицы. Все ученики 4-х классов получают около 45 минут практики в этих областях во время других блоков. открытых учебников | СиявулаМатематикаНаукаНаша книга лицензионнаяЭти книги не просто бесплатные, они также имеют открытую лицензию! Один и тот же контент, но разные версии (брендированные или нет) имеют разные лицензии, как объяснено: CC-BY-ND (фирменные версии) Вам разрешается и поощряется свободное копирование этих версий. Узнайте больше о спонсорстве и партнерстве с другими, которые сделали возможным выпуск каждого из открытых учебников. CC-BY (версии без марочного знака) Эти небрендированные версии одного и того же контента доступны для вас, чтобы вы могли делиться ими, адаптировать, трансформировать, модифицировать или дополнять их любым способом, с единственным требованием — дать соответствующую оценку Siyavula. Сложение и вычитание, часть 1: задачи рассказасюжетные ситуации Как мы упоминали ранее, учащиеся развивают свое понимание операций сложения и вычитания, когда они используют их для решения задач рассказа.Существует несколько категорий сюжетных задач, известных как типов ситуаций , которые описывают отношения между количествами в сюжетных задачах. Четыре типа ситуаций, которые согласно Общим основным государственным стандартам (CCSS) должны изучать учащиеся в классах K-1: Учителя, которые понимают типы ситуаций (а также то, что в них нового и сложного) могут лучше поддержать своих учеников в развитии сильного концептуального понимания сложения и вычитания.По этой причине мы хотим посвятить оставшуюся часть этого ресурса ознакомлению вас с четырьмя сюжетными ситуациями сложения и вычитания. Ситуации сложения и вычитанияЧтобы лучше понять, что мы подразумеваем под «типом ситуации», давайте вернемся к нашему примеру задачи сложения, которая представляет собой добавление к ситуации . В этой задаче одно количество (3 рыбы) добавляется к существующему количеству (5 рыб), в результате чего получается новое количество (что мы обнаруживаем как 8 рыб).Детали проблемы могут измениться (например, это может быть печенье вместо рыбы), как и неизвестное количество (например, возможно, мы знали, сколько рыбы у нас было в итоге, но не сколько мы начали), но соотношение между количествами одинаково для всех дополнительных задач. Ниже мы представляем ситуацию добавления в виде диаграммы и помечаем каждое количество так, как CCSS относится к ним ( начало увеличивается на изменение становится результат ).Мы не рекомендуем представлять диаграмму в качестве модели учащимся, но учителям может быть полезно визуально увидеть, какой тип ситуации представлен. Еще одна важная вещь, которую следует понять, заключается в том, что тип ситуации сам по себе не дает нам определения, использовать ли сложение или вычитание . Скорее, мы определяем необходимую операцию, основываясь на том, какое количество неизвестно. В нашем примере выше 3 рыбы добавляются в аквариум с 5 рыбками, и неизвестным является общее количество рыб (5 + 3 =?), Поэтому это требует добавления.Но если мы добавим 3 рыбок в аквариум, в котором теперь 8 рыб, это все равно «дополнительная» ситуация:? + 3 = 8), но мы использовали бы вычитание, чтобы найти неизвестное (8 — 3 =?). В таблице ниже мы приводим пример проблемы для каждого типа сюжетной ситуации и диаграмму, которая представляет взаимосвязь каждой ситуации между количествами. Урок четвертого класса с использованием обратной операции для сложения и вычитанияВ этом вводном видео с использованием обратной операции я объясняю нашу цель на сегодня. Учащиеся уже научились складывать и вычитать с помощью разряда. Это очень важный навык для студентов. Им нужно знать, что если у вас отсутствует номер, вы можете взять числа, которые они вам дают, и выполнить операцию, которая поможет вам определить недостающий номер.Эта операция является «обратной». Я сообщаю студентам, что сегодня мы изучаем стратегию, которая поможет нам добавить, если есть недостающее слагаемое, и даже найти разницу, если одно из наших чисел отсутствует. Мне нравится использовать свою доску Smart для обсуждения всего класса. Студенты подходят к ковру, чтобы они могли быть рядом, пока мы вместе обсуждаем навык. Мои ученики знают, что они могут задавать вопросы или вносить свой вклад во время прямого обучения всего класса.Обсуждая этот навык, я задаю вопросы на протяжении всего урока. Точка мощности с использованием инверсной операции отображается на интеллектуальной плате. В этом конкретном уроке я начну с обзора стоимости места и того, как мы используем ее для сложения и вычитания. Обзор: 1. Когда мы складываем или вычитаем, мы выстраиваем наши числа в соответствии с разрядными значениями.Цифры в разряде единиц должны совпадать друг с другом, разряды десятков и т. Д. 2. Некоторые номера нужно перегруппировать. Когда мы перегруппировываемся, мы помещаем число в разряды единиц внизу и перегруппируем число в разрядах десятков вверху разряда десятков. Например, с числом 15 5 будет стоять на месте единиц, а 1 будет перегруппировано в разряд десятков, потому что оно оценивается в 10 . 3. Когда мы вычитаем, нам, возможно, также придется перегруппироваться. . Давай попрактикуемся! 45 + ___ = 87 Чтобы найти недостающее слагаемое для этой задачи сложения, мы можем использовать обратную операцию вычитания. Поскольку у нас есть два числа, мы можем взять эти два числа и решить математическую задачу. 87–45 = 42 Отсутствует добавление 42. Давай попробуем с вычитанием! ___ — 53 = 28 Чтобы найти недостающее число, мы можем использовать обратное вычитание. Давайте добавим, чтобы найти недостающий номер. 28 + 53 = 81 Как использование обратной операции помогает находить недостающие числа? Сложение и вычитание: Введение в сложениеУрок 1: Введение в ДополнениеЧто такое сложение? Дополнение — это способ соединить вещи. Что, если бы было еще , четыре, еще кроликов? Как видите, если у вас есть 4 кроликов и добавить еще 4 , у вас будет всего 8 кроликов. Вы могли бы написать это так: 4 + 4 = 8 4 + 4 = 8 — это математическое уравнение . Вы могли прочитать это так: четыре плюс четыре равняются восьми.Математическое уравнение — это, по сути, математическое предложение . Вместо слов используются числа и символов, . Когда мы записываем уравнения со сложением, мы используем два символа: + и = . Знак плюс ( + ) означает, что две вещи складываются. Вот почему мы поместили его между кроликами — у нас было 4 кролика и добавили еще 4. Другой символ в нашем уравнении — равно знак ( = ).Когда вы видите знак равенства в уравнении, это означает, что два больше: равно или эквивалентно . Эквивалентные вещи не всегда выглядят или кажутся абсолютно одинаковыми, но они означают одно и то же. Например, когда вы видите кого-то, кого знаете, вы можете сказать несколько вещей: Эти слова не совсем похожи, но означают одно и то же. Это все способы поприветствовать кого-то. В математике знак равенства показывает, что два числа или выражения означают одно и то же, , даже если они могут выглядеть по-разному.Помните наших кроликов? Поскольку всего кроликов было 8, мы написали 8 справа от знака равенства. Видите, как каждая сторона означает 8? Слева 8 кроликов, а справа цифра 8. Обе стороны равны . Попробуй!Заполните пропуски, чтобы завершить уравнения. Написание выражений На последней странице мы рассмотрели некоторые математические выражения. Любую задачу сложения можно превратить в письменное выражение. Например, предположим, что вы планировали пригласить на ужин троих друзей. В последний момент вы приглашаете еще двоих. Чтобы узнать общее количество друзей, которые приходят к вам домой, вы можете написать такое выражение: 3 + 2 Выражение — это просто другой способ описания ситуации: трое друзей плюс двое еще приходят на обед. Попробуй!Запишите эти ситуации в виде математических выражений. Пока не решайте проблемы — просто установите их. Вы съели на обед трех кусочков пиццы. За ужином вы съели , два, еще : Вы уже ждали пять минут, чтобы обратиться к врачу. Медсестра говорит вам подождать пять еще минут: На вашем пальто четыре пуговицы с правой стороны и три пуговицы с левой стороны: Решение проблем Теперь, когда вы знаете, как писать задачи сложения, давайте решим некоторые из них. Попробуй!Например, можете ли вы использовать счет, чтобы написать и решить эту задачу? С этой проблемой вы смогли подсчитать добавляемые вами объекты. В реальной жизни некоторые люди любят считать пальцами. Другие люди используют мелкие предметы, такие как пуговицы или пенни. Другие могут делать небольшие отметки на листе бумаги. Когда учишься складывать, можно считать! Чем больше вы практикуетесь, тем легче будет складывать без счета. Способы подсчетаДавайте рассмотрим два способа решения задач сложения со счетом. Сначала мы посчитаем с объектами . Другой способ решить проблемы сложения — использовать строку номера . Практика!Попрактикуйтесь в добавлении этих задач. Всего 5 наборов задач, по 3 задач в каждом наборе. Набор 1Набор 2Набор 3Набор 4Набор 5/ ru / addsubtraction / сложение двух- и трехзначных-чисел / content / . Рабочие листы по математике для 4-го классаРабочие листы для сложенияЭто главная страница для рабочих листов для сложения. Перейдите по ссылкам, чтобы найти рабочие листы сложения по математике космического корабля, рабочие листы сложения нескольких цифр, рабочие листы сложения без переноса и другие темы сложения. Эти дополнительные рабочие листы бесплатны для личного или классного использования. Рабочие листы на сложение Рабочие листы на вычитаниеЭто главная страница рабочих листов на вычитание. Перейдите по ссылкам, чтобы найти рабочие листы по математическому вычитанию космического корабля, тесты на вычитание по времени, рабочие листы по вычитанию нескольких цифр, простые рабочие листы по заимствованию и перегруппировке, а также математические рабочие листы со смешанными задачами на сложение и вычитание Рабочие листы по вычитанию Рабочие листы по умножению Это главная страница для рабочих листов по умножению. Рабочие листы на умножение Рабочие листы на делениеЭто главная страница рабочих листов на деление. Сюда входят рабочие листы математического отдела космического корабля, рабочие листы для деления на несколько цифр, рабочие листы для квадратных корней, кубических корней, смешанные рабочие листы для умножения и деления. Эти рабочие листы разделения бесплатны для личного или классного использования. Рабочие листы на деление Таблица умножения Пытаетесь запомнить факты умножения? Эта страница содержит печатные таблицы умножения, которые идеально подходят для справки. Таблица умножения Таблица умноженияВы ищете распечатанную таблицу умножения, в которой есть не только факты? Один с некоторыми дополнительными математическими фактами о множителях? Или уникальный дизайн? В цвете? Все таблицы умножения на этой странице представляют собой файлы SVG с высоким разрешением, которые прекрасно распечатываются на вашем принтере и являются отличным ресурсом для изучения таблицы умножения в классе начальной школы или дома! Таблица умножения Рабочие листы семейства фактов Рабочие листы семейства фактов сосредоточены на наборах связанных математических фактов, а не на конкретных операциях. Рабочие листы семейства фактов Рабочие листы длинного деленияВводные рабочие листы с делением в длинное число, листы с делением в длинное с остатком и без него, деление в длинное с десятичными знаками. Все эти длинные листы деления включают подробные, развернутые ответы. Рабочие листы длинного деления Графические дробиОтличное введение в дроби с использованием круговой графики. Учащихся просят идентифицировать числовые формы дробей на графике или создать свои собственные представления. Графические дроби Сокращение дробей Практические рабочие листы для сокращения дробей. Сокращение дробей Сравнение дробейПрактические рабочие листы для сравнения дробей. Задачи на дроби на этих листах требуют от детей сравнения одинаковых и непохожих знаменателей, неправильных дробей и смешанных дробей. Сравнение дробей Сложение дробейРабочие листы для сложения дробей с общими знаменателями, с разными знаменателями, в виде простых дробей и смешанных дробей. Полная работа с шагами показана для каждой задачи на ключах ответов. Сложение дробей Вычитание дробейРабочие листы для вычитания дробей с общими знаменателями, с разными знаменателями, в виде простых дробей и смешанных дробей. Полные ключи ответов, которые показывают работу! Вычитание дробей Умножение дробей Эти математические рабочие листы служат для практики умножения дробей. Умножение дробей Деление дробейРабочие листы для деления дробей с делением на две дроби. Включает в себя простые дроби, смешанные дроби и неправильные дроби, а также задачи, для решения которых используется шаг перекрестного умножения. Деление дробей Дроби в виде десятичных дробейРабочие листы для преобразования дробей в десятичные, в том числе с использованием деления в большую сторону. Дроби как десятичные числа Задачи со словами На этой странице представлены задачи со словами, охватывающие ряд трудностей для всех основных операций, включая задачи с большими значениями, а также с неиспользованной информацией. Словесные задачи Денежные задачиРеальные задачи на сложение, вычитание, умножение и деление на деньги. Отличное первое введение в прикладную математику для студентов, знакомых с десятичной арифметикой! Задачи на деньги Word Отрицательные числаЭти рабочие листы с отрицательными числами комбинируют отрицательные числа с другими целыми числами (как положительными, так и отрицательными) с использованием основных математических операций, умножения многозначных отрицательных чисел и деления в длинную сторону с отрицательными числами. Отрицательные числа Проценты Рабочие листы для практики использования и вычисления процентов других чисел, включая преобразование между дробями и процентами. Проценты Округление чиселВ этом разделе представлены рабочие листы округления для округления целых чисел и округления десятичных чисел, начиная с относительно простых задач, которые знакомят с алгоритмом округления, а затем переходят к более сложным задачам, где учащиеся должны определить правильную разрядную цифру до проверьте, а также правильную цифру для округления в большую или меньшую сторону.. Округление чисел Упорядочивание чиселПрактика упорядочивания рабочих листов с несколькими числами в порядке возрастания (от наибольшего к наименьшему) и убывания (от наименьшего к наибольшему). Включает в себя целые числа, десятичные числа и отрицательные числа. Аналогичные наборы рабочих листов с порядковыми номерами представлены как в горизонтальном, так и в вертикальном форматах. Номера для заказа Стандартная, расширенная и словесная формы Практические рабочие листы для преобразования чисел между стандартной формой (цифры), расширенной формой (разрядное значение) и формой слова (прописью или устным представлением). Стандартная, расширенная и словесная форма Шаблоны с отрицательными числамиШаблоны чисел, которые пересекают ноль и могут начинаться или заканчиваться отрицательными значениями. Шаблоны с отрицаниями Среднее, медиана, диапазонРабочие листы для определения среднего, медианы, моды и диапазона для наборов чисел. Задачи включают в себя наборы всех положительных целых чисел, все отрицательные целые числа и смешанные наборы знаков, а также практику работы с калькулятором. Среднее, Медиана, Диапазон Отсутствующие операцииРабочие листы, в которых даны ответы, но отсутствует операция. Это отличный способ выучить группы фактов «в обратном порядке» или обеспечить подкрепление, если запоминание с помощью других упражнений кажется застопорившимся. Отсутствующие операции Римские цифры Рабочие листы по римским цифрам, включая преобразование римских цифр, упорядочивание римских цифр и заполнение шаблонов римских цифр. Римские цифры Таблица римских цифрЕсли вы пытаетесь научиться читать и писать римскими цифрами, пытаетесь найти причудливый способ написать свой год рождения, или вам просто нужна «шпаргалка» для быстрого Для справки, каждая таблица с римскими цифрами на этой странице позволит вам работать с этой древней системой счисления в кратчайшие сроки. Все диаграммы печатаются на одной странице в версиях для 1-10, 1-100 и 1-1000 с правилами для римских цифр и без них. Пытаетесь понять, что означает эта странная римская цифра после Суперкубка? Взгляните на новую таблицу римских цифр Super Bowl! Таблица с римскими цифрами СудокуГоловоломки судоку для детей и взрослых, в том числе легкие и сложные, злые судоку, самурайские судоку и многое другое! Судоку Магический квадрат Головоломки с магическим квадратом — отличное введение в логику и решение задач. Волшебный квадрат Головоломки с числовой сеткойВ этом разделе представлены листы математических логических головоломок в виде сетки, включающие сложение, вычитание, умножение и деление для разных классов и уровней навыков. Существуют версии этих логических головоломок с пропущенными числами, а также с пропущенными операциями. Головоломки с числовой сеткой Рабочие листы с показателями степениЗнакомство с квадратами, кубами и показателями степени в сочетании с другими базовыми операциями. Включает в себя практику, которая создаст память сайта общих экспоненциальных терминов Рабочие листы показателей Рабочие листы порядка операций Эти рабочие листы порядка операций смешивают основные арифметические операции, включая круглые скобки и показатели степени. Порядок действий Рабочие листы Базовая геометрияПростая маркировка линий, углов и треугольников. Идентификация фигур Базовая геометрия Определение аналогового времениПрактические рабочие листы для определения времени аналоговых часов, включая чтение времени и рисование циферблата. Определение аналогового времени Прошедшее аналоговое времяРабочие листы для сравнения двух аналоговых часов и определения времени, прошедшего между ними. Прошедшее аналоговое время Больше и меньше Практические рабочие листы для сравнения чисел. Больше и меньше Бумага для рукописного вводаПечатные шаблоны бумаги для рукописного ввода с разной высотой строки, включая 3-строчную тренировочную бумагу в обычном и широком макетах, чистую бумагу для рассказов и обычную разлинованную бумагу для старшего класса ученики. Ознакомьтесь с пронумерованными пустыми шаблонами проверки орфографии! Бумага для рукописного ввода Миллиметровая бумагаБесплатная печатная миллиметровая бумага, бумага с сеткой и точечная бумага для математических задач, ремесел, зентанглинга, ландшафтного дизайна, архитектуры или просто рисования. Все стили графической бумаги включают дюймовые и сантиметровые варианты. Все эти PDF-файлы предназначены для печати на бумаге размером 8,5 x 11 дюймов. Миллиметровая бумага Координатная плоскость Пустые координатные плоскости на этой странице включают варианты с метками либо на оси, либо на краю сетки, а также версии с метками квадрантов. Координатная плоскость Измерение в дюймахЭти листы измерения в дюймах (обычные единицы измерения) помогут развить навыки выполнения линейных измерений либо в одной точке, либо в измерении длины объекта. Существуют различные измерительные рабочие листы с задачами, подходящие для учащихся детского сада, первого, второго или третьего класса по математике. Измерение в дюймах Метрическое измерение Рабочие листы для определения измеренных положений и измерения объектов в сантиметрах и миллиметрах на линейке. Эти рабочие листы являются отличной практикой для учащихся первого, второго, третьего и четвертого классов, а также могут обеспечить практическую практику вычитания при измерении длины объектов на линейке. Метрическая единица измерения Преобразование единиц метрической системы СИВ этих таблицах для преобразования единиц измерения из одной единицы измерения в другую используются единичные дроби. Этот подход более распространен на уроках химии, физики или других естественных наук и требует, чтобы учащиеся сосредоточились на сокращении единиц, чтобы найти решение с правильным значением и правильными единицами. Преобразование единиц метрической системы СИ Преобразование обычных единиц измерения Традиционная практика преобразования единиц измерения расстояния (дюймы в футы), объема (унции в галлоны) и массы (унции в фунты). Эти рабочие листы также используют дроби единицы для преобразования значений единиц измерения из одного измерения в другое. Этот подход более распространен на уроках химии, физики или других естественных наук и требует, чтобы учащиеся сосредоточились на сокращении единиц, чтобы найти решение с правильным значением и правильными единицами. Преобразование обычных единиц измерения Традиционные и метрические единицыВ этих рабочих листах используются единичные дроби для преобразования значений между единицами СИ (метрическими) и обычными единицами. Темы в этом разделе включают практику преобразования дюймов в метры, литров в галлоны и граммов в фунты. Обычное и метрическое деление Изображение Математическое деление В этих печатных рабочих листах используются изображения и группировка для построения концептуального понимания деления, и они являются идеальным первым введением в эту часто запутанную операцию. Эти рабочие листы начинаются с простых задач с изображением деления, где требуются только базовые навыки счета, чтобы придумать предложения с числами вычитания, но более поздние рабочие листы требуют, чтобы учащиеся создали аналогичную иллюстрацию сетки, чтобы продемонстрировать свое понимание концепций деления, включая остатки. Picture Math Division ДеньгиЭти рабочие листы для распечатки денег содержат реалистичные монеты и купюры в задачах на идентификацию монет, внесение сдачи, подсчет монет и сравнение сумм денег. Они формируют базовые навыки распознавания и счета в детском саду и в первом классе, чтобы подготовиться к полной практике с деньгами, необходимой для прохождения второго класса. Деньги Математика космического корабляСтраницы галочки космического корабля (в комплекте с космическим кораблем!) для отслеживания прогресса в рабочих листах математики космического корабля или ракетной математики для каждой из четырех основных операций. Проверка математики космического корабля Дополнение «Раскрась по номеру» Эти рабочие листы с добавлением раскраски требуют, чтобы учащиеся решили простые математические факты, чтобы найти правильный цвет для раскрашивания, чтобы показать изображение их собственного творения. Добавление цвета по номеру Раскраска по номерам с вычитаниемВ этих рабочих листах для раскрашивания с вычитанием учащиеся должны решить простые математические факты, чтобы найти правильный цвет для раскрашивания, чтобы показать изображение собственного творения. Вы найдете растущий набор праздничных и сезонных тематических страниц, которые я буду добавлять со временем… Пожалуйста, заходите почаще на наличие обновлений или, если у вас есть предложения, отправьте мне сообщение по контактной ссылке ниже! Вычитание цвета по номеру Умножение цвета по номеру Ищете рабочие листы, чтобы сделать изучение математики в День святого Валентина более увлекательным? На этой странице собраны листы для умножения в цвете на число, подходящие для учащихся третьего, четвертого или пятого классов. Умножение раскраски по номерам Разделение раскраски по номерамИщете рабочие листы, чтобы сделать изучение математики в День святого Валентина немного веселее? На этой странице собраны листы с цветовым делением по номерам, подходящие для учащихся третьего, четвертого или пятого классов. Раскраска по номерам День святого ВалентинаИщете рабочие листы, чтобы сделать изучение математики в День святого Валентина немного веселее? На этой странице собраны раскрашенные по номерам рабочие листы, подходящие для детей от детского сада до четвертого класса, в которых описаны операции сложения, вычитания, умножения и деления. Есть также коллекция простых математических упражнений с забавными темами Дня святого Валентина. День святого Валентина День Земли Ищете рабочие листы, чтобы сделать изучение математики в День Земли немного веселее? На этой странице собраны раскрашенные по номерам рабочие листы, подходящие для детей от детского сада до четвертого класса, в которых описаны операции сложения, вычитания, умножения и деления. День Земли День Святого ПатрикаКогда дело доходит до математики, нельзя полагаться только на удачу ирландцев, но этот День Святого Патрика делает его немного веселее! На этой странице собраны раскрашенные по номерам рабочие листы, подходящие для детей от детского сада до четвертого класса, в которых описаны операции сложения, вычитания, умножения и деления. Есть также коллекция простых математических упражнений с забавными темами трилистника Дня Святого Патрика. День Святого Патрика ВеснаКакое лучшее время года для развития новых математических навыков, чем весна! На этой странице собраны раскрашенные по номерам рабочие листы, подходящие для детей от детского сада до четвертого класса, в которых описаны операции сложения, вычитания, умножения и деления. Существует также коллекция простых весенних математических листов с забавными весенними цветочными темами, а также таблица умножения, таблица сотен, миллиметровая бумага и координатная плоскость! Пружина Таблица квадратного корня Ищете ли вы список полных квадратных корней или полную таблицу квадратных корней от 1 до 100, таблица квадратных корней на этой странице поможет вам найти радикалы! Существуют как цветные, так и черно-белые версии диаграмм в формате PDF для печати. Таблица квадратного корня Таблица дробейЭта уникальная визуализация эквивалентных дробей объединяет значения дробей на числовой прямой для создания элегантной симметрии. Он не только выделяет дроби в их наименьшей, наиболее сокращенной форме, но и предоставляет удобный десятичный эквивалент для наиболее часто используемых дробей. Это действительно одна из лучших справочных диаграмм, которые я создал за 10 лет создания математических ресурсов! Таблица дробей Головоломки по поиску словИспользуйте эти математические головоломки для поиска слов, чтобы познакомить школьников со словарным запасом и терминами, когда они знакомятся с новыми математическими понятиями! Эти головоломки для поиска слов включают в себя наборы для различных уровней обучения, согласованных с Common Core, а также конкретные темы для геометрии, алгебры и многого другого! Головоломки с поиском слов Таблица вероятностей Таблица привязки вероятностей для решения задач со словами! Эта иллюстрированная таблица описывает сценарии с монетами, костями и игральными картами. Таблица вероятностей Таблица измеренийЭта таблица измерений является хорошим справочным пособием для текстовых задач, связанных с переводом единиц объема, длины или температуры из одной системы в другую. Значения показаны на одной шкале как в обычной, так и в метрической системах. Отлично подходит для измерения кухни и приготовления пищи! Таблица измерений Числовая линейка Числовая линейка может быть мощным инструментом для изучения отрицательных чисел, отношений или просто вводных операций сложения и вычитания. PDF-файлы с числовыми строками на этой странице включают различные диапазоны (10, 12, 15, 20, 15 и 100) как с нуля, так и с отрицательными диапазонами. Полный набор строк чисел дроби, отмеченных общими знаменателями, включен в диапазоны от -5 до 5. Существуют также специальные строки с номерами для прошедшего времени, температуры и денег, а также пустые строки с номерами для обычных диапазонов и дробей. Числовая строка Рабочие листы по математике для четвертого класса Четвертый класс выполнен — это переходный этап, когда основное внимание смещается от многих основных математических фактов к приложениям. По-прежнему большое внимание уделяется более сложным арифметическим задачам, таким как задачи на деление и умножение, и в этом разделе вы найдете множество математических листов по этим темам. Этот набор рабочих листов для 4-го класса содержит больше рабочих листов с дробями, включая уменьшение и сравнение дробей, и обязательно ознакомьтесь с Калькулятором дробей, который поможет решить множество задач с дробями. Проценты — еще одна тема, изучаемая в 4-м классе, и рабочие листы с процентами в этом разделе можно решить с помощью калькулятора процентов, если у учащихся возникнут проблемы с решением этих задач. Учащиеся также будут использовать многие из своих основных математических навыков для преобразования единиц измерения в 4-м классе, и в этом разделе вы также найдете рабочие листы для метрических и обычных единиц измерения. Рабочие листы по математике для 4-го классаПоддерживая обучение и практику, наши рабочие листы по математике для 4-го класса с ключами для ответов прекрасно впишутся в ваш учебный план. При адекватных упражнениях на многозначное умножение и деление, эквивалентные дроби, сложение и вычитание дробей с одинаковыми знаменателями, умножение дробей на целые числа, анализ и классификацию геометрических фигур на основе их свойств, таких как параллельные и перпендикулярные стороны, угол меры и симметрия, преобразование между единицами измерения, построение и интерпретация линейных графиков, эти PDF-файлы становятся наиболее востребованными. Возьмите наши бесплатные рабочие листы по математике для 4 класса, чтобы заглянуть в магазин. All Добавление и вычитание Умножение и разделение Факторы и кратные Паттерны Значение места Фракции и десятилетия Данные и графики , Sephgments & Rays 5 699. Фигуры ФигурыСимметрия Исследуйте более 5600 рабочих листов по математике для четвертого класса Сложение четырехзначных чисел Повторение — верный способ быстро и точно сложить два четырехзначных числа. Тренируйтесь в перегруппировке в единицах, десятках, сотнях и тысячах в процессе. Умножение для начинающих | Факторы До 12 Если вы хотите улучшить навыки умножения, то наши рабочие листы по математике для 4-го класса в формате PDF должны быть очевидным выбором. Находите произведение чисел до 12 и решайте настоящие текстовые задачи. Список факторов | Легко (от 1 до 50) Разбейте каждое число на составляющие, найдя коэффициенты, при умножении которых получается данное число. Перечислите все возможные факторы каждого указанного числа от наименьшего до наибольшего. Завершение построения фигуры Развивайте навыки анализа фигур с помощью наших распечатываемых математических листов. Написание числовых слов | Миллионы Переведите 7-, 8- и 9-значные числа в числовые слова: миллионы, десять миллионов и сто миллионов, по мере того, как вы работаете, удваивая и совершенствуя свои навыки разряда. Запись пропущенных чисел в эквивалентных дробях Чтобы получить эквивалентные дроби, числитель и знаменатель дроби необходимо умножить или разделить на одно и то же число. Примените это правило, чтобы выяснить недостающие числа в этих математических PDF-файлах для 4-го класса. Измерение и преобразование дюймов в футы и дюймы Развить жизненно важный навык, потренировавшись измерять длину полосок бумаги в дюймах с помощью данной линейки и делить длину на 12, чтобы выразить длину в футах и дюймах. Интерпретация линейных графиков Сделайте выводы, интерпретируя данные, организованные в виде линейных графиков в наших печатных листах по математике для 4 класса, и рассчитайте среднее значение, медиану, моду и диапазон, чтобы ответить на вопросы на основе линейного графика. Идентификация точек, линий, лучей и сегментов линий Посмотрите на стрелки и точки и распознайте каждую модель как точку, линию, луч или сегмент линии в Части А. Попытайтесь нарисовать линию, луч и сегмент линии в Часть B. частей угла | Именование вершины и плеч Помогите всезнайкам 4-го класса определить части угла: стороны, два луча, соединяющиеся в угол, и вершину, которая является общей конечной точкой, и назовите их в этих pdf-файлах с математическими таблицами. Классификация треугольников по сторонам Как насчет классификации треугольников по сторонам? Назовите треугольники с тремя равными сторонами равносторонними, треугольники с двумя равными сторонами равнобедренными, а треугольники с неравными сторонами разносторонними. Традиционные единицы США Метрические единицы Рисование линий симметрии | Фигуры Воспользуйтесь нашими печатными таблицами по математике для 4-го класса, чтобы попрактиковаться в рисовании линии поперек фигуры, делящей ее на две одинаковые половины и определяющей, являются ли фигуры симметричными по горизонтали или по вертикали. Решение задач на сложение многозначных слов Вооруженные реальным миром, наши упражнения прививают любовь к математике у детей 4-го класса, поскольку они решают задачи со словами, работают со слагаемыми от 4 до 8 цифр и вычисляют сумму . Мультипликационная дрель | 50 задач Ничто так не способствует повторению умножения, как эти pdf-файлы с заданиями по математике для 4-го класса. Побейте время, выполняя упражнение на умножение на время, состоящее из 50 задач каждое. Факторы поиска | Простые и составные Совершенствуйте свою практику в нахождении множителей чисел и определении, является ли заданное число простым (делящимся только на число 1 или само на себя) или составным. Далее » Рабочие листы по математикеДополнение На этой индексной странице вы найдете ссылки на все типы таблиц сложения, включая основные факты, двухзначные сложения, трехзначные сложения, четырехзначные сложения, сложение дробей, десятичное сложение, семейства фактов и сложение денег. Дополнение: основные факты Рабочие листы с основными однозначными фактами сложения (сумма до 18). Сложение: 3-значные сложения Потренируйтесь складывать 3-значные числа вместе с этими печатными листами, карточками с заданиями и играми. Дополнение: 4- и 5-значное дополнение Предложите своим ученикам решить задачи на сложение с 4- и 5-значными числами. Сложение: 3 или более слагаемых Проблемы сложения столбцов с 3 или более сложениями 1-, 2-, 3- и 4-значных чисел. Сложение и вычитание: основные задачи Рабочие листы, карточки и числовые ряды на этой странице содержат набор основных задач на сложение и вычитание однозначных чисел. Сложение: Дроби Складывание дробей и смешанных чисел с одинаковыми знаменателями, а также с разными знаменателями. Свойства сложения Эти рабочие листы были созданы для обучения учащихся коммутативным и ассоциативным свойствам сложения. Квадраты сложения Развивайте навыки логического мышления с помощью этих рабочих листов-головоломок с добавлением квадратов. Семейства фактов сложения-вычитания Рабочие листы с базовыми треугольниками семейства фактов, числовыми связями и квадратами фактов для сложения и вычитания. Дополнение: Игра с суммой (базовое дополнение) На этих распечатываемых игровых досках учащиеся раскрашивают пары чисел, которые равны заданной сумме. Алгебра и предварительная алгебра Напишите алгебраические выражения, научитесь определять независимые/зависимые переменные, находить переменные в уравнениях, работать с неравенствами и т. д. Углы: типы и измерение Использование транспортира для измерения прямых, острых и тупых углов. Углы: дополнительные, дополнительные, вертикальные Загрузите рабочие листы для отработки геометрических понятий, связанных с вертикальными, дополнительными и дополнительными углами. Площадь треугольников Используйте формулу A = 1/2 x (b x h) для расчета площади треугольников Рабочие листы площади Вычислите площадь (в квадратных единицах) фигур на этих рабочих листах. Коробчатые диаграммы (диаграммы «коробка-и-усы») Используйте эти рабочие листы, чтобы помочь учащимся узнать о статистике и создании диаграмм «коробка-и-усы». Существуют также рабочие листы для расчета Q1, Q3, медианы, минимального и максимального значений. Календари (математика) Календари, чтобы помочь студентам с годами, месяцами, неделями и днями в календаре. Таблицы емкости Таблицы объема или емкости (галлоны, кварты, пинты и чашки). Круги: радиус, диаметр, длина окружности Расчет диаметра и радиуса кругов; также включает листы окружности и площади. Рабочие листы для раскрашивания по номерам Раскрасьте загадочные картинки в соответствии с цифрой внизу. Считать деньги (Австралия) Используйте эти рабочие листы, чтобы попрактиковаться в счете австралийских денег. Подсчет денег (канадский) Считайте мультяшек, луни, четвертаки, пятаки и десятицентовики с помощью этих рабочих листов для канадских валют. Счет денег (британские фунты) Научитесь считать фунты и пенсы, монеты, используемые в Соединенном Королевстве. Счет денег (США) Потренируйтесь считать американские деньги (пенни, пятаки, десять центов и четвертаки). Рабочие листы для подсчета 0–30 (очень простые) Научитесь считать и писать числа до 30. Рабочие листы для подсчета (более сложные) Научитесь точно считать двух-, трех- и четырехзначные числа. Заполните числовые строки, скажите, какая цифра идет впереди, и пропустите счет. Ежедневный обзор математики На этой странице вы найдете более 100 рабочих листов для ежедневного повторения («Math Buzz»), предназначенных для классов с 1 по 5. до 5. Студентам предстоит решить сотни графических текстовых задач, а также достаточно места, чтобы показать свою работу. Десятичное сложение и вычитание Сложение и вычитание десятичных чисел со значениями десятых, сотых и тысячных долей. Десятичное деление Практикуйте деление в длинное с десятичными числами. Десятичное умножение Упражнения на умножение с десятичными множителями и произведениями. Десятичные рабочие листы Именование и работа с десятичными числами. Рабочие листы по разделам: основные Рабочие листы по основным фактам, игры и задания. Рабочие листы деления: длинное деление Рабочие листы длинного деления с 2-, 3- и 4-значными делимыми. Уравнения (базовая алгебра) Научитесь сопоставлять простые алгебраические уравнения и находить значения переменных. Рабочие листы для четных и нечетных чисел Определение нечетных и четных чисел Рабочие листы для показателей степени Найдите показатели степени для однозначных чисел на этих печатных листах и карточках с заданиями. Факторинговые листы Полное дерево множителей, поиск наибольших общих делителей и наименьших общих кратных. Таблицы дробей (дополнительно) Сокращение дробей, упорядочивание дробей, эквивалентные дроби и сравнение дробей. Рабочие листы дробей (базовые) Идентификация основных дробей, полос дробей, манипуляций дробями. Дроби: сложение Нахождение сумм дробей и смешанных чисел. Включает рабочие листы с дробями с одинаковым знаменателем, а также с дробями с разными знаменателями. Дроби: Деление Деление дробей и смешанных чисел. Многие из этих рабочих листов включают иллюстрированные задачи, задачи с графическими моделями, а также текстовые задачи. Дроби: смешанные числа Практикуйте базовые навыки работы со смешанными числами. Дроби: умножение Умножение дробей и смешанных чисел. Многие рабочие листы включают модели и диаграммы, а также текстовые задачи. Дроби: обратные дроби Распечатайте эти рабочие листы, чтобы помочь учащимся узнать об обратных дробях. Дроби: вычитание Практика вычитания дробей и смешанных чисел. Включает подобные и неодинаковые знаменатели. Практика с рамками и стрелками Используйте упражнения с рамками и стрелками для развития навыков логического мышления. Графики: гистограммы Прочитайте гистограммы на рабочих листах и ответьте на вопросы. Графики: линейные графики Интерпретируйте линейные графики на рабочих листах и ответьте на вопросы. Графики: линейные графики Линейные графики — это особый тип числовых линий, представляющих частоту данных. Графики: пиктограммы Изучите пиктограммы на рабочих листах и ответьте на вопросы. Графики: круговые диаграммы Проанализируйте круговые диаграммы на рабочих листах и ответьте на вопросы. Больше, Меньше Рабочие листы Сравните числа больше, меньше и равно. Таблицы сотен Используйте эти полезные таблицы стоимостных значений, таблицы сотен, таблицы девяноста девяти. Ящики ввода и вывода Заполните эти печатаемые поля ввода и вывода или поля правил. Неравенства Решить неравенства и построить график. Включает неравенства с одной переменной, одношаговые и двухшаговые неравенства. Целые числа (базовый) Сравнение, упорядочивание, сложение и вычитание положительных и отрицательных чисел. Наименьшее общее кратное (НОК) Определение наименьшего общего кратного каждого набора чисел Линии, сегменты, лучи Узнайте о линиях, сегментах линий, лучах, параллельных линиях и перпендикулярных линиях. Математические кроссворды Решите математические задачи и используйте ответы, чтобы решить кроссворды. Математические загадки Решите математические задачи, чтобы расшифровать ответ на забавные загадки. Включает широкий спектр математических навыков, включая сложение, вычитание, умножение, деление, разрядность, округление и многое другое. Отрывки из математических рассказов На этой странице есть набор отрывков для чтения на всю страницу. Учащиеся используют информацию из отрывков для решения математических задач. Они намного длиннее, чем «обычные» текстовые задачи. Рабочие листы Mean (Averages) Вычислить среднее или среднее числовых значений. Среднее значение, медиана, мода и диапазон Вычислить моду, медиану, среднее значение и диапазон заданных чисел. Индекс измерений Выберите нужные типы таблиц измерений, включая линейные измерения, емкость и температуру. Измерение: CM, MM и M Практика метрических линейных измерений: сантиметры, миллиметры и метры. Измерение: футы, ярды, дюймы Изучите американские линейные измерения; дюймы, футы и ярды. Измерение: граммы и килограммы Измерение веса и преобразование в граммы и килограммы. Измерение: литры и миллилитры Оценить и преобразовать измерения емкости в литрах и миллилитрах. Измерение: фунты и унции Измерение веса и преобразование в унции и фунты и обратно. Математика средней школы Эта индексная страница содержит ссылки на десятки тем по математике для средней школы на этом сайте. Минимум математических упражнений Листы с практическими упражнениями для сложения, вычитания, умножения и деления. Кратные числа Эти рабочие листы помогут учащимся научиться находить и определять кратные числа. Умножение (Свойства) Узнайте об ассоциативных, дистрибутивных, коммутативных и тождественных свойствах умножения. Таблицы умножения Распечатайте эти таблицы и таблицы умножения, чтобы учащиеся могли использовать их в качестве справочных материалов. Рабочие листы по умножению: продвинутый уровень Решите задачи на умножение двух и трех цифр. Рабочие листы по умножению: основы Изучите основные факты умножения с помощью этих рабочих листов, загадочных картинок и игр. Семейства фактов умножения-деления Связи основных чисел, рабочие листы семейства фактов и треугольники для деления и умножения. Умножение: Решетчатое умножение Умножение на 2-х, 3-х или 4-значные числа с решетчатой сеткой. Mystery Graph Art Нарисуйте упорядоченные пары, чтобы открыть загадочные картинки. Mystery Math Pictures Решите сложение, вычитание, умножение и деление, чтобы открыть загадочную картинку. Детектив чисел (секретные числа) Учащиеся будут использовать подсказки, вывешиваемые каждый день, чтобы вычислить недельный секретный номер. Числовые строки Рабочие листы числовых строк для обучения счету, сложению, вычитанию, числовым образцам, дробям и десятичным числам. Порядок действий Отработайте порядок действий: скобки и возведения в степень, затем умножение и деление, затем сложение и вычитание. Заказные пары; Координатные плоскости Координатные плоскости и упорядоченные парные рабочие листы. Порядковые номера Порядковые номера определяют позицию в серии. (примеры: первый, второй, третий, четвертый и т. д.) Шаблоны: число Учащиеся должны перечислить числа, которые следуют в этих шаблонах. Образцы: Рисунок Учащиеся определяют, какие изображения идут следующими в узорах. Таблицы процентов Преобразование десятичных чисел и дробей в проценты. Рабочие листы периметра Добавьте, чтобы найти периметры многоугольников на этих рабочих листах. Рабочие листы разряда Нахождение значения подчеркнутой цифры; стандартная и расширенная форма; округление. Простые и составные числа Изучите разницу между простыми и составными числами. Полигоны. Рабочие листы Определение многоугольников и работа с ними. Рабочие листы вероятности Определение вероятности определенных исходов. Математические игры-головоломки Распечатываемые кусочки пазла, которые вы можете вырезать, чтобы ученики сопоставили их. Отлично подходит для учебных центров, занятий в небольших группах и самостоятельной практики. Теорема Пифагора Найдите длины сторон прямоугольного треугольника по формуле теоремы Пифагора. Рабочие листы с QR-кодом Учащиеся используют iPad или смартфон для сканирования QR-кодов, чтобы решать или проверять задачи на каждом из этих математических рабочих листов. Соотношения Потренируйтесь сравнивать пары величин с помощью соотношений. Отражение, вращение и перемещение Определение отраженных, повернутых и перемещенных фигур. Римские цифры Научитесь читать и писать римскими цифрами с помощью этих печатных листов и упражнений. Рабочие листы для округления чисел Округление чисел до ближайших десятков и сотен. Научное представление Научитесь записывать числа в научном представлении. Secret Code Math На этих рабочих листах учащиеся будут использовать ключ для расшифровки секретных чисел в каждой задаче на сложение, вычитание, умножение или деление. Похожие и конгруэнтные рабочие листы Определите похожие и конгруэнтные формы. Счет с пропуском сотнями Используйте эти рабочие листы, чтобы научить учащихся считать с пропуском сотнями. Пропустить счет десятками Повторить счет десятками с помощью этих печатных форм. Пропустить счет до 11 Сосчитайте до одиннадцати, умножьте на одиннадцать и вставьте пропущенные числа. Пропустить счет до 12 Заполните пустые ячейки и текстовые задачи, считая до двенадцати. Пропустить счет до 25 Пропустить счет до двадцати пяти очень важно, если вы учите своих учеников считать деньги. Пропустить счет на 2 секунды Используйте эти распечатки, чтобы научить учащихся пропускать счет с интервалом в два. Пропустить счет до трех Набор рабочих листов на этой странице поможет учащимся научиться считать до трех. Пропустить счет до четырех Если вы учите учащихся считать до четырех, попробуйте эти рабочие листы. Пропустить счет пятерками Когда вы учите учащихся считать пятерками или пятерками, эти рабочие листы могут быть вам полезны. Рабочие листы слайдов, переворотов и поворотов Укажите, были ли фигуры перевернуты, сдвинуты или повернуты. Наклон На этих рабочих листах учащиеся будут использовать графики, упорядоченные пары и таблицы для расчета наклонов прямых линий. Рабочие листы с геометрическими телами Назовите геометрические тела: прямоугольные призмы, кубы, сферы и цилиндры. Специальные числа Эти рабочие листы охватывают различные понятия разрядности, включая четные/нечетные значения, нахождение значения цифр и запись чисел в расширенной форме. Вычитание Вычитание однозначных и многозначных чисел. Включает 1, 2, 3 и 4-значные числа. Вычитание: основы Практика основных фактов вычитания однозначных чисел; концепции и рабочие листы. Вычитание дробей Потренируйтесь вычитать дроби и смешанные числа с помощью этих распечатываемых листов и карточек с заданиями. Площадь поверхности Расчет площади поверхности прямоугольных призм и других трехмерных фигур. Рабочие листы по симметрии Найдите линии симметрии, определите симметричные фигуры и завершите симметричные фигуры. Метки учета Научитесь считать объекты с помощью меток учета. Рабочие листы температуры Прочтите показания термометров Цельсия и Фаренгейта и укажите температуру. Математика с десятью рамками Распечатанные задания с десятью рамками для обучения счету, основам сложения и простому вычитанию. Рабочие листы по мозаике Научите учащихся распознавать геометрическую мозаику двумерных фигур. Рабочие листы времени Узнайте, как определять время с точностью до минуты, часа и четверти часа. Время: Прошедшее время Определить количество прошедшего времени. Диаграммы Венна (математика) Эта страница содержит математические рабочие листы диаграммы Венна. Объем — Градуированные цилиндры Эти рабочие листы содержат изображения градуированных цилиндров. Учащиеся должны написать правильный объем в миллилитрах. Таблицы объема Расчет объема объемных фигур. Включает объемные «счетные кубы», прямоугольные призмы, конусы, цилиндры и сферы. Листы задач Word (по типу) Потренируйтесь решать задачи на сложение, вычитание, умножение и деление. Рабочие листы с текстовыми задачами (смешанный) Просмотрите навыки работы со смешанными текстовыми задачами в разных классах. Словесные задачи (несколько шагов) Эти текстовые задачи состоят из нескольких шагов и требуют от учащихся использования навыков критического мышления. Страницы математических указателей Таблицы сложения Здесь вы можете найти ссылки на все типы таблиц сложения, включая основные факты, сложение дробей, сложение 2-х, 3-х и 4-х цифр. Рабочие листы с дробями Указатель наших базовых и расширенных рабочих листов дробей. Рабочие листы по геометрии Изучайте площадь, периметр, симметрию, многоугольники, объемные формы и многое другое. Рабочие листы графиков Выберите из круговых диаграмм, гистограмм и линейных диаграмм. Отношения в математике как решать: Отношение двух чисел — урок. Математика, 6 класс.Отношение ⭐ двух чисел 6 класс: объяснение, примеры решения задачПонятие отношения двух чиселОпределение 1Отношение чисел является частным данных чисел. Запись отношения принято обозначать с помощью арифметического действия деления. Также допускается представление отношения в виде обыкновенной дроби: a:b=ab Здесь записано отношение чисел a и b. Число а может называться предыдущим членом, b играет роль последующего члена. Пример 1Запись отношения пары чисел таких, как 75 и 25, имеет вид: 75:25=7525=3 С помощью объяснения отношения можно выразить следующее: При решении задач на уроках по математике в шестом классе на тему «Отношение чисел» можно часто встретить примеры с процентами. Поэтому важно ознакомиться с особенностью понятия процентного соотношения и записать его в конспект. Вычислить процентное отношение пары чисел можно путем деления одного числа на второе, а полученный результат следует умножить на 100. Пример 2Даны два числа: 52 и 400. Требуется определить, сколько процентов составляет первое число от второго числа. Воспользуемся правилом вычисления процентного соотношения и запишем: 52:400·100%=13% Подобные отношения можно найти в заданиях, где по условию определены некие величины, и требуется вычислить их процентное соотношение. Знание определенных правил вычисления поможет значительно упростить решение. Среди вопросов могут быть такие: и другие вопросы, в которых присутствует понятие «процент». Свойства отношения чиселВ том случае, когда имеется пара чисел или значений одинаковой величины, обозначенных как a и b, справедливы следующие соотношения: Ключевое свойство частного: частное сохраняется без изменений в том случае, когда делимое и делитель умножают или делят на одинаковое число. Основное свойство частного позволяет вывести главное свойство отношения. Определение 3Основное свойство отношения: при умножении или делении членов какого-то отношения на одинаковое число, которое не равно нулю, данное отношение сохранится без изменений. Примеры решения задач с пояснениямиЗадача 1Месячный план производства равен 1200 изделий. В результате предприятие произвело 2300 изделий. Требуется определить процент превышения плана. Решение Данную задачу можно решить двумя способами. Рассмотрим их по отдельности. Способ 1. Запишем, что 1200 изделий являются планом, то есть составляют 100 %. Определим, количество изделий, изготовленных больше плана: 2300−1200=1100 Вычислим разницу между фактом и планом в процентах: 1100 от 1200 ⇒ 1100:1200·100%=91,7%. Попробуем выполнить вычисления другим методом. Способ 2. Сначала найдем разницу между планом и фактом в процентах: 2300 от 1200 ⇒ 2300:1200·100%=191,7%. Далее определим процент перевыполнения плана: 191,7%-100%=91,7%. Ответ: на 91,7 %. Задача 2Поставлена задача вспахать землю на участке поля площадью 500 га. В течение первого дня было обработано 150 га почвы. Требуется вычислить, сколько процентов удалось вспахать от общего запланированного объема. Решение Найдем отношение обработанной земли к общей площади поля и запишем результат в процентном выражении: 150:500·100%=150500·100%=310·100%=0,3·100%=30%. Ответ: 30 % Задача 3Производительность мастера составила 45 деталей, а по плану требовалось изготовить 36 деталей. Нужно найти процент фактически проделанной работы от планируемого объема. Решение Здесь вычислим отношения чисел и запишем результат в процентном выражении: 45:36·100%=1,25·100%=125% Ответ: 125 % Задания для самостоятельной работыЗадача 4Должность председателя желали занять два претендента. Решение 3х+5х=120 х=15 15·5=75 Ответ: 75 Задача 5Отношение количества хвойных деревьев к лиственным в лесу можно выразить как 1:4. Нужно вычислить процент лиственных деревьев. Решение 4:5=0,8=80 % Ответ: 80 % Задача 6Сельскохозяйственные растения высаживают на площади 24 Га. Зерновые культуры и овощные распределены в соответствии с отношением 5:3. Необходимо вычислить площадь в Га, которую занимают овощные культуры. Решение 24·38=9 Ответ: 9 Га. Как решать задачи на отношениеЧто нужно знать об отношении двух чисел в математике за 6 классОтношение чисел является частным данных чисел. Запись отношения принято обозначать с помощью арифметического действия деления. Также допускается представление отношения в виде обыкновенной дроби: Здесь записано отношение чисел a и b. Запись отношения пары чисел таких, как 75 и 25, имеет вид: 75 : 25 = 75 25 = 3 С помощью объяснения отношения можно выразить следующее: При решении задач на уроках по математике в шестом классе на тему «Отношение чисел» можно часто встретить примеры с процентами. Поэтому важно ознакомиться с особенностью понятия процентного соотношения и записать его в конспект. Вычислить процентное отношение пары чисел можно путем деления одного числа на второе, а полученный результат следует умножить на 100. Даны два числа: 52 и 400. Требуется определить, сколько процентов составляет первое число от второго числа. Воспользуемся правилом вычисления процентного соотношения и запишем: 52 : 400 · 100 % = 13 % Подобные отношения можно найти в заданиях, где по условию определены некие величины, и требуется вычислить их процентное соотношение. и другие вопросы, в которых присутствует понятие «процент». Свойства отношения чиселВ том случае, когда имеется пара чисел или значений одинаковой величины, обозначенных как a и b, справедливы следующие соотношения: Ключевое свойство частного: частное сохраняется без изменений в том случае, когда делимое и делитель умножают или делят на одинаковое число. Основное свойство частного позволяет вывести главное свойство отношения. Основное свойство отношения: при умножении или делении членов какого-то отношения на одинаковое число, которое не равно нулю, данное отношение сохранится без изменений. Примеры решения задач с пояснениямиМесячный план производства равен 1200 изделий. В результате предприятие произвело 2300 изделий. Требуется определить процент превышения плана. Данную задачу можно решить двумя способами. Рассмотрим их по отдельности. Способ 1. Запишем, что 1200 изделий являются планом, то есть составляют 100 %. Определим, количество изделий, изготовленных больше плана: Вычислим разницу между фактом и планом в процентах: 1100 от 1200 ⇒ 1100 : 1200 · 100 % = 91 , 7 % . Попробуем выполнить вычисления другим методом. Способ 2. Сначала найдем разницу между планом и фактом в процентах: 2300 от 1200 ⇒ 2300 : 1200 · 100 % = 191 , 7 % . Далее определим процент перевыполнения плана: 191 , 7 % — 100 % = 91 , 7 % . Поставлена задача вспахать землю на участке поля площадью 500 га. В течение первого дня было обработано 150 га почвы. Требуется вычислить, сколько процентов удалось вспахать от общего запланированного объема. Найдем отношение обработанной земли к общей площади поля и запишем результат в процентном выражении: 150 : 500 · 100 % = 150 500 · 100 % = 3 10 · 100 % = 0 , 3 · 100 % = 30 % . Производительность мастера составила 45 деталей, а по плану требовалось изготовить 36 деталей. Нужно найти процент фактически проделанной работы от планируемого объема. Здесь вычислим отношения чисел и запишем результат в процентном выражении: 45 : 36 · 100 % = 1 , 25 · 100 % = 125 % Задания для самостоятельной работыДолжность председателя желали занять два претендента. Отношение количества хвойных деревьев к лиственным в лесу можно выразить как 1:4. Нужно вычислить процент лиственных деревьев. Сельскохозяйственные растения высаживают на площади 24 Га. Зерновые культуры и овощные распределены в соответствии с отношением 5:3. Необходимо вычислить площадь в Га, которую занимают овощные культуры. Урок 21 Бесплатно ОтношенияВ этом уроке мы узнаем, что такое отношения. Также поймем, что нам показывает отношение двух чисел. И в завершение узнаем, как определить часть одного числа от другого. ОтношениеНачнем с определения: Отношением двух чисел называют частное этих двух чисел. Записать отношение числа a к числу b мы можем как \(\mathbf\) или же через дробную черту: \(\mathbf>\) У нас получается дробное выражение, поэтому возможны варианты во что оно преобразуется: Посмотрим на разные примеры. Пример 1 Найдем отношение чисел 256 и 8 По определению, отношением двух чисел будет являться их частное, что мы и посчитаем. Ответом будет 32. Иными словами, 256 относится к 8 как 32 к 1 В последней фразе была как раз упомянута суть отношения, мы акцентируем на этом внимание. Отношение одного числа к другому показывает, как одно число соотносится с другим, иными словами, во сколько раз оно его больше или меньше: Пример 2 Найдите отношение 15 к 12 По определению посчитаем частное, а далее посмотрим на полученный результат. Данный пример иллюстрирует, в каких случая получается смешанное число. Отношение равняется смешанному числу в тех случаях, когда первое число больше второго, и при этом первое на второе не делится. Мы можем прочитать результат так: 15 больше 12 в \(\mathbf>\) раза. Пример 3 Найдем отношение 16 к 24. Снова идем по алгоритму: делим первое число на второе. В этом случае мы получили в ответе правильную дробь. Нам это говорит о том, что первое число меньше второго. А если мы хотим сказать, как именно первое число меньше второго, то это можно сделать так: первое число меньше второго в \(\mathbf>\) раза. Мы можем сформулировать вывод и так: 16 составляет \(\mathbf>\) от 24-х, то есть мы отвечаем на вопрос, какой частью является первое число от второго. Также важно отметить, что отношение числа a к числу b не всегда равно отношению числа b к числу a. Пример 4 Есть два числа, 14 и 28 Посчитаем отношение 14 к 28 И посчитаем отношение 28 к 14 Как вы видите, получились разные значения. Как можно заметить, это взаимно обратные числа. Отметим еще одно свойство отношений: если есть два числа a и b, то отношение a к b взаимно обратно отношению b к a. Если дано отношение первого числа ко второму, то мы без труда сможем найти отношение второго к первому, даже не зная самих чисел, просто посчитав обратное к отношению число. Пример 5 Дано, что отношение числа a к числу b равно \(\mathbf>\), найдем отношение b к a Для этого надо найти обратное число к \(\mathbf>\) Значит, отношение b к a равняется \(\mathbf>\) В конце этой части добавим еще одно простое, но важное свойство. Отношение двух чисел не изменится, если каждое из них домножить или разделить на одно и тоже число. Это легко доказать, показав, что при делении этот множитель сократится. Пример 6 Отношение числа 10 к числу 30 равно \(\mathbf>\) Домножим каждое из чисел на 2 и заметим, что отношение 20 к 60 также равно \(\mathbf>\) Пройти тест и получить оценку можно после входа или регистрации Отношение и часть от числаПосмотрим, какие еще можно сделать выводы, зная отношение. Мы знаем, что, чтобы найти часть от числа (другими словами, дробь от числа), надо умножить число на эту дробь. Так мы получим число, которое будет частью исходного. Допустим, изначально у нас было число 4, и мы решили найти от него \(\mathbf>\) Перемножив, мы получим: А теперь найдите отношение полученного числа к изначальному. Для этого разделите одно на другое: То, что вы получили отношение, равное той дроби, которую мы находили, не совпадение. Действительно, находя дробь от числа мы получаем число, чье отношение к исходному будет равно этой дроби. Сформулируем еще более коротко и четко: отношение числа a к числу b обратно дроби, которую нужно взять от числа а, чтобы получить число b. Пример 1 Известно, что некая дробь от числа 10 равна \(\mathbf>\) Найдем, какая именно это дробь. Решение: Дробь от числа равна отношению полученного числа к изначальному. Теперь разделим одно на другое и получим ответ. Ответ: дробь, взяв которую от 10 получили \(\mathbf>\), равняется \(\mathbf>\) Пример 2 Отношение первого числа ко второму равно \(\mathbf>\), также известно, что первое число равно 6. Найдем второе число. Решение: Мы знаем, что отношение обратно дроби. Найдем обратное число к \(\mathbf>\) Теперь можно найти второе число, домножим первое на эту дробь: Второе число равно 5 Проверка: Найдем отношение первого числа ко второму, то есть 6 к 5 Получилось то же отношение, что и в условии. Пример 3 Решим похожую задачу: Отношение числа а к числу b равно \(\mathbf>\) Известно, что число b равняется 8-ми, надо найти число а. Решение: Найдем, какую дробь число b составляет от числа a, то есть найдем обратное число от отношения: Теперь, чтобы найти число по его дроби, надо разделить часть от числа на эту дробь. В нашем случае на дробь надо делить число b : Ответ: число a равняется 12 Пройти тест и получить оценку можно после входа или регистрации Отношения в задачахТеперь научимся находить отношения в задачах. Сразу перейдем к примерам, чтобы посмотреть, за какими формулировками могут стоять отношения. Задача 1 Длина улицы составляет 25 километров. Освещено 15 километров улицы. а) Найдите, какая часть улицы освещена. б) Во сколько раз вся улица длиннее ее освещенной части? Решение: В начале урока мы находили отношение меньшего числа к большему, тем самым определили, какую часть первое число составляет от второго. Именно это и спрашивается в первом вопросе. Для нахождения отношения длины освещенного участка к длине всей улицы поделим одну величину на другую: Значит, длина освещенного участка составляет \(\mathbf>\) от длины всей улицы. Во втором вопросе нас спрашивают: «Во сколько раз больше?» — это соответствует отношению большего числа к меньшему. Для нахождения этого отношения необходимо поделить длину всей улицы на длину ее освещенной части: Что отвечает на вопрос второго пункта. Также важно помнить, что если подаются какие-либо величины, то всегда надо следить, чтобы мера измерения была одинаковой. То есть если нам подали что-то в тоннах и килограммах и мы хотим найти отношения этих величин, то надо либо тонны переводить в килограммы, либо наоборот. Задача 2 Масса груза составляет 2 тонны. Известно, что часть груза- это одежда и ее масса 350 кг. Найдите, какую часть от массы груза составляет масса одежды. Решение: Для начала преобразуем преобразуем тонны в килограммы. Получается, что масса груза равна 2000 кг. Теперь найдем искомое отношение: Теперь попробуйте порешать задачи самостоятельно, а если будет сложно, используйте подсказки. Пройти тест и получить оценку можно после входа или регистрации Интересная информацияСегодня вы узнаете о математических фокусах! Их идея в том, что можно запутать людей математическими преобразованиями, которые выдадут то, что нужно нам. Фокус 1 Попросите зрителя загадать число и никому не говорить. Теперь попросите его умножить это число на 2, прибавить к результату 8, разделить на 2 и вычесть задуманное число. Теперь вы можете уверенно сказать, что у зрителя получилось число 4. Так получается за счет того, что в процессе преобразований исходное число вообще уходит из цепочки вычислений и остается только четверка. Попробуй доказать это на формулах, взяв за задуманное число Х Фокус 2 В нем вы можете угадать День рождения человека. Попросите зрителя умножить на 2 число дня его рождения, затем пусть он прибавит к результату 5 и умножит это все на 50, после этого попросите зрителя прибавить к этому числу номер месяца рождения (январь- 1, февраль- 2 и т. д.). Для того чтобы сказать по полученному числу День рождения человека, надо вычесть из числа, названного зрителем, 250 — получится трехзначное или четырехзначное число, где первые одна или две цифры — это день рождения, а последние две — месяц. ОтношенияВ данный момент вы не можете посмотреть или раздать видеоурок ученикамЧтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге. Получите невероятные возможностиКонспект урока «Отношения»Для решения практических задач человеку часто приходится сравнивать разные значения одной и той же величины – массы, расстояния, времени, скорости, стоимости, объёма, площади и т.д. Для сравнения чисел и величин существуют, как вы знаете, два способа: 1-ый: вычисление разности и 2-ой: вычисление частного. Оба этих способа используют часто при решении практических задач, но служат они для разных целей. К делению прибегают в тех случаях, когда хотят получить качественную оценку или относительную оценку той или иной ситуации. Задача На экране изображены два отрезка. Вторая задача: на экране изображены эти же два отрезка. Отрезок AB длиной 15 см и отрезок CD, длина которого 6 см. Но поставим вопрос по-другому: какую часть отрезок CD составляет от отрезка АВ? Обе рассмотренные задачи решаются делением, и ответ даётся в виде частного. В таких случаях частное двух чисел называют их отношением. Определение Частное двух не равных нулю чисел (или двух величин) называют отношением. Сами эти числа (величины) называют членами отношения. Иными словами, отношение двух чисел – это другое название их частного. Отношение чисел записывают с помощью знака деления, а также с помощью черты обыкновенной дроби. Частные чисел читают так: Напомним, что отношение двух чисел показывает, во сколько раз одно число больше другого, или какую часть одно число составляет от другого. Черта дроби используется для записи отношения и тогда, когда его члены не являются натуральными числами. Задача Рост дяди Степы 2 м 10 см, а рост мальчика Васи – 105 см. Во сколько раз дядя степа выше мальчика Васи? Но ведь дробную черту мы использовали для записи дробей! А сейчас записана не дробь. Верно. Но вы давно знаете, что при записи деления натуральных чисел вместо знака деления можно использовать дробную черту. Так вот, договариваются о том же и при записи деления любых чисел. Итак, если а и b – любые числа, то Сделаем важное замечание: Если значения двух величин выражены разными единицами измерения, то для нахождения отношения этих величин надо предварительно перейти к одной единице измерения. Отношение величин одного наименования (длин, скоростей, стоимостей и т.д., выраженных одинаковыми единицами измерения) есть число. Отношение величин разных наименований (пути и времени, стоимости товара и его количества, массы тела и его объема и т.д.) есть новая величина. Вот, например, в предыдущей задаче мы находили во сколько раз дядя Степа выше мальчика Васи. Рост Васи и рост дяди Степы – это однородные величины, т.е. длина. Поэтому отношение их роста выраженно натуральным числом. А теперь давайте разберёмся, почему отношение разноимённых величин – это новая величина. Задача Муравей за 20 секунд пробегает 240 сантиметров. Определите скорость движения муравья. Отметим, что обозначения км/ч, м/с и т.п. приняты именно потому, что расстояние делят на время. Их обычно записывают с наклонной чертой. В виде отношений определяются и другие величины: Из основного свойства частного следует свойство отношения. Давайте вспомним основное свойство частного: если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь. Следовательно, получаем свойство отношения: отношение не изменится, если его члены умножить или разделить на одно и то же число, не равное нулю. Пример Мы с вами убедились, что свойство отношения действует. Мы умножили числитель и знаменатель дроби на одно и то же число, само же отношение не изменилось. Итак, сегодня на уроке мы узнали, что частное двух не равных нулю чисел (или двух величин) называют отношением. Сами эти числа (величины) называют членами отношения. Если значения двух величин выражены разными единицами измерения, то для нахождения отношения этих величин надо предварительно перейти к одной единице измерения. И свойство отношения: отношение не изменится, если его члены умножить или разделить на одно и то же число, не равное нулю. Отношения и пропорцииИспользуй поиск, чтобы найти научные материалы и собрать список литературы База статей справочника включает в себя статьи написанные экспертами Автор24, статьи из научных журналов и примеры студенческих работ из различных вузов страны Содержание статьи 1. Отношение двух чисел 2. Понятие пропорции Отношение двух чиселОпределение 1 Отношением двух чисел является их частное. Пример 1 С помощью отношения двух чисел можно показать: При составлении отношения двух чисел в знаменателе дроби записывают то число, с которым проводится сравнение. Чаще всего такое число следует после слов «по сравнению с …» или предлога «к …». Вспомним основное свойство дроби и применим его к отношению: Замечание 1 При умножении или делении обоих членов отношения на одно и то же число, отличное от нуля, получаем отношение, которое равно исходному. Рассмотрим пример, который иллюстрирует использование понятия отношения двух чисел. Пример 2 Количество осадков в предыдущем месяце составляло $195$ мм, а в текущем месяце – $780$ мм. Во сколько раз увеличилось количество осадков в текущем месяце по сравнению с предыдущим месяцем? Решение. Составим отношение количества осадков в текущем месяце к количеству осадков в предыдущем месяце: $\frac{780}{195}=\frac{780\div 5}{195\div 5}=\frac{156\div 3}{39\div 3}=\frac{52}{13}=4$. Ответ: количество осадков в текущем месяце в $4$ раза больше, чем в предыдущем. Пример 3 Найти сколько раз число $1 \frac{1}{2}$ содержится в числе $13 \frac{1}{2}$. Решение. $13 \frac{1}{2}\div 1 \frac{1}{2}=\frac{27}{2}\div \frac{3}{2}=\frac{27}{2} \cdot \frac{2}{3}=\frac{27}{3}=9$. Ответ: $9$ раз. Понятие пропорцииОпределение 2 Пропорцией называется равенство двух отношений: $a\div b=c\div d$ или $\frac{a}{b}=\frac{c}{d}$. Пример 4 $3\div 6=9\div 18$, $5\div 15=9\div 27$, $4\div 2=24\div 12$, $\frac{8}{2}=\frac{36}{9}$, $\frac{10}{40}=\frac{9}{36}$, $\frac{15}{75}=\frac{1}{5}$. В пропорции $\frac{a}{b}=\frac{c}{d}$ (или $a:b = с\div d$) числа a и d называются крайними членами пропорции, а числа $b$ и $c$ – средними членами пропорции. Правильную пропорцию можно преобразовать следующим образом: Замечание 2 Произведение крайних членов правильной пропорции равно произведению средних членов: $a \cdot d=b \cdot c$. Данное утверждение является основным свойством пропорции. Справедливо и обратное утверждение: Замечание 3 Если произведение крайних членов пропорции равно произведению ее средних членов, то пропорция правильная. Замечание 4 Если в правильной пропорции переставить средние члены или крайние члены, то пропорции, которые получатся, также будут правильными. Пример 5 $6\div 3=18\div 9$, $15\div 5=27\div 9$, $2\div 4=12\div 24$, $\frac{2}{8}=\frac{9}{36}$, $\frac{40}{10}=\frac{36}{9}$, $\frac{75}{15}=\frac{5}{1}$. С помощью данного свойства легко из пропорции найти неизвестный член, если известны остальные три: $a=\frac{b \cdot c}{d}$; $b=\frac{a \cdot d}{c}$; $c=\frac{a \cdot d}{b}$; $d=\frac{b \cdot c}{a}$. Пример 6 $\frac{6}{a}=\frac{16}{8}$; $6 \cdot 8=16 \cdot a$; $16 \cdot a=6 \cdot 8$; $16 \cdot a=48$; $a=\frac{48}{16}$; $a=3$. Пример 7 $\frac{a}{21}=\frac{8}{24}$; $a \cdot 24=21 \cdot 8$; $a \cdot 24=168$; $a=\frac{168}{24}$; $a=7$. Пример 8 Для пошива $7$ платьев понадобилось $21,7$ м шелка. Сколько нужно метров такого же шелка, чтобы пошить $18$ платьев? Решение. Пусть $x$ м – количество шелка, необходимого для пошива $18$ платьев. Тогда, по условию: $7$ платьев – $21,7$ м; $18$ платьев – $x$ м. Составим пропорцию: $\frac{7}{18}=\frac{21,7}{x}$. Воспользуемся правилом нахождения неизвестного члена пропорции: $d=\frac{b \cdot c}{a}$; $x=\frac{18 \cdot 21,7}{7}$; $x=18 \cdot 3,1$; $x=55,8$. Ответ: для пошива 18 платьев понадобится 55,8 м шелка. Пример 9 $3$ садовника обрезают в день $108$ деревьев. Сколько нужно садовников, чтобы обрезать $252$ дерева? Решение. Пусть $x$ – количество садовников, необходимое для обрезки $252$ деревьев. Тогда, по условию: $3$ садовника – $108$ деревьев; $x$ садовников – $252$ дерева. Составим пропорцию: $\frac{3}{x}=\frac{108}{252}$. Воспользуемся правилом нахождения неизвестного члена пропорции: $b=\frac{a \cdot d}{c}$; $x=\frac{3 \cdot 252}{108}$; $x=\frac{252}{36}$; $x=7$. Ответ: для обрезки $252$ деревьев потребуется $7$ садовников. Чаще всего свойства пропорции используют на практике в математических вычислениях в случаях, когда необходимо вычислить значение неизвестного члена пропорции, если известны значения трех остальных членов. Сообщество экспертов Автор24 Автор этой статьи Дата последнего обновления статьи: 20.06.2022 Выполнение любых типов работ по математике Решение задач по комбинаторике на заказ Решение задачи Коши онлайн Математика для заочников Контрольная работа на тему числовые неравенства и их свойства Контрольная работа на тему умножение и деление рациональных чисел Контрольная работа на тему действия с рациональными числами Дипломная работа на тему числа Курсовая работа на тему дифференциальные уравнения Контрольная работа на тему приближенные вычисления Решение задач с инвариантами Подбор готовых материалов по теме Дипломные работы Курсовые работы Выпускные квалификационные работы Рефераты Сочинения Доклады Эссе Отчеты по практике Решения задач Контрольные работы Отношения в математике — определение, типы, графики, примеры Отношения в математике помогают установить связь между любыми двумя объектами или вещами. Отношения имеют несколько применений, особенно в области информатики, для создания систем управления реляционными базами данных (RDBMS). В этой статье будут подробно описаны отношения, их типы, как связать элементы из двух наборов с помощью отношений и связанных примеров.
Что такое отношения в математике? Отношения в математике используются для описания связи между элементами двух множеств. Определение отношений в математикеОтношения в математике — это подмножество декартова произведения двух множеств. Предположим, что есть два множества, заданные X и Y. Пусть x ∈ X (x — элемент множества X) и y ∈ Y. Тогда декартово произведение X и Y, представленное как X × Y, задается набором все возможные упорядоченные пары (x, y). Другими словами, отношение говорит о том, что каждый вход будет производить один или несколько выходов. Отношения в математике Пример Предположим, что есть два набора X = {4, 36, 49, 50} и Y = {1, -2, -6, -7, 7, 6, 2}. Отношение, которое утверждает, что «(x, y) находится в отношении R, если x является квадратом y», может быть представлено с использованием упорядоченных пар как R = {(4, -2), (4, 2), (36, -6), (36, 6), (49, -7), (49, 7)}. Представление отношенийОтношения могут быть представлены с использованием различных методов. Существует пять основных представлений отношений. Они представлены следующим образом: Форма конструктора наборов: Это математическая запись, в которой четко указано правило, связывающее два набора X и Y. Если есть два набора X = {5, 6, 7} и Y = {25, 36, 49}. Правило состоит в том, что элементы X являются положительным квадратным корнем элементов Y. В форме построителя множеств это отношение может быть записано как R {(a, b): a — положительный квадратный корень из b, a ∈ X , b ∈ Y}. Форма списка: В форме списка записываются все возможные упорядоченные пары двух наборов, которые следуют заданному отношению. Используя тот же пример, что упоминался выше, отношение элементы множества X являются положительными квадратными корнями элементов множества B представлено как R = {(5, 25), (6, 36), (7, 49)}. Диаграмма-стрелка: Такая диаграмма используется для визуального представления отношения между элементами двух заданных наборов. Табличная форма: Когда ввод и вывод отношения выражаются в форме таблицы, это известно как табличное представление отношения. При этом таблица рисуется с двумя столбцами. Первый обозначает вход, а второй выражает выход. Используя соотношение, согласно которому элементы X = {5, 6, 7} являются положительными квадратными корнями элементов Y = {25, 36, 49} таблица имеет следующий вид:
Пятое представление, использующее графический метод, будет рассмотрено в следующих разделах. Типы отношений Два набора могут иметь разные типы соединений, поэтому для классификации этих соединений необходимы разные виды отношений. Пустое отношениеПустое отношение — это отношение, в котором любой элемент набора не отображается ни на элемент другого набора, ни на себя. Это соотношение обозначается как R = ∅. Например, P = {3, 7, 9} и соотношение на P, R = {(x, y), где x + y = 76}. Это будет пустое отношение, так как никакие два элемента P не суммируются до 76. Универсальное отношениеЕсли все элементы, принадлежащие одному набору, отображаются на все элементы другого набора или на себя самого, то такое отношение известно. как универсальное отношение. Это записывается как R = X × Y, где каждый элемент X связан с каждым элементом Y. Пример, P = {3, 7, 9}, Q = {12, 18, 20} и R = {(x, y), где x < y}. Отношение идентичностиЕсли все элементы в наборе связаны сами с собой, тогда оно становится отношением идентичности. Это записывается как I = {(x, x) : для всех x ∈ X}. Например, P = {3, 7, 9}, тогда I = {(3, 3), (7, 7), (9, 9)} Обратное отношение Если элементы одного множества являются обратными парами другой набор, то такое отношение известно как обратное отношение. Рефлексивное отношениеЕсли в наборе все элементы отображаются сами на себя, то это отношение является рефлексивным. Таким образом, если x ∈ X, то рефлексивное отношение определяется как (x, x) ∈ R. Например, P = {7, 1}, тогда R = {(7, 7), (1, 1)} является рефлексивным связь. Симметричное отношениеОтношение называется симметричным отношением, если одно множество X содержит упорядоченные пары (x, y), а также противоположные этим парам (y, x). Другими словами, если (x, y) ∈ R, то (y, x) ∈ R для того, чтобы отношение было симметричным. Предположим, что P = {3, 4}, тогда симметричным отношением может быть R = {(3, 4), (4, 3)}. Транзитивное отношение Предположим, что (x, y) ∈ R и (y, z) ∈ R, тогда R является транзитивным отношением тогда и только тогда, когда (x, z) ∈ R. Отношение эквивалентностиОтношение эквивалентности — это тип отношения, который является симметричным, транзитивным и рефлексивный. Отношение «один к одному»В отношении «один к одному» каждый элемент одного набора будет сопоставлен с отдельным элементом другого набора. Например, предположим, что есть два множества P = {1, 2, 3} и Q = {a, b, c}. Тогда отношение один к одному может быть R = {(1, a), (2, b), (3, c)} Отношение «один ко многим»В отношении «один ко многим» один элемент одного набора будет сопоставлен более чем с одним элементом другого набора. Например, для двух множеств P = {1, 2, 3} и Q = {a, b, c} отношение «один ко многим» записывается как R = {(2, a), (2, b), ( 2, c)} Отношение «многие к одному» Если более одного элемента одного множества отображаются в один отдельный элемент другого множества, то такое отношение называется отношением «многие к одному». Отношение «многие ко многим»В отношении «многие ко многим» один или несколько элементов одного набора будут сопоставлены с тем же или другим элементом другого набора. Если P = {1, 2, 3} и Q = {a, b, c}, то R = {(2, a), (3, a), (2, c)} является примером множества для многие отношения. Графические отношенияОтношения также могут быть представлены графически с использованием декартовой системы координат. Элемент отношения может быть либо выражен в виде упорядоченной пары (x, y), либо может быть задан в виде уравнения (или неравенства). Упорядоченная пара представляет положение точек на координатной плоскости. Предположим, что отношение задано как y = x — 2 на множестве всех действительных чисел, тогда шаги для построения графика следующие:0005 Важные замечания по отношениям в математике: ☛ Связанные статьи: Часто задаваемые вопросы об отношениях в математикеЧто такое определение отношения в математике? Отношение в математике дает отношение между двумя множествами (скажем, A и B). Что такое функции и отношения в математике?Отношение помогает установить связь между элементами двух множеств так, что вход и выход образуют упорядоченную пару (вход, выход). Функция — это подмножество отношения, которое определяет результат при заданном входе. Все функции являются отношениями, но не все отношения являются функциями. Например, R = {(1, 2), (1, 3), (2, 3)} является отношением, но не функцией, поскольку 1 отображается дважды (и 2, и 3). Какие существуют типы отношений в математике?В математике существует девять различных типов отношений. Они даны следующим образом: Существует четыре других типа отношений, основанных на отображении. Что такое уравнение отношения?Когда отношение выражается в виде уравнения, оно называется уравнением отношения. y = x 2 является примером уравнения отношения. График этой зависимости будет параболой. Как представляются отношения в математике?Существует 5 широко используемых способов представления отношения. Это форма построения набора, форма списка, табличная форма, стрелочная диаграмма и с использованием графика. Как записать отношение на графике?Если существует упорядоченная пара (x, y) такая, что x связано с y, то такое отношение можно изобразить на графике. Чтобы представить отношение на графике, просто отметьте на нем упорядоченные точки. Координата x представляет собой расстояние точки от оси y, а координата y обозначает расстояние от оси x. Что такое симметричные отношения в математике? Симметричное отношение в математике может быть определено как отношение, которое содержит упорядоченную пару (x, y), а также обратную эту пару (y, x). Все ли функции относятся к математике?Все функции являются отношениями. Функция — это отношение, в котором каждый вход будет иметь только один выход. Таким образом, отношение «один к одному» и отношение «многие к одному» образуют функцию. Какие существуют типы математических отношений?Наклонная плоскость, используемая для демонстрации ускорения и квадратичной зависимости Что такое математическая зависимость? Математическое отношение — это отношение между наборами чисел или наборами элементов. Часто взаимосвязи между переменными можно увидеть, просто изучив математическое уравнение. Многие физические соотношения в электростатике, электродинамике, термодинамике и т. д. выражаются математическими уравнениями. Следующие примеры математических взаимосвязей помогут вам в анализе данных для лабораторных работ в этом модуле. Линейные отношения Давайте посмотрим на следующее уравнение: Y = 3X По мере увеличения X Y будет увеличиваться пропорционально. В природе данные не точны, поэтому точки не всегда попадают на линию. Ниже приведен график данных относительно удельной прочности на раздавливание в зависимости от давления (P). Точки падают достаточно близко к прямой линии, чтобы сделать вывод, что это линейная или прямая зависимость.
Что такое независимые и зависимые переменные на графике? Независимая переменная — Независимая переменная — это именно то, на что это похоже. Это переменная, которая стоит особняком и не изменяется другие переменные, которые вы пытаетесь измерить . Например, если время является одной из ваших переменных , это независимая переменная . Время всегда независимая переменная . Ученые любят говорить, что « независимая » переменная идет по оси x (нижняя, горизонтальная), а « зависимая » переменная идет по оси y ( — ) левая сторона, вертикальная). Зависимая переменная — Как и независимая переменная, зависимая переменная – это именно то, на что она похожа. Это то, что зависит от других факторов. Например, результат теста может быть зависимой переменной, потому что он может меняться в зависимости от нескольких факторов, например, от того, сколько вы учились, сколько вы спали в ночь перед сдачей теста или даже от того, насколько вы были голодны, когда сдавали его. Обычно, когда вы ищете взаимосвязь между двумя вещами, вы пытаетесь выяснить, что заставляет зависимую переменную изменяться так, как она это делает. Обратная зависимость Теперь рассмотрим следующее уравнение: Y = 1/X Если X=1, то Y = 1. Если X = 2, то Y = 0,5. Если X = 3, то Y = 0,33. Если X = 4, то Y = 0,25. Обратите внимание, что по мере увеличения X Y уменьшается нелинейным образом. Это обратная зависимость. Пример обратной зависимости в науке: Когда более высокая вязкость приводит к уменьшению расхода, зависимость между вязкостью и расходом обратная. Примеры: Квадратичные отношения обнаруживаются во всех ускоряющихся объектах, например, падающих объектах. Ниже приведен график, демонстрирующий форму квадратного уравнения.
Закон обратных квадратов. силы. Например, объект, расположенный в трех футах от источника света, получит только одну девятую (1/9, обратное 3 в квадрате) столько же освещения, сколько объект находится на расстоянии одного фута от источника света.
В физике законом обратных квадратов называется любой физический закон, утверждающий, что определенная физическая величина или интенсивность обратно пропорциональна квадрату расстояния от источника этой физической величины. Фундаментальную причину этого можно понять как геометрическое разбавление, соответствующее излучению точечного источника, в трехмерном пространстве. Один из известных законов обратных квадратов относится к притяжению двух масс. Подробнее см.: Гравитация: еще один пример закона 1/R2 Подробнее о яркости и законе обратных квадратов Демпфирующее движение эффект уменьшения, ограничения или предотвращения его колебаний. В физических системах затухание вызывается процессами, которые рассеивают энергию, запасенную в колебаниях. Примеры включают вязкое сопротивление в механических системах, сопротивление в электронных генераторах, поглощение и рассеяние света в оптических генераторах. Демпфирование, не основанное на потерях энергии, может быть важным в других колебательных системах, например, в биологических системах.
Зависимость синусоиды Графики функций синуса и косинуса представляют собой синусоиды разных фаз.
Математика, 7 класс, пропорциональные отношения, решение задач на пропорциональные отношенияCCSS.Math.Content.7.RP.A.2b 7 класс, Соотношения и пропорциональные отношения Кластер: Анализ пропорциональных отношений и их использование для решения реальных и математических задач Стандарт: Определение константы пропорциональности (единицы измерения) в таблицах, графиках, уравнениях, диаграммах и словесных описаниях пропорциональных отношений. Степень выравнивания: Без рейтинга (0 пользователей) CCSS.Math.Content.7.RP.A.2 7 класс, Соотношения и пропорциональные отношения Кластер: Анализ пропорциональных отношений и их использование для решения реальных и математических задач Стандарт: Распознавание и представление пропорциональных отношений между величинами. Степень выравнивания: Без рейтинга (0 пользователей) CCSS.Math.Content.7.RP.A.1 7 класс, Соотношения и пропорциональные отношения Кластер: Анализ пропорциональных отношений и их использование для решения реальных и математических задач Стандарт: вычисление удельных расходов, связанных с отношениями дробей, включая отношения длин, площадей и других величин, измеренных в одинаковых или разных единицах. Например, если человек проходит 1/2 мили каждые 1/4 часа, рассчитайте удельную скорость как комплексную дробь (1/2)/(1/4) мили в час, что эквивалентно 2 милям в час. Степень выравнивания: Без рейтинга (0 пользователей) CCSS.Math.Content.7.RP.A.2a 7 класс, Соотношения и пропорциональные отношения Кластер: Анализ пропорциональных отношений и использование их для решения реальных и математических задач. Стандарт: Определите, находятся ли две величины в пропорциональной зависимости, например, путем проверки эквивалентных отношений в таблице или построения графика на координатной плоскости и наблюдения является ли график прямой линией, проходящей через начало координат. Степень выравнивания: Без рейтинга (0 пользователей) CCSS.Math.Content.7.RP.A.2c 7 класс, Соотношения и пропорциональные отношения Кластер: Анализ пропорциональных отношений и их использование для решения реальных и математических задач Стандарт: Представление пропорциональных отношений уравнениями. Например, если общая стоимость t пропорциональна количеству n товаров, купленных по постоянной цене p, соотношение между общей стоимостью и количеством товаров может быть выражено как t = pn. Степень выравнивания: Без рейтинга (0 пользователей) MCCRS.Math.Content. Область обучения: Отношения и пропорциональные отношения Стандарт: Анализ пропорциональных отношений и их использование для решения реальных и математических задач Индикатор: Вычисление удельных показателей, связанных с отношениями дробей, включая отношения длин, площадей и др. величины, измеряемые в одинаковых или разных единицах. Например, если человек проходит 1/2 мили каждые 1/4 часа, рассчитайте удельную скорость как комплексную дробь (1/2)/(1/4) мили в час, что эквивалентно 2 милям в час. Степень выравнивания: Без рейтинга (0 пользователей) MCCRS.Math.Content.7.RP.A.2 7 класс Область обучения: Соотношения и пропорциональные отношения Стандарт: Анализ пропорциональных отношений и их использование для решения реальных и математических задач Показатель: Распознавание и представление пропорциональных отношений между величинами. Степень выравнивания: Без рейтинга (0 пользователей) MCCRS.Math.Content.7.RP.A.2c 7 класс Область обучения: Соотношения и пропорциональные отношения Стандарт: Анализ пропорциональных отношений и их использование для решения реальных и математических задач Индикатор: Представление пропорциональных отношений уравнениями. Например, если общая стоимость t пропорциональна количеству n товаров, купленных по постоянной цене p, соотношение между общей стоимостью и количеством товаров может быть выражено как t = pn. Степень выравнивания: Без рейтинга (0 пользователей) MCCRS.Math.Content.7.RP.A.2b 7 класс Область обучения: Соотношения и пропорциональные отношения Стандарт: Анализ пропорциональных отношений и их использование для решения реальных и математических задач Индикатор: Определение константы пропорциональности (единицы измерения) в таблицах, графиках, уравнениях, диаграммах и словесные описания пропорциональных отношений. Степень выравнивания: Без рейтинга (0 пользователей) MCCRS.Math.Content.7.RP.A.2a 7 класс Область обучения: Отношения и пропорциональные отношения Стандарт: Анализ пропорциональных отношений и их использование для решения реальных и математических задач Индикатор: Определите, находятся ли две величины в пропорциональном отношении, например, путем проверки эквивалентных отношений в таблице или на графике на координатной плоскости и наблюдая, является ли график прямой линией, проходящей через начало координат. Степень выравнивания: Без рейтинга (0 пользователей) WY.Math.7.RP.A.2 7 класс Область обучения: Соотношения и пропорциональные отношения Стандарт: Анализ пропорциональных отношений и их использование для решения реальных и математических задач. Индикатор: Распознавание и представление пропорциональных отношений между величинами. Степень выравнивания: Без рейтинга (0 пользователей) WY.Math.7.RP.A.2a 7 класс Область обучения: Отношения и отношения пропорциональности Стандарт: Индикатор: Определите, находятся ли две величины в таблице или на графике в пропорциональной зависимости. Степень выравнивания: Без рейтинга (0 пользователей) WY.Math.7.RP.A.2c 7 класс Область обучения: соотношения и пропорциональные отношения Стандарт: Индикатор: представление пропорциональных отношений с помощью уравнений. Степень выравнивания: Без рейтинга (0 пользователей) WY.Math.7.RP.A.1 7 класс Область обучения: Соотношения и пропорциональные отношения Стандарт: Анализ пропорциональных отношений и их использование для решения реальных и математических задач. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 Хобби. Досуг
Хобби. Досуг
 Виноделие
Виноделие
 Зарубежная
Зарубежная
 Он содержит текстовые уроки, FlexBooks® (цифровые учебники в форматах PDF, ePub и mobi), видео и викторины по множеству тем по математике и естественным наукам от K до 12 класса.
Он содержит текстовые уроки, FlexBooks® (цифровые учебники в форматах PDF, ePub и mobi), видео и викторины по множеству тем по математике и естественным наукам от K до 12 класса.  Можно смотреть два фильма бесплатно в день или купить годовую подписку для неограниченного доступа.
Можно смотреть два фильма бесплатно в день или купить годовую подписку для неограниченного доступа. 
 Доступна версия для компьютера, iPad и Android. Свободно.
Доступна версия для компьютера, iPad и Android. Свободно.  Несколько уровней доступны примерно для классов K-4.
Несколько уровней доступны примерно для классов K-4.  Это можно использовать для онлайн-учебника по алгебре.
Это можно использовать для онлайн-учебника по алгебре.  Подписка $49 на 12 месяцев.
Подписка $49 на 12 месяцев.  htm
htm Это многостраничные динамические математические исследования, которые ставят вас на место водителя, позволяют вам задавать свои собственные вопросы и позволяют учиться в своем собственном темпе, пока они рассказывают вам свои истории. Для своих WorkBooks вам нужно будет скачать бесплатный плеер. Для работы Microworlds требуется браузер с поддержкой Active-X (Microsoft Internet Explorer 4.0 или выше).
Это многостраничные динамические математические исследования, которые ставят вас на место водителя, позволяют вам задавать свои собственные вопросы и позволяют учиться в своем собственном темпе, пока они рассказывают вам свои истории. Для своих WorkBooks вам нужно будет скачать бесплатный плеер. Для работы Microworlds требуется браузер с поддержкой Active-X (Microsoft Internet Explorer 4.0 или выше).  Включает главы по алгебре и деньгам, алгебре и геометрии, алгебре и физике, алгебре и рычагам и многим другим. Предназначен для детей 4-9 классов.с более высокими математическими способностями и интересом, но может быть использована учащимися старшего возраста и взрослыми. Содержит 22 главы с инструкциями и задачами на трех уровнях сложности.
Включает главы по алгебре и деньгам, алгебре и геометрии, алгебре и физике, алгебре и рычагам и многим другим. Предназначен для детей 4-9 классов.с более высокими математическими способностями и интересом, но может быть использована учащимися старшего возраста и взрослыми. Содержит 22 главы с инструкциями и задачами на трех уровнях сложности. Адаптивная игровая версия
Адаптивная игровая версия 
 Non Non Non Non Non Non Non Non Non Non Non Non Non Non Non Non Non-GAMING7 6 Адаптивная игровая версия
Non Non Non Non Non Non Non Non Non Non Non Non Non Non Non Non Non-GAMING7 6 Адаптивная игровая версия 
 Игровая версия0007 Non-game version Game version
Игровая версия0007 Non-game version Game version 
 Изучайте любой предмет быстро, решая задачи шаг за шагом. Наши уроки помогли тысячам учеников добиться успеха!
Изучайте любой предмет быстро, решая задачи шаг за шагом. Наши уроки помогли тысячам учеников добиться успеха! Мне нравится это приложение. У меня даже сын в 4 классе смотрит лекции по классам! Все так прекрасно организовано и структурировано. 19$ в месяц для меня так дорого стоит по сравнению с тем, что я должен был бы платить за репетитора по часам. Большое спасибо за создание этого удивительного приложения, вы замечательный учитель, и я всегда буду благодарен.
Мне нравится это приложение. У меня даже сын в 4 классе смотрит лекции по классам! Все так прекрасно организовано и структурировано. 19$ в месяц для меня так дорого стоит по сравнению с тем, что я должен был бы платить за репетитора по часам. Большое спасибо за создание этого удивительного приложения, вы замечательный учитель, и я всегда буду благодарен. Он действительно попадает в самую точку, когда дело доходит до объяснения концепций и помогает вам понять, что математика — это навык, который нужно развивать, а не какой-то сверхчеловеческий талант, с которым вы родились.
Он действительно попадает в самую точку, когда дело доходит до объяснения концепций и помогает вам понять, что математика — это навык, который нужно развивать, а не какой-то сверхчеловеческий талант, с которым вы родились. Видео Джейсона действительно тщательно разбивает материал на множество примеров, поэтому его легко понять. Это действительно несправедливо, что мы не можем просто перенаправить зарплату нашего профессора этому человеку!
Видео Джейсона действительно тщательно разбивает материал на множество примеров, поэтому его легко понять. Это действительно несправедливо, что мы не можем просто перенаправить зарплату нашего профессора этому человеку! Наука, занимающаяся изучением чисел, структур, пространств и преобразований.
Наука, занимающаяся изучением чисел, структур, пространств и преобразований.
 Эта теория в совокупности образует математическую модель исследуемого объекта. Т.о. первоначально исходя из пространственных и количественных соотношений, математика получает более абстрактные соотношения, изучение которых также является предметом современной математики.
Эта теория в совокупности образует математическую модель исследуемого объекта. Т.о. первоначально исходя из пространственных и количественных соотношений, математика получает более абстрактные соотношения, изучение которых также является предметом современной математики.



 Наверное, с ней может сравниться только физика, и то она все же уступает. Погружение в какую-либо науку я бы сравнил с такой ситуацией: ты поднимаешься по лестнице, открываешь дверь и выходишь на этаж с множеством других дверей. Это стандартный путь изучения любой дисциплины: ты устал, пока поднимался, но на финише ты собой доволен. Даже можешь открыть много смежных дверей в другие науки и все поймешь.
Наверное, с ней может сравниться только физика, и то она все же уступает. Погружение в какую-либо науку я бы сравнил с такой ситуацией: ты поднимаешься по лестнице, открываешь дверь и выходишь на этаж с множеством других дверей. Это стандартный путь изучения любой дисциплины: ты устал, пока поднимался, но на финише ты собой доволен. Даже можешь открыть много смежных дверей в другие науки и все поймешь. За это мы ее обожаем. Потому что она никогда не дает расслабляться.
За это мы ее обожаем. Потому что она никогда не дает расслабляться. На втором этаже вы спокойно ориентируетесь с неизвестными, применяете формулы сокращенного умножения, разность квадратов, бином Ньютона. В принципе, взойти на этот этаж достаточно легко.
На втором этаже вы спокойно ориентируетесь с неизвестными, применяете формулы сокращенного умножения, разность квадратов, бином Ньютона. В принципе, взойти на этот этаж достаточно легко. Вручается один раз в четыре года на каждом международном математическом конгрессе 2–4 молодым ученым не старше 40 лет (или достигших 40-летия в год вручения премии).
Вручается один раз в четыре года на каждом международном математическом конгрессе 2–4 молодым ученым не старше 40 лет (или достигших 40-летия в год вручения премии). На самом деле, истинная красота непредсказуема, немоделируема и нематематична. Так что золотое сечение переоценено. Но мне бы хотелось отметить, что оно играет ключевую роль при построении правильного пятиугольника циркулем и линейкой, а это важнее любых «народно-хозяйственных задач». Это очень круто и суперкрасиво.
На самом деле, истинная красота непредсказуема, немоделируема и нематематична. Так что золотое сечение переоценено. Но мне бы хотелось отметить, что оно играет ключевую роль при построении правильного пятиугольника циркулем и линейкой, а это важнее любых «народно-хозяйственных задач». Это очень круто и суперкрасиво. Никто не знает, как не знали и при Евклиде. Открытая математическая проблема, казалось бы, доступная школьнику. Таких проблем, на вскидку, штук 30.
Никто не знает, как не знали и при Евклиде. Открытая математическая проблема, казалось бы, доступная школьнику. Таких проблем, на вскидку, штук 30.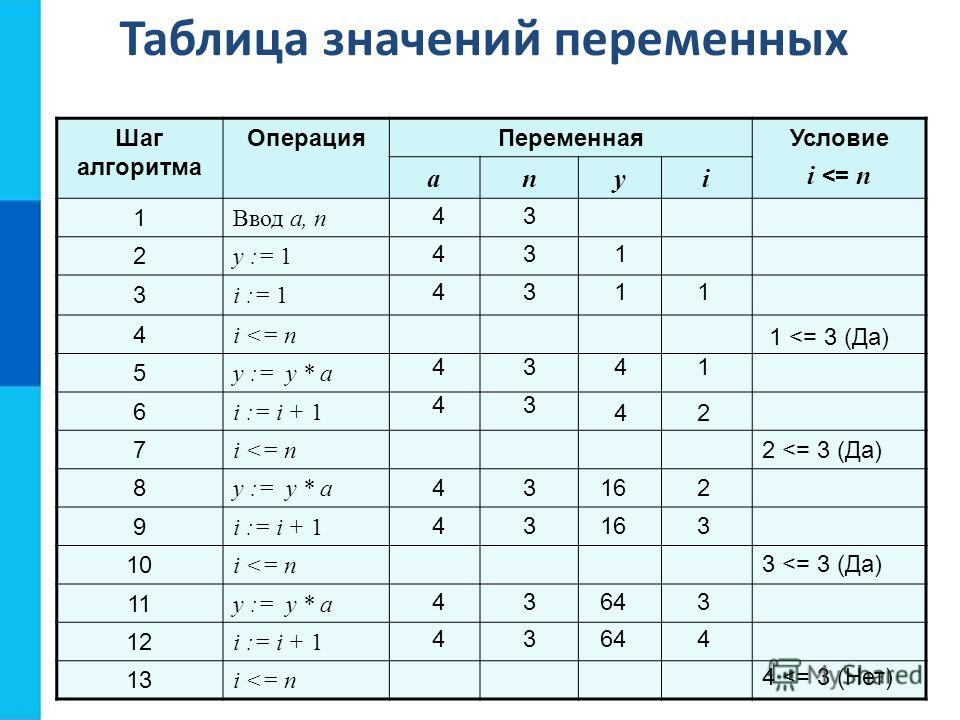 Мне интересно жить в мире, который не описывается математикой.
Мне интересно жить в мире, который не описывается математикой. Если вы попытаетесь математику применить к общению со своим супругом, боюсь, вас ждет развод.
Если вы попытаетесь математику применить к общению со своим супругом, боюсь, вас ждет развод. За ней — «Что такое математика» Куранта и Роббинса. Можно читать Перельмана, но это, скорее, развлекаловка. Потом идет Иэн Стюарт «Величайшие математические задачи» — очень хорошая книга. Кто любит практику — «Кому нужна математика?» Райгородского. Под редакцией моего друга Николая Андреева вышла книга «Математическая составляющая», а недавно еще и новое издание — рекомендую. Уровень выше — математика для первого курса мехмата: «Введение в матанализ» Зорича, «Линейная алгебра и геометрия» Кострикина.
За ней — «Что такое математика» Куранта и Роббинса. Можно читать Перельмана, но это, скорее, развлекаловка. Потом идет Иэн Стюарт «Величайшие математические задачи» — очень хорошая книга. Кто любит практику — «Кому нужна математика?» Райгородского. Под редакцией моего друга Николая Андреева вышла книга «Математическая составляющая», а недавно еще и новое издание — рекомендую. Уровень выше — математика для первого курса мехмата: «Введение в матанализ» Зорича, «Линейная алгебра и геометрия» Кострикина. Однако все основные методы вычисления простого среднего в большинстве случаев дают один и тот же приблизительный результат.
Однако все основные методы вычисления простого среднего в большинстве случаев дают один и тот же приблизительный результат. Применительно к инвестированию среднее значение используется для понимания динамики цены акций компании в течение нескольких дней, месяцев или лет.
Применительно к инвестированию среднее значение используется для понимания динамики цены акций компании в течение нескольких дней, месяцев или лет.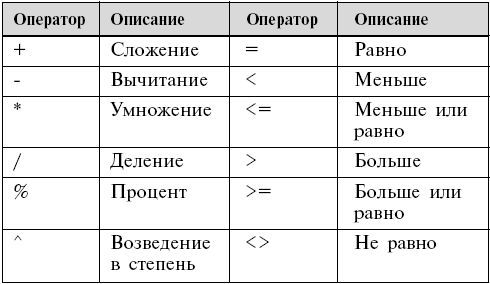 Например, среднее арифметическое чисел 4 и 9находится путем сложения 4 и 9, а затем деления на 2 (количество чисел, которые мы используем). Среднее арифметическое в этом примере равно 6,5.
Например, среднее арифметическое чисел 4 и 9находится путем сложения 4 и 9, а затем деления на 2 (количество чисел, которые мы используем). Среднее арифметическое в этом примере равно 6,5.

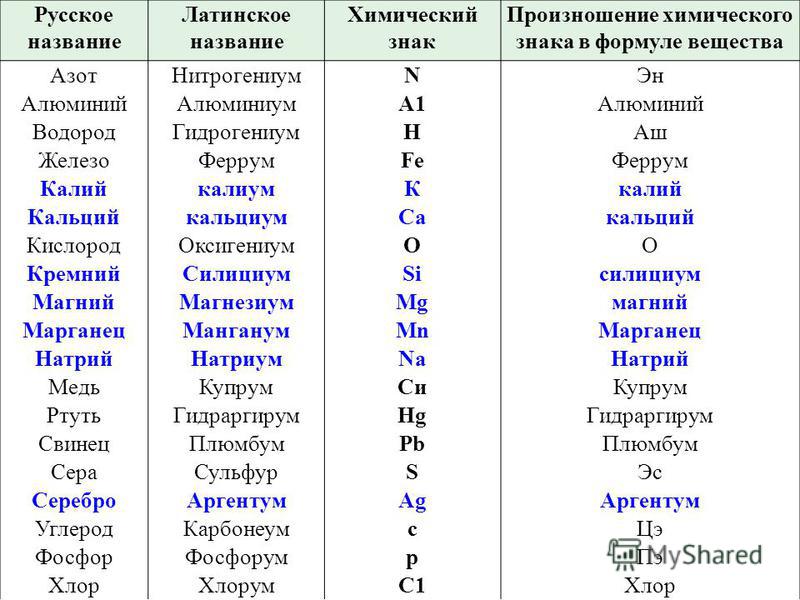 Гармонические средние часто используются в финансах для усреднения данных, представленных в дробях, отношениях или процентах, таких как доходность, доходность или ценовые мультипликаторы.
Гармонические средние часто используются в финансах для усреднения данных, представленных в дробях, отношениях или процентах, таких как доходность, доходность или ценовые мультипликаторы. .. + 0,0043 + (0,0049) + 0,0376} {10} } \\&= 0,0067 \\ &= 0,67\% \\\конец{выровнено}
Среднее арифметическое=10(0,0045)+0,0121+0,0726+…+0,0043+(0,0049)+0,0376=0,0067=0,67%
.. + 0,0043 + (0,0049) + 0,0376} {10} } \\&= 0,0067 \\ &= 0,67\% \\\конец{выровнено}
Среднее арифметическое=10(0,0045)+0,0121+0,0726+…+0,0043+(0,0049)+0,0376=0,0067=0,67% В этом примере и, как это часто бывает во многих расчетах, среднее геометрическое является более точным отражением истинной доходности портфеля.
В этом примере и, как это часто бывает во многих расчетах, среднее геометрическое является более точным отражением истинной доходности портфеля.
 Чтобы найти среднее значение, вы можете вычислить его математически, используя один из нескольких методов, в зависимости от структуры данных и типа необходимого вам среднего значения. Во многих случаях вы также можете визуально определить среднее значение, построив график распределения данных. В нормальном распределении среднее значение, мода и медиана — это одно и то же значение, которое находится в центре графика.
Чтобы найти среднее значение, вы можете вычислить его математически, используя один из нескольких методов, в зависимости от структуры данных и типа необходимого вам среднего значения. Во многих случаях вы также можете визуально определить среднее значение, построив график распределения данных. В нормальном распределении среднее значение, мода и медиана — это одно и то же значение, которое находится в центре графика.
 В статистике среднее арифметическое обычно используется как единственное значение, типичное для набора данных. Для системы частиц, имеющих неравные массы, центр тяжести определяется более общей средней, взвешенной средней арифметической. Если каждому числу ( x ) присвоить соответствующий положительный вес ( w ), взвешенное среднее арифметическое определяется как сумма их произведений ( w x ), деленное на сумму их весов. В этом случае
В статистике среднее арифметическое обычно используется как единственное значение, типичное для набора данных. Для системы частиц, имеющих неравные массы, центр тяжести определяется более общей средней, взвешенной средней арифметической. Если каждому числу ( x ) присвоить соответствующий положительный вес ( w ), взвешенное среднее арифметическое определяется как сумма их произведений ( w x ), деленное на сумму их весов. В этом случае Их средняя площадь составляет (1 2 + 1 2 + 2 2 + 5 2 + 7 2 )/5, или 16 квадратных см, площадь квадрата со стороной 4 см. Число 4 является средним квадратным (или среднеквадратичным) чисел 1, 1, 2, 5 и 7 и отличается от их среднего арифметического, которое составляет 3 1 / 5 . В общем, среднее квадратичное n чисел x 1 , x 2 , …, x n является их средним арифметическим квадратом не указывает, насколько широко данные разбросаны или разбросаны по среднему значению. Меры дисперсии обеспечиваются средними арифметическими и квадратичными N Различия x 1 — x , x 2 — x ,…, x N a N a . Среднеквадратичное значение дает стандартное отклонение x 1 , x 2 , …, x n .
Их средняя площадь составляет (1 2 + 1 2 + 2 2 + 5 2 + 7 2 )/5, или 16 квадратных см, площадь квадрата со стороной 4 см. Число 4 является средним квадратным (или среднеквадратичным) чисел 1, 1, 2, 5 и 7 и отличается от их среднего арифметического, которое составляет 3 1 / 5 . В общем, среднее квадратичное n чисел x 1 , x 2 , …, x n является их средним арифметическим квадратом не указывает, насколько широко данные разбросаны или разбросаны по среднему значению. Меры дисперсии обеспечиваются средними арифметическими и квадратичными N Различия x 1 — x , x 2 — x ,…, x N a N a . Среднеквадратичное значение дает стандартное отклонение x 1 , x 2 , …, x n .
 х 2 или г 2 = x 1 x 2 ; следовательно, это г называется средним геометрическим от х 1 и х 2 . Среднее геометрическое значение N Числа x 1 , x 2 ,…, x N . Подпишитесь на Britannica Premium и получите доступ к эксклюзивному контенту.
Подпишитесь сейчас
х 2 или г 2 = x 1 x 2 ; следовательно, это г называется средним геометрическим от х 1 и х 2 . Среднее геометрическое значение N Числа x 1 , x 2 ,…, x N . Подпишитесь на Britannica Premium и получите доступ к эксклюзивному контенту.
Подпишитесь сейчас
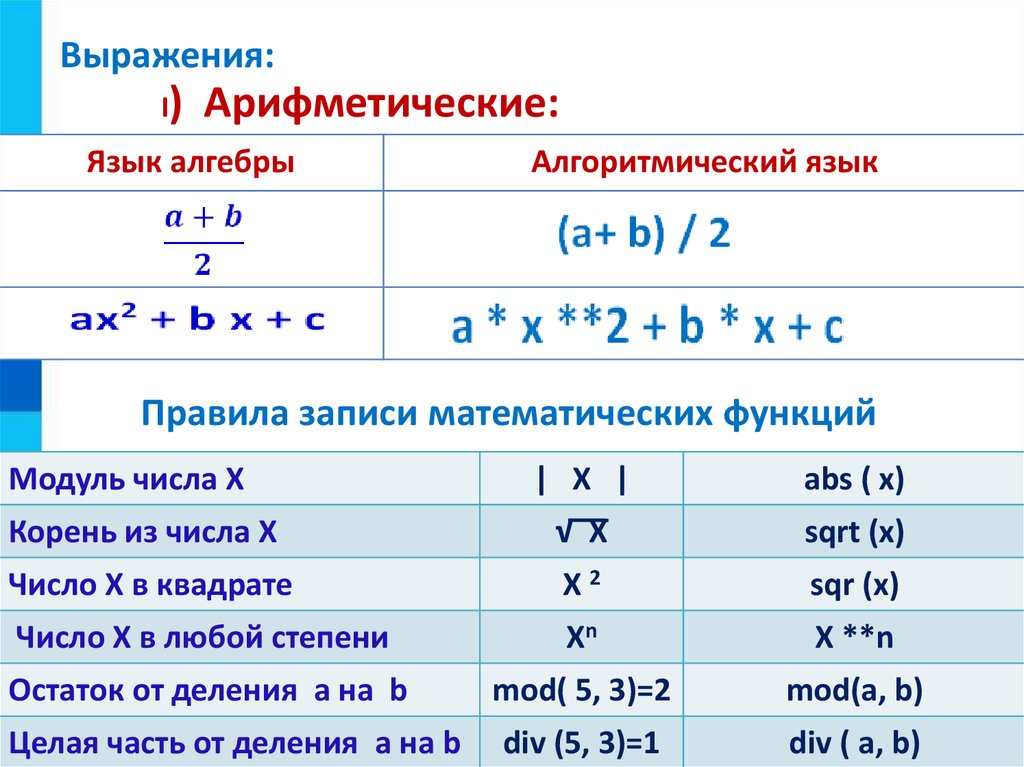 дои: 10.17226/10434.
дои: 10.17226/10434. 0208 математические способности , чтобы выразить то, что, по нашему мнению, означает для любого человека успешное изучение математики.
0208 математические способности , чтобы выразить то, что, по нашему мнению, означает для любого человека успешное изучение математики.
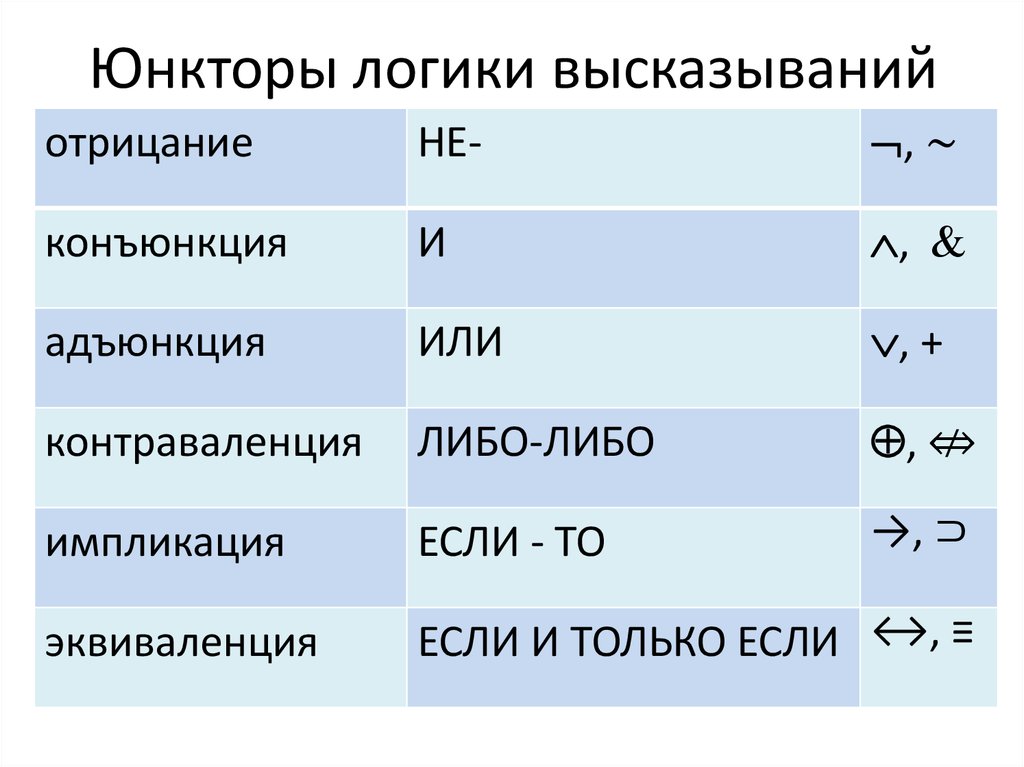 Например, некоторые люди, которые подчеркивали необходимость того, чтобы учащиеся овладевали вычислениями, предполагали, что за этим последует понимание. Другие, сосредотачиваясь на понимании учащимися понятий, предполагали, что навык будет развиваться естественным образом. Используя эти пять направлений, мы попытались дать более полное представление об успешном изучении математики.
Например, некоторые люди, которые подчеркивали необходимость того, чтобы учащиеся овладевали вычислениями, предполагали, что за этим последует понимание. Другие, сосредотачиваясь на понимании учащимися понятий, предполагали, что навык будет развиваться естественным образом. Используя эти пять направлений, мы попытались дать более полное представление об успешном изучении математики.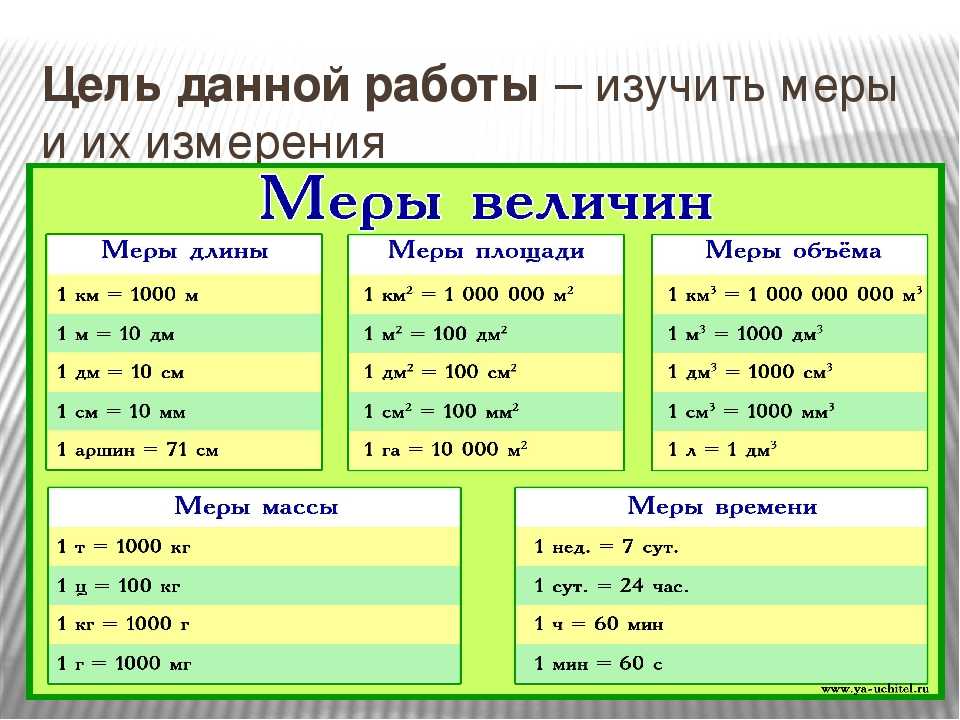
 Или если учащиеся понимают общий принцип, согласно которому умножение размеров трехмерного объекта на коэффициент n увеличивает свой
Или если учащиеся понимают общий принцип, согласно которому умножение размеров трехмерного объекта на коэффициент n увеличивает свой Например, учащиеся, хорошо разбирающиеся в операциях с целыми числами, могут распространить эти понятия и процедуры на операции с десятичными числами.
Например, учащиеся, хорошо разбирающиеся в операциях с целыми числами, могут распространить эти понятия и процедуры на операции с десятичными числами. Свободное владение языком означает умение выполнять процедуру эффективно, точно и гибко.
Свободное владение языком означает умение выполнять процедуру эффективно, точно и гибко. Национальный исследовательский совет. 2002. Помощь детям в изучении математики . Вашингтон, округ Колумбия: Издательство национальных академий. дои: 10.17226/10434.
Национальный исследовательский совет. 2002. Помощь детям в изучении математики . Вашингтон, округ Колумбия: Издательство национальных академий. дои: 10.17226/10434. Оба слишком узкие. Когда люди отстаивают только одну область мастерства, они упускают из виду общую цель. Такое узкое отношение к математике вполне может быть одной из причин плохой успеваемости американских учащихся в национальных и международных оценках.
Оба слишком узкие. Когда люди отстаивают только одну область мастерства, они упускают из виду общую цель. Такое узкое отношение к математике вполне может быть одной из причин плохой успеваемости американских учащихся в национальных и международных оценках.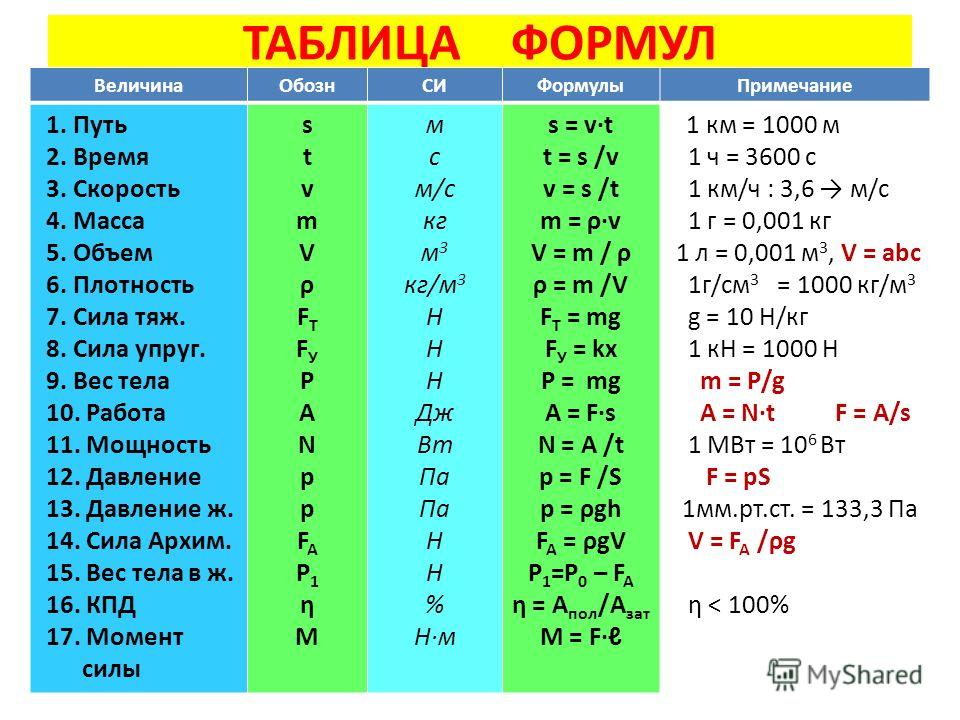 Национальный исследовательский совет. 2002. Помощь детям в изучении математики . Вашингтон, округ Колумбия: Издательство национальных академий. дои: 10.17226/10434.
Национальный исследовательский совет. 2002. Помощь детям в изучении математики . Вашингтон, округ Колумбия: Издательство национальных академий. дои: 10.17226/10434. Например, при вычитании многие дети вычитают меньшее число из большего в каждом столбце, независимо от того, где оно находится, поэтому распространены неправильные ответы, подобные следующим:
Например, при вычитании многие дети вычитают меньшее число из большего в каждом столбце, независимо от того, где оно находится, поэтому распространены неправильные ответы, подобные следующим: В школе учащимся даются конкретные задачи для решения, но вне школы они сталкиваются с ситуациями, в которых одна из трудностей состоит в том, чтобы точно определить, в чем заключается проблема. Следовательно, учащиеся также должны уметь ставить проблемы, разрабатывать стратегии решения и выбирать наиболее полезную стратегию решения проблем. Им нужно знать, как представлять величины в уме или рисовать их на бумаге, и им нужно знать, как отличать известное и актуальное от неизвестного.
В школе учащимся даются конкретные задачи для решения, но вне школы они сталкиваются с ситуациями, в которых одна из трудностей состоит в том, чтобы точно определить, в чем заключается проблема. Следовательно, учащиеся также должны уметь ставить проблемы, разрабатывать стратегии решения и выбирать наиболее полезную стратегию решения проблем. Им нужно знать, как представлять величины в уме или рисовать их на бумаге, и им нужно знать, как отличать известное и актуальное от неизвестного. Например, большинство второклассников знают, что они должны добавить, чтобы ответить на следующий вопрос: «Если в микроавтобусе 12 учеников и еще 7 садятся, сколько учеников в автобусе?» Но для нестандартных задач учащиеся должны изобрести способ понять и решить проблему. Например, второклассникам можно задать следующий вопрос: «В микроавтобусе 7 мест, в каждом по 2-3 ученика. Если есть 19Студенты, сколько человек должно сесть по двое на одно место и сколько должно сесть по трое на одно место?» Чтобы найти ответ, они должны изобрести метод решения. Им необходимо понимать величины в задаче и их взаимосвязь, а также обладать вычислительными навыками, необходимыми для решения задачи.
Например, большинство второклассников знают, что они должны добавить, чтобы ответить на следующий вопрос: «Если в микроавтобусе 12 учеников и еще 7 садятся, сколько учеников в автобусе?» Но для нестандартных задач учащиеся должны изобрести способ понять и решить проблему. Например, второклассникам можно задать следующий вопрос: «В микроавтобусе 7 мест, в каждом по 2-3 ученика. Если есть 19Студенты, сколько человек должно сесть по двое на одно место и сколько должно сесть по трое на одно место?» Чтобы найти ответ, они должны изобрести метод решения. Им необходимо понимать величины в задаче и их взаимосвязь, а также обладать вычислительными навыками, необходимыми для решения задачи.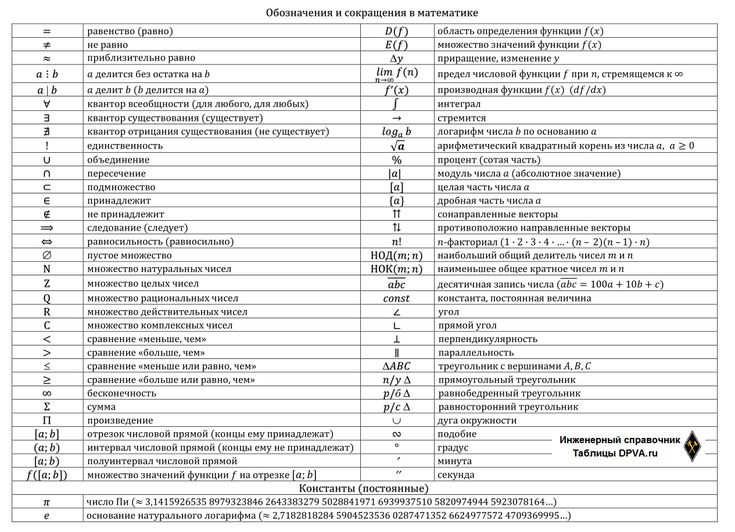 Например, если предоставить возможность изучить и обсудить четные и нечетные числа, четвероклассники могут объяснить, почему сумма любого четного и любого нечетного числа будет нечетной.
Например, если предоставить возможность изучить и обсудить четные и нечетные числа, четвероклассники могут объяснить, почему сумма любого четного и любого нечетного числа будет нечетной.
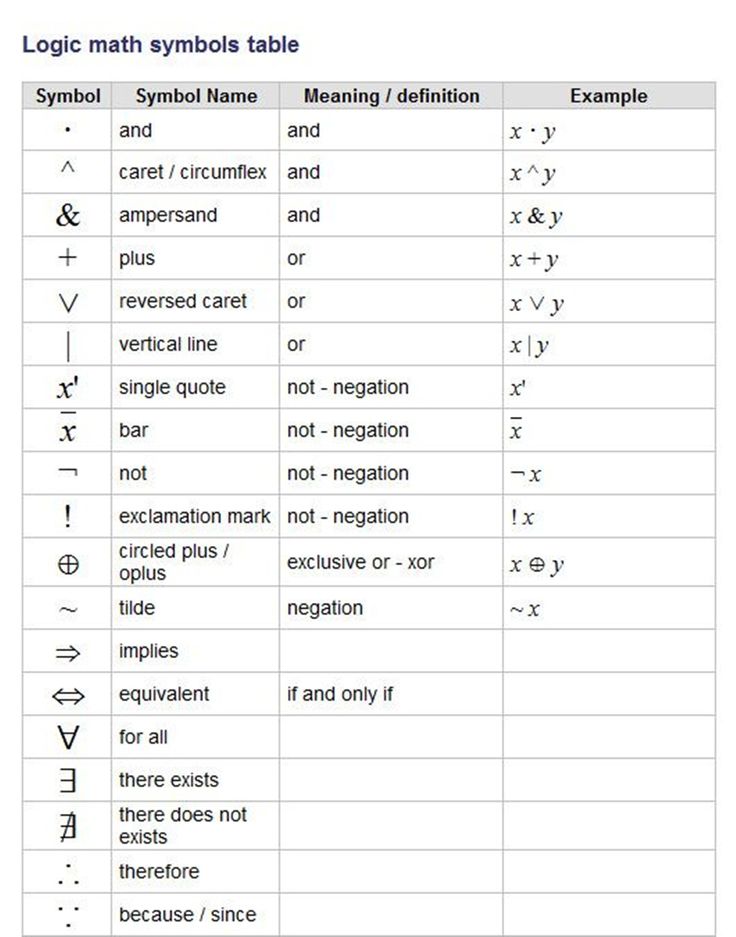 Но учащиеся должны понимать, что происходит в этих сложных вычислениях, и им все еще нужно научиться выполнять более простые вычисления с помощью карандаша и бумаги, потому что это помогает им развить математические навыки. Например, определенный уровень навыков работы с основными комбинациями чисел необходим для понимания процедур умножения двузначных чисел, а беглость вычислений часто необходима при решении задач по алгебре и объяснении их решений. Сколько учебного времени должно быть потрачено на сложные расчеты карандашом и бумагой, — это вопрос, который необходимо будет постоянно пересматривать в течение следующих десятилетий.
Но учащиеся должны понимать, что происходит в этих сложных вычислениях, и им все еще нужно научиться выполнять более простые вычисления с помощью карандаша и бумаги, потому что это помогает им развить математические навыки. Например, определенный уровень навыков работы с основными комбинациями чисел необходим для понимания процедур умножения двузначных чисел, а беглость вычислений часто необходима при решении задач по алгебре и объяснении их решений. Сколько учебного времени должно быть потрачено на сложные расчеты карандашом и бумагой, — это вопрос, который необходимо будет постоянно пересматривать в течение следующих десятилетий.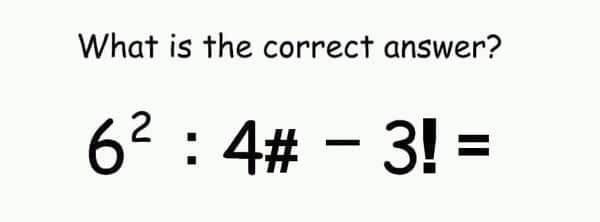 Вашингтон, округ Колумбия: Издательство национальных академий. дои: 10.17226/10434.
Вашингтон, округ Колумбия: Издательство национальных академий. дои: 10.17226/10434.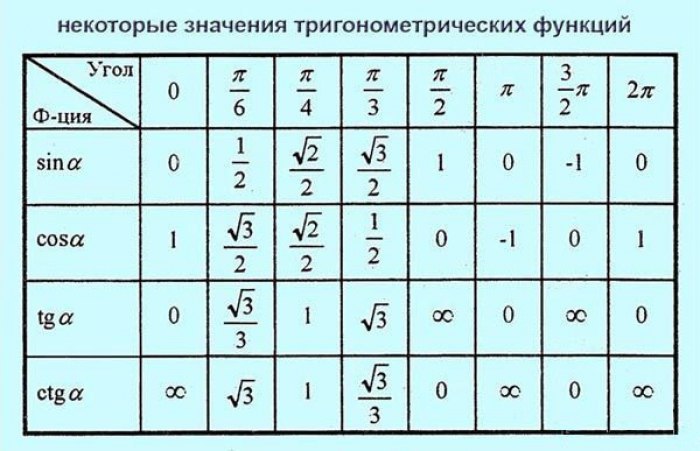 Вместо этого им нужно видеть это как предмет, в котором вещи логически и разумно сочетаются друг с другом, и им нужно верить, что они способны понять это.
Вместо этого им нужно видеть это как предмет, в котором вещи логически и разумно сочетаются друг с другом, и им нужно верить, что они способны понять это. Чтобы овладеть математическими способностями, учащиеся должны развивать все пять направлений в начальной и средней школе.
Чтобы овладеть математическими способностями, учащиеся должны развивать все пять направлений в начальной и средней школе.
 Например, по мере понимания ребенок лучше запоминает вычислительные процедуры и более гибко использует их для решения задач. В свою очередь, по мере того, как процедура становится более автоматической, ребенок может думать о других аспектах проблемы и может решать новые проблемы, что приводит к новому пониманию. В рамке на странице 18 дается дальнейшее описание интеграции направлений математических знаний.
Например, по мере понимания ребенок лучше запоминает вычислительные процедуры и более гибко использует их для решения задач. В свою очередь, по мере того, как процедура становится более автоматической, ребенок может думать о других аспектах проблемы и может решать новые проблемы, что приводит к новому пониманию. В рамке на странице 18 дается дальнейшее описание интеграции направлений математических знаний.

 Распознавание и использование этих связей может сделать изучение комбинаций чисел более легким и менее подверженным забыванию и ошибкам. Например, учащиеся быстро узнают, что 5 файлов cookie плюс 4 файла cookie на единицу больше, чем 4 файла cookie плюс 4 файла cookie. Студенты также узнают некоторые комбинации чисел раньше, чем другие. Например, они часто выучивают двойные числа (например, 6+6, 9+9) и суммирует до десяти (например, 7+3) раньше, чем другие комбинации чисел, и они могут использовать это знание для изучения других комбинаций чисел (например, 6+7 на единицу больше, чем 6+6; 8+5 можно разбивается на 8+2+3).
Распознавание и использование этих связей может сделать изучение комбинаций чисел более легким и менее подверженным забыванию и ошибкам. Например, учащиеся быстро узнают, что 5 файлов cookie плюс 4 файла cookie на единицу больше, чем 4 файла cookie плюс 4 файла cookie. Студенты также узнают некоторые комбинации чисел раньше, чем другие. Например, они часто выучивают двойные числа (например, 6+6, 9+9) и суммирует до десяти (например, 7+3) раньше, чем другие комбинации чисел, и они могут использовать это знание для изучения других комбинаций чисел (например, 6+7 на единицу больше, чем 6+6; 8+5 можно разбивается на 8+2+3).
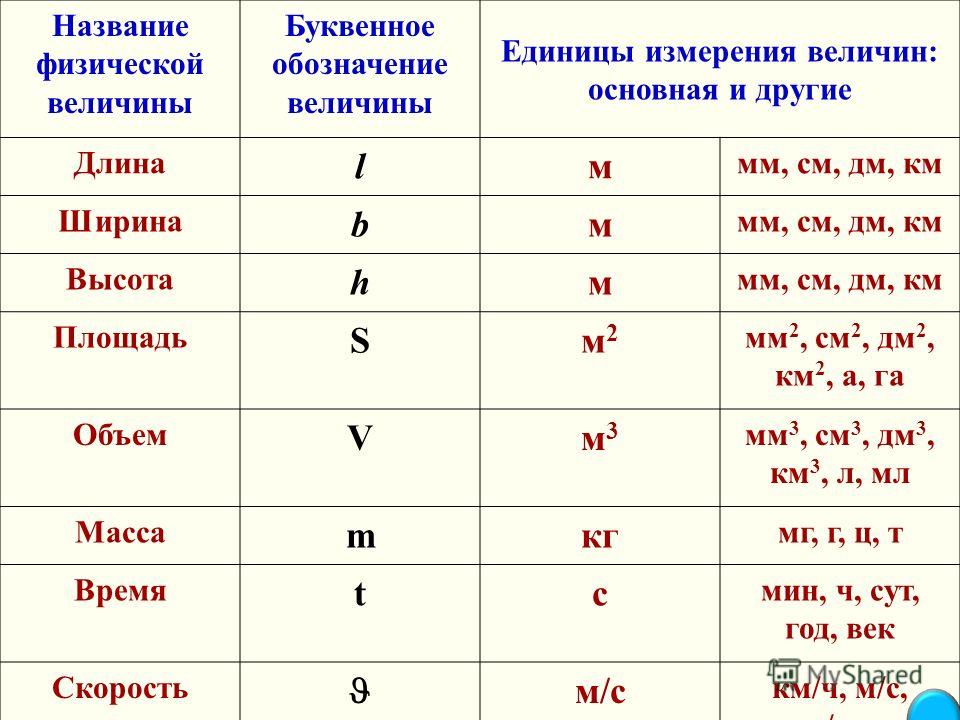 Они начинают считать себя способными использовать числа для решения практических задач.
Они начинают считать себя способными использовать числа для решения практических задач. Однако, когда учащимся предлагается исследовать пропорциональные ситуации в различных контекстах задач, они, естественно, используют все нити математических навыков. Кроме того, поощряя их интегрировать нити, пока они учатся решать пропорции, можно добиться более высоких результатов. 7 Чтобы проиллюстрировать, как учащиеся интегрируют навыки, рассмотрим работу нескольких пятиклассников, которым была задана следующая задача: в 3 за 2 доллара. Они решили вернуться в магазин и купить достаточно воздушных шаров для всех в классе. Сколько бы они заплатили за еще 24 воздушных шара?
Однако, когда учащимся предлагается исследовать пропорциональные ситуации в различных контекстах задач, они, естественно, используют все нити математических навыков. Кроме того, поощряя их интегрировать нити, пока они учатся решать пропорции, можно добиться более высоких результатов. 7 Чтобы проиллюстрировать, как учащиеся интегрируют навыки, рассмотрим работу нескольких пятиклассников, которым была задана следующая задача: в 3 за 2 доллара. Они решили вернуться в магазин и купить достаточно воздушных шаров для всех в классе. Сколько бы они заплатили за еще 24 воздушных шара?  Он объявил, что
Он объявил, что Позже Марти рассказывала своему старшему брату о том, как дети в ее классе по-разному решали задачу о воздушном шаре. Ее брат показал ей другой способ, используя эквивалентные дроби: 2 доллара за три шарика эквивалентны тому, сколько стоит 24 шарика? (То есть .) Он объяснил, что, поскольку вы умножаете 3 на 8, чтобы получить 24, вы должны умножить 2 на 8, чтобы получить недостающий числитель. Итак, ответ: 16 долларов.
Позже Марти рассказывала своему старшему брату о том, как дети в ее классе по-разному решали задачу о воздушном шаре. Ее брат показал ей другой способ, используя эквивалентные дроби: 2 доллара за три шарика эквивалентны тому, сколько стоит 24 шарика? (То есть .) Он объяснил, что, поскольку вы умножаете 3 на 8, чтобы получить 24, вы должны умножить 2 на 8, чтобы получить недостающий числитель. Итак, ответ: 16 долларов. Каждый ребенок также мог рассуждать о ситуации и объяснять другим, что он или она делает. Все они ожидали, что смогут разобраться в проблеме, и упорствовали, пока не пришли к решению, в котором были уверены, хотя Деймон начал с двух разных ответов, а Марти — с «дурацкой цифры».
Каждый ребенок также мог рассуждать о ситуации и объяснять другим, что он или она делает. Все они ожидали, что смогут разобраться в проблеме, и упорствовали, пока не пришли к решению, в котором были уверены, хотя Деймон начал с двух разных ответов, а Марти — с «дурацкой цифры». 2002. Помощь детям в изучении математики . Вашингтон, округ Колумбия: Издательство национальных академий. дои: 10.17226/10434.
2002. Помощь детям в изучении математики . Вашингтон, округ Колумбия: Издательство национальных академий. дои: 10.17226/10434. Но в каждом классе учащиеся должны быть в состоянии продемонстрировать математические способности в той или иной форме.
Но в каждом классе учащиеся должны быть в состоянии продемонстрировать математические способности в той или иной форме.
 Национальный исследовательский совет. 2002. Помощь детям в изучении математики . Вашингтон, округ Колумбия: Издательство национальных академий. дои: 10.17226/10434.
Национальный исследовательский совет. 2002. Помощь детям в изучении математики . Вашингтон, округ Колумбия: Издательство национальных академий. дои: 10.17226/10434.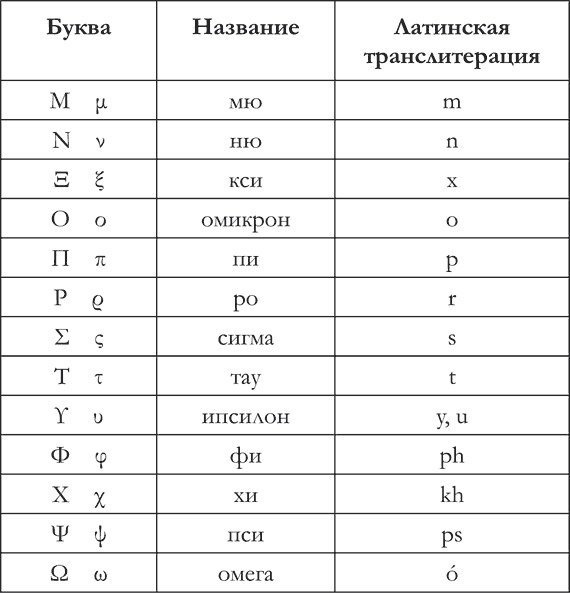
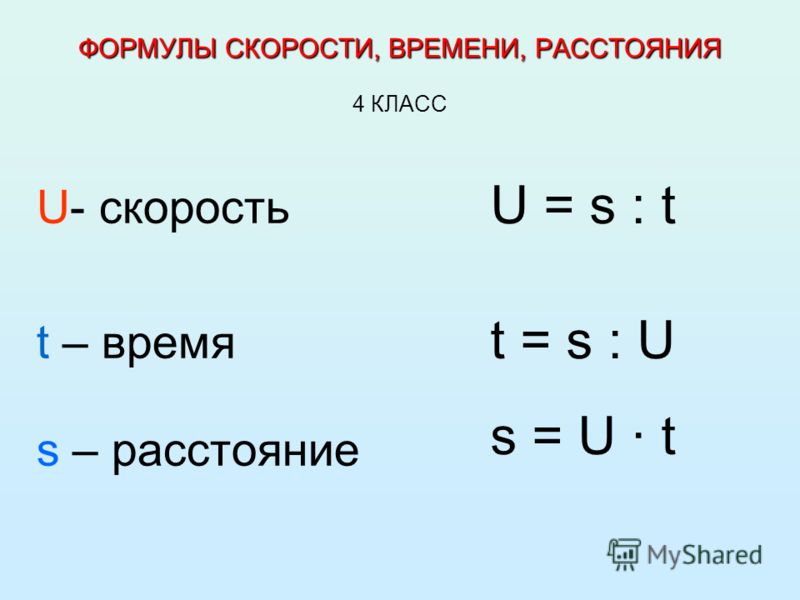 Национальный исследовательский совет. 2002. Помощь детям в изучении математики . Вашингтон, округ Колумбия: Издательство национальных академий. дои: 10.17226/10434.
Национальный исследовательский совет. 2002. Помощь детям в изучении математики . Вашингтон, округ Колумбия: Издательство национальных академий. дои: 10.17226/10434.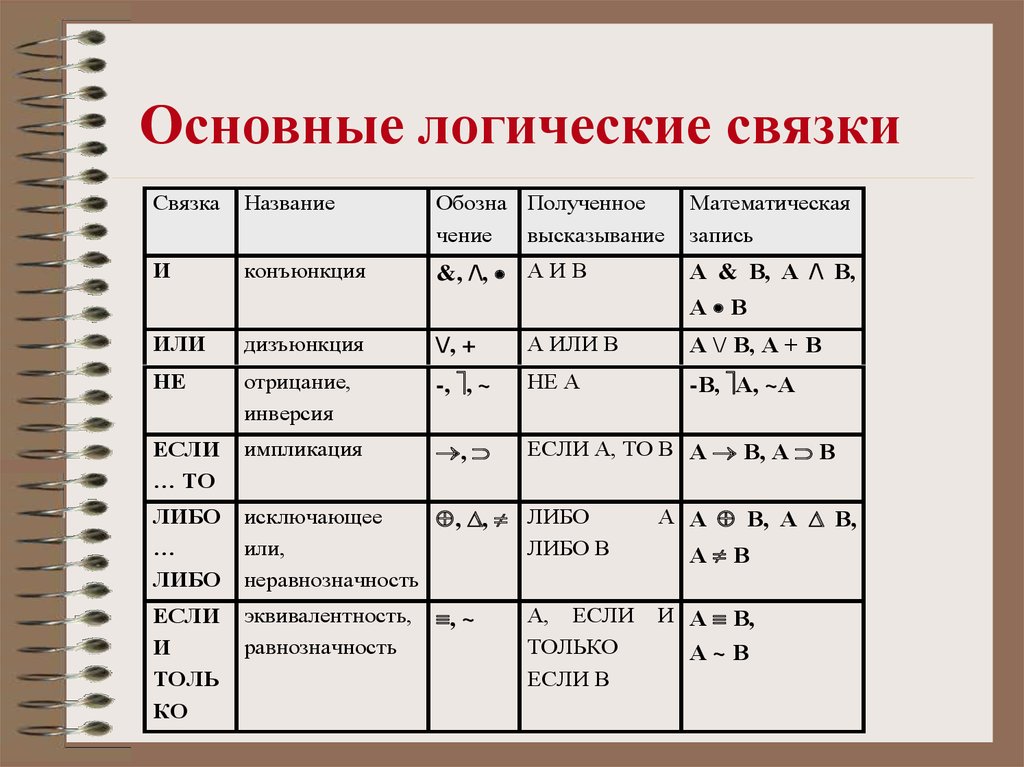 В последних классах учителя использовали несколько представлений математических идей для поддержки понимания, сосредоточивались на нестандартных задачах, чтобы укрепить применение понятий, подчеркивали несколько решений задач для развития беглости вычислений и проводили обсуждения в классе, требующие логических рассуждений, которые исследовали альтернативные решения или значения математические процедуры или результаты.
В последних классах учителя использовали несколько представлений математических идей для поддержки понимания, сосредоточивались на нестандартных задачах, чтобы укрепить применение понятий, подчеркивали несколько решений задач для развития беглости вычислений и проводили обсуждения в классе, требующие логических рассуждений, которые исследовали альтернативные решения или значения математические процедуры или результаты. 11
11  17226/10434.
17226/10434. дои: 10.17226/10434.
дои: 10.17226/10434. дои: 10.17226/10434.
дои: 10.17226/10434. дои: 10.17226/10434.
дои: 10.17226/10434. дои: 10.17226/10434.
дои: 10.17226/10434. дои: 10.17226/10434.
дои: 10.17226/10434.
 Смотрите подробный материал о развитии логики у детей.
Смотрите подробный материал о развитии логики у детей.
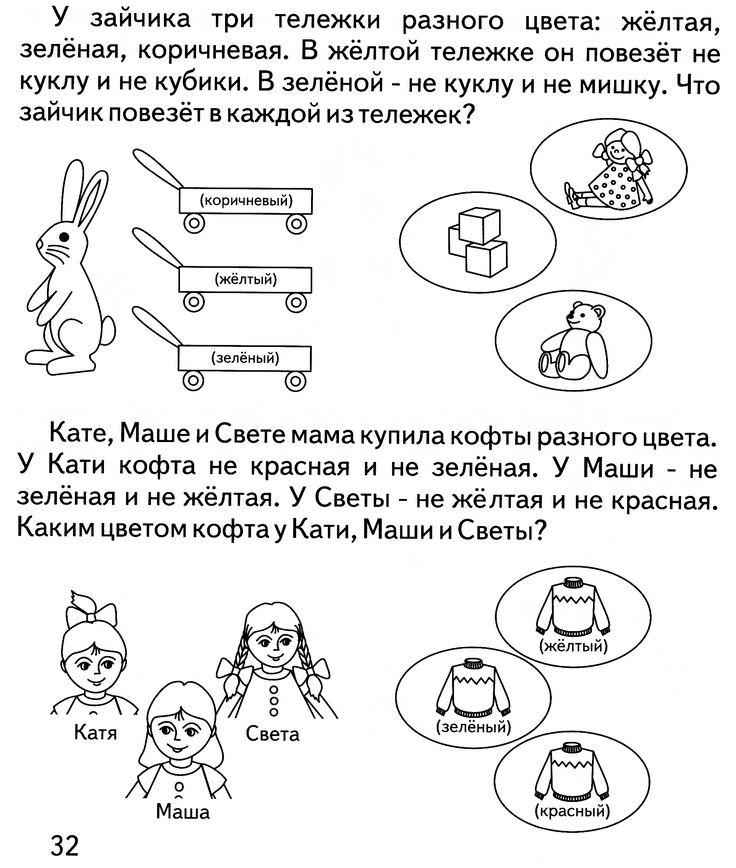 Всего стало 33 стержня.
Всего стало 33 стержня.

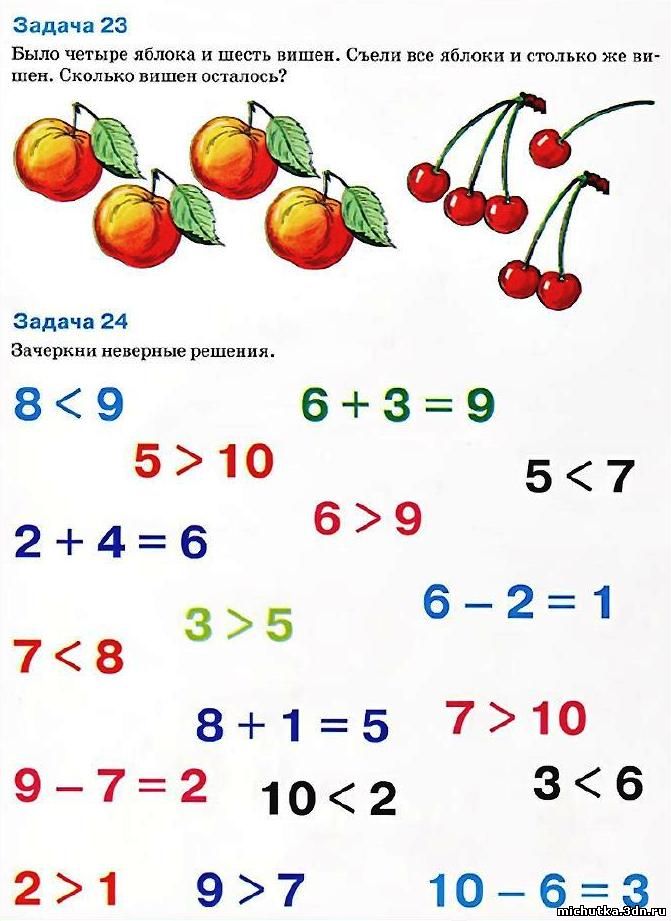

 Следовательно, общее количество кусков
увеличилось на 9 ∙ 4 = 36.
Следовательно, общее количество кусков
увеличилось на 9 ∙ 4 = 36.


 4.2014
4.2014 innerHTML=»
innerHTML=»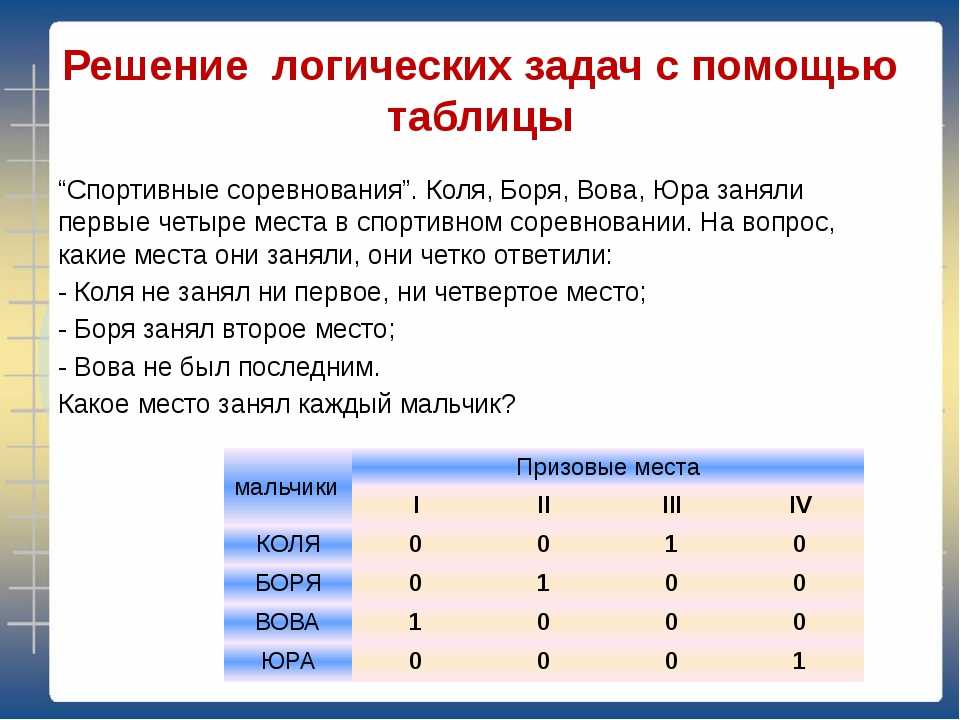 Сколько красок для этого потребовалось ?
Сколько красок для этого потребовалось ?
 Он моложе своей сестры, которой исполнилось 6 лет. Сколько лет может быть Вите ?
Он моложе своей сестры, которой исполнилось 6 лет. Сколько лет может быть Вите ?
 На приключенческий фильм было продано 87 билетов, а на комедию — 63. Сколько ребят посмотрели и тот фильм, и другой? (Каждый посмотрел по меньшей мере один из фильмов.)
На приключенческий фильм было продано 87 билетов, а на комедию — 63. Сколько ребят посмотрели и тот фильм, и другой? (Каждый посмотрел по меньшей мере один из фильмов.)
 к.
к. д.
д. Сколько носков связала бабушка Нине?
Сколько носков связала бабушка Нине? Из пакета взяли 4 красных и 5 жёлтых яблок, и пакет опустел. Сколько яблок было в пакете?
Из пакета взяли 4 красных и 5 жёлтых яблок, и пакет опустел. Сколько яблок было в пакете? На яблоне осталось 6 яблок. Сколько было детей?
На яблоне осталось 6 яблок. Сколько было детей? Шляп 8. Сколько шапок и сколько беретов?
Шляп 8. Сколько шапок и сколько беретов? Сколько журналов выдал ему библиотекарь?
Сколько журналов выдал ему библиотекарь?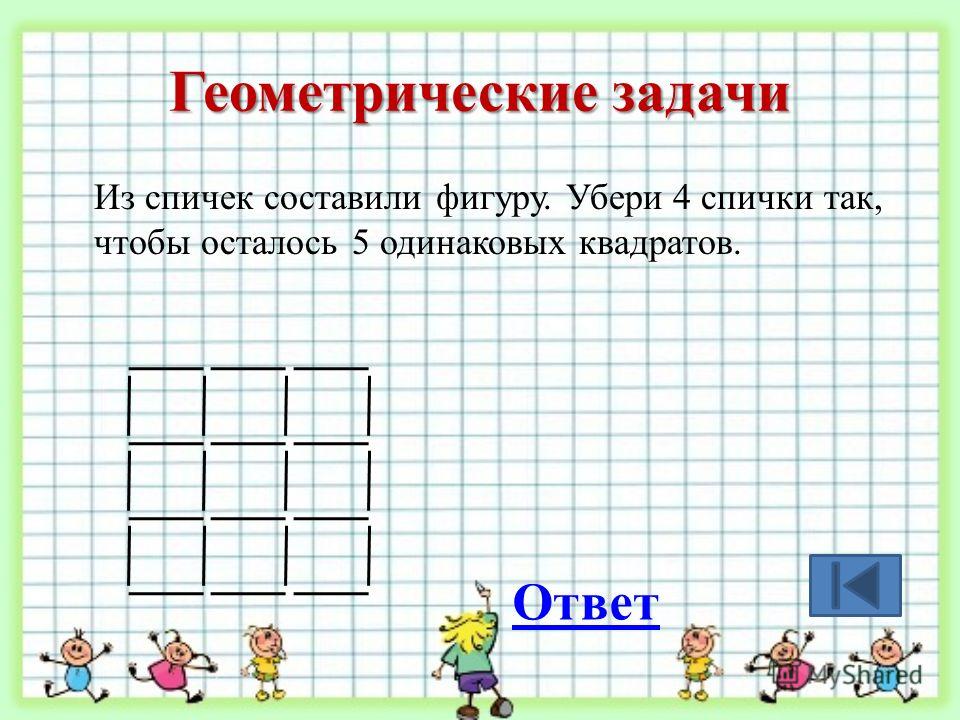 Нина задумала число. Это число она сначала прибавила к 7, а потом отняла его от 7. Ответ оказался одним и тем же – 7. Какое число задумала Нина?
Нина задумала число. Это число она сначала прибавила к 7, а потом отняла его от 7. Ответ оказался одним и тем же – 7. Какое число задумала Нина? Сумма двух чисел равна 8, а их разность 4. Угадайте, какие это числа?
Сумма двух чисел равна 8, а их разность 4. Угадайте, какие это числа? В ящике стола лежат деньги. На эти деньги можно купить 2 одинаковых по цене стула или одно кресло. Что дороже кресло или стул?
В ящике стола лежат деньги. На эти деньги можно купить 2 одинаковых по цене стула или одно кресло. Что дороже кресло или стул? Зелёная лента на 3 м длиннее красной. От зелёной ленты отрезали 5 м, а от красной 2м. Сравните длины оставшихся кусков лент.
Зелёная лента на 3 м длиннее красной. От зелёной ленты отрезали 5 м, а от красной 2м. Сравните длины оставшихся кусков лент. Сколько стаканов кефира было в пакете?
Сколько стаканов кефира было в пакете? Торт разрезали на 4 одинаковые части, а потом каждую часть разрезали на 2 одинаковые части. На сколько человек хватит торта, если каждому положить на блюдце один кусок?
Торт разрезали на 4 одинаковые части, а потом каждую часть разрезали на 2 одинаковые части. На сколько человек хватит торта, если каждому положить на блюдце один кусок?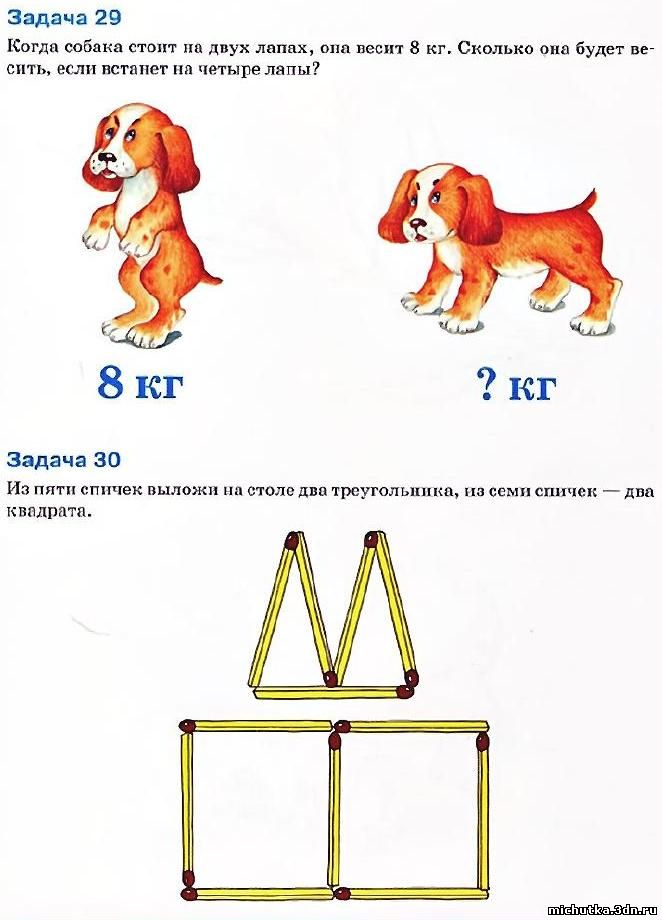 Если одно из слагаемых равно нулю. Например: 5+0=5
Если одно из слагаемых равно нулю. Например: 5+0=5 Если одно из слагаемых равно нулю. Например: 5+0=5
Если одно из слагаемых равно нулю. Например: 5+0=5 Если одно из слагаемых равно нулю. Например: 5+0=5
Если одно из слагаемых равно нулю. Например: 5+0=5
 Этот пост предназначен для тех педагогов или родителей, которые занимаются домашним обучением, которые хотят предоставить проверенные учителями задания для учащихся с логическим математическим интеллектом.
Этот пост предназначен для тех педагогов или родителей, которые занимаются домашним обучением, которые хотят предоставить проверенные учителями задания для учащихся с логическим математическим интеллектом.
 Они редко принимают решения, основанные на чувствах
Они редко принимают решения, основанные на чувствах
 Так почему бы не бросить детям увлекательный исследовательский проект? Просто выберите интересующую тему, например определенного динозавра, насекомое, солнечную систему, вулканы и т. д., и позвольте вашему малышу узнать как можно больше информации по этой теме. Дети постарше могут организовать и структурировать информацию самостоятельно, однако для детей помладше вы можете создать рабочие листы, чтобы направлять их исследования. Мне нравятся материалы Wifeteachermommy.com.
Так почему бы не бросить детям увлекательный исследовательский проект? Просто выберите интересующую тему, например определенного динозавра, насекомое, солнечную систему, вулканы и т. д., и позвольте вашему малышу узнать как можно больше информации по этой теме. Дети постарше могут организовать и структурировать информацию самостоятельно, однако для детей помладше вы можете создать рабочие листы, чтобы направлять их исследования. Мне нравятся материалы Wifeteachermommy.com. Программирование
Программирование  В Интернете можно найти как платные, так и бесплатные игры, которые понравятся вашему ребенку и помогут ему практиковать математику. Например, Math Games — это бесплатный веб-сайт, который содержит множество аркадных игр, рабочих листов, игр типа «Вопросы и ответы» и многое другое, все организовано по навыкам или оценкам.
В Интернете можно найти как платные, так и бесплатные игры, которые понравятся вашему ребенку и помогут ему практиковать математику. Например, Math Games — это бесплатный веб-сайт, который содержит множество аркадных игр, рабочих листов, игр типа «Вопросы и ответы» и многое другое, все организовано по навыкам или оценкам. Так что никогда не рано начинать знакомить вашего ребенка с шаблонными действиями. Не говоря уже о том, что когда дело доходит до логических математических действий, шаблоны очень популярны.
Так что никогда не рано начинать знакомить вашего ребенка с шаблонными действиями. Не говоря уже о том, что когда дело доходит до логических математических действий, шаблоны очень популярны. Вы можете определить количество подсказок. По подсказкам игрок должен угадать животное.
Вы можете определить количество подсказок. По подсказкам игрок должен угадать животное. Удачи!
Удачи!
 The Intruder (Odd one out )
The Intruder (Odd one out ) 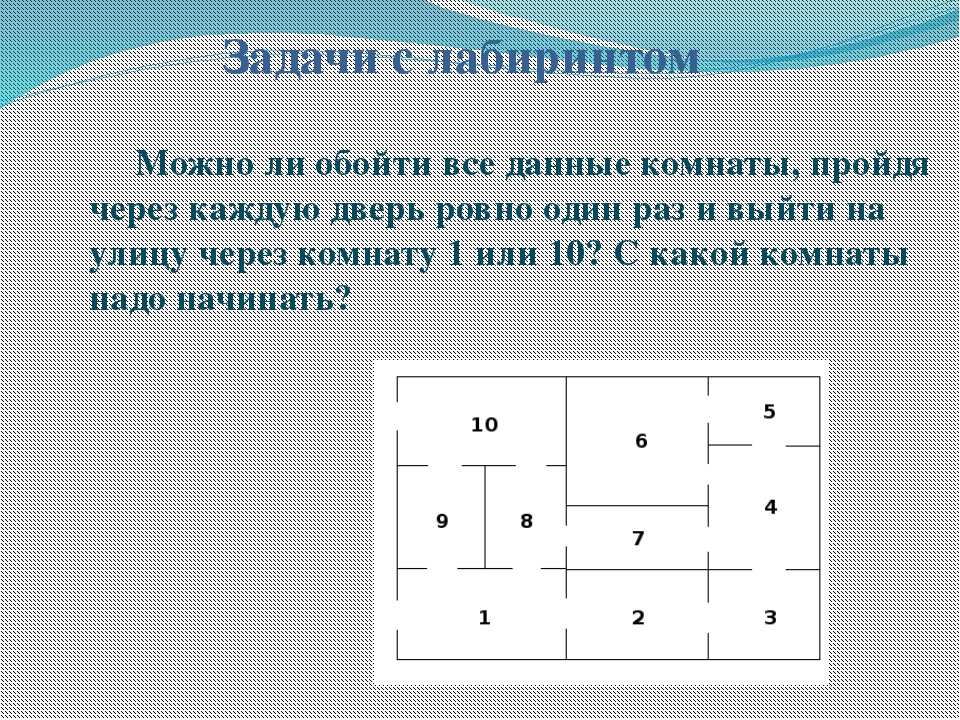 Мы не должны забывать, что мы рождаемся обладающими всеми восемью видами интеллекта, однако в силу биологических и культурных аспектов все мы имеем разные сильные и слабые стороны. В идеальной образовательной системе преподаватели должны представлять материалы таким образом, чтобы задействовать большинство из восьми видов интеллекта, давая своим ученикам возможность усвоить информацию удобным и легким для них способом.
Мы не должны забывать, что мы рождаемся обладающими всеми восемью видами интеллекта, однако в силу биологических и культурных аспектов все мы имеем разные сильные и слабые стороны. В идеальной образовательной системе преподаватели должны представлять материалы таким образом, чтобы задействовать большинство из восьми видов интеллекта, давая своим ученикам возможность усвоить информацию удобным и легким для них способом.
 также: Логика предикатов
также: Логика предикатов Весь картофель в блюде годен для еды; если есть картофель, который нельзя есть, значит, его нет в блюде.
Весь картофель в блюде годен для еды; если есть картофель, который нельзя есть, значит, его нет в блюде.





 Вопрос в том, смогут ли они все перейти мост за 15 минут или меньше?
Вопрос в том, смогут ли они все перейти мост за 15 минут или меньше? Помните наше первоначальное предположение о том, что мы должны свести к минимуму пересечения, поэтому у нас есть пять пересечений — 3 парных пересечения и 2 одиночных пересечения. Предположим, что C и D пересекаются первыми. Но затем C или D должны вернуться, чтобы переместить факел на другую сторону, поэтому тот, кто пересек дорогу в одиночку, должен пересечь снова. Следовательно, они будут пересекаться отдельно. Кроме того, они не могут пересечься вместе последними, поскольку это означает, что один из них должен был пересечь дорогу раньше, иначе на стартовой стороне было бы всего три человека. Таким образом, поскольку есть только три варианта парного пересечения, а C и D не могут пересечься первым или последним, они должны пересечься вместе во втором, или среднем, парном пересечении.
Помните наше первоначальное предположение о том, что мы должны свести к минимуму пересечения, поэтому у нас есть пять пересечений — 3 парных пересечения и 2 одиночных пересечения. Предположим, что C и D пересекаются первыми. Но затем C или D должны вернуться, чтобы переместить факел на другую сторону, поэтому тот, кто пересек дорогу в одиночку, должен пересечь снова. Следовательно, они будут пересекаться отдельно. Кроме того, они не могут пересечься вместе последними, поскольку это означает, что один из них должен был пересечь дорогу раньше, иначе на стартовой стороне было бы всего три человека. Таким образом, поскольку есть только три варианта парного пересечения, а C и D не могут пересечься первым или последним, они должны пересечься вместе во втором, или среднем, парном пересечении. Тогда мы находимся на втором, или среднем, парном пересечении, поэтому C и D должны уйти. Затем мы решаем отправить назад самого быстрого, то есть B. Теперь A и B находятся на стартовой стороне и должны пересечься последней парой. Это дает нам B+A+D+B+B = 2+1+8+2+2 = 15,
Тогда мы находимся на втором, или среднем, парном пересечении, поэтому C и D должны уйти. Затем мы решаем отправить назад самого быстрого, то есть B. Теперь A и B находятся на стартовой стороне и должны пересечься последней парой. Это дает нам B+A+D+B+B = 2+1+8+2+2 = 15,
 Каждый последующий запуск отделяется от других запусков хотя бы одним пустым пространством. Головоломка завершена, когда все числа были удовлетворены. Основным методом решения этих головоломок является процесс исключения. Если головоломка составлена правильно, никаких догадок не требуется.
Каждый последующий запуск отделяется от других запусков хотя бы одним пустым пространством. Головоломка завершена, когда все числа были удовлетворены. Основным методом решения этих головоломок является процесс исключения. Если головоломка составлена правильно, никаких догадок не требуется.



 Каждый открывает свой конверт и проверяет свое число, не видя других чисел.
Каждый открывает свой конверт и проверяет свое число, не видя других чисел. .. я знаю… что ты собирался это сказать!
.. я знаю… что ты собирался это сказать! \text{rd}3-е предположение слишком мало, вы вышли.
\text{rd}3-е предположение слишком мало, вы вышли. org/wiki/логические-пазлы/
org/wiki/логические-пазлы/ 25 — это
25 — это  Как вы можете отмерить 4 литра воды, используя 3-литровые и 5-литровые бутылки???
Как вы можете отмерить 4 литра воды, используя 3-литровые и 5-литровые бутылки??? Теперь у вас есть 4 литра в 5-литровой бутыли. Вот и все.
Теперь у вас есть 4 литра в 5-литровой бутыли. Вот и все. 30 ?????
30 ?????

 С одной стороны, они могут использоваться для выражения того, что член в математическом выражении может быть как положительным, так и отрицательным (например, «± 5» означает, что рассматриваемое число может быть +5 или -5). С другой стороны, знак плюс-минус перед числом может использоваться для обозначения всего диапазона чисел, заключенного в положительное и отрицательное значение числа (например, «± 5» обозначает диапазон от -5 до +5, включая сами эти значения).
С одной стороны, они могут использоваться для выражения того, что член в математическом выражении может быть как положительным, так и отрицательным (например, «± 5» означает, что рассматриваемое число может быть +5 или -5). С другой стороны, знак плюс-минус перед числом может использоваться для обозначения всего диапазона чисел, заключенного в положительное и отрицательное значение числа (например, «± 5» обозначает диапазон от -5 до +5, включая сами эти значения). высота крышки
высота крышки Единицу измерения можно не указывать на чертежах с указанием стандартной единицы измерения: «Размеры в мм. … 304,80 ± 6,35 «.
Единицу измерения можно не указывать на чертежах с указанием стандартной единицы измерения: «Размеры в мм. … 304,80 ± 6,35 «. Таким образом, компактная запись содержит два уравнения
Икс{\ displaystyle x}у{\ displaystyle y}Икс{\ displaystyle x}у{\ displaystyle y}
Таким образом, компактная запись содержит два уравнения
Икс{\ displaystyle x}у{\ displaystyle y}Икс{\ displaystyle x}у{\ displaystyle y} {2} = 4} Икс1знак равно2{\ displaystyle x_ {1} = 2}Икс2знак равно-2{\ displaystyle x_ {2} = — 2}Икс1/2знак равно±4-йзнак равно±2{\ displaystyle x_ {1/2} = \ pm {\ sqrt {4}} = \ pm 2}
{2} = 4} Икс1знак равно2{\ displaystyle x_ {1} = 2}Икс2знак равно-2{\ displaystyle x_ {2} = — 2}Икс1/2знак равно±4-йзнак равно±2{\ displaystyle x_ {1/2} = \ pm {\ sqrt {4}} = \ pm 2} Однако он уже был включен в 1986 году в расширение ASCII ISO 8859-1 (также известное как Latin-1) . Почти все современные компьютеры используют стандарт Unicode, который был представлен в 1991 году, и поэтому могут без проблем обрабатывать и отображать оба символа.
Однако он уже был включен в 1986 году в расширение ASCII ISO 8859-1 (также известное как Latin-1) . Почти все современные компьютеры используют стандарт Unicode, который был представлен в 1991 году, и поэтому могут без проблем обрабатывать и отображать оба символа. 39KB
39KB 14KB
14KB 64KB
64KB Жизнь была бы слишком занятой и трудной, если бы в повседневной работе не помогала математика. Существует множество математических символов, каждый из которых имеет определенную цель и способствует удобству вычислений и целей идентификации. Один из этих символов, плюс-минус, также хорошо известен своей помощью в различных математических расчетах и уравнениях, таких как квадратные формулы, которые имеют жизненно важное значение при решении квадратных уравнений.
Жизнь была бы слишком занятой и трудной, если бы в повседневной работе не помогала математика. Существует множество математических символов, каждый из которых имеет определенную цель и способствует удобству вычислений и целей идентификации. Один из этих символов, плюс-минус, также хорошо известен своей помощью в различных математических расчетах и уравнениях, таких как квадратные формулы, которые имеют жизненно важное значение при решении квадратных уравнений. Только одно из этих двух замененных уравнений верно для любого действительного уравнения.
Только одно из этих двух замененных уравнений верно для любого действительного уравнения. Чтобы написать знак плюс-минус на клавиатуре, одновременно нажмите и удерживайте клавишу alt и альтернативный код, который равен 0177 . Это 0177 называется альтернативным кодом плюс-минус.
Чтобы написать знак плюс-минус на клавиатуре, одновременно нажмите и удерживайте клавишу alt и альтернативный код, который равен 0177 . Это 0177 называется альтернативным кодом плюс-минус.
 Функция обоих символов одинакова. Когда в выражении используются знаки, то положительное значение следует записывать с отрицательным, а отрицательное — с положительным.
Функция обоих символов одинакова. Когда в выражении используются знаки, то положительное значение следует записывать с отрицательным, а отрицательное — с положительным. Если вы хотите ввести этот знак на клавиатуре, MAC или в Word/Excel, вам необходимо следовать определенным методам. Кроме того, коды со знаком плюс-минус необходимы для набора уравнений.
Если вы хотите ввести этот знак на клавиатуре, MAC или в Word/Excel, вам необходимо следовать определенным методам. Кроме того, коды со знаком плюс-минус необходимы для набора уравнений. Ниже -2.0 много игроков на скамейке запасных.
Ниже -2.0 много игроков на скамейке запасных. Некоторые статистические показатели включают следующее: Среднее значение.
Некоторые статистические показатели включают следующее: Среднее значение. Например, скажем, у нас есть проблема -2 — -4.
Например, скажем, у нас есть проблема -2 — -4. Это часто имеет место, особенно для парней, у которых меньше минут.
Это часто имеет место, особенно для парней, у которых меньше минут.
 25KB )
25KB ) 5.2019
5.2019
 Некоторые тесты посвящены теме «Уравнения и неравенства», они включают и более сложные вопросы, посвященные решению показательных неравенств и уравнений.
Некоторые тесты посвящены теме «Уравнения и неравенства», они включают и более сложные вопросы, посвященные решению показательных неравенств и уравнений. 5.2014
5.2014
 А вот 25 примеров порешаем?!
А вот 25 примеров порешаем?!
 Тест включает в себя как задания на перевод величин в различные единицы измерения, так и на действия с ними. В тесте 15 вопросов, из них 11 с открытым ответом и 4 с множественным выбором.
Тест включает в себя как задания на перевод величин в различные единицы измерения, так и на действия с ними. В тесте 15 вопросов, из них 11 с открытым ответом и 4 с множественным выбором. Обязательные ответы на все вопросы теста.
Обязательные ответы на все вопросы теста. Обязательные ответы на все вопросы теста.
Обязательные ответы на все вопросы теста.
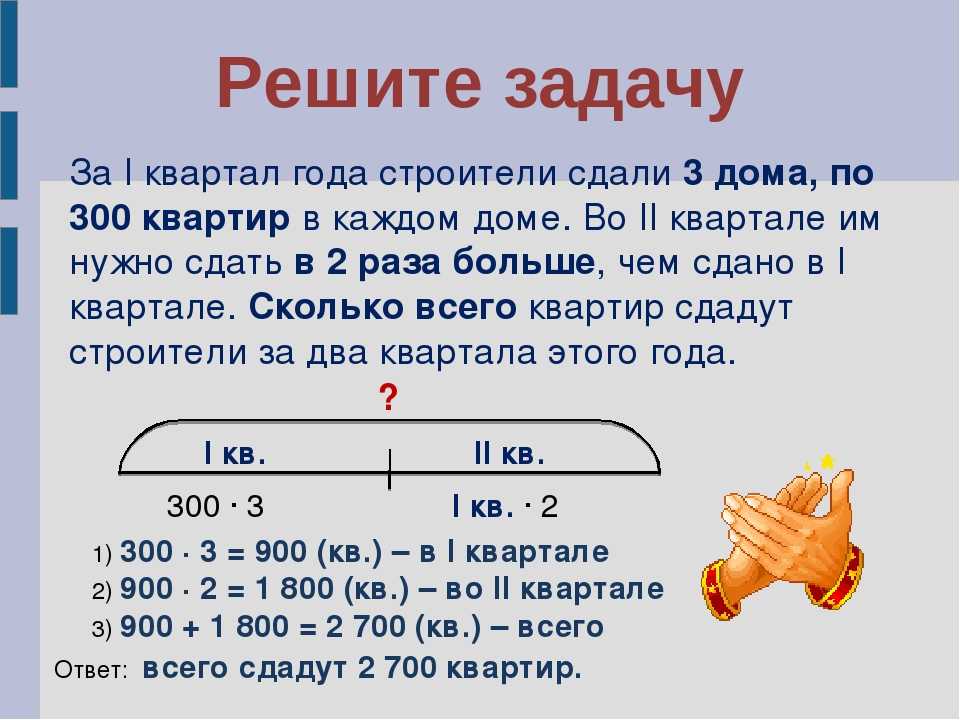 » /> » /> .keyword { color: red; }
» /> » /> .keyword { color: red; }
 Занятия ведут выпускники МГУ и МФТИ.
Занятия ведут выпускники МГУ и МФТИ.
 Наша задача — сделать так чтобы у вашего ребёнка не было проблем с математикой в школе. Для этого мы будем двигаться по школьной программе и разбирать все темы.
Наша задача — сделать так чтобы у вашего ребёнка не было проблем с математикой в школе. Для этого мы будем двигаться по школьной программе и разбирать все темы.
 Вы будете регулярно получать обратную связь об успеваемости и прогрессе вашего ребёнка
Вы будете регулярно получать обратную связь об успеваемости и прогрессе вашего ребёнка

 Также сертификат можно самостоятельно распечатать.
Также сертификат можно самостоятельно распечатать. Для тех, кто любит думать, и увлекается историей.
Для тех, кто любит думать, и увлекается историей. История Древней Индии
История Древней Индии Дети также проводят много времени с дробями и разрядами. Учите всем этим и многим другим понятиям с помощью этих бесплатных и веселых математических игр для четвертого класса!
Дети также проводят много времени с дробями и разрядами. Учите всем этим и многим другим понятиям с помощью этих бесплатных и веселых математических игр для четвертого класса! Первый игрок отмечает число (его счет за этот раунд). Затем второй игрок отмечает все оставшиеся факторы этого числа (которые в сумме составляют его счет за этот раунд). Игра продолжается до тех пор, пока не будут отмечены все числа.
Первый игрок отмечает число (его счет за этот раунд). Затем второй игрок отмечает все оставшиеся факторы этого числа (которые в сумме составляют его счет за этот раунд). Игра продолжается до тех пор, пока не будут отмечены все числа. Сначала они будут просто гадать, но в конце концов начнут замечать появление закономерности.
Сначала они будут просто гадать, но в конце концов начнут замечать появление закономерности. Добавьте несколько кубиков, и вы готовы к игре!
Добавьте несколько кубиков, и вы готовы к игре! Разрешите 30-секундный безопасный «бой снежками», затем пусть каждый учащийся возьмет снежок и прочитает число вслух, правильно округлив его. Повторение!
Разрешите 30-секундный безопасный «бой снежками», затем пусть каждый учащийся возьмет снежок и прочитает число вслух, правильно округлив его. Повторение!
 )
) Как только они выстроятся в очередь, задайте несколько дополнительных вопросов, чтобы подтвердить понимание. Узнайте больше по ссылке.
Как только они выстроятся в очередь, задайте несколько дополнительных вопросов, чтобы подтвердить понимание. Узнайте больше по ссылке. Как только они найдут его, им также необходимо преобразовать измерение в той же системе (например, дюймы в футы).
Как только они найдут его, им также необходимо преобразовать измерение в той же системе (например, дюймы в футы).
 Если вы хотите еще 90 692 математических задач с 90 693 задачами, мы ежедневно публикуем их на нашем удобном для детей сайте: Daily Classroom Hub. Обязательно добавьте ссылку в закладки!
Если вы хотите еще 90 692 математических задач с 90 693 задачами, мы ежедневно публикуем их на нашем удобном для детей сайте: Daily Classroom Hub. Обязательно добавьте ссылку в закладки! 94591
94591 Производная y’=1x, поэтому она никогда не равна 0 и всегда положительна. Следовательно, n должно быть большим.
Производная y’=1x, поэтому она никогда не равна 0 и всегда положительна. Следовательно, n должно быть большим. х). Натуральный журнал — это функция «один к одному».
х). Натуральный журнал — это функция «один к одному».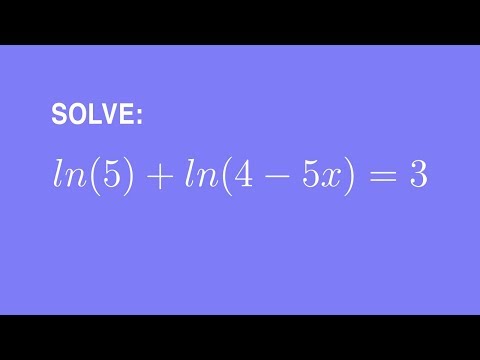 931826
931826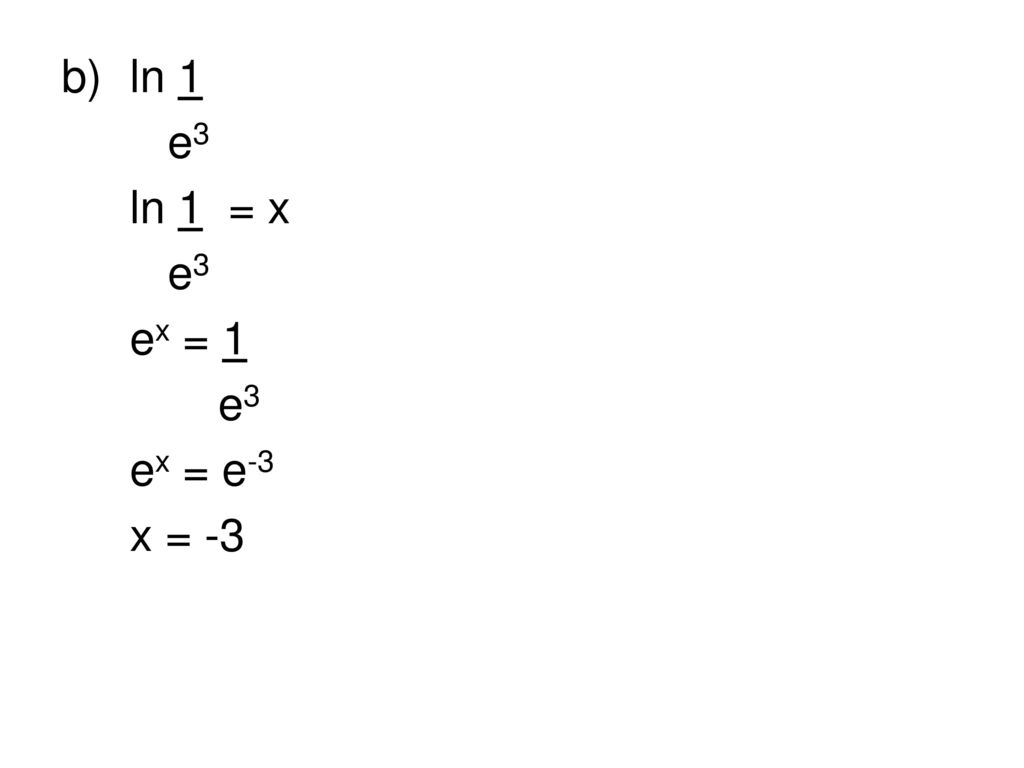 Например, ln(7,389. ) равен 2, потому что e 2 =7,389. . Натуральный логарифм самого числа e (ln(e)) равен 1, потому что e 1 = e, а натуральный логарифм 1 (ln(1)) равен 0, поскольку e 0 = 1.
Например, ln(7,389. ) равен 2, потому что e 2 =7,389. . Натуральный логарифм самого числа e (ln(e)) равен 1, потому что e 1 = e, а натуральный логарифм 1 (ln(1)) равен 0, поскольку e 0 = 1. е. как интеграл:
е. как интеграл: Вспомните: логарифм — это степень, в которую надо возвести основание, чтобы получить аргумент. Именно основание возводится в степень — на картинке оно выделено красным. Получается, что основание всегда находится внизу! Это замечательное правило я рассказываю своим ученикам на первом же занятии — и никакой путаницы не возникает.
Вспомните: логарифм — это степень, в которую надо возвести основание, чтобы получить аргумент. Именно основание возводится в степень — на картинке оно выделено красным. Получается, что основание всегда находится внизу! Это замечательное правило я рассказываю своим ученикам на первом же занятии — и никакой путаницы не возникает. Получается, что ОДЗ логарифма выглядит так: log a x = b ⇒ x > 0, a > 0, a ≠ 1.
Получается, что ОДЗ логарифма выглядит так: log a x = b ⇒ x > 0, a > 0, a ≠ 1.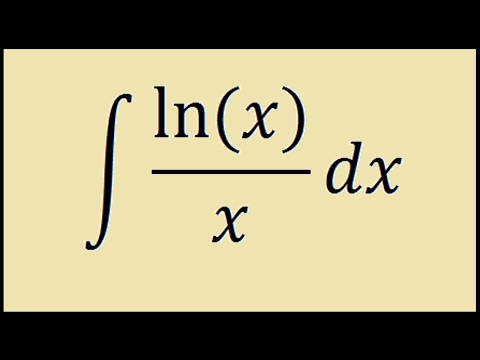
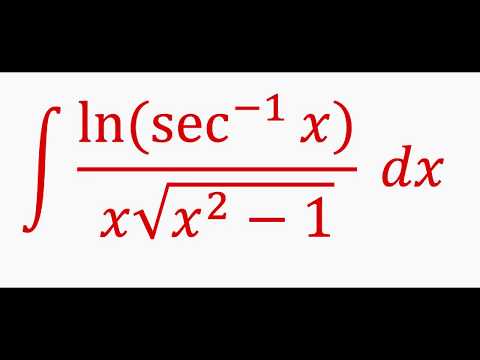

 Обозначение: ln x .
Обозначение: ln x . Например, нам нужно узнать, в какую степень нужно возвести число 2, чтобы получить 8. Если вспомнить степени двойки, то будет ясно, что 2³ = 8, а значит, ответ будет «в третью степень». Мы только что нашли логарифм числа 8 по основанию 2.
Например, нам нужно узнать, в какую степень нужно возвести число 2, чтобы получить 8. Если вспомнить степени двойки, то будет ясно, что 2³ = 8, а значит, ответ будет «в третью степень». Мы только что нашли логарифм числа 8 по основанию 2.
 Вот несколько примеров.
Вот несколько примеров.
 Например, ln(7,389. ) равен 2, потому что e 2 =7,389. . Натуральный логарифм самого числа e (ln(e)) равен 1, потому что e 1 = e, а натуральный логарифм 1 (ln(1)) равен 0, поскольку e 0 = 1.
Например, ln(7,389. ) равен 2, потому что e 2 =7,389. . Натуральный логарифм самого числа e (ln(e)) равен 1, потому что e 1 = e, а натуральный логарифм 1 (ln(1)) равен 0, поскольку e 0 = 1. е. как интеграл:
е. как интеграл: .
.
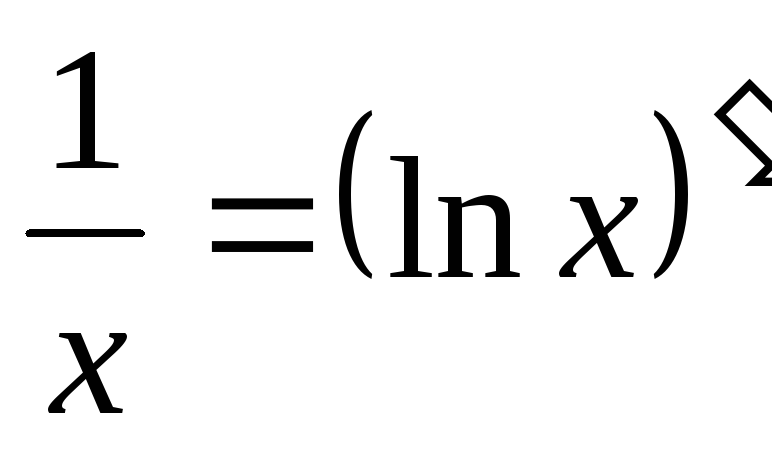
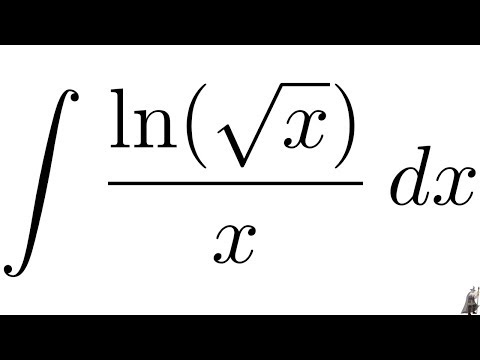 Так, логарифмы употребляются для расчета постоянной распада для известного периода полураспада, или для вычисления времени распада в решении проблем радиоактивности. Они выступают в главной роли во многих разделах математики и практических наук, к ним прибегают в сфере финансов для решения большого числа задач, в том числе и в расчете сложных процентов.
Так, логарифмы употребляются для расчета постоянной распада для известного периода полураспада, или для вычисления времени распада в решении проблем радиоактивности. Они выступают в главной роли во многих разделах математики и практических наук, к ним прибегают в сфере финансов для решения большого числа задач, в том числе и в расчете сложных процентов. Постепенным перемножением мы дойдем до ответа.
Постепенным перемножением мы дойдем до ответа. А мы все в глубине души народ ленивый, так что почему бы себе жизнь не упростить?
А мы все в глубине души народ ленивый, так что почему бы себе жизнь не упростить?



 Если основание логарифма лежит в диапазоне 0 < a < 1 (также как в показательных неравенствах), то после зачеркивания логарифмов знак меняется на противоположный:
Если основание логарифма лежит в диапазоне 0 < a < 1 (также как в показательных неравенствах), то после зачеркивания логарифмов знак меняется на противоположный: Пожалуйста, не используйте этот вопрос как возможность спорить о том, что более «естественно» $\log_e$ или $\log_{10}$. Для целей этого вопроса предположим, что вы находитесь в контексте, в котором нотация $\log$ зарезервирована для $\log_{10}$, а $\log_e$ обозначается как $\ln$. Вопрос не в том, хороша ли эта система обозначений, а в том, что как произносится .
Пожалуйста, не используйте этот вопрос как возможность спорить о том, что более «естественно» $\log_e$ или $\log_{10}$. Для целей этого вопроса предположим, что вы находитесь в контексте, в котором нотация $\log$ зарезервирована для $\log_{10}$, а $\log_e$ обозначается как $\ln$. Вопрос не в том, хороша ли эта система обозначений, а в том, что как произносится . Я произношу его исключительно как /lɑn/.
Я произношу его исключительно как /lɑn/.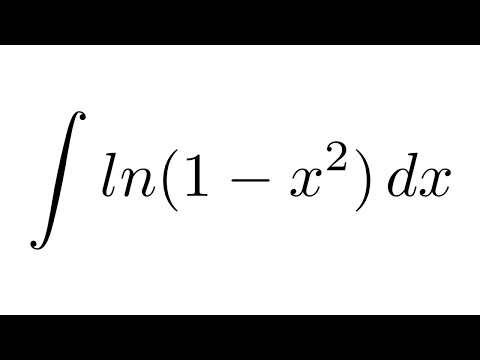
 д. Но только когда основание $e$, а не 6 или 10 или что-то в этом роде} \\
& \ фантом {\ текст {и т. д. }} \text{другое число, кроме $e$, является «константой», равной 1, т.е.} \\[10pt]
& \frac d {dx} \log_e x = \frac 1 x.
\end{выравнивание}
д. Но только когда основание $e$, а не 6 или 10 или что-то в этом роде} \\
& \ фантом {\ текст {и т. д. }} \text{другое число, кроме $e$, является «константой», равной 1, т.е.} \\[10pt]
& \frac d {dx} \log_e x = \frac 1 x.
\end{выравнивание}
 Никто не произносил это так, как мы, израильтяне, как «лан».
Никто не произносил это так, как мы, израильтяне, как «лан».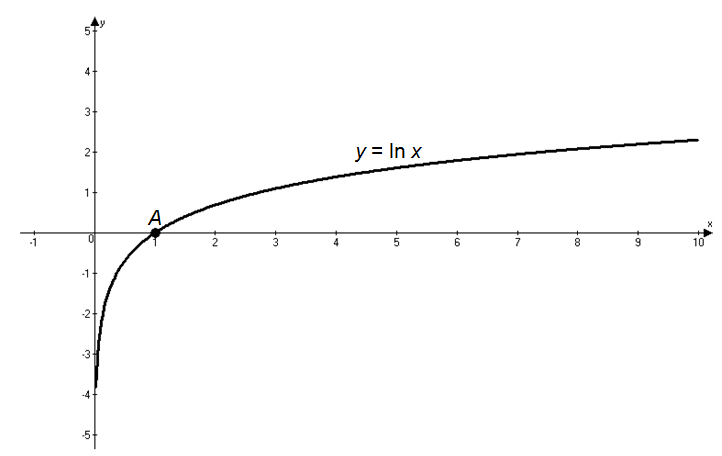 Затем, когда я сдавал AP Stats, моя учительница статистики была из Канады, и она сказала «лужайка бывшего». Я на самом деле приобрел эту привычку различать два:
Затем, когда я сдавал AP Stats, моя учительница статистики была из Канады, и она сказала «лужайка бывшего». Я на самом деле приобрел эту привычку различать два: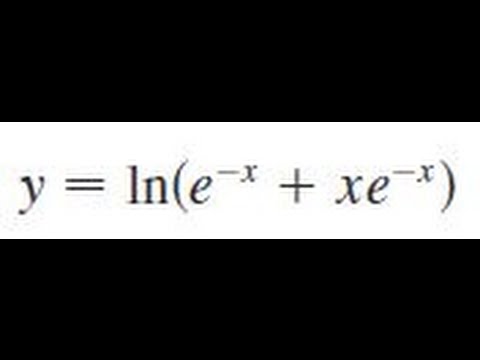 $\endgroup$
$\endgroup$ Я могу только вспомнить, что слышал, как это произносится как el en или log в Австралии, из этого поста на Reddit, где я вижу два ответа, говорящих о произношении этого слова lun, оба из которых являются британскими (один говорит, что слышал это произношение, делая его A-levels , другой прямо говорит об этом).
Я могу только вспомнить, что слышал, как это произносится как el en или log в Австралии, из этого поста на Reddit, где я вижу два ответа, говорящих о произношении этого слова lun, оба из которых являются британскими (один говорит, что слышал это произношение, делая его A-levels , другой прямо говорит об этом). В приложениях, где журнал, являющийся ln, действительно имеет значение, мы просто говорим «натуральный журнал». Я тоже слышал «l n» (el en), но это кажется менее распространенным. Я также слышал «лин», но это достаточно редкое слово, поэтому оно звучит странно, когда я его слышу.
В приложениях, где журнал, являющийся ln, действительно имеет значение, мы просто говорим «натуральный журнал». Я тоже слышал «l n» (el en), но это кажется менее распространенным. Я также слышал «лин», но это достаточно редкое слово, поэтому оно звучит странно, когда я его слышу.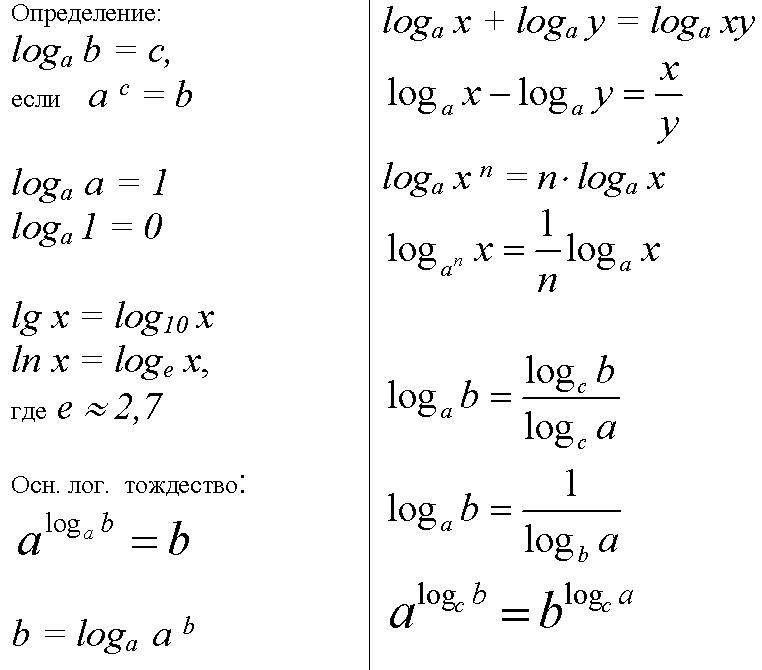
 е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана. Если вы думаете об этом, это будет иметь смысл. Мы возводим положительное число в степень, поэтому результат не может быть ничем иным, как другим положительным числом. Очень важно помнить, что мы не можем логарифмировать ноль или отрицательное число.
Если вы думаете об этом, это будет иметь смысл. Мы возводим положительное число в степень, поэтому результат не может быть ничем иным, как другим положительным числом. Очень важно помнить, что мы не можем логарифмировать ноль или отрицательное число.
 Изменение базы изменит ответ, поэтому нам всегда нужно отслеживать базу.
Изменение базы изменит ответ, поэтому нам всегда нужно отслеживать базу.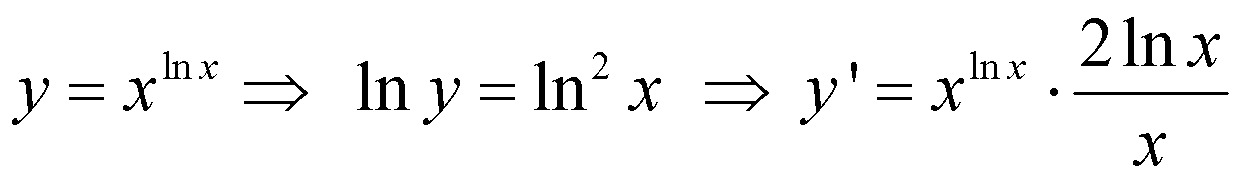 Точно так же натуральный логарифм — это просто логарифмическая база \(\bf{e}\) с другим обозначением, где \(\bf{e}\) — то же число, которое мы видели в предыдущем разделе и определяется как \({\bf{e}} = 2,718281828 \ldots\).
Точно так же натуральный логарифм — это просто логарифмическая база \(\bf{e}\) с другим обозначением, где \(\bf{e}\) — то же число, которое мы видели в предыдущем разделе и определяется как \({\bf{e}} = 2,718281828 \ldots\). 90} = 1\). Опять же, обратите внимание, что база, которую мы здесь используем, не изменит ответ.
90} = 1\). Опять же, обратите внимание, что база, которую мы здесь используем, не изменит ответ.
 Нам просто нужно быть осторожными с этими свойствами и использовать их правильно.
Нам просто нужно быть осторожными с этими свойствами и использовать их правильно. 5}} \вправо)\]
9{\ гидроразрыва {1} {2}}} \]
5}} \вправо)\]
9{\ гидроразрыва {1} {2}}} \] Кроме того, мы можем иметь дело с показателями степени только в том случае, если член в целом возводится в степень. Тот факт, что обе части этого термина возведены в квадрат, не имеет значения. Это должен быть весь член в квадрате, как в первом логарифме.
Кроме того, мы можем иметь дело с показателями степени только в том случае, если член в целом возводится в степень. Тот факт, что обе части этого термина возведены в квадрат, не имеет значения. Это должен быть весь член в квадрате, как в первом логарифме. 8}} \right)\]
98}}}} \справа)\]
8}} \right)\]
98}}}} \справа)\] Если бы 7 было 5, или 25, или 125, и т. д. . мы могли бы сделать это, но это не так. Поэтому приходится использовать формулу замены основания.
Если бы 7 было 5, или 25, или 125, и т. д. . мы могли бы сделать это, но это не так. Поэтому приходится использовать формулу замены основания.
 И. Моро, М.А. Бантова
И. Моро, М.А. Бантова А. Плешаков
А. Плешаков

 п.;
п.; Также зайти на сервис будет полезно обучающемуся среднего звена, чтобы повторить пройденное или заглянуть немного вперед, и, конечно, сборник будет необходим старшекласснику, которому нужно готовиться к ОГЭ или ЕГЭ.
Также зайти на сервис будет полезно обучающемуся среднего звена, чтобы повторить пройденное или заглянуть немного вперед, и, конечно, сборник будет необходим старшекласснику, которому нужно готовиться к ОГЭ или ЕГЭ. Из-за этого всегда нужно быть внимательным на уроке и не пропускать важных занятий. Заданные на дом уроки следует выполнять тщательно и регулярно, в соответствии с пожеланиями школьного преподавателя.
Из-за этого всегда нужно быть внимательным на уроке и не пропускать важных занятий. Заданные на дом уроки следует выполнять тщательно и регулярно, в соответствии с пожеланиями школьного преподавателя.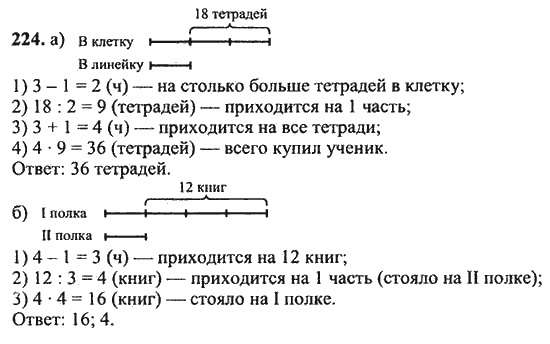
 Координатная прямая.
Координатная прямая.

 Решебник устранит все возникающие трудности и поможет разобраться с решением любой задачи учебника, а также послужит отличным средством для самопроверки.
Решебник устранит все возникающие трудности и поможет разобраться с решением любой задачи учебника, а также послужит отличным средством для самопроверки.
 И. В нём представлены задания по темам и разделам для четырех уровней сложности. Наибольшие трудности, равно как и максимальный интерес у шестиклассников вызывают такие тематики:
И. В нём представлены задания по темам и разделам для четырех уровней сложности. Наибольшие трудности, равно как и максимальный интерес у шестиклассников вызывают такие тематики: 
 И., Мордковича А.Г. окажет шестикласснику большую пользу и позволит улучшить успеваемость без ущерба для отдыха и нервной системы. Использовать книгу можно как дома, так и в школе, а все потому, что она находится в открытом доступе, найти ее можно путем пары переходов по интернет страницам.
И., Мордковича А.Г. окажет шестикласснику большую пользу и позволит улучшить успеваемость без ущерба для отдыха и нервной системы. Использовать книгу можно как дома, так и в школе, а все потому, что она находится в открытом доступе, найти ее можно путем пары переходов по интернет страницам.
 Подробно представлены различия между положительными и отрицательными числами, а также правила математических операций с ними.
Подробно представлены различия между положительными и отрицательными числами, а также правила математических операций с ними. Соответствующие руководства также довольно легко получить в публичных библиотеках. Многие преподаватели формируют на их основе собственные рабочие программы по предмету.
Соответствующие руководства также довольно легко получить в публичных библиотеках. Многие преподаватели формируют на их основе собственные рабочие программы по предмету. Интенсивная работа поможет повысить успеваемость, легко решить контрольно-проверочные работы, зачеты.
Интенсивная работа поможет повысить успеваемость, легко решить контрольно-проверочные работы, зачеты. Пособие с готовыми решениями соответствует требованиям ФГОС.
Пособие с готовыми решениями соответствует требованиям ФГОС. Я. (2018) можно скачать.
Я. (2018) можно скачать. В ГДЗ-онлайн есть как раз такая книжка-решение по математике для Виленкина 6-го класса. С ним шестиклассник действительно разберется в дисциплине и повысит успеваемость.
В ГДЗ-онлайн есть как раз такая книжка-решение по математике для Виленкина 6-го класса. С ним шестиклассник действительно разберется в дисциплине и повысит успеваемость. Я., который представлен на нашем сайте в онлайн-доступе. Каковы его преимущества?
Я., который представлен на нашем сайте в онлайн-доступе. Каковы его преимущества?
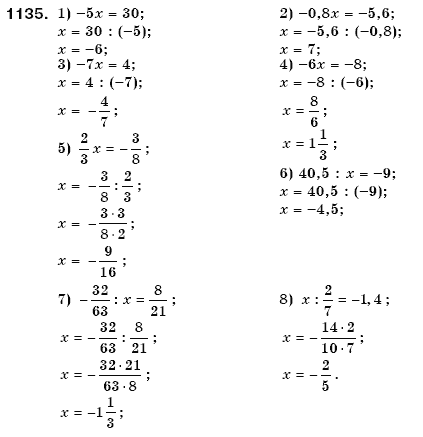 В., Шарыгина И.Ф., Суворова С.Б. и др., которая была опубликована в 2017 году. Сейчас она используется в качестве основного учебного пособия во многих общеобразовательных школах России.
В., Шарыгина И.Ф., Суворова С.Б. и др., которая была опубликована в 2017 году. Сейчас она используется в качестве основного учебного пособия во многих общеобразовательных школах России.

 В связи с этим программа становится достаточно сложной. У некоторых ребят могут возникнуть трудности с решением уравнений, так как они уже не такие простые, как раньше. Поэтому крайне важно убедиться, что ребенок полностью усвоил изучаемую тему. Ведь упустив момент, он может просто не понять алгоритм решения и это приведет к постепенному отставанию от одноклассников. Происходит своего рода цепная реакция, когда непонимание одного приводит к непониманию всего остального. Избежать потери успеваемости поможет решение учебника «Математика 6 класс» Дорофеева, которая окажет качественную поддержку при проверке д/з.
В связи с этим программа становится достаточно сложной. У некоторых ребят могут возникнуть трудности с решением уравнений, так как они уже не такие простые, как раньше. Поэтому крайне важно убедиться, что ребенок полностью усвоил изучаемую тему. Ведь упустив момент, он может просто не понять алгоритм решения и это приведет к постепенному отставанию от одноклассников. Происходит своего рода цепная реакция, когда непонимание одного приводит к непониманию всего остального. Избежать потери успеваемости поможет решение учебника «Математика 6 класс» Дорофеева, которая окажет качественную поддержку при проверке д/з.

 Определение диаметра и площади простейших контурных фигур.
Определение диаметра и площади простейших контурных фигур. Вот почему крайне важно не допускать пробелов в образовании школьников. Этот факт доказывает, насколько значимо использование онлайн-решателя по математике для 5 класса Дорофеева.
Вот почему крайне важно не допускать пробелов в образовании школьников. Этот факт доказывает, насколько значимо использование онлайн-решателя по математике для 5 класса Дорофеева.
 Он учит школьников не только правильно применять арифметические формулы на практике, но и пользоваться практическими пособиями.
Он учит школьников не только правильно применять арифметические формулы на практике, но и пользоваться практическими пособиями. Однако такое знание — не зло, а просто средство, которое можно использовать во благо.
Однако такое знание — не зло, а просто средство, которое можно использовать во благо.
 И можно скачать.
И можно скачать. И только родители могут решить, чем пользоваться при выполнении домашнего задания в их ситуации. Онлайн решение по математике за 3 класс (авторы М.И. Моро, М.А.Бантова и Г.В.Бельтюкова) : — не шпаргалка и не возможность списывания при составлении «домашнего задания». Сегодня даже младшие школьники сверяются с ними в процессе самостоятельной работы. Такая книга поможет:
И только родители могут решить, чем пользоваться при выполнении домашнего задания в их ситуации. Онлайн решение по математике за 3 класс (авторы М.И. Моро, М.А.Бантова и Г.В.Бельтюкова) : — не шпаргалка и не возможность списывания при составлении «домашнего задания». Сегодня даже младшие школьники сверяются с ними в процессе самостоятельной работы. Такая книга поможет: Книга поможет вам быстро подготовить информацию к уроку и станет надежным источником нового для детей. Воспользоваться изданием онлайн можно на нашем сайте – нужно только знать номер нужного упражнения.
Книга поможет вам быстро подготовить информацию к уроку и станет надежным источником нового для детей. Воспользоваться изданием онлайн можно на нашем сайте – нужно только знать номер нужного упражнения. Школьники с разными способностями к точным наукам требуют особого подхода и разного уровня педагогического внимания.
Школьники с разными способностями к точным наукам требуют особого подхода и разного уровня педагогического внимания.
 Две матрицы могут быть перемножены только тогда, когда количество столбцов первой матрицы соответствует количеству рядов второй. Например, вы можете умножить матрицу A размера m, n на матрицу B размера n, p. В результате вы получите матрицу C размера m, p. Формула умножения выглядит вот так:
Две матрицы могут быть перемножены только тогда, когда количество столбцов первой матрицы соответствует количеству рядов второй. Например, вы можете умножить матрицу A размера m, n на матрицу B размера n, p. В результате вы получите матрицу C размера m, p. Формула умножения выглядит вот так: Тензоры получили известность благодаря фреймворку для машинного обучения TensorFlow.
Тензоры получили известность благодаря фреймворку для машинного обучения TensorFlow. Если умножить её на вектор, значения вектора не меняются. Элементы главной диагонали единичной матрицы имеют значение 1, а все остальные равны 0:
Если умножить её на вектор, значения вектора не меняются. Элементы главной диагонали единичной матрицы имеют значение 1, а все остальные равны 0: Но, увы, это работает только с квадратными матрицами.
Но, увы, это работает только с квадратными матрицами. Набор векторов будет линейно зависим, если хотя бы один вектор может быть представлен как комбинация других векторов из набора. Иначе набор будет линейно независим. Обычно векторы x и y будут линейно независимы, только если значения для скаляров a и b, удовлетворяющих ax + by = 0, будут равны a = b = 0.
Набор векторов будет линейно зависим, если хотя бы один вектор может быть представлен как комбинация других векторов из набора. Иначе набор будет линейно независим. Обычно векторы x и y будут линейно независимы, только если значения для скаляров a и b, удовлетворяющих ax + by = 0, будут равны a = b = 0.
 Считается, что система обладает единственным решением. Например, задана система линейных уравнений:
Считается, что система обладает единственным решением. Например, задана система линейных уравнений: Для получения быстрого ответа в представленные поля подставляют переменные числа и их количество. Дополнительно может потребоваться указание вычислительного метода разложения по строке или столбу. Другой вариант заключается в приведении к треугольному виду.
Для получения быстрого ответа в представленные поля подставляют переменные числа и их количество. Дополнительно может потребоваться указание вычислительного метода разложения по строке или столбу. Другой вариант заключается в приведении к треугольному виду. Л. Японцы в реальном и виртуальном мирах: Очерки современной японской массовой культуры. — М.: Восточная литература РАН, 2012. — С. 107. — 357 с. — ISBN 978-5-02-036522-3.
Л. Японцы в реальном и виртуальном мирах: Очерки современной японской массовой культуры. — М.: Восточная литература РАН, 2012. — С. 107. — 357 с. — ISBN 978-5-02-036522-3. Валы, линии и крепости
Валы, линии и крепости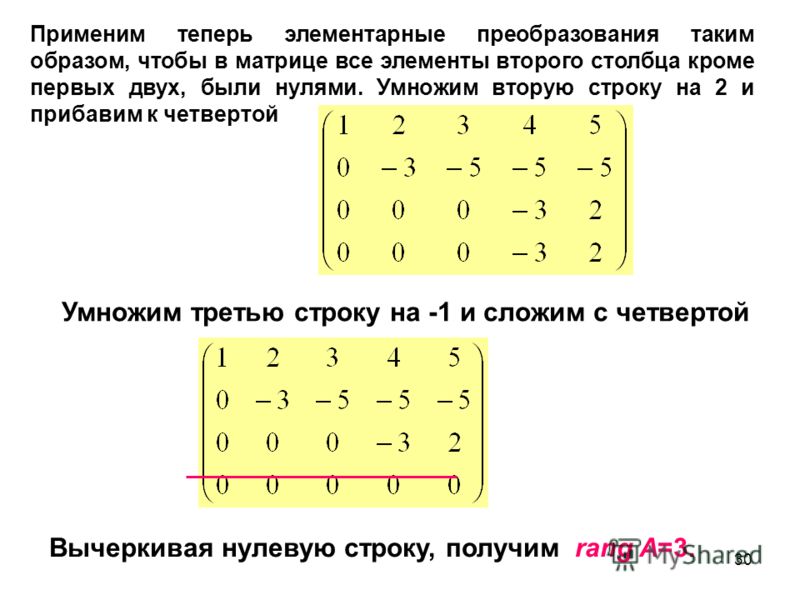 Зачем понадобился?
Зачем понадобился?
 Это образ типичного борца с системой, подпольщика-одиночки, которому не хватает своей «партизанской ячейки». И вскоре она находится – в образе группы Морфеуса, бунтаря, который привык держать в руках оружие потяжелее компьютерной мышки.
Это образ типичного борца с системой, подпольщика-одиночки, которому не хватает своей «партизанской ячейки». И вскоре она находится – в образе группы Морфеуса, бунтаря, который привык держать в руках оружие потяжелее компьютерной мышки. {2}
{2} При помощи данной теоремы можно решать матрицы не только третьего порядка, но и более высших порядков.
При помощи данной теоремы можно решать матрицы не только третьего порядка, но и более высших порядков. Давайте по теореме Лапласа разберём несколько примеров:
Давайте по теореме Лапласа разберём несколько примеров: Part I). Автор сценария и режиссёр: Махиро Маэда
Part I). Автор сценария и режиссёр: Махиро Маэда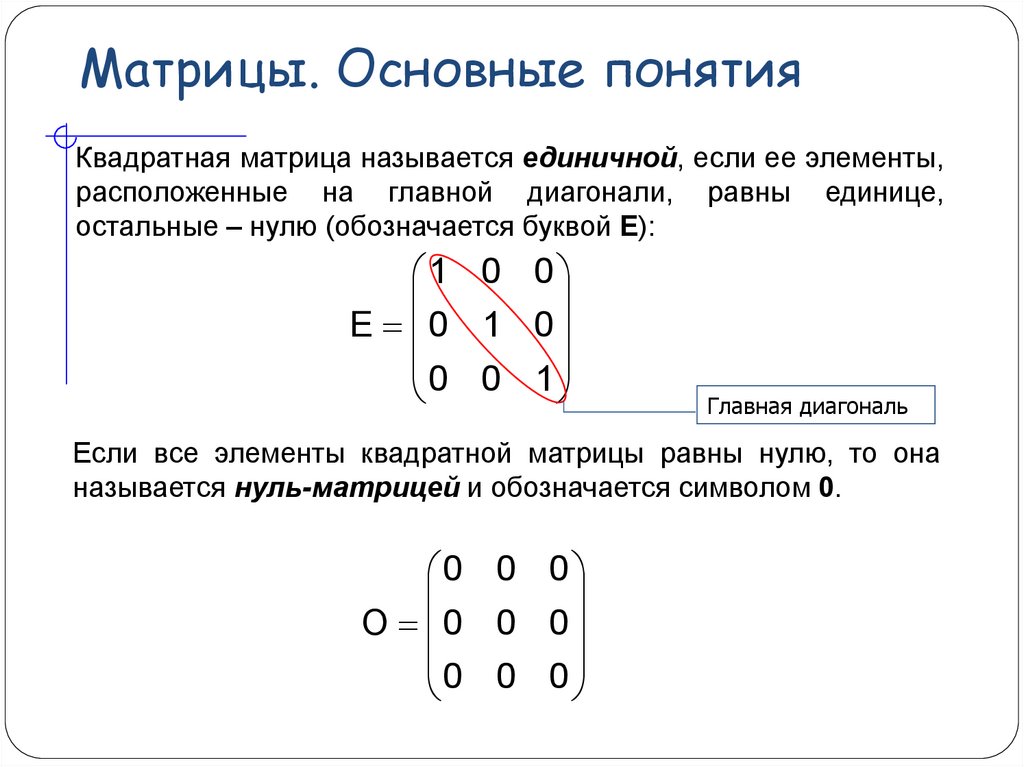
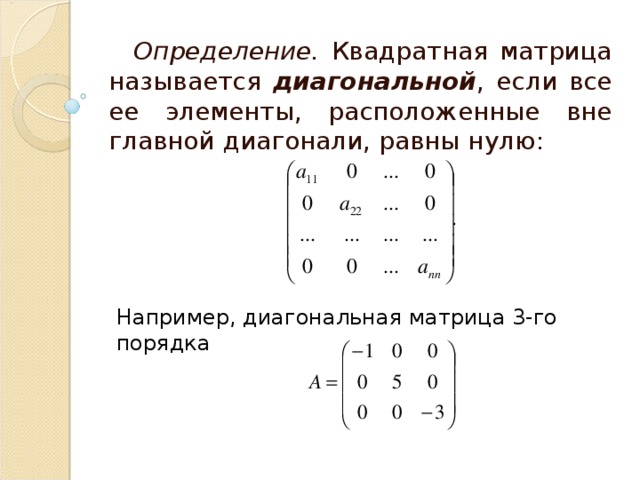
 е. ведущими являются диагональные элементы. В общем виде трапециевидную матрицу можно записать так:
е. ведущими являются диагональные элементы. В общем виде трапециевидную матрицу можно записать так: Например, $\left( \begin{array} {cccc} 3 & 0 & 0 & 0 \\ -5 & 1 & 0 & 0 \\ 8 & 2 & 1 & 0 \\ 5 & 4 & 0 & 6 \end{array} \right)$ – нижняя треугольная матрица. Заметьте, что в определении нижней треугольной матрицы ничего не сказано про значения элементов, расположенных под или на главной диагонали
Например, $\left( \begin{array} {cccc} 3 & 0 & 0 & 0 \\ -5 & 1 & 0 & 0 \\ 8 & 2 & 1 & 0 \\ 5 & 4 & 0 & 6 \end{array} \right)$ – нижняя треугольная матрица. Заметьте, что в определении нижней треугольной матрицы ничего не сказано про значения элементов, расположенных под или на главной диагонали

 ) в Центральной Индии. Это первый из «дьявольских квадратов». Также он называется пандиагональным.
) в Центральной Индии. Это первый из «дьявольских квадратов». Также он называется пандиагональным.
 Нео и Тринити должны сыграть роль своего рода моста, соединяющего все части франшизы.
Нео и Тринити должны сыграть роль своего рода моста, соединяющего все части франшизы.
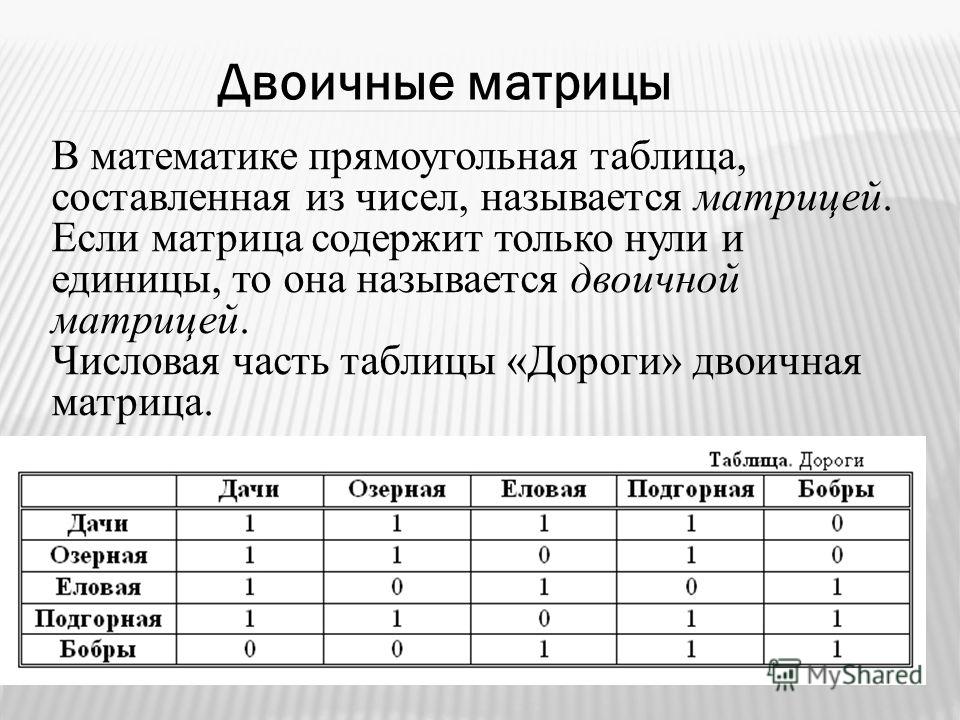 Машины питаются этой энергией, они существуют за счет неё. А «нормальная» жизнь, которую Томас созерцал каждый день, – всего лишь иллюзия, часть программы.
Машины питаются этой энергией, они существуют за счет неё. А «нормальная» жизнь, которую Томас созерцал каждый день, – всего лишь иллюзия, часть программы. Нео узнаёт, что он «избранный», и именно ему предстоит разрушить Матрицу, чтобы освободить людей от власти Машин.
Нео узнаёт, что он «избранный», и именно ему предстоит разрушить Матрицу, чтобы освободить людей от власти Машин. Нео решает отправиться в сердце города Машин, чтобы не допустить падения Зиона и выполнить предначертанное ему. Теперь уже не Матрица контролирует Смита, а Смит контролирует Матрицу, он вышел из-под контроля Машин. Если Нео сможет противостоять Смиту, то у людей и у Зиона появится шанс уцелеть, если же Нео не справится — всё будет кончено.
Нео решает отправиться в сердце города Машин, чтобы не допустить падения Зиона и выполнить предначертанное ему. Теперь уже не Матрица контролирует Смита, а Смит контролирует Матрицу, он вышел из-под контроля Машин. Если Нео сможет противостоять Смиту, то у людей и у Зиона появится шанс уцелеть, если же Нео не справится — всё будет кончено. также: Агенты
также: Агенты Киану Ривз отказался от причитающейся ему доли от продажи билетов, равной примерно 40 млн, после того как продюсеры засомневались, что картина окупит затраты на спецэффекты.
Киану Ривз отказался от причитающейся ему доли от продажи билетов, равной примерно 40 млн, после того как продюсеры засомневались, что картина окупит затраты на спецэффекты. Детерминант самой простой матрицы определяется с помощью вычитания перемноженных элементов из побочной диагонали и главной.
Детерминант самой простой матрицы определяется с помощью вычитания перемноженных элементов из побочной диагонали и главной. Наглядный пример:
Наглядный пример: Валы, линии и крепости
Валы, линии и крепости В этих сложных взаимоотношениях также прослеживается чёткий социальный и психологический смысл: любая система порождает антагонистов и внешних, и внутренних. На счастье Главного Компьютера, Нео и Смит не договорились друг с другом; Нео понял, что победа Смита приведёт ещё к худшим последствиям: тот действительно уничтожит Матрицу, но и человеческий род погубит тоже.
В этих сложных взаимоотношениях также прослеживается чёткий социальный и психологический смысл: любая система порождает антагонистов и внешних, и внутренних. На счастье Главного Компьютера, Нео и Смит не договорились друг с другом; Нео понял, что победа Смита приведёт ещё к худшим последствиям: тот действительно уничтожит Матрицу, но и человеческий род погубит тоже.



 В нашей статье речь пойдет не о знаменитом одноименном фильме, а о математической единице. Сегодня мы расскажем: что это такое и с чем это «есть», как применять на практике.
В нашей статье речь пойдет не о знаменитом одноименном фильме, а о математической единице. Сегодня мы расскажем: что это такое и с чем это «есть», как применять на практике. Например, элемент, находящийся в первой строке и первом столбце обозначают а11, а элемент в первой строке и втором столбце – а12.
Например, элемент, находящийся в первой строке и первом столбце обозначают а11, а элемент в первой строке и втором столбце – а12. Важно отметить, что количество слагаемых (суммируемых или вычитаемых матриц) может быть неограниченно.
Важно отметить, что количество слагаемых (суммируемых или вычитаемых матриц) может быть неограниченно. Данный критерий действителен только в отношении квадратных матриц (когда число строк равно числу столбцов).
Данный критерий действителен только в отношении квадратных матриц (когда число строк равно числу столбцов). В математическом направлении они позволяют просто и быстро решить систему уравнений.
В математическом направлении они позволяют просто и быстро решить систему уравнений. Прямоугольники имеют размеры, которые описываются количеством строк элементов и столбцов элементов, которые они содержат. Матрица «3 на 6» имеет три строки и шесть столбцов; матрица «I на j» имеет I строк и j столбцов. Матрица, имеющая только одну строку, называется «вектор-строка». Матрица, имеющая только один столбец, называется «вектор-столбец».0032
Прямоугольники имеют размеры, которые описываются количеством строк элементов и столбцов элементов, которые они содержат. Матрица «3 на 6» имеет три строки и шесть столбцов; матрица «I на j» имеет I строк и j столбцов. Матрица, имеющая только одну строку, называется «вектор-строка». Матрица, имеющая только один столбец, называется «вектор-столбец».0032 Элемент 1,1 — это запись в первой строке и первом столбце; элемент 13,2 находится в 13-й строке и является вторым элементом этой строки. Адреса ячеек были введены как матричные элементы в двух приведенных выше примерах.
Элемент 1,1 — это запись в первой строке и первом столбце; элемент 13,2 находится в 13-й строке и является вторым элементом этой строки. Адреса ячеек были введены как матричные элементы в двух приведенных выше примерах.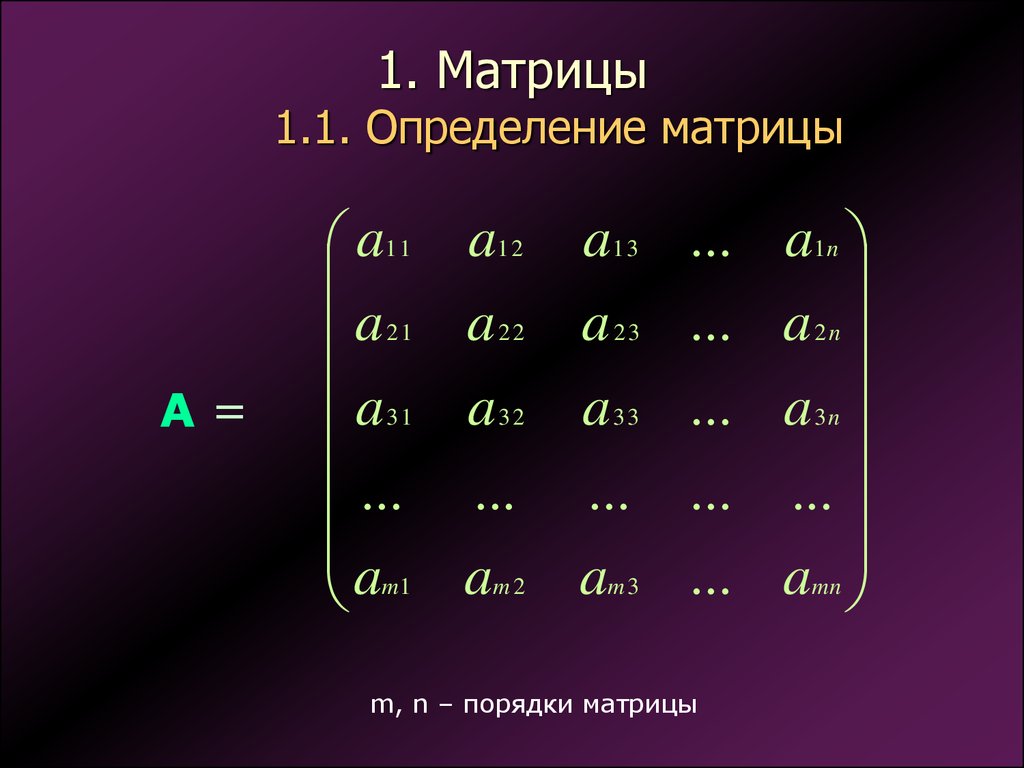 То есть они содержат одинаковое количество строк и столбцов. Но также используются «прямоугольные» матрицы, а также векторы-строки и столбцы. Ко всем этим вариациям применяются одни и те же соглашения.
То есть они содержат одинаковое количество строк и столбцов. Но также используются «прямоугольные» матрицы, а также векторы-строки и столбцы. Ко всем этим вариациям применяются одни и те же соглашения.

 Запись матрицы A , которая находится в строке с номером i и столбце с номером j , называется записью i,j матрицы A . Это пишется как A [ i,j ] или a i,j .
Запись матрицы A , которая находится в строке с номером i и столбце с номером j , называется записью i,j матрицы A . Это пишется как A [ i,j ] или a i,j .


 Кроме того, если матрица M имеет столбец v , который является суммой двух матриц столбцов и , тогда определитель M является суммой определителей M с вместо v и M с вместо против . Эти два условия называются полилинейностью .
Кроме того, если матрица M имеет столбец v , который является суммой двух матриц столбцов и , тогда определитель M является суммой определителей M с вместо v и M с вместо против . Эти два условия называются полилинейностью . Если вы заинтересованы в глубоком погружении в линейную алгебру, вот несколько замечательных ресурсов:
Если вы заинтересованы в глубоком погружении в линейную алгебру, вот несколько замечательных ресурсов:
 Если некоторые записи содержат информацию об апельсинах, а другие о никотине, ваша матрица будет бесполезна.
Если некоторые записи содержат информацию об апельсинах, а другие о никотине, ваша матрица будет бесполезна.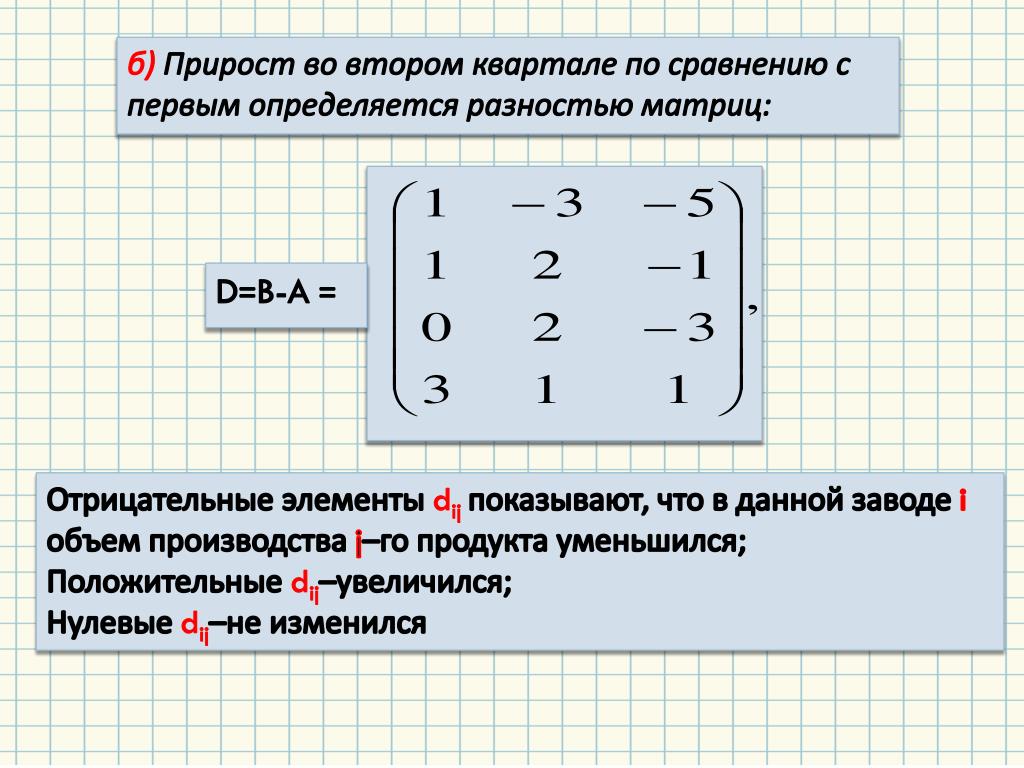 В этом случае мы бы сказали, что матрица имеет размеры (m, n).
В этом случае мы бы сказали, что матрица имеет размеры (m, n).  Здесь нам нужно помнить, что значение математической операции зависит от ее контекста .
Здесь нам нужно помнить, что значение математической операции зависит от ее контекста . е. обе матрицы имеют размерность (m,n)
е. обе матрицы имеют размерность (m,n)  Матрицы можно рассматривать как словари, которые позволяют переводить язык на другой. В нашем примере это означает, что мы переводим неизвестные переменные, чтобы получить правую часть уравнения. Столбцы матрицы представляют язык для перевода, а строки представляют язык, на который необходимо перевести.
Матрицы можно рассматривать как словари, которые позволяют переводить язык на другой. В нашем примере это означает, что мы переводим неизвестные переменные, чтобы получить правую часть уравнения. Столбцы матрицы представляют язык для перевода, а строки представляют язык, на который необходимо перевести. 
 Затем вы повторяете это для каждой строки в левой матрице:
Затем вы повторяете это для каждой строки в левой матрице:

 Из
Из
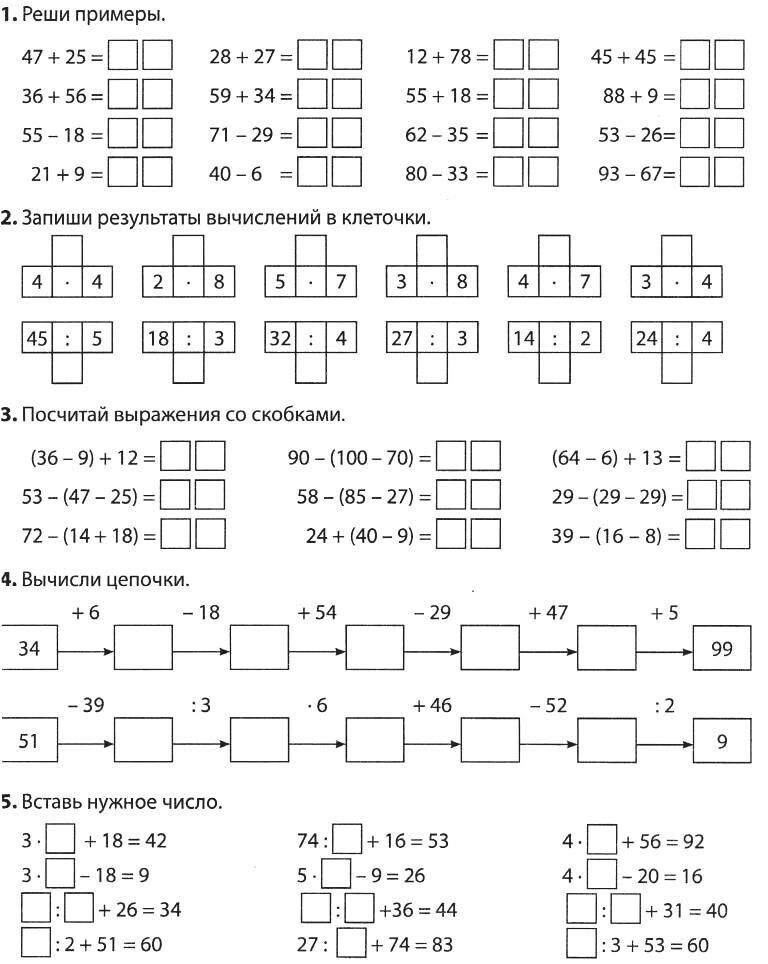

 )
) Например, длина реки Баргузин – 480000 м, реки Селенга – 1024000 м, реки Тыя – 120000 м. Найдите общую длину этих рек? Длину рек выразите в метрах?
Например, длина реки Баргузин – 480000 м, реки Селенга – 1024000 м, реки Тыя – 120000 м. Найдите общую длину этих рек? Длину рек выразите в метрах?
 16. Разноуровневое:
16. Разноуровневое:
 В магазин забрали со склада 30 ящиков. Сколько осталось на складе ящиков с яблоками?
В магазин забрали со склада 30 ящиков. Сколько осталось на складе ящиков с яблоками?


 (Определение знания и незнания на данном этапе)
(Определение знания и незнания на данном этапе)



 Это не исчерпывающий список стратегий, но эта поддержка поможет вам сделать обучение математике более доступным для учащихся. Педагоги должны адаптировать стратегии к потребностям ваших учеников и убедиться, что вы создаете возможности для всех учеников, чтобы они могли взаимодействовать с строгим содержанием.
Это не исчерпывающий список стратегий, но эта поддержка поможет вам сделать обучение математике более доступным для учащихся. Педагоги должны адаптировать стратегии к потребностям ваших учеников и убедиться, что вы создаете возможности для всех учеников, чтобы они могли взаимодействовать с строгим содержанием. 4
%
3503 0 объект
>
эндобдж
xref
3503 72
0000000016 00000 н.
0000006112 00000 п.
0000006307 00000 н.
0000006440 00000 н.
0000007172 00000 н.
0000007210 00000 н.
0000007466 00000 н.
0000008142 00000 п.
0000008280 00000 н.
0000008943 00000 н.
0000009020 00000 н.
0000009090 00000 н.
0000009519 00000 п.
0000010324 00000 п.
0000011851 00000 п.
0000013031 00000 н.
0000014604 00000 п.
0000016145 00000 п.
0000016539 00000 п.
0000016595 00000 п.
0000016931 00000 п.
0000017952 00000 п.
0000019073 00000 п.
0000019600 00000 п.
0000019708 00000 п.
0000019935 00000 п.
0000020514 00000 п.
0000023025 00000 п.
0000034824 00000 п.
0000038876 00000 п.
0000187589 00000 н.
0000353820 00000 н.
0000354040 00000 н.
0000354131 00000 п.
0000354230 00000 н.
0000354330 00000 н.
0000354397 00000 н.
0000354492 00000 н.
0000354515 00000 н.
0000354620 00000 н.
0000354649 00000 н.
0000354736 00000 н.
0000354779 00000 н.
0000354814 00000 н.
0000354844 00000 н.
0000354869 00000 н. Ӯ | > 6 / EW u1HkT $ YӞ 䯬 @ {$ Gϒ | HC {ӪGL5 \:% JKD +% u {) 0rw1 {$ Wϩin / ɾ 䞨 U.
4
%
3503 0 объект
>
эндобдж
xref
3503 72
0000000016 00000 н.
0000006112 00000 п.
0000006307 00000 н.
0000006440 00000 н.
0000007172 00000 н.
0000007210 00000 н.
0000007466 00000 н.
0000008142 00000 п.
0000008280 00000 н.
0000008943 00000 н.
0000009020 00000 н.
0000009090 00000 н.
0000009519 00000 п.
0000010324 00000 п.
0000011851 00000 п.
0000013031 00000 н.
0000014604 00000 п.
0000016145 00000 п.
0000016539 00000 п.
0000016595 00000 п.
0000016931 00000 п.
0000017952 00000 п.
0000019073 00000 п.
0000019600 00000 п.
0000019708 00000 п.
0000019935 00000 п.
0000020514 00000 п.
0000023025 00000 п.
0000034824 00000 п.
0000038876 00000 п.
0000187589 00000 н.
0000353820 00000 н.
0000354040 00000 н.
0000354131 00000 п.
0000354230 00000 н.
0000354330 00000 н.
0000354397 00000 н.
0000354492 00000 н.
0000354515 00000 н.
0000354620 00000 н.
0000354649 00000 н.
0000354736 00000 н.
0000354779 00000 н.
0000354814 00000 н.
0000354844 00000 н.
0000354869 00000 н. Ӯ | > 6 / EW u1HkT $ YӞ 䯬 @ {$ Gϒ | HC {ӪGL5 \:% JKD +% u {) 0rw1 {$ Wϩin / ɾ 䞨 U. b (o` ݮ AsnN + 3jdmJ ejL ׀ afD ը nıt; Y
b (o` ݮ AsnN + 3jdmJ ejL ׀ afD ը nıt; Y Они также решают многоступенчатые задачи со словами, включая сложение и вычитание, используя округление для оценки обоснованности своих ответов.
Они также решают многоступенчатые задачи со словами, включая сложение и вычитание, используя округление для оценки обоснованности своих ответов. Учащиеся измеряют углы и находят неизвестные меры углов, а затем используют это более глубокое понимание для классификации форм и изучения симметрии отражения.
Учащиеся измеряют углы и находят неизвестные меры углов, а затем используют это более глубокое понимание для классификации форм и изучения симметрии отражения.
 Вы можете делать ксерокопии, распечатывать и распространять их сколько угодно раз. Вы можете скачать их на свой мобильный телефон, iPad, ПК или флешку. Вы можете записать их на компакт-диск, отправить по электронной почте или загрузить на свой веб-сайт. Единственным ограничением является то, что вы не можете адаптировать или изменять эти версии учебников, их содержание или обложки, поскольку они содержат соответствующие бренды Siyavula, спонсорские логотипы и одобрены Департаментом базового образования. Для получения дополнительной информации посетите Creative Commons Attribution-NoDerivs 3.0 Непортированный.
Вы можете делать ксерокопии, распечатывать и распространять их сколько угодно раз. Вы можете скачать их на свой мобильный телефон, iPad, ПК или флешку. Вы можете записать их на компакт-диск, отправить по электронной почте или загрузить на свой веб-сайт. Единственным ограничением является то, что вы не можете адаптировать или изменять эти версии учебников, их содержание или обложки, поскольку они содержат соответствующие бренды Siyavula, спонсорские логотипы и одобрены Департаментом базового образования. Для получения дополнительной информации посетите Creative Commons Attribution-NoDerivs 3.0 Непортированный. Для получения дополнительной информации посетите Creative Commons Attribution 3.0 Unported.
Для получения дополнительной информации посетите Creative Commons Attribution 3.0 Unported.
 На сегодняшнем уроке они учатся находить недостающее число в задаче сложения или вычитания с помощью обратной операции. Это согласуется с 4.NBT.4, потому что учащиеся складывают и вычитают многозначные целые числа, используя стандартный алгоритм.
На сегодняшнем уроке они учатся находить недостающее число в задаче сложения или вычитания с помощью обратной операции. Это согласуется с 4.NBT.4, потому что учащиеся складывают и вычитают многозначные целые числа, используя стандартный алгоритм. Если верхнее число меньше нижнего числа, нам нужно убрать 1 с места слева и добавить его к месту справа.Например, 17-8. 7 меньше, чем 8, поэтому мы убираем единицу из разряда десятков (которая становится нулем), затем добавляем эту единицу к разряду единиц. Теперь у нас есть 17.
Если верхнее число меньше нижнего числа, нам нужно убрать 1 с места слева и добавить его к месту справа.Например, 17-8. 7 меньше, чем 8, поэтому мы убираем единицу из разряда десятков (которая становится нулем), затем добавляем эту единицу к разряду единиц. Теперь у нас есть 17. Когда вы прибавляете к двум суммам, вы считаете их вместе как одну большую сумму. В реальной жизни сложение происходит постоянно.
Когда вы прибавляете к двум суммам, вы считаете их вместе как одну большую сумму. В реальной жизни сложение происходит постоянно.
 Выражения полезны, поскольку они помогают отслеживать добавляемые вами суммы.
Выражения полезны, поскольку они помогают отслеживать добавляемые вами суммы. Когда вы только начинаете, вам может быть проще использовать , считая , для решения проблем.
Когда вы только начинаете, вам может быть проще использовать , считая , для решения проблем.
 Уберите пальцы, потому что это первая математическая операция, требующая запоминания фактов. Вы найдете рабочие листы умножения для восьми простых правил папы для освоения таблицы умножения, умножения RocketMath, многозначного умножения, квадратов и других тем рабочего листа умножения. Все эти рабочие листы по умножению содержат ключи для ответов, их можно мгновенно распечатать и использовать в классе или дома.
Уберите пальцы, потому что это первая математическая операция, требующая запоминания фактов. Вы найдете рабочие листы умножения для восьми простых правил папы для освоения таблицы умножения, умножения RocketMath, многозначного умножения, квадратов и других тем рабочего листа умножения. Все эти рабочие листы по умножению содержат ключи для ответов, их можно мгновенно распечатать и использовать в классе или дома. Существуют различные варианты каждой таблицы умножения с фактами от 1 до 9.(продукты 1-81), 1-10 (продукты 1-100), 1-12 (продукты 1-144) и 1-15 (продукты 1-255). Каждая из этих диаграмм умножения представляет собой SVG с высоким разрешением, поэтому факты умножения печатаются красиво!
Существуют различные варианты каждой таблицы умножения с фактами от 1 до 9.(продукты 1-81), 1-10 (продукты 1-100), 1-12 (продукты 1-144) и 1-15 (продукты 1-255). Каждая из этих диаграмм умножения представляет собой SVG с высоким разрешением, поэтому факты умножения печатаются красиво! Научите своих детей сложению и вычитанию одновременно и укрепите отношения в семье фактов! На каждом уровне вводятся два семейства фактов, которые позволяют прогрессивно практиковаться, или просто используйте рабочие листы в конце для всестороннего обзора семейства фактов.
Научите своих детей сложению и вычитанию одновременно и укрепите отношения в семье фактов! На каждом уровне вводятся два семейства фактов, которые позволяют прогрессивно практиковаться, или просто используйте рабочие листы в конце для всестороннего обзора семейства фактов. Рабочие листы с различными дробями в этом разделе посвящены сокращению простых дробей, неправильных дробей и смешанных дробей.
Рабочие листы с различными дробями в этом разделе посвящены сокращению простых дробей, неправильных дробей и смешанных дробей. Включает задачи с целыми и без них, а также с кросс-отменами и без них. Каждый рабочий лист в формате PDF здесь имеет подробный ключ ответа, который показывает работу, необходимую для решения проблемы, а не только окончательный ответ!
Включает задачи с целыми и без них, а также с кросс-отменами и без них. Каждый рабочий лист в формате PDF здесь имеет подробный ключ ответа, который показывает работу, необходимую для решения проблемы, а не только окончательный ответ! Словесные задачи — отличный способ применить эти математические факты на практике и развить реальное понимание того, что означают операции в реальном мире!
Словесные задачи — отличный способ применить эти математические факты на практике и развить реальное понимание того, что означают операции в реальном мире!

 Римские цифры — идеальная тема для учащихся 3-х, 4-х и 5-х классов, и эти рабочие листы обеспечивают практику чтения и письма римскими цифрами, а также базовые навыки восприятия чисел.
Римские цифры — идеальная тема для учащихся 3-х, 4-х и 5-х классов, и эти рабочие листы обеспечивают практику чтения и письма римскими цифрами, а также базовые навыки восприятия чисел. Если вы ищете рабочие листы с порядком операций, которые проверяют знание правил PEMDAS, эти математические листы — хорошее начало. Вы также можете найти рабочие листы порядка операций с отрицательным числом и рабочие листы порядка операций со сравнениями на этих других страницах рабочего листа.
Если вы ищете рабочие листы с порядком операций, которые проверяют знание правил PEMDAS, эти математические листы — хорошее начало. Вы также можете найти рабочие листы порядка операций с отрицательным числом и рабочие листы порядка операций со сравнениями на этих других страницах рабочего листа. Эти рабочие листы содержат больше и меньше операций, сравнений и тестов на равенство для многозначных чисел, времени и многого другого!
Эти рабочие листы содержат больше и меньше операций, сравнений и тестов на равенство для многозначных чисел, времени и многого другого! Вы можете найти полные 4-квадрантные координатные плоскости, а также пустые 1-квадрантные координатные плоскости в настройках макетов для решения нескольких домашних задач на одной странице.
Вы можете найти полные 4-квадрантные координатные плоскости, а также пустые 1-квадрантные координатные плоскости в настройках макетов для решения нескольких домашних задач на одной странице.
 Это идеальное первое введение в деление для учащихся третьего или четвертого класса.
Это идеальное первое введение в деление для учащихся третьего или четвертого класса. Вы найдете растущий набор праздничных и сезонных тематических страниц, которые я буду добавлять со временем… Пожалуйста, заходите почаще на наличие обновлений или, если у вас есть предложения, отправьте мне сообщение по контактной ссылке ниже!
Вы найдете растущий набор праздничных и сезонных тематических страниц, которые я буду добавлять со временем… Пожалуйста, заходите почаще на наличие обновлений или, если у вас есть предложения, отправьте мне сообщение по контактной ссылке ниже!
 Есть также коллекция простых математических упражнений с забавными темами Дня Земли.
Есть также коллекция простых математических упражнений с забавными темами Дня Земли.
 Он включает коэффициенты на наиболее вероятные и наименее вероятные исходы.
Он включает коэффициенты на наиболее вероятные и наименее вероятные исходы.
 Учащиеся 4 класса наблюдают за повторяющимся узором в каждом наборе фигур, предсказывают и рисуют недостающую фигуру в каждой серии.
Учащиеся 4 класса наблюдают за повторяющимся узором в каждом наборе фигур, предсказывают и рисуют недостающую фигуру в каждой серии.










 Темы включают неравенства, абсолютное значение, алгебру и многое другое.
Темы включают неравенства, абсолютное значение, алгебру и многое другое.
 Кроме того, научитесь определять и находить простые числа с помощью разложения на множители или с помощью решета Эратосфена.
Кроме того, научитесь определять и находить простые числа с помощью разложения на множители или с помощью решета Эратосфена.
 Также есть ссылки на десятичную дробь и вычитание денег.
Также есть ссылки на десятичную дробь и вычитание денег.


 Явка на голосовании составила 120 человек. Распределение голосов соответствует пропорции 3:5. Требуется определить количество голосов, которые получил победитель.
Явка на голосовании составила 120 человек. Распределение голосов соответствует пропорции 3:5. Требуется определить количество голосов, которые получил победитель. Число а может называться предыдущим членом, b играет роль последующего члена.
Число а может называться предыдущим членом, b играет роль последующего члена. Знание определенных правил вычисления поможет значительно упростить решение. Среди вопросов могут быть такие:
Знание определенных правил вычисления поможет значительно упростить решение. Среди вопросов могут быть такие:

 Явка на голосовании составила 120 человек. Распределение голосов соответствует пропорции 3:5. Требуется определить количество голосов, которые получил победитель.
Явка на голосовании составила 120 человек. Распределение голосов соответствует пропорции 3:5. Требуется определить количество голосов, которые получил победитель.

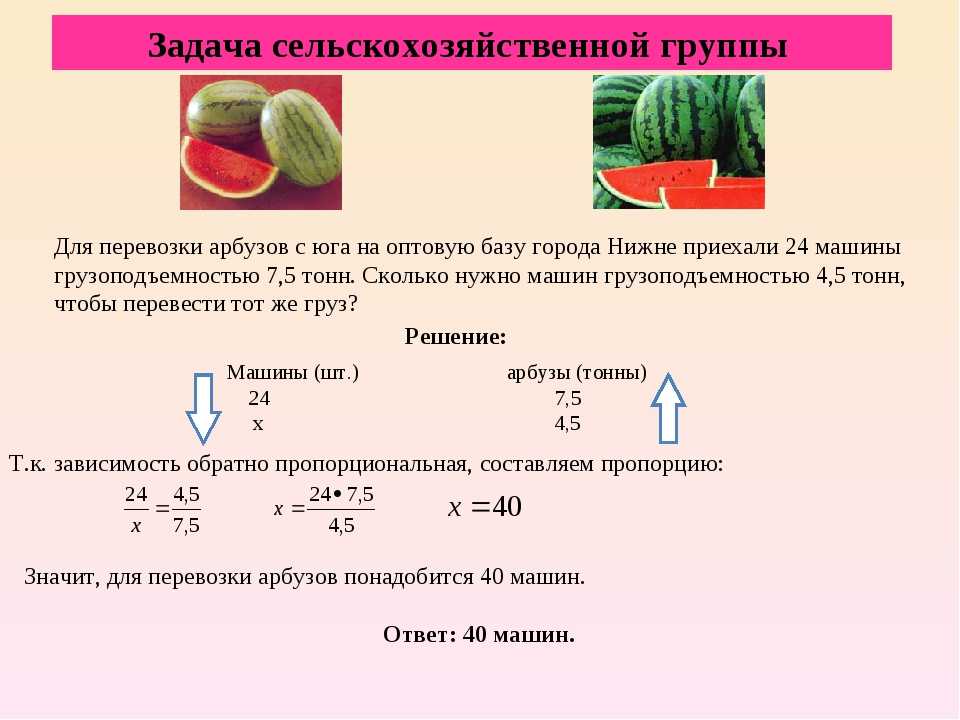







 Отрезок AB длиной 15 см и отрезок CD, длина которого 6 см. Во сколько раз отрезок АВ больше или длиннее отрезка CD?
Отрезок AB длиной 15 см и отрезок CD, длина которого 6 см. Во сколько раз отрезок АВ больше или длиннее отрезка CD?
 Такие величины называют однородными.
Такие величины называют однородными.





 Отношение описывает отношения между двумя объектами, которые обычно представляются в виде упорядоченной пары (вход, выход) или (x, y). Здесь x и y — элементы множеств.
Отношение описывает отношения между двумя объектами, которые обычно представляются в виде упорядоченной пары (вход, выход) или (x, y). Здесь x и y — элементы множеств. Они помогают отображать элементы одного набора (известного как домен) на элементы другого набора (называемого диапазоном), так что результирующие упорядоченные пары имеют форму (вход, выход). Кроме того, специальные типы отношений, которые можно использовать для установления соответствия между двумя величинами, известны как функции. Можно также сказать, что функция является подмножеством отношения.
Они помогают отображать элементы одного набора (известного как домен) на элементы другого набора (называемого диапазоном), так что результирующие упорядоченные пары имеют форму (вход, выход). Кроме того, специальные типы отношений, которые можно использовать для установления соответствия между двумя величинами, известны как функции. Можно также сказать, что функция является подмножеством отношения.
 Стрелочная диаграмма вышеупомянутого примера представлена как
Стрелочная диаграмма вышеупомянутого примера представлена как Основные типы отношений перечислены ниже:
Основные типы отношений перечислены ниже: Другими словами, обратное отношение является обратным отношением. Обратное отношение R обозначается как R -1 . т. е. R -1 = {(y, x) : (x, y) ∈ R}
Другими словами, обратное отношение является обратным отношением. Обратное отношение R обозначается как R -1 . т. е. R -1 = {(y, x) : (x, y) ∈ R} Например, P = {p, q, r}, то транзитивное отношение может быть R = {(p, q), (q, r), (p, r)}
Например, P = {p, q, r}, то транзитивное отношение может быть R = {(p, q), (q, r), (p, r)} Например, P = {1, 2, 3} и Q = {a, b, c}, тогда R = {(1, a), (2, a), (3, a)} является многими к одному связь.
Например, P = {1, 2, 3} и Q = {a, b, c}, тогда R = {(1, a), (2, a), (3, a)} является многими к одному связь.
 Каждый элемент отношения представлен в виде упорядоченной пары (x, y), где x принадлежит A, а y принадлежит B. Другими словами, отношение — это подмножество декартова произведения A и B.
Каждый элемент отношения представлен в виде упорядоченной пары (x, y), где x принадлежит A, а y принадлежит B. Другими словами, отношение — это подмножество декартова произведения A и B.
 Таким образом, для симметричного отношения, если (x, y) ∈ R, то (y, x) ∈ R.
Таким образом, для симметричного отношения, если (x, y) ∈ R, то (y, x) ∈ R. Если мы построим график X-Y, будет сформирована прямая линия.
Если мы построим график X-Y, будет сформирована прямая линия.
 Обратные отношения следуют гиперболическому образцу. Ниже приведен график, показывающий гиперболическую форму обратной зависимости. 92
Обратные отношения следуют гиперболическому образцу. Ниже приведен график, показывающий гиперболическую форму обратной зависимости. 92 Две массы на заданном расстоянии притягивают друг друга равными и противоположными силами. Величина этой силы притяжения определяется выражением: 92), m1 — масса первого объекта в килограммах, m2 — масса второго объекта в килограммах, r — расстояние между центрами двух масс в метрах. График этого уравнения показан ниже.
Две массы на заданном расстоянии притягивают друг друга равными и противоположными силами. Величина этой силы притяжения определяется выражением: 92), m1 — масса первого объекта в килограммах, m2 — масса второго объекта в килограммах, r — расстояние между центрами двух масс в метрах. График этого уравнения показан ниже. Синусоида или синусоида — это математическая кривая, описывающая плавные повторяющиеся колебания. Он назван в честь функции синуса, графиком которой он является.
Синусоида или синусоида — это математическая кривая, описывающая плавные повторяющиеся колебания. Он назван в честь функции синуса, графиком которой он является.

 7.RP.A.1
7 класс
7.RP.A.1
7 класс


