список оригинальных и недорогих подарков на день рождения
День рождения всегда семейный праздник. И если первый год ребенка проходит в самом узком кругу, среди подарков на один год больше полезных для маленькой девочки вещей, приспособления для купания, прогулок и развития, то два года – первый «бал» для маленькой принцессы.
Обычно в два годика девочка уже узнает друзей семьи, эмоционально реагирует на подарки, может даже сама выбрать желанную игрушку и сама сказать «Спасибо!» дарителю.
Ради улыбки маленькой именинницы стоит постараться! Но что же подарить девочке на два года? Чтобы поход по магазинам был приятным, мы составили список идей необычных подарков девочке на день рождения в зависимости от того, кто собирается ее поздравлять.
Топ-10 лучших подарков девочке на 2 год
Подарки от родителей
Мама и папа лучше других знают, что нужно их ребенку на два года. Спросить их мнение важно всем, кто собирается на праздник. Но что выбрать самим родителям на два года девочке?
Но что выбрать самим родителям на два года девочке?
Один из выходов – составить список необходимых, полезных подарков, а отдельно записать приятные непервостепенные – игрушки, развивающие тренажеры, нарядную одежду, аксессуары или даже красивый ночник в детскую комнату.
1. Первое украшение
Фото: pixabay.comРодителям на два года девочке можно подарить особый подарок со смыслом. Например, золотое или серебряное украшение. Многие именно в два годика решаются проколоть ушки дочке, а красивые безопасные сережки будут отличным подарком от родителей. Кстати, маму порадовать в этот особенный день тоже важно. Папа может подарить серьги похожей формы и жене.
2. Красивая мебель
Фото: Curtis Adams, pexels.comДочка выросла из маленькой кроватки. Часто в два года девочке ставят в детской новую мебель. Родители могут приурочить эти изменения к дате празднования двухлетия ребенка. Купить удобный набор мебели, подобрать красивый текстиль, декор. Маленькая принцесса будет рада новому «домику». Можно пригласить к созданию уюта в детской всех близких родственников и друзей. Тогда у дня рождения будет особенный смысл – новоселье для маленькой принцессы.
Маленькая принцесса будет рада новому «домику». Можно пригласить к созданию уюта в детской всех близких родственников и друзей. Тогда у дня рождения будет особенный смысл – новоселье для маленькой принцессы.
3. Развивающий комплект
Фото: pexels.comКак развивается малышка, лучше других знают родители. И они знают, какую игрушку, спортивный инвентарь или приспособление нужно их дочери. Вариантом подарка на два года девочке могут стать развивающие комплекты. Например, спортивный уголок в доме, удобные качели с разными сиденьями и кольцами для игр. А может быть, девочка проявляет интерес к рисованию и ей нужен «уголок художника» — мольберт, удобный стул, подставка для красок и кистей, передник, альбомы, карандаши? Вариантов может быть много. Главное, чтобы подарок был полезным, безопасным и порадовал ребенка.
Подарки от бабушек и дедушек
Все знают, как любят баловать внуков дедушки и бабушки. Выбор подарка становится для них сложной задачей, если у ребенка есть все необходимое. Чем порадовать любимую принцессу?
Чем порадовать любимую принцессу?
4. Сертификат в детский супермаркет
Фото: shutterstock.comСамый простой выход — подарить сертификат с приемлемой для семьи суммой в детский супермаркет или в детский торговый центр. Родители сами выберут подходящий подарок для дочки. А чтобы не приходить на праздник с маленьким конвертом, который в руки ребенку не дашь, бабушка может испечь красивый торт. Ведь самое вкусное, что мы ели в своей жизни – это бабушкины пирожки, торты, печенье, не правда ли?
Торт можно заказать и в специальных кулинарных магазинах или у мастериц, а украсить любыми надписями, шоколадными фигурками и даже фотографиями любимых мультперсонажей девочки.
Подароки от крестных, друзей семьи
Крестные на празднике в честь дня рождения девочки – одни из главных гостей. Подарок от крестных запоминающийся, необычный. Какие идеи необычных подарков на два года девочке можно использовать? Вот небольшой список подарков, который пригодится и другим гостям – близким, друзьям, коллегам родителей, приглашенных на праздник.
5. Бассейн с шариками
Фото: pixabay.comЭто веселое развлечение, развивает ловкость, шарики можно использовать как счетный материал или элементы для других игр. Однозначно полезный и яркий подарок.
6. Магнитный конструктор
Фото: pixabay.comПростые безопасные модели различных фигурок, которые можно собирать в сюжетные картины на специальной доске или цельную фигуру (дом, замок принцессы, ферму с животными, пруд с рыбками и так далее). Именинница оценит!
7. Домашний кукольный театр
Фото: pixabay.comСказки и мультфильмы в два года самое популярное развлечение. Подарите девочке набор кукол, персонажей сказок в комплекте со специальной сценой, занавесом и подсветкой. Ребенок сможет сам устраивать представления.
8. Проектор
Фото: shutterstock.comЕсть модели проекторов со сменными насадками: сегодня у девочки звездное небо, завтра бал снежинок, а послезавтра осенний листопад. Даже взрослых такая подсветка приводит в восторг.
9. Маленький детский компьютер
Фото: pixabay.comЗнакомиться с буквами и цифрами девочка может с помощью компьютера. Никакого излучения — компьютер безопасный, работает на батарейках. Моделей таких игрушек масса, остается выбрать самый интересный и красивый.
10. Сертификат на развивающие занятия
Фото: anastasia-shu, pexels.comУниверсальный подарок девочке на два года. Ребенок любит плавать? Подарите сертификат в детский бассейн. Любит рисовать — сертификат на занятия в детскую художественную школу для самых маленьких. Любит танцевать или ей прочат карьеру модели? Есть и модельные, и танцевальные школы для детей с двух лет. Выбирайте и радуйте именинницу!
Оригинальные идеи подарков девочке на 2 года
- Ручная каталка
- Игровой домик с мягким полом
- Танцевальный коврик
- Пупс
- Комнатные качели
- Санки-коляска
- Небьющаяся посуда с любимыми мультяшными героями
- Музыкальное пианино
- Кукольный домик
- Продуктовая тележка с набором продуктов
- Коляска для кукол
- Магнитная доска
- Детский боулинг
- Механические игрушки для купания
- Велосипед с дополнительными колесиками
- Ростомер
- Интерактивная кухня
- Миниатюрный чемодан на колесиках
- Автокресло
- Игровой набор доктора
- Музыкальная юла
- Детская швейная машинка
- Кукла
- Конструктор с крупными деталями
- Игровой набор детской посуды
- Махровый халат
- Надувной круг для купания
- Интерактивная касса
- Игрушка-грелка
- Принадлежности для песочницы
- Детская подушка
- Заводная фея
- Мягкая игрушка
- Украшения для волос
- Качалка
- Коврик для рисования водными фломастерами
- Рыба-робот для ванны
- Кигуруми
- Набор махровых полотенец
- Теплое одеяльце
- Набор бутылочек для воды
- Садовые качели
- Игрушка-повторялка
- Небольшая горка
- Детский дартс
- Спортивный комплекс
- Мячик с ушками
- Батут
- Домашние тапки в виде лапок
- Игрушечный синтезатор
- Самокат
- Книга с красочными картинкам
- Воздушный змей
- Стол со стулом для творчества
- Беговел
- Детское лото с картинками животных
- Мольберт
- Набор фломастеров или карандашей
- Раскраска с крупным рисунком
- Детский уличный шатер
- Барабан
- Слингобусы
- Мягкая книга
- Развивающие панели
- Аквагрим
- Пирамида
- Гамак
- Маскарадный костюм
- Диадема принцессы
- Резиновые сапожки с принтом
- Набор для выдувания мыльных пузырей
- Гамак
- Праздничное платье
- Дождевик
- Электромобиль розового цвета
- Светящиеся кроссовки
- Набор феи
- Яркий зонт
- Детский пуфик
- Одинаковый набор одежды для мамы и дочки
- Фотоподушки с изображением малышки
- Рюкзачок в виде микки-мауса
- Корзина для игрушек
- Обучающий планшет
- Постельное белье с героями
- Фотопостер
- Игровой холодильник с подсветкой
- Детский альбом для фотографий
- Набор детской косметики
- Игрушечный телефон
- Пальчиковые краски
- Нелопающиеся мыльные пузыри
- Набор для лепки
- Игрушка-шнуровка
- Детский лабиринт
- Большой набор цветных мелков для асфальта
- Игрушки для пальчикового театра
- Игрушечная стиральная машинка
- Качели-балансир
- Надувной игровой центр
- Ветрячок
- Кольцеброс
- Зверошапка
- Комбинезон
- Чудо-чемоданчик
- Комплект фигурок животных
- Полотенце-пончо
- Детский маникюрный набор
- Очиститель воздуха
- Спортивный костюм
- Ингалятор
- Стульчик-горшок
- Детский термометр
- Видеоняня
- Яркий летний сарафан
- Мягкие кубики
- Вязаная шапка и снуд
- Русалка со светящимся хвостом
- Домик лабиринт
- Корзина с детским питанием
- Сквиш
- Электронный термометр для воды и воздуха
- Сборный манеж
- Детский матрас
- Набор носочков
- Плед с капюшоном
- Игрушка-неваляшка
- Мозаичный коврик
- Утюжок с гладильной доской
- Набор для украшения качелей
- Комфортер
- Сенсорная коробка
- Большой калейдоскоп
- Говорящая кукла
- Звуковой плакат
- Поильник-непроливайка
- Игрушка-стучалка
- Гнущаяся мозаика
- Велосипедное кресло
- Набор ярких панамок или платков для головы
- Деревянный лабиринт
- Набор мебели для кукол
- Микрофон
- Игрушечный замок принцесс
- Безопасные ножницы для творчества
- Набор овощей и фруктов на липучке
- Игрушечная бижутерия для самых маленьких
Как выбрать подарок девочке на 2 года
- Одежда, игрушки, мебель и другие подарки для ребенка должны быть безопасными, сертифицированными и соответствовать всем САНПИНам.
 Внимательно читайте упаковку. Материалы не должны быть токсичными, вызывать аллергию. В игрушках не должно быть мелких, колющих, режущих деталей.
Внимательно читайте упаковку. Материалы не должны быть токсичными, вызывать аллергию. В игрушках не должно быть мелких, колющих, режущих деталей. - Будьте внимательны и к внешнему виду игрушек. Излишне агрессивные выражения лиц, рисунки с непонятными животными, слишком яркие, неестественные цвета могут повлиять на эмоциональное и психическое состояние ребенка.
- Не покупайте продукты, конфеты, яркого цвета сладости. Если хоте преподнести девочке на два года что-то вкусное — посоветуйтесь с родителями.
- Пусть ваш подарок принесет только радость и пользу маленькой имениннице!
С 1 мая «Автоваз» повысит цены на свои машины в среднем на 2%
Экономика Сюжет: ДНР, ЛНР, Украина: обострение 2534
Поделиться
Президент компании «Автоваз» Максим Соколов сообщил журналистам в кулуарах Международной выставки «Иннопром. Центральная Азия» о планируемом повышении с 1 мая цен на автомобили Lada в среднем на 2%. При этом он подчеркнул, что речь идет о среднем показателе.
Центральная Азия» о планируемом повышении с 1 мая цен на автомобили Lada в среднем на 2%. При этом он подчеркнул, что речь идет о среднем показателе.
Развивая тему, Соколов отметил, что такой рост цен на машины компании явно не превысит прогнозный уровень инфляции в стране в 2023 году. По расчетам Минэкономразвития инфляция в этом году ожидается на уровне 5,3%.
По опубликованным данным, продажи продукции «Автоваза» в I квартале текущего года увеличились на 22% и составили 64,2 тыс. машин.
Подписаться
Авторы:
- Андрей Степанов
Минэкономразвития ХК Сокол Александр Соколов
Источник: ТАСС
Что еще почитать
Что почитать:Ещё материалы
В регионах
В Рязани из трудового рабства спасли 25-летнюю девушку с грудным ребёнком
Фото 50520
РязаньАнастасия Батищева
В Новосибирске ученики третьего класса устроили забастовку и не пришли в школу
28577
НовосибирскЕлена Балуева
Глава ЧВК «Вагнер» пожаловался на Ярославскую область
Фото 27018
ЯрославльСевастополь снова атаковали дроны утром 24 апреля
22490
Крымфото: МК в Крыму
В США представили снаряд, который поможет Украине бить по Крыму
14866
Крымфото: МК в Крыму
Подоляк заявил, что Украина может уничтожить Крым и Донбасс
12527
Крымcrimea.
 mk.ru
mk.ru
В регионах:Ещё материалы
Натрий | Факты, использование и свойства
натрий
Посмотреть все СМИ
- Ключевые люди:
- сэр Хамфри Дэви Жозеф-Луи Гей-Люссак Рудольф Фиттиг
- Похожие темы:
- химический элемент щелочной металл дефицит натрия натрий-24 натрий-22
Просмотреть весь связанный контент →
натрий (Na) , химический элемент группы щелочных металлов (группа 1 [Ia]) периодической таблицы. Натрий — очень мягкий серебристо-белый металл. Натрий является наиболее распространенным щелочным металлом и шестым по распространенности элементом на Земле, составляющим 2,8 процента земной коры. Он широко встречается в природе в соединениях, особенно в поваренной соли — хлориде натрия (NaCl), который образует минерал галит и составляет около 80% растворенных компонентов морской воды.
| атомный номер | 11 |
|---|---|
| атомный вес | 22,9898 |
| 97,81 °C (208 °F) | |
| точка кипения | 882,9 °C ( 1621 °F) |
| удельный вес | 0,971 (20 °C) |
| степени окисления | +1, −1 (редко) | электронная конфигурация | 2-8-1 или 1 s 2 2 s 2 2 p 6 3 s 1 |
Свойства и производство
Поскольку натрий чрезвычайно активен, он никогда не встречается в свободном состояние в земной коре. В 1807 году сэр Хамфри Дэви первым получил натрий в его элементарной форме, применив электролиз к расплавленному гидроксиду натрия (NaOH). Натрий является важным компонентом ряда силикатных материалов, таких как полевые шпаты и слюды. В разных частях света имеются огромные залежи каменной соли, а в Чили и Перу — месторождения нитрата натрия. Содержание натрия в море составляет примерно 1,05%, что соответствует концентрации примерно 3% галогенидов натрия. Натрий идентифицирован как в атомарной, так и в ионной формах в спектрах звезд, в том числе Солнца, и в межзвездной среде. Анализ метеоритов показывает, что присутствующий силикатный материал имеет среднее содержание примерно 4,6 атома натрия на каждые 100 атомов кремния.
В разных частях света имеются огромные залежи каменной соли, а в Чили и Перу — месторождения нитрата натрия. Содержание натрия в море составляет примерно 1,05%, что соответствует концентрации примерно 3% галогенидов натрия. Натрий идентифицирован как в атомарной, так и в ионной формах в спектрах звезд, в том числе Солнца, и в межзвездной среде. Анализ метеоритов показывает, что присутствующий силикатный материал имеет среднее содержание примерно 4,6 атома натрия на каждые 100 атомов кремния.
Легче воды, натрий можно резать ножом при комнатной температуре, но он становится хрупким при низких температурах. Он легко проводит тепло и электричество и проявляет фотоэлектрический эффект (испускание электронов при воздействии света) в заметной степени.
Натрий является наиболее коммерчески важным щелочным металлом. Большинство процессов производства натрия включают электролиз расплавленного хлорида натрия. Недорогой и доступный в автоцистернах элемент используется для производства присадок к бензину, полимеров, таких как нейлон и синтетический каучук, фармацевтических препаратов и ряда металлов, таких как тантал, титан и кремний. Он также широко используется в качестве теплообменника и в натриевых лампах. Желтый цвет натриевой лампы и натриевого пламени (основа аналитического теста для натрия) определяется двумя заметными линиями в желтой части светового спектра.
Он также широко используется в качестве теплообменника и в натриевых лампах. Желтый цвет натриевой лампы и натриевого пламени (основа аналитического теста для натрия) определяется двумя заметными линиями в желтой части светового спектра.
Викторина «Британника»
Так много химии, так мало времени Викторина
Существенные области применения
Два из первых применений металлического натрия были в производстве цианида натрия и пероксида натрия. Значительные количества тетраэтилсвинца использовались в качестве присадки к бензину, но этот рынок исчез с появлением неэтилированного бензина. Значительные количества натрия используются в производстве алкилсульфатов натрия в качестве основного ингредиента синтетических моющих средств.
Натрий также используется в качестве исходного материала при производстве гидрида натрия (NaH) и боргидрида натрия (NaBH 4 ). Кроме того, натрий используется в производстве красителей и их промежуточных продуктов, в синтезе отдушек и в различных органических восстановителях. Он используется при очистке углеводородов и при полимеризации ненасыщенных углеводородов. Во многих органических применениях натрий используется в виде дисперсий в жидких углеводородных средах.
Он используется при очистке углеводородов и при полимеризации ненасыщенных углеводородов. Во многих органических применениях натрий используется в виде дисперсий в жидких углеводородных средах.
Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту.
Подпишитесь сейчас
Расплавленный натрий является отличным теплоносителем, и благодаря этому свойству он нашел применение в качестве теплоносителя в жидкометаллических реакторах-размножителях на быстрых нейтронах. Натрий широко используется в металлургии в качестве раскислителя и восстановителя для получения кальция, циркония, титана и других переходных металлов. Промышленное производство титана включает восстановление тетрахлорида титана (TiCl 4 ) с натрием. Продукты представляют собой металлический Ti и NaCl.
Основные соединения
Натрий обладает высокой реакционной способностью, образуя широкий спектр соединений почти со всеми неорганическими и органическими анионами (отрицательно заряженными ионами). Обычно он имеет степень окисления +1, и его единственный валентный электрон легко теряется, образуя бесцветный катион натрия (Na + ). Также были синтезированы соединения, содержащие анион натрия Na — . Основными коммерческими соединениями натрия являются хлорид, карбонат и сульфат.
Обычно он имеет степень окисления +1, и его единственный валентный электрон легко теряется, образуя бесцветный катион натрия (Na + ). Также были синтезированы соединения, содержащие анион натрия Na — . Основными коммерческими соединениями натрия являются хлорид, карбонат и сульфат.
Наиболее важным и известным соединением натрия является хлорид натрия, или поваренная соль, NaCl. Большинство других соединений натрия получают прямо или косвенно из хлорида натрия, который содержится в морской воде, в природных рассолах и в виде каменной соли. Большие количества хлорида натрия используются в производстве других тяжелых (промышленных) химикатов, а также используются непосредственно для удаления льда и снега, для кондиционирования воды и в пищевых продуктах.
Другие основные коммерческие применения хлорида натрия включают его использование в производстве хлора и гидроксида натрия путем электролитического разложения и в производстве карбоната натрия (Na 2 CO 3 ) по методу Solvay. Электролиз водного хлорида натрия дает гипохлорит натрия, NaOCl, соединение натрия, кислорода и хлора, используемое в больших количествах в бытовых хлорных отбеливателях. Гипохлорит натрия также используется в качестве промышленного отбеливателя для бумажной массы и текстиля, для хлорирования воды и в некоторых лекарственных препаратах в качестве антисептика и фунгицида. Это нестабильное соединение известно только в водном растворе.
Электролиз водного хлорида натрия дает гипохлорит натрия, NaOCl, соединение натрия, кислорода и хлора, используемое в больших количествах в бытовых хлорных отбеливателях. Гипохлорит натрия также используется в качестве промышленного отбеливателя для бумажной массы и текстиля, для хлорирования воды и в некоторых лекарственных препаратах в качестве антисептика и фунгицида. Это нестабильное соединение известно только в водном растворе.
Карбонаты содержат карбонат-ион (CO 3 2– ). Бикарбонат натрия, также называемый гидрокарбонатом натрия или бикарбонатом соды, NaHCO 3 , является источником двуокиси углерода и поэтому используется в качестве ингредиента разрыхлителей, шипучих солей и напитков, а также в качестве основного компонента сухих напитков. химические огнетушители. Его легкая щелочность делает его полезным при лечении повышенной кислотности желудка или мочевыводящих путей и ацидоза. Он также используется в некоторых промышленных процессах, таких как дубление и подготовка шерсти. Карбонат натрия, или кальцинированная сода, Na 2 CO 3 , широко распространен в природе, встречается в составе минеральных вод и в виде твердых минералов натрона, трона и термонатрита. Большие количества этой щелочной соли используются в производстве стекла, моющих и чистящих средств. Карбонат натрия обрабатывают двуокисью углерода с получением бикарбоната натрия. Моногидрат карбоната натрия Na 2 CO 3 · H 2 O широко используется в фотографии в качестве компонента проявителей.
Карбонат натрия, или кальцинированная сода, Na 2 CO 3 , широко распространен в природе, встречается в составе минеральных вод и в виде твердых минералов натрона, трона и термонатрита. Большие количества этой щелочной соли используются в производстве стекла, моющих и чистящих средств. Карбонат натрия обрабатывают двуокисью углерода с получением бикарбоната натрия. Моногидрат карбоната натрия Na 2 CO 3 · H 2 O широко используется в фотографии в качестве компонента проявителей.
Сульфат натрия, Na 2 SO 4 , представляет собой белое кристаллическое твердое вещество или порошок, используемый в производстве крафт-бумаги, картона, стекла и моющих средств, а также в качестве сырья для производства различных химических веществ. Его получают либо из месторождений сульфатно-натриевых минералов мирабилита и тенардита, либо синтетически путем обработки хлорида натрия серной кислотой. Кристаллизованный продукт представляет собой гидрат Na 2 SO 4 · 10H 2 O, широко известный как глауберова соль. Тиосульфат натрия (гипосульфит натрия), Na 2 S 2 O 3 , используется фотографами для фиксации проявленных негативов и отпечатков; он действует, растворяя часть солей серебра, нанесенных на пленку, которые остаются неизменными под воздействием света.
Тиосульфат натрия (гипосульфит натрия), Na 2 S 2 O 3 , используется фотографами для фиксации проявленных негативов и отпечатков; он действует, растворяя часть солей серебра, нанесенных на пленку, которые остаются неизменными под воздействием света.
Гидроксид натрия (NaOH) представляет собой едкое белое кристаллическое твердое вещество, которое легко поглощает влагу до тех пор, пока не растворится. Гидроксид натрия, обычно называемый едким натром или щелочью, является наиболее широко используемой промышленной щелочью. Он сильно разъедает ткани животных и растений. Щелочные растворы, которые он образует при растворении в воде, нейтрализуют кислоты в различных промышленных процессах: при переработке нефти он удаляет серную и органические кислоты; в мыловарении реагирует с жирными кислотами. Растворы NaOH используются при обработке целлюлозы и в производстве многих химических веществ.
Нитрат натрия, или нитрат натрия, NaNO 3 , обычно называют чилийской селитрой из-за месторождений полезных ископаемых в северной части Чили, основного источника. Нитрат натрия используется как азотное удобрение и как компонент динамита.
Нитрат натрия используется как азотное удобрение и как компонент динамита.
JPMorgan Chase & Co.
JPMorgan Chase обслуживает миллионы заказчиков, клиентов и сообщества на более чем 100 мировых рынках.
Предоставление людям второго шанса: как JPMorgan Chase устраняет барьеры с помощью политики, партнерства с местными сообществами и реформ в собственной практике найма
Нэн Гибсон, исполнительный директор JPMorgan Chase PolicyCenter, и Джаред Эванс, менеджер сообщества Stony Island, Chicago Chase Branch, сели, чтобы поделиться своим опытом продвижения общенациональной программы JPMorgan Chase «Второй шанс».
JPMorgan Chase и Breaking Ground: пожертвование в размере 3,5 миллионов долларов на продвижение стабильного жилья
В детстве Бренда Розен из Breaking Ground из первых рук узнала, что значит бороться за поиск стабильного жилья. Сегодня она борется с проблемой… с помощью пожертвования от JPMorgan Chase.
Разговор о благотворительности с Мишель Р. Томас
Версия этой истории первоначально появилась в Dallas Weekly.
Демистификация нейроразнообразия: пришло время принять разные способы нашего мышления
Брайан Гилл, глава Глобального управления по интеграции инвалидов JPMorgan Chase и глава банка по глобальному нейроразнообразию, обсуждает, как эмпатия является секретом раскрытия потенциала и новых способов добиться положительных результатов в бизнесе.
Все истории Читать больше новостей и историй
Четыре консультанта J.P. Morgan вошли в число 100 лучших финансовых консультантов Barron
17 апреля 2023 г. и сообщества Конгресс-Хайтс.
13 апреля 2023 г.
Рекорд 96 консультантов J.P. Morgan вошли в список лучших консультантов по благосостоянию в штате Forbes за 2023 г.

4 апреля 2023 г.
900 02J.P. Morgan Wealth PlanTM назван «Лучшим продуктом для личных финансов»
23 марта 2023 г.
Новости
16 консультантов по управлению активами J.P. Morgan вошли в рейтинг 1200 лучших компаний Barron
13 марта 2023 г.
Новости
Chase наймет более 500 банкиров малого бизнеса до 2024 года
23 февраля 2023 г.
Узнать больше : открывает главную страницу новостей
Скачать отчет ESG за 2022 г. Нажмите, чтобы просмотреть отчет ESG
JPMorgan Chase объявляет о коэффициенте замещения ценных бумаг, находящихся в обращении, и других инструментов, привязанных к ставкам ледяного свопа LIBOR в долларах США
20 апреля 2023 г.
JPMorgan Chase объявляет дивиденды по привилегированным акциям
14 апреля 2023 г.

 Внимательно читайте упаковку. Материалы не должны быть токсичными, вызывать аллергию. В игрушках не должно быть мелких, колющих, режущих деталей.
Внимательно читайте упаковку. Материалы не должны быть токсичными, вызывать аллергию. В игрушках не должно быть мелких, колющих, режущих деталей. mk.ru
mk.ru
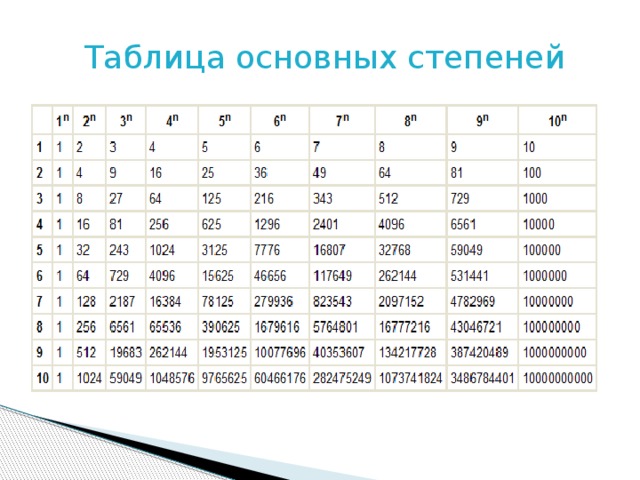
 5. Иллюстрация к задаче
5. Иллюстрация к задаче

 С. и др. Геометрия 7–9 классы. Учебник для общеобразовательных учреждений. – М.: Просвещение, 2010., №№ 959, 960, 962.
С. и др. Геометрия 7–9 классы. Учебник для общеобразовательных учреждений. – М.: Просвещение, 2010., №№ 959, 960, 962. е.является точкой окружности.
е.является точкой окружности. Получили систему уравнений относительно
координат центраокружности:.
Ее решениями будут.
Итак, существует два уравнения,
удовлетворяющих условиям задачи:.
Получили систему уравнений относительно
координат центраокружности:.
Ее решениями будут.
Итак, существует два уравнения,
удовлетворяющих условиям задачи:. Из последнего
равенства следует, что
.Так
как,
то можем обе части уравнения возвести
в квадрат и после эквивалентных
преобразований получим:.
Следовательно,.
Введем новую переменную.
Имеем:.
Из этого равенства следует, что
Из последнего
равенства следует, что
.Так
как,
то можем обе части уравнения возвести
в квадрат и после эквивалентных
преобразований получим:.
Следовательно,.
Введем новую переменную.
Имеем:.
Из этого равенства следует, что
 Если,
ак нулю не стремится, то эллипс вытянут
вдоль большой оси. Таким образом,
эксцентриситет эллипса характеризует
меру его вытянутости вдоль большой оси.
Если,
ак нулю не стремится, то эллипс вытянут
вдоль большой оси. Таким образом,
эксцентриситет эллипса характеризует
меру его вытянутости вдоль большой оси. Большой полуосью является полуось,
поэтому фокусы эллипса расположены на
оси ординат и,
следовательно, фокусы находятся в точкахи.
Эксцентриситет эллипса равен отношению
половины расстояния между фокусами к
большой полуоси, т. е..
Большой полуосью является полуось,
поэтому фокусы эллипса расположены на
оси ординат и,
следовательно, фокусы находятся в точкахи.
Эксцентриситет эллипса равен отношению
половины расстояния между фокусами к
большой полуоси, т. е..

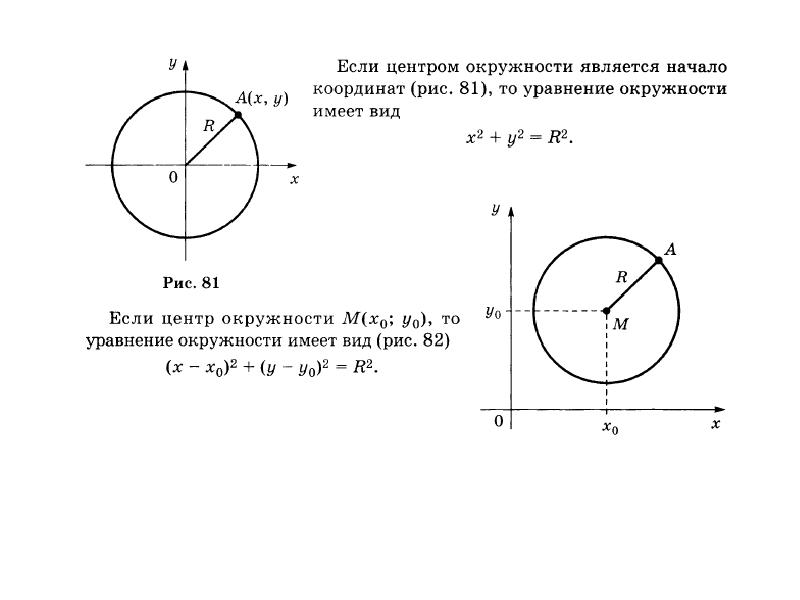
 Если он имеет радиус r , уравнение выглядит так:
Если он имеет радиус r , уравнение выглядит так: См. нашу статью «Уравнение окружности» для справки.
См. нашу статью «Уравнение окружности» для справки. Или любая точка на окружности (rcosθ, rsinθ), где θ — параметр.
Или любая точка на окружности (rcosθ, rsinθ), где θ — параметр.
 Плюсовые собирательные линзы усиливают оптику гиперметропического глаза.
Плюсовые собирательные линзы усиливают оптику гиперметропического глаза. Характерна очень быстрая утомляемость глаз и сильный дискомфорт при работе вблизи.
Характерна очень быстрая утомляемость глаз и сильный дискомфорт при работе вблизи. Это может показаться фантастическим, но мы объясним это без жаргона! Давай сделаем это.
Это может показаться фантастическим, но мы объясним это без жаргона! Давай сделаем это.
 com/calculator/exponent/what-is-25-to-the-3rd-power/.
com/calculator/exponent/what-is-25-to-the-3rd-power/.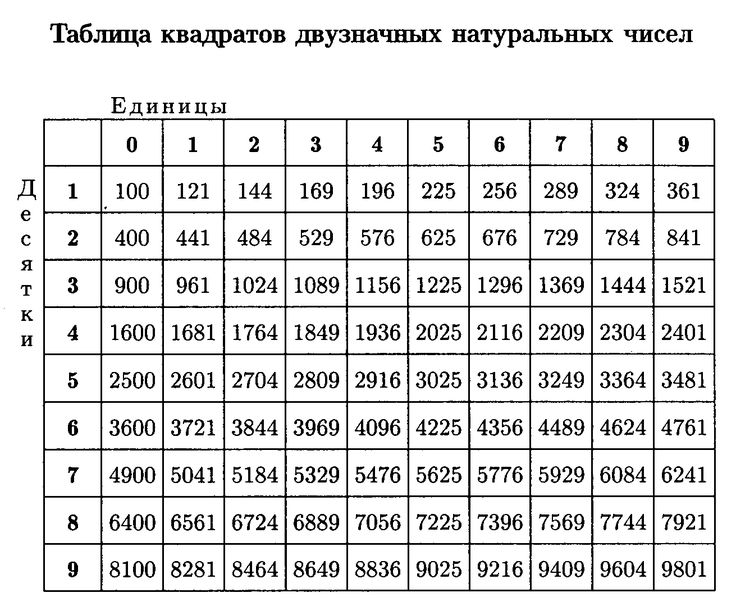 ..
..
 Даже если ваша пусковая батарея слишком разряжена для запуска двигателя, просто нажмите кнопку, чтобы запустить двигатель от второго аккумулятора. Прошли старые времена чтения схем проводов, чтобы выяснить, как добавить вторую батарею к вашему автомобилю с помощью ручного селекторного переключателя или разъединителя. Комплекты с двумя батареями Genesis полностью предварительно смонтированы для вас из коробки, что упрощает установку. Никаких инструментов для зачистки проводов или кримперов не требуется!
Даже если ваша пусковая батарея слишком разряжена для запуска двигателя, просто нажмите кнопку, чтобы запустить двигатель от второго аккумулятора. Прошли старые времена чтения схем проводов, чтобы выяснить, как добавить вторую батарею к вашему автомобилю с помощью ручного селекторного переключателя или разъединителя. Комплекты с двумя батареями Genesis полностью предварительно смонтированы для вас из коробки, что упрощает установку. Никаких инструментов для зачистки проводов или кримперов не требуется!


 66KB
66KB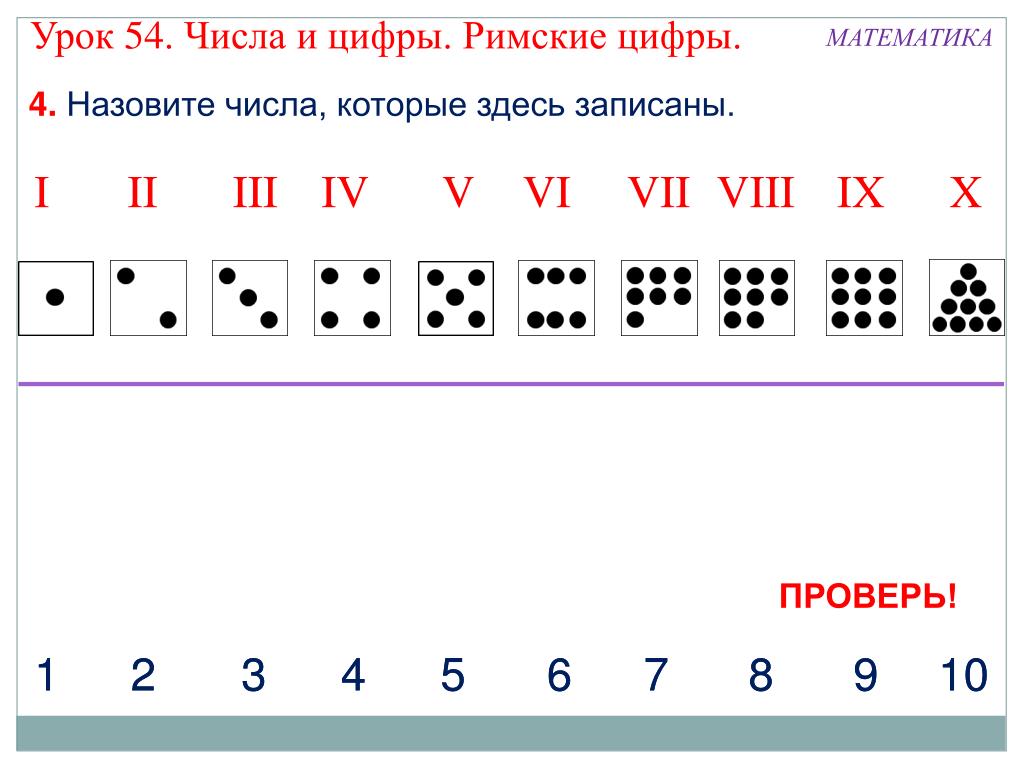 43KB
43KB 12KB
12KB

 При этом в некоторых старых римских документах может встречаться параллельное использование цифр с вычетом (например, IV), и четырёх однотипных символов (например, IIII).
При этом в некоторых старых римских документах может встречаться параллельное использование цифр с вычетом (например, IV), и четырёх однотипных символов (например, IIII). Для больших же чисел понадобятся остальные пять символов римский цифровой модели, причём возможности последней ограничены максимально возможным числом в 3999. Для прохождения данной границы пришлось вводить верхнее подчёркивание цифры (что позволяло умножать такую цифру на тысячу), что делало процесс различных математических операций не очень удобным. Эти и другие недостатки римских цифр в конечном счёте и привели к переходу к более совершенной арабской модели, доминирующей на нашей планете и по сей день. Но это уже совсем другая история.
Для больших же чисел понадобятся остальные пять символов римский цифровой модели, причём возможности последней ограничены максимально возможным числом в 3999. Для прохождения данной границы пришлось вводить верхнее подчёркивание цифры (что позволяло умножать такую цифру на тысячу), что делало процесс различных математических операций не очень удобным. Эти и другие недостатки римских цифр в конечном счёте и привели к переходу к более совершенной арабской модели, доминирующей на нашей планете и по сей день. Но это уже совсем другая история. е. 3 = I + I + I, после чего мы получим 3 = I + I + I = III. В этой статье мы объясним, как правильно преобразовать 3 в римские цифры.
е. 3 = I + I + I, после чего мы получим 3 = I + I + I = III. В этой статье мы объясним, как правильно преобразовать 3 в римские цифры.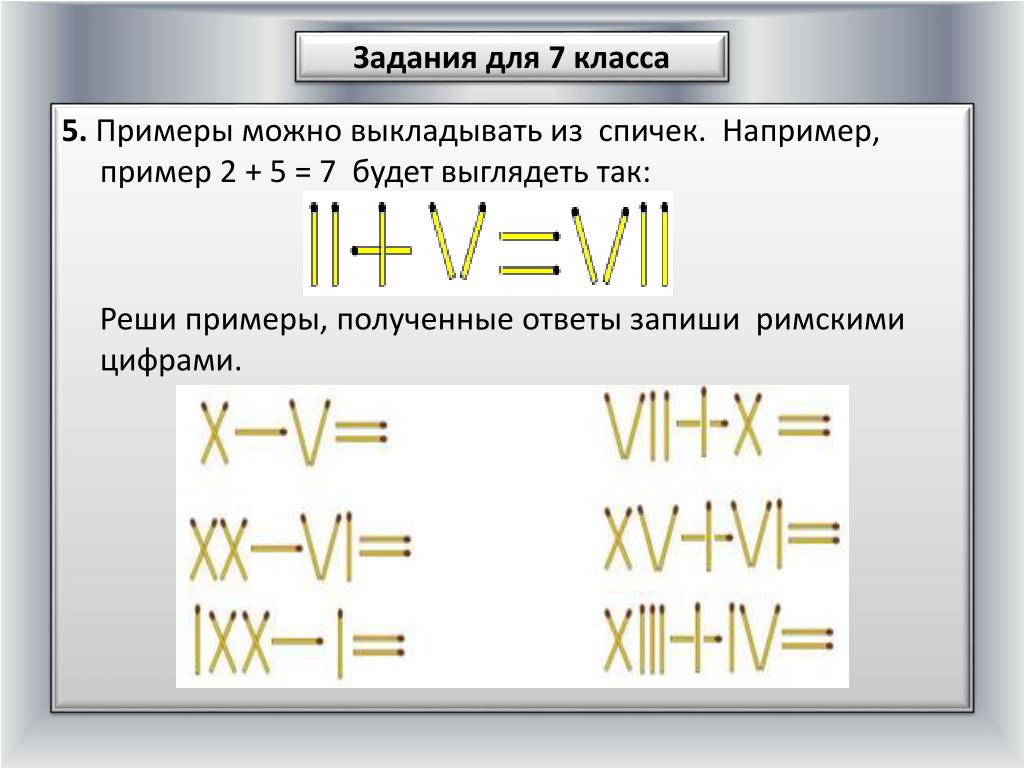 Например: LX, L > X, поэтому LX = L + X = 50 + 10 = 60.
Например: LX, L > X, поэтому LX = L + X = 50 + 10 = 60.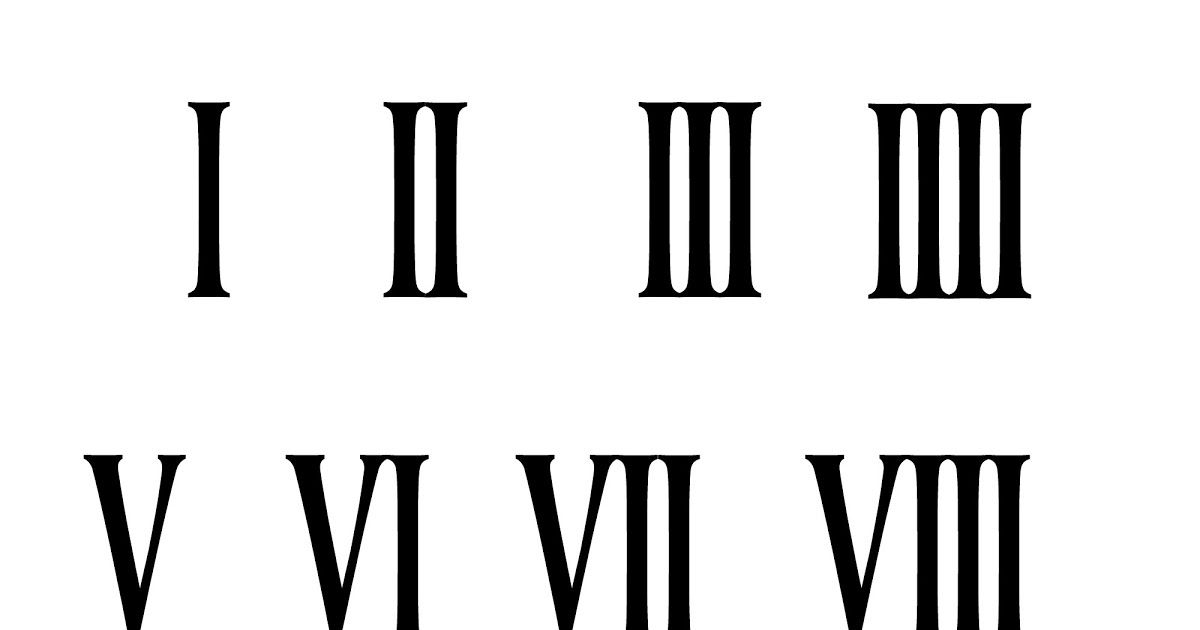

 Следуя той же логике, три единицы, то есть 3 римскими цифрами записывается как 3 = III.
Следуя той же логике, три единицы, то есть 3 римскими цифрами записывается как 3 = III.
 Может показаться, что они отличаются от цифр, но они похожи. Например, римская цифра III эквивалентна числу 3. Римские цифры, относящиеся к III, приведены ниже:
Может показаться, что они отличаются от цифр, но они похожи. Например, римская цифра III эквивалентна числу 3. Римские цифры, относящиеся к III, приведены ниже: Следовательно, значение римских цифр III равно 3.
Следовательно, значение римских цифр III равно 3.


 Калькулятор сохраняет историю даже при переключении режимов, но она удаляется, когда вы закрываете приложение.
Калькулятор сохраняет историю даже при переключении режимов, но она удаляется, когда вы закрываете приложение. Полный список этих сочетаний можно найти на странице «Горячие клавиши Microsoft Windows», но вот несколько наиболее полезных:
Полный список этих сочетаний можно найти на странице «Горячие клавиши Microsoft Windows», но вот несколько наиболее полезных: К тому же оно позволяет выразить соотношение воспринимаемого звукового давления (слухового порога) к предельно переносимому звуковому давлению (болевому порогу) не как 1 : 3 000 000, а гораздо более наглядно – от 0 до 130 дБ. Общий расчет выглядит следующим образом: log (значение/заданное значение). При этом используется десятичный логарифм, обозначенный на калькуляторе символом «log». Сама единица называется «бел», десятая часть обозначается приставкой «деци-», в результате получается децибел. Он выражает соотношение мощностей. Для звукового давления, напряжения, тока используется коэффициент 20.
К тому же оно позволяет выразить соотношение воспринимаемого звукового давления (слухового порога) к предельно переносимому звуковому давлению (болевому порогу) не как 1 : 3 000 000, а гораздо более наглядно – от 0 до 130 дБ. Общий расчет выглядит следующим образом: log (значение/заданное значение). При этом используется десятичный логарифм, обозначенный на калькуляторе символом «log». Сама единица называется «бел», десятая часть обозначается приставкой «деци-», в результате получается децибел. Он выражает соотношение мощностей. Для звукового давления, напряжения, тока используется коэффициент 20. В этом случае заданное значение является постоянным, поэтому к «дБ» добавляется «SPL». В настоящее время появилась тенденция говорить об уровнях звукового давления, не используя «SPL». Другие ссылки:
В этом случае заданное значение является постоянным, поэтому к «дБ» добавляется «SPL». В настоящее время появилась тенденция говорить об уровнях звукового давления, не используя «SPL». Другие ссылки: Следовательно, имеет место тысячекратное усиление (1 000 : 1), или 20 x log (1 000 / 1) = +60 дБ.
Следовательно, имеет место тысячекратное усиление (1 000 : 1), или 20 x log (1 000 / 1) = +60 дБ. В итоге при мощности 6 ватт на расстоянии 1 метр получим 103 дБ SPL. Для расчета также можно использовать математическую формулу, дающую тот же результат: p1 = pn + 10 x log(P)
В итоге при мощности 6 ватт на расстоянии 1 метр получим 103 дБ SPL. Для расчета также можно использовать математическую формулу, дающую тот же результат: p1 = pn + 10 x log(P) Просто введите основание и аргумент, и калькулятор выдаст вам логарифмическое значение. Он также может предоставить объяснения логарифмических вычислений, что делает его отличным ресурсом для образовательных целей. Изучаете ли вы математику, инженерное дело или любую другую область, требующую логарифмических вычислений, калькулятор логарифмов — это полезный и надежный способ получить нужные вам ответы. Это быстро, просто и бесплатно, так что попробуйте прямо сейчас и упростите свои логарифмические вычисления.
Просто введите основание и аргумент, и калькулятор выдаст вам логарифмическое значение. Он также может предоставить объяснения логарифмических вычислений, что делает его отличным ресурсом для образовательных целей. Изучаете ли вы математику, инженерное дело или любую другую область, требующую логарифмических вычислений, калькулятор логарифмов — это полезный и надежный способ получить нужные вам ответы. Это быстро, просто и бесплатно, так что попробуйте прямо сейчас и упростите свои логарифмические вычисления. Чтобы использовать калькулятор, выполните следующие действия:
Чтобы использовать калькулятор, выполните следующие действия:  Они являются важным инструментом, который помогает нам решать сложные уравнения и упрощать математические задачи. В этой статье мы обсудим, что такое логарифмы, их свойства и значение в различных областях.
Они являются важным инструментом, который помогает нам решать сложные уравнения и упрощать математические задачи. В этой статье мы обсудим, что такое логарифмы, их свойства и значение в различных областях.  Некоторые из областей, где используются логарифмы, включают:
Некоторые из областей, где используются логарифмы, включают:  Формула для уровня децибел:
Формула для уровня децибел: 
 x = 8. Логарифмируя обе части уравнения по основанию 2, мы получаем: 9x = 8 равно x = 3.
x = 8. Логарифмируя обе части уравнения по основанию 2, мы получаем: 9x = 8 равно x = 3.  Это значение имеет решающее значение во многих математических формулах и имеет важные приложения в различных областях науки и техники. Каково значение E In Log, можно определить с помощью различных методов, включая исчисление и численные приближения. Знание значения e в log важно для понимания поведения экспоненциальных и логарифмических функций. Независимо от того, работаете ли вы с финансовыми данными, моделируете темпы роста или изучаете поведение сложных систем, важно понимать, в чем ценность E In Log.
Это значение имеет решающее значение во многих математических формулах и имеет важные приложения в различных областях науки и техники. Каково значение E In Log, можно определить с помощью различных методов, включая исчисление и численные приближения. Знание значения e в log важно для понимания поведения экспоненциальных и логарифмических функций. Независимо от того, работаете ли вы с финансовыми данными, моделируете темпы роста или изучаете поведение сложных систем, важно понимать, в чем ценность E In Log.

 Однако использование функции натурального логарифма обычно более просто и удобно.
Однако использование функции натурального логарифма обычно более просто и удобно.
 Экспоненциальная функция обычно используется для моделирования экспоненциального роста и затухания, а также является важной функцией в исчислении и дифференциальных уравнениях.
Экспоненциальная функция обычно используется для моделирования экспоненциального роста и затухания, а также является важной функцией в исчислении и дифференциальных уравнениях. нужно поднять, чтобы получить значение «x». Итак, если мы хотим найти натуральный логарифм самого e, мы имеем ln(e) = 1, потому что e, возведенное в степень 1, равно e.
нужно поднять, чтобы получить значение «x». Итак, если мы хотим найти натуральный логарифм самого e, мы имеем ln(e) = 1, потому что e, возведенное в степень 1, равно e. Их важность заключается в их способности преобразовывать экспоненциальные функции в линейные функции, что делает их мощным инструментом математического анализа и моделирования.
Их важность заключается в их способности преобразовывать экспоненциальные функции в линейные функции, что делает их мощным инструментом математического анализа и моделирования. В натуральном логарифме в качестве основания используется «e», а в логарифме с основанием 10 используется 10 в качестве основания. Они имеют разные свойства и приложения в математике, естественных науках и технике.
В натуральном логарифме в качестве основания используется «e», а в логарифме с основанием 10 используется 10 в качестве основания. Они имеют разные свойства и приложения в математике, естественных науках и технике.





 Во-вторых, вполне ожидаемо рассматривать связанную прямую программу с теневыми затратами в качестве факторов вместо первой прямой программы или связанных с ней, соответственно используя некоторую вычислительную эффективность.
Во-вторых, вполне ожидаемо рассматривать связанную прямую программу с теневыми затратами в качестве факторов вместо первой прямой программы или связанных с ней, соответственно используя некоторую вычислительную эффективность.
 .+a m2 w m d 2
.+a m2 w m d 2  Z W =20w 1 + 4w 2 + 2w 3
Z W =20w 1 + 4w 2 + 2w 3 


 Пришло время узнать о двойной линейной программе! Двойная программа полностью изменит наше понимание проблемы, и именно поэтому она такая классная. Надеюсь, вы так же взволнованы, как и я!
Пришло время узнать о двойной линейной программе! Двойная программа полностью изменит наше понимание проблемы, и именно поэтому она такая классная. Надеюсь, вы так же взволнованы, как и я! Как вы уже поняли, вторая двойная переменная относится к значению одной единицы веса. $value_{\textrm{weight}}$ кажется подходящим названием для него, верно?
Как вы уже поняли, вторая двойная переменная относится к значению одной единицы веса. $value_{\textrm{weight}}$ кажется подходящим названием для него, верно? Если бы ограничения позволили нам украсть еще один объем золота, то дополнительная стоимость ограбления была бы по крайней мере равна стоимости этого одного объема золота, верно? Их может быть больше, если мы воспользуемся новыми ограничениями, чтобы украсть что-то еще, кроме золота, которое стоит больше. Я говорю о том, что если бы общий объем позволил нам украсть еще одну единицу объема золота и если бы мы могли унести еще одну единицу веса одного объема золота, то стоимость этой дополнительной кражи составила бы как минимум стоимость еще одного тома золота. Давайте напишем это.
Если бы ограничения позволили нам украсть еще один объем золота, то дополнительная стоимость ограбления была бы по крайней мере равна стоимости этого одного объема золота, верно? Их может быть больше, если мы воспользуемся новыми ограничениями, чтобы украсть что-то еще, кроме золота, которое стоит больше. Я говорю о том, что если бы общий объем позволил нам украсть еще одну единицу объема золота и если бы мы могли унести еще одну единицу веса одного объема золота, то стоимость этой дополнительной кражи составила бы как минимум стоимость еще одного тома золота. Давайте напишем это. Как видите, любая переменная в основной задаче связана с ограничением в двойственной задаче, и наоборот.
Как видите, любая переменная в основной задаче связана с ограничением в двойственной задаче, и наоборот.
 Попробуйте подумать об этом. Это очень сложное, но еще более интересное упражнение. Это означает, что значение ресурсов двойных ограничений является первичными переменными. В нашем примере, если стоимость золота увеличится на 1 единицу, то стоимость ограбления будет увеличена на количество украденного золота. Это означает, что ценность стоимости золота равна количеству украденного золота!
Попробуйте подумать об этом. Это очень сложное, но еще более интересное упражнение. Это означает, что значение ресурсов двойных ограничений является первичными переменными. В нашем примере, если стоимость золота увеличится на 1 единицу, то стоимость ограбления будет увеличена на количество украденного золота. Это означает, что ценность стоимости золота равна количеству украденного золота! В линейном программировании двойственность дает гораздо больше потрясающих результатов! В частности, существует сильная связь между простыми основаниями и двойственными основаниями.
В линейном программировании двойственность дает гораздо больше потрясающих результатов! В частности, существует сильная связь между простыми основаниями и двойственными основаниями. $$ 9T \\
$$ 9T \\  Кроме того, каждая переменная векторов $e$ и $s$ фигурирует одна в одном из ограничений первичной или двойственной программы.
Кроме того, каждая переменная векторов $e$ и $s$ фигурирует одна в одном из ограничений первичной или двойственной программы. Остальные $n$ переменных являются «базовыми» в обычном их определении.
Остальные $n$ переменных являются «базовыми» в обычном их определении.
 Это значение называется дополняющая ненадежность . Оно равно нулю, если двойственные переменные соответствуют двойственному основанию простых переменных.
Это значение называется дополняющая ненадежность . Оно равно нулю, если двойственные переменные соответствуют двойственному основанию простых переменных. Но его можно в равной степени рассматривать как алгоритм, который переходит от первично допустимых оснований к первично допустимым основаниям с ассоциированным двойным основанием, которое становится все более и более выполнимым. Этот критерий «близости к осуществимости» может, например, означать наличие самой отрицательной переменной как можно ближе к 0. Как только самая отрицательная переменная двойного основания неотрицательна, у нас есть двойное допустимое основание. Таким образом, мы достигли оптимума.
Но его можно в равной степени рассматривать как алгоритм, который переходит от первично допустимых оснований к первично допустимым основаниям с ассоциированным двойным основанием, которое становится все более и более выполнимым. Этот критерий «близости к осуществимости» может, например, означать наличие самой отрицательной переменной как можно ближе к 0. Как только самая отрицательная переменная двойного основания неотрицательна, у нас есть двойное допустимое основание. Таким образом, мы достигли оптимума. с этим ограничением. Эта приведенная стоимость является приращением значения целевой функции при движении по зеленой стрелке.
с этим ограничением. Эта приведенная стоимость является приращением значения целевой функции при движении по зеленой стрелке. Это позволяет избежать возможных многочисленных итераций перехода от экстремальных точек к экстремальным точкам и пропускает проблемы вырождения. Для большого числа переменных метод внутренних точек быстрее, чем симплексный метод.
Это позволяет избежать возможных многочисленных итераций перехода от экстремальных точек к экстремальным точкам и пропускает проблемы вырождения. Для большого числа переменных метод внутренних точек быстрее, чем симплексный метод. Если вы их знаете, вы должны написать о них. Кроме того, полуопределенное программирование позволяет моделировать широкий круг проблем. Я недостаточно знаком с полуопределенным программированием, чтобы писать об этом, поэтому, если вы знаете его, пожалуйста, напишите об этом!
Если вы их знаете, вы должны написать о них. Кроме того, полуопределенное программирование позволяет моделировать широкий круг проблем. Я недостаточно знаком с полуопределенным программированием, чтобы писать об этом, поэтому, если вы знаете его, пожалуйста, напишите об этом! Предположим, что мы находимся на базе ограничений, определяемой зеленым и желтым ограничениями, и что симплекс-алгоритм решает отказаться от зеленого ограничения. Затем мы будем двигаться по желтому ограничению, пока не достигнем черной точки. Эта черная точка может быть определена тем фактом, что мы пересекли ограничение красного или синего цвета. Один из них будет добавлен в базу ограничений. Нам нужно сделать выбор. На самом деле это не проблема. А вот замечание — большая проблема.
Предположим, что мы находимся на базе ограничений, определяемой зеленым и желтым ограничениями, и что симплекс-алгоритм решает отказаться от зеленого ограничения. Затем мы будем двигаться по желтому ограничению, пока не достигнем черной точки. Эта черная точка может быть определена тем фактом, что мы пересекли ограничение красного или синего цвета. Один из них будет добавлен в базу ограничений. Нам нужно сделать выбор. На самом деле это не проблема. А вот замечание — большая проблема. {14}$. Правление Блэнда имеет хорошие шансы посетить половину из них… Это займет целую вечность! Может быть, дни… Это очень-очень плохо. И все же размерность 25 очень маленькая.
{14}$. Правление Блэнда имеет хорошие шансы посетить половину из них… Это займет целую вечность! Может быть, дни… Это очень-очень плохо. И все же размерность 25 очень маленькая. В Монреале также были разработаны несколько методов, таких как агрегация динамических ограничений (DCA), интегральный первичный симплекс (IPS) и улучшенная генерация столбцов (ICG). Короче говоря, я бы сказал, что они классифицируют переменные в зависимости от того, как они появляются в ограничениях, и решают только небольшую группу переменных. Они могут рассматривать другие переменные, если критерий оптимальности не выполняется. Узнайте больше из моей статьи о создании столбцов.
В Монреале также были разработаны несколько методов, таких как агрегация динамических ограничений (DCA), интегральный первичный симплекс (IPS) и улучшенная генерация столбцов (ICG). Короче говоря, я бы сказал, что они классифицируют переменные в зависимости от того, как они появляются в ограничениях, и решают только небольшую группу переменных. Они могут рассматривать другие переменные, если критерий оптимальности не выполняется. Узнайте больше из моей статьи о создании столбцов.
 Поскольку все это векторное пространство соответствует единственной первичной точке, которая имеет единственное целевое значение, все векторное пространство имеет единственное целевое значение. Следовательно, все векторное пространство включено в набор уровней двойной целевой функции.
Поскольку все это векторное пространство соответствует единственной первичной точке, которая имеет единственное целевое значение, все векторное пространство имеет единственное целевое значение. Следовательно, все векторное пространство включено в набор уровней двойной целевой функции. В результате в дуале зеленое ограничение будет ниже (посмотрите на его определение, если хотите убедиться в этом). Получаем следующий график.
В результате в дуале зеленое ограничение будет ниже (посмотрите на его определение, если хотите убедиться в этом). Получаем следующий график.

 Словари
Словари )
) Производные и интегралы. 0 отзывов
Производные и интегралы. 0 отзывов После обучения ее направили в одно из отделений газеты «Асагакэ Таймс». Норико жаждет освещать в своих репортажах самые волнующие проблемы мировой политики и экономики, но хватит ли ей для этого опыта и знаний? Ее непосредственный начальник, Сэки-сан, решил научить ее анализировать происходящие в политике и экономике события используя математику.
После обучения ее направили в одно из отделений газеты «Асагакэ Таймс». Норико жаждет освещать в своих репортажах самые волнующие проблемы мировой политики и экономики, но хватит ли ей для этого опыта и знаний? Ее непосредственный начальник, Сэки-сан, решил научить ее анализировать происходящие в политике и экономике события используя математику.

 Но до того, как вы научились их решать, вы изучили необходимые базовые вычисления, такие как сложение, вычитание, умножение и т. д.
Но до того, как вы научились их решать, вы изучили необходимые базовые вычисления, такие как сложение, вычитание, умножение и т. д. Если вы не можете найти выход из проблемы, отсканируйте ее с помощью приложения Photomath, и мы проведем вас на другую сторону!
Если вы не можете найти выход из проблемы, отсканируйте ее с помощью приложения Photomath, и мы проведем вас на другую сторону!
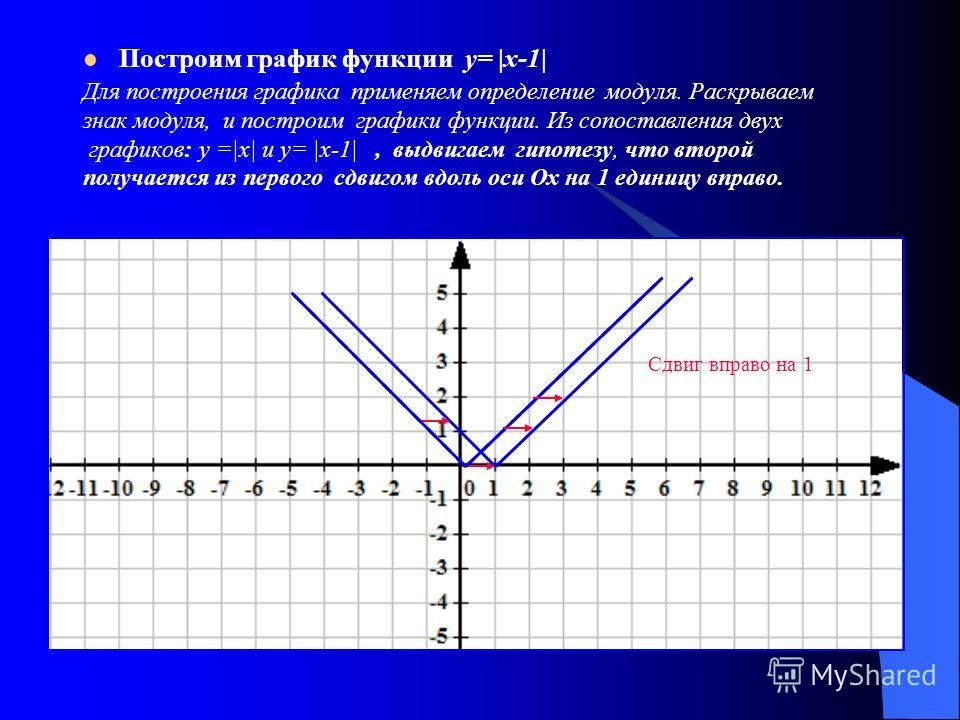
 График — парабола, полученная из параболы y=-x² сжатием к оси абсцисс в 4 раза.
График — парабола, полученная из параболы y=-x² сжатием к оси абсцисс в 4 раза. График — гипербола.
График — гипербола.
 В результате получим график, изображенный на рисунке.
В результате получим график, изображенный на рисунке.

 Поэтому отрезок RS является биссектрисой треугольника PRQ. Поскольку биссектриса равнобедренного треугольника является его высотой и медианой, то PQ ┴RS и PS = QS. А это означает, что точки Р (а; b) и Q (b; а) симметричные относительно прямой у = х.
Поэтому отрезок RS является биссектрисой треугольника PRQ. Поскольку биссектриса равнобедренного треугольника является его высотой и медианой, то PQ ┴RS и PS = QS. А это означает, что точки Р (а; b) и Q (b; а) симметричные относительно прямой у = х.
 Вы получите таблицу значений x и y, которые вам нужно будет нанести на координатную плоскость. Подставим значения x от -2 до 2.
Вы получите таблицу значений x и y, которые вам нужно будет нанести на координатную плоскость. Подставим значения x от -2 до 2. В этом случае (0, -1) становится (0, 1)
В этом случае (0, -1) становится (0, 1) Вам нужно действовать так же, как и раньше, чтобы найти значения x в точках пересечения A и B, которые равны x=2 и x=-43.
Вам нужно действовать так же, как и раньше, чтобы найти значения x в точках пересечения A и B, которые равны x=2 и x=-43. Теперь мы можем найти обратную, потому что этот участок графика является взаимно однозначной функцией.
Теперь мы можем найти обратную, потому что этот участок графика является взаимно однозначной функцией.

 Его уравнение принимает вид , в котором представлено количество единиц, на которые базовый граф переводится вправо и вверх соответственно.
Его уравнение принимает вид , в котором представлено количество единиц, на которые базовый граф переводится вправо и вверх соответственно. Его уравнение принимает вид , в котором представлено количество единиц, на которые базовый граф переводится вправо и вверх соответственно.
Его уравнение принимает вид , в котором представлено количество единиц, на которые базовый граф переводится вправо и вверх соответственно.
 Следовательно, функция четная.
Следовательно, функция четная.
 В режиме Trace учащиеся определяют значения функции для нескольких значений х (0; 0,5; 1; 1,2; 1,4).
В режиме Trace учащиеся определяют значения функции для нескольких значений х (0; 0,5; 1; 1,2; 1,4). (1:5)):
(1:5)): Методика расчета основана на продвинутом алгоритме математической модели с учетом нормативных документов СНиП 2.02.01-83 (СП 22.13330.2011), СНиП 3.03.01-87 (СП 70.13330.2011), СНиП 52-01-2003 (СП 63.13330.2010), СНиП 23-01-99 (СП 131.13330.2012).
Методика расчета основана на продвинутом алгоритме математической модели с учетом нормативных документов СНиП 2.02.01-83 (СП 22.13330.2011), СНиП 3.03.01-87 (СП 70.13330.2011), СНиП 52-01-2003 (СП 63.13330.2010), СНиП 23-01-99 (СП 131.13330.2012).
 Принимая решение о выполнении работ по созданию основания своими руками, важно не допустить ошибок при начальных вычислениях и тем более не нужно пытаться сэкономить на материалах. Помните, что грамотно спроектированный фундамент — залог вашей безопасности.
Принимая решение о выполнении работ по созданию основания своими руками, важно не допустить ошибок при начальных вычислениях и тем более не нужно пытаться сэкономить на материалах. Помните, что грамотно спроектированный фундамент — залог вашей безопасности.
 Соответственно, бетон М100 подходит для легких сооружений – гаражей, бань, оборудования, а М400 – для многоэтажных тяжелых зданий, например, из кирпича. Но в абсолютном большинстве случаев, выбирается бетон марки М300.
Соответственно, бетон М100 подходит для легких сооружений – гаражей, бань, оборудования, а М400 – для многоэтажных тяжелых зданий, например, из кирпича. Но в абсолютном большинстве случаев, выбирается бетон марки М300. Для того чтобы объединить эти качества и повысить эксплуатационные характеристики основания, а также недопустить деформации после возведения сооружения – фундаменты армируют.
Для того чтобы объединить эти качества и повысить эксплуатационные характеристики основания, а также недопустить деформации после возведения сооружения – фундаменты армируют.
 В некоторых случаях доходит до того, что выгоднее купить новый участок, чем вкладываться в преобразование существующего. Поэтому самое первое, что вам необходимо сделать на новом участке – это определить тип грунта.
В некоторых случаях доходит до того, что выгоднее купить новый участок, чем вкладываться в преобразование существующего. Поэтому самое первое, что вам необходимо сделать на новом участке – это определить тип грунта. Поэтому крайне важно строить дом на возвышенностях и избегать низменностей, особенно если рядом находится водотоки и водоемы.
Поэтому крайне важно строить дом на возвышенностях и избегать низменностей, особенно если рядом находится водотоки и водоемы. Вода, содержащаяся в грунте, замерзает и превращается в лед, тем самым увеличивая свой объем.
Вода, содержащаяся в грунте, замерзает и превращается в лед, тем самым увеличивая свой объем. Монолитная или сборная железобетонная полоса проходит под всеми несущими стенами здания, оказывая равномерное давление на грунт.Один из самых простых и доступных в частном строительстве.
Монолитная или сборная железобетонная полоса проходит под всеми несущими стенами здания, оказывая равномерное давление на грунт.Один из самых простых и доступных в частном строительстве. За счет большого объема земляных работ и огромных затрат на бетон, стоимость конструкции возрастает в разы, по сравнению с лентой. Это один из самых дорогих, но в то же время эффективных видов оснований.
За счет большого объема земляных работ и огромных затрат на бетон, стоимость конструкции возрастает в разы, по сравнению с лентой. Это один из самых дорогих, но в то же время эффективных видов оснований. Оно экономично, надежно и не требует работ по гидроизоляции. Защищает ваш дом от плесени и преждевременного разрушения древесины. Тем не менее, фундамент крайне требователен к грунту, ему категорически запрещены подвижки и пучения.
Оно экономично, надежно и не требует работ по гидроизоляции. Защищает ваш дом от плесени и преждевременного разрушения древесины. Тем не менее, фундамент крайне требователен к грунту, ему категорически запрещены подвижки и пучения.
 Ваша программа по алгебре очень помогла ей. Его терпеливые, полные объяснения были почти такими же, как у профессионального репетитора, но гораздо более удобными и, разумеется, менее дорогими.
Ваша программа по алгебре очень помогла ей. Его терпеливые, полные объяснения были почти такими же, как у профессионального репетитора, но гораздо более удобными и, разумеется, менее дорогими.  Вот поисковые фразы, которые сегодняшние поисковики использовали, чтобы найти наш сайт. Сможете ли вы найти среди них свою?
Вот поисковые фразы, которые сегодняшние поисковики использовали, чтобы найти наш сайт. Сможете ли вы найти среди них свою? 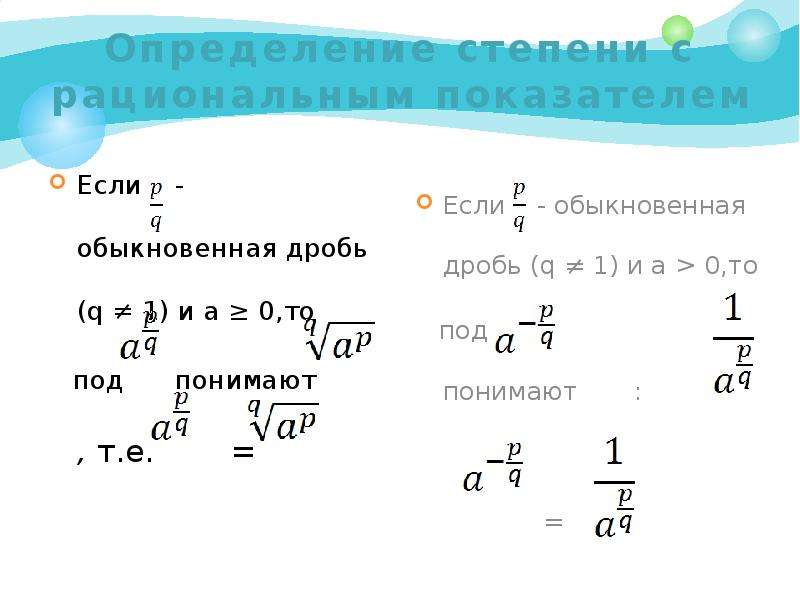
 Просто введите входную дробную экспоненту в поле ввода и нажмите кнопку расчета, чтобы получить упрощенную экспоненту за доли секунд.
Просто введите входную дробную экспоненту в поле ввода и нажмите кнопку расчета, чтобы получить упрощенную экспоненту за доли секунд. Давайте проверим несколько примеров, числитель которых равен 1, и узнаем, как они называются.
Давайте проверим несколько примеров, числитель которых равен 1, и узнаем, как они называются.

 3) = 1/rad64 = 1/8.
3) = 1/rad64 = 1/8.





 Что касаемо икса и игрека, то при подобном положении скобок нужно перемножить степени.
Что касаемо икса и игрека, то при подобном положении скобок нужно перемножить степени. Получается, что число 8 раскладывается, как 2³, а так как у нас степень ещё есть, то получится таким образом: (2³) ⁵. В таком положении степени перемножаются. И теперь можно сделать действия со степенями с одинаковыми основаниями.
Получается, что число 8 раскладывается, как 2³, а так как у нас степень ещё есть, то получится таким образом: (2³) ⁵. В таком положении степени перемножаются. И теперь можно сделать действия со степенями с одинаковыми основаниями.




 Когда числитель и знаменатель имеют разные знаки, частное отрицательно. Если и числитель и знаменатель отрицательны, тогда сама дробь положительна, потому что мы делим отрицательное на отрицательное.
Когда числитель и знаменатель имеют разные знаки, частное отрицательно. Если и числитель и знаменатель отрицательны, тогда сама дробь положительна, потому что мы делим отрицательное на отрицательное. Из перечисленных дробей
Из перечисленных дробей
