Тест. Педагогическая справедливость
Курсы для аттестации учителей 720 ₽ (72 часа). Документы об окончании по почте БЕСПЛАТНО…
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Выбрать материалы
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Пройти тест. Подсчитать свой результат в баллах
Вопрос 1
1 В классе вы назначаете старостой:
Варианты ответов
- а) ученика, который дружит с учителями
- б) ученика, который хорошо учится
- в) ученика с хорошими лидерскими качествами
Вопрос 2
2 Больше всех в классе вы хвалите:
Варианты ответов
- а) тех, кто дружит с учителем, всё им сообщает
- б) тех, кто хорошо учится, у кого высокие результаты
- в) кто очень старается, независимо от результата стараний
Вопрос 3
3 На открытых уроках вы доверите самое ответственное:
Варианты ответов
- а) тому, кто хорошо учится, кто выучит
- б) поработаете дополнительно с двоечниками, чтобы они тоже могли проявить себя
- в) тому, чьи родители хотят видеть своих детей выступающими
Вопрос 4
4 Когда вы отсутствовали, в классе разбили стекло
Варианты ответов
- а) вы поговорите с активом класса тет-а-тет с каждым, они по дружбе с учителем всё расскажут
- б) поговорите с теми, кого подозреваете лично
- в) побудите их самих признаться, расскажете поучительную историю и пообещаете не наказывать виновных
Вопрос 5
5 В классе есть ученик, с которым вы конфликтуете и не можете терпеть его. Вы:
Вы:
Варианты ответов
- а) изживёте его, пока тот не перейдёт в другой класс (школу)
- б) примените строгие меры и исправите его качества, перевоспитаете
- в) будете терпеть дальше, надеясь на лучшее, ища подход к нему
Вопрос 6
6 В учительской рассказывают смешной случай с другим учителем
Варианты ответов
- а) вы смеетесь со всеми
- б) сделаете замечание учителям о недопустимости высмеивания
- в) промолчите, смеяться не будете, постараетесь сменить тему
Вопрос 7
7 Родители считают, что вы ставите любимчикам более высокие отметки:
Варианты ответов
- а) вы не реагируете, пусть думают, что хотят
- б) на родительском собрании постараетесь аргументировать все оценки
- в) пригласите того родителя посмотреть один из уроков
Вопрос 8
Результат тестирования:
А – 0 баллов
Б – 1 балл
В — 3 балла
Варианты ответов
- А – 0 баллов
- Б – 1 балл
- В — 3 балла
Вопрос 9
От 0 до 6 — Вам необходима помощь психолога. Вы не понимаете свои педагогические ошибки. Дети «терпят» Вас, иногда боятся
Вы не понимаете свои педагогические ошибки. Дети «терпят» Вас, иногда боятся
От 7 до 12 – Вы не всегда справедливы в процессе обучения и воспитания. Некоторые свои промахи Вы можете компенсировать пониманием детей, их мотивировки
От 13 до 16 – Вы пример для многих педагогов современности, но вам необходимо совершенствоваться, т.к. мир меняется с каждым днём и Вам нужно успевать за современностью. Старайтесь не спешить действовать и тогда ваши поступки будут более справедливы по отношению к детям
От 17 до 21 – Вы идеально чувствуете все ситуации. У Вас хорошо развито чувство справедливости. Только старайтесь не поучать других педагогов, пусть они сами «вырастут» на вашем молчаливом примере.
Варианты ответов
- От 0 до 6
- От 7 до 12
- От 13 до 16
- От 17 до 21
Вопрос 10
Успехов в работе!
Варианты ответов
- Всегда!
- Иногда.

- Редко.
Пройти тест
Сохранить у себя:
© 2018, Чевокина Елена Анатольевна 500
Шимпанзе оценивают справедливость поступков не хуже людей
https://ria.ru/20130115/918111986.html
Шимпанзе оценивают справедливость поступков не хуже людей
Шимпанзе оценивают справедливость поступков не хуже людей — РИА Новости, 15.01.2013
Шимпанзе оценивают справедливость поступков не хуже людей
Группа психологов под руководством Дарби Проктора из университета штата Джорджия в Атланте (США) научила шимпанзе играть в так называемую игру «ультиматум» — классический психологический тест, который используется для оценки развития чувства справедливости у детей.
2013-01-15T01:33
2013-01-15T01:33
2013-01-15T01:33
/html/head/meta[@name=’og:title’]/@content
/html/head/meta[@name=’og:description’]/@content
https://cdnn21. img.ria.ru/images/sharing/article/918111986.jpg?1358199227
img.ria.ru/images/sharing/article/918111986.jpg?1358199227
сша
америка
весь мир
северная америка
РИА Новости
1
5
4.7
96
7 495 645-6601
ФГУП МИА «Россия сегодня»
https://xn--c1acbl2abdlkab1og.xn--p1ai/awards/
2013
РИА Новости
1
5
4.7
96
7 495 645-6601
ФГУП МИА «Россия сегодня»
https://xn--c1acbl2abdlkab1og.xn--p1ai/awards/
Новости
ru-RU
https://ria.ru/docs/about/copyright.html
https://xn--c1acbl2abdlkab1og.xn--p1ai/
РИА Новости
1
5
4.7
96
7 495 645-6601
ФГУП МИА «Россия сегодня»
https://xn--c1acbl2abdlkab1og.xn--p1ai/awards/
РИА Новости
1
5
4.7
96
7 495 645-6601
ФГУП МИА «Россия сегодня»
https://xn--c1acbl2abdlkab1og. xn--p1ai/awards/
xn--p1ai/awards/
РИА Новости
1
5
4.7
96
7 495 645-6601
ФГУП МИА «Россия сегодня»
https://xn--c1acbl2abdlkab1og.xn--p1ai/awards/
открытия — риа наука, сша
Наука, Открытия — РИА Наука, США, Америка, Весь мир, Северная Америка
МОСКВА, 15 янв — РИА Новости. Психологи научили шимпанзе играть в простейшую экономическую игру, которая продемонстрировала, что эти приматы умеют оценивать щедрость и справедливость своих сородичей, что ранее считалось одним из уникальных качеств человека, говорится в статье, опубликованной в журнале Proceedings of the National Academy of Sciences.
«До нашего исследования никто не верил, что мы можем играть в «ультиматум» (экономическую игру) с животными, так как приматы будут все время поступать самым эгоистичным образом. Мы выяснили, что шимпанзе не только обладают чувством справедливости, но и очень близки в этом отношение к аналогичному качеству человека», — заявил один из авторов статьи Франс де Вааль (Frans de Waal) из университета Эмори в Атланте (США).
Группа психологов под руководством Дарби Проктора (Darby Proctor) из университета штата Джорджия в Атланте (США) научила шимпанзе (Pan troglodytes) играть в так называемую игру «ультиматум» — классический психологический тест, который используется для оценки развития чувства справедливости у детей.
В этой игре участвуют два игрока, исполняющие две разных роли. Экспериментаторы выдают первому из них небольшое количество еды или денег, и спрашивают, какую часть из них он готов отдать партнеру. В том случае, если второй участник не доволен решением своего товарища, он вправе отказаться от дележки «подарка» и тогда оба игрока остаются ни с чем.
Проктор и его коллеги проверили, смогут ли шимпанзе освоить эту игру, и как они себя поведут при «честном» и «нечестном» делении подарков. Параллельно ученые провели аналогичный эксперимент, участие в котором приняло два десятка детей в возрасте от 2 до 7 лет. В качестве призов ученые выдавали обезьянам кусочки еды или сок, а детям — цветные наклейки.
Авторы статьи несколько упростили игру, сделав ее доступной для понимания приматов и маленьких детей. Вместо денег или еды ученые позволяли первому участнику выбрать одну из двух пластиковых игрушек, одна из которых соответствовала равному разделению подарков, а вторая — «нечестному». Обезьяна или ребенок должны были передать ее второму участнику, который либо обменивал ее на еду или наклейки у экспериментаторов, или отказывался от обмена.
К удивлению Проктора и его коллег, обезьяны не хуже детей распознавали несправедливость и отказывались принимать «недостойный» дар.
Первоначально, практически все шимпанзе выбрали «нечестный» вариант раздела подарка, однако серия отказов со стороны их партнеров в соседней клетке заставила их делить добычу пополам. В целом, обезьяны выбирали «честную» дележку более чем в 50% случаев, что сопоставимо с результатами, которые показывают взрослые люди в этой игре.
Таким образом, авторам статьи удалось показать, что шимпанзе умеют оценивать справедливость поступков окружающих их сородичей не хуже, чем это делает человек.
Диким шимпанзе часто приходится вступать в союзы друг с другом для защиты территории племени от других обезьян или поиска пищи. Данный факт мог послужить причиной развития способности к оценке поступков своих соплеменников в ходе эволюции предков шимпанзе или общего предка людей и наших ближайших родичей, заключают ученые.
Оценка справедливости моделей ML в Python (предварительная версия) — Azure Machine Learning
Twitter LinkedIn Facebook Адрес электронной почты
- Статья
- Чтение занимает 7 мин
ОБЛАСТЬ ПРИМЕНЕНИЯ:Пакет SDK для Python для ML Azure версии 1
В этом руководство вы узнаете, как использовать пакет Python Fairlearn с открытым кодом вместе с Машинным обучением Azure для выполнения следующих задач.
- Оценка справедливости прогнозов модели. Дополнительные сведения о справедливости в машинном обучении см. в статье о справедливости в машинном обучении.
- Отправка, перечисление и загрузка аналитических сведений об оценке справедливости в Студию машинного обучения Azure и из нее.
- Просмотр панели мониторинга оценки справедливости в Студии машинного обучения Azure для работы с аналитическими сведениями о справедливости моделей.
Примечание
Оценка справедливости не является чисто технической задачей. Этот пакет поможет вам оценивать справедливость модели машинного обучения, но только вы можете настраивать работу модели и принимать решения о ее работе. Хотя этот пакет помогает определить количественные метрики для оценки справедливости, разработчики моделей машинного обучения должны также выполнять качественный анализ, чтобы оценить справедливость собственных моделей.
Пакет SDK для оценки справедливости Машинного обучения Azure
Пакет SDK для оценки справедливости Машинного обучения Azure azureml-contrib-fairness интегрирует пакет Python Fairlearn с открытым кодом с Машинным обучением Azure. Чтобы узнать больше об интеграции Fairlearn с Машинным обучением Azure, ознакомьтесь с этими примерами записных книжек. Дополнительные сведения о Fairlearn см. в руководстве по примерам и в примерах записных книжек.
Чтобы узнать больше об интеграции Fairlearn с Машинным обучением Azure, ознакомьтесь с этими примерами записных книжек. Дополнительные сведения о Fairlearn см. в руководстве по примерам и в примерах записных книжек.
Для установки пакетов azureml-contrib-fairness и fairlearn используйте следующие команды:
pip install azureml-contrib-fairness pip install fairlearn==0.4.6
Более поздние версии Fairlearn также должны работать в следующем примере кода.
В следующем примере показано, как использовать пакет для оценки справедливости. Мы отправим аналитические сведения о справедливости модели в Машинное обучение Azure и просмотрим панель мониторинга оценки справедливости в Студии машинного обучения Azure.
Обучите пример модели в локальной записной книжке Jupyter Notebook.
В качестве набора данных используется известный набор данных переписи взрослых, который мы получаем из OpenML. Мы разыгрываем ситуацию принятия решения о кредите, в которой есть проблема с меткой, указывающей, погасил ли претендент предыдущий кредит.
 Мы обучим модель предсказывать, выплатят ли кредит люди, ранее не попадавшие в поле зрения. Такую модель можно использовать для принятия решений о кредитах.
Мы обучим модель предсказывать, выплатят ли кредит люди, ранее не попадавшие в поле зрения. Такую модель можно использовать для принятия решений о кредитах.import copy import numpy as np import pandas as pd from sklearn.compose import ColumnTransformer from sklearn.datasets import fetch_openml from sklearn.impute import SimpleImputer from sklearn.linear_model import LogisticRegression from sklearn.model_selection import train_test_split from sklearn.preprocessing import StandardScaler, OneHotEncoder from sklearn.compose import make_column_selector as selector from sklearn.pipeline import Pipeline from raiwidgets import FairnessDashboard # Load the census dataset data = fetch_openml(data_id=1590, as_frame=True) X_raw = data.data y = (data.target == ">50K") * 1 # (Optional) Separate the "sex" and "race" sensitive features out and drop them from the main data prior to training your model X_raw = data.data y = (data.target == ">50K") * 1 A = X_raw[["race", "sex"]] X = X_raw.
 drop(labels=['sex', 'race'],axis = 1)
# Split the data in "train" and "test" sets
(X_train, X_test, y_train, y_test, A_train, A_test) = train_test_split(
X_raw, y, A, test_size=0.3, random_state=12345, stratify=y
)
# Ensure indices are aligned between X, y and A,
# after all the slicing and splitting of DataFrames
# and Series
X_train = X_train.reset_index(drop=True)
X_test = X_test.reset_index(drop=True)
y_train = y_train.reset_index(drop=True)
y_test = y_test.reset_index(drop=True)
A_train = A_train.reset_index(drop=True)
A_test = A_test.reset_index(drop=True)
# Define a processing pipeline. This happens after the split to avoid data leakage
numeric_transformer = Pipeline(
steps=[
("impute", SimpleImputer()),
("scaler", StandardScaler()),
]
)
categorical_transformer = Pipeline(
[
("impute", SimpleImputer(strategy="most_frequent")),
("ohe", OneHotEncoder(handle_unknown="ignore")),
]
)
preprocessor = ColumnTransformer(
transformers=[
("num", numeric_transformer, selector(dtype_exclude="category")),
("cat", categorical_transformer, selector(dtype_include="category")),
]
)
# Put an estimator onto the end of the pipeline
lr_predictor = Pipeline(
steps=[
("preprocessor", copy.
drop(labels=['sex', 'race'],axis = 1)
# Split the data in "train" and "test" sets
(X_train, X_test, y_train, y_test, A_train, A_test) = train_test_split(
X_raw, y, A, test_size=0.3, random_state=12345, stratify=y
)
# Ensure indices are aligned between X, y and A,
# after all the slicing and splitting of DataFrames
# and Series
X_train = X_train.reset_index(drop=True)
X_test = X_test.reset_index(drop=True)
y_train = y_train.reset_index(drop=True)
y_test = y_test.reset_index(drop=True)
A_train = A_train.reset_index(drop=True)
A_test = A_test.reset_index(drop=True)
# Define a processing pipeline. This happens after the split to avoid data leakage
numeric_transformer = Pipeline(
steps=[
("impute", SimpleImputer()),
("scaler", StandardScaler()),
]
)
categorical_transformer = Pipeline(
[
("impute", SimpleImputer(strategy="most_frequent")),
("ohe", OneHotEncoder(handle_unknown="ignore")),
]
)
preprocessor = ColumnTransformer(
transformers=[
("num", numeric_transformer, selector(dtype_exclude="category")),
("cat", categorical_transformer, selector(dtype_include="category")),
]
)
# Put an estimator onto the end of the pipeline
lr_predictor = Pipeline(
steps=[
("preprocessor", copy. deepcopy(preprocessor)),
(
"classifier",
LogisticRegression(solver="liblinear", fit_intercept=True),
),
]
)
# Train the model on the test data
lr_predictor.fit(X_train, y_train)
# (Optional) View this model in the fairness dashboard, and see the disparities which appear:
from raiwidgets import FairnessDashboard
FairnessDashboard(sensitive_features=A_test,
y_true=y_test,
y_pred={"lr_model": lr_predictor.predict(X_test)})
deepcopy(preprocessor)),
(
"classifier",
LogisticRegression(solver="liblinear", fit_intercept=True),
),
]
)
# Train the model on the test data
lr_predictor.fit(X_train, y_train)
# (Optional) View this model in the fairness dashboard, and see the disparities which appear:
from raiwidgets import FairnessDashboard
FairnessDashboard(sensitive_features=A_test,
y_true=y_test,
y_pred={"lr_model": lr_predictor.predict(X_test)})
Войдите в Машинное обучение Azure и зарегистрируйте модель.
Панель мониторинга справедливости может интегрироваться с зарегистрированными или незарегистрированными моделями. Зарегистрируйте свою модель в Машинном обучении Azure с помощью следующих действий:
from azureml.core import Workspace, Experiment, Model import joblib import os ws = Workspace.from_config() ws.get_details() os.makedirs('models', exist_ok=True) # Function to register models into Azure Machine Learning def register_model(name, model): print("Registering ", name) model_path = "models/{0}. pkl".format(name)
joblib.dump(value=model, filename=model_path)
registered_model = Model.register(model_path=model_path,
model_name=name,
workspace=ws)
print("Registered ", registered_model.id)
return registered_model.id
# Call the register_model function
lr_reg_id = register_model("fairness_logistic_regression", lr_predictor)
pkl".format(name)
joblib.dump(value=model, filename=model_path)
registered_model = Model.register(model_path=model_path,
model_name=name,
workspace=ws)
print("Registered ", registered_model.id)
return registered_model.id
# Call the register_model function
lr_reg_id = register_model("fairness_logistic_regression", lr_predictor)
Выполните предварительное вычисление метрик справедливости.
Создайте словарь панели мониторинга с помощью пакета
metricsFairlearn. Метод_create_group_metric_setимеет аргументы, аналогичные конструктору панели мониторинга, за исключением того, что конфиденциальные функции передаются в виде словаря (чтобы обеспечить доступность имен). При вызове этого метода необходимо также указать тип прогноза (в данном случае это двоичная классификация).# Create a dictionary of model(s) you want to assess for fairness sf = { 'Race': A_test. race, 'Sex': A_test.sex}
ys_pred = { lr_reg_id:lr_predictor.predict(X_test) }
from fairlearn.metrics._group_metric_set import _create_group_metric_set
dash_dict = _create_group_metric_set(y_true=y_test,
predictions=ys_pred,
sensitive_features=sf,
prediction_type='binary_classification')
race, 'Sex': A_test.sex}
ys_pred = { lr_reg_id:lr_predictor.predict(X_test) }
from fairlearn.metrics._group_metric_set import _create_group_metric_set
dash_dict = _create_group_metric_set(y_true=y_test,
predictions=ys_pred,
sensitive_features=sf,
prediction_type='binary_classification')
Отправьте предварительно вычисленные метрики справедливости.
Теперь импортируйте пакет
azureml.contrib.fairness, чтобы выполнить отправку:from azureml.contrib.fairness import upload_dashboard_dictionary, download_dashboard_by_upload_id
Создайте эксперимент, затем запуск, и отправьте панель мониторинга:
exp = Experiment(ws, "Test_Fairness_Census_Demo") print(exp) run = exp.start_logging() # Upload the dashboard to Azure Machine Learning try: dashboard_title = "Fairness insights of Logistic Regression Classifier" # Set validate_model_ids parameter of upload_dashboard_dictionary to False if you have not registered your model(s) upload_id = upload_dashboard_dictionary(run, dash_dict, dashboard_name=dashboard_title) print("\nUploaded to id: {0}\n". format(upload_id))
# To test the dashboard, you can download it back and ensure it contains the right information
downloaded_dict = download_dashboard_by_upload_id(run, upload_id)
finally:
run.complete()
format(upload_id))
# To test the dashboard, you can download it back and ensure it contains the right information
downloaded_dict = download_dashboard_by_upload_id(run, upload_id)
finally:
run.complete()
Проверка панели мониторинга справедливости в Студии машинного обучения Azure
Если вы выполните предыдущие действия (отправку созданной аналитики справедливости в Машинное обучение Azure), то сможете просматривать панель мониторинга справедливости в Студии машинного обучения Azure. Эта панель мониторинга — та же панель визуализации, предоставляемая в Fairlearn, которая позволяет анализировать различия между подгруппами признаков, требующих особого обращения (например, между мужчинами и женщинами). Для доступа к панели мониторинга визуализации в Студии машинного обучения Azure используйте один из указанных ниже путей.
- Панель заданий (предварительная версия)
- Выберите Задания на панели слева, чтобы просмотреть список экспериментов, которые были выполнены в Машинном обучении Azure.

- Выберите конкретный эксперимент, чтобы просмотреть все запуски в этом эксперименте.
- Выберите запуск, а затем перейдите на вкладку Fairness (Справедливость), чтобы открыть панель мониторинга визуализации пояснения.
- После перехода на вкладку Fairness (Справедливость) щелкните идентификатор справедливости в меню справа.
- Настройте панель мониторинга, выбрав атрибут конфиденциальности, метрику производительности и метрику справедливости, чтобы попасть на страницу оценки справедливости.
- Переключайтесь с одного типа диаграммы на другой, чтобы наблюдать за негативными эффектами распределения и негативными эффектами качества обслуживания.
- Панель моделей
- Если вы зарегистрировали исходную модель, выполнив предыдущие действия, то можете выбрать пункт Models в левой области, чтобы просмотреть свою модель.

- Выберите модель, а затем откройте вкладку Fairness (Справедливость), чтобы просмотреть панель мониторинга визуализации пояснения.
Дополнительные сведения о панели мониторинга визуализации и содержащихся в ней элементах см. в руководстве пользователя Fairlearn.
Отправка аналитических сведений о справедливости для нескольких моделей
Чтобы сравнить несколько моделей и увидеть, как различаются их оценки справедливости, можно передать на панель мониторинга визуализации несколько моделей и сравнить их компромиссы между эффективностью и справедливостью.
Обучите свои модели.
Теперь мы создадим второй классификатор на основе оценщика, использующего метод опорных векторов, и отправим словарь панели мониторинга справедливости с помощью пакета
metricsFairlearn. Предполагается, что ранее обученная модель по-прежнему доступна.# Put an SVM predictor onto the preprocessing pipeline from sklearn import svm svm_predictor = Pipeline( steps=[ ("preprocessor", copy. deepcopy(preprocessor)),
(
"classifier",
svm.SVC(),
),
]
)
# Train your second classification model
svm_predictor.fit(X_train, y_train)
deepcopy(preprocessor)),
(
"classifier",
svm.SVC(),
),
]
)
# Train your second classification model
svm_predictor.fit(X_train, y_train)
Зарегистрируйте модели
Теперь зарегистрируйте обе модели в Машинном обучении Azure. Для удобства сохраните результаты в словаре, который сопоставляет
idзарегистрированной модели (строку в форматеname:version) с самим прогнозом:model_dict = {} lr_reg_id = register_model("fairness_logistic_regression", lr_predictor) model_dict[lr_reg_id] = lr_predictor svm_reg_id = register_model("fairness_svm", svm_predictor) model_dict[svm_reg_id] = svm_predictorЛокальная загрузка панели мониторинга Fairness
Перед отправкой аналитических сведений о справедливости в Машинное обучение Azure можно проверить эти прогнозы в панели мониторинга Fairness, вызванной локально.
# Generate models' predictions and load the fairness dashboard locally ys_pred = {} for n, p in model_dict. items():
ys_pred[n] = p.predict(X_test)
from raiwidgets import FairnessDashboard
FairnessDashboard(sensitive_features=A_test,
y_true=y_test.tolist(),
y_pred=ys_pred)
items():
ys_pred[n] = p.predict(X_test)
from raiwidgets import FairnessDashboard
FairnessDashboard(sensitive_features=A_test,
y_true=y_test.tolist(),
y_pred=ys_pred)
Выполните предварительное вычисление метрик справедливости.
Создайте словарь панели мониторинга с помощью пакета
metricsFairlearn.sf = { 'Race': A_test.race, 'Sex': A_test.sex } from fairlearn.metrics._group_metric_set import _create_group_metric_set dash_dict = _create_group_metric_set(y_true=Y_test, predictions=ys_pred, sensitive_features=sf, prediction_type='binary_classification')Отправьте предварительно вычисленные метрики справедливости.
Теперь импортируйте пакет
azureml.contrib.fairness, чтобы выполнить отправку:from azureml.contrib.fairness import upload_dashboard_dictionary, download_dashboard_by_upload_id
Создайте эксперимент, затем запуск, и отправьте панель мониторинга:
exp = Experiment(ws, "Compare_Two_Models_Fairness_Census_Demo") print(exp) run = exp.
 start_logging()
# Upload the dashboard to Azure Machine Learning
try:
dashboard_title = "Fairness Assessment of Logistic Regression and SVM Classifiers"
# Set validate_model_ids parameter of upload_dashboard_dictionary to False if you have not registered your model(s)
upload_id = upload_dashboard_dictionary(run,
dash_dict,
dashboard_name=dashboard_title)
print("\nUploaded to id: {0}\n".format(upload_id))
# To test the dashboard, you can download it back and ensure it contains the right information
downloaded_dict = download_dashboard_by_upload_id(run, upload_id)
finally:
run.complete()
start_logging()
# Upload the dashboard to Azure Machine Learning
try:
dashboard_title = "Fairness Assessment of Logistic Regression and SVM Classifiers"
# Set validate_model_ids parameter of upload_dashboard_dictionary to False if you have not registered your model(s)
upload_id = upload_dashboard_dictionary(run,
dash_dict,
dashboard_name=dashboard_title)
print("\nUploaded to id: {0}\n".format(upload_id))
# To test the dashboard, you can download it back and ensure it contains the right information
downloaded_dict = download_dashboard_by_upload_id(run, upload_id)
finally:
run.complete()
Как и в предыдущем разделе, вы можете следовать одному из описанных выше путей (используя эксперименты или модели) в Студии машинного обучения Azure, чтобы получить доступ к панели мониторинга визуализации и сравнить две модели с точки зрения справедливости и эффективности.

Отправка исходных и смягченных аналитических сведений о справедливости
Вы можете использовать алгоритмы смягчения Fairlearn, сравнивать созданные ими смягченные модели с исходной моделью без смягчения и таким образом выбрать компромисс между эффективностью и справедливостью среди сравниваемых моделей.
Пример, демонстрирующий использование алгоритма смягчения Grid Search (поиск по сетке), который создает коллекцию смягчаемых моделей с разными компромиссами между справедливостью и эффективностью, см. в этом примере записной книжки.
Отправка аналитических сведений о справедливости нескольких моделей в один запуск позволяет сравнивать модели с точки зрения справедливости и эффективности. Вы можете щелкнуть любую из моделей, отображаемых на диаграмме сравнения моделей, чтобы просмотреть подробные сведения о справедливости этой конкретной модели.
Дальнейшие действия
Узнайте больше о справедливости моделей
Ознакомьтесь с примерами записных книжек Azure Machine Learning Fairness
IQ-тест — Все об IQ-тестах
Аббревиатура
IQ используется для обозначения
умственного коэффициента,
который представляет собой способ измерения
интеллекта
человека. Шкала IQ
начинается с нуля и не имеет верхней границы, при этом максимально зарегистрированный
уровень IQ составляет около 300 единиц. Средний IQ составляет 100 баллов,
при этом большая часть тестов просто не может оценить знания людей с уровнем
IQ 170 и выше, которые относятся к гениальным людям и требуют особых методик оценки.
Шкала IQ
начинается с нуля и не имеет верхней границы, при этом максимально зарегистрированный
уровень IQ составляет около 300 единиц. Средний IQ составляет 100 баллов,
при этом большая часть тестов просто не может оценить знания людей с уровнем
IQ 170 и выше, которые относятся к гениальным людям и требуют особых методик оценки.
Что измеряет тест IQ?
Все очень просто — интеллект. Интеллект и IQ — это не то же самое, что «отменные знания», а больше относятся к умению решать проблемы и использовать логику. Таким образом, люди, которые спрашивают «Какой IQ у собаки?» просто говорят бессмыслицу. Интеллект собаки невозможно оценить теми же способами, что и интеллект человека.
Как высоко вы оцениваете справедливость ваших тестов?
Некоторые факторы определенно влияют на уровнь справедливости IQ-тестов. Учитывая то, что человека нельзя сравнивать животным, полученные знания
и культурные особенности не должны влиять на результаты IQ-теста.
Проще говоря, англоговорящий человек, принимающий участие в тесте на
английском языке, может набрать 120 баллов. В тех же самых условиях,
проходя тест на французском, он может набрать всего 10 баллов.
Такой человек сможет показать более высокий результат, если он или
она изучал французский, однако, это не будет иметь никакого отношения к интеллекту.
Учитывая то, что человека нельзя сравнивать животным, полученные знания
и культурные особенности не должны влиять на результаты IQ-теста.
Проще говоря, англоговорящий человек, принимающий участие в тесте на
английском языке, может набрать 120 баллов. В тех же самых условиях,
проходя тест на французском, он может набрать всего 10 баллов.
Такой человек сможет показать более высокий результат, если он или
она изучал французский, однако, это не будет иметь никакого отношения к интеллекту.
Таким образом, IQ-тесты должны использовать специальный формат, обеспечивающий их нейтральность. Использование абстрактных изображений и ограниченного количества цветов (чтобы избежать проблем с воприятием цветов) является наиболее точным решением из всех существующих.
История IQ-тестов
Люди всегда интересовались возможностью измерения уровня собственного интеллекта,
но до 1904 года попросту не существовало системы, которая позволяла бы реализовать
задуманное на практике. Британский психолог
Чарльз Спирман
сделал открытие, согласно которому была
обнаружена связь
между определенными когнитивными навыками.
Британский психолог
Чарльз Спирман
сделал открытие, согласно которому была
обнаружена связь
между определенными когнитивными навыками.
Сам термин IQ был предложен другим психологом, Уильямом Штерном, который пытался сравнить физический возраст человека с возрастом его умственного развития. В настоящее время используется совершенно другая методика, однако название остается прежним.
В начале 40-х годов теория общего интеллекта была доработана психологом
Рэймондом Кэттелом,
который ввел такие термины, как подвижный и кристаллический интеллект, которые стали
составными частями общего интеллекта. При этом, IQ-тест уделяет внимание подвижному интеллекту,
навыкам решения задач и аналитическим способностям человека. Вы можете получить более
подробную информацию в разделе
Что такое интеллект?.
Очевидно, что даже до появления современных IQ-тестов люди активно пытались разделить общество на категории в зависимости от уровня знаний. Одним из наиболее успешных решений стал тест Бине-Саймона, который был разработан Альфредом Бине и Теодором Саймоном в 1905 году, и уделял основное внимание вербальным способностям человека.
В период Первой мировой войны Роберт Йеркс сотрудничал с армией США в рамках проведения письменных и невербальных тестов, направленных на оценку интеллекта человека, а не знаний.
В 1939 году
Давид Векслер
создал тест, который состоял из большого количества разделов и позволял получить более
точную оценку, чем отдельные тесты, которые использовались ранее. К началу 60-х годов
тест Векслера стал наиболее популярным IQ-тестом в США и остается таким по сей день.
Дальнейшие исследования привели к обнаружению дополнительных видов интеллекта, включая навыки аудиовизуальной обработки полученных данных и обоснования действий и решений.
IQ-тесты онлайн
Многие IQ-тесты в сети построены на работе Давида Векслера, благодаря чему они позволяют получить всестороннюю оценку интеллекта человека.
Результаты IQ-тестов
Основная задача любого IQ-теста — оценить уровень вашего интеллекта. Результаты IQ-теста могут выражаться как в числовом формате (ваш IQ), цифровом диапазоне (от 100 до 110), наименовании диапазона (средний интеллект) или количества правильных ответов в процентном соотношении к количеству заданных вопросов.
IQ-тесты для детей
Существует множество разговоров о том, что IQ-тесты не работают для людей,
которым еще не исполнилось 16 лет. Даже несмотря на то, что в сети существует
много IQ-тестов для детей, они могут не быть такими же точными и надежными,
как IQ-тесты для взрослых.
Даже несмотря на то, что в сети существует
много IQ-тестов для детей, они могут не быть такими же точными и надежными,
как IQ-тесты для взрослых.
Существуют подтверждения того, что IQ ребенка в возрасте 5-7 лет практически не совпадает с IQ человека, которому исполнилось 17-18 лет. При этом, IQ ребенка в возрасте от 11 до 13 лет ближе к реальному IQ взрослого человека. Другими словами, по мере роста ребенка, он развивает важнейшие навыки и интеллект. Чем моложе ваш ребенок, тем ниже шансы на успешное прохождение IQ-теста.
Бесплатные IQ-тесты
Можно ли полагаться на IQ-тест, особенно если он доступен совершенно бесплатно?
Да, конечно же. Как было сказано выше, IQ-тесты для тех, кому не исполнилось 16 лет,
стоит воспринимать с долей скептицизма. Однако после достижения указанного
возраста результаты онлайн-тестов будут максимально приближены к результатам
классических тестов под чутким контролем медицинских работников.
Кроме того, при проведении тестирования важно учитывать его культурную нейтральность, которая позволяет не учитывать специфические знания человека, ведь тест призван оценить интеллект, а не знания. Каждый человек может прочитать что-то важное, но это не будет признаком интеллекта.
Что представляет собой средний IQ?
Средний IQ всегда равен 100 вне зависимости от условий. Чем больше людей проходят IQ-тестирование, тем выше или ниже становится средний показатель, что приводит к измнению уровня IQ людей, которые уже прошли тест ранее.
Как работает система расчета IQ?
Например, предположим, что три человека прошли IQ-тест и получили 50%, 75% и 100%. Средний результат — 75%. Таким образом, любой человек, получивший 75%, является обладаетем IQ 100.
При этом, если еще 10 человек наберут менее 50%, средний уровень IQ упадет к 50%,
например, составит 57%. Следующий человек, который наберет 60%, получит IQ выше 100.
Следующий человек, который наберет 60%, получит IQ выше 100.
Это вызвано падением среднего уровня IQ, в результате которого IQ 100 составляет около 57%. Учитывая то, что результат IQ зависит от общего уровня умственных способностей, можно смело говорить о том, что, чем больше людей принимает участие в тестировании, тем точнее будет результат IQ-теста.
Какие диапазоны используются в IQ-тестах?
Исходя из вышеизложенного, IQ в пределах от 90 до 109 считается нормальным. IQ ниже 70 может считаться легкой формой слабоумия, а IQ в пределах от 130 до 139 свидетельствует об одаренности.
IQ выше 140 является свидетельством гениальности, и лишь немногие могут попасть
в этот диапазон. То же самое касается и тех, у кого IQ составляет менее 50.
Именно поэтому система средних величин подходит для IQ-тестов как нельзя лучше.
Более подробная информация представлена в разделе Определение.
Какой IQ-тест стоит выбрать?
В сети представлено большое количество тестов, но мы настоятельно рекомендуем пройти Международный IQ-тест. Тест был разработан опытным врачом для тех, кому исполнилось 16 лет, а также является полностью культурно нейтральным. Кроме того, он позволяет принимать участие в тестировании людям, страдающим от проблем с восприятием цветов, поэтому способность воспринимать цвета не является критичной для участия в нашем тесте.
Многие люди слышали о тесте от Mensa и хотят стать участниками этого международного движения. Стоит отметить, что наш тест не позволяет получить членство в Mensa, однако дает реальную оценку ваших шансов на успешное прохождение тестов от Mensa.
IQ-тест от Mensa
Тест Mensa по праву считается одним из самых серьезных в мире. После прохождения теста
вы сможете узнать свой IQ, при этом для успешного прохождения требуется IQ не менее
140 баллов.
После прохождения теста
вы сможете узнать свой IQ, при этом для успешного прохождения требуется IQ не менее
140 баллов.
Более подробная информация о тесте Mensa представлена в нашей статье Тестирование IQ от Mensa.
Ограничения теста от Mensa
На самом деле, для прохождение теста вам нужно оказаться успешнее, чем 98% жителей нашей планеты, поэтому только 2 из 100 могут рассчитывать на успех. Вы не можете делать бесчисленные попытки. У вас будет всего 2 шанса стать участником элитного сообщества Mensa.
Более подробная информация представлена в статье Ограничения IQ-теста от Mensa.
Как подготовиться к прохождению тестирования Mensa
Подготовка является залогом успеха многих вещей и тестирование Mensa не
станет исключением. Вы должны соблюдать правильную диету, которая позволит
улучшить как физическое, так и эмоциональное состояние, которые неразрывно
связаны.
Одним из лучших вариантов подготовки является использование других тестов на определение уровня интеллекта. Это поможет вам привыкнуть к формату проведения тестирования, а также даст возможность понять текущий уровень вашего IQ. Если ваш результат значительно ниже 140 баллов, вам стоит хорошенько потренироваться, прежде чем решиться на этот важный шаг.
Может ли IQ изменяться?
Да, и это может не зависеть от вас. Несмотря на то, что постоянные тренировки повышают общий уровень вашего интеллекта, IQ рассчитывается на основе результатов всех людей, которые принимают участие в тестировании. Как только большая часть людей станет показывать низкий результат, общий IQ станет ниже, и IQ 100 сместится вниз. Таким образом, ваш IQ вырастет по отношению к другим людям.
Тем не менее, это не должно влиять на то, как вы собираетесь готовиться
к прохождению теста Mensa. Чем больше вы тренируетесь перед прохождением теста,
тем лучше. Вы можете найти более подробную информацию о подходах
к тестирования в статье
Как подготовиться к тесту от Mensa.
Чем больше вы тренируетесь перед прохождением теста,
тем лучше. Вы можете найти более подробную информацию о подходах
к тестирования в статье
Как подготовиться к тесту от Mensa.
Эффект Флинна
С момента появления первого варианта IQ-теста методики тестирования умственных способностей постоянно совершентсвуются. Именно поэтому производится постоянный перерасчет среднего IQ, что приводит к относительному повышению отметки в 100 баллов.
При отсутствии подобных мер, начиная с 1920 года общий уровень IQ вырос бы примерно на 3 пункта за каждые десять лет. Многочисленные исследования подтверждают, что это вызвано не генетикой, а развитием окружающей нас среды.
Такие изменение IQ с течением времени получило название эффекта Флинна после того, как
Джеймс Флинн,
автор книги «Кривая Белла» обнаружил этот удивительный феномен.
На протяжении последних десятилетий на территории стран Запада был отмечен эффект, обратный тому, что обнаружил Флинн, и причины вновь скрываются в окружающей нас среде.
3 гения с самым высоким IQ
История человечества знает множество гениев, многие из которых более известны, чем остальные. В первую очередь мы всегда вспоминаем таких ученых, как Альберт Эйнштейн и Исаак Ньютон, однако гении встречаются и в других отраслях. Мы хотим рассказать вам еще о трех гениях, о которых вы могли слышать.
Леонардо Да Винчи
Леонардо Да Винчи родился в Италии в 1452 году. Он был переполнен талантами и новыми идеями, а также постоянно хотел узнать и окрыть что-то новое. Считает, что Леонардо Да Винчи обладал IQ около 220 баллов.
Он написал такие шедевры, как «Мона Лиза» и «Последний ужин», а также сделал
множество изображений в сфере человеческой анатомии, и разработал чертежи
роботов и военных машин, не говоря уже о парашютах и мостах. Многие из его творений являются технически совершенными даже сегодня,
хотя он придумал их более 500 лет назад!
Многие из его творений являются технически совершенными даже сегодня,
хотя он придумал их более 500 лет назад!
Стивен Хокинг
Даже несмотря на то, что его IQ оценивается в более чем 160 баллов, доподлинно неизвестно, проходил ли Стивен Хокинг тестирование хоть раз в своей жизни. Тем не менее, перед своей смертью в марте 2018 года Стивен Хокинг не раз доказывал, что его мозг способен анализировать и решать проблемы любого масштаба и природы.
Несмотря на то, что его тело поразил боковой амиотрофический склероз, Стивен Хокинг
сделал множество открытий в сфере радиационного формирования черных дыр, о которых
не было известно абсолютно ничего. Дальнейшие исследования в области квантовой физики
позволили получить данные, на которых строится наше представление о вселенной.
Он сделал больше, чем Эйнштейн для физики.
Гарри Каспаров
Said to have an IQ of 190, Гарри Каспаров обладает IQ в более чем 190 баллов и прославился тем, что стал чемпионом мира по шахматам. Его аналитический ум сделал его страшным противником и ужасным оппонентом для любого шахматиста. Он получил звание чемпиона в 1984 году и стал самым молодым игроком, получившим такой титул.
После этого он занялся политикой и активно использует свои навыки для решения самых насущных проблем человечества.
3 вещи, которые нужно знать об IQ-тесте
1. Ваш IQ не говорит о том, кем вы являетесь
Ваша работоспособность, умение быть родителем и способность дружить
не зависят от IQ. Ваш IQ — это качественная оценка вашего умения решать
головоломки и задачи в сравнении с остальным населением.
IQ — это оценка вашего интеллекта, но не более того.
2. Вы можете улучшить результаты IQ-теста
Если вы уже прошли тестирование и расстроены его результатом, вы должны использовать продуманный подход к следующему тестированию. Соблюдайте диету, не нарушайте качество сна и активно тренируйтесь. Все, что вы сделаете, чтобы укрепить ваш интеллект, поможет увеличить уровень вашего IQ.
3. Вопросы IQ-тестов должны быть сложными
Тот факт, что вы не смогли ответить на один или несколько вопросов IQ-теста, не означает, что тест слишком сложный. Он создан быть сложным для оценки вашего интеллекта. Каждый бы мог стать гением, если бы вопросы были очень легкими.
Зачем проходить IQ-тест?
Каждый человек хочет развиваться и менять свою жизнь. Зная свой IQ, вы можете определить начальную точку своего развития, к тому же IQ-тесты могут быть просто отличным способом отдохнуть и повеселиться! Так чего же вы ждете? Пройдите ваш первый IQ-тест прямо сейчас!
Хотите узнать свой IQ?
ПРОЙДИТЕ НАШ БЕСПЛАТНЫЙ
IQ-ТЕСТ УЖЕ СЕГОДНЯ! →
Фарма и карма Камилы Валиевой: casus belli или вынужденная справедливость?
За каждой подставой ребенка стоят взрослые — и это то, о чем нужно помнить, несмотря на пока что положительное решение по делу Камилы Валиевой. Фигуристка допущена до личных соревнований, CAS отклонил протесты ISU и МОК. Но праздновать рано. Вопросы и проблемы остаются.
Фигуристка допущена до личных соревнований, CAS отклонил протесты ISU и МОК. Но праздновать рано. Вопросы и проблемы остаются.
Аптечка топ-атлета, и с чем ее едят
Чувство отчаяния от этой истории никуда не ушло. Потому что понятно, что это еще не конец, и спортивная «фармацевтика» наших, да и других спортсменов, еще неоднократно будет предметом расследований. Потому что «невинных» лекарств в аптечке атлета не бывает — иначе зачем они? Чтобы просто что-то съесть или уколоть? Абсурд. Тогда зачем?
Понятно, что большой спорт в наше время — это не только талант спортсмена, хороший тренер и нужная система тренировок. Это и то, что называется «пиком формы», на который как раз и должны выводить атлета члены его команды, включающей не только тренеров, хореографов и дизайнеров костюмов, но и врачей, физиотерапевтов и массажистов.
Золото Чена, олово Ханю и «витаминка для сердца» Валиевой: олимпийское фигурное катание подводит первые итогиВсех тех, кто, учитывая сверхнагрузки при подготовке к главным стартам, должен определять способы поддержки организма спортсмена, чей результат часто зависит именно от объема тренировок, выносливости организма и скорости его восстановления. И именно на эти факторы влияют все эти мельдонии-триметадизины и ноунейм-добавки.
И именно на эти факторы влияют все эти мельдонии-триметадизины и ноунейм-добавки.
Потому что бездарных атлетов на высшем уровне просто не бывает — ни у нас, ни у соперников. Отбор там, наверху, настолько жесткий, что топ-двадцатке спортсменов в любом виде спорта можно вешать медали уже за сам факт их лидерства. Это — для тех, кто «из танка» в прямом и переносном смысле пытается увязать талант с национальностью, расой или конкретной страной.
Среди лидеров фигурного катания сегодня есть и азиаты, и европейцы, и американцы. И да, таких гениев от природы, как Юдзуру Ханю или как раз Камила Валиева — единицы, их находят еще в детстве, а дальше — правильный выбор тренера, трудолюбие и… карма. В том числе травмы, болезни, проблемы роста и — обстоятельства. И это далеко не всегда про звезды, ибо «обстоятельства» создаются конкретными живыми людьми.
«Шветский» синдром
То, что уникальную Камилу в олимпийский сезон будут изучать под лупой, было понятно. Поэтому внезапное появление рядом с ней на финском этапе гран-при скандально известного врача Филиппа Шветского, мягко говоря, шокировало. Сразу уточним: Шветский — очень квалифицированный анестезиолог-реаниматолог, кандидат наук, работавший не только в спорте, но и с ковидными больными.
Сразу уточним: Шветский — очень квалифицированный анестезиолог-реаниматолог, кандидат наук, работавший не только в спорте, но и с ковидными больными.
Вот только пятнадцать лет назад, будучи врачом сборной по гребле, именно он взял на себя вину в допинговом скандале с нашими гребцами, что позволило снизить дисквалификацию спортсменов с четырех до двух лет. А сейчас он консультирует фигуристок, и считается, что свою работу выполняет очень качественно.
ЧМ по фигурному катанию: ледовое побоище или ледяное перемирие?Все это, конечно, хорошо, вот только у репутации нет срока годности, особенно если речь идет о фантастических результатах.
Другая проблема человеческого фактора связана с профессионализмом тех, кто отвечает за правильное оформление всех допусков и документов. То, что результат декабрьского допинг-теста был представлен с опозданием, уже обсуждалось. Но почему люди, которые должны были вести «учет и контроль» допинг-тестов, не забили тревогу, получив — достаточно быстро — результаты тестов с январского Чемпионата Европы, но не имея тестов за декабрь?
И могла ли шведская лаборатория придержать их не столько в рамках «спланированной против России» акции на Олимпиаде (как нас пытаются убедить), сколько по чьей-то просьбе с нашей стороны — если допустить, что у нас об этой пробе все же знали, но договорились о ней «забыть»? А затем, как это бывает, что-то пошло не так? В этом случае становится понятно, почему в нашем штабе никто не бил тревогу, но сама «многоходовка» вызывает вопросы, ведь тайное всегда становится явным.
Соломоново решение
И все же, несмотря на все вопросы, решение CAS о допуске Камилы к соревнованиям, можно только приветствовать. Потому что нельзя добиваться чистоты спорта, нарушая правила — а ведь многочисленные антидопинговые структуры призваны прежде всего защищать здоровье спортсменов. И не допускать «грязной игры» — в том числе со стороны спортивных чиновников всех уровней и национальностей.
Потому что речь идет о девочке-подростке, которая является, в соответствии с Всемирным антидопинговым кодексом (WADC), «защищенным лицом», и результаты ее теста не должны были стать достоянием общественности до решения CAS. А получилось, что ее уже обвинили и распяли, и еще неизвестно, как это скажется на ее катании. К тому же, учитывая космический уровень Камилы, всем понятно, что единичная микродоза не могла хоть как-то повлиять на ее результаты — она давно и совершенно недосягаема.
Почему Олимпиада стала состязанием скандаловК тому же, до сих пор внятного объяснения задержке тех самых результатов нет. Слова лаборатории, что РУСАДА не пометило этот тест как приоритетный для обработки до Олимпиады, звучат как детский лепет. Есть оговоренные сроки «в течение 20 дней», а это — до 15 января. К тому времени закончился уже даже Чемпионат Европы, тесты которого были обработаны оперативно. Потом сборная полетела на сборы в Красноярск, где ее списки были утверждены окончательно.
Слова лаборатории, что РУСАДА не пометило этот тест как приоритетный для обработки до Олимпиады, звучат как детский лепет. Есть оговоренные сроки «в течение 20 дней», а это — до 15 января. К тому времени закончился уже даже Чемпионат Европы, тесты которого были обработаны оперативно. Потом сборная полетела на сборы в Красноярск, где ее списки были утверждены окончательно.
И, кстати, что с тестами других девочек, есть ли их результаты — или нас еще ждут сюрпризы?
К тому же вопрос о золоте нашей команды пока не решен, и это тревожно. Вообще то, что «тест в кустах» возник буквально перед награждением, дает сильный аргумент сторонникам теории заговора — ведь на льду победить Камилу без «спецсредств» действительно невозможно.
Не радует и последняя информация о том, что у девушек церемонии награждения не будет даже в виде вручения панд, а к участию в произвольной программе будет дополнительно допущена 25-я участница — словно МОК заранее готовится к аннуляции результатов.
И все же, несмотря ни на что, хочется верить, что казус Валиевой станет уроком и для допинговой инквизиции — чтобы любые нарушения учитывались лишь при соблюдении правил и самими антидопинговыми организациями. Как там говорится на венчании: «Если кому-то есть, что сказать, пусть говорит сейчас — или замолчит навсегда»?
Как там говорится на венчании: «Если кому-то есть, что сказать, пусть говорит сейчас — или замолчит навсегда»?
В противном случае мировой спорт рискует обогатиться новой зимне-летней дисциплиной — гонкой преследования под совсем неолимпийским девизом «поймай меня, если сможешь».
Тамара Иванова-Исаева
ЧУВСТВО СПРАВЕДЛИВОСТИ У ЛЮДЕЙ И ОБЕЗЬЯН
Ричард Грассо, бывший глава Нью-Йоркской фондовой биржи.
В центральном зале Нью-Йоркской биржи.
Обезьянки капуцины согласны работать с экспериментатором, но за справедливую плату.
‹
›
Открыть в полном размере
Осенью 2003 года на Нью-Йоркской фондовой бирже и шире — во всей Америке разразился скандал. Тогда об этом писали и наши газеты. Ричард Грассо, который занимал должности председателя совета директоров биржи и ее главного исполнительно го директора, получил 139,5 миллиона долларов в виде годовой зарплаты, накопившихся пенсионных сбережений и регулярных, а также специальных премий. Например, только за то, что он быстро наладил работу биржи после терактов 11 сентября 2001 года, ему выписали премию в пять миллионов долларов. Новость вызвала такое возмущение публики, что Грассо пришлось подать в отставку и вернуть почти все полученные деньги.
Например, только за то, что он быстро наладил работу биржи после терактов 11 сентября 2001 года, ему выписали премию в пять миллионов долларов. Новость вызвала такое возмущение публики, что Грассо пришлось подать в отставку и вернуть почти все полученные деньги.
Он стал первым в американской истории руководителем крупного предприятия, которого уволили за то, что он слишком много заработал. Ричард Грассо управлял биржей с 1995 года и, по мнению большинства, управлял хорошо. Он не был некомпетентным или коррумпированным руководителем. Но возмущение общественности оказалось столь громким, что через несколько недель совет директоров Нью-Йоркской биржи, то есть те же самые люди, которые начислили ему такую зарплату, вынужден был попросить Грассо подать в отставку.
Общественное мнение Америки не позволило Грассо остаться в должности. Чем же общественность была так возмущена? В конце концов, миллионы Грассо шли не из кармана граждан США, биржа тратила свои собственные деньги, заработанные продажей и покупкой ценных бумаг. Возврат уже полученных денег никого не делал богаче. Биржа не собиралась раздать возвращенные средства каждому гражданину США (каждому пришлось бы по полдоллара) или направить их на благотворительные цели. С экономической точки зрения реакция публики кажется совершенно неразумной. Может быть, это то, что китайцы называют «болезнью красных глаз», — зависть?
Возврат уже полученных денег никого не делал богаче. Биржа не собиралась раздать возвращенные средства каждому гражданину США (каждому пришлось бы по полдоллара) или направить их на благотворительные цели. С экономической точки зрения реакция публики кажется совершенно неразумной. Может быть, это то, что китайцы называют «болезнью красных глаз», — зависть?
Ответить на такой вопрос помогает несложный психологический эксперимент, проводившийся в самых разных странах.
Двум случайно приглашенным с улицы и незнакомым между собой людям предлагают разделить 10 долларов (или соответствующую сумму в валюте той страны, где проводится опыт). Условия следующие: один из участников опыта будет «банкометом», он предложит пропорцию раздела, а другой должен решить, примет он или не примет предложение первого. Если примет, каждый получит долю, назначенную «банкометом», если не примет — оба не получат ничего.
Самая разумная стратегия для обоих — первый возьмет себе 9, а другому предложит 1 доллар. Другой согласится, ведь иначе ему не достанется вообще ничего.
Другой согласится, ведь иначе ему не достанется вообще ничего.
Однако на практике так бывает редко. Предложения ниже двух долларов отвергаются. Выходит, люди согласны не получить за потраченное время ничего, лишь бы партнер не ушел со «слишком жирным», с точки зрения обиженного, кушем, лишь бы наказать незнакомца, которого сочли слишком эгоистичным или жадным. И что любопытно — «банкомет» такое поведение предвидит. Возможно, он понимает, что на месте второго игрока сам действовал бы так же. Поэтому самый частый предлагаемый вариант раздела — пополам.
Выходит, что в этой игре участники выбирают не тот вариант, что им наиболее выгоден, а тот, который дает им нечто нематериальное — удовлетворение чувства справедливости. Причем так происходит везде, в столь разных странах, как США, Россия, Япония и Франция.
Может быть, увеличив стоящую на кону сумму, можно добиться более рационального поведения? Ведь если бы предлагали разделить миллион долларов, вряд ли кто отказался бы получить ни за что ни про что сто тысяч. Однако в таких странах, как Индонезия, где один-два доллара представляют собой неплохой заработок за три рабочих дня, происходит то же самое.
Однако в таких странах, как Индонезия, где один-два доллара представляют собой неплохой заработок за три рабочих дня, происходит то же самое.
Похоже, что в данном эксперименте реализуется модель известной притчи: «Не надо мне второй коровы, хочу, чтобы соседская сдохла!»
И подобным образом действуют не только люди. Случилось так, что ровно в тот день, когда подал в отставку Ричард Грассо, два американских биолога опубликовали результаты своих опытов с обезьянами капуцинами.
Их научили давать экспериментатору камешки в обмен на пищу. За камешек обезьяна получала ломтик огурца. Капуцины работали в паре, и пока обе обезьяны получали по ломтику огурца за свои камешки, все шло как по маслу. Но когда экспериментаторы изменили правила и стали давать одной обезьяне за камешек сладкую виноградину, а другой — по-прежнему огурец, идиллия нарушилась. Столкнувшись с такой несправедливостью, обделенные капуцины перестали съедать свою порцию огурца, а в 40% случаев вообще перестали «покупать» угощение. Когда же одной из обезьян начали давать виноградину вообще ни за что, без камешка, положение еще более ухудшилось: вторая обезьяна часто стала с гневом выбрасывать свой камешек и меняла его на огурец только в 20% случаев. Иными словами, капуцины перестали участвовать в торговле (в конце концов, ломтик огурца за камешек — неплохая сделка), просто чтобы выразить свое возмущение несправедливостью, «нечестно нажитым богатством» своего партнера по эксперименту. Скорее всего, если бы, как в опыте с разделом 10 долларов, капуцин мог навредить своему партнеру, лишив его виноградины, а заодно себя — огурца, он бы это сделал.
Когда же одной из обезьян начали давать виноградину вообще ни за что, без камешка, положение еще более ухудшилось: вторая обезьяна часто стала с гневом выбрасывать свой камешек и меняла его на огурец только в 20% случаев. Иными словами, капуцины перестали участвовать в торговле (в конце концов, ломтик огурца за камешек — неплохая сделка), просто чтобы выразить свое возмущение несправедливостью, «нечестно нажитым богатством» своего партнера по эксперименту. Скорее всего, если бы, как в опыте с разделом 10 долларов, капуцин мог навредить своему партнеру, лишив его виноградины, а заодно себя — огурца, он бы это сделал.
Похоже, что и люди и обезьяны стремятся к тому, чтобы заработок (особенно если он не мой, а моего партнера) был честным, справедливым. В игре с разделом долларов людям предлагают деньги, пусть небольшие, практически ни за что — за несколько минут, в течение которых надо ответить «да» или «нет». Отказ от плывущей в руки суммы, пусть малой — не повседневное явление, и все же люди на это идут, чтобы обеспечить честную дележку, удовлетворить свое чувство справедливости.
Так же поступают и капуцины. Если только что обезьяна считала вполне нормальным обмен камешка на огурец, но перестала идти на обмен, увидев, что партнер получает не огурец, а виноград, — она, видимо, тоже ищет справедливости. Это чувство, похоже, заложено в нашей биологической природе.
Означает ли это, что мы хотели бы, чтобы в идеальном мире у всех было денег (или винограда) поровну? Нет. Люди просто хотят, чтобы человек получал деньги, которые он честно заслужил. Это доказывает немного усложненный вариант опыта с разделом долларов.
Если в первом варианте экспериментатор сам назначал «банкомета» случайным образом, на этот раз перед игрой проводится какой-либо простенький психологический тест, например на внимание или на быстроту реакции, или на зрительную память. Экспериментатор объявляет (вне зависимости от реальных результатов), что в тесте победил партнер А и именно он будет делить деньги. Оказалось, что при таких правилах партнер Б бывает гораздо уступчивее. Ни одно самое скромное предложение не было отвергнуто. Очевидно, в этом случае люди считают, что «банкомет» заслужил свое привилегированное положение и потому предложенная им дележка в его пользу справедлива.
Ни одно самое скромное предложение не было отвергнуто. Очевидно, в этом случае люди считают, что «банкомет» заслужил свое привилегированное положение и потому предложенная им дележка в его пользу справедлива.
Короче говоря, люди (и обезьяны) хотят, чтобы между достижениями субъекта и его вознаграждением имелось какое-то разумное соотношение. Этого не было, когда несколько никому ранее не известных человек за два-три года «заработали» в России по 10-15 миллиардов долларов. Этого не было и в случае с Ричардом Грассо, хотя тот оказался поскромнее. Директор биржи выполнял свою работу хорошо, но не на 140 миллионов долларов (вообще не очень ясно, что должен сделать человек, чтобы получить столько за год — изобрести лекарство от рака?). И он не был незаменимым, биржа не лопнула, когда ему пришлось уйти. И, пожалуй, есть на свете объекты, управлять которыми сложнее, чем биржей.
Выше было сказано, что эксперимент с разделом денег давал одинаковые результаты во всех странах. И все же традиции, культура страны сильно влияют на то, что считается справедливым и честным. Например, в США главы крупных фирм получают значительно больше, чем в Европе или Японии, и это никого особенно не волнует. Как пишет один американский экономист, «заработки руководителей больших компаний, характерные для Америки, послали бы немцев на баррикады». Хотя из развитых стран наибольшая разница в доходах населения отмечается в США, опросы однозначно показывают, что американцы гораздо меньше других народов беспокоятся насчет неравенства. Возможно, дело в том, что они привыкли считать богатство результатом инициативы, умения, труда, а европейцы, скорее, приписывают его счастливому стечению обстоятельств, удаче, везению. Американцы все еще верят в историю о бедном мальчике из трущоб, который начал с чистки ботинок и благодаря своей предприимчивости стал миллиардером. Ирония в том, что Ричард Грассо действительно происходит из небогатой рабочей семьи итальянских иммигрантов и самостоятельно выбился в люди.
И все же традиции, культура страны сильно влияют на то, что считается справедливым и честным. Например, в США главы крупных фирм получают значительно больше, чем в Европе или Японии, и это никого особенно не волнует. Как пишет один американский экономист, «заработки руководителей больших компаний, характерные для Америки, послали бы немцев на баррикады». Хотя из развитых стран наибольшая разница в доходах населения отмечается в США, опросы однозначно показывают, что американцы гораздо меньше других народов беспокоятся насчет неравенства. Возможно, дело в том, что они привыкли считать богатство результатом инициативы, умения, труда, а европейцы, скорее, приписывают его счастливому стечению обстоятельств, удаче, везению. Американцы все еще верят в историю о бедном мальчике из трущоб, который начал с чистки ботинок и благодаря своей предприимчивости стал миллиардером. Ирония в том, что Ричард Грассо действительно происходит из небогатой рабочей семьи итальянских иммигрантов и самостоятельно выбился в люди. Но, видимо, даже для американцев есть предел такой веры. Прекрасно, молодец, выбился в люди, но не до такой же степени, господа!
Но, видимо, даже для американцев есть предел такой веры. Прекрасно, молодец, выбился в люди, но не до такой же степени, господа!
А все-таки интересно: почему никого особенно не волнует тот факт, что ловкий теннисист иногда зарабатывает за одно состязание больше, чем может получить раз в жизни выдающийся ученый — лауреат Нобелевской премии? Может быть, потому, что борьба спортсмена за первенство видна всем, а чем там занимаются ученые в своих лабораториях, мало кто понимает. Не хватает зрелищности.
Но, видимо, это какой-то другой раздел психологии справедливости, еще не затронутый исследователями.
Проверьте себя на наличие скрытых предубеждений
Стереотип — это преувеличенное убеждение, образ или искаженная правда о человеке или группе — обобщение, которое допускает незначительные индивидуальные различия или социальные вариации или вообще не учитывает их. Стереотипы основаны на изображениях в средствах массовой информации или на репутации, передаваемой родителями, сверстниками и другими членами общества. Стереотипы могут быть положительными или отрицательными.
Стереотипы могут быть положительными или отрицательными.
Предубеждение – это мнение, предубеждение или отношение к группе или ее отдельным членам. Предубеждение может быть положительным, но в нашем понимании оно означает негативное отношение.
Предрассудки часто сопровождаются невежеством, страхом или ненавистью. Предубеждения формируются в результате сложного психологического процесса, который начинается с привязанности к близкому кругу знакомых или «своей группе», такой как семья. Предрассудки часто нацелены на «чужих».
Дискриминация — это поведение, при котором к людям относятся неравномерно из-за их принадлежности к группе. Дискриминационное поведение, начиная от оскорблений и заканчивая преступлениями на почве ненависти, часто начинается с негативных стереотипов и предубеждений.
Как научиться предубеждениям?
Социологи считают, что дети начинают приобретать предубеждения и стереотипы еще в раннем возрасте. Многие исследования показали, что уже в возрасте 3 лет дети усваивают термины расовых предрассудков, не понимая их значения.
Вскоре они начинают привязываться к своей собственной группе и вырабатывают негативное отношение к другим расовым или этническим группам или «чужой группе». В раннем возрасте большинство детей приобретают полный набор предубеждений, которые можно наблюдать в словесных оскорблениях, этнических шутках и актах дискриминации.
Как укрепляются наши предубеждения?
Однажды усвоенные стереотипы и предубеждения сопротивляются изменению, даже если факты не подтверждают их или указывают на обратное.
Люди примут анекдоты, которые укрепляют их предубеждения, но не примут во внимание опыт, который им противоречит. Утверждение «Некоторые из моих лучших друзей _____» отражают эту тенденцию допускать некоторые исключения, не меняя при этом наших предубеждений.
Как сохранить предвзятость?
Предвзятость увековечивается за счет соответствия внутригрупповым установкам и социализации культурой в целом. Тот факт, что белая культура доминирует в Америке, может объяснить, почему цветные люди часто не проявляют сильного предубеждения в пользу своей этнической группы.
Средства массовой информации обычно используют стереотипы как условное обозначение для описания настроения, сцены или персонажа. Пожилые люди, например, обычно изображаются хрупкими и забывчивыми, в то время как молодые люди часто изображаются энергичными и способными.
Стереотипы также могут передаваться через умолчание в популярной культуре, например, когда телешоу представляют полностью белый мир. Психологи предполагают, что предвзятость, передаваемая средствами массовой информации, помогает объяснить, почему дети могут перенимать скрытые предубеждения, даже когда их семейное окружение явно противится им.
О скрытых предубеждениях
Научные исследования показали, что предубеждения, которые считались отсутствующими или угасшими, остаются у большинства из нас в виде «умственного остатка». Исследования показывают, что люди могут сознательно придерживаться эгалитаризма и намеренно работать над тем, чтобы вести себя без предубеждений, но при этом иметь скрытые негативные предубеждения или стереотипы.
«Тесты имплицитных ассоциаций» (IAT) могут выявить скрытые или автоматические стереотипы и предубеждения, которые обходят сознательный контроль. Project Implicit — совместная исследовательская работа исследователей из Гарвардского университета, Университета Вирджинии и Университета Вашингтона — предлагает десятки таких тестов.
Мы считаем, что процедура IAT может быть полезна не только для исследовательских целей, для которых она была первоначально разработана. Это может быть инструмент, который поможет нам начать думать о скрытых предубеждениях: откуда они берутся? Как они влияют на наши действия? Что мы можем с ними сделать?
Предубеждения и поведение
Все больше исследований показывают связь между скрытыми предубеждениями и реальным поведением. Другими словами, скрытые предубеждения могут проявляться в действии, особенно когда усилия человека сознательно контролировать поведение ослабевают в условиях стресса, отвлечения внимания, расслабления или конкуренции.
Было обнаружено, что бессознательные убеждения и установки связаны с речью и определенными видами поведения, такими как зрительный контакт, частота моргания и улыбка.
Исследования показали, например, что школьные учителя явно транслируют предубеждения, настолько, что некоторые исследователи считают, что цветные и белые дети в одном классе фактически получают разное образование.
Ставший уже классическим эксперимент показал, что белые интервьюеры сидели дальше от чернокожих соискателей, чем от белых, допускали больше речевых ошибок и заканчивали интервью на 25% раньше. Было показано, что такая дискриминация снижает эффективность любого, с кем обращаются таким образом, будь то черный или белый.
Проводятся эксперименты, чтобы определить, приводит ли сильное скрытое предубеждение кого-либо к более дискриминационному поведению. Но мы можем кое-что узнать даже из первых исследований:
- Те, кто демонстрировал более высокий уровень неявного предубеждения или стереотипов в отношении чернокожих или геев, были более недружелюбны к ним.

- У испытуемых, у которых были более сильные скрытые расовые предубеждения, была более активна часть мозга, которая, как известно, отвечает за эмоциональное обучение, когда им показывали чернокожие лица, чем когда им показывали белые лица.
Приводит к дискриминации?
Точно не установлено, адекватно ли лабораторные исследования отражают реальные жизненные ситуации. Но, по мнению социологов, появляется все больше свидетельств того, что скрытые предубеждения связаны с дискриминационным поведением в широком диапазоне человеческих взаимодействий, от приема на работу и продвижения по службе до выбора жилья и школы.
В случае с полицией предвзятость может повлиять на принятие решений, которые решают жизнь или смерть за доли секунды. Стрельба по чернокожим, которых ошибочно считали вооруженными, — иммигранту из Нью-Йорка, полицейскому из Род-Айленда — привлекла внимание общественности к этому вопросу.
Возможно, бессознательные предубеждения и стереотипы могут также повлиять на обсуждение в суде присяжных и другие повседневные задачи, требующие суждений человеческого характера.
Люди, утверждающие, что сегодня предрассудки не являются большой проблемой, по иронии судьбы демонстрируют проблему бессознательных предубеждений. Поскольку эти предубеждения находятся вне нашего сознания, их действительно можно отрицать.
Последствия предубеждений и стереотипов
Скрытая предвзятость стала важным ключом к несоответствию между общественным мнением, выражаемым американскими убеждениями и социальными целями, и степенью дискриминации, которая все еще существует.
Несмотря на 30-летнее законодательство о равных правах, уровни бедности, образования и успеха сильно различаются у разных рас. Дискриминация сохраняется при продаже жилья и недвижимости, а расовое профилирование является обычной практикой даже среди простых граждан.
Представители меньшинств продолжают сообщать об унизительном обращении со стороны продавцов, сотрудников и полиции. В то время как афроамериканец может поужинать в хорошем ресторане в любой точке Америки, ему может быть неловко пытаться поймать такси после этого ужина.
Человек, на котором лежит клеймо членства в группе, должен быть готов к его изнурительным последствиям.
Исследования показывают, что афроамериканские подростки осознают, что их стигматизируют как интеллектуально неполноценных, и что они ходят в школу с тем, что психолог Клод Стил назвал «бременем подозрительности». Такое бремя может повлиять на их отношение и достижения.
Точно так же исследования показали, что, когда студенткам колледжа напоминают, что их группа считается плохой по математике, их успеваемость может исполнить это пророчество.
Эти тени нависают над стигматизированными людьми, независимо от их статуса или достижений. Они должны оставаться начеку и нести дополнительное бремя, которое может повлиять на их уверенность в себе, производительность и устремления. Эти стигмы могут лишить их индивидуальности и ослабить их попытки вырваться из стереотипных ролей.
Что вы можете сделать с бессознательными стереотипами и предубеждениями
Сознательные взгляды и убеждения могут измениться.
Например, негативные стереотипы, связанные со многими группами иммигрантов, со временем в значительной степени исчезли. Для афроамериканцев законы о гражданских правах вынуждали к интеграции и недискриминации, что, в свою очередь, помогло изменить общественное мнение.
Но у психологов нет готовой дорожной карты для разрушения таких явных и особенно скрытых стереотипов и предубеждений.
Узнали в раннем возрасте
Первым шагом может быть признание того, что предубеждениям учат рано и они противоречат нашей приверженности справедливому обращению. Родители, учителя, религиозные лидеры и другие лидеры сообщества могут помочь детям подвергнуть сомнению их ценности и убеждения и указать на тонкие стереотипы, используемые сверстниками и в средствах массовой информации. Дети также должны быть окружены намеками на то, что равенство имеет значение.
В своей классической книге « Природа предрассудков » психолог Гордон Олпорт заметил, что дети с большей вероятностью вырастут терпимыми, если они живут в семье, где царит поддержка и любовь. «Они чувствуют себя желанными, принятыми, любимыми, независимо от того, что они делают».
«Они чувствуют себя желанными, принятыми, любимыми, независимо от того, что они делают».
В такой среде приветствуются разные взгляды, наказания не суровы и не капризны, и эти дети в целом положительно относятся к людям и несут в себе чувство доброжелательности и даже привязанности.
Общественные дела
Интеграция сама по себе не приводит к резким изменениям во взглядах и поведении. Но многие исследования показывают, что когда люди работают вместе в структурированной среде для решения общих проблем с помощью общественных работ, их отношение к разнообразию может резко измениться.
Привлекая к выполнению задания членов других групп, дети начинают думать о себе как о части большого сообщества, в котором каждый обладает навыками и может внести свой вклад. Было показано, что такой опыт улучшает отношения между расами и между старыми и молодыми людьми.
Имеются также предварительные данные о том, что бессознательные установки, вопреки первоначальным ожиданиям, могут быть податливыми. Например, было показано, что воображение сильных женщин-лидеров или позитивные образцы для подражания афроамериканцев, по крайней мере временно, изменяют бессознательные предубеждения.
Например, было показано, что воображение сильных женщин-лидеров или позитивные образцы для подражания афроамериканцев, по крайней мере временно, изменяют бессознательные предубеждения.
«Чувство» бессознательного предубеждения
Но есть еще один аспект самого опыта прохождения теста на скрытое предубеждение, который может оказаться полезным. Многие испытуемые могут «чувствовать» свои скрытые предубеждения во время выполнения тестов.
Они могут чувствовать себя неспособными реагировать так же быстро (например) на старые + хорошие концепции, как на молодые + хорошие концепции. Сам акт прохождения тестов может вызвать скрытые предубеждения в сознательной части разума.
Нам хотелось бы верить, что когда человек сознательно настроен на изменение, сам акт обнаружения своих скрытых предубеждений может побудить его действовать, чтобы исправить их. Возможно, невозможно избежать автоматического стереотипа или предубеждения, но, безусловно, возможно сознательно исправить его.
Стремление к изменению
Если люди осознают свои скрытые предубеждения, они могут отслеживать и пытаться улучшить скрытые установки до того, как они выразятся в поведении. Эта компенсация может включать внимание к языку, языку тела и к стигматизации, которую испытывают целевые группы.
Здравый смысл и данные исследований также предполагают, что изменение поведения может изменить убеждения и отношения. Казалось бы логичным, что сознательное решение быть эгалитаристом может привести к расширению круга друзей и знаний о других группах. Такие усилия могут со временем уменьшить силу бессознательных предубеждений.
Может быть легко отвергнуть результаты тестов как «не мои», когда вы столкнетесь с ними впервые. Но это легкий путь. Спросить, откуда берутся эти предубеждения, что они означают и что мы можем с ними сделать, — задача более сложная.
Признание того, что проблема во многих других, а также в нас самих, должно побудить всех нас попытаться понять и действовать.
Проверка материального положения
You are here
Главная » Программа попечителей США
Обновления по электронной почте
Бюро переписи, Данные IRS и множители административных расходов
Должник должен ввести информацию о доходах и расходах в соответствующую форму (, т.е. , формы 122A или формы 122C), а затем произвести расчеты с использованием введенной информации. Некоторая информация, необходимая для заполнения этих форм, например текущий ежемесячный доход должника, берется из личных записей должника. Однако другая информация, необходимая для заполнения форм, поступает от Бюро переписи населения и Налоговой службы (IRS). Этот веб-сайт воспроизводит данные Бюро переписи населения и IRS, необходимые для заполнения форм 122A и 122C. Исходные данные, воспроизведенные здесь, также доступны непосредственно в IRS и Бюро переписи населения по ссылкам в нижней части этой страницы. По вопросам, связанным с этими данными, обращайтесь по электронной почте: [email protected]. Секретарь вашего местного суда по делам о банкротстве или вашей местной коллегии адвокатов штата может получить информацию о лицах или организациях, предлагающих услуги, связанные с банкротством, в том числе за льготную плату или на безвозмездной основе, чтобы получить общую помощь в подаче заявления о банкротстве.
Позиция USTP по юридическим вопросам, возникающим в соответствии с главой 7 «Проверка материального положения» [PDF — 54 КБ] Позиция USTP в отношении главы 13 «Проверка располагаемого дохода» [PDF — 43 КБ] Примечание: Первоначальным источником данных о среднем семейном доходе штата является Бюро переписи населения. Первоначальным источником национальных и местных стандартов является IRS. Чтобы сообщить о любых различиях между данными на этих страницах и их первоисточником, отправьте электронное письмо по адресу: [email protected]. |
|
Обновлено 29 апреля 2022 г.
Была ли эта страница полезной?
Была ли эта страница полезной?
Да
№
Испытательный центр
Центр диагностикиЧтобы зарегистрироваться для участия в тестировании, кандидаты должны сначала создать учетную запись. Создание учетной записи и тестовая регистрация могут быть выполнены ТОЛЬКО онлайн.
Зарегистрируйтесь/войдите в систему для теста PAT & Swim
Зарегистрируйтесь/войдите в систему для теста CJBAT
Обязательно запишите свой логин для дальнейшего использования.
Тест на физическую ловкость. Кандидаты будут парковаться рядом с полосой препятствий в любом другом месте и ждать регистрации на полосе препятствий.
Тест по плаванию — Тест по плаванию проводится в новом месте: Центр водных видов спорта Пайн-Айленд, 3800 SW 92nd Avenue, Davie, FL 33328. (Расположен на SW 92-я авеню от Orange Drive между Pine Island Road и Nob Hill Road.) Более подробную информацию см. в информационном буклете.
(Расположен на SW 92-я авеню от Orange Drive между Pine Island Road и Nob Hill Road.) Более подробную информацию см. в информационном буклете.
Кандидаты должны иметь действительную копию формы медицинского освидетельствования своего врача. Ваша медицинская справка действительна только в течение 6 месяцев с даты ее подписания врачом. Административному персоналу НЕ разрешается делать копии.
До особого распоряжения нет возможности пройти тестирование или получить информацию. См. раздел «Связь с центром тестирования» внизу этой страницы.
После завершения тестирования соискатели должны немедленно освободить помещение.
Центр тестирования Института общественной безопасности (IPS), расположенный в Центральном кампусе колледжа Броуард, является региональным центром тестирования, обслуживающим кандидатов, желающих работать в правоохранительных органах или исправительных учреждениях.
Тесты, проводимые в IPS, соответствуют стандартам Комиссии по стандартам и обучению уголовного правосудия штата Флорида (CJSTC) и стандартам Ассоциации начальников полиции округа Броуард.
Мы не агентство по найму. Пожалуйста, направляйте все запросы о трудоустройстве в правоохранительные органы, в которые вы хотите подать заявление.
Как начать карьеру в правоохранительных органах
- Загрузить информационный буклет (PDF)
- Определите требования агентства, в которое вы хотите подать заявление
- Запланируйте и сдайте необходимый тест здесь, в Центре тестирования IPS
- Распечатайте результаты и следуйте требованиям агентства
Центр тестирования IPS Broward College будет закрыт в следующие дни:
- 11 ноября 2022 г. — День ветеранов
- 23–25 ноября 2022 г. — День благодарения
- 21 декабря 2022 г. — 2 января 2023 г. — зимние каникулы
- 16 января 2023 г. — День рождения Мартина Лютера Кинга-младшего
- 6-10 марта 2023 г. — Весенние каникулы
- 29 мая 2023 г.
 — День памяти
— День памяти - 19 июня 2023 г. — 11 июня
PAT
Регистрация и сдача экзамена PAT проводятся на полосе препятствий, расположенной в северо-восточной части Центрального кампуса Broward College рядом со зданиями 21 и 22. Копия заполненной формы медицинского освидетельствования, удостоверение личности и маска обязательна. Заявители должны припарковаться вдоль полосы препятствий на каждом втором парковочном месте.
Адрес:
3501 Davie Road
Davie, FL 33314
Тест по плаванию
Кандидаты должны явиться в водный центр Пайн-Айленд не позднее, чем за 15-30 минут до начала теста. Требуется форма медицинского освидетельствования, обязательная одежда (см. информационный буклет (PDF)), удостоверение личности и подтверждение оплаты. Заявитель должен проплыть 50 ярдов; 25 ярдов вверх и 25 ярдов назад. Это НЕ тест на время.
Адрес:
Водный центр Пайн-Айленд
3800 SW 92nd Avenue
Дэви, Флорида 33328
Часто задаваемые вопросы
Буклет по тестированию двигательных навыков (PDF)
Руководство по подготовке к физической подготовке (PDF)
Видео теста физической оценки FDLE
Видео с профильными упражнениями Полицейской академии
Видео программы подтягиваний/отжиманий
Кандидаты могут приобрести учебные материалы на сайте Pearson Vue или в Broward College — книжном магазине центрального кампуса в Дэви, корпус 19. Учебные ресурсы недоступны в Центре тестирования.
Учебные ресурсы недоступны в Центре тестирования.
Презентация кандидата Pearson VUE BAT
Форма медицинского освидетельствования действительна в течение 6 месяцев с даты медицинского осмотра. Недействительные или просроченные формы не будут приняты.
CJSTC 75 и 75B больше не являются действительной формой FDLE и не будут приниматься.
Форма медицинского освидетельствования (PDF)
Часы работы:
Понедельник — пятница: с 8:00 до 16:00.
Адрес:
3501 Davie Road
Davie, FL, 33314
Контакты:
Johntae Lowe, административный специалист
здание 22, комната 108
954-201-6931
Электронная почта: jlowe@broward. edu
edu
Denise Warric
954-201-6165
электронная почта: [email protected]
Этот сайт лучше всего просматривать в современном браузере, он несовместим с Internet Explorer (IE). Пожалуйста, используйте другой браузер, такой как Chrome, Safari, Edge или Firefox для лучшего взаимодействия с пользователем.
ИНФОРМАЦИЯ об Академии
| Главная > Обучение > Подготовка к работе в правоохранительных органах Студенты, занимающиеся физической подготовкой Программа предварительной подготовки сотрудников правоохранительных органов В 1989 году 114-й Законодательный орган штата Мэн принял закон, обязывающий Совет попечителей Академии уголовного правосудия штата Мэн установить стандарты предварительной подготовки. В 2009 году Попечительский совет Академии уголовного правосудия штата Мэн предложил внести изменения в действующую программу предварительной подготовки сотрудников правоохранительных органов. Были внесены обновления в существующую программу, а формат и количество часов, необходимых для выпуска, были увеличены. Студенты также должны будут выполнить контрольный компонент. В дополнение к изменениям в учебной программе Академия уголовного правосудия штата Мэн также подготовила процесс сертификации, чтобы стать сотрудником правоохранительных органов, работающим неполный рабочий день. Элементы процесса сертификации включают сертификацию оружия, проверку знаний и надзор со стороны вашего агентства по найму.
Программа предварительной подготовки сотрудников правоохранительных органов Этап I: Для подачи заявки на этот курс учащиеся должны соответствовать возрастным и образовательным требованиям (см. заявку). Студенты должны пройти 40-часовую онлайн-программу предварительной подготовки сотрудников правоохранительных органов. Студенты должны заполнить заявку MCJA для MCJA LEPS Phase I и отправить ее вместе с платой в размере 350 долларов США, наличными или чеком , подлежащим оплате казначею штата Мэн, в Академию уголовного правосудия штата Мэн по адресу: 15 Oak Grove Road, Vassalboro, Maine 049.89. Студентам будет предоставлен логин и пароль для завершения обучения. Это обучение должно быть завершено до посещения Этапа II, и нет ограничения по времени для завершения Этапа I обучения, однако по завершении обучения на Этапе I студент должен будет связаться с MCJA и сдать выпускной экзамен в Вассалборо. Этап II: Учащиеся должны пройти 80-часовую интерактивную программу обучения на основе сценариев. Перед началом этапа II студенты должны заполнить заявку MCJA на участие в MCJA LEPS Phase II. Все студенты должны соответствовать требованиям, перечисленным ниже, и отправить в Академию все необходимые документы, описанные ниже. Стоимость курса 350 долларов.
Фаза III: После приема на работу в правоохранительные органы в качестве сотрудника правоохранительных органов предварительный сертификат будет выдан после получения уведомления о приеме на работу MCJA и формы о знании огнестрельного оружия MCJA, подписанной сертифицированным инструктором по огнестрельному оружию MCJA. Агентство по найму должно обеспечить 80-часовое документированное наблюдение, прежде чем Академия уголовного правосудия выдаст сертификат сотрудника правоохранительных органов. Главный сотрудник правоохранительных органов должен будет подписать нотариально заверенную форму MCJA, в которой будет указано, что сотрудник выполнил 80 часов наблюдения к своему удовлетворению. : Сотрудник правоохранительных органов, работающий неполный рабочий день, будет иметь один год, чтобы отработать 80 часов наблюдения. Офицер может получить продление от Совета MCJA при смягчающих обстоятельствах. Предстоящие подготовительные курсы для правоохранительных органов: Этап 1 можно пройти онлайн в любое время, и он уже доступен. Расписания фазы II: Этот список обновляется по мере появления курсов. Наш годовой календарь завершается в июне для курсов MCJA, и даты будут добавлены после того, как курсы будут запланированы. Пожалуйста, НЕ отправляйте платеж вместе с заявкой на Этап II; подождите, пока вас не примут в класс. Принимаются только полные пакеты заявлений, которые должны быть отправлены за две недели до начала занятий. Стоимость этого курса составляет 350 долларов США (книги не включены, см. ниже)  ниже) ниже) Студенты будут нести ответственность за следующее: Раздел 17A (Уголовное право штата Мэн) и 29A (Дорожное право штата Мэн) обязательны и могут быть приобретены в книжном магазине вашего колледжа или напрямую через Swan Island Press, электронная почта [email protected]. Для целей этого класса вы можете использовать более ранние версии этих книг.
Форма заявки на этап I Форма заявки на этап II Квалификация сотрудника правоохранительных органов штата Мэн В соответствии с разделом 25 Закона штата Мэн: 2804-G претендовать на должность сотрудника правоохранительных органов, если заявитель не имеет степени младшего специалиста или 60 кредитных часов послесреднего образования, и в этом случае заявитель должен быть не моложе 20 лет. Этот курс предлагается абитуриентам в возрасте 19 лет, которые имеют право на участие в программе, в качестве любезности для колледжей и университетов, которые предлагают кредиты курса для этой программы. Если у вас есть дополнительные вопросы о предварительном обслуживании, свяжитесь с Джошуа Дейли в Академии.
|
Оценки | Штат Калифорния – Министерство юстиции
Чтобы подать заявление о приеме на работу в Министерство юстиции, большинство лиц, ранее не служивших в штате, должны сначала сдать экзамен. Раздел ниже включает информацию о текущих экзаменах, проводимых Департаментом. Если после ознакомления с этой информацией у вас возникнут дополнительные вопросы, позвоните в наш отдел привлечения талантов и аналитики по телефону (916) 210-6021.
Обратите внимание, что многие экзамены по классификациям, используемым Департаментом, проводятся Департаментом кадров штата Калифорния, и с ними можно ознакомиться на сайте jobs.ca.gov. Для получения дополнительной информации о подаче заявления о приеме на работу посетите страницу Получение работы штата.
С ежегодным планом экзаменов можно ознакомиться в Плане экзаменов Министерства юстиции на 2022 год, pdf.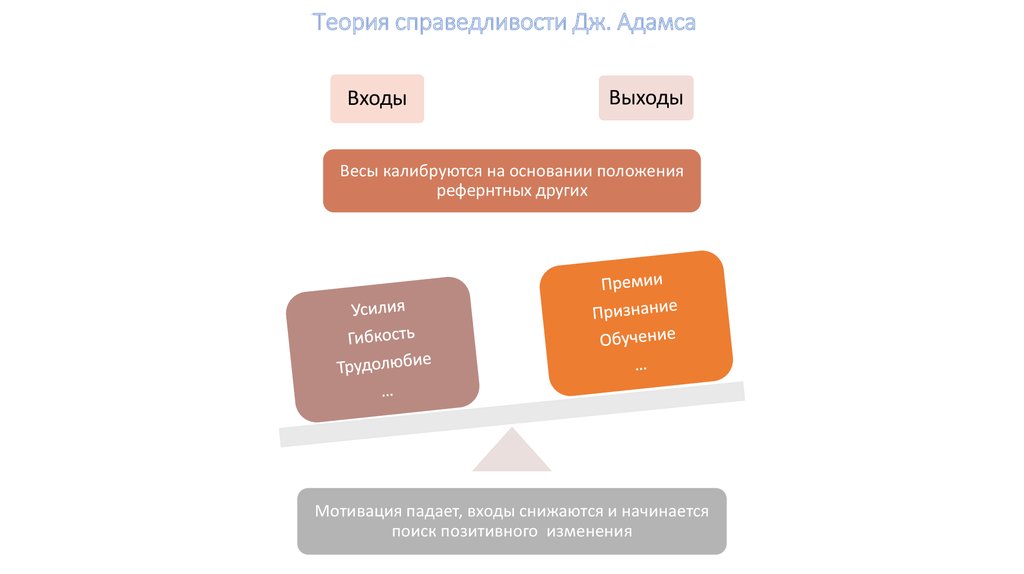
Ссылки на темы ниже
- Непрерывная подача открытых экзаменов
- Другие открытые экзамены
- Рекламные экзамены непрерывной подачи
- Другие рекламные экзамены
- Экзамены Career Executive Assignment (C.E.A)
- Ресурсы
Экзамены Career Executive Assignment (C.E.A)
В настоящее время принимаются заявки на следующие C.E.A. экзамены. Для сдачи этих экзаменов кандидатам не требуется предварительный опыт работы на государственной службе, однако они должны соответствовать желаемой квалификации, указанной в экзаменационном бюллетене. Нажмите на название должности, чтобы просмотреть экзаменационный бюллетень. Экзамен на C.E.A. должностей является оценка заявления о квалификации. Доступен шаблон о том, как заполнить Заявление о квалификации.
| Осмотр | Местоположение | Окончательная дата подачи |
|---|
НЕПРЕРЫВНАЯ ПОДАЧА ОТКРЫТЫХ ЭКЗАМЕНОВ
Экзамены назначаются по мере необходимости. После сдачи запланированного экзамена вы будете помещены в «подходящий список», из которого мы можем принимать решения о приеме на работу.
После сдачи запланированного экзамена вы будете помещены в «подходящий список», из которого мы можем принимать решения о приеме на работу.
Поскольку списки соответствия применимы только к должностям в определенных местах, вы должны внимательно указать детали в экзаменационном бюллетене. Нажмите на названия вакансий ниже, чтобы просмотреть минимальную квалификацию, конкретное местонахождение должности, место проведения экзамена и другую информацию.
ПРИМЕЧАНИЕ. Что касается даты окончания непрерывного экзамена, подача заявления после этой даты не будет принята для текущего экзамена, но будет отложена для следующего запланированного экзамена (см. столбец «Следующая расчетная дата окончания».
| Обследование | Местоположение | Дата окончания | Следующая предполагаемая дата окончания |
|---|---|---|---|
| Криминолог I | По всему штату | Непрерывная подача | Онлайн, 24/7 |
| Криминолог II | По всему штату | Непрерывная подача | Онлайн, 24/7 |
| Криминолог III | По всему штату | Непрерывная подача | Онлайн, 24/7 |
| Криминалист | По всему штату | Непрерывная подача | Онлайн, 24/7 |
| Криминолог Супервайзер | По всему штату | Непрерывная подача | Онлайн, 24/7 |
| Заместитель генерального прокурора | По всему штату | Непрерывная подача | Онлайн, 24/7 |
| Заместитель генерального прокурора III | По всему штату | Непрерывная подача | Онлайн, 24/7 |
| Заместитель генерального прокурора IV | По всему штату | Среда, 10 августа 2022 г. | Пятница, 26 августа 2022 г. |
| Полевой представитель, Министерство юстиции | По всему штату | Понедельник, 25 июля 2022 г. | Понедельник, 24 октября 2022 г. |
| Следственный аудитор II | По всему штату | Непрерывная подача | Онлайн, 24/7 |
| Следственный аудитор III | По всему штату | Непрерывная подача | Онлайн, 24/7 |
| Специальный агент | По всему штату | Среда, 31 августа 2022 г. | пятница, 28 октября 2022 г. |
| Стажер специального агента | По всему штату | 30 марта 2022 г. | ноябрь, 2022 |
| Курирующий заместитель генерального прокурора | По всему штату | Еженедельно | н/д |
ДРУГИЕ ОТКРЫТЫЕ ЭКЗАМЕНЫ
В настоящее время другие открытые экзамены не предлагаются. |
|---|
НЕПРЕРЫВНАЯ ПОДАЧА РЕКЛАМНЫХ ЭКСПЕРТИЗ
В настоящее время на постоянной основе принимаются заявки на следующие ведомственные экзамены по повышению квалификации. Кандидаты должны иметь постоянную должность на государственной службе в Генеральной прокуратуре, Министерстве юстиции или выполнять другие требования для продвижения по службе, как указано в экзаменационном бюллетене, иначе они не будут допущены к экзамену. Экзамены назначаются по мере необходимости и только по требованию программ Министерства юстиции.
ПРИМЕЧАНИЕ. Что касается даты окончания непрерывного экзамена, подача заявки после этой даты не будет принята для текущего экзамена, но будет отложена для следующего запланированного экзамена (см. столбец «Следующая предполагаемая дата окончания».
| Осмотр | Местоположение | Дата окончания | Следующая предполагаемая дата окончания |
|---|---|---|---|
| Младший аналитик по персоналу | Сакраменто | Среда, 30 марта 2022 г. | Сентябрь 2022 |
| Специальный агент (рекламный) | По всему штату | Четверг, 15 сентября 2022 г. | март 2023 |
| Аналитик службы персонала Экзамен | По всему штату | 12 августа 2022 г. | 31 января 2023 г. |
ДРУГИЕ АКЦИОНЕРНЫЕ ЭКЗАМЕНЫ
| В настоящее время другие рекламные экзамены не предлагаются. |
|---|
План экзаменов Министерства юстиции на 2022 год
- План экзаменов Министерства юстиции на 2022 год, pdf
РЕСУРСЫ
- Как пользоваться нашей онлайн-платформой для тестирования (видео)
- Учебное пособие специального агента, pdf
- Форма государственной заявки STD 678, pdf
- Другие экзамены, проводимые Калифорнийским отделом кадров
- Часто задаваемые вопросы об экзамене
- Учебное пособие для аналитиков служб персонала, pdf
- Стать успешным аналитиком штата Калифорния
Back To Top
Расследование документов Трампа представляет собой беспрецедентное испытание для Министерства юстиции
Политика|Расследование документов представляет собой беспрецедентное испытание для Министерства юстиции
https://www. nytimes.com/2022/08/29/us/politics/trump-justice-department-documents.html
nytimes.com/2022/08/29/us/politics/trump-justice-department-documents.html
Реклама
Продолжить чтение основного материала
Анализ новостей
Что началось поскольку попытка получить документы национальной безопасности теперь превратилась в одно из самых сложных и сложных уголовных расследований за последнее время.
Когда Ф.Б.И. обыскав Мар-а-Лаго в этом месяце, федеральные агенты обнаружили 11 наборов секретных материалов. Кредит … Джош Ричи для The New York Times
ВАШИНГТОН. Пока в этом году чиновники Министерства юстиции в течение нескольких месяцев торговались с адвокатами и помощниками бывшего президента Дональда Трампа по поводу возвращения правительственных документов в его дом во Флориде, федеральные прокуроры пришли к выводу, что это не так. говорят всю правду.
Этот вывод помог привести в действие решение, которое станет беспрецедентной проверкой авторитета Министерства юстиции в глубоко поляризованной политической среде: запросить ордер на обыск, чтобы проникнуть в Мар-а-Лаго и получить то, что, по подозрению прокуроров, будет строго засекречено. материалы, помимо сотен страниц, которые г-н Трамп уже вернул.
материалы, помимо сотен страниц, которые г-н Трамп уже вернул.
По мнению правительства, эта авантюра окупилась, с ФБР. агенты вывезли кучу секретных материалов во время обыска три недели назад, включая некоторые документы с грифом «совершенно секретно».
Но на этом дело едва ли закончилось: то, что началось как попытка получить документы национальной безопасности, теперь превратилось в одно из самых сложных, запутанных и потенциально взрывоопасных уголовных расследований за последнее время, с огромными последствиями для Министерства юстиции, мистер , Трамп и общественная вера в правительство.
Генеральному прокурору Меррику Б. Гарланду теперь предстоит решить, предъявлять ли уголовное обвинение бывшему президенту и, вероятно, кандидату от Республиканской партии в 2024 году, шаг, не имеющий исторических аналогов.
Примечательно, что ему, возможно, придется сделать этот выбор дважды, в зависимости от того, какие доказательства его следователи найдут в своем отдельном широком расследовании усилий г-на Трампа по изменению результатов выборов 2020 года и его причастности к нападению 6 января на Капитолий.
Расследование департамента 6 января началось с розыска бунтовщиков, напавших на Капитолий. Но прошлой осенью он расширился, включив в себя действия, имевшие место до штурма, такие как план представить в Конгресс списки выборщиков, в которых ложно утверждалось, что г-н Трамп победил в нескольких ключевых колеблющихся штатах.
Этим летом прокуроры прокуратуры США в Вашингтоне начали напрямую задавать свидетелям вопросы о какой-либо причастности г-на Трампа и членов его ближайшего окружения, в том числе бывшего главы администрации Белого дома Марка Медоуза, к попыткам отменить его избрание потеря.
Несмотря на все свои усилия по дистанцированию отдела от политики, мистер Гарланд не может избежать политических последствий своих решений. То, как он будет обращаться с г-ном Трампом, несомненно, определит его срок пребывания в должности.
Пока неясно, как обернется дело. По словам людей, знакомых с расследованием, прокуроры, работающие над расследованием обращения г-на Трампа с секретной информацией, даже близко не дадут рекомендации г-ну Гарланду. Судебные документы описывают работу как продолжающуюся, с возможностью дополнительных допросов свидетелей и других следственных действий.
Судебные документы описывают работу как продолжающуюся, с возможностью дополнительных допросов свидетелей и других следственных действий.
- Специальный мастер: Федеральный судья удовлетворил просьбу бывшего президента Дональда Дж. Трампа о назначении независимого арбитра, известного как специальный мастер, для рассмотрения документов, которые ФБР предоставило для проверки. изъял у Мар-а-Лаго, назначив судью Рэймонда Дж. Дири из Федерального окружного суда в Бруклине.
- Доступ к конфиденциальным записям: Тот же федеральный судья принял, а затем отказался снять временный запрет на доступ Министерства юстиции к секретным документам, изъятым из дома г-на Трампа. 16 сентября агентство обратилось в апелляционный суд с просьбой разрешить ФБР. восстановить доступ к документам.
- Вводящая в заблуждение информация: Национальный архив сообщил Министерству юстиции, что адвокат, представляющий Трампа, сообщил архивам в прошлом году, что коробки, которые бывший президент взял в Мар-а-Лаго из Белого дома, содержали только незасекреченные материалы.
 лицу, проинструктированному по этому вопросу.
лицу, проинструктированному по этому вопросу.
До сих пор г-н Гарланд давал понять, что ему удобно владеть всеми решениями, связанными с г-ном Трампом. Он сопротивлялся призывам назначить специального прокурора для расследования дела бывшего президента. В своем первом выступлении перед 115 000 сотрудников отдела в прошлом году он выразил уверенность, что вместе они смогут справиться с любым делом. «Всех нас объединяет наша приверженность верховенству закона и поиску равного правосудия перед законом», — сказал он.
В течение этого года, когда прокуроры пытались понять, как конфиденциальные правительственные документы оказались на курорте г-на Трампа во Флориде, они начали проверять, были ли нарушены три закона: Закон о шпионаже, который запрещает несанкционированное хранение или раскрытие информация о национальной безопасности; закон, запрещающий неправильное обращение с конфиденциальными государственными документами; и закон против воспрепятствования федеральному расследованию.
К лету расследование того, как г-н Трамп обращался с секретной информацией, начало давать убедительные доказательства возможного намерения нарушить закон, по словам двух человек, знакомых с работой. Хотя не обязательно имелись железные доказательства, опросы свидетелей и другие материалы стали указывать на возможность преднамеренных попыток ввести следователей в заблуждение. Помимо допросов свидетелей, Министерство юстиции получило от организации Трампа кадры с камер наблюдения в различных частях Мар-а-Лаго.
На что мы обращаем внимание перед использованием анонимных источников. Известна ли информация источникам? Какова их мотивация рассказать нам? Оказались ли они надежными в прошлом? Можем ли мы подтвердить информацию? Даже когда эти вопросы удовлетворены, The Times использует анонимные источники в качестве крайней меры. Репортер и по крайней мере один редактор знают личность источника.
Узнайте больше о нашем процессе.
В сильно отредактированном письме под присягой, объясняющем желание правительства получить ордер на обыск, говорится, что у Министерства юстиции есть «вероятные основания полагать, что в Мар-а-Лаго будут обнаружены доказательства обструкции, и что «правительство имеет вполне обоснованные опасения». что могут быть предприняты шаги, чтобы сорвать или иным образом помешать этому расследованию, если факты, содержащиеся в показаниях под присягой, будут раскрыты преждевременно».
что могут быть предприняты шаги, чтобы сорвать или иным образом помешать этому расследованию, если факты, содержащиеся в показаниях под присягой, будут раскрыты преждевременно».
Но решение о том, предъявлять ли г-ну Трампу обвинения в попытках помешать расследованию или в его обращении с конфиденциальной информацией о национальной безопасности, будет зависеть от множества соображений.
В основе дела лежат улики, обнаруженные ФБР, которое все еще пытается понять, как и почему правительственные документы попали в Мар-а-Лаго и почему некоторые из них остались там, несмотря на неоднократные просьбы об их возвращении со стороны Национального Архивы и более поздняя повестка из Министерства юстиции.
Но строго засекреченный характер некоторых документов, извлеченных из Мар-а-Лаго, и возможные доказательства препятствования — это лишь некоторые элементы, которые будут учитываться при любом окончательном решении о возбуждении уголовного дела.
Карьерные прокуроры национальной безопасности проведут тщательный анализ того, убедительно ли эти доказательства свидетельствуют о нарушении законов. Этот процесс будет включать рассмотрение того, как факты были применены в аналогичных делах, возбужденных по тем же законам, информацию, которую прокуратура изучила, когда они расследовали дела бывшего госсекретаря Хиллари Клинтон и бывшего сотрудника ЦРУ. Режиссер Дэвид Х. Петреус.
Этот процесс будет включать рассмотрение того, как факты были применены в аналогичных делах, возбужденных по тем же законам, информацию, которую прокуратура изучила, когда они расследовали дела бывшего госсекретаря Хиллари Клинтон и бывшего сотрудника ЦРУ. Режиссер Дэвид Х. Петреус.
Например, в деле об использовании г-жой Клинтон частного почтового сервера сотрудники отдела национальной безопасности попросили прокуроров углубиться в историю Закона о шпионаже. Вопрос заключался в том, указывает ли ее обращение с секретной информацией на грубую небрежность. Один убедительный случай грубой небрежности, который они обнаружили, с участием бывшего сотрудника ФБР. агентом, включали куда более серьезные факторы. Изучив прошлые примеры, они обнаружили, что ее случай не соответствует этому стандарту. В конце концов, все согласились не предъявлять обвинения миссис Клинтон.
Но дело г-на Трампа ставит дополнительный вопрос о препятствовании правосудию и возможности того, что доказательства могут показать, что он или его команда юристов бросили вызов Министерству юстиции, чтобы удержать документы, принадлежащие правительству.
Это в некотором роде перекликается с предыдущим расследованием об обструкции, проведенным Робертом С. Мюллером III, специальным прокурором, который изучал вопрос о вмешательстве России в выборы 2016 года. Его окончательный отчет показал, что г-н Трамп пытался сократить или даже прекратить расследование специального прокурора, когда узнал о нем больше. Но г-н Мюллер отказался сообщить, нарушил ли г-н Трамп закон, позволив тогдашнему генеральному прокурору Уильяму П. Барру оправдать г-на Трампа в этом преступлении.
Нет никакого способа узнать, есть ли у Министерства юстиции факты об обструкции, которые соответствуют его стандарту судебного преследования, что является доказательством, которое «вероятно было бы достаточным для получения и подтверждения обвинительного приговора».
Но собственные юридические документы Министерства юстиции поставили вопрос об обструкции перед общественностью. Если г-н Гарланд обнаружит, что нет достаточных доказательств для обвинения г-на Трампа, Министерство юстиции при двух последовательных администрациях решит не рекомендовать преследование г-на Трампа за это преступление.
Если мистер Гарланд решит выдвинуть обвинения, это станет историческим моментом для президентства, бывшего лидера Соединенных Штатов, обвиняемого в совершении преступления и, возможно, вынужденного защищать себя перед судом присяжных своих сограждан. Это процесс, который потенциально может развернуться, даже когда он снова баллотируется в Белый дом против действующего президента, чья администрация преследует его.
Это тоже чревато огромным риском для авторитета департамента, особенно если угроза национальной безопасности, которую представляет наличие у г-на Трампа документов, неизбежно раскрытых, по крайней мере частично, в ходе любого судебного разбирательства, не кажется достаточно существенной, чтобы оправдать такой серьезный поступок.
По словам людей, знакомых с их работой, мистер Гарланд и его следователи полностью осознают последствия своих решений. По их словам, знание того, что они будут подвергнуты тщательной проверке на предмет нарушений и злоупотреблений, подчеркнуло необходимость опираться на факты.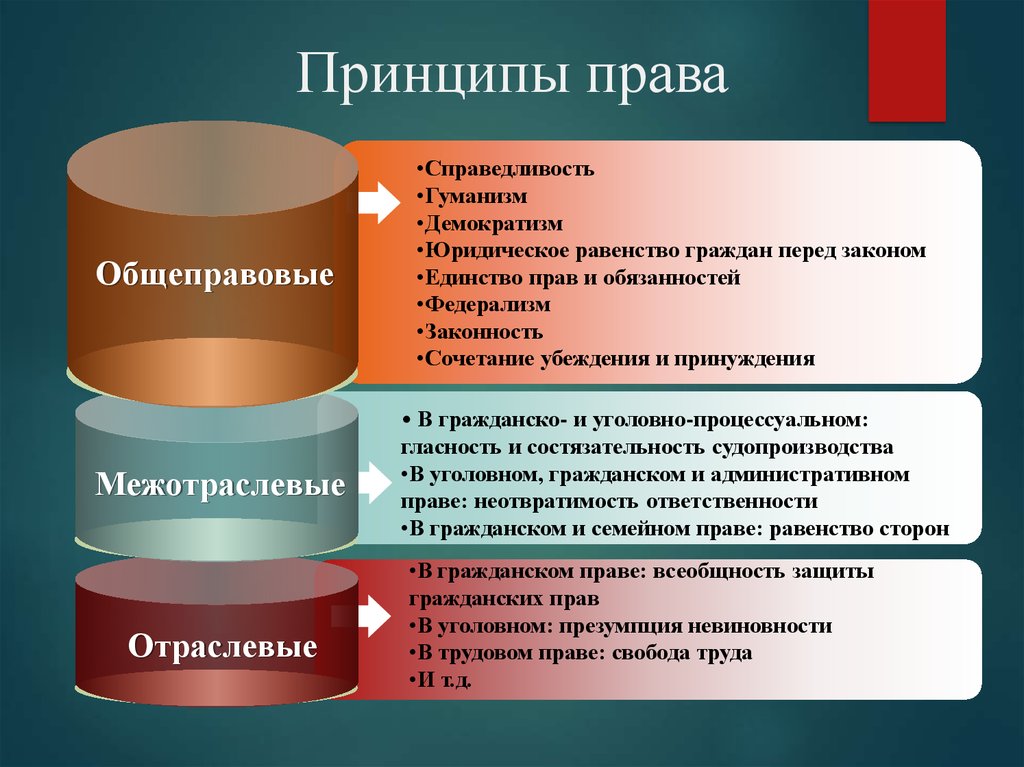


 Мы обучим модель предсказывать, выплатят ли кредит люди, ранее не попадавшие в поле зрения. Такую модель можно использовать для принятия решений о кредитах.
Мы обучим модель предсказывать, выплатят ли кредит люди, ранее не попадавшие в поле зрения. Такую модель можно использовать для принятия решений о кредитах. drop(labels=['sex', 'race'],axis = 1)
# Split the data in "train" and "test" sets
(X_train, X_test, y_train, y_test, A_train, A_test) = train_test_split(
X_raw, y, A, test_size=0.3, random_state=12345, stratify=y
)
# Ensure indices are aligned between X, y and A,
# after all the slicing and splitting of DataFrames
# and Series
X_train = X_train.reset_index(drop=True)
X_test = X_test.reset_index(drop=True)
y_train = y_train.reset_index(drop=True)
y_test = y_test.reset_index(drop=True)
A_train = A_train.reset_index(drop=True)
A_test = A_test.reset_index(drop=True)
# Define a processing pipeline. This happens after the split to avoid data leakage
numeric_transformer = Pipeline(
steps=[
("impute", SimpleImputer()),
("scaler", StandardScaler()),
]
)
categorical_transformer = Pipeline(
[
("impute", SimpleImputer(strategy="most_frequent")),
("ohe", OneHotEncoder(handle_unknown="ignore")),
]
)
preprocessor = ColumnTransformer(
transformers=[
("num", numeric_transformer, selector(dtype_exclude="category")),
("cat", categorical_transformer, selector(dtype_include="category")),
]
)
# Put an estimator onto the end of the pipeline
lr_predictor = Pipeline(
steps=[
("preprocessor", copy.
drop(labels=['sex', 'race'],axis = 1)
# Split the data in "train" and "test" sets
(X_train, X_test, y_train, y_test, A_train, A_test) = train_test_split(
X_raw, y, A, test_size=0.3, random_state=12345, stratify=y
)
# Ensure indices are aligned between X, y and A,
# after all the slicing and splitting of DataFrames
# and Series
X_train = X_train.reset_index(drop=True)
X_test = X_test.reset_index(drop=True)
y_train = y_train.reset_index(drop=True)
y_test = y_test.reset_index(drop=True)
A_train = A_train.reset_index(drop=True)
A_test = A_test.reset_index(drop=True)
# Define a processing pipeline. This happens after the split to avoid data leakage
numeric_transformer = Pipeline(
steps=[
("impute", SimpleImputer()),
("scaler", StandardScaler()),
]
)
categorical_transformer = Pipeline(
[
("impute", SimpleImputer(strategy="most_frequent")),
("ohe", OneHotEncoder(handle_unknown="ignore")),
]
)
preprocessor = ColumnTransformer(
transformers=[
("num", numeric_transformer, selector(dtype_exclude="category")),
("cat", categorical_transformer, selector(dtype_include="category")),
]
)
# Put an estimator onto the end of the pipeline
lr_predictor = Pipeline(
steps=[
("preprocessor", copy. deepcopy(preprocessor)),
(
"classifier",
LogisticRegression(solver="liblinear", fit_intercept=True),
),
]
)
# Train the model on the test data
lr_predictor.fit(X_train, y_train)
# (Optional) View this model in the fairness dashboard, and see the disparities which appear:
from raiwidgets import FairnessDashboard
FairnessDashboard(sensitive_features=A_test,
y_true=y_test,
y_pred={"lr_model": lr_predictor.predict(X_test)})
deepcopy(preprocessor)),
(
"classifier",
LogisticRegression(solver="liblinear", fit_intercept=True),
),
]
)
# Train the model on the test data
lr_predictor.fit(X_train, y_train)
# (Optional) View this model in the fairness dashboard, and see the disparities which appear:
from raiwidgets import FairnessDashboard
FairnessDashboard(sensitive_features=A_test,
y_true=y_test,
y_pred={"lr_model": lr_predictor.predict(X_test)})
 pkl".format(name)
joblib.dump(value=model, filename=model_path)
registered_model = Model.register(model_path=model_path,
model_name=name,
workspace=ws)
print("Registered ", registered_model.id)
return registered_model.id
# Call the register_model function
lr_reg_id = register_model("fairness_logistic_regression", lr_predictor)
pkl".format(name)
joblib.dump(value=model, filename=model_path)
registered_model = Model.register(model_path=model_path,
model_name=name,
workspace=ws)
print("Registered ", registered_model.id)
return registered_model.id
# Call the register_model function
lr_reg_id = register_model("fairness_logistic_regression", lr_predictor)
 race, 'Sex': A_test.sex}
ys_pred = { lr_reg_id:lr_predictor.predict(X_test) }
from fairlearn.metrics._group_metric_set import _create_group_metric_set
dash_dict = _create_group_metric_set(y_true=y_test,
predictions=ys_pred,
sensitive_features=sf,
prediction_type='binary_classification')
race, 'Sex': A_test.sex}
ys_pred = { lr_reg_id:lr_predictor.predict(X_test) }
from fairlearn.metrics._group_metric_set import _create_group_metric_set
dash_dict = _create_group_metric_set(y_true=y_test,
predictions=ys_pred,
sensitive_features=sf,
prediction_type='binary_classification')
 format(upload_id))
# To test the dashboard, you can download it back and ensure it contains the right information
downloaded_dict = download_dashboard_by_upload_id(run, upload_id)
finally:
run.complete()
format(upload_id))
# To test the dashboard, you can download it back and ensure it contains the right information
downloaded_dict = download_dashboard_by_upload_id(run, upload_id)
finally:
run.complete()


 deepcopy(preprocessor)),
(
"classifier",
svm.SVC(),
),
]
)
# Train your second classification model
svm_predictor.fit(X_train, y_train)
deepcopy(preprocessor)),
(
"classifier",
svm.SVC(),
),
]
)
# Train your second classification model
svm_predictor.fit(X_train, y_train)
 items():
ys_pred[n] = p.predict(X_test)
from raiwidgets import FairnessDashboard
FairnessDashboard(sensitive_features=A_test,
y_true=y_test.tolist(),
y_pred=ys_pred)
items():
ys_pred[n] = p.predict(X_test)
from raiwidgets import FairnessDashboard
FairnessDashboard(sensitive_features=A_test,
y_true=y_test.tolist(),
y_pred=ys_pred)
 start_logging()
# Upload the dashboard to Azure Machine Learning
try:
dashboard_title = "Fairness Assessment of Logistic Regression and SVM Classifiers"
# Set validate_model_ids parameter of upload_dashboard_dictionary to False if you have not registered your model(s)
upload_id = upload_dashboard_dictionary(run,
dash_dict,
dashboard_name=dashboard_title)
print("\nUploaded to id: {0}\n".format(upload_id))
# To test the dashboard, you can download it back and ensure it contains the right information
downloaded_dict = download_dashboard_by_upload_id(run, upload_id)
finally:
run.complete()
start_logging()
# Upload the dashboard to Azure Machine Learning
try:
dashboard_title = "Fairness Assessment of Logistic Regression and SVM Classifiers"
# Set validate_model_ids parameter of upload_dashboard_dictionary to False if you have not registered your model(s)
upload_id = upload_dashboard_dictionary(run,
dash_dict,
dashboard_name=dashboard_title)
print("\nUploaded to id: {0}\n".format(upload_id))
# To test the dashboard, you can download it back and ensure it contains the right information
downloaded_dict = download_dashboard_by_upload_id(run, upload_id)
finally:
run.complete()
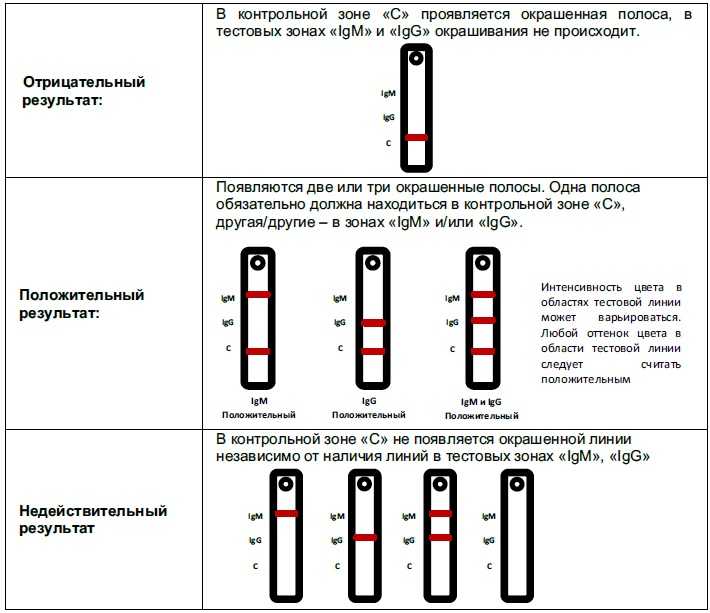

 [Официальные формы банкротства можно найти на веб-сайте Административного управления судов США.]
[Официальные формы банкротства можно найти на веб-сайте Административного управления судов США.] Однако нам и секретарю вашего местного суда по делам о банкротстве запрещено давать какие-либо юридические консультации.
Однако нам и секретарю вашего местного суда по делам о банкротстве запрещено давать какие-либо юридические консультации.
 Пересмотренные множители и стандарты будут применяться к делам, поданным 15 мая 2022 г. или после этой даты9.0005
Пересмотренные множители и стандарты будут применяться к делам, поданным 15 мая 2022 г. или после этой даты9.0005
 — День памяти
— День памяти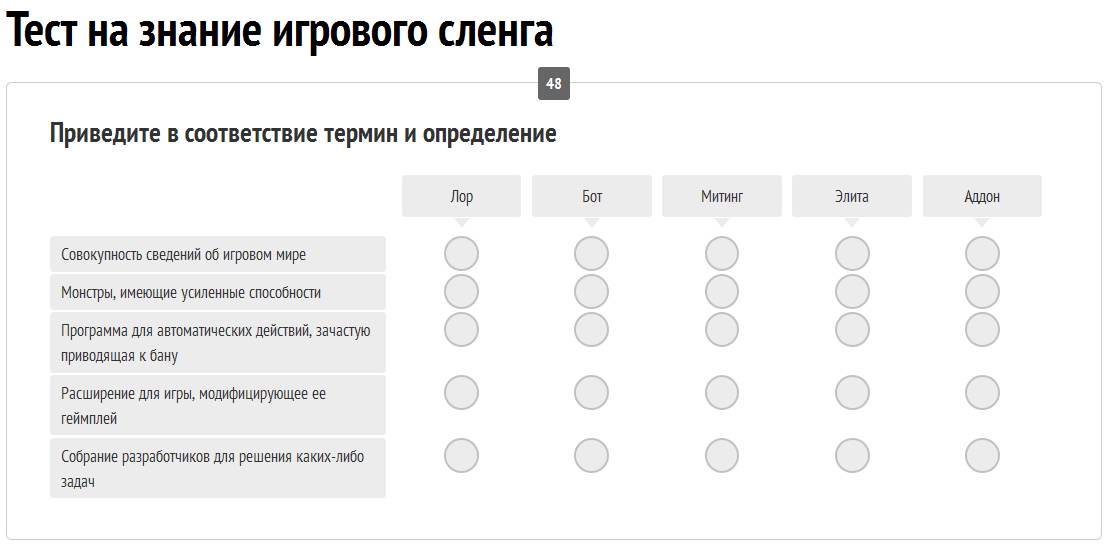 Цель этого мандата состояла в том, чтобы гарантировать, что ни одно лицо не может «служить в качестве сотрудника правоохранительных органов, имеющего право производить аресты или право носить огнестрельное оружие, пока не будет подтверждено соответствие требованиям предварительной подготовки». Это привело к первой программе предварительной подготовки сотрудников правоохранительных органов.
Цель этого мандата состояла в том, чтобы гарантировать, что ни одно лицо не может «служить в качестве сотрудника правоохранительных органов, имеющего право производить аресты или право носить огнестрельное оружие, пока не будет подтверждено соответствие требованиям предварительной подготовки». Это привело к первой программе предварительной подготовки сотрудников правоохранительных органов. Эти требования более полно поясняются следующим образом:
Эти требования более полно поясняются следующим образом: С даты завершения этапа I у студента будет два года, чтобы начать этап II.
С даты завершения этапа I у студента будет два года, чтобы начать этап II. См. справочную форму MCJA . Дисквалифицирующее поведение или судимость лишают заявителей права на участие, если только Совет MCJA не получит отказ.
См. справочную форму MCJA . Дисквалифицирующее поведение или судимость лишают заявителей права на участие, если только Совет MCJA не получит отказ. Следующие три (3) элемента теста представляют собой требования к тесту на физическую пригодность (PFT) для принятия в Программу подготовки к службе в правоохранительных органах, этап II (такую же, как для участия в BLETP): Максимальное отжимание за одну минуту; Одноминутный тест на приседания; и бег на 1,5 км. Студент должен будет сдать экзамен PFT в течение 2 лет до даты начала программы Фазы II .
Следующие три (3) элемента теста представляют собой требования к тесту на физическую пригодность (PFT) для принятия в Программу подготовки к службе в правоохранительных органах, этап II (такую же, как для участия в BLETP): Максимальное отжимание за одну минуту; Одноминутный тест на приседания; и бег на 1,5 км. Студент должен будет сдать экзамен PFT в течение 2 лет до даты начала программы Фазы II .
 Заполните заявку на Фазу I и отправьте ее в академию с оплатой и при необходимости включите выписку из колледжа.
Заполните заявку на Фазу I и отправьте ее в академию с оплатой и при необходимости включите выписку из колледжа.
 лицу, проинструктированному по этому вопросу.
лицу, проинструктированному по этому вопросу. Одна из ключевых особенностей Tabletop Simulator, обеспечившая ей грандиозный успех, заключается в том, что все действия здесь совершаются с использованием продвинутого физического движка на интерактивных игровых столах и с объемными игровыми фигурами, доступными для любых манипуляций. Так что если игра не заладилась, вы всегда можете смести в гневе все фигуры и карты на пол или даже опрокинуть стол.
Одна из ключевых особенностей Tabletop Simulator, обеспечившая ей грандиозный успех, заключается в том, что все действия здесь совершаются с использованием продвинутого физического движка на интерактивных игровых столах и с объемными игровыми фигурами, доступными для любых манипуляций. Так что если игра не заладилась, вы всегда можете смести в гневе все фигуры и карты на пол или даже опрокинуть стол. Все наборы имеют характерное тематическое оформление: классический дизайн, резьба из дерева и камня, Древний Рим, раннее Средневековье, Хэллоуин, мрамор, Моаи, животные и так далее.
Все наборы имеют характерное тематическое оформление: классический дизайн, резьба из дерева и камня, Древний Рим, раннее Средневековье, Хэллоуин, мрамор, Моаи, животные и так далее. Есть свободно вращаемая и масштабируемая камера, приятная анимация ходов и музыка. Для игры с ИИ есть возможность свободно загружать любые современные шахматные движки по своему усмотрению. Также можно играть через Интернет с другими пользователями.
Есть свободно вращаемая и масштабируемая камера, приятная анимация ходов и музыка. Для игры с ИИ есть возможность свободно загружать любые современные шахматные движки по своему усмотрению. Также можно играть через Интернет с другими пользователями. Еще у игры довольно приятный саундтрек, а вызвать на дуэль как всегда можно друзей в локальном мультиплеере.
Еще у игры довольно приятный саундтрек, а вызвать на дуэль как всегда можно друзей в локальном мультиплеере. Из недостатков – отсутствие русского языка и мультиплеера.
Из недостатков – отсутствие русского языка и мультиплеера. org. Конечно, не стоит забывать и про возможность просто приятно пообщаться с соратниками по интересам или понаблюдать в режиме онлайн за партиями признанных мастеров.
org. Конечно, не стоит забывать и про возможность просто приятно пообщаться с соратниками по интересам или понаблюдать в режиме онлайн за партиями признанных мастеров.

 Проект вдохновил многих разработчиков на создание собственных игр в поджанре auto battler.
Проект вдохновил многих разработчиков на создание собственных игр в поджанре auto battler. Проверить, работают они или нет, можно не только в любительской дуэли, но и в рейтинговых матчах, где за достижения присваиваются различные ранги.
Проверить, работают они или нет, можно не только в любительской дуэли, но и в рейтинговых матчах, где за достижения присваиваются различные ранги.
 Кстати, игра является многопользовательской, что делает ее еще более неординарной и любопытной.
Кстати, игра является многопользовательской, что делает ее еще более неординарной и любопытной.
 Имеется несколько наборов фигурок и несколько типов окружения, а при желании можно переключить игру на классический вид.
Имеется несколько наборов фигурок и несколько типов окружения, а при желании можно переключить игру на классический вид. Кроме обилия карт и героев Rooks Keep впечатляет и множеством доступных режимов, варьирующихся от банального экшена до изощренной стратегии. Есть и режим классических шахмат, а также режим шахмат продвинутых, в котором фигурки, оказавшиеся под ударом, будут сражаться друг с другом в реальном времени за возможность сохранить за собой место на шахматном поле.
Кроме обилия карт и героев Rooks Keep впечатляет и множеством доступных режимов, варьирующихся от банального экшена до изощренной стратегии. Есть и режим классических шахмат, а также режим шахмат продвинутых, в котором фигурки, оказавшиеся под ударом, будут сражаться друг с другом в реальном времени за возможность сохранить за собой место на шахматном поле. С героями этого приключения вы уже знакомы, и, чтобы они выжили и прошли дальше, придется задействовать всю свою тактическую хитрость.
С героями этого приключения вы уже знакомы, и, чтобы они выжили и прошли дальше, придется задействовать всю свою тактическую хитрость. Несмотря на более 30 тысяч вариантов ходов, ИИ в игре оставляет желать лучшего, но всегда можно пригласить на партию товарища или сразиться на одном ПК.
Несмотря на более 30 тысяч вариантов ходов, ИИ в игре оставляет желать лучшего, но всегда можно пригласить на партию товарища или сразиться на одном ПК.
 ”
” Скачать обновление можно здесь.
Скачать обновление можно здесь. 3.1
3.1
 02(Размер 30.91 MB)
02(Размер 30.91 MB) Оказалось, что такого количества зерна нет на всей планете. Правда это или нет, теперь уже никто не знает. Но то, что шахматы придумали в Индии – это факт.
Оказалось, что такого количества зерна нет на всей планете. Правда это или нет, теперь уже никто не знает. Но то, что шахматы придумали в Индии – это факт. Сборник задач и встроенный, удобный редактор для их создания
Сборник задач и встроенный, удобный редактор для их создания Играйте онлайн с чемпионами таблицы лидеров, анализируйте сыгранные матчи. Можно выбрать противника для следующей партии — друга или искусственный интеллект. Играйте в бесплатные шахматы онлайн!
Играйте онлайн с чемпионами таблицы лидеров, анализируйте сыгранные матчи. Можно выбрать противника для следующей партии — друга или искусственный интеллект. Играйте в бесплатные шахматы онлайн! Развивайте свои навыки в школе игры, решая шахматные задачи в наших шахматных башнях.
Развивайте свои навыки в школе игры, решая шахматные задачи в наших шахматных башнях.
 Подробнее
Подробнее 07.2022
07.2022 Но для рейтинга лучших мы выбрали только пять таких сайтов, заслуживающих внимания больше остальных.
Но для рейтинга лучших мы выбрали только пять таких сайтов, заслуживающих внимания больше остальных.  А еще у платформы есть мобильная версия для Android и iOS, что позволяет играть и учиться шахматной логике в любом удобном месте.
А еще у платформы есть мобильная версия для Android и iOS, что позволяет играть и учиться шахматной логике в любом удобном месте.  Подписка рекомендована и тем, кто собирается повысить свой уровень мастерства, занимаясь с тренером.
Подписка рекомендована и тем, кто собирается повысить свой уровень мастерства, занимаясь с тренером. 

 Есть тренажер для игры без доски, собственный телеканал и таблица эндшпилей для изучения различных окончаний партий.
Есть тренажер для игры без доски, собственный телеканал и таблица эндшпилей для изучения различных окончаний партий. 
 Простота в установке, отличная графика, удобный интерфейс, приятное музыкальное сопровождение – все это добавляет шахматам Kasparov Chessmate лидирующие позиции среди аналогичных программ. Игра позволяет вести шахматные бои не только в локальной версии (с компьютером), игрокам открывается возможность выбрать достойного противника и в онлайн-игре. Кроме собственно игры, пользователям предлагается пройти виртуальный мастер-класс от великого гроссмейстера, а также потренироваться на упражнениях из исторических матчей Гарри Каспарова.
Простота в установке, отличная графика, удобный интерфейс, приятное музыкальное сопровождение – все это добавляет шахматам Kasparov Chessmate лидирующие позиции среди аналогичных программ. Игра позволяет вести шахматные бои не только в локальной версии (с компьютером), игрокам открывается возможность выбрать достойного противника и в онлайн-игре. Кроме собственно игры, пользователям предлагается пройти виртуальный мастер-класс от великого гроссмейстера, а также потренироваться на упражнениях из исторических матчей Гарри Каспарова.

 В программе целых 15 уровней по силе игры — этого точно будет достаточно не только для любителей, но и для профессионалов!
В программе целых 15 уровней по силе игры — этого точно будет достаточно не только для любителей, но и для профессионалов!
 Пока организована возможность играть с компьютером и решать . В дальнейшем мы планируем сделать еще массу всего полезного для шахматистов. Надеемся, что в каждой сыгранной вами партии, король противника будет повержен также, как и на картинке слева!
Пока организована возможность играть с компьютером и решать . В дальнейшем мы планируем сделать еще массу всего полезного для шахматистов. Надеемся, что в каждой сыгранной вами партии, король противника будет повержен также, как и на картинке слева! В некоторых случаях роль шахматных персон берут на себя схематичные изображения или же шахматы воплощаются в реальных персонажей, делая партии еще более живыми, интересными и насыщенными. В иных случаях можно оценивать гроссмейстерское мастерство на суровом поединке разумов в настоящих соревнованиях. Как играть? Это решает геймер самостоятельно, а портал ИгроУтка просто предоставляет ему огромный выбор и разнообразие игр!
В некоторых случаях роль шахматных персон берут на себя схематичные изображения или же шахматы воплощаются в реальных персонажей, делая партии еще более живыми, интересными и насыщенными. В иных случаях можно оценивать гроссмейстерское мастерство на суровом поединке разумов в настоящих соревнованиях. Как играть? Это решает геймер самостоятельно, а портал ИгроУтка просто предоставляет ему огромный выбор и разнообразие игр!
 Можно выбирать любой из трех уровней сложности, начиная от легкого и заканчивая сложным. Таким образом наши онлайн шахматы будут полезны как новичкам, которые только постигают увлекательный мир шахмат так и опытным игрокам, которые желают “прокачать” свои навыки на скорость игры.
Можно выбирать любой из трех уровней сложности, начиная от легкого и заканчивая сложным. Таким образом наши онлайн шахматы будут полезны как новичкам, которые только постигают увлекательный мир шахмат так и опытным игрокам, которые желают “прокачать” свои навыки на скорость игры. Всем удачной игры!
Всем удачной игры! И данный факт предопределил слабую игру флеш-шахмат аsisChess, поэтому мы не рекомендуем ихопытным шахматистам. Но asisChess станут отличным шахматным тренером для начинающих игроков в шахматы и любителей.
И данный факт предопределил слабую игру флеш-шахмат аsisChess, поэтому мы не рекомендуем ихопытным шахматистам. Но asisChess станут отличным шахматным тренером для начинающих игроков в шахматы и любителей.
 Существует четыре различных стиля доски (двухмерная диаграмма, два фиксированных трехмерных дизайна и вращающаяся трехмерная доска), которые подойдут для любого человека – от развлекающегося ребенка до серьезного турнирного игрока.
Существует четыре различных стиля доски (двухмерная диаграмма, два фиксированных трехмерных дизайна и вращающаяся трехмерная доска), которые подойдут для любого человека – от развлекающегося ребенка до серьезного турнирного игрока. Вы можете скачать SparkChess для PC, Mac, iPad, iPhone, а также телефонов и планшетов Android.
Вы можете скачать SparkChess для PC, Mac, iPad, iPhone, а также телефонов и планшетов Android.
 Обратите внимание, что бесплатные учетные записи могут быть удалены, если они не используются в течение длительного времени. Не разрешается использовать неприличные имена пользователей, они могут быть удалены без предупреждения.
Обратите внимание, что бесплатные учетные записи могут быть удалены, если они не используются в течение длительного времени. Не разрешается использовать неприличные имена пользователей, они могут быть удалены без предупреждения.
 Вы можете отфильтровать противников по разным критериям. Многопользовательский сервис удобен для детей. Если вам не хочется играть, теперь вы можете просто смотреть игры в прямом эфире по мере их развития.
Вы можете отфильтровать противников по разным критериям. Многопользовательский сервис удобен для детей. Если вам не хочется играть, теперь вы можете просто смотреть игры в прямом эфире по мере их развития. Все права защищены.
Все права защищены. 
 Подробнее 🡢
Подробнее 🡢  Подробнее 🡢
Подробнее 🡢  Подробнее 🡢
Подробнее 🡢 
 »
» »
»


 Это отличный способ изучить более продвинутые шахматные стратегии.
Это отличный способ изучить более продвинутые шахматные стратегии. Chess от Chess.com — еще одно хорошее приложение в этом жанре, работающее очень похоже.
Chess от Chess.com — еще одно хорошее приложение в этом жанре, работающее очень похоже. В нем представлены офлайн-наборы головоломок (доступны как покупки в приложении), ежедневные онлайн-головоломки и многое другое. В нем утверждается, что сложность некоторых испытаний может достигать ELO 2000+, и это почти все, что нужно. Это хороший способ проверить свои навыки и изучить новые тактики. Игра бесплатна для скачивания. Вы можете приобрести дополнительный контент через покупки в приложении.
В нем представлены офлайн-наборы головоломок (доступны как покупки в приложении), ежедневные онлайн-головоломки и многое другое. В нем утверждается, что сложность некоторых испытаний может достигать ELO 2000+, и это почти все, что нужно. Это хороший способ проверить свои навыки и изучить новые тактики. Игра бесплатна для скачивания. Вы можете приобрести дополнительный контент через покупки в приложении. Его основная идея — играть в шахматы онлайн против других игроков. Игра может похвастаться базой игроков, насчитывающей более 150 000 игроков. Это не должно сильно усложнить поиск игры с человеком примерно вашего уровня навыков. Также в нем есть несколько режимов игры, турниры, и вы можете видеть свою игровую статистику. Вы также можете играть в автономном режиме против компьютера, если хотите. Приложение также может похвастаться тем, что оно доступно на 80 языках. Его самая большая ничья — цена. Это бесплатно без рекламы или покупок в приложении. Приложение также имеет открытый исходный код, если вы хотите увидеть, как оно работает.
Его основная идея — играть в шахматы онлайн против других игроков. Игра может похвастаться базой игроков, насчитывающей более 150 000 игроков. Это не должно сильно усложнить поиск игры с человеком примерно вашего уровня навыков. Также в нем есть несколько режимов игры, турниры, и вы можете видеть свою игровую статистику. Вы также можете играть в автономном режиме против компьютера, если хотите. Приложение также может похвастаться тем, что оно доступно на 80 языках. Его самая большая ничья — цена. Это бесплатно без рекламы или покупок в приложении. Приложение также имеет открытый исходный код, если вы хотите увидеть, как оно работает. Кроме того, огромное количество головоломок, которые вы получаете за 1,99 доллара, определенно того стоит. В игре есть некоторые ошибки с подсчетом очков, но в этом нет ничего особенно серьезного.
Кроме того, огромное количество головоломок, которые вы получаете за 1,99 доллара, определенно того стоит. В игре есть некоторые ошибки с подсчетом очков, но в этом нет ничего особенно серьезного. Это похоже на довольно стандартную шахматную партию. Тем не менее, этот позволяет вам играть с совершенно случайными фигурами. У вас может быть пять коней и три слона или 3 ферзя и 2 пешки на доске для всех игровых забот. Бесплатная версия позволяет вам сражаться с ИИ в нескольких различных игровых режимах. Премиум-версия добавляет режим сравнения, убирает рекламу, добавляет темы и некоторые другие мелкие изменения. Это шахматная игра для тех, кто всегда задавался вопросом, что было бы, если бы тонкий баланс и идеальная стратегия не имели значения.
Это похоже на довольно стандартную шахматную партию. Тем не менее, этот позволяет вам играть с совершенно случайными фигурами. У вас может быть пять коней и три слона или 3 ферзя и 2 пешки на доске для всех игровых забот. Бесплатная версия позволяет вам сражаться с ИИ в нескольких различных игровых режимах. Премиум-версия добавляет режим сравнения, убирает рекламу, добавляет темы и некоторые другие мелкие изменения. Это шахматная игра для тех, кто всегда задавался вопросом, что было бы, если бы тонкий баланс и идеальная стратегия не имели значения. В ней есть случайные ошибки, но ИИ вполне человекоподобный, и это приятная игра.
В ней есть случайные ошибки, но ИИ вполне человекоподобный, и это приятная игра. В результате у Maia более человеческий стиль, чем у предыдущих движков, и более 50% времени повторяются ходы, выполняемые игроками-людьми в онлайн-играх.
В результате у Maia более человеческий стиль, чем у предыдущих движков, и более 50% времени повторяются ходы, выполняемые игроками-людьми в онлайн-играх.
 Каждая майя делала прогноз для каждой позиции, и мы измеряли результирующую точность сопоставления ходов в каждом наборе. .
Каждая майя делала прогноз для каждой позиции, и мы измеряли результирующую точность сопоставления ходов в каждом наборе. .

 Наши исследовательские цели включают в себя персонализацию Maia для отдельных игроков, определение типов ошибок, которые совершаются на каждом уровне рейтинга, запуск Maia в ваших играх и выявление повторяющихся предсказуемых ошибок и многое другое.
Наши исследовательские цели включают в себя персонализацию Maia для отдельных игроков, определение типов ошибок, которые совершаются на каждом уровне рейтинга, запуск Maia в ваших играх и выявление повторяющихся предсказуемых ошибок и многое другое.
 Сотни миллионов онлайн-игр, в которые играют игроки любого уровня квалификации, представляют собой богатый источник данных, в котором эти решения и их точный контекст записываются в мельчайших деталях. Применяя к этим данным существующие шахматные движки, включая реализацию AlphaZero с открытым исходным кодом, мы обнаруживаем, что они плохо предсказывают ходы человека.
Мы разрабатываем и представляем Maia, специализированную версию Alpha-Zero, обученную на человеческих шахматных играх, которая предсказывает ходы человека с гораздо большей точностью, чем существующие движки, и может достигать максимальной точности при прогнозировании решений, принимаемых игроками с определенным уровнем навыков в игре. настраиваемый способ. Для двойной задачи прогнозирования того, совершит ли человек большую ошибку при следующем шаге, мы разрабатываем глубокую нейронную сеть, которая значительно превосходит конкурентные базовые показатели. Взятые вместе, наши результаты показывают, что существует многообещающая разработка систем искусственного интеллекта с учетом взаимодействия людей путем предварительного точного моделирования детального принятия решений человеком.
Сотни миллионов онлайн-игр, в которые играют игроки любого уровня квалификации, представляют собой богатый источник данных, в котором эти решения и их точный контекст записываются в мельчайших деталях. Применяя к этим данным существующие шахматные движки, включая реализацию AlphaZero с открытым исходным кодом, мы обнаруживаем, что они плохо предсказывают ходы человека.
Мы разрабатываем и представляем Maia, специализированную версию Alpha-Zero, обученную на человеческих шахматных играх, которая предсказывает ходы человека с гораздо большей точностью, чем существующие движки, и может достигать максимальной точности при прогнозировании решений, принимаемых игроками с определенным уровнем навыков в игре. настраиваемый способ. Для двойной задачи прогнозирования того, совершит ли человек большую ошибку при следующем шаге, мы разрабатываем глубокую нейронную сеть, которая значительно превосходит конкурентные базовые показатели. Взятые вместе, наши результаты показывают, что существует многообещающая разработка систем искусственного интеллекта с учетом взаимодействия людей путем предварительного точного моделирования детального принятия решений человеком.
 Джон Клейнберг был частично поддержан премией Саймонса исследователя, стипендией факультета Ванневара Буша, грантом MURI и грантом Фонда Макартура.
Джон Клейнберг был частично поддержан премией Саймонса исследователя, стипендией факультета Ванневара Буша, грантом MURI и грантом Фонда Макартура.
 Раздел ниже для объяснения этого).
Раздел ниже для объяснения этого). (Я сверяюсь с рейтингами с сайта computerchess.org.uk (открывается в новой вкладке).)
(Я сверяюсь с рейтингами с сайта computerchess.org.uk (открывается в новой вкладке).) версия.
версия. Большая часть того, за что вы платите, — это их полнота и качество их учебных инструментов.
Большая часть того, за что вы платите, — это их полнота и качество их учебных инструментов. com (откроется в новой вкладке). Если вам нужен полный пакет и вы не жалеете денег, это разумный выбор. Однако пользоваться им ничуть не проще, чем бесплатными вариантами, поэтому я бы посоветовал поискать несколько руководств (откроется в новой вкладке).
com (откроется в новой вкладке). Если вам нужен полный пакет и вы не жалеете денег, это разумный выбор. Однако пользоваться им ничуть не проще, чем бесплатными вариантами, поэтому я бы посоветовал поискать несколько руководств (откроется в новой вкладке). Эти инструменты не для игры, а для анализа шахматных партий.
Эти инструменты не для игры, а для анализа шахматных партий.
 Он думал, что это нормально. В 2011 году он присоединился к PC Gamer, и сегодня он сосредоточен на новостях сайта. После работы он занимается боксом и добавляет к своим 1200 часам в Rocket League.
Он думал, что это нормально. В 2011 году он присоединился к PC Gamer, и сегодня он сосредоточен на новостях сайта. После работы он занимается боксом и добавляет к своим 1200 часам в Rocket League. Вы можете посмотреть его, если ищете шахматные игры для своего компьютера.
Вы можете посмотреть его, если ищете шахматные игры для своего компьютера. Хотя это забавная игра, стоимость непомерно высока, если мы хотим сыграть в одну игру.
Хотя это забавная игра, стоимость непомерно высока, если мы хотим сыграть в одну игру.
 В результате вы можете выбрать доску на основе ваших предпочтений.
В результате вы можете выбрать доску на основе ваших предпочтений. Без сомнения, это одна из лучших шахматных игр для ПК.
Без сомнения, это одна из лучших шахматных игр для ПК. Это одна из самых визуально ошеломляющих шахматных игр, доступных сегодня.
Это одна из самых визуально ошеломляющих шахматных игр, доступных сегодня.


 В 2015 году игра вышла.
В 2015 году игра вышла. Дайте ребенку карандаш. Пусть он нарисует дорожку, по которой белочке можно добраться до желудя.
Дайте ребенку карандаш. Пусть он нарисует дорожку, по которой белочке можно добраться до желудя. И очень важно сделать все правильно, потому что ошибка в одном месте приведет к неточности в другом.
И очень важно сделать все правильно, потому что ошибка в одном месте приведет к неточности в другом. В этой игре ребенок должен выполнить каждое задание и написать ответ на льдинке. После этого можно проложить путь медведицы к медвежонку по льдинкам, на которых написаны числа 1, 2, 3 и далее по порядку до 10.
В этой игре ребенок должен выполнить каждое задание и написать ответ на льдинке. После этого можно проложить путь медведицы к медвежонку по льдинкам, на которых написаны числа 1, 2, 3 и далее по порядку до 10. Малыш должен решить математический пример, который написан на фрукте, и «положить» его в правильную корзинку.
Малыш должен решить математический пример, который написан на фрукте, и «положить» его в правильную корзинку.


 Наконец-то сын занимается математикой с великим удовольствием и рвением! Побольше бы таких игровых пособий! Процветания вам!
Наконец-то сын занимается математикой с великим удовольствием и рвением! Побольше бы таких игровых пособий! Процветания вам! Подробные сведения доступны в политике конфиденциальности разработчика.
Подробные сведения доступны в политике конфиденциальности разработчика. В их число входит коллекция новогодних игр про Санта-Клауса, Деда Мороза и Снегурочку. Надеемся всем придется по душе кидание снежками и катание на санях в новогодние праздники, которые для детей всегда были настоящими каникулами, ну а для взрослых превратились в полноценный отпуск.
В их число входит коллекция новогодних игр про Санта-Клауса, Деда Мороза и Снегурочку. Надеемся всем придется по душе кидание снежками и катание на санях в новогодние праздники, которые для детей всегда были настоящими каникулами, ну а для взрослых превратились в полноценный отпуск. Это стандартный плагин, вырезающий рекламу внутри игр и на страницах игровых сайтов.
Это стандартный плагин, вырезающий рекламу внутри игр и на страницах игровых сайтов. HTML5 — универсальные и работают независимо от платформы, на которой вы их открываете (ПК, Мак, андроид смартфон, айфон, айпад и т.д.) Также стали убирать с сайта все на движке UNITY3D, т.к. поддержка этого плагина в скором времени также станет ограниченной (об этом заявила компания гугл) и unity3d игры часто вешают ваш браузер, что приводит к тому, что вы уходите с нашего распрекрасного сайта в другие места 🙂
HTML5 — универсальные и работают независимо от платформы, на которой вы их открываете (ПК, Мак, андроид смартфон, айфон, айпад и т.д.) Также стали убирать с сайта все на движке UNITY3D, т.к. поддержка этого плагина в скором времени также станет ограниченной (об этом заявила компания гугл) и unity3d игры часто вешают ваш браузер, что приводит к тому, что вы уходите с нашего распрекрасного сайта в другие места 🙂.png)
 Достаточно выбрать подходящий раздел и нажать в нем на понравившуюся иконку. Всего два клика — и вы наслаждаетесь игрой совершенно бесплатно!
Достаточно выбрать подходящий раздел и нажать в нем на понравившуюся иконку. Всего два клика — и вы наслаждаетесь игрой совершенно бесплатно! Также вам наверняка понравятся спортивные симуляторы из разделов «Гонки», «Хоккей» и «Футбол», ведь ни один мальчик не смыслит своей жизни без духа соревнования или быстрых автомобилей.
Также вам наверняка понравятся спортивные симуляторы из разделов «Гонки», «Хоккей» и «Футбол», ведь ни один мальчик не смыслит своей жизни без духа соревнования или быстрых автомобилей. Среди них есть множество интересных вариантов, геймплей которых действительно затягивает!
Среди них есть множество интересных вариантов, геймплей которых действительно затягивает! Например, вы сможете наслаждаться любимыми играми без рекламы, а также участвовать в ежемесячном конкурсе игроков с денежными призами.
Например, вы сможете наслаждаться любимыми играми без рекламы, а также участвовать в ежемесячном конкурсе игроков с денежными призами. Удачи в прохождении!
Удачи в прохождении! А вот 25 примеров порешаем?!
А вот 25 примеров порешаем?! 2 класс.
2 класс.
 Читаем задание и выполняем. Всего 10 заданий. Внизу в строке можно выбирать № задания самостоятельно.
Читаем задание и выполняем. Всего 10 заданий. Внизу в строке можно выбирать № задания самостоятельно. 03.2018
8032
03.2018
8032
 04.2022
382
04.2022
382


 02.2021
433
02.2021
433
 Связь между компонентами и результатом умножения. Повторение изученного.
Связь между компонентами и результатом умножения. Повторение изученного.
 Единицы измерения: час, сутки, неделя, месяц, год
Единицы измерения: час, сутки, неделя, месяц, год
 4
4
 02.2022
3202
02.2022
3202
 04.2013
2062
04.2013
2062
 09.2016
82787
09.2016
82787
 03.2017
2153
03.2017
2153
 Тема «Умножение и деление».
Тема «Умножение и деление». 04.2020
156
0
04.2020
156
0
 12.2020
589
12.2020
589
 1
1
 6
6
 Решение задач на кратное сравнение
Решение задач на кратное сравнение
 03.2022
600
0
03.2022
600
0

 ..14
..14 262
262
 К этой группе относятся известные учителям игры «Цепочка», «Молчанка», «Угадайка», «Математическая эстафета», «Составь круговые примеры», «Рассели числа в домики» и др.
К этой группе относятся известные учителям игры «Цепочка», «Молчанка», «Угадайка», «Математическая эстафета», «Составь круговые примеры», «Рассели числа в домики» и др.








 M. и П.М.
M. и П.М..png)











 НБТ.4
НБТ.4


 M. и П.М.
M. и П.М.













 Кроме того, игры на определение времени, измерение длины и высоты и сравнение данных с помощью графиков также отлично подходят для развития математических навыков у второклассников. Онлайн-игры, такие как игры на сложение, игры на вычитание, игры с измерениями, игры со счетом, игры с чувством числа, игры со значениями, алгебраические игры и т. д., могут улучшить качество обучения и практики вашего ребенка по математике.
Кроме того, игры на определение времени, измерение длины и высоты и сравнение данных с помощью графиков также отлично подходят для развития математических навыков у второклассников. Онлайн-игры, такие как игры на сложение, игры на вычитание, игры с измерениями, игры со счетом, игры с чувством числа, игры со значениями, алгебраические игры и т. д., могут улучшить качество обучения и практики вашего ребенка по математике. Занимаясь вычислительной практикой, они могут расширить свое знакомство с такими математическими операциями.
Занимаясь вычислительной практикой, они могут расширить свое знакомство с такими математическими операциями.

 Обучение математике с помощью игр, несомненно, является одним из лучших подходов.
Обучение математике с помощью игр, несомненно, является одним из лучших подходов. Узнайте, как в нее играют, по ссылке.
Узнайте, как в нее играют, по ссылке.
 Учащиеся, которые не бросают, подыгрывают, записывая число самостоятельно, зарабатывая балл, если они угадали.
Учащиеся, которые не бросают, подыгрывают, записывая число самостоятельно, зарабатывая балл, если они угадали.
 Соревнуйтесь в Close Call
Соревнуйтесь в Close Call Затем измерьте расстояние в дюймах и сантиметрах.
Затем измерьте расстояние в дюймах и сантиметрах.
 Дети сопоставляют картинки с указанными суммами. Также есть пустая версия, в которой дети могут вместо этого добавлять свои собственные монеты в квадраты.
Дети сопоставляют картинки с указанными суммами. Также есть пустая версия, в которой дети могут вместо этого добавлять свои собственные монеты в квадраты. Играй в Kaboom! с палочками для монет
Играй в Kaboom! с палочками для монет



 Деньги – работа с денежными монетами для подсчета денег и решения задач, связанных с денежными суммами
Деньги – работа с денежными монетами для подсчета денег и решения задач, связанных с денежными суммами 
 0.1
0.1 И ОМГ, это так идеально для нее! Она учится во втором классе, и игры буквально соответствуют главам ее учебной программы. Мы только что начали играть в игры «Время и деньги», особенно со временем, она просто так путалась, что сводила меня с ума. Ей буквально приходилось делать это снова и снова в игре в течение часа, прежде чем она, наконец, получила это! Но она, наконец, поняла, и я сказал, что следующая игра на самом деле соответствует ее следующей главе по математике, которая считает в пределах 1000. Жаль, что я не получил это для нее раньше. Я так взволнован, если честно, это стоит 59 долларов.. По крайней мере, столько мне стоило бы нанять репетитора на один час. Это на удивление того стоило!
И ОМГ, это так идеально для нее! Она учится во втором классе, и игры буквально соответствуют главам ее учебной программы. Мы только что начали играть в игры «Время и деньги», особенно со временем, она просто так путалась, что сводила меня с ума. Ей буквально приходилось делать это снова и снова в игре в течение часа, прежде чем она, наконец, получила это! Но она, наконец, поняла, и я сказал, что следующая игра на самом деле соответствует ее следующей главе по математике, которая считает в пределах 1000. Жаль, что я не получил это для нее раньше. Я так взволнован, если честно, это стоит 59 долларов.. По крайней мере, столько мне стоило бы нанять репетитора на один час. Это на удивление того стоило! Это бросает достаточно вызовов, и она наслаждается этим. Я собирался просто пройти бесплатную пробную версию, но всего через один день решил покупать ее ежемесячно. Абсолютно 💖 это приложение. До сих пор в последние недели некоторые из упражнений действительно помогли ей с математическими навыками. Это проще, чем пытаться использовать рабочие тетради. У некоторых детей есть разные методы обучения, и это приложение затронуло множество различных методов использования. Я очень ценю Splash Math. Я надеюсь, что это поможет и вам, люди!!! 😊😀😀
Это бросает достаточно вызовов, и она наслаждается этим. Я собирался просто пройти бесплатную пробную версию, но всего через один день решил покупать ее ежемесячно. Абсолютно 💖 это приложение. До сих пор в последние недели некоторые из упражнений действительно помогли ей с математическими навыками. Это проще, чем пытаться использовать рабочие тетради. У некоторых детей есть разные методы обучения, и это приложение затронуло множество различных методов использования. Я очень ценю Splash Math. Я надеюсь, что это поможет и вам, люди!!! 😊😀😀 Маленький парень, говорящий «Ты молодец» каждый раз, когда она отвечает на вопрос, немного раздражает, но это исходит от старой мамы. 76 долларов в год кажутся дорогими, но если она сможет лучше понять математические понятия с помощью этого приложения, я с радостью заплачу вдвое больше.
Маленький парень, говорящий «Ты молодец» каждый раз, когда она отвечает на вопрос, немного раздражает, но это исходит от старой мамы. 76 долларов в год кажутся дорогими, но если она сможет лучше понять математические понятия с помощью этого приложения, я с радостью заплачу вдвое больше. Узнать больше
Узнать больше Для меня это оба этих чувства одновременно. Будучи студентом, я находил изучение математики скучным и бессмысленным. Как родитель, я находил преподавание математики непосильным и разочаровывающим. Вы можете задать себе вопрос:
Для меня это оба этих чувства одновременно. Будучи студентом, я находил изучение математики скучным и бессмысленным. Как родитель, я находил преподавание математики непосильным и разочаровывающим. Вы можете задать себе вопрос: Ваш ученик может даже съесть конфету в конце в качестве награды!
Ваш ученик может даже съесть конфету в конце в качестве награды! Соберите солнечные часы и помогите своему второкласснику в этой захватывающей игре определить время по аналоговым часам.
Соберите солнечные часы и помогите своему второкласснику в этой захватывающей игре определить время по аналоговым часам. С.
С.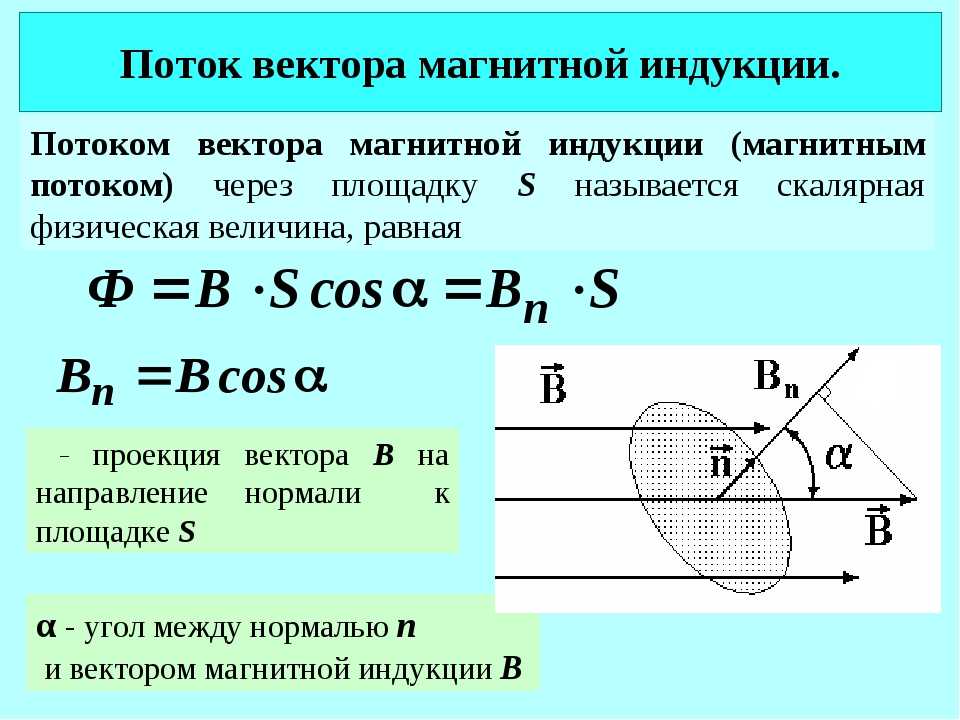 Экономится также время, затраченное учениками на повторение пройденного материала. Но самое главное заключается в том, что учащиеся осваивают единый мощнейший метод изучения тех разделов и тем всех без исключения разделов физики, где встречаются векторные величины (механика, электростатика, электродинамика, магнетизм).
Экономится также время, затраченное учениками на повторение пройденного материала. Но самое главное заключается в том, что учащиеся осваивают единый мощнейший метод изучения тех разделов и тем всех без исключения разделов физики, где встречаются векторные величины (механика, электростатика, электродинамика, магнетизм).
 Действительно, выбрав иное начало отсчета (пулковский меридиан вместо гринвичского, сотворение мира вместо Рождества Христова, среднеевропейское время вместо московского, иную координатную систему, мы получили бы совсем иные числа: ноль градусов, 7195 год (а сам Ньютон получил бы 5675 год) и т. д.
Действительно, выбрав иное начало отсчета (пулковский меридиан вместо гринвичского, сотворение мира вместо Рождества Христова, среднеевропейское время вместо московского, иную координатную систему, мы получили бы совсем иные числа: ноль градусов, 7195 год (а сам Ньютон получил бы 5675 год) и т. д.
 Точно также автору никто не может запретить понимать под числом пи не 3,14…, а, например, 8,395 или измерять расстояние не в метрах, а в попугаях. Находясь в этой своей, если так можно сказать, «понятийной системе координат», автор может весьма комфортно себя чувствовать, делая одно открытие за другим. Но при общении с другими исследователями, находящимися в другой «понятийной системе», ему постоянно придется объяснять, что именно он понимает под тем или иным определением (термином, буквой…).
Точно также автору никто не может запретить понимать под числом пи не 3,14…, а, например, 8,395 или измерять расстояние не в метрах, а в попугаях. Находясь в этой своей, если так можно сказать, «понятийной системе координат», автор может весьма комфортно себя чувствовать, делая одно открытие за другим. Но при общении с другими исследователями, находящимися в другой «понятийной системе», ему постоянно придется объяснять, что именно он понимает под тем или иным определением (термином, буквой…).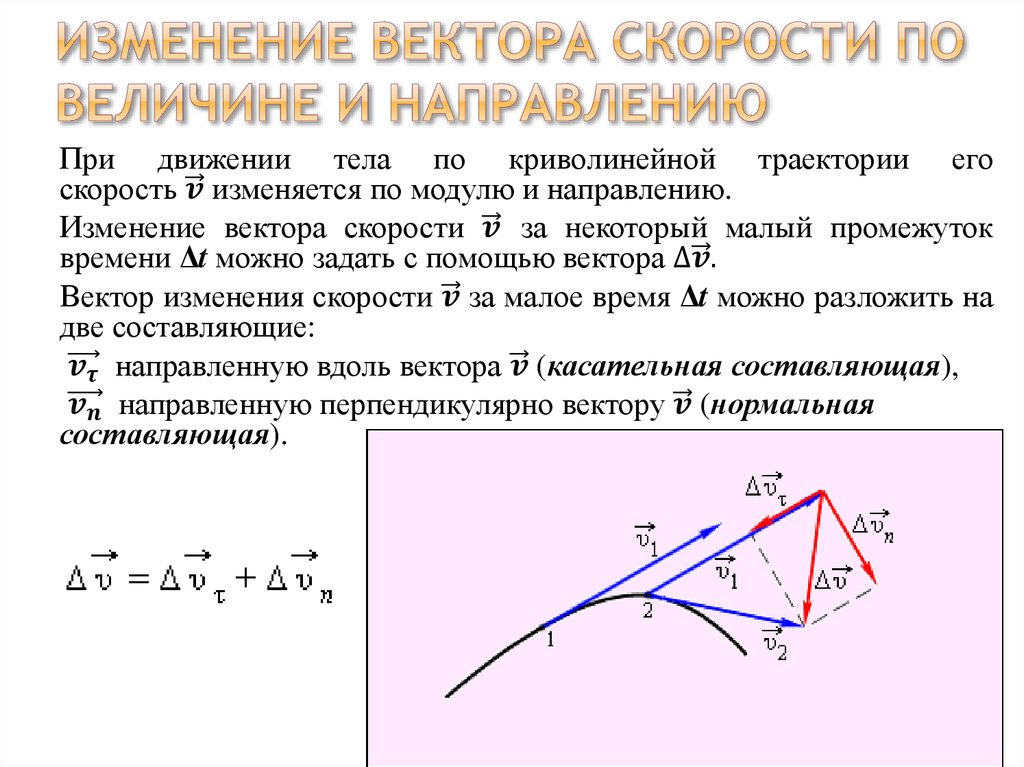 А чего уж говорить, если речь идет об определении каких-то категорий, процессов… Тут и запутаться недолго. В общем, не такая уж это и безобидная вещь – пренебрежение общепринятыми соглашениями. Попробуйте, эксперимента ради, предложить ученикам измерять скорость в попугаях, деленных на секунду или под пи понимать число 8,395. Я догадываюсь, какова будет их реакция.
А чего уж говорить, если речь идет об определении каких-то категорий, процессов… Тут и запутаться недолго. В общем, не такая уж это и безобидная вещь – пренебрежение общепринятыми соглашениями. Попробуйте, эксперимента ради, предложить ученикам измерять скорость в попугаях, деленных на секунду или под пи понимать число 8,395. Я догадываюсь, какова будет их реакция. И, хотя такой символ векторной величины давно ушел в прошлое, все-таки иногда его можно еще встретить. Черточкой над буквой принято обозначать средние значения величин, а для обозначения векторов применяется только стрелка над буквой (речь, конечно, идет о рукописном варианте, в печатном варианте буквы, обозначающие векторы имеют жирный шрифт).
И, хотя такой символ векторной величины давно ушел в прошлое, все-таки иногда его можно еще встретить. Черточкой над буквой принято обозначать средние значения величин, а для обозначения векторов применяется только стрелка над буквой (речь, конечно, идет о рукописном варианте, в печатном варианте буквы, обозначающие векторы имеют жирный шрифт). Но студенты также должны понимать, что эти абстрактные образы являются обобщением конкретных свойств многих физических объектов. Изучив действия над математическими образами, учащимся не составит никакого труда перенести эти действия на реальные свойства: скорости, силы, напряженности полей и т. д.
Но студенты также должны понимать, что эти абстрактные образы являются обобщением конкретных свойств многих физических объектов. Изучив действия над математическими образами, учащимся не составит никакого труда перенести эти действия на реальные свойства: скорости, силы, напряженности полей и т. д.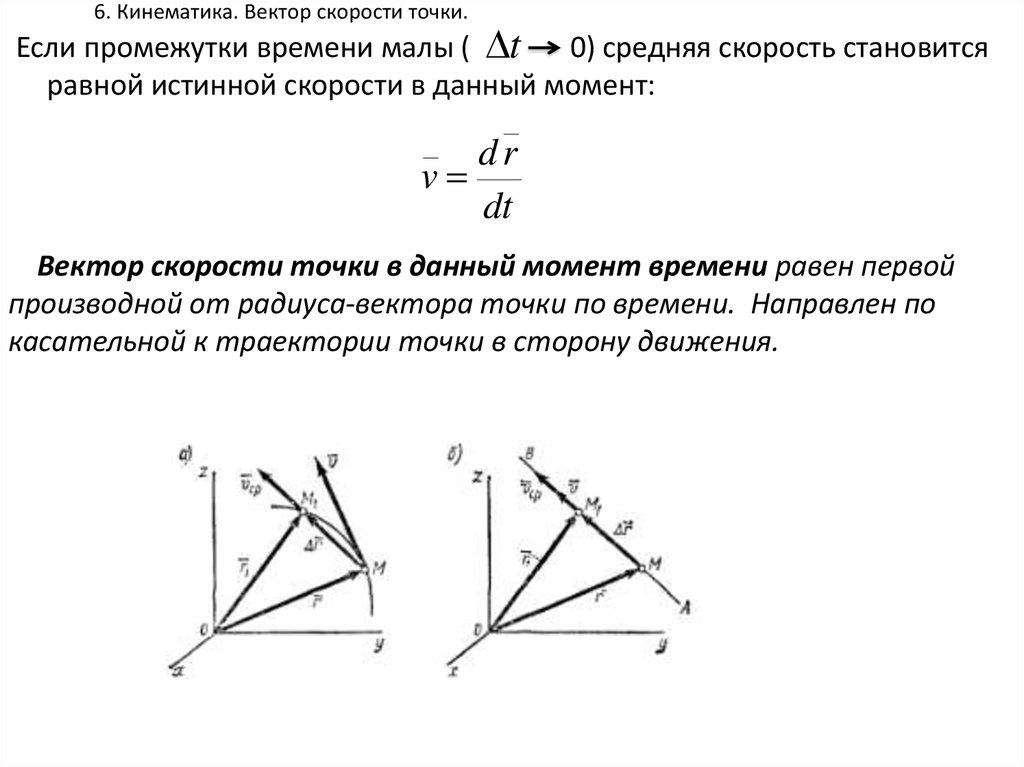
 Но именно при изучении вычитания векторов самое время будет сказать ученикам о том, что не бывает ни положительных, ни отрицательных векторов. Знак же «минус» перед символическом обозначении вектора указывает только на то, что речь идет об обратном векторе, но вовсе не о том, что бывают отрицательные (а, значит, и положительные) векторы.
Но именно при изучении вычитания векторов самое время будет сказать ученикам о том, что не бывает ни положительных, ни отрицательных векторов. Знак же «минус» перед символическом обозначении вектора указывает только на то, что речь идет об обратном векторе, но вовсе не о том, что бывают отрицательные (а, значит, и положительные) векторы.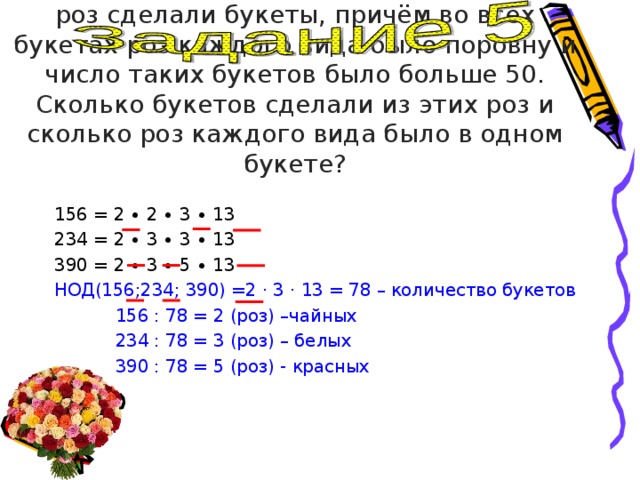 6 мс
6 мс 6%
6% 2
2
 9
9  5
5 1
1 5 мм аудио порт
5 мм аудио порт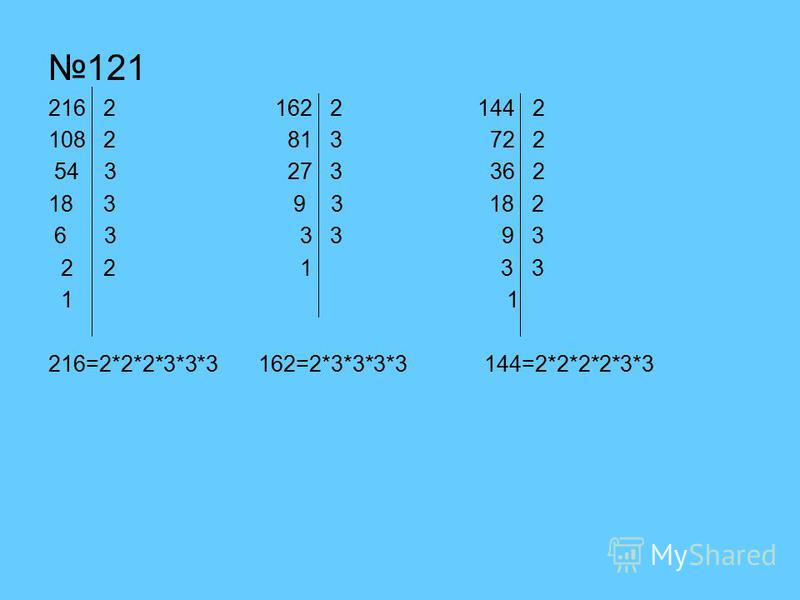
 Мы снова и снова бросаем вызов трудностям, чтобы в очередной раз
превзойти ваши ожидания. Теперь настала ваша очередь!
Разрушьте рамки привычного и узнайте, на что вы способны.
Мы снова и снова бросаем вызов трудностям, чтобы в очередной раз
превзойти ваши ожидания. Теперь настала ваша очередь!
Разрушьте рамки привычного и узнайте, на что вы способны. Ночной режим
Ночной режим

 * Доступность в магазинах может различаться в зависимости от страны. Местные стандарты и законы могут отличаться. Перед покупкой убедитесь, что данный продукт соответствует местным требованиям.
* Доступность в магазинах может различаться в зависимости от страны. Местные стандарты и законы могут отличаться. Перед покупкой убедитесь, что данный продукт соответствует местным требованиям. The testing data may vary slightly due to
The testing data may vary slightly due to Замените произведение степенью:
Замените произведение степенью:
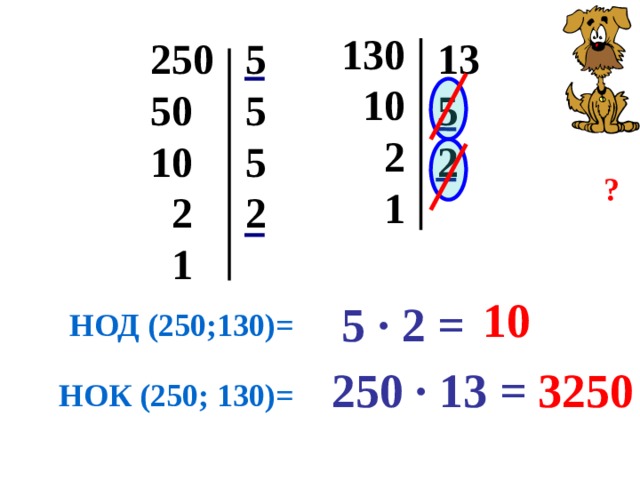
 Однако для больших
чисел находить НОД(а;b) путем перечисления всех
делителей чисел а и b — процесс трудоемкий
и ненадежный.
Однако для больших
чисел находить НОД(а;b) путем перечисления всех
делителей чисел а и b — процесс трудоемкий
и ненадежный. Какое наибольшее число комплектов
можно составить из этих книг так, чтобы в каждом
было одинаковое число книг по математике,
истории и географии? По сколько книг будет в
каждом комплекте?»
Какое наибольшее число комплектов
можно составить из этих книг так, чтобы в каждом
было одинаковое число книг по математике,
истории и географии? По сколько книг будет в
каждом комплекте?» Пусть
требуется найти НОД(102;84). Разделим одно число на
другое и определим остаток.
Пусть
требуется найти НОД(102;84). Разделим одно число на
другое и определим остаток. То есть, все общие
делители пар (а; b) и (b; r) совпадают, а значит,
совпадают и их наибольшие общие делители.
То есть, все общие
делители пар (а; b) и (b; r) совпадают, а значит,
совпадают и их наибольшие общие делители. Последний делитель и есть НОД.
Последний делитель и есть НОД.
 Во всех подарках вместе
было 123 апельсина и 82 яблока. Сколько ребят
присутствовало на елке? Сколько апельсинов и
сколько яблок в каждом подарке?
Во всех подарках вместе
было 123 апельсина и 82 яблока. Сколько ребят
присутствовало на елке? Сколько апельсинов и
сколько яблок в каждом подарке? 84 : л = 14; л = 6 84 : т = 7; т = 12 84 : е = 21; е = 4 84 : л = 4; л = 21 84 : ь = 3; ь = 28 84 : д = 28; д = 3 84 : е = 6; е = 14 84 : и = 12; и = 7 Расположите ответы в порядке возрастания. Назовите, какое слово получилось. Дайте определение делителя натурального числа. 3 4 6 7 12 14 21 28 д е л и т е л ь
84 : л = 14; л = 6 84 : т = 7; т = 12 84 : е = 21; е = 4 84 : л = 4; л = 21 84 : ь = 3; ь = 28 84 : д = 28; д = 3 84 : е = 6; е = 14 84 : и = 12; и = 7 Расположите ответы в порядке возрастания. Назовите, какое слово получилось. Дайте определение делителя натурального числа. 3 4 6 7 12 14 21 28 д е л и т е л ь 2376 : 2 = 1188
2376 : 2 = 1188
 Если все данные числа делятся на одно из них, то это число и является наибольшим общим делителем данных чисел.
Если все данные числа делятся на одно из них, то это число и является наибольшим общим делителем данных чисел.
 Количество апельсинов и яблок должно делиться на одно и то же наибольшее число. НОД (123; 82) = 41, значит, 41 человек. 123 : 41 = 3 ( ап .) 82 : 41 = 2 ( ябл .) Ответ: ребят 41, апельсинов 3, яблок 2. Сколько ребят -? Сколько яблок — ? Сколько апельсинов -?
Количество апельсинов и яблок должно делиться на одно и то же наибольшее число. НОД (123; 82) = 41, значит, 41 человек. 123 : 41 = 3 ( ап .) 82 : 41 = 2 ( ябл .) Ответ: ребят 41, апельсинов 3, яблок 2. Сколько ребят -? Сколько яблок — ? Сколько апельсинов -? 21
21
 Он получил основной модуль Samsung JN1 на 50 Мп, который делает фото с разрешением 8700 x 5800. В предыдущей версии установлен объектив Sony IMX582 на 48 Мп с разрешением фото 8000 х 6000. В то же время предшественник может записывать видео в 4К с частотой 30 кадров в секунду, чего не может предложить новая модель.
Он получил основной модуль Samsung JN1 на 50 Мп, который делает фото с разрешением 8700 x 5800. В предыдущей версии установлен объектив Sony IMX582 на 48 Мп с разрешением фото 8000 х 6000. В то же время предшественник может записывать видео в 4К с частотой 30 кадров в секунду, чего не может предложить новая модель.

 / шт
/ шт Увеличьте свою видимость.
Увеличьте свою видимость. 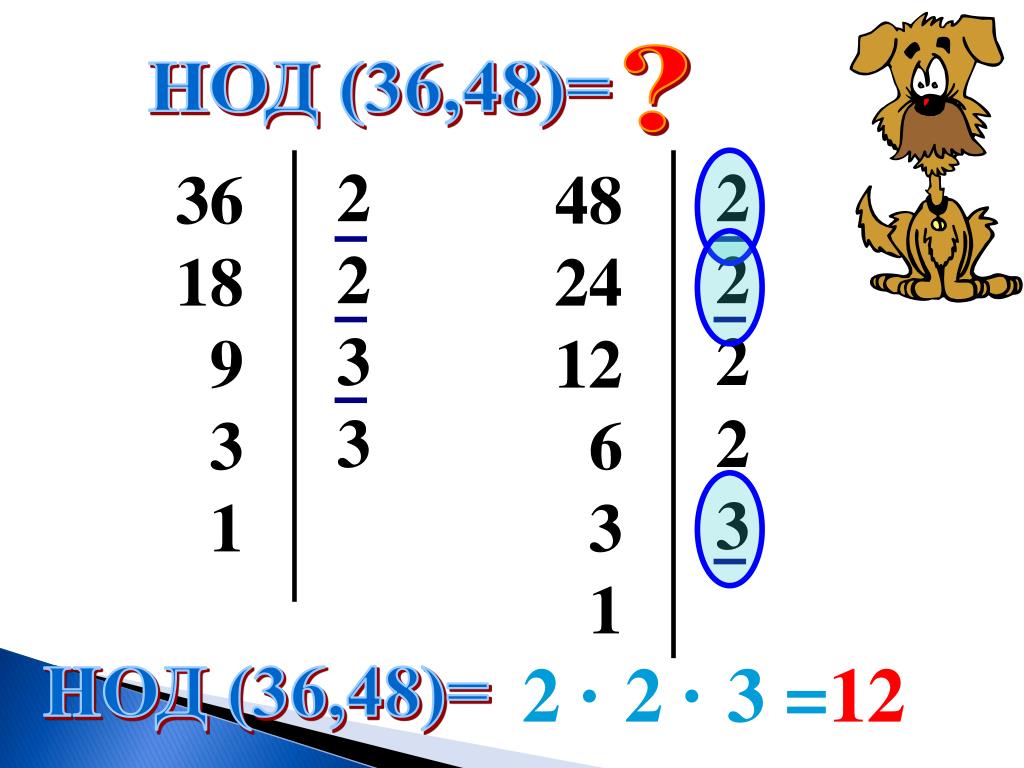 Добавляет CCM, OCB, ChaCha/Poly, scrypt, BLAKE2.
Добавляет CCM, OCB, ChaCha/Poly, scrypt, BLAKE2. В сообщении в блоге, первоначально анонсировавшем N-API, Арунуш Чандра из Microsoft и Майкл Доусон из IBM подсчитали, что зависимость от нативных API повлияла на 30% пакетов через прямые или косвенные зависимости, что привело к большому барьеру для обновления версий Node.js. Саид Чандра и Доусон:
В сообщении в блоге, первоначально анонсировавшем N-API, Арунуш Чандра из Microsoft и Майкл Доусон из IBM подсчитали, что зависимость от нативных API повлияла на 30% пакетов через прямые или косвенные зависимости, что привело к большому барьеру для обновления версий Node.js. Саид Чандра и Доусон: Стандартная поддержка встроена в популярные серверные платформы Hapi и Koa, но для Express все еще требуется некоторая настройка. Разработчики, желающие начать работу с любым из этих инструментов, могут ознакомиться с кратким руководством в блоге Rising Stack.
Стандартная поддержка встроена в популярные серверные платформы Hapi и Koa, но для Express все еще требуется некоторая настройка. Разработчики, желающие начать работу с любым из этих инструментов, могут ознакомиться с кратким руководством в блоге Rising Stack.

 0091 .
0091 . js постоянно работают над исправлением уязвимостей всех уровней серьезности (низкий, средний и высокий). В выпуске безопасности за февраль 2019 года были исправлены все активно поддерживаемые линии выпуска Node.js, включая «Boron». После 30 апреля выпуски безопасности больше не будут применяться к Node.js 6, что увеличивает вероятность вредоносных атак.
js постоянно работают над исправлением уязвимостей всех уровней серьезности (низкий, средний и высокий). В выпуске безопасности за февраль 2019 года были исправлены все активно поддерживаемые линии выпуска Node.js, включая «Boron». После 30 апреля выпуски безопасности больше не будут применяться к Node.js 6, что увеличивает вероятность вредоносных атак. Это также относится к тем, кто имеет дело с конфиденциальными данными, такими как личная информация (PII). Подвергание этих типов данных ненужному риску может привести к серьезным последствиям, начиная от длительных судебных баталий и заканчивая крупными штрафами.
Это также относится к тем, кто имеет дело с конфиденциальными данными, такими как личная информация (PII). Подвергание этих типов данных ненужному риску может привести к серьезным последствиям, начиная от длительных судебных баталий и заканчивая крупными штрафами. js также значительно увеличивает вероятность непредвиденных расходов, связанных с простоем или критической проблемой.
js также значительно увеличивает вероятность непредвиденных расходов, связанных с простоем или критической проблемой.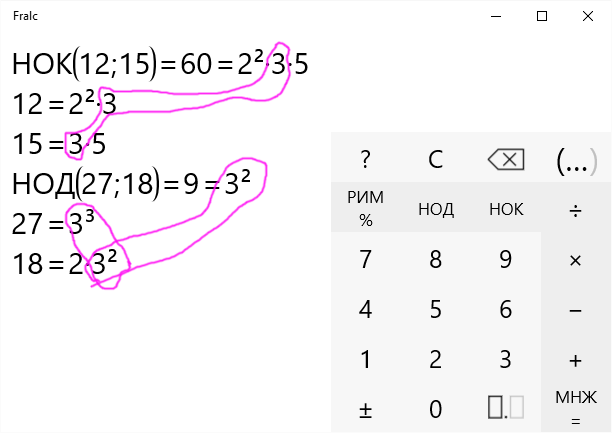 Эта линейка выпусков содержит несколько усовершенствований и улучшений по сравнению с более ранними версиями, в том числе следующие:
Эта линейка выпусков содержит несколько усовершенствований и улучшений по сравнению с более ранними версиями, в том числе следующие: Джеймс Снелл, член технического руководящего комитета Node.js (TSC) [источник цитаты]
Джеймс Снелл, член технического руководящего комитета Node.js (TSC) [источник цитаты]
 js 10 уровень Lambda, предоставляемый NodeSource, включает N|Solid. N|Solid для AWS Lambda обеспечивает практический мониторинг производительности функций Lambda. Чтобы воспользоваться этой функцией, вы также можете зарегистрировать бесплатную учетную запись NodeSource. После регистрации вам просто нужно установить лицензионный ключ N|Solid в качестве переменной среды в вашей функции Lambda.
js 10 уровень Lambda, предоставляемый NodeSource, включает N|Solid. N|Solid для AWS Lambda обеспечивает практический мониторинг производительности функций Lambda. Чтобы воспользоваться этой функцией, вы также можете зарегистрировать бесплатную учетную запись NodeSource. После регистрации вам просто нужно установить лицензионный ключ N|Solid в качестве переменной среды в вашей функции Lambda. js в других вычислительных средах.
js в других вычислительных средах. js:
js: js 6, до Node.js 10, новейшей версии LTS.
js 6, до Node.js 10, новейшей версии LTS.
 Для начала рассмотрим простые манипуляции. Вы можете добавить один узел
за раз,
Для начала рассмотрим простые манипуляции. Вы можете добавить один узел
за раз, Стоит подумать о том, как структурировать ваше приложение, чтобы узлы
являются полезными существами. Конечно, вы всегда можете использовать уникальный идентификатор в
Стоит подумать о том, как структурировать ваше приложение, чтобы узлы
являются полезными существами. Конечно, вы всегда можете использовать уникальный идентификатор в 
 DiGraph()
>>> DG.add_edge(2, 1) # добавляет узлы в порядке 2, 1
>>> DG.add_edge(1, 3)
>>> DG.add_edge(2, 4)
>>> DG.add_edge(1, 2)
>>> список утверждений (DG.successors (2)) == [1, 4]
>>> утвердить список (DG.edges) == [(2, 1), (2, 4), (1, 3), (1, 2)]
DiGraph()
>>> DG.add_edge(2, 1) # добавляет узлы в порядке 2, 1
>>> DG.add_edge(1, 3)
>>> DG.add_edge(2, 4)
>>> DG.add_edge(1, 2)
>>> список утверждений (DG.successors (2)) == [1, 4]
>>> утвердить список (DG.edges) == [(2, 1), (2, 4), (1, 3), (1, 2)]

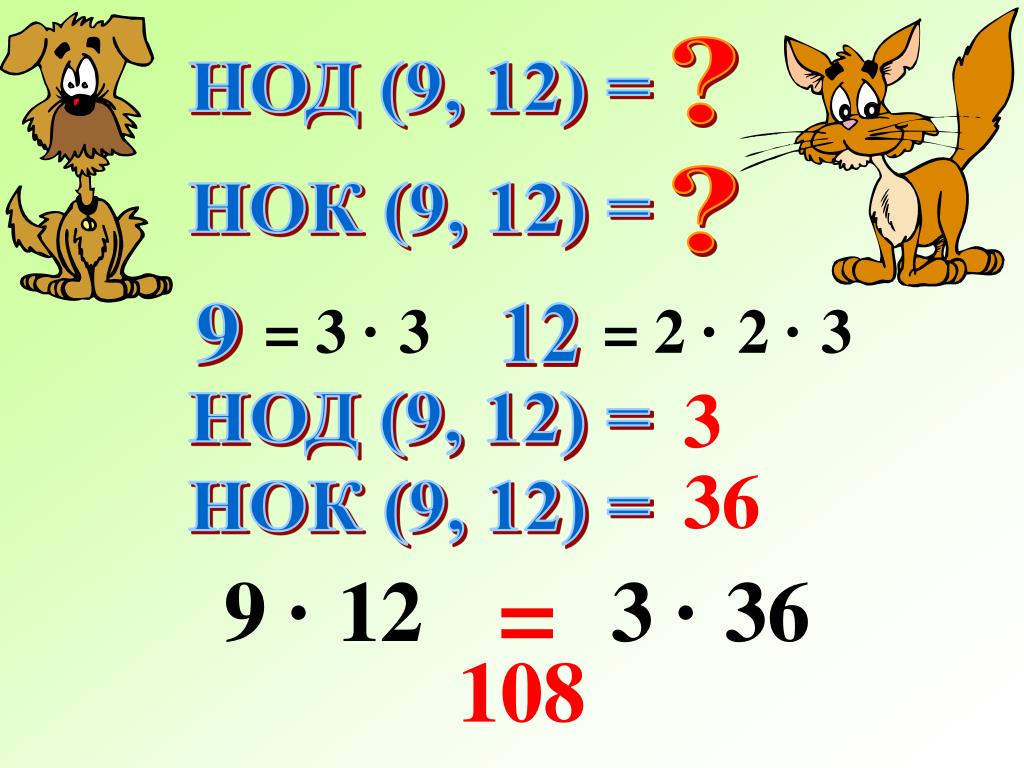 remove_edge(1, 3)
remove_edge(1, 3)
 Наиболее распространенными вариантами являются числа или строки, но узел может
быть любым хешируемым объектом (кроме
Наиболее распространенными вариантами являются числа или строки, но узел может
быть любым хешируемым объектом (кроме 
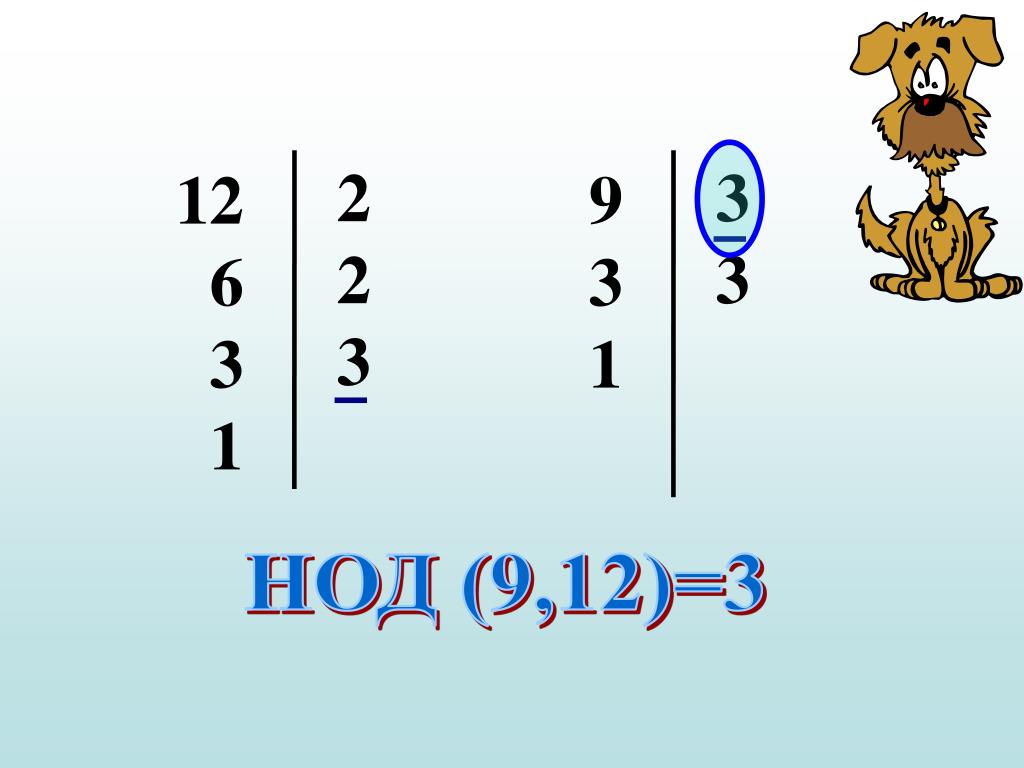
 graph['день'] = "Понедельник"
>>> G.граф
{'день': 'понедельник'}
graph['день'] = "Понедельник"
>>> G.граф
{'день': 'понедельник'}
 edges[3, 4]['вес'] = 4,2
edges[3, 4]['вес'] = 4,2
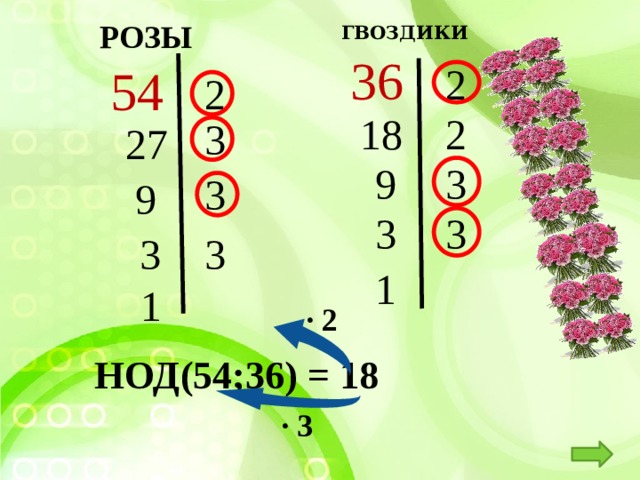 Действительно, тенденция к общей направленности
и неориентированные графы вместе опасны. Если вы хотите лечить
ориентированный граф как неориентированный для некоторых измерений, которые вы, вероятно, должны
преобразовать его с помощью
Действительно, тенденция к общей направленности
и неориентированные графы вместе опасны. Если вы хотите лечить
ориентированный граф как неориентированный для некоторых измерений, которые вы, вероятно, должны
преобразовать его с помощью 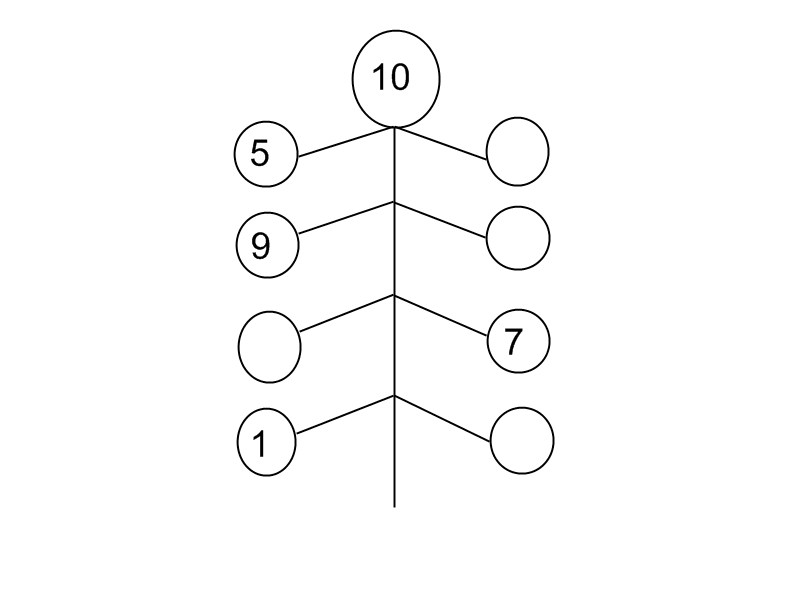 MultiGraph()
>>> MG.add_weighted_edges_from([(1, 2, 0,5), (1, 2, 0,75), (2, 3, 0,5)])
>>> dict(MG.степень(вес='вес'))
{1: 1,25, 2: 1,75, 3: 0,5}
>>> GG = nx.Graph()
>>> для n, nbrs в MG.adjacency():
... для nbr, укажите в nbrs.items():
... minvalue = min([d['weight'] для d в edict.values()])
... GG.add_edge(n, nbr, вес = минимальное значение)
...
>>> nx.shortest_path(GG, 1, 3)
[1, 2, 3]
MultiGraph()
>>> MG.add_weighted_edges_from([(1, 2, 0,5), (1, 2, 0,75), (2, 3, 0,5)])
>>> dict(MG.степень(вес='вес'))
{1: 1,25, 2: 1,75, 3: 0,5}
>>> GG = nx.Graph()
>>> для n, nbrs в MG.adjacency():
... для nbr, укажите в nbrs.items():
... minvalue = min([d['weight'] для d в edict.values()])
... GG.add_edge(n, nbr, вес = минимальное значение)
...
>>> nx.shortest_path(GG, 1, 3)
[1, 2, 3]




 connected_components(G))
[{1, 2, 3}, {'спам'}]
>>> отсортировано (d для n, d для G.степень())
[0, 1, 1, 2]
>>> nx.clustering(G)
{1:0, 2:0, 3:0, "спам": 0}
connected_components(G))
[{1, 2, 3}, {'спам'}]
>>> отсортировано (d для n, d для G.степень())
[0, 1, 1, 2]
>>> nx.clustering(G)
{1:0, 2:0, 3:0, "спам": 0}
 petersen_graph()
>>> subax1 = plt.subplot(121)
>>> nx.draw(G, with_labels=True, font_weight='жирный')
>>> subax2 = plt.subplot(122)
>>> nx.draw_shell(G, nlist=[range(5, 10), range(5)], with_labels=True, font_weight='bold')
petersen_graph()
>>> subax1 = plt.subplot(121)
>>> nx.draw(G, with_labels=True, font_weight='жирный')
>>> subax2 = plt.subplot(122)
>>> nx.draw_shell(G, nlist=[range(5, 10), range(5)], with_labels=True, font_weight='bold')
 Вы можете использовать несколько оболочек с
Вы можете использовать несколько оболочек с  на чертеже.
на чертеже.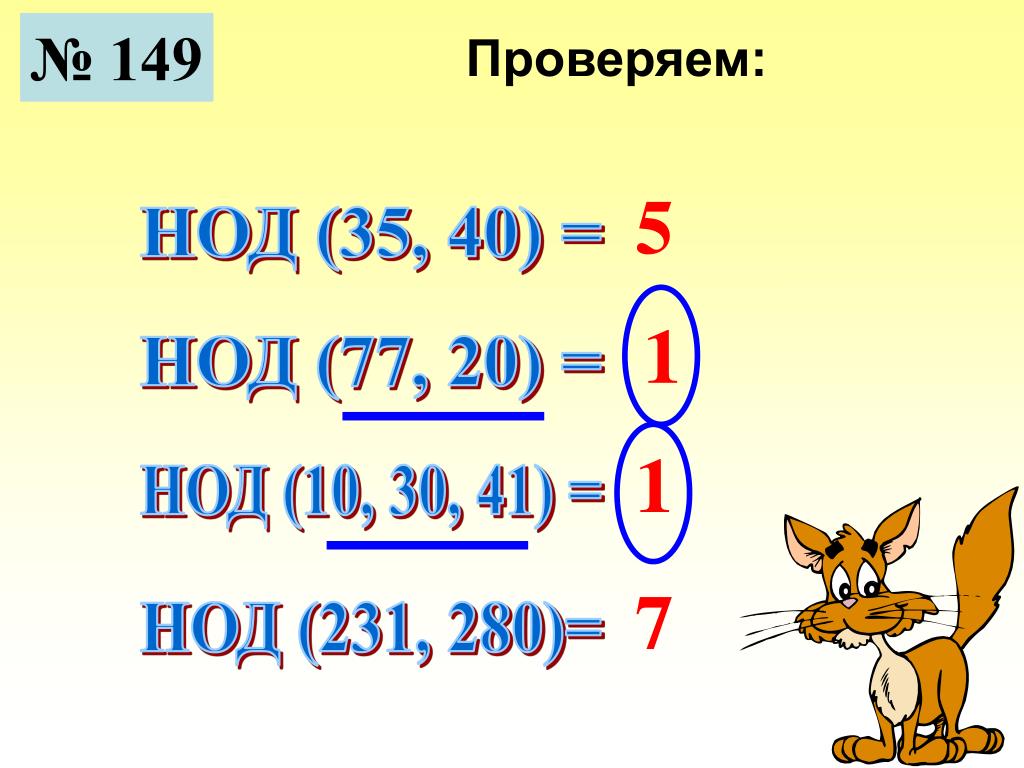 станций лимфоузлов (2).
станций лимфоузлов (2). 
 Субааортальные
Субааортальные 
 Правая верхняя паратрахеальная
Правая верхняя паратрахеальная 
 Нижние паратрахеальные узлы
Нижние паратрахеальные узлы 





 Сильвестри, доктор медицины, FCCP Кристиан Ллойд, доктор медицины, и Джерард А. Сильвестри, доктор медицинских наук, FCCP
Сильвестри, доктор медицины, FCCP Кристиан Ллойд, доктор медицины, и Джерард А. Сильвестри, доктор медицинских наук, FCCP  js | endoflife.date
js | endoflife.date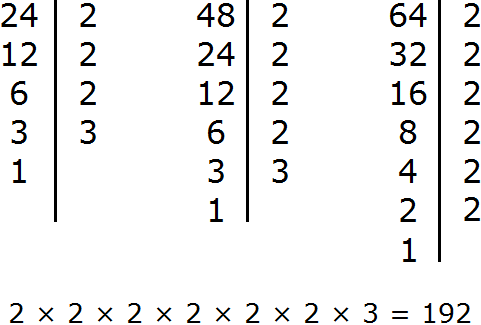 04.2022)
04.2022) )
) 14.0
14.0 )
) )
) )
) )
)

 В частности, быть
в курсе изменений переменных окружения
представлен в среде выполнения Node.js 10.
В частности, быть
в курсе изменений переменных окружения
представлен в среде выполнения Node.js 10.

 js 10 внесены изменения, которые могут потребовать от вас
чтобы изменить исходный код вашей функции для использования более новых сред выполнения.
js 10 внесены изменения, которые могут потребовать от вас
чтобы изменить исходный код вашей функции для использования более новых сред выполнения.
 Ваше кодовое местоположение
Ваше кодовое местоположение 

 3026 =
3026 = 81047 73809 65351 65547 30357…
81047 73809 65351 65547 30357… ru:
ru: Хобби. Досуг
Хобби. Досуг
 Виноделие
Виноделие
 Зарубежная
Зарубежная

 Его приближённое значение — 3,141592653589793238… Вот почему π называют иррациональным числом — его нельзя записать в виде конечного числа цифр после запятой. А вот другое интересное иррациональное число — e. Число e — это «число Эйлера» (от Euler). Вот первые несколько цифр числа e: 2,7182818284590…
Его приближённое значение — 3,141592653589793238… Вот почему π называют иррациональным числом — его нельзя записать в виде конечного числа цифр после запятой. А вот другое интересное иррациональное число — e. Число e — это «число Эйлера» (от Euler). Вот первые несколько цифр числа e: 2,7182818284590…
 Вот тут-то и возникает понятие мнимого числа.
Вот тут-то и возникает понятие мнимого числа. (ix). Наконец, если в формулу Эйлера подставить значение x = π, получаем:
(ix). Наконец, если в формулу Эйлера подставить значение x = π, получаем:

 Например, надо выяснить, в каком отношении находятся суждения: Все люди изучали логику и Некоторые люди не изучали логику. Видя, что первое суждение является общеутвердительным (А), а второе частноотрицательным (О), мы без труда устанавливаем отношение между ними с помощью логического квадрата – противоречие. Также суждения: Все люди изучали логику (А) и Некоторые люди изучали логику (I) находятся в отношении подчинения, а суждения: Все люди изучали логику (А) и Все люди не изучали логику (Е) находятся в отношении противоположности.
Например, надо выяснить, в каком отношении находятся суждения: Все люди изучали логику и Некоторые люди не изучали логику. Видя, что первое суждение является общеутвердительным (А), а второе частноотрицательным (О), мы без труда устанавливаем отношение между ними с помощью логического квадрата – противоречие. Также суждения: Все люди изучали логику (А) и Некоторые люди изучали логику (I) находятся в отношении подчинения, а суждения: Все люди изучали логику (А) и Все люди не изучали логику (Е) находятся в отношении противоположности. е. имеющих сходные с ним субъекты и предикаты) в зависимости от этого (т. е. от истинности или ложности суждения вида А) тоже являются истинными или ложными. Например, если суждение вида А: Все тигры – это хищники является истинным, то суждение вида I: Некоторые тигры – это хищники также является истинным (если все тигры – хищники, то и часть из них, т. е. некоторые тигры – это тоже хищники), суждение вида Е: Все тигры – это не хищники является ложным, и суждение вида О: Некоторые тигры – это не хищники также является ложным. Таким образом, в данном случае из истинности суждения вида А вытекает истинность суждения вида I и ложность суждений вида Е и вида О (разумеется, речь идет о сравнимых суждениях, т. е. имеющих одинаковые субъекты и предикаты).
е. имеющих сходные с ним субъекты и предикаты) в зависимости от этого (т. е. от истинности или ложности суждения вида А) тоже являются истинными или ложными. Например, если суждение вида А: Все тигры – это хищники является истинным, то суждение вида I: Некоторые тигры – это хищники также является истинным (если все тигры – хищники, то и часть из них, т. е. некоторые тигры – это тоже хищники), суждение вида Е: Все тигры – это не хищники является ложным, и суждение вида О: Некоторые тигры – это не хищники также является ложным. Таким образом, в данном случае из истинности суждения вида А вытекает истинность суждения вида I и ложность суждений вида Е и вида О (разумеется, речь идет о сравнимых суждениях, т. е. имеющих одинаковые субъекты и предикаты).
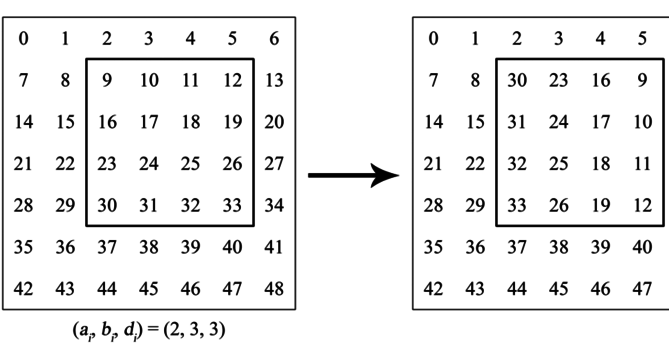 Выше был приведен пример таких выводов на основе суждения вида А: Все тигры являются хищниками, где из его истинности вытекали определенные истинностные значения других суждений – I, Е, О. Рассмотрим еще один пример. Возьмем суждение вида Е: Все треугольники не являются квадратами и сделаем из его истинности выводы об истинностных значениях суждений А, I, О. Когда данное суждение вида Е истинно (см. правила выше), то суждение вида А: Все треугольники являются квадратами ложно, суждение вида I: Некоторые треугольники являются квадратами также ложно, а суждение вида О: Некоторые треугольники не являются квадратами истинно (если все треугольники не являются квадратами, то и часть треугольников, т. е. некоторые треугольники также не являются ими).
Выше был приведен пример таких выводов на основе суждения вида А: Все тигры являются хищниками, где из его истинности вытекали определенные истинностные значения других суждений – I, Е, О. Рассмотрим еще один пример. Возьмем суждение вида Е: Все треугольники не являются квадратами и сделаем из его истинности выводы об истинностных значениях суждений А, I, О. Когда данное суждение вида Е истинно (см. правила выше), то суждение вида А: Все треугольники являются квадратами ложно, суждение вида I: Некоторые треугольники являются квадратами также ложно, а суждение вида О: Некоторые треугольники не являются квадратами истинно (если все треугольники не являются квадратами, то и часть треугольников, т. е. некоторые треугольники также не являются ими). Квадрат коммуникации и генеративная матрица
Квадрат коммуникации и генеративная матрица Логический позитивизм выглядит слабее его в одном важном пункте, но зато сильнее в
Логический позитивизм выглядит слабее его в одном важном пункте, но зато сильнее в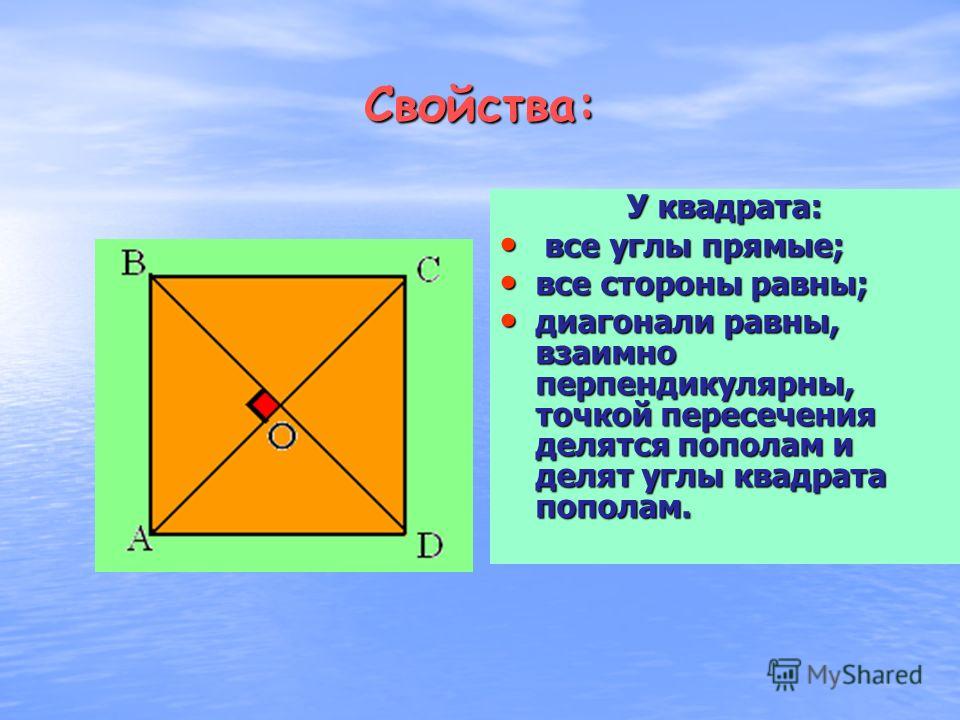 Из колоды игральных карт вытащите десять одной масти — от туза (примем его за единицу) до десятки — и сложите из них квадрат. Причем сложите так, чтобы сумма чисел на
Из колоды игральных карт вытащите десять одной масти — от туза (примем его за единицу) до десятки — и сложите из них квадрат. Причем сложите так, чтобы сумма чисел на Тетрактис и квадрат четырех[119]
В ходе наших исследований нам уже не раз случалось говорить о пифагорейском Тетрактисе, и мы тогда же привели его числовую формулу: 1+2+3+4=10, указав на связь, непосредственно соединяющую денер с кватернером. Известно совершенно особое
Тетрактис и квадрат четырех[119]
В ходе наших исследований нам уже не раз случалось говорить о пифагорейском Тетрактисе, и мы тогда же привели его числовую формулу: 1+2+3+4=10, указав на связь, непосредственно соединяющую денер с кватернером. Известно совершенно особое Тут имеется в виду, что для любого
Тут имеется в виду, что для любого Возведение в квадрат будет очень важно позднее, когда мы будем изучать
Возведение в квадрат будет очень важно позднее, когда мы будем изучать
 Он пошел в банк так же, как все ходят в банк, и вернулся к своему джипу. Поэтому, когда Изабель Роланд, одинокая молодая кассирша, которая помогала ему, выходит из банка по пути на обед, Джо оказывается рядом, когда двое мужчин похищают ее. Джо преследует их, и двое мужчин арестованы. Но вместо того, чтобы положить конец драме, аресты — это только начало проблем для Джо и Иззи.
Он пошел в банк так же, как все ходят в банк, и вернулся к своему джипу. Поэтому, когда Изабель Роланд, одинокая молодая кассирша, которая помогала ему, выходит из банка по пути на обед, Джо оказывается рядом, когда двое мужчин похищают ее. Джо преследует их, и двое мужчин арестованы. Но вместо того, чтобы положить конец драме, аресты — это только начало проблем для Джо и Иззи. На дворе 1969 год, и для семьи Левиных времена меняются. Каждый год дети с нетерпением ждут возможности провести лето в историческом доме своей бабушки в центре Нантакета. Но, как и многое другое в Америке, здесь все по-другому.
На дворе 1969 год, и для семьи Левиных времена меняются. Каждый год дети с нетерпением ждут возможности провести лето в историческом доме своей бабушки в центре Нантакета. Но, как и многое другое в Америке, здесь все по-другому. Нора — непоколебимая пограничница, ожидающая возвращения мужчин в своей жизни — своего мужа, отправившегося на поиски воды для выжженного дома, и старших сыновей, исчезнувших после бурной ссоры. Нора ждет своего часа со своим младшим сыном, который убежден, что таинственный зверь бродит по земле вокруг их дома.
Нора — непоколебимая пограничница, ожидающая возвращения мужчин в своей жизни — своего мужа, отправившегося на поиски воды для выжженного дома, и старших сыновей, исчезнувших после бурной ссоры. Нора ждет своего часа со своим младшим сыном, который убежден, что таинственный зверь бродит по земле вокруг их дома. Все в городе, даже ее лучший друг Энди, думают, что горе держит ее взаперти, и Эвви не поправляет их. Тем временем в Нью-Йорке Дин Тенни, бывший питчер Высшей лиги и лучший друг детства Энди, борется с тем, что несчастные спортсмены, живущие в своих самых страшных кошмарах, называют «улюлюканьем»: он больше не может бросать прямо и, что еще хуже, он не может понять почему.
Все в городе, даже ее лучший друг Энди, думают, что горе держит ее взаперти, и Эвви не поправляет их. Тем временем в Нью-Йорке Дин Тенни, бывший питчер Высшей лиги и лучший друг детства Энди, борется с тем, что несчастные спортсмены, живущие в своих самых страшных кошмарах, называют «улюлюканьем»: он больше не может бросать прямо и, что еще хуже, он не может понять почему. Но когда ее отчужденная и больная мать просит ее разрушить свою жизнь и переехать в Бостон, это чрезвычайное положение, которого Кэсси никогда не ожидала. Жесткая бостонская пожарная часть старой школы настолько отличается от старой работы Кэсси, насколько это возможно. Дедовщина, нехватка финансирования и плохие условия означают, что пожарные не очень рады видеть в бригаде «женщину».
Но когда ее отчужденная и больная мать просит ее разрушить свою жизнь и переехать в Бостон, это чрезвычайное положение, которого Кэсси никогда не ожидала. Жесткая бостонская пожарная часть старой школы настолько отличается от старой работы Кэсси, насколько это возможно. Дедовщина, нехватка финансирования и плохие условия означают, что пожарные не очень рады видеть в бригаде «женщину». Заинтригованный подозрительными обстоятельствами этого события, Стоун объединяет усилия с остроумным и привлекательным местным детективом для расследования. Но они сталкиваются с проблемой: улики продолжают исчезать.
Заинтригованный подозрительными обстоятельствами этого события, Стоун объединяет усилия с остроумным и привлекательным местным детективом для расследования. Но они сталкиваются с проблемой: улики продолжают исчезать.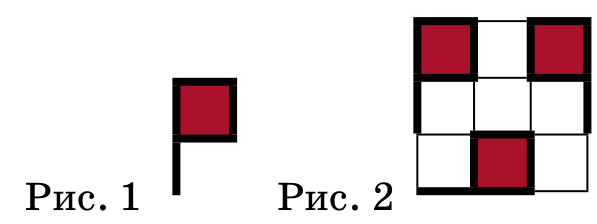 Они не могли быть более разными ни тогда, ни даже сегодня: Линкольн был брокером по коммерческой недвижимости, Тедди — издателем крошечной прессы, а Микки — музыкантом не по возрасту. Но у каждого человека есть свои секреты, в дополнение к монументальной тайне, над которой никто из них не переставал ломать голову со времен Дня поминовения на выходных прямо здесь, на Винограднике, в 1971: исчезновение женщины, которую любил каждый из них — Джейси Кэллоуэй.
Они не могли быть более разными ни тогда, ни даже сегодня: Линкольн был брокером по коммерческой недвижимости, Тедди — издателем крошечной прессы, а Микки — музыкантом не по возрасту. Но у каждого человека есть свои секреты, в дополнение к монументальной тайне, над которой никто из них не переставал ломать голову со времен Дня поминовения на выходных прямо здесь, на Винограднике, в 1971: исчезновение женщины, которую любил каждый из них — Джейси Кэллоуэй. За последние 30 лет Уэстон сменил множество имен и бесчисленное количество маскировок, что позволило ему выманить восемь богатых женщин из своего состояния до того, как они бесследно исчезли, их семьи остались без ответов, а власти — без зацепок. Единственная общая черта среди жертв: новый человек в их жизни, который также исчез, не оставив после себя никаких свидетельств своего существования… кроме одного подписного обычая.
За последние 30 лет Уэстон сменил множество имен и бесчисленное количество маскировок, что позволило ему выманить восемь богатых женщин из своего состояния до того, как они бесследно исчезли, их семьи остались без ответов, а власти — без зацепок. Единственная общая черта среди жертв: новый человек в их жизни, который также исчез, не оставив после себя никаких свидетельств своего существования… кроме одного подписного обычая. У нее была кожаная сумка для книг, а не нейлоновый рюкзак. Ее лакированные балетки были блестящими и яркими. Она была приличной, новенькой, скромной. Но было в ней кое-что еще… В эксклюзивной частной школе в Швейцарии тайна окружает личность красивой темноволосой девушки, которая каждое утро прибывает в кортеже, достойном главы государства. Говорят, что она дочь богатого международного бизнесмена.
У нее была кожаная сумка для книг, а не нейлоновый рюкзак. Ее лакированные балетки были блестящими и яркими. Она была приличной, новенькой, скромной. Но было в ней кое-что еще… В эксклюзивной частной школе в Швейцарии тайна окружает личность красивой темноволосой девушки, которая каждое утро прибывает в кортеже, достойном главы государства. Говорят, что она дочь богатого международного бизнесмена. Он пошел в банк так же, как все ходят в банк, и вернулся к своему джипу. Поэтому, когда Изабель Роланд, одинокая молодая кассирша, которая помогала ему, выходит из банка по пути на обед, Джо оказывается рядом, когда двое мужчин похищают ее. Джо преследует их, и двое мужчин арестованы. Но вместо того, чтобы положить конец драме, аресты — это только начало проблем для Джо и Иззи.
Он пошел в банк так же, как все ходят в банк, и вернулся к своему джипу. Поэтому, когда Изабель Роланд, одинокая молодая кассирша, которая помогала ему, выходит из банка по пути на обед, Джо оказывается рядом, когда двое мужчин похищают ее. Джо преследует их, и двое мужчин арестованы. Но вместо того, чтобы положить конец драме, аресты — это только начало проблем для Джо и Иззи. На дворе 1969 год, и для семьи Левиных времена меняются. Каждый год дети с нетерпением ждут возможности провести лето в историческом доме своей бабушки в центре Нантакета. Но, как и многое другое в Америке, здесь все по-другому.
На дворе 1969 год, и для семьи Левиных времена меняются. Каждый год дети с нетерпением ждут возможности провести лето в историческом доме своей бабушки в центре Нантакета. Но, как и многое другое в Америке, здесь все по-другому. Нора — непоколебимая пограничница, ожидающая возвращения мужчин в своей жизни — своего мужа, отправившегося на поиски воды для выжженного дома, и старших сыновей, исчезнувших после бурной ссоры. Нора ждет своего часа со своим младшим сыном, который убежден, что таинственный зверь бродит по земле вокруг их дома.
Нора — непоколебимая пограничница, ожидающая возвращения мужчин в своей жизни — своего мужа, отправившегося на поиски воды для выжженного дома, и старших сыновей, исчезнувших после бурной ссоры. Нора ждет своего часа со своим младшим сыном, который убежден, что таинственный зверь бродит по земле вокруг их дома.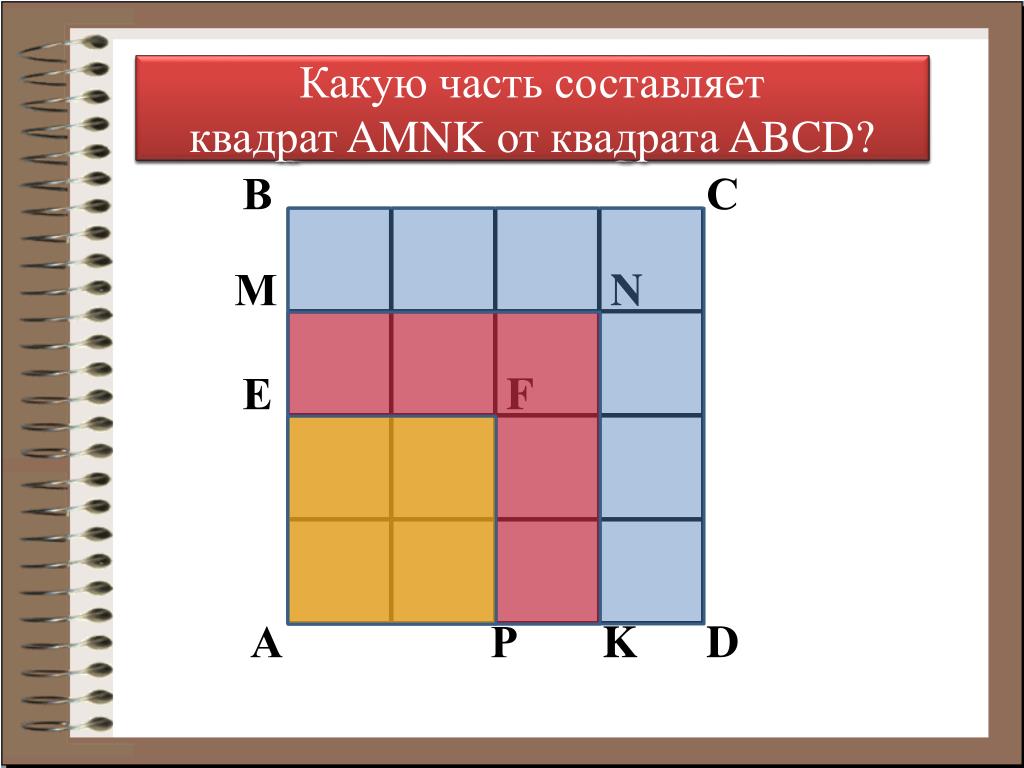 Все в городе, даже ее лучший друг Энди, думают, что горе держит ее взаперти, и Эвви не поправляет их. Тем временем в Нью-Йорке Дин Тенни, бывший питчер Высшей лиги и лучший друг детства Энди, борется с тем, что несчастные спортсмены, живущие в своих самых страшных кошмарах, называют «улюлюканьем»: он больше не может бросать прямо и, что еще хуже, он не может понять почему.
Все в городе, даже ее лучший друг Энди, думают, что горе держит ее взаперти, и Эвви не поправляет их. Тем временем в Нью-Йорке Дин Тенни, бывший питчер Высшей лиги и лучший друг детства Энди, борется с тем, что несчастные спортсмены, живущие в своих самых страшных кошмарах, называют «улюлюканьем»: он больше не может бросать прямо и, что еще хуже, он не может понять почему. Но когда ее отчужденная и больная мать просит ее разрушить свою жизнь и переехать в Бостон, это чрезвычайное положение, которого Кэсси никогда не ожидала. Жесткая бостонская пожарная часть старой школы настолько отличается от старой работы Кэсси, насколько это возможно. Дедовщина, нехватка финансирования и плохие условия означают, что пожарные не очень рады видеть в бригаде «женщину».
Но когда ее отчужденная и больная мать просит ее разрушить свою жизнь и переехать в Бостон, это чрезвычайное положение, которого Кэсси никогда не ожидала. Жесткая бостонская пожарная часть старой школы настолько отличается от старой работы Кэсси, насколько это возможно. Дедовщина, нехватка финансирования и плохие условия означают, что пожарные не очень рады видеть в бригаде «женщину».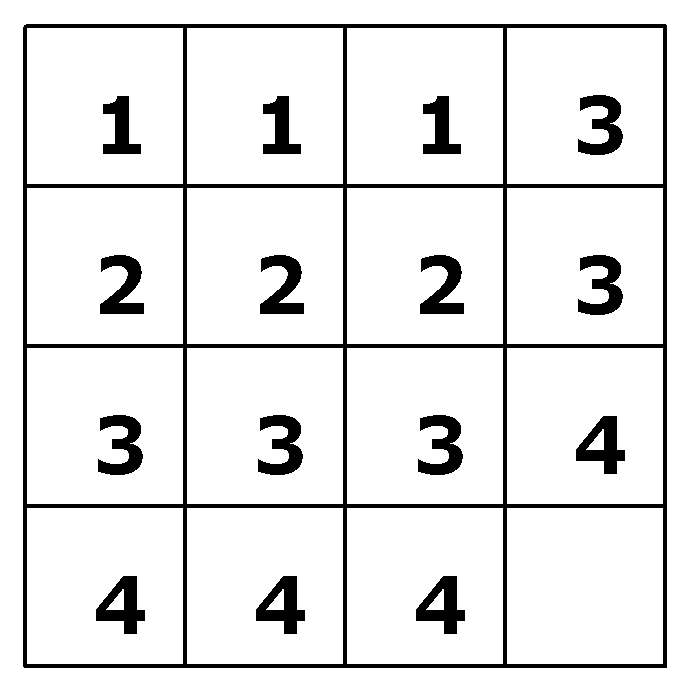 Заинтригованный подозрительными обстоятельствами этого события, Стоун объединяет усилия с остроумным и привлекательным местным детективом для расследования. Но они сталкиваются с проблемой: улики продолжают исчезать.
Заинтригованный подозрительными обстоятельствами этого события, Стоун объединяет усилия с остроумным и привлекательным местным детективом для расследования. Но они сталкиваются с проблемой: улики продолжают исчезать. Они не могли быть более разными ни тогда, ни даже сегодня: Линкольн был брокером по коммерческой недвижимости, Тедди — издателем крошечной прессы, а Микки — музыкантом не по возрасту. Но у каждого человека есть свои секреты, в дополнение к монументальной тайне, над которой никто из них не переставал ломать голову со времен Дня поминовения на выходных прямо здесь, на Винограднике, в 1971: исчезновение женщины, которую любил каждый из них — Джейси Кэллоуэй.
Они не могли быть более разными ни тогда, ни даже сегодня: Линкольн был брокером по коммерческой недвижимости, Тедди — издателем крошечной прессы, а Микки — музыкантом не по возрасту. Но у каждого человека есть свои секреты, в дополнение к монументальной тайне, над которой никто из них не переставал ломать голову со времен Дня поминовения на выходных прямо здесь, на Винограднике, в 1971: исчезновение женщины, которую любил каждый из них — Джейси Кэллоуэй.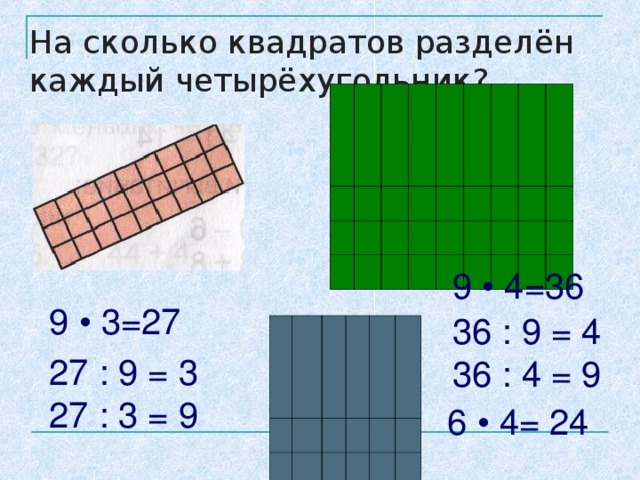 За последние 30 лет Уэстон сменил множество имен и бесчисленное количество маскировок, что позволило ему выманить восемь богатых женщин из своего состояния до того, как они бесследно исчезли, их семьи остались без ответов, а власти — без зацепок. Единственная общая черта среди жертв: новый человек в их жизни, который также исчез, не оставив после себя никаких свидетельств своего существования… кроме одного подписного обычая.
За последние 30 лет Уэстон сменил множество имен и бесчисленное количество маскировок, что позволило ему выманить восемь богатых женщин из своего состояния до того, как они бесследно исчезли, их семьи остались без ответов, а власти — без зацепок. Единственная общая черта среди жертв: новый человек в их жизни, который также исчез, не оставив после себя никаких свидетельств своего существования… кроме одного подписного обычая. У нее была кожаная сумка для книг, а не нейлоновый рюкзак. Ее лакированные балетки были блестящими и яркими. Она была приличной, новенькой, скромной. Но было в ней кое-что еще… В эксклюзивной частной школе в Швейцарии тайна окружает личность красивой темноволосой девушки, которая каждое утро прибывает в кортеже, достойном главы государства. Говорят, что она дочь богатого международного бизнесмена.
У нее была кожаная сумка для книг, а не нейлоновый рюкзак. Ее лакированные балетки были блестящими и яркими. Она была приличной, новенькой, скромной. Но было в ней кое-что еще… В эксклюзивной частной школе в Швейцарии тайна окружает личность красивой темноволосой девушки, которая каждое утро прибывает в кортеже, достойном главы государства. Говорят, что она дочь богатого международного бизнесмена. Когда ветеран войны Алоизиус Арчер выходит из тюрьмы Кардерок, его отправляют в Пока-Сити на условно-досрочное освобождение с коротким списком разрешений и гораздо более длинным списком запретов: регулярно отчитываться перед офицером по условно-досрочному освобождению, не Не ходи в бары, уж точно не пей алкоголь, найди работу и никогда не общайся с распутными женщинами. Маленький городок быстро оказывается более сложным и опасным, чем годы службы Арчера на войне или его время в тюрьме.
Когда ветеран войны Алоизиус Арчер выходит из тюрьмы Кардерок, его отправляют в Пока-Сити на условно-досрочное освобождение с коротким списком разрешений и гораздо более длинным списком запретов: регулярно отчитываться перед офицером по условно-досрочному освобождению, не Не ходи в бары, уж точно не пей алкоголь, найди работу и никогда не общайся с распутными женщинами. Маленький городок быстро оказывается более сложным и опасным, чем годы службы Арчера на войне или его время в тюрьме. Виновная в том, что она не видела своего сына и измученная ночами в засаде, Кэсси, тем не менее, справляется… пока старый друг не просит об одолжении: она хочет, чтобы Кэсси помогла оправдать человека, обвиняемого в нападении на молодую девушку из влиятельной семьи. Вопреки собственному здравому смыслу, Кэсси соглашается. Но в стране Большого Неба в Монтане извращенная семейная верность так же глубока, как и связи с землей, и в этой истории всегда есть что-то большее.
Виновная в том, что она не видела своего сына и измученная ночами в засаде, Кэсси, тем не менее, справляется… пока старый друг не просит об одолжении: она хочет, чтобы Кэсси помогла оправдать человека, обвиняемого в нападении на молодую девушку из влиятельной семьи. Вопреки собственному здравому смыслу, Кэсси соглашается. Но в стране Большого Неба в Монтане извращенная семейная верность так же глубока, как и связи с землей, и в этой истории всегда есть что-то большее. Его уединение подходит бывшему детективу бостонской полиции Биллу Робинсону, начинающему владельцу и трактирщику. Пока дюжина жильцов платит арендную плату, Робинсон не задает никаких вопросов. Как и шериф Клейтон Спирс, живущий на втором этаже. Затем появляется Митчелл Клайн с новым смертельно опасным способом ведения бизнеса. Его команда местных убийц нарушает законы, торгует наркотиками и совершает насилие у дверей гостиницы.
Его уединение подходит бывшему детективу бостонской полиции Биллу Робинсону, начинающему владельцу и трактирщику. Пока дюжина жильцов платит арендную плату, Робинсон не задает никаких вопросов. Как и шериф Клейтон Спирс, живущий на втором этаже. Затем появляется Митчелл Клайн с новым смертельно опасным способом ведения бизнеса. Его команда местных убийц нарушает законы, торгует наркотиками и совершает насилие у дверей гостиницы. Но это кажется слишком хорошей возможностью, чтобы ее упустить — должность няни с проживанием и ошеломляюще щедрой зарплатой. И когда Роуэн Кейн приезжает в Heatherbrae House, она поражена — роскошным «умным» домом, оснащенным всеми современными удобствами, красивым шотландским нагорьем и этой идеальной семьей. Чего она не знает, так это того, что она вступает в кошмар, который закончится смертью ребенка, а она сама окажется в тюрьме в ожидании суда за убийство.
Но это кажется слишком хорошей возможностью, чтобы ее упустить — должность няни с проживанием и ошеломляюще щедрой зарплатой. И когда Роуэн Кейн приезжает в Heatherbrae House, она поражена — роскошным «умным» домом, оснащенным всеми современными удобствами, красивым шотландским нагорьем и этой идеальной семьей. Чего она не знает, так это того, что она вступает в кошмар, который закончится смертью ребенка, а она сама окажется в тюрьме в ожидании суда за убийство. Винегард
Винегард
 С его лысеющей головой, кардиганом и брюками цвета хаки он, кажется, пришел прямо из Центрального кастинга Терапевта. И все же он окажется совсем не таким.
С его лысеющей головой, кардиганом и брюками цвета хаки он, кажется, пришел прямо из Центрального кастинга Терапевта. И все же он окажется совсем не таким.
 Он обнаружил, что в большинстве областей — особенно в сложных и непредсказуемых — универсалы, а не специалисты, стремятся преуспеть. Универсалы часто поздно находят свой путь и жонглируют многими интересами, а не сосредотачиваются на одном. Они также более креативны, более гибки и способны устанавливать связи, которые их более специализированные сверстники не видят.
Он обнаружил, что в большинстве областей — особенно в сложных и непредсказуемых — универсалы, а не специалисты, стремятся преуспеть. Универсалы часто поздно находят свой путь и жонглируют многими интересами, а не сосредотачиваются на одном. Они также более креативны, более гибки и способны устанавливать связи, которые их более специализированные сверстники не видят. Теперь, в этом ослепительном сборнике из девяти совершенно оригинальных эссе, написанных с редким сочетанием подачи и резкости, остроумия и бесстрашия, она углубляется в силы, искажающие наше видение, демонстрируя беспрецедентную стилистическую мощь и критическую ловкость.
Теперь, в этом ослепительном сборнике из девяти совершенно оригинальных эссе, написанных с редким сочетанием подачи и резкости, остроумия и бесстрашия, она углубляется в силы, искажающие наше видение, демонстрируя беспрецедентную стилистическую мощь и критическую ловкость.

 В Северной Дакоте мы встречаем Мэгги, 17-летнюю ученицу средней школы, у которой якобы есть тайные физические отношения с ее красивым женатым учителем английского языка; последующий уголовный процесс перевернет их тихое сообщество с ног на голову.
В Северной Дакоте мы встречаем Мэгги, 17-летнюю ученицу средней школы, у которой якобы есть тайные физические отношения с ее красивым женатым учителем английского языка; последующий уголовный процесс перевернет их тихое сообщество с ног на голову.
 Давать и брать звонит в колокола?
Давать и брать звонит в колокола? Это как современный человек, отказывающийся от электричества. Все, что вам нужно сделать, чтобы получить доступ к электричеству, это найти розетку, подключить электронное устройство или прибор и вуаля! Вы получаете множество крутых штучек: поджаренный хлеб, музыку, транслируемую по радиовышкам, фильмы и новости, а также людей, совершающих всевозможные выходки, например, поедающих слизняков на необитаемых островах.
Это как современный человек, отказывающийся от электричества. Все, что вам нужно сделать, чтобы получить доступ к электричеству, это найти розетку, подключить электронное устройство или прибор и вуаля! Вы получаете множество крутых штучек: поджаренный хлеб, музыку, транслируемую по радиовышкам, фильмы и новости, а также людей, совершающих всевозможные выходки, например, поедающих слизняков на необитаемых островах. »
»
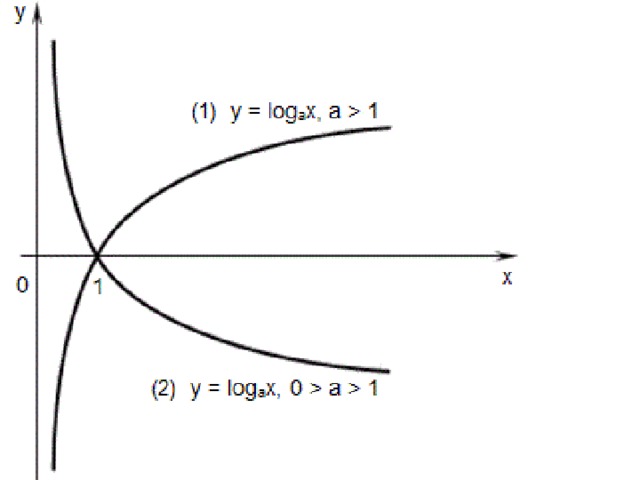
 y = logπ(2x-4).
y = logπ(2x-4).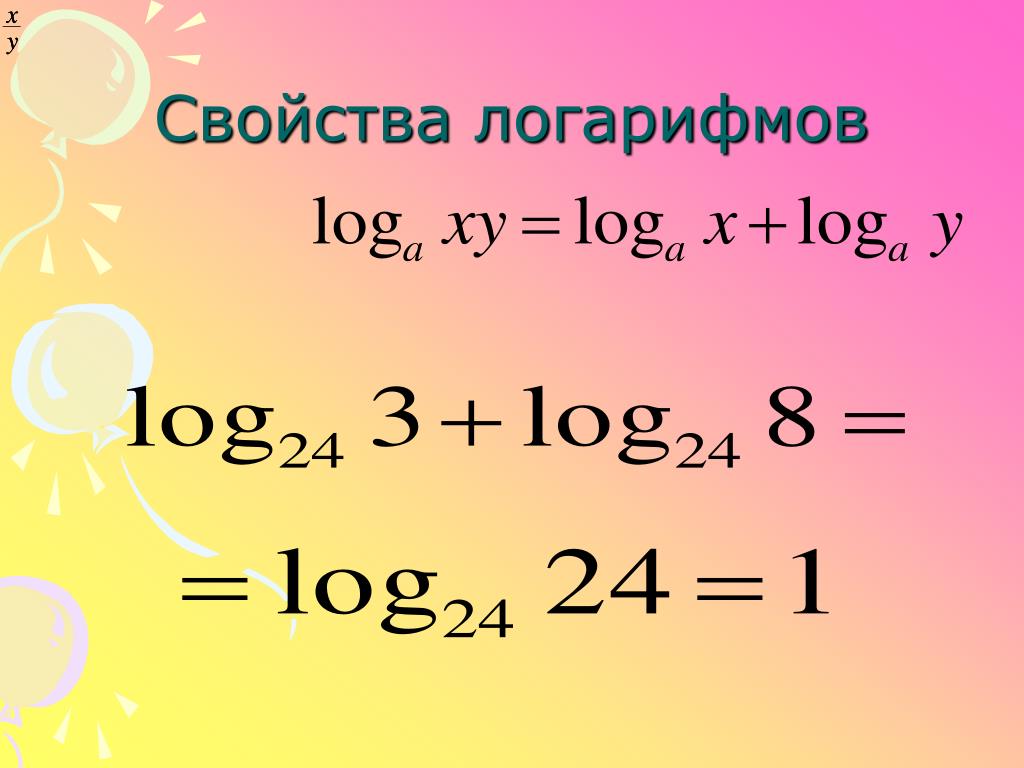 Например, чтобы получить 16, надо два возвести в четвертую степень. А чтобы получить 64, надо два возвести в шестую степень. Это видно из таблицы.
Например, чтобы получить 16, надо два возвести в четвертую степень. А чтобы получить 64, надо два возвести в шестую степень. Это видно из таблицы. Например, попробуйте найти log 2 5 . Числа 5 нет в таблице, но логика подсказывает, что логарифм будет лежать где-то на отрезке . Потому что 2 2 больше степень двойки, тем больше получится число.
Например, попробуйте найти log 2 5 . Числа 5 нет в таблице, но логика подсказывает, что логарифм будет лежать где-то на отрезке . Потому что 2 2 больше степень двойки, тем больше получится число.
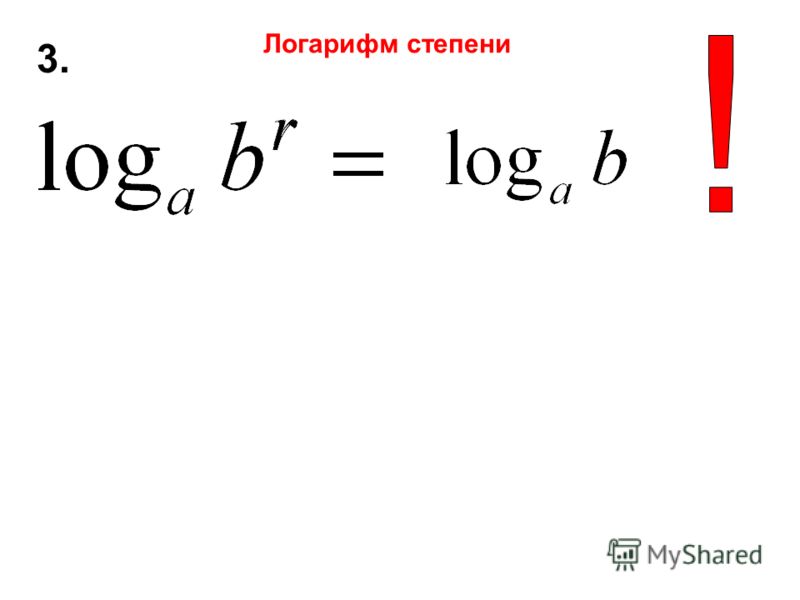 Все ограничения уже учтены составителями задач. Но когда пойдут логарифмические уравнения и неравенства, требования ОДЗ станут обязательными. Ведь в основании и аргументе могут стоять весьма неслабые конструкции, которые совсем необязательно соответствуют приведенным выше ограничениям.
Все ограничения уже учтены составителями задач. Но когда пойдут логарифмические уравнения и неравенства, требования ОДЗ станут обязательными. Ведь в основании и аргументе могут стоять весьма неслабые конструкции, которые совсем необязательно соответствуют приведенным выше ограничениям.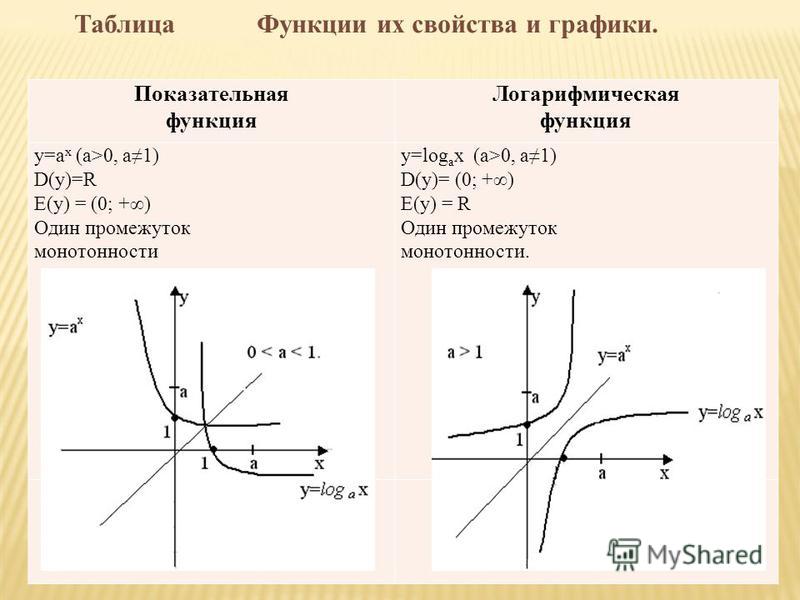 Вычислите логарифм: log 5 25
Вычислите логарифм: log 5 25
 е. степень, в которую надо возвести число 10, чтобы получить число x
. Обозначение: lg x
.
е. степень, в которую надо возвести число 10, чтобы получить число x
. Обозначение: lg x
.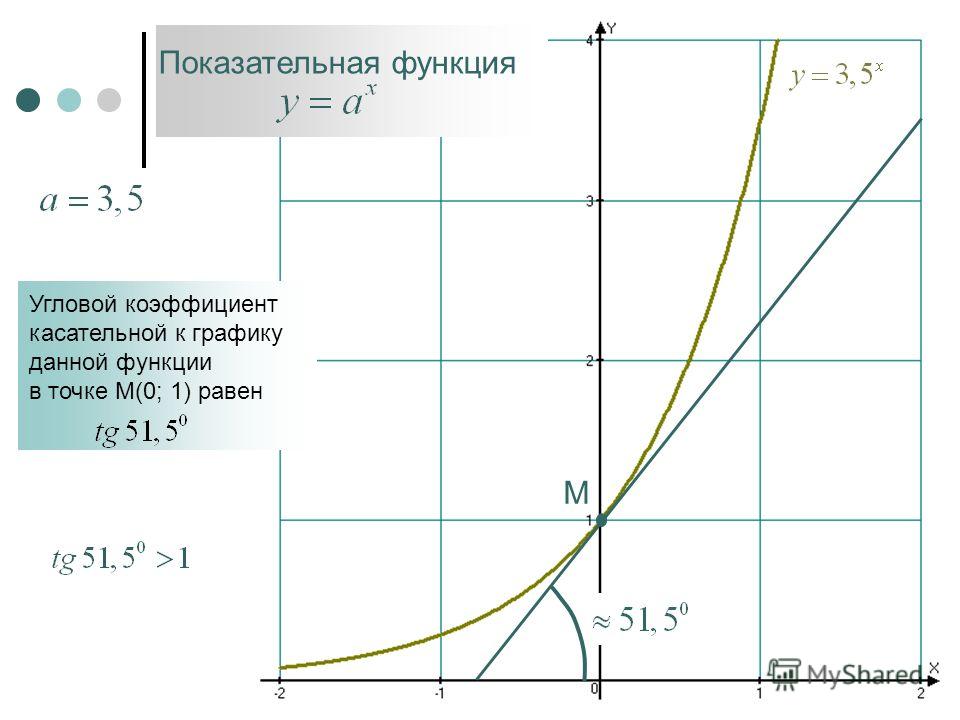 {-5}=\)\(\frac{1}{32}\)
{-5}=\)\(\frac{1}{32}\)  {b}=c\) \(\Leftrightarrow\) \(\log_{a}{c}=b\)
{b}=c\) \(\Leftrightarrow\) \(\log_{a}{c}=b\)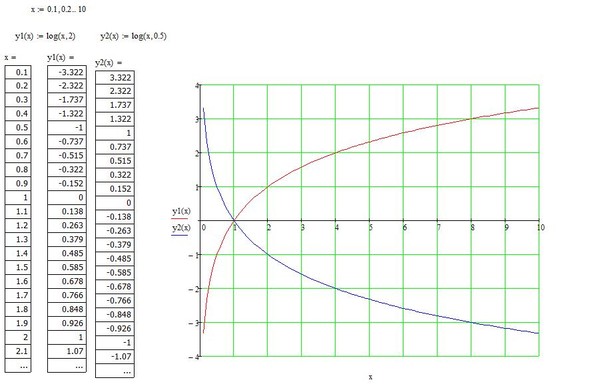 {\log_{6}{5}}\)
{\log_{6}{5}}\)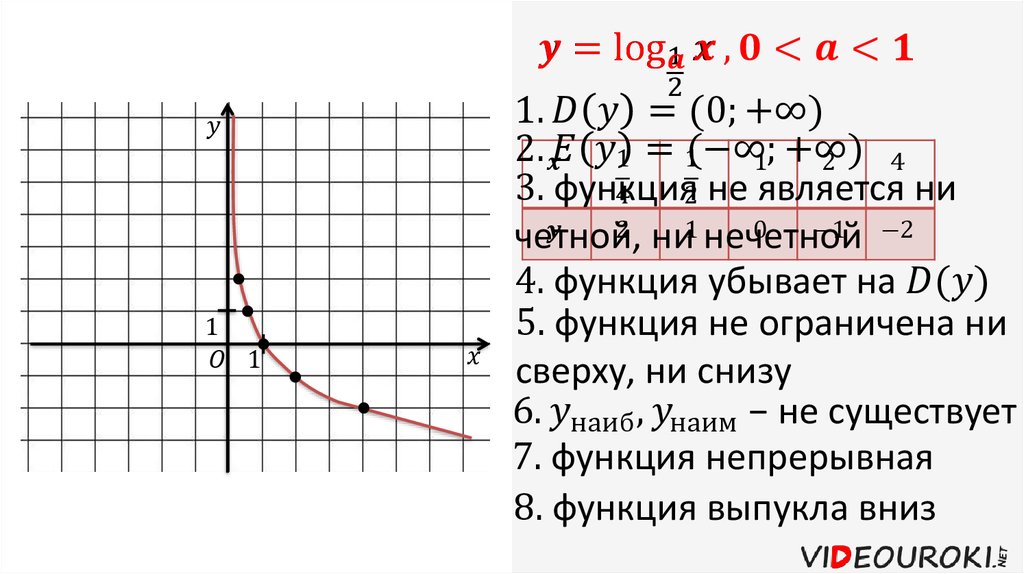 {a}}\)
{a}}\) также в других словарях:
также в других словарях: Если х является логарифмом с основанием у от z, то z=уx. Логарифмы имеют такое свойство, что … Экономический словарь
Если х является логарифмом с основанием у от z, то z=уx. Логарифмы имеют такое свойство, что … Экономический словарь ), чтобы получить N;обозначается logaN, т. е. m=logaN, если am=N. Каждому положительному числу соответствует при данном основании единственный действительный… … Математическая энциклопедия
), чтобы получить N;обозначается logaN, т. е. m=logaN, если am=N. Каждому положительному числу соответствует при данном основании единственный действительный… … Математическая энциклопедия
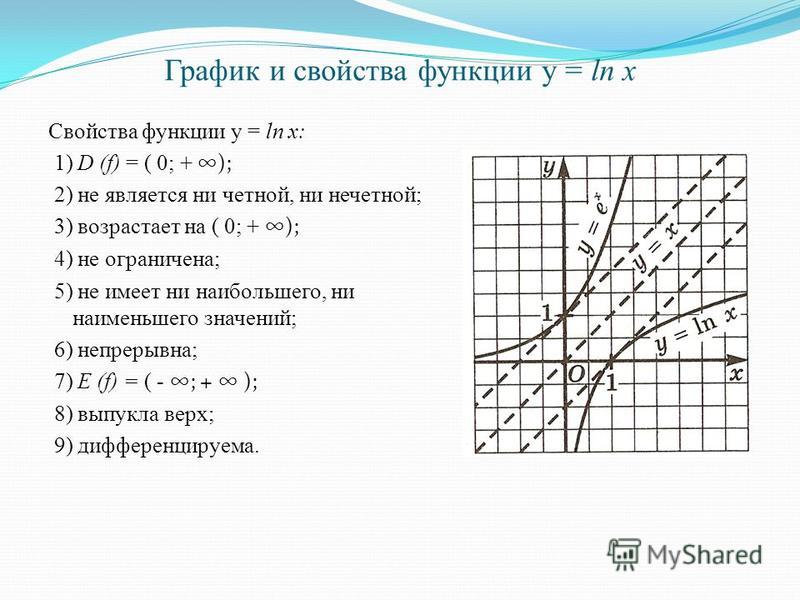 Именно по этой причине и оговорено условие a>0.
Именно по этой причине и оговорено условие a>0.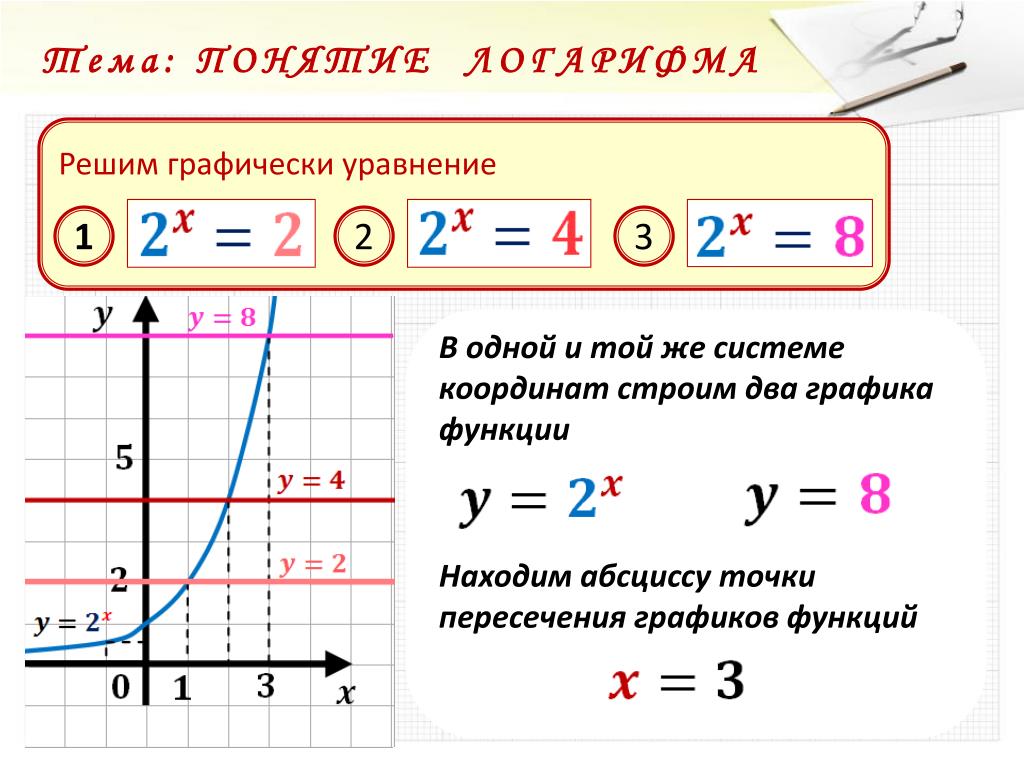 когда вы встречаете простейшую конструкцию, сразу без дополнительных действий и построений можете перейти к решению.
когда вы встречаете простейшую конструкцию, сразу без дополнительных действий и построений можете перейти к решению. Следовательно, на эту букву распространяются все ограничения, которые накладываются на основание логарифма. а именно:
Следовательно, на эту букву распространяются все ограничения, которые накладываются на основание логарифма. а именно: Новая функция уже не содержит логарифма и решается стандартными алгебраическими приемами.
Новая функция уже не содержит логарифма и решается стандартными алгебраическими приемами.
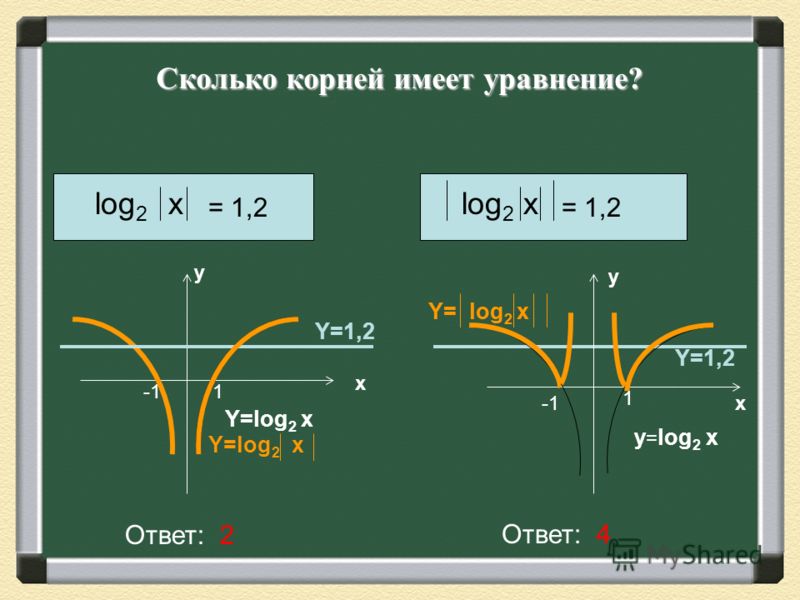 Логарифмические таблицы, увеличенные и детализированные прочими учеными, широко использовались при выполнении научных и инженерных вычислений, и оставались актуальными пока не стали применяться электронные калькуляторы и компьютеры.
Логарифмические таблицы, увеличенные и детализированные прочими учеными, широко использовались при выполнении научных и инженерных вычислений, и оставались актуальными пока не стали применяться электронные калькуляторы и компьютеры.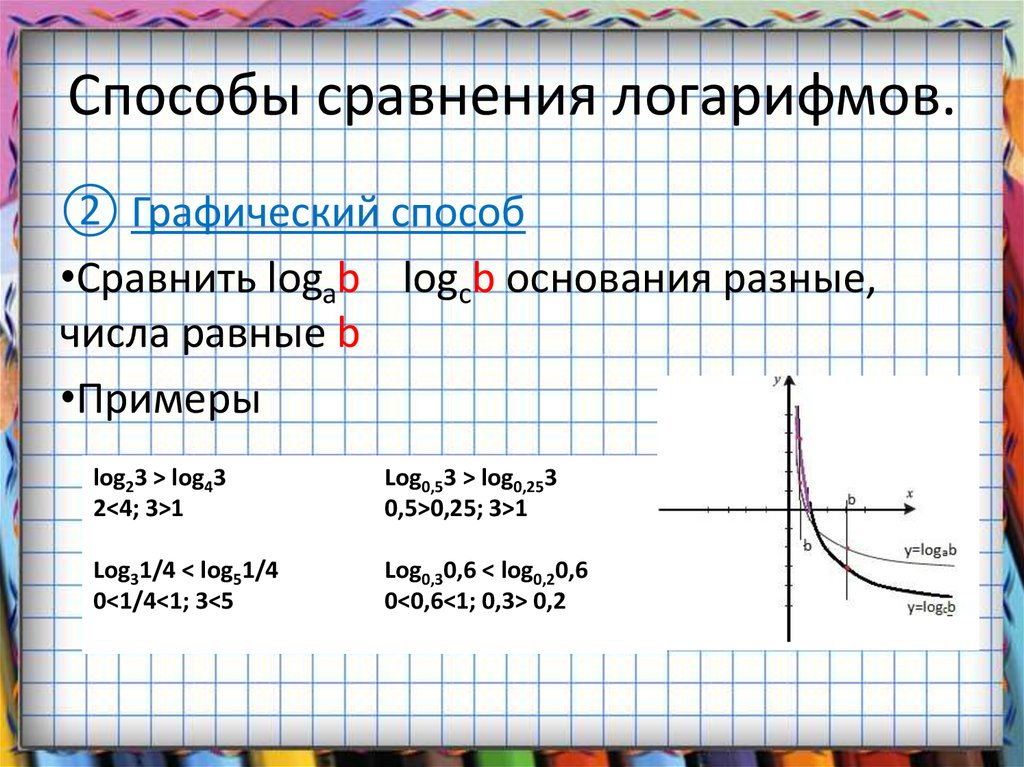
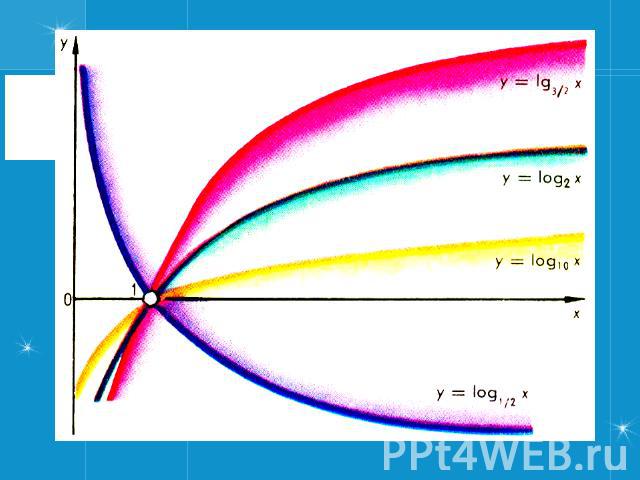
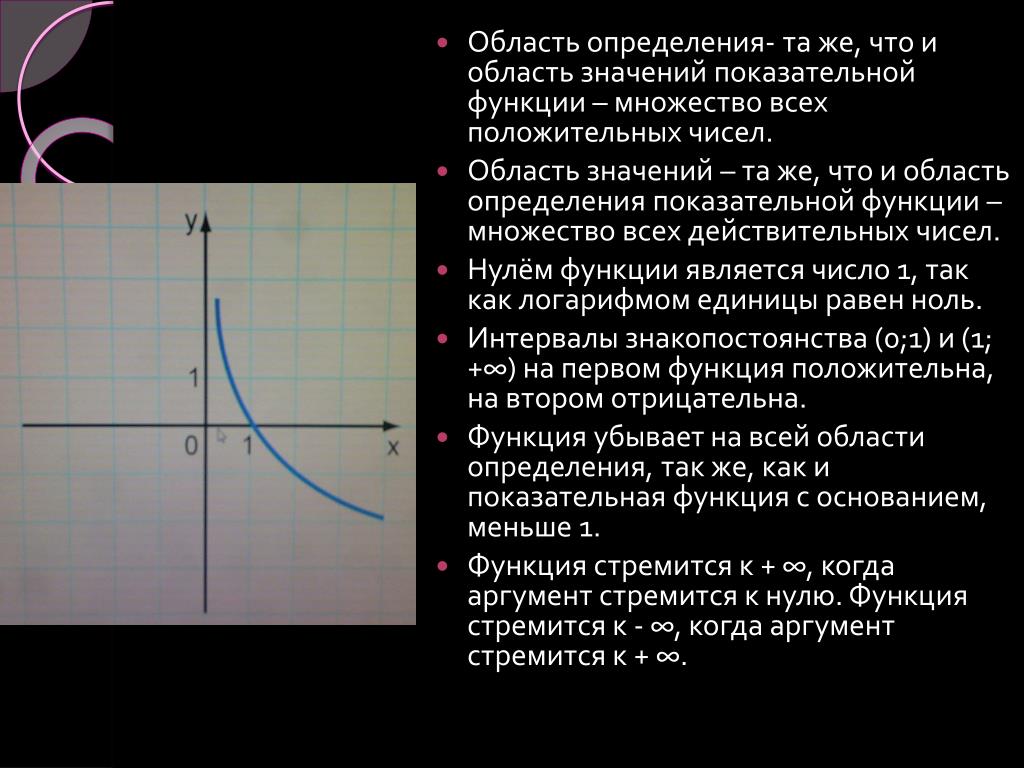 В случае с основаниями происходит следующее:
В случае с основаниями происходит следующее: Вторая задача решена.
Вторая задача решена. е. простейшее логарифмическое уравнение у нас нигде не всплывало.
е. простейшее логарифмическое уравнение у нас нигде не всплывало. Просто знайте, что если в задаче переменная х встречается лишь в одном месте (а точнее — в одном-единственном аргументе одного-единственного логарифма), и больше нигде в нашем случае нет переменной х, то записывать область определения не нужно, потому что она будет выполняться автоматически.
Просто знайте, что если в задаче переменная х встречается лишь в одном месте (а точнее — в одном-единственном аргументе одного-единственного логарифма), и больше нигде в нашем случае нет переменной х, то записывать область определения не нужно, потому что она будет выполняться автоматически. Но это не значит, что такого числа не существует, просто его можно вычислить только на калькуляторе.
Но это не значит, что такого числа не существует, просто его можно вычислить только на калькуляторе. На примере этих уравнения мы увидим, какие ошибки чаще всего допускаются в процессе решения и преобразования исходных выражений.
На примере этих уравнения мы увидим, какие ошибки чаще всего допускаются в процессе решения и преобразования исходных выражений. Но когда вместо них стоят функции, данные выражения перестают быть равноправными. Представьте себе такую гипотетическую ситуацию:
Но когда вместо них стоят функции, данные выражения перестают быть равноправными. Представьте себе такую гипотетическую ситуацию: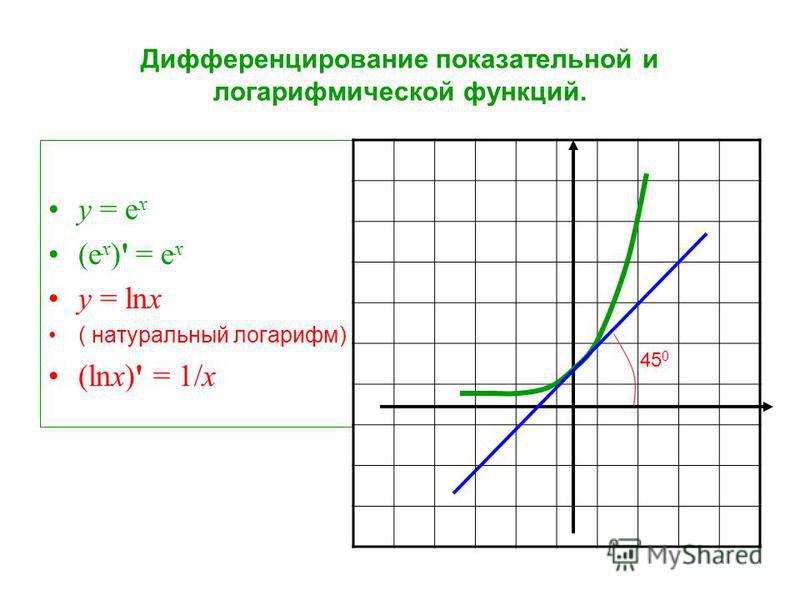 Напротив: количество слагаемых лишь увеличились! Чтобы понять, как действовать дальше, введем новые переменные:
Напротив: количество слагаемых лишь увеличились! Чтобы понять, как действовать дальше, введем новые переменные: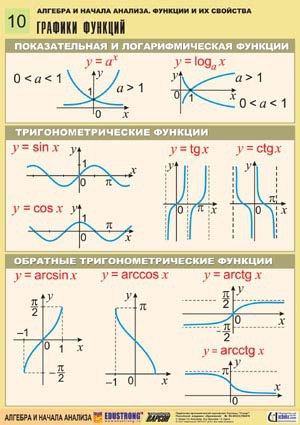 Теперь проверим область определения. Для первого аргумента:
Теперь проверим область определения. Для первого аргумента: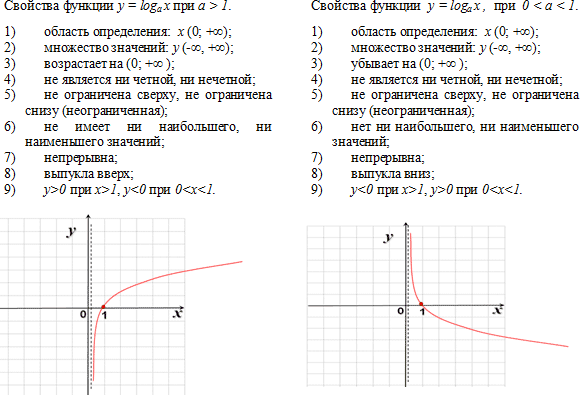

 Область определения и ответы при этом никак не пострадают, а вот объем вычислений существенно сократится.
Область определения и ответы при этом никак не пострадают, а вот объем вычислений существенно сократится.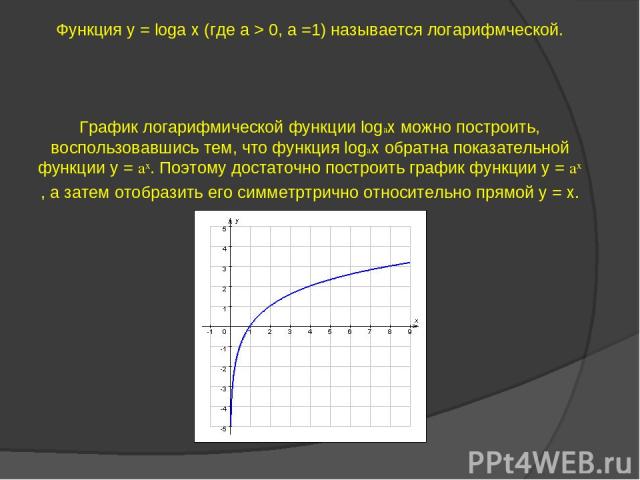
 png" width="130" height="308" data-full="https://exceltut.ru/wp-content/uploads/2020/06/logarifm-exc-10.png"><meta itemprop="width" content="130"><meta itemprop="height" content="308"></td><td class="htLeft htMiddle" data-order=» itemprop=»url image» src=»https://exceltut.ru/wp-content/uploads/2020/06/logarifm-exc-11.png» size-full=»» data-full=»https://exceltut.ru/wp-content/uploads/2020/06/logarifm-exc-11.png»/>‘ data-original-value=’‘ data-cell-type=”text” data-db-index=”6″ data-y=”6″ data-x=”2″ data-cell-id=”C6″>
png" width="130" height="308" data-full="https://exceltut.ru/wp-content/uploads/2020/06/logarifm-exc-10.png"><meta itemprop="width" content="130"><meta itemprop="height" content="308"></td><td class="htLeft htMiddle" data-order=» itemprop=»url image» src=»https://exceltut.ru/wp-content/uploads/2020/06/logarifm-exc-11.png» size-full=»» data-full=»https://exceltut.ru/wp-content/uploads/2020/06/logarifm-exc-11.png»/>‘ data-original-value=’‘ data-cell-type=”text” data-db-index=”6″ data-y=”6″ data-x=”2″ data-cell-id=”C6″> png"><meta itemprop="width" content="130"><meta itemprop="height" content="280"></td><td class="htLeft htMiddle" data-order=» itemprop=»url image» src=»https://exceltut.ru/wp-content/uploads/2020/06/logarifm-exc-5.png» size-full=»» data-full=»https://exceltut.ru/wp-content/uploads/2020/06/logarifm-exc-5.png»/>‘ data-original-value=’‘ data-cell-type=”text” data-db-index=”7″ data-y=”7″ data-x=”2″ data-cell-id=”C7″>
png"><meta itemprop="width" content="130"><meta itemprop="height" content="280"></td><td class="htLeft htMiddle" data-order=» itemprop=»url image» src=»https://exceltut.ru/wp-content/uploads/2020/06/logarifm-exc-5.png» size-full=»» data-full=»https://exceltut.ru/wp-content/uploads/2020/06/logarifm-exc-5.png»/>‘ data-original-value=’‘ data-cell-type=”text” data-db-index=”7″ data-y=”7″ data-x=”2″ data-cell-id=”C7″>
 При этом имеется в виду логарифм по основанию 2.
При этом имеется в виду логарифм по основанию 2.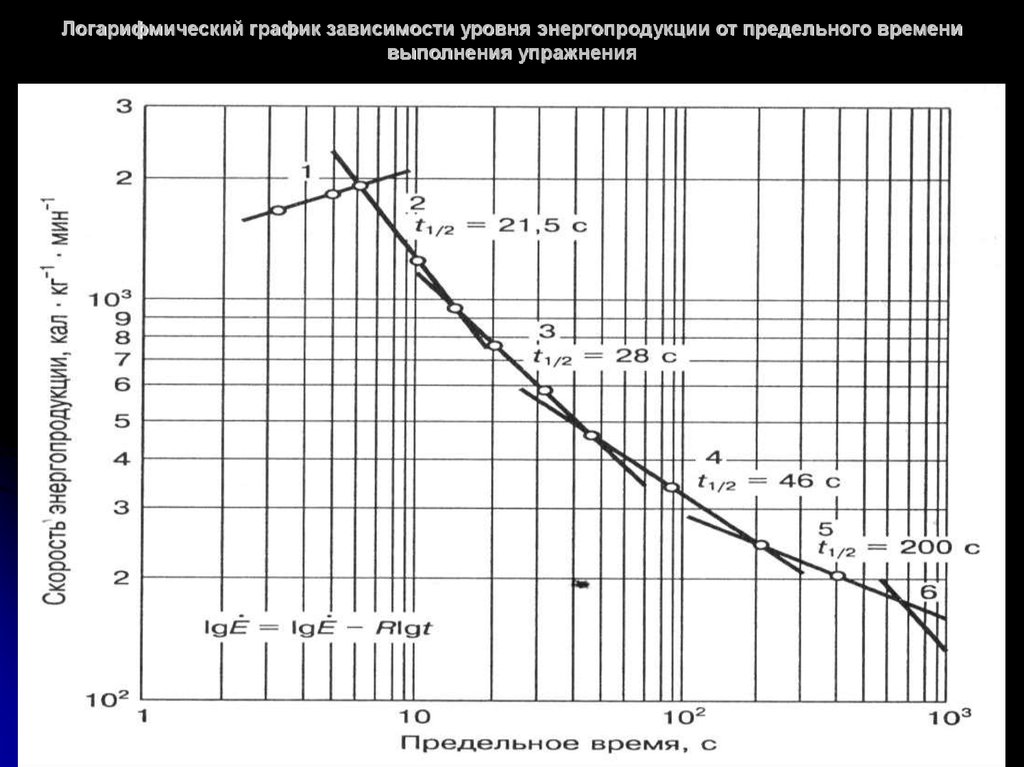 ..» и буду признателен за более развернутый ответ, написанный не для математиков. Разве правило, что «константы в О-большом не имеют значения», относится к основанию логарифма? Разве для бинарного поиска не имеет никакой разницы как записать его сложность — логарифмом по основанию 2 или по основанию 100?
..» и буду признателен за более развернутый ответ, написанный не для математиков. Разве правило, что «константы в О-большом не имеют значения», относится к основанию логарифма? Разве для бинарного поиска не имеет никакой разницы как записать его сложность — логарифмом по основанию 2 или по основанию 100?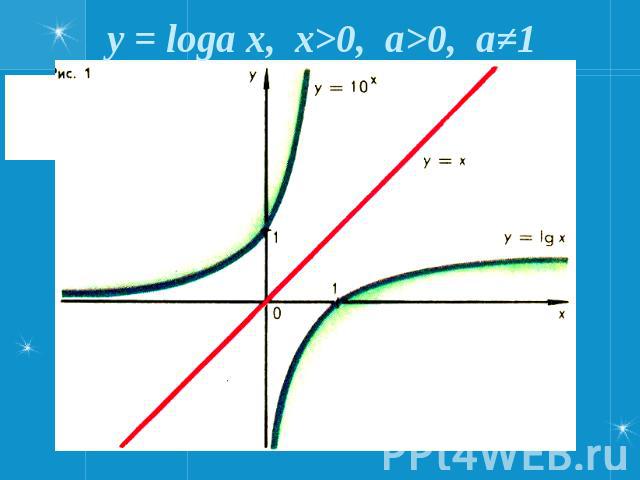 Разве мы можем заменить в его сложности основание у логарифма с два на десять? А с два на 0,5? Мне кажется, не можем. Т.е. мы не можем подставить в выражении log N произвольное основание потому что зависимость будет совершенно другая — это хорошо видно на графике. Т.о. какой именно логарифм использовать важно. Или я не прав?
Разве мы можем заменить в его сложности основание у логарифма с два на десять? А с два на 0,5? Мне кажется, не можем. Т.е. мы не можем подставить в выражении log N произвольное основание потому что зависимость будет совершенно другая — это хорошо видно на графике. Т.о. какой именно логарифм использовать важно. Или я не прав?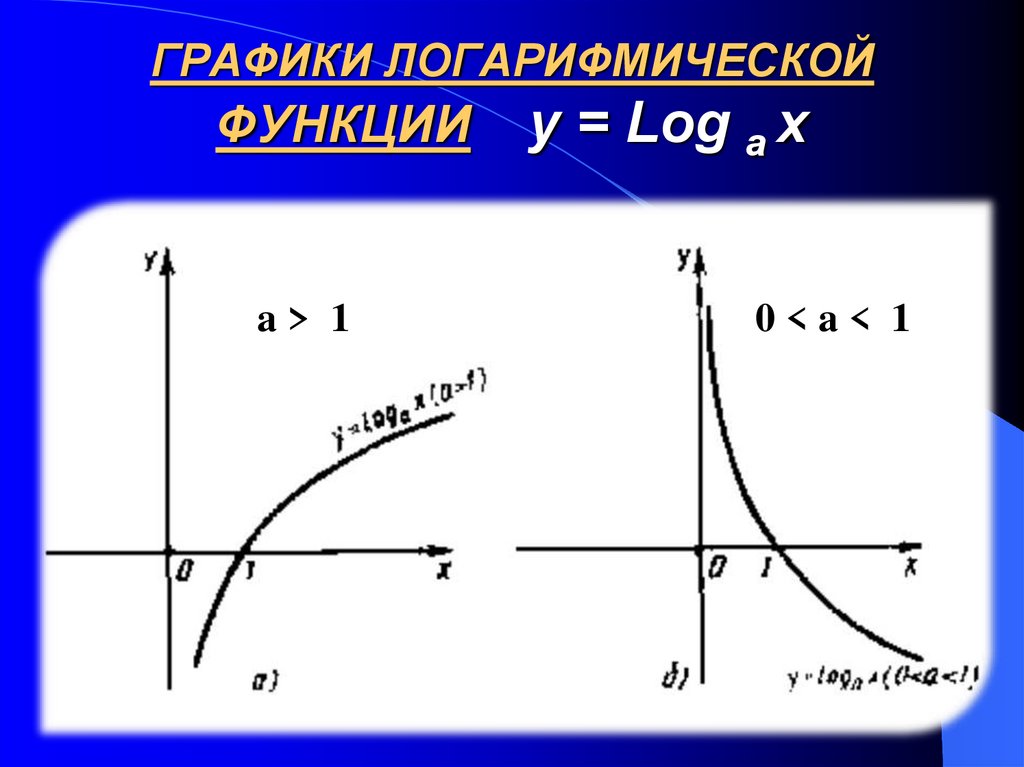 Это — определение записи с большим О.
Это — определение записи с большим О.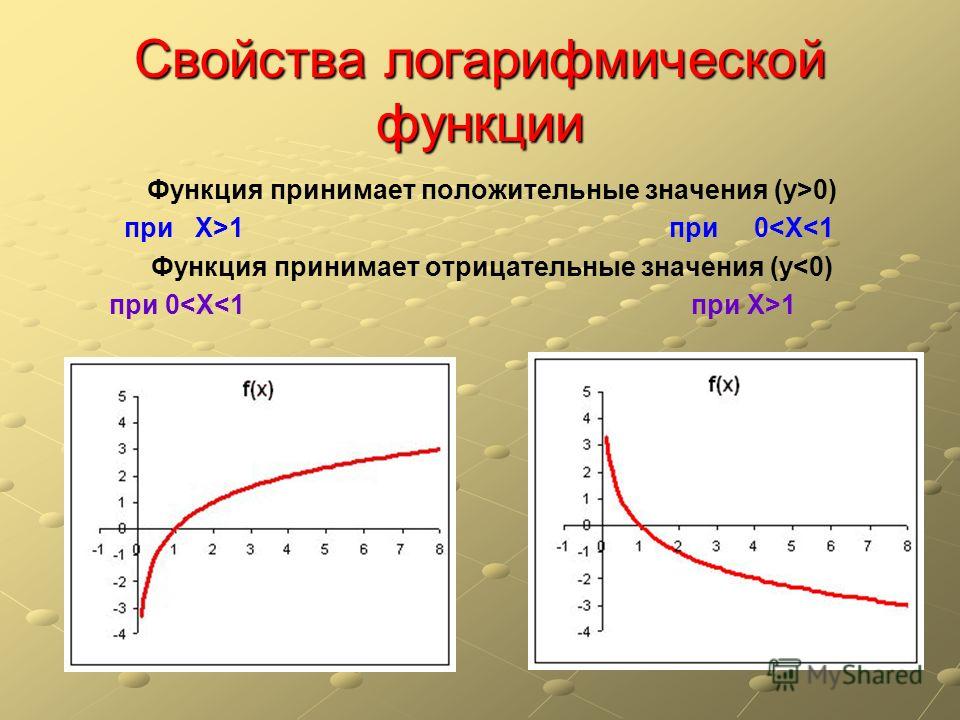 Но и тут — достаточно взять его по модулю или отрицательную константу 🙂
Но и тут — достаточно взять его по модулю или отрицательную константу 🙂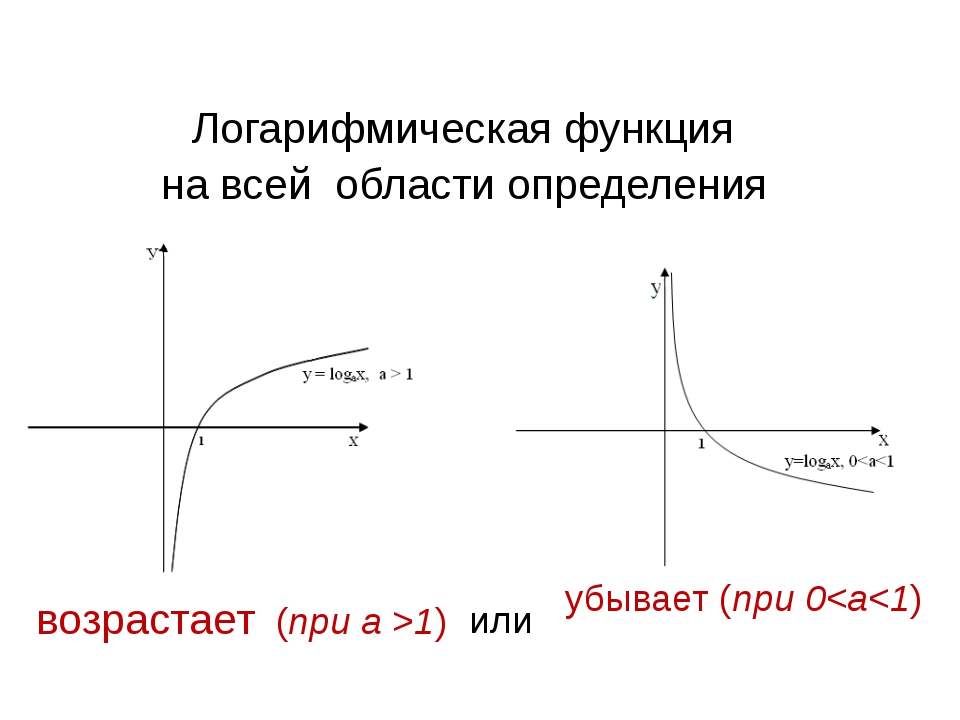 Но, если честно, моих математических знаний на данный момент не хватает, чтобы дать этому утверждению оценку. Поэтому я предпочту пока более общую формулировку про то, что «основание определено контекстом»
Но, если честно, моих математических знаний на данный момент не хватает, чтобы дать этому утверждению оценку. Поэтому я предпочту пока более общую формулировку про то, что «основание определено контекстом»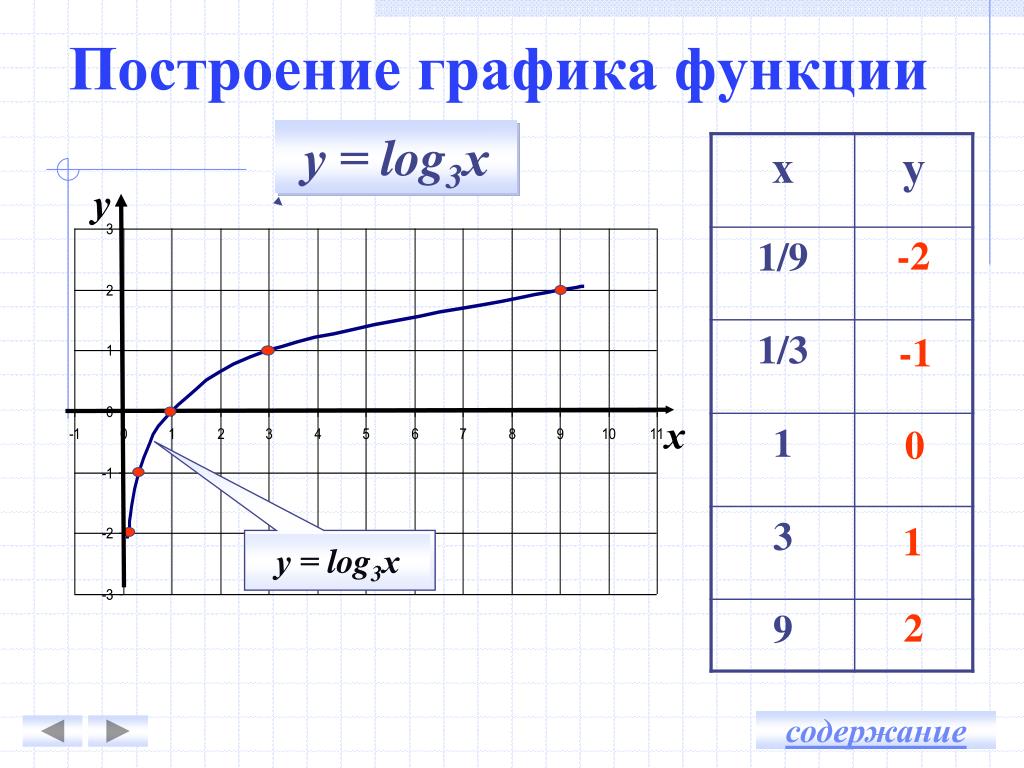 ..
..
 4kb.
4kb.
 98kb.
98kb.
 Формировать навыки общения, диалога, умение работать в коллективе.
Формировать навыки общения, диалога, умение работать в коллективе. 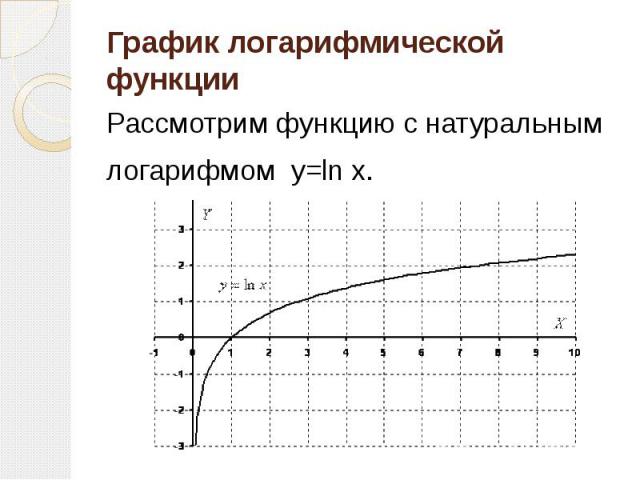 В подтверждение разберём три примера (Приложение 1) Примеры на вычисление логарифма
В подтверждение разберём три примера (Приложение 1) Примеры на вычисление логарифма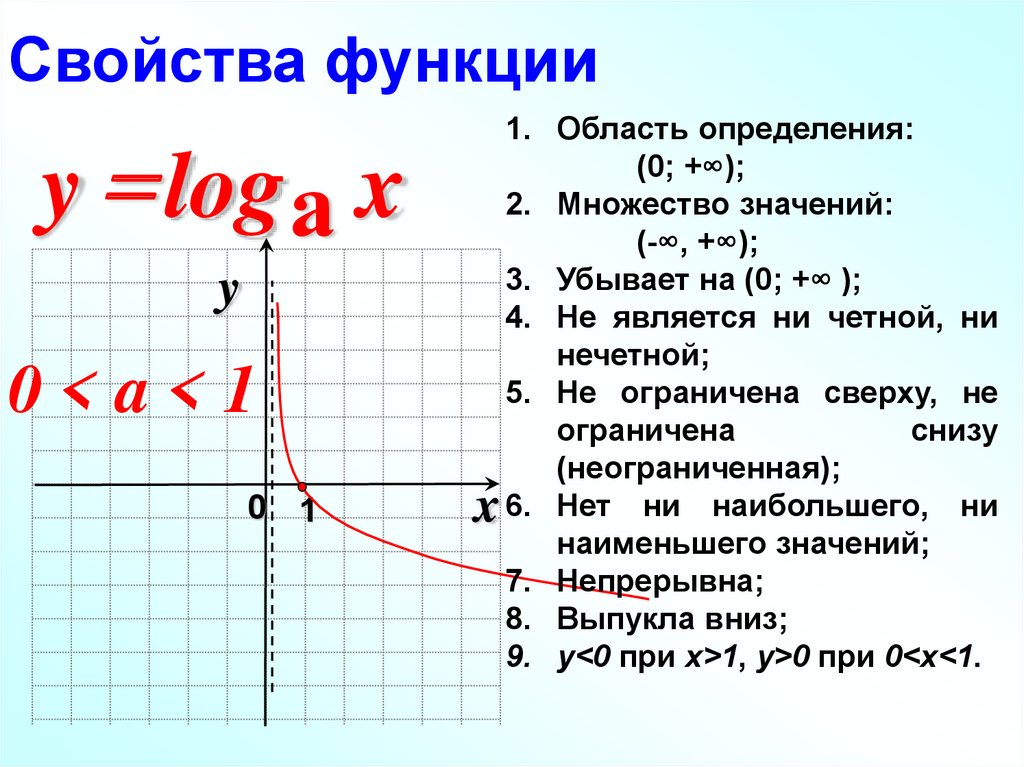
 На вопрос учителя: «Как бы вы назвали эту функции?» учащиеся говорят, что она логарифмическая, так как переменная стоит под знаком логарифма: . На вопрос: «Находит ли эта функция применение в окружающем нас мире?», ответит с помощью своего сообщения о логарифмической спирали учащаяся (Приложение 4).
На вопрос учителя: «Как бы вы назвали эту функции?» учащиеся говорят, что она логарифмическая, так как переменная стоит под знаком логарифма: . На вопрос: «Находит ли эта функция применение в окружающем нас мире?», ответит с помощью своего сообщения о логарифмической спирали учащаяся (Приложение 4). 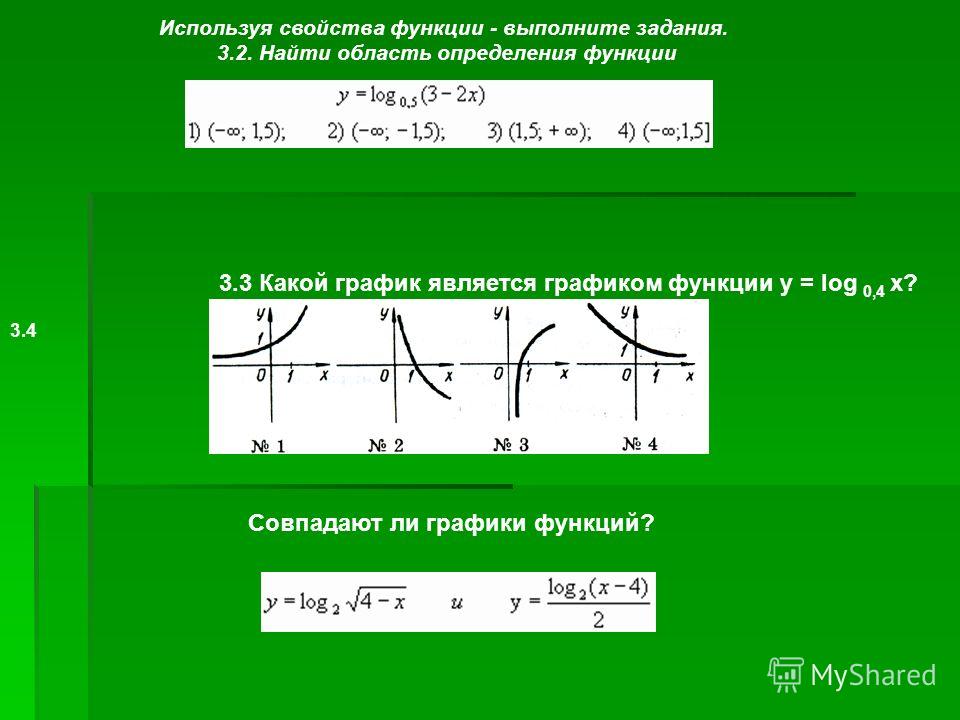

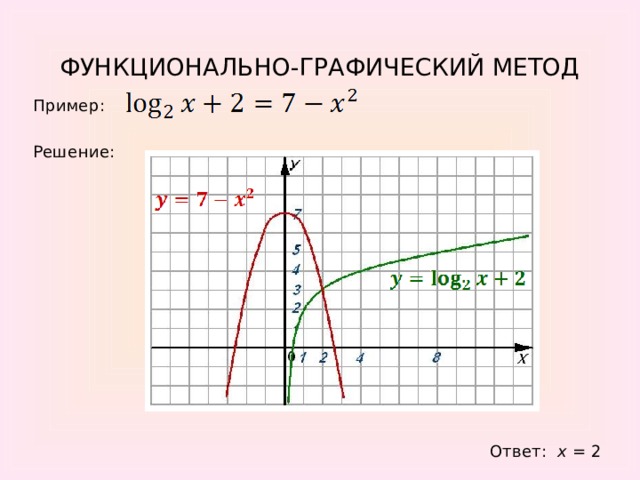


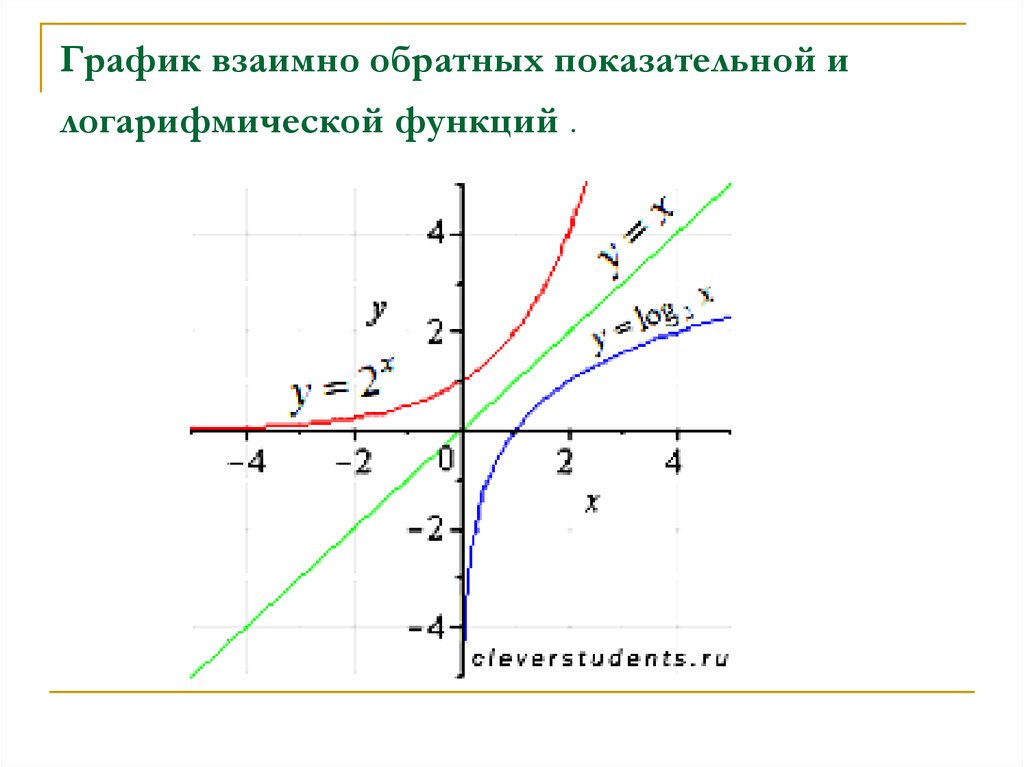 Подводя итоги урока, выясняется, что было известно учащимся, что нового узнали и чему научились на этом уроке.
Подводя итоги урока, выясняется, что было известно учащимся, что нового узнали и чему научились на этом уроке. 


 Вот общая формула для изменения основания —
Вот общая формула для изменения основания —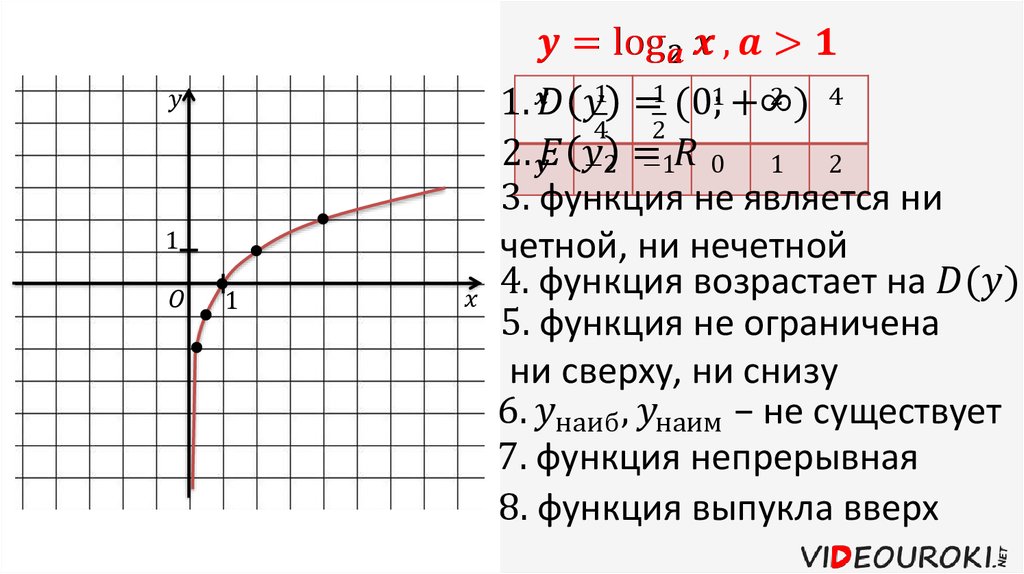


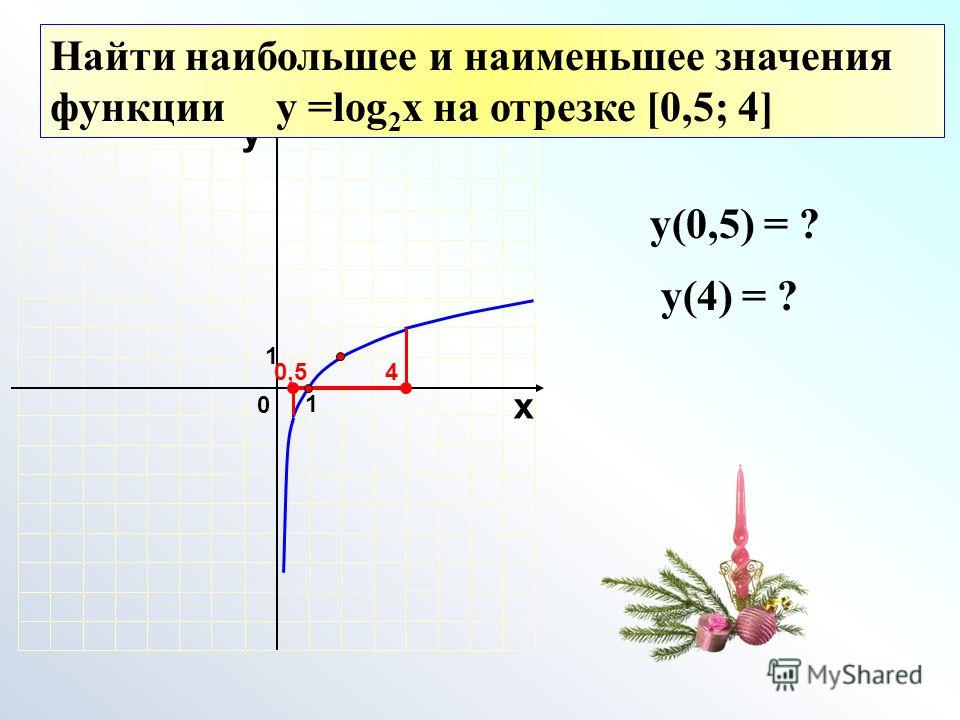
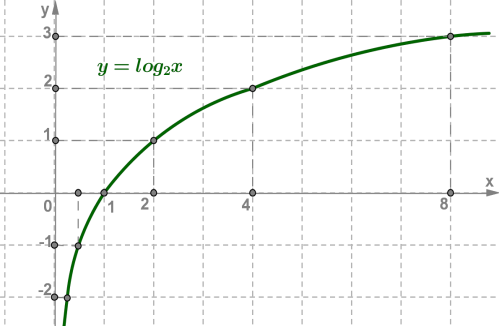
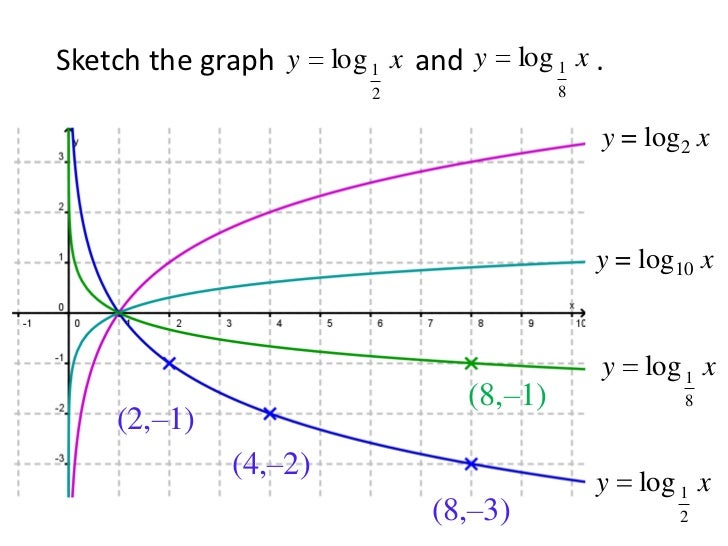
 1 не имеет нулей, так что это 10 0 . А 0,0001 имеет четыре нуля и является отрицательным, поэтому это 10 -4 . Таким образом, логарифмическая шкала не показывает числа на линейной шкале, но показывает величины в линейной форме: 0, 1, 2, 3 и т. д.
1 не имеет нулей, так что это 10 0 . А 0,0001 имеет четыре нуля и является отрицательным, поэтому это 10 -4 . Таким образом, логарифмическая шкала не показывает числа на линейной шкале, но показывает величины в линейной форме: 0, 1, 2, 3 и т. д. богатый зернами пшеницы и шахматной доской: мы все слышали слово «экспоненциальный» раньше. Давайте вспомним, что это значит.
богатый зернами пшеницы и шахматной доской: мы все слышали слово «экспоненциальный» раньше. Давайте вспомним, что это значит.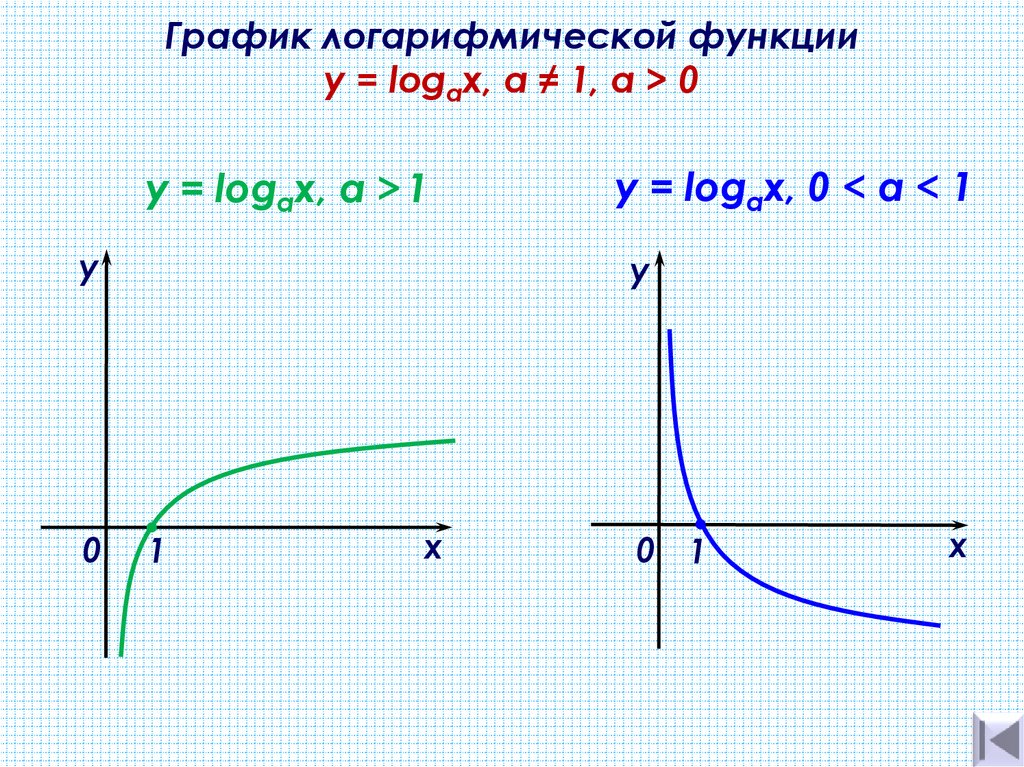 д. Та же сделка. Логарифмическая шкала «растет экспоненциально», если ее показатели степени (= порядок величин) «растут линейно».
д. Та же сделка. Логарифмическая шкала «растет экспоненциально», если ее показатели степени (= порядок величин) «растут линейно». 
 Это означает, что потребовалось 15 лет, чтобы перейти от 1000 транзисторов к 100 000 транзисторов, и потребовалось 15 лет, чтобы перейти от 100 миллионов транзисторов к 10 миллиардам.
Это означает, что потребовалось 15 лет, чтобы перейти от 1000 транзисторов к 100 000 транзисторов, и потребовалось 15 лет, чтобы перейти от 100 миллионов транзисторов к 10 миллиардам.
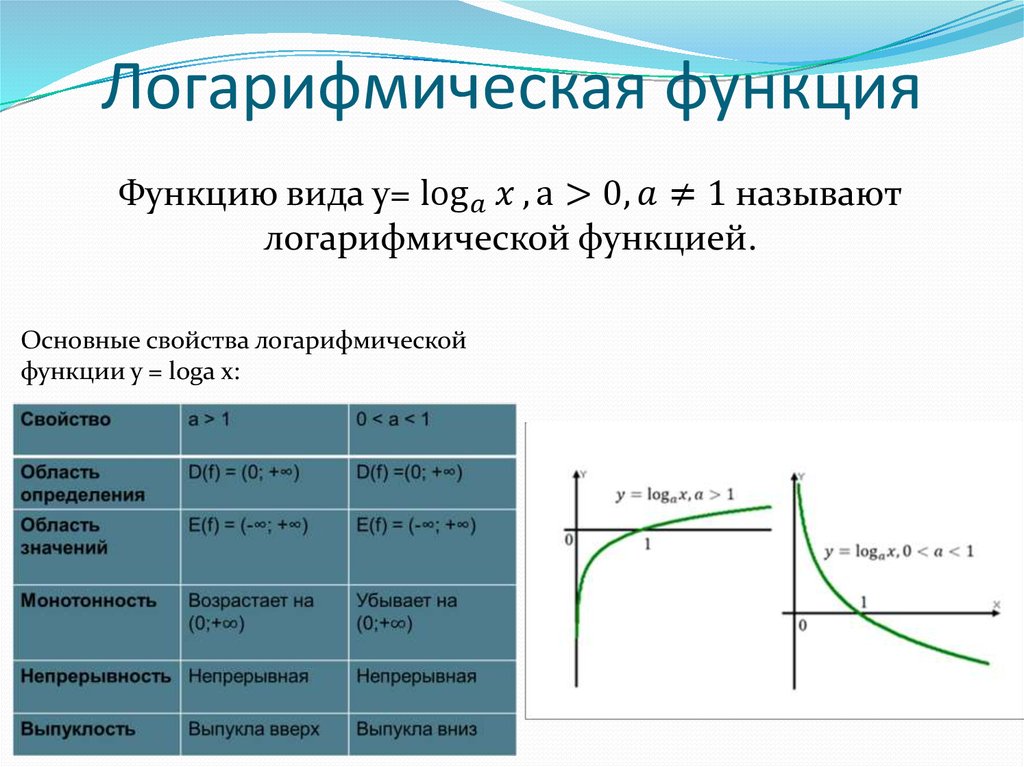 Я поддерживаю это прямо, глядя на положение вещей. В исходном журнале аргумент находится «над» базой (поскольку база индексирована), поэтому я оставлю все так, когда разделю их:
Я поддерживаю это прямо, глядя на положение вещей. В исходном журнале аргумент находится «над» базой (поскольку база индексирована), поэтому я оставлю все так, когда разделю их: Вам не нужно утруждать себя записью этого промежуточного шага.
Вам не нужно утруждать себя записью этого промежуточного шага.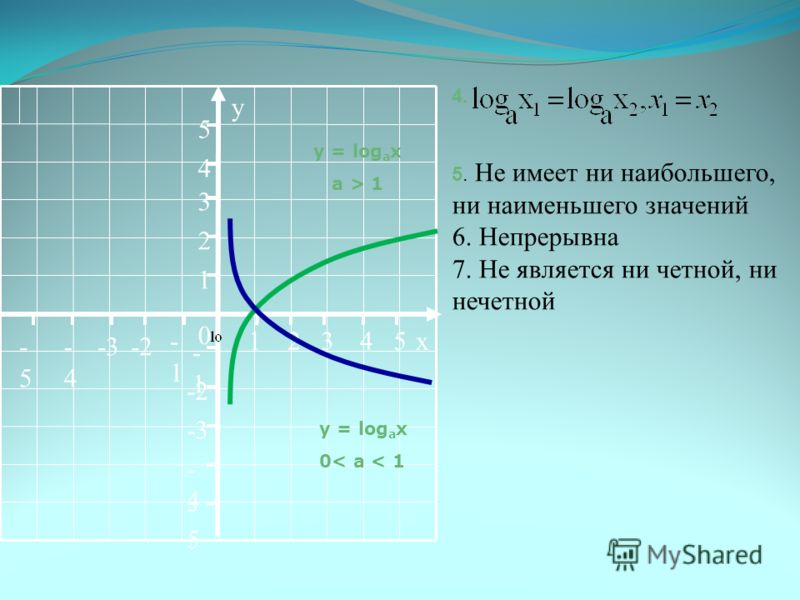

 е. точки I рассчитал бы вручную, как показано выше), чтобы убедиться, что на картинке отображается правильный график:
е. точки I рассчитал бы вручную, как показано выше), чтобы убедиться, что на картинке отображается правильный график: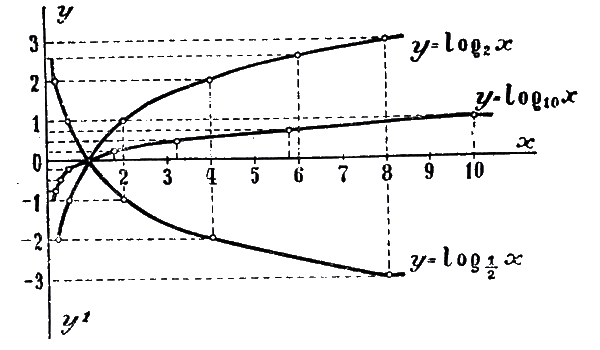 Если вы подгоните что-нибудь к данным, это, вероятно, изменит подходящие значения.
Если вы подгоните что-нибудь к данным, это, вероятно, изменит подходящие значения.
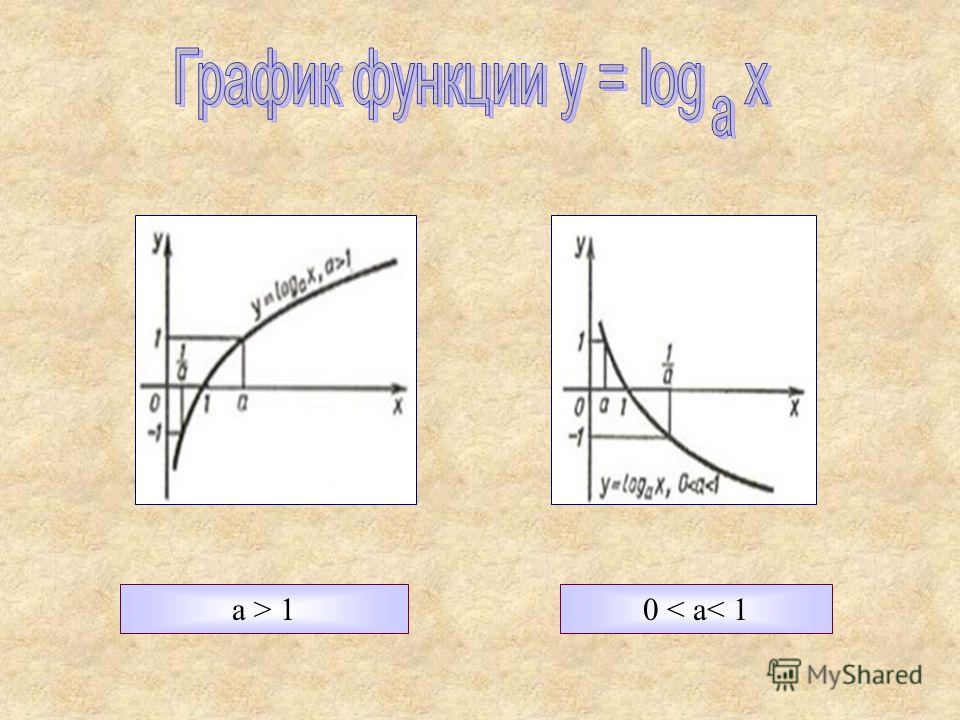 .x))) +
тема_bw()
часть 2
.x))) +
тема_bw()
часть 2 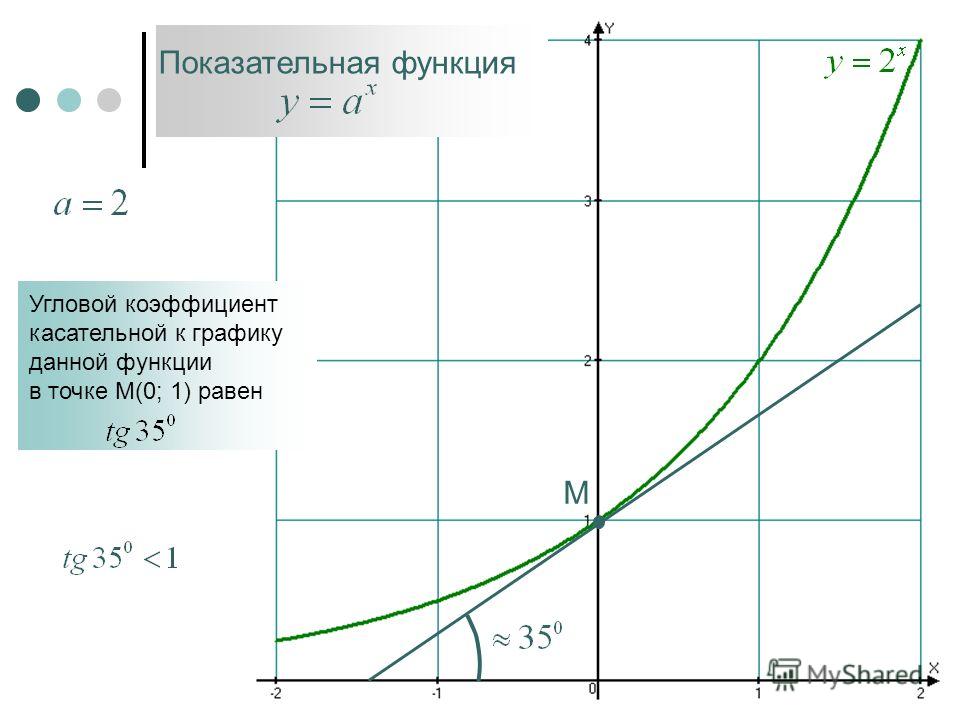 1
1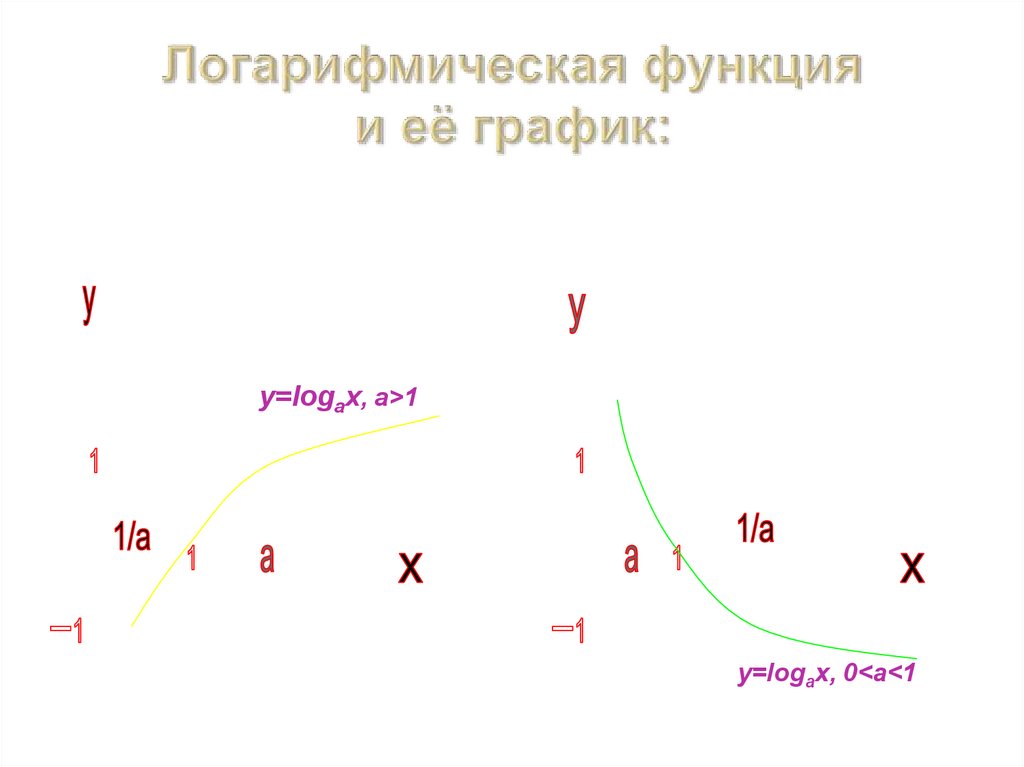 )
)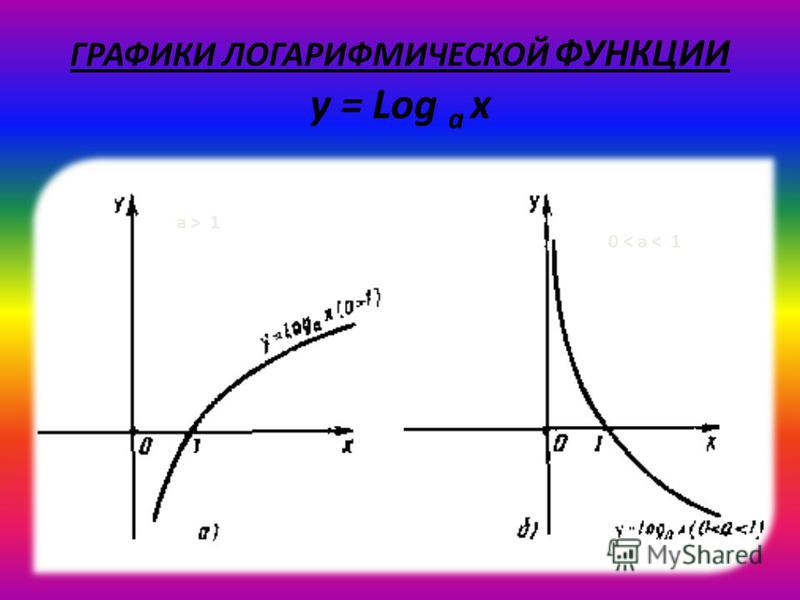 В этом контексте логарифм определяется по основанию 10.
В этом контексте логарифм определяется по основанию 10.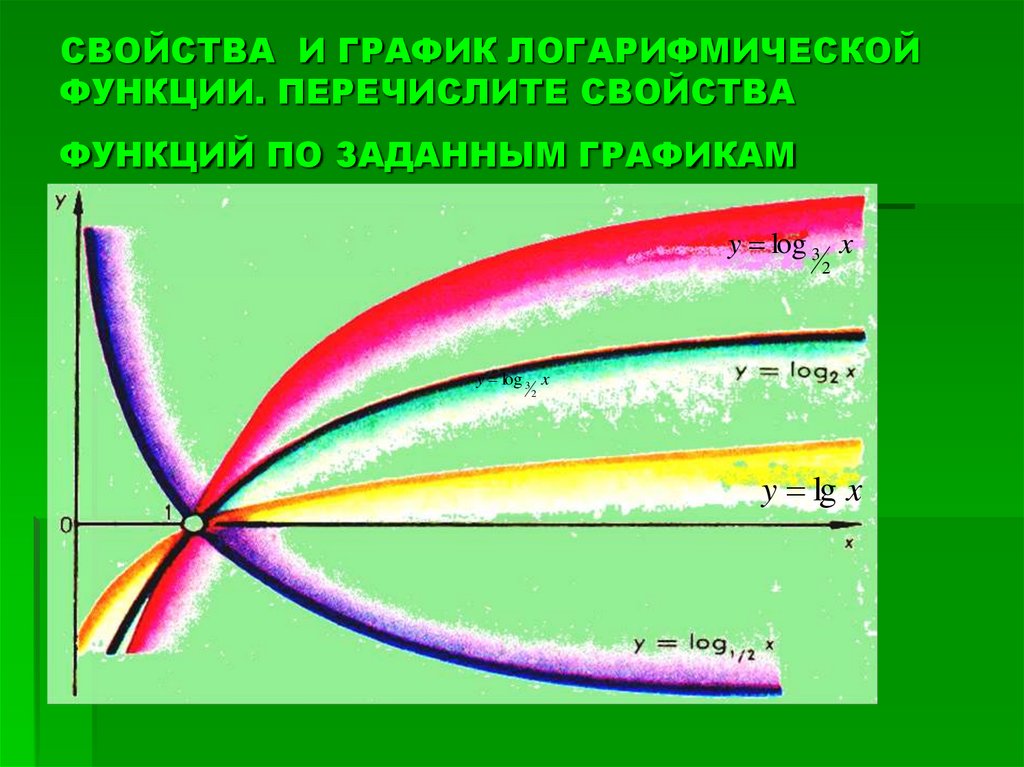 30103… 0 DB11100–3 DB√121210 - 0,30103… −6 DB121410 - 0,60206… -10 DB√110110101121410111010110110 гг. см. значения децибел за пределами этих границ: +80 дБ представляет собой множитель мощности 108
и множитель напряжения 104
. В общем, мы можем просто инвертировать приведенные выше уравнения для A дБ:
30103… 0 DB11100–3 DB√121210 - 0,30103… −6 DB121410 - 0,60206… -10 DB√110110101121410111010110110 гг. см. значения децибел за пределами этих границ: +80 дБ представляет собой множитель мощности 108
и множитель напряжения 104
. В общем, мы можем просто инвертировать приведенные выше уравнения для A дБ: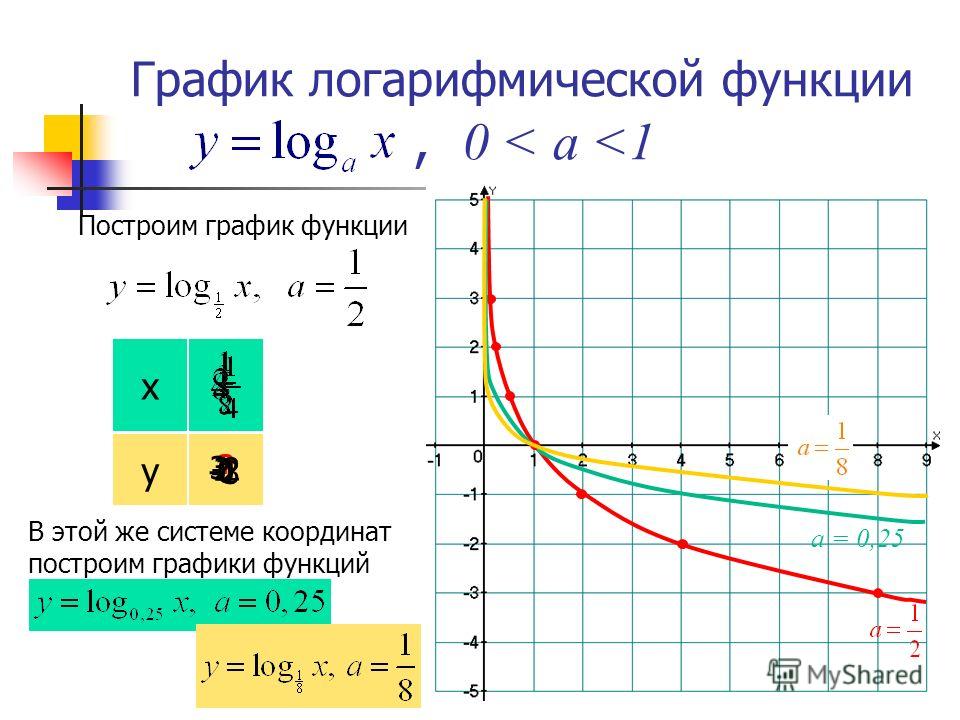 по напряжению и коэффициентом 104
в силе.
по напряжению и коэффициентом 104
в силе.
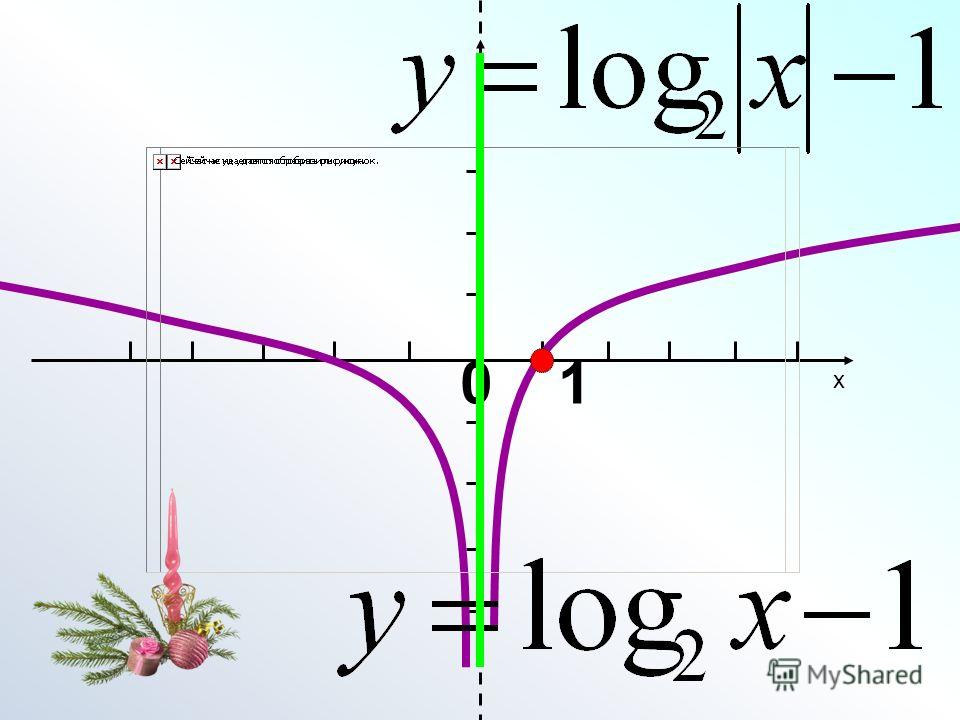 е. подняться на три октавы вверх), мы получим 23⋅f=8⋅f
- почти достаточно, чтобы достичь 10⋅f
, но не совсем. Если мы удвоим f
четыре раза (т.е. подняться на четыре октавы вверх), мы получим 24⋅f=16⋅f
– более десяти лет; мы зашли слишком далеко. Реальное количество октав, необходимое для завершения декады, составляет от трех до четырех и отображается как k.
выше.
е. подняться на три октавы вверх), мы получим 23⋅f=8⋅f
- почти достаточно, чтобы достичь 10⋅f
, но не совсем. Если мы удвоим f
четыре раза (т.е. подняться на четыре октавы вверх), мы получим 24⋅f=16⋅f
– более десяти лет; мы зашли слишком далеко. Реальное количество октав, необходимое для завершения декады, составляет от трех до четырех и отображается как k.
выше.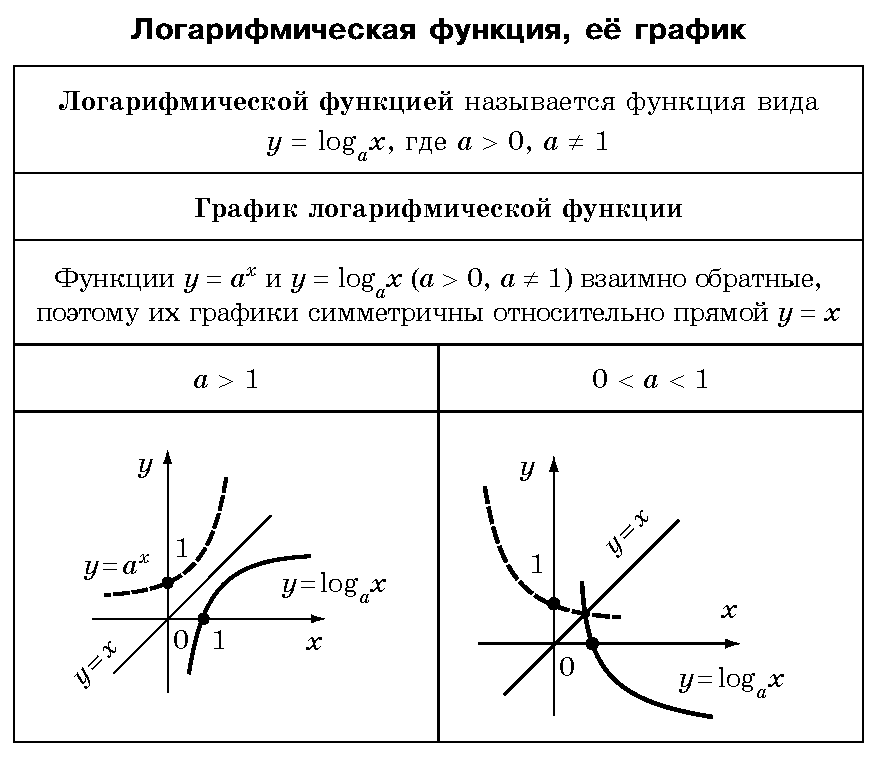
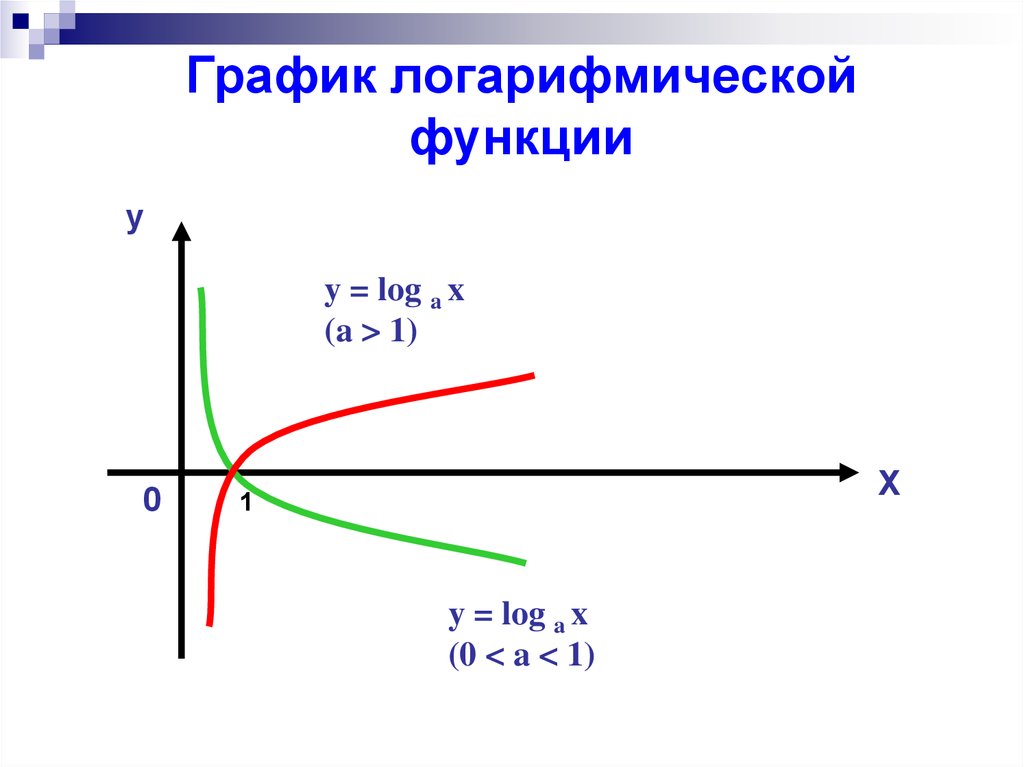 Теперь нажмите «Редактировать график», нажмите «Формат» и установите флажок «Масштаб журнала»; если горизонтальная шкала сбрасывается, вам, возможно, придется снова нажать «Макс». Теперь, хотя это не является гладким, последовательным или безрисковым, вы увидите, что на самом деле общая тенденция роста (в %/годовом смысле роста) присутствовала в течение многих десятилетий.
Теперь нажмите «Редактировать график», нажмите «Формат» и установите флажок «Масштаб журнала»; если горизонтальная шкала сбрасывается, вам, возможно, придется снова нажать «Макс». Теперь, хотя это не является гладким, последовательным или безрисковым, вы увидите, что на самом деле общая тенденция роста (в %/годовом смысле роста) присутствовала в течение многих десятилетий.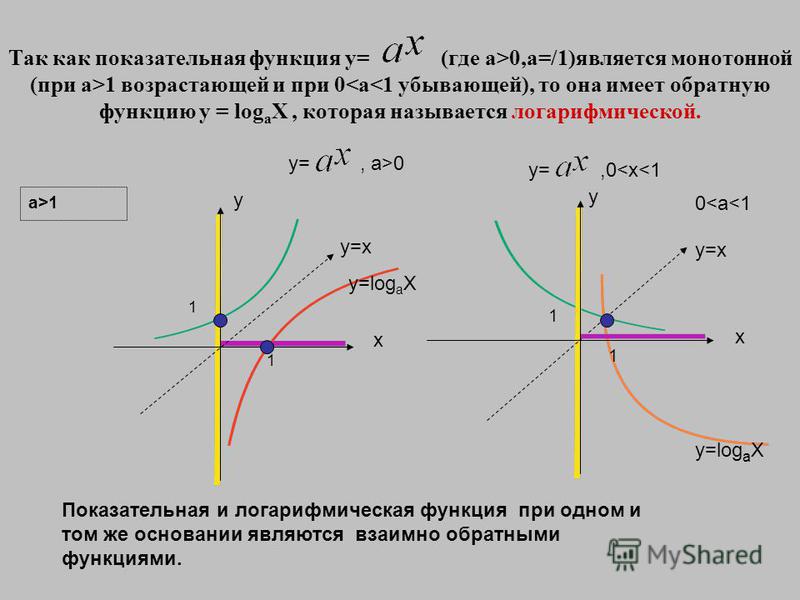 Они представляют собой логарифмически преобразованный x
и ты
оси для черчения.
Они представляют собой логарифмически преобразованный x
и ты
оси для черчения.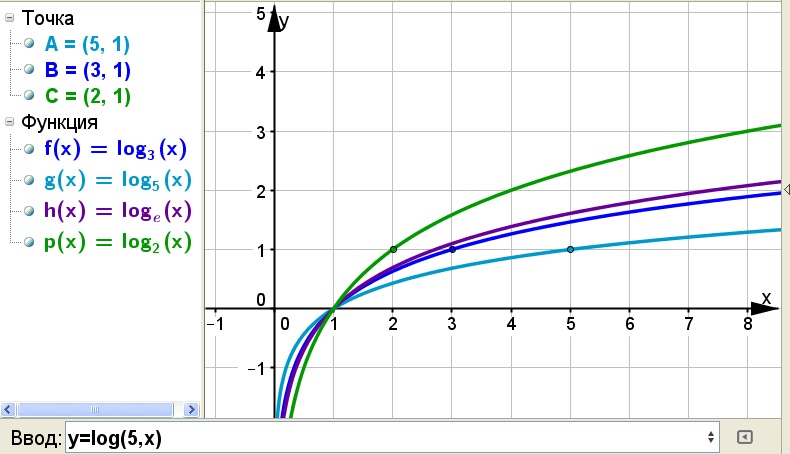 В середине ни одно из приближений не является превосходным, но теперь, когда мы знаем, что ошибка существует, ее можно определить количественно.
В середине ни одно из приближений не является превосходным, но теперь, когда мы знаем, что ошибка существует, ее можно определить количественно. Например, простой RC фильтр нижних частот будет иметь 1/f
амплитудная характеристика для частот выше его угловой частоты, точно отображая пример, который мы только что проиллюстрировали.
Например, простой RC фильтр нижних частот будет иметь 1/f
амплитудная характеристика для частот выше его угловой частоты, точно отображая пример, который мы только что проиллюстрировали.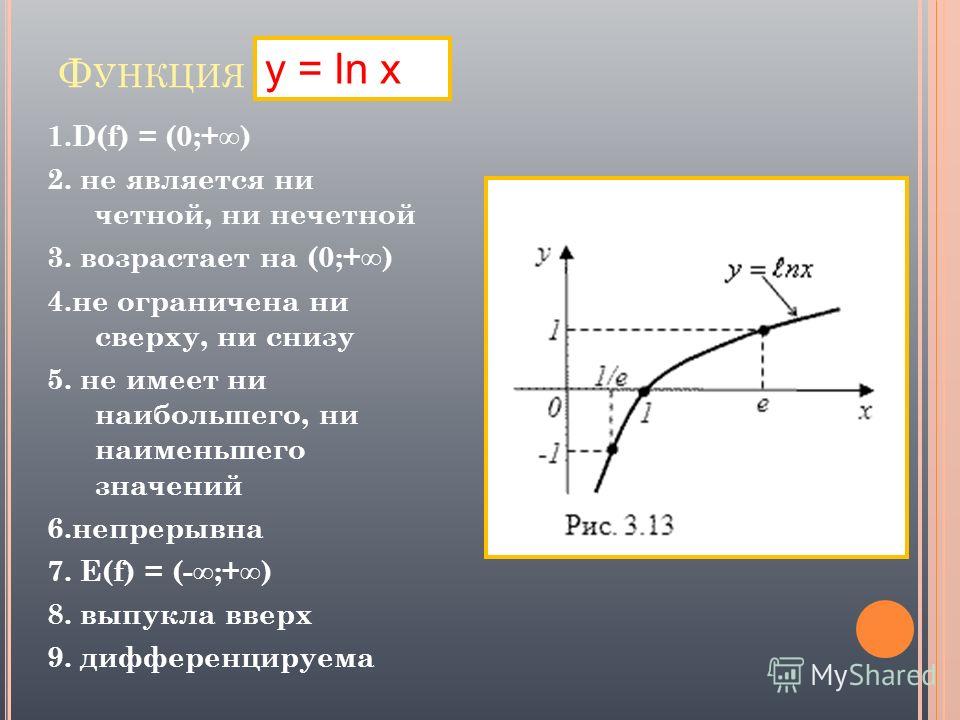 , но произносится вслух как «двадцать два микрофарад» в любом случае.
, но произносится вслух как «двадцать два микрофарад» в любом случае.
 Решение
Решение Сколько получится сухих грибов из 22 кг свежих грибов? Решение
Сколько получится сухих грибов из 22 кг свежих грибов? Решение процентных денег. Добавив 850 р., он оставил деньги еще на один год. По истечении года вклад вместе с процентами составил 4200 р. Какая сумма была положена первоначально и какие годовые проценты дает банк? Ответ: 3000 р, 5%
процентных денег. Добавив 850 р., он оставил деньги еще на один год. По истечении года вклад вместе с процентами составил 4200 р. Какая сумма была положена первоначально и какие годовые проценты дает банк? Ответ: 3000 р, 5% К концу года сумма на этих вкладах выросла до 1340 р., а к концу следующего года — до 1498 р. Было подсчитано, что если бы с самого начала денег вкладчик положил во второй банк, а остальные — в первый, то по итогам первого года сумма на этих вкладах составила бы 1420 р. Определить величину вклада по истечении двух лет, предполагая, что вкладчик положил все деньги в первый банк. Ответ: 1452 р.
К концу года сумма на этих вкладах выросла до 1340 р., а к концу следующего года — до 1498 р. Было подсчитано, что если бы с самого начала денег вкладчик положил во второй банк, а остальные — в первый, то по итогам первого года сумма на этих вкладах составила бы 1420 р. Определить величину вклада по истечении двух лет, предполагая, что вкладчик положил все деньги в первый банк. Ответ: 1452 р. Полученный здесь опыт поможет решить и другие олимпиадные задачи.
Полученный здесь опыт поможет решить и другие олимпиадные задачи. * Вася прочитал в газете, что за последние 3 месяца цены на продукты питания росли в среднем на 10 % за каждый месяц. На сколько процентов выросли цены за 3 месяца?
* Вася прочитал в газете, что за последние 3 месяца цены на продукты питания росли в среднем на 10 % за каждый месяц. На сколько процентов выросли цены за 3 месяца? На сколько процентов увеличилась его площадь?
На сколько процентов увеличилась его площадь? * На некотором участке пути машинист уменьшил скорость поезда на 25 %. На сколько процентов увеличится время движения на этом участке?
* На некотором участке пути машинист уменьшил скорость поезда на 25 %. На сколько процентов увеличится время движения на этом участке? После рубки сосна будет составлять 98% всех деревьев». Какую часть леса может вырубить леспромхоз?
После рубки сосна будет составлять 98% всех деревьев». Какую часть леса может вырубить леспромхоз? Теперь 10 частей воды приходится на 30 частей «сухого вещества» яблок или на 40 частей массы сушеных яблок. Масса воды составляет 10:40 = 0,25, или 25 % массы сушеных яблок?
Теперь 10 частей воды приходится на 30 частей «сухого вещества» яблок или на 40 частей массы сушеных яблок. Масса воды составляет 10:40 = 0,25, или 25 % массы сушеных яблок? * Из 40 т руды выплавили 20 т металла, содержащего 6 % примесей. Сколько процентов примесей в руде?
* Из 40 т руды выплавили 20 т металла, содержащего 6 % примесей. Сколько процентов примесей в руде? Число мальчиков (m) составляют 80 % от числа девочек (d), значит, m = 0,8d. Отсюда d = 1,25m, то есть число девочек составляет 125 % от числа мальчиков.
Число мальчиков (m) составляют 80 % от числа девочек (d), значит, m = 0,8d. Отсюда d = 1,25m, то есть число девочек составляет 125 % от числа мальчиков. Затем все полученные деньги положим еще на полгода. Таким образом через год мы получим:
Затем все полученные деньги положим еще на полгода. Таким образом через год мы получим: Проверьте это.
Проверьте это. На сколько процентов рабочий перевыполнил задание двух дней?
На сколько процентов рабочий перевыполнил задание двух дней?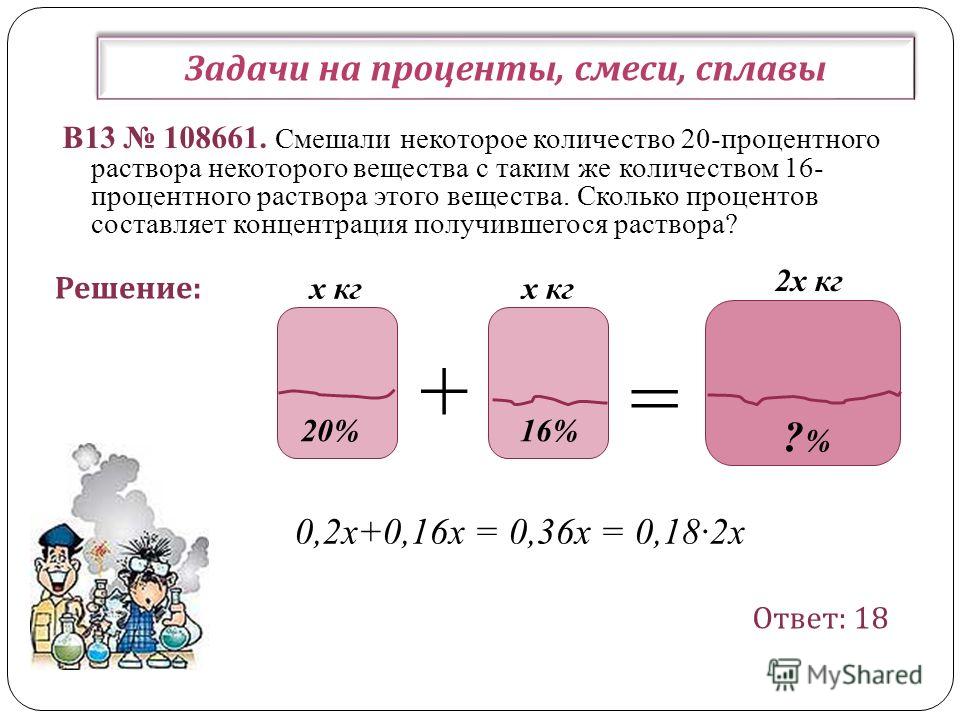 Но понять это решение из-за нагромождения процентов нелегко. Если же число мальчиков обозначитьбуквой x, то те же самые действия легче объяснить и понять. Итак, число девочек равно 0,6x, а число всех участников секции x + 0,6x = 1,6x. Определим, сколько процентов от 1,6х составляет число 0,6х:
Но понять это решение из-за нагромождения процентов нелегко. Если же число мальчиков обозначитьбуквой x, то те же самые действия легче объяснить и понять. Итак, число девочек равно 0,6x, а число всех участников секции x + 0,6x = 1,6x. Определим, сколько процентов от 1,6х составляет число 0,6х: Потеря составила 1 – 20/27 =
Потеря составила 1 – 20/27 = 
 * Вася прочитал в газете, что за последние 3 месяца цены на продукты питания росли в среднем на 10 % за каждый месяц. На сколько процентов выросли цены за 3 месяца?
* Вася прочитал в газете, что за последние 3 месяца цены на продукты питания росли в среднем на 10 % за каждый месяц. На сколько процентов выросли цены за 3 месяца? Как изменилась площадь прямоугольника?
Как изменилась площадь прямоугольника? Какова теперь масса арбуза?
Какова теперь масса арбуза? Какова масса вермишели, если она хранится при влажности 25 %?
Какова масса вермишели, если она хранится при влажности 25 %? С 1 октября 1993 г. за хранение денег на срочном депозите в течение года Сбербанк выплачивал доход из расчета 150 % от вложенной суммы; в течение полугода — 130 % годовых, в течение трех месяцев — 120 % годовых. Каким образом за год на условиях Сбербанка можно было получить наибольший доход на 100 000 р.? Каков этот наибольший доход?
С 1 октября 1993 г. за хранение денег на срочном депозите в течение года Сбербанк выплачивал доход из расчета 150 % от вложенной суммы; в течение полугода — 130 % годовых, в течение трех месяцев — 120 % годовых. Каким образом за год на условиях Сбербанка можно было получить наибольший доход на 100 000 р.? Каков этот наибольший доход? Проверьте это.
Проверьте это. На сколько процентов рабочий перевыполнил задание двух дней?
На сколько процентов рабочий перевыполнил задание двух дней? Сколько процентов прибыли планировал получить торговец при продаже книги?
Сколько процентов прибыли планировал получить торговец при продаже книги? РП.А.1. Вычислить удельные ставки, связанные с отношениями фракций, включая отношения длин, площадей и других величин, измеренных в одинаковых или разных единицах. Например, если человек проходит $1/2$ мили за каждые $1/4$ часа, рассчитайте удельную норму как комплексную дробь $\frac{1/2}{1/4}$ миль в час, что эквивалентно $2$ миль. в час.
РП.А.1. Вычислить удельные ставки, связанные с отношениями фракций, включая отношения длин, площадей и других величин, измеренных в одинаковых или разных единицах. Например, если человек проходит $1/2$ мили за каждые $1/4$ часа, рассчитайте удельную норму как комплексную дробь $\frac{1/2}{1/4}$ миль в час, что эквивалентно $2$ миль. в час. РП.А.2.а. Определите, находятся ли две величины в пропорциональном соотношении, например, проверив эквивалентные отношения в таблице или нарисовав график на координатной плоскости и наблюдая, является ли график прямой линией, проходящей через начало координат.
РП.А.2.а. Определите, находятся ли две величины в пропорциональном соотношении, например, проверив эквивалентные отношения в таблице или нарисовав график на координатной плоскости и наблюдая, является ли график прямой линией, проходящей через начало координат. РП.А.2.д. Объясните, что означает точка $(x, y)$ на графике пропорциональной зависимости с точки зрения ситуации, обратив особое внимание на точки $(0, 0)$ и $(1, r)$, где $r$ является единичной ставкой.
РП.А.2.д. Объясните, что означает точка $(x, y)$ на графике пропорциональной зависимости с точки зрения ситуации, обратив особое внимание на точки $(0, 0)$ и $(1, r)$, где $r$ является единичной ставкой. НС. 7 класс — Система счисления
НС. 7 класс — Система счисления
 НС.А.2.а. Поймите, что умножение распространяется с дробей на рациональные числа, требуя, чтобы операции продолжали удовлетворять свойствам операций, в частности свойству распределения, что приводит к таким продуктам, как $(-1)(-1) = 1$ и правилам умножения со знаком числа. Интерпретируйте произведения рациональных чисел, описывая контексты реального мира.
НС.А.2.а. Поймите, что умножение распространяется с дробей на рациональные числа, требуя, чтобы операции продолжали удовлетворять свойствам операций, в частности свойству распределения, что приводит к таким продуктам, как $(-1)(-1) = 1$ и правилам умножения со знаком числа. Интерпретируйте произведения рациональных чисел, описывая контексты реального мира.
 EE.A.2. Поймите, что переписывание выражения в разных формах в контексте задачи может пролить свет на проблему и на то, как связаны в ней величины. Например, $a + 0,05a = 1,05a$ означает, что «увеличение на $5\%$» равносильно «умножению на $1,05$».
EE.A.2. Поймите, что переписывание выражения в разных формах в контексте задачи может пролить свет на проблему и на то, как связаны в ней величины. Например, $a + 0,05a = 1,05a$ означает, что «увеличение на $5\%$» равносильно «умножению на $1,05$». 50$. Если вы хотите разместить полотенцесушитель $9\frac34$ дюймов в центре двери шириной $27 \frac12$ дюймов, вам нужно будет разместить планку на расстоянии около $9$ дюймов от каждого края; эту оценку можно использовать в качестве проверки точного вычисления.
50$. Если вы хотите разместить полотенцесушитель $9\frac34$ дюймов в центре двери шириной $27 \frac12$ дюймов, вам нужно будет разместить планку на расстоянии около $9$ дюймов от каждого края; эту оценку можно использовать в качестве проверки точного вычисления. Например, периметр прямоугольника равен $54$ см. Его длина $6$ см. Какова его ширина?
Например, периметр прямоугольника равен $54$ см. Его длина $6$ см. Какова его ширина?


 Например, оцените среднюю длину слова в книге путем случайной выборки слов из книги; предсказать победителя школьных выборов на основе случайно выбранных данных опроса. Оцените, насколько далеко может быть оценка или прогноз.
Например, оцените среднюю длину слова в книге путем случайной выборки слов из книги; предсказать победителя школьных выборов на основе случайно выбранных данных опроса. Оцените, насколько далеко может быть оценка или прогноз.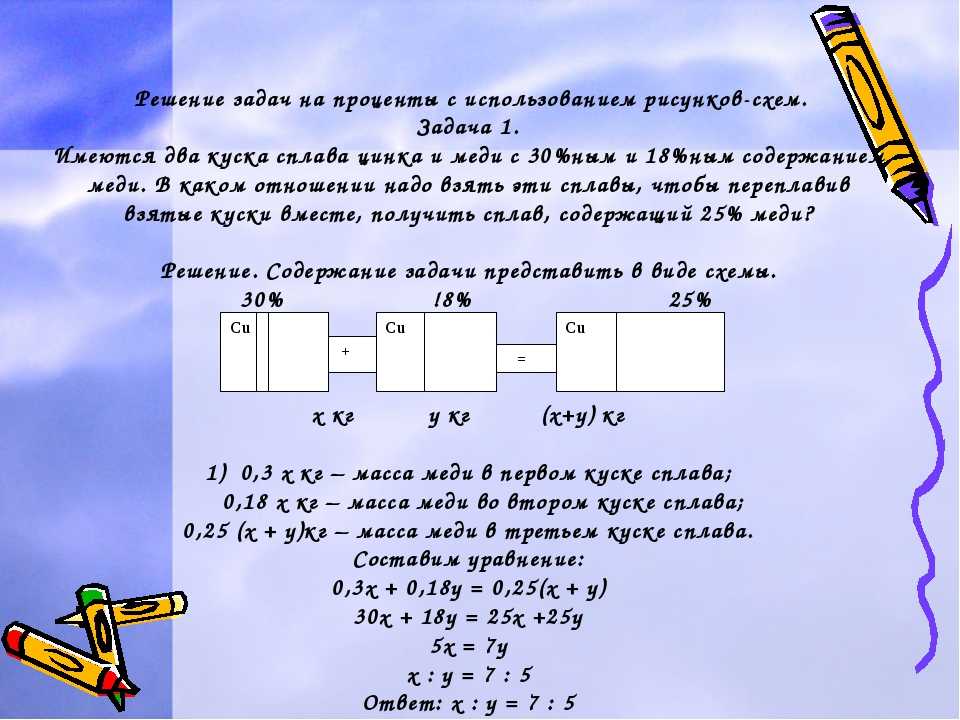 Например, решите, длиннее ли слова в главе учебника по естествознанию для седьмого класса, чем слова в главе из учебника по естествознанию для четвертого класса.
Например, решите, длиннее ли слова в главе учебника по естествознанию для седьмого класса, чем слова в главе из учебника по естествознанию для четвертого класса. Например, подбрасывая числовой куб 600 раз, предскажите, что число 3 или 6 выпадет примерно 200 раз, но, вероятно, не ровно 200 раз.
Например, подбрасывая числовой куб 600 раз, предскажите, что число 3 или 6 выпадет примерно 200 раз, но, вероятно, не ровно 200 раз. Например, найдите приблизительную вероятность того, что крутящийся пенни упадет решкой вверх или что брошенный бумажный стаканчик упадет открытым концом вниз. Судя по наблюдаемым частотам, результаты для крутящегося пенни кажутся равновероятными?
Например, найдите приблизительную вероятность того, что крутящийся пенни упадет решкой вверх или что брошенный бумажный стаканчик упадет открытым концом вниз. Судя по наблюдаемым частотам, результаты для крутящегося пенни кажутся равновероятными? Для события, описанного повседневным языком (например, «выпадение двойных шестерок»), определите исходы в выборочном пространстве, составляющие событие.
Для события, описанного повседневным языком (например, «выпадение двойных шестерок»), определите исходы в выборочном пространстве, составляющие событие. РП.А.3
— Используйте пропорциональные отношения для решения многошаговых задач на соотношение и проценты. Примеры: простые проценты, налоги, надбавки и скидки, чаевые и комиссионные, сборы, процентное увеличение и уменьшение, процентная ошибка.
РП.А.3
— Используйте пропорциональные отношения для решения многошаговых задач на соотношение и проценты. Примеры: простые проценты, налоги, надбавки и скидки, чаевые и комиссионные, сборы, процентное увеличение и уменьшение, процентная ошибка.  RP.3 и рассматривает понятия процента в шестом классе, которые являются основополагающими для этого модуля. Это хорошая возможность вернуться к 7.NS.3 и включить задачи, связанные с операциями с рациональными числами.
RP.3 и рассматривает понятия процента в шестом классе, которые являются основополагающими для этого модуля. Это хорошая возможность вернуться к 7.NS.3 и включить задачи, связанные с операциями с рациональными числами.







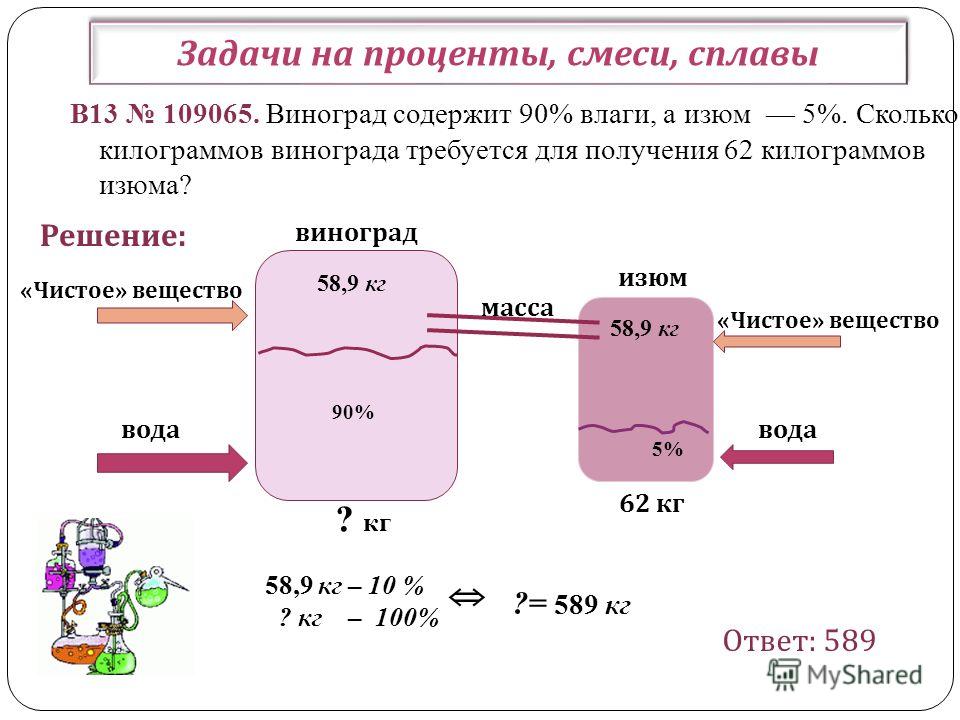



 Это не должно занимать много времени: вы можете спроецировать слайд перед аудиторией и попросить учащихся писать в журнале или на доске, или вы можете распечатать страницы на половину листа и дать каждому учащемуся по одному листу при входе. учебный класс.
Это не должно занимать много времени: вы можете спроецировать слайд перед аудиторией и попросить учащихся писать в журнале или на доске, или вы можете распечатать страницы на половину листа и дать каждому учащемуся по одному листу при входе. учебный класс.

 В математике проценты используются так же, как дроби и десятичные дроби, как способы описания частей целого. Когда вы используете проценты, считается, что целое состоит из ста равных частей. Символ % используется, чтобы показать, что число представляет собой процент, и реже может использоваться аббревиатура «процент».
В математике проценты используются так же, как дроби и десятичные дроби, как способы описания частей целого. Когда вы используете проценты, считается, что целое состоит из ста равных частей. Символ % используется, чтобы показать, что число представляет собой процент, и реже может использоваться аббревиатура «процент».
 А если их больше или меньше?
А если их больше или меньше?  Предположим, вы хотите купить новый портативный компьютер. Вы проверили местных поставщиков, и одна компания предложила вам скидку 20% от прейскурантной цены в 500 фунтов стерлингов. Сколько будет стоить ноутбук от этого поставщика?
Предположим, вы хотите купить новый портативный компьютер. Вы проверили местных поставщиков, и одна компания предложила вам скидку 20% от прейскурантной цены в 500 фунтов стерлингов. Сколько будет стоить ноутбук от этого поставщика?
 500 разделить на 100 = 005, или 5. Начальные нули (нули «снаружи слева» числа, например, в 005, 02, 00014) не имеют значения, поэтому их не нужно записывать.
500 разделить на 100 = 005, или 5. Начальные нули (нули «снаружи слева» числа, например, в 005, 02, 00014) не имеют значения, поэтому их не нужно записывать. нашу страницу на умножение для справки).
нашу страницу на умножение для справки).


 (неповторяющийся) десятичный или процентный.
(неповторяющийся) десятичный или процентный. 
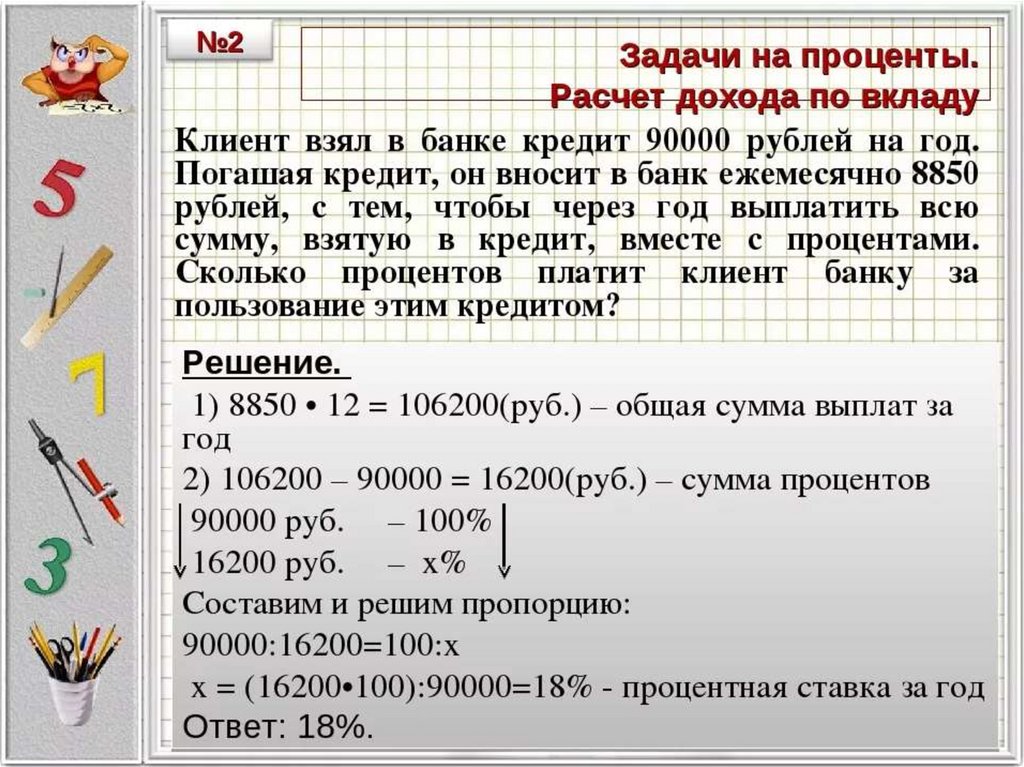 Когда мы используем слова для описания расчета, это может сделать его более понятным.
Когда мы используем слова для описания расчета, это может сделать его более понятным. 0,1 × 100 = 10%.
0,1 × 100 = 10%. Вы можете быстро увидеть пропорции категорий персонала на примере.
Вы можете быстро увидеть пропорции категорий персонала на примере.

 Включает урок с практическими задачами.
 ПОДРОБНЕЕ
Включает урок с практическими задачами.
 ПОДРОБНЕЕ 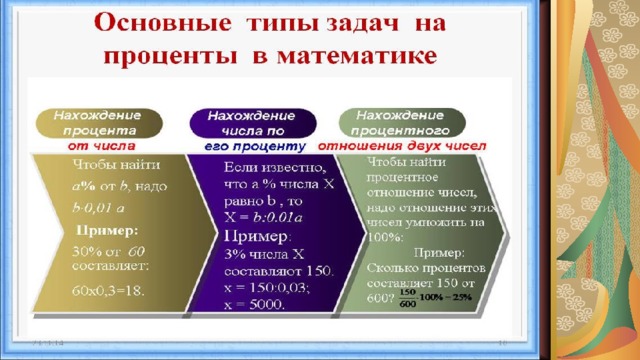  ПОДРОБНЕЕ
 ПОДРОБНЕЕ  Математика в торговом центре.
Математика в торговом центре. Вы должны рассчитать правильные чаевые, чтобы оставить пингвина официанту. Четыре уровня: легкий, средний, сложный и супермозг.
 ПОДРОБНЕЕ
Вы должны рассчитать правильные чаевые, чтобы оставить пингвина официанту. Четыре уровня: легкий, средний, сложный и супермозг.
 ПОДРОБНЕЕ  Проценты от числа (2).
Проценты от числа (2). Ответьте на вопросы правильно, чтобы набрать очки.
 ПОДРОБНЕЕ
Ответьте на вопросы правильно, чтобы набрать очки.
 ПОДРОБНЕЕ   ПОДРОБНЕЕ
 ПОДРОБНЕЕ   ПОДРОБНЕЕ
 ПОДРОБНЕЕ  Уровень 2: Найдите скидку в процентах, когда известны первоначальная цена и цена продажи.]
 ПОДРОБНЕЕ
Уровень 2: Найдите скидку в процентах, когда известны первоначальная цена и цена продажи.]
 ПОДРОБНЕЕ 
 Тогда же, с разницей менее чем в месяц, значение разницы было улучшено до 59 470 640, а затем и вовсе на порядок — до 4 982 086. На данный момент существуют теоретические обоснования бесконечности пар простых чисел с разницей в 12 и 6, однако доказанной является лишь разность в 246. Как и прочие проблемы такого рода, гипотеза о числах-близнецах особенно важна для криптографии. Однако, до сих пор она остается нерешенной математической проблемой, над которой бьются лучшие умы.
Тогда же, с разницей менее чем в месяц, значение разницы было улучшено до 59 470 640, а затем и вовсе на порядок — до 4 982 086. На данный момент существуют теоретические обоснования бесконечности пар простых чисел с разницей в 12 и 6, однако доказанной является лишь разность в 246. Как и прочие проблемы такого рода, гипотеза о числах-близнецах особенно важна для криптографии. Однако, до сих пор она остается нерешенной математической проблемой, над которой бьются лучшие умы.
 Пожалуй, это одна из немногих нерешенных математических задач, которая имеет четкое практическое применение.
Пожалуй, это одна из немногих нерешенных математических задач, которая имеет четкое практическое применение. Более того, он смог доказать разницу в мощностях различных бесконечностей. Проблема тут заключается в доказательстве того, что существует кардинал (или, возможно, кардиналы) с некоторым заданным большим кардинальным свойством. До сих пор эта задача остается нерешенной.
Более того, он смог доказать разницу в мощностях различных бесконечностей. Проблема тут заключается в доказательстве того, что существует кардинал (или, возможно, кардиналы) с некоторым заданным большим кардинальным свойством. До сих пор эта задача остается нерешенной. Согласно теории цепных дробей, если постоянная Эйлера-Маскерони является рациональной дробью, то ее знаменатель должен быть больше 10 в 242 080 степени. Но пока доказать ее рациональность не удалось — для этого нам и нашим компьютерам нужно больше времени. До этих пор рациональность постоянной γ остается нерешенной математической проблемой.
Согласно теории цепных дробей, если постоянная Эйлера-Маскерони является рациональной дробью, то ее знаменатель должен быть больше 10 в 242 080 степени. Но пока доказать ее рациональность не удалось — для этого нам и нашим компьютерам нужно больше времени. До этих пор рациональность постоянной γ остается нерешенной математической проблемой.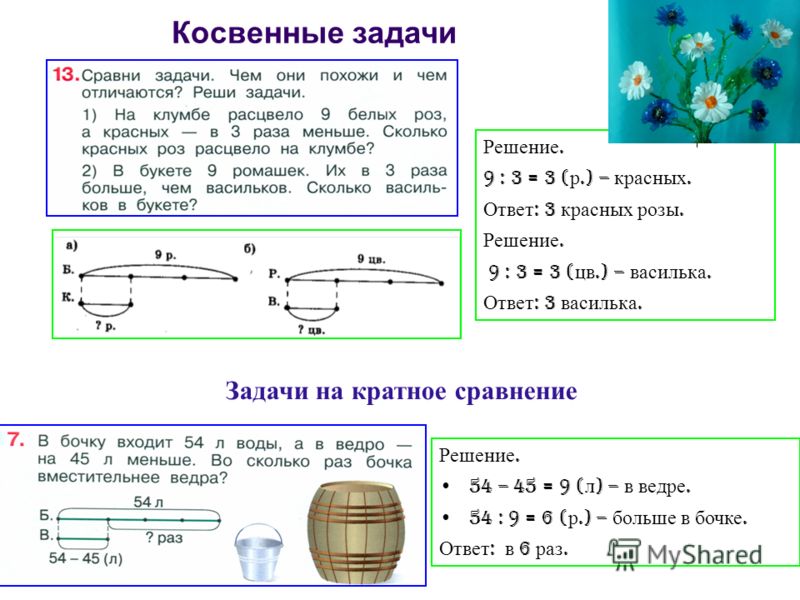 Преподаватель математики Анна Эккерман уверена, что проблемы с математикой часто имеют исключительно психологический характер:
Преподаватель математики Анна Эккерман уверена, что проблемы с математикой часто имеют исключительно психологический характер: И если польза этих знаний вызывает у подростка вопросы, объясните ему, что с их помощью мы тренируем память, развиваем логическое мышление и остроту ума — навыки, в равной степени необходимые как «технарям», так и «гуманитариям».
И если польза этих знаний вызывает у подростка вопросы, объясните ему, что с их помощью мы тренируем память, развиваем логическое мышление и остроту ума — навыки, в равной степени необходимые как «технарям», так и «гуманитариям».  Сколько деревьев съел второй динозавр?». Невнимательно прочитав условия, ребёнок посчитает 16−3, и получит неправильный ответ, ведь эта задача на самом деле требует не вычитания, а сложения.
Сколько деревьев съел второй динозавр?». Невнимательно прочитав условия, ребёнок посчитает 16−3, и получит неправильный ответ, ведь эта задача на самом деле требует не вычитания, а сложения.  Многократное повторение одного и того же вопроса неэффективно.
Многократное повторение одного и того же вопроса неэффективно. 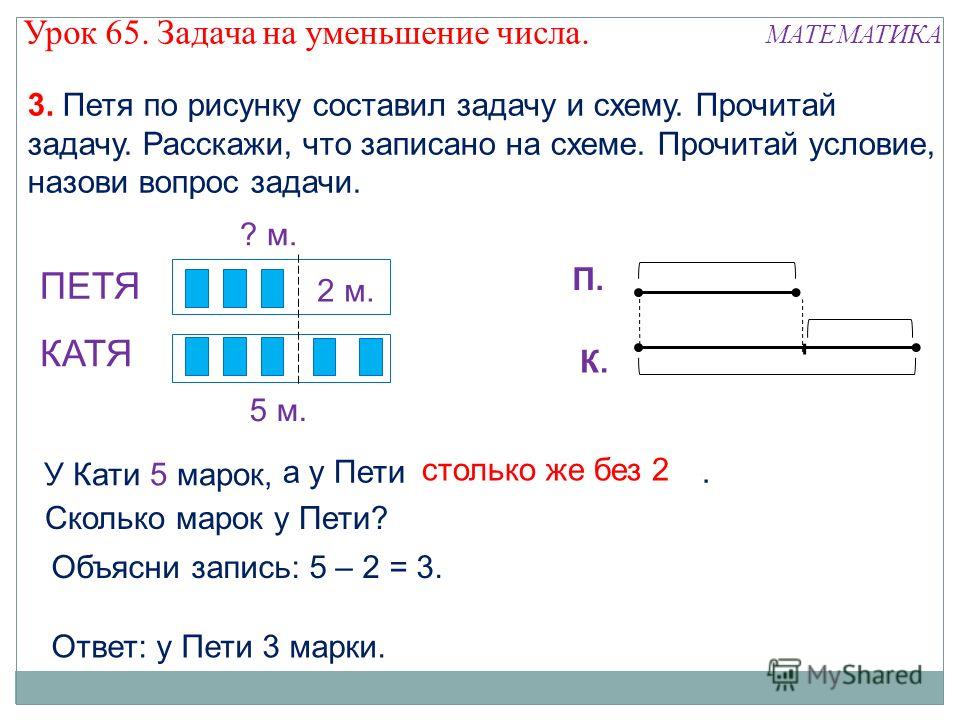 А главное — из описания должна быть понятна логика решения.
А главное — из описания должна быть понятна логика решения.
 Это позволит ему не только закрепить материал, но и проявить творческие способности.
Это позволит ему не только закрепить материал, но и проявить творческие способности.
 Известно, что две машины, выезжающие по разным дорогам из A в B и связанные веревкой некоторой длины, меньшей 2l, смогли проехать из A в B, не порвав веревки. Могут ли разминуться, не коснувшись, два круглых воза радиуса l, центры которых движутся по этим дорогам навстречу друг другу? (Ответ: нет).
Известно, что две машины, выезжающие по разным дорогам из A в B и связанные веревкой некоторой длины, меньшей 2l, смогли проехать из A в B, не порвав веревки. Могут ли разминуться, не коснувшись, два круглых воза радиуса l, центры которых движутся по этим дорогам навстречу друг другу? (Ответ: нет). Если человек читает, то он вполне может быть кандидатом наук, но может быть не в состоянии придумывать что-то простое. Вот задача: есть баллон на 100 литров, в котором имеется газ под высоким давлением. И есть два пустых баллона по 50 литров, нужно газ разлить по этим двум баллоном, но каким-нибудь простым способом, домашними средствами. Константинов пишет, что он давал эту задачу многим кандидатам наук, и большинство так ничего и не придумали, а на самом деле способ очень простой и широко применяется – правда, в чем состоит способ, Константинов не написал. Я думаю, надо в пустой баллон налить воду, соединить с большим баллоном шлангом с краном, открыть кран, баллон с водой поместить наверх, тогда вода перетечет вниз, займет половину места в большом, после чего надо закрыть кран и то же повторить со вторым 50-литровым баллоном. Еще один пример Константинова – разрыв теории с практикой. У них был школьник, отличник по всем предметам. Они приехали на Белое море, он поставил рюкзак и пошел гулять.
Если человек читает, то он вполне может быть кандидатом наук, но может быть не в состоянии придумывать что-то простое. Вот задача: есть баллон на 100 литров, в котором имеется газ под высоким давлением. И есть два пустых баллона по 50 литров, нужно газ разлить по этим двум баллоном, но каким-нибудь простым способом, домашними средствами. Константинов пишет, что он давал эту задачу многим кандидатам наук, и большинство так ничего и не придумали, а на самом деле способ очень простой и широко применяется – правда, в чем состоит способ, Константинов не написал. Я думаю, надо в пустой баллон налить воду, соединить с большим баллоном шлангом с краном, открыть кран, баллон с водой поместить наверх, тогда вода перетечет вниз, займет половину места в большом, после чего надо закрыть кран и то же повторить со вторым 50-литровым баллоном. Еще один пример Константинова – разрыв теории с практикой. У них был школьник, отличник по всем предметам. Они приехали на Белое море, он поставил рюкзак и пошел гулять. Приходит – рюкзака нет. Выяснилось, что, хотя он изучал географию, идея, что бывают приливы, ему в голову не пришла. Другой школьник в том же походе, видя, что вода в море очень чистая, набрал ее для чая, не подумавши, что в море вода соленая, хотя наверняка учился этому на географии.
Приходит – рюкзака нет. Выяснилось, что, хотя он изучал географию, идея, что бывают приливы, ему в голову не пришла. Другой школьник в том же походе, видя, что вода в море очень чистая, набрал ее для чая, не подумавши, что в море вода соленая, хотя наверняка учился этому на географии.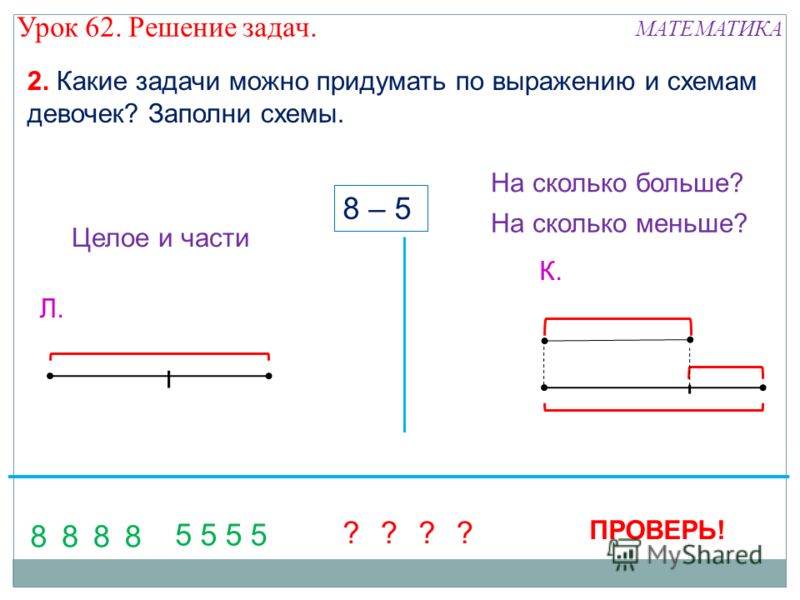 00 (в других кружках Москвы день занятий, конечно, мог отличаться. – Прим.). Для школьников было общее задание, которое мы готовили, листочек с, допустим, шестью задачами. В каждой аудитории – три преподавателя, среди них часто студенты. Школьники решают задачи, когда думают, что решили, поднимают руку, подходит преподаватель, выслушивает решение. Мы старались, чтобы никто не ушел совсем обиженный, то есть было желательно, чтобы большинство людей решили по крайней мере две задачи. Если человек все решил, ему давались дополнительные задачи. Важно, что занятия тематически были более-менее независимыми: школьник не смог прийти в этот раз – придет в следующий (и ему должна быть понятна тема несмотря на пропуск. – Прим.). Смысл кружков состоял в том, чтобы люди поняли, интересно им решать задачи или нет. Так продолжалось в течение учебного года, а в его конце происходило собеседование для желающих попасть в матклассы (которые обычно охватывали последние три года школы, 8–10-й классы).
00 (в других кружках Москвы день занятий, конечно, мог отличаться. – Прим.). Для школьников было общее задание, которое мы готовили, листочек с, допустим, шестью задачами. В каждой аудитории – три преподавателя, среди них часто студенты. Школьники решают задачи, когда думают, что решили, поднимают руку, подходит преподаватель, выслушивает решение. Мы старались, чтобы никто не ушел совсем обиженный, то есть было желательно, чтобы большинство людей решили по крайней мере две задачи. Если человек все решил, ему давались дополнительные задачи. Важно, что занятия тематически были более-менее независимыми: школьник не смог прийти в этот раз – придет в следующий (и ему должна быть понятна тема несмотря на пропуск. – Прим.). Смысл кружков состоял в том, чтобы люди поняли, интересно им решать задачи или нет. Так продолжалось в течение учебного года, а в его конце происходило собеседование для желающих попасть в матклассы (которые обычно охватывали последние три года школы, 8–10-й классы). Школьники приходили на собеседование так же, как на кружок, но тут уже регистрировалось четко, что кто решил, выяснялось, у кого результаты лучше. В конце концов объявлялся список, кто попал в маткласс следующего года (и дети переводились из своих прежних школ в школы, где набирались матклассы. – Прим.). При этом с точки зрения советской власти и органов образования, ВМШ почти не существовала. По вечерам какие-то кружки по математике в школе – это нормально, кто туда приходит – никого не волнует. А матклассы советская власть терпела. Это был сложный политической момент, директора школ как-то договаривались, уговаривали, чтобы матклассы открыли. Райком иногда не разрешал открывать, то есть все всегда было в подвешенном состоянии, но в основном разрешали, они даже не мешали набирать школьников по конкурсу, в это дело не лезли. В школе происходило то же самое, что на кружках, но уже с помощью задач изучалась в целом некоторая теория. Это было параллельно с обычными уроками алгебры и геометрии: обычные уроки – четыре часа в неделю, и еще четыре урока дополнительных.
Школьники приходили на собеседование так же, как на кружок, но тут уже регистрировалось четко, что кто решил, выяснялось, у кого результаты лучше. В конце концов объявлялся список, кто попал в маткласс следующего года (и дети переводились из своих прежних школ в школы, где набирались матклассы. – Прим.). При этом с точки зрения советской власти и органов образования, ВМШ почти не существовала. По вечерам какие-то кружки по математике в школе – это нормально, кто туда приходит – никого не волнует. А матклассы советская власть терпела. Это был сложный политической момент, директора школ как-то договаривались, уговаривали, чтобы матклассы открыли. Райком иногда не разрешал открывать, то есть все всегда было в подвешенном состоянии, но в основном разрешали, они даже не мешали набирать школьников по конкурсу, в это дело не лезли. В школе происходило то же самое, что на кружках, но уже с помощью задач изучалась в целом некоторая теория. Это было параллельно с обычными уроками алгебры и геометрии: обычные уроки – четыре часа в неделю, и еще четыре урока дополнительных.
 Когда его выгнали, другие люди тоже, по-моему, ушли в знак протеста. И Толпыго в Киеве, Анджанс в Риге и Константинов в Москве решили: давайте мы вместо олимпиады сами составим трудные задачи, а все желающие эти задачи придут решать. Советская власть не препятствовала, было разрешено провести турнир в каком-то вузе или в школе. Соответственно, в Москве Константинов потом забрал все работы на проверку, а в Риге и Киеве проверяли тамошние люди. После этого сверили критерии, результаты по всем городам, и школьники могли сравнить свои успехи. Но в отличие от олимпиады, никакой официальной пользы от этого не было. Человек решил задачу, у него есть бумажка, что он решил задачу, но ее особенно предъявлять никуда нельзя было, никаких преимуществ она не давала, бумажка и бумажка. А Турнир Ломоносова был устроен для более младших школьников. Идея была в том, что он – вместо районной олимпиады – привлечет школьников в кружки, и не только по математике, там были физика, химия, биология, астрономия, лингвистика в какой-то момент образовалась.
Когда его выгнали, другие люди тоже, по-моему, ушли в знак протеста. И Толпыго в Киеве, Анджанс в Риге и Константинов в Москве решили: давайте мы вместо олимпиады сами составим трудные задачи, а все желающие эти задачи придут решать. Советская власть не препятствовала, было разрешено провести турнир в каком-то вузе или в школе. Соответственно, в Москве Константинов потом забрал все работы на проверку, а в Риге и Киеве проверяли тамошние люди. После этого сверили критерии, результаты по всем городам, и школьники могли сравнить свои успехи. Но в отличие от олимпиады, никакой официальной пользы от этого не было. Человек решил задачу, у него есть бумажка, что он решил задачу, но ее особенно предъявлять никуда нельзя было, никаких преимуществ она не давала, бумажка и бумажка. А Турнир Ломоносова был устроен для более младших школьников. Идея была в том, что он – вместо районной олимпиады – привлечет школьников в кружки, и не только по математике, там были физика, химия, биология, астрономия, лингвистика в какой-то момент образовалась. Разные люди приходили, говорили: «А давайте мы еще сделаем конкурс по лингвистике». Константинов спрашивал: «А есть ли у вас для этого люди?» – «Человек 15–20 соберем, пришлем своих представителей, потом соберем работы и проверим».
Разные люди приходили, говорили: «А давайте мы еще сделаем конкурс по лингвистике». Константинов спрашивал: «А есть ли у вас для этого люди?» – «Человек 15–20 соберем, пришлем своих представителей, потом соберем работы и проверим». Такое ощущение, что “константиновская”, условно назовем ее, система развилась в этой слепой зоне, куда советская власть не смотрела.
Такое ощущение, что “константиновская”, условно назовем ее, система развилась в этой слепой зоне, куда советская власть не смотрела. Но если из Ленинского райкома объясняли: вы набрали тут класс, слишком много евреев, – невозможно было позвонить какому-то академику, чтобы он перезвонил в ЦК и сказал: что вы делаете? Надо было отвечать: мы в этом году не будем набирать, или вписать каких-нибудь несуществующих школьников, чтобы уменьшить процент евреев, в другой школе набирать класс, другие предпринимать хитрости. По-моему, Гриша Гальперин рассказывал, как Константинов объяснял устойчивость системы математического образования: система действительно требовала сотрудничества с советскими органами образования, чтобы разрешили занятия в школе, кружок в помещении вуза. Но она требовала на таком низком уровне, что это не выглядело вопиющим. Весь размах системы был в каждом отдельном месте неясен. Как якобы говорил Константинов, бывают отдельные понятливые чиновники, которые видят всю угрозу, но не в состоянии объяснить на языке, понятном их начальству.
Но если из Ленинского райкома объясняли: вы набрали тут класс, слишком много евреев, – невозможно было позвонить какому-то академику, чтобы он перезвонил в ЦК и сказал: что вы делаете? Надо было отвечать: мы в этом году не будем набирать, или вписать каких-нибудь несуществующих школьников, чтобы уменьшить процент евреев, в другой школе набирать класс, другие предпринимать хитрости. По-моему, Гриша Гальперин рассказывал, как Константинов объяснял устойчивость системы математического образования: система действительно требовала сотрудничества с советскими органами образования, чтобы разрешили занятия в школе, кружок в помещении вуза. Но она требовала на таком низком уровне, что это не выглядело вопиющим. Весь размах системы был в каждом отдельном месте неясен. Как якобы говорил Константинов, бывают отдельные понятливые чиновники, которые видят всю угрозу, но не в состоянии объяснить на языке, понятном их начальству.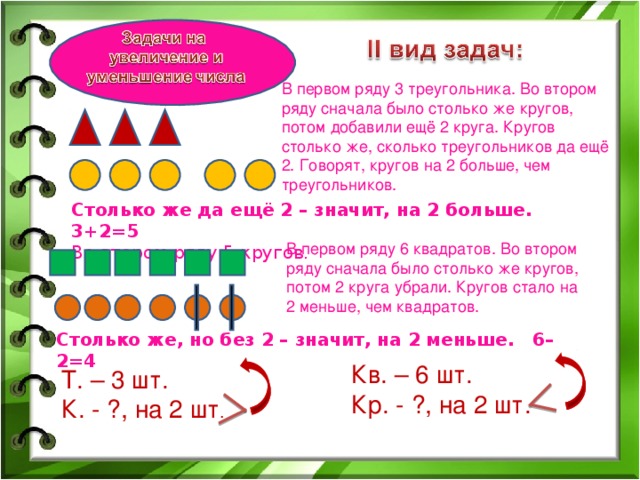 Он был учеником Кронрода, его диссертация по топологии плоскости. Он преподавал какое-то время, его из университета выгнали, кажется, в связи с «письмом девяноста девяти» в защиту Есенина-Вольпина (в 1968 году 99 ученых подписали письмо против принудительной госпитализации математика и диссидента Александра Есенина-Вольпина в психбольницу. – Прим.). Потом Константинов попал в Институт экономики, математическая экономика. Лаборатория Кронрода изначально была лабораторией для расчетов по бомбе, поэтому у них были численные методы, технология программирования, а потом уже не по бомбе, а вообще. У Константинова из работ по информатике – знаменитый фильм с кошкой, но это просто школьный проект. Просто школьникам было интересно, он вместе с ними это делал, получился такой исторический первый мультфильм компьютерный.
Он был учеником Кронрода, его диссертация по топологии плоскости. Он преподавал какое-то время, его из университета выгнали, кажется, в связи с «письмом девяноста девяти» в защиту Есенина-Вольпина (в 1968 году 99 ученых подписали письмо против принудительной госпитализации математика и диссидента Александра Есенина-Вольпина в психбольницу. – Прим.). Потом Константинов попал в Институт экономики, математическая экономика. Лаборатория Кронрода изначально была лабораторией для расчетов по бомбе, поэтому у них были численные методы, технология программирования, а потом уже не по бомбе, а вообще. У Константинова из работ по информатике – знаменитый фильм с кошкой, но это просто школьный проект. Просто школьникам было интересно, он вместе с ними это делал, получился такой исторический первый мультфильм компьютерный. – Прим.)
– Прим.) Были разные математики, которые хотели это по-разному исправить, у них были совершенно завиральные идеи. Колмогоров помимо интерната (школа-интернат при МГУ для одаренных детей, созданный при участии Колмогорова. – Прим.), где он как следует работал, вроде еще пробовал свои идеи в обычной школе, но несерьезно. Конечно, у них не было представления, что учителя могут понять. Они составили программу, и когда составляли программу, говорили: ну нельзя же вот этого не знать. Потом по этой программе начали писать учебники. Потом выяснилось, что никто ничего по программе не успевает, не понимает, поэтому все содержательное постепенно выбрасывалось, оставались только упражнения, которые было легко выполнить, ничего не понимая. Упражнения можно было выполнить, но понимание не совершенствовалось, и в следующем классе проблемы повторялись. Была идея, причем с самыми лучшими побуждениями, что в старых гимназиях решали слишком много задач арифметическими способами: большой бидон, маленький бидон, если бы маленький бидон был как большой, то сколько бы тогда… Зачем это все, мы научим решать уравнения – общий метод, это гораздо проще.
Были разные математики, которые хотели это по-разному исправить, у них были совершенно завиральные идеи. Колмогоров помимо интерната (школа-интернат при МГУ для одаренных детей, созданный при участии Колмогорова. – Прим.), где он как следует работал, вроде еще пробовал свои идеи в обычной школе, но несерьезно. Конечно, у них не было представления, что учителя могут понять. Они составили программу, и когда составляли программу, говорили: ну нельзя же вот этого не знать. Потом по этой программе начали писать учебники. Потом выяснилось, что никто ничего по программе не успевает, не понимает, поэтому все содержательное постепенно выбрасывалось, оставались только упражнения, которые было легко выполнить, ничего не понимая. Упражнения можно было выполнить, но понимание не совершенствовалось, и в следующем классе проблемы повторялись. Была идея, причем с самыми лучшими побуждениями, что в старых гимназиях решали слишком много задач арифметическими способами: большой бидон, маленький бидон, если бы маленький бидон был как большой, то сколько бы тогда… Зачем это все, мы научим решать уравнения – общий метод, это гораздо проще. Но выяснилось, что школьники не понимают, что означает буква «икс» в уравнении, и учителя не в состоянии им это объяснить. Как-то вместо этой скучной, но понятной деятельности с бидонами стало нужно переписывать формулы, писать загадочную ОДЗ – «область допустимых значений», непонятную, но писать ее обязательно надо. Можно было даже поступить в технический вуз, так ничего и не поняв, просто научившись решать по правилам. Хорошие репетиторы тем и славились, что могут плохого школьника научить сдать экзамены по математике без того, чтобы он разобрался, – просто какой-то тип задач будет уметь решать, и хорошо. Тогда это было со вступительными экзаменами, так же сейчас с ЕГЭ происходит. С реформой матобразования получилось плохо, наверное, если бы ее не было, было бы лучше. Но никакого злого умысла, естественно, не было. Хотели как лучше, а получилось как у Черномырдина.
Но выяснилось, что школьники не понимают, что означает буква «икс» в уравнении, и учителя не в состоянии им это объяснить. Как-то вместо этой скучной, но понятной деятельности с бидонами стало нужно переписывать формулы, писать загадочную ОДЗ – «область допустимых значений», непонятную, но писать ее обязательно надо. Можно было даже поступить в технический вуз, так ничего и не поняв, просто научившись решать по правилам. Хорошие репетиторы тем и славились, что могут плохого школьника научить сдать экзамены по математике без того, чтобы он разобрался, – просто какой-то тип задач будет уметь решать, и хорошо. Тогда это было со вступительными экзаменами, так же сейчас с ЕГЭ происходит. С реформой матобразования получилось плохо, наверное, если бы ее не было, было бы лучше. Но никакого злого умысла, естественно, не было. Хотели как лучше, а получилось как у Черномырдина. Их дети шли в эти классы, становились студентами, потом сами преподавали, ну и впоследствии их дети шли в школу. Вы много работали с детьми в кружках и матклассах. Появлялись самородки-Ломоносовы, непонятно откуда вынырнувшие?
Их дети шли в эти классы, становились студентами, потом сами преподавали, ну и впоследствии их дети шли в школу. Вы много работали с детьми в кружках и матклассах. Появлялись самородки-Ломоносовы, непонятно откуда вынырнувшие? Явно школьник должен быть на общем фоне способным, проявлять себя. Учитель или учительница, видя, что есть хороший школьник, говорит: сходи на олимпиаду. Или приятель школьника идет на олимпиаду, и он за компанию решил сходить. В классе, который я набирал в 57-й школе, как-то был школьник с приводом в милицию, потому что он взорвал лифт. Не то что он взорвал лифт в целях теракта, он просто интересовался химическими опытами. Это был чисто научный начальный толчок.
Явно школьник должен быть на общем фоне способным, проявлять себя. Учитель или учительница, видя, что есть хороший школьник, говорит: сходи на олимпиаду. Или приятель школьника идет на олимпиаду, и он за компанию решил сходить. В классе, который я набирал в 57-й школе, как-то был школьник с приводом в милицию, потому что он взорвал лифт. Не то что он взорвал лифт в целях теракта, он просто интересовался химическими опытами. Это был чисто научный начальный толчок. Естественно, со временем я более-менее тоже всех узнал. Никакого оттенка элитного клуба в этом не было.
Естественно, со временем я более-менее тоже всех узнал. Никакого оттенка элитного клуба в этом не было. Если бы можно было устраивать по-другому, может, какая-то другая система была бы более эффективной?
Если бы можно было устраивать по-другому, может, какая-то другая система была бы более эффективной?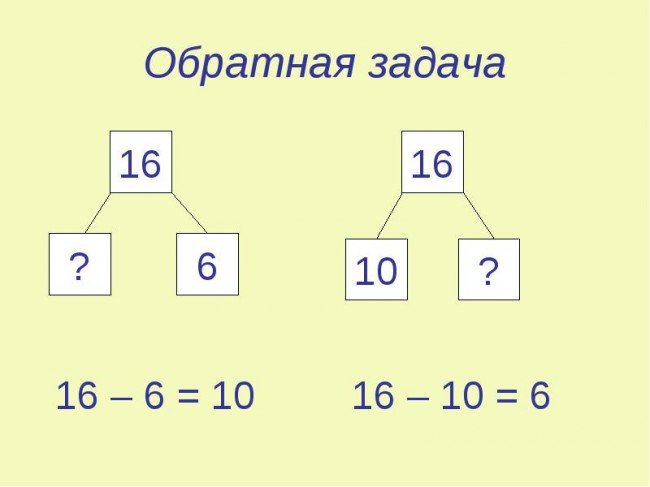 Сейчас есть система олимпиад, но совершенно не такая, как в Советском Союзе. Олимпиады были, но зарплата директора или статус школы зависел от того, сколько в школе победителей олимпиад. Олимпиады, кроме международных, не учитывались при поступлении. Олимпиады были ради удовольствия. Сейчас вокруг олимпиад возникла какая-то параллельная система, довольно неплохо финансируемая, всякие «Сириусы» (Образовательный центр в Сочи по выявлению одаренных детей, созданный по инициативе Путина. – Прим.), сборы такие, сборы сякие. В результате школьники вместо того, чтобы учиться в школе, все время ездят на сборы, и там их тренируют. Появилась дикая идея, что целью и критерием обучения математике в школе является победа на каких-то олимпиадах. Возникли репетиторы, готовящие к олимпиадам. В советское время было бы совершенно невозможно себе представить, кому придет в голову нанимать репетитора для подготовки к олимпиадам, которые ничего не дают. Может, некоторые из репетиторов – квалифицированные преподаватели, хотя, конечно, не очень хорошо, что это зависит от наличия у школьников и их родителей денег.
Сейчас есть система олимпиад, но совершенно не такая, как в Советском Союзе. Олимпиады были, но зарплата директора или статус школы зависел от того, сколько в школе победителей олимпиад. Олимпиады, кроме международных, не учитывались при поступлении. Олимпиады были ради удовольствия. Сейчас вокруг олимпиад возникла какая-то параллельная система, довольно неплохо финансируемая, всякие «Сириусы» (Образовательный центр в Сочи по выявлению одаренных детей, созданный по инициативе Путина. – Прим.), сборы такие, сборы сякие. В результате школьники вместо того, чтобы учиться в школе, все время ездят на сборы, и там их тренируют. Появилась дикая идея, что целью и критерием обучения математике в школе является победа на каких-то олимпиадах. Возникли репетиторы, готовящие к олимпиадам. В советское время было бы совершенно невозможно себе представить, кому придет в голову нанимать репетитора для подготовки к олимпиадам, которые ничего не дают. Может, некоторые из репетиторов – квалифицированные преподаватели, хотя, конечно, не очень хорошо, что это зависит от наличия у школьников и их родителей денег. Благодаря этим олимпиадам в разных местах, где вообще ничего никогда не было, образовались достаточно высокого уровня занятия по математике, но по немного странной и дикой программе вокруг этих олимпиад: если что-то в олимпиаде не встречается, то мы изучать этого не будем, потому что зачем? Средний уровень участников Всероссийской олимпиады от этого стал лучше, но на фоне этого по результатам ЕГЭ, наверное, стало хуже. Хотя все качественное обучение программированию, которое сейчас в России есть, – это результат именно олимпиад. Можно ли было представить в советское время, что вдруг в Петрозаводском университете появится команда студентов, которые знают базовые алгоритмы и умеют их быстро реализовывать. Никогда такого бы не было. А сейчас в совершенно неожиданных городах появляются центры олимпиад. Для программирования это как раз хорошо, потому что они после этого идут работать – это точно пригодится. А для математики это не так хорошо. Лучше, если бы человек занимался в школе тем, что ему интересно, не пытаясь соревноваться, – просто читал бы книжки, разбирался в чем-то.
Благодаря этим олимпиадам в разных местах, где вообще ничего никогда не было, образовались достаточно высокого уровня занятия по математике, но по немного странной и дикой программе вокруг этих олимпиад: если что-то в олимпиаде не встречается, то мы изучать этого не будем, потому что зачем? Средний уровень участников Всероссийской олимпиады от этого стал лучше, но на фоне этого по результатам ЕГЭ, наверное, стало хуже. Хотя все качественное обучение программированию, которое сейчас в России есть, – это результат именно олимпиад. Можно ли было представить в советское время, что вдруг в Петрозаводском университете появится команда студентов, которые знают базовые алгоритмы и умеют их быстро реализовывать. Никогда такого бы не было. А сейчас в совершенно неожиданных городах появляются центры олимпиад. Для программирования это как раз хорошо, потому что они после этого идут работать – это точно пригодится. А для математики это не так хорошо. Лучше, если бы человек занимался в школе тем, что ему интересно, не пытаясь соревноваться, – просто читал бы книжки, разбирался в чем-то. А когда олимпиады вдруг кончаются, то совершенно непонятно, что делать дальше. Это как если бы человек всю жизнь занимался теннисом, стал чемпионом мира среди юниоров, а потом узнал, что соревнования для более старших если и проводятся, то никого не интересуют. В смысле умений – олимпиадная подготовка, безусловно, им способствует, – но в смысле интересов после окончания олимпиад происходит ломка.
А когда олимпиады вдруг кончаются, то совершенно непонятно, что делать дальше. Это как если бы человек всю жизнь занимался теннисом, стал чемпионом мира среди юниоров, а потом узнал, что соревнования для более старших если и проводятся, то никого не интересуют. В смысле умений – олимпиадная подготовка, безусловно, им способствует, – но в смысле интересов после окончания олимпиад происходит ломка.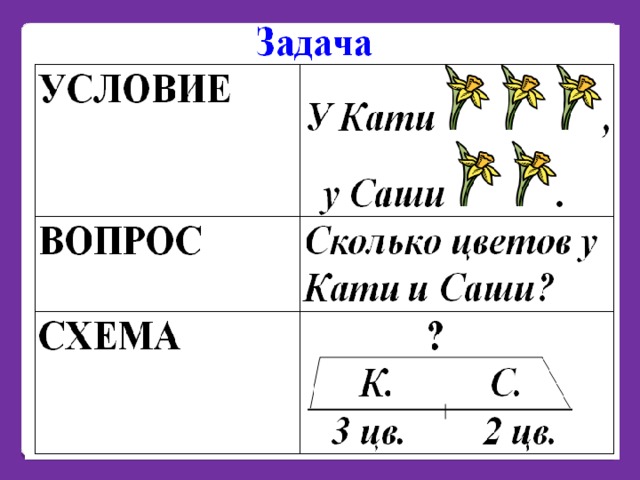 Например, Независимый университет и Московский центр непрерывного математического образования были очень обязаны префекту Центрального округа Москвы Музыкантскому, который организовал для них здание. Боря Музыкантский, его сын, учился в 57-й школе. Мы с ним ходили в поход даже в Карелию, он брал с собой своего отца Александра Ильича, которого я тогда тоже хорошо знал, мы были в походе неделю. Когда потом Константинов пришел к нему, было ясно, что это не жулики. Позже стали финансироваться Турниры городов. В материальном смысле поддержка сейчас гораздо больше. Другое дело, что она связана с политическими играми, с ЕГЭ, с «Сириусом», который вроде как хорош, но там Ролдугин. Все сложно.
Например, Независимый университет и Московский центр непрерывного математического образования были очень обязаны префекту Центрального округа Москвы Музыкантскому, который организовал для них здание. Боря Музыкантский, его сын, учился в 57-й школе. Мы с ним ходили в поход даже в Карелию, он брал с собой своего отца Александра Ильича, которого я тогда тоже хорошо знал, мы были в походе неделю. Когда потом Константинов пришел к нему, было ясно, что это не жулики. Позже стали финансироваться Турниры городов. В материальном смысле поддержка сейчас гораздо больше. Другое дело, что она связана с политическими играми, с ЕГЭ, с «Сириусом», который вроде как хорош, но там Ролдугин. Все сложно.
 Количество. Стоимость
Количество. Стоимость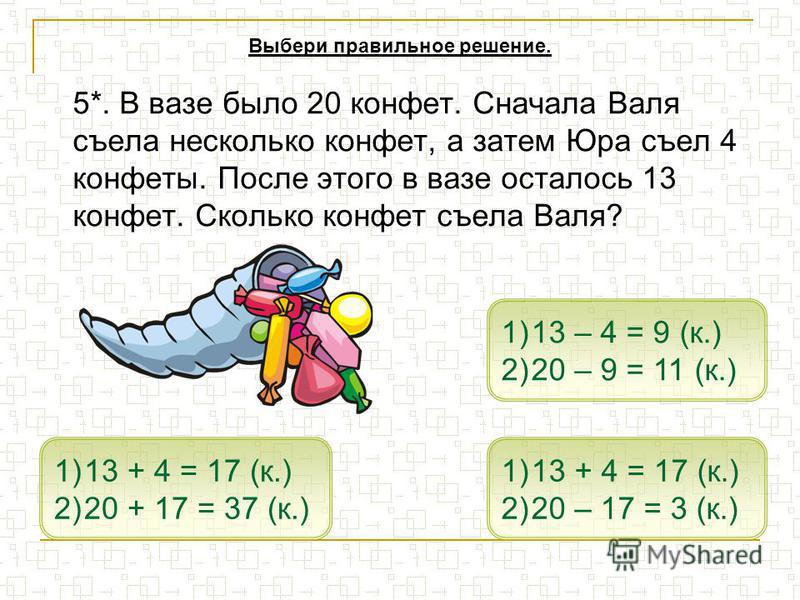 Урок 17,
Петерсон, Учебник, часть 3
Урок 17,
Петерсон, Учебник, часть 3
 Вариант 1. № 1,
Моро, Волкова, Проверочные работы
Вариант 1. № 1,
Моро, Волкова, Проверочные работы
 Урок 13,
Петерсон, Учебник, часть 1
Урок 13,
Петерсон, Учебник, часть 1
 А. 1
А. 1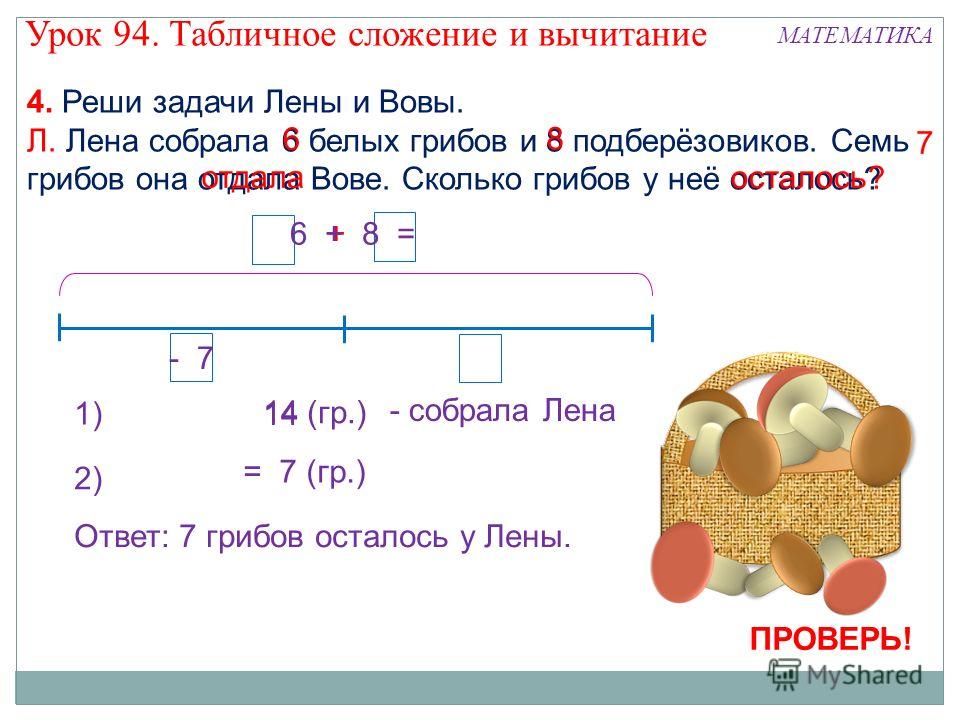 Действительно, дать определение «красивой» задачи, подобрать такие задачи, классифицировать их определенным образом весьма интересно и полезно.
Действительно, дать определение «красивой» задачи, подобрать такие задачи, классифицировать их определенным образом весьма интересно и полезно.


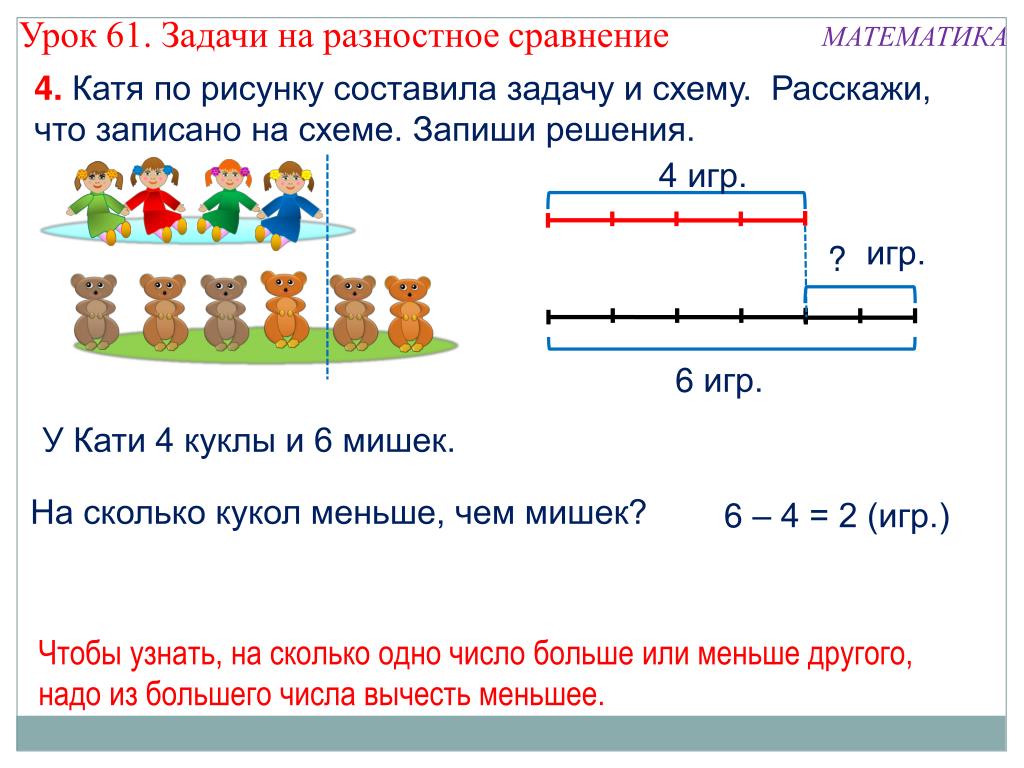
 2). Оказалось, что длины всех кусочков различны и что табурет после этого стоит на полу, пусть наклонно, но по-прежнему касаясь, пола всеми четырьмя концами ножек. Дедушка решил починить табурет, однако нашел только три кусочка с длинами 8, 9 и 10 см. Какой длины может быть четвертый кусочек?
2). Оказалось, что длины всех кусочков различны и что табурет после этого стоит на полу, пусть наклонно, но по-прежнему касаясь, пола всеми четырьмя концами ножек. Дедушка решил починить табурет, однако нашел только три кусочка с длинами 8, 9 и 10 см. Какой длины может быть четвертый кусочек? При этом получим, что длина отпиленной части удовлетворяет одному из равенств:
При этом получим, что длина отпиленной части удовлетворяет одному из равенств: На рисунке образовалось много параллелограммов и трапеций с диагоналями. Расставим номера треугольников, причем одинаковым номером отметим равные треугольники разных цветов. 12 из них разбились на пары, а тринадцатому, который оказался закрашенным, пары не хватило. Значит, закрашенная часть площади девятиугольника больше его незакрашенной части.
На рисунке образовалось много параллелограммов и трапеций с диагоналями. Расставим номера треугольников, причем одинаковым номером отметим равные треугольники разных цветов. 12 из них разбились на пары, а тринадцатому, который оказался закрашенным, пары не хватило. Значит, закрашенная часть площади девятиугольника больше его незакрашенной части.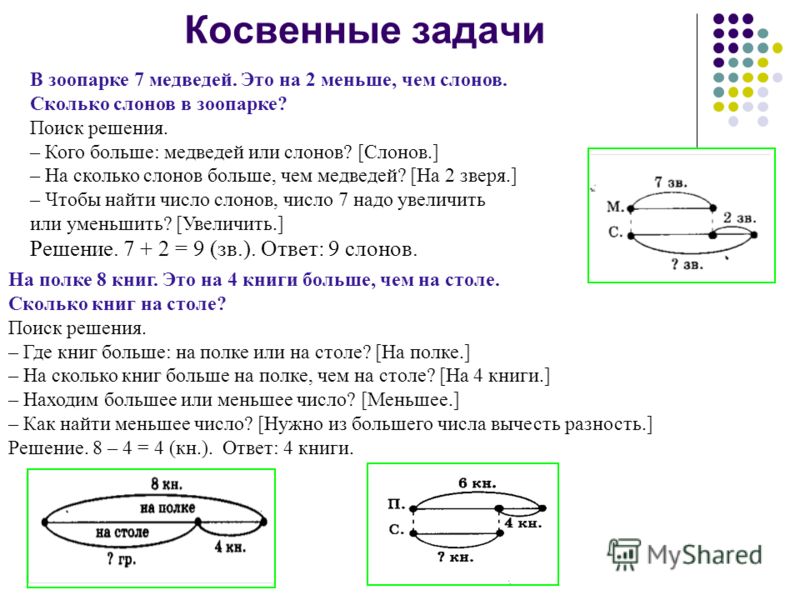
 7). Двое по очереди красят ее клетки в черный цвет, причем первый всегда закрашивает квадрат 2*2, а второй—три клетки, образующие «уголок». Уже покрашенную клетку второй раз красить нельзя. Проигрывает тот, кто не может сделать очередной ход. Кто выигрывает при правильной игре: первый или второй?
7). Двое по очереди красят ее клетки в черный цвет, причем первый всегда закрашивает квадрат 2*2, а второй—три клетки, образующие «уголок». Уже покрашенную клетку второй раз красить нельзя. Проигрывает тот, кто не может сделать очередной ход. Кто выигрывает при правильной игре: первый или второй? Были указаны используемые методы исследования, определена проблема, обоснована актуальность.
Были указаны используемые методы исследования, определена проблема, обоснована актуальность.

 В. А. Стеклова Николаем Андреевым о том, в чем преимущества 3D-графики при иллюстрации задач, реально ли сделать популярное приложение про математику и что нового появилось в «Этюдах» в последнее время.
В. А. Стеклова Николаем Андреевым о том, в чем преимущества 3D-графики при иллюстрации задач, реально ли сделать популярное приложение про математику и что нового появилось в «Этюдах» в последнее время.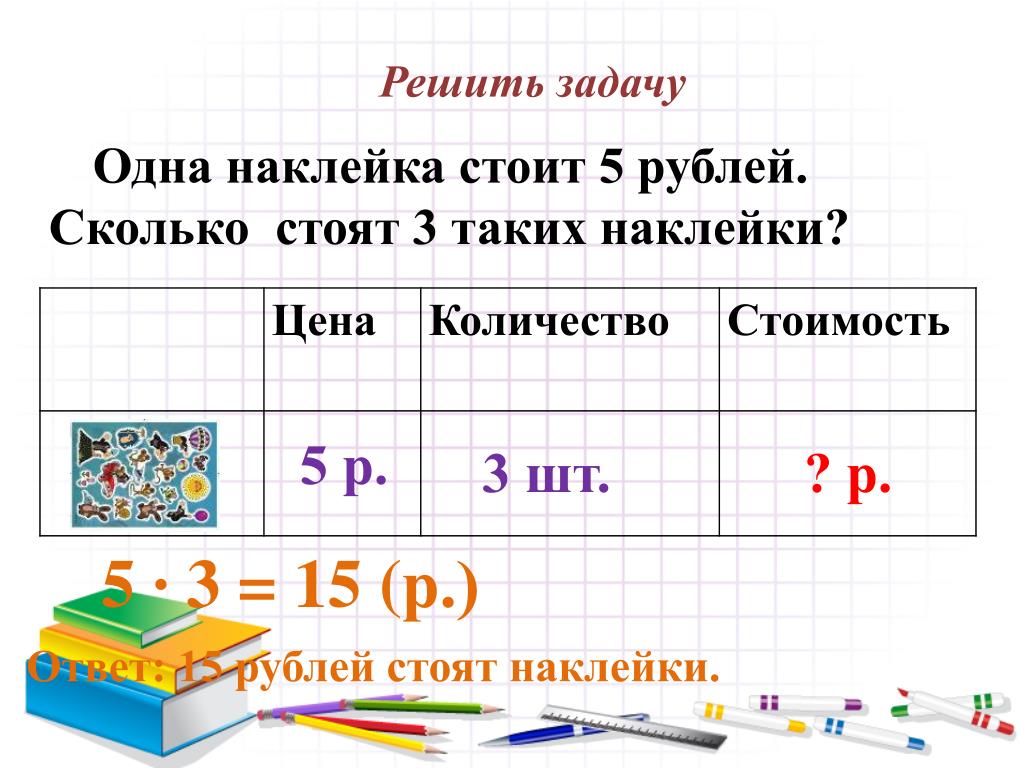 В какой-то момент мне показалось, что о задачах, которыми я занимался в науке, можно красиво и понятно рассказать с использованием 3D-графики. Представления о 3D-графике у меня тогда были только примерные, но было понятно, что это отдельная наука и изучать ее я не готов. Поэтому я кинул клич на интернет-форумах, где обитали специалисты по 3D-графике. Так мы познакомились с мультипликатором Михаилом Калиниченко, с ним мы начали что-то пробовать и, собственно говоря, работаем вместе по сей день. Правда, первые два фильма – про задачу Томсона и про контактное число шаров – я теперь показываю редко, сегодня они кажутся не такими захватывающими. Но в начале 2000-х они очень понравились и учителям, и научному сообществу. Поэтому мы продолжили создавать фильмы, математические расчеты для создания фильма стал делать Никита Панюнин, а в 2005 году совершенно уникальный человек Роман Кокшаров создал нашу полянку с мальчишкой у доски – сайт в интернете.
В какой-то момент мне показалось, что о задачах, которыми я занимался в науке, можно красиво и понятно рассказать с использованием 3D-графики. Представления о 3D-графике у меня тогда были только примерные, но было понятно, что это отдельная наука и изучать ее я не готов. Поэтому я кинул клич на интернет-форумах, где обитали специалисты по 3D-графике. Так мы познакомились с мультипликатором Михаилом Калиниченко, с ним мы начали что-то пробовать и, собственно говоря, работаем вместе по сей день. Правда, первые два фильма – про задачу Томсона и про контактное число шаров – я теперь показываю редко, сегодня они кажутся не такими захватывающими. Но в начале 2000-х они очень понравились и учителям, и научному сообществу. Поэтому мы продолжили создавать фильмы, математические расчеты для создания фильма стал делать Никита Панюнин, а в 2005 году совершенно уникальный человек Роман Кокшаров создал нашу полянку с мальчишкой у доски – сайт в интернете. Это направление очень важно по сей день, сегодня у нас в копилке больше тысячи лекций – вполне себе немаленькая цифра.
Это направление очень важно по сей день, сегодня у нас в копилке больше тысячи лекций – вполне себе немаленькая цифра. В России ежегодно проходит крупнейшее мероприятие по 3D-графике – CG Event. И на первом CG Event представили несколько пленарных докладов, среди выступающих был сотрудник студии Pixar, представитель «Базелевса» – компании Тимура Бекмамбетова, который как раз тогда снял «Дозоры», и были мы с докладом по «Математическим этюдам». И даже на трехмерщиков они тогда произвели огромное впечатление.
В России ежегодно проходит крупнейшее мероприятие по 3D-графике – CG Event. И на первом CG Event представили несколько пленарных докладов, среди выступающих был сотрудник студии Pixar, представитель «Базелевса» – компании Тимура Бекмамбетова, который как раз тогда снял «Дозоры», и были мы с докладом по «Математическим этюдам». И даже на трехмерщиков они тогда произвели огромное впечатление. А что в принципе сегодня представляют собой «Математические этюды» с точки зрения цифр: сколько заданий, сколько посетителей?
А что в принципе сегодня представляют собой «Математические этюды» с точки зрения цифр: сколько заданий, сколько посетителей? Все мы пользуемся транспортом, но далеко не все задумывались, что при повороте радиус внешнего рельса больше, чем радиус внутреннего. Соответственно, путь, которое проходит внешнее колесо, больше, чем путь, которое проходит внутреннее. А между тем колеса вращаются с одной и той же скоростью, они сидят на единой оси! Оказывается, что проблему помогает решить геометрия.
Все мы пользуемся транспортом, но далеко не все задумывались, что при повороте радиус внешнего рельса больше, чем радиус внутреннего. Соответственно, путь, которое проходит внешнее колесо, больше, чем путь, которое проходит внутреннее. А между тем колеса вращаются с одной и той же скоростью, они сидят на единой оси! Оказывается, что проблему помогает решить геометрия. Мне это кажется ценным, потому что у нас пока нет хороших музеев науки, и даже в имеющихся математические отделы очень маленькие: сложно придумать модель, в которой как-то показывается математический факт. Сейчас на рабочей версии сайта собрано больше 400 таких моделей, постепенно мы будем выкладывать их в открытый доступ.
Мне это кажется ценным, потому что у нас пока нет хороших музеев науки, и даже в имеющихся математические отделы очень маленькие: сложно придумать модель, в которой как-то показывается математический факт. Сейчас на рабочей версии сайта собрано больше 400 таких моделей, постепенно мы будем выкладывать их в открытый доступ.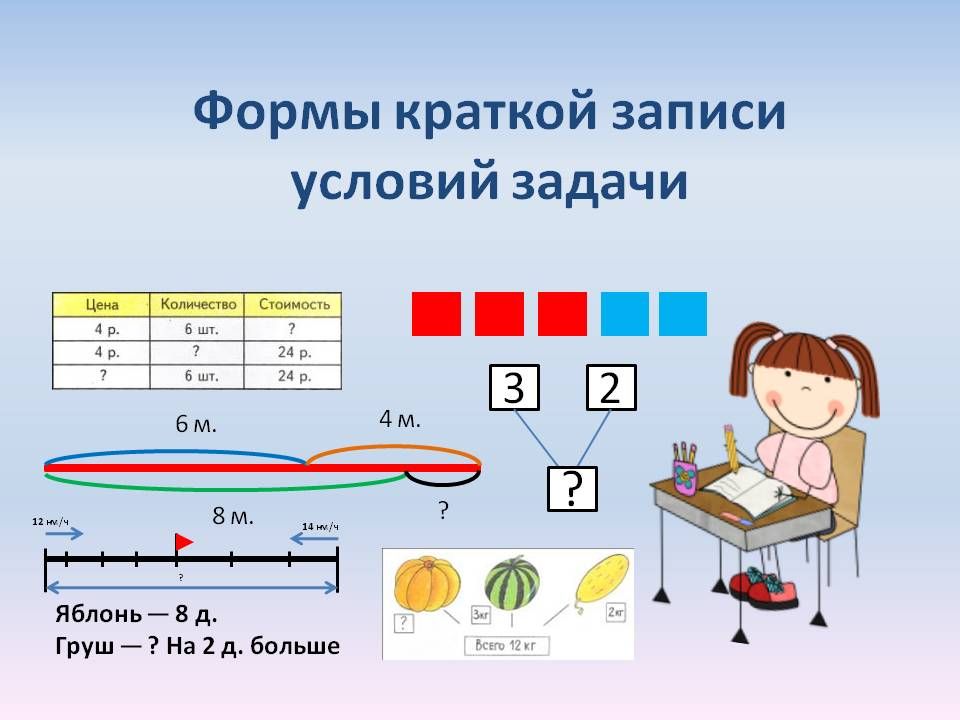 В. А. Стеклова РАН. К нам заходит почти весь институт, все понимают, что наша деятельность важна, делятся своими мыслями. Соответственно, мы можем черпать идеи с переднего края науки, получать их из первых рук, от людей, которые занимаются данной темой. Благодаря этому получается интересно, качественно и неизбито.
В. А. Стеклова РАН. К нам заходит почти весь институт, все понимают, что наша деятельность важна, делятся своими мыслями. Соответственно, мы можем черпать идеи с переднего края науки, получать их из первых рук, от людей, которые занимаются данной темой. Благодаря этому получается интересно, качественно и неизбито. Задача «Математических этюдов» – изменить их мнение, помочь полюбить математику. Потому что, конечно, научить математике никакой сайт не может, он может только вдохновить школьника: возможно, после он в книжках пороется, а главное, поработает сам – в математике это основное. Вторая важная задача – это дать учителям хороший по качеству материал для работы с детьми.
Задача «Математических этюдов» – изменить их мнение, помочь полюбить математику. Потому что, конечно, научить математике никакой сайт не может, он может только вдохновить школьника: возможно, после он в книжках пороется, а главное, поработает сам – в математике это основное. Вторая важная задача – это дать учителям хороший по качеству материал для работы с детьми.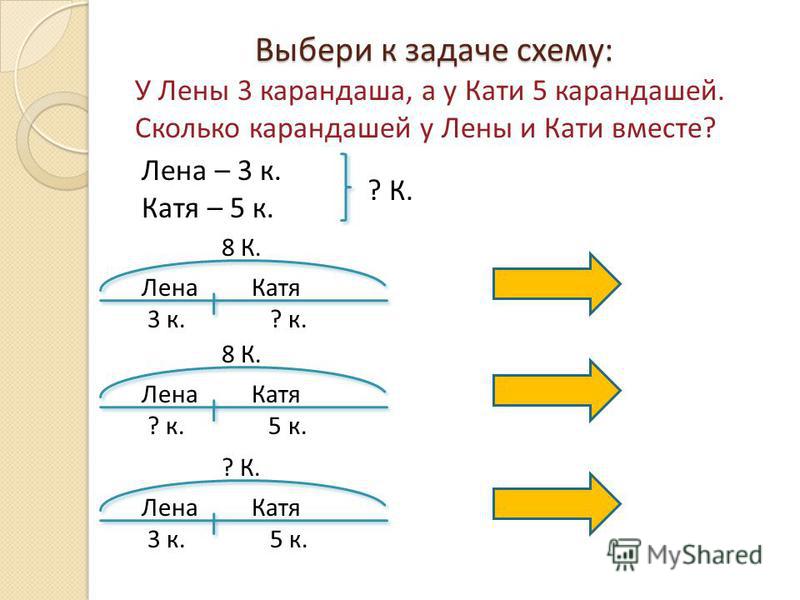 Кто-то просто картинку посмотрит, а кто-то поймет, какая теорема за ней стоит.
Кто-то просто картинку посмотрит, а кто-то поймет, какая теорема за ней стоит. Насколько он популярен среди ваших заграничных коллег? Может быть, у вас есть планы дальнейшего расширения?
Насколько он популярен среди ваших заграничных коллег? Может быть, у вас есть планы дальнейшего расширения?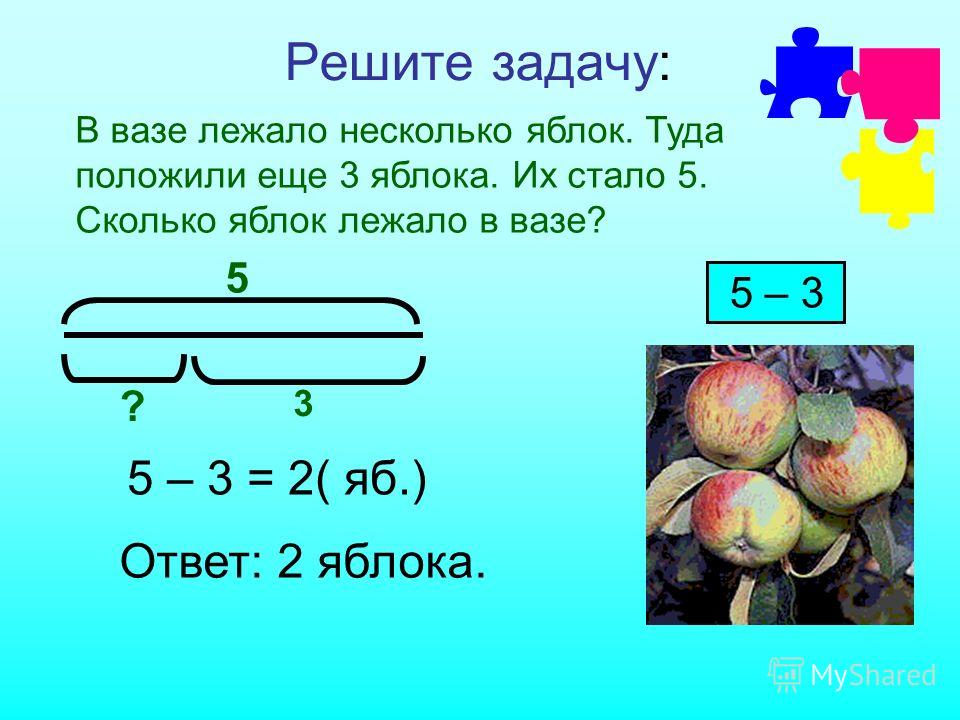 У многих ELL могут возникнуть трудности с чтением и пониманием письменного содержания словесной задачи. Если учащийся изучает английский как второй язык, он может еще не знать ключевую терминологию, необходимую для решения уравнения. Другими словами, ELL, получившие формальное образование в своих странах, как правило, не испытывают математических трудностей; следовательно, их борьба начинается, когда они сталкиваются с проблемами слов на втором языке, который они еще не освоили (Бернардо, 2005). По этой причине рекомендуется, чтобы учащиеся изучили ключевую терминологию, прежде чем пытаться решать математические текстовые задачи.
У многих ELL могут возникнуть трудности с чтением и пониманием письменного содержания словесной задачи. Если учащийся изучает английский как второй язык, он может еще не знать ключевую терминологию, необходимую для решения уравнения. Другими словами, ELL, получившие формальное образование в своих странах, как правило, не испытывают математических трудностей; следовательно, их борьба начинается, когда они сталкиваются с проблемами слов на втором языке, который они еще не освоили (Бернардо, 2005). По этой причине рекомендуется, чтобы учащиеся изучили ключевую терминологию, прежде чем пытаться решать математические текстовые задачи.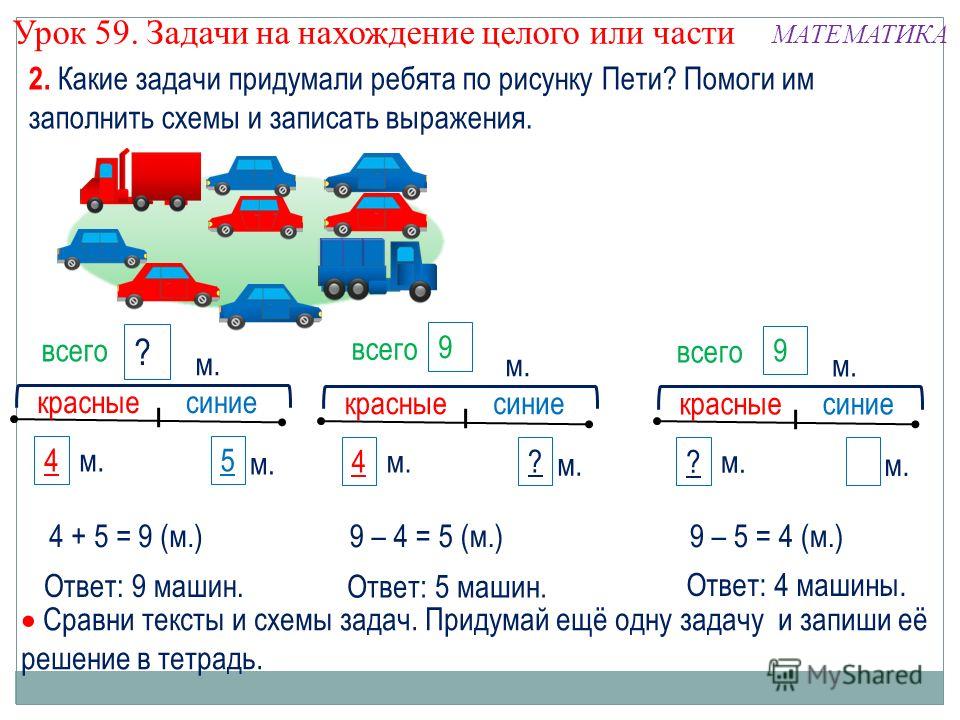 Понимание языка в текстовых задачах имеет решающее значение для всех учащихся. Им нужно знать значение слов. Но поскольку слова часто используются по-разному и проблемы ставятся по-разному, есть некоторые предостерегающие сообщения. Вот пример задачи, в которой используется «меньше чем» для составления уравнения на вычитание.
Понимание языка в текстовых задачах имеет решающее значение для всех учащихся. Им нужно знать значение слов. Но поскольку слова часто используются по-разному и проблемы ставятся по-разному, есть некоторые предостерегающие сообщения. Вот пример задачи, в которой используется «меньше чем» для составления уравнения на вычитание. Это не поможет им впоследствии стать математическими специалистами, даже если они хорошо владеют английским языком.
Это не поможет им впоследствии стать математическими специалистами, даже если они хорошо владеют английским языком. Мы хотим, чтобы учащиеся знали значение слов, а также видели их в контексте всей проблемы.
Мы хотим, чтобы учащиеся знали значение слов, а также видели их в контексте всей проблемы.
 в Учебнике по математике для изучающих английский язык.
в Учебнике по математике для изучающих английский язык.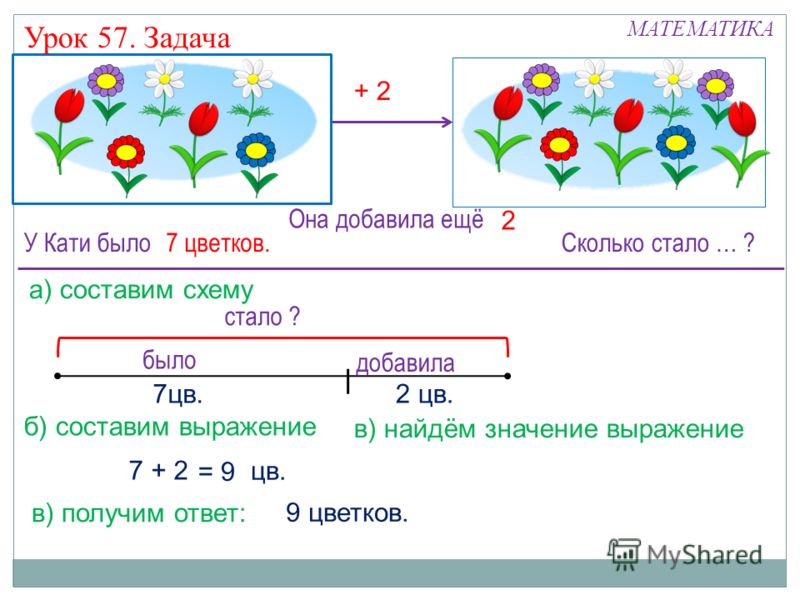 Решение проблем играет центральную роль в мышлении педагогов-теоретиков с момента публикации книги Полиа «Как это решить» в 1945 году. Национальный совет учителей математики (NCTM) последовательно выступает за решение проблем для почти 40 лет, в то время как международные тенденции в преподавании математики показали повышенное внимание к решению задач и математическому моделированию, начиная с начала 19 века.90-е. По мере того, как преподаватели во всем мире все больше осознавали, что предоставление опыта решения задач имеет решающее значение для того, чтобы учащиеся могли осмысленно использовать и применять математические знания (Wu and Zhang, 2006), мало что изменилось на школьном уровне в Соединенных Штатах.
Решение проблем играет центральную роль в мышлении педагогов-теоретиков с момента публикации книги Полиа «Как это решить» в 1945 году. Национальный совет учителей математики (NCTM) последовательно выступает за решение проблем для почти 40 лет, в то время как международные тенденции в преподавании математики показали повышенное внимание к решению задач и математическому моделированию, начиная с начала 19 века.90-е. По мере того, как преподаватели во всем мире все больше осознавали, что предоставление опыта решения задач имеет решающее значение для того, чтобы учащиеся могли осмысленно использовать и применять математические знания (Wu and Zhang, 2006), мало что изменилось на школьном уровне в Соединенных Штатах. Для многих учителей математики это был первый раз, когда они должны были объединить сотрудничество учащихся и обсуждение с решением проблем. Эта практика требует обучения совершенно по-другому, поскольку школы перешли от ориентированного на учителя к более диалогическому подходу к преподаванию и обучению. Задача учителей состоит в том, чтобы научить учащихся не только решать задачи, но и изучать математику посредством решения задач. Хотя многие учащиеся могут развить беглость процедур, им часто не хватает глубокого концептуального понимания, необходимого для решения новых задач или установления связей между математическими идеями.
Для многих учителей математики это был первый раз, когда они должны были объединить сотрудничество учащихся и обсуждение с решением проблем. Эта практика требует обучения совершенно по-другому, поскольку школы перешли от ориентированного на учителя к более диалогическому подходу к преподаванию и обучению. Задача учителей состоит в том, чтобы научить учащихся не только решать задачи, но и изучать математику посредством решения задач. Хотя многие учащиеся могут развить беглость процедур, им часто не хватает глубокого концептуального понимания, необходимого для решения новых задач или установления связей между математическими идеями.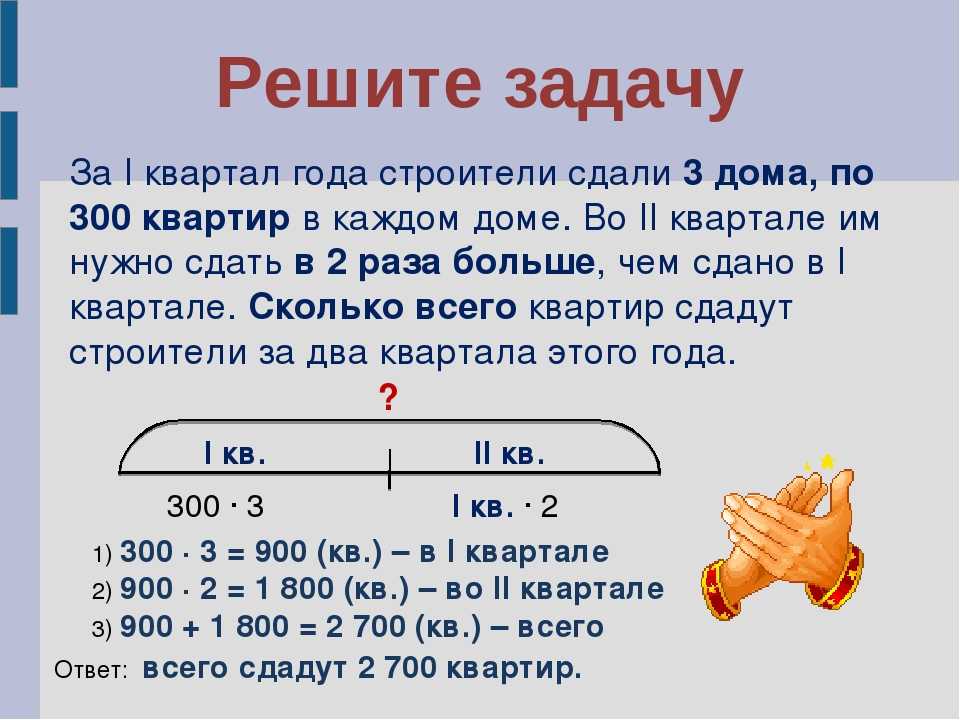
 Учителю необходимо установить связь и опираться на это понимание через опыт, который позволяет учащимся изучать математику и делиться своими идеями в содержательном диалоге с учителем и своими сверстниками.
Учителю необходимо установить связь и опираться на это понимание через опыт, который позволяет учащимся изучать математику и делиться своими идеями в содержательном диалоге с учителем и своими сверстниками.
 Решение задач по математике способствует развитию:
Решение задач по математике способствует развитию: Задача учителей заключается в обеспечении того, чтобы задачи, которые они ставят, были разработаны для поддержки обучения математике и были подходящими и сложными для всех учащихся. Задачи должны быть достаточно сложными, чтобы вызвать затруднения , но не настолько сложными, чтобы учащиеся не смогли добиться успеха. Учителя, которые понимают это правильно, создают устойчивых решателей проблем, которые знают, что при настойчивости они могут добиться успеха. Задачи должны находиться в «зоне ближайшего развития» учащихся (Выготский 19).68). Эти типы сложных проблем предоставят возможности для обсуждения и обучения.
Задача учителей заключается в обеспечении того, чтобы задачи, которые они ставят, были разработаны для поддержки обучения математике и были подходящими и сложными для всех учащихся. Задачи должны быть достаточно сложными, чтобы вызвать затруднения , но не настолько сложными, чтобы учащиеся не смогли добиться успеха. Учителя, которые понимают это правильно, создают устойчивых решателей проблем, которые знают, что при настойчивости они могут добиться успеха. Задачи должны находиться в «зоне ближайшего развития» учащихся (Выготский 19).68). Эти типы сложных проблем предоставят возможности для обсуждения и обучения. Выход из тупика обычно требует времени и включает в себя использование различных подходов. Студенты должны научиться этому на опыте. Эффективных задач:
Выход из тупика обычно требует времени и включает в себя использование различных подходов. Студенты должны научиться этому на опыте. Эффективных задач: Сообщество обеспечивает среду, в которой отдельные математические идеи могут быть выражены и проверены на соответствие идеям других… Это позволяет учащимся стать более ясными и уверенными в том, что они знают и понимают».
Сообщество обеспечивает среду, в которой отдельные математические идеи могут быть выражены и проверены на соответствие идеям других… Это позволяет учащимся стать более ясными и уверенными в том, что они знают и понимают». 
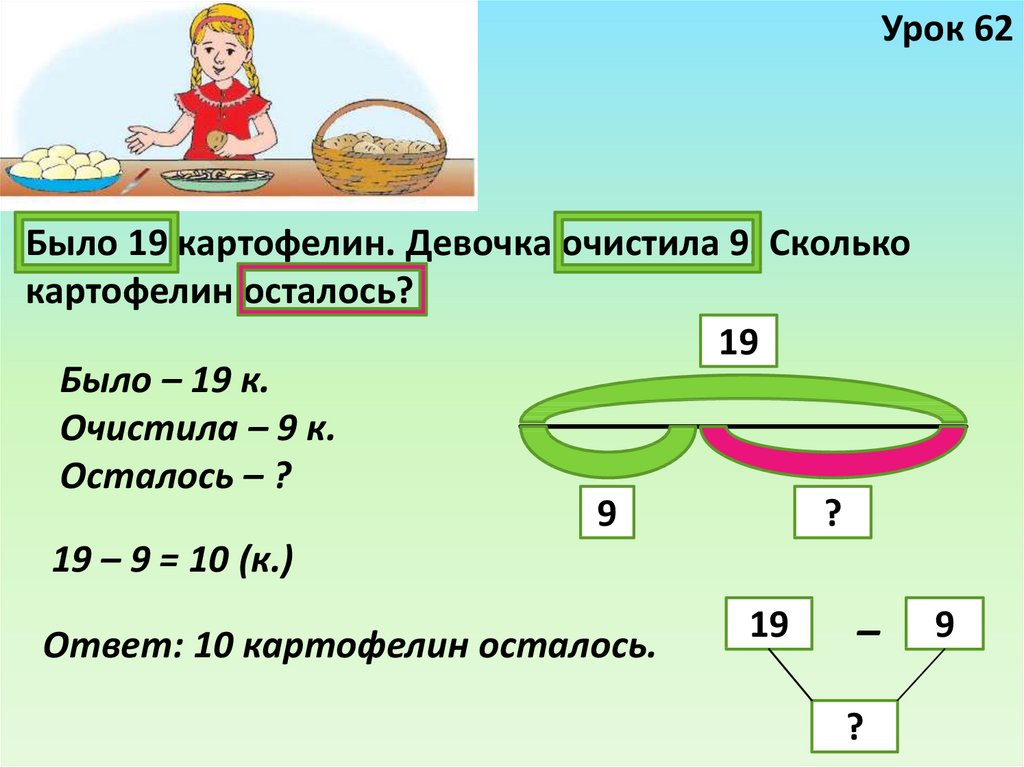 ).
). Будут времена, когда учащиеся должны иметь возможность работать самостоятельно, а иногда им нужно будет иметь возможность работать в небольших группах, чтобы они могли делиться идеями и учиться с другими и у них.
Будут времена, когда учащиеся должны иметь возможность работать самостоятельно, а иногда им нужно будет иметь возможность работать в небольших группах, чтобы они могли делиться идеями и учиться с другими и у них.

 Задача учителей математики состоит в том, чтобы развивать у учащихся процесс математического мышления наряду со знаниями и создавать возможности для представления даже рутинных математических задач в контексте решения проблем.
Задача учителей математики состоит в том, чтобы развивать у учащихся процесс математического мышления наряду со знаниями и создавать возможности для представления даже рутинных математических задач в контексте решения проблем. . Мы пришли к оценке следующих особенностей, которые, по нашему мнению, являются важными компонентами хорошей задачи :
. Мы пришли к оценке следующих особенностей, которые, по нашему мнению, являются важными компонентами хорошей задачи : Существует широкий спектр возможностей для изготовления крючка. что мы не здесь проблемы, которые начинаются с полутора страниц настройки и нескольких подвопросов, прежде чем мы когда-либо доберемся до конечной точки всего этого. Чтобы было ясно, мы не говорим, что большие объемы информации или контекстуальный фон несовместимы с хорошими математическими задачами. Действительно, многие хорошие математические задачи будут включать в себя глубокое погружение в соответствующие контексты и просеивание потенциально полезной информации, чтобы решить, что нужно включить в решение, но наша точка зрения заключается в том, что с хорошими задачами мы уже заранее понимаем цель. on, а не только в конце (или вообще не).
Существует широкий спектр возможностей для изготовления крючка. что мы не здесь проблемы, которые начинаются с полутора страниц настройки и нескольких подвопросов, прежде чем мы когда-либо доберемся до конечной точки всего этого. Чтобы было ясно, мы не говорим, что большие объемы информации или контекстуальный фон несовместимы с хорошими математическими задачами. Действительно, многие хорошие математические задачи будут включать в себя глубокое погружение в соответствующие контексты и просеивание потенциально полезной информации, чтобы решить, что нужно включить в решение, но наша точка зрения заключается в том, что с хорошими задачами мы уже заранее понимаем цель. on, а не только в конце (или вообще не).
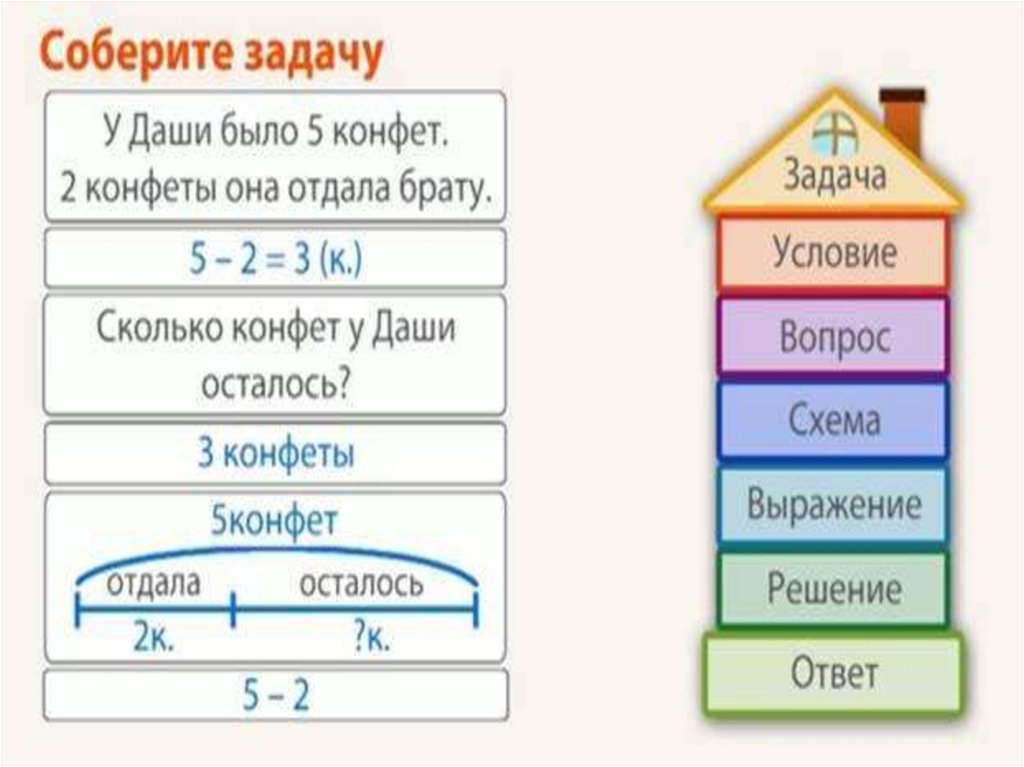

 Один человек может подумать о показателях и определить a § b как a b . Но другие люди могут думать иначе, например, § b = a 4 или
Один человек может подумать о показателях и определить a § b как a b . Но другие люди могут думать иначе, например, § b = a 4 или 
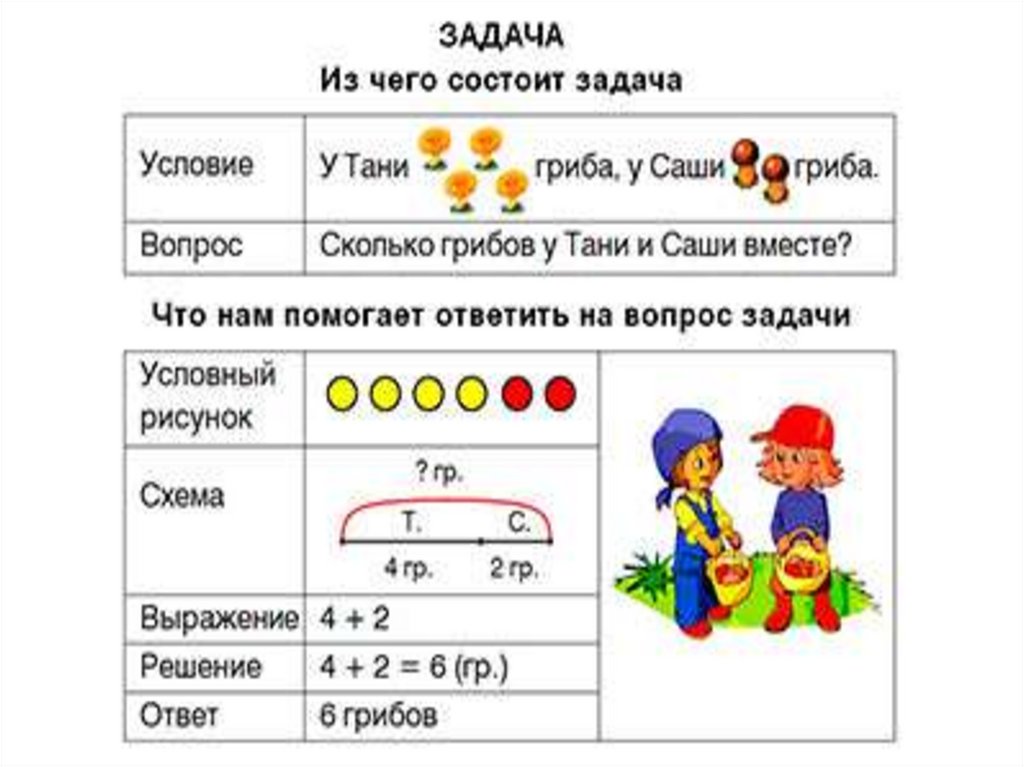 Но, возможно, было бы целесообразно расширить его до более широкой идеи об экспоненциальном росте по сравнению с полиномиальным ростом в целом. Пример задачи равно , вероятно, полезной для многих школьников, изучающих математику, является проблема Красной/Синей области, описанная выше, потому что она может показаться эзотерической на первый взгляд, но на самом деле приводит к важным идеям о связи между треугольной площадью и площадью параллелограмма, а также об инвариантности сравнения площадей. хотя ситуация постоянно меняется.
Но, возможно, было бы целесообразно расширить его до более широкой идеи об экспоненциальном росте по сравнению с полиномиальным ростом в целом. Пример задачи равно , вероятно, полезной для многих школьников, изучающих математику, является проблема Красной/Синей области, описанная выше, потому что она может показаться эзотерической на первый взгляд, но на самом деле приводит к важным идеям о связи между треугольной площадью и площадью параллелограмма, а также об инвариантности сравнения площадей. хотя ситуация постоянно меняется.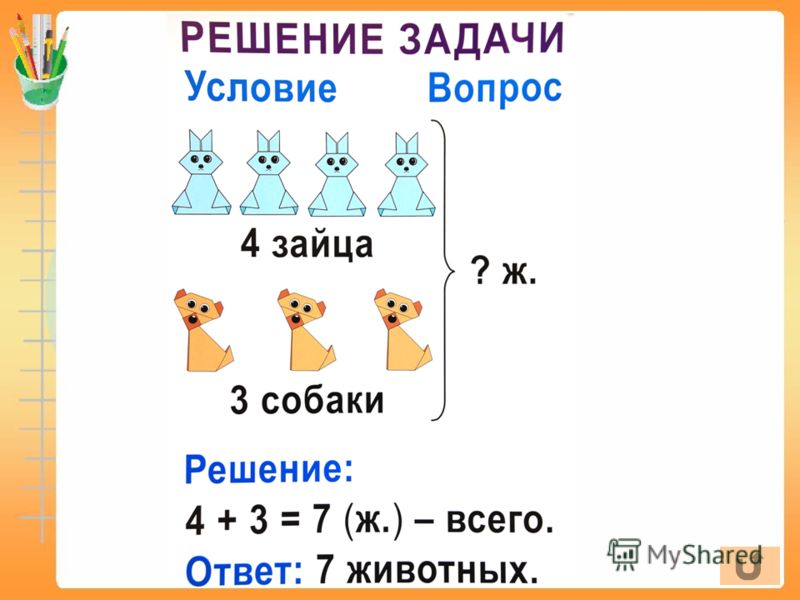
 Он должен иметь отношение к жизни учащихся и, в идеале, должен быть направлен на улучшение мира, в котором мы все живем.
Он должен иметь отношение к жизни учащихся и, в идеале, должен быть направлен на улучшение мира, в котором мы все живем.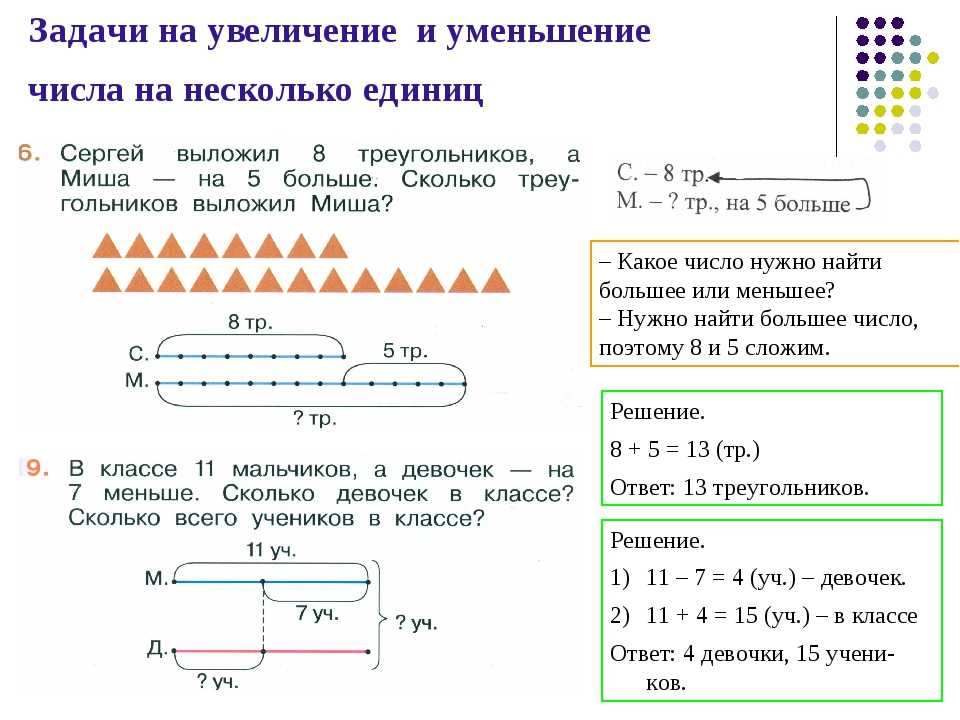
 Вам нужно найти класс посложнее.
Вам нужно найти класс посложнее. Да, проблема сложная. Да вы понятия не имеете, что делать, чтобы решить эту проблему. В какой-то момент вы должны перестать пялиться и начать пробовать что-то новое. Большая часть не будет работать. Примите тот факт, что многие ваши усилия будут потрачены впустую. Но есть шанс, что один из ваших ударов во что-то попадет, и даже если нет, усилия могут подготовить ваш разум к победной идее, когда придет время.
Да, проблема сложная. Да вы понятия не имеете, что делать, чтобы решить эту проблему. В какой-то момент вы должны перестать пялиться и начать пробовать что-то новое. Большая часть не будет работать. Примите тот факт, что многие ваши усилия будут потрачены впустую. Но есть шанс, что один из ваших ударов во что-то попадет, и даже если нет, усилия могут подготовить ваш разум к победной идее, когда придет время.
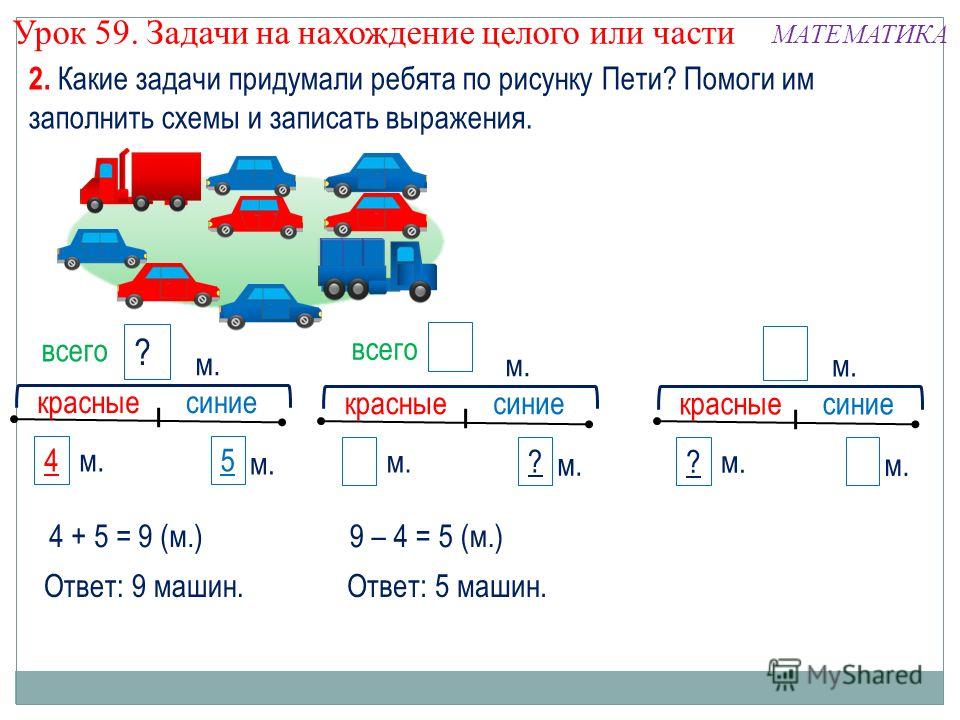 Затем я подумал о том, как сгенерировать этот метод, и путь к решению стал ясен. (Я предполагаю, что некоторые из наших математически продвинутых читателей настолько усвоили процесс решения этого типа диофантова уравнения, что вам не нужно путешествовать с Пифагором, чтобы добраться до него!)
Затем я подумал о том, как сгенерировать этот метод, и путь к решению стал ясен. (Я предполагаю, что некоторые из наших математически продвинутых читателей настолько усвоили процесс решения этого типа диофантова уравнения, что вам не нужно путешествовать с Пифагором, чтобы добраться до него!) Когда я впервые попал в программу математической олимпиады (MOP) на втором курсе, я был выше головы. Я мало что понимал из того, что происходило в классе. Однажды я обратился за помощью к профессору — очень трудно было набраться смелости сделать это. Я ничего не понял из того, что он сказал мне в течение 15 минут, когда он работал со мной наедине. Я просто не мог признать это и просить о дополнительной помощи, поэтому перестал просить. Я мог бы многому, гораздо большему научиться, если бы был более готов признаться людям, которых я просто не понимаю. (Отчасти поэтому в наших классах теперь есть функция, позволяющая учащимся задавать вопросы анонимно.) Преодолей это. Вы застрянете. Вам понадобится помощь. И если вы попросите об этом, вы добьетесь гораздо большего, чем если бы вы этого не сделали.
Когда я впервые попал в программу математической олимпиады (MOP) на втором курсе, я был выше головы. Я мало что понимал из того, что происходило в классе. Однажды я обратился за помощью к профессору — очень трудно было набраться смелости сделать это. Я ничего не понял из того, что он сказал мне в течение 15 минут, когда он работал со мной наедине. Я просто не мог признать это и просить о дополнительной помощи, поэтому перестал просить. Я мог бы многому, гораздо большему научиться, если бы был более готов признаться людям, которых я просто не понимаю. (Отчасти поэтому в наших классах теперь есть функция, позволяющая учащимся задавать вопросы анонимно.) Преодолей это. Вы застрянете. Вам понадобится помощь. И если вы попросите об этом, вы добьетесь гораздо большего, чем если бы вы этого не сделали. Более того, для полного понимания сложных идей требуется много времени. Люди, которых вы знаете, которые кажутся чертовски умными и которые, кажется, придумывают идеи намного быстрее, чем вы могли бы, часто являются людьми, которые просто думали о проблемах гораздо дольше, чем вы. Я использовал эту стратегию в колледже с большим успехом — в первые несколько недель каждого семестра я продвигался вперед во всех своих классах. Поэтому к концу семестра я обдумывал ключевые идеи гораздо дольше, чем большинство моих одноклассников, что значительно облегчало экзамены и тому подобное в конце курса.
Более того, для полного понимания сложных идей требуется много времени. Люди, которых вы знаете, которые кажутся чертовски умными и которые, кажется, придумывают идеи намного быстрее, чем вы могли бы, часто являются людьми, которые просто думали о проблемах гораздо дольше, чем вы. Я использовал эту стратегию в колледже с большим успехом — в первые несколько недель каждого семестра я продвигался вперед во всех своих классах. Поэтому к концу семестра я обдумывал ключевые идеи гораздо дольше, чем большинство моих одноклассников, что значительно облегчало экзамены и тому подобное в конце курса. Ваша другая работа все еще будет там, если вы захотите извлечь из нее позже, и, возможно, она подготовила вас к тому, чтобы извлечь выгоду из идей, которые вы сделаете во время второго раунда.
Ваша другая работа все еще будет там, если вы захотите извлечь из нее позже, и, возможно, она подготовила вас к тому, чтобы извлечь выгоду из идей, которые вы сделаете во время второго раунда. Я был совершенно сбит с толку, когда впервые увидел кучу материала о «модах» в олимпиадном решении — у нас тогда не было интернета, поэтому я не мог легко узнать, насколько проста модульная арифметика! Теперь у вас есть интернет, так что у вас нет оправдания. Если вы решили проблему, не хлопайте себя по спине. Подумайте о ключевых шагах, которые вы сделали, и о том, каковы были признаки того, что вы должны их попробовать. Подумайте о тупиках, которые вы исследовали на пути к решению, и о том, как вы могли их избежать. Эти уроки пригодятся вам позже.
Я был совершенно сбит с толку, когда впервые увидел кучу материала о «модах» в олимпиадном решении — у нас тогда не было интернета, поэтому я не мог легко узнать, насколько проста модульная арифметика! Теперь у вас есть интернет, так что у вас нет оправдания. Если вы решили проблему, не хлопайте себя по спине. Подумайте о ключевых шагах, которые вы сделали, и о том, каковы были признаки того, что вы должны их попробовать. Подумайте о тупиках, которые вы исследовали на пути к решению, и о том, как вы могли их избежать. Эти уроки пригодятся вам позже. Он приписывает этой практике некоторые анекдоты, которые дали Фейнману такую репутацию гения. Это еще одно доказательство того, что быть гением — это очень много усилий, подготовки и способности справляться с трудностями.
Он приписывает этой практике некоторые анекдоты, которые дали Фейнману такую репутацию гения. Это еще одно доказательство того, что быть гением — это очень много усилий, подготовки и способности справляться с трудностями. Для начала, вопрос, относящийся к последней математике, которую вы преподавали в классе, не является проблемой в том смысле, в каком мы будем использовать это слово. Ваши ученики уже знают стратегию, которую можно использовать в таких вопросах.
Для начала, вопрос, относящийся к последней математике, которую вы преподавали в классе, не является проблемой в том смысле, в каком мы будем использовать это слово. Ваши ученики уже знают стратегию, которую можно использовать в таких вопросах. Во-вторых, вы можете не увидеть, как начать работу . У вас может не быть очевидной стратегии , которую вы могли бы использовать. В-третьих, вы можете не знать правильный кусок математики для использования. И в-четвертых, вы можете знать правильную стратегию и правильную математику, но вам может не быть , используя их правильно , иначе вы не сможете понять, как сложить их вместе, чтобы найти решение.
Во-вторых, вы можете не увидеть, как начать работу . У вас может не быть очевидной стратегии , которую вы могли бы использовать. В-третьих, вы можете не знать правильный кусок математики для использования. И в-четвертых, вы можете знать правильную стратегию и правильную математику, но вам может не быть , используя их правильно , иначе вы не сможете понять, как сложить их вместе, чтобы найти решение. Сколько мест у нее сейчас?
Сколько мест у нее сейчас? Сколько игр нужно сыграть?
Сколько игр нужно сыграть?  Что вы могли бы сделать с другими задачами, чтобы приблизить их к интересам ваших учеников?
Что вы могли бы сделать с другими задачами, чтобы приблизить их к интересам ваших учеников? Там он однажды замечает задачу на доске в коридоре, поставленную профессором Джеральдом Ламбо, обладателем медали Филдса. Обладая эйдетической памятью, Уилл запоминает задачу и решает ее перед зеркалом в своей ванной дома в Южном Бостоне. Вернувшись на следующий день в Массачусетский технологический институт, он не может ничего с собой поделать, но анонимно представляет свое решение на доске.
Там он однажды замечает задачу на доске в коридоре, поставленную профессором Джеральдом Ламбо, обладателем медали Филдса. Обладая эйдетической памятью, Уилл запоминает задачу и решает ее перед зеркалом в своей ванной дома в Южном Бостоне. Вернувшись на следующий день в Массачусетский технологический институт, он не может ничего с собой поделать, но анонимно представляет свое решение на доске. Производящая функция для блужданий от i → j
Производящая функция для блужданий от i → j  Все диагональные элементы матрицы равны нулю, поскольку ребра из вершины i в саму себя (петли) не допускаются в простых графах. Для всех ступенчатых обходов длины 1 вдоль множества ребер E это дает нам следующую матрицу смежности для графа G:
Все диагональные элементы матрицы равны нулю, поскольку ребра из вершины i в саму себя (петли) не допускаются в простых графах. Для всех ступенчатых обходов длины 1 вдоль множества ребер E это дает нам следующую матрицу смежности для графа G: Путем матричного умножения, для всех ступенчатых обходов длины 3 от i до j это дает следующую матрицу:
Путем матричного умножения, для всех ступенчатых обходов длины 3 от i до j это дает следующую матрицу: 2). Сумма может быть рассчитана с использованием известного тождества для геометрического степенного ряда, а именно: Согласно Horváth et al (2010) для матрицы M пусть Mᵢⱼ обозначает матрицу, полученную из M удалением i -го столбца и j -й строки. Если мы это сделаем, мы получим матрицу N, ij запись равна
2). Сумма может быть рассчитана с использованием известного тождества для геометрического степенного ряда, а именно: Согласно Horváth et al (2010) для матрицы M пусть Mᵢⱼ обозначает матрицу, полученную из M удалением i -го столбца и j -й строки. Если мы это сделаем, мы получим матрицу N, ij запись равна
 Фото : © 1997 Miramax Pictures
Фото : © 1997 Miramax Pictures Гомоморфно неприводимое дерево — это дерево, не имеющее точек степени 2. Проблема, вероятно, была навеяна статьей Число гомоморфно неприводимых деревьев и других видов Харари и Принса ( 1959).
Гомоморфно неприводимое дерево — это дерево, не имеющее точек степени 2. Проблема, вероятно, была навеяна статьей Число гомоморфно неприводимых деревьев и других видов Харари и Принса ( 1959).
 Например, вместо a × (b + c) можно записать a(b + c). Применив распределительный закон умножения, получим a(b + c) = ab + ac.
Например, вместо a × (b + c) можно записать a(b + c). Применив распределительный закон умножения, получим a(b + c) = ab + ac.

 В этом случае коэффициентом является единица:
В этом случае коэффициентом является единица:
 Найти значение выражения −abc при a=−2, b=−4 и c=−3
Найти значение выражения −abc при a=−2, b=−4 и c=−3 А именно, отдельно перемнóжим числа и отдельно перемнóжим буквы (переменные):
А именно, отдельно перемнóжим числа и отдельно перемнóжим буквы (переменные):

 В итоге получили 12 переменных a
В итоге получили 12 переменных a Стало быть, выражение выглядит следующим образом:
Стало быть, выражение выглядит следующим образом: Привести подобные слагаемые в выражении 6a − 3a + 4a − 8a
Привести подобные слагаемые в выражении 6a − 3a + 4a − 8a То есть сложить коэффициенты и полученный результат умножить на общую буквенную часть. Сделать это нужно для обеих групп слагаемых: для слагаемых, содержащих переменную a и для слагаемых содержащих переменную b.
То есть сложить коэффициенты и полученный результат умножить на общую буквенную часть. Сделать это нужно для обеих групп слагаемых: для слагаемых, содержащих переменную a и для слагаемых содержащих переменную b.
 Поэтому слагаемые, содержащие переменную t, можно записать в начале выражения, а слагаемые содержащие переменную x в конце выражения:
Поэтому слагаемые, содержащие переменную t, можно записать в начале выражения, а слагаемые содержащие переменную x в конце выражения: Если убрать этот ноль из выражения, то значение выражения не изменится, поэтому мы его и уберём. А уберём мы его обычным вычеркиванием слагаемых 3t и (−3t)
Если убрать этот ноль из выражения, то значение выражения не изменится, поэтому мы его и уберём. А уберём мы его обычным вычеркиванием слагаемых 3t и (−3t)
 В итоге получили окончательный ответ 0,5.
В итоге получили окончательный ответ 0,5.
 Другими словами, использовать короткую версию сокращения дроби, в которой мы не расписываем подробно на что был разделен числитель и знаменатель.
Другими словами, использовать короткую версию сокращения дроби, в которой мы не расписываем подробно на что был разделен числитель и знаменатель. Упростить выражение
Упростить выражение Новые множители, которые получаются в результате сокращения предыдущих множителей, тоже допускается сокращать.
Новые множители, которые получаются в результате сокращения предыдущих множителей, тоже допускается сокращать. В первом случае получилось 22, во втором случае 120. Это означает, что упрощение выражения 5a + 4b было выполнено неверно.
В первом случае получилось 22, во втором случае 120. Это означает, что упрощение выражения 5a + 4b было выполнено неверно. Упростить выражение −7,5a − 2,5b + 4a
Упростить выражение −7,5a − 2,5b + 4a Упростить выражение
Упростить выражение Если значение в обоих выражениях будет одинаковым, то это означает, что выражение упрощено верно.
Если значение в обоих выражениях будет одинаковым, то это означает, что выражение упрощено верно. Например, пусть a = 1 и b = 2
Например, пусть a = 1 и b = 2

 Найдите значение выражения при
Найдите значение выражения при Приведите подобные слагаемые в следующем выражении:
Приведите подобные слагаемые в следующем выражении: Формула
Формула Выполнение этих действий называется вычислением значения числового выражения. Перед записью значения числового выражения ставят знак равенства «=». В таблице 1 приведены примеры числовых выражений и их значений.
Выполнение этих действий называется вычислением значения числового выражения. Перед записью значения числового выражения ставят знак равенства «=». В таблице 1 приведены примеры числовых выражений и их значений.


 В этом тесте содержится 70 задач. Но решать задачи можно по выбору, для этого есть оценочная таблица, где указаны простые задачи и посложнее. Ниже приведён тест.
В этом тесте содержится 70 задач. Но решать задачи можно по выбору, для этого есть оценочная таблица, где указаны простые задачи и посложнее. Ниже приведён тест. В каждом из рядов палубы m мест, рядов на палубе на n больше, чем мест в ряду
В каждом из рядов палубы m мест, рядов на палубе на n больше, чем мест в ряду
 Фасетный тест. Числовые и буквенные выражения (ответы под заданиями)
Фасетный тест. Числовые и буквенные выражения (ответы под заданиями) Про порядок выполнения действий можно прочитать в теме
Про порядок выполнения действий можно прочитать в теме 

 Например:
Например:
 К 30 прибавляем 2.
К 30 прибавляем 2.

 Урок 6,
Петерсон, Учебник, часть 2
Урок 6,
Петерсон, Учебник, часть 2
 Вариант 1. № 4,
Моро, Волкова, Проверочные работы
Вариант 1. № 4,
Моро, Волкова, Проверочные работы
 Урок 30,
Петерсон, Учебник, часть 1
Урок 30,
Петерсон, Учебник, часть 1
 Запись условий задач с их помощью приводит к появлению так называемых математических выражений. Можно говорить про числовые, буквенные выражения и математические выражения с переменными. Для удобства и одни, и вторые и третьи называются просто выражениями. В этой статье мы дадим определения и по порядку рассмотрим каждый тип математических выражений.
Запись условий задач с их помощью приводит к появлению так называемых математических выражений. Можно говорить про числовые, буквенные выражения и математические выражения с переменными. Для удобства и одни, и вторые и третьи называются просто выражениями. В этой статье мы дадим определения и по порядку рассмотрим каждый тип математических выражений.
 Например, запись 1,75+2 означает, что к целой части числа 1,75прибавляется число 2.
Например, запись 1,75+2 означает, что к целой части числа 1,75прибавляется число 2.  Буквенное выражение должно содержать по крайней мере одну букву.
Буквенное выражение должно содержать по крайней мере одну букву.
 Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.










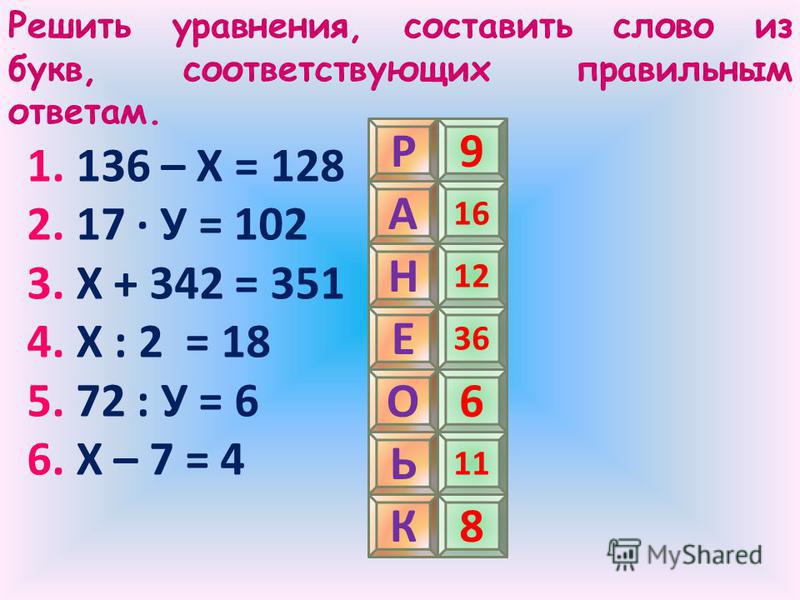
 Мы не согласны. Искусство написания официальных и неформальных писем живет и здравствует, и если в эпоху электронной почты и социальных сетей написание писем происходит реже, это только увеличивает влияние хорошо написанного личного сообщения. Изучите основные типы официальных писем и способы их написания с примерами писем.
Мы не согласны. Искусство написания официальных и неформальных писем живет и здравствует, и если в эпоху электронной почты и социальных сетей написание писем происходит реже, это только увеличивает влияние хорошо написанного личного сообщения. Изучите основные типы официальных писем и способы их написания с примерами писем. Официальные письма имеют формальный тон и имеют определенный формат. Неофициальные письма тоже не нужны.
Официальные письма имеют формальный тон и имеют определенный формат. Неофициальные письма тоже не нужны.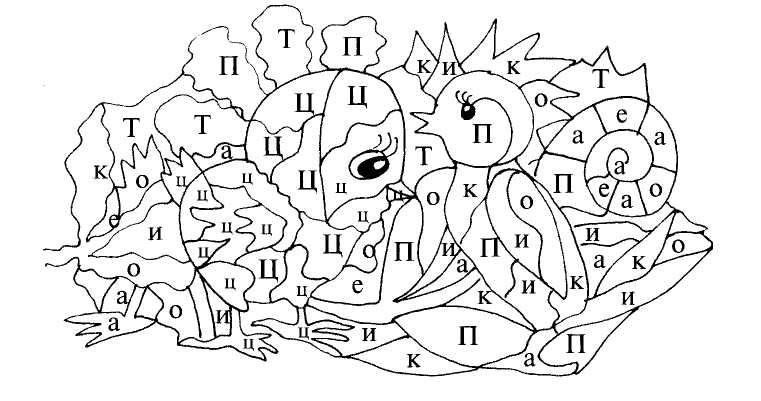 В то же время вы должны быть уверены, что ваша критика носит конструктивный характер, а тон — вежливый.
В то же время вы должны быть уверены, что ваша критика носит конструктивный характер, а тон — вежливый. Для профессионального электронного письма важно сохранять профессиональный тон и не быть слишком длинным. Вы хотите быть ясным, кратким и по существу. Однако также важно обязательно указать имя, приветствие, текст и приветствие, включая ваши учетные данные.
Для профессионального электронного письма важно сохранять профессиональный тон и не быть слишком длинным. Вы хотите быть ясным, кратким и по существу. Однако также важно обязательно указать имя, приветствие, текст и приветствие, включая ваши учетные данные. 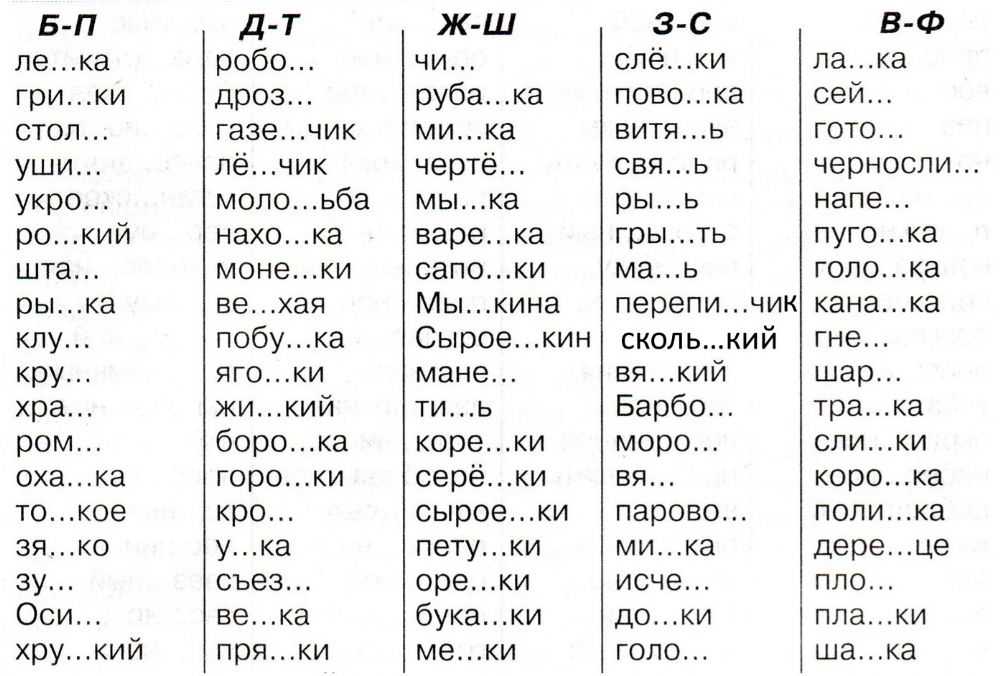 Старайтесь, чтобы ваш тон был легким и профессиональным, и подчеркивайте свой опыт.
Старайтесь, чтобы ваш тон был легким и профессиональным, и подчеркивайте свой опыт. Мы обеспечим вас обоими. Ознакомьтесь с советами о том, как написать рекомендацию для максимального эффекта.
Мы обеспечим вас обоими. Ознакомьтесь с советами о том, как написать рекомендацию для максимального эффекта.

 Элисон основала CareerToolBelt.com и является экспертом в этой области уже более 20 лет.
Элисон основала CareerToolBelt.com и является экспертом в этой области уже более 20 лет.
 Укажите свою контактную информацию в конце письма, после вашей подписи.
Укажите свою контактную информацию в конце письма, после вашей подписи.
 Фамилия,
Фамилия, Фамилия,
Фамилия,