Как правильно рассчитать свой пульс и пульсовую зону
Много ли Вы знаете людей, которые перед тем, как начать заниматься бегом, идут к кардиологу и обследуют свое сердце? Увы, на такой важный момент обращают внимание только те, кто занимается бегом профессионально. Однако, до того, как перейти к тренировкам, Вам просто необходимо узнать, какой потенциал у Вашей сердечной мышцы, какие нагрузки для нее норма, а какие недопустимы.
Эта информация повысит Вашу эффективность на тренировках, поможет добиться более высокой результативности, а так же сохранит вас от получения инфаркта только потому, что в ясный июльский день Вы решите, что сегодня самый подходящий день, чтобы одолеть кросс в 20 километров. Кроме того, ЧСС (частота сердечных сокращений) — даст возможность определить для Вас идеальный темп бега для того, чтобы эффективно сбросить вес.
Достаточно доступно расписано в книге известного тренера из Новой Зеландии Артура Лидьярда «Бег с Лидьярдом». Он очень точно и доступно описывает работу сердечной мышцы и о преобразованиях, которые происходят с ней во время кардиотренировок. В этой статье Вы найдете короткие и наиболее важные выдержки из этой книги о принципах работы сердца. Возможно, материал станет для Вас хорошим помощником в определении своих сердечных зон и составления оптимального плана занятий.
Он очень точно и доступно описывает работу сердечной мышцы и о преобразованиях, которые происходят с ней во время кардиотренировок. В этой статье Вы найдете короткие и наиболее важные выдержки из этой книги о принципах работы сердца. Возможно, материал станет для Вас хорошим помощником в определении своих сердечных зон и составления оптимального плана занятий.
У каждой возрастной категории есть свои, так называемые, пульсовые зоны. Однако, если пульс у Вас немного выше предложенных рамок, это не повод для сильных переживаний. Но при этом обязательно нужно обратить внимание, если Ваш пульс значительно выше этих параметров. Самый лучший вариант привести его в норму – это правильные кардионагрузки. Сердце представляет собой мышцу, которая, сокращаясь, перекачивает кровь по нашему телу. А раз это мышца, то ее можно натренировать как любую другую. Вот здесь и приходит очередь кардиотренировок. Если Вы будете регулярно заниматься бегом, то спустя некоторое время частота Вашего пульса начнет снижаться. Только представьте, у профессиональных бегунов, которые часто пробегают марафоны, пульс в абсолютно спокойном состоянии находится на уровне около 37 ударов в минуту. Чтобы лучше понять эту величину, достаточно помнить, что среднестатистическая норма у обычного человека – 60-100 ударов, а у спортсменов с хорошей физической подготовкой – около 40-60.
Только представьте, у профессиональных бегунов, которые часто пробегают марафоны, пульс в абсолютно спокойном состоянии находится на уровне около 37 ударов в минуту. Чтобы лучше понять эту величину, достаточно помнить, что среднестатистическая норма у обычного человека – 60-100 ударов, а у спортсменов с хорошей физической подготовкой – около 40-60.
Что касается нормальных показателей ЧСС у разных возрастных категорий, то Вы можете ознакомиться с ними ниже:
- Новорождённые от 0 до 3 месяцев — 100-150 ударов в минуту;
- Младенцы от 3 до 6 месяцев — 90–120 ударов в минуту;
- Младенцы от 6 до 12 месяцев — 80-120 ударов в минуту;
- Дети от 1 года до 10 лет — 70–130 ударов в минуту;
- Дети старше 10 лет и взрослые, включая пожилых — 60–100 ударов в минуту;
- Профессиональные спортсмены — 40–60 ударов в минуту.
Каждое человеческое сердце имеет определенный резервный запас на жизнь, который практически никто из нас не использует до конца. Лидьярд, к примеру, утверждает, что этот резерв сохраняется, в том числе, и после нескольких сердечных приступов. Существуют вполне ясные симптомы сердечного перенапряжения – боль в груди и сильная отдышка. Если Вы ощутили нечто подобное, необходимо немного снизить нагрузку.
Лидьярд, к примеру, утверждает, что этот резерв сохраняется, в том числе, и после нескольких сердечных приступов. Существуют вполне ясные симптомы сердечного перенапряжения – боль в груди и сильная отдышка. Если Вы ощутили нечто подобное, необходимо немного снизить нагрузку.
Наше сердце и занятия бегом
Какие же процессы происходят с нашей сердечной мышцей и организмом, во время занятий бегом? Во-первых, частота пульса начинает выравниваться и падать – организм совершает попытки сохранить баланс. Если сердце работает достаточно хорошо, значит, и остальные органы останутся в порядке. Если даже в состоянии покоя Ваш пульс высокий, значит в крови слишком много холестерина, а сосуды недостаточно эластичны.
Во время занятий бегом у Вас увеличивается кровоток, повышается давление в сосудах, температура тела тоже растет. Такое давление даст возможность организму вымыть из артерий некоторые остатки непереработанного жира и других продуктов распада. Если Вы еще немного увеличите нагрузку, то организм возьмет лишний холестерин из крови в качестве «топлива» для выработки энергии.
Спустя некоторое время таких нагрузок, Ваши артерии и кровь постепенно очистятся от всего ненужного, станут более эластичными. Их просветы станут шире, а организм привыкнет к таким нагрузкам и пропадет необходимость так часто гнать кровь, а это значит, что снизится частота пульса. Продолжив тренировки и дальше, Вы дадите возможность Вашему сердцу увеличиться.
Помимо того, в нашем организме великое множество капилляров, которые проникают во все уголочки тела. Они тоже освобождаются и очищаются, появляется все больше свободных путей для притоков крови, а это значит, что ко всем другим органам значительно увеличивается приток кислорода и необходимых элементов. Другими словами, весь Ваш организм словно оживает, пробуждается как деревья после зимы!
Опять же, из статистики, у человека, который в силу каких-либо обстоятельств ведет малоподвижный образ жизни, сердечнососудистая система примерно в 20 раз слабее, чем у того, кто регулярно проводит кардионагрузки.
Дополнительно к тому, что сердце у Вас будет как мотор нового Феррари, очищенная кровь так же повлияет на общий тонус. Повысится количество эритроцитов в крови, они в свою очередь будут активно перемещать по сосудам гемоглобин, а тот начнет активно вырабатывать гликоген. Этот самый гликоген, так сказать, самое качественное горючее для тела. То, как организм может его вырабатывать, напрямую влияет на количество кислорода, которое кровь переносит по телу. Если его недостаточно, то наступает «кислородное голодание», и организм начинает очень быстро истощаться, если физической подготовки человека недостаточно.
Повысится количество эритроцитов в крови, они в свою очередь будут активно перемещать по сосудам гемоглобин, а тот начнет активно вырабатывать гликоген. Этот самый гликоген, так сказать, самое качественное горючее для тела. То, как организм может его вырабатывать, напрямую влияет на количество кислорода, которое кровь переносит по телу. Если его недостаточно, то наступает «кислородное голодание», и организм начинает очень быстро истощаться, если физической подготовки человека недостаточно.
Что нужно, чтобы определить свой максимальный ЧСС
Здесь Вам помогут очень простые расчеты. Вы просто берете цифру 220, и вычитаете из нее Ваш возраст.
ЧССmax= 220 — возраст
На просторах Интернета Вы так же сможете найти массу ресурсов-калькуляторов, которые просчитают для Вас пульсовые зоны.
Все что Вам необходимо сделать, это два параметра – количество полных лет и количество ударов пульса в спокойном состоянии. Далее приложение само рассчитает для Вас пульсовые зоны и даст важные рекомендации о нагрузках для каждой из них.
Есть, к примеру, зона разминки — здесь тренировки проводят с частотой пульса около 50%-60% от максимального ЧСС. Вы разогреваетесь, либо восстанавливаетесь после предыдущей тренировки, пульс постепенно нормализуется, кровь начинает перерабатывать холестерин.
Лишние жировые отложения, а значит и килограммы начинают уходить в тот момент, когда пульс переходит на 60%-70% от максимальной частоты. Нагрузки в этой зоне вполне терпимы, занятия приносят тонус, не изнуряют. Большая часть калорий, которые организм расходует в этой пульсовой зоне, берутся из жировых запасов.
Так называемая аэробная пульсовая зона работает, когда пульс составляет 70%-80% от максимального показателя. Здесь активизируются легкие, это связано с тем, что организм начинает усиленно потреблять кислород. Именно на фоне этого начинается рост сердечной мышцы. Калорий при этом сжигается больше, но если в предыдущей пульсовой зоне около 85% из них были из жировых запасов, то здесь только 50%.
Анаэробная пульсовая зона — это 80%-90% от максимума. Занятия в таком режиме активно улучшают вашу форму, но всего лишь 15% калорий организм будет брать из жировых запасов.
Занятия в таком режиме активно улучшают вашу форму, но всего лишь 15% калорий организм будет брать из жировых запасов.
Последняя, максимально допустимая зона — это тренировки на пределах возможностей сердечной мышцы – 90%-100%, максимально высокие показатели ЧСС. Тренировать в такой зоне могут исключительно хорошо подготовленные профессиональные спортсмены, и притом весьма недолго.
Итак, расчеты для определения максимального ЧСС:
- Максимальная частота пульса: 220 — (возраст) = количество ударов в минуту.
- Выбираем желаемую пульсовую зону. Например, 60%-70% — зона активного жиросжигания. В некоторых источниках указывают 65%-75%.
- Делаем расчет своей пульсовой зоны: ЧСС max (см пункт 1) * 0,6 = нижний порог, а так же ЧСС max * 0,7 = верхний порог. Это значит, что для того, чтобы Ваш организм сжигал жировые клетки, Ваш пульс не должен выходить за рамки первой и второй цифр.
Самый эффективный способ измерить частоту пульса в состоянии покоя – это замерить показатель утром, сразу после пробуждения. Или же необходимо находиться в состоянии полного покоя не менее 10 минут перед тем, как начать замерять. Так же есть очень много приложений для смартофонов, которые могут измерить для Вас этот показатель как на базе iOS, так и на базе Android.
Или же необходимо находиться в состоянии полного покоя не менее 10 минут перед тем, как начать замерять. Так же есть очень много приложений для смартофонов, которые могут измерить для Вас этот показатель как на базе iOS, так и на базе Android.
Чтобы знать и контролировать свою частоту сердечных сокращений во время занятий спортом, существуют специальные устройства. Это могут быть датчики пульса, которые переводят данные непосредственно на смартфон или персональный компьютер. Есть так же специальные часы для спорта с пульсометрами, которые всегда будут выводить Ваш пульс прямо на дисплей у Вас на руке. Вы можете ознакомиться с огромным разнообразием подобных устройств и приобрести одно из них на сайте нашего магазина www.magazin-sportlife.ru. Тренируйтесь эффективно и с удовольствием!
Если хотите получить профессиональную консультацию по подбору подходящего пульсометра, звоните по телефону:
+7 (812) 951-57-82 (СПб), +7 (499) 705-28-56 (Москва).
Просмотров 117. 4K
4K
Помощь студентам в учёбе от Людмилы Фирмаль
Здравствуйте!
Я, Людмила Анатольевна Фирмаль, бывший преподаватель математического факультета Дальневосточного государственного физико-технического института со стажем работы более 17 лет. На данный момент занимаюсь онлайн обучением и помощью по любыми предметам. У меня своя команда грамотных, сильных бывших преподавателей ВУЗов. Мы справимся с любой поставленной перед нами работой технического и гуманитарного плана. И не важно: она по объёму на две формулы или огромная сложно структурированная на 125 страниц! Нам по силам всё, поэтому не стесняйтесь, присылайте.
Срок выполнения разный: возможно онлайн (сразу пишите и сразу помогаю), а если у Вас что-то сложное – то от двух до пяти дней.
Для качественного оформления работы обязательно нужны методические указания и, желательно, лекции. Также я провожу онлайн-занятия и занятия в аудитории для студентов, чтобы дать им более качественные знания.
Моё видео:
youtube.com/embed/4sKc0lcxi7g» frameborder=»0″ allow=»accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»/>Вам нужно написать сообщение в Telegram . После этого я оценю Ваш заказ и укажу срок выполнения. Если условия Вас устроят, Вы оплатите, и преподаватель, который ответственен за заказ, начнёт выполнение и в согласованный срок или, возможно, раньше срока Вы получите файл заказа в личные сообщения.
Сколько может стоить заказ?Стоимость заказа зависит от задания и требований Вашего учебного заведения. На цену влияют: сложность, количество заданий и срок выполнения. Поэтому для оценки стоимости заказа максимально качественно сфотографируйте или пришлите файл задания, при необходимости загружайте поясняющие фотографии лекций, файлы методичек, указывайте свой вариант.
Какой срок выполнения заказа?Минимальный срок выполнения заказа составляет 2-4 дня, но помните, срочные задания оцениваются дороже.
Сначала пришлите задание, я оценю, после вышлю Вам форму оплаты, в которой можно оплатить с баланса мобильного телефона, картой Visa и MasterCard, apple pay, google pay.
Какие гарантии и вы исправляете ошибки?В течение 1 года с момента получения Вами заказа действует гарантия. В течении 1 года я и моя команда исправим любые ошибки в заказе.
Качественно сфотографируйте задание, или если у вас файлы, то прикрепите методички, лекции, примеры решения, и в сообщении напишите дополнительные пояснения, для того, чтобы я сразу поняла, что требуется и не уточняла у вас. Присланное качественное задание моментально изучается и оценивается.
Теперь напишите мне в Telegram или почту и прикрепите задания, методички и лекции с примерами решения, и укажите сроки выполнения. Я и моя команда изучим внимательно задание и сообщим цену.
Если цена Вас устроит, то я вышлю Вам форму оплаты, в которой можно оплатить с баланса мобильного телефона, картой Visa и MasterCard, apple pay, google pay.
Мы приступим к выполнению, соблюдая указанные сроки и требования. 80% заказов сдаются раньше срока.
После выполнения отправлю Вам заказ в чат, если у Вас будут вопросы по заказу – подробно объясню. Гарантия 1 год. В течении 1 года я и моя команда исправим любые ошибки в заказе.
youtube.com/embed/g4ioDc7sLwU» frameborder=»0″ allow=»accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»/>
youtube.com/embed/zW5JhiZ4140″ frameborder=»0″ allow=»accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»/>
Можете смело обращаться к нам, мы вас не подведем. Ошибки бывают у всех, мы готовы дорабатывать бесплатно и в сжатые сроки, а если у вас появятся вопросы, готовы на них ответить.
Ошибки бывают у всех, мы готовы дорабатывать бесплатно и в сжатые сроки, а если у вас появятся вопросы, готовы на них ответить.
В заключение хочу сказать: если Вы выберете меня для помощи на учебно-образовательном пути, у вас останутся только приятные впечатления от работы и от полученного результата!
Жду ваших заказов!
С уважением
Пользовательское соглашение
Политика конфиденциальности
Лучший ответ по мнению автора | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Химия
| Похожие вопросы |
Решено
реагирует ли уксусная кислота с гидроксидом меди (2)? Если реагирует, то какие получаются продукты реакции? Объясните пожалуйста.
Составить схемы электролиза водных растворов h3SO4, CuCl2, Pb(NO3)2 с платиновыми электродами
В каком году была сформулирована теория — предшественница кислородной теории горения.
Как изменится скорость реакции 2NO + O2 = 2NO2, если концентрации исходных веществ увеличить в 4 раза?
Решено
вычислите константу и степень гидролиза 0,01 н. раствора нитрата аммония
Пользуйтесь нашим приложением
Карточки-задания по математике 3-4 класс | Материал по математике (3, 4 класс):
Дидактический материал
«Карточки-задания по математике
для организации математического диктанта в 3-4 классах»
Карточка №1
Первый вариант. | Второй вариант. |
1). Вычислить: 3х6:2= | 1).Вычислить: 4х3:2= |
2). 97 уменьшить на 60. | 2).84 уменьшить на 50. |
3). Найти сумму чисел 26 и 70. | 3). Найти сумму чисел 34 и 40. |
4). Найти разность чисел 95 и 30. | 4). Найти разность чисел 87 и 60. |
5). Уменьшаемое 74, вычитаемое 20. Найти разность. | 5). Уменьшаемое 82, вычитаемое 30. Найти разность. |
6). Первое слагаемое 46, второе слагаемое 30. Найти сумму. | 6). Первое слагаемое 54, второе слагаемое 20. Найти сумму. |
7). | 7). 28 увеличить на 40. |
8). 40 да еще 50 получится… | 8). 30 да еще 60 получится… |
9). 100 без 80 получится… | 9). 90 без 60 получится… |
10). Найти произведение чисел 6 и 10. | 10). Найти произведение чисел 8 и 10. |
11). Первый множитель 2, второй множитель 6. Найти произведение. | 11). Первый множитель 3, второй множитель 4. Найти произведение. |
12). Найти произведение чисел 3 и 5. | 12). Найти произведение чисел 2 и 7. |
13). К какому числу прибавили 60 и получили 75? | 13). |
14). Какое число прибавили к 56 и получили 76? | 14). Какое число прибавили к 34 и получили 94? |
Карточка №2
Первый вариант. | Второй вариант. |
1). Найти разность чисел: 67 и 42. | 1). Найти разность чисел: 89 и 57. |
2). Найти сумму чисел: 34 и 22. | 2). Найти Сумму чисел: 23 и 45. |
3). Вычислить: 90-40+20. | 3). Вычислить: 70-30+50. |
4). Первое слагаемое 24, второе слагаемое 42. Найти сумму. | 4). Первое слагаемое 36, второе слагаемое 43. |
5). Уменьшаемое 86, вычитаемое 52. Найти разность. | 5). Уменьшаемое 78, вычитаемое 46. Найти разность. |
6). 32 увеличить на 43. | 6). 54 увеличить на 23. |
7). Вычислить: 3+4-5+8-6+2= | 7). Вычислить: 5+4-6+7-8+3= |
8). Чему равна сумма чисел 45 и 50? | 8). Чему равна сумма чисел 37 и 60? |
9). Чему равна разность чисел: 92 и 70? | 9). Чему равна разность чисел: 84 и 50? |
10). 57 уменьшить на 26. | 10). 69 уменьшить на 42. |
11). Какое число уменьшили на 67 и получили 97? | 11). |
12). Какое число увеличили на 62 и получили 92? | 12). Какое число увеличили на 57 и получили 77? |
13). К какому числу прибавили 42 и получили 95? | 13). К какому числу прибавили 53 и получили 86? |
14). Из какого числа вычли 35 и получили 23? | 14). Из какого числа вычли 43 и получили 34? |
Карточка №3
Первый вариант. | Второй вариант. |
1). Найти произведение чисел: 3 и 9. | 1). Найти произведение чисел: 8 и 3. |
2). Первый множитель 2, второй 8. | 2). Первый множитель 7, второй — 3. Найти произведение. |
3).Делимое 18, делитель 3. Найти частное. | 3). Делимое 12, делитель 3. Найти частное. |
4). Найти частное чисел: 14 и 7. | 4). Найти частное чисел: 18 и 2. |
5). Во сколько раз 10 больше 2? | 5). Во сколько раз 12 больше 2? |
6). Найти сумму чисел: 44 и 35. | 6).Найти сумму чисел: 25 и 53. |
7). Найти разность чисел: 82 и 50. | 7). Найти разность чисел: 76 и 34. |
8). Вычислить: 15:5х9= | 8). |
9). Какое число умножили на 8 и получили24? | 9). Какое число умножили на 9 и получили 27? |
10). Вычислить: 70+30-60= | 10). Вычислить: 60+40-70= |
11). Во сколько раз 2 меньше 18? | 11). Во сколько раз 2 меньше 16? |
12). На сколько 87 больше 60? | 12). На сколько 76 больше 40? |
13). Вычислить: 7+ 4-6+8-9= | 13). Вычислить: 5+8-9+7-6= |
14). 5см 6мм=…мм | 14). 4дм 8см=…см |
Карточка №4
Первый вариант. | Второй вариант. |
1). Найти сумму чисел: 26 и 50. | 1).Найти сумму чисел: 32 и 60. |
2). Найти разность чисел: 84 и 60. | 2). Найти разность чисел: 73 и 50. |
3). Первое слагаемое 43, второе слагаемое 7. Найти сумму. | 3). Первое слагаемое 52, второе слагаемое 8. Найти сумму. |
4). Уменьшаемое 90, вычитаемое 8. Найти разность. | 4). Уменьшаемое 70, вычитаемое 7. Найти разность. |
5). 58 уменьшить на 32. | 5). 69 уменьшить на 27. |
6). 35 увеличить на 43. | 6). |
7).На сколько 18 больше 7? | 7). На сколько 19 больше 6? |
8). 12 увеличить на 7. | 8). 13 увеличить на 5. |
9). На сколько 58 больше 42? | 9). На сколько 69 больше 53? |
10). Найти произведение чисел: 4 и 3. | 10). Найти произведение чисел: 6 и 3. |
11). Найти частное чисел: 21 и 7. | 11). Найти частное чисел: 27 и 9. |
12). Первый множитель 8, второй множитель 2. Найти произведение. | 12). Первый множитель 6, второй множитель 2. Найти произведение. |
13). | 13). К какому числу прибавили 7 и получили 40? |
14). Найти разность чисел 69 и 27. | 14). Найти разность чисел 58 и 32. |
Карточка №5
Первый вариант. | Второй вариант. |
1). Найти произведение чисел: 4 и 7. | 1). Найти произведение чисел: 6 и 4. |
2). Найти частное чисел: 36 и 9. | 2). Найти частное чисел: 32 и 8. |
3). Во сколько раз 16 больше 4? | 3). Во сколько раз 20 больше 5? |
4). 56 уменьшить на 40. | 4). |
5). Первое слагаемое 32, второе 60. Найти сумму. | 5). Первое слагаемое 24, второе 70. Найти сумму. |
6). Уменьшаемое 89, вычитаемое 57. Найти разность. | 6). Уменьшаемое 98, вычитаемое 65. Найти разность. |
7). Найти разность чисел: 60 и 8. | 7). Найти разность чисел: 70 и 6. |
8). Найти сумму чисел: 24 и 63. | 8). Найти сумму чисел: 32 и 56. |
9). Во сколько раз 27 больше 9? | 9). Во сколько раз 21 больше 7? |
10). Вычислить: 70-40+60-50+20= | 10). Вычислить: 90-70+40-50+90= |
11). | 11). Первый множитель 4, второй множитель 3. Найти произведение. |
12). Делимое 24, делитель 8. Найти частное. | 12). Делимое 27. Делитель 9. Найти частное. |
13). Какое число умножили на 6 и получили 24? | 13). Какое число умножили на 7 и получили 28? |
14). Какое число разделили на 7 и получили 4? | 14). Какое число разделили на 8 и получили 4? |
Карточка №6
Первый вариант. | Второй вариант. |
1). Первый множитель 9, второй множитель 3. Найти произведение. | 1). |
2). Найти произведение чисел 5 и 7. | 2). Найти произведение чисел 8 и 5. |
3). 45 уменьшить в 5 раз. | 3). 20 уменьшить в 4 раза. |
4). Делимое 18, делитель 6. Найти частное. | 4). Делимое 21, делитель 7. Найти частное. |
5). 4 увеличить в 9 раз. | 5). 6 увеличить в 4 раза. |
6). Найти частное чисел: 30 и 5. | 6).. Найти частное чисел: 28 и 7. |
7). Какое число умножили на 3 и получили 18? | 7). Какое число умножили на 4 и получили 12? |
8). | 8). Во сколько раз 9 меньше 27? |
9). Какое число умножили на 8 и получили 32? | 9). Какое число умножили на 5 и получили 45? |
10). Какое число разделили на 7 и получили 3? | 10). Какое число разделили на 9 и получили 4? |
11). Найти сумму чисел: 47 и 30. | 11). Найти сумму чисел: 52 и 40. |
12). Найти разность чисел: 98 и 60. | 12). Найти разность чисел: 87 и 70. |
13). На сколько 56 больше 25? | 13). На сколько 63 больше 31? |
14). На сколько 56 меньше 89? | 14). |
Карточка №7
Первый вариант. | Второй вариант. |
1). Найти сумму чисел: 17 и 16 | 1). Найти сумму чисел: 18 и 14. |
2). Первое слагаемое 36, второе слагаемое 44. Найти сумму. | 2). Первое слагаемое 28, второе слагаемое 52. Найти сумму. |
3). Найти разность чисел: 97 и 35. | 3). Найти разность чисел: 89 и 56. |
4). Первый множитель 8, второй множитель 6. Найти произведение. | 4). Первый множитель 7, второй множитель 6. Найти произведение. |
5).Уменьшаемое 78, вычитаемое 36. | 5).Уменьшаемое 78, вычитаемое 42.Найти разность. |
6). Найти произведение чисел: 6 и 9. | 6). Найти произведение чисел: 8 и 6. |
7). Делимое 54, делитель 6. Найти частное. | 7). Делимое 36, делитель 6. Найти частное. |
8). Найти частное чисел: 42 и 7. | 8). Найти частное чисел: 48 и 6. |
9). На сколько 70 больше 45? | 9). На сколько 60 больше 37? |
10). Во сколько раз 40 больше 8? | 10). Во сколько раз 27 больше 9? |
11). Вычислить: 20+50-30+60-80= | 11). |
12). Какое число разделили на 6 и получили 7? | 12). Какое число разделили на 6 и получили 4? |
13). Вычислить: 7+8-6+4-5+3= | 13). Вычислить: 6+7-8+9-5+3= |
14). Какое число умножили на 4 и получили 36? | 14). Какое число умножили на 6 и получили 30? |
Карточка №8
Первый вариант. | Второй вариант. |
1). Делимое 21, делитель 3. Найти частное. | 1). Делимое 24, делитель 6. Найти частное. |
2). Во сколько раз 63 больше 6? | 2). Во сколько раз 48 больше 8? |
3). | 3). Вычислить: 60+30-70+40+40-90= |
4). Найти произведение чисел: 5 и 9. | 4). Найти произведение чисел: 6 и 4. |
5). Первый множитель 8, второй множитель 2.Найти произведение. | 5). Первый множитель 9. Второй множитель 4. Найти произведение. |
6). Уменьшаемое 80, вычитаемое 59. Найти разность. | 6).Уменьшаемое 60, вычитаемое 26. Найти разность. |
7). Вычислить: 6+5-7+8-3= | 7). Вычислить: 9+4-6+8-9= |
8). Найти сумму чисел:34 и 63. | 8). Найти сумму чисел: 47 и 21. |
9). | 9). Какое число прибавили к 46 и получили 98? |
10). На сколько 48 больше 15? | 10). На сколько 57 больше 13? |
11). Какое число больше 34 на 6? | 11). Какое число больше 53 на 7? |
12). Какое число в 6 раз меньше 54? | 12). Какое число в 8 раз меньше 48? |
13). Первое слагаемое 46, второе слагаемое 54. Найти сумму. | 13). Первое слагаемое 38, второе слагаемое 52. Найти сумму. |
14). Вычислить: 24:4х3:2х4= | 14). Вычислить: 36:6х3:2х5= |
Карточка №9
Первый вариант. | Второй вариант. |
1). Уменьшаемое 93, вычитаемое 70. Найти разность. | 1). Уменьшаемое 82, вычитаемое 50. Найти разность. |
2). К какому числу прибавили 50 и получили 85? | 2). К какому числу прибавили 60 и получили 87? |
3). Из какого числа вычли 6 и получили 64? | 3). Из какого числа вычли 7 и получили 73? |
4). Чему равно первое слагаемое, если второе слагаемое равно 8, а сумма равна 30? | 4). Чему равно первое слагаемое, если второе слагаемое равно 6, а сумма равна 40? |
5). Найти разность чисел: 87 и 32. | 5). Найти разность чисел: 98 и 46. |
6). Вычислить: 4+8-7+6-9= | 6). Вычислить: 5+7-8+9-6= |
7). Вычислить: 20+50-60+80-60= | 7). Вычислить: 30+40-50+60-20= |
8). Найти сумму чисел: 43 и 54. | 8). Найти сумму чисел: 34 и 65. |
9). 82 уменьшить на 50. | 9). 93 уменьшить на 70. |
10). Какое число увеличили на 6 и получили 40? | 10). Какое число увеличили на 8 и получили 30? |
11). Какое число уменьшили на 46 и получили 52? | 11). Какое число уменьшили на 32 и получили 55? |
12). Вычислить:5+7-8+9-6= | 12). |
13). Вычислить: 30+40-50+60-20= | 13). Вычислить: 20+50-60+80-60= |
14). 34 увеличить на 65. | 14). 43 увеличить на 54. |
Карточка №10
Первый вариант. | Второй вариант. |
1). Найти разность чисел: 94 и 60. | 1).Найти разность чисел: 82 и 50. |
2). 5 увеличить в 4 раза. | 2). 6 увеличить в 5 раз. |
3). Уменьшаемое 84, вычитаемое 23. Найти разность. | 3). Уменьшаемое 73, вычитаемое 42. Найти разность. |
4). | 4). Найти частное чисел: 42 и 6. |
5). 27 увеличить на 40. | 5). 25 увеличить на 60. |
6). Из какого числа вычли 4 и получили 76? | 6). Из какого числа вычли 3 и получили 67? |
7). Какое число умножили на 9 и получили63? | 7). Какое число умножили на 9 и получили 54? |
8). 56 уменьшить в 8 раз. | 8). 49 уменьшить в 7 раз. |
9). Чему равно произведение, если первый множитель 6, а второй множитель 5? | 9). Чему равно произведение, если первый множитель 8, а второй множитель 6? |
10). | 10). Какое число уменьшили на 23 и получили 61? |
11). Какое число разделили на 6 и получили 7? | 11).Какое число разделили на 8 и получили6? |
12). Найти произведение чисел: 8 и 4. | 12). Найти произведение чисел: 7 и 4. |
13). 70 уменьшить на 3. | 13). 80 уменьшить на 4. |
14). Вычислить: 3+4-6+5-2+8= | 14). Вычислить: 2+7-6+4-5+8= |
Карточка №11
Первый вариант. | Второй вариант. |
1). Первый множитель 6, второй множитель 4. | 1). Первый множитель 8, Второй множитель 4. Найти произведение. |
2). Делимое 36, делитель 6. Найти частное. | 2) Делимое 54, делитель 9.Найти частное. |
3). 27 уменьшить в 9 раз. | 3). 24 уменьшить в 8 раз. |
4). 4 увеличить в 8 раз. | 4). 3 увеличить в 9 раз. |
5).Найти частное чисел: 63 и 7. | 5). Найти частное чисел: 72 и 8. |
6). 42 уменьшить в 6 раз. | 6). 28 уменьшить в 7 раз. |
7). Какое число умножили на 8 и получили 32? | 7). Какое число умножили на 6 и получили 24? |
8). | 8). Какое число разделили на 6 и получили6? |
9). На какое число разделили 24 и получили 3? | 9). На какое число разделили 27 и получили3? |
10). Какие два числа надо перемножить, чтобы получить 27? | 10). Какие два числа надо перемножить, чтобы получить32? |
11). Найти произведение чисел: 8 и 9. | 11). Найти произведение чисел: 9 и 7. |
12). Первый множитель 3, второй множитель 6.Найти произведение. | 12). Первый множитель 4, второй множитель 3. Найти произведение. |
13). 40 уменьшить в 8 раз. | 13). |
14). Какое число разделили на 9 и получили 6? | 14). Какое число разделили на 9 и получили 4? |
Карточка №12
Первый вариант. | Второй вариант. |
1).Чему равен первый множитель, если второй множитель равен 6,а произведение 42. | 1). Чему равен первый множитель, если второй множитель равен 9,а произведение 54? |
2). Найти произведение чисел: 4 и 8. | 2). Найти произведение чисел: 5 и 6. |
3).Первый множитель 8, второй множитель 7.Найти произведение. | 3). Первый множитель 4, второй множитель 9 Найти произведение. |
4). | 4). Чему равен делитель. Если делимое 42, а частное 6? |
5). Найти частное чисел: 35 и 5. | 5). Найти частное чисел 32 и 8. |
6). Делимое 36, делитель 9. Найти частное. | 6). Делимое 56, делитель 7. Найти частное. |
7). Какое число умножили на 3 и получили 21? | 7). Какое число умножили на 9 и получили 45? |
8). Какое число разделили на 4 и получили 4? | 8). Какое число разделили на 6 и получили 3? |
9). 6 увеличить в 9 раз. | 9). 7 увеличить в 6 раз. |
10). | 10). На какое число разделили54 и получили 9. |
11). На какое число умножили 6 и получили 12? | 11). На какое число умножили 4 и получили 12? |
12). Чему равно произведение чисел: 8 и 3? | 12). Чему равно произведение чисел: 3 и 9? |
13). Чему равно частное дух чисел: 48 и 8? | 13). Чему равно частное двух чисел: 28 и 4? |
14). Вычислить: 45:5:3х6:9х7= | 14). Вычислить: 27:3х2:6х4:8= |
Карточка №13
Первый вариант. | Второй вариант. |
1). | 1). 78 уменьшить на 40. |
2). 27 увеличит на 60. | 2).36 увеличить на 60. |
3). Уменьшаемое 40, вычитаемое 7.Найти разность. | 3). Уменьшаемое 30, вычитаемое 8. Найти разность. |
4). Первое слагаемое 54. Второе слагаемое 6. Найти сумму. | Первое слагаемое 73, второе слагаемое 7. Найти сумму. |
5). Найти разность чисел:50 и 24. | 5). Найти разность чисел: 60 и 32. |
6). На сколько 75 больше 40? | 6). На сколько 84 больше 50? |
7). Из какого числа вычли 20 и получили 64? | 7). |
8). На сколько 5 меньше 26? | 8). На сколько 6 меньше 28? |
9). Какое число вычли из 78 и получили 38? | 9). Какое число вычли из 92 и получили 42? |
10). Какое число прибавили к36 и получили 86? | 10). Какое число прибавили к 27 и получили 87? |
11). Из какого числа вычли 8 и получили 22? | 11). Из какого числа вычли 7 и получили 33? |
12). К какому числу прибавили 7 и получили 80? | 12). К какому числу прибавили 6 и получили 60? |
13). Какое число уменьшили в 6 раз и получили 8? | 13). |
14). Во сколько раз 24 больше 6? | 14). Во сколько раз 54 больше 9? |
Карточка №14
Первый вариант. | Второй вариант. |
1). 48 уменьшить в 6 раз. | 1).54 уменьшить в 9 раз. |
2). 8 увеличить в 7 раз. | 2). 7 увеличить в 9 раз. |
3). Первый множитель 5, второй множитель 4.Найти произведение. | 3).Первый множитель 9, второй множитель 5. Найти произведение. |
4). Найти произведение чисел: 8 и 4. | 4). Найти произведение чисел 4 и 6. |
5). Делимое 54, делитель 9.Найти частное. | 5). Делимое 48, делитель 6. Найти частное. |
6). Чему равен второй множитель, если первый множитель 7, а произведение равно 63? | 6). Чему равен второй множитель, если первый множитель 8, а произведение равно 56? |
7). Чему равен первый множитель, если второй множитель равен 5, а произведение равно 45? | 7). Чему равен первый множитель, второй множитель равен 4, а произведение равно 20? |
8). Чему равно частное, если делимое равно 24. а делитель равен6? | 8). Чему равно частное, если делимое равно 32. а делитель равен 8? |
9). Какое число умножили на 3 и получили 27? | 9). |
10). Какое число разделили на 7 и получили 2? | 10). Какое число разделили на 4 и получили 3? |
11). Найти произведение чисел: 7 и 10. | 11). Найти произведение чисел: 10 и 8. |
12). На какое число умножили 4 и получили 28? | 12). На какое число умножили 3 и получили 27? |
13).Произведение каких двух множителей равно 42? | 13). Произведение каких двух множителей равно 54? |
14). Чему равно произведение двух чисел: 8 и 2? | 14). Чему равно произведение двух чисел: 6 и 3? |
Карточка №15
Первый вариант. | Второй вариант. |
1). Вычислить: 90-70+60-40+30= | 1). Вычислить: 80-50+40-60+90= |
2). Вычислить: 63:9х8= | 2). Вычислить: 42:7х9= |
3). Вычислить: 18:3х7= | 3). Вычислить: 16:4х8= |
4). 76 увеличить на 4. | 4). 62 увеличить на 8. |
5). Найти произведение чисел: 3 и 7. | 5). Найти произведение чисел: 4 и 9. |
6). Делимое 42, делитель 6. Найти частное. | 6). Делимое 48, делитель 8. Найти частное. |
7). Найти сумму чисел: 23 и 45. | 7). Найти сумму чисел: 36 и 42. |
8). Найти разность чисел: 87 и 35. | 8). Найти разность чисел: 78 и 43. |
9). Из какого числа вычли 62 и получили 24? | 9). Из какого числа вычли 54 и получили 33? |
10). Какое число уменьшили на 44 и получили 32? | 10). Какое число уменьшили на 26 и получили 51. |
11). К какому числу прибавили 56 и получили 80? | 11). К какому числу прибавили 62 и получили 90?. |
12). Вычислить: 4х3:6х4х7= | 12). Вычислить: 6х3:9х4х5= |
13). Вычислить: 6+8-7+8-9+7= | 13). |
14). 9 увеличить в 6 раз. | 14).8 увеличить в 7 раз. |
Карточка №16
Первый вариант. | Второй вариант. |
1). 48 уменьшить на 6. | 1). 59 уменьшить на 7. |
2). 26 увеличить на 40. | 2). 34 увеличить на 50. |
3). Уменьшаемое 93, вычитаемое 60. Найти разность. | 3). Уменьшаемое 84. Вычитаемое 70. Найти разность. |
4). Первое слагаемое 36 , второе слагаемое 32. Найти сумму. | 4). Первое слагаемое 54. Второе слагаемое 34. Найти сумму. |
5). | Найти разность чисел: 70 и 64. |
6). Найти сумму чисел: 23 и 64. | Найти сумму чисел: 32 и 57. |
7). На сколько 12 меньше 19? | 7). На сколько 13 меньше 16? |
8). Из какого числа вычли 58 и получили 40? | 8). Из какого числа вычли 43 и получили50? |
9). Какое число прибавили к 20 и получили 74? | 9). Какое число прибавили к 30 и получили 68? |
10). Вычислить: 4+8-7+6-9+7+6= | 10). Вычислить: 3+8-5+6-7+9-8= |
11). Найти произведение чисел: 8 и 7. | 11). |
12). Найти частное чисел: 64 и 8. | 12). Найти частное чисел: 81 и 9. |
13). Чему равно второе слагаемое, если первое слагаемое 47, а сумма равна 89? | 13). Чему равно второе слагаемое, если первое слагаемое 38, а сумма равна 99. |
14). Чему равно уменьшаемое, если вычитаемое равно 67, а разность равна 13? | 14).Чему равно уменьшаемое, если вычитаемое равно 86, вычитаемое равно 14? |
Карточка №17
Первый вариант. | Второй вариант. |
1). Какое число прибавили к 60 и получили 87? | 1).Какое число прибавили к 40 и получили 84? |
2). | 2).какое число прибавили к 54 и получили 94? |
3). Из какого числа вычли 30 и получили 56. | 3). Из какого числа вычли 40 и получили 58. |
4). 64 уменьшили на какое – то число и получили 20. | 4). 75 уменьшили на какое – то число и получили 40. |
5). Вычислить: 90-40+50-70+60= | 5). Вычислить: 80-50+40-20+30= |
6). Вычислить: 7+8-9+5-4+7= | 6). Вычислить: 6+7-8+6-7+8= |
7). Вычислить: 3+2+4-7+6+2= | 7)э Вычислить: 4+3+3-8+5-2= |
8). На сколько 18 больше 5? | 8). |
9). На сколько 12 меньше 19? | 9). На сколько 13 меньше 17? |
10). Уменьшаемое 40, вычитаемое 7. Найти разность. | 10). Уменьшаемое 50, вычитаемое 8. Найти разность. |
11). Первое слагаемое 22, второе слагаемое 8.Найти сумму. | 11). Первое слагаемое 33. Второе слагаемое 7.Найти сумму. |
12). 96 уменьшить на 34. | 12). 87 уменьшить на 53. |
13). Вычислить: 72:8х4:6= | 13). Вычислить: 54:9х6:4= |
14). Вычислить: 8х5:10х7= | 14). Вычислить: 6х5:10х8= |
Карточка №18
Первый вариант. | Второй вариант. |
1). Вычислить: 56:7:2х9= | 1). Вычислить: 42:7:2х9= |
2). Вычислить: 63:9х5= | 2).Вычислить: 54:9х4= |
3). Найти частное чисел: 0и9. | 3). Найти произведение чисел: 0 и 7. |
4). Найти произведение чисел: 6 и 0. | 4). Найти частное чисел: 0 и 5. |
5). Первый множитель 5, второй множитель 8.Найти произведение. | 5). Первый множитель 6, второй множитель 9. Найти произведение. |
6). Какое число разделили на 8 и получили ? | 6). Какое число разделили на 7 и получили 8? |
7). | 7). На какое число разделили на 49 и получили 7? |
8). Какое число умножили на 3 и получили 21? | 8). Какое число умножили на 8 и получили 32? |
9). На какое число умножили 7 и получили 42? | 9). На какое число умножили 9 и получили 27? |
10). Вычислить: 50+40-70+30+40-60= | 10). Вычислить: 30+40+30-80+50-30= |
11). 57 уменьшить на 32. | 11). 78 уменьшить на 46. |
12). 43 увеличить на 34. | 12). 36 увеличить на 53. |
13). Какое число уменьшили на 64 и получили 32? | 13). |
14). На сколько 43 меньше 80? | 14). На сколько 57 меньше 90? |
Карточка №19
Первый вариант. | Второй вариант. |
1). Вычислить: 40+50-70+60-30-40= | 1).Вычислить: 30+50-60+70-40-20= |
2). 54 увеличить на 6. | 2) 56 увеличить на 4. |
3).Вычислить: 7+8-9+5-4+8= | 3) Вычислить: 6+7-5+4-9+8= |
4). Вычислить:6+3-7+6-4+5= | 4). Вычислить: 4+5-7+6-3+5= |
5). Найти разность чисел: 93 и 60. | 5). Найти разность чисел: 85 и 40. |
6). 18 уменьшить на 6. | 6). 19 уменьшить на 5. |
7). Уменьшаемое 30, вычитаемое 7. Найти разность. | 7). Уменьшаемое 40, вычитаемое 7. Найти разность. |
8). На сколько 60 меньше 92? | 8). На сколько 70 меньше 98? |
9). Какое число прибавили к 16 и получили 48? | 9). Какое число прибавили к 14 и получили 57? |
10). На какое число уменьшили 42 и получили 21? | 10) На какое число уменьшили 58 и получили 32? |
11). Уменьшаемое 78, вычитаемое 54. Найти разность. | 11). |
12). Первое слагаемое 16, второе слагаемое 52. Найти сумму. | 12). Первое слагаемое 17. Второе слагаемое 51. Найти сумму. |
13). Вычислить: 40+50-60+70-40-20= | 13). Вычислить: 30+50-70+60-30-40= |
14). Во сколько раз 56 больше 7? | 14). Во сколько раз 48 больше 6? |
Карточка №20
Первый вариант. | Второй вариант. |
1). Найти разность чисел: 64 и 40. | 1). Найти разность чисел: 72 и 30. |
2). Найти сумму чисел: 45 и 50. | 2). |
3). Уменьшаемое 60, вычитаемое 7. Найти разность. | 3). Уменьшаемое 70, вычитаемое 6. Найти разность. |
4). Первое слагаемое 23. Второе слагаемое 6. Найти сумму. | 4). Первое слагаемое 42, второе слагаемое 7. Найти сумму. |
5). Какое число уменьшили на 12 и получили 74? | 5). Какое число уменьшили на 14 и получили 53? |
6). На сколько 85 больше 50? | 6). На сколько 92 больше 70? |
7). Вычислить: 90-60+20+40-70= | 7). Вычислить: 80-30+40-70+50= |
8). К какому числу прибавили 24 и получили 58? | 8). |
9). Вычислить: 6+5-4+8-9= | 9). Вычислить: 7+4-5+8-9= |
10). Вычислить: 2+7-6+5-4+6= | 10). Вычислить: 3+6-5+4-2+3-8= |
11). Найти произведение чисел: 10 и 8. | 11) Найти произведение чисел: 9 и 0. |
12). Найти произведение чисел: 0 и 7. | 12). Найти произведение чисел: 4 и 10. |
13). Какое число умножили на 6 и получили 42? | 13). Какое число умножили на 7 и получили 63? |
14). Какое число разделили на 4 и получили 36? | 14). Какое число разделили на 8 и получили 56? |
Карточка №21
Первый вариант. | Второй вариант. |
1). Вычислить: 64:8:2х7= | 1).Вычислить: 56:7:2х9= |
2). Найти частное чисел: 48 и 6. | 2). Найти частное чисел: 54 и 9. |
3). Во сколько раз 72 больше 8? | 3). Во сколько раз 42 больше 7? |
4). Найти произведение чисел: 40 и 2. | 4). Найти произведение чисел: 30 и 2. |
5). 3 увеличить в 30 раз. | 5). 2 увеличить в 40 раз. |
6). Делимое 0, делитель 7. Найти частное. | 6). Делимое 6, делитель 0. Найти частное. |
7). | 7). Делимое 0, делитель 4. Найти частное. |
8). Во сколько раз 5 меньше 35? | 8). Во сколько раз 9 меньше 27? |
9). Какое число разделили на 3 и получили 8? | 9). Какое число разделили на 6 и получили 4? |
10). Найти произведение чисел: 30 и 3. | 10). Найти произведение чисел: 20 и 4. |
11). На какое число умножили 6 и получили 12? | 11). На какое число умножили 8 и получили 40? |
12). На какое число разделили 30 и получили 6? | 12). На какое число разделили 42 и получили 7? |
13). | 13) Какое число разделили на 4 и получили 8? |
14). Вычислить: 56:7:4х9= | 14). Вычислить: 63:7:3х8= |
Карточка №22
Первый вариант. | Второй вариант. |
1). Найти разность чисел: 74 и 30. | 1). Найти разность чисел: 82 и 60. На сколько 79 больше 56? |
2). 89 уменьшить на 54. | 2). 97 уменьшить на 63. |
3). Уменьшаемое 30, вычитаемое 7. Найти разность. | 3). Уменьшаемое 40, вычитаемое 8. Найти разность. |
4). 54 увеличить на 6. | 4). 63 увеличить на 7. |
5). На сколько 38 больше 15? | 5). На сколько 47 больше 16? |
6). Вычислить: 30+60-70+40-50+20= | 6). Вычислить: 40+30+20-60+50-40= |
7). Вычислить: 6+7-8+9-7+5= | 7). Вычислить: 6+8-7+5-6+9= |
8). Чему равна разность чисел: 18 и 15? | 8). Чему равна разность чисел: 19 и 17? |
9). Вычислить: 5+4-7+6-5+8= | 9). Вычислить: 3+6-7+4+4-8= |
10). Какое число уменьшили на 63 и получили 34? | 10). Какое число уменьшили на 54 и получили 35? |
11). | 11). Какое число увеличили на 14 и получили 57? |
12).К какому числу прибавили 42 и получили 76? | 12). К какому числу прибавили 36 и получили 79? |
13).Какое число уменьшили на 66 и получили 23? | 13). Какое число уменьшили на 55 и получили 34? |
14). Найти произведение чисел: 4 и 10. | 14). Найти произведение чисел: 9 и 0. |
Карточка №23
Первый вариант. | Второй вариант. |
1). Вычмслить:72:8х4= | 1). Вычислить: 56:7х5= |
2). | 2). Найти произведение чисел: 6 и 0. |
3). Найти частное чисел: 0 и 4. | 3). Найти частное чисел: 2 и 0. |
4). 6 увеличить в 100 раз. | 4). ; увеличить в 100 раз. |
5). Вычислить: 49:7х4= | 5). Вычислить: 81:9х7= |
6). Какое число увеличили в 3 раза и получили 18? | 6). Какое число увеличили в 6 раз и получили 42? |
7). Какое число уменьшили в 9 раз и получили 6? | 7). Какое число уменьшили в 8 раз и получили 6? |
8). Во сколько раз 18 больше 2? | 8). |
9). Первый множитель 30, второй множитель 2. Найти произведение. | 9). Первый множитель 30, второй множитель 3. Найти произведение. |
10). Делимое 8. Делитель 0. Найти частное. | 10). Делимое 0, делитель 3. Найти частное. |
11). Какое число разделили на 8 и получили 5? | 11). Какое число разделили на 9 и получили 4? |
12). Вычислить: 56:7х4= | 12). Вычислить: 48:8х9= |
13) Вычислить: 4х100:10= | 13). Вычислить: 7х100:10= |
14). На какое число умножили 8 и получили 32? | 14). |
Карточка №24
Первый вариант. | Второй вариант. |
1). Найти сумму чисел: 17 и 18. | 1). Найти сумму чисел: 16 и 17. |
2). Из 74 вычесть 30. | 2). Из 83 вычесть 50. |
3). 26 увеличить на 60. | 3). 27 увеличить на 70. |
4). 40 уменьшить на7. | 4). 50 уменьшить на 7. |
5). Первое слагаемое 24, второе слагаемое 6.Найти сумму. | 5). Первое слагаемое 72, второе слагаемое 8.Найти сумму. |
6). | 6). Вычислить: 7+5-8+9-6+7= |
7). Из какого числа вычли 60 и получили 34? | 7). Из какого числа вычли 50 и получили 46? |
8). К какому числу прибавили 32 и получили 80? | 8). К какому числу прибавили 44 и получили 70? |
9). На сколько 50 меньше 86? | 9). На сколько 60 меньше 92? |
10). Вычислить: 4+3-6+2+5-4= | 10). Вычислить: 3+5-4+2+3-7= |
11). Какое число вычли из 78 и получили42? | 11). Какое число вычли из 86 и получили 55. |
12). На сколько 79 больше 7? | 12). |
13). Вычислить: 60+30-70+40-50= | 13). Вычислить: 40+50-70+60-50= |
14). Уменьшаемое 48, вычитаемое 25. Найти разность. | 14). Уменьшаемое 76, вычитаемое 42. Найти разность. |
Карточка №25
Первый вариант. | Второй вариант. |
1).Вычислить: 28:7х9= | Вычислить: 54:9х7= |
2). Во сколько раз 9 меньше 63? | 2). Во сколько раз 8 меньше 56? |
3). Вычислить: 72:9:4х8= | 3). Вычислить: 32:4:2х9= |
4). | 4). Какое число умножили на 8 и получили 32? |
5). Во сколько раз 54 больше 6? | 5). Во сколько раз 45 больше 9? |
6). Найти произведение чисел: 80 и 5. | 6). Найти произведение чисел: 60 и 5. |
7). Первый множитель30, второй множитель 7. Найти произведение. | 7). Первый множитель30, второй множитель 4. Найти произведение. |
8). 8 увеличить в 60 раз. | 8). 5 увеличить в 70 раз. |
9). 420 уменьшить в 6 раз. | 9). 540 уменьшить в 9 раз. |
10). Какое число умножили на 3 и получили 18? | Какое число умножили на 9 и получили 27? |
11). | 11). Найти частное чисел: 40 и 8. |
12). Делимое неизвестно, делитель 4 Частное 8.Найти делимое. | 12). Делимое неизвестно, делитель 6. Частное 4. Найти делимое. |
13). Первый множитель 5.второй множитель 100. Найти произведение. | 13). Первый множитель 4, второй множитель100. Найти произведение. |
14). Найти частное чисел: 3 и 0. | 14). Найти частное чисел: 0 и 6. |
Карточка №26
Первый вариант. | Второй вариант. |
1). Первое слагаемое 43, второе слагаемое 54.Найти сумму. | 1). |
2). Уменьшаемое 78. Вычитаемое 26. Найти разность. | 2). Уменьшаемое 89, вычитаемое 57. Найти разность. |
3). Найти разность чисел: 80 и 43. | 3). Найти разность чисел: 60 и 34. |
4). Найти сумму чисел: 28 и 37. | 4). Найти сумму чисел: 46 и 27. |
5). 43 увеличить на 37. | 5). 24 увеличить на 56. |
6). На сколько 72 больше 50? | 6). На сколько 87 больше 60? |
7). Из какого числа вычли 34 и получили 52? | 7). Из какого числа вычли 26 и получили43? |
8). | 8). На сколько 91 больше 60? |
9). Какое число вычли из 83 и получили 31? | 9). Какое число вычли из 94 и получили 42? |
10). Вычислить: 70-40+30-50+90-60-20= | 10). Вычислить: 80-30+20-60+90-70-20= |
11). Вычислить: 7+8-9+5-4+8-9= | 11). Вычислить: 7+6-5+4-7+8-9= |
12). К какому числу прибавили 24 и получили 80? | 12). К какому числу прибавили 35 и получили 70? |
13). Какое число прибавили к 43 и получили 58? | 13). Какое число прибавили к 52 и получили 68? |
14). Чему равна сумма чисел: 14 и 18? | 14). |
Карточка №27
Первый вариант. | Второй вариант. |
1). Во сколько раз 9 меньше 54? | 1). Во сколько раз 8 меньше 56? |
2). Какое число разделили на 7 и получили 4? | 2). Какое число разделили на 6 и получили 8? |
3). На какое число разделили 32 и получили 4? | 3). На какое число разделили 36 и получили 9? |
4). Во сколько раз 400 больше 4? | 4). Во сколько раз 600 больше 6? |
5). Вычислить: 64:8:2х7= | 5). Вычислить: 81:9:3х9= |
6). | 6). Найти произведение чисел: 30 и 2. |
7). Найти частное чисел: 90 и 3. | 7). Найти частное чисел: 80 и 4. |
8). Во сколько раз 50 больше 5? | 8). Во сколько 40 больше 4? |
9). Первый множитель 5, второй множитель 80. Найти произведение. | 9). Первый множитель 6. Второй множитель 50. Найти произведение. |
10). Чему равно произведение чисел: 30 и 4? | 10). Чему равно произведение чисел: 40 и 4? |
11). Найти произведение чисел: 70 и 0. | 11).Найти произведение чисел: 0 и 90. |
12). | 12). Чему равно частное чисел: 450 и 5? |
13). Вычислить: 42:7х5:10х7= | 13). Вычислить: 36:9х5:10х9= |
14). Второй множитель равен 6, произведение равно 24. Чему равен первый множитель? | 14). Второй множитель равен 8. Произведение равно 24. Чему равен первый множитель? |
Карточка №28
Первый вариант. | Второй вариант. |
1). Найти сумму чисел: 32 и 45. | 1). Найти произведение чисел: 53 и36. |
2). Найти разность чисел: 83 и 62. | 2). Найти разность чисел: 75 и 23. |
3). | 3). Вычислить: 50-20+40+20-60= |
4). Вычислить:5+7-6+8-9+7-6= | 4). Вычислить: 8+4-5+6-9+8-7= |
5). Вычислить: 2+4+-7+5-6+4= | 5). 3+5-4+5-7+8= |
6). Какое число уменьшили на 62 и получили 28? | 6). Какое число уменьшили на 57 и получили 43? |
7). На сколько 89 больше 7? | 7). На сколько 78 больше 6? |
8). На какое число уменьшили на 65 и получили 43? | 8). На какое число уменьшили 76 и получили 53? |
9). Первое слагаемое 38. Второе слагаемое 47. Найти сумму. | 9). |
10). Уменьшаемое 40, вычитаемое 18. Найти разность. | 10). Уменьшаемое 50. вычитаемое 16.Найти разность. |
11). 83 уменьшить на 37. | 11). 85 уменьшить на 47. |
12). Какое число прибавили к 26 и получили 59? | 12). Какое число прибавили к 27 и получили 68? |
13). Найти разность чисел: 73 и 60. | 13). Найти разность чисел: 84 и 50. |
14).Найти сумму чисел: 35 и 60. | 14). Найти сумму чисел: 28 и 70. |
Карточка №29
Первый вариант. | Второй вариант. |
1). Вычислить: 36:4:3х6:9= | 1). Вычислить: 48:8:2х4:3= |
2). Какое число умножили на 7 и получили 28? | 2). Какое число умножили на 8 и получили48? |
3). Во сколько раз 56 больше 7? | 3). Во сколько раз 42 больше 6? |
4). Найти произведение чисел: 80 и 9. | 4). Найти произведение чисел: 60 и 5. |
5). 40 увеличить в 5 раз. | 5). 70 увеличить в 70 раз. |
6). Из каких множителей состоит произведение 27? | 6). Из каких множителей состоит произведение 56? |
7). | 7). Из каких множителей состоит произведение 40? |
8). Какое число разделили на 9 и получили 4? | 8). Какое число разделили на 7 и получили 5? |
9). Во сколько раз 7 меньше 14? | 9). Во сколько раз 6 меньше 18? |
10). Найти частное чисел: 90 и 0. | 10). Найти частное чисел: 0 и 60. |
11). Вычислить: 54:9х5:10х7= | 11). Вычислить: 72:9х5:10х8= |
12). Найти частное чисел: 40 и 6. | 12) Найти частное чисел: 36 и 8. |
13). 67 уменьшить в 8 раз. | 13) 59 уменьшить в 7 раз. |
14). Вычислить: 70:7х4:8= | 14).Вычислить:60:6х30:6= |
Карточка №30
Первый вариант. | Второй вариант. |
1). Уменьшаемое 90, вычитаемое 70.Найти разность. | 1). Уменьшаемое 80, Вычитаемое 50. Найти разность. |
2). 84 уменьшить на 40. | 2). 76 уменьшить на 30. |
3). Первое слагаемое 28, второе слагаемое 50. Найти сумму. | 3). Первое слагаемое 36, второе слагаемое 40. Найти сумму. |
4). Найти разность чисел: 30 и 7. | 4). Найти разность чисел: 40 и 8. |
5). | 5). 43 увеличить на 7. |
6). Из какого числа вычли 36 и получили 42? | 6). Из какого числа вычли 57 и получили 32? |
7). Найти сумму чисел:24 и 43. | 7). Найти сумму чисел: 35 и 53. |
8). Какое число вычли из 100 и получили 76? | 8). Какое число вычли из 100 и получили 63? |
9). Найти произведение чисел:11 и 4. | 9). Найти произведение чисел: 6 и 11. |
10). Найти частное чисел: 80 и 8. | 10). Найти частное чисел: 70 и 10. |
11).Делимое 60, делитель 10. Найти частное. | 11). |
12). Первый множитель 12. Второй множитель 3. Найти произведение. | 12). Первый множитель 13. Второй множитель 2. Найти произведение. |
13). Вычислить: 40+30-20-50+80= | 13). Вычислить: 70+20-60+40-50= |
14). Вычислить:7+5-6+8-9= | 14). Вычислить: 8+5-7+4-6= |
Карточка №31
Первый вариант. | Второй вариант. |
1)Первый множитель 7, второй множитель 9. Найти произведение.. | 1). Первый множитель 8, второй множитель 4. Найти произведение. |
2). Делимое 36, делитель 4. | 2). Делимое 48. Делитель 6. Найти частное. |
3). Найти частное чисел: 15 и 5. | 3). Найти частное чисел: 18 и 3. |
4). Найти произведение чисел: 9 и 3. | 4). Найти произведение чисел: 6 и 4. |
5). Какое число умножили на 7 и получили 21? | 5). Какое число умножили на 8 и получили 24? |
6). На какое число разделили 42 и получили 9? | 6). На какое число разделили 72 и получили 9? |
7). Делимое 54. Частное 9. Чему равен делитель? | 7). Делимое 72. Частное 9.Чему равен делитель? |
8). | 8). Первый множитель 6. Произведение 54.Чему равен второй множитель. |
9). Второй множитель 4. Произведение 32. Чему равен первый множитель? | 9). Второй множитель 9. Произведение 63. Чему равен первый множитель? |
10). Делимое 48. Частное 8.Чему равен делитель? | 10). Делимое 36. Частное 9.Чему равен делитель? |
11). 0 уменьшить в 4 раза. | 11). 0 увеличить в 6 раз. |
12). Вычислить: 5х4:10х8:4х6:8= | 12). Вычислить: 5х5:10х6:2:3х9= |
13). Найти произведение чисел: 9 и 0. | 13). |
14). Какое число увеличили в 6 раз и получили 54? | 14). Какое число увеличили в 8 раз и получили 56? |
Карточка №32
Первый вариант. | Второй вариант. |
1). Уменьшаемое 48, вычитаемое 36. Найти разность. | 1). Уменьшаемое 57, вычитаемое 43. Найти разность. |
2). Первое слагаемое 23. Второе слагаемое 56. Найти сумму. | 2). Первое слагаемое 43, второе слагаемое 25. Найти сумму. |
3). 70 уменьшить на 43. | 3). 80 уменьшить на 52. |
4). Найти разность чисел: 30 и 6. | 4). |
5). 32 увеличить на 8. | 5). 63 увеличить на 7. |
6). Какое число уменьшили на 40 и получили 33? | 6). Какое число уменьшили на 60 и получили22? |
7). Уменьшаемое 57. Разность 14. Чему равно вычитаемое? | 7). Уменьшаемое 48. Разность 12. Чему равно вычитаемое? |
8). Первое слагаемое 43. Сумма 68. Чему равно вычитаемое? | 8). Первое слагаемое 23. Сумма 79. Чему равно вычитаемое? |
9). Вычитаемое 7, Разность 33.Чему равно уменьшаемое? | 9). Вычитаемое 6. Разность 24. Чему равно уменьшаемое? |
10). Какое число увеличили на 6 и получили 39? | 10). |
11). На сколько 82 больше 60? | 11). На сколько 73 больше 40? |
12). На сколько 30 меньше 78? | 12). На сколько 40 меньше 97? |
13). Во сколько раз 72 больше 9? | 13). Во сколько раз 35 болдьше7? |
14). Во сколько раз 7 меньше 63?3 | 13). Во сколько раз 8 меньше 56? |
Карточка №33
Первый вариант. | Второй вариант. |
1). 9 увеличить в 3 раза. | 1). 6 увеличить в 4 раза. |
2). | 2). Вычислить: 15:3х4= |
3). Делимое 70, делитель 10.Найти частное. | 3). Делимое 80. Делитель 10.Найти частное. |
4). Найти частное чисел: 60 и 6. | 4). Найти частное чисел: 50 и 5. |
5). Какое число разделили на 3 и получили 8? | 5). Какое число разделили на 7 и получили3? |
6). Какое число умножили на 8 и получили 32? | 6). Какое число умножили на 9 и получили 72? |
7). 0 уменьшить в 4 раза. | 7). 0 увеличить в 7 раз. |
8). На какое число разделили 56 и получили 7? | 8). |
9). Первый множитель 6, второй множитель 4. Найти произведение. | 9). Первый множитель9. Второй множитель 3. Найти произведение. |
10). Вычислить: 16:4х6:3:2х5:10= | 10). Вычислить: 18:3х5:10х4:6= |
11). Делимое 48 .Частное 8. Чему равен делитель? | 11). Делимое 64. Частное 8. Чему равен делитель? |
12). Второй множитель 10. Произведение 70.Чему равен первый множитель? | 12). Второй множитель 6. Произведение 60. Чему равен первый множитель? |
13). Чему равно произведение, если первый множитель 0, а второй множитель7? | 13). Чему равно произведение, если первый множитель 3, а второй множитель 0? |
14). | 14).На какое число разделили 56 и получили 8? |
Карточка №34
Первый вариант. | Второй вариант. |
1). Вычислить: 30+40-50+80-70= | 1). Вычислить: 50+40-70+30+50= |
2). Какое число уменьшили на 48 и получили52? | 2). Какое число уменьшили на 37 и получили 43? |
3). На сколько 74 больше 50? | 3). На сколько 86 больше 60? |
4). Вычислить: 7+8-9+5-7+8= | 4). Вычислить: 6+5-7+8-6+5=- |
5). Какое число вычли из 57 и получили 43? | 5). |
6). Вычислить: 2+3+4-7+6-5= | 6). Вычислить: 4+3-5+7-6+5= |
7). На сколько 43 меньше 59? | 7). На сколько 35 меньше 46? |
8). Какое число прибавили к 64 и получили 59? | 8). Какое число прибавили к 73 и получили 98? |
9). Вычислить: 50+40-70+30+50= | 9). Вычислить: 30+40-50+80-70= |
10). Из какого числа вычли 37 и получили 52? | 10). Из какого числа вычли 48 и получили 52? |
11). Вычислить: 6+6-7+8-6+5= | 11). Вычислить: 7+8-9+5-7+8= |
12). | 12). Из 85 вычли какое – то и получили 13. Какое число вычли? |
13). Второе слагаемое 74. Сумма 98. Найти первое слагаемое. | 13).Второе слагаемое 62. Сумма 85. Найти первое слагаемое. |
14). Уменьшаемое 74.Разность 25.Найти вычитаемое. | 14). Уменьшаемое 63. Разность 34. Найти вычитаемое. |
Карточка №35
Первый вариант. | Второй вариант. |
1). 37 увеличить на 50. | 1).24 увеличить на 70. |
2). 93 уменьшить на 70. | 2). 86 уменьшить на 60. |
3). | 3). Первое слагаемое 44. Второе слагаемое 6.Найти сумму. |
4). Уменьшаемое 60, вычитаемое 6. Найти разность. | 4). Уменьшаемое 70. Вычитаемое 8.Найти Разность. |
5). На сколько 18 больше 12? | 5). На сколько 19 больше 14? |
6). Вычислить: 30+60-70+50-40= | 6). Вычислить: 20+70-60+40-50= |
7). На сколько 7 меньше 17? | 7). На сколько 5 меньше 12? |
8). Вычислить: 4+3+2-6+5 | 8). Вычислить: 4+5-7+3+4-6= |
90. Какое число уменьшили на 16 и получили 44? | 9). |
10). К какому числу прибавили 32 и получили 58? | 10). К какому числу прибавили 43 и получили 69? |
11). Найти разность чисел: 78 и 43. | 11). Найти разность чисел: 87 и 53. |
12). Найти сумму чисел, 45 и 44. | 12). Найти разность чисел: 32 и 56. |
13). На какое число уменьшили 7 и получили 22? | 13). На какое число уменьшили 6 и получили 32? |
14). На какое число увеличили 32 и получили 38? | 14). На какое число увеличили 42 и получили 49? |
Карточка №36
Первый вариант. | Второй вариант. |
1). Первый множитель 6, второй множитель 9. Найти произведение. | 1). Первый множитель 8, второй множитель 4. Найти произведение. |
2). Во сколько раз 28 больше 7? | 2). Во сколько раз 36 больше 4? |
3). Вычислить: 5х8:10х4:2х9= | 3). Вычислить: 5х6:10х8:6х7= |
4). Какое число умножили на 3 и получили 21? | 4). Какое число умножили на 6 и получили 42? |
5). Во сколько раз 5 меньше 45? | 5). Во сколько раз 6 меньше 18? |
6). Найти произведение чисел: 7 и 100. | 6). |
7). Делимое 80, делитель 4. Найти частное. | 7). Делимое 60, делитель 2.Найти частное. |
8). Чему равно произведение чисел: 30 и 3? | 8). Чему равно произведение чисел: 20 и 4? |
9). Какое число умножили на 9 и получили 0? | 9). Какое число разделили на 7 и получили 0? |
10). Вычислить: 32:4:2х6:8х9= | 10). Вычислить: 48:6:4х3х6:9= |
11). Какое число разделили на 8 и получили 0? | 11). Какое число умножили на 6 и получили 0? |
12). Вычислить: 36:4х7= | 11). Вычислить: 42:6х9= |
13). | 13). Найти произведение чисел: 7 и 3. |
14). Делитель 4. Частное 5. Чему равно делимое? | 14) Делитель 7. Частное 9. Чему равно делимое? |
Карточка №37
Первый вариант. | Второй вариант. |
1).84 уменьшить на 50.. | 1). 73 уменьшить на 40. |
2). Первый множитель 7. Второй множитель 8. Найти произведение. | 2). Первый множитель 6, второй множитель 9.Найти произведение. |
3). 25 увеличить на 70. | 3). 34 увеличить на 60. |
4). Делимое 42, делитель 6. | 4). Делимое 36, делитель 4. Найти частное. |
5). Уменьшаемое 80, вычитаемое 26. Найти разность. | 5). Уменьшаемое 70. Вычитаемое 32. Найти разность. |
6). 64 уменьшить в 8 раз. | 6). 49 уменьшить в 7 раз. |
7). Уменьшаемое 59. Разность 43. Найти вычитаемое. | 7). Уменьшаемое 68. Разность 15. Найти вычитаемое. |
8). Какое число разделили на 4 и получили 6? | 8). Какое число разделили на 6 и получили 7? |
9). На сколько 13 больше 8? | 9). На сколько 15 больше 7? |
10). Какое число уменьшили на40 и получили 33? | 10). |
11). Какое число умножили на 9 и получили 54? | 11). Какое число умножили на 7 и получили 56? |
12). Какое число увеличили на 60 и получили 94? | 12). Какое число увеличили на 70 и получили 95? |
13). На сколько 4 меньше 20? | 13).На сколько 6 меньше20? |
14). Какое число увеличили в 2 раза и получили 0? | 14). Какое число увеличили в 6 раз и получили 0? |
Карточка №38
Первый вариант. | Второй вариант. |
1). Вычислить: 12:4х7= | 1). |
2). Какое число умножили на 8 и получили 32? | 2). Какое число умножили на 7 и получили на 7? |
3). Найти произведение чисел: 10 и 6. | 3). Найти произведение чисел: 10 и 4. |
4). Найти разность чисел :97 и 60. | 4). Найти разность чисел: 84 и 50. |
5). Найти сумму чисел: 28 и 7. | 5). Найти сумму чисел: 35 и 40. |
6). Найти уменьшаемое, если вычитаемое 8,а разность 6. | 6). Найти уменьшаемое , если вычитаемое 6. А разность 9. |
7). На сколько 40 больше 18? | 7). На сколько 30 больше 12? |
8). | 8). К какому числу прибавили 40 и получили 83? |
9). Вычислить: 18:6х8= | 9). Вычислить: 12:4х7= |
10). Второй множитель 7. Произведение 28. Чему равен первый множитель? | 10). Второй множитель 8, произведение 32. Найти первый множитель. |
11). Первый множитель 10. Второй множитель 4. Найти произведение. | 11). Первый множитель 10, второй множитель 6. Найти произведение. |
12). 84 уменьшить на 50. | 12). 97 уменьшить на 60. |
13). 35 увеличить на 40. | 13). 27 увеличить на 70. |
14). | 14). На сколько 17 меньше 40? |
Карточка №39
Первый вариант. | Второй вариант. |
1). 11 уменьшить на 5. | 1). 13 уменьшить на 6. |
2). Какое число умножили на 3 и получили 27? | 2). Какое число умножили на 7 и получили 56? |
3). На какое число умножили 4 и получили 36? | 3). На какое число умножили 6 и получили 42? |
4). Найти разность чисел: 94 и 50. | 4). Найти разность чисел: 68 и 30. |
5). Найти сумму чисел: 26 и 70. | 5). |
6). Из какого числа вычли 24 и получили 40? | 6). Из какого числа вычли 37 и получили 50? |
7). На сколько 92 больше 60? | 7). На сколько 87 больше 40? |
8). Вычислить: 24:6х4:8х9= | 8). Вычислить: 36:9х4:8х7= |
9). Уменьшаемое 13. Вычитаемое 6. Найти разность. | 9). Уменьшаемое 11. Вычитаемое 5. Найти разность. |
10). Найти произведение чисел: 8и7. | 10). Найти произведение чисел: 9 и 3. |
11). 68 уменьшить на 30. | 11). 94 уменьшить на 50. |
12). | 12). 26 увеличить на 70. |
13). Из какого числа вычли 37 и получили 50? | 13). Из какого числа вычли 24 и получили 40? |
14). Вычислить: 18:6х8:6х3= | 14). Вычислить: 12:4х6:2х4= |
Карточка №40
Первый вариант. | Второй вариант. |
1). Найти разность чисел: 30 и 8. | 1). Найти разность чисел: 40 и 7. |
2). Найти произведение чисел: 6 и 9. | 2). Найти разность чисел: 7 и 8. |
3). Какое число разделили на 3 и получили 7? | 3). |
4). Какое число умножили на 8 и получили 16? | 4). Какое число умножили на 9 и получили 27? |
5). 63 увеличить на 7 | 5). 82 увеличить на 8. |
6). Из какого числа вычли50 и получили 50? | 6). Из какого числа вычли 40 и получили 57? |
7). На сколько 53 больше 30? | 7). На сколько 46 больше 20? |
8). Вычислить: 70+20-60+40-50= | 8). Вычислить: 90-60=40+30-80= |
9). 40 уменьшить на 7. | 9). 30 уменьшить на 8. |
10). | 10). Первый множитель 6, второй множитель 9. Найти произведение. |
11). 71 увеличить на 8. | 11). 52 увеличить на 7. |
12). Из какого числа вычли 40 и получили 57? | 12). Из какого числа вычли 50 и получили 32? |
13). На сколько 46 больше 20? | 13). На сколько 53 больше 30? |
14). Вычислить: 90-60+30+40-80= | 14). Вычислить: 70-20-60+40-50= |
Карточка №41
Первый вариант. | Второй вариант. |
1). Вычислить:4х6:3:2х7= | 1). |
2). Вычислить: 3+2+4-7+5= | 2). Вычислить: 4+3+3-8+5= |
3). Найти произведение чисел: 8 и 9. | 3). Найти произведение чисел: 6 и 7. |
4). Найти частное чисел:36 и 4. | 4). Найти частное чисел: 48 и 8. |
5). 90 уменьшить на 5. | 5). 80 уменьшить на 6. |
6). Какое число уменьшили на 43 и получили 27? | 6). Какое число уменьшили на 56 и получили 34? |
7). Вычислить: 12:4х7= | 7). Вычислить: 18:3х8= |
8). Вычислить:5х6:10:6= | 8). |
9). Найти произведение чисел: 6 и 7. | 9). Найти произведение чисел: 8 и 9. |
10). Вычислить: 4+3=3-8=5= | 10). Вычислить: 3+2+4-7+5= |
11). Уменьшаемое 80, вычитаемое 6.Найти разность. | 11). Уменьшаемое 90, вычитаемое 5. Найти разность. |
12). Какое число умножили на 8 и получили 56? | 12). Какое число умножили на 6 и получили 54? |
13). Из какого числа вычли 56 и получили 34? | 13). Из какого числа вычли 43 и получили 27? |
14). Вычислить: 12:3х8= | 14). Вычислить: 16:4х7= |
Карточка №42
Первый вариант. | Второй вариант. |
1). 67 уменьшить на 43. | 1). 78 уменьшить на 53. |
2). Уменьшаемое 90. Вычитаемое 60. Найти разность. | 2). Уменьшаемое 80, вычитаемое 50. Найти разность. |
3). Из какого числа вычли 34 и получили 40? | 3). Из какого числа вычли 36 и получили 30? |
4). Какое число умножили на 4 и получили 36? | 4). Какое число умножили на 6 и получили 30? |
5). Вычислить: 6+4+3-7+5= | 5). Вычислить: 8+2+4-8+7= |
6). Какое число разделили на 8 и получили 7? | 6). |
7). Найти сумму чисел: 39 и 40. | 7). Найти сумму чисел: 43 и 50. |
8). Из какого числа вычли 18 и получили 60? | 8). Из какого числа вычли 16 и получили 70? |
9). Уменьшаемое 78. Вычитаемое 53. Найти разность. | 9). Уменьшаемое 67. Вычитаемое 43. Найти разность. |
10). Какое число уменьшили на 36 и получили 40? | 10).Какое число уменьшили на 34 и получили 60. |
11). Найти разность чисел: 80 и 50. | 11). Найти разность чисел: 90 и 60. |
12). Первый множитель 6, второй множитель 9. Найти произведение. | 12). Первый множитель 4. Второй множитель 7. Найти произведение. |
13). Делимое 54, делитель 6. Найти частное. | 13). Делимое 63, делитель 7. Найти частное. |
14). Из какого числа вычли 16 и получили 40? | 14). Из какого числа вычли 18 и получили 60? |
Карточка №43
Первый вариант. | Второй вариант. |
1).84 уменьшить на 40. | 1).95 уменьшить на 50. |
2). 30 увеличить на 67. | 2). 20 увеличить на 68. |
3). Вычислить: 24:6х4:8= | 3). |
4). На сколько 30 меньше 69? | 4). На сколько 40 меньше 93? |
5). Какое число разделили на 5 и получили 9? | 5). Какое число разделили на 8 и получили 8? |
6). Какое число умножили на 3 и получили 21? | 6). Какое число умножили на 4 и получили 32? |
7). Вычислить: 35:7х4:10= | 7) Вычислить: 30:6х8:10= |
8). На сколько 6 меньше 18? | 8). На сколько 4 меньше 16? |
9). Найти разность чисел: 95 и 50. | 9). Найти разность чисел: 84 и 40. |
10. | 10). Найти сумму чисел: 30 и 67. |
11). Вычислить: 40:5х3:6= | 11). Вычислить: 30:6х8:10= |
12). На сколько 40 меньше 93? | 12). На сколько 30 меньше 69? |
13). На какое число разделили 64 и получили 8? | 13). На какое число разделили 45 и получили 9? |
14). На какое число умножили 4 и получили 36? | 14). На какое число умножили 3 и получили 27? |
Карточка №44
Первый вариант. | Второй вариант. |
1).Найти произведение чисел: 7и9. | 1). |
2). Первое слагаемое 24. Второе слагаемое 36. Найти сумму. | 2). Первое слагаемое 38, второе слагаемое 22. Найти сумму. |
3). Уменьшаемое 80. Вычитаемое 8.Найти разность. | 3). Уменьшаемое 80. Вычитаемое 6. Найти разность. |
4). 6 увеличить в 20 раз. | 4). 8 увеличит в 30 раз. |
5). Первый множитель 70. Второй множитель 4. Найти произведение. | 5). Первый множитель 80. Второй множитель 4. Найти произведение. |
6). Вычислить: 100-80+50= | 6). Вычислить: 90-70+30= |
7). 10 увеличить в 7 раз. | 7). |
8). Делимое 80. Делитель 10. Найти частное. | 8). Делимое 60. Делитель 10. Найти частное. |
9). Какое число умножили на 8 и получили 32? | 9). Какое число умножили на 9 и получили 45? |
10). Вычислить: 3+8-6+7= | 10). Вычислить: 4+8-6+7= |
11). Чему равен первый множитель, если второй множитель 8, а произведение 32? | 11). Чему равен первый множитель, если второй множитель 9, произведение 63? |
12). Чему равно уменьшаемое, если вычитаемое 6. Разность 74? | 12). Чему равно уменьшаемое, если вычитаемое 8, разность 62? |
13). | 13). На какое число умножили 6 и получили 120? |
14). Чему равно произведение чисел: 80 и 5? | 14). Чему равно произведение чисел: 70 и 4? |
Карточка №45
Первый вариант. | Второй вариант. |
1). Какое число умножили на 3 и получили 18? | 1). Какое число умножили на 4 и получили 12? |
2). На какое число умножили 8 и получили 24? | 2). На какое число умножили 9 и получили 36? |
3). Какое число разделили на 5 и получили 8? | 3). Какое число разделили на 9 и получили 4? |
4). | 4). На какое число разделили 56 и получили 7? |
5). Вычислить: 20+70-50= | 5).Вычислить: 30+20-40 |
6). Из какого числа вычли 35 и получили 6? | 6). Из какого числа вычли 46 и получили 7? |
7). Вычислить: 3+6-7+4= | 7). Вычислить: 4+5-3+4= |
8). Вычислить: 4х6:3х8= | 8). Вычислить: 6х3:2х7= |
9). Чему равен первый множитель, если второй множитель 4, произведение 12? | 9). Чему равен первый множитель, если второй множитель 3, а произведение 18? |
10). Чему равен второй множитель, если первый множит ель 9. | 10). Чему равен второй множитель, если первый множитель 8, а произведение 24? |
11). Вычислить: 30+20-40= | 11). Вычислить: 20+70-50= |
12). Чему равно уменьшаемое, если вычитаемое 46, разность 7? | 12). Чему равно уменьшаемое, если вычитаемое 35, а разность 6? |
13). Вычислить: 4+5-3+4= | 13) Вычислить: 3+6-7+4= |
14). Вычислить: 6х3:2х7= | 14). Вычислить: 4х6:3х5= |
Карточка №46
Первый вариант. | Второй вариант. |
1).Какое число умножили на 9 и получили 63? | 1). |
2). 56 уменьшить на 40. | 2). 67 уменьшить на 50. |
3). Уменьшаемое 89, вычитаемое 44. Найти разность. | 3). Уменьшаемое 98, вычитаемое 56. Найти разность. |
4). Из какого числа вычли 32 и получили 28? | 4). Из какого числа вычли 48 и получили 22? |
5). Вычислить: 8х3:6= | 5). Вычислить: 6х5:10= |
6). На какое число разделили 54 и получили 9? | 6). На какое число разделили42 и получили 6? |
7). Найти разность чисел: 79 и 8. | 7). Найти разность чисел: 99 и8. |
8). Во сколько раз 32 больше 8? | 8). Во сколько раз 36 больше 4? |
9). На какое число умножили 8 и получили 72? | 9). На какое число умножили9 и получили 63? |
10). На сколько уменьшили 67 и получили 17? | 10). На сколько уменьшили 56 и получили 16? |
11). Уменьшаемое98, вычитаемое 56. Найти разность. | 11). Уменьшаемое 89, вычитаемое 54.Найти разность. |
12). Чему равно уменьшаемое, если вычитаемое 48, а разность 32? | 12). Чему равно уменьшаемое, если вычитаемое 42, а разность 56? |
13). Вычислить: 5х8:10= | 13). |
14). Во сколько раз 4 меньше, чем 36? | 14). Во сколько раз 7 меньше, чем 28? |
Карточка №47
Первый вариант. | Второй вариант. |
1). Чему равен второй множитель, если первый множитель 9, а произведение 36? | 1). Чему равен второй множитель, если первый множитель 7, а произведение56? |
2). Во сколько раз 42 больше 7? | 2). Во сколько раз 32 больше 9? |
3). Чему равно делимое, если делитель 8, а частное 8? | 3). Чему равно делимое, если делитель 6. А частное 7? |
4). Найти разность чисел: 60 и 43. | 4). Найти разность чисел: 50 и 36. |
5). 48 уменьшить на 25. | 5). 57 уменьшить на 34. |
6). На сколько 17 больше 13? | 6). На сколько 19 больше 14? |
7). Вычислить: 70-50+40-30= | 7). Вычислить: 80-40+50-20= |
8). Из какого числа вычли 40 и получили 56? | 8). Из какого числа вычли 60 и получили 38? |
9). Какое число умножили на 7 и получили 28? | 9). Какое число умножили на 9 и получили 54? |
10). Во сколько раз 32 больше 8? | 10). Во сколько раз 63 больше 7? |
11). | 11). Какое число разделили на 9 и получили 8? |
12). Найти разность чисел: 50 и 46. | 12). Найти разность чисел: 60 и 53. |
13). Уменьшаемое 57, вычитаемое 34. Найти разность. | 13). Уменьшаемое 48, вычитаемое 25. Найти разность. |
14). Вычислить: 80-30+50-20= | 14). Вычислить:70-40+50-20= |
Карточка №48
Первый вариант. | Второй вариант. |
1). Найти частное чисел: 48 и 6. | 1). Найти разность чисел: 56 и 8. |
2). Делимое 32, делитель 4. | 2). Делимое 21, делитель7. Найти частное. |
3). Во сколько раз 18 больше 3? | 3). Во сколько раз 12 больше 4? |
4). Вычислить: 36:4:3х8= | 4). Вычислить: 28:7:2х9= |
5). Какое число разделилина7 и получили8? | 5). Какое число разделили на 8 и получили 6? |
6). На какое число разделили 24 и получили6? | 6). На какое число разделили 56 и получили 8? |
7). На сколько 53 больше 40? | 7). На сколько 45 больше 30? |
8). 98 уменьшить на 64. | 8). 89 уменьшить 35. |
9). 56 уменьшить в 8 раз. | 9). 48 уменьшить в 6 раз. |
10). Во сколько раз 3 меньше 12? | 10).Во сколько раз 3 меньше 18? |
11). Вычислить: 28:7:2х9= | 11). Вычислить: 36:4:3х8= |
12). Найти произведение чисел: 9 и 7. | 12). Найти произведение чисел: 6 и 9. |
13). Найти частное чисел: 48 и 8. | 13). Найти частное чисел: 56 и 7. |
14). На сколько 48 больше 30? | 14). На сколько 53 больше 40? |
Карточка №49
Первый вариант. | Второй вариант. |
1). Найти произведение чисел:40 и 3. | 1). Найти произведение чисел: 50 и 3. |
2). Первый множитель 20, второй множитель 6. Найти произведение. | 2). Первый множитель 30, второй множитель4. Найти произведение. |
3). 80 увеличить в 4 раза. | 3). 60 увеличить в 7 раз. |
4). Какое число разделили на 7 и получили9? | 4). Какое число разделили на 6 и получили 9? |
5). Во сколько раз 24 больше 6? | 5). Во сколько раз 36 больше 4? |
6). Из какого числа вычли 40 и получили 28? | 6). |
7). К какому числу прибавили 26 и получили 70? | 7). К какому числу прибавили 36 и получили 80? |
8). Найти произведение чисел: 60 и 3. | 8). Найти произведение чисел: 70 и 4. |
9). Первый множитель 4, второй множитель 60.Найти произведение. | 9). Первый множитель 7, второй множитель 40.Найти произведение. |
10). 60 увеличить в 6 раз. | 10). 80 увеличить в 3 раза. |
11). Какое число разделили на8 и получили 4? | 11). Какое число разделили на 7 и получили 8? |
12). На какое число разделили 56 и получили 7? | 12). |
13). Во сколько раз 36 больше 4? | 13). Во сколько раз 24 больше 8? |
14). К какому числу прибавили 36 и получили 80? | 14).К какому числу прибавили 34 и получили 70? |
Карточка №50
Первый вариант | Второй вариант |
1). Делимое 36, делитель 9. Найти частное. | 1). Делимое 48, делитель 6.Найти частное. |
2). Вычислить: 72:8:3х7= | 2). Вычислить: 3:4:3х8= |
3). Найти произведение чисел: 7 и 40. | 3). Найти произведение чисел: 6 и 90. |
4). Первый множитель, второй множитель 70. Найти произведение. | 4). Первый множитель9, второй множитель 80. Найти произведение. |
5). 3 увеличить в 60 раз. | 5). 4 увеличит в 60 раз. |
6). Во сколько раз 700 больше 100? | 6). Во сколько раз 600 больше 100? |
7). Какое число разделили на 8 и получили 6? | 7). Какое число разделили на 4 и получили9? |
8). На какое число разделили 54 и получили 9? | 8). На какое число разделили 48 и получили 8? |
9). Вычислить: 36:4:3х7= | 9). Вычислить: 72:8:3х9= |
10). | 10) Найти частное чисел 56 и 7. |
11). 9 увеличить в 50 раз. | 11). 7 увеличить в 80 раз. |
12). Первый множитель 40. Второй множитель 6. Найти произведение. | 12). Первый множитель8,второй множитель 30.Найти произведение. |
13). Во сколько раз 100 меньше400? | 13). Во сколько раз 100 меньше 300? |
14). 600 уменьшить в 10 раз. | 14). 900 уменьшить в 10 раз. |
Карточка №51
Первый вариант. | Второй вариант. |
1). 48 уменьшить на 7. | 1). |
2). 36 увеличить на 24. | 2). 43 увеличит на 23. |
3). 30 увеличить в 9 раз. | 3). 40 увеличить в 9 раз. |
4). Какое число увеличили в 50 раз и получили 350? | 4). Какое число увеличили в 70 раз и получили 420? |
5). Какое число умножили на 4 и получили 16? | 5). Какое число умножили на 7 и получили 28? |
6). На какое число разделили 63 и получили9? | 6). На какое число разделили 72 и получили 9? |
7). Из какого числа вычли 32 и получили 28? | 7). Из какого числа вычли 43 и получили 27? |
8). | 8). Во сколько раз 12 больше 3? |
9). 87 уменьшить на 4. | 9). 69 уменьшить на 7. |
10). Найти сумму чисел: 62 и 38. | 10). Найти сумму чисел: 46 и 54. |
11). Найти произведение чисел: 5 и 80. | 11). Найти произведение чисел: 60 и 5. |
12). Во сколько раз 270 больше 9? | 12). Во сколько раз 560 больше 7? |
13). Во сколько раз 4 меньше 160? | 13). Во сколько раз 5 меньше 150? |
14). 4см 5мм= мм | 14). 6дм2см= см |
Карточка №52
Первый вариант. | Второй вариант. |
1). Вычислить:81:9:3х6= | 1). Вычислить:64:8;х7= |
2). Какое число разделили на 7 и получили20? | 2). Какое число разделили на 8 и получили 30? |
3). Найти произведение чисел: 70 и 4. | 3). Найти произведение чисел: 60 и 7. |
4). Найти частное чисел: 360 и 4. | 4). Найти частное чисел: 560 и 8. |
5). Первый множитель 5. Второй множитель 70.Найти произведение. | 5). Первый множитель 6, второй множитель 40.Найти произведение. |
6). На какое число разделили 56 и получили 90? | 6). |
7). Найти разность чисел: 80 и 43. | 7). Найти разность чисел: 70 и 36. |
8). 42 увеличить на7. | 8). 53 увеличить на 6. |
9). Вычислить: 36:6:3х7= | 9). Вычислить: 16:4:2х9= |
10). Найти произведение 40 и 8. | 10). Найти произведение 30 и 8. |
11). 560 уменьшить в 8раз. | 11). 630 уменьшить в 9 раз. |
12). 70 уменьшить на 54. | 12). 90 уменьшить на 73. |
13). 6м7дм= дм | 13). |
14). 3дм 8см= см | 14). 5м 2дм= дм |
Карточка №53
Первый вариант. | Второй вариант. |
1). Найти произведение чисел: 7 и 9. | 1). Найти произведение чисел: 5 и 8. |
2). Чему равен делитель, если делимое 81, а частное 9? | 2). Чему равен делитель, если делимое 64, а частное 8? |
3). Вычислить: 42:7:2х9= | 3). Вычислить: 56:7:2х8= |
4). 3 увеличить в100 раз. | 4). 6 увеличить в 100 раз. |
5). | 5). Какое число умножили на 6 и получили 24? |
6). Из какого числа вычли 12 и получили 28? | 6). Из какого числа вычли 14 и получили 36? |
7). 400 уменьшить в 100 раз | 7). 700 уменьшить в 100 раз. |
8). Какое число вычли из 68 и получили 24? | 8). Какое число вычли из 77 и получили 35? |
9). Найти произведение чисел: 5 и 7. | 9). Найти произведение чисел: 7 и 8. |
10). Какое число разделили на 7 и получили 9? | 10). Какое число разделили на 6 и получили 8? |
11). | 11). 7дм 8см= см |
12). 5дм4см= см | 12). 8м 2дм= дм |
13). 200 уменьшить в 100 раз. | 13). 500 уменьшить в 100 раз. |
14). Вычислить: 8+4-5+6-9= | 14). Вычислить: 3+8-7+9-6= |
Карточка №54
Первый вариант. | Второй вариант. |
1). Найти частное чисел: 49 и 7. | 1). Найти частное чисел: 24 и 8. |
2). Во сколько раз 60 больше 10? | 2). Во сколько раз 40 больше 10? |
3). | 3). Найти произведение чисел: 8 и 7. |
4). На сколько 60 больше 46? | 4). На сколько 80 больше 63? |
5). Во сколько раз 10 меньше 300? | 5). Во сколько раз 10 меньше 600? |
6). 100 увеличить в 2 раза | 6). 100 увеличить в 9 раз. |
7). Какое число разделили на 7 и получили 6? | 7). Какое число разделили н 5 и получили 9? |
8). Из какого числа вычли 53 и получили 17? | 8). Из какого числа вычли 42 и получили 18? |
9). Какое число увеличили на 47 и получили 22? | 9). |
10). 97см= дм см | 10). 48дм= м дм |
11). 4см 7мм= мм | 11). 8дм 5см= см |
12). 56дм= м дм | 12) 63см= дм см |
13). Вычислить: 90-70+40-30+50= | 13). Вычислить: 70-40+50-40+30= |
14). Вычислить: 36:6х5:10= | 14). Вычислить: 20:4х6:10= |
Карточка №55
Первый вариант. | Второй вариант. |
1). На сколько 79 больше56? | 1). |
2). Какое число разделили на 8 и получили 4? | 2). Какое число разделили на 5 и получили 7? |
3). Во сколько раз 56 больше 7? | 3). Во сколько раз 42 больше 6? |
4). 100 увеличить в 5 раз. | 4). 100 увеличить в 8 раз. |
5). Найти сумму чисел: 43 и 52. | 5). Найти сумму чисел: 36 и 55. |
6). Уменьшаемое 97, вычитаемое 43. Найти разность. | 6). Уменьшаемое 89, вычитаемое 52.Найти разность. |
7).Делимое 63. Делитель 9.Найти частное. | 7). Делимое 72. Делитель 9.Найти частное. |
8). Во сколько раз 9 меньше 81? | 8). Во сколько раз 8 меньше 64? |
9). Вычислить: 7+8-9+5-4+6= | Вычислить: 6+5-3+4-7+9= |
10). 2м 7дм= дм | 10). 5дм6см= см |
11). 64дм= м дм | 11). 85см= дм см |
12). Первый множитель 4, второй множитель100.Найти произведение. | 12). Первый множитель 7. Второй множитель 100. Найти произведение. |
13). На сколько 35 меньше 49? | 13). Насколько 43 меньше 58? |
14). Вычислить:100-40-30+50-70= | 14). |
Карточка №56
Первый вариант. | Второй вариант. |
1). 97 уменьшить на 56. | 1). 89 уменьшить на 67. |
2). 45 уменьшить в 5 раз. | 2). 32 уменьшить в 4 раза. |
3). Найти сумму чисел: 43 и 56. | 3). Найти сумму чисел: 35 и 64. |
4). 8 увеличить в 3 раза. | 4). 9 увеличить в 2 раза. |
5). Во сколько раз 700 больше 7? | 5). Во сколько раз 900 больше 9? |
6). Найти разность чисел: 78 и 56. | 6). |
7). 48 уменьшить в 6 раз. | 7). 54 уменьшить в 9 раз. |
8). 2м 4дм= дм | 8). 5см 6 мм = мм |
9). 49мм= см мм | 9). 67дм= м дм |
10). Делимое 400, делитель 4. Найти частное. | 10). Делимое 500. Делитель 5 .Найти частное. |
11). Найти частное чисел: 700 и 100. | 11). Найти частное чисел: 800 и 100. |
12). Вычислить: 48:6:2х4:8х9:3х10= | 12).Вычислить: 36:6:3х8:4х5:10х7= |
13). | 13). Какое число умножили на 100 и получили 700? |
14). Какое число разделили на 6 и получили 9? | 14). Какое число разделили на 8 и получили 4? |
Карточка №57
Первый вариант. | Второй вариант. |
1). Найти произведение чисел: 40 и 8. | 1). Найти произведение чисел: 60 и 7. |
2). Вычислить: 70-50+40-30+60-70. | 2). Вычислить: 80-30+40-70+50-30= |
3). Вычислить: 90:3х2х9= | 3). Вычислить: 60:2х3х7= |
4). Какое число умножили на 8 и получили 480? | 4). |
5). Какое число разделили на 6 и получили 0? | 5). Какое число разделили на 1 и получили 1? |
6). Вычислить: 6+8-7+5-6+9= | 6). Вычислить: 7+8-6+4-7+8= |
7). Во сколько раз 240 больше 60? | 7). Во сколько раз 360 больше 90? |
8).На сколько 28 меньше 70? | 8). На сколько 34 меньше 80? |
9). Найти произведение чисел: 12 и 6. | 9). Найти произведение чисел: 13 и 5. |
10). Найти частное чисел: 96 и 12. | 10). Найти частное чисел: 51 и 17. |
11). | 11). Делимое 84, делитель6. Найти частное. |
12). Во сколько раз 8 меньше 560? | 12). Во сколько раз 7 меньше 280? |
13). Какое число разделили на 1 и получили 1? | 13). Какое число разделили на 8 и получили 0? |
14). На сколько 78 больше 25? | 14). На сколько 89 больше 38? |
Карточка №58
Первый вариант. | Второй вариант. |
1)Вычислить: 72:8:3х6:9х8:4х9:6х9=. | 1). Вычислить: 63:7:3х6:9х8:4х9:6х8= |
2). Какое число разделили на 4 и получили 70? | 2). |
3). Вычислить: 80-60+50-40+20+50-40-50= | 3). Вычислить: 90-70+30+50-40-30+40-50= |
4). Вычислить: 20х3х7= | 4). Вычислить: 40х2х7= |
5). Из какого числа вычли 34 и получили 56. | 5). Из какого числа вычли 43 и получили 57? |
6). Найти сумму чисел: 43 и 39. | 6). Найти сумму чисел: 56 и 27, |
7). Найти разность чисел: 64 и 28. | 7). Найти разность чисел: 76 и 48. |
8). Первый множитель 39, второй множитель 2. Найти произведение. | 8). Первый множитель 36, второй множитель 2. |
9). Делимое 91, делитель 7.Найти частное. | 9). Делимое 96, делитель 8.Найти частное. |
10). Какое число умножили на 0 и получили 0? | 10). Какое число умножили на 1 и получили 1. |
11). На сколько 63 больше 35? | 11). На сколько 72 больше 47? |
12). Какое число умножили на 40 и получили 360? | 12). Какое число умножили на 80 и получили 480? |
13). Вычислить: 60:3х4х7= | 13). Вычислить: 90:3х2х9= |
14). Найти частное чисел: 400 и 10. | 14). Найти частное чисел: 800 и 100. |
Карточка №59
Первый вариант. | Второй вариант. |
1). Во сколько раз 90 меньше 270? | 1). Во сколько раз 40 меньше 240? |
2). Какое число разделили на 50 и получили 8? | 2). Какое число разделили на 60 и получили 5? |
3). Вычислить: 540:6:3:5= | 3). Вычислить: 420:7:3:5= |
4). Вычислить: 6+5-7+8-6+7-8= | 4). Вычислить: 7+6-5+4-6+8-7= |
5). На сколько 70 больше 63? | 5). На сколько 80 больше 72? |
6). Из какого числа вычли 63 и получили 25? | 6). Из какого числа вычли 54 и получили 32? |
7). | 7). Во сколько раз 80 больше4? |
8). Какое число прибавили к 34 и получили 79? | 8). Какое число прибавили к 46 и получили 89? |
9). 91 уменьшить на 57. | 82 уменьшить на 58. |
10). Найти разность чисел: 60 и 28. | 10). Найти разность чисел: 70 и 37. |
11). Вычислить: 36:4:3х4:2х4:3:2х9= | 11). Вычислить: 54:6:3х6:2х4:6х4:6х4:8= |
12). На сколько 27 меньше 69? | 12).На сколько 37 меньше 89? |
13). Вычислить: 2+7-6+5-4+6-8= | 13). Вычислить: 3+6-5+3+2-6+7= |
14). | 14). Из какого числа вычли 46 и получили 14? |
Карточка №60
Первый вариант. | Второй вариант. |
1). Найти произведение чисел: 70 и 8. | 1). Найти произведение чисел: 40 и 9. |
2). Вычислить: 90-70+40-30+50-40= | 2). Вычислить: 80-60+50+30-80+40= |
3). Во сколько раз 12 больше 4? | 3). Во сколько раз 18 больше2? |
4). Найти сумму чисел: 46 и 37. | 4). Найти сумму чисел: 54 и 28. |
5). Найти разность чисел: 80 и 46. | 5). |
6). На сколько 79 больше 24? | 6). На сколько 87 больше 35? |
7). Вычислить: 48:6:2х5:10х8:4х8= | 7). Вычислить: 42:7:2х10:5х6:9х7= |
8). Запишите формулу нахождения периметра прямоугольника. | 8). Запишите формулу нахождения периметра квадрата. |
9). Во сколько раз 420 больше 7? | 9). Во сколько раз 720 больше 9? |
10). Вычислить: 90:3:6х10= | 10). Вычислить: 80:4:5х10= |
11). Найти произведение чисел: 28 и 3. | 11). Найти произведение чисел: 27 и 3. |
12). | 12). Найти частное чисел: 84 и 6. |
13). На сколько 38 меньше 70? | 13). На сколько 43 меньше 90? |
14). Какое число разделили на 9 и получили 70? | 14). Какое число разделили на 8 и получили 90? |
Карточка №61
Первый вариант. | Второй вариант. |
1). Найти произведение чисел:11 и 8. | 1). Найти произведение чисел: 9 и 11. |
2). Найти сумму чисел: 56 и 18. | 2). Найти сумму чисел: 67 и 15. |
3). Вычислить: 6+5-7+8-6+9= | 3). |
4). Вычислить: 12:3х6:8х6:9= | 4). Вычислить: 15:3х6:3:2х8= |
5). Вычислить: 40х2х6= | 5). Вычислить: 30х2х9= |
6). Найти произведение чисел: 17 и 6. | 6). Найти произведение чисел: 18 и 6. |
7). Во сколько раз 6 меньше 300? | 7). Во сколько раз 8 меньше 400? |
8). Найти частное чисел: 400 и 10. | 8). Найти частное чисел: 600 и 10. |
9). Делимое 560, делитель 70. Найти частное. | 9). Делимое 420, делитель 10. Найти частное. |
10). | 10). Первый множитель 80. Второй множитель 7. Найти произведение. |
11). Какое число разделили на 3 и получили 14? | 11). Какое число разделили на 4 и получили 13? |
12). Вычислить: 20+30+40-70+50+30= | 12). Вычислить: 40+30+20-60+50-40= |
13). Уменьшаемое 79, вычитаемое 47.Найти разность. | 13). Уменьшаемое 87. Вычитаемое 54. Найти разность. |
14). Из какого числа вычли 28 и получили 32? | 14). Из какого числа вычли 34 и получили 46? |
Карточка №62
Первый вариант. | Второй вариант. |
1). Вычислить: 56:7:2х3:6х9:3= | 1). Вычислить: 63:7:3х6:2х4:6= |
2). Найти разность чисел: 60 и 18. | 2). Найти разность чисел: 70 и 16. |
3). Вычислить: 9+3-6+5-7+8= | 3). Вычислить: 8+4-6+5-7+9= |
4). 89 уменьшить на 54. | 4). 89 уменьшить на 65. |
5). Во сколько раз 480 больше 8? | 5) Во сколько раз 720 больше 9? |
6). Какое число разделили на 4 и получили 90? | 6). Какое число разделили на 3 и получили 70? |
7). Вычислить: 80-60+50+30-80+40= | 7). |
8). На сколько 32 меньше 85? | 8). На сколько 43 меньше 89? |
9). Уменьшаемое 73, вычитаемое 58. Найти разность. | 9). Уменьшаемое 62, вычитаемое 47. Найти разность. |
10). 38 увеличить в 2 раза. | 10). 39 увеличить в 2 раза. |
11). 96 уменьшить в 3 раза. | 11). 69 уменьшить в 3 раза. |
12) 6см 8мм= мм | 12). 4м 6дм= дм |
13). Делимое 84, делитель 6.Найти частное. | 13). Делимое 96, делитель 8.Найти частное. |
14). | 14). Вычислить: 3+4+2-6+4-2+5= |
Карточка №63
Первый вариант. | Второй вариант. |
1). Найти разность чисел: 73 и 38. | 1). Найти разность чисел: 62 и 27. |
2). Найти сумму чисел: 28 и 46. | 2). Найти сумму чисел: 35 и 58. |
3). 100 уменьшить на 72. | 3). 100 уменьшить на 64. |
4). Вычислить: 20+40-30+60-70+80= | 4). Вычислить: 30+60-70+40_50+80= |
5). Какое число разделили на 90 и получили 6? | 5). |
6). Во сколько раз 700 больше 100? | 6). Во сколько раз 800 больше 100? |
7). Из какого числа вычли 33 и получили 56? | 7). Из какого числа вычли 42 и получили 53? |
8). Найти произведение чисел: 24 и 3. | 8). Найти произведение чисел: 26 и 3. |
9). Найти частное чисел: 84 и 6. | 9). Найти частное чисел: 64 и 4. |
10). Делимое 90, делитель 15.Найти частное. | 10). Делимое 96. Делитель 12. Найти частное. |
11). Вычислить: 56:6:3х8:6х9:6х7= | 11). Вычислить: 63:7:3х8:6х9:6х8= |
12). | 12). На сколько 80 больше 32? |
13). К какому числу прибавили 53 и получили 68? | 13). К какому числу прибавили 64 и получили 78? |
14). Найти ¼ от 28. | 14). Найти 1\3 от 27. |
Карточка №64
Первый вариант. | Второй вариант. |
1). Вычислить: 20х4х3:60= | 1). Вычислить: 30х3х4:60 |
2). Из какого числа вычли 73 и получили 17? | 2). Из какого числа вычли 56 и получили 14? |
3). 42 уменьшить на 18. | 3). |
4). Вычислить: 6+8-7+8-9+5-7= | 4). Вычислить: 5+7-6+8-9+7-6= |
5). Записать формулу нахождения периметра разностороннего треугольника. | 5). Записать формулу нахождения периметра равностороннего треугольника. |
6). Найти площадь квадрата со стороной 8дм. | 6). Найти площадь прямоугольника со сторонами 6дм и 9дм. |
7). Какое число умножили на 40 и получили 120? | 7). Какое число умножили на 30 и получили 180? |
8). На сколько 90 больше 72? | 8). На сколько 80 больше 56? |
9). Вычислить: 10х9:3:6х80= | 9). |
10). Во сколько раз 70 меньше 420? | 10). Во сколько раз 80 больше 320? |
11). Записать формулу нахождения периметра прямоугольника. | 11). Записать формулу нахождения периметра квадрата. |
12). Какое число прибавили к 28 и получили 98? | 12). Какое число прибавили к 35 и получили 85? |
13). Чему равна 1\7 от 28? | 13). Чему равна 1\8 от 56? |
14). Найти произведение чисел: 36 и 3. | 14). Найти произведение чисел: 35 и 3. |
Карточка №65
Первый вариант. | Второй вариант. |
1). Во сколько раз 80 больше 4? | 1). Во сколько раз 90 больше 30? |
2). Из какого числа вычли 62 и получили 18? | 2). Из какого числа вычли 54 и получили 16? |
3). Вычислить: 30+60-70+50-40= | 3). Вычислить:20+80-70+50-40= |
4). Вычислить: 56:7:2х6:3х9= | 4). Вычислить: 42:7:2х8:6х9= |
5). На сколько 49 больше 18? | 5). На сколько 58 больше 16? |
6). Найти произведение чисел:27 и 4. | 6). Найти произведение чисел: 26 и 4. |
7). Первый множитель 18, второй множитель 6. | 7). Первый множитель 17. Второй множитель 6.Найти произведение. |
8). Найти частное чисел: 84 и 14. | 8). Найти частное чисел: 64 и 16. |
9). Найти разность чисел:72 и 56. | 9). Найти разность чисел: 75 и 58. |
10). Найти сумму чисел: 28 и 47. | 10). Найти сумму чисел: 45 и 27. |
11). Найти периметр прямоугольника со сторонами: 7м и 4м. | 11). Найти периметр квадрата со стороной 4дм. |
12). Найти площадь квадрата 6см. | 12). Найти площадь прямоугольника со сторонами 6м и 5м. |
13). | 13). Вычислить: 3х20х7= |
14). Найти 1/9 от 72. | 14). Найти 1/6 от 54. |
Карточка №66
Первый вариант. | Второй вариант. |
1). Вычислить: 20х4:10х8= | 1). Вычислить: 30х3:10х9= |
2). Какое число разделили на 3 и получили 90? | 2). Какое число разделили 7 и получили 30? |
3) На сколько 37 меньше 89? | 3). На сколько 46 меньше 87? |
4). Вычислить: 30+60-70+40-50= | 4). Вычислить: 20+70-60+50-40= |
5). | 5). Во сколько 50 меньше 300? |
6). Вычислить: 18:2:3х5х10= | 6). Вычислить: 16:2:2х7х10= |
7). Вычислить: 4+8-6+7-8+9= | 7). Вычислить: 6+5-4+7-8+9= |
8). Найти ¼ от 36. | 8). Найти 1/3 от 21. |
9). Найти площадь квадрата со стороной 7см. | 9). Найти площадь прямоугольника со сторонами 7 и 9см. |
10). Найти периметр прямоугольника со сторонами 5м и 7м. | 10). Найти периметр квадрата со стороной 6м. |
11). Какое число умножили на 0 и получили 0? | 11). |
12). Найти частное чисел: 900 и 100. | 12). Найти частное чисел: 800 и 100 |
13). Найти произведение чисел: 100 и 6. | 16). Найти произведение чисел: 4 и 100. |
14). Вычислить: 15х2:10= | 14). 25х2:10= |
Карточка №67
Первый вариант. | Второй вариант. |
1). Найти 1/8 от 72. | 1). Найти 1/9 от 54. |
2). 1/6=9. Найти все число. | 2). 1/4=7. Найти все число. |
3). Первый множитель 14, второй множитель 6. | 3). Первый множитель 18, второй множитель 4. Найти произведение. |
4). Найти произведение чисел: 17 и 6. | 4). Найти произведение чисел: 19 и 5. |
5). Делимое 57, делитель 3.Найти частное. | 5). Делимое 64. Делитель 4. Найти частное. |
6). 36 увеличить в 2 раза. | 6). 38 увеличить в 2 раза. |
7). Найти частное чисел: 78 и 13. | 7). Найти частное чисел: 75 и 15. |
8). Вычислить: 54:9:2х10:5= | 8). Вычислить: 56:7:2х10:5= |
9). Вычислить: 90:3х7= | 9). |
10).Вычислить: 4+8-6+7-9+8= | 10). Вычислить: 5+8-7+8-9+6= |
11). Найти периметр квадрата со стороной 9м. | 11). Найти периметр прямоугольника со сторонами 5м и 6м. |
12). Найти периметр разностороннего треугольника со сторонами 2см, 4см и 3см. | 12). Найти периметр равностороннего треугольника со стороной 6см. |
13). На сколько 76 больше 24? | 13). На сколько 87 больше 34? |
14). Во сколько раз 7 меньше 63? | 14). Во сколько раз 8 меньше 32? |
Карточка №68
Первый вариант. | Второй вариант. |
1). Какое число разделили на 40 и получили 7? | 1). Какое число разделили на 60 и получили 7? |
2). К какому числу прибавили 38 и получили 60? | 2). К какому числу прибавили 43 и получили80? |
3). Из какого числа вычли 63 и получили 22? | 3). Из какого числа вычли 74 и получили 25? |
4). Какое число умножили на 8 и получили 320? | 4). Какое число умножили на 7 и получили 350? |
5). Во сколько раз 360 больше 90? | 5). Во сколько раз 560 больше 70? |
6). На сколько 16 меньше 58? | 6). На сколько 14 меньше 48? |
7). | 7). Найти 1/4 от 36? |
8). 1/6=8. Найти все число. | 8). 1/3=6. Найти все число. |
9). Вычислить:50+40-70+80-60= | 9). Вычислить: 90-70+60-40+30= |
10). Найти произведение чисел: 16 и 5. | 10). Найти произведение чисел: 13 и 7. |
11). Найти частное чисел: 65 и 13. | 11). Найти частное чисел: 96:12. |
12). Найти разность чисел:97 и 64. | 12). Найти разность чисел: 89 и 57. |
13). Найти сумму чисел: 26 и 58. | 13). Найти сумму чисел: 37 и 46. |
14). | 14). Вычислить: 48:8:2х10:6х7= |
Карточка №69
Первый вариант. | Второй вариант. |
1). Найти произведение чисел: 19 и 4. | 1). Найти произведение чисел: 18 и 4. |
2). Делимое 57, делитель 3. Найти частное. | 2). Делимое 51, делитель 3.Найти частное. |
3). Найти частное чисел: 84 и 14. | 3). Найти частное чисел: 64 и 16. |
4). Найти 1/5 от 40. | 4). Найти 1/6 от 54. |
5). 1/9=8. Найти все число. | 5). |
6). Вычислить: 80:2х6= | 6).Вычислить: 90:3х7= |
7). Во сколько раз 5 меньше 400? | 7). Во сколько раз 5 меньше 300? |
8). Вычислить: 40+30+30-60+50= | 8). Вычислить: 50+40-70+60-30= |
9). На какое число разделили 560 и получили 80? | 9). На какое число разделили 720 и получили 90? |
10). К какому числу прибавили 42 и получили 79? | 10). К какому числу прибавили 54 и получили 89? |
11). Вычислить: 28:7х5:10х9= | 11). Вычислить: 42:7х5:10х8= |
12). | 12). Из какого числа вычли 38 и получили 60? |
13). Какое число разделили на 9 и получили 77? | 13). Какое число разделили на 6 и получили40? |
14). Во сколько раз 360 больше 9? | 14) Во сколько раз 320 больше 4? |
Карточка №70
Первый вариант. | Второй вариант. |
1). Найти 1/8 от 40. | 1). Найти 1/7 от 56. |
2). Вычислить: 48:6:4х9:3х7= | 2). Вычислить: 63:7:3х6:9х8= |
3). 11 увеличить в 7 раз. | 3). |
4). Найти произведение чисел: 6 и 100. | 4). Найти произведение чисел: 4 и 100. |
5). 1/3=4. Найти все число. | 5). ¼=6. Найти все число. |
6). Во сколько раз 420 больше6? | 6). Во сколько раз 350 больше5? |
7). Какое число умножили на 30 и получили 120? | 7). Какое число умножили на 40 и получили160? |
8). Вычислить: 81:9:3х8:6х4= | 8). Вычислить: 64:8:2х6:3х7= |
9). Найти разность чисел: 72 и 38. | 9). Найти разность чисел: 84 и 37. |
10). | 10). На сколько 32 меньше 75? |
11). Вычислить: 60:2х7= | 11). Вычислить: 90:3х6= |
12). 7см8мм= мм | 12). 9м 6дм= дм. |
13). Найти периметр равностороннего треугольника со стороной 6см. | 13). Найти периметр разностороннего треугольника со сторонами 5мм. 3мм. 2мм. |
14). Вычислить:4+7-5+6-8+9= | 14). Вычислить: 6+5-7+8-6=9= |
Карточка №71
Первый вариант. | Второй вариант. |
1). Найти произведение чисел:80 и 7. | 1). |
2). Вычислить: 30+20+40-70+60-40= | 2). Вычислить: 50+40-70+60-30-40= |
3). Вычислить: 6+8-9+7-6+5= | 3). Вычислить: 7+8-9+5-7+8= |
4). На сколько 27 меньше 89? | 4). На сколько 34 меньше 88? |
5). Во сколько раз 30 меньше 180? | 5). Во сколько раз 40 меньше 240? |
6). Найти разность чисел: 72 и 54. | 6). Найти разность чисел: 83 и 65. |
7). Найти сумму чисел: 28 и 46. | 7). Найти сумму чисел: 37 и 48. |
8). Найти произведение чисел: 16 и 8. | 8). Найти произведение чисел: 17 и 4. |
9). Найти частное чисел: 57 и 19. | 9). Найти частное чисел: 84 и 12. |
10). Найти ¼ от 36. | 10). Найти 1/6 от 48. |
11). 1/9=5.Найти все число. | 11). 1/7=6. Найти все число. |
12). Вычислить: 80:4:5х8= | 12). Вычислить: 90:3:5х9= |
13). 64 уменьшить в 4 раза. | 13). 96 уменьшить в 8 раз. |
14). Какое число разделили на 1 и получили 1? | Какое число разделили на 6 и получили 0? |
Карточка №72
Первый вариант. | Второй вариант. |
1). Вычислить: 6+5-7+8-6+9= | 1). Вычислить: 8+4-6+7-9+8= |
2). Какое число разделили на 40 и получили 7? | 2). Какое число разделили на 60 и получили 7? |
3). Какое число уменьшили на 52 и получили 46? | 3). Какое число уменьшили на 43 и получили 35? |
4). Какое число увеличили на 26 и получили 33? | 4). Какое число увеличили на 37 и получили 43? |
5). На сколько уменьшили 78 и получили 24? | 5). На сколько уменьшили 87 и получили 36? |
6). Вычислить: 54:9х7х10= | 6). |
7). Какое число умножили на 30 и получили 210? | 7). Какое число умножили на 60 и получили 240? |
8). Вычислить: 300:10:5= | 8). Вычислить: 400:10:5= |
9). На сколько умножили на 6 и получили 180? | 9). На сколько умножили 8 и получили 320? |
10). Вычислить: 30х2х7= | 10). Вычислить: 40х2х7= |
11). 7дм= см | 11). 9м= дм |
12). На сколько 84 больше 52? | 12). На сколько 76 больше 35? |
13). Найти произведение чисел: 100 и 7. | 13). Найти произведение чисел: 8 и 100. |
14). Найти частное чисел: 500 и 100. | 14). Найти частное чисел: 400 и 10. |
Карточка №73
Первый вариант. | Второй вариант. |
1). Вычислить: 4+8-7+6-9= | 1). Вычислить: 5+8-7+5-6= |
2). Вычислить: 20+40+30-70+60-50= | 2). 20+40+30-70+40-50= |
3). Вычислить: 42:7х5:10х8= | 3). Вычислить: 48:6х5:10х7= |
4). Найти частное и остаток: 50:6= | 4). Найти частное и остаток: 38:5= |
5). | 5). Найти частное и остаток: 47:6= |
6). 1/9=3. Найти все число. | 6). 1/8=7. Найти все число. |
7). Найти 1/3 от 21. | 7). Найти 1/6 от 54. |
8). Найти произведение чисел: 24 и 4. | 8). Найти произведение чисел: 28 и 3. |
9). Первый множитель 38. Второй множитель 2. Найти произведение. | 9). Первый множитель 39, второй множитель 2. Найти произведение. |
10). Найти частное чисел: 96 и 16. | 10). Найти частное чисел: 96 и 12. |
11). Из какого числа вычли 48 и получили 42? | 11). |
12). Вычислить: 2+8-7+5-4-2= | 12). Вычислить: 3+4+3-8+5-4= |
13). Какое число умножили на 70 и получили 210? | 13). Какое число умножили на 60 и получили 180? |
14). На сколько 78 больше 35? | 14). На сколько 87 больше 24? |
Карточка №74
Первый вариант. | Второй вариант. |
1). Найти 1/ от 21. | 1). Найти ¼ от 36. |
2). 1/8=7. Найти все число. | 2). 1/7=8. Найти все число. |
3). | 3). Найти частное и остаток: 57 и 6. |
4). Найти частное и остаток: 46 и 7 | 4). Найти частное и остаток: 35 и 4. |
5). Записать формулу нахождения периметра прямоугольника. | 5). Записать формулу нахождения периметра квадрата. |
6). Вычислить: 30+40-50+60-70= | 6). Вычислить: 20+70-60+40-50= |
7). Найти произведение чисел: 14 и 7. | 7). Найти произведение чисел: 16 и 6. |
8). Найти частное чисел: 64 и 16. | 8). Найти частное чисел: 84 и 14. |
9). 57 уменьшить в 3 раза. | 9). 51 уменьшить в 3 раза. |
10). На сколько 32 больше 17? | 10). На сколько 34 больше18? |
11). Во сколько раз 7 меньше 420? | 11). Во сколько раз 8 меньше 480? |
12). Какое число разделили на 30 и получили 4? | 12). Какое число разделили на 60 и получили 3? |
13). Найти разность чисел: 93 и 65. | 13). Найти разность чисел: 84 и 47. |
14). Найти сумму чисел: 36 и 28. | 14). Найти сумму чисел: 25 и 47. |
Карточка №75
Первый вариант. | Второй вариант. |
1). Найти произведение чисел: 30 и 9. | 1). Найти произведение чисел: 40 и 8. |
2). Найти частное чисел: 360 и 90, | 2). Найти частное чисел: 480 и 60. |
3). Какое число разделили на 8 и получили 90? | 3). Какое число разделили на 9 и получили 60? |
4). Из какого числа вычли 54 и получили 25? | 4). Из какого числа вычли 43 и получили 35? |
5). 6м 4дм= дм | 5). 46см= дм см |
6). 59мм= см мм | 6). 7м 9дм= дм |
7). Найти периметр прямоугольника со сторонами: 8м и 4м. | 7). Найти площадь квадрата со стороной 7м. |
8). Найти периметр квадрата со стороной 9дм. | 8). Найти периметр прямоугольника со сторонами: 7дм и 7дм. |
9). Вычислить: 30+60-70+50-40= | 9). Вычислить: 20+70-60+50-40= |
10). Вычислить: 50х2х9= | 10). Вычислить: 2х50х7= |
11). На сколько 54 меньше 80? | 11). На сколько 48 меньше 70? |
12). 1/8=9. Найти все число. | 12).1/7=6. Найти все число. |
13). Во сколько раз 80 меньше 320? | 13). Во сколько раз 70 меньше 630? |
14). | 14). Найти 1/9 от 63. |
Карточка №76
Первый вариант. | Второй вариант. |
1). Найти разность чисел: 72 и 47. | 1). Найти разность чисел: 83 и 58. |
2). Найти сумму чисел: 36 и 47. | 2). Найти сумму чисел: 24 и 67. |
3). Из какого числа вычли 32 и получили 56? | 3). Из какого числа вычли 43 и получили 46? |
4). Какое число умножили на 60 и получили 240? | 4). Какое число умножили на 70 и получили 210? |
5). Вычислить: 63:7:3х6:2х7= | 5). |
6). На сколько 83 больше 64? | 6). На сколько 93 больше 78? |
7). Найти сумму чисел: 38 и 47. | 7).Найти сумму чисел: 36 и 57. |
8). Вычислить: 30+70-80+50-40= | 8). Вычислить: 20+60-40+50-70= |
9). Во сколько раз 10 меньше 700? | 9). Во сколько раз 10 меньше 900? |
10). Найти произведение чисел: 18 и 3. | 10). Найти произведение чисел: 19 и 4. |
11). 42 увеличить в 2 раза. | 11). 43 увеличить в 2 раза. |
12). Найти частное чисел: 76 и 19. | 12 Найти частное чисел: 54 и 18. |
13). К какому числу прибавили 46 и получили 89? | 13). К какому числу прибавили 53 и получили 87? |
14). Найти 1/4 от160. | 14). Найти 1/7 от 560. |
Карточка №77
Первый вариант. | Второй вариант. |
1). Найти разность чисел: 63 и 27. | 1). Найти разность чисел: 72 и 35. |
2). Найти сумму чисел: 48 и 24. | 2). Найти сумму чисел: 57 и 26. |
3). Найти произведение чисел: 28 и 3. | 3). Найти произведение чисел: 27 и 3. |
4). Найти частное чисел: 76 и 4. | 4). Найти частное чисел: 72 и 6. |
5). 19 увеличить в 4 раза. | 5). 14 увеличить в 6 раз. |
6). Вычислить:81:9:3х10:5= | 6). 56:7:2х10:5= |
7). Вычислить: 6+5-7+8-6+9= | 7). Вычислить: 7+6-8+9-7+8= |
8). Какое число разделили на 90 и получили 4? | 8) Какое число разделили на 80 и получили 7? |
9). На какое число умножили 7 и получили 490? | 9). На какое число умножили 9 и получили 360? |
10). 1/9 =3. Найти все число. | 10). 1/7=4. Найти все число. |
11). Найти 1/6 от 18. | 11). Найти 1/7 от 35. |
12). Найти периметр квадрата со стороной 8дм. | 12). Найти периметр прямоугольника со сторонами 5дм и 4дм. |
13). На сколько 86 больше 24? | 13). На сколько 97 больше 35? |
14). Найти частное и остаток чисел: 51 и 6. | 14). Найти частное и остаток чисел: 46 и 7. |
Карточка №78
Первый вариант. | Второй вариант. |
1). Найти произведение чисел: 40 и 9. | 1). |
2). Найти разность чисел: 72 и 47. | 2). Найти разность чисел: 81 и 54. |
3). На сколько 23 меньше 47? | 3). На сколько 26 меньше 69? |
4). Найти сумму чисел: 38 и 24. | 4). Найти сумму чисел:46 и 27. |
5). Найти 1/9 от 63. | 5). Найти 1/8 от 48. |
6). 1/8=7. Найти все число. | 6). 1/7=9. Найти все число. |
7). 4м 6дм= дм. | 7). 8дм 4см= см |
8). 7дм= см | 8). 5м= дм |
9). | 9). 15 увеличить в 5 раз. |
10). 75 уменьшить в 5 раз. | 10). 64 уменьшить в 4 раза. |
11). Делимое 51, делитель17. Найти частное. | 11). Делимое 72, делитель12. Найти частное. |
12). Во сколько раз 7 меньше 280? | 12). Во сколько раз 6 меньше 420? |
13). Вычислить: 30+60-70+40-30= | 13). Вычислить: 40+30+20-60+50= |
14). Найти периметр прямоугольника со сторонами 6м и 5м. | 14). Найти периметр квадрата со стороной 6см. |
Карточка №79
Первый вариант. | Второй вариант. |
1). Вычислить: 32:4:4х3х9= | 1). Вычислить: 48:6:4х3х7= |
2). Вычислить: 90:3х8= | 2). Вычислить: 80:2х7= |
3). Найти 1\4 от 32. | 3). Найти 1/6 от 42. |
4). 1/5=8. Найти все число. | 4). 1\6=5. Найти все число. |
5). 600 уменьшить в 10 раз. | 5). 900 уменьшить в 10 раз. |
6). Найти произведение чисел: 30 и 10. | 6). Найти произведение чисел: 40 и 10. |
7). Насколько 35 меньше 70? | 7). |
8). Найти произведение чисел: 14 и 7. | 8). Найти произведение чисел: 16 и 6. |
9). Найти частное чисел: 96 и 12. | 9). Найти частное чисел: 91 и 13. |
10). 36 увеличить в 3 раза. | 10). 34 увеличить в 3 раза. |
11). 200 увеличить на 700. | 11). 300 увеличить на 500. |
12). Найти периметр прямоугольника со сторонами 6дм и 4 дм. | 12)Найти площадь квадрата со стороной 8дм. |
13). 45см= дм см | 13). 72дм= м дм |
14). Из какого числа вычли 43 и получили 54? | 14). |
Карточка №80
Первый вариант. | Второй вариант. |
1). Какое число умножили на 6 и получили 540? | 1). Какое число умножили на 8 и получили 720? |
2). На какое число умножили 6 и получили 0? | 2). На какое число умножили 1 и получили 1? |
3). Из какого числа вычли 27 и получили 13? | 3). Из какого числа вычли 26 и получили 14? |
4). Найти разность чисел: 63 и 28. | 4). Найти разность чисел: 72 и 36. |
5). Найти произведение чисел: 15 и 3. | 5). |
6). Найти частное чисел: 96 и 16. | 6). Найти частное чисел: 64 и 16. |
7). 91 уменьшить в 7 раз. | 7). 84 уменьшить в 6 раз. |
8). Делимое 84, делитель 2. Найти частное. | 8). Делимое 96, делитель 3. Найти частное. |
9). Найти 1/7 от 14. | 9). Найти 1/8 от 24. |
10). 700 уменьшить в 100 раз. | 10). 500 уменьшить в 10 раз. |
11). Найти частное чисел: 900 и 10. | 11). Найти частное чисел: 300 и 100. |
12). Вычислить: 40х4:80= | 12). |
13). Записать формулу нахождения периметра квадрата. | 13). Записать формулу нахождения периметра прямоугольника. |
14). 37мм= см мм | 14). 56см= дм см |
Задача №9. Кодирование звуковой и графической информации. Передача информации.
Автор материалов — Лада Борисовна Есакова.
При оцифровке звука в памяти запоминаются только отдельные значения сигнала. Чем чаще записывается сигнал, тем лучше качество записи.
Частота дискретизации f – это количество раз в секунду, которое происходит преобразование аналогового звукового сигнала в цифровой. Измеряется в Герцах (Гц).
Глубина кодирования (а также, разрешение) – это количество бит, выделяемое на одно преобразование сигнала. Измеряется в битах (Бит).
Возможна запись нескольких каналов: одного (моно), двух (стерео), четырех (квадро).
Обозначим частоту дискретизации – f (Гц), глубину кодирования – B(бит), количество каналов – k, время записи – t(Сек).
Количество уровней дискретизации d можно рассчитать по формуле: d = 2B.
Тогда объем записанного файла V(бит) = f * B * k * t.
Или, если нам дано количество уровней дискретизации,
V(бит) = f * log2d * k * t.
Единицы измерения объемов информации:
1 б (байт) = 8 бит
1 Кб (килобайт) = 210 б
1 Мб (мегабайт) = 220 б
1 Гб (гигабайт) = 230 б
1 Тб (терабайт) = 240 б
1 Пб (петабайт) = 250 б
При оцифровке графического изображения качество картинки зависит от количества точек и количества цветов, в которые можно раскрасить точку.
Если X – количество точек по горизонтали,
Y – количество точек по вертикали,
I – глубина цвета (количество бит, отводимых для кодирования одной точки), то количество различных цветов в палитре N = 2I. Соответственно, I = log2N.
Тогда объем файла, содержащего изображение, V(бит) = X * Y * I
Или, если нам дано количество цветов в палитре, V(бит) = X * Y * log2N.
Скорость передачи информации по каналу связи (пропускная способность канала) вычисляется как количество информации в битах, переданное за 1 секунду (бит/с).
Объем переданной информации вычисляется по формуле V = q * t, где q – пропускная способность канала, а t – время передачи.
Кодирование звука
Пример 1.
Производится двухканальная (стерео) звукозапись с частотой дискретизации 16 кГц и глубиной кодирования 32 бит. Запись длится 12 минут, ее результаты записываются в файл, сжатие данных не производится. Какое из приведенных ниже чисел наиболее близко к размеру полученного файла, выраженному в мегабайтах?
1) 30 2) 45 3) 75 4) 90
Решение:
V(бит) = f(Гц)* B(бит) * k * t(Сек),
где V – размер файла, f – частота дискретизации, B – глубина кодирования, k – количество каналов, t – время.
Значит, V(Мб) = (f * B * k * t ) / 223
Переведем все величины в требуемые единицы измерения:
V(Мб) = (16*1000 * 32 * 2 * 12 * 60 ) / 223
Представим все возможные числа, как степени двойки:
V(Мб) = (24 * 23 * 125 * 25 * 2 * 22 * 3 * 15 * 22) / 223 = (5625 * 217) / 223 = 5625 / 26 =
5625 / 64 ≈ 90.
Ответ: 4
!!! Без представления чисел через степени двойки вычисления становятся намного сложнее.
!!! Частота – это физическая величина, а потому 16 кГц = 16 * 1000 Гц, а не 16 * 210. Иногда этой разницей можно пренебречь, но на последних диагностических работах она влияла на правильность ответа.
Пример 2.
В течение трех минут производилась четырёхканальная (квадро) звукозапись с частотой дискретизации 16 КГц и 24-битным разрешением. Сжатие данных не производилось. Какая из приведенных ниже величин наиболее близка к размеру полученного файла?
1) 25 Мбайт
2) 35 Мбайт
3) 45 Мбайт
4) 55 Мбайт
Решение:
V(бит) = f(Гц)* B(бит) * k * t(Сек),
где V – размер файла, f – частота дискретизации, B – глубина кодирования (или разрешение), k – количество каналов, t – время.
Значит, V(Мб) = (f * B * k * t ) / 223 = (16 * 1000 * 24 * 4 * 3 * 60) / 223 = (24 * 23 * 125 * 3 * 23 * 22 * 3 * 15 * 22) / 223 = (125 * 9 * 15 * 214) / 223 = 16875 / 29 = 32, 96 ≈ 35
Ответ: 2
Пример 3.
Аналоговый звуковой сигнал был записан сначала с использованием 64 уровней дискретизации сигнала, а затем с использованием 4096 уровней дискретизации сигнала. Во сколько раз увеличился информационный объем оцифрованного звука?
1) 64
2) 8
3) 2
4) 12
Решение:
V(бит) = f * log2d * k * t, где V – размер файла, f – частота дискретизации, d – количество уровней дискретизации, k – количество каналов, t – время.
V1 = f * log264 * k * t = f * 6 * k * t
V2 = f * log24096 * k * t = f * 12 * k * t
V2 / V1 = 2
Правильный ответ указан под номером 3.
Ответ: 3
Кодирование изображения
Пример 4.
Какой минимальный объём памяти (в Кбайт) нужно зарезервировать, чтобы можно было сохранить любое растровое изображение размером 64×64 пикселей при условии, что в изображении могут использоваться 256 различных цветов? В ответе запишите только целое число, единицу измерения писать не нужно.
Решение:
V(бит) = X * Y * log2N, где V – объем памяти, X,Y – количество пикселей по горизонтали и вертикали, N – количество цветов.
V (Кб) = (64 * 64 * log2256) / 213 = 212 * 8 / 213 = 4
Ответ: 4
Пример 5.
Для хранения растрового изображения размером 64×32 пикселя отвели
1 килобайт памяти. Каково максимально возможное число цветов в палитре изображения?
Решение:
V(бит) = X * Y * log2N, где V – объем памяти, X,Y – количество пикселей по горизонтали и вертикали, N – количество цветов.
log2N = V /( X*Y) = 213 / (26 * 25) = 4
N = 16
Ответ:16
Сравнение двух способов передачи данных
Пример 6.
Документ объемом 5 Мбайт можно передать с одного компьютера на другой двумя способами:
А) Сжать архиватором, передать архив по каналу связи, распаковать.
Б) Передать по каналу связи без использования архиватора.
Какой способ быстрее и насколько, если
– средняя скорость передачи данных по каналу связи составляет 218 бит в секунду,
– объем сжатого архиватором документа равен 80% от исходного,
– время, требуемое на сжатие документа – 35 секунд, на распаковку – 3 секунды?
В ответе напишите букву А, если способ А быстрее или Б, если быстрее способ Б. Сразу после буквы напишите количество секунд, насколько один способ быстрее другого. Так, например, если способ Б быстрее способа А на 23 секунды, в ответе нужно написать Б23. Слов «секунд», «сек.», «с.» к ответу добавлять не нужно.
Решение:
Способ А. Общее время складывается из времени сжатия, распаковки и передачи. Время передачи t рассчитывается по формуле t = V / q, где V — объём информации, q — скорость передачи данных.
Объем сжатого документа: 5 * 0,8 = 4 Мб =4 * 223 бит.
Найдём общее время: t = 35 с + 3 с + 4 * 223 бит / 218 бит/с = 38 + 27 с = 166 с.
Способ Б. Общее время совпадает с временем передачи: t = 5 * 223 бит / 218 бит/с = 5 * 25 с = 160 с.
Способ Б быстрее на 166 — 160 = 6 с.
Ответ: Б6
Определение времени передачи данных
Пример 7.
Скорость передачи данных через ADSL─соединение равна 128000 бит/c. Через данное соединение передают файл размером 625 Кбайт. Определите время передачи файла в секундах.
Решение:
Время t = V / q, где V — объем файла, q — скорость передачи данных.
t = 625 * 210 байт / (2 7 * 1000) бит/c = 625 * 213 бит / (125 * 210) бит/c = 5 * 23 с = 40 с.
Ответ: 40
Пример 8.
У Васи есть доступ к Интернет по высокоскоростному одностороннему радиоканалу, обеспечивающему скорость получения им информации 217 бит в секунду. У Пети нет скоростного доступа в Интернет, но есть возможность получать информацию от Васи по низкоскоростному телефонному каналу со средней скоростью 215 бит в секунду. Петя договорился с Васей, что тот будет скачивать для него данные объемом 4 Мбайта по высокоскоростному каналу и ретранслировать их Пете по низкоскоростному каналу. Компьютер Васи может начать ретрансляцию данных не раньше, чем им будут получены первые 512 Кбайт этих данных. Каков минимально возможный промежуток времени (в секундах), с момента начала скачивания Васей данных, до полного их получения Петей? В ответе укажите только число, слово «секунд» или букву «с» добавлять не нужно.
Решение:
Нужно определить, сколько времени будет передаваться файл объемом 4 Мбайта по каналу со скоростью передачи данных 215 бит/с; к этому времени нужно добавить задержку файла у Васи (пока он не получит 512 Кбайт данных по каналу со скоростью 217 бит/с).
Время скачивания данных Петей: t1= 4*223 бит / 215 бит/с = 210 c.
Время задержки: t2 = 512 кб / 217 бит/с = 2(9 + 10 + 3) — 17 c = 25 c.
Полное время: t1 + t2 = 210 c + 25 c = (1024 + 32) c = 1056 c.
Ответ: 1056
Пример 9.
Данные объемом 60 Мбайт передаются из пункта А в пункт Б по каналу связи, обеспечивающему скорость передачи данных 219 бит в секунду, а затем из пункта Б в пункт В по каналу связи, обеспечивающему скорость передачи данных 220 бит в секунду. Задержка в пункте Б (время между окончанием приема данных из пункта А и началом передачи в пункт В) составляет 25 секунд. Сколько времени (в секундах) прошло с момента начала передачи данных из пункта А до их полного получения в пункте В? В ответе укажите только число, слово «секунд» или букву «с» добавлять не нужно.
Решение:
Полное время складывается из времени передачи из пункта А в пункт Б (t1), задержки в пункте Б (t2) и времени передачи из пункта Б в пункт В (t3).
t1 = (60 * 223) / 219 =60 * 16 = 960 c
t2 = 25 c
t3 = (60 * 223) / 220 =60 * 8 = 480 c
Полное время t1 + t2 +t3 = 960 + 25 + 480 = 1465 c
Ответ: 1465
Как самостоятельно рассчитать плитку? — новости «Керамин»
Ремонт часто сталкивает нас со специфическими задачами и технологиями, требует особых знаний и навыков. Нередко приходится пользоваться помощью специалистов, в разы увеличивая бюджет даже несущественной переделки.
При укладке плитки можно воспользоваться услугами дизайн-студии, плиточников и даже сделать все «под ключ». А можно попытаться разобраться в некоторых аспектах самостоятельно. Советуем начать с малого, однако, не менее важного – узнать, как правильно рассчитать необходимое количество плитки для будущего интерьера.
Существует несколько способов укладки плитки, соответственно, и затраты материала на разные варианты будут различными.
Базовый способ укладки: плитка выкладывается точно в ряд, параллельно углам и стенам. С точки зрения экономии материала – это самый оптимальный способ укладки, отходов остаётся очень мало.
Способ расчета: площадь помещения / площадь одной плитки = количество плиток. Количество плиток округляется в большую сторону.
Для того, чтобы узнать необходимое количество плитки в метрах квадратных – умножаем количество плиток на площадь одной плитки.
Пример. Необходимо облицевать пол помещения, длиной 2,6 метра и шириной 2,4 метра, плиткой, размером 40*40 см.
Площадь помещения = 2,6м×2,4м = 6,24м.кв.
Площадь 1 плитки = 40см×40см = 1600 см.кв.= 0,16 м.кв.
Количество плиток = 6,24÷0,16 = 39шт.
Метраж плитки = 39шт × 0,16 м.кв. = 6,24 м.кв.
Коллекция «Антик» от «Керамин»
Базовый под углом: плитка выкладывается под углом (например, 45°) относительно стен. Рисунок выглядит интереснее, чем при базовом способе, укладка позволяет скрыть некоторую кривизну поверхности стен. Однако, при таком способе укладки расход плитки больше.
Рисунок выглядит интереснее, чем при базовом способе, укладка позволяет скрыть некоторую кривизну поверхности стен. Однако, при таком способе укладки расход плитки больше.
Способ расчета: площадь помещения / площадь одной плитки = количество плиток. Для учета подрезки добавляем 10% к полученному количеству целых плиток. Округляем количество в большую сторону.
Для того, чтобы узнать необходимое количество плитки в метрах квадратных – умножаем количество плиток на площадь одной плитки.
Пример. Необходимо облицевать пол помещения, длиной 1,6 метра и шириной 1,2 метра, плиткой, размером 30*30 см.
Площадь помещения = 1,6м×1,2м = 1,92 м.кв.
Площадь 1 плитки = 30см×30см = 900 см.кв.= 0,09 м.кв.
Количество плиток = 1,92÷0,09 = 21,3 шт.
Количество плиток с подрезкой = 21,3 + 10% = 23,43шт. = 24шт.
Метраж плитки = 24шт × 0,09 м.кв. = 2,16 м.кв.
Коллекция «Каррара» от «Керамин»
Шахматы: такой способ укладки привносит в интерьер живость и эффектность. Также он может помочь скрыть недостатки стен. В классическом варианте используются два контрастных цвета плитки, однако все зависит от дизайна Вашего помещения – можно использовать смежные оттенки.
Также он может помочь скрыть недостатки стен. В классическом варианте используются два контрастных цвета плитки, однако все зависит от дизайна Вашего помещения – можно использовать смежные оттенки.
Способ расчета: площадь помещения / площадь одной плитки = количество плиток. Полученное число делим на 2 = количество плиток каждого цвета. Округляем количество плиток каждого цвета в большую сторону.
Для того, чтобы узнать необходимое количество плитки каждого цвета в метрах квадратных – умножаем количество плиток на площадь одной плитки.
Пример. Необходимо облицевать пол помещения, длиной 3,6 метра и шириной 3,6 метра, плиткой двух цветов, размером 60*60 см.
Площадь помещения = 3,6м×3,6м = 12,96м.кв.
Площадь 1 плитки = 60см×60см = 3600 см.кв.= 0,36 м.кв.
Количество плиток = 12,96÷0,36 = 36 шт.
Количество плиток каждого цвета: 36 шт ÷ 2 = 18 шт.
Метраж плитки каждого цвета = 18шт × 0,36 м.кв. = 6,48 м.кв.
Общий метраж плитки: 6,48 м. кв × 2 = 12,96 м.кв.
кв × 2 = 12,96 м.кв.
Коллекция «Помпеи» от «Керамин»
Шахматы под углом: плитка укладывается под углом относительно стен, чередуясь в цвете. Такой способ отлично скрывает кривизну стен и позволяет визуально расширить помещение.
Способ расчета: площадь помещения / площадь одной плитки = количество плиток. Полученное число делим на 2 = количество плиток каждого цвета. Для учета подрезки добавляем 10% к полученному количеству целых плиток каждого из цветов. Округляем количество плиток каждого цвета в большую сторону.
Для того, чтобы узнать необходимое количество плитки каждого цвета в метрах квадратных – умножаем количество плиток на площадь одной плитки.
Пример. Необходимо облицевать пол помещения, длиной 2,2 метра и шириной 2,8 метра, плиткой двух цветов в раскладке шахматы под углом, размером 40*40 см.
Площадь помещения = 2,2м×2,8м = 6,16 м. кв.
кв.
Площадь 1 плитки = 40см×40см = 1600 см.кв.= 0,16 м.кв.
Количество плиток = 6,16 ÷0,16 = 38,5 шт. = 39 шт.
Количество плиток каждого цвета: 39 шт ÷ 2 = 19,5 шт. = 20 шт.
Количество плиток каждого цвета с подрезкой = 20 + 10% = 22 шт.
Метраж плитки каждого цвета = 22 шт × 0,16 м.кв. = 3,52 м.кв.
Общий метраж плитки: 3,52 м.кв × 2 = 7,04 м.кв.
Коллекция «Мадейра» от «Керамин»
Укладка со смещением: необычный вариант укладки – он позволяет сочетать плитку даже разных размеров. При таком способе обычная плитка чередуется с декоративными вставками, которые отличаются по цвету, фактуре и размеру.
Способ расчета: площадь помещения / площадь одной плитки = количество плиток. В маленьких помещениях количество плиток совпадает с количеством декоров. В больших помещениях: количество декоров = количество плиток – 5%. Округляем количество плиток и декоров в большую сторону.
Для того, чтобы узнать необходимое количество плитки в метрах квадратных – умножаем количество плиток на площадь одной плитки. Декоры считаются поштучно.
Пример. Необходимо облицевать пол помещения, длиной 2,55 метра и шириной 2,4 метра, плиткой размером 60*60 см. с декоративными вставками, размером 9,8*9,8см
Площадь помещения = 2,55м×2,4м = 6,12м.кв.
Площадь 1 плитки = 60см×60см = 3600 см.кв.= 0,36 м.кв.
Количество плиток = 6,12÷0,36 = 17 шт.
Количество декоров: 17 шт. – 5% = 16 шт.
Количество плитки каждого цвета: 17шт ÷ 2 = 8,5 шт = 9 шт
Метраж плитки каждого цвета = 9шт. × 0,36 = 3,24 м.кв.
Коллекция «Троя» от «Керамин»
Несколько важных моментов:
- учитывайте подрезку при подсчете: некоторые мелкие элементы плиток могут пригодиться;
- не забудьте про пол под ванной и стены за ней: если Вы не собираетесь их облицовывать – отнимите это количество плитки;
- всегда добавляйте несколько плиток «про запас» – при подрезке некоторые элементы могут треснуть.

Подсчет плитки – дело ответственное. Чтобы избежать лишних затрат бюджета или времени на докупку недостающих плиток, лучше воспользоваться услугами профессионалов. В салонах «Керамин» каждому покупателю доступна бесплатная услуга создания 3D дизайн-проекта и подсчета необходимого количества материалов (плитки и строительных смесей) в рамках разработанного проекта.
В «Керамин» ремонт превращается в удовольствие!
Калькулятор процентов: что такое 40 процентов от 60
Воспользуйтесь помощью онлайн-математического калькулятора «Что такое x процентов от y», который легко вычисляет 40% от 60 вместе с пошаговым решением, подробно описывающим, как получен результат 24.
Что составляет
40 процентов*60
= (40/100)*60
= (40*60)/100
= 2400/100 = 24
Теперь мы имеем: 40. проценты от 60 = 24
Вопрос: Чему равно 40 процентов от 60?
Теперь нам нужно определить 40% от 60 и процедуру, объясняющую это.
Шаг 3: Примите во внимание, что выходное значение 60 = 100%.
Шаг 4: Таким же образом, x = 40%.
Шаг 5: Разделив пару простых уравнений, мы получили уравнение вида
60 = 100% (1).
х = 40% (2).
(60%)/(х%) = 100/40
Шаг 6: Обратное значение обеих сторон приводит к следующему уравнению %
Следовательно, 40% из 60 — 24
40 процентов*60
= (40/100)*60
= (40*60)/100
= 2400/100 = 24
Теперь у нас есть: 40 процентов от 60 = 24
Вопрос: Сколько будет 40 процентов от 60?
Теперь нам нужно определить 40% от 60 и процедуру, объясняющую это.
Шаг 3: Примите во внимание, что выходное значение 60 = 100%.
Шаг 4: Таким же образом, x = 40%.
Шаг 5: Разделив пару простых уравнений, мы получили уравнение вида
60 = 100% (1).
х = 40% (2).
(60%)/(х%) = 100/40
Шаг 6: Обратное значение обеих сторон приводит к следующему уравнению %
Следовательно, 40% от 60 равно 24
1. Как рассчитать процент от суммы?
Как рассчитать процент от суммы?
Чтобы вычислить проценты, начните с написания числа, которое вы хотите преобразовать в проценты от общего значения, чтобы в итоге вы получили дробь. Затем превратите дробь в десятичную, разделив верхнее число на нижнее число. Наконец, умножьте десятичную дробь на 100, чтобы найти процент.
2. Сколько составляет 40 процентов от 60?
40 процентов от 60 равно 24.
3. Как вычислить 40 процентов от 60?
Multiply 40/100 with 60 = (40/100)*60 = (40*60)/100 = 24.
| 40% of | Result |
|---|---|
| 60 | 24 |
| 60,01 | 24,004 |
| 60,02 | 24,008 |
| 60,02 2,01300131 | |
| 60.04 | 24.016 |
| 60.05 | 24.02 |
| 60.06 | 24.024 |
| 60.07 | 24.028 |
60. 08 08 | 24.032 |
| 60.09 | 24.036 |
| 60.1 | 24.04 |
| 60.11 | 24.044 |
| 60.12 | 24.048 |
| 60.13 | 24.052 |
| 60.14 | 24.056 |
| 60.15 | 24.06 |
| 60.16 | 24.064 |
| 60.17 | 24.068 |
| 60.18 | 24.072 |
| 60.19 | 24.076 |
| 60.2 | 24.08 |
| 60.21 | 24.084 |
| 60.22 | 24.088 |
| 60.23 | 24.092 |
| 60.24 | 24.096 |
| 40% of | Result |
|---|---|
| 60.25 | 24.1 |
| 60.26 | 24. 104 104 |
| 60.27 | 24.108 |
| 60.28 | 24.112 |
| 60.29 | 24.116 |
| 60.3 | 24.12 |
| 60.31 | 24.124 |
| 60.32 | 24.128 |
| 60.33 | 24.132 |
| 60.34 | 24.136 |
| 60.35 | 24.14 |
| 60.36 | 24.144 |
| 60.37 | 24.148 |
| 60.38 | 24.152 |
| 60.39 | 24.156 |
| 60.4 | 24.16 |
| 60.41 | 24.164 |
| 60.42 | 24.168 |
| 60.43 | 24.172 |
| 60.44 | 24.176 |
| 60.45 | 24.18 |
| 60.46 | 24.184 |
60. 47 47 | 24.188 |
| 60.48 | 24.192 |
| 60.49 | 24.196 |
| 40% of | Result |
|---|---|
| 60.5 | 24.2 |
| 60.51 | 24.204 |
| 60.52 | 24.208 |
| 60.53 | 24.212 |
| 60.54 | 24.216 |
| 60.55 | 24.22 |
| 60.56 | 24.224 |
| 60.57 | 24.228 |
| 60.58 | 24.232 |
| 60.59 | 24.236 |
| 60.6 | 24.24 |
| 60.61 | 24.244 |
| 60.62 | 24.248 |
| 60.63 | 24.252 |
| 60.64 | 24.256 |
| 60.65 | 24. 26 26 |
| 60.66 | 24.264 |
| 60.67 | 24.268 |
| 60.68 | 24.272 |
| 60.69 | 24.276 |
| 60.7 | 24.28 |
| 60.71 | 24.284 |
| 60.72 | 24.288 |
| 60.73 | 24.292 |
| 60.74 | 24.296 |
| 40% of | Result | ||
|---|---|---|---|
| 60.75 | 24.3 | ||
| 60.76 | 24.304 | ||
| 60.77 | 24.308 | ||
| 60.78 | 24.312 | ||
| 60.79 | 24.316 | ||
| 60.8 | 24.32 | ||
| 60.81 | 24.324 | ||
| 60.82 | 24.328 | ||
| 60.83 | 24.332 | ||
60. 84 84 | 24.336 | ||
| 60.85 | 24.34 | ||
| 60.86 | 24.344 | ||
| 60.87 | 24.348 | ||
| 60.88 | 24.352 | ||
| 60.89 | 24.356 | ||
| 60.9 | 24.36 | ||
| 60,91 | 24,364 | ||
| 60,92 | 24,368 | ||
| 60,93 | 24,372 | 1313013824,372 | 131313138424.376 |
| 60.95 | 24.38 | ||
| 60.96 | 24.384 | ||
| 60.97 | 24.388 | ||
| 60.98 | 24.392 | ||
| 60.99 | 24.396 |
Нахождение процентов — Как найти проценты
Главная
Узнать
Бытовая математика
- Процент
- Простые проценты
- Виды простых процентов
- Расчет простых процентов
- Расчет общей суммы простых процентов
- Простой расчет процентного времени
- Расчет основного долга для простых процентов
- Сложные проценты
- Расчет сложных процентов
- Расчет сложного принципала
- Расчет сложной процентной ставки
- Расчет времени
Слово процентов означает одну стотную часть.
Процент — это число или отношение в виде дроби от 100. За числом в процентах всегда следует символ процента (%) . Ниже приведены примеры процентов:
`5%,10%,33 1/3%«,67,5%,100%`
Процент применяется в разных областях. Он обычно используется в бухгалтерском учете и финансах, таких как процентные ставки, прибыль, продажи и налогообложение. Ряд школ и университетов использовали проценты для выражения оценок учащихся. Вероятности, факты о питании и загрузка процесса представлены в процентах.
Процент – это результат умножения определенного числа на процент. В большинстве случаев проценты меньше, чем число, поскольку процент
является частью числа или количества. Но бывают случаи, что процент больше числа. Это произойдет, если процент больше 100%.
Но бывают случаи, что процент больше числа. Это произойдет, если процент больше 100%.
Короче говоря, процент — это определенный процент от числа.
В большинстве случаев за количеством следует фраза «процент».
Например;
70% от 50 равно 35.
В этом утверждении 50 — это количество, 35 — это процент, а 70% — это процент.
Пример 3:
Пример 4:
Чтобы найти процент от числа, разделите процент на количество, затем умножьте произведение на 100. Поставьте символ процента (%) после конечного произведения.
Если процент больше количества, это означает, что процент больше 100%. Процент является фактором увеличения значения количества.
Пример 5:
Пример 6:
Пример 7:
Для получения процентов необходимо преобразовать проценты в десятичную форму, прежде чем умножать их на количество.
Ниже приведены шаги преобразования процентов в десятичные числа:
1. Не обращайте внимания на символ процента (%).
Не обращайте внимания на символ процента (%).
2. Переместите запятую на два знака влево.
Пример 8:
Пример 9:
Пример 10:
Десятичные дроби легко преобразовать в проценты: просто переместите десятичную точку на две позиции вправо, а затем поставьте символ процента (%).
Пример 11:
Пример 12:
Иногда преобразование процентов в дроби является более простым способом получения процентов. Дроби предпочтительнее использовать, чем десятичные дроби, если десятичная дробь имеет много цифр. Это делает умножение более удобным, поскольку для упрощения процента используется только факторизация.
Вот шаги преобразования процентов в дроби:
1. Не обращайте внимания на символ процента (%).
2. Разделите процент на 100. Если числитель имеет цифры справа от десятичной точки, перемещайте десятичную точку, пока числитель не станет целым числом. Переместите десятичную точку знаменателя (равную 100) на то же количество знаков после запятой, на которое переместилась десятичная точка числителя.
Переместите десятичную точку знаменателя (равную 100) на то же количество знаков после запятой, на которое переместилась десятичная точка числителя.
3. Сократить до минимума.
Пример 13:
Пример 14:
Пример 15:
При преобразовании дробей в проценты проще и удобнее сначала преобразовать дробь в десятичную, а затем преобразовать десятичную в проценты.
Вот этапы преобразования дробей в проценты:
1. Разделить числитель дроби на знаменатель. Результат в десятичной форме.
2. Умножьте десятичную форму на 100.
3. Поместите символ процента (%) после последней цифры процента.
В случае смешанных номеров;
1. Примените шаги, описанные выше, только для правильной части смешанного числа.
2. Умножьте целое число смешанной дроби на 100.
3. Сложите произведение (целое число, умноженное на 100) и десятичную форму правильной дроби.
4. Поместите символ процента (%) после последней цифры процента.
Пример 16:
Пример 17:
Пример 18:
Существуют некоторые неправильные представления об использовании слов процент и процент. Два слова имеют
процентов относится к определенному числу.
Например;
Бернадетт правильно ответила на 90 процентов тестовых вопросов.
Она набрала 90% (процентов) в тесте.
процентов — это результат умножения числа на процент. Он обозначает часть и в основном описывается как более низкий или более высокий.
Например;
Бернадетт набрала высокий процент в тесте.
Она набрала 90/100 баллов по тесту.
Обычно слово «процент» стоит после определенного числа, и обычно это целые или счетные числа. Он обычно не используется в предложениях, так как всегда заменяется символом процента (%). Слово «процент» стоит перед дробью или после прилагательного (например, высокий, низкий, большой, маленький).
Пример 1:
Пример 2:
- Процент
- Простые проценты
- Виды простых процентов
- Расчет простых процентов
- Расчет общей суммы простых процентов
- Простой расчет процентного времени
- Расчет основного долга для простых процентов
- Сложные проценты
- Расчет сложных процентов
- Вычисление сложного принципала
- Расчет сложной процентной ставки
- Расчет времени
Свиток
Станьте участником сегодня!
Зарегистрируйтесь (бесплатно)Вы зарегистрированы? Войти!
Войдите в свою учетную запись Изучите основы расчета процентов от количества на этом простом уроке! Чтобы найти процент от любого числа, используйте это общее правило ПЕРЕВОДА: замените процент на десятичную дробь, а слово «от» на умножение. Концепции и идеи этого урока также объясняются в этом видео:
1. «Перевести» выражения в умножение на десятичную дробь. Рассчитать.
2. «Перевести» в другую сторону: запишите умножение как выражение «процент от числа».
3. Используйте калькулятор, чтобы найти проценты от этих величин. а. 17% от $4500 б. 67% от 27 м 4. Используйте ментальную арифметику, чтобы найти проценты этих количества.
5. а. Озеро имеет береговую линию длиной 30 км. 6% это песчаный пляж. Какой процент береговой линии составляет , а не песчаный пляж? 6. Двадцать процентов из 4000 студентов университета имеют стипендия. а. Чем занимаются процентов учащихся , а не имеют стипендия? б. Сколько студентов получают стипендию?
8. Найдите 80% от 50. Решение Глэдис: 9. Найдите выражения с одинаковым значением 20% от 620 долларов.
11. В таблице ниже показано, как Энди использовал время за один день. а. Подсчитайте время, которое он потратил на каждое занятие. б. Пометьте участки круговой диаграммы знаком
название каждой деятельности. Использование времени Энди
См. также такжеПроцент – бесплатный урок Процентное число с использованием ментальной арифметики — бесплатный урок Как считать проценты — бесплатный урок Основы процентной сдачи – бесплатный урок Интерактивный инструмент дроби, десятичной дроби и процента Этот урок взят из книги Марии Миллер Math Mammoth Percent и размещен на сайте www.HomeschoolMath.net с разрешения автора. Авторское право © Мария Миллер. Меню уроков математики |
| 1 процент от 60,00 составляет 59,40 | Разница 0,60 | |
| 2 процента от 60,00 составляет 58,80 | Разница 1,20 | |
| 3 процента от 60,00 составляет 58,20 | Разница 1,80 | |
| 4 процента от 60,00 составляет 57,60 | Разница 2,40 | |
| 5 процентов от 60,00 составляет 57,00 | Разница 3,00 | |
| 6 процентов от 60,00 составляет 56,40 | Разница 3,60 | |
| 7 процентов от 60,00 составляет 55,80 | Разница 4,20 | |
| 8 процентов от 60,00 составляет 55,20 | Разница 4,80 | |
| 9 процентов от 60,00 составляет 54,60 | Разница 5,40 | |
| 10 процентов от 60,00 составляет 54,00 | Разница 6,00 | |
| 11 процентов от 60,00 составляет 53,40 | Разница 6,60 | |
| 12 процентов от 60,00 составляет 52,80 | Разница 7,20 | |
| 13 процентов от 60,00 составляет 52,20 | Разница 7,80 | |
| 14 процентов от 60,00 составляет 51,60 | Разница 8,40 | |
| 15 процентов от 60,00 до 51,00 | Разница 9,00 | |
| 16 процентов от 60,00 составляет 50,40 | Разница 9,60 | |
| 17 процентов от 60,00 составляет 49,80 | Разница 10,20 | |
| 18 процентов от 60,00 составляет 49,20 | Разница 10,80 | |
| 19 процентов от 60,00 составляет 48,60 | Разница 11,40 | |
| 20 процентов от 60,00 составляет 48,00 | Разница 12. 00 00 | |
| 21 процент от 60,00 составляет 47,40 | Разница 12,60 | |
| 22 процента от 60,00 составляет 46,80 | Разница 13,20 | |
| 23 процента от 60,00 составляет 46,20 | Разница 13,80 | |
| 24 процента от 60,00 составляет 45,60 | Разница 14,40 | |
| 25 процентов от 60,00 составляет 45,00 | Разница 15.00 | |
| 26 процентов от 60,00 составляет 44,40 | Разница 15,60 | |
| 27 процентов от 60,00 составляет 43,80 | Разница 16,20 | |
| 28 процентов от 60,00 составляет 43,20 | Разница 16,80 | |
| 29 процентов от 60,00 составляет 42,60 | Разница 17,40 | |
| 30 процентов от 60,00 составляет 42,00 | Разница 18. 00 00 | |
| 31 процент от 60,00 составляет 41,40 | Разница 18,60 | |
| 32 процента от 60,00 составляет 40,80 | Разница 19,20 | |
| 33 процента от 60,00 составляет 40,20 | Разница 19,80 | |
| 34 процента от 60,00 составляет 39,60 | Разница 20,40 | |
| 35 процентов от 60,00 до 39,00 | Разница 21.00 | |
| 36 процентов от 60,00 составляет 38,40 | Разница 21,60 | |
| 37 процентов от 60,00 составляет 37,80 | Разница 22.20 | |
| 38 процентов от 60,00 составляет 37,20 | Разница 22,80 | |
| 39 процентов от 60,00 составляет 36,60 | Разница 23,40 | |
| 40 процентов от 60,00 составляет 36,00 | Разница 24. 00 00 | |
| 41 процент от 60,00 составляет 35,40 | Разница 24,60 | |
| 42 процента от 60,00 составляет 34,80 | Разница 25,20 | |
| 43 процента от 60,00 составляет 34,20 | Разница 25,80 | |
| 44 процента от 60,00 составляет 33,60 | Разница 26.40 | |
| 45 процентов от 60,00 до 33,00 | Разница 27.00 | |
| 46 процентов от 60,00 составляет 32,40 | Разница 27,60 | |
| 47 процентов от 60,00 составляет 31,80 | Разница 28,20 | |
| 48 процентов от 60,00 составляет 31,20 | Разница 28,80 | |
| 49 процентов от 60,00 составляет 30,60 | Разница 29,40 | |
| 50 процентов от 60,00 составляет 30,00 | Разница 30. 00 00 | |
| 51 процент от 60,00 составляет 29,40 | Разница 30,60 | |
| 52 процента от 60,00 составляет 28,80 | Разница 31,20 | |
| 53 процента от 60,00 составляет 28,20 | Разница 31,80 | |
| 54 процента от 60,00 составляет 27,60 | Разница 32,40 | |
| 55 процентов от 60.00 до 27.00 | Разница 33,00 | |
| 56 процентов от 60,00 составляет 26,40 | Разница 33,60 | |
| 57 процентов от 60,00 составляет 25,80 | Разница 34,20 | |
| 58 процентов от 60,00 составляет 25,20 | Разница 34,80 | |
| 59 процентов от 60,00 составляет 24,60 | Разница 35,40 | |
60 процентов от 60. 00 до 24.00 00 до 24.00 | Разница 36,00 | |
| 61 процент от 60,00 составляет 23,40 | Разница 36,60 | |
| 62 процента от 60,00 составляет 22,80 | Разница 37,20 | |
| 63 процента от 60,00 до 22,20 | Разница 37,80 | |
| 64 процента от 60,00 составляет 21,60 | Разница 38,40 | |
| 65 процентов от 60.00 до 21.00 | Разница 39.00 | |
| 66 процентов от 60,00 составляет 20,40 | Разница 39,60 | |
| 67 процентов от 60,00 составляет 19,80 | Разница 40,20 | |
| 68 процентов от 60,00 до 19,20 | Разница 40,80 | |
69 процентов от 60. 00 составляет 18.60 00 составляет 18.60 | Разница 41,40 | |
| 70 процентов от 60.00 до 18.00 | Разница 42,00 | |
| 71 процент от 60.00 составляет 17.40 | Разница 42,60 | |
| 72 процента от 60,00 составляет 16,80 | Разница 43.20 | |
| 73 процента от 60,00 до 16,20 | Разница 43,80 | |
| 74 процента от 60,00 составляет 15,60 | Разница 44,40 | |
| 75 процентов от 60.00 до 15.00 | Разница 45,00 | |
| 76 процентов от 60.00 это 14.40 | Разница 45,60 | |
| 77 процентов от 60,00 составляет 13,80 | Разница 46,20 | |
| 78 процентов от 60,00 до 13,20 | Разница 46,80 | |
| 79 процентов от 60,00 составляет 12,60 | Разница 47. 40 40 | |
| 80 процентов от 60.00 до 12.00 | Разница 48,00 | |
| 81 процент от 60,00 составляет 11,40 | Разница 48,60 | |
| 82 процента от 60,00 составляет 10,80 | Разница 49,20 | |
| 83 процента от 60.00 это 10.20 | Разница 49,80 | |
| 84 процента от 60,00 составляет 9,60 | Разница 50,40 | |
| 85 процентов от 60.00 это 9.00 | Разница 51,00 | |
| 86 процентов от 60,00 составляет 8,40 | Разница 51,60 | |
| 87 процентов от 60,00 составляет 7,80 | Разница 52,20 | |
| 88 процентов от 60,00 это 7,20 | Разница 52,80 | |
| 89 процентов от 60,00 составляет 6,60 | Разница 53,40 | |
| 90 процентов от 60,00 это 6,00 | Разница 54,00 | |
| 91 процент от 60,00 составляет 5,40 | Разница 54,60 | |
| 92 процента от 60,00 составляет 4,80 | Разница 55,20 | |
| 93 процента от 60,00 составляет 4,20 | Разница 55,80 | |
| 94 процента от 60,00 составляет 3,60 | Разница 56,40 | |
| 95 процентов от 60,00 составляет 3,00 | Разница 57,00 | |
| 96 процентов от 60,00 составляет 2,40 | Разница 57,60 | |
| 97 процентов от 60,00 составляет 1,80 | Разница 58,20 | |
| 98 процентов от 60,00 составляет 1,20 | Разница 58,80 | |
| 99 процентов от 60,00 составляет 0,60 | Разница 59,40 | |
| 100-процентная скидка 60,00 равна 0,00 | Разница 60. 00 00 |
Как рассчитать A 60 40 Split
По сути, у вас есть два веса — 60 и 40. Присвойте каждому весу 10 баллов. Итак, 60% = 600 баллов и 40% = 400 баллов.
Содержание
Какое число составляет 80 процентов от 500?
Калькулятор процентов: что такое 80 процентов от 500? = 400.
Как вы работаете 60%?
Чтобы преобразовать дробь 60/100 в проценты, вы должны сначала преобразовать 60/100 в десятичную дробь, разделив числитель 60 на знаменатель 100. Отсюда следует, что 60/100 = 0,6. Затем умножьте 0,6 на 100 = 60%.
Как найти 35 процентов числа?
Если вам нужно найти процент от числа, вот что вы делаете — например, чтобы найти 35% от 240: разделите число на 10, чтобы найти 10%. Умножьте это число на количество десятков в процентах, которые вы ищете — в данном случае это 3, поэтому вы получаете 30% как 24 x 3 = 72.
Как рассчитать сплит 65 на 35?
Что такое 65/35 в процентах? Шаг 1: Разделите 65 на 35, чтобы получить десятичное число. 65/35 = 1,86. Шаг 2: Умножьте 1,86 на 100. 1,86 умножить на 100 = 185,71. Вот и все!.
Что такое 65 как дробь в простейшей форме?
Шаги к упрощению дробей Таким образом, 65/100, упрощенное до наименьших значений, равно 13/20.
Как найти 25% числа?
Чтобы вычислить 25 процентов числа, просто разделите его на 4. Например, 25 процентов от 12 — это 12, деленное на 4, или 3.
Что такое 47 из 60 в процентах?
Калькулятор процентов: 47 сколько процентов от 60? = 78,33.
youtube.com/embed/RaNHV6W1p84″>Что такое 62 из 100 в процентах?
Следовательно, доля 62/100 в процентах составляет 62%.
Насколько 5 баллов влияют на вашу оценку?
Ваш устный экзамен составляет 5% от вашей общей оценки, так что думайте об этом как о 5 баллах. Вы получаете 80 баллов за устный экзамен, поэтому умножаете . 05 (5%) и 80, что дает вам 4 балла. Это означает, что вы заработали 4 балла из 5 возможных.
Каково соотношение 100 к 60?
Следовательно, 100/60, упрощенное до минимума, составляет 5/3.
Как найти процентное соотношение?
Вы делите свой процент на 100. Таким образом, 40 процентов будут 40, разделенными на 100. Получив десятичную версию своего процента, просто умножьте его на заданное число (в данном случае на сумму вашей зарплаты). Если ваша зарплата составляет 750 долларов, вы должны умножить 750 на .
Если ваша зарплата составляет 750 долларов, вы должны умножить 750 на .
Какие 3 способа разделить?
Чтобы разделить доску на три части, выберите любое число, которое делится на три, например девять, 12, 18 и т. д. Положите квадрат или рулетку по диагонали через доску с нулем на одном конце и в данном случае 18 на другом. Чтобы разделить доску на трети, выберите любое число, которое делится на три, например девять, 12, 18 и т. д.
Что упростило 35 65?
Следовательно, 35/65, упрощенное до самых низких значений, равно 7/13.
Как рассчитать итоговую оценку?
Сложите новые числа. После того, как вы умножите каждый балл на его взвешенный процент, добавьте общее количество полученных вами баллов и общее возможное количество баллов. Разделите сумму всех ваших взвешенных баллов на сумму всех на общее взвешенное количество баллов.
Что такое 65 100 в процентах?
Следовательно, доля 65/100 в процентах составляет 65%.
Как найти 70% числа?
Пример 1. Найдите 70% от 80. Следуя сокращению, запишем это как 0,7 × 80. Помните, что при десятичном умножении вы умножаете так, как если бы не было десятичных знаков, и в ответе будет столько «десятичных цифр», сколько справа от запятой как общее количество десятичных цифр всех факторов.
Что такое 40 из 50 в процентах?
40 это 80% от 50.
Какое соотношение между 65 и 35?
Следовательно, 65/35, упрощенное до самых низких значений, равно 13/7.
Какое число составляет 65 процентов от 50?
Калькулятор процентов: что такое 65 процентов от 50? = 32,5.
youtube.com/embed/BefOMNbgKUA»>Что такое 39 из 60 в процентах?
Калькулятор процентов: 39 сколько процентов от 60? = 65.
Чему равно 35 из 100 в виде дроби?
Следовательно, 35/100, упрощенное до минимума, равно 7/20.
Какие 3 способа разделить 100?
В математике «100%» означает не что иное, как «100 на 100», а именно «100/100=1». Таким образом, в математике вы можете разделить 100% на 3, не оставив 0,1%. 100%/3=1/3=13.
Являются ли калькуляторы итоговых оценок точными?
Если ваша текущая оценка не учитывает всю курсовую работу (задания, лабораторные работы, тесты, домашнюю работу и т. д.) до вашего выпускного экзамена, результаты калькулятора не будут точными для вас. В этом случае вес финала просто рассчитывается как 100% минус сумма весов вашей курсовой работы.
Что такое 39 из 50 в процентах?
Калькулятор процентов: 39 сколько процентов от 50? = 78.
Что такое 40 60 в простейшей форме?
Сократите 40/60 до наименьшего члена Найдите НОД (или HCF) числителя и знаменателя. НОД 40 и 60 равен 20. 40 ÷ 2060 ÷ 20. Сокращенная дробь: 23. Следовательно, 40/60, упрощенное до самых низких значений, равно 2/3.
Что такое 41 из 50 в процентах?
Калькулятор процентов: 41 сколько процентов от 50? = 82.
Что такое 42 из 50 в процентах?
Калькулятор процентов: 42 сколько процентов от 50? = 84.
Как найти 80 процентов числа без калькулятора?
Это 10% от 4500. Точно так же вы можете умножить ответ 1% на любое число, чтобы найти любое процентное значение. Например, чтобы найти 80% от 4500, умножьте 45 на 80, чтобы получить 3600.
youtube.com/embed/4eu0zsgr7Gg»>Какое число составляет 65 процентов от 60?
Калькулятор процентов: сколько будет 65 процентов от 60? = 39.
Сколько процентов к 60 40?
Калькулятор процентов: 40 сколько процентов от 60? = 66,67.
Что такое 29 из 60 в процентах?
Калькулятор процентов: 29 сколько процентов от 60? = 48,33.
Какое число составляет 25 процентов от 80?
Калькулятор процентов: сколько будет 25 процентов от 80? = 20.
Что такое 3 от 100%?
Ответ: 1/3 от 100 равно 100/3 или 33⅓.
Какое число составляет 40% от 50?
Калькулятор процентов: что такое 40 процентов от 50? = 20.
Как рассчитываются итоговые оценки за 12 класс в 2020 году?
КАК СЧИТАЮТСЯ МОИ РЕЗУЛЬТАТЫ ЗА 12 КЛАСС? 25% внутренняя школьная оценка (SBA) (оценка, выставляемая вам вашей школой) и 75% внешний экзамен (финал) — за исключением LO, который является 100% внутренней оценкой. ЕСЛИ ОН НА 10% ВЫШЕ ИЛИ НИЖЕ ВАШЕЙ ЭКЗАМЕНАЦИОННОЙ ОЦЕНКИ, ТОЛЬКО ВАШИ ОКОНЧАТЕЛЬНЫЕ ЭКЗАМЕНАЦИОННЫЕ ОЦЕНКИ.
ЕСЛИ ОН НА 10% ВЫШЕ ИЛИ НИЖЕ ВАШЕЙ ЭКЗАМЕНАЦИОННОЙ ОЦЕНКИ, ТОЛЬКО ВАШИ ОКОНЧАТЕЛЬНЫЕ ЭКЗАМЕНАЦИОННЫЕ ОЦЕНКИ.
Каково соотношение 60% к 40%?
Упрощение коэффициентов Соотношение 3:2 такое же, как 6:4, или 15:10, или 60:40. Как и в случае с дробями, отношения имеют простейшую форму, что означает форму, в которой два числа не имеют общих множителей (кроме 1) — нет числа, на которое можно разделить обе части отношения без остатка.
Как получить 60 разделить на 100?
60 разделить на 100 равно 3/5, ответ, который также может быть выражен в десятичной форме как 0,6.
Калькулятор процентов: проценты от числа
Этот бесплатный сервис позволяет вычислять проценты
Преобразование процентов в числа
Что такое % из ?Преобразование числа в проценты
это сколько процентов?
Увеличение/уменьшение в процентах
плюс-минус %= какое значение?
Процентное изменение между двумя значениями
Разница междуи = какой процент?
Как пользоваться нашим калькулятором
Здесь вы найдете несколько простых процентных калькуляторов с примерами. Вы можете использовать наши простые калькуляторы процентов для расчета процентов.
В качестве десятичного разделителя можно использовать запятую или точку. Вам не нужно использовать разделители тысяч, потому что этот калькулятор рассматривает и запятую, и точку как десятичный разделитель.
Для того, чтобы рассчитать проценты онлайн, нажмите на кнопку. Результат появится на следующей странице. Если есть ошибки, поле результата будет пустым.
Попробуйте этот удобный онлайн-инструмент, чтобы проверить свои проблемы с процентами.
Найдите процентное изменение между двумя числами или вычислите процент значения до и после.
Наша цель — предложить лучший онлайн-калькулятор процентов с быстрыми и полезными ответами.
Всякий раз, когда вам нужно рассчитать проценты или узнать, как рассчитать проценты, этот бесплатный веб-сайт поможет вам.
Мы надеемся, что вам понравится время, проведенное на сайте. Пожалуйста, не стесняйтесь, присылайте нам свои комментарии или предложения.
Вы можете использовать наши простые калькуляторы процентов для расчета процентов.
В качестве десятичного разделителя можно использовать запятую или точку. Вам не нужно использовать разделители тысяч, потому что этот калькулятор рассматривает и запятую, и точку как десятичный разделитель.
Для того, чтобы рассчитать проценты онлайн, нажмите на кнопку. Результат появится на следующей странице. Если есть ошибки, поле результата будет пустым.
Попробуйте этот удобный онлайн-инструмент, чтобы проверить свои проблемы с процентами.
Найдите процентное изменение между двумя числами или вычислите процент значения до и после.
Наша цель — предложить лучший онлайн-калькулятор процентов с быстрыми и полезными ответами.
Всякий раз, когда вам нужно рассчитать проценты или узнать, как рассчитать проценты, этот бесплатный веб-сайт поможет вам.
Мы надеемся, что вам понравится время, проведенное на сайте. Пожалуйста, не стесняйтесь, присылайте нам свои комментарии или предложения.
Несколько простых примеров
| Пример 1 60% от 900 = ??? (900/100) х 60 = 540 Сначала проверяем, сколько составляет один процент: делим 900 на 100. | Пример второй 90 = ??? % от 125 90 х (100/125) = 72 % Сначала посчитаем, сколько стоит одна единица: делим 125 на 100. | Пример третий Каково процентное изменение от 150 до 190? (190-150) х (100/150) = 26,66 % 150 соответствует 100%. Таким образом, процент одной единицы представлен 100/150. |
Что такое проценты?
Один процент — это одна сотая. Мы используем %, чтобы указать это. Итак, 5 процентов — это то же самое, что 5%, 0,05, 5/100 или пять сотых. Это так просто!
Это хорошо, но обычно мы используем не только проценты. Иногда мы хотим показать соотношение между двумя числами. Например: что такое 40% от 20? Это 40 сотых от 20, поэтому, если мы разделим 20 печенек на 100 равных частей (удачи в этом!), 40 из этих частей составляют наши 40% от 20 печенек. Давайте посчитаем: 40/100 * 20 = 8. Здесь действует небольшая хитрость: если вы хотите разделить на сто, просто переместите запятую на два знака влево. В нашем расчете 40/100*20 мы могли бы сделать и так: (40*20)/100 (то же самое). 40 * 20 равно 800. Переместите запятую в числе 800 на 2 знака влево, и вы получите 8,00. Введите эти значения в верхней части страницы, 40 и 20. Тогда вы получите «40% от 20 равно 8».
В другом случае вы хотите указать, например, на сколько процентов уменьшилось или увеличилось число. Например, если у вас есть 10 яблок и вы едите 2 из них… То вы потеряли 20% яблок.
Мы используем %, чтобы указать это. Итак, 5 процентов — это то же самое, что 5%, 0,05, 5/100 или пять сотых. Это так просто!
Это хорошо, но обычно мы используем не только проценты. Иногда мы хотим показать соотношение между двумя числами. Например: что такое 40% от 20? Это 40 сотых от 20, поэтому, если мы разделим 20 печенек на 100 равных частей (удачи в этом!), 40 из этих частей составляют наши 40% от 20 печенек. Давайте посчитаем: 40/100 * 20 = 8. Здесь действует небольшая хитрость: если вы хотите разделить на сто, просто переместите запятую на два знака влево. В нашем расчете 40/100*20 мы могли бы сделать и так: (40*20)/100 (то же самое). 40 * 20 равно 800. Переместите запятую в числе 800 на 2 знака влево, и вы получите 8,00. Введите эти значения в верхней части страницы, 40 и 20. Тогда вы получите «40% от 20 равно 8».
В другом случае вы хотите указать, например, на сколько процентов уменьшилось или увеличилось число. Например, если у вас есть 10 яблок и вы едите 2 из них… То вы потеряли 20% яблок. Почему? Потому что 8 — это 80% от 10. Все яблоки были 100%, теперь у нас осталось 80%, поэтому количество яблок уменьшилось на 20% (потому что 100 — 80 = 20). Используйте для этого наш инструмент увеличения процента.
Почему? Потому что 8 — это 80% от 10. Все яблоки были 100%, теперь у нас осталось 80%, поэтому количество яблок уменьшилось на 20% (потому что 100 — 80 = 20). Используйте для этого наш инструмент увеличения процента.
Происхождение
Термин процент происходит от латинского per center (на сотню) и обозначается знаком «%», или просто «процент» или «процент». В математике процент — это число в дробях от 100. Американцы говорят проценты, британцы предпочитают использовать проценты.
Проценты для растворов
Процент не всегда должен обозначать несколько сотых от целого. Таким образом, решения также отображаются в процентах. Физиологический солевой раствор называют, например, раствором 0,9% поваренной соли. Эти 0,9% означают, что раствор содержит 0,9 г соли на 100 мл (= 100 г). Таким образом, процент здесь относится к массе.
Объемный процент часто указывает дополнение: «vol», тогда мы получаем, например: 14% vol или 14% vol.
Процентные пункты
Процентный пункт, также обозначаемый как %-пункт, используется для обозначения абсолютной разницы между значениями, выраженными в процентах. Таким образом, процент — это сотая часть, а процентный пункт — это расчетная единица, выражающая изменение процента.
Пример
Если проценты по вашему сберегательному счету вырастут с 2% до 3%, вы можете выразить это как «увеличение на 50% от старой процентной ставки» или как «увеличение на 1 процентный пункт» (что составляет 1% от первоначальной процентной ставки). весь). «Увеличение на 1%» неясно, потому что это может означать увеличение на 1% от 2 (0,02), в результате чего общее количество составляет 2,02% вместо 3%.
Промилле
1 промилле – это 1 тысячная часть, слово промилле также означает «промилле».

 12.18
12.18
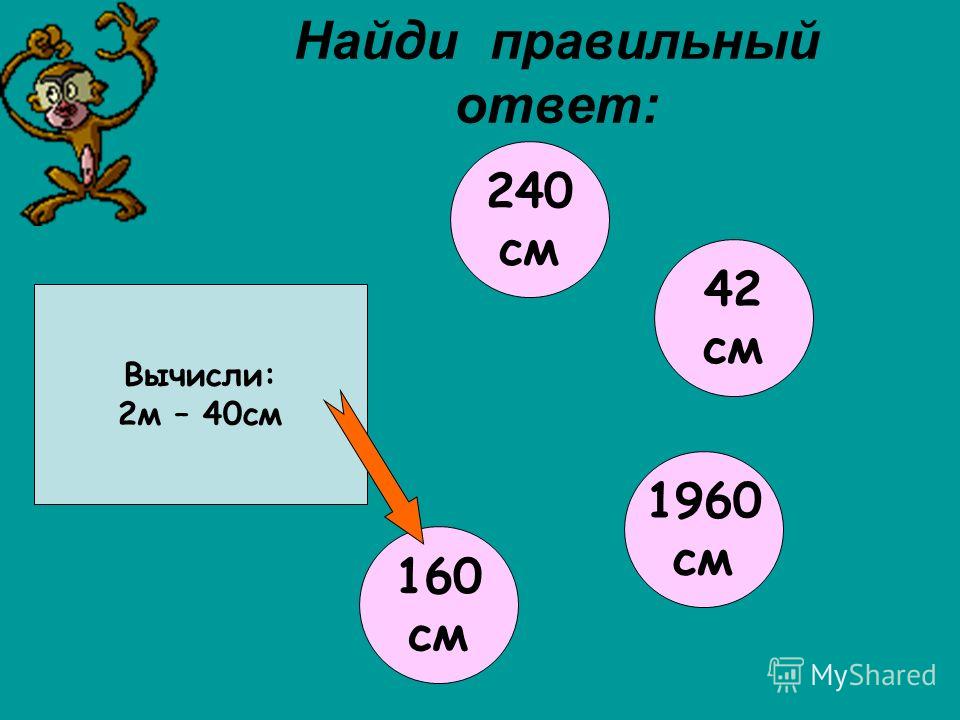 36 увеличить на 60.
36 увеличить на 60. К какому числу прибавили 40 и получили 92?
К какому числу прибавили 40 и получили 92? Найти сумму.
Найти сумму. Какое число уменьшили на 48 и получили78?
Какое число уменьшили на 48 и получили78?  Найти произведение.
Найти произведение. Вычислить: 21:3х2=
Вычислить: 21:3х2=
 42 увеличить на 34.
42 увеличить на 34.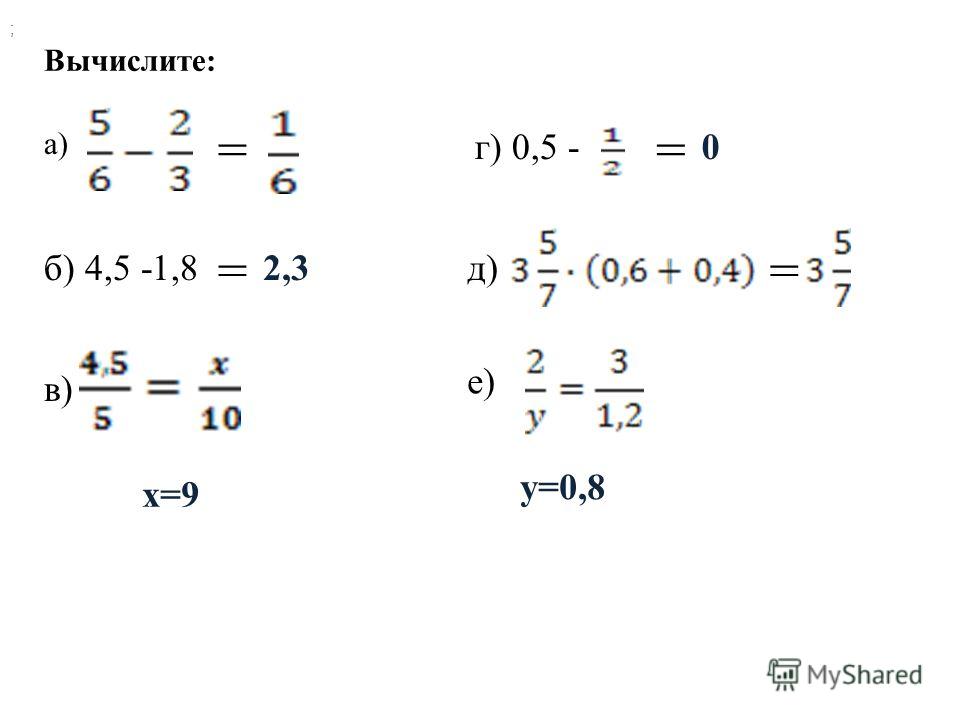 К какому числу прибавили 8 и получили 60?
К какому числу прибавили 8 и получили 60? 78 уменьшить на 50.
78 уменьшить на 50.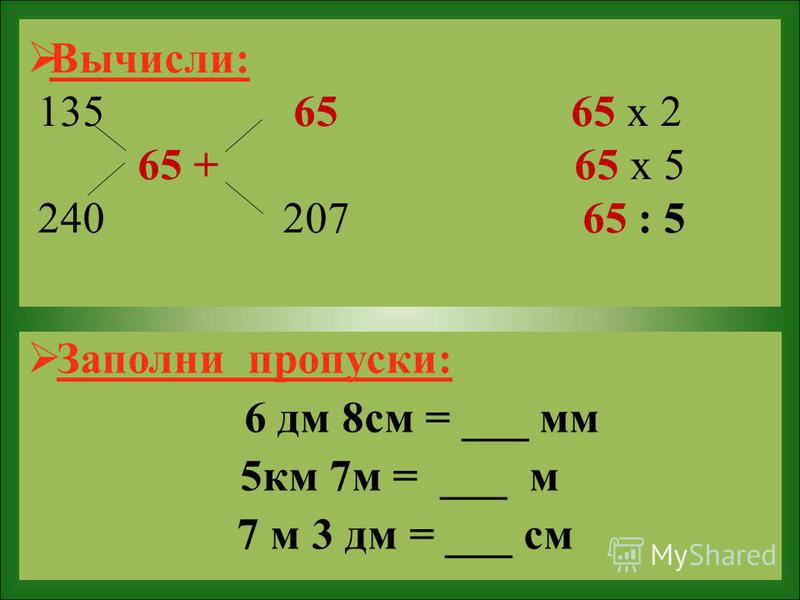 Первый множитель 2, второй множитель 8. Найти произведение.
Первый множитель 2, второй множитель 8. Найти произведение. Первый множитель 8, второй множитель 4. Найти произведение.
Первый множитель 8, второй множитель 4. Найти произведение. Во сколько раз 6 меньше 24?
Во сколько раз 6 меньше 24? На сколько 43 меньше 96
На сколько 43 меньше 96 Найти разность.
Найти разность.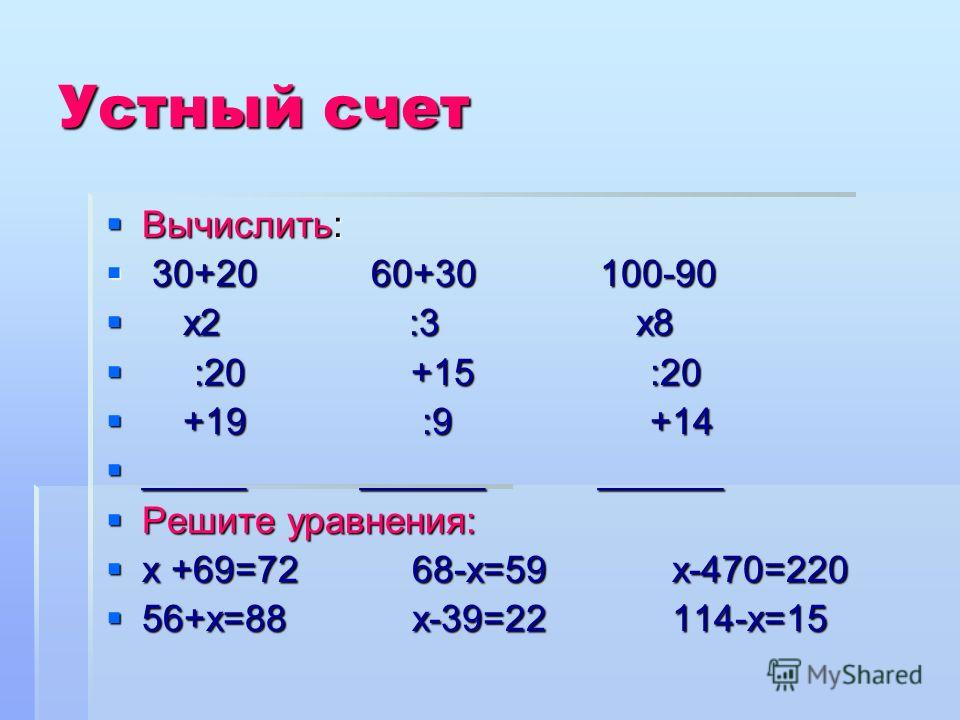 Вычислить: 30+40-50+60-20=
Вычислить: 30+40-50+60-20= Вычислить: 50+40-60+20+50-20=
Вычислить: 50+40-60+20+50-20= Какое число прибавили к 38 и получили 89?
Какое число прибавили к 38 и получили 89?

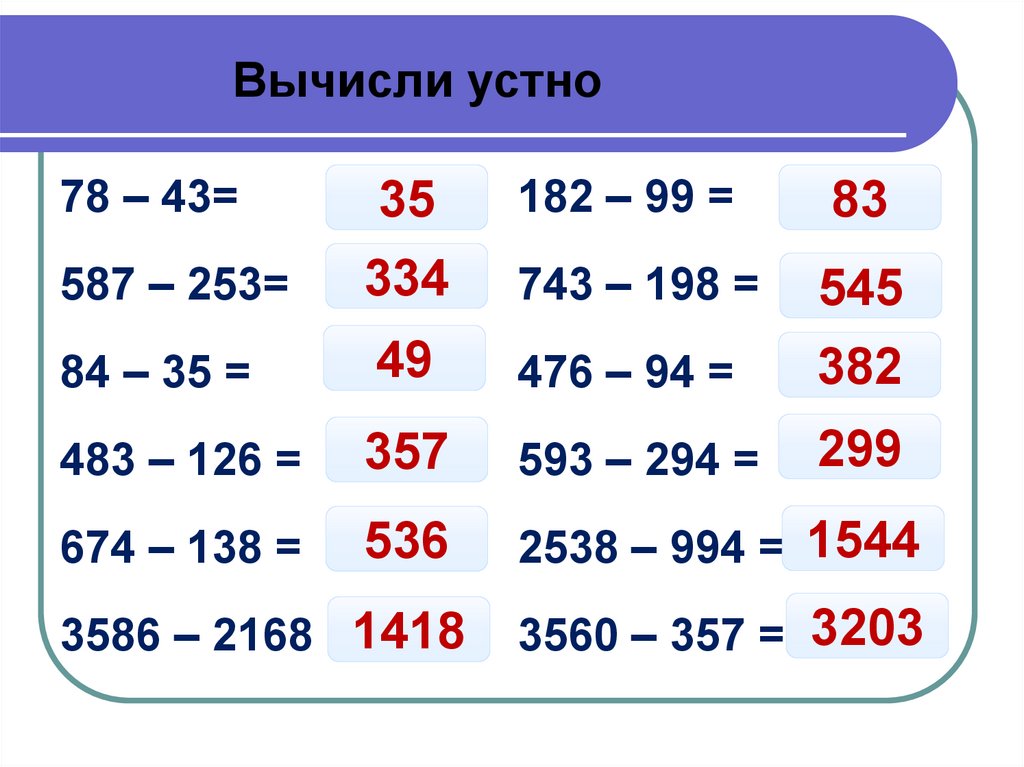 Вычислить: 4+8-7+6-9=
Вычислить: 4+8-7+6-9= Найти частное чисел: 48 и 8.
Найти частное чисел: 48 и 8. Какое число уменьшили на 42 и получили 31?
Какое число уменьшили на 42 и получили 31? Найти произведение.
Найти произведение. Какое число разделили на 9 и получили 6?
Какое число разделили на 9 и получили 6?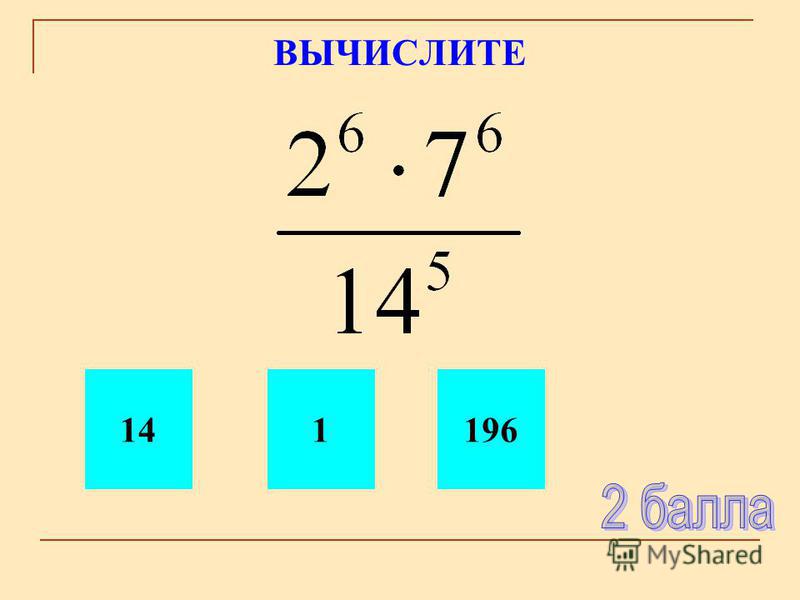 35 уменьшить в 5 раз.
35 уменьшить в 5 раз. Чему равен делитель, если делимое 54,а частное 9.
Чему равен делитель, если делимое 54,а частное 9. На какое число разделили 42 и получили 6?
На какое число разделили 42 и получили 6? 92 уменьшить на 50.
92 уменьшить на 50. Из какого числа вычли 30 и получили67?
Из какого числа вычли 30 и получили67?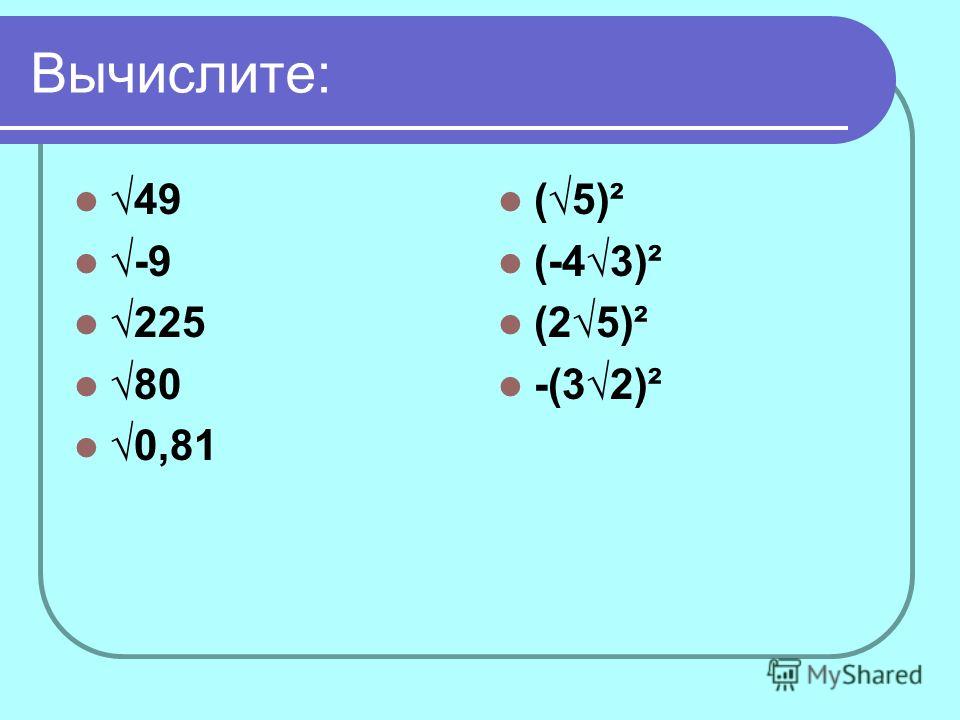 Какое число уменьшили в 8 раз и получили 4?
Какое число уменьшили в 8 раз и получили 4?
 Какое число умножили на 4 и получили 24.
Какое число умножили на 4 и получили 24.

 Вычислить: 7+8-9+5-4+7=
Вычислить: 7+8-9+5-4+7= Найти разность чисел: 50 и 43.
Найти разность чисел: 50 и 43. Найти произведение чисел: 6 и 7.
Найти произведение чисел: 6 и 7. Какое число прибавили к 35 и получили 95?
Какое число прибавили к 35 и получили 95? На сколько 19 больше 7?
На сколько 19 больше 7?
 На какое число разделили 81 и получили 9?
На какое число разделили 81 и получили 9?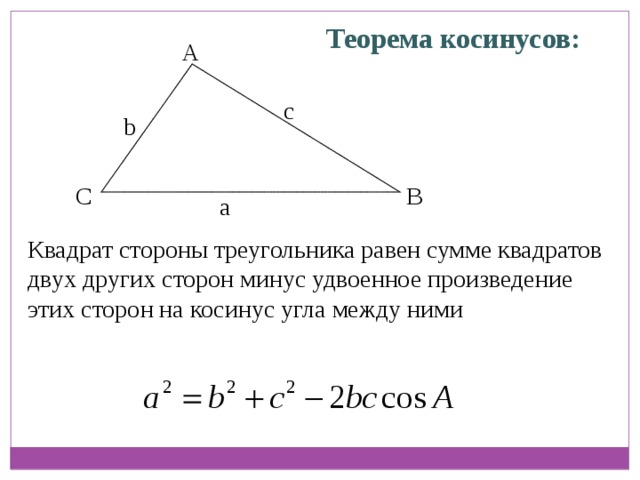 ru
ru ru
ru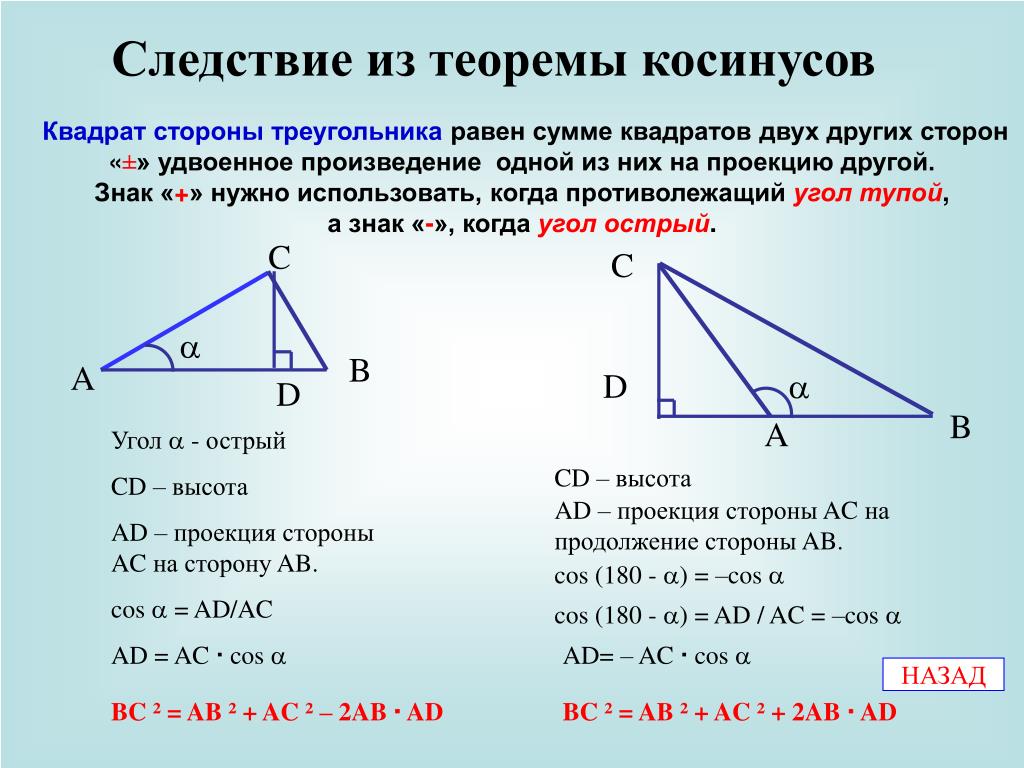

 = 1 2 · a → 2 + b → 2 – b → – a → 2 a → · b →
= 1 2 · a → 2 + b → 2 – b → – a → 2 a → · b → Требуется найти косинус угла между векторами.
Требуется найти косинус угла между векторами.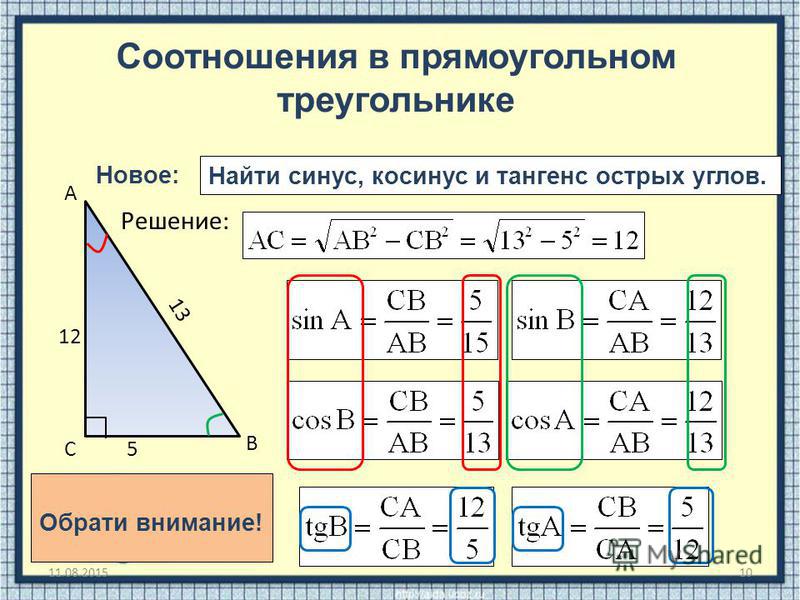 =a→, b→a→·b→
=a→, b→a→·b→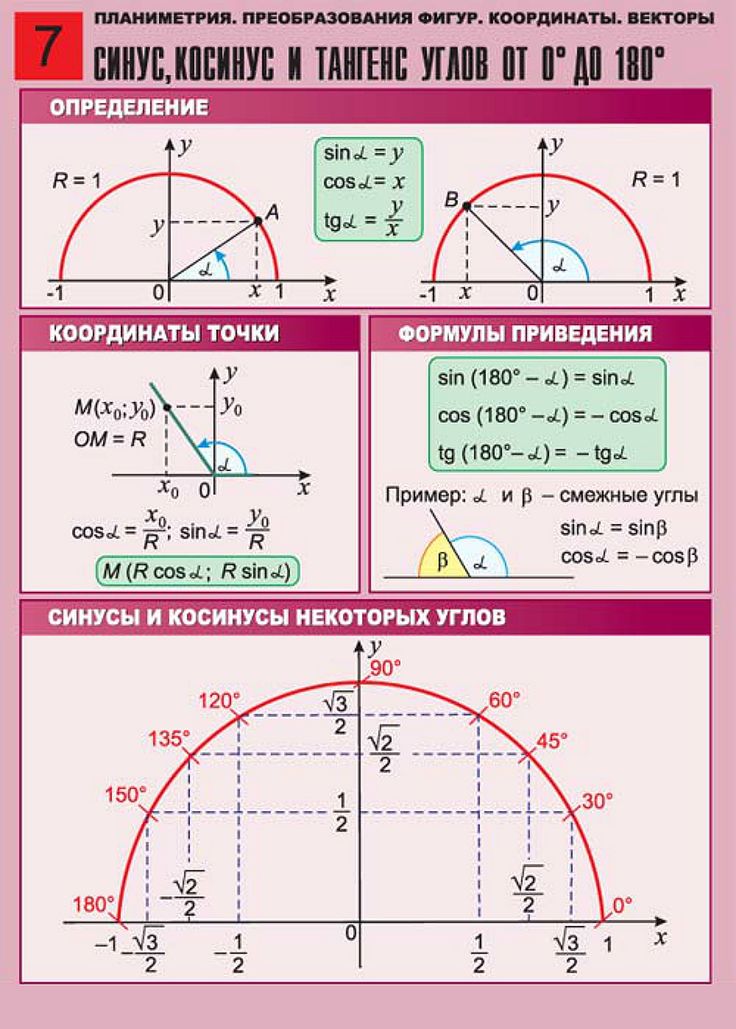

 Для решения задач нам поможет таблица, которая находится чуть ниже. Рассмотрим эти варианты.
Для решения задач нам поможет таблица, которая находится чуть ниже. Рассмотрим эти варианты.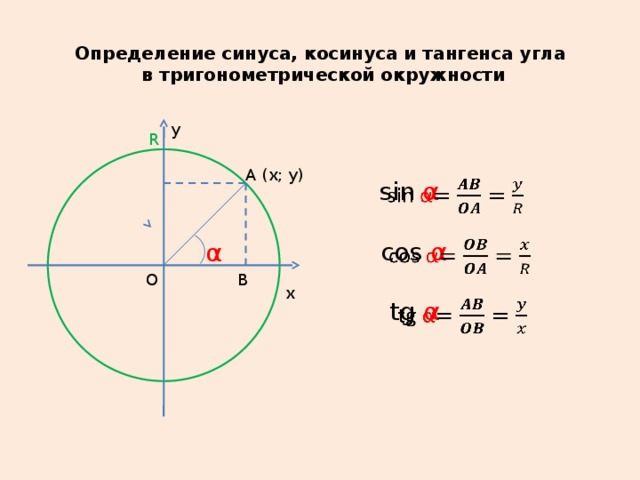 Формула: tg=a/b, где а – противолежащий к углу катет, а b – прилежащий. Преобразуем формулу и получаем: a=tg*b.
Формула: tg=a/b, где а – противолежащий к углу катет, а b – прилежащий. Преобразуем формулу и получаем: a=tg*b. Пусть в нем сторона BC = a, сторона CA = b и S — площадь этого треугольника. Необходимо доказать, что S = (1/2)*a*b*sin(C) .
Пусть в нем сторона BC = a, сторона CA = b и S — площадь этого треугольника. Необходимо доказать, что S = (1/2)*a*b*sin(C) .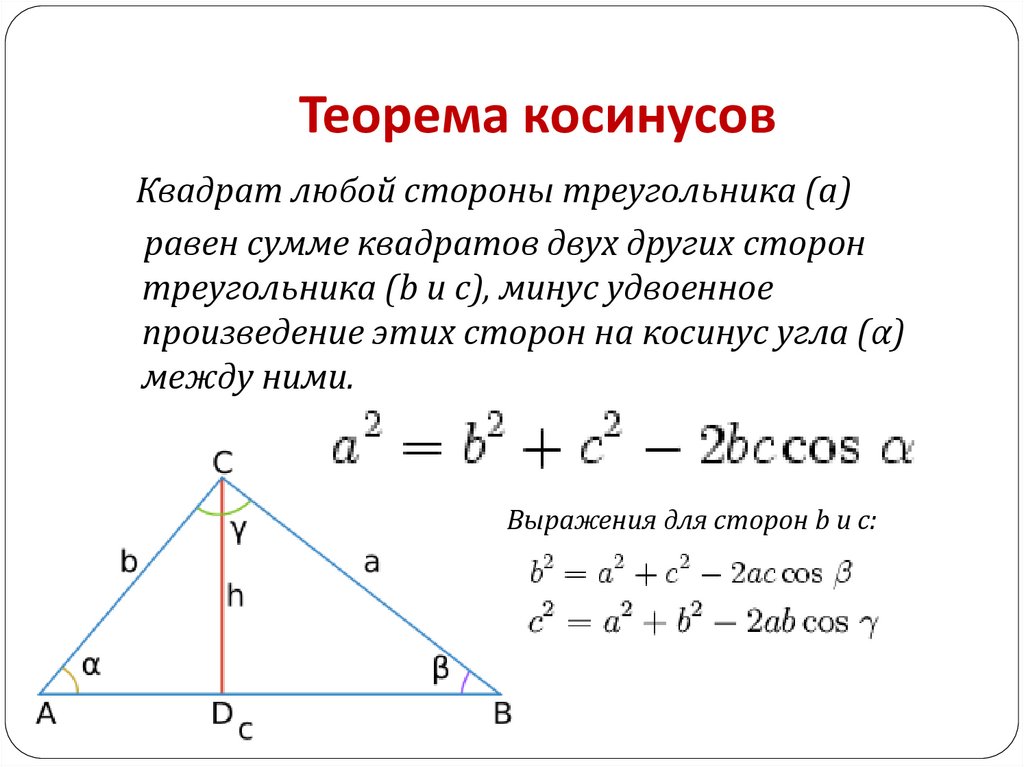 2. Найдите сторону AB, если AC = 15 см, угол А = 30˚.
2. Найдите сторону AB, если AC = 15 см, угол А = 30˚. От того что синус , как знаменито, представляет собой отношение противолежащего катета к гипотенузе, а косинус – отношение прилежащего катета к гипотенузе, для решения поставленной задачи воспользуйтесь дальнейшим соотношением между этими параметрами:sin ?=НB/BCСоответственно, если вы хотите узнать катет прямоугольного треугольника, выразите его через гипотенузу дальнейшим образом:НB=BC*sin ?
От того что синус , как знаменито, представляет собой отношение противолежащего катета к гипотенузе, а косинус – отношение прилежащего катета к гипотенузе, для решения поставленной задачи воспользуйтесь дальнейшим соотношением между этими параметрами:sin ?=НB/BCСоответственно, если вы хотите узнать катет прямоугольного треугольника, выразите его через гипотенузу дальнейшим образом:НB=BC*sin ?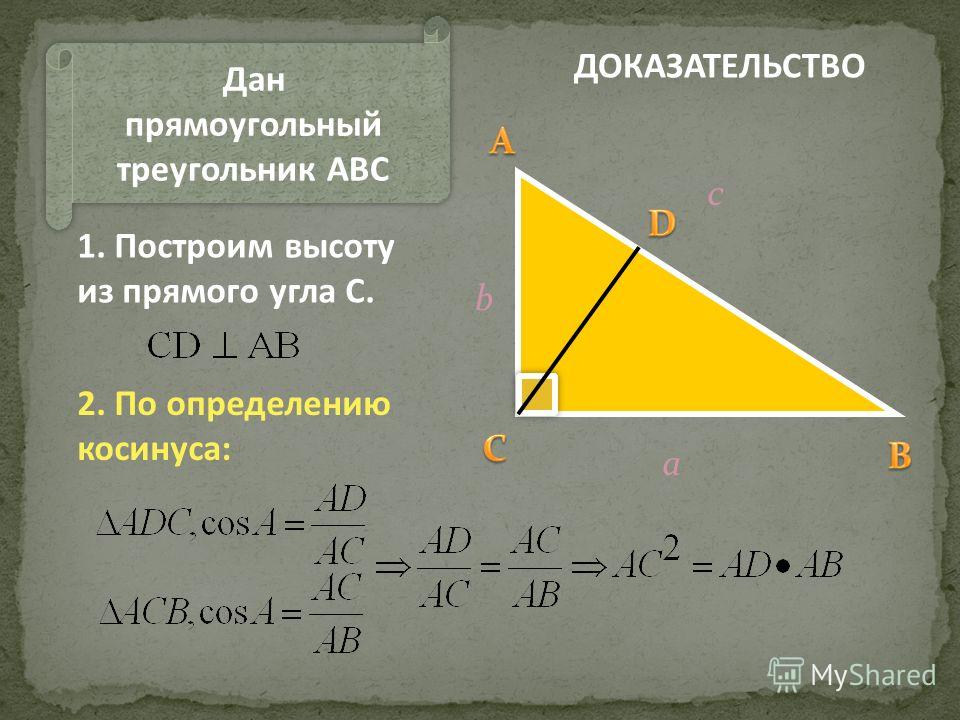 2-2ab*cos ?
2-2ab*cos ?
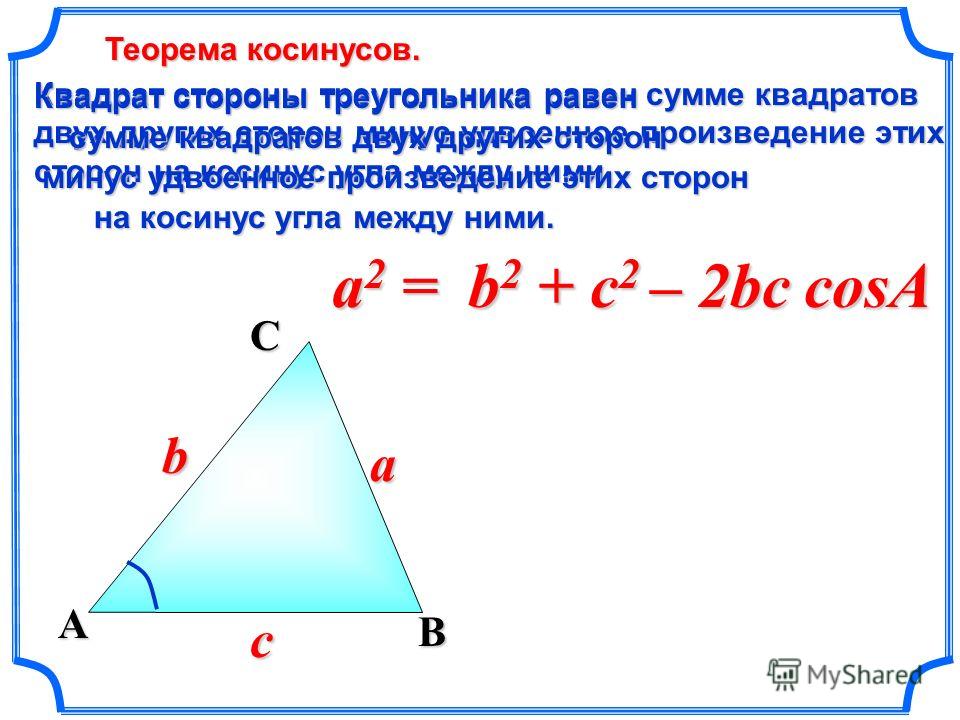 Дабы обнаружить значение тупого либо острого угла, стороны всякого треугольника, довольно применить теорему косинусов и синусов.Теорема косинусов достаточно примитивна: «Квадрат стороны треугольника равен сумме квадратов 2-х других сторон за вычетом удвоенного произведения этих сторон на косинус угла между ними». Существует две трактовки теоремы синусов: малая и расширенная. Согласно малой: «В треугольнике углы пропорциональны противолежащим сторонам». Данную теорему зачастую расширяют за счет свойства описанной около треугольника окружности: «В треугольнике углы пропорциональны противолежащим сторонам, а их отношение равно диаметру описанной окружности».
Дабы обнаружить значение тупого либо острого угла, стороны всякого треугольника, довольно применить теорему косинусов и синусов.Теорема косинусов достаточно примитивна: «Квадрат стороны треугольника равен сумме квадратов 2-х других сторон за вычетом удвоенного произведения этих сторон на косинус угла между ними». Существует две трактовки теоремы синусов: малая и расширенная. Согласно малой: «В треугольнике углы пропорциональны противолежащим сторонам». Данную теорему зачастую расширяют за счет свойства описанной около треугольника окружности: «В треугольнике углы пропорциональны противолежащим сторонам, а их отношение равно диаметру описанной окружности». Производной синуса является косинус, а косинуса – синус, но со знаком «минус».
Производной синуса является косинус, а косинуса – синус, но со знаком «минус». Вообще, вычисление синуса поможет закрепить чертёжные навыки и знание тригонометрических тождеств.
Вообще, вычисление синуса поможет закрепить чертёжные навыки и знание тригонометрических тождеств.
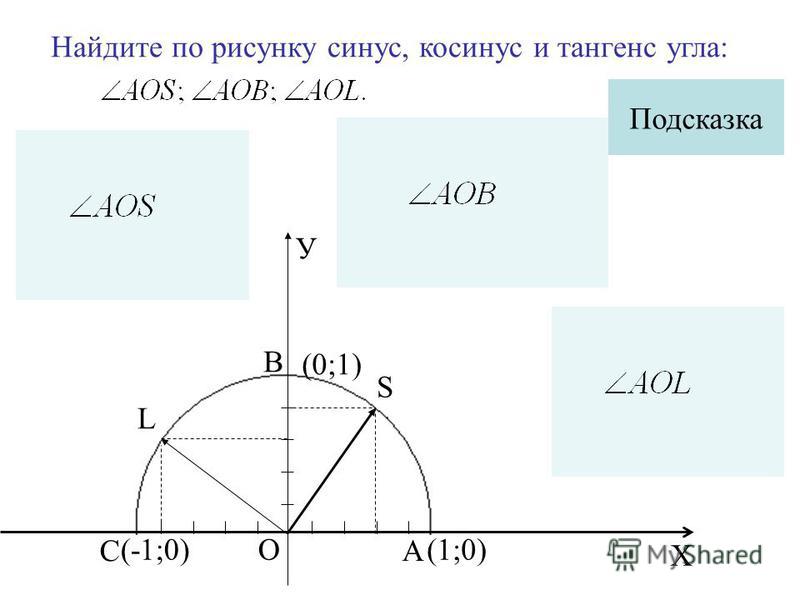

 В ее числителе находится произведение синусов прилегающих углов, а в знаменателе синус противолежащего угла. Теперь рассчитываем площадь по следующим формулам:
В ее числителе находится произведение синусов прилегающих углов, а в знаменателе синус противолежащего угла. Теперь рассчитываем площадь по следующим формулам:
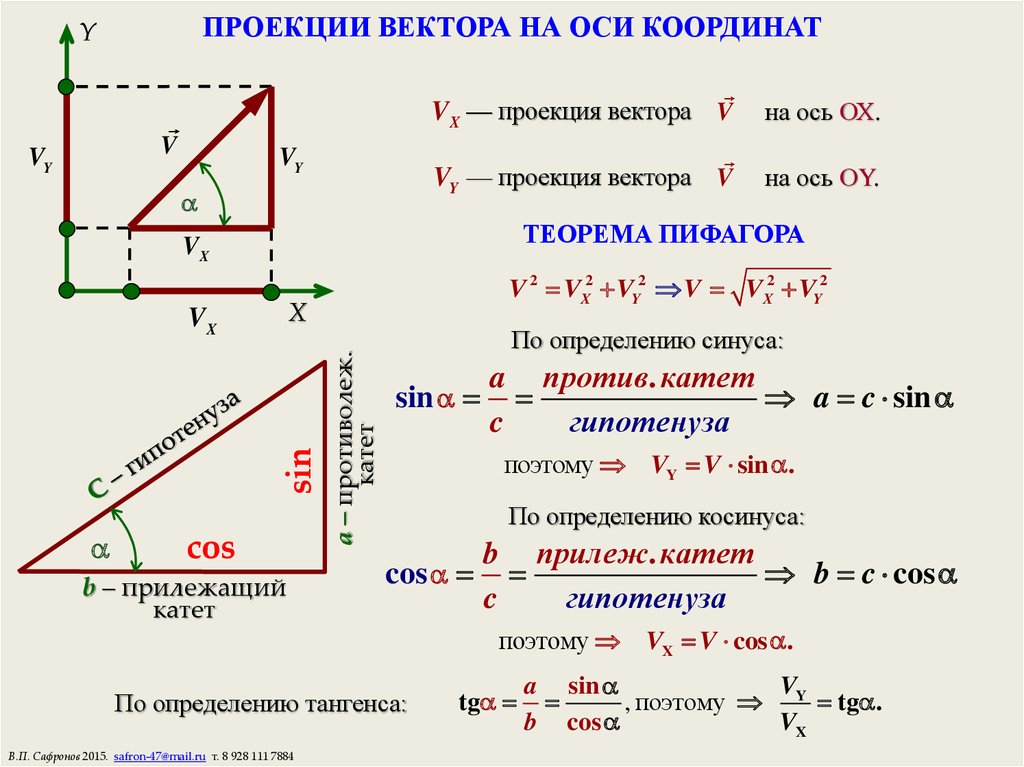 Для любого угла α верно утверждение:
Для любого угла α верно утверждение: А именно:
А именно:
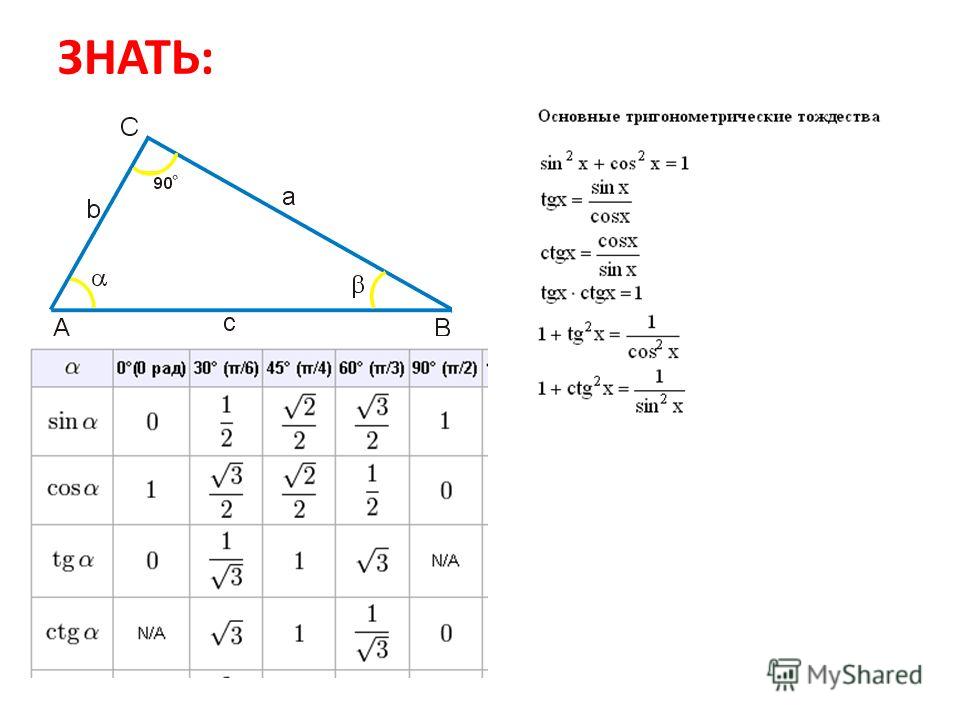 Известно, что α ∈ (3π/2; 2π). Переведем углы из радианной меры в градусную — получим α ∈ (270°; 360°).
Известно, что α ∈ (3π/2; 2π). Переведем углы из радианной меры в градусную — получим α ∈ (270°; 360°). Известно, что угол α ∈ (0; π/2). В градусной мере это записывается так: α ∈ (0°; 90°) — I координатная четверть.
Известно, что угол α ∈ (0; π/2). В градусной мере это записывается так: α ∈ (0°; 90°) — I координатная четверть. А в знаменателе расположено произведение модулей векторов. Каждый модуль равен извлеченному квадратному корню из суммы квадратов координат вектора.
А в знаменателе расположено произведение модулей векторов. Каждый модуль равен извлеченному квадратному корню из суммы квадратов координат вектора. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!
Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!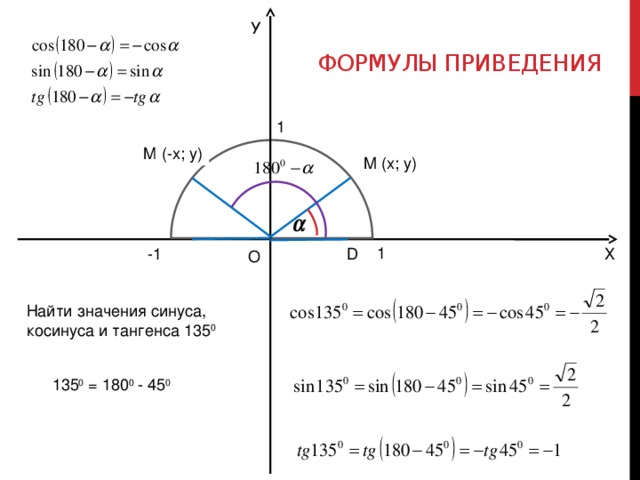

 = 1 2 · a → 2 + b → 2 – b → – a → 2 a → · b →
= 1 2 · a → 2 + b → 2 – b → – a → 2 a → · b → Помимо этой общей формулы, в тригонометрии есть много других формул, которые определяют функцию косинуса, которую вы можете увидеть на следующем изображении.
Помимо этой общей формулы, в тригонометрии есть много других формул, которые определяют функцию косинуса, которую вы можете увидеть на следующем изображении.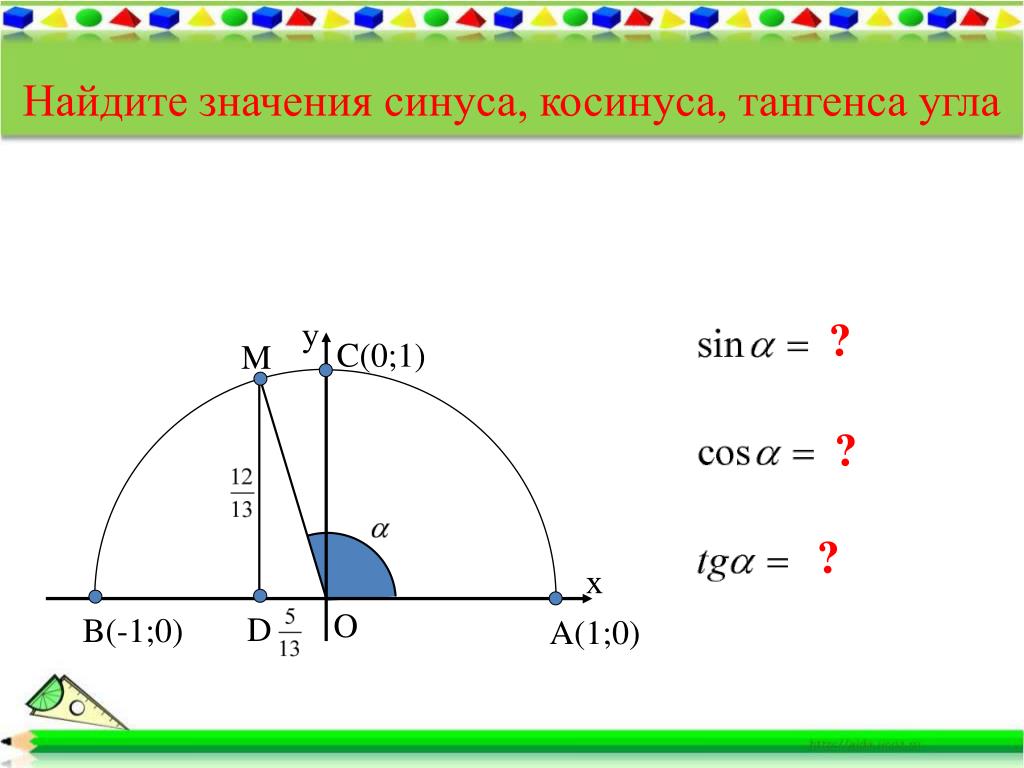 Используя одно из тождеств кофункций,
Используя одно из тождеств кофункций, Среди них формула тройного угла функции косинуса:
Среди них формула тройного угла функции косинуса: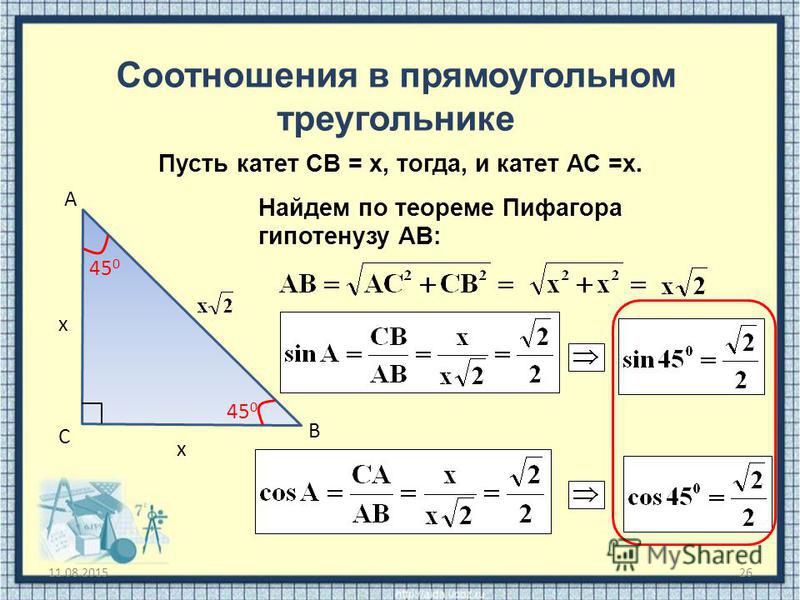 С Cuemath находите решения простыми и легкими шагами.
С Cuemath находите решения простыми и легкими шагами.
 Заменив x на (x/2) с обеих сторон, мы получим cos x = 2 cos 2 (x/2) — 1. . Решая это для cos (x/2), мы получаем cos (x/2) = ± √[ (1 + cos x) / 2 ].
Заменив x на (x/2) с обеих сторон, мы получим cos x = 2 cos 2 (x/2) — 1. . Решая это для cos (x/2), мы получаем cos (x/2) = ± √[ (1 + cos x) / 2 ].
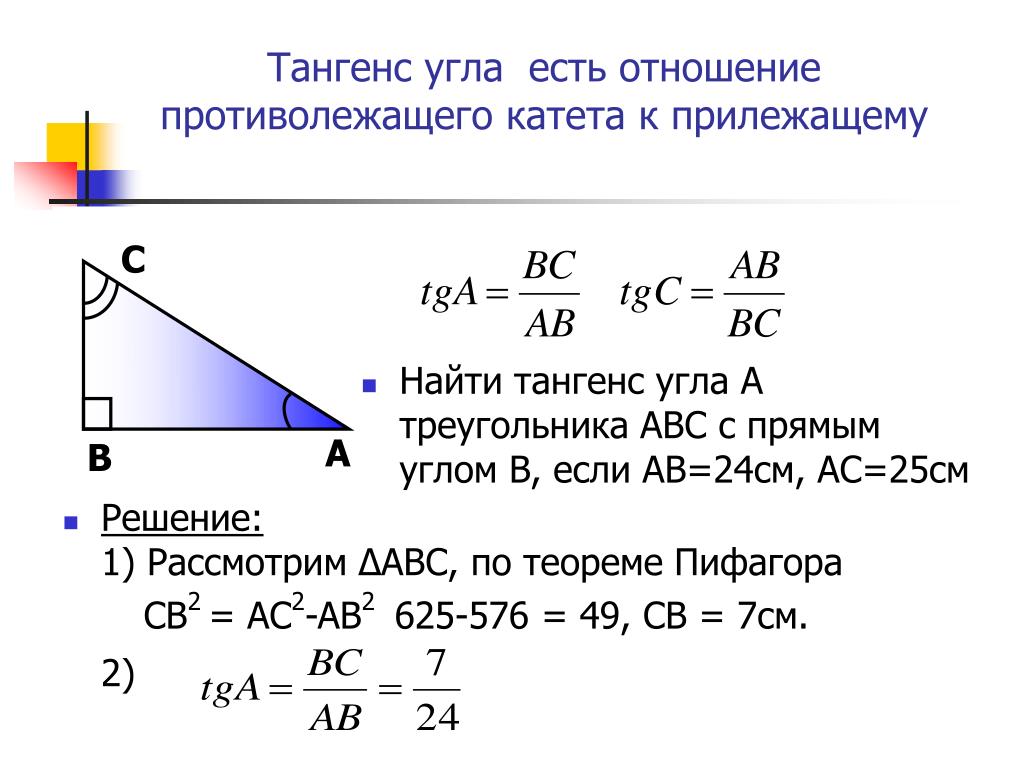 обозначают сторону, противоположную углу B, и мы используем букву c для обозначения стороны, противоположной углу C.
обозначают сторону, противоположную углу B, и мы используем букву c для обозначения стороны, противоположной углу C. Эти и следующие примеры относятся к прямоугольному треугольнику, использованному выше.
Эти и следующие примеры относятся к прямоугольному треугольнику, использованному выше.
 7$°
7$° Таким образом, определение тангенса представляет собой отношение перпендикуляра к основанию и представляется как тангенс θ.
Таким образом, определение тангенса представляет собой отношение перпендикуляра к основанию и представляется как тангенс θ. cot θ = 1
cot θ = 1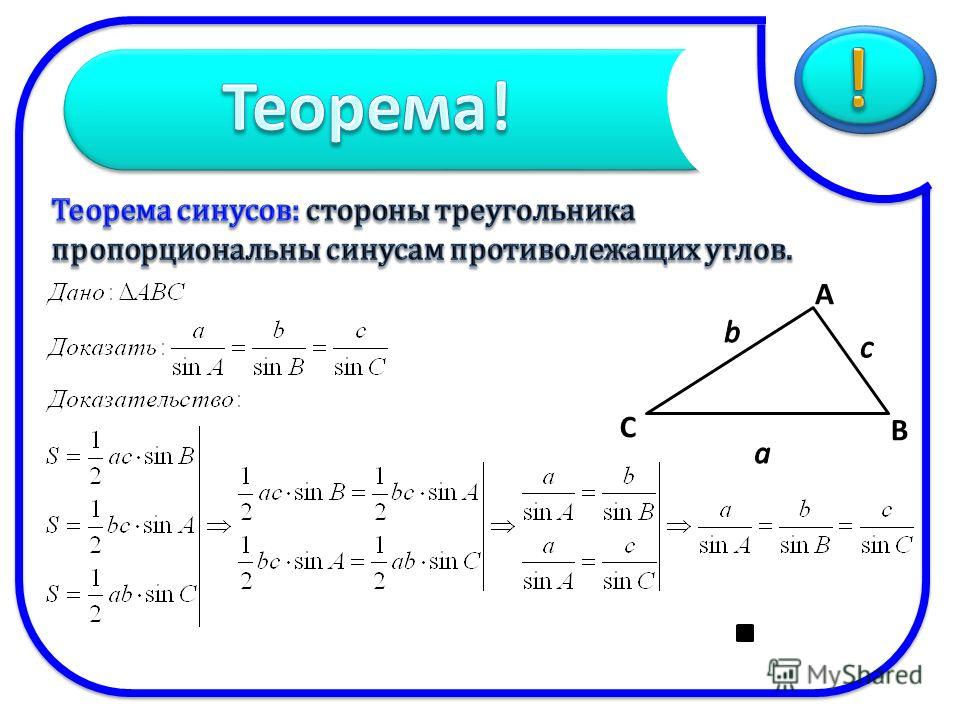
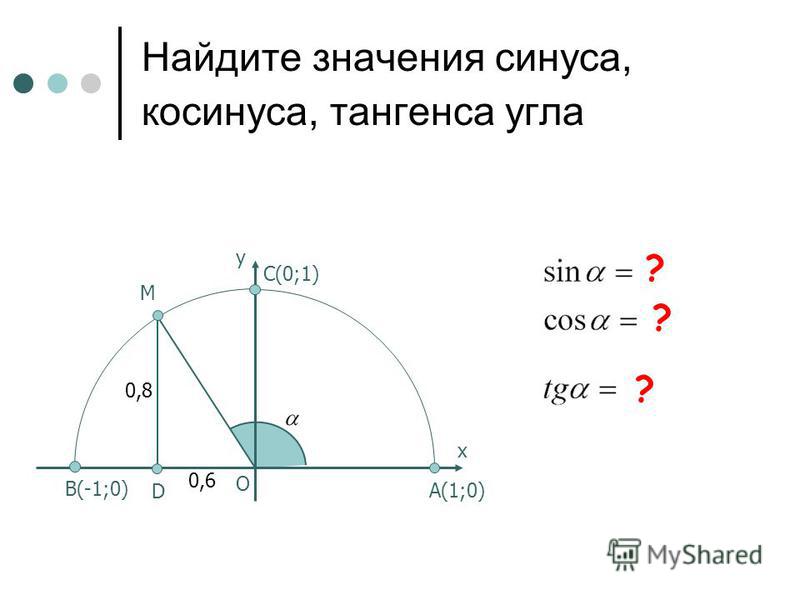



 Теперь еще раз взглянем на те же формулы. Формулы двойного угла являются частным случаем формул суммы, где \(\alpha=\beta\). Вывод формулы двойного угла для синуса начинается с формулы суммы
Теперь еще раз взглянем на те же формулы. Формулы двойного угла являются частным случаем формул суммы, где \(\alpha=\beta\). Вывод формулы двойного угла для синуса начинается с формулы суммы
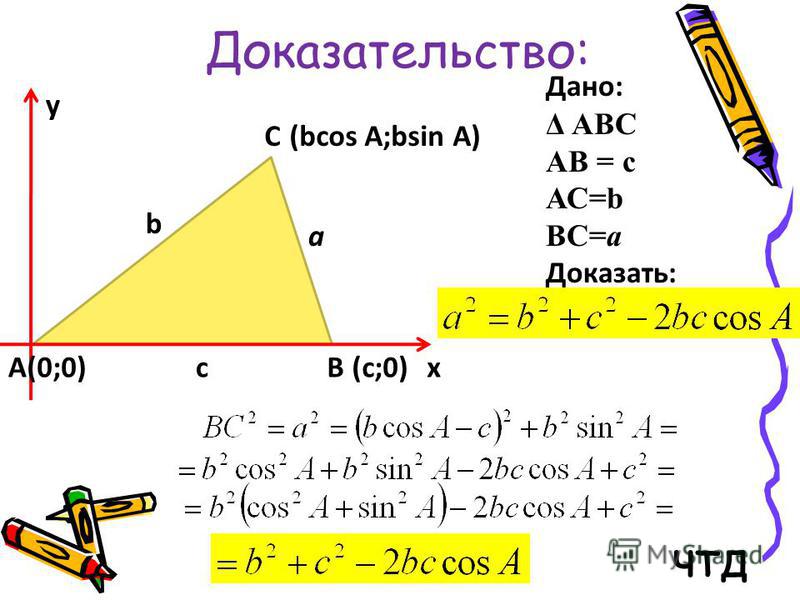
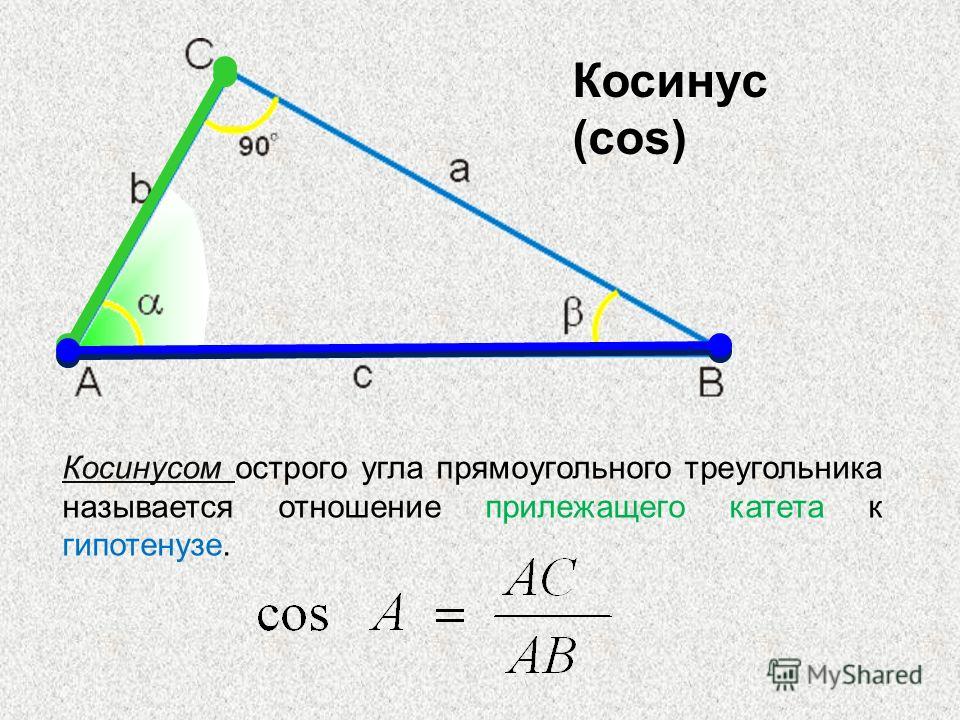 Он подчеркивает, что шаблон — это то, что нам нужно помнить, и что тождества верны для всех значений в области определения тригонометрической функции.
Он подчеркивает, что шаблон — это то, что нам нужно помнить, и что тождества верны для всех значений в области определения тригонометрической функции. 3(2x)=\left[ \dfrac{ 1}{2} \sin(2x) \right] [ 1−\cos(4x) \) 92 x\\[5pt] &= \dfrac{10}{4}+\dfrac{10}{2} \cos(2x)+\dfrac{10}{8}+\dfrac{10}{8}\ cos(4x)\\[5pt] &= \dfrac{30}{8}+5\cos(2x)+\dfrac{10}{8}\cos(4x)\\[5pt] &= \dfrac{ 15}{4}+5\cos(2x)+\dfrac{5}{4}\cos(4x) \end{align*}\]
3(2x)=\left[ \dfrac{ 1}{2} \sin(2x) \right] [ 1−\cos(4x) \) 92 x\\[5pt] &= \dfrac{10}{4}+\dfrac{10}{2} \cos(2x)+\dfrac{10}{8}+\dfrac{10}{8}\ cos(4x)\\[5pt] &= \dfrac{30}{8}+5\cos(2x)+\dfrac{10}{8}\cos(4x)\\[5pt] &= \dfrac{ 15}{4}+5\cos(2x)+\dfrac{5}{4}\cos(4x) \end{align*}\] 92\left(\dfrac{\alpha}{2}\right)&= \dfrac{1-\cos\left(2\cdot \dfrac{\alpha}{2}\right)}{1+\cos\ влево (2 \ cdot \ dfrac {\ alpha} {2} \ right)} \\ \ tan \ left (\ dfrac {\ alpha} {2} \ right) & = \ pm \ sqrt {\ dfrac {1- \ cos \alpha}{1+\cos \alpha}} \end{align*}\]
92\left(\dfrac{\alpha}{2}\right)&= \dfrac{1-\cos\left(2\cdot \dfrac{\alpha}{2}\right)}{1+\cos\ влево (2 \ cdot \ dfrac {\ alpha} {2} \ right)} \\ \ tan \ left (\ dfrac {\ alpha} {2} \ right) & = \ pm \ sqrt {\ dfrac {1- \ cos \alpha}{1+\cos \alpha}} \end{align*}\]
 Используя теорему Пифагора, мы находим, что гипотенуза равна 17. Следовательно, мы можем вычислить {17}\).
Используя теорему Пифагора, мы находим, что гипотенуза равна 17. Следовательно, мы можем вычислить {17}\).

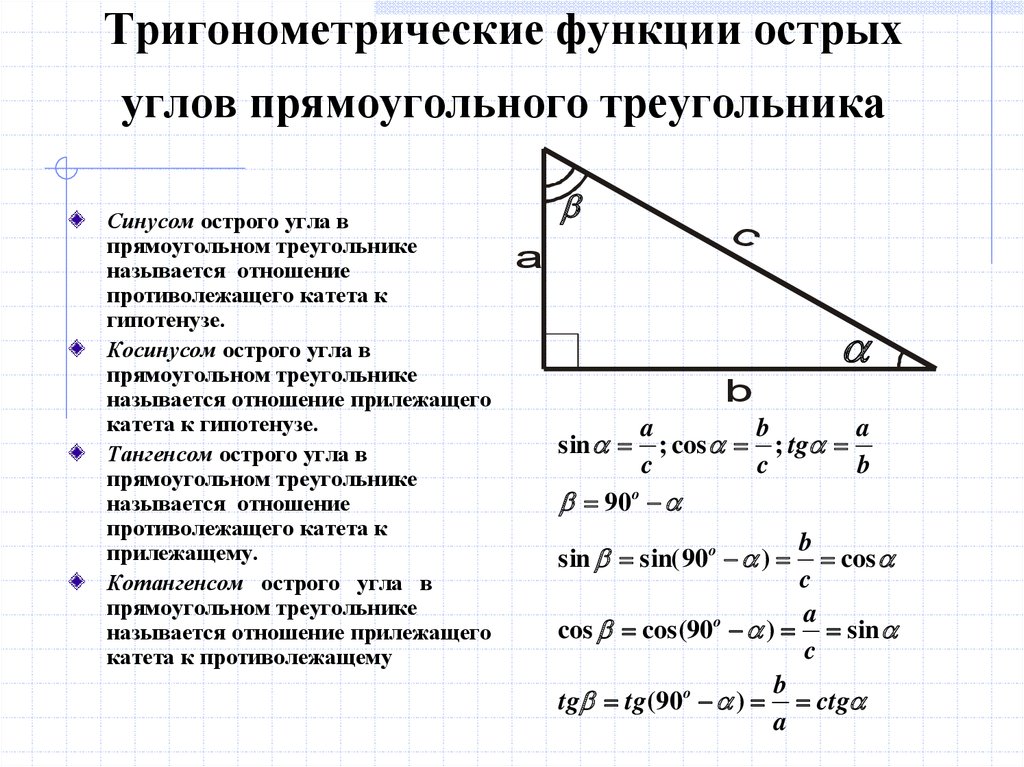
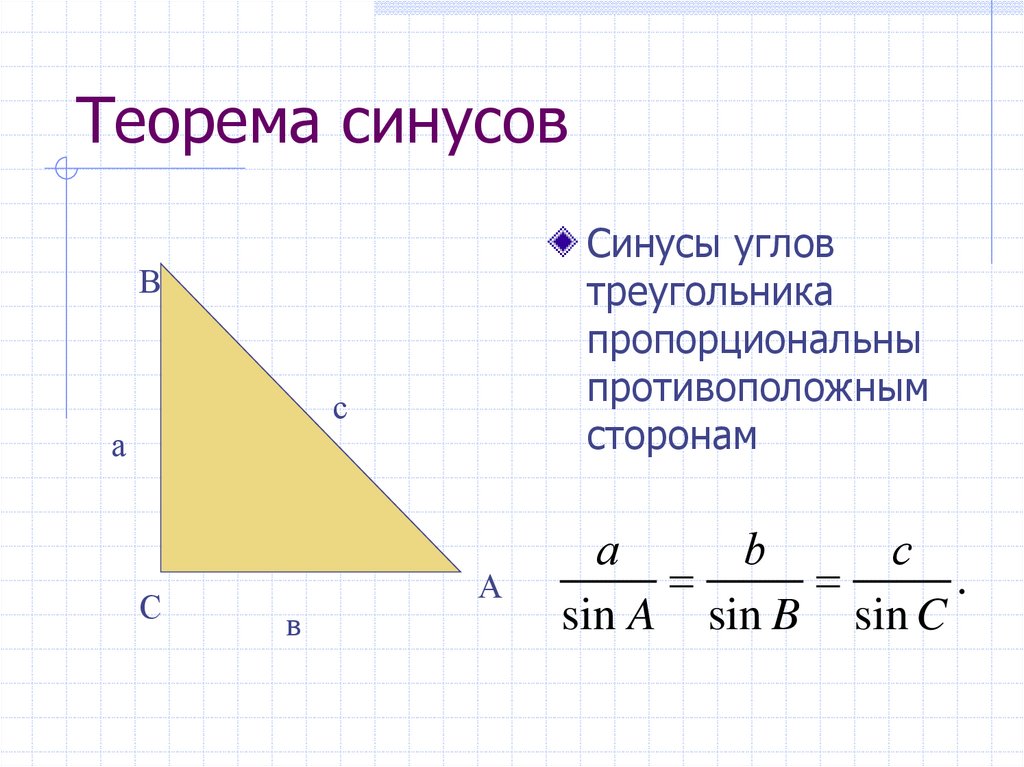 См. Пример \(\PageIndex{1}\), Пример \(\PageIndex{2}\), Пример \(\PageIndex{3}\) и Пример \(\PageIndex{4}\).
См. Пример \(\PageIndex{1}\), Пример \(\PageIndex{2}\), Пример \(\PageIndex{3}\) и Пример \(\PageIndex{4}\).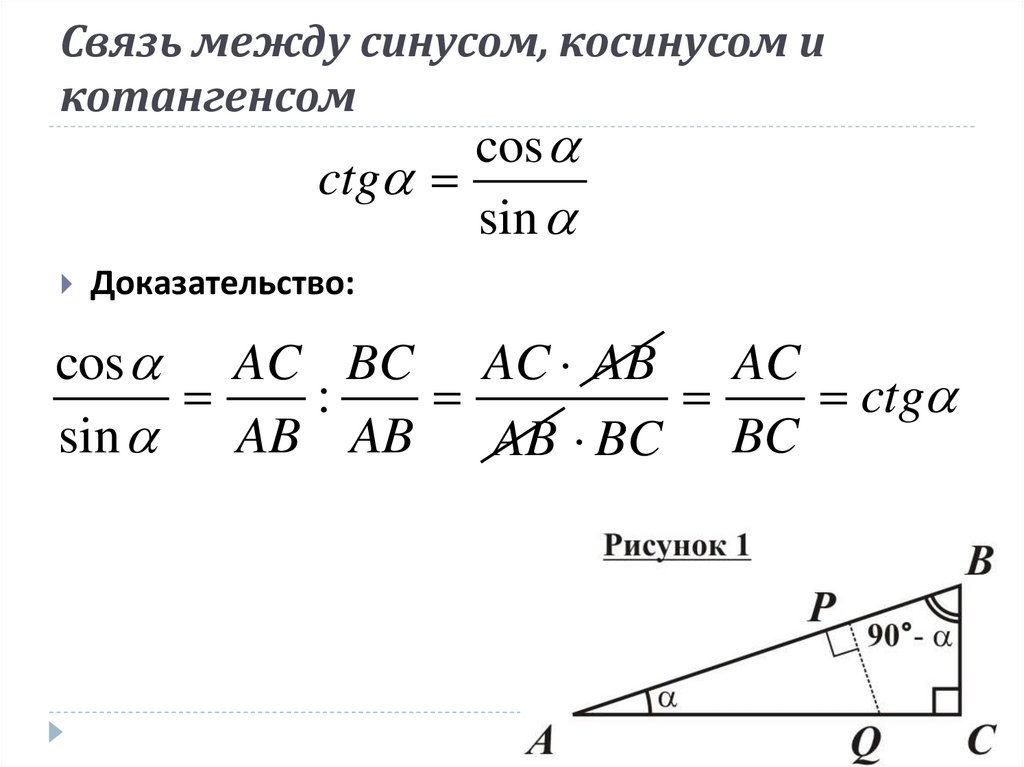 org/details/books/precalculus
org/details/books/precalculus
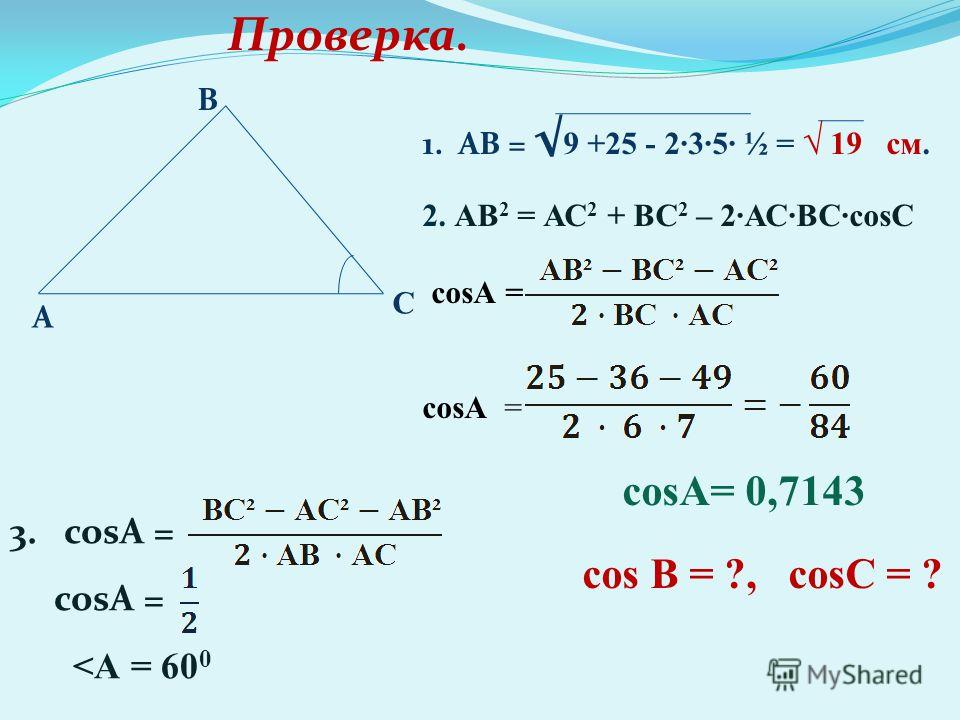
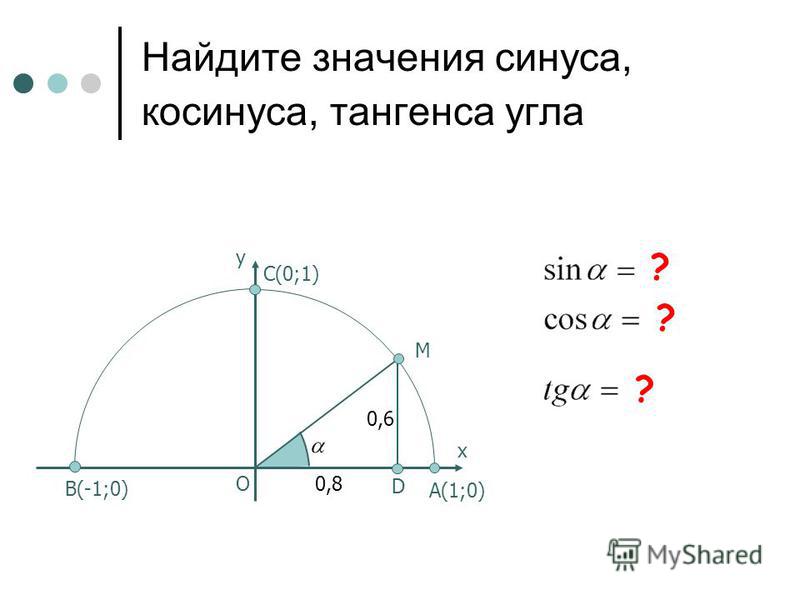
 Включает рассуждения и прикладные вопросы.
Включает рассуждения и прикладные вопросы. Для ответа на этот вопрос нам нужно найти сторону длины x, противоположную углу R. 9{2}&=110619,7432…\\
\\x&=\sqrt{110619.7432…}\\
\\x&=333\mathrm{m}\quad(3sf)\\
\end{aligned}
Для ответа на этот вопрос нам нужно найти сторону длины x, противоположную углу R. 9{2}&=110619,7432…\\
\\x&=\sqrt{110619.7432…}\\
\\x&=333\mathrm{m}\quad(3sf)\\
\end{aligned}

 Обычно вместо угла А используется один из углов треугольника, поэтому расчет будет неверным.
Обычно вместо угла А используется один из углов треугольника, поэтому расчет будет неверным.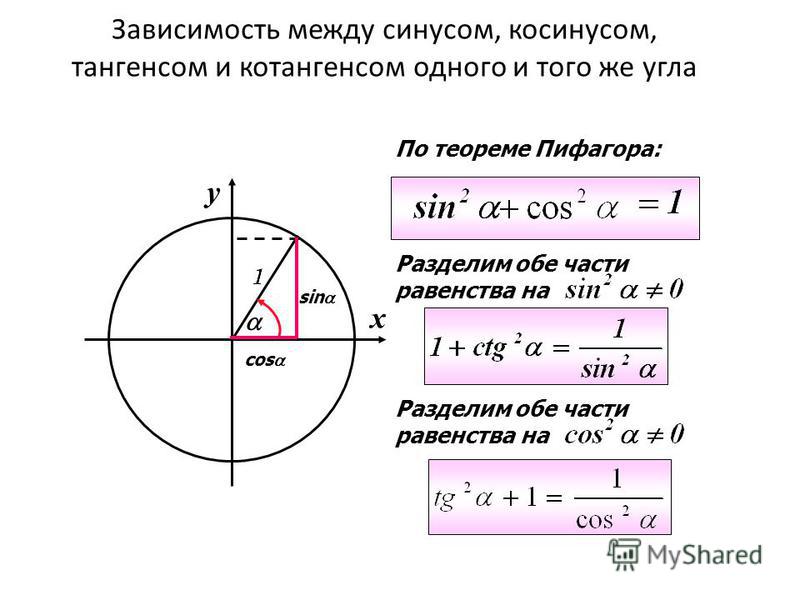 Например.
Например. 


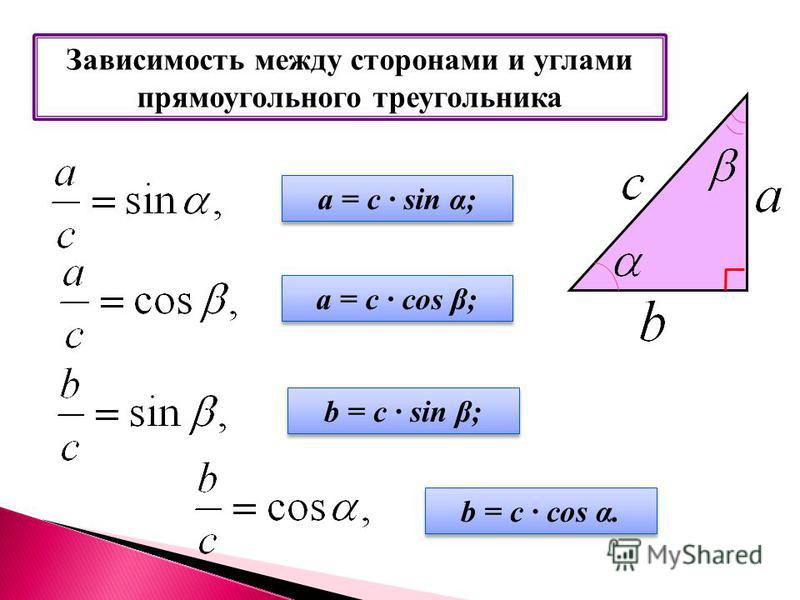 Косинус 90° = 0, поэтому в этом частном случае формула закона косинусов сводится к известному уравнению теоремы Пифагора:
Косинус 90° = 0, поэтому в этом частном случае формула закона косинусов сводится к известному уравнению теоремы Пифагора: В 16 веке закон был популяризирован известным французским математиком Виете, прежде чем он получил свою окончательную форму в 19 веке.
В 16 веке закон был популяризирован известным французским математиком Виете, прежде чем он получил свою окончательную форму в 19 веке.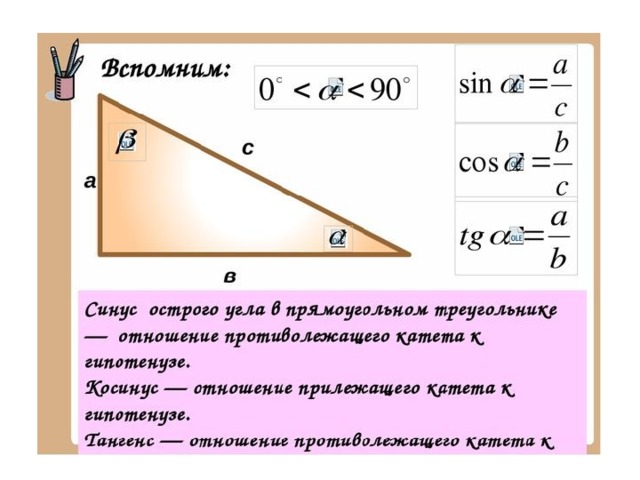 Вот почему мы решили реализовать в этом инструменте SAS и SSS, но не SSA.
Вот почему мы решили реализовать в этом инструменте SAS и SSS, но не SSA. Отсюда:
Отсюда: Теорема Птолемея
Теорема Птолемея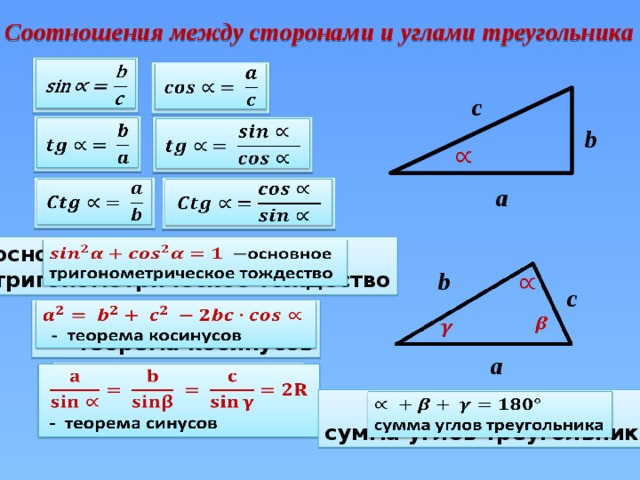
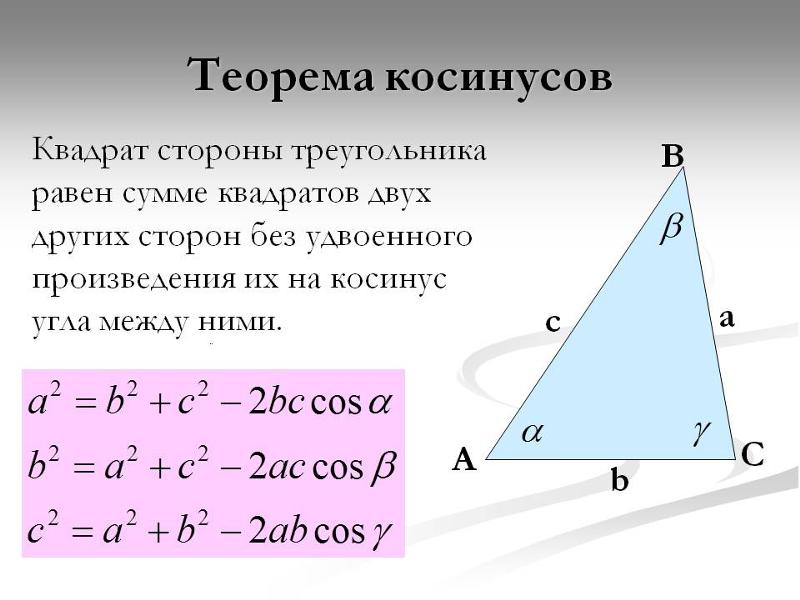 Не забудьте еще раз свериться с рисунком выше, правильно ли вы обозначили стороны и углы правильными символами.
Не забудьте еще раз свериться с рисунком выше, правильно ли вы обозначили стороны и углы правильными символами.


 Тогда дискриминант — это просто число D = b2 − 4ac.
Тогда дискриминант — это просто число D = b2 − 4ac. Аналогично разбираем второе уравнение:
Аналогично разбираем второе уравнение: Наконец, если D < 0, корней нет — ничего считать не надо.
Наконец, если D < 0, корней нет — ничего считать не надо. Например, первую:
Например, первую:
 Если там положительное число — корней будет два. Если отрицательное — корней не будет вообще.
Если там положительное число — корней будет два. Если отрицательное — корней не будет вообще.
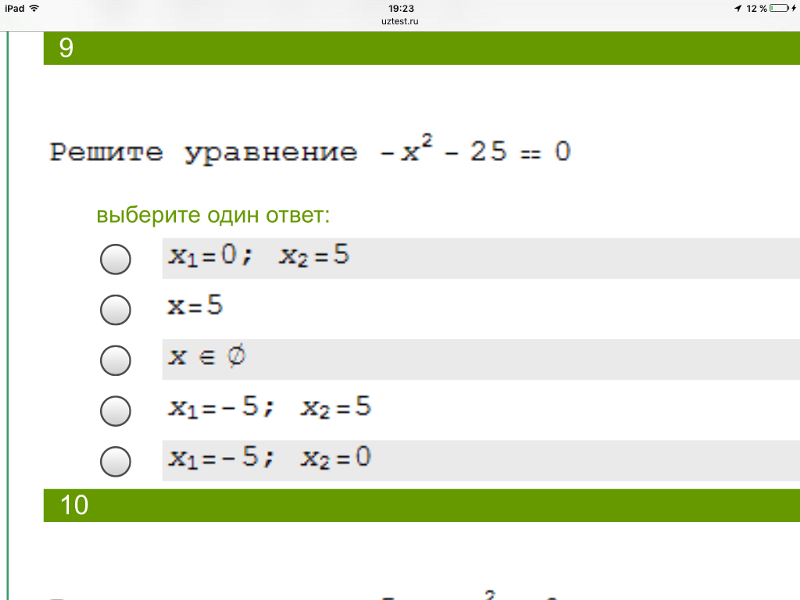 2) 5 ∙ 9 = 45 (кг)
Ответ: 45 кг масса 9 коробок с бананами.
2) 5 ∙ 9 = 45 (кг)
Ответ: 45 кг масса 9 коробок с бананами.
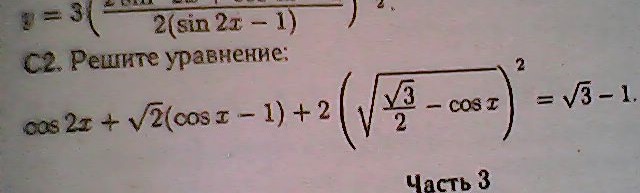 1).
Таня закрасила одну шестую (рис.3).
А Оля закрасила одну двенадцатую (рис. 2).
1).
Таня закрасила одну шестую (рис.3).
А Оля закрасила одну двенадцатую (рис. 2).

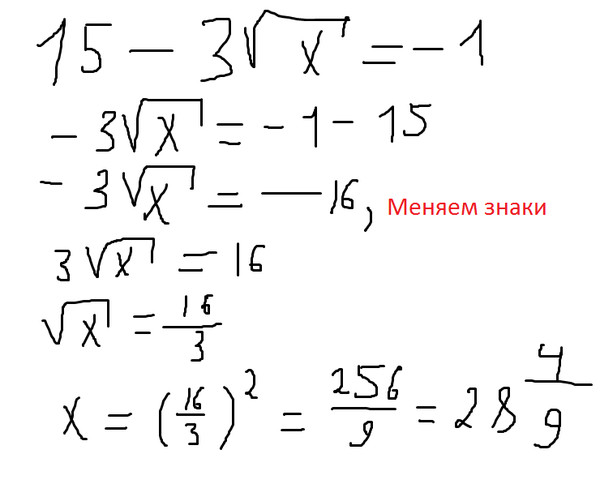 Данные ярче яркого.
Данные ярче яркого. Основание стало плоским. За счёт этого стекло приобрело более надёжную форму с повышенной устойчивостью к трещинам.
Основание стало плоским. За счёт этого стекло приобрело более надёжную форму с повышенной устойчивостью к трещинам. А измерить этот показатель теперь можно с помощью потрясающего датчика и специального приложения на Apple Watch Series 7. Они даже умеют делать это в фоновом режиме днём и ночью.3
А измерить этот показатель теперь можно с помощью потрясающего датчика и специального приложения на Apple Watch Series 7. Они даже умеют делать это в фоновом режиме днём и ночью.3 Или, наоборот, может определить, что у вас синусовый ритм, а значит, сердце бьётся в нормальном режиме.5
Или, наоборот, может определить, что у вас синусовый ритм, а значит, сердце бьётся в нормальном режиме.5 А новая функция «Размышление» в приложении «Осознанность» поможет привести в порядок мысли и обрести баланс. И всё это с невероятно красивой анимацией. Кроме того, в Apple Fitness+ вас ждут медитации с сопровождением — видеосеансы и аудио.9 С их помощью можно улучшить общее самочувствие, фокусируясь на таких темах, как спокойствие, доброта или благодарность.
А новая функция «Размышление» в приложении «Осознанность» поможет привести в порядок мысли и обрести баланс. И всё это с невероятно красивой анимацией. Кроме того, в Apple Fitness+ вас ждут медитации с сопровождением — видеосеансы и аудио.9 С их помощью можно улучшить общее самочувствие, фокусируясь на таких темах, как спокойствие, доброта или благодарность.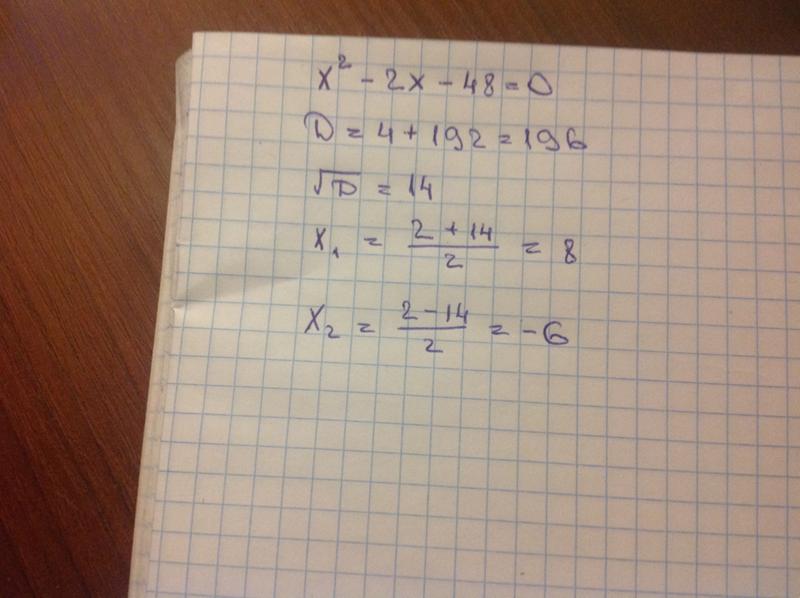 Больше движения, больше эндорфинов. Стартуйте. Прямо с запястья.
Больше движения, больше эндорфинов. Стартуйте. Прямо с запястья.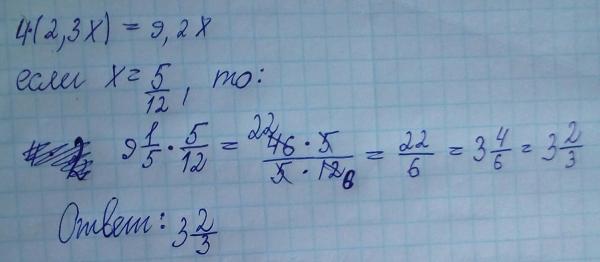
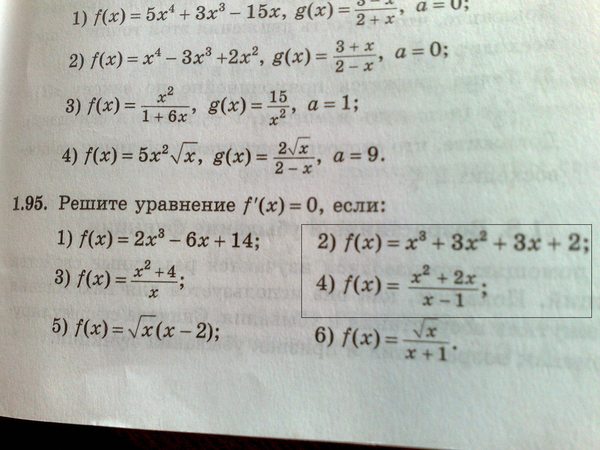 Позвоните в офис, ответьте на срочное письмо, определите верное направление по встроенному компасу, отправьте своим детям сообщение с эмодзи. Когда Apple Watch подключены к iPhone, все важные связи, полезная информация и любимый контент у вас под рукой.
Позвоните в офис, ответьте на срочное письмо, определите верное направление по встроенному компасу, отправьте своим детям сообщение с эмодзи. Когда Apple Watch подключены к iPhone, все важные связи, полезная информация и любимый контент у вас под рукой.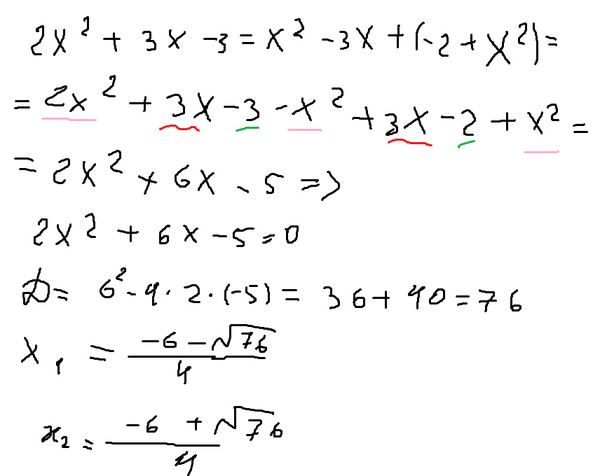
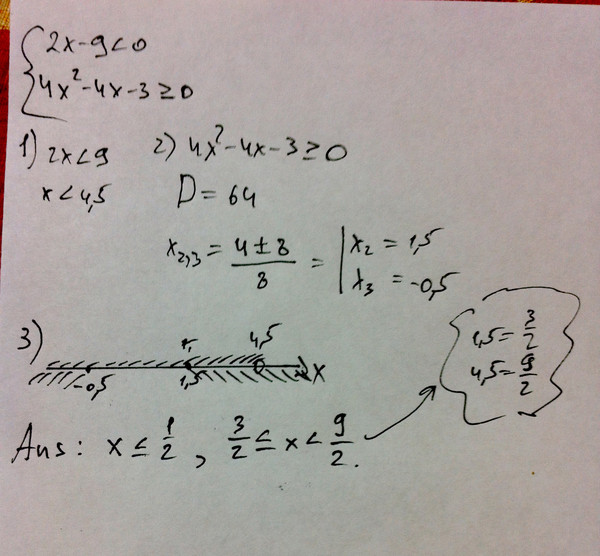
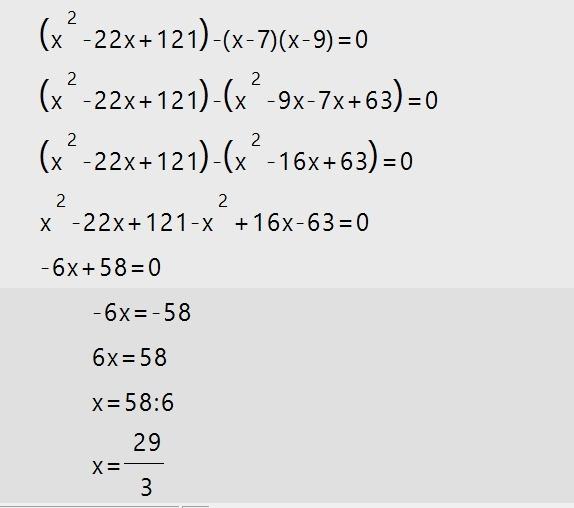
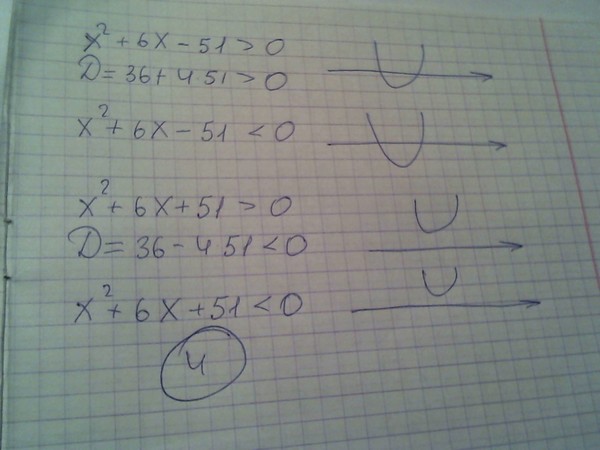 Это изменение сделает сражения более комфортными для всех игроков, особенно для новых.
Это изменение сделает сражения более комфортными для всех игроков, особенно для новых.
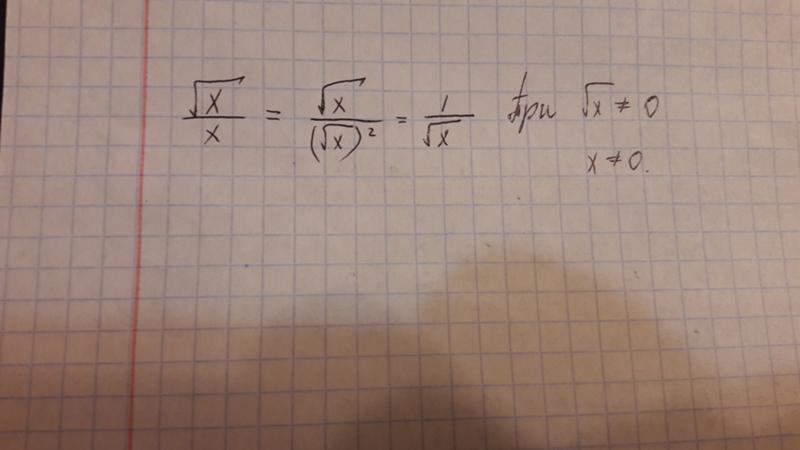

 Квартал зданий в квадрате F9 будет иметь форму, аналогичную кварталу с северной стороны, чтобы обеспечить обеим командам равные возможности для удержания позиций.
Квартал зданий в квадрате F9 будет иметь форму, аналогичную кварталу с северной стороны, чтобы обеспечить обеим командам равные возможности для удержания позиций. 18.1 вместо значений бонусов личного резерва будет отображаться строка текста с надписью «bonus%». Во второй итерации общего теста это будет исправлено. Приносим свои извинения за доставленные неудобства.
18.1 вместо значений бонусов личного резерва будет отображаться строка текста с надписью «bonus%». Во второй итерации общего теста это будет исправлено. Приносим свои извинения за доставленные неудобства.

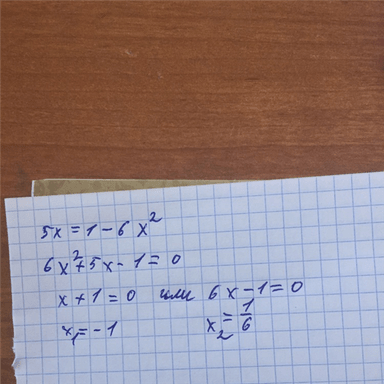
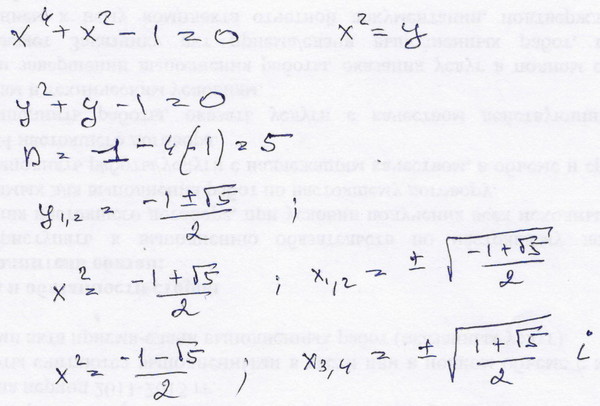 ответил 10.12.14
ответил 10.12.14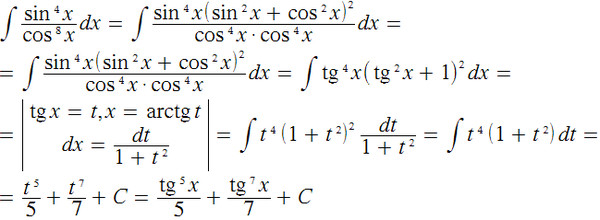 ответил 08.08.13
ответил 08.08.13 7. ac ))/2 a
7. ac ))/2 a 
 также график):
также график): как стандартное квадратное уравнение)
как стандартное квадратное уравнение)
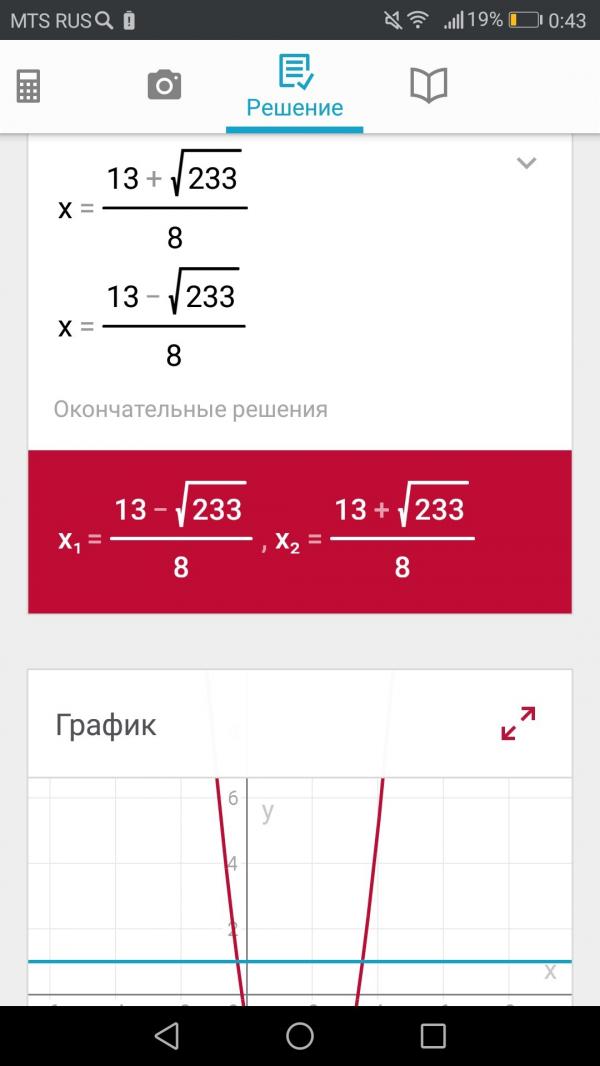 Пожалуйста, включите его, чтобы вы могли испытать все возможности этого сайта.
Пожалуйста, включите его, чтобы вы могли испытать все возможности этого сайта.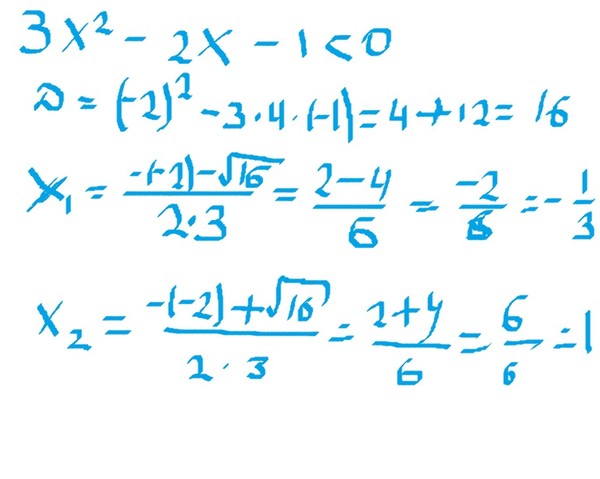
 Вы можете измерить с помощью линейки или просто использовать формулу, включающую координаты каждой конечной точки сегмента. Средняя точка — это просто среднее значение каждой координаты сечения, образующее новую точку координат. Мы проиллюстрируем это ниже.
Вы можете измерить с помощью линейки или просто использовать формулу, включающую координаты каждой конечной точки сегмента. Средняя точка — это просто среднее значение каждой координаты сечения, образующее новую точку координат. Мы проиллюстрируем это ниже.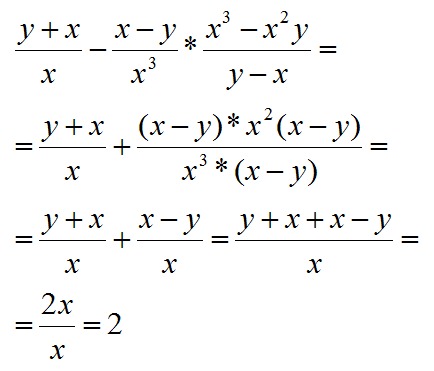
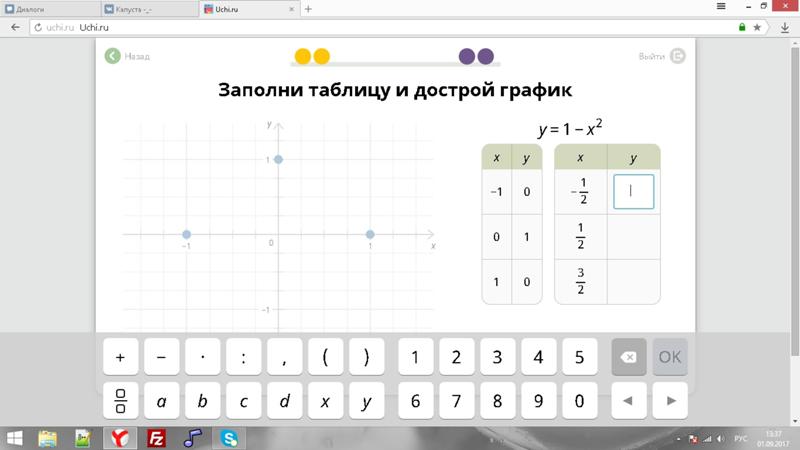


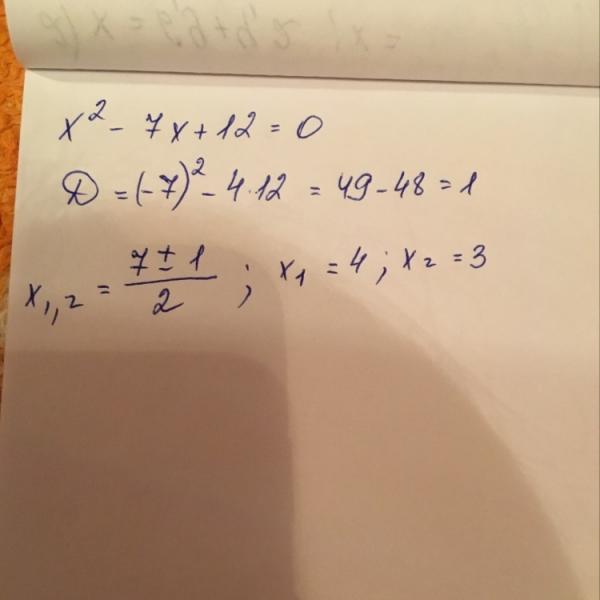
 (22,5 градусов).
Ложку в зубы, калькулятор в руки:
(22,5 градусов).
Ложку в зубы, калькулятор в руки: КИЛОбайта. При этом программисты умудрялись
заталкивать туда аркадные игры с сотнями экранов и отличной графикой (по меркам 8-разрядных машин, конечно). …А ведь с той поры прошло немногим
больше двух десятилетий.
КИЛОбайта. При этом программисты умудрялись
заталкивать туда аркадные игры с сотнями экранов и отличной графикой (по меркам 8-разрядных машин, конечно). …А ведь с той поры прошло немногим
больше двух десятилетий.
 Но только не того, кто прочитал эту книгу! Примерный образец оформления задачи в конце урока.
Но только не того, кто прочитал эту книгу! Примерный образец оформления задачи в конце урока.

 2.4. Кривые в полярной системе координат
2.4. Кривые в полярной системе координат Аналитическая геометрия > 3.2. Аналитическая геометрия на плоскости > 3.2.4. Кривые в полярной системе координат
Аналитическая геометрия > 3.2. Аналитическая геометрия на плоскости > 3.2.4. Кривые в полярной системе координат
 Для всех точек плоскости, не
совпадающих с полюсом .
Для всех точек плоскости, не
совпадающих с полюсом .  32
32 Из уравнения кривой следует, что если мы будем
увеличивать , то будет возрастать. Кривая построена на рисунке
33.
Из уравнения кривой следует, что если мы будем
увеличивать , то будет возрастать. Кривая построена на рисунке
33. 34
34 Поэтому найдем
несколько точек на кривой при из промежутка и нанесем их на плоскость в полярной системе
координат.
Поэтому найдем
несколько точек на кривой при из промежутка и нанесем их на плоскость в полярной системе
координат. 36
36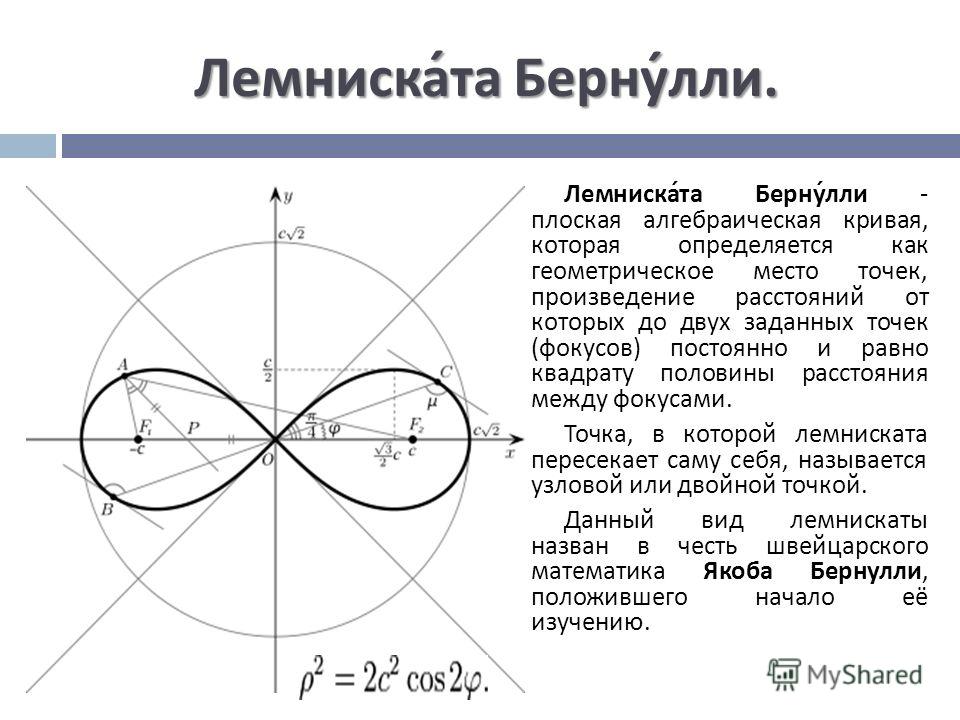 Давно пользовался MathCad . Как построить график чтобы получился как на скриншоте. Ну.
Давно пользовался MathCad . Как построить график чтобы получился как на скриншоте. Ну. Аналогично декартовому графику, для полярного графика можно задать стиль оформления осей (в частности, для наглядности удобно отразить вспомогательные угловые линии), изменить параметры кривой, создать надписи.
Аналогично декартовому графику, для полярного графика можно задать стиль оформления осей (в частности, для наглядности удобно отразить вспомогательные угловые линии), изменить параметры кривой, создать надписи.

 Все выражения должны использовать одну и ту же переменную. Угол вводится в радианах (по умолчанию) или в градусах (указываются единицы – deg).
Все выражения должны использовать одну и ту же переменную. Угол вводится в радианах (по умолчанию) или в градусах (указываются единицы – deg).
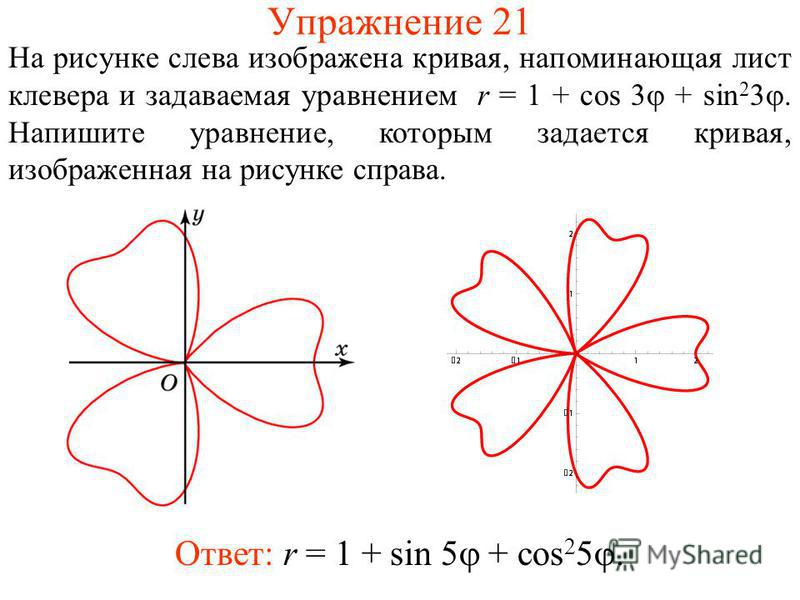 05.2014, 18:40
05.2014, 18:40 
 . 2*Pi, coords = polar)
. 2*Pi, coords = polar)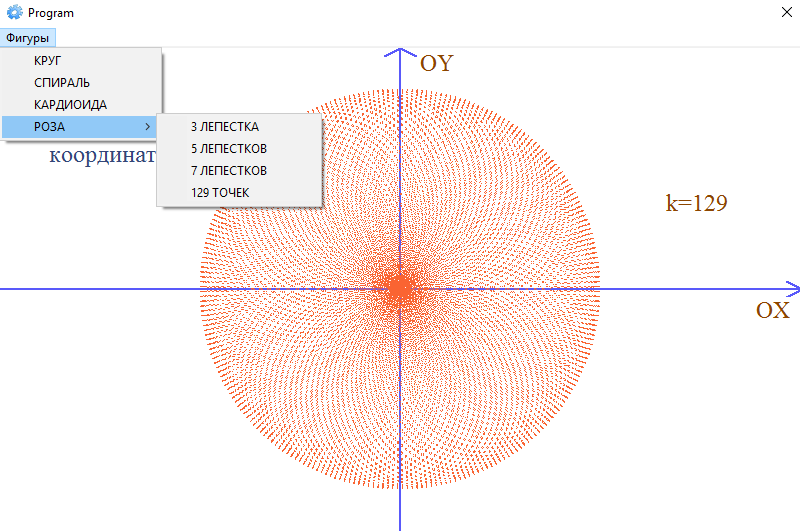 Но выбирая даже между, все равно ничего не показывается. Какая тут может быть ошибка?
Но выбирая даже между, все равно ничего не показывается. Какая тут может быть ошибка?  Как я понимаю это (а может ?). В любом случае ошибка в том, что это иностранные пакеты, и у них тангенс обозначается . Поэтому например для первой функции график строится так
Как я понимаю это (а может ?). В любом случае ошибка в том, что это иностранные пакеты, и у них тангенс обозначается . Поэтому например для первой функции график строится так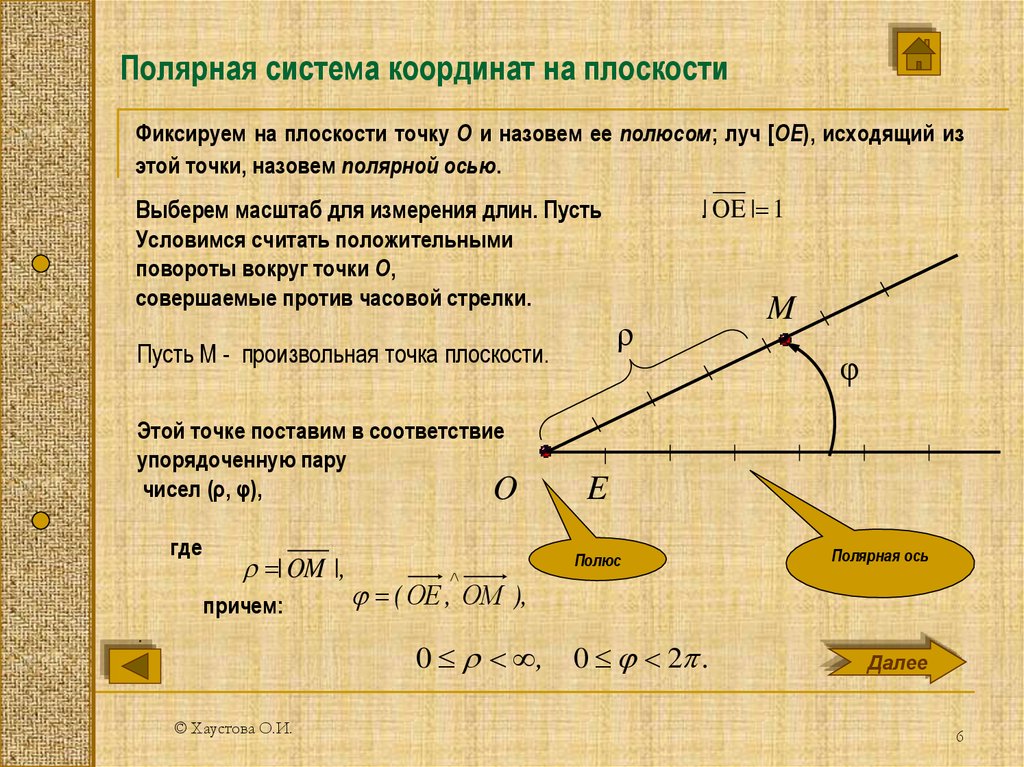 (2*tan((x/2))-x)}, x = (Pi/4) .. (Pi/3), coords = polar, color = red)
(2*tan((x/2))-x)}, x = (Pi/4) .. (Pi/3), coords = polar, color = red)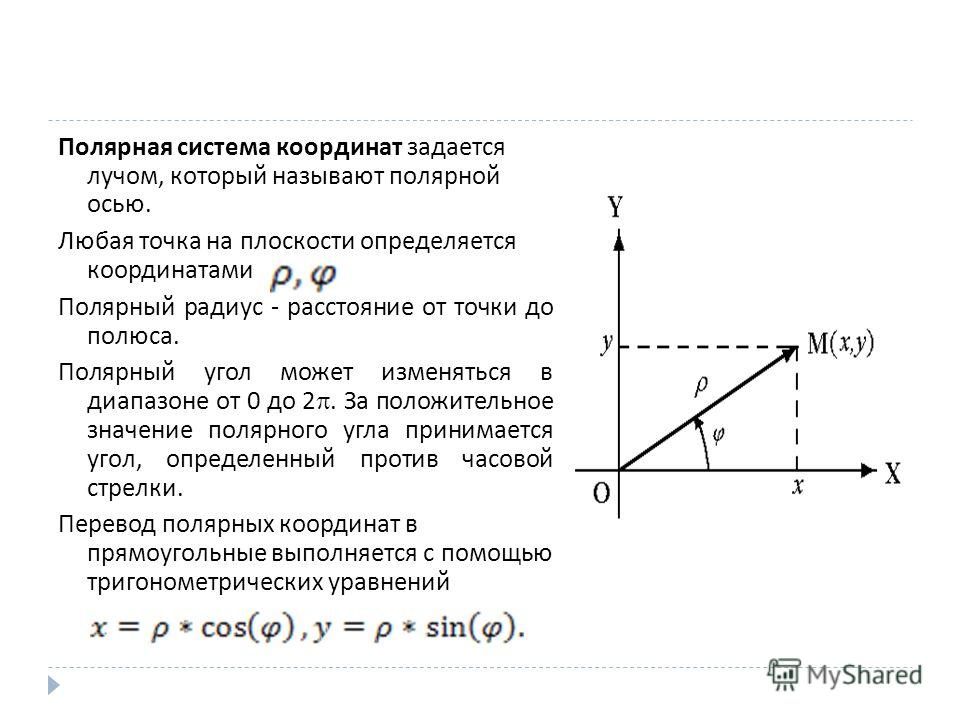 . Для начала вам нужно использовать как положительные, так и отрицательные числа для описания всех точек на плоскости, и вы должны создать сетку (оси скважин), чтобы использовать ее в качестве
ссылка.
. Для начала вам нужно использовать как положительные, так и отрицательные числа для описания всех точек на плоскости, и вы должны создать сетку (оси скважин), чтобы использовать ее в качестве
ссылка. c$ .. , под углом и все равно в конечном итоге указывают в том же направлении! В приведенном выше примере общие координаты для $A$ будут $(90,2n\pi + \frac{\pi}{2})$, где $n$ — целое число.
c$ .. , под углом и все равно в конечном итоге указывают в том же направлении! В приведенном выше примере общие координаты для $A$ будут $(90,2n\pi + \frac{\pi}{2})$, где $n$ — целое число.
 После того, как вы нарисовали полярную диаграмму, используйте графический калькулятор или графопостроитель, чтобы подтвердить свой рисунок.
После того, как вы нарисовали полярную диаграмму, используйте графический калькулятор или графопостроитель, чтобы подтвердить свой рисунок.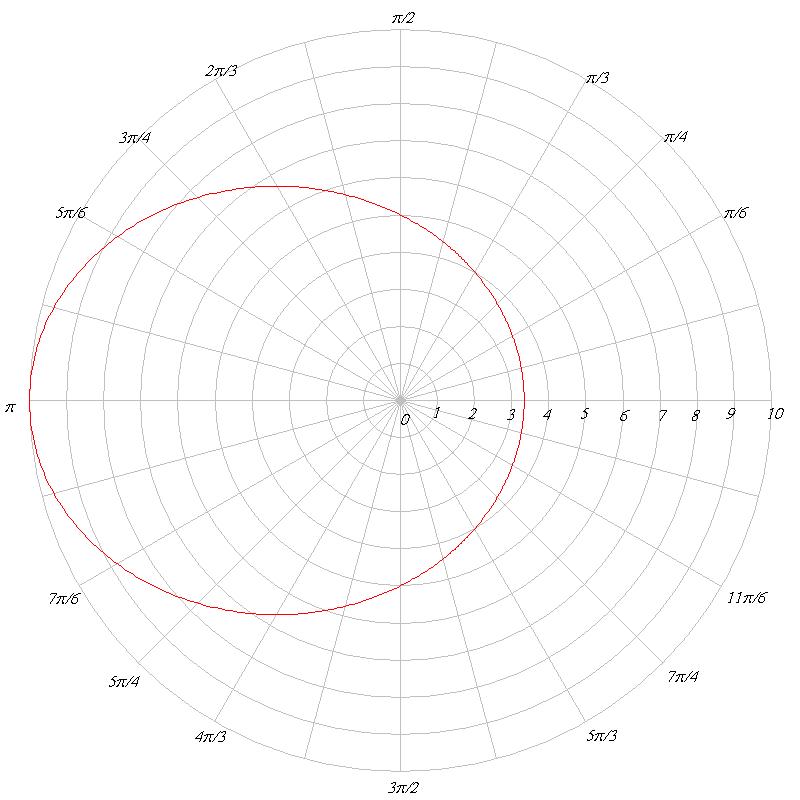 0241
0241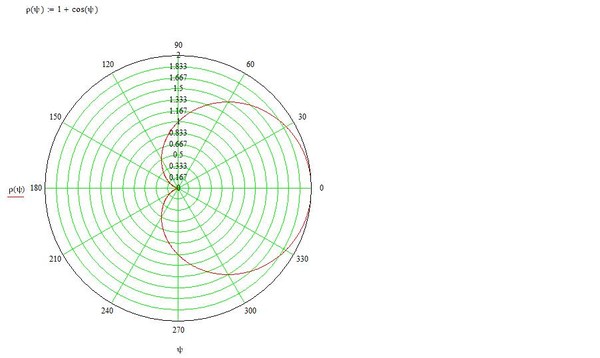 axes( проекция
axes( проекция  pyplot as plt
pyplot as plt 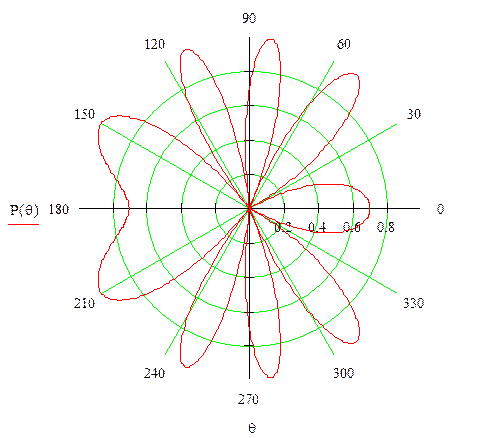 sqrt((a
sqrt((a 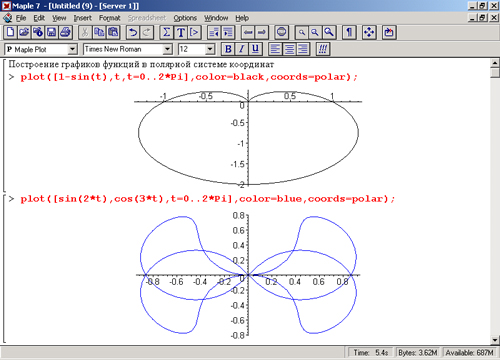 pyplot as plt
pyplot as plt  cos(rad))
cos(rad))  ARNGE
ARNGE  pyplot as plt
pyplot as plt 
 Калькуляторы могут дать неверное значение tan -1 () , когда значения x или y отрицательны... подробнее см. ниже.
Калькуляторы могут дать неверное значение tan -1 () , когда значения x или y отрицательны... подробнее см. ниже. ..
..  ..
.. 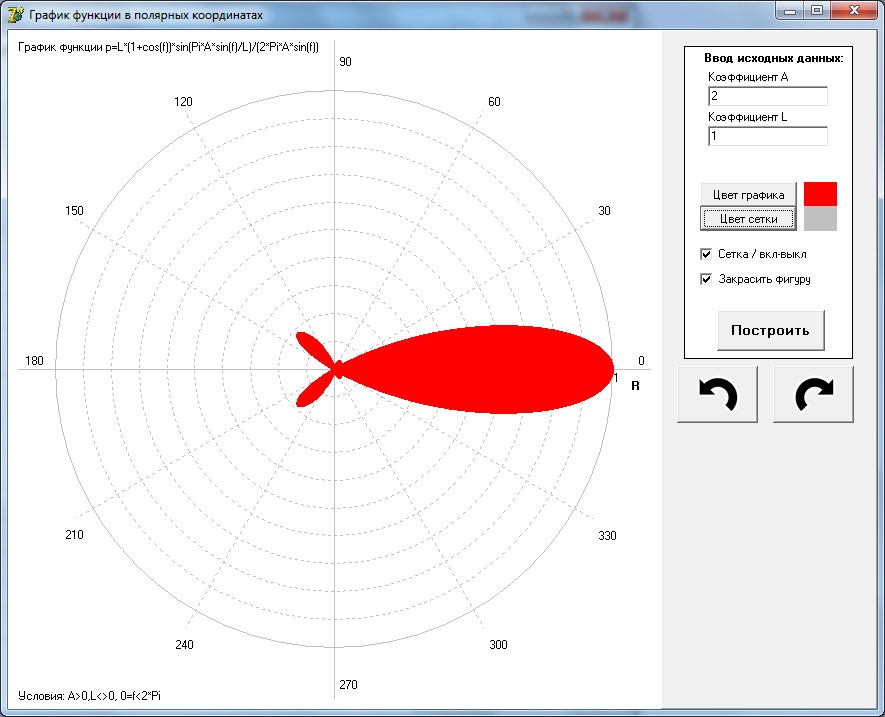 ..)
..) Департамент математического образования J.
Департамент математического образования J. 2.1. Если вы этого не сделаете
Если у вас есть это программное обеспечение, вы можете использовать демо-версию или приобрести
программное обеспечение через Интернет по адресу http://www.pacifict.com. Эти демонстрации также могут быть созданы с использованием других графических
программное обеспечение или графические калькуляторы.
2.1. Если вы этого не сделаете
Если у вас есть это программное обеспечение, вы можете использовать демо-версию или приобрести
программное обеспечение через Интернет по адресу http://www.pacifict.com. Эти демонстрации также могут быть созданы с использованием других графических
программное обеспечение или графические калькуляторы.
 Регулировка
диапазон q производит
следующий график:
Регулировка
диапазон q производит
следующий график:
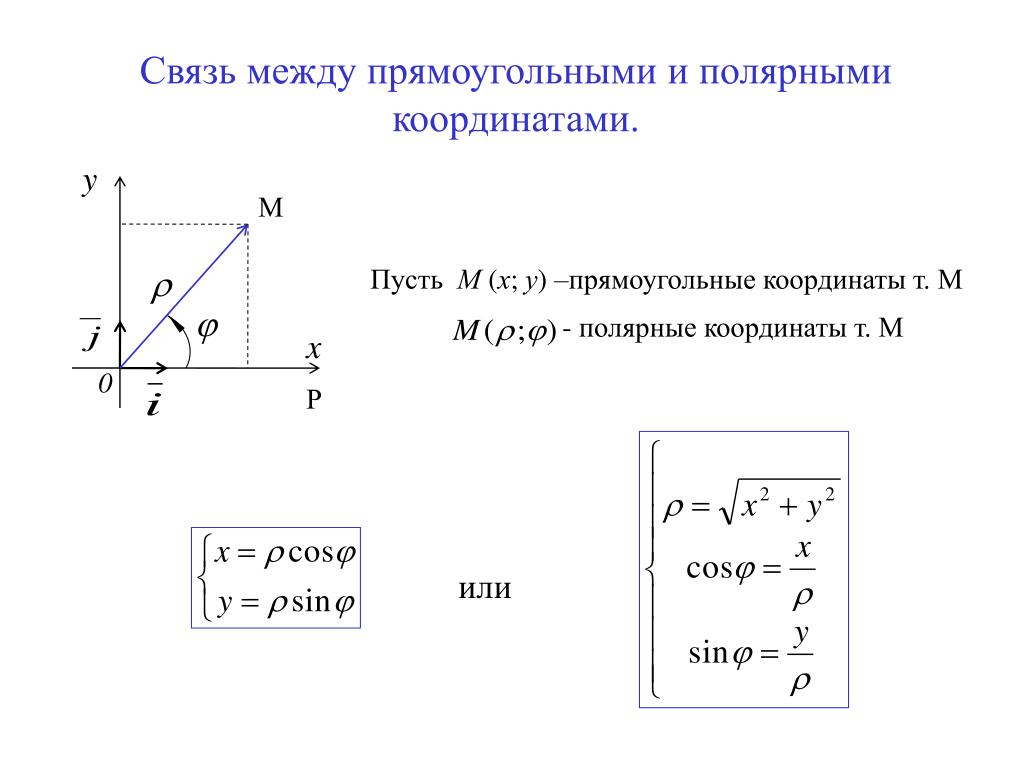
 2.1 в качестве вспомогательного приложения, нажмите здесь .
2.1 в качестве вспомогательного приложения, нажмите здесь .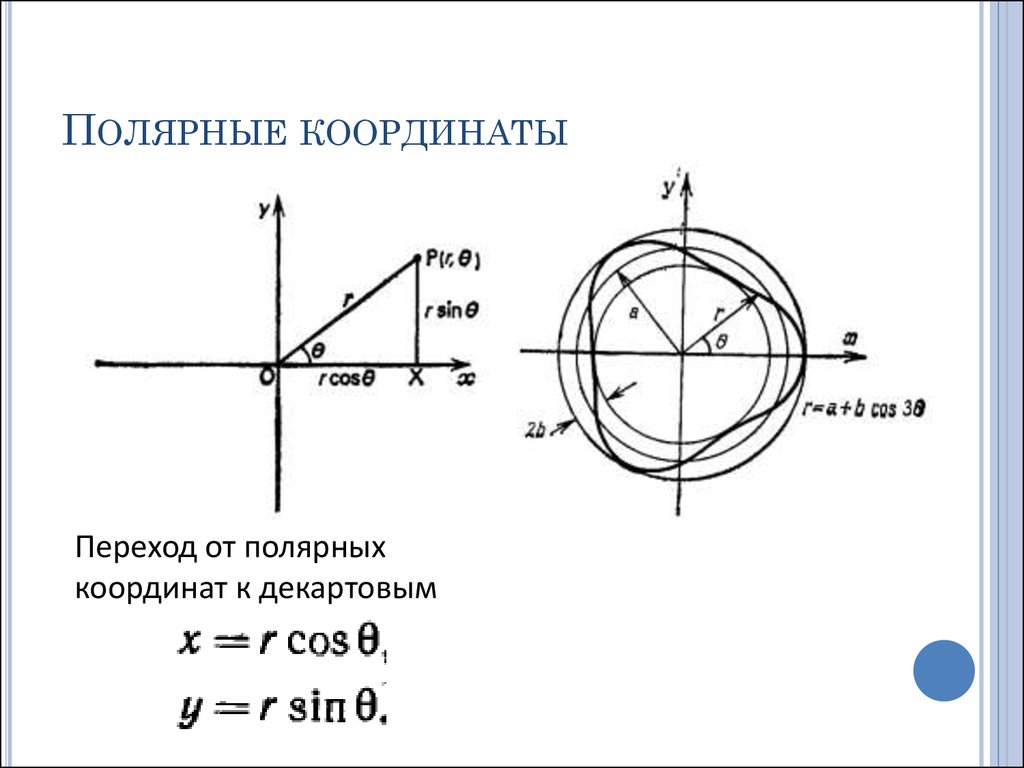 Диапазон может включать любую комбинацию qmin
и qmax,
пока расстояние вращения равно p. Следовательно
стандартное значение по умолчанию qmin = 0 и qmax = 2p
дважды отображает множество всех точек
вокруг кривой. n = количество листьев розы .
При n = 1 возникает частный случай, однолистная роза представляет собой круг.
Обратите внимание, что перехваты находятся на 0 и и .
Диапазон может включать любую комбинацию qmin
и qmax,
пока расстояние вращения равно p. Следовательно
стандартное значение по умолчанию qmin = 0 и qmax = 2p
дважды отображает множество всех точек
вокруг кривой. n = количество листьев розы .
При n = 1 возникает частный случай, однолистная роза представляет собой круг.
Обратите внимание, что перехваты находятся на 0 и и .
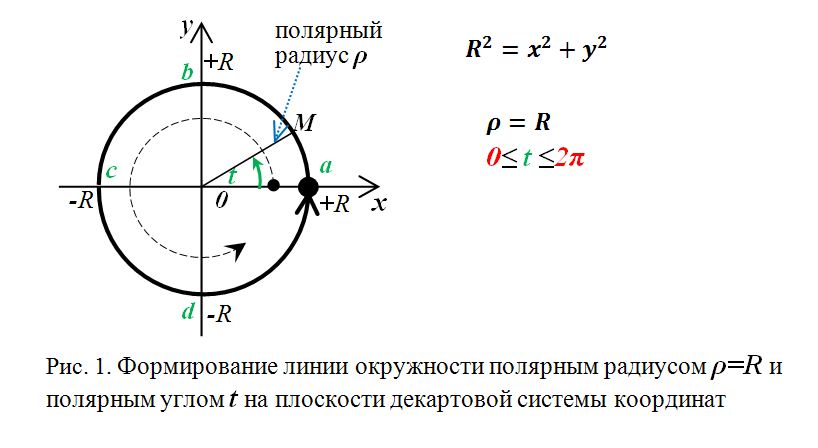 При задании свойств твердых материалов глобальные системные оси вместо этого фиксируются в материале. Другими словами, в этом контексте это система материального каркаса.
При задании свойств твердых материалов глобальные системные оси вместо этого фиксируются в материале. Другими словами, в этом контексте это система материального каркаса.
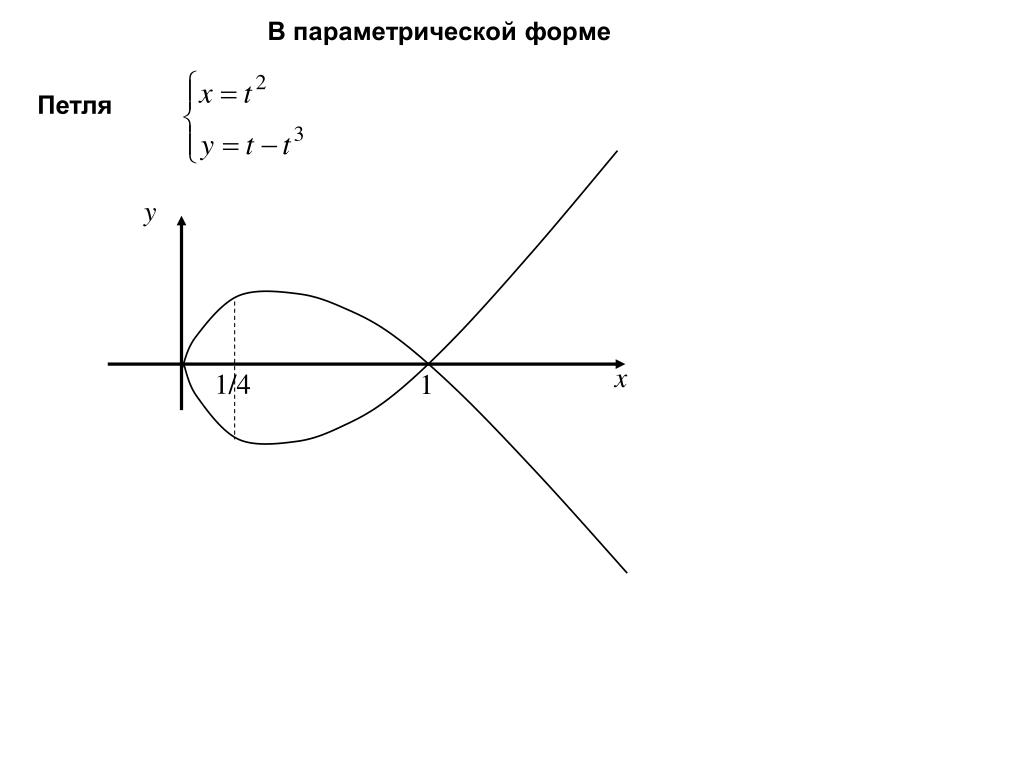
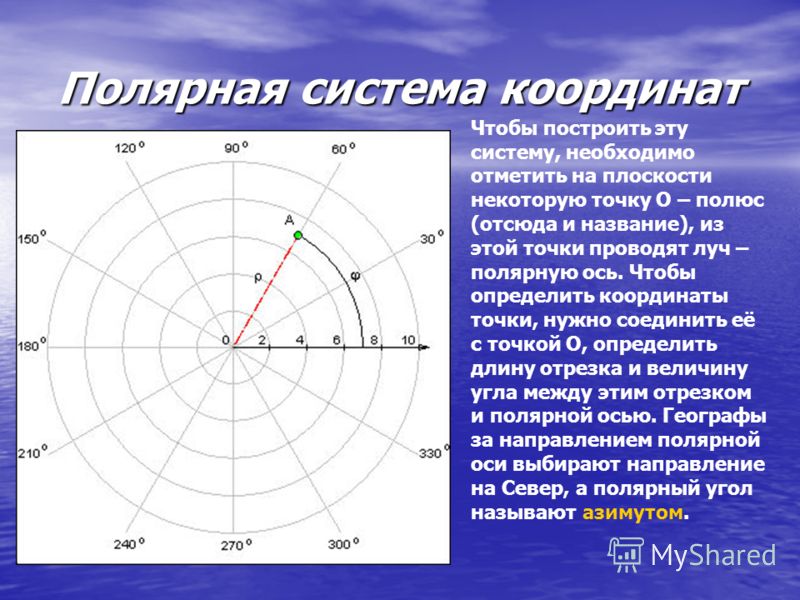 Задайте это, используя набор базовых векторов, чтобы сформировать систему координат.
Задайте это, используя набор базовых векторов, чтобы сформировать систему координат. Используйте комбинированную систему, когда вам нужно использовать разные системы координат в разных областях, например, для представления некоторого свойства материала. Вы можете добавить применимые системы координат в качестве подузлов, каждый с выбором геометрического объекта.
Используйте комбинированную систему, когда вам нужно использовать разные системы координат в разных областях, например, для представления некоторого свойства материала. Вы можете добавить применимые системы координат в качестве подузлов, каждый с выбором геометрического объекта.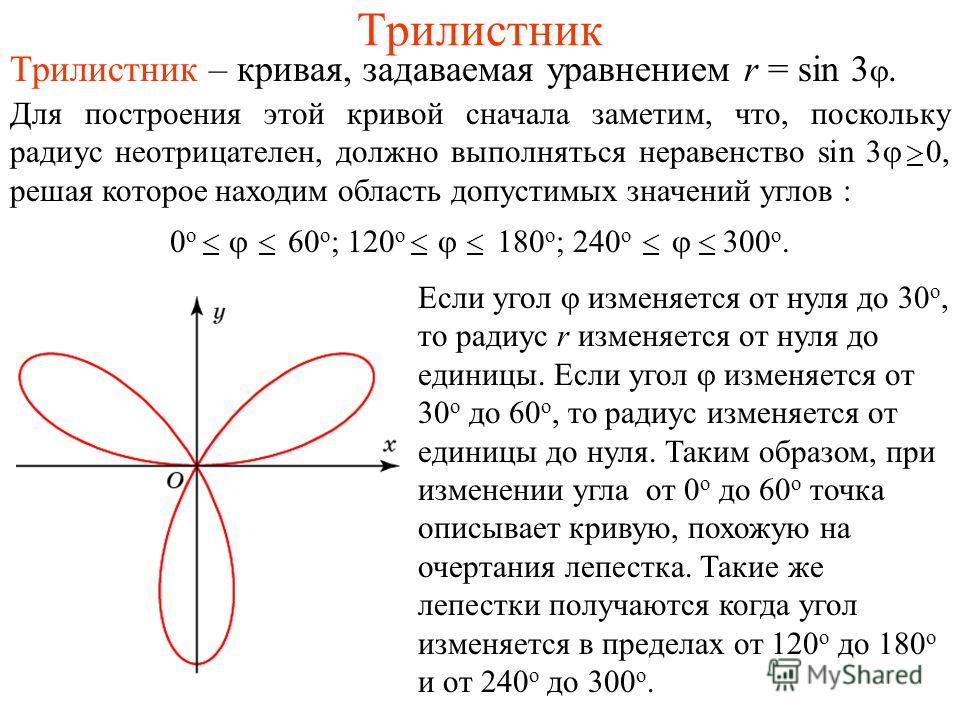 Недоступно в геометриях с двумерной осевой симметрией, где цилиндрическая система координат является системой координат по умолчанию.
Недоступно в геометриях с двумерной осевой симметрией, где цилиндрическая система координат является системой координат по умолчанию. Используйте эту систему координат, похожую на систему координат с картой, для произвольной деформации домена.
Используйте эту систему координат, похожую на систему координат с картой, для произвольной деформации домена.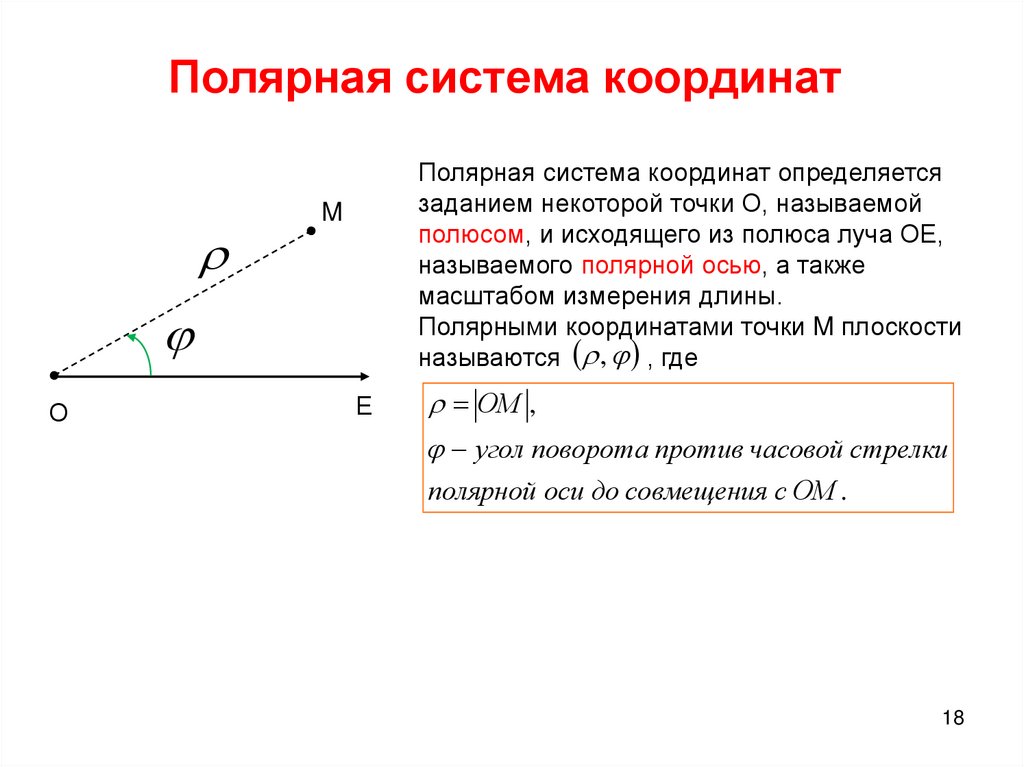 Он переключает положение пикселя по осям X и Y в полярной системе координат.
Он переключает положение пикселя по осям X и Y в полярной системе координат.
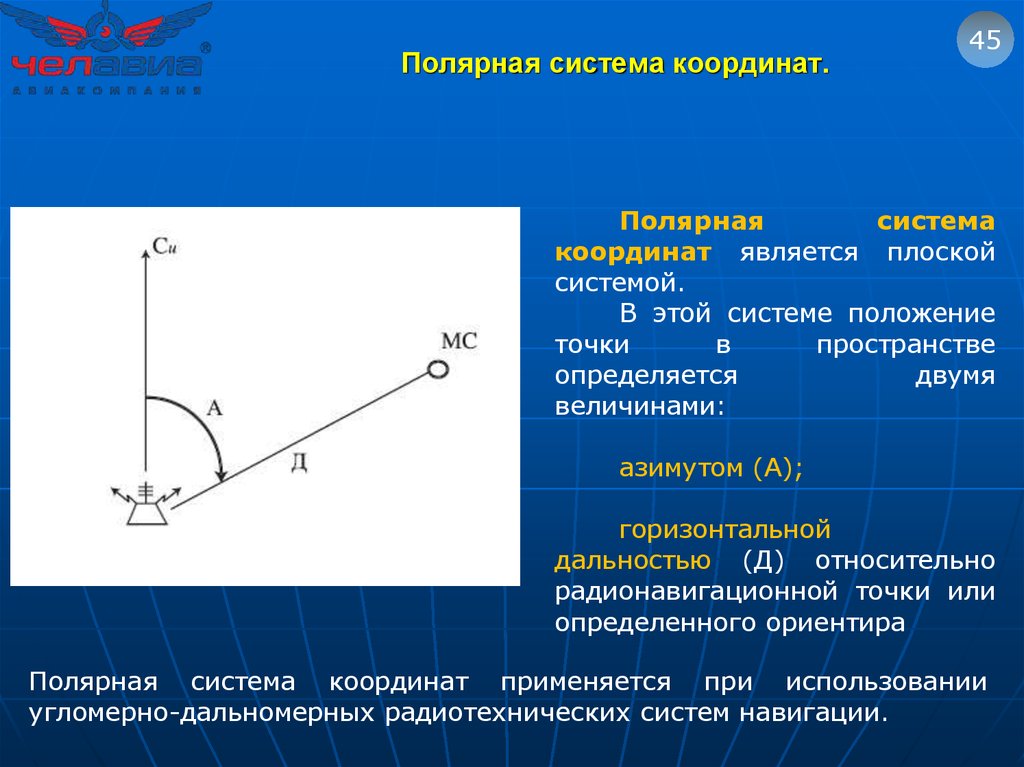 Верх вашего изображения становится центром круга, если вы измените настройку интерполяции на 100%.
Верх вашего изображения становится центром круга, если вы измените настройку интерполяции на 100%.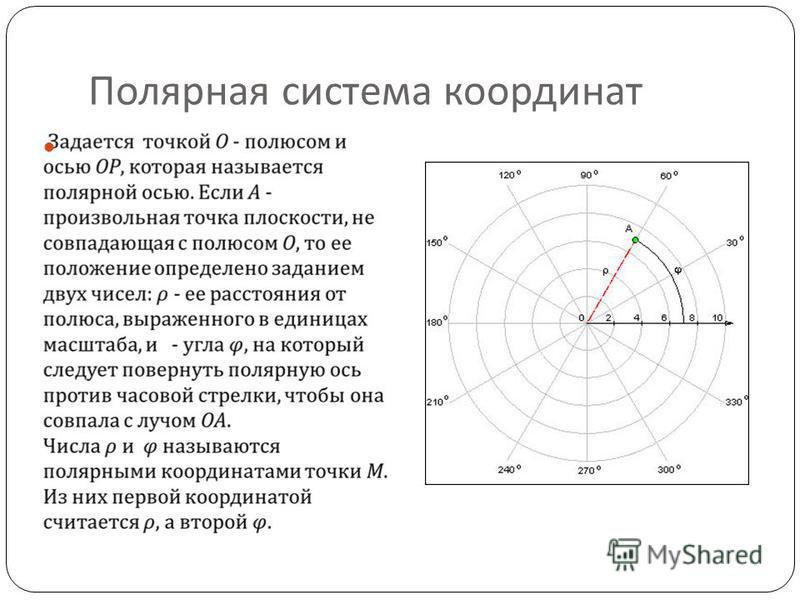
 Когда это применяется, изображение искажается, как если бы оно было снято широкоугольным объективом. Это также может помочь создать эффект туннеля, если вы используете настройку Rect to Polar. Если вы хотите, чтобы центр вашего круга полярных координат был пуст, вы можете создать слой Matte и замаскировать верхнюю часть изображения. Вы можете растушевать край, чтобы создать плавный переход.
Когда это применяется, изображение искажается, как если бы оно было снято широкоугольным объективом. Это также может помочь создать эффект туннеля, если вы используете настройку Rect to Polar. Если вы хотите, чтобы центр вашего круга полярных координат был пуст, вы можете создать слой Matte и замаскировать верхнюю часть изображения. Вы можете растушевать край, чтобы создать плавный переход.
 )
)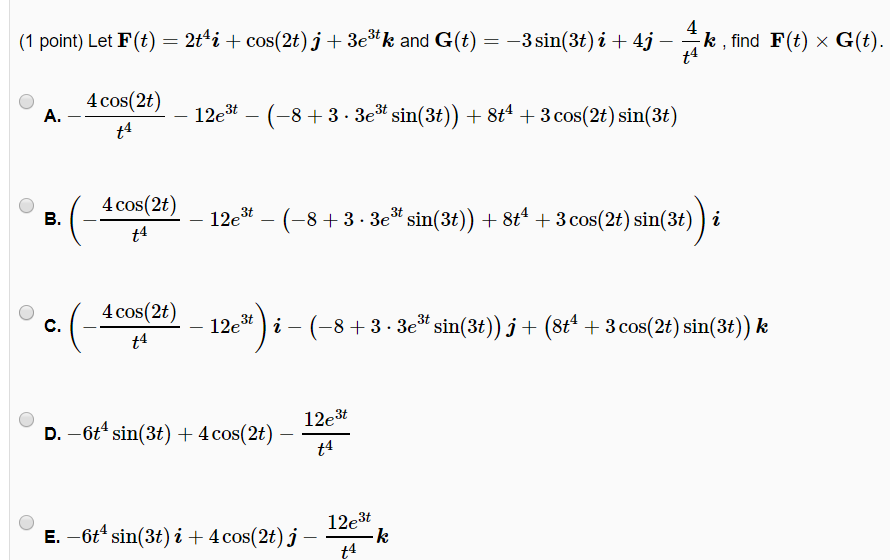 )
)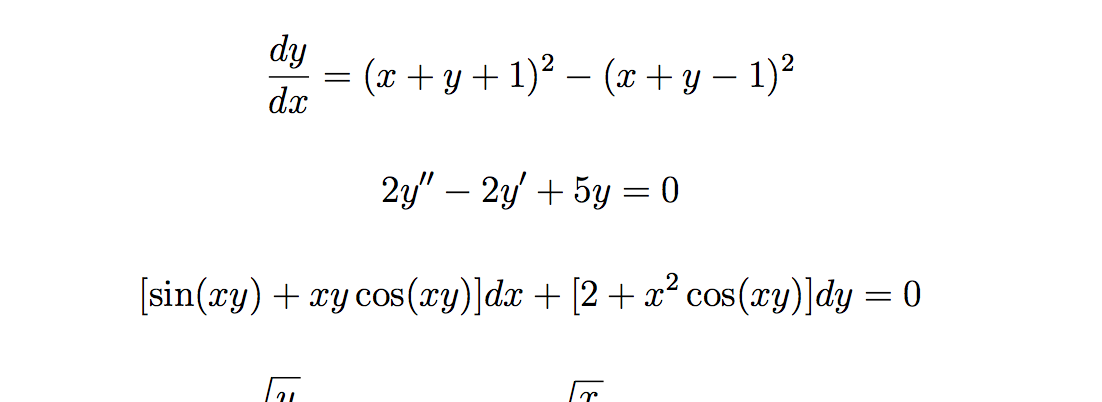 )
) )
)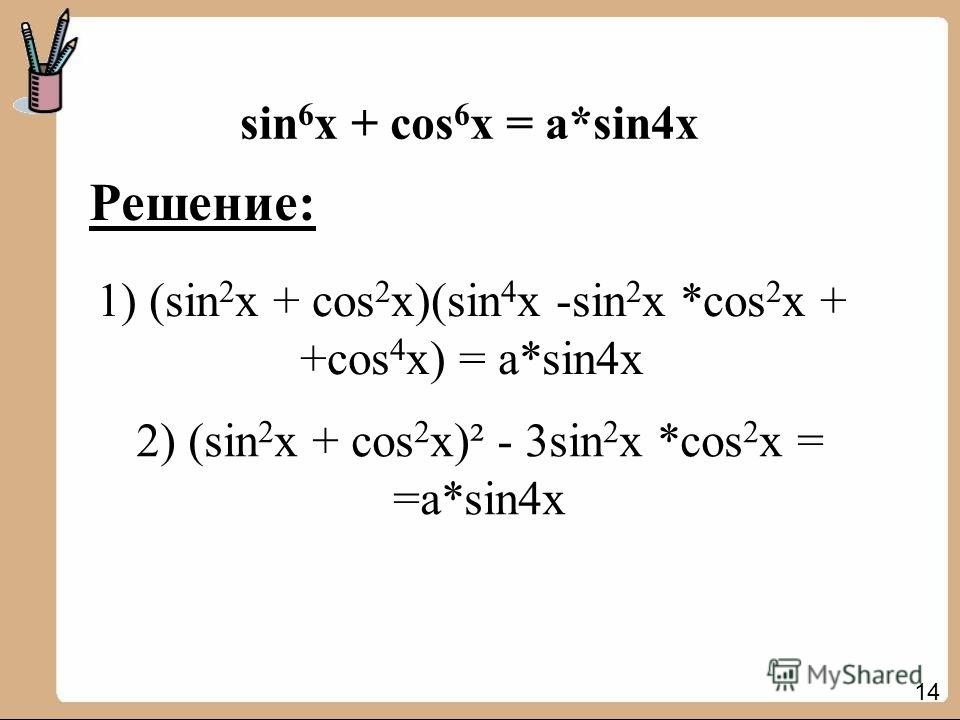 )
) )
) )
) )
)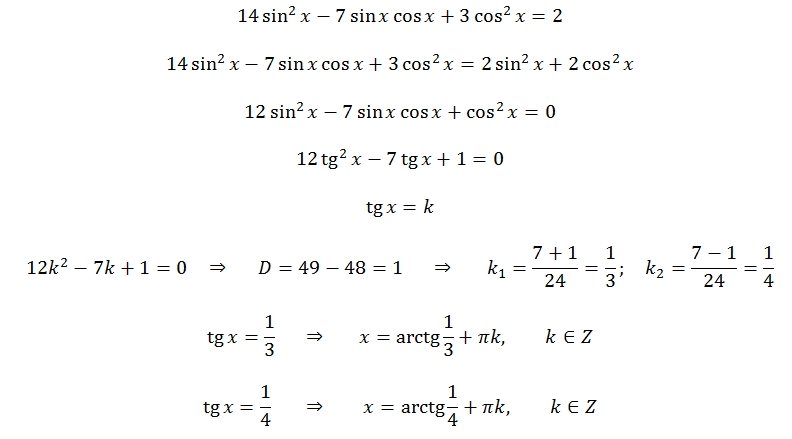 Углы с шагом в 1°. Таблица значений синусов.
Углы с шагом в 1°. Таблица значений синусов. 0175
0175 2079
2079 3907
3907 5592
5592 7071
7071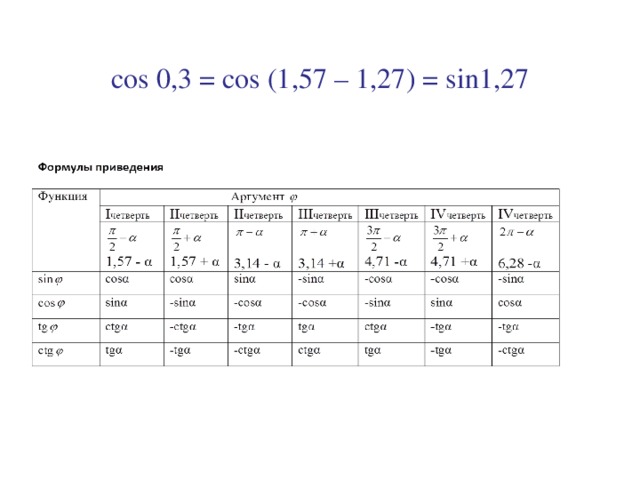 829
829 9205
9205 9781
9781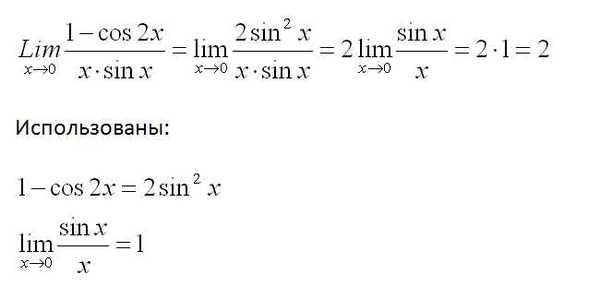 9998
9998 9925
9925 9511
9511 8746
8746 766
766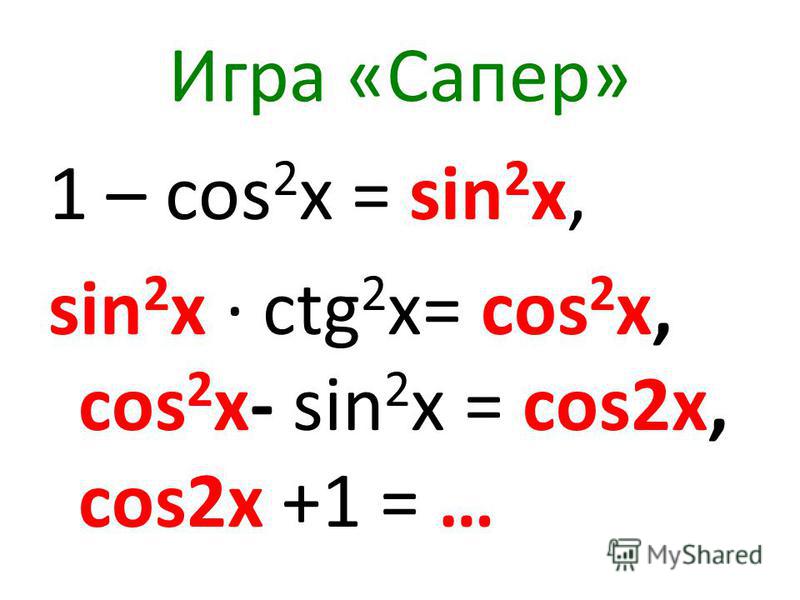 6293
6293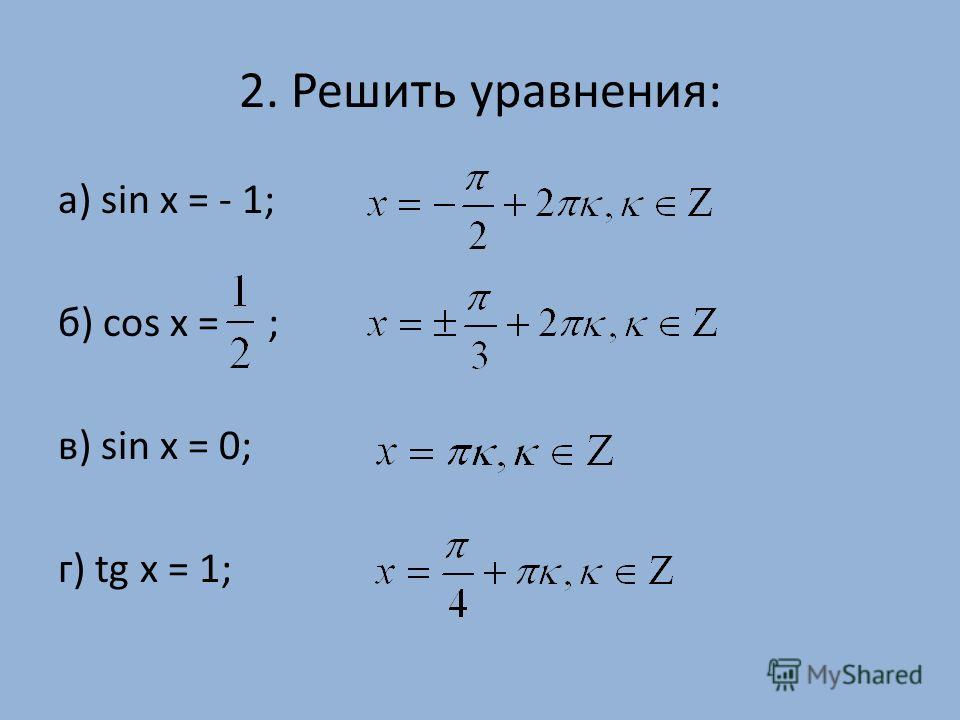 4695
4695 2924
2924 1045
1045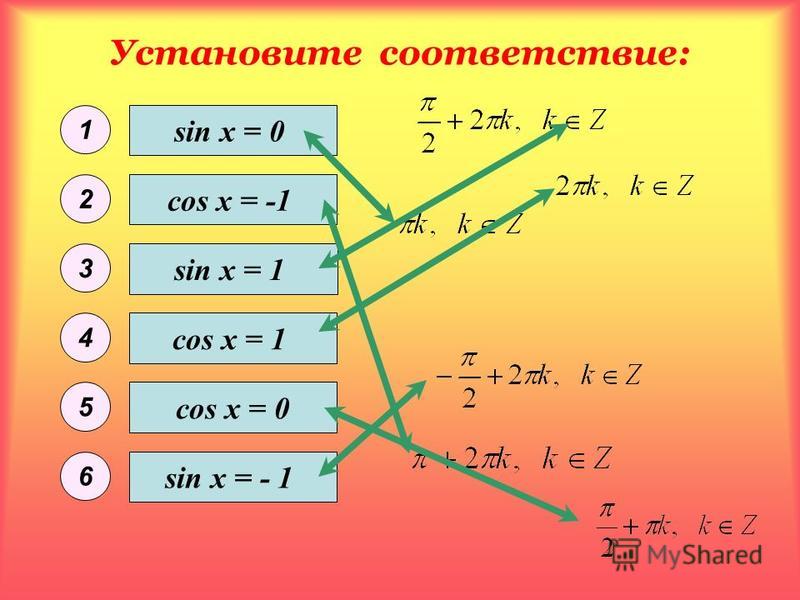 0349
0349 2079
2079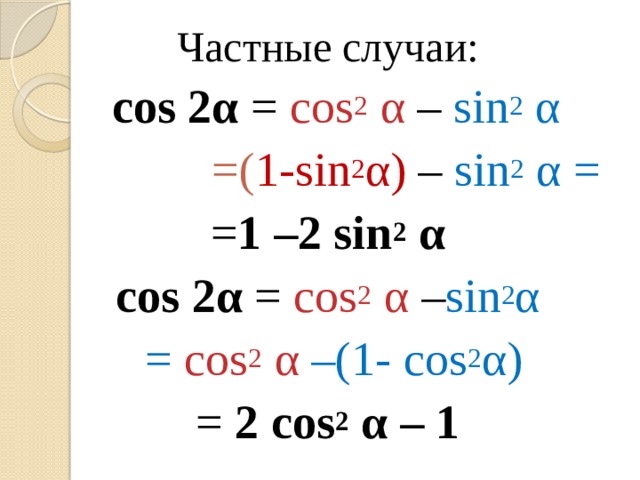 3746
3746 5299
5299 6691
6691 788
788 8829
8829 9511
9511 9903
9903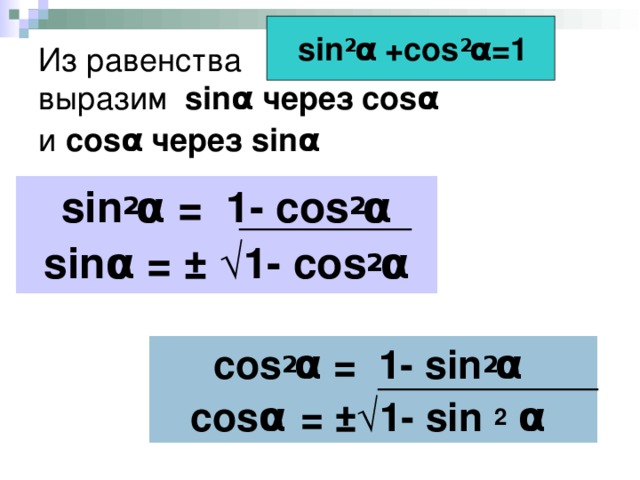 9998
9998 9816
9816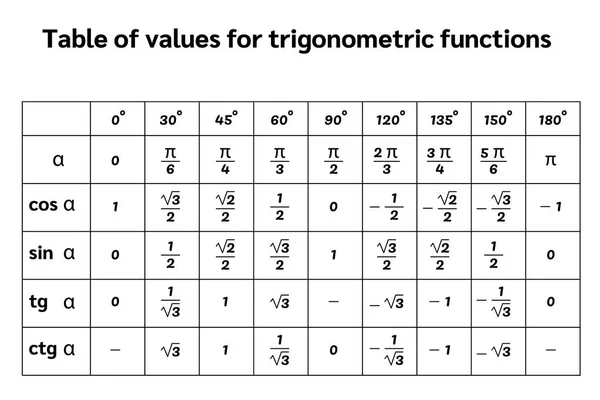 9336
9336 8572
8572 7547
7547 6293
6293 4848
4848 3256
3256 1564
1564 Синусы, косинусы, тангенсы и котангенсы. Таблица значений тригонометрических функций
Синусы, косинусы, тангенсы и котангенсы. Таблица значений тригонометрических функций 8. Однако применение walrus является предметом дискуссий и множество людей испытывают безосновательную неприязнь к нему.
8. Однако применение walrus является предметом дискуссий и множество людей испытывают безосновательную неприязнь к нему.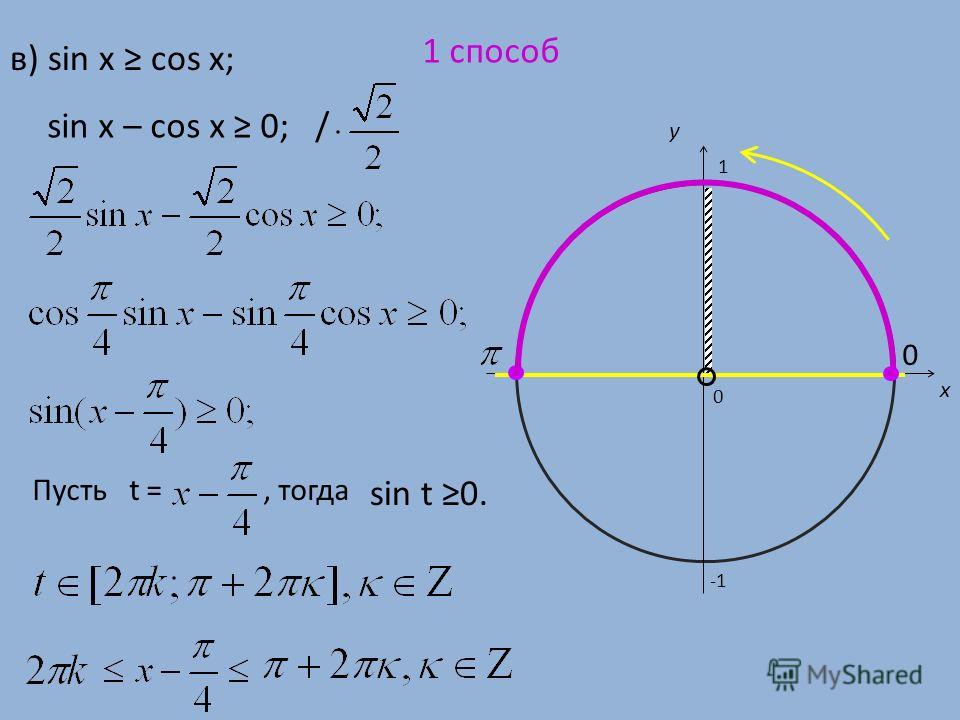 Когда мы перепишем выражение с использованием оператора walrus,
Когда мы перепишем выражение с использованием оператора walrus,  .*(not present).*»
m = re.match(pattern1, test)
if m:
print(f»Matched the 1st pattern: {m.group(1)}»)
else:
m = re.match(pattern2, test)
if m:
print(f»Matched the 2nd pattern: {m.group(1)}»)
# ———————
# Или иначе
if m := (re.match(pattern1, test)):
print(f»Matched 1st pattern: ‘{m.group(1)}'»)
elif m := (re.match(pattern2, test)):
print(f»Matched 2nd pattern: ‘{m.group(1)}'»)
.*(not present).*»
m = re.match(pattern1, test)
if m:
print(f»Matched the 1st pattern: {m.group(1)}»)
else:
m = re.match(pattern2, test)
if m:
print(f»Matched the 2nd pattern: {m.group(1)}»)
# ———————
# Или иначе
if m := (re.match(pattern1, test)):
print(f»Matched 1st pattern: ‘{m.group(1)}'»)
elif m := (re.match(pattern2, test)):
print(f»Matched 2nd pattern: ‘{m.group(1)}'») Вместо этого мы можем задействовать оператор walrus, чтобы заново присвоить значение исполненной команды и затем использовать его в условии остановки цикла на той же строке, делая код более явным и коротким.
Вместо этого мы можем задействовать оператор walrus, чтобы заново присвоить значение исполненной команды и затем использовать его в условии остановки цикла на той же строке, делая код более явным и коротким. В этом простом случае функция
В этом простом случае функция  2f}, {sin(theta) =: .2f}, {cos(theta) =: .2f}')
# angle=60° (theta := radians(angle)) = 1.05, sin(theta) = 0.87, cos(theta) = 0.50
2f}, {sin(theta) =: .2f}, {cos(theta) =: .2f}')
# angle=60° (theta := radians(angle)) = 1.05, sin(theta) = 0.87, cos(theta) = 0.50 А что, если вы захотите также значение, которое оставляет
А что, если вы захотите также значение, которое оставляет 
 .*(present).*»
for test in tests:
m = re.match(pattern1, test)
if m:
print(f»Matched the 1st pattern: {m.group(1)}»)
else:
m = re.match(pattern2, test)
if m:
print(f»Matched the 2nd pattern: {m.group(1)}»)
# Соответствие первому шаблону: thing
# Соответствие второму шаблону: present
for test in tests:
if m := (re.match(pattern1, test) or re.match(pattern2, test)):
print(f»Matched: ‘{m.group(1)}'»)
# Соответствие: ‘thing’
# Соответствие: ‘present’
.*(present).*»
for test in tests:
m = re.match(pattern1, test)
if m:
print(f»Matched the 1st pattern: {m.group(1)}»)
else:
m = re.match(pattern2, test)
if m:
print(f»Matched the 2nd pattern: {m.group(1)}»)
# Соответствие первому шаблону: thing
# Соответствие второму шаблону: present
for test in tests:
if m := (re.match(pattern1, test) or re.match(pattern2, test)):
print(f»Matched: ‘{m.group(1)}'»)
# Соответствие: ‘thing’
# Соответствие: ‘present’ # Она по-прежнему имеет привязку к значению "unmodified"
total = 0
partial_sums = [total := total + v for v in values]
print(total) # 50
# Она по-прежнему имеет привязку к значению "unmodified"
total = 0
partial_sums = [total := total + v for v in values]
print(total) # 50 ..")
with ContextManager() as context:
print(context) # None
with (context := ContextManager()):
print(context) # <__main__.ContextManager object at 0x7fb551cdb9d0>
..")
with ContextManager() as context:
print(context) # None
with (context := ContextManager()):
print(context) # <__main__.ContextManager object at 0x7fb551cdb9d0>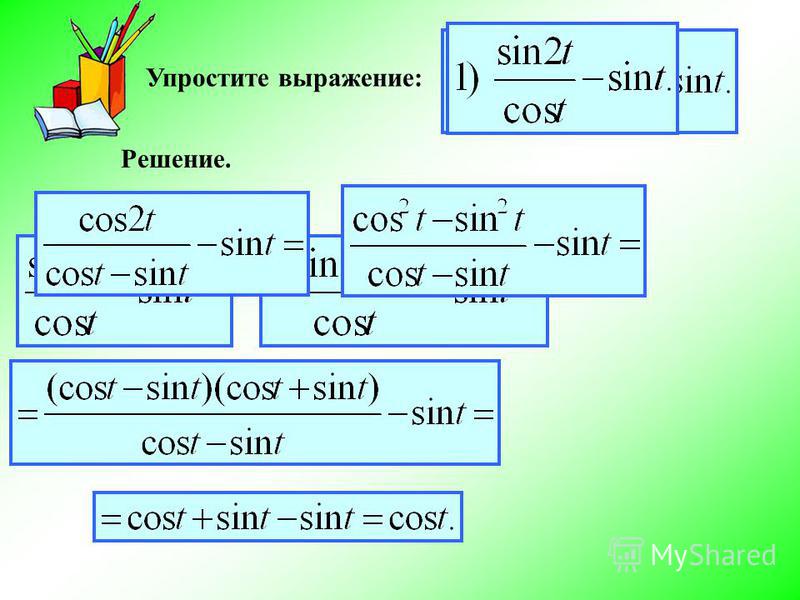 .*(thing).*", text)) and flag:
print(match.groups()) # ('thing',)
.*(thing).*", text)) and flag:
print(match.groups()) # ('thing',)

 Исчисление
Исчисление

 2$ стремятся к нулю, но предел равен $+\infty$. 92$ и $x$ стремятся к нулю, но предел равен $0$.
2$ стремятся к нулю, но предел равен $+\infty$. 92$ и $x$ стремятся к нулю, но предел равен $0$. 

 )/3
)/3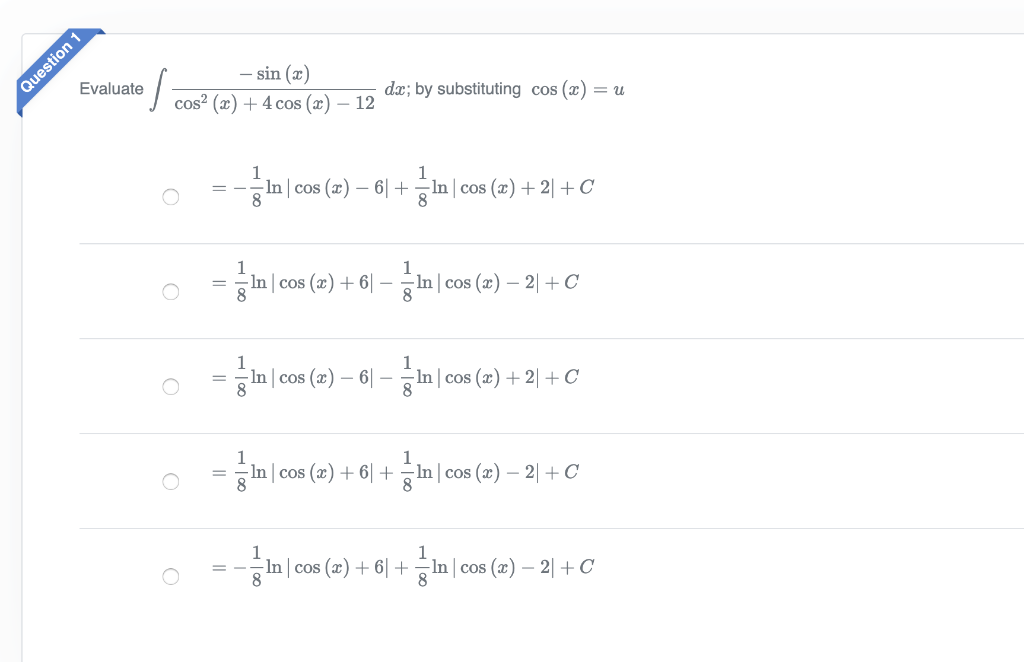 )/4
)/4 )/3
)/3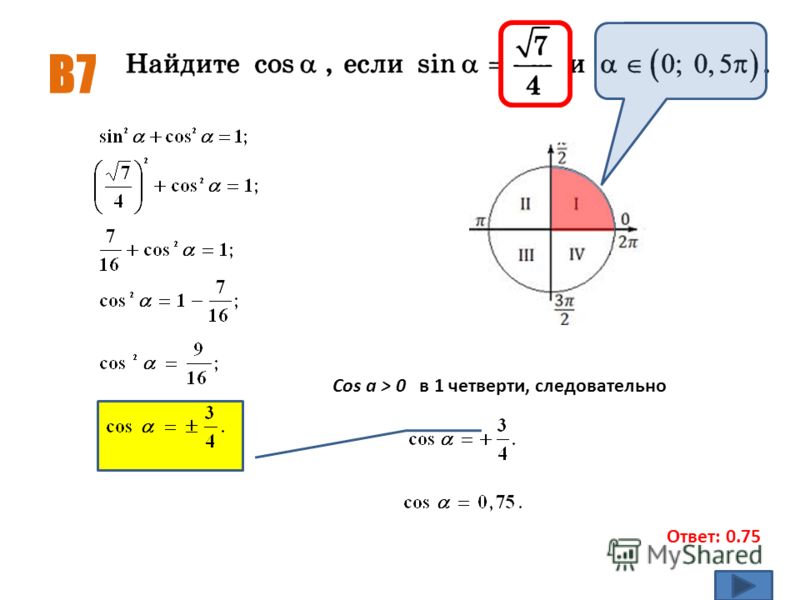 )/4
)/4 (Вы можете сообщить о проблеме с содержанием на этой странице здесь)
(Вы можете сообщить о проблеме с содержанием на этой странице здесь)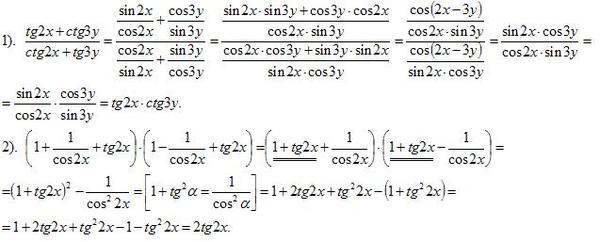
 #lab_color2 Вектор с тремя компонентами, соответствующими другому значению Lab.
#k_L Весовой коэффициент для компонента L.
#k_C Весовой коэффициент для компонента C.
#k_H Весовой коэффициент для компонента H.
#K1 Весовой коэффициент, зависящий от применения.
#K2 Весовой коэффициент, зависящий от применения.
#симметричный Если TRUE, используйте симметричную версию формулы
#lab_color2 Вектор с тремя компонентами, соответствующими другому значению Lab.
#k_L Весовой коэффициент для компонента L.
#k_C Весовой коэффициент для компонента C.
#k_H Весовой коэффициент для компонента H.
#K1 Весовой коэффициент, зависящий от применения.
#K2 Весовой коэффициент, зависящий от применения.
#симметричный Если TRUE, используйте симметричную версию формулы
 2 + термин4)
}
2 + термин4)
} 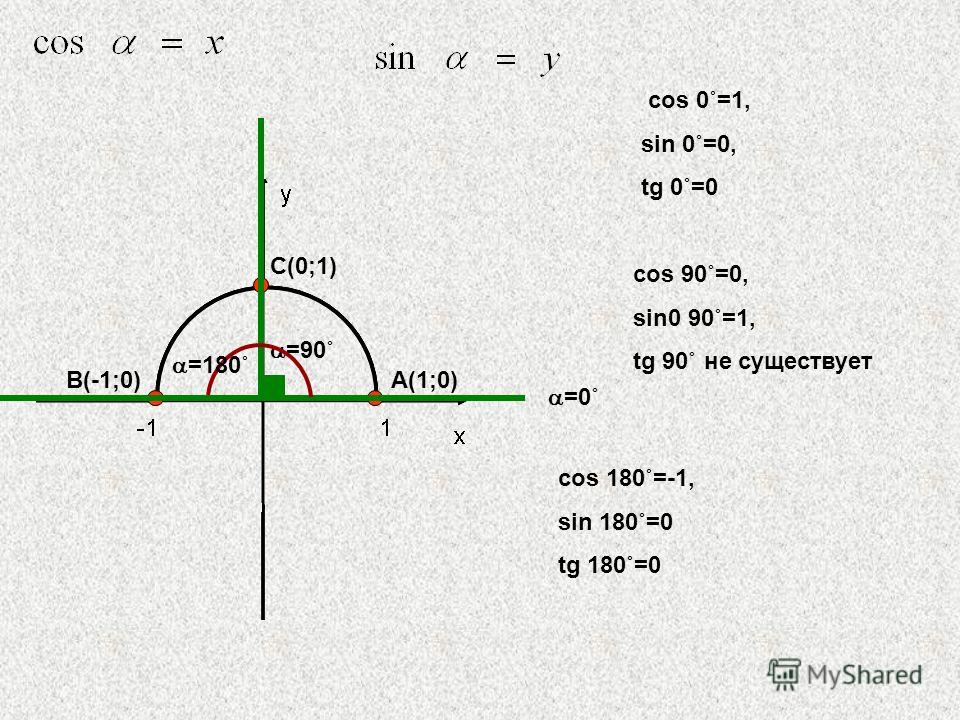 контох
контох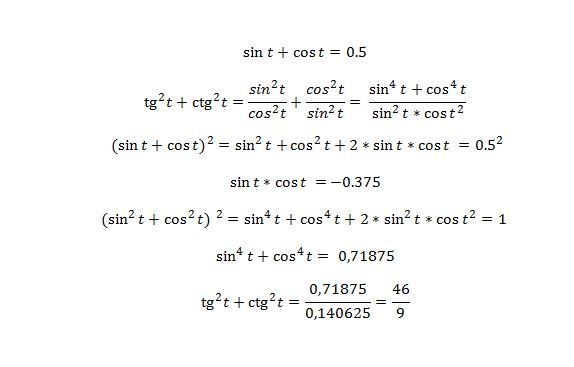 Нилай дари син х дан соз х. Rhanibayu rhanibayu 20.12.2015 математика sekolah menengah atas.
Нилай дари син х дан соз х. Rhanibayu rhanibayu 20.12.2015 математика sekolah menengah atas. Y = x2 + 16x + 18 Fungsi dinyatakan sebagai f dalam kurung x = ax + b jika f dalam kurung 5 = 25 dan f dalam kurung 4 = negatif 11 nilai dari f dalam kurung 2 dikurang f dalam kurung 5 adalah.
Y = x2 + 16x + 18 Fungsi dinyatakan sebagai f dalam kurung x = ax + b jika f dalam kurung 5 = 25 dan f dalam kurung 4 = negatif 11 nilai dari f dalam kurung 2 dikurang f dalam kurung 5 adalah.


 В нём дана функция не трёх, а лишь двух переменных, но несколько
иначе задан направляющий вектор. Так что придётся вновь повторить векторную алгебру.
В нём дана функция не трёх, а лишь двух переменных, но несколько
иначе задан направляющий вектор. Так что придётся вновь повторить векторную алгебру.

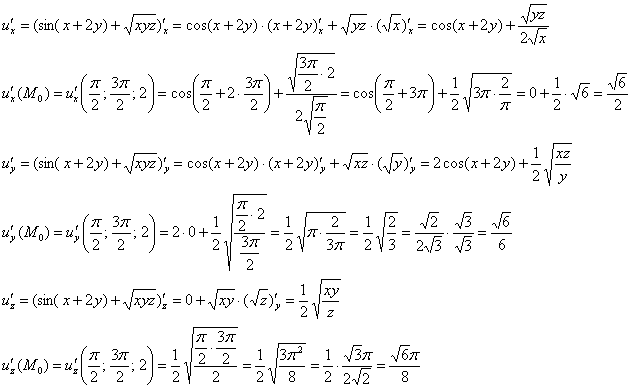
 Что будет, если активированными окажутся больше чем 1 нейрон? Все нейроны из функции активации выведут 1. В таком случае появляются вопросы о том, какой класс должен в итоге получиться для заданного объекта.
Что будет, если активированными окажутся больше чем 1 нейрон? Все нейроны из функции активации выведут 1. В таком случае появляются вопросы о том, какой класс должен в итоге получиться для заданного объекта.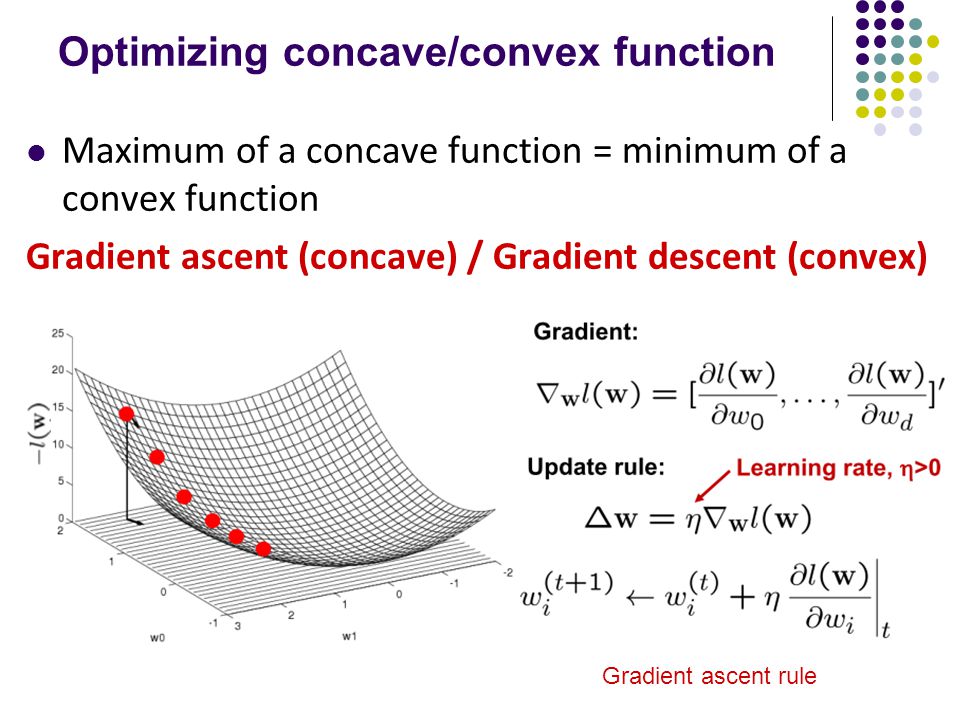
 Если производится ошибочное предсказание, то изменения, сделанные обратным распространением ошибки, тоже постоянны и не зависят от изменения на входе delta(x).
Если производится ошибочное предсказание, то изменения, сделанные обратным распространением ошибки, тоже постоянны и не зависят от изменения на входе delta(x).
 Такое поведение позволяет находить четкие границы при предсказании.
Такое поведение позволяет находить четкие границы при предсказании. Нейросеть отказывается обучаться дальше или делает это крайне медленно (в зависимости от способа использования или до тех пор, пока градиент/вычисление не начнет страдать от ограничений на значение с плавающей точкой). Существуют варианты работы над этими проблемами, а сигмоида всё ещё очень популярна для задач классификации.
Нейросеть отказывается обучаться дальше или делает это крайне медленно (в зависимости от способа использования или до тех пор, пока градиент/вычисление не начнет страдать от ограничений на значение с плавающей точкой). Существуют варианты работы над этими проблемами, а сигмоида всё ещё очень популярна для задач классификации.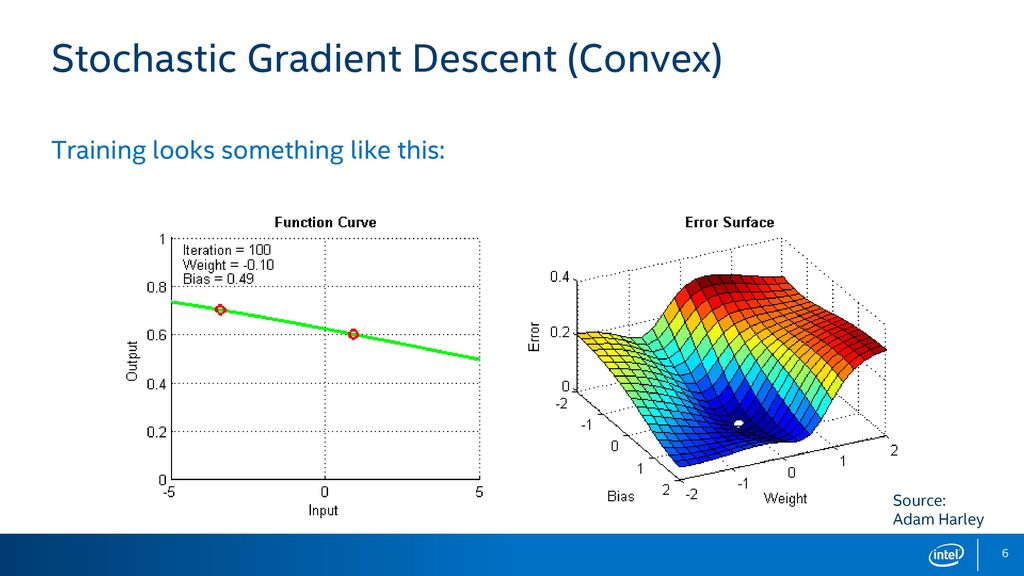 Также как и сигмоиде, гиперболическому тангенсу свойственная проблема исчезновения градиента.
Также как и сигмоиде, гиперболическому тангенсу свойственная проблема исчезновения градиента. Представим большую нейронную сеть с множеством нейронов. Использование сигмоиды или гиперболического тангенса будет влечь за собой активацию всех нейронов аналоговым способом. Это означает, что почти все активации должны быть обработаны для описания выхода сети. Другими словами, активация плотная, а это затратно. В идеале мы хотим, чтобы некоторые нейроны не были активированы, это сделало бы активации разреженными и эффективными.
Представим большую нейронную сеть с множеством нейронов. Использование сигмоиды или гиперболического тангенса будет влечь за собой активацию всех нейронов аналоговым способом. Это означает, что почти все активации должны быть обработаны для описания выхода сети. Другими словами, активация плотная, а это затратно. В идеале мы хотим, чтобы некоторые нейроны не были активированы, это сделало бы активации разреженными и эффективными. Из-за равенства нулю градиента, веса не будут корректироваться во время спуска. Это означает, что пребывающие в таком состоянии нейроны не будут реагировать на изменения в ошибке/входных данных (просто потому, что градиент равен нулю, ничего не будет меняться). Такое явление называется проблемой умирающего ReLu (Dying ReLu problem). Из-за этой проблемы некоторые нейроны просто выключатся и не будут отвечать, делая значительную часть нейросети пассивной. Однако существуют вариации ReLu, которые помогают эту проблему избежать. Например, имеет смысл заменить горизонтальную часть функции на линейную. Если выражение для линейной функции задается выражением y = 0.01x для области x < 0, линия слегка отклоняется от горизонтального положения. Существует и другие способы избежать нулевого градиента. Основная идея здесь — сделать градиент неравным нулю и постепенно восстанавливать его во время тренировки.
Из-за равенства нулю градиента, веса не будут корректироваться во время спуска. Это означает, что пребывающие в таком состоянии нейроны не будут реагировать на изменения в ошибке/входных данных (просто потому, что градиент равен нулю, ничего не будет меняться). Такое явление называется проблемой умирающего ReLu (Dying ReLu problem). Из-за этой проблемы некоторые нейроны просто выключатся и не будут отвечать, делая значительную часть нейросети пассивной. Однако существуют вариации ReLu, которые помогают эту проблему избежать. Например, имеет смысл заменить горизонтальную часть функции на линейную. Если выражение для линейной функции задается выражением y = 0.01x для области x < 0, линия слегка отклоняется от горизонтального положения. Существует и другие способы избежать нулевого градиента. Основная идея здесь — сделать градиент неравным нулю и постепенно восстанавливать его во время тренировки. Поэтому имеет смысл использовать ReLu при создании глубоких нейронных сетей.
Поэтому имеет смысл использовать ReLu при создании глубоких нейронных сетей. В большинстве случаев ReLu работает как хороший аппроксиматор.
В большинстве случаев ReLu работает как хороший аппроксиматор. )
) Алгоритмы в основе циферблата обеспечивают миллионы возможных комбинаций.
Алгоритмы в основе циферблата обеспечивают миллионы возможных комбинаций.

 Прямо с этого циферблата можно запустить секундомер.
Прямо с этого циферблата можно запустить секундомер.
 Шрифт для этого циферблата разработан таким образом, чтобы цифры умещались на гранях дисплея и плавно перетекали от часа к часу.
Шрифт для этого циферблата разработан таким образом, чтобы цифры умещались на гранях дисплея и плавно перетекали от часа к часу.
 Чтобы вернуться к циферблату в стандартном состоянии, коснитесь красной кнопки истекшего времени.
Чтобы вернуться к циферблату в стандартном состоянии, коснитесь красной кнопки истекшего времени.



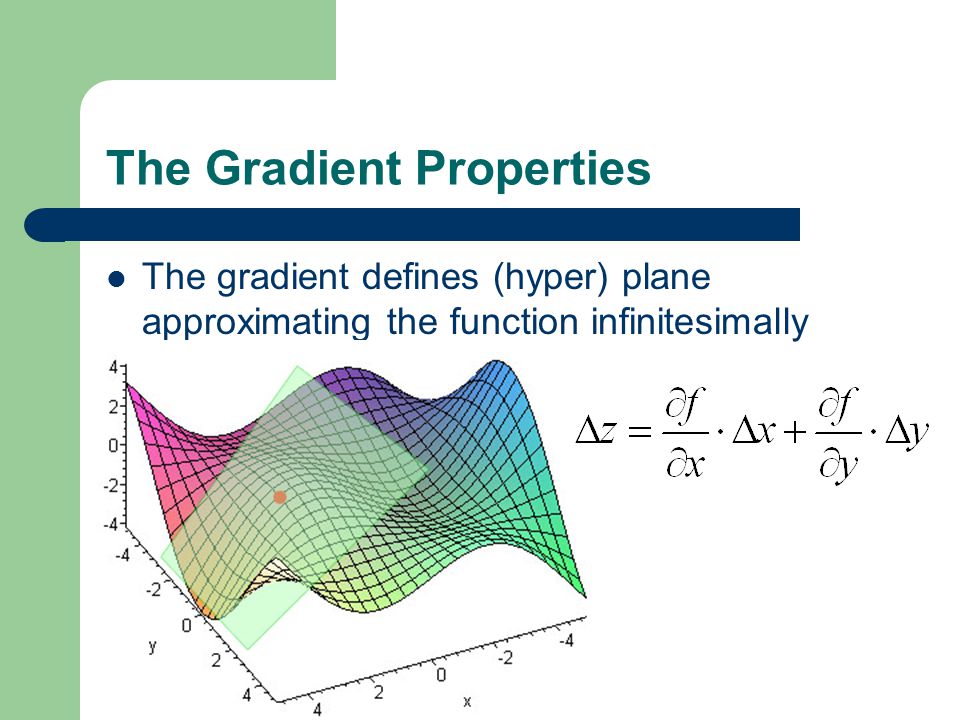 Цифры с настраиваемым дизайном динамически меняют свой стиль и форму с каждым поворотом колесика Digital Crown. Если опустить запястье, цифры, развернувшись, превращаются в черточки.
Цифры с настраиваемым дизайном динамически меняют свой стиль и форму с каждым поворотом колесика Digital Crown. Если опустить запястье, цифры, развернувшись, превращаются в черточки.

 Два из них — прямоугольные элементы, крупный размер которых позволяет показывать важную для Вас информацию более подробно.
Два из них — прямоугольные элементы, крупный размер которых позволяет показывать важную для Вас информацию более подробно. Цифры реагируют на каждый шаг, прыжок или движение запястья. Вы также можете коснуться дисплея или повернуть колесико Digital Crown, чтобы привести объекты в движение.
Цифры реагируют на каждый шаг, прыжок или движение запястья. Вы также можете коснуться дисплея или повернуть колесико Digital Crown, чтобы привести объекты в движение. Центральное место на нем занимают отображение времени и постоянное расширение для запуска приложения Nike Run Club.
Центральное место на нем занимают отображение времени и постоянное расширение для запуска приложения Nike Run Club. Для циферблата доступны персональная настройка и возможность добавить до пяти расширений.
Для циферблата доступны персональная настройка и возможность добавить до пяти расширений. Вы можете выбирать любые из 7 различных шрифтов и многочисленных цветов, чтобы создать идеальное сочетание.
Вы можете выбирать любые из 7 различных шрифтов и многочисленных цветов, чтобы создать идеальное сочетание.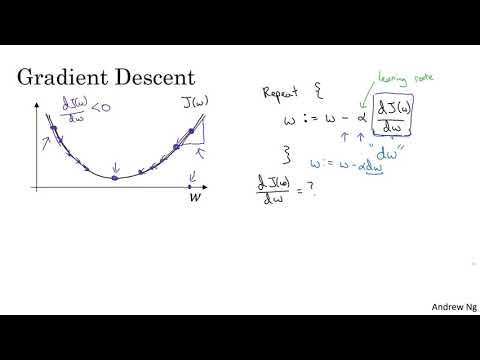
 Когда отображается текущий циферблат, коснитесь и удерживайте дисплей, смахните вправо до конца, коснитесь кнопки «Новый» (+), затем коснитесь «Фото». Или при просмотре фотографий в приложении «Фото» на Apple Watch коснитесь , прокрутите к нижней части экрана, затем коснитесь «Создать циферблат».
Когда отображается текущий циферблат, коснитесь и удерживайте дисплей, смахните вправо до конца, коснитесь кнопки «Новый» (+), затем коснитесь «Фото». Или при просмотре фотографий в приложении «Фото» на Apple Watch коснитесь , прокрутите к нижней части экрана, затем коснитесь «Создать циферблат». Коснитесь , чтобы выбрать из более широкого списка цветов.
Коснитесь , чтобы выбрать из более широкого списка цветов.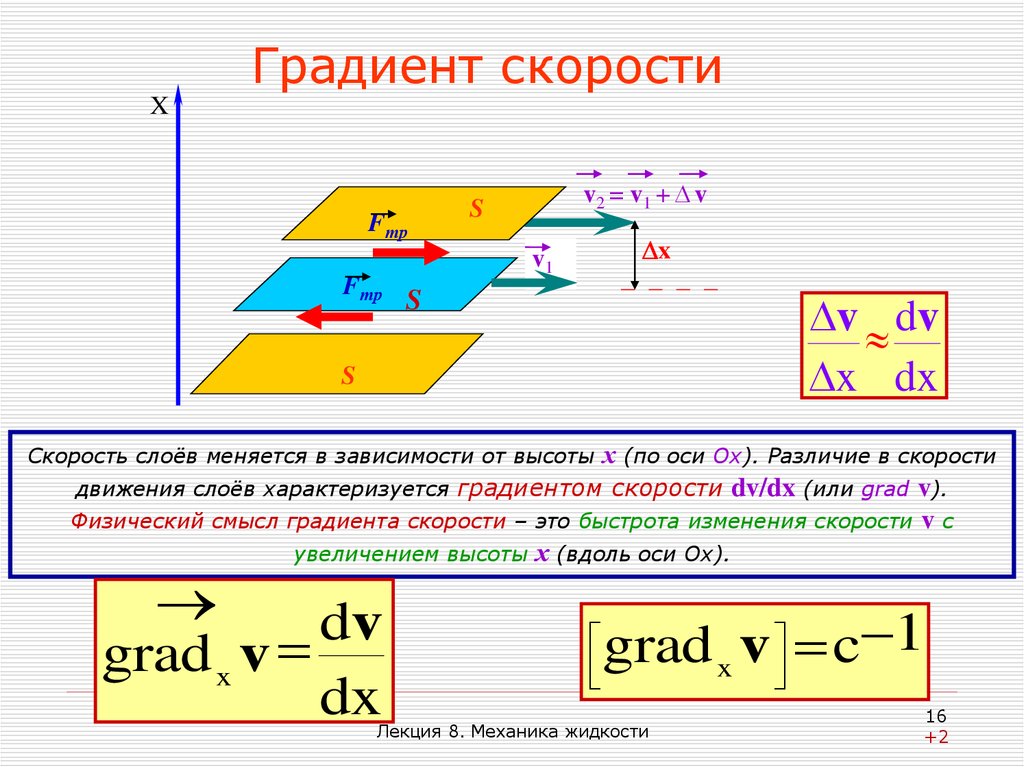 Прокрутите колесико Digital Crown, чтобы увеличить фотографию.
Прокрутите колесико Digital Crown, чтобы увеличить фотографию. Это могут быть ближайшие встречи, пробки по дороге домой или время заката солнца. Можно коснуться экрана и посмотреть подробную информацию. Можно также прокрутить колесико Digital Crown, чтобы пролистать события дня.
Это могут быть ближайшие встречи, пробки по дороге домой или время заката солнца. Можно коснуться экрана и посмотреть подробную информацию. Можно также прокрутить колесико Digital Crown, чтобы пролистать события дня.




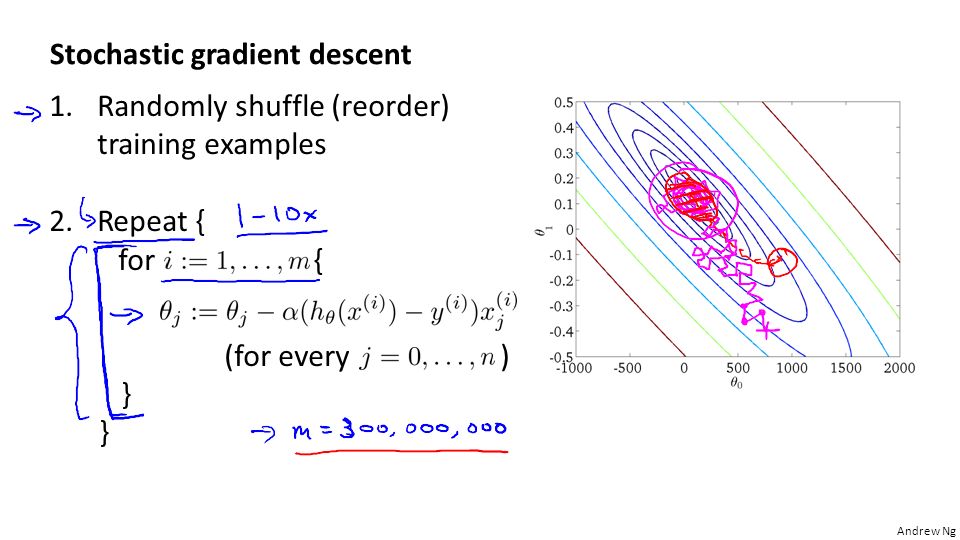 На внешней шкале показаны локации в разных часовых поясах, а на внутренней шкале — текущее время для каждой локации. Коснитесь глобуса, чтобы отобразить в центре текущий часовой пояс, который также обозначен стрелкой, указывающей на 6 часов.
На внешней шкале показаны локации в разных часовых поясах, а на внутренней шкале — текущее время для каждой локации. Коснитесь глобуса, чтобы отобразить в центре текущий часовой пояс, который также обозначен стрелкой, указывающей на 6 часов. Когда Вы добавляете расширение, оно заполняет весь экран.
Когда Вы добавляете расширение, оно заполняет весь экран.

 Здесь мы покажем, как быстро проверить, а если и нужно то и доказать, что поле является потенциальным и соленоидальным. Условия за которых это выполняется детально расписанны в объяснениях к вычислениям.
Здесь мы покажем, как быстро проверить, а если и нужно то и доказать, что поле является потенциальным и соленоидальным. Условия за которых это выполняется детально расписанны в объяснениях к вычислениям.  Если полетпотенциальное, то найти его потенциал.
Если полетпотенциальное, то найти его потенциал. 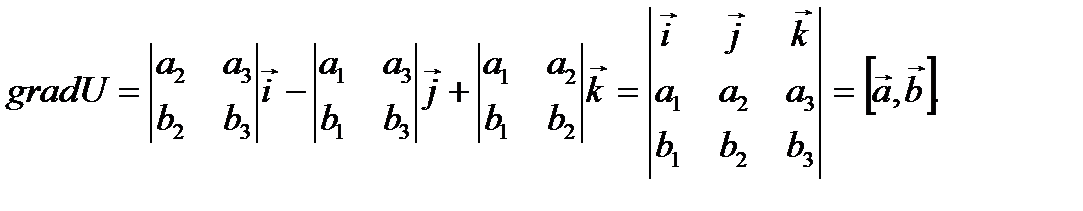



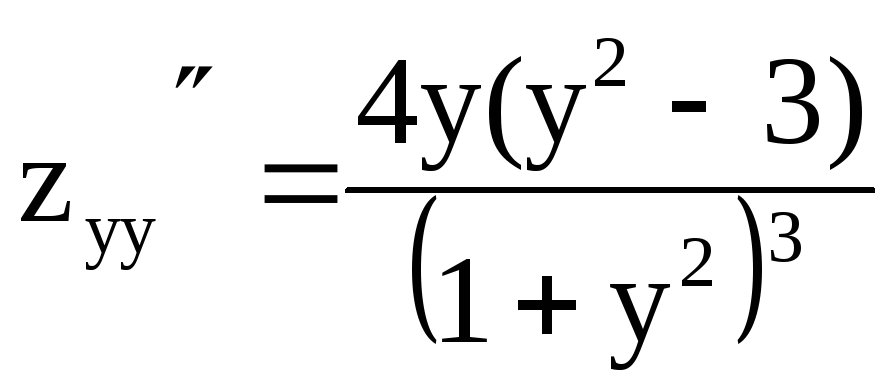
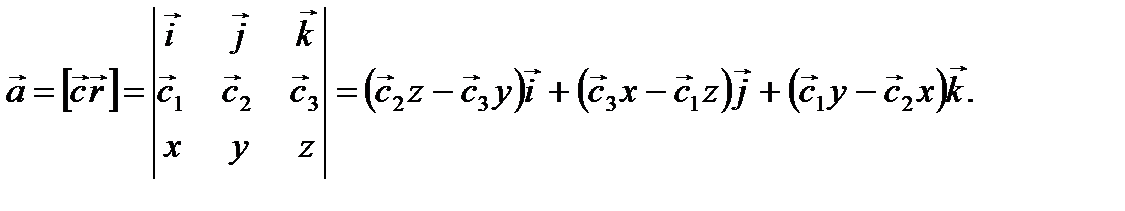


 В конце поста я дам ответ на вопрос одного из читателей блога, связанный с этой темой.
В конце поста я дам ответ на вопрос одного из читателей блога, связанный с этой темой. (3z)}
(3z)} Именно он стал главной причиной этого поста.
Именно он стал главной причиной этого поста. Когда линия наклонена слева направо, ее градиент отрицательный. Вертикальная линия должна иметь неопределенный уклон. Символ m используется для обозначения градиента. В алгебре дифференцирование можно использовать для нахождения градиента линии или функции.
Когда линия наклонена слева направо, ее градиент отрицательный. Вертикальная линия должна иметь неопределенный уклон. Символ m используется для обозначения градиента. В алгебре дифференцирование можно использовать для нахождения градиента линии или функции.
 Подъем — это подъем/спуск второй точки относительно первой точки, а бег — расстояние между ними (по горизонтали). 93) | (x, y) = (1, 3) = (2, 27)$$
Подъем — это подъем/спуск второй точки относительно первой точки, а бег — расстояние между ними (по горизонтали). 93) | (x, y) = (1, 3) = (2, 27)$$ Он получается применением векторного оператора V к скалярной функции f(x, y). Это векторное поле называется градиентным (или консервативным) векторным полем.
Он получается применением векторного оператора V к скалярной функции f(x, y). Это векторное поле называется градиентным (или консервативным) векторным полем. е. F имеет соответствующий потенциал ϕ. Это означает, что кривизна векторного поля, представленная ∇×, исчезает.
е. F имеет соответствующий потенциал ϕ. Это означает, что кривизна векторного поля, представленная ∇×, исчезает.

 Не забудьте считать расстояние между вами двумя по горизонтали, а не параллельно склону . И вот оно! Отношение
Не забудьте считать расстояние между вами двумя по горизонтали, а не параллельно склону . И вот оно! Отношение  И , если вы находитесь на ровной поверхности , это не помогает и не усложняет, поэтому оно нейтрально или имеет нулевой градиент.
И , если вы находитесь на ровной поверхности , это не помогает и не усложняет, поэтому оно нейтрально или имеет нулевой градиент.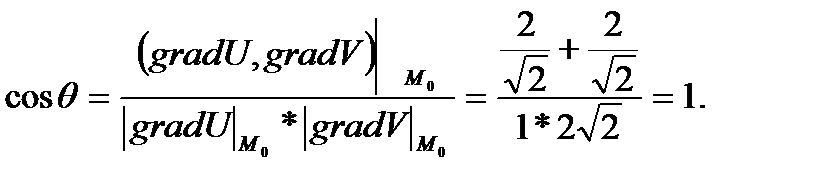 Подъем — насколько выше/ниже вторая точка от первой, а пробег — насколько далеко (по горизонтали) они друг от друга.
Подъем — насколько выше/ниже вторая точка от первой, а пробег — насколько далеко (по горизонтали) они друг от друга. Не происходит ли чего-то подобного при подсчете наклона или подъема над пробегом? » Ты абсолютно прав. Все эти три понятия: градиент, уклон и подъем над пробегом описывают одно и то же , и не волнуйтесь, между ними нет никакой разницы.
Не происходит ли чего-то подобного при подсчете наклона или подъема над пробегом? » Ты абсолютно прав. Все эти три понятия: градиент, уклон и подъем над пробегом описывают одно и то же , и не волнуйтесь, между ними нет никакой разницы. используется для вычисления производной по направлению функции с точки зрения двух переменных x и y в заданной точке.
используется для вычисления производной по направлению функции с точки зрения двух переменных x и y в заданной точке.

 Координата Y по умолчанию равна 2.
Координата Y по умолчанию равна 2.
 Это показано в окне интерпретации ввода выходных данных калькулятора. 9где {1}{4} \]
Это показано в окне интерпретации ввода выходных данных калькулятора. 9где {1}{4} \]
 Этот бесплатный векторный калькулятор градиента также покажет вам, как шаг за шагом вычислять определенные точки. Давайте рассмотрим формулы и примеры, чтобы узнать, как найти производные по направлению.
Этот бесплатный векторный калькулятор градиента также покажет вам, как шаг за шагом вычислять определенные точки. Давайте рассмотрим формулы и примеры, чтобы узнать, как найти производные по направлению. Любое из следующего может быть использовано в калькуляторе производной по направлению, чтобы найти функцию f для p:
Любое из следующего может быть использовано в калькуляторе производной по направлению, чтобы найти функцию f для p:


 Функция падает в этом направлении или растет в противоположном направлении, если производная по направлению отрицательна.
Функция падает в этом направлении или растет в противоположном направлении, если производная по направлению отрицательна. Мы обнаружили, что наша функция стоимости:
Мы обнаружили, что наша функция стоимости:

 Помните, что производная функции по переменной, не входящей в эту функцию, равна нулю, поэтому:
Помните, что производная функции по переменной, не входящей в эту функцию, равна нулю, поэтому: Мы определим наши промежуточные переменные как:
Мы определим наши промежуточные переменные как: Чтобы найти часть C(v), мы перемножаем две производные вместе:
Чтобы найти часть C(v), мы перемножаем две производные вместе: Если мы назовем этот член ошибки ei, наша окончательная производная будет:
Если мы назовем этот член ошибки ei, наша окончательная производная будет: Чем больше скорость обучения, тем больше шаг. Однако установка слишком большой скорости обучения может привести к слишком большому шагу и отклонению от локального минимума. Дополнительные сведения см. в этой статье о градиентном спуске и в этой статье о настройке скорости обучения.
Чем больше скорость обучения, тем больше шаг. Однако установка слишком большой скорости обучения может привести к слишком большому шагу и отклонению от локального минимума. Дополнительные сведения см. в этой статье о градиентном спуске и в этой статье о настройке скорости обучения.

 2x +g(y)\right)\\
&= \sin x + 2yx + \diff{g}{y}(y).
\конец{выравнивание*}
Сравнивая это с условием \eqref{cond2}, нам повезло. Мы можем
легко заставить эту $f(x,y)$ удовлетворять условию \eqref{cond2}, пока
в качестве
\начать{выравнивать*}
\diff{g}{y}(y)=-2y.
\конец{выравнивание*}
Если бы векторное поле $\dlvf$ зависело от пути, мы бы имели
обнаружил невозможность одновременного выполнения условия \eqref{cond1} и условия \eqref{cond2}. Мы бы столкнулись с проблемой в этом
точку, так как мы обнаружили бы, что $\diff{g}{y}$ должна быть функцией
$x$, а также $y$. Поскольку $\diff{g}{y}$ является функцией только $y$,
наш расчет подтверждает, что $\dlvf$ является консервативным. 92, \sin x + 2xy -2y) = \dlvf(x,y).
\конец{выравнивание*}
2x +g(y)\right)\\
&= \sin x + 2yx + \diff{g}{y}(y).
\конец{выравнивание*}
Сравнивая это с условием \eqref{cond2}, нам повезло. Мы можем
легко заставить эту $f(x,y)$ удовлетворять условию \eqref{cond2}, пока
в качестве
\начать{выравнивать*}
\diff{g}{y}(y)=-2y.
\конец{выравнивание*}
Если бы векторное поле $\dlvf$ зависело от пути, мы бы имели
обнаружил невозможность одновременного выполнения условия \eqref{cond1} и условия \eqref{cond2}. Мы бы столкнулись с проблемой в этом
точку, так как мы обнаружили бы, что $\diff{g}{y}$ должна быть функцией
$x$, а также $y$. Поскольку $\diff{g}{y}$ является функцией только $y$,
наш расчет подтверждает, что $\dlvf$ является консервативным. 92, \sin x + 2xy -2y) = \dlvf(x,y).
\конец{выравнивание*}
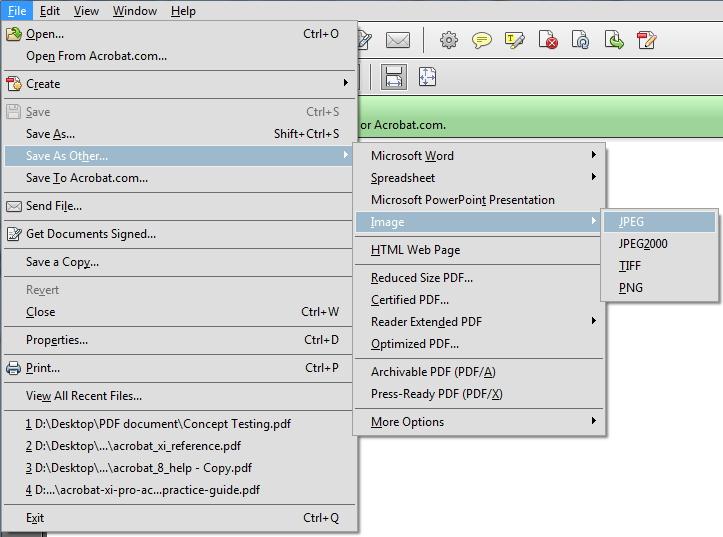
 Мы удаляем загруженные файлы через 24 часа, и ссылки для скачивания перестают работать после этого периода времени. Никто не имеет доступа к вашим файлам. Слияние файлов (включая JPG и PDF) абсолютно безопасно.
Мы удаляем загруженные файлы через 24 часа, и ссылки для скачивания перестают работать после этого периода времени. Никто не имеет доступа к вашим файлам. Слияние файлов (включая JPG и PDF) абсолютно безопасно.
 Также пользователи часто конвертируют файлы изображений в формат PDF. При конвертации JPG в PDF важно учитывать размер, ориентацию и качество выходного PDF-файла. Ниже мы перечислили некоторые инструменты для конвертирования JPG в PDF, включая программу PDFelement, которую можно загрузить бесплатно. Эти инструменты отличаются по своему функционалу и уровню сложности.
Также пользователи часто конвертируют файлы изображений в формат PDF. При конвертации JPG в PDF важно учитывать размер, ориентацию и качество выходного PDF-файла. Ниже мы перечислили некоторые инструменты для конвертирования JPG в PDF, включая программу PDFelement, которую можно загрузить бесплатно. Эти инструменты отличаются по своему функционалу и уровню сложности. Откройте PDFelement
Откройте PDFelement Благодаря простому интерфейсу, преобразование файлов займет у вас минимум времени.
Благодаря простому интерфейсу, преобразование файлов займет у вас минимум времени.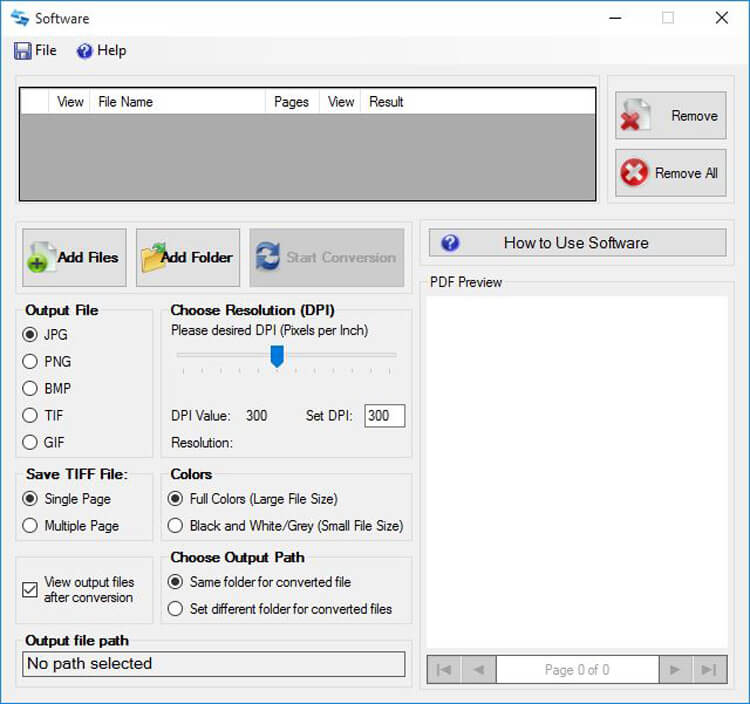
 Откройте PDFelement
Откройте PDFelement




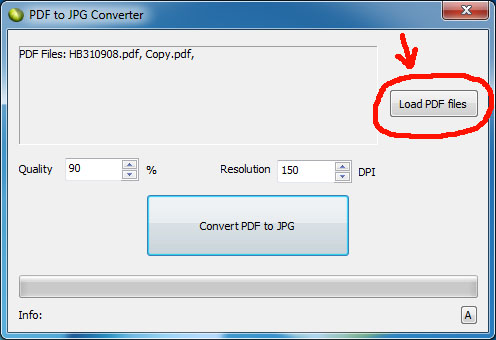 Программа оснащена множеством функций, от основных до продвинутых, таких как распознавание текста . Он поддерживает пакетное преобразование и работает на основных операционных системах и устройствах.
Программа оснащена множеством функций, от основных до продвинутых, таких как распознавание текста . Он поддерживает пакетное преобразование и работает на основных операционных системах и устройствах. Он имеет несколько основных и расширенных функций, необходимых для создания качественной продукции. С легкостью защищайте, сжимайте и редактируйте свои PDF-файлы в нескольких операционных системах.
Он имеет несколько основных и расширенных функций, необходимых для создания качественной продукции. С легкостью защищайте, сжимайте и редактируйте свои PDF-файлы в нескольких операционных системах. Его распространение обусловлено удобством использования, потому что этот формат позволяет хранить множество текстовых и графических файлов в одном документе. С помощью PDF можно создавать журналы, книги или фотоальбомы, а затем комфортно их просматривать.
Его распространение обусловлено удобством использования, потому что этот формат позволяет хранить множество текстовых и графических файлов в одном документе. С помощью PDF можно создавать журналы, книги или фотоальбомы, а затем комфортно их просматривать. Также есть возможность сохранить его в электронном виде. Для сопряжения с копировальной оргтехникой дополнительного программного обеспечения не требуется.
Также есть возможность сохранить его в электронном виде. Для сопряжения с копировальной оргтехникой дополнительного программного обеспечения не требуется. 
 pdf. Обычно они бесплатны, достаточно зайти на сайт и следовать инструкции:
pdf. Обычно они бесплатны, достаточно зайти на сайт и следовать инструкции: Некоторые из них подразумевают взаимодействие с дополнительными программами, а другие позволяют реализовать поставленную задачу через онлайн-сервисы. Предлагаем по очереди изучить каждый доступный момент, чтобы в результате выбрать подходящий.
Некоторые из них подразумевают взаимодействие с дополнительными программами, а другие позволяют реализовать поставленную задачу через онлайн-сервисы. Предлагаем по очереди изучить каждый доступный момент, чтобы в результате выбрать подходящий. Так можно себя обезопасить от случайного заражения вирусами и вовсе обойтись без защитного ПО.
Так можно себя обезопасить от случайного заражения вирусами и вовсе обойтись без защитного ПО.



 Просто перейдите по расположенной в разделе ссылке на сайт, загрузите картинки и обработайте их, что займет буквально несколько секунд.
Просто перейдите по расположенной в разделе ссылке на сайт, загрузите картинки и обработайте их, что займет буквально несколько секунд. Это может быть то, что интересует многих пользователей, которые не знают, как они могут это сделать.
Это может быть то, что интересует многих пользователей, которые не знают, как они могут это сделать.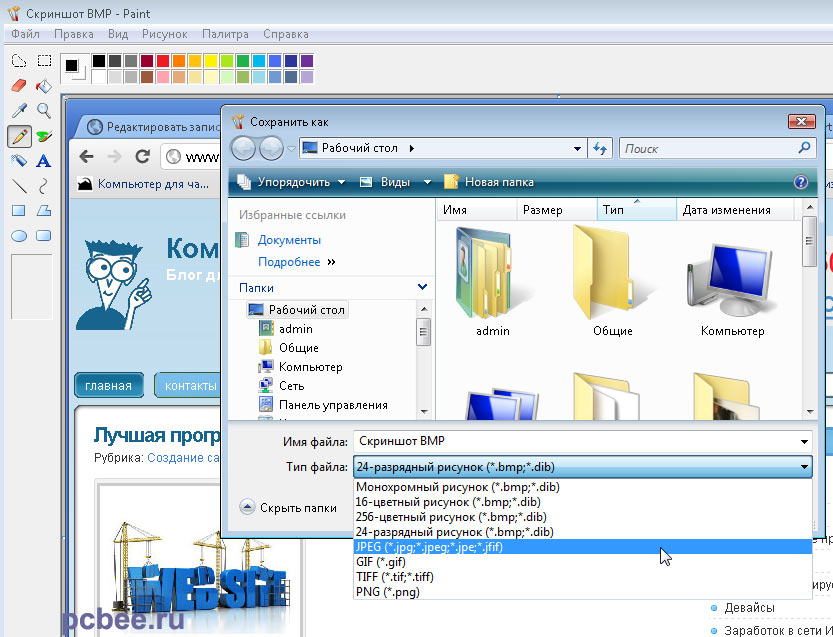 Они представлены как хороший вариант для использования на нашем телефоне или планшете, поскольку делают этот процесс очень простым. Кроме того, они могут позволить вам делать это, например, с несколькими фотографиями одновременно.
Они представлены как хороший вариант для использования на нашем телефоне или планшете, поскольку делают этот процесс очень простым. Кроме того, они могут позволить вам делать это, например, с несколькими фотографиями одновременно.
 Когда дело доходит до преобразования фотографии в PDF на планшете или телефоне, мы сталкиваемся с одним из лучших приложений. Это приложение позволяет конвертировать любую фотографию в PDF, имея поддержка таких форматов, как JPG, PNG или TIFF, среди прочего. Это будет означать, что любой пользователь операционной системы сможет использовать его в любое время.
Когда дело доходит до преобразования фотографии в PDF на планшете или телефоне, мы сталкиваемся с одним из лучших приложений. Это приложение позволяет конвертировать любую фотографию в PDF, имея поддержка таких форматов, как JPG, PNG или TIFF, среди прочего. Это будет означать, что любой пользователь операционной системы сможет использовать его в любое время. Вы можете скачать его по этой ссылке:
Вы можете скачать его по этой ссылке:
 На любой из этих страниц необходимо выполнить следующие действия:
На любой из этих страниц необходимо выполнить следующие действия: Конечно, если используются тяжелые фотографии, может потребоваться большой объем мобильных данных, поэтому в этом случае вам может быть интересно использовать Wi-Fi.
Конечно, если используются тяжелые фотографии, может потребоваться большой объем мобильных данных, поэтому в этом случае вам может быть интересно использовать Wi-Fi. Вы можете проверить, доступна ли эта функция в вашей мобильной галерее, выполнив следующие действия:
Вы можете проверить, доступна ли эта функция в вашей мобильной галерее, выполнив следующие действия: Иногда пользователям необходимо создавать PDF-файлы из изображений JPG/JPEG для уменьшения размера файлов или упрощения печати. Если вы сжимаете файлы JPG, разрешение изображения будет принесено в жертву. Когда дело доходит до документа PDF, исходное качество сохраняется. Это может быть самым значительным преимуществом знания того, как конвертировать JPG в PDF бесплатно .
Иногда пользователям необходимо создавать PDF-файлы из изображений JPG/JPEG для уменьшения размера файлов или упрощения печати. Если вы сжимаете файлы JPG, разрешение изображения будет принесено в жертву. Когда дело доходит до документа PDF, исходное качество сохраняется. Это может быть самым значительным преимуществом знания того, как конвертировать JPG в PDF бесплатно .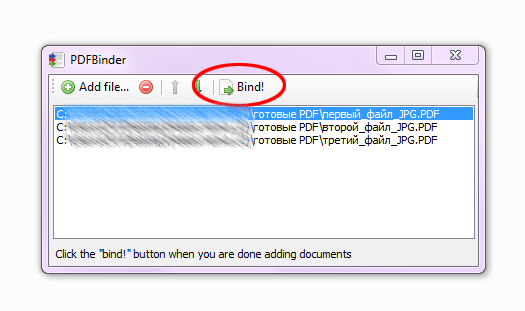 Отличная производительность и стабильность являются критическими факторами, которые мы поставили этот конвертер JPG в PDF в первую очередь. Теперь следуйте инструкциям, чтобы узнать, как легко преобразовать JPG в PDF:
Отличная производительность и стабильность являются критическими факторами, которые мы поставили этот конвертер JPG в PDF в первую очередь. Теперь следуйте инструкциям, чтобы узнать, как легко преобразовать JPG в PDF: . Кроме того, SwifDoo PDF позволяет изменить размер страницы с исходной страницы, A4 книжной, A4 альбомной или нестандартного размера.
. Кроме того, SwifDoo PDF позволяет изменить размер страницы с исходной страницы, A4 книжной, A4 альбомной или нестандартного размера. Найдите изображение JPG/JPEG на компьютере с Windows и откройте его в Microsoft Photos;
Найдите изображение JPG/JPEG на компьютере с Windows и откройте его в Microsoft Photos; Качество изображения хуже, чем у PDF, преобразованного профессиональным конвертером JPG в PDF, например, SwifDoo PDF.
Качество изображения хуже, чем у PDF, преобразованного профессиональным конвертером JPG в PDF, например, SwifDoo PDF. Когда пользователи iPhone конвертируют JPG/JPEG в PDF, они могут изменить только размер страницы и количество копий PDF.
Когда пользователи iPhone конвертируют JPG/JPEG в PDF, они могут изменить только размер страницы и количество копий PDF. Тем не менее, пакетное преобразование JPG/JPEG в PDF неудобно. Вот почему нам нужно рассказать, как конвертировать JPG в PDF онлайн.
Тем не менее, пакетное преобразование JPG/JPEG в PDF неудобно. Вот почему нам нужно рассказать, как конвертировать JPG в PDF онлайн.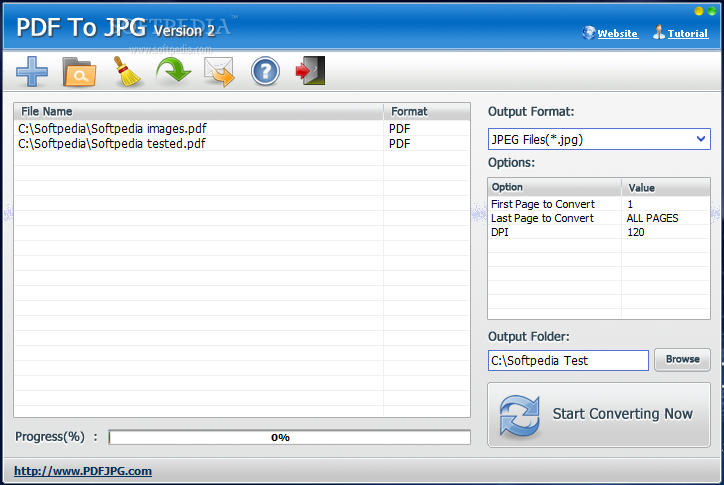 Нажмите кнопку Download , чтобы вывести этот PDF-документ.
Нажмите кнопку Download , чтобы вывести этот PDF-документ. Когда все будет готово, нажмите Преобразовать в PDF , чтобы легко преобразовать этот JPG в PDF.
Когда все будет готово, нажмите Преобразовать в PDF , чтобы легко преобразовать этот JPG в PDF.
 Как конвертировать JPG в PDF в Adobe Acrobat
Как конвертировать JPG в PDF в Adobe Acrobat Выберите параметр « Создать » или выберите « Инструменты » после того, как вы откроете конвертер Adobe JPG в PDF и выберите «9».0243 Создать PDF «.
Выберите параметр « Создать » или выберите « Инструменты » после того, как вы откроете конвертер Adobe JPG в PDF и выберите «9».0243 Создать PDF «.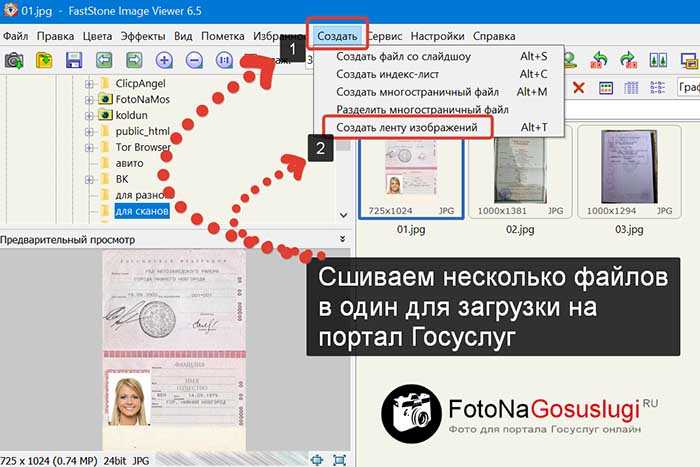 Или вы можете перетащить файлы JPG в PDFelement Pro, чтобы напрямую открывать файлы JPG как PDF.
Или вы можете перетащить файлы JPG в PDFelement Pro, чтобы напрямую открывать файлы JPG как PDF.
 Стандартный стоит от 155,88 до 275,88 долларов в год, а Pro — от 179,88 до 299,88 долларов в год. Разница в цене зависит от того, как вы платите.
Стандартный стоит от 155,88 до 275,88 долларов в год, а Pro — от 179,88 до 299,88 долларов в год. Разница в цене зависит от того, как вы платите.
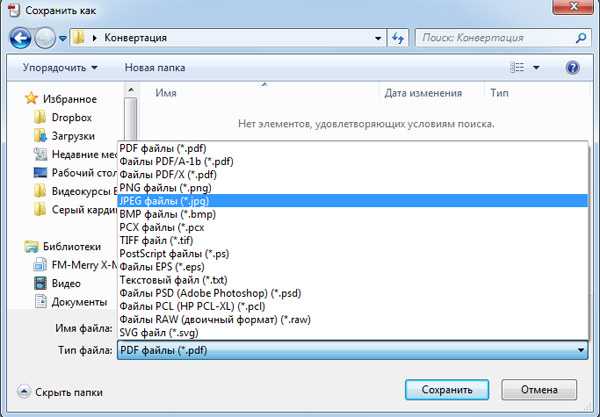 Ниже приведены некоторые из лучших приложений JPG в PDF для iPhone и iPad, которые вы можете использовать.
Ниже приведены некоторые из лучших приложений JPG в PDF для iPhone и iPad, которые вы можете использовать. UPDF имеет встроенный сканер, который позволяет создавать PDF-файлы путем сканирования файла JPG. Он предлагает пользователям возможность удалять, фильтровать или обрезать файлы JPG перед преобразованием. Приложение дает вам возможность конвертировать неограниченное количество JPG в PDF. Вы также можете объединить множество PDF-файлов в один файл. Если вы хотите сжать или распечатать преобразованные PDF-файлы, вы также можете легко сделать это с помощью UPDF.
UPDF имеет встроенный сканер, который позволяет создавать PDF-файлы путем сканирования файла JPG. Он предлагает пользователям возможность удалять, фильтровать или обрезать файлы JPG перед преобразованием. Приложение дает вам возможность конвертировать неограниченное количество JPG в PDF. Вы также можете объединить множество PDF-файлов в один файл. Если вы хотите сжать или распечатать преобразованные PDF-файлы, вы также можете легко сделать это с помощью UPDF. Вы можете быстро преобразовать JPG в PDF. Самое замечательное в приложении то, что вам не нужно подключение к Интернету, чтобы выполнить преобразование. Вы также не ограничены размером JPG, который вы можете конвертировать в PDF.
Вы можете быстро преобразовать JPG в PDF. Самое замечательное в приложении то, что вам не нужно подключение к Интернету, чтобы выполнить преобразование. Вы также не ограничены размером JPG, который вы можете конвертировать в PDF. простая организация и управление вашими файлами
простая организация и управление вашими файлами Приложение также позволяет подключаться к вашим поставщикам хранилищ, таким как iCloud Drive, Dropbox, Google Drive и OneDrive.
Приложение также позволяет подключаться к вашим поставщикам хранилищ, таким как iCloud Drive, Dropbox, Google Drive и OneDrive. Он прост в использовании, хотя рекомендуется ознакомиться с рекомендациями, предоставленными после установки, чтобы помочь вам более эффективно использовать все предоставленные функции. Что вам нравится больше, так это то, что функции кнопок мощные и простые в использовании. Это также позволяет вам захватывать и делиться преобразованными PDF-файлами. С помощью приложения у вас также есть возможность импортировать фотографии, которые вы уже сохранили на своем iPhone или iPad, используя галерею. 9
Он прост в использовании, хотя рекомендуется ознакомиться с рекомендациями, предоставленными после установки, чтобы помочь вам более эффективно использовать все предоставленные функции. Что вам нравится больше, так это то, что функции кнопок мощные и простые в использовании. Это также позволяет вам захватывать и делиться преобразованными PDF-файлами. С помощью приложения у вас также есть возможность импортировать фотографии, которые вы уже сохранили на своем iPhone или iPad, используя галерею. 9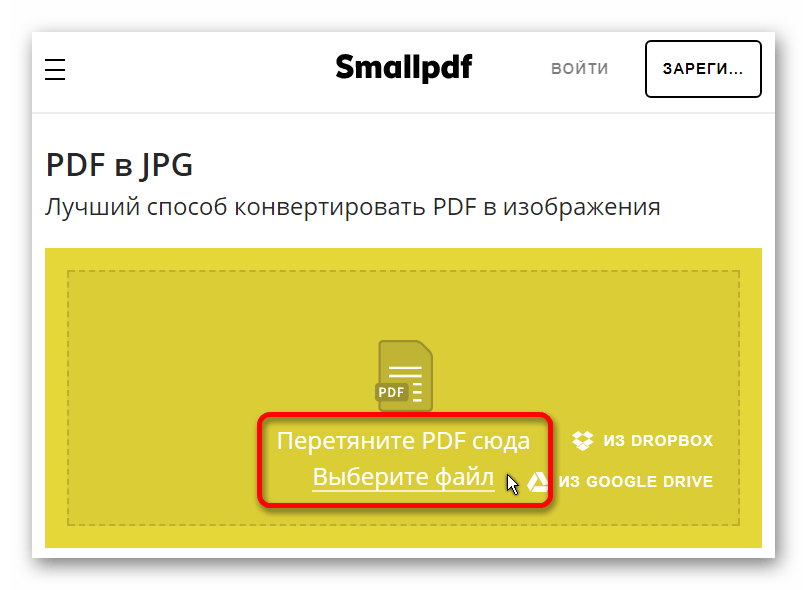
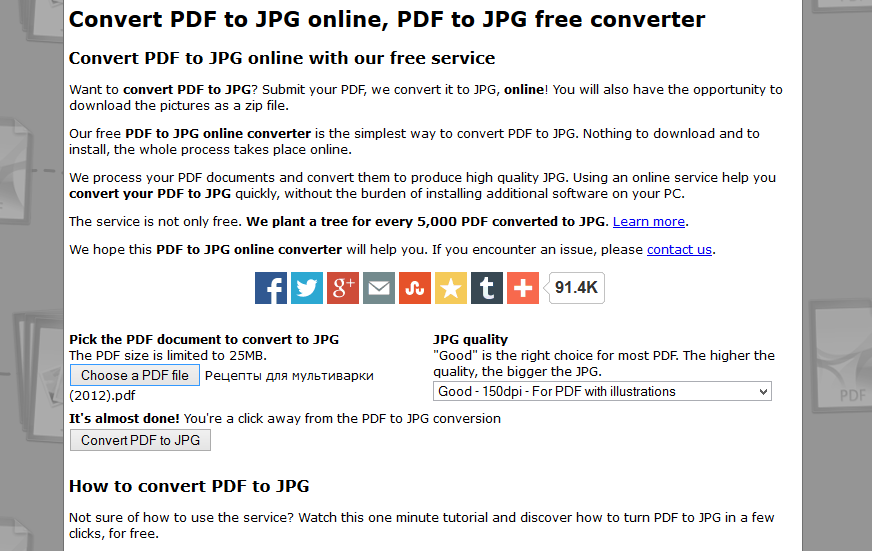 Вы также можете обратно преобразовать PDF-файлы в JPG на своем iPad или iPhone. После того, как вы закончите преобразование, приложение также позволяет вам делиться PDF-файлами или сохранять файлы в iCloud.
Вы также можете обратно преобразовать PDF-файлы в JPG на своем iPad или iPhone. После того, как вы закончите преобразование, приложение также позволяет вам делиться PDF-файлами или сохранять файлы в iCloud.
 Еще одна замечательная вещь заключается в том, что вы можете конвертировать неограниченное количество JPG с помощью приложения.
Еще одна замечательная вещь заключается в том, что вы можете конвертировать неограниченное количество JPG с помощью приложения. После преобразования документа из JPG в PDF вы можете отправлять файлы по электронной почте, загружать их и делиться ими.
После преобразования документа из JPG в PDF вы можете отправлять файлы по электронной почте, загружать их и делиться ими. SwiftScan
SwiftScan 
 Преобразование JPG в PDF очень просто и может быть выполнено на вашем ПК, телефоне Android или iPhone. Вот несколько шагов, чтобы сделать это.
Преобразование JPG в PDF очень просто и может быть выполнено на вашем ПК, телефоне Android или iPhone. Вот несколько шагов, чтобы сделать это.
 Один из самых простых способов выполнить преобразование — использовать приложение Google Photos, которое предустановлено на телефонах Android. Вот как это сделать:
Один из самых простых способов выполнить преобразование — использовать приложение Google Photos, которое предустановлено на телефонах Android. Вот как это сделать:
 , 10:52 [IST]
, 10:52 [IST]
 Он не может заменить средство просмотра PDF, поставляемое с Windows, поскольку оно не отображает все параметры форматирования, например таблицы, и не может выполнять такие задачи, как сжатие страницы или ее поворот. Он также позволяет конвертировать только один файл за раз
Он не может заменить средство просмотра PDF, поставляемое с Windows, поскольку оно не отображает все параметры форматирования, например таблицы, и не может выполнять такие задачи, как сжатие страницы или ее поворот. Он также позволяет конвертировать только один файл за раз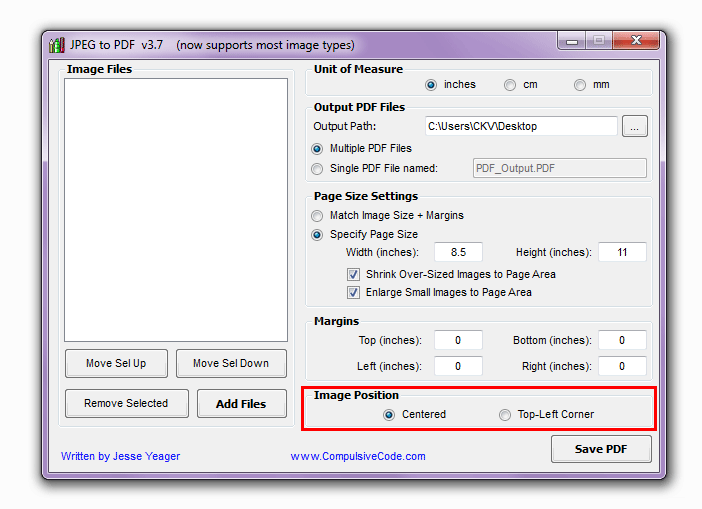 В зависимости от конвертера вы можете получить зараженные вредоносным ПО файлы. Вероятно, стоит помнить, что вы подвергаете риску свой компьютер, передавая документ через ненадежный источник. Если вы используете платный онлайн-конвертер, файл обычно не проверяется на наличие вирусов перед передачей в процесс конвертации.
В зависимости от конвертера вы можете получить зараженные вредоносным ПО файлы. Вероятно, стоит помнить, что вы подвергаете риску свой компьютер, передавая документ через ненадежный источник. Если вы используете платный онлайн-конвертер, файл обычно не проверяется на наличие вирусов перед передачей в процесс конвертации. Вы не хотите потерять какие-либо важные детали ваших фотографий в процессе, поэтому вот несколько советов, как найти подходящее программное обеспечение для преобразования JPG в PDF:
Вы не хотите потерять какие-либо важные детали ваших фотографий в процессе, поэтому вот несколько советов, как найти подходящее программное обеспечение для преобразования JPG в PDF: 
 051 (
051 (


 Однако -2,5 есть больше -5. Кто ответит x=-2,5 тоже может оказаться неправым если окажется, что значение не удовлетворяет ОДЗ. Поэтому, для себя сделайте простой вывод — после вычисления иррациональных уравнений проверяйте решение подстановкой. Поскольку -2,5>-5, то его мы и проверим
Однако -2,5 есть больше -5. Кто ответит x=-2,5 тоже может оказаться неправым если окажется, что значение не удовлетворяет ОДЗ. Поэтому, для себя сделайте простой вывод — после вычисления иррациональных уравнений проверяйте решение подстановкой. Поскольку -2,5>-5, то его мы и проверим
 2 меньше 15 и уравнение не имеет решения. Однако, проверка на калькуляторе показывает
2 меньше 15 и уравнение не имеет решения. Однако, проверка на калькуляторе показывает Приведём примеры иррациональных уравнений:
Приведём примеры иррациональных уравнений: Чтобы проверить, подходит ли нам корень , сделаем проверку: Если , то =>
Чтобы проверить, подходит ли нам корень , сделаем проверку: Если , то => Для того чтобы понять, почему это происходит, давайте решим ещё один пример.
Для того чтобы понять, почему это происходит, давайте решим ещё один пример.
 Тогда, по определению квадратного корня, также такое неравенство должно выполняться . Теперь подставим полученное нами первое значение : – это неравенство неверно, поэтому можем сразу сказать, что не является корнем исходного иррационального уравнения.
Тогда, по определению квадратного корня, также такое неравенство должно выполняться . Теперь подставим полученное нами первое значение : – это неравенство неверно, поэтому можем сразу сказать, что не является корнем исходного иррационального уравнения. Также мы объяснили, почему мы можем получить неверные (посторонние) корни: из равенства квадратов не следует равенство аргументов, однако из равенства аргументов следует равенство квадратов.
Также мы объяснили, почему мы можем получить неверные (посторонние) корни: из равенства квадратов не следует равенство аргументов, однако из равенства аргументов следует равенство квадратов. В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 8. 5 издание. – М.: Просвещение, 2010.
В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 8. 5 издание. – М.: Просвещение, 2010.
 Оно наряду с корнями исходного уравнения может содержать и другие корни, которые называются посторонними. Поэтому после решения уравнения-следствия необходимо найти способ отсеять посторонние корни. Обычно это можно сделать при помощи проверки, которая в данном случае рассматривается как один из этапов решения.
Оно наряду с корнями исходного уравнения может содержать и другие корни, которые называются посторонними. Поэтому после решения уравнения-следствия необходимо найти способ отсеять посторонние корни. Обычно это можно сделать при помощи проверки, которая в данном случае рассматривается как один из этапов решения.




 2$
2$



 Дробно-рациональное неравенство
Дробно-рациональное неравенство Пример, в котором нужно решить систему
Пример, в котором нужно решить систему


 Сложение и вычитание рациональных дробей с одинаковыми знаменателями
Сложение и вычитание рациональных дробей с одинаковыми знаменателями
 Составление программ с разветвлением.
Составление программ с разветвлением.

 Нахождение производной в точке
Нахождение производной в точке После этой исследования построить ее график.
После этой исследования построить ее график. Применение формул приведения
Применение формул приведения Результат тестов по математике засчитывается как балл государственной итоговой
аттестации (ДПА) . Выпускникам, которые прошли ЕГЭ по математике, алгебре, геометрии выдается сертификат
с его результатами, в соответствии с которым вносится соответствующая запись в дополнение к аттестату.
Чтобы набрать необходимое количество баллов недостаточно формально овладеть школьным материалом –
необходимы углубленные знания, практика в решении задач, умение правильно и четко изложить на бумаге
решение задачи, сопровождая его необходимыми схемами, рисунками, формулами.
Результат тестов по математике засчитывается как балл государственной итоговой
аттестации (ДПА) . Выпускникам, которые прошли ЕГЭ по математике, алгебре, геометрии выдается сертификат
с его результатами, в соответствии с которым вносится соответствующая запись в дополнение к аттестату.
Чтобы набрать необходимое количество баллов недостаточно формально овладеть школьным материалом –
необходимы углубленные знания, практика в решении задач, умение правильно и четко изложить на бумаге
решение задачи, сопровождая его необходимыми схемами, рисунками, формулами.
 Специалиста можно найти, обратившись в специальные агентства, поместив объявление в средствах массовой
информации. Однако , попав на этот сайт, вы уже нашли то, что искали. У автора — большой опыт подготовки
к ЗНО по математике, ДПА по математике, ЗНО по физике, ДПА по физике. Вы можете посмотреть отзывы на
соответствующей странице. Все мои ученики успешно сдавали ЗНО с результатом от 180 баллов, а результат
ДПА всегда был не ниже 9. Поэтому вы можете быть уверены в результативности занятий.
Специалиста можно найти, обратившись в специальные агентства, поместив объявление в средствах массовой
информации. Однако , попав на этот сайт, вы уже нашли то, что искали. У автора — большой опыт подготовки
к ЗНО по математике, ДПА по математике, ЗНО по физике, ДПА по физике. Вы можете посмотреть отзывы на
соответствующей странице. Все мои ученики успешно сдавали ЗНО с результатом от 180 баллов, а результат
ДПА всегда был не ниже 9. Поэтому вы можете быть уверены в результативности занятий. ..
..
 В таких уравнениях при возможности лучше проверять корни подстановкой.
В таких уравнениях при возможности лучше проверять корни подстановкой. Значение первой переменной затем нужно найти используя её выражение через уже найденную переменную.
Значение первой переменной затем нужно найти используя её выражение через уже найденную переменную. Ноль можно возводить только в положительную степень. Ну а основное свойство отрицательной степени записывается следующим образом:
Ноль можно возводить только в положительную степень. Ну а основное свойство отрицательной степени записывается следующим образом: Кроме того, нужно отметить, что если используется запись со значком математического корня, то показатель степени этого корня может быть только целым числом, причем это число должно быть больше либо равно двум:
Кроме того, нужно отметить, что если используется запись со значком математического корня, то показатель степени этого корня может быть только целым числом, причем это число должно быть больше либо равно двум: Если под корнем квадратным имеется произведение двух отрицательных величин (т.е. по итогу величина положительная, а значит корень существует), то этот корень раскладывается на множители следующим образом:
Если под корнем квадратным имеется произведение двух отрицательных величин (т.е. по итогу величина положительная, а значит корень существует), то этот корень раскладывается на множители следующим образом: Часть II
Часть II

 com для 5-го класса системы с основанием 5
com для 5-го класса системы с основанием 5 7: Решение радикальных уравнений — Математика LibreTexts
7: Решение радикальных уравнений — Математика LibreTexts Это устранит радикал. 9{п}=а\).
Это устранит радикал. 9{п}=а\).


 6.3
6.3 {m \cdot n}\), мы имеем, например, 9{4}\)
{m \cdot n}\), мы имеем, например, 9{4}\)

 Часто проще всего сначала выделить более сложный радикал. 9{3}\)
Часто проще всего сначала выделить более сложный радикал. 9{3}\)






 6.11
6.11 Используйте формулу \(s=\sqrt{24d}\), чтобы найти скорость автомобиля до включения тормозов. Округлите ответ до десятых.
Используйте формулу \(s=\sqrt{24d}\), чтобы найти скорость автомобиля до включения тормозов. Округлите ответ до десятых.
 9{2}}\конец{массив}\)
9{2}}\конец{массив}\)

 04.2007
04.2007  03.2007
03.2007 
 Все мои сомнения относительно знаменателей и свойств уравнений рассеялись, как только я начал использовать это программное обеспечение. Так что давай, попробуй Алгебратор.
Все мои сомнения относительно знаменателей и свойств уравнений рассеялись, как только я начал использовать это программное обеспечение. Так что давай, попробуй Алгебратор. Даже я столкнулся с похожими проблемами, решая преобразование дробей, преобразование дробей и построение кругов. Просто напечатайте в задачнике и нажмите «Решить» — и пошаговое решение моего домашнего задания по математике будет готово. Я использовал его на нескольких занятиях по алгебре — «Исправительная алгебра», «Алгебра колледжа» и «Основная математика». Очень рекомендую программу.
Даже я столкнулся с похожими проблемами, решая преобразование дробей, преобразование дробей и построение кругов. Просто напечатайте в задачнике и нажмите «Решить» — и пошаговое решение моего домашнего задания по математике будет готово. Я использовал его на нескольких занятиях по алгебре — «Исправительная алгебра», «Алгебра колледжа» и «Основная математика». Очень рекомендую программу. по математике
по математике Вот некоторые из их опытов:
Вот некоторые из их опытов:  В нем есть все, что нужно студенту.
В нем есть все, что нужно студенту.  Вот поисковые фразы, которые сегодняшние поисковики использовали, чтобы найти наш сайт. Сможете ли вы найти среди них свою?
Вот поисковые фразы, которые сегодняшние поисковики использовали, чтобы найти наш сайт. Сможете ли вы найти среди них свою?  практика навыков 17
практика навыков 17 05.18
05.18 2 больше равно 3x. Если корень стоит на всей функции
2 больше равно 3x. Если корень стоит на всей функции Найдите радиус окружности, если OB = 10 см и угол ABO = 30 градусам.
Найдите радиус окружности, если OB = 10 см и угол ABO = 30 градусам. Узоры и орнаменты на посуде»
Узоры и орнаменты на посуде» Продолжение разминкиКаким числом не может быть
Продолжение разминкиКаким числом не может быть Определение функцииФункцией
Определение функцииФункцией Задание: найти область определения функции по ее графику1)
Задание: найти область определения функции по ее графику1)
 Найти область определения функции: y
Найти область определения функции: y  Это трекер объектов на основе модифицированного метода главных компонент: он самообучается на ходу и адаптируется к изменчивым условиям.
Это трекер объектов на основе модифицированного метода главных компонент: он самообучается на ходу и адаптируется к изменчивым условиям. Всего сценариев использования, естественно, гораздо больше.
Всего сценариев использования, естественно, гораздо больше. Преимущество же кодирования “внешнего вида” объекта заключается в том, что эта информация вкупе с координатами объекта улучшает качество трекинга. Визуально разницу между detection-моделью и appearance-моделью можно увидеть на видео ниже.
Преимущество же кодирования “внешнего вида” объекта заключается в том, что эта информация вкупе с координатами объекта улучшает качество трекинга. Визуально разницу между detection-моделью и appearance-моделью можно увидеть на видео ниже.
 Визуализация уменьшения размерности в двумерном пространстве. Исходные данные представляют собой массив векторов , каждый из которых изображается точкой на графике с координатами . Рисунок слева иллюстрирует новую ортогональную систему координат с центром в . Рисунок справа иллюстрирует проекцию исходных данных (красные точки) на систему, состоящую только из первой главной компоненты . Так как разброс проекций для оси заметно меньше разброса оси , мы можем отсечь вторую ось, пожертвовать некоторой информацией, сохранив при этом основную. Таким образом проекция представляется одним числом и мы сократили размерность с 2 до 1.
Визуализация уменьшения размерности в двумерном пространстве. Исходные данные представляют собой массив векторов , каждый из которых изображается точкой на графике с координатами . Рисунок слева иллюстрирует новую ортогональную систему координат с центром в . Рисунок справа иллюстрирует проекцию исходных данных (красные точки) на систему, состоящую только из первой главной компоненты . Так как разброс проекций для оси заметно меньше разброса оси , мы можем отсечь вторую ось, пожертвовать некоторой информацией, сохранив при этом основную. Таким образом проекция представляется одним числом и мы сократили размерность с 2 до 1. В программной реализации, о которой будет рассказано ниже, будут использованы первые 16 главных компонент при исходной длине вектора 32×32=1024. Согласимся, что оперировать матрицами гораздо выгоднее чем матрицами . На рисунке ниже визуально представлены первые четыре главные компоненты для изображений велосипеда.
В программной реализации, о которой будет рассказано ниже, будут использованы первые 16 главных компонент при исходной длине вектора 32×32=1024. Согласимся, что оперировать матрицами гораздо выгоднее чем матрицами . На рисунке ниже визуально представлены первые четыре главные компоненты для изображений велосипеда. Эта вероятность обратно пропорциональна расстоянию от спроецированного объекта до центра базиса . В следующих разделах будет показано, что все чуть сложнее, но для текущего пояснения этого будет достаточно. Очевидно, что объекты, принадлежащие базису будут располагаться близко к центру, в то время как иные объекты будут находиться далеко. Представьте, что на рисунке 1 мы пытаемся спроецировать точку на главную ось . Понятно, что проекция будет находиться далеко от центра , значит маловероятно, что точка принадлежит базису. Теперь предположим, что мы хотим найти участок кадра, в котором находится объект. Для этого я должен найти участок кадра, который лучше всего проецируется на базис объекта ; иными словами, расстояние от которого до базиса минимально.
Эта вероятность обратно пропорциональна расстоянию от спроецированного объекта до центра базиса . В следующих разделах будет показано, что все чуть сложнее, но для текущего пояснения этого будет достаточно. Очевидно, что объекты, принадлежащие базису будут располагаться близко к центру, в то время как иные объекты будут находиться далеко. Представьте, что на рисунке 1 мы пытаемся спроецировать точку на главную ось . Понятно, что проекция будет находиться далеко от центра , значит маловероятно, что точка принадлежит базису. Теперь предположим, что мы хотим найти участок кадра, в котором находится объект. Для этого я должен найти участок кадра, который лучше всего проецируется на базис объекта ; иными словами, расстояние от которого до базиса минимально. Теперь заставим функцию пробежать все изображение, сдвигая наше окно по горизонтали и вертикали. Тогда результатом работы будет новое изображение, в каждой точке которого будет записано расстояние от участка с центром в до базиса.
Теперь заставим функцию пробежать все изображение, сдвигая наше окно по горизонтали и вертикали. Тогда результатом работы будет новое изображение, в каждой точке которого будет записано расстояние от участка с центром в до базиса. И IVT трекер умеет это делать.
И IVT трекер умеет это делать.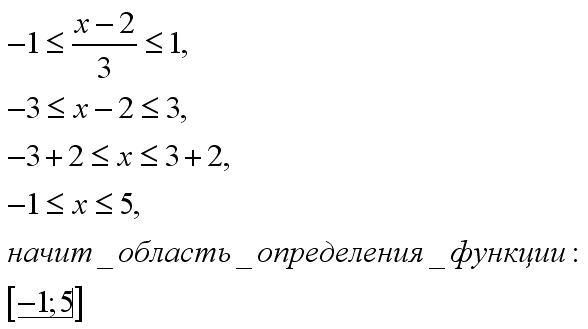
 Кроме этого, авторы вводят в уравнения обновления коэффициент затухания (forgetting factor), снижающий влияние более старых данных на новый базис, уделяя больше внимания более новым данным. Полное описание алгоритма с формулами для вычисления приведено в статье. На видео 2 представлен пример обновления среднего и собственного базиса.
Кроме этого, авторы вводят в уравнения обновления коэффициент затухания (forgetting factor), снижающий влияние более старых данных на новый базис, уделяя больше внимания более новым данным. Полное описание алгоритма с формулами для вычисления приведено в статье. На видео 2 представлен пример обновления среднего и собственного базиса.
 Первый множитель это модель движения или “где будет находиться объект в момент времени , при условии, что в момент времени объект находился в . Второй множитель это модель наблюдения или “насколько правдоподобно было бы наблюдение , если бы в момент времени объект находился в . В следующих разделах мы рассмотрим эти множители подробнее.
Первый множитель это модель движения или “где будет находиться объект в момент времени , при условии, что в момент времени объект находился в . Второй множитель это модель наблюдения или “насколько правдоподобно было бы наблюдение , если бы в момент времени объект находился в . В следующих разделах мы рассмотрим эти множители подробнее. По сути, в выражении содержатся (хоть и в проинтегрированном виде) все предыдущие знания о перемещении объекта (оно соответствует верхней горизонтальной стрелочке в графической модели на рисунке 5). На самом деле байесовский вывод возникает естественным образом для моделей последовательной обработки данных, каковой является и наша марковская модель, из-за способности обновлять апостериорное знание по мере поступления новой информации.
По сути, в выражении содержатся (хоть и в проинтегрированном виде) все предыдущие знания о перемещении объекта (оно соответствует верхней горизонтальной стрелочке в графической модели на рисунке 5). На самом деле байесовский вывод возникает естественным образом для моделей последовательной обработки данных, каковой является и наша марковская модель, из-за способности обновлять апостериорное знание по мере поступления новой информации. Мы можем записать это движение в виде многомерного нормального распределения , где — диагональная ковариационная матрица, каждый элемент которой на главной диагонали равен дисперсии одного из параметров, то есть . Иными словами, каждый параметр распределен нормально вокруг своего центра (предыдущего параметра) со среднеквадратичным отклонением .
Мы можем записать это движение в виде многомерного нормального распределения , где — диагональная ковариационная матрица, каждый элемент которой на главной диагонали равен дисперсии одного из параметров, то есть . Иными словами, каждый параметр распределен нормально вокруг своего центра (предыдущего параметра) со среднеквадратичным отклонением . Это и есть модель наблюдения. В байесовской интерпретации модель наблюдения задается распределением — правдоподобием того, что находясь в позиции , мы пронаблюдаем . Так как для наблюдаемого объекта мы моделируем базис с центром , то мы предполагаем, что наблюдение получено из этого базиса. В этом случае распределение имеет следующий смысл: насколько вероятно получить из пространства нашего объекта. Эта вероятность обратно пропорциональна расстоянию от наблюдения до центра . Это расстояние можно разложить на два: расстояние от наблюдения до пространства и расстояние внутри самого пространства от спроецированного до центра. Но для наших целей достаточно будет посчитать только расстояние, пропорциональное :
Это и есть модель наблюдения. В байесовской интерпретации модель наблюдения задается распределением — правдоподобием того, что находясь в позиции , мы пронаблюдаем . Так как для наблюдаемого объекта мы моделируем базис с центром , то мы предполагаем, что наблюдение получено из этого базиса. В этом случае распределение имеет следующий смысл: насколько вероятно получить из пространства нашего объекта. Эта вероятность обратно пропорциональна расстоянию от наблюдения до центра . Это расстояние можно разложить на два: расстояние от наблюдения до пространства и расстояние внутри самого пространства от спроецированного до центра. Но для наших целей достаточно будет посчитать только расстояние, пропорциональное : Видно, что исходное изображение несколько искажено, из-за потери некоторой составляющей при проецировании, но основной образ сохранен. Тогда разность , называемая также вектором невязки, есть просто разница между исходным изображением и его реконструкцией, а -норма вектора невязки выражает количество информации, которую мы не можем восстановить. Ясно, что чем больше расстояние , тем ниже вероятность и тем хуже будет качество восстановленного изображения.
Видно, что исходное изображение несколько искажено, из-за потери некоторой составляющей при проецировании, но основной образ сохранен. Тогда разность , называемая также вектором невязки, есть просто разница между исходным изображением и его реконструкцией, а -норма вектора невязки выражает количество информации, которую мы не можем восстановить. Ясно, что чем больше расстояние , тем ниже вероятность и тем хуже будет качество восстановленного изображения. Смысл параметра в том, что он задает критическую область, после которой влияние шумов на модель наблюдения начинает уменьшаться [2].
Смысл параметра в том, что он задает критическую область, после которой влияние шумов на модель наблюдения начинает уменьшаться [2]. Видно, что в начале модель уверена в положении объекта (лицо человека в красной рамке), но по мере движения начинают образовываться несколько гипотез. Например, на отметке t=20 на левом графике видно три вершины. Самая левая вершина соответствует цели, вершина посередине соответствует похожему человеку справа от цели и правая вершина соответствует человеку в синей жилетке справа. Так как человек справа находится далеко от цели, то модель справедливо дает ему наименьший вес полагая, что цель не сможет так резко сдвинуться вправо.
Видно, что в начале модель уверена в положении объекта (лицо человека в красной рамке), но по мере движения начинают образовываться несколько гипотез. Например, на отметке t=20 на левом графике видно три вершины. Самая левая вершина соответствует цели, вершина посередине соответствует похожему человеку справа от цели и правая вершина соответствует человеку в синей жилетке справа. Так как человек справа находится далеко от цели, то модель справедливо дает ему наименьший вес полагая, что цель не сможет так резко сдвинуться вправо. На рисунке 8 частицей является каждая темно-синяя точка на левом графике. Если устремить количество частиц в бесконечность, то “рваный” график будет становиться более гладким, а в пределе станет непрерывным. Заметно, что частица с наибольшим весом соответствует наиболее вероятному местоположению объекта. Для генерации и распространения частиц во времени мы воспользуемся алгоритмом сэмплирования CONDENSATION [3].
На рисунке 8 частицей является каждая темно-синяя точка на левом графике. Если устремить количество частиц в бесконечность, то “рваный” график будет становиться более гладким, а в пределе станет непрерывным. Заметно, что частица с наибольшим весом соответствует наиболее вероятному местоположению объекта. Для генерации и распространения частиц во времени мы воспользуемся алгоритмом сэмплирования CONDENSATION [3].
 Задаем всем частицам значение начальной позиции объекта с равным весом .
Задаем всем частицам значение начальной позиции объекта с равным весом . Еще одно ограничение связано с тем, что при переходе координаты некоторых частиц могут “вылететь” за рамки кадра. Мы не будем утруждать себя отдельной обработкой таких случаев, а будем просто возводить такие частицы в нулевой вектор, что эквивалентно обнулению веса частицы.
Еще одно ограничение связано с тем, что при переходе координаты некоторых частиц могут “вылететь” за рамки кадра. Мы не будем утруждать себя отдельной обработкой таких случаев, а будем просто возводить такие частицы в нулевой вектор, что эквивалентно обнулению веса частицы.

 Идею же инкрементного обучения можно подхватить при реализации других CV-алгоритмов.
Идею же инкрементного обучения можно подхватить при реализации других CV-алгоритмов. ..🎶
..🎶 Вместо этого пойте припев как «Домен, домен в диапазоне», и это поможет вам понять, что есть что.
Вместо этого пойте припев как «Домен, домен в диапазоне», и это поможет вам понять, что есть что. Домен — это все значения x , а диапазон — все значения y . Чтобы указать домен и диапазон, я просто перечисляю значения без дублирования:
Домен — это все значения x , а диапазон — все значения y . Чтобы указать домен и диапазон, я просто перечисляю значения без дублирования: Это отношение повторяется, так что оно есть:
Это отношение повторяется, так что оно есть: Но каждое x значение отличается, поэтому, хотя и скучно,
Но каждое x значение отличается, поэтому, хотя и скучно, Таким образом, единственные значения, которые x не могут принимать, это те, которые вызвали бы деление на ноль. Поэтому я приравняю знаменатель к нулю и решу; мой домен будет всем остальным.
Таким образом, единственные значения, которые x не могут принимать, это те, которые вызвали бы деление на ноль. Поэтому я приравняю знаменатель к нулю и решу; мой домен будет всем остальным.
 Тогда:
Тогда: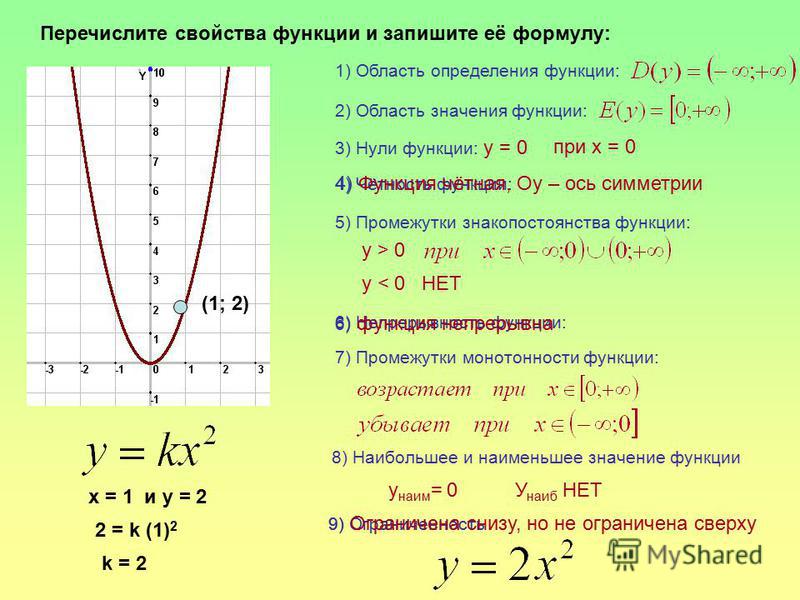 Затем нажмите кнопку и выберите «Найти домен и диапазон», чтобы сравнить свой ответ с ответом Mathway.
Затем нажмите кнопку и выберите «Найти домен и диапазон», чтобы сравнить свой ответ с ответом Mathway.
 Для этого урока нам потребуется, чтобы наши базисы были положительными на данный момент, чтобы мы могли оставаться в реальном мире.
Для этого урока нам потребуется, чтобы наши базисы были положительными на данный момент, чтобы мы могли оставаться в реальном мире.








 Например, если соотношение R = {(1, 2), (2, 2), (3, 3), (4, 3)}, то:
Например, если соотношение R = {(1, 2), (2, 2), (3, 3), (4, 3)}, то: Область определения функции — это набор всех возможных входных данных для функции. Рассмотрим этот ящик как функцию f(x) = 2x . При вводе значений x = {1,2,3,4,…} домен представляет собой просто набор натуральных чисел, а выходные значения называются диапазоном. Но в общем случае f(x) = 2x определено для всех действительных значений x, и, следовательно, его областью определения является множество всех действительных чисел, которое обозначается (-∞, ∞). Вот общие формулы, используемые для нахождения области определения различных типов функций. Здесь R — множество всех действительных чисел.
Область определения функции — это набор всех возможных входных данных для функции. Рассмотрим этот ящик как функцию f(x) = 2x . При вводе значений x = {1,2,3,4,…} домен представляет собой просто набор натуральных чисел, а выходные значения называются диапазоном. Но в общем случае f(x) = 2x определено для всех действительных значений x, и, следовательно, его областью определения является множество всех действительных чисел, которое обозначается (-∞, ∞). Вот общие формулы, используемые для нахождения области определения различных типов функций. Здесь R — множество всех действительных чисел.



 g. http://48ers.com/magnacarta.pdf
g. http://48ers.com/magnacarta.pdf Вы не можете добавлять изображения или объекты — он направлен исключительно на текст. Вы можете создать файл с помощью «Microsoft Word» в «Windows», сохранить его в виде файла в формате RTF (он будет иметь имя файла с суффиксом .rtf) и отправить его кому-либо, кто использует «WordPerfect 6.0» на любой версии «Windows», и они смогут открыть файл и прочитать его. Большинство людей сталкивались с этим форматом, когда писали файлы в «WordPad RTF».
Вы не можете добавлять изображения или объекты — он направлен исключительно на текст. Вы можете создать файл с помощью «Microsoft Word» в «Windows», сохранить его в виде файла в формате RTF (он будет иметь имя файла с суффиксом .rtf) и отправить его кому-либо, кто использует «WordPerfect 6.0» на любой версии «Windows», и они смогут открыть файл и прочитать его. Большинство людей сталкивались с этим форматом, когда писали файлы в «WordPad RTF». При считывании, управляющие слова и символы оформляются читателем RTF, который преобразует язык RTF в форматирование для текстового процессора, который будет отображать документ.
При считывании, управляющие слова и символы оформляются читателем RTF, который преобразует язык RTF в форматирование для текстового процессора, который будет отображать документ. doc
doc DOC файлы могут также содержать информацию о слиянии, что позволяет шаблону обработки слов быть использованным в сочетании с таблицей или базой данных.
DOC файлы могут также содержать информацию о слиянии, что позволяет шаблону обработки слов быть использованным в сочетании с таблицей или базой данных.
 Спецификации формата файлов доступны Microsoft для общедоступной загрузки, и на них можно ссылаться с точки зрения разработчика.
Спецификации формата файлов доступны Microsoft для общедоступной загрузки, и на них можно ссылаться с точки зрения разработчика. Спецификации формата файлов доступны Microsoft для общедоступной загрузки, и на них можно ссылаться с точки зрения разработчика.
Спецификации формата файлов доступны Microsoft для общедоступной загрузки, и на них можно ссылаться с точки зрения разработчика. Когда обработка будет завершена, вы сможете нажать кнопку «Просмотр», чтобы просмотреть документ, или скопировать ссылку, которой вы можете поделиться с друзьями для просмотра файла.
Когда обработка будет завершена, вы сможете нажать кнопку «Просмотр», чтобы просмотреть документ, или скопировать ссылку, которой вы можете поделиться с друзьями для просмотра файла.
 Viewer for .NET
Viewer for .NET Соответственно у пользователя возникает вопрос о том, чем открыть файл RTF на компьютере или онлайн.
Соответственно у пользователя возникает вопрос о том, чем открыть файл RTF на компьютере или онлайн. Потом пути компаний разошлись и за развитие формата стала отвечать одна Майкрософт. В 1985 году был создан язык PostScript. Последнее обновление спецификации формата было выпущено в 2006 году.
Потом пути компаний разошлись и за развитие формата стала отвечать одна Майкрософт. В 1985 году был создан язык PostScript. Последнее обновление спецификации формата было выпущено в 2006 году.

 Если поставить флажок в пункте «Всегда открывать это приложение для открытия .rtf файлов», то файлы данного формата будут автоматически открываться в этом текстовом редакторе.
Если поставить флажок в пункте «Всегда открывать это приложение для открытия .rtf файлов», то файлы данного формата будут автоматически открываться в этом текстовом редакторе. rtf» в приложении LibreOffice Writer.
rtf» в приложении LibreOffice Writer.
 Чтобы бесплатно пользоваться онлайн сервисом в некоммерческих целях необходима регистрация на сайте.
Чтобы бесплатно пользоваться онлайн сервисом в некоммерческих целях необходима регистрация на сайте. aspose.app/words/viewer на веб-страницу «Viewer».
aspose.app/words/viewer на веб-страницу «Viewer».

 com может показывать эскизы или изображения только в том случае, если размер изображения меньше 100 МБ (примерно 12000 x 8000 пикселей).
com может показывать эскизы или изображения только в том случае, если размер изображения меньше 100 МБ (примерно 12000 x 8000 пикселей). DIF, DIFF, ДЛСП, DML, DTD, DTML, EL, EMAKE, ERB, ERL, F90, F95, FS, FSI, FSSCRIPT, FSX, FSX, THESPEC, GITCONFIG, GO,OVOVY, GVY, H, H++, ГАМЛ, HANDLEBARS, HBS, HRL, HS, HTC, HTML, HXX, IDL, IIM, INC, INF, INL, IPP, IRBRC, HTM, JAV, JAVA, JS, JS, JSP, JSX, L, LHS, LHS, LOG, LST, LTX, LUA, M, MAKE, MARKDN, MARKDOWN, MD, MDOWN, MKDN, ML, MLI, MLL, MLY, MM, MM, MUD, NFO, OPML, OSASCRIPT, OUT, P, PAS, PATCH, PHP2, PHP2, PHP3, PHP4, PHP5, PL, PLIST, PM, POD, PP, PROFILE, PROPERTIES, PS, PS1, PT, PYW, R, RAKE, RB, RBX, RC, RE, README, REG, REST, RESW, RESX,РАТML, RJS, RPROFILE, RPY, RSS, RST, RXML, S, SASS, SCALA, SCM, SCONSCRIPT, SCONSTRUCT, SCRIPT, SCSS, SGML, SH, SHTML, SML, SQL, STY, TCL, TEX, TEXT, TLD, TLD, TMPL, TPL, TXT, VB, VI, VI, VIM, WSDL, XAML, XHTML, XOML, XML, XSD, XSL, XSLT, YAML, YAWS, YML, ZSH
DIF, DIFF, ДЛСП, DML, DTD, DTML, EL, EMAKE, ERB, ERL, F90, F95, FS, FSI, FSSCRIPT, FSX, FSX, THESPEC, GITCONFIG, GO,OVOVY, GVY, H, H++, ГАМЛ, HANDLEBARS, HBS, HRL, HS, HTC, HTML, HXX, IDL, IIM, INC, INF, INL, IPP, IRBRC, HTM, JAV, JAVA, JS, JS, JSP, JSX, L, LHS, LHS, LOG, LST, LTX, LUA, M, MAKE, MARKDN, MARKDOWN, MD, MDOWN, MKDN, ML, MLI, MLL, MLY, MM, MM, MUD, NFO, OPML, OSASCRIPT, OUT, P, PAS, PATCH, PHP2, PHP2, PHP3, PHP4, PHP5, PL, PLIST, PM, POD, PP, PROFILE, PROPERTIES, PS, PS1, PT, PYW, R, RAKE, RB, RBX, RC, RE, README, REG, REST, RESW, RESX,РАТML, RJS, RPROFILE, RPY, RSS, RST, RXML, S, SASS, SCALA, SCM, SCONSCRIPT, SCONSTRUCT, SCRIPT, SCSS, SGML, SH, SHTML, SML, SQL, STY, TCL, TEX, TEXT, TLD, TLD, TMPL, TPL, TXT, VB, VI, VI, VIM, WSDL, XAML, XHTML, XOML, XML, XSD, XSL, XSLT, YAML, YAWS, YML, ZSH
 RTF, иначе Rich Text Format, представляет собой формат текстового файла, который сохраняет форматирование документа, такое как полужирный шрифт, курсив и изображения.
RTF, иначе Rich Text Format, представляет собой формат текстового файла, который сохраняет форматирование документа, такое как полужирный шрифт, курсив и изображения. Таким образом, ваш файл будет безопасным, и им будет легко поделиться.
Таким образом, ваш файл будет безопасным, и им будет легко поделиться.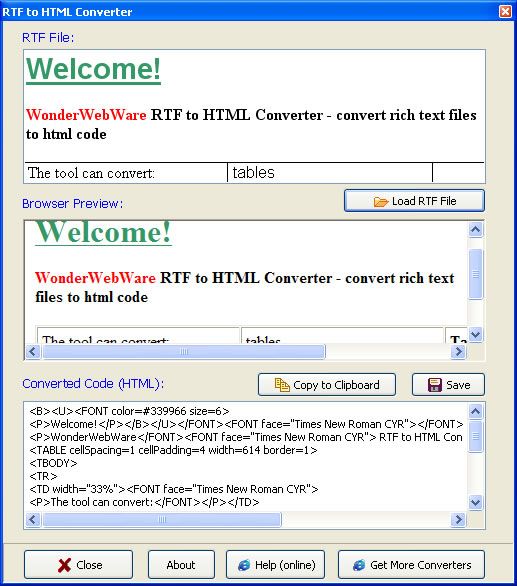
 При необходимости вы можете создать учетную запись Google+, а затем открыть файл RTF в GD, как указано выше.
При необходимости вы можете создать учетную запись Google+, а затем открыть файл RTF в GD, как указано выше.
 cloud
cloud Conholdate Viewer чистый, быстрый, безопасный и поддерживает все современные веб-браузеры. Таким образом, одним щелчком мыши вы можете просматривать, совместно использовать или даже встраивать файлы RTF в свой веб-сайт, блог и т. д. кодирование форматированного текста и графики для использования в приложениях. Этот формат облегчает межплатформенный обмен документами с другими продуктами Microsoft, что служит цели функциональной совместимости. Эта возможность делает его стандартом передачи данных между программным обеспечением для обработки текстов, и, следовательно, содержимое может быть передано из одной операционной системы в другую без потери форматирования документа. Спецификации формата файлов доступны Microsoft для общедоступной загрузки, и на них можно ссылаться с точки зрения разработчика.
Conholdate Viewer чистый, быстрый, безопасный и поддерживает все современные веб-браузеры. Таким образом, одним щелчком мыши вы можете просматривать, совместно использовать или даже встраивать файлы RTF в свой веб-сайт, блог и т. д. кодирование форматированного текста и графики для использования в приложениях. Этот формат облегчает межплатформенный обмен документами с другими продуктами Microsoft, что служит цели функциональной совместимости. Эта возможность делает его стандартом передачи данных между программным обеспечением для обработки текстов, и, следовательно, содержимое может быть передано из одной операционной системы в другую без потери форматирования документа. Спецификации формата файлов доступны Microsoft для общедоступной загрузки, и на них можно ссылаться с точки зрения разработчика. Conholdate Viewer чистый, быстрый, безопасный и поддерживает все современные веб-браузеры. Таким образом, одним щелчком мыши вы можете просматривать, совместно использовать или даже вставлять файлы RTF на свой веб-сайт, в блог и т. д. метод кодирования форматированного текста и графики для использования в приложениях. Этот формат облегчает межплатформенный обмен документами с другими продуктами Microsoft, что служит цели функциональной совместимости. Эта возможность делает его стандартом передачи данных между программным обеспечением для обработки текстов, и, следовательно, содержимое может быть передано из одной операционной системы в другую без потери форматирования документа. Спецификации формата файлов доступны Microsoft для общедоступной загрузки, и на них можно ссылаться с точки зрения разработчика.
Conholdate Viewer чистый, быстрый, безопасный и поддерживает все современные веб-браузеры. Таким образом, одним щелчком мыши вы можете просматривать, совместно использовать или даже вставлять файлы RTF на свой веб-сайт, в блог и т. д. метод кодирования форматированного текста и графики для использования в приложениях. Этот формат облегчает межплатформенный обмен документами с другими продуктами Microsoft, что служит цели функциональной совместимости. Эта возможность делает его стандартом передачи данных между программным обеспечением для обработки текстов, и, следовательно, содержимое может быть передано из одной операционной системы в другую без потери форматирования документа. Спецификации формата файлов доступны Microsoft для общедоступной загрузки, и на них можно ссылаться с точки зрения разработчика. Щелкните внутри области перетаскивания, перетащите или вставьте URL-адрес в файл RTF
Щелкните внутри области перетаскивания, перетащите или вставьте URL-адрес в файл RTF Мы поддерживаем все новейшие браузеры, такие как Chrome, Safari, Opera, Firefox, Edge и Tor.
Мы поддерживаем все новейшие браузеры, такие как Chrome, Safari, Opera, Firefox, Edge и Tor. Viewer
Viewer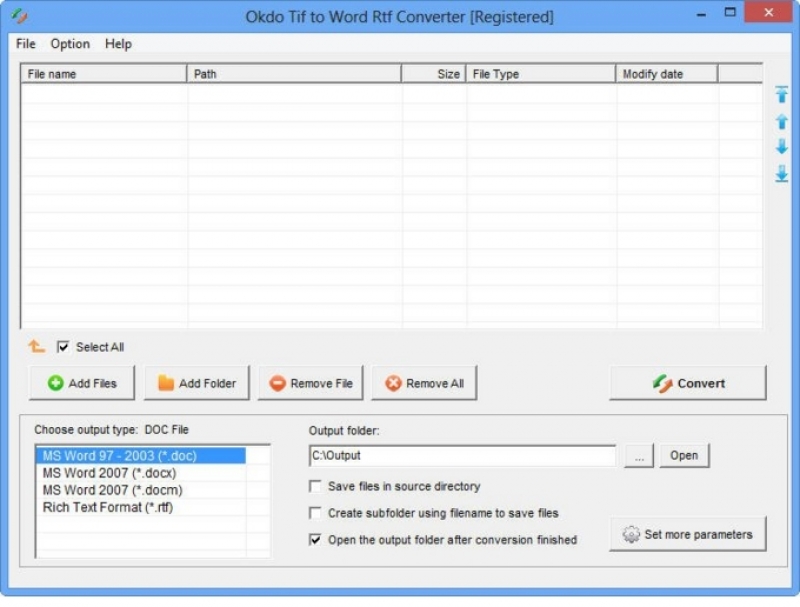


 Кроме того, я предложу альтернативные решения, такие как онлайн-сервисы для просмотра файлов в формате RTF непосредственно из браузера, который вы обычно используете для просмотра Интернета, или приложения, которые будут установлены на вашем мобильном телефоне или планшете для открытия документов с расширением RTF, даже когда у вас нет ПК.
Кроме того, я предложу альтернативные решения, такие как онлайн-сервисы для просмотра файлов в формате RTF непосредственно из браузера, который вы обычно используете для просмотра Интернета, или приложения, которые будут установлены на вашем мобильном телефоне или планшете для открытия документов с расширением RTF, даже когда у вас нет ПК.