Автор: alexxlab

10К сколько это: Калькулятор процентов. Процент от числа

alexxlab / / Разное

Помощь и обучение по Windows

Помощь и обучение по Windows

Обзор с помощью Microsoft Edge в Windows

В Microsoft Edge есть встроенные средства, которые помогают защитить конфиденциальность и безопасность в Интернете при просмотре. Изучите сведения о работоспособности паролей, мониторинге паролей, предотвращении отслеживания и т. д.

Открытие Microsoft Edge

Начало использования мобильных приложений в Windows 11

Amazon Appstore и мобильные приложения теперь доступны в виде предварительной версии. Узнайте, как настроить их на компьютере с Windows 11.

Приступить

Обзор Windows

Подготовка к Windows 11

Найдите ответы на самые распространенные вопросы об обновлении до Windows 11.

Ознакомьтесь с ответами на часто задаваемые вопросы об обновлении

Встречайте мини-приложения

Будьте в курсе своих любимых сведений.

Подробнее о мини-приложениях

Собрание Windows 11

Узнайте, как использовать новые функции Windows 11.

Просмотр серии видео

Изучение панели задач

Научитесь работать с Windows 11.

Получите сведения о панели задач

Пользуйтесь актуальными версиями

Узнайте, как использовать Центр обновления Windows, чтобы поддерживать свой ПК в актуальном состоянии, на ваших условиях.

Подробнее об обновлениях

Освобождение места

Узнайте, как освободить место на диске компьютера.

Освобождение места

Повышение производительности

Мы предлагаем несколько советов, которые помогут повысить эффективность работы вашего ПК с Windows 10.

Повышение производительности ПК

Безопасность

Безопасность Windows обеспечивает новейшую антивирусную защиту для вашего компьютера. Мы покажем, как использовать это приложение.

Убедитесь, что ваше устройство защищено

Windows 8.1 окончания поддержки

Благодарим вас за верность. Мы хотим помочь вам подготовиться и рекомендуем перейти на компьютер с Windows 11, чтобы получать поддержку и защиту.

Дополнительные сведения о завершении поддержки Windoes 8.1

Оптимальное качество изображения на мониторе

Windows анализирует характеристики вашего монитора и определяет оптимальные параметры изображения.

Оптимизация настроек монитора

Поиск параметров компьютера

Установите устройства, персонализируйте свой ПК и выберите конфигурацию Windows в разделе «Параметры».

Поиск параметров компьютера

Поддержка Windows 7 прекращена

Поддержка Windows 7 была прекращена 14 января 2020 г. Получите подробные сведения и узнайте, что это означает для вас.

Сведения

Подготовка к переходу

Переходите на ПК с Windows 10? Мы рады это слышать! У нас есть необходимая информация, чтобы помочь вам плавно выполнить переход.

Руководство по переходу

Возьмите файлы с собой

Узнайте, как переместить файлы с компьютера с Windows 7 на внешнее запоминающее устройство.

Инструкции

Популярные разделы

Требования к системе для Windows 11

Подключение при настройке компьютера с Windows 11

Устранение неполадок Bluetooth в Windows

Персонализация компьютера

Установить быструю поддержку

Все о компьютерных играх на Xbox

Обновление Windows

Резервное копирование ключа восстановления BitLocker

Устранение неполадок с подключением принтера и печатью в Windows 10

Темы рабочего стола

Использование панели задач в Windows 11

Сочетания клавиш в Windows

Установка и активация

Активация Windows 10

Использование средства устранения неполадок активации

Переустановка Windows 10

Установить быструю поддержку

Центр обновления Windows

Обновление Windows 10

Устранение неполадок при обновлении Windows 10

Центр обновления Windows: вопросы и ответы

Содержание последнего обновления Windows 10

Устранение неполадок

Исправление размытости приложений в Windows 10

Резервное копирование ключа восстановления BitLocker

Устранение неполадок с подключением принтера и печатью в Windows 10

Устранение проблем с Bluetooth в Windows 10

Персонализация

Использование панели задач в Windows 10

Закрепление и открепление приложений в меню «Пуск»

Персонализация экрана блокировки

Изменение пароля Windows

Установка и обновления

Обновление с Windows 8 до Windows 8. 1

Требования к системе

Включение автоматического обновления приложений

Приложение «Запись голоса» для Windows: вопросы и ответы

Скачивание и установка драйверов в Windows 8.1

Создание USB-накопителя восстановления

Приложение «Ридер» для Windows: вопросы и ответы

Распространенные термины для компьютеров и устройств

Активация Windows 7 и Windows 8.1

Как найти ключ продукта Windows

Переход на компьютер с Windows 10

Изменение разрешения экрана

Обновление драйвера для оборудования, работающего неправильно

Устранение неполадок с принтерами в Windows 7 и Windows 8. 1

Настройка беспроводной сети

Восстановление утерянных или удаленных файлов

Изменение или сброс пароля Windows

Устранение STOP-ошибок (ошибки типа «синий экран») в Windows 7

Расширенные параметры запуска (включая безопасный режим)

Распространенные термины для компьютеров и устройств

Utair. Сколько стоит дополнительный багаж и как его приобрести

Содержание статьи

  • Багаж
  • Багаж сверх нормы
  • Превышение размеров
  • Превышение веса
  • Превышение веса и размеров
  • Рейсы исключения
  • Полет разными авиакомпаниями
  • Дополнительный багаж для участников программы Utair Status

На рейсах Utair у вас есть несколько способов купить и оплатить сверхнормативный багаж:

— Через сервис «Управлять билетом». В первую строку впишите серию и номер паспорта без пробела, номер заказа или номер билета, во вторую — фамилию пассажира точно как в билете → Нажмите «Найти заказ» → Нажмите «Купить услуги».

— Во время онлайн регистрации на рейс за 36 часов до вылета.

— В аэропорту вылета в агентстве, которое может принимать плату за сверхнормативный багаж.  При оформлении услуги в аэропорту стоимость будет такая же, как и онлайн.

Багаж

Норма провоза багажа, установленная тарифом, по которому вы купили билет на рейс, регулирует три основных параметра — количество мест, вес багажа, габариты. Всё, что выходит за пределы этих параметров, считается сверхнормативным багажом.

Провезти ручную кладь или багаж сверх нормы можно только за отдельную плату. Стоимость меняется в зависимости от момента, когда вы платите — до начала регистрации на рейс, во время регистрации или во время посадки в самолет. Выгоднее всего оплачивать сверхнормативный багаж заранее — на сайте или в мобильном приложении Utair.

Если в билете несколько направлений, то за сверхнормативный багаж придется заплатить отдельно для каждого из них.

Важно! Для рейсов по территории Российской Федерации и при вылете из Российской Федерации стоимость багажа оплачивается в рублях, для рейсов при вылете в Российскую Федерацию — в долларах США.

Багаж сверх нормы

Доплатите, чтобы взять с собой в багаж еще одну сумку, чемодан или коробку.

Место покупки

 Багаж до 10 кг 55х40х25
По России/при вылете из России/при вылете в Россию 

Багаж до 20 кг 203см
По России/при вылете из России/при вылете в Россию 

Багаж от 21 до 30 кг 203 см
По России/при вылете из России/при вылете в Россию 

При покупке билета более чем за 36 до вылета 

1499 ₽ / 1990 ₽ / 35 $

2499 ₽ / 2990 ₽ / 55 $

3499 ₽ / 3990 ₽ / 75 $

При регистрации на рейс на сайте и в мобильном приложении

А так же при покупке билета менее чем за 36 часов до вылета

2000 ₽ / 2450 ₽/ 45 $

3000 ₽ / 3450 ₽ / 65 $

4000 ₽ / 4450 ₽ / 95 $

При регистрации на рейс в аэропорту

2300 ₽ / 3000 ₽ / 50 $

3500 ₽ / 4000 ₽ / 75 $

4500 ₽ / 5000 ₽ / 105 $

При посадке в самолёт

3000 ₽ / 4500 ₽ / 65 $

4000 ₽ / 5500 ₽ / 85 $ 

─

Для трансферных полетов стоимость удваивается.

Превышение размеров

Если сумма трех измерений — длины, ширины, глубины — вашего багажа превышает 203 см, за него придется доплатить.

Место покупки

Превышение габаритов (более 203 см по сумме 3-х измерений),вес не более 20 кг.
По России/при вылете из России/при вылете в Россию 

При покупке билета

─

При регистрации на рейс

3500 ₽ / 4000 ₽ / 75$

При посадке в самолет 

─


Для трансферных полетов стоимость удваивается.

Превышение веса

Если общий вес вашего багажа больше допустимой тарифом нормы, за него придется доплатить.

Место покупки

Багаж от 21 до 30 кг 203см.
По России/при вылете из России/при вылете в Россию 

Багаж от 31 до 50 кг 203см.
По России/при вылете из России/при вылете в Россию 

При покупке билета

─

─

При регистрации на рейс

3500 ₽ / 4000 ₽ / 75 $

7000 ₽ / 7500 ₽ / 145 $

*На маршрутах: Тюмень — Ханты-Мансийск — Тюмень, Тюмень — Березово — Тюмень, Тюмень — Белоярский — Тюмень, Тюмень — Игрим — Тюмень, Тюмень — Советский — Тюмень, Тюмень — Урай — Тюмень, Тюмень — Нягань — Тюмень установлен тариф на превышение нормы багажа по весу от 10 до 20кг — 1500 ₽

Для трансферных полетов стоимость удваивается. Если норма превышена по нескольким категориям, например вес сумок и их количество, то заплатить придется за каждое превышение.

Превышение веса и размеров

Место покупки

Превышение габаритов (более 203 см по сумме 3-х измерений),

вес от 21 кг до 30 кг.
По России/при вылете из России/при вылете в Россию 

Превышение габаритов (более 203 см по сумме 3-х измерений),

вес от 31 кг до 50 кг.
По России/при вылете из России/при вылете в Россию 

При покупке билета

─

─

При регистрации на рейс

7000 ₽ / 8000 ₽ / 150 $

10500 ₽ / 11500 ₽ / 220 $

Негабаритный, тяжеловесный багаж, багаж весом свыше 30 кг можно оплатить только в аэропорту на стойке регистрации.

Рейсы исключения

  1. Москва — Нарьян-Мар — Москва, Москва — Усинск — Москва, Москва — Ухта — Москва, Москва — Ноябрьск — Москва, Москва — Когалым — Москва. На этих рейсах стоимость дополнительного багажа составляет 2 990 ₽. Это одно место весом до 20 кг и габаритами не более 203 см в сумме трех измерений, купленное раньше чем за 36 часов до вылета. 
  2. Москва — Грозный — Москва, Москва — Ханты-Мансийск — Москва, Москва — Самара — Москва, Москва — Санкт Петербург — Москва, Москва — Сыктывкар — Москва, Москва — Тюмень — Москва, Москва — Уфа — Москва. Сургут — Самара — Сургут, Сургут — Екатеринбург — Сургут, Сургут — Тюмень — Сургут, Сургут — Новосибирск — Сургут.
    Новый Уренгой — Тюмень — Новый Уренгой, Новый Уренгой — Уфа — Новый Уренгой.
    Красноярск — Омск — Красноярск, Красноярск — Новосибирск — Красноярск.
    Самара — Екатеринбург — Самара, Самара — Уфа — Самара.
    Уфа — Екатеринбург — Уфа, Уфа — Тюмень — Уфа.
    Нижневартовск — Омск — Нижневартовск.
    На этих рейсах стоимость дополнительного багажа составляет 1999 ₽. Это одно место весом до 20 кг и габаритами не более 203 см в сумме трех измерений, купленное раньше чем за 36 часов до вылета.  
  3. На рейсе Нахичевань — Москва багаж заранее приобрести нельзя. Оплатить багаж можно в аэропорту вылета по стоимости 1$ за килограмм.
    На рейсах Баку-Москва, Гянджа-Москва установлен багажный тариф 4 AZN/кг. Тариф применяется, если вес сверхнормативного багажа пассажира более 30кг.   Если вес сверхнормативного багажа пассажира 30 кг и менее, то оплата взимается за место багажа. Тарифы на сверхнормативный багаж в таблице, расположенной выше.
    На рейсах Баку-Сургут, Баку-Тюмень установлен багажный тариф 4 AZN/кг. Тариф применяется, если вес сверхнормативного багажа пассажира более 30кг.   Если вес сверхнормативного багажа пассажира 30 кг и менее, то оплата взимается за место багажа. Тарифы на сверхнормативный багаж в таблице, расположенной выше.
  4. Если ваш багаж весит больше 30 кг, то на рейсах Стамбул — Грозный — Стамбул,  придется заплатить 3 $ за каждый килограмм. Если вес багажа 30 кг и менее, то оплата взимается за место багажа. Тарифы на места сверхнормативного багажа можно увидеть в таблице выше.
  5. На внутриокружных маршрутах на территории Ханты-Мансийского автономного округа — Югры пассажир оплачивает сверхнормативный багаж за каждый килограмм веса. Уточнить, сколько стоит килограмм сверхнормативного багажа, можно в онлайн-чате службы поддержки Utair или в аэропорту вылета. Оплатить багаж можно только в аэропорту при регистрации на рейс.
    Рейсы по территории ХМАО — Югры:
    Белоярский  — Советский — Белоярский
    Белоярский — Нягань — Белоярский
    Белоярский — Березово — Белоярский
    Сургут — Белоярский — Сургут
    Березово — Игрим — Березово
    Советский — Урай — Советский
    Нягань — Сургут — Нягань
    Ханты-Мансийск — Нижневартовск — Ханты-Мансийск
    Ханты-Мансийск — Игрим — Ханты-Мансийск
    Ханты-Мансийск — Белоярский — Ханты-Мансийск
    Ханты-Мансийск — Березово — Ханты-Мансийск
    Ханты-Мансийск — Когалым — Ханты-Мансийск
    Ханты-Мансийск — Урай — Ханты-Мансийск
    Ханты-Мансийск — Советский — Ханты-Мансийск
    Ханты-Мансийск — Сургут — Ханты-Мансийск
    Ханты-Мансийск — Нягань — Ханты-Мансийск

Полет разными авиакомпаниями

Если вы летите рейсом Utair с пересадкой на рейс другой авиакомпании, учтите, что нормы багажа и ручной клади могут различаться. Почитайте о нормах другой авиакомпании на ее сайте и убедитесь, что ваши багаж и ручная кладь им соответствуют.

Дополнительный багаж для участников программы Utair Status

Владельцы карт элитных уровней программы лояльности Utair Status имеют привилегии в провозе багажа:

Вид багажаSilverGold
Ручная кладь 10 кг (55х40х25см)—бесплатно
Спортинвентарь (до 20 кг)бесплатнобесплатно

 

зачем их нужно делать и какой будет результат, советы фитнес-инструктора

«10 000 шагов в день — это минимум!» — твердят нам фитнес-инструкторы, диетологи и блогеры. Но откуда взялась эта цифра? Почему 10 000, а не 5 или 15? Да и всем ли так необходимо нахаживать эти несчастные шаги? Давай разберемся.

Редакция сайта

Теги:

Здоровье

Похудение

Фитнес

Гаджеты

Фигурное катание

Теория про десять тысяч шагов, которые необходимо проходить ежедневно, стала буквально мантрой современного человека. Но откуда она взялась? Почему именно 10000 шагов в день и действительно ли такое количество оказывает какое-то невероятное влияние на наше здоровье и самочувствие? Столько вопросов, на которые мы попробуем дать ответы.

Не занимайтесь самолечением! В наших статьях мы собираем последние научные данные и мнения авторитетных экспертов в области здоровья. Но помните: поставить диагноз и назначить лечение может только врач.

10 000 шагов: история вопроса 

Существует правило, с утверждением которого мало кто теперь решится спорить. Заключается оно в следующем. Для поддержания мышечного тонуса и нормальной работы сердечно-сосудистой системы в день следует проходить от 10 до 12 тысяч шагов. Это примерно 5-8 км в зависимости от длины шага.

На самом деле, нет научного обоснования тому, что именно ходьба 10 000 шагов в день — универсальный и подходящий всем способ, так как все мы индивидуальны. Например, для тех, кто привык вести малоподвижный образ жизни, такое количество пройденного пути покажется настоящим достижением. А те, кто ведут активный образ жизни, это расстояние даже и не заметят.

Первое упоминание о необходимости преодоления 10 000 шагов каждый день появилось в японской рекламе шагомеров еще в 60-х годах. Так что эта цифра – просто еще один успешный маркетинговый ход. Но, разумеется, лучше стремиться преодолевать подобные дистанции, нежели свести физические упражнения к минимуму.

Можно как совершать прогулки по парку, так и проходить необходимое расстояние на беговой дорожке. Оба вида активности полезны, если набирается норма 10 000 шагов в день.

Как приучить себя проходить 10 000 шагов в день 

Если ты решила кардинально изменить жизнь и начать больше двигаться, не стоит сразу гнаться за большими цифрами. Начинай с малого и постепенно прибавляй по 500-1000 шагов в день, пока не сможешь похвастаться перед подругами и коллегами: «Я хожу 10 000 шагов в день». Отслеживать свои результаты можно как с помощью шагомера, так и применяя различные мобильные приложения.

Разумеется, чтобы делать в день 10000 шагов, необходимо правильно подбирать обувь для длительных пеших прогулок. Она должна быть в первую очередь удобной, не сдерживать движение ноги и нигде не натирать. Обувь на плоской подошве отлично подойдет (кроссовки, туфли без каблука, ботинки и так далее).

Многое зависит от наличия свободного времени и твоего образа жизни. Если тебе не по душе проводить драгоценные минуты после работы в зале или отправляться туда в выходной, прогулка по парку или от работы до дома – отличный выход. К тому же променад на свежем воздухе полезен не только для здоровья (помогает увеличить размер легких, тренирует сердечно-сосудистую систему, снижает развитие варикоза), но и для эмоциональной разгрузки.

Отзывы тренированных людей говорят о том, что 10000 шагов в день помогают им оставаться бодрыми и поддерживать позитивный настрой. А если ты задалась целью похудеть, то просто старайся проходить нужное расстояние со скоростью 6 — 6,5 км/ч.

В современном мире мы больше времени проводим, сидя перед компьютером, в метро, в машине, и практически не двигаемся. Это приводит к большим рискам для здоровья: ожирению, заболеваниям сердца и сосудов, болезням опорно-двигательного аппарата, диабету, раку и другим малоприятным вещам. Поверь, 10 тысяч шагов в день – вполне осуществимая планка. Главное, не зацикливаться на ней. Просто ищи любую возможность провести время активно.

Например, вместо того, чтобы стоять на эскалаторе, поднимайся по нему пешком, пройди на одну остановку больше, чем планировала, спускайся и поднимайся по лестнице, полностью отказавшись от лифта.

К тому же существует множество гаджетов и приложений, с помощью которых ты можешь контролировать, сколько шагов ты сделала за день. В общем, подобная активность действительно способствует поддержанию здоровья. Но убиваться ради достижения этой цифры не стоит. Сколько бы ты шагов ни делала, главное – чтобы все было в удовольствие. А ты получишь его в двойном размере, когда узнаешь, сколько калорий сжигают 10000 шагов в день.

10 000 шагов в день для похудения 

Многие девушки полагают, что если ходить себе каждый день по 10 000 шагов, можно невероятно похудеть или качественно изменить фигуру. К сожалению, это не так. Ничего особенного с талией и организмом не произойдет, просто они наконец-то начнут нормально функционировать.

Когда человеческий организм недополучает нормальной ежедневной нагрузки, это выливается в огромное количество мелких и крупных проблем: от головных болей до варикоза и проблем с суставами и лишним весом. Сами по себе 10 000 шагов в день похудеть не помогут, но вот отсутствие адекватной активности принесет очень серьезные проблемы со здоровьем.

Сколько калорий тратится, если ходить 10 000 шагов в день, и можно ли похудеть? Можно. Но для этого нужно будет еще и нормализовать питание так, чтобы количество потребляемых ежедневно калорий было меньше, чем количество затраченных. А что касается объема затрачиваемых калорий, это зависит от веса, роста и темпа, в котором эти шаги делаются.

Посчитаем в среднем, сколько калорий сжигается, если ходить 10 000 шагов в день. Стоит начать делать это в бодром темпе, можно потратить от трехсот до четырехсот ккал. Можно использовать датчик частоты сердечных сокращений для получения более точного результата.

Личный опыт и отзывы о 10 000 шагах в день

Арина Байбуртян, генеральный директор Лаборатуар Экспансьянс, так рассказывает о своем опыте:

«В детстве я всегда занималась спортом. Фигурное катание, плавание и большой теннис в те далекие советские времена были моими фаворитами. С рождением детей приоритеты изменились. Много лет я живу жизнью работающей мамы под моим любимым девизом «Успеть все!». Семья, дети, профессия занимали все мое время в сутках, но почему-то на спорт почти никогда не оставалось времени.

В один момент я поняла окончательно, что хочу привести себя в порядок и выделить время для себя. Так я попала на мини-тренинг к психологу, который помог мне не только изменить привычки питания, но и вернуть движение в каждый мой день.

При рабочем офисном графике я ежедневно прохожу минимум 10 км (13-14 тысяч шагов), часто 13-15 км. Это стало привычкой, помогают часы, считающие мою активность. Не ложусь спать, пока цель не выполнена. Старший сын смеется иногда, но польза от 10 000 шагов в день очевидна. Как-то за 4 месяца ушло 7 кг! Я не пью алкоголь ни в каком виде, не ем сахар, стала чувствовать себя лучше, ни разу не болела за всю зиму.

Как успеваю? Очень простой подход: бросаю часто машину, иду пешком, пользуюсь метро, занялась скандинавской ходьбой, хожу 2 раза в неделю в зал на дорожку, 1 раз на йогу, в офисе всегда подхожу к коллегам вместо звонков и смс. Так что если ходить 10 000 шагов в день, обязательно похудеешь. Но только в том случае, когда в целом ведешь активную жизнь и следишь за питанием. Запасаться пачкой крекеров или упаковкой глазированных пончиков для восстановления сил во время прогулки точно не стоит.

В итоге лично убедилась, что вопрос совсем не в наличии свободного времени! Когда начинаешь правильно питаться и каждый день ходить 10000 шагов, то не только похудеешь. Но еще отыщешь в себе дополнительные резервы и откроешь огромную силу. Если хочется жить легко и с удовольствием, чтобы близкие увидели приятные перемены в вашем образе и настроении, просто примите для себя решение. А дальше вопрос исполнения, помимо гаджетов помогает личный фокус внимания на свои ощущения. Удачи! Ходите больше, это огромное удовольствие».

Фото: Getty Images

Untitled-1

%PDF-1.5 % 1 0 obj >/OCGs[8 0 R 875 0 R]>>/Pages 3 0 R/Type/Catalog>> endobj 2 0 obj >stream 2018-02-07T10:09:33+03:00Adobe Illustrator CC (Macintosh)2018-02-07T10:09:51+03:002018-02-07T10:09:51+03:00

  • 256176JPEG/9j/4AAQSkZJRgABAgEBLAEsAAD/7QAsUGhvdG9zaG9wIDMuMAA4QklNA+0AAAAAABABLAAAAAEA AQEsAAAAAQAB/+4ADkFkb2JlAGTAAAAAAf/bAIQABgQEBAUEBgUFBgkGBQYJCwgGBggLDAoKCwoK DBAMDAwMDAwQDA4PEA8ODBMTFBQTExwbGxscHx8fHx8fHx8fHwEHBwcNDA0YEBAYGhURFRofHx8f Hx8fHx8fHx8fHx8fHx8fHx8fHx8fHx8fHx8fHx8fHx8fHx8fHx8fHx8fHx8f/8AAEQgAsAEAAwER AAIRAQMRAf/EAaIAAAAHAQEBAQEAAAAAAAAAAAQFAwIGAQAHCAkKCwEAAgIDAQEBAQEAAAAAAAAA AQACAwQFBgcICQoLEAACAQMDAgQCBgcDBAIGAnMBAgMRBAAFIRIxQVEGE2EicYEUMpGhBxWxQiPB UtHhMxZi8CRygvElQzRTkqKyY3PCNUQnk6OzNhdUZHTD0uIIJoMJChgZhJRFRqS0VtNVKBry4/PE 1OT0ZXWFlaW1xdXl9WZ2hpamtsbW5vY3R1dnd4eXp7fh2+f3OEhYaHiImKi4yNjo+Ck5SVlpeYmZ qbnJ2en5KjpKWmp6ipqqusra6voRAAICAQIDBQUEBQYECAMDbQEAAhEDBCESMUEFURNhIgZxgZEy obHwFMHR4SNCFVJicvEzJDRDghaSUyWiY7LCB3PSNeJEgxdUkwgJChgZJjZFGidkdFU38qOzwygp 0+PzhJSktMTU5PRldYWVpbXF1eX1RlZmdoaWprbG1ub2R1dnd4eXp7fh2+f3OEhYaHiImKi4yNjo +DlJWWl5iZmpucnZ6fkqOkpaanqKmqq6ytrq+v/aAAwDAQACEQMRAD8AfYQXdzdx2FhJMLqc8ItP vEMgc0rxR+p2HZjnPiJJ5X7nqp1XFIAgfxRNfMfsCYv+U/mG9crN5emtJf8Af8Dx+mf9ixU/8LmQ MWUcgse0/DHpyCQ7pc/x8UovfyW89xMfq2nyXC9hQI34nj+OWRjPrEudi7bwn6jw/ah/+VOfmX/1 Y5f+RkH/AFUyfhS7m/8AlfTfz/v/AFO/5U3+Zf8A1Y5P+RkH/VTHwpdy/wAr6b+f9/6nf8qb/Mv/ AKscn/IyD/qpj4Uu5f5X038/7/1O/wCVN/mX/wBWOT/kZB/1Ux8KXcv8r6b+f9/6nf8AKm/zL/6s cn/IyD/qpj4Uu5f5X038/wC/9SP0L8pfzBtdUhuLnRZVij5GvOJtypA2VyepyGXDMxoBxdZ2ngni MYy3PvTgflz53NuIn0mUn6vFC+6UJd63H7XZfv7ZT+XnfJ151mLisS/iJ+Q9Kt/yr/zp65lOkzH9 9JMQSm5VPThh3uhG/t3yP5bJ3Nf5rHVcQ+kD7bKmPy787rEFXS5uaxLEsnw1DStW4k69fDD+Xn3M vzeIm7HO/l9IX/8AKvPOvKselywmvoxOOB9GBR1QVPxPT6O/TH8vk7kfm8Vbm+v9aXn5D8c1Bvy3 82VLf4cL8T1lflO1O/McgD4fF92HwMncWz87Dl4h+A9Py/Yt1DyZ5r0yzkvbmxmSCzUSxXEpUsvI gNA5BPINWgO/4DISwzAsigxjqMcjVj1bGuX9Yfj9LKPySMY80XsSfYSyaSD2imkiYD6GDAZkaH6z 7nF7SvwwT1O/vF/opv8AO9lXzHYuZLiGlmKTQDmq/vX/ALxaNUf7HDrvrHuT2YLgRUTvyP6D+1iE PkzzHrFlFeJpC6xYzgmG8gAikIBoaciB1H8wzHhhmd4guaNTHHKhI45Dodx+Pgh7z8k/NJX1LSxn iY7+jKFantyQmn45cIZBzi5OLtyI2nR8x+1Kv+VOfmTUhdElYD9rnEAf+CcHLRjl3OaO19N/P+93 /Km/zL/6scn/ACMg/wCqmPhS7k/yvpv5/wB/6nf8qb/Mv/qxyf8AIyD/AKqY+FLuX+V9N/P+/wDU 7/lTf5l/9WOT/kZB/wBVMfCl3L/K+m/n/f8Aqd/ypv8AMv8A6scn/IyD/qpj4Uu5f5X038/7/wBT v+VN/mX/ANWOT/kZB/1Ux8KXcv8AK+m/n/f+pkkH5a+dUsI7c6TMGW19A0KbNKwMu4bsB179sxjg yXddXTz12IzMuIfXfy5Ir/lX3nM3HqHSpuBuPVI+D7CRcIx1/m3yP5fJ3NP5rHw1xD6a+Zs/Yoj8 u/PHoBf0VMJBAI+QKbSTPW4YfF+z1Hj2w/l59zM6vFfMVxX8Ij0qjfl35yZnX9EzJFIwiIBX4baN fhRfi/bPXwB3x/L5O5iNXjH8Qsb/AOcevwU5Py685yqhm0SSYtssEhUQQKOi8VLcm96U9xj+XyDo WQ1mOPKdeY+qX6g6P8u/OcSu0OiSQsnWGMqYJ1PVeLFeLe9Ke5x/L5D0Ky1eOVXO/M/VH9YSe7s5 tOvZLO5QrJZusTxtufQnPAxt48Hh4DKSCNi2xlxix/F/uo738QmvkKdR5x0iEXUorcp/od0n73b+ RzQtTv8Aa2y3APWNuvRr1UP3cjwjl9UeXxH9j078wPzC1jy/q8NjaWitG6xSCV1dvU5uVYAqKUWm 46+4zaajOMdWQP1fj+x0GDTzyE8I5D8fj7UD5g/Oa60R9Mgm0h2ri/09dQlVryC2MYZnUr6cvxkV Qb9PizJaUph/5yNgnETQ6LFIs684qalAKqqlpCeSKFCCOT4mNCUIBqVBVRdp/wA5B6W96I7yxt7O zWSNJ7t9StyUjdwhk9OgZggIYgb77VxpXpP6at5dLk1OydLmzNmt7ayqfhkR0Z1IPgygUyE5UCe5 MRZpj8vnfUbe5WO4sofTCo8hjlYtxZFk+EMgqeL5hnVSB3Ab/BBGxRS+cpuRU2BJUlSQ0gBIJ6Vi 8Bk/zR7vx8keD5q1p5seWZVntDFD8XqTL6r0p2AEe+9BhjqbO4/HyQcXmjj5k0nhzDyMCCy8YJjU Dbb4Ms8eP4BYeGVzeYNLVirNKCDxP7ibr4VCYfGj+AV8MosXKutvJFvHOdiQQeJQsNjQjp3ywGxb Ah59qH5o3cXnKXRoYbeK2s2ZJxcMVll4blkrxp7UVvE7EZj9o5J6fHHIAJA9Px97fpJ6aQlHJIwm Pp7id/ny5WCs1f8ANq7sNQngFpaNFDIyLzuSkrAFh9gpsfhoR2+7MiBsA97QUw8ya2dV/K251aZI 4xMqOyxv6iBUuVX7RC12XfbMfWf3Z+h4uRpQTkADCvyNjdPNE6sKGPRoI2/1llBI/HMXRh2n4/od t2rIHH78kir/AJ3yiPzFYsZ5baloP3sac4x+9faQUbbw/Xg131j3MOzI3AihLfkdj8GV+WNXu9N/ Ke31O1Rb64gjkdRGpKvW5YFgqmtADXY5m6OvDF/jd1uvBGSQAr3+5LNI/NrVptK1fUrjTBNBpsfq xhWMHNmnEQjMsoWMdTQdaDv1x02XjhZIJvp+D+3nsw1GGWOdEVslP/Qx0HwA6LCjOnrANqdvQQgC srMFKheTBRvv+zWhpkU0rm/5yLiKj0NEimdiOKDU7ZSUdFkRqMoI5IzNQjouNKzfyb+Y2k+aLG4N u8MeqWsbS3FhHOtyET9h/UjAUq2BUZrPmLUbK9lgtraGWOH6sHaSRkbldOyLQKjbArvmLlzyiaA7 vtbYYwRugYvPV0yRV08PK6hikcjkfHHHKlCIz+zMAffIDVnu/G362ZwjvVW863QZCNNJRweNHkJJ AB2pF4Vw/mj3fj5I8Ed6aQ+ZdP8AST6x6kVyE5TRCGdgrAhXAPp/EFY0rlwzxrfn7iwOMqg8w6We jS0JoD6E3Xf/ACPbD48fwCjwyiLTU7O7kaOBmLoKtyjkQU27sqjvko5BLkgxIY75886yeWfLsOor Ejz3JCK0nIRRkxly7UHQcenIfgcvhjMrroGHiRjIcV0T0SR/zO1SHQ7W7e3sXu3kVbstc+nCgY78 WAkUlO/xU2+0M12j1UsplGQoxLl6uOET/cy44fqRnkr8wtS17Wm066trGNBC0qy2d01wTwYKRQxo APiFN9/15zivK/P7q3m7WwNiJBHUfzSTkKPvGaHP9Z95ek0g/dx+P2R3Sb8q9e1K5886LZXEglje 4B5sPjHBS2xFOvGm+ZGPEBMEd7se09FjjhlOIo0+nr7TLK+9L60hf0W5xUd0o3j8BXNq8UrSW1vK waSJHZdlZlBI+ROKrUsrJDVLeNTSlQijalKbDFVi6XpirxW0hVa8uIjQCvj064qqtbQNG8bRqY3T 03SnwlNxxp4b4CLUKJ0rTSQWtYmIZHFVBo0Q4od+6jYZHw49zLiKj/h7Q+fP6jDzNfi4CvxbHI+D DuT4ku9ZH5Y8vxuzpYRBmNW+GoryDdDt1GAYIDoviS72j5X8usatp8B+aA4/l4dwXxJd6aZcwaKq xUkVKmq+xoR+o4qkN/5E8q32sHV7mxVr9uHqyBmUSenuvqKCFanuMjOIkKLXPFGXMLrnyP5Vubp7 qawVp5HaR2DyKC7gKx4qwG4HhkmxKvP+m6dp35b6jZQRmKxiWP8AdAs5o1yjMPiLMeRY5j6v+7P4 6uXob8WNc/2MI/JRm/xTfCQUnezeWcdkLSxCNK+Kou/398wtD9Z9zn9ogeGK5XQ8+dn5pd/zkLqt 9p/mbSntX487M81IBDUlala/PLdXASlv3Ob2HpoZcUuIdf0PTPymuGufy90ed1CtIkrMF2FTO/TM nTCoAfjm6btLGIZ5RHT9TJLHSrCxt2t7aLjC7c2Viz1Y0G5csewy9wV5sLE1rbRGvX4F3/DFWm07 T2dHa1iZ4/sMUUlfkabYquSys41ZY4UjDgh+Chahtz0p1xVqSxs5JDK8KNIxjZnI3JhYtGf9iTUZ EwB3pPEVBtB0VkEZsYeALMF4KBVyCx28aDI+DDuCeOXepv5a0F1CtYxUFdgKdaeHywHBDuT4ku9z +WtAfjysISUFFPHcCtevzxOCHcviS70XZ6fZWSslpAkCueTBBSpycYCPIMTInmr5JCX6xoGk6xpx 07UbcT2nwkRkkEFdgVYbg074oItL4vIHlKO0jtBYBreJneNWeQkNIKE8i3I7dKnbtkYxEeTGGOMB QCto/k3y1o06z6ZZLbSqhiDK8jfC1CRRmIP2Rkmbwvz00aecNYdYzwiu2klHeSegWKNa/Q33Zo8/ 1l6TTAnHEd8a90ep/QxX8ov/ACZGhf8AGdv+TbZl4/qDvO1v8Wn7v0vrjNi+fuxVIvOXnXQvJ+mQ 6nrcjxWU1zHa+rGhk4NLWjMF34qFJNAT7Yqxkf8AOQX5QHp5gHXj/vLedf8AkTimmH+a/wA/baa8 gufJ/mLTobeISxzafq1lfkzyIWAZWghJVStCtXX3p0xWksf8/PNiTSQtr3lNHAQxcrLXTzDxrMGH FG24v33r2xWlST8//MBgieHzF5TLEFZS1nrpXnzbjxIi6FKde/LsMVpRuvz382vZPTzN5Ut2mWSO O4js9bLo4Aqyh5XWqBqjkpBPbFaXJ+fnmQGTh5j8sGN3me1+s2WtCT0mmb0q+lEF48CtO9PtVNcV plflH88vL8OkSz+cdfsmu572ZLN9PtL9YfRSKFwvGSh2Kj1a1bqCN+uK0nJ/5yA/KIMFOvgFq0ra 3nah/wB8++K0znTNRstT0201Kxk9ayvoY7m1loy84pVDo3FgrCqsDQiuKETirF/zOYp5F1Rg6xlV iPqP9laTp8R6dMx9X/dn8dXK0QvKBV+559+SXL/El1xBWE2UjIz/AN5KTNFylYdge3+1mFofrPud h3l9A77HuGx2SP8A5yW/5SPSP+YNv+TpzI1h2fB2ns5/dy/rfoepfk5/5LTQ/wDjFJ/yfky/B9Ad F2v/AIzP3/oDM8udc7FXn1z+fX5X2V9e2Go6q9le2FzPaTwS21wx520hjdlMSSKVLKab/Rimku1z /nIH8uDp1zBpevCPUJ7ecWV49pdGCGfgRC0oMJYjnTojYrTCB+fXnGK3V/0/5WngieGB7t7LWgzt KHo/FUUb+k1eK0ritK0f5/eYzzr5i8pkivEiy17rUAVHp960+eK06L8+PN0gIGv+UeYrt9T17bip dq1jHRBXFaQifnj5wN+0g82eXJA1T9UFhq31eOiU3P1cT0JIavPqfDbFNJv5f/Pi/n13TRrXmHQG 0Yuxvl0yz1dbhg0EvpAG5hZePqhSaUbbwrVRTNR+f/5RlGf9PfApoW+qXtKmv/FPscVpOvKf5m+R /Nt7PZeX9TF7dW0frTx+jPFxQsFrWWOMHc9sUUyjFXYq+cvPLO3nXVfTk9SaO4k9MMKR24P2pJN9 2/lHh9JzR5/rPvej0wHhCxQI+MvIeXf/AGBin5Rf+TI0L/jO3/Jtsy8f1B3va3+LT936X1xmxfP3 Yq7FVOG3t4TIYYkjMrmSUooXk5ABZqdWNOuKsX85fl8nme+s7xte1XSpLGnox6dOkMdeVWcgxs3M oSleWw7YptJ5Pyek/R15bQ+cvMKz3fqs1xJdRvykkSNEaULHG0gRYVWnMVFRUV2VtC6H+TOqWV5b vqPnXVdSs7J45rG0fgFhlglV4mX1fXSiopjICCoJ3HTFbXJ+TGpR3IeLz/5lWBzzuUN4GkdwFAKv xouy0pxPbw3Vtx/JCCS2t7G581a5eaZD6oNnPcrxVWheKH0fSWIRtDzVlqGWq/Zptitsp8i+Tm8p 6Zdad+lbvVoZrp7mCa+cyTRo8aJ6RetGAZC2wXr07lQyPFXYq7FWLfme3HyLqjckTiIjzk+wtJ03 bp0zh2f92fx1crRC8o5/DnyeffklRvM95KA787J63UvwmSksX2E/ZQdv8zmFofrPudj2ltjA2G/I dOfM96Sf85Lf8pHpH/MG3/J05kaj6vg7P2c/u5f1v0PUvyc/8lpof/GKT/k/Jl+D6A6Ltf8Axmfv /QGZ5c652KrXhido2dFZom5xMwBKsVK8lr0PFiPkcVQ+qWLX+nXNkt1PZG5jaL63asqTx8xTnEzK 4Vh3NNsVYDZ/kpBaLbxxeb/MnoWzepFAbyIoGD8lYK0JAPWpHWvbFNoTUvyY8xzai91p/wCYOt2a PCkJDv6srGJTwLyq8PIc2ZivHuaUrXFbRj/krAixR2Xm3zBY28LvLHb291DHGHavGipCootaCtds VtV0n8pLyyurW9m87eYbq7gaBrgtcxCOb0Pi4OjROxjLljwZjsSOtTitobRPySh0fU9L1S18zau1 7ZyJLqXqTlor0g8nDpWoDN2LN8O253xW3peKHYq7FXYq+cfPbep5y1eGpuCLliLRBxFf5p33+HwH h3OaPP8AWfe9JphWKJ+nb6j/AL0fj4MV/KL/AMmRoX/Gdv8Ak22ZeP6g7ztb/Fp+79L64zYvn7sV dirsVdirsVYhN+ZujpAs0dhqE9eQeOOFPUUrI8VCrSKST6dfhrsVr9oVNK3pf5m6HqGqx6YtnqFv cSOsQaa1cRB2VmCmRC6j7ONKy7ArsVdirsVdirFvzPbj5F1RuapQQ/G45KP38e5G1cx9X/dn8dXK 0QvKNr/sef8A5Jgt5nvJSJW5WT/v5vhLfvYtkj24r9AzC0P1n3Ow7S2xgbc+Q+PM9Skf/OS3/KR6 R/zBt/ydOZGo+r4O09nP7uX9b9D1L8nP/JaaH/xik/5PyZfg+gOi7X/xmfv/AEBmeXOudirsVdir sVSnXvNGlaGYhfs6+uk0kZUAgi3UO4JJABodq4qxp/zl8qR3SW0sF+krlQK2xIqy8xRlZg3w/wAt fDrthpWYaRqtnq2nQ6hZszW04JQspRgVYqwKtvUMpGBUXirsVdirsVdir5y89ky+cdXgrJcAXL1t IxwXen99Ke3gK9OxzR5/rPvek0wrHE7R25nf/Sj8e8Mc/K3T76z/ADK0JbmF4v37AEj4T+7bow2O ZOGQMhTt+0c8Mmmnwm9v0voZfNfmOaUfVdDilt5L26sYJXvQhY2jzIXZfRbjy+rk0qc2bwiL/Snn L/qw2/8A0n/9eMVd+lPOX/Vht/8ApP8A+vGKu/SnnL/qw2//AEn/APXjFWFax5Z1Bb1LifSbpZtR vGFIdcmRA9xykccBEECUUjpXChXbyHfm3EB0m64BShI8wXYZgwoeTcKsadzvilUHkzV/r1zeNpty z3LmQx/pyZURmBB4BYV236EnFV3+C7/iK6JI0imNoppNbnkeN4YDbo6M8TUYITU9zua4qkWtnRdB ntLPW7T6vdiNvq88+sXPqkXBkiqJ1g2YmR+NGFD0pihb5d85+VNM1B9RsEs5rq7UWsdzdarJMwAk PKOKWa3LKJJOIZQ1GZV2qMUvR/0p5y/6sNv/ANJ//XjArv0p5y/6sNv/ANJ//XjFXfpTzl/1Ybf/ AKT/APrxirG/POv6jL5V8w2ep2a6ZLZW9lciaOb6yClxcsnT046FTbnseuY+qF4z+Orl6GJlmiAL 8vgw78iNRs7vzbqC2/qyMlixe4mO7Vmj2CjZR8gMxdHAiW/c7ftbTzhiBlQ9XIe4oT/nI+yu7jX9 MeCJpVisz6nAVpylamw37ZPUyAnv3OR7P5oRhISNWf0M/wDyqvL2LyD5ctLW3jlklt7mVjLK0QUR XHGnwxy1J9XMnT/QHTdrf4zP8dAybSNX1vU9JstSjsLaOO9giuERrqTkqyoHANLfqOWXOuRfr6// AMsdr/0lSf8AZPirvX1//ljtf+kqT/snxVJ/Mvl/VPMFvbwXKfVVt5RMr2WoTQSEgEULrb8qb9vl 0Jwqx7TvIE83qXBuL6RfXmBil1m5K8onMRoFtxtWOoxQrv8AlpcNavb/AFq+UPI8nqDWroupcUKo xtzxUdQB+rFK+2/LmWBJI1ku2jl4B0bWbwj4K0p+4267+NMVUNT8nRaZZ3uoXBnj0+O2uFntY9Ru JIhHM8skjLCLVqvyncqdyNqfZFFWMtc+RKR11GYQ26lvqrXuoNCUDh3DRGzKNQr4bV2xQ9K0DzDL rGnrdaPDZz2SERqy3E6AEKDx4vaqRRWHbAlMvX1//ljtf+kqT/snxV3r6/8A8sdr/wBJUn/ZPiql cahrFsI5J7O39J5oYnKXLswE0qxcgDAoNOdaVGKvnn8y9XsLbzhrENw80zLcN/oS/BGK/F8bAAsG rWm/yzTZcZMz73rOz9LOeOJiBHb6uZ+CL8hSqvnHSIRcTpW4T/Q7lavtv8Eh606ndtshgHrHv6NG qjeOR4Ynb6o/pH7A9N8r65c3Gt/oh9PkhgstZ1KSO/aaErN6st+SFiVzKApqKstK5vXmmT655x0P Q7yK11Jp4jNH6iSx2888f2uPEtCklG+eBUvX80fJTPGgurktLIkKf6BfbvJXjv6Gy7faO3virdv+ ZvlC4MKRzzmWdkRIzaXI+KQgAczH6ffryoe1caVX878vQ0orbz3RGoxUhtZFhlP7uTo7SQAf8GMV Qa3ytMYF0bWDMK1iGpW5bbr8P6RrjYTwlj2sz+bZ9Slk0eDUbKztALa8tryeGT/SGRZldJRqkf7E qbUOFC3S5fPFveQT6tb3l7ptxKUiS0lSNjzB9NfUOryjY9Wp9GKshN5DNMbY6Jq8kqEEwnUbcsGQ hh8P6Q6qah3ysZYk0CLTwmrpBaTqUq2LyXmlayT9bvUWR9SgUcY7qVVT4tQX7CqF+jJk0oBKn5hu taltfqOi6Zq1nq1xGbi2uZ7yGWIRQSRetUDUQPiWQKN+9e2KEpsW/MIcZ7lbi5t7eQPeLbyIGMCk Myg/phqOyBgD0rvQ9MKGTHVIQsTPo2sx+uoeJX1K3UlTTeh2h4yuWSMTRIDIRJ5Bj3mmL19P83Rz 6bewK2m6WDbXdwk0rj63dGqMs9wAPbkPlleqP7suVoZGOaJBrzY9+Q+n2Fr5svzbetG72Lc4J1IK 0mjpQ0ofvOYmikTLfudv2tnyTxDioji5j3FGfne4TzHYsZZ4KWgpLCvNB+9f+8WjbfRkdd9Q9zR2 YLgRUTvyOx+CLsvNbaB5Q8sXyX1hC88V9H9bvjItuYxcpJKyrFyYuI42YD2O4zM0g/dj8dXXa0Vl IqvL4M78qXYtvy70a8WGW5EOkW0y28ADzScLZW4RqSOTtSgFeuZDiocfmFbcSToOugrQuv6NnqA3 hQHl78a4q4fmDbsIiuh60fVCtT6hKGXlypzQ0ZfsHcimKpxoOuRazayXMVrdWYjlMJivYWt5SVVS SEf4uPxUr37bb4qkFtbWqxXM09rqYVr28/ex6i0MRJupfsJ9biC/LiMSVAJUtVtEfTuNlHrFvPdk Q2l4moNOqSP9luBvgrDbxxCkMdHlfzy0rW6eZL0ygEKlKyAgblh+lqGnXZR+qhQn2krAulQNqC6r Nco0ltPdHUHtllmt5GilZYzqD8RyjJA5HbITyRjzIDIRJ5BdNaImu2USWmsLayWd3M6DU5OLMklv xev12mwkbv3yVopEBtJYSmO31aQwqzuqao5JVFVmKj698QAcbjbfEG0kEMZudA83PcT3EOu39naX ZMlhbTPzeJH+wC/6Ui50qBuOvffYsU10KzurKOfTtdk1XUNStI0uri9S7eziEM7yLGOH6RlAIMDV PLIykALJoJAth4FtaPFbTQW2plVvbP8Aeyai00QIuovtp9bkDfLicYyEtwbSQRzeMfmZpWmXHnTV 5bmO4gdpz/paDnEaKBuBypTpuBmozTImaer0GpyRxRETGQrlyP4+aK8hTj/GOkwi8kI+spW1uUpN t/Ix41A79dsrwD1jbq4+qh+7keHpzidvj+A9J0WfyVY6hFfPcWFvq/6Z1ZLyZpYlmCGe8+F6tUAl U/DN682zH/FvlX/q82P/AEkw/wDNWBXf4t8q/wDV5sf+kmH/AJqxV3+LfKv/AFebH/pJh/5qxVJ/ MPmryu0ukldYsmCX8bORcxGiiOTc/F0wqwfzBptlJ5xk1TTtXtDNMoKav+kYFZFeUlrYwsxVESiy c4hyJ/yqtlPhniu9m+OSAkZcIsw4ectvOrrz+eydeZL7RdX0/wAw2tvqtlIZL0SC1N7HbrcoNPgT 0/WVgyhn2LA+Na7qb4miC48gDEirsef6Pl1QnlGfS9GsorefVrSOzF5a/UrNry3f0Io1aoHpsRxU FVBY8jx37YmySSbtmTGgAAKFdd/M2Tv9nkiBp/l7/Gra6Nf08LVZPr5vYmmKer6jWggNYlj+AVdS Dv0rUnVS0eQ5AbHCJcX48/x5OxGuiMJhXPp8KEru+81yS/zW2j635dFst5ZahAL++MumtqEdoJBJ fyMHdwwJTh8QG4O2xryXYTgTydaeGUDGQu66kfd+Nk307UNLt7fTdPm8wWhuxpmpRNdtcWxKvNPb tGh5/u+VPAHoftdcMIVGm7LlEsnEIgDu3r77+1j/AJZtLHSNTvbldStLK0kF213H+kYZ1uXZGRJq s8kxeQcCUZuK8epIGWzkSbvpTj4xGMDGhd3dyJ93Oq68vinHmW28va4NFuF1nTpPqqw/upr1Ilt3 jBcXCqnP1JFagCOKe4+Kut1mmnkPpI3Ffj8fs2Oj1ccQNjffzu9q8veN1vmS4sJ9H8xw2l4NWFto +kQyz2skfNnS6ugWrGwVWP2qVGWZYcGHh7gGGmnxZ+IVGyfMD70l/JGUN5nvIxcSy8bJ/wBzcJxk T97h4ovIf51zG0I9Z9zndpxrGDwgb8wdjzX/AJ3yiLzHYsbiS1pZikipzi/vX/vNjT23GOuHrHuX syNwIoS376PwZN5G1TTLPQPLkuo3ttCklpf8JpHSKN2F3Eapzb6euZmk/ux+OrrtaKykUR7018ne aPLMPlHQ4pdXso5Y9PtUkje4iVlZYVBBBaoIOZDipx/i3yr/ANXmx/6SYf8AmrFXf4t8q/8AV5sf +kmH/mrFXf4t8q/9Xmx/6SYf+asVYjr955f1nyneWUes2Zl+sXsi2ZvY4FuKzylYmlVucaycvtKf nUbZGcSeTIEUQRdjvI+75LdCm8uaBoen6cddsJQl9FIkUdzCyW8QUIsKP8DOkYWgZxXxwY4GI3ZZ ZxNCI4RGIHXp13JS9dK0OTzx+nZNfsEMTrKt+L6OSSSIzO5tPQb90i/BGxdKbnxBY2mR4avr5MI8 ImZcINxrnLbzq+fzG52Xa7H5d8weXvqzarp8wTUL9n0+e9W3ilSW/kId5Iyz0VfjUUIbbatCMLV4 ZzoxO4/S5mi1IxSs+++fLyOyawahoEE+n6fJ5jtJWGnajE98Jrf4Wnnt2UUrw+EVC1G4GT0+A48Q gebVkziWXjERW22/T43v72OeW9H0XSLu9vn1nT7aFWu3Nut+l01zK8bRrcl5D6itIjbrzNONN61F mOBBstYlAQMYxomV3ZJ+019nxRnmuy0PzD+iHGtae0UCQ8ed+kRtZY43cXKop4ysrhAqvXc1+EVr fGRF11Hk1ERJjYB4ZXzO/kaP6uZ35Ji935fnudR0z/EVqgOk6ZbLfieFObwTXfOhRlCkileBBWu1 Nsxs+MzgYjn5t+PKIz4q27t/xt5/FR8qQ6Ho2jx2UeqWCyXN3YiHSbW7juEif64rsEkISSRnaSpq PllGj084GUpHeVORrtUMpFDl15XyrbltX63nn5gSiHzpq7+vcWhM5/esvqWzUA6g1C+H7OYOo3me rttLHixRFRlty5S/b9qS/lZr+o3XnnRbO4ZZUa4BEhHxrxUtsRTrShy3HiAmCO92HaehxwwynHbb 4PWp9fvdM0xzpt7PLeHWr9X05VhUGKS+valXaCQ7egxrU7infNu8Wvm86a7VlhW75qIWqxgKnnHy kXazBBjf4a03640hF6d5uup9Rkgvbq8tLVIy31hUil+PkAqFRaKwqpLVpjSpv+ndN/6vl/8A9Iqf 9kmKWNedP8L6v+iYtR1G7u0W9VQJLYAqHjfkVK2y77DFCUSeU/IqazFbRW+oGxIEj6mHdODssgdf TEHMlTFFTt8ZIpxNVVv6B8lrDrSQtf3zW1yiW1oA6F1NvE5Bd4SBRpn69voxVavlnyKtpYXE316x vLiWOG5tz6kpVKsKeoIAGNO+Kok+WfJE+o3NlNHfpp7KSNRUtWQ0QgemtuHBJeQN/qjry2VTxfON wNLa4tr++1C6+uXUHorFFCFiinljjYs1ow2CIG77k9qYqiz5og/S1lbtrV9HFNaXE08f1WMkSRvA FAP1XcASt0xSo2/m2aS2v3ury/sDbq/1Zmihl9TiXo1FtPhHFVbfxp2xQ6fzdNHBYPa3d/f/AFhU Ny6xQxelyaMM1GtPiHBnfb+Wn7VQqlHm3UrGTTvN8/125u4Y9N0oPK6CGRf9Muvs8Y4Pn0zh2Q/d lzez4mWaIFX5+5J/yMvIrnzJdmG9+txrZPRXULKn76P7RHGv3ZhaKNTO1bOx7VxGEBceE38OR/HN B/8AOQurXuneZtKa2cKHsz6iEAhqStSv35Zq4CUt+5yew9NDLilxDr+hlPky5vZvJ3lq8t2uYZTa 3ZeKwSFnIkvoUY8Z45hxQNzNN6DMnTCsYDpu0sfBnlHnX6lfRvMuvTaZp8l4PMUlxc28Ej3Fraaf JbsZY1fmrCHZTy79O++ZDhI067rBRZI08ysnJVdTZ2COvKprxaAVA8QcVbTWtaMxjZPMikPKpb6r p5HGJXYMGEHE8+AC79WGKpto6alqcVxJ+k9WtPq872/C5hsUZ+AB5qPqx+E8tjgViusfl1p19Hde Ybq51e/1M3hWVLOaOF5FhuPqisUiiRG4QoCy0+KmFVD/AJVJoSW2n3ou9Xt5r+S3+sWtxcrJ6fNe RjKMjIGU7bDriqtpv5XaU+r3FqW1q2htFKRXclyjRyqfhBAMRBJDHevIb9Ad1CXX35caZ+i11B31 vU7mO7uLSGK1uByjWzeaGBqCNqVWBI3YDetW2rilmlnoF5pV9p2iWWt3yWh2S6lCstm7BopYAvxt bk/7vatcCrbNvMNzBqTy3mqWBs1b0XnSwKykc91pa9KKrf7KnUHCq65/T9vFppjv9TvProX1pYY7 HjEW4buBasQp5E19sVXmHWxrepWg1q+litLG2uoYkjsQ7STSXKstTbU3EC0wKpQxaxd6Ta315eX9 uTeWZNjcraAkC6i2fhbRON9tiPY0wq8c8/ajax+e9ZhW/a1uVnPKOYc4GqoIpX7O3WjDNJqIHjOz 1GmwSOGJ4OKNdPq/HwLGfyi/8mRoX/Gdv+TbZk4/qDuO1v8AFp+79L1HV9WSa1udKuJobiKDW7x1 sTcW1uzh7y8ZvjkkiKGGgf4iOXQZsnz5Ru7TQ4xLNa2tpPcRLHFGh2Kyj5pNUy8W+sPT0+h5UJ/Z qMVVIm0eG14m3gSa6j/0iKG/sXI4RvEqiRrlBy9NyK7deppsqyfyv5htI7ZrH9L22lWlqqfVlnns 5WcvyMg+CWT7D7faNeo2pVVU8wa5YNLpNPNdi1L+MmjW2w9OTfZ8UpPql3pM/mqC4N7bXLxzRP8A pP63bRxDiYiJPS9Wjenx6cf2ffFCtqN/pN3ba/bXOuWl/BcahbVtllgiMiiC0rIHEimkfEk0O/Gm KXabq1qmkWCtrVrprfpFpntZLi2uXHqzSSPM0gkb+8Zy5HauKFNLjSE85i+XULZZJJS0uq/XLf0g VgdEkMHq8SSJGQADbkSd6YqoX1/p1xpEMcuqQai0epX9xEsVzbWzRSJdTSQycvWRjzanHqN6nbFU 00zVrGK80Ff8Q2dmsOlTxtbmW2l+rnlaUhMvMhyvEjlXfjXFKS+V7rSrWHUfQuoNHU2SRI895b3B akYPohDM9ODMVqOtMULvM0uj30GnGa9ttWkhtQqtHdwW3EOvGSJgJVryU9+1em1VV3n+8gutB86P DqcOqKul6UDLAYyFP126PE+mWHvlOf6C7Lsj/GYe/wDQWJf841/8pZqf/MAf+T0eY+n+r4O/9ov7 qP8AW/QVX/nJb/lI9I/5g2/5OnHUfV8GPs5/dy/rfoZd5Eg0uXyN5UOo6V+l4ktLvjb+glyVL30E RkCP/IJCzU34g0r0zIwfQHRdr/4zP8dAxHRToK6LZf7lNJgX6pE5iuNEs55oyiR+orP6sRPDmA3I FqkEnsbnWpnFfeT7iVkg1TQ5FULUpotmzVmEccdf3xWhlqw8eYHYEqr0fyzerawWl/pAncusjRaL ZytIX4rCsal6A1DHvWtKbYqus7LSNRdbbSr3Tbu6ZSYwug2TciBWg4sR9nevbrQjYKsmXQPLk2hz rbaDBY3X1q4petpdvMqqt29Rweg3UcRvtircug+WobLTkuvLsN3cfXE53KaZbxB1ZmKjioI2Wg96 Yqq2/lrRU1uaaXRrebTnU+np36ItVeM1FD6o+JvpH9ilLV8uaPdaN/uN0eDTrhNSvTJNJpVtcB4l vJgYv3gHh5ehHSnSmKph+hfKi69pkcvleF2+oXZm46dCqu4ktRzCUPiaeFcVQ0HlrSIF1WW90q3v 7doT9WgTR7WFoCENSzpyLVO+KFt35a0m4j0l9P02306MLCbm3fR7Sc3AoCyhn4spYbbYqqyaJ5Xk 8wazDB5bit3OmWfoSNpsEiwyNLeD1fTICnoPnTFKpp+iaPa2du82kwT3w1CzaHUItNt7b0gbiEAc o/A1PL3xQ8M/N3/yZGu/8Z1/5NrmtyfUX0Hsn/Foe79Lvyi/8mRoX/Gdv+TbY4/qC9rf4tP3fpe2 eZfU/wAEDhEs7/p6/pGwmII+v3fQQfveQG44982QfPmKWcGsLBH6r3RhnkHpMBrnrDiSeJLBKeFT 7Yq6B9aiskjgNx6s6gwCV9eOzv8AAX5nkpYJTc+PyxVm+j+Qte+uTHWLkLZ3MZ9ZLPUNRaRZA6uv pmVgFX4ADSny3xSyTXIlhGhwqWZY7+FAXJZiFikG7Hcn3OBU1dr369CqKhsjFKZ3JPqCUNH6QUdO JUycvoxVLdNMwu/MRgAMwvF9IN9kt9QtuNadq4qv1Mzm30s3AUXBuoPWCElA9Dy4k70r0xVHxtfG +mV0jFiI4vq7gn1DKWf1Qw6cQvp8fpxVL/LhcaXNwALfX9QoCaD/AHvm7gHFV1z/AMpVp3/MDff8 nrTFUXqJf9HXnIAD0pONDWo4HrsKYq7Ti/6Ns+IB/dR8qmlBwG42OKvPPzY/44/nD/tk6V/1HXWU 5/oLseyP8Zh7/wBBYF/zjX/ylmp/8wB/5PR5Rp/q+Dv/AGi/uo/1v0FV/wCclv8AlI9I/wCYNv8A k6cdR9XwY+zn93L+t+hmP5fTarD5J8qvppT1RZ3gdXge4qjX0KMQElhpwDcjudgaDMjB9AdF2v8A 4zP3/oDHtBt/MEnl61hdtfEclrDwNvb3bw8TEhBgK36gKePw0UU7AVy51qZTaHr9yoSTUfMhguEK MvoXqBVDmL4qXyuCacvdTU4q02j65eTTTC88xQvSeRU9C/iRapzKRAX/AMNeHGML406Yqmfl+TzT ps/1onUJJL4rEyX1lNKsYD1qqm9qv954Yqnj6XrN/wCXLyC9ltbyzN1dGW1WxnLuY71z8IF4hPxL WncePdSthsNah0XRFsZ7WztHnglhtZbC4SSP1aycZFe8ZgwLHkp6HFV1roV6vmy4u41t49UWP49T fT7n0XU0PBHN7xP96dgP5vfFUtvNGv7zy4x1NYNUgg1O9kjtbewuJJPUF7P8fFL2OorXriqc/o/z FbeYNKt4b6xRIdPu44QLKaiokloOO92Se3fAqX6doV5afpuWw9CzuWjdLmWexuqSqnNFMZe+deP7 uop+yV8cKtahoN1evoR1JLa9lCxPa3CWFy0cEkPH0zJxvVof3pIPE7cq7YqipdP8w3PmLXLae7s5 o5tKso54xZzDnG8t6vBaXakE778vuwKh9Hs7q18vW0tmIrDTpdStvUsZLC4t7jkt9HATSS6mKcvT BUlacaHCrwT83f8AyZGu/wDGdf8Ak2ua3J9RfQOyf8Wh7v0pt+WGgNY+fdElubmJbgT/AAWqnk5q jA+HQb5Vhy3MUHB7Q1viYJCMTw1zek+ZrmYeVJvrVoos7XXLyW3u2eCkjNfXokUrPHMsfFaAsy7g mnHrm3eMYRe3llLbq1m8XEpJ6EyvpbeqQrKj0WzY0qQeh7Hp1KoyGa0mvpNMs0jumvD6GmzrJpJd 2JdFZAbMgGq78q/MmuBWQP5B813cE7LpZsJpXkdI3bSGWMPULGpS0f4U4gqTv8W9RtiqIsfIM8Ot 2t7rVmqwTX1v6dhKlhLByeGT1Fj9GCN1VCo+0xr99VWfSeWNBXUIIU8uWD2ckUrzXfowAxyIUEcf p8Kt6gZzyB24+4wJS6y8s+Xo5/MLw6DZXUsV2vo2/oQLyP1G2PAMy8VqTird15a0GWy0qa68vWVl dS3EBntfRgkMbMDVC6LxantthVFQ+XtJfV57WTyrYx6dGgaHUfTtm9R6LVPRCc1+0258PfAqD0fy zoK6NcSW+gWN1cC+vlSJ4YUBh2+Vd3KNQKu/TtTFVa48q+Vx5o09Bo9jwNjekr9WhoSJrShpx7VO Kr5/LOhPZ6oJ/LthbLD6iWkgigf1ovRVvVoEHD42ZeJ/lr3xVTHl7R4LDTPqfliyvvW9BLhvTtov SjYoHlPNfi4qWbiNzSnfFWKfmXpmnWGh+co7C1htI30rSmdII1jUt9duhUhAN8qz/QXY9kf4zD3/ AKCwv/nGv/lLNT/5gD/yejzH0/1fB3/tF/dR/rfoKaf85A6RJqHmPTW9aOCGGzPqySGgHKVqU/4H K9Xk4ZfBw+xdUMWOQokmXRkvlHSbWbyb5ZgSwtdeWC1ujHDcqnBgb2BZHUyB1DLGzkePTMvTG4B1 HaUzLPIkUe74PMtNg8tpa2sYiiM5gg9eE3lqnxenyd1SawmdN/2S5FO/fL3BV1Hl70WuFhty8Cl3 imvbP0mikIiMjenpsL1VnHHiwFd9wKFVE2+laExeS4jVP3SSTKt5YOkRfk0PTSxtLCryVLfs8RXF Xo35c+XvKWp2V9cnSbG7hNwCkzrbXSq7xrI0UZW1teKRh2A2NfGtcSlObXyd5b/Q9y9r5f0ya8W4 uxAstrDxJW5kCgniNgBirV55O8si00prnQdMju3ntxdLFaw8OZU81Hw7ryxVEQ+T9DOrTxS+WdKX TFQG3uBbQeoz0WoK8T35fhgVK7bynpC6BcS6X5a0q8vxfXyIlxBCi8FvZl68DXiAAFqNu/bCqPuP JvlAeZ9PjGh6eI2sr1mT6rBQlZbUAkceo5HAqxvKGim31T655a0mCGNJPqUsVvCzuo9T4nXh8B4h TsT9HQFW08n6J6OlC08uaVJDJGhvZpbWCqqAnTYEswLdjv1xVSj8n+Vf8U6tHHoWntw02xeGI2sB X1GmvQTQqB8XFQflgVuHyzp0Wj2V7d+XtN03WEvbUkWsMJ4UvkCskiqCCUoeu2FXz1+bv/kyNd/4 zr/ybXNbk+ovoHZP+LQ936WWfl8jQ+cNIUQw2UclwCIWPK4loCak1+k/azF0++QdXR6s8WOW5mQO f8I/Hweia27Q+U7aSOaSB18xX1Jo/iZOd/dqWoZrbYBif7zbqAxAU7x5tjDeZNZlt0Mep6rBIELh 3gUJLQHj11J6cmFDTp4DFDVvrnmCa3jia51Br64kYIRAoJkjMbK6qdVblyRHjTbdqV40xVk2kaF5 21aOSRNav9KaLivp6jaSjkWHIlRHfmtK8T8WKq115V8xW+raXJqmtte2h22JY4YjdQuXMLAsWNxJ xoykin83tirKJbayj1OGw9HU39ZeQukuLo260DGjyer8J+DuO4wJQdhplnDc+YZT9dlEN4pEcV1d GRgLG2NABKORxVu906yubTS7kC+h9a6hb0Z7m6SRK1+FlMuzDCqLitrKTU5rD0dTT0V5fW3uLoW7 7IaJJ6u5+Pw7HwwKgdF06yg0e4nb69Lwvr4enDc3TOf9PlXZVk3p1OKq1zotn/ijT19S6obG9P8A vXdV2mtO/qV74qr3ul2cljqK/wCmp6COnJ7q6Cv+6D8k/enkvxU+YIxVRjtLK0sNNBi1KcXAhi5W 9xdOEL8V5SUl+FByqW6AA4VYf+Z1nFa6L5yWNpGDaVpRPqyyTH/e266GRnIynP8AQXY9kf4zD3/o LCP+ca/+Us1P/mAP/J6PMfT/AFfB3/tF/dR/rfoLI/ztiZ/Mliy28UrJZgiac/u4v3r7kdyf8zlG uPqHudV2bKsZuRG/IcyyLylLo58veXJtWNvc24tLtVuHjVoecl7BEgWvOlXcKMzdL/dh2utjWUiq 97D/AC3rthbeX9PQ3ulBYYrcNHNpqMyKEHOJ3WVatUqOVPGvXMhxUdbeZLSSeKZ7zRrizeojSDSQ zO8UfqScSJn5UQFyANl3rToqvl8y6e7R29teaWbtnljkQ6WhrIYkWOOMhzwZZKsQwcnl02xVGaTL Pqlok0h2S6tnlHq3+l6Ov2VQhgnM3Uda8ep2GKpogsZtLK6boz21wL64Z5JNL9UGIXUnJPs7Ejav bFW5jpkVlp0d9okk90LxfUmXTBGGUu5VeIXstB74qqxQKuttcPpjPpBJK2R0geoKrQfvQo6NuNvv 7KoG3WGfSmXStJ+qzfXdS9SWbSTOOLXNwsfEfDujFTT2piqJjOkx6vpMV1ocs10mm3S3Eq6aEEko e0DSBOFBvXttXFUFDa30IuJdTshc2gt5gbeLRhGeR5lW50qOIKj6OmKq11byXFvZNpWntZwi3jEi vpCysXpUsGZT22p9OKqrto0nmHWY7fRJoZX0yzW3f9HB/SkMt4BJ6ZWnWnXrTFK6wiSC3RNQ09pb t9StHtbpdNFssMZuYeKlgo+yQfixQ8K/N3/yZGu/8Z1/5NrmtyfUX0Hsn/Foe79LK/y7VD5w0qW3 iDQtcDnezkmWY0P2P8n8KdBmLg/vBfe6PWE+GRI719I5R9/495Zd5jj5+X5z+mJGEWt3xl0yVbI2 6CS8vAtfVtLhjy4mgflv4dt480xqy1C1uEVIVtOQQS2sKzaLvD6ixSvT9C/AFNfnQdOyqxb+Ozvf rNIIGtkinsJUm0ZXSVnZT8a6T+7DLRlAHWteuKpvN+YvmEzyQ2Wrz3J5H6sTe6agkjG4Y/7h34Er vTffauNJTHS9b1HXr7T4JvMV0kwvYmt4o5tNuGZfTk5SUXT4CvGq0rUGvtihnctpNDfQ2EnmrUFv LgEww+np5ZgAzE7We2yN18MCUDY6ZeW1x5guLjzLfwQW92rTTFNPA4rY2zFmraHoNtvDxxV17p11 fWOl3lp5o1Ca1u7iCS3nWPT6FHBZXX/RPDxwqrx2c0mqyaUnnLU21CGP1pbcRaZyVDx+I/6DT9sY FQOnW0mmaBc31/5pv7W1gvL/ANSQx2BHw3swJp9UYlmpWg+gUxVF3Ghap/ifT1/xFqBY2V6Q/p6f UAS2uw/0SlDXw7Yq3LbSXlrqUVt5qv55LNJEuYxHp/wsAw4n/Qx3QjY9sVU/h02006K982X9vJdR L6Efp2BrxQFulm1APE4VSTznp0sVl5st7u4uNXEmmaWSJvQSTj9buvhX0I7ddqV3398x9Uf3ZcvQ yMc0SDw+bFvyHsNPtfNuoG1MqM1iweCdSrLSaPoSBUffmJo5Ey37nb9r58k8UeKvq5j3FGfnekT+ ZdPQwNcym0BigrSKolerSdqL7/QMjrvqHuaOzCRjJvhF8+vuDKfKF3a2+g+XhfRm4R7O9UpbW8ty lVuoTThEkpAWnU98zNJ/dh2usrxTV/FgGk6XrV7oFozWd+IHto3g9D62AxWJRE5jFkyfsqR+8PjU dBkuKzi28seWY4oEa513jHMLl4Pql0UMlKMpItAShBoRtUY2q4eWfLQJYX3mASl/U9UWlyHDcg1Q RabEsoNRvjap9oN3pGjWklrCdUnieVpUM9hekoGA+BeNuo4im22BKC/ScN9pJhtrnU9PlW+upPXg 0+8YkfWZfgNYeh5b4VWLqVvp9lYW1xc6pqMgvon+sXOn3gelKcdoR4Yq3HyXVReNrOtvbLcPOtid OuxHxfj+5JFvUovDau+5xVRtb+K90x1t7vU7BlvNSBaHT71gRJfyMCaRU5DjT2qe/RVWtNWtbPVt KtpZdSvJIrC/VrqawvfVctPakEgQ9vbbAqjGxslubmfVtZvYxbzL9Wm0+8EZLBmBP7j9nlQfIYVV bm5XULG2NtqGraf/AKNClINPvSAV+JmH7nqwPH5Yqt/S1tLr+pwJLqMUh07TFF0theeqTHcXbEso hh3+h6V3pgVfBcfVozHPf6nqEl1eWIQ3VjdQxxlbtK0YwoihqitT2wq8c/M7StLuPOery3KzWzmc /wCmKOcTUUD4qcuNOm9M0uaZEzT1nZ+pyRxRETGQr6ev4+aXflzq0+o/mjocjErCs7CGLsq+m3bx y3BDhIcvWaaOLSTHWtz8XuOpeSvMl5aSWC31nHZG+ub2JljuEuONxPLMEMscqEU9ciq0zavEICb8 s/MUoAfVlAViyhJ9RjAqKAUS5WtB4/Tjarpvy38xTSzyvqihrhi7hLjU0UEgghAt0OI37YqmUPlX zdFrA1ZdQtTcAFRG5vpIaFeP929yy+/zxVF3+leebxrVnvNMX6pOtwtLe43Kqy0P77p8WBUSbfz0 WVjcaSWWvEm2uKiuxp++xVD2mmeebae9mW80xjezCdwbe4opWGOGg/feEIOKt3Wm+ebgQA3eloLe VJVC29x1StB/fdMVRHoee+XL6zpXKlK/V7itP+R2KoWx0rzxaW0luLvS5EkmnmblbXHW4meZl/vu gMlMVbk0zzy+pQX5vNMDwQzQKn1e4oRO0Tkn9929AYqqz2PnmWGaI3OlL66lXYW1xXdeNf77wxVb Hp3nZbaK3e40mVIlVV5205+yKV3mxVI/OWlazH5c8xahq0sVxJc2tnbxxWCSQsq29xI9avIx5E3H Y9sx9V/dlytEf3seXx5MV/JGYP5nvEFy83Gyf9zOnCVKyx9dlqPozD0I9Z9zse04VjB4QN+YOx5o D/nIvU7m01mwggPD6zZ0dx1CrK+w+fLLNVC5gnucvsHTxmDKX8JTTQLUT/lr5YdtOOqJBaXkjWiG b1TW7jjrGICHYgPuPCuZen+gOq7X/wAZn7/0BCaVpMVtb2anyvfteWirFJMi6vAsksUYDSlFKRnl 1HbsN8udamCyRSMjN5cvmLxyzyxyDWXKLMGtW9SE8m+JYPgXif5lFTXFVGa1iEdpGfLOoJHEJyiK +rRLEIY1qJJOSKqsLdQoL8WO/euKpzoPmTXNNli0610C8iW+uFU3F1BfMgkKpFzkmdTwWiDc7eGK ppcRa1N5fnXUTYw2QvJzJIJ7iM8zeOoHJUrQu1MVbistesNJ0i2sEsWsRdRyWzGe4kJErNJXkyVo eeKtxWF8PM/NTYnWYxJc+h9ZuuKqyrG7enw4dJR2rviqCkt9Tl0B5tVNjBaW+oagfVE1xGweW6uI WFUSu4kYDFUfa23mSz1fRrS1jsPQg026jt/307gxrJaD7RSp7UxSg7DTbyJ9Xu9Neymu0imtrwG5 uXCEE1XgyceQZKV/hihfqVje3VrpiaqbGJ7mKK3tVFzcxGQkrRfgQVPJhsdsVV5oPMt15g1u2uIr D059Lso7gCSYD02lvRseFa/axSpaXbXiWh22xe0uLHUNStZrmdJ7iVi4u4kfgJFAG69Nhih5f+YE wh86as/1ma0JuD+8kXnbNsPoX71zR6jeZ6vS6WPFiiOGMtum0v2/axT8ov8AyZGhf8Z2/wCTbZlY /qDvO1v8Wn7v0vrjNi+fuxV2KuxV2KuxV2KuxV2KuxV2KuxV2KsW/NGaGHyFq0szOkSpHyaI0cfv k3GUakXjLmaCJlmiBV+fueefkbdx3HmS7MV6LyMWT05KFlWssf2qUr/wOYWijUztWzsO1MRhAXHh N/Dr+OaTf85Lf8pHpH/MG3/J05fqPq+DsvZz+7l/W/Qm9g11F+VHl25gnSIW9tM7pIqMj/7k7YAE vHNQqTyX4ftAVIFcyNP9AdF2v/jM/wAdAx63tbBLiCNrW2ieJybOPlEZAQoAYo1goWvKnU/qy91r UsulRJeQyRW/GRSb5R6dDJFJIFRibAV+B+YI6ciPAlVM9E8wahowddLuIdPt5JDFcvEYXqyJObdQ psk+36Y3JoK0r0wKm0f5ieYGe2MmrusEsqx3EiCCRo1NWZghso+VFHQlf4Y0rNdI0DWbzTHr5ill t5Lm5IU2tm6NS6kIb4oj1I5Ypb1fQfMEa2Cr5in4i7hVV+rWgC9aUAjHTFUcPLGtic3A8wSi4YcT MLSy5ldtuXpVp8IwKleieWtZu9Knin16WSE3t+Gie0s3UkXswqQ8TdTvhVVuNE8xf4n09f8AEdwW NlekP9WtKgCW1qP7um9fwwKr3nlnWoLC+eLX5UaSOR5StpZrzPEmrERAnrhV1l5a1uawsnl1+VzH HG0XK0s24HiDVSYiR0xVB2+h+YG826nGfMM9f0fYFn+rWhLK014ApBjpQUPbvgVF3Xl/VrK2tQNa kktIry0JtBbWscbA3cZI/dxqRUmu2FXjXn7ULePz1rMC6h9WuBOeUM6hoDVQRTpTY/zZpNRE8ZNP T6bBI4YyMOKNcx9X4+DGPyi/8mRoX/Gdv+TbZk4/qDue1v8AFp+79L64zYvn7sVdirsVdirsVdir sVdirsVdirsVdirDPzj/APJaa5/xij/5Px5Tn+gux7I/xmHv/QXlH/ONf/KWan/zAH/k9HlGn+r4 O/8AaL+6j/W/QVX/AJyW/wCUj0j/AJg2/wCTpx1h2fBj7Of3cv636GR+Xob+b8rNASw9T619UmKr EJWYqNTt+YpBST7Fen07VzI0/wBAdF2v/jM/x0CVFPMst6nLTr8xwMBE8aa4FZo1Ab1gh4ryA367 03G1zrV2mJryR+tcWmpSG4P1ecRJrjMrw+lPyMfOkIblTah6oehGKoOG81mMxWeqRTW91e+l6yTP rMAXZ4QyhnBVf3jFmUHoD+yMVZP5Jl8wWnmuBJbC+itZ+dvHPPDq0kYg4I4aT6xI0UcjGJRzfffa tWGKXounfWv0RdfVOh2v1776v6tfT9T6zLw58fi48utMCrtarTT67n65DUjbxxVHD619afkY/qnp r6YAPqepVudT9njx40+nFUl0v9J/oG5/Rno/Xf0hfen9Z5+lT9Iy8+XD4q8K098VRVz/AMpVp3/M Dff8nrTFVe9+tfUdS9coY+D/AFbgCD6fpCvOv7XPl07UxV1mLr6hp3oGMJwj+scwSfT9I/YoR8XP j17VxVB2n/KZ6p/2ztO/5P32Krrv9I/oiH9I+j9b+u23L6vy9Pj9dT06c/irw48veuKvl/8AN3/y ZGu/8Z1/5NrmuyfUX0Dsn/Foe79Kefl3o9sPzC0bULBwLdbgia2b4ZImZGHEr8zlGDIeIAut1mrl +Xljn9VbHoX05m4eRdirsVdirsVdirsVdirsVdirsVdirsVYZ+cf/ktNc/4xR/8AJ+PKc/0F2PZH +Mw9/wCgvKP+ca/+Us1P/mAP/J6PKNP9Xwd/7Rf3Uf636CnH5/afaX2v6fDLKIbn6oPqzt9kn1Xq p+f35VrJGMx7nA7GzzxwJAuN7/rTfR9L1BPy38vWggR5RHJHzc27okq6hDcRnhPNbh6iAleJrXwz M0xuALrO0sgnnlIcj+pS0/8ALO8sg8sWnSpeOq/6QlpY8fVR0cSem+oSL9pNh38cvtwFOL8rr2M2 7/o397DHJE7CxsVDBuBSi/pKg4Mld619u7aso0zyvpdroUGky+U7l4o4o4pFjaziQ+m0jAhUuxx+ K4k6eOKWSx6tfxosaaBfKiAKqh7HYDYD/erAqG0zUdWt7Z45NBvuTT3EopJYn4ZZ3kX/AI+f5WGK rdSv9XuPqvp6DffubiOV6yWI+Fa1/wCPn3xVEy+YLuIKZdFvIw7BE5S2C1Y9AK3XXFUJot7rFnZy RTaDe82uruYcZLEjjPcySp/x89eLiuKumvdYfXLS9Gg3vowWtzC/7yxrymkt2Wg+s9KQtiqIvdU1 SazniTQb7nJG6LWSxpVlIH/HzirrLVNUhs4In0G+5xxojUksaVVQD/x84qhILrWU8xX2oNoN79Xu LO0t4/3ljy5wS3LvUfWelJ1piqKvb3VLxIYF0W8irc2zvLI9nwVI7hHdjwuHbZVPQE4q+ZPzd/8A Jka7/wAZ1/5NrmuyfUX0Dsn/ABaHu/Sy3yEryectHndIroCcBNQhYKaUOzqOv0E79hmJp/rHvdFq SBjlEEx2+k/ofRebx5x2KuxV2KuxV2KuxV2KuxV2KuxV2KuxVhn5x/8AktNc/wCMUf8AyfjynP8A QXY9kf4zD3/oLyj/AJxr/wCUs1P/AJgD/wAno8o0/wBXwd/7Rf3Uf636CyT87BI/mKziQQyh7Ic7 WbYyASv9k70K/LKNd9Y9zqezaECTY9X1Doy3yp5fttY/LnSrKfnaxqHb0iIpSGEj0BMiy7A7/CQf em2Zml/uw6/Wm8st7SlfybuViMf17T2iMpcQvpvJeLEK6sROvLlGOPQU60zJtxFUfk5HGGEF1ZAy fBI7aeCTEpEiKQJhXjKit2xtVC8/JC3nW4jFzpwhmdykUmmmQBWIKK1bkFitNztX2xtKIu/ygaWG eK2u7G15oqxk2BlHIFWLsDOjbsPshuwNdsbQ60/J4QNcK11p7w3cyy3S/o1VLoJkleJeM3wA+nsw 3DGvamNpUF/JidYnK3+ni6kUxSTNpnqVT1AaAG4UrVEQUr1GNoV7b8pb+2imWLUbEco4RGo08qPU tgEiJrcP8Cxl4+FCNwe2NpQz/kxdmUEajp3pxlmt66WecbScPUqwufiDmMeGNqqSfkskzWzy3lgZ IFqxXTAAZAAqutbglaKNxU169d8bVOND8lea9GtJLax160toZSZPSj00FVlZFUtUz/F9nwGKsu06 K9hsoYr64W7u0UCa5SP0Vdv5hHyfj8uWBURirsVfI/5u/wDkyNd/4zr/AMm1zXZPqL6B2T/i0Pd+ llPkkej5u0y7mt4YyJuRvoZAsBop3lBpt/wWYmCVTG/zdHqJXjMRI/1ZDf4fgPVIfNfmuSCMRXvl uW5FfXR72ReJEjdPTWX9jj9ObIZT3x+brpafCDuMoH9UfppePN3mZVUzzeXLZmrxjk1KTlWpA6RU 8OmEZj3x+aBpsJ5eIf8ANH63P5p83K0bc/L/AKIIadlvnaqChb0yyp8TcqLy22NSKjB4x74/NAwY P9sv+qEw0XzXNdW93Le3WkxSVP1GGC9EpGxoLhgKA1p9iuTjm7zH5tWfTxiQAJ+dxr5ftS6384eY YVt1vbjQXmeGs6C+9Fll5ilK+rUen4ftd6ZAZj3x+bcdLiNmPiVf829vsUbvzt5sQEwroKglwrPq QI4gHiSaR/aJHTpT32TnP9H5soaXCeZyf6VMdI83ahdaPd3F5LpEGoBCbGGO9WWPlwqFmdelG2PE 5KObY2Y372nNp4RmAOPh6+mj8ECnnDzPHEkry6BcRNHEOYv/AEqS0Hq1P7xSOX2QPvOR8aXfH5tp 02Emv3gO/wDDezX+NPNi3ih5dFNsi85oo9RQzEcuPw8uCj7Jap2oR3BqPHP9H5r+Ww8POd/1dkTb eeLiTQJZri80W21vl+5tlv45ouFR9pqx/FSu1ae+T8X08xfvRLRAZAAMhh48NFC3fnrW45pFtrjy 9PFzPpSHUghCdgy0NSPGu/gMBzS/o/NnHRQI3GQf5jm8/wCtn0wp0BS1RKTqysFNaKR+7UsKbnHx j/R+a/kYf7Z/pP2oWD8wvNRmCyr5eEZJPqfpVBQVIAIAf4gKHw/gBml/R+bYdBirbxf9Ik/n3zdf 6j5G1611GXSI0e3j+rJY363MzyCdCRwou3HfbwyM8hMSDTkaHSxhngY8fPe40OTFf+ca/wDlLNT/ AOYA/wDJ6PBp/q+Dn+0X91H+t+gsj/O6FpfMNkv1aK6X6mpMTtwfaV94zTqPoyjXh2j3Op7NlwwJ sx359PizL8vtd0Gx8maXBdX8NnKqOPQuriMSr+9fY8nJ+XtmVpskRAWQ4eqxTnlkQOL+qNmTHzBo IXkdStQtK8vXjpT/AILLvFh4j5uJ4Uu4rYvMnl2UExarZyAdeM8TfqbHxYd4ZSwzjziR8Gm8zeW0 cRvqtmrnohuIgT9HLHxYd4UYMhFiJr3L38w6BGpZ9TtEUdWaeMD8Wx8WHePmgYpnYArE8zeW3FU1 azYeK3ER/U2Piw7wk4Mg5xPyaXzP5aaT011ayMn8guIifu5Y+LHvCnT5AL4TXuK//EXl/wBQR/pO 09QioT14+VPGnLHxYd4+aPCnV0a9zX+JfLnFm/StnxQ0dvrEVFPgfi2x8WHeE+BP+afktl80eWom Cy6tZRsRUBriJTT6Ww+LHvCY6fJLlGR+BWf4u8qf9Xqw/wCkmH/mrHxI94T+Vy/zJfIu/wAXeVP+ r1Yf9JMP/NWPiR7wv5XL/Ml8i7/F3lT/AKvVh/0kw/8ANWPiR7wv5XL/ADJfIu/xd5U/6vVh/wBJ MP8AzVj4ke8L+Vy/zJfIvln81Lm2uvzB1qe2lSeCSYGOWNg6MPTXcMtQcwJm5F7rsuJjp4AijSe2 n5L/AJsWjcra0WI9SFuYaH5jnQ4y08jzDh5e1dHP6t/gU3j/ACv/ADIn4jU9DguCvSeO4gSUfIh/ 1EZWdHMcnBlq9NH+7yGPkQSPx80Ufys8/ohWG19WI9be7lt5BTw5iTl99ch+Uyd32uP+dwk77Hvj Y+yv1LYfyn86qKw6c9hJ3WG5t3hJ/wBR3p9yjCdLk7rZT1+M8yJjzBB+f7VrflT55klrdaRFIw6X cFxFDN93qf8AG+P5TJ0h4JGuxAemRHkRY+79Co/5WfmEF4LaJcxf76u2t2I/2aSD8QcH5TJ3fawG twXf0nvjf3EIdPyn8+q3JfL+nxt2cSwsR9FV/Xkjpcnn9n6209oYSP7zIfx8UQ/5U+epErd2RugP s2yTW8MPyYeoWI+ZPyyI0mToGuOuxA+k8PnuT9zX/KrfP5pcSaaklym1tAJ4Fgi7V+3Vj70+VMfy mTu+5fzuH6RKo9TvxFDaj+U/5jGze3s7ANNc73lzJcQKzf5KgOaL2p4ZKGlndkN2n1+n4+KZoR+k UUg/5UR+Zf8A1bo/+kiD/mvL/Bn3O0/lzTfzj8i7/lRH5l/9W6P/AKSIP+a8fBn3L/Lmm/nH5F3/ ACoj8y/+rdH/ANJEH/NePgz7l/lzTfzj8i7/AJUR+Zf/AFbo/wDpIg/5rx8Gfcv8uab+cfkXf8qI /Mv/AKt0f/SRB/zXj4M+5f5c0384/IvRPyU/Ljzb5W8wX15rVqkFvPaGGNlljkq/qI1KIxPRTl2H HISsh0/bPaGLPjAgbIPcqfnV+Xvm7zPrenXmh36yx21uY5HMscRDly23JlPTHPjMjsGPY+vw4YSj kPM91sOtPyv/ADehX05rCG6h6GOaeBqj586/fmJLRk9KcvJq9DI2CYnyBR8H5UedlXlDpr6fL1KQ 3Nu8Nf8AUZ6fcBkDpMndbiz1+PrITHmCD8/2ub8qfPMktbrSIpGHS7t7iKGb7vU/43x/KZOg+5I1 2ID0yI/oyFj7v0Lpfys/MH0+h2FLyA9YLuS3r/yMVz+KnANJk7q+LGOtwXd8B7439x/W6L8qfPEa 1tbOSzb/AHybi3mh+hWkqB8qYnSZOotZa/EfqIn50Qfu/Woy/lR5+dqyaFYTt3kaSJCfo5P+vCNL k8/mP1s46/COU8g/HwVovys/MMLwFjDZxU3W1a35fQzSU/4XAdJk7r+IYS1uDnZkf6V/o/W5fyq8 8qzRwad9Xifee5NxA9xJ7VMhp86/LH8pk7vuU67FzkeI9BREQ0Pyq87AqP0UFtbbe1tBPB8TjcPI xfx+fjj+UydyTrsf871S5yo8u4fjySC+/JX80r26e5msIy7np9ZgoB2A+PoMyI6eQFU7TD2tpMcR EE/Iof8A5UR+Zf8A1bo/+kiD/mvD4M+5t/lzTfzj8i7/AJUR+Zf/AFbo/wDpIg/5rx8Gfcv8uab+ cfkXf8qI/Mv/AKt0f/SRB/zXj4M+5f5c0384/Iu/5UR+Zf8A1bo/+kiD/mvHwZ9y/wAuab+cfkXf 8qI/Mv8A6t0f/SRB/wA14+DPuX+XNN/OPyL/AP/Z
    • Corel PDF Engine Version 16. 3.0.1114application/pdf
  • Alik Sayfutdinov
  • Untitled-1
    • 1TrueTrue104.999997148.000010Millimeters
  • Cyan
  • Magenta
  • Yellow
  • Black
  • PANTONE 872 C
  • Группа образцов по умолчанию0
  • PANTONE 285 CSPOT100.000000CMYK89.99999847.9999990.0000000.000000
  • PANTONE 286 CSPOT100.000000CMYK100.00000072.0000030.0000000.000000
  • PANTONE 368 CSPOT100.000000CMYK63.0000000.00000097.0000030.000000
  • PANTONE 661 CSPOT100.000000CMYK100.00000075.0000000.0000005.000000
  • PANTONE 872 CSPOT100.000000CMYK20.00000030.00000169.99999915.000001
    • xmp. did:4ff34d5e-c0c0-4b06-80ad-2fec4dff10a1uuid:8cf6fd17-8e07-e046-9681-57155ff3428cxmp.did:09c93ebd-df3a-4c97-8094-b97363895d44proof:pdfuuid:1e40b86b-0cab-914d-8801-18f6f8f920bfxmp.did:09c93ebd-df3a-4c97-8094-b97363895d44xmp.did:09c93ebd-df3a-4c97-8094-b97363895d44proof:pdf
  • savedxmp.iid:09c93ebd-df3a-4c97-8094-b97363895d442017-06-30T14:17:44+03:00Adobe Illustrator CC (Macintosh)/
  • savedxmp.iid:4ff34d5e-c0c0-4b06-80ad-2fec4dff10a12018-02-07T10:09:33+03:00Adobe Illustrator CC (Macintosh)/
    • endstream endobj 3 0 obj > endobj 10 0 obj >/Resources>/ExtGState>/ProcSet[/PDF/ImageC]/Properties>/XObject>>>/Thumb 893 0 R/TrimBox[5. 66928 5.66928 303.307 425.197]/Type/Page>> endobj 11 0 obj >/Resources>/ExtGState>/ProcSet[/PDF/ImageC]/Properties>/XObject>>>/Thumb 902 0 R/TrimBox[5.66928 5.66928 303.307 425.197]/Type/Page>> endobj 894 0 obj >stream H|n$ z:zd«xKV`2$A_=t5Q:o?~e-3y{q2[:sG-̃OXC

    Забудьте про 10 000 шагов, есть лучший способ поддержать форму

    • Майкл Мосли
    • Би-би-си

    Подпишитесь на нашу рассылку ”Контекст”: она поможет вам разобраться в событиях.

    Автор фото, Getty Images

    Подпись к фото,

    Уже прошли 10 000 шагов?

    Последнее время и квартала не пройти, чтобы не уткнуться в кого-нибудь, проверяющего на своем гаджете, сколько осталось протопать до заветных 10 000 шагов в сутки. Но стоит ли игра свеч? И откуда взялась эта цифра?

    Вы можете удивиться, но возникла она вследствие маркетинговой кампании 1960-х годов в Японии.

    • Как похудеть при помощи силы мысли
    • Как похудеть: врачи предлагают этикетки с упражнениями
    • Почему ваша попытка похудеть снова провалится

    В преддверии Олимпийских игр в Токио в 1964 году одна фирма начала продвигать устройство для людей, заботящихся о своей физической форме.

    Прибор назывался Manpo-Kei, что в переводе с японского означает «измеритель 10 000 шагов».

    Это был один из первых шагомеров. Основывался он на работе доктора Йосиро Хатано, молодого ученого из университета Кюсю.

    Доктора Хатано беспокоило то, что наряду с модой смотреть бейсбол японцы перенимали у американцев и их малоподвижный образ жизни. Он решил помочь своим соотечественникам стать более активными физически.

    Автор фото, Getty Images

    Подпись к фото,

    Что полезнее — 10 000 шагов в день или 3 короткие, но энергичные прогулки?

    Йосиро Хатано подсчитал, что если сможет убедить своих японских приятелей увеличить количество пройденных за день шагов с обычных четырех до десяти тысяч, они ежедневно будут дополнительно сжигать около 500 килокалорий и таким образом оставаться стройными.

    Так и родилась система «10 000 шагов в день». И это был большой маркетинговый успех.

    Но остается ли она до сих пор наиболее эффективным способом улучшить физическую форму?

    «Мой спорт — вязание»

    Готовя программу «Вся правда о похудении», я отправился вместе с профессором Робом Коуплендом из университета Шеффилд Халлам на фабрику в Шеффилде.

    Мы решили провести небольшой эксперимент и сравнить эффективность «10 000 шагов» с другой программой — Active 10.

    Active 10 не предполагает подсчета шагов. Нужно просто трижды в день идти быстрым шагом в течение 10 минут.

    У каждого из согласившихся нам помочь волонтеров были свои причины заняться своей физической формой.

    Подпись к фото,

    Некоторые из волонтеров, согласившихся принять участие в эксперименте

    «Я понимаю, что уже не такой стройный, как был, я основательно поправился», — сказал нам Дэвид, один из волонтеров.

    «Сейчас я упражняюсь разве что в вязании», — призналась Джули.

    Натана же вдохновила на эксперимент шестилетняя дочь: «Она бегает так быстро, а я так медленно, что не могу ее поймать».

    Мы раздали волонтёрам датчики активности и наблюдали не только за тем, что они делали, но и насколько они старались.

    Одним дали задачу проходить каждый день по 10 000 шагов (около 8 километров), другим — просто быстро ходить три раза в день по 10 минут (что эквивалентно примерно 2,5 км или 3000 шагам).

    Темп ходьбы второй группе задали так: «Идти нужно настолько быстро, чтобы можно было говорить, но невозможно было петь на ходу».

    Энергичная ходьба

    Результаты первой группы показали, что 10 000 шагов в день могли пройти двое из трёх волонтёров. Но им пришлось приложить для этого дополнительные усилия.

    Вторая же группа назвала задание довольно простым. Они собирались и вместе выходили на короткие энергичные 10-минутные прогулки в течение рабочего дня.

    Для просмотра этого контента вам надо включить JavaScript или использовать другой браузер

    Подпись к видео,

    «Скончаться от такой глупой вещи, как похудение» — история девушки, победившей анорексию

    Итак, пройти 10 000 шагов за день оказалось сложнее, чем совершить три небольшие активные прогулки. Но какая техника оказалась эффективнее для здоровья?

    Когда профессор Коупленд проанализировал показатели датчиков активности волонтеров, результаты оказались красноречивы.

    «В группе Active 10 общий объем высокой и умеренной физической нагрузки оказался на 30% больше, чем в группе «10 000 шагов», несмотря на то, что по времени первая группа двигалась меньше», — рассказал профессор.

    «Умеренно интенсивная нагрузка на ваш организм оказывает наиболее благоприятное влияние на здоровье», — говорит ученый.

    Лучше меньше, но активнее

    Члены группы Active 10 в общей сложности двигались меньше, чем группа «10 000 шагов», но зато у них чаще ускорялся пульс и они чувствовали реальную нагрузку.

    «Прежде всего мы хотели ускорить сердцебиение. Множество исследований позволяет предположить, что такие упражнения помогают снизить риск возникновения диабета, сердечно-сосудистых болезней и даже некоторых видов рака», — подытожил учёный.

    Так что три быстрых, активных прогулки в день оказались не только более подходящим вариантом для нашего образа жизни, чем 10 000 шагов ежедневно, но и более полезными для здоровья.

    Это сильно вдохновляет, потому что не каждому хочется каждый день шагать по восемь километров.

    То, что можно добиться такого же, а то и лучшего результата с помощью коротких, но активных прогулок, весьма обнадеживает.

    Сколько листов профнастила потребуется, чтобы огородить 6, 8, 10, 12 соток

    В этой статье мы рассказываем, как посчитать всё самостоятельно и даже без онлайн-калькуляторов.

    Вступление: особенности профнастила и его маркировка

    Профнастил изготавливается из стали методом холодного проката, затем профилируется: получает трапецевидную или волнообразную гофру. Профилирование делает тонкий лист жёстче, увеличивает его прочность и срок службы.

    Профлист кладётся на кровлю, из него делают заборы, облицовывают стены. Это популярный материал: он быстро монтируется и служит 20-40 лет.

    Поставляется в трёх разновидностях:

    1. «чёрный» — простая сталь, которая быстро ржавеет;
    2. оцинкованный — с цинковым покрытием, защищающим металл от ржавчины;
    3. с полимерным покрытием — представлен в 200 цветовых решениях; полимеры предохраняют от коррозии так же, как цинк.

    Черновой профнастил в строительстве ограждений почти не используется. Для надёжного и красивого забора мы рекомендуем сразу брать оцинкованный или полимерный.

    Профнастил по-разному маркируется в зависимости от характеристик и того, где он будет использоваться. Заборы монтируются из стенового профлиста, который промаркирован буквой «С». Цифра после «С» указывает на высоту гофры. Мы используем три варианта: С-8, С-20, С-21. Чем выше гофра, тем жёстче профлист, поэтому С-21 крепче С-8.

    При строительстве забора профилированный лист можно установить вертикально (гофры расположены перпендикулярно земле) и горизонтально (параллельно). Высота забора тоже может быть разной при установке обоими методами.

    Наша компания использует продукцию липецкого ООО «НЛМК», поэтому для расчёта того, сколько листов профнастила нужно, чтобы огородить 6, 8, 10 и 12 соток, возьмём С-8 производства «НЛМК» с монтажной шириной 1150 мм (1,15 м), установленный вертикально. Расчёт универсальный — можно подставить любые значения. Обычно на сайте производителя все эти данные указываются.

    Что такое «сотка», и как перевести её в периметр

    «Сотка» — народное название внесистемной единицы измерения ар, которая используется для измерения участков. Она равна площади квадрата с шириной 10 м. То есть, шесть соток-аров — это 600 кв. м.

    Чтобы узнать длину забора, нужно знать периметр участка, который рассчитывается по формуле:

    Чтобы вычислить периметр прямоугольника из площади, нужно знать длину хотя бы одной стороны. Например, известно, что площадь участка — 600 кв. м, а одна из его сторон равна 60 м. Тогда по формуле b = S / a — 600 / 60 = 10. Периметр участка со сторонами 60 и 10 м будет равен 140 м. Такой будет и приблизительная длина забора без учёта ворот и калиток.

    Сколько листов профнастила нужно, чтобы огородить 6 соток

    6 соток или аров — это 600 квадратных метров. Чтобы рассчитать, сколько листов профнастила нужно, чтобы огородить 6 соток, нужно знать длину сторон. Допустим, это прямоугольный участок со сторонами 30 и 20 метров. Периметр — 100 м.

    Как указывалось выше, для упрощения расчётов берётся конкретный профлист шириной в 1,15 м, который устанавливается вертикально, с гофрами перпендикулярно земле.

    Чтобы выяснить, сколько листов профнастила нужно, используем формулу: N = P / В, где N — количество профлистов, P — периметр территории, а B — ширина листа. Или для участка в шесть соток со сторонами 20 и 30 м: 100 / 1,15 = 86,956, округляется до 87 штук.

    Сколько листов профнастила нужно, чтобы огородить 8 соток

    По такому же принципу рассчитываются все остальные участки.

    8 соток — 800 квадратных метров. Допустим, с одной стороны участок 50 м, с другой — 16 м. По формуле его периметр (P) будет равен 132 м.

    Используем ту же формулу, что и до этого: N (количество) = P (периметр участка) / B (ширина единицы материала). Выходит: 132 / 1,15 = 114,782, округляем до 115 штук. Теперь вы знаете, сколько листов профнастила нужно, чтобы огородить 8 соток.

    Сколько листов профнастила нужно, чтобы огородить 10 соток

    10 соток — 1000 квадратных метров. Предположим, это прямоугольная территория со сторонами 50 и 20 м. Её периметр будет равен 140 м.

    Снова берём универсальную формулу, подставляем значения и получаем N = P (140) / В (1,15) = 121,739 = 122 шт.

    Помните, что участки редко бывают идеальной прямоугольной формы, поэтому так важно измерять каждую отдельную сторону. О том, как лучше измерять землю, поговорим чуть ниже.

    Сколько листов профнастила нужно, чтобы огородить 12 соток

    Посчитать, сколько листов профнастила нужно, чтобы огородить 12 соток, так же просто. Если предположить, что стороны прямоугольника равны 24 и 50 м, то его периметр будет равняться 148 м.

    Дальше рассчитываем: 148 / 1,15 = 128,695 = 129 шт.

    Как самостоятельно рассчитать длину сторон участка

    Точно рассчитать, сколько нужно листов профнастила, можно только зная длину сторон. Посчитать можно без спецприборов, особенно если территория 4–6 соток.

    1. С помощью «кронциркуля» с метровым шагом. Возьмите две палки и приколотите их друг к другу так, чтобы расстояние между ними было метр. После этого пройдитесь вдоль сторон участка и посчитайте вручную. Для этих же целей можно использовать покупной шагомер-землемер.
    2. Строительной рулеткой. После каждого метра втыкайте в землю прутик, чтобы не сбиться и иметь возможность пересчитать всё заново.
    3. По картам Google, с учётом масштаба. Масштаб на картах указывается. Можно оттолкнуться от размеров автомобиля или другого предмета с известными габаритами, который попался на гугл-карты.
    4. По кадастровому паспорту — самый простой вариант. Если вы знаете кадастровый номер участка, то можете оформить электронный запрос через Росреестр или портал Госуслуг. Официальный план можно получить в любом офисе МФК.

    Пара слов напоследок:

    • сразу решите, сколько будет ворот и калиток, прикиньте их размеры и вычтите из метража забора при подсчёте;
    • простой расчёт, сколько листов профнастила нужно, чтобы огородить участок в 12, 10, 8, 6 соток, не учитывает рельефа земли и перепада уровня;
    • самый точный и простой способ узнать количество профлистов — обратиться к замерщику, который выезжает на участок. Мы предлагаем услуги замерщика совершенно бесплатно.

    И наконец, вы можете воспользоваться онлайн-калькулятором, который учитывает всё: материалы, ворота и калитки, а также стоимость работы. Хотя умение самостоятельно сделать расчёты полезно, онлайн-калькулятор профнастила очень упрощает жизнь.

    Желаем вам лёгкого и удачного строительства!

    Среднее время на 10 км и советы по забегу и восстановлению

    Забег на 10 км, который составляет 6,2 мили, идеально подходит для опытных бегунов, которые ищут более сложные задачи. Это второй по популярности забег после полумарафона, требующий уровня физической подготовки, который сочетает в себе силу, энергию и выносливость.

    Если вы уже пробежали несколько 5 км и любите бегать на более длинные дистанции, 10 км могут стать идеальным следующим шагом.

    Пробег на 10 км — это само по себе достижение, и вы должны быть довольны потраченным временем, несмотря ни на что. Тем не менее, это нормально — хотеть знать, как соотносится ваше время с результатами других бегунов и с вашими предыдущими рекордами.

    Ваш возраст, состояние сердечно-сосудистой системы и опорно-двигательного аппарата могут влиять на вашу индивидуальную производительность, но среднее время прохождения 10 км составляет 50–70 минут.

    Продолжайте читать, чтобы узнать больше о средних показателях 10K и о том, как развить скорость и выносливость, необходимые для достижения цели.

    Большинство бегунов, которые находятся в хорошей физической форме и проходят 15–30 миль в неделю, могут рассчитывать на то, что закончат гонку на 10 км за 50–70 минут.

    Более продвинутые бегуны обычно финишируют за 43–50 минут. Исключительно подготовленные бегуны могут пробегать милю каждые 7 минут, в то время как более обычные бегуны могут рассчитывать на пробежку мили каждые 10–14 минут.

    Во всем мире

    Средние показатели 10K в Соединенном Королевстве такие же, как и в Соединенных Штатах: мужчины финишируют примерно за 53 минуты, а женщины — примерно за 63 минуты.

    Что касается 10-километрового забега по всему миру, то в настоящее время первое место среди мужчин занимает бегунья из Уганды, а самые высокие результаты среди женщин занимают бегуны из Нидерландов и Эфиопии (1).

    Как правило, в Эфиопии и Кении одни из самых быстрых бегунов как среди мужчин, так и среди женщин.

    Другие факторы

    Среднее время 10 000 может зависеть от таких факторов, как возраст, пол и уровень физической подготовки.

    Здоровье опорно-двигательного аппарата также играет важную роль, поэтому вам следует принимать меры, чтобы уменьшить боль, избежать травм и бегать в правильной форме.

    Если вы испытываете боль во время бега, рекомендуется проконсультироваться с врачом, чтобы исключить распространенные проблемы, такие как расколотая голень, подошвенный фасциит и колено бегуна. Лучше всего решить эти вопросы до подготовки к гонке.

    Личный рекорд

    Придерживайтесь своей программы тренировок и постепенно доведите ее до достижения целевого времени финиша. Убедитесь, что ваши цели реалистичны и что вы хорошо понимаете свои ограничения.

    Возможно, вы сможете соответствовать средним показателям для вашего возраста и пола, но если они не в пределах досягаемости, исходя из вашего времени в милях, стремитесь к своим личным рекордам.

    Наряду с вашим уровнем физической подготовки и режимом тренировок, возраст и пол являются факторами, которые следует учитывать, когда речь идет о среднем показателе 10 000 раз.

    Ниже приведены средние значения, опубликованные RunRepeat в 2019 году, которые вы можете использовать в качестве указателей, чтобы примерно определить, где вы должны быть в начале и в какое время вы можете стремиться уложиться (2).

    Age Men Women
    0–15 57:08 1:03:14
    16–19 46:36 1:00: 21
    20–24 51:40 59:50
    25–29 53:31 1:02:25
    30–34 54:21 1:02:31
    35–39 54 :27 1:02:19
    40–44 53:31 1:02:37
    45–49 55:35 1:03:27
    50–54 56:12 1:04:04
    55–59 59:00 1:07:41
    60–64 58:48 1:09:51
    65–99 1:03:02 1:18:57

    Если вы только начинаете бегать, вы можете попробовать забег на 5 км, прежде чем переходить на 10 км. Если вы в хорошей физической форме, в добром здравии и привержены своей программе тренировок, вы сможете подготовиться к гонке в течение нескольких недель.

    Подготовка к гонке на 10 км займет в два раза больше времени, чем к гонке на 5 км, поэтому убедитесь, что у вас достаточно времени на подготовку.

    Если это ваша первая гонка, начните с более легкого бега. Медленно повышайте свою выносливость, увеличивая продолжительность и интенсивность занятий.

    Старайтесь не бегать слишком долго или в слишком быстром темпе. Чтобы снизить риск получения травмы, не рискуйте и останавливайтесь каждый раз, когда чувствуете боль или истощение. Сбалансируйте свои беговые тренировки более легкими тренировками, такими как йога, тай-чи или плавание.

    Во время забега на 10 км бегите в темпе, который вы можете поддерживать, чтобы избежать слишком быстрого перенапряжения. Поберегите силы для последней части гонки.

    Среднее время прохождения мили для мужчин, бегущих на 10 км, составляет немногим менее 9 минут, в то время как среднее время для женщин составляет около 10 минут.

    Новичкам может понадобиться 12–15 минут, чтобы пройти милю. Ходоки, которые проходят милю каждые 15–20 минут, могут пройти 10 км за время от 90 минут до 2 часов. Ниже приведена диаграмма, в которой указан средний темп на милю для мужчин и женщин разного возраста (2).

    .
    Age Men Women
    0–15 9:13 10:12
    16–19 7:31 9:44
    20–24 8:20 9:39
    10:05
    35–39 8:47 10:03
    40–44 8:38 10:06
    45–49 8:58 10:14
    50– 54 9:04 10:20
    55–59 9:31. + 10:10 12:44

    Чтобы улучшить скорость, выносливость и работоспособность, вам необходимо повысить общий уровень физической подготовки. Включите различные беговые тренировки в свою программу и часто меняйте ее.

    • Упражнения. Вместо того, чтобы сосредотачиваться исключительно на подсчете миль, выполняйте упражнения, помогающие увеличить скорость, такие как темповые пробежки, интервальные тренировки и бег в гору. Вы можете улучшить свой шаг, пытаясь увеличить количество шагов в минуту.
    • Испытайте себя. Попробуйте сложные трассы с множеством холмов, ручьев или пересеченной местности. Бегайте в неблагоприятных условиях, таких как жара, холод и дождь, чтобы вы могли адаптироваться к различным погодным условиям. Если есть возможность, потренируйтесь на гоночной трассе заранее.
    • Смешайте это. Во избежание травм выберите 1 день в неделю для интенсивных тренировок. В остальные дни выполняйте умеренные упражнения и отдыхайте как минимум 1 полный день в неделю. Сбалансируйте свои беговые тренировки упражнениями на растяжку, которые сделают ваше тело гибким.
    • Стань сильнее. Силовые тренировки для наращивания мышечной массы и повышения устойчивости. Примеры этого включают тяжелую атлетику, тренировки с собственным весом и упражнения с эспандером.
    • Хорошо относитесь к своему телу. Позаботьтесь о своем здоровье в целом, высыпайтесь и повышайте уровень гидратации, выпивая много воды и электролитных напитков. Избегайте или ограничьте потребление кофеина, алкоголя и мочегонных средств, таких как зеленый, черный чай и чай из каркаде.
    • Соблюдайте здоровую диету. Ешьте часто и небольшими порциями, включающими сложные углеводы, свежие фрукты и овощи, нежирные белки и полезные жиры. Избегайте обработанных и сладких продуктов.
    • Знайте свои пределы. Испытайте себя, чтобы полностью раскрыть свой потенциал, но в то же время знайте и работайте в пределах своих возможностей. Вы также можете включить ходьбу в свой распорядок дня, особенно в дни, когда вам не хватает мотивации для интенсивных тренировок.
    • Не забывайте отдыхать. В течение недели, предшествующей гонке, отдыхайте больше, чем обычно. Поддерживайте свою выносливость и расслабьте мышцы, пробежав несколько километров на 3 мили. Обязательно отдохните за 2 дня до гонки.

    За день до забега нет необходимости делать что-либо вроде загрузки углеводами или принимать какие-либо экстремальные диетические меры, поскольку ваши усилия, скорее всего, потребуют менее 90 минут (3).

    Выполняя простые упражнения на подвижность, избегая обезвоживания и пытаясь хорошо выспаться, вы будете чувствовать себя лучше в день гонки.

    Утром перед гонкой, за 1–4 часа до старта, съешьте хороший завтрак, состоящий в основном из углеводов и небольшого количества белка. Это дополнительное количество энергии углеводов поможет пополнить ваш бак, чтобы сохранить достаточное количество гликогена для немедленной энергии (3).

    В зависимости от ваших потребностей рекомендуемое количество углеводов составляет 1–4 грамма на килограмм массы тела. Для человека весом 155 фунтов (около 70 кг) это означает 70–280 граммов углеводов или не менее 280 калорий из углеводов.

    В день соревнований ешьте продукты с высоким гликемическим индексом, которые легче усваиваются. Простые углеводы, белые злаки и сладкие фрукты могут быть хорошим выбором (4).

    Во время тренировки лучше пробовать разные продукты, чтобы знать, что подходит именно вам. Это гарантирует, что в день гонки вы не удивитесь, обнаружив, что что-то не так с вами.

    Пейте много жидкости утром перед забегом, останавливаясь примерно за 1 час до старта, чтобы убедиться, что вы не бежите прямо к горшкам.

    Национальная ассоциация силовой и физической подготовки рекомендует 5–7 мл на кг массы тела не менее чем за 4 часа до гонки (5).

    Подумайте о том, чтобы добавить в воду таблетку электролита, чтобы предотвратить мышечные спазмы и избежать гипонатриемии — опасного потенциального последствия чрезмерного увлажнения только водой (6, 7).

    Если вы пьете кофе, дневная чашка вполне подойдет. Только не переусердствуйте. Однако, если вы не привыкли к кофе и его стимулирующим мочевой пузырь и кишечник эффектам, день гонки может быть не лучшим днем, чтобы начать его пить.

    Кофеин является стимулятором и может помочь вам более эффективно использовать ваши запасы энергии (4).

    Но чрезмерное потребление может отнять у вас время из-за дополнительных перерывов, поэтому экспериментируйте на тренировках, чтобы увидеть, что работает лучше всего.

    После того, как вы в достаточной степени накормлены и выпиты и находитесь на месте, постарайтесь немного расслабиться. Примерно за 10 минут до начала можно выполнить несколько динамических разминочных упражнений.

    Эти упражнения активизируют и разогревают мышцы бедер, ног, ступней и туловища, подготавливая вас к эффективному и комфортному бегу со стартовой линии, вместо того, чтобы использовать первые 10 минут забега для достижения максимальной готовности.

    Хорошая динамическая разминка включает в себя несколько ритмичных движений, таких как перетасовка в сторону, высоко поднятые колени и удары ногами. Это может также включать некоторые динамические растяжки, такие как махи ногой, боковые выпады и касания бегуна.

    Не двигайтесь слишком энергично и не утомляйте себя, но используйте минуты перед гонкой, чтобы разогреться и размяться перед предстоящей задачей.

    Сразу после гонки начинается восстановление. Ваши самые насущные потребности связаны с восстановлением мышц. Вам нужно двигаться медленно и ритмично, чтобы ваше сердце и легкие успокоились.

    Не садитесь сразу — у вас все еще есть большой кровоток в мышцах ног, а ходьба или динамическая растяжка позволят вашему сердцу мягко перенаправить больший поток крови обратно домой и из ваших рук и ног.

    Если вы немедленно плюхнетесь на землю или в кресло, кровь может скапливаться в ваших руках и ногах, что может привести к проблемам с кровяным давлением и даже к потере сознания (8).

    В дополнение к замедлению частоты сердечных сокращений и замедлению дыхания вам потребуется мягко растянуть мышцы. Вам не нужно беспокоиться о глубокой растяжке, но небольшое удлинение этих мышц может улучшить кровообращение и общий комфорт, а также улучшить вашу гибкость.

    Возможно, но это еще не доказано, что растяжка после тренировки может помочь уменьшить болезненность мышц (9).

    Когда дело доходит до уменьшения боли в мышцах с отсроченным началом (DOMS), массаж является лучшим выбором. Одно исследование показало, что массаж через 48 часов после интенсивной тренировки лучше всего помогает облегчить DOMS (10).

    После того, как вы оправитесь от непосредственных последствий вашей гонки, вы получите огромную пользу от приема пищи после тренировки. Ваше восстановление мышц начинается сразу же, поэтому чем раньше вы сможете принять немного углеводов и белков, тем лучше.

    Потребление углеводов и белков в течение 2 часов после окончания гонки важно для восстановления (4).

    Обязательно увлажняйте! Общая рекомендация состоит в том, чтобы выпивать 150% массы тела, потерянной во время гонки, что означает употребление 1,5 л жидкости на каждые 1,0 л потерянной жидкости. Ключ в том, чтобы пить больше воды, чем вы потеряли, чтобы достичь идеального уровня гидратации (11).

    Вам также следует подумать о добавлении электролитов в воду. Исследования показали, что более высокие уровни электролитов натрия в восстановительных напитках (60–80 ммоль/л) оптимальны для восстановления натрия, потерянного с потом (11).

    Как насчет пива? Многим бегунам нравится стакан «жидкого хлеба» после забега, и они наслаждаются ритуалом питья после пробежки.

    Хотя пиво содержит электролиты и углеводы, которые способствуют восстановлению, употребление алкоголя после тренировки препятствует восстановлению мышц (12).

    Итак, если вы решите выпить пиво после гонки, лучше остановиться на одном. Выберите один с более низким содержанием алкоголя и дополните водой.

    Когда вы полностью оправитесь от усилий, дайте своему телу отдохнуть. То, что вы остыли и приняли душ, не означает, что ваше тело готово. Ваши мышцы и кости были перегружены и нуждаются в восстановлении.

    Расслабьтесь до конца дня, но продолжайте периодически двигаться, чтобы ваше тело оставалось гибким.

    Позвольте себе хорошо выспаться после гонки. Хотя восстановление начинается немедленно, ваше тело восстанавливает большую часть мышц во время сна, поэтому вы хотите подарить себе хороший сон, чтобы чувствовать себя сильнее и более восстановленным на следующее утро (13).

    Отдайте себе должное за пробежку на 10 км, независимо от того, сколько у вас времени. Хотя небольшая конкуренция — это нормально, убедитесь, что вы не слишком напрягаетесь или слишком торопитесь. Прислушивайтесь к своему телу и берите дни отдыха, когда это необходимо.

    Запишитесь на фитнес-программу и ожидайте результатов через несколько недель. Наслаждайтесь процессом, когда вы пожинаете плоды того, что получаете или остаетесь в форме, и не удивляйтесь, если вскоре вы обнаружите, что нацелились на полумарафон.

    Среднее время на 10 км и советы по забегу и восстановлению

    Забег на 10 км, который составляет 6,2 мили, идеально подходит для опытных бегунов, которые ищут более сложные задачи. Это второй по популярности забег после полумарафона, требующий уровня физической подготовки, который сочетает в себе силу, энергию и выносливость.

    Если вы уже пробежали несколько 5 км и любите бегать на более длинные дистанции, 10 км могут стать идеальным следующим шагом.

    Пробег на 10 км — это само по себе достижение, и вы должны быть довольны потраченным временем, несмотря ни на что. Тем не менее, это нормально — хотеть знать, как соотносится ваше время с результатами других бегунов и с вашими предыдущими рекордами.

    Ваш возраст, состояние сердечно-сосудистой системы и опорно-двигательного аппарата могут влиять на вашу индивидуальную производительность, но среднее время прохождения 10 км составляет 50–70 минут.

    Продолжайте читать, чтобы узнать больше о средних показателях 10K и о том, как развить скорость и выносливость, необходимые для достижения цели.

    Большинство бегунов, которые находятся в хорошей физической форме и проходят 15–30 миль в неделю, могут рассчитывать на то, что закончат гонку на 10 км за 50–70 минут.

    Более продвинутые бегуны обычно финишируют за 43–50 минут. Исключительно подготовленные бегуны могут пробегать милю каждые 7 минут, в то время как более обычные бегуны могут рассчитывать на пробежку мили каждые 10–14 минут.

    Вокруг света

    Средние результаты в беге на 10 км в Соединенном Королевстве аналогичны показателям в США: мужчины финишируют примерно за 53 минуты, а женщины — за 63 минуты.

    Что касается 10-километрового забега по всему миру, то в настоящее время первое место среди мужчин занимает бегунья из Уганды, а самые высокие результаты среди женщин занимают бегуны из Нидерландов и Эфиопии (1).

    Как правило, в Эфиопии и Кении одни из самых быстрых бегунов как среди мужчин, так и среди женщин.

    Прочие факторы

    Среднее время 10 000 может зависеть от таких факторов, как возраст, пол и уровень физической подготовки.

    Здоровье опорно-двигательного аппарата также играет важную роль, поэтому вам следует принимать меры, чтобы уменьшить боль, избежать травм и бегать в правильной форме.

    Если вы испытываете боль во время бега, рекомендуется проконсультироваться с врачом, чтобы исключить распространенные проблемы, такие как расколотая голень, подошвенный фасциит и колено бегуна. Лучше всего решить эти вопросы до подготовки к гонке.

    Личный рекорд

    Придерживайтесь своей программы тренировок и постепенно доводите ее до достижения целевого времени финиша. Убедитесь, что ваши цели реалистичны и что вы хорошо понимаете свои ограничения.

    Возможно, вы сможете соответствовать средним показателям для вашего возраста и пола, но если они не в пределах досягаемости, исходя из вашего времени в милях, стремитесь к своим личным рекордам.

    Наряду с вашим уровнем физической подготовки и режимом тренировок, возраст и пол являются факторами, которые следует учитывать, когда речь идет о среднем показателе 10 000 раз.

    Ниже приведены средние значения, опубликованные RunRepeat в 2019 году, которые вы можете использовать в качестве указателей, чтобы примерно определить, где вы должны быть в начале и в какое время вы можете стремиться уложиться (2).

    Age Men Women
    0–15 57:08 1:03:14
    16–19 46:36 1:00: 21
    20–24 51:40 59:50
    25–29 53:31 1:02:25
    30–34 54:21 1:02:31
    35–39 54 :27 1:02:19
    40–44 53:31 1:02:37
    45–49 55:35 1:03:27
    50–54 56:12 1:04:04
    55–59 59:00 1:07:41
    60–64 58:48 1:09:51
    65–99 1:03:02 1:18:57

    Если вы только начинаете бегать, вы можете попробовать забег на 5 км, прежде чем переходить на 10 км. Если вы в хорошей физической форме, в добром здравии и привержены своей программе тренировок, вы сможете подготовиться к гонке в течение нескольких недель.

    Подготовка к гонке на 10 км займет в два раза больше времени, чем к гонке на 5 км, поэтому убедитесь, что у вас достаточно времени на подготовку.

    Если это ваша первая гонка, начните с более легкого бега. Медленно повышайте свою выносливость, увеличивая продолжительность и интенсивность занятий.

    Старайтесь не бегать слишком долго или в слишком быстром темпе. Чтобы снизить риск получения травмы, не рискуйте и останавливайтесь каждый раз, когда чувствуете боль или истощение. Сбалансируйте свои беговые тренировки более легкими тренировками, такими как йога, тай-чи или плавание.

    Во время забега на 10 км бегите в темпе, который вы можете поддерживать, чтобы избежать слишком быстрого перенапряжения. Поберегите силы для последней части гонки.

    Среднее время прохождения мили для мужчин, бегущих на 10 км, составляет немногим менее 9 минут, в то время как среднее время для женщин составляет около 10 минут.

    Новичкам может понадобиться 12–15 минут, чтобы пройти милю. Ходоки, которые проходят милю каждые 15–20 минут, могут пройти 10 км за время от 90 минут до 2 часов. Ниже приведена диаграмма, в которой указан средний темп на милю для мужчин и женщин разного возраста (2).

    .
    Age Men Women
    0–15 9:13 10:12
    16–19 7:31 9:44
    20–24 8:20 9:39
    10:05
    35–39 8:47 10:03
    40–44 8:38 10:06
    45–49 8:58 10:14
    50– 54 9:04 10:20
    55–59 9:31. + 10:10 12:44

    Чтобы улучшить скорость, выносливость и работоспособность, вам необходимо повысить общий уровень физической подготовки. Включите различные беговые тренировки в свою программу и часто меняйте ее.

    • Упражнения. Вместо того, чтобы сосредотачиваться исключительно на подсчете миль, выполняйте упражнения, помогающие увеличить скорость, такие как темповые пробежки, интервальные тренировки и бег в гору. Вы можете улучшить свой шаг, пытаясь увеличить количество шагов в минуту.
    • Испытайте себя. Попробуйте сложные трассы с множеством холмов, ручьев или пересеченной местности. Бегайте в неблагоприятных условиях, таких как жара, холод и дождь, чтобы вы могли адаптироваться к различным погодным условиям. Если есть возможность, потренируйтесь на гоночной трассе заранее.
    • Смешайте это. Во избежание травм выберите 1 день в неделю для интенсивных тренировок. В остальные дни выполняйте умеренные упражнения и отдыхайте как минимум 1 полный день в неделю. Сбалансируйте свои беговые тренировки упражнениями на растяжку, которые сделают ваше тело гибким.
    • Стань сильнее. Силовые тренировки для наращивания мышечной массы и повышения устойчивости. Примеры этого включают тяжелую атлетику, тренировки с собственным весом и упражнения с эспандером.
    • Хорошо относитесь к своему телу. Позаботьтесь о своем здоровье в целом, высыпайтесь и повышайте уровень гидратации, выпивая много воды и электролитных напитков. Избегайте или ограничьте потребление кофеина, алкоголя и мочегонных средств, таких как зеленый, черный чай и чай из каркаде.
    • Соблюдайте здоровую диету. Ешьте часто и небольшими порциями, включающими сложные углеводы, свежие фрукты и овощи, нежирные белки и полезные жиры. Избегайте обработанных и сладких продуктов.
    • Знайте свои пределы. Испытайте себя, чтобы полностью раскрыть свой потенциал, но в то же время знайте и работайте в пределах своих возможностей. Вы также можете включить ходьбу в свой распорядок дня, особенно в дни, когда вам не хватает мотивации для интенсивных тренировок.
    • Не забывайте отдыхать. В течение недели, предшествующей гонке, отдыхайте больше, чем обычно. Поддерживайте свою выносливость и расслабьте мышцы, пробежав несколько километров на 3 мили. Обязательно отдохните за 2 дня до гонки.

    За день до забега нет необходимости делать что-либо вроде загрузки углеводами или принимать какие-либо экстремальные диетические меры, поскольку ваши усилия, скорее всего, потребуют менее 90 минут (3).

    Выполняя простые упражнения на подвижность, избегая обезвоживания и пытаясь хорошо выспаться, вы будете чувствовать себя лучше в день гонки.

    Утром перед гонкой, за 1–4 часа до старта, съешьте хороший завтрак, состоящий в основном из углеводов и небольшого количества белка. Это дополнительное количество энергии углеводов поможет пополнить ваш бак, чтобы сохранить достаточное количество гликогена для немедленной энергии (3).

    В зависимости от ваших потребностей рекомендуемое количество углеводов составляет 1–4 грамма на килограмм массы тела. Для человека весом 155 фунтов (около 70 кг) это означает 70–280 граммов углеводов или не менее 280 калорий из углеводов.

    В день соревнований ешьте продукты с высоким гликемическим индексом, которые легче усваиваются. Простые углеводы, белые злаки и сладкие фрукты могут быть хорошим выбором (4).

    Во время тренировки лучше пробовать разные продукты, чтобы знать, что подходит именно вам. Это гарантирует, что в день гонки вы не удивитесь, обнаружив, что что-то не так с вами.

    Пейте много жидкости утром перед забегом, останавливаясь примерно за 1 час до старта, чтобы убедиться, что вы не бежите прямо к горшкам.

    Национальная ассоциация силовой и физической подготовки рекомендует 5–7 мл на кг массы тела не менее чем за 4 часа до гонки (5).

    Подумайте о том, чтобы добавить в воду таблетку электролита, чтобы предотвратить мышечные спазмы и избежать гипонатриемии — опасного потенциального последствия чрезмерного увлажнения только водой (6, 7).

    Если вы пьете кофе, дневная чашка вполне подойдет. Только не переусердствуйте. Однако, если вы не привыкли к кофе и его стимулирующим мочевой пузырь и кишечник эффектам, день гонки может быть не лучшим днем, чтобы начать его пить.

    Кофеин является стимулятором и может помочь вам более эффективно использовать ваши запасы энергии (4).

    Но чрезмерное потребление может отнять у вас время из-за дополнительных перерывов, поэтому экспериментируйте на тренировках, чтобы увидеть, что работает лучше всего.

    После того, как вы в достаточной степени накормлены и выпиты и находитесь на месте, постарайтесь немного расслабиться. Примерно за 10 минут до начала можно выполнить несколько динамических разминочных упражнений.

    Эти упражнения активизируют и разогревают мышцы бедер, ног, ступней и туловища, подготавливая вас к эффективному и комфортному бегу со стартовой линии, вместо того, чтобы использовать первые 10 минут забега для достижения максимальной готовности.

    Хорошая динамическая разминка включает в себя несколько ритмичных движений, таких как перетасовка в сторону, высоко поднятые колени и удары ногами. Это может также включать некоторые динамические растяжки, такие как махи ногой, боковые выпады и касания бегуна.

    Не двигайтесь слишком энергично и не утомляйте себя, но используйте минуты перед гонкой, чтобы разогреться и размяться перед предстоящей задачей.

    Сразу после гонки начинается восстановление. Ваши самые насущные потребности связаны с восстановлением мышц. Вам нужно двигаться медленно и ритмично, чтобы ваше сердце и легкие успокоились.

    Не садитесь сразу — у вас все еще есть большой кровоток в мышцах ног, а ходьба или динамическая растяжка позволят вашему сердцу мягко перенаправить больший поток крови обратно домой и из ваших рук и ног.

    Если вы немедленно плюхнетесь на землю или в кресло, кровь может скапливаться в ваших руках и ногах, что может привести к проблемам с кровяным давлением и даже к потере сознания (8).

    В дополнение к замедлению частоты сердечных сокращений и замедлению дыхания вам потребуется мягко растянуть мышцы. Вам не нужно беспокоиться о глубокой растяжке, но небольшое удлинение этих мышц может улучшить кровообращение и общий комфорт, а также улучшить вашу гибкость.

    Возможно, но это еще не доказано, что растяжка после тренировки может помочь уменьшить болезненность мышц (9).

    Когда дело доходит до уменьшения боли в мышцах с отсроченным началом (DOMS), массаж является лучшим выбором. Одно исследование показало, что массаж через 48 часов после интенсивной тренировки лучше всего помогает облегчить DOMS (10).

    После того, как вы оправитесь от непосредственных последствий вашей гонки, вы получите огромную пользу от приема пищи после тренировки. Ваше восстановление мышц начинается сразу же, поэтому чем раньше вы сможете принять немного углеводов и белков, тем лучше.

    Потребление углеводов и белков в течение 2 часов после окончания гонки важно для восстановления (4).

    Обязательно увлажняйте! Общая рекомендация состоит в том, чтобы выпивать 150% массы тела, потерянной во время гонки, что означает употребление 1,5 л жидкости на каждые 1,0 л потерянной жидкости. Ключ в том, чтобы пить больше воды, чем вы потеряли, чтобы достичь идеального уровня гидратации (11).

    Вам также следует подумать о добавлении электролитов в воду. Исследования показали, что более высокие уровни электролитов натрия в восстановительных напитках (60–80 ммоль/л) оптимальны для восстановления натрия, потерянного с потом (11).

    Как насчет пива? Многим бегунам нравится стакан «жидкого хлеба» после забега, и они наслаждаются ритуалом питья после пробежки.

    Хотя пиво содержит электролиты и углеводы, которые способствуют восстановлению, употребление алкоголя после тренировки препятствует восстановлению мышц (12).

    Итак, если вы решите выпить пиво после гонки, лучше остановиться на одном. Выберите один с более низким содержанием алкоголя и дополните водой.

    Когда вы полностью оправитесь от усилий, дайте своему телу отдохнуть. То, что вы остыли и приняли душ, не означает, что ваше тело готово. Ваши мышцы и кости были перегружены и нуждаются в восстановлении.

    Расслабьтесь до конца дня, но продолжайте периодически двигаться, чтобы ваше тело оставалось гибким.

    Позвольте себе хорошо выспаться после гонки. Хотя восстановление начинается немедленно, ваше тело восстанавливает большую часть мышц во время сна, поэтому вы хотите подарить себе хороший сон, чтобы чувствовать себя сильнее и более восстановленным на следующее утро (13).

    Отдайте себе должное за пробежку на 10 км, независимо от того, сколько у вас времени. Хотя небольшая конкуренция — это нормально, убедитесь, что вы не слишком напрягаетесь или слишком торопитесь. Прислушивайтесь к своему телу и берите дни отдыха, когда это необходимо.

    Запишитесь на фитнес-программу и ожидайте результатов через несколько недель. Наслаждайтесь процессом, когда вы пожинаете плоды того, что получаете или остаетесь в форме, и не удивляйтесь, если вскоре вы обнаружите, что нацелились на полумарафон.

    Среднее время на 10 км и советы по забегу и восстановлению

    Забег на 10 км, который составляет 6,2 мили, идеально подходит для опытных бегунов, которые ищут более сложные задачи. Это второй по популярности забег после полумарафона, требующий уровня физической подготовки, который сочетает в себе силу, энергию и выносливость.

    Если вы уже пробежали несколько 5 км и любите бегать на более длинные дистанции, 10 км могут стать идеальным следующим шагом.

    Пробег на 10 км — это само по себе достижение, и вы должны быть довольны потраченным временем, несмотря ни на что. Тем не менее, это нормально — хотеть знать, как соотносится ваше время с результатами других бегунов и с вашими предыдущими рекордами.

    Ваш возраст, состояние сердечно-сосудистой системы и опорно-двигательного аппарата могут влиять на вашу индивидуальную производительность, но среднее время прохождения 10 км составляет 50–70 минут.

    Продолжайте читать, чтобы узнать больше о средних показателях 10K и о том, как развить скорость и выносливость, необходимые для достижения цели.

    Большинство бегунов, которые находятся в хорошей физической форме и проходят 15–30 миль в неделю, могут рассчитывать на то, что закончат гонку на 10 км за 50–70 минут.

    Более продвинутые бегуны обычно финишируют за 43–50 минут. Исключительно подготовленные бегуны могут пробегать милю каждые 7 минут, в то время как более обычные бегуны могут рассчитывать на пробежку мили каждые 10–14 минут.

    Вокруг света

    Средние результаты в беге на 10 км в Соединенном Королевстве аналогичны показателям в США: мужчины финишируют примерно за 53 минуты, а женщины — за 63 минуты.

    Что касается 10-километрового забега по всему миру, то в настоящее время первое место среди мужчин занимает бегунья из Уганды, а самые высокие результаты среди женщин занимают бегуны из Нидерландов и Эфиопии (1).

    Как правило, в Эфиопии и Кении одни из самых быстрых бегунов как среди мужчин, так и среди женщин.

    Прочие факторы

    Среднее время 10 000 может зависеть от таких факторов, как возраст, пол и уровень физической подготовки.

    Здоровье опорно-двигательного аппарата также играет важную роль, поэтому вам следует принимать меры, чтобы уменьшить боль, избежать травм и бегать в правильной форме.

    Если вы испытываете боль во время бега, рекомендуется проконсультироваться с врачом, чтобы исключить распространенные проблемы, такие как расколотая голень, подошвенный фасциит и колено бегуна. Лучше всего решить эти вопросы до подготовки к гонке.

    Личный рекорд

    Придерживайтесь своей программы тренировок и постепенно доводите ее до достижения целевого времени финиша. Убедитесь, что ваши цели реалистичны и что вы хорошо понимаете свои ограничения.

    Возможно, вы сможете соответствовать средним показателям для вашего возраста и пола, но если они не в пределах досягаемости, исходя из вашего времени в милях, стремитесь к своим личным рекордам.

    Наряду с вашим уровнем физической подготовки и режимом тренировок, возраст и пол являются факторами, которые следует учитывать, когда речь идет о среднем показателе 10 000 раз.

    Ниже приведены средние значения, опубликованные RunRepeat в 2019 году, которые вы можете использовать в качестве указателей, чтобы примерно определить, где вы должны быть в начале и в какое время вы можете стремиться уложиться (2).

    Age Men Women
    0–15 57:08 1:03:14
    16–19 46:36 1:00: 21
    20–24 51:40 59:50
    25–29 53:31 1:02:25
    30–34 54:21 1:02:31
    35–39 54 :27 1:02:19
    40–44 53:31 1:02:37
    45–49 55:35 1:03:27
    50–54 56:12 1:04:04
    55–59 59:00 1:07:41
    60–64 58:48 1:09:51
    65–99 1:03:02 1:18:57

    Если вы только начинаете бегать, вы можете попробовать забег на 5 км, прежде чем переходить на 10 км. Если вы в хорошей физической форме, в добром здравии и привержены своей программе тренировок, вы сможете подготовиться к гонке в течение нескольких недель.

    Подготовка к гонке на 10 км займет в два раза больше времени, чем к гонке на 5 км, поэтому убедитесь, что у вас достаточно времени на подготовку.

    Если это ваша первая гонка, начните с более легкого бега. Медленно повышайте свою выносливость, увеличивая продолжительность и интенсивность занятий.

    Старайтесь не бегать слишком долго или в слишком быстром темпе. Чтобы снизить риск получения травмы, не рискуйте и останавливайтесь каждый раз, когда чувствуете боль или истощение. Сбалансируйте свои беговые тренировки более легкими тренировками, такими как йога, тай-чи или плавание.

    Во время забега на 10 км бегите в темпе, который вы можете поддерживать, чтобы избежать слишком быстрого перенапряжения. Поберегите силы для последней части гонки.

    Среднее время прохождения мили для мужчин, бегущих на 10 км, составляет немногим менее 9 минут, в то время как среднее время для женщин составляет около 10 минут.

    Новичкам может понадобиться 12–15 минут, чтобы пройти милю. Ходоки, которые проходят милю каждые 15–20 минут, могут пройти 10 км за время от 90 минут до 2 часов. Ниже приведена диаграмма, в которой указан средний темп на милю для мужчин и женщин разного возраста (2).

    .
    Age Men Women
    0–15 9:13 10:12
    16–19 7:31 9:44
    20–24 8:20 9:39
    10:05
    35–39 8:47 10:03
    40–44 8:38 10:06
    45–49 8:58 10:14
    50– 54 9:04 10:20
    55–59 9:31. + 10:10 12:44

    Чтобы улучшить скорость, выносливость и работоспособность, вам необходимо повысить общий уровень физической подготовки. Включите различные беговые тренировки в свою программу и часто меняйте ее.

    • Упражнения. Вместо того, чтобы сосредотачиваться исключительно на подсчете миль, выполняйте упражнения, помогающие увеличить скорость, такие как темповые пробежки, интервальные тренировки и бег в гору. Вы можете улучшить свой шаг, пытаясь увеличить количество шагов в минуту.
    • Испытайте себя. Попробуйте сложные трассы с множеством холмов, ручьев или пересеченной местности. Бегайте в неблагоприятных условиях, таких как жара, холод и дождь, чтобы вы могли адаптироваться к различным погодным условиям. Если есть возможность, потренируйтесь на гоночной трассе заранее.
    • Смешайте это. Во избежание травм выберите 1 день в неделю для интенсивных тренировок. В остальные дни выполняйте умеренные упражнения и отдыхайте как минимум 1 полный день в неделю. Сбалансируйте свои беговые тренировки упражнениями на растяжку, которые сделают ваше тело гибким.
    • Стань сильнее. Силовые тренировки для наращивания мышечной массы и повышения устойчивости. Примеры этого включают тяжелую атлетику, тренировки с собственным весом и упражнения с эспандером.
    • Хорошо относитесь к своему телу. Позаботьтесь о своем здоровье в целом, высыпайтесь и повышайте уровень гидратации, выпивая много воды и электролитных напитков. Избегайте или ограничьте потребление кофеина, алкоголя и мочегонных средств, таких как зеленый, черный чай и чай из каркаде.
    • Соблюдайте здоровую диету. Ешьте часто и небольшими порциями, включающими сложные углеводы, свежие фрукты и овощи, нежирные белки и полезные жиры. Избегайте обработанных и сладких продуктов.
    • Знайте свои пределы. Испытайте себя, чтобы полностью раскрыть свой потенциал, но в то же время знайте и работайте в пределах своих возможностей. Вы также можете включить ходьбу в свой распорядок дня, особенно в дни, когда вам не хватает мотивации для интенсивных тренировок.
    • Не забывайте отдыхать. В течение недели, предшествующей гонке, отдыхайте больше, чем обычно. Поддерживайте свою выносливость и расслабьте мышцы, пробежав несколько километров на 3 мили. Обязательно отдохните за 2 дня до гонки.

    За день до забега нет необходимости делать что-либо вроде загрузки углеводами или принимать какие-либо экстремальные диетические меры, поскольку ваши усилия, скорее всего, потребуют менее 90 минут (3).

    Выполняя простые упражнения на подвижность, избегая обезвоживания и пытаясь хорошо выспаться, вы будете чувствовать себя лучше в день гонки.

    Утром перед гонкой, за 1–4 часа до старта, съешьте хороший завтрак, состоящий в основном из углеводов и небольшого количества белка. Это дополнительное количество энергии углеводов поможет пополнить ваш бак, чтобы сохранить достаточное количество гликогена для немедленной энергии (3).

    В зависимости от ваших потребностей рекомендуемое количество углеводов составляет 1–4 грамма на килограмм массы тела. Для человека весом 155 фунтов (около 70 кг) это означает 70–280 граммов углеводов или не менее 280 калорий из углеводов.

    В день соревнований ешьте продукты с высоким гликемическим индексом, которые легче усваиваются. Простые углеводы, белые злаки и сладкие фрукты могут быть хорошим выбором (4).

    Во время тренировки лучше пробовать разные продукты, чтобы знать, что подходит именно вам. Это гарантирует, что в день гонки вы не удивитесь, обнаружив, что что-то не так с вами.

    Пейте много жидкости утром перед забегом, останавливаясь примерно за 1 час до старта, чтобы убедиться, что вы не бежите прямо к горшкам.

    Национальная ассоциация силовой и физической подготовки рекомендует 5–7 мл на кг массы тела не менее чем за 4 часа до гонки (5).

    Подумайте о том, чтобы добавить в воду таблетку электролита, чтобы предотвратить мышечные спазмы и избежать гипонатриемии — опасного потенциального последствия чрезмерного увлажнения только водой (6, 7).

    Если вы пьете кофе, дневная чашка вполне подойдет. Только не переусердствуйте. Однако, если вы не привыкли к кофе и его стимулирующим мочевой пузырь и кишечник эффектам, день гонки может быть не лучшим днем, чтобы начать его пить.

    Кофеин является стимулятором и может помочь вам более эффективно использовать ваши запасы энергии (4).

    Но чрезмерное потребление может отнять у вас время из-за дополнительных перерывов, поэтому экспериментируйте на тренировках, чтобы увидеть, что работает лучше всего.

    После того, как вы в достаточной степени накормлены и выпиты и находитесь на месте, постарайтесь немного расслабиться. Примерно за 10 минут до начала можно выполнить несколько динамических разминочных упражнений.

    Эти упражнения активизируют и разогревают мышцы бедер, ног, ступней и туловища, подготавливая вас к эффективному и комфортному бегу со стартовой линии, вместо того, чтобы использовать первые 10 минут забега для достижения максимальной готовности.

    Хорошая динамическая разминка включает в себя несколько ритмичных движений, таких как перетасовка в сторону, высоко поднятые колени и удары ногами. Это может также включать некоторые динамические растяжки, такие как махи ногой, боковые выпады и касания бегуна.

    Не двигайтесь слишком энергично и не утомляйте себя, но используйте минуты перед гонкой, чтобы разогреться и размяться перед предстоящей задачей.

    Сразу после гонки начинается восстановление. Ваши самые насущные потребности связаны с восстановлением мышц. Вам нужно двигаться медленно и ритмично, чтобы ваше сердце и легкие успокоились.

    Не садитесь сразу — у вас все еще есть большой кровоток в мышцах ног, а ходьба или динамическая растяжка позволят вашему сердцу мягко перенаправить больший поток крови обратно домой и из ваших рук и ног.

    Если вы немедленно плюхнетесь на землю или в кресло, кровь может скапливаться в ваших руках и ногах, что может привести к проблемам с кровяным давлением и даже к потере сознания (8).

    В дополнение к замедлению частоты сердечных сокращений и замедлению дыхания вам потребуется мягко растянуть мышцы. Вам не нужно беспокоиться о глубокой растяжке, но небольшое удлинение этих мышц может улучшить кровообращение и общий комфорт, а также улучшить вашу гибкость.

    Возможно, но это еще не доказано, что растяжка после тренировки может помочь уменьшить болезненность мышц (9).

    Когда дело доходит до уменьшения боли в мышцах с отсроченным началом (DOMS), массаж является лучшим выбором. Одно исследование показало, что массаж через 48 часов после интенсивной тренировки лучше всего помогает облегчить DOMS (10).

    После того, как вы оправитесь от непосредственных последствий вашей гонки, вы получите огромную пользу от приема пищи после тренировки. Ваше восстановление мышц начинается сразу же, поэтому чем раньше вы сможете принять немного углеводов и белков, тем лучше.

    Потребление углеводов и белков в течение 2 часов после окончания гонки важно для восстановления (4).

    Обязательно увлажняйте! Общая рекомендация состоит в том, чтобы выпивать 150% массы тела, потерянной во время гонки, что означает употребление 1,5 л жидкости на каждые 1,0 л потерянной жидкости. Ключ в том, чтобы пить больше воды, чем вы потеряли, чтобы достичь идеального уровня гидратации (11).

    Вам также следует подумать о добавлении электролитов в воду. Исследования показали, что более высокие уровни электролитов натрия в восстановительных напитках (60–80 ммоль/л) оптимальны для восстановления натрия, потерянного с потом (11).

    Как насчет пива? Многим бегунам нравится стакан «жидкого хлеба» после забега, и они наслаждаются ритуалом питья после пробежки.

    Хотя пиво содержит электролиты и углеводы, которые способствуют восстановлению, употребление алкоголя после тренировки препятствует восстановлению мышц (12).

    Итак, если вы решите выпить пиво после гонки, лучше остановиться на одном. Выберите один с более низким содержанием алкоголя и дополните водой.

    Когда вы полностью оправитесь от усилий, дайте своему телу отдохнуть. То, что вы остыли и приняли душ, не означает, что ваше тело готово. Ваши мышцы и кости были перегружены и нуждаются в восстановлении.

    Расслабьтесь до конца дня, но продолжайте периодически двигаться, чтобы ваше тело оставалось гибким.

    Позвольте себе хорошо выспаться после гонки. Хотя восстановление начинается немедленно, ваше тело восстанавливает большую часть мышц во время сна, поэтому вы хотите подарить себе хороший сон, чтобы чувствовать себя сильнее и более восстановленным на следующее утро (13).

    Отдайте себе должное за пробежку на 10 км, независимо от того, сколько у вас времени. Хотя небольшая конкуренция — это нормально, убедитесь, что вы не слишком напрягаетесь или слишком торопитесь. Прислушивайтесь к своему телу и берите дни отдыха, когда это необходимо.

    Запишитесь на фитнес-программу и ожидайте результатов через несколько недель. Наслаждайтесь процессом, когда вы пожинаете плоды того, что получаете или остаетесь в форме, и не удивляйтесь, если вскоре вы обнаружите, что нацелились на полумарафон.

    Среднее время на 10 км и советы по забегу и восстановлению

    Забег на 10 км, который составляет 6,2 мили, идеально подходит для опытных бегунов, которые ищут более сложные задачи. Это второй по популярности забег после полумарафона, требующий уровня физической подготовки, который сочетает в себе силу, энергию и выносливость.

    Если вы уже пробежали несколько 5 км и любите бегать на более длинные дистанции, 10 км могут стать идеальным следующим шагом.

    Пробег на 10 км — это само по себе достижение, и вы должны быть довольны потраченным временем, несмотря ни на что. Тем не менее, это нормально — хотеть знать, как соотносится ваше время с результатами других бегунов и с вашими предыдущими рекордами.

    Ваш возраст, состояние сердечно-сосудистой системы и опорно-двигательного аппарата могут влиять на вашу индивидуальную производительность, но среднее время прохождения 10 км составляет 50–70 минут.

    Продолжайте читать, чтобы узнать больше о средних показателях 10K и о том, как развить скорость и выносливость, необходимые для достижения цели.

    Большинство бегунов, которые находятся в хорошей физической форме и проходят 15–30 миль в неделю, могут рассчитывать на то, что закончат гонку на 10 км за 50–70 минут.

    Более продвинутые бегуны обычно финишируют за 43–50 минут. Исключительно подготовленные бегуны могут пробегать милю каждые 7 минут, в то время как более обычные бегуны могут рассчитывать на пробежку мили каждые 10–14 минут.

    Вокруг света

    Средние результаты в беге на 10 км в Соединенном Королевстве аналогичны показателям в США: мужчины финишируют примерно за 53 минуты, а женщины — за 63 минуты.

    Что касается 10-километрового забега по всему миру, то в настоящее время первое место среди мужчин занимает бегунья из Уганды, а самые высокие результаты среди женщин занимают бегуны из Нидерландов и Эфиопии (1).

    Как правило, в Эфиопии и Кении одни из самых быстрых бегунов как среди мужчин, так и среди женщин.

    Прочие факторы

    Среднее время 10 000 может зависеть от таких факторов, как возраст, пол и уровень физической подготовки.

    Здоровье опорно-двигательного аппарата также играет важную роль, поэтому вам следует принимать меры, чтобы уменьшить боль, избежать травм и бегать в правильной форме.

    Если вы испытываете боль во время бега, рекомендуется проконсультироваться с врачом, чтобы исключить распространенные проблемы, такие как расколотая голень, подошвенный фасциит и колено бегуна. Лучше всего решить эти вопросы до подготовки к гонке.

    Личный рекорд

    Придерживайтесь своей программы тренировок и постепенно доводите ее до достижения целевого времени финиша. Убедитесь, что ваши цели реалистичны и что вы хорошо понимаете свои ограничения.

    Возможно, вы сможете соответствовать средним показателям для вашего возраста и пола, но если они не в пределах досягаемости, исходя из вашего времени в милях, стремитесь к своим личным рекордам.

    Наряду с вашим уровнем физической подготовки и режимом тренировок, возраст и пол являются факторами, которые следует учитывать, когда речь идет о среднем показателе 10 000 раз.

    Ниже приведены средние значения, опубликованные RunRepeat в 2019 году, которые вы можете использовать в качестве указателей, чтобы примерно определить, где вы должны быть в начале и в какое время вы можете стремиться уложиться (2).

    Age Men Women
    0–15 57:08 1:03:14
    16–19 46:36 1:00: 21
    20–24 51:40 59:50
    25–29 53:31 1:02:25
    30–34 54:21 1:02:31
    35–39 54 :27 1:02:19
    40–44 53:31 1:02:37
    45–49 55:35 1:03:27
    50–54 56:12 1:04:04
    55–59 59:00 1:07:41
    60–64 58:48 1:09:51
    65–99 1:03:02 1:18:57

    Если вы только начинаете бегать, вы можете попробовать забег на 5 км, прежде чем переходить на 10 км. Если вы в хорошей физической форме, в добром здравии и привержены своей программе тренировок, вы сможете подготовиться к гонке в течение нескольких недель.

    Подготовка к гонке на 10 км займет в два раза больше времени, чем к гонке на 5 км, поэтому убедитесь, что у вас достаточно времени на подготовку.

    Если это ваша первая гонка, начните с более легкого бега. Медленно повышайте свою выносливость, увеличивая продолжительность и интенсивность занятий.

    Старайтесь не бегать слишком долго или в слишком быстром темпе. Чтобы снизить риск получения травмы, не рискуйте и останавливайтесь каждый раз, когда чувствуете боль или истощение. Сбалансируйте свои беговые тренировки более легкими тренировками, такими как йога, тай-чи или плавание.

    Во время забега на 10 км бегите в темпе, который вы можете поддерживать, чтобы избежать слишком быстрого перенапряжения. Поберегите силы для последней части гонки.

    Среднее время прохождения мили для мужчин, бегущих на 10 км, составляет немногим менее 9 минут, в то время как среднее время для женщин составляет около 10 минут.

    Новичкам может понадобиться 12–15 минут, чтобы пройти милю. Ходоки, которые проходят милю каждые 15–20 минут, могут пройти 10 км за время от 90 минут до 2 часов. Ниже приведена диаграмма, в которой указан средний темп на милю для мужчин и женщин разного возраста (2).

    .
    Age Men Women
    0–15 9:13 10:12
    16–19 7:31 9:44
    20–24 8:20 9:39
    10:05
    35–39 8:47 10:03
    40–44 8:38 10:06
    45–49 8:58 10:14
    50– 54 9:04 10:20
    55–59 9:31. + 10:10 12:44

    Чтобы улучшить скорость, выносливость и работоспособность, вам необходимо повысить общий уровень физической подготовки. Включите различные беговые тренировки в свою программу и часто меняйте ее.

    • Упражнения. Вместо того, чтобы сосредотачиваться исключительно на подсчете миль, выполняйте упражнения, помогающие увеличить скорость, такие как темповые пробежки, интервальные тренировки и бег в гору. Вы можете улучшить свой шаг, пытаясь увеличить количество шагов в минуту.
    • Испытайте себя. Попробуйте сложные трассы с множеством холмов, ручьев или пересеченной местности. Бегайте в неблагоприятных условиях, таких как жара, холод и дождь, чтобы вы могли адаптироваться к различным погодным условиям. Если есть возможность, потренируйтесь на гоночной трассе заранее.
    • Смешайте это. Во избежание травм выберите 1 день в неделю для интенсивных тренировок. В остальные дни выполняйте умеренные упражнения и отдыхайте как минимум 1 полный день в неделю. Сбалансируйте свои беговые тренировки упражнениями на растяжку, которые сделают ваше тело гибким.
    • Стань сильнее. Силовые тренировки для наращивания мышечной массы и повышения устойчивости. Примеры этого включают тяжелую атлетику, тренировки с собственным весом и упражнения с эспандером.
    • Хорошо относитесь к своему телу. Позаботьтесь о своем здоровье в целом, высыпайтесь и повышайте уровень гидратации, выпивая много воды и электролитных напитков. Избегайте или ограничьте потребление кофеина, алкоголя и мочегонных средств, таких как зеленый, черный чай и чай из каркаде.
    • Соблюдайте здоровую диету. Ешьте часто и небольшими порциями, включающими сложные углеводы, свежие фрукты и овощи, нежирные белки и полезные жиры. Избегайте обработанных и сладких продуктов.
    • Знайте свои пределы. Испытайте себя, чтобы полностью раскрыть свой потенциал, но в то же время знайте и работайте в пределах своих возможностей. Вы также можете включить ходьбу в свой распорядок дня, особенно в дни, когда вам не хватает мотивации для интенсивных тренировок.
    • Не забывайте отдыхать. В течение недели, предшествующей гонке, отдыхайте больше, чем обычно. Поддерживайте свою выносливость и расслабьте мышцы, пробежав несколько километров на 3 мили. Обязательно отдохните за 2 дня до гонки.

    За день до забега нет необходимости делать что-либо вроде загрузки углеводами или принимать какие-либо экстремальные диетические меры, поскольку ваши усилия, скорее всего, потребуют менее 90 минут (3).

    Выполняя простые упражнения на подвижность, избегая обезвоживания и пытаясь хорошо выспаться, вы будете чувствовать себя лучше в день гонки.

    Утром перед гонкой, за 1–4 часа до старта, съешьте хороший завтрак, состоящий в основном из углеводов и небольшого количества белка. Это дополнительное количество энергии углеводов поможет пополнить ваш бак, чтобы сохранить достаточное количество гликогена для немедленной энергии (3).

    В зависимости от ваших потребностей рекомендуемое количество углеводов составляет 1–4 грамма на килограмм массы тела. Для человека весом 155 фунтов (около 70 кг) это означает 70–280 граммов углеводов или не менее 280 калорий из углеводов.

    В день соревнований ешьте продукты с высоким гликемическим индексом, которые легче усваиваются. Простые углеводы, белые злаки и сладкие фрукты могут быть хорошим выбором (4).

    Во время тренировки лучше пробовать разные продукты, чтобы знать, что подходит именно вам. Это гарантирует, что в день гонки вы не удивитесь, обнаружив, что что-то не так с вами.

    Пейте много жидкости утром перед забегом, останавливаясь примерно за 1 час до старта, чтобы убедиться, что вы не бежите прямо к горшкам.

    Национальная ассоциация силовой и физической подготовки рекомендует 5–7 мл на кг массы тела не менее чем за 4 часа до гонки (5).

    Подумайте о том, чтобы добавить в воду таблетку электролита, чтобы предотвратить мышечные спазмы и избежать гипонатриемии — опасного потенциального последствия чрезмерного увлажнения только водой (6, 7).

    Если вы пьете кофе, дневная чашка вполне подойдет. Только не переусердствуйте. Однако, если вы не привыкли к кофе и его стимулирующим мочевой пузырь и кишечник эффектам, день гонки может быть не лучшим днем, чтобы начать его пить.

    Кофеин является стимулятором и может помочь вам более эффективно использовать ваши запасы энергии (4).

    Но чрезмерное потребление может отнять у вас время из-за дополнительных перерывов, поэтому экспериментируйте на тренировках, чтобы увидеть, что работает лучше всего.

    После того, как вы в достаточной степени накормлены и выпиты и находитесь на месте, постарайтесь немного расслабиться. Примерно за 10 минут до начала можно выполнить несколько динамических разминочных упражнений.

    Эти упражнения активизируют и разогревают мышцы бедер, ног, ступней и туловища, подготавливая вас к эффективному и комфортному бегу со стартовой линии, вместо того, чтобы использовать первые 10 минут забега для достижения максимальной готовности.

    Хорошая динамическая разминка включает в себя несколько ритмичных движений, таких как перетасовка в сторону, высоко поднятые колени и удары ногами. Это может также включать некоторые динамические растяжки, такие как махи ногой, боковые выпады и касания бегуна.

    Не двигайтесь слишком энергично и не утомляйте себя, но используйте минуты перед гонкой, чтобы разогреться и размяться перед предстоящей задачей.

    Сразу после гонки начинается восстановление. Ваши самые насущные потребности связаны с восстановлением мышц. Вам нужно двигаться медленно и ритмично, чтобы ваше сердце и легкие успокоились.

    Не садитесь сразу — у вас все еще есть большой кровоток в мышцах ног, а ходьба или динамическая растяжка позволят вашему сердцу мягко перенаправить больший поток крови обратно домой и из ваших рук и ног.

    Если вы немедленно плюхнетесь на землю или в кресло, кровь может скапливаться в ваших руках и ногах, что может привести к проблемам с кровяным давлением и даже к потере сознания (8).

    В дополнение к замедлению частоты сердечных сокращений и замедлению дыхания вам потребуется мягко растянуть мышцы. Вам не нужно беспокоиться о глубокой растяжке, но небольшое удлинение этих мышц может улучшить кровообращение и общий комфорт, а также улучшить вашу гибкость.

    Возможно, но это еще не доказано, что растяжка после тренировки может помочь уменьшить болезненность мышц (9).

    Когда дело доходит до уменьшения боли в мышцах с отсроченным началом (DOMS), массаж является лучшим выбором. Одно исследование показало, что массаж через 48 часов после интенсивной тренировки лучше всего помогает облегчить DOMS (10).

    После того, как вы оправитесь от непосредственных последствий вашей гонки, вы получите огромную пользу от приема пищи после тренировки. Ваше восстановление мышц начинается сразу же, поэтому чем раньше вы сможете принять немного углеводов и белков, тем лучше.

    Потребление углеводов и белков в течение 2 часов после окончания гонки важно для восстановления (4).

    Обязательно увлажняйте! Общая рекомендация состоит в том, чтобы выпивать 150% массы тела, потерянной во время гонки, что означает употребление 1,5 л жидкости на каждые 1,0 л потерянной жидкости. Ключ в том, чтобы пить больше воды, чем вы потеряли, чтобы достичь идеального уровня гидратации (11).

    Вам также следует подумать о добавлении электролитов в воду. Исследования показали, что более высокие уровни электролитов натрия в восстановительных напитках (60–80 ммоль/л) оптимальны для восстановления натрия, потерянного с потом (11).

    Как насчет пива? Многим бегунам нравится стакан «жидкого хлеба» после забега, и они наслаждаются ритуалом питья после пробежки.

    Хотя пиво содержит электролиты и углеводы, которые способствуют восстановлению, употребление алкоголя после тренировки препятствует восстановлению мышц (12).

    Итак, если вы решите выпить пиво после гонки, лучше остановиться на одном. Выберите один с более низким содержанием алкоголя и дополните водой.

    Когда вы полностью оправитесь от усилий, дайте своему телу отдохнуть. То, что вы остыли и приняли душ, не означает, что ваше тело готово. Ваши мышцы и кости были перегружены и нуждаются в восстановлении.

    Расслабьтесь до конца дня, но продолжайте периодически двигаться, чтобы ваше тело оставалось гибким.

    Позвольте себе хорошо выспаться после гонки. Хотя восстановление начинается немедленно, ваше тело восстанавливает большую часть мышц во время сна, поэтому вы хотите подарить себе хороший сон, чтобы чувствовать себя сильнее и более восстановленным на следующее утро (13).

    Отдайте себе должное за пробежку на 10 км, независимо от того, сколько у вас времени. Хотя небольшая конкуренция — это нормально, убедитесь, что вы не слишком напрягаетесь или слишком торопитесь. Прислушивайтесь к своему телу и берите дни отдыха, когда это необходимо.

    Запишитесь на фитнес-программу и ожидайте результатов через несколько недель. Наслаждайтесь процессом, когда вы пожинаете плоды того, что получаете или остаетесь в форме, и не удивляйтесь, если вскоре вы обнаружите, что нацелились на полумарафон.

    Среднее время на 10 км и советы по забегу и восстановлению

    Забег на 10 км, который составляет 6,2 мили, идеально подходит для опытных бегунов, которые ищут более сложные задачи. Это второй по популярности забег после полумарафона, требующий уровня физической подготовки, который сочетает в себе силу, энергию и выносливость.

    Если вы уже пробежали несколько 5 км и любите бегать на более длинные дистанции, 10 км могут стать идеальным следующим шагом.

    Пробег на 10 км — это само по себе достижение, и вы должны быть довольны потраченным временем, несмотря ни на что. Тем не менее, это нормально — хотеть знать, как соотносится ваше время с результатами других бегунов и с вашими предыдущими рекордами.

    Ваш возраст, состояние сердечно-сосудистой системы и опорно-двигательного аппарата могут влиять на вашу индивидуальную производительность, но среднее время прохождения 10 км составляет 50–70 минут.

    Продолжайте читать, чтобы узнать больше о средних показателях 10K и о том, как развить скорость и выносливость, необходимые для достижения цели.

    Большинство бегунов, которые находятся в хорошей физической форме и проходят 15–30 миль в неделю, могут рассчитывать на то, что закончат гонку на 10 км за 50–70 минут.

    Более продвинутые бегуны обычно финишируют за 43–50 минут. Исключительно подготовленные бегуны могут пробегать милю каждые 7 минут, в то время как более обычные бегуны могут рассчитывать на пробежку мили каждые 10–14 минут.

    Вокруг света

    Средние результаты в беге на 10 км в Соединенном Королевстве аналогичны показателям в США: мужчины финишируют примерно за 53 минуты, а женщины — за 63 минуты.

    Что касается 10-километрового забега по всему миру, то в настоящее время первое место среди мужчин занимает бегунья из Уганды, а самые высокие результаты среди женщин занимают бегуны из Нидерландов и Эфиопии (1).

    Как правило, в Эфиопии и Кении одни из самых быстрых бегунов как среди мужчин, так и среди женщин.

    Прочие факторы

    Среднее время 10 000 может зависеть от таких факторов, как возраст, пол и уровень физической подготовки.

    Здоровье опорно-двигательного аппарата также играет важную роль, поэтому вам следует принимать меры, чтобы уменьшить боль, избежать травм и бегать в правильной форме.

    Если вы испытываете боль во время бега, рекомендуется проконсультироваться с врачом, чтобы исключить распространенные проблемы, такие как расколотая голень, подошвенный фасциит и колено бегуна. Лучше всего решить эти вопросы до подготовки к гонке.

    Личный рекорд

    Придерживайтесь своей программы тренировок и постепенно доводите ее до достижения целевого времени финиша. Убедитесь, что ваши цели реалистичны и что вы хорошо понимаете свои ограничения.

    Возможно, вы сможете соответствовать средним показателям для вашего возраста и пола, но если они не в пределах досягаемости, исходя из вашего времени в милях, стремитесь к своим личным рекордам.

    Наряду с вашим уровнем физической подготовки и режимом тренировок, возраст и пол являются факторами, которые следует учитывать, когда речь идет о среднем показателе 10 000 раз.

    Ниже приведены средние значения, опубликованные RunRepeat в 2019 году, которые вы можете использовать в качестве указателей, чтобы примерно определить, где вы должны быть в начале и в какое время вы можете стремиться уложиться (2).

    Age Men Women
    0–15 57:08 1:03:14
    16–19 46:36 1:00: 21
    20–24 51:40 59:50
    25–29 53:31 1:02:25
    30–34 54:21 1:02:31
    35–39 54 :27 1:02:19
    40–44 53:31 1:02:37
    45–49 55:35 1:03:27
    50–54 56:12 1:04:04
    55–59 59:00 1:07:41
    60–64 58:48 1:09:51
    65–99 1:03:02 1:18:57

    Если вы только начинаете бегать, вы можете попробовать забег на 5 км, прежде чем переходить на 10 км. Если вы в хорошей физической форме, в добром здравии и привержены своей программе тренировок, вы сможете подготовиться к гонке в течение нескольких недель.

    Подготовка к гонке на 10 км займет в два раза больше времени, чем к гонке на 5 км, поэтому убедитесь, что у вас достаточно времени на подготовку.

    Если это ваша первая гонка, начните с более легкого бега. Медленно повышайте свою выносливость, увеличивая продолжительность и интенсивность занятий.

    Старайтесь не бегать слишком долго или в слишком быстром темпе. Чтобы снизить риск получения травмы, не рискуйте и останавливайтесь каждый раз, когда чувствуете боль или истощение. Сбалансируйте свои беговые тренировки более легкими тренировками, такими как йога, тай-чи или плавание.

    Во время забега на 10 км бегите в темпе, который вы можете поддерживать, чтобы избежать слишком быстрого перенапряжения. Поберегите силы для последней части гонки.

    Среднее время прохождения мили для мужчин, бегущих на 10 км, составляет немногим менее 9 минут, в то время как среднее время для женщин составляет около 10 минут.

    Новичкам может понадобиться 12–15 минут, чтобы пройти милю. Ходоки, которые проходят милю каждые 15–20 минут, могут пройти 10 км за время от 90 минут до 2 часов. Ниже приведена диаграмма, в которой указан средний темп на милю для мужчин и женщин разного возраста (2).

    .
    Age Men Women
    0–15 9:13 10:12
    16–19 7:31 9:44
    20–24 8:20 9:39
    10:05
    35–39 8:47 10:03
    40–44 8:38 10:06
    45–49 8:58 10:14
    50– 54 9:04 10:20
    55–59 9:31. + 10:10 12:44

    Чтобы улучшить скорость, выносливость и работоспособность, вам необходимо повысить общий уровень физической подготовки. Включите различные беговые тренировки в свою программу и часто меняйте ее.

    • Упражнения. Вместо того, чтобы сосредотачиваться исключительно на подсчете миль, выполняйте упражнения, помогающие увеличить скорость, такие как темповые пробежки, интервальные тренировки и бег в гору. Вы можете улучшить свой шаг, пытаясь увеличить количество шагов в минуту.
    • Испытайте себя. Попробуйте сложные трассы с множеством холмов, ручьев или пересеченной местности. Бегайте в неблагоприятных условиях, таких как жара, холод и дождь, чтобы вы могли адаптироваться к различным погодным условиям. Если есть возможность, потренируйтесь на гоночной трассе заранее.
    • Смешайте это. Во избежание травм выберите 1 день в неделю для интенсивных тренировок. В остальные дни выполняйте умеренные упражнения и отдыхайте как минимум 1 полный день в неделю. Сбалансируйте свои беговые тренировки упражнениями на растяжку, которые сделают ваше тело гибким.
    • Стань сильнее. Силовые тренировки для наращивания мышечной массы и повышения устойчивости. Примеры этого включают тяжелую атлетику, тренировки с собственным весом и упражнения с эспандером.
    • Хорошо относитесь к своему телу. Позаботьтесь о своем здоровье в целом, высыпайтесь и повышайте уровень гидратации, выпивая много воды и электролитных напитков. Избегайте или ограничьте потребление кофеина, алкоголя и мочегонных средств, таких как зеленый, черный чай и чай из каркаде.
    • Соблюдайте здоровую диету. Ешьте часто и небольшими порциями, включающими сложные углеводы, свежие фрукты и овощи, нежирные белки и полезные жиры. Избегайте обработанных и сладких продуктов.
    • Знайте свои пределы. Испытайте себя, чтобы полностью раскрыть свой потенциал, но в то же время знайте и работайте в пределах своих возможностей. Вы также можете включить ходьбу в свой распорядок дня, особенно в дни, когда вам не хватает мотивации для интенсивных тренировок.
    • Не забывайте отдыхать. В течение недели, предшествующей гонке, отдыхайте больше, чем обычно. Поддерживайте свою выносливость и расслабьте мышцы, пробежав несколько километров на 3 мили. Обязательно отдохните за 2 дня до гонки.

    За день до забега нет необходимости делать что-либо вроде загрузки углеводами или принимать какие-либо экстремальные диетические меры, поскольку ваши усилия, скорее всего, потребуют менее 90 минут (3).

    Выполняя простые упражнения на подвижность, избегая обезвоживания и пытаясь хорошо выспаться, вы будете чувствовать себя лучше в день гонки.

    Утром перед гонкой, за 1–4 часа до старта, съешьте хороший завтрак, состоящий в основном из углеводов и небольшого количества белка. Это дополнительное количество энергии углеводов поможет пополнить ваш бак, чтобы сохранить достаточное количество гликогена для немедленной энергии (3).

    В зависимости от ваших потребностей рекомендуемое количество углеводов составляет 1–4 грамма на килограмм массы тела. Для человека весом 155 фунтов (около 70 кг) это означает 70–280 граммов углеводов или не менее 280 калорий из углеводов.

    В день соревнований ешьте продукты с высоким гликемическим индексом, которые легче усваиваются. Простые углеводы, белые злаки и сладкие фрукты могут быть хорошим выбором (4).

    Во время тренировки лучше пробовать разные продукты, чтобы знать, что подходит именно вам. Это гарантирует, что в день гонки вы не удивитесь, обнаружив, что что-то не так с вами.

    Пейте много жидкости утром перед забегом, останавливаясь примерно за 1 час до старта, чтобы убедиться, что вы не бежите прямо к горшкам.

    Национальная ассоциация силовой и физической подготовки рекомендует 5–7 мл на кг массы тела не менее чем за 4 часа до гонки (5).

    Подумайте о том, чтобы добавить в воду таблетку электролита, чтобы предотвратить мышечные спазмы и избежать гипонатриемии — опасного потенциального последствия чрезмерного увлажнения только водой (6, 7).

    Если вы пьете кофе, дневная чашка вполне подойдет. Только не переусердствуйте. Однако, если вы не привыкли к кофе и его стимулирующим мочевой пузырь и кишечник эффектам, день гонки может быть не лучшим днем, чтобы начать его пить.

    Кофеин является стимулятором и может помочь вам более эффективно использовать ваши запасы энергии (4).

    Но чрезмерное потребление может отнять у вас время из-за дополнительных перерывов, поэтому экспериментируйте на тренировках, чтобы увидеть, что работает лучше всего.

    После того, как вы в достаточной степени накормлены и выпиты и находитесь на месте, постарайтесь немного расслабиться. Примерно за 10 минут до начала можно выполнить несколько динамических разминочных упражнений.

    Эти упражнения активизируют и разогревают мышцы бедер, ног, ступней и туловища, подготавливая вас к эффективному и комфортному бегу со стартовой линии, вместо того, чтобы использовать первые 10 минут забега для достижения максимальной готовности.

    Хорошая динамическая разминка включает в себя несколько ритмичных движений, таких как перетасовка в сторону, высоко поднятые колени и удары ногами. Это может также включать некоторые динамические растяжки, такие как махи ногой, боковые выпады и касания бегуна.

    Не двигайтесь слишком энергично и не утомляйте себя, но используйте минуты перед гонкой, чтобы разогреться и размяться перед предстоящей задачей.

    Сразу после гонки начинается восстановление. Ваши самые насущные потребности связаны с восстановлением мышц. Вам нужно двигаться медленно и ритмично, чтобы ваше сердце и легкие успокоились.

    Не садитесь сразу — у вас все еще есть большой кровоток в мышцах ног, а ходьба или динамическая растяжка позволят вашему сердцу мягко перенаправить больший поток крови обратно домой и из ваших рук и ног.

    Если вы немедленно плюхнетесь на землю или в кресло, кровь может скапливаться в ваших руках и ногах, что может привести к проблемам с кровяным давлением и даже к потере сознания (8).

    В дополнение к замедлению частоты сердечных сокращений и замедлению дыхания вам потребуется мягко растянуть мышцы. Вам не нужно беспокоиться о глубокой растяжке, но небольшое удлинение этих мышц может улучшить кровообращение и общий комфорт, а также улучшить вашу гибкость.

    Возможно, но это еще не доказано, что растяжка после тренировки может помочь уменьшить болезненность мышц (9).

    Когда дело доходит до уменьшения боли в мышцах с отсроченным началом (DOMS), массаж является лучшим выбором. Одно исследование показало, что массаж через 48 часов после интенсивной тренировки лучше всего помогает облегчить DOMS (10).

    После того, как вы оправитесь от непосредственных последствий вашей гонки, вы получите огромную пользу от приема пищи после тренировки. Ваше восстановление мышц начинается сразу же, поэтому чем раньше вы сможете принять немного углеводов и белков, тем лучше.

    Потребление углеводов и белков в течение 2 часов после окончания гонки важно для восстановления (4).

    Обязательно увлажняйте! Общая рекомендация состоит в том, чтобы выпивать 150% массы тела, потерянной во время гонки, что означает употребление 1,5 л жидкости на каждые 1,0 л потерянной жидкости. Ключ в том, чтобы пить больше воды, чем вы потеряли, чтобы достичь идеального уровня гидратации (11).

    Вам также следует подумать о добавлении электролитов в воду. Исследования показали, что более высокие уровни электролитов натрия в восстановительных напитках (60–80 ммоль/л) оптимальны для восстановления натрия, потерянного с потом (11).

    Как насчет пива? Многим бегунам нравится стакан «жидкого хлеба» после забега, и они наслаждаются ритуалом питья после пробежки.

    Хотя пиво содержит электролиты и углеводы, которые способствуют восстановлению, употребление алкоголя после тренировки препятствует восстановлению мышц (12).

    Итак, если вы решите выпить пиво после гонки, лучше остановиться на одном. Выберите один с более низким содержанием алкоголя и дополните водой.

    Когда вы полностью оправитесь от усилий, дайте своему телу отдохнуть. То, что вы остыли и приняли душ, не означает, что ваше тело готово. Ваши мышцы и кости были перегружены и нуждаются в восстановлении.

    Расслабьтесь до конца дня, но продолжайте периодически двигаться, чтобы ваше тело оставалось гибким.

    Позвольте себе хорошо выспаться после гонки. Хотя восстановление начинается немедленно, ваше тело восстанавливает большую часть мышц во время сна, поэтому вы хотите подарить себе хороший сон, чтобы чувствовать себя сильнее и более восстановленным на следующее утро (13).

    Отдайте себе должное за пробежку на 10 км, независимо от того, сколько у вас времени. Хотя небольшая конкуренция — это нормально, убедитесь, что вы не слишком напрягаетесь или слишком торопитесь. Прислушивайтесь к своему телу и берите дни отдыха, когда это необходимо.

    Запишитесь на фитнес-программу и ожидайте результатов через несколько недель. Наслаждайтесь процессом, когда вы пожинаете плоды того, что получаете или остаетесь в форме, и не удивляйтесь, если вскоре вы обнаружите, что нацелились на полумарафон.

    Калькулятор стоимости расплава 10-каратного золота

    Сколько стоит ваше 10-каратное золото?

    Стоимость 10-каратного золота на основе текущей цены на золото

    Калькулятор стоимости плавления 10-каратного золота, доступный ниже, может рассчитать общее количество золота. стоимость 10 000 золотых изделий, измеренная в выбранной вами единице веса. Стоимость золота рассчитывается исходя из общей суммы фактического содержания золота, не включая другие металлы, используемые при изготовлении 10-каратного золотого сплава. Калькулятор 10K золота покажет только сколько стоит золото (внутренняя ценность), а не какая-либо коллекционная ценность ваших 10 000 золотые предметы.

    Калькулятор стоимости плавления 10-каратного золота рассчитает цену золотых изделий с чистота золота измеряется как 10 частей золота и 14 частей другого металла, используемого для изготовления золотой сплав 10К.

    Используйте калькулятор расплава 10-каратного золота, чтобы узнать, сколько стоят ваши изделия из 10-каратного золота. стоимость, исходя из их общего количества фактического содержания золота, или решить, что вы готов заплатить за любой предмет из 10-каратного золота, исходя из спотовой цены на золото.

    Общая стоимость 10 000 золота рассчитывается на основе суммы в валюте, указанной в Цена золота текстовое поле. Текущая спотовая цена на золото часто обновляется в течение обычные торговые часы. Цена золота может быть изменена на любое значение по вашему выбору.

    1. Выберите единицу измерения (тип веса):

    ГраммыКилограммыЗернаПеннивейтУнциитройские унциифунтытройские фунты

    2. Введите общий вес 10-каратного золота:

    Общий вес в граммах:

    3. (Опция) Изменить цену на золото или оставить как есть:

    Цена золота: за тройскую унцию

    Валюта: AED — Дирхам ОАЭARS — Аргентинское песоAUD — Австралийский долларBRL — Бразильский реалCAD — Канадский долларCHF — Швейцарский франкCNY — Китайский юаньDKK — Датская кронаEUR — ЕвроGBP — Британский фунт HKD — Гонконгский долларIDR — Индонезийская рупияILS — Израильский шекельINR — Индийская рупияJPY — Японская иенаKRW — Южнокорейский вонMXN — Мексиканское песоMYR — Малайзийский ринггитNOK — Норвежская кронаNZD — Новозеландский долларPHP — Филиппинское песоPKR — Пакистанская рупияQAR — Катарский риалRUB — Российский рубльSAR — Саудовский риалSEK — Шведская кронаSGD — Сингапурский долларTRY — Турецкая лираUSD — Доллар СШАZAR — Южноафриканский рэнд

    Последнее обновление спотовой цены на золото на сервере:

    4. (Опция) Введите ценовой спред или оставьте как есть:

    Разброс цен: %

    Общая стоимость золота:

    Общий вес золота

    Граммы:
    Килограммы:
    Зерна:
    Пеннивейт:
    Унции:
    Тройские унции:
    Фунты:
    Тройские фунты:

    Спред цен

    Цена предложения:
    Спроси цену:

    Результирующие значения будут округлены до двух или более знаков после запятой в зависимости от длины.

    Решение показательных уравнений и неравенств: Решение показательных уравнений и неравенств: алгоритм решения и примеры

    alexxlab / / Разное
    {x+2}-1}

    Методы решения показательных уравнений и неравенств

    • Авторы
    • Руководители
    • Файлы работы
    • Наградные документы

    Мамиева М.А. 1

    1МБОУ СОШ 30

    Караева Д.А. 1

    1МБОУ СОШ 30

    Автор работы награжден дипломом победителя III степени

    Диплом школьникаСвидетельство руководителя

    Текст работы размещён без изображений и формул.
    Полная версия работы доступна во вкладке «Файлы работы» в формате PDF

    Аннотация

    Из предложенных тем я выбрала: «Методы решения показательных уравнений и неравенств», так как она наиболее актуальна не только для меня, но и для детей моего возраста. В связи с приближающимися экзаменами, данный проект так же поможет мне при решении заданий из ЕГЭ.                                                                                 

     В данной работе исследуются разные способы решений показательных уравнений и неравенств.

    В процессе выполнения проекта я приобрела навыки проектной деятельности, развила коммуникативные и аналитические способности,  а также навыки самостоятельного поиска необходимого материала с помощью учебной и художественной литературы и интернет­-источников, более того получила знания как по математики, так и по истории.

    Для достижения цели исследовательской работы необходимо было решить следующие задачи:

    — осваивание математических знаний и умений, необходимых для изучения школьных естественнонаучных дисциплин на базовом уровне.

    -изучить различные методы решения показательных уравнений и неравенств.

    — развитие логического мышления и алгоритмической культуры;

     

    Введение

    Обычно математику считают прямой противоположностью поэзии. Однако математика и поэзия — ближайшие родственники, ведь и то и другое — работа воображения. 
    Томас Хилл 


    Определенно, чтобы понять и научиться решать любые математические задания, мало просто знать все многочисленные формулы и свойства, которыми богата данная наука. Если не подходить к заданию творчески, широко и открыто мыслить, то легко попадешь «в тупик», что может привести не только к разочарованию в науке, но и в самом себе. Математика как игра привлекательна свое содержательностью, сложностью и неожиданностью результатов. Так же для овладения почти любой современной профессии требуются математические познания. Строгое и абстрактное мышление, необходимое в реальной действительности, легче развить, занимаясь математикой, поскольку эта наука строга и абстрактна. Именно поэтому, на примере решения показательных уравнений и неравенств, я хочу показать, что данный процесс может не только увлечь вас, но и так же заставить ваш мозг работать куда продуктивнее.

    История Показательных уравнений

    Термин «показатель» для степени ввел в 1553 г. немецкий математик (сначала монах, а затем − профессор) Михаэль Штифель (1487-1567). По-немецки показатель − Exponent: «выставлять напоказ». Штифель же ввел дробные и нулевой показатели степени. Само обозначение ax для натуральных показателей степени ввел Рене Декарт (1637 г.), а свободно обращаться с такими же дробными и отрицательными показателями стал с  1676 г. сэр Исаак Ньютон.
    Степени с произвольными действительными показателями, без всякого общего определения, рассматривали и Готфрид Вильгельм Лейбниц, и Иоганн Бернулли; в 1679 г. Лейбниц ввел понятия экспоненциальной (т.е., по-русски, показательной) функции для зависимости y=ax и экспоненциальной кривой для графика этой функции.

     

    Показательные уравнения

    Уравнение, которое содержит неизвестное в показателе степени, называется показательным уравнением.

    Самое простое показательное уравнение имеет вид:

    ax = b,         

    где a > 0, a ≠ 1.

    Показательные уравнения путём алгебраических преобразований приводят к стандартным уравнениям, которые решаются, используя следующие методы:

    • метод приведения к одному основанию;
    • метод введения новых переменных;
    • метод вынесения общего множителя за скобки;
    • метод почленного деления;
    • метод группировки;
    • метод оценки.

    Метод приведения к одному основанию

    Способ основан на следующем свойстве степеней: если равны две степени и равны их основания, то равны и их показатели, т. е. уравнение надо попытаться свести к виду:

    Пример:

    32x-1 = 7x+1

    Представим правую часть в виде 3 log37x+1

    И запишем уравнение равносильное исходному

    32x-1=3 log37x+1

    Перейдем к уравнению для показательных степеней

    2x-1= log37x+1

    2x-1=xlog37 +log37

    x(2-log37 )=log37 +1

    x=1+log372-log37

    x=log33+log37log332-log37

    x=log321log3  97

    x=log9721≈12. 1144

    Ответ: 12.1144

     

    Метод введения новых переменных

    Введение новой переменной обычно производится после преобразований членов уравнения.

    Пример:

    4x2 -2x2 -2=0

    Обозначим t=2x2 ,где t>0, тогда

    t2 -t-2=0

    t1 =-1

    t2 =2

    Так как -1<0, то остается только корень равный 2

    2x2 =2 , откуда

    x2 =1

    x=1

    x=-1

    Ответ: -1; 1.

     

    Метод вынесения общего множителя за скобки

    Тождественное преобразование, в результате которого многочлен 
    приводится к произведению нескольких множителей, называют 
    разложением многочлена на множители.

    Пример:

    x2·2x+1 + 2|x-3|+2 = x2·2|x-3|+4 + 2x-1

    То, что находится в правой части, мы перенесем в левую часть и сгруппируем многочлены с одинаковыми показателями

    (x2·2x+1 -2x-1)+(2|x-3|+2- x2·2|x-3|+4) = 0

    Вынесем общие множители за скобки

    2x-1(4×2-1) +2|x-3|+2(1-4×2) = 0,

    откуда следует

    (4×2-1)·(2x-1 -2|x-3|+2) = 0.

    Последнее уравнение равносильно совокупности

     

    4×2-1 = 0,

    2x-1 = 2|x-3|+2.

    Из первого уравнения совокупности находим x1 = — 12 ,x2= 12

     

    Из второго уравнения получаем:

    2x-1 = 2|x-3|+2

    x-1=x-3+2

    x-3=x-3

    x-3=x-3, если x≥3x-3=-x+3, если x<3

    0∙x=0, если x≥32x=6, x=3, если x<3

    Ответ: -12  ∪   12  ∪  3; +∞ .

     

     

    Метод почленного деления

    Данный метод заключается в том, чтобы разделить каждый член уравнения, содержащий степени с одинаковыми показателями, но разными основаниями, на одну из степеней. Этот метод применяется для решения однородных показательных уравнений.

     22х+1-7·10х+ 52х+1=0

    22х·2– 7·2х·5х+52х·5=0    /52х≠ 0
    2·25 2х– 7· 25 х +5=0

    Пусть 25 х =t, t>0
    2t2-7t+5=0
    D=b2-4ac=49-4·2·5=9
    t1=1, t2=52
    25 х=1, 25 х =52
    х=0, х=-1

    Ответ: -1; 0.

     

     

     

    Метод группировки

    3·22х+12 ·9х+1– 6·4х+1= — 13 ·9х+2

    Сгруппируем слагаемые следующим образом:

    12 ·9х+1+13 ·9х+2=6·4х+1-3·22х

    12 ·9х·9+13 ·9х·92=6·4х·4-3·4х

    4,5·9х+27·9х=24·4х-3·4х

    31,5·9х=21·4х      /9х≠0        

    31,5= 21·49 х

    49 х=32

    23 2х=23 -1

    2х=-1

    х=-0,5

    Ответ: -0,5.

     

    Метод оценки

    (5)2+4+6+…+2x =545  , x Î N

     Логарифмируя по основанию 5 (обе части уравнения положительны), получим

    12  (2+4+6+…+2x) = 45

     1+2+…+ x= 45.

    Используя формулу суммы первых n членов арифметической прогрессии

    Sn =n(a1+an2 )

    получим уравнение

    x1+x2 =45

    или

    x2+x-90 = 0

    корни которого x1 = -10 и x2 = 9.

    Поскольку x ÎN, остается x = 9.

    Ответ: 9.

     

    Показательные неравенства

    Неравенства, содержащие переменные в показатели степени, называются показательными. Методы применяемы при решении показательных уравнений, мы также можем использовать и при решении показательных неравенств. Приведем несколько примеров.

    Пример 1.

     2x-3≥  4+ 16-2x-3

    В этом неравенстве мы используем метод введения новой переменной.

    Пусть  2x-3 =t, тогда получаем неравенство

    t ≥ 4+16-t

    Преобразуем последнее неравенство

    4+16-t – t ≤ 0

    t2-10t+256-t≤ 0

    (t-5)26-t ≤ 0

     

    Используя метод интервалов, найдем решение неравенства с переменной

    t=5, t> 6. Отсюда 2x-3 =5 и 2x-3> 6.

    Пусть 2x =a, решим уравнение и неравенство с модулем.

    Из уравнения a-3 =5 получаем

    a-3=5   a-3=-5

    a=8   a=-2

    Подставим вместо a=2x

    2x=8   2x=-2

    Получаем x=3

    Модуль a-3  есть расстояние на координатной оси от точки a до точки 3.

    Для решения неравенств a-3> 6 необходимо найти такие точки, расстояние от которых до точки 3 больше 6. Справа от точки 3 расположена точка 9 на расстоянии 6 единиц, а слева — точка (-3). Поэтому из неравенства

    a-3> 6  получаем a< -3 или a> 9.

       2x<-32x>9

    2x>2log29

    x >log29

    Ответ: {3} ∪ (log29 ;+∞).

    Пример 2.

    2(32x+2x∙3x+1+30)> 3(4x-2x∙3x+1+log32)

    Так как  и левая, и правая части неравенства положительны, то от них можно взять  log2 :

    32x+2x∙3x+1>log23(4x-2x∙3x+1+log32)

    32x+2x∙3x+1>(4x-2x∙3x+1+log32)∙log23

    32x+2x∙3x+1>(4x-2x∙3x+1)∙log23+1

    32x+2x∙3x>(4x-2x∙3x+1)∙log23

    Поделим каждое слагаемое неравенства на (2x∙3x) :

    32x+1>23x-3∙log23

    Обозначим: 32x =y, где y >  0:

    y+1 > 1y-3∙log23

    Умножим каждое слагаемое на y:

    y2+y> 1-3y∙log23

    Перенесем многочлен из левой стороны в правую сторону:

    y2+y-1-3y∙log23>0

    Раскроем скобки:

    y2+y-log23+3ylog23>0

    y2+3log23+1y-log23>0

    Решим уравнение:

    y2+3log23+1y-log23=0

    D=3log23+1 2 +  4log23=9log232+10log23+1

    D>0 ,   следовательно

    y=-3log23+1±9log232+10log23+12

    В связи с тем, что log23>0 , то и D >3log23+1 2.

     

    Из этого следует, что только один из корней будет больше нуля:

    y=-3log23+1+9log232+10log23+12

    Отметим точку y на оси, y>0 :

    (Иллюстрация II.)

    y Î -3log23+1+9log232+10log23+12;+∞

    Из этого следует, что  x Î log32-3log23+1+9log232+10log23+12;+∞

    Ответ: x Î log32-3log23+1+9log232+10log23+12;+∞ .

     

    -3log23+1+9log232+10log23+12
                                                                                         

     

    Иллюстрация II.

    Заключение

    Работа над данным проектом была интересной и увлекательной. Но что самое главное — она стала очень полезной для меня, так как совсем скоро мне предстоит сдавать экзамены. Ведь изучение над этой темой не только дало мне новые знания, но также помогло развить логическое мышление и научило находить решение в, казалось бы, безвыходных ситуациях.
    Мне понравилось работать над данной темой, потому что благодаря этому проекту я смогла расширить свои знания в области показательных уравнений и неравенств.

    Список литературы

    Алгебра и начала математического анализа 10-11 класс:/ Ш.А. Алимов, Ю.М. Колягин, М.В. Ткачев, Н.Е.Федоров, М.И.Шабунин

    Алгебра и начала математического анализа. 10-11 класс. Учебник. Базовый и углублённый уровни. Колягин Ю. М.

    ЕГЭ. Математика: типовые экзаменационные варианты: 30 вариантов/ под редакцией И.В. Ященко.

    ЕГЭ 2016. Математика: типовые экзаменационные варианты: 30 вариантов/ под редакцией И.В. Ященко.

    https://shkolkovo. net/catalog/reshenie_neravenstv/pokazatelnye/page-7

    Просмотров работы: 1821

    Показательные уравнения и неравенства. Решение показательных уравнений и неравенств

    Исходя из этого и применяя теорему о корне, получим, что уравнение a x = b иметь один единственный корень, при b>0 и положительном a не равном единице. Чтобы его найти, необходимо представить b в виде b = a c .
    Тогда очевидно, что с будет являться решением уравнения a x = a c .

    Рассмотрим следующий пример: решить уравнение 5 (x 2 — 2*x — 1) = 25.

    Представим 25 как 5 2 , получим:

    5 (x 2 — 2*x — 1) = 5 2 .

    Или что равносильно:

    x 2 — 2*x — 1 = 2.

    Решаем полученное квадратное уравнение любым из известных способов. Получаем два корня x = 3 и x = -1.

    Ответ: 3;-1.

    Решим уравнение 4 x — 5*2 x + 4 = 0. Сделаем замену: t=2 x и получим следующее квадратное уравнение:

    t 2 — 5*t + 4 = 0.
    Решаем это уравнение любым из известных способов. Получаем корни t1 = 1 t2 = 4

    Теперь решаем уравнения 2 x = 1 и 2 x = 4.

    Ответ: 0;2.

    Решение простейших показательных неравенств основывается тоже на свойствах возрастания и убывания функции. Если в показательной функции основание a больше единицы, то функция будет возрастающей на всей области определения. Если в показательной функции для основания а выполнено следующее условие 0, то данная функция будет убывающей на всем множестве вещественных чисел.

    Рассмотрим пример: решить неравенство (0.5) (7 — 3*x)

    Заметим, что 4 = (0.5) 2 . Тогда неравенство примет вид (0.5)(7 — 3*x)

    Получим: 7 — 3*x>-2.

    Отсюда: х

    Ответ: х

    Если бы в неравенстве основание было больше единицы, то при избавлении от основания, знак неравенства менять было бы не нужно.

    Показательными уравнениями и неравенствами считают такие уравнения и неравенства, в которых неизвестное содержится в показателе степени.

    Решение показательных уравнений часто сводится к решению уравнения а х = а b , где а > 0, а ≠ 1, х – неизвестное. Это уравнение имеет единственный корень х = b, так как справедлива следующая теорема:

    Теорема. Если а > 0, а ≠ 1 и а х 1 = а х 2 , то х 1 = х 2 .

    Обоснуем рассмотренное утверждение.

    Предположим, что равенство х 1 = х 2 не выполняется, т.е. х 1 1, то показательная функция у = а х возрастает и поэтому должно выполняться неравенство а х 1 а х 2 . В обоих случаях мы получили противоречие условию а х 1 = а х 2 .

    Рассмотрим несколько задач.

    Решить уравнение 4 ∙ 2 х = 1.

    Решение.

    Запишем уравнение в виде 2 2 ∙ 2 х = 2 0 – 2 х+2 = 2 0 , откуда получаем х + 2 = 0, т.е. х = -2.

    Ответ. х = -2.

    Решить уравнение 2 3х ∙ 3 х = 576.

    Решение.

    Так как 2 3х = (2 3) х = 8 х, 576 = 24 2 , то уравнение можно записать в виде 8 х ∙ 3 х = 24 2 или в виде 24 х = 24 2 .

    Отсюда получаем х = 2.

    Ответ. х = 2.

    Решить уравнение 3 х+1 – 2∙3 х — 2 = 25.

    Решение.

    Вынося в левой части за скобки общий множитель 3 х — 2 , получаем 3 х — 2 ∙ (3 3 – 2) = 25 – 3 х — 2 ∙ 25 = 25,

    откуда 3 х — 2 = 1, т. е. х – 2 = 0, х = 2.

    Ответ. х = 2.

    Решить уравнение 3 х = 7 х.

    Решение.

    Так как 7 х ≠ 0, то уравнение можно записать в виде 3 х /7 х = 1, откуда (3/7) х = 1, х = 0.

    Ответ. х = 0.

    Решить уравнение 9 х – 4 ∙ 3 х – 45 = 0.

    Решение.

    Заменой 3 х = а данное уравнение сводится к квадратному уравнению а 2 – 4а – 45 = 0.

    Решая это уравнение, находим его корни: а 1 = 9, а 2 = -5, откуда 3 х = 9, 3 х = -5.

    Уравнение 3 х = 9 имеет корень 2, а уравнение 3 х = -5 не имеет корней, так как показательная функция не может принимать отрицательные значения.

    Ответ. х = 2.

    Решение показательных неравенств часто сводится к решению неравенств а х > а b или а х

    Рассмотрим некоторые задачи.

    Решить неравенство 3 х

    Решение.

    Запишем неравенство в виде 3 х 1, то функция у = 3 х является возрастающей.

    Следовательно, при х

    Таким образом, при х 3 х

    Ответ. х

    Решить неравенство 16 х +4 х – 2 > 0.

    Решение.

    Обозначим 4 х = t, тогда получим квадратное неравенство t2 + t – 2 > 0.

    Это неравенство выполняется при t 1.

    Так как t = 4 х, то получим два неравенства 4 х 1.

    Первое неравенство не имеет решений, так как 4 х > 0 при всех х € R.

    Второе неравенство запишем в виде 4 х > 4 0 , откуда х > 0.

    Ответ. х > 0.

    Графически решить уравнение (1/3) х = х – 2/3.

    Решение.

    1) Построим графики функций у = (1/3) х и у = х – 2/3.

    2) Опираясь на наш рисунок, можно сделать вывод, что графики рассмотренных функций пересекаются в точке с абсциссой х ≈ 1. Проверка доказывает, что

    х = 1 – корень данного уравнения:

    (1/3) 1 = 1/3 и 1 – 2/3 = 1/3.

    Иными словами, мы нашли один из корней уравнения.

    3) Найдем другие корни или докажем, что таковых нет. Функция (1/3) х убывающая, а функция у = х – 2/3 возрастающая. Следовательно, при х > 1 значения первой функции меньше 1/3, а второй – больше 1/3; при х 1 и х

    Ответ. х = 1.

    Заметим, что из решения этой задачи, в частности, следует, что неравенство (1/3) х > х – 2/3 выполняется при х 1.

    сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.

    Урок 2. Показательные неравенства. Системы показательных уравнений и неравенств. Практика 11 класс онлайн-подготовка на

     

     

     

     

    Подготовка к ЕГЭ по математике

    Эксперимент

    Урок 1. Повторение. Показательная функция. Показательные уравнения

    Практика

     

    Простейшие показательные неравенства

     

     

    Конспект урока

     

    Пример №1. Решить неравенство:

    Правило: привести к одинаковому основанию.

    Так как основание больше 1, знак неравенства не меняется

    Ответ:

     

    Пример №2. Решить неравенство:

    Так как основание больше 1, знак неравенства не меняется

    Ответ:

    Пример №3. Решить неравенство:

    Так как основание меньше 1, знак неравенства меняется

    Ответ:

     

    Пример №4. Решить неравенство:

    Вспоминаем свойства показательной функции: , значит,  Данное неравенство не имеет решений.

     

    Пример №5. Решить неравенство:

    По аналогии с предыдущим неравенством:  (а, значит, ) для всех  из области определения, то есть .

     

    Показательные неравенства, которые сводятся к простейшим

     

     

    Пример №1.

     

    Так как основание меньше 1, знак неравенства меняется

    Ответ:

    Пример №2. Решите неравенство

    Рассмотрим решение данного неравенства двумя способами.

    1 способ:

    Приведем обе части неравенства к основанию 2:

    Так как основание больше 1, знак неравенства не меняется

     

    2 способ:

    Приведем обе части неравенства к основанию :

    Так как основание меньше 1, знак неравенства меняется

    Ответ:

     

    Пример №3. Решите неравенство

    Подсказка: чтобы не ошибиться, лучше приводить обе части неравенства к основанию больше 1, так как в этом случае нет риска забыть о смене знака неравенства.

    Вспомним, что:

    Поэтому:

    Так как основание больше 1, знак неравенства не меняется

    Ответ:

     

    Пример №4. Решите неравенство

    Приведем обе части неравенства к основанию 2:

    Так как основание больше 1, знак неравенства не меняется

    Ответ:

     

    Показательные неравенства, которые решаются с помощью вынесения общего множителя

     

     

    С вынесением общей степени

     

     

    Пример №1.  Решите неравенство

    Так как основание больше 1, знак неравенства не меняется

    Ответ:

     

    Показательное неравенство, которое решается с помощью замены

     

     

    Сводящиеся к квадратным

     

    Пример №1.  Решите неравенство:

    Замена:

    Обратная замена:

    Ответ:

     

    Пример №2. Решите неравенство:

    Замена:

    Обратная замена:

    Ответ:

     

    Пример №3. Решите неравенство:

    Замена:

     

    Обратная замена:

    Левое неравенство, как мы помним, выполняется всегда.

    Ответ:

     

    Однородные показательные неравенства

     

     

    Однородные

     

    Пример №1. Решите неравенство:

    Замена:

     

    Обратная замена:

    Ответ:

     

    Системы показательных уравнений

     

     

    Системы показательных уравнений

     

    Пример №1. Решите систему уравнений:

    «Решаем» каждое из уравнений по отдельности, приводя к обычной линейной системе.

    1)     

    2)     

    Получаем систему:

    Ответ:

     

    Пример №2. Решите систему уравнений:

    1)      Перемножим оба уравнения:

    2)      Поделим второе уравнение на первое:

    Получаем систему:

    Ответ:

     

    Пример №3. Решите систему уравнений:

    Замена:

    —

    Обратная замена:

    Ответ:

     

    Пример №4.

    Замена:

    Рассмотрим решение данной системы двумя способами:

    1 способ:

    Обратная замена:

    2 способ:

    Обратная замена:

    Ответ:

     

    Системы показательных неравенств

     

     

    Пример №1.

     

    Правило: решаем каждое из неравенств по отдельности.

    1)     

    Замена:

    Обратная замена:

    2)     

    3)     

    Ответ: решений нет.

     

    Показательные уравнения в математике с примерами решения и образцами выполнения

    Оглавление:

    Простейшее показательное уравнение — это уравнение вида = b. Пусть основание а>0 и отлично от 1. Так как функция у = строго монотонна, то каждое свое значение она принимает ровно один раз. Это означает, что уравнение = b при b>0 имеет одно решение, которое по определению логарифма равно log0 b. Если 0, то уравнение = b корней не имеет, так как всегда больше нуля. Если число b записано в виде ас, т. е. если уравнение представлено в виде = ас, то оно имеет один корень х = с.

    Сформулируем общий результат о решении простейшего показательного уравнения (схема XI).

    Теорема:

    Пусть а > 0 и а ≠ 1. Уравнение равносильно уравнению f (x) = g (х).

    Доказательство:

    Докажем, что если то f(x) = g(x). Действительно, так как показательная функция строго монотонна, то из равенства ее значений ac = ad следует равенство показателей c = d. Обратно: если f(x) = g(x), то .

    Примеры:

    Простейшее логарифмическое уравнение — это уравнение вида logax=b. Оно имеет единственное решение х — а при любом b.

    Сформулируем общий результат о решении простейшего логарифмического уравнения (схема XI).

    Теорема:

    Уравнение ioga f (х) = loga g (х) равносильно уравнению f(x)=g(x) при ограничениях f (х)> 0, g(x)>0.

    Доказательство:

    Пусть х — решение уравнения

    Тогда определены логарифмы чисел f (х) и g (х), т. е. эти числа должны быть больше нуля. Потенцируя равенство получаем равенство f(x) = g (x). Обратно, пусть х — решение уравнения f (х) = g (х), причем g(x)>0 и f (х)> 0. Тогда равенство f{x) = g(x) можно прологарифмировать, И МЫ получим .

    Примеры:

    Мы решили уравнение х— 1 = 5 — х, а затем проверили, удовлетворяет ли решение условиям х— 1 >0 и 5 — х>0. Заметим, что если f (x) = g (х) и f (х)>0, то тогда и g (x)>0, т. е. из двух неравенств достаточно проверить только одно.

    Показательные уравнения справочные сведения

    Показательная функция где определена на , а множество ее значений — множество всех положительных чисел.

    2.Для любых и при любых значениях и ну верны равенства (основные свойства степени):

    3. Простейшее показательное уравнение

    не имеет корней при и имеет единственный корень при

    В частности, уравнение имеет единственный корень

    4.Уравнение

    равносильно уравнению

    5.Уравнение

    равносильно каждому из уравнений

    Примеры с решениями
    Пример:

    Решить уравнение

    Решение:

    Данное уравнение равносильно каждому из уравнений откуда

    Ответ.

    Пример:

    Решить уравнение

    Решение:

    Это уравнение равносильно каждому из уравнений:

    откуда находим

    Ответ.

    Пример:

    Решить уравнение

    Решение:

    Пусть тогда уравнение примет вид

    Это уравнение равносильно каждому из уравнений: откуда

    Ответ.

    Пример:

    Решить уравнение

    Решение:

    Полагая получаем уравнение или откуда находим

    Следовательно, исходное уравнение равносильно совокупности уравнений Первое из них не имеет корней, второе имеет единственный корень

    Ответ.

    Пример:

    Решить уравнение

    Решение:

    Запишем данное уравнение в виде

    и заметим, что левая часть уравнения (2) — однородный многочлен степени от и где (сумма степеней и в каждом члене этого многочлена равна двум).

    Разделив обе части уравнения (2) на и полагая получим уравнение имеющее корни Исходное уравнение (1) равносильно совокупности уравнений откуда находим

    Ответ.

    Пример:

    Решить уравнение

    Решение:

    Воспользуемся равенством и положим Тогда уравнение примет вид или откуда Исходное уравнение равносильно совокупности уравнении

    откуда

    Ответ,

    Пример:

    Решить уравнение

    Решение:

    Число 2 является корнем этого уравнения. Докажем, что уравнение не имеет других корней. Так как каждая из функций является возрастающей, то и — также возрастающая функция. Поэтому при и при т. е. функция не принимает значение, равное 25, при Это означает, что — единственный корень уравнения.

    Показательные неравенства

    Простейшее показательное неравенство — это неравенство вида >b или < b (или ≥ b, или ≤ b). Решение такого неравенства нетрудно представить себе графически, построив график показательной функции у = и проведя прямую у=b (схема XI). Рассмотрим для примера два из 16 возможных вариантов.

    Пусть а> 1 и b >0. Решением неравенства ≥ b является промежуток , т. е. все числа (схема XI).

    Пусть а>1 и b ≤ 0. Решением неравенства ≥ b является множество всех вещественных чисел R.

    Примеры:

    Можно сказать, что неравенство типа >b мы решаем логарифмированием. При логарифмировании неравенств надо помнить два правила: 1) в обеих частях неравенства должны стоять положительные числа; 2) при логарифмировании по основанию а>1 знак неравенства сохраняется, если же 0<а<1, то знак неравенства меняется на противоположный.

    Простейшее логарифмическое неравенство — это неравенство вида (вместо знака > может стоять ≤ , ≥ . Аналогично показательному неравенству здесь также возможно много вариантов (схема XI). Логарифмическое неравенство решают потенцированием. При этом надо помнить два правила: 1) при переходе от выражения loga f (х) к выражению f (х) надо добавлять условие f (х)>0; 2) если а>1, то при потенцировании знак неравенства сохраняется; если же 0<а<1, то знак неравенства меняется на противоположный.

    Примеры:

    4. Сначала учтем условия x2 — 1>0 и x + 5>0. Решение этой системы неравенств изображено на рисунке 110. Затем потенцируем: x2 — 1 ≤ x+5 ⇔ x2 — х — 6 ≤ 0 ⇔ -2 ≤ x ≤ 3. Соединяя решения вместе, получим ответ: -2 ≤ х<-1 и 1< x ≤ З, или [—2; —1)U(1;3].

    Введение новой неизвестной

    Основной прием, с помощью которого решают показательные и логарифмические уравнения и неравенства,— это введение новой неизвестной. Поясним этот прием на ряде примеров.

    1) Выражение показательных функций друг через друга.

    Рассмотрим выражения . Все они могут быть алгебраически выражены друг через друга. Например, и т. д. Алгебраическая связь между различными степенями может быть осложнена добавлением в показателе степени постоянных слагаемых: Однако и сейчас несложно выразить эти выражения, например, через у1. Получим

    К этому полезно напомнить связь между различными основаниями. Например, и т. п. Поэтому выражения

    также нетрудно выразить через у1:

    Если в уравнении или неравенстве встречается несколько показательных функций, то надо все их выразить через одну. Обычно после этого показательное уравнение или неравенство превращается в алгебраическое.

    Примеры:

    Ответ: xi = 2, x2 = 1.

    Делаем замену =у. Неравенство перепишем таким образом:

    (мы умножили неравенство на у, что можно, так как

    Так как > — 1 верно при всех х, то остается решить неравенство < 2 ⇔ x<1.

    Ответ: х<1. (Иначе ответ можно записать так: (— ∞ ; 1).)

    2) Выражение логарифмических функций друг через друга.

    Рассмотрим выражения

    Используя модуль перехода, легко связать эти выражения между собой:

    Свойства логарифмов позволяют по-разному записать связи между выражениями. Например,

    Если в уравнении или неравенстве встречается несколько логарифмических функций, то надо (если не удается избавиться от логарифмов потенцированием) выразить их через одну и свести логарифмическое уравнение или неравенство к алгебраическому.

    Примеры:

    Делаем замену lg х = у. Получаем уравнение относительно у:

    Возвращаясь к неизвестной х, получим lg х = 2, х=100; lgx = 3, х= 1000.

    Ответ, x1 = 100, x2 =1000.

    Перейдем к основанию 3. Получим

    заменив log3x на у, получим

    Возвpащаясь к неизвестной х, получим log3x = 2, x = 9; log3x =—2,


    Ответ:

    Логарифмируя, получим равносильное данному неравенство (lg x —2) 1g x ≤ 3.

    Положим lg х = у. Получим неравенство (у — 2)y ≤ З ⇔

    Возвращаясь к неизвестной х, получим — l ≤ lg x ≤ 3 ⇔ x 1000

    Ответ: ≤ x ≤ 1000, или в другой записи [ ; 1 ООО].

    Использование свойства монотонности функций при решении показательных уравнений

    Монотонность функций часто позволяет определить число корней уравнения, а иногда и найти их значения. Рассмотрим примеры решения уравнений.

    В левой части уравнения имеем возрастающую функцию, а в правой — убывающую. Следовательно, уравнение не может иметь более одного корня (рис. 111). Один корень можно угадать: х=1. Это число и является окончательным ответом.

    Одно решение х=1 легко найти подбором. Докажем, что других корней нет. Перепишем уравнение так:

    В правой части последнего уравнения сумма убывающих функций т. е. значение у = 1 эта сумма может принять только один раз.

    Ответ: х = 1.

    3. Сколько корней имеет уравнение = ах?

    Изобразим схематически графики функций у = и у = ах (рис. 112). При а<0 графики имеют одну точку пересечения. При а>0 графики могут не пересекаться, касаться друг друга или пересекаться в двух точках. Граничным значением параметра а, при котором происходит разделение основных случаев — две точки пересечения или ни одной, является значение а, при котором прямая у = ах является касательной к графику функции у = некоторой точке. Найдем это значение а. Пусть касание произошло в точке хо, тогда производная функция у = в этой точке равна а. Поэтому получаем уравнение = а, т. е. x0 = ln а. Точка с абсциссой х0 = ln а должна лежать как на графике функции у=, так и на прямой у = ах. Получаем ° = ах, т. е. а = а ln а, так как а ≠ 0, то ln а= 1 и а = е.

    Ответ: при 0 ≤ а<0 один корень, при а>е два корня, при а = е один корень, при корней нет.

    Этот материал взят со страницы решения задач с примерами по всем темам предмета математика:

    Возможно вам будут полезны эти страницы:

    Показательные уравнения и примеры решения

    Определение. Уравнение называется показательным, если неизвестная входит в показатель степени.

    Рассмотрим простейшие приемы решения показательных уравнений на отдельных примерах.

    1. Решить уравнение

    Представим левую и правую части уравнения в виде степеней, имеющих одинаковые основания:

    Отсюда 3х = 2, или .

    Мы здесь воспользовались следующей теоремой:

    Если степени равны и основания равны, положительны и отличны от единицы, то равны и их показатели степеней.

    Докажем эту теорему.

    Пусть а > 1 и . Докажем, что в этом случае

    Допустим противное тому, что требуется доказать, т. е. допустим, что х > у или что х < у. Тогда получим по свойству показательной функции, что либо либо

    Оба эти результата противоречат условию теоремы. Следовательно, х=у, что и требовалось доказать.

    Также доказывается теорема и для случая, когда 0<а<1.

    Замечание. Из равенства не обязательно следует, что

    Из равенства также не обязательно вытекает равенство х=у.

    2. Решить уравнение

    Преобразуя левую и правую части уравнения, получим:

    3. Решить уравнение

    Преобразуя левую часть уравнения, получим:

    или

    или

    Отсюда

    или

    или

    Отсюда

    Значит, данное показательное уравнение имеет два корня:

    4. Решить уравнение

    Примем за новую неизвестную выражение и обозначим это выражение буквой у. Тогда получим:

    Отсюда

    Следовательно,

    либо , либо

    Из уравнения имеем х = 4.
    Из уравнения имеем х = —2.

    Итак, данное показательное уравнение имеет два корня: 4 и — 2.

    5. Решить уравнение

    Снова, обозначая и решая полученное квадратное уравнение, находим:

    Таким образом, получим:

    Как было указано при исследовании показательной функции, степень ни при каком х не может быть отрицательной, следовательно, первое из полученных уравнений не имеет корней. Из второго уравнения находим х = 0. Значит, первоначальное уравнение имеет лишь один корень, равный нулю.

    6. Решить уравнение

    Для решения этого уравнения применим графический метод. Построим на одной координатной плоскости (рис. 148) графики функций:

    Тогда абсциссы точек пересечения этих линий, т. е. абсциссы точек А и В, будут корнями данного уравнения. Абсцисса точки В, равная числу 2, будет точным корнем данного уравнения, а абсцисса точки А, равная приближенно —1,7, будет его приближенным корнем. Других корней данное уравнение не имеет.

    Сведения, изложенные в этой главе, окажутся полезными при изучении логарифмов, которым посвящена следующая глава.

    Примем к сведению без доказательства еще следующую теорему:

    Если а есть положительной число, отличное от единицы, а N — любое положительное число, то уравнение с неизвестным х имеет один и только один действительный корень (рациональный или иррациональный).

    Примеры. Уравнение имеет единственный действительный корень, равный рациональному числу 5.

    Уравнение имеет единственный действительный иррациональный корень, приближенное значение которого с точностью до 0,00001 равно 0,47712.

    Итак, мы можем сделать следующие заключения:

    1. Выражение , где а>0, имеет при каждом действительном значении х одно и только одно действительное значение.
    2. Действия над выражениями вида , в которых х является любым действительным числом, можно выполнять по тем же правилам, по которым они выполняются над степенями с целым положительным показателем. Поэтому выражение при всяком действительном значении х также называется степенью (обобщенной).

    Примеры зависимостей, выражающихся с помощью показательных функций.

    1. (барометрическая формула):
    —давление на уровне моря;
    k —некоторая известная постоянная;
    е —2,718;
    h(м) —высота над уровнем моря;
    р(ат) —давление на высоте А над уровнем моря.

    Здесь h есть независимая переменная, или аргумент, а р есть зависимая переменная, или функция.

    По этой формуле можно определять давление р по заданному значению h.

    2. Если температура воздуха равна 20° С и тело в течение 20 минут охлаждается от 100 до 60°, то зависимость температуры Т охлаждающегося тела от времени t минут (в течение которого будет происходить охлаждение) выразится формулой

    Здесь t есть аргумент, а Т—функция.

    Пользуясь этой формулой, можно узнать, например, что через один час температура тела понизится до 30°.

    Приведенные формулы выводятся в курсах высшей математики.

    Решение заданий и задач по предметам:

    • Математика
    • Высшая математика
    • Математический анализ
    • Линейная алгебра

    Дополнительные лекции по высшей математике:

    1. Тождественные преобразования алгебраических выражений
    2. Функции и графики
    3. Преобразования графиков функций
    4. Квадратная функция и её графики
    5. Алгебраические неравенства
    6. Неравенства
    7. Неравенства с переменными
    8. Прогрессии в математике
    9. Арифметическая прогрессия
    10. Геометрическая прогрессия
    11. Показатели в математике
    12. Логарифмы в математике
    13. Исследование уравнений
    14. Уравнения высших степеней
    15. Уравнения высших степеней с одним неизвестным
    16. Комплексные числа
    17. Непрерывная дробь (цепная дробь)
    18. Алгебраические уравнения
    19. Неопределенные уравнения
    20. Соединения
    21. Бином Ньютона
    22. Число е
    23. Непрерывные дроби
    24. Функция
    25. Исследование функций
    26. Предел
    27. Интеграл
    28. Двойной интеграл
    29. Тройной интеграл
    30. Интегрирование
    31. Неопределённый интеграл
    32. Определенный интеграл
    33. Криволинейные интегралы
    34. Поверхностные интегралы
    35. Несобственные интегралы
    36. Кратные интегралы
    37. Интегралы, зависящие от параметра
    38. Квадратный трехчлен
    39. Производная
    40. Применение производной к исследованию функций
    41. Приложения производной
    42. Дифференциал функции
    43. Дифференцирование в математике
    44. Формулы и правила дифференцирования
    45. Дифференциальное исчисление
    46. Дифференциальные уравнения
    47. Дифференциальные уравнения первого порядка
    48. Дифференциальные уравнения высших порядков
    49. Дифференциальные уравнения в частных производных
    50. Тригонометрические функции
    51. Тригонометрические уравнения и неравенства
    52. Показательная функция
    53. Обобщенная степень
    54. Взаимно обратные функции
    55. Логарифмическая функция
    56. Уравнения и неравенства
    57. Положительные и отрицательные числа
    58. Алгебраические выражения
    59. Иррациональные алгебраические выражения
    60. Преобразование алгебраических выражений
    61. Преобразование дробных алгебраических выражений
    62. Разложение многочленов на множители
    63. Многочлены от одного переменного
    64. Алгебраические дроби
    65. Пропорции
    66. Уравнения
    67. Системы уравнений
    68. Системы уравнений высших степеней
    69. Системы алгебраических уравнений
    70. Системы линейных уравнений
    71. Системы дифференциальных уравнений
    72. Арифметический квадратный корень
    73. Квадратные и кубические корни
    74. Извлечение квадратного корня
    75. Рациональные числа
    76. Иррациональные числа
    77. Арифметический корень
    78. Квадратные уравнения
    79. Иррациональные уравнения
    80. Последовательность
    81. Ряды сходящиеся и расходящиеся
    82. Тригонометрические функции произвольного угла
    83. Тригонометрические формулы
    84. Обратные тригонометрические функции
    85. Теорема Безу
    86. Математическая индукция
    87. Показатель степени
    88. Показательные функции и логарифмы
    89. Множество
    90. Множество действительных чисел
    91. Числовые множества
    92. Преобразование рациональных выражений
    93. Преобразование иррациональных выражений
    94. Геометрия
    95. Действительные числа
    96. Степени и корни
    97. Степень с рациональным показателем
    98. Тригонометрические функции угла
    99. Тригонометрические функции числового аргумента
    100. Тригонометрические выражения и их преобразования
    101. Преобразование тригонометрических выражений
    102. Комбинаторика
    103. Вычислительная математика
    104. Прямая линия на плоскости и ее уравнения
    105. Прямая и плоскость
    106. Линии и уравнения
    107. Прямая линия
    108. Уравнения прямой и плоскости в пространстве
    109. Кривые второго порядка
    110. Кривые и поверхности второго порядка
    111. Числовые ряды
    112. Степенные ряды
    113. Ряды Фурье
    114. Преобразование Фурье
    115. Функциональные ряды
    116. Функции многих переменных
    117. Метод координат
    118. Гармонический анализ
    119. Вещественные числа
    120. Предел последовательности
    121. Аналитическая геометрия
    122. Аналитическая геометрия на плоскости
    123. Аналитическая геометрия в пространстве
    124. Функции одной переменной
    125. Высшая алгебра
    126. Векторная алгебра
    127. Векторный анализ
    128. Векторы
    129. Скалярное произведение векторов
    130. Векторное произведение векторов
    131. Смешанное произведение векторов
    132. Операции над векторами
    133. Непрерывность функций
    134. Предел и непрерывность функций нескольких переменных
    135. Предел и непрерывность функции одной переменной
    136. Производные и дифференциалы функции одной переменной
    137. Частные производные и дифференцируемость функций нескольких переменных
    138. Дифференциальное исчисление функции одной переменной
    139. Матрицы
    140. Линейные и евклидовы пространства
    141. Линейные отображения
    142. Дифференциальные теоремы о среднем
    143. Теория устойчивости дифференциальных уравнений
    144. Функции комплексного переменного
    145. Преобразование Лапласа
    146. Теории поля
    147. Операционное исчисление
    148. Системы координат
    149. Рациональная функция
    150. Интегральное исчисление
    151. Интегральное исчисление функций одной переменной
    152. Дифференциальное исчисление функций нескольких переменных
    153. Отношение в математике
    154. Математическая логика
    155. Графы в математике
    156. Линейные пространства
    157. Первообразная и неопределенный интеграл
    158. Линейная функция
    159. Выпуклые множества точек
    160. Система координат

    Показательные уравнения и неравенства методы их решения.

    Решение систем показательных уравнений

    Способы решения систем уравнений

    Для начала кратко вспомним, какие вообще существуют способы решения систем уравнений.

    Существуют четыре основных способа решения систем уравнений:

      Способ подстановки: берется любое из данных уравнений и выражается $y$ через $x$, затем $y$ подставляется в уравнение системы, откуда и находится переменная $x.$ После этого мы легко можем вычислить переменную $y.$

      Способ сложения: в данном способе необходимо умножать одно или оба уравнения на такие числа, чтобы при сложении вместе обоих одна из переменных «исчезла».

      Графический способ: оба уравнения системы изображается на координатной плоскости и находится точка их пересечения.

      Способ введения новых переменных: в этом способе мы делаем замену каких-либо выражений для упрощения системы, а потом применяем один из выше указанных способов.

    Системы показательных уравнений

    Определение 1

    Системы уравнений, состоящие из показательных уравнений, называются системой показательных уравнений. {n}}$. До тех пор, пока у вас слева или справа есть какие-то левые множители, дополнительные константы и т.д., никакую рационализацию и «зачёркивание» оснований выполнять нельзя ! Бесчисленное множество задач было выполнено неправильно из-за непонимания этого простого факта. Я сам постоянно наблюдаю эту проблему у моих учеников, когда мы только-только приступаем к разбору показательных и логарифмических неравенств.

    Но вернёмся к нашей задаче. Попробуем в этот раз обойтись без рационализации. Вспоминаем: основание степени больше единицы, поэтому тройки можно просто зачеркнуть — знак неравенства при этом не поменяется. Получим:

    \[\begin{align} & -\frac{8x}{3} \lt 4-4x; \\ & 4x-\frac{8x}{3} \lt 4; \\ & \frac{4x}{3} \lt 4; \\ & 4x \lt 12; \\ & x \lt 3. \\\end{align}\]

    Вот и всё. Окончательный ответ: $x\in \left(-\infty ;3 \right)$.

    Выделение устойчивого выражения и замена переменной

    В заключение предлагаю решить ещё четыре показательных неравенства, которые уже являются довольно сложными для неподготовленных учеников. {5}}=3125. \\\end{align}\]

    Конечно, все эти числа при желании можно восстановить в уме, просто последовательно умножая их друг на друга. Однако, когда вам предстоит решить несколько показательных неравенств, причём каждое следующее сложнее предыдущего, то последнее, о чём хочется думать — это степени каких-то там чисел. И в этом смысле данные задачи являются более сложными, нежели «классические» неравенства, которые решаются методом интервалов.

    Надеюсь, этот урок помог вам в освоении данной темы. Если что-то непонятно — спрашивайте в комментариях. И увидимся в следующих уроках.:)

    Способы решения систем уравнений

    Для начала кратко вспомним, какие вообще существуют способы решения систем уравнений.

    Существуют четыре основных способа решения систем уравнений:

      Способ подстановки: берется любое из данных уравнений и выражается $y$ через $x$, затем $y$ подставляется в уравнение системы, откуда и находится переменная $x.$ После этого мы легко можем вычислить переменную $y. $

      Способ сложения: в данном способе необходимо умножать одно или оба уравнения на такие числа, чтобы при сложении вместе обоих одна из переменных «исчезла».

      Графический способ: оба уравнения системы изображается на координатной плоскости и находится точка их пересечения.

      Способ введения новых переменных: в этом способе мы делаем замену каких-либо выражений для упрощения системы, а потом применяем один из выше указанных способов.

    Системы показательных уравнений

    Определение 1

    Системы уравнений, состоящие из показательных уравнений, называются системой показательных уравнений.

    Решение систем показательных уравнений будем рассматривать на примерах.

    Пример 1

    Решить систему уравнений

    Рисунок 1.

    Решение.

    Будем пользоваться первым способом для решения данной системы. Для начала выразим в первом уравнении $y$ через $x$.

    Рисунок 2.

    Подставим $y$ во второе уравнение:

    \ \ \[-2-x=2\] \ \

    Ответ: $(-4,6)$. {\varphi (x)} $, где $a >0,a\ne 1$ равносильна совокупности двух систем

    \}

    6.3: Экспоненциальные уравнения и неравенства

    1. Последнее обновление
    2. Сохранить как PDF
  • Идентификатор страницы
    80789
    • Carl Stitz & Jeff Zeager
    • Общественный колледж Лейкленда и Общественный колледж округа Лорейн 9{x}\right) & = & \ln(129) & \mbox{Возьмем натуральный логарифм обеих сторон.} \\ x \ln(2) & = & \ln(129) & \mbox{степенное правило} \\[4pt] x & = &\dfrac{\ln(129)}{\ln(2)} & \\ \end{массив}\nonumber\]

      «Взять натуральный логарифм» обеих сторон сродни возведению в квадрат обеих сторон: поскольку \(f(x) = \ln(x)\) является функцией , пока две величины равны, их натуральные логарифмы равны равный. 2 Также обратите внимание, что мы рассматриваем \(\ln(2)\) как любое другое ненулевое действительное число и делим его на 3 , чтобы изолировать переменную \(x\). Ниже мы суммируем два распространенных способа решения показательных уравнений, мотивированных нашими примерами.

      Этапы решения уравнения с экспоненциальными функциями

      1. Выделить экспоненциальную функцию.
        1. Если удобно, выразите обе части общим основанием и приравняйте степени.
        2. В противном случае возьмите натуральный логарифм обеих частей уравнения и используйте степенное правило. 9{2x}\справа)\). Правило мощности дает \((x+2)\ln(3) = 2x\ln(7)\). Хотя это уравнение кажется очень сложным, имейте в виду, что \(\ln(3)\) и \(\ln(7)\) — это просто константы. Уравнение \((x+2) \ln(3) = 2x \ln(7)\) на самом деле является линейным уравнением, и поэтому мы собираем все члены с \(x\) на одной стороне, а константы с другой. Затем мы делим обе части на коэффициент \(х\), который мы получаем путем факторизации.

          \[\begin{array}{rclr} (x+2) \ln(3) & = & 2x \ln(7) & \\ x \ln(3) + 2 \ln(3) & = & 2x \ln(7) & \\ 2 \ln(3) & = & 2x \ln(7) — x \ln(3) & \\ 2 \ln(3) & = & x (2 \ln(7) — \ln(3)) & \mbox{Коэффициент.}\\ x & = & \frac{2 \ln(3)}{2\ln(7) — \ln(3)} & \\[4pt] \конец{массив}\номер\] 9{\log_{3}(2)} & \mbox{Изменение базы}\\ 2000 & \stackrel{?}{=} & 1000 \cdot 2 & \mbox{Обратное свойство}\\ 2000 & \stackrel{\ галочка}{=} & 2000 & \\ \end{массив}\номер\]

          Другие решения можно проверить, используя комбинацию логарифмических и обратных свойств. Одни выпадают довольно быстро, а другие более вовлекаются. Оставляем их читателю.

          Поскольку экспоненциальные функции непрерывны в своих областях определения, применима теорема 3.1 о промежуточном значении. Как и в случае с алгебраическими функциями в разделе 5.3, это позволяет нам решать неравенства с помощью диаграмм со знаками, как показано ниже. 9{2x} — 4 = 0\). Чтобы решить последнее, мы изолируем экспоненту и берем журналы, чтобы получить \(2x = \ln(4)\), или \(x = \frac{\ln(4)}{2} = \ln(2)\ ). {\ln\left(\frac{1}{4}\right )}- 4\ln\left(\frac{1}{2}\right) & \\ & = & \frac{1}{4} \ln\left(\frac{1}{2}\right) — 4 \ln\left(\frac{1}{2}\right) = -\frac{15}{4} \ln\left(\frac{1}{2}\right) & \end{array} \номер\] 9{-0.1t} = \frac{1}{3}\), так что \(t = -10\ln\left(\frac{1}{3}\right)\), которое после быстрого применения Правило степени оставляет нам \(t = 10\ln(3)\). Если мы хотим избежать использования калькулятора для выбора тестовых значений, заметим, что, поскольку \(1 < 3\), \(0 = \ln(1) < \ln(3)\), так что \(10\ln( 3) > 0\). Поэтому мы выбираем \(t = 0\) в качестве тестового значения в \([0, 10 \ln(3))\). Поскольку \(3 < 4\), \(10 \ln(3) < 10 \ln(4)\), то последнее является нашим выбором тестового значения для интервала \((10 \ln(3), \infty)\). Наша диаграмма знаков приведена ниже, а рядом с ней — наш график \(y=T(t)\) из примера 6.1.2 с горизонтальной линией \(y = 100\). 9{x}\) растет относительно любого многочлена?

        6.3.2. Ответы

        1. \(x = \frac{3}{4}\)
        2. \(х = 4\)
        3. \(х=2\)
        4. \(х = -\фракция {1}{4}\)
        5. \(х = -\фракция {7}{3}\)
        6. \(х = -1, \, 0, \, 1\)
        7. \(х = \фракция{16}{15}\)
        8. \(х=-\фракция{2}{11}\)
        9. \(х = \frac{\ln(5)}{2\ln(3)}\)
        10. \(х = -\frac{\ln(2)}{\ln(5)}\)
        11. Нет решения.
        12. \(x = \frac{\ln(29) + \ln(3)}{\ln(3)}\)
        13. \(x = \frac{\ln(3)}{12\ln(1,005)}\)
        14. \(k = \frac{\ln\left(\frac{1}{2}\right)}{-5730} = \frac{\ln(2)}{5730}\)
        15. \(t=\frac{\ln(2)}{0,1} = 10\ln(2)\)
        16. \(x=\frac{1}{2}\ln\left(\frac{1}{2}\right) = -\frac{1}{2}\ln(2)\)
        17. \(t = \frac{\ln\left(\frac{1}{18}\right)}{-0,1} =10 \ln(18)\)
        18. \(x=-10\ln\left(\frac{5}{3}\right) = 10\ln\left(\frac{3}{5}\right)\)
        19. \(х=\ln(2)\)
        20. \(t=\frac{1}{3}\ln(2)\)
        21. \(t = \frac{\ln\left(\frac{1}{29}\right)}{-0,8} = \frac{5}{4}\ln(29)\)
        22. \(x = \frac{\ln\left(\frac{2}{5}\right)}{\ln\left(\frac{4}{5}\right)} = \frac{\ln( 2)-\ln(5)}{\ln(4) — \ln(5)}\)
        23. \(х = \ln(2)\)
        24. \(x = -\frac{1}{8} \ln\left(\frac{1}{4} \right) = \frac{1}{4}\ln(2)\)
        25. \(x = \frac{\ln(3)}{\ln(3) — \ln(2)}\)
        26. \(x = \frac{\ln(3) + 5\ln\left(\frac{1}{2}\right)}{\ln(3) — \ln\left(\frac{1}{) 2}\right)} = \frac{\ln(3)-5\ln(2)}{\ln(3)+\ln(2)}\)
        27. \(x = \frac{4 \ln(3) — 3 \ln(7)}{7 \ln(7) + 2 \ln(3)}\)
        28. \(х=\ln(5)\)
        29. \(х=\ln(3)\)
        30. \(x=\frac{\ln(3)}{\ln(2)}\)
        31. \(х=\ln(3)\)
        32. \(х=\лн(3)\), \(\лн(5)\)
        33. \(x=\frac{\ln(5)}{\ln(3)}\)
        34. \((\ln(53), \infty)\)
        35. \(\left[\frac{\ln(3)}{12\ln(1. 005)}, \infty\right)\)
        36. \((-\infty, -1) \чашка (0, 1)\)
        37. \(\left(-\infty, \frac{\ln\left(\frac{2}{5}\right)}{\ln\left(\frac{4}{5}\right)} \right ] = \left(-\infty, \frac{\ln(2)-\ln(5)}{\ln(4)-\ln(5)} \right]\)
        38. \(\left(-\infty, \frac{\ln\left(\frac{2}{377}\right)}{-0,8} \right] = \left(-\infty, \frac{5} {4}\ln\left(\frac{377}{2}\right) \right]\)
        39. \(\left[\ln\left(\frac{1}{18}\right)}{-0.1}, \infty\right) = [10\ln(18), \infty)\)
        40. \(х \приблизительно -0,76666, \, х = 2, \, х = 4\)
        41. \(х \приблизительно 0,01866, \, х \приблизительно 1,7115\)
        42. \(х = 0\)
        43. \((-\infty, 1]\)
        44. \(\приблизительно (-\infty, 2.7095)\)
          45. 9{-1}\) имеют домен \((-\infty, \infty)\) и диапазон \((-\infty, \infty)\).

        Артикул

        1 Можно использовать натуральные бревна или обычные бревна. Мы выбираем натуральные бревна. (Из исчисления вы узнаете, что это самые «математические» логарифмы. )

        2 Это также часть оператора «если» \(\log _{b}(u)=\log _{b}(w)\) тогда и только тогда, когда \(u = w\) в теореме 6.4.

        3  Пожалуйста, не поддавайтесь искушению разделить обе части на «ln» вместо ln(2). Точно так же, как не имеет смысла делить обе части на символ квадратного корня \(‘\sqrt ‘\) при решении \(x \sqrt{2}=5\), нет смысла делить на ‘ln’ .

        4  Это потому, что основание \(\ln (x)\) равно \(e>1\). Если бы основание \(b\) находилось в интервале \(0

        5  Конечно, мы могли бы воспользоваться калькулятором, но разве это было бы весело?

        6  На этом этапе можно использовать калькулятор. Как обычно, мы действуем без извинений аналитическим методом.

        7 Примечание: \(\ln (2) \приблизительно 0,693\).

        8  Критики могут указать, что, поскольку нам все равно нужно было использовать калькулятор для интерпретации нашего ответа, почему бы не использовать его раньше для упрощения вычислений? Справедливый вопрос, на который мы несправедливо отвечаем: это наша книга

        Эта страница под названием 6. 3: Экспоненциальные уравнения и неравенства распространяется под лицензией CC BY-NC-SA 3.0 и была создана, изменена и/или курирована Карлом Стицем и Джеффом Зегером посредством исходного контента, который был отредактирован в соответствии со стилем и стандартами. платформы LibreTexts; подробная история редактирования доступна по запросу.

        1. Наверх
          • Была ли эта статья полезной?
          1. Тип изделия
            Раздел или Страница
            Автор
            Карл Стиц и Джефф Зигер
            Лицензия
            CC BY-NC-SA
            Версия лицензии
            3,0
            Показать страницу TOC
            нет
          2. Теги
            1. источник@https://www. stitz-zeager.com/latex-source-code.html
            2. источник[1]-math-4005

          Экспоненциальные уравнения и неравенства — Предварительный расчет

          Экспоненциальные уравнения и неравенства — Предварительный расчет

          —>

          • Войти
          • Биографии репетитора
          • Подготовка к тесту
            СРЕДНЯЯ ШКОЛА
            • ACT Репетиторство
            • SAT Репетиторство
            • Репетиторство PSAT
            • ASPIRE Репетиторство
            • ШСАТ Репетиторство
            • Репетиторство STAAR
            ВЫСШАЯ ШКОЛА
            • Репетиторство MCAT
            • Репетиторство GRE
            • Репетиторство по LSAT
            • Репетиторство по GMAT
            К-8
            • Репетиторство AIMS
            • Репетиторство по HSPT
            • Репетиторство ISEE
            • Репетиторство ISAT
            • Обучение SSAT
            • Репетиторство STAAR
            Поиск 50+ тестов
          • Академическое обучение
            репетиторство по математике
            • Алгебра
            • Исчисление
            • Элементарная математика
            • Геометрия
            • Предварительный расчет
            • Статистика
            • Тригонометрия
            репетиторство по естественным наукам
            • Анатомия
            • Биология
            • Химия
            • Физика
            • Физиология
            иностранные языки
            • французский
            • немецкий
            • Латинский
            • Китайский диалект
            • Испанский
            начальное обучение
            • Чтение
            • Акустика
            • Элементарная математика
            прочие
            • Бухгалтерский учет
            • Информатика
            • Экономика
            • Английский
            • Финансы
            • История
            • Письмо
            • Лето
            Поиск по 350+ темам
          • О
            • Обзор видео
            • Процесс выбора наставника
            • Онлайн-репетиторство
            • Мобильное обучение
            • Мгновенное обучение
            • Как мы работаем
            • Наша гарантия
            • Влияние репетиторства
            • Обзоры и отзывы
            • Освещение в СМИ
            • О преподавателях университета

          Мы открыты в субботу и воскресенье!

          Звоните прямо сейчас, чтобы записаться на обучение:

          (888) 888-0446

          Все ресурсы Precalculus

          12 диагностических тестов 380 практических тестов Вопрос дня Карточки Learn by Concept

          Precalculus Help » Экспоненциальные и логарифмические функции » Показательные уравнения и неравенства

          Решение показательного уравнения.

          Найдите ,

          .

          Возможные ответы:

          Правильный ответ:

          Пояснение:

          Вспоминаем свойство:

          Теперь, .

          Итак,

          .

          Сообщить об ошибке

          Решение экспоненциального уравнения.

          Решить

          Возможные ответы:

          Правильный ответ:

          Объяснение:

          Используйте  (по соглашению просто ) для решения.

          .

          Сообщить об ошибке

          Решите уравнение для  используя правила логарифмирования.

          Возможные ответы:

          Правильный ответ:

          Объяснение:

          Преобразование логарифмов в суммы логарифмов аннулирует первые два члена x, что приведет к уравнению:

           

          Объединение первого и второго членов, а затем вычитание нового члена позволит вам изолировать переменный член .

          Разделите обе части уравнения на 2, затем возведите в степень 3.

          Численная оценка этого члена даст правильный ответ.

          Сообщить об ошибке

          Решите следующее уравнение:

          Возможные ответы:

          Правильный ответ:

          1 1 1 Объяснение:

          Чтобы решить это уравнение, вспомните следующее свойство:

               Можно переписать как 

          Оцените с помощью калькулятора, чтобы получить

          Сообщить об ошибке

          Решите

          .

          Возможные ответы:

          Правильный ответ:

          Объяснение:

          После использования правила деления для упрощения левой части вы можете взять натуральный логарифм с обеих сторон.

          Если вы затем объедините одинаковые члены, вы получите квадратное уравнение, которое делит на,

           .

          Приравняв каждый бином к нулю и найдя  мы получим решение  .

          Сообщить об ошибке

          Решить x: 

          Возможные ответы:

          Правильный ответ:

          Объяснение:

          Сообщить об ошибке

          Найдите x в следующем уравнении: 

          Возможные ответы:

          Правильный ответ:

          Объяснение:

          Сообщить об ошибке

          Найдите x, используя правила логарифмирования:

          Возможные ответы:

          Правильный ответ:

          1 1 1 Объяснение:

          Сообщить об ошибке

          Решить для x: 

          Возможные ответы:

          Правильный ответ:

          6

          6
          6 Объяснение:

          Отчет о ошибке

          Упростить выражение журнала:

          Возможные ответы:

          нельзя упростить.

          Объяснение:

          Логарифмическое выражение максимально упрощено.

           

          Сообщить об ошибке

          Уведомление об авторских правах

          Посмотреть репетиторов по математике

          Zachary
          Сертифицированный репетитор

          Дартмутский колледж, бакалавр искусств, политических наук и государственного управления. Университет Торонто, магистр гуманитарных наук, политическая наука…

          Посмотреть Преподаватели математического анализа

          Пьер
          Сертифицированный преподаватель

          Университет Бригама Янга в Прово, бакалавр наук, электротехника. Pennsylvania State University-Penn State Fayette…

          View Pre-Calculus Tutors

          Katie
          Сертифицированный преподаватель

          Университет Северной Каролины в Чапел-Хилл, бакалавр наук, биохимия.

          Все ресурсы Precalculus

          12 диагностических тестов 380 практических тестов Вопрос дня Карточки Учись по концепции

          экспоненциальных неравенств | Brilliant Math & Science Wiki

          Содержание
          • Введение
          • Экспоненциальные неравенства — одно и то же основание
          • Экспоненциальные неравенства — основание меньше 1
          • Экспоненциальные неравенства — аналогичное основание
          • Экспоненциальные неравенства — другое основание
          • Экспоненциальные неравенства — несколько терминов 9xf(x)=ax равно монотонно возрастающему (\big((увеличение xxx всегда увеличивает f(x))f(x)\big)f(x)) для a>1a>1a>1 и монотонно убывает (\big((увеличение xxx всегда уменьшает f(x))f(x)\big)f(x)) для 0 2} < \ гидроразрыва {9x ?24332​<(32​)x2<49​⋅(278​)x?

            Когда два основания различны и не связаны общим основанием (как в предыдущем разделе), становится необходимым использование логарифмов. К счастью, логарифмы обладают теми же свойствами, что и экспоненты:

            .

            Если a>1a>1a>1 и x>yx>yx>y, то log⁡ax>log⁡ay\log_ax>\log_ayloga​x>loga​y. В противном случае, если 0(8-5x)\log 5,log25x>log58-5x⟹5xlog2>(8-5x)log5,

            , так что 5xlog⁡2>8log⁡5−5xlog⁡5,5x\log 2>8\log 5-5x\log 5,5xlog2>8log5−5xlog5. Перестановка дает 5x(log⁡2+log⁡5)>8log⁡5,5x(\log2+\log5)>8\log 5,5x(log2+log5)>8log5. Поскольку log⁡2+log⁡5=log⁡10=1,\log 2+\log 5=\log 10=1,log2+log5=log10=1, это эквивалентно 5x>8log⁡5,5x>8 \log 5,5x>8log5, поэтому x>85log⁡5.x>\frac{8}{5}\log 5.x>58​log5. □_\квадрат□​

            В случае нескольких членов, как правило, стоит присвоить другую переменную экспоненциальному члену, решить полученное неравенство, а затем работать с одночленным неравенством. x). 2x(2⋅2x+8)≤8x(5−2x). Каково значение a+b? а + б? а+б? 92-x-4=0 \ подразумевает x=\frac{1 \pm \sqrt{17}}{2}x2−x−4=0⟹x=21±17​​. Только 1−172∈[−2,1]\frac{1-\sqrt{17}}{2} \in [-2, 1] 21−17​​∈[−2,1], так что это единственное решение в этом подслучае.

            При объединении случаев получается набор решений

            .

            х<−2, х=1−172, х=−1, х=0, х>1. □x<-2,\ x=\frac{1-\sqrt{17}}{2},\ x=-1,\ x=0,\ x>1.\ _\squarex<−2, x= 21−17, х=−1, х=0, х>1. □​

            • Экспоненты
            • Правила экспонентов
            • Логарифмы
            • Логарифмические неравенства

            Цитировать как: Экспоненциальные неравенства. Brilliant.org . Извлекаются из https://brilliant.org/wiki/exponential-inequalities/

            неравенство — Экспоненциальные уравнения и неравенства и логарифмы

            спросил

            Изменено 3 года, 5 месяцев назад 9{5}}$=? , поэтому, если у вас также есть хорошая книга в формате PDF с введением и примерами для логарифмов, это будет неплохо. x$ относительно $x$ (то есть $x=\log_2 u$) для каждого решения $u$.

            Для этого конкретного многочлена вы, наверное, сразу заметили, что $u=1$ является решением, так как сумма коэффициентов равна нулю. Это означает, что вы можете разложить полином как $$(u-1)(\textrm{квадратный полином от }u)=0$$ которые вы можете легко решить.

            Для второй задачи напомним, что $\log_b c=\frac{\log_a c}{\log_a b}$ для любого выбора основания $a$, и удобно использовать основание $a=7$, так как оба $b$ и $c$ являются степенями $7$.

            $\endgroup$

            95}}}{\лог 49}\\ &= \frac{\frac53\log 7}{2\log 7}\\ &= \frac56 \end{align*}$$

            Обратите внимание, что в строке $(1)$ нет ничего особенного для логарифмирования по основанию $10$. Базой может быть любая база $c > 0$ и $c \ne 1$. Натуральный логарифм $\ln$ с основанием-$e$ одинаково верен:

            $$\begin{align*} ? &= \frac{\ln a}{\ln b}\\ &= \ гидроразрыва {\ log_c a} {\ log_c b} \end{выравнивание*}$$

            $\endgroup$

            1

            Твой ответ

            Зарегистрируйтесь или войдите в систему

            Зарегистрируйтесь с помощью Google

            Зарегистрироваться через Facebook

            Зарегистрируйтесь, используя электронную почту и пароль

            Опубликовать как гость

            Электронная почта

            Обязательно, но не отображается

            Опубликовать как гость

            Электронная почта

            Требуется, но не отображается

            Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

            . 92-log2)<-log5$$

            Используя правило логарифмирования , мы получаем

            $$x \cdot log\frac{25}{2}< -log5$$

            Деление на $log\frac {25}{2}$,

            $$x<-\frac{log5}{log\frac{25}{2}} \ приблизительно -0,637$$

            Следовательно, решения $x<- \frac {log5}{log\frac{25}{2}} \приблизительно -0,637$, т. е. $x \in \left<-\infty, -\frac{log5}{log\frac{25}{2}} \ правильно>$.

            Другие примеры

            Пример 5:   9x<0$ — это $x \in \left<0, \infty\right>$. Следовательно, решение второго случая есть пересечение решений обоих неравенств: $x \in \left[1, \infty\right>$.

            Окончательное решение является объединением решений первого и второго случая, т.е. решение:

            $$x \in \left<- \infty, 0\right> \cup \left[1, \infty \right>.$$

             

             

             

            Экспоненциальные уравнения — определение, решение, примеры

            Экспоненциальные уравнения , как следует из названия, включают показатели степени. Мы знаем, что показатель степени числа (основания) показывает, сколько раз число (основание) умножается. Но что произойдет, если степень числа является переменной? Когда мощность является переменной и если она является частью уравнения, то это называется показательным уравнением. Нам может понадобиться использовать связь между показателями степени и логарифмами для решения экспоненциальных уравнений.

            Давайте изучим определение показательных уравнений вместе с процессом их решения, когда основания одинаковы и когда основания не совпадают, а также несколько решенных примеров и практических вопросов.

            1. Что такое экспоненциальные уравнения?
            2. Уравнения с показателями
            3. Формулы экспоненциальных уравнений
            4. Решение экспоненциальных уравнений с одинаковыми основаниями
            5. Решение экспоненциальных уравнений с разными основаниями
            6. Часто задаваемые вопросы об экспоненциальных уравнениях

            Что такое экспоненциальные уравнения?

            Показательное уравнение — это уравнение с показателями степени, где показатель степени (или часть показателя степени) является переменной. Например, 3 x = 81, 5 x — 3 = 625, 6 2y — 7 = 121 и т. д. являются примерами экспоненциальных уравнений. Мы можем столкнуться с использованием экспоненциальных уравнений при решении задач алгебры, сложных процентов, экспоненциального роста, экспоненциального убывания и т. д.

            Типы показательных уравнений

            Существует три типа показательных уравнений. Они следующие:

            • Уравнения с одинаковыми основаниями с обеих сторон. (Пример: 4 x = 4 2 )
            • Уравнения с разными базами, которые можно сделать одинаковыми. (Пример: 4 x = 16, что можно записать как 4 x = 4 2 )
            • Уравнения с разными основаниями, которые нельзя сделать одинаковыми. (Пример: 4 х = 15)

            Уравнения с показателями

            Уравнения в алгебре с переменными показателями называются уравнениями с показателями или показательными уравнениями. Другими словами, мы можем сказать, что алгебраические уравнения, в которых переменные входят в качестве показателей, известны как уравнения с показателями. Вот некоторые примеры такого уравнения: 3 x + 4  = 81, -2 3y-7  = -64 и т. д.  

            Формулы экспоненциальных уравнений

            При решении экспоненциального уравнения основания в обеих частях могут совпадать или не совпадать. Вот формулы, которые используются в каждом из этих случаев, которые мы подробно изучим в следующих разделах.

            Свойство равенства для экспоненциальных уравнений

            Это свойство полезно для решения показательного уравнения с теми же основаниями. В нем говорится, что если основания в обеих частях экспоненциального уравнения равны, то показатели степени также должны быть равны. то есть

            a x = a y ⇔ x = y.

            Экспоненциальные уравнения в логарифмической форме

            Мы знаем, что логарифмы не что иное, как показатели степени, и наоборот. Следовательно, показательное уравнение может быть преобразовано в логарифмическую функцию. Это помогает в процессе решения показательного уравнения с разными основаниями. Вот формула для преобразования показательных уравнений в логарифмические уравнения.

            б х = а ⇔ log б а = х

            Решение экспоненциальных уравнений с одинаковыми основаниями

            Иногда показательное уравнение может иметь одинаковые основания в обеих частях уравнения. Например, 5 x = 5 3 имеет одинаковое основание 5 с обеих сторон. Иногда, хотя показатели с обеих сторон неодинаковы, их можно сделать одинаковыми. Например, 5 x = 125. Хотя у него разные основания в обеих частях уравнения, их можно сделать одинаковыми, записав 5 x 9.0035 = 5 3 (так как 125 = 5 3 ). Чтобы решить показательные уравнения в каждом из этих случаев, мы просто применяем свойство равенства показательных уравнений, используя которое, мы устанавливаем показатели равными и решаем для переменной.

            Вот еще один пример, когда базы не одинаковые, но их можно сделать одинаковыми.

            Пример: Решите показательное уравнение 7 y + 1 = 343 y .

            Решение:

            Мы знаем, что 343 = 7 3 . Используя это, данное уравнение может быть записано как

            7 y + 1 = (7 3 ) y

            7 y + 1 = 7 3y

            на обеих сторонах основания 903 9035 подобные. Таким образом, мы можем установить показатели степени одинаковыми.

            y + 1 = 3y

            Вычитание y с обеих сторон,

            2y = 1

            Деление обеих сторон на 2,

            y = 1/2

            .

            Решение экспоненциальных уравнений с разными основаниями

            Иногда основания в обеих частях экспоненциального уравнения могут не совпадать (или) не могут быть сделаны одинаковыми. Мы решаем показательные уравнения с помощью логарифмов, когда основания не совпадают в обеих частях уравнения. Например, 5 x = 3 не имеет одинаковых оснований с обеих сторон, и основания не могут быть одинаковыми. В таких случаях мы можем сделать одну из следующих вещей.

            • Преобразуйте показательное уравнение в логарифмическую форму, используя формулу b x = a ⇔ log b a = x и найдите переменную.
            • Примените логарифм (log) к обеим частям уравнения и найдите переменную. В этом случае нам придется использовать свойство логарифма, log a m = m log a.

            Решим уравнение 5 x = 3 каждым из этих способов.

            Метод 1:

            Преобразуем 5 x = 3 в логарифмическую форму. Тогда мы получаем,

            log 5 3 = x

            Используя изменение базового свойства,

            x = (log 3) / (log 5)

            Метод 2:

            Мы применим log с обеих сторон 5 x = 3. Тогда мы получаем log 5 x = log 3. Используя свойство log a m = m log a в левой части уравнения, получаем x log 5 = log 3. Разделив обе части на log 5,

            x = (log 3) / (log 5)

            Важные примечания к экспоненциальным уравнениям:

            Вот несколько важных замечаний относительно экспоненциальных уравнений.

            • Чтобы решить экспоненциальные уравнения с одним и тем же основанием, просто приравняйте показатели степени.
            • Чтобы решить показательные уравнения с разными основаниями, примените логарифмирование к обеим частям.
            • Показательные уравнения с теми же основаниями также могут быть решены с использованием логарифмов.
            • Если экспоненциальное уравнение имеет 1 с любой стороны, то мы можем записать его как 1 = a 0 для любого ‘a’. Например, чтобы решить 5 х = 1, мы можем записать это как 5 х = 5 0 , тогда мы получим х = 0,
            • Чтобы решить экспоненциальное уравнение с помощью логарифмов, мы можем либо применить «log», либо применить «ln» к обеим сторонам.

            Статьи по теме:

            • Экспоненциальная форма
            • Правила экспоненты
            • Экспоненциальные функции
            • Калькулятор экспоненциальных уравнений

            Часто задаваемые вопросы об экспоненциальных уравнениях

            Что такое экспоненциальные уравнения?

            Экспоненциальное уравнение — это уравнение, которое имеет переменную в показателях степени. Например, 5 2x — 3 = 125, 3 7 — 2x = 91 и т. д. являются показательными уравнениями.

            Какие бывают типы экспоненциальных уравнений?

            Существует три типа экспоненциальных уравнений. Вот они,

            • Показательные уравнения с одинаковыми основаниями с обеих сторон.
            • Показательные уравнения с разными основаниями с обеих сторон, которые можно сделать одинаковыми.
            • Показательные уравнения с разными основаниями с обеих сторон, которые нельзя сделать одинаковыми.

            Как решать экспоненциальные уравнения?

            Для решения показательных уравнений с равными основаниями мы приравниваем показатели степени, тогда как для решения показательных уравнений с разными основаниями мы применяем логарифмы с обеих сторон.

            Как записать экспоненциальное уравнение в логарифмической форме?

            Запись показательного уравнения в логарифмической форме помогает нам решить его. Это можно сделать по формуле b х = а ⇔ log б а = х.

            Что такое свойство равенства экспоненциальных уравнений?

            Свойство равенства экспоненциальных уравнений говорит о том, что степени равны, если основания в обеих частях уравнения равны. т. е. а х = а у ⇔ х = у.

            Как решать экспоненциальные уравнения с одинаковыми основаниями?

            Если экспоненциальное уравнение имеет одинаковые основания с обеих сторон, просто приравняйте показатели степени и найдите переменную.

      Cos x 1 5: Решите уравнение cos(x)=-1,5 (косинус от (х) равно минус 1,5)

      alexxlab / / Разное
      36Risolvere per ?cos(x)=1/27Risolvere per xsin(x)=-1/28Преобразовать из градусов в радианы2259Risolvere per ?cos(x)=( квадратный корень из 2)/210Risolvere per xcos(x)=( квадратный корень из 3)/211Risolvere per xsin(x)=( квадратный корень из 3)/212Графикg(x)=3/4* корень пятой степени из x13Найти центр и радиусx^2+y^2=914Преобразовать из градусов в радианы120 град. 2+n-72)=1/(n+9)

      Mathway | Популярные задачи

      1Найти точное значениеsin(30)
      2Найти точное значениеsin(45)
      3Найти точное значениеsin(30 град. )
      4Найти точное значениеsin(60 град. )
      5Найти точное значениеtan(30 град. )
      6Найти точное значениеarcsin(-1)
      7Найти точное значениеsin(pi/6)
      8Найти точное значениеcos(pi/4)
      9Найти точное значениеsin(45 град. )
      10Найти точное значениеsin(pi/3)
      11Найти точное значениеarctan(-1)
      12Найти точное значениеcos(45 град. )
      13Найти точное значениеcos(30 град. )
      14Найти точное значениеtan(60)
      15Найти точное значениеcsc(45 град. )
      16Найти точное значениеtan(60 град. )
      17Найти точное значениеsec(30 град. )
      18Найти точное значениеcos(60 град. )
      19Найти точное значениеcos(150)
      20Найти точное значениеsin(60)
      21Найти точное значениеcos(pi/2)
      22Найти точное значениеtan(45 град. )
      23Найти точное значениеarctan(- квадратный корень из 3)
      24Найти точное значениеcsc(60 град. )
      25Найти точное значениеsec(45 град. )
      26Найти точное значениеcsc(30 град. )
      27Найти точное значениеsin(0)
      28Найти точное значениеsin(120)
      29Найти точное значениеcos(90)
      30Преобразовать из радианов в градусыpi/3
      31Найти точное значениеtan(30)
      32Преобразовать из градусов в радианы45
      33Найти точное значениеcos(45)
      34Упроститьsin(theta)^2+cos(theta)^2
      35Преобразовать из радианов в градусыpi/6
      36Найти точное значениеcot(30 град. )
      37Найти точное значениеarccos(-1)
      38Найти точное значениеarctan(0)
      39Найти точное значениеcot(60 град. )
      40Преобразовать из градусов в радианы30
      41Преобразовать из радианов в градусы(2pi)/3
      42Найти точное значениеsin((5pi)/3)
      43Найти точное значениеsin((3pi)/4)
      44Найти точное значениеtan(pi/2)
      45Найти точное значениеsin(300)
      46Найти точное значениеcos(30)
      47Найти точное значениеcos(60)
      48Найти точное значениеcos(0)
      49Найти точное значениеcos(135)
      50Найти точное значениеcos((5pi)/3)
      51Найти точное значениеcos(210)
      52Найти точное значениеsec(60 град. )
      53Найти точное значениеsin(300 град. )
      54Преобразовать из градусов в радианы135
      55Преобразовать из градусов в радианы150
      56Преобразовать из радианов в градусы(5pi)/6
      57Преобразовать из радианов в градусы(5pi)/3
      58Преобразовать из градусов в радианы89 град.
      59Преобразовать из градусов в радианы60
      60Найти точное значениеsin(135 град. )
      61Найти точное значениеsin(150)
      62Найти точное значениеsin(240 град. )
      63Найти точное значениеcot(45 град. )
      64Преобразовать из радианов в градусы(5pi)/4
      65Найти точное значениеsin(225)
      66Найти точное значениеsin(240)
      67Найти точное значениеcos(150 град. )
      68Найти точное значениеtan(45)
      69Вычислитьsin(30 град. )
      70Найти точное значениеsec(0)
      71Найти точное значениеcos((5pi)/6)
      72Найти точное значениеcsc(30)
      73Найти точное значениеarcsin(( квадратный корень из 2)/2)
      74Найти точное значениеtan((5pi)/3)
      75Найти точное значениеtan(0)
      76Вычислитьsin(60 град. )
      77Найти точное значениеarctan(-( квадратный корень из 3)/3)
      78Преобразовать из радианов в градусы(3pi)/4
      79Найти точное значениеsin((7pi)/4)
      80Найти точное значениеarcsin(-1/2)
      81Найти точное значениеsin((4pi)/3)
      82Найти точное значениеcsc(45)
      83Упроститьarctan( квадратный корень из 3)
      84Найти точное значениеsin(135)
      85Найти точное значениеsin(105)
      86Найти точное значениеsin(150 град. )
      87Найти точное значениеsin((2pi)/3)
      88Найти точное значениеtan((2pi)/3)
      89Преобразовать из радианов в градусыpi/4
      90Найти точное значениеsin(pi/2)
      91Найти точное значениеsec(45)
      92Найти точное значениеcos((5pi)/4)
      93Найти точное значениеcos((7pi)/6)
      94Найти точное значениеarcsin(0)
      95Найти точное значениеsin(120 град. )
      96Найти точное значениеtan((7pi)/6)
      97Найти точное значениеcos(270)
      98Найти точное значениеsin((7pi)/6)
      99Найти точное значениеarcsin(-( квадратный корень из 2)/2)
      100Преобразовать из градусов в радианы88 град.

      Решение неоднородных уравнений первой степени относительно sin x и cos x

      org/BreadcrumbList»> Разделы: Математика

      При изучении темы «Решение тригонометрических уравнений» в курсе алгебры и начал анализа в 10 классе достаточное внимание уделяется рассмотрению примеров решений уравнений, сводящихся к квадратным и решению однородных уравнений первой и второй степени относительно sin x и cos x. При этом практически не рассматриваются примеры решения уравнений первой степени, являющихся неоднородными относительно функций sin x и cos x.

      Изучая в школьном курсе 10 класса тему «Преобразование тригонометрических выражений», целесообразно ввести формулу a sinx + b cosx = sin(x+), где tg =  . В дальнейшем она будет использоваться при решении неоднородных линейных уравнений. Формулы универсальной подстановки и формулы половинного аргумента выводятся в теме «Преобразование тригонометрических выражений» при выполнении заданий на упрощение тригонометрических выражений.

      Цели:

      • ввести понятие неоднородного тригонометрического уравнения I степени;
      • ознакомить с алгоритмами решения неоднородных тригонометрических уравнений I степени;
      • проверить прочность усвоения ранее изученных формул тригонометрии.

      Тип урока: комбинированный.

      Форма проведения: индивидуальная и фронтальная работа с учащимися.

      I. Организационный момент

      Вступительное слово учителя: Изучение темы «Решение тригонометрических уравнений» кроме рассмотренного нами ранее вопроса о способах решения однородных тригонометрических уравнений I степени предполагает также рассмотрение способов решения неоднородных тригонометрических уравнений. Но прежде, чем мы перейдем к изучению нового материала, необходимо вспомнить применение формул тригонометрии при решении уравнений и неравенств.

      II. Актуализация опорных знаний, умений

      Математический диктант (10-12 минут).

      I вариант II вариант
      1. cos3x =
      2. 1 — cos 2x = sin x
      3. tg x — ctg x = 1,5
      4. sin (– 2x)  —
      5. sin 3x ·cos 3x – cos 3x ·sin x  0
      1. sin 2x =
      2. 1 + cos 2x = cos x
      3. ctg x – tg x = 1,5
      4. cos (– 3x) ≤
      5. cos 2x · cos x – sin 2x · sin x ≤ 0
      Ответы варианта I Ответы варианта II
      1.   + ;  + , n
      2. n; (-1) + n, n
      3. arctg2 + n; arctg(-) + n, n
      4. —  + n ≤ x ≤  + n, n
      5. n ≤ x ≤  + n, n

      1. (-1) + ; (-1)  + , n

      2. + n;  + 2n, n

      3. arctg(-2) + n; arctg + n, n

      4.  +  ≤ x ≤  + , n

      5.  +  ≤ x ≤  + , n

      По окончанию самостоятельной работы учащиеся меняются тетрадями и проводят взаимопроверку. Правильные ответы заранее записаны учителем на закрытой доске.

      III. Формирование новых знаний и понятий

      Слова учителя: Теперь мы переходим к новой теме нашего занятия – решению неоднородных тригонометрических уравнений I степени.

      Дается определение: Уравнение вида a sin x + b cos x = c, где а, b, с не равны 0, называется неоднородным тригонометрическим уравнением I степени.

      Данное уравнение может быть решено тремя способами.

      Первый способ – универсальная подстановка

      sin x =

      cos x =

      Второй способ – введение дополнительного угла

      a sinx + b cosx = sin(x+), где  = arctg  если a + b  c, то уравнение имеет корни

      Третий способ – переход к функциям половинного аргумента

      sin x = 2 sin cos

      cos x = cos — sin

      IV.

      Применение знаний, навыков, понятий

      Задания на отработку применения разобранных способов решения неоднородных тригонометрических уравнений. Решаются у доски учениками с помощью учителя:

      1-й ученик

      1) sin 2x + cos 2x = sin 3x (через введение дополнительного угла)

      Решение

       sin (2x + ) =  sin 3x
      sin (2x + ) = sin 3x
      sin (2x + ) — sin 3x = 0
      2 sin  cos  = 0
      sin () = 0
      sin ( — ) = 0
      x =  + 2n, где n       		 или cos () = 0
      cos ( + ) = 0
      x =  + , где n

      2-й ученик

      2) 3 sin x – 4 cos x = 5 (применение универсальной подстановки)

      Решение

      3  — 4  = 5
      6 tg  — 4 (1 — tg) = 5 (1 + tg)
      (tg — 3) = 0
      x = 2 arctg3 + 2n, где n

      3-й ученик

      3) cos x – sin x = 1 (через переход к функциям половинного аргумента)

      Решение

      cos — sin — 2 sincos = sin + cos
      2 sin(sin + cos) = 0
      sin = 0
      x = 2n      		 или sin + cos = 0 – однородное первой степени
      tg = -1
      x = — + 2n

      Для самостоятельной работы учащихся (перед началом указываются способы решения):

      1) sin x + cos x = (через введение дополнительного угла)

      Решение

      sin (x + ) =
      sin (x + ) = 1
      x =  + 2n, где n

      2) 3 sin x + 5 cos x= 6 (универсальная подстановка)

      Решение

      3 + 5 = 6
      6 tg +5 — 5 tg = 6 + 6 tg
      11 tg — 6 tg + 1= 0
      решений нет, так как D<0

      3) sin x + cos x = 1 (формулы половинного аргумента)

      2 sin cos  + cos — sin = cos + sin
      2 sin cos  — 2 sin = 0
      2 sin( cos  — sin) = 0
      sin  = 0
      x = 2n, где n       		 или cos  — sin = 0
      tg = 1
      x =  + 2n, где n

      V.

      Итог урока

      Подвести итог урока. Сообщить учащимся оценки, отметить наиболее активных.

      VI. Домашняя работа

      Домашняя контрольная работа по учебнику Колмогорова, стр. 285, № 152- 154 (задания а и б), №162 (задания а и в).

      Синус и косинус равны не табличному значению. Как решить уравнение? Часть 2

      Синус равен не стандартному значению

      В прошлой статье мы разобрали как решать простейшие тригонометрические уравнения со стандартными значениями, т.е. вот эти:


      Но бывает так, что нужно решить уравнение, в котором синус равен не табличному значению. Например, как решить уравнение \(\sin⁡x= \frac{1}{3}\)? Давайте обо всем по порядку.

      Сначала действуем, как и при решении стандартных уравнений:
      1. Чертим оси и тригонометрический круг
      2. На оси синусов отмечаем нужное значение
      3. Проводим к оси перпендикуляр


      А что дальше? Какие значения будут получаться на круге? Не \(\frac{π}{6}\), не \(\frac {π}{4}\), и даже не \(\frac{π}{7}\) — вообще никакие привычные числа не подходят. Однако при этом очевидно, что значения эти есть. Но как их записать? Вот тут-то на помощь и приходит арксинус! Значение правой точки равно \(\arcsin⁡\frac{1}{3}\). Почему? Да потому что синус равен \(\frac{1}{3}\) .


      Ок, значение правой точки найдено, как найти значение левой? Давайте подумаем. Значение дуги от нуля до правой точки равно \(\arcsin⁡\frac{1}{3}\).


      Но дуга от \(π\) до левой точки имеет такую же длину:


      Значит, если мы пройдем от \(π\) против часовой стрелки на величину \(\arcsin⁡\frac{1}{3}\) мы попадем в левую точку. Иными словами, значение в левой точке равно \(π-\arcsin⁡\frac{1}{3}\).


      Теперь мы можем записать все корни уравнения: \( \left[ \begin{gathered} x_1=\arcsin⁡\frac{1}{3}+2πn\\ x_2=π-\arcsin⁡\frac{1}{3}+2πn,  \,    n∈Z\end{gathered}\right.\). Не понимаешь откуда появилось «\(2πn\)» и «\(n∈Z\)» ? Смотри это и это видео!

      Готово.

      Без арксинусов решить уравнение \(\sin⁡x=\frac{1}{3}\) не получилось бы, потому что мы не смогли бы записать итоговый ответ. Аналогично и с уравнением \(\sin⁡x=0,125\), \(\sin⁡x=-\frac{1}{9}\), \(\sin⁡x=\frac{1}{\sqrt{3}}\) и многими другими. Фактически без арксинуса мы можем решать только 9 простейших, базовых, уравнений с синусом:


      С арксинусом – бесконечное количество.

      Алгоритм решения простейших уравнений с синусом

      Шаг 1. Построить окружность и оси синусов и косинусов.

      Шаг 2. Отметить на оси синусов значение, которому синус должен быть равен.

      Шаг 3. Провести перпендикуляр и отметить точки пересечения перпендикуляра и круга. Если пересечений нет, то уравнение не имеет решений.

      Шаг 4. Найти по одному значению каждой из полученных точек на круге. Если синус равен не стандартному числу, то правую точку на круге можно отметить, как \(\arcsin⁡a\), а левую как \(π-\arcsin⁡a\).

      Шаг 5. Записать все значения каждой точки используя формулу \(x=t_0+2πn\), \(n∈Z\), где \(t_0\) – как раз те значения точек, которые вы нашли в шаге 4.


      Пример: \(\sin⁡x=-\frac{\sqrt{2}}{4}\)


      Или если воспользоваться свойством арксинуса \(\arcsin⁡(-a)=-\arcsin⁡a\):


      Ответ: \( \left[ \begin{gathered} x=π+\arcsin⁡\frac{\sqrt{2}}{4}+2πn\\ x=-\arcsin⁡\frac{\sqrt{2}}{4}+2πn,  \,    n∈Z\end{gathered}\right.\)

      Как делать не надо:

      \(\sin⁡x=\frac{1}{2}\)

      Ответ: \( \left[ \begin{gathered} x=\arcsin⁡\frac{1}{2}+2πn\\ x=π-\arcsin⁡\frac{1}{2}+2πn,  \,    n∈Z\end{gathered}\right. \)

      Это стандартное уравнение — его можно решить с помощью круга, либо просто вычислить \(\arcsin⁡\frac{1}{2}= \frac{π}{6}\). В любом случае корректным ответом здесь будет:

      \( \left[ \begin{gathered} x=⁡\frac{π}{6}+2πn\\ x=\frac{5π}{6}+2πn,  \,    \end{gathered}\right.\)   \(n∈Z\)

      Запомните! В математике принято вычислять ответы до конца, поэтому если арксинус берется для стандартной точки и может быть посчитан – его надо вычислить. Потому что ответ с \(\arcsin⁡\frac{1}{2}\) и тому подобным будет выглядеть столь же странно, как ответ \(x=\frac{6}{3}\) в линейном уравнении \(3x=6\).

      Больше примеров использования алгоритма читай в этой статье: простейшие уравнения с синусом и косинусом.

      Косинус равен не стандартному значению

      Предположим, надо решить уравнение \(\cos⁡x=\frac{1}{3}\). Как это сделать?


      Тут логика такая же, как и в уравнении с синусом: косинус одной трети равняться может, следовательно, и значение должно быть таким, при котором косинус будет равен \(\frac{1}{3}\). Очевидное решение — использовать арккосинус.



      Несложно заметить, что дуга от нуля до нижней точки имеет такую же длину, как и от нуля до верхней, но только она откладывается в отрицательном направлении (по часовой стрелке). Поэтому одно из значений второй точки: \(-\arccos⁡\frac{1}{3}\)


      И теперь можно записать общий ответ: \(x=±\arccos⁡\frac{1}{3}+2πn\),     \(n∈Z\).

      Алгоритм решения простейших уравнений с косинусом

      Шаг 1. Построить окружность и оси синусов и косинусов.

      Шаг 2. Отметить на оси косинусов значение, которому косинус должен быть равен.

      Шаг 3. Провести перпендикуляр и отметить точки пересечения перпендикуляра и круга. Если пересечений нет, то уравнение не имеет решений.

      Шаг 4. Найти по одному значению каждой из полученных точек на круге. Если косинус равен не стандартному числу, то верхнюю точку на круге можно отметить, как \(\arccos⁡a\), а нижнюю как \(-\arccos⁡a\).

      Шаг 5. Записать все значения каждой точки используя формулу \(x=t_0+2πn\),   \(n∈Z\), где \(t_0\) – как раз те значения точек, которые вы нашли в шаге 4.


      Пример: \(\cos⁡x=-\frac{8}{7}\).

      Решение:


      Важно быть начеку, а не штампованно везде писать аркфункции. Пересечения с окружность нет, значит и решений нет.
      Ответ: нет решений.

      Пример: \(\cos⁡x=-\frac{3}{4}\).


      Или если применить формулу \(\arccos⁡(-a)=π-\arccos⁡a\)


      Ответ: \(π±\arccos \frac{3}{4}+2πn\), \(n∈Z\).

      3 6 Решить для ? cos(x)=1/2 7 Найти x sin(x)=-1/2 8 Преобразование градусов в радианы 225 9 Решить для ? cos(x)=(квадратный корень из 2)/2 10 Найти x cos(x)=(квадратный корень из 3)/2 11 Найти x sin(x)=(квадратный корень из 3)/2 92=9 14 Преобразование градусов в радианы 120 градусов 15 Преобразование градусов в радианы 180 16 Найти точное значение желтовато-коричневый(195) 92-4 38 Найти точное значение грех(255) 39 Оценить лог база 27 из 36 40 Преобразовать из радианов в градусы 2 шт. 92-3sin(x)+1=0 43 Найти x tan(x)+ квадратный корень из 3=0 44 Найти x sin(2x)+cos(x)=0 45 Упростить (1-cos(x))(1+cos(x)) 92=25 59 График f(x)=- натуральный логарифм x-1+3 60 Найдите значение с помощью единичного круга угловой синус(-1/2) 61 Найти домен квадратный корень из 36-4x^2 92=0 66 Найти x cos(2x)=(квадратный корень из 2)/2 67 График у=3 68 График f(x)=- логарифмическая база 3 x-1+3 92 71 Найти x квадратный корень из x+4+ квадратный корень из x-1=5 72 Решить для ? cos(2x)=-1/2 73 Найти x логарифмическая база x из 16=4 9х 75 Упростить (cos(x))/(1-sin(x))+(1-sin(x))/(cos(x)) 76 Упростить сек(х)sin(х) 77 Упростить кубический корень из 24 кубический корень из 18 92=0 96 Найти x 3x+2=(5x-11)/(8г) 97 Решить для ? sin(2x)=-1/2 98 Найти x (2x-1)/(x+2)=4/5 92+n-72)=1/(n+9)

      Мэтуэй | Популярные задачи

      92
      1 Найти точное значение грех(30)
      2 Найти точное значение грех(45)
      3 Найти точное значение грех(30 градусов)
      4 Найти точное значение грех(60 градусов)
      5 Найти точное значение загар (30 градусов)
      6 Найти точное значение угловой синус (-1)
      7 Найти точное значение грех(пи/6)
      8 Найти точное значение cos(pi/4)
      9 Найти точное значение грех(45 градусов)
      10 Найти точное значение грех(пи/3)
      11 Найти точное значение арктан(-1)
      12 Найти точное значение cos(45 градусов)
      13 Найти точное значение cos(30 градусов)
      14 Найти точное значение желтовато-коричневый(60)
      15 Найти точное значение csc(45 градусов)
      16 Найти точное значение загар (60 градусов)
      17 Найти точное значение сек(30 градусов)
      18 Найти точное значение cos(60 градусов)
      19 Найти точное значение соз(150)
      20 Найти точное значение грех(60)
      21 Найти точное значение cos(pi/2)
      22 Найти точное значение загар (45 градусов)
      23 Найти точное значение arctan(- квадратный корень из 3)
      24 Найти точное значение csc(60 градусов)
      25 Найти точное значение сек(45 градусов)
      26 Найти точное значение csc(30 градусов)
      27 Найти точное значение грех(0)
      28 Найти точное значение грех(120)
      29 Найти точное значение соз(90)
      30 Преобразовать из радианов в градусы пи/3
      31 Найти точное значение желтовато-коричневый(30)
      35 Преобразовать из радианов в градусы пи/6
      36 Найти точное значение детская кроватка(30 градусов)
      37 Найти точное значение арккос(-1)
      38 Найти точное значение арктан(0)
      39 Найти точное значение детская кроватка(60 градусов)
      40 Преобразование градусов в радианы 30
      41 Преобразовать из радианов в градусы (2 шт. )/3
      42 Найти точное значение sin((5pi)/3)
      43 Найти точное значение sin((3pi)/4)
      44 Найти точное значение тан(пи/2)
      45 Найти точное значение грех(300)
      46 Найти точное значение соз(30)
      47 Найти точное значение соз(60)
      48 Найти точное значение соз(0)
      49 Найти точное значение соз(135)
      50 Найти точное значение cos((5pi)/3)
      51 Найти точное значение cos(210)
      52 Найти точное значение сек(60 градусов)
      53 Найти точное значение грех(300 градусов)
      54 Преобразование градусов в радианы 135
      55 Преобразование градусов в радианы 150
      56 Преобразовать из радианов в градусы (5 дюймов)/6
      57 Преобразовать из радианов в градусы (5 дюймов)/3
      58 Преобразование градусов в радианы 89 градусов
      59 Преобразование градусов в радианы 60
      60 Найти точное значение грех(135 градусов)
      61 Найти точное значение грех(150)
      62 Найти точное значение грех(240 градусов)
      63 Найти точное значение детская кроватка(45 градусов)
      64 Преобразовать из радианов в градусы (5 дюймов)/4
      65 Найти точное значение грех(225)
      66 Найти точное значение грех(240)
      67 Найти точное значение cos(150 градусов)
      68 Найти точное значение желтовато-коричневый(45)
      69 Оценить грех(30 градусов)
      70 Найти точное значение сек(0)
      71 Найти точное значение cos((5pi)/6)
      72 Найти точное значение КСК(30)
      73 Найти точное значение arcsin(( квадратный корень из 2)/2)
      74 Найти точное значение загар((5pi)/3)
      75 Найти точное значение желтовато-коричневый(0)
      76 Оценить грех(60 градусов)
      77 Найти точное значение arctan(-( квадратный корень из 3)/3)
      78 Преобразовать из радианов в градусы (3 пи)/4 
      79 Найти точное значение sin((7pi)/4)
      80 Найти точное значение угловой синус(-1/2)
      81 Найти точное значение sin((4pi)/3)
      82 Найти точное значение КСК(45)
      83 Упростить арктан( квадратный корень из 3)
      84 Найти точное значение грех(135)
      85 Найти точное значение грех(105)
      86 Найти точное значение грех(150 градусов)
      87 Найти точное значение sin((2pi)/3)
      88 Найти точное значение загар((2pi)/3)
      89 Преобразовать из радианов в градусы пи/4
      90 Найти точное значение грех(пи/2)
      91 Найти точное значение сек(45)
      92 Найти точное значение cos((5pi)/4)
      93 Найти точное значение cos((7pi)/6)
      94 Найти точное значение угловой синус(0)
      95 Найти точное значение грех(120 градусов)
      96 Найти точное значение желтовато-коричневый ((7pi)/6)
      97 Найти точное значение соз(270)
      98 Найти точное значение sin((7pi)/6)
      99 Найти точное значение arcsin(-( квадратный корень из 2)/2)
      100 Преобразование градусов в радианы 88 градусов

      Калькулятор — cos(-1.

      5) — Solumaths

      Cos, расчет онлайн

      Резюме:

      Тригонометрическая функция cos вычисляет cos угла в радианах, градусов или градианов.

      cos online

      Описание:

      Калькулятор позволяет использовать большинство из тригонометрических функций , есть возможность вычислить косинус , синус и касательная угла через одноименные функции.

      Тригонометрическая функция косинус отметил косинус , позволяет вычислить косинус угла онлайн , можно использовать разные угловые единицы: градусы, грады и радианы, которые по умолчанию являются угловыми единицами.

      1. Расчет косинуса

        2. Вычисление косинуса угла в радианах

        Калькулятор косинуса позволяет через функцию cos вычислить г. онлайн косинус угла в радианах, вы должны сначала выберите нужную единицу, нажав на кнопку параметров расчетного модуля. После этого можно приступать к расчетам.

        Чтобы вычислить косинус онлайн от `pi/6`, введите cos(`pi/6`), после вычисления результат `sqrt(3)/2` возвращается.

        Обратите внимание, что функция косинуса способна распознавать некоторые специальные углы и делать расчеты со специальными связанными значениями в точной форме.

        г.

        Вычислить косинус угла в градусах

        Чтобы вычислить косинус угла в градусах, необходимо сначала выбрать нужную единицу измерения нажав на кнопку модуля расчета параметров. После этого можно приступать к вычислениям.

        Чтобы вычислить косинус числа 90, введите cos(90). возвращает 0.

        Вычисление косинуса угла в градианах

        Чтобы вычислить косинус угла в градианах, необходимо сначала выбрать нужную единицу измерения нажав на кнопку модуля расчета параметров. После этого можно приступать к вычислениям.

        г.

        Чтобы вычислить косинус 50, введите cos(50), после вычисления возвращается результат `sqrt(2)/2`.

        Обратите внимание, что функция косинуса способна распознавать некоторые специальные углы и выполнять исчисление со специальными ассоциированными точными значениями.

      2. Специальные значения косинуса

        3. Косинус допускает некоторые специальные значения, которые калькулятор может определить в точных формах. Вот список специальные значения косинуса :

        (90`006 cos `)
        cos(`2*pi`) `1`
        cos(`pi`) `-1`
        cos(`pi/2`) 0 0 0 04 90 90 90
        cos(`pi/4`) `sqrt(2)/2`
        cos(`pi/3`) `1/2`
        `sqrt(3)/2`
        cos(`2*pi/3`) `-1/2`
        cos(`3*pi/4`) `-sqrt(2)/2`
        cos(`5*pi/6`) `-sqrt(3)/2`
        cos(`0`) `1`
        cos(*s) pi`) `1`
        cos(`-pi`) `-1`
        cos(`pi/2`) `09` 90`90`105 90 pi/4`) `sqrt(2)/2`
        cos(`-pi/3`) `1/2`
        cos(`-pi/6`) `sqrt(3)/2`
        cos(`-2*pi/3`) `-1/2`
        cos(`-3*pi/4`) `-sqrt(2)/2`
        cos(`-5*pi/6`) `-sqrt(3)/2`

      3. Основные свойства

        4. `AA x в RR, k в ZZ`,

      • `cos(-x)= cos(x)`
      • `cos(x+2*k*pi)=cos(x)`
      • `cos(pi-x)=-cos(x) `
      • `cos(pi+x)=-cos(x)`
      • `cos(pi/2-x)=sin(x)`
      • `cos(pi/2+x)=-sin(x) )`

    • Производная косинуса

      • Производная косинуса равна -sin(x).

    • Первообразная косинуса

      • Первообразная косинуса равна sin(x).

    • Свойства функции косинуса

      • Функция косинуса является четной функцией для каждого действительного x, `cos(-x)=cos(x)`. Следствием для кривой, представляющей функцию косинуса, является то, что она допускает ось ординат как ось симметрии.

    • Уравнение с косинусом

      • Калькулятор имеет решатель, который позволяет решать уравнение с косинусом вида cos(x)=a . Расчеты для получения результата детализированы, поэтому можно будет решать уравнения типа `cos(x)=1/2` или же `2*cos(x)=sqrt(2)` с этапами расчета.

      Синтаксис:

      cos(x), где x — мера угла в градусах, радианах или градах.

      Примеры:

      cos(`0`), возвращает 1

      Производная косинус :

      Чтобы дифференцировать функцию косинуса онлайн, можно использовать калькулятор производной, который позволяет вычислить производную функции косинуса

      Первообразная косинуса :

      Калькулятор первообразной позволяет вычислить первообразную функции косинуса.

      Первообразная cos(x) есть первопроизводная(`cos(x)`)=`sin(x)`

      Предельный косинус :

      Калькулятор пределов позволяет вычислять пределы функции косинуса.

      предел cos(x) is limit(`cos(x)`)

      Обратная функция косинуса :

      обратная функция косинуса представляет собой функцию арккосинуса, отмеченную как arccos.

      Графический косинус:

      Графический калькулятор может строить косинусоидальную функцию в заданном интервале.

      Свойство функции косинуса:

      Функция косинуса является четной функцией.

      Расчет онлайн с косинусом

      См. также

      Список связанных калькуляторов:

      • г. Арккосинус: арккос. Функция arccos позволяет вычислять арккосинус числа. Функция arccos является обратной функцией функции косинуса.
      • Арксинус : арксинус. Функция arcsin позволяет вычислить арксинус числа. Функция arcsin является обратной функцией функции синуса.
      • Арктангенс: арктангенс. Функция арктангенса позволяет вычислить арктангенс числа. Функция арктангенса является обратной функцией функции тангенса.
      • Тригонометрический калькулятор: simple_trig. Калькулятор, который использует тригонометрическую формулу для упрощения тригонометрического выражения.
      • Косинус: cos. Кос-тригонометрическая функция вычисляет косинус угла в радианах, градусов или градианов.
      • Косеканс: косеканс Тригонометрическая функция sec позволяет вычислить секанс угла, выраженного в радианах, градусах или градусах.
      • Котангенс : котанг. Тригонометрическая функция котана для вычисления котана угла в радианах, градусов или градианов.
      • Тригонометрическое расширение: expand_trigo. Калькулятор позволяет получить тригонометрическое разложение выражения.
      • Тригонометрическая линеаризация : linearization_trigo. Калькулятор, позволяющий линеаризовать тригонометрическое выражение.
      • Упрощение калькулятора: упрощение. Калькулятор, который может упростить алгебраическое выражение онлайн.
      • Секанс : сек. Тригонометрическая функция sec позволяет вычислить секанс угла, выраженного в радианах, градусах или градусах.
      • Синус : син. Тригонометрическая функция sin для вычисления греха угла в радианах, градусов или градианов.
      • Касательная: рыжевато-коричневая. Тригонометрическая функция тангенса для вычисления тангенса угла в радианах, градусов или градианов.

      Тригонометрические функции | Реальные функции

       

      numpy.sum — NumPy v1.23 Manual

      numpy.sum( a , axis=None , dtype=None , out=None , keepdims=<нет значения> , initial=<нет значения> , где=<нет значения> )[источник]

      Сумма элементов массива по заданной оси.

      Параметры
      a array_like

      Элементы для суммирования.

      ось Нет или целое или кортеж целых чисел, необязательный

      Ось или оси, вдоль которых выполняется суммирование. По умолчанию, axis=None, суммирует все элементы входного массива. Если ось отрицательная, она считает от последней до первой оси.

      г.

      Новое в версии 1.7.0.

      Если ось представляет собой набор целых чисел, суммирование выполняется по всем осям указывается в кортеже вместо одной оси или всех осей как до.

      dtype dtype, необязательный

      Тип возвращаемого массива и аккумулятора, в котором элементы суммируются. По умолчанию используется dtype a , если только a имеет целочисленный dtype с меньшей точностью, чем платформа по умолчанию целое число. В таком случае, если a подписывается, затем целое число платформы используется, в то время как если a без знака, то беззнаковое целое число используется та же точность, что и для целого числа платформы.

      out ndarray, необязательный

      Альтернативный выходной массив, в который следует поместить результат. Он должен иметь той же формы, что и ожидаемый результат, но тип вывода значения будут преобразованы в случае необходимости.

      keepdims bool, опционально

      Если установлено значение True, уменьшаемые оси остаются в результате как размеры с размером один. С этой опцией результат будет корректно транслироваться относительно входного массива.

      г.

      Если передано значение по умолчанию, то keepdims не будет прошел через метод сумма подклассов ndarray , однако любое значение, отличное от значения по умолчанию, будет. Если метод подкласса не реализует keepdims любой исключения будут подняты.

      начальный скалярный, необязательный

      Начальное значение для суммы. Подробнее см. уменьшить .

      Новое в версии 1.15.0.

      где array_like of bool, необязательный

      Элементы для включения в сумму. Подробнее см. уменьшить .

      Новое в версии 1.17.0.

      Возвращает
      sum_along_axis ndarray

      Массив той же формы, что и a , с указанным ось снята. Если a является массивом 0-d, или если ось имеет значение None, скаляр возвращается. Если указан выходной массив, ссылка на из возвращается.

      См. также

      ndarray.sum

      Эквивалентный метод.

      add.reduce

      Эквивалентная функциональность add .

      cumsum

      Накопленная сумма элементов массива.

      trapz

      Интегрирование значений массива с помощью составного правила трапеций.

      г.
      среднее , среднее

      Примечания

      Арифметика является модульной при использовании целочисленных типов, и ошибка не возникает. поднимается при переполнении.

      Сумма пустого массива является нейтральным элементом 0:

       >>> np.sum([])
0,0

      Для чисел с плавающей запятой числовая точность суммы (и np.add.reduce ) обычно ограничивается прямым добавлением каждого числа индивидуально к результату, вызывая ошибки округления на каждом шаге. Однако часто numpy будет использовать численно лучший подход (частичный попарное суммирование), что приводит к повышению точности во многих случаях использования. Эта повышенная точность всегда обеспечивается, когда нет ось дана. Когда задается ось , это будет зависеть от того, какая ось суммируется. Технически, чтобы обеспечить максимально возможную скорость, повышенная точность используется только при суммировании по быстрой оси в памяти. Обратите внимание, что точная точность может варьироваться в зависимости от других параметров. В отличие от NumPy, функция Python math.fsum использует более медленную, но более точный подход к суммированию. Особенно при суммировании большого количества чисел с плавающей запятой более низкой точности. числа, например float32 числовые ошибки могут стать значительными. В таких случаях рекомендуется использовать dtype=»float64″ для использования более высокого точность на выходе.

      Примеры

       >>> np.sum([0.5, 1.5])
2.0
>>> np.sum([0,5, 0,7, 0,2, 1,5], dtype=np.int32)
1
>>> np.sum([[0, 1], [0, 5]])
6
>>> np.sum([[0, 1], [0, 5]], ось=0)
массив ([0, 6])
>>> np.sum([[0, 1], [0, 5]], ось = 1)
массив([1, 5])
>>> np.sum([[0, 1], [np.nan, 5]], где=[Ложь, Истина], ось=1)
массив([1., 5.])

      Если аккумулятор слишком мал, происходит переполнение:

       >>> np.ones(128, dtype=np.int8).sum(dtype=np.int8)
-128

      Вы также можете начать суммирование со значения, отличного от нуля:

       >>> np. sum([10], начальный=5)
15

      Важные вопросы для 10 класса по математике Глава 8 Введение в тригонометрию

      Введение в тригонометрию 10 класс Важные вопросы Очень короткий ответ (1 балл)

      Вопрос 1.
      Если tan θ + cot θ = 5, найдите значение tan2θ + раскладушка θ. (2012)
      Решение:
      tan θ + cot θ = 5 … [Дано
      tan 2 θ + cot 2 θ + 2 tan θ cot θ = 25 … [Квадрат обеих сторон θ + 2 = 25
      ∴ tan 2 θ + cot 2 θ = 23

      Вопрос 2.
      Если sec 2A = cosec (A – 27°), где 2A — острый угол, найдите величину ∠A . (2012, 2017D)
      Решение:
      с 2A = cosec (A – 27°)
      cosec(90° – 2A) = cosec(A – 27°) …[∵ sec θ = cosec (90° – θ)
      90 ° – 2А = А – 27° 9{\circ}}{3}\) = 39°

      Вопрос 3.
      Если тангенс α = \(\sqrt{3}\) и тангенс β = \(\frac{1}{\sqrt{3}} \),0 < α, β < 90°, найти значение ctg (α + β). (2012)
      Решение:
      тангенс α = \(\sqrt{3}\) = тангенс 60° … (i)
      тангенс β = \(\frac{1}{\sqrt{3}}\) = тангенс 30 ° …(ii)
      Решение (i) и (ii), α = 60° и β = 30°
      ∴ cot (α + β) = cot (60° + 30°) = cot 90° = 0

      Вопрос 4. {2} \theta+2 \cos \theta}{3 \cos \theta+2}\). (2015)
      Решение:
      \(\sqrt{3}\) sin θ = cos θ … [Дано

      Вопрос 10.
      Вычислить: sin 2 19° + sin 7 71°. (2015)
      Решение:
      sin 2 19° + sin 2 71°
      = sin 2 19° + sin 2 (90° – 19°)…[∵ sin(90° – θ) = cos θ
      = sin 2 19° + cos 2 19° = 1 …[∵ sin 2 θ + cos 2 θ = 1

      Вопрос 11.
      Что происходит при увеличении значения cos от 0° до 9{2}/латекс] = 1 + [латекс]\)
      = \(\frac{144+25}{144}=\frac{169}{144}\)
      cosec B = \(\frac{13} {12}\) ∴ sin B = \(\frac{12}{13}\)
      2-й метод:

      tan B = \(\frac{12}{5}\)
      tan B = \(\frac {AC}{BC}\)
      Пусть AC = 12k, BC = 5k
      In rt. ∆ACB,
      AB 2 = AC 2 + BC 2 …[Pythagoras theorem
      AB 2 = (12k) 2 + (5k) 2
      AB 2 = 144k 2 + 25к 2 2 = 169к 2
      AB = 13k
      ∴ sin B = \(\frac{\mathrm{AC}}{\mathrm{AB}}=\frac{12 \mathrm{k}}{13 \mathrm{k}}= \frac{12}{13}\)

      Вопрос 14.
      Если ∆ABC направлена ​​под прямым углом к ​​B, каково значение sin (A + C). (2015)
      Решение:

      ∠B = 90° …[Дано
      ∠A + ∠B + ∠C = 180° …[Свойство суммы углов a ∆
      ∠A + ∠C + 90° = 180°
      ∠ A + ∠C = 90°
      ∴ sin (A + C) = sin 90° = 1 …(принимая sin с обеих сторон

      Введение в тригонометрию Класс 10 Важные вопросы Краткий ответ-I (2 балла)

      Вопрос 15.
      Оценка: tan 15° . загар 25°, загар 60°. загар 65°. тангенс 75° – тангенс 30°. (2013)
      Решение:
      tan 15°. загар 25°, загар 60°. загар 65°. tan 75° – tan 30°
      = tan(90° – 75°) tan(90° – 65°). \(\sqrt{3}\) . загар 65°. tan 75° – \(\frac{1}{\sqrt{3}}\)

      Вопрос 16.
      Выразите cot 75° + cosec 75° через тригонометрические соотношения углов от 0° до 30°. (2013)
      Решение:
      cot 75° + cosec 75°
      = cot(90° – 15°) + cosec(90° – 15°)
      = tan 15° + sec 15° …[cot(90°-A) = tan A
      cosec(90° – A) = sec A

      Вопрос 17.
      Если cos (A + B) = 0 и sin ( A – B) = 3, затем найдите значения A и B, где A и B — острые углы. (2012)
      Решение:

      Подставляя значение B в (i), получаем
      ⇒ A = 30° + 30° = 60°
      ∴ A = 60°, B = 30°

      Вопрос 18.
      Если A, B и C — внутренние углы ∆ABC, покажите, что sin \(\left(\frac{A+B}{2}\right)\) = cos\(\left(\frac{c}{ 2}\справа)\). (2012)
      Решение:
      В ∆ABC, ∠A + ∠B + ∠C = 180° … (Свойство суммы углов ∆
      ∠A + ∠B = 180° – ∠C

      Вопрос 19.
      Если x = p sec (2014)
      Решение: 2 – y 2
      = (p сек θ + q тангенс θ) 2 – (p тангенс θ + q сек θ) 2
      = p 2 сек θ 6 q θ + 2 PQ Sec 2 TAN 2 -(P 2 TAN 2 θ + Q 2 SEC 2 θ + 2PQ Sec θ Tan θ)
      = P θ + 2PQ Sec θ Tan θ)
      = P θ + 2PQ Sec θ θ)
      = P θ + 2pq Sec θ)
      = P θ + 2pq θ)
      = P θ + 2pq θ)
      = P θ + 2pq Sec θ)
      = P θ + 2pq θ) 2 θ + 2pq θ) 2 Tan 2 θ + 2pq Sec θ tan θ — p 2 Tan 2 θ — Q 2 Sec θ — 2pq Sec θ tan θ
      = P 2 (SEC 2
      = P 2 (SEC 2
      = P 2 (SEC 2
      rail 2       θ) – q 2 (сек? 2 θ – тангенс 2 θ) =
      = p 2 – q 2 …[сек 2 9{2} А}\). (2014)
      Решение:

      Вопрос 22.
      Если x = a cos θ – b sin θ и y = a sin θ + b cos θ, то докажите, что a 2 + b 2 = x 2 + у 2 . (2015)
      Решение:
      R.H.S. = x 2 + y 2
      = (a cos θ – b sin θ) 2 + (a sin θ + b cos θ) 2
      = a 2 + b 8 2 sin 2 θ – 2ab cos θ sin θ + a 2 sin 2 θ + B 2 COS 2 θ + 2AB SIN θ COS θ
      = A 2 (COS 2 θ + SIN 2 θ) + B       2 (SIN 2 θ) + B 2 (SIN 2 θ) + B 2 (SIN 2 θ) + B 2 (SIN 2 . + cos 2 θ)
      = a 2 + b 2 = L.H.S. …[∵ cos 2 θ + sin 2 θ = 1

      Введение в тригонометрию Класс 10 Важные вопросы Краткий ответ – II (3 балла)

      Вопрос 23.
      Учитывая 2 cos 3θ = \(\sqrt{3 }\), найдите значение θ. (2014)
      Решение:
      2 cos 3θ = \(\sqrt{3}\) …[Дано
      cos 3θ = \(\frac{\sqrt{3}}{2}\) ⇒ cos 3θ = cos 30°
      30 = 30° ∴ θ = 10°

      Вопрос 24.
      Если cos x = cos 40° . sin 50° + sin 40°. cos 50°, то найдите значение x. (2014)
      Решение:
      cos x = cos 40° sin 50° + sin 40° cos 50°
      cos x = cos 40° sin(90° – 40°) + sin 40°.cos(90° – 40° )
      cos x = cos 2 40° + sin 2 40°
      cos x = 1 …[∵ cos 2 A + sin 2 A = 1
      cos x = cos 0° ⇒ x = 0°

      Вопрос 25.
      Если sin θ = \(\frac{1}{2}\), то покажите, что 3 cos θ – 4 cos 3 θ = 0 , (2014)
      Решение:
      sin θ = \(\frac{1}{2}\)
      sin θ = sin 30° ⇒ θ = 30°
      LHS = 3 cos θ – 4 cos 3 θ
      = 3 cos 30° – 4 cos 3 (30°)

      Вопрос 26.
      Если 5 sin θ = 4, докажите, что \(\frac{1}{\cos \theta}+\frac{1}{ \cot \theta}\) = 3 (2013
      Решение:
      Дано: 5 sin θ = 4

      Вопрос 27.
      Оценка: сек 41°. sin 49° + cos 29°.cosec 61°  (2012)
      Решение:

      Вопрос 28.
      Оценка: (2012, 2017D)

      Решение:

      Вопрос 29.
      Q, PQ = 6 см и PR = 12 см. Определите ∠QPR и ∠PRQ. (2013)

      Решение:
      В рт. ∆PQR,
      PQ 2 + QR 2 = PR 2 … [By Pythogoras ‘Теорема

      (6) 2 + QR 2
      = (12) 2 2 2 2 2 2 2 2 2 .{3} \theta-\cos \theta}\) = tan θ (2015)
      Решение:

      Вопрос 39.
      Докажите, что: \(\frac{\sin \theta}{1+\cos \theta} +\frac{1+\cos \theta}{\sin \theta}\) = 2 cosec θ (2017OD)
      Решение:

      Введение в тригонометрию Класс 10 Важные вопросы Подробный ответ (4 балла)

      Вопрос 40.
      В остроугольном треугольнике ABC, если sin (A + B – C) = \(\frac{1}{2}\) и cos (B + C – A) = \(\frac{1}{\sqrt {2}}\), найдите ∠A, ∠B и ∠C. (2012)
      Решение:

      Подставляя значения A и B в (iii), получаем
      67,5° + B + 75° = 180°
      B = 180° – 67,5° – 75° = 37,5° 37,5 ° и ♂ = 75 °

      Вопрос 41.
      Оценка: (2013)

      Решение:

      Вопрос 42.
      Оцените следующее: (2015)

      Solution:

      1818.103333333333333333313 гг. = 30°, проверьте следующее: (2014)
      (i) cos 3θ = 4 cos 3 θ – 3 cos θ
      (ii) sin 3θ = 3 sin θ – 4 sin 3 θ
      Решение:

      Вопрос 44.
      Если тангенс (A + B) = \(\sqrt{3}\) и тангенс (A – B) = \(\frac{1}{\sqrt {3}}\) где 0 < A + B < 90°, A > B, найти A и B. Также вычислить: tan A. sin (A + B) + cos A. tan (A – B). (2015)
      Решение:

      Вопрос 45.
      Найдите значение cos 60° геометрически. Отсюда находим cosec 60°. (2012, 2017D)
      Решение:

      Пусть ∆ABC — равносторонний ∆.
      Пусть каждая сторона треугольника равна 2а.
      Поскольку каждый угол равностороннего треугольника ∆ равен 60°
      ∴ ∠A = ∠B = ∠C = 60°
      Draw AD ⊥ BC
      В ∆ADB и A∆ADC,
      AB = AC … [Каждый = 2a
      AD = AD …[Общий
      ∠1 -∠2 … [Каждые 90°
      ∴ ∆ADB = ∆ADC …[правило соответствия RHS
      BD = DC = \(\frac{2 a}{2}\) = a
      In rt. {2}}\) = 2. (2012, 2017D) 9{2}}}\) и d > 0, найти значения cos θ и tan θ. (2013)
      Решение:

      Вопрос 49.
      Если cot B = \(\frac{12}{5}\), докажите, что tan 2 B – sin 2 B = sin 4 B . sec 2 B. (2013)
      Решение:
      cot B = \(\frac{12}{5}\) :: \(\frac{A B}{B C}=\frac{12}{5}\ )

      АВ = 12к, ВС = 5к
      В рт. ∆ABC, …[По теореме Пифагора
      AC 2 = AB 2 + BC 2
      AC 2 = (12k) 2 + (5K) 2
      AC 2 = 144K 2 + 25K 2
      AC 2 = 169K 2 …
      [
      [
      IVELEN.

      Вопрос 50.
      Если \(\sqrt{3}\) кроватка 2 θ – 4 кроватка θ + \(\sqrt{3}\) = 0, то найти значение кроватки 2 θ + tan 2 θ. (2013)
      Решение:

      Вопрос 51.
      Докажите, что b 2 x 2 – a 2 y 2 = a 2 b 2 , если: (2014)
      (i) x = a sec θ, y = b tan θ
      (ii) x = a cosec θ, y = b cot θ
      Решение:
      (i) Л. Х.С. = B 2 x 2 — A 2 Y 2
      = B 2 (Sec θ) 2 — A 2 (B Tan θ) 777868 2 2 2 2 — A 2 (B Tan θ) 777768 — A 2 (B TAN θ) 77768 — A 2 (B TAN θ) — A 2 ) A 2 Sec θ — A 2 B 2 TAN 2 θ
      = B 2 A 2 (г. 2 θ – 2 (г.2363 = b 2 a 2 (1) …[∵ sec 2 θ – tan 2 θ = 1
      = a 2 b 2 = R.H.S.

      (ii) L.H.S. = B 2 x 2 — A 2 Y 2
      = B 2 (A COSEC θ) 2 — A 2 (B COTE θ) 68 — A 2 (B COTE θ) — A 2 (B COTE θ) — A 2 (B COTE θ) — A 2 (B Cot a 2 cosec 2 θ – a 2 b 2 cot 2 θ
      = b 2 a 2 9298{2}+1}\). (2012)
      Решение:
      cosec θ + cot θ = p

      Вопрос 54.
      Если tan θ + sin θ = p; тангенс θ – sin θ = q; докажите, что p 2 – q 2 = \(4 \sqrt{p q}\). (2012)
      Решение:
      Л.Х.С. = p 2 – q 2
      = (tan θ + sin θ) 2 – (tan θ – sin θ) 2
      = (tan 2 θ + 2 2,367 tanθ.sinθ) – (tan 2 θ + sin 2 θ – 2tan θ sin θ)
      = 2 тангенс θ sin θ+ 2 тангенс θ sin θ
      = 4 tan θ sin θ …(i)

      Вопрос 55.
      Если sin θ + cos θ = m и sec θ + cosec θ = n, то докажите, что n(m 2 – 1) = 2m. (2013)
      Решение:
      m 2 – 1 = (sin θ + cos θ) 2 – 1
      = sin 2 θ + cos 2 θ + 2 sin 1 θ1 – 6 θ 3 cos 93 + 2 sin θ cos θ – 1
      = 2 sin θ cos θ …[sin 2 θ + cos 2 θ = 1
      L.H.S. = n(m 2 – 1)
      = (sec θ + cosec θ) 2 sin θ cos θ

      Вопрос 56.
      Докажите, что:  = 2 cosec A (2012)
      Решение:

      Вопрос 57.
      В ∆ABC покажите, что sin 2 \(\frac{\mathbf{A}}{2} \) + sin 2 \(\frac{\mathbf{B}+\mathbf{C}}{\mathbf{2}}\) = 1. (2013)
      Решение:
      In ∆ABC, ∠A + ∠B + ∠C = 180° … [Сумма углов ∆
      ∠B + ∠C = 180° – ∠A

      Вопрос 58.
      Найдите значение: (2013)

      Решение:

      3

      Вопрос 59.
      Докажите, что: (sin θ + cos θ + 1). (sin θ – 1 + cos θ) . сек θ . cosec θ = 2 (2014)
      Решение:
      L.H.S. = (sin θ + cos θ + 1) (sin θ – 1 + cos θ) . sec θ cosec θ
      = [(sin θ + cos θ) + 1] [(sin θ + cos θ) – 1] . sec θ cosec θ
      = [(sin θ + cos θ) 2 – (1) 2 ] sec θ cosec θ …[∵ (a + b)(a – b) = a 2 – b 2
      = (sin 2 θ + cos 2 θ + 2 sin θ cos θ – 1]. sec θ cosec θ
      = (1 + 2 sin θ cos θ – 1). sin 2 θ + cos 2 θ = 1
      = (2 sin θ cos θ). ) 9{2} A}\) (2015)
      Решение:

      Вопрос 62.
      Докажите тождество: (2015)

      Решение:

      Вопрос 63.
      Докажите следующие тригонометрические тождества: sin A (1 + tan A) + cos A (1 + cot A) = sec A + cosec A. (2015)
      Решение:
      L.H.S. Вопрос 64 = 2(cot A. sec B + tan B. cosec A) (2014)
      Решение:
      L.H.S.
      = (кроватка A + сек B) 2 – (загар B – косек A) 2
      = детская кроватка 2 A + сек 2 B + 2 кроватка A сек ​​B – (tan 2 B + cosec 2 A – 2 tan B cosec A)
      = cot 2 A + sec 2 B + 2 cot A sec B – tan 2 B – cosec 2 A + 2 tan B cosec A
      = (sec 2 B – tan 2 B) – (cosec 2 A – cot 2 A) + 2(cot A sec B + tan B cosec A)
      = 1 – 1 + 2(cot A sec B + tan B cosec A) … [∵ sec 2 B – tan 2 B = 1
      cosec 2 A – cot 2 A = 1
      = 2(cot A . sec B + tan B . cosec A) = R.H.S.

      Вопрос 65.
      Если x = r sin A cos C, y = r sin A sin C и z = r cos A, то докажите, что x 2 + y 2 + z 2 = r 2 . (2017OD)
      Решение:
      x = r sin A cos C; y = r sin A sin C; z = r cos A
      Возведение в квадрат и сложение,
      L.H.S. х 2 + y 2 + z 2 = 2 sin 2 A cos 2 C + r 2 sin 2 A sin 2 C + r 2 cos 2 A
      = r 2 sin 2 A(cos 2 C + sin 2 C) + r 2 cos 2 A
      = r 2 sin 2 A + r 2 cos 2 A … [cos 2 θ + sin 2 θ = 1
      = r 2 (sin 2 A + cos 2 A) = r 2 = R.H.S.

      Вопрос 66.
      Докажите, что: (2017OD)

      Решение:

      Вопрос 67.
      На соседнем рисунке ABCD — прямоугольник шириной BC = 7 см и ∠CAB = 30°. Найдите длину стороны АВ прямоугольника и длину диагонали АС. Если ∠CAB = 60°, то какова длина стороны AB прямоугольника. [Используйте \(\sqrt{3}\) = 1,73 и \(\sqrt{2}\) = 1,41, если необходимо) (2014OD)

      Решение:

      Важные вопросы по математике для 10 класса

      Тригонометрические функции: quais são e como calcular?

      As trigonométricas funções são as funções seno, cosseno e tangente . Todas as funções trigonométricas relacionam о доблести сделать angulo em graus ou radianos com о доблести да razão trigonométrica, relação essa дие Pode сер feita пор meio сделать estudo сделать цикло trigonométrico. Com о estudo индивидуальный де cada uma das funções trigonométricas, é possível fazer a репрезентасао графика, estudar о sinal да função пункт cada um dos quadrantes, entre outras características важных.

      Leia tambem: Os 4 erros mais cometidos na trigonometria básica

      Tópicos deste artigo

      • 1 — Quais são as funções trigonométricas?
      • 2 — Função cosseno
        • Domínio
        • Imagem
        • Gráfico da função cosseno
        • Sinal
        • Período da função cosseno
        • Paridade
      • 3 — Arcos notáveis ​​da função cosseno
      • 4 — Função seno
        • Доминио
        • Imagem
        • Gráfico da função seno
        • Sinal
        • Período da função cosseno
        • Paridade
      • 5 — Arcos notáveis ​​da função seno
      • 6 — Função tangente
        • Domínio
        • Imagem
        • Gráfico da função Tangente
        • Sinal
        • Período
        • Paridade
      • 7 — Arcos notáveis ​​da função tangente
      • 8 — Exercícios 91 resolves3464

      Quais são as funções trigonométricas?

      В качестве тригонометрических функций, которые обычно используются в качестве тригонометрических функций, используются как обычные, так и косвенные функции и тангентные функции. O estudo delas está ligado ao ciclo trigonométrico.

      Тригонометрический цикл.

      Para cada valor de angulo, há um único valor para o seno e para o cosseno. As funções trigonométricas nada mais são que a relação entre o angulo e o valor da razão trigonométrica para esse angulo . Vale lembrar que o valor desse angulo pode ser dado em radianos ou em graus e que o valor do seno e do cosseno é semper um número real entre -1 e 1.

      г. Доблесть сделать сено и сделать коссено пара ос principais angulos.

      Note na imagem que, para cada angulo, o cosseno e o seno accepte m um valor. É com base no estudo de cada uma das funções trigonométricas que observamos a relação entre o valor do angulo e o valor da razão trigonométrica.

      Лея тел.: Quais são os angulos notáveis?

      Não pare agora… Tem mais depois da publicidade 😉

      Função cosseno

      A função cosseno é função f : R → R, cuja lei de formação é f (x) = cos (x). Como o cosseno de um angulo é semper um número entre 1 e -1 , então, -1 ≤ cos (x) ≤ 1.

      • Доминио

      O domínio da função cosseno é o conjunto dos números reais , pois não existse nenhuma restrição para o valor de x, em que x é o angulo em radianos. Para todo número real, é possível encontrar o valor de cos(x), então, D ф = р.

      • Имидж

      Sabemos que o contradomínio da função cosseno é o conjunto dos números reais, entretanto, quando analisamos a imagem da função, é possível perceber que ela é semper um valor po 5 1 8 a igual ou -1 e menor o ciclo trigonométrico tem raio 1, então, o maior valor que a função cosseno pode assumir é 1, e, аналог, o menor valor que ela pode assumir é -1. Im = [-1, 1]

      O gráfico da função cosseno está contido entre as retas y = — 1 e y = 1. Vale lembrar que isso acontece porque a imagem da função é semper um número entre -1 e 1 e possui parte crescente e parte decrescente, como podemos ver a seguir:

      Gráfico da função cosseno.

      Fazendo a reportência do valor do angulo com o valor da razão trigonométrica, é possível perceber que o grafico possui um comportamento cíclico ou seja, o comportamento semper se repete de forma Periodica. O grafico да função cosseno é conhecido como cossenoide.

      • Синал

      Sabemos que, no ciclo trigonométrico, o cosseno possui valores positivos no I e IV quadrantes. Первый квадрант между 0° и 90°, четвертый квадрант между 270° и 360°. Em radianos, função é positiva para valores de x entre 0 e π/2 e entre 3π/2 e 2π.

      A função cosseno possui valores negativos no II e III quadrantes ou seja, o angulo está entre 90º e 270º. Em radianos, para que a função cosseno seja negativa, x está entre π/2 e 3π/2.

      Sinal da função cosseno.

      O grafico da função cosseno tem um período de 2π . Аналисандо, é possível perceber que o grafico está contido no intervalo de 0 a 2π. Para valores anteriores ou posteriores a esse intervalo, o grafico se repete.

      • г.

        Паридад

      Função cosseno é рассмотрит uma função par , pois há uma simetria no grafico em relação ao eixo y. Quando uma função é рассматривая пар, temos que f (x) = f (-x), ou seja, cos (x) = cos (-x).

      Arcos notáveis ​​da função cosseno

      Vejamos o valor do cosseno para os principais angulos:

      Arcos notáveis ​​da função cosseno.

      Вежа там: Secante, cossecante e cotangente – razões trigonométricas inversas do seno, cosseno e tangente

      Função seno

      A função cosseno é a função f : R → R, cuja lei de formação é f (x) = сен (х). Como o seno de um angulo, assim como o cosseno, é semper um número entre 1 e -1 , então, -1 ≤ sen (x) ≤ 1.

      • Доминио

      O domínio da função seno г. é o conjunto dos números reais . A função f (x) = sen (x) está definida para todos os números reais, então, D f = R.

      3

      Имидж

      A imagem da função seno possui valor máximo em f (x) = 1 e valor mínimo quando f(x) = -1 . Então, забавный образ или реальный интервал [-1, 1].

      О графике функции é limitado tambem pelas retas horizontalis y = -1 e y = 1 . O comportamento é parecido com o da função seno Periodico, Tendo intervalos crescentes e intervalos decrescentes. Veja представляет график работы, который не имеет плано-картезиано, а затем:

      График работы, имеющийся в сети

      О графике работы, который используется там же, где и периодичность, и é conhecido como senoide.

      • г.

        Синал

      Divenentemente DA Funcáo Cosseno, Funcáo Seno Vosui Valores Positivos № S Quadrante S I EI Primeiro, SEJA, SEJA, SEJA, SEJA, SEJA, SEJA, SEJA, SEJA, SEJA. Em radianos, função é positiva para valores entre 0 e π.

      A função seno possui valores negativos no II I e IV quadrante s , ou seja, o angulo está entre 180º e 360º. Em radianos, para que função seno seja negativa, x está entre π e 2π.

      Sinal da função seno

      O grafico da função seno tem um período de 2π. Isso significa que, posteriormente ou anteriormente ao intervalo de 0 a 2π, o graphico é Periodico, ou seja, repete-se.

      • Паридад

      Удобный номер Função IM пар , pois há uma simetria no grafico em relação à bissetriz dos quadrantes ímpares. Quando uma função é рассмотрит ímpar, temos que f (x) = — f (x), ou seja, sen (-x) = -sen (x).

      Arcos notáveis ​​da função seno

      Vejamos o valor do seno para os principais angulos:

      Arcos notáveis ​​da função seno.

      Função tangente

      Sabemos que a tangente é a razão entre o seno e o cosseno. Diferentemente das duas funções trigonométricas anteriores, função tangente não possui valor de maximo nem valor de minimo. Além disso, existsretrições para o domínio, mas a lei de formação da função tangente é f (x) = tan(x).

      • Доминио

      Касательные функции, которые могут быть ограничены в отношении seu domínio, como ela é formada pela razão entre o seno e o cosseno, não existsem valores para tangente quando cos(x) = 0 . Pesando no ciclo trigonométrico de 0º a 360º, função tangente não está definida para os angulos de 90º e 270º, pois são os valores em que o cosseno é igual a 0. Quando há ângulos maiores que uma volta aqueles, to emdo volta aqueles completa valor de cosseno é 0 não fazem parte do domínio da função cosseno.

      • Имидж

      Различия между отдельными функциями и функциями, и образы дополнительных функций, а также числовое значение , ou seja, ela não é limitada e não possui valor de máximo nem de minimo. Im = R

      Função tangente também é Periodica como as funções seno e cosseno, ou seja, ela semper se repete. Quando comparamos:

      Grafico da função tangente.

      • Синал

      A função tangente possui valor positivo para os quadrantes ímpares, ou seja, I e III quadrantes. Пара ангулос между 0º и 90º e angulos entre 180º e 270º, função possui valores positivos. Em radianos, o valor de x tem que estar entre 0 e π/2 или π e 3π/2.

      Grafico da função tangente

      • Период

      O período da função tangente também é diferente das funções seno e cosseno. O período da função tangente é π .

      • Паридад

      Тангентная функция é uma função ímpar , pois tan(-x) = -tan(x), logo, ha uma simetria no grafico em relação à origem do plano cartesiano.

      Arcos notáveis ​​da função tangente

      Vejamos o valor da tangente para os principais angulos:

      Arcos notáveis ​​da função tangente.

      Veja tambem: Como encontrar seno e cosseno de angulos suplementares?

      Exercícios resolvidos

      Questão 1 — (Enem 2017) Raios de luz solar estão atingindo a superfície de um lago, formando um ângulo x com a superfície in sua superfície.

      Em determinadas condições, pode-se supor que a intensidade luminosa desses raios, na superfície do lago, seja dada aproximadamente por I(x) = k · sen(x), sendo kuma Constante, e supondo-se que X está между 0° и 90°.

      Quando x = 30º, a intensidade luminosa se reduz a qual Percentual de seu valor maximo?

      A) 33%

      B) 50%

      C) 57%

      D) 70%

      E) 86%

      Resolução

      0 Alterniva1813

      No intervalo de 0º a 90º, a função seno tem seu maior valor quando x = 90º, então, temos que:

      i = k · sen(90º)
      я = к · 1
      i = k

      Agora, quando x = 30º, temos que:

      i = k · sem (30º)
      я = к · 1/2
      i = k/2

      Note que a intensidade i foi reduzida pela metade, ou seja, 50%.

      Questão 2 — (Enem 2015) Segundo o Brasileiro de Geografia e Estatística (IBGE), produtos sazonais são aqueles que apresentam ciclos bem definidos de produção, consumo e preço. Resumidamente, existsem épocas do ano em que a sua disponibilidade nos mercados varejistas ora é escassa, com preços elevados, ora é riche, com preços mais baixos, o que ocorre no mês de produção maxima da safra.

      Конвертер jpg в пдф онлайн бесплатно: конвертировать изображения JPEG онлайн (БЕСПЛАТНО)

      alexxlab / / Разное

      Онлайн-конвертер JPG в PDF | Бесплатные приложения GroupDocs

      Вы также можете конвертировать JPG во многие другие форматы файлов. Пожалуйста, смотрите полный список ниже.

      JPG TO TIFF Конвертер (Формат файла изображения с тегами)

      JPG TO TIF Конвертер (Формат файла изображения с тегами)

      JPG TO JPG Конвертер (Файл изображения Объединенной группы экспертов по фотографии)

      JPG TO JPEG Конвертер (Изображение в формате JPEG)

      JPG TO PNG Конвертер (Портативная сетевая графика)

      JPG TO GIF Конвертер (Графический файл формата обмена)

      JPG TO BMP Конвертер (Формат растрового файла)

      JPG TO ICO Конвертер (Файл значка Майкрософт)

      JPG TO PSD Конвертер (Документ Adobe Photoshop)

      JPG TO WMF Конвертер (Метафайл Windows)

      JPG TO EMF Конвертер (Расширенный формат метафайла)

      JPG TO DCM Конвертер (DICOM-изображение)

      JPG TO DICOM Конвертер (Цифровая визуализация и коммуникации в медицине)

      JPG TO WEBP Конвертер (Формат файла растрового веб-изображения)

      JPG TO SVG Конвертер (Файл масштабируемой векторной графики)

      JPG TO JP2 Конвертер (Основной файл изображения JPEG 2000)

      JPG TO EMZ Конвертер (Расширенный сжатый метафайл Windows)

      JPG TO WMZ Конвертер (Метафайл Windows сжат)

      JPG TO SVGZ Конвертер (Сжатый файл масштабируемой векторной графики)

      JPG TO TGA Конвертер (Тарга Графика)

      JPG TO PSB Конвертер (Файл изображения Adobe Photoshop)

      Преобразовать JPG TO PPT (Презентация PowerPoint)

      Преобразовать JPG TO PPS (Слайд-шоу Microsoft PowerPoint)

      Преобразовать JPG TO PPTX (Презентация PowerPoint Open XML)

      Преобразовать JPG TO PPSX (Слайд-шоу PowerPoint Open XML)

      Преобразовать JPG TO ODP (Формат файла презентации OpenDocument)

      Преобразовать JPG TO OTP (Шаблон графика происхождения)

      Преобразовать JPG TO POTX (Открытый XML-шаблон Microsoft PowerPoint)

      Преобразовать JPG TO POT (Шаблон PowerPoint)

      Преобразовать JPG TO POTM (Шаблон Microsoft PowerPoint)

      Преобразовать JPG TO PPTM (Презентация Microsoft PowerPoint)

      Преобразовать JPG TO PPSM (Слайд-шоу Microsoft PowerPoint)

      Преобразовать JPG TO FODP (Плоская XML-презентация OpenDocument)

      Преобразовать JPG TO HTML (Язык гипертекстовой разметки)

      Преобразовать JPG TO HTM (Файл языка гипертекстовой разметки)

      Преобразовать JPG TO MHT (MIME-инкапсуляция совокупного HTML)

      Преобразовать JPG TO MHTML (MIME-инкапсуляция совокупного HTML)

      Преобразовать JPG TO XLS (Формат двоичного файла Microsoft Excel)

      Преобразовать JPG TO XLSX (Электронная таблица Microsoft Excel Open XML)

      Преобразовать JPG TO XLSM (Электронная таблица Microsoft Excel с поддержкой макросов)

      Преобразовать JPG TO XLSB (Двоичный файл электронной таблицы Microsoft Excel)

      Преобразовать JPG TO ODS (Открыть электронную таблицу документов)

      JPG TO XLTX Преобразование (Открытый XML-шаблон Microsoft Excel)

      JPG TO XLT Преобразование (Шаблон Microsoft Excel)

      JPG TO XLTM Преобразование (Шаблон Microsoft Excel с поддержкой макросов)

      JPG TO TSV Преобразование (Файл значений, разделенных табуляцией)

      JPG TO XLAM Преобразование (Надстройка Microsoft Excel с поддержкой макросов)

      JPG TO CSV Преобразование (Файл значений, разделенных запятыми)

      JPG TO FODS Преобразование (Плоская XML-таблица OpenDocument)

      JPG TO SXC Преобразование (Электронная таблица StarOffice Calc)

      JPG TO EPUB Преобразование (Формат файла цифровой электронной книги)

      JPG TO XPS Преобразование (Спецификация документа Open XML)

      JPG TO TEX Преобразование (Исходный документ LaTeX)

      JPG TO DOC Преобразование (Документ Microsoft Word)

      JPG TO DOCM Преобразование (Документ Microsoft Word с поддержкой макросов)

      JPG TO DOCX Преобразование (Документ Microsoft Word с открытым XML)

      JPG TO DOT Преобразование (Шаблон документа Microsoft Word)

      JPG TO DOTM Преобразование (Шаблон Microsoft Word с поддержкой макросов)

      JPG TO DOTX Преобразование (Шаблон документа Word Open XML)

      JPG TO RTF Преобразование (Расширенный текстовый формат файла)

      JPG TO ODT Преобразование (Открыть текст документа)

      JPG TO OTT Преобразование (Открыть шаблон документа)

      JPG TO TXT Преобразование (Формат обычного текстового файла)

      JPG TO MD Преобразование (Уценка)

      JPG-To-PDF-Преобразование изображений в PDF и JPG в PDF бесплатно.

      JPG-To-PDF-Преобразование изображений в PDF и JPG в PDF бесплатно.
      Поделиться сайтом в социальных сетях и блогах
        ПОДПИШИТЕСЬ НА НАС В
      • Twitter
      • Facebook
      • youtube
      • email

      PDF23.com (short url)

      Лучшие бесплатные редакторы PDF и онлайн-инструменты

      Обрезать PDF

      Обрезайте PDF-файлы онлайн бесплатно. Перетащите файл и проведите пальцем по области, которую хотите обрезать. Автоматически обрезайте белые поля или просматривайте страницы PDF и выбирайте области обрезки.

      PDF разблокировать

      pdf защита паролем требует правильного пароля для разблокировки файла pdf. Требуется защищенный пароль pdf. Если вы забыли пароль PDF-файла или пароль владельца, вы можете использовать средство для удаления PDF-файлов, чтобы разблокировать PDF-файл.

      JPG в PDF

      Бесплатный онлайн-конвертер JPG в PDF, позволяющий объединить несколько изображений в один документ PDF

      Сжать PDF

      Простые шаги для сжатия больших файлов PDF в Интернете, сжатия файла PDF для получения того же качества PDF, но меньшего размера файла. Легко и бесплатно сжимайте или оптимизируйте файлы PDF в Интернете.

      Объединить PDF

      Легко объединяйте файлы PDF в Интернете. PDF-editor-free.com — это решение для пользователей, которые хотят объединить несколько файлов в один PDF-документ. Наши инструменты просты в использовании и бесплатны

      Удаление страницы PDF

      Наш онлайн-инструмент PDF можно использовать для удаления одной или нескольких страниц из документа PDF. Просто загружайте, изменяйте и сохраняйте файлы

      Объединить PDF Разделить PDF Сортировка PDF-страниц Удаление страницы PDF Повернуть PDF PDF в OCR Сжать PDF Обрезать PDF Изменить размер PDF Восстановить PDF Защитить PDF PDF для удаления паролей PDF разблокировать PDF в JPG JPG в PDF PNG в PDF Изображение в PDF PDF экспорт изображения Водяной знак PDF Добавить текст в PDF PDF-текст в рамку PDF в RGB PDF в CMYK Iccprofile для PDF в RGB Iccprofile для PDF в CMYK Печать переменных PDF
      Word в PDF Excel в PDF PowerPoint в PDF PDF в Word PDF в текст Конвертер PDF Illustrator в PDF PDF в EPS TIF в PDF PDF в TIF Читатель PDF Word Viewer Excel Viewer PowerPoint Viewer Illustrator Viewer Подписать PDF PDFредактор

      Этот файл хранится всего 30 минут

      Нужен пароль для открытия PDF-файла?

      Подтвердите, что у вас есть право удалить пароль этого PDF-файла, и согласитесь с нами на удаление пароля.

      Если вы согласны, мы попытаемся удалить пароль для вас, используя бесплатную онлайн-программу для удаления паролей в формате PDF.

      Согласен

      У меня есть право удалить пароль этого файла, и я согласен разрешить удаление пароля

      Удаление пароля требует больших вычислений и времени. Когда обработка будет завершена, вы получите уведомление по электронной почте.

      На этот адрес электронной почты будет отправлено письмо с подтверждением.

      Отправка подтверждения по электронной почте …

      Войдите в свой аккаунт

      Забыли или изменить пароль?

      Нет учетной записи? Зарегистрироваться

      Выберите свой любимый тарифный план

      Частота пожертвований:

      • Один раз
      • Ежемесячно
      • Ежегодно

      Сумма пожертвования:

            Privacy Policy

            JPG-To-PDF-Преобразование изображений в PDF и JPG в PDF бесплатно.

            JPG-To-PDF-Преобразование изображений в PDF и JPG в PDF бесплатно.
            Поделиться сайтом в социальных сетях и блогах
              ПОДПИШИТЕСЬ НА НАС В
            • Twitter
            • Facebook
            • youtube
            • email

            PDF23.com (short url)

            Лучшие бесплатные редакторы PDF и онлайн-инструменты

            Обрезать PDF

            Обрезайте PDF-файлы онлайн бесплатно. Перетащите файл и проведите пальцем по области, которую хотите обрезать. Автоматически обрезайте белые поля или просматривайте страницы PDF и выбирайте области обрезки.

            PDF разблокировать

            pdf защита паролем требует правильного пароля для разблокировки файла pdf. Требуется защищенный пароль pdf. Если вы забыли пароль PDF-файла или пароль владельца, вы можете использовать средство для удаления PDF-файлов, чтобы разблокировать PDF-файл.

            JPG в PDF

            Бесплатный онлайн-конвертер JPG в PDF, позволяющий объединить несколько изображений в один документ PDF

            Сжать PDF

            Простые шаги для сжатия больших файлов PDF в Интернете, сжатия файла PDF для получения того же качества PDF, но меньшего размера файла. Легко и бесплатно сжимайте или оптимизируйте файлы PDF в Интернете.

            Объединить PDF

            Легко объединяйте файлы PDF в Интернете. PDF23.com — это решение для пользователей, которые хотят объединить несколько файлов в один PDF-документ. Наши инструменты просты в использовании и бесплатны

            Удаление страницы PDF

            Наш онлайн-инструмент PDF можно использовать для удаления одной или нескольких страниц из документа PDF. Просто загружайте, изменяйте и сохраняйте файлы

            Объединить PDF Разделить PDF Сортировка PDF-страниц Удаление страницы PDF Повернуть PDF PDF в OCR Сжать PDF Обрезать PDF Изменить размер PDF Восстановить PDF Защитить PDF PDF для удаления паролей PDF разблокировать PDF в JPG JPG в PDF PNG в PDF Изображение в PDF PDF экспорт изображения Водяной знак PDF Добавить текст в PDF PDF-текст в рамку PDF в RGB PDF в CMYK Iccprofile для PDF в RGB Iccprofile для PDF в CMYK Печать переменных PDF
            Word в PDF Excel в PDF PowerPoint в PDF PDF в Word PDF в текст Конвертер PDF Illustrator в PDF PDF в EPS TIF в PDF PDF в TIF Читатель PDF Word Viewer Excel Viewer PowerPoint Viewer Illustrator Viewer Подписать PDF PDFредактор

            Этот файл хранится всего 30 минут

            Нужен пароль для открытия PDF-файла?

            Подтвердите, что у вас есть право удалить пароль этого PDF-файла, и согласитесь с нами на удаление пароля.

            Если вы согласны, мы попытаемся удалить пароль для вас, используя бесплатную онлайн-программу для удаления паролей в формате PDF.

            Согласен

            У меня есть право удалить пароль этого файла, и я согласен разрешить удаление пароля

            Удаление пароля требует больших вычислений и времени. Когда обработка будет завершена, вы получите уведомление по электронной почте.

            На этот адрес электронной почты будет отправлено письмо с подтверждением.

            Отправка подтверждения по электронной почте …

            Войдите в свой аккаунт

            Забыли или изменить пароль?

            Нет учетной записи? Зарегистрироваться

            Выберите свой любимый тарифный план

            Частота пожертвований:

            • Один раз
            • Ежемесячно
            • Ежегодно

            Сумма пожертвования:

                  Privacy Policy

                  Преобразование JPG в PDF бесплатно онлайн

                  Перетащите файлы сюда или нажмите, чтобы загрузить.


                  Используйте Ctrl или Shift, чтобы добавить несколько файлов одновременно

                  Оцените нас из 5

                  4.1 / 5 (3772)

                  No votes so far! Be the first to rate this post.

                  We are sorry that our service was not useful for you!

                  Let us improve service!

                  Tell us what issue you are facing?

                  • Почему конвертировать JPG в PDF?
                  • Как конвертировать JPG в PDF онлайн?
                  • Почему наш онлайн инструмент является лучшим JPG в PDF конвертер?
                  • Вопросы и ответы

                  У вас есть важный файл образа, который нужно отправить в виде файла PDF для своего клиента, поставщика, университет, или применения к работе, интересно, как конвертировать JPG в PDF и запутать, что делать?

                  Не волнуйтесь !!

                  Вам не нужно тратить слишком много времени и рыть для быстрого решения.

                  У нас есть быстрое решение преобразования JPG в PDF; Pngtopdf.net лучший JPG в PDF конвертер , который позволяет превратить JPG изображений в PDF с самым передовым онлайным конвертером непринужденно.

                  Независимо от того, используете ли вы операционную систему Windows, или макинтош IOS, вы можете конвертировать JPG в PDF с одним щелчком мыши.

                  Кроме того, сайт позволяет конвертировать JPG в PDF файлы без ущерба для его качества; она выглядит так же, как и оригинальные изображения.

                  JPG является формат файла изображения и PDF является печать дружественный формат документа. Лучше всего в PDF, оно может держать оба изображения и текст, а также.

                  JPG и форматы PDF файлов очень компактные, более годные к употреблению форматов файлов в Интернете.

                  JPG стандартный формат файла, который наиболее часто используется для отображения графики на веб-сайтах, JPG, как правило, имеет меньшие размеры файлов и позволяет высокую степень сжатия изображений, но некоторые из фотографий потеряли свое качество при сжатии и сохраняется.

                  Он считает формат файла с потерями, что означает, что качество не может восстановиться, когда он сжат. Формат JPG основном используется в цифровых камер и сканеров.

                  В то время как PDF является печати формат файла, разработанный Adobe, и это также стандартный формат файла, который использует в Интернете.

                  Он является предшественником PostScript, который обеспечивает отличное качество, когда дело доходит до печати документа.

                  Почему конвертировать JPG в PDF?

                  Есть так много сайтов , которые принимают только формат , специфичный , чтобы они могли распечатать его и представить его как позже файл.
                  Она является наиболее распространенным для написания исследования, резюме, сопроводительные письма, и писать образцы.

                  Что делать, если вы потратили часы, созданные профессиональные резюме в Adobe InDesign, сохраненные в формате JPG, а теперь претендуют на работу, и они только позволяют загружать только файлы PDF.

                  Это происходит много раз, и тогда вы ищете быстрое решение , как конвертировать JPG в PDF?
                  PDF является универсальным форматом файлов , который является к печати и может легко прочитать на всех устройствах, включая смартфоны, персональные ноутбуки и планшеты.
                  Кроме того , так много возможностей, она выделяется своей безопасностью. Вы можете поставить безопасность пользователя и пароль на файл, так как шифрование PDF используется для защиты PDF – файлы файлов , так что вы можете быть отправлены надежно другими.
                  Иногда нам нужно сделать скриншот из основных документов в наших смартфонах, которые в основном сохраненные в формате JPG.
                  Так что теперь, вы также можете конвертировать любые картинки в формате PDF в pngtopdf.net с одним щелчком мыши.

                  Как конвертировать JPG в PDF онлайн?

                  Несмотря на то, что можно конвертировать изображения в PDF без использования какой – либо третьей стороной платформы, но почему нужно пройти через длительный процесс , когда вы можете конвертировать JPG в PDF с одним щелчком мыши?
                  Да, благодаря JPG в PDF конвертер , который позволяет конвертировать JPG в PDF очень легко? Это удобный онлайн – конвертер , который поставляется с функцией перетаскивания мышью.
                  Этот конвертер поддерживает все форматы файлов , такие как JPG, PNG, TIFF, GIF и файлов.

                  • Открыть JPG в PDF конвертер , загружать или использовать функцию перетаскивания мышью , чтобы загрузить изображение
                  • После загрузки изображения, нажмите на кнопку «Convert», чтобы начать процесс преобразования PDF.
                  • Нажмите кнопку преобразовать
                  • Скачать преобразованный PDF на свой компьютер или смартфон
                  • Вы можете загружать несколько файлов одновременно, используя Ctrl или клавишу Shift,

                  Вы можете конвертировать неограниченное JPG в PDF онлайн без входа в систему или зарегистрироваться.

                  Почему наш онлайн инструмент является лучшим JPG в PDF конвертер?

                  Лучший онлайн JPG в PDF конвертер
                  Наш онлайн JPG в PDF конвертер бесплатно , что позволяет превратить неограниченное количество изображений в формате PDF. Мы гарантируем , чтобы сохранить все ваши важные файлы и данные в безопасности. Наш интернет – конвертер PDF поддерживает почти все форматы изображений, включая JPG, PNG, GIF и TIFF. Преобразование вашего JPG в PDF теперь можно с помощью одного клика.
                  Мы не храним файлы
                  Лучшее особенность нашего онлайн JPG в PDF конвертер является автоматическое удаление файлов. Да, после преобразования изображений в PDF, у вас есть всего несколько часов , чтобы загрузить файлы. После этого файлы будут автоматически удалены с сервера. Мы не идти на компромисс в вашей личной жизни.
                  Безопасная загрузка и хранение:
                  Наш интернет – конвертер привержен сохраняет ваши данные и личные файлы безопасны. Для того, чтобы выполнить наши обязательства, мы зашифровать все файлы, загруженные на нашей платформе с помощью шифрования SSL.
                  Таким образом, неавторизованные третьи стороны не могут взломать шифрование SSL. Мы никогда не передаем ваши файлы, информацию третьих лиц.
                  Преобразование JPG в PDF из любой точки мира
                  Вы можете преобразовать свою фотографию в PDF из любого места, в любое время, если у вас есть доступ в Интернет.
                  Наш онлайн бесплатно JPG в PDF конвертер совместим со всеми устройствами, вы можете использовать и преобразовать файл в Windows, Linux, Mac, IOS, Android и т. д.
                  Всегда жить до даты
                  JPG в PDF конвертер на облаке; Вы можете получить доступ к веб-сайт в любое время. Это всегда живет со 100% Провели конвертировать JPG в PDF с несколькими щелчками мыши, не регистрации, или загрузками программного обеспечения не требуется.

                  Вопросы и ответы

                  Как открыть файл PDF в окнах?
                  В окне, то EDGE браузер Microsoft, Chromes или Firefox, или браузер по умолчанию любой позволяет открывать и читать PDF – файлы изначально.
                  У вас также есть возможность открыть его с помощью Adobe Acrobat Reader; Вы можете скачать его бесплатно с Adobe Вебсайта .
                  Если вы используете Windows 10 или версию обновления , которая поддерживает Microsoft EDGE, вы можете дважды щелкнуть на файл PDF, и она будет открыта в браузере Microsoft EDGE.
                  Как открыть PDF – файлы в Linux?
                  Linux имеет в основном для чтения PDF, но если он отсутствует или вы не используете обновленную версию, вы можете установить его.  Откройте терминал и введите «Sudo APT-получить установку Evince» установку в скором времени начнется, а затем вы можете открыть PDF – файлы в Linux.
                  Как открыть файл PDF в Mac Операционная система?
                  Вам необходимо установить Adobe Acrobat Reader от Adobe сайта , чтобы получить доступ к файлу PDF.
                  Как открыть JPG в Windows?
                  Дважды щелкните на файле JPG и изображение откроется в средстве просмотра фотографий Windows. У вас также есть возможность открыть JPEG в браузере.
                  Как открыть JPG в Linux?
                  Вы можете открыть JPG файлов в Linux с помощью GIMP.
                  Как открыть JPG в операционной системе Mac?
                  Операционная система Mac имеет встроенный Photo Viewer , которая будет автоматически открывать файлы JPG.

                  Резюме

                  Если у Вас есть JPG изображения и хотите конвертировать в PDF файлы, бесплатно и быстро JPG в PDF онлайн конвертер делает это очень просто.
                  Наш интернет – конвертер PDF бесплатно; Вы можете включить неограниченное JPG изображений в PDF файлы без каких – либо ограничений.
                  Этот конвертер поддерживает практически все форматы изображения, такие как JPG, TIFF, PNG, GIF, BMP, и т.д., так что теперь вы можете конвертировать ваши фотографии в PDF – файлы в считанные секунды с помощью одного клика.
                  Кроме того, наш онлайн конвертер не разделяет ваши данные или важные файлы в какой – либо третьей стороне; данные автоматически удалять с нашего сервера.

                  Jpg в PDF — Конвертируйте JPG в PDF онлайн бесплатно

                  Jpg в PDF — Конвертируйте JPG в PDF онлайн бесплатно

                   We do not upload any files to server, hence your data is 100% secure. 

                  Конвертируйте jpg в pdf бесплатно онлайн, начните с загрузки вашего файла ниже

                  Download Preview

                  CHOOSE FILE

                  or drop your JPG files here

                  JPG to PDF

                  Add more

                  Простота в использовании

                  JPG в PDF делает процесс преобразования элегантным и простым

                  Точные результаты

                  Результаты являются точными и, следовательно, полностью удовлетворяют потребности пользователей.

                  Кросс-платфор

                  Теперь вы можете использовать этот конвертер в любой операционной системе, например Windows/Mac/Linux/Android/iPhone.

                  Безопасный и надежный

                  Сервер не задействован, поэтому ваши данные и файлы в безопасности

                  Быстро и эффективно

                  Сайт обрабатывает ваш pdf очень быстро и эффективно. Вы можете выполнить свою работу в кратчайших сроках

                  Файлы не загружены

                  Приложение полностью работает в вашем браузере без использования какого-либо сервера. Таким образом, ваши файлы в безопасности

                  Как конвертировать JPG в PDF

                  1. 1.Загрузите файлы изображений или нажмите на стрелку раскрывающегося списка и выберите Dropbox/Google Drive, чтобы выбрать файл
                  2. 2.Выберите настройки страницы для окончательного PDF-файла
                  3. 3.Просматривайте точный предварительный просмотр ваших PDF-страниц в реальном времени
                  4. 4. Нажмите на кнопку конвертировать
                  5. 5.Теперь нажмите «Загрузить», чтобы получить файлы
                  6. 6.Ура! наслаждайтесь нашим сервисом

                  Frequently Asked Questions

                  • Безопасно ли разрешить доступ к моему диску?

                    Да, абсолютно безопасно разрешить и предоставить нам доступ к вашему диску. Мы не будем вносить никаких изменений на ваш сайт, и ваши файлы будут в безопасности с вами.

                  • Как загрузить файлы со своего диска/dropbox?

                    Нажмите на стрелку раскрывающегося списка и выберите Dropbox/Google Drive. Выберите учетную запись Google, к которой вы хотите привязать диск. Теперь вы можете выбрать файлы, которые хотите загрузить.

                  • Какие функции предлагает файл jpg to pdf feature feature feature feature feature feature feature feature feature

                    Функция Jpg to pdf с сайта safepdfkit. com предлагает множество функций при преобразовании jpg-файла в pdf-файл, включая регулировку границ бумаги, полей бумаги и наклона бумаги (в основном альбомной и портретной), и предлагает все эти функции для всех типов jpg-файлов. Однако лучше всего то, что мы можем объединить несколько jpg-файлов (применив все вышеперечисленные функции к каждому jpg файлу) и объединить их в один pdf файл.

                  • Какой формат изображения предпочтительнее среди форматов webp и jpg?

                    Хорошо оптимизированный jpg похож или лучше webp. Однако webp — это новый формат изображений, который поддерживается не всеми браузерами. Типичная разница между ними заключается в качестве, которое составляет 15-25% разницы в размере.

                  • Могу ли я конвертировать jpg в pdf без маржи, используя safepdfkit?

                    Safepdfkit предоставляет возможность конвертировать jpg в pdf без полей. Таким образом, вы можете выполнить эту операцию с помощью safepdfkit для преобразования jpg в pdf без полей!

                  • Можем ли мы обрезать изображение перед загрузкой pdf-файла с помощью функции jpg to pdf с сайта safepdfkit.com?

                    Нет, в настоящее время инструмент конвертации jpg в pdf предлагает редактирование изображений путем настройки типа бумаги (например, A4), а также корректировки границ и полей, которые должны быть включены в файл pdf. Актуальные функции редактирования изображений, такие как обрезка, регулировка яркости изображения, резкость и т. д., будут включены в ближайшие обновления веб-сайта.

                  • Можем ли мы конвертировать jpeg, jpng и форматы изображений в формат pdf с помощью функции jpg в pdf с safepdfkit.com?

                    Нет, в настоящее время мы предлагаем функции преобразования изображений только для формата jpg в формат pdf, а функции редактирования включают настройку границ, наклон страницы и тип страницы. В настоящее время мы можем загрузить несколько jpg файлов и объединить их в один большой pdf или несколько маленьких pdf файлов, эти функции поддерживают только формат jpg. Будущие обновления этого инструмента конвертера предоставят пользователям все интересные функции.

                  • Снизится ли качество моих изображений после загрузки их из функции jpg to pdf с safepdfkit.com?

                    Нет, качество изображения не снизится после загрузки из функции jpg в pdf с safepdfkit.com. Изображения не потеряют своего качества и будут сдвинуты с тем же качеством после преобразования в pdf файл.

                  • Сколько времени требуется для преобразования jpg-файла или коллекции jpg-файлов в pdf-файл с помощью функции jpg в pdf с safepdfkit.com?

                    Время — это захватывающий фактор, присутствующий здесь. В качестве первого шага мы просто выбираем файлы jpg, которые необходимо преобразовать в файлы pdf, и перетаскиваем файлы один за другим, настраиваем параметры и нажимаем кнопку конвертировать. В одно мгновение загруженные файлы преобразуются в pdf-файл. Все, что нужно, это стабильное подключение к Интернету и устройство для работы с поддержкой хорошего веб-браузера.

                  • Могу ли я использовать функцию jpg to pdf с сайта safepdfkit.com на моем яблочном iPhone 10?

                    Да, функция jpg to pdf от safepdfkit.com является кросс-платформенной, где пользователь может использовать этот инструмент конвертера из операционной системы, такой как Android, iOS, Windows и Mac OS. Он не зависит от используемой операционной системы, но зависит только от подключения к Интернету и размера файлов jpg, которые загружаются для преобразования в pdf-файлы.

                  • Сколько jpg-файлов мы можем редактировать и создавать pdf-файлы за один раз, используя функцию jpg to pdf file с safepdfkit.

                    com?

                    За один отрезок пользователь может отредактировать 10 jpg файлов и создать их в один pdf файл или использовать для создания 10 отдельных pdf-файлов в идеальном случае при обычном подключении. Загруженные файлы jpg можно редактировать по границе, наклону и типу бумаги. Однако при медленном подключении рекомендуется использовать 5 или более jpg преобразований. Реальная сделка заключается в том, что он может конвертировать бесконечные jpg в pdf в соответствии с требованиями пользователя.

                  • Какие функции предлагаются в полях страниц при преобразовании jpg-файла в pdf-файл с использованием функции jpg в pdf с сайта safepdfkit.com?

                    Функция Jpg to pdf с сайта safepdfkit.com в настоящее время предлагает пользователям 3 типа полей страницы, включая небольшую маржу, большую маржу и функцию без маржи. Малый запас обеспечивает идеальное пространство для конвертированного jpg файла и создает пространство для загруженного jpg файла, в то время как большая маржа создает еще больше места, уменьшая размер jpg еще больше. С другой стороны, никакие поля не оставляют места и помещается в jpg файл точно на границе страницы.

                  • Сколько наклонов страниц доступно для загруженных jpg-файлов при преобразовании их в pdf-файлы с помощью функции jpg to pdf с safepdfkit.com?

                    Функция Jpg to pdf с сайта safepdfkit.com предлагает наклоны на 2 страницы и автоматический режим. Наклоны страниц включают альбомный и портретный режимы. Альбомный режим используется для горизонтальной установки бумаги, в то время как портретный режим — общий, при котором бумага располагается в вертикальном режиме. Наконец, автоматический режим используется, когда пользователь не может определиться с наклоном страницы. Это настройка, которая применяется ко всем загружаемым файлам, если они не изменены.

                  • Сколько вариантов страниц доступно для загруженных jpg-файлов при преобразовании их в pdf-файлы с помощью функции jpg to pdf с safepdfkit.

                    com?

                    Функция Jpg to pdf file от safepdfkit.com в настоящее время предлагает варианты 3-страничного типа, которые включают тип A4, тип LETTER (US) и автоматический режим (для случайного выбора). Лист формата A4 в общем режиме обычно используется для всех обычных целей. Тем не менее, буквенный тип (US) также используется для высококлассного формального произведения. Дополнительные варианты страниц будут включены в ближайшие обновления.

                  • Почему стоит выбрать JPG в PDF?

                    Ваша безопасность является для нас первостепенной задачей. Чтобы убедиться, что все ваши данные полностью защищены, мы не загружаем ваши файлы на наши серверы. Все обрабатывается в самом клиентском браузере, и на наших серверах ничего не сохраняется. Это делает преобразование JPG в pdf наиболее безопасным инструментом для пользователей.

                  • Как конвертировать несколько JPGS в PDF в Windows?

                    PDF — это одно из очень важных расширений файлов, которое широко используется в Интернете. Это расширение файла используется практически во всех видах ОС, будь то Windows, Mac, Linux, Android, IOS и т. Д., А также на всех видах устройств, таких как мобильные устройства, настольные компьютеры, планшеты и т. д. в этой статье вы изучите различные способы, с помощью которых мы можем конвертировать несколько JPG в один файл PDF в Windows легко, чтобы бесплатно. Наш инструмент JPG to PDF очень прост в использовании и абсолютно безопасен для пользователей. Нажмите, чтобы узнать больше

                  • Безопасны ли конвертеры PDF?

                    Мы часто понимаем, что онлайн-инструменты конвертации небезопасны в использовании, поскольку иногда они хранят вашу личную информацию на своих серверах, что может быть использовано не по назначению. Инструменты онлайн-конвертации широко используются в Интернете, и выбор правильного инструмента конвертации PDF имеет первостепенное значение для пользователей. В этой статье мы расскажем о том, насколько наш инструмент конвертации PDF безопасен для пользователей, какие методы он использует, чтобы сделать его лучшим с точки зрения безопасности и безопасности. Нажмите, чтобы узнать больше.

                  • Как конвертировать несколько JPGS в PDF на MAC?

                    PDF — это одно из очень важных расширений файлов, которое широко используется в Интернете. Это расширение файла используется практически во всех видах ОС, будь то Windows, Mac, Linux, Android, IOS и т. Д., А также на всех видах устройств, таких как мобильные устройства, настольные компьютеры, планшеты и т. д. в этой статье вы изучите различные способы, с помощью которых мы можем конвертировать несколько JPG в один PDF-файл на Mac легко, чтобы бесплатно. Наш инструмент JPG to PDF очень прост в использовании и абсолютно безопасен для пользователей. Нажмите, чтобы узнать больше

                  • Как конвертировать несколько JPG в PDF в Linux?

                    PDF — это одно из очень важных расширений файлов, которое широко используется в Интернете. Это расширение файла используется практически во всех видах ОС, будь то Windows, Mac, Linux, Android, IOS и т. Д., А также на всех видах устройств, таких как мобильные устройства, настольные компьютеры, планшеты и т. д. в этой статье вы изучите различные способы, с помощью которых мы можем конвертировать несколько JPG в один файл PDF на Linux легко, чтобы бесплатно. Наш инструмент JPG to PDF очень прост в использовании и абсолютно безопасен для пользователей. Нажмите, чтобы узнать больше

                  • Как конвертировать изображения в PDF на Ipad или Iphone?

                    PDF — это одно из очень важных расширений файлов, которое широко используется в Интернете. Это расширение файла используется практически во всех видах ОС, будь то Windows, Mac, Linux, Android, IOS и т. Д., А также на всех видах устройств, таких как мобильные устройства, настольные компьютеры, планшеты и т. д. в этой статье вы изучите различные способы, с помощью которых мы можем конвертировать несколько JPG в один PDF-файл на Ipad или Iphone легко, чтобы бесплатно . Наш инструмент JPG to PDF очень прост в использовании и абсолютно безопасен для пользователей. Нажмите, чтобы узнать больше

                  • Лучшие приложения для конвертации PDF для Android?

                    В современном мире преобразование файлов из одного формата в другой осуществляется практически ежедневно. В таких случаях очень важно, чтобы мы, пользователи, тратили свое время только на лучшие приложения и больше ничего. Таким образом мы сэкономим много драгоценного времени и повысим эффективность. В этой статье мы обсудим различные приложения, которые превращаются в PDF для пользователей Android. Упомянутый список сравнивается на основе безопасности, удобства использования и многих других функций. Нажмите, чтобы узнать больше.

                  • Как мне связаться, если у меня возникнут какие-либо проблемы или я хочу дать какие-либо предложения?

                    Мы с радостью примем любые вопросы или предложения, предложенные всеми пользователями, пожалуйста, свяжитесь с нами через наши ручки в социальных сетях для получения дополнительной информации. Просто прокрутите веб-сайт вниз, и вы найдете все порталы, на которые мы ссылаемся.

                  Rate this tool

                  5.00/5   20 votes

                  Наши USP

                  безопасность 100% (файлы не отправляются на сервер для обработки)
                  Ограничения на размер файла Нет (нет ограничений на размер файлов)
                  Ограничения на использование Нет (обрабатывайте столько файлов, сколько хотите)
                  Цена бесплатно
                  Информация о пользователе Нет (мы не запрашиваем информацию о пользователе, такую как адрес электронной почты/номер телефона)
                  Объявления Нет (Мы предоставляем полный опыт без рекламы)

                  ТОП-7 лучших программ для конвертации JPG в PDF

                  ФотоМАСТЕР

                  Откройте нужное изображение в редакторе и нажмите на кнопку «Печать», чтобы переформатировать фотографию в ПДФ.

                  Далее нажмите кнопку «Сохранить макет как…» и выберите необходимый нам PDF формат. После этого останется лишь указать путь для сохранения результата и подтвердить действие. Конвертация пройдет всего за пару секунд.

                  Перевод картинки в формат электронных документов — это не единственная возможность ФотоМАСТЕРа. Эта программа является мощным инструментом для редактирования изображений, построенным на использовании нейросетей и снабженным большим количеством функций для профессиональной обработки снимков. Cкачайте фоторедактор и используйте все его возможности по-максимуму!

                  С ФотоМАСТЕРом вы сможете:

                  • устранить любые дефекты на коже;
                  • скорректировать черты лица;
                  • добавить эффектный макияж;
                  • изменить цвет глаз и волос;
                  • стильно обрабатывать фотоснимки благодаря большой коллекции фильтров;
                  • обрезать и поворачивать изображения;
                  • удалять людей и лишние объекты из кадра;
                  • исправлять геометрические искажения;
                  • менять фон за три простых шага;
                  • наносить текст, украшать фото рамкой или клипартом и многое другое.

                  PDF-XChange Editor

                  Нужна программа конвертации JPG в PDF, с помощью которой можно потом отредактировать результат? PDF-XChange Editor позволит вам работать с содержимым страницы: удалять текст и вставлять новый, добавлять изображения, вносить комментарии и даже снабжать файлы аудиосопровождением. Также есть возможность отправить документ в печать.

                  Само создание ПДФ из фото происходит за три секунды. Вы просто загружаете картинку в программу, нажимаете на иконку в виде дискеты и в выпадающем списке выбираете нужное расширение (по умолчанию установлено PDF). В бесплатной версии программы вы сможете работать только с текстом, к тому же на результате обработки редактор ставит водяной знак, обозначающий, что редактирование проводилось в демо-версии. Бесплатно эту программу можно использовать лишь для перевода JPG в PDF, а также ряда других расширений.

                  Adobe Acrobat Reader

                  Adobe Acrobat Reader — самый популярный просмотрщик PDF файлов. Кроме чтения, в этом приложении можно делать многое. Например, рецензировать документы при помощи стандартного набора инструментов (заметки, линии, формы, штампы), вставлять аудио и видео, объединять разные типы расширений в один формат, защищать содержимое страниц паролем.

                  Компания позаботилась о создании мобильной версии приложения под Android. Однако для разблокировки основного спектра функций, вам придется приобрести платную версию софта Acrobat Pro. Если же вам нужна лишь опция преобразования, сделайте это онлайн. Перейдите по ссылке, выберите пункт «Конвертировать в PDF» и перетащите в окно приложения картинку. Теперь вы знаете как перевести фото в ПДФ формат, не скачивая на компьютер дистрибутив.

                  doPDF

                  doPDF — простое приложение для преобразования фото в ПДФ. Является своеобразным «виртуальным» принтером и позволяет проверить перед печатью тот или иной документ. Распространяется она бесплатно и способна переформатировать любые файлы (документы Word, таблицы Excel, презентации PowerPoint, чертежи AutoCad и другие). К сожалению, в этой программе вы не найдете инструментов для создания и корректуры медиаконтента. Для начала работы откройте JPG в редакторе или средстве просмотра и сохраните в PDF через виртуальный принтер.

                  Smallpdf

                  Думаете, как из фото сделать ПДФ файл онлайн? Тогда воспользуйтесь простым конвертером Smallpdf. Зайдите на страницу сайта, загрузите нужный файл и скачайте, предварительно выбрав место хранения (облачное хранилище или устройство).

                  PDF Candy

                  PDF Candy — еще один онлайн-сервис, предоставляющий инструменты для работы с PDF-файлами. Есть также десктопная версия программы. Приложение поддерживает большое количество расширений, позволяет уменьшать размер документа без потери качества.

                  Между компьютерной и браузерной версиями программы имеются существенные отличия. Например, онлайн вы сможете выполнить только одну конкретную задачу: слить несколько ПДФ файлов в один, отредактировать документ или извлечь текст. Если хотите снять лимит, скачайте стационарный софт. Бесплатная версия позволит вам выполнять одновременно три операции, а платная – вообще снимает какие-либо ограничения.

                  Как приложение для конвертации JPG в PDF этот редактор отлично справляется со своей задачей. Для начала работы перейдите на главную страницу онлайн-ресурса, выберите пункт «JPG в PDF», добавьте один или несколько файлов и примените конвертацию. Вы можете выставить настройки для выходного файла, установить размер страницы и переставлять загруженные картинки в нужной последовательности, поскольку пакетная конвертация объединит все документы в один. Сам процесс занимает несколько секунд.

                  PDF.io

                  Хотите узнать как перевести фото в пдф на компьютере без дополнительного программного обеспечения? Это возможно, если у вас есть интернет. Да, речь пойдет еще об одном онлайн-ресурсе. Все что от вас потребуется – это перейти по ссылке, загрузить картинку, установить ориентацию и поля (опционально) и нажать на кнопку «Конвертировать».

                  Возможна загрузка фото не только с ПК, но и из облачного хранилища, а также при вставке прямой ссылки в специальную строку. Скачанный файл, к сожалению, немного теряет в качестве. Так что, если этот критерий для вас очень важен, рекомендуем воспользоваться другими вышеописанными средствами конвертации.

                  Вывод

                  Теперь вы знаете можно ли фото перевести в ПДФ и как это сделать. Если вы планируете заниматься редактирование документа после его преобразования, то выбирайте премиум-пакеты Adobe Acrobat или PDF-XChange Editor. С обычной конвертацией справятся простые онлайн-сервисы. А если у вас есть желание корректировать не только текстовые файлы, но и изображение выбирайте программу для редактирования фото, о которой мы упоминали в начале статьи. ФотоМАСТЕР имеет встроенный модуль печати, при помощи которого вы при наличии принтера сможете тут же распечатать снимок. Поддержка большинства популярных форматов, режим пакетной обработки и функции автоматического улучшения делают программу незаменимым помощником при работе с фотоснимками.

                  Бесплатный онлайн-конвертер JPG в PDF

                  Другие статьи >

                  • Учебные пособия ,

                    Как объединить JPG в PDF

                    JPG (или JPEG) — один из самых популярных форматов изображений. Иногда вам может потребоваться поделиться серией изображений или снимков экрана в формате JPG, если вы отправляете их по одному, получателям неудобно их просматривать. Хороший способ избежать хлопот — объединить все эти изображения JPG в один файл PDF и отправить их за один раз. Когда дело доходит до объединения файлов JPG в PDF, самым простым способом может быть вставка изображений JPG в документ Word, а затем экспорт Word в формате PDF. Этот метод аналогичен тому, что мы используем для создания PDF-файла с изображениями на Google Диске (как показано в разделе часто задаваемых вопросов в конце поста). Это работает, но не продуктивно. Чтобы эффективно объединить несколько файлов JPG в файл PDF с минимальными усилиями, можно использовать автономные и онлайн-программы. Что касается автономных программ, также известных как настольные программы, пользователи могут выбрать нужный продукт в соответствии со своей операционной системой. В Windows SwifDoo PDF удобен для объединения изображений JPG в один документ PDF. Пользователям macOS может помочь встроенная программа просмотра фотографий и PDF Preview. Что касается любого онлайн-конвертера, jpg2pdf доступен бесплатно. Кроме того, объединение изображений JPG в один PDF-файл легко выполнить с помощью Google Docs на Google Диске, Проводнике и виртуальном принтере Microsoft PDF. В следующем содержании объясняется, как объединить файлы JPG в PDF с помощью этих методов или программ соответственно. ## Как объединить изображения JPG в один PDF-файл с помощью SwifDoo PDF SwifDoo PDF — это многофункциональное PDF-приложение, применимое для пользователей Windows 7 и Windows 8/10/11. Он имеет более 30 инструментов PDF, которые позволяют быстро редактировать, сжимать, разделять, поворачивать документы PDF и многое другое. Программа может выступать в качестве мощного конвертера JPG в PDF. Он позволяет легко объединять группу изображений JPG в один файл PDF или преобразовывать их в несколько отдельных файлов PDF. Если вы хотите упорядочить все изображения на одной странице, используйте функцию создания PDF в приложении, чтобы создать пустую страницу PDF и вставить в нее изображения. ### Шаг 1: Бесплатно загрузите программное обеспечение SwifDoo PDF и запустите его; ### Шаг 2: Нажмите «PDF в Word» или «PDF в изображение» в домашнем интерфейсе; ![??102.png](https://wpsstrapicms.cache.wpscdn.com/102_ba8adf6c1f.png) ### Шаг 3: Во всплывающем окне SwifDoo PDF Converter выберите «Изображение в PDF» на левой панели, затем перетащите изображения JPG в интерфейс. 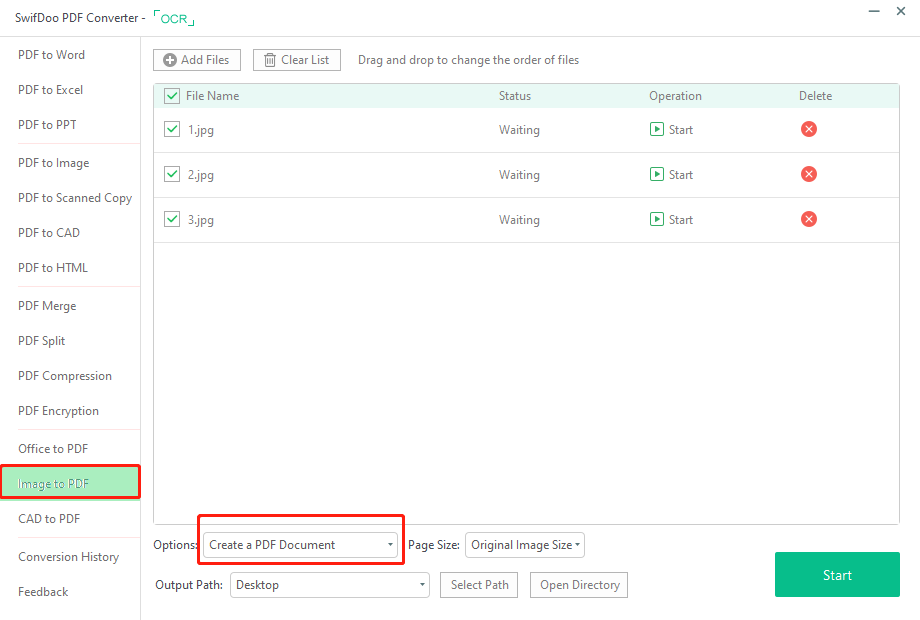В конце концов, изображения добавляются, вы можете перетаскивать их, чтобы изменить порядок; ![??103.png](https://wpsstrapicms.cache.wpscdn.com/103_16eeb5d7ff.png) ### Шаг 4: Убедитесь, что вы выбрали Создать документ PDF. Нажмите раскрывающееся меню «Размер страницы», чтобы установить ориентацию и размер страниц PDF; ### Шаг 5: Выберите выходной путь для сохранения преобразованного PDF. Нажмите кнопку Пуск, чтобы объединить файлы JPG в один файл PDF. Описанный выше метод используется для объединения нескольких файлов JPG (JPEG) в PDF с разными страницами. Это означает, что если вы выберете 2 изображения JPG для слияния, PDF будет создан с 2 страницами. Что делать, если вам нужно объединить 2 изображения JPG на одну страницу в PDF? Читай дальше что бы узнать. ## Вывод Если вы часто работаете с PDF-документами, рекомендуется установить настольное PDF-приложение вместо использования веб-инструмента. Первый всегда мощнее и безопаснее. Для пользователей Windows WPS Office может очень хорошо удовлетворить ваши потребности. Как конвертер JPG в PDF или объединитель PDF, WPS Office позволяет вам объединять несколько изображений или PDF-файлов в один PDF-файл за считанные секунды без потери качества. Кроме того, это также компрессор PDF, разделитель PDF, редактор PDF и т. д. Включая в себя полный набор функций PDF, WPS Office поможет вам работать более продуктивно.

                  • Инструкции ,

                    Как объединить JPG в PDF

                    Иногда, когда у нас есть набор изображений JPG или JPEG и мы можем поделиться ими с другими, мы выбираем сжатие изображений в файл. Но что, если мы не хотим, чтобы эти фотографии были скопированы или даже украдены для коммерческого использования? Можем ли мы объединить изображения JPG в PDF для кросс-платформенного обмена и представления с защитой интеллектуальной собственности? Здесь мы представляем вам решение для слияния и объединения изображений JPG в файл PDF. ## Метод -1 ### Шаг 1. Откройте изображения JPG в приложении «Фото» Перейдите к файлу, в котором находятся ваши изображения JPG, выберите те, которые вы хотите преобразовать. Щелкните правой кнопкой мыши, чтобы открыть меню, теперь выберите «Печать». ![??54.png](https://wpsstrapicms.cache.wpscdn.com/54_af5a608b59.png) ### Шаг 2. «Распечатайте» изображения JPG Появится новое окно с настройками печати. В столбце «Принтер» выберите «Microsoft Print to PDF» в раскрывающемся меню. Установите нужный размер и качество бумаги. Если выбранные вами изображения имеют разный размер, мы рекомендуем вам отметить вкладку «Подогнать изображение к рамке» внизу, чтобы убедиться, что каждая из преобразованных страниц PDF имеет одинаковый размер. 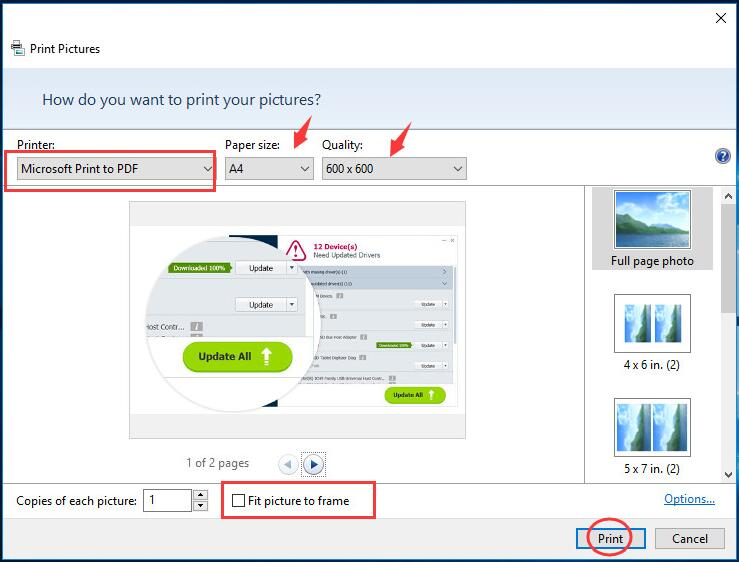![??55.png](https://wpsstrapicms.cache.wpscdn.com/55_f63e585c7c.png) Когда вы закончите все настройки, нажмите «Печать», чтобы сохранить JPG в формате PDF. #### Советы «1. Некоторые пользователи могут обнаружить, что параметр «Microsoft Print to PDF» отсутствует в этом параметре принтера. Это связано с тем, что вы не активировали его. Пожалуйста, следуйте этому видеоруководству «Как добавить Microsoft Print в PDF в Windows 10», чтобы заставить его работать. 2. Как конвертировать JPG в PDF в Windows 7 и Windows 8? Это видеоруководство «Как преобразовать изображения jpg в PDF без программного обеспечения в Windows 7 8 10» поможет вам четко его активировать». ### Шаг 3. Сохраните и объедините изображения JPG в PDF В окне «Сохранить вывод на печать как» выберите место для сохранения преобразованного PDF-файла и дайте ему имя, затем нажмите кнопку «Сохранить». 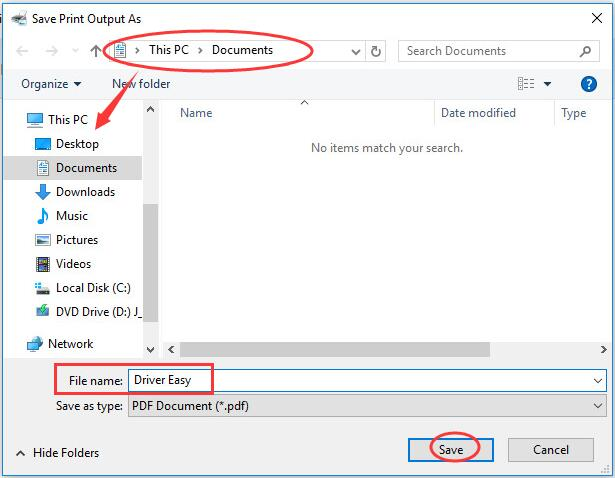![??56.png](https://wpsstrapicms.cache.wpscdn.com/56_943cedab76.png) ХОРОШО. Теперь у вас есть все ваши фотографии JPG, преобразованные в файл PDF, просто перейдите в папку, которую вы выбрали, чтобы открыть ее. Если сложные шаги ошеломляют вас, просто используйте онлайн-конвертер EasePDF, который сэкономит вам много времени. ## Метод -2 Онлайн-конвертер JPG в PDF — это служба, позволяющая конвертировать файлы JPG в PDF в любое время и в любом месте через подключение к Интернету. Здесь мы используем EasePDF в качестве демонстрации. ### Шаг 1. Нажмите JPG в PDF на главной странице EasePDF. ![??57.png](https://wpsstrapicms.cache.wpscdn.com/57_9b69c5dc4f.png) ### Шаг 2. Добавьте изображения JPG Вы можете загрузить фотографии в формате JPG тремя способами: 1. Перетащите изображения в область «Перетащите PDF сюда». 2. Нажмите кнопку «Добавить файл(ы)», чтобы загрузить изображения в формате JPG. 3. Добавьте изображения с вашего Google Диска, Dropbox или других URL-адресов. 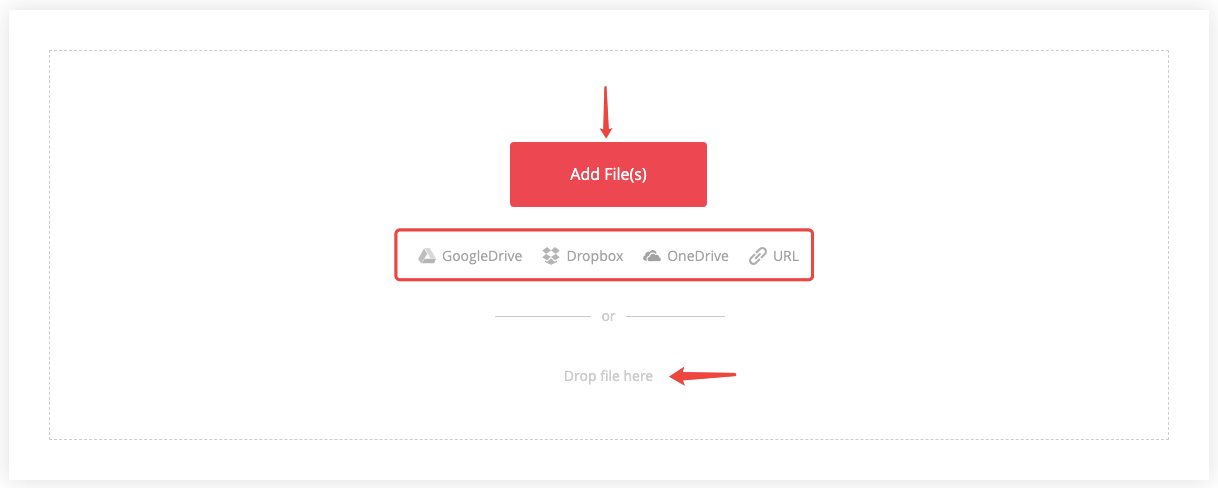![??58.png](https://wpsstrapicms.cache.wpscdn.com/58_eaa762e8fe.png) ### Шаг 3. Создайте PDF из JPG После завершения загрузки выбранных изображений появится новое окно для предварительного просмотра. ![??59.png](https://wpsstrapicms. cache.wpscdn.com/59_35462aae88.png) На этом этапе вы можете внести некоторые коррективы, если это необходимо, например: 1. Измените порядок изображений JPG, перетащив изображения предварительного просмотра. 2. Измените ориентацию изображений с помощью значка «Повернуть». 3. Нажмите на отдельное изображение, чтобы просмотреть информацию об изображении, перезагрузите изображение или увеличьте масштаб, чтобы увидеть подробности. 4. Удалите все изображения, которые вам не нужны для преобразования. 5. Добавьте другие изображения JPG для объединения в PDF. Когда все выглядит нормально для вас, нажмите кнопку «Создать PDF» справа внизу, чтобы начать преобразование и объединение JPG в PDF. ### Шаг 4. Загрузите преобразованный PDF Ваш комбинированный PDF-файл готов. Теперь выберите «Загрузить», чтобы загрузить новый PDF-файл на локальное устройство, или нажмите «Google Диск», «Dropbox», «URL», чтобы сохранить в Интернете или поделиться с другими. Если вам нужно выполнить еще одно преобразование, выберите «Начать сначала», чтобы начать другое задание. 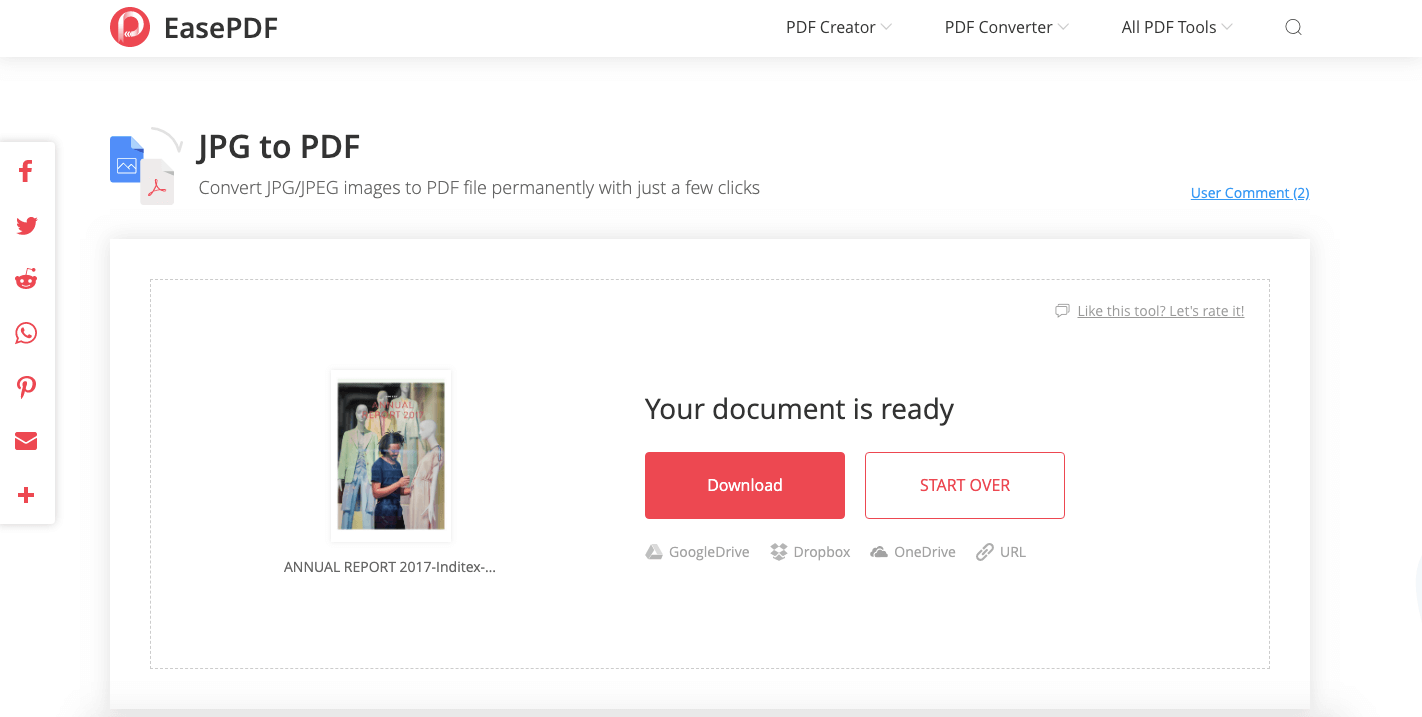![??60.png](https://wpsstrapicms.cache.wpscdn.com/60_a06b0b90da.png) Хотите объединить свои PDF-файлы в WPS Office? Ознакомьтесь с учебным пособием здесь: [Узнайте, как объединить файлы PDF с помощью WPS Office ](https://pdf.wps.com/blog/learn-how-to-merge-pdf-files-using-wps-office-post919/) ## Вывод Независимо от того, используете ли вы компьютер Mac или Windows, вы всегда можете использовать WPS Office — профессиональную программу для создания, преобразования, объединения и редактирования PDF-файлов. WPS Office – хороший выбор для создания, преобразования и объединения файлов JPG в PDF. Это легко и удобно в использовании.

                  • Учебники,

                    Как конвертировать JPG в PDF бесплатно двумя лучшими способами 2022

                    Когда вы делаете снимки и сохраняете их на своих мобильных телефонах и iPhone, они обычно сохраняются в формате JPG. Но если вам нужен PDF-файл вашего изображения, вы можете сделать это с помощью онлайн- и офлайн-программного обеспечения, уже имеющегося на вашем мобильном телефоне или ноутбуке. Преобразование изображений в формат PDF не приведет к потере качества исходного файла. Вы также можете легко объединить несколько фотографий в один файл PDF. Доступно несколько конвертеров JPG в PDF, большинство инструментов бесплатны, и вам не нужно платить ни копейки. Я здесь, чтобы рассказать вам о лучшем решении проблемы «Как бесплатно конвертировать JPG в PDF», используя эти инструменты. ## Как бесплатно конвертировать JPG в PDF с помощью ILovePdf ILovePDF — это бесплатный онлайн-конвертер, который конвертирует файлы JPG в PDF. Особенность этого инструмента доступна и удобна для пользователя. Он также легко регулирует ориентацию и поля документа. **Вот несколько шагов, которые нужно выполнить:** Шаг 1: Зайдите в браузер и выполните поиск «Я люблю pdf». Шаг 2: Внутри инструмента нажмите «Выбрать изображения JPG», а затем выберите изображения вручную с вашего устройства или загрузите изображения с диска Google или Dropbox. ![??52.png](https://wpsstrapicms.cache.wpscdn.com/52_a5bd6320ac. png) Шаг 3: задайте необходимые настройки и нажмите кнопку «Преобразовать в PDF». ![??53.png](https://wpsstrapicms.cache.wpscdn.com/53_510d4d414c.png) Шаг 4: После некоторой обработки преобразование документа начнется автоматически. ## Как бесплатно конвертировать JPG в PDF с помощью Smallpdf Это еще один инструмент, который предоставляет вам ту же функцию, что и инструмент I Love PDF. Он предлагает вам быстрое и простое преобразование файлов, а также гарантирует вам защиту файлов. Основная особенность заключается в том, что этот инструмент поддерживается всеми платформами, такими как мобильные устройства, ноутбуки, MAC и iPhone. Вот несколько шагов, которые помогут вам преобразовать изображения JPG в файлы PDF. Шаг 1: Откройте браузер и выполните поиск «smallpdf jpg to pdf convert». Шаг 2: Внутри конвертера загрузите файл JPG, нажав кнопку «Выбрать файл» или перетащив файлы JPG. ![??54.png](https://wpsstrapicms.cache.wpscdn.com/54_e37c008753.png) Шаг 3: На следующем экране после выполнения некоторых необходимых настроек нажмите кнопку «Преобразовать». ![??55.png](https://wpsstrapicms.cache.wpscdn.com/55_1b046d63b5.png) Шаг 4: Нажмите кнопку «Загрузить», ваш файл начнет загружаться. ## Заключительные слова Некоторые преимущества преобразования JPG в PDF заключаются в том, что вы можете сжимать файл PDF без потери качества изображений. Вы также можете загрузить программное обеспечение WPS Office с официального сайта, которое поможет вам «как бесплатно конвертировать JPG в PDF». Это программное обеспечение позволяет вам управлять документами Word, листами Excel и слайдами и обеспечивать безопасность ваших файлов.

                  15 бесплатных онлайн-конвертеров JPG в PDF

                  Вот список из лучших бесплатных онлайн-конвертеров JPG в PDF . JPG — это распространенный формат файла изображения, который поддерживается большинством устройств и платформ. Принимая во внимание, что PDF является распространенным форматом файлов для документов. Обычно он используется для обмена и печати. Если вы по какой-то причине хотите конвертировать изображения JPG в PDF, вы можете использовать эти веб-сайты для этого в Интернете.

                  Все эти веб-сайты бесплатны для использования, и вам не нужна учетная запись ни на одном из них. Вы можете просто посетить веб-сайт, добавить файлы JPG и преобразовать их в PDF. Этот список представляет собой смесь веб-сайтов, налагающих приличные ограничения для бесплатных пользователей или вообще не имеющих ограничений. Некоторые веб-сайты позволяют вам конвертировать любое количество файлов JPG в PDF, в то время как некоторые дают вам возможность выбрать, хотите ли вы объединить их в один PDF-файл или создать отдельный PDF-файл для каждого файла. Я кратко рассказал о каждом веб-сайте, затем рассказал о процессе преобразования и основных моментах веб-сайта. Вы можете просмотреть список и выбрать веб-сайт, который работает для вас.

                  Мой любимый онлайн-конвертер JPG в PDF

                  11zon — мой любимый онлайн-конвертер JPG в PDF в этом списке. В то время как некоторые конвертеры налагают некоторые ограничения на бесплатных пользователей, этот конвертер не имеет каких-либо ограничений. Нет ограничений на размер загрузки, файлов на конверсию и количество конверсий. Вы можете добавить столько файлов, сколько вам нужно, и преобразовать их все вместе в один файл PDF. Кроме того, вы получаете возможность установить формат страницы, ориентацию и поля, а также ползунок для настройки качества изображения. Этот набор инструментов позволяет создавать PDF-файлы точно в соответствии с вашими потребностями, включая размер PDF-файла.

                  Вы также можете ознакомиться с нашими списками лучших бесплатных онлайн-сайтов для разделения PDF-файлов, онлайн-сайтов для слияния PDF-файлов и онлайн-сайтов для ротации страниц PDF.

                  11zon

                  11zon предлагает различные типы бесплатных онлайн-инструментов, включая конвертеры, компрессоры, редакторы и многое другое. На этом сайте есть конвертер JPG в PDF, который вы можете использовать бесплатно. Этот преобразователь не накладывает никаких ограничений; ни по размеру загрузки, ни по количеству файлов, ни по количеству конверсий. Вы можете добавить любое количество файлов JPG, не беспокоясь о размере изображений. Позже вы можете настроить размер всех изображений с помощью общего ползунка качества. Этот конвертер показывает вам размер каждого изображения в реальном времени, пока вы меняете качество. Помимо качества, вы также можете установить формат, ориентацию и поля страниц для PDF. Когда преобразование завершится, вы получите размер окончательного PDF-файла, указанный чуть ниже кнопки загрузки. Если вы хотите еще больше уменьшить размер, вы можете сделать это прямо здесь. Этот веб-сайт предлагает другое качество изменения размера на странице загрузки. С этим изменением размера вы можете уменьшить размер PDF. Таким образом, вы можете получить окончательный PDF-файл нужного вам размера.

                  Как конвертировать JPG в PDF онлайн с помощью 11zon?

                  • Перейдите по ссылке, указанной ниже, чтобы получить доступ к этому онлайн-конвертеру JPG в PDF.
                  • Нажмите кнопку «Выбрать JPG» и загрузите файлы JPG.
                  • На следующем экране настройте вывод PDF в соответствии с вашими потребностями и при необходимости уменьшите качество.
                  • Запустите преобразование, чтобы получить файл PDF.
                  • Загрузите PDF-файл как есть или используйте ползунок изменения размера, чтобы еще больше уменьшить размер.

                  Моментов:

                  • Этот веб-сайт позволяет загружать любое количество файлов для преобразования JPG в PDF.
                  • Нет ограничений по размеру или конвертации, вы можете выполнять столько конвертаций, сколько вам нужно.
                  • Вы можете установить формат страницы, поля и ориентацию для PDF.
                  • Отрегулируйте качество для всего изображения, получая размер и миниатюру каждого файла.
                  • Показывает размер файла PDF перед загрузкой.
                  • Вы можете уменьшить размер файла PDF, изменив качество.
                  • После преобразования вы получаете ссылки на различные потенциально релевантные инструменты PDF, которые можно использовать сразу.

                  Домашняя страница

                  Инструменты PDF24

                  Инструменты PDF24 — еще один бесплатный сайт для онлайн-конвертации JPG в PDF. Этот веб-сайт также не имеет ограничений для конверсий. Вы можете добавлять и конвертировать любое количество изображений JPG в один PDF-файл. Вы можете добавлять изображения любого размера и выполнять столько преобразований, сколько вам нужно. Чтобы выполнить преобразование, вы можете добавить изображения из локального хранилища и облачных дисков. После этого он показывает все добавленные файлы на экране. Вы можете просмотреть каждый файл, изменить его положение и ориентацию. Затем вы можете преобразовать их в один файл PDF. Вы можете просмотреть файл PDF онлайн. Если вам нужно внести какие-либо изменения, вы можете вернуться и сделать это. В противном случае вы можете загрузить файл, а затем также немедленно удалить его с веб-сайта, если хотите.

                  Как конвертировать JPG в PDF онлайн с помощью инструментов PDF24?

                  • Используйте приведенную ниже ссылку, чтобы открыть этот конвертер.
                  • Добавьте файлы JPG в конвертер.
                  • Перетащите файлы, чтобы изменить порядок и ориентацию файлов.
                  • Запустите преобразование, чтобы получить один PDF-файл.
                  • Просмотрите PDF-файл и загрузите его.

                  Особенности:

                  • Этот веб-сайт может преобразовать любое количество изображений JPG в один файл PDF.
                  • Он поддерживает облачное хранилище (Google Диск и Dropbox) для прямого импорта и экспорта файлов.
                  • Нет ограничений на размер файла и количество преобразований.
                  • Вы можете переупорядочить файлы и изменить ориентацию.
                  • Вы можете просмотреть файлы до и после преобразования.
                  • Этот веб-сайт дает вам возможность удалить файлы с веб-сайта сразу после преобразования.

                  Домашняя страница

                  FormSwift

                  FormSwift — бесплатный онлайн-конвертер JPG в PDF. Этот веб-сайт содержит различные онлайн-инструменты PDF для создания, редактирования, подписи, преобразования и сжатия ваших документов. Конвертер JPG в PDF здесь прост в использовании. Он поддерживает пакетное преобразование. Вы должны добавить каждый файл отдельно; он не позволяет добавлять несколько файлов одновременно. Однако вы можете добавить столько изображений JPG, сколько вам нужно. Когда вы добавляете изображения, он показывает предварительный просмотр того, как каждое изображение будет выглядеть в PDF. Кроме того, он открывает PDF-файл в онлайн-редакторе, где вы можете помечать, подписывать и добавлять в файл основные моменты. Оттуда вы можете скачать файл. Если вы сначала создадите учетную запись, вы также можете отправить преобразованный PDF-файл по электронной почте прямо с этого веб-сайта.

                  Как конвертировать JGP в PDF онлайн с помощью FormSwift?

                  • Воспользуйтесь приведенной ниже ссылкой, чтобы открыть этот онлайн-конвертер JPG в PDF в своем браузере.
                  • Перетащите один файл JPG в конвертер.
                  • На следующем экране используйте кнопку Добавить больше страниц , чтобы добавить дополнительные файлы JPG.
                  • После этого нажмите кнопку Создать PDF , чтобы начать преобразование.
                  • Затем вы можете комментировать, подписывать и выделять страницы. Обрабатывается в соответствии с вашими потребностями.
                  • В конце загрузите PDF-файл, нажав на кнопку в правом верхнем углу.

                  Особенности:

                  • Этот веб-сайт позволяет конвертировать любое количество изображений JPG в один файл. Однако вы должны добавлять изображения JPG одно за другим.
                  • Размер изображений не ограничен, и вы можете выполнять любое количество преобразований по мере необходимости.
                  • При добавлении изображения вы получаете предварительный просмотр того, как каждое изображение будет выглядеть в окончательном PDF-файле.
                  • Вы можете редактировать окончательный PDF-файл, добавлять текст, выделять текст и подписывать страницы цифровой подписью.
                  • Создав учетную запись, вы можете отправлять PDF-файлы по электронной почте прямо с этого веб-сайта.

                  Домашняя страница

                  PDF.Online

                  PDF Online — еще один бесплатный сайт для онлайн-конвертации JPG в PDF. Этот веб-сайт предлагает десятки инструментов и утилит для работы с PDF. Он не имеет ограничений по размеру файла и количеству конвертаций. Вы можете добавить столько изображений JPG, сколько вам нужно, и преобразовать их в PDF. При этом вы можете изменить положение загрузки JPG и повернуть каждый файл по отдельности, чтобы изменить ориентацию. Вы также можете предварительно просмотреть любой файл в полном размере, чтобы просмотреть содержимое. Наконец, этот веб-сайт предлагает два метода преобразования. Либо вы можете объединить все изображения в один файл PDF. Или вы можете создать отдельные PDF-файлы для каждого изображения. Этот веб-сайт также позволяет вам удалить все ваши файлы после преобразования.

                  Как конвертировать JPG в PDF онлайн с помощью PDF Online?

                  • Используйте приведенную ниже ссылку, чтобы получить доступ к этому онлайн-конвертеру JPG в PDF.
                  • Добавьте файлы JPG в конвертер.
                  • Переставьте изображения и при необходимости измените ориентацию.
                  • Нажмите кнопку Создать PDF , чтобы начать преобразование.
                  • В конце нажмите кнопку Загрузить , чтобы получить преобразованный PDF-файл.

                  Основные моменты:

                  • Этот веб-сайт может конвертировать несколько изображений JPG в файлы PDF.
                  • Вы можете выбрать, хотите ли вы объединить все файлы в один PDF-файл или создать новый PDF-файл для каждого изображения.
                  • Нет ограничений на размер загрузки и количество конверсий.
                  • Вы можете добавить столько изображений, сколько вам нужно, изменить их положение и ориентацию в PDF.
                  • Предварительный просмотр каждого изображения, а также предварительный просмотр преобразованных PDF-файлов.
                  • Просмотрите окончательный комбинированный файл PDF перед загрузкой.
                  • После преобразования вы можете удалить свои файлы с веб-сайта, когда закончите.
                  • Этот веб-сайт также предлагает множество других утилит PDF для преобразования, редактирования, разделения, подписи и т. д.

                  Домашняя страница

                  PDF Converter

                  PDF Converter — бесплатный веб-сайт для конвертации JPG в PDF. Этот веб-сайт также поставляется с бесплатными и платными планами. Бесплатный план накладывает некоторые ограничения на размер файла и количество конверсий, которые вы можете выполнять на веб-сайте. Кроме того, в бесплатном плане вам нужно подождать 30 минут, прежде чем начинать следующие преобразования. Кроме того, вы можете загружать любое количество файлов из локального хранилища, Dropbox, Google Диска или через URL-адреса. После добавления файлов вы можете свободно менять их положение в документе и поворачивать их ориентацию. Наряду с PDF вы также можете вставить множество других файлов изображений и документов для объединения в PDF.

                  Как конвертировать JPG в PDF онлайн с помощью PDF Converter?

                  • Перейдите на веб-сайт PDF Converter, используя приведенную ниже ссылку.
                  • Выберите конвертер JPG в PDF , объяснив раздел Инструменты .
                  • Добавьте файлы JPG из локального хранилища или из Интернета.
                  • Измените положение и ориентацию каждого файла PDF.
                  • Нажмите кнопку Создать PDF , чтобы получить файл PDF.

                  Моментов:

                  • Этот веб-сайт может конвертировать несколько файлов JPG в один PDF-файл.
                  • Поддерживает импорт и экспорт для Dropbox и Google Drive.
                  • Вы можете переупорядочить изображения и изменить их ориентацию для PDF.
                  • В бесплатном плане количество конверсий ограничено.
                  • Между преобразованиями должно пройти 30 минут.
                  • Вы можете вставлять файлы других типов для объединения в PDF, включая Word, PowerPoint, Excel, Open Office и т. д.
                  • Удалите свои файлы с сайта сразу после конвертации.

                  Домашняя страница

                  JPG2PDF

                  JPG2PDF — это бесплатный онлайн-конвертер JPG в PDF. Этот веб-сайт предлагает множество конвертеров PDF для различных типов файлов. Все эти конвертеры можно использовать бесплатно без какой-либо регистрации или водяных знаков. Нет ограничений на размер загрузки, что означает, что вы можете легко конвертировать большие изображения JPG. Веб-сайт позволяет конвертировать до 20 файлов за одно преобразование. Это означает, что вы можете создавать файлы PDF до 20 страниц в зависимости от изображений JPG. На веб-сайте есть возможность импорта из облака, поэтому он работает только для локальной загрузки. После преобразования вы можете сохранить PDF и удалить все свои файлы с веб-сайта.

                  Как конвертировать JPG в PDF онлайн с помощью JPG2PDF?

                  • Используйте приведенную ниже ссылку, чтобы получить доступ к этому онлайн-конвертеру JPG в PDF.
                  • Нажмите кнопку «Загрузить файлы» и ваши файлы JPG (максимум 20).
                  • Затем нажмите кнопку «Комбинированный», чтобы преобразовать и загрузить PDF-файл.
                  • В конце очистите очередь файлов, чтобы удалить все ваши файлы с веб-сайта.

                  Особенности:

                  • Этот веб-сайт может конвертировать до 20 файлов за одно преобразование.
                  • Для файла JPG нет ограничений на размер загрузки.
                  • Каждый файл JPG добавляется как новая страница в PDF.
                  • Отсутствуют параметры форматирования, полей, качества и т. д.
                  • Вы можете удалить все свои файлы с сайта после конвертации.

                  Домашняя страница

                  Sejda

                  Sejda  – это бесплатная онлайн-утилита PDF, на которой собрано множество онлайн-инструментов, связанных с PDF. На этом веб-сайте вы можете редактировать, сжимать, разделять, объединять, подписывать, заполнять и конвертировать PDF-файлы онлайн. Вы можете загружать PDF-файлы со своего устройства или получать их из облака. Он предлагает просмотр файлов и просмотр страниц. Вы можете выбрать любой режим, чтобы установить порядок ваших файлов и страниц, а затем объединить их вместе. Вы можете загрузить несколько файлов размером до 200 страниц или 50 МБ. Однако вы ограничены 3 конверсиями в час. После этого нужно подождать час, чтобы слить еще.

                  Как объединить файлы PDF онлайн с Sejda?

                  • Перейдите на сайт Sejda и разверните раздел «Все инструменты».
                  • Выберите оттуда инструмент «Объединить PDF».
                  • Загрузите туда свои PDF-файлы и установите порядок файлов или страниц.
                  • Нажмите «Объединить PDF-файлы», чтобы получить один PDF-файл.

                  Особенности:

                  • Импорт PDF-файлов из Google Диска, Dropbox, OneDrive и Интернета.
                  • Существует ограничение на размер документов до 200 страниц или 50 МБ.
                  • Бесплатно выполнять 3 операции в час.
                  • Файлы остаются закрытыми и автоматически удаляются через 2 часа.

                  Домашняя страница

                  PDFCandy

                  PDFCandy — еще один веб-сайт с набором десятков инструментов и утилит для работы с PDF. Вы можете конвертировать JPG в PDF здесь. Этот веб-сайт позволяет вам установить размер страницы, ориентацию и поля для PDF. Вы также можете просмотреть и изменить порядок загруженных файлов JPG, но в нем отсутствуют параметры для поворота изображений. Бесплатная версия позволяет добавлять столько изображений, сколько хотите, если общий размер не превышает 500 МБ. Вы также можете добавлять файлы из облачного хранилища. После завершения преобразования вы можете загрузить PDF-файл или экспортировать его на облачный диск по вашему выбору. Вы также можете немедленно удалить файлы с веб-сайта.

                  Как конвертировать JPG в PDF онлайн с помощью PDFCandy?

                  • Перейдите по приведенной ниже ссылке, чтобы использовать конвертер JPG в PDF от PDFCandy.
                  • Перетащите файлы JPG в конвертер.
                  • Упорядочить положение файла и установить размер страницы для PDF.
                  • Запустите преобразование, чтобы загрузить файл PDF.

                  Особенности:

                  • Этот веб-сайт может конвертировать несколько файлов JPG в один PDF-файл.
                  • Он может импортировать файлы с Google Диска и Dropbox, а также может экспортировать их после преобразования.
                  • В случае пакетного преобразования общий размер ограничен 500 МБ.
                  • Время от времени вам, возможно, придется ждать своей очереди в очереди.

                  Домашняя страница

                  Online2PDF

                  Online2PDF — бесплатный веб-сайт для онлайн-конвертации JPG в PDF. Этот веб-сайт может обрабатывать несколько файлов одновременно. Вы можете добавить до 20 файлов JPG для конвертации. Но убедитесь, что общий размер всех объединенных файлов не должен превышать 150 МБ. Для одного файла максимальный размер загрузки составляет 100 МБ. Процесс преобразования JPG в PDF прост. Этот веб-сайт не предлагает возможность изменить ориентацию или переупорядочить файлы. Однако после преобразования отображаются другие утилиты PDF, которые можно использовать для просмотра, сжатия и защиты преобразованных PDF-файлов.

                  Как конвертировать JPG в PDF онлайн с помощью Online2PDF?

                  • Перейдите на веб-сайт Online2PDF и выберите PDF-Converter сверху.
                  • Прокрутите вниз до конвертера и добавьте туда файлы JPG.
                  • Нажмите кнопку Convert  , чтобы начать преобразование.

                  Особенности:

                  • Этот веб-сайт может конвертировать до 20 изображений JPG в один файл PDF.
                  • Ограничение общего размера файла на одно преобразование составляет 150 МБ; 100 МБ для одного файла.
                  • После преобразования PDF-файлы можно просматривать онлайн.
                  • Поддерживает импорт и экспорт в Google Drive и Dropbox.
                  • Позволяет защитить PDF-файлы паролем и разблокировать защищенные файлы.
                  • Вы также можете добавить верхние и нижние колонтитулы в PDF, а также изменить макет.

                  Домашняя страница

                  SmallPDF

                  SmallPDF предлагает различные типы конвертеров и утилит для файлов PDF. Вы можете найти бесплатный конвертер JPG в PDF на этом сайте. Этот конкретный конвертер позволяет вам конвертировать столько изображений JPG, сколько вы хотите, в один файл PDF. Вы можете добавлять файлы JPG любого размера из локального хранилища, Google Диска или Dropbox. Перед созданием файла PDF вы можете установить формат страницы и ориентацию в соответствии с вашими требованиями. Таким образом, вы можете конвертировать файлы JPG в отдельные файлы PDF. Обратите внимание, что вы можете выполнять только две конверсии в день. На этом веб-сайте также есть функция просмотра страниц, которая позволяет упорядочивать отдельные страницы из каждого файла PDF. Но эта функция входит в платный план.

                  Как конвертировать JPG в PDF онлайн с помощью SmallPDF?

                  • Перейдите по ссылке, указанной ниже, чтобы открыть этот онлайн-конвертер JPG в PDF.
                  • Загрузите изображение в конвертер JPG в PDF.
                  • Отрегулируйте размер букв, ориентацию и поля в соответствии с вашими потребностями.
                  • Нажмите Создайте PDF прямо сейчас! и дождитесь окончания преобразования.

                  Особенности:

                  • Этот веб-сайт может конвертировать любое количество файлов JPG в один файл PDF.
                  • Вы можете упорядочить файлы, чтобы установить порядок вывода PDF.
                  • Просмотр каждой страницы каждого файла PDF и упорядочивание отдельных страниц. (профессиональная функция)
                  • Этот веб-сайт предлагает 2 бесплатных преобразования в день.
                  • Кроме того, вы также можете легко поворачивать, комментировать, редактировать, обрезать, разделять PDF-файлы онлайн.

                  Домашняя страница

                  ILovePDF

                  ILovePDF — еще один сайт для онлайн-конвертации JPG в PDF. Хотя на этом веб-сайте вы можете найти различные инструменты для работы с PDF, давайте поговорим об этом конкретном конвертере. Он довольно прост в использовании и может конвертировать несколько файлов JPG в один или отдельные файлы PDF. Существует ограничение общего размера на конверсию в 25 МБ. Вы можете добавлять файлы из локального хранилища из Dropbox и Google Drive. После загрузки вы можете изменить порядок файлов и при необходимости повернуть их. Вы также можете настроить размер страницы, ориентацию и поля страницы. Затем вы можете начать преобразование. После конвертации вы можете скачать PDF-файл, скопировать ссылку на него и использовать ее, чтобы поделиться файлом, пока он не будет удален автоматически через 24 часа после конвертации. Но имейте в виду, что вы получаете 20 бесплатных заданий в месяц на ILovePDF. Это означает, что вы можете совершать до 20 конверсий в месяц.

                  Как конвертировать JPG в PDF онлайн с помощью ILovePDF?

                  • Перейдите на веб-сайт ILovePDF и выберите JPG в PDF в разделе Преобразование в PDF .
                  • Добавьте сюда свои файлы JPG или импортируйте изображения прямо из хранилища вашего диска.
                  • Расположите файлы вместе с возможностью поворота всего файла.
                  • Выберите, хотите ли вы объединить все изображения JPG в один PDF-файл или создать отдельный PDF-файл для каждого изображения.
                  • Установите размер страницы, ориентацию и поля для страниц PDF.
                  • Нажмите кнопку Преобразовать в PDF , чтобы получить окончательный PDF-файл.

                  Особенности:

                  • Этот веб-сайт может конвертировать несколько файлов JPG (общий размер до 25 МБ) в PDF.
                  • Позволяет импортировать и экспортировать файлы с Google Диска и Dropbox.
                  • Вы можете объединить все изображения в один файл PDF или создать отдельный файл PDF для каждого изображения.
                  • Вы можете вращать и изменять порядок изображений, а также устанавливать размер страницы, ориентацию и поля для PDF.
                  • Этот сайт предлагает 20 конверсий в месяц бесплатно.

                  Домашняя страница

                  Adobe Acrobat (онлайн)

                  Вы также можете использовать онлайн-версию Adobe Acrobat для преобразования JPG в PDF онлайн. Этот бесплатный инструмент может конвертировать один файл JPG за раз. Он не может объединять несколько изображений в один PDF-файл. Для входного изображения нет ограничений по размеру, и вы также можете выполнять несколько преобразований. Если вам нужно использовать только этот инструмент, вы можете конвертировать несколько изображений JPG одно за другим, а затем объединять все преобразованные PDF-файлы в один PDF-файл. Но это займет некоторое время. После преобразования вы можете предварительно просмотреть объединенный PDF-файл перед его загрузкой. Если все выглядит хорошо, вы можете скачать файл.

                  Как конвертировать JPG в PDF онлайн с помощью Adobe Acrobat?

                  • Используйте приведенную ниже ссылку, чтобы открыть этот конвертер в вашем браузере.
                  • Добавьте файл JPG в конвертер и начните конвертацию.
                  • Нажмите кнопку Загрузить , чтобы сохранить выходной PDF-файл.

                  Особенности:

                  • Этот веб-сайт может одновременно конвертировать только один файл JPG в PDF.
                  • Для входного файла нет ограничения на размер загружаемого файла.
                  • Вы можете получить доступ к другим функциям Adobe Acrobat для редактирования, преобразования, разделения, подписи, комментирования, поворота и защиты PDF-файлов.

                  Домашняя страница

                  PDFChef

                  PDF Chef — это бесплатный веб-сайт с различными инструментами для работы с PDF. Этот веб-сайт предлагает бесплатный онлайн-конвертер JPG в PDF. Конвертер прост в использовании, но он может конвертировать только один файл за раз. Размер вводимого JPG не ограничен. Вы можете преобразовать любое большое изображение в PDF. Но не хватает дополнительных опций. Это означает, что если вы хотите изменить ориентацию изображения, вы должны сделать это самостоятельно перед загрузкой изображения. Однако вы можете получить расширение PDFChef для Chrome для быстрого доступа ко всем инструментам с любой веб-страницы.

                  Как конвертировать JPG в PDF онлайн с помощью PDF Chef?

                  • Перейдите по ссылке, указанной ниже, чтобы открыть этот конвертер JPG в PDF.
                  • Загрузите файл JPG в конвертер. (один файл за раз)
                  • Подождите, пока он будет преобразован, и сохраните его из приглашения на загрузку, которое появляется на вашем экране.

                  Основные моменты:

                  • Этот веб-сайт может конвертировать только один JPG в PDF за раз.
                  • Размер вводимых данных не ограничен, но вы ограничены одним файлом.

                  Домашняя страница

                  AvePDF

                  AvePDF — еще один бесплатный онлайн-конвертер JPG в PDF. Этот веб-сайт может легко преобразовать один файл JPG в один PDF. Он имеет ограничение по размеру 256 МБ. Это означает, что вы можете конвертировать файлы такого размера. Для преобразования вы можете добавить файл из локального хранилища и загрузить его из Интернета. Поскольку это только один файл, нет возможности переупорядочить или изменить ориентацию. После процесса преобразования вы можете загрузить файл PDF или экспортировать его непосредственно на Google Диск или Dropbox.

                  Как конвертировать JPG в PDF онлайн с помощью AvePDF?

                  • Перейдите по ссылке, приведенной ниже, чтобы открыть этот конвертер.
                  • Перетащите файл JPG или загрузите его со своего устройства или из облачного хранилища.
                  • При добавлении файла преобразование начинается автоматически.
                  • Загрузите преобразованный PDF-файл на свой компьютер или сохраните его непосредственно в облачном хранилище.

                  Особенности:

                  • Этот веб-сайт преобразует один файл JPG в файл PDF.
                  • Вы можете добавить и преобразовать файл JPG размером до 256 МБ.
                  • Вы можете импортировать из Google Диска, Dropbox и Интернета (через URL-адрес).
                  • Все файлы автоматически удаляются через 30 минут вместе с возможностью удаления сразу после преобразования.

                  Домашняя страница

                  EasePDF

                  EasePDF — бесплатный веб-сайт для онлайн-конвертации JPG в PDF. Этот веб-сайт может легко конвертировать несколько файлов JPG в один файл PDF. Вы можете добавить до 50 файлов JPG для конвертера, каждый из которых имеет размер менее 10 МБ. После добавления файлов вы получаете возможность изменить расположение файлов для PDF. Кроме того, вы также можете выбрать размер страницы, ориентацию и поля для документов. После завершения преобразования вы можете загрузить результат, отправить его на облачный диск, скопировать ссылку, поделиться по электронной почте или с помощью QR-кода. Обратите внимание, что этот сайт предлагает 2 бесплатные конверсии в течение 24 часов.

                  Как конвертировать JPG в PDF онлайн с помощью EasePDF?

                  • Перейдите на веб-сайт EasePDF и выберите функцию конвертера JPG в PDF в Tools .
                  • Добавьте файлы JPG в конвертер.
                  • При необходимости поверните изображения JPG.
                  • Прокрутите вниз и настройте макет, размер страницы и поля PDF.
                  • Запустите процесс преобразования, чтобы получить один файл PDF.

                  Особенности:

                  • Этот веб-сайт конвертирует несколько файлов JPG в один файл PDF.
                  • Вы можете добавить до 50 файлов JPG за одно преобразование.
                  • Вы можете получать PDF-файлы напрямую из Dropbox и Google Drive.
                  • Размер каждого файла JPG не должен превышать 10 МБ.
                  • Предварительный просмотр каждого файла PDF страница за страницей и установка порядка страниц/файлов.
                  • Экспортируйте выходные данные на свой облачный диск или поделитесь ими по ссылке, QR-коду или электронной почте.
                  • Вы получаете 2 бесплатные конверсии в день.

                  Домашняя страница

                  Похожие сообщения

                  Написать комментарий

                  [5 лучших] Лучшие приложения для конвертации JPG в PDF для различных ОС

                  Ознакомьтесь с лучшими приложениями для конвертации JPG в PDF, доступными для Интернета, Windows, Android, iOS и Mac. Также узнайте, как преобразовать JPG в PDF:

                  PDF и JPG являются широко используемыми форматами, и иногда вам может понадобиться преобразовать JPG в PDF по разным причинам.

                  В этой статье представлены различные инструменты для Интернета, Windows, Android, iOS и Mac, которые можно использовать для преобразования изображений в PDF.

                  Чему вы научитесь:

                  • Приложения для конвертации JPG в PDF
                  • Онлайн-приложения
                    • #1) Free PDF Convert
                    • #2) Adobe Acrobat
                    • #3) Small PDF
                    • #4) PDF.online
                    • #5) PDF.online
                    • #5
                  • Приложения для Windows
                    • #1) TalkHelper PDF Converter
                    • #2) Apowersoft Image to PDF Converter
                    • #3) PDFElement-PDF Editor
                    • #4) Icecream PDF Converter
                      • 5)9005
                  • Приложения для Android
                    • #1) Преобразование изображений в PDF
                    • #2) Преобразование изображений в PDF
                    • #3) Фото в PDF
                    • #4) Фото в PDF – конвертирование одним нажатием
                    • #5) Несколько файлов изображений или фотографий в PDF Converter
                  • Приложения для iOS
                    • #1) Опция печати
                    • #2) Книги
                    • #3) Приложение файлов
                    • #4) PDF Эксперт
                    • #5) Примечания
                  • #5) Примечания
                • 9005 3
                • .
                • #1) Предварительный просмотр
                • #2) JPG в PDF
                • #3) Prizmo5
                • #4) Automator
                • #5) Adobe Acrobat для Mac
              • Часто задаваемые вопросы
              • Заключение
                • Рекомендуемое чтение

                  Онлайн-приложения

                  Многие хорошие веб-сайты позволяют конвертировать JPG в PDF без хлопот с загрузкой приложений. Вот 5 лучших веб-сайтов, на которых вы можете рассчитывать на беспроблемную конвертацию:

                  #1) Free PDF Convert

                  Веб-сайт: Преобразование PDF бесплатно

                  Цена:

                  • 1 месяц — 9 долларов США в месяц
                  • 12 месяцев — 49 долларов в год
                  • Пожизненно — 99 долларов Однократно

                  Чтобы преобразовать JPG в PDF, выполните следующие действия:

                  • Перейдите на веб-сайт.
                  • Щелкните стрелку рядом с онлайн-конвертером PDF.
                  • Выберите JPG в PDF, как показано ниже.

                  • Нажмите «Выбрать файл изображения».
                  • Выберите вариант, откуда вы хотите загрузить файл.

                  • Нажмите на знак «плюс», чтобы добавить столько файлов JPG, сколько хотите.
                  • Отметьте, хотите ли вы объединить все изображения в один PDF-файл или создать отдельные файлы.
                  • Нажмите «Преобразовать PDF».
                  • После завершения преобразования нажмите «Загрузить», чтобы сохранить файл на своем устройстве.
                  • Или нажмите на стрелку рядом с ним, чтобы сохранить его на Google Диске или в Dropbox.

                  #2) Adobe Acrobat

                  Веб-сайт: Adobe Acrobat

                  Цена:

                  • Acrobat Pro DC — 14,99 долларов США в месяц
                  • Acrobat PDF Pack — 9,99 долларов США в месяц

                  Чтобы преобразовать JPG в PDF, выполните следующие действия:

                  • Перейдите на веб-сайт Adobe.
                  • Щелкните PDF и электронные подписи.
                  • Выберите Adobe Acrobat.

                  • Перейдите в раздел «Функции и инструменты».
                  • Нажмите «Преобразовать PDF-файлы», как показано ниже.

                  • Перейдите к опции JPG to PDF и нажмите «Попробовать сейчас».

                  • Нажмите кнопку «Выбрать файл».
                  • Перейдите к файлу JPG, который вы хотите преобразовать в PDF.
                  • Нажмите на JPG, чтобы загрузить его.
                  • Когда файл будет сконвертирован, нажмите «Загрузить».

                  #3) Small PDF

                  Веб-сайт: Small PDF

                  Цена:

                  • Pro — 9 долларов США в месяц за пользователя, оплачивается ежегодно.
                  • Team — 7 долларов США в месяц за пользователя, оплачивается ежегодно.

                  Чтобы преобразовать JPG в PDF, выполните следующие действия:

                  • Перейдите на веб-сайт.
                  • Прокрутите вниз, чтобы найти раздел «Самые популярные инструменты PDF».
                  • Выберите JPG в PDF, как показано на рисунке ниже.

                  • Нажмите «Выбрать файлы».
                  • Выберите, откуда вы хотите загрузить файлы.

                  • Выберите файл JPG, который вы хотите преобразовать.
                  • Нажмите на значок плюса, чтобы добавить больше изображений.
                  • Затем нажмите «Преобразовать».
                  • После преобразования файла нажмите «Загрузить» или выберите один из других вариантов.

                  #4) PDF.online

                  Веб-сайт: PDF.online

                  Цена: Бесплатно

                  Выполните следующие действия, чтобы преобразовать JPG в PDF: 5 12

                  900

                • Нажмите на опцию JPG в PDF

                • Выберите, откуда вы хотите загрузить файл JPG для преобразования.
                • Выберите файл.

                • Когда преобразование будет завершено, нажмите «Загрузить».

                #5) JPG в PDF

                Веб-сайт: JPG в PDF

                Цена: Бесплатно

                Чтобы преобразовать JPG в PDF, выполните следующие действия:

                9003 900

              • Выберите JPG в PDF.
              • Нажмите «Загрузить файлы».

              • Выберите файл JPG, который вы хотите преобразовать, и нажмите «Открыть».
              • После преобразования вы можете загрузить файл PDF.

              Приложения для Windows

              Вот 5 лучших приложений, которые вы можете загрузить на свой ноутбук, чтобы преобразовать JPG в PDF:

              #1) TalkHelper PDF Converter

              Веб -сайт: TalkHelper Pdfter

              Веб -хэм: TalkHelper PdfTer

              Веб -хэм: TalkHelper PdfTer

              . Цена: 29,95 долларов США

              Чтобы преобразовать файлы из JPG в PDF, выполните следующие действия:

              • Загрузите и установите приложение.
              • Запустите TalkHelper PDF Converter.
              • Нажмите «Преобразовать файлы в PDF».
              • Выберите изображение в PDF.

              • Выберите файл изображения или папку, которую вы хотите преобразовать.
              • Нажмите «Преобразовать».

              • Когда файл преобразован, щелкните значок файла, чтобы просмотреть его и параметр папки, чтобы открыть папку, в которой он сохранен.

              #2) Apowersoft Image to PDF Converter

              Веб-сайт: Apowersoft Image to PDF Converter

              Цена: 

              • Персональный
                • Ежемесячно: $19,95
                • Годовой: $29,95
                • Срок службы: $39,95
              • Бизнес
                • Годовой: $79,95
                • Срок службы: $159,90
                • Team Lifetime Version: 119,90 долл. США за пользователя для более чем одного пользователя

              Чтобы преобразовать файлы из JPG в PDF, выполните следующие действия:

              • Загрузите и установите приложение.
              • Запустить конвертер.
              • Нажмите «Преобразовать в PDF», как показано на изображении ниже.

              • Нажмите на изображение в PDF

              • Нажмите на плюс, чтобы добавить файл
              • В нижней части экрана укажите, куда вы хотите сохранить преобразованный файл
              • Нажмите Конвертировать
              • После преобразования файла вы сможете увидеть его в выбранной выходной папке

              #3) Редактор PDFElement-PDF

              Веб-сайт: Редактор PDFElement-PDF

              Цена:

              • Индивидуальный
              1. PDFelement: $69/год
              2. PDFelement Pro: 79 долларов США в год
              • PDFelement Pro для Team
                1. Оплата ежегодно: 109 долл. США/пользователь
                2. Бессрочная лицензия: $139/пользователь

              Чтобы преобразовать JPG в PDF, выполните следующие действия:

              • Загрузите и установите элемент PDF
              • Запустить приложение
              • Нажмите «Создать PDF»
              • Выберите файл, который вы хотите конвертировать
              • Нажмите Открыть

              Теперь вы сможете сохранить PDF-файл или отредактировать его.

              Рекомендуемая литература =>> Обзор лучших редакторов PDF

              #4) Icecream PDF Converter

              Веб-сайт: Icecream PDF Converter

              Цена: PDF Converter PRO: $19 95

              Выполните следующие действия, чтобы преобразовать JPG в PDF:

              • Загрузите и установите PDF Converter.
              • Запустите приложение.
              • Выберите параметр «В PDF» на главном экране.

              • Добавьте файл.
              • Выберите папку назначения для сохранения преобразованного файла.
              • Нажмите «Преобразовать».

              #5) Изображение до PDF

              Веб -сайт: Изображение до PDF

              Цена: БЕСПЛАТНО

              Следуйте шагам ниже, чтобы конвертировать JPG с PDF:

              . приложение.
            • Запустить изображение в PDF.
            • Нажмите «Добавить изображение».
            • Перейдите к изображению, которое вы хотите преобразовать.
            • Выберите Открыть.
            • Нажмите «Начать преобразование».

            • Выберите папку, в которой вы хотите сохранить преобразованный файл.

            Приложения для Android

            Когда дело доходит до смартфонов, наличие приложения всегда полезно. Вот 5 приложений, которые вы можете использовать на своих устройствах Android:

            #1) Конвертер изображений в PDF

            Веб-сайт: Скачать конвертер изображений в PDF

            Цена: Бесплатно

            Выполните следующие действия, чтобы конвертировать Файлы JPG в PDF:

            • Загрузите приложение.
            • Запустить.
            • Щелкните значок изображения.
            • Выберите Преобразовать в PDF в нижней части окна.

            • Выберите настройки и нажмите OK.

            • После завершения преобразования вы можете открыть PDF-файл или поделиться им.

            #2) Конвертер изображений в PDF

            Веб-сайт: Скачать конвертер изображений в PDF

            Цена: Бесплатно

            Чтобы преобразовать JPG в PDF, выполните следующие действия:

            • Загрузите и запустите приложение.
            • Нажмите на знак плюса, чтобы добавить JPG.
            • Теперь выберите значок PDF.

            • Настройте параметры по своему вкусу.
            • Нажмите «Сохранить PDF».

            • После завершения преобразования вы можете либо открыть его, либо отправить.

            #3) Фотографии в PDF

            Веб-сайт: Загрузка фотографий в PDF

            Чтобы преобразовать JPG в PDF, выполните следующие действия:

            • Загрузите и запустите приложение
            • Нажмите кнопку плюс

            • Выберите макет страницы.
            • Щелкните Далее.
            • Выберите параметры документа.
            • Щелкните Далее.
            • Проверьте настройки.
            • Нажмите «Создать и опубликовать PDF».

            #4) Фото в PDF – Преобразование в один клик

            Веб-сайт: Загрузка фото в PDF – Конвертер в один клик

            Цена: Бесплатно

            Чтобы конвертировать JPG в PDF, выполните следующие действия:

            • Загрузите и запустите приложение.
            • Щелкните значок изображения, чтобы загрузить файл из галереи, или щелкните изображение.

            • Выберите файл.
            • Нажмите «Готово».
            • После преобразования JPG в PDF им можно поделиться.

            #5) Конвертер нескольких файлов изображений или фотографий в PDF

            Веб-сайт: Загрузка нескольких файлов изображений или фотографий в конвертер PDF

            Цена: Бесплатно

            Выполните следующие действия, чтобы преобразовать файлы/фотографии JPG в PDF:

            • Загрузите и откройте приложение.
            • Нажмите «Добавить изображения», чтобы добавить несколько изображений, или «Добавить папку», чтобы добавить всю папку.

            • Перейдите к изображению, которое вы хотите преобразовать.
            • Выберите Применить.
            • Нажмите «Создать PDF».

            • После создания PDF-файла его можно открыть или поделиться

            Приложения для iOS

            iOS поставляется с несколькими встроенными приложениями, которые можно использовать для преобразования JPG в PDF.

            #1) Опция печати

            Опция печати — это самый простой способ преобразования JPG в PDF. Выполните следующие действия:

            • Открыть фотографии.
            • Нажмите «Альбомы».
            • Щелкните Выбрать.
            • Выберите изображения, которые вы хотите преобразовать.
            • Нажмите «Поделиться».
            • Выберите Печать.

            [ изображение источник ]

            • Сдвиньте изображение наружу, чтобы превратить все в PDF
            • Проведите по миниатюре страницы на экране предварительного просмотра PDF, чтобы проверить, все ли в порядке
            • Нажмите «Поделиться», чтобы поделиться преобразованным PDF-файлом.

            #2) Книги

            Книги — это встроенное в iOS приложение, которое можно использовать для преобразования JPG в PDF.

            Выполните следующие действия:

            • Выберите изображения, которые вы хотите преобразовать в PDF.
            • Нажмите «Поделиться».
            • Нажмите на Книги.

            [изображение источник ]

            • Изображения будут автоматически преобразованы в PDF и открыты в Книгах

            #3) Приложение Files

            Приложение Files — еще одно встроенное приложение в iOS, которое может быть очень удобным, если вы хотите использовать Apowersoft Image to PDF Converter.

            Выполните следующие действия:

            • Перейдите к фотографиям.
            • Выберите изображения, которые вы хотите преобразовать в PDF.
            • Нажмите «Поделиться».
            • Сохранить в файлы.

            • Перейти к файлам.
            • Чтобы преобразовать одно изображение в PDF, нажмите и удерживайте его и выберите «Создать PDF».

            [изображение источник ]

            • Для преобразования нескольких изображений нажмите на три горизонтальные точки в правом верхнем углу.
            • Выберите несколько фотографий.
            • Нажмите на три горизонтальные точки внизу экрана.
            • Выберите Создать PDF.

            #4) PDF Expert

            Веб-сайт: Скачать PDF Expert

            Цена: Бесплатно

            Выполните следующие действия, чтобы преобразовать JPG в PDF:

          • 0 Открыть PDF1 Expert 2
            • Коснитесь знака плюс внизу

            [изображение источник ]

            • Импортируйте изображение, которое хотите преобразовать, из фотографий, файлов или облака.
            • Коснитесь трех горизонтальных точек, чтобы открыть дополнительные параметры.
            • Выберите Преобразовать в PDF.

            #5) Notes

            Notes — это встроенное приложение, которое можно использовать не только для создания заметок. Вы можете использовать его для преобразования JPG в PDF.

            Следуйте инструкциям:

            • Примечания к запуску.
            • Нажмите на опцию «Новые заметки».
            • Щелкните значок плюса.

            .

            [изображение источник ]

            • Выберите «Библиотека фотографий», если вы хотите преобразовать изображение из библиотеки, или нажмите «Сделать фото»

            [изображение источник ]

            • Выберите изображение, которое вы хотите преобразовать
            • Нажмите «Поделиться»
            • Перейти к опции «Создать PDF»

            [изображение источник ]

            • Если предварительный просмотр в порядке, нажмите кнопку «Готово».
            • Сохраните файл.

            Приложения для Mac

            Как и iOS, Mac поставляется с несколькими приложениями, которые могут удобно конвертировать JPG в PDF.

            #1) Предварительный просмотр

            Предварительный просмотр — это встроенное в Mac приложение, с помощью которого можно легко конвертировать JPG в PDF.

            • Открыть предварительный просмотр.
            • Перейти в меню «Файл».
            • Выберите Открыть.
            • Найдите изображение, которое хотите открыть.
            • После того, как изображение отобразится, снова нажмите на опцию «Файл»
            • Выберите Экспорт в формате PDF

            [изображение источник ]

            Выберите имя файла и место, где вы хотите его сохранить.

            #2) JPG в PDF

            Веб-сайт: Скачать JPG в PDF

            Цена: Бесплатно

            Выполните следующие действия, чтобы преобразовать JPG в PDF:

            3 90 Загрузите приложение.

          • Нажмите Добавить файлы.
          • Импортируйте файл или файлы, которые вы хотите преобразовать.
          • Нажмите на файлы.
          • Выберите Преобразовать.
          • Установите флажок «Объединить в один файл», если вы хотите, чтобы все изображения были в одном файле PDF.
          • Нажмите Экспорт.

          #3) Prizmo5

          Веб-сайт: Скачать Prizmo5

          Цена:

          • Prizmo: $49,99 9001
          • Набор Prizmo+Pro: $74,99

          Чтобы преобразовать JPG в PDF, выполните следующие действия:

          • Запустите Prizmo.
          • Перейти в меню.
          • Нажмите «Создать».

          [изображение источник ]

          • Выберите «Открыть файл изображения».

          • Откройте файл, который вы хотите преобразовать
          • Перейти к опции «Поделиться»
          • Выбрать PDF

          [изображение источник ]

          • Назовите файл и выберите место для его сохранения.
          • Нажмите Сохранить.

          #4) Automator

          Мало кто знает, но вы можете использовать Mac Automator для преобразования JPG в PDF.

          • Перейти к приложению.
          • Выберите Автоматизатор.
          • Щелкните Рабочий процесс.

          .

          [изображение источник ]

          • Перейдите в «Файлы и папки».
          • Щелкните PDF-файлы.
          • Выберите «Новый PDF» в разделе «Изображения».
          • Выберите файл, который хотите преобразовать.
          • Установите флажок Разрешить множественный выбор, если вы хотите преобразовать несколько изображений в один PDF-файл.
          • Выберите выходную папку.
          • Нажмите «Выполнить».

          #5) Adobe Acrobat для MAC

          Веб -сайт: Adobe Acrobat для MAC

          Цена:

          Индивидуальное:

          • .9/мес
          • Acrobat Pro DC: 14,99 долларов США в месяц

          Бизнес:

          • Acrobat DC для команд: 15,70 долларов США в месяц/лицензия

          Студенты и преподаватели

          • Acrobat Pro DC: 14,99 долларов США в месяц
          • Все приложения Creative Cloud: 19,99 долларов США в месяц

          Чтобы преобразовать JPG в PDF, выполните следующие действия:

          • Запустите Adobe Acrobat на Mac.
          • Нажмите «Создать PDF».
          • Выберите «Один файл», чтобы преобразовать одно изображение, и «Несколько файлов», чтобы создать один PDF-файл из нескольких изображений.

          • Выберите файл для преобразования.
          • Нажмите Открыть.

          • Выберите Создать PDF.
          • Когда файл PDF откроется, нажмите «Файлы» и выберите «Сохранить как».
          • Сохраните файл.

          Часто задаваемые вопросы

          Вопрос № 1) Какое приложение лучше всего подходит для преобразования JPG в PDF?

          Ответ: Существует множество приложений, которые можно использовать для преобразования JPG в PDF. Однако Adobe Acrobat — самый безопасный и надежный вариант. Вы также можете использовать параметр «Печать» для преобразования изображений в PDF.

          Читайте также =>> Инструменты для конвертации EPUB в PDF

          Вопрос №2) Как конвертировать JPG в PDF в Windows?

          Ответ: Откройте проводник и найдите файлы JPG, которые вы хотите преобразовать. Теперь щелкните файл правой кнопкой мыши и выберите «Печать». Измените принтер на Microsoft Print to PDF. Вы найдете эту опцию, если у вас установлен Adobe Reader DC. И нажмите «Печать». Ваши изображения будут преобразованы в PDF.

          Q #3) Как конвертировать изображение в PDF бесплатно?

          Ответ: Вы можете использовать такие веб-сайты, как Cloud convert, Free pdf convert, Small pdf и т. д., чтобы конвертировать JPG в PDF бесплатно.

          Q #4) Как преобразовать JPG в PDF на телефоне Android?

          Ответ: Вы можете использовать конвертер JPG в PDF для своего телефона Android. Вы также можете найти различные приложения в своем магазине Google Play, которые могут конвертировать изображения в PDF.

          Вопрос № 5) Могу ли я конвертировать PDF в JPG в Chrome?

          Ответ: Да. В меню Chrome три вертикальные точки перейдите в раздел «Дополнительные инструменты» и нажмите «Расширение». Найдите jpegify и добавьте его в Chrome. Откройте новую вкладку, нажмите «Выбрать файл», загрузите PDF-файл, который хотите преобразовать, и нажмите «Преобразовать в JPG». Вы получите zip-файл для преобразованных файлов.

          Заключение

          С таким количеством приложений, доступных для различных платформ, вы можете легко конвертировать файлы изображений в PDF. Вы можете сделать это онлайн, загрузить приложение или использовать некоторые встроенные приложения и опции для той же цели.

          Читайте также =>> Инструменты конвертера PDF в Word

          Простота использования будет зависеть от того, что отвечает вашим потребностям в данный момент. Каждый из них имеет свой собственный набор преимуществ и недостатков.

          Попробуйте несколько из них и выберите наиболее подходящий для вас.

          Рекомендуемая литература

          Бесплатный инструмент для конвертации JPG в PDF

          Камера не обнаружена или доступ к камере заблокирован. Если заблокировано, включите камеру, щелкнув значок камеры в адресной строке.

          Перетащите сюда изображения JPEG

          Ориентация страницы

          Портрет Пейзаж

          Размер страницы

          Письмо Юридический — А4 — Подробнее …ПисьмоПравительственное письмоЮридическийЮниорский юридический журналБазовая книгаКредитная карта- A1 — A2 — A3 — A4 — A5 — A6 — A7 — B4 — B5 –

          Поля страницы

          Никто Маленький Обычный Большой

          Размер изображения

          Оригинал Посадка по ширине Подгонка по высоте

          %

          Заголовок страницы

          * Для экономии бумаги лучше отправить по электронной почте или распечатать на двух сторонах.

          Вам надоело отправлять несколько изображений на друзья все время? Что, если мы скажем, что у нас есть легкий выход? JustFreetools. com предлагает онлайн-конвертер jpg в pdf, который объединит все ваши изображения в один файл PDF.

          Вы можете легко загрузить этот файл и поделиться им с ваша семья и друзья. Наш конвертер jpg в pdf онлайн сохранит оригинал разрешающая способность. Тем не менее, он оптимизирует и уменьшает изображение в соответствии с требования.

          Теперь давайте посмотрим на некоторые особенности нашего jpg, чтобы конвертер пдф онлайн.

          Особенности

          Быстро и легко Преобразование  


          Наш онлайн-конвертер jpg в pdf можно использовать довольно без труда. Все, что вам нужно сделать, это перетащить изображения в нужные раздел. Выберите необходимые параметры и настройте файл в соответствии с вашими предпочтение, и все, все готово.


          Гарантированная защита файлов


          Безопасность превыше всего. Без задней мысли. Вот почему мы используем SSL-шифрование, чтобы ваши изображения оставались в безопасности на протяжении всего процесса преобразование. Нет даже ни одного человека, который получит доступ к вашему картинки. Они также будут удалены с нашего веб-сайта, когда вы закончите использовать наш инструмент.


          Без ограничений JPG


          Наш инструмент не ограничивает вас, когда он приходит к количеству изображений. Добавьте столько, сколько хотите. Наш преобразователь будет справлюсь со всеми нормально.


          Пользовательский PDF

          Вы сами выбираете формат, ориентация, поля и размер файла PDF. Вы можете выбрать любой вариант хочу.

          Ваш JPG конвертируется быстро

          Вы получите свой PDF-файл в свои руки в мгновение ока. Justfreetools.com не просит вас регистрироваться на веб-сайте и нет никакого другого процесса, через который вам придется пройти. Просто перетащите изображения и дайте им преобразоваться в файл PDF.

          Поддерживаются все платформы

          Наш конвертер jpg в pdf онлайн: поддерживается всеми платформами. Это в основном инструмент на основе браузера, и он не требует какой-либо ОС для эффективной работы. Итак, неважно, если у вас есть Linux, Mac или Windows, вы можете свободно использовать наш конвертер изображений в pdf.

          Добавить дополнительные документы

          Если вы хотите добавить больше файлов в свой уже загруженные, вы можете легко это сделать. Просто повторите шаги, которые вы сделали загрузить предыдущие.

          Другие форматы изображений

          Наш конвертер jpg в pdf онлайн не только поддерживает изображения JPG, но вы также можете добавить множество других форматов, таких как BMP, PNG, GIF и TIFF. Просто бросьте их в нужный ящик и сохраните в PDF формат.

          Бесплатный сервис

          Наш онлайн-инструмент для конвертации jpg в pdf абсолютно бесплатно, и любой, у кого есть хорошее интернет-соединение, может использовать его Сервисы. Все становится лучше, когда это бесплатно, не так ли?

          Как конвертировать JPG в PDF онлайн с помощью нашего инструмента?

          Наш онлайн Конвертер jpg в pdf — очень простой в использовании инструмент. Чтобы преобразовать jpg в pdf онлайн, вам нужно всего лишь выполнить следующие шаги.

          · Тяга и перетащите изображения в нужное поле или откройте их.

          · Выбирать все необходимые параметры, такие как ориентация страницы, размер страницы, поля страницы, размер изображения и, наконец, название вашей страницы.

          · Нажмите на ‘ создайте PDF ‘ .

          · Один раз ваш pdf готов, вы можете нажать ‘ сохранить PDF ‘ и он будет сохранен на вашем компьютер.

          Сейчас, давайте рассмотрим некоторые часто задаваемые вопросы наших пользователей.

          Часто задаваемые вопросы

          Зачем использовать конвертер JPG в PDF?

          JPG менее подходят, чем PDF для печать

          Наиболее предпочтительный формат фотографий: JPG. В большинстве смартфонов ожидаемым типом файла всегда является JPG. Например, приложение галереи вашего телефона поддерживает этот тип. Однако там это один из случаев, когда JPG не работает, и это область печати. Когда дело доходит до получения фотографии на листе, работа кажется проще, но это совершенно противоположный. Многие наши пользователи сталкивались с таким разочарованием, когда они не могли очень хорошо разместить изображения на физическом носителе. Иногда они были слишком большими, иногда слишком короткими.

          Теперь формат pdf намного больше удобно по сравнению с форматом JPG. Алфавит « р » в слово « pdf » означает «для печати» . Поэтому лучше конвертировать ваши изображения в pdf-файл. Это будет не только быть экономически эффективным, но сэкономить много времени, а также.

          Наш онлайн-инструмент для преобразования изображений в PDF: лучше всего использовать для этой конкретной задачи.

          Вместо многих JPG PDF легче ручка

          Мы все знаем, что у вас будет куча фотографии, которыми вы время от времени делитесь с семьей и друзьями. В настоящее время, их можно разделить несколькими способами. Вы можете сделать это по почте или любым другим платформа социальных сетей. Но отправка нескольких фотографий одновременно может быть довольно удобной. раздражающий. Кроме того, на некоторых устройствах и в почтовых приложениях отображение изображений не очень удобно, так как пользователям, возможно, придется открывать изображения по одному.

          С другой стороны, если вы поделитесь своим изображения в pdf-файле, всем было бы гораздо удобнее. Наш инструмент поможет вам сделать именно это. Все, что вам нужно сделать, это взять все ваши изображения и преобразовать их в один файл PDF.

          Как преобразовать JPG в PDF без онлайн-инструменты?

          Вы можете этого не знать, но в Windows 10 есть есть все, что может понадобиться. Он имеет встроенный pdf-принтер, который может распечатать любой pdf-файл, который вы хотите. Теперь в приложении, когда вы откроете «печать settings», вам будет виден список принтеров. Вы также увидите «Майкрософт распечатать в pdf» . (Вы увидите более двух вариантов, если вы установили Adobe Reader DC)

          Таким образом, вы сохраните файл PDF на Ваш жесткий диск вместо настоящего принтера. Если вы хотите сделать JPG в pdf файл самостоятельно. Вот как вы можете это сделать.

          Запустите проводник Windows. Вы можете открыть это с помощью сочетания клавиш Windows+E.

          Добавьте все изображения, которые вы хотите преобразовать в один документ PDF. Есть два способа сделать это. Во-первых, вы можете использовать Клавиша Ctrl. Удерживайте эту клавишу на месте и щелкните каждое изображение, которое вы хотите преобразовать.

          Во-вторых, вы можете выбрать нужные изображения чтобы преобразовать и перетащить прямоугольник вокруг них.

          Если вы хотите сделать один документ, убедитесь, что все изображения находятся в одной папке. В противном случае вы окажетесь создание нескольких PDF-документов.

          Теперь наступает момент, когда вы продолжаете печать. Для этого вам нужно щелкнуть правой кнопкой мыши на любом из изображений, которые вы выбран и нажмите на «печать». Встроенный мастер печати изображений Windows откроется перед вами.

          Здесь вы меняете «принтер» с по «Microsoft print to pdf». Если вы не видите это вариант, установите Adobe Reader DC.

          В мастере вы найдете множество параметры для настройки вашего PDF-документа. Например, вы можете изменить размер страницы от А4 до любого другого, который вы предпочитаете.

          Когда все будет на своих местах, нажмите » print .»

          Когда вы нажмете кнопку печати, вы увидите печать прогресс происходит примерно так же, как когда файл печатается по-настоящему. Однако для этого, когда процесс завершится, появится окно с просьбой выбрать место для сохранения. Не забудьте ввести имя ваш файл.

          Преобразование изображений в pdf-файл вручную. Этот подход требует много времени и усилий. Вот почему мы создали наш онлайн-конвертер изображений в PDF, чтобы помочь вам сэкономить ваше время и энергия!

          Нужна помощь с другим преобразованием PDF инструменты? Тогда ознакомьтесь с нашим PDF раздел инструментов и найти правильный инструмент для вас.

          В настоящее время у нас есть около 5611 калькуляторов, таблиц преобразования и полезных онлайн-инструментов и программных функций для студентов, преподавателей и учителей, дизайнеров и просто для всех.

          Вы можете найти на этой странице финансовые калькуляторы, ипотечные калькуляторы, калькуляторы для кредитов, калькуляторы автокредита и калькуляторы лизинга, калькуляторы процентов, калькуляторы выплат, пенсионные калькуляторы, калькуляторы амортизации, инвестиционные калькуляторы, калькуляторы инфляции, калькуляторы финансов, калькуляторы подоходного налога , калькуляторы сложных процентов, калькулятор зарплаты, калькулятор процентной ставки, калькулятор налога с продаж, калькуляторы фитнеса и здоровья, калькулятор ИМТ, калькуляторы калорий, калькулятор жировых отложений, калькулятор BMR, калькулятор идеального веса, калькулятор темпа, калькулятор беременности, калькулятор зачатия беременности, срок родов калькулятор, математические калькуляторы, научный калькулятор, калькулятор дробей, калькулятор процентов, генератор случайных чисел, калькулятор треугольника, калькулятор стандартного отклонения, другие калькуляторы, калькулятор возраста, калькулятор даты, калькулятор времени, калькулятор часов, калькулятор среднего балла, калькулятор оценок, конкретный калькулятор, подсеть калькулятор, генератор паролей калькулятор преобразования tor и многие другие инструменты, а также для редактирования и форматирования текста, загрузки видео с Facebook (мы создали один из самых известных онлайн-инструментов для загрузки видео с Facebook). Мы также предоставляем вам онлайн-загрузчики для YouTube, Linkedin, Instagram, Twitter, Snapchat, TikTok и других сайтов социальных сетей (обратите внимание, что мы не размещаем видео на своих серверах. Все видео, которые вы загружаете, загружаются с Facebook, YouTube, Linkedin, CDN в Instagram, Twitter, Snapchat, TikTok. Мы также специализируемся на сочетаниях клавиш, ALT-кодах для Mac, Windows и Linux и других полезных советах и ​​инструментах (как написать смайлики онлайн и т. д.)

          Есть много очень полезных бесплатных онлайн-инструментов, и мы будем рады, если вы поделитесь нашей страницей с другими или пришлете нам какие-либо предложения по другим инструментам, которые придут вам на ум. Также, если вы обнаружите, что какой-либо из наших инструментов не работает должным образом или нуждается в лучшем переводе, сообщите нам об этом. Наши инструменты сделают вашу жизнь проще или просто помогут вам выполнять свою работу или обязанности быстрее и эффективнее.

          Ниже перечислены наиболее часто используемые многими пользователями по всему миру.

          • Бесплатные онлайн-калькуляторы и инструменты
          • Калькуляторы часовых поясов/часов/дат
          • Бесплатные онлайн-калькуляторы перевода единиц
          • Бесплатные онлайн-инструменты для веб-дизайна
          • Бесплатные онлайн-инструменты для электричества и электроники
          • Математика 1 Инструменты

            2 Онлайн-инструменты
          • Инструменты PDF
          • Код
          • Экология
          • Прочее
          • Бесплатные онлайн-загрузчики для социальных сетей
          • Преобразователи PDF в изображения
          • Читатели/просмотрщики PDF
          • Преобразователь изображений в PDF
          • Преобразователь JPG в PDF
          • Преобразователь PNG в PDF

          И мы все еще разрабатываем больше. Наша цель — стать универсальным сайтом для людей, которым нужно быстро рассчитать или найти быстрый ответ для основных конверсий.

          Кроме того, мы считаем, что Интернет должен быть источником бесплатной информации. Поэтому все наши инструменты и сервисы абсолютно бесплатны и не требуют регистрации. Мы кодировали и разрабатывали каждый калькулятор индивидуально и подвергали каждый из них строгому всестороннему тестированию. Однако, пожалуйста, сообщите нам, если вы заметите малейшую ошибку — ваш вклад чрезвычайно ценен для нас. Хотя большинство калькуляторов на Justfreetools.com предназначены для универсального использования во всем мире, некоторые из них предназначены только для определенных стран.

          Бесплатная загрузка конвертера JPG в PDF для Windows

          Пакетная обработка

          Преобразование нескольких файлов JPEG одним нажатием кнопки. Перестаньте работать с файлом за файлом, конвертируйте все ваши изображения одновременно.

          Локальное и безопасное преобразование в автономном режиме

          Преобразование JPG в автономном режиме означает, что они не покидают вашу систему, что позволяет конвертировать локально и обеспечивает безопасность файлов.

          Быстрый и надежный

          Интернет не нужен, лучшее автономное программное обеспечение для конвертации JPEG в PDF.

          Перетаскивание

          Легко выбирайте и добавляйте файлы с помощью функции перетаскивания.

          Режим преобразования

          Вы можете подать заявку на сохранение каждого JPG в виде одного PDF-файла или объединить все JPEG в один PDF-документ.

          Изменить порядок изображений

          Перемещайте файл JPEG вверх или вниз, нажимая кнопки «Вверх» и «Вниз», чтобы изменить порядок.

          Самая быстрая и универсальная программа преобразования, которую может предложить современная индустрия программного обеспечения. С помощью этого инструмента вы можете конвертировать тысячи файлов JPEG в документы PDF в пакетном режиме на вашем ПК. Если у вас есть несколько изображений JPEG для преобразования в PDF, вряд ли во всем мире найдется лучшая утилита для преобразования, чем этот конвертер JPG в PDF. Конвертер JPG в PDF имеет ряд опций, которые превратят вашу повседневную работу в удовольствие. Вы можете пометить более тысячи файлов JPEG для преобразования, и вам потребуется всего одно нажатие кнопки и несколько секунд со стороны конвертера, чтобы преобразовать их все в PDF. Чтобы начать работу, запустите JPG to PDF Converter. Выберите папки или файлы, перетащите их в список преобразования. Вы можете либо оставить параметры по умолчанию, либо создать свои собственные параметры. Когда вы закончите с параметрами, нажмите кнопку «Преобразовать».

          Если вы ищете простой способ преобразования изображения в PDF, используйте JPG to PDF Converter — удобную для пользователя программу для Windows с расширенными параметрами, позволяющими пакетно конвертировать файлы JPEG в файлы PDF удобным для вас способом. В параметрах вы можете выбрать преобразование одного файла JPG в один файл PDF или объединить все файлы JPG в один файл PDF. Вы также можете установить процент качества для файла JPG. Он имеет надежный и удобный интерфейс, благодаря которому даже новичок может легко преобразовать JPEG в PDF. Массовое преобразование экономит время и упрощает процедуру преобразования JPG в формат PDF.

          JPEG расшифровывается как Объединенная группа экспертов по фотографии. Это стандартный метод сжатия фотографических изображений. JPEG в основном используется для хранения и передачи фотографий в World Wide Web, но не так хорошо подходит для штриховых рисунков и другой текстовой или пиктографической графики, поскольку его метод сжатия плохо работает с этими типами изображений. Иногда вам нужно преобразовать файлы JPEG в документы PDF. Portable Document Format (PDF) — это формат файла, разработанный Adobe Systems для представления документов таким образом, который не зависит от исходного прикладного программного обеспечения, оборудования и операционной системы, используемых для создания этих документов. Файл PDF может описывать документы, содержащие любую комбинацию текста, графики и изображений в формате, независимом от устройства и разрешения. Эти документы могут состоять из одной страницы или тысяч страниц, очень простых или очень сложных, с богатым использованием шрифтов, графики, цветов и изображений. PDF является открытым стандартом, и любой может писать приложения, которые могут читать или записывать PDF без лицензионных отчислений. Некоторые пользователи предпочитают преобразовывать JPEG в PDF, чтобы сэкономить место на диске и упростить передачу файлов через Интернет.

          1 шт. | Купить сейчас

          24,95 долл. США за шт.

          2 шт. | Купить сейчас

          19,95 долл. США за шт.

          3 шт. | Купить сейчас

          14,95 долл. США за шт.

          5 шт. | Купить сейчас

          12,95 долл. США за шт.

          10 шт. | Купить сейчас

          10,95 долл. США за шт.

          Неограниченный ПК | Купить сейчас

          224,95 долл. США

          Обработка заказов и безопасность: Чтобы обеспечить наиболее безопасные платежные услуги, мы не обрабатываем заказы напрямую. Мы выбрали одну из самых авторитетных компаний электронной коммерции, доступных для этого от нашего имени, BlueSnap Inc. (Waltham, MA 02453, USA) . Формы заказов расположены на защищенном сервере, и все транзакции обрабатываются по безопасному протоколу SSL, гарантируя, что ваши личные данные останутся конфиденциальными. Мы не получаем копию ваших фактических платежных данных (таких как номера кредитных карт или реквизиты банковского перевода). Мы не предоставляем эту информацию третьим лицам. Вы можете узнать больше о нашем провайдере электронной коммерции политики конфиденциальности , посетив их веб-сайт.

          Автоматическая доставка заказа : Вы получите лицензионный ключ и ссылку для скачивания продукта сразу после успешной покупки. Если у вас есть какие-либо проблемы при покупке нашего продукта, пожалуйста, не стесняйтесь обращаться к нам за поддержкой. Если вы произвели платеж, но не получили электронное письмо с регистрационной информацией и лицензионным ключом в разумные сроки, свяжитесь с нами. Обратите внимание, что задержка может означать, что адрес электронной почты, указанный в вашей форме заказа, недействителен (из-за опечатки и т. д.) или регистрационный адрес электронной почты был заблокирован вашими фильтрами спама или нежелательной почты. Если вы используете спам-фильтр, пожалуйста, добавьте наш адрес электронной почты в свой «белый» или «разрешенный список отправителей» перед заказом.

          11 лучших бесплатных приложений для преобразования JPG в PDF на iPhone

          Преобразование файлов JPG в формат PDF весьма полезно, особенно когда речь идет о совместном использовании или печати документа. Есть определенные способы выполнения работы. Но можно с уверенностью сказать, что использование приложений для преобразования JPG в PDF — лучший вариант.

           

          Существуют десятки приложений для создания PDF-файлов из изображений на iPhone. В следующем содержании мы придумали лучшие приложения для конвертации изображений в pdf. Давайте вкратце ознакомимся с их обзорами и подсластим процесс выбора лучшего среди них.

          Бесплатные приложения для преобразования JPG в PDF на iPhone | 11 лучших вариантов

          Приложения iPhone для преобразования JPG в PDF, как правило, состоят из функций, выходящих за рамки опции конвертера PDF. Таким образом, наряду с инструментом преобразования, мы рассмотрели важные важные функции, которые максимизируют качество приложения в целом.

          Вот лучшие бесплатные приложения для преобразования JPG в PDF0012

        • Image Converter: photos to PDF

        • PDFelement – ​​PDF Editor

        • PDF Photos

        • Easy Scanner PDF Document Scan

        • Adobe Scan: Mobile PDF Scanner

        • PDF Converter Documents To PDF

        • iLovePDF – PDF Editor & Scan

        • Web to PDF Converter & Reader

        • ScanPDF: сканер документов PDF

        1. Приложение сканера – редактор PDF

        Цена : Бесплатно (предлагает покупки в приложении)

        Совместимость : iOS 11.0 или более поздней версии

        Приложение сканера – PDF Editor занимает первое место в этом списке первоклассные возможности преобразования PDF для изображений и слов. Легко конвертируйте фотографии в PDF на iPhone, используя лучший инструмент для конвертации PDF, предлагаемый этим приложением. Вы также можете сканировать с помощью камеры, чтобы сохранить изображение в формате PDF на своем iPhone. Благодаря передовой технологии OCR сканирование, чтение и создание PDF-файлов никогда не было проще.

         

        Конвертируйте JPEG в PDF с помощью этого приложения и сохраняйте изображения в формате PDF на вашем iPhone. Кроме того, приложение Scanner имеет лучший PDF-редактор для корректировки документа перед публикацией. Поэтому отредактируйте рамку сканирования и ориентацию, прежде чем преобразовывать изображения в форматы PDF. Вы можете преобразовать оба скриншота в PDF и любую фотографию iPhone в PDF.

         

        Основные функции приложения «Сканер»

        • Преобразование файлов JPG и PNG в PDF на iPhone

        • Сканирование и сохранение изображения в формате PDF

        • Построено с технологией OCR

        • Импорт фотографий из Google Drive, Dropbox, iCloud и т. д. для преобразования в PDF

        • 0 PDF с инструментами настройки

          Добавление электронных подписей

        • Объединение нескольких страниц и изображений в один файл PDF

        • Лучшее приложение для преобразования изображения в pdf и обратно

        Как преобразовать любой файл изображения в PDF (Видеоруководство)

        Подробнее

        2. Сканировать в PDF — приложение для сканирования PDF

        Цена : Бесплатно (предлагает покупки в приложении) 3 Совместимость

        03

         : iOS 13.0 или более поздняя версия

        Другое приложение для сканирования PDF в этом списке, Scan to PDF, может легко преобразовать ваши фотографии в формат PDF или наоборот. Это приложение может легко фотографировать или сканировать юридические документы, договорные бумаги, визитные карточки, удостоверения личности или любые другие документы. А затем превратить их в PDF-файлы. Таким образом, с помощью функции сканирования в PDF вы можете сканировать или импортировать изображения, а затем преобразовывать, упорядочивать и экспортировать их в высококачественный PDF-файл. Кроме того, вы можете редактировать отсканированные документы, добавлять электронные подписи и экспортировать файлы в форматы PDF или JPG.

         

        Основные функции

        • Преобразование документов в PDF или JPG.

        • Интеллектуальная обработка изображений.

        • Экспорт документов через AirDrop, мессенджеры, социальные сети, вложения электронной почты, отправка ссылки на документ и т. д. 3. Конвертер изображений: фото в PDF

          Цена : Бесплатно (Предлагает покупки в приложении)

          Совместимость : iOS 13.0 или более поздней версии

          Приложение Image Converter предназначено исключительно для преобразования фотографий iPhone в файлы PDF. Он поддерживает все форматы изображений, такие как JPG, JPEG, PNG, SVG и другие. Таким образом, вы можете просто выбрать любое изображение и легко преобразовать его в PDF с помощью этого приложения. Более того, он также позволяет импортировать изображения из облачных источников прямо на ваш iPhone для создания PDF-файлов.

           

          Основные характеристики

          • Универсальное приложение для преобразования изображений в PDF

          • Поддерживает почти все форматы изображений (JPG, PNG, SVG, BMP, PSD и т. д.) PDFelement – ​​Редактор PDF

            Цена : Бесплатно (Предлагает покупки в приложении)

            Совместимость : iOS 13.0 или более поздней версии

            PDFelement от Wondershare Technology предлагает фантастические инструменты для преобразования фотографий в PDF на iPhone. Хотите знать, как конвертировать изображение в pdf на iPhone? Это приложение позволяет упорядочивать, импортировать и создавать PDF-файлы из всех изображений. Кроме того, вы можете редактировать текст и границы документа с помощью PDFelement для iPhone.

            Ключевые функции

            • Мощная фотография для PDF App

            • РЕДАКТИРОВАТЬ PDF -перспективы перед публикацией

            • Compase PDF от Blank и RAW Documents

            • PDFS FIND и RAW DOCUNTION 5. PDF Photos

              Цена : Бесплатно (предлагает покупки в приложении)

              Совместимость : iOS 12. 0 или более поздней версии

              PDF Photos — это простое приложение для преобразования фотографий в PDF и обмена ими с коллегами. Интуитивно понятный инструмент конвертера JPG в PDF обеспечивает идеальный результат с возможностью редактирования. Кроме того, вы можете добавлять титульные страницы, изменять размер документов, создавать PDF-файлы из изображений с помощью этого замечательного приложения PDF Photos.

              Ключевые функции

              • Включите изображения в форматы PDF

              • Документы бренда, добавив подпись и покройте страницы

              • РЕДАКТИРОВАНИЕ Ориентации документа и размер файла управления

              . Сканирование документов

              Цена : Бесплатно (предлагает покупки в приложении)

              Совместимость : iOS 11.0 или более поздняя версия

              Easy Scanner — буквально одно из самых простых приложений для преобразования JPG в PDF на iPhone. Превратите свой смартфон в портативный сканер документов и сохраните любое изображение в формате PDF с помощью этого приложения. Вы также можете сканировать документы, бумаги, квитанции, визитные карточки и преобразовывать их в PDF-файлы.

              Ключевые функции

              • Сканирование или импортные изображения из библиотеки iPhone для преобразования в PDF

              • АВТОМАТИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ДОКУМЕНТА Сканирование: Мобильный PDF-сканер

                Цена : Бесплатно (предлагает покупки в приложении)

                Совместимость : iOS 13.0 или более поздней версии

                Adobe Scan — популярный мобильный PDF-сканер и мощный PDF-конвертер. С помощью технологии OCR любые изображения можно преобразовать в редактируемые форматы PDF. Поэтому для сканирования или импорта просто выберите любое изображение, чтобы мгновенно преобразовать его в PDF. Кроме того, улучшайте свои копии с помощью встроенного бесплатного редактора PDF.

                Ключевые функции

                • Документы сканирования в форматах PDF

                • Предварительный просмотр, редактирование и улучшение документов

                • Капля что угодно на бумаге с помощью OCR

                • Документы в PDF

                  Цена : Бесплатно (предлагает покупки в приложении)

                  Совместимость : iOS 11.0 или более поздняя версия

                  Эффективное приложение для преобразования изображений в PDF, этот конвертер PDF бесплатно превращает фотографии iPhone в PDF. В отличие от других приложений в списке, оно может захватывать веб-страницы, вложения электронной почты и веб-контент для создания PDF-файлов. Таким образом, наряду с изображениями конвертируйте текстовые материалы и изображения из любого места и эффективно делитесь ими между приложениями.

                   

                  Key features

                  • Convert photos, pictures, and texts into PDF files

                  • Create PDFs from web pages and email content

                  • Merge multi-page PDF into a single file

                  9.

                  iLovePDF – PDF Editor & Scan

                  Цена : Бесплатно (предлагает покупки в приложении)

                  Совместимость : iOS 13.0 или более поздней версии

                  Когда это приложение так же легко доступно, как с Нравится PDF для их управления документами? С легкостью читайте и конвертируйте любые файлы изображений в форматы PDF с помощью приложения iLovePDF. Например, вам интересно, как сохранить фотографию в формате PDF на iPhone? Просто отсканируйте или выберите существующие изображения с вашего iPhone и мгновенно сохраните их в формате PDF.

                   

                  Key features

                  • JPG to PDF converter app

                  • OCR scanning for accurate text capture

                  • Fill and sign forms with the in-app PDF editor

                  10. Web to PDF Converter & Reader

                  Цена : Бесплатно (предлагает покупки в приложении)

                  Совместимость : iOS 14. 0 или более поздняя версия

                  Когда дело доходит до лучших приложений для преобразования JPG в PDF, это приложение предлагает некоторые мощные инструменты конвертера. Он также эффективен при преобразовании веб-страниц в общедоступные форматы PDF. Кроме того, конвертируйте и сохраняйте изображения в виде файлов PDF, упорядочивайте и редактируйте их в любое время в приложении.

                  Ключевые функции

                  • Изображение в PDF Converter App

                  • Web to PDF Converter

                  • Брейзер в приложении.

                    Цена : Бесплатно (предлагает покупки в приложении)

                    Совместимость : iOS 13.0 или более поздняя версия

                    ScanPDF — еще одно бесплатное приложение для преобразования JPG в PDF на iPhone. Благодаря производительному мобильному сканеру он позволяет мгновенно преобразовывать бумаги и документы в PDF-файлы. С помощью этого приложения вы также можете сканировать для создания PDF, конвертировать JPG в PDF и даже преобразовывать скриншоты в PDF.

      С симплекс метод: Симплекс-метод онлайн

      alexxlab / / Разное

      Подробный разбор симплекс-метода / Хабр

      Пролог

      Недавно появилась необходимость создать с нуля программу, реализующую алгоритм симплекс-метода. Но в ходе решения я столкнулся с проблемой: в интернете не так уж много ресурсов, на которых можно посмотреть подробный теоретический разбор алгоритма (его обоснование: почему мы делаем те или иные шаги) и советы по практической реализации — непосредственно, алгоритм. Тогда я дал себе обещание — как только завершу задачу, напишу свой пост на эту тему. Об этом, собственно, и поговорим.

      Замечание. Пост будет написан достаточно формальным языком, но будет снабжен комментариями, которые должны внести некоторую ясность. Такой формат позволит сохранить научный подход и при этом, возможно, поможет некоторым в изучении данного вопроса.

      §1. Постановка задачи линейного программирования


      Определение:

      Линейное программирование – математическая дисциплина, посвященная теории и методам решения экстремальных задач на множествах n- мерного пространства, задаваемых системами линейными уравнений и неравенств.

      Общая задача линейного программирования (далее – ЛП) имеет вид:

      §2. Каноническая форма задачи ЛП

      Каноническая форма задачи ЛП:

      Замечание: Любая задача ЛП сводится к канонической.

      Алгоритм перехода от произвольной задачи ЛП к канонической форме:

      1. Неравенства с отрицательными умножаем на (-1).
      2. Если неравенство вида (≤), то к левой части добавляем – добавочную переменную, и получаем равенство.
      3. Если неравенство вида (≥), то из левой части вычитаем , и получаем равенство.
      4. Делаем замену переменных:

      • Если , то
      • Если — любой, то , где

      Замечание:

      Будем нумеровать по номеру неравенства, в которое мы его добавили.

      Замечание: ≥0.

      §3. Угловые точки. Базисные/свободные переменные. Базисные решения


      Определение:

      Точка называется угловой точкой, если представление возможно только при .

      Иными словами, невозможно найти две точки в области, интервал проходящий через которые содержит (т.е. – не внутренняя точка).

      Графический способ решения задачи ЛП показывает, что нахождение оптимального решения ассоциируется с угловой точкой. Это является основной концепцией при разработке симплекс-метода.

      Определение: Пусть есть система m уравнений и n неизвестных (m < n). Разделим переменные на два множества: (n-m) переменные положим равными нулю, а остальные m переменных определяются решением системы исходных уравнений. Если это решение единственно, то тогда ненулевые m переменных называют базисными; нулевые (n-m) переменных – свободными (небазисными), а соответствующие результирующие значения переменных называют базисным решением.

      §4. Симплекс-метод

      Симплекс-метод позволяет эффективно найти оптимальное решение, избегая простой перебор всех возможных угловых точек. Основной принцип метода: вычисления начинаются с какого-то «стартового» базисного решения, а затем ведется поиск решений, «улучшающих» значение целевой функции. Это возможно только в том случае, если возрастание какой-то переменной приведет к увеличению значения функционала.

      Необходимые условия для применения симплекс-метода:

      1. Задача должна иметь каноническую форму.
      2. У задачи должен быть явно выделенный базис.

      Определение:

      Явно выделенным базисом будем называть вектора вида:, т.е. только одна координата вектора ненулевая и равна 1.

      Замечание: Базисный вектор имеет размерность (m*1), где m – количество уравнений в системе ограничений.

      Для удобства вычислений и наглядности обычно пользуются симплекс-таблицами:

      • В первой строке указывают «наименование» всех переменных.
      • В первом столбце указывают номера базисных переменных, а в последней ячейке – букву Z (это строка функционала).
      • В «середине таблицы» указывают коэффициенты матрицы ограничений — aij.
      • Последний столбец – вектор правых частей соответствующих уравнений системы ограничений.
      • Крайняя правая ячейка – значение целевой функции. На первой итерации ее полагают равной 0.

      Замечание:

      Базис – переменные, коэффициенты в матрице ограничений при которых образуют базисные вектора.

      Замечание: Если ограничения в исходной задаче представлены неравенствами вида ≤, то при приведении задачи к канонической форме, введенные дополнительные переменные образуют начальное базисное решение.

      Замечание: Коэффициенты в строке функционала берутся со знаком “-”.

      Алгоритм симплекс-метода:

      1. Выбираем переменную, которую будем вводить в базис. Это делается в соответствии с указанным ранее принципом: мы должны выбрать переменную, возрастание которой приведет к росту функционала. Выбор происходит по следующему правилу:

      • Если задача на минимум – выбираем максимальный положительный элемент в последней строке.
      • Если задача на максимум – выбираем минимальный отрицательный.

      Такой выбор, действительно, соответствует упомянутому выше принципу: если задача на минимум, то чем большее число вычитаем – тем быстрее убывает функционал; для максимума наоборот – чем большее число добавляем, тем быстрее функционал растет.

      Замечание: Хотя мы и берем минимальное отрицательное число в задаче на максимум, этот коэффициент показывает направление роста функционала, т.к. строка функционала в симплекс-таблице взята со знаком “-”. Аналогичная ситуация с минимизацией.

      Определение: Столбец симплекс-таблицы, отвечающий выбранному коэффициенту, называется ведущим столбцом.

      2. Выбираем переменную, которую будем вводить в базис. Для этого нужно определить, какая из базисных переменных быстрее всего обратится в нуль при росте новой базисной переменной. Алгебраически это делается так:

      • Вектор правых частей почленно делится на ведущий столбец
      • Среди полученных значений выбирают минимальное положительное (отрицательные и нулевые ответы не рассматривают)

      Определение:

      Такая строка называется ведущей строкой и отвечает переменной, которую нужно вывести из базиса.

      Замечание: Фактически, мы выражаем старые базисные переменные из каждого уравнения системы ограничений через остальные переменные и смотрим, в каком уравнении возрастание новой базисной переменной быстрее всего даст 0. Попадание в такую ситуацию означает, что мы «наткнулись» на новую вершину. Именно поэтому нулевые и отрицательные элементы не рассматриваются, т.к. получение такого результата означает, что выбор такой новой базисной переменной будет уводить нас из области, вне которой решений не существует.

      3. Ищем элемент, стоящий на пересечении ведущих строки и столбца.

      Определение: Такой элемент называется ведущим элементом.

      4. Вместо исключаемой переменной в первом столбце (с названиями базисных переменных) записываем название переменной, которую мы вводим в базис.

      5. Далее начинается процесс вычисления нового базисного решения. Он происходит с помощью метода Жордана-Гаусса.

      • Новая Ведущая строка = Старая ведущая строка / Ведущий элемент
      • Новая строка = Новая строка – Коэффициент строки в ведущем столбце * Новая Ведущая строка

      Замечание:

      Преобразование такого вида направлено на введение выбранной переменной в базис, т. е. представление ведущего столбца в виде базисного вектора.

      6. После этого проверяем условие оптимальности. Если полученное решение неоптимально – повторяем весь процесс снова.

      §5. Интерпретация результата работы симплекс-метода

      1. Оптимальность

      Условие оптимальности полученного решения:

      • Если задача на максимум – в строке функционала нет отрицательных коэффициентов (т.е. при любом изменении переменных значение итогового функционала расти не будет).
      • Если задача на минимум – в строке функционала нет положительных коэффициентов (т.е. при любом изменении переменных значение итогового функционала уменьшаться не будет).

      2. Неограниченность функционала

      Однако, стоит отметить, что заданный функционал может не и достигать максимума/минимума в заданной области. Алгебраический признак этого можно сформулировать следующим образом:

      При выборе ведущей строки (исключаемой переменной) результат почленного деления вектора правых частей на ведущий столбец содержит только нулевые и отрицательные значения.

      Фактически, это значит, что какой бы рост мы не задавали новой базисной переменной, мы никогда не найдем новую вершину. А значит, наша функция не ограничена на множестве допустимых решений.

      3. Альтернативные решения

      При нахождении оптимального решения возможен еще один вариант – есть альтернативные решения (другая угловая точка, дающая то же самое значение функционала).

      Алгебраический признак существования альтернативы:

      После достижения оптимального решения имеются нулевые коэффициенты при свободных переменных в строке функционала.

      Это значит, что при росте соответствующей переменной с нулевым коэффициентом значение функционала не изменится и новое базисное решение будет также давать оптимум функционала.

      Эпилог

      Данная статья направлена на более глубокое понимание теоретической части. В замечаниях и пояснениях здесь можно получить ответы на вопросы, которые обычно опускают при изучении этого метода и принимают априори. Однако, надо понимать, что многие методы численной оптимизации основаны на симплекс-методе (например, метод Гомори, М-Метод) и без фундаментального понимания вряд ли получится сильно продвинуться в дальнейшем изучении и применении всех алгоритмов этого класса.

      Чуть позже напишу статью о практической реализации симплекс-метода, а также несколько статей о Методе искусственных переменных (М-Метод), Методе Гомори и Методе ветвей и границ.

      Спасибо за внимание!

      P.S.

      Если уже сейчас Вы мучаетесь с реализацией симплекс-метода, советую почитать книгу А. Таха Введение в исследование операций — там все неплохо разобрано и в теории, и на примерах; а также посмотрите примеры решения задач matburo.ru — это поможет с реализацией в коде.

      Симплекс метод — процесс решения проблем

      Цель этой минилекции – познакомить вас с практическим применением симплекс-метода решения проблем, предложенного Басадуром. После ее прочтения станут понятны основы этого мощного творческого метода решения проблем.

      Что собой представляет симплекс метод

      Вне всякого сомнения, проблемы бывают разного характера и масштаба. Но важно только то, что они могут быть разрешены. Однако прежде чем предпринять действия для решения проблемы, важно сначала осознать ее. Тем не менее, наиболее значимые шаги в процессе решения проблем часто упускаются из виду. Это означает, что оптимальный выход из ситуации не удается найти или сама проблема определена неверно. Симплекс метод – это метод преодоления трудностей, который учитывает такие ошибки и предотвращает их. Эту модель разработал американский гуру в сфере творчества Марино (Мин) Сидни Басадур, который представил свой метод в книге «Сила инноваций». Он также является изобретателем запатентованной системы мышления Simplexity. Симплекс-метод решения проблем, разработанный Басадуром, включает несколько шагов, пройдя которые группа людей получает возможность найти креативные решения. С помощью Simplex-метода легче определить задачу, а затем предложить и реализовывать способы ее преодоления.

      Алгоритм симплекс метода по Басадуру: три фазы

      Басадур разделил разработанный им симплекс-метод решения задач на три фазы, которые включают восемь шагов.

      Фаза 1: Постановка проблемы

      Эта первая фаза связана с первыми тремя шагами симплекс-процесса решения задач: поиск проблемы, выяснение деталей и формирование четкой задачи. Только после этого задача может быть сформулирована правильно. Когда станет ясно, в чем заключена проблема, появится возможность отследить ее истоки в организационной структуре.

      Фаза 2: Процесс поиска решений

      После фокусировки на описании проблемы симплекс-метод переходит ко второй фазе, заключающейся в поиске возможных решений. Выполняются следующие шаги: поиск идей, способных привести к устранению проблемы, выбор и оценка этих идей. На этом этапе предлагается как можно больше творческих идей, которые могут помочь разрешить сложившуюся ситуацию.

      Фаза 3: Реализация решения

      Когда преодоление проблемы близко, следует третья и последняя фаза. Она содержит три заключительных шага симплекс-процесса Басадура, а именно: планирование всех необходимых действий, обеспечение поддержки с вовлечением в решение проблемы всех сотрудников и последний шаг – принятие требуемых мер и их реализация. В этой фазе важно, чтобы решение было тщательно проработано. Его внедрение должно осуществляться профессионально. Кроме того, при реализации решения нужно позаботиться о пространстве для маневра, чтобы в случае необходимости можно было корректировать свои действия.

      Симплекс-метод решения проблем: восемь шагов

      Шаг 1: Поиск проблемы

      На этом этапе лучше всего не пытаться сразу же найти выход из ситуации. Для начала необходимо прояснить суть проблемы и ее симптомы. Причина выяснится позже. В ходе этого шага, к примеру, потребуется определить желания и потребности не только клиентов и поставщиков, но и сотрудников. В отличие от многих других методов решения проблем в симплекс-процессе Басадура на первом этапе проблема еще не известна. Для ускорения шага 1 могут быть заданы вспомогательные вопросы, например такие:

      • Какие полезные рекомендации могут предложить клиенты?
      • Как отреагируют клиенты на попытку расширить взаимодействие?
      • Что не так в обслуживании клиентов на текущий момент?

      Шаг 2: Выяснение деталей

      Этот этап включает в себя сбор информации, касающейся текущей ситуации и, возможно, самой проблемы. На первом этапе были выяснены симптомы проблемы, и на основе этого понадобится собрать имеющиеся факты. Что организации уже известно о рассматриваемой проблеме? Собранные сведения должны быть проанализированы и оценены. Наиболее значимые данные будут играть важную роль на следующих этапах. Опять же, могут быть полезны дополнительные вопросы, такие как:

      • Какие претензии предъявлялись за последний год?
      • Как клиенты относятся к проблеме?
      • Предпринимались ли какие-либо действия?
      • Существуют ли предложения по улучшению ситуации?

      Шаг 3: Определение проблемы

      Область проблем выяснена, поэтому теперь можно определить конкретную проблему. Важно объяснить проблему не слишком пространно, но и не слишком ограниченно. Ответы на ряд вопросов «почему?» помогают понять ситуацию в целом. Отдельные детали помогают описать проблему. Как это работает, можно понять на следующем примере:

      Вопрос: «Почему мы хотим улучшить обслуживание наших клиентов?»

      Ответ: «Потому что клиентов в настоящее время отсылают туда-обратно в различные контактные центры. Им нужен постоянный человек для контактов, который будет в курсе происходящего».

      Определено, что проблема касается работы отдела обслуживания клиентов, который по большей части не связывает клиента с нужным человеком.

      Шаг 4: Поиск решения

      В рамках симплекс-процесса этот шаг связан с широким кругом идей, которые могли бы способствовать решению проблемы. Структурные подразделения и отдельные сотрудники играют в этом важную роль. Неплохой идеей будет создание проектной группы, которая бы разрабатывала креативные решения. Такой групповой поиск идей по принципу «мозгового штурма» не подразумевает критики идей друг друга. Это препятствовало бы творческому процессу. На этом этапе должны быть разработаны возможные варианты решения проблемы.

      Шаг 5: Выбор и оценка

      Пришло время рассмотреть предложенные идеи более подробно. Цель этапа состоит в том, чтобы решить, какая идея лучше всего подходит для решения задачи. Лучше всего начать с создания критериев оценки, позволяющих провести объективный анализ. Идея, наиболее соответствующая этим критериям, обычно является самым лучшим решением проблемы. На этом этапе вспомогательные вопросы также могут ускорить процесс. В частности, лучше уточнить:

      • Какое влияние окажет выбранное решение?
      • Понадобятся ли какие-либо расходы в связи с выбранным решением?
      • Сколько времени и усилий потребуется для реализации задачи?

      Шаг 6: Планирование

      Теперь, когда выбор сделан, пришло время для составления плана действий. Проще говоря, понадобится четко распределить действия и обязанности, предоставив возможность каждому трудиться над выполнением задачи. Обычно решение незначительных проблем не требует большого количества действий. В случае более серьезных проблем лучшим выбором будет официальное участие в управлении проектом.

      Шаг 7: Обеспечение взаимодействия

      Хотя это может показаться излишним, но важно учитывать вовлеченность сотрудников на протяжении всего процесса. Только при условии согласия с решением они будут стремиться к успешному завершению задачи. Решение проблем часто связано с нововведениями. Сотрудникам нередко трудно изменить привычный стиль работы. Вот почему они должны осознавать негативные последствия проблемы и ценность внедряемых изменений.

      Шаг 8: Принятие мер

      План действий может быть реализован только в том случае, если будет обеспечена достаточная поддержка. Этот шаг заслуживает такого же внимания, как и другие. В конце концов, если план не будет реализован, проблема не будет решена. Будет полезным по ходу дела оценивать результаты и проверять, насколько значительно уменьшилась решаемая проблема.

      Симплекс-метод решения проблем: цикличность метода

      Симплекс-процесс, предложенный Басадуром для преодоления проблем – простая, но мощная модель решения задач. Однако этот процесс не является линейным, он имеет циклический характер. Это означает наличие возможностей для постоянного совершенствования. Вот почему решение задач с помощью симплекс-метода Басадура часто сравнивают с циклом Деминга (PDCA): планирование, действие, проверка, корректировка. После завершения финального этапа следует вернуться к первому шагу для дальнейшей корректировки решения проблемы.

      Симплекс метод решения проблем — презентация в PowerPoint

      Если вы бизнес-тренер и планируете использовать эту мини-лекцию в своих тренингах, то:

      1. Рекомендуем прочитать статью о том как сделать свою мини-лекцию живой и интересной.
      2. Скачайте презентацию в формате PowerPoint для визуальной поддержки вашей мини-лекции.

      Премиальный контент

      Ссылка на скачивание этой презентации и другой премиальный контент доступны подписчикам платных тарифов. Оформите платную подписку на сайте “Технология тренинга” и получите полный доступ к 13 готовым тренингам, 256 слайдам, 112 минилекциям, 619 упражнениям, 41 видео и т.д. Это совсем не дорого.

      Нет аккаунта? Зарегистрируйтесь   Есть аккаунт? Войдите  

       

      Алгоритм и пример симплекс-метода (ММЭ). Пример решения симплекс-методом

      Пример 5.1. Решить следующую задачу линейного программирования симплекс-методом:

      Решение:

      I итерация:

      1 этап: формирование исходной симплекс-таблицы.

      Исходная задача линейного программирования задана в стандартной форме. Приведем ее к каноническому виду путем введения в каждое из ограничений-неравенств дополнительной неотрицательной переменной, т. е.

      В полученной системе уравнений примем в качестве разрешенных (базисных) переменные х3, х4, х5, х6, тогда свободными переменными будут х1,х2. Выразим базисные переменные через свободные:

      Приведем целевую функцию к следующему виду:

      На основе полученной задачи сформируем исходную симплекс-таблицу:

      Таблица 5.3

      Исходная симплекс-таблица

      СП

      БП

      Оценочные отношения

      18

      1

      3

      16

      2

      1

      5

      0

      1

      21

      3

      0

      0

      –2

      –3

      2 этап: определение базисного решения.

      Согласно определению базисного решения свободные переменные равны нулю, а значения базисных переменных – соответствующим значениям свободных чисел, т.е.:

      .

      3 этап: проверка совместности системы ограничений ЗЛП.

      На данной итерации (в таблице 5.3) признак несовместности системы ограничений (признак 1) не выявлен (т.е. нет строки с отрицательным свободным числом (кроме строки целевой функции), в которой не было бы хотя бы одного отрицательного элемента (т.е. отрицательного коэффициента при свободной переменной)).

      4 этап: проверка ограниченности целевой функции.

      На данной итерации (в таблице 5.3) признак неограниченности целевой функции (признак 2) не выявлен (т.е. нет колонки с отрицательным элементом в строке целевой функции (кроме колонки свободных чисел), в которой не было бы хотя бы одного положительного элемента).

      5 этап: проверка допустимости найденного базисного решения.

      Так как найденное базисное решение не содержит отрицательных компонент, то оно является допустимым.

      6 этап: проверка оптимальности.

      Найденное базисное решение не является оптимальным, так как согласно признаку оптимальности (признак 4) в строке целевой функции не должно быть отрицательных элементов (свободное число данной строки при рассмотрении данного признака не учитывается). Следовательно, согласно алгоритму симплекс-метода переходим к 8 этапу.

      8 этап: определение разрешающего элемента.

      8.1. Определение разрешающей колонки.

      Так как найденное базисное решение допустимое, то поиск разрешающей колонки будем производить по следующей схеме: определяем колонки с отрицательными элементами в строке целевой функции (кроме колонки свободных чисел). Согласно таблице 5.3, таких колонок две: колонка «х1» и колонка «х2». Из таких колонок выбирается та, которая содержит наименьший элемент в строке целевой функции. Она и будет разрешающей. Колонка «х2» содержит наименьший элемент (–3) в сравнении с колонкой «х1». Следовательно, ее принимаем в качестве разрешенной.

      8.2. Определение разрешающей строки.

      Для определения разрешающей строки находим положительные оценочные отношения свободных чисел к элементам разрешающей колонки, строка, которой соответствует наименьшее положительное оценочное отношение, принимается в качестве разрешенной.

      Таблица 5.4

      Исходная симплекс-таблица

      В таблице 5.4 наименьшее положительное оценочное отношение соответствует строке «х5», следовательно, она будет разрешающей.

      Элемент, расположенный на пересечение разрешающей колонки и разрешающей строки, принимается в качестве разрешающего. В нашем примере – это элемент , который расположен на пересечении строки «х5» и колонки «х2».

      9 этап: преобразование симплекс-таблицы.

      Разрешающий элемент показывает одну базисную и одну свободную переменные, которые необходимо поменять местами в симплекс-таблице, для перехода к новому «улучшенному» базисному решению. В данном случае это переменные х5 и х2, в новой симплекс-таблице (таблице 5.5) их меняем местами.

      9.1. Преобразование разрешающего элемента.

      Разрешающий элемент таблицы 5.4 преобразовывается следующим образом:

      Полученный результат вписываем в аналогичную клетку таблицы 5.5.

      9.2. Преобразование разрешающей строки.

      Элементы разрешающей строки таблицы 5.4 делим на разрешающий элемент данной симплекс-таблицы, результаты вписываются в аналогичные ячейки новой симплекс-таблицы (таблицы 5.5). Преобразования элементов разрешающей строки приведены в таблице 5.5.

      9.3. Преобразование разрешающей колонки.

      Элементы разрешающей колонки таблицы 5.4 делим на разрешающий элемент данной симплекс-таблицы, а результат берется с обратным знаком. Полученные результаты вписываются в аналогичные ячейки новой симплекс-таблицы (таблицы 5.5). Преобразования элементов разрешающей колонки приведены в таблице 5.5.

      9.4. Преобразование остальных элементов симплекс-таблицы.

      Преобразование остальных элементов симплекс-таблицы (т.е. элементов не расположенных в разрешающей строке и разрешающей колонке) осуществляется по правилу «прямоугольника».

      К примеру, рассмотрим преобразование элемента, расположенного на пересечении строки «х3» и колонки «», условно обозначим его «х3». В таблице 5.4 мысленно вычерчиваем прямоугольник, одна вершина которого располагается в клетке, значение которой преобразуем (т.е. в клетке «х3»), а другая (диагональная вершина) – в клетке с разрешающим элементом. Две другие вершины (второй диагонали) определяются однозначно. Тогда преобразованное значение клетки «х3» будет равно прежнему значению данной клетки минус дробь, в знаменателе которой разрешающий элемент (из таблицы 5. 4), а в числителе произведение двух других неиспользованных вершин, т.е.:

      «х3»: .

      Аналогично преобразуются значения других клеток:

      «х3 х1»: ;

      «х4»: ;

      «х4 х1»: ;

      «х6»: ;

      «х6 х1»: ;

      «»: ;

      «х1»: .

      В результате данных преобразований получили новую симплекс- таблицу (таблица 5.5).

      II итерация:

      1 этап: составление симплекс-таблицы.

      По результатам симплекс-преобразований предыдущей итерации составляем новую симплекс-таблицу:

      Таблица 5.5

      Симплекс-таблица II итерации

      СП

      БП

      Оценочные

      отношения

      –(3/1)=–3

      –(1/1)=–1

      5/1=5

      0/1=0

      (1)–1=1

      –(0/1)=0

      –(–3/1)=3

      2 этап: определение базисного решения.

      В результате проведенных симплекс-преобразований получили новое базисное решение (таблица 5.5):

      .

      Как видно, при данном базисном решении значение целевой функции =15, что больше чем при предыдущем базисном решении.

      3 этап: проверка совместности системы ограничений.

      Не совместность системы ограничений в соответствии с признаком 1 в таблице 5.5 не выявлена.

      4 этап: проверка ограниченности целевой функции.

      Неограниченность целевой функции в соответствии с признаком 2 в таблице 5.5 не выявлена.

      5 этап: проверка допустимости найденного базисного решения.

      Найденное базисное решение в соответствии с признаком 3 допустимое, так как не содержит отрицательных компонент.

      6 этап: проверка оптимальности найденного базисного решения.

      Найденное базисное решение в соответствии с признаком 4 не оптимальное, так как в строке целевой функции симплекс-таблицы (таблица 5. 5) содержится отрицательный элемент: –2 (свободное число данной строки при рассмотрении данного признака не учитывается). Следовательно, переходим к 8 этапу.

      8 этап: определение разрешающего элемента.

      8.1. Определение разрешающей колонки.

      Найденное базисное решение допустимое, определяем колонки с отрицательными элементами в строке целевой функции (кроме колонки свободных чисел). Согласно таблице 5.5, такой колонкой является только одна колонка: «х1». Следовательно, ее принимаем в качестве разрешенной.

      8.2. Определение разрешающей строки.

      Согласно полученным значениям положительных оценочных отношений в таблице 5.6, минимальным является отношение, соответствующее строке «х3». Следовательно, ее принимаем в качестве разрешенной.

      Таблица 5.6

      Симплекс-таблица II итерации

      СП

      БП

      Оценочные

      отношения

      3

      1

      –3

      3/1=3 – min

      11

      2

      –1

      11/2=5,5

      5

      0

      1

      –

      21

      3

      0

      21/3=7

      15

      –2

      3

      9 этап: преобразование симплекс-таблицы.

      Преобразования симплекс-таблицы (таблицы 5.6) выполняются аналогично, как и в предыдущей итерации. Результаты преобразований элементов симплекс-таблицы приведены в таблице 5.7.

      III итерация

      1 этап: построение новой симплекс-таблицы.

      По результатам симплекс-преобразований предыдущей итерации составляем новую симплекс-таблицу:

      Таблица 5.7

      Симплекс-таблица III итерации

      СП

      БП

      Оценочные

      отношения

      3/1=3

      (1)–1=1

      –3/1=–3

      –(2/1)=–2

      –(0/1)=0

      –(3/1)=–3

      –(–2/1)=2

      2 этап: определение базисного решения.

      В результате проведенных симплекс-преобразований получили новое базисное решение (таблица 5.7):

      .

      3 этап: проверка совместности системы ограничений.

      Не совместность системы ограничений в соответствии с признаком 1 в таблице 5.7 не выявлена.

      4 этап: проверка ограниченности целевой функции.

      Неограниченность целевой функции в соответствии с признаком 2 в таблице 5.7 не выявлена.

      5 этап: проверка допустимости найденного базисного решения.

      Найденное базисное решение в соответствии с признаком 3 допустимое, так как не содержит отрицательных компонент.

      6 этап: проверка оптимальности найденного базисного решения.

      Найденное базисное решение в соответствии с признаком 4 не оптимальное, так как в строке целевой функции симплекс-таблицы (таблица 5.7) содержится отрицательный элемент: –3 (свободное число данной строки при рассмотрении данного признака не учитывается). Следовательно, переходим к 8 этапу.

      8 этап: определение разрешающего элемента.

      8.1. Определение разрешающей колонки.

      Найденное базисное решение допустимое, определяем колонки с отрицательными элементами в строке целевой функции (кроме колонки свободных чисел). Согласно таблице 5.7, такой колонкой является только одна колонка: «х5». Следовательно, ее принимаем в качестве разрешенной.

      8.2. Определение разрешающей строки.

      Согласно полученным значениям положительных оценочных отношений в таблице 5.8, минимальным является отношение, соответствующее строке «х4». Следовательно, ее принимаем в качестве разрешенной.

      Таблица 5.8

      Симплекс-таблица III итерации

      СП

      БП

      Оценочные

      отношения

      3

      1

      –3

      –

      5

      –2

      5

      5/5=1 – min

      5

      0

      1

      5/1=5

      12

      –3

      9

      12/9=1?

      21

      2

      –3

      9 этап: преобразование симплекс-таблицы.

      Преобразования симплекс-таблицы (таблицы 5.8) выполняются аналогично, как и в предыдущей итерации. Результаты преобразований элементов симплекс-таблицы приведены в таблице 5.9.

      IV итерация

      1 этап: построение новой симплекс-таблицы.

      По результатам симплекс-преобразований предыдущей итерации составляем новую симплекс-таблицу:

      Таблица 5.9

      Симплекс-таблица IV итерации

      СП

      БП

      Оценочные

      отношения

      –(–3/5)=3/5

      5/5=1

      –2/5

      (5)–1=

      –(1/5)=–1/5

      –(9/5)=–9/5

      –(–3/5)=3/5

      2 этап: определение базисного решения.

      В результате проведенных симплекс-преобразований получили новое базисное решение, согласно таблице 5.9 решение следующее:

      .

      3 этап: проверка совместности системы ограничений.

      Не совместность системы ограничений в соответствии с признаком 1 в таблице 5.9 не выявлена.

      4 этап: проверка ограниченности целевой функции.

      Неограниченность целевой функции в соответствии с признаком 2 в таблице 5.9 не выявлена.

      5 этап: проверка допустимости найденного базисного решения.

      Найденное базисное решение в соответствии с признаком 3 допустимое, так как не содержит отрицательных компонент.

      6 этап: проверка оптимальности найденного базисного решения.

      Найденное базисное решение в соответствии с признаком 4 оптимальное, так как в строке целевой функции симплекс-таблицы (таблица 5.9) нет отрицательных элементов (свободное число данной строки при рассмотрении данного признака не учитывается).

      7 этап: проверка альтернативности решения.

      Найденное решение является единственным, так как в строке целевой функции (таблица 5.9) нет нулевых элементов (свободное число данной строки при рассмотрении данного признака не учитывается).

      Ответ: оптимальное значение целевой функции рассматриваемой задачи =24, которое достигается при .

      Пример 5.2. Решить вышеприведенную задачу линейного программирования при условии, что целевая функция минимизируется:

      Решение:

      I итерация:

      1 этап: формирование исходной симплекс-таблицы.

      Исходная задача линейного программирования задана в стандартной форме. Приведем ее к каноническому виду путем введения в каждое из ограничений-неравенств дополнительной неотрицательной переменной, т. е.

      В полученной системе уравнений примем в качестве разрешенных (базисных) переменные х3, х4, х5, х6, тогда свободными переменными будут х1,х2. Выразим базисные переменные через свободные:

      Приведем целевую функцию к следующему виду:

      На основе полученной задачи сформируем исходную симплекс-таблицу:

      Таблица 5.10

      Исходная симплекс-таблица

      СП

      БП

      Оценочные отношения

      18

      1

      3

      16

      2

      1

      5

      0

      1

      21

      3

      0

      0

      –2

      –3

      2 этап: определение базисного решения.

      Согласно определению базисного решения свободные переменные равны нулю, а значения базисных переменных – соответствующим значениям свободных чисел, т.е.:

      .

      3 этап: проверка совместности системы ограничений ЗЛП.

      На данной итерации (в таблице 5.10) признак несовместности системы ограничений (признак 1) не выявлен (т.е. нет строки с отрицательным свободным числом (кроме строки целевой функции), в которой не было бы хотя бы одного отрицательного элемента (т.е. отрицательного коэффициента при свободной переменной)).

      4 этап: проверка ограниченности целевой функции.

      На данной итерации (в таблице 5.10) признак неограниченности целевой функции (признак 2) не выявлен (т.е. нет колонки с положительным элементом в строке целевой функции (колонка свободных чисел не рассматривается), в которой не было бы хотя бы одного положительного элемента).

      5 этап: проверка допустимости найденного базисного решения.

      Так как найденное базисное решение не содержит отрицательных компонент, то оно является допустимым.

      6 этап: проверка оптимальности найденного базисного решения.

      Найденное базисное решение в соответствии с признаком 4 оптимальное, так как в строке целевой функции симплекс-таблицы (таблица 5.10) нет положительных элементов (свободное число данной строки при рассмотрении данного признака не учитывается).

      7 этап: проверка альтернативности решения.

      Найденное решение является единственным, так как в строке целевой функции (таблица 5.10) нет нулевых элементов (свободное число данной строки при рассмотрении данного признака не учитывается).

      Ответ: оптимальное значение целевой функции рассматриваемой задачи =0, которое достигается при .

      Пример 5.3. Решить следующую задачу линейного программирования симплекс-методом:

      Решение:

      I итерация

      1 этап: составление исходной симплекс-таблицы.

      Задача линейного программирования задана в каноническом виде. Составим расширенную матрицу и выделим с помощью метода Жордана-Гаусса базисные переменные. Примем в качестве базисных – переменные х1 и х2.

      Умножим (поэлементно) первую строку на –3 и сложим со второй:

      .

      Умножим вторую строку на :

      .

      Сложим вторую с первой строкой:

      .

      В результате система ограничений примет следующий вид:

      Выразим базисные переменные через свободные:

      Выразим целевую функцию также через свободные переменные, для этого подставим полученные значения базисных переменных в целевую функцию:

      .

      Запишем целевую функцию в следующем виде:

      .

      Составим исходную симплекс-таблицу:

      Таблица 5.11

      Исходная симплекс-таблица

      СП

      БП

      Оценочные отношения

      –1

      0

      0

      2

      4

      –

      –3

      2 этап: определение базисного решения.

      Согласно определению базисного решения свободные переменные равны нулю, а значения базисных переменных – соответствующим значениям свободных чисел, т.е.:

      .

      Найденное базисное решение является вырожденным, т.к. имеется базисная переменная х2, равная нулю.

      3 этап: проверка совместности системы ограничений ЗЛП.

      Так как в таблице 5.11 имеется строка с отрицательным свободным числом (–1), в которой нет ни одного отрицательного элемента (т.е. отрицательного коэффициента при свободной переменной), то согласно признаку несовместности (признак 1) система ограничений данной задачи не совместна (строка целевой функции при рассмотрении данного признака не учитывается). Следовательно, рассматриваемая задача линейного программирования не имеет решения.

      Ответ: рассматриваемая задача линейного программирования не имеет решения в силу несовместности ее системы ограничений.

      МЕТОД — Энциклопедия по экономике

      Итак, для нахождения оптимальной производственной программы необходимо такое решение системы многих уравнений с многими неизвестными, при котором критерий (целевая функция) достигает оптимума. Система уравнений и неравенств (24.1) — (24.5), (24.7) обладает следующим свойством она линейна относительно неизвестных. Это означает, что неизвестные входят в уравнения, неравенства и критерий лишь в первой степени и что отсутствуют произведения неизвестных. Методом решения подобных задач, которые носят название задач линейного программирования, служит так называемый симплекс-метод. Симплекс-метод изложен в целом ряде книг. Ограничимся лишь его технико-экономической интерпретацией.  [c.413]
      Решение задачи (24.1) — (24.7) нахождения оптимальной производственной программы симплекс-методом осуществляется на ЭВМ в два этапа на первом этапе отыскивается допустимый план на втором — происходит улучшение допустимого плана до оптимального. В целом можно сказать, что решение задачи нахождения  [c. 413]

      Упорядоченный перебор интересующих нас допустимых планов, нахождение допустимых планов требуют огромной вычислительной работы, которая осуществляется на ЭВМ. Симплекс-метод, согласно которому ЭВМ осуществляет упорядоченный перебор и находит оптимальное решение, является наиболее распространенным экономико-математическим методом.  [c.414]

      Наиболее распространенным методом решения важных практических задач планирования и управления является линейное программирование. С помощью симплекс-метода решаются задачи планирования производственной программы предприятия, объединения, способствующие получению максимального эффекта при ограниченных материальных и трудовых ресурсах. Распределительный метод линейного программирования позволяет выбрать оптимальные варианты планов транспортных перевозок решать задачи по оптимизации планов загрузки оборудования и др.  [c.78]


      Для решения задачи (I) автор предлагает использовать метод ветвей и границ, а для нахождения решения семейства задач (II) -использовать методы линейного программирования (например. симплекс -метод).  [c.120]

      Рассмотрим некоторые особенности этого метода. В качестве-основы может быть выбран алгоритм симплекс-метода (например, мультипликативный), в котором на каждой итерации в явном виде вычисляется вектор симплексных множителей по формуле  [c.99]

      Вычислительная схема реализации расчетов по модели (2)— (9) на основе мультипликативного алгоритма симплекс. — метода показана на рисунке.  [c.100]

      Симплекс-метод представляет собой технику решения задач с ограничивающими факторами при помощи компьютера (соответствующие расчеты можно сделать и вручную, но это очень трудоемко, даже при относительно несложных задачах). Будучи ограниченным только аппаратными или программными возможностями (т.е. особенностями прикладной программы или объемом памяти компьютера), симплекс-метод позволяет решать задачи с огромным количеством товаров/услуг и ограни-  [c.370]

      Симплекс-метод — это техника решения многопродуктовых задач в условиях ограничений, чаще реализуемая с помощью компьютера.  [c.378]

      Для решения симплекс-методом (на компьютере) технический консультант спортклуба сформулировал задачу о размещении кресел  [c.389]

      Наконец, рассмотрим многокритериальные симплекс-методы,, основанные на использовании симплекс-таблицы линейного программирования. Эти методы очень близки к методам параметрического программирования и состоят в переходе из некоторой исходной точки (скажем, точки А см. рис. 6.9) в соседнюю эффективную точку. При этом, в отличие от методов взвешивания, понятие весов не используется. Многокритериальные симплекс-методы имеют те же самые достоинства и1 недостатки, что и параметрические методы.  [c.311]

      Стандартные программные пакеты для персональных компьютеров реализуют в этом случае симплекс-метод, который представляет собой итеративный пошаговый процесс. Он начинается с выбора одного возможного решения с последующим замещением его, если результат может быть улучшен. Этот перебор продолжается до тех пор, пока дальнейшее улучшение невозможно. Таким образом будет получено оптимальное решение.  [c.280]


      В этих случаях используется симплекс-метод, который представляет собой итеративную (пошаговую) процедуру для определения оптимального решения задачи линейного программирования. Расчеты по симплекс-методу начинают с определения допустимого решения, а затем отыскиваются другие допустимые решения и проверяются возможности их улучшения. Переход от одного решения к другому продолжается до тех пор, пока новые улучшения не будут невозможны. Широко распространены стандартные компьютерные программы, которые используют симплекс-метод для решения таких управленческих задач, которые можно представить как задачи линейного программирования.  [c.220]

      Нахождение оптимального решения. В случае, когда в целевой функции только две переменные и количество ограничений небольшое, для нахождения оптимального решения можно использовать графический метод и метод проб и ошибок. В более сложных случаях, которые возникают на практике, необходимы специальные пакеты программного обеспечения, например симплекс-метод.  [c.382]

      Следует отметить, что метод проб и ошибок, а также графический метод полезны в случае двух или, возможно, трех переменных. Для решения проблемы линейного программирования со многими переменными эти методы непрактичны. Стандартные программные пакеты для персональных компьютеров реализуют в этом случае симплекс-метод, который представляет собой итеративный пошаговый процесс. Он начинается выбором одного возможного решения с последующим замещением его, если результат можно улучшить. Этот перебор продолжается до тех пор, пока дальнейшее улучшение перестает быть возможным.  [c.385]

      Весьма типичной задачей, решаемой с помощью линейного программирования, является транспортная задача. Ее смысл заключается в минимизации грузооборота при доставке товаров широкого потребления от производителя к потребителю, с оптовых складов и баз в розничные торговые предприятия. Она решается симплекс-методом или распределительным методом.  [c.163]

      Задачи с помощью линейного программирования решаются двумя способами симплекс-методом и распределительном методом.  [c.41]

      Симплекс-метод см. Баканов М. И., Шеремет А. Д. Теория экономического анализа. — М. Финансы и статистика, 1998.-С. 162- 171. Приведенный в учебнике пример также может служить материалом для практических занятий.  [c.42]

      Известно, что в случае двух переменных решение задачи математического программирования можно провести не только аналитически (например, используя симплекс-метод), но и графически. В нашем примере интерес представляет только целочисленное решение.  [c.221]

      Линейное программирование — математический метод, предназначенный для выявления оптимального решения из большого числа возможных вариантов решения задачи, у которой условия позволяют запись в виде линейных соотношений. Линейное программирование применяется для решения задач типа распределение ресурсов, формирование комбинации кормов, составление портфеля инвестиций, выбор производственной программы. Для постановки задачи линейного программирования необходимо ввести переменные (определяемые) величины, выразить через эти переменные ограничивающие условия и целевую функцию. Для решения задач линейного программирования используют симплекс-метод или графический метод (при наличии двух переменных в решаемой задаче).  [c.122]

      Симплекс-метод (аналитическое решение задач линейного программирования) — это алгоритм формального пересчета вариантов решения задачи с последовательным движением к оптимальному решению. Каждый шаг алгоритма расчетов улучшает предыдущее решение.  [c.122]

      Рассмотрим алгоритм симплекс-метода на основе числового примера — оптимизационной задачи, включающей пять неизвестных и три ограничивающих условия.  [c.122]

      Решение. В результате решения задачи симплекс-методом найдем оптимальное решение х = 1 х = 7, 5 1 =29,5, где верхний индекс переменных — номер задачи.  [c.127]

      Результаты решения симплекс-методом задачи 2 х = 1,2 j f = 7 L2 = 29,4 задачи 3 х = 0,75 xf = 8 L3 = 29,25.  [c.128]

      Решение задачи ЛП осуществляется модифицированным симплекс-методом с мультипликативным представлением обратной матрицы и двусторонними границами для переменных и ограничений.  [c.179]

      С учетом возможностей современных ППП, использующих модифицированный симплекс-метод с мультипликативным представлением матрицы, отнесение очередного вектора к классу векторов, обеспечивающих совместность или несовместность, требует проведения всего нескольких итераций после модификации обобщенной матрицы  [c.207]

      Раскрыв любую книгу по управлению финансами, изданную в России, или переведенный с английского учебник по корпоративным финансам, едва ли не с первых страниц натыкаешься на обилие сложных формул, интегралов и производных, а также на множество терминов, таких как финансовый рычаг, модель Дюпона и т. п. Изыски финансовой механики безусловно важны и полезны. Но все симплекс-методы и оптимизационные модели ни на шаг не приближают нас к составлению бюджетов компании. Например, к пониманию того, чем бюджет отличается от сметы.  [c.37]

      Имеется три источника AI, А2, А3 располагающие соответствующими мощностями и четыре потребителей Btj B2, В3 и В4 (мвт). При известных стоимостях передачи единицы мощности С, t от i источника к j потребителю ( без учёта потерь мощности ) найти оптимальный Уед распределения электрической мощности от источников к потребителям, при котором затраты на передачу минимальны и определить оптимальную конфигурацию электрической сети. Решение задачи осуществить можно симплекс методом, либо распределительным методом либо методом потенциалов.  [c.10]

      Блок 6 — машинное решение модели. Для решения данной экономико-математической модели может быть использован алгоритм, разработанный сотрудниками ЦЭМИ АН СССР, который предусматривает решение с помощью мультипликативного симплекс-метода. В результате машинного решения должна быть получена распечатка ленты, описание которой дано а разделе Выходная информация . . . . . . ….  [c.157]

      Данная задача решается с применением симплекс-метода, описание которого приводится ниже.  [c.179]

      Оптимизация компаундирования значительно повышает рентабельность продукции при полном использовании запасов компонентов. Но для получения таких результатов необходимо обеспечить быстроту расчетов, что возможно только при применении ЭЦВМ. Решение простейшего варианта задачи о смешении симплекс-методом вручную продолжается около 15 дней, тогда как решение более сложной задачи на ЭЦВМ при наличии готовой  [c.135]

      Рассмотренный метод оптимизации производственной программы. НПЗ в постановке (2)—(9)-реализован на ЭВМ М-22 . Ниже приводится общая схема вычисления по данному методу. Условия (4)—(8) формируются в виде отдельного. информационного массива. Он используется только при решении вспомогательной задачи (12). Основой предлагаемой вычислительной схемы является алгоритм мультипликативного симплекс-метода, к которому стыкуются алгоритмы решения вспомогательной задачи и усреднения. Для решения вспомогательнбй задачи может использоваться основная программа. Однако в связи/с ее небольшими размерами был разработан и реализован на ЭВМ более экономный прямой алгоритм симплекс метода с верхними ограничениями на переменные. Следует отметить, что предлагаемый подход может реализован и другой вычислительной схемой, отличной от приводимой ниже. Ее отличие состоит в том, что алгоритм решения вспомогательной задачи.подключается только после получения оптимального решения, основной задачи. Практическая проверка обеих вычислительных схем не показала существенного преимущества ни одной из них.  [c.100]

      На /-и итерации процедуры исходной информацией шага а) является положительный вектор весов X = Х15. .., Я ]. Задача (3.9) решается с помощью симплекс-метода ее решение, обозначаемое х1, используется для построения вспомогательной информации, которая состоит в расчете значений вектора критериев в соседних с х вершинах многогранного множества (3.7). При этом рассматриваются только те вершины, которые принадлежат эффективному множеству решений. Пусть на Z-й итерации таких вершин [c.307]

      AB D, содержащий все выпуклые комбинации этих точек (он заштрихован на рис. 6.9), содержит и неэффективные точки. Среди методов построения эффективных вершин можно выделить два основных направления. Это методы взвешивания и многокритериальные симплекс-методы.  [c.310]

      Становление современного математического аппарата оптимальных экономических решений началось в 40-е годы, благодаря первым работам Н. Винера, Р. Беллмана, С. Джонсона, Л. Канторовича. Задача линейного программирования впервые математически сформулирована Л. В. Канторовичем в 1939 г. на примере задачи раскроя материалов для Ленинградского фанерного треста. В 1947 г. Дж. Данциг предложил универсальный алгоритм решения задач линейного программирования, названный им симплекс-методом. В 1941 г. Хичкок и независимо от него в 1947 г. Купсман формулируют транспортную задачу, в 1945 г. Стиглер — задачу о диете. В 1952 г. было проведено первое успешное решение задачи линейного программирования на ЭВМ Sea в Национальном бюро стандартов США.  [c.102]

      М301. Мультипликативный симплекс-метод решения общей задачи линейного программирования  [c.35]

      Симплексный метод, библиотека scipy и нелинейное программирование в линейном программировании на Python

      Симплексный метод, scipy библиотека и нелинейное программирование для решения задач

      • Основное определение симплекс-метода
      • Принцип метода Big M для решения линейного программирования
      • решение Excel
      • Python вызывает optimize package и scipy для решения линейного программирования
      • Программирование на Python для реализации симплексного метода
      • Сравнение
      • Нелинейное программирование

      Основное определение симплекс-метода:
      В общих задачах линейного программирования, когда количество переменных в системе линейных уравнений больше, чем количество уравнений, будет неопределенное количество решений, и симплекс-метод является общим метод решения задач линейного программирования. Конкретные шаги заключаются в том, чтобы найти один за другим симплекс из системы линейных уравнений, и каждый симплекс может получить набор решений, а затем оценить, увеличивает ли решение или уменьшает значение целевой функции, и решить, какой симплекс выбрать в форма следующего шага. Через итерацию оптимизации, пока целевая функция не достигнет максимального или минимального значения. Другими словами, симплекс-метод придерживается основной идеи «гарантировать, что каждая итерация лучше предыдущей»: сначала найдите базовое возможное решение, определите его и посмотрите, является ли оно оптимальным решением; если нет, следовать Преобразовать определенное правило в другое улучшенное и лучшее базовое выполнимое решение, а затем определить; если это все еще не так, преобразовать снова и повторить. Поскольку количество основных возможных решений ограничено, оптимальное решение задачи может быть получено после конечного числа преобразований. Если проблема не имеет оптимального решения, этот метод также можно использовать для оценки.

      Принцип метода Big M для решения линейного программирования:
      Метод Big M сначала преобразует задачу линейного программирования в стандартную форму. Если система уравнений ограничений содержит единичную матрицу I, то был получен начальный допустимый базис. В противном случае добавьте тысячи неотрицательных искусственных переменных в левую часть системы уравнений ограничений, чтобы вектор-столбец коэффициентов, соответствующий искусственной переменной, и вектор-столбец коэффициентов других переменных образовали единичную матрицу. Используя единичную матрицу в качестве начального базиса, можно получить начальное базовое допустимое решение. Чтобы получить начальное базовое возможное решение исходной проблемы, искусственная переменная должна быть заменена из базовой переменной на неосновную переменную посредством итеративного процесса как можно скорее. По этой причине отрицательный коэффициент -M с большим абсолютным значением может быть присвоен искусственной переменной в целевой функции. Таким образом, пока в базовых переменных есть искусственные переменные, целевая функция не может быть максимизирована. Последующие вычисления такие же, как и для решения с симплексной таблицей, и M нужно только рассматривать как большое положительное число. Если искусственные переменные включены в базовые переменные симплексной оптимальной таблицы, это означает, что не существует допустимого решения исходной задачи. В противном случае оставшаяся часть оптимального решения, исключая искусственные переменные, является начальным основным допустимым решением исходной задачи.

      тема:

      Используйте пакет для решения:



      Excel использует метод Big M для решения линейного программирования:

      # Импорт пакета
from scipy import optimize
import numpy as np
#OK c, A_ub, B_ub
c = np.array([50,100])
A_ub = np.array([[1,1],[2,1],[0,1]])
B_ub = np.array([300,400,250])
#Решать
res =optimize.linprog(-c,A_ub,B_ub)
print(res)

      результат:

      import numpy as np
def pivot(d,bn):
    l = list(d[0][:-2])
    jnum = l. index(max(l)) # Номер перевода
    m = []
    for i in range(bn):
        if d[i][jnum] == 0:
            m.append(0.)
        else:
            m.append(d[i][-1]/d[i][jnum])
    inum = m.index(min([x for x in m[1:] if x!=0]))  # Перенести нижний индекс
    s[inum-1] = jnum
    r = d[inum][jnum]
    d[inum] /= r
    for i in [x for x in range(bn) if x !=inum]:
        r = d[i][jnum]
        d[i] -= r * d[inum]        
def solve(d,bn):
    flag = True
    while flag:
        if max(list(d[0][:-1])) <= 0: # Пока все коэффициенты не будут меньше или равны 0
            flag = False
        else:
            pivot(d,bn)            
def printSol(d,cn):
    for i in range(cn - 1):
        if i in s:
            print("x"+str(i)+"=%.2f" % d[s.index(i)+1][-1])
        else:
            print("x"+str(i)+"=0.00")
    print("objective is %.2f"%(-d[0][-1]))
d = np.loadtxt("./data.txt", dtype=np.float)
(bn,cn) = d.shape
s = list(range(cn-bn,cn-1)) # Базовый список переменных
solve(d,bn)
printSol(d,cn)

      данные данные:

      Результаты:

      Сравнивая два результата с точки зрения ценности, два метода в основном одинаковы с небольшой ошибкой, но результат симплексного метода более точен как целочисленное значение.

      # coding=utf-8
from scipy.optimize import minimize
import numpy as np
 
# demo 2
#Calculate (2 + x1) / (1 + x2) - минимальное значение 3 * x1 + 4 * x3 x1, x2, x3 в диапазоне от 0,1 до 0,9
def fun(args):
    a,b,c,d=args
    v=lambda x: (a+x[0])/(b+x[1]) -c*x[0]+d*x[2]
    return v
def con(args):
    # Ограничения делятся на eq и ineq
    #eq означает, что результат функции равен 0; ineq означает, что выражение больше или равно 0  
    x1min, x1max, x2min, x2max,x3min,x3max = args
    cons = ({'type': 'ineq', 'fun': lambda x: x[0] - x1min},\
              {'type': 'ineq', 'fun': lambda x: -x[0] + x1max},\
             {'type': 'ineq', 'fun': lambda x: x[1] - x2min},\
                {'type': 'ineq', 'fun': lambda x: -x[1] + x2max},\
            {'type': 'ineq', 'fun': lambda x: x[2] - x3min},\
             {'type': 'ineq', 'fun': lambda x: -x[2] + x3max})
    return cons
 
if __name__ == "__main__":
    # Определить постоянное значение
    args = (2,1,3,4)  #a,b,c,d
    # Установить диапазон параметров / ограничения
    args1 = (0. 1,0.9,0.1, 0.9,0.1,0.9)  #x1min, x1max, x2min, x2max
    cons = con(args1)
    # Установить первоначальное предположение  
    x0 = np.asarray((0.5,0.5,0.5))
    
    res = minimize(fun(args), x0, method='SLSQP',constraints=cons)
    print(res.fun)
    print(res.success)
    print(res.x)

      результат:

      Симплекс-метод. Алгоритм симплекс-метода. Особенности табличного симплекс-метода. Понятия модифицированного симплекс-метода и двойственного симплекс-метода

      Информатика и выч. техника \ Информатика

      Страницы работы

      16 страниц (Word-файл)

      Посмотреть все страницы

      Скачать файл

      Фрагмент текста работы

      Задачей оптимизации в математике называется задача о нахождении экстремума вещественной функции в некоторой области. Как правило, рассматриваются области, принадлежащие и заданные набором равенств и неравенств.

      3.1. Описание

      Задача линейного программирования состоит в том, что необходимо максимизировать или минимизировать некоторый линейный функционал на многомерном пространстве при заданных линейных ограничениях.

      Каждое из линейных неравенств на переменные ограничивает полупространство в соответствующем линейном пространстве. В результате все неравенства ограничивают некоторый многогранник (возможно, бесконечный), называемый также полиэдральным конусом. 

       

      Уравнение W(x) = c, где W(x) – максимизируемый (или минимизируемый) линейный функционал, порождает гиперплоскость L(c). Зависимость от c порождает семейство параллельных гиперплоскостей. При этом экстремальная задача приобретает следующую формулировку: требуется найти такое наибольшее c, что гиперплоскость L(c) пересекает многогранник хотя бы в одной точке. Заметим, что пересечение оптимальной гиперплоскости и многогранника будет содержать хотя бы одну вершину, причем их будет более одной, если пересечение содержит ребро или k-мерную грань. Поэтому максимум функционала можно искать в вершинах многогранника. Принцип симплекс-метода состоит в том, что выбирается одна из вершин многогранника, после чего начинается движение по его рёбрам от вершины к вершине в сторону увеличения значения функционала. Когда переход по ребру из текущей вершины в другую вершину с более высоким значением функционала невозможен, считается, что оптимальное значение c найдено.

      Сущность симплекс-метода состоит в том, что если число неизвестных больше числа уравнений, то данная система неопределенная с бесчисленным множеством решений. Для решения системы все неизвестные произвольно подразделяются на базисные и свободные. Число базисных переменных определяется числом линейно-независимых уравнений. Остальные неизвестные свободные. Им придаются произвольные значения и затем подставляются в систему. Любому набору свободных неизвестных можно придать бесчисленное множество произвольных значений, которые дадут бесчисленное множество решений. Если все свободные неизвестные приравнять к нулю, то решение будет состоять из значений базисных неизвестных. Такое решение называется базисным.

      В теории линейного программирования существует теорема, которая утверждает, что среди базисных решений системы можно найти оптимальное, а в некоторых случаях – несколько оптимальных решений, причем все они обеспечат экстремум целевой функции. Таким образом, если найти какой-то базисный план и затем улучшить его, то получится оптимальное решение. На этом принципе построен симплекс-метод. 

      Последовательность вычислений симплекс-методом можно разделить на две основные фазы:

      1.  нахождение исходной вершины множества допустимых решений;

      2.  последовательный переход от вершины к вершине, ведущий к оптимизации значения целевой функции.

      В некоторых случаях исходное решение очевидно или его определение не требует сложных вычислений, – например, когда все ограничения представлены неравенствами вида «меньше или равно» (тогда нулевой вектор совершенно точно есть допустимое решение, хотя, скорее всего, далеко не оптимальное). В таких задачах первую фазу симплекс-метода можно вообще не проводить. Симплекс-метод соответственно делится на однофазный и

      двухфазный.

      3.2. Алгоритм симплекс-метода

      Усиленная постановка задачи

      Рассмотрим следующую задачу линейного программирования:

       

      Теперь поставим эту задачу в эквивалентной усиленной форме. Необходимо максимизировать Z, где:

       

      Здесь x – переменные из исходного линейного функционала; xs – новые переменные, дополняющие старые таким образом, что неравенство переходит в равенство; c – коэффициенты исходного линейного функционала; Z – переменная, которую необходимо максимизировать. Полупространства  и  в пересечении образуют многогранник, представляющий множество допустимых решений. Разница между числом переменных и уравнений даёт число степеней свободы. Проще говоря, если рассматривать вершину многогранника, это есть число рёбер, по которым можно продолжать движение.

      Тогда можно присвоить такому числу переменных значение 0 и назвать

      Похожие материалы

      Информация о работе

      Скачать файл

      4.2: Максимизация Симплекс-методом

      1. Последнее обновление
      2. Сохранить как PDF
    • Идентификатор страницы
      37869
      • Рупиндер Секон и Роберта Блум
      • Колледж Де Анза

      Цели обучения

      В этом разделе вы научитесь решать задачи максимизации линейного программирования с использованием симплекс-метода:

      1. Определить и настроить линейную программу в стандартной форме максимизации
      2. Преобразование ограничений неравенства в уравнения с использованием резервных переменных
      3. Настройте начальную симплексную таблицу, используя целевую функцию и уравнения резерва
      4. Найдите оптимальную симплексную таблицу, выполнив операции поворота.
      5. Определите оптимальное решение по оптимальной симплексной таблице.

      В предыдущей главе мы использовали геометрический метод для решения задач линейного программирования, но геометрический подход не работает для задач с более чем двумя переменными. В реальных жизненных ситуациях задачи линейного программирования состоят буквально из тысяч переменных и решаются компьютерами. Мы можем решить эти проблемы алгебраически, но это будет не очень эффективно. Предположим, нам дали задачу, скажем, с 5 переменными и 10 ограничениями. Выбрав все комбинации из пяти уравнений с пятью неизвестными, мы могли бы найти все угловые точки, проверить их на допустимость и найти решение, если оно существует. Но беда в том, что даже для задачи с таким небольшим количеством переменных мы получим более 250 угловых точек, и проверка каждой точки будет очень утомительна. Поэтому нам нужен метод, который имеет систематический алгоритм и может быть запрограммирован для компьютера. Метод должен быть достаточно эффективным, чтобы нам не пришлось оценивать целевую функцию в каждой угловой точке. У нас есть именно такой метод, и он называется симплексный метод .

      Симплекс-метод был разработан во время Второй мировой войны доктором Джорджем Данцигом. Его модели линейного программирования помогли союзным войскам решить проблемы с транспортом и планированием. В 1979 году советский ученый Леонид Хачян разработал метод, названный алгоритмом эллипсоида, который должен был стать революционным, но, как оказалось, ничем не лучше симплексного метода. В 1984 году Нарендра Кармаркар, научный сотрудник AT&T Bell Laboratories, разработал алгоритм Кармаркара, который, как было доказано, в четыре раза быстрее, чем симплекс-метод для определенных задач. Но симплекс-метод по-прежнему работает лучше всего для большинства задач.

      В симплексном методе используется очень эффективный подход. Он не вычисляет значение целевой функции в каждой точке; вместо этого он начинается с угловой точки области выполнимости, где все основные переменные равны нулю, а затем систематически перемещается от угловой точки к угловой точке, улучшая значение целевой функции на каждом этапе. Процесс продолжается до тех пор, пока не будет найдено оптимальное решение.

      Чтобы изучить симплекс-метод, мы попробуем довольно нетрадиционный подход. Сначала мы перечисляем алгоритм, а затем работаем над проблемой. Мы обосновываем обоснование каждого шага в процессе. Тщательное обоснование выходит за рамки данного курса.

      Начнем с примера, который мы решили в предыдущей главе графическим методом. Это даст нам некоторое представление о симплекс-методе и в то же время даст нам возможность сравнить несколько допустимых решений, которые мы получили ранее с помощью графического метода. Но сначала приведем алгоритм симплекс-метода.

      СИМПЛЕКСНЫЙ МЕТОД

      1. Поставьте задачу. То есть запишите целевую функцию и ограничения неравенства.
      2. Преобразуйте неравенства в уравнения. Это делается путем добавления одной резервной переменной для каждого неравенства.
      3. Построить начальную симплексную таблицу. Запишите целевую функцию в нижней строке.
      4. Самая отрицательная запись в нижней строке идентифицирует сводной столбец.
      5. Вычислите частные. Наименьшее частное определяет строку. Элемент на пересечении столбца, определенного на шаге 4, и строки, определенной на этом шаге, идентифицируется как опорный элемент. Частные вычисляются путем деления крайнего правого столбца на столбец, указанный в шаге 4. Частное, являющееся нулем, отрицательным числом или имеющим ноль в знаменателе, игнорируется.
      6. Выполните поворот, чтобы обнулить все остальные записи в этом столбце. Это делается так же, как и с методом Гаусса-Джордана.
      7. Когда в нижней строке больше нет отрицательных значений, мы закончили; в противном случае начинаем снова с шага 4.
      8. Прочитайте свои ответы. Получить переменные, используя столбцы с 1 и 0. Все остальные переменные равны нулю. Максимальное значение, которое вы ищете, отображается в правом нижнем углу.

      Теперь мы используем симплекс-метод для решения примера 3. 1.1, решенного геометрически в разделе 3.1.

      Пример \(\PageIndex{1}\)

      Ники работает на двух работах с частичной занятостью: работа I и работа II. Она никогда не хочет работать больше, чем в общей сложности 12 часов в неделю. Она определила, что на каждый час работы на Работе I ей нужно 2 часа времени на подготовку, а на каждый час работы на Работе II ей нужен один час времени на подготовку, и она не может тратить на подготовку более 16 часов. Если она зарабатывает 40 долларов в час на работе I и 30 долларов в час на работе II, сколько часов в неделю она должна работать на каждой работе, чтобы максимизировать свой доход?

      Решение

      При решении этой задачи будем следовать алгоритму, указанному выше.

      ШАГ 1. Поставьте задачу. Запишите целевую функцию и ограничения.

      Поскольку симплекс-метод используется для задач, состоящих из многих переменных, нецелесообразно использовать переменные \(x\), \(y\), \(z\) и т. д. Мы используем символы \(x_1\ ), \(x_2\), \(x_3\) и так далее.

      Let

      • \(x_1\) = количество часов в неделю, которое Ники будет работать на работе I и 9.0010
      • \(x_2\) = количество часов в неделю, которое Ники будет работать на задании II.

      Принято выбирать переменную, которая должна быть максимизирована как \(Z\).

      Задача формулируется так же, как и в предыдущей главе.

      \[\begin{array}{ll}
      \textbf { Развернуть} & \mathrm{Z}=40 \mathrm{x}_{1}+30 \mathrm{x}_{2} \\
      \ textbf { При условии: } & \mathrm{x}_{1}+\mathrm{x}_{2} \leq 12 \\
      & 2 \mathrm{x}_{1}+\mathrm{x}_ {2} \leq 16 \\
      & \mathrm{x}_{1} \geq 0 ; \mathrm{x}_{2} \geq 0
      \end{array}\nonumber \]

      ШАГ 2. Преобразовать неравенства в уравнения. Это делается путем добавления одной резервной переменной для каждого неравенства.

      Например, чтобы преобразовать неравенство \(x_1 + x_2 ≤ 12\) в уравнение, мы добавляем неотрицательную переменную \(y_1\), и мы получаем

      \[x_1 + x_2 + y_1 = 12 \nonumber \]

      Здесь переменная \(y_1\) восполняет пробел и представляет величину, на которую \(x_1 + x_2\) меньше 12. В этой задаче, если Ники работает менее 12 часов, скажем, 10 , тогда \(y_1\) равно 2. Позже, когда мы прочитаем окончательное решение из симплексной таблицы, значения резервных переменных будут определять неиспользованные суммы.

      Перепишем целевую функцию \(Z = 40x_1 + 30x_2\) в виде \(- 40x_1 — 30x_2 + Z = 0\).

      После добавления резервных переменных наша задача выглядит следующим образом:

      \[\begin{array}{ll}
      \text { Целевая функция } & — 40x_1 — 30x_2 + Z = 0 \\
      \text { С учетом ограничений: } &x_1+x_2+y_1=12\
      &2x_1+x_2+y_2=16\
      &x1 ≥ 0; x2 ≥ 0
      \end{array} \nonumber \]

      ШАГ 3. Построить исходную симплексную таблицу . Каждое ограничение неравенства отображается в отдельной строке. (Ограничения неотрицательности заставляют , а не появляться в виде строк в симплексной таблице.) Запишите целевую функцию в нижней строке.

      Теперь, когда неравенства преобразованы в уравнения, мы можем представить задачу в виде расширенной матрицы, называемой исходной симплексной таблицей, следующим образом.

      Здесь вертикальная линия отделяет левую часть уравнений от правой. Горизонтальная линия отделяет ограничения от целевой функции. Правая часть уравнения представлена ​​столбцом C.

      Читатель должен заметить, что последние четыре столбца этой матрицы выглядят как окончательная матрица для решения системы уравнений. Если мы произвольно выберем \(x_1 = 0\) и \(x_2 = 0\), мы получим

      \[\left[\begin{array}{ccccc}
      y_{1} & y_{2} & Z & | &С\
      1&0&0 & | & 12 \
      0 & 1 & 0 & | & 16 \\
      0 & 0 & 1 & | & 0
      \end{массив}\right]\nonumber \]

      , что читается как

      \[y_1 = 12 \quad y_2 = 16 \quad Z = 0 \nonumber \]

      Решение, полученное путем произвольного присвоения значений некоторым переменным и последующего решения для оставшихся переменных, называется базовым решением , связанным с таблицей . Таким образом, приведенное выше решение является основным решением, связанным с исходной симплексной таблицей. Мы можем пометить базовую переменную решения справа от последнего столбца, как показано в таблице ниже.

      ШАГ 4. Самая отрицательная запись в нижней строке идентифицирует сводной столбец.

      Самая отрицательная запись в нижней строке -40; поэтому столбец 1 идентифицируется.

      Вопрос Почему мы выбираем самую отрицательную запись в нижней строке?

      Ответ Самая отрицательная запись в нижней строке представляет наибольший коэффициент в целевой функции — коэффициент, ввод которого увеличит значение целевой функции быстрее всего.

      Симплекс-метод начинается с угловой точки, где все основные переменные, переменные с такими символами, как \(x_1\), \(x_2\), \(x_3\) и т. д., равны нулю. Затем он перемещается от угловой точки к соседней угловой точке, всегда увеличивая значение целевой функции. В случае целевой функции \(Z = 40x_1+ 30x_2\) имеет смысл увеличить значение \(x_1\), а не \(x_2\). Переменная \(x_1\) представляет количество часов в неделю, которые Ники работает на работе I. Поскольку работа I оплачивается 40 долларов в час, в отличие от работы II, на которой платят всего 30 долларов, переменная \(x_1\) увеличит целевую функцию на $40 за единицу увеличения переменной \(x_1\).

      ШАГ 5. Вычислите частные. Наименьшее частное определяет строку. Элемент на пересечении столбца, определенного на шаге 4, и строки, определенной на этом шаге, идентифицируется как опорный элемент.

      Следуя алгоритму, для вычисления частного делим записи в крайнем правом столбце на записи в столбце 1, исключая запись в нижней строке.

      Наименьшее из двух частных, 12 и 8, равно 8. Следовательно, идентифицируется строка 2. Пересечение столбца 1 и строки 2 является записью 2, которая выделена. Это наш опорный элемент.

      Вопрос Почему мы находим частное и почему наименьшее частное определяет строку?

      Ответ Когда мы выбираем самую отрицательную запись в нижней строке, мы пытаемся увеличить значение целевой функции, вводя переменную \(x_1\). Но мы не можем выбрать любое значение для \(x_1\). Можем ли мы позволить \(x_1 = 100\)? Точно нет! Это потому, что Ники никогда не хочет работать более 12 часов на обеих работах вместе взятых: \(x_1 + x_2 ≤ 12\). Можем ли мы позволить \(x_1 = 12\)? Опять же, ответ отрицательный, потому что время подготовки к работе I в два раза превышает время, затрачиваемое на работу. Поскольку Ники никогда не хочет тратить на подготовку более 16 часов, максимальное время, которое она может работать, составляет 16 ÷ 2 = 8.9.0034

      Теперь вы видите цель вычисления частных; использование частных для определения опорного элемента гарантирует, что мы не нарушаем ограничения.

      Вопрос Почему мы идентифицируем поворотный элемент?

      Ответ Как мы упоминали ранее, симплекс-метод начинается с угловой точки, а затем переходит к следующей угловой точке, всегда улучшая значение целевой функции. Значение целевой функции улучшается за счет изменения количества единиц переменных. Мы можем добавить количество единиц одной переменной, отбросив единицы другой. Поворот позволяет нам сделать именно это.

      Переменная, единицы которой добавляются, называется входной переменной , , а переменная, единицы которой заменяются, называется исходящей переменной . Входной переменной в приведенной выше таблице является \(x_1\), и она определяется самой отрицательной записью в нижней строке. Уходящая переменная \(y_2\) была идентифицирована наименьшим из всех частных.

      ШАГ 6. Выполните поворот, чтобы обнулить все остальные записи в этом столбце.

      В главе 2 мы использовали поворот, чтобы получить эшелонированную форму строк расширенной матрицы. Поворот — это процесс получения 1 в местоположении поворотного элемента, а затем обнуления всех остальных записей в этом столбце. Итак, теперь наша задача состоит в том, чтобы сделать наш опорный элемент равным 1, разделив всю вторую строку на 2. Далее следует результат.

      Чтобы получить ноль в записи первой над опорным элементом, умножаем вторую строку на -1 и прибавляем к строке 1. Получаем

      Чтобы получить ноль в элементе ниже стержня, умножаем вторую строку на 40 и прибавляем к последней строке.

      Теперь мы определяем основное решение, связанное с этой таблицей. Произвольно выбирая \(x_2 = 0\) и \(y_2 = 0\), мы получаем \(x_1 = 8\), \(y_1 = 4\) и \(z = 320\). Если мы напишем расширенную матрицу, левая часть которой представляет собой матрицу со столбцами, в которых одна единица, а все остальные элементы равны нулю, мы получим следующую матрицу, утверждающую то же самое.

      \[\left[\begin{array}{ccccc}
      \mathrm{x}_{1} & \mathrm{y}_1 & \mathrm{Z} & | & \mathrm{C} \\
      0 & 1 & 0 & | & 4 \
      1 & 0 & 0 & | & 8 \
      0 & 0 & 1 & | & 320
      \end{array}\right] \nonumber \]

      Мы можем переформулировать решение, связанное с этой матрицей, как \(x_1 = 8\), \(x_2 = 0\), \(y_1 = 4\) , \(y_2 = 0\) и \(z = 320\). На этом этапе игры написано, что если Ники проработает 8 часов на работе I и ни одного часа на работе II, ее прибыль Z составит 320 долларов. Напомним из примера 3.1.1 в разделе 3.1, что (8, 0) была одной из наших угловых точек. Здесь \(y_1 = 4\) и \(y_2 = 0\) означают, что у нее останется 4 часа рабочего времени и никакого времени на подготовку.

      ШАГ 7. Когда в нижней строке больше нет отрицательных значений, мы закончили; в противном случае мы начинаем снова с шага 4.

      Поскольку в нижней строке все еще есть отрицательная запись, -10, нам нужно снова начать с шага 4. На этот раз мы не будем повторять детали каждого шага. , вместо этого мы укажем столбец и строку, которые дают нам опорный элемент, и выделим опорный элемент. Результат следующий.

      Делаем опорный элемент 1, умножая строку 1 на 2, и получаем

      Теперь, чтобы все остальные записи в этом столбце были равны нулю, мы сначала умножаем строку 1 на -1/2 и прибавляем к строке 2, а затем умножаем строку 1 на 10 и прибавляем к нижней строке.

      У нас больше нет отрицательных записей в нижней строке, поэтому мы закончили.

      Вопрос Почему мы закончили, если в нижней строке нет отрицательных значений?

      Ответ Ответ лежит в нижней строке. Нижняя строка соответствует уравнению:

      \[\begin{array}{l}
      0 x_{1}+0 x_{2}+20 y_{1}+10 y_{2}+Z=400 \quad \text { or } \\
      z=400-20 y 1-10 y 2
      \end{array}\nonumber \]

      Поскольку все переменные неотрицательны, максимальное значение \(Z\) может быть равно 400, и это произойдет только когда \(y_1\) и \(y_2\) равны нулю.

      ШАГ 8. Прочитайте ваши ответы.

      Теперь мы читаем наши ответы, то есть мы определяем базовое решение, связанное с окончательной симплексной таблицей. Опять же, мы смотрим на столбцы, в которых есть 1, а все остальные записи — нули. Поскольку столбцы с метками \(y_1\) и \(y_2\) не являются такими столбцами, мы произвольно выбираем \(y_1 = 0\) и \(y_2 = 0\), и мы получаем

      \[\left[\begin{array}{ccccc}
      \mathrm{x}_{1} & \mathrm{x}_{2} & \mathrm{Z} & | & \mathrm{C} \\
      0 & 1 & 0 & | & 8 \\
      1 & 0 & 0 & | & 4 \
      0 & 0 & 1 & | & 400
      \end{массив}\right] \nonumber \]

      Матрица читается как \(x_1 = 4\), \(x_2= 8\) и \(z = 400\).

      Окончательное решение гласит, что если Ники будет работать 4 часа на работе I и 8 часов на работе II, она максимизирует свой доход до 400 долларов. Поскольку обе переменные slack равны нулю, значит, она израсходовала бы все рабочее время, а также время на подготовку, и ничего не останется.

      Эта страница под названием 4. 2: Максимизация с помощью симплексного метода распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована Рупиндером Секоном и Робертой Блум с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами LibreTexts. Платформа; подробная история редактирования доступна по запросу.

      1. Наверх
        • Была ли эта статья полезной?
        1. Тип изделия
          Раздел или Страница
          Автор
          Рупиндер Сехон и Роберта Блум
          Лицензия
          СС BY
          Версия лицензии
          4,0
          Показать страницу TOC
          нет
        2. Теги
          1. симплексный алгоритм
          2. источник@https://www. deanza.edu/faculty/bloomroberta/math21/afm3files.html.html

        Линейное программирование: пример симплексного метода

        • HOME
        • ИЗБРАННОЕ
        •  КОНТАКТ
        • КРЕДИТЫ
        • Дом
        • PHPСимплекс
          • Помощь PHPSimple
        • Исследование операций
          • История
          • Реальные случаи
        • Теория
          • Проблемы моделирования
          • Симплексный метод
          • Двухфазный симплексный метод
          • Графический метод
        • Примеры
          • Проблемы моделирования
            • Диетическая проблема
            • Проблема перевозки войск
            • Проблема перевозки грузов
            • Проблема фруктовых деревьев
            • Задача распределения персонала
            • Задача минимальной дороги
            • Проблема с местоположением
            • Проблема фондовой биржи
          • Симплексный метод
          • Графический метод
        • Джордж Б. Данциг
          • Биография
          • Интервью
        • Язык
          • Испанский
          • Английский
          • Французский
          • Португальский

        Пример (часть 1): Симплекс-метод

        Решите Симплекс-методом следующую задачу:

        Максимизация Z = f(x,y) = 3x + 2y
        предмет: 2x + у ≤ 18
          2x + 3y ≤ 42
          3x + у ≤ 24
          х ≥ 0, у ≥ 0

        Рассмотрим следующие шаги:

        1. Произведите замену переменных и нормализуйте знак независимых членов.

          Внесено изменение в наименование переменной, устанавливающее следующие соответствия:

          • x становится X1
          • г становится X2

          Поскольку независимые условия всех ограничений положительны, никаких дальнейших действий не требуется. В противном случае было бы умножение на «-1» в обеих частях неравенства (заметим, что эта операция также влияет на тип ограничения).

        2. Нормализация ограничений.

          Неравенства становятся уравнениями путем добавления запаса , избытка и искусственные переменные в виде следующей таблицы:

          Тип неравенства Появляющаяся переменная
          ≥ — избыток + искусственный
          = + искусственный
          ≤ + провисание

          В этом случае в каждое из ограничений типа ≤ вводится резервная переменная (X3, X4 и X5), для преобразования их в равенства, в результате чего получается система линейных уравнений:

          2·Х1 + Х2 + Х3 = 18
          2·Х1 + 3·Х2 + Х4 = 42
          3·Х1 + Х2 + Х5 = 24
        3. Сопоставьте целевую функцию с нулем.

          Z — 3·X1 — 2·X2 — 0·X3 — 0·X4 — 0·X5 = 0

        4. Напишите исходную таблицу симплекс-метода.

          Исходная таблица симплекс-метода состоит из всех коэффициентов переменных решения исходной задачи и резерва, избыточных и искусственных переменных, добавленных на втором этапе (в столбцах, с P0 в качестве постоянного члена и Pi в качестве коэффициентов остальных переменных Xi) и ограничения (в строках). Столбец Cb содержит коэффициенты переменных, которые находятся в базе.

          Первая строка состоит из коэффициентов целевой функции, а последняя строка содержит значение целевой функции и приведенных затрат Zj — Cj.

          Последняя строка вычисляется следующим образом: Zj = Σ(Cbi·Pj) для i = 1..m, где если j = 0, то P0 = bi и C0 = 0, иначе Pj = aij. Хотя это первая таблица симплекс-метода и все Cb нулевые, поэтому расчет можно упростить, и к этому моменту Zj = -Cj.

          Таблица I . 1-я итерация
                3 2 0 0 0
          Основание Кб Р0 Р1 Р2 Р3 Р4 Р5
          Р3 0 18 2 1 1 0 0
          Р4 0 42 2 3 0 1 0
          Р5 0 24 3 1 0 0 1
          З   0 -3 -2 0 0 0

        5. Состояние остановки.

          Если целью является максимизация, когда в последней строке (строке индикатора) нет отрицательного значения между дисконтированными затратами (столбцы P1 ниже), достигается условие остановки.

          В этом случае алгоритм достигает конца, так как возможности улучшения нет. Значение Z (столбец P0) является оптимальным решением задачи.

          Другой возможный сценарий: все значения отрицательные или нулевые в столбце входных переменных базы. Это указывает на то, что проблема не ограничена и решение всегда будет улучшаться.

          В противном случае последовательно выполняются следующие шаги.

        6. Выбор входных и выходных базовых переменных.

          Сначала определяется входная базовая переменная. Для этого выбирается столбец, значение которого в строке Z меньше всех отрицательных значений. В этом примере это будет переменная X1 (P1) с коэффициентом -3.

          Если есть два или более одинаковых коэффициента, удовлетворяющих вышеуказанному условию (случай равенства), то выбрать базовую переменную.

          Столбец входной базовой переменной называется сводным столбцом (выделен зеленым цветом).

          После получения входной базовой переменной определяется выходная базовая переменная. Решение основано на простом вычислении: разделить каждый независимый член (столбец P0) между соответствующим значением в сводном столбце, если оба значения строго положительны (больше нуля). Выбирается строка, результатом которой является минимальный балл.

          Если какое-либо значение меньше или равно нулю, это частное не будет выполнено. Если все значения опорного столбца удовлетворяют этому условию, то будет достигнуто условие остановки и задача имеет неограниченное решение (см. теорию симплекс-метода).

          В этом примере: 18/2 [=9], 42/2 [=21] и 24/3 [=8]

          Член сводного столбца, который привел к меньшему положительному частному в предыдущем делении, указывает строку резервной переменной, выходящую из базы. В данном примере это X5 (P5) с коэффициентом 3. Этот ряд называется поворотный ряд (зеленый).

          Если два или более частных удовлетворяют условию выбора (случай равенства), выбирается другая базовая переменная (где это возможно).

          Пересечение опорного столбца и сводной строки отмечает значение сводки , в этом примере 3.

        7. Обновление таблицы.

          Новые коэффициенты таблицы рассчитываются следующим образом:

          • В сводной строке каждое новое значение рассчитывается как:

            Новое значение = Предыдущее значение / Сводка

          • В остальных строках каждое новое значение рассчитывается как:

            Новое значение = Предыдущее значение — (Предыдущее значение в сводном столбце * Новое значение в сводной строке)

          Таким образом, стержень нормализуется (его значение становится равным 1), а другие значения стержневого столбца отменяются (аналогично методу Гаусса-Жордана).

          Расчеты для строки P4 показаны ниже:

          Предыдущий ряд P4 42 2 3 0 1 0
            — — — — — —
          Предыдущее значение в сводном столбце 2 2 2 2 2 2
            х х х х х х
          Новое значение в сводной строке 8 1 1/3 0 0 1/3
            = = = = = =
          Новый ряд P4 26 0 7/3 0 1 -2/3

          Таблица, соответствующая этой второй итерации:

          Таблица II . 2-я итерация
                3 2 0 0 0
          Основание Кб Р0 Р1 Р2 Р3 Р4 Р5
          Р3 0 2 0 1/3 1 0 -2/3
          Р4 0 26 0 7/3 0 1 -2/3
          Р1 3 8 1 1/3 0 0 1/3
          З   24 0 -1 0 0 1
        8. При проверке наблюдается условие остановки, которое не выполняется, так как в последней строке одно отрицательное значение -1. Итак, снова повторите шаги 6 и 7.
          • 6.1. Входной базовой переменной является X2 (P2), так как это переменная, соответствующая столбцу, где коэффициент равен -1.
          • 6.2. Чтобы вычислить выходную базовую переменную, постоянные члены столбца P0) делятся на члены нового сводного столбца: 2 / 1/3 [= 6], 26 / 7/3 [= 78/7] и 8 / 1/ 3 [=24]. Поскольку меньшее положительное частное равно 6, выходная базовая переменная равна X3 (P3).
          • 6.3. Новый стержень равен 1/3.
          • 7. Обновление значений таблицы снова получается:
            Таблица III. 3-я итерация
                  3 2 0 0 0
            Основание Кб Р0 Р1 Р2 Р3 Р4 Р5
            Р2 2 6 0 1 3 0 -2
            Р4 0 12 0 0 -7 1 4
            Р1 3 6 1 0 -1 0 1
            З   30 0 0 3 0 -1
        9. Повторная проверка условия остановки показывает, что опорная строка имеет одно отрицательное значение, -1. Это означает, что оптимальное решение еще не достигнуто, и мы должны продолжить итерацию (шаги 6 и 7):
          • 6.1. Входной базовой переменной является X5 (P5), так как это переменная, соответствующая столбцу, где коэффициент равен -1.
          • 6.2. Чтобы вычислить выходную базовую переменную, постоянные члены (P0) делятся на члены нового сводного столбца: 6/(-2) [=-3] , 12/4 [=3] и 6/1 [= 6]. В этой итерации выходная базовая переменная равна X4 (P4).
          • 6.3. Новый стержень 4.
          • 7. Обновление значений таблицы снова получается:
            Таблица IV. 4-я итерация
                  3 2 0 0 0
            Основание Кб Р0 Р1 Р2 Р3 Р4 Р5
            Р2 2 12 0 1 -1/2 1/2 0
            Р5 0 3 0 0 -7/4 1/4 1
            Р1 3 3 1 0 3/4 -1/4 0
            З   33 0 0 5/4 1/4 0
        10. Конец алгоритма.

          Отмечено, что в последней строке все коэффициенты положительные, значит, условие остановки выполнено.

          Оптимальное решение задается значением Z в столбце постоянных условий (столбец P0), в примере: 33. В том же столбце показана точка, в которой оно достигает, наблюдая за соответствующими строками входных переменных решения. : X1 = 3 и X2 = 12.

          Отмена изменения имени дает x = 3 и y = 12.

        Решите с помощью PHPSimplex.

        Copyright © 2006-2022 PHPSimplex. Все права защищены.

        X

        PHPSimple
        Версия 0.81

        Copyright © 2006-2022. Все права защищены.

        Разработчик:
        Даниэль Искьердо Гранха
        Хуан Хосе Руис Руис

        английский перевод:
        Лучано Мигель Тобариа

        Французский перевод:
        Эстер Руте Руис

        перевод на португальский:
        Розан Бухес

        Линейное программирование: симплекс-метод

        Линейное программирование: симплекс-метод

        Задача линейного программирования

        Вот первая проблема, с которой мы столкнулись.

        Развернуть Р = 40x 1 + 30x 2    
        Тема:     х 1 + 2x 2 ≤ 16
              х 1 + х 2 ≤ 9
              3x 1 + 2x 2 ≤ 24
              х 1 , х 2 ≥ 0

        Начальная система

        Исходная система находится путем преобразования ограничений ≤ в ограничения = путем добавления резервной переменной.

        Это тот же шаг, который мы предприняли в табличном методе.

        Развернуть Р = 40x 1 + 30x 2                
        Тема:     х 1 + 2x 2 + с 1         = 16
              х 1 + х 2     + с 2     = 9
              3x 1 + 2x 2         + с 3 = 24
              х 1 , х 2 , с 1 , с 2 , с 3 ≥ 0

        Начальная таблица

        Таблицы — это причудливые имена для матриц. Теперь мы преобразуем систему линейных уравнений в матрицы. Однако здесь есть еще одна хитрость… мы перемещаем все переменные в левую часть, поэтому целевая функция становится равной -40×9.1343 1 — 30x 2 + P = 0. Мы также помещаем целевую функцию последней в таблицу и помещаем над ней линию увеличения, чтобы отделить ее от ограничений.

          х 1 x 2 с 1 с 2 с 3 Р справа  
          1 2 1 0 0 0 16  
          1 1 0 1 0 0 9  
          3 2 0 0 1 0 24  
          -40 -30 0 0 0 1 0  

        Базовые и небазовые переменные

        В каждой строке таблицы будет базовая переменная, а целевая функция всегда будет базовой в нижней строке.

        Каждая переменная соответствует столбцу в таблице. Если столбец очищен и содержит только один ненулевой элемент, то эта переменная является базовой переменной. Если столбец не очищен и содержит более одного ненулевого элемента, эта переменная не является базовой и значение этой переменной равно нулю.

        Значения всех неосновных переменных (столбцы, содержащие более одного числа) равны нулю. В этой таблице это будет x 1 и x 2 .

        Значения основных переменных находятся путем считывания решения из матрицы, полученной путем удаления неосновных столбцов.

          с 1 с 2 с 3 Р правая сторона          
          1 0 0 0 16     с 1 = 16
          0 1 0 0 9     с 2 = 9
          0 0 1 0 24     с 3 = 24
          0 0 0 1 0     Р = 0

        Подытожим, что у нас есть.

        Базовый Небазовый
        с 1 =16, с 2 =9, с 3 =24, P=0 х 1 =0, х 2 =0

        Связывание таблицы с таблицей

        Давайте вспомним результаты, которые мы получили от табличного метода.

        Пт х 1 x 2 с 1 с 2 с 3 Выполнимо? P = 40x 1 + 30x 2
        А 0 0 16 9 24 да 0
        Б 0 8 0 1 16 да 240
        С 0 9 -2 0 6 нет н/д
        Д 0 12 -8 -3 0 нет н/д
        Е 16 0 0 -7 -24 нет н/д
        Ф 9 0 7 0 -3 нет н/д
        Г 8 0 8 1 0 да 320
        Н 2 7 0 0 15 да 290
        я 4 6 0 -1 0 нет н/д
        Дж 6 3 4 0 0 да 330

        Если вы сравните значения, полученные при чтении таблицы, вы увидите, что мы находимся в точке A , где x 1 = 0 и x 2 = 0.

        Идентификация основных переменных для каждой строки

        Каждая строка таблицы будет иметь одну базовую переменную для этой строки. Какая это переменная, можно довольно легко определить, не удаляя столбцы, соответствующие неосновным переменным.

        Для столбцов, которые очищены и содержат только одну ненулевую запись, вы перемещаетесь вниз по столбцу, пока не найдете ненулевую запись. Каждый столбец будет иметь ненулевой элемент в другой строке. Переменная в этом столбце будет базовой переменной для строки с ненулевым элементом.

        Это немного сбивает с толку, так что, возможно, это поможет.

        • Столбец s 1 очищен, кроме первой строки. Поэтому s 1 является базовой переменной в первой строке.
        • Столбец s 2 очищен, за исключением второй строки. Поэтому s 2 является базовой переменной во второй строке.
        • Столбец s 3 очищен, за исключением третьей строки. Поэтому s 3 является базовой переменной в третьей строке.
        • Столбец P очищен, за исключением нижней строки. Следовательно, P — основная переменная в нижней строке.
        Базовый   х 1 x 2 с 1 с 2 с 3 Р справа  
        с 1   1 2 1 0 0 0 16  
        с 2   1 1 0 1 0 0 9  
        с 3   3 2 0 0 1 0 24  
        Р   -40 -30 0 0 0 1 0  

        Симплексный метод

        Мы видели, что находимся на пересечении линий x 1 = 0 и x 2 = 0. Это начало координат, а две неосновные переменные: x 1 и x 2 . Чтобы обойти допустимую область, нам нужно сойти с одной из линий x 1 = 0 или x 2 = 0 на одну из линий s 1 = 0, s 2 = 0 или s 3 = 0. Вопрос в том, в каком направлении двигаться?

        Выбор сводной колонки

        Подумайте о целевой функции P = 40x 1 + 30x 2 . На каждую единицу, которую мы двигаем в направлении x 1 , мы получаем 40 в целевой функции. На каждую единицу, которую мы двигаем в направлении x 2 , мы получаем 30 в целевой функции. Думайте об этом как о каждом шаге, который вы делаете вправо (x 1 ), вы получаете 40 долларов, и за каждый сделанный вами шаг (направление x 2 ) вы получаете 30 долларов.

        Что бы вы предпочли? Надеюсь, ваш ответ — зарабатывать 40 долларов за каждый шаг, который вы делаете. Если это не так, вы не очень хорошо поймете симплекс-метод.

        Теперь подумайте о том, как эти 40 представлены в целевой функции таблицы. Когда мы поместили целевую функцию в таблицу, мы переместили переменные решения и их коэффициенты в левую часть и сделали их отрицательными. Следовательно, самое отрицательное число в нижней строке соответствует самому положительному коэффициенту целевой функции и указывает направление, в котором мы должны двигаться.

        Сводной столбец — это столбец с самым отрицательным числом в нижней строке. Если в нижней строке нет минусов, остановитесь, все готово.

        Положительное значение в нижней строке таблицы будет соответствовать отрицательному коэффициенту целевой функции, что означает, что движение в этом направлении фактически уменьшит значение цели. Это не то, что мы хотим сделать, если нам нужно максимальное значение, поэтому мы останавливаемся, когда в нижней строке целевой функции больше нет отрицательных значений.

        Мы уходим от линии, соответствующей неосновной переменной в сводном столбце. Это означает, что переменная выходит из набора базовых переменных и становится небазовой.

        Поместите стрелку под опорную колонку.

        Выбор сводного ряда

        Теперь, когда мы выбрали направление, нам нужно определить, как далеко мы должны двигаться в этом направлении. Помните, что мы сейчас находимся в точке A и движемся в направлении x 1 или вправо. Это означает, что мы можем перейти к пунктам E (16,0), F (9,0) или G (8,0).

        • Точка E находится в точке (16,0) и является пересечением прямых x 2 = 0 и s 1 = 0. x 1 станет основной, а s 1 станет неосновной . Значение x 1 изменится с x 1 = 0 на x 1 = 16, если мы перейдем к точке E .
        • Точка F находится в (9,0) и является пересечением линий x 2 = 0 и s 2 = 0. x 1 станет основным, а s 2 станет неосновным. Значение x 1 изменится с x 1 = 0 на x 1 = 9, если мы перейдем к точке F .
        • Точка G находится в (8,0) и является пересечением прямых x 2 = 0 и s 3 = 0. x 1 станет основной, а s 3 станет неосновной. Значение x 1 изменится с x 1 = 0 до x 1 = 8, если мы перейдем к точке G .

        Давайте посмотрим, как мы можем узнать эту информацию из таблицы. Помните, мы пытаемся сделать это вообще без использования графа.

        Сформируйте отношения между неотрицательными записями в правой части и положительными записями в сводном столбце для каждого из проблемных ограничений. Не найти соотношение для целевой функции. Не находите отношение, если элемент в сводном столбце отрицателен или равен нулю, но найдите отношение, если правая часть равна нулю.

        Базовый   х 1 x 2 с 1 с 2 с 3 Р справа   отношение
        с 1   1 2 1 0 0 0 16   16/1 = 16
        с 2   1 1 0 1 0 0 9   9/1 = 9
        с 3   3 2 0 0 1 0 24   24/3 = 8
        Р   -40 -30 0 0 0 1 0    
            ↑                

        Не могли бы вы посмотреть на эти коэффициенты? 16, 9 и 8. И еще лучше, 16 связано со строкой, где s 1 является базовой, 9 связана со строкой, где s 2 является базовой, а 8 связана со строкой, где s 3 является основным.

        Это означает, что мы можем сказать, насколько изменится x 1 , взглянув на соотношение. Мы также можем сказать, к какой строке мы будем двигаться, взглянув на переменную, которая является базовой для этой строки.

        Какую строку выбрать? Ваша первая мысль может заключаться в том, что, поскольку мы получаем 40 долларов за каждую перемещаемую единицу, мы должны переместить как можно больше единиц. Если мы переместим 8 единиц, мы получим 40 × 8 = 320 долларов, если мы переместим 9 единиц, мы получим 40 × 9 = 360 долларов, а если мы переместим 16 единиц, мы получим 40 × 16 = 640 долларов. Есть одна очень большая проблема с однако такая цепочка рассуждений. Если мы переместимся больше, чем на 8, мы покинем достижимую область. Следовательно, мы должны переместиться на наименьшее возможное расстояние, чтобы остаться в допустимой области.

        Сводная строка — это строка с наименьшим неотрицательным отношением. Если не удается найти неотрицательных отношений, останавливайтесь, задача не имеет решения.

        Если одно из соотношений равно 0, это считается неотрицательным значением. Используй это.

        Поместите стрелку рядом с наименьшим соотношением, чтобы указать основную строку.

        Базовый   х 1 x 2 с 1 с 2 с 3 Р справа   отношение  
        с 1   1 2 1 0 0 0 16   16/1 = 16  
        с 2   1 1 0 1 0 0 9   9/1 = 9  
        с 3   3 2 0 0 1 0 24   24/3 = 8 ←
        Р   -40 -30 0 0 0 1 0      
            ↑                  

        Переменная, являющаяся базовой для сводной строки, будет исключена из набора базовых. Ее заменит переменная из сводного столбца, входящая в набор базовых переменных.

        Пересечение опорной строки и опорного столбца называется опорным элементом. Обведите это.

        вещей, которые мы можем сказать перед разворотом

        Нам известно следующее.

        • Целевая функция увеличивается на 40 на каждую единицу, которую мы перемещаем в x 1 направление и мы движемся на 8 единиц. Это означает, что целевая функция увеличится на 40×8 = 320. Поскольку сейчас она равна 0, она станет равной 320.
        • Переменная x 1 заменит s 3 в качестве базовой переменной в третьей строке. Остальные строки сохранят свои основные переменные.
        • Опорный столбец будет очищен, за исключением опорного элемента, который станет 1.
        • Опорная строка не изменится, кроме как путем деления, чтобы сделать опорный элемент равным 1. В этом случае мы разделим все на 3.
        • Увеличение x 1 будет 8.
        • Графически мы будем в точке G , где x 2 и s 3 — неосновные.
        • Столбцы s 1 , s 2 и P останутся очищенными, а их основные строки останутся прежними.
        Базовый   х 1 x 2 с 1 с 2 с 3 Р справа  
        с 1   0   1 0   0    
        с 2   0   0 1   0    
        x 1   1 2/3 0 0 1/3 0 8  
        Р   0   0 0   1 320  

        Поворот!

        Используйте операции со строками, чтобы очистить сводной столбец. То есть, когда вы закончите, единственной записью в сводном столбце будет элемент в 3-й строке, где был опорный элемент.

        Базовый   х 1 x 2 с 1 с 2 с 3 Р справа  
        с 1   0 4/3 1 0 -1/3 0 8  
        с 2   0 1/3 0 1 -1/3 0 1  
        х 1   1 2/3 0 0 1/3 0 8  
        Р   0 -10/3 0 0 40/3 1 320  

        Интерпретация новой таблицы

        На этот раз x 2 и s 3 столбцы не очищаются, поэтому они неосновные и их значение равно 0. x 1 является основным в третьей строке и его значение равно 8. s 1 является основным в первой строке и его значение равно 8. s 2 является основным во второй строке и его значение равно 1.

        Базовый Небазовый
        x 1 =8, с 1 =8, с 2 =1, P=320 х 2 =0, с 3 =0

        Сравните это с таблицей, которую мы имели раньше, и вы увидите, что мы действительно находимся в точке G .

        Пт х 1 x 2 с 1 с 2 с 3 Выполнимо? P = 40x 1 + 30x 2
        Г 8 0 8 1 0 да 320

        Повторение процесса

        Пока в нижней строке есть отрицательные значения, значение целевой функции можно увеличить, переместив ее в новую точку.

        Если вы посмотрите на целевую функцию, вы заметите, что есть только одно отрицательное значение, -10/3 в столбце x 2 . Это означает, что, двигаясь вверх (в x 2 направление), мы можем увеличить значение целевой функции. Мы будем двигаться от линии x 2 = 0, что означает, что мы будем двигаться вдоль линии s 3 = 0. Где бы мы ни оказались, x 2 займет место этой базовой переменной. Если бы мы двигались в направлении s 3 , это движение навредило бы нам.

        Как далеко мы можем двигаться?

        • Мы можем перейти к точке J , которая равна (6,3), так что увеличение x 2 будет 3. Эта точка находится на пересечении прямых s 3 = 0 и s 1 = 0, поэтому s 1 станет неосновным и будет заменено на x 2 как основное.
        • Мы могли бы перейти к точке I , которая находится в точке (5,6), поэтому увеличение x 2 будет равно 6. Эта точка находится на пересечении прямых s 3 = 0 и s 2 = 0, поэтому s 2 станет неосновным и будет заменено на x 2 в качестве основного.
        • Мы могли бы перейти к точке D , которая находится в точке (0,12), так что увеличение x 2 будет 12. Эта точка находится на пересечении линий s 3 = 0 и x 1 = 0, поэтому x 1 станет неосновным и будет заменен на x 2 в качестве основного.

        Обратите внимание, что когда мы формируем отношения между неотрицательными элементами в правой части и положительными элементами в основной строке, мы получаем 6 при переходе к s 1 = 0 (точка I ), 3 при переходе к s 2 = 0 (точка J ) и 12 при переходе к x 1 = 0 (точка D ). Мы снова выбираем наименьшее отношение, чтобы оставаться в допустимой области.

        Базовый   х 1 x 2 с 1 с 2 с 3 С справа   отношение  
        с 1   0 4/3 1 0 -1/3 0 8   8/(4/3) = 6  
        с 2   0 1/3 0 1 -1/3 0 1   1/(1/3) = 3 ←
        x 1   1 2/3 0 0 1/3 0 8   8/(2/3) = 12  
        Р   0 -10/3 0 0 40/3 1 320      
              ↑                

        Вещи, которые мы можем сказать перед поворотом

        Нам известно следующее.

        • Целевая функция увеличивается на 10/3 на каждую единицу, которую мы перемещаем в направлении x 2 , и мы перемещаемся на 3 единицы. Это означает, что целевая функция увеличится на (10/3)×3 = 10. Поскольку сейчас 320, она станет 330.
        • Переменная x 2 заменит s 2 в качестве базовой переменной во второй строке. Остальные строки сохранят свои основные переменные.
        • Опорный столбец будет очищен, за исключением опорного элемента, который станет 1.
        • Опорная строка не изменится, кроме как путем умножения, чтобы сделать опорный элемент равным 1. В этом случае мы умножим все на 3.
        • Увеличение x 2 будет 3.
        • Графически мы будем в точке J , где s 2 и s 3 неосновные.
        • Столбцы s 1 , x 1 и P останутся очищенными, а их основные строки останутся прежними.
        Базовый   х 1 x 2 с 1 с 2 с 3 Р справа  
        с 1   0 0 1     0    
        х 2   0 1 0 3 -1 0 3  
        x 1   1 0 0     0    
        Р   0 0 0     1 330  

        Шарнир

        Хорошо, теперь мы развернёмся и найдём остальную информацию.

        Базовый   х 1 x 2 с 1 с 2 с 3 Р справа  
        с 1   0 0 1 -4 1 0 4  
        х 2   0 1 0 3 -1 0 3  
        x 1   1 0 0 -2 1 0 6  
        Р   0 0 0 10 10 1 330  

        Интерпретация новой таблицы

        На этот раз столбцы s 2 и s 3 не очищаются, поэтому они неосновные и их значение равно 0. x 1 является основным в третьей строке и его значение равно 6. s 1 является основным в первой строке и его значение равно 4. x 2 является основным во второй строке и его значение равно 3.

        Базовый Небазовый
        х 1 = 6, х 2 = 3, с 1 = 4, Р=330 с 2 =0, с 3 =0

        Сравните это с таблицей, которую мы имели ранее, и вы увидите, что мы действительно находимся в точке J .

        Пт х 1 x 2 с 1 с 2 с 3 Выполнимо? P = 40x 1 + 30x 2
        Дж 6 3 4 0 0 да 330

        Готово!

        Поскольку в нижней строке нет отрицательных значений, перемещение в другую точку понизит значение целевой функции, а не повысит его. Поскольку мы пытаемся максимизировать значение целевой функции, это было бы контрпродуктивно. Мы останавливаемся, мы закончили.

        Решение

        Максимальное значение P равно 330, когда x 1 = 6 и x 2 = 3. Значения резервных переменных: s 1 = 4, s 2 = 0 и s 3 = 0,

        Оптимизация: симплексный метод максимизации. | Свапнил Бандгар | Analytics Vidhya

        Фото взято из Википедии

        Симплекс-метод — это подход к ручному решению моделей линейного программирования с использованием резервных переменных, таблиц и сводных переменных в качестве средства поиска оптимального решения задачи оптимизации. Линейная программа — это метод достижения наилучшего результата при максимальном или минимальном уравнении с линейными ограничениями. Большинство линейных программ можно решить с помощью онлайн-решателя, такого как MatLab, но симплекс-метод — это метод решения линейных программ вручную. Для решения модели линейного программирования с помощью симплекс-метода необходимо выполнить следующие шаги:

        ● Стандартная форма

        ● Введение резервных переменных

        ● Создание таблицы

        ● Переменные сводки

        ● Создание новой таблицы

        ● Проверка оптимальности методов в вышеуказанные шаги и следует примеру модели линейного программирования, показанной ниже, на протяжении всего документа, чтобы найти оптимальное решение.

        Максимизировать:

        Чтобы определить Максимум, мы должны выполнить следующие шаги.

        Шаги:

        1. Преобразование всех основных уравнений неравенства путем добавления резервных переменных. Также создайте целевую функцию, равную нулю, переместив все значения в одну сторону.
          Уравнения после добавления резервной переменной (u,v,w)
          Где u,v,w≥0

        2. Симплексная таблица используется для выполнения строковых операций в модели линейного программирования, а также для проверки решения на оптимальность . Таблица состоит из коэффициента, соответствующего переменным линейного ограничения, и коэффициента целевой функции. В таблице ниже выделенная полужирным шрифтом верхняя строка таблицы указывает, что представляет каждый столбец. Следующие две строки представляют коэффициенты переменных линейного ограничения из модели линейного программирования, а последняя строка представляет коэффициенты переменных целевой функции.

        Теперь создайте симплексную таблицу, создав коэффициенты всех уравнений субъекта и добавив уравнение объекта внизу.

        3. Чтобы рассчитать коэффициент, мы можем выбрать минимальное значение из последней строки и выполнить следующие шаги.

        Как идентифицировать столбец Pivot:

        В приведенной выше таблице -6 — это наименьшее отрицательное число в последней строке. Это укажет, что столбец z будет содержать сводную переменную, которая выделена желтым цветом.

        Как идентифицировать сводную строку:

        Сводная переменная используется в операциях со строками, чтобы определить, какая переменная станет значением единицы, и является ключевым фактором при преобразовании значения единицы. Опорную переменную можно определить, посмотрев на нижнюю строку таблицы и индикатор. Предполагая, что решение не является оптимальным, выберите наименьшее отрицательное значение в нижней строке. Одно из значений, лежащих в столбце этого значения, будет опорной переменной. Чтобы найти индикатор, разделите бета-значения линейных ограничений на соответствующие им значения из столбца, содержащего возможную сводную переменную. Пересечение строки с наименьшим неотрицательным показателем и наименьшим отрицательным значением в нижней строке станет опорной переменной.

        Разделите сводной столбец на константу в соответствующей строке и определите значения.

        Решение отношения дает нам значение (900/1 = 900) для первого ограничения, значение (350/1 = 350) для второго ограничения и значение третьего ограничения (400 /1 = 400) . Поскольку 350 является наименьшим неотрицательным отношением, опорное значение будет во второй строке, выделенной зеленым цветом, а пересечение опорной строки и столбца будет опорным элементом со значением 1, выделенным красным цветом.

        Теперь, когда опорная переменная определена, мы можем работать над дальнейшим решением, чтобы оптимизировать ее.

        4. Чтобы оптимизировать сводную переменную, ее необходимо преобразовать в единичное значение (значение 1). Так как здесь опорный элемент уже равен 1, нам не нужно делать его единичным значением.

        5. После того, как значение единицы было определено, поработайте над формулой, которая сделает другие значения в столбце, содержащем значение единицы, равными нулю. Это связано с тем, что переменная резерва и другое значение переменной могут быть идентифицированы, и решение оптимизируется.

        Формулы: R1=R1-R2 , R3=R3-R2 и R4=R4+6R2

        Применение приведенных выше формул к нашей симплексной таблице приведет к приведенной ниже таблице.

        Получено оптимальное решение, поскольку все значения в нижней строке больше или равны нулю.

        Здесь основными переменными являются u, z, w и p.
        Неосновными переменными являются x, v и y.

        Отсюда мы можем получить значения переменных, как показано ниже:

        x=0, y=0, v=0, u=550, w = 50, p = 2100, z = 350.

        Теперь, чтобы проверить уравнение,

        Максимальное оптимальное значение равно 2100 и находится при (0,0, 350) целевой функции.

        Симплекс-метод — это метод определения оптимального значения линейной программы вручную. Метод дает оптимальное решение, удовлетворяющее заданным ограничениям, и дает максимальное значение дзета. Чтобы использовать симплекс-метод, данная модель линейного программирования должна иметь стандартную форму, в которую затем могут быть введены резервные переменные. Используя табличные и сводные переменные, можно найти оптимальное решение.

        Базовые переменные — это переменные, которые неотрицательны с точки зрения оптимального решения.

        Ограничения представляют собой ряд равенств и неравенств, являющихся набором критериев, которым необходимо удовлетворять при поиске оптимального решения.

        Неравенство — это выражение, которое не имеет однозначного решения и отличается символами «больше» или «меньше» вместо традиционного знака равенства.

        Линейная программа — это модель, используемая для достижения наилучшего результата при максимальном или минимальном уравнении с линейными ограничениями.

        Неосновные переменные — это переменные, равные нулю с точки зрения оптимального решения.

        Оптимальное решение модели линейного программирования максимизации — это значения, присвоенные переменным в целевой функции, чтобы получить наибольшее значение дзета. Оптимальное решение существовало бы в угловых точках графика всей модели.

        Сводная переменная используется в операциях со строками для определения того, какая переменная станет значением единицы, и является ключевым фактором при преобразовании значения единицы.

        Симплекс-метод — это подход к ручному решению моделей линейного программирования с использованием резервных переменных, таблиц и сводных переменных в качестве средства поиска оптимального решения задачи оптимизации.

        Симплексная таблица используется для выполнения строковых операций в модели линейного программирования, а также для проверки оптимальности.

        Переменные Slack — это дополнительные переменные, которые вводятся в линейные ограничения линейной программы для преобразования их из ограничений неравенства в ограничения равенства.

        Стандартная форма является базовым форматом для всех линейных программ перед поиском оптимального решения.

        Ссылка: Либретексты, Книга: Блитцер, Математическое мышление | Пирсон.

        Симплексный алгоритм — табличный метод

        import numpy as np

        from fractions import Fraction

         

        print ("\n                 * * * * SiMplex Алгоритм * * * * \ n \ n ")

        A

        A

        A

        A

        . 4017 1 , 1 , 0 , 1 ], [ 2 , 1 , 1 , 0 ]] )

        b = np.array([ 8 , 10 ])          

        c = np.array([ 1 , 1 , 0 , 0 ])            

         

        cb = np.array(c[ 3 ])

        B = np.array([[ 3 ], [ 2 ]])         

         

        cb = np. vstack((cb, c[ 2 ]))       

        xb = np.transpose([b])                

        table = np.hstack((B, cb))            

        table = np.hstack ((Таблица, XB))

        Таблица = NP.HSTACK ((Таблица, A)

        TABLE = NP.AR.RARAPE (TABLE = . поплавок )

         

        MIN = 0

         

        print ("Table at itr = 0 ")

        print ("B \tCB \tXB \ty1 \ty2 \ty3 \ty4")

        for row in table:

             for el in row:

                        

                 print (Fraction( str (el)). limit_denominator( 100 ), end = '\t' )

             print ()

        print ()

        print ("Simplex Working....")

         

        reached = 0     

        itr = 1

        unbounded = 0

        alternate = 0

         

        while reached = = 0 :

         

             print ("Iteration: ", end = ' ' )

             print (itr)

             print ("B \tCB \tXB \ty1 \ty2 \ty3 \ty4")

             for row in table:

                 for el in row:

                     print (Fraction( str (el)). limit_denominator( 100 ), end = '\t' )

                 print ()

         

            

             i = 0

             rel_prof = []

        В то время как I < LEN (A [ 0 ]): 018018]: A [ 0 ]): 018]): ]: ]: ]): ( 0 ( 0 ( .4018 rel_prof.append(c[i] - np. sum (table[:, 1 ] * table[:, 3 + i]))

                 i = i + 1

         

             print ("rel profit: ", end = " ")

             for profit in rel_prof:

                 print (Fraction( str (profit)).limit_denominator( 100 ), end = ", ")

             print ()

             i = 0

              

             b_var = table[:, 0 ]

            

             while i< len (A[ 0 ]):

                 j = 0

                 present = 0

                 while j< len (b_var):

                     if int (b_var[j]) = = i:

                         present = 1

                         перерыв ;

        J + = 1

        , если . 4018 = = 0 :

                     if rel_prof[i] = = 0 :

                         alternate = 1

                         print ("Case of Alternate found")

                        

                 i + = 1

             print ()

             flag = 0

             for profit in rel_prof:

                 if profit> 0 :

                     flag = 1

                     break

                

             if flag = = 0 :

                 print (" All profits are < = 0 , оптимальность достигнута")

                 достигнуто = 1

        4017          break

         

            

             k = rel_prof. index( max (rel_prof))

             min = 99999

             i = 0 ;

             r = - 1

            

             while i< len (table):

                 if (table[:, 2 ][i]> 0 and table[:, 3 + k][i]> 0 ):

                     val = table[:, 2 ] [я] / table[:, 3 + k][i]

                     if val< min :

                         min = val

                         r = i    

                 i + = 1

         

                

             if r = = - 1 :

                 unbounded = 1

                 print ("Case of Unbounded")

                 break

         

             print : индекс элемента ("end pivot 9 element":4018 = ' ' )

             print (np. array([r, 3 + k]))

         

             pivot = table[r][ 3 + k]

             print ("pivot element: ", end = " ")

             print (Fraction(pivot).limit_denominator( 100 ))

                  

                

            

             table[r, 2 : len ( table[ 0 ])] = table[

                     r, 2 : len (table[ 0 ])] / pivot

                      

            

             i = 0

             while i< len (таблица):

                 если i ! = r:

                     таблица[i, 2 : len (table[ 0 ])] = table[i,

                          2 : len (table[ 0 ])] - table[i][ 3 + k] *

                          table[r, 2 : len (table[ 0 ])]

                 i + = 1

         

              

            

             table[r][ 0 ] = k

             table[r][ 1 ] = c[k]

              

             print ()

             print ()

             itr + = 1

              

         

        print ()

         

        print (" * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * ")

        if unbounded = = 1 :

             print ("UNBOUNDED LPP")

             exit()

        if alternate = = 1 :

             print ("ALTERNATE Solution")

         

        Печать («Оптимальная таблица:»

        Печать («B \ TCB \ TXB \ TY1 \ TY2 \ TY3 \ TY4»)

        для

        для

        для

        для

        для

        для

        для

             for el in row:

                 print (Fraction( str (el)). limit_denominator( 100 ), end = '\ t' )

        Печать ()

        Печать ()

        Печать ()

        Печать ()

        .4018 = " ")

         

        basis = []

        i = 0

        sum = 0

        while i< len (table):

             sum + = c[ int (table[i][ 0 ])] * table[i][ 2 ]

             temp = "x" + str ( int (table[i][ 0 ]) + 1 )

             basis. append(temp)

             i + = 1

        if MIN = = 1 :

             print ( - Fraction( str ( sum )).limit_denominator( 100 )

        else :

        Печать (фракция ( STR ( .4018 ))

        Печать («Последняя основа:», END = »")

        PRINT (Основная база)

        . ...")

        print ()

        Симплексный метод - Брайан Вейтч

        Симплексный метод - Брайан Вейтч

        решить систему неравенств

        Описание

        Спасибо за проверку моего приложения Row Reduction. Ознакомьтесь с симплексным методом на приложение хранить сейчас!

        Посмотрите демонстрационное видео от того, как использовать это приложение.

        Особенности:

        - Решает стандартное максимальное, стандартное минимальное и нестандартное

        - Позволяет вам самостоятельно работать с этим методом

        - Предлагает подсказки по запросу

        - Отменить операцию, если вы допустили ошибку

        Нужно решить задачу линейного программирования? Закончили использовать симплекс-метод, но вы не получающий правильный ответ? Один из основных недостатков симплекс-метода заключается в том, что вы должны отслеживать а страница, полная утомительных вычислений И выберите правильные операции со строками. Когда вы впервые узнаете это технику трудно сделать и то, и другое правильно.

        Симплекс-метод включает в себя использование последовательности «Если/Тогда», которая приводит вас к начальному Симплексному методу. Стол. Это приложение проведет вас через настройку и создаст исходную таблицу. Оттуда вы можете либо использовать метод самостоятельно или он поможет вам с помощью подсказок. Выберите операцию, и приложение создать новую таблицу для вас. Вы можете сосредоточиться исключительно на практике и экспериментировании.

        Что делать, если вы делаете всю эту рукописную работу и все еще не можете получить ответ?

        Вы также можете приобрести обновление Instant Solution. Введите систему уравнений и нажмите РЕШЕНИЕ. Он сгенерирует все правильные операции со строками и таблицы и отобразит их все в однажды. Теперь вы можете продолжить и попытаться найти свою ошибку.

        Счастливого обучения

        Симплексный метод

        Подборка скриншотов

        Навыки и умения

        Что я выучил...

        Мое второе приложение!

        Приложение симплексного метода было продолжением приложения Row Приложение «Уменьшение». Структура и поток были идентичными, поэтому я смог повторно использовать большую часть сокращения строк. код. я написал это app таким образом, чтобы я мог повторно использовать большую часть кода. Вот чему я научился... писать код в таком случае чтобы его можно было использовать в других проектах.

        Что было сложно

        Разница между приложением Row Reduction и Приложение «Симплексный метод» писал код для подсказок. Симплекс-метод достаточно сложно объяснить, и даже сложнее кодировать. Я узнал, что составление подробной блок-схемы метода помогло мне создать классы, методы и т.д. В основном Я узнал, что вы действительно должны планировать заранее.

        Что я мог бы сделать лучше

        Теперь, когда я узнал больше, я хотел бы вернуться и переделать это приложение. Я хочу очистить классы, работающие с симплексным алгоритмом. Опция мгновенного решения распечатывает каждый шаг алгоритма. Мне пришлось создавать подпредставления программно. И я уверен, что смогу это сделать очиститель и более эффективным.

        Политика конфиденциальности

        В основном... я не собираю данные

        Файлы cookie

        Файлы cookie — это файлы с небольшим объемом данных, которые обычно используются как анонимные уникальные идентификаторы. Они отправляются в ваш браузер с веб-сайтов, которые вы посещаете, и хранятся во внутренней памяти вашего устройства.

        Эта Служба не использует эти файлы cookie в явном виде. Однако приложение может использовать сторонние код и библиотеки, которые используют файлы cookie для сбора информации и улучшения своих услуг. У вас есть возможность либо принять, либо отказаться от этих файлов cookie и узнать, когда файл cookie отправляются на ваше устройство. Если вы решите отказаться от наших файлов cookie, вы не сможете использовать некоторые части этой Услуги.

        Поставщики услуг

        Я могу нанимать сторонние компании и частных лиц по следующим причинам:

        Для облегчения нашего Сервиса; Для предоставления Сервиса от нашего имени; Для оказания услуг, связанных с Сервисом; или же Чтобы помочь нам проанализировать, как используется наш Сервис. Я хочу сообщить пользователям этого Сервиса, что эти третьи лица имеют доступ к вашим Персональные данные. Причина в том, чтобы выполнять возложенные на них задачи от нашего имени. Однако они обязаны не разглашать и не использовать информацию для каких-либо других целей.

        Безопасность

        Я ценю ваше доверие в предоставлении нам вашей личной информации, поэтому мы стремимся использовать коммерчески приемлемые средства защиты. Но помните, что ни один метод передача через Интернет или метод электронного хранения на 100% безопасен и надежным, и я не могу гарантировать его абсолютную безопасность.

        Ссылки на другие сайты

        Эта служба может содержать ссылки на другие сайты. Если вы нажмете на стороннюю ссылку, вы быть направлены на этот сайт. Обратите внимание, что эти внешние сайты не управляются мной. Поэтому я настоятельно рекомендую вам ознакомиться с Политикой конфиденциальности этих веб-сайтов. У меня нет контролировать и не нести ответственности за содержание, политику конфиденциальности или практику любых сторонних сайтов или сервисов.

        Конфиденциальность детей

        Эти Услуги не предназначены для лиц моложе 13 лет. Я не собираю намеренно личную информацию от детей младше 13 лет. В случае, если я узнаю, что ребенок младше 13 лет предоставил мне личную информацию, я немедленно удаляю ее из наши серверы. Если вы являетесь родителем или опекуном и знаете, что у вашего ребенка предоставил нам личную информацию, пожалуйста, свяжитесь со мной, чтобы я мог сделать необходимые действия.

        Изменения в настоящей Политике конфиденциальности

        Я могу время от времени обновлять нашу Политику конфиденциальности. Таким образом, вам рекомендуется просмотреть эту страницу периодически на любые изменения. Я сообщу вам о любых изменениях, опубликовав новую Политику конфиденциальности. Политика на этой странице. Эти изменения вступают в силу сразу после их публикации на этом сайте. страница.

        Свяжитесь с нами

        Если у вас есть какие-либо вопросы или предложения относительно моей Политики конфиденциальности, не стесняйтесь обращаться к нам мне на jankyapps@gmail.

        Площадь по диагоналям: Площадь прямоугольника — калькулятор онлайн и формула

        alexxlab / / Разное

        Площадь четырехугольника

        Главная

         → 

        Геометрия

         → 

        Площадь четырехугольника

        Площадь произвольного четырехугольника, формулы и калькулятор для вычисления в режиме онлайн. Для вычисления площади произвольного четырехугольника применяются различные формулы, в зависимости от известных исходных данных. Ниже приведены формулы и калькулятор, который поможет вычислить площадь произвольного четырехугольника или проверить уже выполненные вычисления.

        В окончании статьи приведены ссылки для вычисления частных случаев четырехугольников: квадрата, трапеции, параллелограмма, прямоугольника, ромба.

        Таблица с формулами площади четырехугольника (в конце страницы)

        — Вычисления   (показано)   (скрыто)

        — примечания   (показано)   (скрыто)


        1

        Площадь четырехугольника по диагоналям и углу между ними

        . .. подготовка …

        d1 — диагональ

        d2 — диагональ

        α° — угол между диагоналями


        2

        Площадь четырехугольника через стороны и углы между этими сторонами

        При вычислении площади четырехугольника с использованием данной формулы, необходимо предварительно вычислить полупериметр четырехугольника по формуле:

        … подготовка …

        a — сторона

        b — сторона

        c — сторона

        d — сторона

        α° — угол между сторонами

        β° — угол между сторонами


        3

        Площадь четырехугольника вписанного в окружность, вычисляемая по Формуле Брахмагупты

        Данная формула справедлива только для четырехугольников, вокруг которых можно описать окружность.

        При вычислении площади четырехугольника с использованием данной формулы, необходимо предварительно вычислить полупериметр четырехугольника по формуле:

        . .. подготовка …

        a — сторона

        b — сторона

        c — сторона

        d — сторона


        4

        Площадь четырехугольника в который можно вписать окружность

        Данная формула справедлива только для четырехугольников, в которые можно вписать окружность. Вписанная окружность должна иметь точки соприкосновения со всеми четырьмя сторонами четырехугольника.

        При вычислении площади четырехугольника с использованием данной формулы, необходимо предварительно вычислить полупериметр четырехугольника по формуле:

        … подготовка …

        a — сторона

        b — сторона

        c — сторона

        d — сторона

        r — радиус вписанной окружности


        5

        Площадь четырехугольника в который можно вписать окружность, определяемая через стороны и углы между ними

        Данная формула справедлива только для четырехугольников, в которые можно вписать окружность. Вписанная окружность должна иметь точки соприкосновения со всеми четырьмя сторонами четырехугольника.

        … подготовка …

        a — сторона

        b — сторона

        c — сторона

        d — сторона

        α° — угол между сторонами

        β° — угол между сторонами

        Примечание:

        Если в исходных данных угол задан в радианах, то для перевода в градусы вы можете воспользоваться «Конвертером величин». Или вычислить самостоятельно по формуле: 1 рад × (180/π) ° = 57,296°


        Таблица с формулами площади четырехугольника


        исходные данные
        (активная ссылка для перехода к калькулятору)        		эскизформула
        1диагональ и угол между ними
        2стороны и углы между этими сторонами

        где  ,

        3стороны
        (по Формуле Брахмагупты)

        где 

        4стороны и радиус вписанной окружности

        где 

        5стороны и углы между ними

        Площадь частных случаев четырехугольников

        Для вычисления частных случаев четырехугольников можно воспользоваться формулами и калькуляторами, приведенными в других статьях сайта:

        • площадь квадрата
        • площадь трапеции
        • площадь параллелограмма
        • площадь прямоугольника
        • площадь ромба

        Определения

        Четырехугольник – это геометрическая плоская фигура, образованная четырьмя последовательно соединенными отрезками.

        Площадь – это численная характеристика, характеризующая размер плоскости, ограниченной замкнутой геометрической фигурой.

        Площадь четырехугольника — это численная характеристика, характеризующая размер плоскости, ограниченной геометрической фигурой, образованной четырьмя последовательно соединенными отрезками.

        Площадь измеряется в единицах измерения в квадрате: км2, м2, см2, мм2 и т.д.


        Как найти площадь прямоугольника – 9 формул с лайфхаками и примерами

        Самый простой способ – перемножить две стороны. Но иногда эти две стороны неизвестны.

        Умножьте его ширину на высоту. Это самый простой способ найти площадь прямоугольника. Например, если ширина прямоугольника равна 4 см, а высота – 2 см, то площадь будет равна 4*2 = 8 см.

        По диагонали и стороне

        Должна быть известна диагональ и любая из сторон. Действия:

        1. Найти квадрат диагонали, то есть умножить ее на саму себя.
        2. Найти квадрат известной стороны.
        3. Из квадрата диагонали вычесть квадрат стороны.
        4. Найти квадратный корень получившейся разности.
        5. Умножить его на известную сторону.

        Пример. Сторона прямоугольника равна 3 см, а диагональ – 5 см. Найдите площадь.

        1. Квадрат стороны = 3*3 = 9 см.
        2. Квадрат диагонали = 5*5 = 25 см.
        3. Вычитаю из квадрата диагонали квадрат стороны: 25-9 = 16 см.
        4. Нахожу квадратный корень получившейся разности. Корень из 16 = 4 см.
        5. Умножаю корень разности на известную сторону: 16*9 = 144 см.

        Ответ: 144 см.

        Обратите внимание

        Диагональ в прямоугольнике – это гипотенуза, потому что она всегда находится напротив угла в 90 градусов. Найти диагональ можно по формуле нахождения гипотенузы, например, поделив катет угла A на синус угла A.

        По стороне и диаметру описанной окружности

        Вокруг любого прямоугольника можно описать окружность. Вам надо знать диаметр этой окружности и любую из сторон прямоугольника.

        Действия:

        1. Найдите квадрат диаметра – умножьте диаметр на диаметр.
        2. Найдите квадрат известной стороны.
        3. Отнимите от квадрата диаметра квадрат стороны.
        4. Найдите квадратный корень разности.
        5. Умножьте квадратный корень на известную сторону.

        Пример. Найдите площадь прямоугольника, если диаметр описанной окружности равен 10 см, а одна из сторон равна 8 см.

        1. Квадрат диаметра: 10*10 = 100 см.
        2. Квадрат стороны: 8*8 = 64 см.
        3. Отнимаю от квадрата диаметра квадрат стороны: 100-64 = 36 см.
        4. Квадратный корень из 36 равен 6 см (потому что 6*6 = 36).
        5. Умножаю сторону на корень из разности: 8*6 = 48 см.

        Ответ: 48 см.

        Лайфхак

        Диаметр описанной окружности всегда равен диагонали прямоугольника. Смотрите:

        А найти диагональ можно по формуле гипотенузы прямоугольного треугольника.

        Диаметр равен двум радиусам, потому что радиус – это половина диаметра.

        По радиусу описанной окружности и стороне

        Можно просто найти диаметр (умножить радиус на два) и использовать формулу выше.

        Другой способ:

        1. Найти квадрат радиуса (умножьте радиус на радиус).
        2. Умножить квадрат радиуса на 4.
        3. Найти квадрат известной стороны.
        4. Отнять от четырех радиусов в квадрате квадрат известной стороны (из второго отнять третье).
        5. Найти квадратный корень разности.
        6. Умножить корень на известную сторону.

        Пример. Найдите площадь прямоугольника, если радиус описанной окружности равен 5 см, а одна из сторон равна 6 см.

        1. Квадрат радиуса: 5*5=25 см.
        2. Четыре квадрата радиуса: 4*25 = 100 см.
        3. Квадрат стороны: 6*6 = 36 см.
        4. Отнимаю от четырех радиусов в квадрате квадрат стороны: 100-36 = 64 см.
        5. Нахожу квадратный корень разности. Корень из 64 равен 8 см.
        6. Умножаю корень на сторону: 8*6 = 48 см.

        Ответ: 48 см.

        Помните

        Радиус = половине диаметра.

        Радиус = половине гипотенузы прямоугольного треугольника, вокруг которого описана окружность. Потому что эта гипотенуза = диагонали прямоугольника = диаметру.

        По стороне и периметру – 1 способ

        Периметр – это сумма всех сторон прямоугольника. P=a+b+a+b. Другая формула периметра: P=2(a+b).

        Если известен периметр и одна сторона, надо найти вторую сторону и перемножить их.

        Пример. Периметр прямоугольника равен 14 см, а одна из  сторон равна 3 см. Найдите площадь.

        1. Нахожу вторую сторону прямоугольника:
          1. P=2(a+b).
          2. P=2a+2b.
          3. 14= 2*3+2b.
          4. 14 = 6+2b.
          5. 2b = 14-6 = 8.
          6. b = 8/2.
          7. b = 4.
        2. Нахожу площадь по основной формуле. S = 3*4 = 12 см.

        Ответ: 12 см.

        По стороне и периметру – 2 способ

        Действия такие:

        1. Умножьте периметр на сторону.
        2. Найдите квадрат стороны.
        3. Умножьте квадрат стороны на 2.
        4. Отнимите от произведения периметра и стороны два квадрата стороны (от первого отнимите третье).
        5. Поделите на 2.

        Пример. Сторона прямоугольника равна 8, а периметр равен 28. Найдите площадь.

        1. Умножаю периметр на сторону: 8*28 = 224 см.
        2. Нахожу квадрат стороны: 8*8 = 64 см.
        3. Умножаю квадрат стороны на два: 64*2 = 84 см.
        4. Отнимаю из первого третье: 224-84 = 140 см.
        5. Делю разность на два: 140/2 = 70 см.

        Ответ: 70 см.

        По диагонали и углу между диагоналями

        Диагонали прямоугольника всегда равны.

        Действия:

        1. Найти квадрат диагонали (умножить диагональ на саму себя).
        2. Найти половину этого квадрата – умножить его на 0,5.
        3. Найти синус угла между диагоналями.
        4. Умножить половину квадрата диагонали на синус угла между диагоналями.

        Пример. Найдите площадь прямоугольника, диагональ которого равна 10 см, а угол между диагоналями – 30 градусов.

        1. Квадрат диагонали: 10*10 = 100 см.
        2. Половина этого квадрата: 0,5*100 = 50 см.
        3. Синус угла между диагоналями: sin 30 градусов = 0,5.
        4. Перемножаю половину квадрата и синус угла, чтобы найти площадь: 50*0,5 = 25 см.

        Ответ: 25 см.

        Вот еще вам таблица основных значений из тригонометрии. Там как раз отмечено, что синус 30 градусов всегда равен 0,5 (1/2).

        По радиусу описанной окружности и углу между диагоналями – первый способ

        Радиус описанной окружности равен половине ее диаметра, а диаметр равен диагонали прямоугольника. Надо найти диаметр и посчитать площадь по формуле выше.

        Пример. Найдите площадь прямоугольника, если радиус описанной окружности равен 6 см, а угол между диагоналями – 30 градусов.

        1. Находим длину диагонали: 6*2 =12 см.
        2. Квадрат диагонали равен 144 см.
        3. Половина квадрата: 72 см.
        4. Синус 30 градусов равен 0,5.
        5. Умножаем половину квадрата на синус: 72*0,5 = 36 см.

        Ответ: 36 см.

        По радиусу описанной окружности и углу между диагоналями – второй способ

        Действия:

        1. Найти квадрат радиуса (умножить радиус на радиус).
        2. Умножить квадрат радиуса на два.
        3. Найти синус угла между диагоналями.
        4. Умножить синус угла на два радиуса в квадрате.

        Пример. Найдите площадь прямоугольника, если радиус описанной окружности равен 6, а угол между диагоналями – 30 градусов.

        1. Квадрат радиуса: 6*6 = 36.
        2. Два радиуса в квадрате: 36*2 = 72.
        3. Синус 30 градусов равен 0,5.
        4. Произведение синуса и двух радиусов в квадрате: 72*0,5 = 36 см.

        Ответ: 36 см.

        Покритикуйте статью и стиль подачи материала в комментариях, я внесу правки. Это моя вторая статья по математике, я хочу, чтобы они все были образцовыми.

        ЕЖЕНЕДЕЛЬНАЯ РАССЫЛКА

        Получайте самые интересные статьи по почте и подписывайтесь на наши социальные сети

        ПОДПИСАТЬСЯ

        Ваш браузер устарел рекомендуем обновить его до последней версии
        или использовать другой более современный.

        порядок ее нахождения, свойства фигуры и пример решения

        Геометрия

        12.11.21

        14 мин.

        В геометрии при решении задач иногда требуется найти площадь прямоугольника через диагонали. Формула и ее применение позволяют вычислить эту величину. Однако с самого начала фигуру требуется идентифицировать, руководствуясь определенными признаками. Кроме того, полезно будет знать основные свойства и соотношения для расчета других параметров (периметра, сторон и т. д.).

        Оглавление:

        • Общие сведения
        • Информация о фигуре
        • Соотношения для вычислений
        • Пример задания

        В геометрии при решении задач иногда требуется найти площадь прямоугольника через диагонали. Формула и ее применение позволяют вычислить эту величину. Однако с самого начала фигуру требуется идентифицировать, руководствуясь определенными признаками. Кроме того, полезно будет знать основные свойства и соотношения для расчета других параметров (периметра, сторон и т. д.).

        Общие сведения

        В геометрии, как и во всех дисциплинах с физико-математическим уклоном, существует взаимосвязь между параметрами. Например, базовая формула площади прямоугольника зависит от длин его противоположных сторон. Впервые ее используют в пятом классе для решения простейших задач.

        Однако на начальном уровне дается название фигуры, т. е. прямоугольник или квадрат. В старших классах встречаются задачи на идентификацию последних. На основании исследования принадлежности четырехугольника к определенному виду требуется вычислить некоторые его параметры. Если фигура определена неверно, расчеты будут выполнены некорректно.

        Навык решения задач по геометрии необходим не только на вступительных экзаменах, тестировании и зачетах, но и для выполнения ремонта. Например, для комнаты прямоугольной формы нужно купить плитку и обои. Для этого необходимо вычислить площадь и правильно идентифицировать форму основания, т. е. пола или стены.

        Однако перед рассмотрением признаков, свойств и формул, которые нужны для нахождения параметров фигуры, следует ознакомиться с теорией, дающей общее представление о прямоугольнике.

        Четырехугольник, состоящий из равных и параллельных между собой противоположных сторон, которые образуют прямые углы, называется прямоугольником. Обозначается он четырьмя литерами — именами вершин. Например, UVWX. Специалисты рекомендуют соблюдать очередность в алфавитном порядке, поскольку в высших учебных заведениях преподавательский состав это требует от студентов.

        Многие учащиеся делают ошибку, используя в качестве идентификации фигуры определение. Для примера следует рассмотреть квадрат и прямоугольник. У первого противолежащие стороны параллельны и будут равняться одному значению, а углы, образованные ими, равны 90 градусов. Признаки фигур позволяют точно классифицировать вид четырехугольника, а затем применить к нему соответствующие соотношения.

        Признаки прямоугольника

        Признак или идентификация — набор критериев, на основании которых четырехугольник можно отнести к определенному типу. Первоначальное определение было сформулировано на основании теоремы из евклидовой геометрии, которая гласит, что если у искомого четырехугольника 3 угла прямые, то он прямоугольник. Доказать утверждение довольно просто:

        1. Обозначить прямоугольник — UVWX. У него ∠U=∠V=∠W=90.
        2. На основании утверждения о сумме внутренних углов найти ∠Х: ∠Х = 360-90-90-90=90.
        3. Утверждение доказано.

        Однако математики вывели 3 признака, которые помогут отличить прямоугольник от квадрата. К ним относятся:

        1. Смежные стороны не равны между собой.
        2. Диагонали при пересечении не образуют прямые углы.
        3. В прямоугольник невозможно вписать окружность, поскольку он не является правильным четырехугольником.

        Первый признак строится из определения самой фигуры. Доказывается это очень просто. Следует начертить прямоугольник и обозначить его UVWX. Он состоит из следующих сторон: первая пара противоположных — UV=WX и вторая — VW=UX. Пусть UV и VX равны между собой. В этом случае будет выполняться такое равенство: UV=WX=VW=UX, т. е. фигура является правильной, поскольку у нее все стороны равны одному значению. Следовательно, она квадрат. Признак доказан.

        Диагонали в квадрате и прямоугольнике равны между собой. В этом случае для вычисления такого параметра, как площадь, можно брать любую диагональ (UW и VX). Основное отличие свойства пересечения последних — в квадрате они образуют прямой угол.

        Если рассмотреть последний признак, нужно учесть, что окружность можно вписать только в правильные фигуры, т. е. их стороны должны быть эквивалентны между собой. Так можно легко идентифицировать прямоугольник. Однако требуется рассмотреть его основные свойства, которые могут быть полезными при решении задач по геометрии.

        Основные свойства

        Прямоугольник обладает такими же свойствами, что и квадрат. Однако есть некоторые отличия, состоящие из доказанных математиками утверждений и соотношений. Например, возможно найти площадь прямоугольника, зная диагонали. К свойствам можно отнести:

        1. Вершины фигуры — основания прямых внутренних углов, сумма которых составляет 360 градусов.
        2. Равенство и параллельность взаимно противоположных сторон.
        3. Центр симметрии и окружности — точка пересечения диагоналей, которая делит их пополам. Кроме того, через нее можно провести среднюю линию.
        4. Подобие и равенство всех треугольников, которые образуются в результате пересечения его диагоналей.

        5. Вычисление диагонали (UW=q) через известные смежные стороны (UV=u и VW=v). q 2 = u 2 + v 2.

        6. Диагональ — диаметр описанной окружности, D = q.
        7. Если диагонали пересекаются, образуются большие прямоугольные и малые равнобедренные треугольники.
        8. Медиана и высота, которые проведены из любой вершины, равны половине q.
        9. Диагональ не является биссектрисой.

        Этих свойств недостаточно при решении задач. В этом случае могут пригодиться формулы.

        Соотношения для вычислений

        В геометрии для удобства решения задач и описания формул применяются сокращенные записи. Пусть прямоугольник обозначается литерами UVWX. Его стороны — UV=u и VW=v, а диагонали — q. Все углы при вершинах эквивалентны 90 градусам. Если рассматривать градусные меры ∠, образованных пересечением двух диагоналей q, острый — w, а тупой — z. Кроме того, вокруг фигуры можно описать окружность с радиусом (R) и диаметром (D).

        Начинающие математики часто путают ∠w и ∠z, подставляя в формулу площади через диагональ, размерность не того ∠. У прямоугольника существуют следующие параметры, являющиеся дополнительными: площадь (обозначается литерой «S» и является его размерностью) и периметр «P» (алгебраическая сумма длин 4 сторон).

        Нахождение размерности и периметра

        Базовое соотношение, по которому возможно вычислить периметр, имеет следующий вид: P=2u+2v. (0.5)=54,64 (м).

        Задача любого типа должна решаться с минимальных количеством формул и вычислений. Алгоритм ее решения должен быть оптимален.

        Таким образом, нахождение площади прямоугольника через диагональ позволяет существенно сократить объемы вычислений и время, потраченное на решение этой задачи.

        Площадь прямоугольника формула 4. Как посчитать площадь прямоугольника: практические советы

        Площадь прямоугольника, как не будет дерзко звучать, но это важное понятие. В повседневной жизни мы постоянно сталкиваемся с ним. Узнать размер полей, огородов, рассчитать количество краски, необходимой для побелки потолка, сколько понадобится обоев для оклейки ко

        мнаты и другое.

        Геометрическая фигура

        Для начала поговорим о прямоугольнике. Это фигура на плоскости, которая имеет четыре прямых угла, а ее противоположные стороны равны. Стороны его привыкли называть длиной и шириной. Измеряют их в миллиметрах, сантиметрах, дециметрах, метрах и т. д. Теперь ответим на вопрос: «Как найти площадь прямоугольника?» Для этого необходимо длину умножить на ширину.

        Площадь=длина*ширина

        Но еще одна оговорка: длина и ширина должны быть выражены в одинаковых единицах измерения, то есть метр и метр, а не метр и сантиметр. Записывается площадь латинской буквой S. Для удобства обозначим длину латинской буквой b, а ширину латинской буквой a, как показано на рисунке. Отсюда мы делаем вывод, что единицей измерения площади является мм 2 , см 2 , м 2 и т. д.

        Рассмотрим на конкретном примере, как найти площадь прямоугольника. Длина b=10 ед. Ширина a=6 ед. Решение: S=a*b, S=10 ед.*6 ед., S=60 ед 2 . Задача. Как узнать площадь прямоугольника, если длина в 2 раза больше ширины и составляет 18 м? Решение: если b=18 м, тогда а=b/2, a=9 м. Как найти площадь прямоугольника, если известны обе стороны? Правильно, подставить в формулу. S=a*b, S=18*9, S=162 м 2 . Ответ: 162 м 2 . Задача. Сколько необходимо купить рулонов обоев для комнаты, если ее размеры составляют: длина 5,5 м ширина 3,5, а высота 3 м? Размеры рулона обоев: длина 10 м, ширина 50 см. Решение: сделаем рисунок комнаты.

        Площади противоположных сторон равны. Вычислим площадь стены с размерами 5,5 м и 3 м. S стены 1 =5,5*3,

        S стены 1 =16,5 м 2 . Следовательно, противоположная стена имеет площадь равную 16,5 м 2 . Найдем площади следующих двух стен. Стороны их, соответственно, равны 3,5 м и 3 м. S стены 2 =3,5*3, S стены 2 =10,5 м 2 . Значит, и противоположная сторона равна 10,5 м 2 . Сложим все результаты. 16,5+16,5+10,5+10,5=54 м 2 . Как вычислить площадь прямоугольника, если стороны выражены в разных единицах измерения. Ранее мы вычисляли площади в м 2 , то и в этом случае будем использовать метры. Тогда ширина рулона обоев будет равна 0,5 м. S рулона =10*0,5, S рулона =5 м 2 . Теперь узнаем, сколько рулонов необходимо для оклейки комнаты. 54:5=10,8 (рулонов). Так как они измеряются целыми числами, то нужно купить 11 рулонов обоев. Ответ: 11 рулонов обоев. Задача. Как вычислить площадь прямоугольника, если известно, что ширина на 3 см короче длины, а сумма сторон прямоугольника составляет 14 см? Решение: пусть длина х см, тогда ширина (х-3) см. х+(х-3)+х+(х-3)=14, 4х-6=14, 4х=20, х=5 см — длина прямоугольника, 5-3=2 см — ширина прямоугольника, S=5*2, S=10 см 2 Ответ: 10 см 2 .

        Резюме

        Рассмотрев примеры, надеюсь, стало понятно, как найти площадь прямоугольника. Напомню, что единицы измерения длины и ширины должны совпадать, иначе получится неправильный результат, чтобы не допустить ошибок, читайте задание внимательно. Иногда сторона может быть выражена через другую сторону, не стоит бояться. Обратитесь к нашим решенным задачам, вполне возможно, они могут помочь. Но хоть раз в жизни мы сталкиваемся с нахождением площади прямоугольника.

        Инструкция

        Например, вам , что длина одной из сторон (а) равна 7 см, а периметр прямоугольника (P) равен 20 см. Так как периметр любой фигуры равен сумме длин ее сторон, а у прямоугольника противоположные стороны равны, то его периметр а будет выглядеть следующим образом: P = 2 x (a + b), или P = 2a + 2b. Из этой формулы следует, что найти длину второй стороны (b) можно с помощью несложной операции: b = (P – 2a) : 2. Так, в нашем случае сторона b будет равна (20 – 2 х 7) : 2 = 3 см.

        Теперь, зная длины обеих смежных сторон (a и b), вы сможете подставить их в формулу площади S = ab. В данном случае прямоугольника будет равна 7х3 = 21. Обратите на то, что единицами измерения будут уже не , а сантиметры квадратные, так как длин двух сторон единицы их измерения (сантиметры) вы тоже умножали друг на друга.

        Источники:

        • как находится периметр прямоугольника

        Плоская фигура, состоящая из четырех сторон и четырех прямых углов. Из всех фигур площадь прямоугольника приходится вычислять чаще других. Это и площадь квартиры, и площадь садового участка, и площадь поверхности стола или полки. Например, чтобы просто оклеить комнату обоями, вычисляют площадь ее прямоугольных стен.

        Инструкция

        Кстати, из прямоугольника можно легко вычислить площадь . Достаточно достроить прямоугольный до прямоугольника так, чтобы гипотенуза стала диагональю прямоугольника . Тогда будет очевидно, что площадь такого прямоугольника равна произведению катетов треугольника, а площадь самого треугольника, соответственно, равна половине произведения катетов.

        Видео по теме

        Частный случай параллелограмма — прямоугольник – известен только в геометрии Евклида. У прямоугольника равны все углы, и каждый из них по отдельности составляет 90 градусов. Исходя из частных свойств прямоугольника , а также из свойств параллелограмма о параллельности противолежащих сторон можно найти стороны фигуры по заданным диагоналям и углу от их пересечения. Вычисление сторон прямоугольника основывается на дополнительных построениях и применении свойств получаемых фигур.

        Инструкция

        Буквой А отметьте точку пересечения диагоналей. Рассмотрите образованный построениями EFА. Согласно свойству прямоугольника его диагонали равны и пополам точкой пересечения А. Вычислите значения FА и EА. Так как треугольник EFА равнобедренным и его стороны EА и FА равны между собой и соответственно равны половине диагонали EG.

        Далее вычислите первую EF прямоугольника . Данная сторона является третьей неизвестной стороной рассматриваемого треугольника EFА. Согласно теореме косинусов по соответствующей формуле найдите сторону EF. Для этого подставьте в формулу косинусов полученные ранее значения сторон FА EА и косинус известного угла между ними α. Вычислите и запишите полученное значение EF.

        Найдите вторую сторону прямоугольника FG. Для этого рассмотрите другой треугольник EFG. Он является прямоугольным, где известны гипотенуза EG и катет EF. Согласно теореме Пифагора найдите второй катет FG по соответствующей формуле.

        Относится к простейшим плоским геометрическим фигурам и является одним из частных случаев параллелограмма. Отличительная черта такого параллелограмма — прямые углы во всех четырех вершинах. Ограниченную сторонами прямоугольника площадь можно вычислить несколькими способами, используя размеры его сторон, диагонали и углы между ними, радиус вписанной окружности и т. д.

        Инструкция

        Если известна величина угла (α), который составляет диагональ прямоугольника с одной из его сторон, а также длина (С) этой диагонали, то для вычисления площади можно задействовать определения тригонометрических в прямоугольном . Прямоугольный треугольник здесь образуют две стороны четырехугольника и его диагональ. Из определения косинуса вытекает, что длина одной из сторон будет равна произведению длины диагонали на угла, величина известна. Из определения синуса можно вывести формулу длины другой стороны — она равна произведению длины диагонали на синус все того же угла. Подставьте эти тождества в формулу из предыдущего шага, и получится, что для нахождения площади надо перемножить синус и косинус известного угла, а также длины диагонали прямоугольника : S=sin(α)*cos(α)*С².

        Если кроме длины диагонали (С) прямоугольника известна величина угла (β), который образуют диагонали, то для вычисления площади фигуры можно тоже задействовать одну из тригонометрических функций — синус. Возведите в квадрат длину диагонали и умножьте полученный результат на половину синуса известного угла: S=С²*sin(β)/2.

        Если известен (r) вписанной в прямоугольник окружности, то для вычисления площади возведите эту величину во вторую степень и увеличьте результат в четыре раза: S=4*r². Четырехугольник, в который можно , будет являться квадратом, а длина его стороны равна диаметру вписанной окружности, то есть удвоенному радиусу. Формула получена подстановкой длин сторон, выраженных через радиус в тождество из первого шага.

        Если известны длины (P) и одной из сторон (A) прямоугольника , то для нахождения площади внутри этого периметра вычислите половину произведения длины стороны на разницу между длиной периметра и двумя длинами этой стороны: S=A*(P-2*A)/2.

        Видео по теме

        С задачей найти периметр или площадь многоугольника сталкиваются не только ученики на уроках геометрии. Порой ее случается решать и взрослому человеку. Приходилось ли вам рассчитывать необходимое количество обоев для комнаты? Или, может быть, вы измеряли протяженность дачного участка, чтобы огородить его забором? Так знания основ геометрии иногда незаменимы для осуществления важных проектов.

        Площадь геометрической фигуры — численная характеристика геометрической фигуры показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц.

        Формулы площади треугольника

        1. Формула площади треугольника по стороне и высоте
          Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты
        2. Формула площади треугольника по трем сторонам и радиусу описанной окружности
        3. Формула площади треугольника по трем сторонам и радиусу вписанной окружности
          Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.
          4. где S — площадь треугольника,
          — длины сторон треугольника,
          — высота треугольника,
          — угол между сторонами и,
          — радиус вписанной окружности,
          R — радиус описанной окружности,

        Формулы площади квадрата

        1. Формула площади квадрата по длине стороны
          Площадь квадрата равна квадрату длины его стороны.
        2. Формула площади квадрата по длине диагонали
          Площадь квадрата равна половине квадрата длины его диагонали.
          S =1 2
          2
          3. где S — Площадь квадрата,
          — длина стороны квадрата,
          — длина диагонали квадрата.

        Формула площади прямоугольника

          Площадь прямоугольника равна произведению длин двух его смежных сторон

          где S — Площадь прямоугольника,
          — длины сторон прямоугольника.

        Формулы площади параллелограмма

        1. Формула площади параллелограмма по длине стороны и высоте
          Площадь параллелограмма
        2. Формула площади параллелограмма по двум сторонам и углу между ними
          Площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними.

          a · b · sin α

          3. где S — Площадь параллелограмма,
          — длины сторон параллелограмма,
          — длина высоты параллелограмма,
          — угол между сторонами параллелограмма.

        Формулы площади ромба

        1. Формула площади ромба по длине стороны и высоте
          Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты.
        2. Формула площади ромба по длине стороны и углу
          Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба.
        3. Формула площади ромба по длинам его диагоналей
          Площадь ромба равна половине произведению длин его диагоналей.
          4. где S — Площадь ромба,
          — длина стороны ромба,
          — длина высоты ромба,
          — угол между сторонами ромба,
          1 , 2 — длины диагоналей.

        Формулы площади трапеции

        1. Формула Герона для трапеции

          Где S — Площадь трапеции,
          — длины основ трапеции,
          — длины боковых сторон трапеции,

        Начиная с 5 класса, ученики начинают знакомиться с понятием площадей разных фигур. 2$.

        Диагонали разделяет прямоугольник на 4 фигуры – 4 треугольника. При этом треугольники попарно равны. Если провести диагональ в прямоугольнике, то она разделяет фигуру на два равных прямоугольных треугольника. Средняя оценка: 4.4 . Всего получено оценок: 214.

        Полезный калькулятор для школьников и взрослых позволяет быстро вычислить площадь прямоугольника по двум его сторонам. Подобный расчет мы часто производим не только в рамках школьного курса геометрии, но и в повседневной жизни. Например, если нужно посчитать площадь комнаты при ремонте квартиры, для расчета необходимого количества материалов.

        Удобная навигация по статье:

        Как рассчитать площадь прямоугольника

        Прямоугольником принято называть геометрическую плоскую фигуру, которая имеет параллельно расположенные противоположные стороны при углах в 90 градусов. В качестве длины этой геометрической фигуры выступает величина, которая имеет большую сторону. При этом, за ширину принимается величина меньшей стороны. Для правильного вычисления площади прямоугольника Вам необходимо знать определённые параметры, которыми обладает данная фигура. В их числе:

        • диагональ;
        • ширина;
        • так называемый угол наклона к одной из сторон диагонали;
        • длина.

        Таким образом, произвести расчёт площади прямоугольника можно различными способами. Всё зависит от количества информации о фигуре, а именно, какие величины нам точно известны.

        Как вычислить площадь прямоугольника, имея линейные параметры его сторон?

        Давайте в качестве обозначения длины прямоугольника будем использовать букву «а», для его ширины – букву «b», а площадь геометрической фигуры обозначим буквой «S». Согласно этому, наша формула будет выглядеть следующим образом: S = a x b.

        Зная линейные параметры прямоугольника, можно легко определить его периметр последующей формуле: P = 2(a + b), где в качестве обозначения периметра мы используем букву «P».

        Как можно вычислить площадь прямоугольника, зная величину одну из его сторон и диагональ?

        Как нам известно, диагональ делит любой прямоугольник на два так называемых прямоугольных треугольника. Давайте присвоим диагонали индекс «с», а длину стороны обозначим буквой «а». Теперь необходимо произвести следующий порядок действий:

        1. для начала необходимо найти длину неизвестной стороны. Для этого мы используем формулу Пифагора: b = V c2 – a2.
        2. После этого, нам следует определить площадь нашей основной геометрической фигуры (прямоугольника) как площадь треугольника, умноженную на два: Sтр = ½ (а х в).
        3. Согласно вышеописанной схеме расчёта площадь прямоугольника в данном случае будет равна: S = 2 x Sтр = а х в.

        В том случае, если нам известны периметр прямоугольника, а также длина одной из его сторон, то площадь этой геометрической фигуры можно вычислить, определив длину второй стороны (b = (P – 2xa), по такой формуле: S = a x b.

        Если же нам известны размер диагонали прямоугольника, а также угол между стороной и самой диагональю, то площадь можно вычислить при помощи следующих тригонометрических функций: Sтр = ½ х с2 х sinФ х cosФ.

        При этом, общая площадь в данном случае будет составлять S = 2 x Sтр.

        Площадь прямоугольника. Видео-урок.

        Площадь ромба по 2 диагоналям. Площадь ромба

        Несмотря на то, что математика – царица наук, а арифметика – царица математики, самую большую сложность в изучении у школьников вызывает геометрия. Планиметрия – раздел геометрии, который изучает плоские фигуры. Одной из таких фигур является ромб. Большинство задач по решению четырехугольников сводятся к нахождению их площадей. Систематизируем известные формулы и различные способы расчета площади ромба.

        Ромб – это параллелограмм, все четыре стороны которого равны. Напомним, что у параллелограмма есть четыре угла и четыре попарно параллельные равные стороны. Как любой четырехугольник, ромб имеет ряд свойств, которые сводятся к следующим: при пересечении диагонали образуют угол, равный 90 градусов (AC ⊥ BD), точка пересечения делит каждую на два равных отрезка. Диагонали ромба также являются биссектрисами его углов (∠DCA = ∠BCA, ∠ABD = ∠CBD и т. д.). Отсюда следует, что они делят ромб на четыре равных прямоугольных треугольника. Сумма длин диагоналей, возведенных во вторую степень, равна длине стороны во второй степени, умноженной на 4, т.е. BD 2 + AC 2 = 4AB 2 . Существует множество методов, используемых в планиметрии для расчета площади ромба, применение которых зависит от исходных данных. Если известны длина стороны и любой угол, можно воспользоваться следующей формулой: площадь ромба равна квадрату стороны, умноженному на синус угла. Из курса тригонометрии известно, что sin (π – α) = sin α, а значит, в расчетах можно использовать синус любого угла – как острого, так и тупого. Частным случаем является ромб, у которого все углы прямые. Это квадрат. Известно, что синус прямого угларавен единице, поэтому площадь квадрата равна длине его стороны, возведенной во вторую степень.

        Если величина сторон неизвестна, воспользуемся длиной диагоналей. В этом случае площадь ромба равна половине произведения большой и малой диагоналей.

        При известной длине диагоналей и величине любого угла площадь ромба определяется двумя способами. Первый: площадь – это половина квадрата большей диагонали, умноженная на тангенс половины градусной меры острого угла, т.е. S = 1/2*D 2 *tg(α/2), где D – большая диагональ, α – острый угол. Если вам известен размер меньшей диагонали, воспользуемся формулой 1/2*d 2 *tg(β/2), где d – меньшая диагональ, β – тупой угол. Напомним, что мера острого угла меньше 90 градусов (меры прямого угла), а тупой угол соответственно – больше 90 0 .

        Площадь ромба можно отыскать, используя длину стороны (напомним, все стороны у ромба равны) и высоты. Высота – это перпендикуляр, опущенный на противоположную углу сторону или на ее продолжение. Чтобы основание высоты располагалось внутри ромба, ее следует опускать из тупого угла.

        Иногда в задаче требуется отыскать площадь ромба, исходя из данных, относящихся к вписанной окружности. В этом случае необходимо знать ее радиус. Существуют две формулы, которыми можно воспользоваться для расчета. Итак, чтобы ответить на поставленный вопрос, можно удвоить произведение стороны ромба и радиуса вписанной окружности. Другими словами, необходимо умножить диаметр вписанной окружности на сторону ромба. Если в условии задачи представлена величина угла, то площадь находится через частное между квадратом радиуса, умноженном на четыре, и синусом угла.

        Как видите, существует множество способов для нахождения площади ромба. Конечно, чтобы запомнить каждый из них, потребуется терпение, внимательность и, конечно же, время. Но в дальнейшем вы сможете легко выбрать метод, подходящий для вашей задачи, и убедитесь, что геометрия – это несложно.

        Площадь геометрической фигуры — численная характеристика геометрической фигуры показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц.

        Формулы площади треугольника

        1. Формула площади треугольника по стороне и высоте
          Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты
        2. Формула площади треугольника по трем сторонам и радиусу описанной окружности
        3. Формула площади треугольника по трем сторонам и радиусу вписанной окружности
          Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.
          4. где S — площадь треугольника,
          — длины сторон треугольника,
          — высота треугольника,
          — угол между сторонами и,
          — радиус вписанной окружности,
          R — радиус описанной окружности,

        Формулы площади квадрата

        1. Формула площади квадрата по длине стороны
          Площадь квадрата равна квадрату длины его стороны.
        2. Формула площади квадрата по длине диагонали
          Площадь квадрата равна половине квадрата длины его диагонали.
          S =1 2
          2
          3. где S — Площадь квадрата,
          — длина стороны квадрата,
          — длина диагонали квадрата.

        Формула площади прямоугольника

          Площадь прямоугольника равна произведению длин двух его смежных сторон

          где S — Площадь прямоугольника,
          — длины сторон прямоугольника.

        Формулы площади параллелограмма

        1. Формула площади параллелограмма по длине стороны и высоте
          Площадь параллелограмма
        2. Формула площади параллелограмма по двум сторонам и углу между ними
          Площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними.

          a · b · sin α

          3. где S — Площадь параллелограмма,
          — длины сторон параллелограмма,
          — длина высоты параллелограмма,
          — угол между сторонами параллелограмма.

        Формулы площади ромба

        1. Формула площади ромба по длине стороны и высоте
          Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты.
        2. Формула площади ромба по длине стороны и углу
          Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба.
        3. Формула площади ромба по длинам его диагоналей
          Площадь ромба равна половине произведению длин его диагоналей.
          4. где S — Площадь ромба,
          — длина стороны ромба,
          — длина высоты ромба,
          — угол между сторонами ромба,
          1 , 2 — длины диагоналей.

        Формулы площади трапеции

        1. Формула Герона для трапеции

          Где S — Площадь трапеции,
          — длины основ трапеции,
          — длины боковых сторон трапеции,

        – это параллелограмм, у которого все стороны равны.

        Ромб с прямыми углами называется квадратом и считается частным случаем ромба. Найти площадь ромба можно различными способами, используя все его элементы – стороны, диагонали, высоту. Классической формулой площади ромба считается расчет значения через высоту.

        Пример расчета площади ромба по этой формуле очень прост. Необходимо только подставить данные и высчитать площадь.

        Площадь ромба через диагонали


        Диагонали ромба пересекаются под прямым углом и в точке пересечения делятся пополам.

        Формула площади ромба через диагонали представляет собой произведение его диагоналей, разделенное на 2.

        Рассмотрим пример расчета площади ромба через диагонали. Пусть дан ромб с диагоналями
        d1 =5 см и d2 =4. Найдем площадь.

        Формула площади ромба через стороны подразумевает и применение других элементов. Если в ромб вписана окружность, то площадь фигуры можно просчитать по сторонам и ее радиусу:

        Пример расчета площади ромба через стороны также весьма прост. Требуется только просчитать радиус вписанной окружности. Его можно вывести из теоремы Пифагора и по формуле .

        Площади ромба через сторону и угол


        Формула площади ромба через сторону и угол используется очень часто.

        Рассмотрим пример расчета площади ромба через сторону и угол.

        Задача: Дан ромб, диагонали которого равны d1 =4 см,d2 =6 см. Острый угол равен α = 30°. Найдите площадь фигуры через сторону и угол.
        Для начала найдем сторону ромба. Используем для этого теорему Пифагора. Мы знаем, что в точке пересечения диагонали делятся пополам и образуют прямой угол. Следовательно:
        Подставим значения:
        Теперь мы знаем сторону и угол. Найдем площадь:

        – это параллелограмм , у которого все стороны равны, то для него действуют все те же формулы, как и для параллелограмма, включая формулу нахождения площади через произведение высоты и стороны .

        Площадь ромба можно найти, также зная его диагонали . Диагонали делят ромб на четыре абсолютно одинаковых прямоугольных треугольника . Если мы их рассортируем, так чтобы получить прямоугольник , то его длина и ширина будут равны одной целой диагонали и половине второй диагонали. Поэтому площадь ромба находится умножением диагоналей ромба, сокращенных на два (как площади получившегося прямоугольника).

        Если в распоряжении только угол и сторона , то можно вооружиться диагональю в качестве помощника и начертить ее напротив известного угла. Тогда она разделит ромб на два конгруэнтных треугольника, площади которых в сумме дадут нам площадь ромба. Площадь каждого из треугольников будет равна половине произведения квадрата стороны на синус известного угла, как площадь равнобедренного треугольника . Поскольку таких треугольников два, то коэффициенты сокращаются, оставив только сторону во второй степени и синус:

        Если внутри ромба вписать окружность , то его радиус будет относиться к стороне под углом 90° , что значит, что удвоенный радиус будет равен высоте ромба . Подставив вместо высоты h=2r в предыдущую формулу, получим площадь S=ha=2ra

        Если же вместе с радиусом вписанной окружности, дана не сторона, а угол, то следует сначала найти сторону, проведя высоту таким образом, чтобы получить прямоугольный треугольник с заданным углом. Тогда сторона a может быть найдена из тригонометрических отношений по формуле . Подставляя это выражение в ту же стандартную формулу площади ромба, выходит

        Ромб — это частный случай параллелограмма. Он представляет собой плоскую четырехугольную фигуру, в которой все стороны равны. Данное свойство определяет то, что у ромбов параллельны противоположные стороны и равны противолежащие углы. Диагонали ромба пресекаются под прямым углом, точке их пересечения приходится на середину каждой диагонали, а углы из который они выходят делятся пополам. То есть они диагонали ромба являются биссектрисами углов. Исходя из приведенных определений и перечисленных свойств ромбов их площадь может быть определена различными способами.

        1. Если известны обе диагонали ромба AC и BD, то площадь ромба может быть определена как половина произведения диагоналей.

        S = ½ ∙ AC ∙ BD

        где AC, BD — длина диагоналей ромба.

        Чтобы понять почему это так, можно мысленно вписать в ромб прямоугольник таким образом, чтобы стороны последнего были перпендикулярны диагоналям ромба. Становится очевидным, что площадь ромба будет равна половине площади вписанного данным образом в ромб прямоугольника, длина и ширина которого будут соответствовать величине диагоналей ромба.

        2. По аналогии с параллелепипедом площадь ромба может быть на найдена как произведение его стороны, на высоту перпендикуляра с опущенного к данной стороне с противолежащей стороны.

        S = а ∙ h

        где а — сторона ромба;
        h — высота перпендикуляра, опущенного на данную сторону.

        3. Площадь ромба также равна квадрату его стороны, умноженному на синус угла α .

        S = a 2 ∙ sinα

        где, a — сторона ромба;
        α — угол между сторонами.

        4. Также площадь ромба может быть найдена через его сторону и радиус вписанной в него окружности.

        S = 2 ∙ a ∙ r

        где, a — сторона ромба;
        r — радиус вписанной в ромб окружности.

        Интересные факты
        Слово ромб произошло от древнегреческого rombus, что в переводе означает «бубен». В те времена бубны действительно имели ромбовидную форму, а не круглую, как мы привыкли видеть их в настоящее время. С тех же времен произошло и название карточной масти «бубны». Очень широко ромбы различных видов используются в геральдике.

        Найти площадь квадрата по диагонали

        Квадрат — это правильный четырёхугольник, у которого все стороны и углы равны. У квадрата две диагонали, соединяющие несмежные вершины фигуры. Расчет площади квадрата по диагонали онлайн-калькулятором производится по формуле S=12*d2, где d — диагональ квадрата

        Чтобы найти площадь квадрата по диагонали онлайн, понадобится несколько простых действий:

        • указать размер диагонали и единицы измерения;
        • выбрать, в каких единицах необходимо рассчитать площадь;
        • получить ответ после нажатия на кнопку «Найти».

        Нахождение площади квадрата по диагонали

        Чтобы найти площадь квадрата по диагонали с помощью онлайн-калькулятора, нужно:

        1. Задать диагональ квадрата. Для наглядности возьмем квадрат со стороной 8 см и введем это значение в пустое поле калькулятора:

          Отметим, что при вводе некорректного значения калькулятор выдает предупреждение. Например, вот что будет, если ввести в поле для диагонали отрицательное значение:
        2. Выберем размерности величин. Онлайн калькулятор позволяет работать с миллиметрами, сантиметрами и метрами, а также осуществляет конвертацию этих величин.
        3. Теперь нажмем «Найти» и получим решение с ответом:

        Материалы, которые помогут вам лучше разобраться в теме:

        • Площадь фигуры: понятие площади, свойства площади, квадрируемые фигуры
        • Вычисление площади фигуры в полярных координатах

        Ответ:

        Решение

        Ответ:

        • list» :key=»`error-${eIdx}`» v-html=»e»/>

        Похожие калькуляторы:

        • Площадь треугольника (по 3 сторонам)
        • Площадь треугольника (по 2 сторонам и углу)
        • Площадь треугольника (по стороне и высоте)
        • Площадь прямоугольного треугольника
        • Площадь равнобедренного треугольника
        • Площадь равностороннего треугольника
        • Площадь квадрата (по стороне квадрата)
        • Площадь прямоугольника
        • Площадь треугольника (по 3 сторонам и радиусу описанной окружности)
        • Площадь треугольника (по 3 сторонам и радиусу вписанной окружности)
        • Площадь треугольника (по полупериметру и радиусу вписанной окружности)
        • Площадь треугольника (по двум сторонам и одному углу)
        • Площадь треугольника (по одной стороне и двум углам)
        • Площадь треугольника (по радиусу описанной окружности и двум углам)
        • Площадь круга (по радиусу)
        • Площадь круга (по диаметру)
        • Площадь круга (по длине окружности)
        • Площадь ромба (по сторонам и углу между ними)
        • Площадь ромба (по стороне и высоте)
        • Площадь ромба (по диагоналям)
        • Площадь параллелограмма (по сторонам и углу между ними)
        • Площадь параллелограмма (по стороне и высоте)
        • Площадь параллелограмма (по диагоналям и углу между ними)
        • Площадь трапеции (по основаниям и высоте)
        • Площадь трапеции (по средней линии и высоте)
        • Площадь трапеции (по диагоналям и углу между ними)
        • Площадь эллипса
        • Площадь поверхности куба
        • Площадь поверхности параллелепипеда
        • Площадь поверхности сферы
        • Площадь поверхности цилиндра
        • Площадь поверхности конуса

        Вычисление площади квадрата по диагонали онлайн

        При отсутствии данных о длине стороны квадрата можно найти площадь фигуры другим способом. В данном случае можно не прибегать к услугам программных средств и все действия произвести самостоятельно. Но если величина диагонали содержит несколько знаков, то при возведении ее в квадрат есть вероятность допустить ошибку.

        Рассчитать площадь квадрата по диагонали онлайн понадобится:

        • школьникам, которые выполняют домашнее задание по геометрии;
        • родителям для быстрого контроля;
        • учителям, проверяющим работы класса;
        • студентам, которым важен точный ответ, на который опираются дальнейшие вычисления.

        Сервис выдает последовательное решение задачи с точным ответом. С помощью сайта Zaochnik можно осуществлять подготовку к занятиям без привлечения репетиторов, траты средств и лишнего времени.

        Понравился калькулятор? Поделись с друзьями!

        Площадь квадрата по диагонали

        Площадь любой геометрической фигуры – это пространство, занимаемое двумерным объектом. Квадрат представляет собой двумерную геометрическую фигуру, которая определяется сторонами, которые равны по длине и перпендикулярны друг другу (угол между двумя сторонами составляет 90 градусов). Площадь квадрата — это количество квадратных единиц, необходимых для полного заполнения квадрата. Существуют разные способы вычисления площади квадрата.

        Один из обычных и стандартных способов вычисления площади квадрата — это использование его диагоналей или сторон. Поскольку все стороны квадрата одинаковы, мы можем напрямую найти квадрат его стороны. Следовательно, площадь квадрата равна произведению любой из двух его сторон.

        Но иногда длина стороны не указана, и мы знаем только длину диагонали квадрата. Зная прямоугольные треугольники, мы можем найти площадь квадрата по диагонали.

        Что такое диагональ квадрата?

        Диагональ — это линия, идущая от одного угла фигуры к противоположному углу и проходящая через центр фигуры. Диагонали квадрата всегда равны друг другу. В многоугольнике диагонали можно определить как линию, соединяющую две его несмежные вершины.

        Связь между диагональю и стороной квадрата

        Квадрат можно разделить на два прямоугольных треугольника, где диагональ квадрата равна длине гипотенузы треугольника. Теорема Пифагора, применимая к прямоугольным треугольникам, показывает связь между гипотенузой и сторонами прямоугольного треугольника.

        Таким образом, он также представляет отношение между диагональю квадрата (гипотенузой треугольника) и его сторонами.

        (Изображение скоро будет загружено) 9{2}}\]

        = \[a\sqrt{2}\]

        = сторона \[\sqrt{2}\]

        Формула площади квадрата по диагонали

        По длине диагонали , площадь квадрата можно рассчитать как:

        Площадь квадрата = ½ × d 2 единицы 2

        Здесь «d» — длина любой из диагоналей. Также помните, что в квадрате диагонали равны.

        Вычисление площади квадрата по диагонали

        Мы знаем формулу нахождения площади квадрата по диагоналям. Теперь мы выведем эту формулу, используя следующие два метода.

        1. Использование теоремы Пифагора

        (Изображение будет загружено в ближайшее время)

        На данном рисунке диагональ единиц длины «d» делит квадрат стороны «a» единиц на два прямоугольных треугольника. Теперь, применяя теорему Pythagoras в любом правом треугольнике,

        (гипотенуза) 2 = (основа) 2 + (перпендикуляр) 2

        здесь,

        Perpendicular = A

        = A

        = A

        =

        =

        =

        Гипотенуза = d

        SO,

        A 2 + A 2 = D 2

        2A 2 = D 2

        или, A 2 = D 2 /2

        WELY 2 = D 2 /2 что площадь квадрата = a 2 = d 2 / 2

        Таким образом, площадь квадрата с использованием диагоналей = ½ × d 2 квадратных единиц.

        1. Используя отношение между стороной и диагональю

        Для квадрата со стороной «a» и диагональю «d», мы знаем, что

        Площадь квадрата = сторона x сторона = a 2

        Теперь, как мы получили выше,

        Диагональ квадрата = сторона x √2 = a√2

        Тогда, сторона квадрата, a = 1 /√2 x диагональ = d/√2

        Таким образом, площадь квадрата = a 2

        Площадь = (d/√2) 2

        Площадь = d 2 /2

        3 Площадь = 90½ x d 2

        Площадь = ½ x (диагональ) 2

        Таким образом, площадь квадрата с использованием диагоналей = ½ × d 2 квадратных шт.

        Решенные примеры

        Пример 1. Найдите стороны и площадь квадрата, если диагональ равна 6 см.

        Решение: Возьмем квадрат со стороной x. Если квадрат разделить на два прямоугольных треугольника, то гипотенуза каждого треугольника равна диагонали квадрата. Как известно, диагональ равна 6 см.

        Согласно теореме Пифагора,

        x 2 + x 2 = 6 2  

        9Таким образом, длина сторона квадрата равна 3\[\sqrt{2}\]  единиц.

        Чтобы найти площадь квадрата, когда дана диагональ, мы можем использовать любой из следующих методов:

        1. Метод 1 

         Площадь квадрата = сторона x сторона =3\[\sqrt{2 }\]  x 3\[\sqrt{2}\]

         = 9 x 2 = 18 см 2

        1. Метод 2

        Площадь квадрата = ½ x d 2 =  ½ x 6 x 6 

        =  ½ x 36 = 18 см 2

        92002 Пример длины диагонали квадрата по теореме Пифагора, если сторона равна 4 см.

        Решение: Мы знаем, что все стороны квадрата равны по длине. Мы также знаем, что каждая вершина образует угол 90°. Теперь давайте разделим квадрат на два прямоугольных треугольника со сторонами, равными 4 см. Используя теорему Пифагора в одном из треугольников найдем третью сторону треугольника, являющуюся диагональю квадрата.

        Пусть гипотенуза/диагональ равна ‘c’ см.

        Следовательно, (гипотенуза) 2 = (основание) 2 + (перпендикулярный) 2

        C 2 = 4 2 + 4 2

        = C 2 + 160023 2

        = C 2 + = 16024 = 16024 = 160023 2

        = C 2 + 4 2

        = C 2 + 4 2

        = C 2 + 4 2

        = C 2 + 4 2

        = C 2 + 16 

        c = \[\sqrt{32}\] см

        c = 4\[\sqrt{2}\]см

        Длина диагонали 4\[\sqrt{2}\]см

        Диагональ прямоугольника.

        Калькулятор

        Автор Доминик Черня, кандидат наук

        Отзыв от Bogna Szyk

        Последнее обновление: 11 марта 2022 г.

        Содержание:
        • Как найти диагональ прямоугольника?
        • Какова диагональ прямоугольника?

        Наш калькулятор диагонали прямоугольника — это обширный инструмент, который быстро находит диагональ и другие параметры прямоугольника. Вы столкнулись с конкретной проблемой прямоугольника, и вы не знаете , как найти диагональ прямоугольника ? Попробуйте ввести пару параметров в поля рядом с текстом или продолжайте читать, чтобы узнать возможные 9 параметров.0269 диагональ прямоугольника формулы .

        Типичный прямоугольник показан на рисунке ниже. Мы отметили пять основных величин, описывающих конкретный прямоугольник. Вы можете использовать их для получения формулы диагонали прямоугольника. Это:

        • l — длина ,
        • ширина ,
        • α — угол между диагоналями ,
        • r — радиус описанной окружности ,
        • д — диагональ ,

        и два других параметра, которые не показаны на картинке:

        • A — площадь ,
        • П — периметр .

        Термин прямоугольник происходит от латинского rectangulus , который представляет собой комбинацию двух слов: rectus (правый, правильный) и angulus (угол). Это название происходит от того факта, что прямоугольник представляет собой четырехугольник с четырьмя прямыми углами (4 * 90° = 360°). Его противоположные стороны параллельны и имеют одинаковую длину, а две его диагонали пересекаются посередине и также имеют одинаковую длину.

        Квадрат — это частный случай прямоугольника. Его определение состоит в том, что у него все четыре стороны одинаковой длины, или, альтернативно, угол между двумя диагоналями прямой. Попробуйте наши калькуляторы, посвященные квадратам. Они могут быстро оценить периметр, площадь и диагональ любого квадрата, который вам нужен, только по длине его стороны.

        Центр прямоугольника равноудален от его вершин, поэтому на нем всегда можно описать окружность . С другой стороны, вы можете вписать окружность в прямоугольник, только если это квадрат .

        Как найти диагональ прямоугольника?

        Чтобы найти диагональ прямоугольника по формуле, вы можете разделить прямоугольник на два конгруэнтных прямоугольных треугольника, т. е. треугольники с одним углом 90°. Каждый треугольник будет иметь стороны длиной l и w и гипотенузой длины d . Вы можете использовать теорему Пифагора для оценки диагонали прямоугольника, которая может быть выражена следующей формулой:

        d² = l² + w² ,

        и теперь вы должны знать, как найти диагональ прямоугольника по явной формуле — просто извлеките квадратный корень:

        d = √(l² + w²) .

        Наш калькулятор диагонали прямоугольника позволяет использовать практически любые единицы измерения. Воспользуйтесь нашим конвертером длины или конвертером площади, чтобы узнать, как переключаться между различными единицами измерения (СИ и имперскими).

        Какова диагональ прямоугольника?

        Иногда вы не можете указать все две стороны прямоугольника. Как найти диагональ прямоугольника в этом случае? Ответ дает наш калькулятор диагонали прямоугольника. Сначала запишем три основных уравнения для площади, периметра и радиуса описанной окружности:

        1. Площадь прямоугольника: A = w * l ,
        2. Периметр прямоугольника P = 2 * w + 2 * l ,
        3. Радиус окружности прямоугольника r = d/2 .

        С помощью приведенных выше уравнений мы теперь можем вывести различные формулы диагонали прямоугольника , которые используются калькулятором этой диагонали прямоугольника:

        1. Учитывая длину и ширину : д = √(l² + w²) ,
        2. Дано длина/ширина и площадь : d = √(A²/l² + l²) или d = √(A²/w² + w²) ,
        3. Дано длина/ширина и периметр : d = √(2l² - P*l + P²/4)) или d = √(2w² - P*w + P²/4) ,
        4. Даны длина/ширина и угол : d = w / sin(α/2) или d = l / cos(α/2) ,
        5. Учитывая площадь и периметр : d = √(P² - 2*A) ,
        6. Учитывая площадь и угол : d = √(2 * A / sin(α)) ,
        7. Учитывая периметр и угол : d = P / (2*sin(α/2) + 2*cos(α/2)) ,
        8. Дан радиус описанной окружности : d = 2 * r .

        Примечание: Угол α между диагоналями лежит перед длиной , как и на первом рисунке. Также помните, что калькулятор диагонали прямоугольника предполагает, что длина больше ширины!

        Знаете ли вы, что существует особый прямоугольник, называемый золотым прямоугольником? Если нет, то воспользуйтесь нашим калькулятором золотых прямоугольников и узнайте, как построить золотые прямоугольники!

        Доминик Черня, кандидат наук

        Длинная сторона (l)

        Короткая сторона (w)

        Площадь (A)

        Периметр (P)

        Угол между диагоналями окружности (06)

        Диагональ

        Диагональ (d)

        Посмотрите 21 похожий калькулятор 2d геометрии 📏

        ПлощадьПлощадь прямоугольникаПлощадь полумесяца… Еще 18

        Диагональ квадрата — формула, свойства, примеры

        LearnPracticeDownload

        Диагональ квадрата представляет собой отрезок, соединяющий любые две несмежные вершины. Квадрат имеет две диагонали, которые равны по длине и делят друг друга пополам под прямым углом. Формула диагонали квадрата используется для вычисления длины диагонали квадрата, когда известна длина его стороны.

        1. Какова диагональ квадрата?
        2. Что такое Диагональ формулы квадрата?
        3. Вывод диагонали квадрата по формуле
        4. Примеры использования диагональной формулы квадрата
        5. Часто задаваемые вопросы о диагонали квадратной формулы

        Что такое диагональ квадрата?

        Квадрат имеет две диагонали, каждая из которых образована соединением противоположных вершин квадрата. Обратите внимание на следующий квадрат, чтобы соотнести свойства диагоналей, приведенные ниже.

        • Диагонали квадрата равны по длине.
        • Они перпендикулярны друг другу.
        • Они делят квадрат на два равных равнобедренных прямоугольных треугольника.

        Что такое Диагональ формулы квадрата?

        Диагональ формулы квадрата равна d = a√2; где «d» — диагональ, а «а» — сторона квадрата. Формула диагонали квадрата выводится по теореме Пифагора. Диагональ делит квадрат на два равнобедренных прямоугольных треугольника. Обе диагонали равны и делят друг друга пополам под прямым углом. Давайте разберемся, как вывести формулу для нахождения диагонали квадрата.

        Вывод диагонали квадрата по формуле

        В квадрате длина обеих диагоналей одинакова. Длина диагонали «d» квадрата со стороной «а» вычисляется по теореме Пифагора. Обратите внимание на следующий квадрат, чтобы увидеть, что длина диагонали обозначена буквой «d», а длина стороны обозначена буквой «a».

        Диагональ квадрата Формула

        Рассмотрим треугольник ADC в квадрате. Мы знаем, что все углы квадрата равны 9.0 °, поэтому, используя теорему Пифагора, мы можем найти гипотенузу, которая в данном случае равна «d».

        D 2 = A 2 + A 2

        D = √ (A 2 + A 2 )

        D = √ (2A 2 )

        D = √ (2A 2 )

        9666 D = √ (2A 2 )

        966 D = √ (2A 2 )

        9

        D = √ (2A 2 ) 9000 3

        D = √ (2A 2 )

        D = √ (2A 2 )

        D = √ (2A 2 )

        D = √ (2A 2 ) √a 2

        = √2a

        Следовательно, диагональ квадрата равна: d = a√2

        ☛ Похожие статьи

        • Диагонали прямоугольника 9006
        • Диагональ куба Формула
        • Диагональ формулы параллелограмма
        • Диагональ многоугольника Формула
        • Диагональ ромба

         

        Примеры использования диагональной формулы квадрата

        1. Пример 1: Найдите длину диагонали квадрата со стороной 14 единиц.

          Решение:

          Длина стороны квадрата: а = 14 единиц.

          Используя формулу вычисления диагонали квадрата, длина диагонали d равна:

          d = a√2

          d = 14√2 или 19,8 единицы

          Ответ: Длина каждой диагонали данного квадрата равна 19,8 единицы.

        2. Пример 2: Длина диагонали квадрата составляет 3√2 единицы. Найдите длину стороны квадрата.

          Решение:

          Дано, что диагональ квадрата = 3√2 единицы.

          Предположим, что длина стороны квадрата равна «а».

          Согласно формуле диагонали квадрата, длина диагонали d равна:

          d = a √2

          3√2 = a √2

          a = 3

          Ответ: Длина стороны данного квадрата = 3 единицы.

        3. Пример 3: Найдите длину диагонали квадрата, если его площадь 36 квадратных единиц.

          Решение:

          Площадь квадрата = 36 квадратных единиц

          Мы знаем, что площадь квадрата = a 2 = 36

          Следовательно, a = 6 единиц

          Мы знаем, что диагональ формула квадрата: d = a√2

          Следовательно, длина диагонали = a√2 = 6√2 = 8,49 ед.

          Ответ: Длина диагонали квадрата = 8,49 ед.

        перейти к слайдуперейти к слайдуперейти к слайду

        Есть вопросы по основным математическим понятиям?

        Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, что стоит за математикой, с нашими сертифицированными экспертами

        Запишитесь на бесплатный пробный урок

        Практические вопросы по диагонали квадрата

         

        перейти к слайдуперейти к слайду

        Часто задаваемые вопросы о диагонали квадратной формулы

        Что такое диагональ квадрата в математике?

        Диагональ квадрата — это отрезок, соединяющий две несмежные вершины. Квадрат имеет две диагонали, которые равны по длине и делят друг друга пополам под прямым углом. Свойства диагоналей квадрата следующие:

        • Они равны по длине.
        • Они перпендикулярны друг другу.
        • Они делят квадрат на два равных равнобедренных прямоугольных треугольника.

        Какова формула диагонали квадрата?

        Квадрат имеет две диагонали одинаковой длины, которые можно рассчитать по формуле d = a√2, где а — сторона квадрата.

        Как рассчитать диагональ квадрата по формуле диагонали?

        Чтобы вычислить длину диагонали квадрата, мы используем следующие шаги:

        • Шаг 1: Проверьте длину стороны квадрата, a.
        • Шаг 2: Подставьте значение «а» в формулу диагонали квадрата, d = a√2.
        • Шаг 3: Запишите полученное значение в соответствующей единице измерения.

        Как получить диагональ квадратной формулы?

        Диагональ квадратной формулы можно вывести с помощью теоремы Пифагора.

        • Шаг 1: Проведите диагонали квадрата.
        • Шаг 2: Образуются два прямоугольных треугольника. Рассмотрим один из треугольников.
        • Шаг 3: Две стороны прямоугольного треугольника будут одинаковыми, так как все стороны квадрата равны.
        • Шаг 4: Примените теорему Пифагора и вычислите длину гипотенузы треугольника, являющегося диагональю квадрата.

        Таким образом, диагональ d = √(a 2 + a 2 ) = (√2)a = a√2; где «а» — сторона квадрата.

        Что такое «а» в диагонали квадратной формулы?

        Так как квадрат имеет четыре равные стороны, поэтому в формуле диагонали квадрата «а» представляет сторону квадрата. Таким образом, диагональ квадратной формулы задается как d = a√2.

        Диагональ квадрата равна его стороне?

        Нет, диагональ квадрата не равна его стороне. Поскольку все углы квадрата равны 90°, диагональ квадрата становится гипотенузой треугольников, образуемых в квадрате.

        Как найти диагональ квадрата, зная площадь?

        Если известна площадь квадрата, можно вычислить длину стороны квадрата. Затем значение длины стороны можно использовать для нахождения диагонали квадрата с помощью формулы d = a√2. Например, если площадь квадрата составляет 81 кв. Сначала найдем длину его стороны, так как мы знаем, что площадь квадрата = a 2 . Следовательно, сторона «а» = √81 = 9 единиц. Теперь мы будем использовать это значение в формуле d = a√2, d = 9√2 = 12,72 единицы.

        Как найти диагональ квадрата, если дана сторона?

        Диагональ квадрата можно вычислить, если известна сторона. Диагональ квадратной формулы = a√2; где «а» — длина стороны. Данную длину стороны подставляют в эту формулу, чтобы получить длину диагонали. Например, если длина стороны квадрата равна 10 см, мы подставим в формулу значение d = a√2. Это означает, что длина диагонали (d) = a√2 = 10√2 = 14,14 см.

        Как найти диагональ квадрата с периметром?

        Диагональ квадрата можно вычислить, если известен периметр квадрата. Давайте разберемся в этом на примере. Например, если периметр квадрата равен 32 единицам, найдем диагональ, выполнив следующие шаги:

        • Шаг 1: Мы знаем, что формула для нахождения периметра квадрата = 4 × длина стороны. После подстановки заданного значения периметра можно вычислить длину стороны квадрата. Здесь это будет Периметр квадрата = 4 × длина стороны. Это будет 32 = 4 × длина стороны. Следовательно, длина стороны будет равна 8 единицам.
        • Шаг 2: Зная длину стороны, можно вычислить диагональ квадрата по формуле Диагональ квадрата = a√2; где «а» — длина стороны. Теперь мы можем подставить это значение в формулу Диагональ квадрата = a√2 = 8 × √2 = 11,313 единиц.

        Рабочие листы по математике и визуальный учебный план

        Как найти длину диагонали прямоугольника

        Все ресурсы по базовой геометрии

        9 Диагностические тесты 164 практических теста Вопрос дня Карточки Учитесь по концепции

        ← Предыдущая 1 2 3 4 Следующая →

        Справка по базовой геометрии » Плоская геометрия » Четырехугольники » Прямоугольники » Как найти длину диагонали прямоугольника

        Длина прямоугольника 12 дюймов, а ширина 5 дюймов. Чему равна диагональ прямоугольника?

        Возможные ответы:

        Правильный ответ:

        Пояснение:

        Чтобы найти диагональ, воспользуемся теоремой Пифагора:

        где = гипотенуза

        или

        Сообщить об ошибке

        Одна сторона прямоугольника 7 дюймов, а другая 9 дюймов. Сколько сантиметров длина диагонали прямоугольника?

        Возможные ответы:

        Правильный ответ:

        Объяснение:

        Вы можете найти диагональ прямоугольника, если у вас есть ширина и высота. Диагональ равна квадратному корню из квадрата ширины плюс квадрат высоты.

        Сообщить об ошибке

        Найдите длину диагонали.

        Возможные ответы:

        Правильный ответ:

        Пояснение:

        Прямоугольник можно разрезать на два равных прямоугольных треугольника, гипотенуза которых является диагональю прямоугольника.

        Используйте теорему Пифагора, чтобы найти гипотенузу:

        , где a и b — катеты, а c — гипотенуза

         

        Сообщить об ошибке

        Стандартная школьная баскетбольная площадка имеет длину 84 фута и ширину 50 футов. Во время тренировки тренер К. заставляет Кайри бежать из одного правого угла на одном конце площадки в левый угол на другом конце площадки. С точностью до фута, сколько пробежал Кирие?

        Возможные ответы:

        Правильный ответ:

        Объяснение:

        Картинка очень помогает решить эту задачу, поэтому мы начнем с прямоугольной баскетбольной площадки.

        Заметим, что расстояние, пройденное Кирие (обозначено красным), является диагональю нашего прямоугольника, который мы назовем . Нам также не следует, что эта диагональ делит наш прямоугольник на два конгруэнтных прямоугольных треугольника. Поэтому мы можем найти длину нашей диагонали, сосредоточившись на одном из этих треугольников и определив гипотенузу. Это можно сделать с помощью теоремы Пифагора, которая дает нам:

        Извлечение квадратного корня дает нам

        Округление до ближайшего фута дает ответ 98.

        Сообщить об ошибке

        Прямоугольник имеет высоту . Какова длина его диагонали, округленная до десятых?

        Возможные ответы:

        Правильный ответ:

        Объяснение:

        1. Используйте теорему Пифагора с  и .

        Сообщить об ошибке

        Стороны прямоугольника ABCD равны 4 дюймам и 13 дюймам. 

        Какова длина диагонали прямоугольника ABCD?

        Возможные ответы:

        Правильный ответ:

        Объяснение:

        Диагональ прямоугольника делит прямоугольник на 2 прямоугольных треугольника со сторонами, равными сторонам прямоугольника, и с гипотенузой, являющейся диагональю. Все, что вам нужно сделать, это использовать теорему Пифагора:

         где a и b — стороны прямоугольника, а c — длина диагонали.

        Сообщить об ошибке

        Найдите длину диагонали прямоугольника, имеющего длину  и ширину .

        Возможные ответы:

        Правильный ответ:

        Пояснение:

        Диагональ прямоугольника также является гипотенузой прямоугольного треугольника, катетами которого являются длина и ширина прямоугольника.

        Затем мы можем использовать теорему Пифгора, чтобы найти диагональ.

        Для заданного прямоугольника

        Сообщить об ошибке

        Найдите длину диагонали прямоугольника, имеющего длину  и ширину  .

        Возможные ответы:

        Правильный ответ:

        Пояснение:

        Диагональ прямоугольника также является гипотенузой прямоугольного треугольника, катетами которого являются длина и ширина прямоугольника.

        Затем мы можем использовать теорему Пифгора, чтобы найти диагональ.

        Для заданного прямоугольника

        Сообщить об ошибке

        Найдите длину диагонали прямоугольника, имеющего длину  и ширину  .

        Возможные ответы:

        Правильный ответ:

        Пояснение:

        Диагональ прямоугольника также является гипотенузой прямоугольного треугольника, катетами которого являются длина и ширина прямоугольника.

        Затем мы можем использовать теорему Пифгора, чтобы найти диагональ.

        Для заданного прямоугольника

        Сообщить об ошибке

        Найдите длину диагонали прямоугольника, имеющего длину  и ширину  .

        Возможные ответы:

        Правильный ответ:

        Пояснение:

        Диагональ прямоугольника также является гипотенузой прямоугольного треугольника, катетами которого являются длина и ширина прямоугольника.

        Затем мы можем использовать теорему Пифгора, чтобы найти диагональ.

        Для заданного прямоугольника

        Сообщить об ошибке

        ← Предыдущий 1 2 3 4 Далее →

        Уведомление об авторских правах

        Все ресурсы по базовой геометрии

        9 Диагностические тесты 164 практических теста Вопрос дня Карточки Изучите концепцию

        Площадь прямоугольника размером 24 x 16 и геометрические свойства, такие как симметрия, периметр прямоугольника, диагонали

        Нам дано, что длина прямоугольника = 24,0 единицы, а ширина = 16,0 единицы.

        н.э. = до н.э. = 24,0 ед.

        А АВ = CD = 16,0 ед.

        Единицами могут быть любые единицы длины: дюймы, см, футы, мили, км и т. д.

        Геометрические свойства, которые мы вычислим 

        Вычислим площадь, периметр, длину диагонали, радиус описанной окружности, площадь описанной окружности и углы, образуемые диагональю со сторонами.

        Вычисление площади прямоугольника

        Площадь этого прямоугольника = длина х ширина (длина х ширина) = 24,0 х 16,0 = 384,0 кв. шт.

        Вычисление периметра прямоугольника

        Периметр этого прямоугольника = 2 * (длина + ширина) = 2 * (24,0 + 16,0) = 80,0 единиц

        Диагональ этого прямоугольника может быть вычислена с помощью теоремы Пифагора (или теоремы Пифагора).

        Треугольники ADC (или BDC) являются прямоугольными треугольниками.

        Итак, диагональ(и) можно рассматривать как гипотенузу прямоугольного треугольника. Таким образом, квадрат длины диагонали равен сумме квадратов длины и ширины.

        Длина диагоналей AC и BD =  (24,0 2 + 16,0 2 ) (1/2)

        Итак, длина диагонали = 28,84 единицы

        Вычисление радиуса и площади описанной окружности

        На самом деле у прямоугольника нет вписанной окружности, которая касается каждой стороны. Это возможно только в предельном случае, когда длина и ширина равны и это квадрат.

        Однако действительно возможно нарисовать окружность, проходящую через все 4 вершины прямоугольника. Обе диагонали являются диаметрами окружности.

        Угол в полуокружности является прямым углом: каждый из 4 углов прямоугольника становится углом полукруга, когда мы рисуем описанную окружность.

        Радиус описанной окружности = половина длины диагонали = 28,84/2 единицы = 14,42 единицы

        Площадь описанной окружности = PI x радиус окружности2 = PI * 14,42 * 14,42 = 653,45 квадратных единиц


        Симметрия и оси симметрии

        Прямоугольник имеет 2 оси симметрии: прямую, проходящую через середины сторон AB и CD, и другую прямую, проходящую через середины сторон AD и BC.

        Оба проходят через точку E. Прямоугольник также является «изогональным» по своей природе, хотя это понятие вы, возможно, изучите или столкнетесь с ним позже.


        Вычисление угла, образованного диагональю со сторонами

        Мы можем использовать немного тригонометрии, чтобы вычислить это.

        Тангенс угла CAD = Тангенс угла ACB  = ширина прямоугольника / длина прямоугольника = 16,0/24,0 = 0,67

        Угол CAD = Угол ACB = tan -1 0,67  = 0,59 радиан = 33,69градусов

        и угол BAC = угол ACD = 90 градусов — угол CAD   = 0,98 радиана = 56,31 градуса

        Примеры конгруэнтности и конгруэнтных треугольников

        Каждая диагональ делит прямоугольник на пару конгруэнтных треугольников.

        Диагональ

        BD делит прямоугольник на равные треугольники BAD и BCD.

        Доказательство:

        (a) Угол BAD = угол BCD = 90 градусов (прямой угол)

        (b) BD общая сторона обоих (гипотенуза)

        (c) BA = CD = 16,0 единиц (противоположные стороны прямоугольника равны)

        (d) AD = BC  = 24,0 единицы (противоположные стороны прямоугольника равны) 

        Используя (a) (b) и (c), два треугольника конгруэнтны, используя конгруэнтность RHS или HL (гипотенуза-катет).

        Или с использованием (c) (a) и (d) два треугольника конгруэнтны с использованием конгруэнтности SAS (сторона-угол-сторона)

        Аналогично можно доказать, что АС делит прямоугольник на два равных треугольника.

        Кроме того, две диагонали делят прямоугольник на две пары конгруэнтных треугольников

         (Треугольник AEB и треугольник CED конгруэнтны, треугольник BEC и треугольник AED конгруэнтны)

        Чтобы доказать, что треугольники AEB и треугольники CED равны:

        (a) AB = CD = 16,0 единиц (противоположные стороны прямоугольника равны)

        (б) Угол ABD = Угол CDB (AB параллелен CD, а BD — их секущая, это противоположные углы, значит, они равны)

        (c) Угол BAC = угол DCA (по той же причине, что и выше)

        (d) Угол BEA = угол CED (противоположные или вертикальные углы равны)

        Итак, мы можем доказать конгруэнтность двух треугольников с помощью ASA Congruence (используя (c) (a) (b)) 

        Или мы можем доказать конгруэнтность двух треугольников с помощью конгруэнтности AAS (используя (d)(b)(a)) 

        Аналогичным образом мы можем доказать, что треугольники BEC и AED равны.

        Геометрические свойства прямоугольников

        Помните: прямоугольник — это четырехугольник с 4 прямыми углами. Противоположные стороны равны. Все свойства, применимые к параллелограммам, применимы и к прямоугольникам.

        Квадрат можно рассматривать как частный случай прямоугольника, у которого все стороны равны.

        Каждый прямоугольник представляет собой выпуклый многоугольник и вписанный четырехугольник, диагональ которого представляет собой диаметр описанной окружности.


        Несколько примеров для иллюстрации похожих прямоугольников, преобразования размеров, коэффициента масштабирования и геометрического подобия.

        Эти учебные пособия по подобным треугольникам, масштабному коэффициенту и преобразованию размеров также могут быть полезны.

        Несколько примеров для иллюстрации подобных прямоугольников, преобразования размеров, масштабного коэффициента и геометрического подобия

        Пример:

        Пусть текущий прямоугольник (с размерами 24,0 x 16,0) будет прямоугольником A.

        Теперь рассмотрим другой прямоугольник B (размерами 12,0 x 8,0)

        Оба эти прямоугольника геометрически подобны, так как отношения длин соответствующих сторон равны.

        Длина прямоугольника A : Длина прямоугольника B = Ширина прямоугольника A : Ширина прямоугольника B

        24,0 : 12,0 = 16,0 : 8,0 = 2,0 : 1

        А отношение их площадей:

        Площадь прямоугольника A : Площадь прямоугольника B = 384,0 : 96,0  = 4,0 : 1

        Масштабный коэффициент между A:B  = длина прямоугольника A : длина прямоугольника B = 24,0 : 12,0 = 2,0

        Обратите внимание, что отношение площадей равно квадрату отношения соответствующих сторон (или масштабному коэффициенту).

        Это пример преобразования размера в 2D-фигурах: 

        , когда все стороны фигуры умножаются на отношение R , площадь новой фигуры в R 2 умножается на площадь исходной фигуры.

        Несколько примеров для иллюстрации подобных прямоугольников, преобразования размеров, масштабного коэффициента и геометрического подобия

        Пример:

        Пусть текущий прямоугольник (с размерами 24,0 x 16,0) будет прямоугольником A.

        Теперь рассмотрим другой прямоугольник B (размерами 6,0 x 4,0)

        Оба эти прямоугольника геометрически подобны, так как отношения длин соответствующих сторон равны.

        Длина прямоугольника A : Длина прямоугольника B = Ширина прямоугольника A : Ширина прямоугольника B

        24,0 : 6,0 = 16,0 : 4,0 = 4,0 : 1

        А отношение их площадей:

        Площадь прямоугольника A : Площадь прямоугольника B = 384,0 : 24,0  = 16,0 : 1

        Масштабный коэффициент между A:B  = длина прямоугольника A : длина прямоугольника B = 24,0 : 6,0 = 4,0

        Обратите внимание, что отношение площадей равно квадрату отношения соответствующих сторон (или масштабному коэффициенту).

        Это пример преобразования размера в 2D-фигурах: 

        , когда все стороны фигуры умножаются на отношение R , площадь новой фигуры в R 2 умножается на площадь исходной фигуры.

        Несколько примеров для иллюстрации подобных прямоугольников, преобразования размеров, масштабного коэффициента и геометрического подобия

        Пример:

        Пусть текущий прямоугольник (с размерами 24,0 x 16,0) будет прямоугольником A.

        Теперь рассмотрим другой прямоугольник B (размерами 3,0 x 2,0)

        Оба эти прямоугольника геометрически подобны, так как отношения длин соответствующих сторон равны.

        Длина прямоугольника A : Длина прямоугольника B = Ширина прямоугольника A : Ширина прямоугольника B

        24,0 : 3,0 = 16,0 : 2,0 = 8,0 : 1

        А отношение их площадей:

        Площадь прямоугольника A : Площадь прямоугольника B = 384,0 : 6,0  = 64,0 : 1

        Масштабный коэффициент между A:B  = длина прямоугольника A : длина прямоугольника B = 24,0 : 3,0 = 8,0

        Обратите внимание, что отношение площадей равно квадрату отношения соответствующих сторон (или масштабному коэффициенту).

        Это пример преобразования размера в 2D-фигурах: 

        если все стороны фигуры умножить на коэффициент R площадь новой фигуры равна R 2 площадь исходной фигуры.

        Еще несколько примеров:

        Геометрические свойства прямоугольника размером 25 x 16.

        Геометрические свойства прямоугольника размером 25 x 17.

        Чтобы узнать больше о геометрических особенностях и свойствах прямоугольников, формулах, связанных с измерением и т. д., вы можете найти это полезным. чтобы прочитать свойства учебника Rectangle здесь. Многие из этих концепций являются частью программы по математике для 9 и 10 классов программы GCSE в Великобритании, Common Core Standards в США, программы ICSE/CBSE/SSC в Индии. Вы можете ознакомиться с нашими бесплатными и печатными рабочими листами для Common Core и GCSE.

        Что такое диагональ? — Определение, факты и примеры

        Диагонали в геометрии

        Многоугольник определяется как плоская или плоская двумерная замкнутая форма, ограниченная прямыми сторонами. Диагональ — это отрезок, соединяющий противоположные вершины (или углы) многоугольника. Другими словами, диагональ — это отрезок, соединяющий две несмежные вершины многоугольника. Он соединяет вершины многоугольника, исключая ребра фигуры. На следующих фигурах нарисованы диагонали:

        История диагонали

        Слово «диагональ» происходит от древнегреческого слова diagonios , что означает «от угла к углу». И Евклид, и Страбон использовали его для описания линии, соединяющей две вершины прямоугольного параллелепипеда или ромба; позже он стал известен на латыни как diagonus (наклонная линия).

        Диагонали многоугольника

        Формула диагонали

        Диагонали для многоугольников всех форм и размеров могут быть изготовлены и для любой формы; есть формула для определения количества диагоналей.

        Количество диагоналей в многоугольнике с n вершинами = $\frac{n(n-3)}{2}$

        Итак, по этой формуле мы можем легко вычислить количество диагоналей в многоугольнике.

        В данной таблице показано количество диагоналей в различных многоугольниках:

        Диагонали объемных фигур

        Как и у многоугольников, у объемных фигур также есть диагонали. В зависимости от количества ребер количество и свойства диагоналей различаются для разных тел. На следующих телах проведены диагонали:

        Длина диагонали

        Длина диагоналей любой формы зависит от размеров их сторон.

        Длина диагонали квадрата

        Длину диагонали квадрата можно определить по теореме Пифагора. Диагональ квадрата делит его на два прямоугольных треугольника. Применяя теорему Пифагора, мы можем найти длину диагонали (d) квадрата со стороной (a) как a$\sqrt{2}$.

        Длина диагонали квадрата с каждой стороной a единиц = a$\sqrt{2}$ единиц 9{2}}$, где d — диагональ, l — длина, а b — ширина прямоугольника.

        Решенные примеры

        1. Каково общее количество диагоналей в многоугольнике с 12 сторонами?

        Решение:

        Количество диагоналей в многоугольнике с n вершинами = $\frac{n(n-3)}{2}$

        Следовательно, количество диагоналей в многоугольнике с 12 сторонами = $\frac{12(12-3)}{2}$ = 54

        1. Какова длина диагонали квадрата со стороной 6 см?

        Решение:

        Сторона, A = 6 см

        Длина диагонала = a $ \ times \ sqrt {2} $

        = 6 $ \ times \ sqrt {2} $ 9000 39666 = 6 $ \ times \ sqrt {2} $

        66 = 6 $ \ times \ sqrt {2} $

        66 = 6 $ \ times \ sqrt {2} $

        66 = 6 $ \ sqrt {2} $

        6 = 6 $ \ times \ sqrt {2} $

        6 = 6 $ \ times \ sqrt {2} $

        6 = 6 $ \ sqrt $\sqrt{2}$ см

        1. Рахул прогуливается по прямоугольному парку длиной 20 и шириной 15 метров. Определить диагональ прямоугольного парка.

        Решение:

        Длина прямоугольного парка = 20 м, Ширина прямоугольного парка = 15 м 9{2}}$

                                                   = $\sqrt{400 + 225}$

                                              = $\sqrt{625}$

                                                   = 25 m

        Practice Problems

        5

        6

        8

        9

        Правильный ответ: 9
        Количество диагоналей в шестиугольнике (6 вершин) = $\frac{6(6-3)}{2}$ = 9

        $\sqrt{10}$ см

        2$\sqrt{ 10}$ см

        10 см

        20 см 9{2}}$ = $\sqrt{4+36}$ = $\sqrt{40}$ = $2\sqrt{10}$ см

        6 см

        24 см

        3$\sqrt{2}$ см

        24$\sqrt{2}$ см

        Правильный ответ: 24 см
        Диагональ квадрата со стороной a равна a$\sqrt{2}$ . Поскольку a$\sqrt{2}$ = 6$\sqrt{2}$, a должно быть 6 см.
        Следовательно, периметр квадрата должен быть 4 × 6 см или 24 см.

        Nano2 степень окисления: 2. В каком из перечисленных соединений степень окисления азота равна +4: А) NO; Б) NaNO3;…

        alexxlab / / Разное

        Помощь студентам в учёбе от Людмилы Фирмаль

        Здравствуйте!

        Я, Людмила Анатольевна Фирмаль, бывший преподаватель математического факультета Дальневосточного государственного физико-технического института со стажем работы более 17 лет. На данный момент занимаюсь онлайн обучением и помощью по любыми предметам. У меня своя команда грамотных, сильных бывших преподавателей ВУЗов. Мы справимся с любой поставленной перед нами работой технического и гуманитарного плана. И не важно: она по объёму на две формулы или огромная сложно структурированная на 125 страниц! Нам по силам всё, поэтому не стесняйтесь, присылайте.

        Срок выполнения разный: возможно онлайн (сразу пишите и сразу помогаю), а если у Вас что-то сложное – то от двух до пяти дней.

        Для качественного оформления работы обязательно нужны методические указания и, желательно, лекции. Также я провожу онлайн-занятия и занятия в аудитории для студентов, чтобы дать им более качественные знания.

        Моё видео:

        Вам нужно написать сообщение в Telegram . После этого я оценю Ваш заказ и укажу срок выполнения. Если условия Вас устроят, Вы оплатите, и преподаватель, который ответственен за заказ, начнёт выполнение и в согласованный срок или, возможно, раньше срока Вы получите файл заказа в личные сообщения.

        Сколько может стоить заказ?

        Стоимость заказа зависит от задания и требований Вашего учебного заведения. На цену влияют: сложность, количество заданий и срок выполнения. Поэтому для оценки стоимости заказа максимально качественно сфотографируйте или пришлите файл задания, при необходимости загружайте поясняющие фотографии лекций, файлы методичек, указывайте свой вариант.

        Какой срок выполнения заказа?

        Минимальный срок выполнения заказа составляет 2-4 дня, но помните, срочные задания оцениваются дороже.

        Как оплатить заказ?

        Сначала пришлите задание, я оценю, после вышлю Вам форму оплаты, в которой можно оплатить с баланса мобильного телефона, картой Visa и MasterCard, apple pay, google pay.

        Какие гарантии и вы исправляете ошибки?

        В течение 1 года с момента получения Вами заказа действует гарантия. В течении 1 года я и моя команда исправим любые ошибки в заказе.

        Качественно сфотографируйте задание, или если у вас файлы, то прикрепите методички, лекции, примеры решения, и в сообщении напишите дополнительные пояснения, для того, чтобы я сразу поняла, что требуется и не уточняла у вас. Присланное качественное задание моментально изучается и оценивается.

        Теперь напишите мне в Telegram или почту и прикрепите задания, методички и лекции с примерами решения, и укажите сроки выполнения. Я и моя команда изучим внимательно задание и сообщим цену.

        Если цена Вас устроит, то я вышлю Вам форму оплаты, в которой можно оплатить с баланса мобильного телефона, картой Visa и MasterCard, apple pay, google pay.

        Мы приступим к выполнению, соблюдая указанные сроки и требования. 80% заказов сдаются раньше срока.

        После выполнения отправлю Вам заказ в чат, если у Вас будут вопросы по заказу – подробно объясню. Гарантия 1 год. В течении 1 года я и моя команда исправим любые ошибки в заказе.
















        Можете смело обращаться к нам, мы вас не подведем. Ошибки бывают у всех, мы готовы дорабатывать бесплатно и в сжатые сроки, а если у вас появятся вопросы, готовы на них ответить.

        В заключение хочу сказать: если Вы выберете меня для помощи на учебно-образовательном пути, у вас останутся только приятные впечатления от работы и от полученного результата!

        Жду ваших заказов!

        С уважением

        Пользовательское соглашение

        Политика конфиденциальности


        Степень окисления n в nh5cl. Задания ЕГЭ химия: Электроотрицательность

        Электроотрицательность. Степень окисления и валентность химических элементов.

        Реакции окислительно-восстановительные.

        1) Установите соответствие между схемой изменения степени окисления элемента и уравнением реакции, в которой это изменение происходит.

        3) Установите соответствие между уравнением окислительно-восстановительной реакции и свойством азота, которое он проявляет в этой реакции.

        4) Установите соответствие между формулой вещества и степенью окисления хлора в нем.

        6) Установите соответствие между свойствами азота и уравнением окислительно-восстановительной реакции, в которой он проявляет в эти свойства.

        7) Установите соответствие между формулой вещества и степенью окисления азота в нем.

        ФОРМУЛА ВЕЩЕСТВА
        А) NaNO 2        		СТЕПЕНЬ ОКИСЛЕНИЯ АЗОТА
        1) +5
        2) +3
        3) –3, +5
        4) 0, +2
        5) –3, +3
        6) +4, +2

        8) Установите соответствие между схемой реакции и изменением степени окисления окислителя в ней.

        10. Установите соответствие между формулой соли и степенью окисления хрома в ней.

        12. Установите соответствие между схемой реакции и формулой восстановителя в ней

        14. Установите соответствие между формулой вещества и степенью окисления азота в нем.

        16. Установите соответствие между формулой соли и степенью окисления хрома в ней.

        18. Установите соответствие между схемой реакции и формулой восстановителя в ней

        19. Установите соответствие между схемой реакции и изменением степени окисления восстановителя.

        СХЕМА РЕАКЦИИ

        А) Cl 2 + P → PCl 5

        Б) HCl+ KMnO 4 → Cl 2 + MnCl 2 + KCl + H 2 O

        В) HClO + H 2 O 2 → O 2 + H 2 O + HCl

        Г) Cl 2 + KOH → KCl + KClO 3 + H 2 O

        		ИЗМЕНЕНИЕ СО ВОССТАНОВИТЕЛЯ
        1) Cl 0 → Cl -1

        2) Cl -1 →Cl 0

        3) Cl 0 → Cl +1

        		5) Cl 0 → Cl +5

        6) Mn +7 → Mn +2

        20. Установите соответствие между схемой реакции и изменением степени окисления окислителя.

        СХЕМА РЕАКЦИИ

        А) Na 2 SO 3 + I 2 +NaOH → Na 2 SO 4 + NaI + H 2 O

        Б) I 2 + H 2 S → S + HI

        В) SO 2 + NaIO 3 + H 2 O → H 2 SO 4 + NaI

        Г) H 2 S + SO 2 → S + H 2 O

        		ИЗМЕНЕНИЕ СО ОКИСЛИТЕЛЯ
        1) S -2 → S 0

        3) S +4 → S +6

        		 5) I +5 → I -1

        21. Установите соответствие между схемой реакции и изменением степени окисления восстановителя.

        23. Установите соответствие между формулой вещества и степенью окисления хрома в нем.

        25. Установите соответствие между схемой реакции и изменением степени окисления восстановителя.

        27. Установите соответствие между схемой реакции и изменением степени окисления окислителя.

        ОПРЕДЕЛЕНИЕ

        Хлорид аммония (нашатырь) в обычных условиях представляет собой белые кристаллы (рис. 1).

        Летуч, термически мало устойчив (температура плавления — 400 o С при давлении). Брутто-формула — NH 4 Cl. Молярная масса хлорида аммония равна 53,49 г/моль.

        Рис. 1. Хлорид аммония. Внешний вид.

        Хорошо растворяется в воде (гидролизуется по катиону). Кристаллогидратов не образует. Разлагается концентрированной серной кислотой и щелочами.

        Nh5Cl, степени окисления элементов в нем

        Чтобы определить степени окисления элементов, входящих в состав хлорида аммония, сначала необходимо разобраться с тем, для каких элементов эта величина точно известна.

        Степень окисления кислотного остатка определяется числом атомов водорода, входящих в состав образующей его кислоты, указанных со знаком минус. Хлорид-ион — это кислотный остаток хлороводородной (соляной) кислоты, формула которой HCl. В её составе имеется один атом водорода, следовательно, степень окисления хлора в хлорид ионе равна (-1).

        Ион-аммония является производным аммиака (NH 3), представляющим собой гидрид. А, как известно, степень окисления водорода в гидридах всегда равна (+1). Для нахождения степени окисления азота примем её значение за «х» и определим его при помощи уравнения электронейтральности:

        x + 4× (+1) + (-1) = 0;

        x + 4 — 1 = 0;

        Значит степень окисления азота в хлориде аммония равна (-3):

        N -3 H +1 4 Cl -1 .

        Примеры решения задач

        ПРИМЕР 1

        ЗаданиеОпределите степени окисления азота в следующих соединениях: а) NH 3 ; б) Li 3 N; в) NO 2 .
        Ответа) Аммиак представляет собой гидрид азота, а, как известно, в данных соединениях водород проявляет степень окисления (+1). Для нахождения степени окисления азота примем её значение за «х» и определим его при помощи уравнения электронейтральности:

        x + 3× (+1) = 0;

        Степень окисления азота в аммиаке равна (-3): N -3 H 3 .

        б) Литий проявляет постоянную степень окисления, совпадающую с номером группы в Периодической системе Д.И. Менделеева, в которой он расположен, т.е. равна (+1) (литий — металл). Для нахождения степени окисления азота примем её значение за «х» и определим его при помощи уравнения электронейтральности:

        3× (+1) + х = 0;

        Степень окисления азота в нитриде лития равна (-3): Li 3 N -3 .

        в)Степень окисления кислорода в составе оксидов всегда равна (-2). Для нахождения степени окисления азота примем её значение за «х» и определим его при помощи уравнения электронейтральности:

        x + 2×(-2) = 0;

        Степень окисления азота в диоксиде азота равна (+4): N +4 O 2 .

        ПРИМЕР 2

        ЗаданиеОпределите степени окисления азота в следующих соединениях: а) N 2 ; б) HNO 3 ; в) Ba(NO 2) 2 .
        Ответа)В соединениях с неполярными связями степень окисления элементов равна нулю. Это означает, что степень окисления азота в его двухатомной молекуле равна нулю: N 0 2 .

        б) Степени окисления водорода и кислорода в составе неорганических кислот всегда равны (+1) и (-2) соответственно. Для нахождения степени окисления азота примем её значение за «х» и определим его при помощи уравнения электронейтральности:

        (+1) + х + 3×(-2) = 0;

        1 + х — 6 = 0;

        Степень окисления азота в азотной кислоте равна (+5): HN +5 O 3 .

        в)Барий проявляет постоянную степень окисления, совпадающую с номером группы в Периодической системе Д.И. Менделеева, в которой он расположен, т.е. равна (+2) (барий — металл). Степень окисления кислорода в составе неорганических кислот и их остатков всегда равна (-2). Для нахождения степени окисления азота примем её значение за «х» и определим его при помощи уравнения электронейтральности:

        (+2) + 2×х + 4×(-2) = 0;

        2 + 2х — 8 = 0;

        Степень окисления азота в нитрите бария равна (+3):Ba(N +3 O 2) 2 .

        Обязательный минимум знаний

        Степень окисления

        Закономерности изменения электроотрицательности в периодах и группах Периодической системы рассматривались в § 36.

        Правила для расчёта степени окисления (с. о.) химических элементов:

        1. Наименее электроотрицательным является химический элемент
          1. железо
          2. магний
          3. кальций

          Следует обратить внимание на словосочетание «наименее электроотрицательный», т. е. элемент с наибольшими металлическими свойствами. Этот аргумент позволит исключить из возможных ответов азот, как неметалл, и остановиться на кальции, как наиболее активном из предложенных в задании металлов. Ответ: 4.

        2. Наиболее полярна химическая связь в одной из молекул
          1. ССl 4
          2. СВr 4

          Знание закономерностей изменения электроотрицательности в периодах и группах Периодической системы Д. И. Менделеева позволяет исключить из списка четырёхвалентных соединений углерода метан СН 4 , а из оставшихся галогенидов остановиться на CF 4 , как на соединении углерода с наиболее электроотрицательным из всех химических элементов — фтором. Ответ: 2.

        3. В молекулах хлороводорода и хлора химическая связь соответственно
          1. ионная и ковалентная полярная
          2. ионная и ковалентная неполярная
          3. ковалентная полярная и ковалентная неполярная
          4. водородная и ковалентная неполярная

          Ключевым словом для быстрого и верного выполнения этого задания является слово «соответственно». В предложенных вариантах только один из ответов начинается со слов «ковалентная полярная», т. е. связи, характерной для хлороводорода. Ответ: 3.

        4. Степень окисления марганца в соединении, формула которого К 2 МnO 4 , равна

          Знание правил расчёта степеней окисления элементов по формуле позволит выбрать верный ответ. Ответ: 3.

        5. Наименьшую степень окисления имеет сера в соли
          1. сульфат калия
          2. сульфит калия
          3. сульфид калия
          4. гидросульфат калия

          Очевидно, быстрому выполнению этого задания будет способствовать перевод названий солей в формулы. Так как сера — элемент VIA группы, то её наименьшая степень окисления равна -2. Этому значению соответствует соединение с формулой K 2 S — сульфид калия. Ответ: 3.

        6. Степень окисления +5 атом хлора имеет в ионе
          1. С1O — 4
          2. С1O —
          3. С1O — 3
          4. С1O — 2

          При выполнении этого задания следует обратить внимание на то, что в условии даны не электронейтральные соединения, а ионы хлора с единичным отрицательным зарядом («-»). Поскольку сумма степеней окисления атомов в ионе равна заряду иона, суммарный отрицательный заряд атомов кислорода в искомом ионе должен иметь значение -6 (+5 — 6 = -1). Ответ: 3.

        7. Степень окисления -3 азот имеет в каждом из двух соединений
          1. NF 3 И NH 3
          2. NH 4 Cl и N 2 O 3
          3. NH 4 Cl и NH 3
          4. HNO 2 и NF 3

          Для определения верного ответа необходимо мысленно разделить варианты ответов на левый и правый подстолбики. Затем выбрать тот, в котором соединения имеют более простой состав, — в нашем случае это правый подстолбик бинарных соединений. Анализ позволит исключить ответы 2 и 4, так как в оксиде и фториде у азота положительная степень окисления, как у менее электроотрицательного элемента. Этот аргумент позволяет исключить и ответ 1, так как в нём первое вещество — всё тот же фторид азота. Ответ: 3.

        8. К веществам молекулярного строения не относятся
          1. углекислый газ
          2. метан
          3. хлороводород
          4. карбонат кальция

          Следует обратить внимание на отрицательное суждение, заложенное в условии задания. Так как газообразные при обычных условиях вещества имеют в твёрдом состоянии молекулярную кристаллическую решётку, то условию задания не отвечают варианты 1-3. Отнесение карбоната кальция к солям ещё раз подтвердит верный ответ. Ответ: 4.

        9. Верны ли следующие суждения о свойствах веществ и их строении?

          А. Мокрое бельё высыхает на морозе потому, что вещества молекулярного строения способны к сублимации (возгонке).

          Б. Мокрое бельё высыхает на морозе потому, что молекулы воды имеют низкую молекулярную массу.

          1. верно только А
          2. верно только Б
          3. верны оба суждения
          4. оба суждения не верны

          Знание физических свойств веществ молекулярного строения позволяет решить, что причиной высыхания мокрого белья на морозе является способность льда к сублимации, а не дипольное строение молекул воды. Ответ: 1.

        10. Молекулярное строение имеет каждое из веществ, формулы которых приведены в ряду
          1. СO 2 , HNO 3 , СаО
          2. Na 2 S, Br 2 , NO 2
          3. H 2 SO 4 , Сu, O 3
          4. SO 2 , I 2 , НСl

          Так как предложенные варианты содержат по три вещества, логично мысленно разделить эти варианты на три вертикальных подстолбика. Анализ каждого из них, начиная с веществ более простого состава (средний подстолбик), позволит исключить ответ 3, так как в нём содержится металл медь, имеющий металлическую кристаллическую решётку. Аналогичный анализ правого подстолбика позволит исключить ответ 1, так как он содержит оксид щёлочноземельного металла (ионная решётка). Из двух оставшихся вариантов необходимо исключить вариант 2, так как он содержит соль щелочного металла — сульфид натрия (ионная решётка). Ответ: 4.

        Задания для самостоятельной работы

        1. Степень окисления +5 азот проявляет в соединении, формула которого
          1. N 2 O 5
          2. N 2 O 4
          3. N 2 O
        2. Степень окисления хрома в соединении, формула которого (NH 4) 2 Cr 2 O 7 , равна
        3. Степень окисления азота уменьшается в ряду веществ, формулы которых
          1. NH 3 , NO 2 , KNO 3
          2. N 2 O 4 , KNO 2 , NH 4 Cl
          3. N 2 , N 2 O,NH 3
          4. HNO 3 , HNO 2 , NO 2
        4. Степень окисления хлора увеличивается в ряду веществ, формулы которых
          1. НСlO, НСlO 4 , КСlO 3
          2. Сl 2 , С1 2 O 7 , КСlO 3
          3. Са(С1O) 2 , КСlO 3 , НСlO 4
          4. КСl, КСlO 3 , КСlO
        5. Наиболее полярна химическая связь в молекуле
          1. аммиака
          2. сероводорода
          3. бромоводорода
          4. фтороводорода
        6. Вещество с ковалентной неполярной связью
          1. белый фосфор
          2. фосфид алюминия
          3. хлорид фосфора (V)
          4. фосфат кальция
        7. Формулы веществ только с ионной связью записаны в ряду
          1. хлорид натрия, хлорид фосфора (V), фосфат натрия
          2. оксид натрия, гидроксид натрия, пероксид натрия
          3. сероуглерод, карбид кальция, оксид кальция
          4. фторид кальция, оксид кальция, хлорид кальция
        8. Атомную кристаллическую решётку имеет
          1. оксид натрия
          2. оксид кальция
          3. оксид серы (IV)
          4. оксид алюминия
        9. Соединение с ионной кристаллической решёткой образуется при взаимодействии хлора с
          1. фосфором
          2. барием
          3. водородом
          4. серой
        10. Верны ли следующие суждения о хлориде аммония?

          А. Хлорид аммония — вещество ионного строения, образованное за счёт ковалентной полярной и ионной связей.

          Б. Хлорид аммония — вещество ионного строения, а потому твёрдое, тугоплавкое и нелетучее.

          1. верно только А
          2. верно только Б
          3. верны оба суждения
          4. оба суждения неверны

        Поделиться с друзьями:

        Интерактивный тест по химии Степень окисления. (9 -11 класс) доклад, проект

        • Главная
        • Разное
        • Образование
        • Спорт
        • Естествознание
        • Природоведение
        • Религиоведение
        • Французский язык
        • Черчение
        • Английский язык
        • Астрономия
        • Алгебра
        • Биология
        • География
        • Геометрия
        • Детские презентации
        • Информатика
        • История
        • Литература
        • Математика
        • Музыка
        • МХК
        • Немецкий язык
        • ОБЖ
        • Обществознание
        • Окружающий мир
        • Педагогика
        • Русский язык
        • Технология
        • Физика
        • Философия
        • Химия
        • Шаблоны, фоны, картинки для презентаций
        • Экология
        • Экономика

        Презентация на тему Интерактивный тест по химии Степень окисления. (9 -11 класс), предмет презентации: Химия. Этот материал в формате pptx (PowerPoint) содержит 23 слайдов, для просмотра воспользуйтесь проигрывателем. Презентацию на заданную тему можно скачать внизу страницы, поделившись ссылкой в социальных сетях! Презентации взяты из открытого доступа или загружены их авторами, администрация сайта не отвечает за достоверность информации в них, все права принадлежат авторам презентаций и могут быть удалены по их требованию.

        Слайд 1
        Текст слайда:

        Степень окисления.

        Тест по химии

        Готовимся к ЕГЭ.

        Слайд 2
        Текст слайда:

        Аннотация

        Ресурс по химии адресован учащихся 9,11-классов для организации самостоятельной работы в период подготовки к итоговой аттестации, а также для текущей проверки знаний учащихся в форме тестирования.
        Ресурс содержит 20 вопросов на выбор одного правильного ответа из нескольких по теме: «Степень окисления». Если дан правильный ответ, то кнопка выбора ответа окрашивается в зелёный цвет. Если ответ неправильный, то кнопка выбора ответа окрашивается в красный цвет. При каждом ответе появляется соответствующая анимация.

        Слайд 3
        Текст слайда:

        Cl2 O7, HClO4, KClO4


        Cl2, PCl5, HCl

        HCl, NaCl, Cl2

        HCl, HClO, HClO4

        В каком ряду степень окисления хлора не изменяется?

        Вопрос 1.

        Слайд 4
        Текст слайда:

        HNO3, NaNO3, NaNO2


        Nh4, NO, NO2

        NO2, HNO2, HNO3

        Mg3N2, Nh4, Nh5Cl

        В каком ряду степень окисления азота не изменяется?

        Вопрос 2.

        Слайд 5
        Текст слайда:

        Ca3(PO4)2, P, P2O5


        HPO3, h4PO4, Na3PO4

        P, PCl3, h4PO3

        Ph4, h4PO3, h4PO4

        В каком ряду степень окисления фосфора не изменяется?

        Вопрос 3.

        Слайд 6
        Текст слайда:

        Cl2, KClO3, KClO4


        Cl2, PCl5, HCl

        Cl2O7, HClO, HClO4

        HCl, KCl, AgCl

        В каком ряду степень окисления хлора увеличивается?

        Вопрос 4.

        Слайд 7
        Текст слайда:

        h3S, Na2S, S


        SO2, SO3, h3SO4

        h3SO4, SO2, S

        h3S, h3SO3, h3SO4

        В каком ряду степень окисления серы уменьшается?

        Вопрос 5.

        Слайд 8
        Текст слайда:

        Nh4, N2, Mg3N2


        HNO3, NO2, NO

        Nh4, NO, NO2

        NO2, HNO2, HNO3

        В каком ряду степень окисления азота уменьшается?

        Вопрос 6.

        Слайд 9
        Текст слайда:

        Ca3(PO4)2, P, P2O5


        P2O5,h4PO4,Ca3(PO4)2

        PCl5, PCl3, h4PO3

        Рh4, h4PO3, h4PO4

        В каком ряду степень окисления фосфора увеличивается?

        Вопрос 7.

        Слайд 10
        Текст слайда:

        PCl3, PCl5


        Ca3(PO4)2, P4O10

        Ca3P2, Ca3(PO4)2

        Р4O6, Ph4

        Одну и ту же степень окисления фосфор имеет в каждом из двух соединений?

        Вопрос 8.

        Слайд 11
        Текст слайда:

        Na2S


        SO3

        h3SO4

        CaSO3

        В каком соединении атом серы имеет минимальную возможную степень окисления?

        Вопрос 9.

        Слайд 12
        Текст слайда:

        Mn2(SO4)3


        MnS

        MnO2

        KMnO4

        В каком соединении атом марганца имеет максимальную возможную степень окисления?

        Вопрос 10.

        Слайд 13
        Текст слайда:

        Cu(NO3)2


        NO

        N2O

        Li3N

        В каком соединении атом азота имеет минимальную возможную степень окисления?

        Вопрос 11.

        Слайд 14
        Текст слайда:

        KClO4


        KClO3

        AlCl3

        Cl2O

        В каком соединении атом хлора имеет минимальную возможную степень окисления?

        Вопрос 12.

        Слайд 15
        Текст слайда:

        Nh4


        LiH

        HCl

        h3

        В каком соединении атом водорода имеет отрицательную степень окисления?

        Вопрос 13.

        Слайд 16
        Текст слайда:

        CF4


        CO2

        Ch5

        C60

        В каком веществе элемент углерод имеет отрицательную степень окисления?

        Вопрос 14.

        Слайд 17
        Текст слайда:

        железо


        натрий

        хлор

        фтор

        Какой элемент может проявлять в соединениях как положительную, так и отрицательную степень окисления?

        Вопрос 15.

        Слайд 18
        Текст слайда:

        магний


        азот

        кислород

        фтор

        Какой элемент может проявлять в соединениях только положительную степень окисления?

        Вопрос 16.

        Слайд 19
        Текст слайда:

        Fe2(SO4)3 K2SO4 CaSO4

        h3S Na2S MnS

        Na2SO3 BaSO3 SO2

        h3S SO2 SO3

        Укажите схему превращений, в которой степень окисления серы изменяется:

        Вопрос 17.

        Слайд 20
        Текст слайда:

        Li3N Nh4 NO

        N2O5 HNO3 Ba(NO3)2

        HNO3 Ba(NO3)2 NO2

        Nh4 NO NO2

        Укажите схему превращений, в которой степень окисления азота не изменяется:

        Вопрос 18.

        Слайд 21
        Текст слайда:

        +4, 0

        +5, 0

        +4, -3

        +5, -3

        Определите высшую и низшую степень окисления азота в соединениях.

        Вопрос 19.

        Слайд 22
        Текст слайда:

        +6, 0

        0, -2

        +6, -2

        +2, -2

        Определите высшую и низшую степень окисления кислорода в соединениях.

        Вопрос 20.

        Слайд 23
        Текст слайда:

        Список использованных ресурсов:

        А.А. Дроздов, В.В. Еремин «Пособие для подготовки к ЕГЭ по химии». — М. : БИНОМ. Лаборатория знаний, 2010.
        http://smayli. ru/data/smiles/emocii-2154.gif
        http://smayli.ru/data/smiles/emocii-2198.gif
        http://smayli.ru/data/smiles/emocii-2035.gif
        http://www.smayli.ru/data/smiles/emocii-1634.gif

        Скачать презентацию

        Что такое shareslide.ru?

        Это сайт презентаций, где можно хранить и обмениваться своими презентациями, докладами, проектами, шаблонами в формате PowerPoint с другими пользователями. Мы помогаем школьникам, студентам, учителям, преподавателям хранить и обмениваться учебными материалами.

        Для правообладателей

        Обратная связь

        Email: Нажмите что бы посмотреть 

        Степень окисления

        Дидактический материал

        Тренировочные тесты ЕГЭ по химии

        Электроотрицательность. Степень окисления и валентность химических элементов.

        1. Электроотрицательность  атома – это

        1) отрицательный заряд атома в молекуле

        2) способность атома переходить в возбужденное состояние

        3) способность атома, участвующего в химической связи, смещать к себе электронную пару, участвующую в образовании химической связи

        4) потенциал ионизации атома

         

        2. Элементы расположены в порядке возрастания электроотрицательности в ряду

        1) O, H, Br, Te

        2) C, I, B, P

        3) Sn, Se, Br, F

        4) H, Br, C, B

         

        3. Степень окисления атома – это

        1) условный заряд, вычисленный из предположения, что все полярные ковалентные связи являются ионными

        2) число отданных в ходе химической реакции электронов

        3) отрицательный заряд, сосредоточенный на какой-либо части молекулы

        4) заряд иона в нерастворимом веществе

         

        4. Степень окисления элемента в простом веществе равна

        1) нулю

        2) числу электронов во внешнем электронном слое

        3) числу неспаренных электронов

        4) номеру группы

        5. Высшую степень окисления марганец проявляет в соединении

        1) КМnО4           2) МnО2              3) К2MnО4         4) MnSO4

         

        6. Наибольшую степень окисления марганец проявляет в соединении
        1) МпС12             2) МnО               3) К2МnО4          4) МnСO3

        7. Наибольшую степень окисления марганец имеет в соединении

        1) MnSO4    2) МnО2              3) К2МnО4           4) Мn2Оз

         

        8. Степень окисления  — 3 фосфор проявляет в соединении

        1) РН3         2) Р2Оз                3) NaH2PO4         4) Н3РО4

         

        9. Наименьшую степень окисления сера проявляет в соединении

        1) Na2S                  2) Na2SO3            3) Na2SO4           4) SO3

         

        10. Степень окисления  — 3 фосфор проявляет в соединении

        1) РН3                 2) Р2Оз                3) NaH2PO4       4) НзРО4

         

        11. Наибольшую степень окисления сера проявляет в соединении

        I )  Na2S              2) Na2SO3           3) Na2SO4           4) SO2

         

        12. Одинаковую степень окисления азот проявляет в веществах, указанных в РЯДУ:

        1) N2O5, HNO3, NaNO3

        2) NО2,  HNO3, KNO3

        3) NO, NO2, N2O3

        4) HNO3,HNO2,NO2

        13. В порядке увеличения электроотрицательности элементы расположены в ряду:

        1) O-N-C-B

        2) Si-Ge-Sn-Pb

        3) Li-Na-K-Rb

        4) Sb-P-S-Cl

         

        14. Степень окисления азота увеличивается в ряду веществ:

        1) NH3,NO,HNO3

        2) NO,NO2,NH3

        3) NH3,HNO3,NO2

        4) KNO3, KNO2, NO2

         

        15.  Электроотрицательность химических элементов увеличивается в ряду:

        1) Be,Mg,Ca

        2) F,Cl,Br

        3) P,S,C1

        4) Cl.S.P

         

        16. В порядке возрастания относительной электроотрицательности элементы расположены в ряду:

        1) Na, Mg,Al                         2) N,P,As           3) O,N,C             4) Cl, Br, I

         

        17. Из перечисленных элементов наиболее электроотрицательным является
        1) азот                2) кислород       3) хлор            4) фтор

         

        18. Степень окисления хлора в Са(С1О)2 равна

        1)+1                    2) +3                    3) +5                    4) +7

         

        19. Степень окисления хлора в Ва(СlOз)2 равна

        1) + 1                     2) + 3                     3) +5                     4) + 7

         

        20. Минимальную степень окисления хлор проявляет в соединении

        1) NH4Cl              2) Сl2                    3)  Ca(OCl)2          4} NaCIO

         

        21. Степень окисления   + 3 азот проявляет в каждом из двух соединений:

        1)   HNO2 и NH3

        2)   NH4C1 и N203

        3)   NaNO2 и NF3

        4)   HNO3 и N2

         

        22. В каком соединении степень окисления серы равна +4?

        1) H2SO4                2) FeS                    3) H2SO3                4)  SO3

         

        23. Наиболее электроотрицательным элементом является

        1)  кремний

        2)  свинец

        3)  олово

        4)  углерод

         

        24. Азот проявляет степень окисления +3 в каждом соединении, указанном в ряду:

        1)   N203, HNO2, NH3

        2)   NH4C1, N20, NF3

        3)   HNO2,N2H4,N2

        4)   NaNO2, NF3, N2O3

         

        25. Наиболее электроотрицательным элементом является

        I) кремний             2) азот                   3)  фосфор              4) селен

         

        26. В порядке возрастания электроотрицательности элементы расположены в ряду

        1) H-Se-S-O-F

        2) F-O-C1-S-H

        3) H-CI-S-O-F

        4) H-S-C1-F-O

         

        27. Хлор проявляет положительную степень окисления в соединении с

        1)  серой

        2)  водородом

        3)   кислородом

        4)  железом

         

        28. Степень окисления + 3 азот проявляет в соединении

        1) NН4С1                2) NaNO3               3) N2O4                  4) KNO2

         

        29. Степень окисления  + 3 хром имеет в соединении

        1) СrО                   2) Сr2О3                 3) СrО3                  4) Н2СrО4

         

        30. Степень окисления азота в сульфате аммония равна

        1) — 3                     2) — 1                     3)  + 1                     4) + 3

         

        Ответы: 1-3, 2-3, 3-1, 4-1, 5-1, 6-3, 7-3, 8-1, 9-1, 10-1, 11-3, 12-1, 13-4, 14-1, 15-3, 16-1, 17-4, 18-1, 19-3, 20-1, 21-3, 22-3, 23-4, 24-4, 25-2, 26-1, 27-3, 28-4, 29-2, 30-1

        Контрольная работа по теме «Многообразие химических реакций»

        Контрольная работа № 1.

        по теме «Многообразие химических реакций».

        Вариант 1

        Часть 1

        I. Тест.

        1. К электролитам относится:

        а) АgCl  б) BaCl2 в) BaО г) О2

        2. В каком из соединений степень окисления азота +3

        а) NaNO2  б) NaNO3 в) N2О г) N2О5

        3. При диссоциации Na2SO4 образуются ионы:

        а) Na+ и SO42-  б) 2Na+ и SO42- в) 2Na+ и 4SO2-  г) Na+ и 4SO-

        4. Скорость реакции, уравнение которой N2+3H2=2NH3, увеличится при

        а) увеличении концентрации аммиака

        б) понижение температуры

        в) уменьшении концентрации аммиака

        г) увеличении концентрации водорода

        5. Равновесие реакции сместится в сторону прямой реакции СО(г)+Н2О(г) ↔ CO2(г)+Н2(г)+Q

        а) при повышении температуры

        б) при понижении температуры

        в) при увеличении концентрации СО2

        г) при увеличении давления.

        6. Выберите все верные высказывания относительно реакции

        CaCO3 (тв ) ↔ CaO(тв ) + CO2 (г ) -157 кДж

        а) реакция разложения б) реакция соединения в) эндотермическая

        г) экзотермическая д) окислительно-восстановительная ж) обратимая

        7. Признаками реакции между сульфатом натрия и хлоридом бария является:

        а) выделение газа; б) образование белого осадка; в) образование желтого осадка;

        в) воды

        8.Составьте уравнения разложения на ионы для данных веществ. Для многоосновной кислоты составьте уравнение полной и ступенчатой диссоциации:

        а) HNO3→_______________________ г) h3SO4→____________________(полная)

        б)K3PO4→_______________________ ____________________________(1 ступень)

        в) Ba(OH)2→_____________________ ___________________________(2 ступень)

        9.Допишите число электронов, принимающих участие в данных процессах. Укажите, какие из процессов являются окислением, а какие восстановлением.

        Схема

        Процесс (окисление или восстановление)

        h30______________→2H+

        		 

        Mn+7____________→Mn+2

        		 

        N-3______________→N+5

        		 

        Ca+2____________→Ca0

        		 

        Часть 2.

        10.Установите соответствие между схемой окислительно-восстанови​тель​ной ре​ак​ции и ве​ществом-окис​ли​те​лем в ней.

        11. Закончите уравнения реакций. Составьте для них полные и сокращенные ионные уравнения:

        а) HNO3+Ba(OH)2→ б) NaOH+FeCl3→ в) Na2CO3+HCl→

        Часть 3

        12.Используя метод электронного баланса, составьте уравнение ре​ак​ции::

        P+HNO3+h3O→h4PO4+NO

        Опре​де​ли​те окис​ли​тель и вос​ста​но​ви​тель.

        13. Составить уравнение в молекулярной форме, которое бы соответствовало следующему уравнению в ионной форме:

        H++OH-→h3O

        14. В ре­зуль­та­те реакции, тер­мо­хи­ми­че­ское урав­не­ние которой

         

         

        выделилось 968 кДж теплоты. Вы­чис­ли­те массу об­ра­зо­вав­шей­ся при этом воды. Ответ ука­жи­те в грам­мах с точ­но­стью до целых.


         

        Контрольная работа № 1.

        по теме «Многообразие химических реакций».

        Вариант 2

        I. Тест

        1. К неэлектролитам относится

        а) h3O  б) HNO3 в) AgNO3  г) CaCl2

        2. В каком из соединений степень окисления хлора +5

        а) HCl  б) HClO4 в) Cl2O7  г) NaClO3

        3. При диссоциации К2SO4 образуются ионы:

        а) К+ и SO42-  б) 2К+ и SO42- в) 2К+ и 4SO2-  г) К+ и 4SO-

        4. Скорость реакции, уравнение которой Zn+H2SO4=H2+ZnSO4 понизится при:

        а) увеличении концентрации серной кислоты

        б) нагревании

        в) увеличении концентрации водорода

        г) уменьшении концентрации сульфата цинка

        5. Равновесие реакции сместится в сторону обратной реакции 2Н2(г)+О2(г)↔2Н2О(г)+Q

        а) при понижении температуры

        б) при повышении температуры

        в) при уменьшении давления

        г) при увеличении концентрации Н2

        6.  Выберите все верные высказывания относительно реакции

        S(тв ) + O2 (г ) ↔ SO2(г) + 297 кДж

        а) реакция разложения б) реакция замещения в) эндотермическая

        г) экзотермическая д) окислительно-восстановительная ж) обратимая

        7. Признаками реакции между хлоридом натрия и нитратом серебра является:

        а) выделение газа; б) образование белого осадка; в) образование желтого осадка;

        в) воды

        8.Составьте уравнения разложения на ионы для данных веществ. Для многоосновной кислоты составьте уравнение полной и ступенчатой диссоциации:

        а) KNO3→_______________________ г) h3CO3→______________(полная)

        б)Al2(SO4)3→____________________ _____________________________(1 ступень)

        в) Ca(OH)2→_____________________ ___________________________(2 ступень)

        9.Допишите число электронов, принимающих участие в данных процессах. Укажите, какие из процессов являются окислением, а какие восстановлением.

        Схема

        Процесс(окисление или восстановление)

        S+6_____________→S-2

        		 

        O20____________→2O-2

        		 

        N-3_____________→N+2

        		 

        Pb0____________→Pb+2

        		 

        Часть 2.

        10.Установите соответствие между схемой окислительно-восстанови​тель​ной ре​ак​ции и ве​ще​ством-вос​ста​но​ви​те​лем в ней.

        11.Закончите уравнения реакций. Составьте для них полные и сокращенные ионные уравнения:

        а) K2CO3+BaCl2 → б) KOH+ Mg(NO3)2→ в) BaCO3+HCl→

        Часть 3.

        12. Используя метод электронного баланса, составьте уравнение ре​ак​ции::

        KNO2+KJ +h3SO4→J2+NO+K2SO4+h3O

        Опре​де​ли​те окис​ли​тель и вос​ста​но​ви​тель.

        13. Составить уравнение в молекулярной форме, которое бы соответствовало следующему уравнению в ионной форме:

        Са+2 +СО32- = СаСО3

        14. В результате реакции, термохимическое уравнение которой

         

         

        выделилось 1452 кДж теплоты. Вычислите массу образовавшейся при этом воды (в граммах). Запишите число с точностью до целых.

        Правильные ответы:

         

        1

        2

        3

        4

        5

        6

        7

        В-1

        б

        а

        б

        в, г

        б

        а, в

        б

        В-2

        а

        г

        б

        в

        б, в

        г, д

        б

         

        В-1

        8. а) HNO3→H++NO3- г) h3SO4→2H+ + SO4 2-

        б)K3PO4→ 3K++PO43- h3SO4 →H+ + HSO4 – (1 ступень)

        в) Ba(OH)2→Ba2++2OH- HSO4 – → H+ + SO4 2-_(2 ступень)

        9..

        Схема

        Процесс (окисление или восстановление)

        h30-2ē→2H+

        окисление

        Mn+7+5ē_→Mn+2

        восстановление

        N-3-8ē→N+5

        окисление

        Ca+2+2ē→Ca0

        восстановление

        10. А)2; Б)1; В)5

        12. 3P+5HNO3+2h3O=3h4PO4+5NO

        14. Ответ:72г.

        В-2

        8. а) KNO3→ K+ + NO3- г) h3CO3→2H+ + CO3 2- (полная)

        б)Al2(SO4)3→2Al3+ +3SO42- h3CO3 →H+ + HCO3 – _(1 ступень)

        в) Ca(OH)2→ Ca2+ +2OH- HCO3 – → H+ + CO3 2-_( (2 ступень)

        9.

        Схема

        Процесс(окисление или восстановление)

        S+6+8ē→S-2

        восстановление

        O20+4ē→2O-2

        восстановление

        N-3-5ē→N+2

        окисление

        Pb0-2ē→Pb+2

        окисление

        10. А)2; Б)3; В)5

        12. 2KNO2 +2 KI +2h3SO4=I2+2NO+2K2SO4+2h3O

        14. Ответ:108г.

        Критерии оценивания

        Всего 30 баллов

        За задания части 1

        1-7 – 7 баллов (1 балл за каждое правильно выполненное задание )

        8 – 4 балла ( 1 балла за каждое правильное написание диссоциацию веществ)

        9— 4 балла ( 1 балл за каждое правильное написание схемы реакции и определение процесса)

        За задания части 2

        10 – 3 балла(за каждое правильное соответствие 1 б)

        11. – 3 балла (за каждое правильно написанное уравнение 1 б )

        За задания части 3

        12. – 3 балла (за правильное написание баланса, определение процесса окисления и восстановления, расставление коэффициентов)

        13. – 3 балла (1 балл за правильное написанное уравнение, 2 балла за ионное уравнение)

        14. – 3 балла – за правильное решение задачи

        — отметка «5» выставляется обучающемуся, если 24-30 баллов;

        — отметка «4» выставляется обучающемуся, если 18-23 баллов;

        — отметка «3» выставляется обучающемуся, если 13-17 баллов;

        — отметка «2» выставляется обучающемуся, если менее 13 баллов.

        Получение и использование азотистой кислоты | Азотная(iii) кислота

        Азотистая кислота может быть получена в лаборатории в несколько этапов. Азотистую кислоту нельзя хранить в бутылках как азотную кислоту, потому что азотистая кислота легко разлагается на азотную кислоту, оксид азота (NO) и воду. Твердый нитрат натрия и холодная разбавленная соляная кислота (HCl) хочу приготовить азотную кислоту. Азотистая кислота — слабая одноосновная кислота.

        В этом уроке мы узнаем, как приготовить азотистую кислоту и для чего она нужна.


        Азотистая кислота | азотная(iii) кислота | HNO

        2 этапы подготовки

        В качестве основного метода приготовления мы используем твердый NaNO 3 . В этом методе есть три этапа для получения HNO 2 . Обычно мы готовим азотистую кислоту, когда она нам нужна. В противном случае мы не храним его в лабораториях, потому что он легко разлагается.


        Нагревание нитрата натрия как первая стадия получения азотистой кислоты

        Твердый нитрат натрия (NaNO 3 ) нагревают до разложения до твердого нитрита натрия (NaNO 2 ) и кислород (O 2 ) газ. Эта реакция является окислительно-восстановительная реакция (окислительно-восстановительная реакция), так как при протекании реакции изменяются степени окисления атомов азота и кислорода.

        Растворение нитрита натрия в воде для приготовления водного раствора нитрита натрия

        Твердый нитрит натрия растворяют в воде для приготовления водного раствора нитрита натрия . На этом этапе реакции не происходит. Только происходит растворение.

        Холодная разбавленная HCl и NaNO

        2 реакция

        Добавьте холодную разбавленную HCl в водный раствор нитрита натрия. Дает разбавленную азотистую кислоту и раствор NaCl.

        Почему к водному раствору
        NaNO 2 добавляют разбавленную HCl?

        ПРИМЕЧАНИЕ

        Если разбавленной HCl добавить к твердого NaNO 2 , NO 2 образуется коричневый газ. Тогда нет возможности подготовиться. азотная кислота кроме того.

        Почему
        холодная разбавленная HCl добавляется к водному раствору NaNO 2

        Азотистая кислота стабильна в холодном состоянии. При высокой температуре раствора образующаяся азотистая кислота разлагается на азотную кислоту (HNO 3 ), окись азота (NO) и воду. Поэтому мы должны использовать холодную HCl при получении азотистой кислоты.

        Реакция трехокиси азота и воды | N

        2 O 3 + H 2 O

        Триоксид азота реагирует с водой с образованием азотистой кислоты. Он показывает N 2 О 3 имеет слабые кислотные характеристики из-за образования слабой кислоты. В этой реакции N 2 O 3 реагирует с водой, защищая степени окисления атомов.

        Хранение раствора в холодном состоянии важно для защиты образующейся HNO 2 кислоты и предотвращения разложения.


        Степень окисления азота в азотистой кислоте

        Нарисовав структуру Льюиса HNO 2 , мы можем увидеть степень окисления, если азот равен +3.


        Из уравнения

        Принять степень окисления азота за x. Степень окисления атома кислорода и водорода равна -2 и +1.

        • +1 + x + (-2)*2 = 0
        • x = 0

        Применение азотистой кислоты

        Азотистая кислота используется во многих областях органической химии для производства очень многих химических веществ. Теперь мы узнаем, каковы эти области применения азотистой кислоты.

        Для получения спиртов

        Азотистая кислота реагирует с первичными алифатическими аминами для получения первичного спирта . Но помните, что для этой реакции NaNO 2 и разбавленная HCl используются для получения кислоты HNO 2 .


        Для приготовления N-нитрозамина

        N-нитрозамина представляет собой масло желтого цвета. Когда соединение вторичного амина обрабатывают азотистой кислотой, в качестве продукта получают N-нитрозамин.

        Получение хлорида бензолдиазония

        Хлорид бензолдиазония используется для изготовления пигментов. При обработке анилина NaNO 2 и разбавить HCl ниже 5 0 C , в качестве продукта получают хлорид бензолдиазония.

        Вопросы

        Задайте свой вопрос по химии и найдите ответы бесплатно

        Как определить водный раствор NaNO

        2 и HNO 2 ?

        Вопрос

        Классный руководитель посоветовал вам и вашему другу приготовить раствор азотистой кислоты из твердого нитрата натрия для провести больше экспериментов. Но вы не можете прийти на подготовительный день и ваш друг сказал, что сделает подготовку один. Придя на следующий день в лабораторию, вы должны провести дальнейшие эксперименты с приготовленным раствором азотной кислоты. Когда на следующий день вы пошли в лабораторию, вы видите, что ваш друг сделал некоторые приготовления, но он забыл пометить два решения. Итак, вы хотите знать, в каком растворе содержится приготовленная азотная кислота. Как отличить азотистую кислоту от водной? раствор нитрита натрия. Дайте пояснения.

        Ответ

        При получении азотистой кислоты из твердого нитрата натрия в водном растворе присутствует NaCl при перегонке или других метод химического разделения не используется для удаления NaCl.


        Добавлять нитрат серебра к растворам NaNO
        2 и HNO 2 Белый осадок AgCl образуется в растворе, в то время как в водном растворе NaNO 2 изменений нет.
        pH растворов NaNO
        2 и HNO 2

        HNO 2 является слабой кислотой, а NaNO 2 имеет слабоосновные характеристики. Таким образом, значение pH раствора HNO 2 равно меньше, чем раствор NaNO 2 .

        NaNO

        2 кислота или основание?

        NaNO 2 имеет слабые основные характеристики. NaNO 2 полностью диссоциирует в воде на ион натрия и NO 2 — ионы. Ион натрия стабилен в воде и не участвует в гидролизе воды.


        Стабилен или нестабилен нитрит-ион в воде?

        Ион нитрита не является стабильной водой и принимает протон от молекулы воды и образует азотистую кислоту и ион гидроксила. За счет образования гидроксильного иона водный раствор становится щелочным.

        Согласно приведенным выше объяснениям, водный раствор NaNO 2 является основным раствором.

        Почему мы должны готовить азотную кислоту в лаборатории, когда это требуется?

        Азотистая кислота является нестабильной кислотой. Поэтому хранить его долгое время невозможно, потому что он легко разлагается.

        Что такое азотная (iii) кислота

        Азотная (iii) кислота представляет собой оксокислоту азота. Эта кислота является слабой кислотой. В скобках указана степень окисления атома азота (iii). Так называют неорганические кислоты по номенклатуре ИЮПАК.


        Одноосновная кислота

        Когда кислота имеет только один атом водорода для реакции с основанием, мы говорим, что это одноосновная кислота.


        Можно ли сделать азотную кислоту из азотистой кислоты?

        Да, можно. Нагрейте раствор азотистой кислоты. Из-за нестабильности азотистая кислота разлагается на азотную кислоту, NO и воду.


        Какова степень окисления азота в hno2

        Мы можем найти степень окисления азота по алгебраическому уравнению. В большинстве случаев степень окисления кислорода равна -2, а водорода +1. За х примем степень окисления азота.

        HNO 2 представляет собой нейтральную молекулу. Таким образом, сумма степеней окисления каждого элемента должна быть ноль .

        • +1 + x + (-2)*2 = 0
        • x = +3

        Итак, степень окисления азота в HNO 3 это +3.

        какова степень окисления азота в nano2?

        Мы можем использовать алгебраическое уравнение, чтобы найти степень окисления азота в NaNO 2 . Щелочные металлы всегда имеют только +1 степень окисления. Таким образом, степень окисления натрия равна +1. В большинстве случаев кислород находится в степени окисления -2. Тогда неизвестная степень окисления азота равна х.

        +1 + x + (x)*2 = 0

        x = +3

        Похожие темы

        Диоксид серы подготовка и реакции Оствальдский процесс — HNO 3 Производство Характеристики газообразного азота и подготовка Подготовка и характеристики газообразного аммиака Оксиды азота HNO 3 и HNO 2 Кислоты Какой оксид азота является нейтральным, NO или NO 2

        Нитрит натрия – обзор

        ScienceDirect

        RegisterSign in

        эффективный ингибитор окисления липидов и антимикробное средство.

        Из: Окисление липидов (второе издание), 2012 г.

        PlusAdd to Mendeley

        М. Абдоллахи, М. Р. Хаксар, в Энциклопедии токсикологии (третье издание), 2014 г. по названию и применению похож на нитрат натрия. Оба являются консервантами, используемыми в переработанном мясе, таком как салями, хот-доги и бекон. Нитрит натрия был синтезирован с помощью нескольких химических реакций, включающих восстановление нитрата натрия. Промышленное производство нитрита натрия осуществляется в основном путем абсорбции оксидов азота водным раствором карбоната натрия или гидроксида натрия. За прошедшие годы нитрит натрия вызвал некоторые опасения по поводу его безопасности в пищевых продуктах, но он по-прежнему используется, и есть признаки того, что он действительно может быть полезен для здоровья. Нитрит натрия был разработан в 1960-е годы. В 1977 году Министерство сельского хозяйства США (USDA) рассматривало вопрос о ее запрете, но окончательное решение Министерства сельского хозяйства США о добавке вышло в 1984 году, разрешив ее использование. Исследования, проведенные в 1990-х годах, показали некоторые побочные эффекты нитрита натрия, например, способность вызывать у детей лейкемию и рак мозга. В конце 1990-х годов Национальная программа по токсичности (NTP) начала обзор нитрита натрия и предложила включить нитрит натрия в список токсикантов для развития и репродуктивной системы, но в отчете NTP от 2000 года было предложено, чтобы нитрит натрия не был токсичным веществом, и он был удален из список токсикантов развития и репродуктивной системы. В настоящее время считается, что он может помочь при пересадке органов и проблемах с сосудами ног, а также предотвращает сердечные приступы и серповидно-клеточную анемию.

        Просмотреть главуКнига покупок

        Прочитать всю главу

        URL: https://www.sciencedirect.com/science/article/pii/B9780123864543012069

        Wood 1982

        2-экзо-карбометокси-6-экзо-метилбицикло[3.3.0]окт-3-ен-7-экзо-илацетат (

        47 )
        Метод А

        Нитрит натрия (4 г) добавляли небольшими порциями в течение 1,5 ч к амиду ( 46 ) (560 мг) в уксусной кислоте (2,5 мл) и уксусном ангидриде (12 мл) при 0° и смесь выдерживали при 0–3° в течение 16 ч. К осажденному твердому веществу добавляли холодный насыщенный водный раствор ацетата натрия (20 мл) и смесь перемешивали на бане со льдом в течение 0,5 часа, а затем при комнатной температуре в течение 2 часов. Смесь экстрагировали дихлорметаном (5 х 20 мл), экстракты упаривали. Остаток растворяли в метаноле и добавляли избыток эфирного диазометана. Через 0,5 ч при комнатной температуре избыток диазометана разлагали уксусной кислотой, смесь промывали водой, сушили (Na 2 SO 4 ), и выпарили. Растворимую в четыреххлористом углероде часть остатка очищали методом ТСХ (SiO 2 , эфир, R f 0,6) с последующей перегонкой (температура бани (130–140°, 0,07 мм) с получением сложного эфира ( 47 ) (410 мг, 69%) (Найдено: C 65,44; H 7,85. C 13 H 18 O 4 требуется: C 65,5; H 7,6%), v max (пленка) 1740s см − 1 δ (CCl 4 ) 0,96 (3 Н, д, J 7 Гц, Ме), 1,38–2,24 (7 Н, м, с синглетом 1,96), 2,95, 3,08 (каждый 1 Н, м, аллильный Н), 3,60 (3H, с, ОМе), 5,03 (1H, кв, J 8 и 4 Гц, AcOC H ), 5,52 и 5,75 (каждый 1H, м, CH=CH).

        Метод В

        Хлорсульфонилизоцианат (500 мг, 3,5 ммоль) добавляли по каплям к силану ( 43 ) (715 мг, 2,8 ммоль) в четыреххлористом углероде (1,2 мл) при 0°. После выдерживания при 0° в течение 10 мин и затем при комнатной температуре в течение 2,5 ч растворитель выпаривали. Остаток перемешивали при 0° с уксусной кислотой (3 мл) в уксусном ангидриде (15 мл) и порциями добавляли нитрит натрия (4,5 г) в течение 1 часа. Смесь выдерживали в атмосфере азота при 0–3° в течение 16 ч и отделяли осадок. К осадку добавляли ацетат натрия (10 г) в воде (25 мл) при 0°; смесь перемешивали при 0° в течение 2 ч, затем при комнатной температуре в течение 3 ч, затем экстрагировали дихлорметаном (5 х 25 мл), остаток обрабатывали диазометаном и очищали, как указано выше, с получением сложного эфира ( 47 ) (410 мг, 61%).

        Просмотреть главуКнига покупок

        Прочитать главу полностью

        URL: https://www.sciencedirect. com/science/article/pii/B9780080292380500099

        P.W.G. СМИТ, А.Р. TATCHELL, в Fundamental Aliphatic Chemistry, 1965

        4 Реакция с азотистой кислотой

        Добавление нитрита натрия к щелочному раствору первичного или вторичного нитроалкана с последующим подкислением дает азотную кислоту и псевдонитрол соответственно.

        Алкилнитроловые кислоты представляют собой кристаллические твердые вещества, дающие красные растворы при растворении в щелочи. Псевдонитролы распознаются по темно-синему раствору, полученному экстракцией хлороформом. Поскольку третичные нитроалканы не вступают в реакцию, приведенная выше реакция использовалась в качестве диагностического теста для первичных, вторичных и третичных нитроалканов. Исторический интерес этой реакции состоит в том, что первичные, вторичные и третичные спирты первоначально классифицировались путем превращения сначала в алкилгалогенид, а затем с помощью нитрита серебра в соответствующий нитроалкан.

        Просмотреть главуКнига покупок

        Прочитать главу полностью

        URL: https://www.sciencedirect.com/science/article/pii/B9780080107462500168

        PG JEFFERY, D. HUTCHISON Chemical Method of Edition, D. HUTCHISON. ), 1981

        Реактивы:

        Периодат калия.

        Нитрит натрия.

        Раствор азотной кислоты, кипятят 1 литр 0,2 н. азотной кислоты с примерно 0,1 г перйодата калия, охлаждают и хранят в цельностеклянной промывной бутыли.

        Стандартный маточный раствор марганца, точно взвесьте 0,155 г чистого марганца в небольшой химический стакан, растворите в 50 мл 0,5 N серной кислоты, перенесите в мерную колбу на 1 л и доведите до нужного объема водой. Этот раствор содержит 200 мкг MnO на мл.

        Стандартный рабочий раствор марганца, перенесите 25 мл исходного раствора в мерную колбу вместимостью 100 мл и доведите до нужного объема водой. Этот раствор содержит 50 мкг MnO на мл и должен использоваться для калибровки 1-сантиметровых кювет спектрофотометра. Если будут использоваться 4-см ячейки, рабочий раствор можно приготовить, разбавив 5 мл маточного раствора до 100 мл, давая 10 мкг на мл.

        Просмотреть главуКнига покупок

        Прочитать главу полностью

        URL: https://www.sciencedirect.com/science/article/pii/B9780080238067500336

        D.L.H. WILLIAMS, в Nitrosation Reactions and the Chemistry of Nitric Oxide, 2004

        Нитрозилкарбоксилаты (ацилнитриты) RCOONO

        Обычно считается, что когда нитрит натрия растворяется в карбоновой кислоте, образуется равновесная концентрация нитрозилкарбоксилата. , который действует как нитрозирующий агент [119]. Многие реакции нитрозирования были проведены препаративно с использованием, например, нитрит натрия, растворенный в уксусной или муравьиной кислотах, уравнение (77). Впоследствии из ацетата серебра и нитрозилхлорида был синтезирован нитрозилацетат

        (77)HNO2+h4O++RCOO-⇄RCOONO+2h3O

        (78)Ch4COOAg+ClNO=Ch4COONO+AgCl

        (ацетилнитрит) [120]. , уравнение (78) при температурах жидкого азота. Это бледно-коричневая жидкость при комнатной температуре, зеленая жидкость при -78°C и зеленое твердое вещество при -19°C.6°С. Он быстро гидролизуется в воде, но достаточно стабилен в растворителях, таких как пиридин или уксусная кислота, чтобы действовать как эффективный нитрозирующий агент. Он превращает 1-октанол в нитритовый эфир пиридина, уравнение (79) и дает такое же распределение продуктов дезаминирования из 1-октиламина, как и при использовании реагента нитрит натрия/уксусная кислота, уравнение. (80).

        (79)Ch4(Ch3)6Ch3OH+Ch4COONO→Ch4(Ch3)6Ch3ONO

        (80)

        Кинетические результаты реакции в присутствии карбоксилатных буферов часто показывают путь, который протекает через нитрозилкарбоксилат. Стедман [121] показал, что реакция между азотистой кислотой и азотистоводородной кислотой в ацетатных буферах протекает по двум путям с участием как нитрозилацетата, так и триоксида диазота в качестве нитрозирующих частиц. Позже [122] более детальная кинетическая работа по нитрозированию N-метиланилина и пиперазина в сходных условиях выявила пути через CH 3 COONO, N 2 O 3 и H 2 NO2+/NO + . По сравнению с другими субстратами оказывается, что CH 3 COONO может реагировать на пределе диффузии, что обеспечивает константу равновесия для образования нитрозилацетата, уравнение. (77), который можно оценить как ~1,4 × 10 90 144 -8 90 145 M 90 144 -1 90 145 . Такое малое значение не позволило бы обнаружить нитрозилацетат в этих растворах ни одним спектроскопическим методом.

        Было показано, что нитрит натрия в трифторуксусной кислоте эффективен при нитрозировании водонерастворимых амидов [123]. Тот же самый реагент был успешно использован для диазотирования (и последующей реакции с ионом азида) сильно дезактивированных производных анилина, таких как перфторанилин и 2,6-дифторанилин, уравнение (81). Точно так же нитрит натрия в безводной пропионовой

        (81)

        кислота образует 2-нитрозопродукты из фенолов региоселективно [124], возможно, посредством образования нитрозилпропионата in situ.

        Просмотреть главуКнига покупок

        Прочитать главу полностью

        URL: https://www.sciencedirect.com/science/article/pii/B9780444517210500025

        Betty J. Locey, 20000 Betty J. Locey, в энциклопедии

        Хроническая токсичность (или воздействие)

        Животные

        В одном исследовании крысы получали нитрит натрия в дозе 100 мг кг -1 в питьевой воде ежедневно в течение всей жизни на протяжении трех поколений, и не наблюдалось никаких признаков хронической токсичности, канцерогенности или тератогенности.

        Человек

        Длительное воздействие нитритов и нитратов в достаточно высоких концентрациях может вызвать увеличение образования мочи почками (диурез), увеличение отложений крахмала и кровотечение из селезенки.

        Нитриты обычно не классифицируются как канцерогены для человека. При определенных условиях нитриты могут соединяться с аминами в организме с образованием нитрозаминов. Существует ряд различных нитрозаминов; многие из них регулируются как человеческие канцерогены. Некоторые химические вещества, такие как витамин С (аскорбиновая кислота), могут ограничивать превращение нитритов в нитрозамины. Министерство сельского хозяйства США (USDA) требует добавления аскорбиновой кислоты или эриторбиновой кислоты в бекон, чтобы снизить риск образования нитрозаминов.

        Просмотр книги Глава покупки

        Читать полную главу

        URL: https://www.sciendirect.com/science/article/pii/b0123694000006864

        Yang-heon Song, в комплект Heteroccricl 202920595050595929299595959595959595959595969296969695959595959695969296959692969596959595959596969695959596959696969695969596959695969596959695969596969

        12.15.2.4 Пиридазиновое центральное кольцо

        Обработка аминопиррола 257 нитритом натрия с последующей циклизацией полученного диазосоединения 258 при обработке 25% серной кислотой с получением пирроло[3,4- c ]тиено[2,3- e ]пиридазин 259 (схема 18). 108

        схема 18 5 H -тиазоло[5,4- c ][1,2,4]триазоло[1,2- a ]пиридазин-7,9(8 H ,10a H )-дион 262 с количественным выходом (уравнение 73). 109

        (73)

        Бис([1,2,4]триазоло)[3,4- a :4′3′- c ]фталазин 264 – антибактериальный агент, синтезированный окислительная циклизация бис(2-бензилиденгидразинил)нафталина 263 диацетатом иодбензола (уравнение 74). 110

        (74)

        Дегидратационная циклизация ацилгидразида 265 в пиридине с обратным холодильником дала 3,9-диметилизоксазоло[4,5- d ][1,2,4]триазоло[4 — d ]пиридазин 266 (ур. 75). 111

        (75)

        View chapterPurchase book

        Read full chapter

        URL: https://www. sciencedirect.com/science/article/pii/B9780124095472148991

        K. Hemming, in Comprehensive Heterocyclic Chemistry III, 2008

        10.20.11 Дальнейшие разработки

        Недавняя работа продемонстрировала, что опосредованная нитритом натрия циклизация ряда гликозидов гидразиноурацила дает ряд гликозидов токсофлавина вместе с их 4-оксидными аналогами, где последние могут восстанавливаться до первого гипосульфитом. Метод циклизации описан в разделе 10.20.9..2.3(i) в уравнениях (22)–(24). Образующиеся таким образом гликозиды токсофлавина являются потенциальными пролекарствами для направленной антителами ферментативной терапии опухолей <2007CAR1254>. Ряд токсофлавиноподобных соединений (азаптеридинов) был идентифицирован как ингибиторы РНК-зависимой РНК-полимеразы гепатита С, что представляет определенный интерес, учитывая, что использование токсофлавинов, как обсуждалось в разделе 10.20.10.3, было ограничено их токсичностью. 2007MI1>. Чувство кворума ацил-гомосерин-лактона (см. Раздел 10.20.10.3) и его значение в биосинтезе фитотоксина токсофлавина были изучены дополнительно, что дало дополнительную информацию о производстве и роли токсофлавина в больном рисе <2007MI4950>. Фервенулин, 2-метилфервенулин-3-он и их 4-N-оксиды были подвергнуты подробному изучению с помощью рентгеновской дифракции, 1 Н ЯМР и 13 С ЯМР спектроскопии, при этом те же исследователи провели углубленное исследование. изучение их химической активности к окислению, хлорированию, алкилированию и нуклеофильной атаке <2006KFZ49>. Более поздние работы установили исход реакции тех же трех видов с индолами <2007KFZ49>.

        Просмотр главыКнига покупок

        Прочитать главу полностью

        URL: https://www.sciencedirect.com/science/article/pii/B9780080449920009202

        Ричард Н. Батлер, Всесторонняя химия гетероциклов II, 1996 3,7 0005 5-диазоний и 5-диазотетразолы

        Диазотирование 5-аминотетразола нитритом натрия и водным раствором HCl дает хлорид тетразол-5-диазония ( 199 ), который взрывоопасен в твердом состоянии или если он кристаллизуется из раствора, но хранится в растворе является важным синтетическим промежуточным продуктом в химии тетразолов 〈75CRV241〉. Его можно легко восстановить до гидразина или N 2 можно заменить галогеном, OH или H 〈77AHC(21)323, 84CHEC-I(5)791, 84CHEC-I(5)822〉. Удаление протона дает диазоформу, которая использовалась для контролируемого образования атомарного углерода 〈74JA7830〉. Теоретические исследования ряда диазоазолов позволяют предположить, что 5-диазотетразол должен легко входить в переходное состояние циклоприсоединения с электронно-богатыми алкенами 〈90JCS(P2)1943〉. Соль диазония ( 199 ) соединяется с малонодинитрилом в основных условиях с образованием производного 3-азидо-1,2,4-триазина ( 201 ). Эта реакция формально включает последовательность раскрытия тетразольного кольца, прототропных таутомеризаций и внутримолекулярного нуклеофильного присоединения к исходному диазопродукту, представленному как ( 200 ) на схеме 32 для иллюстрации процесса, хотя этот конкретный вид не обязательно должен быть промежуточным продуктом 〈84KGS557〉. Также сообщалось о гидрате 5-[(диазометил)-азо]тетразола, HN 4 C-NN-CHN 2 H 2 O, который восстанавливается до 5-гидразинотетразола и до тетразол-5-илдиазометанола. , ХН 4 C-NN-CH 2 ОН 〈92KGS1351〉. В более ранней литературе было показано, что замещенные по кольцу 5-аминотетразолы претерпевают окислительную димеризацию до азотетразолов и диазотирование до 5-нитрозаминотетразолов или 1,3-бистетразол-5-илтриазенов, в зависимости от условий диазотирования 〈75CRV241, 84CHEC-I(5 )791〉.

        Схема 32.

        Просмотр главыКнига покупок65185000952

        Тадао Сугимото, в монодисперсных частицах (второе издание), 2019 г.

        Радикальная полимеризация, инициируемая поверхностно-связанными группами как 2-нафталинтиол,

        фенил-диазогруппа образуется на поверхности кремнезема, которые разлагаются при нагревании при повышенных температурах, таких как 60°C, с образованием фенильных радикалов, химически связанных с поверхностью кремнезема, и несвязанных тиорадикалов, оба из которых способны инициировать свободнорадикальную полимеризацию виниловых мономеров. 197 Схема 3 представляет такие реакции. С помощью этой радикальной полимеризации к поверхностям кремнезема прививают различные полимеры; например, полистирол (в толуоле или в массе), поли(метилметакрилат) (в толуоле или в массе), полиакриламид (в воде), полиакрилонитрил (в ДМФА), полиакриловая кислота (в воде). ) и поли(4-винилпиридин) (в этаноле или в массе). Фенилдиазогруппы, связанные с диоксидом кремния, также использовались для реакций сочетания с одноцепочечными DNA , и ожидалось, что продукт будет полезен для реакций гибридизации ДНК. 190

        Схема 3.

        Радикальную привитую полимеризацию акриламида с поверхности ультрадисперсного кремнезема проводили в окислительно-восстановительной системе, состоящей из ионов церия и восстановителей, таких как спиртовые гидроксильные, амино- и меркаптогруппы, сопряженные с гидроксилом группы на поверхности кремнезема. 201 В результате гидрофильный диоксид кремния с привитым полиакриламидом был синтезирован. Эти восстанавливающие группы, связанные с поверхностью диоксида кремния, были введены реакциями поверхностных силанольных групп с 3-глицидоксипропилтриметоксисиланом (ГПС), 3-аминопропилтриэтоксисиланом (АПС) и 3-меркаптопропилтриметоксисиланом (МПС) соответственно. Аналогичным образом была получена сажа с привитым полиакриламидом . 202 Схема 4 представляет такие реакции.

        Схема 4.

        Посмотреть главуКнига покупок

        Читать всю главу

        URL: https://www.sciencedirect.com/science/article/pii/B97804446274

        089

        Термодинамическое моделирование процессов окисления Ag2Se под действием NaNO2

        Заголовки статей

        Характеристика гамма-облученной смеси ПП/ПЭНП
        стр. 90

        Экспериментальное исследование скорости распространения пламени в золе рисовой шелухи в неподвижных слоях
        стр.96

        Сжатие агрегатов двумерных монодисперсных материалов для оценки распространения дефектов
        стр.101

        Интерактивная сила двумерной деформации сжатия методом дискретных элементов (DEM)
        стр.106

        Термодинамическое моделирование процессов окисления Ag 2 Se NaNO 2
        стр.111

        Сушка промышленных керамических кирпичей: экспериментальное исследование в печи
        стр. 116

        Оценка корреляции Нуссельта для численного прогноза мощности промерзания на трубчатых валах треугольного расположения
        стр.121

        Математическое моделирование процесса высокоэнергетического шарового измельчения (HEBM)
        стр.126

        In Situ Оптический анализ структурных изменений в полимолочной кислоте (ПМК) в процессе растворения газа
        стр.131

        Главная Форум дефектов и диффузии Форум дефектов и диффузии Vol. 353 Термодинамическое моделирование окисления…

        Предварительный просмотр статьи

        Abstract:

        Проведено термодинамическое моделирование процессов окисления селенида серебра такими реагентами, как NaNO 2 , NaNO 3 и NaOH при их термообработке. Оценена энергия Гиббса реакций окисления селенида серебра. Показано, что в качестве реагента-окислителя селенида серебра рационально использовать смесь нитрита натрия и гидроксида натрия. Окисление селенида серебра при термообработке совместно с нитритом натрия и гидроксидом натрия сопровождается образованием растворимых соединений типа Na 2 SeO 3 и Na 2 SeO 4 , серебро проходит в металлическом состоянии. Оценены коэффициенты разделения, характеризующие эффективность окисления и уровень перехода селена в растворимые соединения. С использованием полученных данных предложен метод разделения материалов, содержащих селениды, путем их спекания с натрийсодержащими реагентами. Метод основан на переводе селена в водорастворимые соединения с последующим выщелачиванием, при этом драгоценные металлы находятся в элементарном состоянии. Полученные продукты пригодны для производства селена и драгоценных металлов по традиционным технологиям.

        Доступ через ваше учреждение

        * — Автор, ответственный за переписку

        использованная литература

        [1] Кудрявцев А. А. Химия и технология селена и теллура. Москва, Металлургическая, 1968. 340 с.

        [2] М.А. Ласточкина, С.А. Мастюгин, Т.В. Вергизова, Т.Н. Грейвер, В.В. Ашихин. Влияние условий автоклавного окислительного выщелачивания медеэлектролитных шламов на их поведение при флотации / Цветные металлы, 2012. № 8, с.50-56.

        [3] Грейвер Т.Н. Некоторые особенности образования шламов при электролитическом рафинировании меди и никеля/цветных металлов. 1965. № 1. С. 28-33.

        [4] Букетов Е. А., Малышев В.П. Удаление селена и теллура из медного электролитного шлама. Алма-Ата: Наука. 1969. 206.

        [5] Грейвер Т.Н., Зайцева И.Г., Косовер В.М. Селен и теллур. Новая технология производства и переработки. Москва: Металлургия. 1977. 296 с.

        [6] Патент РФ № 2451759/ М.А. Ласточкина, Т.Н. Грейвер, Т.В. Вергизова, С.А. Мастюгин, В.В. Ашихин, С.А. Краюхин, А.Т. Крестьянинов. Способ переработки свинцового шлама электролитной меди (варианты). Опубл. 27. 05. (2012).

        [7] Патент РФ № 2458159. Способ получения металлического серебра из халькогенида серебра. Громов О.Г., Локшин Е.П., Савельев Ю.А., Мастюгин С.А. по 20.03.(2011).

        Цитируется

        ОКИСЛЕНИЕ ПЛУТОНИЯ (III) НИТРИТОМ НАТРИЯ (Технический отчет)

        ОКИСЛЕНИЕ ПЛУТОНИЯ (III) НИТРИТОМ НАТРИЯ (Технический отчет) | ОСТИ.GOV

        перейти к основному содержанию

        • Полная запись
        • Другие родственные исследования

        Приведена константа скорости реакции окисления Pu(III) нитритом в растворе HNO/sub 3/, содержащем сульфанат железа. Было обнаружено, что скорость реакции можно измерить с помощью спектрофотометрии. Данные показывают, что реакция является реакцией псевдопервого порядка в интересующей области концентрации HNO/sub 3/ и нитрита. Константа скорости реакции, выраженная как реакция первого порядка по Pu, была найдена для нескольких значений концентрации HNO/sub 3/ и нитрита. Дана зависимость HNC/sub 3/константы скорости реакции. Окисление сульфамата железа — раствор Pu(III) Pu(III) протекает последовательно через ионы сульфамата, железа и Pu(III). С окислением как ионов железа, так и ионов Pu(III) связан автокаталитический механизм, что исключает возможность простые расчеты констант на основе концентрации нитрита.Дана эмпирическая связь между константой скорости реакции и концентрацией (добавленного) нитрита.(авт.)

        Авторов:
        Брюнстад, А
        Дата публикации:
        Исследовательская организация:
        General Electric Co. Hanford Atomic Products Operation, Ричленд, Вашингтон
        Идентификатор ОСТИ:
        4345806
        Номер(а) отчета:
        HW-51655
        Номер АНБ:
        НСА-12-003620
        Номер контракта Министерства энергетики:  
        W-31-109-ENG-52
        Тип ресурса:
        Технический отчет
        Отношение ресурсов:
        Другая информация: Децл. 12 ноября 1957 г. Ориг. Дата поступления: 31 декабря 1958 г.
        Страна публикации:
        США
        Язык:
        Английский
        Тема:
        ХИМИЯ; КАТАЛИЗ; ХИМИЧЕСКИЕ РЕАКЦИИ; СОЕДИНЕНИЯ ЖЕЛЕЗА; АЗОТНАЯ КИСЛОТА; НИТРИТЫ; ОКИСЛЕНИЕ; ФОТОМЕТРИЯ; ПЛУТОНИЙ; КИНЕТИКА РЕАКЦИИ; СОЕДИНЕНИЯ НАТРИЯ; РЕШЕНИЯ; СПЕКТРОСКОПИЯ; СУЛЬФАМИНОВАЯ КИСЛОТА; СУЛЬФОКИСЛОТЫ; СОЕДИНЕНИЯ СЕРЫ; СКОРОСТЬ

        Форматы цитирования

        • MLA
        • АПА
        • Чикаго
        • БибТекс

        Брунстад, А. ОКИСЛЕНИЕ ПЛУТОНИЯ (III) НИТРИТОМ НАТРИЯ . США: Н. П., 1957. Веб. дои: 10.2172/4345806.

        Копировать в буфер обмена

        Брюнстад, А. ОКИСЛЕНИЕ ПЛУТОНИЯ (III) НИТРИТОМ НАТРИЯ . Соединенные Штаты. https://doi.org/10.2172/4345806

        Копировать в буфер обмена

        Бранстад, А. 1957. «ОКИСЛЕНИЕ ПЛУТОНИЯ (III) НИТРИТОМ НАТРИЯ». Соединенные Штаты. https://doi.org/10.2172/4345806. https://www.osti.gov/servlets/purl/4345806.

        Копировать в буфер обмена

        @статья{osti_4345806,
        title = {ОКИСЛЕНИЕ ПЛУТОНИЯ (III) НИТРИТОМ НАТРИЯ},
        автор = {Брунстад, А},
        abstractNote = {Дана константа скорости реакции окисления Pu(III) нитритом в растворе HNO/sub 3/, содержащем сульфанат железа. Было обнаружено, что скорость реакции можно измерить с помощью спектрофотометрии. Данные показывают, что реакция является реакцией псевдопервого порядка в интересующей области концентрации HNO/sub 3/ и нитрита. Константа скорости реакции, выраженная как реакция первого порядка по Pu, была найдена для нескольких значений концентрации HNO/sub 3/ и нитрита. Дана зависимость HNC/sub 3/константы скорости реакции. Окисление сульфамата железа - раствор Pu(III) Pu(III) протекает последовательно через ионы сульфамата, железа и Pu(III). С окислением как ионов железа, так и ионов Pu(III) связан автокаталитический механизм, что исключает возможность простые расчеты констант на основе концентрации нитрита.Дана эмпирическая связь между константой скорости реакции и концентрацией (добавленного) нитрита.(авт.)},
        дои = {10.2172/4345806},
        URL-адрес = {https://www.osti.gov/biblio/4345806}, журнал = {},
        номер =,
        объем = ,
        место = {США},
        год = {1957},
        месяц = ​​{7}
        }

        Копировать в буфер обмена

        Посмотреть технический отчет (5,46 МБ)

        https://doi. org/10.2172/4345806

        Экспорт метаданных

        Сохранить в моей библиотеке

        Вы должны войти в систему или создать учетную запись, чтобы сохранять документы в своей библиотеке.

        Аналогичных записей в сборниках OSTI.GOV:

        • Аналогичные записи

        кислородная кислота | химическое соединение | Британика

        оксикислота

        См. все средства массовой информации

        Связанные темы:
        сульфоновая кислота серная кислота фосфорная кислота азотная кислота пероксикислота

        Просмотреть весь соответствующий контент →

        Резюме

        Прочтите краткий обзор этой темы

        оксикислота , любая кислородсодержащая кислота. Большинство ковалентных оксидов неметаллов реагируют с водой с образованием кислых оксидов; то есть они реагируют с водой с образованием оксикислот, которые дают ионы гидроксония (H 3 O + ) в растворе. Есть некоторые исключения, такие как окись углерода, CO, закись азота, N 2 O, и окись азота, NO.

        Сила оксикислоты определяется степенью ее диссоциации в воде (т. е. ее способностью образовывать H + 9ионов 0145). В общем, относительную силу оксикислот можно предсказать на основе электроотрицательности и степени окисления центрального атома неметалла. Сила кислоты увеличивается по мере увеличения электроотрицательности центрального атома. Например, поскольку электроотрицательность хлора (Cl) выше, чем у серы (S), которая, в свою очередь, выше, чем у фосфора (P), можно предположить, что хлорная кислота HClO 4 является более сильной кислота, чем серная кислота, H 2 SO 4 , которая должна быть более сильной кислотой, чем фосфорная кислота, H 3 PO 4 . Для данного центрального атома неметалла сила кислоты увеличивается по мере увеличения степени окисления центрального атома. Например, азотная кислота HNO 3 , в которой атом азота (N) имеет степень окисления +5, является более сильной кислотой, чем азотистая кислота HNO 2 , где степень окисления азота равна +3. Таким же образом серная кислота H 2 SO 4 с серой в степени окисления +6 является более сильной кислотой, чем сернистая кислота, H 2 SO 3 , где существует степень окисления серы +4.

        Соль оксикислоты представляет собой соединение, образующееся при взаимодействии кислоты с основанием: кислота + основание → соль + вода. Этот тип реакции называется нейтрализацией, потому что раствор становится нейтральным.

        Оксикислоты азота

        Азотная кислота, HNO 3 , была известна алхимикам 8-го века как «aqua fortis» (сильная вода). Он образуется в результате реакции как пятиокиси азота (N 2 O 5 ) и диоксид азота (NO 2 ) с водой. Небольшие количества азотной кислоты обнаруживаются в атмосфере после гроз, а ее соли, называемые нитратами, широко распространены в природе. Огромные залежи нитрата натрия, NaNO 3 , также известного как чилийская селитра, находятся в пустынной области недалеко от границы Чили и Перу. Эти отложения могут иметь ширину 3 км (2 мили), длину 300 км (200 миль) и толщину до 2 метров (7 футов). Нитрат калия, KNO 3 , иногда называемая бенгальской селитрой, встречается в Индии и других странах Восточной Азии. Азотную кислоту можно получить в лаборатории путем нагревания азотнокислой соли, такой как упомянутые выше, с концентрированной серной кислотой; Например, NaNO 3 + H 2 SO 4 + тепло → NaHSO 4 + HNO 3 . Поскольку HNO 3 кипит при 86 °C (187 °F), а H 2 SO 4 кипит при 338 °C (640 °F), NaNO 3 и NaHSO 4 – нелетучие соли, азотная кислота легко удаляется перегонкой.

        Викторина «Британника»

        Наука: правда или вымысел?

        Вас увлекает физика? Устали от геологии? С помощью этих вопросов отделите научный факт от вымысла.

        В промышленных масштабах азотная кислота производится по процессу Оствальда. Этот процесс включает окисление аммиака NH 3 до оксида азота NO и дальнейшее окисление NO до диоксида азота NO 2 9.0012, а затем превращение NO 2 в азотную кислоту (HNO 3 ). Это поточный процесс, при котором смесь аммиака и избыточного воздуха нагревается до 600–700 °C (от 1100 до 1300 °F) и проходит через платино-родиевый катализатор. (Катализатор увеличивает скорость реакции, не расходуясь при этом сам.) Когда происходит окисление до NO, эта газообразная смесь буквально горит пламенем. Добавляется дополнительный воздух для окисления NO до NO 2 . № 2 , избыток кислорода и нереакционноспособный азот из воздуха пропускают через распыляемую воду, где образуются HNO 3 и NO в виде диспропорционирования NO 2 . Газообразный NO рециркулирует в процессе с большим количеством воздуха, а жидкая HNO 3 отбирается и концентрируется. Около 7 миллиардов кг (16 миллиардов фунтов) HNO 3 ежегодно производится в Соединенных Штатах в промышленных масштабах, причем основная часть производится по процессу Оствальда.

        В чистом виде азотная кислота представляет собой бесцветную жидкость, которая кипит при 86 ° C (187 ° F) и замерзает при -42 ° C (-44 ° F). Под воздействием света или тепла он разлагается с образованием кислорода, воды и смеси оксидов азота (в основном NO 2 ). 4HNO 3 + свет (или тепло) → 4ΝΟ 2 + 2H 2 O + O 2 Следовательно, азотная кислота часто имеет желтый или коричневый цвет из-за NO 2 , который образуется при ее разложении. Азотная кислота стабильна в водном растворе, и 68-процентные растворы кислоты (т. е. 68 граммов HNO 3 на 100 граммов раствора) продаются как концентрированная HNO 3 . Это одновременно сильный окислитель и сильная кислота. Неметаллические элементы, такие как углерод (C), йод (I), фосфор (P) и сера (S), окисляются концентрированной HNO 3 до их оксидов или оксикислот с образованием NO 2 ; Например, S + 6HNO 3 → H 2 SO 4 + 6NO 2 + 2H 2 O. Кроме того, многие соединения окисляются HNO 3 . Соляная кислота, водный раствор HCl, легко окисляется концентрированной HNO 3 до хлора Cl 2 и диоксида хлора ClO 2 . Царская водка («царская вода»), смесь одной части концентрированной HNO 3 и три части концентрированной HCl, энергично реагирует с металлами. Использование этой смеси алхимиками для растворения золота задокументировано еще в 13 веке.

        Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчас

        Действие азотной кислоты на металл обычно приводит к восстановлению кислоты (т. е. к уменьшению степени окисления азота). Продукты реакции определяют по концентрации HNO 3 , задействованный металл (т. е. его реакционная способность) и температура. В большинстве случаев образуется смесь оксидов азота, нитратов и других продуктов восстановления. Относительно нереакционноспособные металлы, такие как медь (Cu), серебро (Ag) и свинец (Pb), восстанавливают концентрированную HNO 3 прежде всего до NO 2 . Реакция разбавленной HNO 3 с медью дает NO, тогда как более активные металлы, такие как цинк (Zn) и железо (Fe), реагируют с разбавленной HNO 3 с образованием N 2 O. При использовании чрезвычайно разбавленной HNO 3 может образовываться либо газообразный азот (N 2 ), либо ион аммония (NH 4 + ). Азотная кислота реагирует с белками, например, с белками кожи человека, с образованием желтого вещества, называемого ксантопротеином.

        Нитраты, представляющие собой соли азотной кислоты, образуются при взаимодействии металлов или их оксидов, гидроксидов или карбонатов с азотной кислотой. Большинство нитратов растворимы в воде, и азотная кислота в основном используется для получения растворимых нитратов металлов. Все нитраты разлагаются при нагревании и могут происходить со взрывом. Например, когда нитрат калия (KNO 3 ) нагревается, образуется нитрит (соединение, содержащее NO 2 − ) и выделяется газообразный кислород. 2КНО 3 + нагрев → 2КНО 2 + О 2 При нагревании нитратов тяжелых металлов образуется оксид металла, как, например, в 2Cu(NO 3 ) 2 + тепло → 2CuO + 4NO 2 + O 2 . Нитрат аммония (NH 4 ) 2 NO 3 производит закись азота N 2 O и особенно опасен для нагревания или детонации.

        Азотная кислота широко используется в лаборатории и в химической промышленности как сильная кислота и как окислитель. Кислота широко используется в производстве взрывчатых веществ, красителей, пластмасс и лекарств. Нитраты ценны как удобрения. Порох представляет собой смесь нитрата калия, серы и древесного угля. Аммонал, взрывчатое вещество, представляет собой смесь аммиачной селитры и алюминиевой пудры.

        Реакции солей диазония: Зандмейера и родственные реакции

        Соли диазония из аминов и реакции солей диазония

        Сегодня поговорим о наборе реакций ароматических аминов, которые по-разному классифицируются как «амины» и «ароматические соединения», в зависимости от учебника.

        Он включает преобразование ароматической аминогруппы (NH 2 ) в очень хорошую уходящую группу (N 2 ), которую затем можно заменить различными нуклеофилами. Однако N 2 представляет собой , такую ​​как , хорошую уходящую группу, так что метод хорошо работает только для ароматических аминов; алкильные («алифатические») амины склонны терять N 2   слишком быстро , что делает метод в этом случае гораздо менее полезным.

        СОДЕРЖАНИЕ

        1. Образование солей диазония из ароматических аминов
        2. Реакции диазония Соли: Сэндмейер и другие реакции
        3. Механизм: формирование диазония.
        4. (Дополнительно) Ссылки и дополнительная литература

        1. Образование солей диазония из ароматических аминов

        Вот процесс. Обработка ароматического амина азотистой кислотой ( или нитритом натрия, который превращается в азотистую кислоту в присутствии кислоты ) в присутствии сильной кислоты, такой как HCl, приводит к потере H 2 O и образованию новая тройная связь N-N. Полученный вид называется «ионом диазония»:

        (Как это работает? Мы рассмотрим механизм внизу поста) 903:30 .

        2. Реакции солей диазония: обзор

        Так почему же это важно?

        Это важно, потому что полученные соли диазония могут быть преобразованы во всевозможные полезные функциональные группы. Вместо того, чтобы описывать все словами, сначала давайте просто покажем 7 примеров на диаграмме:

        Любой процесс, в котором используется один исходный материал, который может быть преобразован в семь различных потенциальных продуктов, можно с полным основанием назвать «универсальным».

        Эти реакции можно условно разделить на две категории: реакции Зандмейера и все остальное.

        Реакции Сандмейера

        Одним из способов преобразования солей диазония является их обработка различными соединениями меди. Они известны как реакции Зандмейера в честь Трауготта Зандмейера, который впервые открыл реакцию в 1884 году (с ацетилидом меди!).

        Три ключевых примера:

        • CuCl превращает соли арилдиазония в арилхлориды
        • CuBr превращает соли арилдиазония в арилбромиды
        • CuCN превращает соли арилдиазония в арилцианиды (нитрилы).

        Механизм, о котором вы можете прочитать в другом месте, вероятно, происходит через арильный радикал, который окисляется до арильного катиона, а затем атакуется нуклеофилом.

        Другие реакции

        Медь не требуется для замещения, если присутствует достаточно сильный нуклеофил или если смесь достаточно нагрета:

        • Арилиодиды также могут быть получены из солей арилдиазония путем обработки йодидом калия (KI).
        • Гидроксильные группы (ОН) могут быть установлены на соли арилдиазония путем нагревания с водой и кислотой. (ранее мы видели один пример в работе Джона Робертса по аринам, которую мы рассмотрели здесь.)
        • Арил фториды  можно установить с помощью двухэтапного процесса. Первый включает замену противоиона (X – ) на арилдиазониевую соль ионом тетрафторбората ( BF 4 – ) путем обработки диазониевой соли HBF 4 . Тогда при нагревании фтор может действовать как нуклеофил, вытесняя N 2 и выделяя в качестве побочного продукта BF 3 .
        • Соль диазония также может быть восстановлена ​​ до C– H путем обработки соли арилдиазония гипофосфористой кислотой (H 3 PO 2 ).

        Не так уж и плохо из одной функциональной группы!

        3. Механизм: образование ионов диазония

        1. образование ионов нитрозония из HNO 2

        Теперь давайте рассмотрим, как работают некоторые из этих реакций.

        Во-первых, давайте пройдем через образование соли диазония, процесс, называемый «диазотированием».

        Первым ключевым реагентом для этого процесса является либо нитрит натрия (NaNO 2 ), либо азотистая кислота (HNO 2 ). Преимущество нитрита натрия состоит в том, что с ним легко обращаться, в то время как HNO 2  — несколько нестабильная жидкость.

        Вторым ключевым реагентом является сильная минеральная кислота, такая как HCl; если используется NaNO 2 , HCl превращает его в HNO 2 .

        Основной целью HCl является дальнейшее преобразование HNO 2 в мощный электрофил NO + , «ион нитрозония», который является ключевым электрофилом в реакции, в результате которой образуется соль диазония.

        Ион нитрозония образуется в результате протонирования ОН и последующей потери воды:

        2. Образование иона диазония

        Следующим этапом является образование иона диазония в результате реакции между амином и ионом нитрозония, для которой также требуется кислота.

        Как это работает?

        Первая стадия – образование новой связи N–N, которое происходит в результате атаки иона нитрозония ароматическим амином (, стадия 1 ). За этим следуют два переноса протона от азота к кислороду (, шаги 2 и 3, ), сопровождающиеся реорганизацией каркаса пи-связей [с образованием N-N (pi), разрывом N-O (pi)]. Заключительный этап – образование тройной связи азот-азот, сопровождающееся вытеснением воды ( Шаг 4 ).

        Будучи довольно нестабильными (и потенциально взрывоопасными), соли диазония обычно не выделяют (относительно безопасно обращаться с тетрафторборатными солями в виде твердых веществ, но это все). После образования их обычно сразу же обрабатывают соответствующим реагентом по пути к желаемому продукту.

        4. Бонусная реакция: Диазосочетание

        Стоит упомянуть еще одну последнюю реакцию солей диазония. Удивительно много красителей в нашем повседневном опыте являются производными диазобензол , основная структура которого представляет собой две молекулы бензола, соединенные двойной связью азот-азот. См., например, эту статью об азокрасителях . Желтый, красный и оранжевый — обычные цвета азокрасителей.

        Азокрасители получают в результате реакции богатого электронами ароматического компонента с солью диазония. Только богатые электронами ароматические соединения являются достаточно хорошими нуклеофилами, чтобы атаковать соли диазония.

        Проверьте себя!

        (Дополнительно) Ссылки и дополнительная литература
        1. Ueber die Ersetzung der Amidgruppe durch Хлор в ароматических веществах
          Bergot.           1884 17 (2), 1633-1635
          Он пытался синтезировать фенилацетилен, соединив хлорид бензолдиазония и ацетилид меди, и вместо этого получил хлорбензол.
        2. Ueber die Ersetzung der Amid-gruppe durch Chlor, Brom und Cyan в ароматических веществах
          Traugott Sandmeyer
          Ber. 1884 17 (2), 2650-2653
          DOI: 10.1002/cber.188401702202
          Зандмейер обобщает реакцию, включив в нее синтез бромбензола и CuCN и CuCN.
        3. Реакция Сандмейера.
          Герберт Х. Ходжсон
          Химические обзоры 1947, 40 (2), 251-277
          DOI : 10.1021/cr60126a003
          Это старый обзор, полезный, если вы хотите найти некоторые оригинальные ссылки на эту химию.
        4. Über flavortische Fluorverbindungen, I.: Ein neues Verfahren zu ihrer Darstellung
          Günther Balz, Günther Schiemann
          Ber. 1927 , 60 (5), 1186-1190
          DOI : 10.1002/cber.19270600539
          . который первым описал реакцию.
        5. The Mechanism of the Sandmeyer and Meerwein Reactions
          Jay K. Kochi
          Journal of the American Chemical Society 1957, 79 (11), 2942-2948
          DOI : 10.1021/ja01568a066
          Kochi был выдающимся физико-химиком-органиком в 20 -м -м веке. В этой статье он исследует механизм реакции Зандмейера, предоставляя дополнительные доказательства того, что она протекает через промежуточный арильный радикал.
        6. Radical reactions of arenediazonium ions: An easy entry into the chemistry of the aryl radical
          Carlo Galli
          Chemical Reviews 1988, 88 (5), 765-792
          DOI : 10.1021/cr00087a004
          This обзор охватывает результаты различных исследований механизма реакции Зандмейера и родственных реакций — предполагается, что они проходят через промежуточные соединения арильных радикалов.
        7. Исследование двухстадийности реакции Зандмейера
          Карло Галли
          Хим. Soc., Perkin Trans. 2 , 1981 , 1459-1461
          DOI : 10.1039/P29810001459
          Роль солей Cu в реакции Зандмейера заключается в передаче электрона промежуточному арильному катиону с образованием арильного радикала. Если это так, то другие соли и соединения металлов (например, ферроцен) должны быть способны восстанавливать соли диазония, и это рассматривается здесь.
        8. Дезаминирование фосфорноватистой кислотой солей диазония в оксиде дейтерия
          Эллиот Р. Александр и Роберт Э. Бердж младший
          Журнал Американского химического общества 1950, 72 (7), 3100-3103
          DOI : 10.1021/ja01163A082 DOI : 10.1021/ja01163A082 . соли с H 3 PO 3 могут показаться бесполезной реакцией, в этой статье показано очень полезное применение – если вы сделаете это в D 2 O, вы сможете получить ipso -дейтерирование!
        9. Простое получение фенолов из ионов диазония путем образования и окисления арильных радикалов солями меди
          Теодор Коэн, Альберт Г. Дитц-младший, и Джейн Р. Мизер
          Журнал органической химии 1977, 42 (12), 2053-2058
          DOI : 10.1021/1043A00 39313A00 3

          A. Во введении к этой статье говорится, что превращение ионов арилдиазония в фенолы просто на бумаге, но не обязательно на практике. Для подавления побочных реакций, таких как азосочетание, требуется высокая кислотность. Использование солей Cu для этой реакции также обеспечивает более чистые реакции, более высокие выходы и упрощенную обработку.
        10. Mechanism of formation of aryl fluorides from arenediazonium fluoborates
          Gardner Swain and Randall J. Rogers
          Journal of the American Chemical Society 1975, 97 (4), 799-800
          DOI : 10.1021 /ja00837a019
          Элегантное кинетическое исследование для определения механизма реакции Бальца-Шимана. Из-за нечувствительности распределения продукта к избытку BF 3 предполагается, что фторбензол образуется путем прямого захвата из BF 4 – интермедиатом Ar + , образующимся при дедиазонировании.

        2000 мм это сколько см: 2000 мм сколько метров — решение и ответ!

        alexxlab / / Разное
        2\).

         

         

         

        Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!

        Запишитесь на бесплатное тестирование знаний!

        Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности

        Наши преподаватели

        Далер Евгеньевич Мануилов

        Репетитор по математике

        Стаж (лет)

        Образование:

        Самаркандский Государственный Университет

        Проведенных занятий:

        Форма обучения:

        Дистанционно (Скайп)

        Репетитор по физике 5-9 класс. На своих уроках постараюсь доступно и ясно изложить сложный материал на основе простых истин и примеров из жизни. Контакт с учеником устанавливаю быстро. Урок провожу в дружественной и непринужденной атмосфере. Не пренебрегая синтез с классическим изложением физики, что позволяет на моих уроках раскрыть полный потенциал ученика.

        Вера Александровна Бондаренко

        Репетитор по математике

        Стаж (лет)

        Образование:

        Ульяновский государственный педагогический университет имени ИН Ульянова

        Проведенных занятий:

        Форма обучения:

        Дистанционно (Скайп)

        Я считаю, что знать русский язык, грамотно писать и говорить на нём – это гражданский долг каждого человека, проживающего в Российской Федерации. Тем самым мы проявляем уважение к языку и сохраняем его для будущих поколений. Беру в работу как начальные, так и средние классы; осуществляю подготовку детей в ВПР, ОГЭ, олимпиадам, проектам; даю консультации. Методы преподавания, которые используются в работе с учеником, направлены на определение целей и задач обучения русскому языку как родному и их результативность.

        Анна Казимировна Пятчиц

        Репетитор по математике

        Стаж (лет)

        Образование:

        Барановичский государственный университет

        Проведенных занятий:

        Форма обучения:

        Дистанционно (Скайп)

        Репетитор по русскому языку для 1-4 классов и по математике для 1-5 классов. Доброжелательна, позитивно настроена, всегда в хорошем настроении с улыбкой на лице. На занятии учитываю психотип ребёнка и его «язык» коммуникаций. Встречаю учеников с хорошим и доброжелательным настроением, настраиваю ребят на отличную тренировку. Проявляю интерес к увлечениям учеников, поддерживаю их достижения. Использую юмор, задания на внимание, игры на скорость. Имею опыт взаимодействия с группами детей разных возрастов. Опыт с детьми более 20 лет

        Похожие статьи

        • Примеры решения уравнений: логарифм с переменным основанием
        • Признак делимости на 19
        • ИВТ (МИФИ)
        • РУДН: Геология
        • ЕГЭ по математике, базовый уровень. Текстовые задачи (вариант 7)
        • 10 способов помириться с другом/подругой
        • Топ 20 бесполезных покупок к школе
        • Как выбрать ребенку коньки и научить кататься

        Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности

        Стандартные и нестандартные размеры межкомнатных дверей Какие бывают? Как измерить?

        ДвериО магазинеВыбор дверей Размеры межкомнатных дверей

        Назад

         

        Перед заказом межкомнатных дверей, всех начинают интересовать технические вопросы. Большая часть этих вопросов связана с размерами. Часто спрашивают, какие бывают стандартные и нестандартные размеры дверей? Проемы каких размеров должны сделать ремонтники? Если проемы готовы, какие двери в них можно поставить?

        По опыту наших клиентов, рабочие, которые делают им ремонт, иногда вообще не думают о том, как потом в эти проемы впишутся двери стандартных размеров. И бывает – они не вписываются. А если заказывать двери нестандартных размеров, то это переплата минимум в 30%. Поэтому, приходится проемы зашивать или расширять, и это в конце ремонта, когда вся чистовая отделка закончена. Что бы избежать этих проблем, рекомендуем заранее ознакомиться с информацией, которую мы собрали в этой статье.

         

        Содержание:
        1. Стандартные и нестандартные размеры межкомнатных дверей
        2. Размер проема для межкомнатных дверей
        3. Как правильно замерить проем для двери
        4. Двери левые или правые как определить
        5. Что сначала устанавливают двери или ламинат
        6. Толщина межкомнатной двери

         

        Стандартные размеры межкомнатных дверей

         

        Стандартные размеры дверных проемов определяются гостами. Эти госты были разработаны еще в советское время, именно по ним, в наших квартирах делали дверные проемы. Сейчас, нас интересуют стандартные размеры по тому, что именно таких размеров двери выпускаются фабриками по стандартной стоимости. Любое отклонение, по высоте или ширине, происходит за доплату. Объясняется это тем, что поточное производство дверей надо останавливать, регулировать оборудование, переналаживать его для выпуска нестандартной продукции.

         

        Большинство фабрик считает стандартными следующие размеры дверных полотен:

          высота: 2000мм.

          ширина: 600, 700, 800, 900мм.

        Есть фабрики, у которых в стандартные размеры включены:

          высота: 1900мм.

          ширина: 550, 600мм.

         

        Двери высотой 1900 используются в ванную и туалет в некоторых сериях домов советской постройки, например, в домах 137 серии.

        Двери шириной до 600мм. используют для установки в ванную и туалет. Двери 700мм. ставят обычно на кухню, 800 и 900мм. в комнаты и вторая входная. В большие по площади гостиные иногда устанавливают двустворчатые двери, у которых 2 полотна по 700 или 800 мм.

        Все размеры, которые отличаются от приведенных выше, считаются нестандартными. Не все фабрики делают двери нестандартных размеров. На тех фабриках, которые их выпускают, этот процесс и условия могут сильно отличаться.

        Чаще всего требуются двери нестандартной высоты: 2100, 2200, 2300мм. Двери до 2300мм. заказать легко, многие фабрики делают такие размеры за доплату от 30% до 50% к стандартной стоимости. Двери выше 2300 практически ни кто не делает, только на маленьких производствах, вручную, под заказ.

        Иногда нужны полотна нестандартной ширины, при стандартной высоте. Это либо очень широкие двери, например 1000мм., либо с каким-то нестандартным размером, например 840мм..  Производителей таких дверей найти сложнее. Но есть фабрики, например, ульяновская фабрика «Варадор», которые делают двери любых размеров (шириной до 1000мм., высотой до 2300мм. ) с шагом в 10мм., и это большая редкость.

         

        Размер проема для межкомнатных дверей

         

        Чтобы рассчитать размер проема, который необходим для нормальной установки дверного блока, надо знать толщину коробки. Коробки, скажем сразу, бывают разные. Производители очень хорошо считают издержки, и никто не будет для легкой щитовой двери делать толстую, массивную коробку. И наоборот, если дверь тяжелая, например из массива дерева, то тонкая коробка просто не выдержит.

        Как рассчитать проем для двери? Для расчета ширины проема надо сложить ширину дверного полотна, прибавить 2 толщины коробки без притвора, прибавить 2 зазора между коробкой и полотном (2-3мм.), прибавить 2 зазора между коробкой и стеной (для нормального запенивания надо оставить минимум 10мм. с каждой стороны).

        Давайте рассчитаем, какой проем нужен для двери 60 см., 70 см., 80 см., если толщина коробки 25мм. Получаем:

          600 + 25*2 + 3*2 +10*2 = 676 мм.

          700 + 25*2 + 3*2 +10*2 = 776 мм.

          800 + 25*2 + 3*2 +10*2 = 876 мм.

         

        Высота проема рассчитывается аналогично, только надо не забыть про нижний зазор между дверным полотном и напольным покрытием, обычно его делают 10мм.. Получается: высота дверного полотна, прибавить толщину коробки, прибавить зазор между коробкой и полотном, прибавить зазор между коробкой и проемом, прибавить нижний зазор между полотном и полом.

         

        Для двери стандартной высоты 2000мм. и коробки толщиной 25мм. получаем:

         

        Рассчитывать дверные проемы надо на этапе проектирования ремонта. Но как мы говорили ранее, обычно все получается наоборот – есть уже готовый проем, в который надо вписать дверь. Чтобы произвести расчеты в таком случае, необходимо правильно измерить дверной проем.

         

        Как правильно замерить проем для двери?

         

        Чтобы понять какого размера дверь встанет в тот или иной проем, необходимо грамотно его измерить.

        Проемы обычно никто не выравнивает и они получаются кривые. Кривизна может быть любой. Бывают непараллельные боковины, он может быть в форме бочонка или песочных часов. Верхняя часть может быть не горизонтальной. Но вписывать, в кривой проем, мы будем прямоугольник с идеальной геометрией и по уровню. Поэтому наша задача найти самые узкие места, и измерить их ширину и высоту. Проще всего это делать с помощью лазерного уровня.

        Надо не забыть про толщину стен. Стандартная глубина коробки 70мм. Это значит, что такая коробка может перекрыть стену толщиной в 70мм. Если погонаж телескопический, то можно за счет Г-образных выступов на наличниках закрыть еще 20мм. Но стены обычно толще. Поэтому необходимо замерить и толщину стен проема, чтобы рассчитать ширину доборного элемента. Добор – это погонажный элемент, который заказывают вместе с дверями. На месте, мастер его обрезает вдоль, до нужной ширины и стыкует с коробкой. Таким образом, ширина коробки добирается до толщины стены.

         

        Важно! Уделите проемам достаточно внимания на стадии ремонта. Пропишите в условиях, какого размера они должны быть.

         

        Есть еще нюансы, которые иногда приходится учитывать. Например, кривизну стен или неравномерность толщины стены. Часто проемы делают слишком близко к углу комнаты. Если это никак не компенсировать расположением коробки в проеме, приходится обрезать наличники вдоль, чтобы сделать их уже. Бывают проемы такой ширины, что вписав туда стандартную дверь, никак не перекрыть наличниками расстояние от коробки до начала обоев, и это тоже надо учитывать.

        После того, как все размеры сняты, необходимо сделать расчет. Расчет включает в себя количество коробок в стойках, наличников в штуках, количество и ширину доборных элементов, ширину и высоту дверных полотен, которые будут заказаны на производстве. В 60% случаев такая продукция делается под заказ. Это значит, что поменять что-то, если не подошло из-за ошибки в расчетах, не получится.

        Попробуем рассчитать ширину дверного полотна, зная размеры проема. В этом случае все делаем наоборот: от ширины проема отнимаем зазоры, толщину коробки и получаем ширину, например 785мм. Если заказать полотно шириной 700мм. получатся зазоры по 52.5 мм. с каждой стороны, и это в самых узких местах. Это многовато, и наличник, например, шириной 60мм. может не закрыть. Если заказать полотно 800 мм., с каждой стороны останется по 2.5 мм., этого может быть недостаточно для нормального крепления коробки. Как лучше поступить в таком случае? Для того, чтобы ответить на этот вопрос, мастер установщик должен на месте оценить ситуацию, а потом совместно со специалистом по дверям подобрать варианты из ассортимента.

        Как вы поняли, нюансов в замере проемов и последующем расчете много. Даже если вам все понятно и кажется, что проемы идеальные, мы рекомендуем вызывать замерщика из организации, где вы будете заказывать двери. Это снимет с вас всю ответственность. А выезд мастера на замер, при заказе установки, обычно получается бесплатным.

         

        Важно! Любая ошибка на стадии замера проемов приводит к ошибкам в расчетах. А ошибки приводят к дополнительным денежным тратам на перезаказ и обмен готовых изделий.

         

        По тому, как сильно отличаются зазоры и толщина пены вверху и внизу, можно понять насколько кривой проем. Ширины наличников едва хватило чтобы закрыть верхнюю часть.

        Крепление короба производилось под петлями и под ответной частью защелки. Это, так называемый, скрытый монтаж, когда ни одного крепежного элемента не видно. На фото только предварительное запенивание, окончательное производилось после монтажа доборников.

        Если вам нужно подобрать и установить межкомнатные двери в Санкт-Петербурге обращайтесь, мы предоставляем гарантию на нашу установку 5 лет.

         

        Двери левые или правые как определить?

         

        Двери в комнаты обычно открываются вовнутрь помещения. Двери в ванную и туалет открываются в коридор. Если возле проема есть перпендикулярная стена, то дверь в открытом положении должна располагаться вдоль этой стены. То, как будут открываться двери необходимо учесть в момент замера проемов, т.к. от этого зависит какие петли надо заказать.

        Если дверь открывается на вас, а петли с правой стороны дверного полотна – петли правые, если слева – петли левые.

         

        Что сначала устанавливают двери или ламинат?

         

        Что сначала: двери или ламинат, двери или плитка? Такие вопросы можно услышать довольно часто. Ответим сразу, все отделочные работы должны быть закончены к моменту установки межкомнатных дверей. Двери устанавливаются в самую последнюю очередь.

        Можно ли сделать замер проемов, если нет ламината или плитки, чтобы потом не ждать, пока двери будут делать под заказ несколько недель?

        Ламинат или любое другое напольное покрытие поднимет уровень пола. Соответственно, высота проема уменьшится. Из предыдущей части статьи мы знаем, что расчет ведется с точностью до миллиметров. На сколько поднимется уровень пола с точностью до миллиметров? Какой толщины будет напольное покрытие, какая толщина будет у подложки и как она сожмется? Какой толщины будет плитка вместе с клеем? Мы не рекомендуем гадать, лучше измерять полностью готовый проем.

         

        Толщина межкомнатной двери

         

        Стандартов толщины дверных полотен нет. Толщина недорогих ламинированных дверей, с отделкой из экошпона или пленок ПВХ, обычно в пределах 35 — 37 мм. Двери подороже, например шпонированные или из массива дерева, могут быть от 37 до 42 мм. Толще 42 мм. межкомнатные двери встречаются редко, обычно это дорогой массив или двери, изготовленные по индивидуальному проекту. Есть фабрики, которые могут сделать дверное полотно и коробку к нему, толщиной, например, 50 мм. Естественно, такие двери делаются под заказ и цена будет соответствующей.

        • 11 июля 2022 Минимальный заказ

          Просим обратить Ваше внимание, не принимаются заказы на один дверной блок. Минимальный заказ — три двери в комплекте.

        • 01 июля 2022 Повышение цен!

          В связи с проведением работ на сайте просим уточнять действующие цены на двери и фурнитуру у менеджеров. Цены на сайте могут быть не актуальны.

        • 28 июня 2022 Наши СКИДКИ

          Смотрите в последней редакции: новая скидочная программа магазина, скидки от производителей Варадор, Альберо, Turen Becker, Задор.

        • Все новости

        Как изменение размера влияет на разрешение изображения и размеры в пикселях в Photoshop?

        С помощью Photoshop изменить размер фотографии и откадрировать ее можно несколькими способами. Для достижения наилучших результатов при кадрировании или изменении размера изображений следует понимать концепции, лежащие в основе методов изменения размера, и то, как изменение размера влияет на кадрирование.

        Инструкции по изменению размера фотографии см. в статье Размер и разрешение изображения.

        Инструкции по кадрированию фотографий см. в статье Кадрирование и выравнивание фотографий.

        Размер изображения при просмотре на экране отличается от его размера при печати. Если вы представляете эти различия, вы сможете лучше понять, какие настройки следует изменить при изменении размера изображения.

        Размер экрана

        Разрешение экрана монитора — это количество пикселей, которое он может отобразить. Например, монитор с разрешением экрана 640 x 480 пикселей отображает 640 пикселей в ширину и 480 пикселей в высоту. Можно использовать несколько различных разрешений экрана, а физический размер экрана монитора обычно определяет доступные разрешения. Например, большие мониторы обычно отображают более высокое разрешение, чем маленькие, поскольку они имеют больше пикселей.

        Чтобы узнать разрешение экрана, выберите Пуск > Панель управления > Экран > Свойства и просмотрите разрешение экрана (Windows) или выберите Параметры системы > Экраны и посмотрите список Разрешения (macOS).

        Размер изображения на экране

        Когда изображения появляются на экране, они имеют фиксированный размер в пикселях. Разрешение экрана определяет размер изображения на экране. Например, монитор с разрешением 640 x 480 отображает меньше пикселей, чем монитор с разрешением 1024 x 768. Поэтому размер каждого пикселя, отображаемого на экране с разрешением 640 x 480, больше, чем размер пикселя, отображаемого на экране с разрешением 1024 x 768.

        Изображение размером 100 x 100 пикселей занимает примерно одну шестую площади экрана с разрешением 640 x 480 и всего одну десятую площади экрана с разрешением 1024 x 768. Поэтому на экране с разрешением 1024 x 768 пикселей изображение выглядит меньше, чем на экране с разрешением 640 x 480 пикселей.

        Размер изображения при печати

        Другие значения, используемые для изменения размера изображений — физический размер изображения при печати и разрешение — не применятся до печати изображения. Тогда физический размер изображения, разрешение и размеры в пикселях определяют объем данных в изображении и его качество при печати. Как правило, более высокое разрешение изображения позволяет выполнить печать в более высоком качестве. Дополнительную информацию о разрешении и физическом размере см. в следующих разделах.

        Диалоговое окно «Размер изображения»

        При использовании диалогового окна Размер изображения для изменения размера изображения (выберите Изображение > Размер изображения) могут измениться четыре параметра изображения:

        • Размеры в пикселях: ширина и высота изображения.
        • Размер изображения, когда оно открыто в Photoshop: это значение появляется в верхней части диалогового окна.
        • Размер документа: физический размер изображения при печати, включая ширину и высоту.
        • Разрешение изображения при печати: это значение отображается в пикселях на дюйм или пикселях на сантиметр.

        Photoshop вычисляет физический размер, разрешение и размеры изображения в пикселях следующим образом:

        • Физический размер = разрешения x размеры в пикселях
        • Разрешение = физический размер / размеры в пикселях
        • Размеры в пикселях = физический размер / разрешение

        Диалоговое окно Размер изображения позволяет изменить размер изображения двумя способами. Можно увеличить или уменьшить объем данных в изображении (ресамплинг). Также можно сохранить тот же объем данных в изображении (изменение размера без ресамплинга). При ресамплинге качество изображения может ухудшиться в некоторой степени. Возможно, придется выполнить дополнительную работу, например, использовать фильтр Контурная резкость, чтобы увеличить резкость изображения и компенсировать ресамплинг.

        Совет: для сброса диалогового окна Изменить размер изображения к его исходному состоянию нажмите клавишу Alt (Windows) или Option (macOS). При нажатии этих клавиш кнопка «Отмена» изменяется на кнопку «Сброс».

        При изменении размера и ресамплинге изображения изменяется объем данных в этом файле. Для ресамплинга изображения убедитесь, что выбран параметр Ресамплинг в нижней части диалогового окна Размер изображения. По умолчанию ресамплинг включен.

        Ресамплинг изменяет общее количество пикселей в изображении, которые отображаются как ширина и высота в пикселях в диалоговом окне Размер изображения. При увеличении количества пикселей в этой части диалогового окна (повышение разрешения) приложение добавляет данные к изображению. При уменьшении количества пикселей (понижение разрешения) приложение удаляет данные. При каждом удалении или добавлении данных к изображению качество изображения ухудшается в некоторой степени. Удаление данных из изображения обычно является предпочтительным по отношению к добавлению данных. Это связано с тем, что при повышении разрешения Photoshop приходится «угадывать», какие пиксели необходимо добавить. Эта процедура более сложна, чем «угадывание» пикселей для удаления при понижении разрешения. Для получения наилучших результатов рекомендуется брать для работы в Photoshop изображения с разрешением, необходимым для вывода. Иногда желаемые результаты можно получить изменением размера изображения без ресамплинга. Однако, если вы делаете ресамплинг изображения, делайте его только один раз.

        При включении параметра Ресамплинг можно изменить любое значение в диалоговом окне Размер изображения: размеры в пикселях, физический размер или разрешение. Изменение одного значения влияет на другие. Размеры в пикселях изменяются в любом случае.

        • Изменение размеров в пикселях влияет на физический размер, но не на разрешение.
        • Изменение разрешения влияет на размеры в пикселях, но не на физический размер.
        • Изменение физического размера влияет на размеры в пикселях, но не на разрешение.

        Вы не можете установить размер файла. Он изменяется при изменении общего объема данных в изображении (размер в пикселях). Обратите внимание на значение «Размер файла», прежде чем изменить любые другие значения в диалоговом окне. Информация о размере файла поможет понять, сколько данных удаляется или добавляется к изображению при ресамплинге. Например, если размер файла меняется с 250 кБ на 500 кБ, к изображению добавляется вдвое больше данных, что может привести к ухудшению изображения. Такие изображения могут выглядеть размытыми, неровными или зернистым.

        При изменении размера изображения без ресамплинга изменяется размер изображения без изменения объема данных в нем. Изменение размера без ресамплинга изменяет физический размер изображения без изменения размеров изображения в пикселях. Данные не добавляются и не удаляются из изображения. При снятии флажка или деактивации параметра Ресамплинг поля размеров в пикселях недоступны. Два значения, которые можно изменить — это физический размер (ширина и высота в размере документа) или разрешение (пикселей/дюйм). При изменении размера без ресамплинга можно установить физический размер или разрешение изображения. Чтобы сохранить общее количество пикселей в изображении, Photoshop компенсирует измененное значение увеличением или уменьшением другого значения. Например, при установке физического размера, Photoshop меняет разрешение.

        Если размеры в пикселях являются постоянными, при уменьшении физического размера изображения соответственно увеличивается разрешение. При уменьшении физического размера изображения на половину, разрешение увеличивается вдвое. В то же самое пространство помещается в два раза больше пикселей. При увеличении размера изображения вдвое, разрешение уменьшается на половину, поскольку пиксели теперь находятся в два раза дальше друг от друга для заполнения того же физического размера.

        Например, изображение размером 400 x 400 пикселей имеет физический размер 4 x 4 дюйма и разрешение 100 пикселей на дюйм (ppi). Для уменьшения физического размера изображения на половину без ресамплинга можно задать физический размер 2 x 2 дюйма. Photoshop увеличит разрешение до 200 пикселей на дюйм. Изменение размера изображения таким образом оставляет общее количество пикселей неизменным (200 пикселей на дюйм x 2 x 2 дюйма = 400 x 400 пикселей). При увеличении физического размера вдвое (до 8 x 8 дюймов) разрешение уменьшается до 50 пикселей на дюйм. Добавление дюймов к размеру изображения означает, что теперь в дюйме может быть вдове меньше пикселей. При изменении разрешения изображения, физический размер также изменяется.

        Важно. Размеры в пикселях регулируют объем данных, а разрешение и физический размер используются только для печати.

        Примечание. Пиксели на дюйм (ppi) — это количество пикселей в каждом дюйме изображения. Количество точек на дюйм (dpi) относится только к принтерам и отличается в зависимости от принтера. Как правило, оно составляет от 2,5 до 3 точек краски на пиксель. Например, принтеру со значением 600 точек на дюйм необходимо изображение со значением от 150 до 300 пикселей на дюйм для наилучшего качества печати.

        Дополнительные сведения о параметрах в диалоговом окне Размер изображения см. в разделе Размеры в пикселях и разрешение печатного изображения в справке Photoshop.

        При использовании инструмента «Кадрирование» для изменения размера изображения размеры изображения в пикселях и размер файла изменяются, но ресамплинг изображения не выполняется. При использовании инструмента «Кадрирование» размеры в пикселях и разрешение включают больше пикселей на дюйм на основе размера области кадрирования. Однако Photoshop специально не добавляет и не удаляет данные из изображения.

        При кадрировании изображения данные удаляются или добавляются из исходного изображения или к нему, чтобы создать другое изображение. Поскольку данные удаляются или добавляются относительно исходного изображения, ресамплинг теряет свое значение. Это связано с тем, что количество пикселей на дюйм может отличаться в зависимости от количества пикселей в области фрагмента кадрирования. Если количество пикселей в области кадрирования позволяет, Photoshop пытается сохранить разрешение исходного изображения. Этот метод считается кадрированием без ресамплинга. Однако, если количество пикселей выбрано неточно, размеры в пикселях и размер файла изменяются в новом изображении.

        Параметры инструмента «Кадрирование»

        Набор параметров, доступных на панели параметров инструмента «Кадрирование» изменится после выбора области. При первом выборе инструмента «Кадрирование» можно задать значения высоты и ширины, а также разрешение. Высоту и ширину можно измерять в дюймах, сантиметрах, миллиметрах, точках и пайках. Введите единицу измерения или ее сокращение после числа в поле значения. Например, 100 пикселей, 1 дюйм, 1 д, 10 см, 200 мм, 100 точек или 100 паек.Если не указать единицы измерения ширины и высоты на панели кадрирования, по умолчанию используются дюймы.

        Можно также установить значение разрешения кадрированного изображения в поле Разрешение. Выберите пиксели/дюйм или пиксели/см во всплывающем меню.

        Дополнительные сведения о параметрах инструмента «Кадрирование» см. в разделе Кадрирование и выравнивание изображений.

        Изменение только размера в дюймах

        Если изменить физический размер изображения в дюймах в параметрах инструмента «Кадрирование» и не изменять разрешение, размеры в пикселях изменяются. Размеры изменяются в зависимости от пропорций количества пикселей в области кадрирования к размеру в пикселях исходного изображения. Разрешение изменяется, чтобы добавить дополнительные пиксели в каждый дюйм изображения на основе исходного размера изображения.

        Примечание. Параметры исходного изображения, используемого в примерах ниже: 4 x 4 дюйма, 100 пикселей на дюйм, 400 x 400 пикселей, 468,8 кБ.

        Размер в дюймах
        (задает пользователь)

        Разрешение
        (изменяется приложением Photoshop)

        Размеры в пикселях
        (размер заданного пользователем фрагмента кадрирования)

        Размер файла

        2 x 2 дюйма

        104 пикселя на дюйм
        (исходное разрешение = 100 пикселей на дюйм)

        208 x 208 пикселей
        (исходное = 400 x 400 пикселей)

        125,8 КБ
        (исходный размер 468,8 КБ)

        В этом примере Photoshop уменьшает изображение на половину физического размера (с квадрата со стороной 4 дюйма до квадрата со стороной 2 дюйма). Photoshop также уменьшает размеры в пикселях на 50%. Исходное разрешение сохраняется (100 пикселей на дюйм), но при этом увеличивается, чтобы компенсировать дополнительные пиксели (8 пикселей на дюйм), добавленные к прямоугольнику выделения.

        Изменение размера в дюймах и разрешения

        При установке физического размера изображения в дюймах в параметрах инструмента «Кадрирование» и изменении количества пикселей на дюйм размеры в пикселях изменяются. Во всем документе результирующего изображения будет больше или меньше пикселей. Задается размер в дюймах и количество пикселей в каждом из этих дюймов. Photoshop удаляет или добавляет данные для соответствия количества пикселей в каждом дюйме.

        Примечание. Параметры исходного изображения, используемого в примерах ниже: 4 x 4 дюйма, 100 пикселей на дюйм, 400 x 400 пикселей, 468,8 кБ.

        Размер в дюймах
        (задает пользователь)

        Разрешение
        (задает пользователь)

        Размеры в пикселях
        (изменяются)

        Размер файла

        2 x 2 дюйма

        200 ppi

        400 x 400 пикселей

        468,8 кБ

        2 x 2 дюйма

        300 ppi

        600 x 600 пикселей

        1,03 МБ

        2 x 2 дюйма

        50 ppi

        100 x 100 пикселей

        29,3 кБ

        В первом примере физический размер уменьшен в два раза, но это компенсировано удвоением разрешения. Поэтому размеры в пикселях и размер файла остались прежними.

        Во втором примере физический размер уменьшен в два раза, а разрешение увеличено. Поэтому размеры в пикселях увеличены, чтобы вместить дополнительного количество пикселей на дюйм. Также увеличен размер файла.

        В третьем примере физический размер уменьшен в два раза, разрешение также уменьшено (ppi). Поэтому размеры в пикселях уменьшены, поскольку в изображении стало меньше пикселей. Размер файла также уменьшен.

        Изменение только размера в пикселях

        Если указать размер в пикселях, но не указывать разрешение, разрешение стабилизируется до того же значения, что было у исходного изображения. Устанавливается новый физический размер, чтобы вместить указанное количество пикселей в изображении и на дюйм. Размер файла изменяется, поскольку изменяются размеры в пикселях, что позволяет Photoshop стабилизировать количество пикселей на дюйм.

        Примечание. Параметры исходного изображения, используемого в примерах ниже: 4 x 4 дюйма, 100 пикселей на дюйм, 400 x 400 пикселей, 468,8 кБ.

        Размер в дюймах
        (изменяется)

        Разрешение
        (изменяется)

        Размеры в пикселях
        (задает пользователь)

        Размер файла

        2 x 2 дюйма

        100 ppi

        200 x 200 пикселей

        117,2 кБ

        3 x 3 дюйма

        100 ppi

        300 x 300 пикселей

        263,7 кБ

        6 x 6 дюймов

        100 ppi

        600 x 600 пикселей

        1,03 МБ

        В этих примерах разрешение осталось без изменений, но размеры в пикселях изменились. Физический размер изменяется, чтобы соответствовать указанному количеству пикселей на дюйм (размеры в пикселях).

        Изменение размера в пикселях и разрешения

        При установке размера в пикселях и разрешения Photoshop создает другой физический размер. Изображение содержит указанное количество пикселей в изображении и на дюйм. Размер файла изменяется, поскольку изменено общее количество пикселей в изображении и количестве пикселов на дюйм.

        Примечание. Параметры исходного изображения, используемого в примерах ниже: 4 x 4 дюйма, 100 пикселей на дюйм, 400 x 400 пикселей, 468,8 кБ.

        Размер в дюймах
        (изменяется)

        Разрешение
        (изменяется)

        Размеры в пикселях
        (задает пользователь)

        Размер файла

        1 x 1 дюйм

        600 ppi

        600 x 600 пикселей

        1,03 МБ

        2 x 2 дюйма

        300 ppi

        600 x 600 пикселей

        1,03 МБ

        0,667 x 0,667 дюйма

        300 ppi

        200 x 200 пикселей

        117,2 кБ

        В этих примерах изменены как размеры в пикселях, так и разрешение. Физический размер изменяется, чтобы соответствовать общему количеству пикселей и количеству пикселей на дюйм (размеры в пикселях и разрешение).

        Изменение только разрешения

        При изменении только разрешения в параметрах инструмента «Кадрирование» размер изображения зависит от количества пикселей в области кадрирования.

        Совет: обратите внимание на панель «Информация», чтобы видеть, какое количество пикселей входит в область кадрирования.

        Примечание. Параметры исходного изображения, используемого в примерах ниже: 4 x 4 дюйма, 100 пикселей на дюйм, 400 x 400 пикселей, 468,8 КБ.

        Размер в дюймах
        (результат)

        Разрешение
        (задает пользователь)

        Размеры в пикселях
        (результат)

        Размер кадрирования
        (задает пользователь)

        Размер файла

        0,767 x 0,767 дюйма

        300 ppi

        230 x 230 пикселей

        2,3 x 2,3 дюйма

        115 кБ

        1 x 1 дюйм

        300 ppi

        300 x 300 пикселей

        3 x 3 дюйма

        263,7 кБ

        0,75 x 0,75 дюйма

        400 ppi

        300 x 300 пикселей

        3 x 3 дюйма

        263,7 кБ

        1 x 1 дюйм

        200 ppi

        200 x 200 пикселей

        2 x 2 дюйма

        117,2 кБ

        0,5 x 0,5 дюйма

        200 ppi

        100 x 100 пикселей

        1 x 1 дюйм

        29,3 кБ

        1,5 x 1,5 дюйма

        200 ppi

        300 x 300 пикселей

        3 x 3 дюйма

        263,7 кБ

        В этих примерах Photoshop использует размер фрагмента кадрирования и разрешение, указанные пользователем, для изменения размера изображения. Физический размер нового изображения и размеры в дюймах соответствуют количеству пикселей в заданном фрагменте кадрирования и новому разрешению.

        Похожие темы

        • Ключевая концепция: разрешение
        • Ключевая концепция: ресамплинг
        • Кадрирование и выравнивание фотографий
        • Бесплатное изменение размера изображений в Интернете

        Вход в учетную запись

        Войти

        Управление учетной записью

        Размеры межкомнатных дверей, размеры коробки: ширина, высота, толщина дверного проёма

         

        Жилище с дверными проёмами, имеющими размер межкомнатной двери стандарт – это в некотором роде приятный бонус, так как подобрать модель по вкусу будет несложно. В магазинах и на рынке представлено многообразие вариантов полотна стандартных размеров из древесно-стружечных, древесно-волоконных плит. А также разнообразие ассортимента обеспечивается межкомнатными конструкциями, материалом для производства которых послужил клееный или цельный массив дерева. В случае если дом частный и строился по индивидуальным эскизам, изготавливаются изделия на заказ.

         

        Какие стандарты являются общепринятыми


        Стандартные размеры межкомнатной двери составляют 200 сантиметров в высоту и 80 (70 или 60) сантиметров в ширину. Некоторые компании наладили производство межкомнатных створок, размер которых слегка отличается от параметров стандартного полотна: 190 сантиметров в высоту и 55 сантиметров в ширину. Кроме высоты и ширины значимой является ширина дверной коробки, которая может варьировать от пятнадцати до сорока пяти миллиметров.
        Стандартные размеры межкомнатных дверей упрощают монтаж, так как большинство отверстий в стене для установки межкомнатных конструкций в квартирах делались в соответствии с ГОСТом и имеют схожие параметры.

        Что является стандартом


        Размер стандартного межкомнатного проема в стене определяется в соответствии с вышеописанными параметрами, если ими пренебречь, то велика вероятность, что коробка будет слишком большой или напротив – маленькой. Увеличение размеров проема повлечёт за собой дополнительные траты, а имеющиеся коммуникации или перегородки из гипсокартона с металлическим каркасом дополнительно усложнят процесс.


        Размеры отверстия в стене находятся в прямой зависимости от того, какие размеры имеет межкомнатная створка:

        1. Полотно шириной 550 мм и высотой 1900 мм – оно идеально подойдёт для проема высотой 1950–2000 мм и шириной 650 мм.
        2. Проему высотой 1950 – 2000 мм и шириной 640 – 700 мм подойдут габариты полотна 600 (ширина) и 1900 (высота) миллиметров.<.li>
        3. Дверь высотой 2000 мм и шириной 600 мм идеально войдёт в проём шириной 640–700 миллиметров и высотой 2050–2100 мм.


        Даже если размеры отверстия в стене стандартные и выполнены по ГОСТу, замер каждого из них производится индивидуально.

         

        Как производится замер

        Правильное измерение параметров дверного проема отвечает следующим требованиям:

        • Высота измеряется от пола, на котором уже имеется отделочное покрытие.
        • Ширина меряется от края одной до края другой стенки.
        • Толщина стены определяется с учётом положенной на неё керамической плитки. Стенки в ванной тоньше, чем в других комнатах на четыре или пять сантиметров.


        Между стенкой и дверной коробкой должно оставаться расстояние приблизительно от десяти до пятнадцати миллиметров. Между коробом и самой межкомнатной створкой оставляется промежуток 0,3 сантиметра (3 мм). Ширина дверного бруса составляет двадцать пять миллиметров, что также необходимо учитывать. Чтобы размеры были точными нужно умножить эти параметры на два, потому что у двери имеется левый и правый край.


        Параметры выбора


        Модели межкомнатных створок представлены четырьмя вариантами в соответствии с конструкцией: комбинированные, глухие, одно- и двухдверные. По способу открывания встречаются распашные, маятниковые и раздвижные. Форма изделий бывает закруглённая, прямоугольная и арочная. При выборе учитывается сколько нужно створок установить, размер и форма отверстия в стене для монтажа, материал из которого производится изготовление. 
        Размер проёма более 90 сантиметров предполагает установку двухдверной модели, так как однодверная в открытом виде займёт много места и может перекрыть проход.


        Система открывания подбирается в соответствии с планировкой квартиры. При этом учитывается:

        • Размер комнаты.
        • Наличие смежных комнат и расстояние между ними.


        Чтобы верно подобрать межкомнатную конструкцию, нужно принимать во внимание внешний вид, соответствие общей концепции дизайнерского решения, назначение комнаты, цветовую гамму, надежность изделия, имеющиеся комплектующие, производителя, материал, из которого изделие изготовлено, его цену.

        Преимущества STATUS:

        Уважение и забота о покупателе

        Европейское качество Чтобы обеспечить высокое качество и безопасность наших дверей, мы используем импортные комплектующие и материалы: экошпон производства Германии и Италии, клей из Германии, интерьерное стекло из Бельгии. Подробнее

        Сертифицированные материалы При изготовлении продукции используются только те изделия, которые прошли сертификацию. Подробнее

        Экологичность В производстве дверей применяется экошпон на основе полипропилена. Этот материал имеет высокий профиль безопасности и используется также в трубопроводах для питьевой воды. Подробнее

        Окутка на 360° Благодаря использованию экошпона доступна технология полной окутки изделия. Это повышает прочность двери, устойчивость к механическим повреждениям и воздействию влаги, исключает возможность отслаивания материала на торцах. Подробнее

        Долгосрочная гарантия
        Мы уверены в надежности и долговечности нашей продукции, поэтому предоставляем на двери гарантию сроком на 5 лет. А также выдаем сертификат качества с контактами сервисной службы. Подробнее

        Стойкость к химическим средствам Двери бренда STATUS легко чистить с использованием привычных моющих средств. Они устойчивы ко многим химическим соединениям. Подробнее

        Ремонтопригодность Мы используем принцип взаимозаменяемости деталей, поэтому испорченную часть двери легко заменить даже в домашних условиях.Подробнее

        Соответствие требованиям Межкомнатные двери и перегородки собираются вручную и проходят строгий контроль качества. Подробнее

        Стабильность цвета Используемая технология производства и качественные материалы позволяют добиться стабильности цвета и структуры экошпона в разных партиях дверей. Подробнее

             

         

        Чтобы купить понравившиеся двери в Москве и других городах России, позвоните по контактному телефону.

         

        Премиальные качество и безопасность

        Status Life

        10.09.2022, суббота

        АКЦИЯ! 4+1=4 Пятая дверь в подарок!

        Выберите 5 дверей TM STATUS  и получите одно из полотен в подарок!

        Подробнее

        13.07.2022, среда

        Акция ЖАРКИЕ НЕДЕЛИ!

        С 11 по 25 июля, получите скидку до 20%!

        Подробнее

        17.02.2022, четверг

        Обновление выставки на Рябиновой улице в Москве

        Здесь Вы сможете увидеть наш новый цвет — СЕРЕБРО!

        Подробнее

        Металл листовой — сколько весит 1 металлический лист, 1 м2, предельные отклонения

        ГлавнаяСтатьиТеоретический вес стального листа и предельные отклонения

        Статьи

        Цены на металлический лист

        • Горячекатаный
        • Рифленый
        • Оцинкованный
        • Профильный
        • Холоднокатаный
        • Просечно-вытяжной
        • Рулон оцинкованный
        • Рулон холоднокатаный

        Теоретическая масса металлического листа

        Зная стоимость тонны, легко подсчитать цену 1 металлического листа. Для этого необходимо знать вес единицы продукции. В таблице ниже приводится теоретический вес для листов толщиной 0,5 — 60 мм наиболее популярного и востребованного раскроя — 1250х2500, 1500х6000 и 2000х6000 мм (в зависимости от толщины металла).

        Следует учесть, что данной таблицей можно воспользоваться для определения приблизительной стоимости металлического листа, так как вес проката определяется для стандартной плотности стали 7,85 кг/м3 и может незначительно отличаться в зависимости от марки стали и технических условий завода — изготовителя.

        Толщина листа Вес 1 м2 Вес 1 листа, кг Толщина листа Вес 1 м2 Вес 1 листа, кг
        мм кг 1250 x 2500 мм 1500 x 6000 мм мм кг 1250 x 2500 мм 1500 x 6000 мм
        0,5 3,93 12,28 - 5,0 39,3 353,25 471,00
        0,55 4,32 13,50 - 6,0 47,1 423,90 565,20
        0,6 4,72 14,75 - 7,0 55,0 494,55 659,40
        0. 7 5,50 17,19 - 8,0 62,8 565,20 753,60
        0,8 6,28 19,63 - 9,0 70,7 635,85 847,80
        0,9 7,06 22,06 - 10,0 78,5 706,50 942,00
        1,0 7,85 24,53 - 12,0 94,2 847,80 1130,4
        1,2 9,49 29,66 - 14,0 109,9 989,10 1318,8
        1,4 10,99 34,34 - 16,0 125,9 1133,1 1510,8
        1,5 11,77 36,78 - 18,0 141,3 1271,7 1695,6
        1,7 13,34 41,69 - 20,0 157,0 1413,0 1884,0
        1,8 14,13 44,16 - 22,0 172,7 1554,3 2072,4
        1,9 14,91 46,59 - 25,0 196,3 1766,3 2355,0
        2,0 15,70 49,06 - 30,0 235,5 2119,5 2826,0
        2,5 19,62 61,31 - 40,0 314,0 2826,0 3768,0
        3,0 23,55 73,59 211,95 50,0 392,5 3532,5 4710,0
        4,0 31,04 97,00 279,36 60,0 471,0 4239,0 5652,0

        Предельные отклонения при производстве листового металла

        Любой листовой металл выполняется с размерными отклонениями по длине, ширине, толщине, величина которых зависит от прокатного оборудования. Для горячекатаной продукции по ГОСТ 19903, произведенной в листах, существуют следующие предельные отклонения:

        • по ширине составляет +10 мм (для проката с обрезной кромкой) или + 20 мм (для проката с необрезной кромкой)
        • по длине может варьироваться от +10 (при длине листов до 1500 мм) и до +15 мм (при длине листов свыше 1500 мм)

        Кроме того, величины допусков в размерах металлических листов зависят от:

        • точности прокатки (повышенная, нормальная точность)
        • назначения проката (прокат для авиационной промышленности допускается производить с минусовыми допусками)

        Продажа металла с учетом возможных допусков

        Изменения размерных параметров на величину предельных отклонений сказывается на увеличении веса единицы проката. В результате после взвешивания и при отгрузке продукции цена может незначительно увеличиться по сравнению с теоретически рассчитанной величиной.

        APEX METAL продает листовой прокат не только в рулонах и листах стандартного раскроя, но оказывает услугу плазменной, газовой, лазерной резки, продольно -поперечной рубки. Стоимость листового металла зависит от марки стали (качественные стали, легированные стали или углеродистые стали обыкновенного качества), способа обработки поверхности и объема закупаемой продукции.


        Резка листа по чертежу

        Продольно — поперечная резка листовой стали по индивидуальным проектам с использованием лазерной, плазменной и газовой установки .

        Рубка листа в размер

        Цены на рубку металлических листов из стали 3 сп/пс, 09Г2С толщиной от 1 мм до 160 мм при помощи специализированной гильотины.

        Форматы А1, A2, A0 (1189 х 841 мм), метрические (ISO), форматы А1, А2, А0, JIS (B1, B2, B3), Дюймовые архитектурные ARCH, инженерные ANSI, DIN, Чему равны размеры формата А1?

        Форматы бумаги для печати и форматы оригиналов для сканирования

        В данном разделе приведены все форматы размеры бумаги и форматы размеры оригиналов, поддерживаемые инженерными системами, плоттерами, сканерами, копировальными аппаратами и принтерами, предлагаемыми компанией Jetcom.

        • Метрические форматы и кратные метрические форматы
        • Инженерные системы Seiko LP-1020
        • Инженерные системы MPW5100 / 7140
        • Струйный плоттер Seiko IPE-3020
        • Сканеры Graphtec IS 210 /CS 510/610 CSX300

        Метрические форматы и кратные метрические форматы

        Метрические форматы
        Кратные метрические форматы
        Формат А0 = 1189 х 841 мм А0 х 2 = 1189 х 1682 мм А0 х 3 = 1189 х 2523 мм
        Формат А1 = 841 х 594 мм А1 х 3 = 841 х 1782 мм А1 х 4 = 841 х 2376 мм
        Формат А2 = 594 х 420 мм А2 х 3 = 594 х 1261 мм А2 х 4 = 594 х 1682 мм А2 х 5 = 594 х 2102 мм
        Формат А3 = 420 х 297 мм А3 х 3 = 420 х 891 мм А3 х 4 = 420 х 1189 мм А3 х 5 = 420 х 1486 мм
        А3 х 6 = 420 х 1783 мм А3 х 7 = 420 х 2080 мм
        Формат А4 = 297 х 210 мм А4 х 3 = 297 х 610 мм А4 х 4 = 297 х 841 мм А4 х 5 = 297 х 1051 мм
        А4 х 6 = 297 х 1261 мм А4 х 7 = 297 х 1471 мм А4 х 8 = 297 х 1682 мм
        А4 х 9 = 297 х 1892 мм
        Формат А5 = 210 х 148 мм
        Формат А6 = 148 х 105 мм
        Формат А7 = 105 х 74 мм

        Инженерные системы Seiko LP-1020
        Форматы бумаги для печати
        А0 1189 x 841 мм ANSI E 44 x 34″
        А1 841 х 594 мм ANSI D 34 x 22″
        А2 594 х 420 мм ANSI C 22 x 17″
        А3 420 х 297 мм ANSI B 17 x 11″
        А4 297 х 210 мм ANSI A 11 x 8,5″
        MAP B1 1000 х 700 мм DIN B1 1000 x 707 мм
        MAP B2 700 х 500 мм DIN B2 707 х 500 мм
        30 x 42 « 30 x 42″ DIN B3 500 х 353 мм
        Нестандартный размер Длина от 75 до 10000 мм Ширина от 50 до 914 мм
        Поддерживаемая ширина рулонов
        A-серия
        MAP-серия
        A0 841 мм В1 700 мм
        A1 594 мм В2 500 мм
        A2 420 мм
        DIN-серия
        A3 297 мм В1 707 мм
        9х12″-серия
        		 В2 500 мм
        36″ 914,4 мм
        China-серия
        24″ 609,6 мм А0 914 мм
        18″ 457,2 мм А0 910 мм
        12″ 304. 8 мм А0 900 мм
        8,5х11″-серия
        		 А0 800 мм
        34″ 683,6 мм А1 620 мм
        22″ 558,8 мм А1 610 мм
        17″ 431.8 мм А2 450 мм
        11″ 279,4 мм А2 440 мм
        30х42″-серия
        		 А3 310 мм
        30″ 762 мм А3 297 мм
        Форматы оригиналов для сканирования
        A-серия
        Распознаваемые листовые форматы Распознаваемая ширина оригинала
        A0 портрет 1189 x 841 мм 841 мм
        Минимальная длина оригинала 210 мм

        Максимальная длина оригинала 10000 мм
        A1 портрет /альбом 841 х 594 мм 594 мм
        A2 портрет /альбом 594 х 420 мм 420 мм
        A3 портрет /альбом 420 х 297 мм 297 мм
        A4 портрет /альбом 297 х 210 мм 210 мм
        9 х 12-серия
        Распознаваемые листовые форматы Распознаваемая ширина оригинала
        E портрет 1219 x 914 мм (48×36″) 914 мм
        Минимальная длина оригинала 210 мм

        Максимальная длина оригинала 10000 мм
        D портрет /альбом 914 х 610 мм (36×24″) 610 мм
        C портрет /альбом 610 х 457 мм (24×18″) 457 мм
        B портрет /альбом 457 х 305 мм (18×12″) 305 мм
        A портрет /альбом 305 х 228 мм (12×9″) 228 мм
        8,5 х 11-серия
        Распознаваемые листовые форматы Распознаваемая ширина оригинала
        E портрет 1117 x 863 мм (44×34″) 863 мм
        Минимальная длина оригинала 210 мм

        Максимальная длина оригинала 10000 мм
        D портрет /альбом 863 х 559 мм (34×22″) 559 мм
        C портрет /альбом 559 х 432 мм (22×17″) 432 мм
        B портрет /альбом 432 х 279 мм (17×11″) 279 мм
        A портрет /альбом 279 х 216 мм (11×8,5″) 216 мм
        30 х 42-серия
        Распознаваемые листовые форматы Распознаваемая ширина оригинала
        30 х 42 портрет 1067 x 762 мм (42×30″) 914 мм Минимальная длина оригинала 210 мм
        Максимальная длина оригинала 10000 мм
        MAP-серия
        Распознаваемые листовые форматы Распознаваемая ширина оригинала
        B1 портрет 1000 x 700 мм 700 мм Минимальная длина оригинала 210 мм

        Максимальная длина оригинала 10000 мм
        B2 портрет /альбом 700 х 500 мм 500 мм
        DIN-серия
        Распознаваемые листовые форматы Распознаваемая ширина оригинала
        B1 портрет 1000 x 707 мм 707 мм
        Минимальная длина оригинала 210 мм

        Максимальная длина оригинала 10000 мм
        B2 портрет /альбом 707 х 500 мм 500 мм
        B3 портрет /альбом 500 х 353 мм 353 мм
        China-серия
        Распознаваемая ширина оригинала
        914 мм 620 мм 440 мм
        Минимальная длина оригинала 210 мм

        Максимальная длина оригинала 10000 мм
        910 мм 610 мм 310 мм
        900 мм 450 мм 297 мм
        880 мм

        Инженерные системы MPW 5100 / 7140
        Форматы бумаги для печати
        A0 1189 x 841 мм ANSI E 44 x 34″
        A1 841 х 594 мм ANSI D 34 x 22″
        A2 594 х 420 мм ANSI C 22 x 17″
        A3 420 х 297 мм ANSI B 17 x 11″
        A4 297 х 210 мм ANSI A 11 x 8,5″
        B1 JIS 1030 х 728 мм ARCH E 48 x 36″
        B2 JIS 728 х 515 мм ARCH D 36 x 24″
        B3 JIS 515 x 364 мм ARCH C 24 x 18″
        B4 JIS 364 х 257 мм ARCH B 18 x 12″
        ARCH A 12 x 9″
        Нестандартный размер Рулон: Д от 210 до 15000 мм; Ш от 210 до 914 мм
        Ручной лоток: Д от 210 до 2000 мм; Ш от 210 до 914 мм
        Поддерживаемая ширина рулонов
        Метрические форматы
        A0 841 мм

        Прочие

        		 880 мм
        A1 594 мм 800 мм
        A2 420 мм

        757 мм
        A3 297 мм 680 мм
        А4 210 мм 660 мм
        B1 JIS 914,4 мм 625 мм
        B2 JIS 609,6 мм 620 мм
        B3 JIS 457,2 мм 490 мм
        B4 JIS 304. 8 мм 440 мм
        Дюймовые форматы
        Инженерные
        Архитектурные
        ANSI E 34″ 683,6 мм ARCH E 36″ 914.4 мм
        ANSI D 22″ 558,8 мм ARCH D 24″ 609.6 мм
        ANSI C 17″ 431.8 мм ARCH C 18″ 457.2 мм
        ANSI B 11″ 279,4 мм ARCH B 12″ 304.8мм
        ANSI A 8,5″ 216 мм ARCH A 9″ 228.6 мм

        Прочие
        42х30″ 762 мм
        Форматы оригиналов для сканирования
        Распознаваемые листовые форматы Распознаваемая ширина оригинала
        A0 портрет 1189 x 841 мм 841 мм
        Минимальная длина оригинала 210 мм

        Максимальная длина оригинала 15000 мм
        A1 портрет /альбом 841 х 594 мм 594 мм
        A2 портрет /альбом 594 х 420 мм 420 мм
        A3 портрет /альбом 420 х 297 мм 297 мм
        A4 портрет /альбом 297 х 210 мм 210 мм
        B1 JIS портрет 1030 х 728 мм 728 мм
        B2 JIS портрет /альбом 728 х 515 мм 515 мм
        B3 JIS портрет /альбом 515 x 364 мм 364 мм
        B4 JIS портрет /альбом 364 х 257 мм 257 мм
        1189 x 880 мм портрет 1189 x 880 мм 880 мм
        1085 х 765 мм портрет 1085 х 765 мм 765 мм
        880 х 625 мм порт. /альб. 880 х 625 мм 625 мм
        36 х 48″ портрет 1219 x 914 мм 914 мм
        34 х 44″ портрет 1117 x 863 мм 863 мм
        24 х 36″ портрет 914 х 610 мм 610 мм
        22 х 34″ портрет 863 х 559 мм 559 мм
        21 х 30″ портрет 762 х533 мм 533 мм
        18 х 24″ портрет /альбом 610 х 457 мм 457 мм
        17 х 22″ портрет /альбом 559 х 432 мм 432 мм
        12 х 18″ портрет /альбом 457 х 305 мм 305 мм
        9 х 12″ портрет /альбом 305 х 228 мм 228 мм
        8,5 х 14″ портрет /альбом 355 х 216 мм 216 мм
        8,5 х 11″ портрет /альбом 279 х 216 мм 216 мм

        Струйный плоттер Seiko IPE-3020
        Форматы бумаги для печати
        A0 1189 x 841 мм ARCH E 48 x 36″
        A1 841 х 594 мм ARCH D 36 x 24″
        A2 594 х 420 мм ARCH C 24 x 18″
        A3 420 х 297 мм ARCH B 18 x 12″
        A4 297 х 210 мм ARCH A 12 x 9″
        B1 1030 х 728 мм ARCH E1 42″ х 30″
        В2 728 x 515 мм ARCH E2 38″ x 26″
        В3 515 х 364 мм ARCH E3 39″x27″
        B4 364 х 257 мм
        В5 257 x 182 мм
        Нестандартный размер Длина от 150 до 18000 мм Ширина от 150 до 1080 мм

        Сканеры Graphtec IS 210 CS 510/610 CSX300
        Форматы оригиналов
        A0 1189 x 841 мм ARCH E 48 x 36″ (1219. 2 х 914,4 мм)
        A1 841 х 594 мм ARCH D 36 x 24″ (914,4 х 609,6 мм)
        A2 594 х 420 мм ARCH C 24 x 18″ (609,6 х 457,2 мм)
        A3 420 х 297 мм ARCH B 18 x 12″ (457,2 х 304,8 мм)
        A4 297 х 210 мм ARCH A 12 x 9″ (304,8 х 228,6 мм)
        B0 1456 х 1030 мм ANSI E 44 х 34″ (1117,6 х 863,6 мм)
        B1 1030 х 728 мм ANSI D 34″ х 22″ (863,6 х 558,8 мм)
        В2 728 x 515 мм ANSI C 22″ x 17″ (558,8 х 431,8 мм)
        В3 515 х 364 мм ANSI B 17″x 11″ (431,8 х 279,4 мм)
        B4 364 х 257 мм ANSI A 11″ x 8. 5″ (279,4 х 215,9 мм)
        DIN A0 1230 x 880 мм
        DIN A1 880 х 625 мм
        DIN A2 625 х 450 мм
        DIN A3 450 х 330 мм
        DIN A4 330 x 240 мм

        2000 Миллиметры в Сантиметры Преобразование — Конвертировать 2000 Миллиметры в Сантиметры (мм в см)

        Посетите 2000 сантиметров в миллиметры Преобразование

        миллиметров : Миллиметр (символ СИ мм) — единица длины в метрической системе, равная 1/1000 метра (или 1Е-3 метра), которая также является стандартной инженерной единицей. 1 дюйм=25,4 мм.

        см : Сантиметр (обозначается см) — единица длины в метрической системе. Это также основная единица в системе единиц сантиметр-грамм-секунда. Сантиметр практическая единица длины для многих повседневных измерений. Сантиметр равен 0,01 (или 1Е-2) метра.

        Калькулятор преобразования длины и расстояния

        Результат:

        2000 Миллиметр = 200 сантиметров

        Как перевести миллиметры в сантиметры?

        1 миллиметр равен 0,1 сантиметра:

        1 мм = 0,1 см

        Расстояние d в сантиметрах (см) равно расстоянию d в миллиметрах (мм), умноженному на 0,1, эта формула преобразования:

        d(см) = d(мм) × 0,1

        Как сколько сантиметров в миллиметре?

        Один миллиметр равен 0,1 сантиметра:

        1 мм = 1 мм × 0,1 = 0,1 см

        Сколько миллиметров в сантиметре?

        Один сантиметр равен 10 миллиметрам:

        1 см = 1 см × 10 = 10 мм

        Как преобразовать 30 миллиметров в сантиметры?

        d(см) = 30(мм) × 0,1 = 3 см

        Преобразование футов и дюймов в метры

        Таблица преобразования длины

        миллиметр (мм) сантиметр (см) метр (м) километр (км) дюйм (дюйм) фут / фут (фут) ярд (ярд) миля (ми)
        1 миллиметр (мм) 1 0,1 0,001 0,000001 0,03937 0,003281 0,0010936 0,0000006214
        1 сантиметр (см) 10 1 0,01 0,00001 0,3937 0,03281 0,010936 0,000006214
        1 метр (м) 1000 100 1 0,001 39,37 3,281 1. 0936 0,0006214
        1 километр (км) 1000000 100000 1000 1 39370 3281 1093,6 0,6214
        1 дюйм (дюйм) 25,4 2,54 0,0254 0,0000254 1 0,08333 0,02778 0,000015783
        1 фут / фут (фут) 304,8 30,48 0,3048 0,0003048 12 1 0,33333 0,0001894
        1 ярд (ярд) 914,4 91,44 0,9144 0,0009144 36 3 1 0,0005682
        1 миля 1609344 160934 1609.3 1,6093 63360 5280 1760 1
        1 морская миля (нми) 1852000 185200 1852 1,852 72913 6076 2025. 4 1.1508

        Мы решили округлить некоторые переводные коэффициенты, чтобы они соответствовали этой таблице. Поэтому некоторые из этих значений неточны, но все же имеют разумную точность.

        Самые популярные пары для перевода расстояния и длины

        • Сантиметр в фут
        • Сантиметр в Дюйм
        • Сантиметров в
          • Километров
        • Сантиметр в Метр
        • Сантиметр в Миля (США)
        • Сантиметр в Миллиметр
        • Сантиметр в Морская Миля
        • Сантиметр в Ярд
        • Фут в Сантиметр
        • Футов в Дюймы
        • Футов в Километров
        • Футов в Метров
        • Футов в Миля (США)
        • Футов в Миллиметры
        • Футов в Морская Миля
        • Футов до двора
        • Дюймов в Сантиметров
        • Дюймов в Футы
        • Дюйм в Километр
        • Дюйм в Метр
        • Дюймов в Миля (США)
        • Дюйм в Миллиметр
        • Дюйм в Морская Миля
        • дюймов в ярдах
        • Километров в
          • Сантиметров
        • Километров в Футов
        • Километров в Дюйм
        • Километров в
          • Метров
        • Километров в Миля (США)
        • Километр в Миллиметр
        • Километров в Морская Миля
        • км до двора
        • Метр в Сантиметр
        • Метр в Фут
        • Метр в Дюйм
        • Метр в Километр
        • Метр в Миля (США)
        • Метр в Миллиметр
        • Метр в Морская Миля
        • Метр в двор
        • миль (США) в
          • сантиметров
        • миль (США) в
          • футов
        • миль (США) в
          • дюймов
        • миль (США) в
          • километров
        • миль (США) в Метр
        • Миля (США) в Миллиметр
        • Миля (США) в Морская Миля
        • миль (США) до двора
        • Миллиметр в Сантиметр
        • Миллиметр в Фут
        • Миллиметр в Дюйм
        • Миллиметр в Километр
        • Миллиметр в Метр
        • Миллиметр в Миля (США)
        • Миллиметр в Морская Миля
        • Миллиметр в Ярд
        • Морская Миля в Сантиметр
        • Морская миля в фут
        • Морская Миля в Дюйм
        • Морская Миля в Километр
        • Морская Миля в Метр
        • Морская Миля в Миля (США)
        • Морская Миля в Миллиметр
        • Морская миля до верфи
        • Ярдов в Сантиметр
        • Ярдов в фут
        • Ярдов в Дюйм
        • Ярдов в Километр
        • Ярд в Метр
        • Ярдов в Миля (США)
        • Ярд в Миллиметр
        • Ярдов в Морские мили

        Последние запросы на конвертацию

        Что такое 2000 миллиметров в сантиметрах? Преобразовать 2000 мм в см

        2000 миллиметров =

        200 сантиметров

        Конвертер единиц измерения

        Сумма

        От Сантиметры (см)Футы (футы)Дюймы (дюймы)Километры (км)Метры (м)Мили (мили)Морские мили (нми)Миллиметры (мм)Нанометры (нм)Ярды (ярды)Граммы (г)Миллиграммы (мг)Унции (oz)Фунты (lb)Стоуны (st)Длинные тонны (uk ton)Метрические тонны (tonne)Короткие тонны (ton)Килограммы (kg)Дни (d)Месяцы (mo)Годы (yr)Часы (hr)Миллисекунды (ms) )Минуты (min)Наносекунды (ns)Секунды (s)Недели (wk)Акры (ac)Гектары (га)Квадратные футы (ft2)Квадратные дюймы (in2)Квадратные километры (km2)Квадратные метры (m2)Квадратные мили (mi2) Квадратные ярды (yd2) Футы в секунду (ft/s) Километры в час (km/h) Узлы (kt) Метры в секунду (m/s) Мили в час (mph) Нефтяные баррели (bbl) Кубические сантиметры (cm3) Кубические Футы (ft3)Кубические дюймы (in3)Кубические метры (м3)Империйские чашки (uk cup)Чашки (cup)Децилитры (dL)Британские галлоны (uk gal)Галлоны (gal)Литры (L)Миллилитры (ml)Империйские жидкие унции ( британские жидкие унции)жидкие унции (жидкие унции)имперские пинты (uk pt)пинты (pt)имперские кварты (uk qt)кварты (qt)имперские столовые ложки (uk tbsp)столовые ложки (tbsp)имперские чайные ложки (uk tsp)чайные ложки (tsp)

        Кому Сантиметры (см)Футы (футы)Дюймы (дюймы)Километры (км)Метры (м)Мили (мили)Морские мили (нми)Миллиметры (мм)Нанометры (нм)Ярды (ярды)Граммы (г)Миллиграммы (мг)Унции (oz)Фунты (lb)Стоуны (st)Длинные тонны (uk ton)Метрические тонны (tonne)Короткие тонны (ton)Килограммы (kg)Дни (d)Месяцы (mo)Годы (yr)Часы (hr)Миллисекунды (ms) )Минуты (min)Наносекунды (ns)Секунды (s)Недели (wk)Акры (ac)Гектары (га)Квадратные футы (ft2)Квадратные дюймы (in2)Квадратные километры (km2)Квадратные метры (m2)Квадратные мили (mi2) Квадратные ярды (yd2) Футы в секунду (ft/s) Километры в час (km/h) Узлы (kt) Метры в секунду (m/s) Мили в час (mph) Нефтяные баррели (bbl) Кубические сантиметры (cm3) Кубические Футы (ft3)Кубические дюймы (in3)Кубические метры (м3)Империйские чашки (uk cup)Чашки (cup)Децилитры (dL)Британские галлоны (uk gal)Галлоны (gal)Литры (L)Миллилитры (ml)Империйские жидкие унции ( британские жидкие унции)жидкие унции (жидкие унции)имперские пинты (uk pt)пинты (pt)имперские кварты (uk qt)кварты (qt)имперские столовые ложки (uk tbsp)столовые ложки (tbsp)имперские чайные ложки (uk tsp)чайные ложки (tsp)

        Перевести 2000 миллиметров в сантиметры

        Чтобы преобразовать 2000 миллиметров в соответствующее значение в сантиметрах, умножьте количество в миллиметрах на 0,1 (коэффициент преобразования). В этом случае мы должны умножить 2000 миллиметров на 0,1, чтобы получить эквивалентный результат в сантиметрах:

        .

        2000 миллиметров x 0,1 = 200 сантиметров

        2000 миллиметров эквивалентно 200 сантиметрам.

        Коэффициент преобразования миллиметров в сантиметры равен 0,1. Чтобы узнать, сколько миллиметров в сантиметрах, умножьте на коэффициент преобразования или используйте конвертер длины выше. Две тысячи миллиметров равны двум сотням сантиметров.

        Миллиметр (обозначение: мм) — единица измерения длины в метрической системе, равная 1/1000 метра (или 1Е-3 метра), которая также является стандартной единицей инженерного искусства. 1 дюйм=25,4 мм.

        Сантиметр (обозначение: см) — единица длины в метрической системе. Это также основная единица в системе единиц сантиметр-грамм-секунда. Сантиметр практическая единица длины для многих повседневных измерений. Сантиметр равен 0,01 (или 1Е-2) метра.

        С помощью конвертера Миллиметры в Сантиметры вы можете получить ответы на следующие вопросы:

        • Сколько сантиметров в 2000 миллиметрах?
        • 2000 миллиметров равно скольким сантиметрам?
        • Как преобразовать 2000 миллиметров в сантиметры?
        • Сколько будет 2000 миллиметров в сантиметрах?
        • Сколько будет 2000 миллиметров в сантиметрах?
        • Сколько будет 2000 миллиметров в сантиметрах?
        • Сколько см в 2000 мм?
        • 2000 мм это сколько см?
        • Как перевести 2000 мм в см?
        • Сколько 2000 мм в см?
        • Что такое 2000 мм в см?
        • Сколько будет 2000 мм в см?

        Что такое 2000 миллиметров в других единицах измерения длины?

        • 2000 миллиметров в футах
        • 2000 миллиметров в дюймах
        • 2000 миллиметров в километрах
        • 2000 миллиметров в метрах
        • 2000 миллиметров в милях
        • 2000 миллиметров в морских милях
        • 2000 миллиметров в нанометрах
        • 2000 миллиметров в ярдах

        Преобразования, аналогичные 2000 Миллиметры в Сантиметры

        • 2001 Миллиметры в сантиметрах
        • 2002 Миллиметры в сантиметрах
        • 2003 Миллиметры в сантиметрах
        • 2004 Миллиметры в сантиметрах
        • 2005 Миллиметры в сантиметрах
        • 2006 Миллиметры в сантиметрах
        • 2007 Миллиметры в сантиметрах
        • 2008 Миллиметры в сантиметрах
        • 2009 Миллиметры в сантиметрах
        • 2010 Миллиметры в сантиметрах

        Предыдущие преобразования Миллиметры в Сантиметры

        • 977 Миллиметры в сантиметрах
        • 258 миллиметров в сантиметрах
        • 161 миллиметр в сантиметрах
        • 113 миллиметров в сантиметрах
        • 539 миллиметров в сантиметрах
        • 453 миллиметра в сантиметрах
        • 134 миллиметра в сантиметрах
        • 176 миллиметров в сантиметрах
        • 473 миллиметра в сантиметрах
        • 200 миллиметров в сантиметрах

        Сколько мм в см? Преобразовать см в мм

        Сантиметр (обозначение см) или сантиметр (американское правописание) — единица длины, равная одной сотой метра.

        Этот инструмент преобразует сантиметры в миллиметры (см в миллиметры) и наоборот. 1 сантиметр = 10 миллиметров . Пользователь должен заполнить одно из двух полей и преобразование произойдет автоматически.

        футы (футы) миллиметры (мм) сантиметры (см) метры (м) километры (км) ярды (ярды) мили (ми) морские мили (морские мили) дюймы (дюймы)   футы (футы) миллиметры (мм) сантиметры (см) метры (м) километры (км) ярды (ярды) мили (ми) морские мили (морские мили) дюймы (дюймы)
         <=> 
           

        точность:авто0 десятичное1 десятичное2 десятичное число3 десятичное число4 десятичное число5 десятичное число6 десятичное число7 десятичное число8 десятичное число9 десятичное число10 десятичное число11 десятичное число12 десятичное число

        1 сантиметры = 10 миллиметров

         

        Формула сантиметры в миллиметрах (см в мм). Миллиметр = см*10

         

        Преобразование сантиметров в другие единицы измерения

        Сантиметр в Фут Сантиметр в Миллиметр Сантиметр в Метр
        Сантиметр в Километр Сантиметр в Ярд Сантиметр в Миля
        Сантиметр в Морская миля Сантиметр в Дюйм

          

        Table centimeters to millimeters

        1 cm = 10 mm 11 cm = 110 mm 21 cm = 210 mm
        2 cm = 20 мм 12 см = 120 мм 22 cm = 220 mm
        3 cm = 30 mm 13 cm = 130 mm 23 cm = 230 mm
        4 cm = 40 mm 14 cm = 140 mm 24 cm = 240 mm
        5 cm = 50 mm 15 cm = 150 mm 25 cm = 250 mm
        6 cm = 60 mm 16 cm = 160 mm 26 cm = 260 mm
        7 см = 70 мм 17 см = 170 мм 27 см = 270 мм
        8 cm = 80 mm 18 cm = 180 mm 28 cm = 280 mm
        9 cm = 90 mm 19 cm = 190 mm 29 cm = 290 mm
        10 см = 100 мм 20 см = 200 мм 30 см = 300 мм
        40 см = 400 мм 70 см = 700 мм 100 CM = 1000 мм
        9. мм 80 см = 800 мм 110 см = 1100 мм
        60 cm = 600 mm 90 cm = 900 mm 120 cm = 1200 mm
        200 cm = 2000 mm 500 cm = 5000 mm 800 cm = 8000 mm
        300 cm = 3000 mm 600 cm = 6000 mm 900 cm = 9000 mm
        400 cm = 4000 mm 700 cm = 7000 mm 1000 cm = 10000 mm

        Length Conversions

        Фут в Миллиметр Фут в Сантиметр Фут в Метр
        Фут в Километр фут во двор Фут в Милю
        Фут в Морская миля Фут в Дюйм Миллиметр в Фут
        Миллиметр в Сантиметр Миллиметр в Метр Миллиметр в Километр
        Миллиметр в Ярд Миллиметр в Миля Миллиметр в Морская миля
        Миллиметр в Дюйм метр в фут Метр в Миллиметр
        Метр в Сантиметр Метр в Километр Метр в Ярд
        Метр в Миля Метр в Морская миля Метр в Дюйм
        Километр в Фут Километр в Миллиметр Километр в Сантиметр
        Километр в Метр Километр в Двор Километр в Миля
        Километр в Морская миля Километр в Дюйм Двор в фут
        Ярд в Миллиметр Ярд в Сантиметр Ярд в Метр
        Ярд в Километр Ярд в Миля Ярд в Морская миля
        Ярд в Дюйм Миля в фут Миля в Миллиметр
        Миля в Сантиметр Миля в Метр Миля в Километр
        Миля в Ярд Миля в Морская миля Миля в Дюйм
        Морская миля в Фут Морская миля в Миллиметр Морская миля в Сантиметр
        Морская миля в Метр Морская миля в Километр Морская миля в Верфь
        Морская миля в Миля Морская миля в Дюйм Дюйм в фут
        Дюйм в Миллиметр Дюйм в Сантиметр Дюйм в Метр
        Дюйм в Километр Дюйм в Ярд Дюйм в Миля
        Дюйм в Морская миля

         

         

        Преобразование мм в см, см в мм, преобразование миллиметров

        Основные факты


         
         
         
         

        Сантиметров в Миллиметры Преобразование

        см = 10 мм

        Преобразование миллиметров в сантиметры

        мм = 0,1 см
        Таблица перевода
        см в мм:
        1 см  = 10 мм 21 см = 210 мм 41 см = 410 мм 70 см = 700 мм
        2 см  = 20 мм 22 см = 220 мм 42 см = 420 мм 80 см = 800 мм
        3 см  = 30 мм 23 см = 230 мм 43 см = 430 мм 90 см = 900 мм
        4 см = 40 мм 24 см = 240 мм 44 см = 440 мм 100 см  = 1000 мм
        5 см  = 50 мм 25 см = 250 мм 45 см = 450 мм 110 см = 1100 мм
        6 см  = 60 мм 26 см = 260 мм 46 см = 460 мм 120 см  = 1200 мм
        7 см  = 70 мм 27 см = 270 мм 47 см = 470 мм 130 см = 1300 мм
        8 см  = 80 мм 28 см = 280 мм 48 см = 480 мм 140 см = 1400 мм
        9 см  = 90 мм 29 см = 290 мм 49 см = 490 мм 150 см = 1500 мм
        10 см  = 100 мм 30 см = 300 мм 50 см = 500 мм 160 см = 1600 мм
        11 см  = 110 мм 31 см = 310 мм 51 см = 510 мм 170 см = 1700 мм
        12 см  = 120 мм 32 см = 320 мм 52 см = 520 мм 180 см = 1800 мм
        13 см  = 130 мм 33 см = 330 мм 53 см = 530 мм 190 см = 1900 мм
        14 см  = 140 мм 34 см = 340 мм 54 см = 540 мм 200 см  = 2000 мм
        15 см  = 150 мм 35 см = 350 мм 55 см = 550 мм 300 см = 3000 мм
        16 см  = 160 мм 36 см = 360 мм 56 см = 560 мм 400 см = 4000 мм
        17 см  = 170 мм 37 см = 370 мм 57 см  = 570 мм 500 см  = 5000 мм
        18 см  = 180 мм 38 см = 380 мм 58 см = 580 мм 700 см  = 7000 мм
        19 см  = 190 мм 39 см = 390 мм 59 см = 590 мм 900 см  = 9000 мм
        20 см  = 200 мм 40 см = 400 мм 60 см = 600 мм 1000 см  = 10000 мм
        Таблица преобразования мм в см:
        1 мм  = 0,1 см 21 мм = 2,1 см 41 мм = 4,1 см 70 мм = 7 см
        2 мм  = 0,2 см 22 мм = 2,2 см 42 мм = 4,2 см 80 мм = 8 см
        3 мм  = 0,3 см 23 мм = 2,3 см 43 мм = 4,3 см 90 мм = 9 см
        4 мм  = 0,4 см 24 мм = 2,4 см 44 мм = 4,4 см 100 мм = 10 см
        5 мм  = 0,5 см 25 мм = 2,5 см 45 мм = 4,5 см 110 мм = 11 см
        6 мм  = 0,6 см 26 мм = 2,6 см 46 мм = 4,6 см 120 мм = 12 см
        7 мм  = 0,7 см 27 мм = 2,7 см 47 мм = 4,7 см 130 мм = 13 см
        8 мм  = 0,8 см 28 мм = 2,8 см 48 мм = 4,8 см 140 мм = 14 см
        9 мм  = 0,9 см 29 мм = 2,9 см 49 мм = 4,9 см 150 мм = 15 см
        10 мм  = 1 см 30 мм = 3 см 50 мм = 5 см 160 мм = 16 см
        11 мм  = 1,1 см 31 мм = 3,1 см 51 мм = 5,1 см 170 мм = 17 см
        12 мм  = 1,2 см 32 мм = 3,2 см 52 мм = 5,2 см 180 мм = 18 см
        13 мм  = 1,3 см 33 мм = 3,3 см 53 мм = 5,3 см 190 мм = 19 см
        14 мм  = 1,4 см 34 мм = 3,4 см 54 мм = 5,4 см 200 мм = 20 см
        15 мм  = 1,5 см 35 мм = 3,5 см 55 мм = 5,5 см 300 мм = 30 см
        16 мм  = 1,6 см 36 мм = 3,6 см 56 мм = 5,6 см 400 мм = 40 см
        17 мм  = 1,7 см 37 мм = 3,7 см 57 мм = 5,7 см 500 мм = 50 см
        18 мм  = 1,8 см 38 мм = 3,8 см 58 мм = 5,8 см 700 мм = 70 см
        19мм  = 1,9 см 39 мм = 3,9 см 59 мм = 5,9 см 900 мм = 90 см
        20 мм  = 2 см 40 мм = 4 см 60 мм = 6 см 1000 мм  = 100 см


        Конвертер миллиметров в метры

        Выберите тип преобразования:
        миллиметры => метры метры => миллиметры

        Варианты округления:
        1 знак после запятой2 знака после запятой3 знака после запятой4 знака после запятой5 знаков после запятой6 знаков после запятой7 знаков после запятой8 цифр после запятой9 знаков после запятой10 знаков после запятой



        Преобразовать метры в миллиметры (м в мм) ▶

        Таблица преобразования

        1750 1. 2
        миллиметров до метров
        мм м
        100 0,1
        200 0,2
        300 0. 3
        400 0.4
        500 0.5
        600 0.6
        700 0.7
        800 0.8
        900 0,9
        1000 1
        1,1
        1200
        1200
        1200
        1300 1.3
        1400 1.4
        1500 1.5
        1600 1.6
        1700 1.7
        1800 1.8
        1900 1,9
        2000 2

        Как преобразовать

        1 миллиметр (мм) = 0,001 метра (м). Миллиметр (мм) — единица длины, используемая в метрической системе. Метр (м) — единица длины, используемая в метрической системе. Миллиметры также могут быть обозначены как миллиметров .

        Метр

        — Единица измерения расстояния/длины

        Условное обозначение / сокращение: м

        Где используется единица измерения в мире:

        Счетчик используется как единица измерения средних расстояний или длин.
        Это стандартная мера для коротких расстояний (длиной до 1 км), в сфере недвижимости и строительства, поставок материалов, габаритов транспортных средств и самолетов, коротких географических расстояний и направлений в большинстве стран, за исключением США, где для этого все еще широко используются футы и ярды. цель.
        Метр широко используется в большинстве стран и является официальной единицей для средних длин и расстояний (например, дорожные знаки в континентальной Европе показывают максимальную высоту транспортного средства в метрах). Основными исключениями являются Соединенные Штаты Америки и некоторые страны, где футы и ярды используются в ограниченной степени: Великобритания и Канада, где ярд остается в ограниченном использовании как часть имперской системы (например, ярды используются на дорогах). знаки для более коротких расстояний в Соединенном Королевстве и ноги широко используются в строительстве и недвижимости в Канаде).

        Определение единицы измерения:

        Метр (метр в английском правописании) — единица длины/расстояния в метрической системе (система единиц СИ), эквивалентная длине пути, пройденного светом за интервал времени 1/299 792 458 секунды (в вакууме, определяется с 1983 г.).

        1 м эквивалентен 3,28084 фута или 0,000621371 мили.

        История подразделения:

        В результате Французской революции 1789 г., старые единицы измерения, которые были связаны с монархией, были заменены новыми единицами. Введена новая единица длины, получившая название метра. В 1795 году метр был определен как 1/10 000 000 часть четверти меридиана, проходящего через Париж. Метр приобрел популярность в континентальной Европе в девятнадцатом веке, особенно в научной сфере, и был официально принят в качестве международной единицы измерения в 1875 году. В 1960 году метр был определен как 1 650 763,73 длины волны света от определенного перехода в криптоне-86. В 1983 окончательное определение метра было принято как длина пути, пройденного светом в вакууме за 1/299 792 458 секунды.

        Где используется:

        Счетчик широко используется в различных профессиях и отраслях (например, в машиностроении), на дорожных знаках для указания ограничений высоты транспортного средства, расстояния до определенного места (например, в голосовых подсказках автомобильной GPS-навигации), на картах. для обозначения малых размеров, размеров транспортных средств, судов и самолетов в промышленности и торговле. Это также самая популярная единица измерения для описания расстояний и измерений торговой недвижимости (размеры комнат, размеры этажей и т. д.).

        Эквиваленты в других единицах и масштабах:

        • 1 м = 1000 миллиметров (мм)
        • 1 м = 100 сантиметров (см)
        • 1 м = 10 дециметров (дм)
        • 1 м = 0,001 километра (км)
        • 1 м = 3,28084 фута (фута)
        • 1 мегаметр = 1000000 м
        • 1 гигаметр = 1000000000 м
        • Единицы длины в метрической системе СИ основаны на кратных или долях метра.
        • Существуют измерения длины/расстояния в метрической системе СИ, превышающие метр, которые могут быть выражены в метрах.

        1 м равен 3,28084 фута или 1,09361 ярда.

        Метр — единица длины в метрической системе СИ, эквивалентная длине пути, пройденного светом за промежуток времени 1/299 792 458 секунды (в вакууме, определено с 1983 г.).

        Метры также могут быть обозначены как метров (в британском английском написании).

        Испанский Русский французский

        Калькулятор

        мм в дюймы [Конвертировать мм в дюймы и 1/16]

        Преобразование мм в дюймы и 1/16 калькулятор.
        1 дюйм = 25,4 миллиметра
        1/16 дюйма в мм = 1,5875 мм. 1/8 дюйма в мм = 3,175 мм.
        3/16 дюйма в мм = 4,7625 мм. 1/4 дюйма в мм = 6,35 мм.
        5/16 дюйма в мм = 7,9375 мм. 3/8 дюйма в мм = 9,525 мм.
        7/16 дюйма в мм = 11,1125 мм. 1/2 дюйма в мм = 12,7 мм.
        9/16 дюйма в мм = 14,2875 мм. 5/8 дюйма в мм = 15,875 мм.
        11/16 дюйма в мм = 17,4625 мм. 3/4 дюйма в мм = 19,05 мм.
        13/16 дюйма в мм = 20,6375 мм. 7/8 дюйма в мм = 22,225 мм.
        15/16 дюйма в мм = 23,8125 мм.

        Список преобразования 10–2000 мм в дюймы

        10 мм в дюймы равно 0 . Также 10 мм равны 0 дюймам и 6 шестнадцатым зубьям (6/16).
        20 мм в дюймы равно 0 . Также 20 мм равны 0 дюймам и 12 шестнадцатым зубьям (12/16).
        30 мм в дюйм равно 1 . Также 30 мм равны 1 дюйму и 2 шестнадцатым зубьям (2/16).
        40 мм в дюйм равно 1 . Также 40 мм равняется 1 дюйму и 9шестнадцатый (9/16).
        50 мм в дюйм равно 1 . Также 50 мм равны 1 дюйму и 15 шестнадцатым зубьям (15/16).
        60 мм в дюйм равно 2 . Также 60 мм равняется 2 дюймам и 5 шестнадцатым зубьям (5/16).
        70 мм в дюйм равно 2 . Также 70 мм равняется 2 дюймам и 12 шестнадцатым зубьям (12/16).
        80 мм в дюйм равно 3 . Также 80 мм равняется 3 дюймам и 2 шестнадцатым зубьям (2/16).
        90 мм в дюйм равно 3 . Также 90 мм равняется 3 дюймам и 8 шестнадцатым зубьям (8/16).
        100 мм в дюйм равно 3 . Также 100 мм равны 3 дюймам и 14 шестнадцатым зубьям (14/16).
        110 мм в дюйм равно 4 . Также 110 мм равняется 4 дюймам и 5 шестнадцатым зубьям (5/16).
        120 мм в дюйм равно 4 . Также 120 мм равняется 4 дюймам и 11 шестнадцатым зубьям (11/16).
        130 мм в дюйм равно 5 . Также 130 мм равняется 5 дюймам и 1 шестнадцатой части (1/16).
        140 мм в дюйм равно 5 . Также 140 мм равняется 5 дюймам и 8 шестнадцатым зубьям (8/16).
        150 мм в дюйм равно 5 . Также 150 мм равняется 5 дюймам и 14 шестнадцатым зубьям (14/16).
        160 мм в дюйм равно 6 . Также 160 мм равняется 6 дюймам и 4 шестнадцатым зубьям (4/16).
        170 мм в дюйм равно 6 . Также 170 мм равняется 6 дюймам и 11 шестнадцатым зубьям (11/16).
        180 мм в дюйм равно 7 . Также 180 мм равняется 7 дюймам и 1 шестнадцатой части (1/16).
        190 мм в дюйм равно 7 . Также 190 мм равняется 7 дюймам и 7 шестнадцатым зубьям (7/16).
        200 мм в дюйм равно 7 . Также 200 мм равняются 7 дюймам и 13 шестнадцатым зубьям (13/16).
        210 мм в дюйм равно 8 . Также 210 мм равняется 8 дюймам и 4 шестнадцатым зубьям (4/16).
        220 мм в дюйм равно 8 . Также 220 мм равняется 8 дюймам и 10 шестнадцатым зубьям (10/16).
        230 мм в дюйм равно 9 . Также 230 мм равны 9 дюймам и 0 шестнадцатым зубьям (0/16).
        240 мм в дюйм равно 9 . Также 240 мм равняются 9 дюймам и 7 шестнадцатым зубьям (7/16).
        250 мм в дюйм равно 9 . Также 250 мм равняются 9 дюймам и 13 шестнадцатым зубьям (13/16).
        260 мм в дюйм равно 10 . Также 260 мм равны 10 дюймам и 3 шестнадцатым зубьям (3/16).
        270 мм в дюйм равно 10 . Также 270 мм равны 10 дюймам и 10 шестнадцатым зубьям (10/16).
        280 мм в дюйм равно 11 . Также 280 мм равны 11 дюймам и 0 шестнадцатым зубьям (0/16).
        290 мм в дюйм равно 11 . Также 290 мм равняются 11 дюймам и 6 шестнадцатым зубьям (6/16).
        300 мм в дюйм равно 11 . Также 300 мм равны 11 дюймам и 12 шестнадцатым зубьям (12/16).
        310 мм в дюйм равно 12 . Также 310 мм равняется 12 дюймам и 3 шестнадцатым зубьям (3/16).
        320 мм в дюйм равно 12 . Также 320 мм равняются 12 дюймам и 9 шестнадцатым зубьям (9/16).
        330 мм в дюйм равно 12 . Также 330 мм равняются 12 дюймам и 15 шестнадцатым (15/16).
        340 мм в дюйм равно 13 . Также 340 мм равняются 13 дюймам и 6 шестнадцатым зубьям (6/16).
        350 мм в дюйм равно 13 . Также 350 мм равняется 13 дюймам и 12 шестнадцатым зубьям (12/16).
        360 мм в дюйм равно 14 . Также 360 мм равняются 14 дюймам и 2 шестнадцатым зубьям (2/16).
        370 мм в дюйм равно 14 . Также 370 мм равняется 14 дюймам и 9 шестнадцатым зубьям (9/16).
        380 мм в дюйм равно 14 . Также 380 мм равняются 14 дюймам и 15 шестнадцатым (15/16).
        390 мм в дюйм равно 15 . Также 390 мм равняется 15 дюймам и 5 шестнадцатым зубьям (5/16).
        400 мм в дюйм равно 15 . Также 400 мм равняются 15 дюймам и 11 шестнадцатым зубьям (11/16).
        410 мм в дюйм равно 16 . Также 410 мм равняется 16 дюймам и 2 шестнадцатым зубьям (2/16).
        420 мм в дюйм равно 16 . Также 420 мм равняется 16 дюймам и 8 шестнадцатым зубьям (8/16).
        430 мм в дюйм равно 16 . Также 430 мм равняется 16 дюймам и 14 шестнадцатым (14/16).
        440 мм в дюйм равно 17 . Также 440 мм равняется 17 дюймам и 5 шестнадцатым зубьям (5/16).
        450 мм в дюйм равно 17 . Также 450 мм равняется 17 дюймам и 11 шестнадцатым (11/16).
        460 мм в дюйм равно 18 . Также 460 мм равняется 18 дюймам и 1 шестнадцатой части (1/16).
        470 мм в дюйм равно 18 . Также 470 мм равняется 18 дюймам и 8 шестнадцатым зубьям (8/16).
        480 мм в дюйм равно 18 . Также 480 мм равняется 18 дюймам и 14 шестнадцатым (14/16).
        490 мм в дюйм равно 19 . Также 490 мм равняется 19 дюймам и 4 шестнадцатым зубьям (4/16).
        500 мм в дюйм равно 19 . Также 500 мм равны 19 дюймам и 10 шестнадцатым зубьям (10/16).
        510 мм в дюйм равно 20 . Также 510 мм равняется 20 дюймам и 1 шестнадцатой части (1/16).
        520 мм в дюйм равно 20 . Также 520 мм равняется 20 дюймам и 7 шестнадцатым зубьям (7/16).
        530 мм в дюйм равно 20 . Также 530 мм равняются 20 дюймам и 13 шестнадцатым (13/16).
        540 мм в дюйм равно 21 . Также 540 мм равняется 21 дюйму и 4 шестнадцатым зубьям (4/16).
        550 мм в дюйм равно 21 . Также 550 мм равняется 21 дюйму и 10 шестнадцатым зубьям (10/16).
        560 мм в дюйм равно 22 . Также 560 мм равняется 22 дюймам и 0 шестнадцатым зубьям (0/16).
        570 мм в дюйм равно 22 . Также 570 мм равняется 22 дюймам и 7 шестнадцатым зубьям (7/16).
        580 мм в дюйм равно 22 . Также 580 мм равняются 22 дюймам и 13 шестнадцатым зубьям (13/16).
        590 мм в дюйм равно 23 . Также 590 мм равняется 23 дюймам и 3 шестнадцатым зубьям (3/16).
        600 мм в дюйм равно 23 . Также 600 мм равняются 23 дюймам и 9 шестнадцатым зубьям (9/16).
        610 мм в дюйм равно 24 . Также 610 мм равняется 24 дюймам и 0 шестнадцатым зубьям (0/16).
        620 мм в дюйм равно 24 . Также 620 мм равняется 24 дюймам и 6 шестнадцатым зубьям (6/16).
        630 мм в дюйм равно 24 . Также 630 мм равняется 24 дюймам и 12 шестнадцатым зубьям (12/16).
        640 мм в дюйм равно 25 . Также 640 мм равняется 25 дюймам и 3 шестнадцатым зубьям (3/16).
        650 мм в дюйм равно 25 . Также 650 мм равняется 25 дюймам и 9 шестнадцатым зубьям (9/16).
        660 мм в дюйм равно 25 . Также 660 мм равняется 25 дюймам и 15 шестнадцатым (15/16).
        670 мм в дюйм равно 26 . Также 670 мм равняется 26 дюймам и 6 шестнадцатым (6/16).
        680 мм в дюйм равно 26 . Также 680 мм равняется 26 дюймам и 12 шестнадцатым зубьям (12/16).
        690 мм в дюйм равно 27 . Также 690 мм равняется 27 дюймам и 2 шестнадцатым зубьям (2/16).
        700 мм в дюйм равно 27 . Также 700 мм равняется 27 дюймам и 8 шестнадцатым зубьям (8/16).
        710 мм в дюйм равно 27 . Также 710 мм равняется 27 дюймам и 15 шестнадцатым (15/16).
        720 мм в дюйм равно 28 . Также 720 мм равняется 28 дюймам и 5 шестнадцатым зубьям (5/16).
        730 мм в дюйм равно 28 . Также 730 мм равняется 28 дюймам и 11 шестнадцатым (11/16).
        740 мм в дюйм равно 29 . Также 740 мм равняется 29 дюймам и 2 шестнадцатым зубьям (2/16).
        750 мм в дюйм равно 29 . Также 750 мм равняется 29 дюймам и 8 шестнадцатым зубьям (8/16).
        760 мм в дюйм равно 29 . Также 760 мм равняется 29 дюймам и 14 шестнадцатым (14/16).
        770 мм в дюйм равно 30 . Также 770 мм равняется 30 дюймам и 5 шестнадцатым зубьям (5/16).
        780 мм в дюйм равно 30 . Также 780 мм равняется 30 дюймам и 11 шестнадцатым зубьям (11/16).
        790 мм в дюйм равно 31 . Также 790 мм равняется 31 дюйму и 1 шестнадцатой части (1/16).
        800 мм в дюйм равно 31 . Также 800 мм равняется 31 дюйму и 7 шестнадцатым зубьям (7/16).
        810 мм в дюйм равно 31 . Также 810 мм равняется 31 дюйму и 14 шестнадцатым зубьям (14/16).
        820 мм в дюйм равно 32 . Также 820 мм равняется 32 дюймам и 4 шестнадцатым зубьям (4/16).
        830 мм в дюйм равно 32 . Также 830 мм равняется 32 дюймам и 10 шестнадцатым (10/16).
        840 мм в дюйм равно 33 . Также 840 мм равняется 33 дюймам и 1 шестнадцатой части (1/16).
        850 мм в дюйм равно 33 . Также 850 мм равняется 33 дюймам и 7 шестнадцатым зубьям (7/16).
        860 мм в дюйм равно 33 . Также 860 мм равняется 33 дюймам и 13 шестнадцатым (13/16).
        870 мм в дюйм равно 34 . Также 870 мм равняется 34 дюймам и 4 шестнадцатым зубьям (4/16).
        880 мм в дюйм равно 34 . Также 880 мм равняется 34 дюймам и 10 шестнадцатым (10/16).
        890 мм в дюйм равно 35 . Также 890 мм равняется 35 дюймам и 0 шестнадцатым зубьям (0/16).
        900 мм в дюйм равно 35 . Также 900 мм равняется 35 дюймам и 6 шестнадцатым зубьям (6/16).
        910 мм в дюйм равно 35 . Также 910 мм равняется 35 дюймам и 13 шестнадцатым (13/16).
        920 мм в дюйм равно 36 . Также 920 мм равняется 36 дюймам и 3 шестнадцатым зубьям (3/16).
        930 мм в дюйм равно 36 . Также 930 мм равняется 36 дюймам и 9 шестнадцатым зубьям (9/16).
        940 мм в дюйм равно 37 . Также 940 мм равняется 37 дюймам и 0 шестнадцатым зубьям (0/16).
        950 мм в дюйм равно 37 . Также 950 мм равняется 37 дюймам и 6 шестнадцатым зубьям (6/16).
        960 мм в дюйм равно 37 . Также 960 мм равняется 37 дюймам и 12 шестнадцатым (12/16).
        970 мм в дюйм равно 38 . Также 970 мм равняется 38 дюймам и 3 шестнадцатым зубьям (3/16).
        980 мм в дюйм равно 38 . Также 980 мм равняется 38 дюймам и 9 шестнадцатым зубьям (9/16).
        990 мм в дюйм равно 38 . Также 990 мм равняется 38 дюймам и 15 шестнадцатым (15/16).
        1000 мм в дюйм равно 39 . Также 1000 мм равняется 39 дюймам и 5 шестнадцатым зубьям (5/16).
        1010 мм в дюйм равно 39 . Также 1010 мм равняется 39 дюймам и 12 шестнадцатым зубьям (12/16).
        1020 мм в дюйм равно 40 . Также 1020 мм равняется 40 дюймам и 2 шестнадцатым (2/16).
        1030 мм в дюйм равно 40 . Также 1030 мм равняется 40 дюймам и 8 шестнадцатым зубьям (8/16).
        1040 мм в дюйм равно 40 . Также 1040 мм равняется 40 дюймам и 15 шестнадцатым (15/16).
        1050 мм в дюйм равно 41 . Также 1050 мм равняется 41 дюйму и 5 шестнадцатым зубьям (5/16).
        1060 мм в дюйм равно 41 . Также 1060 мм равняется 41 дюйму и 11 шестнадцатым зубьям (11/16).
        1070 мм в дюйм равно 42 . Также 1070 мм равняется 42 дюймам и 2 шестнадцатым зубьям (2/16).
        1080 мм в дюйм равно 42 . Также 1080 мм равняется 42 дюймам и 8 шестнадцатым (8/16).
        1090 мм в дюйм равно 42 . Также 1090 мм равняется 42 дюймам и 14 шестнадцатым (14/16).
        1100 мм в дюйм равно 43 . Также 1100 мм равняется 43 дюймам и 4 шестнадцатым зубьям (4/16).
        1110 мм в дюйм равно 43 . Также 1110 мм равняется 43 дюймам и 11 шестнадцатым (11/16).
        1120 мм в дюйм равно 44 . Также 1120 мм равняется 44 дюймам и 1 шестнадцатой части (1/16).
        1130 мм в дюйм равно 44 . Также 1130 мм равняется 44 дюймам и 7 шестнадцатым (7/16).
        1140 мм в дюйм равно 44 . Также 1140 мм равняются 44 дюймам и 14 шестнадцатым (14/16).
        1150 мм в дюйм равно 45 . Также 1150 мм равняется 45 дюймам и 4 шестнадцатым зубьям (4/16).
        1160 мм в дюйм равно 45 . Также 1160 мм равняется 45 дюймам и 10 шестнадцатым (10/16).
        1170 мм в дюйм равно 46 . Также 1170 мм равняется 46 дюймам и 1 шестнадцатой части (1/16).
        1180 мм в дюйм равно 46 . Также 1180 мм равняется 46 дюймам и 7 шестнадцатым (7/16).
        1190 мм в дюйм равно 46 . Также 1190 мм равняется 46 дюймам и 13 шестнадцатым (13/16).
        1200 мм в дюйм равно 47 . Также 1200 мм равняется 47 дюймам и 3 шестнадцатым зубьям (3/16).
        1210 мм в дюйм равно 47 . Также 1210 мм равняется 47 дюймам и 10 шестнадцатым зубьям (10/16).
        1220 мм в дюйм равно 48 . Также 1220 мм равняется 48 дюймам и 0 шестнадцатым (0/16).
        1230 мм в дюйм равно 48 . Также 1230 мм равняется 48 дюймам и 6 шестнадцатым (6/16).
        1240 мм в дюйм равно 48 . Также 1240 мм равняется 48 дюймам и 13 шестнадцатым (13/16).
        1250 мм в дюйм равно 49 . Также 1250 мм равняется 49 дюймам и 3 шестнадцатым зубьям (3/16).
        1260 мм в дюйм равно 49 . Также 1260 мм равняется 49 дюймам и 9 шестнадцатым (9/16).
        1270 мм в дюйм равно 50 . Также 1270 мм равняется 50 дюймам и 0 шестнадцатым (0/16).
        1280 мм в дюйм равно 50 . Также 1280 мм равняется 50 дюймам и 6 шестнадцатым (6/16).
        1290 мм в дюйм равно 50 . Также 1290 мм равняется 50 дюймам и 12 шестнадцатым зубьям (12/16).
        1300 мм в дюйм равно 51 . Также 1300 мм равняется 51 дюйму и 2 шестнадцатым зубьям (2/16).
        1310 мм в дюйм равно 51 . Также 1310 мм равняется 51 дюйму и 9 шестнадцатым зубьям (9/16).
        1320 мм в дюйм равно 51 . Также 1320 мм равняется 51 дюйму и 15 шестнадцатым зубьям (15/16).
        1330 мм в дюйм равно 52 . Также 1330 мм равняется 52 дюймам и 5 шестнадцатым (5/16).
        1340 мм в дюйм равно 52 . Также 1340 мм равняется 52 дюймам и 12 шестнадцатым (12/16).
        1350 мм в дюйм равно 53 . Также 1350 мм равняется 53 дюймам и 2 шестнадцатым зубьям (2/16).
        1360 мм в дюйм равно 53 . Также 1360 мм равняется 53 дюймам и 8 шестнадцатым (8/16).
        1370 мм в дюйм равно 53 . Также 1370 мм равняются 53 дюймам и 14 шестнадцатым (14/16).
        1380 мм в дюйм равно 54 . Также 1380 мм равняется 54 дюймам и 5 шестнадцатым (5/16).
        1390 мм в дюйм равно 54 . Также 1390 мм равняется 54 дюймам и 11 шестнадцатым (11/16).
        1400 мм в дюйм равно 55 . Также 1400 мм равняется 55 дюймам и 1 шестнадцатой части (1/16).
        1410 мм в дюйм равно 55 . Также 1410 мм равняется 55 дюймам и 8 шестнадцатым зубьям (8/16).
        1420 мм в дюйм равно 55 . Также 1420 мм равняется 55 дюймам и 14 шестнадцатым (14/16).
        1430 мм в дюйм равно 56 . Также 1430 мм равняется 56 дюймам и 4 шестнадцатым зубьям (4/16).
        1440 мм в дюйм равно 56 . Также 1440 мм равняется 56 дюймам и 11 шестнадцатым (11/16).
        1450 мм в дюйм равно 57 . Также 1450 мм равняется 57 дюймам и 1 шестнадцатой части (1/16).
        1460 мм в дюйм равно 57 . Также 1460 мм равняется 57 дюймам и 7 шестнадцатым (7/16).
        1470 мм в дюйм равно 57 . Также 1470 мм равняются 57 дюймам и 13 шестнадцатым (13/16).
        1480 мм в дюйм равно 58 . Также 1480 мм равняется 58 дюймам и 4 шестнадцатым (4/16).
        1490 мм в дюйм равно 58 . Также 1490 мм равняется 58 дюймам и 10 шестнадцатым (10/16).
        1500 мм в дюйм равно 59 . Также 1500 мм равняется 59 дюймам и 0 шестнадцатым зубьям (0/16).
        1510 мм в дюйм равно 59 . Также 1510 мм равняется 59 дюймам и 7 шестнадцатым (7/16).
        1520 мм в дюйм равно 59 . Также 1520 мм равняется 59 дюймам и 13 шестнадцатым (13/16).
        1530 мм в дюйм равно 60 . Также 1530 мм равняется 60 дюймам и 3 шестнадцатым зубьям (3/16).
        1540 мм в дюйм равно 60 . Также 1540 мм равняется 60 дюймам и 10 шестнадцатым зубьям (10/16).
        1550 мм в дюйм равно 61 . Также 1550 мм равняется 61 дюйму и 0 шестнадцатым зубьям (0/16).
        1560 мм в дюйм равно 61 . Также 1560 мм равняется 61 дюйму и 6 шестнадцатым зубьям (6/16).
        1570 мм в дюйм равно 61 . Также 1570 мм равняется 61 дюйму и 12 шестнадцатым зубьям (12/16).
        1580 мм в дюйм равно 62 . Также 1580 мм равняется 62 дюймам и 3 шестнадцатым зубьям (3/16).
        1590 мм в дюйм равно 62 . Также 1590 мм равняется 62 дюймам и 9 шестнадцатым зубьям (9/16).
        1600 мм в дюйм равно 62 . Также 1600 мм равняется 62 дюймам и 15 шестнадцатым (15/16).
        1610 мм в дюйм равно 63 . Также 1610 мм равняется 63 дюймам и 6 шестнадцатым (6/16).
        1620 мм в дюйм равно 63 . Также 1620 мм равняется 63 дюймам и 12 шестнадцатым зубьям (12/16).
        1630 мм в дюйм равно 64 . Также 1630 мм равняется 64 дюймам и 2 шестнадцатым зубьям (2/16).
        1640 мм в дюйм равно 64 . Также 1640 мм равняется 64 дюймам и 9 шестнадцатым (9/16).
        1650 мм в дюйм равно 64 . Также 1650 мм равняется 64 дюймам и 15 шестнадцатым (15/16).
        1660 мм в дюйм равно 65 . Также 1660 мм равняется 65 дюймам и 5 шестнадцатым зубьям (5/16).
        1670 мм в дюйм равно 65 . Также 1670 мм равняется 65 дюймам и 11 шестнадцатым зубьям (11/16).
        1680 мм в дюйм равно 66 . Также 1680 мм равняется 66 дюймам и 2 шестнадцатым зубьям (2/16).
        1690 мм в дюйм равно 66 . Также 1690 мм равняется 66 дюймам и 8 шестнадцатым (8/16).
        1700 мм в дюйм равно 66 . Также 1700 мм равняется 66 дюймам и 14 шестнадцатым (14/16).
        1710 мм в дюйм равно 67 . Также 1710 мм равняется 67 дюймам и 5 шестнадцатым зубьям (5/16).
        1720 мм в дюйм равно 67 . Также 1720 мм равняется 67 дюймам и 11 шестнадцатым (11/16).
        1730 мм в дюйм равно 68 . Также 1730 мм равняется 68 дюймам и 1 шестнадцатой части (1/16).
        1740 мм в дюйм равно 68 . Также 1740 мм равняется 68 дюймам и 8 шестнадцатым (8/16).
        1750 мм в дюйм равно 68 . Также 1750 мм равняется 68 дюймам и 14 шестнадцатым (14/16).
        1760 мм в дюйм равно 69 . Также 1760 мм равняется 69 дюймам и 4 шестнадцатым зубьям (4/16).
        1770 мм в дюйм равно 69 . Также 1770 мм равняется 69 дюймам и 10 шестнадцатым (10/16).
        1780 мм в дюйм равно 70 . Также 1780 мм равняется 70 дюймам и 1 шестнадцатой части (1/16).
        1790 мм в дюйм равно 70 . Также 1790 мм равняется 70 дюймам и 7 шестнадцатым зубьям (7/16).
        1800 мм в дюйм равно 70 . Также 1800 мм равняется 70 дюймам и 13 шестнадцатым (13/16).
        1810 мм в дюйм равно 71 . Также 1810 мм равняется 71 дюйму и 4 шестнадцатым зубьям (4/16).
        1820 мм в дюйм равно 71 . Также 1820 мм равняется 71 дюйму и 10 шестнадцатым (10/16).
        1830 мм в дюйм равно 72 . Также 1830 мм равняется 72 дюймам и 0 шестнадцатым (0/16).
        1840 мм в дюйм равно 72 . Также 1840 мм равняется 72 дюймам и 7 шестнадцатым (7/16).
        1850 мм в дюйм равно 72 . Также 1850 мм равняется 72 дюймам и 13 шестнадцатым (13/16).
        1860 мм в дюйм равно 73 . Также 1860 мм равняется 73 дюймам и 3 шестнадцатым зубьям (3/16).
        1870 мм в дюйм равно 73 . Также 1870 мм равняется 73 дюймам и 9 шестнадцатым зубьям (9/16).
        1880 мм в дюйм равно 74 . Также 1880 мм равняется 74 дюймам и 0 шестнадцатым (0/16).
        1890 мм в дюйм равно 74 . Также 1890 мм равняется 74 дюймам и 6 шестнадцатым (6/16).
        1900 мм в дюйм равно 74 . Также 1900 мм равняется 74 дюймам и 12 шестнадцатым зубьям (12/16).
        1910 мм в дюйм равно 75 . Также 1910 мм равняется 75 дюймам и 3 шестнадцатым зубьям (3/16).
        1920 мм в дюйм равно 75 . Также 1920 мм равняется 75 дюймам и 9 шестнадцатым зубьям (9/16).
        1930 мм в дюйм равно 75 . Также 1930 мм равняется 75 дюймам и 15 шестнадцатым (15/16).
        1940 мм в дюйм равно 76 . Также 1940 мм равняется 76 дюймам и 6 шестнадцатым (6/16).
        1950 мм в дюйм равно 76 . Также 1950 мм равняется 76 дюймам и 12 шестнадцатым (12/16).
        1960 мм в дюйм равно 77 . Также 1960 мм равняется 77 дюймам и 2 шестнадцатым зубьям (2/16).
        1970 мм в дюйм равно 77 . Также 1970 мм равняется 77 дюймам и 8 шестнадцатым (8/16).
        1980 мм в дюйм равно 77 . Также 1980 мм равняется 77 дюймам и 15 шестнадцатым (15/16).
        1990 мм в дюйм равно 78 . Также 1990 мм равняется 78 дюймам и 5 шестнадцатым (5/16).
        2000 мм в дюйм равно 78 . Также 2000 мм равняются 78 дюймам и 11 шестнадцатым зубьям (11/16).

        мм в дюймы Часто задаваемые вопросы

        43 мм в дюймы дробь

        43 мм = 1 дюйм и 11/16. С помощью вышеуказанного калькулятора.

        мм в дробь дюймов

        Используя приведенный выше калькулятор, введите мм (миллиметры), нажмите «Получить результаты», результаты появятся ниже в дюймах (дюймах) и шестнадцатых зубьях (1/16).

        Любое ли иррациональное число является действительным числом: а) Любое ли иррациональное число является действительным числом?б) Каждое ли действительное число является иррацион

        alexxlab / / Разное

        определение, примеры, представления, координатная прямая

        Данная статья посвящена теме «Действительные числа». В статье дается определение действительных чисел, иллюстрируется их положение на координатной прямой, рассматриваются способы задания действительных чисел числовыми выражениями.

        Определение действительных чисел

        Целые и дробные числа вместе составляют рациональные числа. В свою очередь, рациональные и иррациональные числа составляют действительные числа. Как дать определение, что такое действительные числа?

        Определение 1

        Действительные числа — это рациональные и иррациональные числа. Множество действительных чисел обозначается через R.

        Данное определение можно записать иначе с учетом следующего:

        1. Рациональные числа можно представить в виде конечной десятичной дроби или бесконечной периодической десятичной дроби.
        2. Иррациональные числа представляют собой бесконечные непериодические десятичные дроби.
        Определение 2

        Действительные числа — числа, которые можно записать в виде конечной или бесконечной (периодической или непериодической) десятичной дроби. 

        Действительные числа — это любые рациональные и иррациональные числа. Приведем примеры таких чисел: 0; 6; 458; 1863; 0,578; -38; 265; 0,145(3); log512.

        Нуль также является действительным числом. Согласно определению, существуют как положительные, так и отрицательные действительные числа. Нуль является единственным действительным числом, которое не положительно и не отрицательно.

        Еще одно название для действительных чисел — вещественные числа. Эти числа позволяют описывать значение непрерывно меняющейся величины без введения эталонного (единичного) значения этой величины.

        Координатная прямая и действительные числа

        Каждой точке не координатной прямой соответствует определенное и единственное действительное число. Иными словами, действительные числа занимают всю координатную прямую, а между точками кривой и числами присутствует взаимно-однозначное соответствие.

        Представления действительных чисел

        Под определение дейситвительных чисел попадают:

        1. Натуральные числа.
        2. Целые числа.
        3. Десятичные дроби.
        4. Обыкновенные дроби.
        5. Смешанные числа.

        Также действительные числа часто представляются в виде выражений со степенями, корнями и логарифмами. Сумма, разность произведение и частное действительных чисел также являются действительными числами. 

        Значение любого выражения, составленного из действительных чисел, также будет являться действительным числом.

        Например, значения выражений sin23π·e-285·10log32 и tg676693-8π32  — действительные числа.

        Решение задач от 1 дня / от 150 р. Курсовая работа от 5 дней / от 1800 р. Реферат от 1 дня / от 700 р.

        Автор: Ирина Мальцевская

        Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

        Навигация по статьям

        Предыдущая статья

        Вычитание целых чисел

        Следующая статья

        Рациональные числа

        • Арифметические операции над действительными числами
        • Взаимно обратные числа
        • Вычитание десятичных дробей
        • Вычитание натуральных чисел
        • Вычитание натуральных чисел
        • Все темы по математике
        • Курсовые работы
        • Рефераты
        • Контрольные работы
        • Отчет по практике
        • Эссе

        Узнать подробнее

      3. ПЛАСТИНЧАТЫЙ ТЕПЛООБМЕННИК В Компас А Бумага теплообменник кожухотрубчатый

        • Вид работы:

          Чертёж

        • Выполнена:

          27 июня 2022 г.

        • Стоимость:

          2 400 руб

        Заказать такую же работу

      4. Математические модели инфодемии

        Заказать такую же работу

      5. Нужно рассчитать теплообменник

        • Вид работы:

          Контрольная работа

        • Выполнена:

          28 апреля 2022 г.

        • Стоимость:

          3 600 руб

        Заказать такую же работу

      6. Задания прикреплены

        • Вид работы:

          Контрольная работа

        • Выполнена:

          21 января 2022 г.

        • Стоимость:

          1 400 руб

        Заказать такую же работу

      7. Особенности исторической застройки Красноярска от появления острога до конца века

        • Вид работы:

          Реферат

        • Выполнена:

          27 декабря 2021 г.

        • Стоимость:

          1 000 руб

        Заказать такую же работу

      8. по Строительным материалам

        • Вид работы:

          Решение задач

        • Выполнена:

          30 ноября 2021 г.

        • Стоимость:

          1 100 руб

        Заказать такую же работу

        9. Смотреть все работы по чертежам в компас

        Урок 8. иррациональные числа. понятие действительного числа. сравнение действительных чисел — Алгебра — 7 класс

        Алгебра

        7 класс

        Урок № 8

        Иррациональные числа. Понятие действительного числа.

        Сравнение действительных чисел

        Перечень вопросов, рассматриваемых в теме:

        • Иррациональные числа.
        • Понятие действительного числа.
        • Абсолютная величина (модуль) числа.
        • Сравнение действительных чисел.

        Тезаурус:

        Число, которое можно записать в виде конечной или бесконечной периодической десятичной дроби, называют рациональным.

        Бесконечная периодическая десятичная дробь – это бесконечная дробь, у которой одна цифра или группа цифр повторяются. Повторяющаяся группа цифр называется периодом и записывается в скобках.

        Число, которое можно записать в виде бесконечной непериодической десятичной дроби, называют иррациональным числом.

        Рациональные и иррациональные числа называются действительными числами.

        Основная литература:

        1. Никольский С. М. Алгебра: 7 класс. // Никольский С. М., Потапов М. К., Решетников Н. Н., Шевкин А. В. – М.: Просвещение, 2017. – 287 с.

        Дополнительная литература:

        1. Чулков П. В. Алгебра: тематические тесты 7 класс. // Чулков П. В. – М.: Просвещение, 2014 – 95 с.

        2. Потапов М. К. Алгебра: дидактические материалы 7 класс. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 96 с.

        3. Потапов М. К. Рабочая тетрадь по алгебре 7 класс: к учебнику С. М. Никольского и др. «Алгебра: 7 класс». 1, 2 ч. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 160 с.

        Теоретический материал для самостоятельного изучения.

        Рассмотрим положительную бесконечную непериодическую дробь 0,10110111011110…

        После запятой записаны группы единиц, разделённые нулём. Эта дробь не может быть десятичным разложением какого – либо рационального числа.

        Её называют иррациональным (нерациональным) числом.

        Иррациональное число – бесконечная непериодическая десятичная дробь.

        Примеры иррациональных чисел:

        0,010010001…

        -17,1234567…

        Самое знаменитое иррациональное число π = 3,1415926…

        Понятие действительного числа:

        Рациональные и иррациональные числа называют действительными.

        Таким образом, любое действительное число можно представить в виде бесконечной (периодической или непериодической) десятичной дроби.

        Если дробь периодическая – число рациональное.

        Если дробь непериодическая – число иррациональное.

        Число, образованное цифрами до запятой, называют целой частью, после запятой дробной частью.

        Для записи произвольной бесконечной десятичной дроби, отличной от нуля, пользуются буквами:

        α0,α1 α2 α3… αn…, причем хотя бы одна из цифр отлична от нуля.

        Противоположные числа

        Противоположные числа отличаются только знаками:

        α0, α1, α2, α3,… αn…, и — α0,α1, α2, α3,… αn…,

        Обозначают: а, если а положительное число,

        -а, если а отрицательное число.

        Абсолютная величина числа (модуль) числа

        Абсолютной величиной числа (модулем) действительного числа называют:

        • само число а, если а – положительное
        • 0, если а = 0
        • число -а, если а – отрицательное число.

        Обозначается: а, если а > 0,

        |а| = 0, если а = 0,

        -а, если а < 0.

        Примеры:

        а = 0,10110111… |а| = 0,10110111…

        b = -2,1234567…… |b| = 2,1234567…

        c = 0,(0) |c| = 0

        Сравнение действительных чисел.

        Правило 1.

        Два действительных числа равны, если они имеют одинаковые знаки и их абсолютные величины имеют одинаковые целые и дробные части.

        Правило 2.

        Отрицательное число меньше 0 и меньше любого положительного числа.

        Число 0 меньше любого положительного числа.

        Правило 3.

        Если целые части положительных чисел разные, то больше то, у которого целая часть больше.

        Если целые части положительных чисел одинаковые, то больше то, у которого цифра в наименьшем разряде дробной части больше.

        Из двух отрицательных чисел больше то, у которого абсолютная величина меньше.

        Сравнение чисел обозначают с помощью знаков: > = <

        Разбор решения заданий тренировочного модуля.

        Задача 1.

        Изобразите числовые множества с помощью кругов Эйлера.

        Определите, какому множеству принадлежат числа: 2,(3) и 2,1234?

        Решение:

        Число 2,(3) принадлежит множествам рациональных и действительных чисел.

        Число 2,1234 принадлежит множествам иррациональных и действительных чисел.

        Задача 2.

        Сравните числа:

        1. 0,(27) > 0,2727, т. к. 0,(27) = 0,272727…
        2. -3,(5) < -3,(4), т. к. абсолютная величина первого числа меньше.
        3. 8,273273 > 8,(27), т. к. 8,273 и 8,272, первая отличная цифра в третьем разряде больше.

        Все ли иррациональные числа действительные числа да или нет? – Обзоры Вики

        Да. Иррациональные числа определяются как те действительные числа, которые не являются рациональными.

        Отсюда, почему каждое иррациональное число не является действительным числом? Таким образом, каждое иррациональное число является действительным числом. … Поскольку никакое отрицательное значение не может быть квадратным корнем натурального числа, поэтому каждая точка на числовой прямой не может быть в форме u221am, где m — натуральное число.

        Является ли каждое действительное число рациональным или иррациональным? Это действительные числа, которые мы не можем записать как отношение pq, где p и q — целые числа, при этом q≠0. По факту, каждое действительное число является либо рациональным числом, либо иррациональным числом. Никакое число не может быть одновременно рациональным и иррациональным!

        Кроме того, каждое ли иррациональное число является рациональным числом? «Является каждый иррациональный рациональное число?» Нет. Рациональные числа — это те, которые могут быть выражены как отношение (доля) двух целых чисел; иррациональные числа — это те, которые не могут быть выражены таким образом. Между этими двумя категориями нет пересечения.

        Всякое ли натуральное число является действительным числом? Да, цель не каждое действительное число является натуральным числом. Натуральные числа — это набор целых положительных чисел {1, 2, 3,…}, которые также являются действительными числами. Однако действительные числа также включают отрицательные числа, дроби и т. д., ни одно из которых не является натуральным числом.

        Что такое каждое иррациональное число?

        иррациональное число, любое действительное число, которое не может быть выражено как частное двух целых чисел. Например, среди целых чисел и дробей нет числа, равного квадратному корню из 2. … Каждое иррациональное число может быть выражено как бесконечное десятичное расширение без регулярно повторяющихся цифр или групп цифр.

        Является ли каждое целое число действительным числом? Мы знаем, что целые числа не включают десятичные числа. Иррациональное число определяется как число, которое не может быть выражено в виде дробей. … Каждое целое число реальное число и Рациональное число, но не иррациональные числа и натуральные числа. Следовательно, каждое целое число является действительным числом и рациональным числом.

        Как иррациональные числа используются в реальной жизни? Инженерные револьверы по конструированию вещей для реальной жизни и несколько вещей, таких как обработка сигналов, расчет силы, спидометр и т. д. использовать иррациональные числа. Исчисление и другие области математики, в которых используются эти иррациональные числа, широко используются в реальной жизни. Иррациональные числа используются косвенно.

        Что такое каждое рациональное число?

        Каждое рациональное число целое число.

        Также является ли каждое иррациональное число целым числом? Поскольку иррациональные числа не могут быть выражены как отношение двух целых чисел, отсюда следует, что иррациональные числа не могут быть целыми числами, и наоборот.

        Каждое ли число является рациональным числом?

        Поскольку любое целое число можно представить как отношение двух целых чисел, все целые числа являются рациональными числами. Помните, что все счетные числа и все целые числа тоже целые, а значит, они тоже рациональны.

        Что такое действительные и рациональные числа? Рациональными считаются числа, которые можно представить в виде отношения двух целых чисел, причем знаменатель не равен нулю. Действительные числа – это те, которые может быть представлен на действительной числовой прямой. … не может быть выражено как отношение двух целых чисел, как рациональные числа, но может быть представлено в прямой числовой строке.

        Как действительные числа используются в реальной жизни?

        Большинство чисел, с которыми мы работаем каждый день, являются действительными числами.. К ним относятся все деньги в вашем кошельке, статистика, которую вы видите в спорте, или измерения, которые мы видим в поваренных книгах. Все эти числа можно представить в виде дроби (нравится нам это или нет).

        Каковы примеры действительных чисел?

        В математике действительное число — это значение непрерывной величины, которое может представлять расстояние вдоль линии. Реальные числа включают как рациональные, так и иррациональные числа. Рациональные числа, такие как целые числа (-5, 0, 9), дроби (1/2,7, 8/2.5, 7) и иррациональные числа, такие как √XNUMX, π и т. д., являются действительными числами.

        Всякое ли целое число является рациональным числом? Рациональное число — это число, которое может быть выражено в виде p/q, где q не должно быть равно 0… Но это не целое число, а десятичное. Таким образом, рациональное число может быть или не быть целым числом, но каждое целое число является рациональным числом.

        Реально или рационально? Число рациональное (записывается как отношение двух целых чисел), но оно также реальные . Все рациональные числа также являются действительными числами.
        …

        Тип десятичной дроби Рациональный или иррациональный Примеры
        Нагрузочный Рациональный 0.25 (золото) 1.3 (золото)
        Непрерывный и повторяющийся Рациональный 0. 66… (золото) 3.242424… (золото)

        Что такое действительные числа и недействительные числа?

        Реальные числа могут быть положительными или отрицательными.и включите число ноль. Их называют действительными числами, потому что они не являются мнимыми, а это другая система чисел. Мнимые числа — это числа, которые невозможно определить количественно, например квадратный корень из -1.

        Что такое недействительные числа? Чай числа не действительные, а мнимые называются недействительными или недействительными числами. Недействительные числа не могут быть представлены на числовой прямой. I. Комплексные числа: 4+i5 , где «i» представляет йоту, которая равна √−1 .

        Как найти настоящие числа?

        Абсолютное значение числа — это его расстояние от нуля на числовой прямой. Действительные числа — это числа, которые не являются мнимыми, то есть все числа, кроме квадратного корня из -1 и бесконечности. Чтобы найти абсолютное значение действительного числа, найдите его расстояние от нуль в числовой строке.

        Что такое рациональное и иррациональное число? Рациональные числа – это те числа, которые целые и может быть выражено в виде x/y, где и числитель, и знаменатель являются целыми числами, тогда как иррациональные числа — это те числа, которые не могут быть выражены дробью. … Иррациональные числа включают surds и специальные числа, такие как π.

        Что такое рациональное и иррациональное число на примере?

        Рациональное число — это число, которое можно представить в виде P/Q, где P и Q — целые числа, а Q ≠ 0. Но иррациональное число нельзя записать в виде простых дробей. ⅔ это пример рациональных чисел, тогда как √2 — иррациональное число.

        Почему каждое рациональное число является действительным числом? Верно или ложно? Ага это правда….

        Что такое действительное число в математике?

        действительное число, в математике, количество, которое может быть выражено в виде бесконечного десятичного разложения. … Действительные числа включают положительные и отрицательные целые числа и дроби (или рациональные числа), а также иррациональные числа.

        Что такое рациональные и иррациональные числа? Рациональные числа — это числа, которые можно представить в виде дроби или части целого числа.. (примеры: -7, 2/3, 3.75) Иррациональные числа — это числа, которые нельзя представить в виде дроби или отношения двух целых чисел. Нет конечного способа выразить их. (примеры: √2, π, е)

        Что такое реальное число 10-го класса?

        Реальные числа просто комбинация рациональных и иррациональных чисел, в системе счисления. В общем, над этими числами можно производить все арифметические действия, и их можно представить в числовой строке.

        404 Cтраница не найдена

        Размер:

        AAA

        Цвет: C C C

        Изображения Вкл. Выкл.

        Обычная версия сайта

        Найти ближайший филиал Версия для слабовидящих Версия для слабовидящих

        КАМЕНСК-УРАЛЬСКИЙ
        АГРОПРОМЫШЛЕННЫЙ ТЕХНИКУМ


        Сохраняя традиции, вместе создаем будущее!

        Не хватает прав доступа к веб-форме.

        Выше сщщбщение успешно отправлено.

        • Сведения об ОО
          • Основные сведения
          • Структура и органы управления
          • Документы
          • Образование
          • Образовательные стандарты
          • Руководство. Педагогический состав
          • Педагогический состав
          • МТО и оснащенность ОП
          • Стипендия и иные виды материальной поддержки
          • Платные образовательные услуги
          • Финансово-хозяйственная деятельность
          • Вакантные места для приёма (перевода)
          • Противодействие коррупции
          • Бесплатная юридическая помощь
          • Награды, достижения ОО
          • Инновационная деятельность
          • Доступная среда
          • Международное сотрудничество
        • Летопись техникума
          • Страницы летописи
          • Руководители
          • Нам есть у кого учиться
          • Педагоги техникума
          • Наша гордость — выпускники
          • Достижения
          • СМИ о техникуме
          • Хранители нашей истории
        • Абитуриентам
          • Прием 2022
          • Дни открытых дверей
          • Специальности/профессии
          • Общежитие
          • Правила и условия приема
          • Документы для поступления
          • Подать заявление онлайн
          • Студенческая жизнь
          • Приемная комиссия
          • Мониторинг подачи заявлений и документов
          • Зачисление
          • Фото-экскурсия
          • Инклюзивное образование
          • Целевое обучение
        • Студентам
          • Расписание
          • Заочное отделение
          • Документы
          • Студенческая жизнь
          • Государственная итоговая аттестация
          • Центр профориентологии
          • Стипендия и иные виды материальной поддержки
          • Спорт
          • Конференции и олимпиады
          • Советы психолога
          • Сайты преподавателей
          • ЕГЭ для студентов учреждений СПО
          • Воспитательная работа
          • Целевое обучение
        • Выпускникам
        • Сотрудникам
          • Документы
          • Методическая служба
        • Родителям
          • Телефонный справочник
          • Информация для Родителей
          • Специальности / профессии
        • Главная
        • ›
        • uploads
        • ›
        • about_the_university
        • ›
        • 14_sistema-distantsionnogo-obucheniya
        • ›
        • raspisanie-na-05-09-2020g-subbota

        определение и сравнение • BUOM

        Автор: редакционная команда Indeed

        30 апреля 2021 г.

        Категории чисел показывают, насколько некоторые группы чисел отличаются или похожи на другие группы чисел. Некоторые из этих категорий перекрываются и включают в себя подмножества друг друга, потому что они имеют схожие характеристики, в то время как другие категории уникальны и не пересекаются. Действительные числа и целые числа принадлежат к двум различным категориям чисел. В этой статье мы обсудим, что такое действительные числа, что такое целые числа, действительные числа и целые числа, а также сравним действительные и целые числа на диаграмме.

        Что такое действительное число?

        Вещественное число — это любое число на числовой прямой, которое включает в себя подмножества чисел, включая натуральные, целые, целые, рациональные и иррациональные числа. Проще говоря, все числа являются действительными числами, за исключением мнимых чисел, которые представляют собой набор комплексных чисел, которые когда-то считались невозможными для вычисления.

        Вы можете разделить действительные числа на две категории, рациональные числа и иррациональные числа. Вы можете дополнительно разделить категорию рациональных чисел на подмножество целых чисел, которые содержат подмножество, целые числа; который содержит подмножество натуральных чисел. Существует множество наглядных пособий и диаграмм того, как работают эти категории и подмножества чисел. Если вы хотите найти один в Интернете, вы найдете его легко.

        Вот определения чисел, из которых состоят все действительные числа:

        Иррациональные числа

        Иррациональное число — это действительное число, которое нельзя записать в виде простой дроби. Числа, которые вы не можете записать в виде дроби, — это десятичные числа, которые продолжаются вечно без повторяющегося шаблона.

        Например, некоторые известные иррациональные числа:

        • Число пи, или «π», является иррациональным числом, потому что это десятичная дробь, которая продолжается бесконечно, не повторяясь, и вы не можете записать ее в виде дроби.

        • Квадратный корень из двух, или «√2», — это еще одна бесконечная десятичная дробь, которая никогда не повторяется.

        • Число Эйлера, или «е», — это десятичная дробь без шаблона или конца.

        • Золотое сечение, или «φ», — это еще одна десятичная дробь без конца и без видимой закономерности.

        Рациональное число

        Рациональное число — это число, которое можно записать как отношение двух целых чисел, или, другими словами, как простую дробь. Рациональные числа включают подмножества: целые числа, целые числа и натуральные числа.

        Например, следующие числа являются рациональными числами:

        • Десятичное число 2,5 можно записать как дробь 6/2.

        • Дробь 0,33 — это повторяющаяся десятичная дробь, которую можно записать как дробь 1/3.

        • Целое число -4 также можно записать в виде дроби -4/1.

        • Целое число 32 также можно записать в виде дроби 32/1.

        • Натуральное число 1 также можно записать в виде дроби 1/1.

        Целые числа

        Целое число — это положительное или отрицательное целое число без дробной или десятичной части. Целые числа включают подмножества, целые числа и натуральные числа.

        Например, следующие числа являются целыми:

        • Отрицательное число, -16

        • Целое число, 0

        • Счетное число, 57

        Целые числа

        Целое число — это положительное целое число без дробной или десятичной части. Целые числа включают подмножество натуральных чисел. Целые числа представляют целые объекты без каких-либо частей или фрагментов.

        Например, следующие числа являются целыми числами:

        • Целое число, 0

        • Целое число, 1258

        • Натуральное число, 7

        Натуральные числа

        Натуральное число иногда также называют «счетным числом» и оно похоже на целое число, за исключением того, что вы не включаете ноль в набор. Если бы вы естественным образом начали подсчитывать количество предметов в сумке, вы бы начали с единицы, а не с нуля.

        Например, следующие числа являются натуральными числами:

        • Натуральное число, 1

        • Натуральное число 513

        • Натуральное число 3 482 389.

        Что такое целое число?

        Целое число — это положительное или отрицательное целое число без дробной или десятичной части. Целые числа представляют собой подмножество действительных чисел и включают в себя целые числа подмножества и натуральные числа. Обычно целые числа представляются как: «-3, -2, -1, 0, 1, 2, 3», поскольку это показывает, что числа бесконечны в любом направлении, целые числа и содержат число ноль.

        Целые числа имеют следующие характеристики:

        • Целые числа положительны, поэтому вы видите их в правой части числовой строки, а положительные целые числа имеют более высокое значение, чем их отрицательные аналоги или противоположности.

        • Целые числа отрицательны, поэтому вы видите их в левой части числовой строки, а отрицательные целые числа имеют меньшее значение, чем их положительные аналоги или противоположности.

        • Есть одно целое число — ноль — нейтральное, то есть ни положительное, ни отрицательное, и вы видите его в центре числовой прямой.

        • Целые числа не имеют фрагментов, то есть это целые числа без дробных или десятичных частей.

        Действительные числа против целых чисел

        Целые числа являются действительными числами, но не все действительные числа являются целыми числами. Вот некоторые отличия:

        • Действительные числа включают целые числа, но также включают рациональные, иррациональные, целые и натуральные числа.

        • Целые числа — это тип вещественных чисел, который включает в себя только положительные и отрицательные целые числа и натуральные числа.

        • Действительные числа могут включать дроби из-за рациональных и иррациональных чисел, но целые числа не могут включать дроби.

        • Действительные числа обладают «свойством наименьшей верхней границы», или полнотой, но целые числа не обладают этим свойством.

        Таблица сравнения целых и действительных чисел

        Вот таблица, которая поможет вам легче сравнивать целые числа с действительными числами:

        Параметры сравнения Целые числа Действительные числа Происхождение Арбермут Холст изобрел систему счисления целых чисел в 1563 году. Слово целое имеет латинские корни 16-го века, означая целое или неповрежденное. Рене Декарт ввел термин «действительный» в 17 веке для описания всех чисел, которые не считались мнимыми числами. Классификация Математики классифицируют целые числа только как целые числа и их отрицательные числа. Математики классифицируют действительные числа как рациональные числа, иррациональные числа, целые числа, целые числа и натуральные числа. Счетность Целые числа могут образовывать счетное бесконечное множество. Нотационный символ «Z» представляет собой набор всех целых чисел. Действительные числа могут образовывать неисчисляемое бесконечное множество. «R» представляет собой набор всех действительных чисел. Представление в числовой строке Целые числа в числовой строке — это все целые числа и их отрицательные числа. Действительные числа на числовой прямой — это любая точка на числовой прямой. Наличие дробей или десятичных знаков Дробное или десятичное число не является целым числом. Дробное или десятичное число является действительным числом.

        Поиск материала «Числа рациональные и иррациональные, Нивен А., 1966» для чтения, скачивания и покупки

        Ниже показаны результаты поиска поисковой системы Яндекс. В результатах могут быть показаны как эта книга, так и похожие на нее по названию или автору.

        Search results:

        1. Числа рациональные и иррациональные | Нивен А., Яглом…

          Эта книга посвящена одному из основных понятий математики — понятию действительного числа. Ученики старших классов (именно на них она в первую очередь и рассчитана) узнают из нее некоторые свойства чисел, о которых они раньше и не подозревали, и познакомятся с доказательствами

          Оно сопровождается рядом вопросов и задач, облегчающих активное усвоение материала.Автор книги — известный американский специалист по теории чисел. Скачать книгу бесплатно (djvu, 3.86 Mb) | Читать «Числа рациональные и иррациональные».

          bookscat. org

        2. А. нивен. числа рациональные и иррациональные…

          А. НИВЕН. ЧИСЛА РАЦИОНАЛЬНЫЕ И ИРРАЦИОНАЛЬНЫЕ Москва: «Мир», 1966 #книги_math_досуг. Аннотация издательства: Эта книга посвящена одному из основных понятий математики — понятию действительного числа. Ученики старших классов (именно на них она в первую очередь и рассчитана) узнают из нее некоторые свойства чисел, о которых они раньше и не подозревали, и познакомятся с доказательствами теорем, принимаемых в школьном курсе алгебры на веру. Изложение очень простое и живое. Оно сопровождается рядом вопросов и…

          vk.com

        3. Купить эту книгу

        4. Канцтовары

          Канцтовары: бумага, ручки, карандаши, тетради. Ранцы, рюкзаки, сумки. И многое другое.

          my-shop.ru

        6. А. НИВЕН числа РАШИОНАЛЬНЫЕ ИРРАШИОНАЛЬНЫЕ 3 1415 9

          3. (Действительные) алгебраические числа. 4. Числа, допускающие построение 5. Рациональные числа.

          ikfia.ysn.ru

        7. Числа рациональные и иррациональные — Нивен А. — быстро…

          Числа рациональные и иррациональные.djvu. Читать онлайн. Нивен А. (посмотреть).

          klex.ru

        8. Нивен А. Числа рациональные и иррациональные. — 1966

          Нивен А. Числа рациональные и иррациональные / пер. с англ. В. В. Сазонова ; под ред. И. М. Яглома. — М. : Мир, 1966.

          Рациональные числа. 33§ 1. Определение рациональных чисел 36§ 2. Конечные и бесконечные десятичные дроби 39§ 3. Различные способы формулировки и доказательства предложений 45§ 4. Периодические десятичные дроби 50§ 5. Всякую конечную десятичную дробь можно представить в виде периодической десятичной дроби 53§ 6. 718 2818, 37 коп. kj 1. Комплексные числа 2. Действительные числа 3. (Действительные) алгебраические числа 4. Числа, допускающие построение 5. Рациональные числа 6. Целые числа 7

          Действительные числа образуются всеми рациональными и иррациональными числами и являются основной числовой системой в математике. Любое геометрическое рассуждение, касающееся длин, площадей или объемов, сразу приводит к действительным числам.

          b-ok.xyz

        9. Числа рациональные и иррациональные » Litgu.ru…

          Название: Числа рациональные и иррациональные Автор: Нивен Айвен Издательство: Мир Год: 1966 Формат: PDF/Djvu Страниц: 201 Размер: 24.3 MB Язык: Русский. Эта книга посвящена одному из основных понятий математики — понятию действительного числа. Ученики старших классов (именно на них она в первую очередь и рассчитана) узнают из нее некоторые свойства чисел, о которых они раньше и не подозревали, и познакомятся с доказательствами теорем, принимаемых в школьном курсе алгебры на веру.

          litgu.ru

        10. А. нивен. числа рациональные и иррациональные…

          А. НИВЕН. ЧИСЛА РАЦИОНАЛЬНЫЕ И ИРРАЦИОНАЛЬНЫЕ Москва: «Мир», 1966 #книги_math_досуг. Аннотация издательства: Эта книга посвящена одному из основных понятий математики — понятию действительного числа. Ученики старших классов (именно на них она в первую очередь и рассчитана) узнают из нее некоторые свойства чисел, о которых они раньше и не подозревали, и познакомятся с доказательствами теорем, принимаемых в школьном курсе алгебры на веру. Изложение очень простое и живое.

          vk.com

        11. Числа рациональные и иррациональные

          Название: Числа рациональные и иррациональные Автор: Нивен Айвен Издательство: Мир Год: 1966 Страниц: 201 Формат: PDF, DJVU Размер: 24,3 МБ Качество: Отличное. Числа рациональные и иррациональные — Эта книга посвящена одному из основных понятий математики — понятию действительного числа. Ученики старших классов (именно на них она в первую очередь и рассчитана) узнают из нее некоторые свойства чисел, о которых они раньше и не подозревали, и познакомятся с доказательствами теорем, принимаемых в школьном курсе…

          bookskeeper.ru

        12. Скачать Нивен А. Числа рациональные и иррациональные [PDF]

          Нивен А. Числа рациональные и иррациональные. Файл формата pdf. размером 4,80 МБ.

          Дополнительные главы», содержащие классическое изложение понятий и результатов математической логики с элементами теории множеств, теории алгоритмов и оснований математики….

          eruditor.io

        13. А. нивен. числа рациональные и иррациональные…

          А. Нивен. Числа рациональные и иррациональные.

          vk. com

        14. Скачать Числа рациональные и иррациональные — Нивен…

          Нивен А. Числа рациональные и иррациональные. Формат: Электронная/бумажная книга Жанр: Теория чисел Автор(ы): Нивен А. Название: Числа рациональные и иррациональные Издательство: Мир Город: Москва Год: 1966. Аннотация: Эта книга посвящена одному из основных понятий математики — понятию действительного числа.

          dislyget.ru

        15. Числа рациональные и иррациональные | Нивен Айвен

          Нивен Айвен. Скачать книгу бесплатно (djvu, 4.40 Mb) | Читать «Числа рациональные и иррациональные».

          bookscat.org

        16. Числа рациональные и иррациональные | Нивен А. | download

          A НИВЕН ЧИСЛА РАЦИОНАЛЬНЫЕ и ИРРАиИОНАЛЬНЫЕ 3-4 7С= 3 1Л15927. 718 2818, 37 коп. kj 1. Комплексные числа 2. Действительные числа 3. (Действительные) алгебраические числа 4. Числа, допускающие построение 5. Рациональные числа 6. Целые числа 7

          Действительные числа образуются всеми рациональными и иррациональными числами и являются основной числовой системой в математике. Любое геометрическое рассуждение, касающееся длин, площадей или объемов, сразу приводит к действительным числам.

          b-ok.cc

        17. Скачать Нивен А. Числа рациональные и иррациональные…

          Нивен А. Числа рациональные и иррациональные. Файл формата djvu. размером 3,00 МБ.

          Чтобы скачать этот файл зарегистрируйтесь и/или войдите на сайт используя форму сверху.

          eruditor.io

        18. Скачать книгу Числа рациональные и иррациональные — Нивен. 718 2818, 37 коп. kj 1. Комплексные числа 2. Действительные числа 3. (Действительные) алгебраические числа 4. Числа, допускающие построение 5. Рациональные числа 6. Целые числа 7

          Действительные числа образуются всеми рациональными и иррациональными числами и являются основной числовой системой в математике. Любое геометрическое рассуждение, касающееся длин, площадей или объемов, сразу приводит к действительным числам.

          b-ok.cc

        19. Числа рациональные и иррациональные

          Числа рациональные и иррациональные. Айвен Нивен. Числа рациональные и иррациональные. Эта книга посвящена одному из основных понятий математики — понятию действительного числа. Ученики старших классов (именно на них она в первую очередь и рассчитана) узнают из нее некоторые свойства чисел, о которых они раньше и не подозревали, и познакомятся с доказательствами теорем, принимаемых в школьном курсе алгебры на веру. 718 2818, 37 коп. kj 1. Комплексные числа 2. Действительные числа 3. (Действительные) алгебраические числа 4. Числа, допускающие построение 5. Рациональные числа 6. Целые числа 7. Натуральные числа.

          СОВРЕМЕННАЯ МАТЕМАТИКА» Популярная серая АЙВЕН НИВЕН Числа рациональные и иррациональные Перевод с английского В, В, Сазонова Под редакцией И. М. Яглома ИЗДАТЕЛЬСТВО «МИР» Москва 1966.

          b-ok.global

        20. Книга Числа рациональные и иррациональные (Нивен…

          Читать онлайн книгу Числа рациональные и иррациональные автора Нивен А., Яглом И.М. (ред.)

          bookree.org

        21. Числа рациональные и иррациональные — Нивен А.

          Числа рациональные и иррациональные. Нивен А. | Математика. Эта книга посвящена одному из основных понятий математики — понятию действительного числа. Ученики старших классов (именно на них она в первую очередь и рассчитана) узнают из нее некоторые свойства чисел, о которых они раньше и не подозревали, и познакомятся с доказательствами теорем, принимаемых в школьном курсе алгебры на веру. Изложение очень простое и живое. Оно сопровождается рядом вопросов и задач, облегчающих активное усвоение материала.

          www.koob.ru

        22. Айвен Нивен «Числа рациональные и иррациональные«

          ] Книга двести тридцать вторая. Айвен Нивен «Числа рациональные и иррациональные» (Ivan Niven «Numbers: Rational and Irrational», 1961) М: Мир, 1966 г., 200 стр. От прошлой жизни осталась куча книг по математике — элементарной и не очень. Эта — из элементарных. Не читал раньше, почему бы и не. Тем более в ней доказывается существование трансцендентных чисел прямым лиувиллевским построением — даже не помню, знал ли я это доказательство раньше.

          timur0.livejournal.com

        23. Числа рациональные и иррациональные | Нивен Айвен

          Нивен Айвен. Скачать (djvu, 4.40 Mb) Читать.

          www.bookfi.net

        24. Целые числа. Рациональные и иррациональные числа

          Рациональные и иррациональные числа. Шилепина Надежда Ивановна. преподаватель. Новокузнецк, 2019. Что такое число. Число — основное понятие математики, используемое для количественной характеристики, сравнения, нумерации объектов и их частей.

          Рациональные числа. Множество чисел, которое можно представить в виде ,называется множеством рациональных чисел и обозначается — Q первой буквой французского слова Quotient — «отношение».

          multiurok.ru

        25. Нивен А., Числа рациональные и иррациональные. .

          Нивен А., Числа рациональные и иррациональные. Серия: Современная математика. 1966, изд-во: Мир, город: М., стр. : 198 с., обложка: Мягкая издательская обложка, формат: Обычный, состояние: Хорошее (следы влаги). Книга известного американского специалиста по теории чисел посвящена понятию действительного числа.

          4. Иррациональные числа. 5. Значения тригонометрических и логарифмической функций. Приближение иррациональных функций рациональными. 7. Существование трансцендентных чисел.

          www.gornitsa.ru

        26. Разница между рациональными и иррациональными числами…

          Рациональные и иррациональные числа. Рациональное число – это такое число, которое можно записать в виде дроби с целыми числителем и знаменателем.

          Иррациональное число – это число, которое невозможно записать в виде дроби с целыми числителем и знаменателем. Невозможно, потому что это бесконечные дроби, да еще и непериодические. Поэтому нет таких целых чисел, которые бы поделившись друг на друга, дали бы иррациональное число.

          cos-cos.ru

        27. Числа: натуральные, целые, рациональные, иррациональные…

          Рациональные числа — это целые числа и дроби. Любое рациональное число может быть представлено в виде периодической дроби.

          Действительные числа – это все рациональные и все иррациональные числа. Множество действительных чисел обозначается латинской буквой R. Школьная алгебра Школьная геометрия.

          sbp-program.ru

        28. Какие числа называются Иррациональные?

          Просмотры. 43252. Определение иррациональных чисел. Иррациональное число — это действительное число, которое невозможно выразить в форме деления двух целых чисел, то есть в рациональной дроби: Оно может быть выражено в форме бесконечной

          Множество иррациональных чисел договорились обозначать латинской буквой I. Действительныеили вещественные числа — это все рациональные и иррациональные числа: положительные, отрицательные и нуль. Если натуральное число n не является точным квадратом, т. е. n ≠ k2…

          skysmart.ru

        29. Рациональные и иррациональные числа. Понятие…

          Множество рациональных и иррациональных чисел составляют множество вещественных (действительных) чисел.

          Это число, как и любое другое иррациональное число, изображается бесконечной непериодической десятичной дробью. Последовательностью десятичных приближений числа с недостатком называют последовательность конечных десятичных дробей, которая получится, если у числа отбросить все десятичные знаки, начиная, сначала с первого десятичного знака, затем со второго десятичного знака, потом с третьего…

          www.resolventa.ru

        30. Числовая ось, рациональные, иррациональные числа

          Такие числа называются иррациональными числами. Иррациональное число невозможно представить в виде Приведём примеры иррациональных чисел

          Например, иррациональные числа. Множество иррациональных чисел обозначается буквой I. Арифметические действия над иррациональными числами и их свойства аналогичны рациональным числам. Множество, состоящее из рациональных и иррациональных чисел, называется множеством действительных чисел, которое обозначается буквой R.

          www.evkova.org

        31. Рациональные и иррациональные числа, множество…

          Множество рациональных чисел замкнуто, относительно операций сложения, вычитания, умножения и деления (исключая деление на 0). В алгебре говорят, что рациональные числа образуют поле. Иррациональные числа. Иррациональное число – это число, которое нельзя представить обыкновенной дробью m/n, где числитель m – целое число, а знаменатель n – натуральное число. Иррациональное число может быть представлено в виде бесконечной непериодической десятичной дроби.

          reshator.com


        На данной странице Вы можете найти лучшие результаты поиска для чтения, скачивания и покупки на интернет сайтах материалов, документов, бумажных и электронных книг и файлов похожих на материал «Числа рациональные и иррациональные, Нивен А., 1966»

        Для формирования результатов поиска документов использован сервис Яндекс.XML.

        Нашлось 13 млн ответов. Показаны первые 32 результата(ов).

        Дата генерации страницы:

        Классифицировать реальное число | Колледж Алгебра

        Результаты обучения

        • Запись целых чисел в виде рациональных чисел
        • Определение рациональных чисел
        • Классифицировать действительные числа по наборам

        Числа, которые мы используем для счета или перечисления предметов, — это натуральных чисел : 1, 2, 3, 4, 5 и так далее. Мы описываем их в системе обозначений как {1, 2, 3, …}, где многоточие (…) указывает, что числа продолжаются до бесконечности. Натуральные числа, конечно же, также называются 9.0015 подсчет чисел . Всякий раз, когда мы перечисляем членов команды, считаем монеты в коллекции или подсчитываем деревья в роще, мы используем набор натуральных чисел. Набор из целых чисел — это набор натуральных чисел плюс ноль: {0, 1, 2, 3,…}.

        Набор из целых чисел добавляет противоположные натуральные числа к набору целых чисел: {…,-3, -2, -1, 0, 1, 2, 3,…}. Полезно отметить, что набор целых чисел состоит из трех различных подмножеств: отрицательных целых чисел, нуля и положительных целых чисел. В этом смысле положительные целые числа — это просто натуральные числа. Другой способ думать об этом состоит в том, что натуральные числа являются подмножеством целых чисел.

        [латекс]\begin{align}&{\text{целые отрицательные}} && {\text{ноль}} && {\text{целые положительные}}\\&{\dots ,-3,-2,- 1,} && {0,} && {1,2,3,\dots }\\ \text{ }\end{align}[/latex]

        Набор из рациональных чисел записывается как [латекс]\ left\{\frac{m}{n}|m\text{ и }{n}\text{ являются целыми числами, а }{n}\ne{ 0 }\right\}[/latex]. Обратите внимание на то, что из определения рациональные числа — это дроби (или частные), содержащие целые числа как в числителе, так и в знаменателе, а знаменатель никогда не равен 0. Мы также можем видеть, что каждое натуральное, целое и целое число является рациональным числом с знаменатель 1,

        Поскольку это дроби, любое рациональное число также может быть представлено в десятичной форме. Любое рациональное число может быть представлено как:

        1. завершающая десятичная дробь: [латекс]\фракция{15}{8}=1,875[/латекс] или
        2. повторяющееся десятичное число: [латекс]\frac{4}{11}=0,36363636\dots =0.\overline{36}[/latex]

        Мы используем линию, проведенную над повторяющимся блоком чисел, вместо многократного написания группы.

        Пример: запись целых чисел в виде рациональных чисел

        Каждое из следующих чисел запишите в виде рационального числа.

        1. 7
        2. 0
        3. –8

        Показать решение

        Попробуйте

        Каждое из следующих чисел запишите в виде рационального числа.

        1. 11
        2. 3
        3. –4

        Показать решение

        Пример: Идентификация рациональных чисел

        Запишите каждое из следующих рациональных чисел как завершающее или повторяющееся десятичное число.

        1. [латекс]-\dfrac{5}{7}[/латекс]
        2. [латекс]\dfrac{15}{5}[/латекс]
        3. [латекс]\dfrac{13}{25}[/латекс]

        Показать решение

        Иррациональные числа

        В какой-то момент в далеком прошлом кто-то обнаружил, что не все числа являются рациональными числами. Строитель, например, мог обнаружить, что диагональ квадрата с единицей стороны равна не 2 и даже не [латекс]\фрак{3}{2}[/латекс], а чему-то другому. Или швейник мог заметить, что отношение длины окружности к диаметру рулона ткани чуть больше 3, но все же это не рациональное число. Такие числа называются 9.0015 иррационально , потому что их нельзя записать в виде дробей. Эти числа составляют набор из иррациональных чисел . Иррациональные числа не могут быть представлены в виде дроби от двух целых чисел. Невозможно описать этот набор чисел одним правилом, кроме как сказать, что число иррационально, если оно не рационально. Итак, мы пишем это, как показано.

        {ч | h не является рациональным числом}

        Пример: дифференцирование рациональных и иррациональных чисел

        Определите, является ли каждое из следующих чисел рациональным или иррациональным. Если оно рационально, определите, является ли оно завершающим или повторяющимся десятичным числом.

        1. [латекс]\sqrt{25}[/латекс]
        2. [латекс]\dfrac{33}{9}[/латекс]
        3. [латекс]\sqrt{11}[/латекс]
        4. [латекс]\dfrac{17}{34}[/латекс]
        5. [латекс]0.3033033303333\точки[/латекс]

        Показать решение

        Попробуйте

        Вещественные числа

        Для любого числа n мы знаем, что n либо рационально, либо иррационально. Не может быть и того, и другого. Наборы рациональных и иррациональных чисел вместе составляют набор действительные числа . Как мы видели с целыми числами, действительные числа можно разделить на три подмножества: отрицательные действительные числа, ноль и положительные действительные числа. Каждое подмножество включает дроби, десятичные числа и иррациональные числа в соответствии с их алгебраическим знаком (+ или –). Ноль не считается ни положительным, ни отрицательным.

        Действительные числа можно изобразить на горизонтальной числовой линии с произвольной точкой, выбранной как 0, с отрицательными числами слева от 0 и положительными числами справа от 0. Затем для обозначения каждого целого числа используется фиксированное единичное расстояние. (или другое базовое значение) по обе стороны от 0. Любое действительное число соответствует уникальной позиции на числовой прямой. Верно и обратное: каждое место на числовой прямой соответствует ровно одному вещественному числу. Это известно как переписка один на один. Мы называем это действительная числовая строка .

        Строка действительных чисел

        Пример: Классификация действительных чисел

        Классифицируйте каждое число как положительное или отрицательное, а также как рациональное или иррациональное. Находится ли число слева или справа от 0 на числовой прямой?

        1. [латекс]-\dfrac{10}{3}[/латекс]
        2. [латекс]\sqrt{5}[/латекс]
        3. [латекс]-\sqrt{289}[/латекс]
        4. [латекс]-6\пи[/латекс]
        5. [латекс]0.615384615384\точки[/латекс]

        Показать раствор

        Попробуйте

        Классифицируйте каждое число как положительное или отрицательное, а также как рациональное или иррациональное. Находится ли число слева или справа от 0 на числовой прямой?

        1. [латекс]\sqrt{73}[/латекс]
        2. [латекс]-11.411411411\точки [/латекс]
        3. [латекс]\dfrac{47}{19}[/латекс]
        4. [латекс]-\dfrac{\sqrt{5}}{2}[/латекс]
        5. [латекс]6. 210735[/латекс]

        Показать решение

        Наборы чисел как подмножества

        Начав с натуральных чисел, мы расширили каждый набор, чтобы сформировать больший набор, а это означает, что существует отношение подмножества между наборами чисел, с которыми мы сталкивались до сих пор. Эти отношения становятся более очевидными, если рассматривать их в виде диаграммы.

        Наборы цифр. N : множество натуральных чисел W : множество целых чисел I : множество целых чисел Q : множество рациональных чисел Q´ : множество иррациональных чисел

        Общее примечание: наборы чисел

        Набор из натуральных чисел включает числа, используемые для счета: [латекс]\{1,2,3,\точки\}[/латекс].

        Набор из целых чисел — это набор натуральных чисел плюс ноль: [латекс]\{0,1,2,3,\точки\}[/латекс].

        Набор из целых чисел добавляет отрицательные натуральные числа к набору целых чисел: [латекс]\{\dots,-3,-2,-1,0,1,2,3,\dots\}[ /латекс].

        Набор из рациональных чисел включает дроби, записанные как [латекс]\{\frac{m}{n}|m\text{ и }n\text{ являются целыми числами, а }n\ne 0\}[/latex].

        Набор из иррациональных чисел — это набор нерациональных, неповторяющихся и непрерывных чисел: [латекс]\{ч|ч\текст{ не является рациональным числом}\}[/латекс].

        Пример: дифференцирование наборов чисел

        Классифицируйте каждое число как натуральное число ( N ), целое число ( W ), целое число ( I ), рациональное число ( Q ) и/или иррациональное число ( Q’ ).

        1. [латекс]\sqrt{36}[/латекс]
        2. [латекс]\dfrac{8}{3}[/латекс]
        3. [латекс]\sqrt{73}[/латекс]
        4. [латекс]-6[/латекс]
        5. [латекс]3.2121121112\точки [/латекс]

        Показать решение

        Попробуйте

        Классифицируйте каждое число как натуральное число ( N ), целое число ( W ), целое число ( I ), рациональное число ( Q ) и/или иррациональное число ( Q’ ).

        1. [латекс]-\dfrac{35}{7}[/латекс]
        2. [латекс]0[/латекс]
        3. [латекс]\sqrt{169}[/латекс]
        4. [латекс]\sqrt{24}[/латекс]
        5. [латекс]4.763763763\точки [/латекс]

        Показать решение

         

        Внесите свой вклад!

        У вас есть идеи по улучшению этого контента? Мы будем признательны за ваш вклад.

        Улучшить эту страницуПодробнее

        Рациональные и иррациональные числа — математический обзор (видео и практика)

        TranscriptFAQsPractice

        Привет и добро пожаловать в это видео о рациональных и иррациональных числах!

        Рациональные и иррациональные числа составляют систему действительных чисел . Эта диаграмма Венна показывает визуальное представление того, как классифицируются действительные числа.

        натуральных чисел составляют наименьшее подмножество, также известное как множество «счетных» чисел. Это все положительные недесятичные значения, начинающиеся с единицы. Целые числа — это натуральные числа плюс значение нуля. Набор чисел integer включает целые числа и все отрицательные недесятичные значения.

        Рациональные числа включают наборы, показанные здесь, в дополнение к дробным значениям между ними.

        Простой способ запомнить это — слово ratio в названии этой классификации. Все числа, входящие в набор рациональных чисел, можно записать в виде отношения целых чисел:

        Если \(a\) и \(b\) являются целыми числами: рациональные числа могут быть записаны как \(\frac{a}{b}\), если \(b\neq 0\).

        Ясно, что множество целых чисел можно записать в виде отношений, потому что любое целое число, деленное на 1, дает исходное целое число. Как показано здесь, целые числа могут быть выражены в виде дробей бесконечным числом способов.

        Целое число 3 можно представить в виде дробей \(\frac{3}{1}\), \(\frac{6}{2}\), \(\frac{-24}{-8) }\)
        Целое число -5 может быть представлено в виде следующих дробей \(\frac{-5}{1}\), \(\frac{5}{-1}\), \(\frac{-25 {5}\)
        Целое число 0 может быть представлено в виде дробей \(\frac{0}{3}\), \(\frac{0}{-2}\), \(\frac{0}{123}\)

        В качестве примечания, это не единственные дроби, которые приводят к этим целым числам, это лишь некоторые из множества существующих примеров.

        Дроби также могут быть записаны в виде десятичных дробей. Например:

        .1 эквивалентно \(\frac{1}{10}\), поскольку 1 находится в десятых десятичных разрядах

        .13 эквивалентно \(\frac{13}{100} \) потому что 3 находится в сотых десятичных разрядах, а единица — в десятых десятичных разрядах

        . 237 эквивалентно \(\frac{237}{1,000}\), потому что 7 находится в тысячных десятичных долях, и так далее.

        Эти десятичные дроби можно записать в виде дробей, поэтому они считаются рациональными.

        Другие десятичные числа имеют повторяющихся шаблонов. Они также считаются рациональными, поскольку могут быть выражены в виде дроби на основе следующего доказательства:

        Повторяющаяся десятичная дробь \(2.\overline{17}\) представляет цифры \(2.1717171717\)…

        Давайте попробуем это в качестве практической задачи.

        Пусть \(x=2.\overline{17}\). Повторяющаяся десятичная дробь состоит из двух цифр, что представляет сотые доли.

        Итак, давайте умножим обе части уравнения на 100:

        В результате получится \(100x=217,17171717\)…, что равно \(217,17\) повторения.

        Мы перемещаем десятичную дробь на две точки, потому что мы умножили на 100. Теперь давайте вычтем исходное уравнение из этого:

        \(100x\) \ (= 217,171717 \)…
        \ ( — \) \ (x \) \ (= 002. 171717 \)…
        \) (
        \) (
        \)…
        \)…
        \)…
        \)…
        \)… )

        Обратите внимание, что повторяющаяся часть десятичной дроби теперь удалена.

        Решение для \(x\) дает \(x=\frac{215}{99}\).

        Итак, \(99x\) равно \(215\). Обратите внимание, что повторяющаяся часть десятичной дроби теперь удалена. Решение для \(x\) приводит к делению обеих частей на \(99\): \(x = \frac{215}{99}\).

        Это дробное представление \(x=2.\overline{17}\).

        Это доказательство показывает, что повторяющиеся десятичные числа также считаются рациональными, поскольку их можно записать в виде дроби целых чисел. Если вы подключите это к своему калькулятору, вы получите что-то близкое, возможно, округленное, к 2,17 повторения.

        Важно отметить, что не все десятичные знаки повторяются. Некоторые десятичные дроби имеют бесконечное число неповторяющихся цифр и, следовательно, не могут быть выражены как часть целых чисел. Эти типы действительных чисел классифицируются как иррациональный . Хотя в действительной системе счисления существует бесконечное количество иррациональных чисел, в математике чаще всего используются квадратные корни несовершенных квадратов, например, квадратный корень из 2, а также константы π и e. Обозначение иррациональных чисел позволяет повысить эффективность математических приложений.

        Для геометрии вы можете вспомнить, что π = 3,14159… для бесконечности. Это получено из длины окружности любого круга и его диаметра. Поскольку десятичное значение неповторяющееся и бесконечное, мы используем приблизительное значение в математических приложениях. Бизнес-приложения, касающиеся непрерывного начисления процентов, используют иррациональное значение e, которое снова имеет приблизительное значение 2,718 для бесконечности.

        Спасибо за просмотр и удачной учебы!

        Часто задаваемые вопросы

        Q

        Все ли целые числа рациональные?

        A

        Да, рациональное число — это любое число, которое можно представить в виде дроби. Все целые числа подходят под это определение.

        Q

        Рациональны ли отрицательные числа?

        A

        Да, большинство отрицательных чисел рациональны. Рациональное число — это любое число, которое можно представить в виде дроби. К ним относятся целые числа, дроби, десятичные дроби, которые заканчиваются, и десятичные дроби, которые повторяются. Положительное и отрицательное не влияют на рациональность.

        Q

        Все ли рациональные числа являются целыми числами?

        A

        Нет, не все рациональные числа являются целыми числами. К рациональным числам относятся все числа, которые заканчиваются или повторяются. Целое число — это любое число без дробной части, которое больше или равно нулю.
        пр. 2,7 — рациональное число, но не целое.

        Q

        В чем разница между рациональными и иррациональными числами?

        A

        Разница между рациональными и иррациональными числами заключается в том, что рациональное число можно представить в виде точной дроби, а иррациональное число — нет. Рациональное число включает в себя любое целое число, дробь или десятичное число, которое заканчивается или повторяется. Иррациональное число — это любое число, которое нельзя превратить в дробь, то есть любое число, не подпадающее под определение рационального числа.

        Практические вопросы

        Вопрос №1:

         
        Рационально ли число π?

        Да

        Нет

        Иногда

        Невозможно определить

        Показать Ответ

        Ответ:

        Правильный ответ — нет. Пи (π) — иррациональное число, потому что это бесконечная десятичная дробь, которую нельзя упростить до точной дроби.

        Скрыть ответ

        Вопрос № 2:

         
        Является ли \(1.\overline{3}\) рациональным числом?

        Да

        Нет

        Иногда

        Невозможно определить

        Показать ответ

        Ответ:

        Правильный ответ — да. \(1.\overline{3}\) можно представить в виде дроби \(1\frac{1}{3}\), что означает, что оно рационально. Любое число, которое можно представить в виде дроби, считается рациональным.

        Скрыть ответ

        Вопрос № 3:

         
        Какое из следующих чисел является примером рационального числа?

        π

        \(\sqrt{2}\)

        4.17

        \(4-\sqrt{7}\)

        Показать ответ

        Ответ:

        9 Правильный ответ:

        9 90. Это единственное число из этого списка, которое можно превратить в дробь, \(4\frac{17}{100}\).

        Скрыть ответ

        Вопрос № 4:

         
        Какое из следующих чисел является иррациональным?

        \(\frac{17}{3}\)

        13

        \(2.\overline{97}\)

        \(\sqrt{3}\)

        Показать ответ

        Ответ:

        Правильный ответ: \(\sqrt{3}\). Квадратные корни несовершенных квадратов нерациональны, потому что они равны бесконечному десятичному числу, а это значит, что это число нельзя превратить в дробь.

        Скрыть ответ

        Вопрос № 5:

         
        Является ли \(\frac{7}{9}\) рациональным?

        Да

        Нет

        Иногда

        Невозможно определить

        Показать Ответ

        Ответ:

        Правильный ответ — да. Рациональное число — это любое число, которое можно превратить в дробь, а \(\frac{7}{9}\) — это дробь.

        Скрыть ответ

         

        Вернуться к видео по основам арифметики

        280645255557515712

        Вещественное число, которое нельзя точно выразить как отношение двух целых чисел.

        Произношение: /ɪˈræ.ʃə.nl ˈnʌm.bər/ Объяснение

        Иррациональное число – это настоящий номер которое не может быть выражено как отношение двух целые числа. Поскольку Рациональное число это действительное число, которое можно выразить как отношение двух целых чисел, это означает, что любое действительное число либо рационально, либо иррационально, но не может быть и то, и другое.

        В математике можно представлять номера способами, которые маскируют их настоящую личность. Например, квадратный корень можно уменьшить до 2, и поэтому не является иррациональным числом, даже если оно представлено используя квадратный корень.

        Примеры иррациональных чисел включают π , , а также .

        Вот несколько примеров неиррациональных чисел: 5,2 , , 3 и .

        Свойства иррациональных чисел

        Свойство Описание
        Непрерывность Множество иррациональных чисел не является непрерывным множеством.
        Дополнение Сложение иррациональных чисел такое же, как сложение действительных чисел.
        Закрытие в отношении дополнения Множество иррациональных чисел , а не замкнуто относительно сложения так как + — = 0. 0 не является иррациональным числом.
        Ассоциативное свойство дополнения Множество иррациональных чисел ассоциативно относительно сложения. Так как все иррациональные числа также являются действительными числами, а множество действительных чисел ассоциативно по отношению к сложению ассоциативное свойство сложения относится к иррациональным числа.
        Дополнительный идентификатор Аддитивная идентичность для действительных чисел равна нулю. Ноль это а не в наборе иррациональных чисел. Множество иррациональных чисел не обладает свойством идентичность по отношению к дополнению.
        Добавка, обратная Аддитивная инверсия иррационального числа есть — а т.к. a + (- a ) = 0. Множество иррациональные числа обратимы относительно сложения.
        Группа в отношении дополнения Поскольку аддитивная идентичность иррациональных чисел сама по себе не является иррациональной число, набор иррациональных чисел , а не образует группу с относительно доп.
        Умножение Умножение иррациональных чисел такое же, как умножение действительных числа.
        Замыкание по умножению 903:50 Множество иррациональных чисел , а не замкнуто относительно умножение с · = 2. 2 не является иррациональное число.
        Ассоциативное свойство умножения Множество иррациональных чисел ассоциативно относительно умножения. С все иррациональные числа также являются действительными числами, а множество действительных чисел равно ассоциативный по отношению к умножению, ассоциативное свойство умножения относится к иррациональным числам.
        Мультипликативная идентичность Мультипликативное тождество для действительных чисел равно единице. Один , а не в множество иррациональных чисел. Множество иррациональных чисел не обладает свойством тождества относительно умножения.
        Мультипликативный обратный Мультипликативная инверсия иррационального числа а это 1/ с · 1/ a = 1, a ≠ 0. Множество иррациональных чисел равно обратимым относительно умножения.
        Группа по умножению Поскольку мультипликативное тождество иррациональных чисел само по себе не является иррациональное число, набор иррациональных чисел , а не образует группу относительно умножения.
        МощностьМощность иррациональных чисел равна ℵ 1 = 2 ℵ0 . Множество иррациональных чисел несчетно.
        Таблица 1: Свойства иррациональных чисел.

        Доказательство существования иррациональных чисел

        Первое доказательство существования иррациональных чисел приписывается пифагорейцу, представитель древнегреческой религии. Это происходит следующим образом:

        Шаг Уравнения/диаграммы Обсуждение
        1 Претензия Предположим, что длина гипотенузы и длина катетов равнобедренного оба прямоугольных треугольника являются рациональными числами. Так как отношение двух рациональных чисел можно уменьшить к другому рациональному числу существует отношение двух целых чисел c : b , которые могут представлять отношение любых двух рациональных чисел. 903:50
        2 Пусть c : b будет отношением длины гипотенузы к катету равнобедренного прямоугольного треугольника, выраженные в наименьшие члены, где c и b оба являются целыми числами. С c : b выражается в наименьшем термины, c и б имеют № общих факторов.
        3
        А 2 + Б 2 = C 2 Теорема Пифагора c 2 Замените значения из диаграммы
        2 b 2 = с 2 Объединить подобные термины
        		 Начните с теоремы Пифагора: A 2 + В 2 = С 2 . Затем замените переменные из диаграммы на шаге 1. Замените б в для А и Б . Заменять c дюймов для С . Затем объедините похожие термины, чтобы получить уравнение 2 б 2 = в 2 .
        4 2 б 2 = с 2 Определение четного числа — это число, которое имеет 2 как фактор. С с 2 = 2 б 2 , 2 является фактором с 2 . Это означает, что c 2 — четное число.
        5 c четно. Так как c 2 имеет коэффициент из 2 и с 2 = с · с , c также должен иметь коэффициент 2. Итак, c четно.
        6 б нечетное. Начиная с c : b находится в низшей условия, b имеет нет факторов общего с c . Так b может , а не иметь коэффициент 2. Это означает, что b должно быть нечетным.
        7 с = 2 г Поскольку c четно, существует целое число и такие, что с = 2 у .
        8 4 у 2 = 2 б 2 Начиная с c 2 = 2 б 2 , заменитель 2 и в для с . Это дает уравнение (2 y ) 2 = 2 б 2 . Расширьте показатель степени в левой части уравнения, чтобы получить 4 y 2 = 2 b 2 .
        9 2 у 2 = б 2 Возьмем уравнение 4 y 2 = 2 б 2 и упростите. Это дает уравнение 2 y 2 = b 2 .
        10 b четно. По аналогии с шагами 3 и 4, b должно быть четным.
        11 Противоречие Так как b может ли не быть одновременно четным и странно, есть противоречие. Это означает, что размеры как ноги, так и гипотенузы равнобедренного прямоугольного треугольника не могут быть рациональными числами. Итак, число это , а не , должно существовать рациональное число.
        Таблица 2: Доказательство существования иррациональных чисел.

        Ссылки

        1. МакАдамс, Дэвид Э.. Словарь всех математических слов, иррациональное число . Издание 2-го класса 20150108-4799968. стр. 103. Life is a Story Problem LLC. 8 января 2015. Купить книгу

        Цитируйте эту статью как:

        МакАдамс, Дэвид Э. Иррациональное число . 23.04.2019. Вся энциклопедия математических слов. ООО «Жизнь — это проблема истории». https://www.allmathwords.org/en/i/irrational.html.

        Авторы изображений

        • Все изображения и манипуляции принадлежат Дэвиду МакАдамсу, если не указано иное. Все изображения Дэвида МакАдамса защищены авторским правом © Life is a Story Problem LLC и находятся под лицензией Creative Commons Attribution-ShareAlike 4.0 International License.

        История изменений

        23. 04.2019:

        Уравнения и выражения обновлены до нового формата.

        (МакАдамс, Дэвид Э.)

        22.03.2019:

        Исправлена ​​мультипликативная инверсия.

        (МакАдамс, Дэвид Э.)

        21.12.2018:

        Пересмотрено и исправлено произношение МФА.

        (МакАдамс, Дэвид Э.)

        28.08.2018:

        Исправлена ​​орфография.

        (МакАдамс, Дэвид Э.)

        07.08.2018:

        Словарные ссылки изменены на формат WORDLINK.

        (МакАдамс, Дэвид Э.)

        06. 08.2018:

        Удалены битые ссылки, обновлена ​​лицензия, реализована новая разметка, реализован новый протокол Geogebra.

        (МакАдамс, Дэвид Э.)

        03.03.2010:

        Добавлен «Справочник», добавлен раздел о доказательстве существования иррациональных чисел.

        (МакАдамс, Дэвид Э.)

        13.08.2008:

        Некоторые математические конструкции заменены изображениями. Добавлена ​​проверка понимания

        (МакАдамс, Дэвид Э.)

        12.07.2007:

        Первоначальная версия.

        (МакАдамс, Дэвид Э.)

        √4 — рациональное или иррациональное число?

        Действительные числа, которые не могут быть выражены простой дробью, известны как иррациональных чисел. Его нельзя представить в виде отношения типа p/q, где p и q — целые числа, q≠0. Это несоответствие рациональных чисел. Иррациональные числа обычно записываются как R \ Q, где знак обратной косой черты означает «установить минус». Его также можно записать как R-Q, что представляет собой разницу между набором действительных и рациональных чисел.

        Вычисления, основанные на этих цифрах, немного сложнее. К иррациональным числам относятся √5, √11, √21 и так далее. Если такие числа используются в арифметических операциях, сначала должны быть оценены значения под корнем.

        Что такое рациональные числа?

        Рациональные числа имеют форму p/q, где p и q — целые числа, а q ≠ 0. Из-за лежащей в основе структуры чисел, формы p/q, большинству людей трудно отличить дроби от рациональных чисел. Когда рациональное число делится, вывод находится в десятичной форме, которая может быть как оканчивающейся, так и повторяющейся. 3, 4, 5 и т. д. — некоторые примеры рациональных чисел, поскольку они могут быть выражены дробью как 3/1, 4/1 и 5/1.

        Что такое иррациональные числа?

        Иррациональные числа — это любые числа, не являющиеся рациональными числами. Иррациональные числа могут быть представлены десятичными знаками, но не дробями, что означает, что они не могут быть представлены как отношение двух целых чисел. После запятой иррациональные числа имеют бесконечное количество неповторяющихся цифр.

        Вещественное число, которое не может быть представлено как отношение целых чисел, называется иррациональным числом. Например, √2 — иррациональное число.

        Десятичное расширение иррационального числа не заканчивается и не повторяется. Определение иррационального — это число, которое не имеет отношения или для которого нельзя установить отношение, то есть число, которое не может быть представлено никаким другим способом, кроме как с использованием корней. Иными словами, иррациональные числа нельзя представить в виде отношения двух целых чисел.

        Примеры иррациональных чисел

        √2, √3, √5 и т. д. — некоторые примеры иррациональных чисел, поскольку они не могут быть выражены в форме p ⁄ q. Число Эйлера, золотое сечение, π и т. д. также являются примерами иррациональных чисел. 1/0, 2/0, 3/0 и т. д. иррациональны, потому что дают нам неограниченные значения.

        Является ли число √4 рациональным или иррациональным?

        Решение:

        Иррациональные числа — это действительные числа, которые нельзя записать в виде p/q, где p и q — целые числа, а q≠0. Например, √2 и √3 и так далее иррациональны. Рациональное число — это любое число, которое можно записать в виде p/q, где p и q — целые числа, а q≠0.

        Здесь данное число √4 равно 2; число 2 является целым числом, а целые числа всегда рациональны. Кроме того, его можно выразить в форме дроби как 2 ⁄ 1, что означает, что это рациональное число. Следовательно, √4 равно не иррациональное число .

        Похожие вопросы

        Вопрос 1: Является ли √5 рациональным или иррациональным числом?

        Ответ:

        Рациональное число — это действительное число, имеющее форму p/q, где q≠0. Когда рациональное число разбивается, результатом является десятичное число, которое может быть как завершающим, так и повторяющимся десятичным числом. Здесь данное число √5 не может быть выражено в виде p/q. Кроме того, 5 является простым числом. Это означает, что число 5 не имеет пары и не делится на 2. Следовательно, √5 — иррациональное число.

        Вопрос 2: Определите, является ли 4.152152…. является рациональным числом.

        Ответ:

        Рациональное число — это действительное число, имеющее форму p/q, где q≠0. Когда рациональное число разбивается, результатом является десятичное число, которое может быть как завершающим, так и повторяющимся десятичным числом. Здесь заданное число 4.152152…. имеет повторяющиеся цифры. Следовательно, 4,152152…. является рациональным числом.

        Вопрос 3: Является ли √11 рациональным или иррациональным числом?

        Ответ:

        Рациональное число — это действительное число, имеющее форму p/q, где q≠0. Когда рациональное число разбивается, результатом является десятичное число, которое может быть как завершающим, так и повторяющимся десятичным числом. Здесь данное число √11 не может быть выражено в виде p/q. Альтернативно, 11 — простое число. Это означает, что число 11 не имеет пары и не делится на 2. Следовательно, √11 — иррациональное число.

        Вопрос 4: Определите, является ли 7,23 рациональным числом.

        Ответ:

        Рациональное число — это действительное число, имеющее форму p/q, где q≠0. Когда рациональное число разбивается, результатом является десятичное число, которое может быть как завершающим, так и повторяющимся десятичным числом. Здесь заданное число, 7.23…. имеет конечные цифры. Следовательно, 7,23 — рациональное число.

        Что такое иррациональные числа? | Живая наука

        Живая наука поддерживается своей аудиторией. Когда вы покупаете по ссылкам на нашем сайте, мы можем получать партнерскую комиссию. Вот почему вы можете доверять нам.

        Иррациональные числа — это действительные числа, которые при выражении в виде десятичной дроби всегда идут после десятичной дроби и никогда не повторяются. (Изображение предоставлено Shutterstock)

        Иррациональные числа — это числа, которые нельзя представить как отношение двух целых чисел. Это противоположно рациональным числам, таким как 2, 7, одна пятая и -13/9, которые могут выражаться и выражаются как отношение двух целых чисел. При выражении в виде десятичного числа иррациональные числа всегда идут после десятичной точки и никогда не повторяются.

        Связанный: 9 самых больших существующих чисел

        Кто вычислил иррациональные числа?

        Греческому математику Гиппасу из Метапонта приписывают открытие иррациональных чисел в V веке до нашей эры, согласно статье Кембриджского университета . Говорят, что во время работы над отдельной задачей Гиппас наткнулся на тот факт, что равнобедренный прямоугольный треугольник, две стороны которого имеют длину 1 единицу, будет иметь гипотенузу, равную √2, что является иррациональным числом. 2.)

        Легенда гласит, что Гиппас был брошен в море в награду за его великое открытие. Это потому, что он был членом пифагорейцев, квазирелигиозного ордена, которые верили, что «все есть число» и что вселенная состоит из целых чисел и их соотношений. Обеспокоенные открытием Гиппаса, группа приговорила его к смертной казни через утопление.

        Связанный: Фотографии: Большие числа, определяющие Вселенную

        Страх перед иррациональными числами позже утих, и в конце концов они были включены в математику. Вместе рациональные и иррациональные числа составляют число 9.1260 действительных чисел , которые включают любое число на числовой прямой и в которых отсутствует мнимое число i.

        Большинство действительных чисел иррациональны. Немецкий математик Георг Кантор окончательно доказал это в 19 веке, показав, что рациональные числа счетны , а действительные числа несчетны. Это означает, что реальных больше, чем рациональных, согласно веб-сайту по истории, математике и другим темам от образовательного карикатуриста Чарльза Фишера Купера. Поскольку иррациональные числа — это все те действительные числа, которые не являются рациональными, иррациональные числа значительно перевешивают рациональные числа; они составляют все остальные несчетные действительные числа.

        Известные иррациональные числа: 

        Квадратный корень из 2

        Несмотря на судьбу Гиппаса, √2 является одним из самых известных иррациональных чисел и иногда называется константой Пифагора, согласно веб-сайту Wolfram MathWorld .

        Постоянная Пифагора равна 1,4142135623… (точки означают, что она продолжается вечно).

        Все это может звучать теоретически, но число имеет и очень конкретное применение. Международные форматы бумаги включают √2. Международная организация по стандартизации (ИСО) 216 определение серии размеров бумаги A гласит, что длина листа, деленная на его ширину, должна составлять 1,4142. Это приводит к тому, что лист бумаги формата А1, разделенный пополам по ширине, дает два листа бумаги формата А2. Разделите лист формата А2 еще раз пополам, и вы получите два листа бумаги формата А3 и так далее.

        Пи

        Пи — это отношение длины окружности к ее диаметру. Математикам известно число пи со времен древних вавилонян, 4000 лет назад.

        Пи равно 3,1415926535… 

        Некоторые фанаты числа Пи очень гордятся тем, что могут запомнить как можно больше цифр числа Пи. Суреш Кумар Шарма из Индии установил мировой рекорд в 2015 году, запомнив 70 030 цифр числа Пи, согласно мировому рейтингу числа Пи .

        Phi

        Phi также известен как золотое сечение . Его можно найти, взяв палку и разломив ее на две части; если соотношение между этими двумя частями такое же, как соотношение между общей палочкой и большим сегментом, говорят, что части находятся в золотом сечении.

        Фи равняется 1,6180339887…

        На протяжении столетий вокруг понятия фи накопилось множество преданий, например идея о том, что оно представляет совершенную красоту или может быть найдено повсюду в природе. Но большая часть этого неверна. Фи тесно связана с последовательностью Фибоначчи , еще одним источником многих заблуждений.

        e

        Основание натуральных логарифмов названо e в честь своего тезки, швейцарского математика 18-го века Леонарда Эйлера.

        e равно 2,7182818284…

        Наряду с логарифмами, e появляется в уравнениях , включающих комплексных чисел и экспоненциальный рост. Подобно тому, как День Пи отмечается 14 марта (14 марта), г. и День отмечается 7 февраля (7 февраля) или 27 января (27 января), в зависимости от того, какую календарную систему вы используете.

        Дополнительные ресурсы:

        • В Академии Хана есть много полезных видеороликов, объясняющих иррациональные числа. Вот с чего начать: « Введение в рациональные и иррациональные числа.

          Адам Манн — независимый журналист с более чем десятилетним стажем, специализирующийся на астрономии и физике. Он имеет степень бакалавра астрофизики Калифорнийского университета в Беркли. Его работы публиковались в New Yorker, New York Times, National Geographic, Wall Street Journal, Wired, Nature, Science и многих других изданиях. Он живет в Окленде, штат Калифорния, где любит кататься на велосипеде.

          Это может показаться скорее иррациональным, чем рациональным | Алекс Лин

          Как иррациональных чисел больше, чем рациональных.

          Photo by Danny Lines on Unsplash

          Мир математики может быть довольно загадочным. В зависимости от того, куда смотреть, некоторые истины, кажется, просто бросают вызов нашей базовой интуиции.

          Тот факт, что иррациональных чисел больше, чем рациональных, не имел для меня особого смысла. Вероятно, можно с уверенностью предположить, что оба набора бесконечны, так как же один набор может быть больше?

          Сегодня мы исследуем, как исчисляемые и неисчисляемые бесконечности помогают нам прийти к этому, казалось бы, странному заключению.

          Содержание

          Фоновый контекст

          Что происходит с действительными числами?

          Как насчет рациональных чисел?

          Собираем все вместе

          Прежде чем мы погрузимся в сочную математику, давайте на минутку дадим определение паре терминов.

          Что такое рациональные числа?

          Любое число, которое может быть получено путем деления двух целых чисел (целых чисел) является рациональным.

          Например, 10 разделить на 4 равно 2,5, поэтому 2,5 рационально. Деление на 1 тоже считается, поэтому все целые числа рациональны.

          Что такое иррациональные числа?

          Иррациональные числа противоположны рациональным. Любое число, которое не может быть получено путем деления двух целых чисел, является иррациональным.

          Рассмотрим π. Хотя такие оценки, как 22/7, близки, мы никогда не сможем разделить два целых числа, чтобы получить точное значение π.

          Вещественные числа

          Любое число, которое вы можете нанести на числовую строку ниже, считается действительным.

          Одномерная числовая линия, расширяющаяся в сторону отрицательной и положительной бесконечности.

          Комбинация всех рациональных и иррациональных чисел образует наши действительные числа. Однако мнимые числа и бесконечность не считаются реальными.

          Наша цель — показать взаимосвязь между размерами рациональных и иррациональных множеств. Поскольку действительные числа являются объединением или комбинацией двух наборов, возможно, стоит попытаться на мгновение изучить действительные числа.

          Насколько велики действительные числа?

          Давайте сначала рассмотрим действительные числа от 0 до 1. Скажем, у нас есть набор, назовем его X, , который содержит всех действительных чисел в пределах нашего интервала.

          Набор всех действительных чисел от 0 до 1.

          Наш набор явно бесконечен по размеру, поскольку он будет продолжать расширяться вниз.

          Хотя наш набор содержит все возможные действительные числа от 0 до 1, я утверждаю, что мы всегда можем найти новое действительное число, которого нет в нашем наборе.

          Начнем с изучения первого числа в наборе X. Мы построим новое число, увеличив значение первой цифры после запятой.

          Создание нашего уникального реального номера из набора реальных номеров.

          Обратите внимание, что наш новый номер уникален из первого значения набора X . Давайте продолжим развивать наше новое число, увеличив вторую цифру второго числа из набора X .

          Создание нашего уникального реального номера из набора реальных номеров.

          Интересно… Наш новый номер уникален как из первых , так и из вторых значений нашего набора. Если мы продолжим повторять этот диагональный узор бесконечно, мы найдем уникальное действительное число, которого нет в нашем исходном наборе!

          Продолжение диагонального узора показывает уникальное действительное число.

          На самом деле увеличение диагональных цифр было не единственным нашим вариантом. Мы могли бы добавить или вычесть любое число по диагонали, чтобы получить уникальное действительное значение.

          Различные уникальные действительные числа и их операции.

          Итак, мы показали, что наш набор всех действительных чисел от 0 до 1 каким-то образом пропускает множество других действительных значений. Этот образец известен как диагональный аргумент Кантора.

          Как бы мы ни пытались подсчитать размер нашего набора, мы всегда будем упускать больше значений. Этот тип бесконечности и есть то, что мы называем неисчислимым.

          Напротив, счетные бесконечности являются перечислимыми бесконечными множествами. Рассмотрим множество целых чисел — мы всегда можем подсчитать все целые числа, не пропуская ни одного значения.

          Теперь мы знаем, что между 0 и 1 множество действительных чисел несчетно бесконечно. Отсюда следует, что множество всех действительных чисел также несчетно бесконечно.

          Теперь рассмотрим рациональные числа. Мы надеемся, что определяя размер его множества, мы сможем пролить свет на наше доказательство.

          С нашим новым пониманием счетных и несчетных бесконечностей, можем ли мы определить, возможно ли окончательно подсчитать все значения в множестве рациональных чисел?

          Подсчет рациональных чисел

          Рассмотрим это расположение положительных рациональных чисел.

          Предложение по отображению всех рациональных чисел.

          Увеличив числитель для каждого столбца и знаменатель для каждой строки, эта сетка в конечном итоге будет включать все положительные рациональные числа.

          Теперь, можем ли мы найти способ абсолютного подсчета всех значений в нашей сетке?

          Существует бесконечное количество строк и столбцов. Если бы мы попытались просто считать по каждой строке/столбцу, мы бы никогда не достигли «конца» первой строки/столбца. Таким образом, этого метода подсчета будет недостаточно.

          Ну, если прямо поперек или вниз нельзя, то как насчет диагонали? Рассмотрим следующий способ обхода.

          Подсчет сетки по диагонали

          Начав с красного круга, мы можем пройти рациональные числа по диагональному пути, отмеченному зелеными стрелками. Бесконечно следуя этому зигзагообразному шаблону, мы можем увидеть, что в конечном итоге будут встречаться все положительные рациональные значения!

          Мы можем применить тот же шаблон обхода, чтобы включить и отрицательные рациональные числа!

          Включение отрицательного пути обхода

          Этот путь обхода дает нам четкий метод подсчета размера рациональных чисел. Хотя мы будем считать до бесконечности, мы по крайней мере знаем, что не будет пропущенных рациональных значений.

          Как видим, множество рациональных чисел счетно бесконечно!

          На данный момент мы знаем пару важных фактов.

          1. Вещественные числа неисчислимо бесконечны.
          2. Рациональные числа счетно бесконечны.
          3. Действительные числа представляют собой объединение множества рациональных и иррациональных чисел.

          Если мы удалим все рациональные числа из нашего набора действительных чисел, у нас все равно останется несчетно бесконечное множество, состоящее только из иррациональных чисел. Следовательно, множество иррациональных чисел также несчетно бесконечно!

          Поскольку несчетно бесконечные множества всегда больше счетно бесконечных множеств, мы можем в конце концов заключить, что иррациональных чисел больше, чем рациональных.

          Вот оно! То, что начиналось как неинтуитивный факт, теперь помогло нам немного больше понять о бесконечностях и их различных размерах.

        Если известен диаметр как найти радиус: Онлайн калькулятор радиуса круга. Как узнать радиус круга, окружности.

        alexxlab / / Разное
        2»).

        Зная лишь длину диаметра окружности, можно вычислить не только площадь круга, но и площади некоторых других геометрических фигур. Это вытекает из того, что диаметры вписанных или описанных вокруг таких фигур окружностей совпадают с длинами их сторон либо диагоналей.

        Инструкция

        Если надо найти площадь (S) по известной длине его диаметра (D), умножайте число пи (π) на возведенную в длину диаметра , а результат делите на четыре: S=π ²*D²/4. Например, круга равен двадцати сантиметрам, то его площадь можно вычислить так: 3,14² * 20² / 4 = 9,86 * 400 / 4 = 986 сантиметров.

        Если надо найти площадь квадрата (S) по диаметру вокруг него окружности (D), возводите длину диаметра в квадрат, а результат разделите пополам: S=D²/2. Например, если диаметр описанной окружности равен двадцати сантиметрам, то площадь квадрата можно вычислить так: 20² / 2 = 400 / 2 = 200 квадратных сантиметров.

        Если площадь квадрата (S) нужно найти по диаметру вписанной в него окружности (D), достаточно возвести длину диаметра в квадрат: S=D². 2 / 4 + 20*10/2», а нажать клавишу Enter.

        Источники:

        • как найти площадь окружности по диаметру

        Круг — это плоская геометрическая фигура, все точки которой находятся на одинаковом и отличном от нуля удалении от выбранной точки, которую называют центром окружности. Прямую, соединяющую любые две точки круга и проходящую через центр, называют его диаметром . Суммарная длина всех границ двухмерной фигуры, которую обычно называют периметром, у круга чаще обозначается как «длина окружности». Зная длину окружности можно вычислить и ее диаметр.

        Инструкция

        Используйте для нахождения диаметра одно из основных свойств окружности, которое заключается в том, что соотношение длины ее периметра к диаметру одинаково для абсолютно всех окружностей. Конечно, постоянство не осталось не отмеченным математиками, и эта пропорция давно уже получила собственное — это число Пи (π — первая греческих слов «окружность » и «периметр»). Числовое этой определяется длиной окружности, у которой диаметр равен единице.

        Используйте какой-либо , чтобы рассчитать длину диаметра, если сделать это в уме не получается. Например, можно воспользоваться тем, который встроен в поисковую систему Nigma или Google — он математические операции, вводимые на «человеческом» . Например, если известная длина окружности составляет четыре метра, то для нахождения диаметра можно «по-человечески» попросить поисковик: «4 метра разделить на пи». Но если вы введете в поле поискового запроса, например, «4/пи», то поисковик поймет и такую постановку задачи. В любом случае ответом будет «1.27323954 метра».

        Воспользуйтесь программным калькулятором Windows, если вам более привычны интерфейсы с обычными кнопками. Чтобы не искать ссылку на его запуск в глубинных уровнях главного меню системы, нажмите сочетание клавиш WIN + R, введите команду calc и нажмите клавишу Enter. Интерфейс этой программы очень незначительно отличается от обычных калькуляторов, поэтому операция деления длины окружности на число Пи вряд ли вызовет какие-либо затруднения.

        Вопрос о диаметре земного шара не так прост, как может показаться на первый взгляд, ведь само понятие «земной шар» весьма условно. У настоящего шара диаметр всегда будет одинаковым, в каком бы месте ни был проведен отрезок, соединяющий две точки на поверхности сферы и проходящий через центр.

        Применительно к Земле не представляется возможным, поскольку ее шарообразность далеко не идеальна (в природе вообще не бывает идеальных геометрических фигур и тел, они представляют собой абстрактные геометрические понятия). Для точного обозначения Земли ученым даже пришлось ввести специальное понятие – «геоид».

        Официальный диаметр Земли

        Величина диаметра Земли определяется тем, в каком месте его будут измерять. Для удобства за официально признанный диаметр принимаются два показателя: диаметр Земли по экватору и расстояние между Северным и Южным полюсами. Первый показатель равен 12 756,274 км, а второй – 12 714, разница между ними составляет немногим менее 43 км.

        Данные числа не производят особого впечатления, они уступают даже расстоянию между Москвой и Краснодаром – двумя городами, расположенными на территории одной страны. Тем не менее, вычислить их было непросто.

        Вычисление диаметра Земли

        Диаметр планеты высчитывается по такой же геометрической формуле, как и любой другой диаметр.

        Чтобы найти периметр окружности, необходимо умножить ее диаметр на число πи. Следовательно, для нахождения диаметра Земли нужно измерить ее окружность в соответствующем сечении (по экватору или в плоскости полюсов) и разделить ее на число πи.

        Первым человеком, попытавшимся измерить окружность Земли, был древнегреческий ученый Эратосфен Киренский. Он обратил внимание, что в Сиене (ныне – Асуан) в день летнего солнцестояния Солнце находится в зените, освещая дно глубокого колодца. В Александрии же в этот день оно отстояло от зенита на 1/50 окружности. Из этого ученый сделал вывод, что расстояние от Александрии до Сиена составляет 1/50 окружности Земли. Расстояние между этими городами равно 5 000 греческим стадиям (приблизительно 787,5 км), следовательно, окружность Земли равна 250 000 стадий (примерно 39 375 км).

        В распоряжении современных ученых имеются более совершенные средства измерения, но их теоретическая основа соответствует идее Эратосфена. В двух точках, расположенных в нескольких сотнях километров друг от друга, фиксируют положение Солнца или определенных звезд на небосводе и вычисляют разницу между результатами двух измерений в градусах. Зная расстояние в километрах, несложно вычислить длину одного градуса, а затем умножить ее на 360.

        Для уточнения размеров Земли используется и лазерная дальнометрия, и спутниковые системы наблюдения.

        На сегодняшний день считается, что окружность Земли по экватору составляет 40 075,017 км, а по – 40 007,86. Эратосфен лишь немного ошибся.

        Величина и окружности, и диаметра Земли увеличивается из-за метеоритного вещества, постоянно выпадающего на Землю, но процесс этот идет очень медленно.

        Источники:

        • Как измерили Землю в 2019

        Окружность — замкнутая кривая, все точки которой находятся на одинаковом расстоянии от центра. Эта фигура является плоской. Поэтому решение задачи, вопрос которой состоит в том, как найти длину окружности, является достаточно простым. Все имеющиеся способы, мы рассмотрим в сегодняшней статье.

        Описания фигуры

        Кроме достаточно простого описательного определения существуют еще три математических характеристики окружности, которые уже сами по себе содержат ответ на вопрос, как найти длину окружности:

        • Состоит из точек A и B и всех других, из которых AB можно увидеть под прямым углом. Диаметр данной фигуры равен длине рассматриваемого отрезка.
        • Включает исключительно такие точки X, что отношение AX/BX неизменно и не равно единице. Если это условие не соблюдается, то это не окружность.
        • Состоит из точек, для каждой из которых выполняется следующее равенство: сумма квадратов расстояний до двух других — это заданная величина, которая всегда больше половине длины отрезка между ними.

        Терминология

        Не у всех в школе был хороший учитель математики. Поэтому ответ на вопрос, как найти длину окружности, осложняется еще и тем, что не все знают основные геометрические понятия. Радиус — отрезок, который соединяет центр фигуры с точкой на кривой. Особым случаем в тригонометрии является единичная окружность. Хорда — отрезок, который соединяет две точки кривой. Например, под это определение подпадает уже рассмотренный AB. Диаметр — это хорда, проходящая через центр. Число π равно длине единичной полуокружности.

        Основные формулы

        Из определений непосредственно следуют геометрические формулы, которые позволяют рассчитать основные характеристики окружности:

        1. Длина равна произведению числа π и диаметра. Формулу обычно записывают следующим образом: C = π*D.
        2. Радиус равен половине диаметра. Его также можно рассчитать, вычислив частное от деления длины окружности на удвоенное число π. Формула выглядит так: R = C/(2* π) = D/2.
        3. Диаметр равен частному от деления длины окружности на π или удвоенному радиусу. Формула является достаточно простой и выглядит так: D = C/π = 2*R.
        4. Площадь круга равна произведению числа π и квадрата радиуса. Аналогично в этой формуле можно использовать диаметр. В этом случае площадь будет равна частному от деления произведения числа π и квадрата диаметра на четыре. Формулу можно записать следующим образом: S = π*R 2 = π*D 2 /4.

        Как найти длину окружности по диаметру

        Для простоты объяснения обозначим буквами необходимые для расчета характеристики фигуры. Пусть C — это искомая длина, D — ее диаметр, а число π приблизительно равно 3,14. Если у нас есть всего одна известная величина, то задачу можно считать решенной. Зачем это нужно в жизни? Предположим мы решили обнести круглый бассейн забором. Как вычислить необходимое количество столбиков? И тут на помощь приходит умение, как вычислить длину окружности. Формула выглядит следующим образом: C = π D. В нашем примере диаметр определяется на основе радиуса бассейна и необходимого расстояния до забора. Например, предположим, что наш домашний искусственный водоем составляет 20 метров в ширину, а столбики мы собираемся ставить на десятиметровом расстоянии от него. Диаметр получившейся окружности равен 20 + 10*2 = 40 м. Длина — 3,14*40 = 125,6 метров. Нам понадобятся 25 столбиков, если промежуток между ними будет около 5 м.

        Длина через радиус

        Как всегда, начнем с присвоения характеристикам окружности букв. На самом деле они являются универсальными, поэтому математикам из разных стран вовсе не обязательно знать язык друг друга. Предположим, что C — это длина окружности, r — ее радиус, а π приблизительно равно 3,14. Формула выглядит в этом случае следующим образом: C = 2*π*r. Очевидно, что это абсолютно правильное равенство. Как мы уже разобрались диаметр окружности равен ее удвоенному радиусу, поэтому эта формула так и выглядит. В жизни этот способ тоже может часто пригодиться. Например, мы печем торт в специальной раздвижной форме. Чтобы он не испачкался, нам нужна декоративная обертка. Но как вырезать круг нужного размера. Здесь на помощь и приходит математика. Те, кто знают, как узнать длину окружности, сразу скажут, что нужно умножить число π на удвоенный радиус формы. Если ее радиус равен 25 см, то длина будет составлять 157 сантиметров.

        Примеры задач

        Мы уже рассмотрели несколько практических случаев полученных знаний о том, как узнать длину окружности. Но зачастую нас заботят не они, а реальные математические задачи, которые содержатся в учебнике. Ведь за них учитель выставляет баллы! Поэтому давайте рассмотрим задачу повышенной сложности. Предположим, что длина окружности составляет 26 см. Как найти радиус такой фигуры?

        Решение примера

        Для начала запишем, что нам дано: C = 26 см, π = 3,14. Также вспомним формулу: C = 2* π*R. Из нее можно извлечь радиус окружности. Таким образом, R= C/2/π. Теперь приступим к непосредственному расчету. Сначала делим длину на два. Получаем 13. Теперь нужно разделить на значение числа π: 13/3,14 = 4,14 см. Важно не забыть записать ответ правильно, то есть с единицами измерения, иначе теряется весь практический смысл подобных задач. К тому же за подобную невнимательность можно получить оценку на один балл ниже. И как бы досадно ни было, придется мириться с таким положением вещей.

        Не так страшен зверь, как его малюют

        Вот мы и разобрались с такой непростой на первый взгляд задачей. Как оказалось, нужно просто понимать значение терминов и запомнить несколько легких формул. Математика — это не так страшно, нужно только приложить немного усилий. Так что геометрия ждет вас!

        Для начала дадим определение радиуса. В переводе с латинского radius — это «луч, спица колеса». Радиус окружности — это отрезок прямой, соединяющий центр окружности с точкой, которая находится на ней. Длина данного отрезка — это значение радиуса. В математических расчётах для обозначения данной величины используют R.

        Советы по нахождению радиуса:

        1. является отрезком прямой, проходящей через ее центр и соединяющей точки, лежащие на окружности, которые максимально удалены друг от друга. Радиус окружности равняется половине её диаметра, следовательно, если вам известен диаметр окружности, то для нахождения её радиуса следует применить формулу: R = D/2, где D — диаметр.
        2. Длина закрытой кривой, которая образуется на плоскости — это длина окружности. Если вы знаете ее длину, то для нахождения радиуса окружности вы можете применить универсальную в своем роде формулу: R = L/(2*π), где L является длиной окружности, а π — константой, равной 3,14. Константа π представляет собой отношение длины окружности к длине ее диаметра, она одинакова для всех окружностей.
        3. Круг представляет собой геометрическую фигуру, являющуюся частью плоскости, ограниченной кривой — окружностью. В том случае, если вы знаете площадь какого либо круга, то радиус окружности может быть найден по специальной формуле R = √(S/π), где S является площадью круга.
        4. Радиус вписаной окружности (в квадрат) находится следующим образом: r = a/2, где а является стороной квадрата.
        5. Радиус описанной окружности (вокруг прямоугольника) вычисляют по формуле: R = √ (a2 + b 2)/2, где а и b являются сторонами прямоугольника.
        6. В том случае, если вы не знаете длину окружности, но знаете высоту и длину какого-либо ее сегмента, то вид формулы будет таков:

        R = (4*h3 + L2)/8*h, где h является высотой сегмента, а L является его длиной.

        Находим радиус окружности, вписанной в треугольник (прямоугольный). В треугольник, какой бы вид он не имел, может быть вписана лишь одна-единственная окружность, центр которой будет одновременно той точкой, где пересекаются биссектрисы его углов. имеет множество свойств, которые должны быть учтены, когда вычисляется радиус вписанной окружности. В задаче могут быть приведены различные данные, следовательно, требуется выполнить дополнительные вычисления, необходимые для ее решения.

        Советы по нахождению радиуса вписанной окружности:

        1. Сначала нужно построить треугольник с теми размерами, которые уже были заданы в вашей задаче. Это необходимо делать, зная размеры всех трёх сторон или двух сторон и угла между ними. Так как размер одного угла вам уже известен, то в условии должны быть два катета. Катеты, которые противолежат углам, должны быть обозначены, как а и b, а гипотенуза — как с. Что касается радиуса вписанной окружности, то он обозначается как r.
        2. Для применения стандартной формулы определения радиуса вписанной окружности требуется найти все три стороны прямоугольного треугольника. Зная размеры всех сторон, вы сможете найти полупериметр треугольника из формулы: p = (a + b+ c)/2.
        3. Если вы знаете один угол и катет, то вам следует определить, прилежащий он или противолежащий. Если он прилежащий, то гипотенузу можно вычислить, используя теорему косинусов: c = a/cosCBA. Если он противолежащий, то тогда требуется воспользоваться c=a/sinCAB.
        4. Если у вас есть полупериметр, то вы можете определить радиус вписанной окружности. Вид формулы для радиуса будет таким: r=√(p-b)(p-a)(p-c)/p.
        5. Следует отметить, что найти радиус можно по формуле: r = S/p. Так что если вам известны два катета, то процедура вычисления будет более лёгкой. Гипотенуза, требуемая для полупериметра, может быть найдена по сумме квадратов его катетов. Вычислить площадь вы можете, перемножив все имеющиеся катеты и разделив надвое число, которое вы получили.

        Зачастую, когда школьник сдает выпускные экзамены в школе либо вступительные в какой-либо ВУЗ, ему необходимы определенные знания в области геометрии. Причем, задания бывают не такие уж сложные, просто нужно помнить базовые формулы, чтобы применить их в решении. Задачи, в которых необходимо найти радиус окружности, не являются исключением. В принципе, они достаточно просты в решении. В данной статье мы расскажем вам, как найти радиус окружности разными способами.

        Находим радиус окружности, исходя из формул

        Когда вы получаете задание на контрольной или на экзамене, в котором надо найти радиус окружности, в первую очередь необходимо проанализировать имеющиеся данные. Потому что именно от них будет зависеть ход решения в целом. Так, например, найти рассматриваемую величину можно, используя такие параметры: длину окружности, ее площадь, диаметр и др. Мы рассмотрим самые простые и часто встречающиеся способы решения задач, в которых радиус окружности является неизвестным.

        Все мы знаем, что радиусом окружности является длина от ее центра до какой-либо точки,которая расположена на самой окружности. В связи с этим, решения могут быть следующими:

        1. Когда вам в исходных данных задачи дан диаметр окружности, то решение здесь будет проще простого. Ведь нам известно, что диаметром является отрезок, который соединяет несколько точек на окружности, проходя при этом через ее центр. Из этого следует, что диаметр – это 2 радиуса. Тогда радиус мы находим по формуле: r=D/2, где r – это радиус окружности, а D, соответственно, ее диаметр. Например, диаметр по условию равен 32 см, тогда радиус мы вычисляем так: 32/2=16 см.
        2. Переходим к следующему способу решения. Допустим, вам в условии дана длина окружности. Выражаясь математическим языком, это так называемый периметр. Мы прекрасно знаем, что есть специальная формула нахождения длины окружности: P=2πr. Отсюда, мы можем вывести формулу радиуса: r=P/2π. Теперь рассмотрим это на примере. Допустим, по условию задачи вам дана длина окружности, равная 31,4 см, а π в математике – величина постоянная и всегда равна 3,14; тогда радиус находим следующим образом: 31,4/2*3,14=5 см.
        3. Теперь рассмотрим, как найти радиус окружности, если дана ее площадь. Формула площади окружности имеет такой вид: S=πr2. Отсюда находим формулу радиуса: r=√(S/π). Опять же рассмотрим все в цифровом исчислении. Пусть вам дана в условии задачи площадь, к примеру – 28,26 см2. Подставляем данные в выведенную нами формулу и получаем: √28,26/3,14=3 см.

        Теперь вам не составит труда решить любую задачу с нахождением радиуса окружности. Главное – четко проанализировать исходные данные, а потом применить подходящую формулу, и можете считать себя великим математиком.

        через диаметр и радиус. Терминология, основные формулы и характеристика фигуры

        Таким образом, длину окружности (C ) можно вычислить, умножив константу π на диаметр (D ), или умножив π на удвоенный радиус, так как диаметр равен двум радиусам. Следовательно, формула длины окружности будет выглядеть так:

        C = πD = 2πR

        где C — длина окружности, π — константа, D — диаметр окружности , R — радиус окружности.

        Так как окружность является границей круга , то длину окружности можно также назвать длиной круга или периметром круга.

        Задачи на длину окружности

        Задача 1. Найти длину окружности, если её диаметр равен 5 см.

        Так как длина окружности равна π умноженное на диаметр, то длина окружности с диаметром 5 см будет равна:

        C ≈ 3,14 · 5 = 15,7 (см)

        Задача 2. Найти длину окружности, радиус которой равен 3,5 м.

        Сначала найдём диаметр окружности, умножив длину радиуса на 2:

        D = 3,5 · 2 = 7 (м)

        теперь найдём длину окружности, умножив π на диаметр:

        C ≈ 3,14 · 7 = 21,98 (м)

        Задача 3. Найти радиус окружности, длина которой равна 7,85 м.

        Чтобы найти радиус окружности по её длине, надо длину окружности разделить на 2π

        Площадь круга

        Площадь круга равна произведению числа π на квадрат радиуса. Формула нахождения площади круга :

        S = πr 2

        где S — площадь круга, а r — радиус круга.

        Так как диаметр круга равен удвоенному радиусу, то радиус равен диаметру, разделённому на 2:

        Задачи на площадь круга

        Задача 1. Найти площадь круга, если его радиус равен 2 см.

        Так как площадь круга равна π умноженное на радиус в квадрате, то площадь круга с радиусом 2 см будет равна:

        S ≈ 3,14 · 2 2 = 3,14 · 4 = 12,56 (см 2)

        Задача 2. Найти площадь круга, если его диаметр равен 7 см.

        Сначала найдём радиус круга, разделив его диаметр на 2:

        7: 2 = 3,5 (см)

        теперь вычислим площадь круга по формуле:

        S = πr 2 ≈ 3,14 · 3,5 2 = 3,14 · 12,25 = 38,465 (см 2)

        Данную задачу можно решить и другим способом. Вместо того чтобы сначала находить радиус, можно воспользоваться формулой нахождения площади круга через диаметр:

        S = π D 2 ≈ 3,147 2 = 3,1449 =153,86 = 38,465 (см 2)
        4444

        Задача 3. Найти радиус круга, если его площадь равна 12,56 м 2 .

        Чтобы найти радиус круга по его площади, надо площадь круга разделить π , а затем из полученного результата извлечь квадратный корень:

        r = √S : π

        следовательно радиус будет равен:

        r ≈ √12,56: 3,14 = √4 = 2 (м)

        Число

        π

        Длину окружности предметов, окружающих нас, можно измерить с помощью сантиметровой ленты или верёвки (нитки), длину которой потом можно померить отдельно. Но в некоторых случаях померить длину окружности трудно или практически невозможно, например, внутреннюю окружность бутылки или просто длину окружности начерченной на бумаге. В таких случаях можно вычислить длину окружности, если известна длина её диаметра или радиуса.

        Чтобы понять, как это можно сделать, возьмём несколько круглых предметов, у которых можно измерить и длину окружности и диаметр. Вычислим отношение длины к диаметру, в итоге получим следующий ряд чисел:

        Из этого можно сделать вывод, что отношение длины окружности к её диаметру это постоянная величина для каждой отдельной окружности и для всех окружностей в целом. Это отношение и обозначается буквой π .

        Используя эти знания, можно по радиусу или диаметру окружности находить её длину. Например, для вычисления длины окружности с радиусом 3 см нужно умножить радиус на 2 (так мы получим диаметр), а полученный диаметр умножить на π . В итоге, с помощью числа π мы узнали, что длина окружности с радиусом 3 см равна 18,84 см.

        Инструкция

        Сначала надо исходные данные к задаче. Дело в том, что ее условии не может быть явно сказано, какова радиуса окружности . Вместо этого в задаче может быть дана длина диаметра окружности . Диаметр окружности — отрезок, который объединяет между собой две противоположные точки окружности , проходя через ее центр. Проанализировав определения окружности , можно сказать, что длина диаметра удвоенной длине радиуса.

        Теперь можно принять радиус окружности равным R. Тогда для длины окружности необходимо воспользоваться формулой:
        L = 2πR = πD, где L — длина окружности , D — диаметр окружности , который всегда в 2 раза радиуса.

        Обратите внимание

        Окружность можно вписать в многоугольник, либо описать вокруг него. При этом, если окружность вписана, то она в точках касания со сторонами многоугольника будет делить их пополам. Чтобы узнать радиус вписанной окружности, нужно поделить площадь многоугольника на половину его периметра:
        R = S/p.
        Если окружность описана вокруг треугольника, то ее радиус находится по следующей формуле:
        R = a*b*c/4S, где a, b, c — это стороны данного треугольника, S — площадь треугольника, вокруг которого описана окружность.
        Если требуется описать окружность вокруг четырехугольника, то это можно будет сделать при соблюдении двух условий:
        Четырехугольник должен быть выпуклым.
        В сумме противоположные углы четырехугольника должны составлять 180°

        Полезный совет

        Помимо традиционного штангенциркуля, для начертания окружности можно применять и трафареты. В современных трафаретах включены окружность разных диаметров. Данные трафареты можно приобрести в любом магазине канцтоваров.

        Источники:

        • Как найти длину окружности?

        Окружность — замкнутая кривая линия, все точки которой находятся на равном расстоянии от одной точки. Эта точка — центр окружности, а отрезок между точкой на кривой и ее центром называется радиусом окружности.

        Инструкция

        Если через центр окружности провести прямую линию, то ее отрезок между двумя точками пересечения этой прямой с окружностью называется диаметром данной окружности. Половина диаметра, от центра до точки пересечения диаметра с окружность — это радиус
        окружности. Если окружность разрезать в произвольной точке, выпрямить и измерить, то полученная величина является длиной данной окружности.

        Начертите несколько окружностей разным раствором циркуля. Визуальное сравнение позволяет сделать вывод, что больший диаметр очерчивает больший круг, ограниченный окружностью с большей длиной. Следовательно, между диаметром окружности и ее длиной существует прямо пропорциональная зависимость.

        По физическому смыслу параметр «длина окружности» соответствует , ограниченного ломаной линией. Если вписать в окружность правильный n-угольник со стороной b, то периметр такой фигуры Р равен произведению стороны b на число сторон n: Р=b*n. Сторона b может быть определена по формуле: b=2R*Sin (π/n), где R — радиус окружности, в которую вписали n-угольник.

        При увеличении числа сторон периметр вписанного многоугольника будет все больше приближаться к L. Р= b*n=2n*R*Sin (π/n)=n*D*Sin (π/n). Зависимость между длиной окружности L и ее диаметром D постоянна. Отношение L/D=n*Sin (π/n) при стремлении числа сторон вписанного многоугольника к бесконечности стремится к числу π, постоянной величине, называемой «число пи» и выраженной бесконечной десятичной дробью. Для расчетов без применения вычислительной техники принимается значение π=3,14. Длина окружности и ее диаметр связаны формулой: L= πD. Для окружности разделите ее длину на число π=3,14.

        Окружностью называют кривую линию, которая ограничивает собой круг. В геометрии фигуры плоские, поэтому определение относится к двухмерному изображению. Предполагается, что все точки этой кривой удалены от центра круга на равное расстояние.

        У окружности есть несколько характеристик, на основе которых производят расчеты, связанные с этой геометрической фигурой. В их число входит: диаметр, радиус, площадь и длина окружности. Эти характеристики взаимосвязаны, то есть для их вычисления достаточно информации хотя бы об одной из составляющих. Например, зная только радиус геометрической фигуры по формуле можно найти длину окружности, диаметр, и ее площадь.

        • Радиус окружности – это отрезок внутри окружности, соединённый с ее центром.
        • Диаметр – это отрезок внутри окружности, соединяющий ее точки и проходящий через центр. По сути, диаметр – это два радиуса. Именно так выглядит формула для его вычисления: D=2r.
        • Есть еще одна составляющая окружности – хорда. Эта прямая, которая соединяет две точки окружности, но не всегда проходит через центр. Так вот ту хорду, которая через него проходит, тоже называют диаметром.

        Как узнать длину окружности? Сейчас выясним.

        Длина окружности: формула

        Для обозначения этой характеристики выбрана латинская буква p. Еще Архимед доказал, что отношение длины окружности к ее диаметру является одним и тем же числом для всех окружностей: это число π, которое приблизительно равно 3,14159. Формула для вычисления π выглядит так: π = p/d. Согласно этой формуле, величина p равна πd, то есть длина окружности: p= πd. Поскольку d (диаметр) равен двум радиусам, то эту же формулу длины окружности можно записать как p=2πr.Рассмотрим применение формулы на примере простых задач:

        Задача 1

        У основания царь-колокола диаметр равен 6,6 метров. Какова длина окружности основания колокола?

        1. Итак, формула для вычисления окружности — p= πd
        2. Подставляем имеющееся значение в формулу: p=3,14*6,6= 20,724

        Ответ: длина окружности основания колокола 20,7 метра.

        Задача 2

        Искусственный спутник Земли вращается на расстоянии 320 км от планеты. Радиус Земли – 6370 км. Какова длина круговой орбиты спутника?

        1. 1.Вычислим радиус круговой орбиты спутника Земли: 6370+320=6690 (км)
        2. 2.Вычислим длину круговой орбиты спутника по формуле: P=2πr
        3. 3.P=2*3,14*6690=42013,2

        Ответ: длина круговой орбиты спутника Земли 42013,2 км.

        Способы измерения длины окружности

        Вычисление длины окружности на практике используется не часто. Причиной тому приблизительное значение числа π. В быту для поиска длины круга используют специальный прибор – курвиметр. На окружности отмечают произвольную точку отсчета и ведут от нее прибор строго по линии, пока опять не дойдут до этой точки.

        Как найти длину окружности? Нужно просто держать в голове незамысловатые формуля для вычислений.

        Одной линейкой здесь не обойтись, необходимо знать специальные формулы. Единственное, что от нас потребуется — это определить диаметр или радиус круга. В некоторых задачах эти величины обозначены. Но что делать, если у нас нет ничего, кроме рисунка? Не беда. Диаметр и радиус можно вычислить с помощью обычной линейки. Теперь приступим к самому основному.

        Формулы, которые должен знать каждый

        Еще в почти 4 000 лет назад, учёные выявили удивительное соотношение: если длину окружности разделить на ее диаметр, то получается одно и то же число, которое равно примерно 3,14. Это значение назвали именно с этой буквы в древнегреческом языке начиналось слово «периметр» и «окружность». На основании того открытия, которое совершили древние ученые, можно рассчитать длину любой окружности:

        Где P означает длину (периметр) окружности,

        D — диаметр, П — число «Пи».

        Длина окружности круга может также быть посчитана через ее радиус (r), который равен половине длины диаметра. Вот и вторая формула, которую нужно запомнить:

        Как узнать диаметр окружности?

        Представляет собой хорду, которая проходит через центр фигуры. При этом она соединяет две наиболее удалённые точки в круге. Исходя из этого, можно самостоятельно прочертить диаметр (радиус) и измерить его длину с помощью линейки.

        Способ 1: вписываем прямоугольный треугольник в круг

        Рассчитать длину окружности будет несложно, если мы найдем ее диаметр. Необходимо начертить в круге где гипотенуза будет равна диаметру окружности. Для этого необходимо иметь под рукой линейку и угольник, иначе ничего не получится.

        Способ 2: вписываем любой треугольник

        На стороне круга отмечаем три любые точки, соединяем их — получаем треугольник. Важно, чтобы центр окружности лежал в области треугольника, это можно сделать на глаз. Проводим к каждой стороне треугольника медианы, точка их пересечения совпадёт с центром окружности. А когда нам известен центр, можно с помощью линейки легко провести диаметр.

        Данный способ очень похож на первый, но может применяться при отсутствии угольника или в тех случаях, когда нет возможности чертить на фигуре, например на тарелке. Необходимо взять лист бумаги с прямыми углами. Прикладываем лист к кругу так, чтобы одна вершина его угла соприкасалась с краем круга. Далее отмечаем точками места, где стороны бумаги пересекаются с линией окружности. Соединяем эти точки с помощью карандаша и линейки. Если под рукой ничего нет, просто согните бумагу. Эта линия и будет равна длине диаметра.

        Пример задачи

        1. Ищем диаметр с помощью угольника, линейки и карандаша по способу № 1. Предположим, получилось 5 см.
        2. Зная диаметр, мы легко можем его вставить в нашу формулу: P = d П = 5*3,14 = 15,7В нашем случае получилось около 15,7. Теперь вы без особых проблем сможете объяснить, как рассчитать длину окружности.

        1. Сложнее найти длину окружности через диаметр , по этому сначала разберём этот вариант.

        Пример: Найдите длину окружности диаметр которой равен 6 см . Мы используем приведённую выше формулу длины окружности, только сначала нам необходимо найти радиус. Для этого мы делим диаметр 6 см на 2 и получаем радиус окружности 3 см.

        После этого всё предельно просто: Умножаем число Пи на 2 и на полученный радиус в 3 см.
        2 * 3,14 * 3 см = 6,28 * 3см = 18,84 см.

        2. А теперь ещё раз разберём простой вариант найдите длину окружности радиус равен 5 см

        Решение: Радиус 5 см умножаем на 2 и умножаем на 3,14. Не пугайтесь, ведь перестановка местами множителей не влияет на результат, и формулу длины окружности можно применять в любой последовательности.

        5см * 2 * 3,14 = 10 см * 3,14 = 31.4 см — это найденная длина окружности для радиуса 5 см!

        Онлайн калькулятор длины окружности

        Наш калькулятор длины окружности произведёт все эти не хитрые вычисления мгновенно и распишет решение в строку и с комментариями. Мы рассчитаем длину окружности для радиуса 3, 5, 6, 8 или 1 см, или диаметр равен 4, 10, 15, 20 дм, нашему калькулятору без разницы для какого значения радиуса найти длину окружности.

        Все вычисления будут точными, оттестированными специалистами математиками. Результаты можно использовать в решении школьных задач по геометрии или математике, а также при рабочих расчётах в строительстве или в ремонте и отделке помещений, когда требуются точные вычисления по этой формуле.

        Как узнать длину окружности зная диаметр формула. Как рассчитать длину окружности, если не указан диаметр и радиус круга

        Одной линейкой здесь не обойтись, необходимо знать специальные формулы. Единственное, что от нас потребуется — это определить диаметр или радиус круга. В некоторых задачах эти величины обозначены. Но что делать, если у нас нет ничего, кроме рисунка? Не беда. Диаметр и радиус можно вычислить с помощью обычной линейки. Теперь приступим к самому основному.

        Формулы, которые должен знать каждый

        Еще в почти 4 000 лет назад, учёные выявили удивительное соотношение: если длину окружности разделить на ее диаметр, то получается одно и то же число, которое равно примерно 3,14. Это значение назвали именно с этой буквы в древнегреческом языке начиналось слово «периметр» и «окружность». На основании того открытия, которое совершили древние ученые, можно рассчитать длину любой окружности:

        Где P означает длину (периметр) окружности,

        D — диаметр, П — число «Пи».

        Длина окружности круга может также быть посчитана через ее радиус (r), который равен половине длины диаметра. Вот и вторая формула, которую нужно запомнить:

        Как узнать диаметр окружности?

        Представляет собой хорду, которая проходит через центр фигуры. При этом она соединяет две наиболее удалённые точки в круге. Исходя из этого, можно самостоятельно прочертить диаметр (радиус) и измерить его длину с помощью линейки.

        Способ 1: вписываем прямоугольный треугольник в круг

        Рассчитать длину окружности будет несложно, если мы найдем ее диаметр. Необходимо начертить в круге где гипотенуза будет равна диаметру окружности. Для этого необходимо иметь под рукой линейку и угольник, иначе ничего не получится.

        Способ 2: вписываем любой треугольник

        На стороне круга отмечаем три любые точки, соединяем их — получаем треугольник. Важно, чтобы центр окружности лежал в области треугольника, это можно сделать на глаз. Проводим к каждой стороне треугольника медианы, точка их пересечения совпадёт с центром окружности. А когда нам известен центр, можно с помощью линейки легко провести диаметр.

        Данный способ очень похож на первый, но может применяться при отсутствии угольника или в тех случаях, когда нет возможности чертить на фигуре, например на тарелке. Необходимо взять лист бумаги с прямыми углами. Прикладываем лист к кругу так, чтобы одна вершина его угла соприкасалась с краем круга. Далее отмечаем точками места, где стороны бумаги пересекаются с линией окружности. Соединяем эти точки с помощью карандаша и линейки. Если под рукой ничего нет, просто согните бумагу. Эта линия и будет равна длине диаметра.

        Пример задачи

        1. Ищем диаметр с помощью угольника, линейки и карандаша по способу № 1. Предположим, получилось 5 см.
        2. Зная диаметр, мы легко можем его вставить в нашу формулу: P = d П = 5*3,14 = 15,7В нашем случае получилось около 15,7. Теперь вы без особых проблем сможете объяснить, как рассчитать длину окружности.

        Окружность состоит из множества точек, которые находятся на равном расстоянии от центра. Это плоская геометрическая фигура, и найти ее длину не составит труда. С окружностью и кругом человек сталкивается ежедневно независимо от того, в какой сфере он работает. Многие овощи и фрукты , устройства и механизмы, посуда и мебель имеют круглую форму. Кругом называют то множество точек, которое находится в границах окружности. Поэтому длина фигуры равна периметру круга.

        Характеристики фигуры

        Кроме того, что описание понятия окружности достаточно простое, её характеристики также несложные для понимания. С их помощью можно вычислить её длину. Внутренняя часть окружности состоит из множества точек, среди которых две — А и В — можно увидеть под прямым углом. Этот отрезок называют диаметром, он состоит из двух радиусов.

        В пределах окружности имеются точки Х такие , что не изменяется и не равняется единице отношение АХ/ВХ. В окружности это условие обязательно соблюдается, в ином случае эта фигура не имеет форму круга. На каждую точку, из которых состоит фигура, распространяется правило: сумма квадратов расстояний от этих точек до двух других всегда превышает половину длины отрезка между ними.

        Основные термины окружности

        Для того чтобы уметь находить длину фигуры, необходимо знать основные термины, касающиеся её. Основные параметры фигуры — это диаметр, радиус и хорда . Радиусом называют отрезок, соединяющий центр круга с любой точкой на её кривой. Величина хорды равна расстоянию между двумя точками на кривой фигуры. Диаметр — расстояние между точками , проходящее через центр фигуры.

        Основные формулы для вычислений

        Параметры используются в формулах вычислений величин окружности:

        Диаметр в формулах вычисления

        В экономике и математике нередко появляется необходимость поиска длины окружности. Но и в повседневной жизни можно столкнуться с этой надобностью, к примеру, во время постройки забора вокруг бассейна круглой формы. Как рассчитать длину окружности по диаметру? В этом случае используют формулу C = π*D, где С — это искомая величина, D — диаметр.

        Например, ширина бассейна равна 30 метрам, а столбики забора планируют поставить на расстоянии десяти метров от него. В этом случае формула расчёта диаметра: 30+10*2 = 50 метров. Искомая величина (в этом примере — длина забора): 3,14*50 = 157 метров. Если столбики забора будут стоять на расстоянии трёх метров друг от друга, то всего их понадобится 52.

        Расчёты по радиусу

        Как вычислить длину окружности по известному радиусу? Для этого используется формула C = 2*π*r, где С — длина, r — радиус. Радиус в круге меньше диаметра в два раза, и это правило может пригодиться в повседневной жизни. К примеру, в случае приготовления пирога в раздвижной форме.

        Для того чтобы кулинарное изделие не испачкалось, необходимо использовать декоративную обёртку. А как вырезать бумажный круг подходящего размера?

        Те, кто немного знаком с математикой, понимают, что в этом случае нужно умножить число π на удвоенный радиус используемой формы. Например, диаметр формы равен 20 сантиметрам, соответственно, её радиус составляет 10 сантиметров. По этим параметрам находится необходимый размер круга: 2*10*3, 14 = 62,8 сантиметра.

        Подручные способы вычисления

        Если найти длину окружности по формуле нет возможности, то стоит воспользоваться подручными методами расчёта этой величины:

        • При небольших размерах круглого предмета его длину можно найти с помощью верёвки, обёрнутой вокруг один раз.
        • Величину большого предмета измеряют так: на ровной плоскости раскладывают верёвку, и по ней прокатывают круг один раз.
        • Современные студенты и школьники для расчётов используют калькуляторы. В режиме онлайн по известным параметрам можно узнавать неизвестные величины.

        Круглые предметы в истории человеческой жизни

        Первое изделие круглой формы, которое изобрёл человек — это колесо. Первые конструкции представляли собой небольшие округлые бревна, насаженные на оси. Затем появились колёса, сделанные из деревянных спиц и обода. Постепенно в изделие добавляли металлические детали для уменьшения износа. Именно для того, чтобы узнать длину металлических полос для обивки колёса, учёные прошлых веков искали формулу расчёта этой величины.

        Форму колеса имеет гончарный круг , большинство деталей в сложных механизмах, конструкциях водяных мельниц и прялок. Нередко встречаются круглые предметы в строительстве — рамки круглых окон в романском архитектурном стиле, иллюминаторы в суднах. Архитекторы, инженеры, учёные, механики и проектировщики ежедневно в сфере своей профессиональной деятельности сталкиваются с надобностью расчёта размеров окружности.

        Множество предметов в окружающем мире имеют круглую форму. Это колеса, круглые оконные проемы, трубы, различная посуда и многое другое. Подсчитать, чему равна длина окружности, можно, зная ее диаметр или радиус.

        Существует несколько определений этой геометрической фигуры.

        • Это замкнутая кривая, состоящая из точек, которые располагаются на одинаковом расстоянии от заданной точки.
        • Это кривая, состоящая из точек А и В, являющихся концами отрезка, и всех точек, из которых А и В видны под прямым углом. При этом отрезок АВ – диаметр.
        • Для того же отрезка АВ эта кривая включает все точки С, такие, что отношение АС/ВС неизменно и не равняется 1.
        • Это кривая, состоящая из точек, для которых справедливо следующее: если сложить квадраты расстояний от одной точки до двух данных других точек А и В, получится постоянное число, большее 1/2 соединяющего А и В отрезка. Это определение выводится из теоремы Пифагора.

        Обратите внимание! Есть и другие определения. Круг – это область внутри окружности. Периметр круга и есть ее длина. По разным определениям круг может включать или не включать саму кривую, являющуюся его границей.

        Определение окружности

        Формулы

        Как вычислить длину окружности через радиус? Это делается по простой формуле:

        где L – искомая величина,

        π – число пи, примерно равное 3,1413926.

        Обычно для нахождения нужной величины достаточно использовать π до второго знака, то есть 3,14, это обеспечит нужную точность. На калькуляторах, в частности инженерных, может быть кнопка, которая автоматически вводит значение числа π.

        Обозначения

        Для нахождения через диаметр существует следующая формула:

        Если L уже известно, можно легко узнать радиус или диаметр. Для этого L нужно поделить на 2π или на π соответственно.

        Если уже дана круга, нужно понимать, как найти длину окружности по этим данным. Площадь круга равняется S = πR2. Отсюда находим радиус: R = √(S/π). Тогда

        L = 2πR = 2π√(S/π) = 2√(Sπ).

        Вычислить площадь через L также несложно: S = πR2 = π(L/(2π))2 = L2/(4π)

        Резюмируя, можно сказать, что существует три основных формулы:

        • через радиус – L = 2πR;
        • через диаметр – L = πD;
        • через площадь круга – L = 2√(Sπ).

        Число пи

        Без числа π решить рассматриваемую задачу не получится. Число π впервые и было найдено как отношение длины окружности к ее диаметру. Это сделали еще древние вавилоняне, египтяне и индийцы. Нашли они его довольно точно – их результаты отличались от известного сейчас значения π не больше, чем на 1%. Постоянную приближали такими дробями как 25/8, 256/81, 339/108.

        Далее значение этой постоянной считали не только с позиции геометрии, но и с точки зрения математического анализа через суммы рядов. Обозначение этой константы греческой буквой π впервые использовал Уильям Джонс в 1706 году, а популярно оно стало после работ Эйлера.

        Сейчас известно, что эта постоянная представляет собой бесконечную непериодическую десятичную дробь, она иррациональна, то есть ее нельзя представить в виде отношения двух целых чисел. С помощью вычислений на суперкомпьютерах в 2011 году узнали 10-триллионный знак константы.

        Это интересно! Для запоминания нескольких первых знаков числа π были придуманы различные мнемонические правила. Некоторые позволяют хранить в памяти большое число цифр, например, одно французское стихотворение поможет запомнить пи до 126 знака.

        Если вам необходима длина окружности, онлайн-калькулятор поможет в этом. Таких калькуляторов существует множество, в них нужно только ввести радиус или диаметр. У некоторых из них есть обе эти опции, другие вычисляют результат только через R. Некоторые калькуляторы могут рассчитать искомую величину с разной точностью, нужно указать число знаков после запятой. Также с помощью онлайн-калькуляторов можно посчитать площадь круга.

        Такие калькуляторы легко найти любым поисковиком. Также существуют мобильные приложения, которые помогут решить задачу, как найти длину окружности.

        Полезное видео: длина окружности

        Практическое применение

        Решать такую задачу чаще всего необходимо инженерам и архитекторам, но и в быту знание нужных формул тоже может пригодиться. Например, требуется обернуть бумажной полоской торт, испеченный в форме с поперечником 20 см. Тогда не составит труда найти длину этой полоски:

        L = πD = 3,14 * 20 = 62,8 см.

        Другой пример: нужно построить забор вокруг круглого бассейна на определенном расстоянии. Если радиус бассейна 10 м, а забор нужно поставить на расстоянии 3 м, то R для полученной окружности будет 13 м. Тогда ее длина равна:

        L = 2πR = 2 * 3,14 * 13 = 81,68 м.

        Полезное видео: круг — радиус, диаметр, длина окружности

        Итог

        Периметр круга легко рассчитать по простым формулам, включающим диаметр или радиус. Также можно найти искомую величину через площадь круга. Решить эту задачу помогут онлайн-калькуляторы или мобильные приложения, в которые нужно ввести единственное число – диаметр или радиус.

        И в чем ее отличие от круга. Возьмите ручку или цвета и нарисуйте на листке бумаги обычный круг. Закрасьте всю середину полученной фигуры синим карандашом. Красный контур, обозначающий границы фигуры, — это окружность. А вот синее содержимое внутри нее — и есть круг.

        Размеры круга и окружности определяются диаметром. На красной линии, обозначающей окружность, отметьте две точки таким образом, чтобы они оказались зеркальным отражением друг друга. Соедините их линией. Отрезок обязательно пройдет через точку в центре окружности. Этот отрезок, соединяющий противоположные части окружности, и называется в геометрии диаметром.

        Отрезок, который тянется не через центр окружности, но смыкается с ней противоположными концами, называется хордой. Следовательно, хорда, пролегающая через точку центра окружности, и является ее диаметром.

        Обозначается диаметр латинской буквой D. Находить диаметр окружности можно по таким значениям, как площадь, длина и радиус круга.

        Расстояние от центральной точки до точки, отложенной на окружности, называется радиусом и обозначается буквой R. Знание величины радиуса помогает вычислить диаметр окружности одним несложным действием:

        К примеру, радиус — 7 см. Умножаем 7 см на 2 и получаем величину, равную 14 см. Ответ: D заданной фигуры равен 14 см.

        Иногда приходится определять диаметр окружности лишь по ее длине. Здесь необходимо применить специальную формулу, помогающую определить Формула L = 2 Пи * R, где 2 — это неизменная величина (константа), а Пи = 3,14. А так как известно, что R = D * 2, то формулу можно представить и другим способом

        Данное выражение применимо и как формула диаметра окружности. Подставив известные в задаче величины, решаем уравнение с одним неизвестным. Допустим, длина равна 7 м. Следовательно:

        Ответ: диаметр равен 21,98 метрам.

        Если известно значение площади, то также можно определить диаметр окружности. Формула, которая применяется в данном случае, выглядит так:

        D = 2 * (S / Пи) * (1 / 2)

        S — в данном случае Допустим, в задаче она равна 30 кв. м. Получаем:

        D = 2 * (30 / 3, 14) * (1 / 2) D = 9, 55414

        При обозначенной в задаче величине, равной объему (V) шара, применяется следующая формула нахождения диаметра: D = (6 V / Пи) * 1 / 3.

        Иногда приходится находить диаметр окружности, вписанной в треугольник. Для этого по формуле находим радиус представленной окружности:

        R = S / p (S — площадь заданного треугольника, а p — периметр, разделенный на 2).

        Полученный результат увеличиваем вдвое, учитывая, что D = 2 * R.

        Нередко находить диаметр окружности приходится и в быту. К примеру, при определении что равносильно его диаметру. Для этого необходимо обмотать палец потенциального обладателя кольца ниткой. Отметить точки соприкосновения двух концов. Измерить линейкой длину от точки до точки. Полученное значение умножаем на 3,14, следуя формуле определения диаметра при известной длине. Так что, утверждение о том, что познания в геометрии и алгебре в жизни не пригодятся, не всегда соответствует действительности. А это является серьезным поводом для того, чтобы более ответственно относиться к школьным предметам.

        Таким образом, длину окружности (C ) можно вычислить, умножив константу π на диаметр (D ), или умножив π на удвоенный радиус, так как диаметр равен двум радиусам. Следовательно, формула длины окружности будет выглядеть так:

        C = πD = 2πR

        где C — длина окружности, π — константа, D — диаметр окружности , R — радиус окружности.

        Так как окружность является границей круга , то длину окружности можно также назвать длиной круга или периметром круга.

        Задачи на длину окружности

        Задача 1. Найти длину окружности, если её диаметр равен 5 см.

        Так как длина окружности равна π умноженное на диаметр, то длина окружности с диаметром 5 см будет равна:

        C ≈ 3,14 · 5 = 15,7 (см)

        Задача 2. Найти длину окружности, радиус которой равен 3,5 м.

        Сначала найдём диаметр окружности, умножив длину радиуса на 2:

        D = 3,5 · 2 = 7 (м)

        теперь найдём длину окружности, умножив π на диаметр:

        C ≈ 3,14 · 7 = 21,98 (м)

        Задача 3. Найти радиус окружности, длина которой равна 7,85 м.

        Чтобы найти радиус окружности по её длине, надо длину окружности разделить на 2π

        Площадь круга

        Площадь круга равна произведению числа π на квадрат радиуса. Формула нахождения площади круга :

        S = πr 2

        где S — площадь круга, а r — радиус круга.

        Так как диаметр круга равен удвоенному радиусу, то радиус равен диаметру, разделённому на 2:

        Задачи на площадь круга

        Задача 1. Найти площадь круга, если его радиус равен 2 см.

        Так как площадь круга равна π умноженное на радиус в квадрате, то площадь круга с радиусом 2 см будет равна:

        S ≈ 3,14 · 2 2 = 3,14 · 4 = 12,56 (см 2)

        Задача 2. Найти площадь круга, если его диаметр равен 7 см.

        Сначала найдём радиус круга, разделив его диаметр на 2:

        7: 2 = 3,5 (см)

        теперь вычислим площадь круга по формуле:

        S = πr 2 ≈ 3,14 · 3,5 2 = 3,14 · 12,25 = 38,465 (см 2)

        Данную задачу можно решить и другим способом. Вместо того чтобы сначала находить радиус, можно воспользоваться формулой нахождения площади круга через диаметр:

        S = π D 2 ≈ 3,147 2 = 3,1449 =153,86 = 38,465 (см 2)
        4444

        Задача 3. Найти радиус круга, если его площадь равна 12,56 м 2 .

        Чтобы найти радиус круга по его площади, надо площадь круга разделить π , а затем из полученного результата извлечь квадратный корень:

        r = √S : π

        следовательно радиус будет равен:

        r ≈ √12,56: 3,14 = √4 = 2 (м)

        Число

        π

        Длину окружности предметов, окружающих нас, можно измерить с помощью сантиметровой ленты или верёвки (нитки), длину которой потом можно померить отдельно. Но в некоторых случаях померить длину окружности трудно или практически невозможно, например, внутреннюю окружность бутылки или просто длину окружности начерченной на бумаге. В таких случаях можно вычислить длину окружности, если известна длина её диаметра или радиуса.

        Чтобы понять, как это можно сделать, возьмём несколько круглых предметов, у которых можно измерить и длину окружности и диаметр. Вычислим отношение длины к диаметру, в итоге получим следующий ряд чисел:

        Из этого можно сделать вывод, что отношение длины окружности к её диаметру это постоянная величина для каждой отдельной окружности и для всех окружностей в целом. Это отношение и обозначается буквой π .

        Используя эти знания, можно по радиусу или диаметру окружности находить её длину. Например, для вычисления длины окружности с радиусом 3 см нужно умножить радиус на 2 (так мы получим диаметр), а полученный диаметр умножить на π . В итоге, с помощью числа π мы узнали, что длина окружности с радиусом 3 см равна 18,84 см.

        Как найти длину окружности зная радиус и диаметр: формула, как найти длину круга и разницу между величинами

        Очень часто при решении школьных заданий по математике или физике возникает вопрос — как найти длину окружности, зная диаметр? На самом деле никаких сложностей в решении этой проблемы нет, нужно только чётко представлять себе, какие формулы, понятия и определения требуются для этого….

        Содержание

        Основные понятия и определения

        1. Радиус — это линия, соединяющая центр окружности и её произвольную точку. Он обозначается латинской буквой r.
        2. Хордой называется линия, соединяющая две произвольные точки лежащие на окружности.
        3. Диаметр — это линия, соединяющая два пункта окружности и проходящая через её центр. Он обозначается латинской буквой d.
        4. Окружность — это линия, состоящая из всех точек, находящихся на равном расстоянии от одной избранной точки, именуемой её центром. Её длину будем обозначать латинской буквой l.

        Площадь круга — это вся территория, заключённая внутри окружности. Она измеряется в квадратных единицах и обозначается латинской буквой s.

        Пользуясь нашими определениями, приходим к выводу, что диаметр круга равен его самой большой хорде.

        Внимание! Из определения, что такое радиус круга можно узнать, что такое диаметр круга. Это два радиуса отложенные в противоположных направлениях! Диаметр окружности.

        Нахождение длины окружности и её площади

        Если нам дан радиус окружности, то диаметр окружности описывает формула d = 2*r. Таким образом, для ответа на вопрос, как найти диаметр круга, зная его радиус, достаточно последний умножить на два.

        Формула длины окружности, выраженная через её радиус, имеет вид l = 2*П*r.

        Внимание! Латинской буквой П (Пи) обозначается отношение длины окружности к её диаметру, и это есть непериодическая десятичная дробь. 2 = 4*s/П. Для определения самого диаметра потребуется извлечь корень квадратный из правой части. Получится d = 2*sqrt(s/П).

        Это интересно! Первый признак равенства треугольников: доказательство

        Решение типовых заданий

        1. Узнаем, как найти диаметр, если дана длина окружности. Пусть она равняется 778,72 километра. Требуется найти d. d = 778,72/3,14 = 248 километров. Вспомним, что такое диаметр и сразу определим радиус, для этого определённое выше значение d разделим пополам. Получится r = 248/2 = 124 километра.
        2. Рассмотрим, как найти длину данной окружности, зная её радиус. Пусть r имеет значение 8 дм 7 см. Переведём это все в сантиметры, тогда r будет равняться 87 сантиметров. Воспользуемся формулой, как найти неизвестную длину круга . Тогда наше искомое будет равняться l = 2*3,14*87 = 546,36 см. Переведём наше полученное значение в целые числа метрических величин l = 546,36 см = 5 м 4 дм 6 см 3,6 мм. 2/(4П) = 2209/12,56 = 175,87 кв. м.

        Это интересно! Что такое биссектриса треугольника: свойства, связанные с отношением сторон

        Длина окружности

        Окружность, диаметр, хорда геометрия 7 класс

        Заключение

        Исходя из приведённых выше рассуждений, можно прийти к выводу, что никаких сложностей в задачах, связанных с нахождением всевозможных характеристик окружности, нет. Достаточно хорошо выучить понятия и формулы, а также уметь производить арифметические действия, причём все выражения выводятся друг из друга.

        Это интересно! Чему равна и как найти площадь равностороннего треугольника

        Как найти окружность зная диаметр. Как найти длину окружности: через диаметр и радиус

        Таким образом, длину окружности (C ) можно вычислить, умножив константу π на диаметр (D ), или умножив π на удвоенный радиус, так как диаметр равен двум радиусам. Следовательно, формула длины окружности будет выглядеть так:

        C = πD = 2πR

        где C — длина окружности, π — константа, D — диаметр окружности , R — радиус окружности.

        Так как окружность является границей круга , то длину окружности можно также назвать длиной круга или периметром круга.

        Задачи на длину окружности

        Задача 1. Найти длину окружности, если её диаметр равен 5 см.

        Так как длина окружности равна π умноженное на диаметр, то длина окружности с диаметром 5 см будет равна:

        C ≈ 3,14 · 5 = 15,7 (см)

        Задача 2. Найти длину окружности, радиус которой равен 3,5 м.

        Сначала найдём диаметр окружности, умножив длину радиуса на 2:

        D = 3,5 · 2 = 7 (м)

        теперь найдём длину окружности, умножив π на диаметр:

        C ≈ 3,14 · 7 = 21,98 (м)

        Задача 3. Найти радиус окружности, длина которой равна 7,85 м.

        Чтобы найти радиус окружности по её длине, надо длину окружности разделить на 2π

        Площадь круга

        Площадь круга равна произведению числа π на квадрат радиуса. Формула нахождения площади круга :

        S = πr 2

        где S — площадь круга, а r — радиус круга.

        Так как диаметр круга равен удвоенному радиусу, то радиус равен диаметру, разделённому на 2:

        Задачи на площадь круга

        Задача 1. Найти площадь круга, если его радиус равен 2 см.

        Так как площадь круга равна π умноженное на радиус в квадрате, то площадь круга с радиусом 2 см будет равна:

        S ≈ 3,14 · 2 2 = 3,14 · 4 = 12,56 (см 2)

        Задача 2. Найти площадь круга, если его диаметр равен 7 см.

        Сначала найдём радиус круга, разделив его диаметр на 2:

        7: 2 = 3,5 (см)

        теперь вычислим площадь круга по формуле:

        S = πr 2 ≈ 3,14 · 3,5 2 = 3,14 · 12,25 = 38,465 (см 2)

        Данную задачу можно решить и другим способом. Вместо того чтобы сначала находить радиус, можно воспользоваться формулой нахождения площади круга через диаметр:

        S = π D 2 ≈ 3,147 2 = 3,1449 =153,86 = 38,465 (см 2)
        4444

        Задача 3. Найти радиус круга, если его площадь равна 12,56 м 2 .

        Чтобы найти радиус круга по его площади, надо площадь круга разделить π , а затем из полученного результата извлечь квадратный корень:

        r = √S : π

        следовательно радиус будет равен:

        r ≈ √12,56: 3,14 = √4 = 2 (м)

        Число

        π

        Длину окружности предметов, окружающих нас, можно измерить с помощью сантиметровой ленты или верёвки (нитки), длину которой потом можно померить отдельно. Но в некоторых случаях померить длину окружности трудно или практически невозможно, например, внутреннюю окружность бутылки или просто длину окружности начерченной на бумаге. В таких случаях можно вычислить длину окружности, если известна длина её диаметра или радиуса.

        Чтобы понять, как это можно сделать, возьмём несколько круглых предметов, у которых можно измерить и длину окружности и диаметр. Вычислим отношение длины к диаметру, в итоге получим следующий ряд чисел:

        Из этого можно сделать вывод, что отношение длины окружности к её диаметру это постоянная величина для каждой отдельной окружности и для всех окружностей в целом. 2»).

        Зная лишь длину диаметра окружности, можно вычислить не только площадь круга, но и площади некоторых других геометрических фигур. Это вытекает из того, что диаметры вписанных или описанных вокруг таких фигур окружностей совпадают с длинами их сторон либо диагоналей.

        Инструкция

        Если надо найти площадь (S) по известной длине его диаметра (D), умножайте число пи (π) на возведенную в длину диаметра , а результат делите на четыре: S=π ²*D²/4. Например, круга равен двадцати сантиметрам, то его площадь можно вычислить так: 3,14² * 20² / 4 = 9,86 * 400 / 4 = 986 сантиметров.

        Если надо найти площадь квадрата (S) по диаметру вокруг него окружности (D), возводите длину диаметра в квадрат, а результат разделите пополам: S=D²/2. Например, если диаметр описанной окружности равен двадцати сантиметрам, то площадь квадрата можно вычислить так: 20² / 2 = 400 / 2 = 200 квадратных сантиметров.

        Если площадь квадрата (S) нужно найти по диаметру вписанной в него окружности (D), достаточно возвести длину диаметра в квадрат: S=D². 2 / 4 + 20*10/2», а нажать клавишу Enter.

        Источники:

        • как найти площадь окружности по диаметру

        Круг — это плоская геометрическая фигура, все точки которой находятся на одинаковом и отличном от нуля удалении от выбранной точки, которую называют центром окружности. Прямую, соединяющую любые две точки круга и проходящую через центр, называют его диаметром . Суммарная длина всех границ двухмерной фигуры, которую обычно называют периметром, у круга чаще обозначается как «длина окружности». Зная длину окружности можно вычислить и ее диаметр.

        Инструкция

        Используйте для нахождения диаметра одно из основных свойств окружности, которое заключается в том, что соотношение длины ее периметра к диаметру одинаково для абсолютно всех окружностей. Конечно, постоянство не осталось не отмеченным математиками, и эта пропорция давно уже получила собственное — это число Пи (π — первая греческих слов «окружность » и «периметр»). Числовое этой определяется длиной окружности, у которой диаметр равен единице.

        Делите известную длину окружности на число Пи, чтобы вычислить ее диаметр. Так как это число является « », то не имеет конечного значения — это дробь. Округляйте число Пи в соответствии с точностью результата, которую вам необходимо получить.

        Используйте какой-либо , чтобы рассчитать длину диаметра, если сделать это в уме не получается. Например, можно воспользоваться тем, который встроен в поисковую систему Nigma или Google — он математические операции, вводимые на «человеческом» . Например, если известная длина окружности составляет четыре метра, то для нахождения диаметра можно «по-человечески» попросить поисковик: «4 метра разделить на пи». Но если вы введете в поле поискового запроса, например, «4/пи», то поисковик поймет и такую постановку задачи. В любом случае ответом будет «1.27323954 метра».

        Вопрос о диаметре земного шара не так прост, как может показаться на первый взгляд, ведь само понятие «земной шар» весьма условно. У настоящего шара диаметр всегда будет одинаковым, в каком бы месте ни был проведен отрезок, соединяющий две точки на поверхности сферы и проходящий через центр.

        Применительно к Земле не представляется возможным, поскольку ее шарообразность далеко не идеальна (в природе вообще не бывает идеальных геометрических фигур и тел, они представляют собой абстрактные геометрические понятия). Для точного обозначения Земли ученым даже пришлось ввести специальное понятие – «геоид».

        Официальный диаметр Земли

        Величина диаметра Земли определяется тем, в каком месте его будут измерять. Для удобства за официально признанный диаметр принимаются два показателя: диаметр Земли по экватору и расстояние между Северным и Южным полюсами. Первый показатель равен 12 756,274 км, а второй – 12 714, разница между ними составляет немногим менее 43 км.

        Данные числа не производят особого впечатления, они уступают даже расстоянию между Москвой и Краснодаром – двумя городами, расположенными на территории одной страны. Тем не менее, вычислить их было непросто.

        Вычисление диаметра Земли

        Диаметр планеты высчитывается по такой же геометрической формуле, как и любой другой диаметр.

        Чтобы найти периметр окружности, необходимо умножить ее диаметр на число πи. Следовательно, для нахождения диаметра Земли нужно измерить ее окружность в соответствующем сечении (по экватору или в плоскости полюсов) и разделить ее на число πи.

        Первым человеком, попытавшимся измерить окружность Земли, был древнегреческий ученый Эратосфен Киренский. Он обратил внимание, что в Сиене (ныне – Асуан) в день летнего солнцестояния Солнце находится в зените, освещая дно глубокого колодца. В Александрии же в этот день оно отстояло от зенита на 1/50 окружности. Из этого ученый сделал вывод, что расстояние от Александрии до Сиена составляет 1/50 окружности Земли. Расстояние между этими городами равно 5 000 греческим стадиям (приблизительно 787,5 км), следовательно, окружность Земли равна 250 000 стадий (примерно 39 375 км).

        В распоряжении современных ученых имеются более совершенные средства измерения, но их теоретическая основа соответствует идее Эратосфена. В двух точках, расположенных в нескольких сотнях километров друг от друга, фиксируют положение Солнца или определенных звезд на небосводе и вычисляют разницу между результатами двух измерений в градусах. Зная расстояние в километрах, несложно вычислить длину одного градуса, а затем умножить ее на 360.

        Для уточнения размеров Земли используется и лазерная дальнометрия, и спутниковые системы наблюдения.

        На сегодняшний день считается, что окружность Земли по экватору составляет 40 075,017 км, а по – 40 007,86. Эратосфен лишь немного ошибся.

        Величина и окружности, и диаметра Земли увеличивается из-за метеоритного вещества, постоянно выпадающего на Землю, но процесс этот идет очень медленно.

        Источники:

        • Как измерили Землю в 2019

        Окружностью называется ряд равноудалённых точек от одной точки, которая, в свою очередь, является центром этой окружности. Окружность имеет также свой радиус, равный расстоянию этих точек от центра.

        Отношение длины, какой либо окружности к её диаметру, для всех окружностей одинаково. Это отношение есть число, являющееся математической константой, которое обозначается греческой буквой π .

        Определение длины окружности

        Произвести расчёт окружности можно по следующей формуле:

        L = π D = 2 π r

        r — радиус окружности

        D — диаметр окружности

        L — длина окружности

        π — 3. 14

        Задача:

        Вычислить длину окружности , имеющей радиус 10 сантиметров.

        Решение:

        Формула для вычисления дины окружности имеет вид:

        L = π D = 2 π r

        где L – длина окружности, π – 3,14 , r – радиус окружности, D – диаметр окружности.

        Таким образом, длина окружности, имеющей радиус 10 сантиметров равна:

        L = 2 × 3,14 × 10 = 62,8 сантиметра

        Окружность представляет собой геометрическую фигуру, являющуюся совокупностью всех точек на плоскости, удаленных от заданной точки, которая называется ее центром, на некоторое расстояние, не равное нулю и именуемое радиусом. Определять ее длину с различной степенью точности ученые умели уже в глубокой древности: историки науки считают, что первая формула для вычисления длины окружности была составлена примерно в 1900 году до нашей эры в древнем Вавилоне.

        С такими геометрическими фигурами, как окружности, мы сталкиваемся ежедневно и повсеместно. Именно ее форму имеет внешняя поверхность колес, которыми оснащаются различные транспортные средства. Эта деталь, несмотря на свою внешнюю простоту и незатейливость, считаются одним из величайших изобретений человечества, причем интересно, что аборигены Австралии и американские индейцы вплоть до прихода европейцев совершенно не имели понятия о том, что это такое.

        По всей вероятности, самые первые колеса представляли собой отрезки бревен, которые насаживались на ось. Постепенно конструкция колеса совершенствовалась, их конструкция становилась все более и более сложной, а для их изготовления требовалось использовать массу различных инструментов. Сначала появились колеса, состоящие из деревянного обода и спиц, а затем, для того, чтобы уменьшить износ их внешней поверхности, ее стали обивать металлическими полосами. Для того чтобы определить длины этих элементов, и требуется использовать формулу расчета длины окружности (хотя на практике, вероятнее всего, мастера это делали «на глаз» или просто опоясывая колесо полосой и отрезая требуемый ее участок).

        Следует заметить, что колесо используется отнюдь не только в транспортных средствах. Например, его форму имеет гончарный круг, а также элементы шестеренок зубчатых передач, широко применяемых в технике. Издавна колеса использовались в конструкциях водяных мельниц (самые древние из известных ученым сооружений такого рода строились в Месопотамии), а также прялок, применявшихся для изготовления нитей из шерсти животных и растительных волокон.

        Окружности нередко можно встретить и в строительстве. Их форму имеют достаточно широко распространенные круглые окна, очень характерные для романского архитектурного стиля. Изготовление этих конструкций – дело весьма непростое и требует высокого мастерства, а также наличия специального инструмента. Одной из разновидностей круглых окон являются иллюминаторы, устанавливаемые в морских и воздушных судах.

        Таким образом, решать задачу определения длины окружности часто приходится инженерам-конструкторам, разрабатывающим различные машины, механизмы и агрегаты, а также архитекторам и проектировщикам. Поскольку число π , необходимое для этого, является бесконечным, то с абсолютной точностью определить этот параметр не представляется возможным, и поэтому при вычислениях учитывается та ее степень, которая в том или ином конкретном случае является необходимой и достаточной.

        Найти длину круга если средняя скорость. Составление системы уравнений

        Окружность состоит из множества точек, которые находятся на равном расстоянии от центра. Это плоская геометрическая фигура, и найти ее длину не составит труда. С окружностью и кругом человек сталкивается ежедневно независимо от того, в какой сфере он работает. Многие овощи и фрукты , устройства и механизмы, посуда и мебель имеют круглую форму. Кругом называют то множество точек, которое находится в границах окружности. Поэтому длина фигуры равна периметру круга.

        Характеристики фигуры

        Кроме того, что описание понятия окружности достаточно простое, её характеристики также несложные для понимания. С их помощью можно вычислить её длину. Внутренняя часть окружности состоит из множества точек, среди которых две — А и В — можно увидеть под прямым углом. Этот отрезок называют диаметром, он состоит из двух радиусов.

        В пределах окружности имеются точки Х такие , что не изменяется и не равняется единице отношение АХ/ВХ. В окружности это условие обязательно соблюдается, в ином случае эта фигура не имеет форму круга. На каждую точку, из которых состоит фигура, распространяется правило: сумма квадратов расстояний от этих точек до двух других всегда превышает половину длины отрезка между ними.

        Основные термины окружности

        Для того чтобы уметь находить длину фигуры, необходимо знать основные термины, касающиеся её. Основные параметры фигуры — это диаметр, радиус и хорда . Радиусом называют отрезок, соединяющий центр круга с любой точкой на её кривой. Величина хорды равна расстоянию между двумя точками на кривой фигуры. Диаметр — расстояние между точками , проходящее через центр фигуры.

        Основные формулы для вычислений

        Параметры используются в формулах вычислений величин окружности:

        Диаметр в формулах вычисления

        В экономике и математике нередко появляется необходимость поиска длины окружности. Но и в повседневной жизни можно столкнуться с этой надобностью, к примеру, во время постройки забора вокруг бассейна круглой формы. Как рассчитать длину окружности по диаметру? В этом случае используют формулу C = π*D, где С — это искомая величина, D — диаметр.

        Например, ширина бассейна равна 30 метрам, а столбики забора планируют поставить на расстоянии десяти метров от него. В этом случае формула расчёта диаметра: 30+10*2 = 50 метров. Искомая величина (в этом примере — длина забора): 3,14*50 = 157 метров. Если столбики забора будут стоять на расстоянии трёх метров друг от друга, то всего их понадобится 52.

        Расчёты по радиусу

        Как вычислить длину окружности по известному радиусу? Для этого используется формула C = 2*π*r, где С — длина, r — радиус. Радиус в круге меньше диаметра в два раза, и это правило может пригодиться в повседневной жизни. К примеру, в случае приготовления пирога в раздвижной форме.

        Для того чтобы кулинарное изделие не испачкалось, необходимо использовать декоративную обёртку. А как вырезать бумажный круг подходящего размера?

        Те, кто немного знаком с математикой, понимают, что в этом случае нужно умножить число π на удвоенный радиус используемой формы. Например, диаметр формы равен 20 сантиметрам, соответственно, её радиус составляет 10 сантиметров. По этим параметрам находится необходимый размер круга: 2*10*3, 14 = 62,8 сантиметра.

        Подручные способы вычисления

        Если найти длину окружности по формуле нет возможности, то стоит воспользоваться подручными методами расчёта этой величины:

        • При небольших размерах круглого предмета его длину можно найти с помощью верёвки, обёрнутой вокруг один раз.
        • Величину большого предмета измеряют так: на ровной плоскости раскладывают верёвку, и по ней прокатывают круг один раз.
        • Современные студенты и школьники для расчётов используют калькуляторы. В режиме онлайн по известным параметрам можно узнавать неизвестные величины.

        Круглые предметы в истории человеческой жизни

        Первое изделие круглой формы, которое изобрёл человек — это колесо. Первые конструкции представляли собой небольшие округлые бревна, насаженные на оси. Затем появились колёса, сделанные из деревянных спиц и обода. Постепенно в изделие добавляли металлические детали для уменьшения износа. Именно для того, чтобы узнать длину металлических полос для обивки колёса, учёные прошлых веков искали формулу расчёта этой величины.

        Форму колеса имеет гончарный круг , большинство деталей в сложных механизмах, конструкциях водяных мельниц и прялок. Нередко встречаются круглые предметы в строительстве — рамки круглых окон в романском архитектурном стиле, иллюминаторы в суднах. Архитекторы, инженеры, учёные, механики и проектировщики ежедневно в сфере своей профессиональной деятельности сталкиваются с надобностью расчёта размеров окружности.

        § 117. Длина окружности и площадь круга.

        1. Длина окружности. Окружностью называется замкнутая плоская кривая линия, все точки которой находятся на равном расстоянии от одной точки (О), называемой центром окружности (рис. 27).

        Окружность вычерчивается с помощью циркуля. Для этого острую ножку циркуля ставят в центр, а другую (с карандашом) вращают вокруг первой до тех пор, пока конец карандаша не вычертит полной окружности. Расстояние от центра до любой точки окружности называется её радиусом. Из определения следует, что все радиусы одной окружности равны между собой.

        Отрезок прямой линии (АВ), соединяющий две любые точки окружности и проходящий через её центр, называется диаметром . Все диаметры одной окружности равны между собой; диаметр равен двум радиусам.

        Как найти длину окружности? Практически в некоторых случаях длину окружности можно найти путём непосредственного измерения. Это можно сделать, например, при измерении окружности сравнительно небольших предметов (ведро, стакан и т. п.). Для этого можно воспользоваться рулеткой, тесьмой или шнуром.

        В математике применяется приём косвенного определения длины окружности. Он состоит в вычислении по готовой формуле, которую мы сейчас выведем.

        Если мы возьмём несколько больших и малых круглых предметов (монета, стакан, ведро, бочка и т. д.) и измерим у каждого из них длину окружности и длину диаметра, то получим для каждого предмета два числа (одно, измеряющее длину окружности, и другое — длину диаметра). Естественно, что для малых предметов эти числа будут небольшими, а для крупных — большими.

        Однако если мы в каждом из этих случаев возьмём отношение полученных двух чисел (длины окружности и диаметра), то при тщательном выполнении измерения найдём почти одно и то же число. Обозначим длину окружности буквой С , длину диаметра буквой D , тогда отношение их будет иметь вид С: D . Фактические измерения всегда сопровождаются неизбежными неточностями. Но, выполнив указанный опыт и произведя необходимые вычисления, мы получим для отношения С: D примерно следующие числа: 3,13; 3,14; 3,15. Эти числа очень мало отличаются одно от другого.

        В математике путём теоретических соображений установлено, что искомое отношение С: D никогда не меняется и оно равно бесконечной непериодической дроби, приближённое значение которой с точностью до десятитысячных долей равно 3,1416 . Это значит, что всякая окружность длиннее своего диаметра в одно и то же число раз. Это число принято обозначать греческой буквой π (пи). Тогда отношение длины окружности к диаметру запишется так: С: D = π . Мы будем ограничивать это число только сотыми долями, т. е. брать π = 3,14.

        Напишем формулу для определения длины окружности.

        Так как С: D = π , то

        C = πD

        т. е. длина окружности равна произведению числа π на диаметр.

        Задача 1. Найти длину окружности (С ) круглой комнаты, если диаметр её D = 5,5 м.

        Принимая во внимание изложенное выше, мы должны для решения этой задачи увеличить диаметр в 3,14 раза:

        5,5 3,14 = 17,27 {м).

        Задача 2. Найти радиус колеса, у которого длина окружности 125,6 см.

        Эта задача обратна предыдущей. Найдём диаметр колеса:

        125,6: 3,14 = 40 (см).

        Найдём теперь радиус колеса:

        40: 2 = 20 (см).

        2. Площадь круга. Чтобы определить площадь круга, можно было бы начертить на бумаге круг данного радиуса, покрыть его прозрачной клетчатой бумагой и потом сосчитать клетки, находящиеся внутри окружности (рис. 28).

        Но такой способ неудобен по многим причинам. Во-первых, вблизи контура круга получается ряд неполных клеток, о величине которых судить трудно. Во-вторых, нельзя покрыть листом бумаги большой предмет (круглую клумбу, бассейн, фонтан и др.). В-третьих, подсчитав клетки, мы всё-таки не получаем никакого правила, позволяющего нам решать другую подобную задачу. В силу этого поступим иначе. Сравним круг с какой-нибудь знакомой нам фигурой и сделаем это следующим образом: вырежем круг из бумаги, разрежем его сначала по диаметру пополам, затем каждую половину разрежем ещё пополам, каждую четверть — ещё пополам и т. д., пока не разрежем круг, например, на 32 части, имеющие форму зубцов (рис. 29).

        Затем сложим их так, как показано на рисунке 30, т. е. сначала расположим 16 зубцов в виде пилы, а затем в образовавшиеся отверстия вложим 15 зубцов и, наконец, последний оставшийся зубец разрежем по радиусу пополам и приложим одну часть слева, другую — справа. Тогда получится фигура, напоминающая прямоугольник.

        Длина этой фигуры (основание) равна приблизительно длине полуокружности, а высота — приблизительно радиусу. Тогда площадь такой фигуры можно найти путём умножения чисел, выражающих длину полуокружности и длину радиуса. Если обозначим площадь круга буквой S , длину окружности буквой С , радиус буквой r , то можем записать формулу для определения площади круга:

        которая читается так: площадь круга равна длине полуокружности, умноженной на радиус.

        Задача. Найти площадь круга, радиус которого равен 4 см. Найдём сначала длину окружности, потом длину полуокружности, а затем умножим её на радиус.

        1) Длина окружности С = π D = 3,14 8 = 25,12 (см).

        2) Длина половины окружности C / 2 = 25,12: 2= 12,56 (см).

        3) Площадь круга S = C / 2 r = 12,56 4 = 50,24 (кв. см).

        § 118. Поверхность и объём цилиндра.

        Задача 1. Найти полную поверхность цилиндра, у которого диаметр основания 20,6 см и высота 30,5 см.

        Форму цилиндра (рис. 31) имеют: ведро, стакан (не гранёный), кастрюля и множество других предметов.

        Полная поверхность цилиндра (как и полная поверхность прямоугольного параллелепипеда) состоит из боковой поверхности и площадей двух оснований (рис. 32).

        Чтобы наглядно представить себе, о чём идёт речь, необходимо аккуратно сделать модель цилиндра из бумаги. Если мы от этой модели отнимем два основания, т. е. два круга, а боковую поверхность разрежем вдоль и развернём, то будет совершенно ясно, как нужно вычислять полную поверхность цилиндра. Боковая поверхность развернётся в прямоугольник, основание которого равно длине окружности. Поэтому решение задачи будет иметь вид:

        1) Длина окружности: 20,6 3,14 = 64,684 (см).

        2) Площадь боковой поверхности: 64,684 30,5= 1972,862(кв.см).

        3) Площадь одного основания: 32,342 10,3 = 333,1226 (кв.см).

        4) Полная поверхность цилиндра:

        1972,862 + 333,1226 + 333,1226 = 2639,1072 (кв. см) ≈ 2639 (кв. см).

        Задача 2. Найти объём железной бочки, имеющей форму цилиндра с размерами: диаметр основания 60 см и высота 110 см.

        Чтобы вычислить объём цилиндра, нужно припомнить, как мы вычисляли объём прямоугольного параллелепипеда (полезно прочитать § 61).

        Единицей измерения объёма у нас будет кубический сантиметр. Сначала надо узнать, сколько кубических сантиметров можно расположить на площади основания, а затем найденное число умножить на высоту.

        Чтобы узнать, сколько кубических сантиметров можно уложить на площади основания, надо вычислить площадь основания цилиндра. Так как основанием служит круг, то нужно найти площадь круга. Затем для определения объёма умножить её на высоту. Решение задачи имеет вид:

        1) Длина окружности: 60 3,14 = 188,4 (см).

        2) Площадь круга: 94,2 30 = 2826 (кв. см).

        3) Объём цилиндра: 2826 110 = 310 860 (куб. см).

        Ответ. Объём бочки 310,86 куб. дм.

        Если обозначим объём цилиндра буквой V , площадь основания S , высоту цилиндра H , то можно написать формулу для определения объёма цилиндра:

        V = S H

        которая читается так: объём цилиндра равен площади основания, умноженной на высоту.

        § 119. Таблицы для вычисления длины окружности по диаметру.

        При решении различных производственных задач часто приходится вычислять длину окружности. Представим себе рабочего, который изготовляет круглые детали по указанным ему диаметрам. Он должен всякий раз, зная диаметр, вычислить длину окружности. Чтобы сэкономить время и застраховать себя от ошибок, он обращается к готовым таблицам, в которых указаны диаметры и соответствующие им длины окружностей.

        Приведём небольшую часть таких таблиц и расскажем, как ими пользоваться.

        Пусть известно, что диаметр окружности равен 5 м. Ищем в таблице в вертикальном столбце под буквой D число 5. Это длина диаметра. Рядом с этим числом (вправо, в столбце под названием «Длина окружности») увидим число 15,708 (м). Совершенно так же найдём, что если D = 10 см, то длина окружности равна 31,416 см.

        По этим же таблицам можно производить и обратные вычисления. Если известна длина окружности, то можно найти в таблице соответствующий ей диаметр. Пусть длина окружности равна приблизительно 34,56 см. Найдём в таблице число, наиболее близкое к данному. Таковым будет 34,558 (разница 0,002). Соответствующий такой длине окружности диаметр равен приблизительно 11 см.

        Таблицы, о которых здесь сказано, имеются в различных справочниках. В частности, их можно найти в книжке «Четырёхзначные математические таблицы» В. М. Брадиса. и в задачнике по арифметике С. А. Пономарёва и Н. И. Сырнева.

        Окружность встречается в повседневной жизни не реже, чем прямоугольник. А у многих людей задача о том, как рассчитать длину окружности, вызывает затруднение. И все потому, что у нее нет углов. При их наличии все стало бы намного проще.

        Что такое окружность и где она встречается?

        Эта плоская фигура представляет собой некоторое количество точек, которые расположены на одинаковом удалении от еще одной, которая является центром. Это расстояние называется радиусом.

        В повседневной жизни нечасто приходится вычислять длину окружности, кроме людей, которые являются инженерами и конструкторами. Они создают проекты механизмов, в которых используются, например, шестеренки, иллюминаторы и колеса. Архитекторы создают дома, имеющие круглые или арочные окна.

        В каждом из этих и других случаях требуется своя точность. Причем высчитать длину окружности совершенно точно оказывается невозможно. Связано это с бесконечностью основного числа, имеющегося в формуле. «Пи» до сих пор уточняется. И используется чаще всего округленное значение. Степень точности выбирается такой, чтобы дать максимально верный ответ.

        Обозначения величин и формулы

        Теперь легко ответить на вопрос о том, как рассчитать длину окружности по радиусу, для этого потребуется такая формула:

        Поскольку радиус и диаметр связаны друг с другом, то есть и другая формула для расчетов. Так как радиус в два раза меньше, то выражение немного видоизменится. И формула того, как рассчитать длину окружности, зная диаметр, будет следующей:

        l = π * d.

        Как быть, если нужно вычислить периметр круга?

        Просто вспомнить, что круг включает в себя все точки внутри окружности. А значит, его периметр совпадает с ее длиной. И после того, как рассчитать длину окружности, поставить знак равенства с периметром круга.

        Кстати, и обозначения у них такие же. Это касается радиуса и диаметра, а периметром является латинская буква P.

        Примеры заданий

        Задача первая

        Условие. Узнать длину окружности, радиус которой равен 5 см.

        Решение. Здесь несложно понять, как рассчитать длину окружности. Нужно только воспользоваться первой формулой. Поскольку радиус известен, то потребуется только подставить значения и сосчитать. 2 умноженное на радиус, равный 5 см, даст 10. Осталось еще умножить его на значение π. 3,14 * 10 = 31,4 (см).

        Ответ: l = 31,4 см.

        Задача вторая

        Условие. Имеется колесо, длина окружности которого известна и равна 1256 мм. Необходимо вычислить его радиус.

        Решение. В этом задании потребуется воспользоваться той же формулой. Но только известную длину нужно будет разделить на произведение 2 и π. Получается, что произведение даст результат: 6,28. После деления остается число: 200. Это искомая величина.

        Ответ: r = 200 мм.

        Задача третья

        Условие. Вычислить диаметр, если известна длина окружности, которая равна 56,52 см.

        Решение. Аналогично предыдущей задаче потребуется разделить известную длину на значение π, округленное до сотых. В результате такого действия получается число 18. Результат получен.

        Ответ: d = 18 см.

        Задача четвертая

        Условие. Стрелки часов имеют длину 3 и 5 см. Нужно вычислить длины окружностей, которые описывают их концы.

        Решение. Поскольку стрелки совпадают с радиусами окружностей, то потребуется первая формула. Ею нужно воспользоваться два раза.

        Для первой длины произведение будет состоять из множителей: 2; 3,14 и 3. Итогом будет число 18,84 см.

        Для второго ответа нужно перемножить 2, π и 5. Произведение даст число: 31,4 см.

        Ответ: l 1 = 18,84 см, l 2 = 31,4 см.

        Задача пятая

        Условие. Белка бегает в колесе диаметром 2 м. Какое расстояние она пробегает за один полный оборот колеса?

        Решение. Это расстояние равно длине окружности. Поэтому нужно воспользоваться подходящей формулой. А именно перемножить значение π и 2 м. Подсчеты дают результат: 6,28 м.

        Ответ: Белка пробегает 6,28 м.

          Известно, что независимо от длины окружности, ее отношение к диаметру является постоянным числом. Если известен диаметр окружности, то нужно эту величину умножить на число Пи (3,14).

          Формула выглядит так:

          Если известен радиус, то чтобы найти диаметр, умножаем его на два, а для нахождения длины окружности опять же на число Пи.

          Окружностью в геометрии называют фигуру на плоскости, все точки, лежащие на окружности круга, удалены на равном расстоянии от центра окружности

          Радиусом окружности называют в геометрии величину расстояния, отрезок от центра окружности до ее любой точки на окружности.

          Длину окружности с радиусом вычисляют по формуле

          Длина окружности L равно 2pi умножить на R.

          Или выглядит формула так. Чтобы не путаться, запомните, что длина окружности это есть периметр круга.

          r — это радиус

          D — диаметр

          Приблизительно 3,14

          Но окружность — это не круг

          Смотрите картинку, на которой видна разница между кругом и окружностью

          Окружность это кривая, ограничивающая круг. Все ее точки находятся на равном от центра расстоянии. В формуле вычисления длины окружности используются значения радиуса или двойная величина радиуса — диаметр и число, всегда имеющее значение 3,14.

          Формула, таким образом, выглядит так: L=d или L=2R , где L — значение длины окружности, получаемое умножением числа (3,14) на величину радиуса окружности или двойного диаметра.

          Еще из средней школьной программы отчетливо помню формулу измерения длины окружности. Эта формула выглядит так- 2Пr, где r- это радиус окружности, которая равна половине диаметра, а число П неизменна и равна 3.14.

          Формула длины окружности равна Пи умноженное на Диаметр или Пи умноженное на Радиус умноженный на 2.

          Длину окружности можно найти одним из представленных способов:

          • если известен диаметр окружности, то формула выглядит так L = ПD
          • если известен радиус окружности, то формула имеет следующий вид L = 2Пr.

        • Формула длины окружности

          Если воспользоваться Яндексом, то длину окружности можно посчитать в самом поисковом интерфейсе. Введите в Яндексе формула длины окружности , он вам выдаст формулу расчета и окошко для ввода значения. Дальше нужно будет нажать кнопку quot;Посчитатьquot;.

          Окружность это такая геометрическая фигура, которая является совокупностью всех своих точек на плоскости, равноудаленных от ее центра, на расстояние, называемое радиусом.

          Для того, чтобы вычислить длину окружности, обозначаемую обычно как L, надо радиус, обозначаемый как R, умножить на 2 и на число Пи. L=2ПиR. Пи — величина постоянная и равна 3,14.

          Или можно взять удвоенный радиус, то есть диаметр (D) и тогда формула будет выглядеть так: L=ПиD.

          Можно найти длину окружности не зная радиуса. Для этого нужно знать площадь круга.

          Формула для расчета длины окружности по известной площади круга выглядит так:

          L=2*корень квадратный пи*S

          где S площадь круга.

          Длина окружности

          Можете скопировать себе на компьютер нижеприведенную табличку с основными формулами окружности и круга. Она вас, при решении геометрических задач, еще не раз выручит.

          Здесь же присутствует формула длины окружности. Она имеет вид: L=2ПR

          На сайте quot;Сборник формулquot;, можно посчитать длину окружности, введя имеющиеся у вас данные. Там же,

          Решение уравнений:

          Геометрическая прогрессия:

          Комбинаторика:

          Решить химическое уравнение

          Арифметическая прогрессия.

        Возьмем циркуль. Установим ножку циркуля с иглой в точку «O », а ножку циркуля с карандашом будем вращать вокруг этой точки. Таким образом, мы получим замкнутую линию. Такую замкнутую линию называют — окружность .

        Рассмотрим более подробно окружность. Разберёмся, что называют центром, радиусом и диаметром окружности.

        Число π и длина окружности

        Прежде чем разобраться, как считается длина окружности, необходимо выяснить, что такое число π (читается как «Пи»), которое так часто упоминают на уроках.

        В далекие времена математики Древней Греции внимательно изучали окружность и пришли к выводу, что длина окружности и её диаметр взаимосвязаны.

        Запомните!

        Отношение длины окружности к её диаметру является одинаковым для всех окружностей и обозначается греческой буквой π («Пи»).
        π ≈ 3,14…

        Число «Пи» относится к числам, точное значение которых записать невозможно ни с помощью обыкновенных дробей, ни с помощью десятичных дробей. Нам для наших вычислений достаточно использовать значение π ,
        округленное до разряда сотых π ≈ 3,14…

        Теперь, зная, что такое число π , мы можем записать формулу длины окружности.

        Запомните!

        Длина окружности — это произведение числа π и диаметра окружности. Длина окружности обозначается буквой «С » (читается как «Це»).
        C = π D
        C = 2π R , так как D = 2R

        Как найти длину окружности

        Чтобы закрепить полученные знания, решим задачу на окружности.

        Виленкин 6 класс. Номер 831

        Условие задачи:

        Найдите длину окружности, радиус которой равен 24 см. Число π округлите до сотых.

        Воспользуемся формулой длины окружности:

        C = 2π R ≈ 2 · 3,14 · 24 ≈ 150,72 см

        Разберем обратную задачу, когда мы знаем длину окружности, а нас просят найти её диаметр.

        Виленкин 6 класс. Номер 835

        Условие задачи:

        Определите диаметр окружности, если её длина равна 56,52 дм. (π ≈ 3,14 ).

        Выразим из формулы длины окружности диаметр.

        C = π D
        D = С / π
        D = 56,52 / 3,14 = 18 дм

        Хорда и дуга окружности

        На рисунке ниже отметим на окружности две точки «A » и «B ». Эти точки делят окружность на две части, каждую из которых называют дугой . Это синяя дуга «AB » и черная дуга «AB ». Точки «A » и «B » называют концами дуг .

        Радиус круга – формула, определение

        Радиус определяется как отрезок, соединяющий центр с границей круга или сферы. Длина радиуса остается неизменной от центра до любой точки на окружности круга или сферы. Это половина длины диаметра. Давайте узнаем больше о радиусе в этой статье.

        1. Что такое радиус?
        2. Формулы радиуса
        3. Радиус окружности
        4. Как найти радиус окружности?
        5. Уравнение радиуса окружности
        6. Радиус сферы
        7. Часто задаваемые вопросы о Radius

        Что такое радиус?

        В геометрии радиус определяется как отрезок, соединяющий центр круга или сферы с его окружностью или границей. Это важная часть кругов и сфер, которая обычно обозначается аббревиатурой «r». Множественное число радиуса — « радиусов », которое используется, когда мы говорим о более чем одном радиусе одновременно. Наибольший отрезок в окружности или сфере, соединяющий любые точки, лежащие на противоположной стороне от центра, является диаметром, а длина радиуса составляет половину длины диаметра. Его можно выразить как d/2, где d — диаметр круга или сферы. Посмотрите на изображение круга, приведенное ниже, показывающее соотношение между радиусом и диаметром.

        Теперь давайте изучим формулы радиуса, которые помогут вам вычислить его длину с учетом данной информации.

        Формулы радиуса

        Радиус круга и сферы можно рассчитать с помощью определенных формул, которые вы изучите в этом разделе. Здесь мы поговорим о формулах радиуса для окружности. Формула радиуса сферы обсуждается в разделе ниже.

        Формула радиуса от диаметра: Диаметр представляет собой прямую линию, проходящую через центр и соединяющую точку на одном конце с точкой на другом конце окружности. Диаметр в два раза больше длины радиуса. Математически это записывается как диаметр = 2 × радиус. Это также самая длинная хорда окружности. Когда диаметр круга дан, тогда формула радиуса выражается как:

        Радиус = Диаметр/2 или D/2 единиц

        Формула радиуса из окружности: Периметр круга называется его окружностью. Это граница круга и может быть выражена формулой: C = 2πr единиц. Здесь C — длина окружности, r — радиус окружности, а π — константа, равная 3,14159.. Радиус равен отношению длины окружности к 2π. Формула радиуса с использованием длины окружности выражается следующим образом:

        Радиус = Окружность/2π или C/2π единиц

        Формула радиуса с площадью: Площадь круга – это пространство, занимаемое кругом. Связь между радиусом и площадью определяется формулой Площадь круга = πr 2 квадратных единиц. Здесь r — радиус, а π — константа, равная 3,14159. Формула радиуса с использованием площади круга выражается как:

        Радиус = √(Площадь/π) единиц

        Радиус окружности

        Радиус — одна из важных частей окружности. Это расстояние от центра круга до любой точки на его границе. Другими словами, когда мы соединяем центр круга с любой точкой его окружности с помощью прямой линии, этот отрезок линии является радиусом этого круга. Круг может иметь более одного радиуса, потому что на его окружности бесконечное количество точек. Это означает, что круг имеет бесконечное число радиусов и все радиусы круга равноудалены от центра круга. Размер круга меняется при изменении длины радиуса.

        На приведенном ниже рисунке точки A, B, M, N, P, Q, X и Y лежат на границе окружности. Заметим, что эти точки равноудалены от центра O. Итак, все отрезки OA, OB, OM, ON, OY, OX, OP и OQ называются радиусами окружности. Обратите внимание, что OA = OB = OM = ON = OP = OQ = OX = OY.

        Как найти радиус окружности?

        Радиус круга можно найти с помощью трех основных формул радиуса, т.е. когда известны диаметр, площадь или длина окружности. Воспользуемся этими формулами, чтобы найти радиус окружности.

        • Когда диаметр известен, формула Радиус = Диаметр/2.
        • Если длина окружности известна, формула Радиус = Длина окружности/2π.
        • Когда площадь известна, формула для радиуса: Радиус = ⎷(Площадь круга/π).

        Например, если диаметр равен 24 единицам, то радиус равен 24/2 = 12 единицам. Если длина окружности равна 44 единицам, то ее радиус можно рассчитать как 44/2π. Отсюда следует, что (44×7)/(2×22) = 7 единиц. И, если площадь круга равна 616 квадратных единиц, то радиус равен ⎷(616×7)/22 = ⎷28×7 = ⎷196 = 14 единиц.

        Уравнение радиуса окружности

        Радиус уравнения окружности на декартовой плоскости с центром (h, k) определяется как (x − h) 2 + (y − k) 2 = r 2 . Здесь (x, y) — точки на окружности окружности, находящиеся на расстоянии «r» (радиус) от центра (h, k). Когда центр окружности находится в начале координат (0,0), уравнение окружности сводится к x 2 + y 2 = r 2 . Обратите внимание на схему окружности на декартовой плоскости, показанную ниже. Здесь координаты центра равны (0, b), а радиус окружности представлен буквой «r», соединяющей центр с точкой (x, y) на окружности. Итак, нам просто нужно подставить эти значения в приведенное выше уравнение, чтобы получить радиус уравнения окружности. Уравнение для нахождения радиуса этой окружности:0085 2 .

        Радиус сферы

        Сфера — трехмерная объемная фигура. Радиус сферы — это отрезок от центра до любой точки на границе сферы. Это определяющий фактор при рисовании сферы, так как ее размер зависит от ее радиуса. Как и в случае с кругом, внутри сферы могут быть нарисованы бесконечные радиусы, и все эти радиусы будут равны по длине. Чтобы вычислить объем и площадь поверхности сферы, нам нужно знать ее радиус. И мы можем легко вычислить радиус сферы по формулам ее объема и площади поверхности.

        Радиус сферы от объема = 3 ⎷(3V)/4π единиц, где V представляет объем, а значение π приблизительно равно 3,14.

        Радиус сферы с использованием площади поверхности = ⎷(A/4π) единиц, где A представляет собой площадь поверхности.

        Используйте наш бесплатный онлайн-калькулятор радиуса сферы, чтобы рассчитать радиус с заданным объемом, площадью поверхности или диаметром сферы.

        ☛ Статьи по теме

        Проверьте эти интересные статьи, связанные с радиусом и его формулами.

        • Формула радиуса кривизны
        • Сегмент круга
        • Сектор круга

        Часто задаваемые вопросы о радиусе окружности

        Что такое радиус круга в геометрии?

        Радиус окружности — это длина отрезка от центра до точки на окружности окружности. Обычно обозначается аббревиатурой «р». В круге может быть бесконечное количество радиусов, и длина всех этих радиусов будет одинаковой. Это половина диаметра круга.

        Как диаметр связан с радиусом окружности?

        Диаметр круга в два раза больше радиуса, или радиус равен половине диаметра. Связь между радиусом и диаметром можно выразить формулой: Диаметр = 2 × радиус. Используйте бесплатный онлайн-калькулятор радиуса, чтобы рассчитать радиус с заданным диаметром.

        Как найти радиус окружности с помощью длины окружности?

        Длина окружности и радиус связаны друг с другом, и их отношение можно выразить как Длина окружности = 2πR, где R — радиус. Итак, когда длина окружности известна, формула, используемая для расчета радиуса круга, выглядит следующим образом: Радиус = Окружность / 2π.

        Что такое радиус кривой?

        Радиус кривой или дуги — это радиус окружности, частью которой они являются. Когда длина хорды, определяющей основание (W), и высота, измеренная в середине основания дуги (H), даны, формула для нахождения радиуса: Радиус = (H / 2) + (W 2 / 8Н).

        Что такое формула радиуса?

        Радиус круга можно рассчитать с помощью различных формул. Соблюдайте следующие формулы для расчета радиуса:

        • Когда диаметр известен, формула Радиус = Диаметр / 2.
        • Когда длина окружности известна, формула для радиуса равна Окружность / 2π.
        • Если площадь известна, формула Радиус = ⎷(Площадь круга / π).

        Как рассчитать радиус окружности с помощью калькулятора?

        Длина радиуса равна половине длины диаметра, который можно рассчитать с помощью онлайн-калькулятора Cuemath, просто введя любое заданное значение среди диаметра, окружности или площади круга.

        Как найти радиус круга с площадью?

        Если известна площадь круга, то формула для нахождения радиуса дается как Радиус = ⎷(A/π) единиц, где A – заданная площадь.

        Определение диаметра окружности и расчет — Math Open Reference

        r

        Определение диаметра круга и калькулятор — Math Open Reference

        Math Open Reference

        Главная Контакт О Тематический указатель

        Расстояние по окружности через ее центр.

        Попробуйте это Перетащите оранжевую точку. Синяя линия всегда будет диаметром круга.

        Диаметр круга — это длина линии, проходящей через центр и касающейся двух точек на его краю. На рисунке выше перетащите оранжевые точки и убедитесь, что диаметр никогда не меняется.

        Иногда слово «диаметр» используется для обозначения самой линии. В этом смысле вы можете увидеть «нарисуйте диаметр круга». В более позднем смысле это длина линии, поэтому его называют «диаметром круга 3,4 сантиметра».

        Диаметр тоже есть аккорд. Хорда – это линия, соединяющая любые две точки окружности. Диаметр – это хорда, проходящая через центр окружности. Это самая длинная хорда любого круга.

        Центр круга является серединой его диаметра. То есть делит его на две равные части, каждая из которых представляет собой радиус окружности. Радиус равен половине диаметра.

        Если вы знаете радиус

        Зная радиус окружности, диаметр можно рассчитать по формуле где:
        R  радиус окружности

        Если вы знаете длину окружности

        Если известна длина окружности, то диаметр можно найти по формуле
        , где:
        C  это длина окружности
        π  это Пи, примерно 3,142

        Если вы знаете район

        Если известна площадь круга, диаметр можно найти по формуле
        , где:
        A  – площадь круга
          π  – число Пи, примерно 3,142.

        Калькулятор

        Радиус прозрачный
        Диаметр прозрачный
        Зона прозрачный
        Окружность прозрачный
         

        Используйте калькулятор выше, чтобы рассчитать свойства круга.

        Введите любое отдельное значение, и остальные три будут рассчитаны. Например: введите диаметр и нажмите «Рассчитать». Будут рассчитаны площадь, радиус и окружность.

        Точно так же, если вы введете область, радиус, необходимый для получения этой области, будет рассчитан вместе с диаметром и окружностью.

        Связанные предметы

        Радиус Радиус — это расстояние от центра до любой точки края. Как видно из рисунка выше, диаметр равен двум радиусным линиям, расположенным вплотную друг к другу, поэтому диаметр всегда в два раза больше радиуса. См. радиус круга

        Окружность Окружность — это расстояние вокруг края круга. Видеть Окружность круга для получения дополнительной информации.

        Что попробовать

        1. На рисунке выше нажмите «Сброс» и перетащите любую оранжевую точку. Обратите внимание, что диаметр имеет одинаковую длину в любой точке окружности.
        2. Нажмите «показать радиус». Перетащите оранжевую точку в конце линии радиуса. Обратите внимание, что радиус всегда равен половине диаметра.
        3. Снимите флажок «фиксированный размер». Повторите вышеописанное и обратите внимание, что радиус всегда равен половине диаметра независимо от размера круга.

        Теорема Фалеса

        Теорема Фалеса утверждает, что диаметр окружности содержит прямой угол в любую точку окружности. (см. рисунок справа).

        Независимо от того, где находится точка, треугольник образуется всегда прямоугольный треугольник. См. Теорему Фалеса для интерактивной анимации этой концепции.

        Другие темы кружка

        Общий

        • Определение круга
        • Радиус окружности
        • Диаметр окружности
        • Длина окружности
        • Части круга (схема)
        • Определение полукруга
        • Касательная
        • Секанс
        • Аккорд
        • Теорема о пересекающихся хордах
        • Теорема о пересекающихся секущих длинах
        • Теорема о пересекающихся секущих углах
        • Площадь круга
        • Концентрические окружности
        • Кольцо
        • Площадь кольца
        • Сектор круга
        • Площадь сектора круга
        • Сегмент круга
        • Площадь сегмента окружности (данный центральный угол)
        • Площадь сегмента круга (данная высота сегмента)

        Уравнения окружности

        • Основное уравнение окружности (центр в начале координат)
        • Общее уравнение окружности (центр в любом месте)
        • Параметрическое уравнение окружности

        Уголки по окружности

        • Угол вписанный
        • Центральный уголок
        • Теорема о центральном угле

        Дуги

        • Дуга
        • Длина дуги
        • Измеритель угла дуги
        • Смежные дуги
        • Большая/малая дуги
        • Перехваченная дуга
        • Сектор круга
        • Радиус дуги или сегмента при заданной высоте/ширине
        • Стрела — высота дуги или сегмента

        (C) 2011 Copyright Math Open Reference.
        Все права защищены

        Как вычислить длину окружности, если я знаю диаметр?

        33 ответа

        Джеймс Фитцджеральд ответил

        Чтобы рассчитать это, вам нужна правильная формула. Формула длины окружности классифицируется как пи х диаметр. Его также можно записать как pi.d.

        Окружность — это, по сути, расстояние или длина по окружности. _, правильно произносимое как пирог, является иррациональным числом, а это значит, что его нельзя записать в виде дроби. Поэтому, чтобы быть уверенным, хорошее приближение π равно 3,14 при использовании в конкретных формулах.

        Круговая диаграмма, или число Пи, необходима для вычисления длины окружности. Убедитесь, что вы знаете, где находится центр круга. Вам нужно будет найти диаметр, который является линией, которая касается двух концов круга и центра.

        Затем вы можете использовать эту линию соответственно или радиус вместе с π для вычисления длины окружности. Все, что вам нужно сделать, это умножить радиус на 2, чтобы получить диаметр.

        Другие вещи, которые следует учитывать в круге, включают радиус, который представляет собой линию, которая касается внешней части круга и центра. Он не соприкасается более чем с одной частью внешней среды. Вы сможете заменить диаметр на это для альтернативной формулы. Чтобы получить радиус, вам нужно разделить диаметр на 2, чтобы получить радиус.

        Есть две формулы и, учитывая, что вы уже знаете диаметр, то будет намного проще сделать окружность. В математических терминах длина окружности в алгебре описывается как:

        C = π x диаметр
        или

        C = π x (2 x радиус)

        поблагодарил автора.

        выпалил это.

        Оддман ответил

        36*Pi ≈ 113,1

        поблагодарил автора.

        выпалил это.

        Mainul Hussain ответил

        113,04 дюйма, принимая pi=3,14

        поблагодарил автора.

        выпалил это.

        Кэти Гарри ответила

        Окружность на самом деле похожа на периметр круга. Формула нахождения длины окружности:
        C = Pi x r 2
        Где,
        C = длина окружности
        pi = 3,14
        r = радиус

        Нам дан диаметр. Радиус равен половине диаметра, поэтому:
        Радиус = Диаметр
        2
        Радиус = 28
        2
        Радиус = 14 дюймов

        Теперь вычислим длину окружности:

        C = Pi x r 2
        6 903,14 (14) 2
        C = 3,14 x 196
        C = 615,4 дюйма ——ОТВЕТ

        поблагодарил автора.

        выпалил это.

        Кэти Гарри ответила

        Формула для нахождения длины окружности:

        C = 2 x pi x r
        Где
        C = длина окружности
        r = радиус
        pi = 3,14

        Теперь у нас нет значение радиуса здесь, хотя оно используется в формуле.
        Итак, нам нужно сначала найти радиус этой окружности. Радиус всегда вдвое меньше диаметра, поэтому:
        радиус = диаметр/2
        радиус = 11/2
        радиус = 5,5 футов

        Теперь найдем длину окружности:
        C = 2 x pi x r
        C = 2(3,14 x 5,5)
        C = 2(17,27)
        C = 34,54 фута

        Следовательно, длина окружности этого круга равна 34,54 фута.

        поблагодарил автора.

        выпалил это.

        Аноним ответил

        25.13

        поблагодарил автора.

        выпалил это.

        Анонимный ответил

        Чтобы найти длину окружности, зная диаметр. Все, что вам нужно сделать, это умножить диаметр на пи (пи равно 3,14!!) и вы получили его. ХОРОШО ТЫ СДЕЛАЛА ЭТО!!!!
        Формула:(пример) 3.14-pi
        x 2-диаметр
        »»»»»»’
        6.28-длина окружности

        поблагодарил автора.

        выпалил это.

        Робин Ротман ответила

        Классическая формула для нахождения длины окружности C=2pi r или длина окружности равна 2 умножить на пи (пи равно 3,14) умножить на радиус. Радиус круга составляет половину диаметра, поэтому вы можете просто умножить диаметр на 3,14 (пи). Это ваша окружность.

        поблагодарил автора.

        выпалил это.

        Аноним ответил

        Для диаметра 36 дюймов

        поблагодарил автора.

        выпалил это.

        Аноним ответил

        25.13

        поблагодарил автора.

        выпалил это.

        Оддман ответил

        Да, и вы сможете, если умножите 8 см на число Пи.
        окружность = 8*3,1416 см = 25,1328 см

        поблагодарил автора.

        выпалил это.

        Аноним ответил

        25.12

        поблагодарил автора.

        выпалил это.

        Анонимный ответил

        Если я сделаю круг диаметром 3 фута из 12-дюймовых кирпичей, сколько мне понадобится?

        поблагодарил автора.

        выпалил это.

        янтарный Джон ответил

        Длина окружности равна удвоенному произведению постоянной пи на радиус окружности.

        Окружность = 2 * пи * радиус

        Пи = 3,14

        Диаметр = 2 * радиус

        Радиус = диаметр/2 ед.

        Окружность = 43,96 шт.

        Требуемая длина окружности 43,96.

        поблагодарил автора.

        выпалил это.

        Анонимный ответил

        Да

        поблагодарил автора.

        выпалил это.

        Аноним ответил

        Какова площадь круга, длина окружности которого равна 8

        поблагодарил автора.

        выпалил это.

        Аноним ответил

        А 6.28

        поблагодарил автора.

        выпалил это.

        Анонимный ответил

        R=5

        поблагодарил автора.

        выпалил это.

        Аноним ответил

        2 раза диаметр равен окружности

        поблагодарил автора.

        выпалил это.

        Анонимный ответил

        100,48

        поблагодарил автора.

        выпалил это.

        Аноним ответил

        16м

        поблагодарил автора.

        выпалил это.

        Анонимный ответил

        34,54 фута

        поблагодарил автора.

        выпалил это.

        Пэт Меррифилд ответил

        Ближайший ответ, который у вас есть, d, поскольку я придумал 50,27.

        поблагодарил автора.

        выпалил это.

        Анонимный ответил

        Думаю, 2 X (круг) X r = длина окружности. Круг равен 3,14, а R — радиус, равный 1/2 диаметра.

        поблагодарил автора.

        выпалил это.

        Аноним ответил

        Если диаметр круга равен 8, длина окружности равна 25,1327: 
          Окружность = (Диаметр)(pi)
        = Окружность = (8)(pi)
        = Окружность = 25,1327 92

        поблагодарил автора.

        выпалил это.

        Аноним ответил

        Умножить диаметр на 3,14

        поблагодарил автора.

        выпалил это.

        Аноним ответил

        Умножить на 3

        поблагодарил автора.

        выпалил это.

        Анонимный ответил

        25.13

        поблагодарил автора.

        выпалил это.

        Аноним ответил

        Да помогите мне плз

        поблагодарил автора.

        выпалил это.

        Мерил Харгривз ответила

        Умножьте диаметр на пи (греческая буква!)
        Значение приблизительно равно 22/7 или 3,1416 или даже точнее, в зависимости от того, что вам дали.
        C= Pd или c=2Pr
        (Нет символа пи!!)

        поблагодарил автора.

        выпалил это.

        Майк Каталанотто-младший ответил

        Периметр = пи (3,1416) x диаметр.

        поблагодарил автора.

        выпалил это.

        Кёко Катаяма ответила

        C = (pi) D; Вы делаете математику.

        поблагодарил автора.

        выпалил это.

        Вам также может понравиться…

        Ответить на вопрос

        Измерение кругов

        Блок № 4
        Измерение кругов

        День 1

        Изучение кругов

        . В качестве введения в решающие проблемы, связанные с цирками, связанные с цирками. диаметр и окружность.

        Радиус — прямая линия, проходящая от центра круга к внешнему краю. Он равен половине расстояния по окружности.

        Диаметр — прямая линия, которая проходит от одного края круга, проходит через центр круга и касается другой стороны. Это в два раза больше длины радиуса.

        Окружность — это расстояние вокруг внешнего края окружности. Он примерно в 3 раза длиннее диаметра.

        Хорда — прямая, соединяющая любые две точки на окружности.

        Дуга — участок окружности, лежащий между двумя концами хорды (каждая хорда образует две дуги).

        День 2

        ВЫЧИСЛЕНИЕ ОКРУЖНОСТИ        

        Вчера мы узнали, что длина окружности примерно в три раза больше ее диаметра. При нахождении приблизительного ответа на вопрос мы используем символ (≈), чтобы указать, что ответ близок к правильному, но не совсем правильный.
        Часто измерение окружности нецелесообразно или требуется более точная формула, чем «примерно в 3 раза». Сегодня студенты узнают точную формулу расчета расстояния по окружности (окружности) с использованием константы Пи
        (π = 3,14).
        Для получения дополнительной информации об истории и использовании числа π
        в математике посетите следующую веб-ссылку:  http://bit.ly/brYCsl

        Формула для оценки приблизительной длины окружности: C = 3d, где C обозначает окружность, а d обозначает диаметр
        Формула для расчета точной длины длины окружности круга – это C = πd, где C – длина окружности,       – символ 3.14, а d – диаметр.
         
        ** Когда известен только радиус, вам нужно умножить его на 2 (2r = d), чтобы найти диаметр.
        Если вы хотите найти забавную (но познавательную) песню, которая поможет вам запомнить длину окружности, число π и диаметр, перейдите по этой ссылке на веб-сайт Teachertube, в котором текст песни Томми Тутоне 86953o9 заменен на 3.14159. http://bit.ly/vWeyfR
        Должен: 13 декабря

        День 3 Средний обзор
        Page 160-161 #1-7
        . Повторные. и число 3, когда оценивается как .
        Не забудьте использовать число Пи (π) при вычислении точных ответов .

        День 4                   

        ОБЛАСТЬ РАСЧЕТА
                                           стр. 166-167 #4-9

        Площадь фигуры показывает, сколько места она занимает.

        При оценке площади круга мы используем формулу: A = 3r²
        При расчете площади круга мы используем формулу: A = πr²

        **1) Не забывайте всегда использовать квадратные единицы в ответах на вопросы о площади .

        **2) Если в вопросе указан только диаметр, вам нужно не забыть разделить его на два, чтобы найти радиус.

        День 5 Решение проблем, работая назад
        19 декабря. работая в обратном порядке, начиная со значений, которые они знают, чтобы найти значения, которые они не знают. Чтобы работать в обратном направлении для решения задач измерения окружности, учащиеся должны хорошо понимать формулы для нахождения длины окружности и площади круга. Учащиеся также должны распознавать отношения радиуса, диаметра, окружности и/или площади в формуле.

        При решении задач в обратном порядке полезно, если учащиеся следуют плану. Я рекомендую четырехэтапный план.
        Шаг 1 — Внимательно прочитайте вопрос и скопируйте предоставленную информацию.
        Если дана длина окружности, скопируйте формулу длины окружности (C = πd). Если дана площадь круга, скопируйте формулу площади (A = πr²).
        Шаг 2 — Замените символы и переменные в формуле известными числами из вопроса.
        Шаг 3 — Сгруппируйте числа по одну сторону знака равенства и переменные (буквы) по другую.
        **Когда числа переходят на другую сторону знака равенства, выполняемая операция становится противоположной тому, что было в исходной части уравнения. Другими словами, если вы умножили число справа от знака равенства, вы разделите это число слева от знака равенства.

        Шаг 4 — Решите уравнение, чтобы найти неизвестную переменную. Пример — Разбрызгиватель для газонов вращается и разбрызгивает воду по кругу. Он распыляет на площади 283 м². Каков радиус круга, в котором он распыляется.
        Шаг 1. Скопируйте предоставленную информацию.
                           A = 283 м²      π = 3,14            A = πr²      
                  
        Шаг 2. Замените символы и переменные в формуле известными числами.
                           A = πr²                
                            283 м²  = (3,14) (r²)

        Шаг 3. Сгруппируйте числа по одну сторону от знака равенства и переменные по другую.
        a = πr²
        283 м² = (3,14) (R²)
        283 м² ÷ 3,14 = R²

        Шаг 4 -Решите уравнение, чтобы найти неизвестную переменную
        A = πr²
        283 M² = (3,14) (R²)
        44833333333 283 M² = (3,14) (R²) m² ÷ 3,14 = r²
                           90,13 = r²                     0244                    (квадратный корень из) 90,13 = r
                             8,49 м = r

        Спринклер вращается с радиусом 8,49 м.


        ДЕНЬ 6 Обзор кругов
        Page 174-175 #1-10
        Запомните
        #1-10
        Запомните
        #1-10
        . Запомните
        .
        Всегда записывайте формулу для начала решения задачи.
        Радиус = 1/2 диаметра (r = 1/2d) или диаметр в два раза больше радиуса (d = 2r)
        Формула окружности       C = πd

         

        Нарисуйте круг диаметром (по всей окружности) 1

        Тогда длина окружности (по всей окружности) равна 3.14159265… число известное как Пи

         

        Пи (произносится как «пирог») часто пишется с использованием греческого символа π

        .

        Определение π:

        Окружность
        , разделенная на Диаметр
        Окружности.

        Длина окружности, деленная на диаметр круга, всегда равна π, независимо от того, насколько большой или маленький круг!

         

        Чтобы помочь вам вспомнить, что такое π… просто нарисуйте эту диаграмму.

        В поисках Пи самостоятельно

        Нарисуйте круг или используйте что-то круглое, например тарелку.

        Измерение по краю ( окружность ):


        У меня 82 см

        Измерение по кругу ( диаметр ):


        У меня 26 см

        Разделить:

        82 см / 26 см = 3,1538…

        Это довольно близко к π. Может быть, если бы я измерил более точно?

        Использование Пи

        Мы можем использовать π, чтобы найти Окружность, когда мы знаем Диаметр

        Длина окружности = π × диаметр

        Пример: Вы идете по кругу диаметром 100 м, какое расстояние вы прошли?

        Пройденное расстояние = Окружность

         = π × 100 м

          = 314,159. .. м

         = 314 м (с точностью до м)

        Также мы можем использовать π, чтобы найти Диаметр, когда мы знаем Окружность

        Диаметр = Окружность / π

        Пример: Сэм измерил 94 мм по внешней стороне трубы… каков ее диаметр?

        Диаметр = Окружность / π

         = 94 мм / π

          = 29,92… мм

         = 30 мм (с точностью до миллиметра)

        Радиус

        Радиус равен половине диаметра, поэтому мы также можем сказать:

         

        Для круга с радиусом из 1

        Расстояние на полпути вокруг окружности равно π = 3,14159265…

        Цифры

        π примерно равно:

        3.14159265358979323846…

        Цифры идут беспорядочно.

        π было рассчитано с точностью до 100 триллионов знаков после запятой, и все же нет шаблона  в цифрах, см. Pi Normal.

        Приблизительно

        Быстрое и простое приближение числа π равно 22/7

        22/7 = 3,1428571. ..

        Но, как видите, 22/7 — это не совсем правильно . На самом деле π не равно отношению любых двух чисел, что делает его иррациональным числом.

         

        Действительно хорошее приближение, лучше, чем 1 часть на 10 миллионов:

        355/113 = 3,1415929…
        (представьте «113355», косую черту в середине «113/355», затем переверните «355/113»)

        Резюме:

        22/7 = 3,14 28571…
        355/113 = 3.141592 9…
        № = 3.14159265 …

        Запоминание цифр

        Обычно я просто запоминаю «3.14159», но вы также можете посчитать буквы:

        «Можно мне сегодня большой контейнер масла»
        3 1 4 1 5 9 2 6 5

        До 100 знаков после запятой

        Вот число π с первыми 100 знаками после запятой:

        3. 14159265358979323846264338327950288
        4197169399375105820974944592307816
        406986704608998825380

         

        Самостоятельное вычисление числа Пи

        Существует много специальных методов, используемых для вычисления числа π, и вот один из них, который вы можете попробовать самостоятельно: он называется Нилакантха, серия (в честь индийского математика, жившего в 1444–1544 годах).

        Это продолжается вечно и имеет следующую схему:

        3 + 4 2×3×4 − 4 4×5×6 + 4 6×7×8 − 4 8×9×10 + …

        (Обратите внимание на шаблон + и -, а также на шаблон чисел под строками.)

        Это дает следующие результаты:

        Термин Результат (до 12 знаков после запятой)
        1 3
        2 3,166666666667
        3 3. 133333333333
        4 3.145238095238
        … … и т.д.! …

        Возьмите калькулятор (или используйте электронную таблицу) и посмотрите, сможете ли вы добиться лучших результатов.

         

        День Пи

        День Пи отмечается 14 марта. Март — 3-й месяц, поэтому он выглядит как 14 марта

         

        5839,5050,5052,1745,2106,5473,5477,1744,3236,3237

        Упражнение: Найдите приблизительное значение числа Пи

        Column Pi (отношение длины окружности к ее диаметру)

        Все окружности подобны, и «длина окружности, деленная на диаметр», дает одно и то же значение независимо от их радиуса. Эта величина представляет собой отношение длины окружности к ее диаметру и называется π (Пи). Эта константа появляется при вычислении площади круга и является типом иррационального числа, известного как трансцендентное число , которое не может быть выражено ни дробью, ни каким-либо подкоренным знаком, таким как квадратный корень, или их комбинацией. . Число имеет бесконечное количество знаков после запятой, а именно 3,14159.26535…, и теперь компьютеры вычислили его с точностью до 5 триллионов знаков после запятой.

        Длина окружности больше 6 от указанной на рисунке. Поскольку диаметр круга равен 2, число Пи больше 3.

        Что касается значения π, древние цивилизации использовали свое собственное значение. Так как правильный шестиугольник, вписанный в окружность радиусом 1, имеет периметр 6, то получается, что число Пи больше 3. В Древнем Египте получили приближение

        (примерно, 3,16)

        путем размещения правильного восьмиугольника на окружности, а в древней Вавилонии использовали

        .

        Архимед в своей работе Kyklu metresis (мера окружности) пришел к выводу, что Пи удовлетворяет

        .

        В древней Индии мы можем найти пример использования =3,1622776 или

        .

        В Китае они использовали

        или

        или

        для Pi.
        В период Эдо в Японии, 9 г.0245 Jinkoki (1627) Ёсида Мицуёси использовал 3,16 для числа Пи, но поскольку люди признали, что это значение было неточным, в которые были рассчитаны более точные значения для Pi, начали развиваться. Ученые-васан, такие как Мурамацу Шигекиё, Секи Такакадзу, Камата Тошикиё, Такебе Катахиро и Мацунага Йошисуке, рассчитали более точные значения числа Пи и достигли результатов, которые можно сравнить с европейской математикой.

        в Европе, Viete (1540-1603) обнаружила первую формулу, которая выражает π:

        После этого Wallis (1616-1703) Формула:

        . 1675) и Лейбниц (1646-1716) Формула:

        Кроме того, Ньютон (1642-1727) и Эйлер (1707-1783) открыли ряд, который сходится быстрее, что позволило им вычислить значения числа Пи с большей точностью места. Если использовать соотношение

        , обнаруженный Дж. Мачином (1680-1752),

        , мы можем получить значение 3,14159 для π с точностью до пяти знаков после запятой с первыми 4 членами разложения Тейлора tan -1 . В недавнем компьютерном расчете , использовались следующие уравнения:

        или

        * tan -1 : Арктангенс. Обратная функция тангенса.

        Вычисление Пи в Васане

        В конце Санпо сёдзё появляется метод вычисления Пи. Подводя итог тому, что описано в книге, метод выглядит следующим образом: Предположим, исходное число = 3, 9.0003

        Продолжайте до тех пор, пока не будет создана разница 100. Затем Пи получается путем сложения исходного числа, разности 1, разности 2, разности 3… и так далее. Переписывая это как математическое выражение, мы видим, что оно имеет следующую закономерность:

        • «Кю энсю хидзюцу киген» (Происхождение тайного искусства нахождения Пи) из Санпо сёдзё
          В книге утверждается, что этот метод является прямым и ясным решением вычисления Пи без использования Kakujutsu или Kaiho (эволюция), но не объясняет, почему это формула для вычисления числа π.
          Цифровые коллекции NDL

          Санпо сёдзё

        Эта формула аналогична формуле, описанной в Hoen sankei (1739) Мацунаги Ёсисуке. Формирование этой формулы также включено в Koshigen koutei (1819) Нинчжоу.

        В эпоху Мэйдзи Кикути Дайроку опубликовал четыре статьи на английском языке, в которых вводил вычисление числа Пи в васан в Токио сугаку бусури гаккай кидзи Том. 7 (1896 г.). В первом трактате он представил вычисление в Sanpo kyuseki tsuko (1844) Хасэгавы Хирому и объяснил Enrikatsujutsu , тип исчисления, первоначально начатый Вада Ясуси (1787-1840) с западными расчетными формулами.

        • «Какова площадь круга диаметром 1?» from Sanpo kyuseki tsuko
          В этой книге
          он получает площадь круга с диаметром 1 и находит Пи, разделив площадь на 4. В этом вычислении, используется.
          Цифровые коллекции NDL

          Санпо Кюсэки Цуко

        При увеличении n для (сумма степеней натуральных чисел),

        верно; Хасэгава использует это, чтобы получить результат

        Мы ничего не знаем о регулярности числа только из этого результата. Однако на самом деле между терминами существует связь. Каждый член определяется путем умножения предыдущего члена на правильную дробь следующим образом:

        Кикучи заметил, что такой ряд был тем, что К. Ф. Гаусс (1777-1855) назвал гипергеометрическим рядом . Гипергеометрическая серия определяется следующим образом:

        Следовательно, Kikuchi доказал в следующей статье, что расчет

        в Enri Shinko Wada Yasushi был эквивалентен

        Hasegawa’s Calculation

        Hasegawa’s Calculation

        . на

        и что Мацунага

        был эквивалентен

        .

        В Васан, Секи Такакадзу, Такебе Катахиро и др. искали формулы для вычисления π 2 .

        , выведенная Такебе, является первой формулой для вычисления Пи в истории Васана. С помощью этой формулы Такебе вычислил число π с точностью до 41 знака после запятой. В следующем трактате Кикучи вывел

        , чтобы выразить квадрат s или дугу окружности со стрелой c и диаметром d , который был описан Ямадзи Нусидзуми в Kenkon no maki (c 1765), и доказано

        , потому что

        когда

        .

        Дуга, стрела и диаметр окружности

        На рисунке часть окружности называется ko (дуга), отрезок AB называется gen (хорда), а отрезок PR — ya (сагитта). Диаметр PQ по-японски называется kei.
        Когда мы рисуем хорду для дуги PB и сагитту для хорды и продолжаем повторять этот процесс с более короткими хордами, форма, полученная путем соединения этих хорд, приближается к форме круга. Таким образом, Ямадзи вычисляет s, длину дуги, когда диаметр равен d и длина сагитты c .

        В последней статье он доказал, что

        , полученное Адзимой Наонобу в Kohai jutsukai , может быть упрощено до

        В следующем году Кикучи также написал статью, в которой представил метод вычисления длины дуга, созданная Такебе Катахиро в Tokyo Sugaku Butsuri Gakkai Kiji Vol.

        1 … 3 138 3 139 3 140 3 141 3 142 … 3 230