Метод Крамера онлайн
Примеры решенийРанг матрицыОбратная матрица Метод Гаусса Производная онлайн Определитель матрицыЭкстремум функции Линейная алгебра онлайн Правило СаррюсаМетод обратной матрицы
- Шаг №1
- Шаг №2
- Видеоинструкция
- Также решают
Инструкция. Выберите количество переменных, нажмите Далее. Полученное решение сохраняется в файле Word (см. пример решения СЛАУ методом Крамера). Для проверки решения автоматически генерируется шаблон в Excel.
Выберите количество переменных
234567
Вместе с этим калькулятором также используют следующие:
По координатам вершин треугольника найти площадь, уравнения сторон, уравнение медианы, уравнение биссектрисы
По координатам вершин пирамиды найти
Построение графика функции методом дифференциального исчисления
Экстремум функции двух переменных
Вычисление пределов
Кратко алгоритм метода Крамера можно описать тремя шагами:
- Находим определитель D исходной матрицы A.

- В цикле от 1 до n заменяем i-ый столбец матрицы на столбец результатов B. Находим текущий определитель Di полученной матрицы.
- xi находится делением Di на D:
xi = Di / D.
Суть метода Крамера демонстрирует пример нахождения переменных системы линейных уравнений.
Пример. Решить систему линейных уравнений методом Крамера.
x1 + 4x2 = 5
-2x1 + x3 = -1
2x1 + x2 + x3 = 4
Решение. Запишем систему в виде:
| A = |
|
BT = (5,-1,4)
Главный определитель:
∆ = 1 • (0 • 1-1 • 1)-(-2 • (4 • 1-1 • 0))+2 • (4 • 1-0 • 0) = 15
Заменим первый столбец матрицы А на вектор результата B.

| 5 | 4 | 0 |
| -1 | 0 | 1 |
| 4 | 1 | 1 |
Найдем определитель полученной матрицы:
∆1 = 5 • (0 • 1-1 • 1)-(-1 • (4 • 1-1 • 0))+4 • (4 • 1-0 • 0) = 15
x1 = 15/15 = 1
Заменим 2-ый столбец матрицы А на вектор результата B.
| 1 | 5 | 0 |
| -2 | -1 | 1 |
| 2 | 4 | 1 |
Определитель полученной матрицы равен
∆2 = 1 • (-1 • 1-4 • 1)-(-2 • (5 • 1-4 • 0))+2 • (5 • 1-(-1 • 0)) = 15
x2 = 15/15 = 1
Заменим третий столбец матрицы А на вектор результата B.
| 1 | 4 | 5 |
| -2 | 0 | -1 |
| 2 | 1 | 4 |
Определитель этой матрицы равен
∆3 = 1 • (0 • 4-1 • (-1))-(-2 • (4 • 4-1 • 5))+2 • (4 • (-1)-0 • 5) = 15
x3 = 15/15 = 1
Проверка решения:
1•1+4•1+0•1 = 5
-2•1+0•1+1•1 = -1
2•1+1•1+1•1 = 4
Вывод:
- Смысл метода Крамера: находим определитель Di, получаемый из заменой i-го столбца на столбец свободных членов и делим его на главный определитель D.

xi = Di / D - Метод Крамера относится к простым для реализации методам решения СЛАУ и получил широкое распространение в разных областях знаний (например, при нахождении уравнений регрессий). Недостатком метода является его практическая непригодность для вычисления СЛАУ с большим количеством переменных (от 5 и выше). Для этого случая используют приближенные методы (например, метод простой итерации).
Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).
калькулятор крамер
калькулятор крамерВы искали калькулятор крамер? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и калькулятор крамера, не
исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «калькулятор крамер».
Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «калькулятор крамер».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как калькулятор крамер,калькулятор крамера,калькулятор крамера матрицы онлайн,калькулятор крамера онлайн,калькулятор крамера с решением,калькулятор матриц крамера,калькулятор матриц метод крамера,калькулятор матриц метод крамера онлайн,калькулятор матриц методом крамера,калькулятор матриц онлайн метод крамера,калькулятор матриц онлайн методом крамера,калькулятор матриц онлайн с решением метод крамера,калькулятор матриц онлайн с решением методом крамера,калькулятор матриц с решением методом крамера онлайн,калькулятор матрица метод крамера,калькулятор матрицы крамера онлайн,калькулятор матрицы метод крамера,калькулятор матрицы метод крамера онлайн,калькулятор матрицы методом крамера,калькулятор матрицы онлайн метод крамера,калькулятор матрицы онлайн методом крамера,калькулятор матрицы онлайн с решением метод крамера,калькулятор матричный метод крамера,калькулятор метод крамера,калькулятор метод крамера онлайн с решением,калькулятор метода крамера,калькулятор методом крамера,калькулятор методом крамера онлайн,калькулятор онлайн для метода крамера,калькулятор онлайн матриц метод крамера,калькулятор онлайн матрицы метод крамера,калькулятор онлайн матрицы методом крамера,калькулятор онлайн методом крамера,калькулятор онлайн по формуле крамера онлайн калькулятор,калькулятор онлайн правило крамера,калькулятор онлайн решение матриц методом крамера,калькулятор онлайн решение систем методом крамера,калькулятор по методу крамера,калькулятор по формуле крамера,калькулятор решение методом крамера,калькулятор решение систем линейных уравнений методом крамера,калькулятор решение систем методом крамера,калькулятор решение уравнений методом крамера,калькулятор решения методом крамера,калькулятор системы уравнений онлайн методом крамера онлайн,калькулятор слау методом крамера,калькулятор формула крамера,калькулятор формула крамера онлайн,крамер калькулятор,крамер калькулятор онлайн,крамер онлайн,крамер онлайн калькулятор,крамера онлайн,крамера онлайн калькулятор,крамера решение онлайн,линейное уравнение методом крамера онлайн,матрица калькулятор метод крамера,матрица калькулятор онлайн метод крамера,матрица крамера онлайн,матрица метод крамера калькулятор,матрица метод крамера онлайн,матрица метод крамера онлайн калькулятор,матрица методом крамера онлайн,матрица онлайн калькулятор метод крамера,матрица онлайн крамера,матрица онлайн метод крамера,матрица онлайн методом крамера,матрицы калькулятор метод крамера,матрицы калькулятор методом крамера,матрицы калькулятор онлайн крамера,матрицы калькулятор онлайн метод крамера,матрицы метод крамера калькулятор,матрицы метод крамера онлайн,матрицы метод крамера онлайн калькулятор,матрицы метод крамера онлайн калькулятор с подробным решением,матрицы методом крамера калькулятор,матрицы онлайн калькулятор крамера,матрицы онлайн калькулятор метод крамера,матрицы онлайн калькулятор методом крамера,матрицы онлайн калькулятор с подробным решением метод крамера,матрицы онлайн калькулятор с решением метод крамера,матрицы онлайн метод крамера,матрицы онлайн методом крамера онлайн,матрицы онлайн решение методом крамера,матрицы онлайн решение методом крамера онлайн с,матрицы решение методом крамера онлайн,матрицы решение методом крамера онлайн с решением,матрицы решение онлайн методом крамера,матрицы решение онлайн методом крамера онлайн с,матричный калькулятор метод крамера,метод крамера калькулятор,метод крамера калькулятор онлайн,метод крамера калькулятор с подробным решением,метод крамера матриц онлайн калькулятор,метод крамера матрица онлайн,метод крамера матрицы калькулятор,метод крамера матрицы онлайн,метод крамера матрицы онлайн калькулятор,метод крамера матричный калькулятор,метод крамера онлайн,метод крамера онлайн калькулятор,метод крамера онлайн калькулятор матрицы,метод крамера онлайн калькулятор с подробным решением,метод крамера онлайн калькулятор с подробным решением и с проверкой,метод крамера онлайн калькулятор с подробным решением матрицы,метод крамера онлайн калькулятор с решением,метод крамера онлайн решение,метод крамера онлайн решение матриц,метод крамера онлайн с решением,метод крамера примеры с решением калькулятор,метод крамера примеры с решением онлайн,метод крамера решение матриц онлайн,метод крамера решение онлайн,метод крамера решения систем линейных уравнений онлайн,метод крамера с решением онлайн,метод решение матриц крамера онлайн,метода крамера калькулятор,методом крамера калькулятор,методом крамера онлайн,методом крамера онлайн калькулятор,методом крамера решить онлайн,методом крамера решить уравнение онлайн,онлайн калькулятор для метода крамера,онлайн калькулятор крамер,онлайн калькулятор крамера,онлайн калькулятор линейных уравнений методом крамера онлайн,онлайн калькулятор матриц метод крамера,онлайн калькулятор матриц метод крамера с решением,онлайн калькулятор матриц методом крамера,онлайн калькулятор матриц с решением метод крамера,онлайн калькулятор матрицы крамера,онлайн калькулятор матрицы метод крамера,онлайн калькулятор матрицы методом крамера,онлайн калькулятор метод крамера,онлайн калькулятор метод крамера матрицы,онлайн калькулятор метод крамера с решением,онлайн калькулятор методом крамера,онлайн калькулятор правило крамера,онлайн калькулятор решение линейных уравнений методом крамера,онлайн калькулятор решение матриц методом крамера,онлайн калькулятор решение методом крамера,онлайн калькулятор решение систем линейных уравнений методом крамера,онлайн калькулятор решение систем методом крамера,онлайн калькулятор решение систем уравнений методом крамера,онлайн калькулятор решение системы уравнений методом крамера,онлайн калькулятор решить систему методом крамера,онлайн калькулятор решить систему по правилу крамера,онлайн калькулятор систем линейных уравнений методом крамера онлайн,онлайн калькулятор систем методом крамера онлайн,онлайн калькулятор систем уравнений методом крамера онлайн,онлайн калькулятор система уравнений методом крамера онлайн,онлайн калькулятор системы уравнений методом крамера онлайн,онлайн калькулятор формула крамера,онлайн калькулятор формулы крамера,онлайн крамера,онлайн матрица крамера,онлайн матрица метод крамера,онлайн матрица методом крамера,онлайн матрицы метод крамера,онлайн методом крамера,онлайн правило крамера,онлайн решение крамера,онлайн решение крамера метод,онлайн решение линейных уравнений методом крамера,онлайн решение матриц крамера,онлайн решение матриц метод крамера,онлайн решение матрицы методом крамера,онлайн решение метод крамера,онлайн решение методом крамера,онлайн решение по крамеру,онлайн решение по формулам крамера онлайн,онлайн решение по формуле крамера,онлайн решение систем линейных уравнений методом крамера,онлайн решение систем линейных уравнений методом крамера онлайн,онлайн решение систем методом крамера,онлайн решение систем методом крамера онлайн с подробным решением,онлайн решение систем уравнений методом крамера,онлайн решение системы линейных уравнений методом крамера,онлайн решение системы линейных уравнений методом крамера онлайн,онлайн решение системы методом крамера,онлайн решение системы методом крамера онлайн калькулятор,онлайн решение системы уравнений методом крамера,онлайн решение слау методом крамера,онлайн решение уравнений крамера,онлайн решение уравнений методом крамера,онлайн решение уравнения методом крамера,онлайн решить систему линейных уравнений методом крамера,онлайн система крамера,онлайн система линейных уравнений методом крамера онлайн,онлайн система уравнений методом крамера,онлайн формула крамера,определитель онлайн методом крамера онлайн,по крамеру решение онлайн,по формулам крамера решить систему онлайн,по формуле крамера калькулятор,по формуле крамера решить систему уравнений онлайн,правило крамера калькулятор онлайн,правило крамера онлайн,правило крамера онлайн калькулятор,решение крамера онлайн,решение линейных систем уравнений методом крамера онлайн,решение линейных уравнений методом крамера калькулятор онлайн,решение линейных уравнений методом крамера онлайн,решение линейных уравнений методом крамера онлайн калькулятор,решение линейных уравнений онлайн методом крамера,решение матриц крамера онлайн,решение матриц метод крамера онлайн,решение матриц методом крамера онлайн,решение матриц методом крамера онлайн калькулятор,решение матриц методом крамера онлайн с подробным решением,решение матриц онлайн калькулятор методом крамера,решение матриц онлайн крамера,решение матриц онлайн метод крамера,решение матриц онлайн метод крамера онлайн,решение матриц онлайн методом крамера,решение матриц онлайн методом крамера онлайн,решение матриц онлайн методом крамера с подробным решением,решение матриц онлайн с подробным решением методом крамера,решение матрицы крамера онлайн,решение матрицы методом крамера онлайн,решение матрицы методом крамера онлайн с подробным решением,решение матрицы методом крамера онлайн с решением,решение матрицы онлайн крамера,решение матрицы онлайн методом крамера,решение матрицы онлайн методом крамера онлайн,решение матрицы онлайн методом крамера онлайн с,решение матрицы онлайн с подробным решением методом крамера,решение матричных уравнений методом крамера онлайн,решение матричных уравнений онлайн методом крамера,решение метод крамера онлайн,решение метод крамера решение онлайн,решение методом крамера калькулятор,решение методом крамера калькулятор онлайн,решение методом крамера матрицы онлайн,решение методом крамера матрицы онлайн калькулятор,решение методом крамера онлайн,решение методом крамера онлайн калькулятор,решение методом крамера онлайн с подробным решением,решение онлайн крамера,решение онлайн линейных уравнений методом крамера,решение онлайн матриц метод крамера,решение онлайн матрицы методом крамера,решение онлайн метод крамера,решение онлайн метод крамера онлайн,решение онлайн методом крамера,решение онлайн по крамеру,решение онлайн по формуле крамера,решение онлайн систем линейных уравнений методом крамера,решение онлайн систем линейных уравнений методом крамера онлайн,решение онлайн систем методом крамера,решение онлайн систем методом крамера онлайн с подробным решением,решение онлайн системы методом крамера онлайн калькулятор,решение онлайн слау методом крамера,решение по крамеру онлайн,решение по методу крамера онлайн,решение по формуле крамера онлайн,решение систем линейных уравнений методом крамера калькулятор,решение систем линейных уравнений методом крамера калькулятор онлайн,решение систем линейных уравнений методом крамера онлайн,решение систем линейных уравнений методом крамера онлайн калькулятор,решение систем линейных уравнений методом крамера онлайн с решением,решение систем линейных уравнений онлайн методом крамера,решение систем линейных уравнений онлайн методом крамера онлайн,решение систем линейных уравнений онлайн методом крамера онлайн с,решение систем методом крамера калькулятор,решение систем методом крамера калькулятор онлайн,решение систем методом крамера онлайн,решение систем методом крамера онлайн калькулятор,решение систем онлайн методом крамера,решение систем онлайн методом крамера онлайн с подробным решением,решение систем уравнений метод крамера онлайн,решение систем уравнений методом крамера онлайн,решение систем уравнений методом крамера онлайн калькулятор,решение систем уравнений методом крамера онлайн с подробным решением,решение систем уравнений онлайн метод крамера,решение систем уравнений онлайн методом крамера,решение систем уравнений онлайн методом крамера онлайн,решение систем уравнений онлайн с подробным решением методом крамера,решение системы линейных уравнений методом крамера онлайн,решение системы линейных уравнений методом крамера онлайн с решением,решение системы линейных уравнений онлайн методом крамера,решение системы линейных уравнений онлайн методом крамера онлайн,решение системы линейных уравнений онлайн методом крамера с решением,решение системы методом крамера онлайн,решение системы онлайн методом крамера,решение системы уравнений методом крамера онлайн,решение системы уравнений методом крамера онлайн калькулятор,решение системы уравнений методом крамера онлайн с решением,решение системы уравнений онлайн методом крамера,решение слау методом крамера онлайн,решение слау методом крамера онлайн с решением,решение слау онлайн методом крамера,решение уравнений крамера онлайн,решение уравнений методом крамера калькулятор,решение уравнений методом крамера онлайн,решение уравнений онлайн крамера,решение уравнений онлайн методом крамера,решение уравнений онлайн по формуле крамера онлайн,решение уравнения методом крамера онлайн,решение уравнения онлайн методом крамера,решить линейное уравнение методом крамера онлайн,решить линейное уравнение онлайн методом крамера,решить матрицу методом крамера онлайн,решить матрицу методом крамера онлайн калькулятор,решить матрицу методом крамера онлайн с подробным решением,решить матрицу онлайн калькулятор методом крамера,решить матрицу онлайн методом крамера,решить матрицу онлайн методом крамера онлайн,решить методом крамера онлайн,решить методом крамера систему линейных уравнений онлайн,решить онлайн матрицу методом крамера,решить онлайн систему линейных уравнений методом крамера,решить онлайн слау методом крамера,решить онлайн уравнение методом крамера,решить онлайн уравнение методом крамера с подробным решением,решить по формуле крамера онлайн,решить систему линейных уравнений методом крамера онлайн,решить систему линейных уравнений методом крамера онлайн с решением,решить систему линейных уравнений методом крамера решить онлайн,решить систему линейных уравнений онлайн методом крамера,решить систему линейных уравнений онлайн по формулам крамера,решить систему линейных уравнений по формулам крамера онлайн,решить систему методом крамера онлайн,решить систему методом крамера онлайн калькулятор,решить систему методом крамера онлайн с подробным решением,решить систему онлайн методом крамера,решить систему по правилу крамера онлайн,решить систему по правилу крамера онлайн калькулятор,решить систему по формулам крамера онлайн,решить систему по формулам крамера онлайн калькулятор,решить систему уравнений методом крамера онлайн,решить систему уравнений методом крамера онлайн с подробным решением,решить систему уравнений онлайн методом крамера,решить систему уравнений онлайн по формуле крамера,решить систему уравнений по формулам крамера онлайн с решением,решить систему уравнений по формуле крамера онлайн,решить слау методом крамера онлайн,решить слау онлайн методом крамера,решить уравнение методом крамера онлайн,решить уравнение методом крамера онлайн с подробным решением,решить уравнение онлайн методом крамера,система линейных уравнений методом крамера онлайн,система линейных уравнений методом крамера онлайн калькулятор,система линейных уравнений онлайн калькулятор методом крамера,система линейных уравнений онлайн методом крамера,система линейных уравнений онлайн методом крамера онлайн,система методом крамера онлайн,система уравнений методом крамера онлайн,система уравнений онлайн методом крамера,систему линейных уравнений решить по формулам крамера онлайн,слау методом крамера калькулятор,слау методом крамера онлайн,слау методом крамера онлайн решение,слау онлайн методом крамера онлайн,слау решение методом крамера онлайн,спецкласс ру онлайн калькулятор,формула крамера для решения системы линейных уравнений онлайн,формула крамера калькулятор,формула крамера онлайн,формула крамера онлайн калькулятор,формулы крамера онлайн калькулятор..png) На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и калькулятор крамер. Просто введите задачу в окошко и нажмите
«решить» здесь (например, калькулятор крамера матрицы онлайн).
На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и калькулятор крамер. Просто введите задачу в окошко и нажмите
«решить» здесь (например, калькулятор крамера матрицы онлайн).
Решить задачу калькулятор крамер вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Метод Крамера — правило и примеры решения систем линейных уравнений
Распространённый в математике метод Крамера отлично себя зарекомендовал как способ поиска неизвестных величин из систем уравнений. Но использовать этот подход можно только тогда, когда число искомых значений эквивалентно реальному количеству алгебраических уравнений.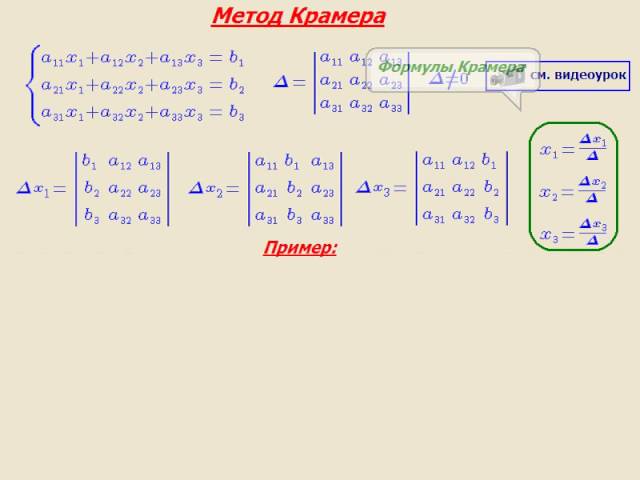 Формируемая в системе основная матрица обязательно должна быть квадратной, наличие нулевых строчек просто недопустимо.
Формируемая в системе основная матрица обязательно должна быть квадратной, наличие нулевых строчек просто недопустимо.
Содержание
- Краткое описание
- Ключевые нюансы
- Практическое применение
- Разнообразие математических подходов
- Помощь онлайн-калькуляторов
- Актуальные примеры решения
- Присутствующая вычислительная сложность
Краткое описание
Широко востребованный метод Крамера активно используется специалистами для решения распространённых алгебраических уравнений (СЛАУ). Итоговая точность полученного результата обусловлена применением определённой математической матрицы, а также некоторыми вспомогательными ограничениями, которые неизбежно накладываются во время доказательства конкретной теоремы.
Набором выражений вида yr 2 x1+ yr 2 x2 +… yr n xn = b r при r =1, 2,…, m принято называть универсальную систему линейных алгебраических уравнений. В этом случае также присутствуют определённые коэффициенты, которые могут принадлежать множеству W -действительных чисел, от неизвестных x 1… xn.
Чаще всего в роли действенных чисел выступают yr и br. Каждое из представленных значений называется линейным уравнением. Элементарные коэффициенты при неизвестных — это yr, а вот bi — свободные коэффициенты уравнений. Стандартный n -мерный вектор k ° = (k 1°, k 2°,…, k n°) называют решением системы. При правильной подстановке в систему вместо неизвестных элементов каждая из строчек становится верным равенством.
Если у системы присутствует минимум одно решение, то она называется совместной. Речь касается несовместного примера только в том случае, если многочисленные алгоритмы решения совпадают с пустым множеством. Классическая формула Крамера используется в том случае, если необходимо отыскать верное решение для линейных уравнений. Для получения достоверного результата матрицы должны быть исключительно квадратными. А на практике такой подход означает одинаковое количество уравнений и неизвестных в системе.
Ключевые нюансы
Востребованный в математике метод Крамера для решения систем линейных уравнений можно успешно использовать только в том случае, если ученик хорошо понимает, что такое матрица алгебраических примеров и каким образом она выписывается. В противном случае будет сложно избежать распространённых ошибок. Если необходимые навыки имеются, то в итоге остаётся только правильно запомнить формулы, которые определяют метод Крамера. Чтобы лучше усвоить все тонкости этой темы, необходимо воспользоваться следующими обозначениями:
В противном случае будет сложно избежать распространённых ошибок. Если необходимые навыки имеются, то в итоге остаётся только правильно запомнить формулы, которые определяют метод Крамера. Чтобы лучше усвоить все тонкости этой темы, необходимо воспользоваться следующими обозначениями:
- Главный определитель совместности матрицы системы — Det.
- Определитель матрицы, который получен из основного элемента — deti. Если ученик попробует заменить последний столбец матрицы, задействовав для этого первые части линейных алгебраических уравнений, тогда следует использовать понятие deti.
- Для количества неизвестных и уравнений в системе используется символ n.
com/embed/jWFt1d5XpoQ»>Если учесть все перечисленные нюансы, то в итоге правило Крамера для вычисления компонентов n -мерного вектора можно записать в следующей формулировке: xi = deti / Det. В этом случае DET максимально отличен от нуля.
Практическое применение
Для решения многих математических задач принято использовать теорему Кронекера — Капелли. Если основной определитель G главной матрицы, которая была составлена за счёт коэффициентов уравнений, не равен нулю, тогда система уравнений будет совместна. Но такое решение является единственным. Для поиска верного результата принято вычислять систему через формулу Крамера для линейных уравнений: x i = D i / D.
Метод Крамера основан на нескольких основных нюансах, которые в сочетании друг с другом дают отличный результат:
- Если решено найти правильное исчисление системы по методике талантливого учёного, тогда первым делом обязательно вычисляют главный определитель обращения матрицы (J). Если при подсчёте детерминант основной матрицы оказался равен нулю, то такая система просто не имеет решения, либо речь касается нескончаемого количества решений. В такой ситуации получить достоверный результат можно только благодаря универсальному методу Гаусса.

- На втором этапе ученику нужно постараться заменить крайний столбец главной матрицы столбцом свободных членов, чтобы отыскать определитель (J 1).
- Остаётся повторить аналогичные действия для всех оставшихся столбцов. За счёт этого можно получить определители от J 1 до J n. В этом случае символ n указывает на номер последнего справа столбца.
- Как только будут найдены абсолютно все детерминанты, нужно постараться высчитать неизвестные переменные по элементарной формуле: х i = B i / B.
Разнообразие математических подходов
Немного иные приёмы используются в том случае, когда предстоит работать с определителем матрицы. Если нужно рассчитать правильные данные на основе конструкции с соразмерностью больше чем 2 на 2, тогда можно использовать сразу несколько проверенных временем способов:
- Метод Гаусса. Некоторые специалисты привыкли называть это математическое направление понижением порядка основного определителя.
 Несколько простых действий помогают преобразить матрицу и привести её к треугольному виду. Все комплексные числа, которые расположены на основной диагонали, перемножаются. Но при таком поиске определителя запрещено выполнять арифметические действия со строчками или столбцами без предварительного вынесения чисел как множителя/делителя. Предварительно умножают вычитаемую строку на нулевой множитель, а уже потом вычитают и складывают все элементы между собой. Конечный знак у обратной матрицы подвергают изменениям только в том случае, когда происходит перестановка столбцов или строчек.
Несколько простых действий помогают преобразить матрицу и привести её к треугольному виду. Все комплексные числа, которые расположены на основной диагонали, перемножаются. Но при таком поиске определителя запрещено выполнять арифметические действия со строчками или столбцами без предварительного вынесения чисел как множителя/делителя. Предварительно умножают вычитаемую строку на нулевой множитель, а уже потом вычитают и складывают все элементы между собой. Конечный знак у обратной матрицы подвергают изменениям только в том случае, когда происходит перестановка столбцов или строчек. - Правило Саррюса. Суть метода треугольников в том, чтобы ученик мог при вычислении дискриминанта и определителя произведения всех чисел, которые были соединены одной линией, записывать примеры только с положительным значением. Это утверждение идеально подходит для матриц размером 3х3. Но если следовать всем нормам правила Саррюса, то первым делом переписывают саму матрицу, а рядом с ней располагают первый и второй столбец.
 В итоге через сформированную конструкцию проводятся диагональные линии. Члены матрицы, которые расположены на основной диагонали или на параллельной ей плоскости всегда записываются со знаком +, а вот элементы, лежащие на побочной диагонали, имеют знак -.
В итоге через сформированную конструкцию проводятся диагональные линии. Члены матрицы, которые расположены на основной диагонали или на параллельной ей плоскости всегда записываются со знаком +, а вот элементы, лежащие на побочной диагонали, имеют знак -. - Если ученик решит использовать универсальный метод Крамера СЛАУ, для которого свойственно присутствие сразу четырёх неизвестных, тогда лучше всего выполнить комбинацию с технологией Гаусса. В этом случае можно гарантированно отыскать детерминант через поиск миноров.
Для каждого направления свойственны свои нюансы и правила теории, которые должен знать каждый ученик. В противном случае решить правильно поставленную задачу практически невозможно.
Помощь онлайн-калькуляторов
Созданные программистами программы пользуются огромным спросом даже среди опытных математиков, так как всего за несколько минут можно правильно решить задачу. Многофункциональные онлайн-калькуляторы с подробным решением по методу Крамера позволяют быстро и качественно решить целую систему различных уравнений. Для этого пользователю необходимо правильно указать количество неизвестных величин.
Многофункциональные онлайн-калькуляторы с подробным решением по методу Крамера позволяют быстро и качественно решить целую систему различных уравнений. Для этого пользователю необходимо правильно указать количество неизвестных величин.
Для быстрого переключения в уравнении с положительных знаков на отрицательные нужно вводить соответствующие числа. Если в задаче отсутствует коэффициент, то на его место в калькулятор вводят ноль. Указывать можно не только числа, но и дроби. К примеру: 4,7 или 1/5.
На специальных сайтах можно решать различные системы уравнений по методу талантливого учёного Крамера в режиме онлайн. Решение будет отображено на экране моментально, к тому же его можно расширить. При решении системы уравнений крайне важно найти определители и присоединить сразу несколько разных матриц. Для существенного сокращения решения эта математическая операция упрощена, что существенно облегчает работу учеников.
Актуальные примеры решения
Единственность арифметических действий с системой при её совместимости обеспечивает условие неравенства нулю основного определителя. Но если сумма точек, которые были возведены в квадрат, строго положительна, то полученный СЛАУ будет несовместим с квадратной матрицей. Такая ситуация может произойти тогда, когда минимум один из присутствующих элементов deti отличён от нуля.
Но если сумма точек, которые были возведены в квадрат, строго положительна, то полученный СЛАУ будет несовместим с квадратной матрицей. Такая ситуация может произойти тогда, когда минимум один из присутствующих элементов deti отличён от нуля.
В качестве примера можно рассмотреть задачу, по условиям которой необходимо решить трёхмерную систему ЛАУ, используя для этого формулы Крамера:
- x1 + 2 x2 + 4 x3 = 31.
- 5 x1 + x2 + 2 x3 = 29.
- 3 x1 — x2 + x3 =10.
Для решения следует выписать матрицу системы построчно. Строку матрицы принято обозначать символом i. После этого можно получить формулу A1=(1 2 4), A2=(5 1 2), A3=(3 -1 1). Существование значения b = (31 29 10) помогает отобразить столбец свободных коэффициентов. Основной определитель Det будет соответствовать следующим данным: a11 a22 a33 + a12 a23 a31 + a31 a21 a32 — a13 a22 a31 — a11 a32 a23 — a33 a21 a12 = 1—20 + 12 — 12 + 2—10 = -27.
В соответствии с формулой Крамера можно найти: x1 = -81/(-27) = 3, x2 = -108/(-27) = 4, x3 = -135/(-27) = 5.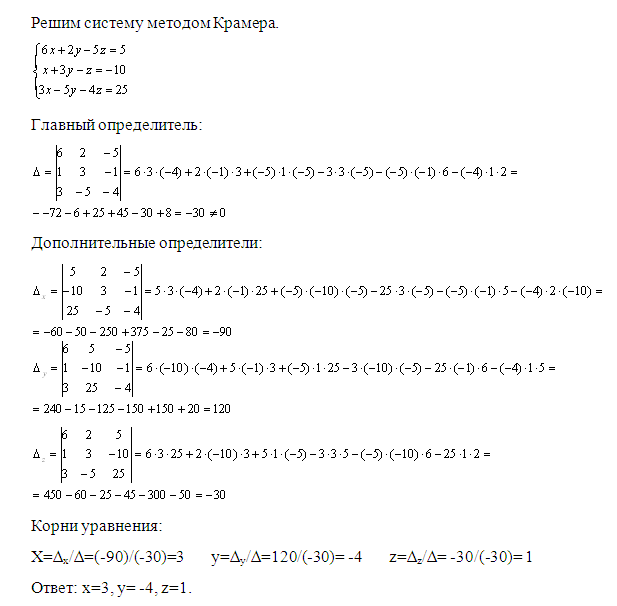 Если всё сделать правильно, то можно получить следующий ответ: x° = (3,4,5). Если руководствоваться базовыми понятиями, то многочисленные средства Крамера для решения сложных линейных уравнений можно использовать опосредованно.
Если всё сделать правильно, то можно получить следующий ответ: x° = (3,4,5). Если руководствоваться базовыми понятиями, то многочисленные средства Крамера для решения сложных линейных уравнений можно использовать опосредованно.
Нелишним также будет рассмотреть следующий пример, где ученику нужно определить то, при каких показателях параметра F неравенство формулы | F x — y — 4|+|x + F y + 4|<=0 будет иметь ровно одно логическое решение. В силу определения модуля функции представленное неравенство может быть выполнено только в том случае, если оба выражения равны нулю. Именно поэтому рассматриваемая задача сводится только к нахождению решения линейной системы алгебраических уравнений. Соблюдаемый принцип действий должен соответствовать двум следующим формулам:
- F x — y = 4.
- x + F y = -4.
Для этого примера свойственно единственное решение, но только в том случае, если главный определитель отличен от нуля.
Это условие выполняется абсолютно для всех действительных значений параметра F. Стоит отметить, что к математическим задачам этого типа могут быть сведены многочисленные практические примеры из области физики, математики и даже химии.
Присутствующая вычислительная сложность
Рассматриваемый метод решения задач требует стандартного вычисления определителей размерности. Если практиковать использование метода Гаусса для поиска всех необходимых определителей, то возникшие в итоге сложности будут связаны с электронными операциями порядка сложения-умножения. В этом случае придётся столкнуться с более сложными формулами, нежели с методом Гаусса.
Именно поэтому, с точки зрения затрат времени на вычисления, метод Гаусса является непрактичным. Специалистами в 2010 году было доказано, что метод Крамера вполне может быть реализован со сложностью O (n 3), а это очень важно в математике.
В распространённых задачах на системы линейных уравнений обязательно встречаются и такие, в которых помимо букв существуют ещё и другие символы. Они обозначают некоторое число (чаще всего действительное). Математики к таким задачам и системам уравнений приводят примеры, которые основаны на поиске общих свойств каких-либо явлений и предметов. Это очень удобно в том случае, если учёными был изобретён какой-либо агрегат или материал, а для описания всех его свойств необходимо решить целую систему линейных уравнений, где вместо коэффициентов используются буквы.
Они обозначают некоторое число (чаще всего действительное). Математики к таким задачам и системам уравнений приводят примеры, которые основаны на поиске общих свойств каких-либо явлений и предметов. Это очень удобно в том случае, если учёными был изобретён какой-либо агрегат или материал, а для описания всех его свойств необходимо решить целую систему линейных уравнений, где вместо коэффициентов используются буквы.
Предыдущая
МатематикаЛуч в математике — определение, форма и свойства
Следующая
МатематикаМатематические диктанты для 4 класса
Решение системы по формулам крамера. Правило Крамера. Метод обратной матрицы
Методы Крамера и Гаусса – одни из самых популярных методов решения СЛАУ . К тому же, в ряде случаев целесообразно использовать именно конкретные методы. Сессия близка, и сейчас самое время повторить или освоить их с нуля. Сегодня разбираемся с решением методом Крамера. Ведь решение системы линейных уравнений методом Крамера — весьма полезный навык.
Сегодня разбираемся с решением методом Крамера. Ведь решение системы линейных уравнений методом Крамера — весьма полезный навык.
Системы линейных алгебраических уравнений
Система линейных алгебраических уравнений – система уравнений вида:
Набор значений x , при котором уравнения системы обращаются в тождества, называется решением системы, a и b – вещественные коэффициенты. Простенькую систему, состоящую из двух уравнений с двумя неизвестными, можно решить в уме либо выразив одну переменную через другую. Но переменных (иксов) в СЛАУ может быть гораздо больше двух, и здесь простыми школьными манипуляциями не обойтись. Что же делать? Например, решать СЛАУ методом Крамера!
Итак, пусть система состоит из n уравнений с n неизвестными.
Такую систему можно переписать в матричном виде
Здесь A – основная матрица системы, X и B , соответственно, матрицы-столбцы неизвестных переменных и свободных членов.
Решение СЛАУ методом Крамера
Если определитель главной матрицы не равен нулю (матрица невырожденная), систему можно решать по методу Крамера.
Согласно методу Крамера, решение находится по формулам:
Здесь дельта – определитель главной матрицы, а дельта x n-ное – определитель, полученный из определителя главной матрицы путем заменой n-ного столбца на столбец свободных членов.
В этом и заключается вся суть метода Крамера. Подставляя найденные по вышеприведенным формулам значения x в искомую систему, убеждаемся в правильности (или наоборот) нашего решения. Чтобы Вы быстрее уловили суть, приведем ниже пример подробного решения СЛАУ методом Крамера:
Даже если у Вас не получится с первого раза, не расстраивайтесь! Немного практики, и Вы начнете щелкать СЛАУ как орешки. Более того, сейчас совершенно необязательно корпеть над тетрадью, решая громоздкие выкладки и исписывая стержень. Можно легко решить СЛАУ методом Крамера в режиме онлайн, лишь подставив в готовую форму коэффициенты. Испробовать онлайн калькулятор решения методом Крамера можно, к примеру, на этом сайте .
Испробовать онлайн калькулятор решения методом Крамера можно, к примеру, на этом сайте .
А если система оказалась упорной и не сдается, Вы всегда можете обратиться за помощью к нашим авторам, например, чтобы . Будь в системе хоть 100 неизвестных, мы обязательно решим ее верно и точно в срок!
Метод Крамера основан на использовании определителей в решении систем линейных уравнений. Это значительно ускоряет процесс решения.
Метод Крамера может быть использован в решении системы стольких линейных уравнений, сколько в каждом уравнении неизвестных. Если определитель системы не равен нулю, то метод Крамера может быть использован в решении, если же равен нулю, то не может. Кроме того, метод Крамера может быть использован в решении систем линейных уравнений, имеющих единственное решение.
Определение . Определитель, составленный из коэффициентов при неизвестных, называется определителем системы и обозначается (дельта).
Определители
получаются путём замены коэффициентов при соответствующих неизвестных свободными членами:
;
.
Теорема Крамера . Если определитель системы отличен от нуля, то система линейных уравнений имеет одно единственное решение, причём неизвестное равно отношению определителей. В знаменателе – определитель системы, а в числителе – определитель, полученный из определителя системы путём замены коэффициентов при этом неизвестном свободными членами. Эта теорема имеет место для системы линейных уравнений любого порядка.
Пример 1. Решить систему линейных уравнений:
Согласно теореме Крамера имеем:
Итак, решение системы (2):
онлайн-калькулятором , решающим методом Крамера.
Три случая при решении систем линейных уравнений
Как явствует из теоремы Крамера , при решении системы линейных уравнений могут встретиться три случая:
Первый случай: система линейных уравнений имеет единственное решение
(система совместна и определённа)
Второй случай: система линейных уравнений имеет бесчисленное множество решений
(система совместна и неопределённа)
** ,
т. е. коэффициенты при неизвестных и свободные члены пропорциональны.
е. коэффициенты при неизвестных и свободные члены пропорциональны.
Третий случай: система линейных уравнений решений не имеет
(система несовместна)
Итак, система m линейных уравнений с n переменными называется несовместной , если у неё нет ни одного решения, и совместной , если она имеет хотя бы одно решение. Совместная система уравнений, имеющая только одно решение, называется определённой , а более одного – неопределённой .
Примеры решения систем линейных уравнений методом Крамера
Пусть дана система
.
На основании теоремы Крамера
………….
,
где
—
определитель системы. Остальные определители получим, заменяя столбец с коэффициентами соответствующей переменной (неизвестного) свободными членами:
Пример 2.
.
Следовательно, система является определённой. Для нахождения её решения вычисляем определители
По формулам Крамера находим:
Итак, (1; 0; -1) – единственное решение системы.
Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.
Если в системе линейных уравнений в одном или нескольких уравнениях отсутствуют какие-либо переменные, то в определителе соответствующие им элементы равны нулю! Таков следующий пример.
Пример 3. Решить систему линейных уравнений методом Крамера:
.
Решение. Находим определитель системы:
Посмотрите внимательно на систему уравнений и на определитель системы и повторите ответ на вопрос, в каких случаях один или несколько элементов определителя равны нулю. Итак, определитель не равен нулю, следовательно, система является определённой. Для нахождения её решения вычисляем определители при неизвестных
По формулам Крамера находим:
Итак, решение системы — (2; -1; 1).
Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.
К началу страницы
Продолжаем решать системы методом Крамера вместе
Как уже говорилось, если определитель системы равен нулю, а определители при неизвестных не равны нулю, система несовместна, то есть решений не имеет. Проиллюстрируем следующим примером.
Пример 6. Решить систему линейных уравнений методом Крамера:
Решение. Находим определитель системы:
Определитель системы равен нулю, следовательно, система линейных уравнений либо несовместна и определённа, либо несовместна, то есть не имеет решений. Для уточнения вычисляем определители при неизвестных
Определители при неизвестных не равны нулю, следовательно, система несовместна, то есть не имеет решений.
Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.
В задачах на системы линейных уравнений встречаются и такие, где кроме букв, обозначающих
переменные, есть ещё и другие буквы. Эти буквы обозначают некоторое число, чаще всего действительное.
На практике к таким уравнениям и системам уравнений приводят задачи на поиск общих свойств каких-либо явлений и предметов.
То есть, изобрели вы какой-либо новый материал или устройство, а для описания его свойств, общих независимо от величины или количества
экземпляра, нужно решить систему линейных уравнений, где вместо некоторых коэффициентов при переменных — буквы. За примерами далеко
ходить не надо.
Эти буквы обозначают некоторое число, чаще всего действительное.
На практике к таким уравнениям и системам уравнений приводят задачи на поиск общих свойств каких-либо явлений и предметов.
То есть, изобрели вы какой-либо новый материал или устройство, а для описания его свойств, общих независимо от величины или количества
экземпляра, нужно решить систему линейных уравнений, где вместо некоторых коэффициентов при переменных — буквы. За примерами далеко
ходить не надо.
Следующий пример — на аналогичную задачу, только увеличивается количество уравнений, переменных, и букв, обозначающих некоторое действительное число.
Пример 8. Решить систему линейных уравнений методом Крамера:
Решение. Находим определитель системы:
Находим определители при неизвестных
Для того чтобы освоить данный параграф Вы должны уметь раскрывать определители «два на два» и «три на три». Если с определителями плохо, пожалуйста, изучите урок Как вычислить определитель?
Сначала мы подробно рассмотрим правило Крамера для системы двух линейных уравнений с двумя неизвестными. Зачем? – Ведь простейшую систему можно решить школьным методом, методом почленного сложения!
Зачем? – Ведь простейшую систему можно решить школьным методом, методом почленного сложения!
Дело в том, что пусть иногда, но встречается такое задание – решить систему двух линейных уравнений с двумя неизвестными по формулам Крамера. Во-вторых, более простой пример поможет понять, как использовать правило Крамера для более сложного случая – системы трех уравнений с тремя неизвестными.
Кроме того, существуют системы линейных уравнений с двумя переменными, которые целесообразно решать именно по правилу Крамера!
Рассмотрим систему уравнений
На первом шаге вычислим определитель , его называют главным определителем системы .
метод Гаусса .
Если , то система имеет единственное решение, и для нахождения корней мы должны вычислить еще два определителя:
и
На практике вышеуказанные определители также могут обозначаться латинской буквой .
Корни уравнения находим по формулам:
,
Пример 7
Решить систему линейных уравнений
Решение : Мы видим, что коэффициенты уравнения достаточно велики, в правой части присутствуют десятичные дроби с запятой. Запятая – довольно редкий гость в практических заданиях по математике, эту систему я взял из эконометрической задачи.
Запятая – довольно редкий гость в практических заданиях по математике, эту систему я взял из эконометрической задачи.
Как решить такую систему? Можно попытаться выразить одну переменную через другую, но в этом случае наверняка получатся страшные навороченные дроби, с которыми крайне неудобно работать, да и оформление решения будет выглядеть просто ужасно. Можно умножить второе уравнение на 6 и провести почленное вычитание, но и здесь возникнут те же самые дроби.
Что делать? В подобных случаях и приходят на помощь формулы Крамера.
;
;
Ответ : ,
Оба корня обладают бесконечными хвостами, и найдены приближенно, что вполне приемлемо (и даже обыденно) для задач эконометрики.
Комментарии здесь не нужны, поскольку задание решается по готовым формулам, однако, есть один нюанс. Когда используете данный метод, обязательным фрагментом оформления задания является следующий фрагмент: «, значит, система имеет единственное решение» . В противном случае рецензент может Вас наказать за неуважение к теореме Крамера.
В противном случае рецензент может Вас наказать за неуважение к теореме Крамера.
Совсем не лишней будет проверка, которую удобно провести на калькуляторе: подставляем приближенные значения в левую часть каждого уравнения системы. В результате с небольшой погрешностью должны получиться числа, которые находятся в правых частях.
Пример 8
Ответ представить в обыкновенных неправильных дробях. Сделать проверку.
Это пример для самостоятельного решения (пример чистового оформления и ответ в конце урока).
Переходим к рассмотрению правила Крамера для системы трех уравнений с тремя неизвестными:
Находим главный определитель системы:
Если , то система имеет бесконечно много решений или несовместна (не имеет решений). В этом случае правило Крамера не поможет, нужно использовать метод Гаусса .
Если , то система имеет единственное решение и для нахождения корней мы должны вычислить еще три определителя:
, ,
И, наконец, ответ рассчитывается по формулам:
Как видите, случай «три на три» принципиально ничем не отличается от случая «два на два», столбец свободных членов последовательно «прогуливается» слева направо по столбцам главного определителя.
Пример 9
Решить систему по формулам Крамера.
Решение : Решим систему по формулам Крамера.
, значит, система имеет единственное решение.
Ответ : .
Собственно, здесь опять комментировать особо нечего, ввиду того, что решение проходит по готовым формулам. Но есть пара замечаний.
Бывает так, что в результате вычислений получаются «плохие» несократимые дроби, например: .
Я рекомендую следующий алгоритм «лечения». Если под рукой нет компьютера, поступаем так:
1) Возможно, допущена ошибка в вычислениях. Как только Вы столкнулись с «плохой» дробью, сразу необходимо проверить, правильно ли переписано условие . Если условие переписано без ошибок, то нужно пересчитать определители, используя разложение по другой строке (столбцу).
2) Если в результате проверки ошибок не выявлено, то вероятнее всего, допущена опечатка в условии задания. В этом случае спокойно и ВНИМАТЕЛЬНО прорешиваем задание до конца, а затем обязательно делаем проверку и оформляем ее на чистовике после решения. Конечно, проверка дробного ответа – занятие неприятное, но зато будет обезоруживающий аргумент для преподавателя, который ну очень любит ставить минус за всякую бяку вроде . Как управляться с дробями, подробно расписано в ответе для Примера 8.
Конечно, проверка дробного ответа – занятие неприятное, но зато будет обезоруживающий аргумент для преподавателя, который ну очень любит ставить минус за всякую бяку вроде . Как управляться с дробями, подробно расписано в ответе для Примера 8.
Если под рукой есть компьютер, то для проверки используйте автоматизированную программу, которую можно бесплатно скачать в самом начале урока. Кстати, выгоднее всего сразу воспользоваться программой (еще до начала решения), Вы сразу будете видеть промежуточный шаг, на котором допустили ошибку! Этот же калькулятор автоматически рассчитывает решение системы матричным методом.
Замечание второе. Время от времени встречаются системы в уравнениях которых отсутствуют некоторые переменные, например:
Здесь в первом уравнении отсутствует переменная , во втором – переменная . В таких случаях очень важно правильно и ВНИМАТЕЛЬНО записать главный определитель:
– на месте отсутствующих переменных ставятся нули.
Кстати определители с нулями рационально раскрывать по той строке (столбцу), в которой находится ноль, так как вычислений получается заметно меньше.
Пример 10
Решить систему по формулам Крамера.
Это пример для самостоятельного решения (образец чистового оформления и ответ в конце урока).
Для случая системы 4 уравнений с 4 неизвестными формулы Крамера записываются по аналогичным принципам. Живой пример можно посмотреть на уроке Свойства определителя. Понижение порядка определителя – пять определителей 4-го порядка вполне решабельны. Хотя задача уже весьма напоминает ботинок профессора на груди у студента-счастливчика.
Решение системы с помощью обратной матрицы
Метод обратной матрицы – это, по существу, частный случай матричного уравнения (см. Пример №3 указанного урока).
Для изучения данного параграфа необходимо уметь раскрывать определители, находить обратную матрицу и выполнять матричное умножение. Соответствующие ссылки будут даны по ходу объяснений.
Пример 11
Решить систему с матричным методом
Решение : Запишем систему в матричной форме:
, где
Пожалуйста, посмотрите на систему уравнений и на матрицы. По какому принципу записываем элементы в матрицы, думаю, всем понятно. Единственный комментарий: если бы в уравнениях отсутствовали некоторые переменные, то на соответствующих местах в матрице нужно было бы поставить нули.
По какому принципу записываем элементы в матрицы, думаю, всем понятно. Единственный комментарий: если бы в уравнениях отсутствовали некоторые переменные, то на соответствующих местах в матрице нужно было бы поставить нули.
Обратную матрицу найдем по формуле:
, где – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .
Сначала разбираемся с определителем:
Здесь определитель раскрыт по первой строке.
Внимание! Если , то обратной матрицы не существует, и решить систему матричным методом невозможно. В этом случае система решается методом исключения неизвестных (методом Гаусса) .
Теперь нужно вычислить 9 миноров и записать их в матрицу миноров
Справка: Полезно знать смысл двойных подстрочных индексов в линейной алгебре. Первая цифра – это номер строки, в которой находится данный элемент. Вторая цифра – это номер столбца, в котором находится данный элемент:
То есть, двойной подстрочный индекс указывает, что элемент находится в первой строке, третьем столбце, а, например, элемент находится в 3 строке, 2 столбце
В ходе решения расчет миноров лучше расписать подробно, хотя, при определенном опыте их можно приноровиться считать с ошибками устно.
В первой части мы рассмотрели немного теоретического материала, метод подстановки, а также метод почленного сложения уравнений системы. Всем, кто зашел на сайт через эту страницу рекомендую ознакомиться с первой частью. Возможно, некоторым посетителям покажется материал слишком простым, но по ходу решения систем линейных уравнений я сделал ряд очень важных замечаний и выводов, касающихся решения математических задач в целом.
А сейчас мы разберём правило Крамера, а также решение системы линейных уравнений с помощью обратной матрицы (матричный метод). Все материалы изложены просто, подробно и понятно, практически все читатели смогут научиться решать системы вышеуказанными способами.
Сначала мы подробно рассмотрим правило Крамера для системы двух линейных уравнений с двумя неизвестными. Зачем? – Ведь простейшую систему можно решить школьным методом, методом почленного сложения!
Дело в том, что пусть иногда, но встречается такое задание – решить систему двух линейных уравнений с двумя неизвестными по формулам Крамера. Во-вторых, более простой пример поможет понять, как использовать правило Крамера для более сложного случая – системы трех уравнений с тремя неизвестными.
Во-вторых, более простой пример поможет понять, как использовать правило Крамера для более сложного случая – системы трех уравнений с тремя неизвестными.
Кроме того, существуют системы линейных уравнений с двумя переменными, которые целесообразно решать именно по правилу Крамера!
Рассмотрим систему уравнений
На первом шаге вычислим определитель , его называют главным определителем системы .
метод Гаусса .
Если , то система имеет единственное решение, и для нахождения корней мы должны вычислить еще два определителя:
и
На практике вышеуказанные определители также могут обозначаться латинской буквой .
Корни уравнения находим по формулам:
,
Пример 7
Решить систему линейных уравнений
Решение : Мы видим, что коэффициенты уравнения достаточно велики, в правой части присутствуют десятичные дроби с запятой. Запятая – довольно редкий гость в практических заданиях по математике, эту систему я взял из эконометрической задачи.
Как решить такую систему? Можно попытаться выразить одну переменную через другую, но в этом случае наверняка получатся страшные навороченные дроби, с которыми крайне неудобно работать, да и оформление решения будет выглядеть просто ужасно. Можно умножить второе уравнение на 6 и провести почленное вычитание, но и здесь возникнут те же самые дроби.
Что делать? В подобных случаях и приходят на помощь формулы Крамера.
;
;
Ответ : ,
Оба корня обладают бесконечными хвостами, и найдены приближенно, что вполне приемлемо (и даже обыденно) для задач эконометрики.
Комментарии здесь не нужны, поскольку задание решается по готовым формулам, однако, есть один нюанс. Когда используете данный метод, обязательным фрагментом оформления задания является следующий фрагмент: «, значит, система имеет единственное решение» . В противном случае рецензент может Вас наказать за неуважение к теореме Крамера.
Совсем не лишней будет проверка, которую удобно провести на калькуляторе: подставляем приближенные значения в левую часть каждого уравнения системы. В результате с небольшой погрешностью должны получиться числа, которые находятся в правых частях.
В результате с небольшой погрешностью должны получиться числа, которые находятся в правых частях.
Пример 8
Ответ представить в обыкновенных неправильных дробях. Сделать проверку.
Это пример для самостоятельного решения (пример чистового оформления и ответ в конце урока).
Переходим к рассмотрению правила Крамера для системы трех уравнений с тремя неизвестными:
Находим главный определитель системы:
Если , то система имеет бесконечно много решений или несовместна (не имеет решений). В этом случае правило Крамера не поможет, нужно использовать метод Гаусса .
Если , то система имеет единственное решение и для нахождения корней мы должны вычислить еще три определителя:
, ,
И, наконец, ответ рассчитывается по формулам:
Как видите, случай «три на три» принципиально ничем не отличается от случая «два на два», столбец свободных членов последовательно «прогуливается» слева направо по столбцам главного определителя.
Пример 9
Решить систему по формулам Крамера.
Решение : Решим систему по формулам Крамера.
, значит, система имеет единственное решение.
Ответ : .
Собственно, здесь опять комментировать особо нечего, ввиду того, что решение проходит по готовым формулам. Но есть пара замечаний.
Бывает так, что в результате вычислений получаются «плохие» несократимые дроби, например: .
Я рекомендую следующий алгоритм «лечения». Если под рукой нет компьютера, поступаем так:
1) Возможно, допущена ошибка в вычислениях. Как только Вы столкнулись с «плохой» дробью, сразу необходимо проверить, правильно ли переписано условие . Если условие переписано без ошибок, то нужно пересчитать определители, используя разложение по другой строке (столбцу).
2) Если в результате проверки ошибок не выявлено, то вероятнее всего, допущена опечатка в условии задания. В этом случае спокойно и ВНИМАТЕЛЬНО прорешиваем задание до конца, а затем обязательно делаем проверку и оформляем ее на чистовике после решения. Конечно, проверка дробного ответа – занятие неприятное, но зато будет обезоруживающий аргумент для преподавателя, который ну очень любит ставить минус за всякую бяку вроде . Как управляться с дробями, подробно расписано в ответе для Примера 8.
В этом случае спокойно и ВНИМАТЕЛЬНО прорешиваем задание до конца, а затем обязательно делаем проверку и оформляем ее на чистовике после решения. Конечно, проверка дробного ответа – занятие неприятное, но зато будет обезоруживающий аргумент для преподавателя, который ну очень любит ставить минус за всякую бяку вроде . Как управляться с дробями, подробно расписано в ответе для Примера 8.
Если под рукой есть компьютер, то для проверки используйте автоматизированную программу, которую можно бесплатно скачать в самом начале урока. Кстати, выгоднее всего сразу воспользоваться программой (еще до начала решения), Вы сразу будете видеть промежуточный шаг, на котором допустили ошибку! Этот же калькулятор автоматически рассчитывает решение системы матричным методом.
Замечание второе. Время от времени встречаются системы в уравнениях которых отсутствуют некоторые переменные, например:
Здесь в первом уравнении отсутствует переменная , во втором – переменная . В таких случаях очень важно правильно и ВНИМАТЕЛЬНО записать главный определитель:
– на месте отсутствующих переменных ставятся нули.
Кстати определители с нулями рационально раскрывать по той строке (столбцу), в которой находится ноль, так как вычислений получается заметно меньше.
Пример 10
Решить систему по формулам Крамера.
Это пример для самостоятельного решения (образец чистового оформления и ответ в конце урока).
Для случая системы 4 уравнений с 4 неизвестными формулы Крамера записываются по аналогичным принципам. Живой пример можно посмотреть на уроке Свойства определителя. Понижение порядка определителя – пять определителей 4-го порядка вполне решабельны. Хотя задача уже весьма напоминает ботинок профессора на груди у студента-счастливчика.
Решение системы с помощью обратной матрицыМетод обратной матрицы – это, по существу, частный случай матричного уравнения (см. Пример №3 указанного урока).
Для изучения данного параграфа необходимо уметь раскрывать определители, находить обратную матрицу и выполнять матричное умножение. Соответствующие ссылки будут даны по ходу объяснений.
Соответствующие ссылки будут даны по ходу объяснений.
Пример 11
Решить систему с матричным методом
Решение : Запишем систему в матричной форме:
, где
Пожалуйста, посмотрите на систему уравнений и на матрицы. По какому принципу записываем элементы в матрицы, думаю, всем понятно. Единственный комментарий: если бы в уравнениях отсутствовали некоторые переменные, то на соответствующих местах в матрице нужно было бы поставить нули.
Обратную матрицу найдем по формуле:
, где – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .
Сначала разбираемся с определителем:
Здесь определитель раскрыт по первой строке.
Внимание! Если , то обратной матрицы не существует, и решить систему матричным методом невозможно. В этом случае система решается методом исключения неизвестных (методом Гаусса) .
Теперь нужно вычислить 9 миноров и записать их в матрицу миноров
Справка: Полезно знать смысл двойных подстрочных индексов в линейной алгебре. Первая цифра – это номер строки, в которой находится данный элемент. Вторая цифра – это номер столбца, в котором находится данный элемент:
Первая цифра – это номер строки, в которой находится данный элемент. Вторая цифра – это номер столбца, в котором находится данный элемент:
То есть, двойной подстрочный индекс указывает, что элемент находится в первой строке, третьем столбце, а, например, элемент находится в 3 строке, 2 столбце
Математика | Онлайн калькулятор
Математика – включающая многие разделы фундаментальная базисная для физики, астрономии и иных научных направлений наука, исследующая пространственные формы существующего мира. Различные методы математики также направлены на определение количественных отношений элементов окружающей действительности.
В математике через описание, выявление структуры, порядка и отношений, операции подсчета и измерения определяются свойства реальных объектов и через запись их формальным языком формируются идеализированные математические объекты.
Методы математики дают возможности нахождения общих для всего сущего законов и являются языковыми средствами и инструментарием для многих иных наук.
Ниже представлен список различных онлайн калькуляторов, которые помогут в решении математических задач.
Геометрия Площадь фигур Плоские фигуры
Объемные фигуры
Объем фигур Периметр фигур Сторона Высота Диагональ Радиус Медиана Биссектриса Углы Теоремы Ещё Еще разделы Комбинаторика Теория множеств Статистика Теория вероятности Логика Конвертеры | Арифметика Арифметические действия Проценты Простые и составные числа Решение дробей Линейная алгебра Операции с матрицами Действия с векторами Решение СЛУ | Математический анализ Решение уравнений Решение неравенств Решение интегралов Решение логарифмов Решение комплексных чисел Решение функций Производные функции Графические построения Решение прогрессии Аналитическая геометрия Точка, прямая, плоскость Решить уравнения |
Select rating12345
Рейтинг: 5 (Голосов 6)
Сообщить об ошибке
Вам помог этот калькулятор?
Предложения и пожелания пишите на [email protected]
Поделитесь этим калькулятором на форуме или в сети!
Это помогает делать новые калькуляторы.
НЕТ
Смотрите также
| Финансы | Физика | Химия | Астрономия | Прочее |
решаем системы линейных алгебраических уравнений (слау)
В первой части мы рассмотрели немного теоретического материала, метод подстановки, а также метод почленного сложения уравнений системы. Всем, кто зашел на сайт через эту страницу рекомендую ознакомиться с первой частью. Возможно, некоторым посетителям покажется материал слишком простым, но по ходу решения систем линейных уравнений я сделал ряд очень важных замечаний и выводов, касающихся решения математических задач в целом.
А сейчас мы разберём правило Крамера, а также решение системы линейных уравнений с помощью обратной матрицы (матричный метод). Все материалы изложены просто, подробно и понятно, практически все читатели смогут научиться решать системы вышеуказанными способами.
Сначала мы подробно рассмотрим правило Крамера для системы двух линейных уравнений с двумя неизвестными. Зачем? – Ведь простейшую систему можно решить школьным методом, методом почленного сложения!
Зачем? – Ведь простейшую систему можно решить школьным методом, методом почленного сложения!
Дело в том, что пусть иногда, но встречается такое задание – решить систему двух линейных уравнений с двумя неизвестными по формулам Крамера. Во-вторых, более простой пример поможет понять, как использовать правило Крамера для более сложного случая – системы трех уравнений с тремя неизвестными.
Кроме того, существуют системы линейных уравнений с двумя переменными, которые целесообразно решать именно по правилу Крамера!
Рассмотрим систему уравнений
На первом шаге вычислим определитель , его называют главным определителем системы .
метод Гаусса .
Если , то система имеет единственное решение, и для нахождения корней мы должны вычислить еще два определителя:
и
На практике вышеуказанные определители также могут обозначаться латинской буквой .
Корни уравнения находим по формулам:
,
Пример 7
Решить систему линейных уравнений
Решение : Мы видим, что коэффициенты уравнения достаточно велики, в правой части присутствуют десятичные дроби с запятой. Запятая – довольно редкий гость в практических заданиях по математике, эту систему я взял из эконометрической задачи.
Запятая – довольно редкий гость в практических заданиях по математике, эту систему я взял из эконометрической задачи.
Как решить такую систему? Можно попытаться выразить одну переменную через другую, но в этом случае наверняка получатся страшные навороченные дроби, с которыми крайне неудобно работать, да и оформление решения будет выглядеть просто ужасно. Можно умножить второе уравнение на 6 и провести почленное вычитание, но и здесь возникнут те же самые дроби.
Что делать? В подобных случаях и приходят на помощь формулы Крамера.
;
;
Ответ : ,
Оба корня обладают бесконечными хвостами, и найдены приближенно, что вполне приемлемо (и даже обыденно) для задач эконометрики.
Комментарии здесь не нужны, поскольку задание решается по готовым формулам, однако, есть один нюанс. Когда используете данный метод, обязательным фрагментом оформления задания является следующий фрагмент: «, значит, система имеет единственное решение» . В противном случае рецензент может Вас наказать за неуважение к теореме Крамера.
В противном случае рецензент может Вас наказать за неуважение к теореме Крамера.
Совсем не лишней будет проверка, которую удобно провести на калькуляторе: подставляем приближенные значения в левую часть каждого уравнения системы. В результате с небольшой погрешностью должны получиться числа, которые находятся в правых частях.
Пример 8
Ответ представить в обыкновенных неправильных дробях. Сделать проверку.
Это пример для самостоятельного решения (пример чистового оформления и ответ в конце урока).
Переходим к рассмотрению правила Крамера для системы трех уравнений с тремя неизвестными:
Находим главный определитель системы:
Если , то система имеет бесконечно много решений или несовместна (не имеет решений). В этом случае правило Крамера не поможет, нужно использовать метод Гаусса .
Если , то система имеет единственное решение и для нахождения корней мы должны вычислить еще три определителя:
, ,
И, наконец, ответ рассчитывается по формулам:
Как видите, случай «три на три» принципиально ничем не отличается от случая «два на два», столбец свободных членов последовательно «прогуливается» слева направо по столбцам главного определителя.
Пример 9
Решить систему по формулам Крамера.
Решение : Решим систему по формулам Крамера.
, значит, система имеет единственное решение.
Ответ : .
Собственно, здесь опять комментировать особо нечего, ввиду того, что решение проходит по готовым формулам. Но есть пара замечаний.
Бывает так, что в результате вычислений получаются «плохие» несократимые дроби, например: .
Я рекомендую следующий алгоритм «лечения». Если под рукой нет компьютера, поступаем так:
1) Возможно, допущена ошибка в вычислениях. Как только Вы столкнулись с «плохой» дробью, сразу необходимо проверить, правильно ли переписано условие . Если условие переписано без ошибок, то нужно пересчитать определители, используя разложение по другой строке (столбцу).
2) Если в результате проверки ошибок не выявлено, то вероятнее всего, допущена опечатка в условии задания. В этом случае спокойно и ВНИМАТЕЛЬНО прорешиваем задание до конца, а затем обязательно делаем проверку и оформляем ее на чистовике после решения. Конечно, проверка дробного ответа – занятие неприятное, но зато будет обезоруживающий аргумент для преподавателя, который ну очень любит ставить минус за всякую бяку вроде . Как управляться с дробями, подробно расписано в ответе для Примера 8.
Конечно, проверка дробного ответа – занятие неприятное, но зато будет обезоруживающий аргумент для преподавателя, который ну очень любит ставить минус за всякую бяку вроде . Как управляться с дробями, подробно расписано в ответе для Примера 8.
Если под рукой есть компьютер, то для проверки используйте автоматизированную программу, которую можно бесплатно скачать в самом начале урока. Кстати, выгоднее всего сразу воспользоваться программой (еще до начала решения), Вы сразу будете видеть промежуточный шаг, на котором допустили ошибку! Этот же калькулятор автоматически рассчитывает решение системы матричным методом.
Замечание второе. Время от времени встречаются системы в уравнениях которых отсутствуют некоторые переменные, например:
Здесь в первом уравнении отсутствует переменная , во втором – переменная . В таких случаях очень важно правильно и ВНИМАТЕЛЬНО записать главный определитель:
– на месте отсутствующих переменных ставятся нули.
Кстати определители с нулями рационально раскрывать по той строке (столбцу), в которой находится ноль, так как вычислений получается заметно меньше.
Пример 10
Решить систему по формулам Крамера.
Это пример для самостоятельного решения (образец чистового оформления и ответ в конце урока).
Для случая системы 4 уравнений с 4 неизвестными формулы Крамера записываются по аналогичным принципам. Живой пример можно посмотреть на уроке Свойства определителя. Понижение порядка определителя – пять определителей 4-го порядка вполне решабельны. Хотя задача уже весьма напоминает ботинок профессора на груди у студента-счастливчика.
Решение системы с помощью обратной матрицыМетод обратной матрицы – это, по существу, частный случай матричного уравнения (см. Пример №3 указанного урока).
Для изучения данного параграфа необходимо уметь раскрывать определители, находить обратную матрицу и выполнять матричное умножение. Соответствующие ссылки будут даны по ходу объяснений.
Пример 11
Решить систему с матричным методом
Решение : Запишем систему в матричной форме:
, где
Пожалуйста, посмотрите на систему уравнений и на матрицы. По какому принципу записываем элементы в матрицы, думаю, всем понятно. Единственный комментарий: если бы в уравнениях отсутствовали некоторые переменные, то на соответствующих местах в матрице нужно было бы поставить нули.
По какому принципу записываем элементы в матрицы, думаю, всем понятно. Единственный комментарий: если бы в уравнениях отсутствовали некоторые переменные, то на соответствующих местах в матрице нужно было бы поставить нули.
Обратную матрицу найдем по формуле:
, где – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .
Сначала разбираемся с определителем:
Здесь определитель раскрыт по первой строке.
Внимание! Если , то обратной матрицы не существует, и решить систему матричным методом невозможно. В этом случае система решается методом исключения неизвестных (методом Гаусса) .
Теперь нужно вычислить 9 миноров и записать их в матрицу миноров
Справка: Полезно знать смысл двойных подстрочных индексов в линейной алгебре. Первая цифра – это номер строки, в которой находится данный элемент. Вторая цифра – это номер столбца, в котором находится данный элемент:
То есть, двойной подстрочный индекс указывает, что элемент находится в первой строке, третьем столбце, а, например, элемент находится в 3 строке, 2 столбце
2. Решение систем уравнений матричным методом (при помощи обратной матрицы).
Решение систем уравнений матричным методом (при помощи обратной матрицы).
3. Метод Гаусса решения систем уравнений.
Метод Крамера.
Метод Крамера применяется для решения систем линейных алгебраических уравнений (СЛАУ ).
Формулы на примере системы из двух уравнений с двумя переменными.
Дано: Решить методом Крамера систему
Относительно переменных х и у .
Решение:
Найдем определитель матрицы, составленный из коэффициентов системы Вычисление определителей. :
Применим формулы Крамера и найдем значения переменных:
и .
Пример 1:
Решить систему уравнений:
относительно переменных х и у .
Решение:
Заменим в этом определителе первый столбец столбцом коэффициентов из правой части системы и найдем его значение:
Сделаем аналогичное действие, заменив в первом определителе второй столбец:
Применим формулы Крамера и найдем значения переменных:
и .
Ответ:
Замечание: Этим методом можно решать системы и большей размерности.
Замечание: Если получается, что , а делить на ноль нельзя, то говорят, что система не имеет единственного решения. В этом случае система имеет или бесконечно много решений или не имеет решений вообще.
Пример 2 (бесконечное количество решений):
Решить систему уравнений:
относительно переменных х и у .
Решение:
Найдем определитель матрицы, составленный из коэффициентов системы:
Решение систем методом подстановки.
Первое из уравнений системы — равенство, верное при любых значениях переменных (потому что 4 всегда равно 4). Значит, остается только одно уравнение. Это уравнение связи между переменными .
Получили, решением системы являются любые пары значений переменных, связанных между собой равенством .
Общее решение запишется так:
Частные решения можно определять выбирая произвольное значение у и вычисляя х по этому равенству связи.
и т.д.
Таких решений бесконечно много.
Ответ: общее решение
Частные решения:
Пример 3 (решений нет, система несовместна):
Решить систему уравнений:
Решение:
Найдем определитель матрицы, составленный из коэффициентов системы:
Применять формулы Крамера нельзя. Решим эту систему методом подстановки
Второе уравнение системы — равенство, неверное ни при каких значениях переменных (конечно же, так как -15 не равно 2). Если одно из уравнений системы не верно ни при каких значениях переменных, то и вся системы не имеет решений.
Ответ: решений нет
Рассмотрим систему 3-х уравнений с тремя неизвестными
Используя определители 3-го порядка, решение такой системы можно записать в таком же виде, как и для системы двух уравнений, т.е.
(2.4)
если 0. Здесь
Это есть правило Крамера решения системы трех линейных уравнений с тремя неизвестными .
Пример
2. 3. Решить
систему линейных уравнений при помощи
правила Крамера:
3. Решить
систему линейных уравнений при помощи
правила Крамера:
Решение . Находим определитель основной матрицы системы
Поскольку 0, то для нахождения решения системы можно применить правило Крамера, но предварительно вычислим еще три определителя:
Проверка:
Следовательно, решение найдено правильно.
Правила Крамера, полученные для линейных систем 2-го и 3-го порядка, наводят на мысль, что такие же правила можно сформулировать и для линейных систем любого порядка. Действительно имеет место
Теорема Крамера. Квадратная система линейных уравнений с отличным от нуля определителем основной матрицы системы (0) имеет одно и только одно решение и это решение вычисляется по формулам
(2.5)
где
– определитель
основной матрицы ,
i – определитель
матрицы , полученной
из основной, заменой i -го
столбца столбцом свободных членов .
Отметим, что если =0, то правило Крамера не применимо. Это означает, что система либо не имеет вообще решений, либо имеет бесконечно много решений.
Сформулировав теорему Крамера, естественно возникает вопрос о вычислении определителей высших порядков.
2.4. Определители n-го порядка
Дополнительным минором M ij элемента a ij называется определитель, получаемый из данного путем вычеркивания i -й строки и j -го столбца. Алгебраическим дополнением A ij элемента a ij называется минор этого элемента, взятого со знаком (–1) i + j , т.е. A ij = (–1) i + j M ij .
Например, найдем миноры и алгебраические дополнения элементов a 23 и a 31 определителя
Получаем
Используя
понятие алгебраического дополнения
можно сформулировать теорему
о разложении определителя n -го
порядка по строке или столбцу .
Теорема 2.1. Определитель матрицы A равен сумме произведений всех элементов некоторой строки (или столбца) на их алгебраические дополнения:
(2.6)
Данная теорема лежит в основе одного из основных методов вычисления определителей, т.н. метода понижения порядка . В результате разложения определителя n -го порядка по какой-либо строке или столбцу, получается n определителей (n –1)-го порядка. Чтобы таких определителей было меньше, целесообразно выбирать ту строку или столбец, в которой больше всего нулей. На практике формулу разложения определителя обычно записывают в виде:
т.е. алгебраические дополнения записывают в явном виде через миноры.
Примеры 2.4. Вычислить определители, предварительно разложив их по какой-либо строке или столбцу. Обычно в таких случаях выбирают такой столбец или строку, в которой больше всего нулей. Выбранную строку или столбец будем обозначать стрелкой.
2.
 5. Основные свойства определителей
5. Основные свойства определителейРазлагая определитель по какой-либо строке или столбцу, мы получим n определителей (n –1)-го порядка. Затем каждый из этих определителей (n –1)-го порядка также можно разложить в сумму определителей (n –2)-го порядка. Продолжая этот процесс, можно дойти до определителей 1-го порядка, т.е. до элементов матрицы, определитель которой вычисляется. Так, для вычисления определителей 2-го порядка придется вычислить сумму двух слагаемых, для определителей 3-го порядка – сумму 6 слагаемых, для определителей 4-го порядка – 24 слагаемых. Число слагаемых будет резко возрастать по мере увеличения порядка определителя. Это означает, что вычисление определителей очень высоких порядков становится довольно трудоемкой задачей, непосильной даже для ЭВМ. Однако вычислять определители можно и по-другому, используя свойства определителей.
Свойство
1 . Определитель
не изменится, если в нем поменять местами
строки и столбцы, т. е. при транспонировании
матрицы :
е. при транспонировании
матрицы :
.
Данное свойство свидетельствует о равноправии строк и столбцов определителя. Иначе говоря, любое утверждение о столбцах определителя справедливо и для его строк и наоборот.
Свойство 2 . Определитель меняет знак при перестановке двух строк (столбцов).
Следствие . Если определитель имеет две одинаковые строки (столбца), то он равен нулю.
Свойство 3 . Общий множитель всех элементов в какой-либо строке (столбце) можно вынести за знак определителя .
Например,
Следствие . Если все элементы некоторой строки (столбца) определителя равны нулю, то и сам определитель равен нулю .
Свойство
4 . Определитель
не изменится, если к элементам одной
строки (столбца), прибавить элементы
другой строки (столбца), умноженной на
какое-либо число .
Например,
Свойство 5 . Определитель произведения матриц равен произведению определителей матриц:
Метод Крамера основан на использовании определителей в решении систем линейных уравнений. Это значительно ускоряет процесс решения.
Метод Крамера может быть использован в решении системы стольких линейных уравнений, сколько в каждом уравнении неизвестных. Если определитель системы не равен нулю, то метод Крамера может быть использован в решении, если же равен нулю, то не может. Кроме того, метод Крамера может быть использован в решении систем линейных уравнений, имеющих единственное решение.
Определение . Определитель, составленный из коэффициентов при неизвестных, называется определителем системы и обозначается (дельта).
Определители
получаются путём замены коэффициентов при соответствующих неизвестных свободными членами:
;
.
Теорема Крамера . Если определитель системы отличен от нуля, то система линейных уравнений имеет одно единственное решение, причём неизвестное равно отношению определителей. В знаменателе – определитель системы, а в числителе – определитель, полученный из определителя системы путём замены коэффициентов при этом неизвестном свободными членами. Эта теорема имеет место для системы линейных уравнений любого порядка.
В знаменателе – определитель системы, а в числителе – определитель, полученный из определителя системы путём замены коэффициентов при этом неизвестном свободными членами. Эта теорема имеет место для системы линейных уравнений любого порядка.
Пример 1. Решить систему линейных уравнений:
Согласно теореме Крамера имеем:
Итак, решение системы (2):
онлайн-калькулятором , решающим методом Крамера.
Три случая при решении систем линейных уравнений
Как явствует из теоремы Крамера , при решении системы линейных уравнений могут встретиться три случая:
Первый случай: система линейных уравнений имеет единственное решение
(система совместна и определённа)
Второй случай: система линейных уравнений имеет бесчисленное множество решений
(система совместна и неопределённа)
** ,
т.е. коэффициенты при неизвестных и свободные члены пропорциональны.
Третий случай: система линейных уравнений решений не имеет
(система несовместна)
Итак, система m линейных уравнений с n переменными называется несовместной , если у неё нет ни одного решения, и совместной , если она имеет хотя бы одно решение. Совместная система уравнений, имеющая только одно решение, называется определённой , а более одного – неопределённой .
Совместная система уравнений, имеющая только одно решение, называется определённой , а более одного – неопределённой .
Примеры решения систем линейных уравнений методом Крамера
Пусть дана система
.
На основании теоремы Крамера
………….
,
где
—
определитель системы. Остальные определители получим, заменяя столбец с коэффициентами соответствующей переменной (неизвестного) свободными членами:
Пример 2.
.
Следовательно, система является определённой. Для нахождения её решения вычисляем определители
По формулам Крамера находим:
Итак, (1; 0; -1) – единственное решение системы.
Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.
Если в системе линейных уравнений в одном или нескольких уравнениях отсутствуют
какие-либо переменные, то в определителе соответствующие им элементы равны нулю! Таков следующий пример.
Пример 3. Решить систему линейных уравнений методом Крамера:
.
Решение. Находим определитель системы:
Посмотрите внимательно на систему уравнений и на определитель системы и повторите ответ на вопрос, в каких случаях один или несколько элементов определителя равны нулю. Итак, определитель не равен нулю, следовательно, система является определённой. Для нахождения её решения вычисляем определители при неизвестных
По формулам Крамера находим:
Итак, решение системы — (2; -1; 1).
Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.
К началу страницы
Продолжаем решать системы методом Крамера вместе
Как уже говорилось, если определитель системы равен нулю, а определители при неизвестных не равны нулю, система несовместна, то есть решений не имеет. Проиллюстрируем следующим примером.
Пример 6. Решить систему линейных уравнений методом Крамера:
Решение. Находим определитель системы:
Находим определитель системы:
Определитель системы равен нулю, следовательно, система линейных уравнений либо несовместна и определённа, либо несовместна, то есть не имеет решений. Для уточнения вычисляем определители при неизвестных
Определители при неизвестных не равны нулю, следовательно, система несовместна, то есть не имеет решений.
Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.
В задачах на системы линейных уравнений встречаются и такие, где кроме букв, обозначающих
переменные, есть ещё и другие буквы. Эти буквы обозначают некоторое число, чаще всего действительное.
На практике к таким уравнениям и системам уравнений приводят задачи на поиск общих свойств каких-либо явлений и предметов.
То есть, изобрели вы какой-либо новый материал или устройство, а для описания его свойств, общих независимо от величины или количества
экземпляра, нужно решить систему линейных уравнений, где вместо некоторых коэффициентов при переменных — буквы. За примерами далеко
ходить не надо.
За примерами далеко
ходить не надо.
Следующий пример — на аналогичную задачу, только увеличивается количество уравнений, переменных, и букв, обозначающих некоторое действительное число.
Пример 8. Решить систему линейных уравнений методом Крамера:
Решение. Находим определитель системы:
Находим определители при неизвестных
С количеством уравнений одинаковым с количеством неизвестных с главным определителем матрицы, который не равен нулю, коэффициентов системы (для подобных уравнений решение есть и оно только одно).
Теорема Крамера.
Когда определитель матрицы квадратной системы ненулевой, значит, система совместна и у нее есть одно решение и его можно найти по формулам Крамера :
где Δ — определитель матрицы системы ,
Δ i — определитель матрицы системы, в котором вместо i -го столбца находится столбец правых частей.
Когда определитель системы нулевой, значит, система может стать совместной или несовместной.
Этот способ обычно применяют для небольших систем с объемными вычислениями и если когда необходимо определить 1-ну из неизвестных. Сложность метода в том, что нужно вычислять много определителей.
Описание метода Крамера.
Есть система уравнений:
Систему 3-х уравнений можно решить методом Крамера, который рассмотрен выше для системы 2-х уравнений.
Составляем определитель из коэффициентов у неизвестных:
Это будет определитель системы . Когда D≠0 , значит, система совместна. Теперь составим 3 дополнительных определителя:
,,
Решаем систему по формулам Крамера :
Примеры решения систем уравнений методом Крамера.
Пример 1 .
Дана система:
Решим ее методом Крамера.
Сначала нужно вычислить определитель матрицы системы:
Т.к. Δ≠0, значит, из теоремы Крамера система совместна и у нее есть одно решение. Вычисляем дополнительные определители. Определитель Δ 1 получаем из определителя Δ, заменяя его первый столбец столбцом свободных коэффициентов. Получаем:
Получаем:
Таким же путем получаем определитель Δ 2 из определителя матрицы системы заменяя второй столбец столбцом свободных коэффициентов:
Калькулятор правила Крамера
Вспомним пример путешествия из второго раздела и систему уравнений, которую мы получили из него после упрощения каждой строки:
x + y + z = 26 ;
у - 2з = 6 ; и
2x - z = 12 .
Напомним также расширенную матрицу коэффициентов:
| ⌈ | 1 | 1 | 1 | ⁞ | 26 | ⌉ |
| | | 0 | 1 | -2 | ⁞ | 6 | ~ |
| ⌊ | 2 | 0 | -1 | ⁞ | 12 | ⌋ |
Прежде чем мы перейдем к построению четырех матриц, используемых в правиле Крамера для систем 3×3, давайте уделим некоторое время описанию того, как мы можем вводить данные в калькулятор правила Крамера 9. 0072 .
0072 .
У нас есть три уравнения, поэтому давайте сообщим калькулятору, что , выбрав правильный вариант в поле » Число уравнений «. Это превратит наш инструмент в средство решения системы уравнений с тремя переменными и покажет нам изображение того, как такая система выглядит , с несколькими загадочными символами, например a₁ или c₂ . Они обозначают коэффициенты нашей системы , т. е. числа, стоящие слева от переменных в каждой строке, и числа справа от = знак.
Это обозначение указано в калькуляторе , где вы можете ввести значения из задачи, которую хотите решить. и соответствуют номерам рядом с x , b — y , c — z , d . числа справа, а индексы сообщают нам номер строки. Обратите внимание, что наш калькулятор правила Крамера принимает только линейные уравнения . Это означает, что у нас не может быть, например, квадратного, или выражения с переменной под квадратным корнем.
Это означает, что у нас не может быть, например, квадратного, или выражения с переменной под квадратным корнем.
Обратите внимание, что эти коэффициенты также находятся в нашей расширенной матрице коэффициентов . На самом деле достаточно скопировать их в калькулятор правила Крамера. Например, в первой строке матрицы есть числа 1 , 1 , 1 и 26 . Соответствует первому уравнению , коэффициенты которого обозначены индексом ₁ . Следовательно, имеем:
а₁ = 1 , b₁ = 1 , c₁ = 1 , d₁ = 26 .
Точно так же две другие строки дают нам:
a₂ = 0 , b₂ = 1 , c₂ = -2 , d₂ = 6 ; и
a₃ = 2 , b₃ = 0 , c₃ = -1 , d₃ = 12 .
Как только вы введете все эти данные в калькулятор правила Крамера, он должен выдать значения четырех определителей, а затем решение системы . Посмотрим, как это выяснилось.
Посмотрим, как это выяснилось.
Как мы упоминали в предыдущем разделе, правило Крамера для систем 2×2 и 3×3 означает, что мы должны вычислить определители нескольких матриц . Первый, так называемый основной , представляет собой просто матрицу коэффициентов, которую мы определили во втором разделе:
| . | ⌈ | 1 | 1 | 1 | ⌉ | |
| Вт | = | | | 0 | 1 | -2 | ~ |
| ⌊ | 2 | 0 | -1 | ⌋ |
Чтобы построить остальные три, нам нужно заменить один столбец этой матрицы на четвертый дополнительный столбец расширенной матрицы коэффициентов , который в нашем случае имеет номера 26 , 6 и 12 . Чтобы получить
Чтобы получить Wₓ , матрицу x , мы подставляем эти числа вместо столбца, соответствующего переменной x , а именно первого:
| ⌈ | 26 | 1 | 1 | ⌉ | ||
| Втₓ | = | | | 6 | 1 | -2 | ~ |
| ⌊ | 12 | 0 | -1 | ⌋ |
Аналогично получаем
| ⌈ | 1 | 26 | 1 | ⌉ | ||
| Втᵧ | = | | | 0 | 6 | -2 | ~ |
| ⌊ | 2 | 12 | -1 | ⌋ |
| ⌈ | 1 | 1 | 26 | ⌉ | ||
| Ш З | = | | | 0 | 1 | 6 | ~ |
| ⌊ | 2 | 0 | 12 | ⌋ |
Все, что нам нужно сделать, это использовать формулу определителя из раздела выше для всех четырех матриц:
|W| = 1*1*(-1) + 1*(-2)*2 + 1*0*0 - 1*1*2 - 1*0*(-1) - 1*(-2)*0 = - 7 ,
|Втₓ| = 26*1*(-1) + 1*(-2)*12 + 1*6*0 - 1*1*26 - 1*6*(-1) - 26*(-2)*0 = - 56 ,
|Wᵧ| = 1*26*(-1) + 26*(-2)*2 + 1*0*12 - 1*6*2 - 26*0*(-1) - 1*(-2)*12 = - 98 ,
|W z | = 1 1 12 + 1 6 2 + 26 0 0 - 26 1 2 - 1 0 12 - 1 6 0 = -28 .

Наконец, мы используем правило Крамера для систем 3x3 и получаем решение :
x = |Wₓ| / |В| = -56 / (-7) = 8 ,
y = |Wᵧ| / |В| = -98 / (-7) = 14 ,
z = |W z | / |В| = -28 / (-7) = 4 .
Возвращаясь к задаче, с которой мы начали, это означает, что велосипед равен 8 , автомобиль равен 14 , а самолет равен 4 .
Вам хочется отправиться в путешествие, не так ли?
Cramers Calculator
Δ = 12
Δ x = -80
Δ y = 100
Δ z = -8
Δ z = -8
X = -6,6667
Y = 8,3333
Z = -0,6667
ВЫЧИСЛИТЬ
сообщить об этом объявлении
ВЫЧИСЛИТЬ
сообщить об этом объявлении
ВЫЧИСЛИТЬ
9002 Понятие о матрице почти идентичных раз появилось в Японии и в матрице2.
 Секи впервые написал об этом в 1683 году в своем «Методе решения скрытых проблем» . Секи разработал шаблон для определителей для $2 \times 2$, $3 \times 3$,
Матрицы $4\times 4$ и $5\times 5$ и использовали их для решения уравнений. В том же году Г. Лейбниц написал о методе решения
система уравнений. Этот метод известен как Правило Крамера . Определитель квадратной матрицы $A$ — это уникальное действительное число, являющееся атрибутом матрицы $A$. Определитель матрицы $A$ обозначается через $det(A)$ или $|A|$.
Секи впервые написал об этом в 1683 году в своем «Методе решения скрытых проблем» . Секи разработал шаблон для определителей для $2 \times 2$, $3 \times 3$,
Матрицы $4\times 4$ и $5\times 5$ и использовали их для решения уравнений. В том же году Г. Лейбниц написал о методе решения
система уравнений. Этот метод известен как Правило Крамера . Определитель квадратной матрицы $A$ — это уникальное действительное число, являющееся атрибутом матрицы $A$. Определитель матрицы $A$ обозначается через $det(A)$ или $|A|$.Правило Крамера — это формула решения системы линейных уравнений. Он выводит решение в терминах определителей матрицы и матриц, полученных из нее, заменой одного столбца вектором-столбцом правых частей уравнений. Оно названо Габриэлем Крамером (1704–1752), а правило для произвольного числа неизвестных опубликовано в статье [Cramer, G. (1750), 9{th}$ столбца основной матрицы вектором правых частей уравнений и вычислить его определитель $D_x$.
Если главный определитель равен нулю, то система линейных уравнений либо несовместна, либо имеет бесконечно много решений.
: Рассмотрим систему уравнений:
$$\begin{align} &a_1x+b_1y=\color{blue}{c_1}\\
&a_2x+b_2y=\color{синий}{c_2}\end{align} $$
Главный определитель равен $$D=\left|
\begin{массив}{cc}
а_1 и б_1 \\
а_2 &b_2 \\
\конец{массив}
\право|$$
а два других определителя равны
$$D_x=\влево|
\begin{массив}{cc}
\цвет{синий}{c_1} и b_1 \\
\цвет{синий}{c_2} &b_2 \\
\конец{массив}
\right|\quad\mbox{and}\quad D_y=\left|
\begin{массив}{cc}
a_1 & \color{синий}{c_1} \\
a_2 &\color{синий}{c_2} \\
\конец{массив}
\право|$$
С помощью определителей $x$ и $y$ можно найти по правилу Крамера как
$$x=\frac{D_x}{D}=
\ гидроразрыва {\ влево |
\begin{массив}{cc}
\цвет{синий}{c_1} и b_1 \\
\цвет{синий}{c_2} &b_2 \\
\конец{массив}
\право|}{\лево|
\begin{массив}{cc}
а_1 и б_1 \\
а_2 &b_2 \\
\конец{массив}
\right|}\quad\mbox{and}\quad y=\frac{D_y}{D}=\frac{\left|
\begin{массив}{cc}
a_1 & \color{синий}{c_1} \\
a_2 &\color{синий}{c_2} \\
\конец{массив}
\право|}{\лево|
\begin{массив}{cc}
а_1 и б_1 \\
а_2 &b_2 \\
\конец{массив}
\право|}$$
Если каждый определитель равен нулю, система непротиворечива, а уравнения зависимы. Система имеет бесконечно много решений. Если $D=0$ и $D_x$ или $D_y$ не равно нулю, система несовместна и не имеет решения.
Система имеет бесконечно много решений. Если $D=0$ и $D_x$ или $D_y$ не равно нулю, система несовместна и не имеет решения.
: Рассмотрим систему уравнений:
$$\begin{align} &a_1x+b_1y+c_1z=\color{синий}{d_1}\\
&a_2x+b_2y+c_2z=\цвет{синий}{d_2}\\
&a_3x+b_3y+c_3z=\цвет{синий}{d_3}\\
\end{выравнивание} $$
Главный определитель равен $$D=\left|
\begin{массив}{ccc}
a_1 & b_1 &c_1\\
а_2 &b_2 &c_2\\
а_3 &b_3 &c_3\\
\конец{массив}
\право|$$
а остальные три определителя равны
$$D_x=\влево|
\begin{массив}{ccc}
\цвет{синий}{d_1} & b_1 &c_1\\
\цвет{синий}{d_2} &b_2 &c_2\\
\цвет{синий}{d_3} &b_3 &c_3\\
\конец{массив}
\право|\quad D_y=\лево|
\begin{массив}{ccc}
a_1 & \color{синий}{d_1} &c_1\\
a_2 &\color{синий}{d_2} &c_2\\
a_3 &\color{синий}{d_3} &c_3\\
\конец{массив}
\right|\quad\mbox{and}\quad D_z=\left|
\begin{массив}{ccc}
a_1 & b_1 &\color{синий}{d_1}\\
a_2 &b_2 &\color{синий}{d_2}\\
a_3 &b_3 &\color{синий}{d_3}\\
\конец{массив}
\право|$$
Решение системы трех уравнений есть
$$x=\frac{D_x}{D},\quad y=\frac{D_y}{D},\quad \mbox{and}\quad z=\frac{D_z}{D}$$
Например, решим систему линейных уравнений:
$$\begin{align} &3x+4y+5z=10\\
&5x+6y+7z=12\\
&4x+5y+0z=15\\
\end{выравнивание} $$
Сначала вычислим главный определитель:
$$\begin{align} D&=\left|
\begin{массив}{ccc}
3 и 4 и 5\\
5 &6 &7\\
4 &5 &0\\
\конец{массив}
\right|\&=\left|\begin{массив}{ccc|cc}
3 и 4 и 5&3 и 4 \\
5 и 6 и 7 и 5 и 6 \\
4 & 5 & 0 & 4 & 5 \\
\конец{массив}
\right. =3\cdot6\cdot0+4\cdot7\cdot4+5\cdot5\cdot 5-5\cdot6\cdot4-3\cdot7\cdot5-4\cdot6\cdot0=12\end{align}$$
Сходным образом,
$$ D_x=\left|
\begin{массив}{ccc}
\цвет{синий}{10} & 4 &5\\
\цвет{синий}{12} &6 &7\\
\цвет{синий}{15} &5 &0\\
\конец{массив}
\right|=-80,\quad D_y=\left|
\begin{массив}{ccc}
3 & \цвет{синий}{10} &5\\
5 &\цвет{синий}{12} &7\\
4 &\цвет{синий}{15} &0\\
\конец{массив}
\right|=100,\quad D_z=\left|
\begin{массив}{ccc}
3 и 4 &\цвет{синий}{10}\\
5 &6 &\цвет{синий}{12}\\
4 &5 &\цвет{синий}{15}\\
\конец{массив}
\право|=-8$$
=3\cdot6\cdot0+4\cdot7\cdot4+5\cdot5\cdot 5-5\cdot6\cdot4-3\cdot7\cdot5-4\cdot6\cdot0=12\end{align}$$
Сходным образом,
$$ D_x=\left|
\begin{массив}{ccc}
\цвет{синий}{10} & 4 &5\\
\цвет{синий}{12} &6 &7\\
\цвет{синий}{15} &5 &0\\
\конец{массив}
\right|=-80,\quad D_y=\left|
\begin{массив}{ccc}
3 & \цвет{синий}{10} &5\\
5 &\цвет{синий}{12} &7\\
4 &\цвет{синий}{15} &0\\
\конец{массив}
\right|=100,\quad D_z=\left|
\begin{массив}{ccc}
3 и 4 &\цвет{синий}{10}\\
5 &6 &\цвет{синий}{12}\\
4 &5 &\цвет{синий}{15}\\
\конец{массив}
\право|=-8$$
Практические задачи по правилу Крамера
Практическая задача 1:
Используя правило Крамера, решите систему уравнений
$$\begin{align} &2x+4y-z=-1\\
&х+3у+7г=2\\
&х+2у+г=-5\\
\end{выравнивание} $$ Практическая задача 2:
Используя правило Крамера, разделите инвестиции $\$20 500$ между облигацией с годовой доходностью $10\%$ и облигацией с годовой доходностью $8\%$ так, чтобы совокупный годовой доход от инвестиций составил $8,5. \%$.
\%$.
Калькулятор правила Крамерса, формула, примеры расчетов и практические задачи будут очень полезны учащимся начальной школы K-12 для понимания концепции решения систем линейных уравнений. Эта концепция используется практически во всех областях науки, поэтому она будет полезна при решении более сложных задач.
Калькулятор правила Крамера - Система уравнений 2 и 3
Сегодня мы поделимся еще одним простым, но мощным методом анализа цепей, известным как « Правило Крамера ».
- Анализ цепи SUPERMESH | Шаг за шагом с решенным примером
Обновление: Мы добавили онлайн-калькулятор правил Крамера, где вы можете решить систему двух уравнений, а также систему трех уравнений. Проверьте оба калькулятора правил Крамера в обоих разделах поста. Спасибо
Ниже приведено пошаговое руководство с примерами решения, в котором подробно рассматривается, как решить сложную электрическую цепь и сеть по правилу Крамера.
Калькулятор правила Крамера 2 x 2 (2 системы уравнений):
х + у = |
х + у = |
х = |
у = |
Пример 1:
(В нашем случае неизвестными значениями являются два тока: i 1 и i 2 ) по правилу Крамера. Теперь давайте начнем.
Как показано ниже, это простая электрическая цепь, и мы собираемся решить ее по правилу Крамера.
Правило Крамера для анализа линейных цепей | 2 переменные (2×2) Пример решения.
Решение:
Во-первых, переставьте схему с соответствующими метками (поскольку два резистора по 5 Ом соединены последовательно, поэтому мы заменим его на 10 Ом.
Примените анализ сетки и упростите по правилу Крамера, чтобы найти неизвестные значения токов и 1 и и 2 .Теперь напишем уравнения КВЛ неизвестных для данной схемы
Применить KVL на сетке (1).
6 = 14 i 1 + 10( i 1 – i 2 )
6 = 24 i 1 – 10 i 2 ….. → Уравнение (1)
Также примените KVL к сетке (2).
-5 = 10 i 2 + 10( и 2 – и 1 )
-5 = – 10 i 1 + 20 i 2 ….. → Уравнение (2)
Здесь мы получили два уравнения, т.е.
24 i 1 – 10 i 2 = 6
– 10 и 1 + 20 и 2 = -5
Теперь решим эти два уравнения по правилу Крамера, чтобы найти неизвестные значения (токов), которые равны i 1 и i 2 .
Решение по правилу Крамера:
Шаг 1:
Прежде всего, запишите приведенные выше уравнения в матричной форме. то есть
Шаг 2:
Теперь напишите матрицу коэффициентов приведенных выше уравнений и назовите ее ∆. Убедитесь, что он квадратный, т.е. количество строк x количество столбцов. В приведенном выше случае он имеет 2 строки и 2 столбца.
Шаг 3:
Теперь найдите определитель |∆| матрицы коэффициентов ∆ следующим методом. (Приведенный ниже рисунок поможет вам в этом.)
Нажмите на картинку, чтобы увеличить
Нахождение матрицы коэффициентов ∆ по правилу Крамера. Простое объяснение.В соответствии с приведенным выше рис. последний шаг будет таким.
Шаг 4:
Теперь найдите определитель коэффициента Δ 1 тем же способом, что и выше, но замените первый столбец Δ на «Столбец ответов» (Если вы не уловили суть столбца ответов, см. рис. на шаге 2 выше или проверьте инфографику на в конце примера просто обратитесь ко второму примеру ниже, где мы сделали то же самое, чтобы найти Δ 1 ), то есть
рис. на шаге 2 выше или проверьте инфографику на в конце примера просто обратитесь ко второму примеру ниже, где мы сделали то же самое, чтобы найти Δ 1 ), то есть
Шаг 5:
Теперь найдите определитель коэффициента Δ 2 , просто замените второй столбец на «Столбец ответов», то есть
.Шаг 6:
As Cramer's rule tells that i 1 = Δ 1 / Δ and i 2 = Δ 2 / Δ .
Теперь найди i 1 и i 2 по правилу Крамера.
i 1 = 0,184,2 А или 184,2 мА
А,
i 2 = 0,157,9 А или 157,9 мА
Ниже представлена сводка инфографики по правилу Крамера для определения двух переменных или неизвестных значений.
Правило Крамера: простые шаги, инфографика, диаграммаХорошо, это было легко… Теперь, как насчет 3 переменных…. Попробуем решить линейные уравнения с тремя переменными с помощью правила Крамера.
Нахождение трех переменных по правилу Крамера: (In our case, these unknown values are three currents which are i 1 , i 2 and i 3 ) by Правило Крамера. Теперь давайте начнем.
Теперь давайте начнем.
Калькулятор правила Крамера 3 x 3 (3 системы уравнений):
х + у + z = |
х + у + z = |
х + у + z = |
х = |
у = |
г = |
Пример 2:
Используйте анализ сетки для определения трех токов сетки в схеме ниже. Используйте правило Крамера для упрощения.
Найдите три неизвестных значения токов по правилу Крамера. Прежде всего, примените KVL к каждому мешу один за другим и напишите его уравнения.
-7+1( i 1 – i 2 ) +6+2( i 1 – i 3 ) = 0
1( i 2 - I 1 ) + 2 I 2 + 3 ( I 2 - I 3 ) = 0
9007 2 ( 3 ) = 0, 9007 2 ( 3 ). 1 ) – 6+3( и 3 – и 2 ) + 1 I 3 = 0Упрощение,
3 I 1 - I 2 - 2 I 9078 2 - 2 I 3 36363 3 2 - 2 I 3 . 1)
– i 1 + 6 i 2 – 3 i 3 = 0 … Eq….. (2)
-2 i 1 – 3 i 2 + 6 i 3 = 6 … Уравнение…. . (3)
. (3)
Теперь запишите приведенные выше уравнения в матричной форме.
3 I 1 - I 2 - 2 I 3 = 1
- I 1 + 6 7 I 1 + 6 7 I 1 + 6 7 I 1 + 6 I 1 + 700077 7 1 + 7000777 1 . = 0
-2 i 1 – 3 i 2 + 6 i 3 = 6
Now, we will find the coefficient determinant of ∆. Как мы это сделаем? Просто проверьте рисунок ниже для лучшего объяснения.
Щелкните изображение, чтобы увеличить его.
Итак, полный шаг показан ниже.
∆ = +3 (6 x 6) – (- 3 x –3) – (-1 (-1 x 6)-(-2 x –3) + (-2 (-1 x –3) – ( -2 x 6)
∆ = 81 -12 -30 = 39
Теперь найдите ∆ 1 так же, как описано выше, но просто замените первый столбец матрицы на "Столбец ответов". Подробности см. на рис., показанном ниже.
Подробности см. на рис., показанном ниже.
Итак, вот полный шаг, чтобы найти ∆ 1 . Здесь мы заменили "Синих парней" в первом столбце на "Черных парней" 🙂
= +1(36-9) – (–1[0+18]) –2(0-36)
= 27 + 18 + 72
∆ 1 = 117
Снова найти ∆ 2 тем же методом, который описан ранее. Просто замените второй столбец матрицы на «Столбец ответов», т.е. замените «Красных парней» в центральном столбце на «Черных парней», как показано ниже.
= +3 (0 +18) -1[(-6)-(+6)] –2(-6-0)
= 54+12+12 = 78
∆ 2 = 78
Наконец, найдите последнее ∆ 3 . Просто замените третий столбец на «Столбец ответов», то есть замените «Зеленых парней в третьем столбце» на «Черных парней», как показано ниже.
= +3 (6 х 6) – (-3 х 0) – [-1(-1 х 6) – (-2 х 0)] + [1(-1) х (-3) – (- 2) x (6)]
= 108 + 6 + 15
∆ 3 = 117
Сейчас, решайте и найдите неизвестные значения тока, т. е. I 1 , I 1 , I 62 1 , I 2 1 , I 2 1 , I 9 1 , I 9 2 и я 3 .
е. I 1 , I 1 , I 62 1 , I 2 1 , I 2 1 , I 9 1 , I 9 2 и я 3 .
As, Cramer's rule says that, variables i.e. i 1 = ∆1/∆ 1 , i 2 = ∆/∆ 2 and i 3 = ∆/∆ 3 .
Therefore,
i 1 = ∆1/∆ 1
= 117/39
i 1 = 3A
And i 2 ,
i 2 = = ∆/∆ 2
= 78/39
i 2 = 2А
И, наконец, i 3 ;
i 3 = ∆/∆ 3
= 117/39
i 3 = 3А.
Надеюсь, вы хорошо поняли правило Крамера и вам понравилось пошаговое руководство. Пожалуйста, не забудьте поделиться с друзьями. Кроме того, введите свой адрес электронной почты в поле ниже, чтобы подписаться. Итак, мы вышлем вам больше руководств, подобных приведенному выше. Спасибо.
Похожие посты и инструменты для анализа цепей:
- Теорема Нортона. Простая пошаговая процедура с примером (иллюстрации) 905:00
- Теорема Тевенина. Простая пошаговая процедура с примером (иллюстрации)
- Калькуляторы для электротехники и электроники онлайн
- 10+ инструментов проектирования и моделирования для инженеров-электриков/электронщиков онлайн
- Проектирование печатных плат: как спроектировать печатную плату (пошаговые и графические изображения)
- 15 обязательных приложений для Android для инженеров-электриков и электронщиков и студентов
- Анализ схемы СУПЕРУЗЛА | Шаг за шагом с решенным примером 905:00
- Анализ цепей SUPERMESH | Шаг за шагом с решенным примером
- Электротехника и электроника Eng Калькуляторы
Решение уравнений в Excel с использованием метода итераций Крамера и Гаусса
В Excel имеется обширный инструментарий для решения различных типов уравнений различными методами. Рассмотрим некоторые решения на примерах.
Рассмотрим некоторые решения на примерах.
Решение уравнений методом проб и ошибок в Excel
Инструмент "Поиск цели" используется в ситуации, когда известен результат, но неизвестны аргументы. Excel подбирает значения до тех пор, пока вычисление не даст желаемую сумму.
Путь к команде: «ДАННЫЕ» — «Инструменты данных» — «Анализ «что если»» — «Поиск цели».
Рассмотрим, например, решение квадратного уравнения х 2 + 3х + 2 = 0. Порядок нахождения корня в Excel:
- Вводим в ячейку В2 формулу нахождения значения функция. Применяем ссылку на ячейку B1 в качестве аргумента.
- Открыть меню инструмента "Поиск цели". В поле «Установить ячейку» есть ссылка на ячейку B2, где находится формула. Введите 0 в поле «К значению». Это значение, которое вы хотите получить. В столбце «По смене ячейки» стоит B1. Здесь должен отображаться выбранный параметр. 905:00
- После нажатия OK отображается результат выбора.
 Если вы хотите сохранить его, нажмите OK еще раз. В противном случае нажмите «Отмена».
Если вы хотите сохранить его, нажмите OK еще раз. В противном случае нажмите «Отмена».
Программа использует циклический процесс для поиска параметра. Вам нужно ввести параметры Excel, чтобы изменить количество итераций и ошибку.
Установить максимальное количество итераций и относительную погрешность на вкладке "Формулы". Установите галочку в поле, чтобы включить итерационные вычисления.
Как решить систему уравнений матричным методом в Excel?
Дана система уравнений:
- Вносим значения элементов в ячейки Excel в виде таблицы.
- Найдем обратную матрицу. Выделите диапазон B6:E9, куда в дальнейшем будут помещены элементы матрицы (ориентируемся на количество строк и столбцов в исходной матрице). Откройте список функций (fx). В категории «Математика и триггер» мы находим функцию MINVERS. Аргумент представляет собой массив ячеек с элементами исходной матрицы.
- Нажмите OK, и в левом верхнем углу диапазона появится значение.
 Последовательно нажмите кнопку F2 и Ctrl+Shift+Enter.
Последовательно нажмите кнопку F2 и Ctrl+Shift+Enter. - Умножаем обратную матрицу Ах -1х на матрицу В (только в таком порядке умножения!). Выделяем диапазон h2:h5, где впоследствии появятся элементы получившейся матрицы (ориентируемся на количество строк и столбцов матрицы B). Откройте диалоговое окно математической функции МУМНОЖ. Первый диапазон — это обратная матрица. Вторая – матрица B. 905:00
- Закройте окно с аргументами функции, нажав кнопку ОК. Последовательно нажимайте кнопку F2 и комбинацию Ctrl+Shift+Enter.
Получены корни уравнений.
Решение системы уравнений методом Крамера в Excel
Возьмем систему уравнений из предыдущего примера:
Вычислим определители матриц, полученных заменой одного столбца в матрице A на столбец матрицы B. И она будет решена методом Крамера.
Используйте функцию MDETERM для вычисления определителей. Аргумент представляет собой диапазон с соответствующей матрицей.
Вычислим также определитель матрицы A (массив — это диапазон матрицы A).
Определитель системы больше 0, и решение можно найти по формуле Крамера (D x / |A|).
Для расчета Х 1 : =K2/$K$1, где K2 равно D1. Для расчета Х 2 : =K3/$K$1 и т.д. Получаем корни уравнений:
Решение систем уравнений методом Гаусса в Excel
Для примера возьмем простейшую систему уравнений:
3а + 2в – 5с = -1
2а – в – 3с = 13
а + 2в – с = 9
Запишем коэффициенты в матрицу А. И запишем постоянный член в матрицу В.
Для наглядности свободные члены выберем заливкой. Вам нужно поменять местами строки, если в первой ячейке матрицы A было 0, чтобы там было значение, отличное от 0.
- Присвоим 0 всем коэффициентам матрицы A, кроме первого уравнения. Копируем значения первой строки двух матриц в ячейки B6:E6. В ячейку B7 вводим формулу:
Затем выберите диапазон B7:E7. Нажмите F2 и нажмите Ctrl + Shift + Enter. Мы вычли из второй строки первую, которая умножается на отношение первых элементов второго и первого уравнения.

- Скопируйте введенную формулу в строку 7. Таким образом, мы избавились от коэффициентов перед A. Осталось только первое уравнение. 905:00
- Приводим к 0 все коэффициенты при B в третьем и четвертом уравнениях. Копируем строки 5 и 6 (только значения). Затем переносим их ниже в строки 9 и 10. Эти данные должны остаться без изменений. Затем вводим формулу массива в ячейку А11
- Прямой прогон выполнен по методу Гаусса. В обратном порядке начинаем прогон с последней строки получившейся матрицы. Все элементы этой строки нужно разделить на коэффициент C. В строку вводим формулу массива:
- В строке 15: из второй строки вычитаем третью, умноженную на коэффициент С из второй строки В строке 14: из первой строки вычитаем вторую и третью, умноженные на соответствующие коэффициенты В последнем столбце новой матрицы мы получаем корни уравнения.
Примеры решения уравнений методом итерации в Excel
Расчеты в рабочей книге должны быть настроены следующим образом:
Это можно сделать на вкладке «Формулы» в «Параметры Excel». Найдем корень уравнения х – х 3 + 1 = 0 (а = 1, b = 2) итерацией по циклическим ссылкам. Формула:
Найдем корень уравнения х – х 3 + 1 = 0 (а = 1, b = 2) итерацией по циклическим ссылкам. Формула:
Х n+1 = X n – F (X n ) / M, n = 0, 1, 2, … .
M — максимальное значение производной по модулю. Выполняем вычисления, чтобы найти M:
f’ (1) = -2 * f’ (2) = -11.
Полученное значение меньше 0. Следовательно, функция будет иметь обратный знак: f(х) = -х + х 3 – 1. М = 11.
Вводим в ячейку A1 значение: a =1. Точность - три десятичных знака. Затем вводим формулу для вычисления текущего значения x в соседней ячейке (B1):
Мы контролируем значение f(x) в ячейке C1 по формуле:
Скачать решения уравнений в Excel
Корень уравнения равен 1. Вводим значение 2 в ячейку A1. Получаем тот же результат. В данном интервале имеется только один корень.
3.5 Детерминанты и правило Крамера – Колледжская алгебра для управленческих наук
[1]
Мы научились решать системы уравнений с двумя переменными и тремя переменными, а также несколькими методами: подстановкой, сложением, методом исключения Гаусса, использованием обратной матрицы и построением графика. Некоторые из этих методов легче применять, чем другие, и они более подходят в определенных ситуациях. В этом разделе мы изучим еще две стратегии решения систем уравнений.
Некоторые из этих методов легче применять, чем другие, и они более подходят в определенных ситуациях. В этом разделе мы изучим еще две стратегии решения систем уравнений.
Вычисление определителя матрицы 2×2
Определитель — это действительное число, которое может быть очень полезно в математике, поскольку имеет множество применений, например, для вычисления площади, объема и других величин. Здесь мы будем использовать определители, чтобы определить, является ли матрица обратимой, используя элементы квадратной матрицы, чтобы определить, существует ли решение системы уравнений. Однако, возможно, одним из наиболее интересных приложений является их использование в криптографии. Защищенные сигналы или сообщения иногда отправляются закодированными в матрице. Данные можно расшифровать только с помощью обратимой матрицы и определителя. Для наших целей мы сосредоточимся на определителе как признаке обратимости матрицы. Вычисление определителя матрицы включает в себя следование определенным шаблонам, описанным в этом разделе.
Определитель матрицы 2 2, заданный
, определяется как:
det
Обратите внимание, что для определителей мы используем прямые вертикальные линии. Другими словами, дет.
Выглядит знакомо? Должно. Помните, что это был знаменатель в скаляре, который мы умножаем на матрицу 2 2 с переключенными диагоналями и противоположными диагоналями, чтобы создать обратную. Таким образом, обратная матрица 2 2, как показано выше, будет:
.
Найти определитель данной матрицы
det
Использование правила Крамера для решения системы двух уравнений с двумя переменными
Теперь мы представим последний метод решения систем уравнений, использующий определители. Этот метод, известный как правило Крамера, восходит к середине 18 века и назван в честь его новатора, швейцарского математика Габриэля Крамера (1704–1752), который представил его в 1750 году. системы с любым числом неизвестных при условии, что у нас есть такое же количество уравнений, что и неизвестных.
Правило Крамера даст нам единственное решение системы уравнений, если она существует. Однако, если система не имеет решения или имеет бесконечное число решений, на это будет указывать определитель . Несогласованные решения имеют по крайней мере один определитель числителя, отличный от нуля. Зависимые решения имеют ноль в качестве определителя в обоих числителях. Для нахождения общего решения необходимо использовать другой метод.
Чтобы понять, как и почему работает правило Крамера, мы направим вас к исходному материалу в OpenStax College Algebra.
Короче говоря, правило Крамера начинается с системы уравнений, например:
, и мы можем показать, что
Обратите внимание, что знаменатель для обоих и является определителем матрицы коэффициентов.
Мы можем использовать эти формулы для решения, но правило Крамера также вводит новое обозначение:
- : определитель матрицы коэффициентов
- : определитель матрицы, созданной матрицей коэффициентов с заменой -коэффициента константами 905:00
- : определитель матрицы, созданной матрицей коэффициентов с заменой -коэффициента константами
Обратите внимание, что ключом к правилу Крамера является замена интересующего столбца переменных столбцом констант и вычисление определителей. Затем мы можем выразить и как:
Затем мы можем выразить и как:
Правило Крамера — это метод, использующий определители для решения систем уравнений, в которых число уравнений равно числу переменных.
Рассмотрим систему двух линейных уравнений с двумя переменными.
Решение с использованием правила Крамера дается как: Если мы ищем для , столбец заменяется постоянным столбцом.
Решите следующую систему, используя правило Крамера
Найти
Найти
Найти
Решение (2,-3).
Используйте правило Крамера, чтобы решить систему уравнений.
Вычисление определителя матрицы
Найти определитель матрицы несложно, но найти определитель матрицы сложнее. Один из методов состоит в том, чтобы дополнить матрицу повторением первых двух столбцов, получив матрицу. Затем мы вычисляем сумму произведений записей вниз по каждой из трех диагоналей (слева вверху справа внизу) и вычитаем произведения записей вверх по каждой из трех противоположных диагоналей (слева внизу справа вверху). Это легче понять с визуальным и пример.
Это легче понять с визуальным и пример.
Найдите определитель матрицы.
Шаг 1: Дополнить первыми двумя столбцами:
Шаг 2: От верхнего левого угла к нижнему правому: Умножьте числа по первой диагонали. , затем начните с и умножьте слева направо по диагонали, а затем . Добавьте эти три продукта.
Шаг 3: Теперь сверху справа: умножьте записи по обратной диагонали. , затем начните с и умножьте справа налево по диагонали, а затем . Добавьте эти три продукта и вычтите это значение из значения на шаге 2.
Алгебра выглядит следующим образом:
Найдите определитель матрицы:
Дополните матрицу первыми двумя столбцами и следуйте формуле. Таким образом,
Детерминанты также можно найти с помощью технологий. После того, как матрица введена в ваш калькулятор. Переход к МАТРИЦА – МАТЕМАТИКА и det и вызов рассматриваемой матрицы предоставит определитель для матрицы. В Excel =mdeterm также найдет определитель матрицы. Методы, упомянутые в этом разделе, работают только для указанного размера. Для больших матриц рекомендуется использовать калькулятор, Excel или другую программу.
В Excel =mdeterm также найдет определитель матрицы. Методы, упомянутые в этом разделе, работают только для указанного размера. Для больших матриц рекомендуется использовать калькулятор, Excel или другую программу.
Найдите определитель матрицы .
от
Использование правила Крамера для решения системы трех уравнений с тремя переменными
Теперь, когда мы можем найти определитель матрицы, мы можем применить правило Крамера для решения системы из трех уравнений и трех неизвестных. Правило Крамера для систем следует той же схеме, что и для систем. Однако требуются дополнительные расчеты.
Рассмотрим систему:
где:
Если мы записываем определитель, мы заменяем столбец постоянным столбцом. Если мы записываем определитель, мы заменяем столбец постоянным столбцом. Если мы записываем определитель, мы заменяем столбец постоянным столбцом. Всегда проверяйте ответ.
Решите следующую систему, используя правило Крамера.
Используйте правило Крамера.
Затем
Решение (1,3,-2).
Используйте правило Крамера для решения системы:
а. Решите систему уравнений (если возможно), используя правило Крамера.
Начнем с нахождения определителей:
Теперь мы знаем, что оно либо зависимо, либо несовместно. Давайте посмотрим на один из других определителей.
Поскольку -16 \neq 0, мы имеем противоречивое решение.
б. Решите следующую систему уравнений (если возможно, или дайте общее решение, если зависит).
Найдем D с помощью технологии, калькулятора или Excel.
Мы знаем, что это зависимая или непоследовательная система. Мы могли бы найти все три других определителя, чтобы увидеть, является ли он зависимым, и если да, то нам пришлось бы использовать rref в калькуляторе, чтобы найти общее решение. По этой причине сейчас быстрее просто использовать rref. Существует онлайн-версия от planetcalc.
По этой причине сейчас быстрее просто использовать rref. Существует онлайн-версия от planetcalc.
Сокращенная эшелонная форма строки матрицы:
В виде уравнений это:
Таким образом, если любое действительное число, то:
Вот несколько свойств, которые могут упростить и ускорить поиск определителей.
- Если матрица имеет форму верхнего треугольника (в нижнем треугольнике под диагональю все нули), то определитель равен произведению элементов по главной диагонали.
- При перестановке двух строк определитель меняет знак.
- Если две строки или два столбца идентичны, определитель равен нулю. 905:00
- Если матрица содержит строку или столбец из нулей, определитель равен 0.
- Определитель обратной матрицы равен обратной величине определителя матрицы .
- Если какая-либо строка или столбец умножается на константу, определитель умножается на тот же коэффициент.
Media Attributions
- clipartmax.com/max/m2i8d3Z5N4i8b1m2/"> takenote находится под лицензией Public Domain
- др. по лицензии Creative Commons License 4.0 CC-BY ↵
Калькулятор системы уравнений и решение Step by Step
Калькулятор системы уравнений доступен для решения линейных уравнений из 2 и 3 линейных уравнений. уравнения.
Решить систему уравнений алгебраическим методом может быть довольно удивительно. Мы знаем, что есть 4 метода решения системы линейных уравнений. Здесь мы только решаем матричный метод с помощью калькулятора системы уравнений.
Система линейных уравнений представляет собой набор линейных уравнений из 2 или более 2, обычно эти уравнения представляют собой две переменные. Решение систем линейных уравнений
Примеры:
5x+6y=3
6x+9y=12
Мы можем решить систему уравнений с помощью калькулятора системы уравнений.
Метод решения алгебраического уравнения:
Мы можем решить алгебраическое уравнение следующими основными методами:
- Графический метод 905:00
- Алгебраический метод:
Алгебраический метод:
Алгебраический метод решения линейного уравнения подразделяется на четыре основных метода:
- Метод подстановки
- Метод исключения
- Метод перекрестного умножения
- Матричный метод
Метод подстановки:
«В методе подстановки мы вычисляем значение одной переменной из одного уравнения и подставляем его в другое уравнение».
Калькулятор системы уравнений быстро находит ответ линейного уравнения. Калькулятор метода подстановки делает задачу простой и сложной для нас, и мы можем быстро найти значения «x» и «y».
Метод исключения:
В методе исключения мы делаем коэффициенты уравнения равными, а затем вычитаем их, чтобы найти ответ таких переменных, как «x» и «y». Решение системы линейных уравнений может быть легко вычислено, если мы сможем сделать коэффициент равным.
Метод перекрестного умножения:
Метод перекрестного умножения обычно используется при решении систем линейных уравнений. Метод перекрестного умножения является наиболее простым методом решения линейных уравнений. Этот метод можно использовать для решения системы линейных уравнений из 2 или 3.
Матричный метод:
Существует три основных метода решения системы линейных уравнений, когда вы решаете линейное уравнение матричным методом:
Правило Крамера:
Правило Крамера — важный метод решения систем линейных уравнений. В правилах Крамера мы используем определитель матриц. Это основная причина, по которой правило Крамера также известно как определитель матриц. .
В правилах Крамера мы используем определитель матриц. Это основная причина, по которой правило Крамера также известно как определитель матриц. .
Решение систем уравнений по правилу Крамера.
ax+by= k
cx+dy= l
$$ \left[ \begin{array}{cc|c}a & b & k\\c & d & l\\\end{array}\right] $$
Определитель в этом случае равен”
$$ D = \begin{vmatrix}a & b \\ c & d\\\end{vmatrix} $$
$$D_x = \begin{vmatrix} a & b \\c & d\\\end{vmatrix} $$
$$D_y = \begin{vmatrix} a & b \\c & d\\\end{ vmatrix} $$
Окончательные значения переменных «x» и «y», рассчитанные калькулятором системы уравнений.
$$ x = \dfrac{D_x}{D} $$
$$ y = \dfrac{D_y}{D} $$
Правило Крамера широко используется для решения системы уравнений, так как его легко найти окончательный результат переменных по правилам Крамера. Калькулятор системы уравнений разрабатывает правильное решение линейных уравнений.
Метод обратной матрицы:
В методе обратной матрицы мы умножаем на обратную матрицу с обеих сторон уравнения. Это простая система уравнений с обратной матрицей. Возможно, вы столкнетесь с трудностями при решении систем уравнений. Вы можете быть поражены, увидев стиль работы калькулятора системы линейных уравнений.
Это простая система уравнений с обратной матрицей. Возможно, вы столкнетесь с трудностями при решении систем уравнений. Вы можете быть поражены, увидев стиль работы калькулятора системы линейных уравнений.
Рассмотрим систему линейных уравнений, представленную следующим образом:
ax+by=L
cx+dy=K 91 \begin{bmatrix}L\\K \\\end{bmatrix} $$
Нам нужно только вставить значения коэффициентов и переменных, чтобы найти их при использовании калькулятора системы уравнений.
Исключение Гаусса-Жордана:
Рассматривайте это как метод, который можно использовать для решения системы линейных уравнений. Мы можем найти редуцированную форму эшелона методом исключения Гаусса-Жордана.
Основные шаги, связанные с исключением Гаусса-Жордана, следующие:
- Изменить положение двух строк 905:00
- Умножить одну из строк с ненулевым скалярным значением
- Сложите и вычтите все строки
Мы можем найти уменьшенную форму эшелона с помощью калькулятора исключения Гаусса.
Мы можем представить исключение Гаусса-Жордана следующим образом:
Рассмотрим линейное уравнение:
ax+by=L
cx+dy=K
$$ \left[ \begin{array}{cc|c}a & b & L\\c & d & K\\\end{массив}\right] $$
Практические примеры:
Шаг 1:
x+3y=5
7x+9y=11
нам нужно расставить значения коэффициентов переменных «x» и «y». Постоянные значения помещаются в правую часть матрицы.
$$ \left[ \begin{array}{cc|c}1 & 3 & 5\\7 & 9 & 11\\\end{array}\right] $$
Шаг 2:
Определитель в в этом случае»
$$ D = \begin{vmatrix}1 & 3 \\7 & 9\\\end{vmatrix} = -12 $$
Шаг 3:
Нам нужно разделить значения Dx и Dy:
D_x = \begin{vmatrix}5 и 3 \\11 и 9\\\end{vmatrix} = 12
D_y = \begin{vmatrix}1 & 5 \\7 & 11\\\end{vmatrix} = -24
Шаг 4:
Окончательные значения переменных «x» и «y», рассчитанный решателем системы уравнений.
$$ x = \dfrac{D_x}{D} = \dfrac{12}{-12} = -1 $$
$$ y = \dfrac{D_y}{D} = \dfrac{-24}{- 12} = 2 $$
x=-1, y=2
Калькулятор решения уравнений - простой способ решения системы линейных уравнений всеми 3-мя известными матричными методами.
Работа калькулятора системы уравнений:
Система решателей уравнений обеспечивает решение 2-х или 3-х линейных уравнений наиболее простым и сложным способом.
Ввод:
- Вставьте коэффициент переменных и константу.
- Выберите метод решения уравнения.
- Нажмите кнопку расчета
Вывод:
Когда мы используем калькулятор системы линейных уравнений. Легко решить систему линейных уравнений.
- Окончательное отображаемое значение переменных
- Все этапы представлены различными способами
Часто задаваемые вопросы:
Зачем нужна система одновременных уравнений?
Когда нам нужно найти общее решение 2 или 3 линейных уравнений. Тогда нам нужно решить их вместе, и мы называем их одновременными уравнениями, так как они имеют общее решение. Калькулятор систем уравнений легко может найти решения одновременных уравнений.
Можете ли вы решить системное линейное уравнение без построения графика?
Да, линейное уравнение можно решить без построения графика. Существуют различные методы решения линейного уравнения, такие как замена, исключение и матричный метод решения линейного уравнения.
Как решить систему уравнений с показателями?
Вы можете решить систему уравнений с показателями, если основания двух или более показательных уравнений совпадают.
Каковы условия решения уравнения системы методом исключения?
Есть определенные условия для решения системы линейных уравнений
Запишите оба уравнения в стандартной форме
Сделайте коэффициенты одной переменной противоположными.
Добавьте уравнения, полученные в результате второго шага 2, чтобы исключить одну переменную.
Найдите оставшуюся переменную.
Подставьте решение из четвертого шага 4 в одно из исходных уравнений.
Как проще всего решить систему уравнений?
Решить систему с помощью графика — самый простой способ решить линейное уравнение.



 Несколько простых действий помогают преобразить матрицу и привести её к треугольному виду. Все комплексные числа, которые расположены на основной диагонали, перемножаются. Но при таком поиске определителя запрещено выполнять арифметические действия со строчками или столбцами без предварительного вынесения чисел как множителя/делителя. Предварительно умножают вычитаемую строку на нулевой множитель, а уже потом вычитают и складывают все элементы между собой. Конечный знак у обратной матрицы подвергают изменениям только в том случае, когда происходит перестановка столбцов или строчек.
Несколько простых действий помогают преобразить матрицу и привести её к треугольному виду. Все комплексные числа, которые расположены на основной диагонали, перемножаются. Но при таком поиске определителя запрещено выполнять арифметические действия со строчками или столбцами без предварительного вынесения чисел как множителя/делителя. Предварительно умножают вычитаемую строку на нулевой множитель, а уже потом вычитают и складывают все элементы между собой. Конечный знак у обратной матрицы подвергают изменениям только в том случае, когда происходит перестановка столбцов или строчек. В итоге через сформированную конструкцию проводятся диагональные линии. Члены матрицы, которые расположены на основной диагонали или на параллельной ей плоскости всегда записываются со знаком +, а вот элементы, лежащие на побочной диагонали, имеют знак -.
В итоге через сформированную конструкцию проводятся диагональные линии. Члены матрицы, которые расположены на основной диагонали или на параллельной ей плоскости всегда записываются со знаком +, а вот элементы, лежащие на побочной диагонали, имеют знак -.
 Процесс усвоения индивидом социального опыта, системы общественных связей и отношений называется?
Процесс усвоения индивидом социального опыта, системы общественных связей и отношений называется? Что из нижеперечисленного относится к педагогике?
Что из нижеперечисленного относится к педагогике? Какие науки изучают образование?
Какие науки изучают образование? Какая интерпретация феномена образования трактует его с точки зрения осуществления человека как телесного, душевного и духовного существа на протяжении всей его жизни в его онтогенетическом развитии в пространстве культуры и социальных отношений?
Какая интерпретация феномена образования трактует его с точки зрения осуществления человека как телесного, душевного и духовного существа на протяжении всей его жизни в его онтогенетическом развитии в пространстве культуры и социальных отношений? Укажите какие:
Укажите какие: д.)
д.)
 Совокупность
полученных на практике умений, навыков и приемов воспитания и обучения
Совокупность
полученных на практике умений, навыков и приемов воспитания и обучения Ратке
Ратке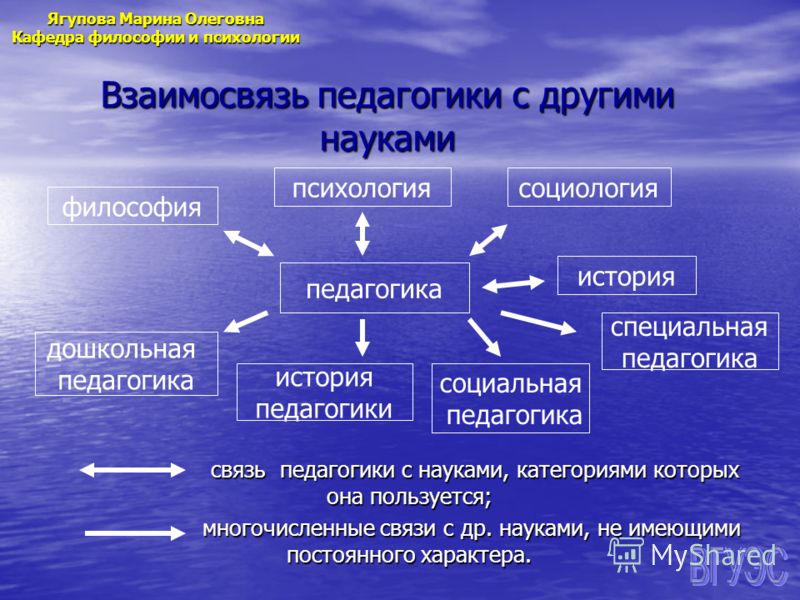 А. Коменский
А. Коменский программированного
программированного
 средства
психологии
средства
психологии  рассказ, беседа,
лекция, диспут, метод примера
рассказ, беседа,
лекция, диспут, метод примера
 словом
словом  Г. Белинский, «создает человека
природа, но развивает и образует его ___________»
Г. Белинский, «создает человека
природа, но развивает и образует его ___________» преемственные
образовательные программы и государственные образовательные стандарты различных
уровней и направленности
преемственные
образовательные программы и государственные образовательные стандарты различных
уровней и направленности в стимулировании
собственной активности воспитанников.
в стимулировании
собственной активности воспитанников.
 testent.ru
testent.ru


 B) Волевые качества. C) Образ жизни. D) Черты характера E) Нравственные качества.
B) Волевые качества. C) Образ жизни. D) Черты характера E) Нравственные качества. B) Акселерация. C) Персонализация. D) Урбанизация. E) Индивидуализация.
B) Акселерация. C) Персонализация. D) Урбанизация. E) Индивидуализация.
 B) Формирующий. C) Констатирующий. D) Лабораторный. E) Мысленный.
B) Формирующий. C) Констатирующий. D) Лабораторный. E) Мысленный.

 Оптовые цены единицы продукции равна: 5 д.е. для П1 и 4 д.е. для П2. Расход сырья на единицу продукции вида П1 и вида П2 дан в таблице.
Оптовые цены единицы продукции равна: 5 д.е. для П1 и 4 д.е. для П2. Расход сырья на единицу продукции вида П1 и вида П2 дан в таблице.



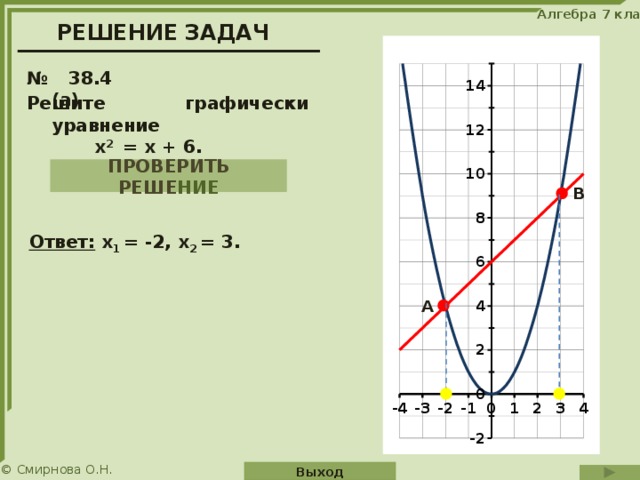 Записать задачу в стандартной форме и решить ее графическим методом.
Записать задачу в стандартной форме и решить ее графическим методом.
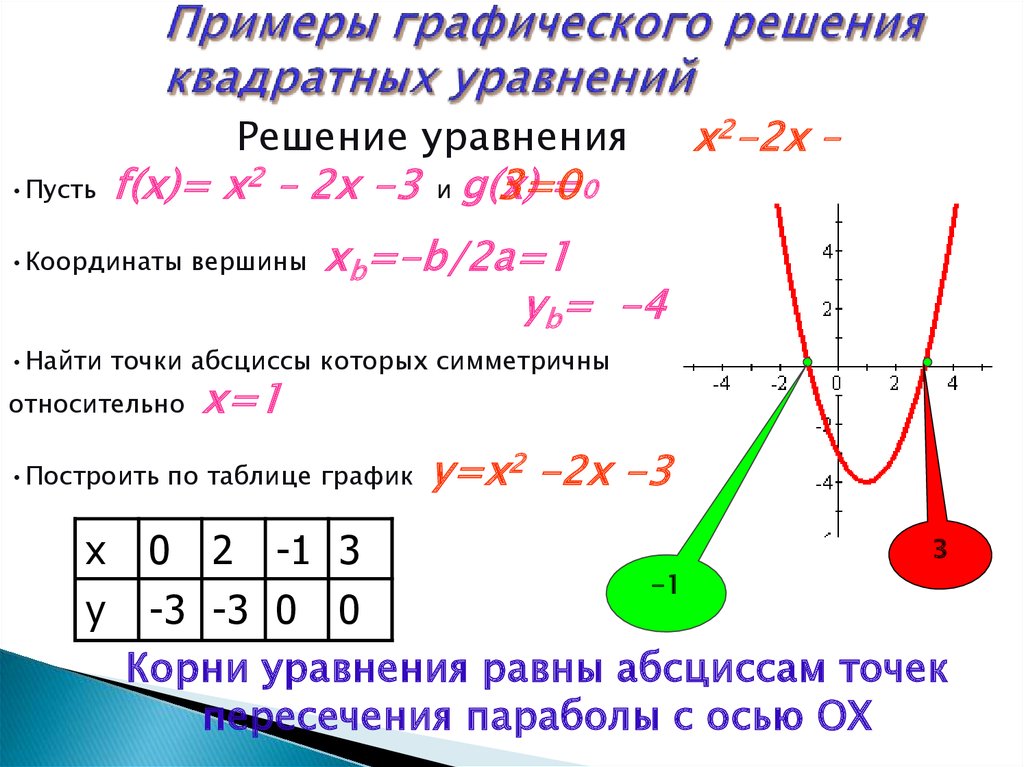

 Составить математическую модель задачи линейного программирования и найти решение геометрическим способом.
Составить математическую модель задачи линейного программирования и найти решение геометрическим способом.
 5
5
 Это представление пригодно для системы ограничений-неравенств с двумя
переменными или для систем уравнений, в которых число переменных на 2 превышает число
уравнений, то есть число свободных переменных равно двум.
Это представление пригодно для системы ограничений-неравенств с двумя
переменными или для систем уравнений, в которых число переменных на 2 превышает число
уравнений, то есть число свободных переменных равно двум. Допустим, что это пятиугольник ABCDE (рисунок внизу).
Допустим, что это пятиугольник ABCDE (рисунок внизу). Опорными обычно
называют такие прямые, которые имеют с многоугольником ABCDE хотя бы одну общую точку,
и многоугольник ABCDE целиком лежит по одну сторону от этой прямой. Как видно из
чертежа, прямая mn является опорной, так как она касается многоугольника в точке A и многоугольник целиком лежит правее (или выше) этой прямой. Прямая MN также является опорной, так как имеет с многоугольником общую точку С и
многоугольник целиком лежит левее этой прямой.
Опорными обычно
называют такие прямые, которые имеют с многоугольником ABCDE хотя бы одну общую точку,
и многоугольник ABCDE целиком лежит по одну сторону от этой прямой. Как видно из
чертежа, прямая mn является опорной, так как она касается многоугольника в точке A и многоугольник целиком лежит правее (или выше) этой прямой. Прямая MN также является опорной, так как имеет с многоугольником общую точку С и
многоугольник целиком лежит левее этой прямой.
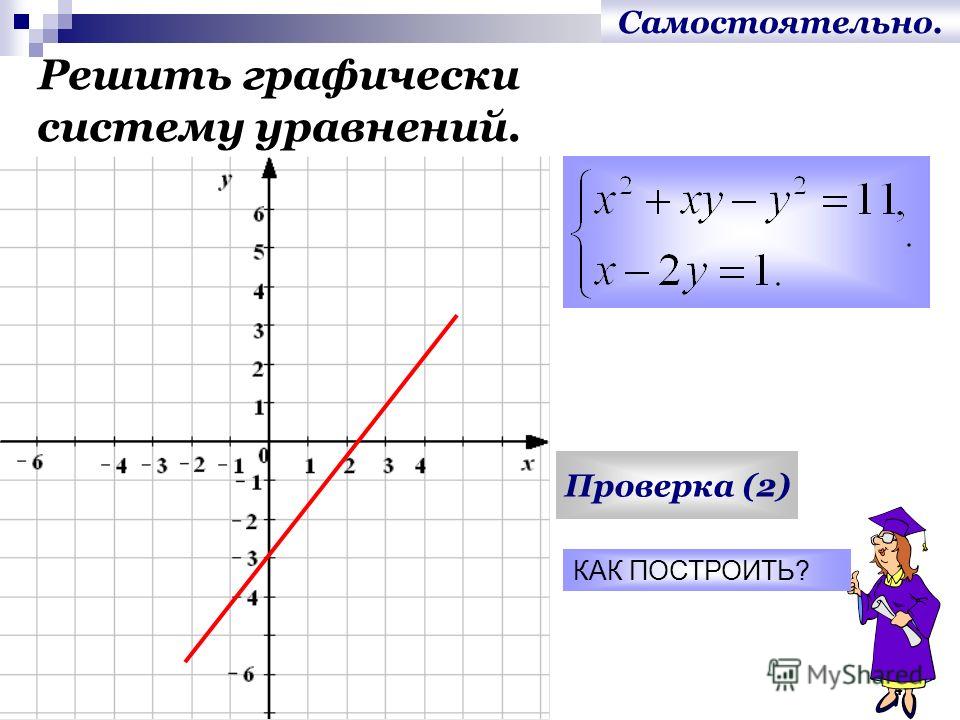

 Здесь функция цели достигает минимума. Двигаясь дальше, придём к точке В.
Здесь максимум. Координаты точки В: (2, 4). Подставляя в функцию цели координаты
точки В, т. е. ,
,
получим максимальное значение функции цели: .
Здесь функция цели достигает минимума. Двигаясь дальше, придём к точке В.
Здесь максимум. Координаты точки В: (2, 4). Подставляя в функцию цели координаты
точки В, т. е. ,
,
получим максимальное значение функции цели: .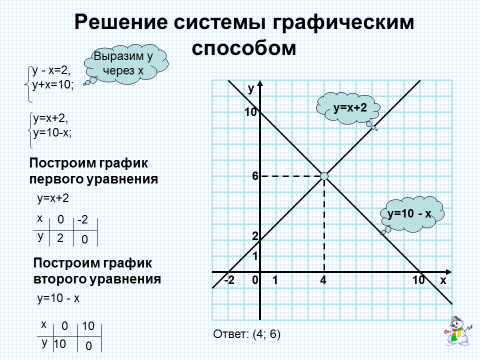

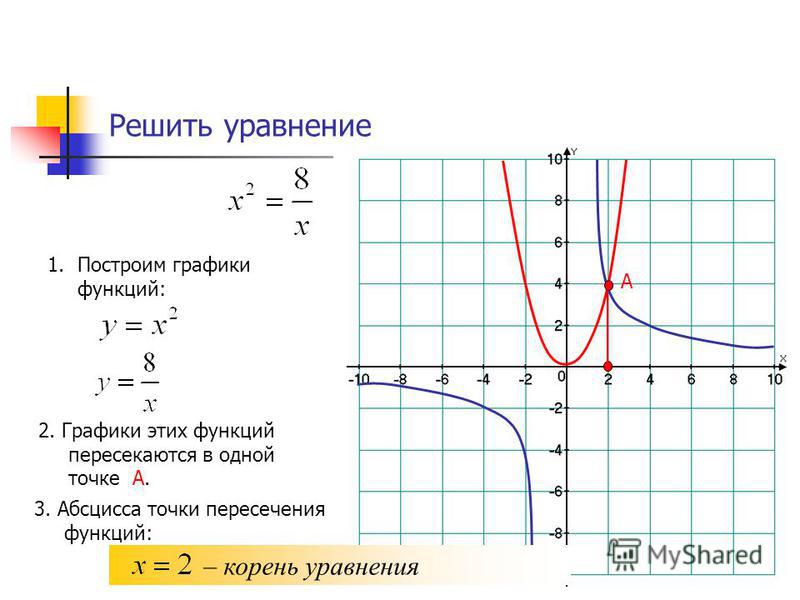 Изображённая на рисунке ниже область не содержит ни одной общей точки,
которая бы удовлетворяла всем неравенствам системы ограничений. То есть система ограничений противоречива
и не может содержать ни одного решения, в том числе и оптимального.
Изображённая на рисунке ниже область не содержит ни одной общей точки,
которая бы удовлетворяла всем неравенствам системы ограничений. То есть система ограничений противоречива
и не может содержать ни одного решения, в том числе и оптимального. Таким
образом, этот пример отличается от предыдущих тем, что одно из неравенств системы ограничений оказалось
лишним.
Таким
образом, этот пример отличается от предыдущих тем, что одно из неравенств системы ограничений оказалось
лишним. Этот пример показывает,
что в некоторых случаях единственность оптимального решения нарушается.
Этот пример показывает,
что в некоторых случаях единственность оптимального решения нарушается. Наш калькулятор позволит вам проверить правильность решения любого линейного уравнения.
Наш калькулятор позволит вам проверить правильность решения любого линейного уравнения. Помимо линейных уравнений существуют квадратные, кубические, тригонометрические, показательные и многие другие типы отношений. Опознать линейное довольно просто – оно должно выглядеть как ax + b = 0 или приводиться к этому виду. Если неизвестный x находится в знаменателе, в показатели степени или имеет степень, отличную от единицы – это не линейное уравнение.
Помимо линейных уравнений существуют квадратные, кубические, тригонометрические, показательные и многие другие типы отношений. Опознать линейное довольно просто – оно должно выглядеть как ax + b = 0 или приводиться к этому виду. Если неизвестный x находится в знаменателе, в показатели степени или имеет степень, отличную от единицы – это не линейное уравнение. Например, в примере x + 2 = 5 мы просто переносим двойку через знак равенства со знаком минус и получаем ответ x = 5 − 2 или x = 3. Однако данная операция выглядит как вычитание двойки из каждой части уравнения:
Например, в примере x + 2 = 5 мы просто переносим двойку через знак равенства со знаком минус и получаем ответ x = 5 − 2 или x = 3. Однако данная операция выглядит как вычитание двойки из каждой части уравнения: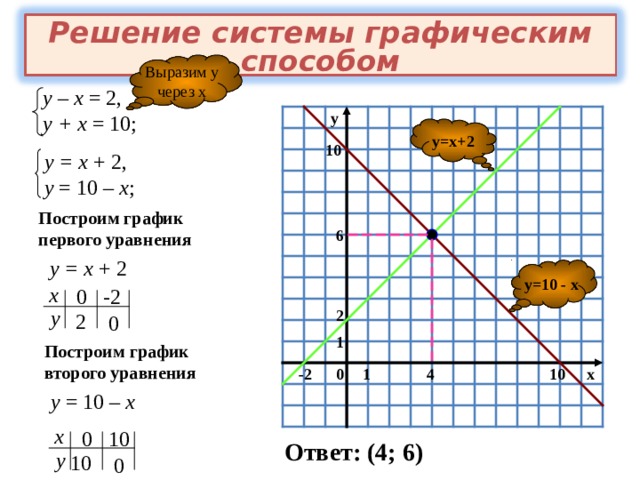 Мы получим:
Мы получим: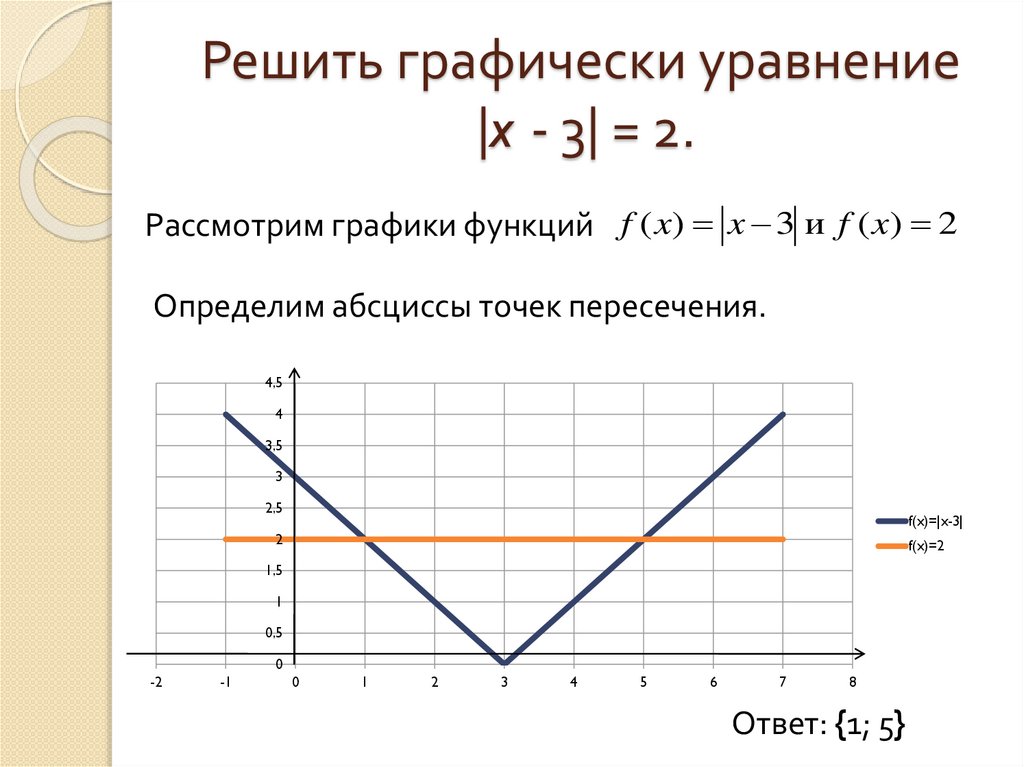
 Так как это одна и та же сумма, мы можем составить следующее уравнение:
Так как это одна и та же сумма, мы можем составить следующее уравнение: Такие равенства широко применяются для решения самых разных бытовых задач. Пользуйтесь калькуляторами из нашего каталога для проверки своих решений.
Такие равенства широко применяются для решения самых разных бытовых задач. Пользуйтесь калькуляторами из нашего каталога для проверки своих решений.
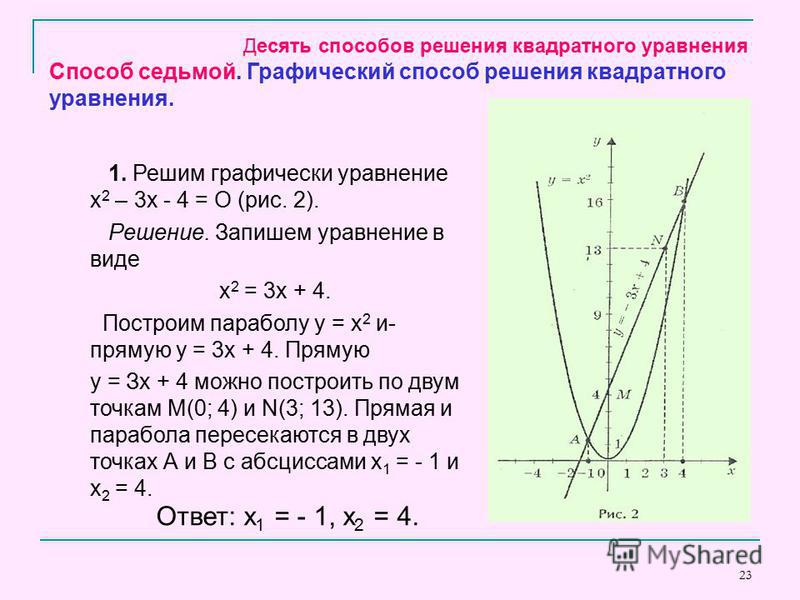 Решим несколько примеров чтоб Вы понимали насколько эффективная методика графического раскрытия модулей.
Решим несколько примеров чтоб Вы понимали насколько эффективная методика графического раскрытия модулей.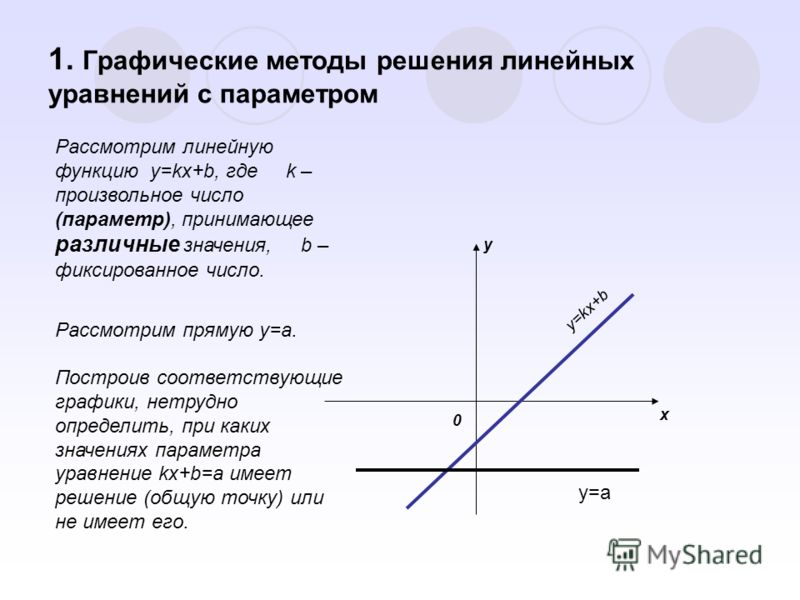 Далее параллельно переносим полученный график вниз на 3 и отразим относительно оси Ox все минусовые y. Полученный график снова опускаем вниз, на этот раз на 5 клеток и симметрично отражаем все что находится ниже оси Ox. Выполняем построение правой стороны уравнения – прямой y=2.
Далее параллельно переносим полученный график вниз на 3 и отразим относительно оси Ox все минусовые y. Полученный график снова опускаем вниз, на этот раз на 5 клеток и симметрично отражаем все что находится ниже оси Ox. Выполняем построение правой стороны уравнения – прямой y=2. Если от 0 до 2 не учитывая краев – 4 корни уравнения. Отсюда получим уравнение для определеения параметра
Если от 0 до 2 не учитывая краев – 4 корни уравнения. Отсюда получим уравнение для определеения параметра Способ, используемый для решения уравнения, — это метод Крамера.Пожалуйста, заполните форму ниже с параметрами для обоих линейных уравнений:
Способ, используемый для решения уравнения, — это метод Крамера.Пожалуйста, заполните форму ниже с параметрами для обоих линейных уравнений:

 Важно то, что у нас есть два линейных уравнения с двумя переменными (неизвестными)
Важно то, что у нас есть два линейных уравнения с двумя переменными (неизвестными)
 Этот метод естественным образом ограничивает приближения в большинстве случаев
Этот метод естественным образом ограничивает приближения в большинстве случаев
 В некотором смысле,
Это более общий способ использования метода замещения
В некотором смысле,
Это более общий способ использования метода замещения
 С
который работает независимо от размера системы, и количество переменных такое же, как количество уравнений.
С
который работает независимо от размера системы, и количество переменных такое же, как количество уравнений.
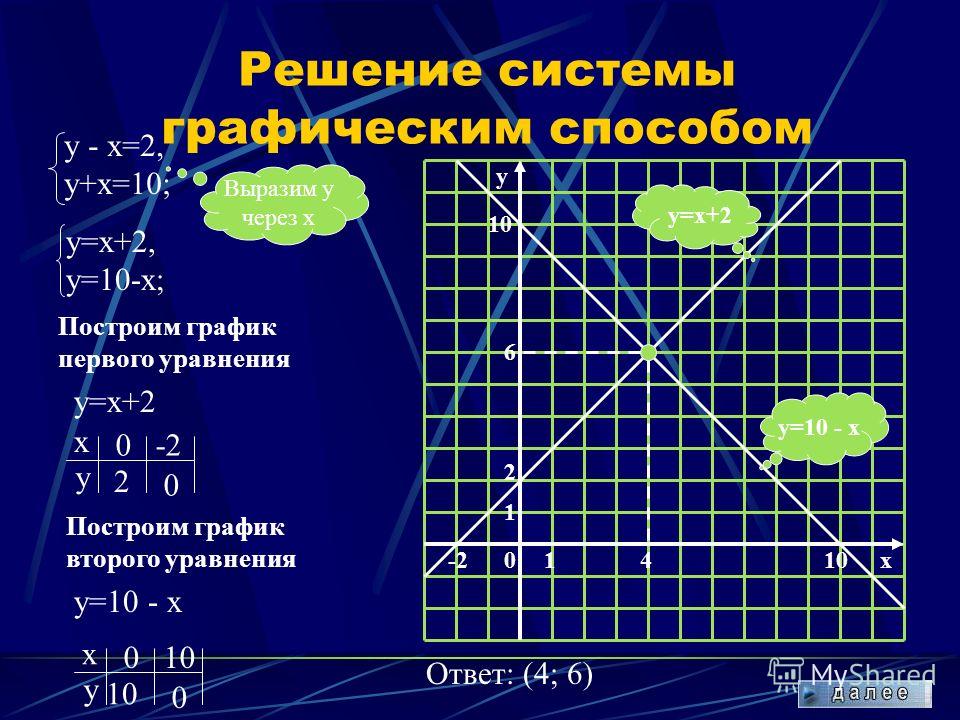 11.2002
11.2002 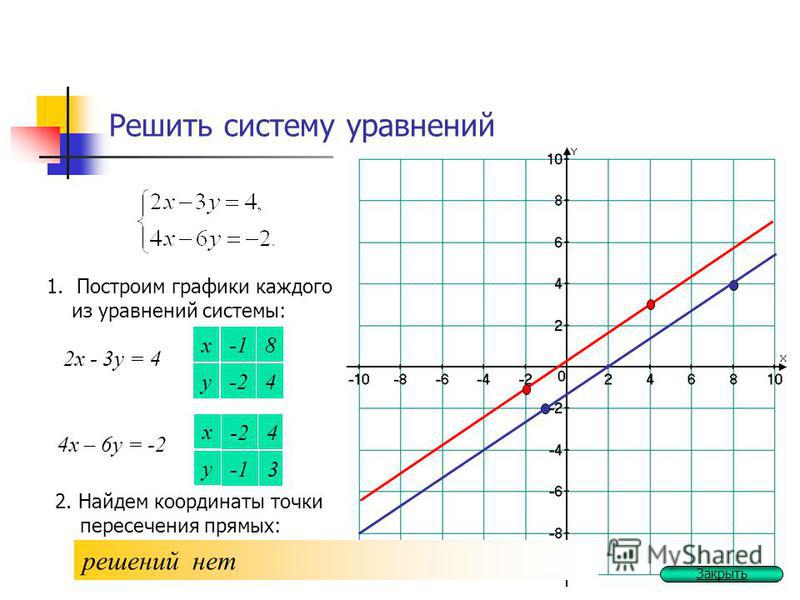
 Вы полюбите математику, как только начнете ее использовать, и увидите, насколько это просто. Я помню, как мне было трудно на уроках Pre Algebra, а теперь с помощью Algebrator учиться стало так весело. Я уверен, что здесь вы получите помощь в решении задач онлайн-калькулятора графических полярных уравнений.
Вы полюбите математику, как только начнете ее использовать, и увидите, насколько это просто. Я помню, как мне было трудно на уроках Pre Algebra, а теперь с помощью Algebrator учиться стало так весело. Я уверен, что здесь вы получите помощь в решении задач онлайн-калькулятора графических полярных уравнений.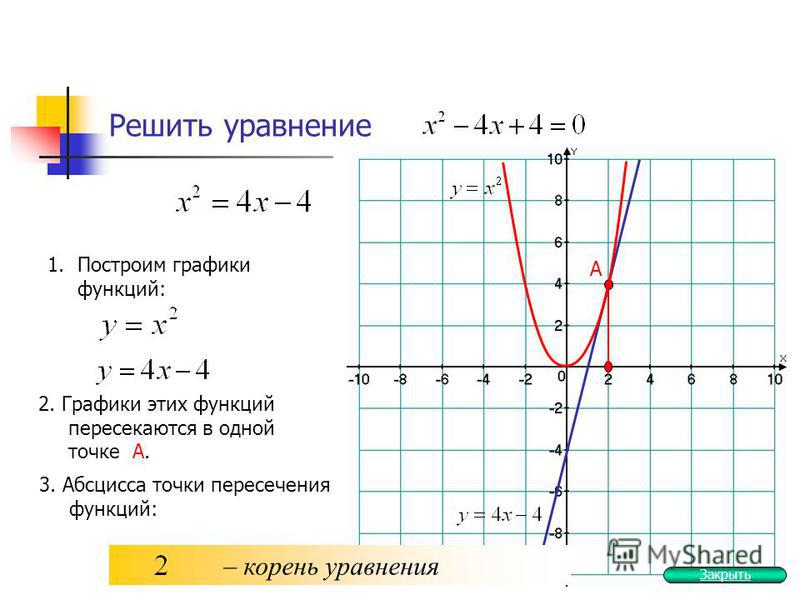 Эй, приятель, ты в теме Алгебратора! Это просто потрясающе! Недавно я скачал его с https://mathsite.org/laws-of-exponents.html после того, как коллега порекомендовал его мне. Теперь все, что я делаю, это набираю задачу, заданную моим учителем, и нажимаю «Решить». Бинго! Я получаю пошаговое решение моей домашней работы по математике. Это похоже на то, как репетитор учит вас этому. Я использую его уже три недели и до сих пор не сталкивался ни с одной проблемой, которую Алгебратор не смог бы решить. Я так многому научился благодаря этому!
Эй, приятель, ты в теме Алгебратора! Это просто потрясающе! Недавно я скачал его с https://mathsite.org/laws-of-exponents.html после того, как коллега порекомендовал его мне. Теперь все, что я делаю, это набираю задачу, заданную моим учителем, и нажимаю «Решить». Бинго! Я получаю пошаговое решение моей домашней работы по математике. Это похоже на то, как репетитор учит вас этому. Я использую его уже три недели и до сих пор не сталкивался ни с одной проблемой, которую Алгебратор не смог бы решить. Я так многому научился благодаря этому! Это действительно отличная программа для алгебры. Я помню, как решал задачи с графической функцией, наименьшей общей мерой и линейной алгеброй. Я просто набирал домашнее задание, нажимал «Решить» — и пошагово решал домашнее задание по алгебре. Очень рекомендую программу.
Это действительно отличная программа для алгебры. Я помню, как решал задачи с графической функцией, наименьшей общей мерой и линейной алгеброй. Я просто набирал домашнее задание, нажимал «Решить» — и пошагово решал домашнее задание по алгебре. Очень рекомендую программу. Графические онлайн-калькуляторы появились относительно недавно и часто бесплатны. Мы рассмотрим лучшие физические и графические онлайн-калькуляторы, чтобы помочь вам решить, какой из них подходит именно вам.
Графические онлайн-калькуляторы появились относительно недавно и часто бесплатны. Мы рассмотрим лучшие физические и графические онлайн-калькуляторы, чтобы помочь вам решить, какой из них подходит именно вам.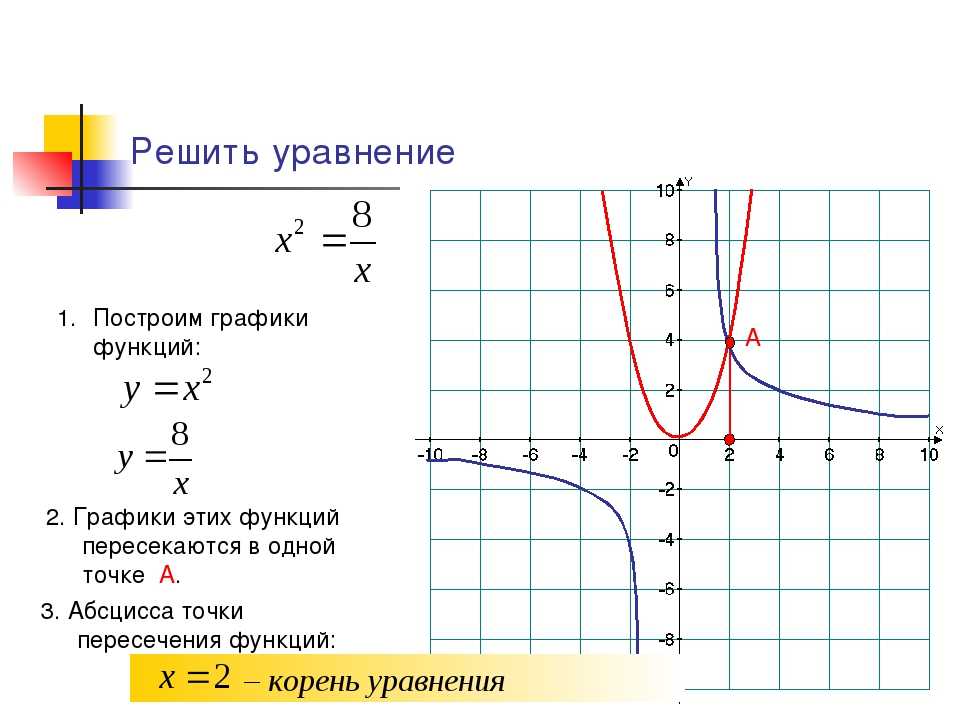
 Некоторые исследователи используют графические калькуляторы вместе с другим оборудованием. Они подключаются к компьютерам или другим машинам и собирают информацию, которая впоследствии может быть доступна и учтена в уравнениях. Помните, графические калькуляторы могут решать несколько уравнений одновременно, поэтому это может помочь сэкономить много времени и труда.
Некоторые исследователи используют графические калькуляторы вместе с другим оборудованием. Они подключаются к компьютерам или другим машинам и собирают информацию, которая впоследствии может быть доступна и учтена в уравнениях. Помните, графические калькуляторы могут решать несколько уравнений одновременно, поэтому это может помочь сэкономить много времени и труда. Этот калькулятор одобрен для экзаменов SAT, PSAT, ACT, IB и AP.
Этот калькулятор одобрен для экзаменов SAT, PSAT, ACT, IB и AP. Этот калькулятор одобрен для тестов SAT, PSAT, ACT и AP.
Этот калькулятор одобрен для тестов SAT, PSAT, ACT и AP.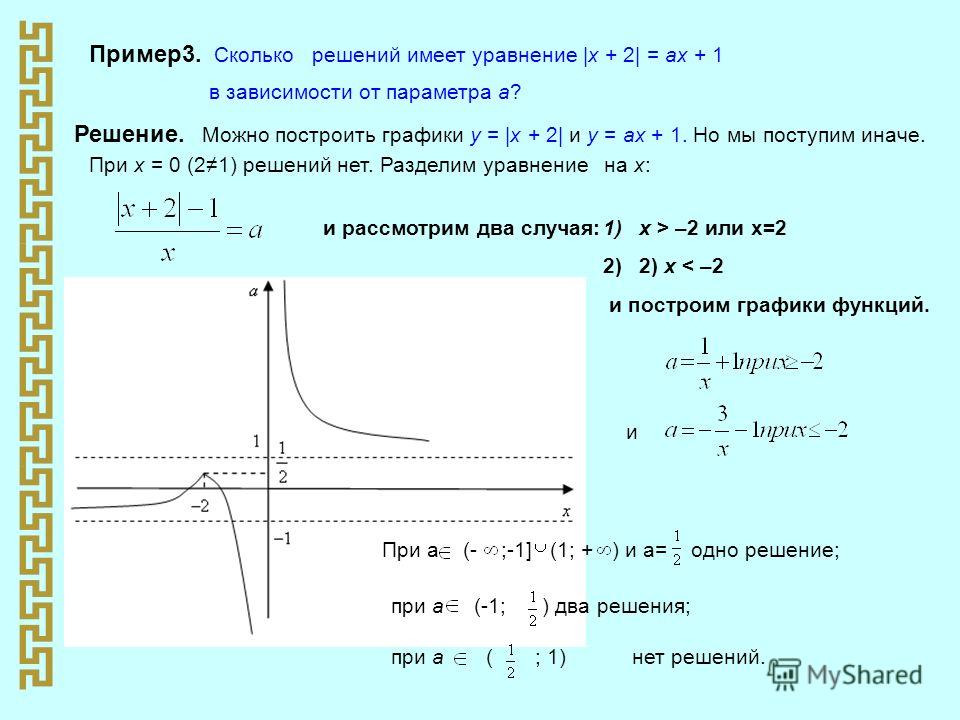 Интерфейс похож на смартфон и имеет дополнительные функции, такие как режим экзамена. Этот калькулятор одобрен для SAT.
Интерфейс похож на смартфон и имеет дополнительные функции, такие как режим экзамена. Этот калькулятор одобрен для SAT.

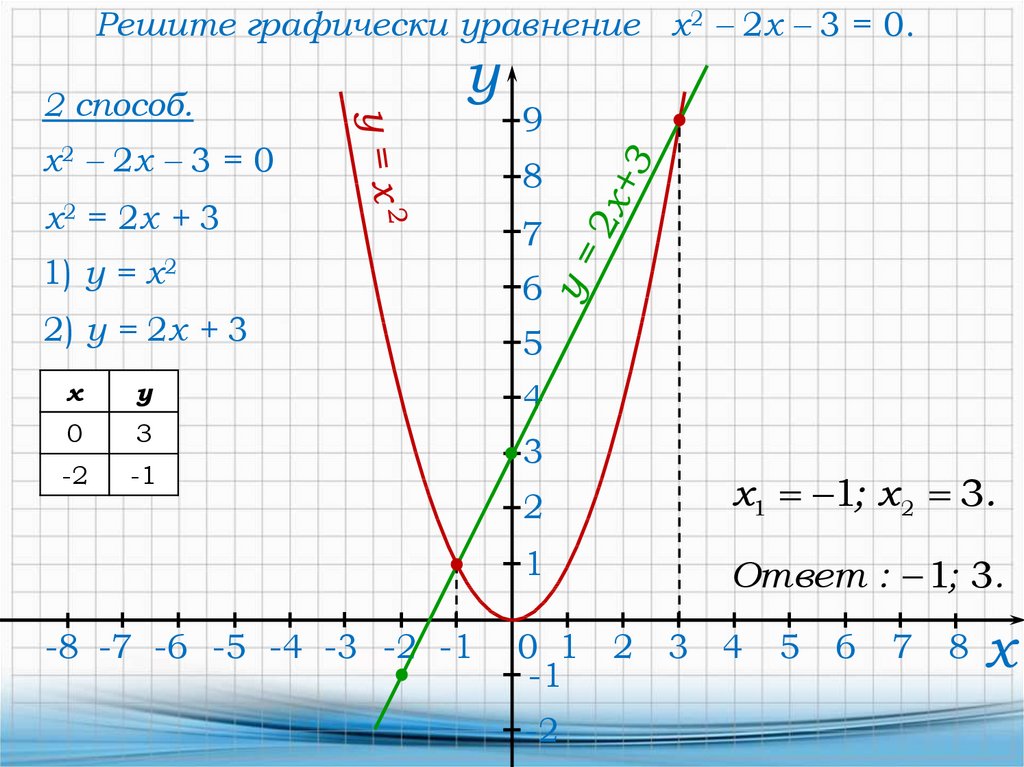 Функция калькулятора позволяет вводить и просматривать уравнения в диалоговом окне слева и просматривать график справа. В нем также есть раскрывающееся меню со знакомыми параметрами, которые вы найдете в большинстве программ (сохранение, экспорт и т. д.), и вы можете создать учетную запись для сохранения своей работы.
Функция калькулятора позволяет вводить и просматривать уравнения в диалоговом окне слева и просматривать график справа. В нем также есть раскрывающееся меню со знакомыми параметрами, которые вы найдете в большинстве программ (сохранение, экспорт и т. д.), и вы можете создать учетную запись для сохранения своей работы.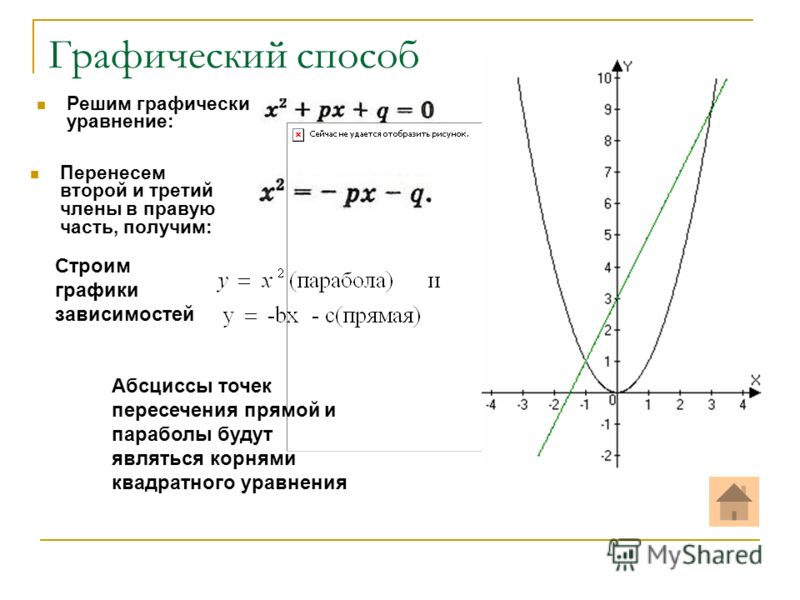 В этом случае можно воспользоваться онлайн-калькулятором. Для этих курсов проконсультируйтесь со своим учителем или профессором, чтобы узнать, можете ли вы использовать онлайн-курс в классе.
В этом случае можно воспользоваться онлайн-калькулятором. Для этих курсов проконсультируйтесь со своим учителем или профессором, чтобы узнать, можете ли вы использовать онлайн-курс в классе. Если вам нужно что-то взять с собой на длительные экзамены в колледже, такие факторы, как дисплей, скорость обработки и время автономной работы, также являются важными факторами. Кроме того, убедитесь, что вы знаете, нужен ли вам калькулятор с CAS или нет.
Если вам нужно что-то взять с собой на длительные экзамены в колледже, такие факторы, как дисплей, скорость обработки и время автономной работы, также являются важными факторами. Кроме того, убедитесь, что вы знаете, нужен ли вам калькулятор с CAS или нет.
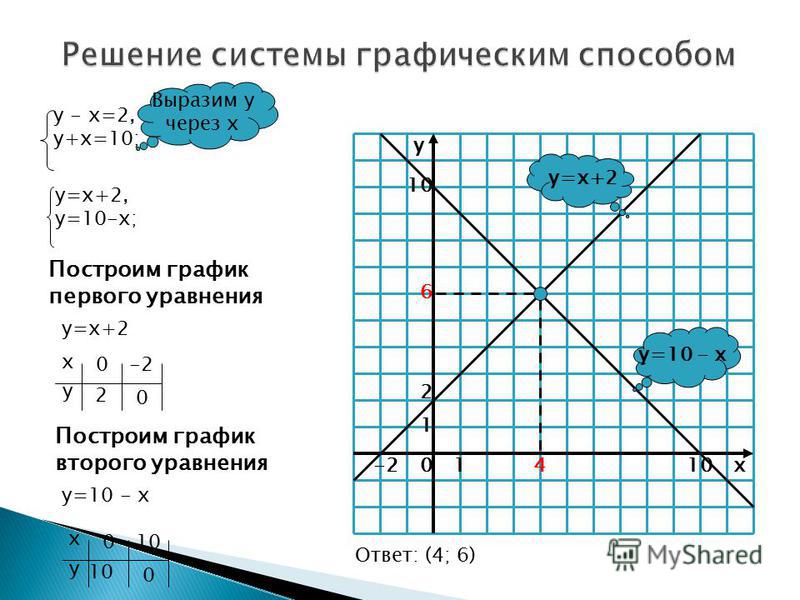
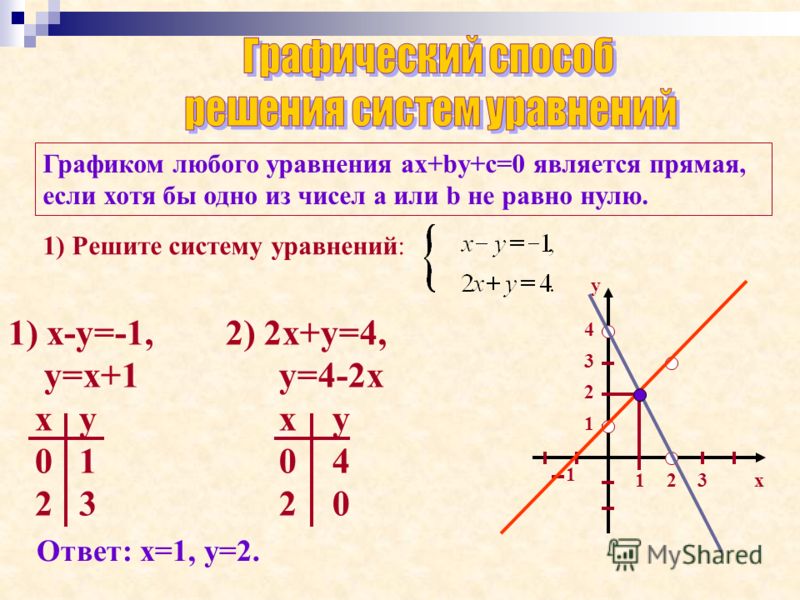 9
9 8 кружков по математике
8 кружков по математике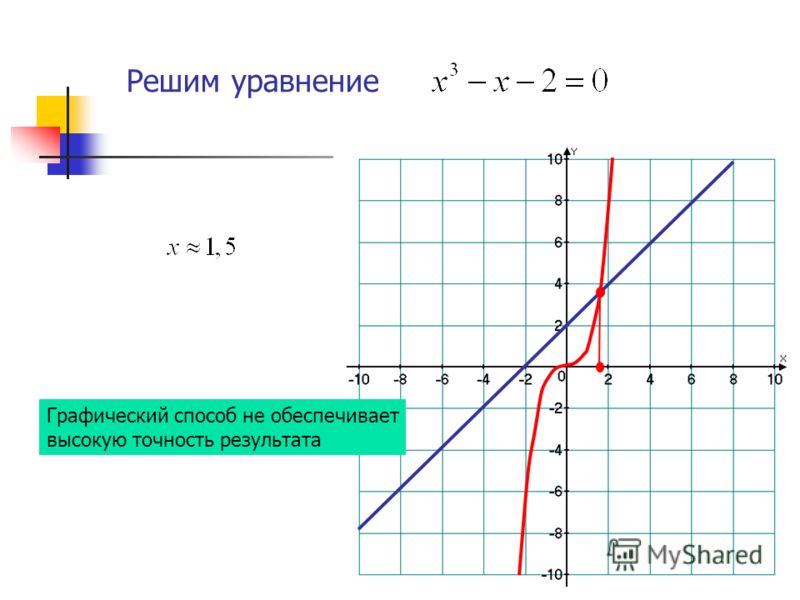 apptitude загрузить тестовые документы
apptitude загрузить тестовые документы pdf скачать бесплатно
pdf скачать бесплатно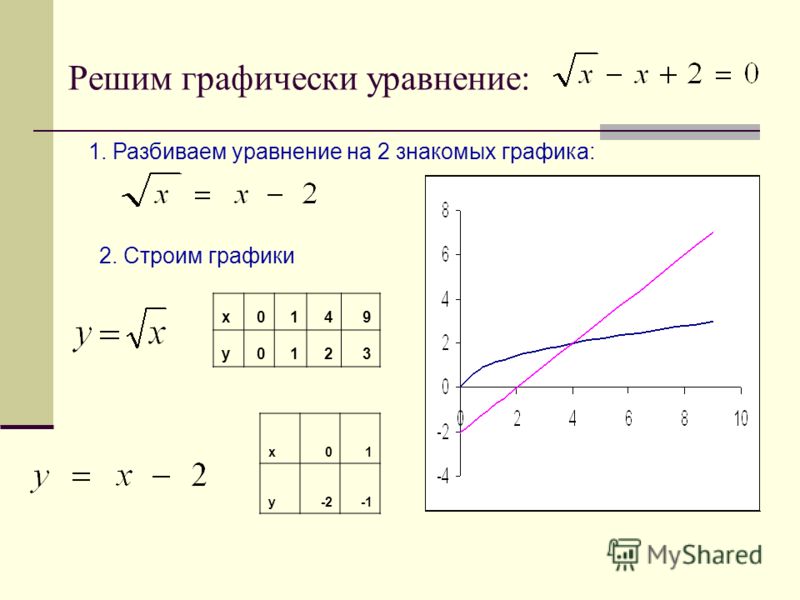 Когда у вас есть 2 точки на линии на графике, наклон представляет собой изменение y, деленное на изменение x.
Когда у вас есть 2 точки на линии на графике, наклон представляет собой изменение y, деленное на изменение x.
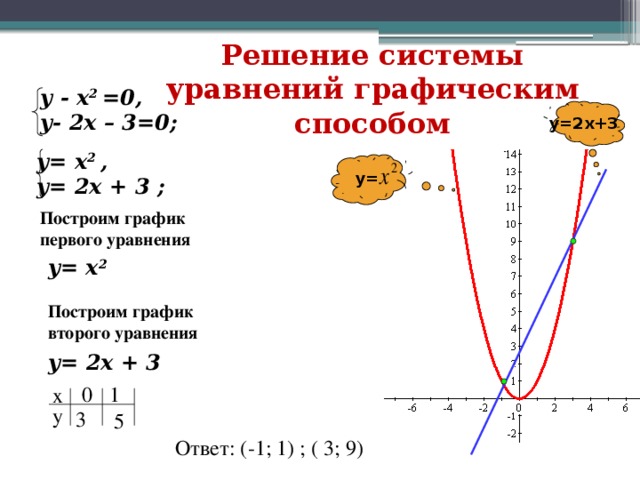 Найдите наклон, найдя разницу в точках y, и разделите ее на разницу в точках x.
Найдите наклон, найдя разницу в точках y, и разделите ее на разницу в точках x.
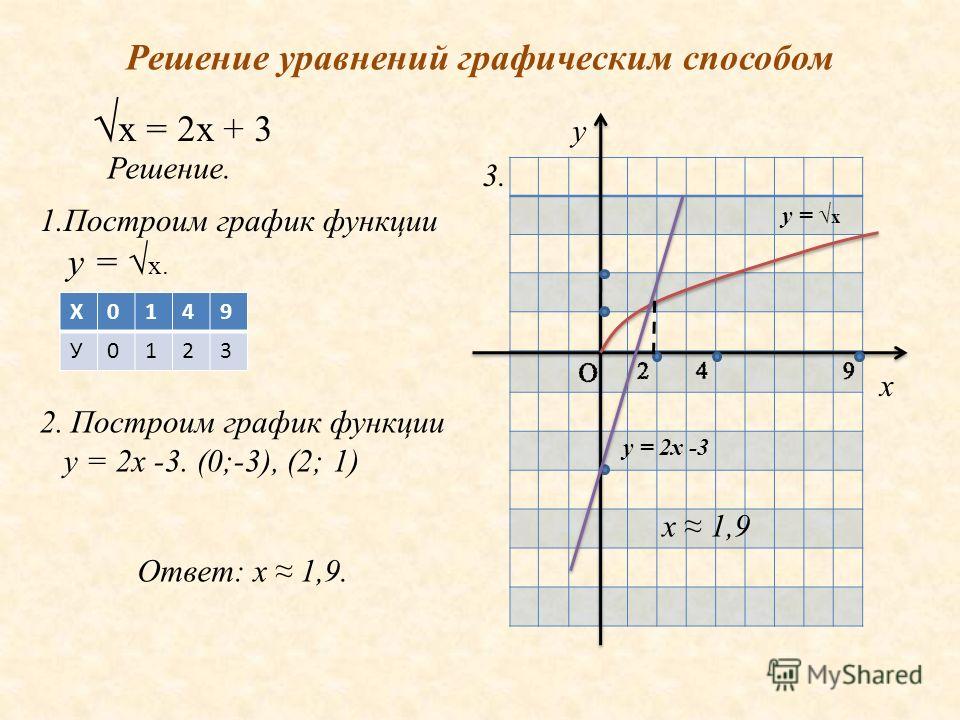
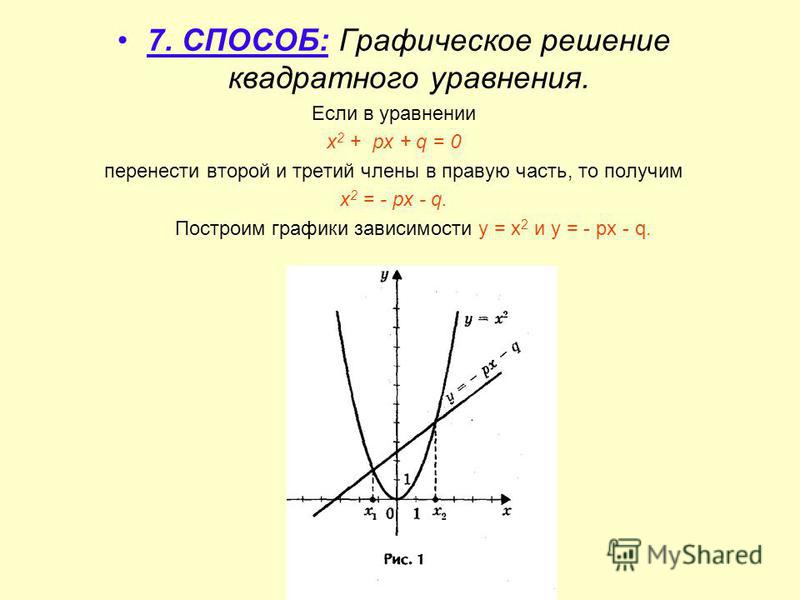 Наклон — это коэффициент x, поэтому в этом случае наклон = 3 906:40
Наклон — это коэффициент x, поэтому в этом случае наклон = 3 906:40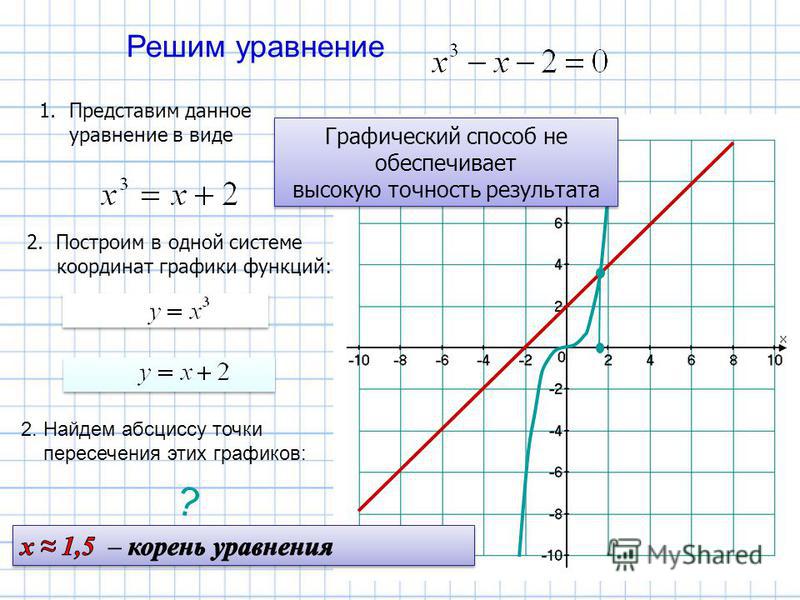
 Я купил ваш продукт Algebrator и могу честно сказать, что это причина, по которой я сдаю уроки математики!
Я купил ваш продукт Algebrator и могу честно сказать, что это причина, по которой я сдаю уроки математики!  Решатель также может решать уравнение для одной переменной при заданных значениях других переменных. Имейте в виду, что Solver может производить только решения с действительными числами.
Решатель также может решать уравнение для одной переменной при заданных значениях других переменных. Имейте в виду, что Solver может производить только решения с действительными числами. Установите исходное уравнение равным нулю и введите полученное уравнение в Решатель.
Установите исходное уравнение равным нулю и введите полученное уравнение в Решатель.



 Вычислите молярную и молярную концентрацию эквивалента (нормальность) 20 % раствора хлорида кальция плотностью 1,178 г/мл.
Вычислите молярную и молярную концентрацию эквивалента (нормальность) 20 % раствора хлорида кальция плотностью 1,178 г/мл. Чему равна нормальность 30% раствора NaOH плотностью 1,328 г/мл? К 1 л этого раствора прибавили 5 л воды. Вычислите массовую долю полученного раствора.
Чему равна нормальность 30% раствора NaOH плотностью 1,328 г/мл? К 1 л этого раствора прибавили 5 л воды. Вычислите массовую долю полученного раствора.
 Определить молярность, нормальность, моляльность и титр 4 % раствора FeSO4 объем которого равен 1,5 л, плотность 1037 кг/м3
Определить молярность, нормальность, моляльность и титр 4 % раствора FeSO4 объем которого равен 1,5 л, плотность 1037 кг/м3 Суть его заключается в составлении «креста», в виде которого располагают две прямые линии. В центре пишут ту концентрацию, которую надо получить, у концов линий креста слева – концентрации исходных растворов (большую – сверху, меньшую — снизу), у концов линий креста справа – искомые концентрации (или массы) растворов, которые получают вычитанием по направлению линий из большей величины меньшей. В общем виде схема решения задач по правилу креста имеет вид:
Суть его заключается в составлении «креста», в виде которого располагают две прямые линии. В центре пишут ту концентрацию, которую надо получить, у концов линий креста слева – концентрации исходных растворов (большую – сверху, меньшую — снизу), у концов линий креста справа – искомые концентрации (или массы) растворов, которые получают вычитанием по направлению линий из большей величины меньшей. В общем виде схема решения задач по правилу креста имеет вид:
 Для этого разделим 1 л на две части в соотношении 1:3, составив пропорции:
Для этого разделим 1 л на две части в соотношении 1:3, составив пропорции: 11.15г.
11.15г.
 Изучение нового материала и решение задач.
Изучение нового материала и решение задач. 10 г нитрата калия добавили в 80 г воды. Определите процентную концентрацию полученного раствора. (11%)
10 г нитрата калия добавили в 80 г воды. Определите процентную концентрацию полученного раствора. (11%)  (27%)
(27%) 
 На уроке я работал…______________________________________
На уроке я работал…______________________________________ Урок для меня показался…__________________________________
Урок для меня показался…__________________________________ Мое настроение…__________________________________________
Мое настроение…__________________________________________
 Для реакции Одна частица А эквивалентна b/a
частицам вещества B.
.
Для реакции Одна частица А эквивалентна b/a
частицам вещества B.
. При разных нормальностях
объемы растворов реагирующих веществ
обратно пропорциональны их нормальностям,
т.е. V1CН1 =V2CН2
.
При разных нормальностях
объемы растворов реагирующих веществ
обратно пропорциональны их нормальностям,
т.е. V1CН1 =V2CН2
. 


 Сколько граммов кислоты содержится в
4 л этого раствора?
Сколько граммов кислоты содержится в
4 л этого раствора? В
150 г воды растворено 30 г кристаллогидрата
.
Вычислить массовую долю кристаллогидрата
и безводного сульфата железа (II)
в растворе.
В
150 г воды растворено 30 г кристаллогидрата
.
Вычислить массовую долю кристаллогидрата
и безводного сульфата железа (II)
в растворе.


 Определить
массовую долю вещества в растворе,
полученном смещением 300 г 25%-ного и 400 г
40%-ного (по массе) растворов этого
вещества
Определить
массовую долю вещества в растворе,
полученном смещением 300 г 25%-ного и 400 г
40%-ного (по массе) растворов этого
вещества Вычислите массовую долю и моляльную
концентрацию этого раствора, если
r=1,28 г/мл.
Вычислите массовую долю и моляльную
концентрацию этого раствора, если
r=1,28 г/мл.
 Из 1
л раствора действием соляной кислоты
выделено 33,6 л СО2.Вычислите
моляльную концентрацию раствора и
мольную долю соли.
Из 1
л раствора действием соляной кислоты
выделено 33,6 л СО2.Вычислите
моляльную концентрацию раствора и
мольную долю соли. Рассчитать массовую
долю и молярную долю соли в новом
растворе.
Рассчитать массовую
долю и молярную долю соли в новом
растворе.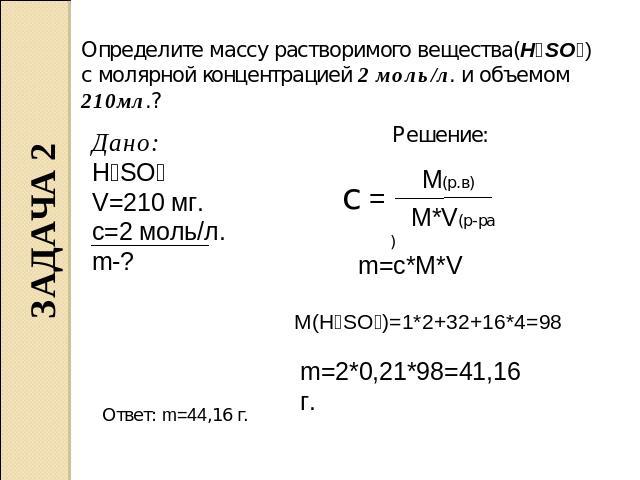




 Записать выражение для ПРи вычислить его величину.
Записать выражение для ПРи вычислить его величину. М(Ag2CrO4) =332 г/моль. См = 9,48.10-5 моль/л. Растворение хромата серебра (I) сопровождается полной (a=1) диссоциацией соли:
М(Ag2CrO4) =332 г/моль. См = 9,48.10-5 моль/л. Растворение хромата серебра (I) сопровождается полной (a=1) диссоциацией соли: Растворение карбоната кальция протекает по схеме CaCO3 ↔ Ca2+ +CO32- В данном уравнении n = m = 1, тогда
Растворение карбоната кальция протекает по схеме CaCO3 ↔ Ca2+ +CO32- В данном уравнении n = m = 1, тогда

 Криоскопическая константа воды 1,86.
Криоскопическая константа воды 1,86.

 Учтём, что
Учтём, что

 Определите величины общей, временной и постоянной жёсткости воды.
Определите величины общей, временной и постоянной жёсткости воды.

 По закону эквивалентов число эквивалентов израсходованного фосфата натрия должно быть равно числу эквивалентов солей жёсткости, бывших в бочке.
По закону эквивалентов число эквивалентов израсходованного фосфата натрия должно быть равно числу эквивалентов солей жёсткости, бывших в бочке.
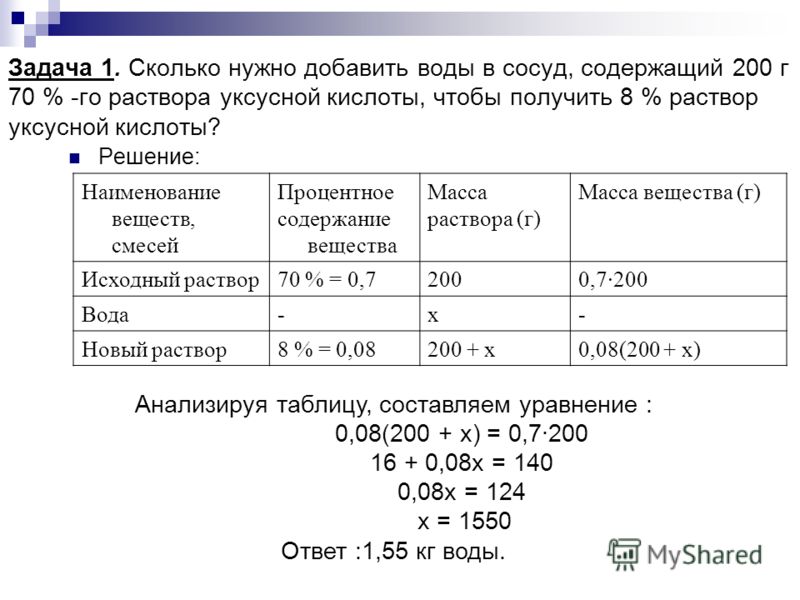

 е. 0,25 x 200 = 50 г.
е. 0,25 x 200 = 50 г. , значит масса (М растворителя) = (М раствора) — (M вещества) = 250 — 12,5 = 237,5 г.
, значит масса (М растворителя) = (М раствора) — (M вещества) = 250 — 12,5 = 237,5 г. Нам нужно обезвредить кислую среду. Вы случайно разлили 200 мл соляной кислоты (HCl), а под руками оказалась стиральная сода (Na2CO3) (или второе её название — кальцинированная сода). Так вот: сколько нужно взять стиральной соды, чтобы обезвредить 200 мл соляной кислоты!?
Нам нужно обезвредить кислую среду. Вы случайно разлили 200 мл соляной кислоты (HCl), а под руками оказалась стиральная сода (Na2CO3) (или второе её название — кальцинированная сода). Так вот: сколько нужно взять стиральной соды, чтобы обезвредить 200 мл соляной кислоты!?

 Вот и всё.
Вот и всё.

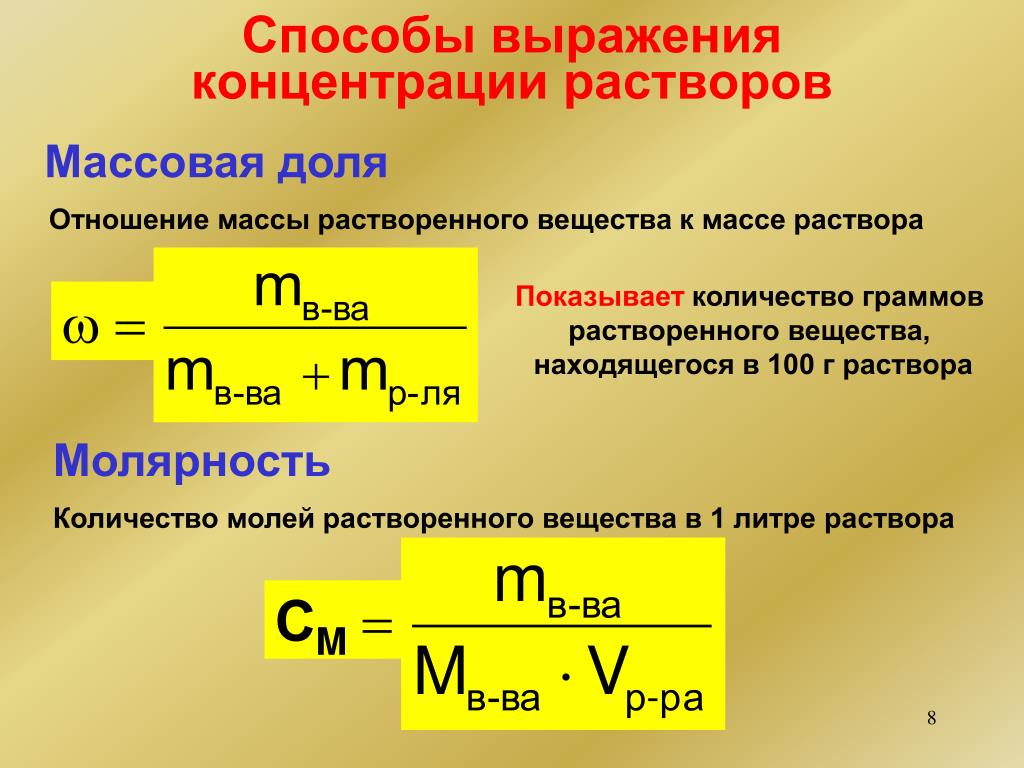
 Какова молярность Ca 2+ в молоке?
Какова молярность Ca 2+ в молоке? Предельные значения установлены для ряда веществ, в том числе для шестивалентного хрома, который ограничивается 0,50 мг/л. Если промышленность сбрасывает шестивалентный хром в виде дихромата калия (K 2 Cr 2 O 7 ), какова максимально допустимая молярность этого вещества?
Предельные значения установлены для ряда веществ, в том числе для шестивалентного хрома, который ограничивается 0,50 мг/л. Если промышленность сбрасывает шестивалентный хром в виде дихромата калия (K 2 Cr 2 O 7 ), какова максимально допустимая молярность этого вещества? org/contents/85abf193-2бд…
org/contents/85abf193-2бд…



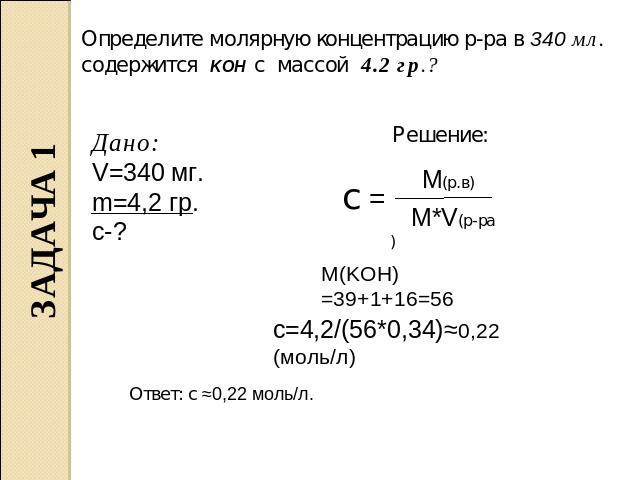 Рассчитать молярность и молярную долю H 2 SO 4 плотностью 1,91 г см -3 . Дано H = 1, S = 32, O = 16.
Рассчитать молярность и молярную долю H 2 SO 4 плотностью 1,91 г см -3 . Дано H = 1, S = 32, O = 16. Если его плотность 1,1 г см -3 ,
рассчитать молярность раствора HCl, а также рассчитать мольную долю HCl
и Н 2 O.
Если его плотность 1,1 г см -3 ,
рассчитать молярность раствора HCl, а также рассчитать мольную долю HCl
и Н 2 O.  Если его плотность 1,2 г см -3 ,
рассчитать молярность раствора HCl.
Если его плотность 1,2 г см -3 ,
рассчитать молярность раствора HCl. 



 моль растворенного вещества на литр раствора
моль растворенного вещества на литр раствора  0,25 литра = 20 M
0,25 литра = 20 M В этой лекции мы рассмотрим молярность, единицы концентрации и процесс разбавления.
В этой лекции мы рассмотрим молярность, единицы концентрации и процесс разбавления. Молярность обозначается заглавной «М».
Молярность обозначается заглавной «М». В настоящее время PDF используется при публикации, распространении факсов, налоговой отчетности, в образовательных, юридических, финансовых учреждениях, а также обычными пользователями ПК по электронной почте, в сообщениях и других типах корреспонденции.
Такой файл легко распечатать и затем использовать для совместной работы. Кроме того, документы в формате PDF достаточно проблематично изменить и взломать. Это формат — взаимно бенефициарное соглашение между отправителем и получателем, таким образом если вы отправите документ в формате PDF, то получатель не сможет редактировать документ. Он будет использоваться, де-факто, как окончательный тип документа и должен быть принят, как он есть – без изменений. Учитывая изложенное выше, онлайн конвертер DOC в PDF — это верный способ избежать больших расходов при документообороте и простой способ получить окончательный документ в формате PDF без установки дополнительного программного обеспечения.
В настоящее время PDF используется при публикации, распространении факсов, налоговой отчетности, в образовательных, юридических, финансовых учреждениях, а также обычными пользователями ПК по электронной почте, в сообщениях и других типах корреспонденции.
Такой файл легко распечатать и затем использовать для совместной работы. Кроме того, документы в формате PDF достаточно проблематично изменить и взломать. Это формат — взаимно бенефициарное соглашение между отправителем и получателем, таким образом если вы отправите документ в формате PDF, то получатель не сможет редактировать документ. Он будет использоваться, де-факто, как окончательный тип документа и должен быть принят, как он есть – без изменений. Учитывая изложенное выше, онлайн конвертер DOC в PDF — это верный способ избежать больших расходов при документообороте и простой способ получить окончательный документ в формате PDF без установки дополнительного программного обеспечения.
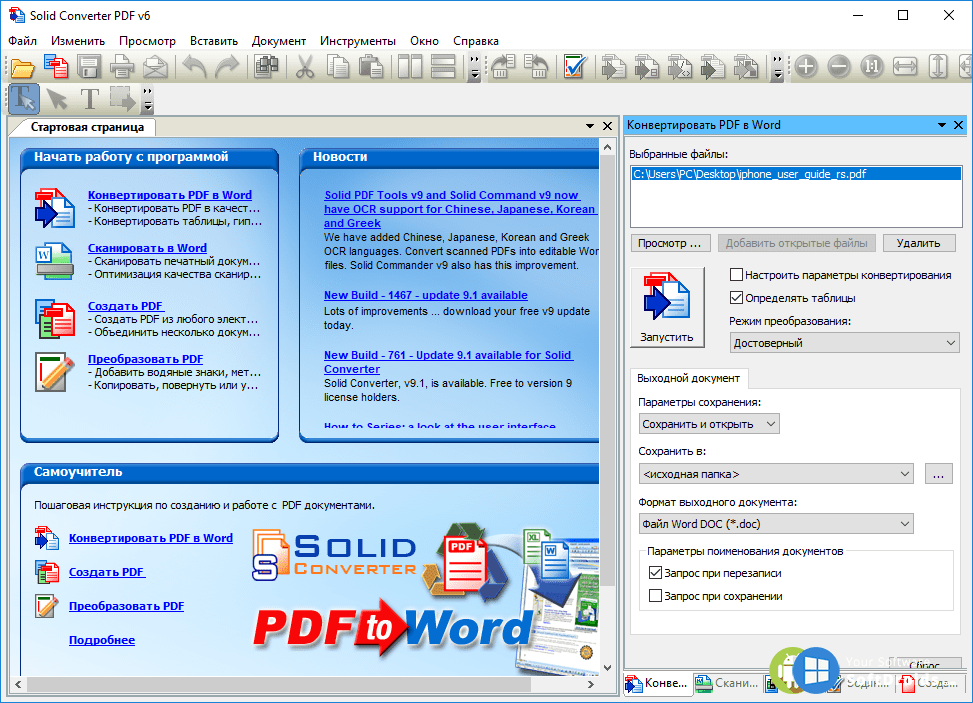 Стандартизация и популярность: PDF документ может быть открыт на любых устройствах с любыми операционными системами точно так, как он был создан — один к одному;
Стандартизация и популярность: PDF документ может быть открыт на любых устройствах с любыми операционными системами точно так, как он был создан — один к одному; Word формат, к сожалению, не гарантирует совместимость отображения формата в разных системах.
Word формат, к сожалению, не гарантирует совместимость отображения формата в разных системах. Мощный бесплатный онлайн DOC в PDF конвертер документов легко. Установка программного обеспечения для настольных ПК, таких как Microsoft Word, OpenOffice или Adobe Acrobat, не требуется. Все конверсии вы можете сделать онлайн с любой платформы: Windows, Linux, macOS и Android. Мы не требуем регистрации. Этот инструмент абсолютно бесплатный.
Мощный бесплатный онлайн DOC в PDF конвертер документов легко. Установка программного обеспечения для настольных ПК, таких как Microsoft Word, OpenOffice или Adobe Acrobat, не требуется. Все конверсии вы можете сделать онлайн с любой платформы: Windows, Linux, macOS и Android. Мы не требуем регистрации. Этот инструмент абсолютно бесплатный. 
 Мы удаляем загруженные файлы через 24 часа, и ссылки для скачивания перестают работать. Никто не имеет доступа к вашим файлам. Преобразование файлов (включая DOC в PDF) абсолютно безопасно.
Мы удаляем загруженные файлы через 24 часа, и ссылки для скачивания перестают работать. Никто не имеет доступа к вашим файлам. Преобразование файлов (включая DOC в PDF) абсолютно безопасно.

 Вы можете разделить большие файлы и использовать инструмент слияния, чтобы объединить их в один PDF-файл.
Вы можете разделить большие файлы и использовать инструмент слияния, чтобы объединить их в один PDF-файл.


 В других случаях вы можете захотеть отправить счета, финансовые отчеты или конфиденциальную информацию по сети, поэтому преобразование DOC и DOCX в PDF кажется лучшим решением для обеспечения безопасности данных в режиме только для чтения. Кроме того, вы можете зашифровать PDF-файл и безопасно поделиться им с другими.
В других случаях вы можете захотеть отправить счета, финансовые отчеты или конфиденциальную информацию по сети, поэтому преобразование DOC и DOCX в PDF кажется лучшим решением для обеспечения безопасности данных в режиме только для чтения. Кроме того, вы можете зашифровать PDF-файл и безопасно поделиться им с другими. Вы получаете PDF-файл высокого разрешения из документа Word.
Вы получаете PDF-файл высокого разрешения из документа Word.

 WPS Office
WPS Office Программа хорошо работает с любой программой обработки текстов, облачным хранилищем или приложением электронной почты
Программа хорошо работает с любой программой обработки текстов, облачным хранилищем или приложением электронной почты Его пользовательский интерфейс прост, но профессионально разработан. Word to PDF Converter совместим с Android 2.3 и выше. Познакомьтесь с функциями этого приложения ниже:
Его пользовательский интерфейс прост, но профессионально разработан. Word to PDF Converter совместим с Android 2.3 и выше. Познакомьтесь с функциями этого приложения ниже: Он не только обеспечивает вертикальный и горизонтальный режим чтения, но также предоставляет широкий выбор инструментов для комментирования, таких как маркер, карандаш, подчеркивание, фигуры и добавление текстовых сносок и многое другое. Вы можете легко управлять PDF-файлами,переименовывая, создавая и перемещая папки по своему усмотрению.
Он не только обеспечивает вертикальный и горизонтальный режим чтения, но также предоставляет широкий выбор инструментов для комментирования, таких как маркер, карандаш, подчеркивание, фигуры и добавление текстовых сносок и многое другое. Вы можете легко управлять PDF-файлами,переименовывая, создавая и перемещая папки по своему усмотрению.

 Итак, вам нужно перевести из ворда в пдф, чтобы сохранить форматирование документа.
Итак, вам нужно перевести из ворда в пдф, чтобы сохранить форматирование документа.
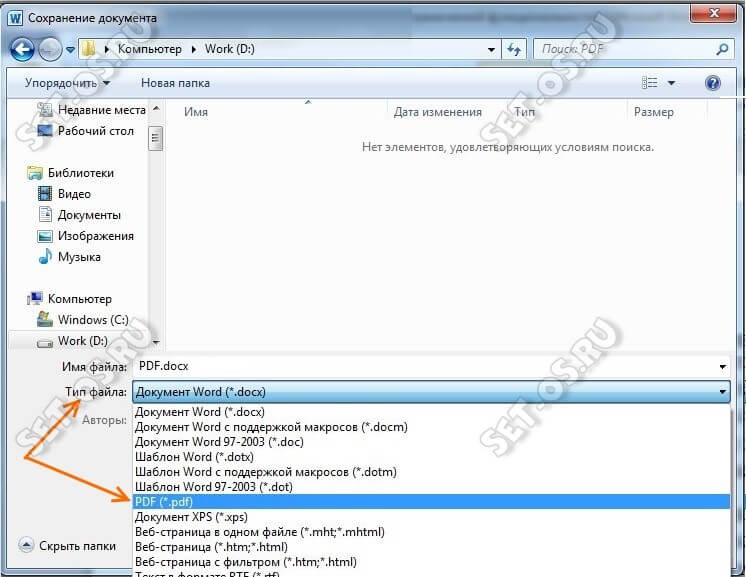 Что ж, если вы предпочитаете, чтобы документ был просмотрен большой аудиторией, перевести ворд в пдф с помощью онлайн-кперевод ворд в пдф.
Что ж, если вы предпочитаете, чтобы документ был просмотрен большой аудиторией, перевести ворд в пдф с помощью онлайн-кперевод ворд в пдф.
 Использование онлайн-конвертер из ворд в пдф позволяет преобразовывать файлы MS DOC в совместимый формат PDF без ущерба для форматирования исходного файла. Что ж, с выпуском MS Word 2007 поддержка Microsoft представила новое расширение файла DOCX, основанное на стандарте Open XML (Extensible Markup Language). Вы можете использовать онлайн-кперевести из ворд в пдф бесплатно, чтобы мгновенно конвертировать docx в pdf без каких-либо ограничений. Если у вас все еще есть MS Word 2003 или более ранняя версия, вам следует загрузить бесплатный пакет обеспечения совместимости с MS Office, чтобы открывать, редактировать и сохранять файлы DOCX прямо сейчас!
Использование онлайн-конвертер из ворд в пдф позволяет преобразовывать файлы MS DOC в совместимый формат PDF без ущерба для форматирования исходного файла. Что ж, с выпуском MS Word 2007 поддержка Microsoft представила новое расширение файла DOCX, основанное на стандарте Open XML (Extensible Markup Language). Вы можете использовать онлайн-кперевести из ворд в пдф бесплатно, чтобы мгновенно конвертировать docx в pdf без каких-либо ограничений. Если у вас все еще есть MS Word 2003 или более ранняя версия, вам следует загрузить бесплатный пакет обеспечения совместимости с MS Office, чтобы открывать, редактировать и сохранять файлы DOCX прямо сейчас!


 pdf).
pdf).



 Корень
из отношения равен отношению корней делимого и делителя:
Корень
из отношения равен отношению корней делимого и делителя: 

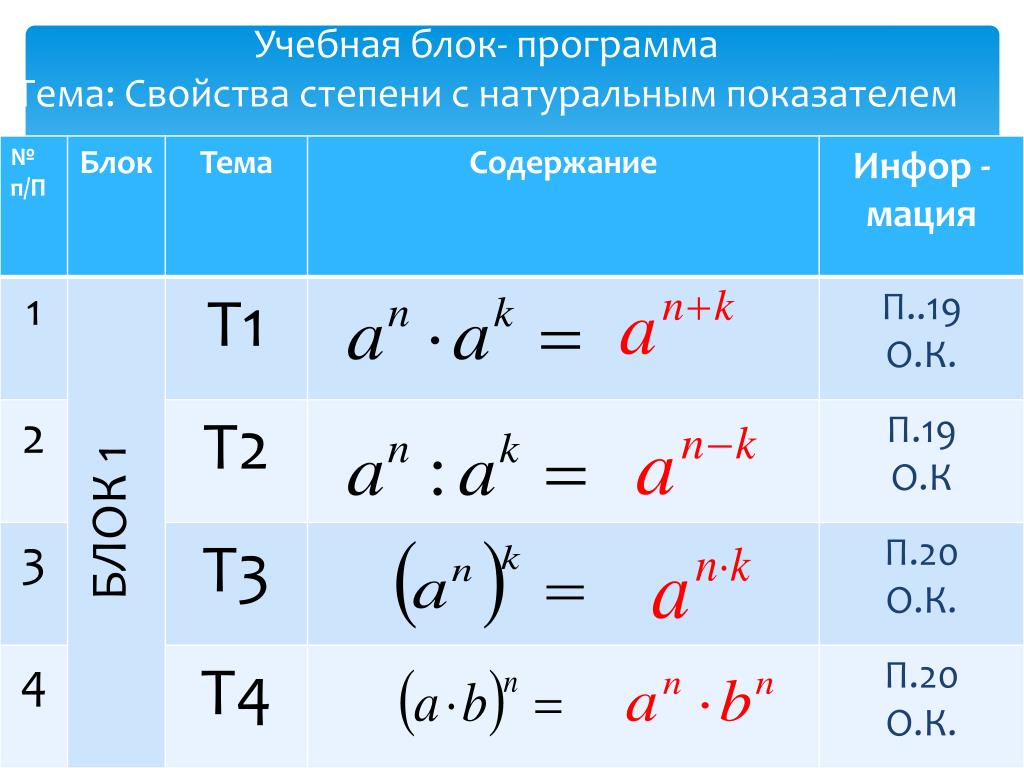



 3$
3$ Степени с рациональными показателями и их свойства будут рассмотрены в уроках для 8 классов.
Степени с рациональными показателями и их свойства будут рассмотрены в уроках для 8 классов.



 Корень из отношения равен отношению корней делимого и делителя:
Корень из отношения равен отношению корней делимого и делителя: 

 По определению степени
По определению степени Поэтому из доказанного пока нельзя делать, например, таких выводов:
Поэтому из доказанного пока нельзя делать, например, таких выводов:







 Нужно перемножить два в квадрате четыре раза. Но в каждом квадрате две двойки, значит всего двоек будет восемь.
Нужно перемножить два в квадрате четыре раза. Но в каждом квадрате две двойки, значит всего двоек будет восемь.
 Тема относится к категории сложных. Здесь необходимо использовать весь арсенал полученных ранее знаний.
Тема относится к категории сложных. Здесь необходимо использовать весь арсенал полученных ранее знаний. А чтобы понять какой модуль больше, а какой меньше, нужно суметь сравнить модули этих дробей до их вычисления:
А чтобы понять какой модуль больше, а какой меньше, нужно суметь сравнить модули этих дробей до их вычисления: Чтобы сложить отрицательные рациональные числа, нужно сложить их модули и перед полученным ответом поставить минус:
Чтобы сложить отрицательные рациональные числа, нужно сложить их модули и перед полученным ответом поставить минус: Найти значение выражения
Найти значение выражения Можно сразу записать ответ, записав вместе числа?7 и дробь (спрятав минус этой дроби)
Можно сразу записать ответ, записав вместе числа?7 и дробь (спрятав минус этой дроби) Делать это нужно очень аккуратно, чтобы не перепутать знаки слагаемых.
Делать это нужно очень аккуратно, чтобы не перепутать знаки слагаемых. Сложим их модули и перед полученным ответом поставим минус:
Сложим их модули и перед полученным ответом поставим минус:
 А чтобы сравнить модули смешанных чисел, нужно перевести их в неправильные дроби и сравнить, как обычные дроби.
А чтобы сравнить модули смешанных чисел, нужно перевести их в неправильные дроби и сравнить, как обычные дроби. А чтобы понять какой модуль больше, а какой меньше, нужно суметь сравнить модули этих десятичных дробей до их вычисления:
А чтобы понять какой модуль больше, а какой меньше, нужно суметь сравнить модули этих десятичных дробей до их вычисления: Запись с модулями можно пропустить, чтобы не загромождать выражение:
Запись с модулями можно пропустить, чтобы не загромождать выражение: Сложить их модули и перед полученным ответом поставим минус. Запись с модулями можно пропустить, чтобы не загромождать выражение:
Сложить их модули и перед полученным ответом поставим минус. Запись с модулями можно пропустить, чтобы не загромождать выражение: Вычтем из большего модуля меньший и перед ответом поставим тот знак, модуль которого больше:
Вычтем из большего модуля меньший и перед ответом поставим тот знак, модуль которого больше: Запись с модулями пропустим, чтобы не загромождать выражения.
Запись с модулями пропустим, чтобы не загромождать выражения.
 Попутно переведём десятичную дробь (?4,4) в неправильную дробь
Попутно переведём десятичную дробь (?4,4) в неправильную дробь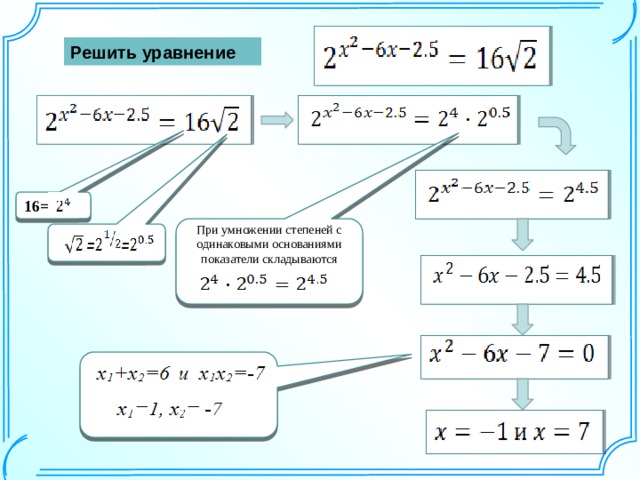 Вычтем из большего модуля меньший и перед полученным ответом поставим тот знак, модуль которого больше:
Вычтем из большего модуля меньший и перед полученным ответом поставим тот знак, модуль которого больше: Это следует из сочетательного закона сложения.
Это следует из сочетательного закона сложения.
 На рисунке можно увидеть как это происходит:
На рисунке можно увидеть как это происходит: В результате мы окажемся в точке, где располагается положительное число 2.
В результате мы окажемся в точке, где располагается положительное число 2. Для этого из точки, где располагается отрицательное число?2 нужно сдвинуться вправо на два шага. В результате мы окажемся в точке, где располагается число 0
Для этого из точки, где располагается отрицательное число?2 нужно сдвинуться вправо на два шага. В результате мы окажемся в точке, где располагается число 0 Для таких случаев предусмотрено следующее правило:
Для таких случаев предусмотрено следующее правило: У числа 3 модуль больше, поэтому знак этого числа и поставлен в ответе. То есть, ответ положительный.
У числа 3 модуль больше, поэтому знак этого числа и поставлен в ответе. То есть, ответ положительный.
 Новое правило говорит, что вычесть одно число из другого означает прибавить к уменьшаемому такое число, которое будет противоположно вычитаемому.
Новое правило говорит, что вычесть одно число из другого означает прибавить к уменьшаемому такое число, которое будет противоположно вычитаемому. Это связано с тем, что положительные числа записываются без своего знака плюс.
Это связано с тем, что положительные числа записываются без своего знака плюс.
 Так мы обеспечим минус, который должен стоять перед ответом:
Так мы обеспечим минус, который должен стоять перед ответом: Сложение оставляем как есть, а вычитание заменяем сложением:
Сложение оставляем как есть, а вычитание заменяем сложением:
 Все […]
Все […] Оформлением данных полисов занимаются многие страховые компании, которые получили соответствующую лицензию на ведение подобной деятельности. Однако, […]
Оформлением данных полисов занимаются многие страховые компании, которые получили соответствующую лицензию на ведение подобной деятельности. Однако, […]


 И x 3 .x 2 .x = x 3+2+1 = x 6 .
И x 3 .x 2 .x = x 3+2+1 = x 6 . 3$
3$ Степени с рациональными показателями и их свойства будут рассмотрены в уроках для 8 классов.
Степени с рациональными показателями и их свойства будут рассмотрены в уроках для 8 классов.



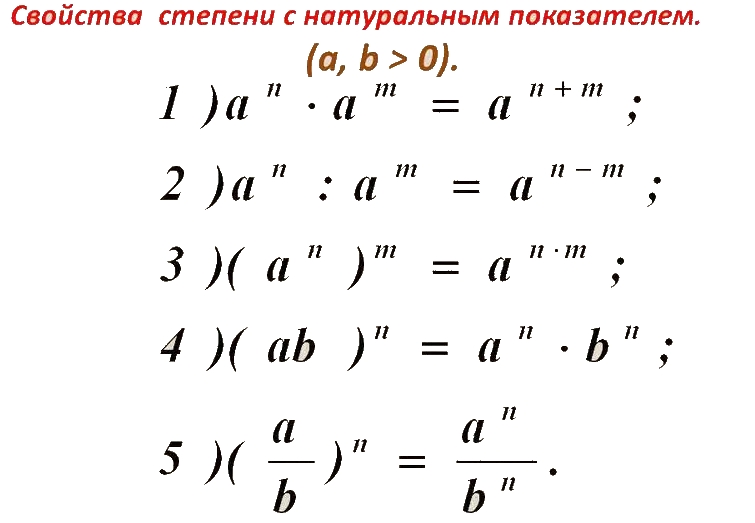 Корень из отношения равен отношению корней делимого и делителя:
Корень из отношения равен отношению корней делимого и делителя: 

 По определению степени
По определению степени Поэтому из доказанного пока нельзя делать, например, таких выводов:
Поэтому из доказанного пока нельзя делать, например, таких выводов:
 Оно не относится к их сложению.
Оно не относится к их сложению.




 О том, как это делается, мы расскажем в отдельной статье.
О том, как это делается, мы расскажем в отдельной статье. В итоге получим следующее:
В итоге получим следующее: Запишем и получим нужный ответ:
Запишем и получим нужный ответ:


 )
)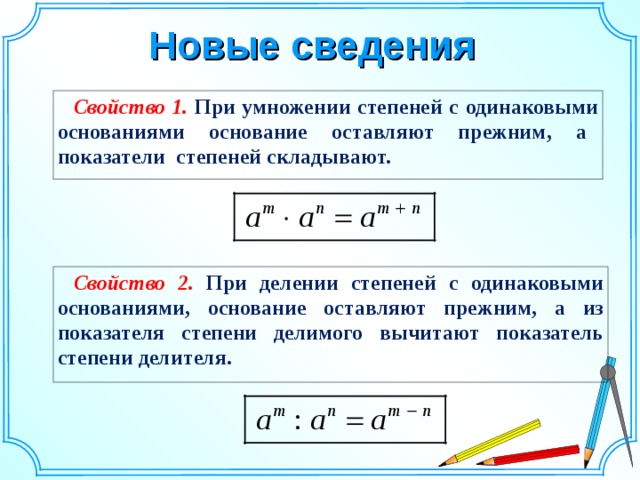 Такой способ изложения, типичный для науки стран древнего Востока, наводит на мысль о том, что математика там развивалась путём обобщений и догадок, не образующих никакой общей теории. Тем не менее, в папирусе есть целый ряд свидетельств того, что египетские математики умели извлекать корни и возводить в степень, решать уравнения, и даже владели зачатками алгебры.
Такой способ изложения, типичный для науки стран древнего Востока, наводит на мысль о том, что математика там развивалась путём обобщений и догадок, не образующих никакой общей теории. Тем не менее, в папирусе есть целый ряд свидетельств того, что египетские математики умели извлекать корни и возводить в степень, решать уравнения, и даже владели зачатками алгебры.
 Если уменьшить степень корня в n раз и в тоже время извлечь корень n -ой степени из подкоренного числа, то значение корня не поменяется:
Если уменьшить степень корня в n раз и в тоже время извлечь корень n -ой степени из подкоренного числа, то значение корня не поменяется: — деление степеней;
— деление степеней; 2 2 2 5 =2 2+5 =2 7 =128. Пример 10. (a – 4c +x) 2 (a – 4c +x) 3 =(a – 4c + x) 5 .
2 2 2 5 =2 2+5 =2 7 =128. Пример 10. (a – 4c +x) 2 (a – 4c +x) 3 =(a – 4c + x) 5 .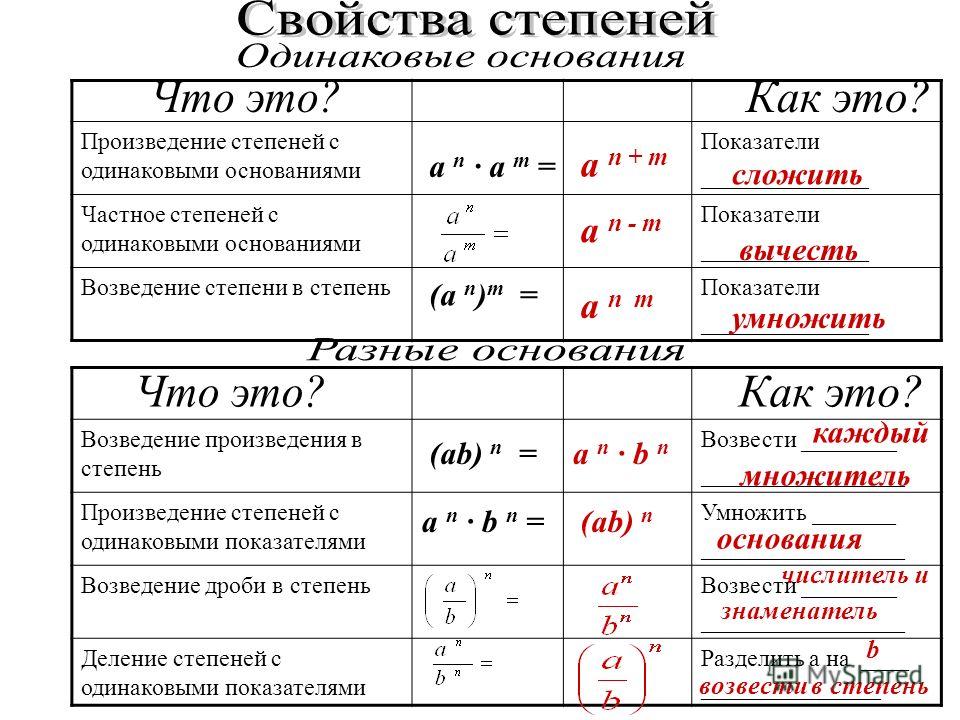
 Если уменьшить степень корня в m раз и одновременно извлечь корень m -ой степени из подкоренного числа, то значение корня не изменится:
Если уменьшить степень корня в m раз и одновременно извлечь корень m -ой степени из подкоренного числа, то значение корня не изменится: 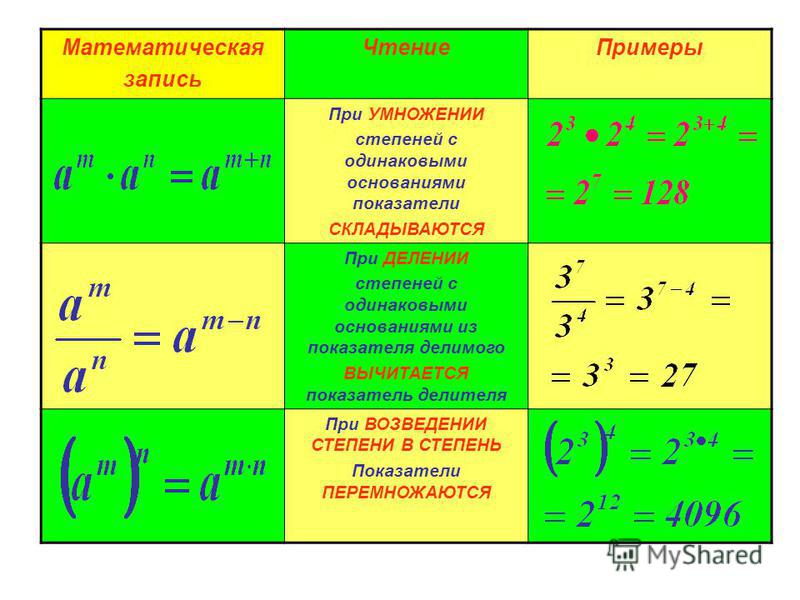
 Но это равенство имеет место при любом числе x , что и требовалось доказать.
Но это равенство имеет место при любом числе x , что и требовалось доказать.

 Представить 3 20 в виде степени с основанием 3 2 .
Представить 3 20 в виде степени с основанием 3 2 . Вычислить.
Вычислить. 


 5}$. Ответ: $\frac{2x}{1}$ или 2x.
5}$. Ответ: $\frac{2x}{1}$ или 2x.


 Например, (2 + 0 , 3 · 7) 5 − 3 , 7 и . Работать с такими записями сложно. Намного проще заменить выражение в основании степени или выражение в показателе тождественно равным выражением.
Например, (2 + 0 , 3 · 7) 5 − 3 , 7 и . Работать с такими записями сложно. Намного проще заменить выражение в основании степени или выражение в показателе тождественно равным выражением.
 Больше информации по вопросу можно найти в теме «Преобразование выражений с использованием свойств степеней».
Больше информации по вопросу можно найти в теме «Преобразование выражений с использованием свойств степеней». Сложим показатели при умножении степеней с одинаковыми основаниями: 21 1 3 · 21 2 3 = 21 1 3 + 2 3 = 21 1 = 21 .
Сложим показатели при умножении степеней с одинаковыми основаниями: 21 1 3 · 21 2 3 = 21 1 3 + 2 3 = 21 1 = 21 . К таким выражениям применимы все основные преобразования дробей без ограничений. Их можно сокращать, приводить к новому знаменателю, работать отдельно с числителем и знаменателем. Проиллюстрируем это примерами.
К таким выражениям применимы все основные преобразования дробей без ограничений. Их можно сокращать, приводить к новому знаменателю, работать отдельно с числителем и знаменателем. Проиллюстрируем это примерами. Подбирать дополнительный множитель необходимо таким образом, чтобы он не обращался в нуль ни при каких значениях переменных из ОДЗ переменных для исходного выражения.
Подбирать дополнительный множитель необходимо таким образом, чтобы он не обращался в нуль ни при каких значениях переменных из ОДЗ переменных для исходного выражения. е. x + 8 · y 1 2 . Это наш новый знаменатель, к которому нам надо привести исходную дробь.
е. x + 8 · y 1 2 . Это наш новый знаменатель, к которому нам надо привести исходную дробь. Также мы можем произвести сокращение на x 0 , 5 + 1 и на x + 2 · x 1 1 3 — 5 3 .
Также мы можем произвести сокращение на x 0 , 5 + 1 и на x + 2 · x 1 1 3 — 5 3 . Знаменатель остается прежним. Результатом наших действий является новая дробь, числитель которой является произведением числителей, а знаменатель есть произведение знаменателей.
Знаменатель остается прежним. Результатом наших действий является новая дробь, числитель которой является произведением числителей, а знаменатель есть произведение знаменателей.
 Это действие позволяет упростить дальнейшее решение. Приведем пример: степенное выражение (x + 1) — 0 , 2 3 · x — 1 можно заменить на x 3 · (x + 1) 0 , 2 .
Это действие позволяет упростить дальнейшее решение. Приведем пример: степенное выражение (x + 1) — 0 , 2 3 · x — 1 можно заменить на x 3 · (x + 1) 0 , 2 .