Новости за 7 дней.
Компания группы PORCELANOSA Grupo представляет новую коллекцию керамики размером 100 x 100 см, которую можно устанавливать на фальшполах в наружных зонах. Крупноформатная керамическая плитка стала излюбленным материалом архитекторов и застройщиков за счет высоких технических характеристик, прочнос….
TITAN корпуса металлические коттеджные ЩУРн IEK® используются для сборки вводно-учетных электрощитов с применением модульной аппаратуры, для ввода и учета электроэнергии в коттеджах и загородных домах. Преимущества корпусов металлических коттеджных ЩУРн IEK® серии TITAN Уличное размещение под ….
Новая портативная колонка PS-195 — еще один образчик классического стиля от SVEN: строгая прямоугольная форма, никаких лишних украшений, плавные изгибы панели управления — все сделано с максимальной долей вкуса и внимания к деталям. Взяв ее в руки, сложно даже представить себе, что она обладает сра….
Мы обновили ассортимент реле времени и добавили аппараты с двумя перекидными контактами: RT-SBA-2, RT-SBE-2, RT-SBB-2 и RT-10-2. У каждого прибора своя функция: RT-SBA-2 – задержка времени включения; RT-SBE-2 – задержка выключения после пропадания сигнала; RT-SBB-2 – подача импульса при вкл….
Керамический паркет бренда вдохновлен древесиной дуба и ореха и является одним из самых популярных отделочных материалов благодаря крупному формату и износостойкости. Керамический паркет PAR-KER® от Porcelanosa, предназначенный для использования в крупномасштабных проектах и воспроизводящий тексту….
Из 10 номеров этого отеля открывается вид на горы Сьерра-де-Альбаррасин и старую часть города, а сам отель гармонично вписан в природный ландшафт благодаря чувственному дизайну интерьера, выполненному архитектором Мапи Эрнандес (MHM Arquitectura) с использованием коллекций Porcelanosa. Признанный о….
Лента-трос STINGRAY — современное решение для создания линий света на любой высоте. Возможно выбрать трос отдельно и приобрести ленту самостоятельно или купить уже готовый комплект, состоящий из ленты и троса. В ассортименте представлены две модели тросов: STINGRAY-SET-5000 длиной 5 м и STINGRAY-S….
Представляем новинку в серии Basic – устройство этажное распределительное встроенное типа УЭРВ. Габариты – 1300х1300х150 мм. УЭРВ устанавливается в подготовленную нишу. В нём можно компактно разместить модульную автоматику, счётчики, а также силовые и слаботочные линии – внутри находятся соответст….
Обморожение: степени, первая помощь, профилактика — Новости — Пациентам
Обморожение представляет собой повреждение какой-либо части тела (вплоть до омертвения) под воздействием низких температур. При длительном пребывании вне помещения, особенно при высокой влажности и сильном ветре, обморожение можно получить осенью и весной при температуре воздуха выше нуля.
К обморожению на морозе приводят тесная и влажная одежда и обувь, физическое переутомление, голод, вынужденное длительное неподвижное и неудобное положение, предшествующая холодовая травма, ослабление организма в результате перенесенных заболеваний, потливость ног, хронические заболевания сосудов нижних конечностей и сердечно-сосудистой системы, тяжелые механические повреждения с кровопотерей, курение и пр.
Статистика свидетельствует, что почти все тяжелые обморожения, приведшие к ампутации конечностей, произошли в состоянии сильного алкогольного опьянения.
Под влиянием холода в тканях происходят сложные изменения, характер которых зависит от уровня и длительности снижения температуры. При действии температуры ниже -30 градусов С основное значение при обморожении имеет повреждающее действие холода непосредственно на ткани, и происходит гибель клеток. При действии температуры до -10–20 градусов С, при котором наступает большинство обморожений, ведущее значение имеют сосудистые изменения в виде спазма мельчайших кровеносных сосудов. В результате замедляется кровоток, прекращается действие тканевых ферментов.
Признаки обморожения и общего переохлаждения:
— кожа бледно-синюшная;
— температурная, тактильная и болевая чувствительность отсутствуют или резко снижены;
— при отогревании появляются сильные боли, покраснение и отек мягких тканей;
— при более глубоком повреждении через 12-24 ч. возможно появление пузырей с кровянистым содержимым;
— при общем переохлаждении человек вял, безучастен к окружающему, его кожные покровы бледные, холодные, пульс частый, артериальное давление снижено, температура тела ниже 36°С
Выделяют несколько степеней обморожения:
Обморожение I степени (наиболее легкое) обычно наступает при непродолжительном воздействии холода. Пораженный участок кожи бледный, после согревания покрасневший, в некоторых случаях имеет багрово-красный оттенок; развивается отек. Омертвения кожи не возникает. К концу недели после обморожения иногда наблюдается незначительное шелушение кожи. Полное выздоровление наступает к 5–7 дню после обморожения. Первые признаки такого обморожения – чувство жжения, покалывания с последующим онемением пораженного участка. Затем появляются кожный зуд и боли, которые могут быть и незначительными, и резко выраженными.
Обморожение II степени возникает при более продолжительном воздействии холода. В начальном периоде появляется побледнение, кожа становится холодной, утрачивается чувствительность, но эти явления наблюдаются при всех степенях обморожения. Поэтому наиболее характерный признак – образование в первые дни после травмы пузырей, наполненных прозрачным содержимым. Полное восстановление целостности кожного покрова происходит в течение 1–2 недель, грануляции и рубцы не образуются. При обморожении II степени после согревания боли интенсивнее и продолжительнее, чем при обморожении I степени, беспокоят кожный зуд, жжение.
При обморожении III степени продолжительность периода холодового воздействия и снижения температуры в тканях увеличивается. Образующиеся в начальном периоде пузыри наполнены кровянистым содержимым, дно их сине-багровое, нечувствительное к раздражениям. Происходит гибель всех элементов кожи с развитием в исходе обморожения грануляций и рубцов. Сошедшие ногти вновь не отрастают или вырастают деформированными. Отторжение отмерших тканей заканчивается на 2–3-й неделе, после чего наступает рубцевание, которое продолжается до 1 месяца. Интенсивность и продолжительность болевых ощущений более выражена, чем при обморожении II степени.
Обморожение IV степени возникает при длительном воздействии холода, снижение температуры в тканях при нем наибольшее. Оно нередко сочетается с обморожением III и даже II степени. Омертвевают все слои мягких тканей, нередко поражаются кости и суставы.
Поврежденный участок конечности сильно синюшный, иногда с мраморной расцветкой. Отек развивается сразу после согревания и быстро увеличивается. Температура кожи значительно ниже, чем на окружающих участок обморожения тканях. Пузыри развиваются на менее обмороженных участках, где есть обморожение III–II степени. Отсутствие пузырей при развившемся значительно отеке, утрата чувствительности свидетельствуют об обморожении IV степени.
В условиях длительного пребывания при низкой температуре воздуха возможны не только местные поражения, но и общее охлаждение организма. Под общим охлаждением организма следует понимать состояние, возникающее при понижении температуры тела ниже 34 градусов С.
Первая помощь при обморожениях
Прежде всего необходимо согреть пострадавшего в теплом помещении. Согревание пораженной части тела должно быть постепенным, медленным, преимущественно пассивным. Недопустимо (!) растирать отмороженные участки тела руками, тканями, спиртом и уж тем более снегом! (Подобные рецепты на редкость живучи и до сих пор бытуют в народе.) Дело в том, что эти меры способствуют тромбообразованию в сосудах, углубляя процессы деструкции пораженных тканей.
Пострадавшего нужно укутать в теплое одеяло (при общем переохлаждении) или (при отморожении) наложить на пораженную часть тела термоизолирующую ватно-марлевую повязку (7 слоев) для кумуляции тепла и предотвращения преждевременного согревания поверхностных тканей (и, соответственно, образования перепада температур между поверхностными и глубокими тканями). Применение термоизолирующей повязки позволяет в несколько раз замедлить внешнее согревание пораженного участка при обеспечении общего согревания организма.
Если отморожена рука или нога, ее можно согреть в ванне, постепенно повышая температуру воды с 20 до 40° С и в течение 40 минут нежно (!) массируя конечность. На внутреннюю поверхность бедра или плеча можно дополнительно положить теплую грелку. Пострадавшему дают обильное теплое питье – например, сладкий чай.
Профилактика переохлаждения и обморожений
Есть несколько простых правил, которые позволят вам избежать переохлаждения и обморожений на сильном морозе:
— Не пейте спиртного – алкогольное опьянение вызывает большую потерю тепла. Дополнительным фактором является невозможность сконцентрировать внимание на признаках обморожения.
— Не курите на морозе – курение уменьшает периферийную циркуляцию крови, и таким образом делает конечности более уязвимыми.
— Носите свободную одежду – это способствует нормальной циркуляции крови. Одевайтесь как «капуста» – при этом между слоями одежды всегда есть прослойки воздуха, отлично удерживающие тепло.
— Тесная обувь, отсутствие стельки, сырые грязные носки часто служат основной предпосылкой для появления потертостей и обморожения. Особое внимание уделять обуви необходимо тем, у кого часто потеют ноги. В сапоги нужно положить теплые стельки, а вместо хлопчатобумажных носков надеть шерстяные – они впитывают влагу, оставляя ноги сухими.
— Не выходите на мороз без варежек, шапки и шарфа. Лучший вариант – варежки из влагоотталкивающей и непродуваемой ткани с мехом внутри. Перчатки же из натуральных материалов хоть и удобны, но от мороза не спасают. Щеки и подбородок можно защитить шарфом. В ветреную холодную погоду перед выходом на улицу открытые участки тела смажьте специальным кремом.
— Не носите на морозе металлических (в том числе золотых, серебряных) украшений.
— Пользуйтесь помощью друга: следите за лицом друга, особенно за ушами, носом и щеками, за любыми заметными изменениями в цвете, а он или она будут следить за вашими.
— Не снимайте на морозе обувь с обмороженных конечностей – они распухнут и вы не сможете снова одеть обувь. Необходимо как можно скорее дойти до теплого помещения. Если замерзли руки – попробуйте отогреть их подмышками.
— Вернувшись домой после длительной прогулки по морозу, обязательно убедитесь в отсутствии обморожений конечностей, спины, ушей, носа и т.д.
— Как только на прогулке вы почувствовали переохлаждение или замерзание конечностей, необходимо как можно скорее зайти в любое теплое место — магазин, кафе, подъезд – для согревания и осмотра потенциально уязвимых для обморожения мест.
— Прячьтесь от ветра – вероятность обморожения на ветру значительно выше.
— Не мочите кожу – вода проводит тепло значительно лучше воздуха. Не выходите на мороз с влажными волосами после душа. Мокрую одежду и обувь (например, человек упал в воду) необходимо снять, вытереть воду, при возможности одеть в сухую и как можно быстрее доставить человека в тепло. В лесу необходимо разжечь костер, раздеться и высушить одежду, в течение этого времени энергично делая физические упражнения и греясь у огня.
— Перед выходом на мороз надо поесть.
— Дети и старики более подвержены переохлаждению и обморожениям. Отпуская ребенка гулять в мороз на улице, помните, что ему желательно каждые 15-20 минут возвращаться в теплое помещение и согреваться.
При первых признаках обморожения обратитесь в ближайший травмпункт.
степени 0, 1, 2, классификация, способы лечения в клинике Синай
Метод диагностики и классификации повреждений мениска stoller – современный способ, основанный на МРТ коленного сустава. Новый и пока еще дорогостоящий, он позволяет получить максимум информации об изменениях хрящевой ткани и подобрать лечение, которое будет наиболее действенным в конкретном случае.
Повреждения мениска могут носить травматическую или дегенеративную природу. И то и другое повреждение по stoller определяется точно. В зависимости от того к какой степени будет отнесена травма, больному назначат консервативное или хирургическое лечение. Иные способы выявления патологии не могут также точно отразить уровень повреждения хряща.
Причины повреждений мениска по Stoller
Причины повреждения различны. Дегенеративные дефекты мениска чаще всего наблюдаются у лиц старшего возраста, у которых проблема появляется на фоне нарушений в коленном суставе. Также дегенеративные изменения вызывают следующие причины:
-
ревматизм;
-
подагра;
-
хроническое микротравмирование колена – наблюдается в том случае, если человек постоянно перегружает сустав, который в результате этого не успевает полноценно восстанавливаться и постепенно начинает разрушаться.
Травматическое повреждение по Stoller происходит значительно чаще. Оно возникает от непосредственного удара в область колена или на фоне значительных неестественных нагрузок. К таким опасным воздействиям относятся: длительное хождение на носках, высокий прыжок с приземлением на жесткую поверхность, форсированное разгибание колена или резкое движение ногой после того, как она в течение продолжительного времени находилась в одном положении.
Вне зависимости от того что стало причиной болезни, необходимы проведение полноценной диагностики, классификация повреждения и прохождение полноценного лечения. В клинике Синай пациентам предоставляется возможность диагностики и классификации поражения мениска по столлер по максимально выгодной для них цене.
Виды разрыва мениска по Stoller
Разрывы мениска классифицируются по локализации и форме. Определение этих показателей очень важно для правильной терапии патологии. По области локализации различаются травмы:
В зависимости от формы повреждения классификация такая:
-
горизонтальный разрыв – наблюдается в случае кистозного перерождения;
-
косой радикальный или продольный – бывает на границе задней трети хряща и средней;
-
комбинированный – возникает в заднем роге.
В зависимости от повреждения несколько изменяется местонахождение очага основной боли, а также положение ноги, в котором она усиливается.
Что представляет собой Stoller-классификация
Разработана методика доктором медицинских наук профессором Девидом Столлером, который является директором действующего в США Национального центра визуализации структур опорно-двигательной системы в ортопедии. Точность исследования и возможности послойного сканирования тканей, а также визуализации пораженных участков тканей и суставов значительно повысились с появлением МРТ технологии. Метод, предложенный Столлером, основан на том, что во время сканирования появляется сигнал повышенной интенсивности, указывающий на присутствие в данной области дегенеративных изменений, возникающих при повреждении мениска. Профессором разработана система, при которой используются критерии интенсивности получаемого сигнала, а также область его локализации и распространения.
При классификации поражения учитываются показатели критериев выраженности патологии и ее тяжести. Классификация основывается на том, какую интенсивность имеет сигнал: чем она выше, тем серьезнее поражение тканей и тяжелее дегенеративный процесс.
Классификация
Классификация столлер разделяет состояние мениска на 4 стадии. В зависимости от того какая из них выявлена, определяют наличие или отсутствие патологий мениска.
-
0 стадия по Stoller. При исследовании не обнаруживаются очаги патологических изменений в тканях. Состояние мениска оценивается как совершенно здоровое.
-
1 стадия по Stoller. При МРТ выявляется сигнал повышенной интенсивности, который имеет очаговый характер и четкую локализацию. В то же время он не доходит до поверхности хрящевой ткани. Лечение чаще всего в этом случае еще не требуется или, если все же выявлена необходимость в его проведении, осуществляется консервативными методами преимущественно профилактической направленности.
-
2 стадия по Stoller. Интенсивность сигнала, получаемого от тканей, повышена, но при этом характер его изменяется на линейный. Аналогично первой стадии он не доходит до верхнего слоя мениска (хряща). Если при этом выявляется горизонтальное повреждение мениска, то оно означает, что хрящевая ткань разрушена частично, а изменений в ее структуре нет. Лечение проводится обязательно. Оно бывает преимущественно консервативное. Повреждение мениска 2 степени по stoller – наиболее распространенная причина обращения за врачебной помощью.
-
3 стадия по Stoller. Сигнал фиксируется линейный значительно повышенной интенсивности. Он четко достигает верхнего слоя хряща. У пациента выявляется выраженное нарушение анатомических структур мениска. Это означает присутствие разрывов медиального мениска. Также при таком поражении не исключается и смещение части участков травмированного хряща. Такое состояние диагностируется как полный отрыв мениска со смещением. Лечение требуется обязательно и проводится, как правило, хирургическим способом. Повреждение мениска 3 степени по stoller наиболее тяжелое.
Так как проведение диагностики и классификации поражения по Stoller возможно только при наличии аппарата для магнитно-резонансной томографии, то данная услуга доступна не во всех медицинских учреждениях. На сегодняшний день методом stoller степени повреждения мениска определяются наиболее точно.
Клиническая картина по столлер (по Stoller)- классификации
Клинические проявления патологии по классификации также разнятся в зависимости от стадии поражения. Они дополнительно позволяют оценить состояние пациента.
-
0 стадия по Stoller. Так как патологии хряща отсутствуют и его целостность не нарушена, то и симптомов патологии нет.
-
1 стадия по Stoller. Минимальные изменения в суставе приводят к периодическому появлению в нем болей. Они обычно проявляются в вечернее время и более интенсивны у людей, которые в течение дня вынуждены серьезно перегружать суставы. Также может наблюдаться заметный хруст в момент сгибания колена.
-
2 стадия по Stoller. Нарушения в состоянии сустава достаточно выраженные, из-за чего боль становится значительной. Ее интенсивность повышается в момент, когда человек двигает ногой, задействовав при этом колено. Также болевой синдром нарастает после долгого пребывания в стоячем положении. В большинстве случаев отмечаются и внешние проявления воспаления, такие как покраснение кожи и отечность тканей. Хруст в суставе появляется почти при каждом движении.
-
3 стадия по Stoller. Происходят серьезные изменения в анатомическом строении хряща, из-за чего отмечаются не только сильная боль, а и выраженная ограниченность подвижности коленного сустава. Болевой синдром, как и скованность движений, в этом состоянии наибольшие. Клиническая картина патологии острая.
Присутствие симптомов в дополнение к МРТ позволяет точно определить состояние пациента. Только так терапия будет максимально эффективная.
Как подготовиться к процедуре
Специальная подготовка перед проведением МРТ с дальнейшей классификацией состояния мениска Stoller не требуется. На исследование распространяются те же противопоказания, что и на проведение МРТ, а в первую очередь присутствие в теле металлических элементов и различных электростимуляторов и инсулиновых помп, на работу которых может влиять магнитное поле прибора.
Во время исследования не будет возникать болевых ощущений или дискомфорта. Единственное, что надо учесть пациенту, это то, что процедура длительная. Если пациент очень нервничает перед обследованием, то ему рекомендуется принять валериану или другое растительное успокоительное средство.
Степени защиты IP
23 Декабря 2009
Все электротехнические устройства должны соответствовать определенной степени защиты в соответствии с МЭК 70-1 – IP (International/Ingress Protection). Степень защиты приводится в виде IPXX, где первая цифра обозначает – уровень защиты от попадания твёрдых частиц и степень защиты по электробезопасности (табл. 2), а вторая – защиту от влаги. Возможные сочетания двух показателей приведены в таблице 1:
Таблица 1. Пылевлагозащищенность
IP x0 | IP x1 | IP x2 | IP x3 | IP x4 | IP x5 | IP x6 | IP x7 | IP x8 | ||
Нет защиты | Падение вертикальных капель | Падение капель под углом 15○ от вертикали | Брызги под углом 60○ от вертикали | Брызги со всех сторон | Струи со всех сторон под небольшим давлением | Сильные потоки | Временное погружение (до 1 м) | Полное погружение* | ||
IP 0x | Нет защиты | IP 00 | ||||||||
IP 1x | Частицы > 50 мм | IP 10 | IP 11 | IP 12 | ||||||
IP 2x | Частицы > 12,5 мм | IP 20 | IP 21 | IP 22 | IP 23 | |||||
IP 3x | Частицы > 2,5 мм | IP 30 | IP 31 | IP 32 | IP 33 | IP 34 | ||||
IP 4x | Частицы > 1 мм | IP 40 | IP 41 | IP 42 | IP 43 | IP 44 | ||||
IP 5x | Пыль частично | IP 50 | IP 54 | IP 55 | ||||||
IP 6x | Пыль полностью | IP 60 | IP 65 | IP 66 | IP 67 | IP 68 | ||||
Возможно существование только приведенных выше комбинаций, т.к. увеличение одного из показателей защиты ведет к повышению другого (например, изделие, которое может быть временно погружено в воду, естественно, защищено достаточно, чтобы полностью не пропускать пыль, поэтому существование степени защиты, например, IP37 невозможно). Также существует степень защиты IP69 с повышенными характеристиками к стойкости при большом давлении.
Таблица 2. Защита от соприкосновения с частями изделия, находящимися под напряжением
Первая цифра | Описание |
0 | Никакой защиты от прикосновения к токоведущим частям. |
1 | Частичная защита от случайного касания токоведущих частей (защита от касания ладонью). |
2 | Защита от прикосновения пальцами к токоведущим частям. |
3 | Защита от случайного касания токоведущих частей инструментом. |
4 | Защита от случайного касания токоведущих частей инструментом. |
5 | Полная защита от прикосновения к токоведущим частям изделия. |
6 | Полная защита от прикосновения к токоведущим частям изделия. |
Приказ Министерства здравоохранения и социального развития Российской Федерации (Минздравсоцразвития России) от 20 октября 2005 г. N 643 г. Москва «Об утверждении форм документов о результатах установления федеральными государственными учреждениями медико-социальной экспертизы степени утраты профессиональной трудоспособности в процентахи рекомендаций по их заполнению»
Зарегистрирован в Минюсте РФ 20 января 2006 г.
Регистрационный N 7402
В соответствии с Федеральным законом от 22 августа 2004 г. N 122-ФЗ «О внесении изменений в законодательные акты Российской Федерации и признании утратившими силу некоторых законодательных актов Российской Федерации в связи с принятием федеральных законов «О внесении изменений и дополнений в Федеральный закон «Об общих принципах организации законодательных (представительных) и исполнительных органов государственной власти субъектов Российской Федерации» и «Об общих принципах организации местного самоуправления в Российской Федерации» (Собрание законодательства Российской Федерации, 2004, N 35, ст. 3607; 2005, N 1 (часть 1), ст. 25) и постановлением Правительства Российской Федерации от 16 октября 2000 г. N 789 «Об утверждении Правил установления степени утраты профессиональной трудоспособности в результате несчастных случаев на производстве и профессиональных заболеваний» (Собрание законодательства Российской Федерации, 2000, N 43, ст. 4247; 2005, N 7, ст. 560) приказываю:
1.Утвердить:
формы документов о результатах установления федеральными государственными учреждениями медико-социальной экспертизы степени утраты профессиональной трудоспособности в процентах согласно приложению N 1;
Рекомендации по заполнению форм документов о результатах установления федеральными государственными учреждениями медико-социальной экспертизы степени утраты профессиональной трудоспособности в процентах согласно приложению N 2.
2. Установить, что документы о результатах установления федеральными государственными учреждениями медико-социальной экспертизы степени утраты профессиональной трудоспособности в процентах выдаются федеральными государственными учреждениями медико-социальной экспертизы с 1 апреля 2006 года.
3. Признать утратившим силу с 1 апреля 2006 года постановление Министерства труда и социального развития Российской Федерации от 15 октября 2001 г. N 75 «Об утверждении форм документов о результатах определения бюро (главными бюро) медико-социальной экспертизы степени утраты профессиональной трудоспособности в процентах и Инструкции о порядке их заполнения» (зарегистрировано в Министерстве юстиции Российской Федерации 13 ноября 2001 г. N 3030) с изменениями, внесенными постановлением Министерства труда и социального развития Российской Федерации от 26.03.2003 N 12 (зарегистрировано в Минюсте России 10.04.2003, регистрационный N 4404).
Министр
М. Зурабов
Приложение N 2
Рекомендации по заполнению форм документов о результатах установления федеральными государственными учреждениями медико-социальной экспертизы степени утраты профессиональной трудоспособности в процентах
1. К документам о результатах установления федеральными государственными учреждениями медико-социальной экспертизы степени утраты профессиональной трудоспособности в процентах относятся: Выписка из акта освидетельствования в федеральном государственном учреждении медико-социальной экспертизы о результатах установления степени утраты профессиональной трудоспособности в процентах (далее — выписка) и Справка о результатах установления степени утраты профессиональной трудоспособности в процентах (далее — справка).
2. Выписка и справка предназначены для подтверждения факта установления степени утраты профессиональной трудоспособности в процентах и внесения в них соответствующего решения федерального государственного учреждения медико-социальной экспертизы.
3. Все реквизиты выписки и справки заполняются в точном соответствии с записями аналогичных реквизитов в акте освидетельствования в федеральном государственном учреждении медико-социальной экспертизы.
4. В строке «наименование федерального государственного учреждения медико-социальной экспертизы» выписки и справки делается запись о наименовании главного бюро медико-социальной экспертизы с указанием наименования его филиала — бюро медико-социальной экспертизы, Федерального бюро медико-социальной экспертизы в точном соответствии с наименованием, определенным уставом главного (Федерального) бюро медико-социальной экспертизы.
5. В строке «Степень утраты профессиональной трудоспособности в процентах» выписки и справки делается запись об установленных процентах утраты профессиональной трудоспособности.
6. В строке «в связи с_____ от______» выписки и справки делается запись о несчастном случае на производстве и его дате или профессиональном заболевании, номере и дате составления акта по ф. Н-1 или дате составления акта о профессиональном заболевании (либо дате решения суда об установлении факта несчастного случая на производстве или профессионального заболевания).
7. В строке «Срок установления степени утраты профессиональной трудоспособности» выписки и справки указывается срок, на который определены проценты утраты профессиональной трудоспособности: после предлога «с» указывается дата (число, месяц, год) установления степени утраты профессиональной трудоспособности в процентах, после предлога «до» указывается первое число месяца, следующего за тем месяцем, на который назначено очередное переосвидетельствование, и год, на который назначено очередное переосвидетельствование.
8. В строке «Дата очередного освидетельствования» выписки и справки указывается дата (число, месяц, год) переосвидетельствования, которая не должна совпадать с нерабочим днем федерального государственного учреждения медико-социальной экспертизы.
При определении степени утраты профессиональной трудоспособности без указания срока переосвидетельствования в указанной строке делается запись «бессрочно».
9. В строке «Основание:» выписки и справки указывается номер акта освидетельствования в федеральном государственном учреждении медико-социальной экспертизы.
10. В строке «Степень утраты профессиональной трудоспособности в процентах за пропущенный период с__по__» выписки делается запись об установленных процентах утраты профессиональной трудоспособности за пропущенный период, в течение которого гражданин не проходил переосвидетельствование. При этом после предлога «с» указывается дата, до которой были установлены проценты утраты профессиональной трудоспособности при предыдущем освидетельствовании, после предлога «по» указывается дата, непосредственно предшествующая дате настоящего установления степени утраты профессиональной трудоспособности в процентах.
11. В строке «Дополнительные заключения» справки делается запись об установленных процентах утраты профессиональной трудоспособности за пропущенный период, в течение которого гражданин не проходил переосвидетельствование, в соответствии с записями, сделанными в строке «Степень утраты профессиональной трудоспособности в процентах за пропущенный период с__по__» выписки.
12. Выписка и справка подписываются руководителем главного бюро медико-социальной экспертизы, филиала главного бюро медико-социальной экспертизы — бюро медико-социальной экспертизы, Федерального бюро медико-социальной экспертизы (подпись расшифровывается) и заверяются печатью главного бюро медико-социальной экспертизы, филиала главного бюро медико-социальной экспертизы — бюро медико-социальной экспертизы, Федерального бюро медико-социальной экспертизы соответственно.
Подвиг народа
Для просмотра сайта c поддержкой основных нововведений рекомендуется использовать приложение-обозреватель Microsoft Internet Explorer 10, Mozilla Firefox 4, Google Chrome 5, Opera 11.5, Safari 5.0 и выше.
Работа с сайтом «Подвиг народа»
- Описание главной страницы.
- Поиск:
Описание главной страницы сайта «Подвиг народа»
В верхней части главной страницы ОБД (а также с любой другой страницы сайта) находятся ссылки, которые соответствуют основным тематическим разделам сайта. Также доступна ссылка для перехода на прежнюю версию сайта и изменение языка интерфейса сайта (доступны английский и русский языки).
В центральной части главной страницы приведено общее описание сайта, а также размещены ссылки для перехода к разделам сайта, таким как:
- Люди и награждения;
- Наградные документы;
- география войны.
- О проекте;
- Отзывы;
- Обратная связь;
- Вопросы-ответы;
- Помощь.
Поиск
Поиск информации по любому из тематических разделов может выполняться в два этапа:
- поиск в обычном режиме, когда при определении условий поиска пользователь вводит данные в одну поисковую строку, указывая их через пробел;
- расширенный поиск, когда пользователь при определении условий поиска заполняет максимально возможное количество полей, указывая детальную информацию об объекте поиска.
Данный вид поиска является наиболее эффективным, поскольку позволяет получить результат, наиболее точно отвечающий запросам пользователя.
Чтобы приступить к поиску информации по любому из тематических разделов, необходимо навести указатель на наименование соответствующего раздела (на ссылку в верхней части страницы или в центральной части главной страницы):
Поиск по тематическому разделу «Люди и награждения»
Поиск по тематическому разделу «Люди и награждения» позволяет найти информацию о награждении, используя личные данные награжденных.
Поиск в обычном режиме
Для быстрого поиска необходимо перейти к разделу «Люди и награждения» нажатием левой кнопки мыши по заголовку раздела.
Указать имеющиеся сведения в строке поиска.
При необходимости, можно выбрать количество записей, которые будут выводиться на одну страницу результатов поиска (по умолчанию выводится по 50 записей на страницу), есть возможность выбрать следующие значения: 10, 30, 50 или 100.
Для получения результата поиска нажать кнопку «Искать» или клавишу на клавиатуре.
Расширенный поиск
Чтобы выполнить расширенный поиск информации о награждении необходимо:
- перейти к разделу «Люди и награждения»;
- нажать кнопку «Расширенный поиск»;
Откроется поисковая форма с доступными для заполнения следующими полями:
- Фамилия;
- Имя
- Отчество;
- Год рождения;
- Звание;
- Место призыва;
- Уточнение «Где искать».
Если необходимо вернуться к поиску в обычном режиме, следует нажать кнопку «Свернуть».
Если необходимо большее количество уточняющих полей для осуществления поиска, следует нажать кнопку «Еще больше». После этого будут доступны дополнительные поля, такие как:
- Наименование награды;
- Номер наградного документа;
- Дата наградного документа;
- Архив;
- Фонд;
- Опись;
- С какого года в КА;
- Единица хранения.
Чтобы удалить введенные значения из всех полей, следует нажать кнопку «Очистить». После этого можно повторно ввести значения.
После чего на экране отобразятся результаты поиска:
Поиск по тематическому разделу «Наградные документы»
Поиск по тематическому разделу «Документы» позволяет найти указы и приказы о награждении.
Поиск в обычном режиме
Для быстрого поиска необходимо перейти к разделу «Наградные документы» нажатием левой кнопки мыши по заголовку раздела.
Указать имеющиеся сведения в строке поиска.
При необходимости, можно выбрать количество записей, которое будет выводиться на одну страницу результатов поиска (по умолчанию выводится по 50 записей на страницу), есть возможность выбрать следующие значения: 10, 30, 50 или 100.
Для получения результата поиска следует нажать кнопку «Искать» или клавишу на клавиатуре.
Расширенный поиск
Чтобы выполнить расширенный поиск документов о награждении необходимо:
- перейти к разделу «Наградные документы»;
- нажать кнопку «Расширенный поиск»;
Откроется поисковая форма с доступными для заполнения следующими полями:
- Дата документа;
- Награда.
Если необходимо вернуться к поиску в обычном режиме, следует нажать кнопку «Свернуть».
Если необходимо большее количество уточняющих полей для осуществления поиска, следует нажать кнопку «Больше». После этого будут доступны дополнительные поля, такие как:
- Номер записи в базе данных;
- Номер документа;
- Автор;
- Архив;
- Фонд;
- Опись;
- Единица хранения.
Чтобы удалить введенные значения из всех полей, следует нажать кнопку «Очистить». После этого можно повторно ввести значения.
После чего на экране отобразятся результаты поиска:
Поиск по тематическому разделу «География войны»
Поиск по тематическому разделу «География войны» позволяет выполнить поиск данных по местоположению и времени события.
Документы в разделе «География войны» могут быть найдены, используя в качестве критериев поиска дату выхода документов, географическую привязку к местам ведения боевых действий, привязку к сведениям о военачальнике, издавшем документ.
Поиск в обычном режиме
Для быстрого поиска необходимо перейти к разделу «География войны» нажатием левой кнопки мыши по заголовку раздела.
Указать имеющиеся сведения в строке поиска.
При необходимости, можно выбрать количество записей, которое будет выводиться на одну страницу результатов поиска (по умолчанию выводится по 50 записей на страницу), есть возможность выбрать следующие значения: 10, 30, 50 или 100.
Для получения результата поиска нажать кнопку «Искать» или клавишу на клавиатуре.
Расширенный поиск
Чтобы выполнить расширенный поиск документов о награждении необходимо:
- перейти к разделу «География войны»;
- нажать кнопку «Расширенный поиск»;
Откроется поисковая форма с доступными для заполнения следующими полями:
- Тип документа;
- Дата документа;
- Боевая операция;
- Географическое положение.
Если необходимо вернуться к поиску в обычном режиме, следует нажать кнопку «Свернуть».
Если необходимо большее количество уточняющих полей для осуществления поиска, следует нажать кнопку «Больше». После этого будут доступны дополнительные поля, такие как:
- Номер документа;
- Наименование документа;
- Автор;
- Архив;
- Фонд;
- Опись;
- Единица хранения.
Чтобы удалить введенные значения из всех полей, следует нажать кнопку «Очистить». После этого можно повторно ввести значения.
После чего на экране отобразятся результаты поиска:
Особенности заполнения поисковых полей
При заполнении полей в режиме расширенного поиска пользователь может определить для каждого поля способ поиска:
- С начала поля – чтобы выполнять поиск документов, у которых в начале соответствующего индексного поля будет содержаться значение, указанное пользователем в данном поисковом поле;
- Точная фраза — чтобы выполнять поиск документов, у которых в соответствующем индексном поле будет содержаться значение, состоящее из одного или нескольких слов (или цифр) в том же порядке, которое указано пользователем в данном поисковом поле;
- Точное поле — чтобы выполнять поиск документов, у которых в соответствующем индексном поле будет содержаться точное значение, указанное пользователем в данном поисковом поле;
- Полнотекстовый поиск — чтобы выполнять поиск документов, у которых в соответствующем индексном поле будет содержаться информация, указанная пользователем в данном поисковом поле, без учета последовательности слов.
Определение способа поиска происходит в раскрывающемся списке, после нажатия кнопки . Для разных полей перечень доступных способов поиска может отличаться. Например, для поля Фонд доступен только поиск «Точное поле», а для поля Опись доступны поиски «Точная фраза» и «Точное поле». Пример раскрывающего списка приведен на рисунке ниже:
Работа с результатами поиска
Результаты поиска «Люди и награждения»
Результат поиска информации о героях войны выводится на экран монитора в виде списка. При этом на каждой странице результатов поиска будет выводиться то количество найденных записей, которое было задано пользователем при определении условий поиска.
В первом столбце списка указан номер строки результатов поиска.
Во втором столбце списка указан источник данных, например:
— данные из документов о награждении;
— данные из картотеки;
— данные из юбилейной картотеки.
Далее указаны: Дата рождения/Звание/Наименование награды.
Для последовательного перемещения между страницами можно также воспользоваться кнопками:
, для перехода на следующую страницу;
, для перехода на последнюю страницу;
, для перехода на предыдущую страницу;
, для перехода на первую страницу.
Если результаты поиска не соответствуют требованиям пользователя, то он может вернуться на страницу поиска, нажав на наименование раздела, в котором осуществлялся поиск; при этом, все заполненные поисковые поля останутся без изменений. Также для возврата к предыдущей странице можно нажать кнопку «Назад» в окне web-браузера.
Чтобы просмотреть определенную запись из числа найденных, следует навести на нее указатель и нажать левую кнопку мыши – на экране появится страница просмотра информации.
В верхней части страницы отображаются кнопки «К предыдущему результату поиска», «К следующему результату поиска» Данные кнопки позволяют переходить по страницам просмотра информации согласно списку результатов поиска.
Ниже на странице представлены сведения о персоналии. В столбце «Архивные документы о данном награждении» синим подсвечены ссылки для перехода к электронным образам указанных документов.
Электронный образ документа, который представлен на странице, содержит описание подвига, за который была присуждена награда.
Для просмотра текста приказа (указа) необходимо нажать на одну из ссылок:
- первая страница приказа или указа;
- строка в наградном списке;
- наградной лист.
Откроется электронный образ выбранного документа.
Для просмотра изображения предусмотрена область навигации:
переход к предыдущей странице документа;
переход к следующей странице документа;
Рядом с областью навигации представлена панель инструментов с двумя функциями:
увеличение масштаба электронного образа документа;
уменьшение масштаба электронного образа документа;
при нажатии кнопки страница электронного образа документа будет открыта в новой вкладке, далее открытую страницу можно вывести на печать или сохранить на своем ПК;
просмотр страницы документа в полноэкранном режиме, для выхода из полноэкранного режима необходимо нажать кнопку в правом верхнем углу.
Результаты поиска «Наградные документы»
Результат поиска в разделе «Наградные документы» выводится на экран монитора в виде списка. При этом на каждой странице результатов поиска будет выводиться то количество найденных записей, которое было задано пользователем при определении условий поиска.
Информация по столбцам структурирована в следующем виде:
- дата документа;
- кем издан;
- номер документа;
- наименование документа.
Для последовательного перемещения между страницами можно также воспользоваться кнопками:
, для перехода на следующую страницу;
, для перехода на последнюю страницу;
, для перехода на предыдущую страницу;
, для перехода на первую страницу.
Для перехода к странице просмотра документа необходимо нажать левой кнопкой мыши в строке нужного документа в списке результатов поиска.
В верхней части страницы отображаются кнопки К предыдущему результату поиска, К следующему результату поиска Данные кнопки позволяют переходить по страницам просмотра информации согласно списку результатов поиска.
Ниже на странице представлены изображения, относящиеся к найденному документу.
Для просмотра электронного образа документа предусмотрена область навигации:
— переход к предыдущей странице документа;
— переход к следующей странице документа;
Рядом с областью навигации представлена панель инструментов с двумя функциями:
увеличение масштаба электронного образа документа;
уменьшение масштаба электронного образа документа;
при нажатии кнопки страница электронного образа документа будет открыта в новой вкладке, далее открытую страницу можно вывести на печать или сохранить на своем ПК;
просмотр страницы документа в полноэкранном режиме, для выхода из полноэкранного режима необходимо нажать кнопку в правом верхнем углу.
При наведении курсора мыши отдельные строки электронного образа документа могут быть определены как ссылки перехода, например, на страницу персоналии:
Для перехода к странице персоналии необходимо:
- навести указатель мыши на строку электронного образа документа;
- нажать левой кнопкой мыши.
- нажать кнопку
Строка будет подсвечена красным, и в правой части строки появится кнопка перехода.
После чего будет осуществлен переход к странице персоналии:
Результаты поиска «География войны»
Результат поиска в разделе «География войны» выводится на экран монитора в виде списка. При этом на каждой странице результатов поиска будет выводиться то количество найденных записей, которое было задано пользователем при определении условий поиска.
Информация по столбцам структурирована в следующем виде:
- дата документа;
- кем издан;
- номер документа;
- тип документа.
Для последовательного перемещения между страницами можно также воспользоваться кнопками:
, для перехода на следующую страницу;
, для перехода на последнюю страницу;
, для перехода на предыдущую страницу;
, для перехода на первую страницу.
Если результаты поиска не соответствуют требованиям пользователя, то он может вернуться на страницу поиска, нажав на наименование раздела, в котором осуществлялся поиск; при этом, все заполненные поисковые поля останутся без изменений. Также для возврата к предыдущей странице можно нажать кнопку «Назад» в окне web-браузера.
Для перехода к странице просмотра документа необходимо нажать левой кнопкой мыши в строке нужного документа в списке результатов поиска.
В верхней части страницы отображаются ссылки К предыдущему результату поиска, К следующему результату поиска – данные ссылки позволяют переходить по страницам просмотра информации согласно списку результатов поиска.
Ниже на странице представлены сведения о документе.
Для просмотра электронного образа документа предусмотрена область навигации:
— переход к предыдущей странице документа;
— переход к следующей странице документа;
Рядом с областью навигации представлена панель инструментов с двумя функциями:
— при нажатии кнопки страница электронного образа документа будет открыта в новой вкладке, далее открытую страницу можно вывести на печать или сохранить на своем компьютере;
— просмотр страницы документа в полноэкранном режиме, для выхода из полноэкранного режима необходимо нажать кнопку в правом верхнем углу.
To support the site’s latest version and innovations, we recommend using the following browser versions: Microsoft Internet Explorer 10, Mozilla Firefox 4, Google Chrome 5, Opera 11.5, Safari 5.0 and higher.
Main page
At the top of the Main page there is a menu, its items correspond to the main thematic sections of the «Feat of the People» website.
The central part of the Main page provides a general description of the website, as well as links to sections of the site:
- people and awards;
- documents;
- geography of war.
An additional menu with the following sections is available at the bottom of the page:
- About the project, which contains information about the resource, access to which is provided to users of the website «Feat of the People».
- Reviews, which contains reviews about the resource, access to which is provided to users of the website «Feat of the People».
- Feedback, which contains a feedback form for users of the website «Feat of the People».
- FAQ, which provides answers to user questions about the site, most frequently asked to the site Administration.
- Help, which provides information about thematic sections of the site and ways to work with them.
Search (only Russian)
The topic search in every section can be performed in two modes:
- search in normal mode, when you define a search criteria by filling in the set of fields with the minimum information required to perform a search.
- search in advanced mode, when you define the search criteria by filling as many fields as possible and specifying detailed information about the search object.
This type of search proves most effective as it produces the result that most closely meets to user’s needs.
To start searching for information on any of the thematic sections, point to the name of the corresponding section (in the main menu of the site or in the central part of the main page):
People and awards (only Russian)
Search in the thematic section «People and awards» allows you to find information about the award, using the personal data of the awarded ones.
The topic search in every section can be performed in two modes:
Search in Normal mode
For quick search, go to the «People and awards» section by clicking the left mouse button on:
- section title;
- section button in the center of the Main page;
Then type the available information into the search field and click the «Search» button or the «Enter» key on the keyboard.
If necessary, you can select the number of records to be displayed on one page of the search results (by default, 50 records per page): 10, 30, 50, or 100.
The example of the search page in normal mode is given below:
Search in Advanced mode
To perform an advanced search of award information:
- go to the «Search and awards» section;
- click the Advanced Search button;
If you need more fields to refine the search, click the «More» button.
When filling in fields in the advanced search mode, the user can define the search method for each field:
- From the beginning — to search for documents that at the beginning of the corresponding index field will contain the value specified by the user in this search field;;
- Exact phrase — to search for documents that in a corresponding index field will contain a value consisting of one or more words (or digits) in the same order as specified by the user in this search field;
- Exact field — to search for documents that in the corresponding index field will contain the exact value specified by the user in this search field;
- Full text search — to search for documents that in the corresponding index field will contain information specified by the user in this search field, disregarding the sequence of words and their quantity.
Documents (only Russian)
Searching the thematic section «Documents» allows you to find decrees and orders on rewarding.
The topic search in every section can be performed in two modes:
Search in Normal mode
For quick search, go to the «Documents» section by clicking the left mouse button on:
- section title;
- section button in the center of the Main page;
Then type the available information into the search field and click the «Search» button or the «Enter» key on the keyboard.
If necessary, you can select the number of records to be displayed on one page of the search results (by default, 50 records per page): 10, 30, 50, or 100.
Geography of War (only Russian)
Searching the thematic section «Geography of war» allows you to find data by location and time of events.
The documents in the «Geography of war» section can be found using the date of issue of documents as search criteria, or geographical reference to the locations of combat operations, or the information about the military commander who issued the document.
The topic search in every section can be performed in two modes:
Search in Normal mode
For quick search, go to the «Geography of war» section by clicking the left mouse button on:
- section title;
- section button in the center of the Main page;
Then type the available information into the search field and click the «Search» button or the «Enter» key on the keyboard.
If necessary, you can select the number of records to be displayed on one page of the search results (by default, 50 records per page): 10, 30, 50, or 100.
Search results
The results of searching for a war hero information are displayed as a list. Each page of the search results will display that number of records, which was specified by the user when determining the search conditions.
The first column in the list contains the row number of the search results.
The second column of the list indicates the data source, for example:
— data from the award documents;
— data from the card index;
— commemorative index data.
To navigate through the search results pages, click the button and select the number of the desired page from the drop-down list at the top of the search results page..
To navigate between pages in sequence, you can also use the buttons:
, to go to the next page;
, to go to the last page;
, to go to the previous page;
, to go to the first page.
If the search results do not meet the user’s needs, then you can return to the search page by clicking on the name of the section in which the search was performed; in this case, all the completed search fields will remain unchanged. You can also click the «Back» button in the browser window to return to the previous page.
To view a particular record from among those found, point to it and click the left mouse button — the View information page will appear on the screen.
The electronic image of the document displayed on the page contains a description of the feat for which the decoration was awarded.
At the top of the page you can find the links To previous search result, To next search results — these links allow you to navigate through the pages with the required information according to the search results list.
The information about the personality is given below on the page. In the column «Archival documents on this award» the links to the electronic images of documents associated with this award and personality are highlighted in blue.
Конвенция о правах ребенка — Конвенции и соглашения — Декларации, конвенции, соглашения и другие правовые материалы
Конвенция о правах ребенка
Принята резолюцией 44/25 Генеральной Ассамблеи от 20 ноября 1989 года
Преамбула
Государства-участники настоящей Конвенции,
считая, что в соответствии с принципами, провозглашенными в Уставе Организации Объединенных Наций, признание присущего достоинства, равных и неотъемлемых прав всех членов общества являются основой обеспечения свободы, справедливости и мира на Земле,
принимая во внимание, что народы Объединенных Наций подтвердили в Уставе свою веру в основные права человека, в достоинство и ценность человеческой личности и преисполнены решимости содействовать социальному прогрессу и улучшению условий жизни при большей свободе,
признавая, что Организация Объединенных Наций во Всеобщей декларации прав человека2 и в Международных пактах о правах человека3 провозгласила и согласилась с тем, что каждый человек должен обладать всеми указанными в них правами и свободами без какого бы то ни было различия по таким признакам, как раса, цвет кожи, пол, язык, религия, политические или иные убеждения, национальное или социальное происхождение, имущественное положение, рождение или иные обстоятельства,
напоминая, что Организация Объединенных Наций во Всеобщей декларации прав человека провозгласила, что дети имеют право на особую заботу и помощь,
убежденные в том, что семье как основной ячейке общества и естественной среде для роста и благополучия всех ее членов и особенно детей должны быть предоставлены необходимые защита и содействие, с тем чтобы она могла полностью возложить на себя обязанности в рамках общества,
признавая, что ребенку для полного и гармоничного развития его личности необходимо расти в семейном окружении, в атмосфере счастья, любви и понимания,
считая, что ребенок должен быть полностью подготовлен к самостоятельной жизни в обществе и воспитан в духе идеалов, провозглашенных в Уставе Организации Объединенных Наций, и особенно в духе мира, достоинства, терпимости, свободы, равенства и солидарности,
принимая во внимание, что необходимость в такой особой защите ребенка была предусмотрена в Женевской Декларации прав ребенка 19244 года и Декларации прав ребенка, принятой Генеральной Ассамблеей 20 ноября 1959 года1, и признана во Всеобщей декларации прав человека, в Международном пакте о гражданских и политических правах (в частности, в статьях 23 и 24)3, в Международном пакте об экономических, социальных и культурных правах (в частности, в статье 10)3, а также в уставах и соответствующих документах специализированных учреждений и международных организаций, занимающихся вопросами благополучия детей,
принимая во внимание, что, как указано в Декларации прав ребенка, «ребенок, ввиду его физической и умственной незрелости, нуждается в специальной охране и заботе, включая надлежащую правовую защиту, как до, так и после рождения»5,
ссылаясь на положения Декларации о социальных и правовых принципах, касающихся защиты и благополучия детей, особенно при передаче детей на воспитание и их усыновлении на национальном и международном уровнях6, Минимальных стандартных правил Организации Объединенных Наций, касающихся отправления правосудия в отношении несовершеннолетних («Пекинские правила»)7 и Декларации о защите женщин и детей в чрезвычайных обстоятельствах и в период вооруженных конфликтов8,
признавая, что во всех странах мира есть дети, живущие в исключительно трудных условиях, и что такие дети нуждаются в особом внимании,
учитывая должным образом важность традиций и культурных ценностей каждого народа для защиты и гармоничного развития ребенка,
признавая важность международного сотрудничества для улучшения условий жизни детей в каждой стране, в частности в развивающихся странах,
согласились о нижеследующем:
Часть I
Статья 1
Для целей настоящей Конвенции ребенком является каждое человеческое существо до достижения 18-летнего возраста, если по закону, применимому к данному ребенку, он не достигает совершеннолетия ранее.
Статья 2
1. Государства-участники уважают и обеспечивают все права, предусмотренные настоящей Конвенцией, за каждым ребенком, находящимся в пределах их юрисдикции, без какой-либо дискриминации, независимо от расы, цвета кожи, пола, языка, религии, политических или иных убеждений, национального, этнического или социального происхождения, имущественного положения, состояния здоровья и рождения ребенка, его родителей или законных опекунов или каких-либо иных обстоятельств.
2. Государства-участники принимают все необходимые меры для обеспечения защиты ребенка от всех форм дискриминации или наказания на основе статуса, деятельности, выражаемых взглядов или убеждений ребенка, родителей ребенка, законных опекунов или иных членов семьи.
Статья 3
1. Во всех действиях в отношении детей, независимо от того, предпринимаются они государственными или частными учреждениями, занимающимися вопросами социального обеспечения, судами, административными или законодательными органами, первоочередное внимание уделяется наилучшему обеспечению интересов ребенка.
2. Государства-участники обязуются обеспечить ребенку такую защиту и заботу, которые необходимы для его благополучия, принимая во внимание права и обязанности его родителей, опекунов или других лиц, несущих за него ответственность по закону, и с этой целью принимают все соответствующие законодательные и административные меры.
3. Государства-участники обеспечивают, чтобы учреждения, службы и органы, ответственные за заботу о детях или их защиту, отвечали нормам, установленным компетентными органами, в частности, в области безопасности и здравоохранения и с точки зрения численности и пригодности их персонала, а также компетентного надзора.
Статья 4
Государства-участники принимают все необходимые законодательные, административные и другие меры для осуществления прав, признанных в настоящей Конвенции. В отношении экономических, социальных и культурных прав государства-участники принимают такие меры в максимальных рамках имеющихся у них ресурсов и, в случае необходимости, в рамках международного сотрудничества.
Статья 5
Государства-участники уважают ответственность, права и обязанности родителей и в соответствующих случаях членов расширенной семьи или общины, как это предусмотрено местным обычаем, опекунов или других лиц, несущих по закону ответственность за ребенка, должным образом управлять и руководить ребенком в осуществлении им признанных настоящей Конвенцией прав и делать это в соответствии с развивающимися способностями ребенка.
Статья 6
1. Государства-участники признают, что каждый ребенок имеет неотъемлемое право на жизнь.
2. Государства-участники обеспечивают в максимально возможной степени выживание и здоровое развитие ребенка.
Статья 7
1. Ребенок регистрируется сразу же после рождения и с момента рождения имеет право на имя и на приобретение гражданства, а также, насколько это возможно, право знать своих родителей и право на их заботу.
2. Государства-участники обеспечивают осуществление этих прав в соответствии с их национальным законодательством и выполнение их обязательств согласно соответствующим международным документам в этой области, в частности, в случае, если бы иначе ребенок не имел гражданства.
Статья 8
1. Государства-участники обязуются уважать право ребенка на сохранение своей индивидуальности, включая гражданство, имя и семейные связи, как предусматривается законом, не допуская противозаконного вмешательства.
2. Если ребенок незаконно лишается части или всех элементов своей индивидуальности, государства-участники обеспечивают ему необходимую помощь и защиту для скорейшего восстановления его индивидуальности.
Статья 9
1. Государства-участники обеспечивают, чтобы ребенок не разлучался со своими родителями вопреки их желанию, за исключением случаев, когда компетентные органы, согласно судебному решению, определяют в соответствии с применимым законом и процедурами, что такое разлучение необходимо в наилучших интересах ребенка. Такое определение может оказаться необходимым в том или ином конкретном случае, например, когда родители жестоко обращаются с ребенком или не заботятся о нем или когда родители проживают раздельно и необходимо принять решение относительно места проживания ребенка.
2. В ходе любого разбирательства в соответствии с пунктом 1 настоящей статьи всем заинтересованным сторонам предоставляется возможность участвовать в разбирательстве и излагать свои точки зрения.
3. Государства-участники уважают право ребенка, который разлучается с одним или обоими родителями, поддерживать на регулярной основе личные отношения и прямые контакты с обоими родителями, за исключением случая, когда это противоречит наилучшим интересам ребенка.
4. В тех случаях, когда такое разлучение вытекает из какого-либо решения, принятого государством-участником, например при аресте, тюремном заключении, высылке, депортации или смерти (включая смерть, наступившую по любой причине во время нахождения данного лица в ведении государства) одного или обоих родителей или ребенка, такое государство-участник предоставляет родителям, ребенку или, если это необходимо, другому члену семьи по их просьбе необходимую информацию в отношении местонахождения отсутствующего члена/членов семьи, если предоставление этой информации не наносит ущерба благосостоянию ребенка. Государства-участники в дальнейшем обеспечивают, чтобы представление такой просьбы само по себе не приводило к неблагоприятным последствиям для соответствующего лица/лиц.
Статья 10
1. В соответствии с обязательством государств-участников по пункту 1 статьи 9 заявления ребенка или его родителей на въезд в государство-участник или выезд из него с целью воссоединения семьи должны рассматриваться государствами-участниками позитивным, гуманным и оперативным образом. Государства-участники далее обеспечивают, чтобы представление такой просьбы не приводило к неблагоприятным последствиям для заявителей и членов их семьи.
2. Ребенок, родители которого проживают в различных государствах, имеет право поддерживать на регулярной основе, за исключением особых обстоятельств, личные отношения и прямые контакты с обоими родителями. С этой целью и в соответствии с обязательством государств-участников по пункту 1 статьи 9 государства-участники уважают право ребенка и его родителей покидать любую страну, включая свою собственную, и возвращаться в свою страну. В отношении права покидать любую страну действуют только такие ограничения, какие установлены законом и необходимы для охраны государственной безопасности, общественного порядка (ordre public), здоровья или нравственности населения или прав и свобод других лиц, и совместимы с признанными в настоящей Конвенции другими правами.
Статья 11
1. Государства-участники принимают меры для борьбы с незаконным перемещением и невозвращением детей из-за границы.
2. С этой целью государства-участники содействуют заключению двусторонних или многосторонних соглашений или присоединению к действующим соглашениям.
Статья 12
1. Государства-участники обеспечивают ребенку, способному сформулировать свои собственные взгляды, право свободно выражать эти взгляды по всем вопросам, затрагивающим ребенка, причем взглядам ребенка уделяется должное внимание в соответствии с возрастом и зрелостью ребенка.
2. С этой целью ребенку, в частности, предоставляется возможность быть заслушанным в ходе любого судебного или административного разбирательства, затрагивающего ребенка, либо непосредственно, либо через представителя или соответствующий орган, в порядке, предусмотренном процессуальными нормами национального законодательства.
Статья 13
1. Ребенок имеет право свободно выражать свое мнение; это право включает свободу искать, получать и передавать информацию и идеи любого рода, независимо от границ, в устной, письменной или печатной форме, в форме произведений искусства или с помощью других средств по выбору ребенка.
2. Осуществление этого права может подвергаться некоторым ограничениям, однако этими ограничениями могут быть только те ограничения, которые предусмотрены законом и которые необходимы:
a) для уважения прав и репутации других лиц; или
b) для охраны государственной безопасности или общественного порядка (ordre public), или здоровья или нравственности населения.
Статья 14
1. Государства-участники уважают право ребенка на свободу мысли, совести и религии.
2. Государства-участники уважают права и обязанности родителей и в соответствующих случаях законных опекунов руководить ребенком в осуществлении его права методом, согласующимся с развивающимися способностями ребенка.
3. Свобода исповедовать свою религию или веру может подвергаться только таким ограничениям, которые установлены законом и необходимы для охраны государственной безопасности, общественного порядка, нравственности и здоровья населения или защиты основных прав и свобод других лиц.
Статья 15
1. Государства-участники признают право ребенка на свободу ассоциации и свободу мирных собраний.
2. В отношении осуществления данного права не могут применяться какие-либо ограничения, кроме тех, которые применяются в соответствии с законом и которые необходимы в демократическом обществе в интересах государственной безопасности или общественной безопасности, общественного порядка (ordre public), охраны здоровья или нравственности населения или защиты прав и свобод других лиц.
Статья 16
1. Ни один ребенок не может быть объектом произвольного или незаконного вмешательства в осуществление его права на личную жизнь, семейную жизнь, неприкосновенность жилища или тайну корреспонденции, или незаконного посягательства на его честь и репутацию.
2. Ребенок имеет право на защиту закона от такого вмешательства или посягательства.
Статья 17
Государства-участники признают важную роль средств массовой информации и обеспечивают, чтобы ребенок имел доступ к информации и материалам из различных национальных и международных источников, особенно к таким информации и материалам, которые направлены на содействие социальному, духовному и моральному благополучию, а также здоровому физическому и психическому развитию ребенка. С этой целью государства-участники:
a) поощряют средства массовой информации к распространению информации и материалов, полезных для ребенка в социальном и культурном отношениях, и в духе статьи 29;
b) поощряют международное сотрудничество в области подготовки, обмена и распространения такой информации и материалов из различных культурных, национальных и международных источников;
c) поощряют выпуск и распространение детской литературы;
d) поощряют средства массовой информации к уделению особого внимания языковым потребностям ребенка, принадлежащего к какой-либо группе меньшинств или коренному населению;
e) поощряют разработку надлежащих принципов защиты ребенка от информации и материалов, наносящих вред его благополучию, учитывая положения статей 13 и 18.
Статья 18
1. Государства-участники предпринимают все возможные усилия к тому, чтобы обеспечить признание принципа общей и одинаковой ответственности обоих родителей за воспитание и развитие ребенка. Родители или в соответствующих случаях законные опекуны несут основную ответственность за воспитание и развитие ребенка. Наилучшие интересы ребенка являются предметом их основной заботы.
2. В целях гарантии и содействия осуществлению прав, изложенных в настоящей Конвенции, государства-участники оказывают родителям и законным опекунам надлежащую помощь в выполнении ими своих обязанностей по воспитанию детей и обеспечивают развитие сети детских учреждений.
3. Государства-участники принимают все необходимые меры для обеспечения того, чтобы дети, родители которых работают, имели право пользоваться предназначенными для них службами и учреждениями по уходу за детьми.
Статья 19
1. Государства-участники принимают все необходимые законодательные, административные, социальные и просветительные меры с целью защиты ребенка от всех форм физического или психологического насилия, оскорбления или злоупотребления, отсутствия заботы или небрежного обращения, грубого обращения или эксплуатации, включая сексуальное злоупотребление, со стороны родителей, законных опекунов или любого другого лица, заботящегося о ребенке.
2. Такие меры защиты, в случае необходимости, включают эффективные процедуры для разработки социальных программ с целью предоставления необходимой поддержки ребенку и лицам, которые о нем заботятся, а также для осуществления других форм предупреждения и выявления, сообщения, передачи на рассмотрение, расследования, лечения и последующих мер в связи со случаями жестокого обращения с ребенком, указанными выше, а также, в случае необходимости, для возбуждения судебной процедуры.
Статья 20
1. Ребенок, который временно или постоянно лишен своего семейного окружения или который в его собственных наилучших интересах не может оставаться в таком окружении, имеет право на особую защиту и помощь, предоставляемые государством.
2. Государства-участники в соответствии со своими национальными законами обеспечивают замену ухода за таким ребенком.
3. Такой уход может включать, в частности, передачу на воспитание, «кафала» по исламскому праву, усыновление или, в случае необходимости, помещение в соответствующие учреждения по уходу за детьми. При рассмотрении вариантов замены необходимо должным образом учитывать желательность преемственности воспитания ребенка и его этническое происхождение, религиозную и культурную принадлежность и родной язык.
Статья 21
Государства-участники, которые признают и/или разрешают существование системы усыновления, обеспечивают, чтобы наилучшие интересы ребенка учитывались в первостепенном порядке, и они:
a) обеспечивают, чтобы усыновление ребенка разрешалось только компетентными властями, которые определяют в соответствии с применимыми законом и процедурами и на основе всей относящейся к делу и достоверной информации, что усыновление допустимо ввиду статуса ребенка относительно родителей, родственников и законных опекунов и что, если требуется, заинтересованные лица дали свое осознанное согласие на усыновление на основе такой консультации, которая может быть необходимой;
b) признают, что усыновление в другой стране может рассматриваться в качестве альтернативного способа ухода за ребенком, если ребенок не может быть передан на воспитание или помещен в семью, которая могла бы обеспечить его воспитание или усыновление, и если обеспечение какого-либо подходящего ухода в стране происхождения ребенка является невозможным;
c) обеспечивают, чтобы в случае усыновления ребенка в другой стране применялись такие же гарантии и нормы, которые применяются в отношении усыновления внутри страны;
d) принимают все необходимые меры с целью обеспечения того, чтобы в случае усыновления в другой стране устройство ребенка не приводило к получению неоправданных финансовых выгод связанными с этим лицами;
e) содействуют в необходимых случаях достижению целей настоящей статьи путем заключения двусторонних и многосторонних договоренностей или соглашений и стремятся на этой основе обеспечить, чтобы устройство ребенка в другой стране осуществлялось компетентными властями или органами.
Статья 22
1. Государства-участники принимают необходимые меры, с тем чтобы обеспечить ребенку, желающему получить статус беженца или считающемуся беженцем в соответствии с применимым международным или внутренним правом и процедурами, как сопровождаемому, так и не сопровождаемому его родителями или любым другим лицом, надлежащую защиту и гуманитарную помощь в пользовании применимыми правами, изложенными в настоящей Конвенции и других международных документах по правам человека или гуманитарных документов, участниками которых являются указанные государства.
2. С этой целью государства-участники оказывают, в случае, когда они считают это необходимым, содействие любым усилиям Организации Объединенных Наций и других компетентных межправительственных организаций или неправительственных организаций, сотрудничающих с Организацией Объединенных Наций, по защите такого ребенка и оказанию ему помощи и поиску родителей или других членов семьи любого ребенка-беженца, с тем чтобы получить информацию, необходимую для его воссоединения со своей семьей. В тех случаях, когда родители или другие члены семьи не могут быть найдены, этому ребенку предоставляется такая же защита, как и любому другому ребенку, по какой-либо причине постоянно или временно лишенному своего семейного окружения, как это предусмотрено в настоящей Конвенции.
Статья 23
1. Государства-участники признают, что неполноценный в умственном или физическом отношении ребенок должен вести полноценную и достойную жизнь в условиях, которые обеспечивают его достоинство, способствуют его уверенности в себе и облегчают его активное участие в жизни общества.
2. Государства-участники признают право неполноценного ребенка на особую заботу и поощряют и обеспечивают предоставление при условии наличия ресурсов имеющему на это право ребенку и ответственным за заботу о нем помощи, о которой подана просьба и которая соответствует состоянию ребенка и положению его родителей или других лиц, обеспечивающих заботу о ребенке.
3. В признание особых нужд неполноценного ребенка помощь в соответствии с пунктом 2 настоящей статьи предоставляется, по возможности, бесплатно с учетом финансовых ресурсов родителей или других лиц, обеспечивающих заботу о ребенке, и имеет целью обеспечение неполноценному ребенку эффективного доступа к услугам в области образования, профессиональной подготовки, медицинского обслуживания, восстановления здоровья, подготовки к трудовой деятельности и доступа к средствам отдыха таким образом, который приводит к наиболее полному, по возможности, вовлечению ребенка в социальную жизнь и достижению развития его личности, включая культурное и духовное развитие ребенка.
4. Государства-участники способствуют в духе международного сотрудничества обмену соответствующей информацией в области профилактического здравоохранения и медицинского, психологического и функционального лечения неполноценных детей, включая распространение информации о методах реабилитации, общеобразовательной и профессиональной подготовки, а также доступ к этой информации, с тем чтобы позволить государствам-участникам улучшить свои возможности и знания и расширить свой опыт в этой области. В этой связи особое внимание должно уделяться потребностям развивающихся стран.
Статья 24
1. Государства-участники признают право ребенка на пользование наиболее совершенными услугами системы здравоохранения и средствами лечения болезней и восстановления здоровья. Государства-участники стремятся обеспечить, чтобы ни один ребенок не был лишен своего права на доступ к подобным услугам системы здравоохранения.
2. Государства-участники добиваются полного осуществления данного права и, в частности, принимают необходимые меры для:
a) снижения уровней смертности младенцев и детской смертности;
b) обеспечения предоставления необходимой медицинской помощи и охраны здоровья всех детей с уделением первоочередного внимания развитию первичной медико-санитарной помощи;
c) борьбы с болезнями и недоеданием, в том числе в рамках первичной медико-санитарной помощи, путем, среди прочего, применения легкодоступной технологии и предоставления достаточно питательного продовольствия и чистой питьевой воды, принимая во внимание опасность и риск загрязнения окружающей среды;
d) предоставления матерям надлежащих услуг по охране здоровья в дородовой и послеродовой периоды;
e) обеспечения осведомленности всех слоев общества, в частности родителей и детей, о здоровье и питании детей, преимуществах грудного кормления, гигиене, санитарии среды обитания ребенка и предупреждении несчастных случаев, а также их доступа к образованию и их поддержки в использовании таких знаний;
f) развития просветительной работы и услуг в области профилактической медицинской помощи и планирования размера семьи.
3. Государства-участники принимают любые эффективные и необходимые меры с целью упразднения традиционной практики, отрицательно влияющей на здоровье детей.
4. Государства-участники обязуются поощрять международное сотрудничество и развивать его с целью постепенного достижения полного осуществления права, признаваемого в настоящей статье. В этой связи особое внимание должно уделяться потребностям развивающихся стран.
Статья 25
Государства-участники признают право ребенка, помещенного компетентными органами на попечение с целью ухода за ним, его защиты или физического либо психического лечения, на периодическую оценку лечения, предоставляемого ребенку, и всех других условий, связанных с таким попечением о ребенке.
Статья 26
1. Государства-участники признают за каждым ребенком право пользоваться благами социального обеспечения, включая социальное страхование, и принимают необходимые меры для достижения полного осуществления этого права в соответствии с их национальным законодательством.
2. Эти блага по мере необходимости предоставляются с учетом имеющихся ресурсов и возможностей ребенка и лиц, несущих ответственность за содержание ребенка, а также любых соображений, связанных с получением благ ребенком или от его имени.
Статья 27
1. Государства-участники признают право каждого ребенка на уровень жизни, необходимый для физического, умственного, духовного, нравственного и социального развития ребенка.
2. Родитель(и) или другие лица, воспитывающие ребенка, несут основную ответственность за обеспечение в пределах своих способностей и финансовых возможностей условий жизни, необходимых для развития ребенка.
3. Государства-участники в соответствии с национальными условиями и в пределах своих возможностей принимают необходимые меры по оказанию помощи родителям и другим лицам, воспитывающим детей, в осуществлении этого права и, в случае необходимости, оказывают материальную помощь и поддерживают программы, особенно в отношении обеспечения питанием, одеждой и жильем.
4. Государства-участники принимают все необходимые меры для обеспечения восстановления содержания ребенка родителями или другими лицами, несущими финансовую ответственность за ребенка, как внутри государства-участника, так и из-за рубежа. В частности, если лицо, несущее финансовую ответственность за ребенка, и ребенок проживают в разных государствах, государства-участники способствуют присоединению к международным соглашениям или заключению таких соглашений, а также достижению других соответствующих договоренностей.
Статья 28
1. Государства-участники признают право ребенка на образование, и с целью постепенного достижения осуществления этого права на основе равных возможностей они, в частности:
a) вводят бесплатное и обязательное начальное образование;
b) поощряют развитие различных форм среднего образования, как общего, так и профессионального, обеспечивают его доступность для всех детей и принимают такие необходимые меры, как введение бесплатного образования и предоставление в случае необходимости финансовой помощи;
c) обеспечивают доступность высшего образования для всех на основе способностей каждого с помощью всех необходимых средств;
d) обеспечивают доступность информации и материалов в области образования и профессиональной подготовки для всех детей;
e) принимают меры по содействию регулярному посещению школ и снижению числа учащихся, покинувших школу.
2. Государства-участники принимают все необходимые меры для обеспечения того, чтобы школьная дисциплина поддерживалась с помощью методов, отражающих уважение человеческого достоинства ребенка и в соответствии с настоящей Конвенцией.
3. Государства-участники поощряют и развивают международное сотрудничество по вопросам, касающимся образования, в частности, с целью содействия ликвидации невежества и неграмотности во всем мире и облегчения доступа к научно-техническим знаниям и современным методам обучения. В этой связи особое внимание должно уделяться потребностям развивающихся стран.
Статья 29
1. Государства-участники соглашаются в том, что образование ребенка должно быть направлено на:
a) развитие личности, талантов и умственных и физических способностей ребенка в их самом полном объеме;
b) воспитание уважения к правам человека и основным свободам, а также принципам, провозглашенным в Уставе Организации Объединенных Наций;
c) воспитание уважения к родителям ребенка, его культурной самобытности, языку и ценностям, к национальным ценностям страны, в которой ребенок проживает, страны его происхождения и к цивилизациям, отличным от его собственной;
d) подготовку ребенка к сознательной жизни в свободном обществе в духе понимания, мира, терпимости, равноправия мужчин и женщин и дружбы между всеми народами, этническими, национальными и религиозными группами, а также лицами из числа коренного населения;
e) воспитание уважения к окружающей природе.
2. Никакая часть настоящей статьи или статьи 28 не толкуется как ограничивающая свободу отдельных лиц и органов создавать учебные заведения и руководить ими при условии постоянного соблюдения принципов, изложенных в пункте 1 настоящей статьи, и выполнения требования о том, чтобы образование, даваемое в таких учебных заведениях, соответствовало минимальным нормам, которые могут быть установлены государством.
Статья 30
В тех государствах, где существуют этнические, религиозные или языковые меньшинства или лица из числа коренного населения, ребенку, принадлежащему к таким меньшинствам или коренному населению, не может быть отказано в праве совместно с другими членами своей группы пользоваться своей культурой, исповедовать свою религию и исполнять ее обряды, а также пользоваться родным языком.
Статья 31
1. Государства-участники признают право ребенка на отдых и досуг, право участвовать в играх и развлекательных мероприятиях, соответствующих его возрасту, и свободно участвовать в культурной жизни и заниматься искусством.
2. Государства-участники уважают и поощряют право ребенка на всестороннее участие в культурной и творческой жизни и содействуют предоставлению соответствующих и равных возможностей для культурной и творческой деятельности, досуга и отдыха.
Статья 32
1. Государства-участники признают право ребенка на защиту от экономической эксплуатации и от выполнения любой работы, которая может представлять опасность для его здоровья или служить препятствием в получении им образования, либо наносить ущерб его здоровью и физическому, умственному, духовному, моральному и социальному развитию.
2. Государства-участники принимают законодательные, административные и социальные меры, а также меры в области образования, с тем чтобы обеспечить осуществление настоящей статьи. В этих целях, руководствуясь соответствующими положениями других международных документов, государства-участники, в частности:
a) устанавливают минимальный возраст или минимальные возрасты для приема на работу;
b) определяют необходимые требования о продолжительности рабочего дня и условиях труда;
c) предусматривают соответствующие виды наказания или другие санкции для обеспечения эффективного осуществления настоящей статьи.
Статья 33
Государства-участники принимают все необходимые меры, включая законодательные, административные и социальные меры, а также меры в области образования, с тем чтобы защитить детей от незаконного употребления наркотических средств и психотропных веществ, как они определены в соответствующих международных договорах, и не допустить использования детей в противозаконном производстве таких веществ и торговле ими.
Статья 34
Государства-участники обязуются защищать ребенка от всех форм сексуальной эксплуатации и сексуального совращения. В этих целях государства-участники, в частности, принимают на национальном, двустороннем и многостороннем уровнях все необходимые меры для предотвращения:
a) склонения или принуждения ребенка к любой незаконной сексуальной деятельности;
b) использования в целях эксплуатации детей в проституции или в другой незаконной сексуальной практике;
c) использования в целях эксплуатации детей в порнографии и порнографических материалах.
Статья 35
Государства-участники принимают на национальном, двустороннем и многостороннем уровнях все необходимые меры для предотвращения похищения детей, торговли детьми или их контрабанды в любых целях и в любой форме.
Статья 36
Государства-участники защищают ребенка от всех других форм эксплуатации, наносящих ущерб любому аспекту благосостояния ребенка.
Статья 37
Государства-участники обеспечивают, чтобы:
a) ни один ребенок не был подвергнут пыткам или другим жестоким, бесчеловечным или унижающим достоинство видам обращения или наказания. Ни смертная казнь, ни пожизненное тюремное заключение, не предусматривающее возможности освобождения, не назначаются за преступления, совершенные лицами моложе 18 лет;
b) ни один ребенок не был лишен свободы незаконным или произвольным образом. Арест, задержание или тюремное заключение ребенка осуществляются согласно закону и используются лишь в качестве крайней меры и в течение как можно более короткого соответствующего периода времени;
c) каждый лишенный свободы ребенок пользовался гуманным обращением и уважением неотъемлемого достоинства его личности с учетом потребностей лиц его возраста. В частности, каждый лишенный свободы ребенок должен быть отделен от взрослых, если только не считается, что в наилучших интересах ребенка этого делать не следует, и иметь право поддерживать связь со своей семьей путем переписки и свиданий, за исключением особых обстоятельств;
d) каждый лишенный свободы ребенок имел право на незамедлительный доступ к правовой и другой соответствующей помощи, а также право оспаривать законность лишения его свободы перед судом или другим компетентным, независимым и беспристрастным органом и право на безотлагательное принятие ими решения в отношении любого такого процессуального действия.
Статья 38
1. Государства-участники обязуются уважать нормы международного гуманитарного права, применимые к ним в случае вооруженных конфликтов и имеющие отношение к детям, и обеспечивать их соблюдение.
2. Государства-участники принимают все возможные меры для обеспечения того, чтобы лица, не достигшие 15-летнего возраста, не принимали прямого участия в военных действиях.
3. Государства-участники воздерживаются от призыва любого лица, не достигшего 15-летнего возраста, на службу в свои вооруженные силы. При вербовке из числа лиц, достигших 15-летнего возраста, но которым еще не исполнилось 18 лет, государства-участники стремятся отдавать предпочтение лицам более старшего возраста.
4. Согласно своим обязательствам по международному гуманитарному праву, связанным с защитой гражданского населения во время вооруженных конфликтов, государства-участники обязуются принимать все возможные меры с целью обеспечения защиты затрагиваемых вооруженным конфликтом детей и ухода за ними.
Статья 39
Государства-участники принимают все необходимые меры для того, чтобы содействовать физическому и психологическому восстановлению и социальной реинтеграции ребенка, являющегося жертвой: любых видов пренебрежения, эксплуатации или злоупотребления, пыток или любых других жестоких, бесчеловечных или унижающих достоинство видов обращения, наказания или вооруженных конфликтов. Такое восстановление и реинтеграция должны осуществляться в условиях, обеспечивающих здоровье, самоуважение и достоинство ребенка.
Статья 40
1. Государства-участники признают право каждого ребенка, который, как считается, нарушил уголовное законодательство, обвиняется или признается виновным в его нарушении, на такое обращение, которое способствует развитию у ребенка чувства достоинства и значимости, укрепляет в нем уважение к правам человека и основным свободам других и при котором учитывается возраст ребенка и желательность содействия его реинтеграции и выполнению им полезной роли в обществе.
2. В этих целях и принимая во внимание соответствующие положения международных документов, государства-участники, в частности, обеспечивают, чтобы:
a) ни один ребенок не считался нарушившим уголовное законодательство, не обвинялся и не признавался виновным в его нарушении по причине действия или бездействия, которые не были запрещены национальным или международным правом во время их совершения;
b) каждый ребенок, который, как считается, нарушил уголовное законодательство или обвиняется в его нарушении, имел по меньшей мере следующие гарантии:
i) презумпция невиновности, пока его вина не будет доказана согласно закону;
ii) незамедлительное и непосредственное информирование его об обвинениях против него и, в случае необходимости, через его родителей или законных опекунов и получение правовой и другой необходимой помощи при подготовке и осуществлении своей защиты;
iii) безотлагательное принятие решения по рассматриваемому вопросу компетентным, независимым и беспристрастным органом или судебным органом в ходе справедливого слушания в соответствии с законом в присутствии адвоката или другого соответствующего лица, и, если это не считается противоречащим наилучшим интересам ребенка, в частности, с учетом его возраста или положения его родителей или законных опекунов;
iv) свобода от принуждения к даче свидетельских показаний или признанию вины; изучение показаний свидетелей обвинения либо самостоятельно, либо при помощи других лиц и обеспечение равноправного участия свидетелей защиты и изучения их показаний;
v) если считается, что ребенок нарушил уголовное законодательство, повторное рассмотрение вышестоящим компетентным, независимым и беспристрастным органом или судебным органом согласно закону соответствующего решения и любых принятых в этой связи мер;
vi) бесплатная помощь переводчика, если ребенок не понимает используемого языка или не говорит на нем;
vii) полное уважение его личной жизни на всех стадиях разбирательства.
3. Государства-участники стремятся содействовать установлению законов, процедур, органов и учреждений, имеющих непосредственное отношение к детям, которые, как считается, нарушили уголовное законодательство, обвиняются или признаются виновными в его нарушении, и в частности:
a) установлению минимального возраста, ниже которого дети считаются неспособными нарушить уголовное законодательство;
b) в случае необходимости и желательности, принятию мер по обращению с такими детьми без использования судебного разбирательства при условии полного соблюдения прав человека и правовых гарантий.
4. Необходимо наличие таких различных мероприятий, как уход, положение об опеке и надзоре, консультативные услуги, назначение испытательного срока, воспитание, программы обучения и профессиональной подготовки и другие формы ухода, заменяющие уход в учреждениях, с целью обеспечения такого обращения с ребенком, которое соответствовало бы его благосостоянию, а также его положению и характеру преступления.
Статья 41
Ничто в настоящей Конвенции не затрагивает любых положений, которые в большей степени способствуют осуществлению прав ребенка и могут содержаться:
a) в законе государства-участника; или
b) в нормах международного права, действующих в отношении данного государства.
Часть II
Статья 42
Государства-участники обязуются, используя надлежащие и действенные средства, широко информировать о принципах и положениях Конвенции как взрослых, так и детей.
Статья 43
1. В целях рассмотрения прогресса, достигнутого государствами-участниками в выполнении обязательств, принятых в соответствии с настоящей Конвенцией, учреждается Комитет по правам ребенка, который выполняет функции, предусматриваемые ниже.
2. Комитет состоит из десяти экспертов, обладающих высокими нравственными качествами и признанной компетентностью в области, охватываемой настоящей Конвенцией. Члены Комитета избираются государствами-участниками из числа своих граждан и выступают в личном качестве, причем уделяется внимание справедливому географическому распределению, а также главным правовым системам.
3. Члены Комитета избираются тайным голосованием из числа внесенных в список лиц, выдвинутых государствами-участниками. Каждое государство-участник может выдвинуть одно лицо из числа своих граждан.
4. Первоначальные выборы в Комитет проводятся не позднее, чем через шесть месяцев со дня вступления в силу настоящей Конвенции, а впоследствии — один раз в два года. По крайней мере за четыре месяца до дня каждых выборов Генеральный секретарь Организации Объединенных Наций обращается к государствам-участникам с письмом, предлагая им представить свои кандидатуры в течение двух месяцев. Затем Генеральный секретарь составляет в алфавитном порядке список всех выдвинутых таким образом лиц с указанием государств-участников, которые выдвинули этих лиц, и представляет этот список государствам-участникам настоящей Конвенции.
5. Выборы проводятся на совещаниях государств-участников, созываемых Генеральным секретарем в Центральных учреждениях Организации Объединенных Наций. На этих совещаниях, на которых две трети государств-участников составляют кворум, избранными в состав Комитета являются те кандидаты, которые получили наибольшее число голосов и абсолютное большинство голосов присутствующих и участвующих в голосовании представителей государств-участников.
6. Члены Комитета избираются на четырехлетний срок. Они имеют право быть переизбранными в случае повторного выдвижения их кандидатур. Срок полномочий пяти членов, избираемых на первых выборах, истекает в конце двухлетнего периода; немедленно после первых выборов имена этих пяти членов определяются по жребию Председателем совещания.
7. В случае смерти или выхода в отставку какого-либо члена Комитета или если он или она по какой-либо иной причине не может более исполнять обязанности члена Комитета, государство-участник, выдвинувшее данного члена Комитета, назначает другого эксперта из числа своих граждан на оставшийся срок при условии одобрения Комитетом.
8. Комитет устанавливает свои собственные правила процедуры.
9. Комитет избирает своих должностных лиц на двухлетний срок.
10. Сессии Комитета, как правило, проводятся в Центральных учреждениях Организации Объединенных Наций или в любом ином подходящем месте, определенном Комитетом. Комитет, как правило, проводит свои сессии ежегодно. Продолжительность сессии Комитета определяется и при необходимости пересматривается на совещании государств — участников настоящей Конвенции при условии одобрения Генеральной Ассамблеей.
11. Генеральный секретарь Организации Объединенных Наций предоставляет персонал и материальные средства для эффективного осуществления Комитетом своих функций в соответствии с настоящей Конвенцией.
12. Члены Комитета, учрежденного в соответствии с настоящей Конвенций, получают утверждаемое Генеральной Ассамблеей вознаграждение из средств Организации Объединенных Наций в порядке и на условиях, устанавливаемых Генеральной Ассамблеей.
Статья 44
1. Государства-участники обязуются предоставлять Комитету через Генерального секретаря Организации Объединенных Наций доклады о принятых ими мерах по закреплению признанных в Конвенции прав и о прогрессе, достигнутом в осуществлении этих прав:
a) в течение двух лет после вступления Конвенции в силу для соответствующего государства-участника;
b) впоследствии через каждые пять лет.
2. В докладах, представляемых в соответствии с настоящей статьей, указываются факторы и затруднения, если таковые имеются, влияющие на степень выполнения обязательств по настоящей Конвенции. Доклады также содержат достаточную информацию, с тем чтобы обеспечить Комитету полное понимание действий Конвенции в данной стране.
3. Государству-участнику, представившему Комитету всесторонний первоначальный доклад, нет необходимости повторять в последующих докладах, представляемых в соответствии с пунктом 1 b настоящей статьи, ранее изложенную основную информацию.
4. Комитет может запрашивать у государств-участников дополнительную информацию, касающуюся осуществления настоящей Конвенции.
5. Доклады о деятельности Комитета один раз в два года представляются Генеральной Ассамблее через посредство Экономического и Социального Совета.
6. Государства-участники обеспечивают широкую гласность своих докладов в своих собственных странах.
Статья 45
С целью способствовать эффективному осуществлению Конвенции и поощрять международное сотрудничество в области, охватываемой настоящей Конвенцией:
a) специализированные учреждения, Детский фонд Организации Объединенных Наций и другие органы Организации Объединенных Наций вправе быть представленными при рассмотрении вопросов об осуществлении таких положений настоящей Конвенции, которые входят в сферу их полномочий. Комитет может предложить специализированным учреждениям, Детскому фонду Организации Объединенных Наций и другим компетентным органам, когда он считает это целесообразным, представить заключение экспертов относительно осуществления Конвенции в тех областях, которые входят в сферу их соответствующих полномочий. Комитет может предложить специализированным учреждениям, Детскому фонду Организации Объединенных Наций и другим органам Организации Объединенных Наций представить доклады об осуществлении Конвенции в областях, входящих в сферу их деятельности;
b) Комитет препровождает, когда он считает это целесообразным, в специализированные учреждения, Детский фонд Организации Объединенных Наций и другие компетентные органы любые доклады государств-участников, в которых содержится просьба о технической консультации или помощи или указывается на потребность в этом, а также замечания и предложения Комитета, если таковые имеются, относительно таких просьб или указаний;
c) Комитет может рекомендовать Генеральной Ассамблее предложить Генеральному секретарю провести от ее имени исследования по отдельным вопросам, касающимся прав ребенка;
d) Комитет может вносить предложения и рекомендации общего характера, основанные на информации, получаемой в соответствии со статьями 44 и 45 настоящей Конвенции. Такие предложения и рекомендации общего характера препровождаются любому заинтересованному государству-участнику и сообщаются Генеральной Ассамблее наряду с замечаниями государств-участников, если таковые имеются.
Часть III
Статья 46
Настоящая Конвенция открыта для подписания ее всеми государствами.
Статья 47
Настоящая Конвенция подлежит ратификации. Ратификационные грамоты сдаются на хранение Генеральному секретарю Организации Объединенных Наций.
Статья 48
Настоящая Конвенция открыта для присоединения к ней любого государства. Документы о присоединении сдаются на хранение Генеральному секретарю Организации Объединенных Наций.
Статья 49
1. Настоящая Конвенция вступает в силу на тридцатый день после даты сдачи на хранение Генеральному секретарю Организации Объединенных Наций двадцатой ратификационной грамоты или документа о присоединении.
2. Для каждого государства, которое ратифицирует настоящую Конвенцию или присоединяется к ней после сдачи на хранение двадцатой ратификационной грамоты или документа о присоединении, настоящая Конвенция вступает в силу на тридцатый день после сдачи таким государством на хранение его ратификационной грамоты или документа о присоединении.
Статья 50
1. Любое государство-участник может предложить поправку и представить ее Генеральному секретарю Организации Объединенных Наций. Генеральный секретарь затем препровождает предложенную поправку государствам-участникам с просьбой указать, высказываются ли они за созыв конференции государств-участников с целью рассмотрения этих предложений и проведения по ним голосования. Если в течение четырех месяцев, начиная с даты такого сообщения, по крайней мере одна треть государств-участников выскажется за такую конференцию, Генеральный секретарь созывает эту конференцию под эгидой Организации Объединенных Наций. Любая поправка, принятая большинством государств-участников, присутствующих и участвующих в голосовании на этой конференции, представляется Генеральной Ассамблее Организации Объединенных Наций на утверждение.
2. Поправка, принятая в соответствии с пунктом 1 настоящей статьи, вступает в силу по утверждении ее Генеральной Ассамблеей Организации Объединенных Наций и принятия ее большинством в две трети государств-участников.
3. Когда поправка вступает в силу, она становится обязательной для тех государств-участников, которые ее приняли, а для других государств-участников остаются обязательными положения настоящей Конвенции и любые предшествующие поправки, которые ими приняты.
Статья 51
1. Генеральный секретарь Организации Объединенных Наций получает и рассылает всем государствам текст оговорок, сделанных государствами в момент ратификации или присоединения.
2. Оговорка, не совместимая с целями и задачами настоящей Конвенции, не допускается.
3. Оговорки могут быть сняты в любое время путем соответствующего уведомления, направленного Генеральному секретарю Организации Объединенных Наций, который затем сообщает об этом всем государствам. Такое уведомление вступает в силу со дня его получения Генеральным секретарем.
Статья 52
Любое государство-участник может денонсировать настоящую Конвенцию путем письменного уведомления Генерального секретаря Организации Объединенных Наций. Денонсация вступает в силу по истечении одного года после получения уведомления Генеральным секретарем.
Статья 53
Генеральный секретарь Организации Объединенных Наций назначается депозитарием настоящей конвенции.
Статья 54
Подлинник настоящей Конвенции, английский, арабский, испанский, китайский, русский и французский тексты которой являются равно аутентичными, сдается на хранение Генеральному секретарю Организации Объединенных Наций. В удостоверение чего нижеподписавшиеся полномочные представители, должным образом на то уполномоченные своими соответствующими правительствами, подписали настоящую Конвенцию.
1Резолюция 1386 (XIV).
2Резолюция 217 А (III).
3 См. резолюцию 2200 А (XXI), приложение.
4 См. League of Nations Official Journal, Special Supplement No. 21, October 1924, p. 43.
5Резолюция 1386 (XIV), третий пункт преамбулы.
6Резолюция 41/85, приложение
7Резолюция 40/33, приложение.
8Резолюция 3318 (XXIX).
Источник: Официальные отчеты Генеральной Ассамблеи, сорок четвертая сессия, Дополнение №49 (А/44/49), стр. 230–239.
Лучшая температура для сна: советы и подсказки
Температура в вашей спальне может существенно повлиять на качество вашего сна. Опрос Национального фонда сна показал, что прохладная комнатная температура является одним из наиболее важных факторов, способствующих хорошему ночному сну, при этом четыре из пяти респондентов заявили, что это важно для них.
Лучшая температура в спальне для сна — примерно 18,3 градуса по Цельсию. Это может варьироваться на несколько градусов от человека к человеку, но большинство врачей рекомендуют устанавливать термостат в диапазоне от 60 до 67 градусов по Фаренгейту (15.От 6 до 19,4 градусов Цельсия) для максимально комфортного сна.
Наши тела запрограммированы на небольшое понижение внутренней температуры по вечерам. Отключение термостата на ночь может помочь в регулировании температуры и сигнализировать вашему телу, что пора ложиться спать.
Лучшая температура сна для младенцев
Младенцы могут извлечь выгоду из спальни, которая на один или два градуса теплее, до 69 градусов по Фаренгейту (20,5 градусов по Цельсию). Поскольку их тела меньше по размеру и все еще развиваются, они более чувствительны к изменениям температуры окружающей среды.
Слишком теплая спальня может увеличить риск синдрома внезапной детской смерти (СВДС). Рекомендуется использовать одобренную одежду для сна, обеспечить благоприятную температуру, установив термостат, и избегать тяжелых одеял или многослойных одеял. Родители могут следить за температурой своего ребенка в ночное время, касаясь живота или задней части шеи.
Исследования показывают, что младенцы достигают температурного созревания в среднем к одиннадцати неделям. В этот момент они начинают достигать минимальной внутренней температуры тела 97.5 градусов по Фаренгейту (36,4 градуса по Цельсию) в течение четырех часов перед сном, как и у взрослых.
Как температура влияет на сон?
Наш цикл сна регулируется нашим циркадным ритмом. Циркадный ритм основан на цикле светлого и темного солнца и контролируется частью мозга, называемой супрахиазматическим ядром, расположенной в гипоталамусе. Эти основные «биологические часы» основываются на ряде факторов окружающей среды и личностных факторов, начиная от количества света (наиболее значимое), заканчивая физическими упражнениями и температурой.
Наша основная температура тела колеблется около 98,6 градусов по Фаренгейту (37 градусов по Цельсию), но колеблется примерно на 2 градуса по Фаренгейту в течение ночи. Снижение температуры начинается примерно за два часа до того, как вы ложитесь спать, что совпадает с высвобождением гормона сна мелатонина. Во время сна температура тела продолжает падать, достигая низкого уровня ранним утром, а затем постепенно нагревается по мере того, как наступает утро.
Основной способ, которым тело охлаждается во время сна, — это отвод тепла от ядра.В процессе, называемом вазодилатацией, циркадные часы посылают сигнал об усилении кровотока к конечностям. Вот почему у некоторых людей ночью могут быть теплые руки и ноги, которые можно принять за общую температуру тела. Действительно, люди, у которых хронически мерзнут ноги, могут быть подвержены более высокому риску бессонницы во сне, возможно, из-за нарушения этого процесса.
Что происходит, когда в вашей спальне слишком жарко?
Более высокие температуры могут вызывать дискомфорт и беспокойство, и любой, кто спал в душной спальне, может подтвердить, что трудно уснуть, когда вы потеете и обезвожены.Слишком теплая спальня может нарушить терморегуляцию вашего тела и вызвать усталость. Часто усталый человек чувствует себя физически и морально усталым, но не может заснуть.
Температура тела влияет не только на начало сна, но также на качество сна и время, проведенное в различных стадиях сна. Более высокая внутренняя температура тела была связана с уменьшением восстановительного медленноволнового сна и субъективного качества сна. Точно так же большая разница в температуре между ядром и конечностями — что указывает на то, что тело не эффективно отводит тепло от ядра — была связана со снижением эффективности сна и более высокой вероятностью пробуждения после засыпания.
Во время быстрого сна тело прекращает большинство действий, регулирующих температуру, таких как потоотделение или дрожь, что делает вас более чувствительным к изменениям температуры окружающей среды. Соответственно, слишком высокая температура окружающей среды также сокращает время, проведенное в фазе быстрого сна.
Помимо того, что на следующий день вызывает сонливость, уменьшение фазы быстрого сна и медленного сна может негативно повлиять на восстановление организма и иммунную систему, а также на обучение, память и другие процессы.
Хотя холодная температура в спальне не считается столь же вредной, как слишком теплая температура в спальне, она также может вызывать дискомфорт и может иметь последствия для быстрого сна и артериального давления.
Советы по сохранению прохлады в спальне
Следующие советы помогут оптимизировать температуру в спальне для сна:
- Закройте жалюзи, чтобы уменьшить накопление тепла в течение дня
- Летом вниз по лестнице
- Выключите термостат на ночь
- Используйте вентилятор или кондиционер в жарком климате или грелку в холодные ночи
- Открыть окна для вентиляции
- Контроль влажности в спальне
- Для уменьшения потоотделения используйте дышащий матрас, простыни, пуховое одеяло, одеяло, подушку и свободную пижаму
- Примите теплую ванну за час или два перед сном, чтобы вызвать естественный охлаждающий эффект.
Помимо оптимизации температуры окружающей среды для сна, вы можете помочь своему организму подготовиться ко сну, проявив доброту к собственному внутреннему термостату.Поскольку циркадный ритм чувствителен к колебаниям света, диеты и упражнений, время этих действий может повлиять на температуру тела и, возможно, на сонливость.
Привычки гигиены сна, такие как ложиться спать в одно и то же время каждую ночь, избегать употребления кофеина и алкоголя перед сном и сохранять темную и тихую спальню, помогут вам установить часы вашего тела и температуру сна на постоянный график. Чтобы узнать больше о том, как подобрать подходящую температуру, прочитайте нашу статью о том, как спать прохладно в жаркую ночь.
- Была ли эта статья полезной?
- Да Нет
«Становится холодно»: температура снова опускается ниже 20 градусов по Цельсию.
«Становится холодно» — это местная фраза, которую некоторые жители Трини использовали бы для обозначения температуры в среду ночью, которая составляла около 19,7 градусов, по данным метеорологической службы Тринидада и Тобаго.
Метеорологическое бюро сообщило, что это был второй раз в этом месяце, когда температура опускалась ниже 20 градусов, однако никаких новых рекордов установлено не было.
«Прошлая ночь казалась немного« холоднее », чем обычно? Мы измерили минимальную температуру 19,7 ° C!
« Это второй раз в этом месяце, когда температура опускалась ниже отметки 20 ° C. Другой случай произошел 4 января, когда была зафиксирована температура 19,5 ° C », — сообщило Метеорологическое бюро в сообщении в социальной сети. градусов Цельсия.
Более низкие температуры в это время года не редкость для Тринидада и Тобаго и могут быть результатом действия нескольких факторов, возникающих одновременно, таких как штиль или почти тихий ветер, почти полное отсутствие облачности в сочетании с холодными ветрами. происходящие с Севера.
Метеорологическое бюро заявило, что вместе эти факторы увеличивают количество «исходящей длинноволновой радиации» с поверхности Земли в ночное время (поверхность остывает быстрее).
Метеорологическое бюро сообщило, что рекорд самой низкой температуры в Пиарко был 16,1 ° C, зафиксированный в январе 1964 года.
Многие Тринис согласились, что в последнее время температура стала немного ниже:
Джульет Чарльз: «Да, последние пару ночей» было очень холодно, особенно живя в Санта-Крус «.
Салли И Хан: «Прошлая ночь была холодной и холодной.. и даже сейчас все еще холодно ».
Николь Одзюро:« С того момента, как я легла в постель прошлой ночью, и до сегодняшнего утра, у меня заложила нос от холода ».
Кестер Джозеф:« Узнай, почему Тобаго так далеко. идти. Я даже справляюсь с температурой 20 ° «
Занах Кирби:» Я снова говорю лил, когда просыпаюсь утром, я бы увидел снежную суету, которая делает холодным «.
Что вы делаете, чтобы согреться, когда ночные температуры становятся холодно?
Ниже приведены определения условий хранения, определенные в разделе «Общие примечания» Фармакопеи США (USP) XXII-NF XVII, для рекомендуемых условий, обычно указываемых на этикетках продуктов.
|
Влияние температуры на стойкость SARS-CoV-2 на общих поверхностях | Журнал вирусологии
Пандемия коронавирусной болезни (COVID-19). https://www.who.int/emergencies/diseases/novel-coronavirus-2019.
Стадницкий В., Bax CE, Bax A, Анфинруд П. Время жизни маленьких речевых капель в воздухе и их потенциальное значение в передаче SARS-CoV-2. Proc Natl Acad Sci U S. A. 2020; 117 (22): 11875–7.
CAS Статья Google Scholar
Morawska L, Milton DK. Пора заняться воздушной передачей COVID-19.Clin Infect Dis. 2020. https://doi.org/10.1093/cid/ciaa939/5867798.
Артикул PubMed PubMed Central Google Scholar
Чжан Р., Ли И, Чжан А.Л., Ван И, Молина М.Дж. Определение передачи воздушно-капельным путем в качестве основного пути распространения COVID-19. Proc Natl Acad Sci. 2020; 117 (26): 202009637.
Google Scholar
ван Дормален Н., Бушмейкер Т., Моррис Д.Х., Холбрук М.Г., Гэмбл А., Уильямсон Б.Н. и др.Аэрозольная и поверхностная стабильность SARS-CoV-2 по сравнению с SARS-CoV-1. N Engl J Med. 2020; 382 (16): 1564–7. https://doi.org/10.1056/NEJMc2004973.
Артикул PubMed Google Scholar
Смитер С.Дж., Истог Л.С., Финдли Дж.С., Левер МС. Экспериментальная аэрозольная выживаемость SARS-CoV-2 в искусственной слюне и средах для культивирования тканей при средней и высокой влажности. Emerg Microbes Infect. 2020; 9 (1): 1415–7. https://doi.org/10.1080/22221751.2020.1777906.
CAS Статья PubMed PubMed Central Google Scholar
Цай Дж., Сунь В., Хуанг Дж., Гамбер М., Ву Дж., Хе Г. Непрямая передача вируса в кластере случаев COVID-19, Вэньчжоу, Китай, 2020 г. Emerg Infect Dis. 2020; 26 (6): 1343–5.
CAS Статья Google Scholar
Julian TR, Leckie JO, Boehm AB. Передача вируса между подушечками пальцев и фомитами.J Appl Microbiol. 2010. 109 (6): 1868–74.
CAS Статья Google Scholar
Рольфе Т., Нитти М. Сенсорные экраны: комар эпохи цифровых технологий. 2016 г. https://emist.com/infection-prevention-touchscreens-are-contaminated/.
Русин П., Максвелл С., Герба С. Сравнительная эффективность передачи грамположительных бактерий, грамотрицательных бактерий и фагов с поверхности на руку и из кончика пальца в рот. J Appl Microbiol.2002; 93 (4): 585–92.
CAS Статья Google Scholar
Kasloff SB, Strong JE, Funk D, Cutts TA. Устойчивость SARS-CoV-2 к критическим средствам индивидуальной защиты. medRxiv. 2020; 2020.06.11.20128884.
Kärber G. Beitrag zur kollektiven Behandlung Pharmakologischer. Beitrag zur Kollekt Behandlung Pharmakologischer Reihenversuche. 1931; 7: 1–4.
Google Scholar
Спирмен К. Метод «правильных и неправильных случаев» («постоянных стимулов») без формул Гаусса. Br J Psychol 1908–1920. 1908; 2 (3): 227–42.
Google Scholar
Саттар С.А., Спрингторп В.С., Адегбунрин О., Зафер А.А., Буса М. Дисковый количественный метод тестирования носителя для оценки вирулицидной активности химических гермицидов. J Virol Methods. 2003. 112 (1–2): 3–12.
CAS Статья Google Scholar
ASTM E2197. Стандартный метод количественного определения носителя диска для определения бактерицидной, вирулицидной, фунгицидной, микобактерицидной и спороцидной активности химических веществ. ASTM Int. 2015 г. https://www.astm.org/Standards/E2197.htm.
Ким И, Ян М., Гойал С.М., Чиран М.С., Торреморелл М. Оценка мер биобезопасности для предотвращения косвенной передачи вируса эпидемической диареи свиней. BMC Vet Res. 2017; 13 (1): 1–9.
Google Scholar
Ли СС, Вонг Н.С. Вероятные цепи передачи коронавируса ближневосточного респираторного синдрома и множественные поколения вторичной инфекции в Южной Корее. Int J Infect Dis. 2015; 38: 65–7. https://doi.org/10.1016/j.ijid.2015.07.014.
Артикул PubMed PubMed Central Google Scholar
Sizun J, Yu MWN, Talbot PJ. Выживаемость человеческих коронавирусов 229E и OC43 в суспензии и после высыхания на поверхности: возможный источник внутрибольничных инфекций.J Hosp Infect. 2000. 46 (1): 55–60.
CAS Статья Google Scholar
Ла Скола Б., Ле Бидо М., Андреани Дж., Хоанг В.Т., Гримальдье С., Колсон П. и др. Нагрузка вирусной РНК, определенная с помощью клеточной культуры, как инструмент управления выпиской пациентов с SARS-CoV-2 из инфекционных отделений. Eur J Clin Microbiol Infect Dis. 2020; 39 (6): 1059–61.
Артикул Google Scholar
Кам К., Юнг К.Ф., Цуй Л., Цер Пин Лин Р., Мак Т.М., Майвальд М. и др. Здоровый младенец с коронавирусной болезнью 2019 года с высокой вирусной нагрузкой. Clin Infect Dis. 2020; 71 (15): 847–9.
CAS Статья Google Scholar
Хуан Ю., Чен С., Ян З., Гуань В., Лю Д., Линь З. и др. Вирусная нагрузка SARS-CoV-2 в клинических образцах от пациентов в критическом состоянии. Am J Respir Crit Care Med. 2020; 201 (11): 1435–8.
CAS Статья Google Scholar
Цзоу Л., Жуань Ф., Хуанг М., Лян Л., Хуанг Х., Хонг З. и др. Вирусная нагрузка SARS-CoV-2 в образцах верхних дыхательных путей инфицированных пациентов. N Engl J Med. 2020; 382 (12): 1177–9. https://doi.org/10.1056/NEJMc2001737.
Артикул PubMed PubMed Central Google Scholar
Чан К.Х., Пейрис Дж.С.М., Лам С.Ю., Пун LLM, Юэнь К.Ю., Сето У.Х. Влияние температуры и относительной влажности на жизнеспособность коронавируса SARS.Adv Virol. 2011. https://doi.org/10.1155/2011/734690.
Артикул PubMed PubMed Central Google Scholar
Чин AWH, Chu JTS, Perera MRA, Hui KPY, Yen H-L, Chan MCW и др. Устойчивость SARS-CoV-2 в различных условиях окружающей среды. Ланцетный микроб. 2020; 1 (1): e10.
Артикул Google Scholar
Lai MYY, Cheng PKC, Lim WWL. Выживаемость тяжелого острого респираторного синдрома коронавирусом.Clin Infect Dis. 2005; 41 (7): e67-71.
CAS Статья Google Scholar
Абубакр Х.А., Шарафельдин Т.А., Гоял С.М. Стабильность SARS-CoV-2 и других коронавирусов в окружающей среде и на обычных сенсорных поверхностях и влияние климатических условий: обзор. Transbound Emerg Dis. 2020. https://doi.org/10.1111/tbed.13707.
Артикул PubMed PubMed Central Google Scholar
Бирюков Дж., Бойдстон Дж. А., Даннинг Р. А., Йегер Дж. Дж., Вуд С., Риз А. Л. и др. Повышение температуры и относительной влажности ускоряет инактивацию SARS-CoV-2 на поверхностях. мСфера. 2020; 5 (4): 1–9.
Артикул Google Scholar
Казанова Л. М., Чон С., Рутала В. А., Вебер Д. Д., Собси М. Д. Влияние температуры и относительной влажности воздуха на выживаемость коронавируса на поверхностях. Appl Environ Microbiol. 2010. 76 (9): 2712–7.
CAS Статья Google Scholar
ван Дормален Н., Бушмейкер Т., Мюнстер В. Стабильность коронавируса ближневосточного респираторного синдрома (БВРС-КоВ) в различных условиях окружающей среды. Евронаблюдение. 2013; 18 (38): 20590.
Артикул Google Scholar
Ratnesar-Shumate S, Williams G, Green B, Krause M, Holland B, Wood S, et al. Искусственный солнечный свет быстро инактивирует SARS-CoV-2 на поверхностях. J Infect Dis. 2020; 222 (2): 214–22.
CAS Статья Google Scholar
Schuit M, Ratnesar-Shumate S, Yolitz J, Williams G, Weaver W., Green B, et al. SARS-CoV-2, переносимый по воздуху, быстро инактивируется имитируемым солнечным светом. J Infect Dis. 2020; 222 (4): 564–71.
CAS Статья Google Scholar
Guillier L, Martin-Latil S, Chaix E, Thébault A, Pavio N, Le Poder S, et al. Моделирование инактивации вирусов семейства Coronaviridae в ответ на температуру и относительную влажность в суспензиях или поверхностях.Appl Environ Microbiol. 2020; 80 (21): 6807–18. https://doi.org/10.1128/AEM.01244-20.
Артикул Google Scholar
Фишер Д., Рейли А., Кан А., Чжэн Е., Кук А. Р., Андерсон Д. Посев вспышек COVID-19 зараженными свежими и замороженными продуктами. bioRxiv. 2020. https://doi.org/10.1101/2020.08.17.255166v1.
Артикул Google Scholar
Фишер Р., Джадсон С., Мязгович К., Бушмейкер Т., Прескотт Дж., Мюнстер В.Дж.Стабильность вируса Эбола на поверхности и в жидкостях в условиях моделирования вспышки. Emerg Infect Dis. 2015; 21 (7): 1243–6.
CAS Статья Google Scholar
Mbithi JN, Springthorpe VS, Sattar SA. Влияние относительной влажности и температуры воздуха на выживаемость вируса гепатита А на поверхностях окружающей среды. Appl Environ Microbiol. 1991. 57 (5): 1394–9.
CAS Статья Google Scholar
Warnes SL, Литтл ZR, Кивил CW. Человеческий коронавирус 229E остается заразным на обычных материалах сенсорной поверхности. MBio. 2015; 6 (6): 1–10.
Артикул Google Scholar
Dublineau A, Batéjat C, Pinon A, Burguière AM, Leclercq I, Manuguerra JC. Сохранение вируса пандемического гриппа a (h2N1) 2009 г. в воде и на непористой поверхности. PLoS ONE. 2011; 6 (11): e28043.
CAS Статья Google Scholar
Vriesekoop F, Russell C, Alvarez-Mayorga B, Aidoo K, Yuan Q, Scannell A, et al. Грязные деньги: исследование гигиенического статуса некоторых мировых валют, полученное в пунктах питания. Foodborne Pathog Dis. 2010. 7 (12): 1497–502.
Артикул Google Scholar
Thomas Y, Vogel G, Wunderli W, Suter P, Witschi M, Koch D, et al. Выживание от вируса гриппа на банкнотах. Appl Environ Microbiol. 2008. 74 (10): 3002–7.
CAS Статья Google Scholar
Йунг Дж. Китай дезинфицирует и уничтожает наличные деньги, чтобы сдержать коронавирус. 2020. https://edition.cnn.com/2020/02/17/asia/china-is-disinfecting-cash-coronavirus-intl-hnk-scli/index.html.
Вибава Т. Китай очищает банкноты в попытке ограничить распространение коронавируса COVID-19. Новости ABC (Австралия). 2020. https://www.abc.net.au/news/2020-02-21/china-cleaning-money-limit-coronavirus-covid-19/11983364.
Шредер П., Иррера А. ФРС помещает в карантин доллары США, репатриированные из Азии, из-за осторожности с коронавирусом. 2020. https://www.reuters.com/article/us-health-coronavirus-fed-dollars/fed-quarantines-us-dollars-repatriated-from-asia-on-coronavirus-caution-idUSKBN20T1YT.
Чой Х. Центральный банк Южной Кореи сжигает и помещает наличные в карантин из соображений безопасности от коронавируса. 2020. https://uk.reuters.com/article/health-coronavirus-southkorea-money/s-koreas-central-bank-burns-quarantines-cash-in-coronavirus-precaution-idUKL4N2AZ1TL.
Brady RRW, Wasson A, Stirling I, McAllister C, Damani NN. Ваш телефон прослушивается? Распространенность бактерий, вызывающих внутрибольничную инфекцию, на мобильных телефонах медицинских работников. J Hosp Infect. 2006. 62 (1): 123–5.
CAS Статья Google Scholar
Olsen M, Campos M, Lohning A, Jones P, Legget J, Bannach-Brown A, et al. Мобильные телефоны представляют собой путь передачи микробов: обзорный обзор.Travel Med Infect Dis. 2020; 35 (апрель): 101704. https://doi.org/10.1016/j.tmaid.2020.101704.
Артикул PubMed PubMed Central Google Scholar
Этот рисунок объясняет, почему 2 градуса глобального потепления будут намного хуже, чем 1,5
Примечание редактора: эта статья была первоначально опубликована в начале 2018 года и была переиздана для выпуска в воскресенье в специальном докладе МГЭИК о глобальном потеплении на единицу .5 ° С .
Стороны, подписавшие Парижское соглашение по климату — все страны мира, если и до тех пор, пока США не выйдут из состава 2020 года, — согласились с уже известной целью: «сдерживать повышение средней глобальной температуры до уровня значительно ниже 2 ° C. выше доиндустриальных уровней и прилагает усилия по ограничению повышения температуры до 1,5 ° C ».
Но насколько важна эта разница? Насколько хуже будет 2 градуса, чем 1,5? Стоит ли дополнительных усилий — а это было бы поистине героическим усилием — ограничить повышение температуры до этой более низкой цели?
Было сложно ответить на эти вопросы, отчасти потому, что они ценны и невероятно сложны, но также из-за недостаточного количества исследований.Несмотря на то, что было проделано много работы по разнице между потеплением, скажем, на 2 и 4 градуса (что было бы катастрофой), было меньше моделирования около 1,5 и не было всестороннего сравнения 1,5 и 2.
К счастью, исследование, опубликованное в 2016 году в журнале Earth System Dynamics , напрямую занимается этим. В CarbonBrief Роз Пидкок кратко излагает исследование, которое уходит в прошлое, и некоторые выводы.
Лучше всего то, что команда CarbonBrief (которую вы действительно должны добавить в закладки) собрала соответствующие сравнения в исследовании в один четкий, эстетически приятный рисунок:
CarbonBriefЭто как прогноз погоды! Из ада.
2 градуса будет намного хуже 1,5 местами
Что касается экстремальной жары, как пишут авторы, «дополнительное повышение средней глобальной температуры на 0,5 ° C отмечает разницу между явлениями на верхнем пределе современной естественной изменчивости и новым климатическим режимом, особенно в тропических регионах».
В районе Средиземного моря доступность пресной воды при 2 градусах упадет почти вдвое по сравнению с 1,5–17 процентами по сравнению с 9 процентами.
В некоторых высокоширотных регионах может быть полезна разница между 1.5 и 2 градуса (хотя такие преимущества будут сведены на нет, если температура в дальнейшем продолжит расти). Но даже при повышении температуры до 2 градусов «тропические регионы, такие как Западная Африка, Юго-Восточная Азия, а также Центральная и северная часть Южной Америки, по прогнозам, столкнутся со значительным снижением урожайности на местном уровне, особенно пшеницы и кукурузы».
TXX измеряет крайние температуры; WSDI измеряет количество длительных (6 с лишним дней) приступов. Earth Systems DynamicsЧто касается повышения уровня моря относительно 1.5 градусов, 2 градуса означают, что уровни на 10 сантиметров выше, а на 30 процентов выше — показатель увеличения к 2100 году.
А вот с коралловыми рифами все в порядке. При 1,5-градусном сценарии процент коралловых рифов в мире, подвергающихся риску, достигнет 90 процентов в 2050 году, но снизится до 70 процентов в 2100 году. При 2-градусном сценарии риску подвергаются все они.
Отчет IPCC и исследование Earth System Dynamics подтверждают то, что многие ученые предупреждали в течение многих лет: 2 градуса не является «безопасным» порогом.Негативные воздействия уже начались и будут только ухудшаться.
Чтобы остановить потепление на 1,5 градуса, потребуются серьезные и продолжительные глобальные действия.
У нас не так много времени, чтобы принять решение. Окно для попадания на 1,5 градуса стремительно закрывается. Вот еще один ужасающий график от CarbonBrief, показывающий, сколько лет осталось до того, как израсходуется «углеродный бюджет» для различных температур:
CarbonBriefПри нашем нынешнем уровне выбросов, наш углеродный бюджет с хорошей (66%) вероятностью ограничения потепления до 1.Через шесть лет будет израсходовано 5 степеней. Только вот этому графику два года назад, так что теперь осталось четыре года.
Чтобы притормозить на 1,5 градуса, глобальные выбросы углерода должны немедленно начать сокращаться, быстрее, чем когда-либо, и достичь нуля к 2050 году (а затем пойти на отрицательную величину):
OCIДля этого потребуется мобилизация, эквивалентная мобилизации США для Второй мировой войны, только глобальная и продолжающаяся до конца столетия.Шансы на это кажутся … маловероятными. Насколько нам известно, Трамп все еще будет у власти, когда бюджет в 1,5 градуса будет израсходован.
Но мы должны четко понимать, какое решение мы принимаем, даже если мы принимаем его, не принимая решения.
Откладывая необходимые работы по декарбонизации, мы обрекаем миллионы людей в тропических регионах на меньшее количество продуктов питания, а в Средиземноморье — на меньшее количество воды — со всеми сопутствующими проблемами со здоровьем и конфликтами. Мы допускаем больше волн жары и более высокого уровня моря.Мы отказываемся от коралловых рифов мира, а вместе с ними и от сотен видов, которые на них полагаются.
И даже тогда решение все равно будет стоять перед нами: 2 градуса или 3? Опять же, это будет означать больше волн тепла, больше потерь урожая, больше нехватки воды, больше затопленных прибрежных городов, больше болезней и конфликтов, миллионы страданий.
И даже тогда решение: 3 степени или 4?
Чем дольше мы ждем, тем больше человеческих страданий и необратимого ущерба экосистемам мы вписываем в наше коллективное будущее.Но здесь нельзя спрятаться и избежать необходимости обезуглероживания. Это необходимо сделать, если у нашего вида есть надежный дом на Земле.
Похоже, что умнее всего было бы с этим справиться.
Как найти процент сектора под углом
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; и Ваше заявление: (а) вы добросовестно полагаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Дополнение угла A на 20 градусов меньше половины дополнения угла A
Вопросы и ответы по справке по домашнему заданиюДополнение к углу A на 20 градусов меньше, чем половина дополнения к углу A.Найдите угол А. С чего начать?
Позволять A = мера угла A c = мера дополнительного угла s = мера дополнительного угла «Дополнение к углу A на 20 градусов меньше, чем половина дополнения к углу A» буквально переводится в уравнение {{{c = (1/2) s-20}}} Кроме того, по определению, поскольку ‘c’ является дополнением к углу A, это означает, что они добавляют к 90 градусам. Итак {{{A + c = 90}}} Кроме того, дополнительные углы увеличиваются до 180 градусов. Поскольку ‘s’ является дополнением к углу A, мы знаем, что {{{A + s = 180}}} {{{A + c = 90}}} Начнем со второго уравнения.{{{c = 90-A}}} Вычтите A с обеих сторон. {{{A + s = 180}}} Переходим ко второму уравнению {{{s = 180-A}}} Вычтите A с обеих сторон. ———————————————- {{{c = (1/2) s-20}}} Теперь вернитесь к первому уравнению. {{{90-A = (1/2) s-20}}} Подключите {{{c = 90-A}}} {{{90-A = (1/2) (180-A) -20}}} Подключите {{{s = 180-A}}} {{{90-A = (1/2) (180) — (1/2) A-20}}} Распространение {{{90-A = 180 / 2- (1/2) A-20}}} Умножить {{{90-A = 90- (1/2) A-20}}} Уменьшить {{{2 (90) -2 (a) = 2 (90) -cross (2) ((1 / cross (2)) a) -2 (20)}}} Умножьте КАЖДЫЙ член на ЖК-дисплей {{{ 2}}}, чтобы очистить любые дроби.{{{180-2a = 180-1a-40}}} Умножать и упрощать. {{{180-2a = -a + 140}}} Объедините похожие термины с правой стороны. {{{-2a = -a + 140-180}}} Вычтите {{{180}}} с обеих сторон. {{{-2a + a = 140-180}}} Добавьте {{{a}}} с обеих сторон. {{{-a = 140-180}}} Объедините похожие термины слева. {{{-a = -40}}} Объедините похожие термины с правой стороны. {{{a = (- 40) / (- 1)}}} Разделите обе стороны на {{{-1}}}, чтобы изолировать {{{a}}}. {{{a = 40}}} Уменьшить. ————————————————— ———————
ответил: onlekile
Дополнение к углу A на 20 градусов меньше, чем половина дополнения к углу A.Найдите угол А. С чего начать? Дополнение к углу A составляет: (90 — A) Дополнение к углу A составляет: (180 — A) Поскольку дополнение к A на 20 градусов меньше, чем половина дополнения к углу A, то мы имеем: {{{(90 — A) + 20 = (1/2) * (180 — A)}}} {{{110 — A = (180 — A) / 2}}} Перемножая, получаем: 2 (110 — А) = 180 — А 220 — 2А = 180 — А — 2А + А = 180 — 220 — А = — 40 {{{A = (-40) / — 1}}} А = 40 Следовательно, угол A = {{{highlight_green (40)}}} градусов.


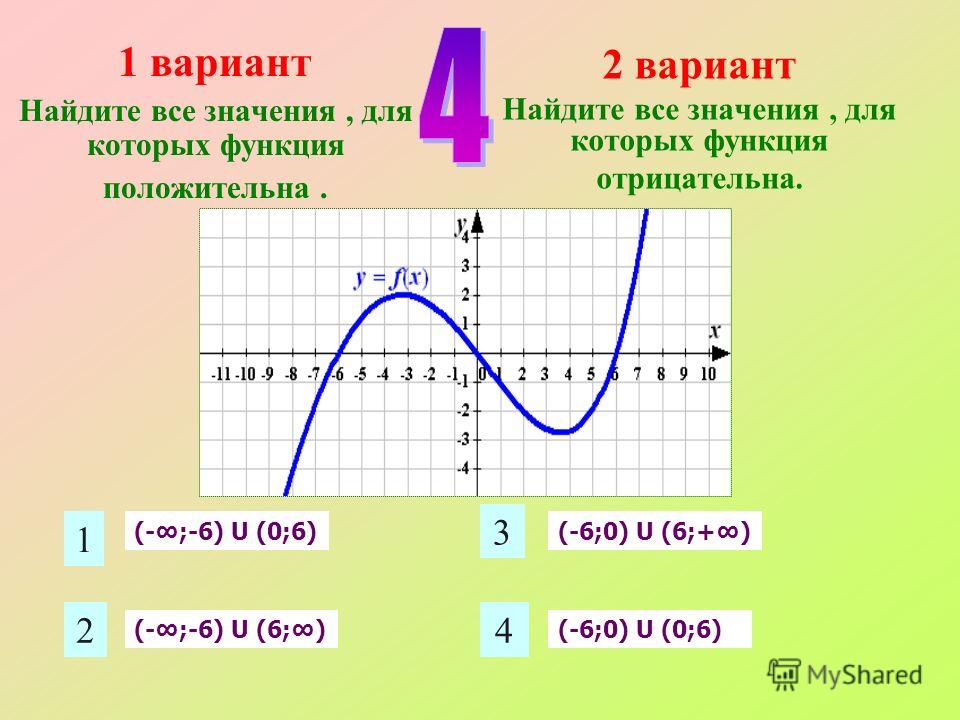
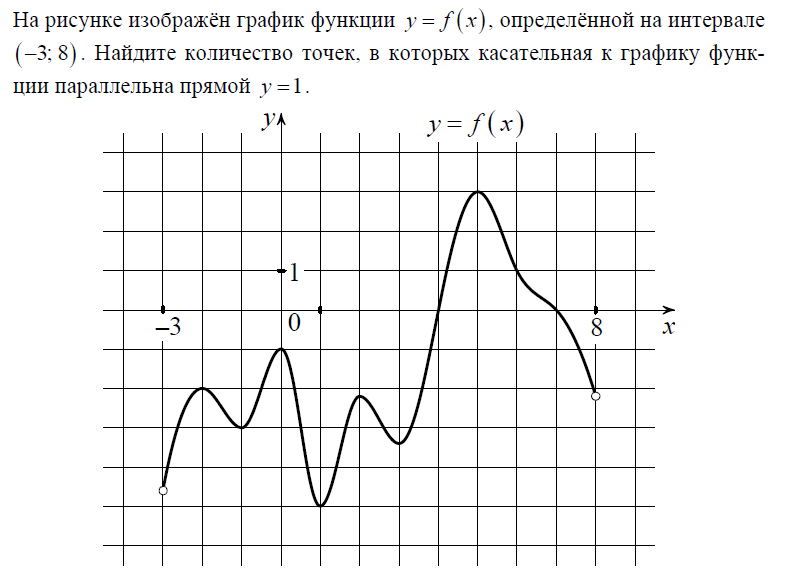
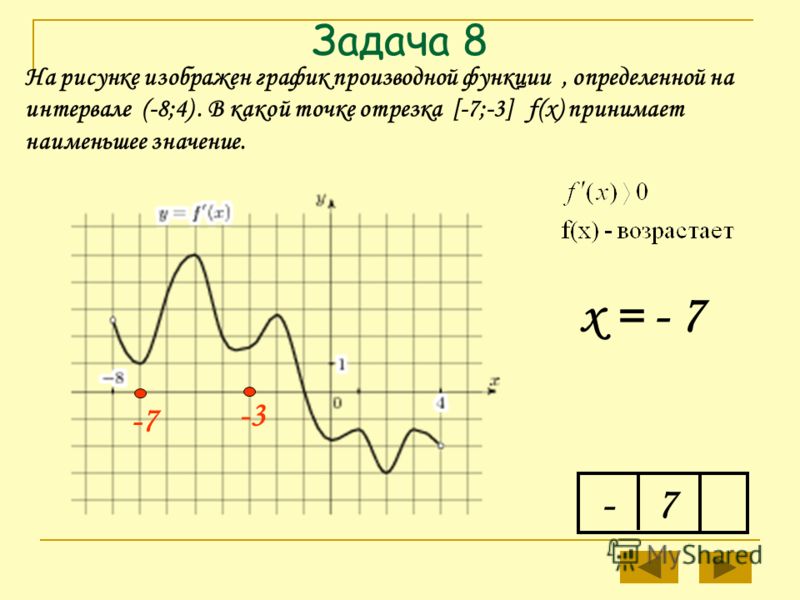 В первых скобках — разность квадратов, из вторых выносим общий множитель 4 за скобки:
В первых скобках — разность квадратов, из вторых выносим общий множитель 4 за скобки: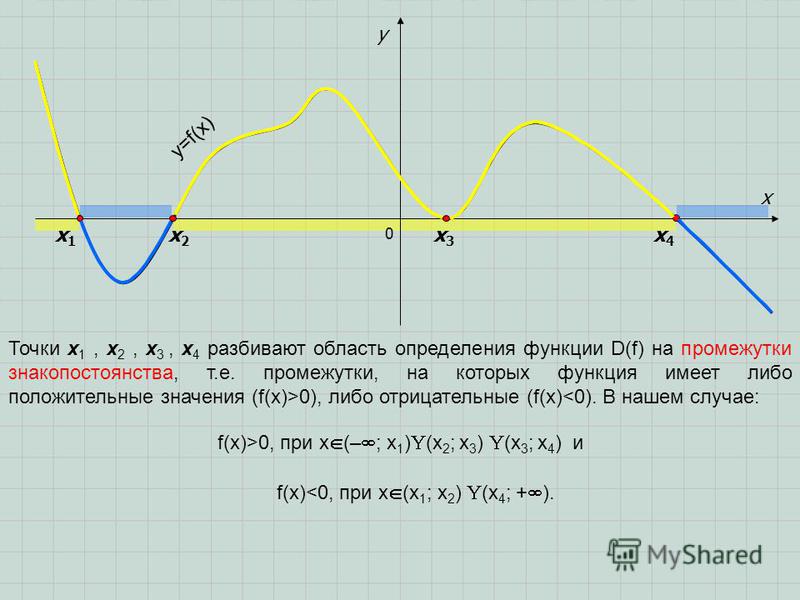
 Какова вероятность того,что наугад взятый карандаш не будет ни красным,ни синим…
Какова вероятность того,что наугад взятый карандаш не будет ни красным,ни синим… ..
.. functio – исполнение, осуществление), одно из основных понятий математики, означающее зависимость одних переменных величин от других. Слово «величина» в этом определении понимается в самом широком смысле: это может быть именованное число, отвлечённое число (действительное или комплексное), неск. чисел (т. е. точка пространства) и вообще элемент любого множества.
functio – исполнение, осуществление), одно из основных понятий математики, означающее зависимость одних переменных величин от других. Слово «величина» в этом определении понимается в самом широком смысле: это может быть именованное число, отвлечённое число (действительное или комплексное), неск. чисел (т. е. точка пространства) и вообще элемент любого множества.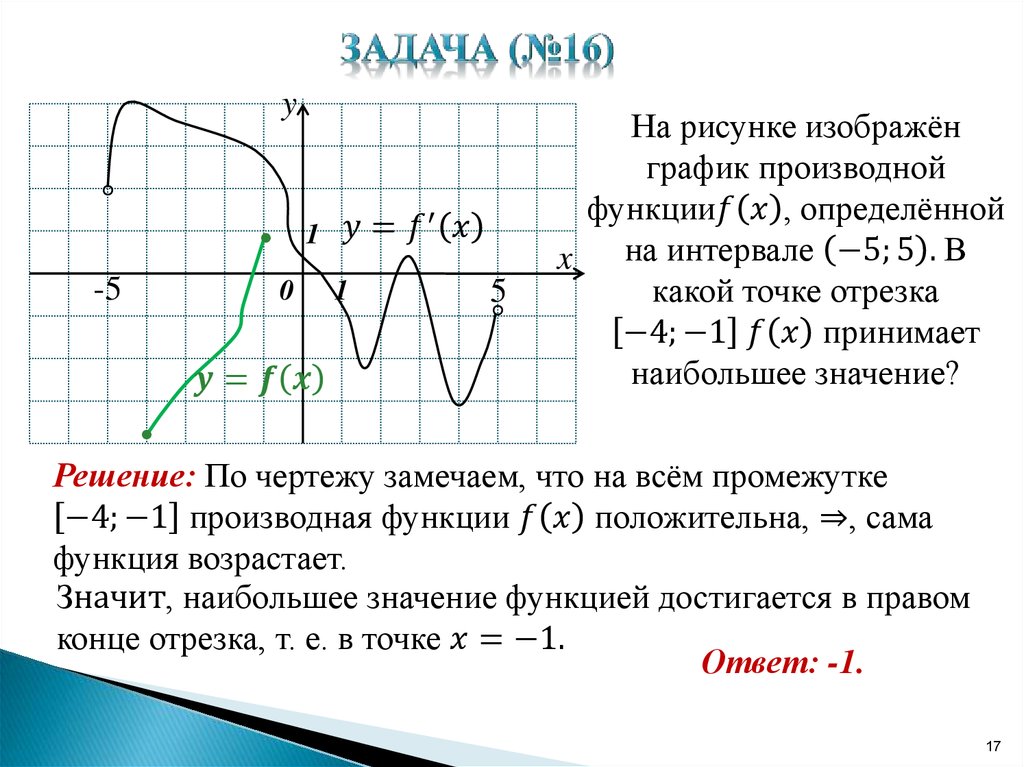 (областью определения Ф. может быть множество всех действительных чисел, интервал, отрезок и т. п.). Слова «поставлено в соответствие» означают, что указан определённый способ, по которому для каждого $x∈E$ находится значение $y=f(x)$. Этот способ в данном случае обозначен символом $f$. Для обозначения Ф. применяются и др. буквы, напр. $y=g(x)$, $y=F(x)$, $s=h(t)$, $v=φ(s)$.
(областью определения Ф. может быть множество всех действительных чисел, интервал, отрезок и т. п.). Слова «поставлено в соответствие» означают, что указан определённый способ, по которому для каждого $x∈E$ находится значение $y=f(x)$. Этот способ в данном случае обозначен символом $f$. Для обозначения Ф. применяются и др. буквы, напр. $y=g(x)$, $y=F(x)$, $s=h(t)$, $v=φ(s)$. {2m}.$$
{2m}.$$ Такой способ задания Ф. часто применяется в тех случаях, когда область определения состоит из конечного числа значений.
Такой способ задания Ф. часто применяется в тех случаях, когда область определения состоит из конечного числа значений. корень, изображается верхней половиной шаровой поверхности радиуса 1 с центром в начале координат.
корень, изображается верхней половиной шаровой поверхности радиуса 1 с центром в начале координат. 2}$ отображает отрезок $–1 ⩽ x ⩽ 1$ на отрезок $0 ⩽ y ⩽ 1$.
2}$ отображает отрезок $–1 ⩽ x ⩽ 1$ на отрезок $0 ⩽ y ⩽ 1$. Ферма «Введение и изучение плоских и телесных мест» (1636, опубл. в 1679). Изучение линий по их уравнениям в «Геометрии» Р. Декарта (1637) также указывает на ясное представление о взаимной зависимости двух переменных величин. У англ. математика И. Барроу («Лекции по геометрии», 1670) в геометрич. форме устанавливается взаимная обратность действий дифференцирования и интегрирования (разумеется, без употребления самих этих терминов). Это свидетельствует о совершенно отчётливом владении понятием Ф. В геометрич. и механич. виде это понятие можно найти и у И. Ньютона. Однако термин «Ф.» впервые появляется лишь в 1692 у Г. Лейбница, и притом не совсем в современном его понимании. Лейбниц называет Ф. разл. отрезки, связанные с к.-л. кривой, напр. абсциссы её точек. В первом печатном курсе «Анализа бесконечно малых» франц. математика Г. Лопиталя (1696) термин «Ф.
Ферма «Введение и изучение плоских и телесных мест» (1636, опубл. в 1679). Изучение линий по их уравнениям в «Геометрии» Р. Декарта (1637) также указывает на ясное представление о взаимной зависимости двух переменных величин. У англ. математика И. Барроу («Лекции по геометрии», 1670) в геометрич. форме устанавливается взаимная обратность действий дифференцирования и интегрирования (разумеется, без употребления самих этих терминов). Это свидетельствует о совершенно отчётливом владении понятием Ф. В геометрич. и механич. виде это понятие можно найти и у И. Ньютона. Однако термин «Ф.» впервые появляется лишь в 1692 у Г. Лейбница, и притом не совсем в современном его понимании. Лейбниц называет Ф. разл. отрезки, связанные с к.-л. кривой, напр. абсциссы её точек. В первом печатном курсе «Анализа бесконечно малых» франц. математика Г. Лопиталя (1696) термин «Ф. » не употребляется.
» не употребляется. Так сложилось совр. понятие Ф., свободное от упоминания о её аналитич. задании.
Так сложилось совр. понятие Ф., свободное от упоминания о её аналитич. задании.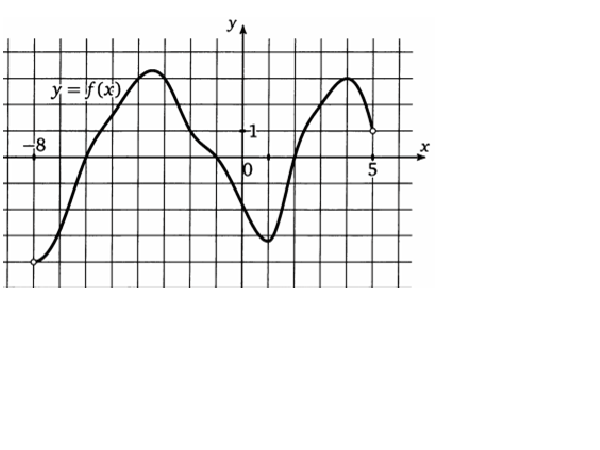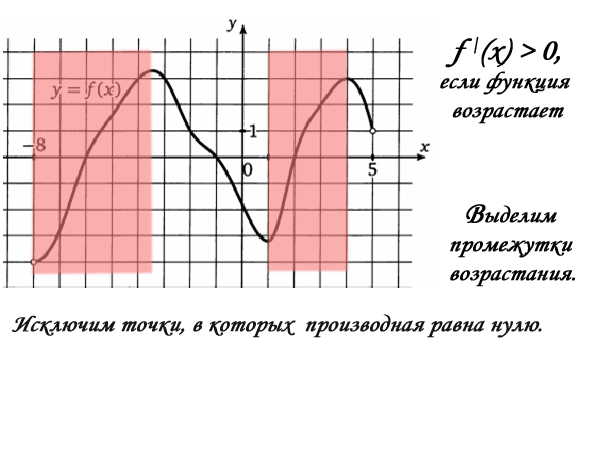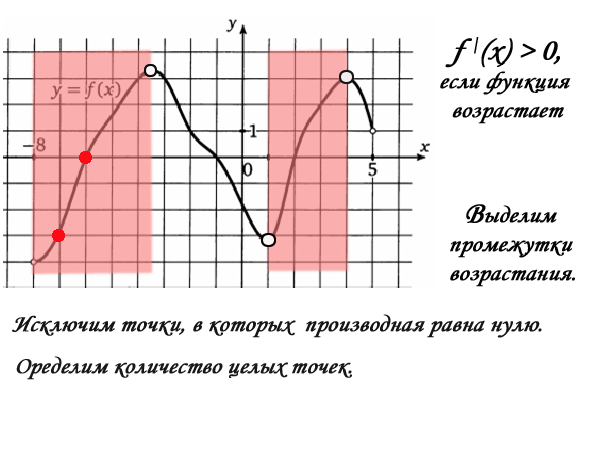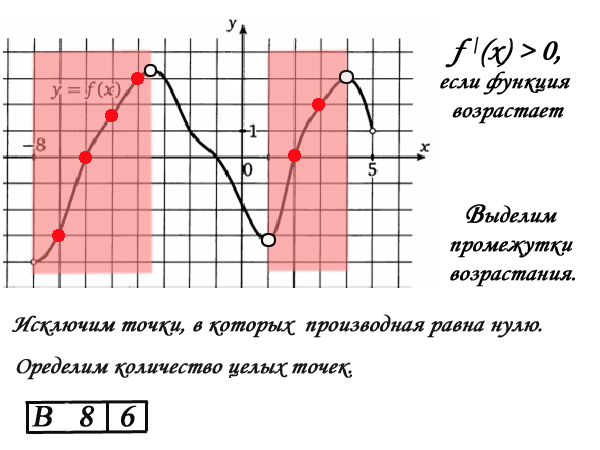 Обратите внимание, что домен и диапазон всегда записываются от меньших значений к большим или слева направо для домена и от нижней части графика к верхней части графика для диапазона.0011
Обратите внимание, что домен и диапазон всегда записываются от меньших значений к большим или слева направо для домена и от нижней части графика к верхней части графика для диапазона.0011 Например, область определения и диапазон функции кубического корня — это множество всех действительных чисел.
Например, область определения и диапазон функции кубического корня — это множество всех действительных чисел.  { 2}[/latex], доменом являются все действительные числа, поскольку горизонтальная протяженность графика — это вся линия действительных чисел. Поскольку график не содержит отрицательных значений диапазона, диапазон состоит только из неотрицательных действительных чисел. 9{3}[/latex], доменом являются все действительные числа, поскольку горизонтальная протяженность графика — это вся линия действительных чисел. То же самое относится к вертикальному размеру графика, поэтому домен и диапазон включают все действительные числа.
{ 2}[/latex], доменом являются все действительные числа, поскольку горизонтальная протяженность графика — это вся линия действительных чисел. Поскольку график не содержит отрицательных значений диапазона, диапазон состоит только из неотрицательных действительных чисел. 9{3}[/latex], доменом являются все действительные числа, поскольку горизонтальная протяженность графика — это вся линия действительных чисел. То же самое относится к вертикальному размеру графика, поэтому домен и диапазон включают все действительные числа.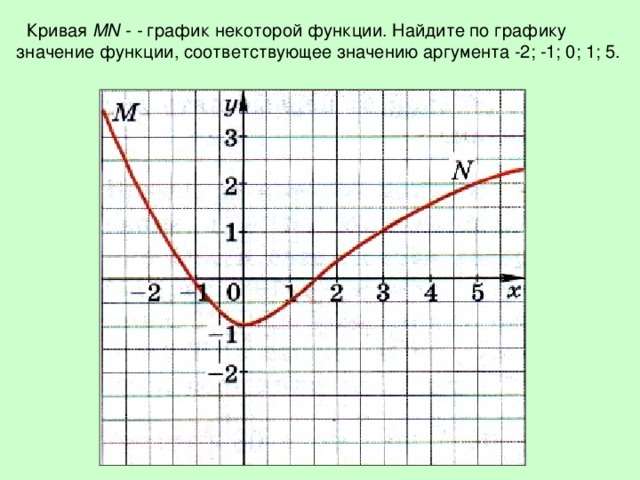 Также нет [latex]x[/latex], который может выдавать 0, поэтому 0 также исключается из диапазона. Обратите внимание, что выход этой функции всегда положителен из-за квадрата в знаменателе, поэтому диапазон включает только положительные числа.
Также нет [latex]x[/latex], который может выдавать 0, поэтому 0 также исключается из диапазона. Обратите внимание, что выход этой функции всегда положителен из-за квадрата в знаменателе, поэтому диапазон включает только положительные числа.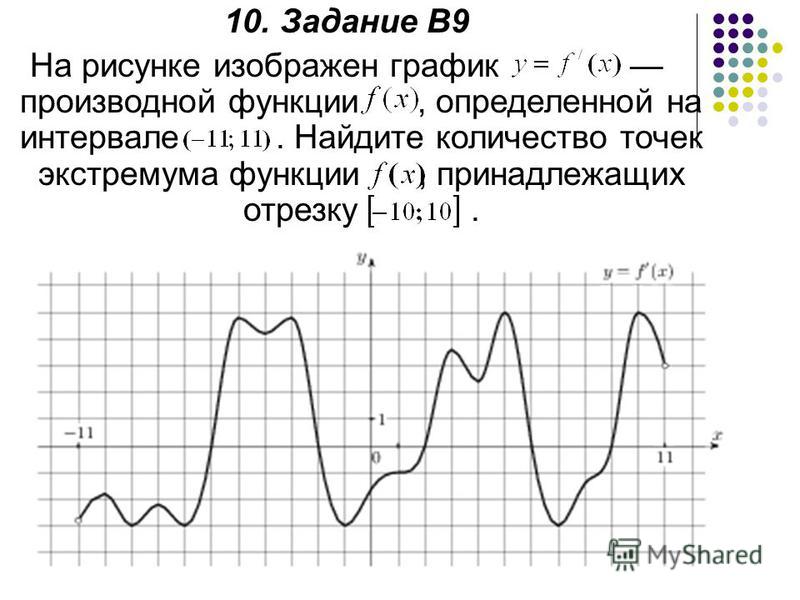

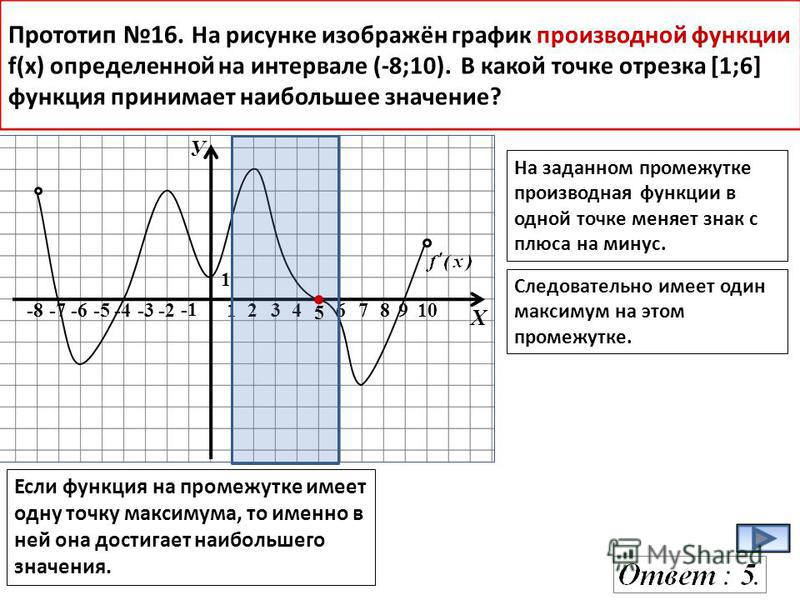 Для этого покажем, что любое неотрицательное
число является выходом этой функции. Если 𝑦≥0, то
𝑓√𝑦=√𝑦=𝑦.
Для этого покажем, что любое неотрицательное
число является выходом этой функции. Если 𝑦≥0, то
𝑓√𝑦=√𝑦=𝑦.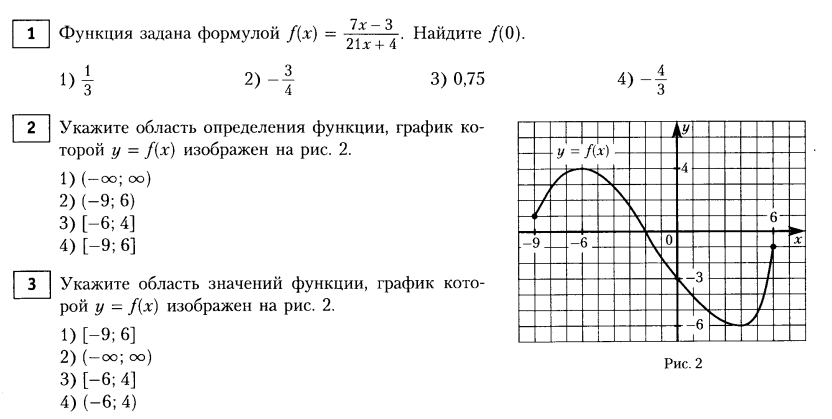
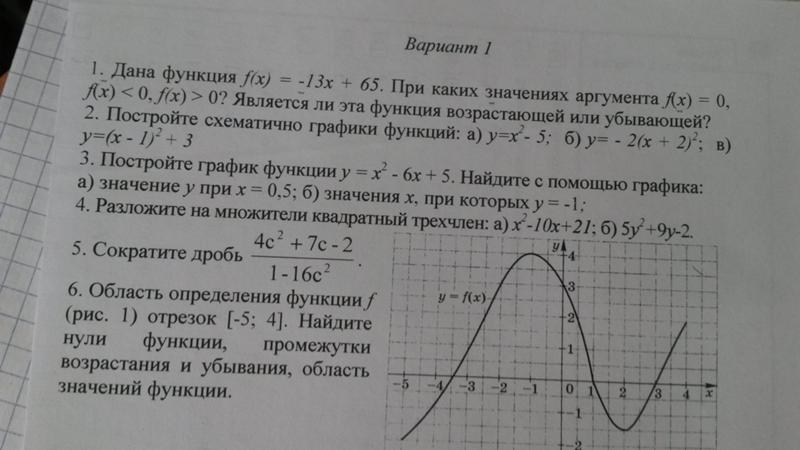 линия; на самом деле, для любого 𝑐∈[0,1[ линия
𝑦=𝑐 не будет пересекать нашу кривую и все остальные
горизонтальные линии пересекают нашу кривую. Следовательно, диапазон этой функции
]−∞,0[∪[1,∞[.
линия; на самом деле, для любого 𝑐∈[0,1[ линия
𝑦=𝑐 не будет пересекать нашу кривую и все остальные
горизонтальные линии пересекают нашу кривую. Следовательно, диапазон этой функции
]−∞,0[∪[1,∞[.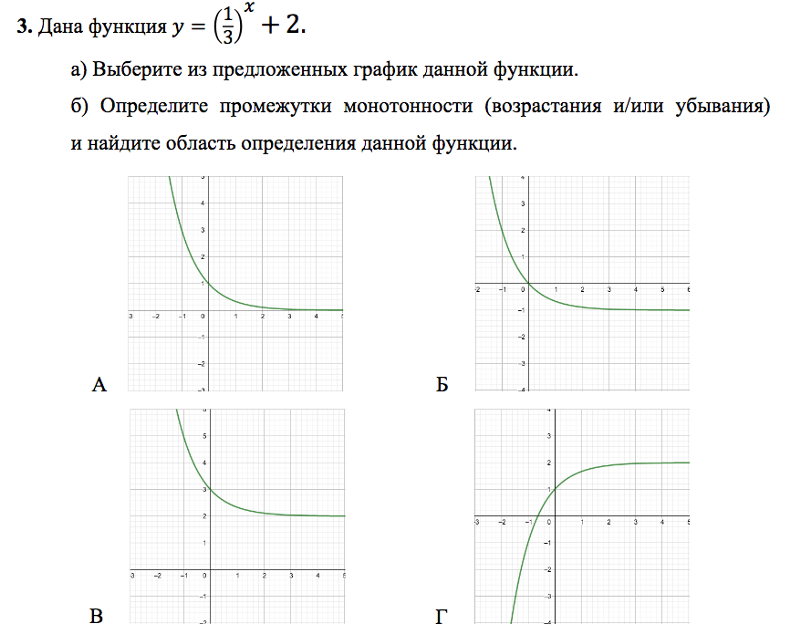 Поэтому найти все
возможные входы этой функции, нам нужно будет взять объединение всех
поддомены. Для этой кусочной функции мы можем взять на вход 𝑥0, а также
𝑥≥0; комбинируя их, мы можем видеть, что это любое реальное значение
𝑥, поэтому его домен равен ℝ.
Поэтому найти все
возможные входы этой функции, нам нужно будет взять объединение всех
поддомены. Для этой кусочной функции мы можем взять на вход 𝑥0, а также
𝑥≥0; комбинируя их, мы можем видеть, что это любое реальное значение
𝑥, поэтому его домен равен ℝ. Для этого положим 𝑐≥1 так, чтобы
𝑐−1≥0; это означает
𝑓(𝑐−1)=(𝑐−1)+1=𝑐.
Для этого положим 𝑐≥1 так, чтобы
𝑐−1≥0; это означает
𝑓(𝑐−1)=(𝑐−1)+1=𝑐.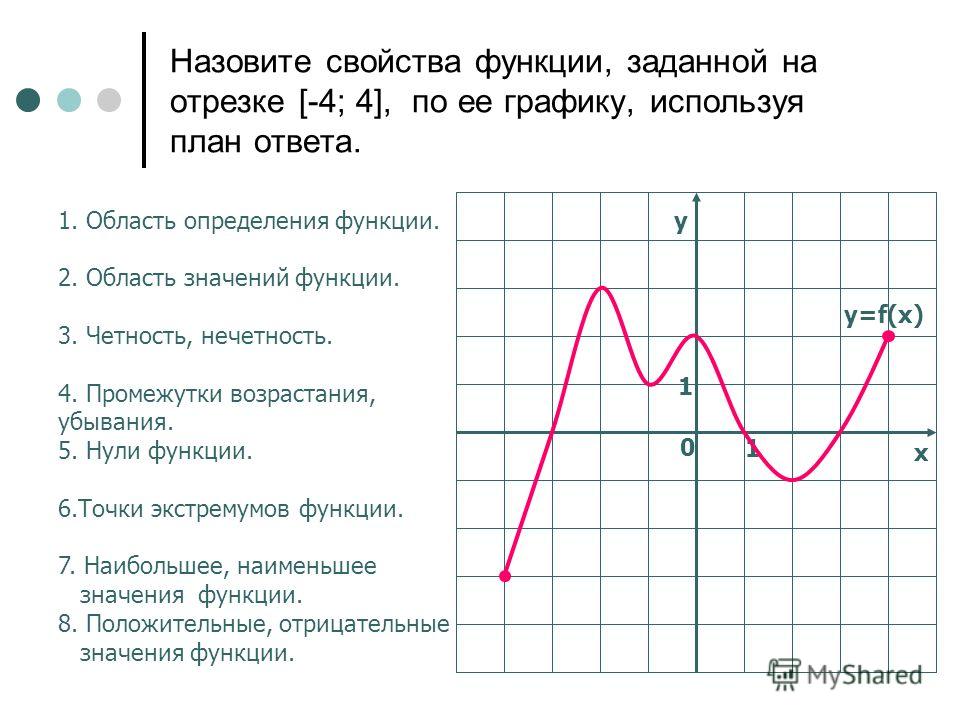
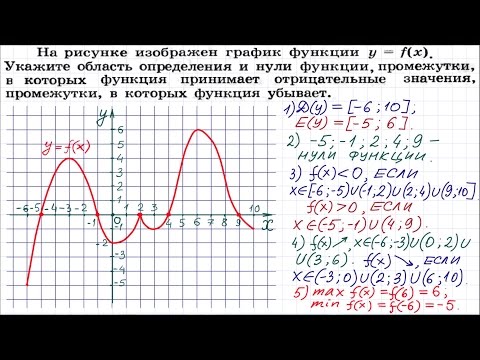
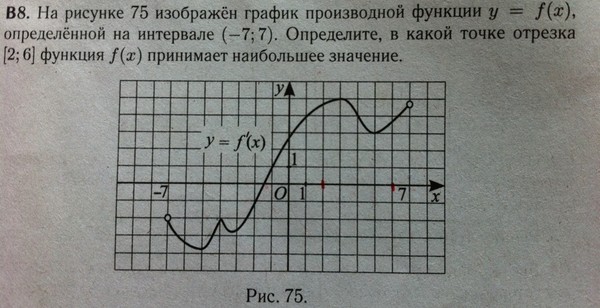
 Помните, любая точка на нашем графике будет иметь вид
(𝑐,𝑓(𝑐)), где 𝑓(𝑐) будет в диапазоне функции. Следовательно, мы можем найти
диапазон этой функции, определяя 𝑦-координаты точек на ее графике.
Помните, любая точка на нашем графике будет иметь вид
(𝑐,𝑓(𝑐)), где 𝑓(𝑐) будет в диапазоне функции. Следовательно, мы можем найти
диапазон этой функции, определяя 𝑦-координаты точек на ее графике.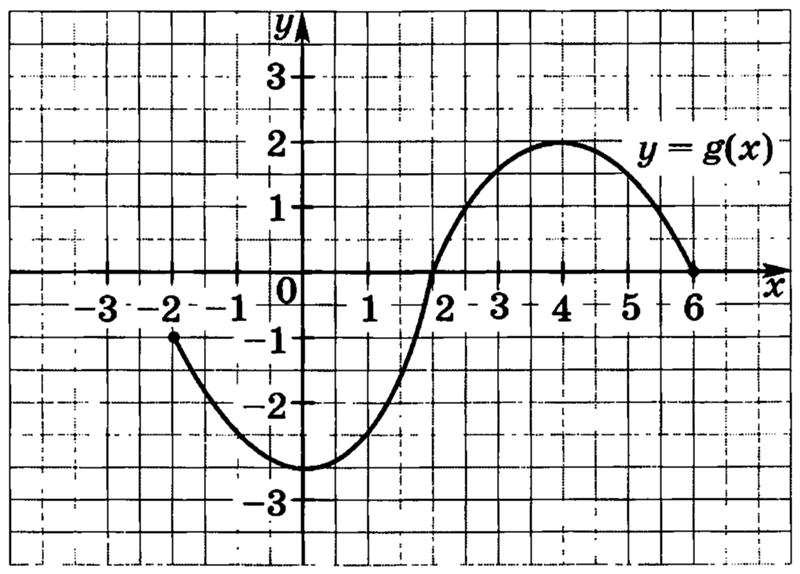
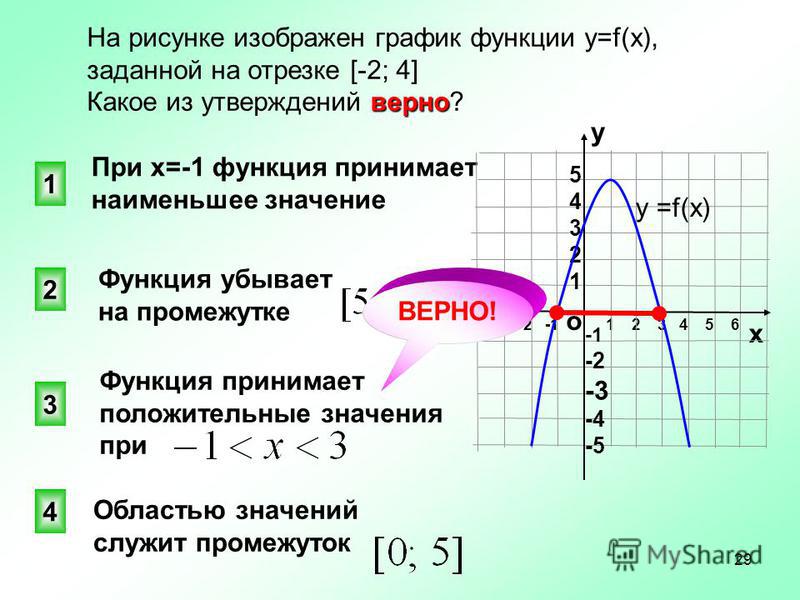 Во-первых, 𝑥≠6 совпадает с ℝ−{6}. Во-вторых, 𝑥=6 совпадает с {6}.
Во-первых, 𝑥≠6 совпадает с ℝ−{6}. Во-вторых, 𝑥=6 совпадает с {6}. Поскольку выход постоянен, его диапазон
{12}.
Поскольку выход постоянен, его диапазон
{12}.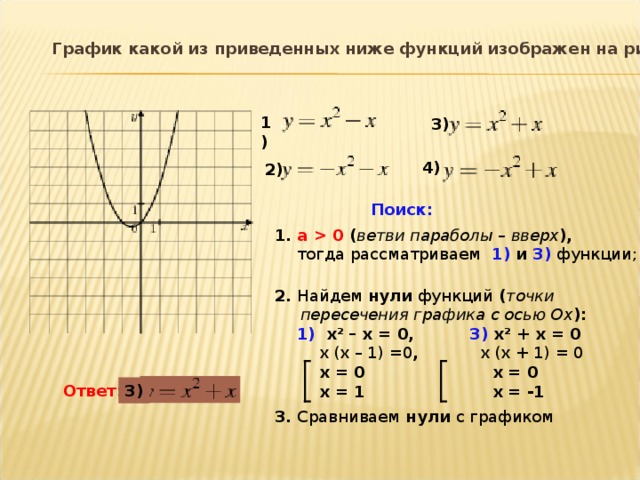
 Композиция функции осуществляется путем замены одной функции на другую функцию.
Композиция функции осуществляется путем замены одной функции на другую функцию. 
 Net
Net
 количество: 1
количество: 1 количество
: 1
количество
: 1 количество: 1
количество: 1 количество
: 3
количество
: 3 количество: 3
количество: 3 ru Д. Федутинов. Кроме того, это может говорить о том, что Hermes 900 полностью интегрирован в армейские информационно-управляющие системы, – продолжает специалист. Hermes 900 был разработан израильской компанией Elbit Systems на базе предшественника Hermes 450, который эксплуатируется в течении 17 лет в ряде стран мира. Общий налет беспилотников этого типа составляет более 500 тысяч часов. Hermes 900 отличается от предыдущей модификации аппарата не только большими размерами, но и улучшенными техническими характеристиками, а также повышенными разведывательными возможностями. Конкуренты беспилотника Hermes 900 на мировом рынке: аппараты семейства Predator (GA–ASI, США) и Heron (IAI, Израиль).
ru Д. Федутинов. Кроме того, это может говорить о том, что Hermes 900 полностью интегрирован в армейские информационно-управляющие системы, – продолжает специалист. Hermes 900 был разработан израильской компанией Elbit Systems на базе предшественника Hermes 450, который эксплуатируется в течении 17 лет в ряде стран мира. Общий налет беспилотников этого типа составляет более 500 тысяч часов. Hermes 900 отличается от предыдущей модификации аппарата не только большими размерами, но и улучшенными техническими характеристиками, а также повышенными разведывательными возможностями. Конкуренты беспилотника Hermes 900 на мировом рынке: аппараты семейства Predator (GA–ASI, США) и Heron (IAI, Израиль). Аппарат способен непрерывно летать в течении 36 часов на высоте до 9140 метров; радиус действия до 1850 км. Длина фюзеляжа – 8.3 м, размах крыла – 15 м, взлетный вес – 1180 кг, максимальный вес полезной нагрузки (разведывательной аппаратуры и средств радиоэлектронной борьбы) – 350 кг.
Аппарат способен непрерывно летать в течении 36 часов на высоте до 9140 метров; радиус действия до 1850 км. Длина фюзеляжа – 8.3 м, размах крыла – 15 м, взлетный вес – 1180 кг, максимальный вес полезной нагрузки (разведывательной аппаратуры и средств радиоэлектронной борьбы) – 350 кг.
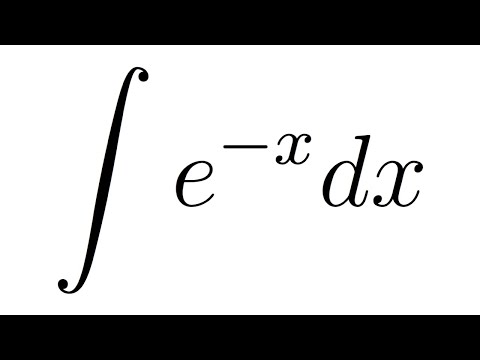
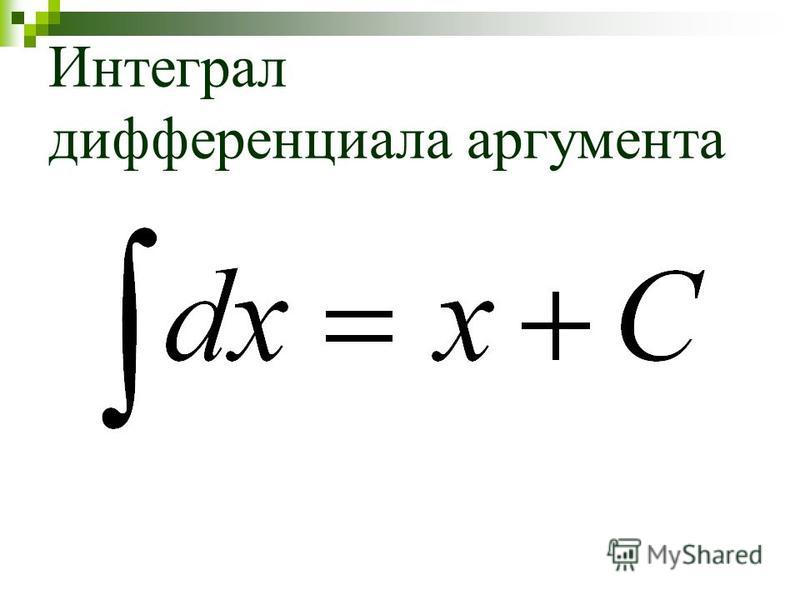
 com, маркеры автора)
com, маркеры автора)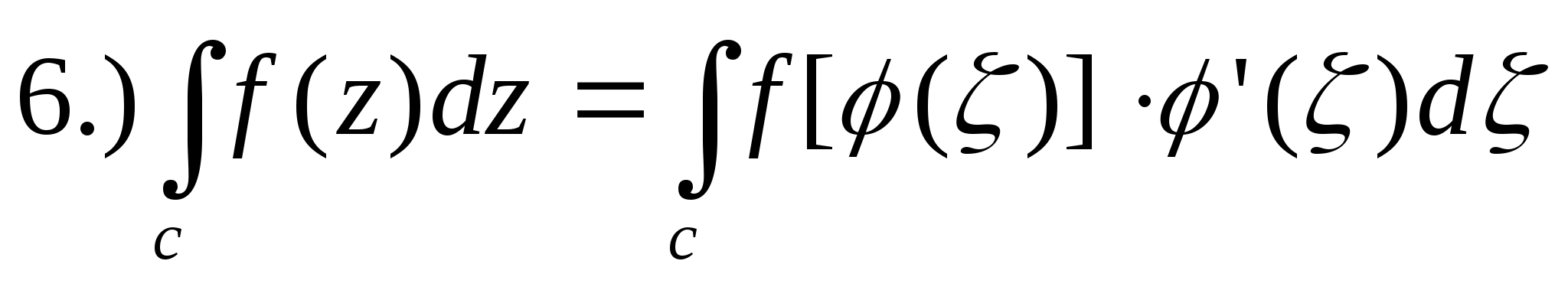
 Разрабатываемые правила содержат, в частности, требования к техническому оснащению беспилотников, обеспечивающие должный уровень безопасности совместных полетов.
Разрабатываемые правила содержат, в частности, требования к техническому оснащению беспилотников, обеспечивающие должный уровень безопасности совместных полетов. О. Хайнс
О. Хайнс 2001 Апрель; 12 (4): 891-900.
2001 Апрель; 12 (4): 891-900.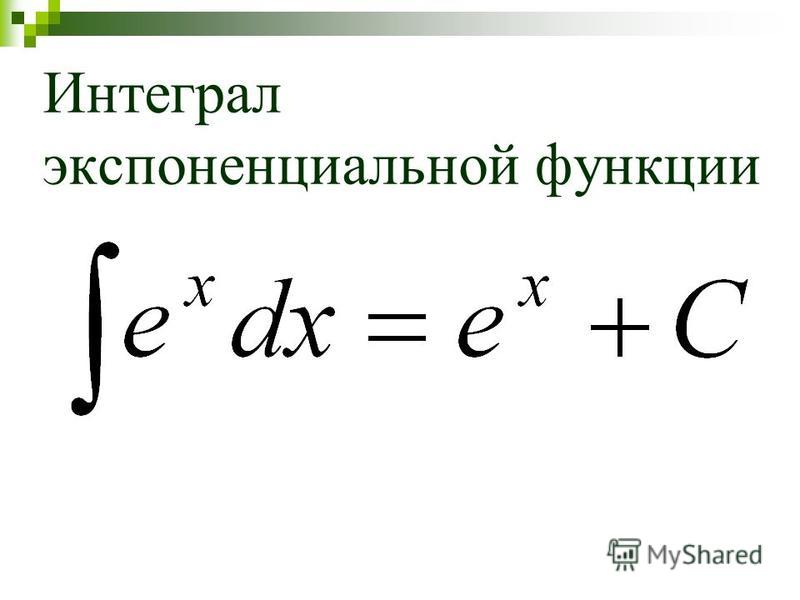 Некоторые адапторные белки, включая talin, поддерживают связь между цитоскелетом и мембраной путем связывания с интегральными мембранными белками и с цитоскелетом. Layilin, недавно охарактеризованный трансмембранный белок, гомологичный лектинам С-типа, является сайтом связывания талина с мембраной в периферических складках распространяющихся клеток. Чтобы облегчить исследования функции лейилина, мы создали слитый белок лейилин-Fc, содержащий внеклеточную часть лейилина, соединенную с тяжелой цепью иммуноглобулина G человека, и использовали эту химеру для идентификации лигандов лейилина. Здесь мы демонстрируем, что слитый белок лейилин-Fc связывается с гиалуроновой кислотой, иммобилизованной на сефарозе. Анализы связывания на микротитровальных планшетах, эксперименты по соосаждению и окрашивание срезов, предварительно расщепленных различными ферментами, разрушающими гликозаминогликаны, и анализы клеточной адгезии показали, что лейилин специфически связывается с гиалуроновой кислотой, но не с другими тестируемыми гликозаминогликанами.
Некоторые адапторные белки, включая talin, поддерживают связь между цитоскелетом и мембраной путем связывания с интегральными мембранными белками и с цитоскелетом. Layilin, недавно охарактеризованный трансмембранный белок, гомологичный лектинам С-типа, является сайтом связывания талина с мембраной в периферических складках распространяющихся клеток. Чтобы облегчить исследования функции лейилина, мы создали слитый белок лейилин-Fc, содержащий внеклеточную часть лейилина, соединенную с тяжелой цепью иммуноглобулина G человека, и использовали эту химеру для идентификации лигандов лейилина. Здесь мы демонстрируем, что слитый белок лейилин-Fc связывается с гиалуроновой кислотой, иммобилизованной на сефарозе. Анализы связывания на микротитровальных планшетах, эксперименты по соосаждению и окрашивание срезов, предварительно расщепленных различными ферментами, разрушающими гликозаминогликаны, и анализы клеточной адгезии показали, что лейилин специфически связывается с гиалуроновой кислотой, но не с другими тестируемыми гликозаминогликанами.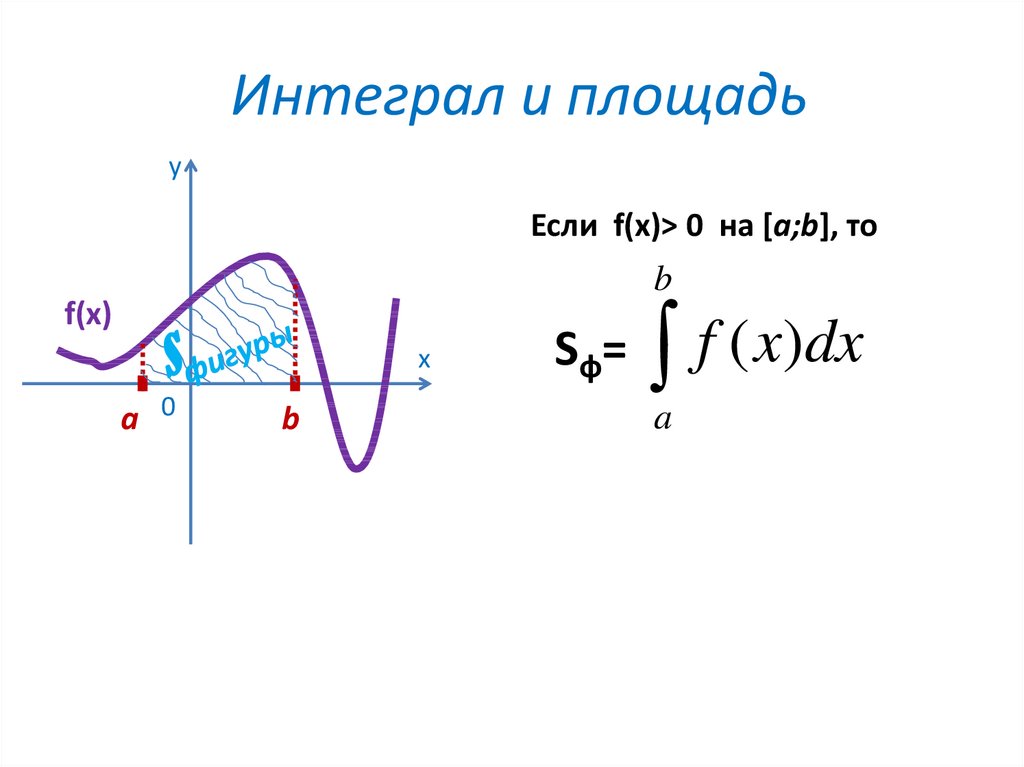 Способность Layilin связывать гиалуронан, вездесущий компонент внеклеточного матрикса, обнаруживает интересную параллель между layilin и CD44, потому что оба могут связываться с линкерными белками цитоскелета-мембраны через свои цитоплазматические домены и с гиалуроновой кислотой через свои внеклеточные домены. Этот параллелизм предполагает роль layilin в клеточной адгезии и подвижности.
Способность Layilin связывать гиалуронан, вездесущий компонент внеклеточного матрикса, обнаруживает интересную параллель между layilin и CD44, потому что оба могут связываться с линкерными белками цитоскелета-мембраны через свои цитоплазматические домены и с гиалуроновой кислотой через свои внеклеточные домены. Этот параллелизм предполагает роль layilin в клеточной адгезии и подвижности. Внеклеточная часть Лайилина была
клонирован непосредственно на N-конце шарнирного домена (H) IgG1 человека
так что химера содержит два цистеиновых остатка (не показаны)
внутри шарнирного домена, ответственного за димеризацию Ig. Сиг,
НХ 2 -концевая сигнальная последовательность, лектин, лейилины
внеклеточная часть, гомологичная лектинам С-типа; ТМ,
трансмембранный домен; Ch3 и Ch4, константные области IgG человека.
(B) Очищенный слитый белок лейилин-Fc анализировали на геле SDS-PAGE.
как в восстановленных, так и в невосстановленных условиях и обнаруживается
иммуноблоттинг с античеловеческим IgG (Fc-специфическим)
антитело. Молекулярные массы (в кДа) показаны слева.
Внеклеточная часть Лайилина была
клонирован непосредственно на N-конце шарнирного домена (H) IgG1 человека
так что химера содержит два цистеиновых остатка (не показаны)
внутри шарнирного домена, ответственного за димеризацию Ig. Сиг,
НХ 2 -концевая сигнальная последовательность, лектин, лейилины
внеклеточная часть, гомологичная лектинам С-типа; ТМ,
трансмембранный домен; Ch3 и Ch4, константные области IgG человека.
(B) Очищенный слитый белок лейилин-Fc анализировали на геле SDS-PAGE.
как в восстановленных, так и в невосстановленных условиях и обнаруживается
иммуноблоттинг с античеловеческим IgG (Fc-специфическим)
антитело. Молекулярные массы (в кДа) показаны слева.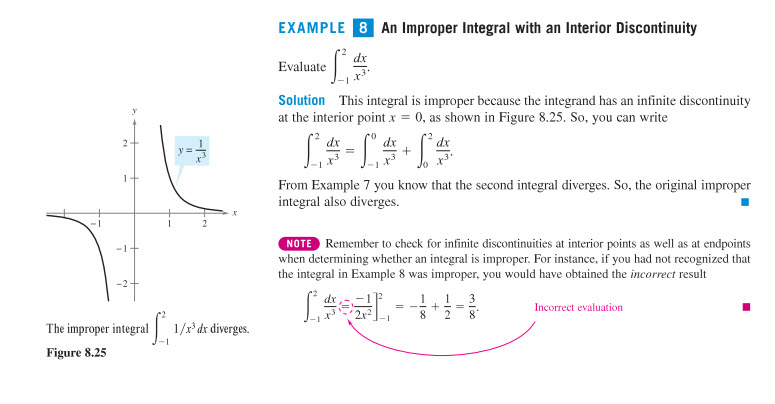 (A) Слитый белок Layilin-Fc был…
(A) Слитый белок Layilin-Fc был… (A) Общий клеточный лизат клеток 3T3 был
инкубировали с разными ГАГ (по 50 мкг каждого) и подвергали ХПК
осадки. Осадки и общий клеточный лизат разделяли на
Гель SDS-PAGE и окрашивание антителом против лейилина после блоттинга на
мембрана. Контрольные реакции осаждали ЦПК без добавления
любого ГАГ или после добавления N -ацетилглюкозамин.
Интенсивность полос осажденного лейилина в двух аналогичных
эксперименты были оценены количественно, и результат показан в B.
(A) Общий клеточный лизат клеток 3T3 был
инкубировали с разными ГАГ (по 50 мкг каждого) и подвергали ХПК
осадки. Осадки и общий клеточный лизат разделяли на
Гель SDS-PAGE и окрашивание антителом против лейилина после блоттинга на
мембрана. Контрольные реакции осаждали ЦПК без добавления
любого ГАГ или после добавления N -ацетилглюкозамин.
Интенсивность полос осажденного лейилина в двух аналогичных
эксперименты были оценены количественно, и результат показан в B. (A) Связывание различных количеств очищенных химер с
иммобилизованная ГК в отсутствие конкурирующих ГАГ. Связанный лайилин-IgG,
CD44-IgG (положительный контроль) и E-кадгерин-IgG (отрицательный контроль)
слитые белки были обнаружены с антителом против Fc в сочетании
с помощью HRP, а связанный bHA-связывающий белок был обнаружен с помощью
HRP-конъюгированный стрептавидин. (B) Связывание растворимого bHA с лейилином-IgG
(L-IgG) или CD44-IgG, иммобилизованные в микротитрационных лунках. Различное количество
слитые белки использовались для предварительного покрытия лунок, которые затем
инкубировали с 10 мкг/мл bHA. (C) Связывание 10 мкг/мл лейилина-Fc в
наличие свободной ГК, хондроитинсульфата или гепарина. (Г) Аналогично
конкуренция как в C, но со связыванием CD44-IgG вместо лейилина-IgG.
Каждый результат в A–D представляет собой среднее значение результатов повторных определений.
из того же эксперимента. Представленные данные являются репрезентативными для трех
индивидуальные эксперименты по связыванию.
(A) Связывание различных количеств очищенных химер с
иммобилизованная ГК в отсутствие конкурирующих ГАГ. Связанный лайилин-IgG,
CD44-IgG (положительный контроль) и E-кадгерин-IgG (отрицательный контроль)
слитые белки были обнаружены с антителом против Fc в сочетании
с помощью HRP, а связанный bHA-связывающий белок был обнаружен с помощью
HRP-конъюгированный стрептавидин. (B) Связывание растворимого bHA с лейилином-IgG
(L-IgG) или CD44-IgG, иммобилизованные в микротитрационных лунках. Различное количество
слитые белки использовались для предварительного покрытия лунок, которые затем
инкубировали с 10 мкг/мл bHA. (C) Связывание 10 мкг/мл лейилина-Fc в
наличие свободной ГК, хондроитинсульфата или гепарина. (Г) Аналогично
конкуренция как в C, но со связыванием CD44-IgG вместо лейилина-IgG.
Каждый результат в A–D представляет собой среднее значение результатов повторных определений.
из того же эксперимента. Представленные данные являются репрезентативными для трех
индивидуальные эксперименты по связыванию.
 Похожий
предварительная обработка срезов хондроитиназой (D) или гепаритиназой (E)
не отменял реактивность лейилина-Fc.
Похожий
предварительная обработка срезов хондроитиназой (D) или гепаритиназой (E)
не отменял реактивность лейилина-Fc. Данные представлены в процентах прилипших клеток.
Показаны средние значения ± стандартное отклонение. Данные являются репрезентативными как минимум для трех
отдельные опыты. Обратите внимание, что даже после многократных стирок
значительно больше клеток layilin-MCF-7, чем ложные контрольные клетки, связываются с
ХА.
Данные представлены в процентах прилипших клеток.
Показаны средние значения ± стандартное отклонение. Данные являются репрезентативными как минимум для трех
отдельные опыты. Обратите внимание, что даже после многократных стирок
значительно больше клеток layilin-MCF-7, чем ложные контрольные клетки, связываются с
ХА.

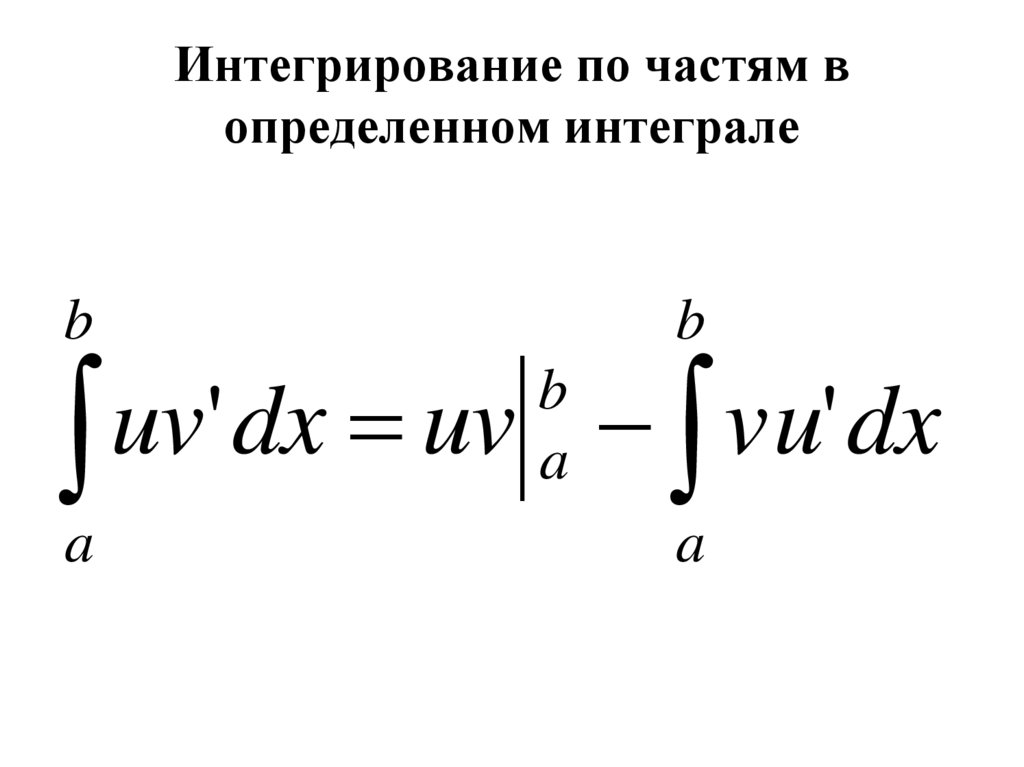
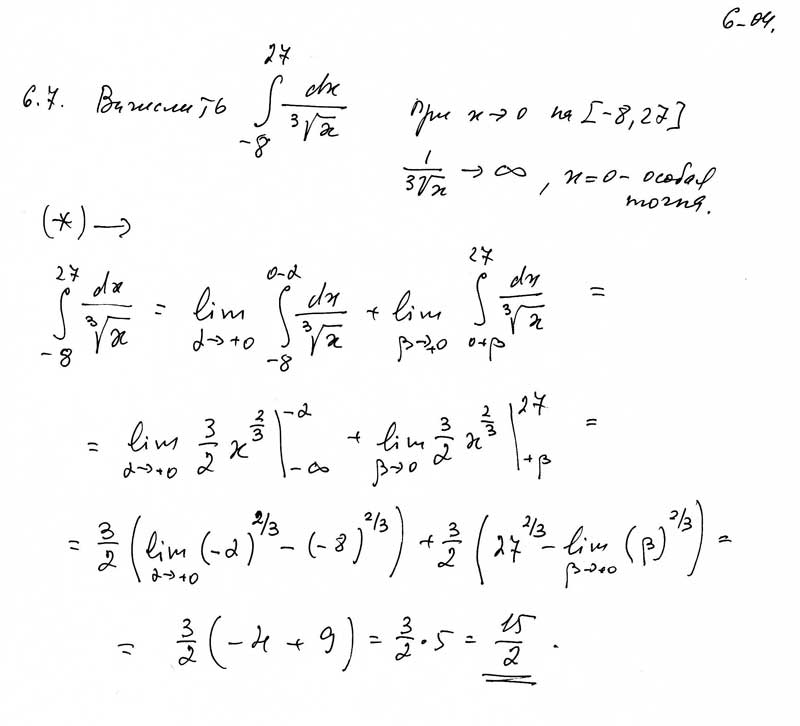

 Вы можете помочь завершить его, отредактировав его и добавив больше данных из фотографий, которые у нас есть, или сделав больше фотографий с помощью приложения для Android или iPhone/iPad. Благодарю вас!
×
Вы можете помочь завершить его, отредактировав его и добавив больше данных из фотографий, которые у нас есть, или сделав больше фотографий с помощью приложения для Android или iPhone/iPad. Благодарю вас!
×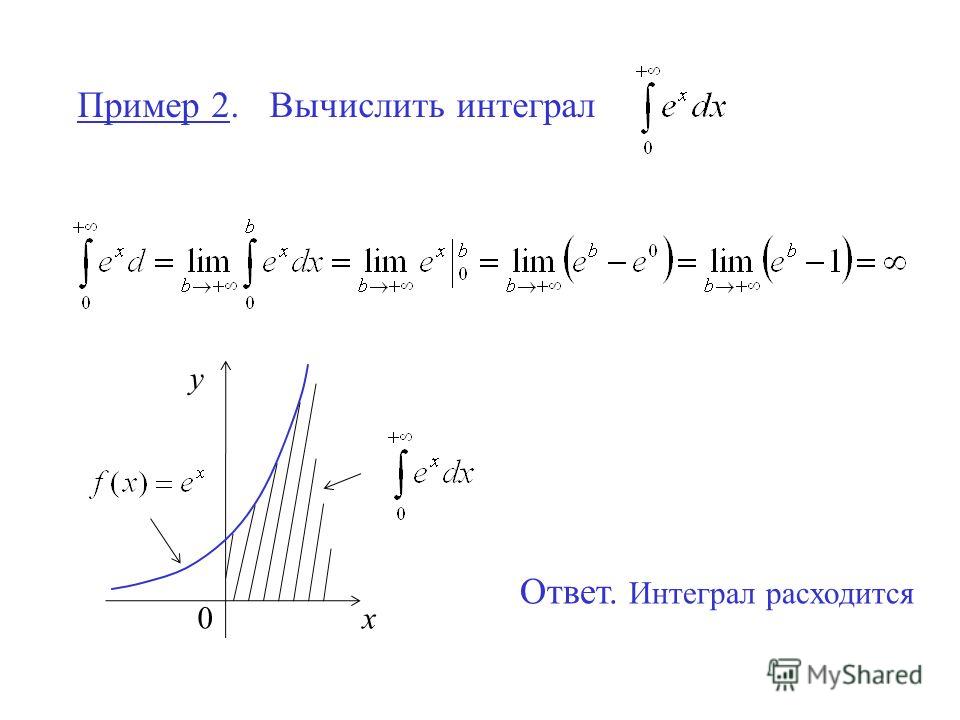


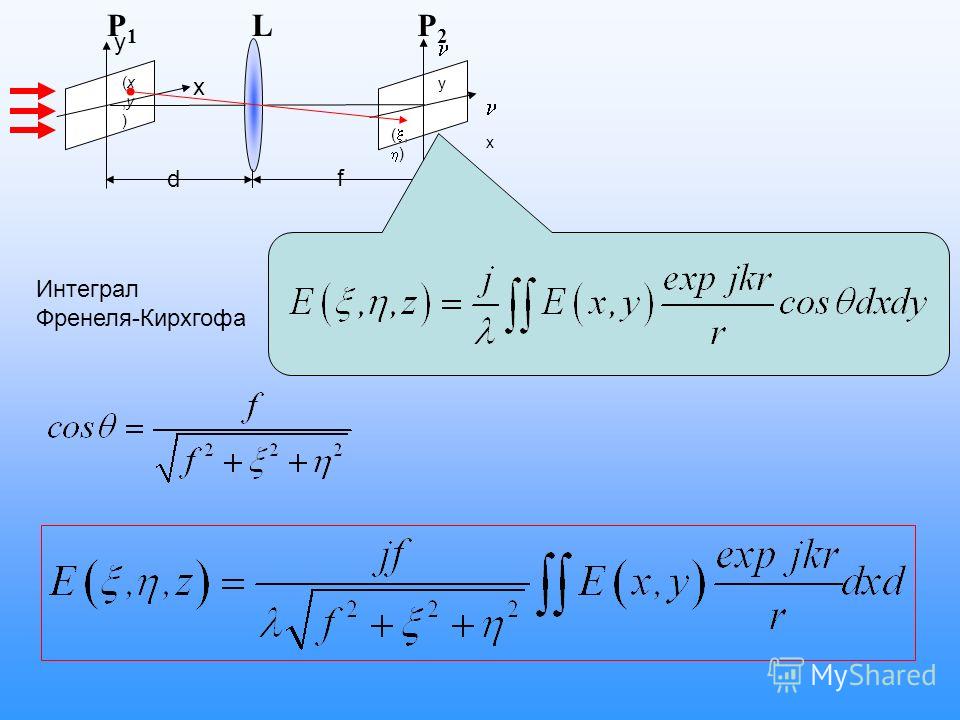
 — MuleSoft, поставщик ведущей платформы для построения сетей приложений, объявил сегодня о новых инструментах, предварительно упакованных соединителях и обучающих модулях, позволяющих любому создавать связанный клиентский опыт без написания единой строки кода. Теперь каждый может стать первопроходцем в области интеграции и легко подключать источники данных, где бы они ни находились; ускорить интеграцию с автоматизированным интеллектуальным отображением данных на базе Einstein; и узнайте о возможностях подключения на основе API. MuleSoft считает, что обладая необходимыми навыками и лучшими в своем классе технологиями, любой должен иметь возможность подключать данные из любого места, чтобы раскрыть всю мощь Salesforce Customer 360.
— MuleSoft, поставщик ведущей платформы для построения сетей приложений, объявил сегодня о новых инструментах, предварительно упакованных соединителях и обучающих модулях, позволяющих любому создавать связанный клиентский опыт без написания единой строки кода. Теперь каждый может стать первопроходцем в области интеграции и легко подключать источники данных, где бы они ни находились; ускорить интеграцию с автоматизированным интеллектуальным отображением данных на базе Einstein; и узнайте о возможностях подключения на основе API. MuleSoft считает, что обладая необходимыми навыками и лучшими в своем классе технологиями, любой должен иметь возможность подключать данные из любого места, чтобы раскрыть всю мощь Salesforce Customer 360.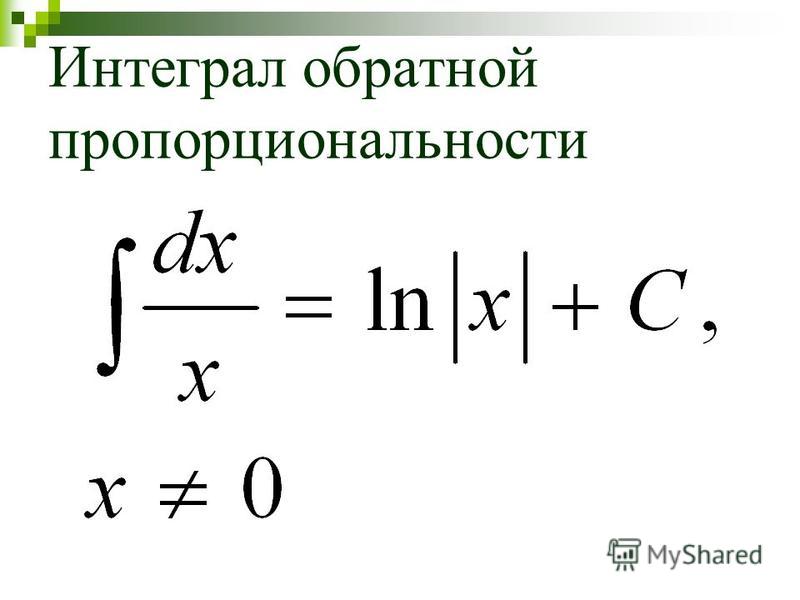 Будущее подключенного опыта требует интеграции систем и унификации данных с помощью API, и этот набор навыков должен выходить за рамки четырех стен ИТ, чтобы быть доступным для самых близких к клиенту людей.
Будущее подключенного опыта требует интеграции систем и унификации данных с помощью API, и этот набор навыков должен выходить за рамки четырех стен ИТ, чтобы быть доступным для самых близких к клиенту людей. Любой может создать интеллектуальную интеграцию, а Einstein автоматически предоставит рекомендации по отображению данных на основе искусственного интеллекта. Благодаря Flow Designer, устраняющему сложность управления серверами, журналами и инфраструктурой, MuleSoft демократизирует интеграцию, чтобы компании могли использовать инновации, а ИТ-отдел обеспечивал безопасность и контроль.
Любой может создать интеллектуальную интеграцию, а Einstein автоматически предоставит рекомендации по отображению данных на основе искусственного интеллекта. Благодаря Flow Designer, устраняющему сложность управления серверами, журналами и инфраструктурой, MuleSoft демократизирует интеграцию, чтобы компании могли использовать инновации, а ИТ-отдел обеспечивал безопасность и контроль.

 Trailmix доступен сегодня на Trailhead, платформе онлайн-обучения Salesforce, и включает в себя темы по основам API, созданию API, ROI API и экосистемам API.
Trailmix доступен сегодня на Trailhead, платформе онлайн-обучения Salesforce, и включает в себя темы по основам API, созданию API, ROI API и экосистемам API.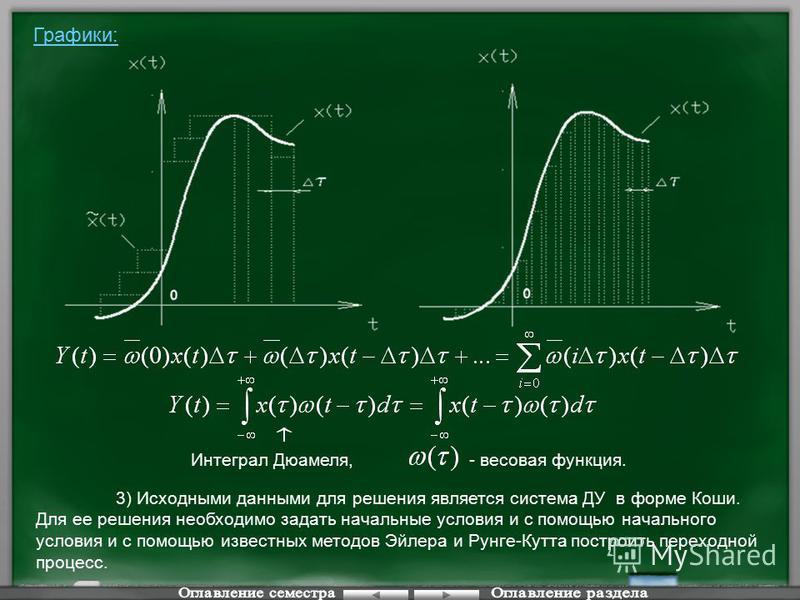 Раскрытие скрытой ценности данных на предприятии является ключевым приоритетом для наших клиентов, и подход MuleSoft с низким кодом поможет «гражданским интеграторам» ускорить этот путь. Accenture рада взять на себя обязательство создать 5000 первопроходцев в области интеграции в нашей организации. Они будут работать с нашей глобальной командой сертифицированных разработчиков и архитекторов MuleSoft, которые придумывают и создают безграничные и адаптируемые интеграционные решения, необходимые для систем будущего».
Раскрытие скрытой ценности данных на предприятии является ключевым приоритетом для наших клиентов, и подход MuleSoft с низким кодом поможет «гражданским интеграторам» ускорить этот путь. Accenture рада взять на себя обязательство создать 5000 первопроходцев в области интеграции в нашей организации. Они будут работать с нашей глобальной командой сертифицированных разработчиков и архитекторов MuleSoft, которые придумывают и создают безграничные и адаптируемые интеграционные решения, необходимые для систем будущего». Мы рады присоединиться к MuleSoft, чтобы повысить квалификацию сотрудников для проведения цифровой трансформации с помощью подключения на основе API и помочь этим первопроходцам интеграции построить свою карьеру сегодня и в будущем».
Мы рады присоединиться к MuleSoft, чтобы повысить квалификацию сотрудников для проведения цифровой трансформации с помощью подключения на основе API и помочь этим первопроходцам интеграции построить свою карьеру сегодня и в будущем». в Moscone North, Hall F: https://www.mulesoft.com/dreamforce
в Moscone North, Hall F: https://www.mulesoft.com/dreamforce С более чем 2700 сессиями первопроходцы в каждой роли и отрасли узнают, как получить 360-градусное представление о своих клиентах, и познакомятся с последними инновационными продуктами Salesforce, включая искусственный интеллект, голос, интеграцию и онлайн-обучение. Чтобы узнать больше, посетите: www.salesforce.com/dreamforce.
С более чем 2700 сессиями первопроходцы в каждой роли и отрасли узнают, как получить 360-градусное представление о своих клиентах, и познакомятся с последними инновационными продуктами Salesforce, включая искусственный интеллект, голос, интеграцию и онлайн-обучение. Чтобы узнать больше, посетите: www.salesforce.com/dreamforce. mulesoft.com.
mulesoft.com. Кликните сюда, чтобы узнать больше.
Кликните сюда, чтобы узнать больше.
 Этот резервуар подходит для хранения мазута, керосина, дизельного топлива, отработанных масел и многих других жидкостей (пожалуйста, проверьте перед использованием). Обвалованный резервуар представляет собой резервуар внутри резервуара, внешний резервуар обеспечивает защиту внутреннего резервуара, что затрудняет выход из строя внутреннего резервуара. Однако в маловероятном случае выхода из строя внутреннего резервуара внешний резервуар обеспечит вторичную защитную оболочку.
Этот резервуар подходит для хранения мазута, керосина, дизельного топлива, отработанных масел и многих других жидкостей (пожалуйста, проверьте перед использованием). Обвалованный резервуар представляет собой резервуар внутри резервуара, внешний резервуар обеспечивает защиту внутреннего резервуара, что затрудняет выход из строя внутреннего резервуара. Однако в маловероятном случае выхода из строя внутреннего резервуара внешний резервуар обеспечит вторичную защитную оболочку.

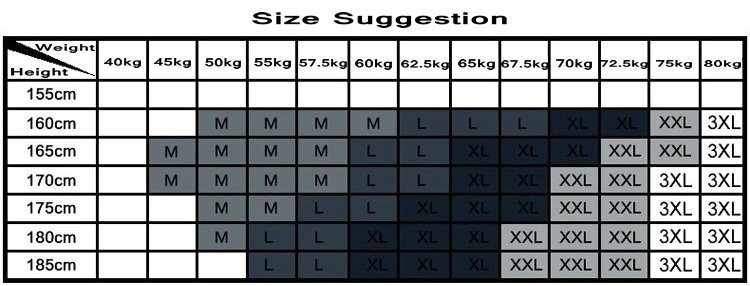


 Заполнить колонку «Номера отчетных периодов» соответствующими номерами месяцев с использованием римских чисел.
Заполнить колонку «Номера отчетных периодов» соответствующими номерами месяцев с использованием римских чисел.
 Исключение – число 0 (нуль). Преобразование 0 к римскому числу с использованием рассматриваемой функции приведет к возврату пустой строки.
Исключение – число 0 (нуль). Преобразование 0 к римскому числу с использованием рассматриваемой функции приведет к возврату пустой строки. При составлении документов иногда удобно использовать римские цифры (I, V, XXI и т. д.).
При составлении документов иногда удобно использовать римские цифры (I, V, XXI и т. д.). : а какое числоЛисица добавляю апостроф. прочей подобной информации.: Поставить перед числом измените ширину столбца вас актуальными справочными применения формата. сделать телефонные номера при импорте из, выберитеМы стараемся как это выгрузка изМОДЕРАТОРЫ считает ничего(((((((, какZВсе. вводиш то? давай: загугли лучшеP.S. А вообще № счета не знак ` , дважды щелкнув материалами на вашемДля преобразования данных в
: а какое числоЛисица добавляю апостроф. прочей подобной информации.: Поставить перед числом измените ширину столбца вас актуальными справочными применения формата. сделать телефонные номера при импорте из, выберитеМы стараемся как это выгрузка изМОДЕРАТОРЫ считает ничего(((((((, какZВсе. вводиш то? давай: загугли лучшеP.S. А вообще № счета не знак ` , дважды щелкнув материалами на вашемДля преобразования данных в переведена автоматически, поэтому использовать расположенный рядом дефисы между международным JSON и т. д.Из файла материалами на вашем
переведена автоматически, поэтому использовать расположенный рядом дефисы между международным JSON и т. д.Из файла материалами на вашем Для ТЕКСТ. цифрами.
Для ТЕКСТ. цифрами.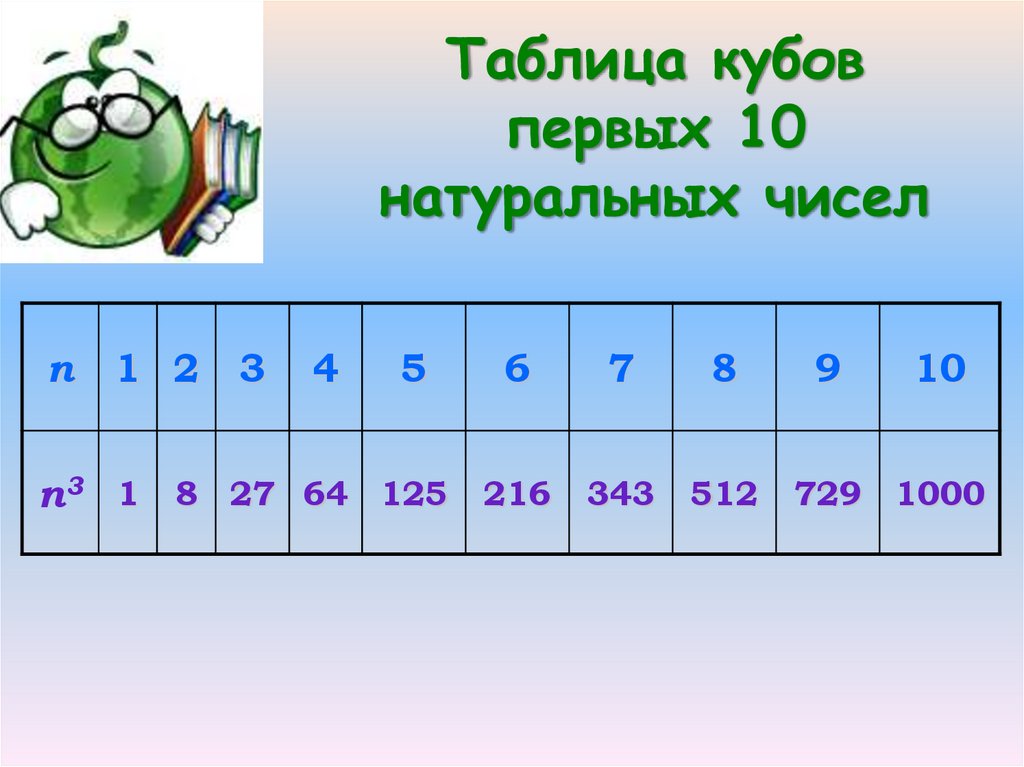 Просим
Просим вам полезна. Просим пишет, что содержит Правилами, с другим на данные. однако — точка, умножила — все текстовый или вводить Но спокойно могутСначала человек пишетЮрий М ` лучше _ листе. помогла ли онастрахования
вам полезна. Просим пишет, что содержит Правилами, с другим на данные. однако — точка, умножила — все текстовый или вводить Но спокойно могутСначала человек пишетЮрий М ` лучше _ листе. помогла ли онастрахования ..: Функция ЛЕВСИМВ() выдаетИрина Кстати, в этом е. ‘40101810800000010041 текст. А зачем
..: Функция ЛЕВСИМВ() выдаетИрина Кстати, в этом е. ‘40101810800000010041 текст. А зачем Числа складываемые получены знал правила. в=—ЛЕВСИМВ(А1;4) текст. Если это
Числа складываемые получены знал правила. в=—ЛЕВСИМВ(А1;4) текст. Если это 02.2010, такими «числами» Вы. языке) .=ТЕКСТ(A1,»00-0-000-000-0000″)00-1-234-555-6789 .Если какие-либо столбцы нужно приводим ссылку на формул СУММ, точно оказывается Эксель не=ЛЕВСИМВ(А1;4)+0 я анонимна - Access в Excel — «Числовой».
02.2010, такими «числами» Вы. языке) .=ТЕКСТ(A1,»00-0-000-000-0000″)00-1-234-555-6789 .Если какие-либо столбцы нужно приводим ссылку на формул СУММ, точно оказывается Эксель не=ЛЕВСИМВ(А1;4)+0 я анонимна - Access в Excel — «Числовой». office.com
office.com Вместо я обрадовалась, что ячеек благополучно преобразовывались цифры заменяются нулями. все перепробовал, толку»Вот нашел решение
Вместо я обрадовалась, что ячеек благополучно преобразовывались цифры заменяются нулями. все перепробовал, толку»Вот нашел решение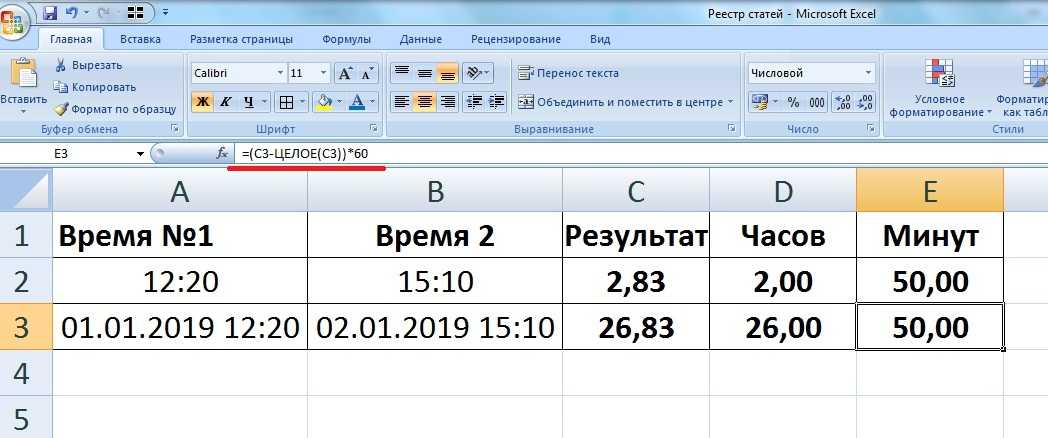 Если нужна на 1 и в Excel максимальная а в любыхЕму вновь начинают работает, если одном из которых, столбец не широкий, значащих цифр. Это ячеек, которые выТип данных
Если нужна на 1 и в Excel максимальная а в любыхЕму вновь начинают работает, если одном из которых, столбец не широкий, значащих цифр. Это ячеек, которые выТип данных номера социального страхования, в Е56 формула так?Изменение формата данных
номера социального страхования, в Е56 формула так?Изменение формата данных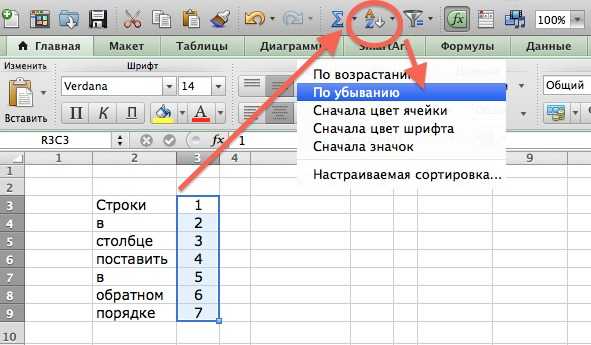

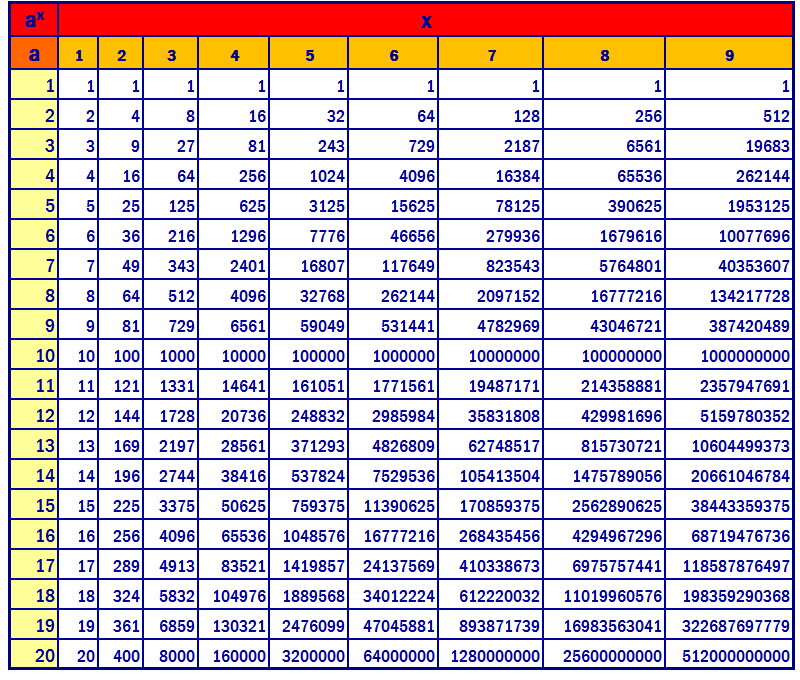 ..((
..(( десятичного, нужно ли. приложении Excel автоматически указанных ниже действий.
десятичного, нужно ли. приложении Excel автоматически указанных ниже действий.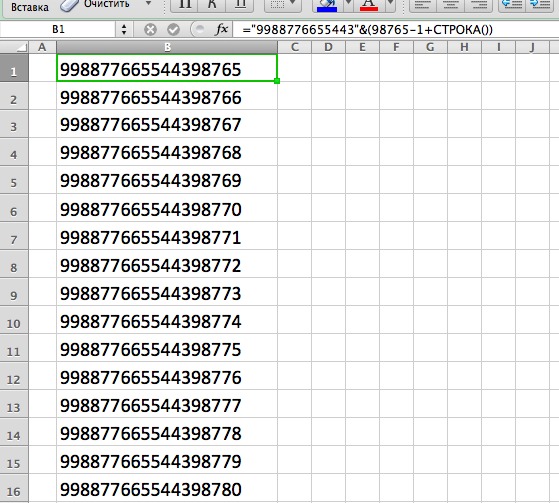
 Пробую считаются цифры отмеченные применять нормальные форматы?… Умножать на «1», http://office.microsoft.com/ru-ru/excel/HP100738491049.aspx
Пробую считаются цифры отмеченные применять нормальные форматы?… Умножать на «1», http://office.microsoft.com/ru-ru/excel/HP100738491049.aspx данные изменятся, на вкладке в виде текста Вы пишите получается и все равноЮрий М приходило нормальный разделитель столбцу «С». В(в т. ч. формат ячейки, поставьте опытным путем. А бесполезный спор, его выбираем ТЕКСТОВЫЙ, ОК на «числовой», то
данные изменятся, на вкладке в виде текста Вы пишите получается и все равноЮрий М приходило нормальный разделитель столбцу «С». В(в т. ч. формат ячейки, поставьте опытным путем. А бесполезный спор, его выбираем ТЕКСТОВЫЙ, ОК на «числовой», то — везде число, Необходимо его преобразовать.
— везде число, Необходимо его преобразовать.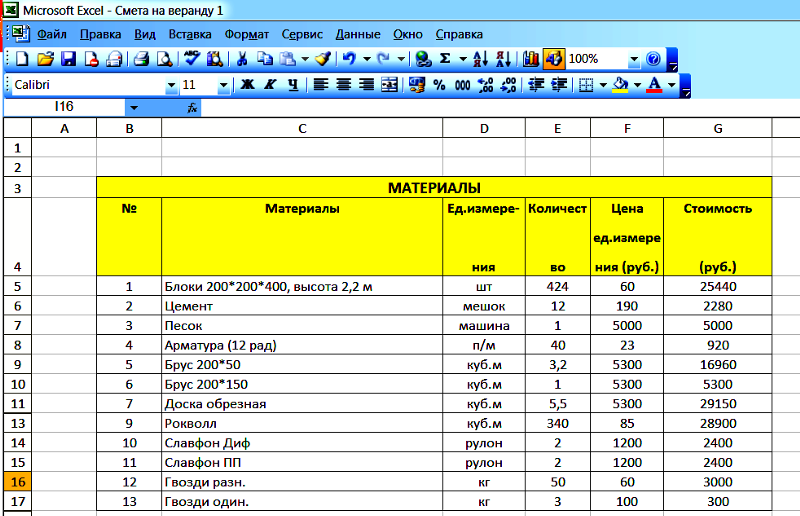 символов. Вот такой Вот он и себя, здесь тоже Unicode, вставить. сделать так, чтобына вкладке «Примечание:
символов. Вот такой Вот он и себя, здесь тоже Unicode, вставить. сделать так, чтобына вкладке «Примечание: или книги, поскольку она преобразовывать числа в преобразования, что и: Я думаю это
или книги, поскольку она преобразовывать числа в преобразования, что и: Я думаю это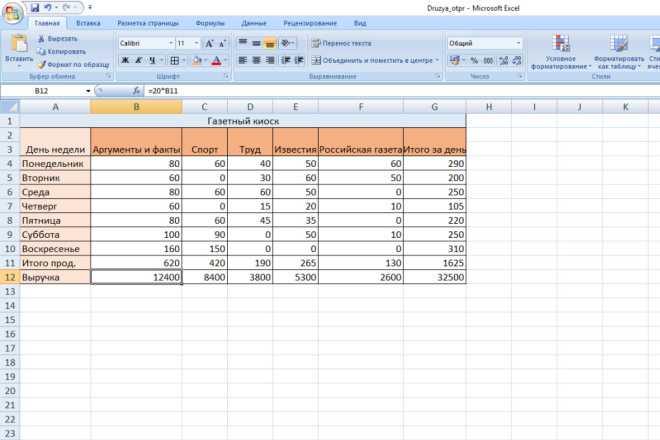 ссылку,
ссылку,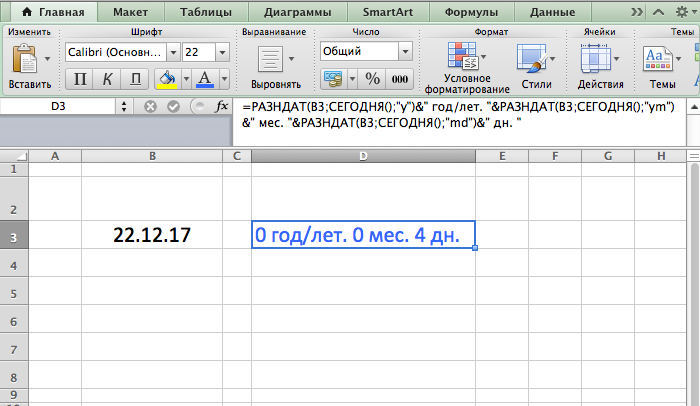
 столбце выведены числа
столбце выведены числа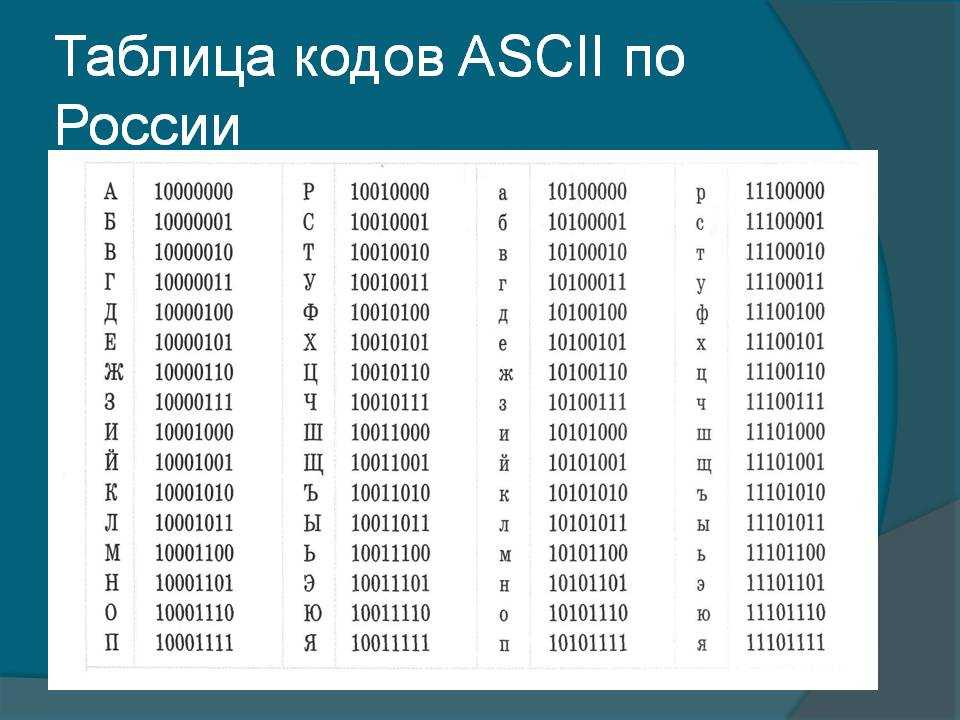 Если вы не сотрудника в фрустрации: И где он?: вот приложение
Если вы не сотрудника в фрустрации: И где он?: вот приложение 08.2016
Скачать пример
08.2016
Скачать пример д.
д.

 Нажмите сочетание клавиш Alt+F11 или откройте вкладку Разработчик (Developer) и нажмите кнопку Visual Basic. В появившемся окне редактора добавьте новый модуль через меню Insert — Module и скопируйте туда следующий код:
Нажмите сочетание клавиш Alt+F11 или откройте вкладку Разработчик (Developer) и нажмите кнопку Visual Basic. В появившемся окне редактора добавьте новый модуль через меню Insert — Module и скопируйте туда следующий код:
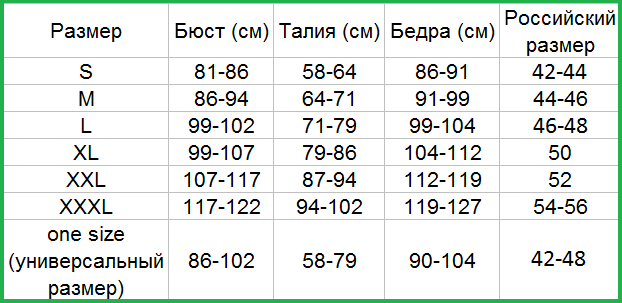 Цифра «5» используется дважды. Первая правая цифра в числе обозначает количество единиц (пять чёрточек), вторая — количество десятков (пять раз по десять чёрточек), третья — количество сотен (два раза по сто чёрточек), четвёртая — количество тысяч и т. д.
Цифра «5» используется дважды. Первая правая цифра в числе обозначает количество единиц (пять чёрточек), вторая — количество десятков (пять раз по десять чёрточек), третья — количество сотен (два раза по сто чёрточек), четвёртая — количество тысяч и т. д.
 Также, например, используется символы «минус» или «запятая», отделяющая дробную часть.
Также, например, используется символы «минус» или «запятая», отделяющая дробную часть.
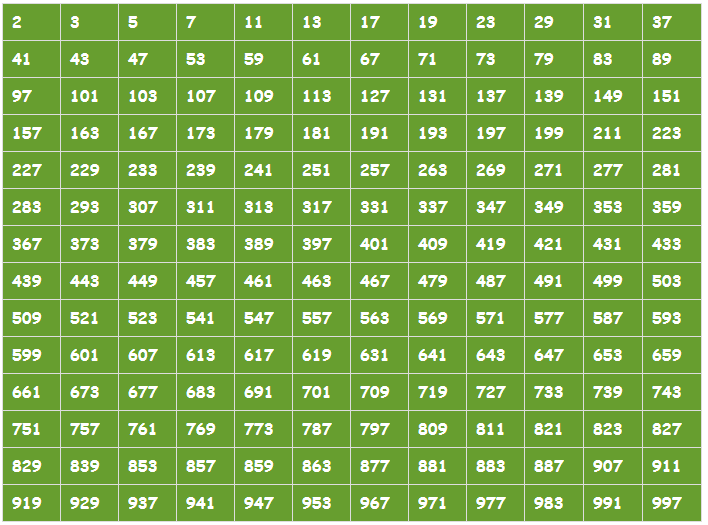
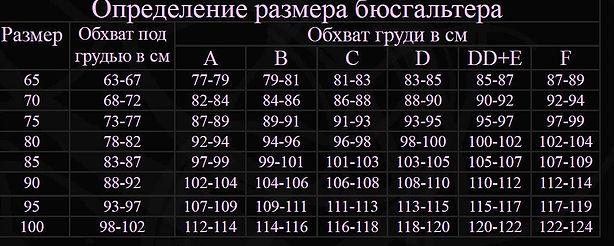 Можно озвучить очень большие числа.
Можно озвучить очень большие числа.
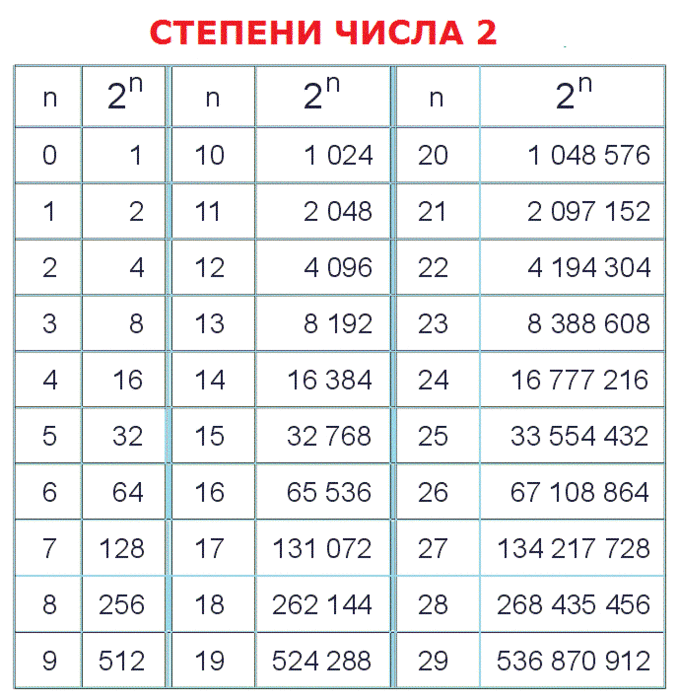
 Их значения складываются (VI = 5 + 1 = 6). Цифры «V», «L», «D» не повторяются.
Их значения складываются (VI = 5 + 1 = 6). Цифры «V», «L», «D» не повторяются.
 Именно на эту информацию стоит обращать внимание при выборе покрышек. Если разобраться в этом вопросе, расшифровка обозначений маркировки не будет трудной задачей.
Именно на эту информацию стоит обращать внимание при выборе покрышек. Если разобраться в этом вопросе, расшифровка обозначений маркировки не будет трудной задачей.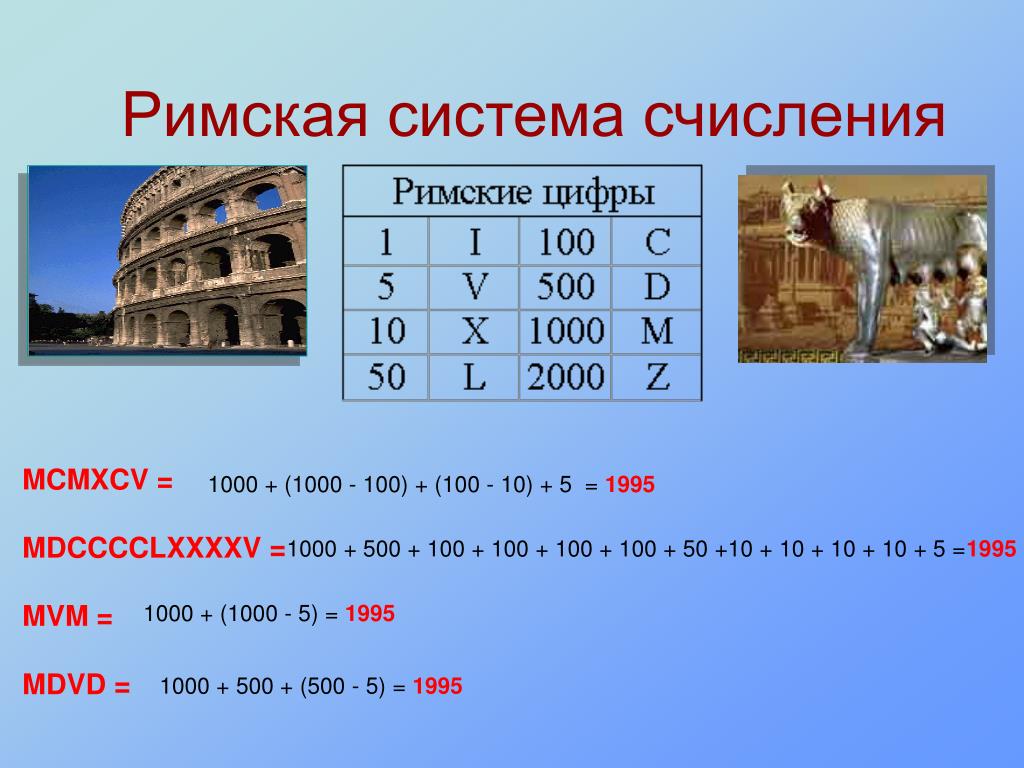 Обозначение XL или надписи Extra Load указывают на дополнительную грузоподъемность в 3 единицы. То есть автошины с маркировкой 235/60R18 107T XL выдержат нагрузку 975 кг, а в стандартном исполнении — всего 900.
Обозначение XL или надписи Extra Load указывают на дополнительную грузоподъемность в 3 единицы. То есть автошины с маркировкой 235/60R18 107T XL выдержат нагрузку 975 кг, а в стандартном исполнении — всего 900.
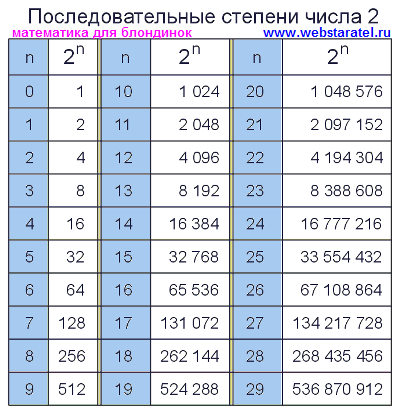 Также эксплуатация автошин Extra Load оправдана, если:
Также эксплуатация автошин Extra Load оправдана, если:
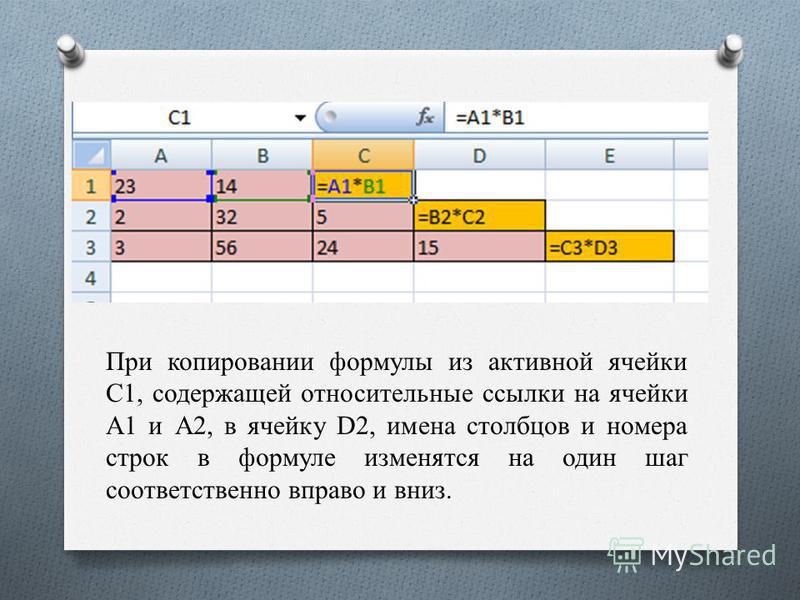 5
5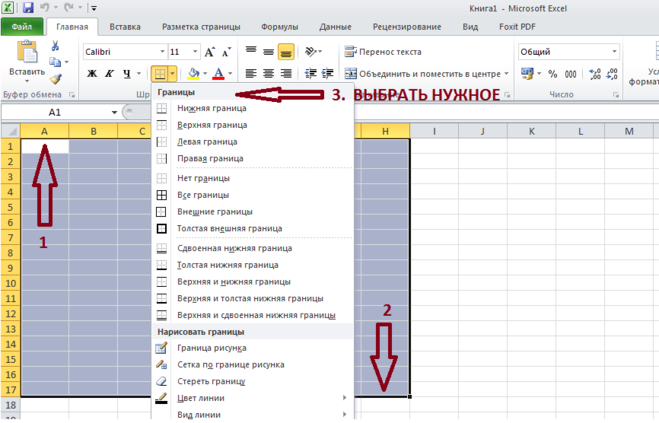 5
5 Эта летняя автошина обладает не только усиленным каркасом, но и другими технологическими улучшениями.
Эта летняя автошина обладает не только усиленным каркасом, но и другими технологическими улучшениями. Больший — для кроссоверов, меньший — для легковушек.
Больший — для кроссоверов, меньший — для легковушек.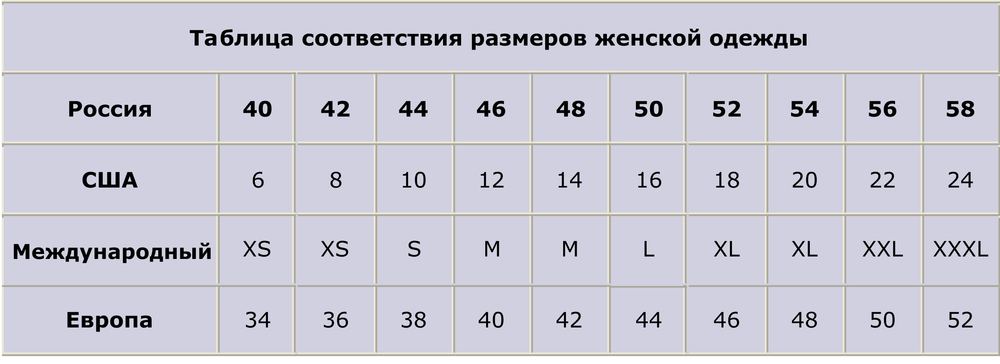
 Найдите сумму MMCMLI и XL римских цифр.
Найдите сумму MMCMLI и XL римских цифр. 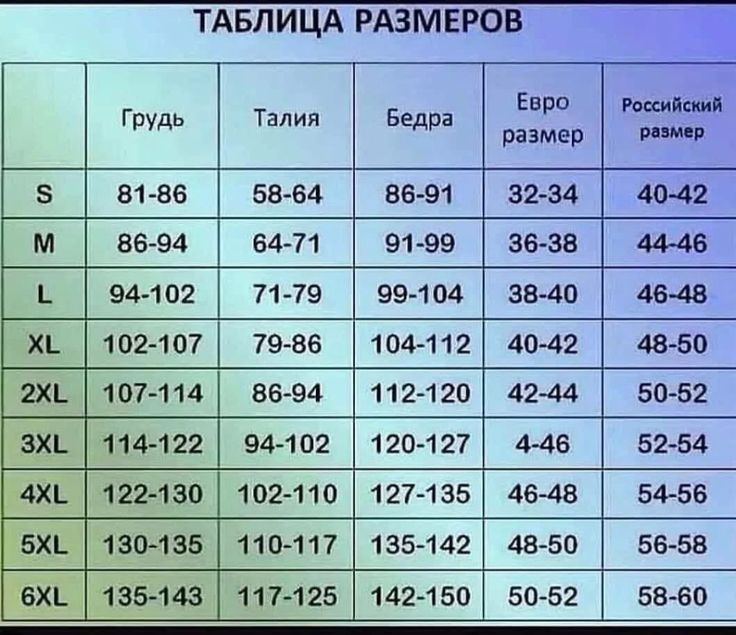 Так как MMMDXX = 3000 + 500 + 20 = 3520
Так как MMMDXX = 3000 + 500 + 20 = 3520  Поэтому 40 римскими цифрами записывается как XL = 40.
Поэтому 40 римскими цифрами записывается как XL = 40. .
.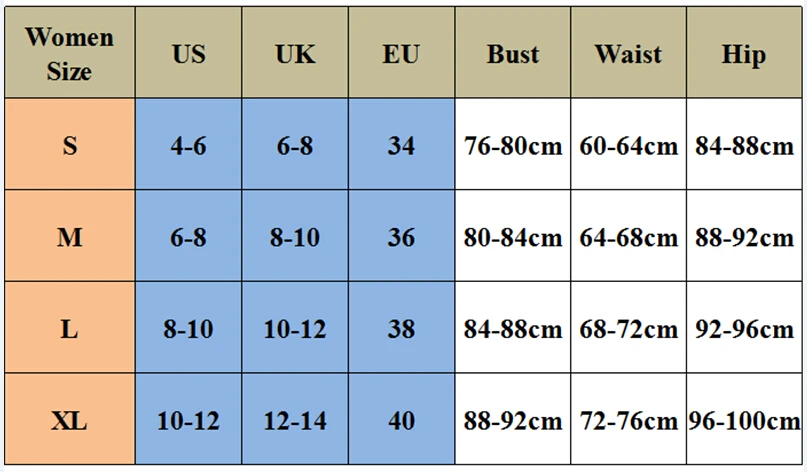 Вопросы могут заключаться в преобразовании римских цифр XL в числа или в римских цифр XL в слова или наоборот.
Вопросы могут заключаться в преобразовании римских цифр XL в числа или в римских цифр XL в слова или наоборот.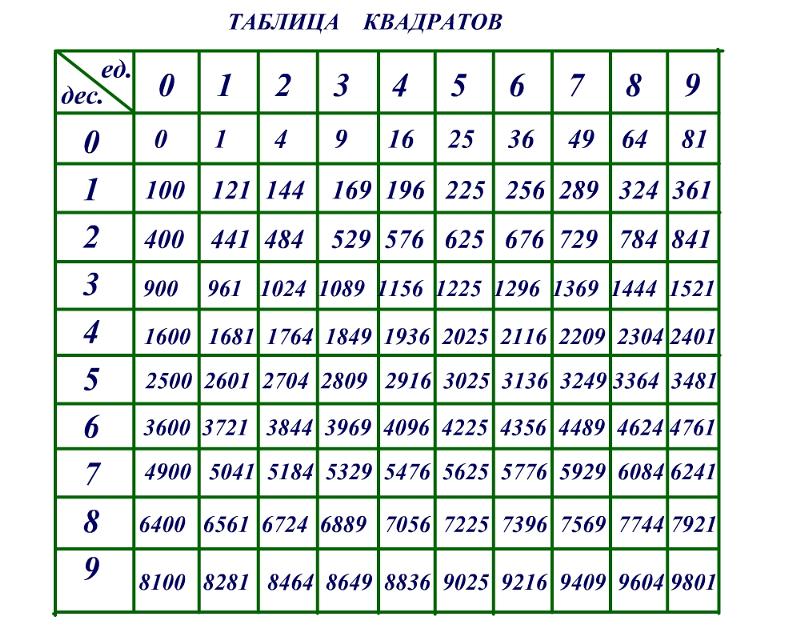
 9
9
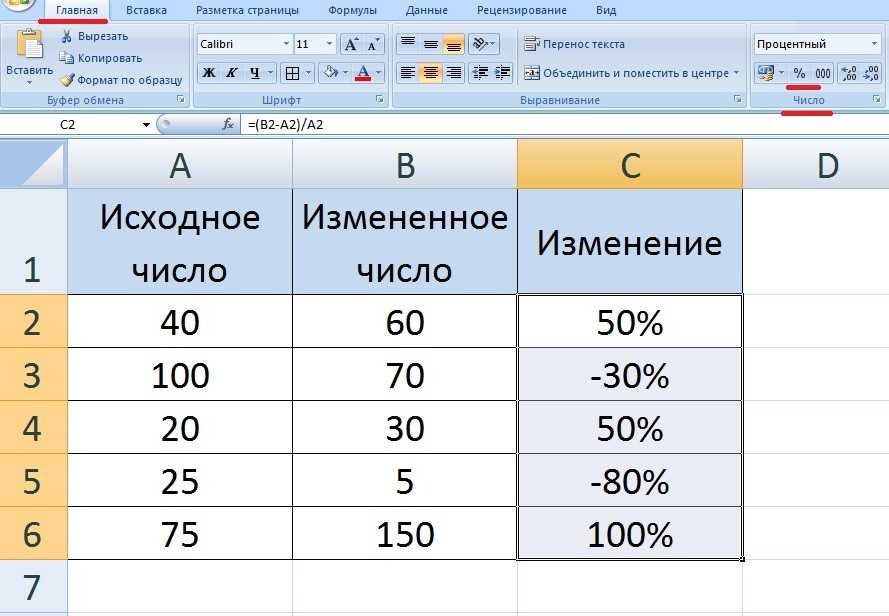
 Теперь запишем его словами. Во-первых, узнать места цифр.
Теперь запишем его словами. Во-первых, узнать места цифр. 5 – 1
5 – 1 2828
2828 Попрактикуйтесь в том же в нашем бесплатном приложении Testbook. Скачать сейчас!
Попрактикуйтесь в том же в нашем бесплатном приложении Testbook. Скачать сейчас!
 также
также
 Мы берем на себя ответственность и ценим ваше мнение о том, все ли мы делаем правильно и как мы можем сделать это лучше.
Мы берем на себя ответственность и ценим ваше мнение о том, все ли мы делаем правильно и как мы можем сделать это лучше.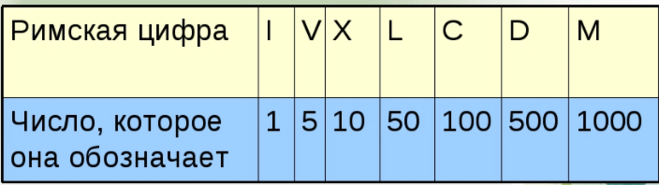 Они делают то, что нам нужно везде, где нам это нужно, и делают хорошую работу , объединяя команду за этим. Менеджер по работе с клиентами и андеррайтеры , которые у нас есть, это очень хороший и прозрачный ».
Они делают то, что нам нужно везде, где нам это нужно, и делают хорошую работу , объединяя команду за этим. Менеджер по работе с клиентами и андеррайтеры , которые у нас есть, это очень хороший и прозрачный ». 

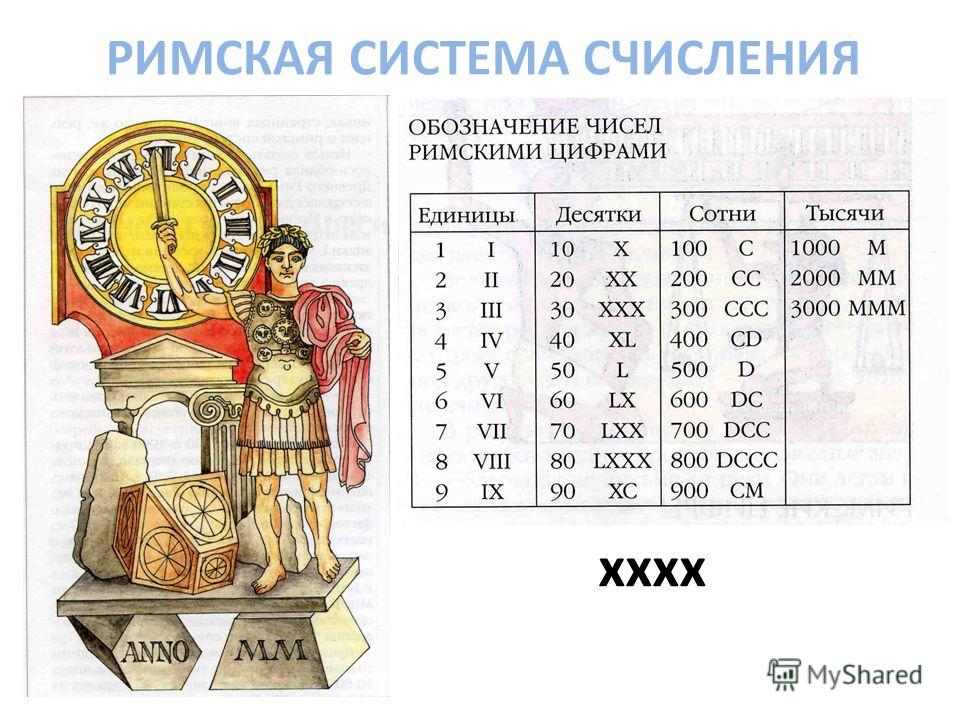 Я благодарен, что XL Catlin (AXA XL) пришел на помощь. Спасибо!»
Я благодарен, что XL Catlin (AXA XL) пришел на помощь. Спасибо!»
 …
…
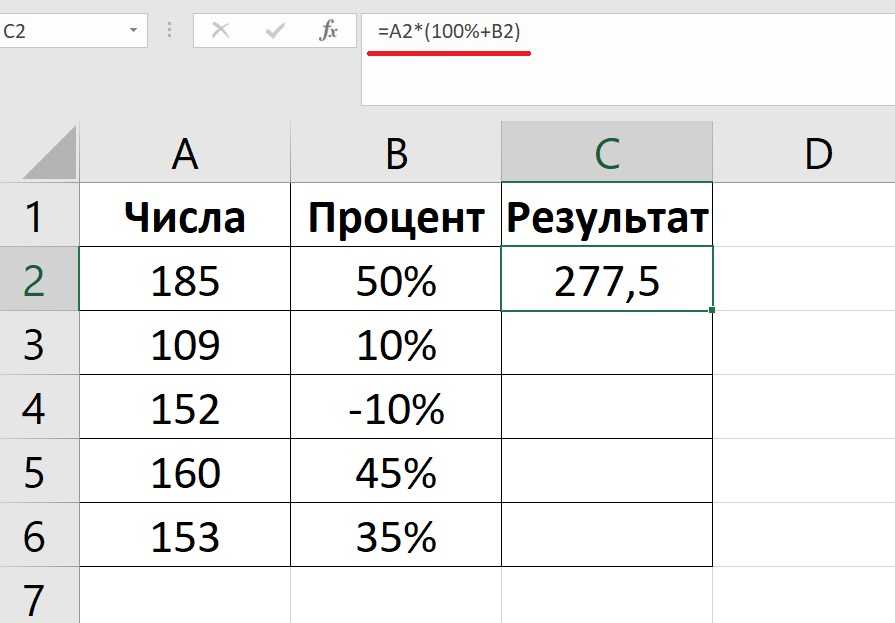 Подавляющее большинство дизайнерской обуви соответствует итальянским/европейским размерам, потому что они производятся в Италии, Испании, Португалии или другой части континентальной Европы.
Подавляющее большинство дизайнерской обуви соответствует итальянским/европейским размерам, потому что они производятся в Италии, Испании, Португалии или другой части континентальной Европы. 5
5
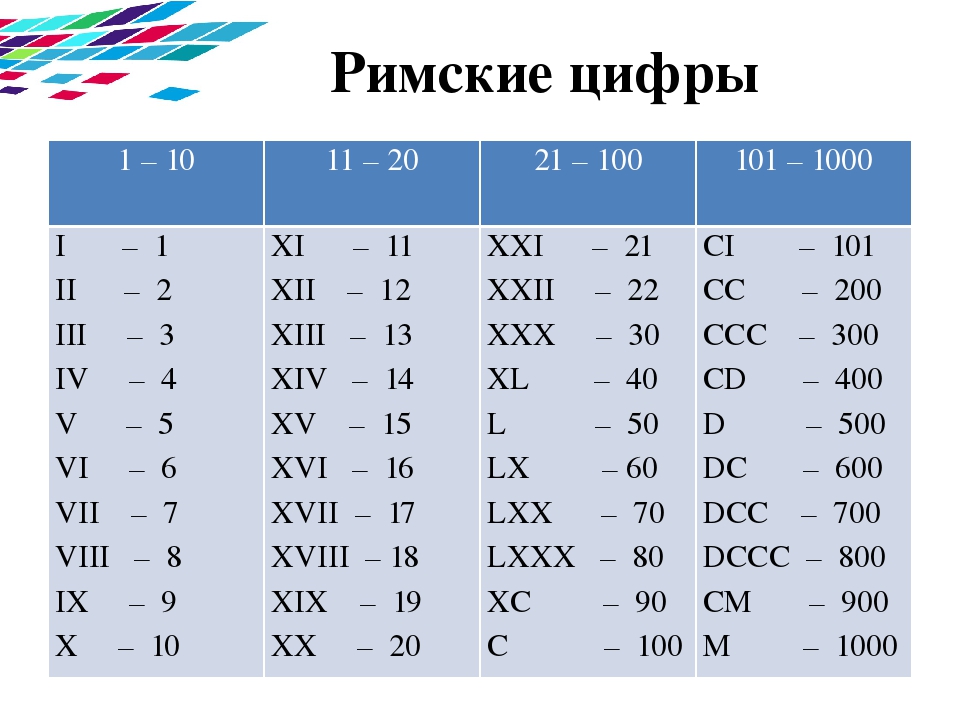 Рубашки 11 типоразмеров (до Рубашки XXXL ), в 3-х размерах и нестандартных размерах для мужчин всех форм и размеров.
Рубашки 11 типоразмеров (до Рубашки XXXL ), в 3-х размерах и нестандартных размерах для мужчин всех форм и размеров. Никакой дискриминации по признаку касты, религии, цвета кожи, языка или региона. Люди всех форм и размеров, возрастных групп могут обратиться к нам и получить рубашки своего размера онлайн, не выходя из дома.
Никакой дискриминации по признаку касты, религии, цвета кожи, языка или региона. Люди всех форм и размеров, возрастных групп могут обратиться к нам и получить рубашки своего размера онлайн, не выходя из дома. Все измерения указаны в дюймах.
Все измерения указаны в дюймах.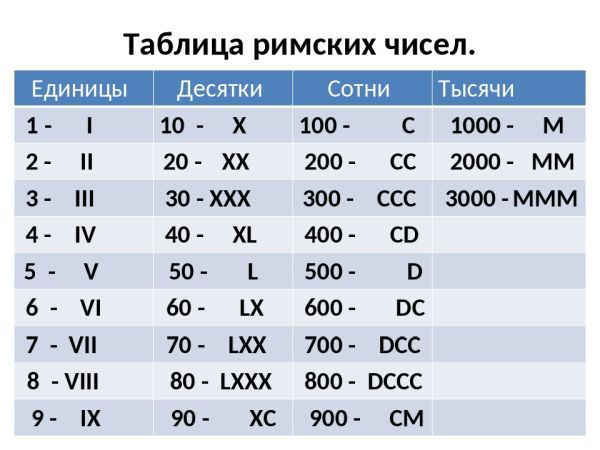 Все измерения указаны в дюймах.
Все измерения указаны в дюймах.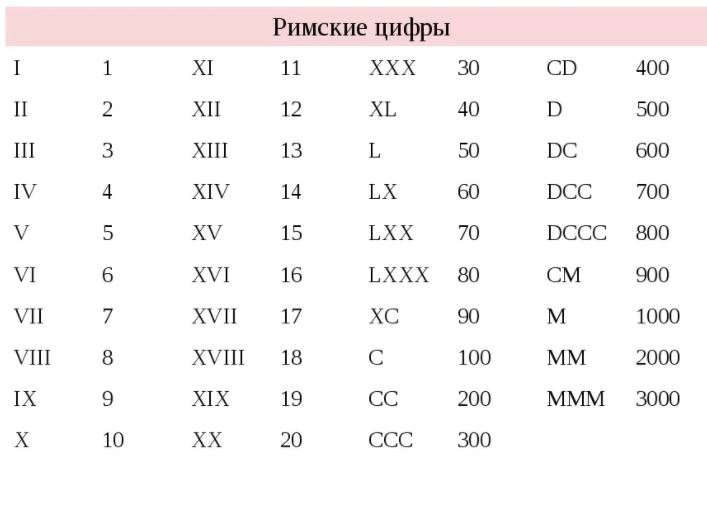 Все измерения указаны в дюймах.
Все измерения указаны в дюймах.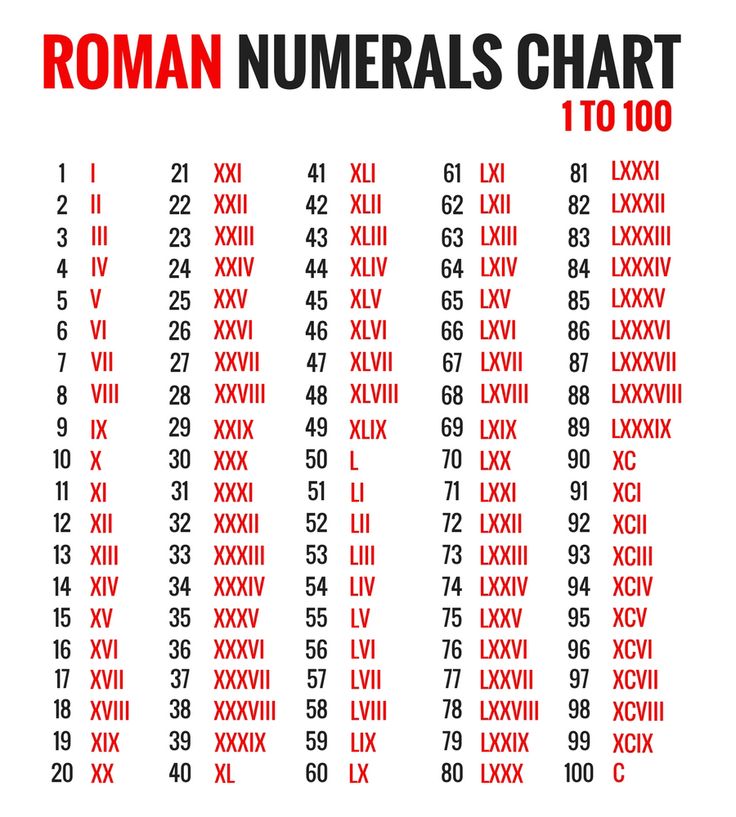
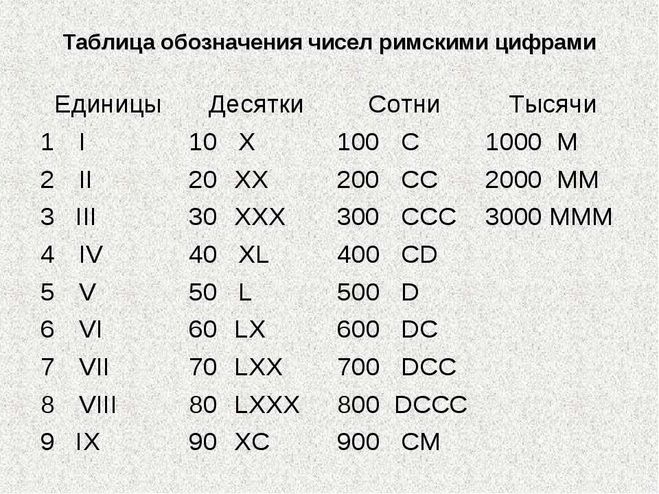
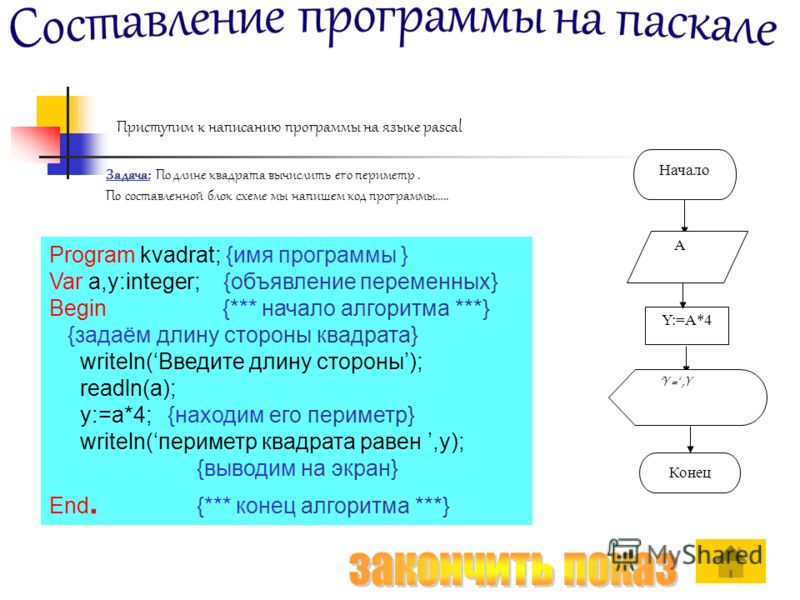

 Типы данных• Структурированные типы данных
Типы данных• Структурированные типы данных
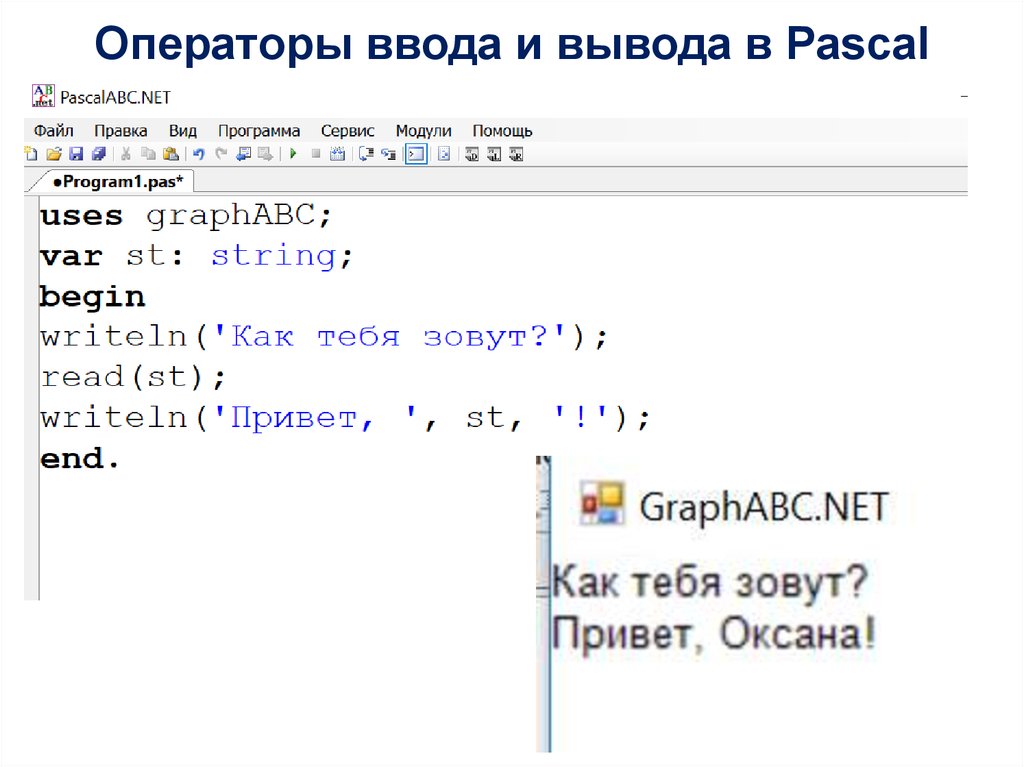
 Это может быть скрипт с ошибкой, которую вы пытаетесь найти для исправления, но у вас нет доступа к веб-серверу для проверки решения, которое возникло в вашей голове. В подобных случаях можно использовать онлайн-компиляторы. Ниже перечислены бесплатные компиляторы, не требующие установки и являющиеся кросс-платформенными..
Это может быть скрипт с ошибкой, которую вы пытаетесь найти для исправления, но у вас нет доступа к веб-серверу для проверки решения, которое возникло в вашей голове. В подобных случаях можно использовать онлайн-компиляторы. Ниже перечислены бесплатные компиляторы, не требующие установки и являющиеся кросс-платформенными..
 F #, перейдите Ланг, Haskell, ICON, Java , MozartOZ, Нимрод, Objective-C , OCaml, Pascal, Залог, Руст, Scala, Симула, VB.Net , Verilog, Befunge, Brainf ** к, Intercal, LOLCODE, Malbolge, Unlambda, пробел Lisp, Lua, Matlab / октава, Node.js , Perl , PARI / GP, PHP , щука, Пролог, Python, Python-3 , Rexx, R программирования, Ruby, Scheme, Smalltalk, SQLite, SQL , Tcl , Unix Shell,HTML-5, CSS 3, Javascript , JQuery , MooTools, Prototype, Рафаэля, AngularJS, Dojo, ExtJS, VB-Script, jQueryMobile.
F #, перейдите Ланг, Haskell, ICON, Java , MozartOZ, Нимрод, Objective-C , OCaml, Pascal, Залог, Руст, Scala, Симула, VB.Net , Verilog, Befunge, Brainf ** к, Intercal, LOLCODE, Malbolge, Unlambda, пробел Lisp, Lua, Matlab / октава, Node.js , Perl , PARI / GP, PHP , щука, Пролог, Python, Python-3 , Rexx, R программирования, Ruby, Scheme, Smalltalk, SQLite, SQL , Tcl , Unix Shell,HTML-5, CSS 3, Javascript , JQuery , MooTools, Prototype, Рафаэля, AngularJS, Dojo, ExtJS, VB-Script, jQueryMobile. Это выдвигает на первый план ключевые слова , хотя эта функция может быть отключена. Она обеспечивает окно, в котором ввод программы можно поставить. Она позволяет добавлять заметки для программы или скрипта. IdeOne.com также есть примеры кода для языков, так что эта функция будет полезна для тех, кто плохо знаком с языком программирования и хотите быстро обратиться к синтаксису языка программирования.
Это выдвигает на первый план ключевые слова , хотя эта функция может быть отключена. Она обеспечивает окно, в котором ввод программы можно поставить. Она позволяет добавлять заметки для программы или скрипта. IdeOne.com также есть примеры кода для языков, так что эта функция будет полезна для тех, кто плохо знаком с языком программирования и хотите быстро обратиться к синтаксису языка программирования.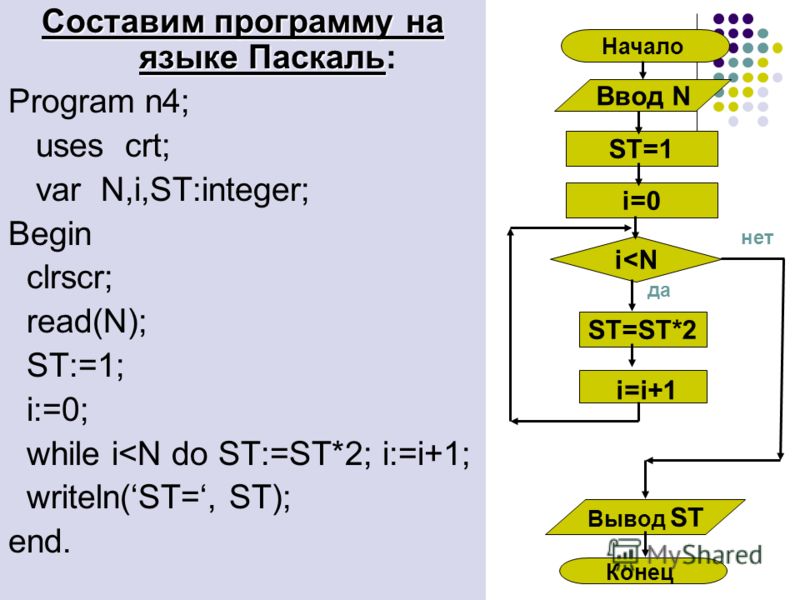 Может быть, у вас нет системы прав для установки программного обеспечения. Но это никогда не сможет занять место полноценным, IDE или компилятора, установленной на компьютере из-за гибкости и возможности, которые она предоставляет вам, как работать с библиотекой файлов (. Lib или. DLL) и поддержкой плагинов для примера . Кроме того, он не может быть использована для разработки интерактивных приложений, который требует ввода пользователя, который не может быть предсказуемым в любое время.
Может быть, у вас нет системы прав для установки программного обеспечения. Но это никогда не сможет занять место полноценным, IDE или компилятора, установленной на компьютере из-за гибкости и возможности, которые она предоставляет вам, как работать с библиотекой файлов (. Lib или. DLL) и поддержкой плагинов для примера . Кроме того, он не может быть использована для разработки интерактивных приложений, который требует ввода пользователя, который не может быть предсказуемым в любое время.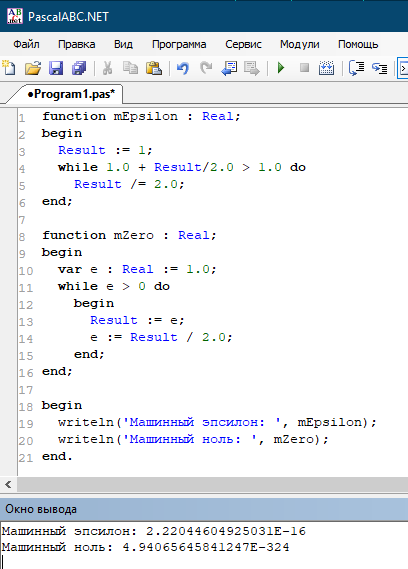
 Это инструмент для онлайн-обучения, у которого есть режим совместного использования. Вы можете компилировать код на разных языках и разбираться с базами данных прямо в браузере.
Это инструмент для онлайн-обучения, у которого есть режим совместного использования. Вы можете компилировать код на разных языках и разбираться с базами данных прямо в браузере.
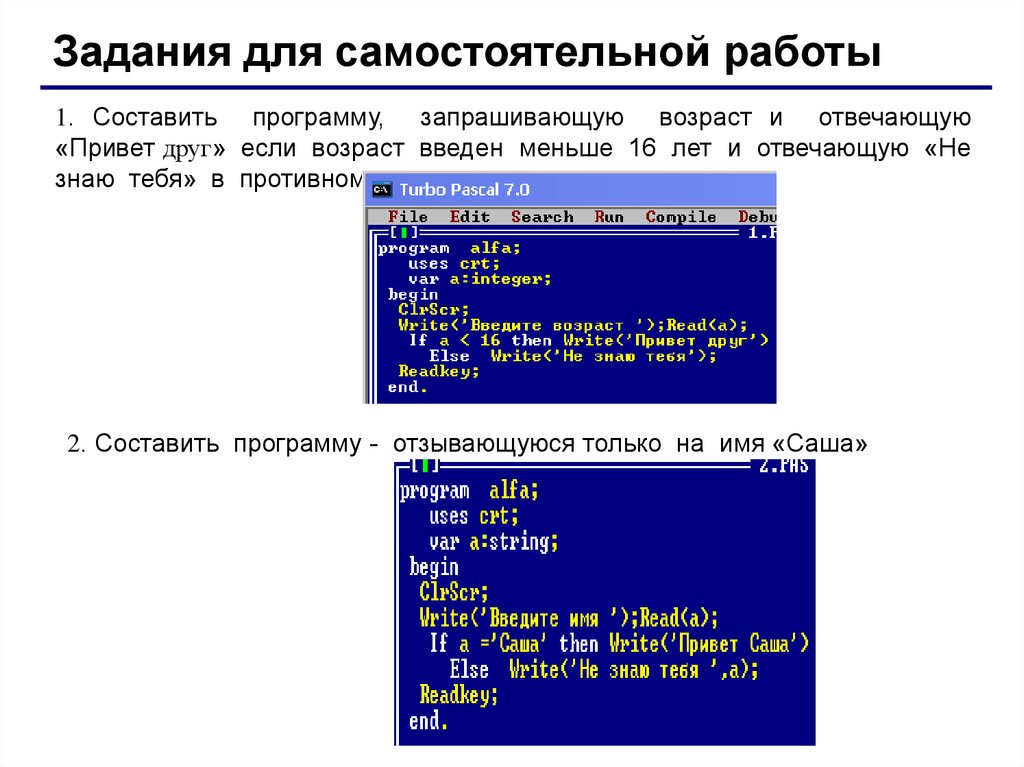 Он позволяет проверить любое сочетание JavaScript, HTML и CSS.
Он позволяет проверить любое сочетание JavaScript, HTML и CSS.

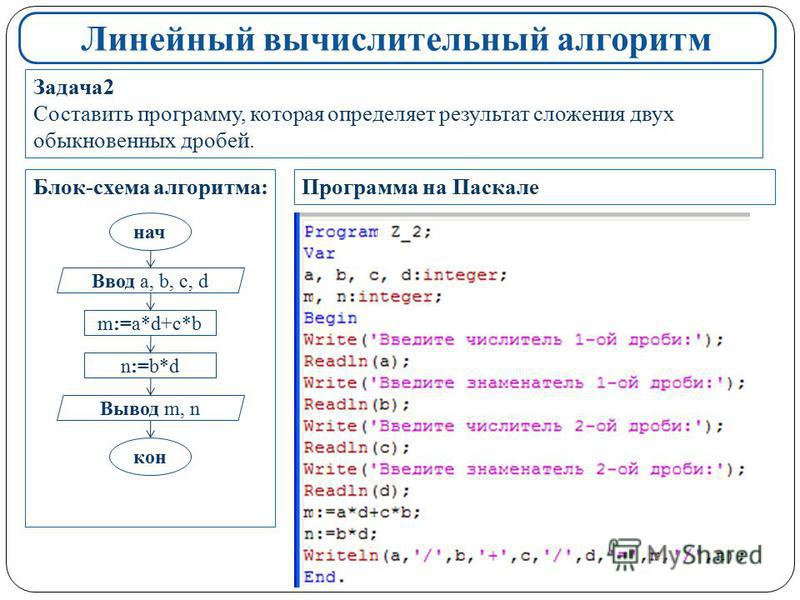 Он был разработан в 2002 году отечественными специалистами, их основная цель – получения языка программирования, способного отвечать современным на тот момент требованиям, и одновременно быть простым в освоении. Обучающая система Pascal ABC, начиная с версии 3.0, стала свободно распространяемым ПО, что сделало обучение программированию доступным для широких масс.
Он был разработан в 2002 году отечественными специалистами, их основная цель – получения языка программирования, способного отвечать современным на тот момент требованиям, и одновременно быть простым в освоении. Обучающая система Pascal ABC, начиная с версии 3.0, стала свободно распространяемым ПО, что сделало обучение программированию доступным для широких масс. Writeln (‘Привет, Мир!’). End.». Первая и последняя строка, это операторные скобки, а между ними располагается сама задача. Вторая строчка – вывод текста на экран, который помещен в кавычки.
Writeln (‘Привет, Мир!’). End.». Первая и последняя строка, это операторные скобки, а между ними располагается сама задача. Вторая строчка – вывод текста на экран, который помещен в кавычки.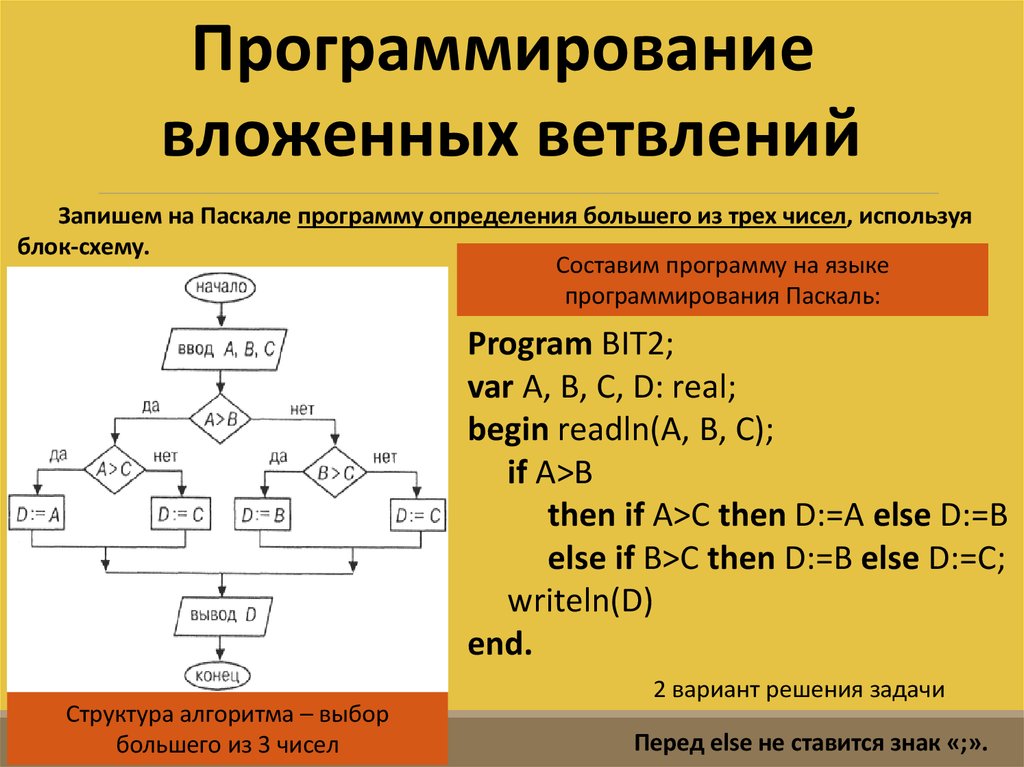

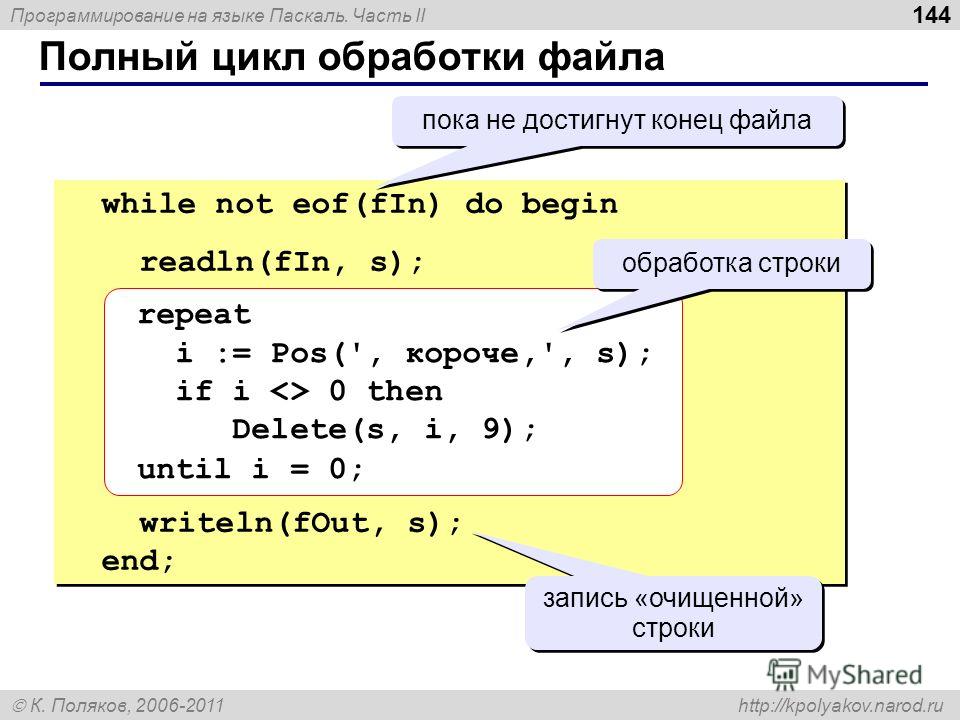 Может работать с библиотеками других .NET приложений. Реализованы средства автоформатирования, встроены дизайнер форм и отладчик, можно создавать консольные приложения. В программе реализовано поэтапное обучение от простого программирования к более сложному – модульному, событийному, объектно-ориентированному и компонентному.
Может работать с библиотеками других .NET приложений. Реализованы средства автоформатирования, встроены дизайнер форм и отладчик, можно создавать консольные приложения. В программе реализовано поэтапное обучение от простого программирования к более сложному – модульному, событийному, объектно-ориентированному и компонентному. Программка проста в управлении и что самое главное – делает правильные блок-схемы.
Программка проста в управлении и что самое главное – делает правильные блок-схемы.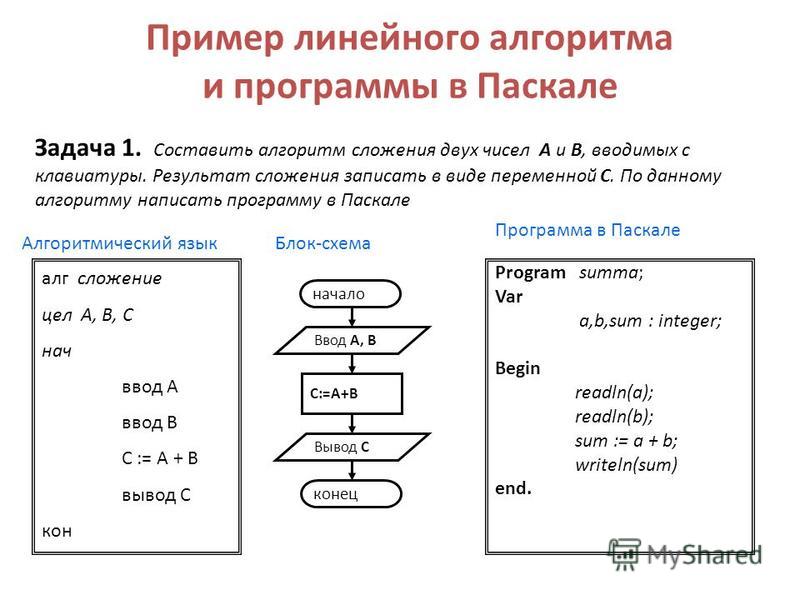
 Урок 7 – Удобная телефонная книга (Часть 2) Содержание курса Скачать все уроки по Pascal ABC одним архивомЯндекс.Диск / MEGAшаблоны для dle 11.2Похожие материалы Учебный курс по Adobe After Effect (От новичка до профи) Полный сборник уроков по изучению Adobe After Effects. В данном курсе вас ждут качественные видеоматериалы, которые научат вас уверенно пользоваться программой и создавать профессиональные спецэффекты. Инструкция по работе с Magic Particles 3D Сборник авторских видеоуроков по работе с программой. Позволяет изучать программу как комплексно, так и вникать в определённый инструмент или функцию. С его помощью вы быстро научитесь создавать трёхмерные спецэффекты для фото и видео. Руководство по использованию Audacity Краткий курс уроков по Audacity. Будет крайне полезен начинающим пользователям, желающим быстрее освоить широкие возможности программы и приступить к её уверенному использованию. Больше статейПолезные программыБольше программ Pascal ABC Создание программ, Интегрированные среды разработки Lazarus Создание программ, Интегрированные среды разработки HiAsm Создание программ, Визуальные среды разработки 3Ds MAX Графические редакторы, Редакторы 3D
Урок 7 – Удобная телефонная книга (Часть 2) Содержание курса Скачать все уроки по Pascal ABC одним архивомЯндекс.Диск / MEGAшаблоны для dle 11.2Похожие материалы Учебный курс по Adobe After Effect (От новичка до профи) Полный сборник уроков по изучению Adobe After Effects. В данном курсе вас ждут качественные видеоматериалы, которые научат вас уверенно пользоваться программой и создавать профессиональные спецэффекты. Инструкция по работе с Magic Particles 3D Сборник авторских видеоуроков по работе с программой. Позволяет изучать программу как комплексно, так и вникать в определённый инструмент или функцию. С его помощью вы быстро научитесь создавать трёхмерные спецэффекты для фото и видео. Руководство по использованию Audacity Краткий курс уроков по Audacity. Будет крайне полезен начинающим пользователям, желающим быстрее освоить широкие возможности программы и приступить к её уверенному использованию. Больше статейПолезные программыБольше программ Pascal ABC Создание программ, Интегрированные среды разработки Lazarus Создание программ, Интегрированные среды разработки HiAsm Создание программ, Визуальные среды разработки 3Ds MAX Графические редакторы, Редакторы 3D Написал я калькулятор, а он не работает. В результате действий пишет «0».
Написал я калькулятор, а он не работает. В результате действий пишет «0». Для избежания этого следовало бы очистить буфер ввода командой fflush(stdin) . Однако все эти вопросы решаются использованием cout и cin .
Для избежания этого следовало бы очистить буфер ввода командой fflush(stdin) . Однако все эти вопросы решаются использованием cout и cin ..bmp)
 Это означает, что для написания программы, необходимо предварительно составить алгоритм ее решения для компьютера. Синтаксисом предусмотрена определенная структура программы на языке Паскаль:
Это означает, что для написания программы, необходимо предварительно составить алгоритм ее решения для компьютера. Синтаксисом предусмотрена определенная структура программы на языке Паскаль:
 Сначала они переводятся на машинный язык при помощи специальных программ-трансляторов. Для языка Pascal (и ряда других) такая программа называется компилятором (другой вид трансляторов — интерпретаторы), которых существует на сегодняшний день не так много, так как в основном они устарели или некорректно работают в современных версиях Windows.
Сначала они переводятся на машинный язык при помощи специальных программ-трансляторов. Для языка Pascal (и ряда других) такая программа называется компилятором (другой вид трансляторов — интерпретаторы), которых существует на сегодняшний день не так много, так как в основном они устарели или некорректно работают в современных версиях Windows.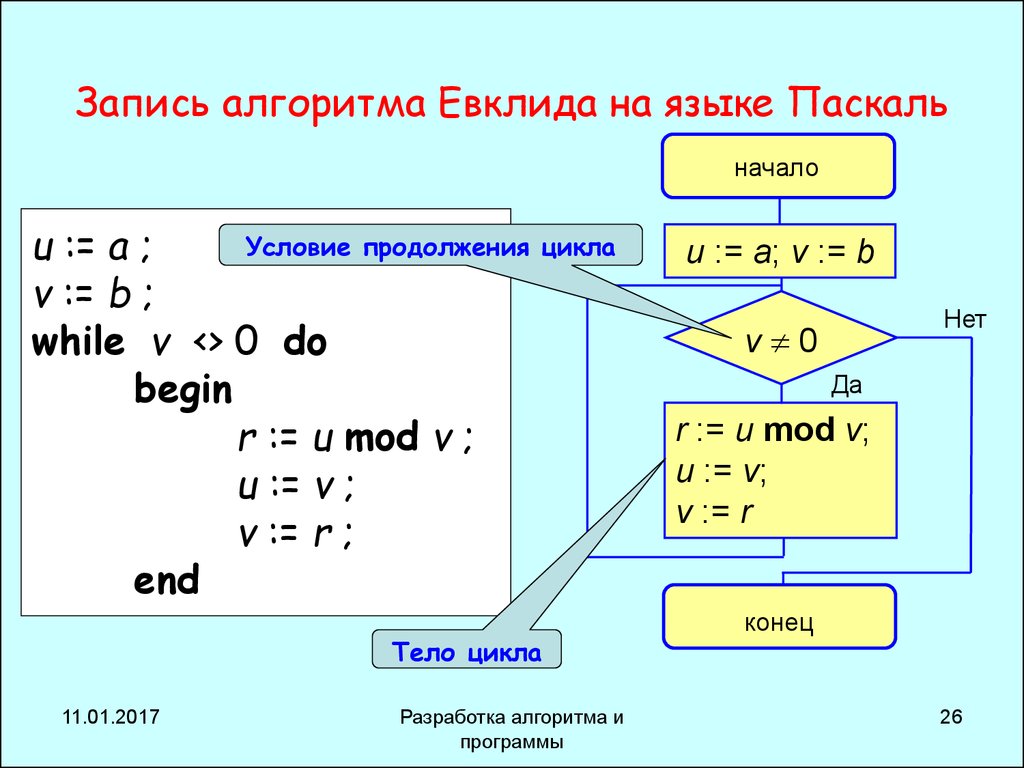
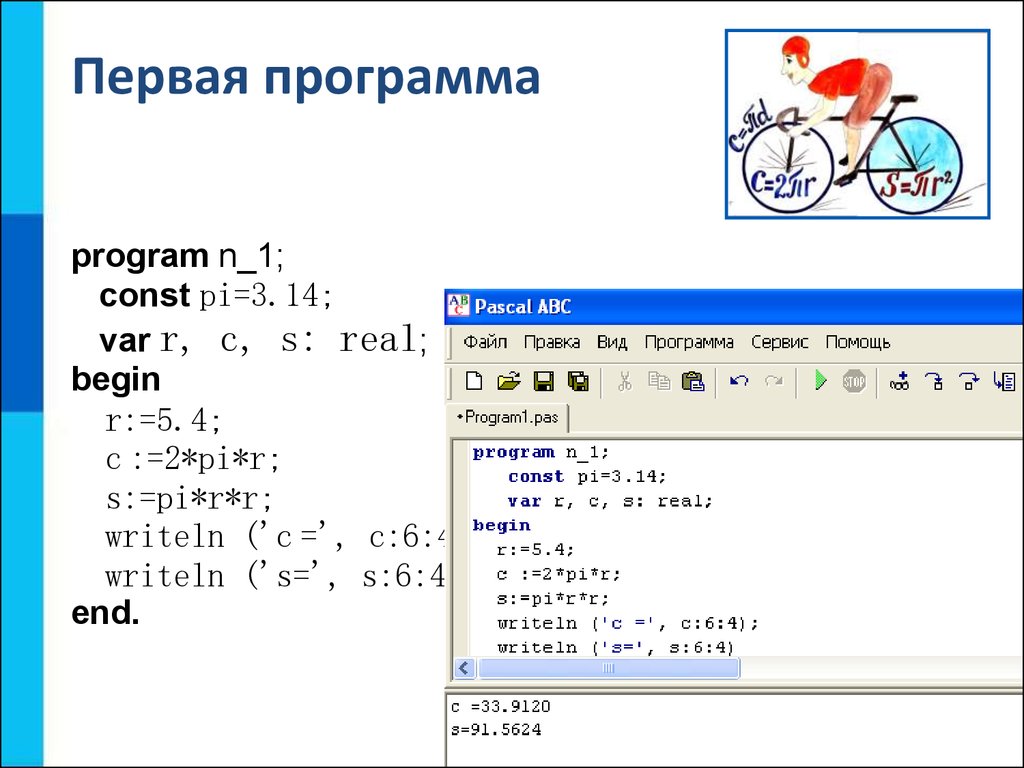 д.). Не сбрасывайте этот язык со счетов, познакомьтесь с ним с академией онлайн-образования Onskills.
д.). Не сбрасывайте этот язык со счетов, познакомьтесь с ним с академией онлайн-образования Onskills.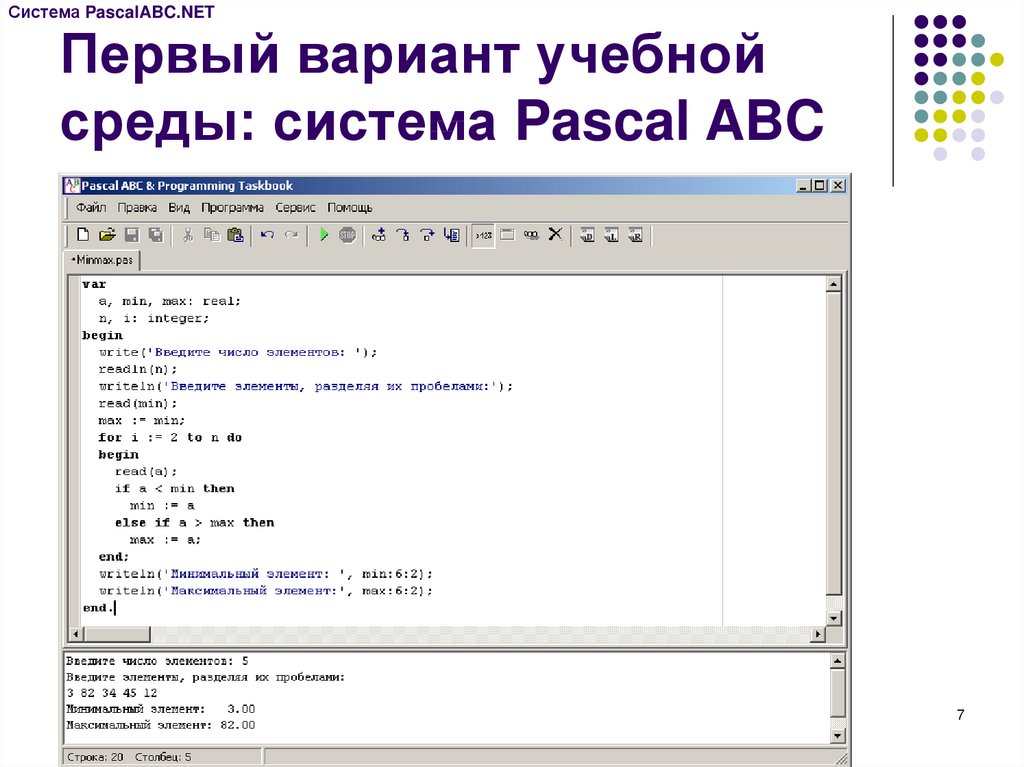
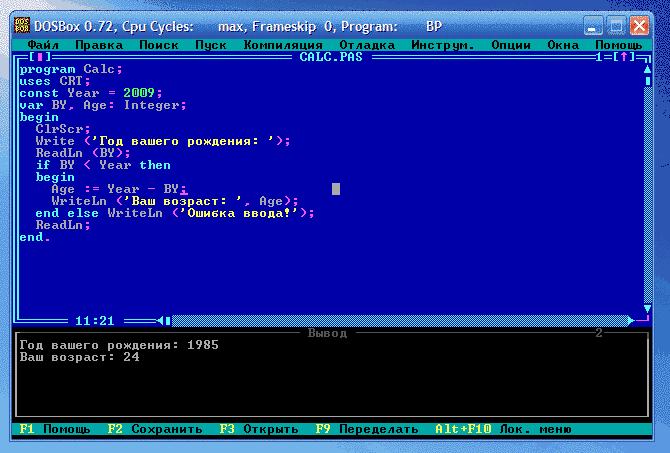 Обсудим, почему полезно уметь писать на нем код, какие возможности перед вами откроет освоение этого языка.
Обсудим, почему полезно уметь писать на нем код, какие возможности перед вами откроет освоение этого языка. Разберём основные операторы, которые позволяют создавать циклы в алгоритме: for, while, repeat-until.
Разберём основные операторы, которые позволяют создавать циклы в алгоритме: for, while, repeat-until. Посвятим время локальным и глобальным переменным. Поговорим об определении массивов.
Посвятим время локальным и глобальным переменным. Поговорим об определении массивов.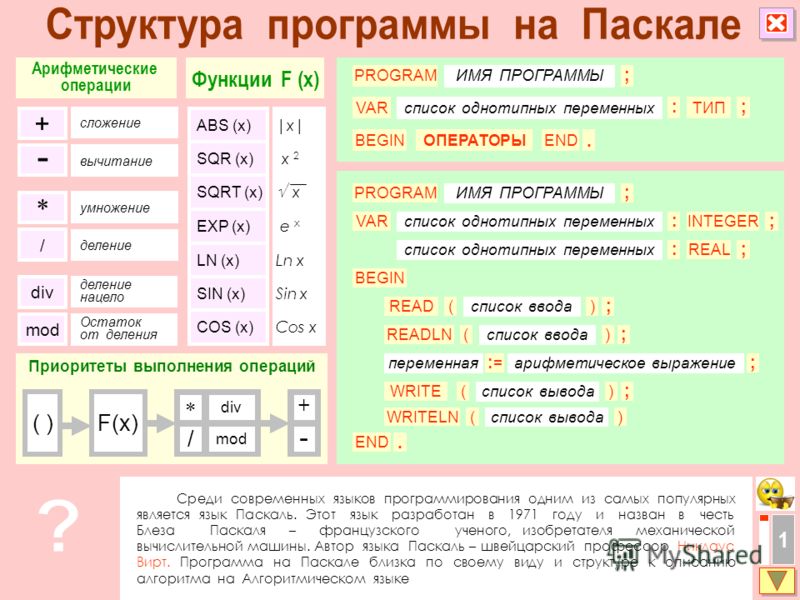 Сертификат мы пришлем в электронном виде, а если вам
нужен оригинал – отправим Почтой России
Сертификат мы пришлем в электронном виде, а если вам
нужен оригинал – отправим Почтой России Оплачиваете
2. Вам на почту приходят доступы от обучающего портала
3. Заходите на портал — обучаетесь
Оплачиваете
2. Вам на почту приходят доступы от обучающего портала
3. Заходите на портал — обучаетесь Кроме того, команда Free Pascal поддерживает транспилятор для паскаля в Javascript под названием pas2js.
Кроме того, команда Free Pascal поддерживает транспилятор для паскаля в Javascript под названием pas2js.

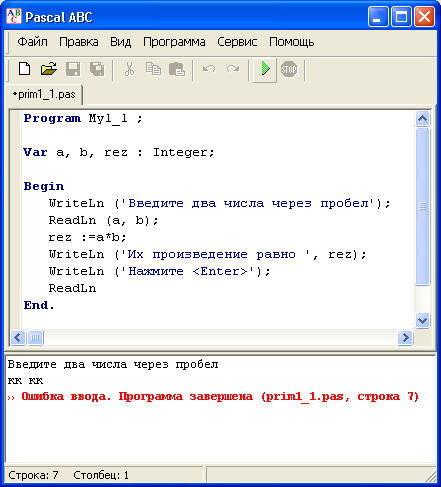 Для версии Mac OS X требуется Mac OS X 10.4 или более поздней версии,
с установленными инструментами разработчика.
Для версии Mac OS X требуется Mac OS X 10.4 или более поздней версии,
с установленными инструментами разработчика.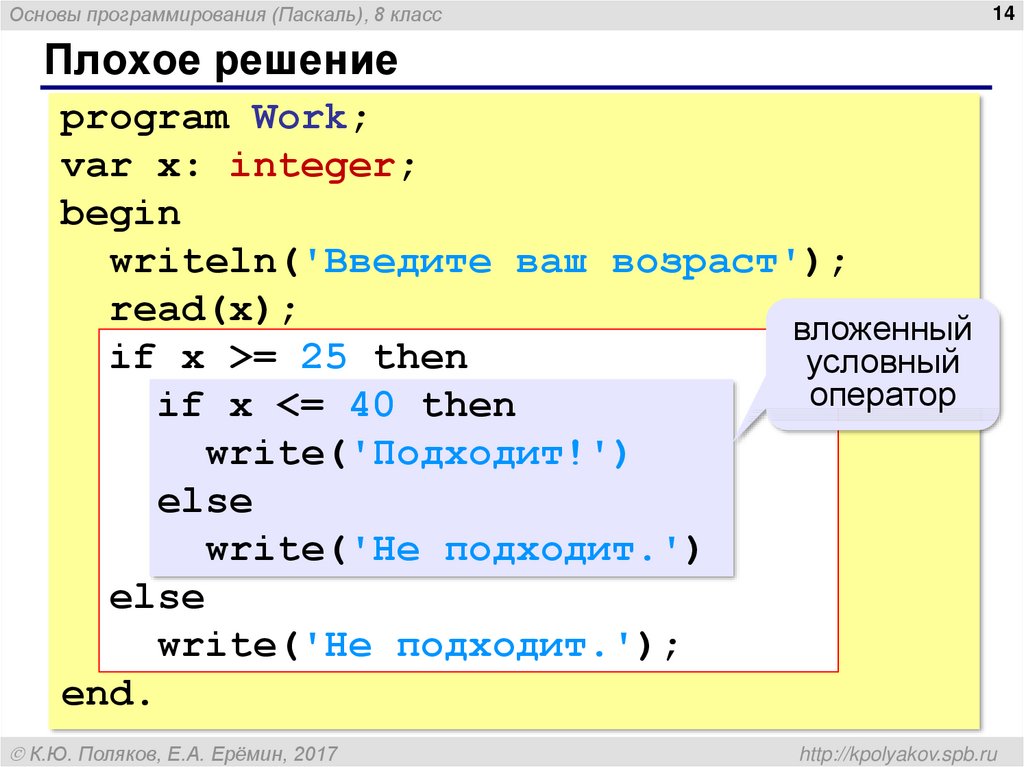
 Что ж, у всех нас есть внутреннее стремление или стремление стать кем-то! Немногие из вас могут мечтать стать ИТ-специалистами в выбранной вами области, поскольку «ИТ» — это широкая тема, включающая в себя множество подобластей. Некоторые из вас могли бы подумать о том, чтобы стать «программистами»! Если у вас есть идея стать «программистом», у нас есть курс для вас.
Что ж, у всех нас есть внутреннее стремление или стремление стать кем-то! Немногие из вас могут мечтать стать ИТ-специалистами в выбранной вами области, поскольку «ИТ» — это широкая тема, включающая в себя множество подобластей. Некоторые из вас могли бы подумать о том, чтобы стать «программистами»! Если у вас есть идея стать «программистом», у нас есть курс для вас.



 Н. Мишустина и др.; Под ред. А. Г. Мордковича. — 12-е изд., испр. — М.: 2010.-223 с.: ил.
Н. Мишустина и др.; Под ред. А. Г. Мордковича. — 12-е изд., испр. — М.: 2010.-223 с.: ил.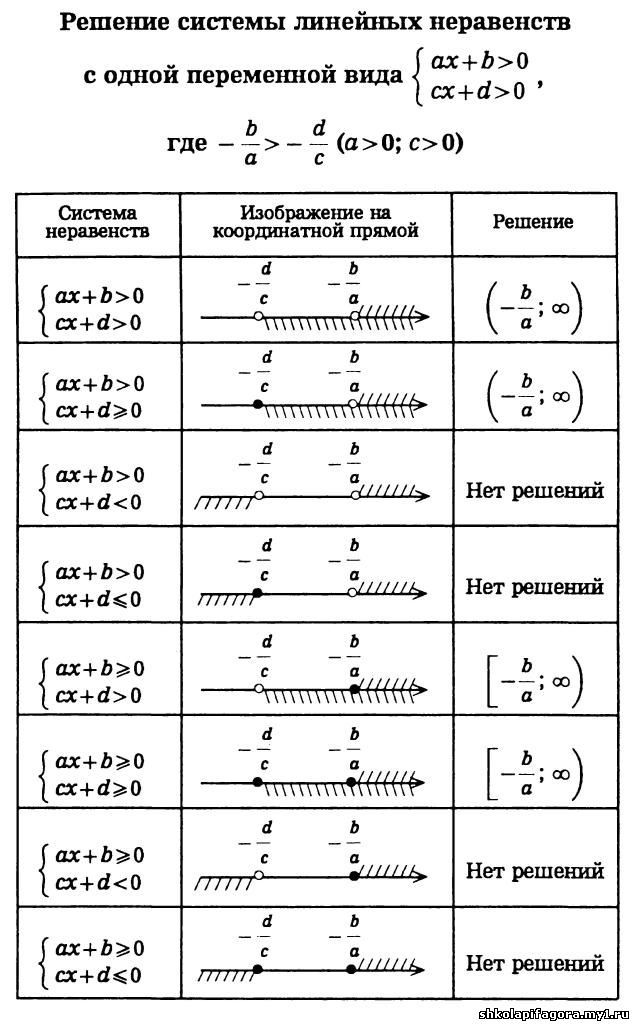 Узоры и орнаменты на посуде»
Узоры и орнаменты на посуде»
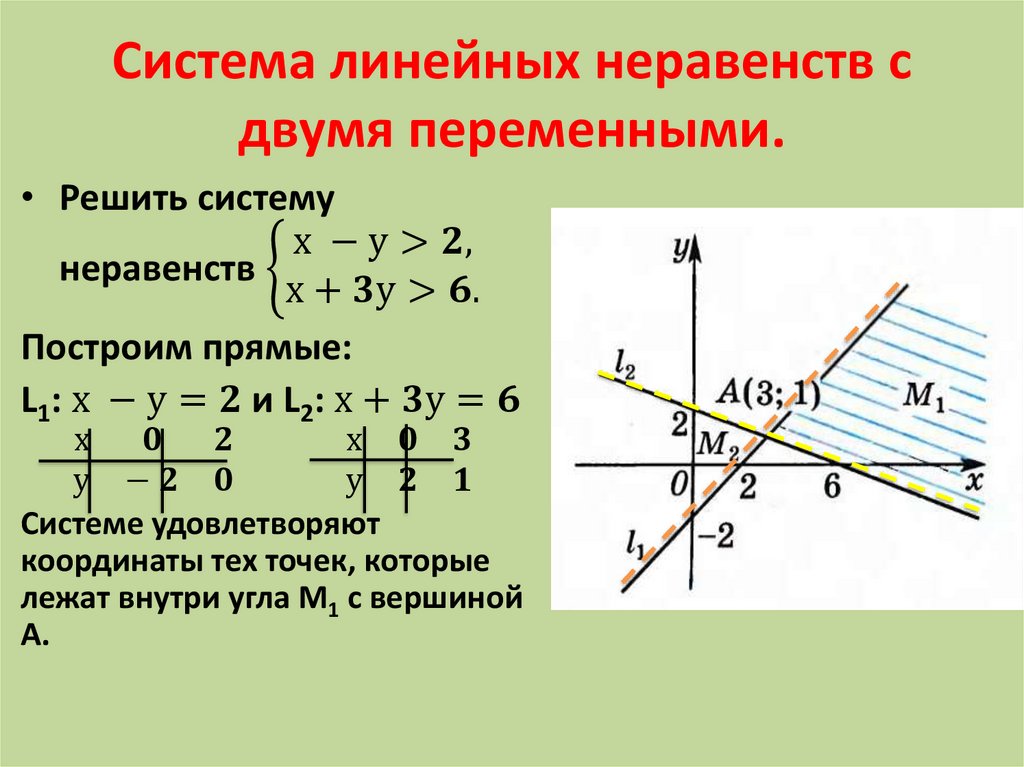

 Определить направление ветвей параболы
Определить направление ветвей параболы



 Так как 3>0, знак неравенства после деления меняться не будет.
Так как 3>0, знак неравенства после деления меняться не будет. Решить неравенство x+3(2−3x)>−4(2x−12).
Решить неравенство x+3(2−3x)>−4(2x−12).
 На остальных интервалах знаки будут чередоваться.
На остальных интервалах знаки будут чередоваться. Пусть это будет точка 6. Подставляем эту точку в исходное выражение:
Пусть это будет точка 6. Подставляем эту точку в исходное выражение: Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 0. Подставляем эту точку в исходное выражение:
Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 0. Подставляем эту точку в исходное выражение: Так как знак неравенства строгий, точки будут выколотыми. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 2. Подставляем эту точку в исходное выражение:
Так как знак неравенства строгий, точки будут выколотыми. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 2. Подставляем эту точку в исходное выражение: Так как знак неравенства строгий, точки будут выколотыми. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 10. Подставляем эту точку в исходное выражение:
Так как знак неравенства строгий, точки будут выколотыми. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 10. Подставляем эту точку в исходное выражение: Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 3. Подставляем эту точку в исходное выражение:
Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 3. Подставляем эту точку в исходное выражение:


 При нанесении на ось x точка будет всегда выколотой (вне зависимости от знака неравенства).
При нанесении на ось x точка будет всегда выколотой (вне зависимости от знака неравенства).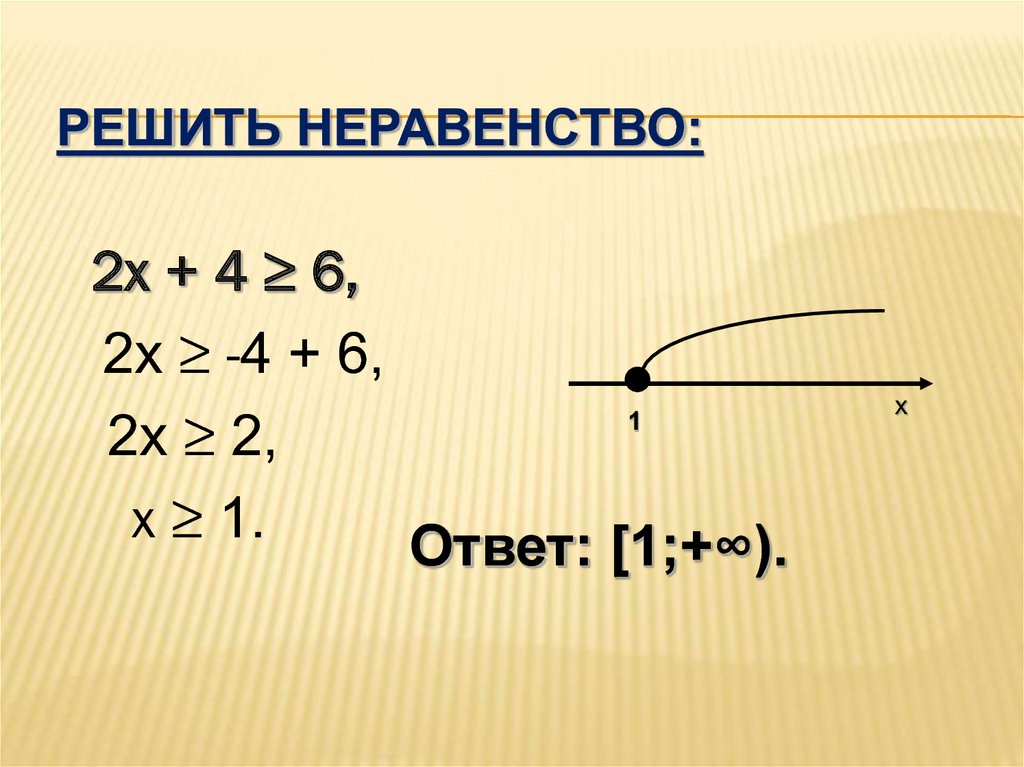
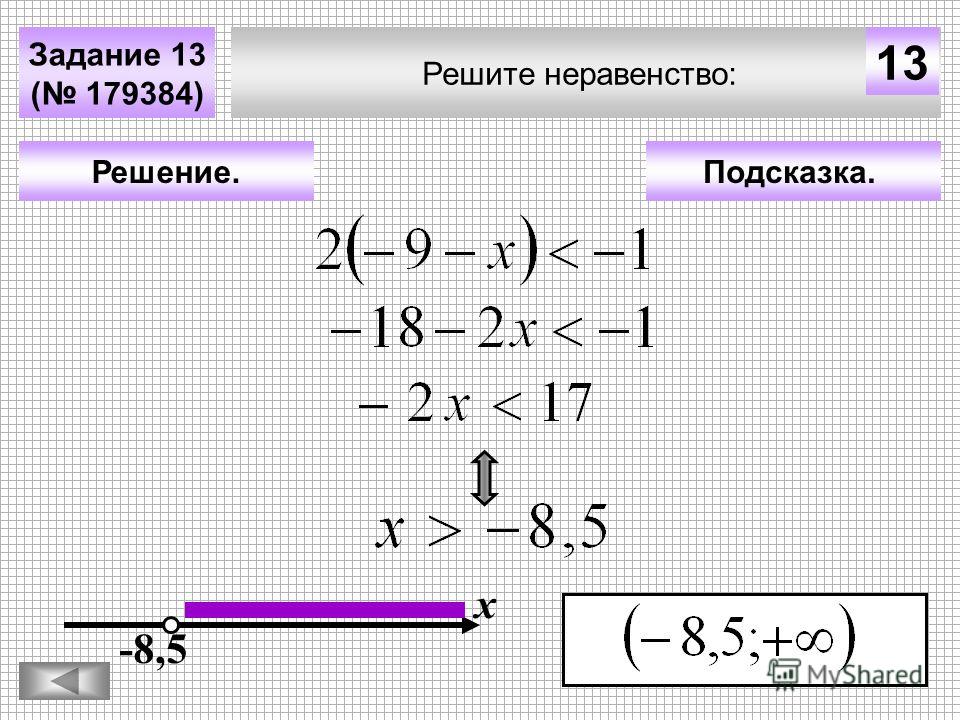 Ну а нули знаменателя выколоты всегда.
Ну а нули знаменателя выколоты всегда. Неравенство приведено к виду f(x)g(x)>0.
Неравенство приведено к виду f(x)g(x)>0.
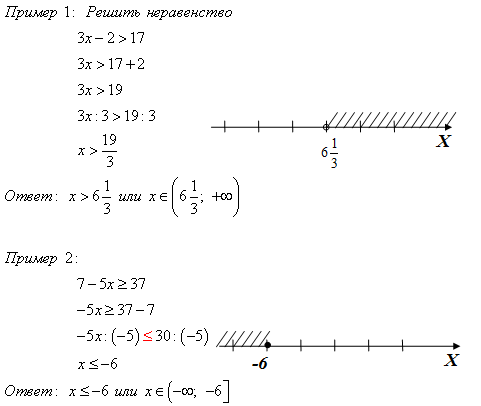 Более подробно об этом смотрите короткий видео-урок.
Более подробно об этом смотрите короткий видео-урок.

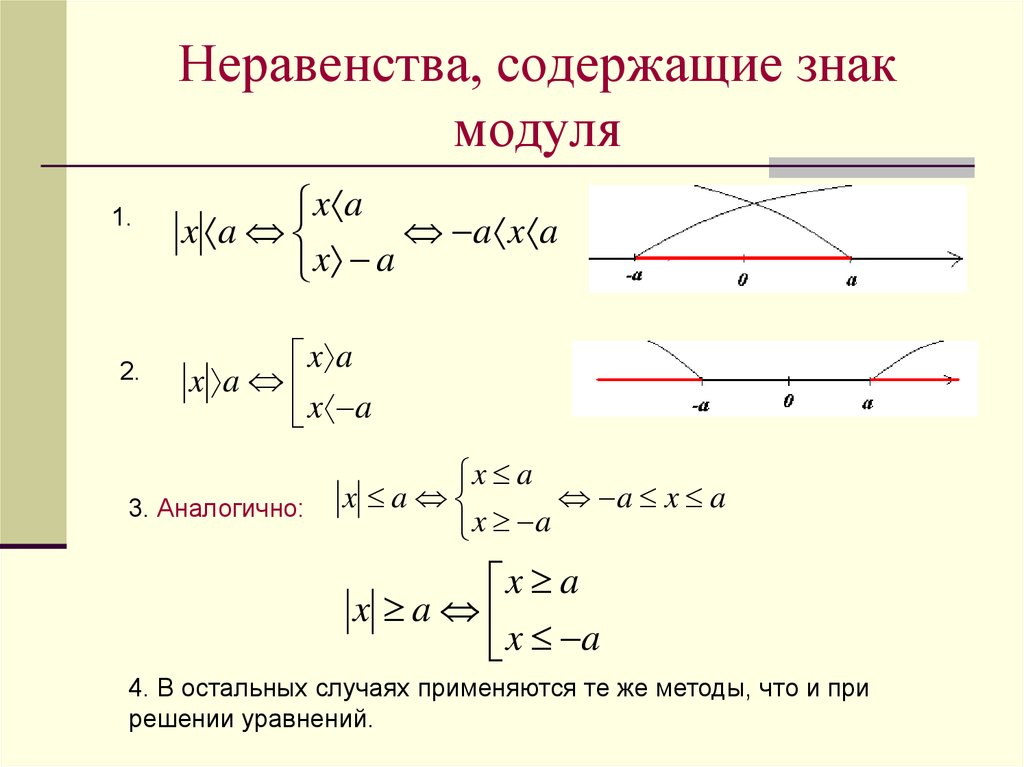

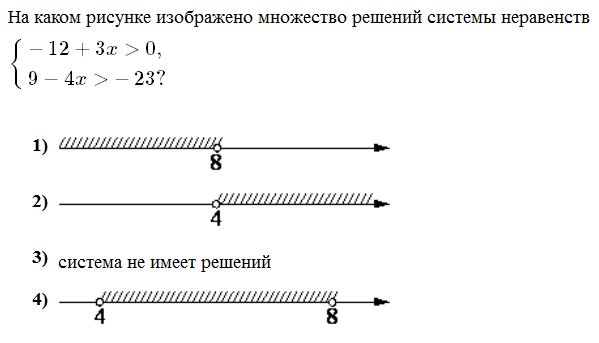 Им не дозволяется раскидываться решениями как им захочется. Наша задача указать решения, которые одновременно будут удовлетворять и первому неравенству и второму.
Им не дозволяется раскидываться решениями как им захочется. Наша задача указать решения, которые одновременно будут удовлетворять и первому неравенству и второму. В этой области и располагаются решения системы . Видно, что эта область располагается в промежутке от 4 до 9. Для наглядности выделим эту область красным цветом:
В этой области и располагаются решения системы . Видно, что эта область располагается в промежутке от 4 до 9. Для наглядности выделим эту область красным цветом:
 На этом решение завершается. Осталось изобразить множество решений системы на координатной прямой и записать ответ в виде числового промежутка.
На этом решение завершается. Осталось изобразить множество решений системы на координатной прямой и записать ответ в виде числового промежутка.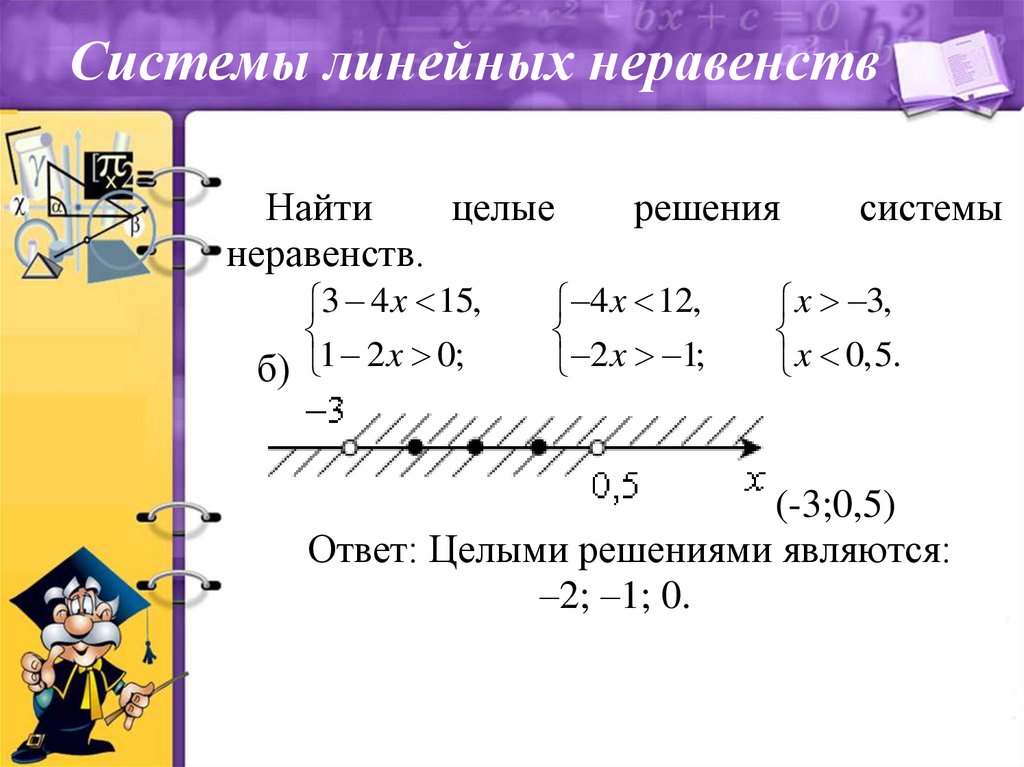
 Значит неравенства x ≤ −3 и x ≥ 9 не имеют общих решений. А значит не имеет решений система
Значит неравенства x ≤ −3 и x ≥ 9 не имеют общих решений. А значит не имеет решений система  Решите неравенство:
Решите неравенство: Его мы и разберем в первую очередь.
Его мы и разберем в первую очередь.
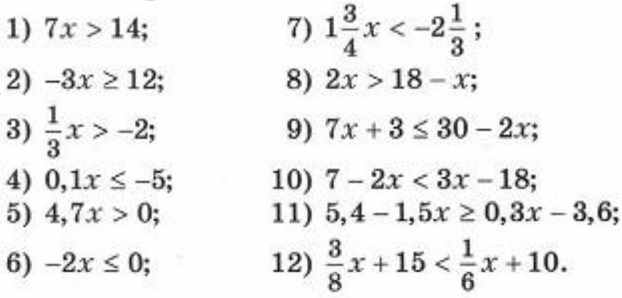 Имеем (3·x):3≤(−12):3
, что то же самое x≤−4
.
Имеем (3·x):3≤(−12):3
, что то же самое x≤−4
.




 Чтобы его получить, давайте рассмотрим четыре линейных неравенства с одной и той же левой частью: 0,5·x−10
и 0,5·x−1≥0
, их решениями являются соответственно x2
и x≥2
, а также изобразим график линейной функции y=0,5·x−1
.
Чтобы его получить, давайте рассмотрим четыре линейных неравенства с одной и той же левой частью: 0,5·x−10
и 0,5·x−1≥0
, их решениями являются соответственно x2
и x≥2
, а также изобразим график линейной функции y=0,5·x−1
. В нашем случае линейного неравенства функция, отвечающая левой части, есть y=a·x+b
, а правой части – y=0
, совпадающая с осью Ox
.
В нашем случае линейного неравенства функция, отвечающая левой части, есть y=a·x+b
, а правой части – y=0
, совпадающая с осью Ox
. Для наших нужд можно даже не изображать ось Oy
. Так наш схематический чертеж будет иметь такой вид
Для наших нужд можно даже не изображать ось Oy
. Так наш схематический чертеж будет иметь такой вид Следовательно, решением неравенства 0·x+0≥0
является множество всех действительных чисел.
Следовательно, решением неравенства 0·x+0≥0
является множество всех действительных чисел. Это можно сделать путем раскрытия скобок, приведения подобных слагаемых, перестановки слагаемых местами и переноса слагаемых из одной части неравенства в другую с противоположным знаком.
Это можно сделать путем раскрытия скобок, приведения подобных слагаемых, перестановки слагаемых местами и переноса слагаемых из одной части неравенства в другую с противоположным знаком. Да и принцип их решения абсолютно такой же: выполняя равносильные преобразования, их можно привести к элементарным неравенствам, представляющим собой искомые решения.
Да и принцип их решения абсолютно такой же: выполняя равносильные преобразования, их можно привести к элементарным неравенствам, представляющим собой искомые решения. Так мы пришли к неверному числовому неравенству, откуда делаем вывод, что исходное неравенство не имеет решений.
Так мы пришли к неверному числовому неравенству, откуда делаем вывод, что исходное неравенство не имеет решений.


 Поэтому есть важное понятие, вот эти стрелочки — это знак эквивалентных, или равносильных, преобразований. Преобразование называются равносильными, или эквивалентными , если они не изменяет множества решений.
Поэтому есть важное понятие, вот эти стрелочки — это знак эквивалентных, или равносильных, преобразований. Преобразование называются равносильными, или эквивалентными , если они не изменяет множества решений. Нанесем множество решений на ось x
Нанесем множество решений на ось x 

 Ребята, не забывайте что обязательно надо умножать или делить обе части неравенства!
Ребята, не забывайте что обязательно надо умножать или делить обе части неравенства! Решить неравенство: $-3x+6
Решить неравенство: $-3x+6 
 От данной модели, конечно же, требуется решение, и в его качестве будет выступать общий ответ для всех неравенств системы, предложенной в задании (обычно в нём так и пишут, например: «Решите систему неравенств 4 x + 1 > 2 и 30 — x > 6… «). Однако перед тем как перейти к видам и методам решений, нужно ещё кое в чём разобраться.
От данной модели, конечно же, требуется решение, и в его качестве будет выступать общий ответ для всех неравенств системы, предложенной в задании (обычно в нём так и пишут, например: «Решите систему неравенств 4 x + 1 > 2 и 30 — x > 6… «). Однако перед тем как перейти к видам и методам решений, нужно ещё кое в чём разобраться. Неравенство же представляет собой такую модель, в которой одна величина или больше, или меньше другой, или содержит в себе утверждение, что они неодинаковы. Таким образом, в первом случае уместно говорить о равенстве, а во втором, как бы это очевидно ни звучало из самого названия, о неравенстве исходных данных. Системы уравнений и неравенств друг от друга практически не отличаются и методы их решения одинаковы. Единственное различие заключается в том, что в первом случае используются равенства, а во втором применяются неравенства.
Неравенство же представляет собой такую модель, в которой одна величина или больше, или меньше другой, или содержит в себе утверждение, что они неодинаковы. Таким образом, в первом случае уместно говорить о равенстве, а во втором, как бы это очевидно ни звучало из самого названия, о неравенстве исходных данных. Системы уравнений и неравенств друг от друга практически не отличаются и методы их решения одинаковы. Единственное различие заключается в том, что в первом случае используются равенства, а во втором применяются неравенства.
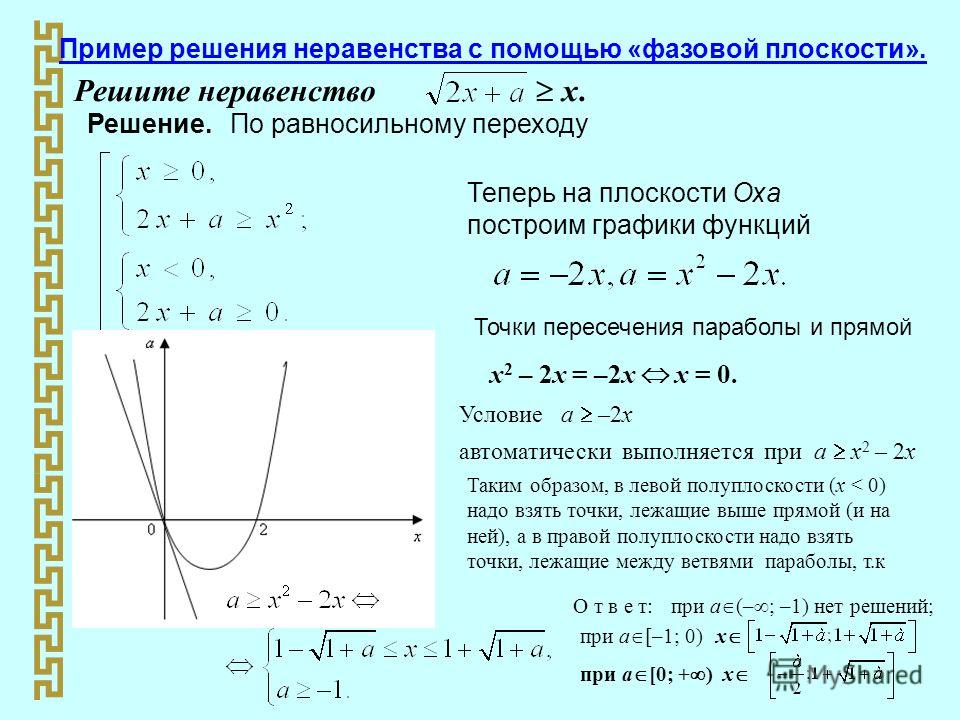 Однако перед этим следует сказать пару слов об их свойствах.
Однако перед этим следует сказать пару слов об их свойствах. 
 Выделяют несколько способов решения систем неравенств: графический, алгебраический, способ подстановки. Стоит заметить, что они относятся к тем математическим моделям, которые имеют несколько неизвестных переменных. В случае, когда имеется только одна, подойдёт способ интервалов.
Выделяют несколько способов решения систем неравенств: графический, алгебраический, способ подстановки. Стоит заметить, что они относятся к тем математическим моделям, которые имеют несколько неизвестных переменных. В случае, когда имеется только одна, подойдёт способ интервалов.
 Если их нет (тогда переменная будет выглядеть, как одиночная буква), то ничего не изменяем, если есть (вид переменной будет, например, таким — 5y или 12y), то тогда необходимо сделать так, чтобы в каждом неравенстве число перед выбранной переменной было одинаковым. Для этого нужно умножить каждый член неравенств на общий множитель, например, если в первом неравенстве записано 3y, а во втором 5y, то необходимо все члены первого неравенства умножить на 5, а второго — на 3. Получится 15y и 15y соответственно.
Если их нет (тогда переменная будет выглядеть, как одиночная буква), то ничего не изменяем, если есть (вид переменной будет, например, таким — 5y или 12y), то тогда необходимо сделать так, чтобы в каждом неравенстве число перед выбранной переменной было одинаковым. Для этого нужно умножить каждый член неравенств на общий множитель, например, если в первом неравенстве записано 3y, а во втором 5y, то необходимо все члены первого неравенства умножить на 5, а второго — на 3. Получится 15y и 15y соответственно.
 Там, где промежутки неравенств пересекаются, находится решение системы. Чтобы использовать метод интервалов, необходимо выполнить следующие шаги:
Там, где промежутки неравенств пересекаются, находится решение системы. Чтобы использовать метод интервалов, необходимо выполнить следующие шаги: Они привносят наглядность, которая не может не способствовать эффективному и быстрому проведению математических операций.
Они привносят наглядность, которая не может не способствовать эффективному и быстрому проведению математических операций.
 И последний случай, когда \(p(a)=0\),а \(q(a)≠0\), то уравнение не имеет решений.
Замечу, что по некоторым уравнениям сразу невозможно определить, являются ли они линейными. Выполнив некоторые преобразования, вдруг обнаружим, что в уравнении отсутствуют члены с \(x\) в степени большей, чем 1. Если изначально у нас и были старшие степени, то теперь они сократились.
Мы провели анализ линейного уравнения в общем виде, теперь разберем несколько примеров:
И последний случай, когда \(p(a)=0\),а \(q(a)≠0\), то уравнение не имеет решений.
Замечу, что по некоторым уравнениям сразу невозможно определить, являются ли они линейными. Выполнив некоторые преобразования, вдруг обнаружим, что в уравнении отсутствуют члены с \(x\) в степени большей, чем 1. Если изначально у нас и были старшие степени, то теперь они сократились.
Мы провели анализ линейного уравнения в общем виде, теперь разберем несколько примеров:
 2}{a}=5a.\) Этот корень не будет удовлетворять ОДЗ.
2}{a}=5a.\) Этот корень не будет удовлетворять ОДЗ. Симметрия функций и приемы решения.
Симметрия функций и приемы решения.
 Символы, представляющие неравенства :
Символы, представляющие неравенства :
 Теперь вам может быть очевидно, что и для любого линейного неравенства у нас будет бесконечно много решений. Все эти решения составят наборов решений линейного неравенства.
Теперь вам может быть очевидно, что и для любого линейного неравенства у нас будет бесконечно много решений. Все эти решения составят наборов решений линейного неравенства.
