Почему «минус на минус даёт плюс»? Простейшие доказательства » uCrazy.ru
В книге Владимира Левшина «Магистр рассеянных наук» есть математическая притча, в которой к богатому человеку пришел бедняк и предложил умножить имущество миллионщика. Правда, бедняк сразу же оговорился, что умножая состояние богача, он на то же число умножит и собственные средства. Движимый алчностью богач согласился на это условие, действие по умножению было совершено….
Миллионщик бросился к своим сундукам, но вместо золота обнаружил только долговые расписки, согласно которым он обязался вернуть различным людям крупные суммы денег.
Источник изображения: shutterstock.com
На вопрос, где моё золото? Бедняк ответил: «Теперь у меня. Мы договорились умножить наши состояния, вот я и умножил… на отрицательное число.»
Это притча прямо иллюстрирует закон умножения на отрицательное число. У бедняка были исключительно долги (отрицательная сумма денег) и при умножении на отрицательное число получилось крупное состояние. Ну а богач при умножении своего состояния на отрицательное число оказался в долгах как в шелках. Приведенная притча как нельзя лучше иллюстрирует математическое правило умножения на отрицательное число. Но как это обосновать и объяснить наглядно?
Ну а богач при умножении своего состояния на отрицательное число оказался в долгах как в шелках. Приведенная притча как нельзя лучше иллюстрирует математическое правило умножения на отрицательное число. Но как это обосновать и объяснить наглядно?
Строгое доказательство того, что умножение двух отрицательных чисел даст в итоге положительный результат, приводится в таком разделе математики как «Теория чисел». Однако вряд ли среди читателей канала много людей знакомых с математическим понятием «кольцо», а тем более с его бинарными операциями. Поэтому оставим строго математическое доказательство через аксиоматику кольца для математиков, а сами обратимся к доказательствам логическим.
Доказательство первое
Сейчас мы воспользуемся «математической логикой». Есть там «закон отрицания отрицания», который гласит, что если неверное утверждение неверно, то оно — истинное. На примере это можно пояснить так: неверно, что неверно, что Москва столица Российской Федерации. Значит утверждение «Москва является столицей РФ» правдиво. Знак «минус» можно трактовать как отрицание, тогда «минус» «минус» есть подтверждение.
Знак «минус» можно трактовать как отрицание, тогда «минус» «минус» есть подтверждение.
Проще говоря:
-(-2)=2
Теперь проведем несложные вычисления:
-2*(-3)= -1*2*(-1)*3 пока мы просто математически переписали наш пример,
а сейчас используем ассоциативность (сочетательный закон) умножения:
-1*(-1)*2*3=-(-1)*6 (мы просто перемножили единицы и умножили 2 на 3, а знаки пока не трогали)= 6 (для -(-1) мы использовали закон отрицания отрицания).
Доказательство второе
Решим несложное уравнение 6х+6=4х+8
Для начала соберем неизвестные слева от знака равенства, а константы справа, при этом, соблюдая, правило смены знака при переносе через равно. Получим:
6х-4х=8-6
Отсюда, 2х=2, х=2/2
Сейчас мы вспомним, что деление, это операция обратная умножению, и разделить на 2 это то же самое, что умножить на 1/2. Перепишем последнюю строчку:
х=2*(1/2)
Имеем, х=1.
Мы уже знаем правильный ответ. А сейчас повторно решим наше уравнение, вот только постоянные соберем слева от знака равенства, а переменные справа. Получим:
Получим:
6-8=4х-6х
Отсюда -2=-2х, следовательно, -2/(-2)=х, или же -2*(-1/2)=х.
Но мы уже знаем, что х=1, а значит -2*(-1/2)=1.
Получили, что при умножении двух отрицательных чисел результат оказывается положительный.
Доказательство третье
Возьмем обыкновенный уличный термометр. Пусть каждый час температура поднимается ровно на 2 градуса по Цельсию. Сейчас полдень и на термометре 0 градусов. Какая температура будет в 15 часов?
Источник изображения: istockphoto.com
Задача абсолютно несложная — при постоянном увеличении температуры за три часа она повысится на 6 градусов, поскольку 15ч-12ч = 3ч, а 3*2=6. Так что в 15 часов термометр покажет 6 градусов.
Усложним вопрос: а какая температура была в 8 часов утра, при условии, что ее рост был точно таким же?
Логика подсказывает, что 8 часов утра по сравнению с полднем это -4 часа, так как 8ч-12ч=-4ч. Спустимся по температурной шкале по 2 градуса вниз от 0 градусов 4 раза. Мы получим 8 градусов мороза, или попросту -8 градусов Цельсия. Таким образом получается -4*2=-8. Пока все просто и логично.
Мы получим 8 градусов мороза, или попросту -8 градусов Цельсия. Таким образом получается -4*2=-8. Пока все просто и логично.
Теперь представим ситуацию, когда температура не повышается со временем, а понижается (бывает и такое) на те же 2 градуса в час.
Понижение температуры означает ее изменение на -2 градуса каждый час. Для большей правдоподобности у нас на часах 23-00, а на термометре все тот же 0 градусов по Цельсию. А какая температура была в 20-00? Посчитаем, 20ч-23ч=-3ч. Далее -3*(-2)=6.
Проверим, двигаясь вверх по шкале на два градуса за каждый час. В итоге имеем те же 6 градусов по Цельсию. Следовательно, при умножении двух отрицательных чисел мы получаем положительное.
Минус на минус дает плюс? В поисках эмоционального баланса
«Если жизнь тебя обманет,
Не печалься, не сердись,
В день уныния смирись,
День веселья, верь, настанет!»
(А.С. Пушкин)
Добрый день! В ходе марафона мы часто говорим о важности оптимизма и позитивного настроя, жизнелюбия и приятия мира. Сегодня – для разнообразия – я хочу рассмотреть некоторые неочевидные плюсы пессимизма. (Ведь во всем плохом должно быть что-то хорошее:)).
Сегодня – для разнообразия – я хочу рассмотреть некоторые неочевидные плюсы пессимизма. (Ведь во всем плохом должно быть что-то хорошее:)).
Психологи утверждают, что пессимистам удается лучше удерживать концентрацию в трудные, стрессовые моменты жизни, по сравнению с оптимистами, поскольку негативные эмоции для них привычны и не выбивают их из колеи. Пока оптимисты ищут, чем бы прекрасным им вдохновиться на грядущие подвиги, пессимисты используют «топливо» негативной мотивации. А поскольку в реальном мире постоянно присутствуют те или иные сложности, проблемы и поводы для недовольства, то пессимистам всегда есть чем «вдохновляться». В этом плане им чаще удается быть более работоспособными!
Неуверенность в собственном будущем, тревога по поводу завтрашнего дня порождает большую ответственность, то есть пессимисты реже пускают дела на самотек, в отличие от оптимистов, преисполненных уверенности, что все и так образуется! Это полезно во многих сферах, особенно в финансовой. Пока оптимист надеется на лучшее, пессимист просчитывает риски и откладывает средства «на черный день».
Пока оптимист надеется на лучшее, пессимист просчитывает риски и откладывает средства «на черный день».
В своей работе пессимисты нередко излишне осторожничают и склонны останавливаться на полпути, не веря, что из задуманного выйдет что-то путное. Это вроде бы сугубо негативное качество, но и оно может быть благом, в случае если речь идет о заведомо провальном проекте, на который не стоит тратить свою энергию. Кроме того, именно у пессимистов всегда бывает в запасе «план Б», на случай провала основного.
Известно, что оптимисты быстрее вылечиваются от разных недугов. В то же время пессимисты реже подвергают себя рискам, поскольку более тщательно следят за здоровьем и не медлят с лечением. Они всегда склонны драматизировать ситуацию, видеть все в гипертрофированном виде, поэтому скорее перестрахуются, чем недобдеют!
Так же осторожен пессимист и в выбираемым им словах: мало ли кто и как на них отреагирует?.. Он пытается всё предусмотреть и потому возьмет с собой в дорогу зонтик, даже если дождя не было в прогнозе, захватит дополнительные вещи в поездку и т. д.
д.
Наконец, именно пессимисты чаще проявляют эмпатию, сочувствие по отношению к окружающим их людям. Если кто-то делится с ними своими проблемами, то они глубоко их осознают, а также всегда готовы поделиться историей собственных неудач, в то время как оптимисты могут отделаться парой дежурных фраз в стиле «Все наладится» и «Ты справишься!».
***
В большинстве своем взрослые люди не видят мир в исключительно белых или черных тонах. В зависимости от ситуации, настроения, погоды, самочувствия, все мы подчас проявляем полярные оценки обстановки и людей. Тем не менее, по выбору более типичных реакций конкретного человека, можно судить, насколько он оптимистичен или пессимистичен.
А кем вы чаще себя ощущаете: оптимистом, пессимистом или реалистом? В жизни вы воспитываете в себе здоровый авантюризм или разумную осторожность, безусловное приятие ситуаций или же полезную критичность? Если вам претит позитивное мышление, то вспомните о том, что и пессимизм может быть вашим другом, а не врагом: «Чаще всего люди пытаются отогнать от себя негативные мысли или избегать сложных ситуаций. Но есть и другой способ — включить защитный пессимизм»: https://secretmag.ru/practice/perestante-borotsya-s-pessimizmom-kak-mysli-o-plokhom-pomogayut-dobitsya-uspekha.htm
Но есть и другой способ — включить защитный пессимизм»: https://secretmag.ru/practice/perestante-borotsya-s-pessimizmom-kak-mysli-o-plokhom-pomogayut-dobitsya-uspekha.htm
Желаю всем радостного воскресенья и отсутствия поводов для пессимизма! ))) Поделитесь, попробовали ли вы на этой неделе вести разные виды дневников? Какие из них вас больше всего вдохновили? Не забывайте про творческое задание предыдущей недели («Один день из жизни…»), с которым пока что мало кто справился!
Тему дневников продолжит романтичный «Дневник памяти» и завораживающая песня Лары Фабиан “You are not from here”:
марафон, отчаянные домохозяйки, дневник, творчество, оптимизм, пессимизм, реализм, эмоциональный баланс, эмпатия, новый взгляд
Умножение отрицаний — знаки, примеры, правила, решенные примеры и часто задаваемые вопросы
Дата последнего обновления: 21 апреля 2023 г. 6.11k
6.11k
Числа меньше нуля называются отрицательными числами. Числа выше нуля являются положительными числами. Существуют правила сложения, вычитания, умножения или деления положительных и отрицательных чисел.
Учащиеся могут загрузить PDF-файл «Умножение отрицаний — знаки, примеры, правила, решенные примеры и часто задаваемые вопросы» с веб-сайта Vedantu. Любой желающий может бесплатно загрузить PDF-файл «Умножение отрицаний — знаки, примеры, правила, решенные примеры и часто задаваемые вопросы» с веб-сайта. Умножение отрицаний — очень важная тема математики, по которой на экзаменах задают много вопросов. Правильное понимание темы необходимо для студентов, чтобы получить хорошие оценки на экзаменах. Эта тема важна для конкурсных экзаменов, таких как IIT и NEET. Таким образом, студенты должны приложить надлежащие усилия при изучении темы. Преподавательский состав Веданту, имеющий большой опыт обучения студентов, подготовил PDF-файл «Умножение отрицаний — знаки, примеры, правила, примеры решения и часто задаваемые вопросы».
Учащиеся могут использовать PDF-файл «Умножение отрицаний — знаки, примеры, правила, решенные примеры и часто задаваемые вопросы» для многих целей. Они могут использовать его для проверки перед экзаменами или для изучения темы.
Таким образом, учащиеся могут получить много преимуществ, загрузив PDF-файл «Умножение отрицаний — знаки, примеры, правила, решенные примеры и часто задаваемые вопросы».
Некоторые из тем, которые были объяснены в PDF-файле «Умножение отрицаний — знаки, примеры, правила, решенные примеры и часто задаваемые вопросы», следующие:
Знаки
Правила умножения отрицательных чисел
Деление отрицательных чисел
Что происходит, когда мы умножаем складывать негативы с матрицами?
Знаки
Мы знаем, что «+» — положительный знак, «-» — отрицательный. Когда знак не обозначается перед числом, это обычно означает, что оно положительное.
Когда знак не обозначается перед числом, это обычно означает, что оно положительное.
Пример: 8 на самом деле +8
Примечание: Чтобы избежать путаницы со знаками, мы можем поставить () вокруг цифр. Например, 5 × −8 можно записать как 5 × (−8)
Правила умножения отрицательных чисел
Мы можем иметь положительные и отрицательные целые значения при работе с целыми числами при умножении. Существуют правила умножения и деления целых чисел, которые очень похожи на правила сложения и вычитания.
Если знаки разные, то ответ отрицательный.
Если знаки совпадают, ответ положительный.
См. описание ниже для лучшего понимания.
(Изображение будет загружено в ближайшее время)
Плюс Times Plus is Plus
Пример: 2 × 5 = 10
(Мы уже обсуждали, что когда число не имеет знака, это обычно означает, что оно положительное. )
)
(Изображение будет загружено в ближайшее время)
Минус Умножить Минус на Плюс
Пример: (-10) × (-5) = 50
Отрицательное, умноженное на Отрицательное, является положительным числом, что означает, что произведение двух отрицательных целых чисел всегда положительный.
(Изображение скоро будет загружено)
Плюс, умноженный на минус, равно минус
Пример: 5 x (-5) = — 25
Умножение отрицательных чисел на положительное число всегда дает отрицательное число.
(Изображение будет загружено в ближайшее время)
Минус Умножить Плюс на Минус
Примечание: Эти правила работают так же, как правила деления целых чисел; вам просто нужно заменить «раз» на «делится на».
Деление отрицательных чисел
Деление отрицательных чисел работает так же, как и деление положительных чисел, за исключением того, что результаты иногда бывают отрицательными. От двух чисел, участвующих в этом делении, зависит, будет ли ответ отрицательным. Ответ также будет отрицательным, если только одно из чисел отрицательное. Результат будет положительным, если оба числа отрицательны. 9
От двух чисел, участвующих в этом делении, зависит, будет ли ответ отрицательным. Ответ также будет отрицательным, если только одно из чисел отрицательное. Результат будет положительным, если оба числа отрицательны. 9
Частное
Пример 9 0003
Положительный ÷ Положительный
Положительный
25 ÷ 5 = + 5
Отрицательный ÷ Отрицательный
Положительный
— 25 ÷ — 5 = +5
Отрицательный ÷ Положительный
Отрицательный
-25 ÷ 5 = -5
Положительный ÷ Отрицательный
Отрицательный
25 ÷ -5 = — 5
Что происходит, когда мы Умножать негативы с помощью матриц?
Целочисленная матрица — это матрица, все элементы которой являются целыми элементами. Отрицательное значение матрицы получается путем ее умножения на -1.
Отрицательное значение матрицы получается путем ее умножения на -1.
Итак, если A — заданная матрица
Тогда − A = − 1 A
Решенные примеры
1. Что такое −6 × 3?
Ответ: 6 х 3 равно 18. Но здесь у нас есть одно отрицательное и одно положительное число. Следовательно, знак ответа будет минус.
Следовательно, ответ равен −18.
2. Что такое −80 ÷ 8?
Ответ: 80 ÷ 8 равно 10. Опять же, у нас есть положительное и отрицательное число. Следовательно, в окончательном ответе знак будет отрицательным.
Следовательно, ответ равен −10.
3. Что такое −50 x −5?
Ответ: 50 x 5 равно 250. На этот раз у нас есть 2 отрицательных числа. Значит, в ответе будет положительный знак. Следовательно, ответ равен 250.
Заключение
Помните только 2 вещи, когда перемножаете отрицательные числа.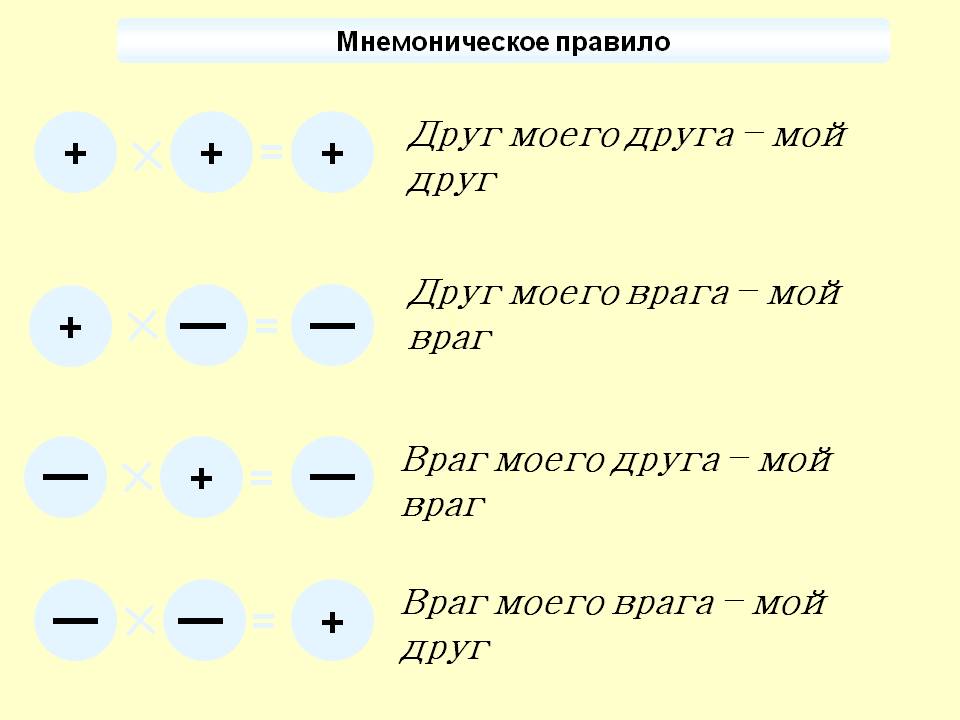
Почему студенты должны присоединиться к Веданту?
Учащиеся могут посещать онлайн-занятия для сдачи школьного экзамена или конкурсных экзаменов, таких как NEET или JEE. Они могут посещать занятия, не выходя из дома. Им просто нужно иметь работающее подключение к Интернету и устройство, такое как ноутбук, планшет или смартфон. У них также есть возможность скачать классы, чтобы просмотреть их позже для повторения. Студенты могут получить доступ к этим классам по очень доступным ценам, что делает их доступными для многих студентов.
На веб-сайте есть обширный банк вопросов с вопросами, основанными на шаблоне экзаменов, к которым они готовятся. Помимо этого, студенты могут получить доступ к другим ресурсам, таким как заметки о пересмотре, решения NCERT, решения для других книг, образцы документов, PYQ и онлайн-тесты.
Таким образом, присоединение к Веданту будет очень полезно для студентов.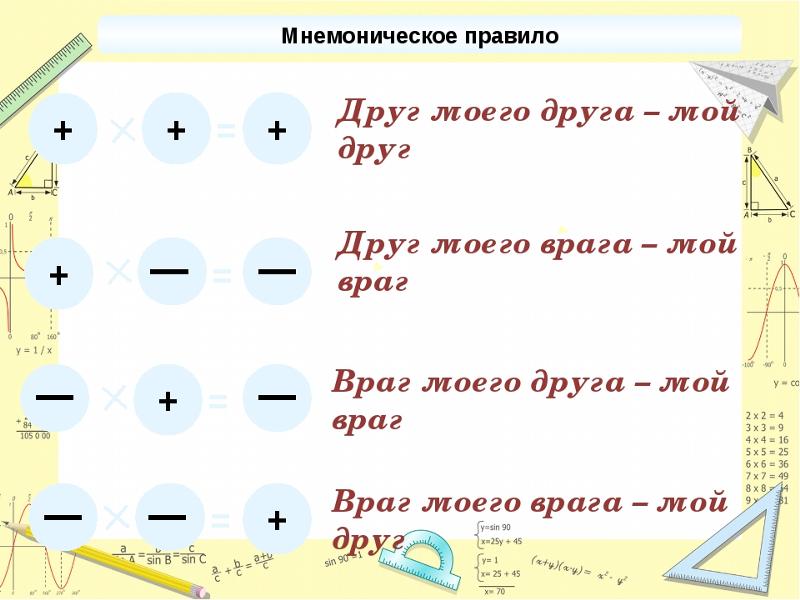
Минус, умноженный на минус, будет плюсом
Я видел несколько недавних сообщений, в которых задавались вопросом об интуитивном объяснении того факта, что «минус, умноженный на минус, равен плюсу». Я понимаю, почему люди задаются этим вопросом — как часто учат, это кажется просто произвольным правилом без «почему»! Но на самом деле это вполне логично.
Пол с сайта crossedstreams.com дает объяснение, включающее две величины с реальными интерпретациями, связанными с отрицательными значениями: чистая стоимость (отрицательное значение означает уменьшение чистой стоимости) и время (прошлое отрицательное). Это довольно интуитивно понятно, но в каком-то смысле оно только показывает , почему это хорошо , что минус, умноженный на минус, является плюсом, поскольку это позволяет нам смоделировать эту реальную ситуацию; это на самом деле не показывает , почему это правда в глубоком смысле. Майк из Walking Randomly приводит доказательство, в основном основанное на аксиомах поля, но (как он сам признает) оно не особенно интуитивно понятно.
Вот как бы я это объяснил. Это совсем не строго, и я даже не полностью удовлетворен этим, но я надеюсь, что это поможет развить некоторую интуицию.
Подумайте о знакомой «числовой прямой»: положительные числа отходят вправо, а отрицательные — влево. Добавление положительного числа соответствует перемещению вправо по числовой прямой. Прибавление отрицательного числа (то есть вычитание положительного) соответствует перемещению влево по числовой прямой. Таким образом, с добавлением мы уже видим эту идею негатива, соответствующую действию «в противоположном направлении».
Итак, чему соответствует умножение на числовой прямой? Конечно, умножение соответствует масштабированию или растяжению: например, если мы начнем с точки на числовой прямой и умножим на 3, мы окажемся в точке, которая в три раза дальше от нуля, чем мы начали. А как насчет умножения на отрицательное число? Это соответствует шкале в другом направлении : например, если мы начнем с точки на числовой прямой и умножим на -3, мы закончим в точке на другая сторона нуля, и в три раза дальше. То есть умножение на отрицательное число означает, что мы переворачиваем с одной стороны нуля на другую. Итак, конечно, если мы начнем с левых нулевых (отрицательное число) и умножим на отрицательное, мы получим правых нулевых (положительное число)!
То есть умножение на отрицательное число означает, что мы переворачиваем с одной стороны нуля на другую. Итак, конечно, если мы начнем с левых нулевых (отрицательное число) и умножим на отрицательное, мы получим правых нулевых (положительное число)!
[Впрочем, я думаю, что попытка объяснить это более глубоко, чем это, действительно требует некоторого введения распределительного свойства — это единственное, что формально связывает сложение (помните, что отрицательные числа определяются как сложение обратное) и умножение. Мне очень нравится идея, опубликованная Эриком в качестве комментария к сообщению Майка относительно иллюстрации дистрибутивной собственности.
Кроме того, я хотел разместить в этом посте красивые картинки, но сейчас, если я подожду, чтобы сделать красивые картинки, этого никогда не произойдет. Так что я просто опубликую это сейчас, и, возможно, я вернусь и добавлю несколько фотографий позже.]
Нравится:
Нравится Загрузка.




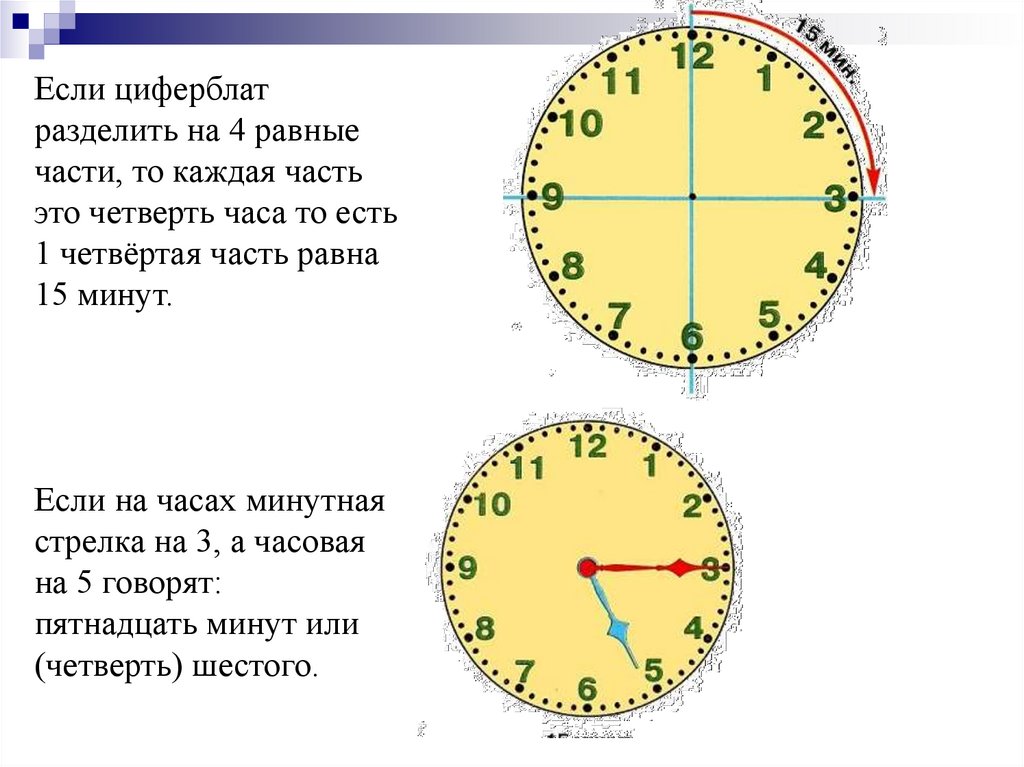

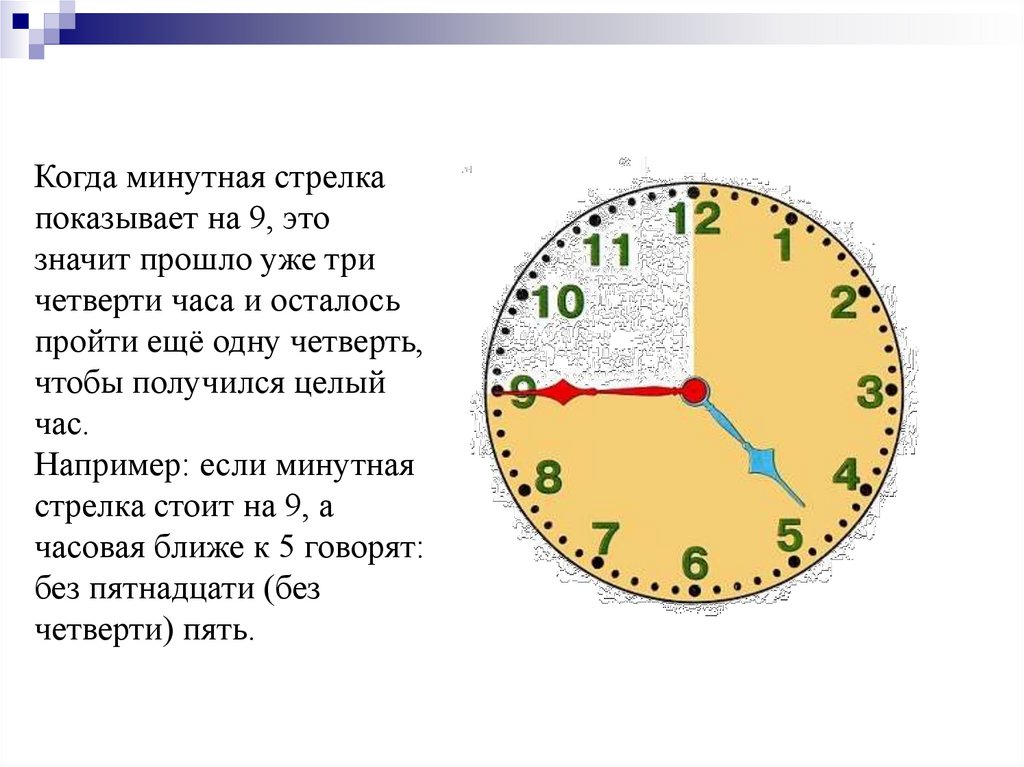




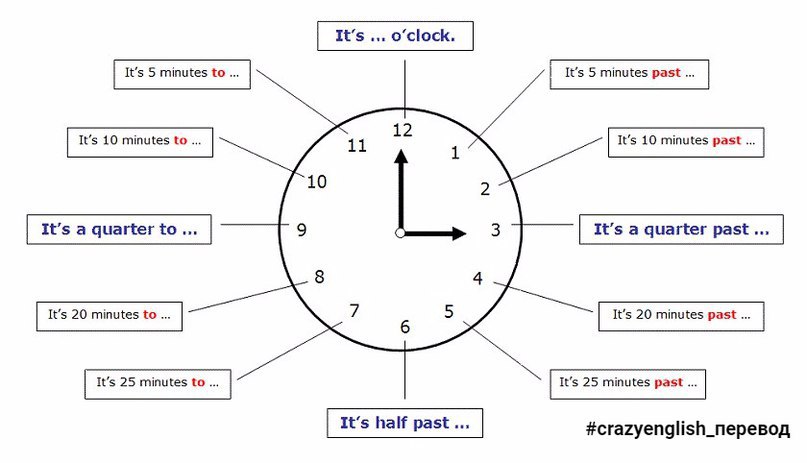
 Без четверти пять утра.Без четверти четыре часа.С пяти до девяти вечера.Без десяти восемь утра.Без двадцати трех утра. Часы утра. С десяти до шести вечера. Половина девятого вечера. Пять минут третьего. Половина первого ночи. Сейчас четверть первого. Без четверти пять утра. Без четверти четыре часа. С пяти до девяти вечера. утра Без двадцати три утра
Без четверти пять утра.Без четверти четыре часа.С пяти до девяти вечера.Без десяти восемь утра.Без двадцати трех утра. Часы утра. С десяти до шести вечера. Половина девятого вечера. Пять минут третьего. Половина первого ночи. Сейчас четверть первого. Без четверти пять утра. Без четверти четыре часа. С пяти до девяти вечера. утра Без двадцати три утра Половина первого ночи. Сейчас четверть первого. Без четверти пять утра. Без четверти четыре часа. С пяти до девяти вечера. утра Без двадцати три утра
Половина первого ночи. Сейчас четверть первого. Без четверти пять утра. Без четверти четыре часа. С пяти до девяти вечера. утра Без двадцати три утра

 Наступило время вызовов и вместе с тем больших возможностей»
Наступило время вызовов и вместе с тем больших возможностей»
 Ни один из трудов или записей Мадхавы не сохранился до наших дней. Другие математики основывали свои работы на открытиях Мадхавы и продолжали работать с этими рядами вплоть до 1500-х годов.
Ни один из трудов или записей Мадхавы не сохранился до наших дней. Другие математики основывали свои работы на открытиях Мадхавы и продолжали работать с этими рядами вплоть до 1500-х годов. {5}}{15}}+\cdots {\text{ for }}|x|<{\frac {\pi }{2}}\! }
{5}}{15}}+\cdots {\text{ for }}|x|<{\frac {\pi }{2}}\! } Поэтому при подстановке также возникает повторение:
Поэтому при подстановке также возникает повторение: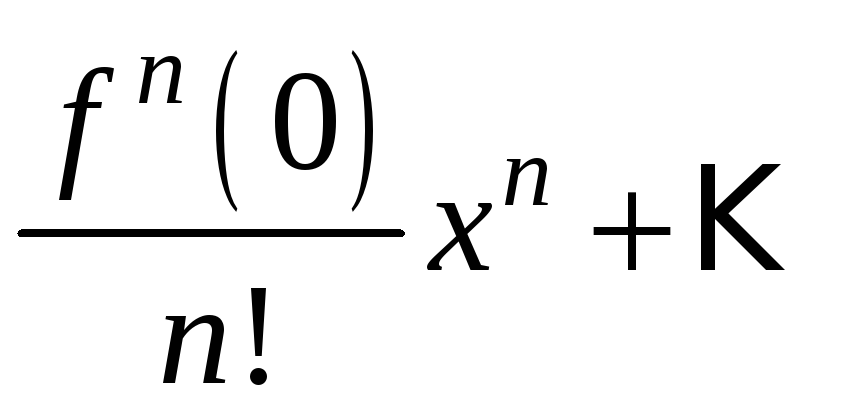 Вычислите значения этих производных при и коэффициенты Тейлора. Покажите, что имеет место разложение
Вычислите значения этих производных при и коэффициенты Тейлора. Покажите, что имеет место разложение Так что её искомое разложение найдено.
Так что её искомое разложение найдено. 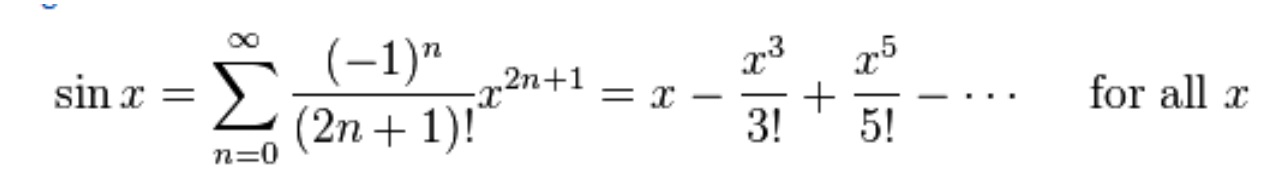
 время()
В = 0
для я в диапазоне (с):
коэффициент = (-1)**i
число = десятичное число (R) ** (2 * i)
denom = math.factorial(2*i)
V = V + (коэффициент) * ((число) / (номинал))
печать(В)
конец = время.время()
print("Время выполнения \n", конец - начало)
# Печатает с точностью до 16 цифр
# print(math.sqrt(1)/2)
n = int(input("Введите положительное целое число, чтобы получить количество циклов для вычисления cos80\n"))
х = Десятичный (2).sqrt ()
начало = время.время()
для я в диапазоне (n):
х = десятичный (2 + х).sqrt()
х = десятичный (2 + х).sqrt()
х = десятичное число (2 - х).sqrt()
печать (x/2)
конец = время.время()
print("Время выполнения \n", конец - начало)
время()
В = 0
для я в диапазоне (с):
коэффициент = (-1)**i
число = десятичное число (R) ** (2 * i)
denom = math.factorial(2*i)
V = V + (коэффициент) * ((число) / (номинал))
печать(В)
конец = время.время()
print("Время выполнения \n", конец - начало)
# Печатает с точностью до 16 цифр
# print(math.sqrt(1)/2)
n = int(input("Введите положительное целое число, чтобы получить количество циклов для вычисления cos80\n"))
х = Десятичный (2).sqrt ()
начало = время.время()
для я в диапазоне (n):
х = десятичный (2 + х).sqrt()
х = десятичный (2 + х).sqrt()
х = десятичное число (2 - х).sqrt()
печать (x/2)
конец = время.время()
print("Время выполнения \n", конец - начало)

 Не забывайте, что вы играете с виртуальным интеллектом компьютера и постарайтесь обхитрить все его планы. На правой стороне находиться игровая консоль, на которой вы сможете вернуть поспешно сделанный ход, начать игру заново, сохранить матч и продолжить его позже и даже сменить вид игровых фигур и шахматной доски. Желаем вам приятного времяпровождения в игре «Шахматы с Компьютером» и легких побед.
Не забывайте, что вы играете с виртуальным интеллектом компьютера и постарайтесь обхитрить все его планы. На правой стороне находиться игровая консоль, на которой вы сможете вернуть поспешно сделанный ход, начать игру заново, сохранить матч и продолжить его позже и даже сменить вид игровых фигур и шахматной доски. Желаем вам приятного времяпровождения в игре «Шахматы с Компьютером» и легких побед.

 Само слово шахматы происходит из двух персидских слов шах и мат. Игра происходит на доске, поделенной на равные поля. Размер доски — 8х8 клеток. Вертикальные ряды полей обозначаются латинскими буквами от a до h слева направо, горизонтальные ряды — цифрами от 1 до 8 снизу вверх; каждое поле обозначается сочетанием соответствующих буквы и цифры. Доска располагается так, чтобы ближнее угловое поле справа от игрока было белым. Шахматную партию начинают белые, дальше стороны делают поочерёдные ходы, каждым ходом перемещая одну фигуру. Ход на поле, занятое своей фигурой, невозможен. При ходе на поле, занятое чужой фигурой, она снимается с доски. При рокировке король сдвигается на 2 клетки по направлению к ладье, а ладья ставится на поле между начальной и конечной позицией короля. Этапы шахматной партии: дебют, миттельшпиль и эндшпиль.
Само слово шахматы происходит из двух персидских слов шах и мат. Игра происходит на доске, поделенной на равные поля. Размер доски — 8х8 клеток. Вертикальные ряды полей обозначаются латинскими буквами от a до h слева направо, горизонтальные ряды — цифрами от 1 до 8 снизу вверх; каждое поле обозначается сочетанием соответствующих буквы и цифры. Доска располагается так, чтобы ближнее угловое поле справа от игрока было белым. Шахматную партию начинают белые, дальше стороны делают поочерёдные ходы, каждым ходом перемещая одну фигуру. Ход на поле, занятое своей фигурой, невозможен. При ходе на поле, занятое чужой фигурой, она снимается с доски. При рокировке король сдвигается на 2 клетки по направлению к ладье, а ладья ставится на поле между начальной и конечной позицией короля. Этапы шахматной партии: дебют, миттельшпиль и эндшпиль.

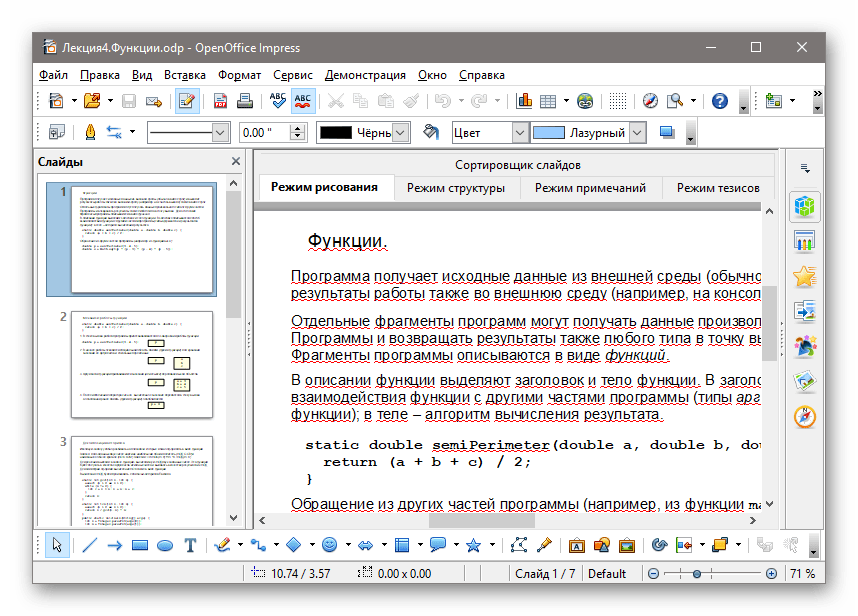 Мы поддерживаем все новейшие браузеры, такие как Chrome, Safari, Opera, Firefox, Edge и Tor.
Мы поддерживаем все новейшие браузеры, такие как Chrome, Safari, Opera, Firefox, Edge и Tor. Если вы являетесь зарегистрированным пользователем, вы можете щелкнуть значок общего доступа справа от элемента документа в сетке списка документов и создать ссылку для общего доступа.
Если вы являетесь зарегистрированным пользователем, вы можете щелкнуть значок общего доступа справа от элемента документа в сетке списка документов и создать ссылку для общего доступа. Выберите файлы для конвертации.
Выберите файлы для конвертации. Ваши данные. Вы в контроле.
Ваши данные. Вы в контроле. ODP используется файлами Open Document Presentation, созданных с помощью программного пакета OpenOffice. Формат Open Document является основой XM и, следовательно, легко переносимым.
ODP используется файлами Open Document Presentation, созданных с помощью программного пакета OpenOffice. Формат Open Document является основой XM и, следовательно, легко переносимым. oasis.opendocument.presentation
oasis.opendocument.presentation
 ms-powerpoint
ms-powerpoint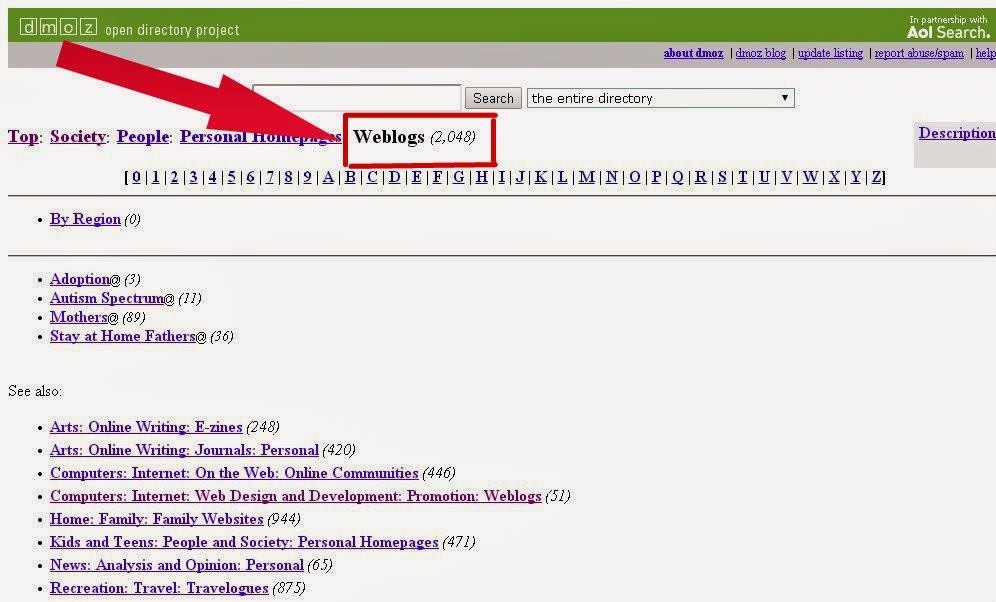 Выберите файлы для преобразования
Выберите файлы для преобразования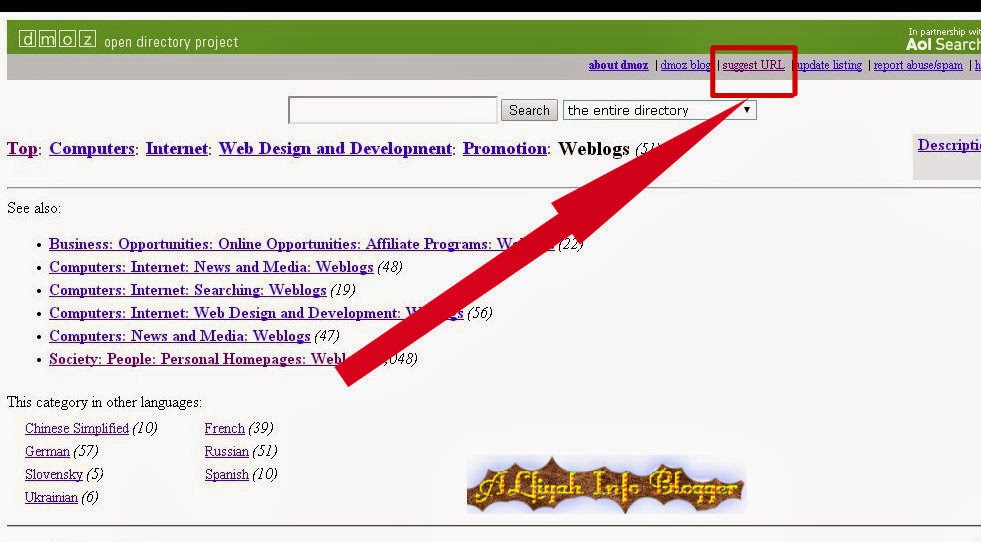 Мы обеспечиваем безопасность ваших файлов и данных и предлагаем выбор и контроль над удалением файлов.
Мы обеспечиваем безопасность ваших файлов и данных и предлагаем выбор и контроль над удалением файлов. Файлы ODP можно открывать в Windows и можно открывать практически любым программным обеспечением на основе презентаций, включая Microsoft PowerPoint. Файлы ODP являются одними из многих файлов в стиле Office с открытым исходным кодом и невероятно популярны, потому что они бесплатны и легко доступны, но при этом включают большую часть популярных функций, которые поставляются с альтернативой Microsoft или Apple.
Файлы ODP можно открывать в Windows и можно открывать практически любым программным обеспечением на основе презентаций, включая Microsoft PowerPoint. Файлы ODP являются одними из многих файлов в стиле Office с открытым исходным кодом и невероятно популярны, потому что они бесплатны и легко доступны, но при этом включают большую часть популярных функций, которые поставляются с альтернативой Microsoft или Apple.
 org. Это файл презентации с открытым исходным кодом на основе XML, который поддерживает несколько вариантов текстового формата. Он также может содержать изображения, тексты, простые анимации и т. д. Все содержимое файлов ODP сжато и заархивировано.
org. Это файл презентации с открытым исходным кодом на основе XML, который поддерживает несколько вариантов текстового формата. Он также может содержать изображения, тексты, простые анимации и т. д. Все содержимое файлов ODP сжато и заархивировано. Мы поддерживаем почти все аудио, видео,
форматы документов, электронных книг, архивов, изображений, электронных таблиц и презентаций. Кроме того, вы можете использовать наш онлайн
инструмент без загрузки какого-либо программного обеспечения.
Мы поддерживаем почти все аудио, видео,
форматы документов, электронных книг, архивов, изображений, электронных таблиц и презентаций. Кроме того, вы можете использовать наш онлайн
инструмент без загрузки какого-либо программного обеспечения.




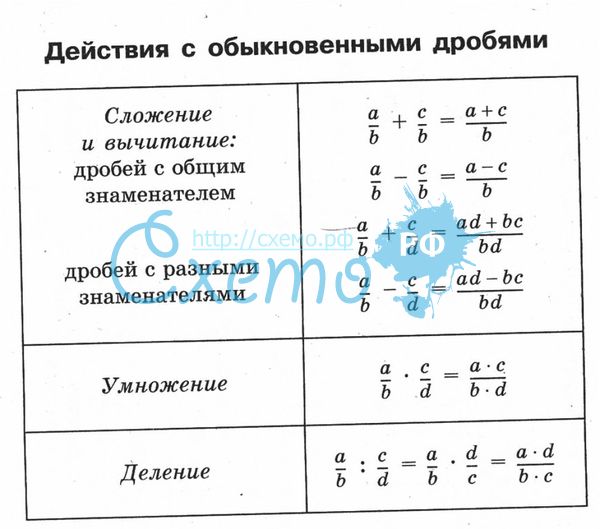
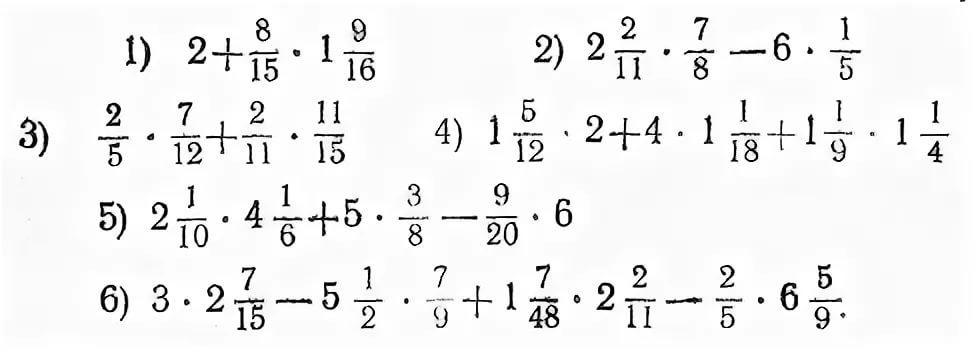 В этой статье мы рассмотрим, как складывать, вычитать, умножать и делить две дроби, а также дробь и целое число. Мы также введем сложные дроби вместе с методами их упрощения. Прежде чем продолжить, убедитесь, что вы полностью понимаете четыре основных математических операции: сложение, вычитание, умножение и деление.
В этой статье мы рассмотрим, как складывать, вычитать, умножать и делить две дроби, а также дробь и целое число. Мы также введем сложные дроби вместе с методами их упрощения. Прежде чем продолжить, убедитесь, что вы полностью понимаете четыре основных математических операции: сложение, вычитание, умножение и деление. Например, добавление одной трети и одной трети, очевидно, дает нам две трети. Точно так же три пятых минус две пятых — это одна пятая. Первый случай проиллюстрирован ниже.
Например, добавление одной трети и одной трети, очевидно, дает нам две трети. Точно так же три пятых минус две пятых — это одна пятая. Первый случай проиллюстрирован ниже. Хотя этот подход концептуально прост, он может быть математически сложным, когда знаменатели велики. Тем не менее, давайте попробуем этот подход для иллюстрации. Обратите внимание на упомянутое выше дополнение.
Хотя этот подход концептуально прост, он может быть математически сложным, когда знаменатели велики. Тем не менее, давайте попробуем этот подход для иллюстрации. Обратите внимание на упомянутое выше дополнение. Общий знаменатель: 45
Общий знаменатель: 45 б. в.
б. в.
 б. г.
б. г.
 Поскольку знаменатель становится равным 1, результатом является просто значение числителя.
Поскольку знаменатель становится равным 1, результатом является просто значение числителя.

 .. И то же самое для суммы вычитания, за исключением того, что вместо этого вы вычитаете числители:
.. И то же самое для суммы вычитания, за исключением того, что вместо этого вы вычитаете числители:
 20/32 можно упростить до 5/8. Намного лучше!
20/32 можно упростить до 5/8. Намного лучше!

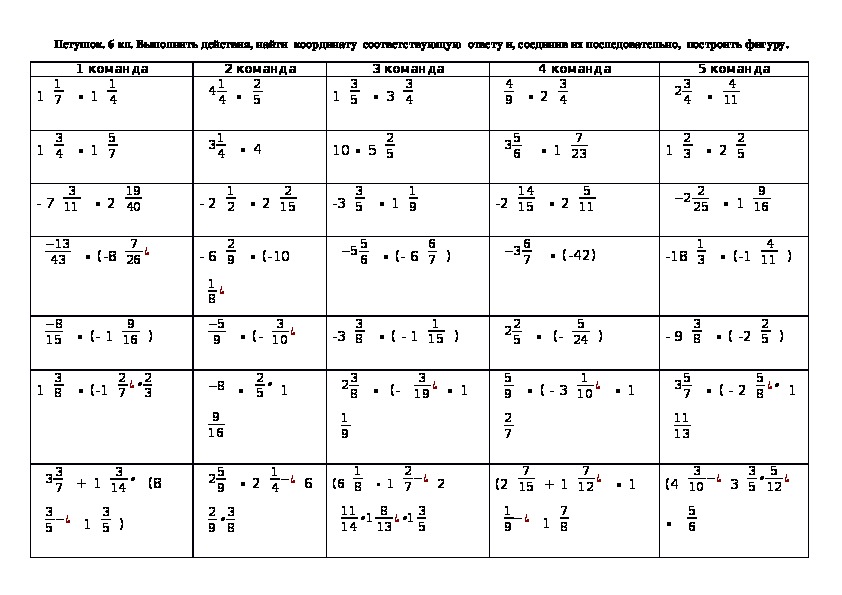
 2. Арифметические действия с переменными, имеющими предел
2. Арифметические действия с переменными, имеющими предел Дифференциальное исчисление функций одной переменной
Дифференциальное исчисление функций одной переменной Точка перегиба
Точка перегиба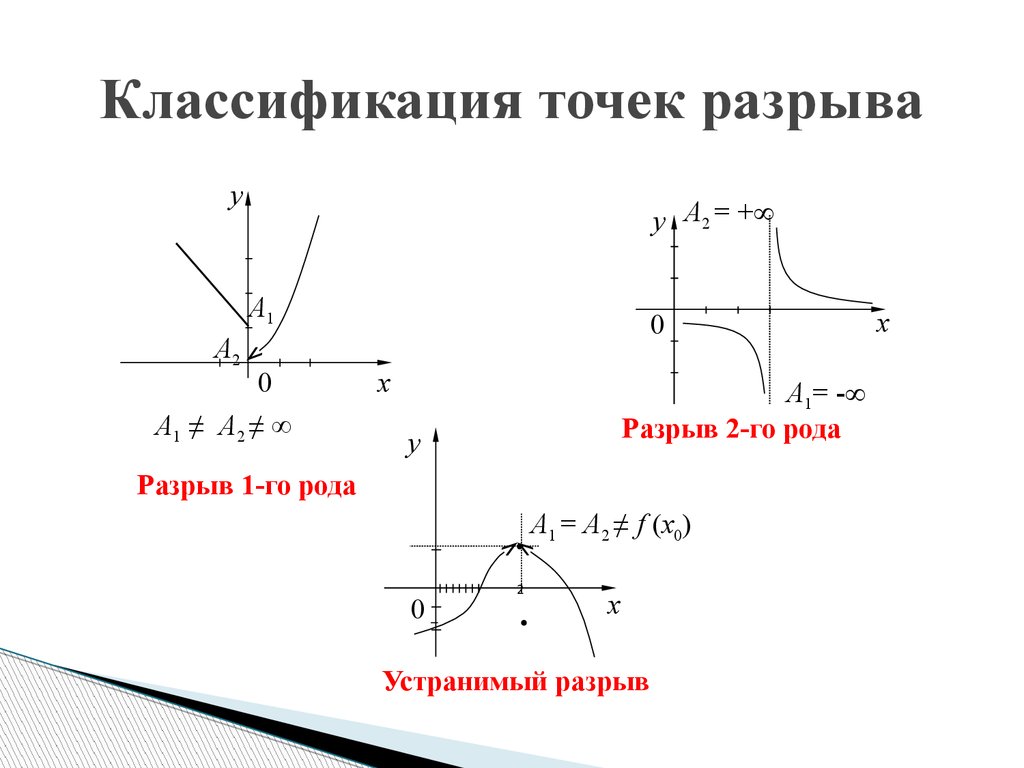 9. Несобственные интегралы от неотрицательных функций
9. Несобственные интегралы от неотрицательных функций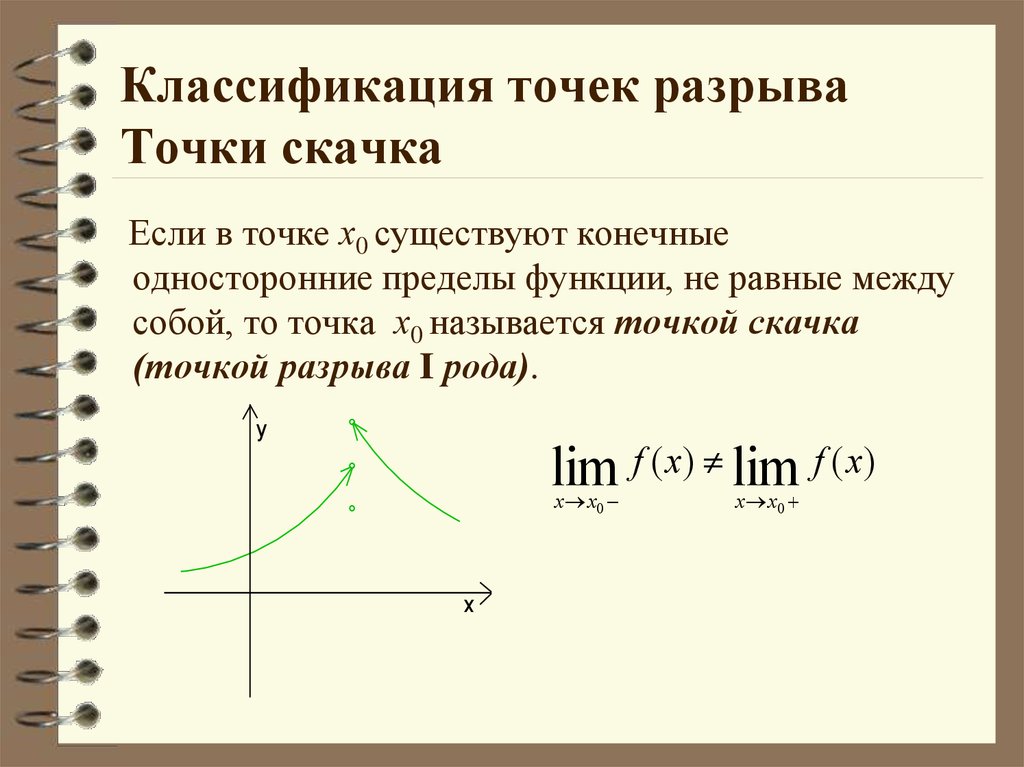 8. Производная сложной функции. Производная по направлению. Градиент
8. Производная сложной функции. Производная по направлению. Градиент Равномерная сходимость
Равномерная сходимость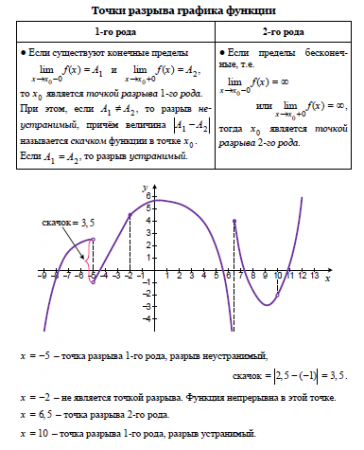
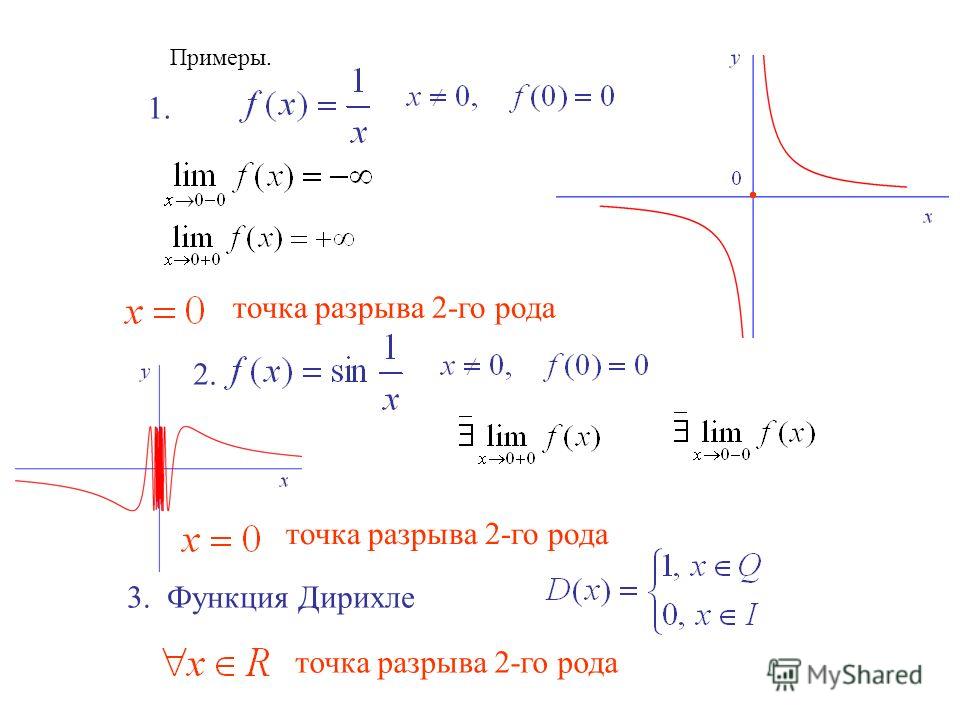
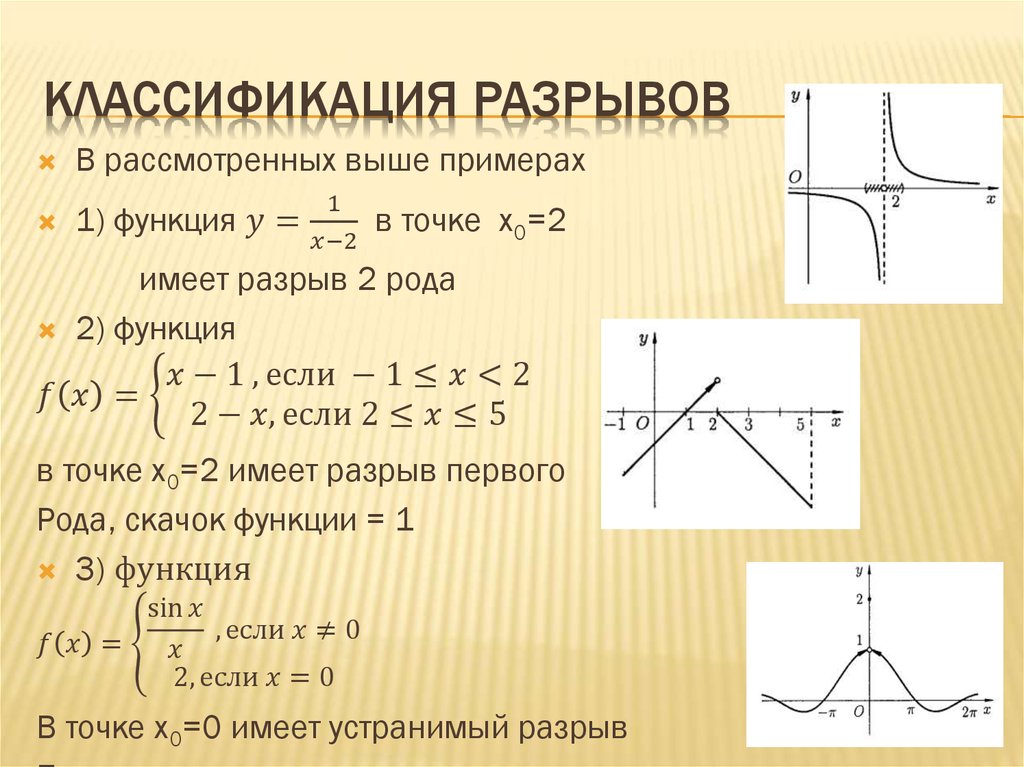 Достаточно лишь иметь возможность измерять расстояния. Множества, на которых указан способ измерять расстояния, называются метрическими пространствами. Отображение метрического пространства (X,ρX) в метрическое пространство (Y,ρY) называется непрерывным в точке a, если
Достаточно лишь иметь возможность измерять расстояния. Множества, на которых указан способ измерять расстояния, называются метрическими пространствами. Отображение метрического пространства (X,ρX) в метрическое пространство (Y,ρY) называется непрерывным в точке a, если Положив можно добиться непрерывности функции в этой точке. Такое изменение значения функции в точке, превращающее функцию в непрерывную в этой точке, называется доопределением по непрерывности.
Положив можно добиться непрерывности функции в этой точке. Такое изменение значения функции в точке, превращающее функцию в непрерывную в этой точке, называется доопределением по непрерывности.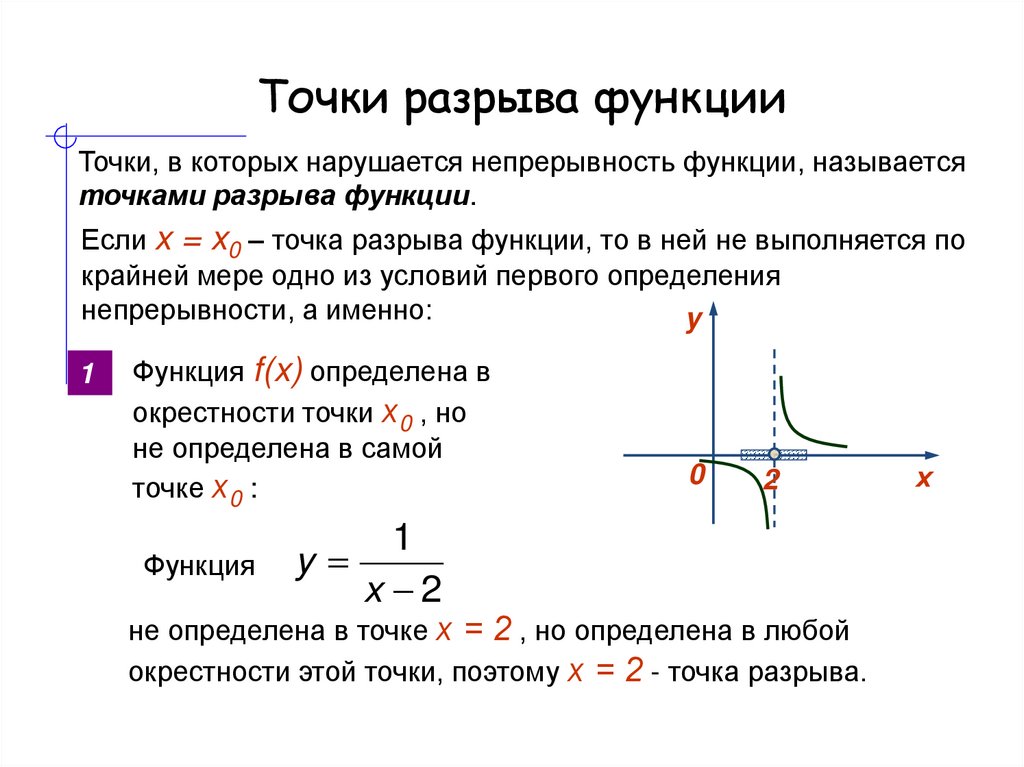 Пусть Тогда существует окрестность U(a) такая, что
Пусть Тогда существует окрестность U(a) такая, что
 Различают четыре степени разрывов промежности. Они оцениваются по степени тяжести разрыва, причем разрыв четвертой степени является худшим. Эпизиотомия может быть сделана, чтобы помочь контролировать слезотечение.
Различают четыре степени разрывов промежности. Они оцениваются по степени тяжести разрыва, причем разрыв четвертой степени является худшим. Эпизиотомия может быть сделана, чтобы помочь контролировать слезотечение. Это может быть сделано, чтобы уменьшить количество крови, которую вы теряете из-за сильного разрыва, или если вашему ребенку нужно быстро родить.
Это может быть сделано, чтобы уменьшить количество крови, которую вы теряете из-за сильного разрыва, или если вашему ребенку нужно быстро родить.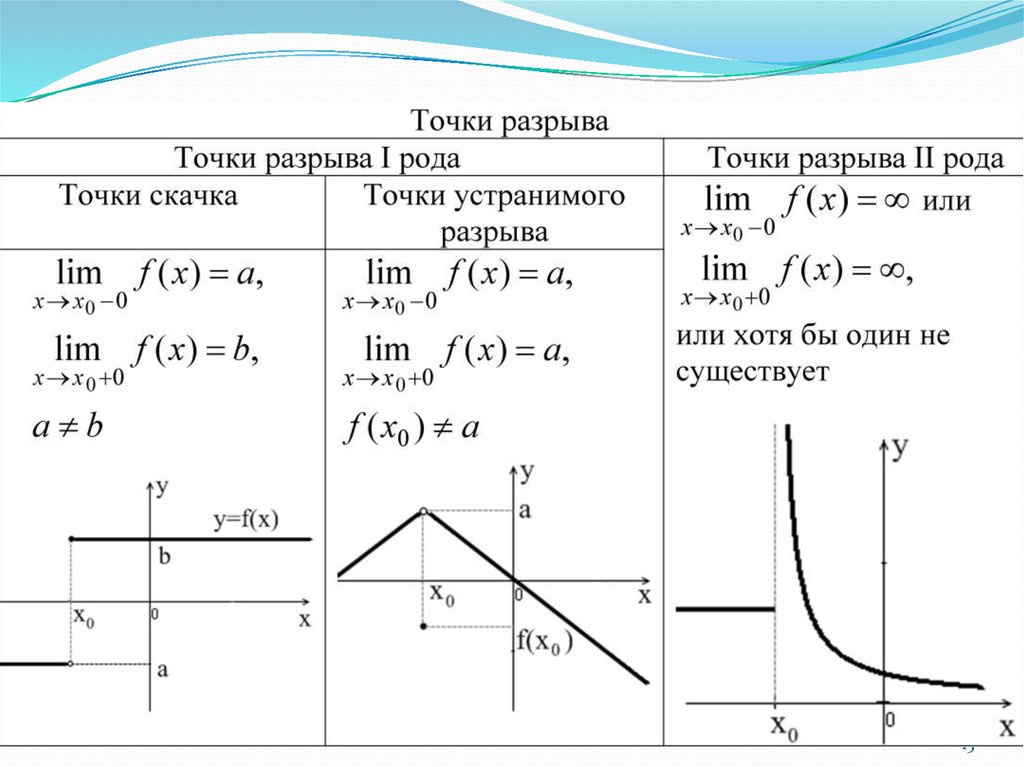 Разрыв второй степени обычно требует наложения швов и обычно заживает в течение нескольких недель.
Разрыв второй степени обычно требует наложения швов и обычно заживает в течение нескольких недель.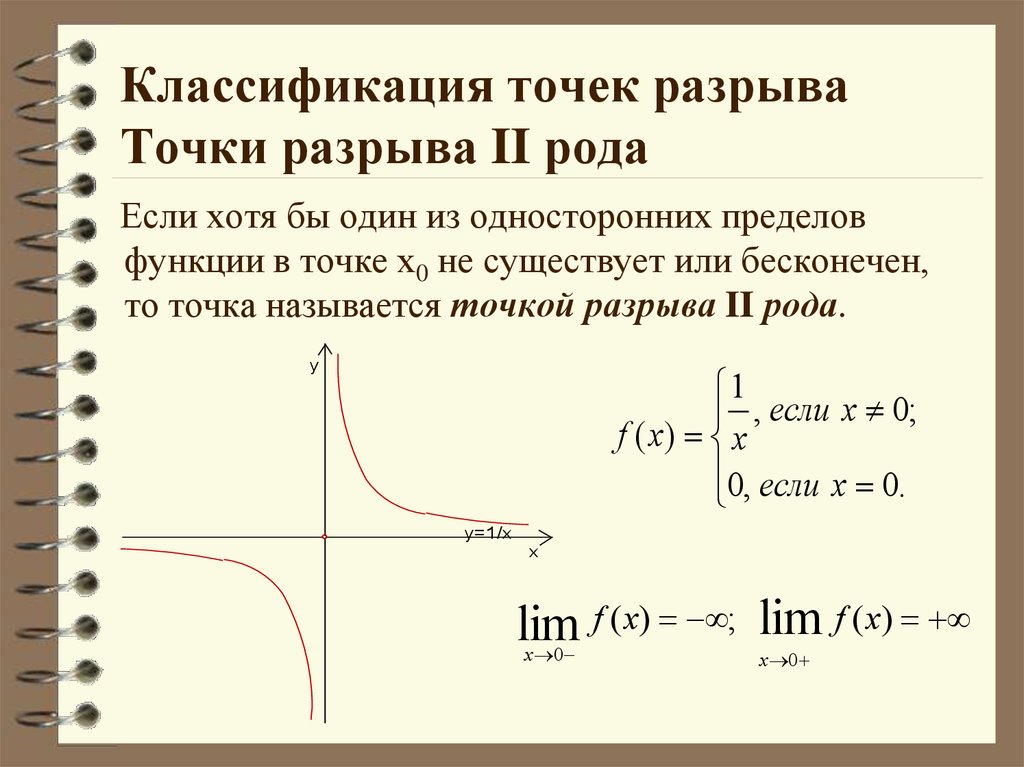 Разрыв первой степени может не потребовать наложения швов, но более серьезные разрывы промежности потребуют. Если вам нужно наложить швы для устранения разрыва промежности, эти швы рассосутся сами по себе в течение шести недель.
Разрыв первой степени может не потребовать наложения швов, но более серьезные разрывы промежности потребуют. Если вам нужно наложить швы для устранения разрыва промежности, эти швы рассосутся сами по себе в течение шести недель. В большинстве случаев эти оболочки разрываются во время родов или в течение 24 часов до начала родов. Говорят, что преждевременный разрыв плодных оболочек (PROM) происходит, когда плодные оболочки разрываются до 37-й недели беременности.
В большинстве случаев эти оболочки разрываются во время родов или в течение 24 часов до начала родов. Говорят, что преждевременный разрыв плодных оболочек (PROM) происходит, когда плодные оболочки разрываются до 37-й недели беременности. Некоторыми причинами или факторами риска могут быть:
Некоторыми причинами или факторами риска могут быть:

 Если в месте, где вы рожаете, нет отделения для недоношенных, вас и вашего ребенка переведут в больницу, где оно есть.
Если в месте, где вы рожаете, нет отделения для недоношенных, вас и вашего ребенка переведут в больницу, где оно есть.
 После этого она разрезала в некотором месте
После этого она разрезала в некотором месте



 Проще говоря, мы можем сказать, что квадратный корень — это процесс, обратный квадрату числа. Итак, здесь, чтобы найти квадратный корень из 4, нам нужно найти число, квадрат которого равен 4.
Проще говоря, мы можем сказать, что квадратный корень — это процесс, обратный квадрату числа. Итак, здесь, чтобы найти квадратный корень из 4, нам нужно найти число, квадрат которого равен 4.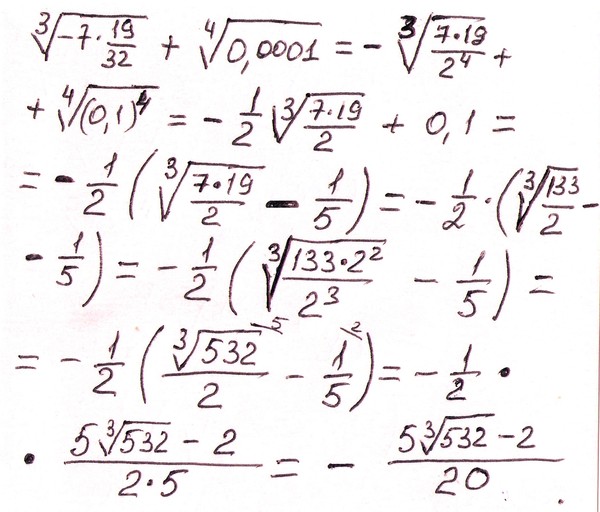



 14159..
14159.. ВОКАЛЬНЫЕ ЖАНРЫ:
ВОКАЛЬНЫЕ ЖАНРЫ: x+1 y(0)=2; y'(0)=1.
x+1 y(0)=2; y'(0)=1. Решение квадратных неравенств
Решение квадратных неравенств Кто упадёт первым?
Кто упадёт первым?