Синус и косинус
Я решил, что не будем слишком долго разжевывать теоретическую часть введения в тригонометрию так, как в любом случае мало кто ее будет читать и уж тем более маловероятно, что он там все поймет. Я считаю, что лучший способ изучения математики — это не зубрежка, а работа с конкретными примерами и чем больше тем лучше. Поэтому я решил опустить несколько скучных лекций и приступить сразу к главному.
Определение синуса и косинуса
Итак, в первую очередь, начнем с определения.
Во-первых построим числовую окружность и отметим на ней некоторые точки:
Если точка М числовой единичной окружности соответствует числу t, то абсциссу точки М называют косинусом числа и обозначают , а ординату точки М называют синусом числа и обозначают .
Итак, судя по нашему рисунку мы видим, что
если , то
Отсюда следует, что
Вспомним, что каждая точка числовой окружности имеет в системе свои координаты, причем для точек:
- первой четверти:
- второй четверти
- третьей четверти:
- четвертой четверти:
Это нам с вами поможет составить таблицу знаков синуса и косинуса по четвертям окружности:
| I | II | III | IV | |
| синус | + | + | – | – |
| косинус | + | – | – | + |
В дальнейшем эту таблицу мы с вами продолжим, а также разберемся в каких случаях она применяется.
Основное тригонометрическое тождество
Надеюсь, все вы помните, что уравнение числовой окружности имеет вид:
Тем самым фактически мы можем получить важнейшее равенство, связывающее синус и косинус между собой, а именно:
В дальнейшем мы будем называть это равенство основным тригонометрическим тождеством. А если оно «основное», то знать его нужно всем обязательно, в отличие от большинства других формул тригонометрии.
Ну и последнее, что я хочу сказать по теории, это, конечно, таблицы значений синусов и косинусов, с которыми вы, наверное, уже сталкивались, если изучали курс геометрии.
Но для тех, у кого их нет, я выложу основные из значений:
1 часть таблицы (значения от 0 до 180º):
| 0 | |||||||||
| 0º | 30º | 45º | 60º | 90º | 120º | 135º | 150º | 180º | |
| sin t | 0 | 1 | 0 | ||||||
| cos t | 1 | 0 | –1 |
2 часть таблицы (значения до 360º):
| 210º | 225º | 240º | 270º | 300º | 315º | 330º | 360º | |
| sin t | –1 | 0 | ||||||
| cos t | 0 | 1 |
С теорией покончено, давайте решим несколько примеров:
Решение уравнений и неравенств
ПРИМЕР 1 Вычислить и , если
а) ; б) ; в)
Решение
а) В первую очередь смотрим в таблицу значений синуса и косинуса и видим сразу, что такого значения t там нет, но, как вы должны знать, данная таблица составлена по числовой окружности, поэтому 0º = 360º. Т.е. все значения после будут повторяться. Остается лишь найти, в какой четверти находится .
Т.е. все значения после будут повторяться. Остается лишь найти, в какой четверти находится .
Имеем,
Если, кому не понято, то вначале я неправильную дробь перевел в смешанное число, а дальше в принципе все понятно, если целая часть четная — то ее опускаем, т.к. будет (), а если нечетная — то в конце концов останется еще и его будем прибавлять к нашей обыкновенной дроби.
Отсюда следует, что числу соответствует та же точка числовой окружности, что и .
Теперь заглянем в таблицу и видим, что
, а
б) Также переписываем неправильную дробь в виде смешанного числа:
;
-12 — четное число, поэтому забываем про него и значения смотрим по второму слагаемому —. В итоге у нас вышло отрицательное число, а значит, отсчитывать значения мы будет по часовой стрелке, т.е. начиная с четвертой четверти, а не с первой. Отсчитав, видим, что соответствует , (чтобы было понятнее соответствует -60º, а 360º — 60º = 300º, поэтому и смотрим ответ у , значит,
,
в) Здесь все вообще супер — просто. . Как видите, в значении целая часть и причем она четная, а это значит, она будет соответствовать значению . Как видим представленное значение t соответствует значению нуля, т.е.
. Как видите, в значении целая часть и причем она четная, а это значит, она будет соответствовать значению . Как видим представленное значение t соответствует значению нуля, т.е.
.
ПРИМЕР 2 Решить уравнение:
Решение:
Учтем, что sin t — это ордината точки M(t) числовой окружности. Значит, нам нужно найти на числовой окружности точки с ординатой и записать, каким числам t они соответствуют.
В нашем случае, если посмотреть в таблицу мы видим, что данной ординате соответствуют точки и
Следовательно,
Ответ: ;
Как вы, надеюсь, понимаете с косинусом все будет наоборот, вы будете искать значение абсциссы (т.е. в таблице смотреть значения косинуса).
С уравнениями, думаю, все понятно. Перейдем к неравенствам. С ними обстоят дела похоже, но кое-чем отличаются.
ПРИМЕР 3 Решить неравенство
Решение:
Учтем, что cos t — абсцисса точки M(t) числовой окружности. Значит, нам нужно найти на числовой окружности точку с абсциссой и записать, каким числам t они соответствуют. Прямая пересекает числовую окружность в двух точках. Неравенству же соответствуют все точки открытой дуги (т.е. все что находится между этими точками пересечения). Согласно таблице, это точки и . Получается, решением неравенства будут все точки, входящие в данный интервал.
Значит, нам нужно найти на числовой окружности точку с абсциссой и записать, каким числам t они соответствуют. Прямая пересекает числовую окружность в двух точках. Неравенству же соответствуют все точки открытой дуги (т.е. все что находится между этими точками пересечения). Согласно таблице, это точки и . Получается, решением неравенства будут все точки, входящие в данный интервал.
Ответ: .
Завершая в данном уроке разговор о синусе и косинусе хотел бы вам также представить еще несколько важных формул, которые справедливы для любого значения t.
1. sin (-t) = -sin t; cos (-t) = cos t
К примеру,
2. sin (t + 2πk) = sin t; cos (t + 2πk) = cos t
Это очевидно, так как 2π — это период функции, равный одному кругу, а k — это количество таких периодов. И вы, уже должны были понять, что, когда первый круг заканчивается 360º, то все начинается сначала, т.е. 390º будут соответствовать 30º
3. sin (t + π) = -sin t; cos (t + π) = -cos t
Это также очевидно, если вы внимательно изучали таблицу, то заметили, что значения после половины периода π соответствуют другому периоду, но с противоположным знаком.
4. sin (t + = cos t; cos (t + = -sin t
Также, если внимательно изучали таблицу, то и эту закономерность вы должны были заметить.
Ну вот с основными закономерностями таблицы синусов и косинусов мы ознакомились и на этом можно заканчивать.
Всем спасибо, если есть вопросы по теме пишите, обязательно отвечу!!!
Что такое тригонометрическая окружность? | О математике понятно
Итак, друзья, я вас поздравляю! Начальный этап знакомства с тригонометрией благополучно пройден. Подытожим его. Теперь мы с вами:
1. Знаем, что такое синус, косинус, тангенс и котангенс в прямоугольном треугольнике.
2. Знаем, как устроена связь между тригонометрическими функциями одного и того же угла и умеем находить полный набор функций, если известна хотя бы одна из них. Кроме того, ещё мы умеем (надеюсь) пользоваться основными тригонометрическими формулами. А чего? Зря, что ли, примеры разбирали?)
Это — самые азы тригонометрии. Без этих элементарных знаний и навыков — дальше никуда. Так что, прошу прогуляться и почитать, пока не поздно. Тем более там всё очень просто и доступно.)
Без этих элементарных знаний и навыков — дальше никуда. Так что, прошу прогуляться и почитать, пока не поздно. Тем более там всё очень просто и доступно.)
Идём дальше.
Как мы уже с вами знаем, у каждого острого угла в прямоугольном треугольнике имеется свой джентльменский набор тригонометрических функций. Знаем длины катетов и гипотенузу, делим друг на друга и считаем себе. И так для любого острого угла. Всё элементарно.
Вопрос: а если угол сделать тупым? Скажем, вот таким:
Что делать? Развалился наш прямоугольный треугольник. Ни катетов больше нет, ни гипотенузы… А тригонометрические функции тоже ушли в небытие, да?
Если бы древние математики не нашли выход из этой ситуации, то, возможно, вы бы сейчас и не читали этот сайт. Ибо не было бы у нас тогда ни планшетов, ни компьютеров, ни смартфонов, ни многих других полезных штучек…
Так как можно определять любые тригонометрические функции любых углов без прямоугольного треугольника? Что ж, пришла пора взрослеть дальше. Знакомимся!
Знакомимся!
Тригонометрическая окружность. Единичная окружность. Числовая окружность. Что всё это значит?
Это очень простые понятия. Более того, эти понятия — верный друг и надёжный помощник во всех разделах тригонометрии! От простой работы с углами в градусах или в радианах до тригонометрических уравнений и неравенств. Почему? А потому, что эта штука — своего рода шпаргалка! Причём совершенно законная! Обычно ведь что бывает: за шпоры выгоняют, двойки ставят… А тут нарисовал окружность, угол, функцию — и сразу увидел всё что тебя интересует.
Например, такое простое задание:
Что больше — sin200° или sin(-100°)?
Кто не в теме, тот отдыхает в сторонке. А кто в теме, тот нацарапает что-то типа вот такого наскального рисунка:
и сразу же увидит всю необходимую информацию!
И никто слова не скажет! Даже суровая комиссия в боевой обстановке ЕГЭ.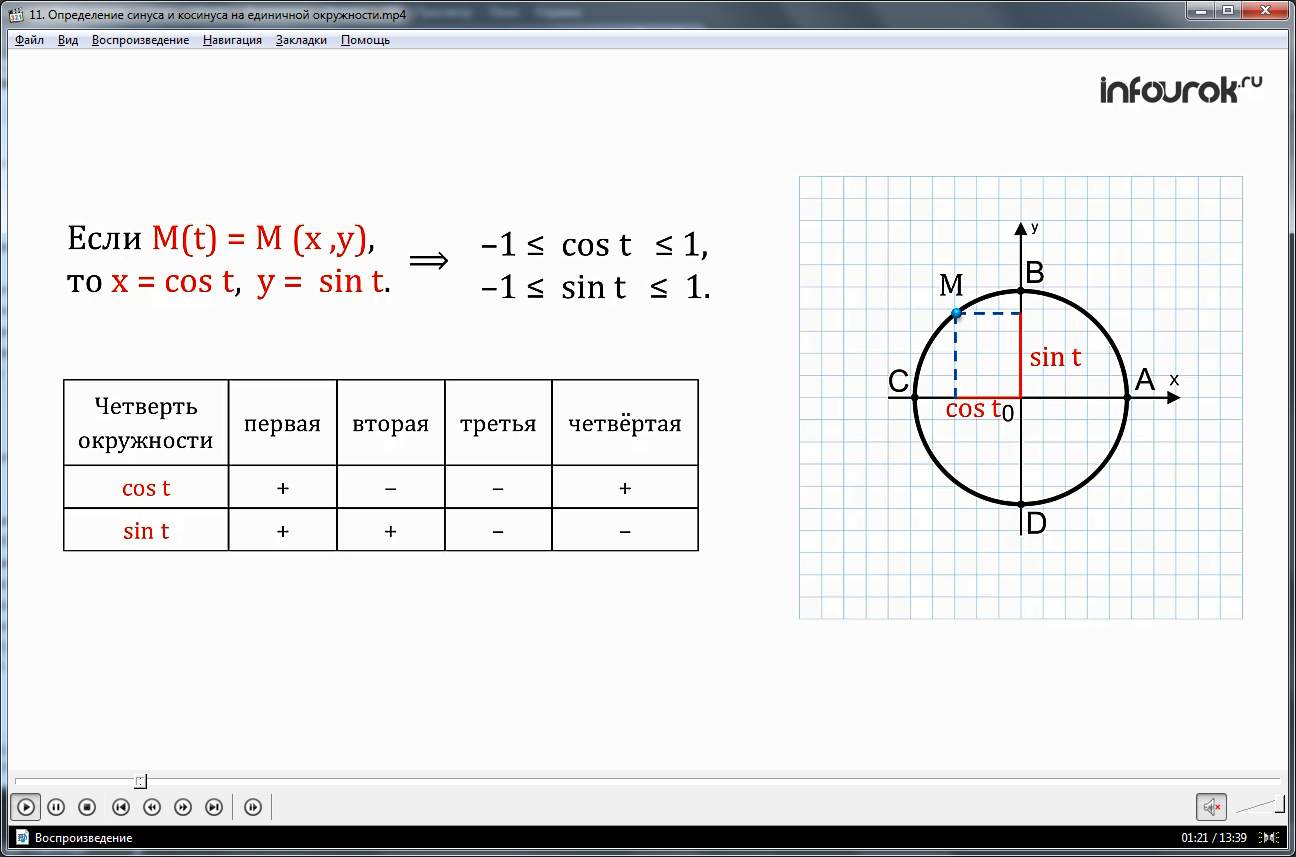 Так зачем же такой шанс упускать, правда?
Так зачем же такой шанс упускать, правда?
Чуть позже, в соответствующем уроке, мы разберём эту страшную задачку. И про злые углы типа -100 градусов тоже поговорим.)
А пока начнём. Для начала нарисуем самый обычный привычный нам острый угол. Назовём его, как обычно, «альфа». Вот так:
Угол как угол, пока ничего выдающегося, но… Раз есть угол (пока что острый), то у него должны быть и свои тригонометрические функции! Косинус там или тангенс… А где их взять? Ни гипотенузы, ни катетов больше нет, только угол. Тупик?
Спокойствие! Сейчас всё увидите.)
Для начала нарисуем самые обычные и знакомые нам координатные оси. OX по горизонтали, OY — по вертикали, всё чин-чинарём… Нарисуем и… приколотим горизонтальную сторону угла к положительной полуоси OX. Приколотим покрепче, дабы не оторвать ненароком.) Вершину угла поместим в начало координат, точку О. А вот вторую сторону угла прибивать не будем и оставим подвижной. Зачем? А чтобы угол менять можно было. Хотим побольше, хотим поменьше. Хотим острый, хотим тупой — любой! Раздвижной у нас угол будет. Как угол раствора циркуля, только одна из его ножек будет прибитой.) Конец подвижной стороны обозначим буквой А.
Зачем? А чтобы угол менять можно было. Хотим побольше, хотим поменьше. Хотим острый, хотим тупой — любой! Раздвижной у нас угол будет. Как угол раствора циркуля, только одна из его ножек будет прибитой.) Конец подвижной стороны обозначим буквой А.
Получим вот такой незамысловатый рисунок:
Итак, угол у нас пристроен, это хорошо. А где же его синус и косинус — спросите вы? Потерпите минутку, торопыги, сейчас всё увидите! Я же только начал.)
Введём теперь координаты x и y конца подвижной стороны угла (точки А) и отметим их на осях. Это будут точки В и С соответственно. Ясное дело, что ОВ и ОС — какие-то числа. Длины отрезков. Или координаты точки А.
ОВ = х
ОС = у
Так вот, оказывается, иксовая координата точки А (отрезок ОВ) будет косинусом угла альфа, а игрековая координата (отрезок ОС) — его синусом!
Смотрим на рисунок:
Стоп-стоп! С какого такого перепугу-то? Ведь мы же чётко зарубили себе на носу из прошлых двух уроков, что синус и косинус — это отношения сторон в прямоугольном треугольнике! Которые от длин этих самых сторон никак не зависят.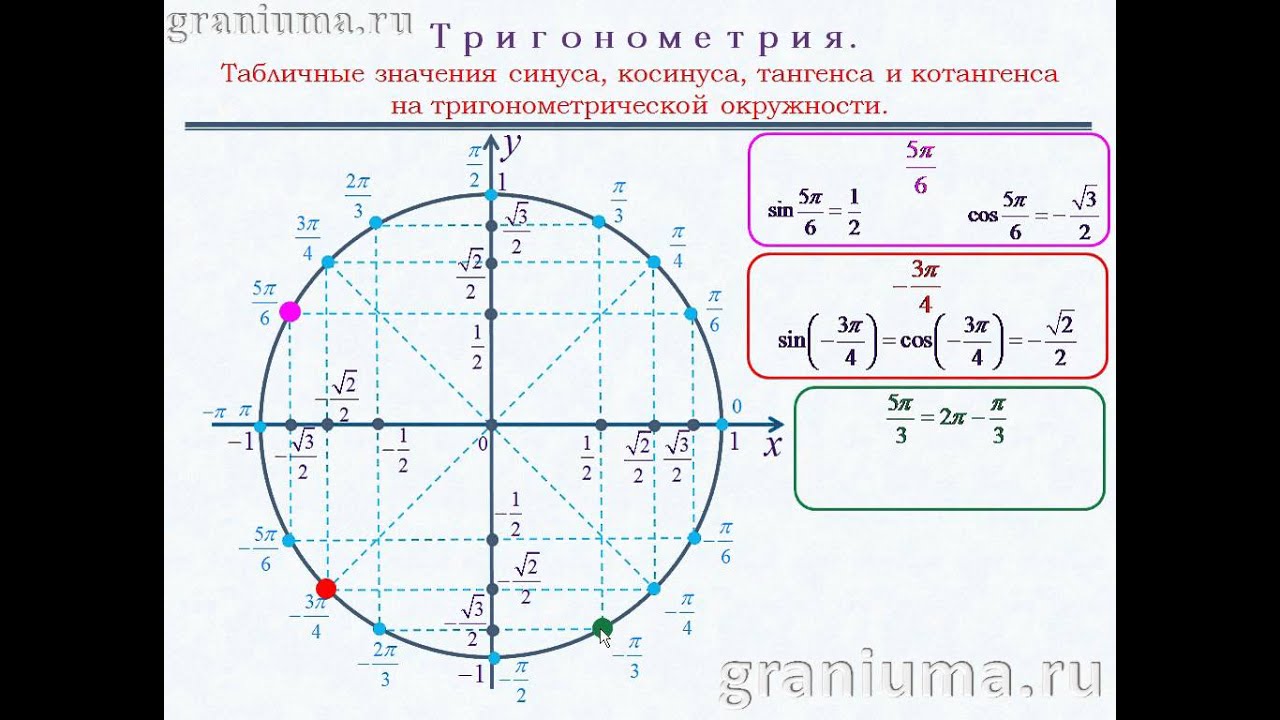 А у нас тут координаты точки А присутствуют. Которые могут быть любыми!
А у нас тут координаты точки А присутствуют. Которые могут быть любыми!
Всё верно. Любыми. Но! Давайте посмотрим внимательнее на треугольник АВО. Прямоугольный, между прочим.) Ибо координаты точки, они обычно перпендикулярами отмечаются на осях, да… По нашему заклинанию косинус угла альфа — это отношение прилежащего катета к гипотенузе. Или ОВ/ОА. Синус альфа — соответственно ОС/ОА. Причём мы с вами помним, что синус/косинус никак не зависят от длин сторон. А это совсем прекрасно! Почему? А потому, что мы имеем полное право выбирать длины сторон как хотим. Как нам удобно, так и выберем. В частности, мы имеем полное право принять длину гипотенузы ОА за единичку (ОА=1)! Причём единицы измерения нас вообще не волнуют — миллиметр, километр, миля, дюйм… Синус и косинус от этого всё равно не изменятся.)
Почему именно гипотенуза (а не катеты) и именно единичка (а не 2, 10, 157 и т.д)? Потому, что так нам (и древним людям) очень удобно! Именно при таком выборе у нас достигаются максимальные упрощения. Смотрите, что получается:
Смотрите, что получается:
Вот и все дела.) Косинус — иксовая координата точки А, а синус — игрековая (если гипотенуза ОА — единичка). Да, ненаучно, да нестрого, но зато понятно. И запоминается проще. А запомнить очень важно. Причём, запомнить надёжно!
Запоминаем:
Косинус — по Х, синус — по Y.
Именно в таком порядке. Не путаемся!
Как видите, всё просто. Пока что всё идёт в рамках геометрии восьмого класса. С той лишь разницей, что катеты превратились у нас в координаты х и у точки А, а гипотенуза — та и вовсе превратилась в единичку. Очень удобное число.) Однако… Тема урока называется «Тригонометрическая окружность», не так ли? Пока ни слова про окружность не было!
Всё правильно. Но остались совсем пустяки. Сейчас мы с вами резко повзрослеем и колоссально расширим наши возможности всего одним движением руки! Как? Очень просто. Берём подвижную сторону угла (т.е. ОА) и… проворачиваем её вокруг точки О на полный оборот! Как вы думаете, какую линию при этом опишет точка А? Ну, конечно! Окружность!
Берём подвижную сторону угла (т.е. ОА) и… проворачиваем её вокруг точки О на полный оборот! Как вы думаете, какую линию при этом опишет точка А? Ну, конечно! Окружность!
Вот так:
Вот и всё. Это и есть тригонометрическая окружность!
Это научное название. А на математическом сленге обычно говорят «тригонометрический круг». Или совсем коротко — просто «круг». Или — «радар» :).
Ну хорошо, окружность начертили. Но почему — тригонометрическая? Окружность как окружность… Вскрою тайну. Любой точке на окружности соответствуют два числа — координаты этой точки по X и координаты этой точки по Y. То есть, А(х; у). А икс и игрек у нас что? Только что разбирались… Да! Косинус и синус угла альфа. То есть, не что иное, как его тригонометрические функции. Вот и весь смысл.
А теперь, вспомнив, что ОА = 1 и что ОА — радиус окружности, можно сообразить, что это же самое понятие — и единичная окружность тоже.
А если вспомнить самый первый урок по тригонометрии (а чуть конкретнее — то, что синус и косинус — просто какие-то числа), то наша с вами тригонометрическая окружность будет ещё и числовой окружностью.
Вот так. Сразу три термина в одном. Очень удобно и практично.
Запоминаем:
Тригонометрическая, единичная и числовая окружности — это всё одно и то же понятие. В рамках тригонометрии.
Так, ну хорошо. Окружность изобразили. Угол у нас крутящийся, меняющийся. А раз крутящийся, то нам уже ничто не запрещает прокрутить подвижную сторону ОА куда угодно. Например, так, чтобы угол альфа стал каким-нибудь тупым!
Хотя бы вот так:
А как увидеть его синус и косинус? Не вопрос! Всё точно так же. Опускаем перпендикуляры из точки А на оси OX и OY и всё видим:
Самые глазастые, возможно, уже заметили, что синус угла альфа у нас положительный (точка С лежит на положительной полуоси OY). А вот косинус альфа — отрицательный! Ибо точка В, иксовая координата точки А (т.е. не что иное, как косинус альфа!), лежит на отрицательной полуоси OХ. Значит, у любого тупого угла синус положительный, а косинус — отрицательный. Чего, кстати, принципиально не бывает в прямоугольном треугольнике: там все тригонометрические функции — синус, косинус, тангенс, котангенс — положительные.
А вот косинус альфа — отрицательный! Ибо точка В, иксовая координата точки А (т.е. не что иное, как косинус альфа!), лежит на отрицательной полуоси OХ. Значит, у любого тупого угла синус положительный, а косинус — отрицательный. Чего, кстати, принципиально не бывает в прямоугольном треугольнике: там все тригонометрические функции — синус, косинус, тангенс, котангенс — положительные.
А здесь — пожалуйста! Не зря же мы с вами расширили наши возможности!) Ну а коли так, раз уж мы столкнулись с отрицательным косинусом у тупого угла, то пришла пора разобраться и с такой важной штукой, как знаки синуса/косинуса по четвертям. До кучи и знаки тангенса/котангенса разберём сразу же.
Знаки синуса и косинуса, тангенса и котангенса по четвертям.
Всё проще простого. Для начала напомню, что координатные четверти (или по-другому квадранты) в тригонометрии нумеруются точно так же, как и при работе с обычными задачами на координаты точек — против часовой стрелки.
Вот так:
А что же со знаками синуса/косинуса по четвертям? Тоже всё элементарно, Ватсон.) С первой и второй четвертями мы уже разобрались выше. Незаметно для себя.) С первой четвертью вообще вопросов нет. Там только острые углы, у которых все функции (в том числе и синус с косинусом) — положительные. Со второй четвертью тоже всё ясно: синус положительный, а косинус — отрицательный. Это мы уже выяснили, когда тупой угол рисовали.
Осталось лишь разобраться с третьей и четвёртой четвертями. Как? Точно так же! Не зря же мы с вами тут углы мотать учимся потихоньку.)
Мы же знаем, что ОА — подвижная сторона нашего угла альфа. Вот и продолжим её крутить от положительной полуоси ОХ в нужную нам сторону! В третью четверть. Получим вот такую картинку:
Как видно из рисунка, для любого угла в третьей четверти уже станет отрицательным не только косинус, но и синус тоже:
Для четвёртой четверти тоже ничего хитрого. Крутим и рисуем:
Крутим и рисуем:
И видим, что синус в четвёртой четверти остаётся по-прежнему отрицательным. А косинус? Да! Косинус снова становится положительным:
Так, по всем четвертям пробежались. Как видите, всё просто. Для лучшего запоминания можно нарисовать знаки синуса/косинуса прямо на нашем круге.
Запоминаются обе картинки достаточно просто и быстро. Особенно если железно помнить наше секретное заклинание: «Косинус — по икс, синус — по игрек.» Кстати, сопоставьте заклинание с картинками! Очень полезно.)
Ну хорошо, с синусом/косинусом всё понятно. А тангенс и котангенс? Тоже никаких проблем. Если, конечно, помнить из второго урока, что тангенс — это синус поделить на косинус:
А котангенс — наоборот.
Вот теперь и прикинем. В первой четверти у нас всё шоколадно. Всё с плюсом — и синус и косинус. А плюс поделить на плюс — что будет? Конечно же, плюс! Во второй четверти знаки синуса и косинуса — разные. Плюс и минус. А это значит, что их отношение (что синуса к косинусу, что наоборот) будет всегда отрицательным. Ибо в борьбе минуса с плюсом всегда выигрывает минус. Так уж повелось в математике.) В третьей четверти как синус, так и косинус имеют знак «минус». А их отношение? Минус на минус — будет… будет… плюс! А в четвёртой четверти знаки синуса/косинуса опять разные. Стало быть, их отношение (тангенс с котангенсом) снова будет с минусом! Вот и все дела.)
Плюс и минус. А это значит, что их отношение (что синуса к косинусу, что наоборот) будет всегда отрицательным. Ибо в борьбе минуса с плюсом всегда выигрывает минус. Так уж повелось в математике.) В третьей четверти как синус, так и косинус имеют знак «минус». А их отношение? Минус на минус — будет… будет… плюс! А в четвёртой четверти знаки синуса/косинуса опять разные. Стало быть, их отношение (тангенс с котангенсом) снова будет с минусом! Вот и все дела.)
Получаем для тангенса/котангенса вот такую картинку:
Запомнить знаки тоже проще простого: плюс-минус-плюс-минус. Простое чередование знаков.)
И вот тут у некоторых назревает закономерный вопрос:
А можно ли увидеть тангенс и котангенс на круге? Синус — по игрек, косинус — по икс. Это понятно.) А тангенс и котангенс???
Ух, какие вы любопытные, оказывается! Все-то секреты вам раскрой сразу же! Да, можно! Можно увидеть тангенс и котангенс на числовой окружности! Любого угла.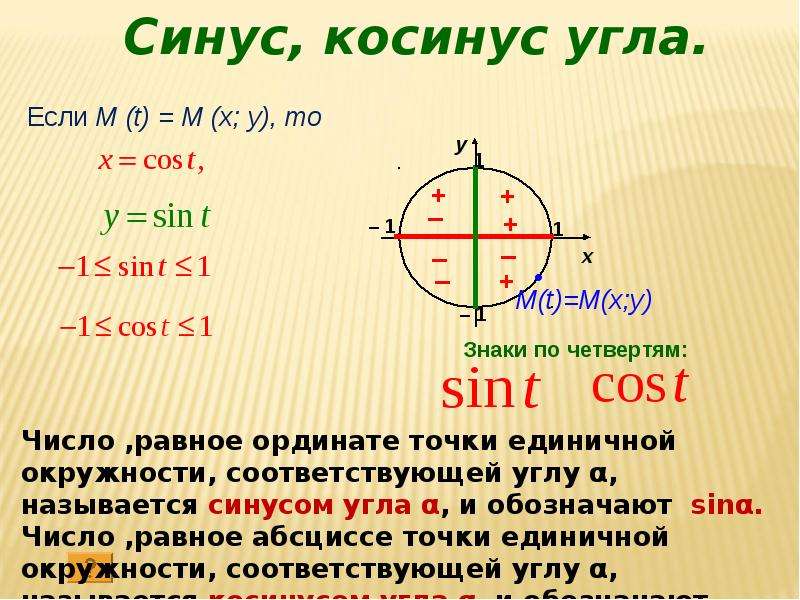 Только для этого на нашем рисунке необходим ещё один дополнительный взмах пера. Всего один. Какой именно — в спецтеме «Тангенс и котангенс на тригонометрической окружности».
Только для этого на нашем рисунке необходим ещё один дополнительный взмах пера. Всего один. Какой именно — в спецтеме «Тангенс и котангенс на тригонометрической окружности».
Итак, полдела сделали. Нарисовали угол, с его помощью начертили окружность. Осталась вторая половина дела. А именно — научиться проделывать обратную операцию. По любой произвольной точке на окружности научиться определять сам угол! А вот эта задачка та ещё…
Об этом — в следующей теме: «Как отсчитывать углы на тригонометрической окружности?».
APC Функции синуса и косинуса
Мотивирующие вопросы
Что такое функции синуса и косинуса и как они возникают из точки, пересекающей единичный круг?
Какими важными свойствами обладают функции синуса и косинуса?
Как точно или приблизительно вычислить значения \(\sin(t)\) и \(\cos(t)\text{,}\)?
В разделе 2.1 мы увидели, как отслеживание высоты точки, пересекающей окружность, генерирует периодическую функцию, как показано на рисунке 2.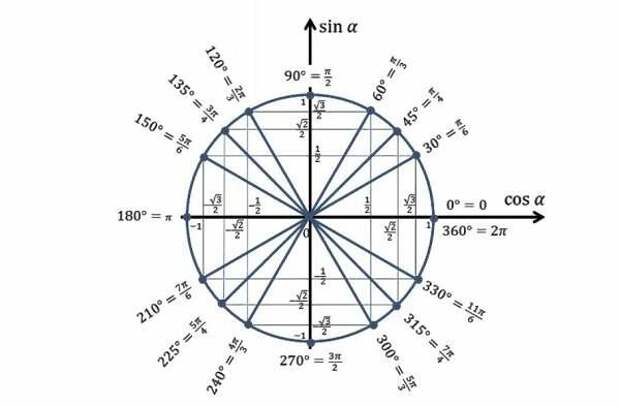 1.10. Затем в разделе 2.2 мы определили набор \(16\) особых точек на единичной окружности, как показано на рисунке 2.3.1.
1.10. Затем в разделе 2.2 мы определили набор \(16\) особых точек на единичной окружности, как показано на рисунке 2.3.1.
Вы также можете использовать файл Desmos по адресу http://gvsu.edu/s/0xt 1 для обзора и изучения особых точек на единичной окружности.
Предварительный просмотр 2.3.1.
Если мы рассмотрим единичный круг на рисунке 2.3.1, начнем с \(t = 0\text{,}\) и пройдем круг против часовой стрелки, мы можем увидеть высоту, \(h\text{,}\) точка пересечения как функция угла, \(t\text{,}\) в радианах. Оттуда мы можем построить получившиеся \((t,h)\) упорядоченные пары и соединить их, чтобы создать круговую функцию, изображенную на рисунке 2.3.2.
Рисунок 2.3.2. График круговой функции, которая отслеживает высоту точки, пересекающей единичный круг.Каково точное значение \(f( \frac{\pi}{4})\text{?}\) для \(f( \frac{\pi}{3} )\text{?} \)
Заполните следующую таблицу точными значениями \(h\), которые соответствуют указанным входам.
Таблица 2.3.3.
\(т\) \(0\) \(\ гидроразрыва {\pi}{6}\) \(\ гидроразрыва {\pi}{4}\) \(\frac{\pi}{3}\) \(\ гидроразрыва {\pi}{2}\) \(\frac{2\pi}{3}\) \(\frac{3\pi}{4}\) \(\frac{5\pi}{6}\) \(\пи\) \(ч\) \(т\) \(\пи\) \(\frac{7\pi}{6}\) \(\frac{5\pi}{4}\) \(\frac{4\pi}{3}\) \(\frac{3\pi}{2}\) \(\frac{5\pi}{3}\) \(\frac{7\pi}{4}\) \(\frac{11\pi}{6}\) \(2\пи\) \(ч\) Каково точное значение \(f( \frac{11\pi}{4} )\text{?}\) для \(f( \frac{14\pi}{3} )\text{? }\)
Приведите четыре различных значения \(t\), для которых \(f(t) = -\frac{\sqrt{3}}{2}\text{.
 }\)
}\)
Подраздел 2.3.1 Определение функции синуса
Круговая функция, которая отслеживает высоту точки на единичной окружности, проходящей против часовой стрелки из \((1,0)\) как функцию соответствующего центрального угла (в радианах), является одной из самых важных функций в математике. Таким образом, мы даем функции имя: функция sine .
Определение 2.3.4.
Дан центральный угол в единичной окружности, который измеряет \(t\) радиан и пересекает окружность в точках \((1,0)\) и \((a,b)\text{,}\), как показано на рисунке 2.3.5 мы определяем синус \(t\) , обозначенный \(\sin(t)\text{,}\) по правилу
\begin{уравнение*} \sin(t) = b\text{.} \end{equation*}
Рисунок 2.3.5. Определение синуса угла \(t\text{.}\) Из-за соответствия между мерой угла в радианах и расстоянием, пройденным на единичной окружности, мы можем также думать о \(\sin(t)\) как об идентификации \(y\)-координаты точки после того, как она прошла \( t\) единиц против часовой стрелки по окружности от \((1,0)\text{. }\) Обратите внимание, что мы можем рассматривать синус отрицательных входных данных: например, \(\sin(-\frac{\pi} {2}) = -1\текст{.}\)
}\) Обратите внимание, что мы можем рассматривать синус отрицательных входных данных: например, \(\sin(-\frac{\pi} {2}) = -1\текст{.}\)
Основываясь на нашей предыдущей работе с единичным кругом, мы знаем много различных точных значений синусоидальной функции и суммируем их в Таблице 2.3.6.
Таблица 2.3.6.| \(т\) | \(0\) | \(\ гидроразрыва {\pi}{6}\) | \(\ гидроразрыва {\pi}{4}\) | \(\ гидроразрыва {\pi}{3}\) | \(\ гидроразрыва {\pi}{2}\) | \(\frac{2\pi}{3}\) | \(\frac{3\pi}{4}\) | \(\frac{5\pi}{6}\) | \(\пи\) |
| \(\грех(т)\) | \(0\) | \(\ гидроразрыва{1}{2}\) | \(\ гидроразрыва {\ sqrt {2}} {2} \) | \(\ гидроразрыва {\ sqrt {3}} {2} \) | \(1\) | \(\ гидроразрыва {\ sqrt {3}} {2} \) | \(\ гидроразрыва {\ sqrt {2}} {2} \) | \(\ гидроразрыва{1}{2}\) | \(0\) |
| \(т\) | \(\пи\) | \(\frac{7\pi}{6}\) | \(\frac{5\pi}{4}\) | \(\frac{4\pi}{3}\) | \(\frac{3\pi}{2}\) | \(\frac{5\pi}{3}\) | \(\frac{7\pi}{4}\) | \(\frac{11\pi}{6}\) | \(2\пи\) |
| \(\sin(t)\) | \(0\) | \(-\frac{1}{2}\) | \(-\frac{\sqrt{2}}{2}\) | \(-\frac{\sqrt{3}}{2}\) | \(-1\) | \(-\frac{\sqrt{3}}{2}\) | \(-\frac{\sqrt{2}}{2}\) | \(-\frac{1}{2}\) | \(0\) |
Более того, если мы теперь нанесем эти точки обычным способом, как мы это делали в предварительном просмотре 2. 3.1, мы получим знакомую круговую волновую функцию, которая получается при отслеживании высоты точки, пересекающей окружность. Мы часто называем график на рисунке 2.3.7 синусоида .
3.1, мы получим знакомую круговую волновую функцию, которая получается при отслеживании высоты точки, пересекающей окружность. Мы часто называем график на рисунке 2.3.7 синусоида .
Подраздел 2.3.2 Определение функции косинуса
Для любого центрального угла в радианах \(t\) в единичной окружности с одной стороной, проходящей через точку \((1,0)\text{,}\), угол порождает единственную точку \((a,b )\), лежащий на окружности. Точно так же, как мы можем рассматривать \(y\)-координату как функцию \(t\text{,}\), \(x\)-координата также является функцией \(t\text{.}\) Поэтому мы даем следующее определение.
Определение 2.3.8.
Дан центральный угол в единичной окружности, который измеряет \(t\) радиан и пересекает окружность в точках \((1,0)\) и \((a,b)\text{,}\), как показано на рисунке 2.3.9 мы определяем косинус \(t\) , обозначаемый \(\cos(t)\text{,}\) по правилу
\begin{уравнение*}
\cos(t) = а\текст{. }
\end{equation*}
}
\end{equation*}
Опять же, из-за соответствия между радианной мерой угла и длиной дуги вдоль единичной окружности, мы можем рассматривать значение \(\cos(t)\) как отслеживание \(x\)-координаты точки, пересекающей единичный круг по часовой стрелке на расстоянии \(t\) единиц вдоль круга от \((1,0)\text{.}\) Теперь мы используем данные и информацию, которые мы получили о единичном круге, чтобы построить таблицу значения \(\cos(t)\), а также график кривой, которую он генерирует.
Мероприятие 2.3.2.
Пусть \(k = g(t)\) будет функцией, которая отслеживает координату \(x\) точки, пересекающей единичный круг против часовой стрелки от \((1,0)\text{.}\). То есть , \(g(t) = \cos(t)\text{.}\) Используйте информацию, известную нам о единичном круге, которая представлена на рисунке 2.3.1, чтобы ответить на следующие вопросы.
Каково точное значение \(\cos(\frac{\pi}{6})\text{?}\) из \(\cos(\frac{5\pi}{6})\text {?}\) \(\cos(-\frac{\pi}{3})\text{?}\)
Заполните следующую таблицу точными значениями \(k\), которые соответствуют указанным входам.
Таблица 2.3.10.
\(т\) \(0\) \(\ гидроразрыва {\pi}{6}\) \(\ гидроразрыва {\pi}{4}\) \(\ гидроразрыва {\pi}{3}\) \(\ гидроразрыва {\pi}{2}\) \(\frac{2\pi}{3}\) \(\frac{3\pi}{4}\) \(\frac{5\pi}{6}\) \(\пи\) \(к\) \(т\) \(\пи\) \(\frac{7\pi}{6}\) \(\frac{5\pi}{4}\) \(\frac{4\pi}{3}\) \(\frac{3\pi}{2}\) \(\frac{5\pi}{3}\) \(\frac{7\pi}{4}\) \(\frac{11\pi}{6}\) \(2\пи\) \(к\) На осях, показанных на рисунке 2.3.11, нарисуйте точный график \(k = \cos(t)\text{.}\) Отметьте точное расположение нескольких ключевых точек на кривой.
Рисунок 2.3.11. Оси для построения \(k = \cos(t)\text{.}\)
Каково точное значение \(\cos( \frac{11\pi}{4} )\text{?}\) для \(\cos( \frac{14\pi}{3} )\text {?}\)
Приведите четыре различных значения \(t\), для которых \(\cos(t) = -\frac{\sqrt{3}}{2}\text{.}\)
Чем график \(k = \cos(t)\) отличается от графика \(h = \sin(t)\text{?}\) Чем графики похожи?
Когда мы работаем с функциями синуса и косинуса, всегда полезно помнить их определения в терминах единичной окружности и движения точки, пересекающей окружность. На http://gvsu.edu/s/0xe 2 вы можете изучить и изучить полезную анимацию Desmos , которая показывает, как это движение по кругу генерирует каждый из соответствующих графиков.
Подраздел 2.3.3 Свойства функций синуса и косинуса
Поскольку функция синуса является результатом отслеживания координаты \(y\) точки, пересекающей единичный круг, а функция косинуса — координаты \(x\), эти две функции имеют несколько общих свойств круговых функций.
Свойства функций синуса и косинуса.
Для обоих \(f(t) = \sin(t)\) и \(g(t) = \cos(t)\text{,}\)
домен функции — все действительные числа;
диапазон функции: \([-1,1]\text{;}\)
средняя линия функции равна \(y = 0\text{;}\)
амплитуда функции равна \(a = 1\text{;}\)
период функции равен \(p = 2\pi\text{.}\)
Также полезно сопоставить графики функций синуса и косинуса на одних и тех же координатных осях. Когда мы это делаем, как показано на рисунке 2.3.12, мы видим, что кривые можно рассматривать как горизонтальные переносы друг друга.
Рисунок 2.3.12. Графики функций синуса и косинуса.В частности, поскольку график синуса можно рассматривать как график косинуса, сдвинутый на \(\frac{\pi}{2}\) единиц вправо, отсюда следует, что для любого значения \(t\text{,}\ )
\begin{уравнение*} \sin(t) = \cos(t-\frac{\pi}{2})\text{.} \end{уравнение*}
Аналогично, поскольку график косинуса можно рассматривать как график синуса, сдвинутый влево,
\begin{уравнение*}
\cos(t) = \sin(t + \frac{\pi}{2})\text{.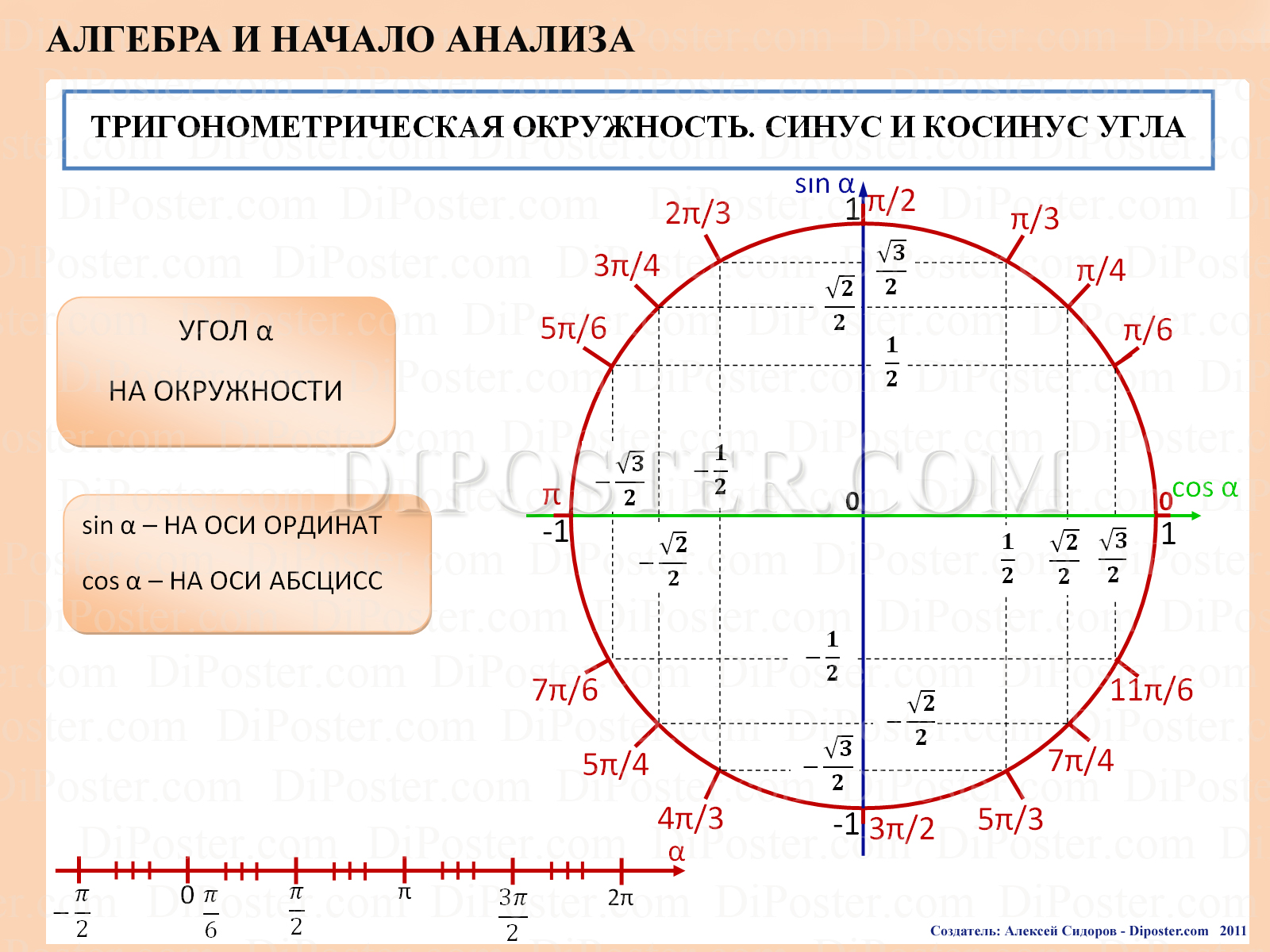 }
\end{уравнение*} 92(т) = 1\текст{.}
\end{equation*}
}
\end{уравнение*} 92(т) = 1\текст{.}
\end{equation*}
На графиках двух функций есть дополнительные тенденции и закономерности, которые мы рассмотрим подробнее в следующем упражнении.
Мероприятие 2.3.3.
Используйте Рисунок 2.3.12, чтобы помочь ответить на следующие вопросы.
Приведите пример наибольшего из найденных интервалов, на котором \(f(t) = \sin(t)\) убывает.
Приведите пример наибольшего интервала, который вы можете найти, на котором \(f(t) = \sin(t)\) убывает и вогнут вниз.
Приведите пример наибольшего из найденных интервалов, на котором \(g(t) = \cos(t)\) возрастает.
Приведите пример наибольшего интервала, который вы можете найти, на котором \(g(t) = \cos(t)\) возрастает и вогнут вверх.
Без каких-либо вычислений, на каком интервале средняя скорость изменения \(g(t) = \cos(t)\) больше: \([\pi, \pi+0,1]\) или \([ \frac{3\pi}{2}, \frac{3\pi}{2} + 0.
 1]\text{?}\) Почему?
1]\text{?}\) Почему?В общем, как бы вы охарактеризовали места на графиках синуса и косинуса, где функции возрастают или убывают быстрее всего?
Думая с точки зрения единичного круга, для которого квадранты плоскости \(x\)-\(y\) являются \(\cos(t)\) отрицательными для угла \(t\), лежащего в этот квадрант?
Подраздел 2.3.4 Использование вычислительной техники
Мы установили, что знаем точное значение \(\sin(t)\) и \(\cos(t)\) для любого из \(t\)-значений в таблице 2.3.6, а также для любого такого \(t \pm 2j\pi\text{,}\), где \(j\) — целое число, из-за периодичности функций. Но что, если мы хотим узнать \(\sin(1.35)\) или \(\cos(\frac{\pi}{5})\) или значения для других входных данных, которых нет в таблице?
Любое стандартное вычислительное устройство, такое как научный калькулятор, Desmos , Geogebra или WolframAlpha , имеет возможность вычислять функции синуса и косинуса при любом входном сигнале, который мы пожелаем. Поскольку ввод рассматривается как угол, каждое вычислительное устройство может учитывать угол в радианах или градусах. Всегда важно знать, какой тип ввода ожидает ваше устройство. Наше вычислительное устройство — 9.0021 Десмос . В Desmos вы можете изменить тип ввода между радианами и градусами, щелкнув значок гаечного ключа в правом верхнем углу и выбрав нужные единицы измерения. Радианная мера используется по умолчанию.
Поскольку ввод рассматривается как угол, каждое вычислительное устройство может учитывать угол в радианах или градусах. Всегда важно знать, какой тип ввода ожидает ваше устройство. Наше вычислительное устройство — 9.0021 Десмос . В Desmos вы можете изменить тип ввода между радианами и градусами, щелкнув значок гаечного ключа в правом верхнем углу и выбрав нужные единицы измерения. Радианная мера используется по умолчанию.
Требуются основательные и сложные математические вычисления, чтобы вычислительное устройство могло вычислить функции синуса и косинуса при любом значении, которое мы захотим; алгоритмы включают идею исчисления, известную как бесконечный ряд. Несмотря на то, что ваше вычислительное устройство является мощным, полезно и важно понимать значение этих значений на единичной окружности и помнить специальные точки, для которых мы точно знаем выходные значения функций синуса и косинуса.
Мероприятие 2.3.4.
По возможности точно ответьте на следующие вопросы. Если вы оцениваете значение, делайте это с точностью не менее \(5\) знаков после запятой.
Если вы оцениваете значение, делайте это с точностью не менее \(5\) знаков после запятой.
Координата \(x\) точки на единичной окружности, лежащей в третьем квадранте и координата \(y\) которой равна \(y = -\frac{3}{4}\text{. }\)
\(y\)-координата точки на единичной окружности, образованной центральным углом в стандартном положении, который измеряет \(t = 2\) радиан.
\(x\)-координата точки на единичной окружности, образованной центральным углом в стандартном положении, который измеряет \(t = -3,05\) радиан.
Значение \(\cos(t)\), где \(t\) — угол в квадранте II, удовлетворяющий условию \(\sin(t) = \frac{1}{2}\text{.}\ )
Значение \(\sin(t)\), где \(t\) — угол в квадранте III, для которого \(\cos(t) = -0,7\text{.}\)
Средняя скорость изменения \(f(t) = \sin(t)\) на интервалах \([0,1,0,2]\) и \([0,8,0,9]\текст{.}\)
Средняя скорость изменения \(g(t) = \cos(t)\) на интервалах \([0.
 1,0.2]\) и \([0.8,0.9]\text{.}\)
1,0.2]\) и \([0.8,0.9]\text{.}\)
Подраздел 2.3.5 Резюме
Функции синуса и косинуса являются результатом отслеживания \(y\)- и \(x\)-координат точки, пересекающей единичный круг против часовой стрелки от \((1,0)\text{.}\) значением \(\sin(t)\) является \(y\)-координата точки, которая прошла \(t\) единиц по окружности от \((1,0)\) (или, что то же самое, соответствует к углу \(t\) радиан), а значение \(\cos(t)\) является \(x\)-координатой той же точки.
Функции синуса и косинуса являются периодическими функциями, которые имеют одну и ту же область определения (множество всех действительных чисел), диапазон (интервал \([-1,1]\)), среднюю линию (\(y = 0\) ), амплитуда (\(a = 1\)) и период (\(P = 2\pi\)). Кроме того, функция синуса представляет собой горизонтальный сдвиг функции косинуса на \(\frac{\pi}{2}\) единиц вправо, поэтому \(\sin(t) = \cos(t-\frac{\ pi}{2})\) для любого значения \(t\text{.}\)
Если \(t\) соответствует одному из известных нам специальных углов на единичной окружности (как на рис.
 2.3.1), мы можем вычислить значения \(\sin(t)\) и \(\ cos(t)\) точно. Для других значений \(t\text{,}\) мы можем использовать вычислительное устройство для оценки значения любой функции при данном входе; когда мы это делаем, мы должны позаботиться о том, в каких единицах мы вычисляем: в радианах или в градусах. 9\circ)\)
2.3.1), мы можем вычислить значения \(\sin(t)\) и \(\ cos(t)\) точно. Для других значений \(t\text{,}\) мы можем использовать вычислительное устройство для оценки значения любой функции при данном входе; когда мы это делаем, мы должны позаботиться о том, в каких единицах мы вычисляем: в радианах или в градусах. 9\circ)\)Отрицательный
Положительный
\(\sin(\frac{15\pi}{16})\)
Положительный
Отрицательный
\(\cos(\frac{20\pi}{21})\)
Отрицательный
Положительный
4.
Вопрос 30:
a) Напишите выражение (включая переменные \(a\) и \(h\)) для наклона отрезка, соединяющего \(S\) и \(T\) на рисунке выше .
Slope = (выражение, включающее переменные a и h )
b) Оцените выражение для \(a = 1,6\) и \(h = 0,01\text{.}\) Округлите ответ до два десятичных знака.
Наклон = (значение, округленное до двух знаков после запятой)
5.
 2(t) = 1\text{.}\) Ниже приведены несколько предложенных тождеств. Для каждого ваша задача состоит в том, чтобы решить, является ли тождество истинным или ложным. Если это так, приведите убедительные аргументы в пользу того, почему это так; если неверно, приведите пример \(t\)-значения, для которого уравнение не выполняется. 92(т)\)
2(t) = 1\text{.}\) Ниже приведены несколько предложенных тождеств. Для каждого ваша задача состоит в том, чтобы решить, является ли тождество истинным или ложным. Если это так, приведите убедительные аргументы в пользу того, почему это так; если неверно, приведите пример \(t\)-значения, для которого уравнение не выполняется. 92(т)\)\(\displaystyle \sin(t) + \cos(t) = 1\)
\(\displaystyle \sin(t) + \sin(\frac{\pi}{2}) = \cos(t)\)
- Проведите единичную окружность через две точки \(A=(0,0)\) и \(B=(1,0)\).
- Введите точку \(C\) на окружности и отметьте угол \(\угол BAC\).

- Убедитесь, что радианы
выбрано на вкладке
Advancedв разделеOptions->Settings.... - Используйте инструмент Дуга окружности в точках \(A, B, C\).
- Изменить радиус окружности и угол. Обратите внимание на длину дуги.
- Удалить дугу.
- Используйте инструмент Круговой сектор на точках \(A, B, C\).
- Изменить радиус окружности и угол. Обратите внимание на площадь сектора.
www.desmos.com/calculator/jgddn7tzxg
gvsu.edu/s/0xe
Тригонометрия — единичный круг
Поскольку тригонометрические отношения не зависят от размера треугольника, всегда можно использовать
прямоугольный треугольник, в котором длина гипотенузы равна единице. Такой треугольник можно расположить в декартовой системе таким образом, что одна его вершина будет лежать на окружности с радиусом единица. Окружность, имеющая радиус
один называется единичный круг . Когда гипотенуза равна единице, значения синуса и косинуса:
Окружность, имеющая радиус
один называется единичный круг . Когда гипотенуза равна единице, значения синуса и косинуса:
\[\sin\alpha = \frac{\text{opp}}{\text{hyp}}=\text{opp} \hspace{1cm} \cos \alpha = \frac{\text{adj}}{ \текст{гип}}=\текст{прил.}\]
Загрузить рабочий лист GeoGebra
Перетащите красную точку!Как видно из рабочего листа, также верно, что \(\sin \alpha = y(A)\) и \(\cos \alpha = x(A)\), где \(x(A)\) и \(y(A)\) — это \(x\)- и \(y\)-координата соответственно \(A\). Используя координаты \(A\), вместо отношения сторон в прямоугольном треугольнике мы можем расширить определение синуса и косинуса, чтобы они были определены для всех углов. 9\круг\).
Если \(f(x)\) периодическая функция с периодом \(P\), то \(f(x)=f(x+P)\) для всех \(x\).
Построение тригонометрических функций с использованием градусов в GeoGebra
Вы можете заметить, что шкала по оси \(x\) не соответствует
к углу. Причина этого в том, что GeoGebra использует радианы вместо градусов для углов.
Если вы хотите, чтобы GeoGebra использовала градусы, вы должны ввести символ градуса, нажать Ctrl + O для записи знака степени.
Введенный код должен быть
Причина этого в том, что GeoGebra использует радианы вместо градусов для углов.
Если вы хотите, чтобы GeoGebra использовала градусы, вы должны ввести символ градуса, нажать Ctrl + O для записи знака степени.
Введенный код должен быть sin(x°) или cos(x°) .
Изменение масштаба оси \(x\) нажав Shift , а затем перетащите ось \(x\). В окне свойств для графического представления вы можете изменить расстояние между метками и добавить символ градуса как единицу измерения.
Расширение определения тангенса и котангенса
Используя определение треугольника, тангенс и котангенс определяются как
\[\tan \alpha = \frac{\text{opp}}{\text{adj}} \hspace{1cm} \cot \alpha = \frac{\text{adj}}{\text{opp}}\ ] 907:35 Загрузить рабочий лист GeoGebra Перетащите красную точку! Используя подобные треугольники, вы можете показать, что конструкция на листе верна для углов, образующих прямоугольный треугольник. \circ \). 9\circ, n \in \mathbb{Z} \).
\circ \). 9\circ, n \in \mathbb{Z} \).
радиан
Загрузить рабочий лист GeoGebra
Координаты x задаются углом. Угловая единица — радиан.На приведенном выше листе \(x\)-координаты синей, зеленой и оранжевой точек задаются углом. Как видно по меткам на оси \(x\), один оборот соответствует не 360, а \(2\pi\). Другими словами, один оборот соответствует полному пути, пройденному красной точкой, т. е. длина окружности единичного круга.
При использовании радиан в качестве единицы измерения углов,
один оборот
соответствует \(2\pi\).
Вы можете изменить единицу измерения угла на радианы в GeoGebra в разделе Options->Settings... , затем выберите
вкладку Advanced .
Упражнения
Упражнение 1
Дуги
Какова длина дуги с точки зрения радиуса \(r\) и угла \(\alpha\), если радианы используются в качестве угловая единица?
Чему равна длина, если в качестве единицы угла используются градусы?
Упражнение 2
секторов
Чему равна площадь сектора по радиусу \(r\) и углу \(\alpha\), если в качестве угловая единица?
Чему равна площадь, если в качестве единицы угла используются градусы?
Малин Кристерссон в рамках Creative Commons Attribution-Noncommercial-Share
Аналогично 2.


 }\)
}\)

 1]\text{?}\) Почему?
1]\text{?}\) Почему? 1,0.2]\) и \([0.8,0.9]\text{.}\)
1,0.2]\) и \([0.8,0.9]\text{.}\) 2.3.1), мы можем вычислить значения \(\sin(t)\) и \(\ cos(t)\) точно. Для других значений \(t\text{,}\) мы можем использовать вычислительное устройство для оценки значения любой функции при данном входе; когда мы это делаем, мы должны позаботиться о том, в каких единицах мы вычисляем: в радианах или в градусах. 9\circ)\)
2.3.1), мы можем вычислить значения \(\sin(t)\) и \(\ cos(t)\) точно. Для других значений \(t\text{,}\) мы можем использовать вычислительное устройство для оценки значения любой функции при данном входе; когда мы это делаем, мы должны позаботиться о том, в каких единицах мы вычисляем: в радианах или в градусах. 9\circ)\)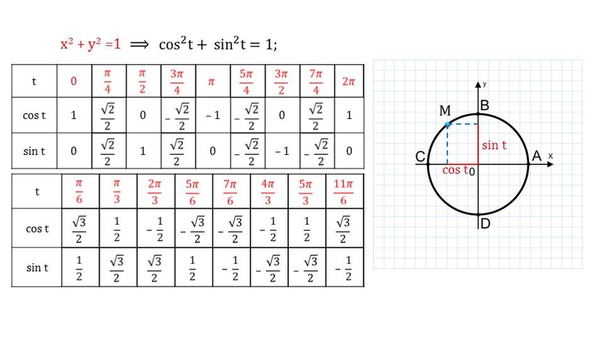 2(t) = 1\text{.}\) Ниже приведены несколько предложенных тождеств. Для каждого ваша задача состоит в том, чтобы решить, является ли тождество истинным или ложным. Если это так, приведите убедительные аргументы в пользу того, почему это так; если неверно, приведите пример \(t\)-значения, для которого уравнение не выполняется. 92(т)\)
2(t) = 1\text{.}\) Ниже приведены несколько предложенных тождеств. Для каждого ваша задача состоит в том, чтобы решить, является ли тождество истинным или ложным. Если это так, приведите убедительные аргументы в пользу того, почему это так; если неверно, приведите пример \(t\)-значения, для которого уравнение не выполняется. 92(т)\)
 )
) )
) )
) )
) )
)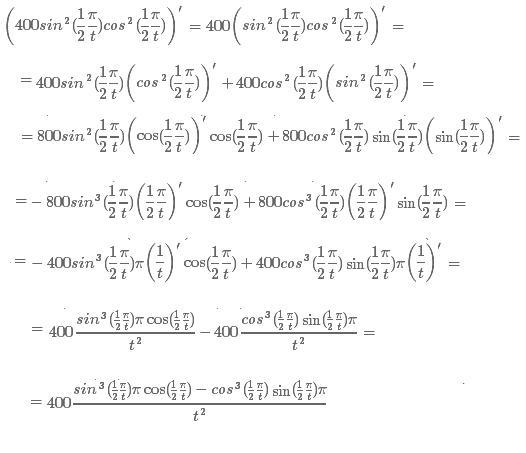 )
) )
) )
) 04.2023
04.2023 и t в секундах. Длина волны равна
и t в секундах. Длина волны равна Скорость волны
Скорость волны




 Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса.
Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса.
 Работа в парах. Карандашом ставится оценка. Данную оценку отметьте на графике.
Работа в парах. Карандашом ставится оценка. Данную оценку отметьте на графике.
 Такая громадная разница биомассы растений суши и океана объясняется следующей причиной. Основные продуценты суши — деревья, а океана — мелкие одноклеточные водоросли.
Такая громадная разница биомассы растений суши и океана объясняется следующей причиной. Основные продуценты суши — деревья, а океана — мелкие одноклеточные водоросли. По мере решения карточек учитель открывает буквы на доске. В итоге получается фамилия русского биолога. Параллельно выставляются оценки учащимся, которые они выставляют в листе самоконтроля.
По мере решения карточек учитель открывает буквы на доске. В итоге получается фамилия русского биолога. Параллельно выставляются оценки учащимся, которые они выставляют в листе самоконтроля. Учёный-энциклопедист, естествоиспытатель, общественный деятель, академик. Занимался геологией, историей науки, философией естествознания. Разработал научные методы поиска месторождений полезных ископаемых, изучил физическое строение важнейших породообразующих минералов, создал учение о биосфере, обосновал понятие «ноосфера», создал ряд новых научных направлений (биогеохимию и др.). Одним из первых рассматривал производственную деятельность человека как фактор дальнейшей эволюции Земли. Труды, научная и общественная деятельность Вернадского оказали огромное влияние на развитие во 2-й половине 20 в. биосферно-экологического направления в науке.
Учёный-энциклопедист, естествоиспытатель, общественный деятель, академик. Занимался геологией, историей науки, философией естествознания. Разработал научные методы поиска месторождений полезных ископаемых, изучил физическое строение важнейших породообразующих минералов, создал учение о биосфере, обосновал понятие «ноосфера», создал ряд новых научных направлений (биогеохимию и др.). Одним из первых рассматривал производственную деятельность человека как фактор дальнейшей эволюции Земли. Труды, научная и общественная деятельность Вернадского оказали огромное влияние на развитие во 2-й половине 20 в. биосферно-экологического направления в науке. Итог урока
Итог урока График показывает зависимость
между количеством ударов о землю и высотой
мяча.
График показывает зависимость
между количеством ударов о землю и высотой
мяча. 














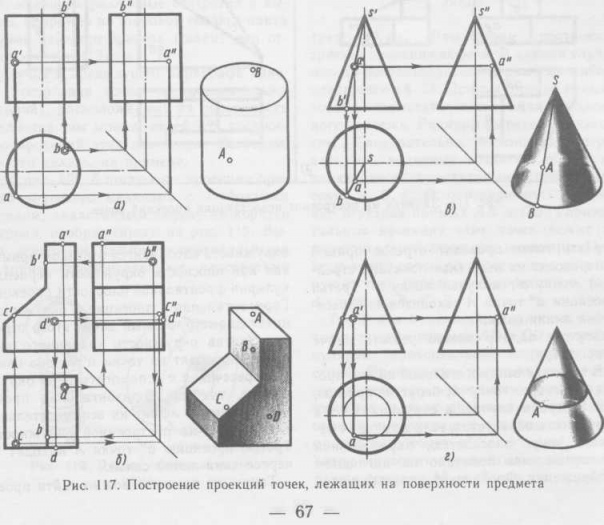
 Плоскость является частным случаем поверхности.
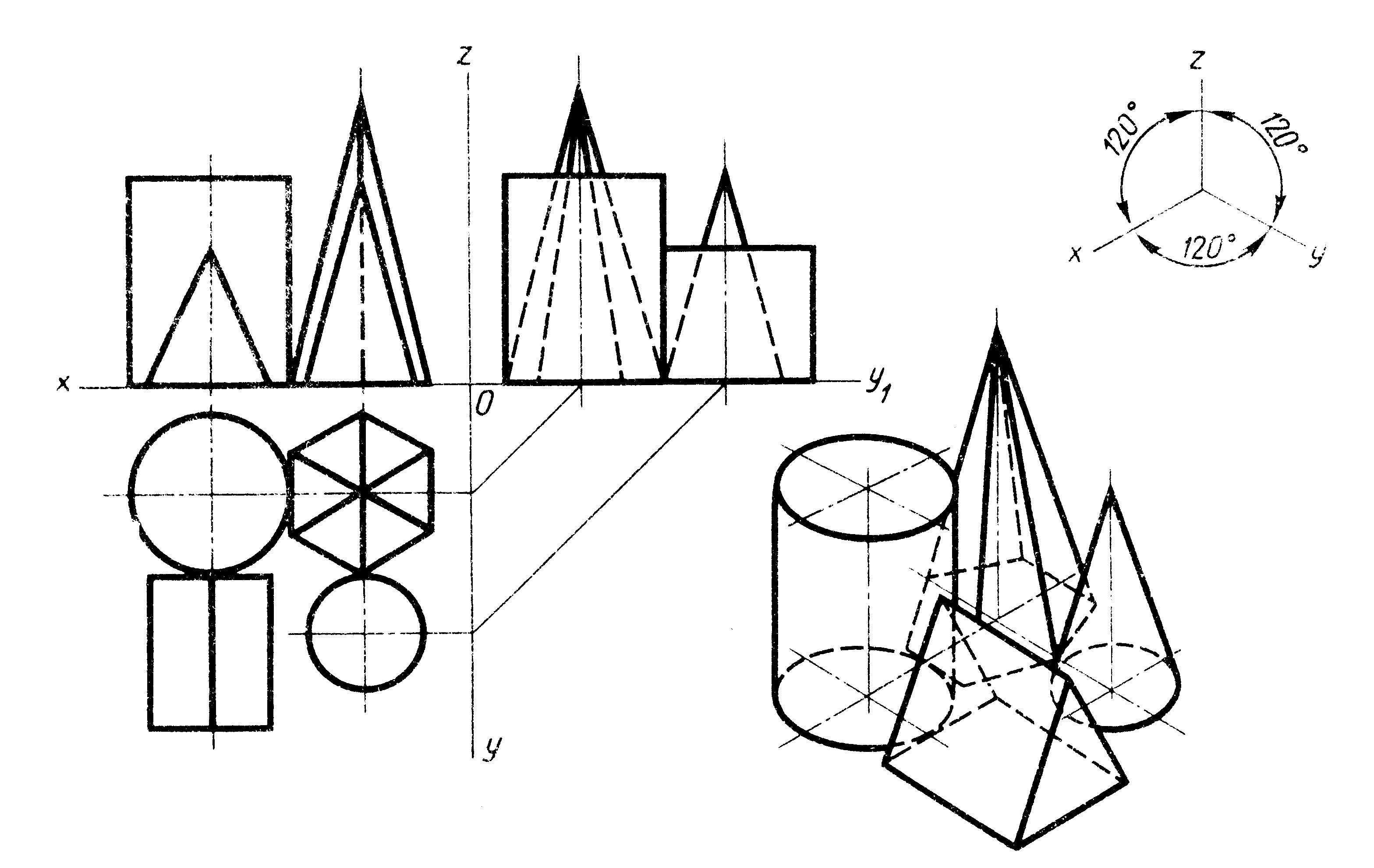
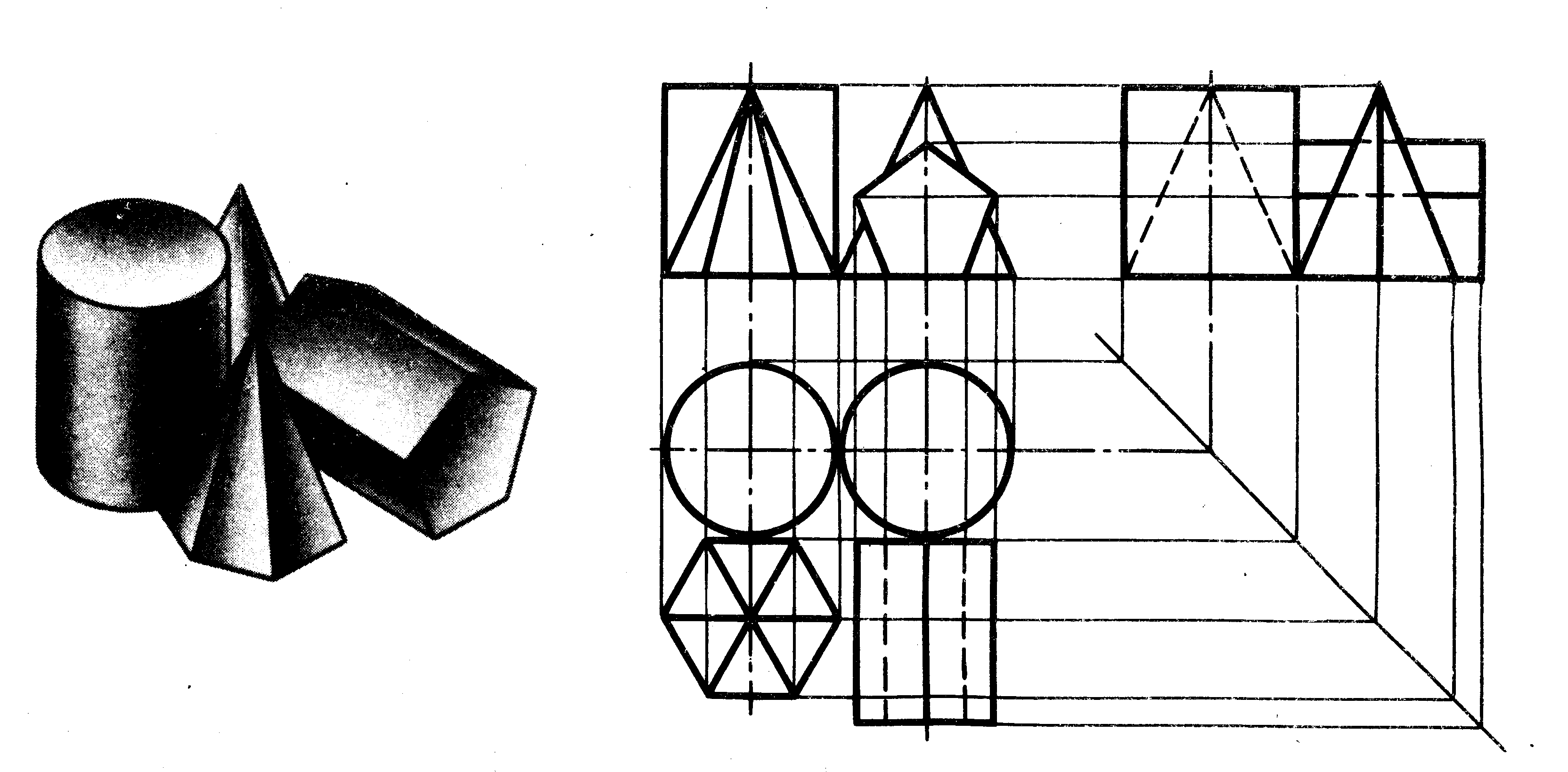
Плоскость является частным случаем поверхности.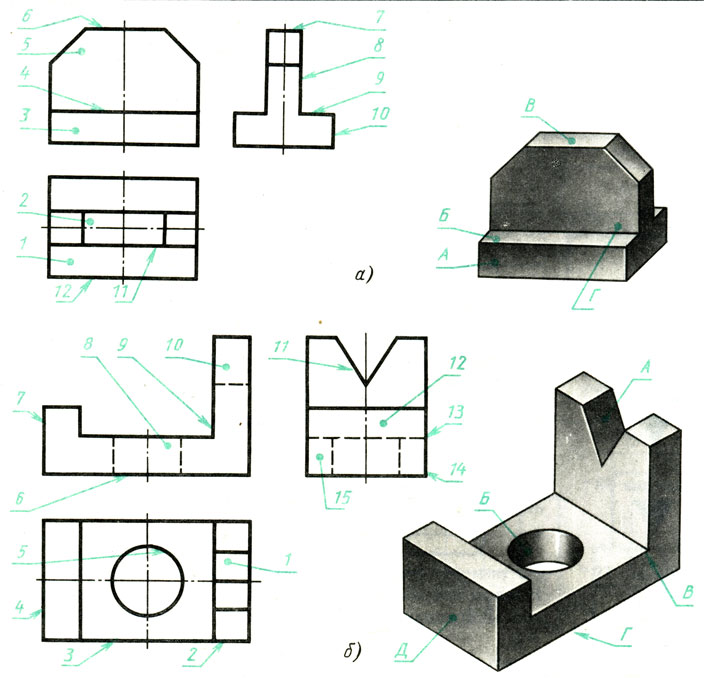 Поэтому рассмотрим сначала построение чертежей и аксонометрических проекций простых тел. Это тем более необходимо, так как в сложной форме любого предмета всегда можно выделить простые геометрические тела, которые помогают представить форму предмета по его чертежу.
Поэтому рассмотрим сначала построение чертежей и аксонометрических проекций простых тел. Это тем более необходимо, так как в сложной форме любого предмета всегда можно выделить простые геометрические тела, которые помогают представить форму предмета по его чертежу. 3. Шестиугольная призма.
3. Шестиугольная призма. 5. Цилиндр
5. Цилиндр
 К геометрическим свойствам предметов относятся: размеры, пропорции, взаимное расположение составляющих элементов формы.
К геометрическим свойствам предметов относятся: размеры, пропорции, взаимное расположение составляющих элементов формы. Для этой цели сложную по форме деталь мысленно разделяют на отдельные конструктивные части, имеющие форму различных геометрических тел. Мысленное разделение предмета на основные геометрические тела называют анализом геометрической формы предмета. Используя изображение детали, размерные числа, условные знаки и надписи, можно воссоздать образ детали, т. е. представить по чертежу ее пространственную форму.
Для этой цели сложную по форме деталь мысленно разделяют на отдельные конструктивные части, имеющие форму различных геометрических тел. Мысленное разделение предмета на основные геометрические тела называют анализом геометрической формы предмета. Используя изображение детали, размерные числа, условные знаки и надписи, можно воссоздать образ детали, т. е. представить по чертежу ее пространственную форму.

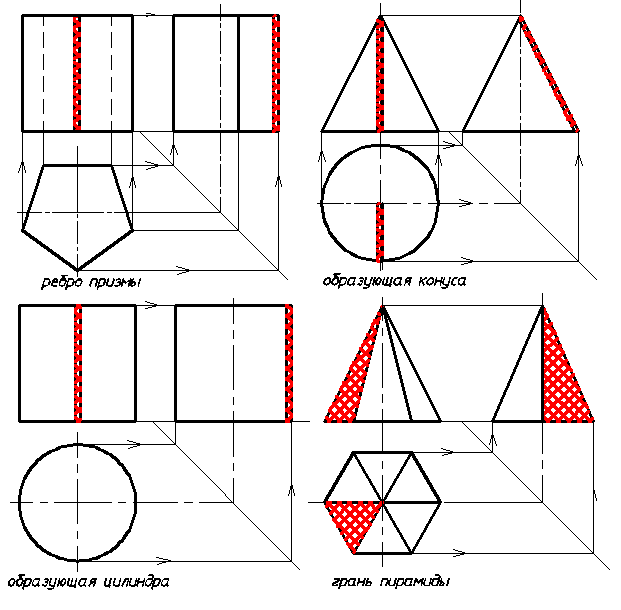
 Через полученные засечки проводят прямые, параллельные одной из осей, и на них откладывают длину стороны шестиугольника. Соединяют полученные засечки отрезками прямых.
Через полученные засечки проводят прямые, параллельные одной из осей, и на них откладывают длину стороны шестиугольника. Соединяют полученные засечки отрезками прямых. 10).
10). 113).
113). 115 Построение изометрической проекции детали на основе последовательного приращения объемов
115 Построение изометрической проекции детали на основе последовательного приращения объемов
 Мы должны видеть это много раз.
Мы должны видеть это много раз.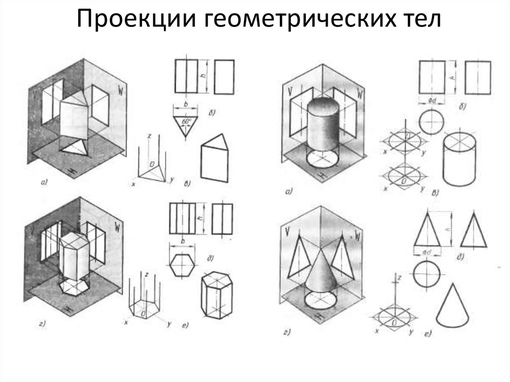 Но я обнаружил, что курс имеет подходящую длину и глубину, чтобы сделать его достаточно надежным, но в то же время выполнимым для тех, кто пытается вписать художественное образование в плотный график.
Учебная программа очень хорошо продумана, и я научился многим принципам и навыкам, которые применимы ко всему рисованию, а не только к рисованию фигур. Структура курса позволила мне сделать самый большой скачок в навыках рисования, который я когда-либо делал. Я закончил с действительно хорошим визуализированным рисунком в дополнение к множеству красивых эскизов фигур.
Я проходил курсы у других замечательных художников и преподавателей, но видео Стэна имеют лучшее качество и являются самыми интересными.
Я рекомендую этот курс! Навыки, полученные в этом курсе, будут служить вам всю жизнь, независимо от того, какие другие курсы или школы вы прошли или планируете пройти.
Спасибо Стэну и команде Proko! Вы создали что-то великое здесь, и я глубоко благодарен.
Но я обнаружил, что курс имеет подходящую длину и глубину, чтобы сделать его достаточно надежным, но в то же время выполнимым для тех, кто пытается вписать художественное образование в плотный график.
Учебная программа очень хорошо продумана, и я научился многим принципам и навыкам, которые применимы ко всему рисованию, а не только к рисованию фигур. Структура курса позволила мне сделать самый большой скачок в навыках рисования, который я когда-либо делал. Я закончил с действительно хорошим визуализированным рисунком в дополнение к множеству красивых эскизов фигур.
Я проходил курсы у других замечательных художников и преподавателей, но видео Стэна имеют лучшее качество и являются самыми интересными.
Я рекомендую этот курс! Навыки, полученные в этом курсе, будут служить вам всю жизнь, независимо от того, какие другие курсы или школы вы прошли или планируете пройти.
Спасибо Стэну и команде Proko! Вы создали что-то великое здесь, и я глубоко благодарен. Эти чувства ушли, потому что я прошел этот курс дважды и каждый раз получаю от него больше. Мне нравится, что я могу вернуться и повторить весь курс или только его часть снова и снова, и срок его действия не истекает, как на сайтах с подпиской. Мне нравится, что это был разовый платеж, и мне не нужно было подписываться на ежемесячную схему.
Уроки преподаются короткими, лаконичными кусками, чтобы можно было попрактиковаться и усвоить один из них, прежде чем переходить к следующему, тем самым укрепляя знания учащегося.
Стэн очень хорошо осведомлен с правильным сочетанием информации и юмора. Я очень рекомендую этот курс всем, кто хочет расширить свои знания в рисовании фигур. Он содержит достаточно инструкций и справочного материала, чтобы занять вас и практиковать в течение длительного времени.
Большое спасибо за создание этих курсов.
Эти чувства ушли, потому что я прошел этот курс дважды и каждый раз получаю от него больше. Мне нравится, что я могу вернуться и повторить весь курс или только его часть снова и снова, и срок его действия не истекает, как на сайтах с подпиской. Мне нравится, что это был разовый платеж, и мне не нужно было подписываться на ежемесячную схему.
Уроки преподаются короткими, лаконичными кусками, чтобы можно было попрактиковаться и усвоить один из них, прежде чем переходить к следующему, тем самым укрепляя знания учащегося.
Стэн очень хорошо осведомлен с правильным сочетанием информации и юмора. Я очень рекомендую этот курс всем, кто хочет расширить свои знания в рисовании фигур. Он содержит достаточно инструкций и справочного материала, чтобы занять вас и практиковать в течение длительного времени.
Большое спасибо за создание этих курсов. Что помогло, так это то, что курс очень структурирован, поскольку кажется, что каждый раздел основан на предыдущем. С четкими инструкциями, примерами для подражания и заданиями.
Мне нравится привлекательный инструктор с чувством юмора. В принципе, Стэн не скучный чувак. Другие курсы теряют меня, если они не обеспечивают структуру, простоту понимания и веселье. Это был отличный курс, который стоил потраченного времени и денег.
Что помогло, так это то, что курс очень структурирован, поскольку кажется, что каждый раздел основан на предыдущем. С четкими инструкциями, примерами для подражания и заданиями.
Мне нравится привлекательный инструктор с чувством юмора. В принципе, Стэн не скучный чувак. Другие курсы теряют меня, если они не обеспечивают структуру, простоту понимания и веселье. Это был отличный курс, который стоил потраченного времени и денег. Это включает в себя дополнительные примеры каждого урока и критические видео. Бесплатный курс длится 5 часов, а премиум-курс — 15 часов. Версии нескольких диаграмм в высоком разрешении также будут в разделе «Премиум», которые вы можете скачать и распечатать для справки.
Видео также можно загрузить, поэтому вы можете смотреть их без доступа в Интернет и переносить на планшет, например iPad. Собираетесь в отпуск? Загрузите их, чтобы вы могли смотреть их в самолете и в той хижине в лесу.
Это включает в себя дополнительные примеры каждого урока и критические видео. Бесплатный курс длится 5 часов, а премиум-курс — 15 часов. Версии нескольких диаграмм в высоком разрешении также будут в разделе «Премиум», которые вы можете скачать и распечатать для справки.
Видео также можно загрузить, поэтому вы можете смотреть их без доступа в Интернет и переносить на планшет, например iPad. Собираетесь в отпуск? Загрузите их, чтобы вы могли смотреть их в самолете и в той хижине в лесу.
 Очень сложно
позы можно упростить, начав с «конверта» для обозначения области
которую занимает фигура, а также основные углы позы. Это
но несколько примеров возможностей.
Очень сложно
позы можно упростить, начав с «конверта» для обозначения области
которую занимает фигура, а также основные углы позы. Это
но несколько примеров возможностей. 


 Обратите внимание на
повторение этого движения в левой стороне тела и в изгибе
позвоночника.
Обратите внимание на
повторение этого движения в левой стороне тела и в изгибе
позвоночника.  в которую вписывается поза.
в которую вписывается поза. 

 Независимо от используемого вами устройства, можно конвертировать файлы XLS и XLSX в PDF для просмотра когда и где угодно.
Независимо от используемого вами устройства, можно конвертировать файлы XLS и XLSX в PDF для просмотра когда и где угодно.




 innerHTML = «
innerHTML = «

 В этой статье мы рассмотрим входы и выходы Kotlin и когда какие использовать.
В этой статье мы рассмотрим входы и выходы Kotlin и когда какие использовать.

 При этом слагаемое берется со знаком
“+”, если перестановка, составленная
из номеров строк и номеров столбцов,
входящих в это произведение – чётное
и со знаком “-”, если она не четная.
При этом слагаемое берется со знаком
“+”, если перестановка, составленная
из номеров строк и номеров столбцов,
входящих в это произведение – чётное
и со знаком “-”, если она не четная. А данная строка в первом
слагаемом заменяется на первое слагаемое
матричной строки, а во втором на вторую.
А данная строка в первом
слагаемом заменяется на первое слагаемое
матричной строки, а во втором на вторую.
 Знак члена (4)
в
Знак члена (4)
в 2)
2) 2), а их алгебраические дополнения.
2), а их алгебраические дополнения.
 Вынося коэффициент пропорциональности за знак определителя, получим определитель с двумя одинаковыми строками, который по свойству 3 равен нулю.
Вынося коэффициент пропорциональности за знак определителя, получим определитель с двумя одинаковыми строками, который по свойству 3 равен нулю. е.:
е.:
 Возьмем, к примеру, производные, поскольку большинство из нас знает, что такое производные:
Возьмем, к примеру, производные, поскольку большинство из нас знает, что такое производные:
 Вернемся к нашему примеру:
Вернемся к нашему примеру: «Что это теперь вообще значит?», спросите вы с полным правом. Давайте посмотрим:
«Что это теперь вообще значит?», спросите вы с полным правом. Давайте посмотрим: Например, вы могли слышать или не слышать следующий факт:
Например, вы могли слышать или не слышать следующий факт:

 2. В этом подразделе мы также покажем, что определитель связан с обратимостью, а в разделе 4.3 — с объемами.
2. В этом подразделе мы также покажем, что определитель связан с обратимостью, а в разделе 4.3 — с объемами.
 Таким образом, определитель исходной матрицы равен 7,9.0005
Таким образом, определитель исходной матрицы равен 7,9.0005
 е. если он одновременно является верхнетреугольным и нижнетреугольным. AAAA0AAA00AA000AGKKKIHLLLJверхний треугольныйA000AA00AAA0AAAAGKKKIHLLLJнижний треугольныйA0000A0000A0000AGKKKIHLLLJдиагональный
е. если он одновременно является верхнетреугольным и нижнетреугольным. AAAA0AAA00AA000AGKKKIHLLLJверхний треугольныйA000AA00AAA0AAAAGKKKIHLLLJнижний треугольныйA0000A0000A0000AGKKKIHLLLJдиагональный Поскольку операции со строками не меняются, если определитель равен нулю, мы заключаем, что det(A)=0.
Поскольку операции со строками не меняются, если определитель равен нулю, мы заключаем, что det(A)=0.


 Если A обратим, то уравнение верно и для всех n≤0; в частности,
Если A обратим, то уравнение верно и для всех n≤0; в частности, Другими словами, элемент ij матрицы AT равен aji.
Другими словами, элемент ij матрицы AT равен aji.

 10 — 11 класс.
10 — 11 класс.



 2
2 ru
ru


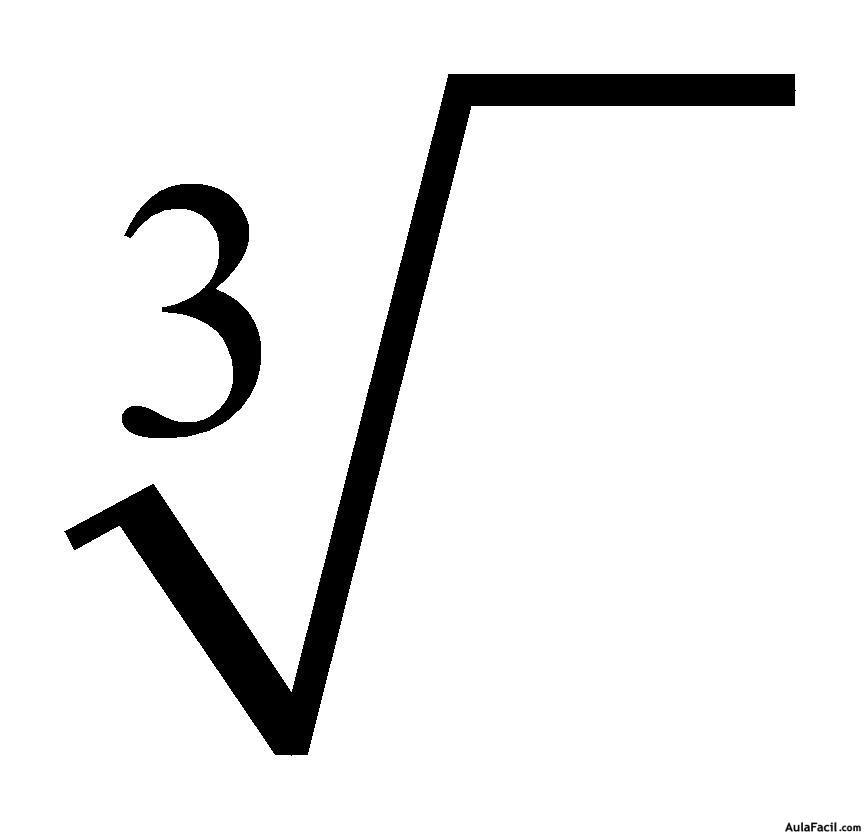
 Подкорневые числа можно перемножать между собой только в том случае, если они имеют одинаковые степени (см. умножение корней без множителей). В случае отсутствия множителя, он равен единице.
Подкорневые числа можно перемножать между собой только в том случае, если они имеют одинаковые степени (см. умножение корней без множителей). В случае отсутствия множителя, он равен единице. Подкорневые числа можно делить между собой только в том случае, если они имеют одинаковые степени. В случае отсутствия множителя, он равен единице.
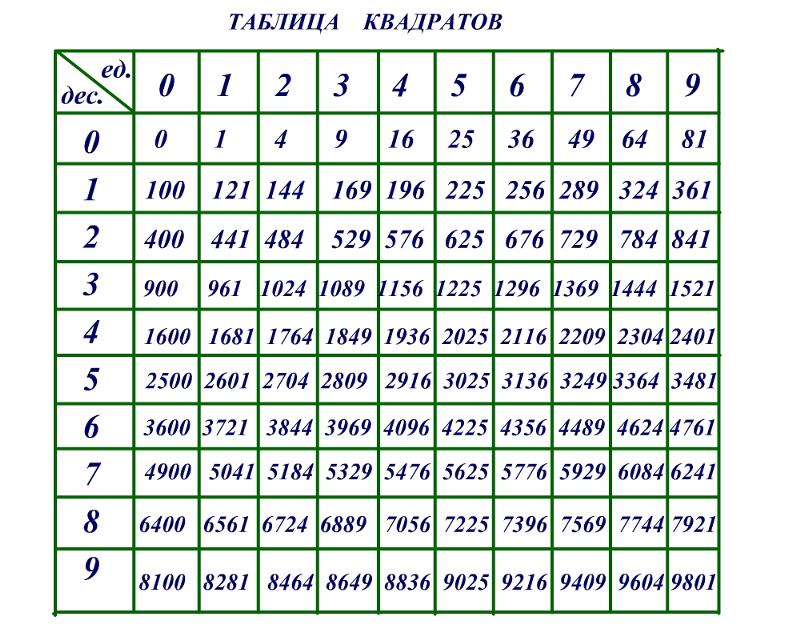
Подкорневые числа можно делить между собой только в том случае, если они имеют одинаковые степени. В случае отсутствия множителя, он равен единице. Ниже приведен неполный список совершенных (целых) квадратных корней.
Ниже приведен неполный список совершенных (целых) квадратных корней. (В квадратном корне индекс 2 понимается и обычно не записывается.) Ниже приводится неполный список совершенных (целых) кубических корней.
(В квадратном корне индекс 2 понимается и обычно не записывается.) Ниже приводится неполный список совершенных (целых) кубических корней. Вы можете иметь в виду эти два, потому что они обычно используются.
Вы можете иметь в виду эти два, потому что они обычно используются.
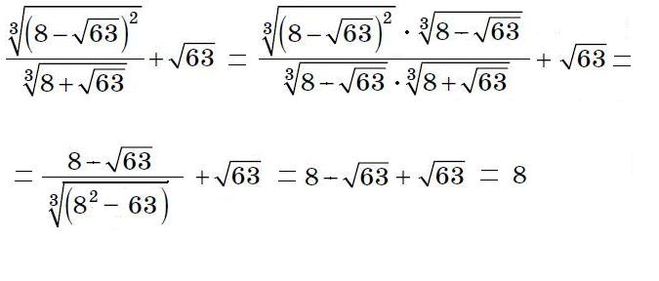



 7: Нахождение кубических корней
7: Нахождение кубических корней 8. Нахождение квадратных корней дробей и
десятичные дроби
8. Нахождение квадратных корней дробей и
десятичные дроби Итак, \(\sqrt{\frac{4}{9}} = \frac{\sqrt{4}}{\sqrt{9}} =
\фракция{2}{3}\).
Итак, \(\sqrt{\frac{4}{9}} = \frac{\sqrt{4}}{\sqrt{9}} =
\фракция{2}{3}\).

 Переместите запятую наполовину
количество мест в ответе.
Переместите запятую наполовину
количество мест в ответе.

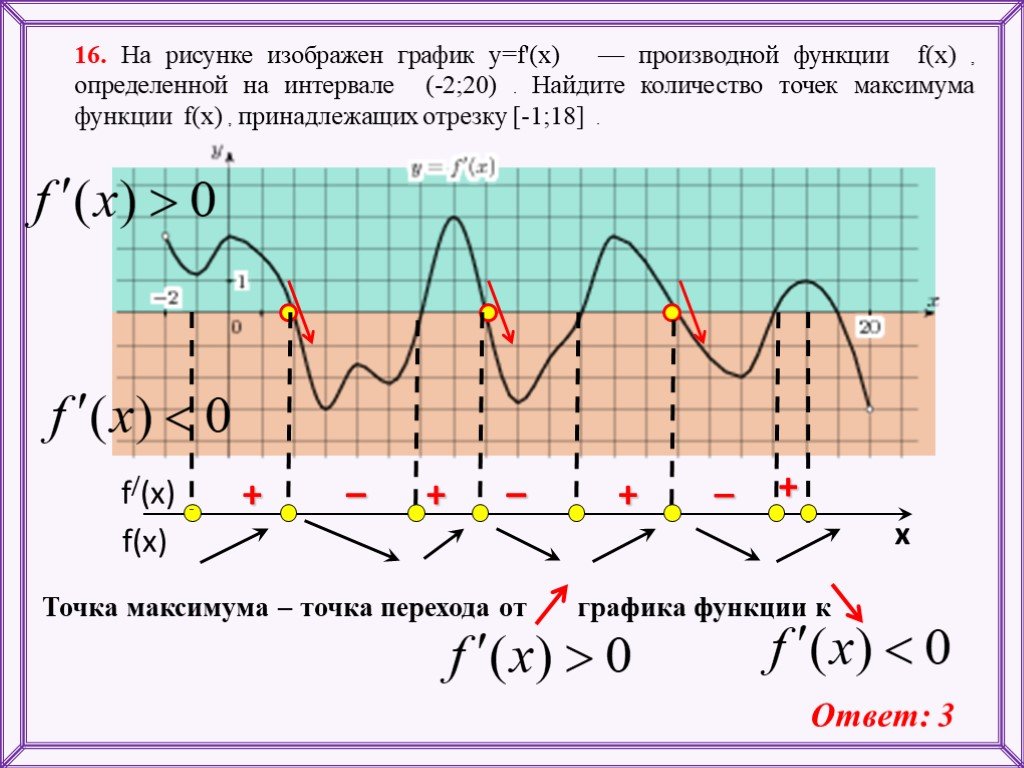
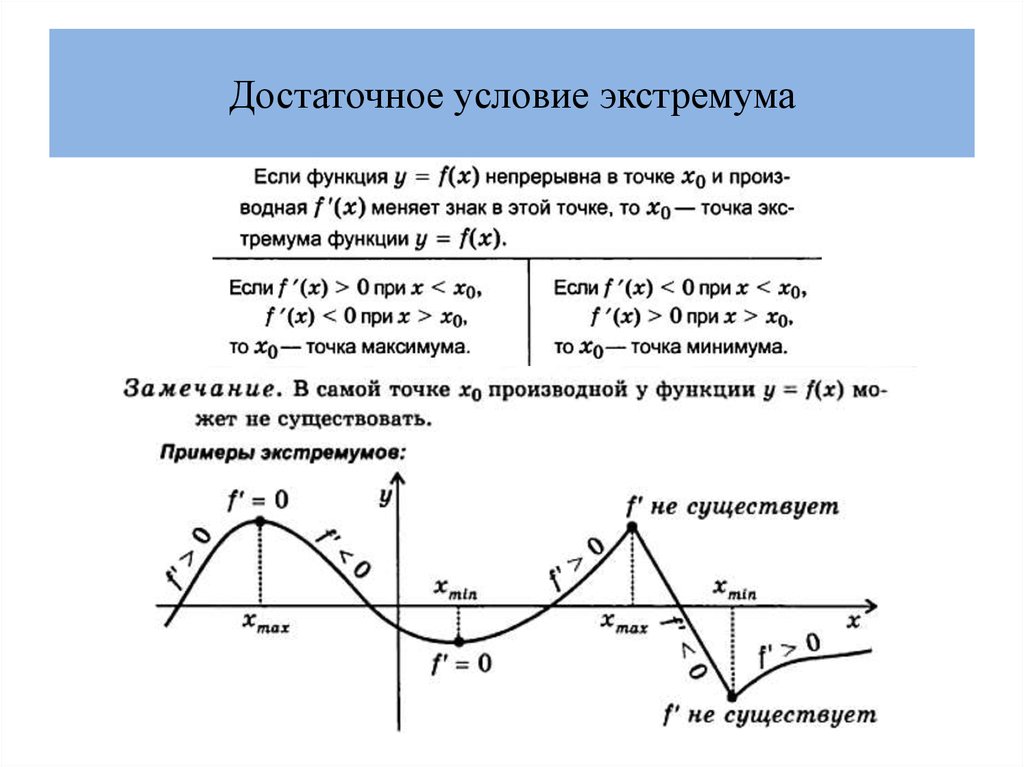
 Здесь функция принадлежала промежутку [-3;2]. Чтобы найти наибольшее и наименьшее в таком случае, предстоит учитывать абсциссы. В них достигаются соответствующие пределы.
Здесь функция принадлежала промежутку [-3;2]. Чтобы найти наибольшее и наименьшее в таком случае, предстоит учитывать абсциссы. В них достигаются соответствующие пределы. А вот максимум – не определен.
А вот максимум – не определен. А еще – закончить тематические дистанционные онлайн курсы.
А еще – закончить тематические дистанционные онлайн курсы. Для глобального максимума эта область расширяется до всей области допустимых аргументов. Для минимума всё наоборот. Экстремум — это локальное экстремальное — минимальное или максимальное — значение.
Для глобального максимума эта область расширяется до всей области допустимых аргументов. Для минимума всё наоборот. Экстремум — это локальное экстремальное — минимальное или максимальное — значение. 2 определена на всей оси аргументов. А y = 1/x определена для всех аргументов, кроме x = 0.
2 определена на всей оси аргументов. А y = 1/x определена для всех аргументов, кроме x = 0. 3. У неё не может быть экстремумов, она убывает на всей оси аргументов.
3. У неё не может быть экстремумов, она убывает на всей оси аргументов. 3 — 3xy + 2$ 92 = 4$
3 — 3xy + 2$ 92 = 4$ 2 &= 4.
\end{выравнивание}
2 &= 4.
\end{выравнивание}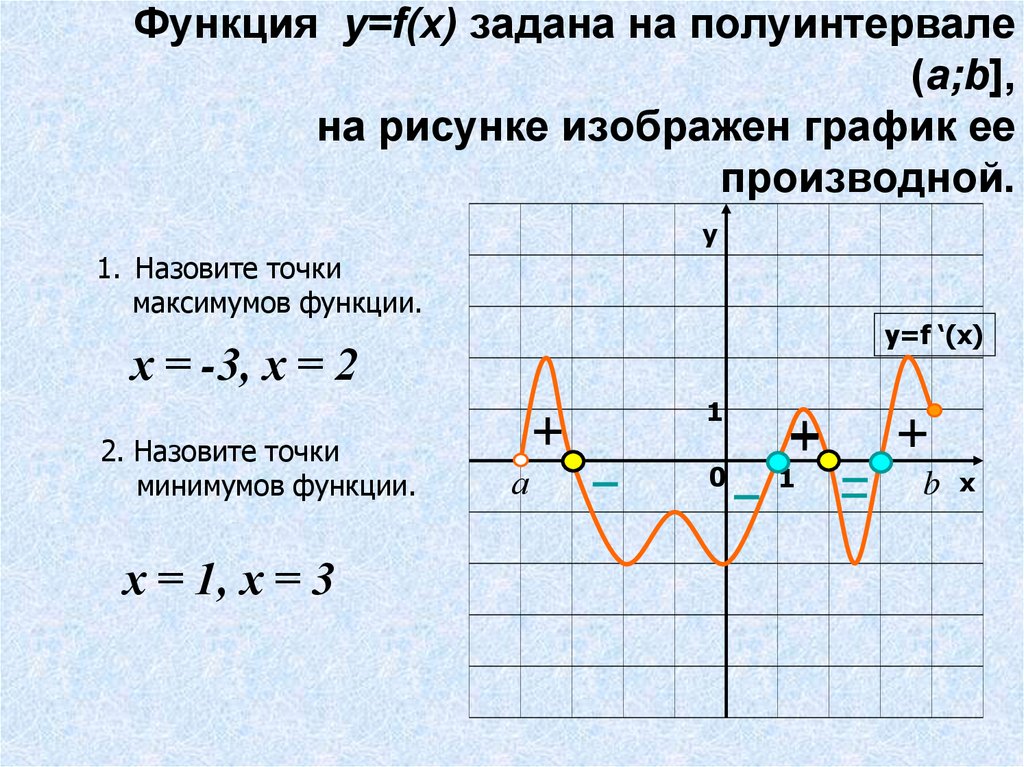






 Однако при умножении двух ненулевых матриц можно получить нулевую матрицу, смотрите:
Однако при умножении двух ненулевых матриц можно получить нулевую матрицу, смотрите: Также
Также 




