Урок 3. Традиционное умножение в уме
Давайте рассмотрим, как можно умножать двузначные числа, используя традиционные методы, которым нас обучают в школе. Некоторые из этих методов, могут позволить вам быстро перемножать в уме двузначные числа при достаточной тренировке. Знать эти методы полезно. Однако важно понимать, что это лишь вершина айсберга.
В данном уроке рассмотрены наиболее популярные приемы умножения двузначных чисел.
Первый способ – раскладка на десятки и единицы
Самым простым для понимания способом умножения двузначных чисел является тот, которому нас научили в школе. Он заключается в разбиении обоих множителей на десятки и единицы с последующим перемножением получившихся четырех чисел. Этот метод достаточно прост, но требует умения удерживать в памяти одновременно до трех чисел и при этом параллельно производить арифметические действия.
Например: 63*85 = (60+3)*(80+5) = 60*80 + 60*5 +3*80 + 3*5=4800+300+240+15=5355
Проще такие примеры решаются в 3 действия. Сначала умножаются десятки друг на друга. Потом складываются 2 произведения единиц на десятки. Затем прибавляется произведение единиц. Схематично это можно описать так:
Сначала умножаются десятки друг на друга. Потом складываются 2 произведения единиц на десятки. Затем прибавляется произведение единиц. Схематично это можно описать так:
- Первое действие: 60*80 = 4800 — запоминаем
- Второе действие: 60*5+3*80 = 540 – запоминаем
- Третье действие: (4800+540)+3*5= 5355 – ответ
Вывод. Не трудно убедиться в том, что этот способ не является самым эффективным, то есть позволяющим при наименьших действиях получить правильный результат. Следует принять во внимание другие способы.
Второй способ – арифметические подгонки
Приведение примера к удобному виду является достаточно распространенным способом счета в уме. Подгонять пример удобно, когда вам нужно быстро найти примерный или точный ответ. Желание подгонять примеры под определенные математические закономерности часто воспитывается на математических кафедрах в университетах или в школах в классах с математическим уклоном. Людей учат находить простые и удобные алгоритмы решения различных задач. Вот некоторые примеры подгонки:
Вот некоторые примеры подгонки:
Пример 49*49 может решаться так: (49*100)/2-49. Сначала считается 49 на сто – 4900. Затем 4900 делится на 2, что равняется 2450, затем вычитается 49. Итого 2401.
Произведение 56*92 решается так: 56*100-56*2*2*2. Получается: 56*2= 112*2=224*2=448. Из 5600 вычитаем 448, получаем 5152.
Этот способ может оказаться эффективнее предыдущего только в случае, если вы владеете устным счетом на базе перемножения двузначных чисел на однозначные и можете держать в уме одновременно несколько результатов. К тому же приходится тратить время на поиск алгоритма решения, а также уходит много внимания за правильным соблюдением этого алгоритма.
Вывод. Способ, когда вы стараетесь умножить 2 числа, раскладывая их на более простые арифметические процедуры, отлично тренирует ваши мозги, но связан с большими мысленными затратами, а риск получить неправильный результат выше, чем при первом методе.
Третий способ — мысленная визуализация умножения в столбик
56*67 – посчитаем в столбик.
Наверное, счет столбиком содержит максимальное количество действий и требует постоянно держать в уме вспомогательные числа. Но его можно упростить. Во втором уроке рассказывалось, что важно уметь быстро умножать однозначные числа на двузначные. Если вы уже умеете это делать на автомате, то счет в столбик в уме для вас будет не таким уж и трудным. Алгоритм таков
Первое действие: 56*7 = 350+42=392 – запомните и не забывайте до третьего действия.
Второе действие: 56*6=300+36=336 (ну или 392-56)
Третье действие: 336*10+392=3360+392=3 752 – тут посложнее, но вы можете начинать называть первое число, в котором уверены – «три тысячи…», а пока говорите, складывайте 360 и 392.
Вывод: счет в столбик напрямую сложен, но вы можете, при наличии навыка быстрого умножения двузначных чисел на однозначные, его упросить. Добавьте в свой арсенал и этот метод. В упрощенном виде счет в столбик является некоторой модификацией первого метода. Что лучше – вопрос на любителя.
Как можно заметить, ни один из описанных выше способов не позволяет считать в уме достаточно быстро и точно все примеры умножения двузначных чисел. Нужно понимать, что использование традиционных способов умножения для счета в уме не всегда является рациональным, то есть позволяющим при наименьших усилиях достигать максимального результата.
Евгений Буянов← 2 Простая арифметика4 Частные методики →
Table of 49 — Learn 49 Times Table
30-DAY PROMIS | ПОЛУЧИТЕ 100% ВОЗВРАТ ДЕНЕГ*
*T&C ApplyLearnPracticeDownload
Таблица 49 показывает значения, которые мы получаем, когда число 49 умножается на другие целые числа. Повторное сложение 49 — это таблица умножения 49. Например, 49 + 49 + 49 = 3 × 49 = 147. На этой странице вы можете найти таблицу от 49 до 20.
Таблица 49 Таблица
| 1. | Стол из 49 |
| 2. | Таблица из 49 Скачать PDF |
3. | Часто задаваемые вопросы по таблице из 49 |
Стол из 49
Таблица умножения на 49 до 20 приведена ниже. Изучение таблицы 49 помогает детям глубже понять умножение, что полезно в долгосрочной перспективе.
Таблица от 49 до 10
| 49 × 1 = 49 | 49 × 6 = 294 |
| 49 × 2 = 98 | 49 × 7 = 343 |
| 49 × 3 = 147 | 49 × 8 = 392 |
| 49 × 4 = 196 | 49 × 9 = 441 |
| 49 × 5 = 245 | 49 × 10 = 490 |
Таблица от 49 до 20
| 49 × 11 = 539 | 49 × 16 = 784 |
| 49 × 12 = 588 | 49 × 17 = 833 |
| 49 × 13 = 637 | 49 × 18 = 882 |
| 49 × 14 = 686 | 49 × 19 = 931 |
| 49 × 15 = 735 | 49 × 20 = 980 |
Вы можете распечатать или сохранить эту таблицу умножения в формате PDF, нажав на ссылку, указанную ниже.
☛ Таблица из 49 PDF Скачать
Таблица из 49 до 10 в словах
- Сорок девять раз Один равен Сороку Девяти
- Сорок девять умножить на два равно девяносто восемь
- Сорок девять умножить на три равно сто сорок семь
- Сорок девять раз четыре равно сто девяносто шести
- Сорок девять умножить на пять равно двести сорок пять
- Сорок девять умножить на шесть равно двести девяносто четыре
- Сорок девять умножить на семь равно триста сорок три
- Сорок девять раз восемь равно триста девяносто два
- Сорок девять раз девять равно четыреста сорок один
- Сорок девять раз десять равно четыреста девяносто
☛ Также проверьте:
- Таблица из 2
- Таблица из 7
- Таблица из 22
- Стол из 36
- Стол из 6
- Таблица из 4
- Таблица из 28
Таблицы из 49 примеров
Пример 1: Дуглас совершает пробежку по 2 мили в день.
 Воспользуйтесь таблицей 49 и найдите, сколько миль он пробежит за 49 дней.
Воспользуйтесь таблицей 49 и найдите, сколько миль он пробежит за 49 дней.Решение:
Дуглас пробегает 2 мили в день. Следовательно, общее количество миль, пройденных за 49 дней, равно 2 × 49 = 98 миль.
Пример 2: Клиент покупает 3 апельсина каждый день. Сколько апельсинов покупатель купит за 49 дней?
Решение:
Клиент покупает 3 апельсина в день. Следовательно, используя таблицу 49, общее количество апельсинов, купленных покупателем за 49 дней, равно 3 × 49 = 147 апельсинов.
Пример 3: Кеннет зарабатывает 20 долларов в час. Сколько денег он заработает, если будет работать 49 часов?
Решение:
Кеннет зарабатывает 20 долларов в час. Следовательно, используя таблицу 49, общая сумма денег, заработанных Кеннетом за 49 часов, составляет 20 × 49 = 980 долларов.
перейти к слайдуперейти к слайдуперейти к слайду
Готовы увидеть мир глазами математика?
Математика лежит в основе всего, что мы делаем. Наслаждайтесь решением реальных математических задач на живых уроках и станьте экспертом во всем.
Наслаждайтесь решением реальных математических задач на живых уроках и станьте экспертом во всем.
Записаться на бесплатный пробный урок
Часто задаваемые вопросы о таблицах из 49
Найдите значение 49, умноженное на 11, используя таблицу 49.
Значение 49, умноженное на 11, из таблицы 49 равно 49 × 11 = 539
Подсчитайте, сколько раз нужно умножить 49, чтобы получить 490.
Из таблицы 49 имеем 49 × 10 = 490. Следовательно, 49 нужно умножить на 10, чтобы получить 490.
Сколько будет 49 умножить на 12 минус 8 плюс 18?
Из таблицы 49, 49 умножить на 12 будет 588. Следовательно, 49 × 12 — 8 + 18 = 588 — 8 + 18 = 598
Используя таблицу 49, найдите значение 11 плюс 49 умножить на 7 минус 49 умножить на 13.
Из таблицы 49, 49 умножить на 7 = 343 и 49 умножить на 13 = 637. Следовательно, 11 + 49 × 7 — 49 × 13 = -283.
☛ Статьи по теме:
Скачать БЕСПЛАТНО учебные материалы
Таблица умножения
Рабочие листы по математике и
наглядный учебный план
Калькулятор дробей
90 243 Этот калькулятор дробей выполняет базовые и расширенные операции с дробями, выражения с дробями в сочетании с целыми числами. , десятичные и смешанные числа. Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении.
, десятичные и смешанные числа. Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении.
Правила выражений с дробями:
Дроби — для деления числителя на знаменатель используйте косую черту, т.е. для пятисотых введите 5/100 . Если вы используете смешанные числа, оставьте пробел между целой и дробной частями. Смешанные числа (смешанные числа или дроби) сохраняют один пробел между целым числом и дробью
и используют косую черту для ввода дробей, например, 1 2/3 . Пример отрицательной смешанной дроби: -5 1/2 .
Поскольку косая черта одновременно является знаком дробной части и деления, используйте двоеточие (:) в качестве оператора деления дробей, т. е. 1/2 : 1/3 .
Decimals (десятичные числа) вводятся с десятичной точкой . и они автоматически преобразуются в дроби — т. е. 1,45 .
е. 1,45 .
Математические символы
| Символ | Имя символа | Символ Значение | Пример | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| + | знак плюс | сложение | 1/2 + 1/3 | ||||||||||
| — | знак минус | вычитание | 90 253 1 1/2 — 2/3 | ||||||||||
| * | звездочка | умножение | 2/3 * 3/4 | ||||||||||
| × | знак умножения | умножение | 2/3 × 5/6 | ||||||||||
| : | знак деления | деление 91/2 • сложение дробей и смешанных чисел: 8/5 + 6 2/7 • деление целых чисел и дробей: 5 ÷ 1/2 • сложные дроби: 5/8 : 2 2/3 • десятичная дробь: 0,625 • Преобразование дроби в десятичную: 1/4 • Преобразование дроби в процент: 1/8 % • сравнение дробей: 1/4 2/3 • умножение дроби на целое число: 6 * 3/4 • квадратный корень дроби: sqrt(1/16) • уменьшение или упрощение дроби (упрощение) — деление числителя и знаменателя дроби на одно и то же ненулевое число — эквивалентная дробь: 4/22 • выражение со скобками: 1/3 * (1/2 — 3 3/8) • составная дробь: 3/4 от 5/7 • кратные дроби: 2/3 от 3/5 • разделить, чтобы найти частное: 3/5 ÷ 2/3 Калькулятор следует известным правилам для порядка операций .  Наиболее распространенные мнемоники для запоминания этого порядка операций: Наиболее распространенные мнемоники для запоминания этого порядка операций: PEMDAS — Скобки, Экспоненты, Умножение, Деление, Сложение, Вычитание. BEDMAS — Скобки, Экспоненты, Деление, Умножение, Сложение, Вычитание BODMAS — Скобки, Порядок, Деление, Умножение, Сложение, Вычитание. GEMDAS — символы группировки — скобки (){}, показатели степени, умножение, деление, сложение, вычитание. MDAS — Умножение и деление имеют тот же приоритет, что и сложение и вычитание. Правило MDAS является частью порядка операций правила PEMDAS. Будь осторожен; всегда выполняйте умножение и деление перед сложением и вычитанием . Некоторые операторы (+ и -) и (* и /) имеют одинаковый приоритет и должны оцениваться слева направо.
| |||||||||||
| ⇌ | |||||||||||||
Найдите другие преобразования здесь:
Определение миллиметра
единица длины, равная 1/1000 метра и равная 0,03937 дюйма. Аббревиатура: mm
Аббревиатура: mm
Насколько велик миллиметр?
Вот примеры вещей размером около 1 мм:
- Толщина кредитной карты
- Типичный наконечник механического карандаша имеет размеры, например, 0,5, 0,7 или 0,9 мм
- Средний размер наконечника ручки обеспечивает линию шириной около 1,0 мм для шариковой ручки.
Вот еще примеры вещей размером около одного миллиметра (порядка величины):
Ширина грифеля механического карандаша
Толщина кредитной карты
Длина блохи
Ширина крупинки соли
Ширина скобы
Диаметр кончика шариковой ручки
Толщина одна прядь человеческого волоса
Высота надписи на монете
Определение сантиметра
сантиметр (см) – десятичная дробь метра, единица длины в Международной системе единиц (СИ), приблизительно эквивалентно 0,39дюймы. Сантиметр (см) — единица длины, которая ранее была базовой единицей длины в системе единиц сантиметр-грамм-секунда (СГС). Хотя технические специалисты предпочитают префиксы SI для коэффициентов 10 3 , сантиметр остается практической единицей длины для повседневных измерений. Ширина ногтя среднего взрослого человека примерно равна одному сантиметру, что делает его удобным для измерения небольших предметов или расстояний. Узнайте больше о сантиметре и его использовании в повседневной жизни.
Хотя технические специалисты предпочитают префиксы SI для коэффициентов 10 3 , сантиметр остается практической единицей длины для повседневных измерений. Ширина ногтя среднего взрослого человека примерно равна одному сантиметру, что делает его удобным для измерения небольших предметов или расстояний. Узнайте больше о сантиметре и его использовании в повседневной жизни.
Вот несколько примеров вещей размером около одного сантиметра (порядок величины):
Ширина ногтя взрослого человека
Диаметр стандартного стержня карандаша
Толщина кредитной карты
Высота маленького кубика Lego
Диаметр батарейки АА
Длина муравья
Ширина маленькая кнопка
Толщина защитной пленки для экрана смартфона
Ширина рисового зерна
Высота маленькой скрепки.
Как преобразовать 72 миллиметра в сантиметры
Чтобы рассчитать значение в сантиметрах, вам просто нужно использовать следующую формулу :
Значение в сантиметрах = значение в миллиметрах × 1 / 10
Другими словами, вам нужно умножить значение емкости в миллиметрах на 1 / 10 , чтобы получить эквивалентное значение в сантиметрах.
Например, чтобы преобразовать 72 мм в сантиметры, вы можете подставить значение 72 в приведенную выше формулу, чтобы получить
сантиметра = 72 × 1 / 10 = 7 1 / 5
Следовательно, емкость конденсатора равна 7 1 / 50 сантиметра 8. Обратите внимание, что полученное значение, возможно, придется округлить до практического или стандартного значения, в зависимости от приложения.
С помощью этого конвертера вы можете получить ответы на такие вопросы, как:
- Сколько 72 миллиметра в сантиметрах;
- Как перевести миллиметры в сантиметры и
- Какая формула для перевода миллиметров в сантиметры?
Millimeters to Centimeters Conversion Chart Near 66 millimeters
| Millimeters to Centimeters | ||
|---|---|---|
| 66 millimeters | equals | 6.6 centimeters |
| 67 millimeters | equals | 6. 7 centimeters 7 centimeters |
| 68 millimeters | равно | 6,8 см |
| 69 millimeters | equals | 6.9 centimeters |
| 70 millimeters | equals | 7 centimeters |
| 71 millimeters | equals | 7.1 centimeters |
| 72 millimeters | equals | 7,2 сантиметра |
| 73 миллиметра | равно | 7,3 сантиметра |
| 74 миллиметра | equals | 7.4 centimeters |
| 75 millimeters | equals | 7.5 centimeters |
| 76 millimeters | equals | 7.6 centimeters |
| 77 millimeters | equals | 7.7 centimeters |
| 78 миллиметров | равно | 7,8 сантиметра |
Примечание. Значения округлены до 4 значащих цифр. Дроби округляются до ближайшей восьмой дроби.
Дроби округляются до ближайшей восьмой дроби.
Преобразование образцов
Отказ от ответственности
Несмотря на усилия по предоставлению точной информации на этом веб-сайте, мы не гарантируем ее точность. Поэтому контент не должен использоваться для принятия решений, касающихся здоровья, финансов или имущества.
О нас | Свяжитесь с нами | КонфиденциальностьCopyright © 2016 — 2023 HowMany.wiki
Сколько см в 72 мм?
72 мм равно 7 1 / 5 см
Универсальный преобразователь единиц измерения
| ⇆ | ||
Пожалуйста, выберите физическую величину, две единицы, затем введите значение в любом из полей выше. | ||
Чтобы вычислить значение в миллиметрах для соответствующего значения в см, просто умножьте количество в мм на 0,1 (коэффициент преобразования). Вот формула :
Вот формула :
Значение в см = значение в мм × 0,1
Предположим, вы хотите преобразовать 72 мм в сантиметры. Используя приведенную выше формулу преобразования, вы получите:
Значение в см = 72 × 0,1 = 7 1 / 5 см
Определение миллиметра
Миллиметр (мм) — это десятичная дробь метра. международная стандартная единица длины, приблизительно эквивалентная 39,37 дюймам.
Определение сантиметра
сантиметр (см) – десятичная дробь метра, международная стандартная единица длины, примерно равная 390,37 дюйма.
Этот конвертер поможет вам получить ответы на такие вопросы, как:
- Сколько мм в 72 см?
- 72 мм равны скольким см?
- Сколько 72 мм в см?
- Как преобразовать мм в см?
- Какой коэффициент преобразования мм в см?
- Как преобразовать мм в см?
- По какой формуле перевести миллиметры в см? Среди прочих.
Таблица перевода миллиметров в см около 72 мм
| Mm to cm conversion chart | ||
|---|---|---|
| 65 mm | = | 6 1 / 2 cm |
| 66 mm | = | 6. 6 cm 6 cm |
| 67 mm | = | 6.7 cm |
| 68 mm | = | 6.8 cm |
| 69 mm | = | 6.9 cm |
| 70 mm | = | 7 cm |
| 71 mm | = | 7.1 cm |
| 72 mm | = | 7 1 / 5 cm |
| Mm to cm conversion chart | ||
|---|---|---|
| 72 mm | = | 7 1 / 5 cm |
| 73 mm | = | 7.3 cm |
| 74 mm | = | 7.4 cm |
| 75 mm | = | 7 1 / 2 cm |
| 76 mm | = | 7.6 cm |
| 77 mm | = | 7.7 cm |
| 78 мм | = | 7,8 см |
| 79 мм | = | 7,9 см |
Примечание.

 Воспользуйтесь таблицей 49 и найдите, сколько миль он пробежит за 49 дней.
Воспользуйтесь таблицей 49 и найдите, сколько миль он пробежит за 49 дней. Шесть детей — девочки. Какую часть детей составляют девочки?
Шесть детей — девочки. Какую часть детей составляют девочки?
 В итоге, пороховыми газами, выходящими из ствола в передней части кожуха, создаётся зона разрежения. А при стрельбе через эти канавки прогоняется холодный воздух. Благодаря постоянному охлаждению передней части ствола, снижается рассеивание огня, и увеличивается долговечность ствола, что является большим преимуществом перед прошлыми моделями. Также применяется регулируемый газоотводный механизм, позволяющий использовать «Печенег» в неблагоприятных климатических условиях (северные широты, тропические джунгли).
В итоге, пороховыми газами, выходящими из ствола в передней части кожуха, создаётся зона разрежения. А при стрельбе через эти канавки прогоняется холодный воздух. Благодаря постоянному охлаждению передней части ствола, снижается рассеивание огня, и увеличивается долговечность ствола, что является большим преимуществом перед прошлыми моделями. Также применяется регулируемый газоотводный механизм, позволяющий использовать «Печенег» в неблагоприятных климатических условиях (северные широты, тропические джунгли). Поэтому у его потомка 6П69 сошки можно вручную смещать. Улучшение охлаждения ствола позволило повысить его ресурс до уровня всего пулемёта, или в 2 раза выше, чем у ПКМ (и это при 80% общих деталей!). Также это снизило смещение точки прицеливания при продолжительной стрельбе. Всё это позволило отказаться от запасного ствола (но крепление ствола у «Печенега» решили оставить быстроразъёмным, для ускорения ремонта в полевых условиях), что снизило походный вес оружия.
Поэтому у его потомка 6П69 сошки можно вручную смещать. Улучшение охлаждения ствола позволило повысить его ресурс до уровня всего пулемёта, или в 2 раза выше, чем у ПКМ (и это при 80% общих деталей!). Также это снизило смещение точки прицеливания при продолжительной стрельбе. Всё это позволило отказаться от запасного ствола (но крепление ствола у «Печенега» решили оставить быстроразъёмным, для ускорения ремонта в полевых условиях), что снизило походный вес оружия.


 В число приспособлений входят ПМС (именуемый также тактическим глушителем), удобная передняя рукоятка (которую можно переставлять в разные стороны), быстросъёмные сошки. Отдельно стоит сказать про переднюю рукоятку, на видео блогера Razvedos, он показывает, что положения слева и справа от ствола не совсем удобны, в отличие от положения снизу. Патронный короб имеет внутри резиновое покрытие, оно тоже показано на видео, позволяющее пулемёту не громыхать при беге (особенно при неполной загрузке короба). Имеется и планка Пикатинни для крепления специального оптического прицела 1П89-3, а механический прицел размечен до 800 метров. Приклад складной и настраиваемый по длине. Оба ствола позволяют переставлять сошки в удобное для стрелка положение. Печенег-СП (6П69) впервые появился перед общественностью в августе 2014 года на выставке «Рособоронэкспо-2014» в Жуковском. Ресурс короткого ствола с тактическим глушителем (ПМС) составляет около 15 000 выстрелов. Все перечисленные модели пулемётов активно используются в зоне СВО на Украине.
В число приспособлений входят ПМС (именуемый также тактическим глушителем), удобная передняя рукоятка (которую можно переставлять в разные стороны), быстросъёмные сошки. Отдельно стоит сказать про переднюю рукоятку, на видео блогера Razvedos, он показывает, что положения слева и справа от ствола не совсем удобны, в отличие от положения снизу. Патронный короб имеет внутри резиновое покрытие, оно тоже показано на видео, позволяющее пулемёту не громыхать при беге (особенно при неполной загрузке короба). Имеется и планка Пикатинни для крепления специального оптического прицела 1П89-3, а механический прицел размечен до 800 метров. Приклад складной и настраиваемый по длине. Оба ствола позволяют переставлять сошки в удобное для стрелка положение. Печенег-СП (6П69) впервые появился перед общественностью в августе 2014 года на выставке «Рособоронэкспо-2014» в Жуковском. Ресурс короткого ствола с тактическим глушителем (ПМС) составляет около 15 000 выстрелов. Все перечисленные модели пулемётов активно используются в зоне СВО на Украине.


 02
02 11
11 016
016 02
02 13
13 , а также азота и кислорода / Combustion products
, а также азота и кислорода / Combustion products 3311)
3311) 15
15 09
09 5
5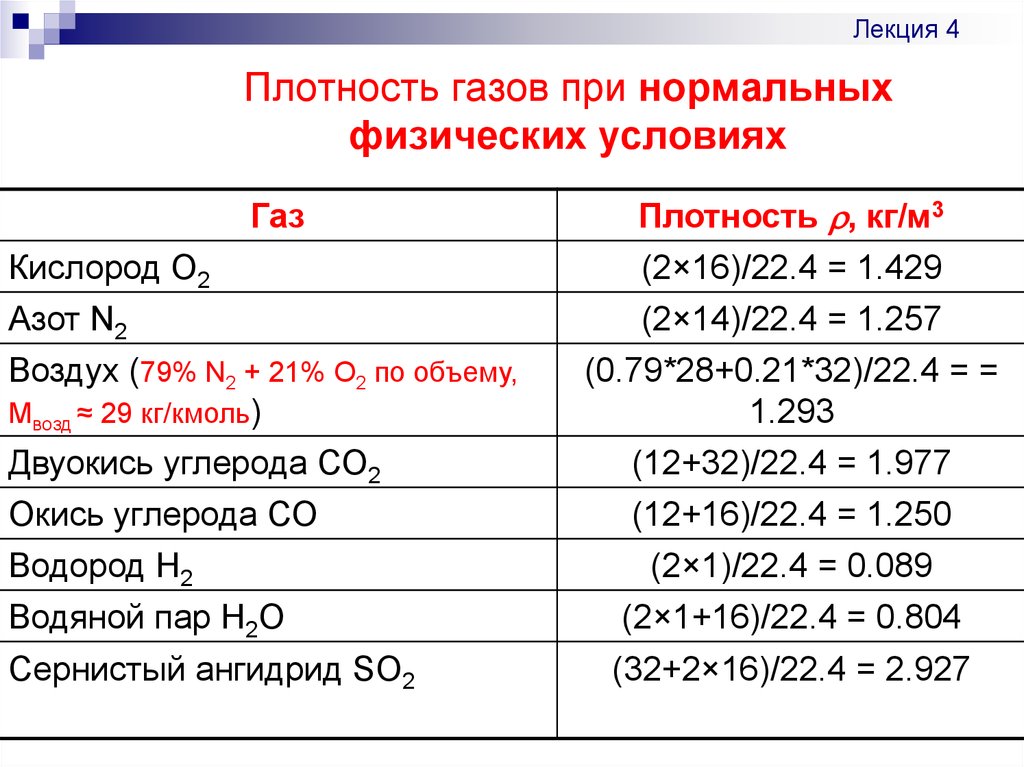 37
37 906
906 325 кН/м2, 101.325 кПа, 14.7 psia, 0 psig, 30 in Hg, 760 мм.рт.ст)
325 кН/м2, 101.325 кПа, 14.7 psia, 0 psig, 30 in Hg, 760 мм.рт.ст)
 д.
д.
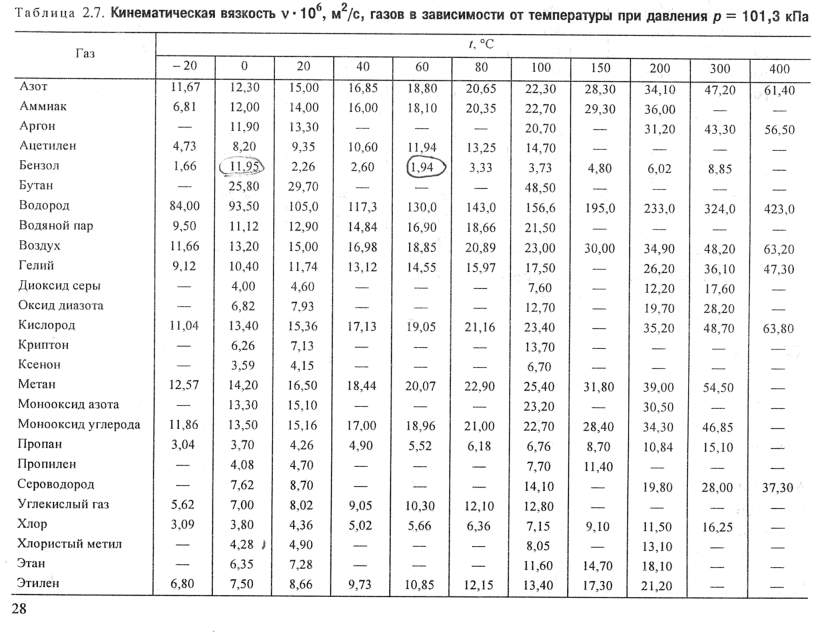 0
0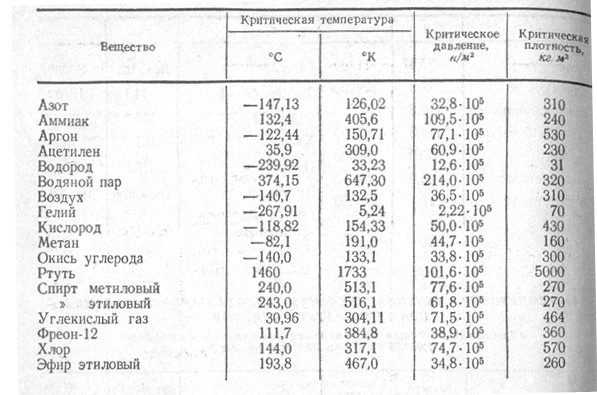 03
03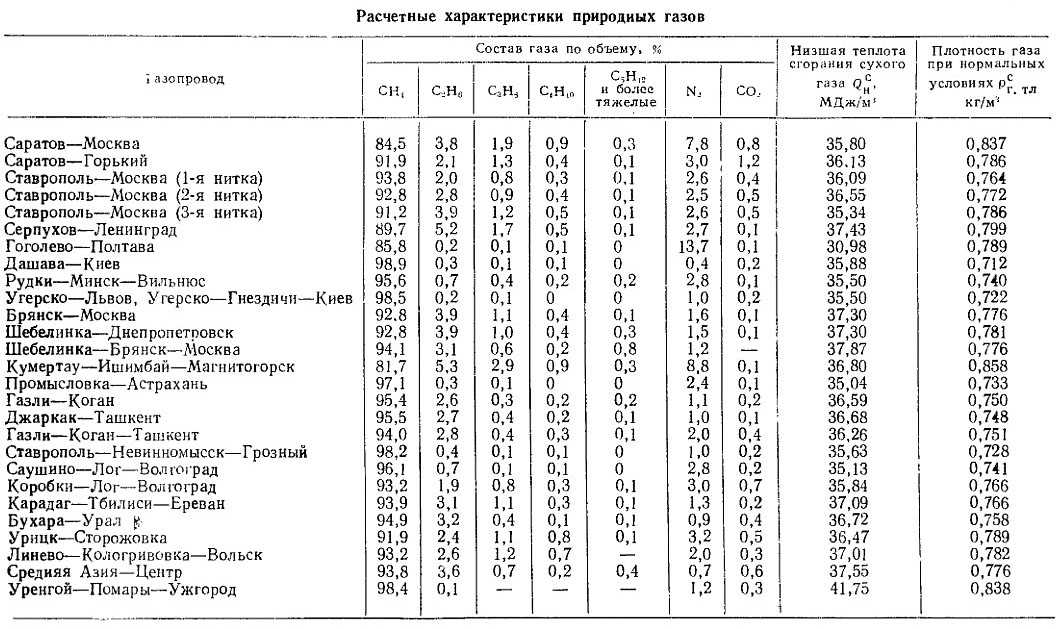 12
12 01
01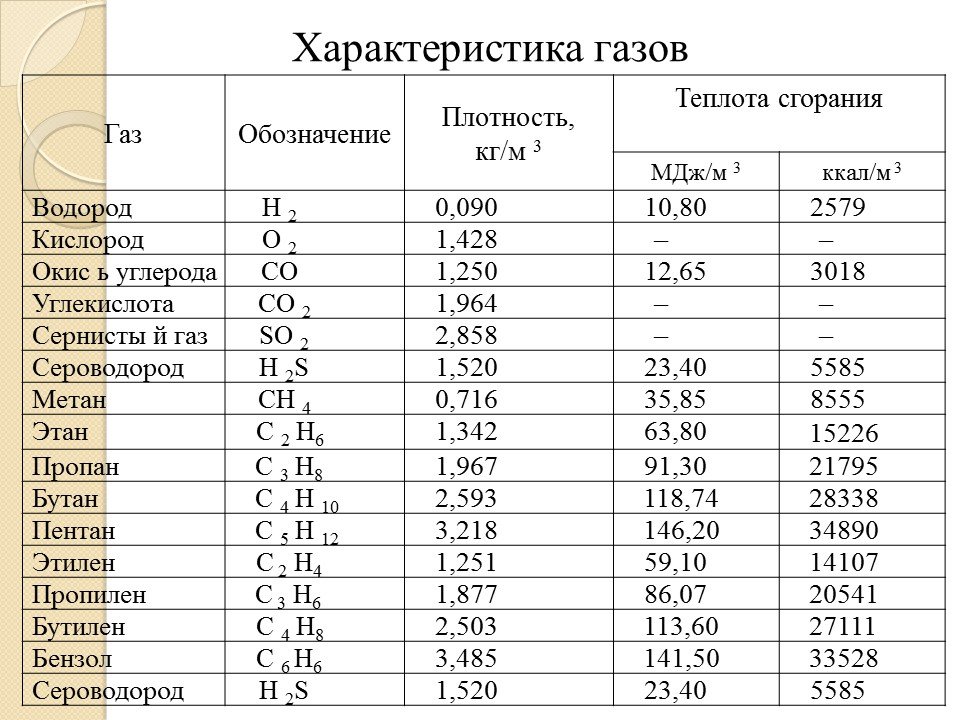 217
217 5Е-6
5Е-6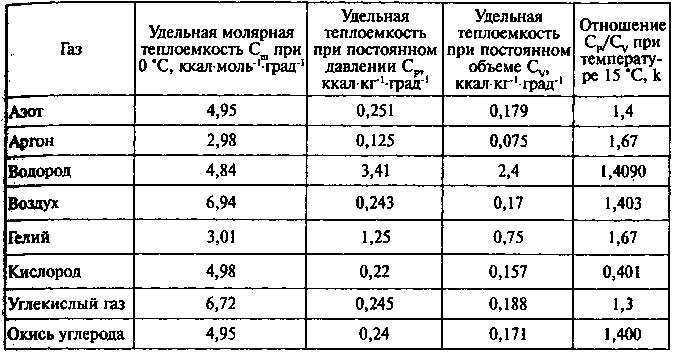 13
13 0
0 708
708 1Е-5
1Е-5 89Е-6
89Е-6 7Е-5
7Е-5 03Е-5
03Е-5 13
13 0
0 03
03


 {2}-4ac}}{2a}.
{2}-4ac}}{2a}. {2}+2 x-3}
{2}+2 x-3}

 Мы очень ценим вашу поддержку!
Мы очень ценим вашу поддержку!
 Вот формула и математика:
Вот формула и математика:
 МОК 33 и 12 можно, например, использовать для сложения и вычитания дробей со знаменателем 33 и 12.
НОК 33 и 12 – это произведение 33 и 12, деленное на НГК 33 и 12. Вот математический результат:
МОК 33 и 12 можно, например, использовать для сложения и вычитания дробей со знаменателем 33 и 12.
НОК 33 и 12 – это произведение 33 и 12, деленное на НГК 33 и 12. Вот математический результат:
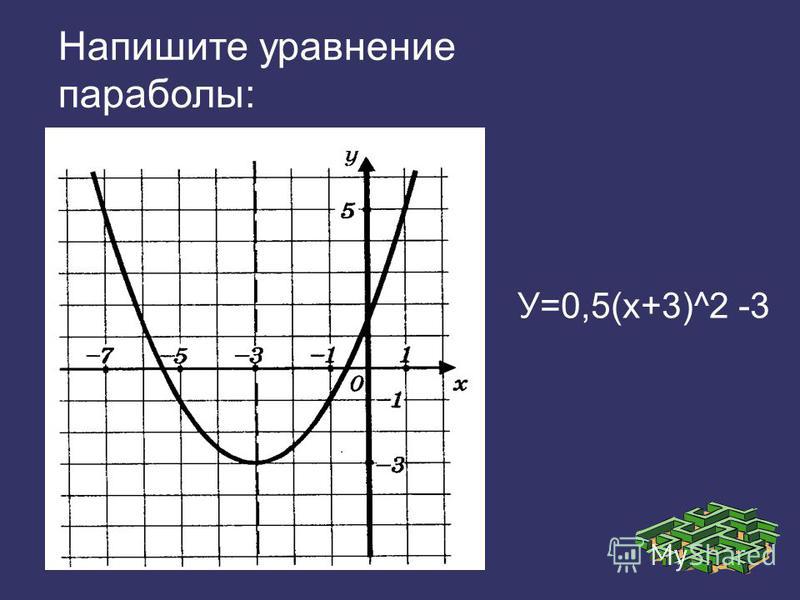 Составить уравнение параболы, если
расстояние от фокуса до директрисы равно 2.
Составить уравнение параболы, если
расстояние от фокуса до директрисы равно 2. Пучок параллельных лучей,
двигающийся вдоль оси параболы, отражаясь, собирается в её фокусе.
Пучок параллельных лучей,
двигающийся вдоль оси параболы, отражаясь, собирается в её фокусе.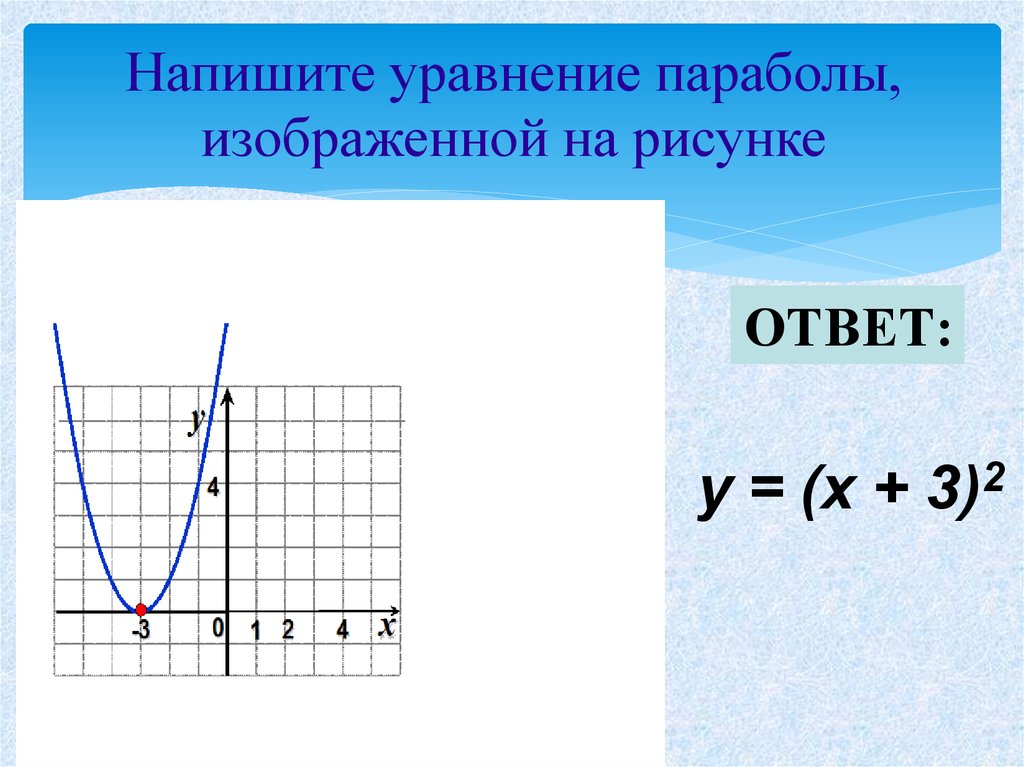 ответил 20.09.13
ответил 20.09.13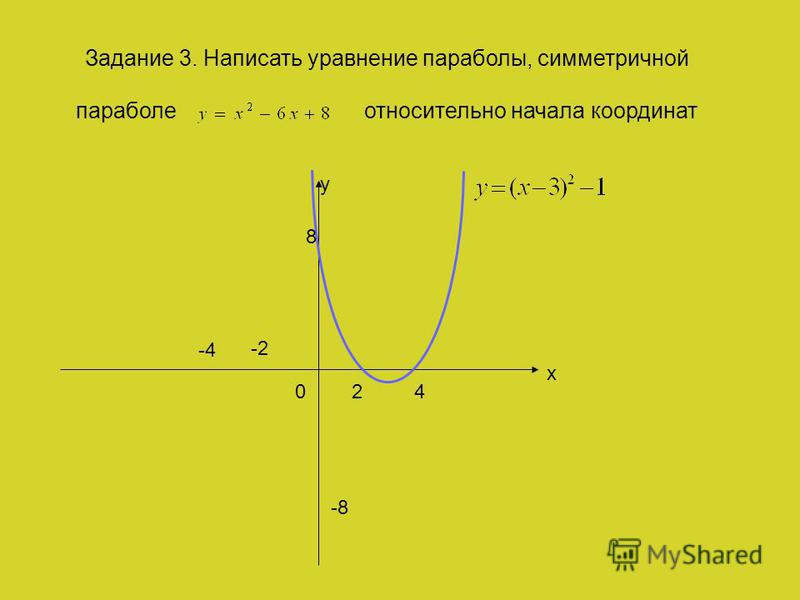 ответил 24.09.13
ответил 24.09.13
 Самый простой способ найти уравнение параболы — использовать знания о специальной точке, называемой вершиной, которая расположена на самой параболе.
Самый простой способ найти уравнение параболы — использовать знания о специальной точке, называемой вершиной, которая расположена на самой параболе. Или, другими словами, если бы вы сложили параболу пополам прямо посередине, вершина была бы «вершиной» параболы, прямо там, где она пересекала бы сгиб бумаги.
Или, другими словами, если бы вы сложили параболу пополам прямо посередине, вершина была бы «вершиной» параболы, прямо там, где она пересекала бы сгиб бумаги.
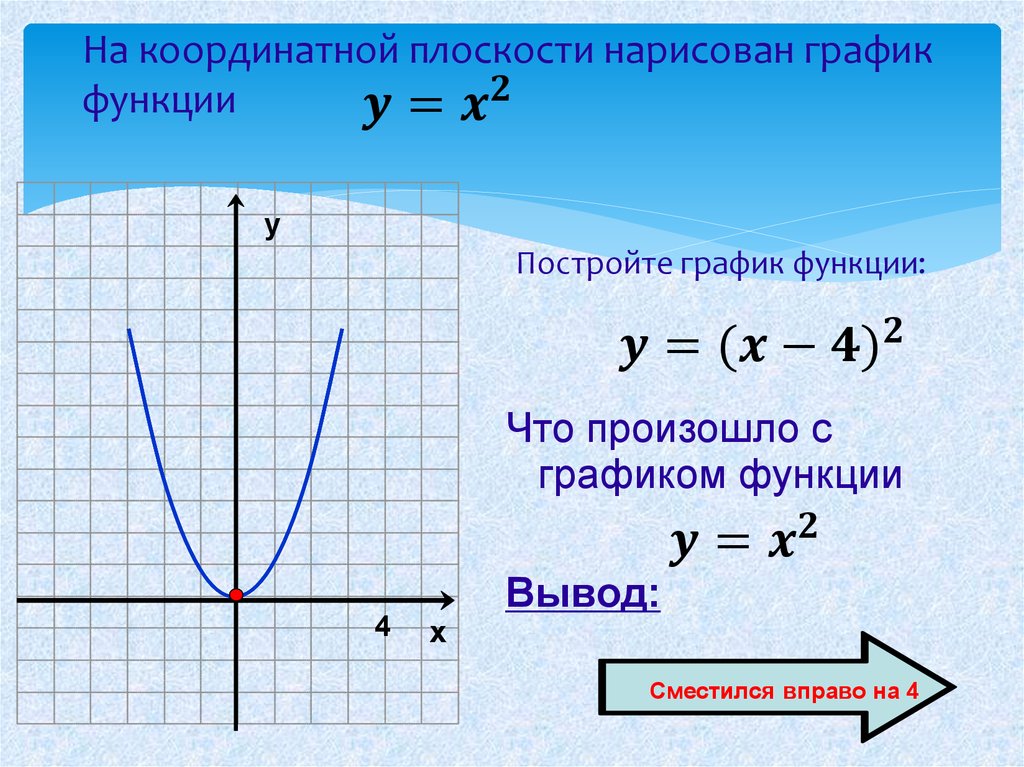
 Для этого пробуем вычислить значение выражения при . Что нужно выполнить в первую очередь? В первую очередь нужно сосчитать чему равно основание: , значит, многочлен – и есть вложенная функция. И, только потом выполняется возведение в степень , следовательно, степенная функция – это внешняя функция.
Для этого пробуем вычислить значение выражения при . Что нужно выполнить в первую очередь? В первую очередь нужно сосчитать чему равно основание: , значит, многочлен – и есть вложенная функция. И, только потом выполняется возведение в степень , следовательно, степенная функция – это внешняя функция. Пробуем вычислить выражение подставив значение . Если использовать для вычислений калькулятор, то сначала нужно найти , значит, арксинус – самое глубокое вложение.
Пробуем вычислить выражение подставив значение . Если использовать для вычислений калькулятор, то сначала нужно найти , значит, арксинус – самое глубокое вложение.



 Даля 166
Даля 166 Дегтярева 174
Дегтярева 174 Макарова 543
Макарова 543 Герцена 123
Герцена 123 Гагарина 114
Гагарина 114 Каразина 305
Каразина 305 Здесь у вас есть константа, умноженная на 8 функцию, функция равна 7 -θ , поэтому сначала применяется правило константы. Затем вычисление производной от 7 -θ , вы пытаетесь использовать правило степени, но это правило для случаев, когда показатель степени является константой. Здесь показатель степени является функцией переменной θ, а основание является константой. Таким образом, мы используем правило d/dx e x = e x , объединенное сначала с тождеством, а затем с цепным правилом следующим образом: θ = e — (ln 7) θ .
Здесь у вас есть константа, умноженная на 8 функцию, функция равна 7 -θ , поэтому сначала применяется правило константы. Затем вычисление производной от 7 -θ , вы пытаетесь использовать правило степени, но это правило для случаев, когда показатель степени является константой. Здесь показатель степени является функцией переменной θ, а основание является константой. Таким образом, мы используем правило d/dx e x = e x , объединенное сначала с тождеством, а затем с цепным правилом следующим образом: θ = e — (ln 7) θ . Производная от 5z равна 5, а не 5z. Также у вас есть сложенные дроби, поэтому используйте общий знаменатель в числителе, и у вас есть множитель e 5z , которое можно вынести из числителя, а затем сократить с чем-то в знаменателе, что даст
Производная от 5z равна 5, а не 5z. Также у вас есть сложенные дроби, поэтому используйте общий знаменатель в числителе, и у вас есть множитель e 5z , которое можно вынести из числителя, а затем сократить с чем-то в знаменателе, что даст В противном случае ваш ответ правильный.
В противном случае ваш ответ правильный. Никаких пакетов или подписок, платите только за то время, которое вам нужно.
Никаких пакетов или подписок, платите только за то время, которое вам нужно.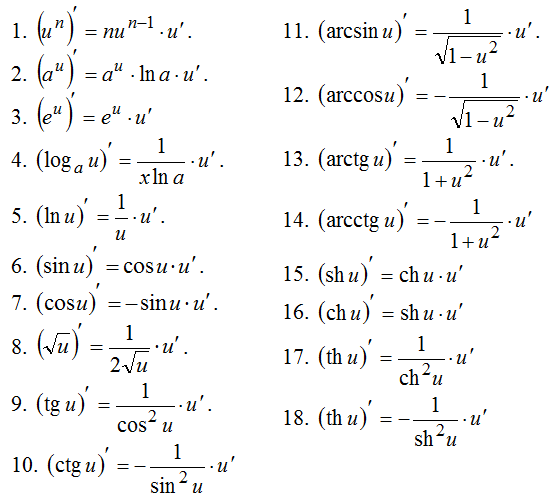 Некоторыми важными пунктами списка являются последовательности , непрерывность и производные для реальных функций. Тогда мы всегда будем расширять понятия до сложной сферы. Теперь в следующем видео давайте обсудим, что такое производная для сложной функции .
Некоторыми важными пунктами списка являются последовательности , непрерывность и производные для реальных функций. Тогда мы всегда будем расширять понятия до сложной сферы. Теперь в следующем видео давайте обсудим, что такое производная для сложной функции . Комплексная производная и примеры
Комплексная производная и примеры Примеры уравнений Коши-Римана
Примеры уравнений Коши-Римана Равномерная сходимость
Равномерная сходимость Комплексный логарифм
Комплексный логарифм Изолированные сингулярности
Изолированные сингулярности Комплексный контурный интеграл
Комплексный контурный интеграл Более подходящее название — просто первопроизводных . Их можно использовать для вычисления контурных интегралов.
Более подходящее название — просто первопроизводных . Их можно использовать для вычисления контурных интегралов.
 Следовательно, чтобы обобщить теорему, нужно говорить о номер обмотки для кривых и точек.
Следовательно, чтобы обобщить теорему, нужно говорить о номер обмотки для кривых и точек. Используя интегральную теорему Коши, мы можем показать очень важный факт для голоморфных функций с изолированной особенностью.
Используя интегральную теорему Коши, мы можем показать очень важный факт для голоморфных функций с изолированной особенностью. Теорема Лиувилля
Теорема Лиувилля

 )
) )
) )
) )
) )
) )
) )
) )
) Узоры и орнаменты на посуде»
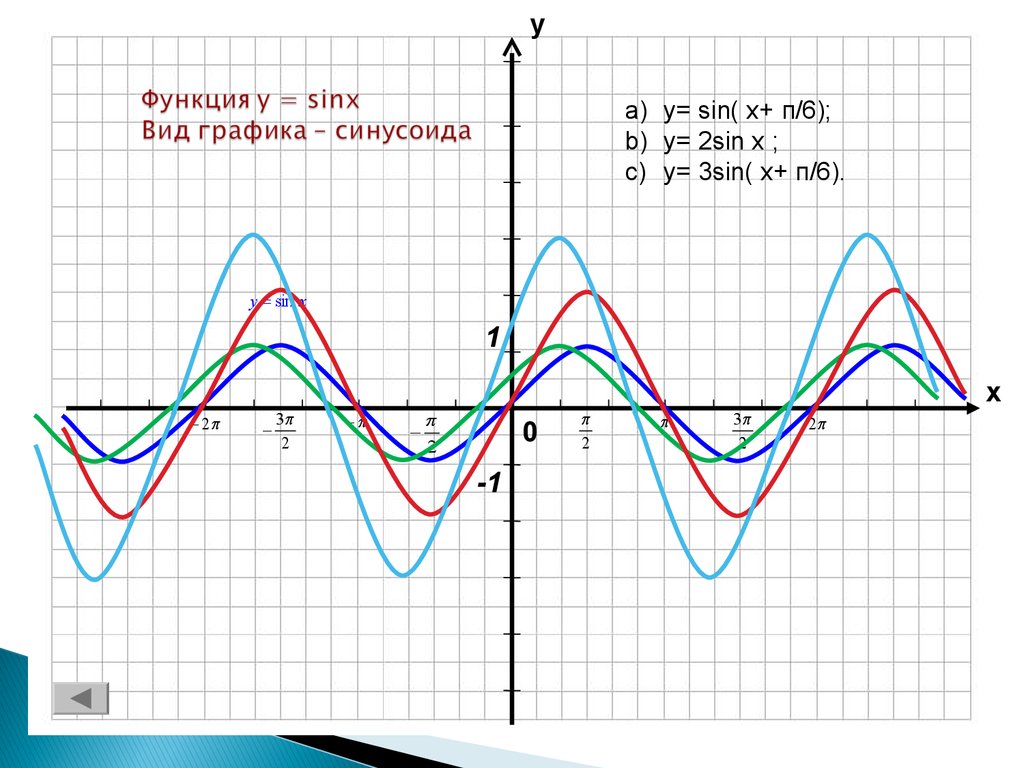
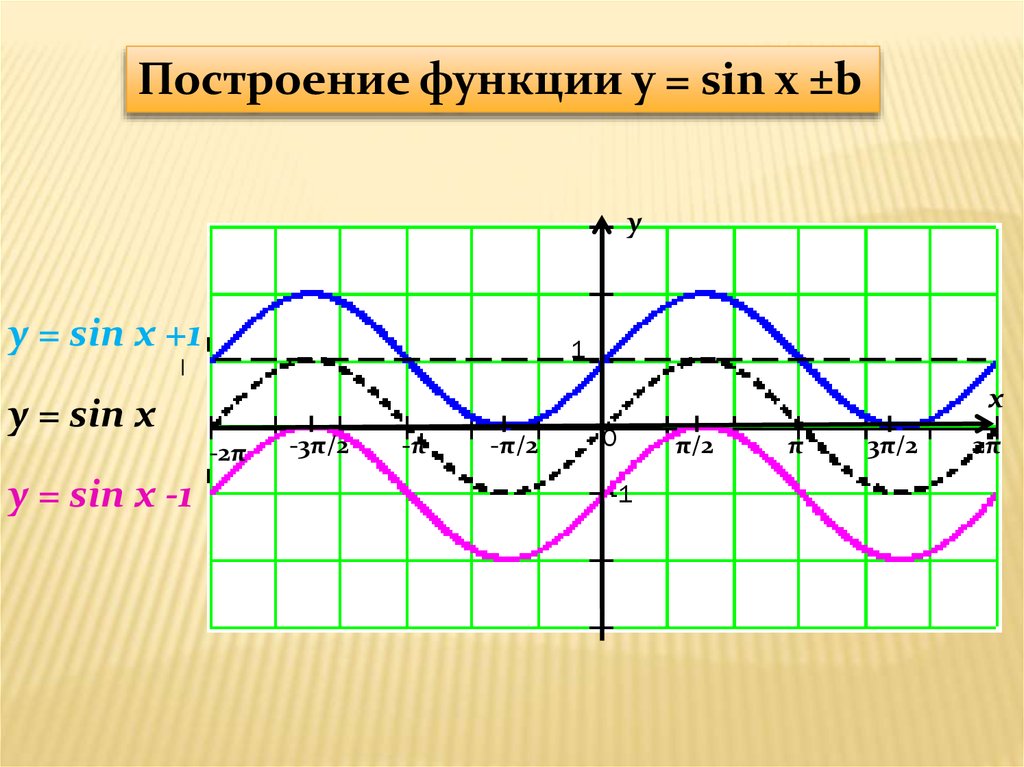
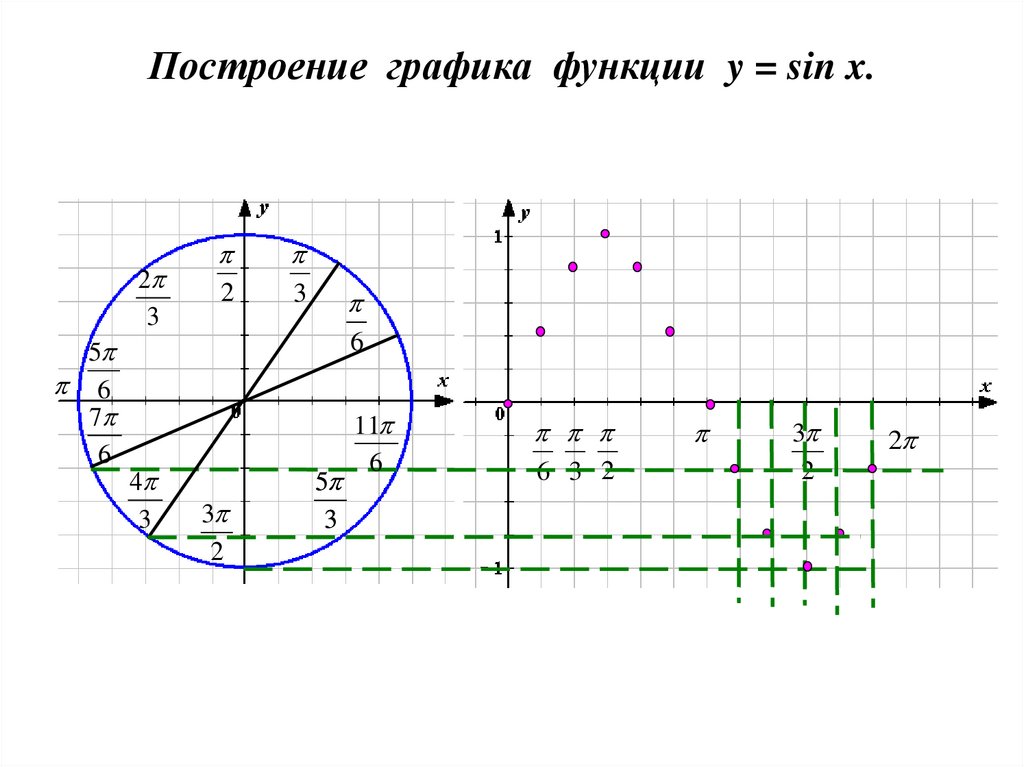
Узоры и орнаменты на посуде» y = sin xy
y = sin xy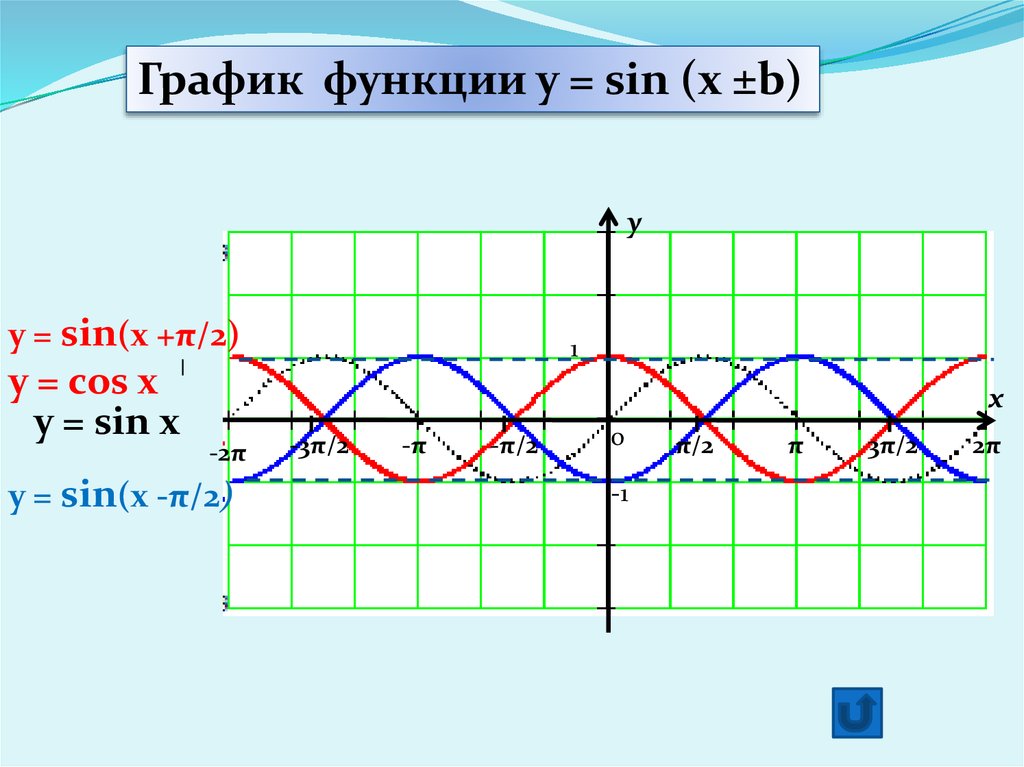 y = sin на отрезкеПостроение графика функции
y = sin на отрезкеПостроение графика функции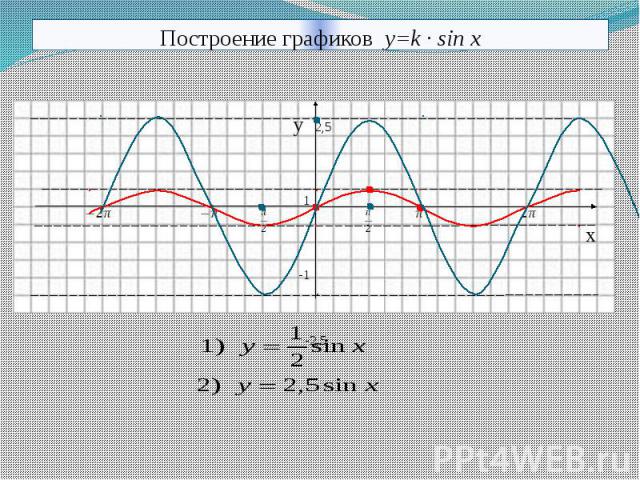 y = sin x.
y = sin x.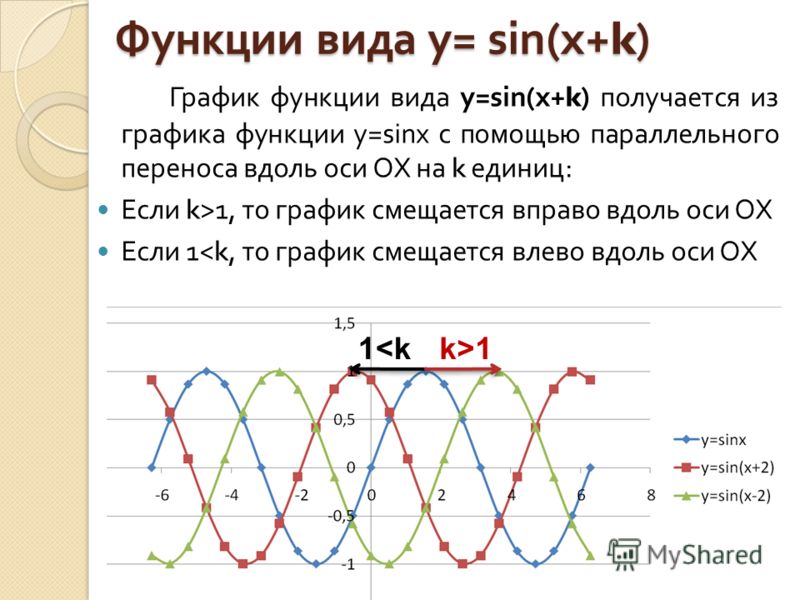 com
com
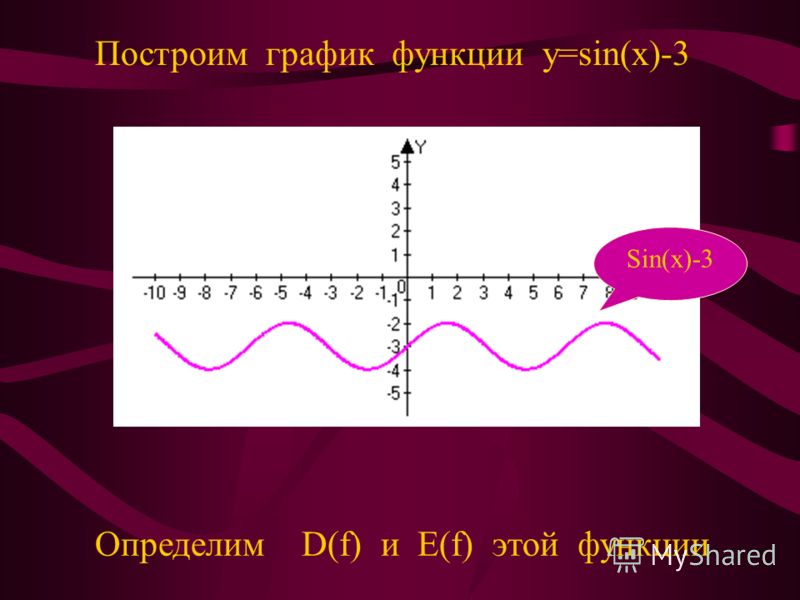 Например, приведенный выше график начинает повторять свою форму через 2π единиц по оси x , поэтому его период равен 2π.
Например, приведенный выше график начинает повторять свою форму через 2π единиц по оси x , поэтому его период равен 2π.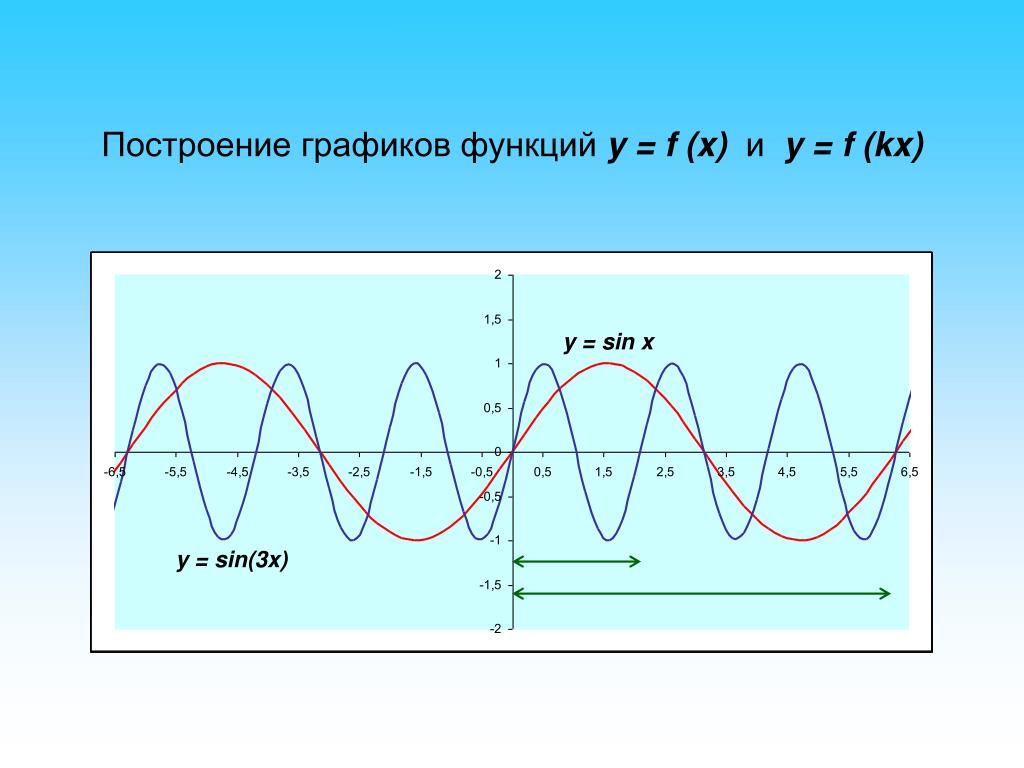 График выше имеет пики при y = 1 и y = -1, поэтому его амплитуда равна всего 1. | и |. Также важно отметить, что если a < 0, график переворачивается (инвертируется).
График выше имеет пики при y = 1 и y = -1, поэтому его амплитуда равна всего 1. | и |. Также важно отметить, что если a < 0, график переворачивается (инвертируется).

 "lab"
"lab"  ]
]  0010
0010 1
1  append(stud_avg)
append(stud_avg)  (i)))
(i)))  Шкалы среднего балла можно найти здесь: Шкала среднего балла 4.33 и Шкала среднего балла 4.0.
Шкалы среднего балла можно найти здесь: Шкала среднего балла 4.33 и Шкала среднего балла 4.0. 33 Шкала среднего балла
33 Шкала среднего балла


 Далее перемножаем полученное и получаем НОК.
Далее перемножаем полученное и получаем НОК.  Для этого нужно действовать поэтапно:
Для этого нужно действовать поэтапно: 3K
3K
 {2}}{11}-\frac{1}{22}\right)=$$
$$=4+\frac{7 \cdot 2-1 \cdot 1}{22}=4+\frac{14-1}{22}=4+\frac{13}{22}=4 \frac{13}{22}$$
{2}}{11}-\frac{1}{22}\right)=$$
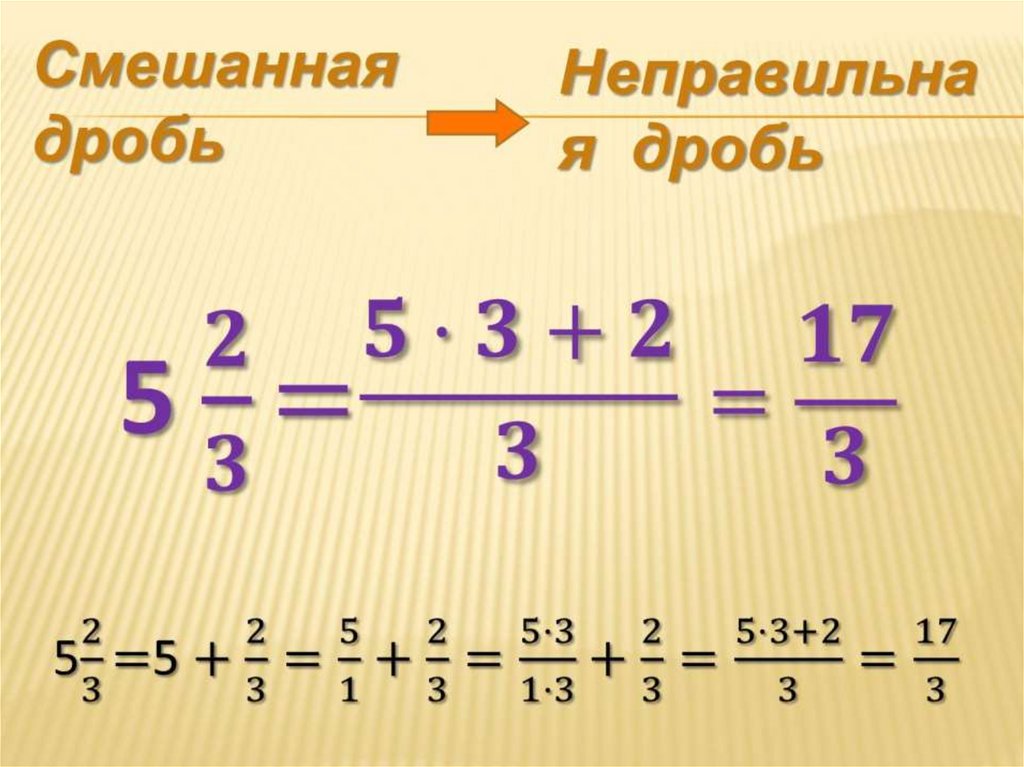
$$=4+\frac{7 \cdot 2-1 \cdot 1}{22}=4+\frac{14-1}{22}=4+\frac{13}{22}=4 \frac{13}{22}$$ $5 \frac{4}{9}-1 \frac{11}{12}=3 \frac{19}{36}$
$5 \frac{4}{9}-1 \frac{11}{12}=3 \frac{19}{36}$ Также известные как дробные числа, они обычно используются для измерения частей целого, например:
Также известные как дробные числа, они обычно используются для измерения частей целого, например:
 Смешанные дроби также известны как смешанные числа.
Смешанные дроби также известны как смешанные числа. Мы рассмотрим, как преобразовать дроби в приведенных ниже примерах уравнений.
Мы рассмотрим, как преобразовать дроби в приведенных ниже примерах уравнений.

 Это наименьшее число, которое полностью делится на оба существующих знаменателя.
Это наименьшее число, которое полностью делится на оба существующих знаменателя. Как умножать дроби
Как умножать дроби


 Во-первых, давайте рассмотрим три разных типа дробей:
Во-первых, давайте рассмотрим три разных типа дробей: Например, 2/3 равно 4/6.
Например, 2/3 равно 4/6. В этом примере мы будем использовать смешанную дробь семи и четырех пятых, записанную численно как 7⅘.
В этом примере мы будем использовать смешанную дробь семи и четырех пятых, записанную численно как 7⅘.
 Нужно просто вычесть второй числитель из первого, сохранив нижнее число тем же.
Нужно просто вычесть второй числитель из первого, сохранив нижнее число тем же. По сути, найти наименьшую возможную эквивалентную дробь.
По сути, найти наименьшую возможную эквивалентную дробь.
 2+bx+c
2+bx+c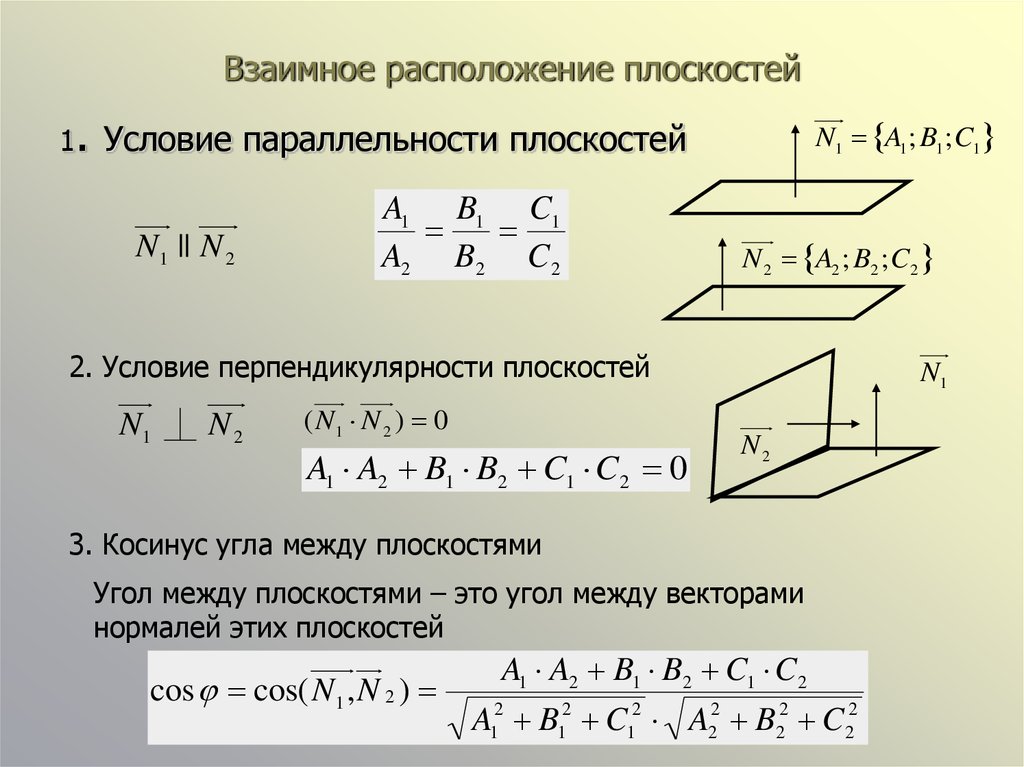 Равносторонняя гипербола как график уравнения y=k/x
Равносторонняя гипербола как график уравнения y=k/x Координаты точки
Координаты точки Выражение векторного произведения через координаты сомножителей
Выражение векторного произведения через координаты сомножителей Точка пересечения трех плоскостей
Точка пересечения трех плоскостей Уравнение плоскости, проходящей через данную точку перпендикулярно данной прямой
Уравнение плоскости, проходящей через данную точку перпендикулярно данной прямой Цилиндрические поверхности, у которых образующие параллельны одной из осей координат
Цилиндрические поверхности, у которых образующие параллельны одной из осей координат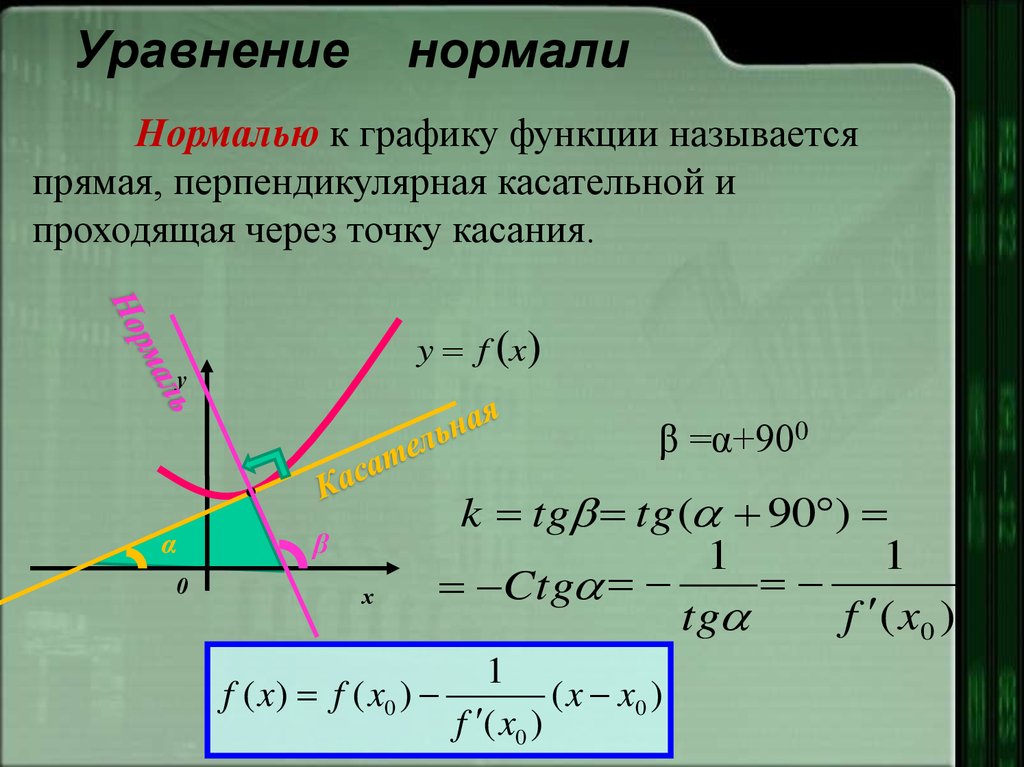 Два уравнения с двумя неизвестными
Два уравнения с двумя неизвестными Эквивалентные бесконечно малые величины
Эквивалентные бесконечно малые величины Производная сложной функции
Производная сложной функции Выражение высших производных через дифференциалы
Выражение высших производных через дифференциалы Второе достаточное условие максимума и минимума
Второе достаточное условие максимума и минимума Интегрирование по частям
Интегрирование по частям Дифференциал интеграла
Дифференциал интеграла Кривизна
Кривизна О знаке кривизны
О знаке кривизны Интегрирование рядов
Интегрирование рядов Ортогональность системы функций cos nx, sin nx
Ортогональность системы функций cos nx, sin nx Касательная плоскость и нормаль к поверхности
Касательная плоскость и нормаль к поверхности Вычисление двойного интеграла (общий случай)
Вычисление двойного интеграла (общий случай) Изоклины
Изоклины Линейное уравнение второго порядка с постоянными коэффициентами с правой частью
Линейное уравнение второго порядка с постоянными коэффициентами с правой частью Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «как найти уравнение прямой перпендикулярной данной».
Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «как найти уравнение прямой перпендикулярной данной». На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и как найти уравнение прямой перпендикулярной данной. Просто введите задачу в окошко и нажмите
«решить» здесь (например, найти уравнение прямой перпендикулярной данной прямой).
На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и как найти уравнение прямой перпендикулярной данной. Просто введите задачу в окошко и нажмите
«решить» здесь (например, найти уравнение прямой перпендикулярной данной прямой).


 Для перпендикулярных линий наклоны являются отрицательными обратными величинами. Наклон равен 5, поэтому наклон перпендикулярной линии будет иметь наклон . Мы знаем, что перпендикулярная линия должна содержать точку (5,3), поэтому у нас есть вся необходимая информация. Теперь мы можем использовать уравнение
Для перпендикулярных линий наклоны являются отрицательными обратными величинами. Наклон равен 5, поэтому наклон перпендикулярной линии будет иметь наклон . Мы знаем, что перпендикулярная линия должна содержать точку (5,3), поэтому у нас есть вся необходимая информация. Теперь мы можем использовать уравнение 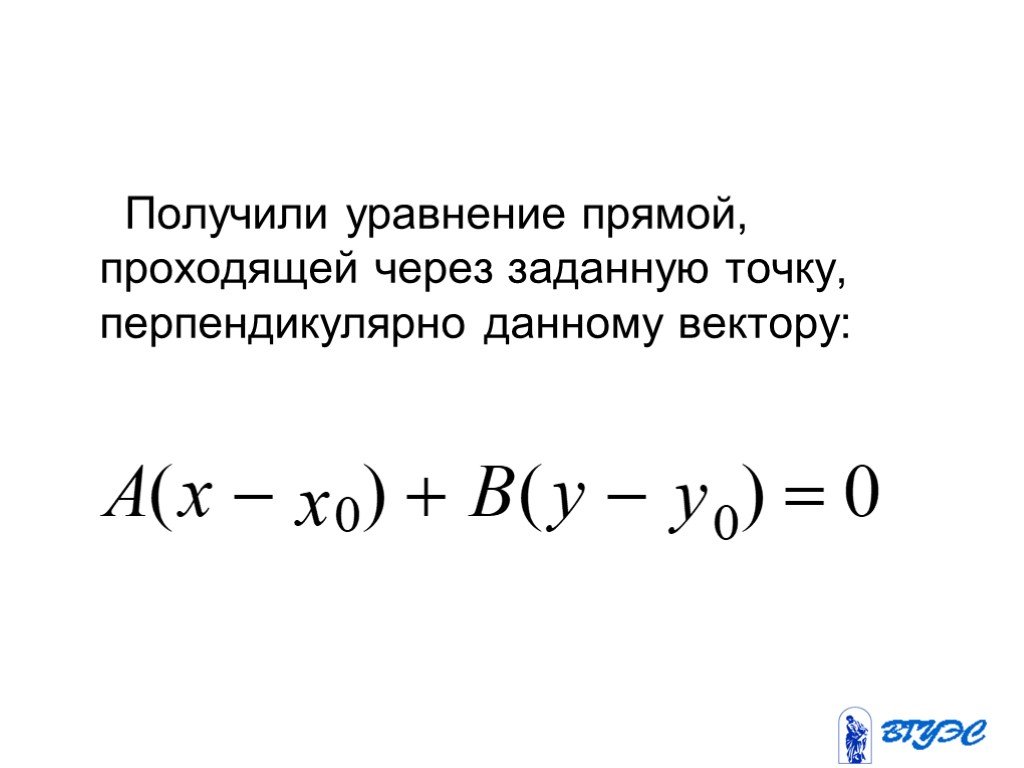



 Например, если задан наклон
Например, если задан наклон Ниже приведены некоторые примеры
Ниже приведены некоторые примеры Таким образом, наклон любой линии, параллельной данной линии, должен быть одинаковым, \(m_{∥}=−5\). Математическая запись \(m_{∥}\) читается как «\(m\) параллельно».
Таким образом, наклон любой линии, параллельной данной линии, должен быть одинаковым, \(m_{∥}=−5\). Математическая запись \(m_{∥}\) читается как «\(m\) параллельно». Часто вас будут просить найти уравнение линии с учетом некоторого геометрического соотношения, например, параллельна ли линия другой линии или перпендикулярна ей.
Часто вас будут просить найти уравнение линии с учетом некоторого геометрического соотношения, например, параллельна ли линия другой линии или перпендикулярна ей. Обратите внимание, что наклон такой же, как у данной линии, но точка пересечения \(y\) отличается. Если иметь в виду геометрическую интерпретацию, то будет легче запомнить процесс, необходимый для решения задачи.
Обратите внимание, что наклон такой же, как у данной линии, но точка пересечения \(y\) отличается. Если иметь в виду геометрическую интерпретацию, то будет легче запомнить процесс, необходимый для решения задачи. Часто приходится выполнять дополнительные действия для определения уклона. Общие шаги для нахождения уравнения линии изложены в следующем примере.
Часто приходится выполнять дополнительные действия для определения уклона. Общие шаги для нахождения уравнения линии изложены в следующем примере. В этом случае наклон равен \(m_{⊥}=\frac{1}{2}\), а заданная точка равна \((8, −2)\).
В этом случае наклон равен \(m_{⊥}=\frac{1}{2}\), а заданная точка равна \((8, −2)\).


 \(m_{∥}=4\) и \(m_{⊥}=−\frac{1}{4}\)
\(m_{∥}=4\) и \(m_{⊥}=−\frac{1}{4}\) \)
\) \)
\)

