Сколько дней до 21 декабря 2024?
Калькулятор «Дней до даты»
Сколько дней до
Через сколько времени будет 21 декабря 2024?
Ответ: Осталось 1 год, 9 месяцев и 11 дней до
(сегодня (10 марта 2023) это 1 год, 9 месяцев и 1 неделю до 21 декабря 2024)
это также
- 1,781 Год
- или
- 21,355 Месяц
- или
- 93,143 Недели
- или
- 652 Дня
- или
- 15 648 Часов
- или
- 938 880 Минут
- или
- 56 332 800 Секунд
- или
- 1 год, 9 месяцев и 11 дней
21 декабря 2024 — Отсчет времени
Временная шкала
10 марта 2023
21.35 месяц
21 декабря 2024
93.14 недели
Информация о дне: 21 декабря 2024
Календарь на Декабрь 2024
Поделитесь текущим расчетом
Печать
https://calculat. io/ru/date/how-many-until/21-december-2024
io/ru/date/how-many-until/21-december-2024
<a href=»https://calculat.io/ru/date/how-many-until/21-december-2024″>Сколько дней до 21 декабря 2024? — Calculatio</a>
О калькуляторе «Дней до даты»
Онлайн калькулятор времени до даты поможет узнать сколько времени осталось до заданной даты. Например, легко узнать сколько времени осталось до вашего Дня Рождения. Также, можно узнать сколько времени прошло с заданной даты. Например, он может помочь узнать через сколько времени будет 21 декабря 2024? Выберите нужную дату, (например ’21 декабря 2024′) и нажмите кнопку ‘Посчитать’.
Калькулятор «Дней до даты»
Сколько дней до
Таблица конвертации
| Дата | Время до даты |
|---|---|
| 07 декабря 2024 | 1 год, 8 месяцев и 28 дней |
| 08 декабря 2024 | 1 год, 8 месяцев и 29 дней |
| 09 декабря 2024 | 1 год, 8 месяцев и 30 дней |
| 10 декабря 2024 | 1 год и 9 месяцев |
| 11 декабря 2024 | 1 год, 9 месяцев и 1 день |
| 12 декабря 2024 | 1 год, 9 месяцев и 2 дня |
| 13 декабря 2024 | 1 год, 9 месяцев и 3 дня |
| 14 декабря 2024 | 1 год, 9 месяцев и 4 дня |
| 15 декабря 2024 | 1 год, 9 месяцев и 5 дней |
| 16 декабря 2024 | 1 год, 9 месяцев и 6 дней |
| 17 декабря 2024 | 1 год, 9 месяцев и 7 дней |
| 18 декабря 2024 | 1 год, 9 месяцев и 8 дней |
| 19 декабря 2024 | 1 год, 9 месяцев и 9 дней |
| 20 декабря 2024 | 1 год, 9 месяцев и 10 дней |
| 21 декабря 2024 | 1 год, 9 месяцев и 11 дней |
| 22 декабря 2024 | 1 год, 9 месяцев и 12 дней |
| 23 декабря 2024 | 1 год, 9 месяцев и 13 дней |
| 24 декабря 2024 | 1 год, 9 месяцев и 14 дней |
| 25 декабря 2024 | 1 год, 9 месяцев и 15 дней |
| 26 декабря 2024 | 1 год, 9 месяцев и 16 дней |
| 27 декабря 2024 | 1 год, 9 месяцев и 17 дней |
| 28 декабря 2024 | 1 год, 9 месяцев и 18 дней |
| 29 декабря 2024 | 1 год, 9 месяцев и 19 дней |
| 30 декабря 2024 | 1 год, 9 месяцев и 20 дней |
| 31 декабря 2024 | 1 год, 9 месяцев и 21 день |
| 01 января 2025 | 1 год, 9 месяцев и 22 дня |
| 02 января 2025 | 1 год, 9 месяцев и 23 дня |
| 03 января 2025 | 1 год, 9 месяцев и 24 дня |
| 04 января 2025 | 1 год, 9 месяцев и 25 дней |
| 05 января 2025 | 1 год, 9 месяцев и 26 дней |
Сколько времени прошло с 21 декабря 60 года до сегодняшнего дня
Калькулятор делает расчет: сколько дней, лет, часов, минут или секунд прошло с 21. 12.0060 по текущий момент времени.
12.0060 по текущий момент времени.
Сколько прошло с 21 декабря 60 года?
В общем
- 1962 года
- 2 месяца
- 20 дней
- 20 часов
- 11 минут
- 18 секунд
В целых величинах
- 1962 года
- 23546 месяцев
- 102383 недели
- 716684 дня
- 17200436 часов
- 1032026171 минута
- 61921570278 секунд
Часовой пояс: Europe/Berlin
Сегодняшняя дата
10 марта 2023 года
Информация о дне: 21 декабря 60 года
- 21 декабря 60 года — это Вторник (Рабочий день)
- Дней в декабре: 31
- 60 — это Високосный год (366 дней)
- Декабрь: пора года — Зима
- Знак зодиака 21 декабря 60 года — Стрелец (sagittarius)
- Unix Timestamp: -60243091200
Календарь на декабрь 60 года
Ближайшие даты
15. 12.0060
12.0060
16.12.0060
17.12.0060
18.12.0060
19.12.0060
20.12.0060
22.12.0060
23.12.0060
24.12.0060
25.12.0060
26.12.0060
27.12.0060
Все даты 60 года
Другие даты
21.12.0060 — 04.03.2023
21.12.0060 — 05.03.2023
21.12.0060 — 06.03.2023
21.12.0060 — 07.03.2023
21.12.0060 — 08.03.2023
21.12.0060 — 09.03.2023
21.12.0060 — 10.03.2023
21.12.0060 — 11.03.2023
21.12.0060 — 12.03.2023
21. 12.0060 — 13.03.2023
12.0060 — 13.03.2023
21.12.0060 — 14.03.2023
21.12.0060 — 15.03.2023
Вопросы и ответы
Данный инструмент является калькулятором дат. Он вычисляет количество времени, которое прошло с заданной даты на текущий момент. Результат можно отобразить в разных единицах измерения.
Просто выберите нужную вам дату с помощью календаря и сразу получайте результат!
Рекомендуем посмотреть
Спасибо за обратную связь!
Если потребуется, мы вышлем ответ на указанную почту.×
Обратная связь
Оставьте сообщение и мы обязательно вам ответим!
Сообщение *
Имя
E-mail *
Я даю согласие на обработку персональных данных в соответствии с политикой конфиденциальности.
Отправить
Поддержите нас!
Мы рады, что вы пользуетесь нашим сервисом!
Чтобы отблагодарить нас за бесплатные инструменты — отключите блокировщик рекламы на сайте или сделайте пожертвование! Это очень поможет развитию наших проектов!
Спасибо 🙂
99₽
99₽199₽
199₽499₽
499₽Любая сумма
Пожертвовать- Ether: 0x2764e55bbbc6e60fa0678da98aae46635e850bdc
- Bitcoin cash: qzm2pkf9sdzc0lpe39lgh52u2gc52majqcnxc0uz8j
Сколько дней до 21 декабря?
Подсчитайте, сколько дней осталось до 21 декабря
21 декабря 2023 года составляет 286 дней от сегодня
Сколько осталось до 21 декабря?
С сегодняшнего дня до 21 декабря осталось 286 дней. Это означает, что до этого момента осталось 40,86 недель, 6864,0 часа и 10,21 месяца. Мы используем этот расчет довольно часто в календаре, даже если
мы этого не осознаем. Обратный отсчет чьего-то дня рождения, юбилея или особой даты важен, чтобы вовремя заказать подарки!
Если 21 декабря имеет для вас особое значение, сделайте одолжение себе в будущем и установите напоминание в календаре на день раньше и
сделай это повторяющимся. Пожалуйста.
Это означает, что до этого момента осталось 40,86 недель, 6864,0 часа и 10,21 месяца. Мы используем этот расчет довольно часто в календаре, даже если
мы этого не осознаем. Обратный отсчет чьего-то дня рождения, юбилея или особой даты важен, чтобы вовремя заказать подарки!
Если 21 декабря имеет для вас особое значение, сделайте одолжение себе в будущем и установите напоминание в календаре на день раньше и
сделай это повторяющимся. Пожалуйста.
Обратный отсчет до 21 декабря
Дней до 21 декабря?
286 дней
Недели до 21 декабря?
40,86 недели
Часов до 21 декабря?
6864,0 часов
Месяцев до 21 декабря?
10,21 месяца
Сколько минут до 21 декабря
411840 минут
Сколько секунд до 21 декабря
004790 секунд0019
Сколько лет до 21 декабря?
До 21 декабря осталось 204 рабочих дня.
В деловом мире время до определенной даты совершенно другое. Десять рабочих дней составляют две календарные недели. и один месяц составляет всего двадцать дней производства. Это меняет то, сколько времени корпорация отрабатывает традиционный 9-5 система подсчета времени реально можно потратить на проекты или работу. Это может добавить слой сложность на расчеты времени.
Чрезмерное упрощение расчета рабочих дней до 21 декабря заключается в подсчете общего количества дней 286 и вычитании общего количества выходных.
Самый простой способ настроить разницу во времени? Используйте калькулятор даты и времени, подобный этому, и мгновенно получите отвечать.
В период с 21 декабря среднестатистический человек потратил…
- 61432,8 часа Сон
- 8168,16 часов Еда и питье
- 13384,8 часов Домашняя деятельность
- 3981,12 часа Работа по дому
- 4392,96 часа Приготовление пищи и уборка
- 1372,8 часа Уход за газоном и садом
- 24024,0 часа Трудовая и связанная с работой деятельность
- 22102,08 часа Рабочий
- 36173,28 часов Отдых и спорт
- 19631,04 часа Просмотр телевизора
21 декабря Статистика:
- В этом году 21 декабря — четверг
- В следующем году 21 декабря будет пятницей
- День недели: Четверг
- День года: 355
- День месяца: 21
В четверг, 21 декабря, было 355, что составляет 97% до 2023 года. и 67,74% в декабре.
и 67,74% в декабре.
Известные спортивные и музыкальные события 21 декабря
- 1947 Актриса Эстель Гетти (24 года) выходит замуж за Артура Геттлмана
- 1891 1-я игра в баскетбол, основанная на правилах, созданных Джеймсом Нейсмитом, сыгранная 18 студентами в Спрингфилде, Массачусетс
Другие даты около 21 декабря
Сколько дней до 16 декабря? Сколько дней до 17 декабря? Сколько дней до 18 декабря? Сколько дней до 19 декабря? Сколько дней до 20 декабря? Сколько дней до 22 декабря? Сколько дней до 23 декабря? Сколько дней до 24 декабря? Сколько дней до 25 декабря? Сколько дней до 26 декабря?
Обратный отсчет до даты, похожей на 21 декабря
Сколько дней до 21 января?
Сколько дней до 21 февраля?
Сколько дней до 20 марта?
Сколько дней до 20 апреля?
Сколько дней до 20 мая?
Сколько дней до 20 июня?
Сколько дней до 20 июля?
Сколько дней до 20 августа?
Сколько дней до 20 сентября?
Сколько дней до 20 октября?
Сколько дней осталось до 21 декабря 2024 года?
Калькулятор «Дней до даты»
Сколько дней осталось до
Сколько осталось до 21 декабря 2024 года?
Ответ: Есть 1 год, 9 месяцев и 11 дней до
Он же
- 1.781 Год
- or
- 21.355 Months
- or
- 93.143 Weeks
- or
- 652 Days
- or
- 15,648 Hours
- or
- 938,880 Minutes
- or
- 56 332 800 Секунды
- или
- 1 год, 9 месяцев и 11 дней
21 декабря 2024 г. — Обратный отсчет времени
2
03
10 марта 2023 г.
21,35 месяца
21 декабря, 2024
93,14 недели
Около дня: 21 декабря 2024
- декабрь 21, 2024
8 декабрь 21, 2024
8 декабрь 21, 2024
8
- декабря 21, 2024
8 декабрь 21, 2024
8
- декабрь 21, 2024
8.
 )
)- Этот день 51-й (пятьдесят первый) Неделя 2024 года
- Это 356-й (триста пятьдесят шестой) День года
- До 10 дней осталось 2024
- 21 декабря 2024 года 97,27% года завершено
- Это 21-й (двадцать первый) День зимы 2024
- 2024 год дней 70 90 дней в високосном году 60 90 дней в 2024: 31
- The Zodiac Sign of December 21, 2024 is Sagittarius (sagittarius)
- December 21, 2024 as a Unix Timestamp : 1734739200
Add December 21, 2024 в свой Календарь Google
- декабря 21, 2024
Календарь на декабрь 2024 года
Поделиться этим расчетом
https://calculat.io/en/date/how-many-until/21-december-2024
io/en/date/how-many-until/21-december-2024″>Сколько дней до 21 декабря 2024 года? — Расчет
О калькуляторе «Дней до даты»
Этот онлайн-калькулятор дат поможет вам рассчитать, сколько дней осталось до определенной даты. Например, легко узнать, сколько времени осталось до дня рождения. Вы также можете узнать, сколько времени прошло с определенной даты. Например, это может помочь вам узнать, сколько осталось до 21 декабря 2024 года? Выберите нужную дату (например, «21 декабря 2024 г.») и нажмите кнопку «Рассчитать».
«Days until Date» Calculator
How Many Days Until
Conversion Table
| Date | Time to Date | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| December 07, 2024 | 1 year, 8 месяцев и 28 дней | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 08 декабря 2024 г. | 1 год, 8 месяцев и 29 дней | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 09 декабря 2024 г. | 1 год, 8 месяцев и 30 дней0333 December 10, 2024| 1 year and 9 months | December 11, 2024 | 1 year, 9 months and 1 day | December 12, 2024 | 1 year, 9 months and 2 days | December 13, 2024 | 1 year, 9 months and 3 days | December 14, 2024 | 1 year, 9 months and 4 days | December 15, 2024 | 1 year, 9 months and 5 дней | December 16, 2024 | 1 year, 9 months and 6 days | December 17, 2024 | 1 year, 9 months and 7 days | December 18, 2024 | 1 year, 9 months and 8 Дни | 19 декабря 2024 г. |  Площадь параллелограмма через вектора: Площадь параллелограмма онлайнПлощадь параллелограмма по координатам векторов. Векторное произведение векторовВспомним в начале, что такое векторное произведение. Замечание 1 Векторным произведением для $\vec{a}$ и $\vec{b}$ является $\vec{c}$, представляющий собой некоторый третий вектор $\vec{c}= ||$, причём этот вектор обладает особенными свойствами:
Если для векторов присутствуют некоторые координаты ($\vec{a}=\{x_1; y_1; z_1\}$ и $\vec{b}= \{x_2; y_2; z_2\}$), то их векторное произведение в декартовой системе координат можно определить по формуле: $ = \{y_1 \cdot z_2 – y_2 \cdot z_1; z_1 \cdot x_2 – z_2 \cdot x_1; x_2 \cdot y_2 – x_2 \cdot y_1\}$ Легче всего запомнить эту формулу записав в форме определителя: $ = \begin{array} {|ccc|} i & j & k \\ x_1 & y_1 & z_1 \\ x_2 & y_2 & z_2 \\ \end{array}$. Эта формула весьма удобна для использования, но чтобы понимать, как её использовать, для начала следует ознакомиться с темой матриц и их определителей. Площадь параллелограмма , стороны которого определяются двумя векторами $\vec{a}$ и $vec{b}$ равна скаляру векторного произведения данных двух векторов. Это соотношение совсем несложно вывести. Вспомним формулу для нахождения площади обычного параллелограмма, который можно охарактеризовать образующими его отрезками $a$ и $b$: $S = a \cdot b \cdot \sin α$ При этом длины сторон равны скалярным значениям векторов $\vec{a}$ и $\vec{b}$, что вполне себе подходит нам, то есть, скаляр векторного произведения данных векторов и будет площадью рассматриваемой фигуры. Пример 1 Даны векторы $\vec{c}$ c координатами $\{5;3; 7\}$ и вектор $\vec{g}$ с координатами $\{3; 7;10 \}$ в декартовой системе координат. Найти, чему равна площадь параллелограмма, образованного $\vec{c}$ и $\vec{g}$. Данный ход рассуждений справедлив не только для нахождения площади в 3-хмерном пространстве, но и для двухмерного. Познакомьтесь со следующей задачкой на эту тему. Пример 2 Вычислить площадь параллелограмма, если его образующие отрезки задаются векторами $\vec{m}$ с координатами $\{2; 3\}$ и $\vec{d}$ с координатами $\{-5; 6\}$. Решение: Эта задача представляет собой частный пример задачки 1, решённой выше, но при этом оба вектора лежат в одной плоскости, а это значит, что третью координату, $z$, можно принять за нуль. Подведём итоги по всему вышесказанному, площадь параллелограмма составит: $S = \begin{array} {||cc||} 2 & 3\\ -5 & 6 \\ \end{array} = \sqrt{12 + 15} =3 \sqrt3$. Пример 3 Даны векторы $\vec{a} = 3i – j + k; \vec{b}= 5i$. Определите площадь образуемого ими параллелограмма. $[ \vec{a} \times \vec{b}] = (3i – j + k) \times 5i = 15 – 5 + $ Упростим согласно приведённой таблице для единичных векторов: Рисунок 1. Предыдущие задачи были о векторах, координаты которых заданы в декартовой системе координат, но рассмотрим также случай, если угол между базисными векторами отличается от $90°$: Пример 4 Вектор $\vec{d} = 2a + 3b$, $\vec{f}= a – 4b$, длины $\vec{a}$ и $\vec{b}$ равны между собой и равны единице, а угол между $\vec{a}$ и $\vec{b}$ равен 45°. Решение: Вычислим векторное произведение $\vec{d} \times \vec{f}$: $[\vec{d} \times \vec{f} ]= (2a + 3b) \times (a – 4b) = 2 – 8 + 3 – 12 $. Для векторных произведений согласно их свойствам справедливо следующее: $$ и $$ равны нулю, $ = — $. Используем это для упрощения: $[\vec{d} \times \vec{f} ]= -8 + 3 = -8 — 3 =-11$. Теперь воспользуемся формулой $(1)$ : $[\vec{d} \times \vec{f} ] = |-11 | = 11 \cdot |a| \cdot |b| \cdot \sin α = 11 \cdot 1 \cdot 1 \cdot \frac12=5,5$. Площадь параллелограмма, построенного на векторах, равняется произведению длин этих векторов на угол угла, который лежит между ними. Хорошо, когда по условиям даны длины этих самых векторов. Однако бывает и так, что применить формулу площади параллелограмма, построенного на векторах можно только после расчетов по координатам. Рассмотрим пример расчета площади параллелограмма построенного на векторах. Задача: параллелограмм построен на векторах и . Найдите площадь, если , а угол между ними 30°. Возможно, у вас возник вопрос – откуда взялись нули? Стоит вспомнить, что мы работаем с векторами, а для них . также обратите внимание, что если в результате мы получаем выражение ,то оно будет преобразовано в. Теперь проводим итоговые вычисления: Вернемся к проблеме, когда длины векторов не указаны в условиях. Если ваш параллелограмм лежит в декартовой системе координат, то потребуется сделать следующее. Расчет длин сторон фигуры, заданной координатамиДля начала находим координаты векторов и отнимаем от координат конца соответствующие координаты начала. Допустим координаты вектора a
(x1;y1;z1), а вектора b
(x3;y3;z3). Имея длины векторов и их скалярное произведение, мы можем найти косинус угла, лежащего между ними . На данном уроке мы рассмотрим ещё две операции с векторами: векторное произведение векторов и смешанное произведение векторов (сразу ссылка, кому нужно именно оно) . Если векторы сверкают где-то далеко, как молнии на горизонте, не беда, начните с урока Векторы для чайников , чтобы восстановить или вновь приобрести базовые знания о векторах. Более подготовленные читатели могут знакомиться с информацией выборочно, я постарался собрать максимально полную коллекцию примеров, которые часто встречаются в практических работах Чем вас сразу порадовать? Когда я был маленьким, то умел жонглировать двумя и даже тремя шариками. В данной операции, точно так же, как и в скалярном произведении, участвуют два вектора . Пусть это будут нетленные буквы . Само действие обозначается следующим образом: . Существуют и другие варианты, но я привык обозначать векторное произведение векторов именно так, в квадратных скобках с крестиком. И сразу вопрос : если в скалярном произведении векторов участвуют два вектора, и здесь тоже умножаются два вектора, тогда в чём разница ? Явная разница, прежде всего, в РЕЗУЛЬТАТЕ: Результатом скалярного произведения векторов является ЧИСЛО: Результатом векторного произведения векторов является ВЕКТОР : , то есть умножаем векторы и получаем снова вектор. Сначала будет определение с картинкой, затем комментарии. Определение : Векторным произведением неколлинеарных векторов , взятых в данном порядке , называется ВЕКТОР , длина которого численно равна площади параллелограмма , построенного на данных векторах; вектор ортогонален векторам , и направлен так, что базис имеет правую ориентацию: Разбираем определение по косточкам, тут много интересного! Итак, можно выделить следующие существенные моменты: 1) Исходные векторы , обозначенные красными стрелками, по определению не коллинеарны . Случай коллинеарных векторов будет уместно рассмотреть чуть позже. 2) Векторы взяты в строго определённом порядке : – «а» умножается на «бэ» , а не «бэ» на «а». 3) Теперь познакомимся с геометрическим смыслом векторного произведения. Это очень важный пункт! ДЛИНА синего вектора (а, значит, и малинового вектора ) численно равна ПЛОЩАДИ параллелограмма, построенного на векторах . На рисунке данный параллелограмм заштрихован чёрным цветом. Примечание : чертёж является схематическим, и, естественно, номинальная длина векторного произведения не равна площади параллелограмма. Вспоминаем одну из геометрических формул: площадь параллелограмма равна произведению смежных сторон на синус угла между ними . Поэтому, исходя из вышесказанного, справедлива формула вычисления ДЛИНЫ векторного произведения: Подчёркиваю, что в формуле речь идёт о ДЛИНЕ вектора, а не о самом векторе . Получим вторую важную формулу. Диагональ параллелограмма (красный пунктир) делит его на два равных треугольника. Следовательно, площадь треугольника, построенного на векторах (красная штриховка), можно найти по формуле: 4) Не менее важный факт состоит в том, что вектор ортогонален векторам , то есть . Разумеется, противоположно направленный вектор (малиновая стрелка) тоже ортогонален исходным векторам . 5) Вектор направлен так, что базис имеет правую ориентацию. На уроке о переходе к новому базису я достаточно подробно рассказал об ориентации плоскости , и сейчас мы разберёмся, что такое ориентация пространства. Объяснять буду на пальцах вашей правой руки . Мысленно совместите указательный палец с вектором и средний палец с вектором . Безымянный палец и мизинец прижмите к ладони. …как всё-таки хорошо, что вы теперь знаете о право- и левоориентированных базисах, ибо страшнЫ высказывания некоторых лекторов о смене ориентации =) Векторное произведение коллинеарных векторовОпределение подробно разобрано, осталось выяснить, что происходит, когда векторы коллинеарны. Таким образом, если , то и . Обратите внимание, что само векторное произведение равно нулевому вектору, но на практике этим часто пренебрегают и пишут, что оно тоже равно нулю. Частный случай – векторное произведение вектора на самого себя: С помощью векторного произведения можно проверять коллинеарность трёхмерных векторов, и данную задачу среди прочих мы тоже разберём. Для решения практических примеров может потребоваться тригонометрическая таблица , чтобы находить по ней значения синусов. Ну что же, разжигаем огонь: Пример 1 а) Найти длину векторного произведения векторов , если б) Найти площадь параллелограмма, построенного на векторах , если Решение : Нет, это не опечатка, исходные данные в пунктах условия я намеренно сделал одинаковыми. а) По условию требуется найти длину вектора (векторного произведения). По соответствующей формуле: Ответ : Коль скоро спрашивалось о длине, то в ответе указываем размерность – единицы. б) По условию требуется найти площадь параллелограмма, построенного на векторах . Площадь данного параллелограмма численно равна длине векторного произведения: Ответ : Обратите внимание, что в ответе о векторном произведении речи не идёт вообще, нас спрашивали о площади фигуры , соответственно, размерность – квадратные единицы. Всегда смотрим, ЧТО требуется найти по условию, и, исходя из этого, формулируем чёткий ответ. Может показаться буквоедством, но буквоедов среди преподавателей хватает, и задание с хорошими шансами вернётся на доработку. Хотя это не особо натянутая придирка – если ответ некорректен, то складывается впечатление, что человек не разбирается в простых вещах и/или не вник в суть задания. Куда подевалась большая буковка «эн»? В принципе, её можно было дополнительно прилепить в решение, но в целях сократить запись, я этого не сделал. Надеюсь, всем понятно, что и – это обозначение одного и того же. Популярный пример для самостоятельного решения: Пример 2 Найти площадь треугольника, построенного на векторах , если Формула нахождения площади треугольника через векторное произведение дана в комментариях к определению. Решение и ответ в конце урока. На практике задача действительно очень распространена, треугольниками вообще могут замучить. Для решения других задач нам понадобятся: Свойства векторного произведения векторовНекоторые свойства векторного произведения мы уже рассмотрели, тем не менее, я их включу в данный список. Для произвольных векторов и произвольного числа справедливы следующие свойства: 1) В других источниках информации данный пункт обычно не выделяют в свойствах, но он очень важен в практическом плане. 2) – свойство тоже разобрано выше, иногда его называют антикоммутативностью . Иными словами, порядок векторов имеет значение. 3) – сочетательные или ассоциативные законы векторного произведения. Константы безпроблемно выносятся за пределы векторного произведения. Действительно, чего им там делать? 4) – распределительные или дистрибутивные законы векторного произведения. С раскрытием скобок тоже нет проблем. В качестве демонстрации рассмотрим коротенький пример: Пример 3 Найти , если Решение: По условию снова требуется найти длину векторного произведения. Распишем нашу миниатюру: (1) Согласно ассоциативным законам, выносим константы за переделы векторного произведения. (2) Выносим константу за пределы модуля, при этом модуль «съедает» знак «минус». Длина же не может быть отрицательной. (3) Дальнейшее понятно. Ответ : Пора подбросить дров в огонь: Пример 4 Вычислить площадь треугольника, построенного на векторах , если Решение : Площадь треугольника найдём по формуле . 1) На первом шаге выразим векторное произведение через векторное произведение , по сути, выразим вектор через вектор . О длинах пока ни слова! (1) Подставляем выражения векторов . (2) Используя дистрибутивные законы, раскрываем скобки по правилу умножения многочленов. (3) Используя ассоциативные законы, выносим все константы за пределы векторных произведений. При маломальском опыте действия 2 и 3 можно выполнять одновременно. (4) Первое и последнее слагаемое равно нулю (нулевому вектору) благодаря приятному свойству . Во втором слагаемом используем свойство антикоммутативности векторного произведения: (5) Приводим подобные слагаемые. В результате вектор оказался выражен через вектор, чего и требовалось достичь: 2) На втором шаге найдем длину нужного нам векторного произведения. 3) Найдём площадь искомого треугольника: Этапы 2-3 решения можно было оформить и одной строкой. Ответ : Рассмотренная задача достаточно распространена в контрольных работах, вот пример для самостоятельного решения: Пример 5 Найти , если Краткое решение и ответ в конце урока. Посмотрим, насколько вы были внимательны при изучении предыдущих примеров;-) Векторное произведение векторов в координатах, заданных в ортонормированном базисе , выражается формулой : Формула и правда простецкая: в верхнюю строку определителя записываем координатные векторы, во вторую и третью строки «укладываем» координаты векторов , причём укладываем в строгом порядке – сначала координаты вектора «вэ», затем координаты вектора «дубль-вэ». Если векторы нужно умножить в другом порядке, то и строки следует поменять местами: Пример 10 Проверить, будут ли коллинеарны следующие векторы пространства: Решение : Проверка основана на одном из утверждений данного урока: если векторы коллинеарны, то их векторное произведение равно нулю (нулевому вектору): . а) Найдём векторное произведение: Таким образом, векторы не коллинеарны. б) Найдём векторное произведение: Ответ : а) не коллинеарны, б) Вот, пожалуй, и все основные сведения о векторном произведении векторов. Данный раздел будет не очень большим, так как задач, где используется смешанное произведение векторов, немного. Фактически всё будет упираться в определение, геометрический смысл и пару рабочих формул. Смешанное произведение векторов – это произведение трёх векторов : Вот так вот они выстроились паровозиком и ждут, не дождутся, когда их вычислят. Сначала опять определение и картинка: Определение : Смешанным произведением некомпланарных векторов , взятых в данном порядке , называется объём параллелепипеда , построенного на данных векторах, снабжённый знаком «+», если базис правый, и знаком «–», если базис левый. Выполним рисунок. Невидимые нам линии прочерчены пунктиром: Погружаемся в определение: 2) Векторы взяты в определённом порядке , то есть перестановка векторов в произведении , как вы догадываетесь, не проходит без последствий. 3) Перед тем, как прокомментировать геометрический смысл, отмечу очевидный факт: смешанное произведение векторов является ЧИСЛОМ : . В учебной литературе оформление может быть несколько другим, я привык обозначать смешанное произведение через , а результат вычислений буквой «пэ». По определению смешанное произведение – это объем параллелепипеда , построенного на векторах (фигура прочерчена красными векторами и линиями чёрного цвета). То есть, число равно объему данного параллелепипеда. Примечание : чертёж является схематическим. 4) Не будем заново париться с понятием ориентации базиса и пространства. Смысл заключительной части состоит в том, что к объёму может добавляться знак минус. Простыми словами, смешанное произведение может быть отрицательным: . Непосредственно из определения следует формула вычисления объема параллелепипеда, построенного на векторах .
Посмотреть всех экспертов из раздела Учеба и наука > Математика
Решено В треугольнике АВС точка М – середина стороны АВ, точка N – середина стороны АС, отрезки СМ и BN пересекаются в точке О, ВА = а, ВС = b. Выразите вектор ВО через векторы а и b. Дана правильная четырёхугольная усечённая пирамида высотой 9 см. Решено Даны вершины треугольника М(1,-1,5), N(4,-3,2), P(0,-5,5). Найти внутренний угол при вершине M Решено Модуль вектора а равен — 2. Известно, что она образует с осью ОХ — острый угол, осью ОУ-угол 60, а осью ОZ -135. Найдите координату вектора а Решено Точка пересечения диагоналей куба — O. Сторона куба равна 3 дм. Пользуйтесь нашим приложением Вопрос Видео: Нахождение площади параллелограмма в трех измеренияхСтенограмма видео 𝐴𝐵𝐶𝐷 представляет собой параллелограмм, в котором вектор 𝐴𝐵 имеет отрицательные компоненты один, один, три, а вектор 𝐴𝐷 имеет компоненты три, четыре, один. В вопросе сказано, что 𝐴𝐵𝐶𝐷 — параллелограмм. Итак, давайте нарисуем его. Вот наш параллелограмм. Теперь нам просто нужно пометить его вершины. Как только мы назвали одну из вершин 𝐴, у нас есть только два варианта, куда пойдет 𝐵. Он должен быть рядом с 𝐴. Так что 𝐵 нужно идти либо сюда, либо сюда. И как только мы выбрали, куда идти 𝐴 и 𝐵, у нас нет выбора для 𝐶 и 𝐷. 𝐶 должен быть рядом с 𝐵. А на 𝐷 осталось всего одно место. Итак, начиная с 𝐴, мы можем обойти параллелограмм, сначала посетив 𝐵, затем 𝐶 и, наконец, 𝐷, прежде чем снова окажемся в 𝐴. Другими словами, мы можем посещать вершины в том же порядке, в котором они встречаются в названии параллелограмма 𝐴𝐵𝐶𝐷. Хорошо, а что еще нам говорят в тексте задачи? Нам даны компоненты вектора 𝐴𝐵. Отметим их на нашей картинке, а также компоненты вектора 𝐴𝐷. И что мы ищем? Мы хотим найти площадь параллелограмма 𝐴𝐵𝐶𝐷. Чтобы найти эту площадь, мы используем тот факт, что величина векторного произведения двух векторов 𝑢 и 𝑣 является площадью параллелограмма, смежные стороны которого равны 𝑢 и 𝑣. Прежде чем найти величину векторного произведения, конечно, нам нужно найти само векторное произведение. И мы можем записать это перекрестное произведение как определитель матрицы три на три, первая строка которой содержит единичные векторы в 𝑥-, 𝑦- и 𝑧-направлениях 𝑖, 𝑗 и 𝑘. Вторая строка содержит компоненты первого вектора в наших перекрестных произведениях минус один, один и три. И третья строка содержит компоненты второго вектора в нашем перекрестном произведении три, четыре и один. Можно разложить определитель по первой строке. И оценивая каждое два на два, вот как это означает, что мы получаем отрицательное 11 𝑖 плюс 10 𝑗 минус семь 𝑘, что мы можем записать в компонентах как отрицательное 11, 10, отрицательное семь. А величина вектора — это просто квадратный корень из суммы квадратов компонентов. Итак, у нас есть квадратный корень из минус 11 в квадрате плюс 10 в квадрате плюс минус семь в квадрате. Мы можем записать это в точности как квадратный корень из 270 или как три умноженный на квадратный корень из 30. Но нас не спрашивают о точном ответе. Нас просят дать правильный ответ до одного знака после запятой. И с точностью до одного десятичного знака квадратный корень из 270 равен 16,4. Итак, наш параллелограмм 𝐴𝐵𝐶𝐷 имеет площадь 16,4 единицы с точностью до одного десятичного знака. Мы нашли это, вычислив величину векторного произведения векторов вдоль двух смежных сторон параллелограмма. И нам повезло, что нам дали компоненты двух смежных сторон в задаче. Нам не даны, например, компоненты одной из диагоналей ни 𝐴𝐶, ни 𝐵𝐷. Параллелограмм, который я только что нарисовал, не является правильной диаграммой для параллелограмма 𝐴𝐵𝐶𝐷. Обходя вершины по порядку, мы можем получить 𝐴𝐵𝐷𝐶 или 𝐴𝐶𝐷𝐵, но не 𝐴𝐵𝐶𝐷. Если бы мы использовали эту неверную диаграмму, мы бы получили неверный ответ, поэтому стоило вначале потратить некоторое время на то, чтобы правильно пометить наши вершины. Как найти площадь параллелограмма с вершинами••• Jupiterimages/Polka Dot/Getty Images Обновлено 10 июня 2019 г. быть вычислено с помощью векторного векторного произведения. Площадь параллелограмма равна произведению его основания на высоту. Используя векторные значения, полученные из вершин, произведение основания и высоты параллелограмма равно перекрестному произведению двух его смежных сторон. Вычислите площадь параллелограмма, найдя векторные значения его сторон и оценив векторное произведение. Найдите векторные значения двух смежных сторон параллелограмма, вычитая значения x и y двух вершин, образующих сторону. Например, чтобы найти длину DC параллелограмма ABCD с вершинами A (0, -1), B (3, 0), C (5, 2) и D (2, 1), из (5) вычтите (2, 1) , 2) чтобы получить (5 — 2, 2 — 1) или (3, 1). Чтобы найти длину AD, вычтите (2, 1) из (0, -1), чтобы получить (-2, -2). Напишите матрицу из двух строк по три столбца. Заполните первую строку векторными значениями одной стороны параллелограмма (значение x в первом столбце и значение y во втором) и запишите ноль в третьем столбце. Заполните значения второй строки векторными значениями другой стороны и нулем в третьем столбце. В приведенном выше примере напишите матрицу со значениями {{3 1 0}, {-2 -2 0}}. Найдите значение x перекрестного произведения двух векторов, заблокировав первый столбец матрицы 2 x 3 и вычислив определитель полученной матрицы 2 x 2. Определитель матрицы 2 x 2 {{a b}, {c d}} равен ad — bc. В приведенном выше примере значение x перекрестного произведения является определителем матрицы {{1 0}, {-2 0}}, которая равна 0. Найдите значение y и значение z перекрестное произведение, блокируя второй и третий столбцы матрицы, соответственно, и вычисляя определитель результирующих матриц 2 x 2. Значение y перекрестного произведения равно определителю матрицы {{3 0}, {-2 0}}, который равен нулю. Z-значение векторного произведения равно определителю матрицы {{3 1}, {-2 -2}}, который равен -4. 92), что равно 4. Нахождение площади параллелограмма может быть полезно во многих областях науки, включая математику, физику и биологию. Математика Математические исследования, пожалуй, наиболее очевидный способ нахождения площади параллелограмма. Знание того, как найти площадь параллелограмма в координатной геометрии, часто является одной из первых вещей, которые вы должны сделать, прежде чем переходить к более сложным формам. Это также может познакомить вас с более сложной графикой и математикой на основе векторов/вершин, которую вы увидите на уроках математики старшего уровня, геометрии, координатной геометрии, исчисления и многого другого. Физика Физика и математика идут рука об руку, и это, безусловно, верно для вершин. Знание того, как найти площадь параллелограмма таким образом, может распространяться на поиск других площадей, а также на задачу, которая требует от вас найти площадь треугольника с вершинами в физической задаче о скорости или электромагнитной силе, например. Та же концепция координатной геометрии и вычисления площади может применяться к ряду физических задач. Связанные статьиСсылки
Об авторе 5 9004 Он написал для веб-сайта «Путеводитель по онлайн-школам», освещая академические и профессиональные темы для молодых людей, ищущих возможности получения высшего образования. Валлулис имеет степень бакалавра психологии колледжа Уитмена. Sin 7x: Mathway | Популярные задачи
MikroTik Routers and Wireless — Products: RB5009UG+S+INRB5009UG+S+IN
The ultimate heavy-duty home lab router with USB 3.0, 1G and 2.5G Ethernet and a 10G SFP+ cage. You can mount four of these new routers in a single 1U rackmount space! Unprecedented processing power in such a small form factor. Double the usual performance: we took your feedback from the MikroTik User Meetings to create the perfect home lab router: compact, powerful, with multiple powering options and efficient cooling.RB5009 has it all, and even more! The board features 9 wired ports and a full-sized USB 3.0. Seven of the ports are Gigabit Ethernet, another one is 2.5 Gigabit Ethernet, and the last one is a 10G SFP+ cage. All the ports are connected to a powerful Marvell Amethyst family switch-chip with a 10 Gbps full-duplex line leading to the Marvell Armada Quad-core ARMv8 1.4 GHz CPU. Both CPU and the switch-chip are located on the bottom of the board – so the case acts as a massive heat-sink! RB5009UG+S+IN can be powered in 3 different ways: a) PoE-in from Ethernet port #1 b) DC Jack c) 2-pin terminal on the side Boards come with 1GB of DDR4 RAM and 1GB NAND storage. This combination of ports and components, compared to our other products in a similar form factor, provides almost double the performance in configurations with heavy CPU loads. With a simple set of mounting accessories, you can mount FOUR of these routers in a single 1U rackmount space! No more server-room-Tetris, just pure productivity. Send purchase questions
Specifications
Powering
Ethernet
Fiber
Peripherals
Other
Certification & Approvals
Included parts
BrochureOpen Quick GuideOpen User ManualOpen RouterOS current releaseDownload Block DiagramOpen DimensionsOpen SFP compatibility listOpen RouterOS software manualOpen Declaration of conformityOpen (CE) High resolution imagesEthernet test results
IPsec test results
The device has an operating system preinstalled and licensed. Related productsDownload: Full CE declaration (PDF) Information about RB5009UG+S+IN
×
Математика. НОД и НОК: наибольший общий делитель и наименьшее общее кратноеМножество делителей Рассмотрим такую задачу: найти делитель числа $140$. Очевидно, что у числа $140$ не один делитель, а несколько. В таких случаях говорят, что задача имеет множество решений. Найдем их все. Прежде всего разложим данное число на простые множители: $140 = 2 \cdot 2 \cdot 5 \cdot 7$. Теперь мы без труда можем выписать все делители. Начнем с простых делителей, то есть тех, которые присутствуют в разложении, приведенном выше: $2, ~5, ~7$. Затем выпишем те, которые получаются попарным умножением простых делителей: $2\cdot 2 = 4, ~~~2\cdot 5 = 10, ~~~2\cdot 7 = 14, ~~~5\cdot 7 = 35$. Затем — те, которые содержат в себе три простых делителя: $2\cdot 2\cdot 5 = 20, ~~~2\cdot 2\cdot 7 = 28, ~~~2\cdot 5\cdot 7 = 70$. Наконец, не забудем единицу и само разлагаемое число: $1, ~140$. Все найденные нами делители образуют множество делителей числа $140$, которое записывается с помощью фигурных скобок: Множество делителей числа $140~=$ $\{1, ~2, ~4, ~5, ~7, ~10, ~14, ~20, ~28, ~35, ~70, ~140\}$. Для удобства восприятия мы выписали здесь делители (элементы множества) в порядке возрастания, но, вообще говоря, это делать необязательно. Кроме того, введем сокращение записи. Вместо «Множество делителей числа $140$» будем писать «Д$(140)$» (читается «Дэ от $140$»). Таким образом, Д$(140) = \{1, ~2, ~4, ~5, ~7, ~10, ~14, ~20, ~28, ~35, ~70, ~140\}$. Точно так же можно найти множество делителей для любого другого натурального числа. Например, из разложения $105 = 3 \cdot 5 \cdot 7$ мы получаем: Д$(105) = \{1, ~3, ~5, ~7, ~15, ~21, ~35, ~105\}$. От множества всех делителей следует отличать множество простых делителей, которые для чисел $140$ и $105$ равны соответственно: ПД$(140) = \{2, ~5, ~7\}$. ПД$(105) = \{3, ~5, ~7\}$. Следует особо подчеркнуть, что в разложении числа $140$ на простые множители двойка присутствует два раза, в то время как во множестве ПД$(140)$ — только один. Множество ПД$(140)$ — это, по своей сути, все ответы на задачу: «Найти простой множитель числа $140$». Ясно, что один и тот же ответ не следует повторять больше одного раза. Сокращение дробей. Наибольший общий делитель Рассмотрим дробь $\dfrac{105}{140}$. Мы знаем, что эту дробь можно сократить на такое число, которое одновременно является и делителем числителя ($105$) и делителем знаменателя ($140$). Взглянем на множества Д$(105)$ и Д$(140)$ и выпишем их общие элементы.
Д$(105) = \{1, ~3, ~5, ~7, ~15, ~21, ~35, ~105\}$; Д$(140) = \{1, ~2, ~4, ~5, ~7, ~10, ~14, ~20, ~28, ~35, ~70, ~140\}$.
Общие элементы множеств Д$(105)$ и Д$(140)~=$ $\{1, ~5, ~7, ~35\}$.
Последнее равенство можно записать короче, а именно: Д$(105)~\cap~$Д$(140)~=~\{1, ~5, ~7, ~35\}$. Здесь специальный значок «$\cap$» («мешок отверстием вниз») как раз и указывает на то, что из двух множеств, записанных по разные стороны от него, надо выбрать только общие элементы. Запись «Д$(105)~\cap~$Д$(140)$» читается «пересечение множеств Дэ от $105$ и Дэ от $140$». Замечание. Отметим по ходу дела, что с множествами можно производить разные бинарные операции, почти как с числами. Другой распространенной бинарной операцией является объединение, которое обозначается значком «$\cup$» («мешок отверстием вверх»). В объединение двух множеств входят все элементы как того, так и другого множества: ПД$(105) = \{3, ~5, ~7\}$; ПД$(140) = \{2, ~5, ~7\}$; ПД$(105)~\cup~$ПД$(140) = \{2, ~3, ~5, ~7\}$. Итак, мы выяснили, что дробь $\dfrac{105}{140}$ можно сократить на любое из чисел, принадлежащих множеству Д$(105)~\cap~$Д$(140) = \{1, ~5, ~7, ~35\}$ и нельзя сократить ни на какое другое натуральное число. Вот все возможные способы сокращения (за исключением неинтересного сокращения на единицу): $\begin{align}
&\frac{105}{140} = \frac{105/5}{140/5} = \frac{21}{28},\\
&\frac{105}{140} = \frac{105/7}{140/7} = \frac{15}{20},\\
&\frac{105}{140} = \frac{105/35}{140/35} = \frac{\,3\,}{4}. Очевидно, что практичнее всего сокращать дробь на число, по возможности большее. В данном случае это число $35$, про которое говорят, что оно является наибольшим общим делителем (НОД) чисел $105$ и $140$. Это записывается как НОД$(105, ~140) = 35$. Впрочем, на практике, если нам даны два числа и требуется найти их наибольший общий делитель, мы вовсе не должны строить какие-либо множества. Достаточно просто разложить оба числа на простые множители и подчеркнуть те из этих множителей, которые являются общими для обоих разложений, например: $105 = 3 \cdot \underline{\,5\,} \cdot \underline{\,7\,}$; $140 = 2 \cdot 2 \cdot \underline{\,5\,} \cdot \underline{\,7\,}$. Перемножая подчеркнутые числа (в любом из разложений), получаем: НОД$(105, ~140) = 5 \cdot 7 = 35$. Разумеется, возможен случай, когда подчеркнутых множителей окажется больше двух: $168 = \underline{\,2\,} \cdot \underline{\,2\,} \cdot 2 \cdot \underline{\,3\,} \cdot 7$; $396 = \underline{\,2\,} \cdot \underline{\,2\,} \cdot \underline{\,3\,} \cdot 3 \cdot 11$. Отсюда видно, что НОД$(168, ~396) = \underline{\,2\,} \cdot \underline{\,2\,} \cdot \underline{\,3\,} = 12$. Особого упоминания заслуживает ситуация, когда общих множителей совсем нет и подчеркивать нечего, например: $42 = 2 \cdot 3 \cdot 7$; $55 = 5 \cdot 11$. В этом случае, НОД$(42, \,55) = 1$. Два натуральных числа, для которых НОД равен единице, называются взаимно простыми. Если из таких чисел составить дробь, например, $\dfrac{42}{55}$, то такая дробь является несократимой. Вообще говоря, правило сокращения дробей можно записать в таком виде: $\dfrac{\,a\,}{b} = \dfrac{a/\text{НОД}(a, b)}{b/\text{НОД}(a, b)}\,$. Здесь предполагается, что $a$ и $b$ — натуральные числа, а вся дробь положительна. Если мы теперь припишем знак «минус» к обоим частям этого равенства, то получим соответствующее правило для отрицательных дробей. Сложение и вычитание дробей. Наименьшее общее кратное Пусть требуется вычислить сумму двух дробей: $\dfrac{1}{105} + \dfrac{1}{140}$. Нетрудно видеть, что оба исходных знаменателя (как $105$, так и $140$) являются делителями числа $420$, а число $420$, в свою очередь, кратно обоим знаменателям, — и не просто кратно, оно является наименьшим общим кратным (НОК) чисел $105$ и $140$. Это записывается так: НОК$(105, ~140) = 420$. Итак, чтобы получить НОК чисел $105$ и $140$, мы разложили их на простые множители, подчеркнули те множители, которые являются общими для обоих чисел, а далее написали: НОК $=$ все множители первого числа $\times$ неподчеркнутые множители второго числа. Отсюда следует, что НОК$(105, 140) = 105 \cdot 140 /~$НОД$(105, 140)$. Это можно также переписать в несколько более изящной, «симметричной» форме: $105 \cdot 140~=~$НОК$(105, 140)~\cdot~$НОД$(105, 140)$. Точно так же, для произвольных натуральных чисел $b$ и $d$: $b \cdot d~=~$НОК$(b, d)~\cdot~$НОД$(b, d)$. Теперь давайте доведем до конца суммирование наших дробей: $\begin{align}
&\dfrac{1}{105} + \dfrac{1}{140} =\\[2mm]
&= \dfrac{1}{3 \cdot \underline{\,5\,} \cdot \underline{\,7\,}} + \frac{1}{2 \cdot 2 \cdot \underline{\,5\,} \cdot \underline{\,7\,}} =\\[2mm]
&= \dfrac{2 \cdot 2 }{2 \cdot 2 \cdot 3 \cdot \underline{\,5\,} \cdot \underline{\,7\,}}
+ \dfrac{3}{3 \cdot 2 \cdot 2 \cdot \underline{\,5\,} \cdot \underline{\,7\,}} =\\[2mm]
&= \dfrac{4 + 3}{2 \cdot 2 \cdot 3 \cdot \underline{\,5\,} \cdot \underline{\,7\,}}
= \dfrac{7}{2 \cdot 2 \cdot 3 \cdot \underline{\,5\,} \cdot \underline{\,7\,}}
= \dfrac{1}{2 \cdot 2 \cdot 3 \cdot \underline{\,5\,}} = \dfrac{1}{60}\,. Подобным же образом можно посчитать разность: $\dfrac{1}{105} — \dfrac{1}{140} = \dfrac{4}{4 \cdot 105} — \dfrac{3}{3 \cdot 140} = \dfrac{4}{420} — \dfrac{3}{420} = \dfrac{1}{420}$. Для того чтобы получить общий знаменатель двух дробей $\frac{\,a\,}{b}$ и $\frac{\,c\,}{d}$, мы фактически проделываем ту же самую процедуру, что и при вычислении НОК$(b, d)$. Именно НОК$(b, d)$ и оказывается общим знаменателем. (Предполагается, что $a$, $b$, $c$ и $d$ — натуральные числа.) Конспект 1. Правило сокращения дробей. Пусть $a$ и $b$ — натуральные числа (${b \ne 0}$). Тогда $\dfrac{\,a\,}{b} = \dfrac{a/\text{НОД}(a, b)}{b/\text{НОД}(a, b)}$ , где НОД$(a, b)$ — наибольший общий делитель чисел $a$ и $b$. Чтобы найти НОД, надо разложить числа $a$ и $b$ на простые множители и подчеркнуть те множители, которые являются общими для обоих чисел. НОД равен произведению подчеркнутых множителей, взятых в любом из разложений. 2. Приведение дробей к общему знаменателю. НОК $=$ все множители числа $b~\times$ неподчеркнутые множители числа $d$. 3. НОК и НОД связаны соотношением $b \cdot d = \text{НОК}(b, d) \cdot \text{НОД}(b, d)$. Из «бесконечного» сборника типовых упражнений Задачи, где требуется разлагать числа на простые множители Примечание. Для решения некоторых задач требуется знать, что такое квадрат числа. Квадратом числа $a$ называется число $a$, помноженное само на себя, то есть $a \cdot a$. (Оно называется так, потому что равно площади квадрата со стороной $a$).
Нахождение наименьшего общего кратного двух чиселРезультаты обучения
Одна из причин, по которой мы находим кратные и простые числа, заключается в том, что мы используем их для нахождения наименьшего общего кратного двух чисел. Перечисление множителей МетодОбщее кратное двух чисел — это число, кратное обоим числам. Предположим, мы хотим найти общие кратные [латекс]10[/латекс] и [латекс]25[/латекс]. Мы можем перечислить первые несколько кратных каждого числа. Затем мы ищем кратные, общие для обоих списков — это общие кратные. [латекс]\begin{array}{c}10\text{ : }10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 110\ldots \hfill \\ 25\text{ : }25, 50,75, 100, 125\ldots\hfill\end{массив}[/latex] Мы видим, что [latex]50[/latex] и [latex]100[/latex] присутствуют в обоих списках. Они являются кратными [латекс]10[/латекс] и [латекс]25[/латекс]. Мы бы нашли больше общих кратных, если бы продолжили список кратных для каждого. Наименьшее число, кратное двум числам, называется наименьшим общим кратным (НОК). Таким образом, наименьший LCM [латекс]10[/латекс] и [латекс]25[/латекс] составляет [латекс]50[/латекс]. Найдите наименьшее общее кратное (НОК) двух чисел, перечислив кратные
примерНайдите LCM [латекс]15[/латекс] и [латекс]20[/латекс], перечислив кратные. Решение: [латекс]\begin{array}{l}\text{15: }15,30,45,60,75,90,105,120\hfill \\ \text{20: }20,40,60,80,100,120,140,160\hfill \ end{array}[/latex] Наименьшее число, появляющееся в обоих списках, равно [latex]60[/latex], поэтому [latex]60[/latex] является наименьшим общим кратным [latex]15[/latex] ] и [латекс]20[/латекс]. Обратите внимание, что [latex]120[/latex] также присутствует в обоих списках.
попробуйтеВ следующем видео мы покажем пример того, как найти наименьшее общее кратное, перечислив кратные каждого числа. Метод простых множителейДругой способ найти наименьшее общее кратное двух чисел — использовать их простые множители. Мы будем использовать этот метод, чтобы найти LCM [latex]12[/latex] и [latex]18[/latex]. Начнем с нахождения разложения каждого числа на простые множители. [латекс]12=2\cdot 2\cdot 318=2\cdot 3\cdot 3[/latex] Затем мы записываем каждое число как произведение простых чисел, по возможности сопоставляя простые числа по вертикали. [латекс]\begin{массив}{l}12=2\cdot 2\cdot 3\hfill \\ 18=2\cdot 3\cdot 3\end{массив}[/latex] Теперь выведем простые числа в каждом столбце. LCM является продуктом этих факторов. Найдите НОК с помощью метода простых множителей
примерНайдите LCM [латекс]15[/латекс] и [латекс]18[/латекс], используя метод простых множителей. Показать раствор
попробуйте
пример Найдите LCM [латекс]50[/латекс] и [латекс]100[/латекс], используя метод простых множителей. Показать раствор
попробуйтеВ следующем видео мы покажем, как найти наименьшее общее кратное с помощью простой факторизации. Найдите первые два общих кратных 12 и 18…Перейти к
Главная >
РД Шарма Решения
Класс 6
Математика
>
Глава 2. Вопрос 4 Игра с числами Упражнение 2.2 Найдите первые два общих числа, кратных 12 и 18. Ответ: Мы знаем, что Число, кратное 12, равно 12, 24, 0 36. , 72, 84, 96, 108, 12 ….. Кратность 18 равна 18, 36, 54, 72, 90, 108, 126, 144, 162, 180 …. Следовательно, первые два общих кратных 12 и 18 равны 36 и 72. Родственные вопросы Найдите общие делители: (i) 15 и 25 (ii) 35 и 50 (iii) 20 и 28 Найдите общие делители: (i) 5, 15 и 25 (ii) 2, 6 и 8 Найдите первые три общих кратных числам 6 и 8. Число делится как на 7, так и на 16. На какое другое число это число всегда делится? Число делится на 24. Нок 16 8: НОД и НОК для 8 и 16 (с решением) 2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Наименьшее общее кратное 8 и 16
Второй способ нахождения НОК для чисел 8 и 16 заключается в перечислении всех кратных для обоих чисел и выбор первого совпадающего:
Кратные числа 8: 8, 16, 24, 32
Кратные числа 16: 16, 32, 48, 64, 80, 96, 112, 128, 144, 160, 176, 192, 208, 224, 240, 256, 272, 288, 304, 320, 336, 352, 368, 384, 400, 416, 432, 448, 464, 480, 496, 512, 528, 544, 560, 576, 592, 608, 624, 640, 656, 672, 688, 704, 720, 736, 752, 768, 784, 800, 816, 832, 848, 864, 880, 896, 912, 928, 944, 960, 976, 992, 1008, 1024, 1040, 1056, 1072, 1088, 1104, 1120, 1136, 1152, 1168, 1184, 1200, 1216, 1232, 1248, 1264, 1280, 1296, 1312, 1328, 1344, 1360, 1376, 1392, 1408, 1424, 1440, 1456, 1472, 1488, 1504, 1520, 1536, 1552, 1568, 1584, 1600, 1616, 1632, 1648, 1664, 1680, 1696, 1712, 1728, 1744, 1760, 1776, 1792, 1808, 1824, 1840, 1856, 1872, 1888, 1904, 1920, 1936, 1952, 1968, 1984, 2000, 2016, 2032, 2048, 2064, 2080, 2096, 2112, 2128, 2144, 2160, 2176, 2192, 2208, 2224, 2240, 2256, 2272, 2288, 2304, 2320, 2336, 2352, 2368, 2384, 2400, 2416, 2432, 2448, 2464, 2480, 2496, 2512, 2528, 2544, 2560, 2576, 2592, 2608, 2624, 2640, 2656, 2672, 2688, 2704, 2720, 2736, 2752, 2768, 2784, 2800, 2816, 2832, 2848, 2864, 2880, 2896, 2912, 2928, 2944, 2960, 2976, 2992, 3008, 3024, 3040, 3056, 3072, 3088, 3104, 3120, 3136, 3152, 3168, 3184, 3200, 3216, 3232, 3248, 3264, 3280, 3296, 3312, 3328, 3344, 3360, 3376, 3392, 3408, 3424, 3440, 3456, 3472, 3488, 3504, 3520, 3536, 3552, 3568, 3584, 3600, 3616, 3632, 3648, 3664, 3680, 3696, 3712, 3728, 3744, 3760, 3776, 3792, 3808, 3824, 3840, 3856, 3872, 3888, 3904, 3920, 3936, 3952, 3968, 3984, 4000, 4016, 4032, 4048, 4064, 4080, 4096, 4112, 4128, 4144, 4160, 4176, 4192, 4208, 4224, 4240, 4256, 4272, 4288, 4304, 4320, 4336, 4352, 4368, 4384, 4400, 4416, 4432, 4448, 4464, 4480, 4496, 4512, 4528, 4544, 4560, 4576, 4592, 4608, 4624, 4640, 4656, 4672, 4688, 4704, 4720, 4736, 4752, 4768, 4784, 4800, 4816, 4832, 4848, 4864, 4880, 4896, 4912, 4928, 4944, 4960, 4976, 4992, 5008, 5024, 5040, 5056, 5072, 5088, 5104, 5120, 5136, 5152, 5168, 5184, 5200, 5216, 5232, 5248, 5264, 5280, 5296, 5312, 5328, 5344, 5360, 5376, 5392, 5408, 5424, 5440, 5456, 5472, 5488, 5504, 5520, 5536, 5552, 5568, 5584, 5600, 5616, 5632, 5648, 5664, 5680, 5696, 5712, 5728, 5744, 5760, 5776, 5792, 5808, 5824, 5840, 5856, 5872, 5888, 5904, 5920, 5936, 5952, 5968, 5984, 6000, 6016, 6032, 6048, 6064, 6080, 6096, 6112, 6128, 6144, 6160, 6176, 6192, 6208, 6224, 6240, 6256, 6272, 6288, 6304, 6320, 6336, 6352, 6368, 6384, 6400, 6416, 6432, 6448, 6464, 6480, 6496, 6512, 6528, 6544, 6560, 6576, 6592, 6608, 6624, 6640, 6656, 6672, 6688, 6704, 6720, 6736, 6752, 6768, 6784, 6800, 6816, 6832, 6848, 6864, 6880, 6896, 6912, 6928, 6944, 6960, 6976, 6992, 7008, 7024, 7040, 7056, 7072, 7088, 7104, 7120, 7136, 7152, 7168, 7184, 7200, 7216, 7232, 7248, 7264, 7280, 7296, 7312, 7328, 7344, 7360, 7376, 7392, 7408, 7424, 7440, 7456, 7472, 7488, 7504, 7520, 7536, 7552, 7568, 7584, 7600, 7616, 7632, 7648, 7664, 7680, 7696, 7712, 7728, 7744, 7760, 7776, 7792, 7808, 7824, 7840, 7856, 7872, 7888, 7904, 7920, 7936, 7952, 7968, 7984, 8000, 8016, 8032, 8048, 8064, 8080, 8096, 8112, 8128, 8144, 8160, 8176, 8192, 8208, 8224, 8240, 8256, 8272, 8288, 8304, 8320, 8336, 8352, 8368, 8384, 8400, 8416, 8432, 8448, 8464, 8480, 8496, 8512, 8528, 8544, 8560, 8576, 8592, 8608, 8624, 8640, 8656, 8672, 8688, 8704, 8720, 8736, 8752, 8768, 8784, 8800, 8816, 8832, 8848, 8864, 8880, 8896, 8912, 8928, 8944, 8960, 8976, 8992, 9008, 9024, 9040, 9056, 9072, 9088, 9104, 9120, 9136, 9152, 9168, 9184, 9200, 9216, 9232, 9248, 9264, 9280, 9296, 9312, 9328, 9344, 9360, 9376, 9392, 9408, 9424, 9440, 9456, 9472, 9488, 9504, 9520, 9536, 9552, 9568, 9584, 9600, 9616, 9632, 9648, 9664, 9680, 9696, 9712, 9728, 9744, 9760, 9776, 9792, 9808, 9824, 9840, 9856, 9872, 9888, 9904, 9920, 9936, 9952, 9968, 9984, 10000, 10016, 10032, 10048, 10064, 10080, 10096, 10112, 10128, 10144, 10160, 10176, 10192, 10208, 10224, 10240, 10256, 10272, 10288, 10304, 10320, 10336, 10352, 10368, 10384, 10400, 10416, 10432, 10448, 10464, 10480, 10496, 10512, 10528, 10544, 10560, 10576, 10592, 10608, 10624, 10640, 10656, 10672, 10688, 10704, 10720, 10736, 10752, 10768, 10784, 10800, 10816, 10832, 10848, 10864, 10880, 10896, 10912, 10928, 10944, 10960, 10976, 10992, 11008, 11024, 11040, 11056, 11072, 11088, 11104, 11120, 11136, 11152, 11168, 11184, 11200, 11216, 11232, 11248, 11264, 11280, 11296, 11312, 11328, 11344, 11360, 11376, 11392, 11408, 11424, 11440, 11456, 11472, 11488, 11504, 11520, 11536, 11552, 11568, 11584, 11600, 11616, 11632, 11648, 11664, 11680, 11696, 11712, 11728, 11744, 11760, 11776, 11792, 11808, 11824, 11840, 11856, 11872, 11888, 11904, 11920, 11936, 11952, 11968, 11984, 12000, 12016, 12032, 12048, 12064, 12080, 12096, 12112, 12128, 12144, 12160, 12176, 12192, 12208, 12224, 12240, 12256, 12272, 12288, 12304, 12320, 12336, 12352, 12368, 12384, 12400, 12416, 12432, 12448, 12464, 12480, 12496, 12512, 12528, 12544, 12560, 12576, 12592, 12608, 12624, 12640, 12656, 12672, 12688, 12704, 12720, 12736, 12752, 12768, 12784, 12800, 12816, 12832, 12848, 12864, 12880, 12896, 12912, 12928, 12944, 12960, 12976, 12992, 13008, 13024, 13040, 13056, 13072, 13088, 13104, 13120, 13136, 13152, 13168, 13184, 13200, 13216, 13232, 13248, 13264, 13280, 13296, 13312, 13328, 13344, 13360, 13376, 13392, 13408, 13424, 13440, 13456, 13472, 13488, 13504, 13520, 13536, 13552, 13568, 13584, 13600, 13616, 13632, 13648, 13664, 13680, 13696, 13712, 13728, 13744, 13760, 13776, 13792, 13808, 13824, 13840, 13856, 13872, 13888, 13904, 13920, 13936, 13952, 13968, 13984, 14000, 14016, 14032, 14048, 14064, 14080, 14096, 14112, 14128, 14144, 14160, 14176, 14192, 14208, 14224, 14240, 14256, 14272, 14288, 14304, 14320, 14336, 14352, 14368, 14384, 14400, 14416, 14432, 14448, 14464, 14480, 14496, 14512, 14528, 14544, 14560, 14576, 14592, 14608, 14624, 14640, 14656, 14672, 14688, 14704, 14720, 14736, 14752, 14768, 14784, 14800, 14816, 14832, 14848, 14864, 14880, 14896, 14912, 14928, 14944, 14960, 14976, 14992, 15008, 15024, 15040, 15056, 15072, 15088, 15104, 15120, 15136, 15152, 15168, 15184, 15200, 15216, 15232, 15248, 15264, 15280, 15296, 15312, 15328, 15344, 15360, 15376, 15392, 15408, 15424, 15440, 15456, 15472, 15488, 15504, 15520, 15536, 15552, 15568, 15584, 15600, 15616, 15632, 15648, 15664, 15680, 15696, 15712, 15728, 15744, 15760, 15776, 15792, 15808, 15824, 15840, 15856, 15872, 15888, 15904, 15920, 15936, 15952, 15968, 15984, 16000, [. ..], 16
..], 16
Следовательно, НОК для 8 и 16 равняется 16
16 новых профессий получат право на экспресс-въезд, когда Канада пересмотрит NOC
В результате пересмотра Канадой системы Национальной классификации занятий (NOC) 16 новых профессий получат право на экспресс-въезд.
Министерский меморандум от 21 февраля 2022 г., с которым ознакомился сайт иммиграции.ca, показывает, что в систему отбора должны быть включены рабочие места, включая водителей грузовиков и автобусов, санитаров, помощников преподавателей и ассистентов стоматолога. Полный список ниже.
Министерство иммиграции, беженцев и гражданства Канады (IRCC) завершит переход от NOC 2016 к NOC 2021 в ноябре 2022 года, подтверждается в меморандуме.
При этом система перейдет от текущей классификации, основанной на уровне навыков, к новой классификации TEER, обозначающей обучение, образование, опыт и обязанности.
Однако текущий тип навыка 0 и уровни навыков от A до D напрямую не соответствуют уровням TEER от 0 до 5.
Приблизительные эквиваленты следующие:
НОК 2016 | НОК 2021 |
Тип навыка 0 | ТЕЕР 0 |
Уровень навыка А | ТЕЕР 1 |
Уровень навыка B | ТЕЕР 2 |
ТЭР 3 | |
Уровень навыка C | ТЕЕР 4 |
Уровень навыка D | ТЕЕР5 |
При использовании NOC 2016 профессии имеют право на участие в программе Express Entry от уровня квалификации B и выше. В рамках NOC 2021 квалифицируются TEER 3 и выше.
Это означает, что будут добавлены следующие профессии:
- Администраторы расчета заработной платы
- Ассистенты стоматолога и зубные лаборанты
- Помощницы медсестер, санитары и помощники по обслуживанию пациентов
- Технические ассистенты аптеки и помощники аптекаря
- Помощники учителей начальной и средней школы
- Шерифы и судебные приставы
- Сотрудники исправительной службы
- Сотрудники правоохранительных органов и других регулирующих органов
- Косметологи, электрологи и смежные профессии
- Жилые и коммерческие установщики и сервисные службы
- Средства борьбы с вредителями и фумигаторы
- Прочие ремонтники и сервисные службы
- Водители грузовиков
- Водители автобусов, операторы метро и другие операторы общественного транспорта
- Операторы тяжелого оборудования
- Сборщики самолетов и инспекторы по сборке самолетов.
Между тем, три другие профессии, которые имеют право на участие в Express Entry в соответствии с NOC 2016, станут неприемлемыми в соответствии с NOC 2021. Эти профессии:
Эти профессии:
- Другие исполнители
- Руководители программ и инструкторы по отдыху, спорту и фитнесу
- Портные, портные, меховщики и модистки.
Подробнее
Новые изменения в Canada Express Entry, позволяющие принимать приглашения по роду занятий
Капитальный ремонт канадской системы NOC имеет серьезные последствия для иммиграционной службы Резкое падение числа ITA по мере того, как IRCC справляется с отставанием
Атлантическая иммиграционная программа
В рамках перехода от NOC 2016 к NOC 2021 также будут затронуты соответствующие профессии в рамках Атлантической иммиграционной программы (AIP).
AIP — это программа, возглавляемая работодателями и предназначенная для привлечения новых квалифицированных иммигрантов в провинции Новая Шотландия, Нью-Брансуик, Остров Принца Эдуарда, Ньюфаундленд и Лабрадор.
В настоящее время он открыт для профессий с уровнем квалификации C или выше в рамках NOC 2016. В соответствии с NOC 2021 он будет открыт для профессий с TEER 4 или выше.
В соответствии с NOC 2021 он будет открыт для профессий с TEER 4 или выше.
В результате следующие профессии станут неприемлемыми :
- Прочие вспомогательные профессии в сфере личных услуг
- Портовые рабочие
- Перегружатели материалов
- Водители такси и лимузинов и шоферы
- Водители службы доставки и дистрибьюторы «от двери до двери»
- Операторы лодок и канатных паромов и связанные с ними профессии
- Рабочие скота
- Работники питомников и теплиц
- Звероловы и охотники
- Серверы для продуктов питания и напитков
- Рабочие по обработке и раскрою текстиля.
Грядут дальнейшие изменения в системе Express Entry
Существенные изменения в системе Express Entry, которые позволят получать приглашения по роду занятий, были изложены в поправках к Закону об иммиграции и защите беженцев, предложенных IRCC.
Поправки, предложенные в соответствии с законопроектом C-19, конкретизируют некоторые детали, впервые опубликованные иммиграционным сайтом иммиграции.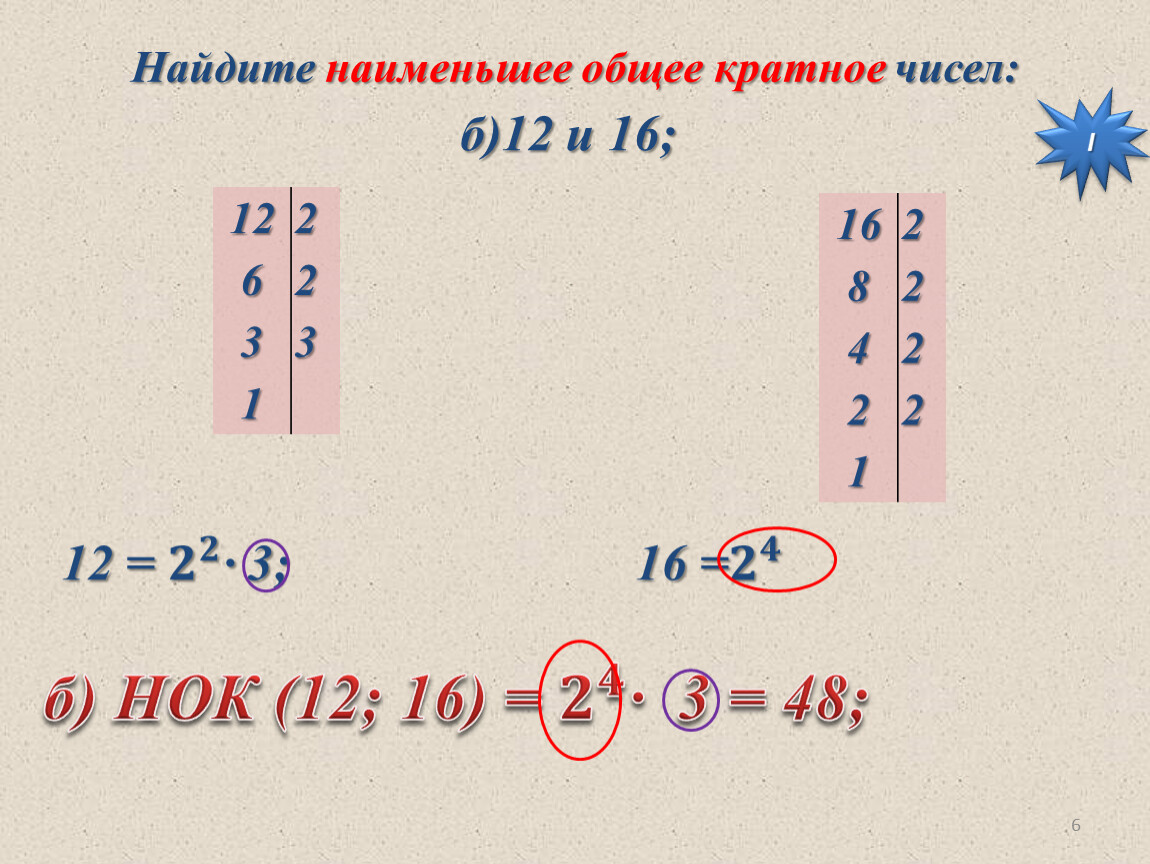 ca в ноябре 2021 года, предоставляя министру иммиграционной службы больше гибкости в отношении того, кого можно пригласить из пула Express Entry.
ca в ноябре 2021 года, предоставляя министру иммиграционной службы больше гибкости в отношении того, кого можно пригласить из пула Express Entry.
Это дает министру право определять конкретную экономическую цель и приглашать кандидатов, которые помогут достичь этой цели, исходя из таких факторов, как опыт работы, образование или знание языков.
Это позволит проводить розыгрыши, нацеленные на конкретные коды Национальной классификации занятий (NOC).
Смотреть видео
Филип Сомогивари, генеральный директор по стратегической политике и планированию IRCC, недавно принял участие в заседании Постоянного комитета по вопросам гражданства и иммиграции, чтобы ответить на вопросы о предлагаемых изменениях.
«Предлагаемые поправки будут основываться на существующей гибкости Express Entry и поддерживать восстановление экономики Канады и будущий рост, позволяя департаменту легче выбирать кандидатов, отвечающих ряду экономических потребностей и приоритетов», — сказал Сомогивари комитету.
«В частности, поправки уполномочивают министра гражданства и иммиграции приглашать иностранных граждан подавать заявления на постоянное проживание через экспресс-въезд на новом основании: право быть членами категории, которая будет поддерживать экономическую цель, определенную министром. ».
Сомогивари привел пример использования иммиграции для поддержки роста технологического сектора Канады.
«Категория кандидатов Express Entry будет создана на основе таких критериев, как наличие у них опыта работы и их отраслевая принадлежность и / или наличие у них соответствующего образования», — сказал он Комитету.
«Затем можно будет разослать приглашения лучшим кандидатам в этой категории».
Конкретная категория будет установлена министром посредством министерских инструкций, так же, как в настоящее время проводятся регулярные розыгрыши через Express Entry.
Однако действующее законодательство разрешает проводить жеребьевки только для конкретных иммиграционных программ, включая федеральную программу Skilled Work, Federal Skilled Trades, Canadian Experience Class и провинциальную программу иммиграции.
Каждый раз, когда создается определенная категория, министр должен будет определить целевую экономическую цель, сказал Шомогивари. Использование новых полномочий также должно быть включено в «Ежегодный отчет парламенту об иммиграции» .
Новый NOC вступает в силу для заявлений на получение разрешения на работу
Новый NOC вступает в силу для заявлений на получение разрешения на работу или иммиграции в Канаду
16 ноября Канада перешла на новый Национальная классификация занятий (NOC) система для иммиграционных программ разрешений на работу. В нем делается вывод, что все заявители должны будут ввести другой код NOC для классификации своей профессии. Кандидатам, подавшим заявки до 16 ноября, не нужно волноваться, так как их заявки будут рассмотрены в соответствии с предыдущим NOC 2016.
Кандидаты, имеющие свой профиль в пуле Express Entry, должны будут обновить его с помощью нового NOC 2021, так как Canadian Experience Class ( ЦИК) , Федеральная программа квалифицированных рабочих (FSWP), Федеральная программа квалифицированных профессий (FSTP) и программы PNP, связанные с экспресс-въездом, будут использовать обновленный NOC.
NOC 2021 также включает больше профессий в список востребованных вакансий и открывает двери для большего количества кандидатов в рамках этих программ. Согласно министерскому меморандуму, опубликованному в конце февраля, Express Entry будет включать водителей грузовиков и автобусов, санитаров, ассистентов преподавателей и ассистентов стоматолога.
В рамках NOC 2021 16 профессий добавлены в список востребованных, а три профессии удаленыДобавляются следующие профессии:
- Администраторы расчета заработной платы;
- Ассистенты стоматолога и зубные лаборанты;
- Помощницы медсестер, санитары и помощники по обслуживанию пациентов;
- Технические помощники аптек и фельдшеры аптек;
- Помощники учителей начальной и средней школы;
- Шерифы и судебные приставы;
- Сотрудники исправительной службы;
- Сотрудники правоохранительных органов и других регулирующих органов;
- Косметологи, электрологи и смежные профессии;
- Установщики и специалисты по обслуживанию жилых и коммерческих помещений;
- Средства борьбы с вредителями и фумигаторы;
- Прочие ремонтники и сервисные службы;
- Водители транспортных грузовиков;
- Водители автобусов, операторы метро и другие операторы общественного транспорта;
- Операторы тяжелого оборудования и;
- Сборщики самолетов и инспекторы по сборке самолетов.

Три профессии исключены из NOC 2021:
- Другие исполнители;
- Руководители программ и инструкторы по отдыху, спорту и фитнесу;
- Портные, портные, меховщики и модистки.
На веб-сайте Министерства занятости и социального развития Канады (ESDC) заявители на иммиграцию и разрешение на работу должны будут искать свою профессию в соответствии с NOC 2021.
Начиная с NOC 2021, IRCC будет использовать пятизначный код для классификации каждого профессия вместо четырехзначного числа.
Новый пятизначный NOC 2021 делит каждую профессию на шесть категорий вместо нынешних четырех, чтобы отразить уровень подготовки, образования, опыта и ответственности, или TEER, этой профессии.
В обновленном NOC категории TEER заменяют предыдущие уровни навыков.
Кроме того, новый NOC ранжирует профессиональные группы на основе пяти иерархических уровней: широкие профессиональные категории, основные профессиональные группы, подосновные профессиональные группы, второстепенные профессиональные группы и единичные профессиональные группы.
Иностранные граждане должны искать свой код NOC, используя свою должность. Важно убедиться, что основные обязанности, перечисленные в списке, совпадают с обязанностями работы после того, как будет выбрано наиболее близкое совпадение. Всякий раз, когда обязанности не совпадают, пользователям рекомендуется использовать другое название должности с более близкими обязанностями.
Новый NOC вводился поэтапно, чтобы предоставить организациям и программам достаточно времени для плавного перехода от NOC 2016 к NOC 2021.
Каждое десятилетие NOC претерпевает серьезные изменения после консультацииКод NOC является одним из наиболее важных компонентов иммиграционного заявления, поскольку это признанная на национальном уровне и стандартизированная система, используемая IRCC для оценки опыта работы заявителей.
После того, как новая система NOC будет введена в действие, во всех заявках от заявителя потребуется ввести надлежащий — и новый — пятизначный код NOC.

 )
) 2} = \sqrt{1878} ≈ 43, 34$.
2} = \sqrt{1878} ≈ 43, 34$. 2} = 5\sqrt{2}$.
2} = 5\sqrt{2}$.
 Ничего страшного, так иногда бывает, что для полного счастья, помимо скалярного произведения векторов , требуется ещё и ещё. Такая вот векторная наркомания. Может сложиться впечатление, что мы залезаем в дебри аналитической геометрии. Это не так. В данном разделе высшей математики вообще мало дров, разве что на Буратино хватит. На самом деле материал очень распространенный и простой – вряд ли сложнее, чем то же скалярное произведение , даже типовых задач поменьше будет. Главное в аналитической геометрии, как многие убедятся или уже убедились, НЕ ОШИБАТЬСЯ В ВЫЧИСЛЕНИЯХ. Повторяйте как заклинание, и будет вам счастье =)
Ничего страшного, так иногда бывает, что для полного счастья, помимо скалярного произведения векторов , требуется ещё и ещё. Такая вот векторная наркомания. Может сложиться впечатление, что мы залезаем в дебри аналитической геометрии. Это не так. В данном разделе высшей математики вообще мало дров, разве что на Буратино хватит. На самом деле материал очень распространенный и простой – вряд ли сложнее, чем то же скалярное произведение , даже типовых задач поменьше будет. Главное в аналитической геометрии, как многие убедятся или уже убедились, НЕ ОШИБАТЬСЯ В ВЫЧИСЛЕНИЯХ. Повторяйте как заклинание, и будет вам счастье =)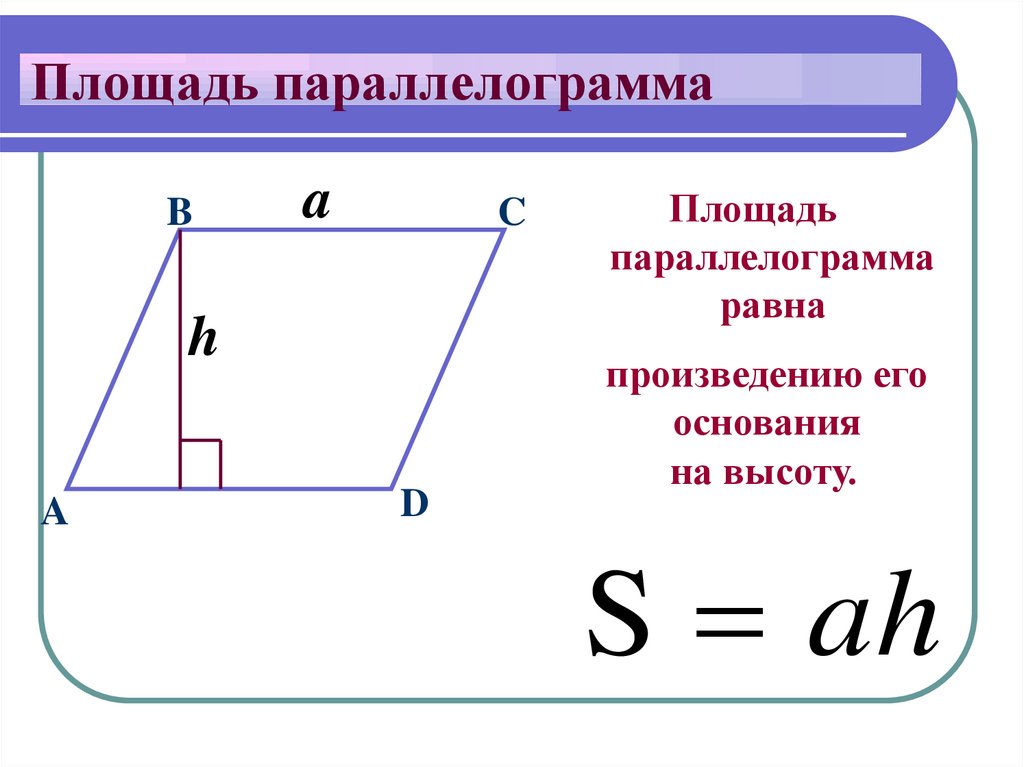 Ловко получалось. Сейчас жонглировать не придётся вообще, поскольку мы будем рассматривать только пространственные векторы , а плоские векторы с двумя координатами останутся за бортом. Почему? Такими уж родились данные действия – векторное и смешанное произведение векторов определены и работают в трёхмерном пространстве. Уже проще!
Ловко получалось. Сейчас жонглировать не придётся вообще, поскольку мы будем рассматривать только пространственные векторы , а плоские векторы с двумя координатами останутся за бортом. Почему? Такими уж родились данные действия – векторное и смешанное произведение векторов определены и работают в трёхмерном пространстве. Уже проще! Закрытый клуб. Собственно, отсюда и название операции. В различной учебной литературе обозначения тоже могут варьироваться, я буду использовать букву .
Закрытый клуб. Собственно, отсюда и название операции. В различной учебной литературе обозначения тоже могут варьироваться, я буду использовать букву . Результатом умножения векторов является ВЕКТОР , который обозначен синим цветом. Если векторы умножить в обратном порядке, то получим равный по длине и противоположный по направлению вектор (малиновый цвет). То есть, справедливо равенство .
Результатом умножения векторов является ВЕКТОР , который обозначен синим цветом. Если векторы умножить в обратном порядке, то получим равный по длине и противоположный по направлению вектор (малиновый цвет). То есть, справедливо равенство . Каков практический смысл? А смысл таков, что в задачах аналитической геометрии площадь параллелограмма часто находят через понятие векторного произведения:
Каков практический смысл? А смысл таков, что в задачах аналитической геометрии площадь параллелограмма часто находят через понятие векторного произведения: В результате большой палец – векторное произведение будет смотреть вверх. Это и есть правоориентированный базис (на рисунке именно он). Теперь поменяйте векторы (указательный и средний пальцы ) местами, в результате большой палец развернётся, и векторное произведение уже будет смотреть вниз. Это тоже правоориентированный базис. Возможно, у вас возник вопрос: а какой базис имеет левую ориентацию? «Присвойте» тем же пальцам левой руки векторы , и полУчите левый базис и левую ориентацию пространства (в этом случае большой палец расположится по направлению нижнего вектора) . Образно говоря, данные базисы «закручивают» или ориентируют пространство в разные стороны. И это понятие не следует считать чем-то надуманным или абстрактным – так, например, ориентацию пространства меняет самое обычное зеркало, и если «вытащить отражённый объект из зазеркалья», то его в общем случае не удастся совместить с «оригиналом». Кстати, поднесите к зеркалу три пальца и проанализируйте отражение;-)
В результате большой палец – векторное произведение будет смотреть вверх. Это и есть правоориентированный базис (на рисунке именно он). Теперь поменяйте векторы (указательный и средний пальцы ) местами, в результате большой палец развернётся, и векторное произведение уже будет смотреть вниз. Это тоже правоориентированный базис. Возможно, у вас возник вопрос: а какой базис имеет левую ориентацию? «Присвойте» тем же пальцам левой руки векторы , и полУчите левый базис и левую ориентацию пространства (в этом случае большой палец расположится по направлению нижнего вектора) . Образно говоря, данные базисы «закручивают» или ориентируют пространство в разные стороны. И это понятие не следует считать чем-то надуманным или абстрактным – так, например, ориентацию пространства меняет самое обычное зеркало, и если «вытащить отражённый объект из зазеркалья», то его в общем случае не удастся совместить с «оригиналом». Кстати, поднесите к зеркалу три пальца и проанализируйте отражение;-) Если векторы коллинеарны, то их можно расположить на одной прямой и наш параллелограмм тоже «складывается» в одну прямую. Площадь такого, как говорят математики, вырожденного параллелограмма равна нулю. Это же следует и из формулы – синус нуля или 180-ти градусов равен нулю, а значит, и площадь нулевая
Если векторы коллинеарны, то их можно расположить на одной прямой и наш параллелограмм тоже «складывается» в одну прямую. Площадь такого, как говорят математики, вырожденного параллелограмма равна нулю. Это же следует и из формулы – синус нуля или 180-ти градусов равен нулю, а значит, и площадь нулевая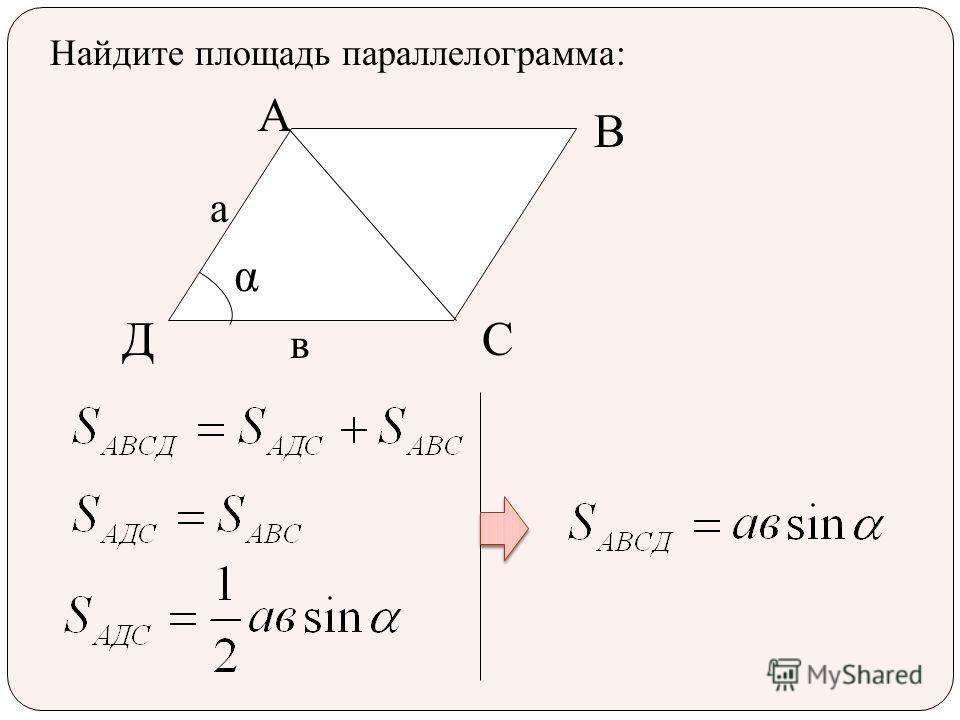 Потому что оформление решений будет отличаться!
Потому что оформление решений будет отличаться!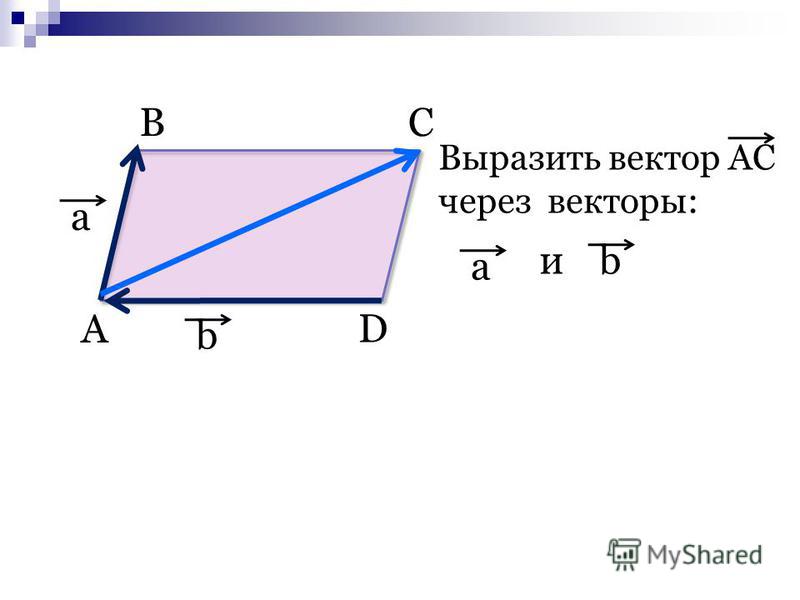 Этот момент всегда нужно держать на контроле, решая любую задачу по высшей математике, да и по другим предметам тоже.
Этот момент всегда нужно держать на контроле, решая любую задачу по высшей математике, да и по другим предметам тоже. Поэтому пусть будет.
Поэтому пусть будет.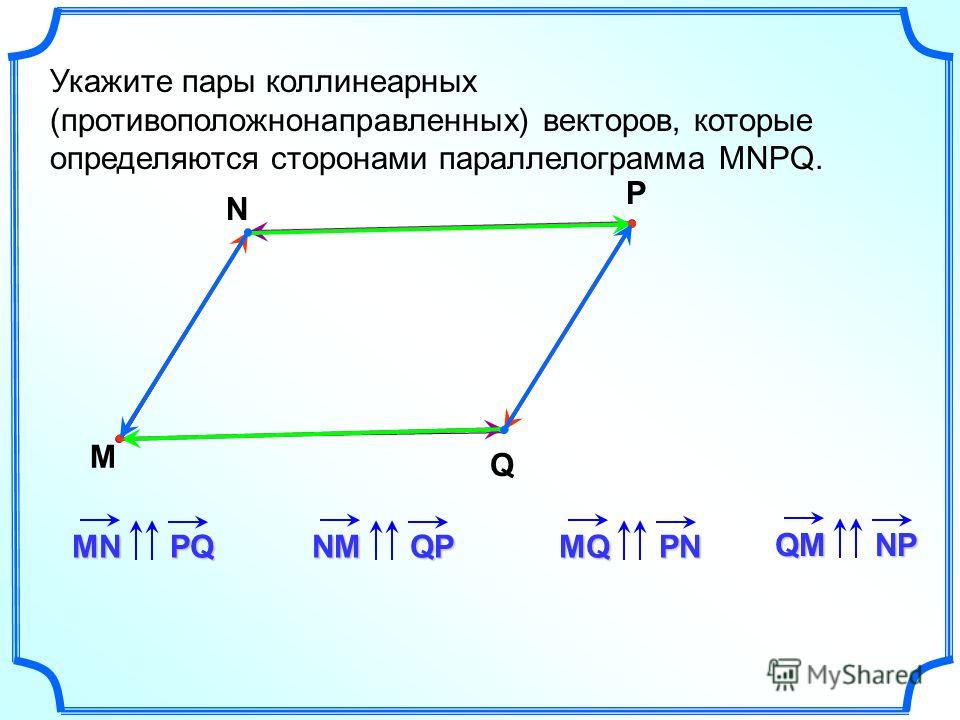 Загвоздка состоит в том, что векторы «цэ» и «дэ» сами представлены в виде сумм векторов. Алгоритм здесь стандартен и чем-то напоминает примеры № 3 и 4 урока Скалярное произведение векторов . Решение для ясности разобьём на три этапа:
Загвоздка состоит в том, что векторы «цэ» и «дэ» сами представлены в виде сумм векторов. Алгоритм здесь стандартен и чем-то напоминает примеры № 3 и 4 урока Скалярное произведение векторов . Решение для ясности разобьём на три этапа: Данное действие напоминает Пример 3:
Данное действие напоминает Пример 3: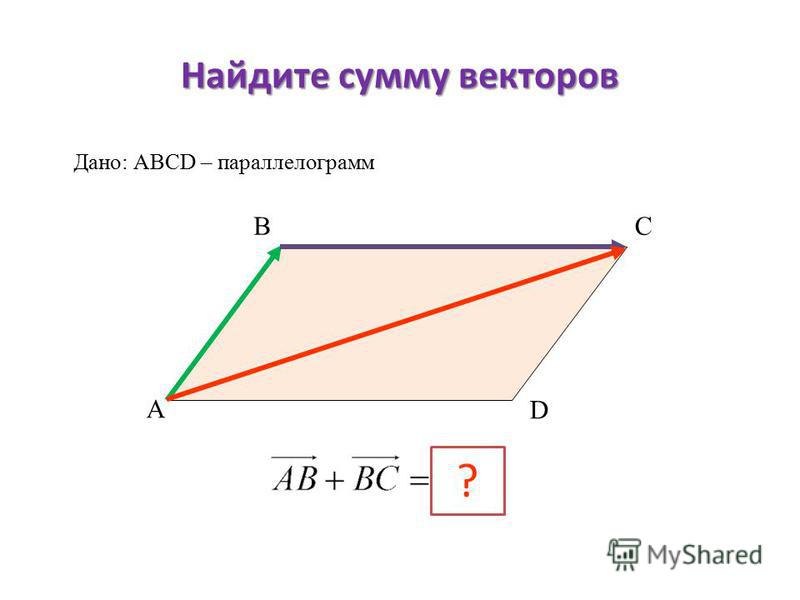
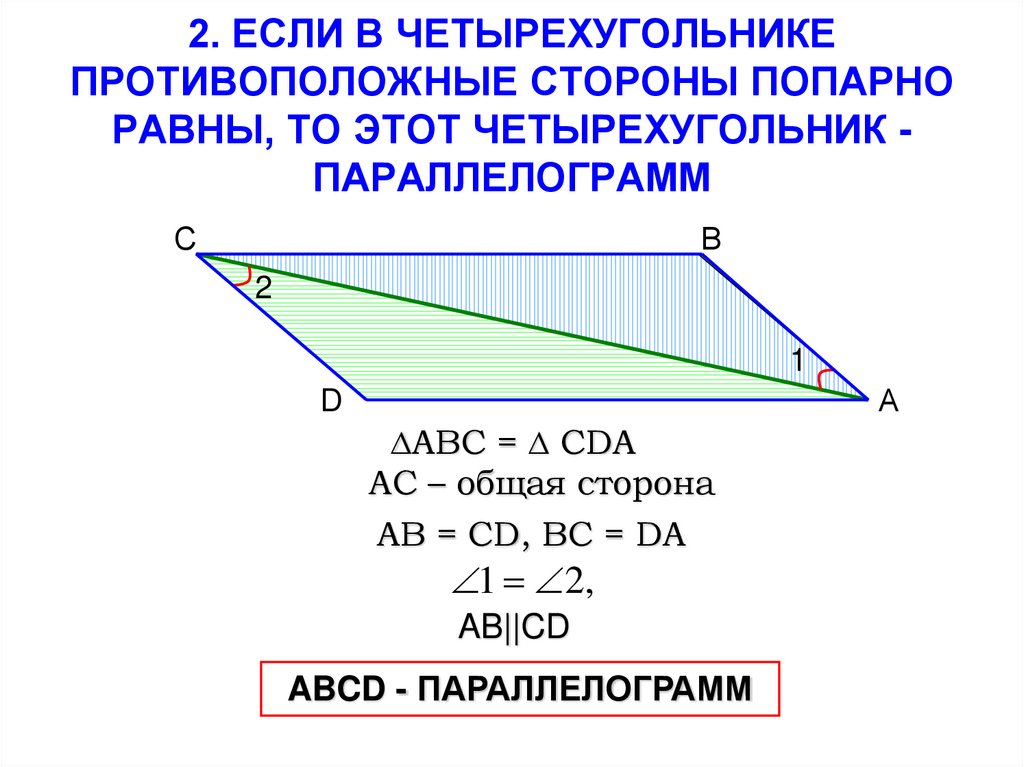
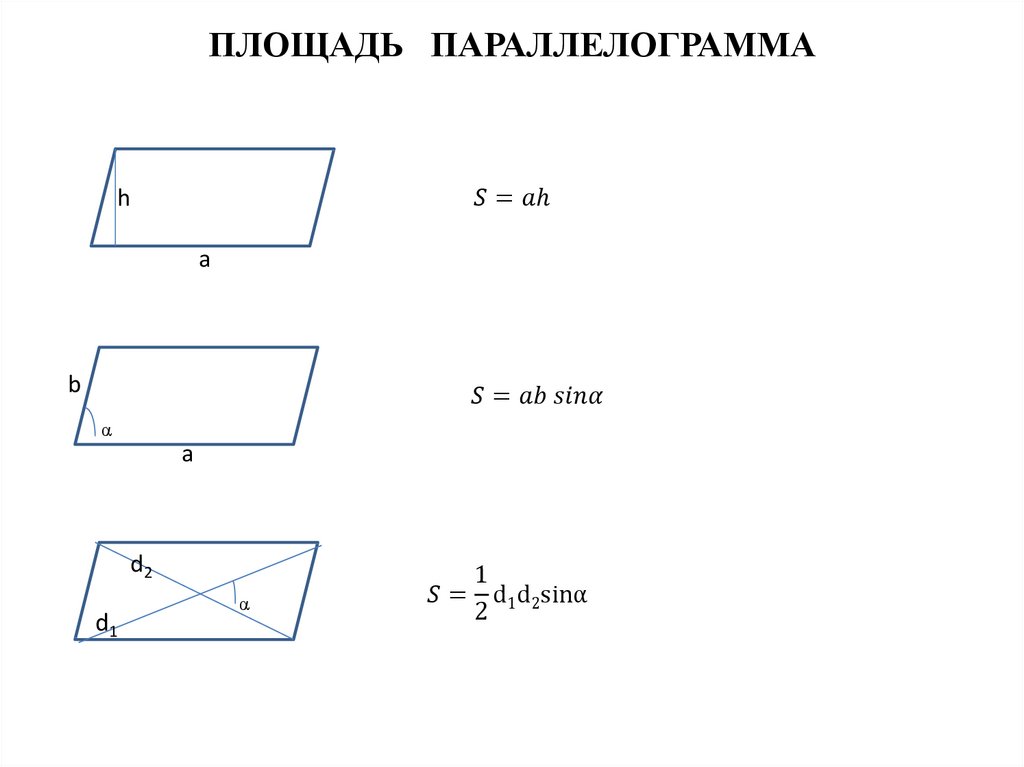 — вопрос №2179254 — Учеба и наука
— вопрос №2179254 — Учеба и наука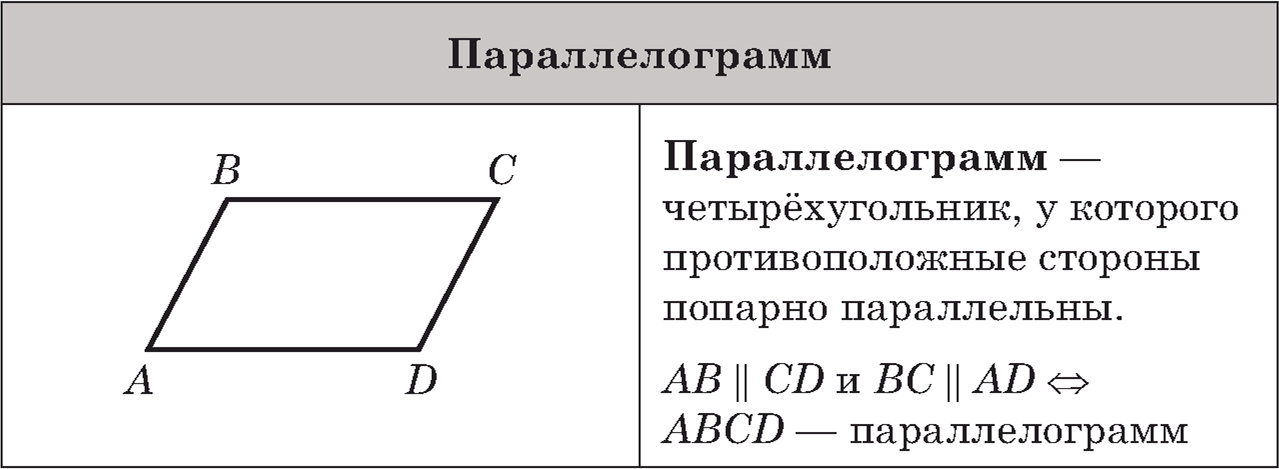 10.16
10.16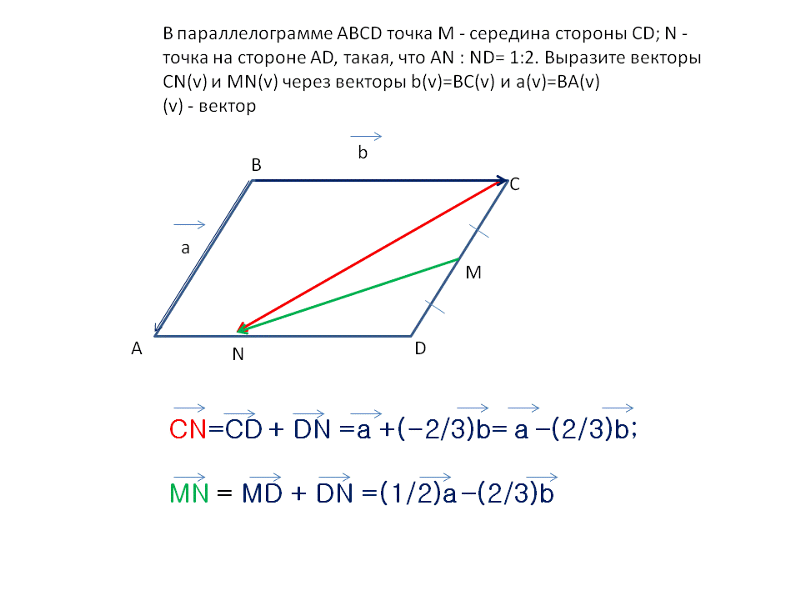


 В основаниях лежат квадраты со сторонами 4 см и 8 см. Найдите:
A) 1/2AC — BO + BB1 + 2B1O1
Б) [OD + DD1 — O1D1]
В) OO1 *OB1
(вектора)
В основаниях лежат квадраты со сторонами 4 см и 8 см. Найдите:
A) 1/2AC — BO + BB1 + 2B1O1
Б) [OD + DD1 — O1D1]
В) OO1 *OB1
(вектора)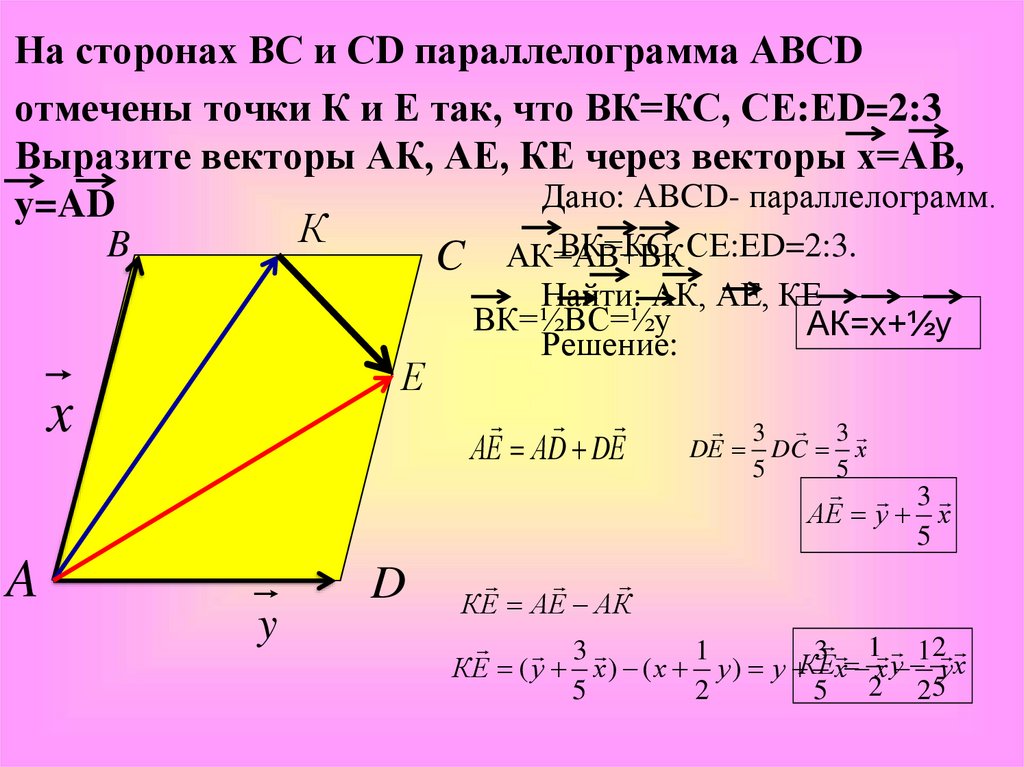 Найдите площадь 𝐴𝐵𝐶𝐷. Дайте ответ с точностью до одного десятичного знака.
Найдите площадь 𝐴𝐵𝐶𝐷. Дайте ответ с точностью до одного десятичного знака. )
) )
) )
) )
) )
) )
)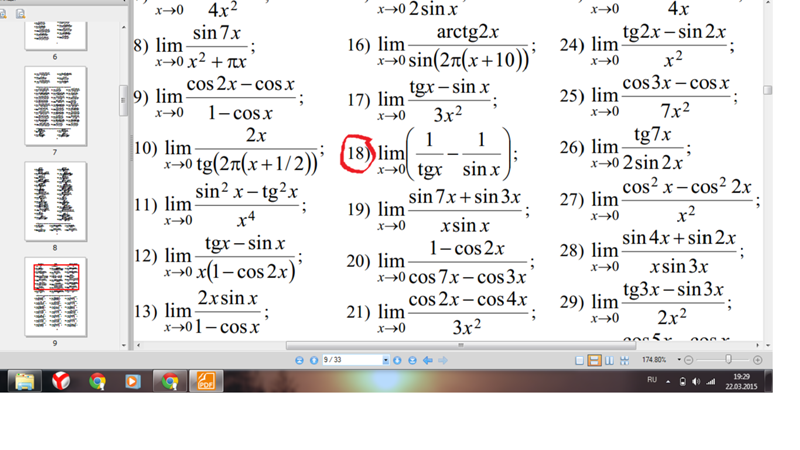 )
) )
)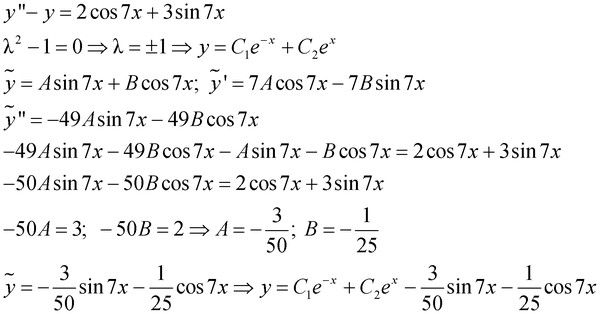

 00
00 5G Ethernet ports
5G Ethernet ports 5A power adapter
5A power adapter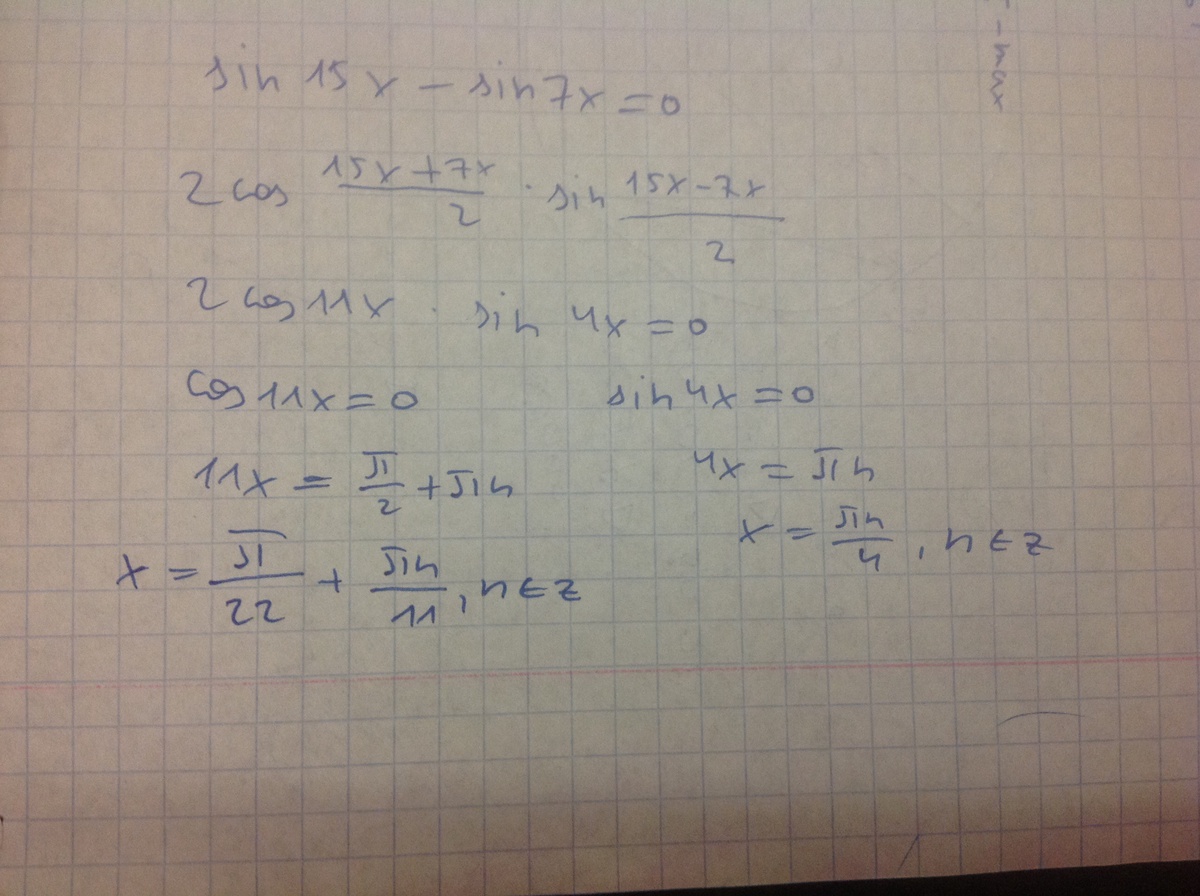 3
3 9
9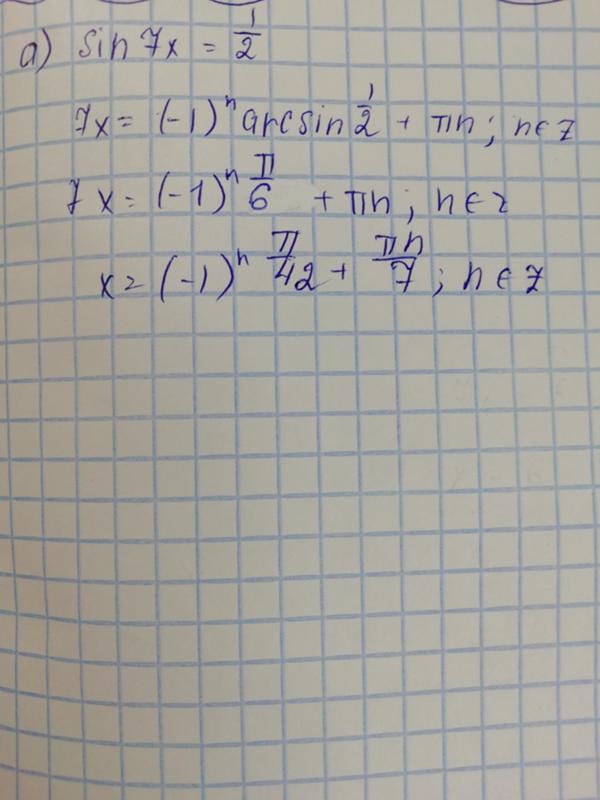 No separate purchase is necessary and the product is ready to use. The device includes free software updates for the life of the product or a minimum of 5 years starting from date of purchase..
No separate purchase is necessary and the product is ready to use. The device includes free software updates for the life of the product or a minimum of 5 years starting from date of purchase.. 




 (237). Читается, как «5 в двести тридцать седьмой степени».
(237). Читается, как «5 в двести тридцать седьмой степени».


 Чтобы её объяснить, ещё раз приведём правило по делению степеней с равными основаниями.
Чтобы её объяснить, ещё раз приведём правило по делению степеней с равными основаниями.
 е. помимо целых и отрицательных значений, может иметь ещё и дробные. Записывается это в виде am/n. Из определения дробной степени известно, что am/n можно записать в виде n√am. n не должно быть равно нулю, ведь на ноль делить нельзя.
е. помимо целых и отрицательных значений, может иметь ещё и дробные. Записывается это в виде am/n. Из определения дробной степени известно, что am/n можно записать в виде n√am. n не должно быть равно нулю, ведь на ноль делить нельзя. Основание может быть и многозначным числом, в частности, 128-2/7 тоже степень с рациональным.
Основание может быть и многозначным числом, в частности, 128-2/7 тоже степень с рациональным. Это делает запись более наглядной и позволяет избежать многих ошибок.
Это делает запись более наглядной и позволяет избежать многих ошибок.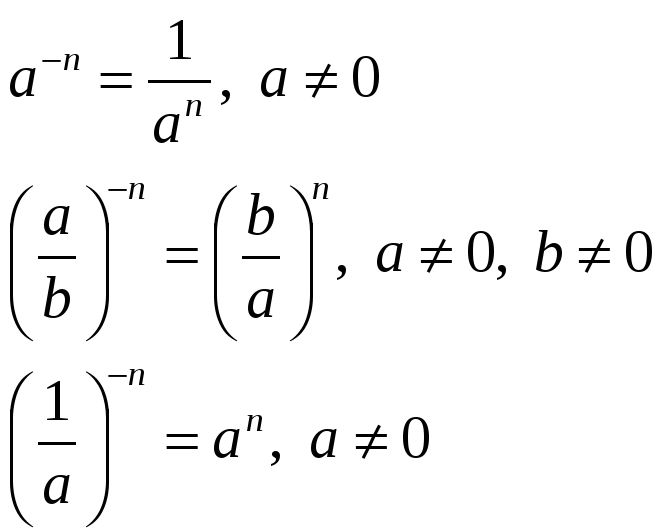 Они с недостатком либо с избытком приближаются к степени иррациональным n.
Они с недостатком либо с избытком приближаются к степени иррациональным n. В частности, сложение показателей при перемножении, сравнение иррациональных степеней происходят аналогичным образом. Нужно только иметь в виду, что при бесконечности и апериодичности иррациональной дроби вы имеете дело с приближёнными с той или иной точностью значениями. Впрочем, в зависимости от поставленной задачи, нужной точности достичь можно в любом случае. Очень осторожны будьте с приближениями. У новичков здесь очень часто случаются ошибки. После некоторого опыта и практики действия совершаются автоматически. Старайтесь на первых порах порешать как можно больше примеров. Пусть они кажутся вам однотипным, но навык отточить и закрепить позволяют.
В частности, сложение показателей при перемножении, сравнение иррациональных степеней происходят аналогичным образом. Нужно только иметь в виду, что при бесконечности и апериодичности иррациональной дроби вы имеете дело с приближёнными с той или иной точностью значениями. Впрочем, в зависимости от поставленной задачи, нужной точности достичь можно в любом случае. Очень осторожны будьте с приближениями. У новичков здесь очень часто случаются ошибки. После некоторого опыта и практики действия совершаются автоматически. Старайтесь на первых порах порешать как можно больше примеров. Пусть они кажутся вам однотипным, но навык отточить и закрепить позволяют. Причем степень числа 10 может быть и положительной, и отрицательной.
Причем степень числа 10 может быть и положительной, и отрицательной.
 Это уже знакомо с начальных классов. Какова положительная степень числа 10 – столько ноликов и приписываем к единичке. Умножение и деление таких чисел не вызывает труда.
Это уже знакомо с начальных классов. Какова положительная степень числа 10 – столько ноликов и приписываем к единичке. Умножение и деление таких чисел не вызывает труда.


 Почти всегда это значительно удобнее!
Почти всегда это значительно удобнее!




 \end{align}$
\end{align}$
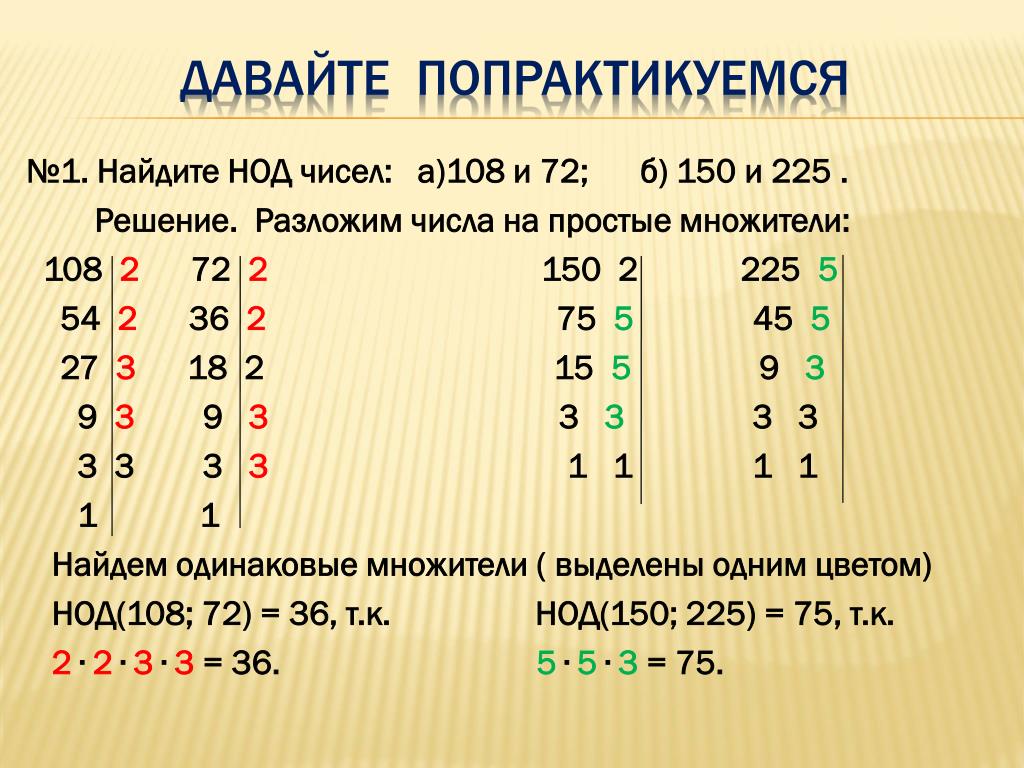 {1}}$
{1}}$ \end{align}$
\end{align}$ Пусть $\,a$, $\,b$, $\,c$ и $\,d$ — натуральные числа (${b \ne 0}$, ${\,d \ne 0}$). В качестве общего знаменателя двух дробей $\frac{\,a\,}{b}$ и $\frac{\,c\,}{d}$ удобно брать НОК$(b, d)$ — наименьшее общее кратное знаменателей $b$ и $d$. Чтобы получить НОК$(b, d)$, мы раскладываем числа $b$ и $d$ на простые множители, причем общие множители подчеркиваем. Тогда
Пусть $\,a$, $\,b$, $\,c$ и $\,d$ — натуральные числа (${b \ne 0}$, ${\,d \ne 0}$). В качестве общего знаменателя двух дробей $\frac{\,a\,}{b}$ и $\frac{\,c\,}{d}$ удобно брать НОК$(b, d)$ — наименьшее общее кратное знаменателей $b$ и $d$. Чтобы получить НОК$(b, d)$, мы раскладываем числа $b$ и $d$ на простые множители, причем общие множители подчеркиваем. Тогда Это будет полезно, когда мы будем складывать и вычитать дроби с разными знаменателями.
Это будет полезно, когда мы будем складывать и вычитать дроби с разными знаменателями.
 Это общее кратное, но не наименьшее общее кратное.
Это общее кратное, но не наименьшее общее кратное.

 Упражнение 2.4.
Упражнение 2.4. Упражнение 2.11.
Упражнение 2.11. Игра с числами
>
Игра с числами. Упражнение 2.2.
>
Вопрос 4
Игра с числами
>
Игра с числами. Упражнение 2.2.
>
Вопрос 4


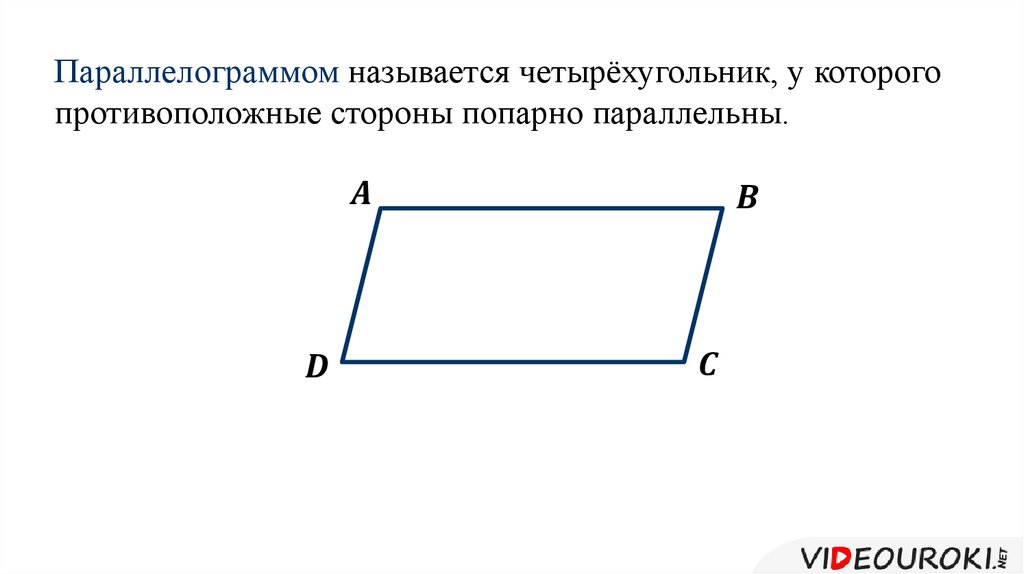 Ромб представляет собой параллелограмм, все четыре стороны которого имеют одинаковую длину; прямоугольник является параллелограммом, смежные стороны которого перпендикулярны ; а квадрат — это параллелограмм, смежные стороны которого перпендикулярны и равны по длине.
Ромб представляет собой параллелограмм, все четыре стороны которого имеют одинаковую длину; прямоугольник является параллелограммом, смежные стороны которого перпендикулярны ; а квадрат — это параллелограмм, смежные стороны которого перпендикулярны и равны по длине. Оба противоположных угла параллелограмма также равны. Его площадь равна произведению одной стороны на перпендикулярное расстояние от противоположной стороны. Параллелограмм, у которого все четыре стороны равны, является ромбом.
Оба противоположных угла параллелограмма также равны. Его площадь равна произведению одной стороны на перпендикулярное расстояние от противоположной стороны. Параллелограмм, у которого все четыре стороны равны, является ромбом. 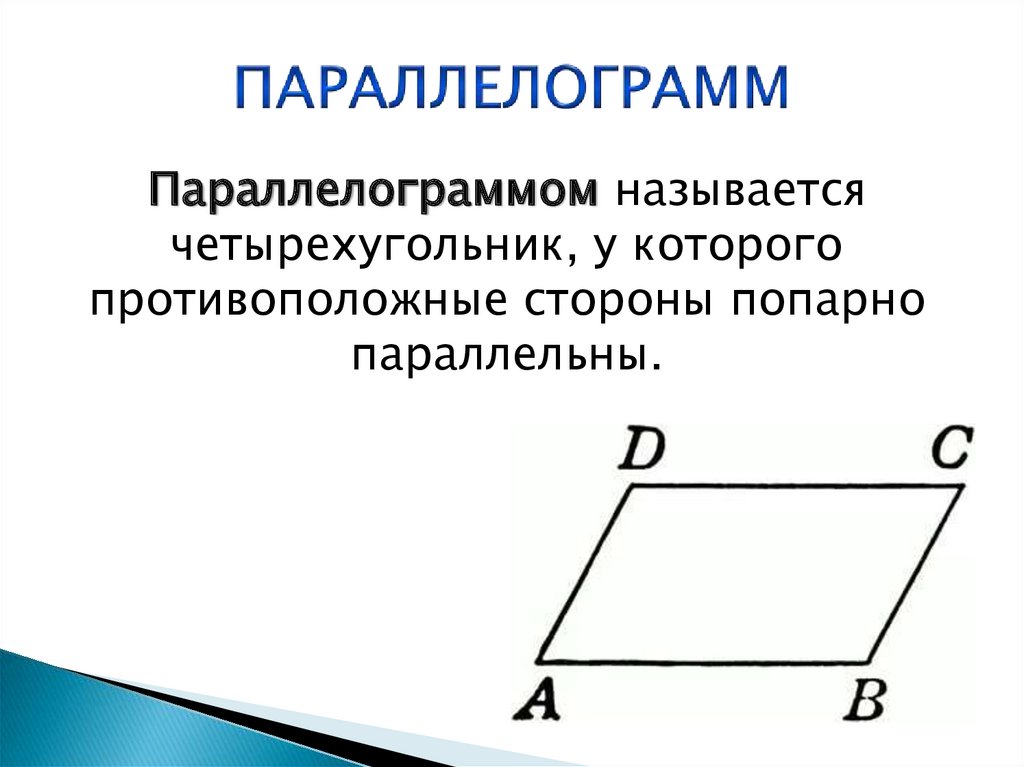
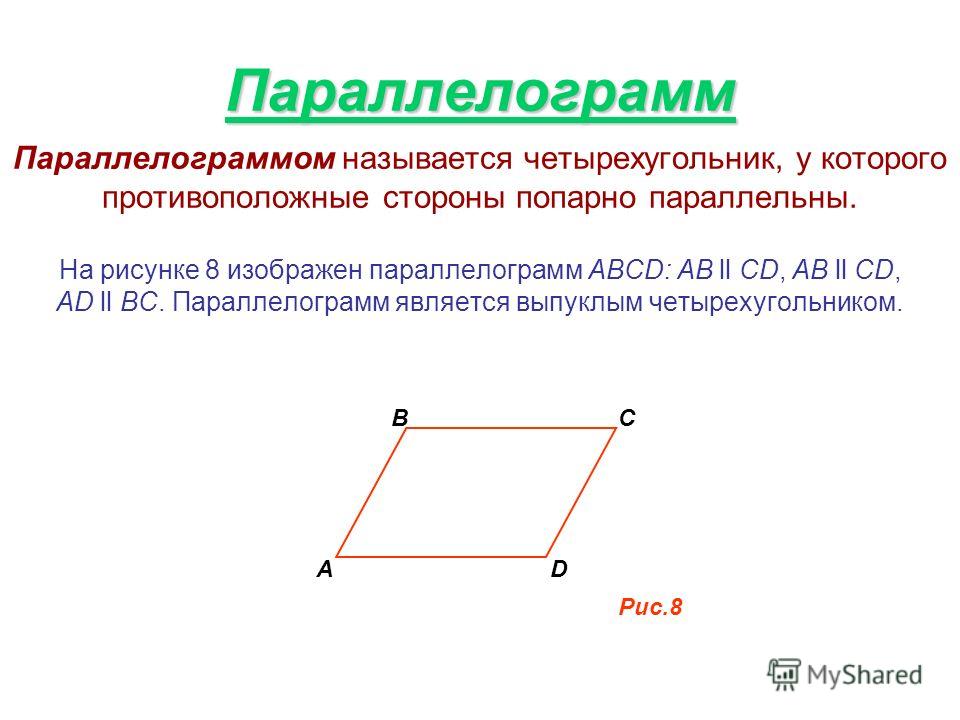 Он имеет плоскую форму и четыре стороны; при этом обращенные стороны параллельны друг другу (см. рисунок ниже).
Он имеет плоскую форму и четыре стороны; при этом обращенные стороны параллельны друг другу (см. рисунок ниже).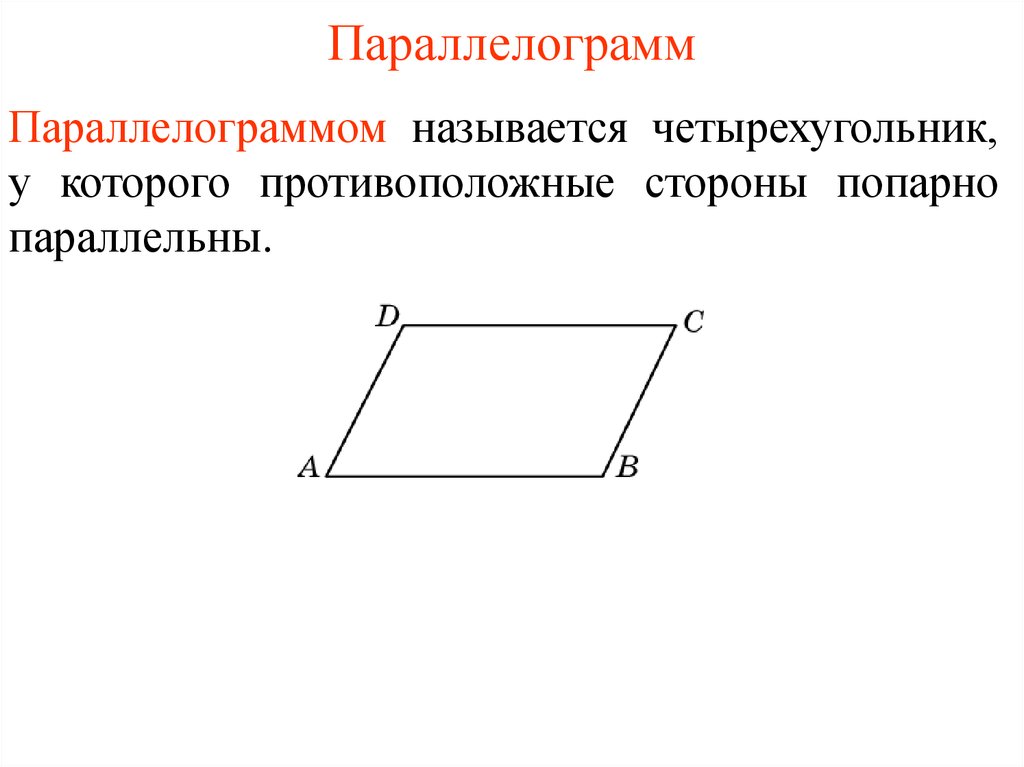
 О нем и будет первая часть теорий.
О нем и будет первая часть теорий.

 2.Морфеус знал о грядущем предательстве
2.Морфеус знал о грядущем предательстве

 Даже если бы и можно, это было рискованно, поскольку кто угодно мог увидеть его в кресле и прочитать на мониторе что происходит.
Даже если бы и можно, это было рискованно, поскольку кто угодно мог увидеть его в кресле и прочитать на мониторе что происходит. Возможно именно за написанием этой программы Нео и застал Сайфера. Если вы согласны, что Морфеус знал о грядущем предательстве, то можно даже предположить, что он сделал все, чтоб план Сайфера удался.
Возможно именно за написанием этой программы Нео и застал Сайфера. Если вы согласны, что Морфеус знал о грядущем предательстве, то можно даже предположить, что он сделал все, чтоб план Сайфера удался. Все это длилось до тех пор пока один из роботов не убил человека. Это подстегнуло ненависть к машинам и по всему миру прокатилась волна насилия. Тогда машины ушли и построили свой город под названием 0,1 (можно оценить всю скромность машин). Далее — акции компаний 0.1 резко росли и их экономика процветала, сильное производство уничтожило производство людей, вызвало безработицу, что привело к вооруженному конфликту. Машины сильно превосходили людей и тогда они(люди) решились на отчаянный шаг: навсегда скрыть солнце за тучами. Машины захватили людей и начали использовать их как источник энергии. Через какое-то время, людей начали выращивать.
Все это длилось до тех пор пока один из роботов не убил человека. Это подстегнуло ненависть к машинам и по всему миру прокатилась волна насилия. Тогда машины ушли и построили свой город под названием 0,1 (можно оценить всю скромность машин). Далее — акции компаний 0.1 резко росли и их экономика процветала, сильное производство уничтожило производство людей, вызвало безработицу, что привело к вооруженному конфликту. Машины сильно превосходили людей и тогда они(люди) решились на отчаянный шаг: навсегда скрыть солнце за тучами. Машины захватили людей и начали использовать их как источник энергии. Через какое-то время, людей начали выращивать. Какой противник поступал так с побеждённым врагом? И не просто врагом, давайте называть вещи своими именами, закрыть небо — это была попытка геноцида.
Какой противник поступал так с побеждённым врагом? И не просто врагом, давайте называть вещи своими именами, закрыть небо — это была попытка геноцида. Потому, чем больше Смитов, тем все хуже. В момент, когда агенты наваливаются на Нео, мы снова видим приличную картинку. Видимо, из-за того, что объекты перестали двигаться.
Потому, чем больше Смитов, тем все хуже. В момент, когда агенты наваливаются на Нео, мы снова видим приличную картинку. Видимо, из-за того, что объекты перестали двигаться.  Зачем? Согласно архитектору это нужно было для того, чтоб выявлять людей, которые не примут программу. Теперь представьте эти две дюжины людей с атрофированными мышцами, которые каким-то образом выбрались из города машин и добрались до безопасного места, а затем построили город и.т.д. Довольно трудно себе такое представить. Зион, как и корабли и вся технология не была создана людьми сбежавшими из первой матрицы.
Зачем? Согласно архитектору это нужно было для того, чтоб выявлять людей, которые не примут программу. Теперь представьте эти две дюжины людей с атрофированными мышцами, которые каким-то образом выбрались из города машин и добрались до безопасного места, а затем построили город и.т.д. Довольно трудно себе такое представить. Зион, как и корабли и вся технология не была создана людьми сбежавшими из первой матрицы.


 Они должны были спасти человечество. Мне кажется, именно этим они и были заняты.
Они должны были спасти человечество. Мне кажется, именно этим они и были заняты. Пришлось искать другой выход.
Пришлось искать другой выход. Когда же последний предлагает мир, злобный бог-машина тут же подключает его к матрице. Позже, если вы посмотрите сцену прямо перед тем, как все Смиты будут уничтожены, вы заметите, что импульс(или что бы это ни было) запустивший цепную реакцию шел по проводам к Нео, а не от него. Если бы Нео каким-то образом уничтожил Смита — сигнал должен был идти от Нео к серверу, а не наоборот. Получается именно машины в итоге уничтожили Смита и Нео, по большому счету, не был для этого нужен.
Когда же последний предлагает мир, злобный бог-машина тут же подключает его к матрице. Позже, если вы посмотрите сцену прямо перед тем, как все Смиты будут уничтожены, вы заметите, что импульс(или что бы это ни было) запустивший цепную реакцию шел по проводам к Нео, а не от него. Если бы Нео каким-то образом уничтожил Смита — сигнал должен был идти от Нео к серверу, а не наоборот. Получается именно машины в итоге уничтожили Смита и Нео, по большому счету, не был для этого нужен. Название корабля, прозвища героев, название города, общий сюжет, все это могло быть тем или иным способом, навеяно машинами, для того, чтоб люди подсознательно чувствовали схожесть.
Название корабля, прозвища героев, название города, общий сюжет, все это могло быть тем или иным способом, навеяно машинами, для того, чтоб люди подсознательно чувствовали схожесть.
 Мне кажется, на то две причины. В конце 20-го столетия, были две темы, которые в том или ином виде волновали весь мир.
Мне кажется, на то две причины. В конце 20-го столетия, были две темы, которые в том или ином виде волновали весь мир.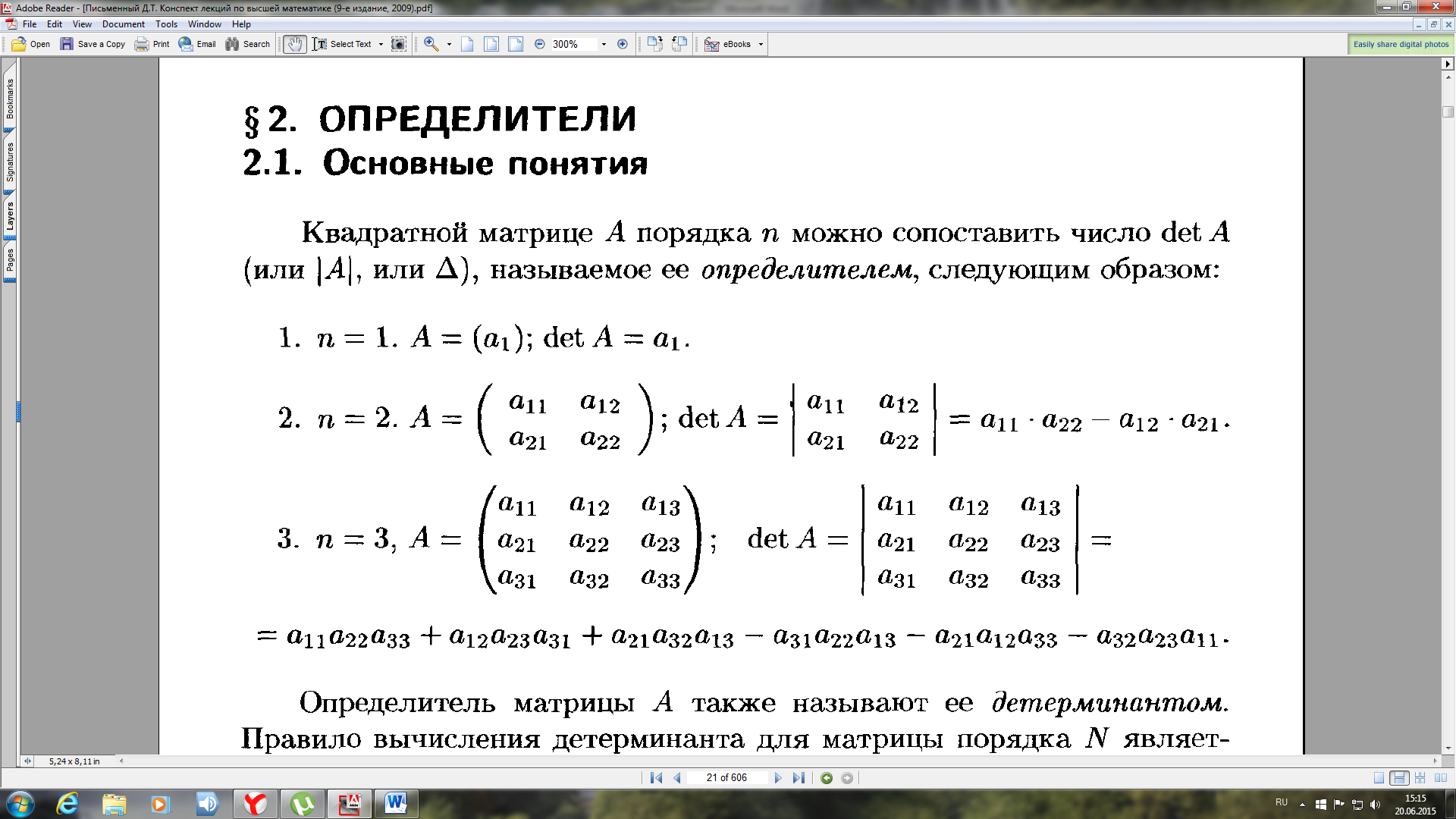 {\frac{{n\left( {n + 1} \right)}}{2}}},
$$
{\frac{{n\left( {n + 1} \right)}}{2}}},
$$
 Как вы знаете, если вы прошли модули OmniStudio, OmniScript — это инструмент для разработки и создания управляемых бизнес-процессов для пользователей, а процедуры интеграции OmniStudio — это инструмент, который извлекает, сохраняет и манипулирует данными за кулисами. Вы можете вызвать матрицу расчета из любого инструмента с помощью действия матрицы.
Как вы знаете, если вы прошли модули OmniStudio, OmniScript — это инструмент для разработки и создания управляемых бизнес-процессов для пользователей, а процедуры интеграции OmniStudio — это инструмент, который извлекает, сохраняет и манипулирует данными за кулисами. Вы можете вызвать матрицу расчета из любого инструмента с помощью действия матрицы. Давайте посмотрим, как он был создан и что вы найдете, когда просмотрите его.
Давайте посмотрим, как он был создан и что вы найдете, когда просмотрите его.


 Появится диалоговое окно «Входной файл классификации».
Появится диалоговое окно «Входной файл классификации». Два имени класса снова появляются в списках в верхней части диалогового окна.
Два имени класса снова появляются в списках в верхней части диалогового окна. Последняя полоса изображения ошибки показывает все неправильно классифицированные пиксели для всех объединенных классов .
Последняя полоса изображения ошибки показывает все неправильно классифицированные пиксели для всех объединенных классов . Появится диалоговое окно «Входной файл классификации».
Появится диалоговое окно «Входной файл классификации».
 Ошибки пропуска представляют собой ложноотрицательные результаты.
Ошибки пропуска представляют собой ложноотрицательные результаты.



 Найти соответствующий положительный угол
Найти соответствующий положительный угол  {\circ}$
{\circ}$  Найти количество кругов пройденных объектом при данных углах
Найти количество кругов пройденных объектом при данных углах  Например, очень высокая кровля в местности с сильными ветрами будет постоянно подвергаться большим нагрузкам и в итоге с большой долей вероятности будет разрушена. Следовательно, чтобы этого избежать, иногда стоит отдать предпочтение не слишком эффектной, но устойчивой низкой крыше. Таких примеров можно привести множество, но рассмотрим сами факторы, влияющие на высоту кровли. От чего она может зависеть?
Например, очень высокая кровля в местности с сильными ветрами будет постоянно подвергаться большим нагрузкам и в итоге с большой долей вероятности будет разрушена. Следовательно, чтобы этого избежать, иногда стоит отдать предпочтение не слишком эффектной, но устойчивой низкой крыше. Таких примеров можно привести множество, но рассмотрим сами факторы, влияющие на высоту кровли. От чего она может зависеть?
 В мансарде иногда бывает сложно использовать некоторые участки пространства, где располагается самая низкая точка потолочной обшивки. Впрочем, такие места как раз можно отвести под хранение вещей, сделав там встроенные шкафчики и тумбы. Другое дело – зона свободного передвижения, ее площадь напрямую зависит от высоты конька, а значит – и угла крыши.
В мансарде иногда бывает сложно использовать некоторые участки пространства, где располагается самая низкая точка потолочной обшивки. Впрочем, такие места как раз можно отвести под хранение вещей, сделав там встроенные шкафчики и тумбы. Другое дело – зона свободного передвижения, ее площадь напрямую зависит от высоты конька, а значит – и угла крыши.
 Возьмем ту же ширину фронтона 9.5 метров, половина его будет соответствовать 4.75, на это значение делим высоту конька, которую сочтем комфортной, например, 4 метра. В итоге получаем 4/4.75 = 0.84, заглядываем в таблицу Брадиса, ищем соответствующую позицию в таблице тангенсов и видим, что нам нужен угол 40°.
Возьмем ту же ширину фронтона 9.5 метров, половина его будет соответствовать 4.75, на это значение делим высоту конька, которую сочтем комфортной, например, 4 метра. В итоге получаем 4/4.75 = 0.84, заглядываем в таблицу Брадиса, ищем соответствующую позицию в таблице тангенсов и видим, что нам нужен угол 40°. Если же кровля делается трехслойной, она должна быть еще более пологой, около 5 градусов, при этом требуется дополнительная обрешетка для повышения прочности на случай увеличения временной нагрузки (снег, дождь). Но есть и исключение – мембранное покрытие, которое можно использовать при любом наклоне крыши.
Если же кровля делается трехслойной, она должна быть еще более пологой, около 5 градусов, при этом требуется дополнительная обрешетка для повышения прочности на случай увеличения временной нагрузки (снег, дождь). Но есть и исключение – мембранное покрытие, которое можно использовать при любом наклоне крыши.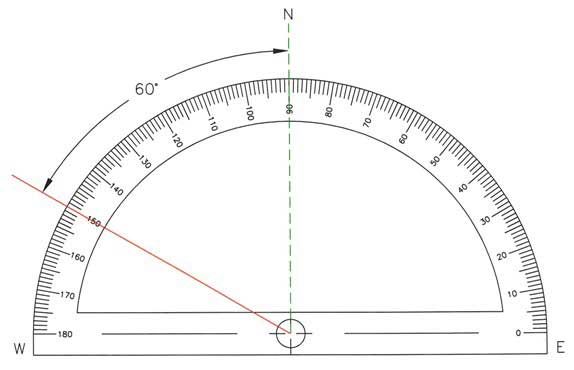 В большую сторону крутизна может увеличиваться без ограничений, однако с учетом того, что большая площадь кровли имеет солидную массу. Также не следует забывать про ветровую нагрузку и высокую парусность крыш с углом, близким к 45 градусам. Оптимальный наклон – порядка 27-30 градусов.
В большую сторону крутизна может увеличиваться без ограничений, однако с учетом того, что большая площадь кровли имеет солидную массу. Также не следует забывать про ветровую нагрузку и высокую парусность крыш с углом, близким к 45 градусам. Оптимальный наклон – порядка 27-30 градусов. В этой статье мы рассмотрим, как построить и понять угол 35 градусов, включая его свойства, приложения и конструкции.
В этой статье мы рассмотрим, как построить и понять угол 35 градусов, включая его свойства, приложения и конструкции. Вот шаги:
Вот шаги:
 Например, вы можете разделить прямой угол (90 градусов) на четыре равные части, каждая из которых равна 22,5 градуса.
Например, вы можете разделить прямой угол (90 градусов) на четыре равные части, каждая из которых равна 22,5 градуса.
 Они размножаются посредством процесса, называемого опылением, при котором пыльца мужского растения…
Они размножаются посредством процесса, называемого опылением, при котором пыльца мужского растения…

 Синий цвет вокруг радара вызван помехами от земли, грязью, насекомыми и т. д. в VCP 32. Режим
Синий цвет вокруг радара вызван помехами от земли, грязью, насекомыми и т. д. в VCP 32. Режим

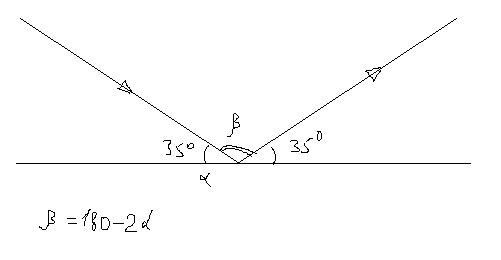
 В то время как вертикальное разрешение отсутствует, он сканирует нижние уровни несколько раз и в разных ПРФ -е. Результатом является значительное улучшение данных о скорости. Полное сканирование тома происходит примерно каждые шесть минут.
В то время как вертикальное разрешение отсутствует, он сканирует нижние уровни несколько раз и в разных ПРФ -е. Результатом является значительное улучшение данных о скорости. Полное сканирование тома происходит примерно каждые шесть минут.

 ..}
..}
 ..}
..}

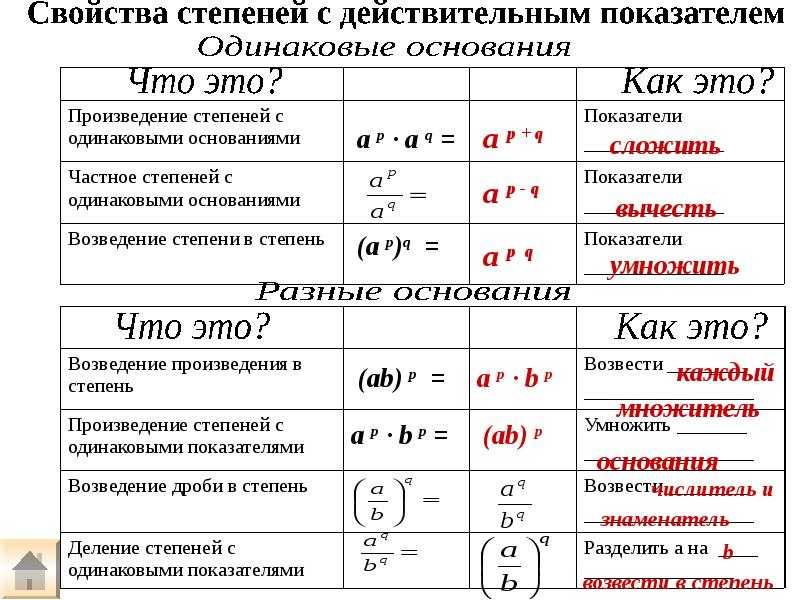

 Онлайн калькулятор расстояния между точками
Онлайн калькулятор расстояния между точками Найди правильный ответ.
Найди правильный ответ. Для плоского, цилиндрического и сферического конденсаторов
Для плоского, цилиндрического и сферического конденсаторов Показатели помогают вам выполнять вычисления с вашими данными, когда вы взаимодействуете со своими отчетами. Это руководство поможет вам понять меры и создать собственные базовые меры в Power BI Desktop.
Показатели помогают вам выполнять вычисления с вашими данными, когда вы взаимодействуете со своими отчетами. Это руководство поможет вам понять меры и создать собственные базовые меры в Power BI Desktop.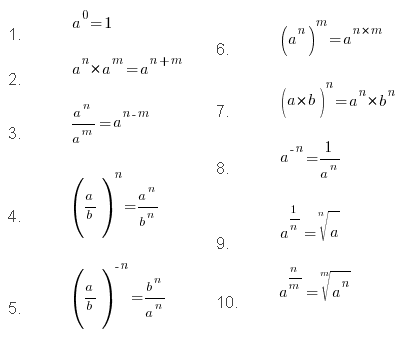 Вместо того, чтобы отображать таблицу со многими значениями (2 000 000 строк для SalesAmount ), Power BI Desktop автоматически создает и вычисляет меру для агрегирования данных, если обнаруживает числовой тип данных. Сумма — это агрегация по умолчанию для числового типа данных, но вы можете легко применять другие агрегации, такие как среднее или количество. Понимание агрегации имеет основополагающее значение для понимания мер, поскольку каждая мера выполняет определенный тип агрегации.
Вместо того, чтобы отображать таблицу со многими значениями (2 000 000 строк для SalesAmount ), Power BI Desktop автоматически создает и вычисляет меру для агрегирования данных, если обнаруживает числовой тип данных. Сумма — это агрегация по умолчанию для числового типа данных, но вы можете легко применять другие агрегации, такие как среднее или количество. Понимание агрегации имеет основополагающее значение для понимания мер, поскольку каждая мера выполняет определенный тип агрегации.



 .. ).
.. ). д. Поскольку мы хотим, чтобы этот показатель был более идентифицируемым, выделите Показатель в строке формул, а затем измените его на Чистый объем продаж .
д. Поскольку мы хотим, чтобы этот показатель был более идентифицируемым, выделите Показатель в строке формул, а затем измените его на Чистый объем продаж .



 В списке предложений показаны только меры, которые нужно добавить в формулу.
В списке предложений показаны только меры, которые нужно добавить в формулу.
 Вы также познакомились с контекстом, в котором результаты вычислений в показателях изменяются в соответствии с другими полями или другими выражениями в вашей формуле.
Вы также познакомились с контекстом, в котором результаты вычислений в показателях изменяются в соответствии с другими полями или другими выражениями в вашей формуле.