Построение графика функции с помощью производной, сопутствующие задачи 10 класс онлайн-подготовка на Ростелеком Лицей |
Введение
Методика исследования функции, построение ее графика, включает в себя 2 этапа:
1. исследование без производной;
2. исследование с помощью производной.
Построение графика и исследование функции без производной
При исследовании функции без производной нахождение интервалов знакопостоянства и определение знаков функции на них выполнить очень затруднительно. Однако некоторые свойства данной функции можно узнать:
1. Область определения функции – это множество всех действительных чисел.
2. Если x стремится к , то и данная функция стремится к . Следовательно, множество значений функции – это вся числовая ось.
3. График этой функции симметричен относительно точки .
График этой функции симметричен относительно точки .
Пояснение
Рассмотрим функцию
Эта функция позволяет найти интервалы знакопостоянства и построить эскиз графика (см. Рис. 1).
Эта функция нечетная:
График нечетной функции симметричен относительно точки с координатами .
Рис. 1. График функции
При прибавлении 4 к функции график сдвинется на 4 единицы вверх по оси (см. Рис. 2): корни и пропадают, а корень сдвигается влево. Следовательно, график функции будет симметричен относительно точки .
Рис. 2. Схематичное изображение графиков функции и
Нам удалось установить, что функция имеет как минимум один корень, который меньше чем .
Построение графика и исследование функции с помощью производной
Приравниваем производную к 0 и находим критические точки:
– критические точки
Выделим интервалы знакопостоянства производной, которые определяют интервалы монотонности самой функции (см. Рис. 3).
Рис. 3).
До точки функция возрастала (производная была положительна), после этой точки функция убывает (производная отрицательная), следовательно, – это точка максимума.
До точки функция убывала, после этой точки функция возрастает, следовательно, – это точка минимума.
Рис. 3. График производной функции
Найдем значения функции в точках минимума и максимума:
Можно сделать вывод, что функция возрастает от до 6 и от 2 до ; функция убывает от 6 до 2.
На рисунке 4 показан график функции . Этот график читается следующим образом:
Если аргумент возрастает от до , то функция возрастает от до 6; если аргумент от до 1, то функция убывает от 6 до 2; если аргумент возрастает от 1 до , то функция возрастает от 2 до .
Рис. 4. График функции
Результаты исследования функции
1.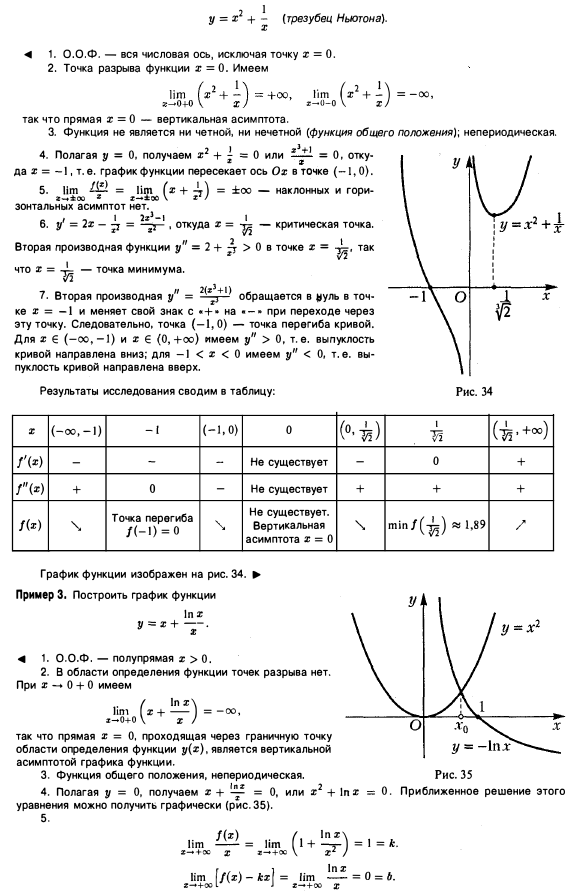 при и при
при и при
2. при
3. – т. max
– т. min
3. . Наибольшего и наименьшего значения функции не существует.
Задача
Найти число корней уравнения в зависимости от параметра .
Решение
1. Перенесем в правую часть уравнения:
2. Построим график функции (см. Рис. 5) (как построить график этой функции см. выше).
Рис. 5. Иллюстрация к задаче
3. Рассечем этот график семейством прямых , при разных . Найдем точки пересечения этих прямых с графиком функции (см. Рис. 6).
Рис. 6. Иллюстрация к задаче
Уравнение имеет один корень при каждом из множества , а также из множества .
Уравнение имеет два корня при и при .
Уравнение имеет три корня при всех из множества .
Ответ: 1 корень:
2 корня: ; ;
3 корня: .
Частные случаи для задачи
1. Найти все значения параметра , при каждом из которых данное уравнение имеет ровно два различных корня.
Ответ: уравнение имеет два корня при и при .
2. Найти наибольшее натуральное значение параметра a, при котором уравнение имеет три различных корня.
Решение
Уравнение имеет три корня при всех из множества . В это множество входят такие натуральные числа: 3, 4, 5. Наибольшее из них – это 5.
Ответ: .
Общий план построения графика и исследования функции
Общий план состоит из двух этапов:
1. Этап А: исследование без производной.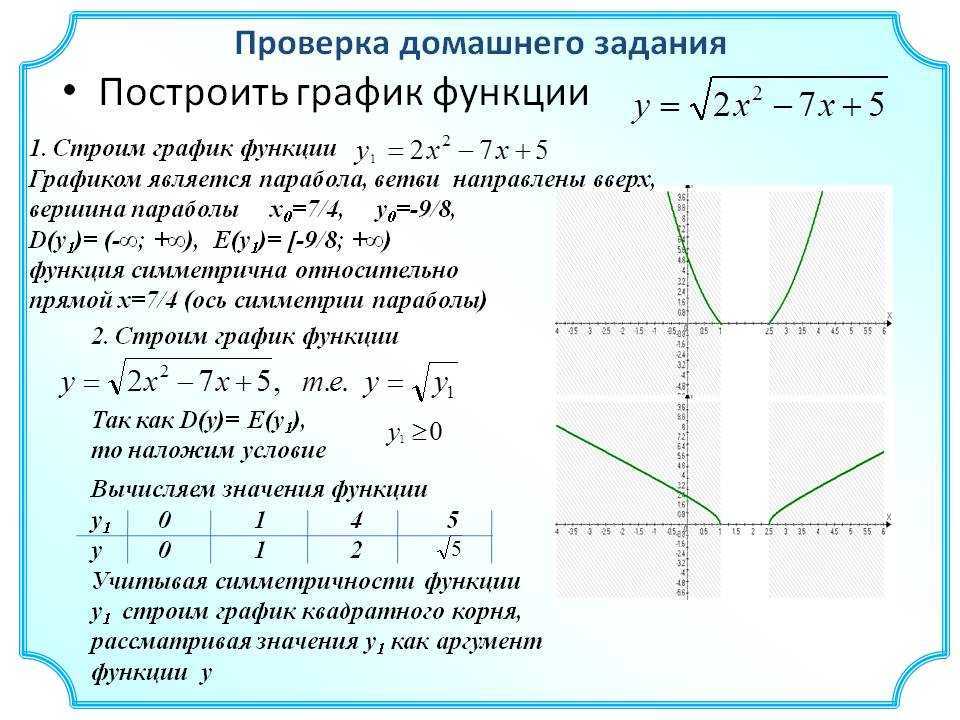
2. Этап Б: исследование с производной.
Этап А
1. Найти область определения функции .
2. Выделить интервалы знакопостоянства функции и определить знаки функции на них (для этого нужно приблизительно оценить расположение корней или точно найти их).
3. Найти точку пересечения графика с осью , для этого приравнять и вычислить .
4. Выяснить специфику функции:
— четность, нечетность, периодичность;
— наличие центра или оси симметрии.
5. Построить эскиз графика в окрестностях каждого корня (в окрестностях корня функция может возрастать, убывать, иметь точку максимума или минимума (см. Рис. 7)).
Рис. 7. Эскиз графиков в окрестностях корня
6. Построить эскиз графика функции в окрестностях точек разрыва области определения . Точки разрыва – это, как правило, корни знаменателя.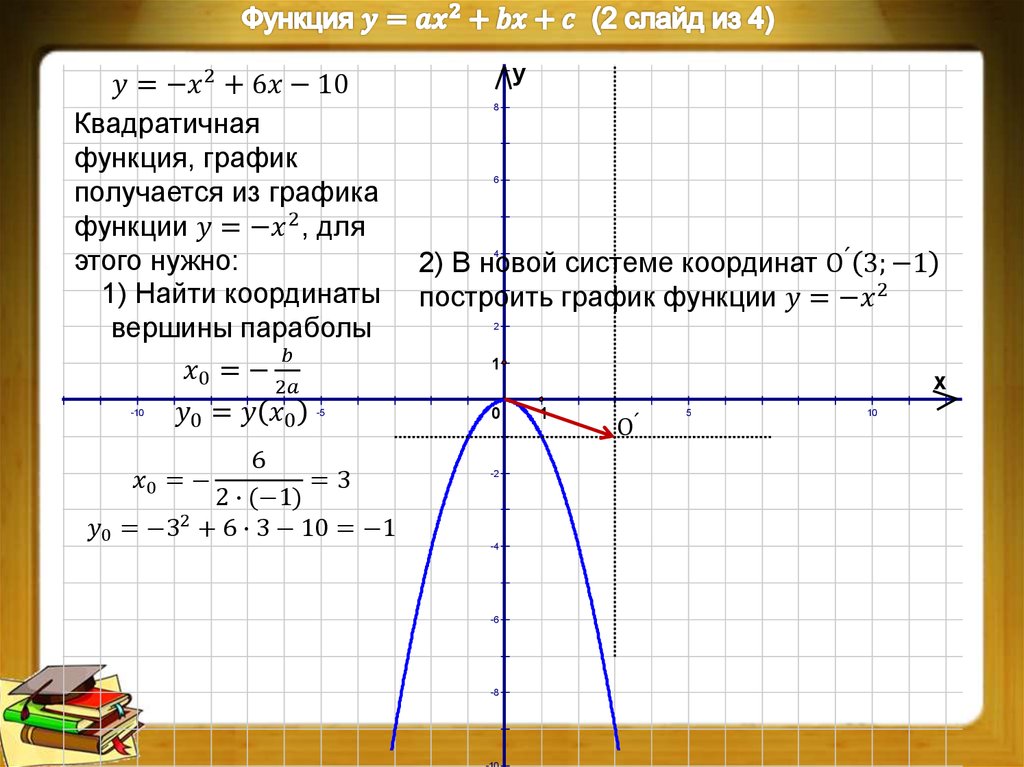 Они могут определять вертикальные асимптоты.
Они могут определять вертикальные асимптоты.
7. Построить график функции в окрестностях бесконечно удаленных точек: .
Этап Б
1. Найти производную функции .
2. Найти интервалы знакопостоянства производной и определить знаки производной на них. Эти интервалы определяют интервалы монотонности самой функции.
3. Найти критические точки, исследовать их на экстремум.
4. Построить и описать график функции .
Предложенная схема работает особенно хорошо для функций вида: , где и – многочлены.
Список литературы
1. Мордкович А.Г., Семенов П. В. Алгебра и начала математического анализа, 10 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений. – М.: Мнемозина, 2009.
2. Мордкович А.Г. Алгебра и начала математического анализа, 10 класс.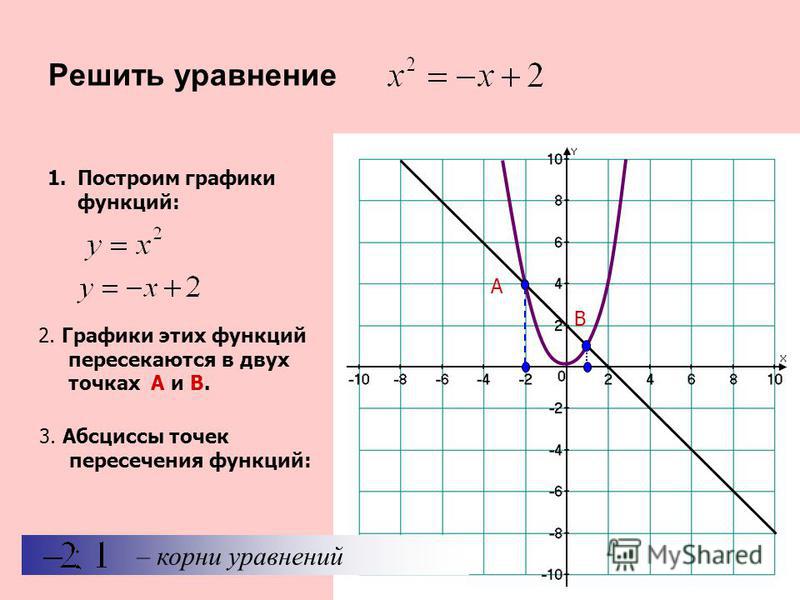 В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений. – М.: Мнемозина, 2009.
В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений. – М.: Мнемозина, 2009.
3. Виленкин Н.Я., Ивашев-Мусатов О.С., Шварцбурд С.И. Алгебра и математический анализ для 10 класса (учебное пособие для учащихся школ и классов с углубленным изучением математики). – М.: Просвещение, 1996.
4. Колягин Ю.М., Сидоров Ю.В., Ткачева М.В., Федорова М.В., Шабунин М.И. Алгебра и начала математического анализа, 10 класс. Учебник для учащихся общеобразовательных учреждений (профильный уровень). – М.: Мнемозина, 2009.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
1. Интернет-сайт «ЯКласс» (Источник)
2. Интернет-сайт «Вся элементарная математика» (Источник)
3. Интернет-сайт YouTube (Источник)
Домашнее задание
1. Задание 45.13, 45.15(а), 45.3 (б) (стр. 265) – Мордкович А.Г. Алгебра и начала математического анализа, 10 класс. В 2 ч. Ч. 2. Задачник (Источник)
265) – Мордкович А.Г. Алгебра и начала математического анализа, 10 класс. В 2 ч. Ч. 2. Задачник (Источник)
2. Исследуйте функцию и постройте ее график .
График Функции — Mathcracker.Com
Инструкции: Используйте этот калькулятор графиков функций для построения графика заданной вами функции. Пожалуйста, введите любую действительную функцию, график которой вы хотите построить, в поле формы ниже.
График функции
Этот калькулятор графиков функций позволит вам построить график любой функции, которую вы предоставите. Вам необходимо указать действительную функцию в x.
Это может быть функция, которая уже упрощена, например, f(x) = sin(2x), или что-то более сложное, например, ‘f(x) = sin((1/3 x +1/4 x^2)(1/5 x +1/6))’, и этот калькулятор сделает следующее
упрощение функций
для вас.
После того, как вы ввели действительную функцию в соответствующую форму, вам нужно просто нажать кнопку «Рассчитать», чтобы получить построенный график.
Работа с график функции может помочь вам понять его основные свойства. Действительно, наличие график функции может рассказать вам в конечном итоге все, что нужно, о поведении функции: возрастает ли она? Уменьшается ли она? Пересекает ли она ось x? Имеет ли она какую-либо симметрию?
Что такое график функции?
График функции f(x)- это множество точек (x, f(x)). При построении по осям x-y это выглядит как «кривая» (может быть линией), которая течет слева направо.
При построении по осям x-y это выглядит как «кривая» (может быть линией), которая течет слева направо.
Теперь у этого потока слева направо есть одно очень специфическое свойство: он проходит тест на вертикальную линию, который показывает, что график функции при пересечении с любой вертикальной линией будет иметь не более одной точки пересечения. Например, график ниже соответствует графику функции, потому что он проходит тест на вертикальную линию.
С другой стороны, график ниже не соответствует графику функции, потому что мы видим вертикальную линию, пересекающую кривую в двух точках.
Каковы этапы нахождения графика функции?
-
Шаг 1: Определите функцию, график которой вы хотите построить.
 Путем осмотра оцените, является ли функция действительной
Путем осмотра оцените, является ли функция действительной
- Шаг 2: Если функция является допустимым выражением, найдите потенциальные точки, в которых функция не может быть оценена (деление на ноль или квадратные корни из отрицательных чисел)
- Шаг 3: Упростите как можно больше, чтобы представить функцию в ее простейшей форме
-
Шаг 4: Попытайтесь выявить известные закономерности. Является ли функция в своей простейшей форме многочленом? Полиномы имеют определенную форму.
 Является ли функция тригонометрической функцией? Они также имеют очень хорошо известную и характерную форму
Является ли функция тригонометрической функцией? Они также имеют очень хорошо известную и характерную форму
- Шаг 5: Если у вас нет простой, узнаваемой модели или известной функции, создайте таблицу точек (x, f(x)), столько точек, сколько это практически возможно
- Шаг 6: Постройте точки из таблицы на плоскости XY. Проведите кривую через эти точки, чтобы получить представление о том, как выглядит график функции
Упрощение функции
в простейшей форме поможет вам легче определить все известные функции, которые появляются и могут быть легко изображены на графике. 2\) (простая парабола) или \(f(x) = x\) (простая линия), но у вас могут быть переводы масштабированных версий этих основных версий. Действительно, например, любой
квадратичная функция
может быть помещена в
Вершинная форма
, что помогает определить кривую как простую параболу, которая переводится.
2\) (простая парабола) или \(f(x) = x\) (простая линия), но у вас могут быть переводы масштабированных версий этих основных версий. Действительно, например, любой
квадратичная функция
может быть помещена в
Вершинная форма
, что помогает определить кривую как простую параболу, которая переводится.
Каковы этапы выполнения преобразований графиков функций?
- Шаг 1: Определите функцию, график которой вы хотите построить
- Шаг 2: Упрощайте как можно больше, избегая ловушки деление на ноль и извлечение квадратного корня из отрицательных значений
- Шаг 3: Используя простейшую версию функции, посмотрите, можно ли распознать какие-либо элементарные функции
-
Шаг 4: Если нет, посмотрите, есть ли преобразования обычных функций (полиномов, линий,
триггерные функции
и т.
 д.) могут быть идентифицированы, поскольку их тоже легко изобразить на графике
д.) могут быть идентифицированы, поскольку их тоже легко изобразить на графике
- Шаг 5: Если все вышеперечисленное не помогает, просто постройте таблицу со значениями (x, f(x)) и вручную проследите форму графика
Конечно, вам не обязательно строить график вручную, вы можете использовать следующее график функции онлайн инструмент для получения точного и аккуратного графика.
Почему вы хотите узнать о типах графиков функций?
График функции может рассказать о ней практически все. 2\), который был сдвинут влево на 4 единицы, сдвинут вниз на \(\frac{5}{6}\) и повторно масштабирован.
2\), который был сдвинут влево на 4 единицы, сдвинут вниз на \(\frac{5}{6}\) и повторно масштабирован.
Пример: еще один пример графика функции
Вычислите график \( f(x) = \displaystyle \frac{\sin(x)}{x}\).
Отвечать: Была предоставлена следующая функция: \(\displaystyle f(x) = \frac{\sin\left(x\right)}{x}\), тогда получается следующий график, интервал \([-10, 10]\):
Другие функциональные калькуляторы
Получив функцию, вы должны быть в состоянии
упростить функцию
, если выразить это в простейшей форме. Мы уже видели, что полезно определить более простым способом потенциальное преобразование графика функции от базовых функций, которые там могут быть.
Мы уже видели, что полезно определить более простым способом потенциальное преобразование графика функции от базовых функций, которые там могут быть.
Графическое представление функции sqrt(x)
Программное обеспечение для построения графиков онлайн , также известное как графопостроитель , это онлайн-график , который позволяет отображать функции в режиме онлайн. Просто введите выражение в соответствии с x функции, которую нужно построить, используя обычные математические операторы. Построитель кривых особенно подходит для функционального исследования , позволяет получить графическое представление функции из уравнения кривой, его можно использовать для определения вариации, минимума, максимума функции.
Онлайн-плоттер также может рисовать параметрические кривые.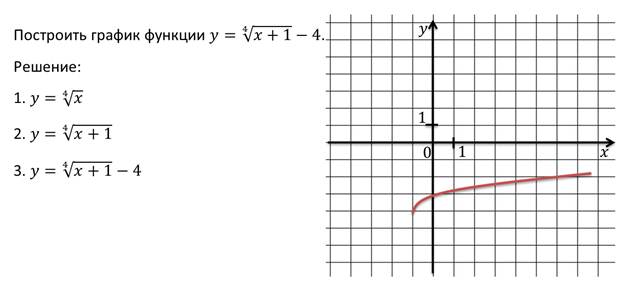 и рисовать полярные кривые, а для функций достаточно ввести выражение для представления по параметру t.
и рисовать полярные кривые, а для функций достаточно ввести выражение для представления по параметру t.
В графическом калькуляторе для записи математических функций должны использоваться следующие операторы: 9Для питания
Это программное обеспечение для построения кривых позволяет использовать следующие обычных математических функций :
- абс (абсолютное значение), график абсолютного значения
- арккос (арккосинус), арккосинус графика
- арксинус (арксинус), арксинус графика
- арктангенс (арктангенс), арктангенс графика
- ch (гиперболический косинус), построить гиперболический косинус
- cos (косинус), график косинус
- cosec (косеканс), косеканс участка
- котан (котангенс), котангенс участка
- coth (гиперболический котангенс), построить гиперболический котангенс
- cube_root (кубический корень), построить кубический корень
- опыта (экспоненциальный), экспоненциальный график
- ln (напировский логарифм), построить напьеровский логарифм логарифм
- (логарифм), логарифм графика
- сек (секанс), секущая участка
- ш (гиперболический синус), построить гиперболический синус
- sin (синус), график синуса
- sqrt (квадратный корень), участок квадратный корень
- тангенс (тангенс), участок касательной
- -й (гиперболический тангенс), построить гиперболический тангенс
- абс.
 (абсолютное значение),
график абсолютного значения
(абсолютное значение),
график абсолютного значения - арккос (арккосинус), арккосинус графика
- арксинус (арксинус), арксинус графика
- арктангенс (арктангенс), арктангенс графика
- ch (гиперболический косинус), построить гиперболический косинус
- cos (косинус), график косинус
- cosec (косеканс), косеканс участка
- котан (котангенс), котангенс участка
- coth (гиперболический котангенс), построить гиперболический котангенс
- cube_root (кубический корень), построить кубический корень
- опыта (экспоненциальный), экспоненциальный график
- ln (напировский логарифм), построить напьеровский логарифм логарифм
- (логарифм), логарифм графика
- сек (секанс), секущая участка
- ш (гиперболический синус), построить гиперболический синус
- sin (синус), график синуса
- sqrt (квадратный корень), участок квадратный корень
- тангенс (тангенс), участок касательной
- -й (гиперболический тангенс), построить гиперболический тангенс
- Графические функции онлайн
Этот онлайн-плоттер позволяет вам рисовать несколько кривых одновременно ,
просто введите выражение функции, которую нужно построить, и нажмите «Добавить», графическое представление функции появляется мгновенно, можно повторить операцию для построения других кривых онлайн .
Переменная, которая будет использоваться для представления функций, — «x».
Координаты точек на кривой можно получить с помощью курсора. Для этого нажмите на кривую, чтобы появился этот курсор, а затем перетащите вдоль кривой, чтобы увидеть ее координаты.
Кривые можно удалить из плоттера:
- Чтобы удалить кривую, выберите кривую, затем нажмите кнопку удаления в меню.
- Чтобы удалить все кривые с графика, нажмите кнопку удалить все в меню.
Можно изменить кривую, представленную на графике, выбрав ее, отредактировав ее выражение и затем щелкнув на кнопку редактирования.
онлайн-плоттер имеет несколько опций, позволяющих настроить график.
Чтобы получить доступ к этим параметрам, нажмите кнопку параметров. Затем можно определить границы графов,
чтобы подтвердить эти изменения, необходимо снова нажать кнопку параметров.
- Проведение касательной функции к точке
- График производной функции
Онлайн-плоттер позволяет провести тангенс функции в точке для этого, вы просто рисуете нужную функцию, затем, как только функция нарисована, нажмите на меню, параметры, а затем кнопку касательной, которая появляется на экране, после чего будет нарисована касательная, можно изменить точку касательной, что приводит к перерисовке касательной. Калькулятор позволяет определить уравнение касательной очень просто, с уравнением кривой.
Онлайн-плоттер позволяет вам построить производную функции для этого,
вы просто рисуете нужную функцию, затем после того, как функция нарисована,
нажмите на меню, на параметры, затем на появившуюся производную кнопку,
затем строится производная функции.
9Построитель кривых 0003 также можно использовать для вычисления производной функции и к участок он для этого, вам нужно нарисовать нужную функцию, затем, как только функция будет нарисована, выберите ее, щелкнув по ней, на кривой появится красный курсор. Затем нажмите на меню, на параметры, затем на производную кнопку «выражение», которая появляется на экране, затем строится и вычисляется производная функции. («Выражение» представляет собой выражение, которое необходимо получить и нанести на график).
Плоттер позволяет рисовать параметрическую кривую , для этого
вам просто нужно ввести абсциссу, ординату как функцию от t,
затем нажмите кнопку «Построить параметрическую кривую»,
кривая автоматически отображается с двумя курсорами для отображения нужных точек.
Построитель кривых можно использовать для построения полярной кривой . Для этого просто введите выражение полярной кривой в зависимости от t, затем нажмите кнопку «Построить полярную кривую», кривая автоматически отобразится с двумя курсорами для отображения нужных точек.
Есть возможность двигаться по кривым и получать координаты точки, на которой находится курсор, Для этого необходимо ввести курсор и перемещать его по графику, координаты X и Y отображаются под графиком.
Можно изменить область графика, для этого необходимо зайти в меню, затем нажать на опции, Затем можно изменить пределы графического дисплея.
Графический калькулятор предлагает возможность масштабировать и перемещать область графика. Сделать это,
используйте область в правом нижнем углу графиков.
Сделать это,
используйте область в правом нижнем углу графиков.
- Кнопка + позволяет увеличить масштаб кривых,
- — позволяет уменьшить масштаб кривых,
- Стрелки используются для перемещения кривых,
Можно экспортировать построенные кривые с помощью графического калькулятора , экспорт осуществляется как
изображение в формате PNG. Для этого вам нужно зайти в меню графика, затем в подменю экспорта графиков.
Затем калькулятор отображает построенные кривые в виде изображения, просто щелкните правой кнопкой мыши, чтобы экспортировать изображение,
также возможно скопировать изображение.
Чтобы вернуться к обычному отображению калькулятора, используйте кнопку Выход из режима изображения.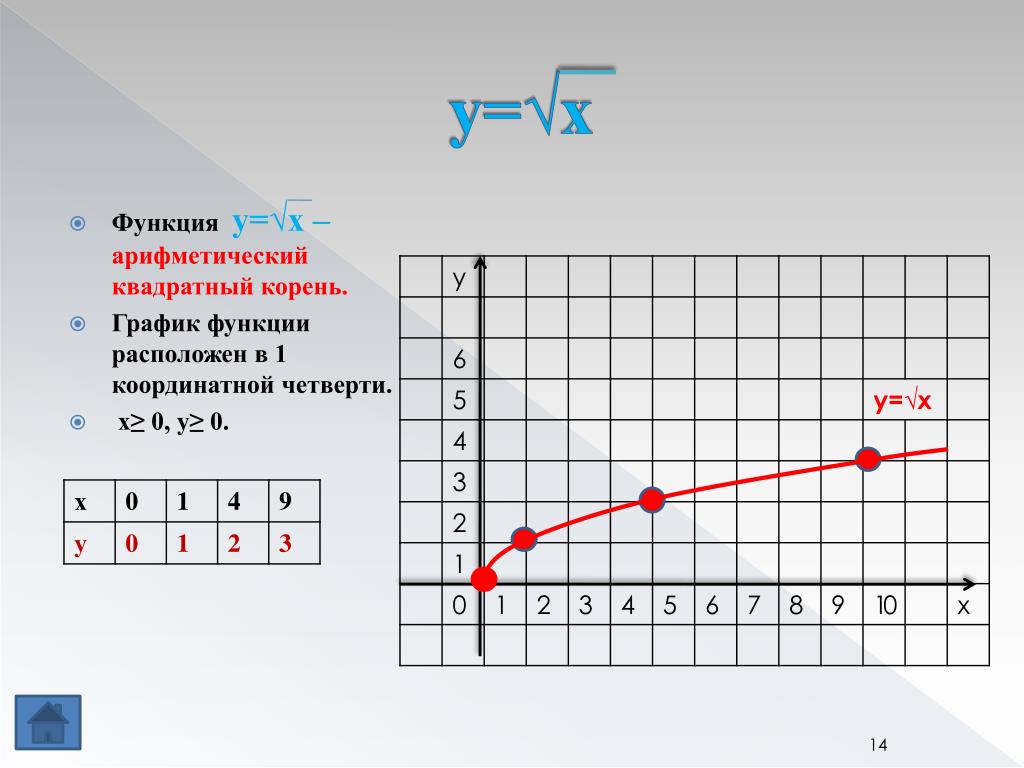 9y теперь анализируются без ошибок.
9y теперь анализируются без ошибок.
24 августа 2021 г.
Исправлено
Кусочные функции больше не вызывают сбой при определенных комбинациях настроек интервала и сетки.
Исправлено
Стрелки на верхнем и нижнем краях функций теперь последовательно указывают в правильном направлении.
Исправлено
Неправильные стрелки больше не появляются на левом и правом краях некоторых кусочных функций.
21 августа 2021 г.
Новая функция
Теперь вы можете выбирать цвет надписей.
Новая функция
Теперь вы можете размещать подписи над или под диаграммой.
Новая функция
Сломанные топоры теперь представлены как таковые. Например, если в вашем окне просмотра x ∈ [5, 10], ось Y появится слева, а символ сломанной оси покажет, что ось X разорвана между 0 и 5.
Новая функция
Все поля ввода текста теперь имеют кнопку для очистки текущего ввода.
93.Изменено
Неявные графики и поля наклона больше не являются опциями для полулогарифмической сетки. Это предотвращает застревание интерфейса в непреднамеренных длительных вычислениях.
Это предотвращает застревание интерфейса в непреднамеренных длительных вычислениях.
Изменено
Внесены небольшие изменения в ширину линий графиков и размер текста.
Фиксированная
Типы графиков функции больше не пропускают части кривой для некоторых графиков.
Исправлено
Открытые круги на прозрачном фоне теперь отображаются правильно, а не залиты белым.
Фиксированная
Затенение на полярной сетке теперь ограничивается круговой полярной сеткой, а не распространяется на поля.
Исправлено
Затенение с типом графика Implicit теперь должно работать последовательно. Раньше затенение иногда просачивалось через неявные кривые.
Исправлено
Символ круга для точечных диаграмм теперь правильно отображается в легендах.
29 июня 2021 г.
Исправлено
Сетка больше не пропадает при определенных настройках окна просмотра.
Большое обновление (18 июня 2021 г.)
Новая функция
По многочисленным просьбам я полностью восстановил ручной контроль интервалов между линиями сетки и надписями. Четыре числовых параметра на панели «Сетка» теперь дают вам полный контроль над наличием и расстоянием между линиями и метками. Вы можете оставить некоторые или все из них пустыми, если вам не нужны линии или метки на этой оси.
Четыре числовых параметра на панели «Сетка» теперь дают вам полный контроль над наличием и расстоянием между линиями и метками. Вы можете оставить некоторые или все из них пустыми, если вам не нужны линии или метки на этой оси.
Новая функция
Теперь стало проще перетаскивать заголовки, аннотации и метки именно туда, куда вы хотите. Вы можете видеть контуры текстов, когда перетаскиваете их, и обычно вы можете изменить график без сброса позиций текстов.
Новая функция
Теперь вы можете вводить гораздо более широкий спектр специальных символов в заголовках, легендах и аннотациях. Вместо небольшого набора кнопок теперь вы используете объекты HTML. Это позволяет использовать огромное количество специальных символов, включая греческие буквы, математические символы и стрелки. Более подробная информация приведена в разделе «Специальные символы в тексте» данного руководства.
Новая функция
Теперь вы можете выбрать прозрачный фон вместо сплошного белого. Этот параметр находится на панели «Общий вид и специальные возможности» внизу.
Этот параметр находится на панели «Общий вид и специальные возможности» внизу.
Новая функция
Теперь вы можете изменять размеры текста и толщину линий. Эти настройки также находятся на новой панели «Общий вид и специальные возможности».
Новая функция
Свернутые панели графиков теперь отображают сводку того, что вы ввели на этой панели.
Новая функция
Я добавил открытый кружок к возможным символам на графиках XY Scatter.
Изменено
Аннотации снова вводятся в отдельные поля вместо одного поля с разделителями с запятой. Я изменил это, потому что объекты HTML, которые теперь поддерживаются в аннотациях, содержат свои собственные точки с запятой, а использование точек с запятой для двух разных целей в одном выражении просто сбивает с толку.
Изменено
Хотя вы больше не используете точку с запятой для разделения аннотаций, теперь вы должны использовать точку с запятой для разделения упорядоченных пар, асимптот и интервалов. (Примеры на экране напомнят вам об этом.) Это изменение предотвращает неправильный разбор некоторых выражений GraphFree.
(Примеры на экране напомнят вам об этом.) Это изменение предотвращает неправильный разбор некоторых выражений GraphFree.
Изменено
Я изменил стрелки на концах функций со сплошных треугольников на простые V-образные линии. Сомневаюсь, что все согласятся, какой стиль лучше. Но бесконечные интервалы на числовой прямой выглядят в новом стиле намного лучше, поэтому я использовал его повсеместно.
Исправлено
На полях графика больше не появляются случайные стрелки.
Фиксированная
В декартовой (триггерной) сетке дроби, не распознаваемые автоматической маркировкой триггера GraphFree, теперь отображаются как десятичные приближения. (Раньше они отображались как дроби, но не были правильными, если GraphFree их не распознавал.)
Ввод функций
Новый GraphFree разработан для удобного использования клавиатуры, что ускоряет ввод данных в большинстве ситуаций. Если на традиционном калькуляторе есть кнопка для этого, то сейчас, вероятно, есть способ ввести его. 9x
9x
Обязательно используйте заглавную E!
Нет, вам не нужен знак умножения.
Полный список функций
| Категория | Доступные функции | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Базовая математика и алгебра | абс. | абс. (квадратный корень), cbrt (кубический корень) | |||||||||||
| Логарифмический | Ln (натуральный логарифмический) и логарифмический (основание 10) | ||||||||||||
| Тригонометрический | sin , cos , tan , cot , sec , csc | ||||||||||||
| Гиперболический | sinh , cosh , tanh , coth , чщ | ||||||||||||
| Обратная гипербола | arcsinh , arccosh , arctanh , arccoth , arcsech , arccsch 9032 9032 487Графики кусочных функций Вы можете выразить условия кусочной функции, используя либо неравенства или интервальные обозначения. Окружности, эллипсы, гиперболы и т. д.Чтобы построить график конических сечений, выберите тип графика Неявный и введите полное уравнение, знак равенства и все остальное. Если у вас медленный компьютер, имейте в виду, что неявный тип графика может выполняться немного дольше, особенно если вы установите большие значения ширины и высоты графика. Вертикальные линииЕсли вам нужна пунктирная вертикальная линия для асимптоты, введите уравнение (например, x = 4 ) с типом графика Асимптота. Вы даже можете ввести несколько асимптот одновременно. Если вместо этого вы хотите сплошную вертикальную линию, введите уравнение в тип графика Неявный. Однако в неявном типе графика вы можете ввести только одно уравнение на каждом графике. Декартова (триггерная) сетка Этот тип сетки идеален, когда ваши соответствующие значения x будут выражены через π. Многоугольники и полилинииТип графика Полилиния имеет два совершенно разных применения. Одним из них является создание многоугольников, таких как те, которые можно использовать в вопросах геометрии координат. Для этого вы обычно включаете опцию Connect Endpoints Без подключенных конечных точек полилинейный график отлично подходит для создания некоторых графиков, которые было бы неудобно собирать в виде кусочных функций. Вместо указания уравнений и интервалов различных сегментов просто укажите точки, которые вы хотите соединить. Когда вы вводите упорядоченные пары, вам действительно нужны круглые скобки, а также точки с запятой между парами. Специальные символы в текстеСпециальные символы поддерживаются в метках осей, заголовке, тексте легенды и аннотациях. Кнопки для копирования и вставки определенных специальных символов заменены поддержкой объектов HTML. Это может быть не так удобно, как кнопки, но они позволяют использовать гораздо более широкий спектр специальных символов, чем раньше. Объекты HTML представляют собой текстовые последовательности, начинающиеся с амперсанда и заканчивающиеся точкой с запятой. Например, объект HTML для числа π имеет вид π . Существуют объекты HTML для греческих букв, математических символов, стрелок и многого другого. Вы можете увидеть внешний список доступных сущностей здесь. (Я не могу гарантировать, что каждый объект, который кто-то захочет использовать, будет доступен в шрифте, который использует GraphFree, но наиболее часто используемые математические символы таковы. Вот еще несколько примеров:
Обратите внимание на то, что сущности для заглавных греческих букв сами пишутся с заглавной буквы, а сущности для строчных греческих букв — нет. Например, сущность Σ заставляет заглавную Σ использоваться для суммирования, а σ использует нижний регистр σ для стандартного отклонения. Существует также шаблон для стрелок. Это → , ← , ↑ и ↓ , где начальные буквы r, l, u и d обозначают право, лево, вверх и вниз. Заголовок, легенда и аннотацииЗаголовок или заголовок отображается над или под диаграммой. Легенда поясняет значение различных линий или символов точечной диаграммы. Он отображается либо справа от графика, либо под ним, в зависимости от ширины графика. Аннотации используются для любых других заметок, которые вы хотите добавить. Вы можете использовать мышь, чтобы перетащить их в любое место на графике. (Если на то пошло, вы также можете перемещать заголовки и легенды, если считаете это необходимым.) Вы можете включать различные математические символы и другие специальные символы, используя объекты HTML, как описано в разделе «Специальные символы в тексте» это руководство. Затенение областиЧтобы закрасить область вашего графика, укажите упорядоченную пару внутри области, которую вы хотите затенить. Чтобы затенить несколько областей, введите точку внутри каждой области, разделенную точкой с запятой. Убедитесь, что вы выбрали точки, которые не находятся слишком близко к краям вашей области (или к краю окна просмотра). АсимптотыТип графика Асимптоты можно использовать для ввода уравнений нескольких горизонтальных, вертикальных и/или наклонных асимптот в одной строке. Линии будут пунктирными, как это принято для асимптот. (Если вам не нужны пунктирные линии, используйте вместо них обычный тип графика «Функция» или тип графика «Неявный» для вертикальных асимптот.) Поскольку этот тип графика разработан специально для асимптот, вам необходимо записать уравнения асимптот «нормальным» способом, что означает x = c , y = c , и y = mx + b . Альтернативные формы обычно не работают. Числовая линия Чтобы построить числовую линию, выберите числовую линию в качестве типа сетки на панели «Оси и сетка». Панели графика теперь будут содержать параметр для графика числовой линии вместо других типов графиков. Чтобы ввести данные в числовой график, вы можете ввести несколько точек и/или интервалов, разделенных точкой с запятой. Как и в кусочном графике, вы можете использовать обозначение интервалов или неравенства для выражения ваших интервалов. В записи интервала вы можете использовать inf для выражения бесконечного интервала. Проблема со вставкой графика?Во-первых, пользователи Windows, вероятно, не смогут копировать и вставлять графики с прозрачным фоном. Это ограничение самой Windows. Пользователям Windows потребуется сохранять изображения с прозрачным фоном на диск, чтобы вставлять их в другие программы. Для изображений с обычным белым фоном обычная процедура — щелчок правой кнопкой мыши, копирование и вставка в программу — работает точно так, как ожидается в большинстве программ. Однако некоторым программам требуется небольшая помощь, чтобы правильно выполнить вставку. Microsoft Word может быть одной из таких программ. Если вставка в Word не работает, используйте команду «Специальная вставка» вместо обычной вставки, а затем выберите «Независимое от устройства растровое изображение». |
Действия в случае потери или кражи iPhone, iPad или iPod touch
Если вы потеряли свое устройство iPhone, iPad или iPod touch либо считаете, что его могли украсть, воспользуйтесь приложением «Локатор» и защитите свои данные.
Поиск устройства на карте
Чтобы найти устройство, выполните вход на странице iCloud.com/find. Можно также воспользоваться приложением «Локатор» на другом принадлежащем вам устройстве Apple.
Если устройство iPhone, iPad или iPod touch не отображается в списке устройств, это означает, что на нем не был включен Локатор. Но вы все равно можете защитить свою учетную запись, даже если Локатор не был включен.
Обозначение устройства как пропавшего
Обозначив устройство как пропавшее, вы удаленно заблокируете его с помощью код-пароля, что позволит защитить данные на устройстве. При этом на утерянном устройстве также отключится служба Apple Pay. Кроме того, на утерянном устройстве можно отобразить произвольное сообщение со своей контактной информацией.
Обозначьте устройство как пропавшее
Подача заявления о пропавшем устройстве в местные правоохранительные органы
Сотрудники правоохранительных органов могут запросить серийный номер вашего устройства.
Определите серийный номер
Подача заявления о краже и потере
Если на утерянный iPhone распространяется действие соглашения AppleCare+ с покрытием кражи и потери, подайте заявление для замены iPhone.
Подайте заявление
Удаленное стирание данных с устройства
Если вы стерли данные с устройства с установленной iOS 15, iPadOS 15 или более поздней версии, вы все равно можете найти устройство или воспроизвести на нем звук с помощью программы «Локатор». В противном случае вы не сможете найти устройство или воспроизвести звук после стирания данных.
Если на устройство распространяется действие соглашения AppleCare+ с покрытием кражи и потери, не удаляйте его из приложения «Локатор» или идентификатора Apple ID.
Стирание данных с устройства
Обращение к оператору сотовой связи
Если у вас пропал iPhone или iPad с поддержкой сотовой связи, сообщите об этом оператору сотовой связи. Попросите оператора заблокировать вашу учетную запись, чтобы предотвратить совершение звонков, отправку текстовых сообщений и передачу данных. Если ваше устройство защищено по программе оператора сотовой связи, подайте соответствующее заявление.
Попросите оператора заблокировать вашу учетную запись, чтобы предотвратить совершение звонков, отправку текстовых сообщений и передачу данных. Если ваше устройство защищено по программе оператора сотовой связи, подайте соответствующее заявление.
Удаление утерянного устройства из учетной записи
Если на устройство распространяется действие соглашения AppleCare+ с покрытием кражи и потери, не удаляйте iPhone из приложения «Локатор» или идентификатора Apple ID, пока ваше заявление не будет одобрено.
Чтобы удалить утерянное устройство из списка доверенных, перейдите на страницу appleid.apple.com.
Соглашение AppleCare+ с покрытием кражи и потери доступно не во всех странах и регионах.
Информация о продуктах, произведенных не компанией Apple, или о независимых веб-сайтах, неподконтрольных и не тестируемых компанией Apple, не носит рекомендательного или одобрительного характера. Компания Apple не несет никакой ответственности за выбор, функциональность и использование веб-сайтов или продукции сторонних производителей. Компания Apple также не несет ответственности за точность или достоверность данных, размещенных на веб-сайтах сторонних производителей. Обратитесь к поставщику за дополнительной информацией.
Компания Apple также не несет ответственности за точность или достоверность данных, размещенных на веб-сайтах сторонних производителей. Обратитесь к поставщику за дополнительной информацией.
Дата публикации:
Простая регрессия
Простая регрессияPPA 696 МЕТОДЫ ИССЛЕДОВАНИЯ
ПРОСТАЯ РЕГРЕССИЯ
Регрессия
Элементы уравнения регрессии
Оценка уравнения регрессии
шагов линейной регрессии
предположений
линейной регрессии
Время
Серийная регрессия
РЕГРЕССИЯ
Наиболее часто используемая форма регрессии представляет собой линейную регрессию, и наиболее распространенным типом линейной регрессии является называется обычной регрессией методом наименьших квадратов.
Линейная регрессия использует значения из
существующий набор данных, состоящий из измерений значений двух переменных,
X и Y, чтобы разработать модель, полезную для прогнозирования значения
зависимая переменная Y для заданных значений X.
ЭЛЕМЕНТЫ УРАВНЕНИЕ РЕГРЕССИИ
Уравнение регрессии записывается как Y = а + бХ + еY — значение зависимой переменной (Y), что предсказывается или объясняется
а или Альфа, константа; равно значению Y, когда значение X=0
б или Бета, коэффициент Х; склон линии регрессии; насколько изменяется Y при каждом изменении на одну единицу ИКС.
X — значение независимой переменной (X), что предсказывает или объясняет значение Y
e — ошибка; ошибка в предсказании значения Y, учитывая значение X (оно не отображается в большинстве регрессионных уравнения).
Например, предположим, что мы знаем среднее
скорость автомобилей на автостраде, когда у нас есть 2 дорожных патруля
(средняя скорость = 75 миль в час) или развернуто 10 дорожных патрулей (средняя скорость = 35 миль в час).
миль/ч). Но какова будет средняя скорость автомобилей на автостраде, когда мы
развернуть 5 дорожных патрулей?
| Средняя скорость на шоссе (Y) | Количество развернутых патрульных машин (X) |
| 75 | 2 |
| 35 | 10 |
Из наших известных данных мы можем использовать регрессию формула (расчеты не показаны) для вычисления значений и и получения следующее уравнение: Y= 85 + (-5) X, где
Y средняя скорость автомобилей на автостраде
a=85 или средняя скорость при X=0
b=(-5), влияние на Y каждого дополнительного патруля автомобиль развернут
X — количество развернутых патрульных машин
То есть средняя скорость автомобилей на
шоссе, когда не работают дорожные патрули (X = 0), будет 85
миль в час Для каждой дополнительной патрульной машины, работающей на шоссе, средняя скорость
упадет на 5 км/ч. ) на
это, или называется Y-шляпа. Это относится к прогнозируемому значению Y. Обычная
Y относится к наблюдаемым значениям Y в наборе данных, используемом для расчета
уравнение регрессии.
) на
это, или называется Y-шляпа. Это относится к прогнозируемому значению Y. Обычная
Y относится к наблюдаемым значениям Y в наборе данных, используемом для расчета
уравнение регрессии.
Вы можете увидеть символы альфа (а)
и бета (b) написаны греческими буквами, или вы можете увидеть их написанными английскими буквами
буквы. Коэффициент независимой переменной может иметь нижний индекс,
как и термин для X, например, b 1 X 1 (это часто встречается при множественной регрессии).
ОЦЕНКА УРАВНЕНИЕ РЕГРЕССИИ
Теперь у нас есть уравнение регрессии. Но как хорошо это уравнение при прогнозировании значений Y для заданных значений X? Для этого оценки, обратимся к мерам ассоциации и мерам статистической значения, которые используются с уравнениями регрессии.
р 2
r 2 является мерой ассоциации;
он представляет собой процент дисперсии значений Y, который может быть
объясняется знанием значения X. r 2 варьируется от минимума
0,0 (ни одна из дисперсий не объяснена), до максимума +1,0 (все
разница объясняется).
r 2 варьируется от минимума
0,0 (ни одна из дисперсий не объяснена), до максимума +1,0 (все
разница объясняется).
СЭБ
s.e.b — стандартная ошибка вычисленного
значение б. Стьюдентный критерий статистической значимости коэффициента
проводится путем деления значения b на его стандартную ошибку. По правилу
thumb, значение t больше 2,0 обычно является статистически значимым.
но вы должны проконсультироваться с t-таблицей, чтобы быть уверенным. Если
значение t указывает на то, что коэффициент b является статистически значимым,
это означает, что независимая переменная или X (количество развернутых патрульных машин)
следует сохранить в уравнении регрессии, так как оно имеет статистически
значимая связь с зависимой переменной или Y (средняя скорость
в милях в час). Если отношений не было
статистически значимым, значение коэффициента b будет (статистически
говоря) неотличимы от нуля.
Ф
F — тест на статистическую значимость
уравнения регрессии в целом. Получается путем деления объясненного
дисперсия необъяснимой дисперсией. По эмпирическому правилу значение F больше
чем 4,0, как правило, статистически значимо, но вы должны свериться с F-таблицей
быть уверенным. Если F значимо, то уравнение регрессии помогает нам
понять связь между X и Y.
Получается путем деления объясненного
дисперсия необъяснимой дисперсией. По эмпирическому правилу значение F больше
чем 4,0, как правило, статистически значимо, но вы должны свериться с F-таблицей
быть уверенным. Если F значимо, то уравнение регрессии помогает нам
понять связь между X и Y.
Допустим, для нашего примера выше мы получили следующие значения:
г 2 = .9
Зная значение X (количество
автомобилей), мы можем объяснить 90% дисперсии Y (средняя скорость
автомобилистов на трассе).
СЭБ = 1,5
Разделив b на s.e.b, получим значение t
= -5/1,5 = -3,3. Просматривая t-таблицу, мы находим, что коэффициент равен
статистически значимый. Это означает, что независимая переменная X (число
развернутых патрульных машин) следует оставить в уравнении регрессии, поскольку
имеет статистически значимую связь с зависимой переменной
Y (средняя скорость в милях в час).
Ф= 8,4
Из F-таблицы мы видим, что регрессия
уравнение в целом является статистически значимым. Это означает, что уравнение регрессии помогает нам понять
отношения между X и Y.
Это означает, что уравнение регрессии помогает нам понять
отношения между X и Y.
ЭТАПЫ ЛИНЕЙНОЙ РЕГРЕССИИ
1. Сформулируйте гипотезу.2. Сформулируйте нулевую гипотезу
3. Соберите данные.
4. Вычислить уравнение регрессии
5. Изучить тесты статистически значимых и меры ассоциации
6. Свяжите статистические данные с гипотезой. Примите или отклоните нулевую гипотезу.
7. Отклонить, принять или пересмотреть исходную гипотезу. Вносить предложения по дизайну исследования и управлению аспектами проблемы.
Пример: автопарк хочет знать, стоит ли больше для обслуживания автомобилей, которые ездят чаще.
Гипотеза: затраты на обслуживание зависят от
пробег автомобиля
Нулевая гипотеза: нет связи между
пробег и стоимость обслуживания
Зависимая переменная: Y — стоимость в долларах
ежегодное техническое обслуживание автомобиля
Независимая переменная: X — годовой пробег. на том же автомобиле
на том же автомобиле
Данные собираются по каждому автомобилю автопарка,
относительно количества миль, пройденных в данном году, и затрат на техническое обслуживание
для этого года. Вот образец собранных данных.
| Номер автомобиля | Пройдено миль (X) | Затраты на ремонт (Д) |
| 1 | 80 000 | 1200 долларов |
| 2 | 29 000 | 150 долларов |
| 3 | 53 000 | 650 долларов |
| 4 | 13 000 | 200 долларов |
| 5 | 45 000 | 325 долларов |
Уравнение регрессии вычисляется как (вычисления не показано): Y = 50 + 0,03 X
Например, если X=50 000, то Y = 50 + 0,03 (50 000) = 1550 долларов США
а=50 или стоимость обслуживания при X=0; если на машине нет пробега, то годовая стоимость обслуживания = $50
b=. 03 значение, которое Y увеличивается для каждой единицы
увеличение Х; за каждую дополнительную милю пробега (X) стоимость годового обслуживания
увеличивается на 0,03 доллара США
03 значение, которое Y увеличивается для каждой единицы
увеличение Х; за каждую дополнительную милю пробега (X) стоимость годового обслуживания
увеличивается на 0,03 доллара США
s.e.b = .0005; значение b разделить по с.э.б=60,0; t-таблица показывает, что коэффициент b для X статистически значимый (это связано с Y)
r 2 = 0,90 мы можем объяснить 90% разницы в стоимости ремонта разных автомобилей если мы знаем пробег каждого автомобиля
Заключение: отвергнуть нулевую гипотезу об отсутствии связи
и принять исследовательскую гипотезу о том, что пробег влияет на стоимость ремонта.
ПРЕДПОЛОЖЕНИЯ ЛИНЕЙНОЙ РЕГРЕССИИ
- Теоретически существует несколько важных предположений. это должно быть выполнено, если будет использоваться линейная регрессия. Это:
- 1. И независимый (X), и зависимый
(Y) переменные измеряются на уровне интервалов или отношений.

- 2. Отношения между независимыми (X) и зависимой (Y) переменных является линейной.
- 3. Ошибки предсказания значения Y распределены так, что приближаются к нормальной кривой.
- 4. Ошибки предсказания значения Y все независимы друг от друга.
- 5. Распределение ошибок предсказания значения Y остается постоянным независимо от значения X.
Существует ряд расширенных статистических
тесты, которые можно использовать для проверки того, верны ли эти предположения.
истинно для любого заданного уравнения регрессии. Однако они выходят за рамки
этого обсуждения.
ВРЕМЯ СЕРИЯ РЕГРЕССИЯ
Линейная регрессия полезна для изучения взаимосвязи независимой переменной, которая отмечает переход времени к зависимой переменной при линейной зависимости; то есть, когда в данных очевидна нисходящая или восходящая тенденция через некоторое время.
Однако, если тренд зависимой переменной во времени нелинейна, то линейная регрессия не зафиксирует отношения. Линейная регрессия не может уловить сезонные, циклические и контрциклические тенденции в данных временных рядов. Ни то, ни другое линейная регрессия фиксирует влияние изменений направления временных рядов данные, ни изменения скорости изменения во времени. Для регрессии временных рядов важно получить график данных с течением времени и проверить его на предмет возможные нелинейные тенденции.
Тоже проблема
если значения в одной точке временного ряда детерминированы или сильно
под влиянием значений в предыдущий момент времени. Это называется автокорреляцией.
Это происходит, когда значения зависимой переменной во времени не
случайно распределены.
- Линейная регрессия может
использоваться с прерванными исследованиями временных рядов. Например, скажите
реализуется политика по снижению количества несчастных случаев среди подростков
водители.

- 1. Данные собираются как минимум за 20 или 30 периоды времени (месяцы или кварталы) до реализации политики, и затем еще в течение 20 или 30 периодов времени после реализации политики.
- 2. Одна линейная регрессия выполняется для данные аварийности за дополитические периоды времени.
- 3. Выполняется еще одна линейная регрессия для данных аварийности за постполитический период времени.
- 4. Должны быть различия в значениях константы, коэффициента b, s.e.b и r 2 для двух уравнений.
Если есть разница
между двумя уравнениями, то политика оказала влияние. Если все
точки данных (как до, так и после) были включены в уравнение регрессии,
сумма объясненной дисперсии (r 2 ) была бы довольно низкой. Этот
потому что, если есть изменение после того, как политика введена, тенденция
уже не является линейным. Вместо этого есть два разных линейных тренда, один
до того, как политика была введена, и другая, другая, после того, как она была
представил.
При настройке данных
для регрессии временных рядов исследователь должен помнить о нумерации
лет (или других периодов времени) последовательно с 1 по n. Эти
значения для независимой (X) переменной. Значение зависимой переменной
это аварийность. Например,
| Независимая переменная (X) — Год | Зависимая переменная (Y) — аварийность |
| 1 | 50 000 |
| 2 | 51 000 |
| 3 | 52 000 |
| 4 | 53 000 |
Линейная регрессия
Линейная регрессияК документам
Уравнение регрессии
Прогнозируемые значения и остатки
- Фактическое значение зависимой переменной равно
у 9 и .

- несмещенными: имеют нулевое среднее значение в любой тонкой вертикали
полоса и
homoscedastic , что означает «тот же участок»: распространение остатки должны быть одинаковыми в любой тонкой вертикальной полосе.
- (а) Беспристрастный и гомоскедастический. Остатки в среднем равны нулю в каждом
тонкая вертикальная полоса, а SD одинакова по всему участку.
(b) Смещенный и гомоскедастический. Остатки имеют линейный характер, вероятно, из-за скрытой переменной, не включенной в эксперимент.
(c) Смещенный и гомоскедастический. Остатки показывают квадратичный образец,
возможно, из-за нелинейной зависимости. Иногда переменная
преобразование устранит предвзятость.
г) беспристрастный, но гомоскедастический. SD мал для слева от графика и большой справа: остатки гетероскадастичны.
(e) Смещенный и гетероскедастический. Узор линейный.
(f) Смещенный и гетероскедастический. Схема квадратичная.
Среднеквадратическая ошибка
- Среднеквадратическая ошибка (RMSE) для регрессионной модели равна похожий на стандартное отклонение (SD) для идеальной модели измерения.
- Мы можем записать это как аналогию Миллера:
- RMSE : регрессионная модель :: SD : идеальная модель измерения
- SD оценивает отклонение от выборочного среднего Икс.
- RMSE оценивает отклонение фактических значений y от
линия регрессии. Другой способ сказать, что это
оценивает стандартное отклонение значений y
в тонкий вертикальный прямоугольник.


 Путем осмотра оцените, является ли функция действительной
Путем осмотра оцените, является ли функция действительной
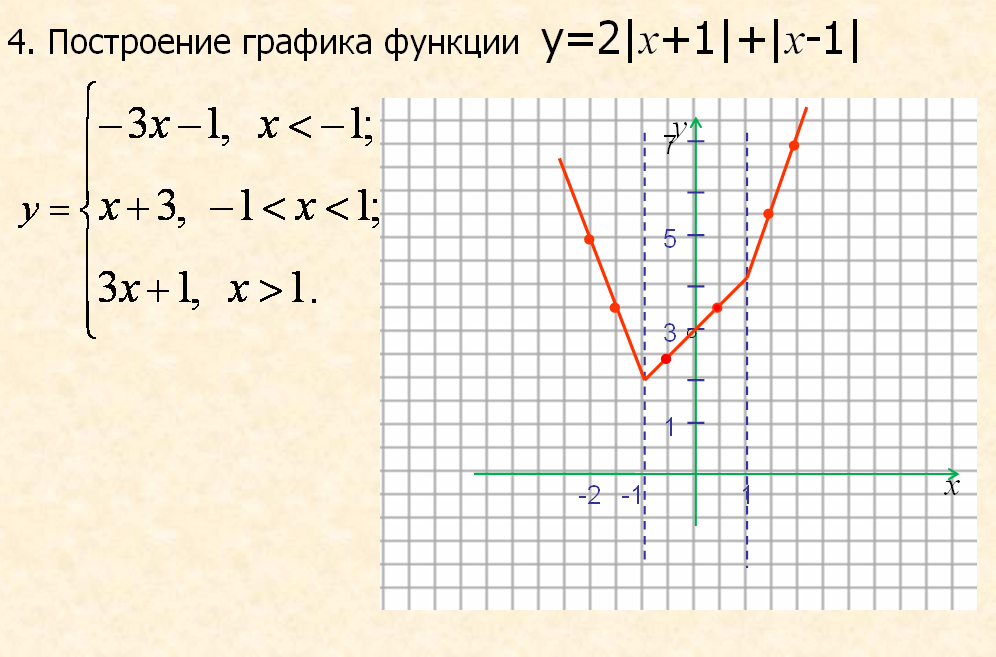 Является ли функция тригонометрической функцией? Они также имеют очень хорошо известную и характерную форму
Является ли функция тригонометрической функцией? Они также имеют очень хорошо известную и характерную форму
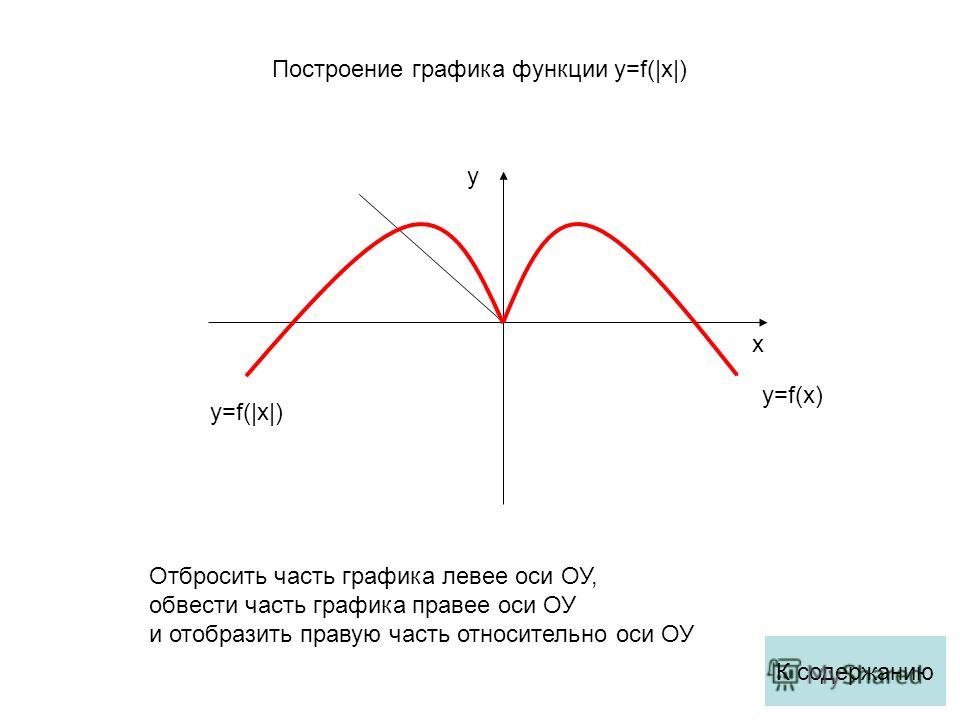 д.) могут быть идентифицированы, поскольку их тоже легко изобразить на графике
д.) могут быть идентифицированы, поскольку их тоже легко изобразить на графике
 (абсолютное значение),
график абсолютного значения
(абсолютное значение),
график абсолютного значения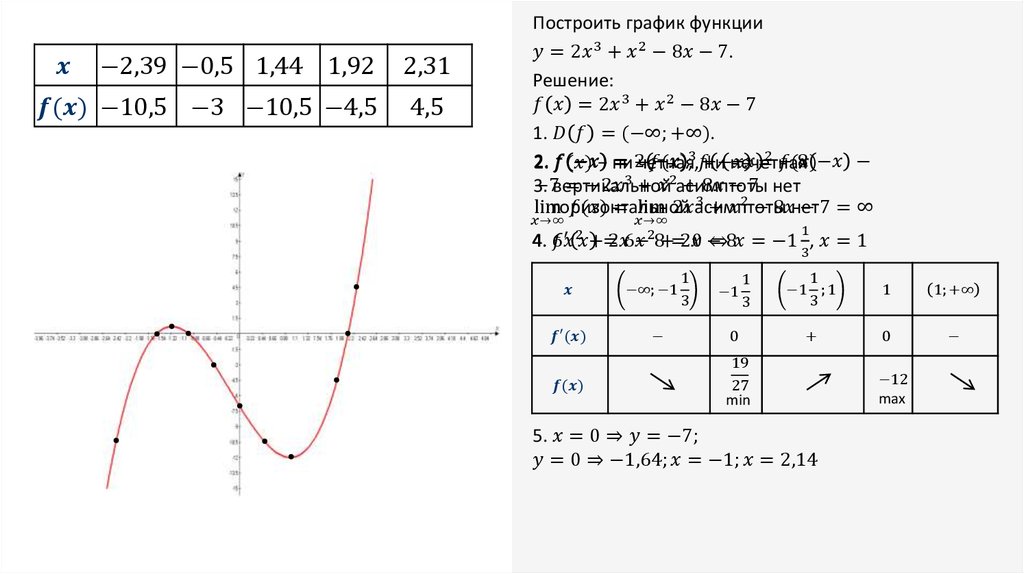 Вы можете выразить бесконечные интервалы в записи интервалов, используя inf для бесконечности.
Вы можете выразить бесконечные интервалы в записи интервалов, используя inf для бесконечности.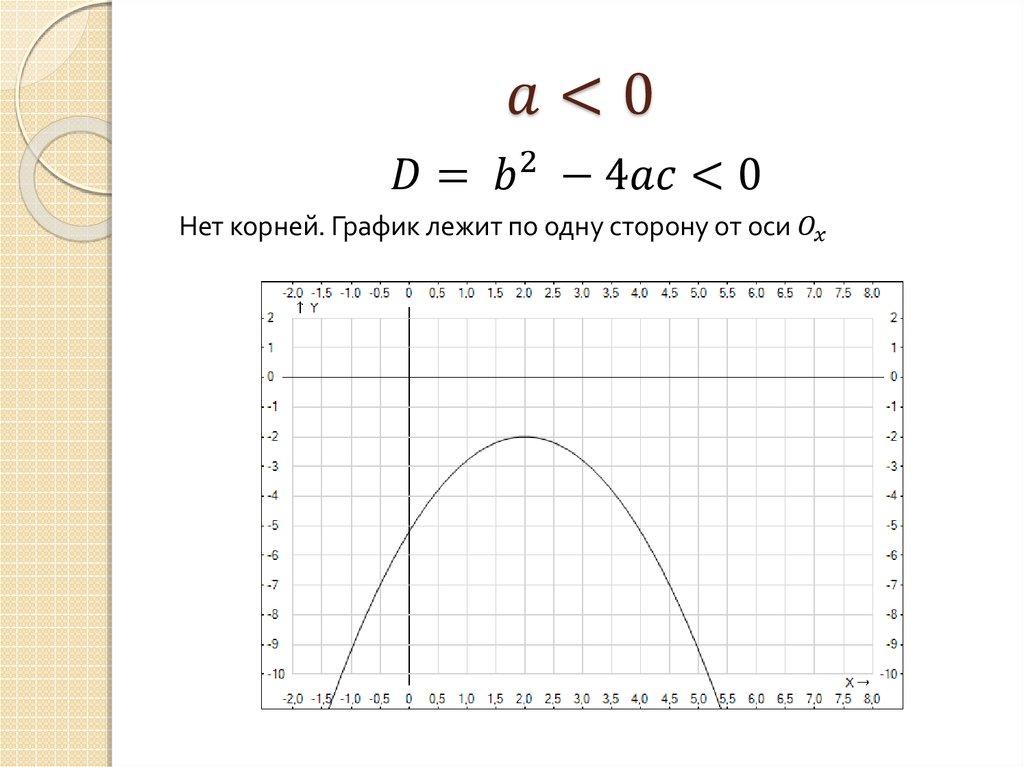 В декартовой (триггерной) сетке вы вводите границы сетки по оси x в терминах π, и метки сетки для обыкновенных дробей π будут отображаться как точные значения (например, π/6), а не десятичные приближения. Если расстояние между метками не имеет общепринятого знаменателя, метка по-прежнему будет выражаться в виде π, но с использованием десятичных приближений вместо точных дробей. GraphFree считает целые числа и дроби со знаменателем 2, 3, 4, 6, 8, 12, 16, 24 и 48 широко используемыми дробями, которые могут отображаться как точные значения.
В декартовой (триггерной) сетке вы вводите границы сетки по оси x в терминах π, и метки сетки для обыкновенных дробей π будут отображаться как точные значения (например, π/6), а не десятичные приближения. Если расстояние между метками не имеет общепринятого знаменателя, метка по-прежнему будет выражаться в виде π, но с использованием десятичных приближений вместо точных дробей. GraphFree считает целые числа и дроби со знаменателем 2, 3, 4, 6, 8, 12, 16, 24 и 48 широко используемыми дробями, которые могут отображаться как точные значения.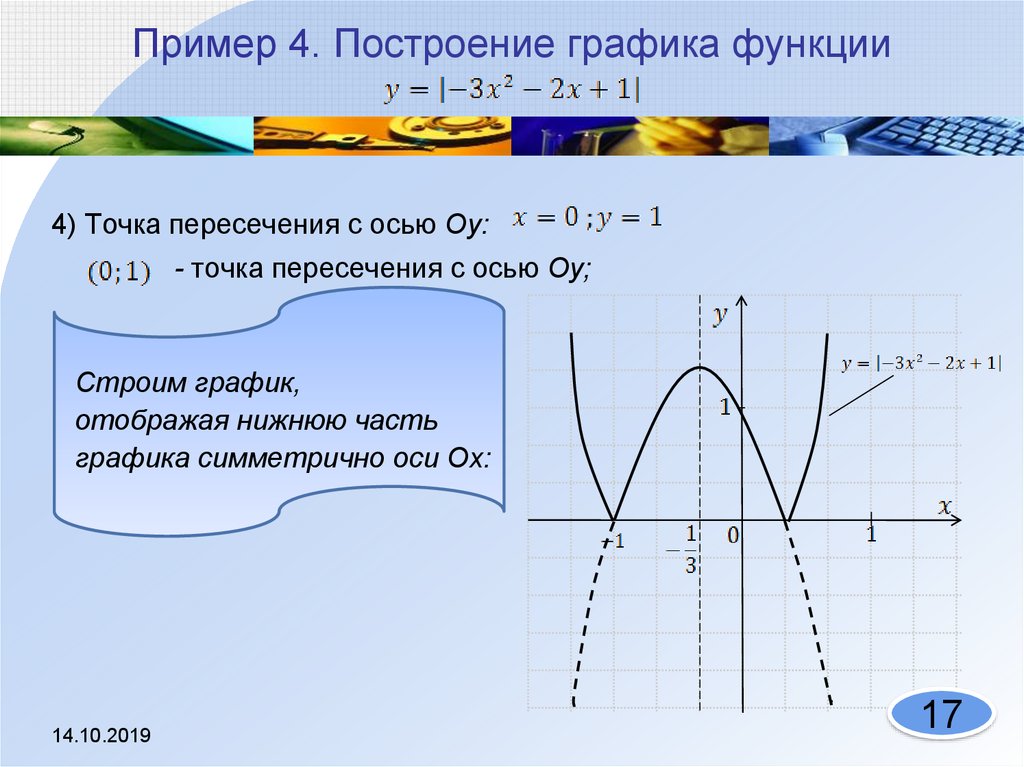
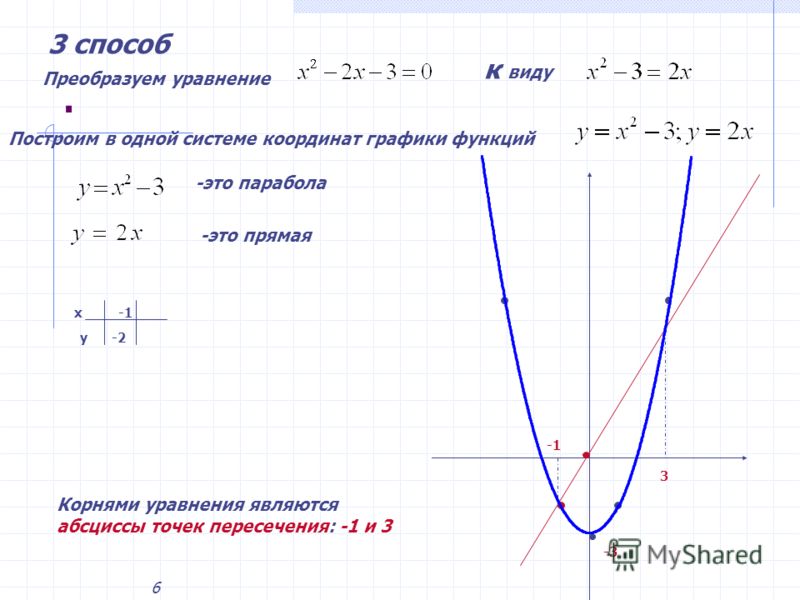 )
)
 Если вы введете точки слишком близко к границам области, GraphFree может ошибочно подумать, что область уже закрашена, и поэтому не закрасит ее «снова».
Если вы введете точки слишком близко к границам области, GraphFree может ошибочно подумать, что область уже закрашена, и поэтому не закрасит ее «снова».




 Если квадрат должен быть, то результат: … = (а8 + b8)2 — 2а8b8 = а16 + b16.
Если квадрат должен быть, то результат: … = (а8 + b8)2 — 2а8b8 = а16 + b16. С-21. № 6. ГДЗ Алгебра 7 класс Звавич. Замените значок * таким выражением, чтобы выполнялось равенство
С-21. № 6. ГДЗ Алгебра 7 класс Звавич. Замените значок * таким выражением, чтобы выполнялось равенство

 Применяем тот же прием, что и в предыдущей задаче.
Применяем тот же прием, что и в предыдущей задаче.
 Сравним значения функции в точке максимума и на конце отрезка, то есть при и
Сравним значения функции в точке максимума и на конце отрезка, то есть при и Значит, точка — точка максимума функции . Других точек экстремума на отрезке функция не имеет, и наибольшее значение функции на отрезке достигается при
Значит, точка — точка максимума функции . Других точек экстремума на отрезке функция не имеет, и наибольшее значение функции на отрезке достигается при
 Презентация содержит 17 слайдов. Можно
использовать презентацию на нескольких уроках,
она содержит дополнительный материал (слайды
14-17). Со слайда 8 есть гиперссылка на Презентацию 2
(развертки куба). Презентация 2 содержит 1 слайд,
на котором изображены 11 разверток куба (они
являются ссылками на видеоролики). На уроке
использована интерактивная доска MIMIO, а также
учащиеся работают на компьютерах (выполнение
практической работы).
Презентация содержит 17 слайдов. Можно
использовать презентацию на нескольких уроках,
она содержит дополнительный материал (слайды
14-17). Со слайда 8 есть гиперссылка на Презентацию 2
(развертки куба). Презентация 2 содержит 1 слайд,
на котором изображены 11 разверток куба (они
являются ссылками на видеоролики). На уроке
использована интерактивная доска MIMIO, а также
учащиеся работают на компьютерах (выполнение
практической работы). 3).
3). Анимация построения правильной
шестиугольной призмы с обозначением ее основных
элементов (Рис. 5).
Анимация построения правильной
шестиугольной призмы с обозначением ее основных
элементов (Рис. 5). Конус – тело вращения,
образованное вращением прямоугольного
треугольника вокруг оси, проходящей через один
из его катетов (Рис.9).
Конус – тело вращения,
образованное вращением прямоугольного
треугольника вокруг оси, проходящей через один
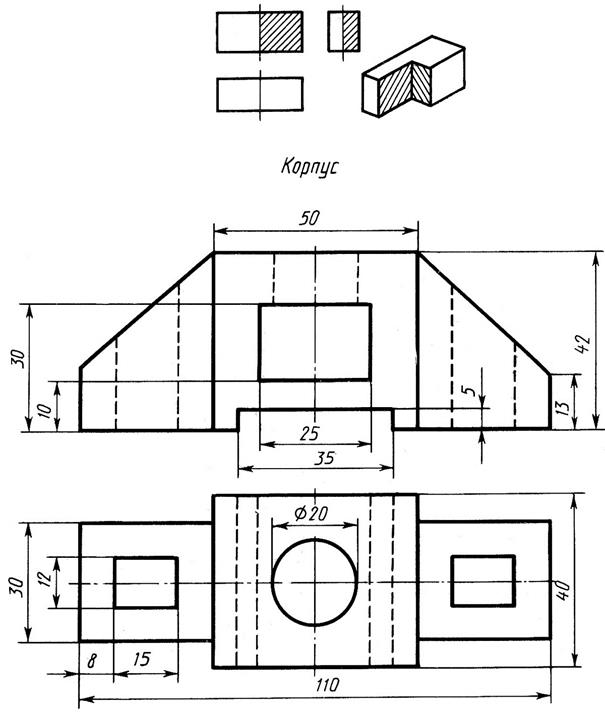
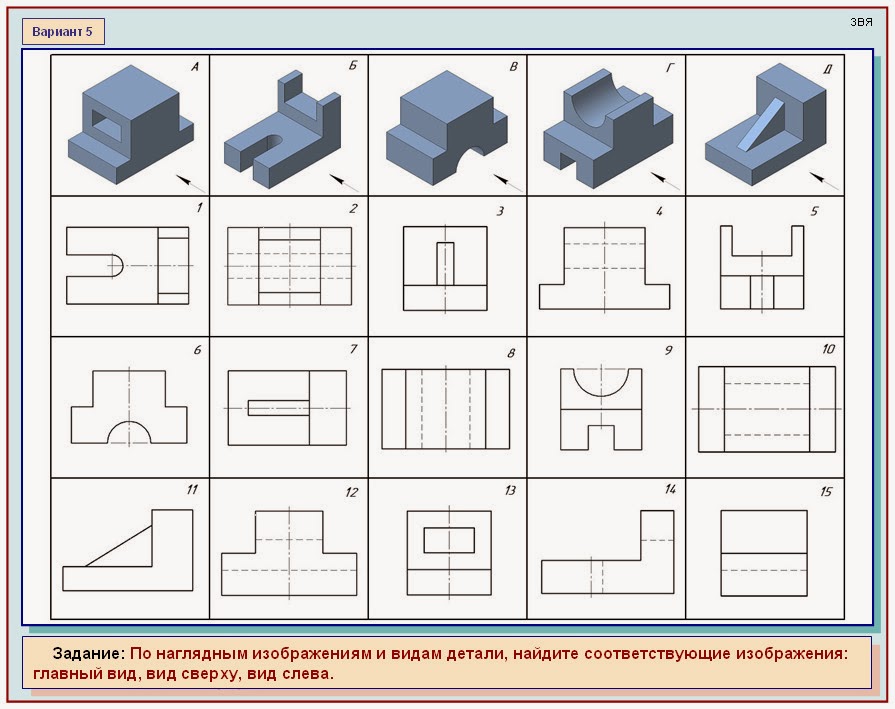
из его катетов (Рис.9). Дана треугольная правильная
призма. В основании лежит правильный
треугольник. Высота призмы = 70 мм, а сторона
основания = 40 мм. Рассматриваем призму
(направление главного вида показано стрелкой),
определяем плоские фигуры, который мы увидим на
виде спереди, сверху и слева. Вытаскиваем
изображения видов и расставляем на поле чертежа
(Рис. 13).
Дана треугольная правильная
призма. В основании лежит правильный
треугольник. Высота призмы = 70 мм, а сторона
основания = 40 мм. Рассматриваем призму
(направление главного вида показано стрелкой),
определяем плоские фигуры, который мы увидим на
виде спереди, сверху и слева. Вытаскиваем
изображения видов и расставляем на поле чертежа
(Рис. 13).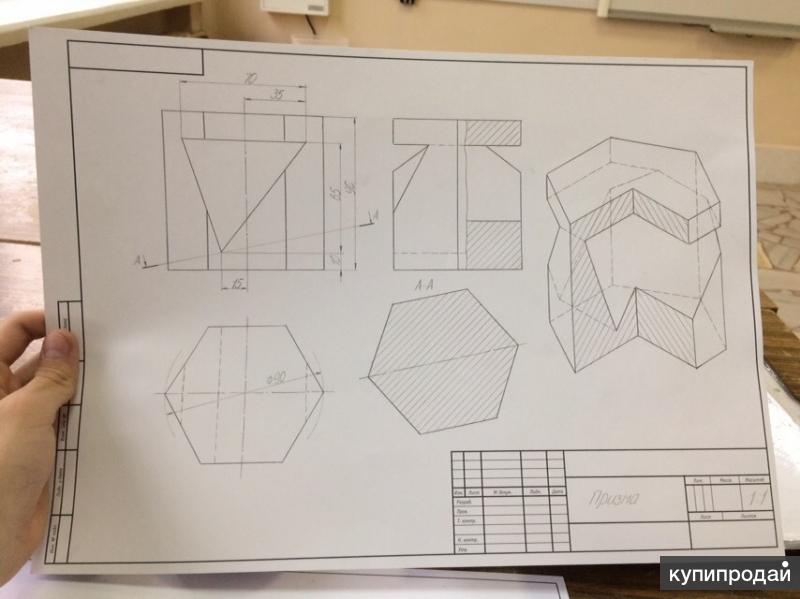
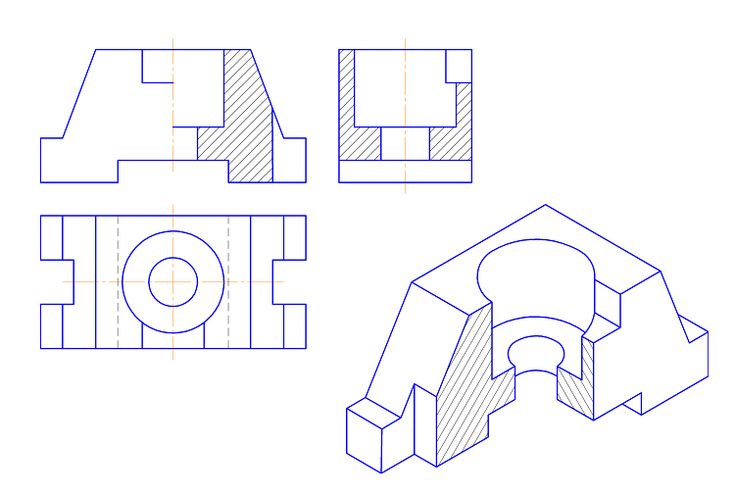
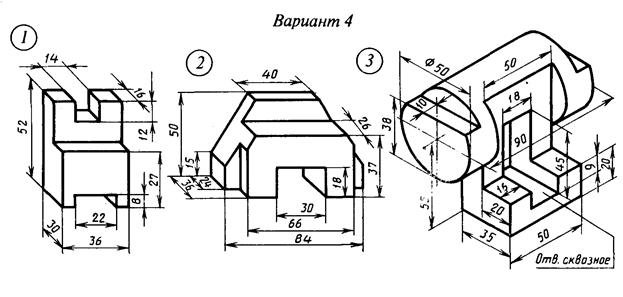 Под фигурой понимают любую совокупность (множество) точек. Всякую сложную фигуру можно разделить на более простые.
Под фигурой понимают любую совокупность (множество) точек. Всякую сложную фигуру можно разделить на более простые.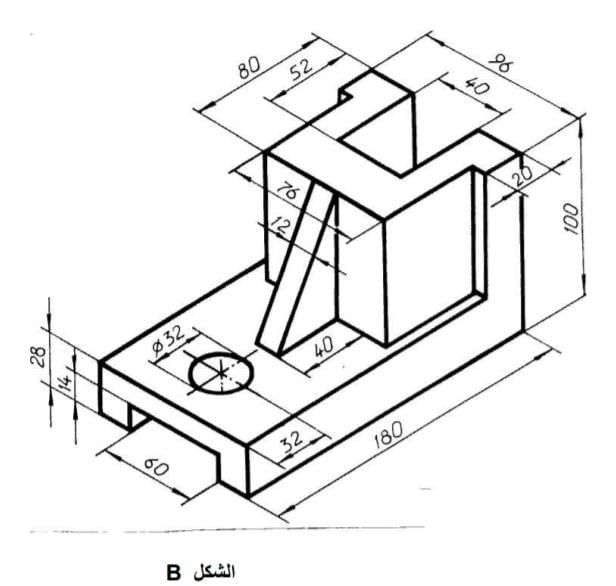 Плоскость является частным случаем поверхности.
Плоскость является частным случаем поверхности. Поэтому рассмотрим сначала построение чертежей и аксонометрических проекций простых тел. Это тем более необходимо, так как в сложной форме любого предмета всегда можно выделить простые геометрические тела, которые помогают представить форму предмета по его чертежу.
Поэтому рассмотрим сначала построение чертежей и аксонометрических проекций простых тел. Это тем более необходимо, так как в сложной форме любого предмета всегда можно выделить простые геометрические тела, которые помогают представить форму предмета по его чертежу.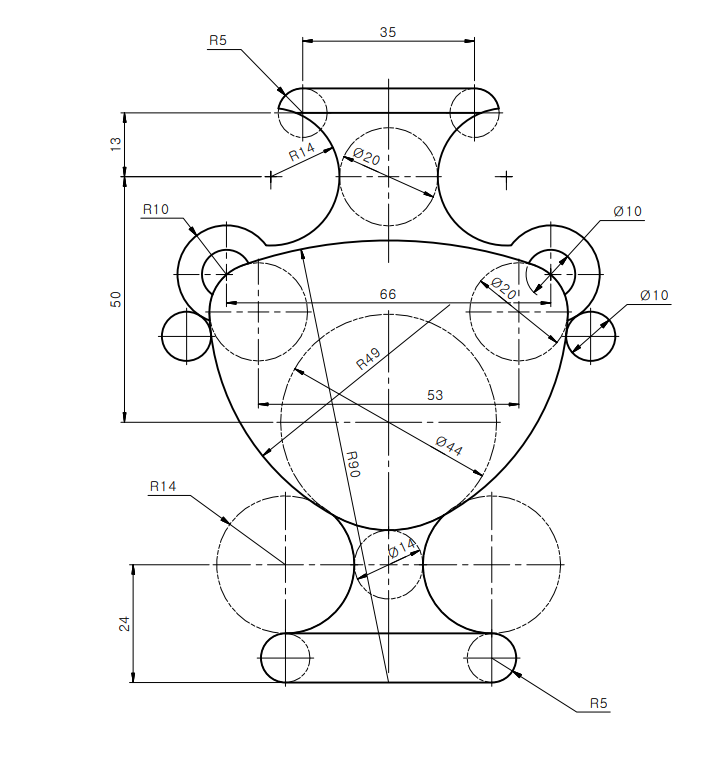 3. Шестиугольная призма.
3. Шестиугольная призма. 5. Цилиндр
5. Цилиндр
 К геометрическим свойствам предметов относятся: размеры, пропорции, взаимное расположение составляющих элементов формы.
К геометрическим свойствам предметов относятся: размеры, пропорции, взаимное расположение составляющих элементов формы.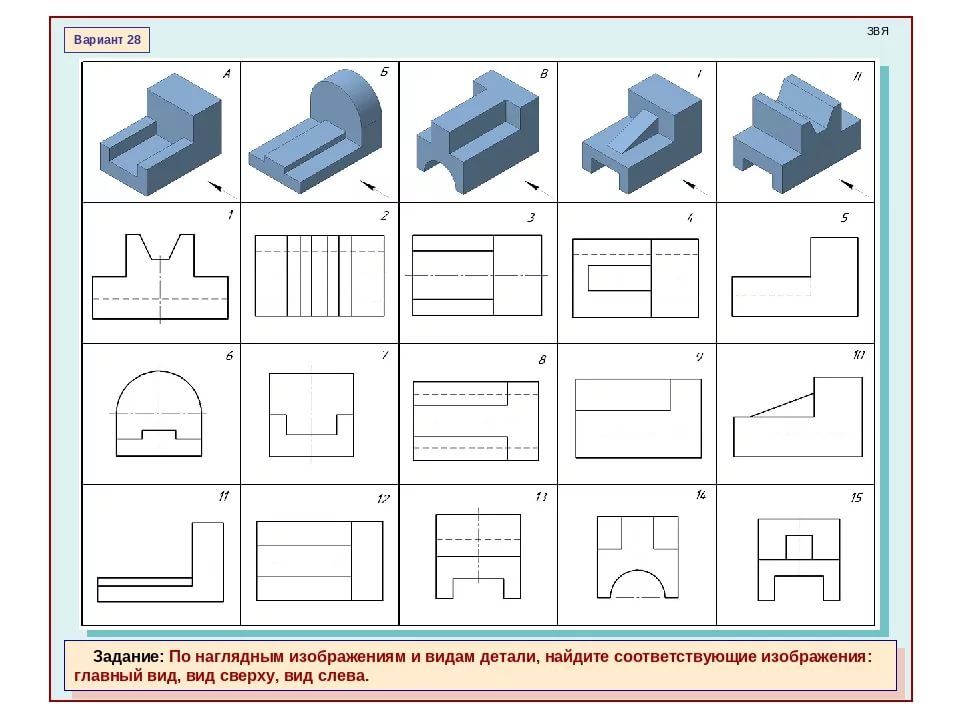 Для этой цели сложную по форме деталь мысленно разделяют на отдельные конструктивные части, имеющие форму различных геометрических тел. Мысленное разделение предмета на основные геометрические тела называют анализом геометрической формы предмета. Используя изображение детали, размерные числа, условные знаки и надписи, можно воссоздать образ детали, т. е. представить по чертежу ее пространственную форму.
Для этой цели сложную по форме деталь мысленно разделяют на отдельные конструктивные части, имеющие форму различных геометрических тел. Мысленное разделение предмета на основные геометрические тела называют анализом геометрической формы предмета. Используя изображение детали, размерные числа, условные знаки и надписи, можно воссоздать образ детали, т. е. представить по чертежу ее пространственную форму.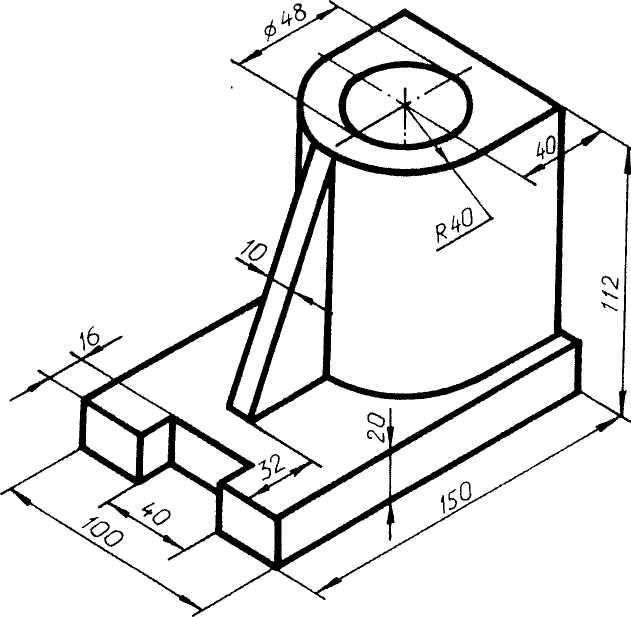
 Этот предмет не только почитается за его эстетические качества, но и является долгожданным вызовом для художников. Постоянно меняющиеся положения и позы фигуры лишают возможности формул и заставляют художника сосредоточиться на чистом наблюдательном рисунке.
Этот предмет не только почитается за его эстетические качества, но и является долгожданным вызовом для художников. Постоянно меняющиеся положения и позы фигуры лишают возможности формул и заставляют художника сосредоточиться на чистом наблюдательном рисунке.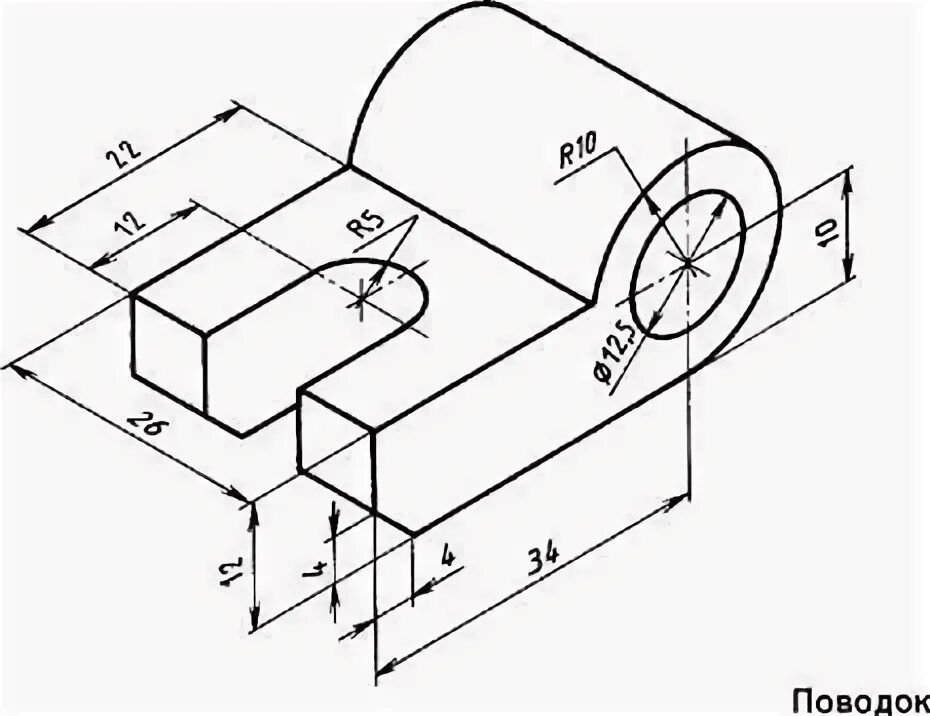 Это отлично подходит для практики, делая рисунки жестами подходящим способом быстро заполнить альбом для рисования.
Это отлично подходит для практики, делая рисунки жестами подходящим способом быстро заполнить альбом для рисования.
 Если вы начнете стирать ошибки или случайные линии во время работы, вы потеряете этот поток и будете отвлекаться. Помните, что суть не в том, чтобы создать законченный рисунок.
Если вы начнете стирать ошибки или случайные линии во время работы, вы потеряете этот поток и будете отвлекаться. Помните, что суть не в том, чтобы создать законченный рисунок.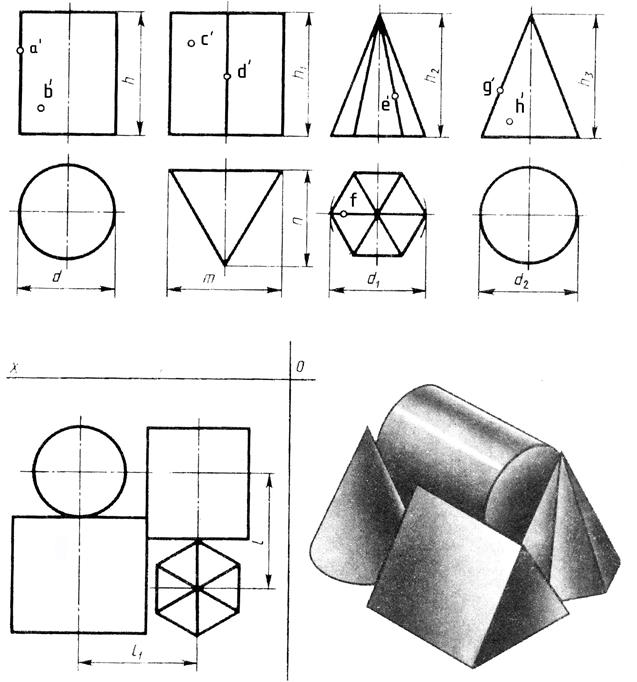

 3
(70)
3
(70)


 Рене покажет нам, как структура тела является ключом к расширению в различных стилях.
Рене покажет нам, как структура тела является ключом к расширению в различных стилях.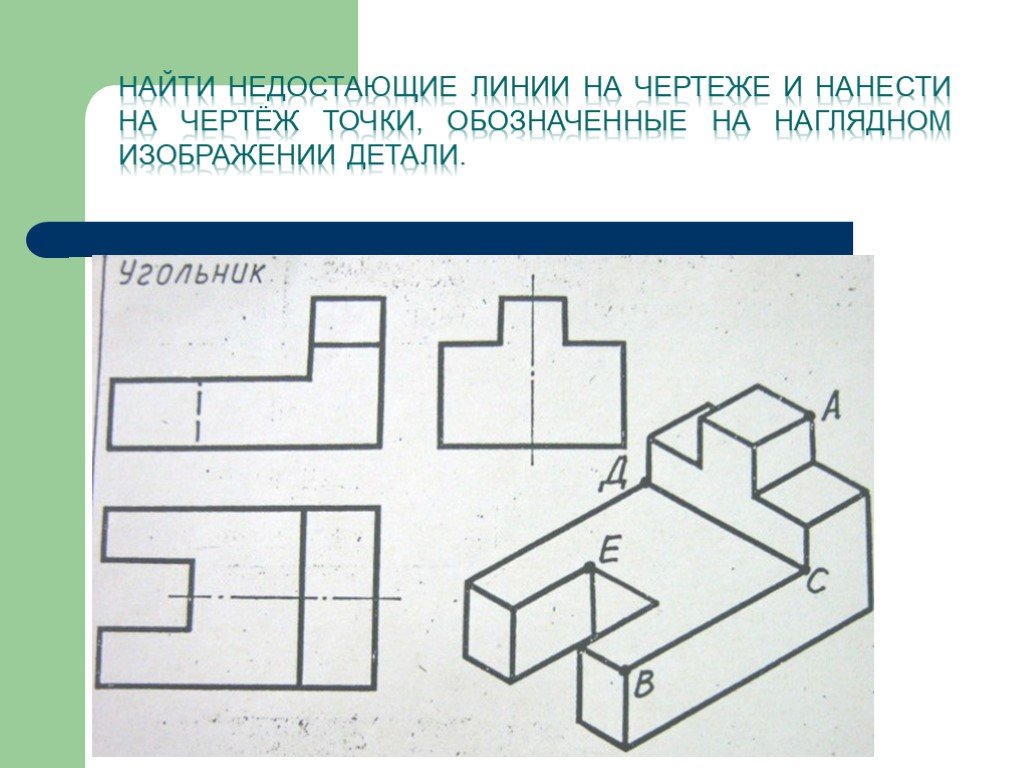
 Рене научит нас, как использовать измерения и собственный здравый смысл для получения желаемых результатов.
Рене научит нас, как использовать измерения и собственный здравый смысл для получения желаемых результатов.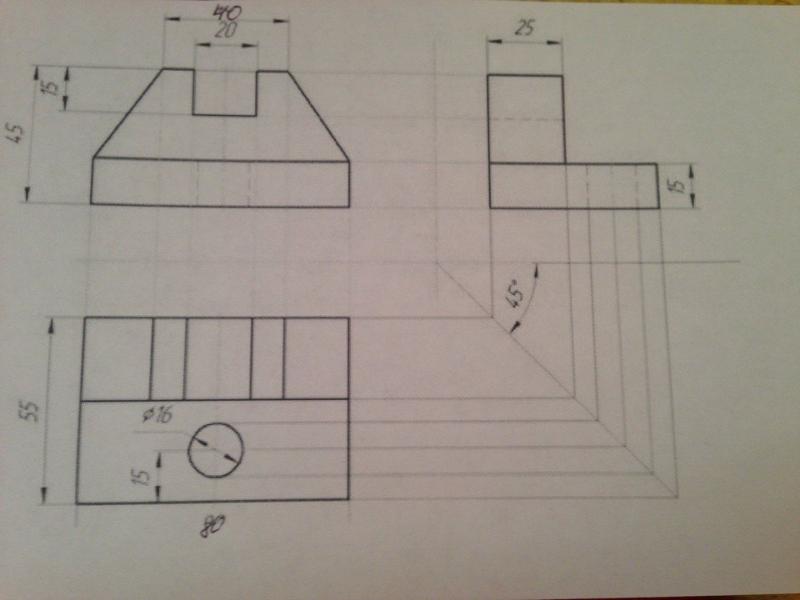 Мы также узнаем, как Рене лично использует свой альбом для рисования, и методы, которые он использует, чтобы получить максимальную отдачу от своих эскизов.
Мы также узнаем, как Рене лично использует свой альбом для рисования, и методы, которые он использует, чтобы получить максимальную отдачу от своих эскизов. У него есть несколько отличных советов, которые я ожидал бы от учителя рисования. Спасибо! Не могу дождаться, чтобы посмотреть больше!
У него есть несколько отличных советов, которые я ожидал бы от учителя рисования. Спасибо! Не могу дождаться, чтобы посмотреть больше!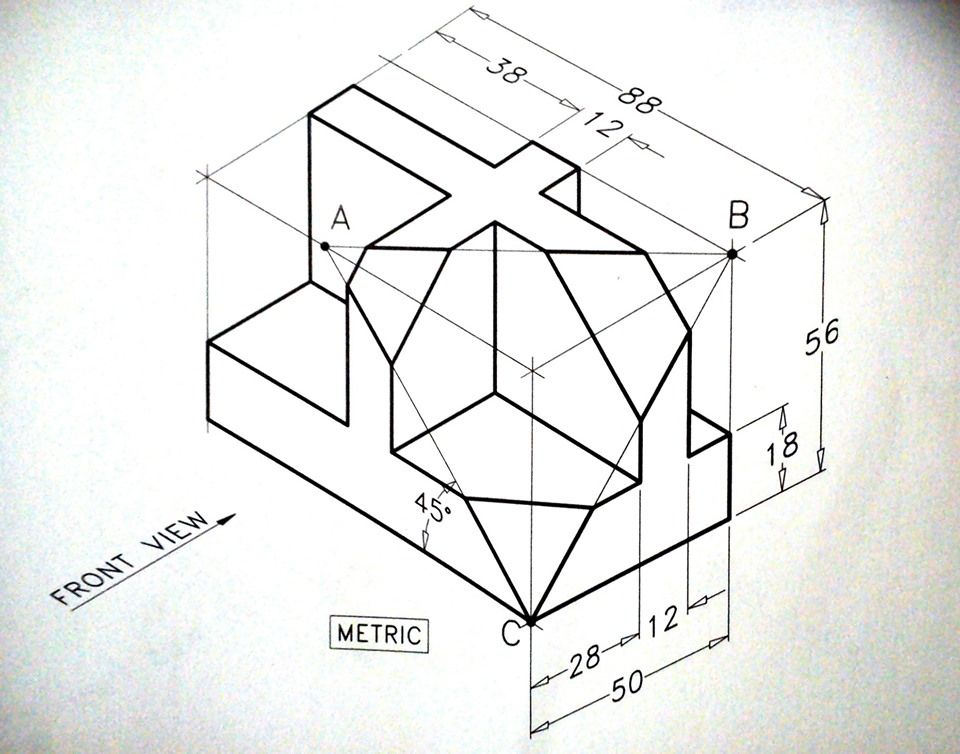 Большое спасибо!
Большое спасибо!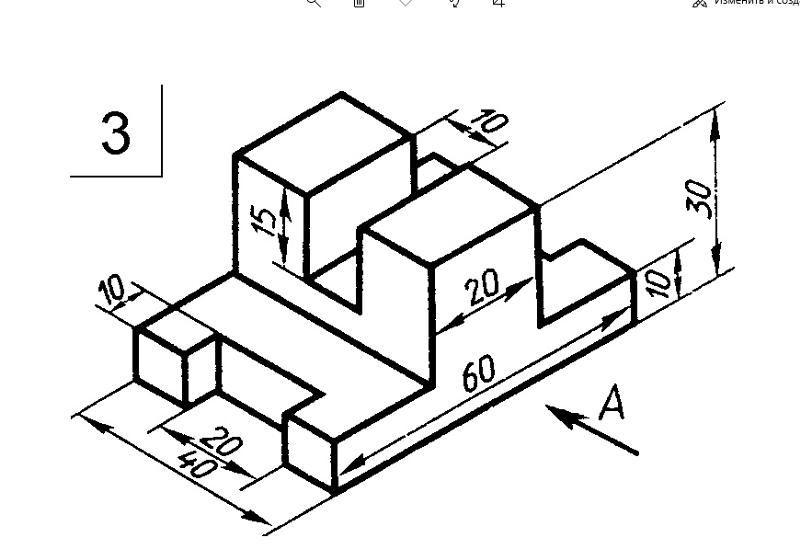 Мне очень, очень понравились эти занятия
Мне очень, очень понравились эти занятия Членство дает полный доступ к нашей потоковой платформе.
Членство дает полный доступ к нашей потоковой платформе.
 д.) с сайта, но не можете скачать видеоуроки на свой компьютер.
д.) с сайта, но не можете скачать видеоуроки на свой компьютер. Мы будем более чем рады предоставить вам полный возврат средств в течение 30 дней с момента вашей первой покупки. Никаких вопросов не было задано. Просто гарантия, которой можно доверять.
Мы будем более чем рады предоставить вам полный возврат средств в течение 30 дней с момента вашей первой покупки. Никаких вопросов не было задано. Просто гарантия, которой можно доверять.

 Чтобы получить единицу заполняем выражение соответствующими коэффициентами: y’ = 1 = 0 ⋅ x + 1 ⋅ 1
Чтобы получить единицу заполняем выражение соответствующими коэффициентами: y’ = 1 = 0 ⋅ x + 1 ⋅ 1
 Изменяя значения элементов матрицы преобразования, к объектам можно применять любые трансформации (например: масштабирование, зеркальное отражение, поворот, перемещение и т. п.). При любой трансформации сохраняется параллельность линий объекта.
Изменяя значения элементов матрицы преобразования, к объектам можно применять любые трансформации (например: масштабирование, зеркальное отражение, поворот, перемещение и т. п.). При любой трансформации сохраняется параллельность линий объекта.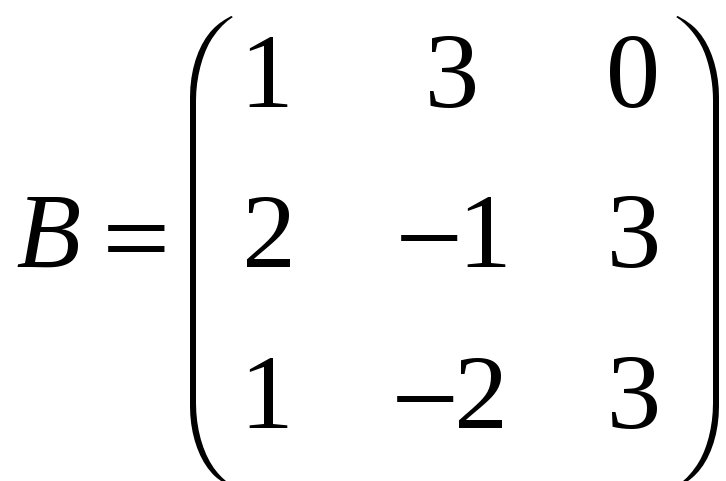 Такая матрица применяется по умолчанию, так как не приводит к трансформации. Поэтому единичную матрицу используют как основу.
Такая матрица применяется по умолчанию, так как не приводит к трансформации. Поэтому единичную матрицу используют как основу. Изменение значения b/-b — наклон вверх/вниз, c/-c – вправо/влево.
Изменение значения b/-b — наклон вверх/вниз, c/-c – вправо/влево.

 Если значение матрицы больше 1, объект расширяется, меньше 1 — сжимается.
Если значение матрицы больше 1, объект расширяется, меньше 1 — сжимается.

 У нас также есть квадратные матрицы более высоких порядков, например 4×4, 5×5 и так далее. Мы используем символ вертикальных линий || для обозначения матрицы.
У нас также есть квадратные матрицы более высоких порядков, например 4×4, 5×5 и так далее. Мы используем символ вертикальных линий || для обозначения матрицы.
 Матрица 2×2 будет получена после исключения строки и столбца, в которых присутствует элемент.
Матрица 2×2 будет получена после исключения строки и столбца, в которых присутствует элемент.






 Приглашайте членов команды, клиентов или заинтересованных лиц через Slack, электронную почту, общедоступную или частную гиперссылку по мере необходимости, чтобы каждый мог узнать подробности.
Приглашайте членов команды, клиентов или заинтересованных лиц через Slack, электронную почту, общедоступную или частную гиперссылку по мере необходимости, чтобы каждый мог узнать подробности. Используйте временную шкалу в качестве общей ссылки для дат начала, окончания и вех.
Используйте временную шкалу в качестве общей ссылки для дат начала, окончания и вех. Это отличное упражнение, когда должно произойти большое деловое событие — например, выпуск нового продукта или сессия стратегического планирования.
Это отличное упражнение, когда должно произойти большое деловое событие — например, выпуск нового продукта или сессия стратегического планирования.
 — графическое сокращение фразы С конца десятого по двенадцатый века и читаться она должна именно так. В редких контекстах возможны конструкции конец двенадцатого — четырнадцатый века, но и там двусмысленностей не возникает из-за разных падежей числительных. При этом в. — это сокращение от век, а вв. — от векА.
— графическое сокращение фразы С конца десятого по двенадцатый века и читаться она должна именно так. В редких контекстах возможны конструкции конец двенадцатого — четырнадцатый века, но и там двусмысленностей не возникает из-за разных падежей числительных. При этом в. — это сокращение от век, а вв. — от векА. Источник: http://rosental-book.ru/styli_xliv.html#sect195
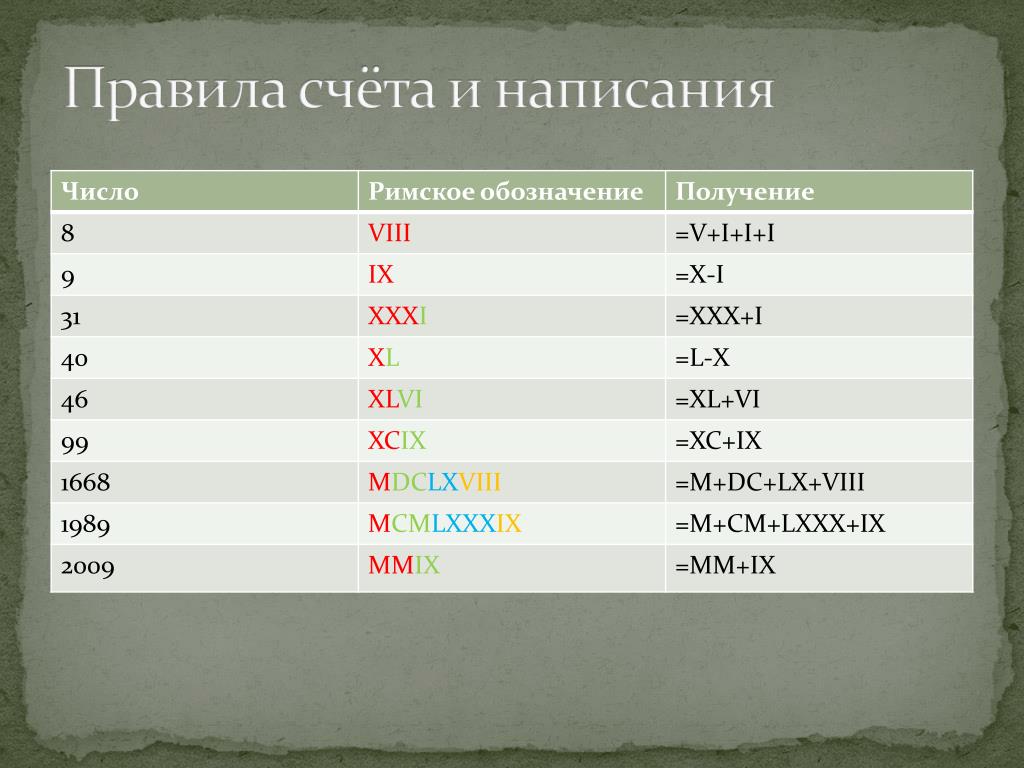
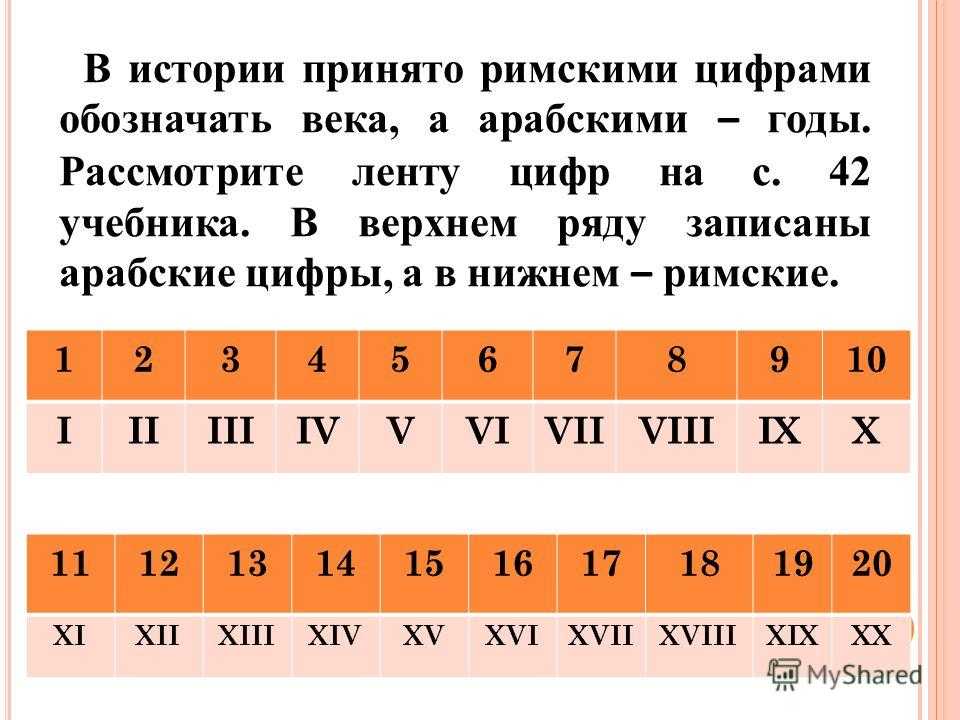
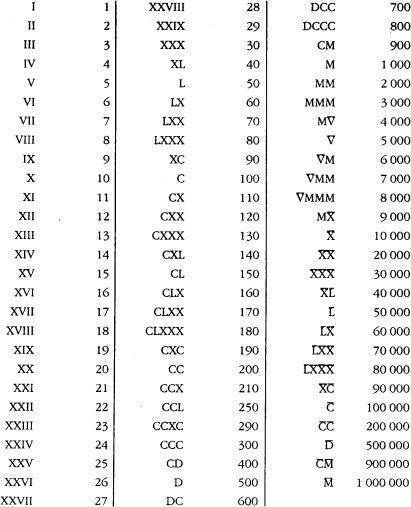
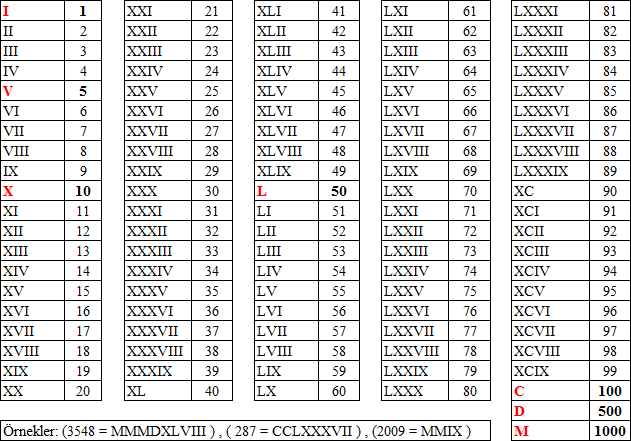
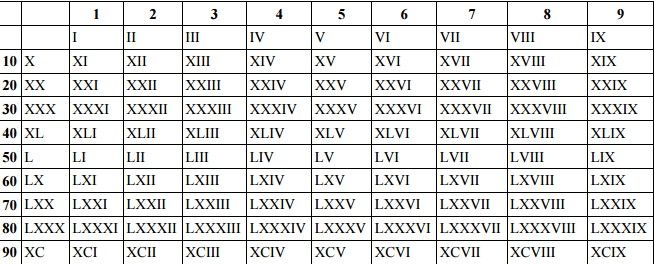
Источник: http://rosental-book.ru/styli_xliv.html#sect195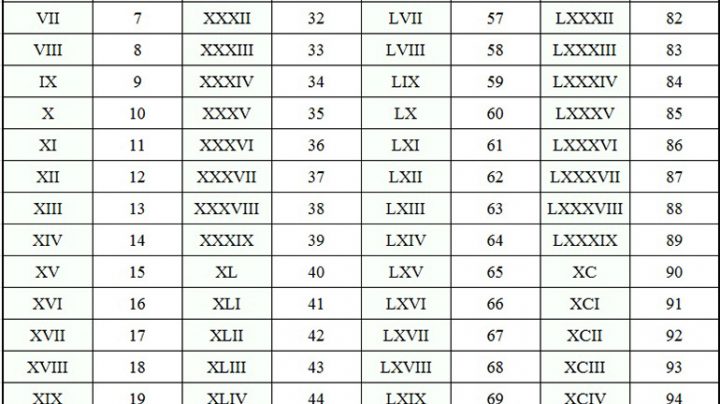 ru”. Изначально у меня не было идеи описывать римские цифры и говорить вообще про них. Цифры и цифры ничего в них такого нет. Но как-то в одном техническом отчете об инженерно-геологических изысканиях пришлось столкнуться с такими римскими цифрами как LXXVIII. Что это за число знаете? LXXVIII – это оказывается 78.
ru”. Изначально у меня не было идеи описывать римские цифры и говорить вообще про них. Цифры и цифры ничего в них такого нет. Но как-то в одном техническом отчете об инженерно-геологических изысканиях пришлось столкнуться с такими римскими цифрами как LXXVIII. Что это за число знаете? LXXVIII – это оказывается 78.
 Конкретный век начинается с года 01: двадцатый век начался в 1901 году и закончился в конце 2000 года, двадцать первый век начался в 2001 году и так далее. Столетия могут быть написаны разными стилями: цифрами, словами или их комбинацией, с апострофом или без него.
Конкретный век начинается с года 01: двадцатый век начался в 1901 году и закончился в конце 2000 года, двадцать первый век начался в 2001 году и так далее. Столетия могут быть написаны разными стилями: цифрами, словами или их комбинацией, с апострофом или без него.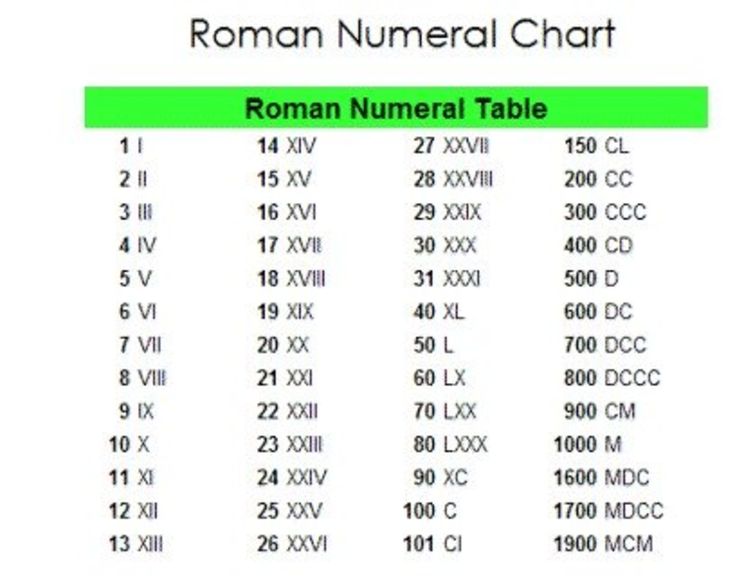 часто считается, что новое столетие начинается в год изменения цифр, например, когда год изменился с 9 на0014 19 99 до 20 00.
часто считается, что новое столетие начинается в год изменения цифр, например, когда год изменился с 9 на0014 19 99 до 20 00.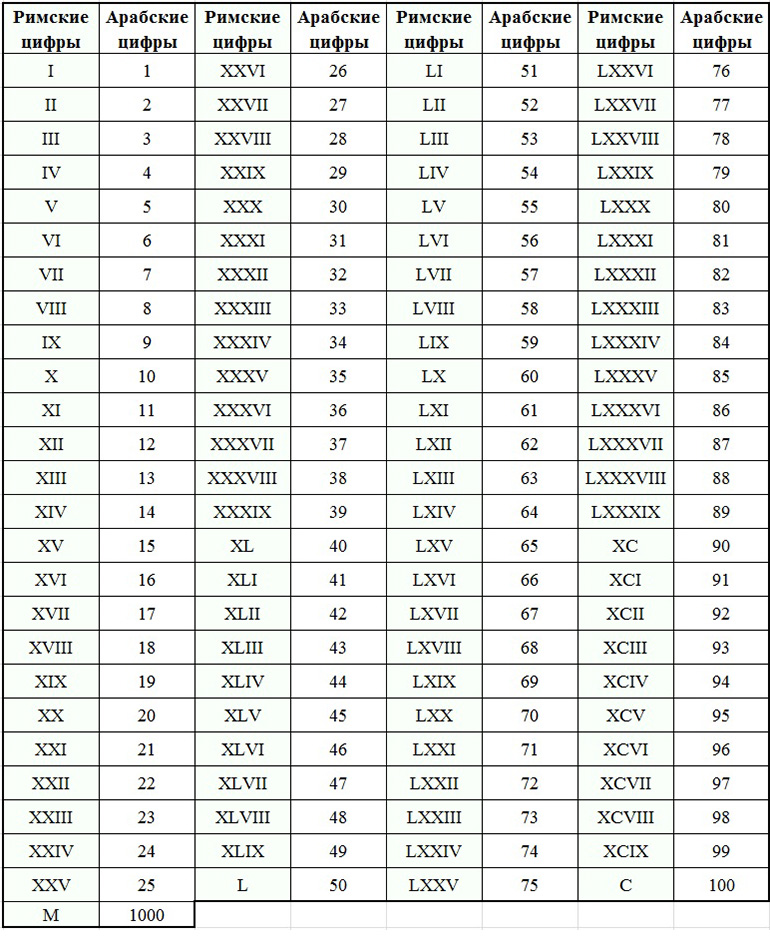 Обе системы численно эквивалентны.
Обе системы численно эквивалентны.
 Однако обратите внимание, что в формальном письме века с одной цифрой (например, девятый век) обычно пишутся прописью, а не цифрами. Двузначные века могут быть записаны любым способом (например, 21-й или 21-й век).
Однако обратите внимание, что в формальном письме века с одной цифрой (например, девятый век) обычно пишутся прописью, а не цифрами. Двузначные века могут быть записаны любым способом (например, 21-й или 21-й век).



 Используйте слово единственного числа века , если они соединены с или или .
Используйте слово единственного числа века , если они соединены с или или . Правильный
Правильный Не копируйте никакие изображения с этой страницы или этого веб-сайта. Если вы цитируете эту статью, вы должны дать ссылку на эту страницу. См. также наши Условия использования.
Не копируйте никакие изображения с этой страницы или этого веб-сайта. Если вы цитируете эту статью, вы должны дать ссылку на эту страницу. См. также наши Условия использования.  Таким образом, при обсуждении прошлых событий важно знать, как правильно их использовать.
Таким образом, при обсуждении прошлых событий важно знать, как правильно их использовать. :
:




 Окончательно получаем х1 = у1/а и х1 = у2/а.
Окончательно получаем х1 = у1/а и х1 = у2/а.



 4).
4). Тогда по теореме о секущих имеем OB • OD = OA • OC, откуда OC = OB • OD/ OA= х1х2/ 1 = c/a.
Тогда по теореме о секущих имеем OB • OD = OA • OC, откуда OC = OB • OD/ OA= х1х2/ 1 = c/a. 6,б) в точке В(х1; 0), где х1 — корень квадратного уравнения.
6,б) в точке В(х1; 0), где х1 — корень квадратного уравнения.

 е. S = х2 + 10х + 25. Заменяя
е. S = х2 + 10х + 25. Заменяя Значит, если к выражению у2 — 6у прибавить 9, то получим площадь квадрата со стороной у — 3. Заменяя выражение у2 — 6у равным ему числом 16,
Значит, если к выражению у2 — 6у прибавить 9, то получим площадь квадрата со стороной у — 3. Заменяя выражение у2 — 6у равным ему числом 16,
 и др. Алгебра, 6-8. / Пробный учебник для 6-8 классов средней школы. — М., Просвещение, 1981.
и др. Алгебра, 6-8. / Пробный учебник для 6-8 классов средней школы. — М., Просвещение, 1981. – 2-е издание, испр. и доп. – М.:Педагогика, 1989.
– 2-е издание, испр. и доп. – М.:Педагогика, 1989.




 е. у²+3у+3у+9.Откуда после примения формулы сокращенного умножения и получаем, что( у + 3)² = 25,
е. у²+3у+3у+9.Откуда после примения формулы сокращенного умножения и получаем, что( у + 3)² = 25, Попытки Кеплера объяснить основные причины таких движений больше не принимаются; тем не менее, сами фактические законы по-прежнему считаются точным описанием движения любой планеты и любого спутника.
Попытки Кеплера объяснить основные причины таких движений больше не принимаются; тем не менее, сами фактические законы по-прежнему считаются точным описанием движения любой планеты и любого спутника. Прикрепите лист бумаги к картону двумя кнопками. Затем завяжите нить в петлю и оберните петлю вокруг двух кнопок. Возьмите карандаш и тяните за нитку, пока карандаш и две кнопки не образуют треугольник (см. рисунок справа). Затем начните обводить путь карандашом, плотно обмотав нитку вокруг кнопок. В результате получится эллипс. Эллипс — это особая кривая, в которой сумма расстояний от каждой точки кривой до двух других точек является постоянной величиной. Две другие точки (обозначенные здесь положениями галса) известны как 9-я точка.0018 фокусов эллипса. Чем ближе друг к другу эти точки, тем больше эллипс напоминает форму круга. На самом деле круг — это частный случай эллипса, в котором два фокуса находятся в одном месте. Первый закон Кеплера довольно прост: все планеты вращаются вокруг Солнца по траектории, напоминающей эллипс, причем Солнце находится в одном из фокусов этого эллипса.
Прикрепите лист бумаги к картону двумя кнопками. Затем завяжите нить в петлю и оберните петлю вокруг двух кнопок. Возьмите карандаш и тяните за нитку, пока карандаш и две кнопки не образуют треугольник (см. рисунок справа). Затем начните обводить путь карандашом, плотно обмотав нитку вокруг кнопок. В результате получится эллипс. Эллипс — это особая кривая, в которой сумма расстояний от каждой точки кривой до двух других точек является постоянной величиной. Две другие точки (обозначенные здесь положениями галса) известны как 9-я точка.0018 фокусов эллипса. Чем ближе друг к другу эти точки, тем больше эллипс напоминает форму круга. На самом деле круг — это частный случай эллипса, в котором два фокуса находятся в одном месте. Первый закон Кеплера довольно прост: все планеты вращаются вокруг Солнца по траектории, напоминающей эллипс, причем Солнце находится в одном из фокусов этого эллипса. Скорость, с которой любая планета движется в космосе, постоянно меняется. Планета движется быстрее всего, когда она находится ближе всего к Солнцу, и медленнее всего, когда она дальше всего от него. Однако если воображаемую линию провести от центра планеты к центру Солнца, то эта линия охватит ту же площадь за равные промежутки времени. Например, если воображаемую линию провести от земли к солнцу, то площадь, заметаемая этой линией за каждый 31-дневный месяц, будет одинаковой. Это изображено на диаграмме ниже. Как видно на диаграмме, области, образованные, когда Земля находится ближе всего к Солнцу, можно аппроксимировать широким, но коротким треугольником; тогда как области, образованные, когда Земля находится дальше всего от Солнца, можно приблизительно представить в виде узкого, но длинного треугольника. Эти области имеют одинаковый размер. С с основанием этих треугольников являются самыми короткими, когда Земля находится дальше всего от Солнца, Земля должна двигаться медленнее, чтобы эта воображаемая площадь была того же размера, что и когда Земля находится ближе всего к Солнцу.
Скорость, с которой любая планета движется в космосе, постоянно меняется. Планета движется быстрее всего, когда она находится ближе всего к Солнцу, и медленнее всего, когда она дальше всего от него. Однако если воображаемую линию провести от центра планеты к центру Солнца, то эта линия охватит ту же площадь за равные промежутки времени. Например, если воображаемую линию провести от земли к солнцу, то площадь, заметаемая этой линией за каждый 31-дневный месяц, будет одинаковой. Это изображено на диаграмме ниже. Как видно на диаграмме, области, образованные, когда Земля находится ближе всего к Солнцу, можно аппроксимировать широким, но коротким треугольником; тогда как области, образованные, когда Земля находится дальше всего от Солнца, можно приблизительно представить в виде узкого, но длинного треугольника. Эти области имеют одинаковый размер. С с основанием этих треугольников являются самыми короткими, когда Земля находится дальше всего от Солнца, Земля должна двигаться медленнее, чтобы эта воображаемая площадь была того же размера, что и когда Земля находится ближе всего к Солнцу.
 На самом деле, если такое же отношение T 2 /R 3 вычислить для других планет, можно обнаружить, что это отношение является почти одинаковым значением для всех планет (см. таблицу ниже). Удивительно, но на каждой планете один и тот же T 2 9Соотношение 0079/R 3 .
На самом деле, если такое же отношение T 2 /R 3 вычислить для других планет, можно обнаружить, что это отношение является почти одинаковым значением для всех планет (см. таблицу ниже). Удивительно, но на каждой планете один и тот же T 2 9Соотношение 0079/R 3 . 615
615 06
06 В следующей части Урока 4 эти принципы будут исследованы по мере того, как мы будем проводить связь между принципами кругового движения, обсуждавшимися в Уроке 1, и движением спутника.
В следующей части Урока 4 эти принципы будут исследованы по мере того, как мы будем проводить связь между принципами кругового движения, обсуждавшимися в Уроке 1, и движением спутника. солнце. Известные данные для вращающихся планет предполагают следующее среднее соотношение:
солнце. Известные данные для вращающихся планет предполагают следующее среднее соотношение: Таким образом,
Таким образом, Следовательно, разумно, что отношение T 2 /R 3 будет одинаковым для всех планет, если сила, которая удерживает планеты на их орбитах, является силой гравитации. Универсальный закон всемирного тяготения Ньютона предсказывает результаты, которые согласуются с известными планетарными данными и обеспечивают теоретическое объяснение закона гармонии Кеплера.
Следовательно, разумно, что отношение T 2 /R 3 будет одинаковым для всех планет, если сила, которая удерживает планеты на их орбитах, является силой гравитации. Универсальный закон всемирного тяготения Ньютона предсказывает результаты, которые согласуются с известными планетарными данными и обеспечивают теоретическое объяснение закона гармонии Кеплера. Какому ученому приписывают точное объяснение данных?
Какому ученому приписывают точное объяснение данных? Среднее орбитальное расстояние Марса в 1,52 раза больше среднего орбитального расстояния Земли. Зная, что Земля совершает оборот вокруг Солнца примерно за 365 дней, используйте закон гармоний Кеплера, чтобы предсказать время обращения Марса вокруг Солнца.
Среднее орбитальное расстояние Марса в 1,52 раза больше среднего орбитального расстояния Земли. Зная, что Земля совершает оборот вокруг Солнца примерно за 365 дней, используйте закон гармоний Кеплера, чтобы предсказать время обращения Марса вокруг Солнца.
 Используйте графические возможности калькулятора TI для построения графика T 2 в сравнении с R 3 (T 2 следует отложить по вертикальной оси) и определить уравнение прямой. Запишите уравнение в форме пересечения наклона ниже.
Используйте графические возможности калькулятора TI для построения графика T 2 в сравнении с R 3 (T 2 следует отложить по вертикальной оси) и определить уравнение прямой. Запишите уравнение в форме пересечения наклона ниже. .. Читать всеВ 19В 60-е сверхсильные люди Чарльз Ксавьер и Эрик Леншерр работают вместе, чтобы найти таких же, как они, но мстительная погоня Эрика за амбициозным мутантом, который разрушил его жизнь, приводит к расколу между ними. найти других, подобных им, но мстительная погоня Эрика за амбициозным мутантом, разрушившим его жизнь, вызывает раскол, разделяющий их.
.. Читать всеВ 19В 60-е сверхсильные люди Чарльз Ксавьер и Эрик Леншерр работают вместе, чтобы найти таких же, как они, но мстительная погоня Эрика за амбициозным мутантом, который разрушил его жизнь, приводит к расколу между ними. найти других, подобных им, но мстительная погоня Эрика за амбициозным мутантом, разрушившим его жизнь, вызывает раскол, разделяющий их. производство, кассовые сборы и информацию о компании
производство, кассовые сборы и информацию о компании . Пока
. Пока

 Возвращение Шторма в серию было бы личным событием для меня, но не обязательно. Я очень рекомендую этот фильм всем, кто смотрел оригинальные фильмы, и даже новичкам.
Возвращение Шторма в серию было бы личным событием для меня, но не обязательно. Я очень рекомендую этот фильм всем, кто смотрел оригинальные фильмы, и даже новичкам. (США)
(США) другие кредиты компаний на IMDbPro
другие кредиты компаний на IMDbPro
 14159..
14159..
 Давайте и мы с вами её бахнем:
Опа, мы с вами достигли интересного результата! Коэффициент при у нас сейчас равен единице, а это значит, что мы с вами можем выразить эту неизвестную через остальные неизвестные в этом уравнении без всяких делений (чем грешили в самом начале статьи). Сделаем это:
Обращу внимание, что это говорит нам о том, что какие бы не были (в рамках диофантовых уравнений), всё равно останется целым числом, и это прекрасно.
Давайте и мы с вами её бахнем:
Опа, мы с вами достигли интересного результата! Коэффициент при у нас сейчас равен единице, а это значит, что мы с вами можем выразить эту неизвестную через остальные неизвестные в этом уравнении без всяких делений (чем грешили в самом начале статьи). Сделаем это:
Обращу внимание, что это говорит нам о том, что какие бы не были (в рамках диофантовых уравнений), всё равно останется целым числом, и это прекрасно. Попробуем найти частное решение исходного уравнения, положив, к примеру, что :
Подставим в исходное уравнение:
Тождественно, круто! Давайте попробуем ещё разок на другом примере?
Тут мы видим отрицательный коэффициент, он может доставить нам изрядных проблем, так что давайте от греха избавимся от него заменой , тогда уравнение будет следующим:
Как мы помним, наша задача сделать такие преобразования, чтобы в нашем уравнении оказалась неизвестная с единичным коэффициентом при ней (чтобы затем выразить её через остальные без любого деления). Для этого мы должны снова что-нибудь взять «за скобку», самое быстрое — это брать коэффициенты из уравнения которые самые близкие к единице. Однако нужно понимать, что за скобку можно взять только лишь то число, которое обязательно является каким-либо коэффициентом уравнения (ни больше, ни меньше), иначе наткнемся на тавтологию/противоречие или дроби (иными словами, нельзя чтобы свободные переменные появились где-то кроме как в последней замене).
Попробуем найти частное решение исходного уравнения, положив, к примеру, что :
Подставим в исходное уравнение:
Тождественно, круто! Давайте попробуем ещё разок на другом примере?
Тут мы видим отрицательный коэффициент, он может доставить нам изрядных проблем, так что давайте от греха избавимся от него заменой , тогда уравнение будет следующим:
Как мы помним, наша задача сделать такие преобразования, чтобы в нашем уравнении оказалась неизвестная с единичным коэффициентом при ней (чтобы затем выразить её через остальные без любого деления). Для этого мы должны снова что-нибудь взять «за скобку», самое быстрое — это брать коэффициенты из уравнения которые самые близкие к единице. Однако нужно понимать, что за скобку можно взять только лишь то число, которое обязательно является каким-либо коэффициентом уравнения (ни больше, ни меньше), иначе наткнемся на тавтологию/противоречие или дроби (иными словами, нельзя чтобы свободные переменные появились где-то кроме как в последней замене). Итак:
Введем замену , тогда получим:
Вновь возьмем за скобку и наконец получим в уравнении неизвестную с единичным коэффициентом:
Введем замену , тогда:
Выразим отсюда нашу одинокую неизвестную :
Из этого следует, что какие бы мы не взяли, все равно останется целым числом. Тогда найдем из соотношения :
Аналогичным образом найдем из соотношения :
На этом наша система решений созрела — мы выразили абсолютно все неизвестные, не прибегая к делению, тем самым показывая, что решение точно будет целочисленным. Также не забываем, что , и нам надо ввести обратную замену. Тогда окончательная система решений следующая:
Итак:
Введем замену , тогда получим:
Вновь возьмем за скобку и наконец получим в уравнении неизвестную с единичным коэффициентом:
Введем замену , тогда:
Выразим отсюда нашу одинокую неизвестную :
Из этого следует, что какие бы мы не взяли, все равно останется целым числом. Тогда найдем из соотношения :
Аналогичным образом найдем из соотношения :
На этом наша система решений созрела — мы выразили абсолютно все неизвестные, не прибегая к делению, тем самым показывая, что решение точно будет целочисленным. Также не забываем, что , и нам надо ввести обратную замену. Тогда окончательная система решений следующая: Доказательство
Доказательство Наконец, объявляем все переменные, через которые выражена оная, как свободные.
Наконец, объявляем все переменные, через которые выражена оная, как свободные. Утверждение 3 верно, только если равно 8. Утверждение 4 верно, только если x равно -3 или 6. Такие утверждения называются уравнениями.
Утверждение 3 верно, только если равно 8. Утверждение 4 верно, только если x равно -3 или 6. Такие утверждения называются уравнениями.



 Нажмите кнопку «Решить подобное», чтобы увидеть больше примеров.
Нажмите кнопку «Решить подобное», чтобы увидеть больше примеров. Чтобы выполнить это. умножьте обе части уравнения на наименьшее общее кратное знаменателей дробей.
Чтобы выполнить это. умножьте обе части уравнения на наименьшее общее кратное знаменателей дробей.
 Чтобы найти набор решений уравнения, составьте эквивалентное уравнение, в котором все члены с переменной в качестве множителя находятся на одной стороне уравнения. Члены, не имеющие переменной в качестве фактора, должны появиться на другой стороне.
Чтобы найти набор решений уравнения, составьте эквивалентное уравнение, в котором все члены с переменной в качестве множителя находятся на одной стороне уравнения. Члены, не имеющие переменной в качестве фактора, должны появиться на другой стороне.

 Часть II
Часть II :: Sxeco ::.
:: Sxeco ::.  03.2002
03.2002  Я не нашел математического задания, которое не смог бы выполнить через Алгебратор. Это просто потрясающе. Самое приятное то, что программное обеспечение дает вам пошаговое объяснение того, как сделать это самостоятельно. Таким образом, вы на самом деле узнаете, как решить эту проблему самостоятельно. Разве это не круто? 905:00
Я не нашел математического задания, которое не смог бы выполнить через Алгебратор. Это просто потрясающе. Самое приятное то, что программное обеспечение дает вам пошаговое объяснение того, как сделать это самостоятельно. Таким образом, вы на самом деле узнаете, как решить эту проблему самостоятельно. Разве это не круто? 905:00 Он охватывает все, что вам нужно знать о внешнем сходстве, в простой и всеобъемлющей форме. алгебра никогда не была легкой для меня, но это программное обеспечение сделало ее очень легкой для изучения. Логичный и пошаговый метод решения проблем действительно является преимуществом, и вскоре вы обнаружите, что вам нравится решать проблемы. 905:00
Он охватывает все, что вам нужно знать о внешнем сходстве, в простой и всеобъемлющей форме. алгебра никогда не была легкой для меня, но это программное обеспечение сделало ее очень легкой для изучения. Логичный и пошаговый метод решения проблем действительно является преимуществом, и вскоре вы обнаружите, что вам нравится решать проблемы. 905:00 Это действительно отличная математическая программа. Я помню, как решал задачи с вычитанием дробей, линейными уравнениями и линейными неравенствами. Я просто набирал домашнее задание, нажимал «Решить» — и пошагово решал домашнее задание по алгебре. Очень рекомендую программу. 905:00
Это действительно отличная математическая программа. Я помню, как решал задачи с вычитанием дробей, линейными уравнениями и линейными неравенствами. Я просто набирал домашнее задание, нажимал «Решить» — и пошагово решал домашнее задание по алгебре. Очень рекомендую программу. 905:00
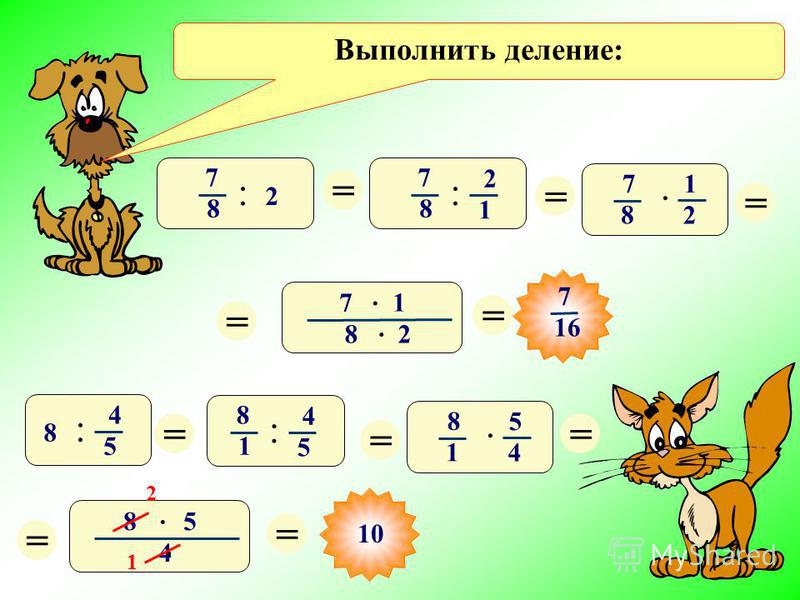 2
2
 io/ru/number/percentage/5—2
io/ru/number/percentage/5—2 02+17.19
02+17.19 Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении.
Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении. е. 1,45 .
е. 1,45 . Наиболее распространенные мнемоники для запоминания этого порядка операций:
Наиболее распространенные мнемоники для запоминания этого порядка операций:  На какую часть вопроса Энди ответил правильно?
На какую часть вопроса Энди ответил правильно?