Свойства степени с натуральным показателем / Алгебра / Справочник по математике 5-9 класс
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Алгебра
- Свойства степени с натуральным показателем
Основное свойство степени
| Для любого числа и любых натуральных чисел и справедливо равенство: . |
Тождество выражает основное свойство степени.
Основное свойство степени распространяется и на произведение трех и более степеней: .
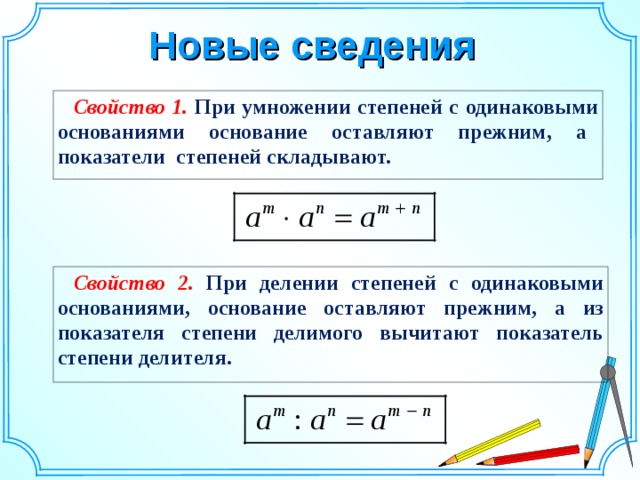
Из основного свойства степеней получаем правило умножения степеней:
| при умножении степеней с одинаковыми основаниями основание оставляют прежним, а показатели степеней складывают. |
Примеры:
Частное степеней
Для любого числа и любых натуральных чисел и , таких, что , справедливо равенство: . |
Правило деления степеней:
| при делении степеней с одинаковыми основаниями основание оставляют прежним, а из показателя степени делимого вычитают показатель степени делителя. |
Примеры:
Если правило деления применить к частному (т.е. когда ), то получится
.
Степень с нулевым показателем не была определена, но при всяком и любом натуральном справедливо равенство:
.
Получается, можно считать, что при , справедливо равенство:
.
| Степень числа , не равного нулю, с нулевым показателем равна единице. |
Примеры:
Возведение степени в степень
Для любого числа и любых натуральных чисел и справедливо равенство: . |
Правило возведения степени в степень:
| при возведении степени в степень показатели перемножают, а основание оставляют прежним. |
Пример:
.
Возведение произведения в степень
Для любых чисел и и любого натурального числа справедливо равенство: . |
Аналогичное свойство справедливо и для произведения трех и более множителей: .
Правило возведения произведения в степень:
| при возведении произведения в степень каждый множитель возводят в эту степень и полученные результаты перемножают. |
Пример:
.
Советуем посмотреть:
Введение в алгебру
Линейное уравнение с одной переменной
Решение задач с помощью уравнений
Тождественно равные выражения. Тождества
Тождества
Степень с натуральным показателем
Одночлены
Многочлены
Сложение и вычитание многочленов
Умножение одночлена на многочлен
Умножение многочлена на многочлен
Разложение многочленов на множители
Формулы сокращенного умножения
Функции
Системы линейных уравнений с двумя переменными
Алгебра
Правило встречается в следующих упражнениях:
7 класс
Номер 214, Мерзляк, Полонский, Якир, Учебник
Номер 244, Мерзляк, Полонский, Якир, Учебник
Номер 416, Мерзляк, Полонский, Якир, Учебник
Номер 511, Мерзляк, Полонский, Якир, Учебник
Номер 584, Мерзляк, Полонский, Якир, Учебник
Номер 591, Мерзляк, Полонский, Якир, Учебник
Номер 668, Мерзляк, Полонский, Якир, Учебник
Номер 1142, Мерзляк, Полонский, Якир, Учебник
Номер 1147, Мерзляк, Полонский, Якир, Учебник
Номер 4, Мерзляк, Полонский, Якир, Учебник
8 класс
Номер 27, Мерзляк, Полонский, Якир, Учебник
Номер 29, Мерзляк, Полонский, Якир, Учебник
Номер 79, Мерзляк, Полонский, Якир, Учебник
Номер 86, Мерзляк, Полонский, Якир, Учебник
Номер 112, Мерзляк, Полонский, Якир, Учебник
Номер 119, Мерзляк, Полонский, Якир, Учебник
Номер 125, Мерзляк, Полонский, Якир, Учебник
Номер 185, Мерзляк, Полонский, Якир, Учебник
Номер 217, Мерзляк, Полонский, Якир, Учебник
Номер 388, Мерзляк, Полонский, Якир, Учебник
Повторяем и систематизируем школьный курс алгебры и начал анализа
Повторяем и систематизируем школьный курс алгебры и начал анализа
ОглавлениеПРЕДИСЛОВИЕГЛАВА I. § 1. НАТУРАЛЬНЫЕ ЧИСЛА И ДЕЙСТВИЯ НАД НИМИ § 2. СЛОЖЕНИЕ И ЗАКОНЫ СЛОЖЕНИЯ § 3. ВЫЧИТАНИЕ § 4. УМНОЖЕНИЕ И ЗАКОНЫ УМНОЖЕНИЯ § 5. ДЕЛЕНИЕ § 6. ПРИЗНАКИ ДЕЛИМОСТИ ЧИСЕЛ § 7. ПОНЯТИЕ МНОЖЕСТВА § 8. ОПЕРАЦИИ НАД МНОЖЕСТВАМИ § 9. ВЗАИМНО ОДНОЗНАЧНОЕ СООТВЕТСТВИЕ § 10. ПРОСТЫЕ И СОСТАВНЫЕ ЧИСЛА § 11. НАИБОЛЬШИЙ ОБЩИЙ ДЕЛИТЕЛЬ § 12. НАИМЕНЬШЕЕ ОБЩЕЕ КРАТНОЕ Контрольные вопросы ГЛАВА II § 1. ОБЫКНОВЕННЫЕ ДРОБИ § 2. 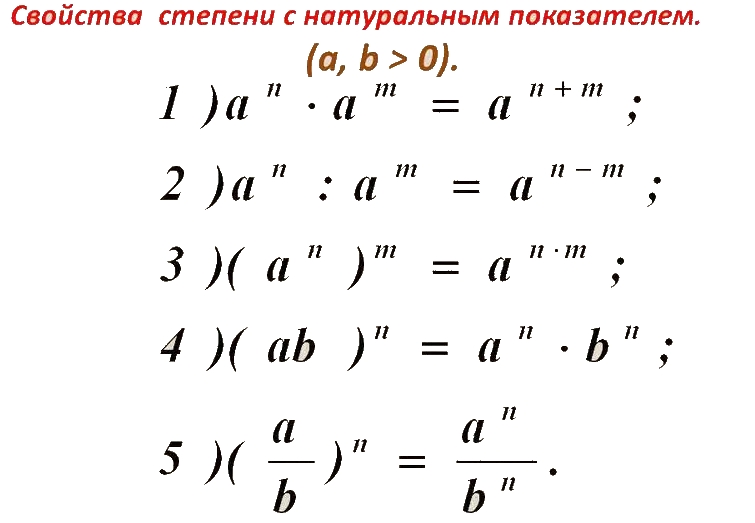 ПРАВИЛЬНЫЕ И НЕПРАВИЛЬНЫЕ ДРОБИ ПРАВИЛЬНЫЕ И НЕПРАВИЛЬНЫЕ ДРОБИ§ 3. ОСНОВНОЕ СВОЙСТВО ДРОБИ § 4. СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДРОБЕЙ § 5. УМНОЖЕНИЕ ДРОБЕЙ § 6. ДЕЛЕНИЕ ДРОБЕЙ § 7. ДЕСЯТИЧНЫЕ ДРОБИ § 8. ОБРАЩЕНИЕ ДЕСЯТИЧНОЙ ДРОБИ В ОБЫКНОВЕННУЮ И ОБЫКНОВЕННОЙ В ДЕСЯТИЧНУЮ. ПЕРИОДИЧЕСКИЕ ДРОБИ § 9. ОТНОШЕНИЕ. ПРОПОРЦИЯ § 10. СВОЙСТВА ПРОПОРЦИИ § 11. ПРОЦЕНТ. ОСНОВНЫЕ ЗАДАЧИ НА ПРОЦЕНТЫ § 12. ДЕЛЕНИЕ ЧИСЛА НА ЧАСТИ, ПРЯМО И ОБРАТНО ПРОПОРЦИОНАЛЬНЫЕ ДАННЫМ ЧИСЛАМ Контрольные вопросы ГЛАВА III § 1. КООРДИНАТНАЯ ПРЯМАЯ § 2. МНОЖЕСТВО ЦЕЛЫХ ЧИСЕЛ § 3. МНОЖЕСТВО РАЦИОНАЛЬНЫХ ЧИСЕЛ § 4. МОДУЛЬ ЧИСЛА § 5. СРАВНЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ § 6. СЛОЖЕНИЕ И ВЫЧИТАНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ § 7. УМНОЖЕНИЕ И ДЕЛЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ § 8. ВОЗВЕДЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ В СТЕПЕНЬ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ Контрольные вопросы ГЛАВА IV § 1. СВОЙСТВА СТЕПЕНИ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ § 2. ЧИСЛОВЫЕ ВЫРАЖЕНИЯ § 3. ВЫРАЖЕНИЯ С ПЕРЕМЕННЫМИ § 4. ТОЖДЕСТВЕННО РАВНЫЕ ВЫРАЖЕНИЯ § 5.  ОДНОЧЛЕНЫ ОДНОЧЛЕНЫ§ 6. МНОГОЧЛЕНЫ § 7. ПРЕОБРАЗОВАНИЕ СУММЫ И РАЗНОСТИ МНОГОЧЛЕНОВ § 8. УМНОЖЕНИЕ МНОГОЧЛЕНА НА ОДНОЧЛЕН И МНОГОЧЛЕНА НА МНОГОЧЛЕН § 9. РАЗЛОЖЕНИЕ МНОГОЧЛЕНА НА МНОЖИТЕЛИ СПОСОБОМ ВЫНЕСЕНИЯ ОБЩЕГО МНОЖИТЕЛЯ ЗА СКОБКИ § 10. РАЗЛОЖЕНИЕ МНОГОЧЛЕНА НА МНОЖИТЕЛИ СПОСОБОМ ГРУППИРОВКИ § 11. ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ Контрольные вопросы ГЛАВА V § 1. ДРОБЬ § 2. ЦЕЛЫЕ И ДРОБНЫЕ ВЫРАЖЕНИЯ § 3. ТОЖДЕСТВЕННОЕ ПРЕОБРАЗОВАНИЕ СУММЫ И РАЗНОСТИ ДВУХ ДРОБЕЙ § 4. ТОЖДЕСТВЕННОЕ ПРЕОБРАЗОВАНИЕ ПРОИЗВЕДЕНИЯ И ЧАСТНОГО ДВУХ ДРОБЕЙ § 5. СТЕПЕНЬ ДРОБИ Контрольные вопросы ГЛАВА VI § 1. ПОНЯТИЕ ОБ ИРРАЦИОНАЛЬНОМ ЧИСЛЕ § 2. РАЗВИТИЕ ПОНЯТИЯ О ЧИСЛЕ. МНОЖЕСТВО ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ § 3. КОРЕНЬ СТЕПЕНИ ИЗ ДЕЙСТВИТЕЛЬНОГО ЧИСЛА § 4. АЛГОРИТМ ИЗВЛЕЧЕНИЯ КВАДРАТНОГО КОРНЯ ИЗ ЧИСЛА § 5. АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ С ДЕЙСТВИТЕЛЬНЫМИ ЧИСЛАМИ § 6. ПРЕОБРАЗОВАНИЯ АРИФМЕТИЧЕСКИХ КОРНЕЙ § 7. СТЕПЕНЬ С ЦЕЛЫМ И ДРОБНЫМ ПОКАЗАТЕЛЕМ Контрольные вопросы ГЛАВА VII § 1.  УРАВНЕНИЯ С ОДНОЙ ПЕРЕМЕННОЙ УРАВНЕНИЯ С ОДНОЙ ПЕРЕМЕННОЙ§ 2. ПОНЯТИЕ О РАВНОСИЛЬНОСТИ УРАВНЕНИЙ § 3. СВОЙСТВА ЧИСЛОВЫХ РАВЕНСТВ И ТЕОРЕМЫ О РАВНОСИЛЬНОСТИ УРАВНЕНИЙ § 4. ЛИНЕЙНОЕ УРАВНЕНИЕ С ОДНОЙ ПЕРЕМЕННОЙ, СОДЕРЖАЩЕЕ ПАРАМЕТР Контрольные вопросы ГЛАВА VIII § 1. ПОНЯТИЕ ФУНКЦИИ § 2. СПОСОБЫ ЗАДАНИЯ ФУНКЦИИ § 3. МОНОТОННОСТЬ ФУНКЦИИ § 4. ЧЕТНЫЕ И НЕЧЕТНЫЕ ФУНКЦИИ СПРАВОЧНЫЙ МАТЕРИАЛ § 5. ПЕРИОДИЧЕСКИЕ ФУНКЦИИ § 6. ПРОМЕЖУТКИ ЗНАКОПОСТОЯНСТВА И КОРНИ ФУНКЦИИ Контрольные вопросы ГЛАВА IX § 1. ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ ГРАФИКОВ ФУНКЦИЙ § 2. ЛИНЕЙНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК § 3. КВАДРАТИЧНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК § 4. ФУНКЦИЯ y=k/x И ЕЕ ГРАФИК § 5. ДРОБНО-ЛИНЕЙНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК Контрольные вопросы ГЛАВА X § 1. КВАДРАТНЫЕ УРАВНЕНИЯ § 2. ТЕОРЕМА ВИЕТА § 3. ГРАФИЧЕСКИЙ СПОСОБ РЕШЕНИЯ КВАДРАТНЫХ УРАВНЕНИЙ § 4. УРАВНЕНИЕ СО МНОГИМИ ПЕРЕМЕННЫМИ § 5. СИСТЕМЫ УРАВНЕНИЙ Контрольные вопросы ГЛАВА XI § 1. НЕРАВЕНСТВА § 2.  ОСНОВНЫЕ СВОЙСТВА НЕРАВЕНСТВ ОСНОВНЫЕ СВОЙСТВА НЕРАВЕНСТВ§ 3. ДЕЙСТВИЯ С НЕРАВЕНСТВАМИ § 4. ДОКАЗАТЕЛЬСТВА НЕРАВЕНСТВ § 5. НЕРАВЕНСТВА, СОДЕРЖАЩИЕ ПЕРЕМЕННУЮ § 6. РЕШЕНИЕ ЛИНЕЙНЫХ И КВАДРАТНЫХ НЕРАВЕНСТВ Контрольные вопросы ГЛАВА XII § 1. СИСТЕМЫ И СОВОКУПНОСТИ НЕРАВЕНСТВ § 2. НЕРАВЕНСТВА И СИСТЕМЫ НЕРАВЕНСТВ С ДВУМЯ ПЕРЕМЕННЫМИ § 3. РЕШЕНИЕ НЕРАВЕНСТВ, СОДЕРЖАЩИХ ПЕРЕМЕННУЮ ПОД ЗНАКОМ МОДУЛЯ § 4. РЕШЕНИЕ РАЦИОНАЛЬНЫХ НЕРАВЕНСТВ МЕТОДОМ ПРОМЕЖУТКОВ Контрольные вопросы ГЛАВА XIII § 1. ЧИСЛОВАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ § 2. АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯ § 3. ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ § 4. СУММА БЕСКОНЕЧНОЙ ГЕОМЕТРИЧЕСКОЙ ПРОГРЕССИИ ПРИ |q|Контрольные вопросы ГЛАВА XIV § 1. ГРАДУСНОЕ ИЗМЕРЕНИЕ УГЛОВЫХ ВЕЛИЧИН § 2. РАДИАННОЕ ИЗМЕРЕНИЕ УГЛОВЫХ ВЕЛИЧИН § 3. СИНУС И КОСИНУС ЧИСЛОВОГО АРГУМЕНТА § 4. ТАНГЕНС И КОТАНГЕНС ЧИСЛОВОГО АРГУМЕНТА. СЕКАНС И КОСЕКАНС ЧИСЛА а § 5. ОСНОВНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ТОЖДЕСТВА § 6. ДОПОЛНИТЕЛЬНЫЕ СВОЙСТВА ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ Контрольные вопросы ГЛАВА XV § 1.  ФОРМУЛЫ ПРИВЕДЕНИЯ ФОРМУЛЫ ПРИВЕДЕНИЯ§ 2. ФОРМУЛЫ СЛОЖЕНИЯ § 3. ФОРМУЛЫ ДВОЙНОГО УГЛА СПРАВОЧНЫЙ МАТЕРИАЛ § 4. ПРЕОБРАЗОВАНИЕ ПРОИЗВЕДЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ В СУММУ § 5. ФОРМУЛЫ СУММЫ И РАЗНОСТИ ОДНОИМЕННЫХ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ § 6. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ПОЛОВИННОГО АРГУМЕНТА § 7. ВЫРАЖЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ ЧЕРЕЗ ТАНГЕНС ПОЛОВИННОГО АРГУМЕНТА Контрольные вопросы ГЛАВА XVI § 1. СВОЙСТВА ФУНКЦИИ y = sin(x) И ЕЕ ГРАФИК § 2. СВОЙСТВА ФУНКЦИ И у = cos(x) И ЕЕ ГРАФИК § 3. СВОЙСТВА ФУНКЦИ И у=tg(x) И ЕЕ ГРАФИК § 4. СВОЙСТВА ФУНКЦИ И y=ctg(x) И ЕЕ ГРАФИК § 5. НАХОЖДЕНИЕ ПЕРИОДОВ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ Контрольные вопросы ГЛАВА XVII § 1. АРКСИНУС И АРККОСИНУС § 2. АРКТАНГЕНС И АРККОТАНГЕНС Контрольные вопросы ГЛАВА XVIII § 1. РЕШЕНИЕ УРАВНЕНИЙ ВИДА cos(x)=а § 2. РЕШЕНИЕ УРАВНЕНИЙ ВИДА sin(x)=a § 3. РЕШЕНИЕ УРАВНЕНИЙ ВИДА tg(х)=а § 4. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ, ПРИВОДИМЫХ К КВАДРАТНОМУ § 5.  РЕШЕНИЕ ОДНОРОДНЫХ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ РЕШЕНИЕ ОДНОРОДНЫХ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ§ 6. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ, РЕШАЕМЫЕ С ПОМОЩЬЮ ФОРМУЛ СЛОЖЕНИЯ, ПОНИЖЕНИЯ СТЕПЕНИ § 7. РЕШЕНИЕ СИСТЕМ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ Контрольные вопросы ГЛАВА XIX § 1. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ВИДА sin(х) > а, sin(х) § 2. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ВИДА cos(x) > a, cos(x) § 3. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ВИДА tg(х) > a, tg(х) § 4. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ГЛАВА XX § 1. ПРИРАЩЕНИЕ АРГУМЕНТА И ПРИРАЩЕНИЕ ФУНКЦИИ § 2. ПРЕДЕЛ ФУНКЦИИ § 3. НЕПРЕРЫВНОСТЬ ФУНКЦИИ § 4. ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ § 5. ПРОИЗВОДНАЯ СУММЫ, ПРОИЗВЕДЕНИЯ, ЧАСТНОГО § 6. ПРОИЗВОДНАЯ СТЕПЕННОЙ И СЛОЖНОЙ ФУНКЦИИ § 7. ПРОИЗВОДНЫЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ Контрольные вопросы ГЛАВА XXI § 1. ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ К НАХОЖДЕНИЮ ПРОМЕЖУТКОВ МОНОТОННОСТИ ФУНКЦИИ § 2. КРИТИЧЕСКИЕ ТОЧКИ ФУНКЦИИ, ЕЕ МАКСИМУМЫ И МИНИМУМЫ § 3. ОБЩАЯ СХЕМА ИССЛЕДОВАНИЯ ФУНКЦИИ § 4.  ЗАДАЧИ НА НАХОЖДЕНИЕ НАИМЕНЬШЕГО И НАИБОЛЬШЕГО ЗНАЧЕНИЯ ФУНКЦИИ ЗАДАЧИ НА НАХОЖДЕНИЕ НАИМЕНЬШЕГО И НАИБОЛЬШЕГО ЗНАЧЕНИЯ ФУНКЦИИКонтрольные вопросы ГЛАВА XXII § 1. ФОРМУЛЫ ПРИБЛИЖЕННЫХ ВЫЧИСЛЕНИЙ СПРАВОЧНЫЙ МАТЕРИАЛ § 2. КАСАТЕЛЬНАЯ К ГРАФИКУ ФУНКЦИИ § 3. СКОРОСТЬ И УСКОРЕНИЕ В ДАННЫЙ МОМЕНТ ВРЕМЕНИ § 4. ГРАФИКИ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ Контрольные вопросы ГЛАВА XXIII § 1. ПОТЕРЯННЫЕ И ПОСТОРОННИЕ КОРНИ ПРИ РЕШЕНИИ УРАВНЕНИЙ (НА ПРИМЕРАХ) § 2. ПОСТОРОННИЕ КОРНИ ИРРАЦИОНАЛЬНОГО УРАВНЕНИЯ (НА ПРИМЕРАХ) § 3. РЕШЕНИЕ ИРРАЦИОНАЛЬНЫХ УРАВНЕНИЙ § 4. РЕШЕНИЕ ИРРАЦИОНАЛЬНЫХ НЕРАВЕНСТВ СПРАВОЧНЫЙ МАТЕРИАЛ Контрольные вопросы ГЛАВА XXIV § 1. ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯ, ЕЕ СВОЙСТВА И ГРАФИК § 2. ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ § 3. ПОКАЗАТЕЛЬНЫЕ НЕРАВЕНСТВА § 4. СИСТЕМЫ ПОКАЗАТЕЛЬНЫХ УРАВНЕНИЙ И НЕРАВЕНСТВ Контрольные вопросы ГЛАВА XXV § 1. ОБРАТНАЯ ФУНКЦИЯ § 2. ПОНЯТИЕ ЛОГАРИФМА § 3. СВОЙСТВА ЛОГАРИФМОВ § 4. ЛОГАРИФМИЧЕСКАЯ ФУНКЦИЯ, ЕЕ СВОЙСТВА И ГРАФИК § 5. ТЕОРЕМЫ О ЛОГАРИФМЕ ПРОИЗВЕДЕНИЯ, ЧАСТНОГО И СТЕПЕНИ.  ФОРМУЛА ПЕРЕХОДА К НОВОМУ ОСНОВАНИЮ ФОРМУЛА ПЕРЕХОДА К НОВОМУ ОСНОВАНИЮ§ 6. ДЕСЯТИЧНЫЕ ЛОГАРИФМЫ И ИХ СВОЙСТВА § 7. ЛОГАРИФМИРОВАНИЕ И ПОТЕНЦИРОВАНИЕ Контрольные вопросы ГЛАВА XXVI § 1. ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ § 2. ЛОГАРИФМИЧЕСКИЕ НЕРАВЕНСТВА § 3. СИСТЕМЫ ЛОГАРИФМИЧЕСКИХ УРАВНЕНИЙ И НЕРАВЕНСТВ § 4. ПРОИЗВОДНЫЕ ЛОГАРИФМИЧЕСКОЙ И ПОКАЗАТЕЛЬНОЙ ФУНКЦИЙ. ЧИСЛО e Контрольные вопросы ГЛАВА XXVII § 1. ПОНЯТИЕ ПЕРВООБРАЗНОЙ ФУНКЦИИ § 2. ОСНОВНОЕ СВОЙСТВО ПЕРВООБРАЗНОЙ ФУНКЦИИ § 3. ТРИ ПРАВИЛА НАХОЖДЕНИЯ ПЕРВООБРАЗНЫХ § 4. КРИВОЛИНЕЙНАЯ ТРАПЕЦИЯ И ЕЕ ПЛОЩАДЬ Контрольные вопросы ГЛАВА XXVIII § 1. ФОРМУЛА НЬЮТОНА—ЛЕЙБНИЦА § 2. ОСНОВНЫЕ ПРАВИЛА ИНТЕГРИРОВАНИЯ § 3. ВЫЧИСЛЕНИЕ ПЛОЩАДЕЙ С ПОМОЩЬЮ ИНТЕГРАЛА § 4. МЕХАНИЧЕСКИЕ И ФИЗИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА ПРИЛОЖЕНИЕ Введение 1. Задачи на движение 2. Задачи на совместную работу 3. Задачи на планирование 4. Задачи на зависимость между компонентами арифметических действий 5.  Задачи на проценты Задачи на проценты6. Задачи на смеси (сплавы) 7. Задачи на разбавление |
Сложение и вычитание показателей степени — GeeksforGeeks
В математике показатели степени используются для представления большего числа в терминах степени. Он показывает, во сколько раз основание умножается само на себя. Где основанием является любое число или любое математическое выражение. Например, A 3 здесь основание равно A, а степень равна 3, что означает, что A умножится само на себя три раза, то есть A 3 = A x A x A. Общий член показателя степени равен
Y n. = Y × Y × Y ×………n раз
Здесь y известен как основание, а n известен как степень или показатель степени. Типы показателей степени:
- Отрицательная степень: Отрицательные степени — это те степени, которые показывают, во сколько раз обратная величина основания умножается сама на себя.
 Он представлен как -n или 1/a n . Например, 23 -2 , 4 -2 .
Он представлен как -n или 1/a n . Например, 23 -2 , 4 -2 . - Дробная экспонента: Когда экспонента представлена в виде дроби, такие типы экспоненты известны как дробные экспоненты. Он представлен как 1/n . Например, 3 1/2 , 4 1/3 .
- Десятичный показатель степени: Когда показатель степени представлен десятичными цифрами, такие типы показателей называются десятичными показателями степени. Он представлен как 1.3 . Например, 3 1,5 , 4 12,3 .
Сложение и вычитание показателей степени
Сложение и вычитание — две основные математические операции. Сложение означает нахождение суммы двух цифр, а вычитание — нахождение разницы между двумя цифрами. Но мы не можем напрямую складывать или вычитать показатели степени, мы можем выполнять сложение или вычитание только с коэффициентами или переменными, имеющими одинаковое основание и одинаковую мощность. Мы можем только складывать показатели степени при умножении и вычитать степени степени при делении.
Мы можем только складывать показатели степени при умножении и вычитать степени степени при делении.
Шаги для сложения или вычитания между показателями степени в алгебре:
Чтобы выполнить сложение или вычитание, мы будем следовать тем же шагам:
Шаг 1: основание и показатели совпадают или нет.
Шаг 2: Расположите похожие переменные/члены вместе.
Шаг 3: Теперь выполните сложение или вычитание по мере необходимости между коэффициентами слагаемых.
Пример 1: решить 6x 3 + 12x 3 .
Решение:
Здесь основание одинаковое, т. е. x и показатели степени двух слагаемых также одинаковы, т. е. 3
Таким образом, мы можем сложить коэффициенты двух слагаемых, чтобы получить результат.
6x 3 + 12x 3 = (6 + 12)x 3
= 18x 3
9 0018 Пример 2: решить 9x 3 -13x 3 .
Решение:
Здесь основание одинаковое, т. е. x и показатели степени двух слагаемых также одинаковы, т. е. 3
Таким образом, мы можем вычесть коэффициенты двух слагаемых, чтобы получить результат.
9x 3 – 13x 3 = (9 – 13)x 3
= -4x 3
90 018 Шаги для сложения или вычитания между показателями степени в числах:
сложение или вычитание мы будем следовать тем же шагам:
Шаг 1: Перед выполнением любого сложения или вычитания между показателями степени мы должны наблюдать, совпадают ли основание и показатели степени.
Шаг 2: Расположите одинаковые члены основания и степени вместе. Если члены имеют разные основание и показатель степени, то решите их по отдельности.
Шаг 3: Теперь выполните сложение или вычитание по мере необходимости между базой терминов.
Пример 1: решить 6 3 + 6 3 .
Решение:
Здесь одно и то же основание, т.е. 6 и показатели степени двух членов также одинаковы, т.е. 3
Итак, мы решаем их вместе + 6 3 = 2(6) 3
= 2 x 6 x 6 x 6
= 432
Пример 2: решить 9 2 – 13 3 900 04 .
Решение:
Здесь основание и показатели разные
Итак, мы решаем их индивидуально.
9 2 – 13 3 = 9 x 9 -13 x 13 x 13
= 81 – 2197
= -2116
Аналогично Вопросы
Вопрос 1: решить 5x 3 + 3x 3 .
Решение:
Здесь основание одинаковое, т. е. x и показатели степени двух слагаемых также одинаковы, т. е. 3
Таким образом, мы можем сложить коэффициенты двух слагаемых, чтобы получить результат.
5x 3 + 3x 3 = (5 + 3)x 3
= 8x 3
Итак, 5x 3 9000 4 + 3x 3 = 8x 3
Вопрос 2: Что является результатом выражения -11a 2 + 4a 2 .
Решение:
Здесь основание одинаковое, т. е. a и показатели степени двух слагаемых также одинаковы, т. е. 2
Таким образом, мы можем сложить коэффициенты двух слагаемых, чтобы получить результат.
-11а 2 + 4а 2 = (-11 + 4)а 2
= (4 – 11)а 2
= -7а 2
Так, -11а 2 + 4a 2 = -7a 2
Вопрос 3: Решите выражение 4x 3 + 4x 2 – 2x 3 + х 2 – х + 1
Решение:
Здесь у нас разные термины (x 3 , x 2 , x), т.
е. основания одинаковые, но разные показатели степени.
Итак, идентифицируйте похожие переменные, сгруппируйте их и выполните сложение/вычитание на основе знаков и расположите в полиномиальном порядке, т.
4x 3 + 4x 2 – 2x 3 + x 2 – x + 1 = (4x 3 – 2x 3 ) + (4x 2 + x 2 )- х + 1
= (4 – 2)х 3 + (4 + 1)х 2 – x + 1
= 2x 3 + 5x 2 – x + 1
Вопрос 4: Каков результат x 3 y + 4x 3 г?
Решение:
Здесь у нас есть 2 разные переменные в 2 терминах x, y и степени x, y в двух терминах одинаковы, т.е. 3,1 соответственно.
Итак, мы можем считать, что эти 2 термина имеют совпадающие переменные, и мы можем добавить/вычесть коэффициент 2 терминов в зависимости от требований.
x 3 y + 4x 3 y = (1 + 4)x 3 y
= 5x 3 y
Вопрос 5: решить x 3 y + 4x 3 y 2 + 4x – x + 1
Решение:
Здесь у нас есть 2 разные переменные в 2 терминах x, y и показатель степени x в 2 терминах одинаковы, т.
е. 3, но показатель степени y не одно и то же, поэтому мы не можем считать два термина одинаковыми и не будем выполнять между ними никаких операций. (осталось как есть)
Но есть еще два члена с той же базовой переменной x и показателем степени, что и 1. Поэтому мы группируем их и выполняем вычисления с их коэффициентами.
x 3 у + 4х 3 у 2 + 4х – х + 1 = 4х 3 у 2 + х 3 у + (4х – х) + 1
= 4х 3 y 2 + x 3 y + (4 – 1)x + 1
= 4x 3 y 2 + x 3 y + 3x + 1
Вопрос 6: Решить х 5 y 2 – x 4 y 4
Решение:
Здесь два члена x 9000 3 5 у 2 , х 4 у 4 и в два термина у нас есть 2 переменные x, y, но показатели переменных не совпадают при сравнении между терминами.
Следовательно, первое слагаемое совершенно не похоже на второе и не может быть вычтено друг из друга.
Оставляем как есть.
х 5 y 2 – x 4 y 4 дальнейшее упрощение невозможно.
6 простых шагов для сложения и вычитания в экспоненте
Вот как складывать и вычитать в экспоненте Когда числа, которые вы добавляете или вычитаете, должны быть равным. Если они уже равны, то можно просто сложить коэффициенты. Если показатели степени не равны, то вы должны сделать их равными, переместив один из десятичных знаков. Самый простой способ сделать десятичные дроби равными — сделать меньшую степень равной большей, переместив десятичную дробь влево. Вы добавляете единицу к показателю степени для каждого пробела, на который вы перемещаете десятичную точку влево. Когда показатели равны, вы можете добавить или вычесть коэффициенты. Последний шаг для Сложение и вычитание в экспоненциальном представлении должно гарантировать, что коэффициент находится между 1 и 10. Если это не так, вы должны переместить десятичную точку так, чтобы она была.
Если это не так, вы должны переместить десятичную точку так, чтобы она была.
Общий базовый стандарт: 8.EE.A.3
Связанные темы: Квадратные корни, кубические корни, иррациональные числа, степени 10, введение в экспоненциальную запись, преобразование чисел в экспоненциальную запись, преобразование чисел из экспоненциальной записи , Умножение в экспоненциальном представлении, Деление в экспоненциальном представлении
Выполнение любого сложения и вычитания в экспоненциальном представлении Пример задачи При сложении и вычитании в экспоненциальном представлении степени чисел, которые вы складываете или вычитаете, должны быть эквивалентны. В том случае, если они эквивалентны, можно просто объединить коэффициенты вместе. Если степени не эквивалентны, вы должны сделать их эквивалентными, переместив один из десятичных знаков так, чтобы степени стали эквивалентными. Как только степени эквивалентны, вы можете либо добавить коэффициенты для добавления научного обозначения, либо вычесть коэффициенты для вычитания научного обозначения. Последним шагом для сложения и вычитания в экспоненциальном представлении является проверка того, что коэффициент находится где-то в диапазоне от 1 до 10. Это самый простой способ решить, как складывать и вычитать экспоненциальное представление.
Последним шагом для сложения и вычитания в экспоненциальном представлении является проверка того, что коэффициент находится где-то в диапазоне от 1 до 10. Это самый простой способ решить, как складывать и вычитать экспоненциальное представление.
- Проверьте, равны ли степени в степени десятков.
- Если степени равны, то вы можете добавить или вычесть коэффициенты.
- Если степени не равны, вы должны сделать их равными, переместив десятичную точку.
- Перемещение десятичной точки влево будет прибавлять к показателю степени для каждой цифры, которую она перемещает влево.
- Когда степени равны, вы можете складывать или вычитать коэффициенты.
- Убедитесь, что ваш коэффициент находится между единицей и десятью, так как он должен быть записан в научной нотации.
Практические задачи на сложение и вычитание
Сложение и вычитание в экспоненциальном представлении
Нажмите «Старт», чтобы начать практический тест!
1 / 5
Добавьте или вычтите следующее в научной записи: 94
Ваш счет
Посмотрите объяснение сложения и вычитания в экспоненциальном представлении видео Посмотрите наше бесплатное видео о том, как решить сложение и вычитание в экспоненциальном представлении . В этом видео показано, как добавить экспоненциальную запись и как вычесть экспоненциальную запись. Вы также можете попробовать решить некоторые практические задачи из нашего бесплатного листа Добавление и вычитание научной нотации , который вы можете получить, отправив свое электронное письмо выше.
В этом видео показано, как добавить экспоненциальную запись и как вычесть экспоненциальную запись. Вы также можете попробовать решить некоторые практические задачи из нашего бесплатного листа Добавление и вычитание научной нотации , который вы можете получить, отправив свое электронное письмо выше.
Посмотрите бесплатное видео о сложении и вычитании в научном представлении на YouTube здесь: Сложение и вычитание в научном представлении
Расшифровка видео:
Это видео о сложении и вычитании в научном не ация. Вы можете бесплатно получить рабочий лист сложения и вычитания научных обозначений, который мы используем в этом видео, нажав на ссылку в описании ниже. Посмотрите это видео, чтобы узнать, как складывать и вычитать экспоненциальные записи.
Первая задача, которую мы собираемся использовать, чтобы показать вам сложение и вычитание экспоненциальной записи, дает нам 9 умножить на 10 до 9 минус 2 умножить на 10 до 9.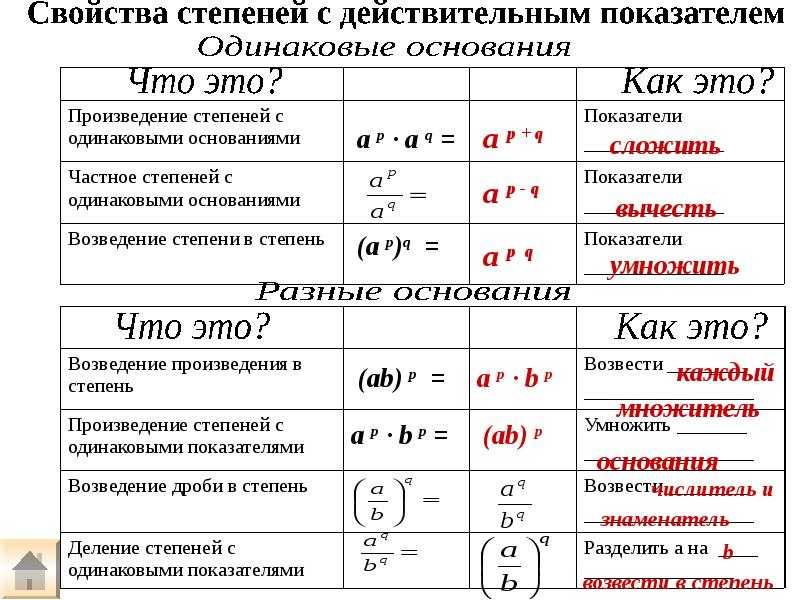 При сложении или вычитании в экспоненциальном представлении вы будете брать коэффициенты каждого числа, которое добавляется или вычитается, и вы собираетесь либо складывать, либо вычитать эти два вместе. В этом случае у нас есть 9 и 2, которые мы в конечном итоге будем складывать или вычитать вместе. Вторая часть добавления или вычитания научной записи, о которой вам нужно знать, заключается в том, что наши степени 10 должны быть равны. Другими словами, показатель степени 10 должен быть одинаковым. Например, если бы это было, скажем, 10 в седьмой степени, мы не могли бы вычесть их, потому что этот показатель равен 9.и этот показатель равен 7. Нам нужно было бы изменить 7 на 9, и когда это было 9, мы могли бы складывать или вычитать, но в случае нашего первого примера у нас есть совпадающие показатели степени.
При сложении или вычитании в экспоненциальном представлении вы будете брать коэффициенты каждого числа, которое добавляется или вычитается, и вы собираетесь либо складывать, либо вычитать эти два вместе. В этом случае у нас есть 9 и 2, которые мы в конечном итоге будем складывать или вычитать вместе. Вторая часть добавления или вычитания научной записи, о которой вам нужно знать, заключается в том, что наши степени 10 должны быть равны. Другими словами, показатель степени 10 должен быть одинаковым. Например, если бы это было, скажем, 10 в седьмой степени, мы не могли бы вычесть их, потому что этот показатель равен 9.и этот показатель равен 7. Нам нужно было бы изменить 7 на 9, и когда это было 9, мы могли бы складывать или вычитать, но в случае нашего первого примера у нас есть совпадающие показатели степени.
Итак, мы собираемся решить эту проблему. При решении этой задачи мы возьмем наши коэффициенты, равные 9 и 2, и вычтем их друг из друга, а затем перепишем нашу степень числа 10 прямо рядом с ним. Мы будем делать 10 раз в 9-й степени, при сложении или вычитании степень 10 должна быть равна. Как только показатель степени равен, вы сохраните показатель степени в своем ответе. Следующим шагом будет фактически пойти дальше и вычесть коэффициент. 9минус 2 равно 7, а затем мы перепишем времена, а затем нашу степень 10, которая равна 10 в 9-й степени. Таким образом, наш ответ в научных обозначениях будет 7 умножить на 10 в 9-й степени, потому что мы не меняем степень 10 в нашем ответе.
Мы будем делать 10 раз в 9-й степени, при сложении или вычитании степень 10 должна быть равна. Как только показатель степени равен, вы сохраните показатель степени в своем ответе. Следующим шагом будет фактически пойти дальше и вычесть коэффициент. 9минус 2 равно 7, а затем мы перепишем времена, а затем нашу степень 10, которая равна 10 в 9-й степени. Таким образом, наш ответ в научных обозначениях будет 7 умножить на 10 в 9-й степени, потому что мы не меняем степень 10 в нашем ответе.
Число 2 очень похоже на число 1. Эта задача покажет вам, как складывать экспоненциальное представление с разными показателями. Нам дано 3 шесть раз по десять до семи плюс две целых один раз по десять до седьмого. Мы знаем, что добавляем, теперь мы собираемся сложить наши коэффициенты вместе, что составляет три целых шесть десятых плюс две целых один десятых. Мы продолжим и напишем, что три целых шесть десятых плюс две целых десятых. Теперь, если вы посмотрите на нашу степень 10, наш показатель степени одинаков для каждой степени 10. 10 в седьмой здесь и десять в седьмой здесь. Нам не нужно менять показатель в степени 10, потому что он уже равен, мы просто перепишем 10 в седьмой степени под нашей задачей. Затем мы продолжим и добавим наши коэффициенты: три целых шесть десятых плюс две целых десятых — это пять целых семь десятых, а затем умножим на 10, а затем уменьшим семерку. Таким образом, наше решение будет пять целых семь десятых в седьмой степени. Все эти задачи можно найти в нашем листе сложения и вычитания с экспоненциальной записью, который можно скачать по ссылке ниже.
10 в седьмой здесь и десять в седьмой здесь. Нам не нужно менять показатель в степени 10, потому что он уже равен, мы просто перепишем 10 в седьмой степени под нашей задачей. Затем мы продолжим и добавим наши коэффициенты: три целых шесть десятых плюс две целых десятых — это пять целых семь десятых, а затем умножим на 10, а затем уменьшим семерку. Таким образом, наше решение будет пять целых семь десятых в седьмой степени. Все эти задачи можно найти в нашем листе сложения и вычитания с экспоненциальной записью, который можно скачать по ссылке ниже.
Число три немного сложнее, потому что оно имеет один дополнительный шаг: семь целых семь целых трижды десять до пятой минус пять целых три десятых до четвертой. Теперь в этом случае мы не можем вычесть их друг из друга, потому что наши показатели степени не совпадают. Вы заметите, что у этого есть четыре, и у этого есть показатель степени пять. Они не равны, что означает, что мы не можем их вычесть, мы должны изменить одно из них на другое, а затем, когда они равны, вы можете их вычесть.
Самый простой способ изменить показатель степени в 10-й степени — это всегда превращать меньший показатель в больший. Что мы собираемся сделать, так это изменить это 4 на 5. Как мы это делаем, мы перемещаем десятичную дробь влево и ставим ее здесь, а затем добавляем единицу к нашему показателю степени. Каждый раз, когда вы перемещаете десятичную дробь влево, вы добавляете единицу к показателю степени. Например, предположим, что мы перемещаем десятичную дробь вместо того, чтобы перемещать ее сразу, мы перемещаем ее один раз два раза, а затем добавляем два к этому показателю степени. Это было бы четыре плюс два, но если бы мы сделали 4 плюс 2, это было бы 6, и мы не пытаемся получить 6, мы пытаемся получить пять, поэтому добавление двух не имеет смысла. Что мы собираемся сделать, так это сдвинуть его влево один раз, а затем добавить один, потому что четыре плюс один равно пяти, и мы пытаемся получить пять. Мы пытаемся сделать показатели равными, поэтому давайте перепишем нашу задачу.

 С. Повторяем и систематизируем школьный курс алгебры и начал анализа.—М.: Просвещение, 1990.— 416 с.
С. Повторяем и систематизируем школьный курс алгебры и начал анализа.—М.: Просвещение, 1990.— 416 с.
 Он представлен как -n или 1/a n . Например, 23 -2 , 4 -2 .
Он представлен как -n или 1/a n . Например, 23 -2 , 4 -2 .

 е. основания одинаковые, но разные показатели степени.
е. основания одинаковые, но разные показатели степени.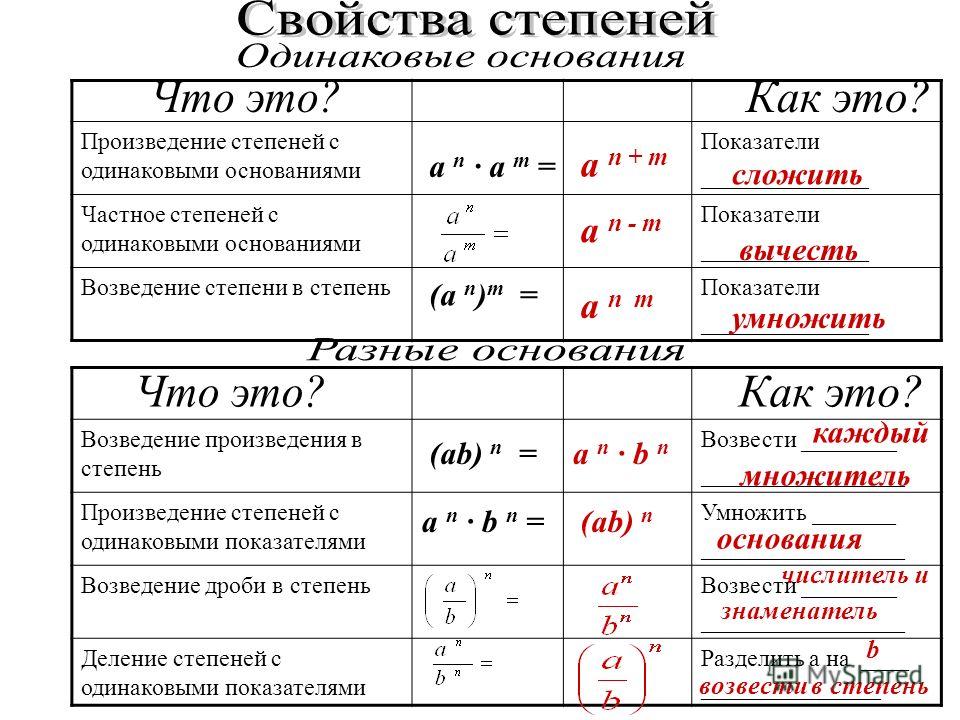 е. 3, но показатель степени y не одно и то же, поэтому мы не можем считать два термина одинаковыми и не будем выполнять между ними никаких операций. (осталось как есть)
е. 3, но показатель степени y не одно и то же, поэтому мы не можем считать два термина одинаковыми и не будем выполнять между ними никаких операций. (осталось как есть)
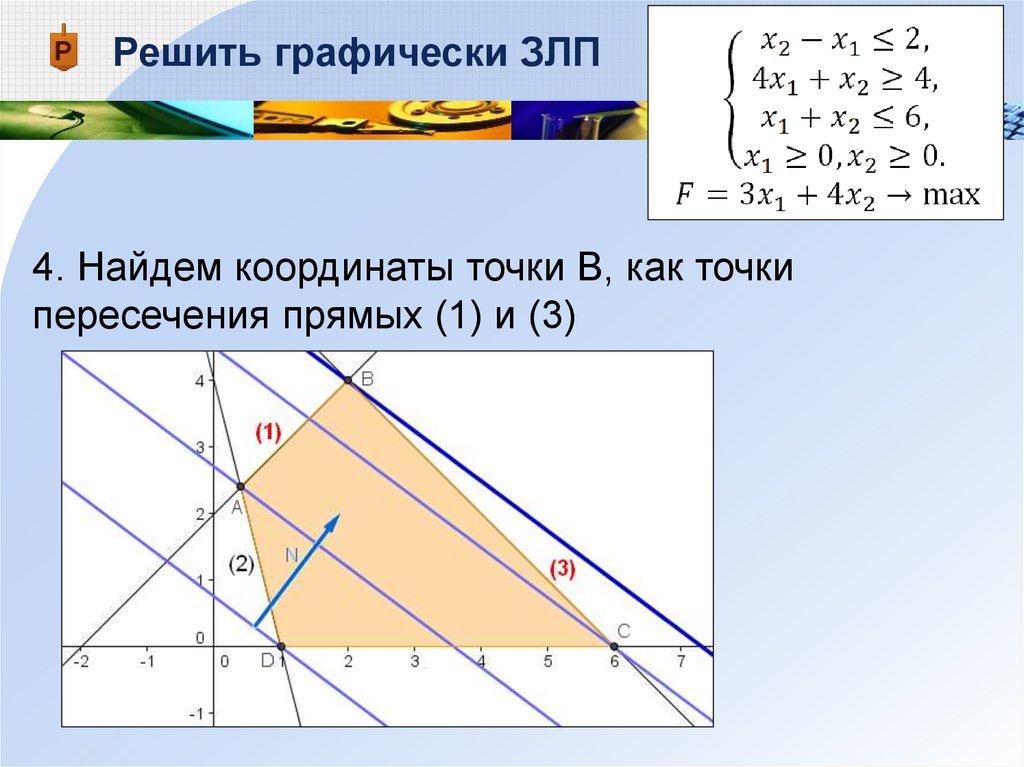
 Чертёж «б» дополним отрезком DВ3 до образования треугольника. На чертеже «в» придадим отрезку направление от вычитаемого (синего вектора) к уменьшаемому (красному вектору), создав вектор разности DВ3.
Чертёж «б» дополним отрезком DВ3 до образования треугольника. На чертеже «в» придадим отрезку направление от вычитаемого (синего вектора) к уменьшаемому (красному вектору), создав вектор разности DВ3. Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и вектор правило треугольника, не
исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «алгебраическое сложение векторов».
Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и вектор правило треугольника, не
исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «алгебраическое сложение векторов». На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и алгебраическое сложение векторов. Просто введите задачу в окошко и нажмите
«решить» здесь (например, вектор суммы).
На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и алгебраическое сложение векторов. Просто введите задачу в окошко и нажмите
«решить» здесь (например, вектор суммы).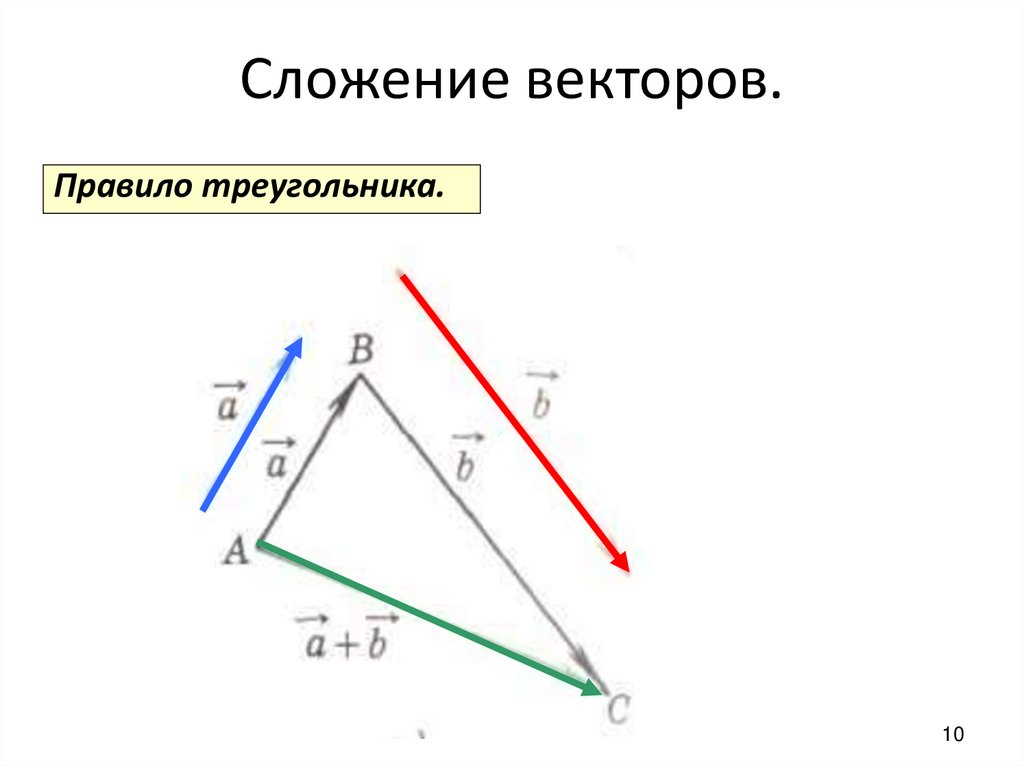 Скаляр, с другой стороны, — это величина, которая имеет только величину и не имеет направления. В физике важны векторы и скаляры. Смещение — фантастический пример векторной величины. Смещение указывает наше расстояние от данной точки, а также нашу ориентацию по отношению к этой точке. Расстояние является примером скаляра и показывает нам, как далеко мы находимся от фиксированного местоположения, но не говорит нам, как туда добраться.
Скаляр, с другой стороны, — это величина, которая имеет только величину и не имеет направления. В физике важны векторы и скаляры. Смещение — фантастический пример векторной величины. Смещение указывает наше расстояние от данной точки, а также нашу ориентацию по отношению к этой точке. Расстояние является примером скаляра и показывает нам, как далеко мы находимся от фиксированного местоположения, но не говорит нам, как туда добраться.


 Векторы складываются геометрически. Закон треугольника, закон параллелограмма и закон многоугольника — это три закона сложения векторов.
Векторы складываются геометрически. Закон треугольника, закон параллелограмма и закон многоугольника — это три закона сложения векторов.
 Это помогает в формировании треугольника ABC, а третья сторона AC дает нам сумму двух векторов a и b соответственно. В результате на основании рис. 2 (ii) мы можем записать
Это помогает в формировании треугольника ABC, а третья сторона AC дает нам сумму двух векторов a и b соответственно. В результате на основании рис. 2 (ii) мы можем записать



 Но на практике специалисты полагают, что 50 тысяч лет — тот предел, за которым точность датировки резко снижается (из-за слишком малого количества исходного изотопа и поступления современных атомов 14C в приборы).
Но на практике специалисты полагают, что 50 тысяч лет — тот предел, за которым точность датировки резко снижается (из-за слишком малого количества исходного изотопа и поступления современных атомов 14C в приборы).

 С., Галкин Г. Н., Маловецкая В. М.
С., Галкин Г. Н., Маловецкая В. М. К.
К.
 Никакое из положений настоящих Правил не дает прав третьим лицам на использование материалов правообладателей, прямо указанных на
конкретном материале, размещенном на Сайте, или в непосредственной близости от указанного материала.
Никакое из положений настоящих Правил не дает прав третьим лицам на использование материалов правообладателей, прямо указанных на
конкретном материале, размещенном на Сайте, или в непосредственной близости от указанного материала.



 ru направляется претензия, содержащая информацию об объекте интеллектуальной собственности, права на который
принадлежат
заявителю и который используется незаконно посредством Сайта или с нарушением правил использования, или иным образом права заявителя как обладателя исключительного права на объект интеллектуальной
собственности, размещенный на Сайте, нарушены посредством Сайта, с приложением документов, подтверждающих правомочия заявителя, данные о правообладателе и копия доверенности на действия от лица
правообладателя, если лицо, направляющее претензию, не является руководителем компании правообладателя или непосредственно физическим лицом — правообладателем. В претензии также указывается адрес
страницы
Сайта, которая содержит данные, нарушающие права, и излагается полное описание сути нарушения прав;
ru направляется претензия, содержащая информацию об объекте интеллектуальной собственности, права на который
принадлежат
заявителю и который используется незаконно посредством Сайта или с нарушением правил использования, или иным образом права заявителя как обладателя исключительного права на объект интеллектуальной
собственности, размещенный на Сайте, нарушены посредством Сайта, с приложением документов, подтверждающих правомочия заявителя, данные о правообладателе и копия доверенности на действия от лица
правообладателя, если лицо, направляющее претензию, не является руководителем компании правообладателя или непосредственно физическим лицом — правообладателем. В претензии также указывается адрес
страницы
Сайта, которая содержит данные, нарушающие права, и излагается полное описание сути нарушения прав;
 Администрация Сайта обязуется
уведомить
заявителя о результатах рассмотрения его заявления (претензии) посредством отправки письма по электронной почте на адрес, указанный заявителем, а также направить ответ в письменном виде на адрес,
указанный заявителем (в случае неуказания такового адреса отправки, обязательство по предоставлению письменного ответа на претензию с Администрации Сайта снимается). В том числе, Администрация
Сайта
вправе запросить дополнительные документы, свидетельства, данные, подтверждающие законность предъявляемой претензии. В случае признания претензии правомерной, Администрация Сайта примет все
возможные
меры, необходимые для прекращения нарушения прав заявителя и урегулирования претензии;
Администрация Сайта обязуется
уведомить
заявителя о результатах рассмотрения его заявления (претензии) посредством отправки письма по электронной почте на адрес, указанный заявителем, а также направить ответ в письменном виде на адрес,
указанный заявителем (в случае неуказания такового адреса отправки, обязательство по предоставлению письменного ответа на претензию с Администрации Сайта снимается). В том числе, Администрация
Сайта
вправе запросить дополнительные документы, свидетельства, данные, подтверждающие законность предъявляемой претензии. В случае признания претензии правомерной, Администрация Сайта примет все
возможные
меры, необходимые для прекращения нарушения прав заявителя и урегулирования претензии;


 Этот распад означает, что количество углерода-14 в объекте служит часами, показывающими возраст объекта в процессе, называемом «углеродное датирование».
Этот распад означает, что количество углерода-14 в объекте служит часами, показывающими возраст объекта в процессе, называемом «углеродное датирование».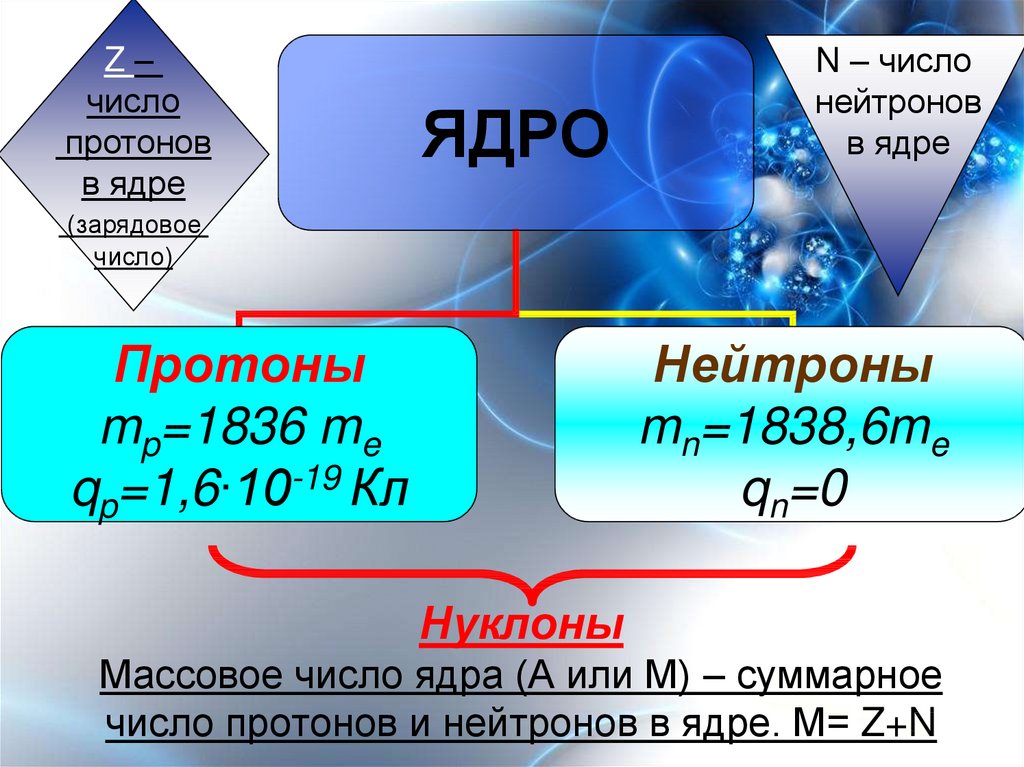 Наконец, он проводит исследования и разработки в области новых и усовершенствованных методов производства и обработки изотопов.
Наконец, он проводит исследования и разработки в области новых и усовершенствованных методов производства и обработки изотопов.
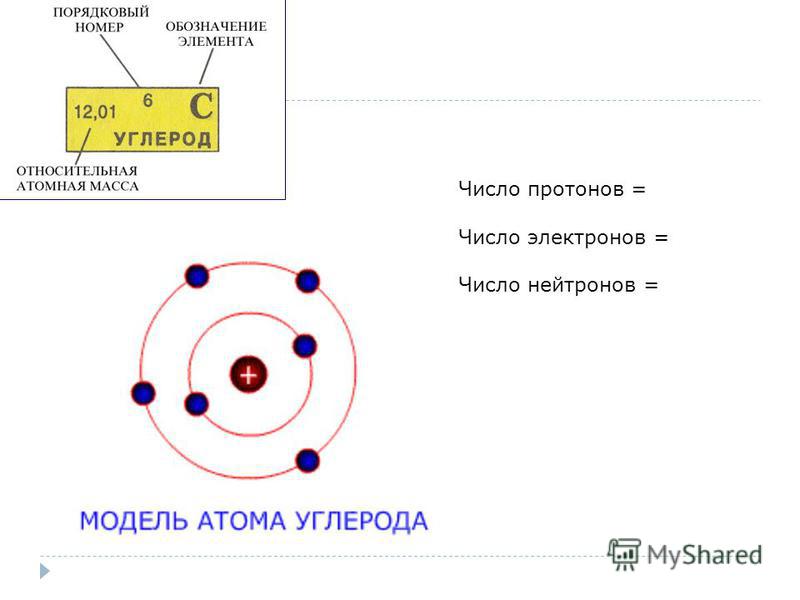
 Однако атом остается одним и тем же элементом независимо от того, имеет ли он положительный, отрицательный или нейтральный заряд.
Однако атом остается одним и тем же элементом независимо от того, имеет ли он положительный, отрицательный или нейтральный заряд. Эти различия в содержании изотопов используются в качестве «меток» для идентификации различных источников CO 2 обнаружен в пробе атмосферного CO 2 . Атмосферные ученые NOAA используют эти изотопные метки, чтобы определить, какой процент этого углерода был получен из ископаемого топлива, земной биосферы или из океана.
Эти различия в содержании изотопов используются в качестве «меток» для идентификации различных источников CO 2 обнаружен в пробе атмосферного CO 2 . Атмосферные ученые NOAA используют эти изотопные метки, чтобы определить, какой процент этого углерода был получен из ископаемого топлива, земной биосферы или из океана.
 Графически могут
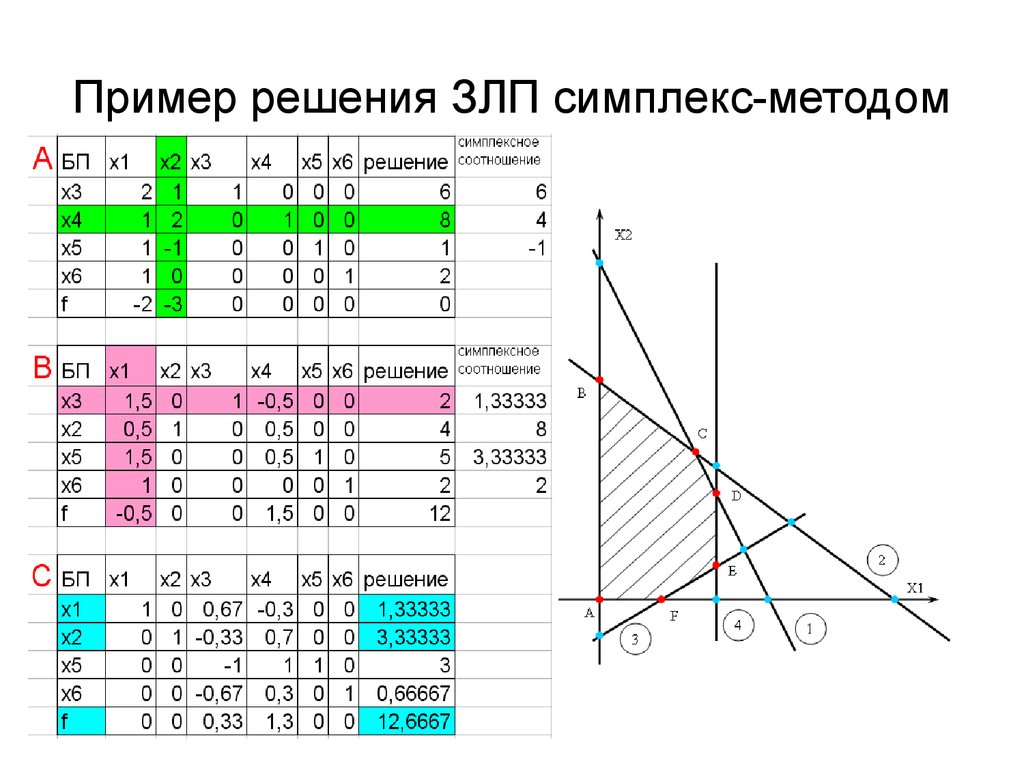
решаться задачи, с числом свободных переменных
𝑛−𝑚 2
(1)
где
n количество переменных;
m количество ограничений.
Задача линейного программирования ставиться следующим образом: Найти точку многогранника решений, в которой целевая функция у = const в зависимости от условий решения
задачи достигает экстремального значения.
Для геометрической интерпретации ЗЛП на плоскости необходимо произвести выбор
координатных переменных. Если в ЗЛП число неизвестных переменных равняется двум, то
данные переменные являются координатными. Если в ЗЛП число переменных больше трёх, то
необходимо выбрать две линейно-независимые неизвестные переменные, которые будем
называть координатными переменными.
Неизвестные переменные считаются линейно-независимыми, когда определители, составленный из коэффициентов при них отличны от нуля.
Далее, используя элементарные методы преобразования, осуществляется представление целевой функции и ограничений через координатные переменные. После преобразования
ЗЛП через координатные переменные можно приступить к решению задачи.
Графически могут
решаться задачи, с числом свободных переменных
𝑛−𝑚 2
(1)
где
n количество переменных;
m количество ограничений.
Задача линейного программирования ставиться следующим образом: Найти точку многогранника решений, в которой целевая функция у = const в зависимости от условий решения
задачи достигает экстремального значения.
Для геометрической интерпретации ЗЛП на плоскости необходимо произвести выбор
координатных переменных. Если в ЗЛП число неизвестных переменных равняется двум, то
данные переменные являются координатными. Если в ЗЛП число переменных больше трёх, то
необходимо выбрать две линейно-независимые неизвестные переменные, которые будем
называть координатными переменными.
Неизвестные переменные считаются линейно-независимыми, когда определители, составленный из коэффициентов при них отличны от нуля.
Далее, используя элементарные методы преобразования, осуществляется представление целевой функции и ограничений через координатные переменные. После преобразования
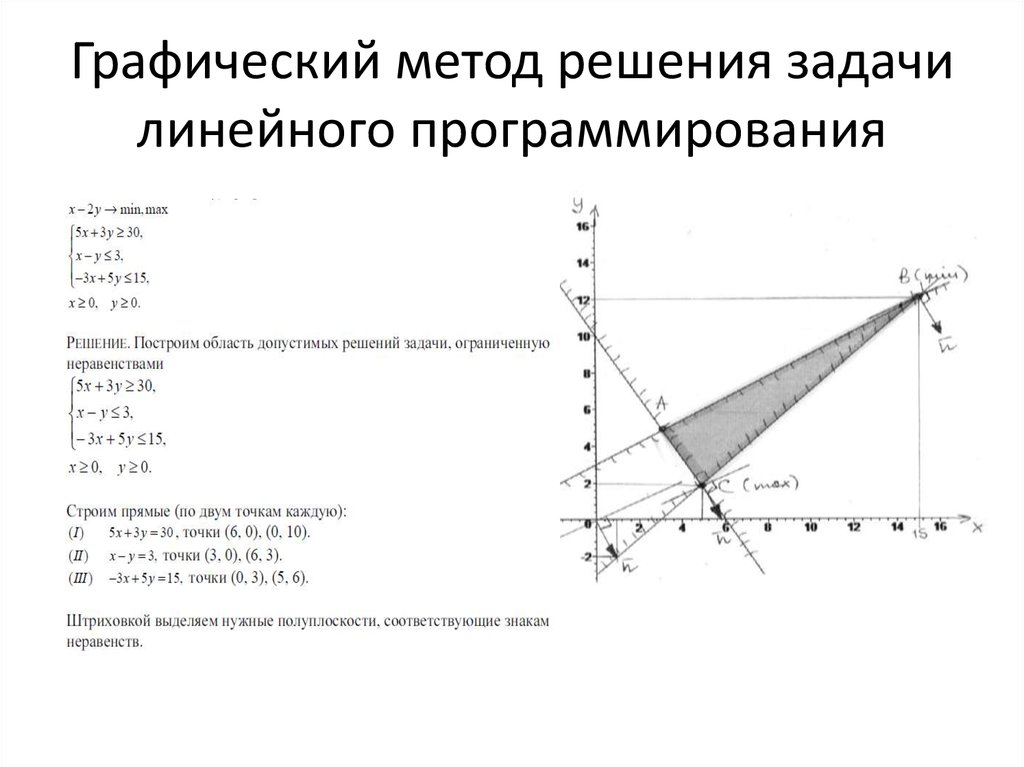
ЗЛП через координатные переменные можно приступить к решению задачи. Графический метод решения ЗЛП состоит из двух этапов:
1. Первый этап построение области допустимых решений (выпуклого многогранника решений).
2. Второй этап нахождение оптимального решения среди всех точек области допустимых
решений.
3
2. ПОСТРОЕНИЕ ОБЛАСТИ ДОПУСТИМЫХ РЕШЕНИЙ
По двум точкам осуществляется построение преобразованных линейных ограничений
на плоскости. Все построенные ограничения нумеруются в той последовательности, как они
записаны в ЗЛП. Из свойств ЗЛП Вы знаете, что каждое ограничение, выраженное через координатные переменные, определяет на плоскости некоторую полуплоскость.
Для нахождения полуплоскостей, в которых выполняется условие решения задачи, выбирается пробная точка. Для этого в любой полуплоскости ограничения необходимо взять
произвольную точку, через которую не проходит соответствующая граничная прямая, и проверить удовлетворяет ли пробная точка данному ограничению. Если удовлетворяет, то данное
ограничение выполняется в соответствующей полуплоскости. В противном случае выбирается
полуплоскость, не содержащая пробной точки.
Графический метод решения ЗЛП состоит из двух этапов:
1. Первый этап построение области допустимых решений (выпуклого многогранника решений).
2. Второй этап нахождение оптимального решения среди всех точек области допустимых
решений.
3
2. ПОСТРОЕНИЕ ОБЛАСТИ ДОПУСТИМЫХ РЕШЕНИЙ
По двум точкам осуществляется построение преобразованных линейных ограничений
на плоскости. Все построенные ограничения нумеруются в той последовательности, как они
записаны в ЗЛП. Из свойств ЗЛП Вы знаете, что каждое ограничение, выраженное через координатные переменные, определяет на плоскости некоторую полуплоскость.
Для нахождения полуплоскостей, в которых выполняется условие решения задачи, выбирается пробная точка. Для этого в любой полуплоскости ограничения необходимо взять
произвольную точку, через которую не проходит соответствующая граничная прямая, и проверить удовлетворяет ли пробная точка данному ограничению. Если удовлетворяет, то данное
ограничение выполняется в соответствующей полуплоскости. В противном случае выбирается
полуплоскость, не содержащая пробной точки. Полуплоскости, в которых не выполняются
условия ограничений, показывают штриховкой.
Так как система линейных ограничений совместна, то прямые, соответствующие ограничениям, пересекаясь, образуют замкнутую область (выпуклый многогранник), который является областью допустимых решений (см. рис. 1.).
Рисунок 1. – Построение ОДР, представляющее выпуклый многогранник
Кроме выпуклого многогранника ОДР может представлять собой неограниченную выпуклую область как сверху, так и снизу (см. рис. 2.), быть пустым множеством (см. рис. 3.), а
также точкой (см. рис. 4.).
Рисунок 2. – ОДР не ограниченная сверху
Рисунок 3. – ОДР, представляющее пустое множество
4
Рисунок 4. – ОДР, представляющее точку
Для построения ОДР ограничения лучше переписать в отрезках.
Например:
3х1 + 2х2 ≤ 27 →
х1
9
+
х2
13.5
≤1
(2)
Как известно, числа, стоящие в знаменателе, показывают, сколько отсекает прямая, соответствующая данному ограничению на той или иной координатной оси.
Например:
Для выражения (1) на оси 0Х1 9 единиц, на оси 0Х2 13,5 единиц.
Полуплоскости, в которых не выполняются
условия ограничений, показывают штриховкой.
Так как система линейных ограничений совместна, то прямые, соответствующие ограничениям, пересекаясь, образуют замкнутую область (выпуклый многогранник), который является областью допустимых решений (см. рис. 1.).
Рисунок 1. – Построение ОДР, представляющее выпуклый многогранник
Кроме выпуклого многогранника ОДР может представлять собой неограниченную выпуклую область как сверху, так и снизу (см. рис. 2.), быть пустым множеством (см. рис. 3.), а
также точкой (см. рис. 4.).
Рисунок 2. – ОДР не ограниченная сверху
Рисунок 3. – ОДР, представляющее пустое множество
4
Рисунок 4. – ОДР, представляющее точку
Для построения ОДР ограничения лучше переписать в отрезках.
Например:
3х1 + 2х2 ≤ 27 →
х1
9
+
х2
13.5
≤1
(2)
Как известно, числа, стоящие в знаменателе, показывают, сколько отсекает прямая, соответствующая данному ограничению на той или иной координатной оси.
Например:
Для выражения (1) на оси 0Х1 9 единиц, на оси 0Х2 13,5 единиц. 3. НАХОЖДЕНИЕ ОПТИМАЛЬНОГО РЕШЕНИЯ
Поскольку оптимальное значение целевой функции достигается на границе, то решение
задачи линейного программирования фактически сводится к поиску вершины многогранника
решений, в которой целевая функция имеет оптимальное (наибольшее в задачах на max или
наименьшее в задачах на min) значение. Т.е. используя метод перебора можно найти оптимальное решение ЗЛП. Однако, при большой размерности задачи (при большом количестве
ограничений и переменных) перебор вершин представляется слишком трудоёмким процессом.
Поэтому задача состоит в том, чтобы избежать перебора вершин, а сделать нахождение оптимального решения целенаправленным.
Уравнение целевой функции при фиксированном значении определяется на плоскости
прямой линией. При у = 0, получаем целевую функцию нулевого уровня. При изменении значения целевой функции получим семейство параллельных прямых, называемых линиями
уровня. При целенаправленном решении оптимизационной задачи вначале строят линию
уровня, приравнивая ЦФ к некоторому малому значению у = Z.
3. НАХОЖДЕНИЕ ОПТИМАЛЬНОГО РЕШЕНИЯ
Поскольку оптимальное значение целевой функции достигается на границе, то решение
задачи линейного программирования фактически сводится к поиску вершины многогранника
решений, в которой целевая функция имеет оптимальное (наибольшее в задачах на max или
наименьшее в задачах на min) значение. Т.е. используя метод перебора можно найти оптимальное решение ЗЛП. Однако, при большой размерности задачи (при большом количестве
ограничений и переменных) перебор вершин представляется слишком трудоёмким процессом.
Поэтому задача состоит в том, чтобы избежать перебора вершин, а сделать нахождение оптимального решения целенаправленным.
Уравнение целевой функции при фиксированном значении определяется на плоскости
прямой линией. При у = 0, получаем целевую функцию нулевого уровня. При изменении значения целевой функции получим семейство параллельных прямых, называемых линиями
уровня. При целенаправленном решении оптимизационной задачи вначале строят линию
уровня, приравнивая ЦФ к некоторому малому значению у = Z. Далее вычисляют координаты
двух точек удовлетворяющие данному уравнению, и через эти две точки проводят пунктирной
линией (или другим цветом) начальную прямую ЦФ, представляющую линию уровня у = Z.
Для определения направления перемещения начальной прямой к оптимальной точки
строят вектор-градиент , координаты которого являются частными производными преобразованной целевой функции:
f
f
k с1 ,
с
(3)
2
k
x
x
2
1
Чтобы построить данный вектор нужно соединить точку (c1, c2) с началом координат.
Осуществляя параллельный сдвиг начальной прямой, перпендикулярной вектору-градиенту
по направлению данного вектора до крайней угловой точки многогранника решений до тех
пор, пока начальная прямая не покинет пределов многоугольной области (до касания с ОДР),
в результате находят точку (см. рис. 5), в которой ЦФ принимает максимальное значение.
5
Осуществляя параллельный сдвиг начальной прямой в противоположном направлении
вектора-градиента до крайней угловой точки многогранника решений, в результате находят
точку, в которой ЦФ принимает минимальное значение.
Далее вычисляют координаты
двух точек удовлетворяющие данному уравнению, и через эти две точки проводят пунктирной
линией (или другим цветом) начальную прямую ЦФ, представляющую линию уровня у = Z.
Для определения направления перемещения начальной прямой к оптимальной точки
строят вектор-градиент , координаты которого являются частными производными преобразованной целевой функции:
f
f
k с1 ,
с
(3)
2
k
x
x
2
1
Чтобы построить данный вектор нужно соединить точку (c1, c2) с началом координат.
Осуществляя параллельный сдвиг начальной прямой, перпендикулярной вектору-градиенту
по направлению данного вектора до крайней угловой точки многогранника решений до тех
пор, пока начальная прямая не покинет пределов многоугольной области (до касания с ОДР),
в результате находят точку (см. рис. 5), в которой ЦФ принимает максимальное значение.
5
Осуществляя параллельный сдвиг начальной прямой в противоположном направлении
вектора-градиента до крайней угловой точки многогранника решений, в результате находят
точку, в которой ЦФ принимает минимальное значение. Определив координаты оптимальной
точки, вычисляют значение ЦФ и оставшиеся неизвестные переменные (см.
рис. 5.).
В данном случае ЗЛП разрешима, и мы имеем единственное решение.
Рисунок 5. – Нахождение оптимальной точки
ЗЛП может иметь и бесконечное множество решений – альтернативный оптимум. В
этом случае прямая, соответствующая целевой функции, параллельна грани многоугольника,
соответствующая одному из активных ограничений ЗЛП (см. рис. 6.).
Рисунок 6. – ЗЛП имеет множество решений
Ограничения называются активными (связывающими), если прямая, его представляющая проходит через оптимальную точку, в противном случае соответствующие ограничения
не являются связывающими.
Если ОДР представляет собой неограниченную выпуклую область, то в зависимости от
условий ЗЛП может и не иметь решения (см. рис. 7, 8)
6
Рисунок 7. – ЗЛП имеет единственное решение точку-минимум
Рисунок 8. – ЗЛП не имеет решения
Если ОДР представляет собой пустое множество, то ЗЛП не разрешима. Если ОДР
представляет собой точку, то говорить об оптимальности не имеет смысла.
Определив координаты оптимальной
точки, вычисляют значение ЦФ и оставшиеся неизвестные переменные (см.
рис. 5.).
В данном случае ЗЛП разрешима, и мы имеем единственное решение.
Рисунок 5. – Нахождение оптимальной точки
ЗЛП может иметь и бесконечное множество решений – альтернативный оптимум. В
этом случае прямая, соответствующая целевой функции, параллельна грани многоугольника,
соответствующая одному из активных ограничений ЗЛП (см. рис. 6.).
Рисунок 6. – ЗЛП имеет множество решений
Ограничения называются активными (связывающими), если прямая, его представляющая проходит через оптимальную точку, в противном случае соответствующие ограничения
не являются связывающими.
Если ОДР представляет собой неограниченную выпуклую область, то в зависимости от
условий ЗЛП может и не иметь решения (см. рис. 7, 8)
6
Рисунок 7. – ЗЛП имеет единственное решение точку-минимум
Рисунок 8. – ЗЛП не имеет решения
Если ОДР представляет собой пустое множество, то ЗЛП не разрешима. Если ОДР
представляет собой точку, то говорить об оптимальности не имеет смысла. Пример:
1. Постановка задачи
Для перевозки изделий, состоящих из двух контейнеров А и В, у компании «Транзит» имеются три транспортных средства разных типов, возможности которых приведены в таблице № 1. Необходимо разработать план
перевозок, обеспечивающий доставку максимального числа изделий в комплекте в течение 24 часов, при условии, что:
— простои и обратные перевозки не допускаются;
— перевозка двух различных контейнеров на одном транспортном средстве не допускается техническими условиями.
Таблица № 1 – Исходные данные задачи
Тип
транспортных средств
Производительность (ед./ч)
Контейнер А
Контейнер В
5
6
5
5
2
3
Т1
Т2
Т3
2. Уяснение экономико-математической постановки задачи
Цель действий: Максимальная перевозка числа изделий в комплекте за сутки.
Цель математического моделирования: Определение эффективного плана перевозок.
Показатель эффективности определим из цели действия – ежедневное число перевезённых изделий в комплекте.
7
3. Разработка математической модели
По условию задачи нам неизвестно время перевозки транспортными средствами соответствующего типа
контейнеров А и В.
Пример:
1. Постановка задачи
Для перевозки изделий, состоящих из двух контейнеров А и В, у компании «Транзит» имеются три транспортных средства разных типов, возможности которых приведены в таблице № 1. Необходимо разработать план
перевозок, обеспечивающий доставку максимального числа изделий в комплекте в течение 24 часов, при условии, что:
— простои и обратные перевозки не допускаются;
— перевозка двух различных контейнеров на одном транспортном средстве не допускается техническими условиями.
Таблица № 1 – Исходные данные задачи
Тип
транспортных средств
Производительность (ед./ч)
Контейнер А
Контейнер В
5
6
5
5
2
3
Т1
Т2
Т3
2. Уяснение экономико-математической постановки задачи
Цель действий: Максимальная перевозка числа изделий в комплекте за сутки.
Цель математического моделирования: Определение эффективного плана перевозок.
Показатель эффективности определим из цели действия – ежедневное число перевезённых изделий в комплекте.
7
3. Разработка математической модели
По условию задачи нам неизвестно время перевозки транспортными средствами соответствующего типа
контейнеров А и В. Обозначим это время как неизвестные переменные модели:
х1 – перевозка контейнера А транспортным средством первого типа;
х2 — перевозка контейнера А транспортным средством второго типа;
х3 — перевозка контейнера А транспортным средством третьего типа;
х4 – перевозка контейнера В транспортным средством первого тип;
х5 — перевозка контейнера В транспортное средство второго типа;
х6 — перевозка контейнера В транспортным средством третьего тип.
Доход, получаемый от перевозки изделий, является условной стоимостью. Обозначим его как с j. По условию задачи с1 = 5, с2 = 6, с3 = 5, с4 = 5, с5 = 2, с6 = 3. Тогда общий доход, получаемый от ежедневного числа
перевезённых изделий можно представить в виде целевой функции:
y 5 x1 6 x 2 5 х3
Условие комплектности изделий является ограничивающим фактором на их перевозку и предполагает,
что за 24 часа транспортные средства перевезут равное число контейнеров А и В. Это условие можно записать
следующим образом:
5 х1 6 х2 5 х3 5 х4 2 х5 3х6
Ещё одним ограничивающим фактором являются требования отсутствия простоев и обратных перевозок.
Обозначим это время как неизвестные переменные модели:
х1 – перевозка контейнера А транспортным средством первого типа;
х2 — перевозка контейнера А транспортным средством второго типа;
х3 — перевозка контейнера А транспортным средством третьего типа;
х4 – перевозка контейнера В транспортным средством первого тип;
х5 — перевозка контейнера В транспортное средство второго типа;
х6 — перевозка контейнера В транспортным средством третьего тип.
Доход, получаемый от перевозки изделий, является условной стоимостью. Обозначим его как с j. По условию задачи с1 = 5, с2 = 6, с3 = 5, с4 = 5, с5 = 2, с6 = 3. Тогда общий доход, получаемый от ежедневного числа
перевезённых изделий можно представить в виде целевой функции:
y 5 x1 6 x 2 5 х3
Условие комплектности изделий является ограничивающим фактором на их перевозку и предполагает,
что за 24 часа транспортные средства перевезут равное число контейнеров А и В. Это условие можно записать
следующим образом:
5 х1 6 х2 5 х3 5 х4 2 х5 3х6
Ещё одним ограничивающим фактором являются требования отсутствия простоев и обратных перевозок.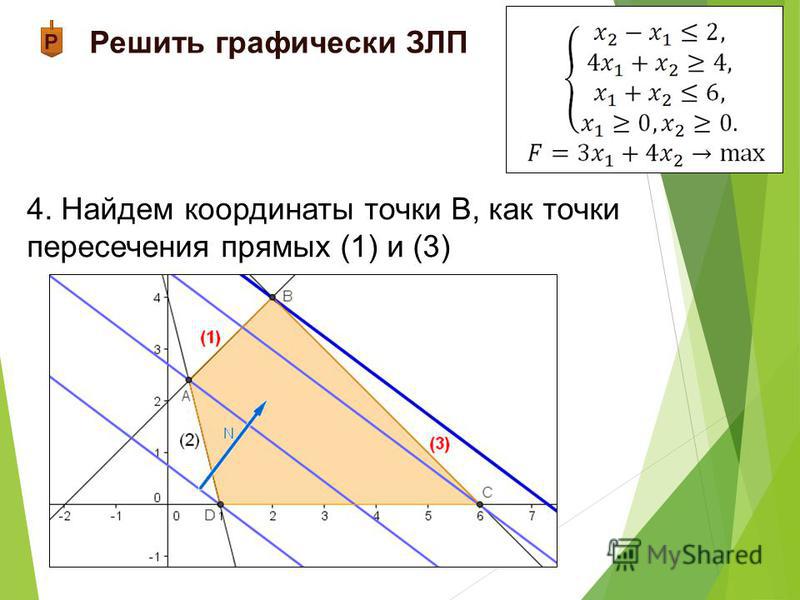 Требование отсутствия простоев, т.е. непрерывного использования всех транспортных средств в течение суток,
можно записать следующим образом:
x1 х4 24
х2 х5 24
х3 х6 24
Требование отсутствия обратных перевозок можно представить в виде общих ограничений:
х j 0 , при j 1,6
Так как ПЭ и ограничения линейны, то данную задачу можно решить методом линейного программирования.
Таким образом, задача нахождения эффективного плана перевозок, обеспечивающего максимум перевозимых изделий в комплекте может быть сформулирована следующим образом:
Найти неотрицательные значения неизвестных переменных х1, х2, х3, х4, х5, х6обращающих ЦФ в максимум:
y 5 x1 6 x2 5 х3 max , при x j X
удовлетворяющих системе линейных ограничений:
уравнений, задающих условия решения задачи
x1 х4 24
x 2 х5 24
x3 х6 24
5 х1 6 х2 5 х3 5 х4 2 х5 3х6 0
ограничений на переменные
х j 0 , при j 1,6
4. Производство расчётов графическим методом
Ввиду того, что неизвестное число переменных не превосходит число линейных уравнений-ограничений
системы на два (6 – 4 = 2), то данная простейшая ЗЛП может быть решена графическим способом.
Требование отсутствия простоев, т.е. непрерывного использования всех транспортных средств в течение суток,
можно записать следующим образом:
x1 х4 24
х2 х5 24
х3 х6 24
Требование отсутствия обратных перевозок можно представить в виде общих ограничений:
х j 0 , при j 1,6
Так как ПЭ и ограничения линейны, то данную задачу можно решить методом линейного программирования.
Таким образом, задача нахождения эффективного плана перевозок, обеспечивающего максимум перевозимых изделий в комплекте может быть сформулирована следующим образом:
Найти неотрицательные значения неизвестных переменных х1, х2, х3, х4, х5, х6обращающих ЦФ в максимум:
y 5 x1 6 x2 5 х3 max , при x j X
удовлетворяющих системе линейных ограничений:
уравнений, задающих условия решения задачи
x1 х4 24
x 2 х5 24
x3 х6 24
5 х1 6 х2 5 х3 5 х4 2 х5 3х6 0
ограничений на переменные
х j 0 , при j 1,6
4. Производство расчётов графическим методом
Ввиду того, что неизвестное число переменных не превосходит число линейных уравнений-ограничений
системы на два (6 – 4 = 2), то данная простейшая ЗЛП может быть решена графическим способом. 4.1
Построение области допустимых решений
8
Т.к. ЗЛП уже представлена в смешанной форме, то сразу перейдём к определению координатных переменных. Неизвестные переменные х1и х2 линейно-независимы, т.к. определитель, составленный из коэффициентов при них, отличен от нуля
1
1
11 0 0 1 0
поэтому их можно использовать в качестве координатных переменных.
Выразим все неизвестные переменные и целевую функцию через координатные переменные, условно
обозначив ограничения:
y 1.25 x1 x 2 150 max
x3 1.25 х1 х2 30
х4 24 х1
х5 24 х2
х6 1.25 х1 х2 6
Из условия не отрицательности всех неизвестных находим следующие выражения, соответствующие линейным ограничениям:
x3 1.25 х1 х2 30 0
х4 24 х1 0
х5 24 х2 0
х6 1.25 х1 х2 6 0
Эти выражения позволяют все ограничения выразить через координатные переменные, условно обозначив их как:
х1 0
х2 0
1.25 х1 х2 30
(1)
х1 24
(2)
х2 24
(3)
1.25 х1 х2 6
(4)
Приравняв левые и правые части неравенств и нанеся прямые на график, определим область допустимых
решений (см.
4.1
Построение области допустимых решений
8
Т.к. ЗЛП уже представлена в смешанной форме, то сразу перейдём к определению координатных переменных. Неизвестные переменные х1и х2 линейно-независимы, т.к. определитель, составленный из коэффициентов при них, отличен от нуля
1
1
11 0 0 1 0
поэтому их можно использовать в качестве координатных переменных.
Выразим все неизвестные переменные и целевую функцию через координатные переменные, условно
обозначив ограничения:
y 1.25 x1 x 2 150 max
x3 1.25 х1 х2 30
х4 24 х1
х5 24 х2
х6 1.25 х1 х2 6
Из условия не отрицательности всех неизвестных находим следующие выражения, соответствующие линейным ограничениям:
x3 1.25 х1 х2 30 0
х4 24 х1 0
х5 24 х2 0
х6 1.25 х1 х2 6 0
Эти выражения позволяют все ограничения выразить через координатные переменные, условно обозначив их как:
х1 0
х2 0
1.25 х1 х2 30
(1)
х1 24
(2)
х2 24
(3)
1.25 х1 х2 6
(4)
Приравняв левые и правые части неравенств и нанеся прямые на график, определим область допустимых
решений (см. рис. 9.).
Х2
32
28
1
2
24
3
20
4
16
12
О
Д
Р
8
4
4
8
12
16
20
24
Х1
Рисунок 9. – Определение ОДР
Нахождение оптимального решения
Для определения направления возрастания ЦФ построим вектор-градиент с координатами (-1.25,1). Далее построим начальную прямую и перемещая по направлению вектора-градиента определим оптимальную граничную экстремальную точку ОДР (см. рис. 10.).
4.2
9
Х2
1
32
28
2
24
3
20
4
16
12
О
Д
Р
8
4
4
8
12
16
20
24
Х1
У=0
Рисунок 10. – Нахождение оптимального решения
Определив координаты оптимальной точки (0, 24), подставив их в уравнение ЦФ и в уравнения линейных
ограничений, получим, что: у = 174, х3 6 , х4 24 , х5 0 , х6 18
5. Анализ полученных результатов
Таким образом при заданных условиях для компании «Транзит» оптимальным решением перевозок
числа изделий в комплекте будет являться: первое транспортное средство должно быть выделено на перевозку
контейнеров «В» в течении 24 часов, второе транспортное средство должно быть выделено на перевозку контейнеров «А» в течении 24 часов и третье транспортное средство должно быть выделено на перевозку контейнеров
«А» и «В» в течении 6 и 18 часов соответственно.
рис. 9.).
Х2
32
28
1
2
24
3
20
4
16
12
О
Д
Р
8
4
4
8
12
16
20
24
Х1
Рисунок 9. – Определение ОДР
Нахождение оптимального решения
Для определения направления возрастания ЦФ построим вектор-градиент с координатами (-1.25,1). Далее построим начальную прямую и перемещая по направлению вектора-градиента определим оптимальную граничную экстремальную точку ОДР (см. рис. 10.).
4.2
9
Х2
1
32
28
2
24
3
20
4
16
12
О
Д
Р
8
4
4
8
12
16
20
24
Х1
У=0
Рисунок 10. – Нахождение оптимального решения
Определив координаты оптимальной точки (0, 24), подставив их в уравнение ЦФ и в уравнения линейных
ограничений, получим, что: у = 174, х3 6 , х4 24 , х5 0 , х6 18
5. Анализ полученных результатов
Таким образом при заданных условиях для компании «Транзит» оптимальным решением перевозок
числа изделий в комплекте будет являться: первое транспортное средство должно быть выделено на перевозку
контейнеров «В» в течении 24 часов, второе транспортное средство должно быть выделено на перевозку контейнеров «А» в течении 24 часов и третье транспортное средство должно быть выделено на перевозку контейнеров
«А» и «В» в течении 6 и 18 часов соответственно. При таком плане перевозок компания «Транзит» перевезёт максимальное количество изделий в комплекте 174 един.
ЗАКЛЮЧЕНИЕ
Таким образом, в процессе изучения лекции Вы практически ознакомились с применением графического метода для решения задачи линейного программирования.
ЛИТЕРАТУРА
Основная:
1. Экономико-математические методы и модели в управлении водным транспортом: Линейное программирование: Учебное пособие / под редакцией профессора В.А. Бабурина.
СПБ.: СПГУВК, 2012. 206 с.
2. Кремер Н.Ш., Исследование операций в экономике: Учебное пособие. М.: Юрайт, 2010.
432с.
3. Есипов Б.А., Методы исследования операций: Учебник для Вузов. М.: Лань, 2010. 256с.
б) Дополнительная:
4. Кремер Н.Ш, Путко Б.А., Фридман М.Н., Исследование операций в экономике: Учебное
пособие. М.: ЮНИТИ, 2006.
5. Хэмди А. Таха, Введение в исследование операций. М.: ВИЛЬЯМС, 2001.
6. Бережная Е.В, Бережной В.И., Математические методы моделирования экономических
систем: Учебное пособие. М.: Финансы и кредит, 2001.
а)
10
7.
При таком плане перевозок компания «Транзит» перевезёт максимальное количество изделий в комплекте 174 един.
ЗАКЛЮЧЕНИЕ
Таким образом, в процессе изучения лекции Вы практически ознакомились с применением графического метода для решения задачи линейного программирования.
ЛИТЕРАТУРА
Основная:
1. Экономико-математические методы и модели в управлении водным транспортом: Линейное программирование: Учебное пособие / под редакцией профессора В.А. Бабурина.
СПБ.: СПГУВК, 2012. 206 с.
2. Кремер Н.Ш., Исследование операций в экономике: Учебное пособие. М.: Юрайт, 2010.
432с.
3. Есипов Б.А., Методы исследования операций: Учебник для Вузов. М.: Лань, 2010. 256с.
б) Дополнительная:
4. Кремер Н.Ш, Путко Б.А., Фридман М.Н., Исследование операций в экономике: Учебное
пособие. М.: ЮНИТИ, 2006.
5. Хэмди А. Таха, Введение в исследование операций. М.: ВИЛЬЯМС, 2001.
6. Бережная Е.В, Бережной В.И., Математические методы моделирования экономических
систем: Учебное пособие. М.: Финансы и кредит, 2001.
а)
10
7. Вентцель Е.С., Исследование операций: Учебное пособие. М.: Советское радио, 1972.
Профессор кафедры математического моделирования
и прикладной информатики, к.в.н., доцент
31 август 2020г.
11
А.А. БУРЫКИН
Вентцель Е.С., Исследование операций: Учебное пособие. М.: Советское радио, 1972.
Профессор кафедры математического моделирования
и прикладной информатики, к.в.н., доцент
31 август 2020г.
11
А.А. БУРЫКИН



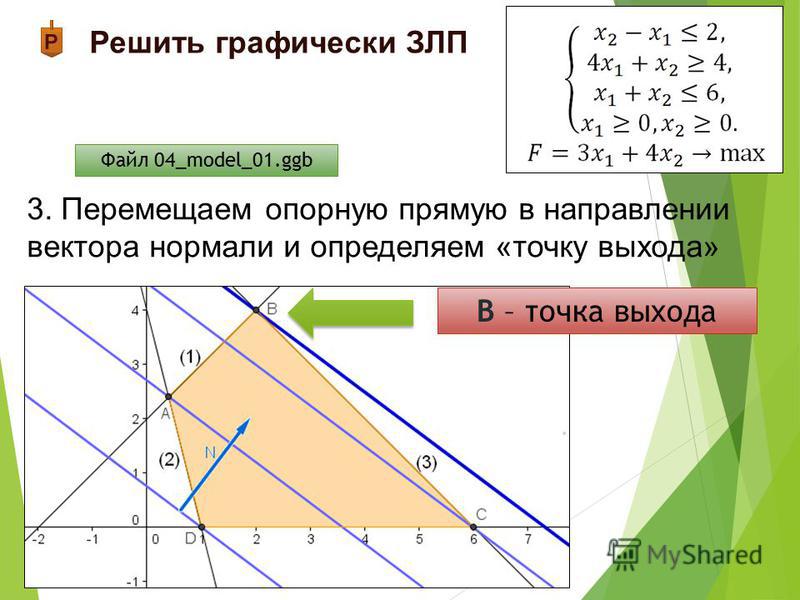
 И эту линию уровня будем передвигать параллельно ей в направлении вектора, если решаем задачу на максимум, и в противном направлении, если на минимум, до тех пор, пока не получим точку выхода из ОДР(если max) или точку входа(если min).
И эту линию уровня будем передвигать параллельно ей в направлении вектора, если решаем задачу на максимум, и в противном направлении, если на минимум, до тех пор, пока не получим точку выхода из ОДР(если max) или точку входа(если min).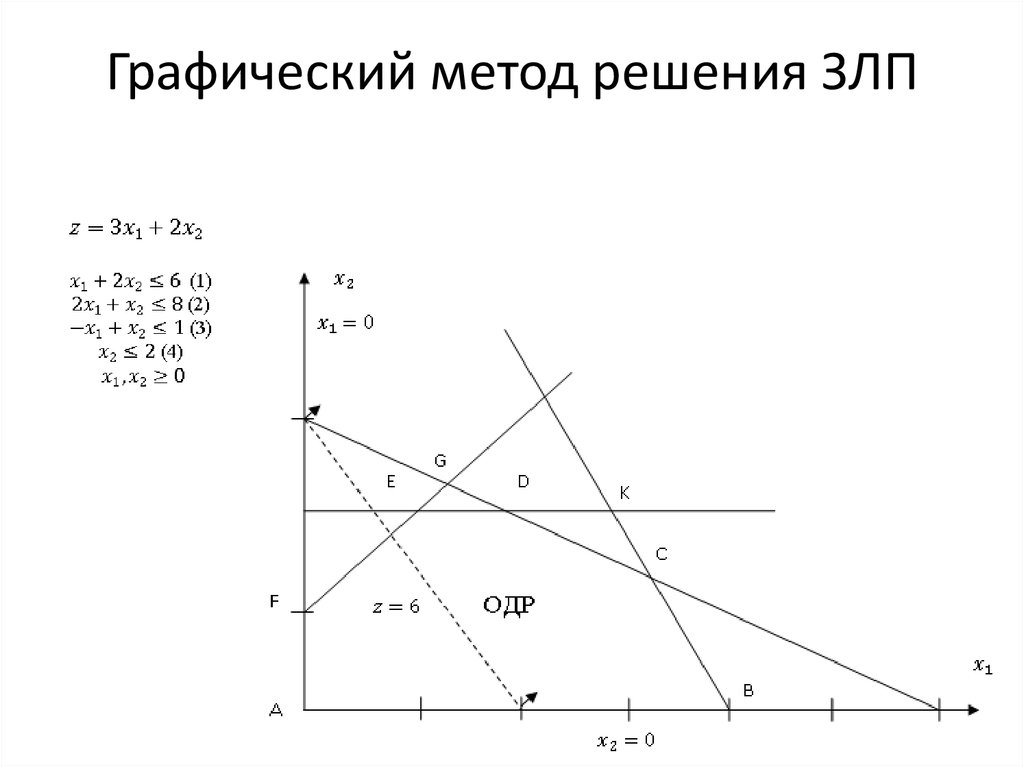 Кроме того, установлено, что спрос на шоколадное мороженое не превышает 350 кг в сутки. Отпускная цена 1 кг сливочного мороженого 16 ден. ед., шоколадного мороженого 14 ден. ед. Требуется определить, какое количество мороженого каждого вида должна производить фирма, чтобы доход от реализации продукции был максимальным?
Кроме того, установлено, что спрос на шоколадное мороженое не превышает 350 кг в сутки. Отпускная цена 1 кг сливочного мороженого 16 ден. ед., шоколадного мороженого 14 ден. ед. Требуется определить, какое количество мороженого каждого вида должна производить фирма, чтобы доход от реализации продукции был максимальным?


 Соединяем их и получаем прямую (2).
Соединяем их и получаем прямую (2). е. x1 = 2; x2 = 3
е. x1 = 2; x2 = 3

 0
0  Fusce dui lectus, congue vel laoreet ac, dictum vitae odio. Донец Аликет. Lorem ipsum
Fusce dui lectus, congue vel laoreet ac, dictum vitae odio. Донец Аликет. Lorem ipsum Fusce dui lectus, congue vel laoreet ac, dictum vitae odio. Донец Аликет. Lorem ipsum dolor sit amet, consectetur adipiscing elit. Nam lacinia pulvinar tortor nec facilisis. Pellentesque dapibus efficitur laoreet. Nam risus ante, dapibus a molestie consequat, ultrices ac magna. Fusce dui lectus, congue vel laoreet ac, dictum vitae odio. Донец Аликет. Lorem ipsum dolor sit amet, consectetur adipiscing elit. Nam lacinia pulvinar tortor nec facilisis. Pellentesque dapibus efficitur laoreet. Nam risus ante, dapibus a molestie consequat, ultrices ac magna. Fusce dui lectus, congue vel laoreet ac, dictum vitae odio. Донец Аликет. Lorem ipsum dolor sit amet, consectetur adipiscing elit. Nam lacinia pulvinar tortor nec facilisis. Pellentesque dapibus efficitur laoreet. Nam risus ante, dapibus a molestie consequat, ultrices ac magna. Fusce dui lectus, congue vel laoreet ac, dictum vitae odio. Донец Аликет. Lorem ipsum dolor sit amet, consectetur adipiscing elit. Nam lacinia pulvinar tortor nec facilisis.
Fusce dui lectus, congue vel laoreet ac, dictum vitae odio. Донец Аликет. Lorem ipsum dolor sit amet, consectetur adipiscing elit. Nam lacinia pulvinar tortor nec facilisis. Pellentesque dapibus efficitur laoreet. Nam risus ante, dapibus a molestie consequat, ultrices ac magna. Fusce dui lectus, congue vel laoreet ac, dictum vitae odio. Донец Аликет. Lorem ipsum dolor sit amet, consectetur adipiscing elit. Nam lacinia pulvinar tortor nec facilisis. Pellentesque dapibus efficitur laoreet. Nam risus ante, dapibus a molestie consequat, ultrices ac magna. Fusce dui lectus, congue vel laoreet ac, dictum vitae odio. Донец Аликет. Lorem ipsum dolor sit amet, consectetur adipiscing elit. Nam lacinia pulvinar tortor nec facilisis. Pellentesque dapibus efficitur laoreet. Nam risus ante, dapibus a molestie consequat, ultrices ac magna. Fusce dui lectus, congue vel laoreet ac, dictum vitae odio. Донец Аликет. Lorem ipsum dolor sit amet, consectetur adipiscing elit. Nam lacinia pulvinar tortor nec facilisis.

 1 мм
1 мм

 Чтобы ознакомиться с ними, выберите соответствующий раздел в меню нашего сайта. Так вы увидите товары со скидками и наиболее выгодные предложения в нашем ассортименте.
Чтобы ознакомиться с ними, выберите соответствующий раздел в меню нашего сайта. Так вы увидите товары со скидками и наиболее выгодные предложения в нашем ассортименте. Оршанская, 5, офис 2/2. Там вы сможете лично оценить качество фурнитуры для душевых кабин, ограждений и стеклянных перегородок.
Оршанская, 5, офис 2/2. Там вы сможете лично оценить качество фурнитуры для душевых кабин, ограждений и стеклянных перегородок. Толщина стенки ровно 1,5 мм – проверил лично
Толщина стенки ровно 1,5 мм – проверил лично 2×6000 мм, GRIT 600Труба круглая AISI 304 ASTM A554 Ø25.0×1.2×6000 мм GRIT 600
2×6000 мм, GRIT 600Труба круглая AISI 304 ASTM A554 Ø25.0×1.2×6000 мм GRIT 600 0×1.5×6000 мм GRIT 320
0×1.5×6000 мм GRIT 320 8×1.5×4000-600
8×1.5×4000-600 2×6000-800
2×6000-800 8
8  4 Миллиметры
4 Миллиметры 8 Миллиметры
8 Миллиметры


 Fe(OH) 3 (водн.) + H 2 SO 3 (водн.) → Fe 2 (SO 3 ) +
Fe(OH) 3 (водн.) + H 2 SO 3 (водн.) → Fe 2 (SO 3 ) + с числом молей Fe(OH) 3 , 3 с числом молей H 2 SO 3 на стороне реагента и 6 с числом молей H 2 O на стороне продукта.
с числом молей Fe(OH) 3 , 3 с числом молей H 2 SO 3 на стороне реагента и 6 с числом молей H 2 O на стороне продукта.  ) + 3SO 3 2- (водн.) + 6H 2 O (л)
) + 3SO 3 2- (водн.) + 6H 2 O (л)  В решетке гидроксида железа ион железа (Fe 3+ ) OH – ) притягиваются друг к другу этой сильной межионной колумбовой силой.
В решетке гидроксида железа ион железа (Fe 3+ ) OH – ) притягиваются друг к другу этой сильной межионной колумбовой силой.  45 KJ/mol ( 𐤃H liquid )
45 KJ/mol ( 𐤃H liquid ) Если вместе с реагентами будут записаны фактические продукты, такие как вода и сульфит железа, то это будет считаться полной реакцией. Поэтому полная реакция написана ниже-
Если вместе с реагентами будут записаны фактические продукты, такие как вода и сульфит железа, то это будет считаться полной реакцией. Поэтому полная реакция написана ниже-  Следовательно, степень окисления Fe, H, O и S не меняется. Все элементы сохраняют свою степень окисления на протяжении всей реакции.
Следовательно, степень окисления Fe, H, O и S не меняется. Все элементы сохраняют свою степень окисления на протяжении всей реакции.  к. завершение реакции. Продукт, сульфит железа [Fe 2 (SO 3 ) 3 ], полностью растворим в воде. Это скорее реакция смещения.
к. завершение реакции. Продукт, сульфит железа [Fe 2 (SO 3 ) 3 ], полностью растворим в воде. Это скорее реакция смещения.  Двойная реакция смещения
Двойная реакция смещения  Добавление энтальпий дает нам наш ответ:
Добавление энтальпий дает нам наш ответ: Напишите (и сбалансируйте) это:
Напишите (и сбалансируйте) это:

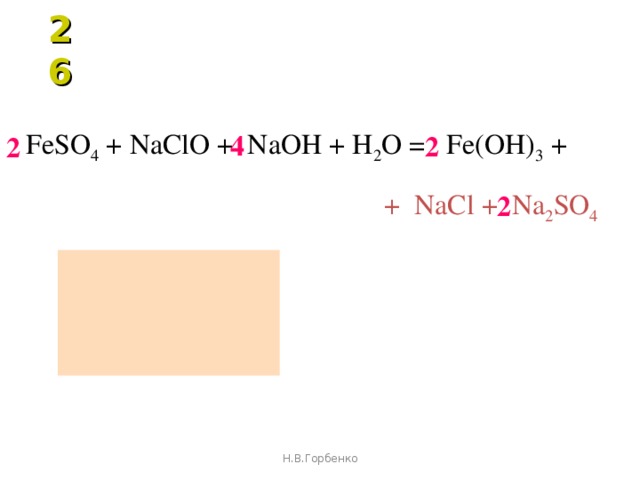

 5ΔH 3
5ΔH 3 
 Сложение трех энтальпий дает энтальпию образования ацетилена:
Сложение трех энтальпий дает энтальпию образования ацетилена: Вот почему я справился с этим, чтобы вы могли проанализировать, как другой мозг подходит к этим проблемам. Обратите особое внимание на рассуждения, происходящие в шаге 4.
Вот почему я справился с этим, чтобы вы могли проанализировать, как другой мозг подходит к этим проблемам. Обратите особое внимание на рассуждения, происходящие в шаге 4.
 Например, если в PDF-файле есть рисунки, диаграммы или таблицы, они будут отображаться в документе Word в том же виде.
Например, если в PDF-файле есть рисунки, диаграммы или таблицы, они будут отображаться в документе Word в том же виде. Если вы предоставите отсканированный PDF-файл, он извлечет из него текст с помощью OCR и включит его в макет.
Если вы предоставите отсканированный PDF-файл, он извлечет из него текст с помощью OCR и включит его в макет.
 Есть много функций: защита, подпись, комментарий, распознавание текста и т. д., которые значительно удовлетворят ваши потребности в редактировании ваших файлов. Он поддерживает все системы Windows.
Есть много функций: защита, подпись, комментарий, распознавание текста и т. д., которые значительно удовлетворят ваши потребности в редактировании ваших файлов. Он поддерживает все системы Windows. Чтобы узнать, как преобразовать документ в PDF с помощью этой программы, просто прочитайте:
Чтобы узнать, как преобразовать документ в PDF с помощью этой программы, просто прочитайте:

 6 класс. Часть 1.
6 класс. Часть 1. ..
.. 7 не делится нацело на 3.
7 не делится нацело на 3. 7 и 15 — взаимно простые.
7 и 15 — взаимно простые.


 Разложим числа на простые множители. Выпишем разложение первого числа. Дополним числами из разложения второго числа без повторений
Разложим числа на простые множители. Выпишем разложение первого числа. Дополним числами из разложения второго числа без повторений Посчитать дополнительные множители
Посчитать дополнительные множители Модули противоположных чисел равны:
Модули противоположных чисел равны:
 Числа, прошедшие тест, считаются делящимися на это число, в противном случае они не делятся.
Числа, прошедшие тест, считаются делящимися на это число, в противном случае они не делятся. Следует помнить, что в настоящее время дешевых транспортных средств нет вовсе — можно лишь говорить о тех или иных видовых преимуществах в конкретных ситуациях.
[c.210]
Следует помнить, что в настоящее время дешевых транспортных средств нет вовсе — можно лишь говорить о тех или иных видовых преимуществах в конкретных ситуациях.
[c.210] Но в случае указанной процедуры равенство суммы значений теоретического и эмпирического рядов соблюдается лишь по отношению к прямой в логарифмах, найденной методом наименьших квадратов, но не должно обязательно иметь место для этих рядов в натуральном масштабе теоретические значения показательной кривой для первоначального ряда обнаруживают часто систематическое, смещение, и их сумма и сумма членов исходного ряда разнятся и иногда очень существенно.
[c.128]
Но в случае указанной процедуры равенство суммы значений теоретического и эмпирического рядов соблюдается лишь по отношению к прямой в логарифмах, найденной методом наименьших квадратов, но не должно обязательно иметь место для этих рядов в натуральном масштабе теоретические значения показательной кривой для первоначального ряда обнаруживают часто систематическое, смещение, и их сумма и сумма членов исходного ряда разнятся и иногда очень существенно.
[c.128] 85]
85] Скобки будут единственным оператором группировки, и они могут быть использованы для ясности выражения, даже если в них математически нет необходимости. В качестве оператора группировки также могут использоваться фигурные скобки. Большинство математических функций, используемых в книге, довольно просты (например, функция абсолютного значения и функция натурального логарифма). Есть одна функция, которая может быть знакома не всем читателям, — это экспоненциальная функция, обозначаемая в книге ЕХР(). Математически она чаще выражается как постоянная е, равная 2,7182818285, возведенная в степень. Таким образом [c.9]
Скобки будут единственным оператором группировки, и они могут быть использованы для ясности выражения, даже если в них математически нет необходимости. В качестве оператора группировки также могут использоваться фигурные скобки. Большинство математических функций, используемых в книге, довольно просты (например, функция абсолютного значения и функция натурального логарифма). Есть одна функция, которая может быть знакома не всем читателям, — это экспоненциальная функция, обозначаемая в книге ЕХР(). Математически она чаще выражается как постоянная е, равная 2,7182818285, возведенная в степень. Таким образом [c.9] Таким же образом мы можем преобразовать десятичный логарифм в натуральный путем умножения десятичного логарифма на 2,3026.
[c.101]
Таким же образом мы можем преобразовать десятичный логарифм в натуральный путем умножения десятичного логарифма на 2,3026.
[c.101] Число 2,718, или, как его обозначают, е — это основание натурального логарифма.
[c.39]
Число 2,718, или, как его обозначают, е — это основание натурального логарифма.
[c.39]


 Так, логарифмы употребляются для расчета постоянной распада для известного периода полураспада, или для вычисления времени распада в решении проблем радиоактивности. Они выступают в главной роли во многих разделах математики и практических наук, к ним прибегают в сфере финансов для решения большого числа задач, в том числе и в расчете сложных процентов.
Так, логарифмы употребляются для расчета постоянной распада для известного периода полураспада, или для вычисления времени распада в решении проблем радиоактивности. Они выступают в главной роли во многих разделах математики и практических наук, к ним прибегают в сфере финансов для решения большого числа задач, в том числе и в расчете сложных процентов. Например, ln(7,389…) равен 2, потому что e 2 =7,389… . Натуральный логарифм самого числа e (ln(e) ) равен 1, потому что e 1 = e , а натуральный логарифм 1 (ln(1) ) равен 0, поскольку e 0 = 1.
Например, ln(7,389…) равен 2, потому что e 2 =7,389… . Натуральный логарифм самого числа e (ln(e) ) равен 1, потому что e 1 = e , а натуральный логарифм 1 (ln(1) ) равен 0, поскольку e 0 = 1. Логарифмы полезны для решения уравнений, в которых неизвестные присутствуют в качестве показателя степени. Например, логарифмы используются для нахождения постоянной распада для известного периода полураспада, или для нахождения времени распада в решении проблем радиоактивности . Они играют важную роль во многих областях математики и прикладных наук, применяются в сфере финансов для решения многих задач, включая нахождение сложных процентов.
Логарифмы полезны для решения уравнений, в которых неизвестные присутствуют в качестве показателя степени. Например, логарифмы используются для нахождения постоянной распада для известного периода полураспада, или для нахождения времени распада в решении проблем радиоактивности . Они играют важную роль во многих областях математики и прикладных наук, применяются в сфере финансов для решения многих задач, включая нахождение сложных процентов.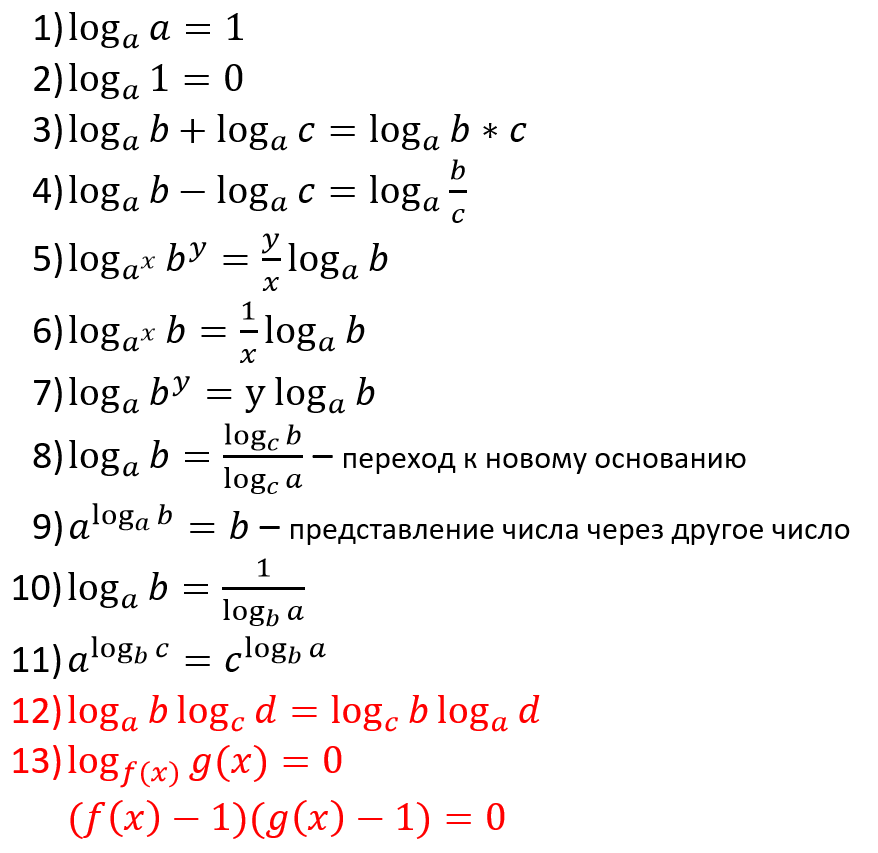

 е. как интеграл :
е. как интеграл :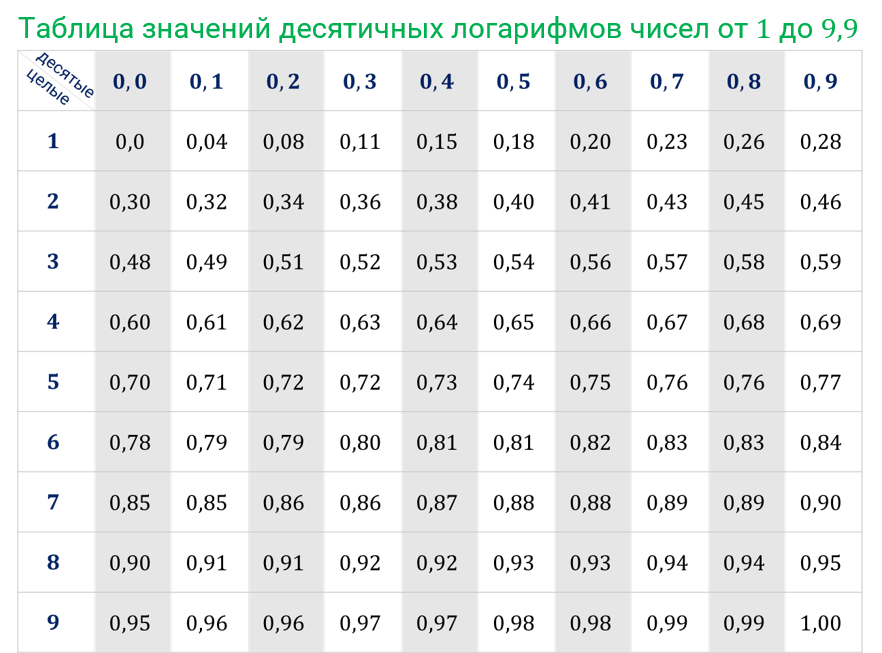 Альтернативой является использование метода Ньютона , чтобы инвертировать в экспоненциальную функцию, ряд которой сходится быстрее.
Альтернативой является использование метода Ньютона , чтобы инвертировать в экспоненциальную функцию, ряд которой сходится быстрее.
 Комплексный логарифм может быть однозначным только на срезе комплексной плоскости. Например, ln i = 1/2 πi или 5/2 πi или −3/2 πi , и т.д., и хотя i 4 = 1, 4 log i может быть определена как 2πi , или 10πi или −6 πi , и так далее.
Комплексный логарифм может быть однозначным только на срезе комплексной плоскости. Например, ln i = 1/2 πi или 5/2 πi или −3/2 πi , и т.д., и хотя i 4 = 1, 4 log i может быть определена как 2πi , или 10πi или −6 πi , и так далее.
 Кстати, о причудах; по латыни он называется logarithmus naturali
, отсюда и появилась аббревиатура ln.
Кстати, о причудах; по латыни он называется logarithmus naturali
, отсюда и появилась аббревиатура ln. Нуль. Нисколько. У вас уже
это есть единожды. Не требуется нисколько времени, чтобы от уровня 1 дорости до уровня 1.
Нуль. Нисколько. У вас уже
это есть единожды. Не требуется нисколько времени, чтобы от уровня 1 дорости до уровня 1.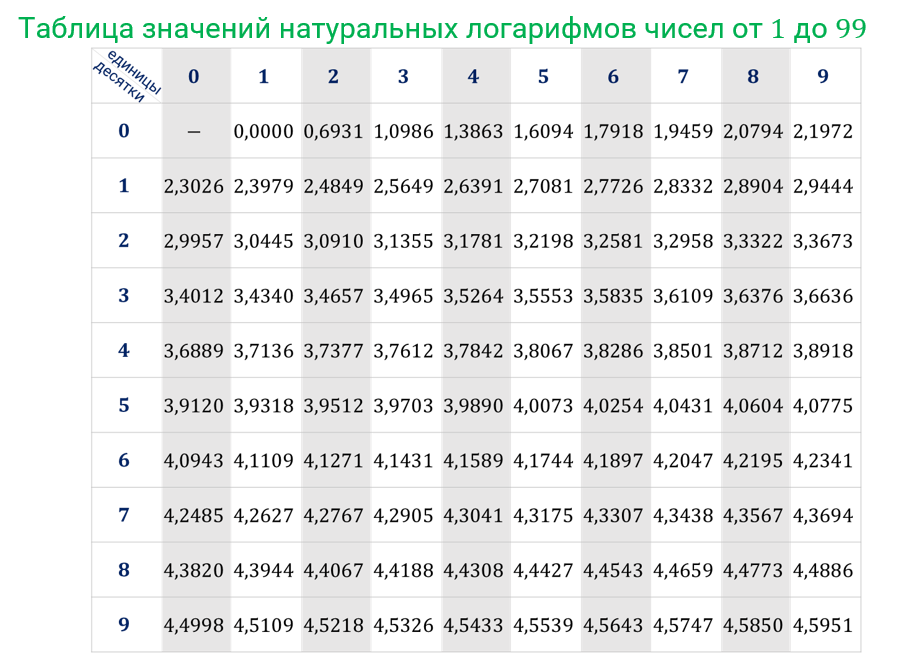 .. минимум) нуль, но вам никак не получить отрицательное число этих маленьких тварей. В отрицательном числе бактерий просто нет смысла.
.. минимум) нуль, но вам никак не получить отрицательное число этих маленьких тварей. В отрицательном числе бактерий просто нет смысла. Это отношение сразу обретает смысл, если оперировать в терминах роста.
Это отношение сразу обретает смысл, если оперировать в терминах роста. Не надо запоминать правила, попробуйте осознать их.
Не надо запоминать правила, попробуйте осознать их. 4
4 Мы использовали натуральный логарифм для случая с непрерывным ростом, а теперь ты ведёшь речь о ежегодном начислении? Не станет ли это формула непригодной для такого случая? Да, станет, однако для реальных процентных ставок вроде 5%, 6% или даже 15%, разница между ежегодным начислением процентов и непрерывным ростом будет невелика. Так что грубая оценка работает, мм, грубо, так что мы сделаем вид, что у нас полностью непрерывное начисление.
Мы использовали натуральный логарифм для случая с непрерывным ростом, а теперь ты ведёшь речь о ежегодном начислении? Не станет ли это формула непригодной для такого случая? Да, станет, однако для реальных процентных ставок вроде 5%, 6% или даже 15%, разница между ежегодным начислением процентов и непрерывным ростом будет невелика. Так что грубая оценка работает, мм, грубо, так что мы сделаем вид, что у нас полностью непрерывное начисление. 10″:
10″:

 Следовательно, log0 10 или log of 0 не определены. Никакое число не может соответствовать уравнению, если x равно любому значению. Следовательно, log 0 равен не определено.
Следовательно, log0 10 или log of 0 не определены. Никакое число не может соответствовать уравнению, если x равно любому значению. Следовательно, log 0 равен не определено.
 Итак, log a (по основанию 1) не определен.
Итак, log a (по основанию 1) не определен. Логарифм отрицательных чисел не определен.
Логарифм отрицательных чисел не определен.


 log(matrix) для применения функции натурального логарифма, но я получаю nan, когда запись матрицы равна нулю, и я хотел бы, чтобы вместо этого она была равна нулю
log(matrix) для применения функции натурального логарифма, но я получаю nan, когда запись матрицы равна нулю, и я хотел бы, чтобы вместо этого она была равна нулю log (матрица))
log (матрица))

 … Просмотреть урок
… Просмотреть урок Эти задачи будут иметь более сложные функции, которые научат учащегося подходить к более сложным задачам…. Просмотреть урок
Эти задачи будут иметь более сложные функции, которые научат учащегося подходить к более сложным задачам…. Просмотреть урок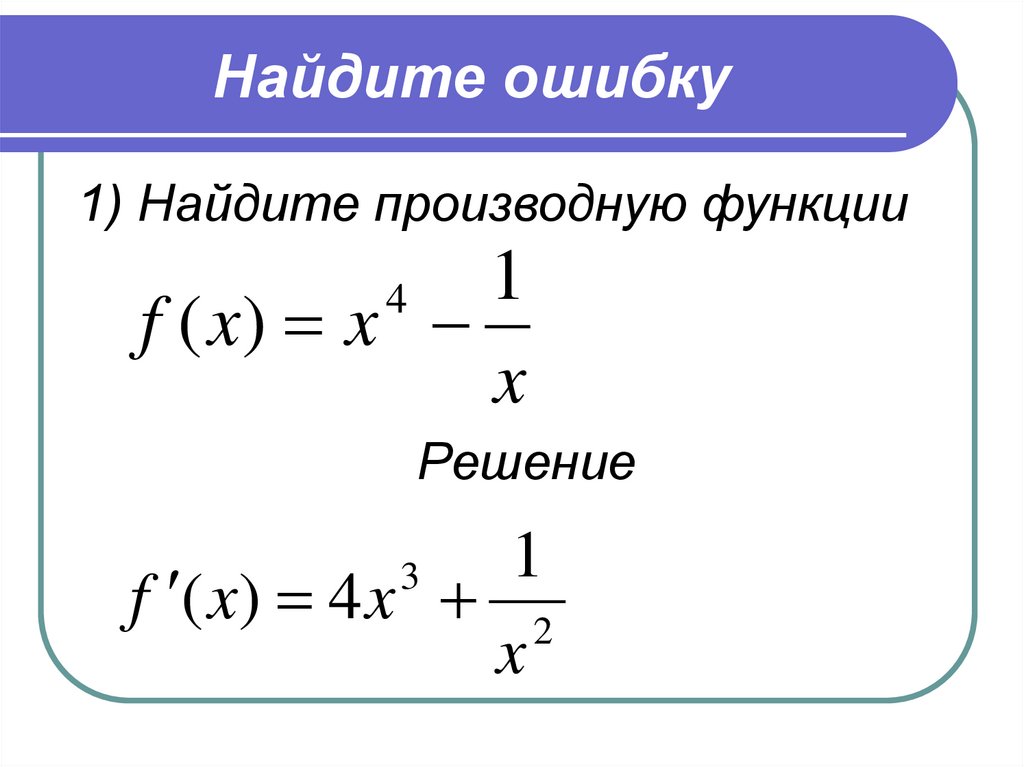 … Посмотреть урок
… Посмотреть урок … Посмотреть урок
… Посмотреть урок Проработаны многочисленные примеры, показывающие пошаговое решение…. Посмотреть урок
Проработаны многочисленные примеры, показывающие пошаговое решение…. Посмотреть урок Спасибо за создание этого приложения; это потрясающе. Лучшее математическое приложение на данный момент. Не позволяйте вашим учителям математики видеть это, иначе они получат сердечный приступ и НЕ БОЛЬШЕ ТРУДНОСТЕЙ В ДОМАШНИХ ЗАДАНИЯХ.
Спасибо за создание этого приложения; это потрясающе. Лучшее математическое приложение на данный момент. Не позволяйте вашим учителям математики видеть это, иначе они получат сердечный приступ и НЕ БОЛЬШЕ ТРУДНОСТЕЙ В ДОМАШНИХ ЗАДАНИЯХ. Когда
Когда Головоломки начинаются с некоторых чисел, уже находящихся на сетке, и остальные числа должны быть заполнены вами. 4 октября 2019 г.
Головоломки начинаются с некоторых чисел, уже находящихся на сетке, и остальные числа должны быть заполнены вами. 4 октября 2019 г.
 Они могут помочь вам понять материал и улучшить свои оценки.
Они могут помочь вам понять материал и улучшить свои оценки.