Статистика хи-квадрата с учетом выборки и дисперсии генеральной совокупности Калькулятор
✖Размер выборки — это общее количество лиц, присутствующих в данной выборке в исследуемой популяции.ⓘ Размер образца [N] | +10% -10% | ||
✖Выборочная дисперсия — это математическое ожидание квадрата отклонения случайной величины, связанной с данной выборкой, от генеральной совокупности.ⓘ Выборочная дисперсия [Vs] | +10% -10% | ||
✖Дисперсия населения — это математическое ожидание квадрата отклонения случайной величины, связанной с данным населением.ⓘ Дисперсия населения [Vσ] | +10% -10% |
|
✖Статистика хи-квадрат — это стандартный параметр, который характеризует выборку из совокупности с использованием стандартного отклонения выборки и стандартного отклонения совокупности. |
⎘ копия |
👎
Формула
сбросить
👍
Статистика хи-квадрата с учетом выборки и дисперсии генеральной совокупности Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1. Преобразование входов в базовый блок
Размер образца: 20 —> Конверсия не требуется
Выборочная дисперсия: 12 —> Конверсия не требуется
Дисперсия населения: 6 —> Конверсия не требуется
ШАГ 2: Оцените формулу
ШАГ 3: Преобразуйте результат в единицу вывода
38 —> Конверсия не требуется
< 16 Основные формулы в статистике Калькуляторы
Значение P образца
Идти Значение P образца = (Образец пропорции-Предполагаемая доля населения)/sqrt((Предполагаемая доля населения*(1-Предполагаемая доля населения))/Размер образца)
Размер выборки с учетом значения P
Идти Размер образца = ((Значение P образца^2)*Предполагаемая доля населения*(1-Предполагаемая доля населения))/((Образец пропорции-Предполагаемая доля населения)^2)
т Статистика
Идти т Статистика = (Наблюдаемое среднее значение выборки-Теоретическое среднее значение выборки)/(Стандартное отклонение выборки/sqrt(Размер образца))
t Статистика нормального распределения
Идти t Статистика нормального распределения = (Выборочное среднее-Средняя численность населения)/(Стандартное отклонение выборки/sqrt(Размер образца))
Чи-квадрат Статистика
Идти Чи-квадрат Статистика = ((Размер образца-1)*Стандартное отклонение выборки^2)/(Стандартное отклонение населения^2)
Количество классов с учетом ширины класса
Идти Количество классов = (Самый большой элемент в данных-Наименьший элемент данных)/Ширина класса данных
Ширина класса данных
Идти Ширина класса данных = (Самый большой элемент в данных-Наименьший элемент данных)/Количество классов
Статистика хи-квадрата с учетом выборки и дисперсии генеральной совокупности
Идти Чи-квадрат Статистика = ((Размер образца-1)*Выборочная дисперсия)/Дисперсия населения
Количество отдельных значений с учетом остаточной стандартной ошибки
Идти Количество отдельных значений = (Остаточная сумма квадратов/(Остаточная стандартная ошибка данных^2))+1
Ожидание разности случайных величин
Идти Ожидание разности случайных величин = Ожидание случайной величины X-Ожидание случайной величины Y
F Значение двух образцов с заданными стандартными отклонениями выборки
Идти Значение F двух образцов = (Стандартное отклонение образца X/Стандартное отклонение образца Y)^2
Ожидание суммы случайных величин
Идти Ожидание суммы случайных величин = Ожидание случайной величины X+Ожидание случайной величины Y
Диапазон данных с учетом наибольшего и наименьшего элементов
Идти Диапазон данных = Самый большой элемент в данных-Наименьший элемент данных
Самый большой элемент в заданном диапазоне данных
Идти Самый большой элемент в данных = Диапазон данных+Наименьший элемент данных
Наименьший элемент в заданном диапазоне данных
Идти Наименьший элемент данных = Самый большой элемент в данных-Диапазон данных
Значение F двух образцов
Идти Значение F двух образцов = Дисперсия образца X/Дисперсия образца Y
Статистика хи-квадрата с учетом выборки и дисперсии генеральной совокупности формула
Чи-квадрат Статистика = ((Размер образца-1)*Выборочная дисперсия)/Дисперсия населения
χ2 = ((N-1)*Vs)/Vσ
Каково значение критерия хи-квадрат в статистике?
Тест хи-квадрат — это проверка статистической гипотезы, используемая при анализе таблиц непредвиденных обстоятельств при больших размерах выборки. Проще говоря, этот тест в основном используется для проверки того, являются ли две категориальные переменные или два измерения таблицы непредвиденных обстоятельств независимыми в влиянии на статистику теста, то есть на значения в таблице. В стандартных приложениях этого теста наблюдения классифицируются во взаимоисключающие классы. Если нулевая гипотеза об отсутствии различий между классами в популяции верна, тестовая статистика, вычисленная на основе наблюдений, соответствует частотному распределению хи-квадрат. Цель теста — оценить, насколько вероятными будут наблюдаемые частоты, если предположить, что нулевая гипотеза верна.
Проще говоря, этот тест в основном используется для проверки того, являются ли две категориальные переменные или два измерения таблицы непредвиденных обстоятельств независимыми в влиянии на статистику теста, то есть на значения в таблице. В стандартных приложениях этого теста наблюдения классифицируются во взаимоисключающие классы. Если нулевая гипотеза об отсутствии различий между классами в популяции верна, тестовая статистика, вычисленная на основе наблюдений, соответствует частотному распределению хи-квадрат. Цель теста — оценить, насколько вероятными будут наблюдаемые частоты, если предположить, что нулевая гипотеза верна.
Share
Copied!
Калькулятор CASIO FX-9750GII • Графические калькуляторы
Калькулятор CASIO FX-9750GII • Графические калькуляторыNavigation
by Fmeaddons
Современный графический калькулятор
с контрастным монохромным дисплеем,
основной памятью 61 Кбайт
и USB-разъемом
Серия: Графические
- Описание
- Технические характеристики
- Инструкция
Описание
- программная память 61 Кбайт
- большой контрастный монохромный дисплей
- 8 строк по 21 знаку
- символьное меню для выбора режима
- размер (В x Ш x Г): прим.
 21,3 x 87,5 x 180,5 мм
21,3 x 87,5 x 180,5 мм - масса: прим. 205 г с элементом питания
- элементы питания: 4 x AAA
- решение уравнений с интегральными, дифференциальными и вероятностными функциями
- Команда Ref и Rref для диагонализации матрицы или преобразования в уменьшенную ступенчатую матрицу
- случайные целые числа
- перевод единиц измерения
- функция НОД и НОК
- функция вычисления остатка (остаток)
- функция хи-квадрата согласия
- круговая и столбчатая диаграмма
- финансовая математика
– займы, списания - установленное приложение для регистрации результатов измерений ECON2
- дополнительный дисплей OH-9860 может использоваться со всеми FX-9750GII
- USB-разъем
Технические характеристики
Экран
- Строки x позиции: 8 x 21
- Размер экрана (в пикселях): 64 x 128
Память / Memory
- Доступный объем памяти RAM/флэш-памяти: 61 kB
- Память значений/постоянная память: 28
- Вызов последнего введенного значения
Элементарная математика
- Нормализованный формат записи чисел: 10+2
- sin, cos, tan и arc
- Гиперболические и обратные гиперболические функции
- Пересчет единиц угловой меры (гоны, угловые градусы и радианы)
- Перевод из шестидесятеричной системы < > десятеричную
- Переключения между прямоугольной < > полярной системой координат
- Перевод единиц измерения
- Расчеты на основе n
- Экспоненциальные/логарифмические функции
- Таблицы значений
- Системы линейных уравнений: до 6
- Полиномиальные уравнения высшего порядка: до 6 градусов
- Логические операторы (AND/OR/…)
- Вычисления с комплексными числами
- Интерактивная программа решения уравнений
- Матрицы
- Функция REF/RREF
- Память повторений/ответов
- Рекурсивные последовательности
- Функция НОД и НОК
- Расчеты с остатком (Remainder)
Графическое изображение
- Количество прямоугольных функций: 20
- Количество параметрических функций: 20
- Количество полярных функций: 20
- X=f(Y) граф
- Неравенства
- Масштабирование, функция следа
- Режим кривых второго порядка (конические сечения)
Статистика
- Среднее значение, стандартное отклонение
- Линейная регрессия
- Медиана, квартиль
- Описательная статистика
- Комбинаторика и перестановки
- Модели регрессии: 12
- Гистограммы, дисперсия
- Диаграмма размаха
- Секторная/столбчатая диаграмма
- Количество списков: 26×6
- Макс.
 длина списков: 999
длина списков: 999 - Оценочная статистика
- Генератор случайных чисел
- Случайные целые числа
- Хи-квадрат, дисперсионный тест, F-тест
- Определение доверительных интервалов (Z и t)
- Распределение вероятностей
Дифференцирование и интегрирование
- Интегрирование
- Дифференцирование
- Максимум, минимум
Программирование
- Память формул
- Программирование/пользовательское
- Строковая функция
Финансовая математика
- N, %, I, PMT, PV, FV
- Амортизация
- Преобразование процент. <> эффект. ставок
- Исчисление процентов и сложных процентов
- Сроки ежегодных платежей
- Расчет количества дней или даты
- Займы
- Амортизация
- Оценка капиталовложений
- Расчет точки безубыточности
Прочее
- Защитная жесткая крышка
- Кабель для соединения двух калькуляторов: необязательный
- Автоматическое отключение
- Возможно подключение к ПК
- Программа-эмулятор с идентичным управлением: необязательный
- Возможно соединение с EA-200/ECON2
- Главная батарея: 4 x AAA
- Размер (В x Ш x Г мм): 21,3 x 87,5 x 180,5
- Масса: 205 г
Инструкция
Спецификация может быть изменена без уведомления
© CASIO Europe Gmbh
Введите текст и нажмите “enter” для поиска
Информация об использовании файлов cookie на веб-сайте CASIO
Мы используем файлы cookie, чтобы максимально адаптировать наш веб-сайт к потребностям пользователей.
Нажмите «Подтвердить и продолжить», если вы хотите продолжить работу с нашим веб-сайтом.
Подтвердить и продолжить
Критерий хи-квадрат
| Холост: 47 Женат: 71 Разведен: 35 |
| Холост: 44 В браке: 85 Разведен: 40 |
Группы и числа
Вы исследуете две группы и распределяете их по категориям одинокие, женатые или разведенные:
Числа определенно разные, но…
- Это просто случайность?
- Или вы нашли что-то интересное?
Тест хи-квадрат дает значение «p», чтобы помочь вам принять решение!
Пример: «Какой праздник вы предпочитаете?»
| Пляж | Круиз | |
| Мужчины | 209 | 280 |
| Женщины | 225 | 248 |
Влияет ли пол на предпочтительный отпуск?
Если пол (мужской или женский) влияет ли на предпочтительный отпуск, мы говорим, что они зависимы .
Выполнив некоторые специальные вычисления (поясняемые позже), мы получаем значение «p»:
значение p равно 0,132
Теперь p < 0,05 является обычным тестом для зависимости .
В этом случае p больше, чем 0,05 , поэтому мы считаем, что переменные равны независимые (т.е. не связанные между собой).
Другими словами, мужчины и женщины, вероятно, , а не , по-разному предпочитают пляжный отдых или круизы.
Это были просто случайные различия, которые мы ожидаем при сборе данных.
Значение «p»
«p» — это вероятность того, что переменные независимы .
Представьте, что предыдущий пример на самом деле был двумя случайными выборками из мужчин каждый раз:
| Мужчины: Пляж 209, Круиз 280 | Мужчины: Пляж 225, Круиз 248 |
Неужели вероятно вы бы каждый раз получали такие разные результаты, опрашивая мужчин?
Что ж, значение «p» 0,132 говорит о том, что это действительно может происходить время от времени.
В конце концов, опросы случайны. Мы ожидаем немного разных результатов каждый раз, верно?
Таким образом, большинство людей хотят видеть значение p меньше, чем 0,05 , прежде чем они будут счастливы сказать, что результаты показывают, что группы имеют разные ответы.
Давайте посмотрим на другой пример:
Пример: «Какого питомца вы предпочитаете?»
| Кат | Собака | |
| Мужчины | 207 | 282 |
| Женщины | 231 | 242 |
Выполняя вычисления (показаны позже), мы получаем:
Значение P равно 0,043
являются независимыми от , а не от .
Другими словами, поскольку 0,043 < 0,05 , мы считаем, что пол связан с предпочтениями домашних животных (мужчины и женщины по-разному относятся к кошкам и собакам).
Просто из интереса заметьте, что числа в наших двух примерах похожи, но результирующие значения p очень разные: 0,132 и 0,043 . Это показывает, насколько чувствителен тест!
Это показывает, насколько чувствителен тест!
Почему p
<0,05 ?Это просто выбор! Использование p<0,05 является обычным явлением , но мы могли бы выбрать p<0,01, чтобы быть еще более уверенными в том, что группы ведут себя по-разному, или любое значение на самом деле.
Расчет P-значения
Итак, как мы можем рассчитать это p-значение? Мы используем тест хи-квадрат!
Тест хи-квадрат
Примечание: Хи Звучит как «Привет», но с K , так что это звучит как « Ki квадрат»
И Chi это греческая буква Χ, так что мы можем также написать это Χ 2
Важные моменты, прежде чем мы начнем:
- Этот тест работает только для категориальных данных (данных в категориях), таких как пол {мужчины, женщины} или цвет {красный, желтый, зеленый, синий} и т. д., но не числовых данных, таких как рост или вес.
- Числа должны быть достаточно большими. Каждая запись должна быть 5 или больше.
 В нашем примере у нас есть такие значения, как 209, 282 и т. д., так что все готово.
В нашем примере у нас есть такие значения, как 209, 282 и т. д., так что все готово.
Наш первый шаг — сформулировать наши
гипотезы :Гипотеза : Утверждение, которое может быть верным, которое затем можно проверить.
Две гипотезы есть.
- Пол и предпочтение кошек или собак не зависят друг от друга .
- Пол и предпочтение кошек или собак не являются независимыми .
Занесите данные в таблицу:
| Кот | Собака | |
| Мужчины | 207 | 282 |
| Женщины | 231 | 242 |
Сложить строки и столбцы:
| Кот | Собака | ||
| Мужчины | 207 | 282 | 489 |
| Женщины | 231 | 242 | 473 |
| 438 | 524 | 962 |
Рассчитайте «ожидаемое значение» для каждой записи:
Умножьте сумму каждой строки на сумму каждого столбца и разделите на общую сумму:
| Кот | Собака | ||
| Мужчины | 489×438 962 | 489×524 962 | 489 |
| Женщины | 473×438 962 | 473×524 962 | 473 |
| 438 | 524 | 962 |
Что дает нам:
| Кот | Собака | ||
| Мужчины | 222,64 | 266,36 | 489 |
| Женщины | 215,36 | 257,64 | 473 |
| 438 | 524 | 962 |
Вычесть ожидаемое из наблюдаемого, возвести его в квадрат, затем разделить на ожидаемое:
Другими словами, используйте формулу (O−E) 2 E где
- O = Наблюдаемое (фактическое) значение
- E = Ожидаемое значение
| Кот | Собака | ||
| Мужчины | (207−222,64) 2 222,64 | (282−266,36) 2 266,36 | 489 |
| Женщины | (231−215,36) 2 215,36 | (242−257,64) 2 257,64 | 473 |
| 438 | 524 | 962 |
Получается:
| Кот | Собака | ||
| Мужчины | 1,099 | 0,918 | 489 |
| Женщины | 1,136 | 0,949 | 473 |
| 438 | 524 | 962 |
Теперь сложите полученные значения:
1,099 + 0,918 + 1,136 + 0,949 = 4,102
Хи-квадрат равен 4,102
От хи-квадрата до p
Степени свободы
Сначала нам нужна «Степень свободы»
Степень свободы = (строки — 1) × (столбцы — 1 )
Для нашего примера у нас есть 2 строки и 2 столбца:
DF = (2 − 1)(2 − 1) = 1×1 = 1
p-значение
Остальная часть вычисления сложно, поэтому либо найдите его в таблице, либо воспользуйтесь калькулятором хи-квадрат.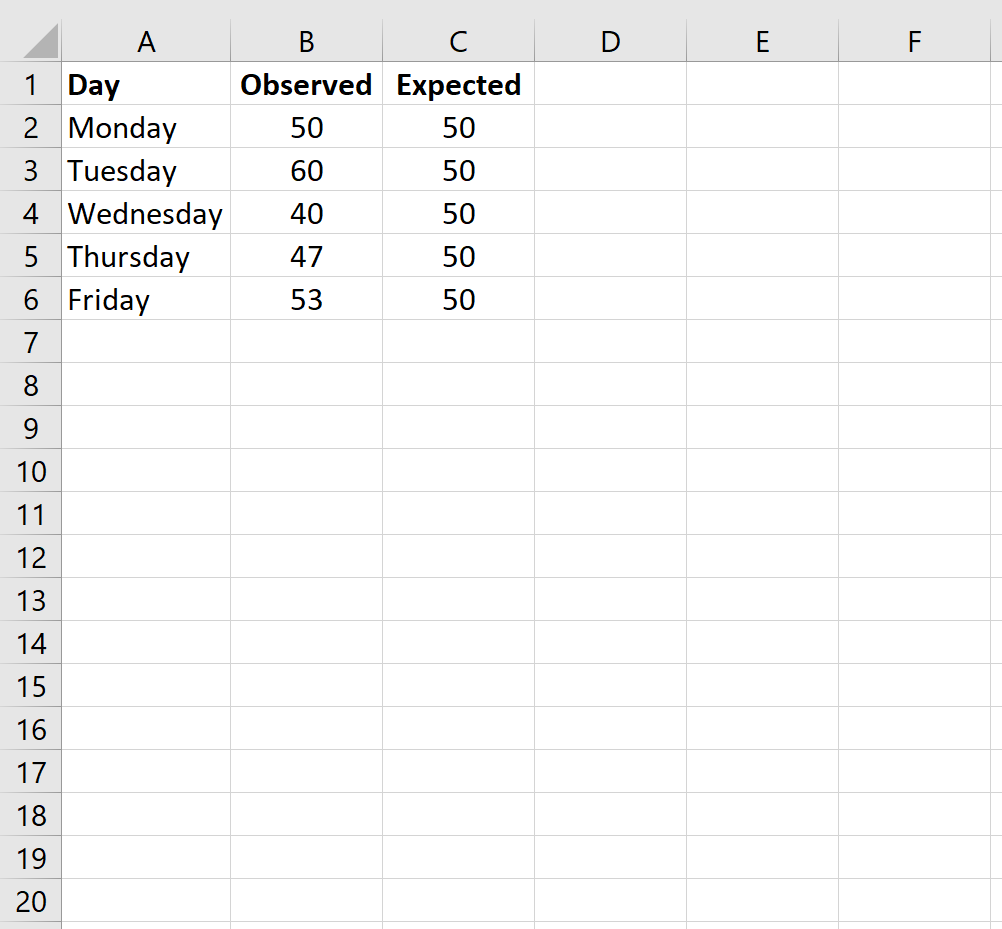
Результат:
p = 0,04283
Готово!
Сигма-нотация)Итак, мы вычисляем (O−E) 2 E для каждой пары наблюдаемых и ожидаемых значений, затем суммируйте их все.
Значение P из калькулятора хи-квадрат
Онлайн-калькулятор значения хи-квадрат P предназначен для определения значения P с использованием стандартного метода хи-квадрат. Прежде чем мы продолжим обсуждение калькулятора, давайте сначала обратим внимание на концепцию значения P.
Что такое значение P?
В статистике значение P на самом деле представляет собой вероятность обнаружения наиболее экстремальных результатов, когда предполагаемая нулевая гипотеза верна. Мы не можем определить значение P с точки зрения прямой вероятности состояния.
Нулевая гипотеза (H0):
Состояние, при котором мы предполагаем, что нет разницы между наблюдаемым значением и ожидаемым значением данных.
Нам нужно определять нулевую гипотезу каждый раз, когда мы ищем решение проблемы.
Например:
Предположим, что Джек и Гарри — два друга. Оба они идут в больницу для вакцинации, но, к сожалению, Джек не получил вакцину. Теперь, после того, как Гарри введут дозу, мы скажем, что разницы в кровяном давлении у обоих друзей нет.
Альтернативная гипотеза (h2):
Если мы принимаем какие-либо значительные изменения в популяции после анализа, то мы должны принять альтернативную гипотезу, которая поддерживает любую дисперсию данных.
Например:
Вопрос:
Будет ли разница между кровяными давлениями двух сестер, если мы дадим одной сестре сахарную таблетку и панадол другой сестре?
Альтернативная гипотеза утверждает, что существуют существенные различия в физическом здоровье обеих сестер, потому что сахарная таблетка и панадол по-разному влияют на физическое и психическое здоровье тела. 92}{E} $$
92}{E} $$
Где;
O = наблюдаемое значение
E = ожидаемое значение
Чтобы рассчитать ожидаемое значение, мы должны следовать следующей формуле:
E = RT * CT / N
Где;
RT = сумма корней для строки, содержащей ячейки
CT = сумма столбца для столбца, содержащего ячейки
N = общее количество наблюдений
Калькулятор значения хи-квадрат P использует значение хи-квадрат для определения значения P.
Условия применения теста хи-квадрат:
Вам не разрешается каждый раз применять тест хи-квадрат для определения вероятности. Тест хи-квадрат применим только при следующих условиях:
- Каждая ячейка должна содержать 5 наблюдений, обычно предпочтительно 10 наблюдений. Если он <5, X2 завышен, что приводит к отклонению нулевой гипотезы.
- Все отдельные наблюдения должны быть случайными и полностью независимыми.

- Общий размер выборки (N) должен составлять не менее 50 наблюдений.
- Данные должны быть выражены в исходных единицах, что означает, что вы не можете выразить данные в процентах или отношениях.
Наш бесплатный онлайн-калькулятор значения хи-квадрат P работает для значения p, если выполняются вышеуказанные условия.
Значение P из хи-квадрата:
Тест хи-квадрат дает нам значение p. Чтобы определить значение p из теста хи-квадрат, вам необходимо понять несколько следующих терминов:
Степень свободы:
Максимальное количество значений в данных, которые могут свободно изменяться, называется степенью свободы. Вы можете оценить этот термин, используя следующее уравнение:
df = (r-1)(c-1)
где ;
r = количество строк
c = количество столбцов
Уровень значимости (α):
Когда нулевая гипотеза верна, то вероятность ее отклонения называется уровнем значимости.
Всякий раз, когда вы отвергаете нулевую гипотезу, выбор уровня значимости является произвольным. Обычно используются уровни 5%, 1% и 0,1%. Если вам не указан уровень значимости проблемы, то вы должны предположить, что это значение равно 5% (0,05)
Большинство авторов называют статистически значимое значение P < 0,05, а статистически высокозначимое значение P < 0,001 (менее один шанс из тысячи ошибиться).
Таблица хи-квадрат:
Вы можете легко определить значение p по диаграмме значения p хи-квадрат следующим образом:
Как рассчитать значение P из теста хи-квадрат?
Давайте обратим внимание на задачу по нахождению значения p с помощью метода хи-квадрат:
Задача:
Во время противомалярийной кампании в Америке хинин вводили людям из всего населения в 2000 человек.
число случаев лихорадки показано ниже:
| Лечение | Лихорадка | Без лихорадки | Всего |
| хинин | 20 | 480 | 500 |
| Без хинина | 100 | 1400 | 1500 |
| Всего | 120 | 1880 | 2000 |
92}{E} $$
Итак, для данных, приведенных в таблице, нам нужно определить ожидаемые значения для лиц, страдающих лихорадкой, и тех, кто не страдает лихорадкой.
E11 = E = RT * CT / N
= 500 * 120 / 2000
= 30
E12 = RT * CT / N
= 1500 * 120 / 2000
= 90
E21 = RT * CT / N
= 500 * 1880 / 2000
= 470
E22 = RT * CT / N
= 1500 * 1880 /2000
= 1410
Приведенные выше данные могут быть таблицы следующим образом:
| Лихорадка | Ожидаемое значение | Без лихорадки | Ожидаемое значение | Итого | |
| хинин | 20 | 30 | 480 | 470 | 500 |
| Без хинина | 100 | 90 | 1400 | 1410 | 1500 |
| Всего | 120 | – | 1880 | – | 2000 |
Для расчета хи-квадрата составим таблицу, содержащую наблюдаемые и ожидаемые значения:
| O наблюдаемое значение (O) | Ожидаемое значение (E) | (О – Э) | (О–Е)2 | (О – Е)2 / Е | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 20 | 30 | -10 | 100 | 3,33 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 100 | 90 | +10 | 100 | 1. 11 11 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 480 | 470 | +10 | 100 | 0,21 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1400 | 1410 | 92}{E} = 4,72 $$ Степень свободы вычисляется следующим образом: df = (r-1)(c-1) Поскольку у нас есть 2 строки и 2 столбца, мы имеем ; df = (2-1) * (2-1) Итак, для 1 степени свободы с уровнем значимости 5% (0,05) , значение хи-квадрат рассчитывается из диаграммы хи следующим образом: X20,05 = 3,84 (табличное значение хи-квадрат) Поскольку табличное значение хи-квадрат < расчетного значения хи-квадрат, мы отвергаем нулевую гипотезу. Следовательно, хинин эффективен при борьбе с малярией. Теперь мы должны вычислить значение chi -значения P, используя таблицу: Два хвостового значения P = 0,100087 левый хвост P Все значения значимы только при p < 0,05. Как работает калькулятор значения хи-квадрат?Вы можете легко найти двустороннее, левостороннее и правостороннее значение p с помощью калькулятора хи-квадрат значения p. Для получения результатов необходимо выполнить следующие шаги: Ввод:
Вывод: В зависимости от выбранных вами входных данных калькулятор вычисляет:
Часто задаваемые вопросы:Что нам говорит значение P? Значение p говорит нам, являются ли полученные нами результаты значимыми или нет. Что означает p-значение 0,05?Значение p меньше . 05 означает, что вероятность увидеть эти результаты составляет менее 5 процентов, когда нулевая гипотеза верна. Что подразумевается под низким значимым значением P?Низкое значимое значение p означает, что у нас есть достаточно доказательств, чтобы доказать, что наблюдаемое распределение не совпадает с ожидаемым распределением. Каково значимое значение P из хи-квадрат?На практике значение p 0,05 или выше считается значимым значением p для хи-квадрат. Заключение:Хи-квадрат позволяет нам сравнить наблюдаемые частоты и ожидаемые частоты. Статистики широко используют метод хи-квадрат для расчета хи-квадрат. Использование бесплатного онлайн-калькулятора значения хи-квадрат сводит к минимуму вероятность ошибки в вычислениях. Ссылки: Из источника википедии: критерий хи-квадрат Пирсона, поправка Йейтса на непрерывность. Посмотреть видео и загрузить технические заметки с веб-сайта Education in Chemistry: rsc.li/3oBNyqC При обучении серии реактивности учащиеся обычно проводят практические занятия, чтобы изучить закономерности в химии. реакции кислот с менее активными металлами. Точно так же они могут увидеть демонстрацию более реакционноспособных металлов с водой или даже сами исследовать их на практике. Такой подход создает у некоторых учеников впечатление, что эти два типа реакций несопоставимы. Как металл средней реактивности, магний можно использовать, чтобы помочь учащимся провести ментальный мост между этими типами реакции. Лента магния удовлетворительно реагирует с сильными кислотами и практически не реагирует с водой комнатной температуры. Однако он будет быстро реагировать с паром. Установка защитных экранов для защиты зрителей и демонстрантов. Рисунок 1: Установка, готовая к реакции магниевой ленты с паром Зрители должны находиться на расстоянии не менее 2 метров, в защитных очках. Демонстратор должен носить защитные очки. Нагрейте трубку горелкой Бунзена прямо под магнием, пока лента не загорится. Затем переместите горелку Бунзена на пропитанную водой минеральную вату, чтобы начать испарение воды. Магний светится ярче, когда над ним проходит пар, и можно использовать лучину, чтобы зажечь выделившийся водород на конце стеклянной трубки. Учащиеся, вероятно, уже видели реакцию магния с кислотами с образованием газообразного водорода и соли (уравнение 1). Они также могли наблюдать реакцию лития с водой с образованием газообразного водорода и гидроксида, о чем свидетельствует использование универсального индикатора или фенолфталеина (уравнение 2). Эта демонстрация показывает, как можно резко ускорить реакцию металлов с водой за счет повышения температуры. Здесь реакция первоначально дает оксид магния (уравнение 3), который может продолжать производить гидроксид при реакции с жидкая вода (уравнение 4). Затем учащимся можно предложить сделать предположения о том, какие реагенты и продукты образуются в реакции магния и воды при комнатной температуре, и какие данные мы можем собрать для проведения реакции. место (уравнение 5), если у них было несколько дней, чтобы ждать результатов. Увидев использование индикатора в реакциях металл-вода и производстве газообразного водорода в реакциях металл-кислота, учащиеся могут предположить, что это возможные признаки того, что реакции связаны. Вы можете проверить это, оставив перевернутую воронку и сборную трубку над магниевой лентой, погруженной в воду с несколькими каплями фенолфталеина. Индикатор начнет менять цвет в течение нескольких минут (Рисунок 2), но может потребоваться несколько дней, чтобы собрать значительный объем газа, который можно будет протестировать на следующем уроке. Рисунок 2: Испытания на производство водорода Там, где горящий магний контактировал со стеклом, мог образовываться силицид магния. Пробирку для кипячения нельзя использовать повторно, но ее можно промыть в 500 см 3 воды для преобразования любых силицидов в силаны. Могут быть видны небольшие хлопки или вспышки от пирофорных силанов. Промытую стеклянную посуду можно выбросить в контейнер для битого стекла. Деклан ФлемингДеклан Флеминг — учитель химии и автор рубрики «Химия на выставке». оксид магния 90 142 (Источник: Wikimedia Commons) Что вы наблюдаете, когда к твердому оксиду магния MgO добавляют воду? Я часто спрашиваю об этом своих студентов, и обычно они отвечают, что они ожидают, что часть, если не весь, твердый MgO растворится с образованием прозрачного щелочного раствора. Правда, они сделали правильный выбор только со щелочным раствором. Я должен отметить, что при добавлении воды к белому твердому образцу MgO видимых изменений не наблюдается. Реакция, без сомнения, ЕСТЬ, но ее нельзя «наблюдать» невооруженным глазом; вы узнаете, что реакция произошла, только если вы проверите рН смеси с помощью лакмусовой или рН-бумаги. Перед добавлением воды в пробирке находится белый твердый образец MgO. После добавления воды наблюдается суспензия белого твердого вещества. Объяснение : MgO(s) + H 2 O( l ) → Mg(OH) 2 (s) При стоянии белое твердое вещество Mg(OH) 2 оседает. (Обратите внимание, что также нет заметного изменения количества белого твердого вещества после «реакции».) Пояснение вода. Таким образом, количество твердого вещества не уменьшается значительно, чтобы можно было наблюдать изменение. Mg(OH) 2 (т) ⇌ Mg 2+ (водн.) + 2OH – (водн.) Раствор над белым твердым веществом оказался щелочным из-за присутствия очень низкой концентрации ионов OH – , образующихся при растворении небольшого количества Mg(OH) 2 . Несмотря на то, что кальций находится чуть ниже магния в группе 2, что интересно, существует ОГРОМНЫЙ скачок в «наблюдаемой реакционной способности» от MgO до оксида кальция, CaO. В то время как нет видимых изменений, когда MgO реагирует с водой, CaO настолько энергично реагирует с водой, что количества выделяемого тепла достаточно, чтобы довести смесь до кипения, как демонстрирует следующее домашнее видео ниже! Больше и ближе, как правило, лучше, когда речь заходит о выборе идеального телевизора для вашей комнаты. Диагональ и расстояние до экрана одни из самых важных факторов, влияющие на цену и оказывающие огромное влияние на качество воспринимаемого изображения. Подберите идеальный размер, передвигая ползунки настроек. Расстояние до телевизора: Диагональ: Рекомендованные телевизоры Поскольку сегодняшние разрешения экранов почти всегда 4k / Ultra HD, чтобы увидеть недостатки, связанные с разрешением, потребуется очень большой телевизор с близким расстоянием обзора. Поэтому, оценить качество картинки и получить захватывающий опыт можно лишь находясь близко к экрану. Представьте кинотеатр, чем больше телевизор заполняет ваш взгляд, тем более яркие ощущения вы получите. Это не значит, что вы должны сидеть в полуметре от телевизора. Как можно больший экран не всегда предпочтителен. Зрительная система человека имеет угол обзора около 135 градусов по горизонтали, и хотя для просмотра фильмов имеет смысл заполнить все поле зрения, не каждому типу контента такой подход будет эффективен. Руководство от общества инженеров кино и телевидения рекомендует сидеть на расстоянии, где экран заполняет как минимум 30° вашего поля зрения или около того. Это сделает просмотр ТВ максимально качественным и подойдет для большинства режимов просмотра. Для пользователей, которые используют свои телевизоры в основном для просмотра фильмов может быть полезно сесть немного ближе, чтобы получить более «театральный» вид. В таком случае специалисты рекомендуют использовать угол обзора 40°. Наш калькулятор высчитывает значения исходя из угла обзора в 30°, который подходит для смешанного использования, но по таблицы ниже можно подобрать нужные расстояния для различных размеров при обзоре в 40°. Использование более высокого поля зрения впервые стало возможным благодаря разрешениям Full HD, но 4k еще больше увеличил эту способность. Сидя рядом с телевизором с разрешением 1080p, часто создается впечатление, что вы смотрите телевизор через ширму, даже если он воспроизводит высококачественный фильм 1080p HD. При увеличении расстояния от телевизора плотность деталей также будет увеличиваться, создавая лучшее изображение. Это и называется угловым разрешением: количество пикселей на угол. Чем дальше, тем выше будет угловое разрешение и тем четче картинка. Поскольку телевизоры 4k имеют очень высокую плотность пикселей, то проблема нечеткости изображения может возникнуть только при очень близком расположении к экрану для весьма большого телевизора. Предел, до которого вы можете увеличить угловое разрешение, отступив назад, зависит от вашей остроты зрения. В какой-то момент ваши глаза перестанут различать все детали на экране. Исследования показывают, что человек со здоровым зрением может различать что-то на 1/60 градуса. Это означает 60 пикселей на градус или 32 градуса для телевизора с разрешением 1080p. 4K UHD телевизоры удваивают это значение до 64 градусов. То есть, ваша задача сводится к тому, чтобы найти оптимальное расстояние при котором дополнительные пиксели более высокого разрешения будут различимы глазом и картинка станем более четкой. На диаграмме показаны области, при которых просмотр телевизора с этими параметрами будет наиболее эффективным и различимым. Если же точка не входит в указанную область, покупка телевизора с бОльшим разрешением не имеет смысла.
Например график показывает, что приобретение 4k телевизора не стоит того, если вы сидите на расстоянии более 1.8 метра и диагональ экрана 50 дюймов. Ваши глаза не смогут увидеть разницу. Ultra HD имеет смысл только в том случае, если вы хотите действительно большой экран и планируете сидеть довольно близко к нему. Вы, вероятно, сейчас думаете что-то вроде: «мой диван находится в 3х метрах от моего телевизора, что согласно диаграмме означает, что мне нужен телевизор с диаганалью 75-дюймов. Мы рекомендуем угол обзора 30 градусов для смешанного использования. В общем, мы также рекомендуем приобрести телевизор 4k, так как выбор 1080p стал довольно ограниченным и не хватает современных функций, таких как HDR. Чтобы легко узнать, телевизор какого размера купить, вы можете разделить расстояние просмотра телевизора (в дюймах) на 1,6 (или использовать наш калькулятор размера телевизора выше), который примерно равен углу 30 градусов. Если подходящий размер выходит за рамки вашего бюджета, просто купите самый большой телевизор, который вы можете себе позволить. Производитель LG каждой модели телевизора при изготовлении на заводе присваивает серийный номер, идентификационный код, по которому можно узнать характеристики устройства. На задней стенке возле панели с разъемами у каждой модели телевизора LG есть табличка с информацией о технических характеристиках устройства или сбоку, если телевизор старой модели с толстым корпусом. Табличка отображает серийный номер, идентификационный код телевизора, дату изготовления, адрес и телефон завода производителя. Однако этикетка может быть повреждена или содрана. Либо же ее нельзя увидеть по причине того, что корпус телевизора был плотно закреплен на стене. В таком случае нужную информацию придется искать другим способом. Рассмотрим, как же узнать модель телевизора LG. В комплектации с каждым устройством поставляется техническая документация и гарантийный талон. В инструкции подробно описаны возможности телевизора, его настройка и, конечно, номер модели. Если вы не успели выкинуть коробку от телевизора, внимательно осмотрите ее. Производитель LG маркирует упаковку, указывая наименование модели и тип устройства. У современных моделей телевизоров LG можно найти этикетку с QR-кодом. В зашифрованном изображении содержится информация об устройстве. Чтобы считать идентификатор, наведите камеру мобильного устройства на QR-код. Для идентификации вам понадобится приложение для работы с QR-кодами, которое можно скачать в Плеймаркете. Если ни один из перечисленных способов не сработал, на помощь приходит внутреннее меню телевизора. Точные сведения о модели устройства можно узнать через меню телевизора. Данный способ подходит для моделей устройств младше 2011 года выпуска. Для владельцев таких моделей телевизоров LG порядок действий следующий: Чтобы в будущем не забыть, запишите последовательность символов серийного номера на отдельном листке. Лучше, если вы запишите на пустой лист сервисной книжки, которую производитель LG прилагает при покупке техники. Каждая модель телевизора LG маркируется в виде идентификационного кода, состоящего из нескольких цифр и букв. В собственную маркировку телевизоров производитель LG, как и другие производители, кодирует определенную техническую информацию о модели. Из расшифровки маркировки телевизора LG можно узнать размер диагонали экрана, год выпуска, номер серии, наличие и вид тюнера, для какой страны выпущена модель. Выберите проектор Поиск по проекционному расстоянию/размеру экрана * = снято с производства ДиагональШиринаВысота Метрика Императорский — Совместимость с принтером для FireFox Калькулятор проекции используется для расчета размера экрана, когда проектор находится на определенном расстоянии от экрана. Когда вы перемещаете проектор
вдали от экрана или стены изображение будет увеличиваться, а по мере приближения проектора к экрану или стене изображение будет уменьшаться. Чтобы правильно
поместите ваше изображение на экран, вам нужен инструмент калькулятора проекций или бросовая диаграмма, чтобы сказать вам размеры размера изображения в соответствующем
расстояние броска. Чтобы определить Размер изображения (размер экрана), введите число измерения расстояния в поле значения Throw Distance и нажмите Enter. Чтобы определить проекционное расстояние , где вы должны разместить проектор в комнате, введите число измерения диагонали изображения в поле Размер изображения значение и нажмите клавишу Enter на клавиатуре или перемещайте ползунок Image Size назад и вперед, пока не найдете число в поле значения, которое
представляет диагональное расстояние между верхним правым углом вашего изображения (экрана) и нижним левым углом вашего изображения (экрана). На
графическое изображение проектора в середине калькулятора, вы увидите размерные линии, которые подскажут вам Расстояние выброса расстояние между передней частью объектива проектора и поверхностью стены или экрана. Если выбранный вами проектор оснащен зум-объективом, то параметр проекционного расстояния или размер изображения проектора можно точно отрегулировать, перемещая
Кольцо зум-объектива на проекторе. Ползунок Zoom Range в калькуляторе поможет вам рассчитать изменения, сделанные зум-объективом. Используя значки синего замка рядом со значением Throw Distance или Image Size , вы можете получить
Ползунок диапазона масштабирования влияет только на один из двух элементов управления. Если вы нажмете значок синего замка рядом со значением Throw Distance , чтобы
показывает символ замка, затем перемещение ползунка масштабирования только отрегулирует размер изображения больше или меньше, как это было бы визуально представлено, если
вы повернули кольцо зум-объектива на зум-объективе проектора, чтобы увеличить или уменьшить изображение. Если щелкнуть замок рядом с Размер изображения значение так, чтобы на значке отображался символ блокировки, затем перемещение ползунка масштабирования будет регулировать только положение проектора Throw Distance в вашей комнате. LG Electronics Air Conditioning and Energy Solutions Инструмент моделирования CAD для систем прямого испарения недавно интегрированной функции для расчета соответствия EN378 приходит на помощь проектировщикам HVAC. Приложение под названием LatsCAD действует как «надстройка» AUTOCAD для 2D-проектирования систем прямого расширения, экономя до 60% времени проектирования. Это приложение было специально разработано для консультационных инженерных компаний в области HVAC, которые хотят повысить эффективность и точность систем прямого испарения в своих проектах, и теперь оно поднимает простоту проектирования на новый уровень. Проверить ответ поможет калькулятор . Sign in Password recovery Восстановите свой пароль Ваш адрес электронной почты MicroExcel.ru Математика Геометрия Нахождение объема цилиндра: формула и задачи В данной публикации мы рассмотрим, как можно найти объем цилиндра и разберем примеры решения задач. Объем (V) цилиндра равняется произведению его высоты и площади основания. V = S ⋅ H Как мы знаем, в качестве оснований цилиндра (равны между собой) выступает круг, площадь которого вычисляется так: S = π ⋅ R2. V = π ⋅ R2 ⋅ H Примечание: в расчетах значение числа π округляется до 3,14. Как нам известно, диаметр круга равняется двум его радиусам: d = 2R. А значит, вычислить объем цилиндра можно следующим образом: V = π ⋅ (d/2)2 ⋅ H Задание 1 Решение: Задание 2 Решение: Таблица знаков зодиака Нахождение площади трапеции: формула и примеры Нахождение длины окружности: формула и задачи Римские цифры: таблицы Таблица синусов Тригонометрическая функция: Тангенс угла (tg) Нахождение площади ромба: формула и примеры Нахождение объема цилиндра: формула и задачи Тригонометрическая функция: Синус угла (sin) Геометрическая фигура: треугольник Нахождение объема шара: формула и задачи Тригонометрическая функция: Косинус угла (cos) Нахождение объема конуса: формула и задачи Таблица сложения чисел Нахождение площади квадрата: формула и примеры Что такое тетраэдр: определение, виды, формулы площади и объема Нахождение объема пирамиды: формула и задачи Признаки подобия треугольников Нахождение периметра прямоугольника: формула и задачи Формула Герона для треугольника Что такое средняя линия треугольника Нахождение площади треугольника: формула и примеры Нахождение площади поверхности конуса: формула и задачи Что такое прямоугольник: определение, свойства, признаки, формулы Разность кубов: формула и примеры Степени натуральных чисел Нахождение площади правильного шестиугольника: формула и примеры Тригонометрические значения углов: sin, cos, tg, ctg Нахождение периметра квадрата: формула и задачи Теорема Фалеса: формулировка и пример решения задачи Сумма кубов: формула и примеры Нахождение объема куба: формула и задачи Куб разности: формула и примеры Нахождение площади шарового сегмента Что такое окружность: определение, свойства, формулы Этот онлайн-калькулятор рассчитает различные свойства цилиндра по двум известным значениям. Единицы: Обратите внимание, что единицы измерения показаны для удобства, но не влияют на расчеты. Единицы используются для указания порядка результатов, таких как футы, футы 2 или фут 3 . Например, если вы начинаете с мм и знаете r и h в мм, ваши расчеты дадут V в мм 3 , L в мм 2 , T в мм 2 , B в мм 2 и A в мм 2 . Ниже приведены стандартные формулы для цилиндра. Расчеты основаны на алгебраических манипуляциях с этими стандартными формулами. ** Рассчитывается площадь только боковой поверхности наружной стенки цилиндра. Используйте следующие дополнительные формулы вместе с формулами выше. %PDF-1.5
%
1 0 объект
>
эндообъект
190 объект
>поток
приложение/pdf Анна Малкова Иррациональными называются уравнения, содержащие знак корня – квадратного, кубического или n-ной степени. Мы помним из школьной программы: как только в уравнении или неравенстве встретились корни, дроби или логарифмы – пора вспомнить про область допустимых значений (ОДЗ) уравнения или неравенства. По определению, ОДЗ уравнения (или неравенства) – это пересечение областей определения всех функций, входящих в уравнение или неравенство. Например, в уравнении присутствует арифметический квадратный корень . Он определен В 2018-2019 году среди учителей появилось такое мнение, что писать слова «область допустимых значений» уже не модно. И что за это даже могут снизить оценку на экзамене. Нет, оценку не снизят. И основных понятий школьной математики никто не отменял. Однако есть еще лучший способ оформления решения – в виде цепочки равносильных переходов. Смотрите, как решать и оформлять иррациональные уравнения: 1. Выражение под корнем должно быть неотрицательно. И сам корень – величина неотрицательная. Значит, и правая часть должна быть больше или равна нуля. Следовательно, уравнение равносильно системе: Повторим, что решение таких уравнений лучше всего записывать в виде цепочки равносильных переходов. Если вы не очень хорошо понимаете, что такое система уравнений и совокупность уравнений, — повторите эту тему. или В ответ запишем меньший из корней: — 9. Теперь уравнение, в котором есть ловушка. 2. Решите уравнение . Если уравнение имеет более одного корня, в ответе запишите меньший из корней. Что получилось у вас? Правильный ответ: . Если у вас получилось – это был посторонний корень. Запишите решение в виде цепочки равносильных переходов, как в задаче 1, и вы поймете, что 3. Запишем решение как цепочку равносильных преобразований. Учитесь читать такую запись и применять ее. Произведение двух (или нескольких) множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю, а другие при этом не теряют смысла. 4. Решите уравнение: Ответ: или . А теперь сложное уравнение. Как это часто бывает, нас выручит замена переменной. Причем новая переменная будет не одна, а целых две. 5. Решите уравнение Найдем ОДЗ: Мы можем, как в задаче 10, возвести обе части уравнения в квадрат. Но после этого придется еще раз возводить в квадрат, а это долгий способ. Есть короткий путь! Сделаем замену: , . Выразим через и : и . Это выражения можно приравнять друг к другу. Получим систему Решим одно из уравнений. Все равно, какое, — ведь нам надо найти . Ответ: . Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Иррациональные уравнения. Можно ли писать ОДЗ?» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта. Публикация обновлена:
08.05.2023 Уважаемые школьники, выпускники, абитуриенты, этот раздел поможет подготовиться к экзаменам, тестам, внешнему независимому тестированию по математике в 2015 году. Ответы к тестам помогут Вам понять материал и методику вычислений, систематизировать и повысить накопленный уровень знаний по математике. Решение примеров будут интересны для школьников 9, 10, 11 классов, а так же их родителей. Задача 2.34 Решите уравнение с корнями Задача 2.35 Решите уравнение Задача 2.36 Решите уравнение ConceptsSimple EqnsHarder EqnsPainful Eqns Хотя большинство («почти все»?) радикальных уравнений, которые вам предстоит решить, будут включать квадратные корни, вы также можете увидеть некоторые уравнения с более высоким индексом. Они работают примерно одинаково. Например, если вам дано уравнение, в котором радикал является кубическим корнем, вы возведете в куб обе части (после выделения радикала), чтобы преобразовать уравнение в полином, который вы сможете решить. Так как это КУБИЧЕСКИЙ корень, а не квадратный корень , я отменю радикал, возведя в куб обе части уравнения, а не возводя в квадрат: винг Расширенные радикальные уравнения Мой ответ: x = 16 Вы можете удивиться, почему я не проверил свое решение. Я должен проверить свои решения для уравнений, где я возведен в квадрат или где я возвел обе части уравнения в какую-то другую четную степень. Почему? Потому что возведение в квадрат и тому подобное избавляет от знаков минус, которые могут создавать решения, которых на самом деле не существует. Но процесс решения в приведенном выше упражнении включал кубирование, которое сохраняет знаки минус. Вот почему мне не нужно было проверять. (Примечание: если ваш инструктор хочет, чтобы вы проверяли и показывали чек для каждого упражнения, независимо от индекса вовлеченных радикалов, то проверка каждый раз является «правильным способом» для этого класса. Я заметил, что «плюс один» в левой части уравнения находится за пределами кубического корня. Мне нужно переместить его в правую часть уравнения, прежде чем я возьму в куб обе стороны. Это решение включало в себя кубирование, а не возведение в квадрат, поэтому мне (технически) не нужно проверять свое решение. Мой ответ: x = 1/3 Поскольку это корень четвертой степени, я возведу обе части в четвертую степень. (Кроме того, поскольку это корень с четным индексом, мне обязательно нужно проверить свой ответ.) Исходное уравнение представляло собой корень четвертой степени, и в процессе решения я возводил обе части уравнения в четвертую степень (в частности, в степень и даже ). Так что мне придется проверить свои ответы. Вот одна из проверок: x = −1 / 2 : Левая часть (LHS) оказалась равной правой части (RHS), так что это решение проверяет. x = -½, -1/3 Между прочим, график показывает, что оба решения верны. Если мы рассмотрим левую и правую части исходного уравнения как свои собственные функции, мы получим: График, мы получим это: Это довольно трудно увидеть, поэтому мы увеличим среднюю часть. пока мы не будем уверены, что видим две точки пересечения (и, следовательно, два решения исходного уравнения): Если вам интересно, почему график радикальной стороны разбит на три части, то это потому, что у нас не может быть отрицательных значений внутри корня четвертой степени. График существует только в том случае, если аргумент радикала, представляющий собой полином x 4 + 4 x 3 − x , неотрицательный. Это происходит в трех частях, когда график аргумента находится на оси x или выше: Не стесняйтесь использовать свой графический калькулятор для подтверждения (или исправления) ваших решений. От вас может требоваться или не требоваться графическое представление решений, но если у вас есть графический калькулятор (поэтому для рисования графиков достаточно быстро нажать несколько кнопок), вы можете использовать графики для проверки своей работы на тестах . Поскольку кубические корни могут содержать отрицательные числа, у вас не возникнет проблем с проверкой ответов, которые вы делали с квадратными корнями. Однако у вас будут трудности с корнями четвертой, шестой, восьмой и т. д.; а именно, любой корень с четным индексом. Будьте осторожны и не забывайте проверять свои решения, когда этого требует указатель. И помните, что у вас квадрат (или куб, или что угодно) стороны уравнения, а не отдельные члены. Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в решении радикальных уравнений. Попробуйте введенное упражнение или введите свое собственное упражнение. Затем нажмите кнопку и выберите «Найти x», чтобы сравнить свой ответ с ответом Mathway. Пожалуйста, примите куки «предпочтения», чтобы включить этот виджет. (Нажмите «Нажмите, чтобы просмотреть шаги», чтобы перейти непосредственно на сайт Mathway для платного обновления.) URL: https://www.purplemath.com/modules/solverad5.htm Страница 1 Страница 2 Страница 3 Страница 4 Задачи на квадратные корни незаменимы в инженерии, вычислениях и практически во всех областях современного мира. Тот факт, что умножение двух отрицательных чисел вместе дает положительное число, важен в мире квадратных корней, поскольку подразумевает, что положительные числа на самом деле имеют два квадратных корня (например, квадратные корни из 16 равны 4 и −4, даже если только первый интуитивно понятен). Точно так же отрицательные числа не имеют действительных квадратных корней, потому что не существует действительного числа, которое принимает отрицательное значение при умножении само на себя. В этой презентации отрицательный квадратный корень из положительного числа будет игнорироваться, поэтому «квадратный корень из 361» можно принять за «19». Кроме того, при попытке оценить значение квадратного корня, когда нет под рукой калькулятора, важно понимать, что функции, включающие квадраты и квадратные корни, не являются линейными. Вы увидите подробнее об этом в разделе о графиках позже, но в качестве грубого примера вы уже заметили, что квадратный корень из 100 равен 10, а квадратный корень из 0 равен 0. На первый взгляд это может привести вас к предположению, что квадратный корень для 50 (что находится на полпути между 0 и 100) должно быть 5 (что находится на полпути между 0 и 10).Но вы также уже узнали, что квадратный корень из 50 равен 7,071. Наконец, вы, возможно, усвоили идею о том, что умножение двух чисел дает число, большее, чем оно само, а это означает, что квадратные корни чисел всегда меньше исходного числа. Это не вариант! У чисел от 0 до 1 тоже есть квадратные корни, и в каждом случае квадратный корень больше, чем исходное число. Это легче всего показать с помощью дробей. Например, 16/25, или 0,64, имеет полный квадрат как в числителе, так и в знаменателе. «Квадратный корень из x » обычно записывается с использованием так называемого подкоренного знака или просто подкореня (√ ). Таким образом, для любого x : \sqrt{x} представляет собой его квадратный корень. Переворачивая это, квадрат числа x записывается с использованием показателя степени 2 ( x 2 ). Показатели принимают надстрочные индексы в текстовых процессорах и связанных с ними приложениях и также называются степенями. Поскольку радикальные знаки не всегда легко изготовить по запросу, другой способ записи «квадратный корень из 9{(y/z)} означает «возвести x в степень y , затем взять из него корень z ». Таким образом, x 1/2 означает «возвести x в первую степень, что равно просто x , а затем извлечь из него корень 2 или квадратный корень». Радикалы могут использоваться для представления корней, отличных от 2, квадратного корня. Это делается простым добавлением надстрочного индекса в верхнем левом углу радикала. 95} представляет то же число, что и x (5/3) из предыдущего абзаца. Большинство квадратных корней являются иррациональными числами. Это означает, что они не только не являются красивыми, аккуратными целыми числами (например, 1, 2, 3, 4…), но и не могут быть выражены в виде аккуратного десятичного числа, которое заканчивается без округления. Рациональное число можно представить в виде дроби. Таким образом, хотя 2,75 не является целым числом, это рациональное число, потому что это то же самое, что и дробь 11/4. Ранее вам сказали, что квадратный корень из 50 равен 7,071, но на самом деле это округление от бесконечного числа знаков после запятой. Вы уже видели, что уравнения с квадратными корнями нелинейны. Один простой способ запомнить это состоит в том, что графики решений этих уравнений не являются линиями. Это имеет смысл, потому что, если, как уже отмечалось, квадрат 0 равен 0, а квадрат 10 равен 100, но квадрат 5 не равен 50, график, полученный в результате простого возведения числа в квадрат, должен изогнуться до правильных значений. Это случай с графиком 92 в чем вы сами можете убедиться, посетив калькулятор в Ресурсах и изменив параметры. Линия проходит через точку (0,0), а y не опускается ниже 0, чего и следовало ожидать, поскольку известно, что x 2 никогда не бывает отрицательным. Вы также можете видеть, что график симметричен относительно оси y , что также имеет смысл, поскольку каждый положительный квадратный корень данного числа сопровождается отрицательным квадратным корнем равной величины. Один из способов решения основных задач на квадратный корень вручную — это поиск идеальных квадратов, «спрятанных» внутри задачи. Во-первых, важно знать о некоторых жизненно важных свойствах квадратов и квадратных корней. Один из них заключается в том, что √ x 2 просто равно x (поскольку радикал и показатель степени компенсируют друг друга): 92y} = x\sqrt{y} То есть, если у вас есть полный квадрат под радикалом, умножающим другое число, вы можете его «вытащить» и использовать как коэффициент того, что осталось. Например, возвращаясь к квадратному корню из 50 \sqrt{50} = \sqrt{(25)(2)} = 5\sqrt{2} Иногда вы можете получить число, включающее квадратные корни, которое равно выражается в виде дроби, но все же является иррациональным числом, потому что знаменатель, числитель или оба содержат радикал. Методическая разработка урока геометрии в 9 классе по теме « Синус, косинус, тангенс» Учебник: «Геометрия» 7-9 класс. Авт.: Л.С. Атанасян, В.Б. Бутузов и др.;М.,Просвещение, 2014 План урока Организационный момент Актуализация знаний. Объяснение нового материала. Физкультминутка Закрепление нового материала. Подведение итогов урока. Домашнее задание. Тип урока: Урок ознакомления с новым материалом (1 час) Цели урока: 1. Образовательные -углубить изученные в 8 классе сведения о синусе, косинусе и тангенсе угла; -сформировать понятия «тригонометрический круг»; -ввести понятие синуса, косинуса и тангенса для углов от 0º до 180º; -научить использовать определение синуса, косинуса и тангенса при решении задач. -повторить основное тригонометрическое тождество ( доказательство запланировано на следующий урок) 2. Развивающие: -развитие мышления учащихся: учить детей анализировать, выделять главное; -развитие сенсорной сферы: развитие глазомера, развитие формы и точности; -развитие навыков самоконтроля. 3. Воспитательные: -развитие нравственных качеств личности: ответственности, дисциплинированности, аккуратности, требовательности к себе, умения работать в коллективе. Ход урока. Организационный момент (сведения из истории). Введение (зарождение тригонометрии) Впервые график тригонометрической функции — синусоида была вычерчена в конце 30-х годов XVII в. французским математиком Робельвалем.. Волновые процессы находят проявление во многих областях физики и технике, и для описания их используется тригонометрическая функция. В физике изучаются: механические колебания, электромагнитные колебания в контуре, переменный ток, звуковые волны и т. Актуализация знаний Повторение – мать учения (Сведения из курса 8 класса) Что называется синусом, косинусом, тангенсом острого угла прямоугольного треугольника? Какое равенство называют основным тригонометрическим тождеством? Чему равны значения синуса, косинуса и тангенса для углов 30 , 45 и 60 градусов ? 3 Изучение нового материала Введем прямоугольную систему координат Оху . Построим полуокружность радиуса 1 с центром в начале координат, расположенном в I и II четвертях Назовем ее единичной полуокружностью Выполнить в тетрадях рисунок 290 (страница 252 учебника) Дать новые определения синуса, косинуса и тангенса для любого угла а из промежутка от 0º до 180º . Подчеркнуть, какие значения могут принимать синус, косинус и тангенс для угла а из промежутка от 0º до 180º . Вывести, используя единичную полуокружность, основное тригонометрическое тождество. 4.Физкультминутка 5 Закрепление нового материала. Тест 1. Синус – это: a) абсцисса точки, лежащей на единичной полуокружности; b) ордината точки, лежащей на единичной полуокружности; с) угол между осью Ох и осью Оy. 2. Выберите из списка значения, которые может принимать sina 1; 1,0001; 2; 0,0001; 2,0001: a) 1; 2; 1,0001; b) 1; 0,0001; с) 1,0001; 0,0001; 2,0001. 3. Выберите из списка значения, которые может принимать cos: -1; 1; 0,5; -0,5; 1,5. a) 1; 0,5; 1,5; b) 1; 0,5; -0,5; с) -1; 1; 0,5; -0,5. 4. Чему равен tga, если sina=0; cosa=1? a)не определен; b)) tga = 0; с) tga = 1. 5 Чему равен cosa , если угол a — прямой? a) 0; b) 1; с) 90⁰.’ 6. Выберите из списка значения, по которым можно утверждать, что угол a острый: cosa = 0,03; sina=0,03 cosa = — 0,03; sina=-0. a) sina = 0.03 или sina =-0.03 b) cosa= — 0,03 или cosa = 0,03; с) cosa = 0,03. 7. Если угол a — тупой, то a)0 < cosa < 1; b)cosa ˃ 1; с) -1 Письменная работа в классе № 1013 в, № 1014 б, № 1015 в Подведение итогов урока. Выставление оценок. Рефлексия. -Достигли цели? Введены определения синуса, косинуса и тангенса для углов промежутка от 0º до 180º , основного тригонометрического тождества, даны некоторые формулы приведения; научились использовать определение синуса, косинуса и тангенса при решении задач. Какие выводы сделали? -Вывели понятие синуса, косинуса, тангенса используя единичную полуокружность, -Объяснили смысл некоторых формул приведения, вспомнили основное тригонометрическое тождество. -Как мы это делали? -Обсуждали -Анализировали Домашнее задание. П.93. № 1013а; № 1014а (по желанию № 1015 а ) Адрес публикации: https://www.
Тригонометрические формулы
Решение тригонометрических уравнений и неравенств
Предел последовательности. Предел функции
Производная
Применение непрерывности и производной
Применение производной к использованию функций
Показать все темы
Алгебра
7
8
9
10
11
Поделиться
0
0
05:40 В первом уроке мы вспомним основные положения по теме “Числовая функция” и методы исследования функции, пройденные в курсе алгебры: какие значения может принимать функция y=f(x), какова область её допустимых значений, при каких условиях функция будет возрастающей или убывающей, четной или нечетной, ограниченной или неограниченной. Графики Тангенса — это тип графика, который помогает найти функцию касательной для заданного диапазона углов. Они обычно представлены в виде ряда точек, соединенных линиями, и могут использоваться для определения конкретных углов и соответствующих значений их касательных. Они показывают отношение между тангенсом угла и самим углом. Тангенс угла – это отношение длины стороны, противолежащей углу, к длине стороны, прилежащей к углу. Диаграмма тангенса обычно рисуется как ряд точек, соединенных линиями, что позволяет легко идентифицировать определенные углы и соответствующие значения тангенсов. Они помогают найти функцию касательной для заданного диапазона углов. Тангенс угла – это отношение длины стороны, противолежащей углу, к длине стороны, прилежащей к углу. Тангенс диаграммы показывает отношение между тангенсом угла и самим углом. Они показывают связь между тангенсом угла и самим углом, что может быть полезно при решении задач, связанных с тригонометрией. Чтобы использовать диаграмму тангенса, вам сначала нужно определить угол, для которого вы хотите найти тангенс. Затем найдите соответствующую точку на графике и прочтите значение по оси Y. Это тангенс этого угла. Тан-графы могут быть применены к множеству тригонометрических задач. Некоторые специальные приложения включают нахождение тангенса заданного угла, решение задач, связанных с обратными тригонометрическими функциями, и нахождение точного значения тригонометрической функции. Танграф может быть особенно полезен при решении задач, связанных с обратными тригонометрическими функциями. Обратные тригонометрические функции применяются для нахождения углов, когда известно значение соответствующей тригонометрической функции. График тангенса можно использовать для определения угла, соответствующего заданному значению касательной, просто рисуя линии от начала координат до различных точек на кривой. Это выгодно с точки зрения правильного и быстрого решения вопросов. Кроме того, график тангенса можно использовать для нахождения точного значения тригонометрической функции. Когда вы знаете значение угла и соответствующий ему тангенс, вы можете использовать график тангенса, чтобы найти точное значение тригонометрической функции. При решении задачи, связанной с тригонометрией, вы можете использовать график тангенса, чтобы найти точное значение тригонометрической функции. Когда вы знаете значение угла и соответствующий ему тангенс, вы можете использовать график тангенса, чтобы найти точное значение тригонометрической функции. Это может быть полезно при решении сложных задач по тригонометрии. Например, допустим, что вам дано уравнение y = sin(x) + 1. Вы знаете, что тангенс х равен 45 градусам, и вы хотите найти значение тангенса y, когда тангенс х равен 45 градусов. Вы можете использовать график загара, чтобы найти точное значение y. Сначала определите угол, который соответствует 45 градусам на графике тангенса. Затем найдите соответствующую точку на графике и прочтите значение по оси Y. Это значение тангенса у, когда тангенс х равен 45 градусам. Следовательно, y = sin(45 градусов) + 1 = 0,72 + 1 = 1,72. Диаграмма тангенса может помочь в точном и эффективном решении проблем. Их также можно использовать для нахождения точного значения тригонометрической функции, что может оказаться полезным при решении сложных тригонометрических задач. Необходимость понимать, как использовать тангенс-график при решении задач по тригонометрии, невозможно переоценить. Танграфы являются важным инструментом для правильного разрешения тригонометрических ситуаций. С помощью диаграммы тангенса можно легко определить угол, соответствующий заданному значению касательной. Это может помочь вам решить проблемы правильно и быстро. Кроме того, график тангенса можно использовать для нахождения точного значения тригонометрической функции. Когда вы знаете значение угла и соответствующий ему тангенс, вы можете использовать график тангенса, чтобы найти точное значение тригонометрической функции. Таким образом, для точного и эффективного решения тригонометрических задач необходимо понимание того, как использовать диаграммы тангенса. Танграф может использоваться в различных задачах тригонометрии и особенно полезен при решении задач, связанных с обратными тригонометрическими функциями. С помощью диаграммы тангенса можно легко определить угол, соответствующий заданному значению тангенса, что может быть полезно при решении сложных задач тригонометрии. Кроме того, график тангенса можно использовать для нахождения точного значения тригонометрической функции. Зная значение угла и соответствующий ему тангенс, можно использовать график тангенса, чтобы найти точное значение тригонометрической функции. Понимание того, как использовать тангенс-график, необходимо для точного и эффективного решения тригонометрических задач. Диаграмма тангенса — ценный инструмент, который можно использовать в различных задачах тригонометрии. Если вы понимаете, как их использовать, они могут помочь в точном и эффективном решении проблем. Итак, в следующий раз, когда вы столкнетесь с проблемой тригонометрии, не забудьте свериться со своим верным графиком загара! Обязательно ознакомьтесь с другими статьями в SchoolOnline, зайдя на нашу страницу GCSE Maths Foundation, чтобы узнать больше о математике! Когда координаты выражаются дробью, они называются тета. Функция тангенса принимает угол в радианах и возвращает отношение длины противоположной стороны к длине соседней стороны. Слово «тангенс» происходит от латинского слова «tangens», что означает «касание». Это потому, что линия, которая касается кривой только в одной точке, называется касательной. Есть несколько способов найти тангенс угла. Самый распространенный метод — использовать калькулятор, но вы также можете использовать таблицу значений или график тангенса. Обратной функцией тангенса является функция арктангенса. Эта функция принимает отношение и возвращает угол в радианах, который имеет это отношение. Функция тангенса имеет множество приложений в математике, физике и технике. Касательную функцию можно построить вручную или с помощью компьютерной программы. Чтобы построить график функции вручную, вам нужно будет использовать таблицу значений или график тангенса. Если вы используете компьютерную программу, вам нужно будет ввести уравнение в программу, а затем построить график. Тангенс угла – это отношение длины противолежащей стороны к длине прилежащей стороны. Это можно рассчитать с помощью калькулятора, таблицы значений или графика тангенса. Нет, функция котангенса не стремится к положительной или отрицательной бесконечности (влево или вправо) от нуля. Функция котангенса не определена в нуле, но она стремится к бесконечности, когда угол приближается к нулю слева или справа. Нет, функция тангенса не является многочленом. Это иррациональное число, которое не может быть выражено как рациональное число. Область определения функции тангенса — все действительные числа, кроме нуля. Это связано с тем, что функция тангенса не определена в нуле. Диапазон функции тангенса — все действительные числа. 0 Сохранить В тригонометрии значение тангенса 0 градусов равно нулю. Функция тангенса является периодической функцией и является одной из шести основных тригонометрических функций. Тангенс функции угла определяется как отношение синуса и косинуса этого угла в прямоугольном треугольнике. Касательная функция угла также определяется как отношение противолежащей стороны к прилежащей по отношению к углу прямоугольного треугольника. Значение тангенса 0 градусов получается из отношения sin 0 градусов к cos 0 градусов и равно нулю. Это значение выражается для угла в градусах. Мы также можем представить это значение, когда угол берется в радианах. Мы преобразуем меру угла из градусов в радианы, умножая значение градуса на отношение π/180. Таким образом, ноль градусов эквивалентен нулю радиан. Итак, у нас есть значение tan 0 градусов = tan 0 радиан = 0 Значение тангенса 0 можно найти следующими способами: \(tan\theta\) определяется как отношение \(sin\theta\) к \(cos\theta\). На приведенном выше изображении дан единичный круг, где мы видим, что отмечены стандартные углы для sin и cos. Теперь, чтобы найти значение tan 0, мы просто находим отношение sin 0 к cos 0. Таким образом, \( \tan0=\frac{\sin0}{\cos0}=\frac{0}{1}= 0 \) Здесь мы используем различные тригонометрические тождества, чтобы получить значение tan 0. В приведенной выше таблице мы видим, что вычисляются значения, соответствующие функции y=tan x. Если хотите чтобы набрать хороший балл на экзамене по математике, то вы находитесь в правильном месте. Здесь вы получите еженедельную подготовку к тестам, живые уроки и серию экзаменов. Загрузите приложение Testbook прямо сейчас, чтобы подготовить умную и высокорейтинговую стратегию к экзамену. В.1 Какое значение имеет Tan 0? Ответ 1 Значение тангенса 0 равно 0, Q.2 Что такое tan 0 на единичном круге? Ответ 2 На единичной окружности тангенс o равен sin o, деленному на cos o, где o/1=1. Q.3 Как найти тангенс 0 треугольника? Ответ 3 Мы находим отношение sin 0 к cos 0, чтобы получить тангенс 0. В.4. Тангенс 0 не определен? Ответ 4 Нет, тангенс 0 не является неопределенным. Число прямых
измерений всегда конечно. Поэтому
средняя квадратичная погрешность
заведомо меньше истинной абсолютной
погрешности. Чтобы получить близкое к
реальности значение абсолютной
погрешности, нужно увеличить среднюю
квадратичную погрешность, умножив ее
на коэффициент Стьюдента
.
В теории Стьюдента рассчитаны значения
этого коэффициента в зависимости от
доверительной вероятности α и числа
измерений n.
С ростом доверительной вероятности, то
есть надежности значения абсолютной
погрешности, коэффициент Стьюдента
увеличивается. А с ростом числа измерений,
увеличивающим надежность самих
результатов измерения, коэффициент
Стьюдента уменьшается. Ниже приведены
значения коэффициента Стьюдента для
доверительной вероятности α = 0,95. n 2 3 4 5 6 tα (n) 12,71 4,303 3,182 2,776 2,571 n 7 8 9 10 20 tα (n) 2,447 2,365 2,306 2,262 2,093 Отметим, что запись
результата измерения в форме (7) означает,
что значение измеренной величины x с заданной вероятностью α не выйдет за
пределы интервала (xср – Δx, xср + Δx). часто называют полушириной
доверительного интервала. Результат косвенного
измерения есть результат расчета по заданной
формуле. Оценка относительной погрешности
результата расчета уже описана выше.
Относительная погрешность рассчитывается
по формуле (2), если величины, полученные
в результаты прямых измерений, входят
в заданную формулу в качестве множителей
или делителей. Для примера
рассмотрим косвенное измерение объема
прямого цилиндра высоты h с диаметром d.
Объем такого цилиндра можно вычислить
по формуле Для вычисления
объема цилиндра по формуле (9) нужно
иметь результаты измерения его диаметра
и высоты. Пусть в результате прямых
измерений получены значения диаметра
и высоты цилиндра в соответствии с (7): В этом случае
известны и относительные погрешности
значений диаметра и высоты цилиндра: и Прежде, чем
приступать к вычислению объема, оценим
относительную погрешность результата
вычисления по формуле (9). Таким образом,
источниками погрешности являются
значения диаметра и высоты цилиндра.
Обе эти величины входят множителями в
формулу (9), но диаметр входит множителем
два раза (в квадрате), а высота – один
раз. Следовательно, подстановка этих
величин в формулу (9) приведет к сложению
двух относительных погрешностей диаметра
и одной относительной погрешности
высоты. Согласно формуле (2), относительная
погрешность объема составит Как видим, наибольший
вклад в относительную погрешность
объема цилиндра вносит неточность
измерения диаметра цилиндра. Чтобы число π не внесло дополнительную погрешность
в результат вычисления объема, нужно
взять его значение с относительной
погрешностью, много меньшей погрешностей
диаметра и высоты цилиндра. Поскольку,
как нам известно, точность числа зависит
от количества значащих цифр в нем, нужно
взять столько цифр числа π,
чтобы их количество на одну цифру
превышало бы максимальное число значащих
цифр в средних значениях диаметра и
высоты. Вот запись округленного числа π,
содержащая 7 значащих цифр: π = 3,141593. Теперь, взяв число π с необходимым количеством значащих
цифр, можно выполнить расчет среднего
значения объема цилиндра по формуле
(9): После этого нужно
выполнить расчет относительной
погрешности значения объема по формуле
(14). Затем вычислить абсолютную погрешность
объема по формуле Значение этой
погрешности нужно округлить, оставив
только две значащие цифры. Например, мы
получили следующие величины: среднее
значение = 3867,395 мм3, = 4,258 мм3.
Округляем значение до двух значащих цифр, получаем = 4,3 мм3.
Вторая значащая цифра находится в
разряде десятых долей миллиметра.
Значит, последней оставленной цифрой
в записи должна быть цифра 3, стоящая в этом же
разряде. Первой отбрасываемой цифрой
является 9 ˃ 5, следовательно, нужно
добавить 1 к оставленной тройке. В итоге
получим: V = (3867,4 4,3) мм3 = (3,8674 0,0043)
мм3 = (3,8674 0,0043)
= (3,8674 0,0043). с относительной
погрешностью, равной КОЕ-ЧТО ИЗ МАТЕМАТИКИ Для успешного
освоения предлагаемого курса физики нужно
вспомнить, что такое вектор и как с ним
работать,
поскольку в описании физической
реальности нельзя обойтись без векторных
величин. Многие
физические величины являются векторами. Вектор можно изобразить в виде направленного
отрезка определенной длины. Вектор имеет две характеристики: модуль (абсолютную величину или просто величину)
и направление. Каждая из
этих характеристик может быть постоянной
или изменяться независимо от другой. Векторы складываются
по правилу
треугольника,
как это показано на рисунке. При
умножении вектора на число получается
новый вектор,
который направлен в ту же сторону, что
и старый, если число положительное, и в
противоположную сторону, если число
отрицательное. При
умножении вектора на число 0, получается нулевой
вектор,
не имеющий ни величины, ни направления. Любой вектор можно
спроецировать на ось координат. Проекция
вектора на ось координат равна произведению
модуля этого вектора на косинус угла
между вектором и осью. Если угол острый,
то его косинус и соответственно проекция
вектора положительны. Если угол тупой,
то его косинус и соответственно проекция
вектора отрицательны. Если вектор
перпендикулярен оси, то его проекция
на эту ось равна нулю. α 0 Любой вектор можно
представить в виде суммы трех его
составляющих по осям координат: где
,
,
и – проекции вектора, а – единичные векторы (орты) соответствующих
осей координат. Вектор
равен сумме трех векторов
,
,
,
каждый из которых направлен вдоль своей
оси координат. 0 Допустим некоторая
векторная физическая величина, например
скорость
,
изменилась с течением времени. Тогда
изменение скорости тоже будет вектором: Для нахождения
вектора это векторное равенство перепишем
по-другому и найдем этот
вектор по правилу треугольника.
Откладываем из одной точки два вектора и
. Существуют
два разных умножения вектора на вектор:
скалярное и векторное. Результатом скалярного
произведения вектора на вектор является число,
равное произведению модуля первого
вектора на модуль второго и на косинус
угла между ними: или равное сумме
одноименных проекций этих векторов на
оси координат: Скалярное умножение
обозначается точкой. Результатом векторного
произведения вектора на вектор является вектор.
Векторное умножение обозначается косым
крестиком. Например, вектор равен векторному произведению векторов и
: Вектор перпендикулярен векторам и и его направление определяется по
правилу буравчика (правого винта), как
это показано на рисунке. Буравчик
вращается от первого вектора в сторону второго вектора
.
Если векторы – множители поменять
местами, то вектор изменит направление на противоположное. Модуль
вектора
равен произведению модуля первого
вектора на модуль второго и на синус
угла между ними: α Если два вектора
параллельны, то их векторное произведение
равно нулевому вектору
. Для успешного
освоения предлагаемого курса физики
нужно также вспомнить основы математического
анализа и, как минимум, уметь
найти производную от комбинации
элементарных функций и взять табличный
интеграл. Напомню определение
производной.
Пусть некоторая физическая величина,
например вектор скорости, меняется с
течением времени. Тогда время t является независимой переменной, то
есть аргументом (играет роль x из математики). А скорость является зависимой переменной, то есть
функцией (играет роль y из математики). Производной называется
предел Если
,
то и Существует обозначение для величины,
которая стремится к 0, но не равна 0. Эта
величина называется бесконечно малой.
Все дело в том, что она
не имеет конкретного значения.
Зато она всегда меньше любого сколь
угодно малого числа, какое бы мы ни
назвали. Для такой бесконечно малой
величины существует обозначение:
. которая обладает
всеми свойствами дроби из математики,
за исключением того, что ее значение
нельзя получить обычным делением
числителя на знаменатель, а нужно перейти
к пределам и раскрыть получившуюся
неопределенность. Для любой функции в
математике это все проделано и сведено
в правила
взятия производной от элементарной
функции. Например, некоторое
тело движется так, что модуль его скорости
зависит от времени по уравнению: где и – константы. Найдем производную от
модуля скорости по времени: Как Вы вероятно
помните, эта производная является
ускорением. Настоятельно
рекомендую каждую производную от функции y по аргументу x,
которая встретится Вам в физике,
обозначать только такой дробью: Для успешного
освоения предлагаемого курса физики
нужно также вспомнить, что такое степень и логарифм. Показатель степени Степень b a Основание степени Для удобства
обозначим эту степень буквой у.
Имеем равенство где а – основание
степени у,
а b – показатель
степени у.
Чтобы выразить а и b из этого равенства, нужно применить
разные правила. Основание а степени у равно корню
из этой степени: а показатель b степени у равен логарифму
этой степени по основанию а: Итак, показатель
степени и логарифм степени – это
практически одно и то же. Чтобы убедиться,
проверьте тождество: и левая и правая
части которого равны у. Число
измерений N Надежность Р 0,5 0,6 0,7 0,8 0,9 0,95 0,99 2 1,00 1,38 2,0 3,1 6,3 12,7 637 3 0,82 1,06 1,5 1,9 2,9 4,3 35 4 0,77 0,98 1,3 1,6 2,4 3,2 12,9 5 0,74 0,94 1,2 1,5 2,1 2,8 8,6 6 0,73 0,92 1,2 1,5 2,0 2,6 6,9 7 0,72 0,91 1,1 1,4 1,9 2,4 6,0 8 0,71 0,90 1,1 1,4 1,9 2,4 5,4 9 0,71 0,89 1,1 1,4 1,9 2,3 5,0 10 0,70 0,88 1,1 1,4 1,8 2,3 4,8 При обработке прямых измерений результаты
наблюдений и вычислений удобно оформлять
в виде табл. 2. Таблица 2 № ai ai ai2 P tPN aсл 1 2 3 4 5 6 7 8 9 1 2 3 В колонке 1указывается номер опыта
по порядку (обычно проводится 3-7
измерений). В колонке 2 записываютсязначения измеряемой величины. В колонку 3вноситсясреднее
значениеизмеряемой величины,
рассчитанное по формуле: . (1) В колонке 4представленыотклонениякаждого значенияизмеряемой величины от среднего: .
(2) Каждый результат, полученный по последней
формуле, возводится в квадрат и заносится в колонку 5. В колонке 6следует расположитьсреднеквадратичную погрешность ,
рассчитанную по формуле: . (3) Она характеризует разброс средних
значений измеряемой величины.
Среднеквадратичная погрешность тем
больше, чем сильнее измеренные величины
отличаются друг от друга. В колонку 7заносится значение
доверительной вероятности (или надежности)
Обычно достаточно выбрать значениеР= 0,95 (или, что то же самое, 95%). Коэффициент Стьюдента, учитывающий
заданную доверительную вероятность и
число измерений tPN ,находится по табл. 1 и располагаетсяв
колонке 8. Случайная погрешностьрассчитывается
по формуле aсл=tPN S(4) и заносится в колонку 9. К учитываемым систематическим погрешностям
относятся погрешности средств измерения
и погрешности отсчета. В форме абсолютных погрешностейзадаются погрешности линеек,
штангенциркулей, секундомеров, термометров
и т.п. Абсолютная погрешность средства
измерения в этом случае может быть
вычислена по формуле , (5) где -
цена деления прибора. В форме приведенных погрешностейзадаются пределы допускаемых погрешностей
электроизмерительных приборов,
манометров. , где ап—нормирующее
значениеприбора илипредел измерений; — предел допускаемой приведенной
погрешности прибора в процентах от
нормирующего значения; аси— абсолютная погрешность
прибора. Пользуясь этой формулой, можно определить
абсолютную погрешность измерительного
прибора: . (6) Полная абсолютная погрешностьпрямых измерений рассчитывается по
формуле . (7) Чаще всего случайная погрешность и
погрешность средств измерения — величины
разных порядков; в таких случаях меньшей
погрешностью пренебрегают. Например,
если
,
то для \(-\infty Кстати, распределение \(t\) впервые было обнаружено человеком по имени В.С. Госсет. Он открыл для себя этот дистрибутив, когда работал на ирландской пивоварне. Поскольку он публиковался под псевдонимом Стьюдент, распределение \(t\) часто называют распределением Стьюдента \(t\). Если оставить в стороне историю, приведенное выше определение, вероятно, не особенно информативно. Давайте попробуем почувствовать распределение \(t\) с помощью моделирования. Давайте случайным образом сгенерируем 1000 стандартных нормальных значений (\(Z\)) и 1000 значений хи-квадрат(3) (\(U\)). Затем приведенное выше определение говорит нам, что если мы возьмем эти случайно сгенерированные значения, вычислим: \(T=\dfrac{Z}{\sqrt{U/3}}\) и создадим гистограмму из 1000 результирующих значений \(T\), мы должны получить гистограмму, которая выглядит как \( t\) распределение с 3 степенями свободы. Итак, вот подмножество результирующих значений одного такого моделирования: Обратите внимание, например, в первой строке: \(T(3)=\dfrac{-2.60481}{\sqrt{10.2497/3}}=-1.4092\) ‘ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| P ( T ≤ т ) | |||||||
| 0,60 | 0,75 | 0,90 | 0,95 | 0,975 | 0,99 | 0,995 | |
| р | т 0,40 ( р ) | т 0,25 ( р ) | т 0,10 ( р ) | т 0,05 ( р ) | т 0,025 ( р ) | т 0,01 ( р ) | т 0,005 ( р ) |
| 1 | 0,325 | 1. 000 000 | 3.078 | 6.314 | 12.706 | 31.821 | 63,657 |
| 2 | 0,289 | 0,816 | 1,886 | 2,920 | 4.303 | 6,965 | 9,925 |
| 3 | 0,277 | 0,765 | 1,638 | 2,353 | 3,182 | 4,541 | 5.841 |
| 4 | 0,271 | 0,741 | 1,533 | 2,132 | 2,776 | 3,747 | 4.604 |
| 5 | 0,267 | 0,727 | 1,476 | 2,015 | 2,571 | 3,365 | 4. 032 032 |
| 6 | 0,265 | 0,718 | 1.440 | 1,943 | 2,447 | 3,143 | 3,707 |
| 7 | 0,263 | 0,711 | 1,415 | 1,895 | 2,365 | 2,998 | 3,499 |
| 8 | 0,262 | 0,706 | 1,397 | 1,860 | 2,306 | 2,896 | 3,355 |
| 9 | 0,261 | 0,703 | 1,383 | 1,833 | 2,262 | 2,821 | 3.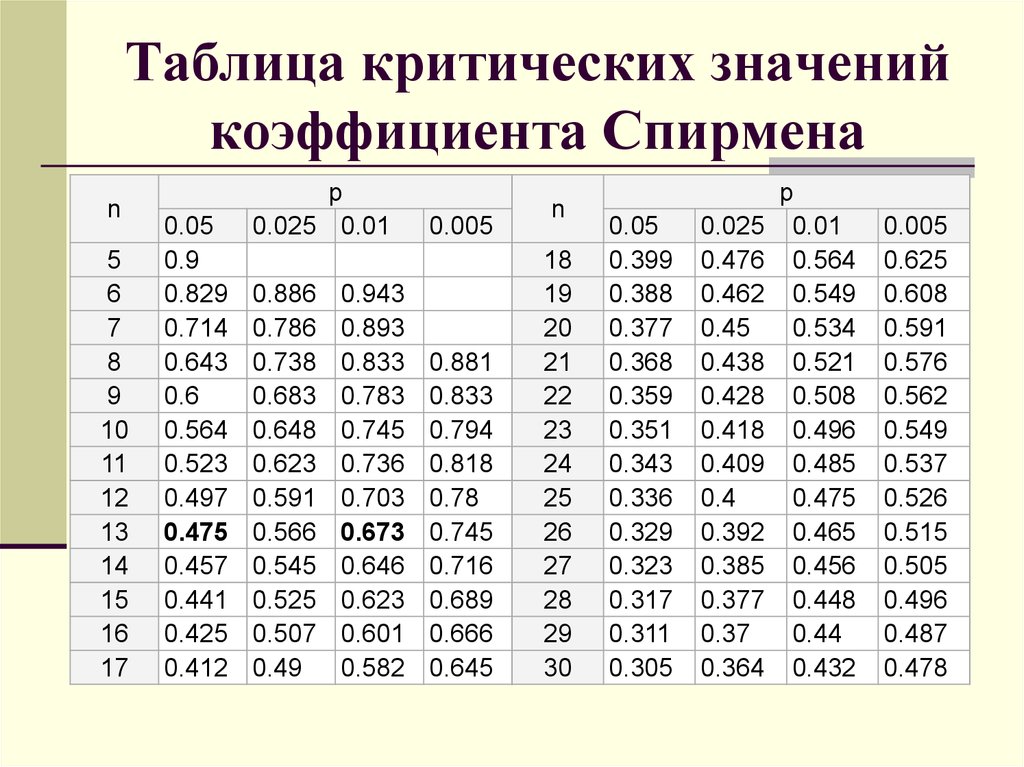 250 250 |
| 10 | 0,260 | 0,700 | 1,372 | 1,812 | 2,228 | 2,764 | 3,169 |
\(t\)-таблица похожа на таблицу хи-квадрат тем, что внутри \(t\)-таблицы (заштрихованной фиолетовым цветом ) содержится \(t\)- значения для различных кумулятивных вероятностей (заштрихованы красным цветом ), таких как 0,60, 0,75, 0,90, 0,95, 0,975, 0,99 и 0,995, а также для различных распределений \(t\) с \(r\) степенями свободы (заштрихованы в синий ). Строка, заштрихованная зеленым цветом , указывает верхнюю \(\альфа\) вероятность, которая соответствует \(1-\альфа\) кумулятивной вероятности. Например, если вас интересует кумулятивная вероятность 0,60 или верхняя вероятность 0,40, вам нужно найти значение \(t\) в первом столбце.
Давайте воспользуемся \(t\)-таблицей, чтобы прочитать несколько вероятностей и \(t\)-значений из таблицы:
Давайте рассмотрим еще несколько примеров.
Пусть \(T\) следует \(t\)-распределению с \(r=8\) ф.р. Какова вероятность того, что абсолютное значение \(T\) меньше 2,306?
Решение
Расчет вероятности очень похож на расчет, который мы должны сделать для обычной случайной величины. Во-первых, переписав вероятность через \(T\) вместо абсолютного значения \(T\), мы получим:
\(P(|T|<2,306)=P(-2,306 Затем мы должны переписать вероятность в терминах кумулятивных вероятностей, которые мы действительно можем найти, то есть: \(P(|T|<2,306)=P(T<2,306)-P(T<-2,306)\) Графически искомая вероятность выглядит примерно так: Но \(t\)-таблица не содержит отрицательных \(t\)-значений, поэтому нам придется воспользоваться симметрией \(T\)-распределения. То есть: >\(P(|T|<2,306)=P(T<2,306)-P(T>2,306)\) Можете ли вы найти необходимые \(t\)-значения на \(t \)-стол? 30602.306
30602.306 Р ( Т ≤ т ) 0,60 0,75 0,90 0,95 0,975 0,99 0,995 р т 0,40 ( р ) т 0,25 ( р ) т 0,10 ( р ) т 0,05 ( р ) т 0,025 ( р ) т 0,01 ( р ) т 0,005 ( р ) 1 0,325 1.  000
000 3,078 6.314 12.706 31.821 63,657 2 0,289 0,816 1,886 2,920 4.303 6,965 9,925 3 0,277 0,765 1,638 2,353 3.182 4,541 5,841 4 0,271 0,741 1,533 2,132 2,776 3,747 4,604 5 0,267 0,727 1,476 2,015 2,571 3,365 4.032 6 0,265 0,718 1.440 1,943 2,447 3,143 3,707 7 0,263 0,711 1,415 1,895 2,365 2,998 3,499 8 0,262 0,706 1,397 1,860 2,306 2,896 3,355 9 0,261 0,703 1,383 1,833 2,262 2,821 3.  250
250 10 0,260 0,700 1,372 1,812 2,228 2,764 3,169 P ( T ≤ t ) 0,60 0,75 0,90 0,95 0,975 0,99 0,995 р т 0,40 ( р ) т 0,25 ( р ) т 0,10 ( р ) т 0,05 ( р ) т 0,025 ( р ) т 0,01 ( р ) т 0,005 ( р ) 1 0,325 1.000 3,078 6.314 12.706 31.821 63,657 2 0,289 0,816 1,886 2,920 4.  303
303 6,965 9,925 3 0,277 0,765 1,638 2,353 3,182 4,541 5,841 4 0,271 0,741 1,533 2,132 2,776 3,747 4,604 5 0,267 0,727 1,476 2,015 2,571 3,365 4.032 6 0,265 0,718 1.440 1,943 2,447 3,143 3,707 7 0,263 0,711 1,415 1,895 2,365 2,998 3,499 8 0,262 0,706 1,397 1,860 2,306 2,896 3,355 9 0,261 0,703 1,383 1,833 2,262 2,821 3.  250
250 10 0,260 0,700 1,372 1,812 2,228 2,764 3,169
Таблица \(t\) говорит нам, что \(P(T<2,306)=0,975\) и \(P(T>2,306)=0,025\). Следовательно:
\(P(|T|>2,306)=0,975-0,025=0,95\)
Что такое \(t_{0,05}(8)\)?
Решение
Значение \(t_{0,05}(8)\) — это значение \(t_{0,05}\), такое, что вероятность того, что \(T\) случайная величина с 8 степенями свободы больше, чем значение \(t_{0,05}\) равно 0,05. То есть:
T(8)0t0.050.05Можете ли вы найти значение \(t_{0.05}\) в таблице \(t\)?
| P ( T ≤ t ) | |||||||
| 0,60 | 0,75 | 0,90 | 0,95 | 0,975 | 0,99 | 0,995 | |
| р | т 0,40 ( р ) | т 0,25 ( р ) | т 0,10 ( р ) | т 0,05 ( р ) | т 0,025 ( р ) | т 0,01 ( р ) | т 0,005 ( р ) |
| 1 | 0,325 | 1. 000 000 | 3,078 | 6.314 | 12.706 | 31.821 | 63,657 |
| 2 | 0,289 | 0,816 | 1,886 | 2,920 | 4.303 | 6,965 | 9,925 |
| 3 | 0,277 | 0,765 | 1,638 | 2,353 | 3,182 | 4,541 | 5,841 |
| 4 | 0,271 | 0,741 | 1,533 | 2,132 | 2,776 | 3,747 | 4,604 |
| 5 | 0,267 | 0,727 | 1,476 | 2,015 | 2,571 | 3,365 | 4.032 |
| 6 | 0,265 | 0,718 | 1.440 | 1,943 | 2,447 | 3,143 | 3,707 |
| 7 | 0,263 | 0,711 | 1,415 | 1,895 | 2,365 | 2,998 | 3,499 |
| 8 | 0,262 | 0,706 | 1,397 | 1,860 | 2,306 | 2,896 | 3,355 |
| 9 | 0,261 | 0,703 | 1,383 | 1,833 | 2,262 | 2,821 | 3. 250 250 |
| 10 | 0,260 | 0,700 | 1,372 | 1,812 | 2,228 | 2,764 | 3,169 |
| P ( T ≤ т ) | |||||||
| 0,60 | 0,75 | 0,90 | 0,95 | 0,975 | 0,99 | 0,995 | |
| р | т 0,40 ( р ) | т 0,25 ( р ) | т 0,10 ( р ) | т 0,05 ( р ) | т 0,025 ( р ) | т 0,01 ( р ) | т 0,005 ( р ) |
| 1 | 0,325 | 1.000 | 3,078 | 6.314 | 12.706 | 31. 821 821 | 63,657 |
| 2 | 0,289 | 0,816 | 1,886 | 2,920 | 4.303 | 6,965 | 9,925 |
| 3 | 0,277 | 0,765 | 1,638 | 2,353 | 3,182 | 4,541 | 5,841 |
| 4 | 0,271 | 0,741 | 1,533 | 2,132 | 2,776 | 3,747 | 4,604 |
| 5 | 0,267 | 0,727 | 1,476 | 2,015 | 2,571 | 3,365 | 4.032 |
| 6 | 0,265 | 0,718 | 1.440 | 1,943 | 2,447 | 3,143 | 3,707 |
| 7 | 0,263 | 0,711 | 1,415 | 1,895 | 2,365 | 2,998 | 3,499 |
| 8 | 0,262 | 0,706 | 1,397 | 1,860 | 2,306 | 2,896 | 3,355 |
| 9 | 0,261 | 0,703 | 1,383 | 1,833 | 2,262 | 2,821 | 3. 250 250 |
| 10 | 0,260 | 0,700 | 1,372 | 1,812 | 2,228 | 2,764 | 3,169 |
Мы определили, что вероятность того, что \(T\) случайная величина с 8 степенями свободы больше значения 1,860, равна 0,05. 92}\)
следует распределению хи-квадрат с \(n-1\) степенями свободы. Мы также узнали, что \(Z\) и \(U\) независимы. Следовательно, используя определение случайной величины \(T\), мы получаем:
Это результирующая величина, то есть:
\(T=\dfrac{\bar{X}-\mu}{ s/\sqrt{n}}\)
, что поможет нам в Stat 415 использовать среднее из случайной выборки, то есть \(\bar{X}\), с уверенностью узнать что-то о население означает \(\mu\).
Т-распределение | Введение в статистику
Что такое
t -распределение?Распределение t- описывает стандартизированные расстояния выборочных средних значений от средних значений генеральной совокупности, когда стандартное отклонение генеральной совокупности неизвестно, а наблюдения происходят из нормально распределенной генеральной совокупности.
Распределение
t- совпадает с распределением Стьюдента t ?Да.
В чем основное различие между
t- и z-распределения?Стандартное нормальное или z-распределение предполагает, что известно стандартное отклонение генеральной совокупности. Распределение t- основано на стандартном отклонении выборки.
t -Распределение по сравнению с нормальным распределением t -распределение аналогично нормальному распределению. Он имеет точное математическое определение. Вместо того, чтобы углубляться в сложную математику, давайте посмотрим на полезные свойства т-9.Распределение 0005 и почему оно важно для анализа.
Вместо того, чтобы углубляться в сложную математику, давайте посмотрим на полезные свойства т-9.Распределение 0005 и почему оно важно для анализа.
- Как и нормальное распределение, распределение t- имеет гладкую форму.
- Как и нормальное распределение, распределение t- является симметричным. Если вы подумаете о том, чтобы сложить его пополам в среднем, каждая сторона будет одинаковой.
- Подобно стандартному нормальному распределению (или z-распределению), распределение t- имеет нулевое среднее значение.
- Нормальное распределение предполагает, что стандартное отклонение генеральной совокупности известно. 9Распределение 0004 t- не делает этого предположения.
- Распределение t- определяется степенями свободы . Они связаны с размером выборки.
- Распределение t- наиболее полезно для небольших размеров выборки, когда неизвестно стандартное отклонение генеральной совокупности или и то, и другое.

- По мере увеличения размера выборки распределение t- становится более похожим на нормальное распределение.
Рассмотрим следующий график, на котором сравниваются три t- распределений со стандартным нормальным распределением:
Рис. 1: Три t-распределения и стандартное нормальное (z-) распределение.
Все распределения имеют плавную форму. Все симметричны. У всех среднее нулевое.
Форма распределения t- зависит от степеней свободы. Кривые с большим количеством степеней свободы выше и имеют более тонкие хвосты. Все три распределения t- имеют «более тяжелые хвосты», чем z-распределение.
Вы можете видеть, что кривые с большим количеством степеней свободы больше похожи на z-распределение. Сравните розовую кривую с одной степенью свободы с зеленой кривой для z-распределения. Распределение t- с одной степенью свободы короче и имеет более толстые хвосты, чем z-распределение. Затем сравните синюю кривую с 10 степенями свободы с зеленой кривой для z-распределения. Эти два дистрибутива очень похожи.
Затем сравните синюю кривую с 10 степенями свободы с зеленой кривой для z-распределения. Эти два дистрибутива очень похожи.
Общепринятое эмпирическое правило заключается в том, что для размера выборки не менее 30 можно использовать z-распределение вместо т- раздача. На рисунке 2 ниже показано распределение t- с 30 степенями свободы и z-распределение. На рисунке используется зеленая кривая из пунктирных линий для z, так что вы можете видеть обе кривые. Это сходство является одной из причин, по которой z-распределение используется в статистических методах вместо распределения t , когда размеры выборки достаточно велики.
Рис. 2: z-распределение и t-распределение с 30 степенями свободы
Хвосты для тестов гипотез и распределения
t Когда вы выполняете t -тест, вы проверяете, является ли ваша тестовая статистика более экстремальным значением, чем ожидалось для распределения t-.
Для двустороннего теста вы смотрите на оба хвоста распределения. На рисунке 3 ниже показан процесс принятия решения для двустороннего теста. Кривая представляет собой распределение t- с 21 степенью свободы. Значение из распределения t- с α = 0,05/2 = 0,025 равно 2,080. Для двустороннего теста вы отклоняете нулевую гипотезу, если статистика теста больше, чем абсолютное значение эталонного значения. Если значение тестовой статистики находится либо в нижнем хвосте, либо в верхнем хвосте, вы отклоняете нулевую гипотезу. Если тестовая статистика находится в пределах двух контрольных линий, вы не можете отвергнуть нулевую гипотезу.
Рисунок 3: Процесс принятия решения для двустороннего теста
Для одностороннего теста вы смотрите только на один хвост распределения. Например, на рис. 4 ниже показан процесс принятия решения для одностороннего теста. Кривая снова представляет собой распределение t- с 21 степенью свободы. Для одностороннего теста значение из распределения t- с α = 0,05 равно 1,721. Вы отклоняете нулевую гипотезу, если статистика теста больше опорного значения. Если тестовая статистика ниже контрольной линии, вы не можете отвергнуть нулевую гипотезу.
Для одностороннего теста значение из распределения t- с α = 0,05 равно 1,721. Вы отклоняете нулевую гипотезу, если статистика теста больше опорного значения. Если тестовая статистика ниже контрольной линии, вы не можете отвергнуть нулевую гипотезу.
Рисунок 4: Процесс принятия решения для одностороннего теста
Как использовать таблицу
t-Большинство людей используют программное обеспечение для выполнения расчетов, необходимых для t -тестов. Но во многих книгах по статистике по-прежнему приводятся таблицы t-, поэтому понимание того, как пользоваться таблицей, может быть полезным. Шаги ниже описывают, как использовать типичный стол t-.
- Определите, предназначена ли таблица для двусторонних или односторонних тестов. Затем решите, какой у вас тест: односторонний или двусторонний. Столбцы для 9Таблица 0004 t- определяет различные альфа-уровни.

Нод 12 и 9: НОД и НОК для 9 и 12 (с решением)
Наибольший общий делитель 9 и 12
Калькулятор «Наибольший общий делитель»
Какой наибольший общий делитель у чисел 9 и 12?
Ответ: НОД чисел 9 и 12 это 3
(три)
Нахождение наибольшего общего делителя для чисел 9 и 12 используя перечисление всех делителей
Первый способ нахождения НОД для чисел 9 и 12 — это перечисление всех делителей для обоих чисел и выбор из них наибольшего общего:
Все делители числа 9: 1, 3, 9
Все делители числа 12: 1, 2, 3, 4, 6, 12
Следовательно, наибольший общий делитель для чисел 9 и 12 это 3
Нахождение наибольшего общего делителя для чисел 9 и 12 используя разложение чисел на простые множители
Второй способ нахождения наибольшего общего делителя для числе 9 и 12 — это перечисление всех простых множителей для чисел и перемножение общих.
Смотрите также: Наименьшее общее кратное (НОК) для чисел 9 и 12
Поделитесь текущим расчетом
Печать
https://calculat.
 io/ru/number/greatest-common-factor-of/9—12
io/ru/number/greatest-common-factor-of/9—12<a href=»https://calculat.io/ru/number/greatest-common-factor-of/9—12″>Наибольший общий делитель 9 и 12 — Calculatio</a>
О калькуляторе «Наибольший общий делитель»
Данный калькулятор поможет найти наибольший общий делитель двух чисел. Например, он может помочь узнать какой наибольший общий делитель у чисел 9 и 12? Выберите первое число (например ‘9’) и второе число (например ’12’). После чего нажмите кнопку ‘Посчитать’.
Наибольший общий делитель (НОД) для двух чисел - это наибольшее положительное целое число, которое делит каждое из целых чисел с нулевым остатком.
Калькулятор «Наибольший общий делитель»
Таблица наибольших общих делителей
Число 1 Число 2 НОД 1 12 1 2 12 2 3 12 3 4 12 4 5 12 1 6 12 6 7 12 1 8 12 4 9 12 3 10 12 2 11 12 1 12 12 12 13 12 1 14 12 2 15 12 3 16 12 4 17 12 1 18 12 6 19 12 1 20 12 4 21 12 3 22 12 2 23 12 1 24 12 12 25 12 1 26 12 2 27 12 3 28 12 4 29 12 1 30 12 6 Текстовые задачи на проценты — что это, определение и ответ
Для быстрого и верного решения задач на проценты нужно понимание сути процента, умение считать проценты и внимательно читать условие.

С процентами нам постоянно приходится сталкиваться в повседневной жизни. «Скидка 30%», «Кредит без процентов за 5 минут», «Арендная плата выросла на 12%» — со всех сторон на нас сыплются рекламные слоганы и призывы. Но что же значит слово «проценты»? И как ими оперировать?
Проценты являются удобным инструментом. Нужны они для нахождения части от чего-то. Вообще говоря, звучит похоже на определение дроби. И действительно, проценты очень тесно связаны с дробями, по сути, основываются на них.
Что такое процент?
Процент – это всегда доля какого-то числа.
100% — все число
50% — половина
25% — четверть
Чтобы найти 1%, необходимо поделить всё число на 100.
Один процент – одна сотая доля.
Нахождение процента через деление на 100:
1. Делим изначальное число на 100 (таким образом получаем величину 1 процента от числа).
2. Умножаем на нужное нам количество процентов.
Например, чтобы найти 25% от 200, нужно:
Сначала найти, сколько составляет 1% от 200:
\(200:100 = 2\)
2.
 Умножить полученное значение на нужное нам количество процентов, то есть на 25:
Умножить полученное значение на нужное нам количество процентов, то есть на 25:\(2 \cdot 25 = 50\)
Нахождение процента через умножение на десятичную дробь:
Принцип действия тот же, однако 2 действия объединяем в одно – умножаем исходное число сразу на дробь.
1. Превращаем процент в дробь (отсчитываем 2 символа справа и ставим запятую), например:
\(115\% = 1,15\)
\(82\% = 0,82\)
\(7\% = 0,07\)
\(25\% = 0,25\)
2. Умножаем число на полученную дробь:
25% от \(200 = 200 \cdot 0,25 = 50\)
Нахождение процента упрощённым способом «по кубикам»
Пользуясь правилом перевода процента в десятичную дробь, а затем – правилом перевода десятичной дроби в обыкновенную, можем вывести стандартные соотношения:
\(1\% = \frac{1}{100}\)
\(\ 10\% = \frac{1}{10}\)
\(\ 20\% = \frac{1}{5}\)
\(\ 25\% = \frac{1}{4}\)
\(\ 50\% = \frac{1}{2}\)
\(\ 75\%\ = \frac{3}{4}\)
Тогда работу с дробями мы можем заменить простым умножением или делением.

Например, чтобы найти 25% от 200, можно 200 поделить на 4 и получить 50.
Итак, пользуясь методом кубиков всегда можно найти 50%, 25%, а также 1%,10% и 20%. Например:
Для вычисления 1% нужно поставить запятую после второго символа, а для нахождения 10% поставить запятую после первого символа.
Далее, чтобы получить иной процент, нужно умножить полученное значение на нужное количество процентов. Например:
Как работать с процентами в текстовых задачах?
Для работы с процентами используется пропорция, в которой в одном столбце записываются реальные значения, в другом – соответствующие проценты.
Исходя из правил работы с дробями, получаем правила работы с пропорцией.
1. Внутри одной дроби можно сокращать значения.
2. Произведение накрест лежащих значений равно.
Например, если известно, что всего на прилавке имеется 200 груш, и нужно найти, сколько груш составляет 1%.
Составляем пропорцию:
200 груш – 100 %
x груш – 1 %
Пользуемся правилом произведения накрест лежащих значений:
\(200 \cdot 1 = x \cdot 100\)
Выражаем искомую величину:
\(x = \frac{200 \cdot 1}{100} = 2\)
Получаем готовое соотношение:
200 груш – 100 %
2 груши – 1 %
Итак, 1% от всего количества составляет 2 груши.

Или другая задача: известно, что 20% от всего количества составляет 40 груш. Сколько всего груш на прилавке?
Составляем пропорцию:
x груш – 100 %
40 груш – 20 %
Пользуемся правилом произведения накрест лежащих значений:
\(x \cdot 20 = 40 \cdot 100\)
Выражаем искомую величину:
\(x = \frac{40 \cdot 100}{20} = 200\)
Получаем готовое соотношение:
200 груш – 100 %
40 груш – 20 %
Итак, 100% — это 200 груш.
Видим, что пропорция отражает зависимость величин, по-другому это можно записать в виде двух дробей:
\(\frac{200}{2} = \frac{100}{1}\) или \(\frac{200}{40} = \frac{100}{20}\)
Рак молочной железы и состояние лимфатических узлов
Состояние лимфатических узлов показывает, содержат ли лимфатические узлы в подмышечной области (подмышечные лимфатические узлы) рак:
- Отрицательный лимфатический узел означает, что ни один из подмышечных лимфатических узлов не содержит рака.

- Лимфатический узел положительный означает, что по крайней мере один подмышечный лимфатический узел содержит рак.
Прогноз (шанс на выживание) лучше, если рак не распространился на лимфатические узлы (негативное поражение лимфатических узлов) [12].
Чем больше раковых лимфатических узлов, тем хуже прогноз [12].
Количество положительных лимфоузлов определяет лечение и помогает предсказать прогноз.
См. рис. 4.4 ниже, где показан рисунок молочной железы и лимфатических узлов.
Узнайте больше о состоянии лимфатических узлов.
Патологическое состояние лимфатических узлов
Патологоанатомическое исследование — лучший способ оценить состояние лимфатических узлов. Это называется патологическим состоянием лимфатических узлов.
Обычно хирург удаляет один или несколько подмышечных лимфатических узлов с помощью метода, называемого биопсией сторожевого узла. Патолог исследует эти узлы под микроскопом, чтобы определить, содержат ли они рак.

Эти результаты помогают определить стадию рака молочной железы и назначить лечение.
Узнайте больше о биопсии сигнального лимфатического узла и оценке лимфатических узлов.
Клиническое состояние лимфатических узлов
Физическое обследование (также называемое клиническим обследованием) может дать первую оценку состояния лимфатических узлов. Это называется клиническим статусом лимфатических узлов. Увеличенные узлы могут быть признаком того, что рак молочной железы распространился на узлы.
Клинический статус лимфатических узлов используется только при отсутствии патологических данных.
Категории состояния лимфатических узлов
См. рис. 4.4, где показан рисунок молочной железы и лимфатических узлов.
Патологическое состояние лимфатических узлов
Клинический статус лимфатических узлов
(используется только при отсутствии патологических данных)NX
Подмышечные и другие близлежащие лимфатические узлы не могут быть оценены (например, они не были удалены во время операции)
Подмышечные и другие близлежащие лимфатические узлы не могут быть оценены (например, они были удалены в прошлом)
N0
Подмышечные и другие близлежащие лимфатические узлы не поражены раком или имеют только изолированные опухолевые клетки (отдельные раковые клетки) при исследовании под микроскопом
Подмышечные и другие близлежащие лимфатические узлы не поражены раком
N1
Микрометастазы (очень маленькие скопления раковых клеток) ИЛИ
1–3 подмышечных лимфатических узла имеют рак И/ИЛИ
Внутренние узлы молочной железы имеют рак или микрометастазы, обнаруженные при биопсии сигнального узла
Подмышечные лимфатические узлы поражены раком, но могут перемещаться
N2
4–9 подмышечных лимфатических узлов поражены раком ИЛИ
Внутренние узлы молочной железы поражены раком, но подмышечные лимфатические узлы не поражены раком
Подмышечные лимфатические узлы поражены раком и спаяны друг с другом или прикреплены к другим структурам (например, к грудной стенке) ИЛИ
Внутренние узлы молочной железы поражены раком, но подмышечные лимфатические узлы, по-видимому, не поражены раком
N3
Рак 10 или более подмышечных лимфатических узлов ИЛИ
Рак подключичных (подключичных) узлов ИЛИ
Рак внутренних узлов молочной железы плюс рак 1 или более подмышечных лимфатических узлов ИЛИ
4 или более подмышечных лимфатических узла имеют рак плюс внутренние узлы молочной железы имеют рак или микрометастазы (очень маленькие скопления раковых клеток), обнаруженные при биопсии сигнального узла ИЛИ
Надключичные (над ключицей) узлы имеют рак
Подключичные (подключичные) узлы имеют рак (подмышечные лимфатические узлы могут быть или не быть раковыми) ИЛИ
Внутренние грудные узлы и подмышечные лимфатические узлы имеют рак ИЛИ
Надключичные (над ключицей) узлы имеют рак (подмышечные лимфатические узлы может быть рак, а может и не быть)
Адаптировано из материалов Американского объединенного комитета по раку [30].

Обновлено 20.12.22
УЗИ злокачественных шейных лимфатических узлов
[1] Ishii JI, Amagasa T, Tachibana T, Shinozuka K, Shioda S. УЗИ и КТ оценка метастазов в шейных лимфатических узлах рака полости рта . J Cranio-Max-Fac Surg. 1991;19:123. [PubMed] [Google Scholar]
[2] Вассалло П., Эдель Г., Роос Н., Нагиб А., Петерс П.Е. Ультрасонография доброкачественных и злокачественных лимфатических узлов с высоким разрешением in vitro. Сонографо-патологическая корреляция. Инвестируйте Радиол. 1993;28:698. [PubMed] [Google Scholar]
[3] Сом PM. Выявление метастазов в шейных лимфатических узлах: КТ- и МРТ-критерии и дифференциальная диагностика. Am J Рентгенол. 1992; 158:961. [PubMed] [Google Scholar]
[4] Сом PM. Лимфатические узлы шеи. Радиология. 1987; 165:593. [PubMed] [Google Scholar]
[5] DePena CA, Van Tassel P, Lee YY. Лимфома головы и шеи. Радиол Клин Норт Ам. 1990;28:723. [PubMed] [Google Scholar]
[6] Bruneton JN, Normand F.
 Шейные лимфатические узлы. В: Брунетон Дж. Н., редактор. УЗИ шеи. Берлин: Springer-Verlag. 1987; с. 81 [Google Scholar]
Шейные лимфатические узлы. В: Брунетон Дж. Н., редактор. УЗИ шеи. Берлин: Springer-Verlag. 1987; с. 81 [Google Scholar][7] Baatenburg de Jong RJ, Rongen RJ, Lameris JS, Harthoorn M, Verwoerd CD, Knegt P. Метастатическая болезнь шеи. Пальпация против УЗИ. Arch Otolaryngol Head Neck Surg. 1989;115:689. [PubMed] [Google Scholar]
[8] Сом П.М., Брандвейн М., Лидов М., Лоусон В., Биллер Х.Ф. Разнообразные проявления папиллярной карциномы щитовидной железы с поражением шейных узлов: данные КТ и МРТ. Am J Нейрорадиол. 1994;15:1123. [Бесплатная статья PMC] [PubMed] [Google Scholar]
[9] Ахуджа А., Ин М. Обзор сонографии шейных узлов. Инвестируйте Радиол. 2002; 37:333. [PubMed] [Google Scholar]
[10] Jeong HS, Baek CH, Son YI, et al. Использование интегрированной 18 F-FDG ПЭТ/КТ для повышения точности начальной оценки шейных лимфоузлов у пациентов с плоскоклеточным раком головы и шеи. Шея головы. 2007; 29:203. [PubMed] [Google Scholar]
[11] Суми М.
 , Ван Каутерен М., Накамура Т. МРТ-микровизуализация доброкачественных и злокачественных узлов на шее. AJR Am J Рентгенол. 2006;186:749. [PubMed] [Google Scholar]
, Ван Каутерен М., Накамура Т. МРТ-микровизуализация доброкачественных и злокачественных узлов на шее. AJR Am J Рентгенол. 2006;186:749. [PubMed] [Google Scholar][12] Ахуджа А., Ин М. Ультрасонография в шкале серого в оценке шейной лимфаденопатии: обзор сонографических проявлений и особенностей, которые могут помочь новичку. Br J Oral Maxillofac Surg. 2000;38:451. [PubMed] [Google Scholar]
[13] Линдберг Р. Распространение метастазов в шейные лимфатические узлы плоскоклеточного рака верхних дыхательных и пищеварительных путей. Рак. 1972; 29:1446. [PubMed] [Google Scholar]
[14] Комисар А. Лечение узловой отрицательной шейки. В: Vogl SE, редактор. Рак головы и шеи. Нью-Йорк: Черчилль Ливингстон; 1988. с. 19. [Google Scholar]
[15] van Overhagen H, Lameris JS, Berger MY, et al. Метастазы в надключичные лимфатические узлы при карциноме пищевода и желудочно-пищеводного перехода: оценка с помощью КТ, УЗИ и тонкоигольной аспирационной биопсии под контролем УЗИ.
 Радиология. 1991;179:155. [PubMed] [Google Scholar]
Радиология. 1991;179:155. [PubMed] [Google Scholar][16] ван Оверхаген Х., Ламерис Дж. С., Зондерланд Х. М., Тиланус Х. В., ван Пел Р., Шютте Х. Е. Ультразвуковая и тонкоигольная аспирационная биопсия надключичных лимфатических узлов под ультразвуковым контролем у пациентов с раком пищевода. Рак. 1991;67:585. [PubMed] [Google Scholar]
[17] Van Overhagen H, Lameris JS, Berger MY, et al. Улучшенная оценка надключичных и абдоминальных метастазов при раке пищевода и желудочно-пищеводного перехода с помощью комбинации ультразвука и компьютерной томографии. Бр Дж Радиол. 1993;66:203. [PubMed] [Google Scholar]
[18] Ахуджа А., Ин М., Кинг В., Метревели С. Практический подход к УЗИ шейных лимфатических узлов. Ж Ларынгол Отол. 1997; 111:245. [PubMed] [Академия Google]
[19] Ying M, Ahuja AT, Evans R, King W, Metreweli C. Шейная лимфаденопатия: сонографическая дифференциация между туберкулезными узлами и узловыми метастазами от карциномы не головы и шеи. Дж. Клин Ультразвук.
 1998; 26:383. [PubMed] [Google Scholar]
1998; 26:383. [PubMed] [Google Scholar][20] Sugama Y, Kitamura S. УЗИ шеи и надключичных лимфатических узлов с метастазами рака легких. Интерн Мед. 1992; 31:160. [PubMed] [Google Scholar]
[21] Yao ZH, Wu AR. Метастазы рака шейки матки в надключичные лимфатические узлы после лучевой терапии – анализ 219пациенты. Чунг Хуа Чунг Лю Ца Чжи. 1988;10:230. [PubMed] [Google Scholar]
[22] Kiricuta IC, Willner J, Kolbl O, Bohndorf W. Прогностическое значение метастазов в надключичные лимфатические узлы у больных раком молочной железы. Int J Radiat Oncol Biol Phys. 1994; 28:387. [PubMed] [Google Scholar]
[23] Cervin JR, Silverman JF, Loggie BW, Geisinger KR. Повторное посещение узла Вирхова. Анализ с клинико-патологической корреляцией 152 тонкоигольной аспирационной биопсии надключичных лимфатических узлов. Arch Pathol Lab Med. 1995;119:727. [PubMed] [Google Scholar]
[24] Ахуджа А., Ин М., Эванс Р., Кинг В., Метревели С. Применение ультразвуковых критериев злокачественности при дифференциации туберкулезного шейного аденита от метастатической карциномы носоглотки.
 Клин Радиол. 1995;50:391. [PubMed] [Google Scholar]
Клин Радиол. 1995;50:391. [PubMed] [Google Scholar][25] Swartz JD, Yussen PS, Popky GL. Визуализация шеи: узловая болезнь. Критическая диагностика визуализации. 1991; 31:413. [PubMed] [Google Scholar]
[26] Ахуджа А.Т., Чоу Л., Чик В., Кинг В., Метревели С. Метастатические шейные узлы при папиллярной карциноме щитовидной железы: УЗИ и гистологическая корреляция. Клин Радиол. 1995;50:229. [PubMed] [Google Scholar]
[27] Attie JN, Setzin M, Klein I. Карцинома щитовидной железы в виде увеличенного шейного лимфатического узла. Am J Surg. 1993; 166:428. [PubMed] [Google Scholar]
[28] De Jong SA, Demeter JG, Jarosz H, Lawrence AM, Paloyan E. Первичная папиллярная карцинома щитовидной железы, проявляющаяся шейной лимфаденопатией: оперативный подход к «латеральной аберрантной щитовидной железе» Am Surg. 1993; 59:172. [PubMed] [Google Scholar]
[29] Ahuja A, Ying M, Yang WT, Evans R, King W, Metreweli C. Использование сонографии для дифференциации шейных лимфоматозных лимфатических узлов от шейных метастатических лимфатических узлов.
 Клин Радиол. 1996;51:186. [PubMed] [Google Scholar]
Клин Радиол. 1996;51:186. [PubMed] [Google Scholar][30] Hajek PC, Salomonowitz E, Turk R, Tscholakoff D, Kumpan W, Czembirek H. Лимфатические узлы шеи: оценка с помощью УЗИ. Радиология. 1986; 158:739. [PubMed] [Google Scholar]
[31] Shozushima M, Suzuki M, Nakasima T, Yanagisawa Y, Sakamaki K, Takeda Y. Ультразвуковая диагностика метастазов в лимфатические узлы при раке головы и шеи. Дентомаксиллофак Радиол. 1990;19:165. [PubMed] [Google Scholar]
[32] Solbiati L, Rizzatto G, Bellotti E, Montali G, Cioffi V, Croce F. УЗИ шейных лимфатических узлов с высоким разрешением при раке головы и шеи: критерии дифференциации реактивного и злокачественные узлы. Радиология. 1988;169(П):113. [Google Scholar]
[33] Ying M, Ahuja A, Metreweli C. Диагностическая точность сонографических критериев для оценки шейной лимфаденопатии. J УЗИ Мед. 1998;17:437. [PubMed] [Google Scholar]
[34] Ahuja A, Leung SF, Ying M, Metreweli C. Эхография метастатических узлов, леченных лучевой терапией.
 Ж Ларынгол Отол. 1999;113:993. [PubMed] [Google Scholar]
Ж Ларынгол Отол. 1999;113:993. [PubMed] [Google Scholar][35] Tohnosu N, Onoda S, Isono K. Ультрасонографическая оценка метастазов в шейных лимфатических узлах при раке пищевода с особым упором на взаимосвязь между отношением короткой оси к длинной (S/L) и раковое содержание. Дж. Клин Ультразвук. 1989;17:101. [PubMed] [Google Scholar]
[36] Ин М., Ахуджа А., Брук Ф., Браун Б., Метревели С. Сонографический вид и распределение нормальных шейных лимфатических узлов у населения Китая. J УЗИ Мед. 1996; 15:431. [PubMed] [Google Scholar]
[37] Vassallo P, Wernecke K, Roos N, Peters PE. Дифференциация доброкачественной поверхностной лимфаденопатии от злокачественной: роль УЗИ высокого разрешения. Радиология. 1992;183:215. [PubMed] [Google Scholar]
[38] Johnson JT. Хирург осматривает шейные лимфатические узлы. Радиология. 1990;175:607. [PubMed] [Google Scholar]
[39] van den Brekel MW, Stel HV, Castelijns JA, et al. Метастазирование шейных лимфатических узлов: оценка радиологических критериев.
 Радиология. 1990;177:379. [PubMed] [Google Scholar]
Радиология. 1990;177:379. [PubMed] [Google Scholar][40] Evans RM, Ahuja A, Metreweli C. Линейные эхогенные ворота при шейной лимфаденопатии – признак доброкачественности или злокачественности? Клин Радиол. 1993;47:262. [PubMed] [Google Scholar]
[41] Sakai F, Kiyono K, Sone S, et al. Ультразвуковая оценка метастатической лимфаденопатии шейки матки. J УЗИ Мед. 1988;7:305. [PubMed] [Google Scholar]
[42] Rubaltelli L, Proto E, Salmaso R, Bortoletto P, Candiani F, Cagol P. Сонография аномальных лимфатических узлов in vitro: корреляция сонографических и гистологических данных. Am J Рентгенол. 1990;155:1241. [PubMed] [Google Scholar]
[43] Ying M, Ahuja A, Brook F, Metreweli C. Сосудистые и серые сонографические особенности нормальных шейных лимфатических узлов: изменения в зависимости от размера узла. Клин Радиол. 2001; 56:416. [PubMed] [Академия Google]
[44] Solbiati L, Cioffi V, Ballarati E. УЗИ шеи. Радиол Клин Норт Ам. 1992;30:941. [PubMed] [Google Scholar]
[45] Ahuja A, Ying M, Leung SF, Metreweli C.
 Сонографический вид и значение метастатических узлов шейки матки после лучевой терапии рака носоглотки. Клин Радиол. 1996; 51:698. [PubMed] [Google Scholar]
Сонографический вид и значение метастатических узлов шейки матки после лучевой терапии рака носоглотки. Клин Радиол. 1996; 51:698. [PubMed] [Google Scholar][46] Ин М., Ахуджа А., Брук Ф. Повторяемость энергетической допплерографии шейных лимфатических узлов. Ультразвук Медицина Биол. 2002; 28:737. [PubMed] [Академия Google]
[47] Ariji Y, Kimura Y, Hayashi N, et al. Энергетическая допплерография шейных лимфатических узлов у больных раком головы и шеи. Am J Нейрорадиол. 1998;19:303. [Бесплатная статья PMC] [PubMed] [Google Scholar]
[48] Na DG, Lim HK, Byun HS, Kim HD, Ko YH, Baek JH. Дифференциальный диагноз шейной лимфаденопатии: полезность цветной допплерографии. Am J Рентгенол. 1997; 168:1311. [PubMed] [Google Scholar]
[49] Wu CH, Chang YL, Hsu WC, Ko JY, Sheen TS, Hsieh FJ. Полезность допплеровского спектрального анализа и энергетической допплерографии в дифференциации шейных лимфаденопатий. Am J Рентгенол. 1998;171:503. [PubMed] [Google Scholar]
[50] Ying M, Ahuja A, Brook F, Metreweli C.
 Энергетическая допплерография нормальных шейных лимфатических узлов. J УЗИ Мед. 2000;19:511. [PubMed] [Google Scholar]
Энергетическая допплерография нормальных шейных лимфатических узлов. J УЗИ Мед. 2000;19:511. [PubMed] [Google Scholar][51] Steinkamp HJ, Maurer J, Cornehl M, Knobber D, Hettwer H, Felix R. Рецидивирующая шейная лимфаденопатия: дифференциальный диагноз с помощью цветной дуплексной сонографии. Eur Arch Оториноларингол. 1994; 251:404. [PubMed] [Google Scholar]
[52] Ahuja AT, Ying M, Ho SS, Metreweli C. Распределение внутриузловых сосудов при дифференциации доброкачественных узлов шеи от метастатических. Клин Радиол. 2001;56:197. [PubMed] [Google Scholar]
[53] Maurer J, Willam C, Schroeder R, et al. Оценка метастазов и реактивных лимфатических узлов при допплерографии с использованием ультразвукового усилителя контраста. Инвестируйте Радиол. 1997; 32:441. [PubMed] [Google Scholar]
[54] Dragoni F, Cartoni C, Pescarmona E, et al. Роль высокоразрешающей импульсной и цветной допплерографии в дифференциальной диагностике доброкачественной и злокачественной лимфаденопатии: результаты многофакторного анализа.
 Рак. 1999;85:2485. [PubMed] [Академия Google]
Рак. 1999;85:2485. [PubMed] [Академия Google][55] Chang DB, Yuan A, Yu CJ, Luh KT, Kuo SH, Yang PC. Дифференциация доброкачественных и злокачественных шейных лимфатических узлов с помощью цветной допплерографии. Am J Рентгенол. 1994; 162:965. [PubMed] [Google Scholar]
[56] Adibelli ZH, Unal G, Gul E, Uslu F, Kocak U, Abali Y. Дифференциация доброкачественных и злокачественных шейных лимфатических узлов: значение B-режима и цветная допплерография. Евр Дж Радиол. 1998;28:230. [PubMed] [Google Scholar]
[57] Ishii J, Fujii E, Suzuki H, Shinozuka K, Kawase N, Amagasa T. Ультразвуковая диагностика злокачественной лимфомы полости рта и шеи. Bull Tokyo Med Dent Univ. 1992;39:63. [PubMed] [Google Scholar]
[58] Lee YY, Van Tassel P, Nauert C, North LB, Jing BS. Лимфомы головы и шеи: данные КТ при первичном обращении. Am J Рентгенол. 1987; 149:575. [PubMed] [Google Scholar]
[59] Bruneton JN, Normand F, Balu-Maestro C, et al. Лимфоматозные поверхностные лимфатические узлы: УЗИ.
 Радиология. 1987; 165:233. [PubMed] [Google Scholar]
Радиология. 1987; 165:233. [PubMed] [Google Scholar][60] Ho SS, Ahuja AT, Yeo W, Chan TC, Kew J, Metreweli C. Продольное цветное допплеровское исследование поверхностных лимфатических узлов у пациентов с неходжкинской лимфомой, получающих химиотерапию. Клин Радиол. 2000;55:110. [PubMed] [Академия Google]
[61] Ин МТС. Кафедра оптометрии и рентгенографии Гонконгского политехнического университета, Гонконг; 1996. Ультразвуковая оценка шейных лимфатических узлов у населения Китая. п. 235. MPhil thesis [Google Scholar]
[62] Callen PW, Marks WM. Лимфоматозные массы, имитирующие кисту при УЗИ. J Can Assoc Radiol. 1979; 30:244. [PubMed] [Google Scholar]
[63] Bruneton JN, Roux P, Caramella E, Demard F, Vallicioni J, Chauvel P. Рак уха, носа и горла: ультразвуковая диагностика метастазов в шейные лимфатические узлы. Радиология. 1984;152:771. [PubMed] [Google Scholar]
[64] Ahuja AT, Ying M, Yuen HY, Metreweli C. «Псевдокистозный» вид неходжкинских лимфоматозных узлов: нечастая находка с датчиками высокого разрешения.
 Клин Радиол. 2001; 56:111. [PubMed] [Google Scholar]
Клин Радиол. 2001; 56:111. [PubMed] [Google Scholar][65] Steinkamp HJ, Mueffelmann M, Bock JC, Thiel T, Kenzel P, Felix R. Дифференциальная диагностика поражений лимфатических узлов: полуколичественный подход с цветным допплеровским ультразвуком. Бр Дж Радиол. 1998;71:828. [PubMed] [Академия Google]
[66] Ин МТС. Кафедра оптометрии и рентгенографии Гонконгского политехнического университета, Гонконг; 2002. Энергетическая допплерография нормальных и патологических шейных лимфатических узлов; п. 236. в докторской диссертации [Google Scholar]
[67] Moritz JD, Ludwig A, Oestmann JW. Цветная допплерография с контрастным усилением для оценки увеличенных шейных лимфатических узлов при опухолях головы и шеи. Am J Рентгенол. 2000;174:1279. [PubMed] [Google Scholar]
[68] Rubaltelli L, Khadivi Y, Tregnaghi A, et al. Оценка перфузии лимфатических узлов с помощью гармонической ультрасонографии в непрерывном режиме с контрастным веществом второго поколения. J УЗИ Мед.

2 в 5 степени сколько: Два в пятой степени — решение и ответ!
3-89 Оценить квадратный корень из 12 10 Оценить квадратный корень из 20 11 Оценить квадратный корень из 50 94 18 Оценить квадратный корень из 45 19 Оценить квадратный корень из 32 20 Оценить квадратный корень из 18 92
Степени и степени
Обновлено 21 февраля 2017 г.

 21,3 x 87,5 x 180,5 мм
21,3 x 87,5 x 180,5 мм длина списков: 999
длина списков: 999 В нашем примере у нас есть такие значения, как 209, 282 и т. д., так что все готово.
В нашем примере у нас есть такие значения, как 209, 282 и т. д., так что все готово.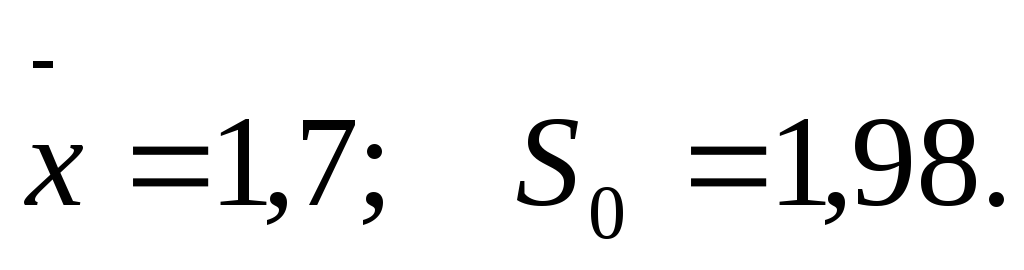
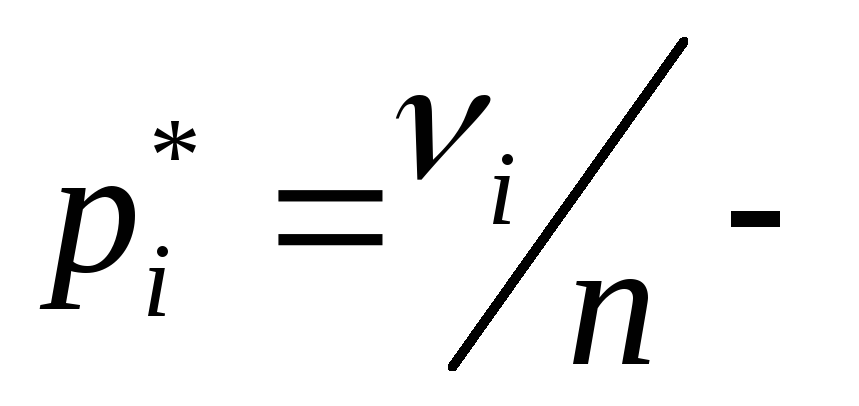
 Калькулятор значения хи-квадрат p позволяет найти точное значение p.
Калькулятор значения хи-квадрат p позволяет найти точное значение p.
 Учащиеся должны оставаться на расстоянии 2 м и носить защитные очки.
Учащиеся должны оставаться на расстоянии 2 м и носить защитные очки. Учащиеся могут увидеть образование газообразного водорода и провести мысленную связь между реакциями, показанными в уравнении 1 и уравнении 2.
Учащиеся могут увидеть образование газообразного водорода и провести мысленную связь между реакциями, показанными в уравнении 1 и уравнении 2.
 Надосадочная жидкость над твердым веществом считается щелочной, когда красная лакмусовая бумажка становится синей.
Надосадочная жидкость над твердым веществом считается щелочной, когда красная лакмусовая бумажка становится синей. 7 см
7 см 3 дм
3 дм 9 см
9 см Это становится очевидным, например, если вы будете смотреть спорт с близкого расстояния, фиксируя одну часть экрана. Через какое-то время это становится довольно тошнотворным.
Это становится очевидным, например, если вы будете смотреть спорт с близкого расстояния, фиксируя одну часть экрана. Через какое-то время это становится довольно тошнотворным.
 1′ (1.86 м)
1′ (1.86 м) 5′ (2.29 м)
5′ (2.29 м)
 К счастью у нас есть сводная таблица оптимального расстояния при различных разрешениях и размерах, на которую мы советуем ориентироваться.
К счастью у нас есть сводная таблица оптимального расстояния при различных разрешениях и размерах, на которую мы советуем ориентироваться. Это безумие!». Да, если вы хотите ощутить мощность более высоких разрешений по максимуму, это идеальный размер. Это подводит нас к главному ограничению для большинства людей — бюджету.
Обратите внимание, что цена телевизора экспоненциальна к его размеру, как показано на графике. Ниже показан ценовой диапазон светодиодных телевизоров 2016 года по их размерам. Как вы можете видеть, переход к 70-дюймовому телевизору довольно резкий вверх.
Это безумие!». Да, если вы хотите ощутить мощность более высоких разрешений по максимуму, это идеальный размер. Это подводит нас к главному ограничению для большинства людей — бюджету.
Обратите внимание, что цена телевизора экспоненциальна к его размеру, как показано на графике. Ниже показан ценовой диапазон светодиодных телевизоров 2016 года по их размерам. Как вы можете видеть, переход к 70-дюймовому телевизору довольно резкий вверх.
 Старайтесь не выкидывать документы, они могут пригодиться.
Старайтесь не выкидывать документы, они могут пригодиться.
 Увеличение размера диагонали экрана на несколько дюймов может сильно повлиять на цену, поэтому нужно предварительно выбрать размер телевизора по тому расстоянию, с которого вы будете его смотреть. Наибольшей популярностью у покупателей пользуются телевизоры с размерами диагонали экрана от 32 до 50 дюймов.
Увеличение размера диагонали экрана на несколько дюймов может сильно повлиять на цену, поэтому нужно предварительно выбрать размер телевизора по тому расстоянию, с которого вы будете его смотреть. Наибольшей популярностью у покупателей пользуются телевизоры с размерами диагонали экрана от 32 до 50 дюймов.

 /макс. проекционное отношение
/макс. проекционное отношение на клавиатуре или перемещайте ползунок Throw Distance назад и вперед, пока не найдете число в поле значения, которое представляет
расстояние между объективом проектора и поверхностью экрана. На графическом изображении экрана в середине
калькулятор, вы увидите размерные линии, которые сообщат вам размеры высоты, ширины и диагонали вашего изображения.
на клавиатуре или перемещайте ползунок Throw Distance назад и вперед, пока не найдете число в поле значения, которое представляет
расстояние между объективом проектора и поверхностью экрана. На графическом изображении экрана в середине
калькулятор, вы увидите размерные линии, которые сообщат вам размеры высоты, ширины и диагонали вашего изображения.
 Положение проектора в вашей комнате меняется, потому что вам нужно переместить проектор ближе или дальше от экрана.
чтобы сохранить тот же размер изображения, чтобы соответствовать вашему экрану при повороте кольца трансфокатора.
Положение проектора в вашей комнате меняется, потому что вам нужно переместить проектор ближе или дальше от экрана.
чтобы сохранить тот же размер изображения, чтобы соответствовать вашему экрану при повороте кольца трансфокатора. Регламент вступил в силу с 1 октября 2000 г. и имеет прямое юридическое действие во всех странах ЕС. В нем говорится, что должны быть приняты все возможные меры предосторожности для предотвращения и сведения к минимуму утечек хладагентов из систем охлаждения и кондиционирования воздуха.
Регламент вступил в силу с 1 октября 2000 г. и имеет прямое юридическое действие во всех странах ЕС. В нем говорится, что должны быть приняты все возможные меры предосторожности для предотвращения и сведения к минимуму утечек хладагентов из систем охлаждения и кондиционирования воздуха. 


 Он также рассчитает эти свойства с точки зрения PI π. Это правильный круглый цилиндр, верхняя и нижняя поверхности которого параллельны, но его обычно называют «цилиндром».
Он также рассчитает эти свойства с точки зрения PI π. Это правильный круглый цилиндр, верхняя и нижняя поверхности которого параллельны, но его обычно называют «цилиндром».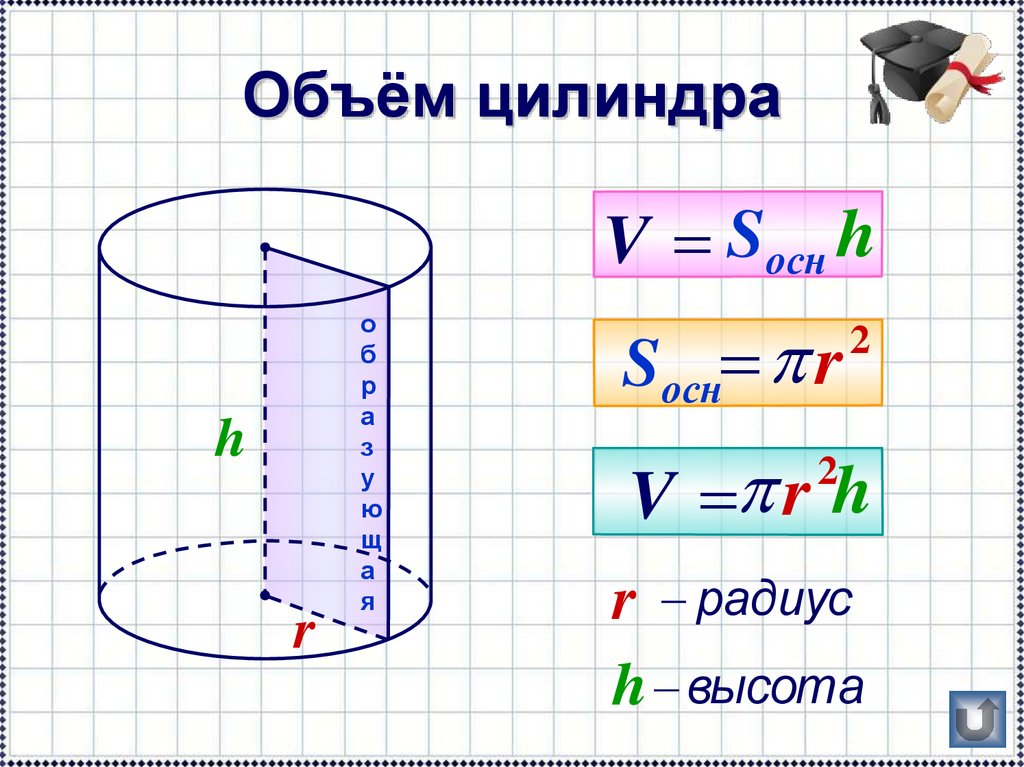 Чтобы рассчитать общую площадь поверхности, вам нужно будет также рассчитать площадь верха и низа. Вы можете сделать это с помощью
круговой калькулятор.
Чтобы рассчитать общую площадь поверхности, вам нужно будет также рассчитать площадь верха и низа. Вы можете сделать это с помощью
круговой калькулятор.

 Решите уравнение:
Решите уравнение: Заметим, что является также и корнем уравнения
Заметим, что является также и корнем уравнения



 Если вы не знаете, что делать, спросите сейчас, до следующего теста.)
Если вы не знаете, что делать, спросите сейчас, до следующего теста.) (Я оставлю вам проверку другого решения.) Мой ответ:
(Я оставлю вам проверку другого решения.) Мой ответ:

 Хотя вы можете легко найти онлайн-калькуляторы уравнений с квадратным корнем (пример см. в разделе Ресурсы), решение уравнений с квадратным корнем — важный навык в алгебре, поскольку он позволяет вам ознакомиться с использованием радикалов и работать с рядом типов задач за пределами области. квадратных корней как таковых.
Хотя вы можете легко найти онлайн-калькуляторы уравнений с квадратным корнем (пример см. в разделе Ресурсы), решение уравнений с квадратным корнем — важный навык в алгебре, поскольку он позволяет вам ознакомиться с использованием радикалов и работать с рядом типов задач за пределами области. квадратных корней как таковых. » вместо » -19 и 19″.
» вместо » -19 и 19″. Это означает, что квадратный корень дроби — это квадратный корень из ее верхней и нижней частей, то есть 4/5. Это равно 0,80, что больше, чем 0,64.
Это означает, что квадратный корень дроби — это квадратный корень из ее верхней и нижней частей, то есть 4/5. Это равно 0,80, что больше, чем 0,64. Расширяя это, x (5/3) означает «возвести x в степень 5, затем найти третий корень (или кубический корень) результата».
Расширяя это, x (5/3) означает «возвести x в степень 5, затем найти третий корень (или кубический корень) результата». Точное значение √50 равно 5√2, и вы скоро увидите, как оно определяется.
Точное значение √50 равно 5√2, и вы скоро увидите, как оно определяется. Следовательно, за исключением 0, каждые 9Значение 0009 y на графике y = x 2 связано с двумя x -значениями.
Следовательно, за исключением 0, каждые 9Значение 0009 y на графике y = x 2 связано с двумя x -значениями.
 д. При изучении колебаний пружинного и математического маятников вводится понятия амплитуды, фазы, циклической чистоты.
д. При изучении колебаний пружинного и математического маятников вводится понятия амплитуды, фазы, циклической чистоты. Записать формулы приведения, объяснить их смысл, используя единичную полуокружность
Записать формулы приведения, объяснить их смысл, используя единичную полуокружность 03
03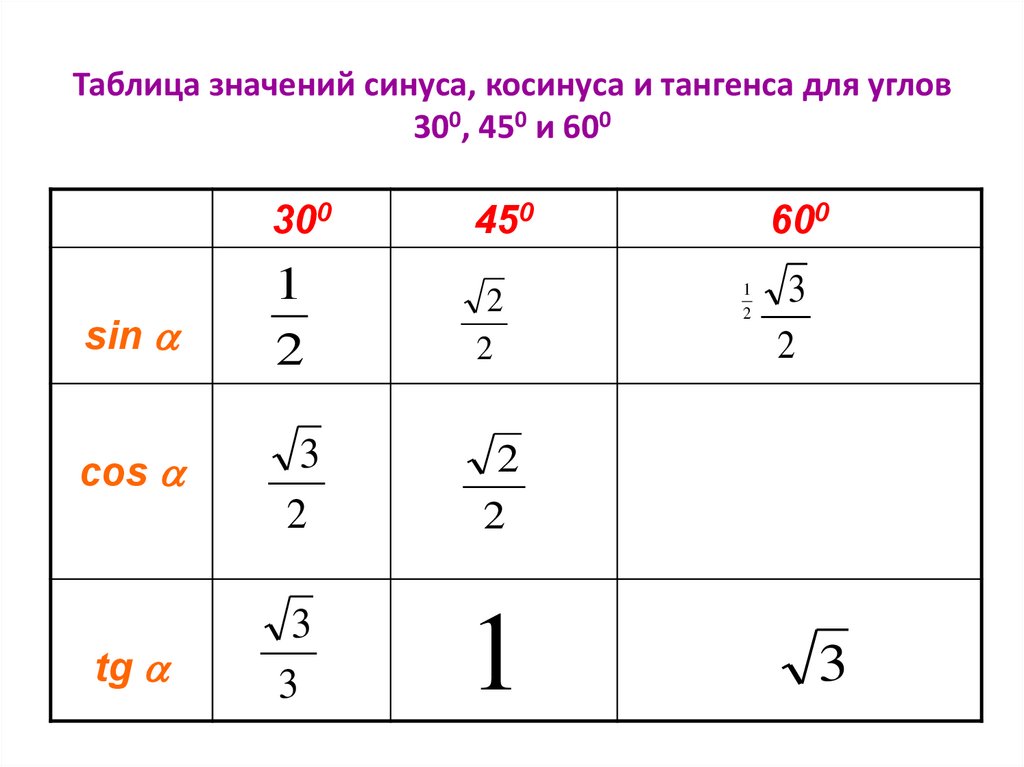 prodlenka.org/metodicheskie-razrabotki/291844-metodicheskaja-razrabotka-uroka-po-geometrii-
prodlenka.org/metodicheskie-razrabotki/291844-metodicheskaja-razrabotka-uroka-po-geometrii-

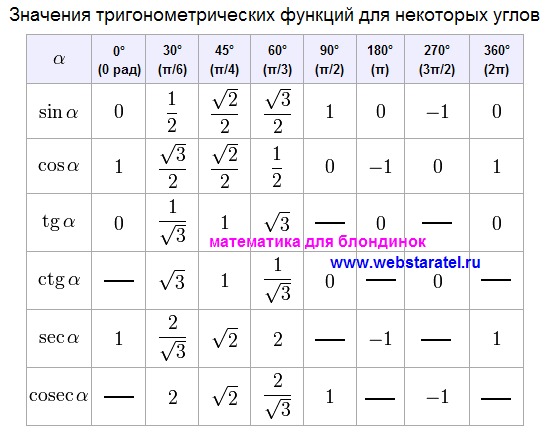


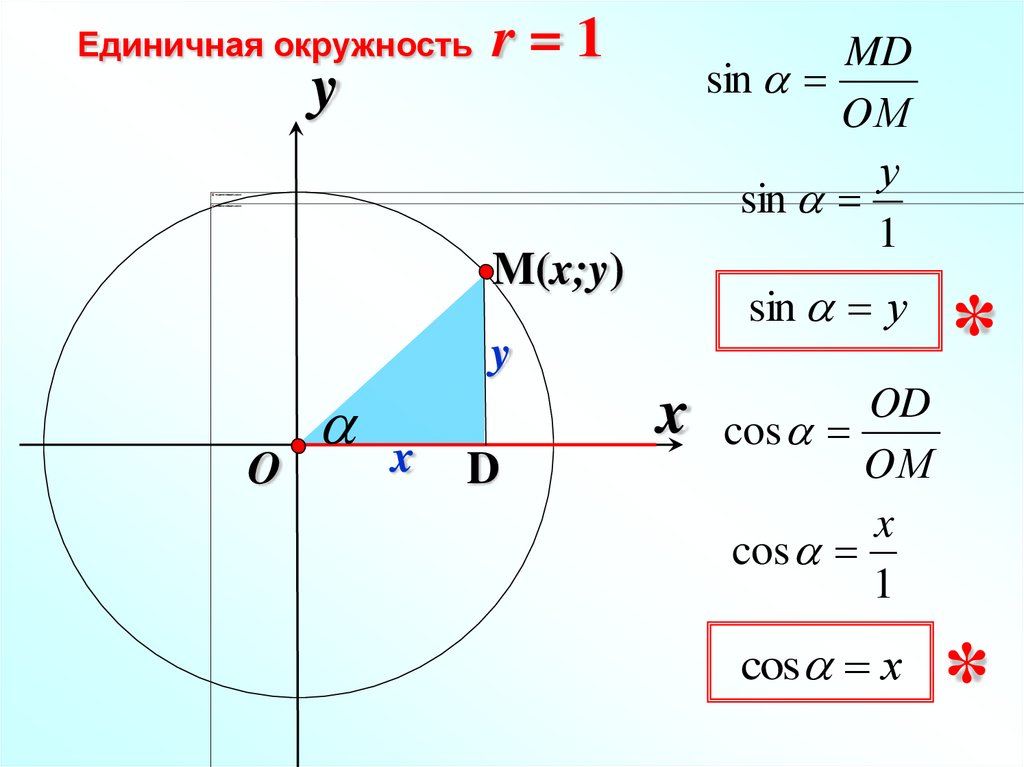
 Тангенс тета равен y относительно x, когда эти переменные заменены на y и x.
Тангенс тета равен y относительно x, когда эти переменные заменены на y и x. Он используется для расчета таких вещей, как амплитуда волны, скорость и ускорение. Он также используется в навигации и астрономии.
Он используется для расчета таких вещей, как амплитуда волны, скорость и ускорение. Он также используется в навигации и астрономии.
 Значение Tan 0 представляет собой отношение sin 0 к cos 0. Это значение tan 0 может быть получено либо из других тригонометрических функций, либо из единичного круга.
Значение Tan 0 представляет собой отношение sin 0 к cos 0. Это значение tan 0 может быть получено либо из других тригонометрических функций, либо из единичного круга.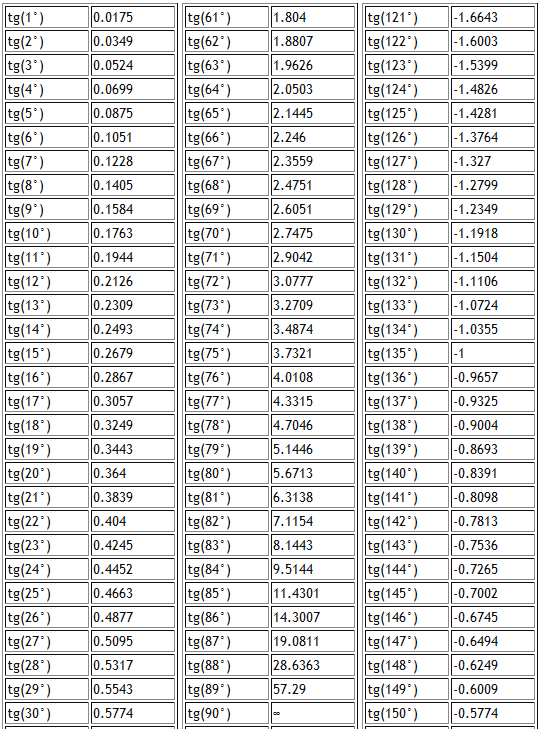 В единичном круге абсцисса, т. Е. Координата x, представляет значение cos, а ордината, т. е. координата y, представляет значение sin. Теперь, чтобы получить значение тангенса, мы просто делим соответствующее значение sin на значение cos, т. е. ординату на абсциссу.
В единичном круге абсцисса, т. Е. Координата x, представляет значение cos, а ордината, т. е. координата y, представляет значение sin. Теперь, чтобы получить значение тангенса, мы просто делим соответствующее значение sin на значение cos, т. е. ординату на абсциссу.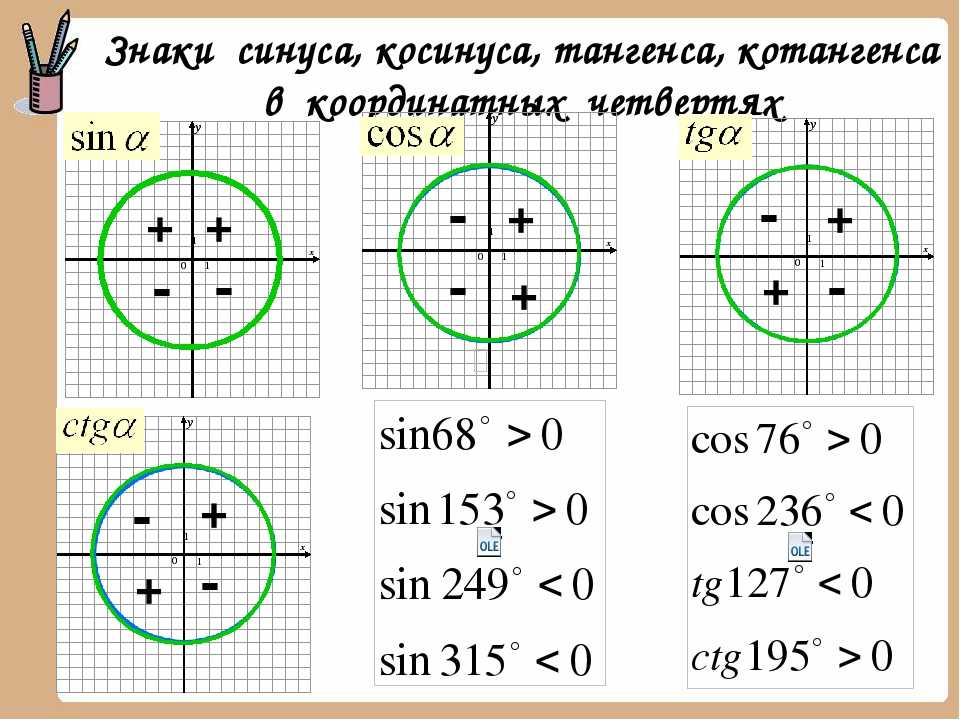 {\circ} \) или \ (\пи\) 9{\circ}}=\frac{1\left(1-0\right)}{\frac{1}{2}}=\frac{2\times1}{1}=2 \)
{\circ} \) или \ (\пи\) 9{\circ}}=\frac{1\left(1-0\right)}{\frac{1}{2}}=\frac{2\times1}{1}=2 \)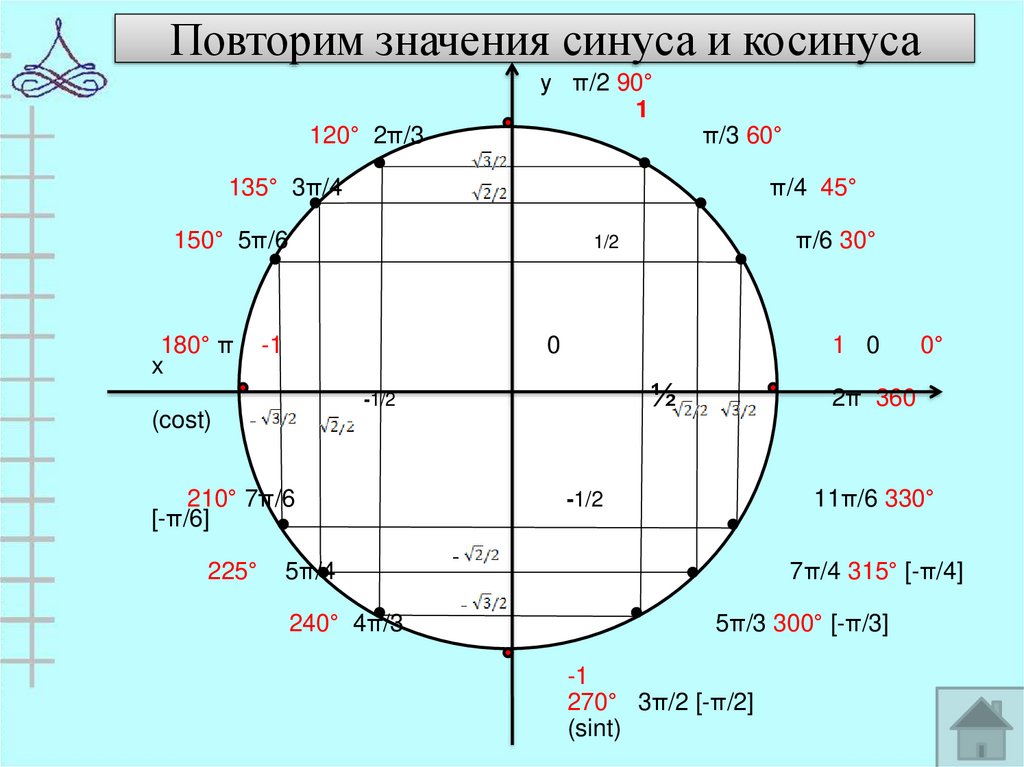
 В эту формулу
входят четыре величины (числа). Два числа
из них пришли из математики и являются,
а скорее считаются, абсолютно точными:
это числа 4 и π.
Но число 4 – конечное число, а число π – является бесконечной непериодической
дробью. Как это будет показано, можно
взять округленное значение числа π с таким количеством значащих цифр, что
это число практически не внесет никакой
погрешности в окончательный результат
расчета значения объема цилиндра.
В эту формулу
входят четыре величины (числа). Два числа
из них пришли из математики и являются,
а скорее считаются, абсолютно точными:
это числа 4 и π.
Но число 4 – конечное число, а число π – является бесконечной непериодической
дробью. Как это будет показано, можно
взять округленное значение числа π с таким количеством значащих цифр, что
это число практически не внесет никакой
погрешности в окончательный результат
расчета значения объема цилиндра. Поэтому
для уменьшения погрешности результата
необходимо именно диаметр цилиндра
измерить с как можно большей точностью.
Поэтому
для уменьшения погрешности результата
необходимо именно диаметр цилиндра
измерить с как можно большей точностью. Затем нужно
уточнить запись среднего значения
объема, сопоставив его с величиной
абсолютной погрешности (16). Число,
обозначающее среднее значение объема,
нужно округлить, оставив в нем все цифры
вплоть до разряда, являющегося последним
в окончательной записи абсолютной
погрешности. Записываем результат
измерений в виде суммы округленного
среднего значения и абсолютной
погрешности:
Затем нужно
уточнить запись среднего значения
объема, сопоставив его с величиной
абсолютной погрешности (16). Число,
обозначающее среднее значение объема,
нужно округлить, оставив в нем все цифры
вплоть до разряда, являющегося последним
в окончательной записи абсолютной
погрешности. Записываем результат
измерений в виде суммы округленного
среднего значения и абсолютной
погрешности: Окончательно:
Окончательно: Модуль нового вектора
равен произведению модуля старого
вектора на модуль этого числа.
Модуль нового вектора
равен произведению модуля старого
вектора на модуль этого числа.
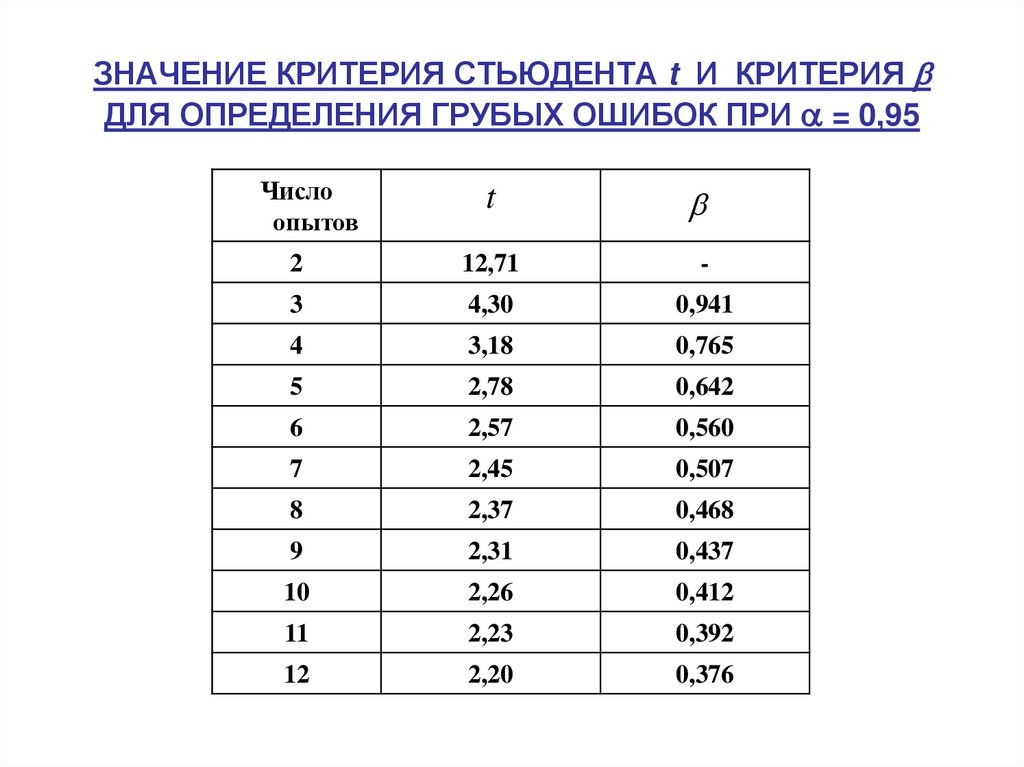 По правилу треугольника строим вектор
.
Обратите внимание, какой физический
смысл здесь раскрывается: Вектор изменения
скорости соединяет конец первого вектора с концом
второго, то есть показывает, как изменился вектор скорости (увеличился или уменьшился
и в какую сторону повернулся).
По правилу треугольника строим вектор
.
Обратите внимание, какой физический
смысл здесь раскрывается: Вектор изменения
скорости соединяет конец первого вектора с концом
второго, то есть показывает, как изменился вектор скорости (увеличился или уменьшился
и в какую сторону повернулся).

 Это выражение называется дифференциалом и является в данном случае бесконечно
малым промежутком времени. – бесконечно малое приращение вектора
скорости. Имеем дробь:
Это выражение называется дифференциалом и является в данном случае бесконечно
малым промежутком времени. – бесконечно малое приращение вектора
скорости. Имеем дробь: Степенью называется двухуровневое
выражение вида
,
нижняя и верхняя части которого
неравнозначны.
Степенью называется двухуровневое
выражение вида
,
нижняя и верхняя части которого
неравнозначны.
 2. Расчет случайной погрешности
2. Расчет случайной погрешности

 Этим приборам присваиваются
классы точности.Класс точностиравен пределу допускаемой приведенной
погрешности, выраженной в процентах,
которая определяется по формуле
Этим приборам присваиваются
классы точности.Класс точностиравен пределу допускаемой приведенной
погрешности, выраженной в процентах,
которая определяется по формуле 2497
2497 1265
1265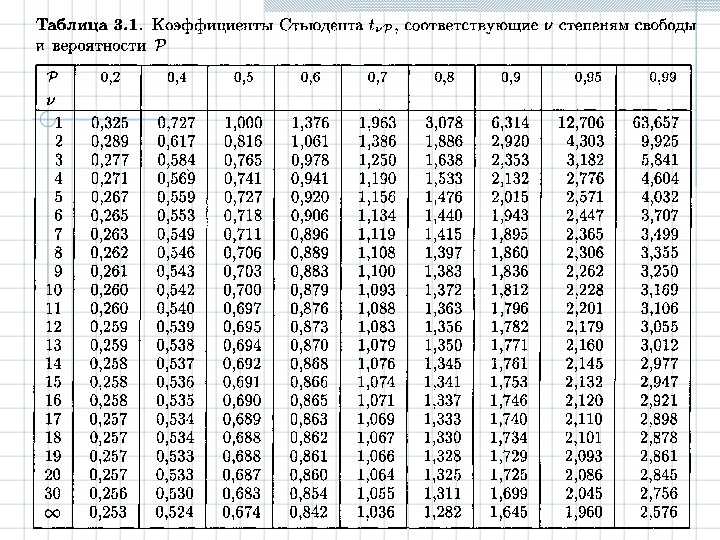 \(t\)-распределение похоже на стандартное нормальное распределение. Используя приведенную выше формулу для p.d.f. \(T\), мы можем построить кривую плотности различных \(t\) случайных величин, скажем, когда \(r=1, r=4\) и \(r=7\), чтобы увидеть, что это действительно так:
\(t\)-распределение похоже на стандартное нормальное распределение. Используя приведенную выше формулу для p.d.f. \(T\), мы можем построить кривую плотности различных \(t\) случайных величин, скажем, когда \(r=1, r=4\) и \(r=7\), чтобы увидеть, что это действительно так: То есть мы с большей вероятностью получим экстремальные \(t\)-значения, чем экстремальные \(z\)-значения.
То есть мы с большей вероятностью получим экстремальные \(t\)-значения, чем экстремальные \(z\)-значения.


 Умножить полученное значение на нужное нам количество процентов, то есть на 25:
Умножить полученное значение на нужное нам количество процентов, то есть на 25:



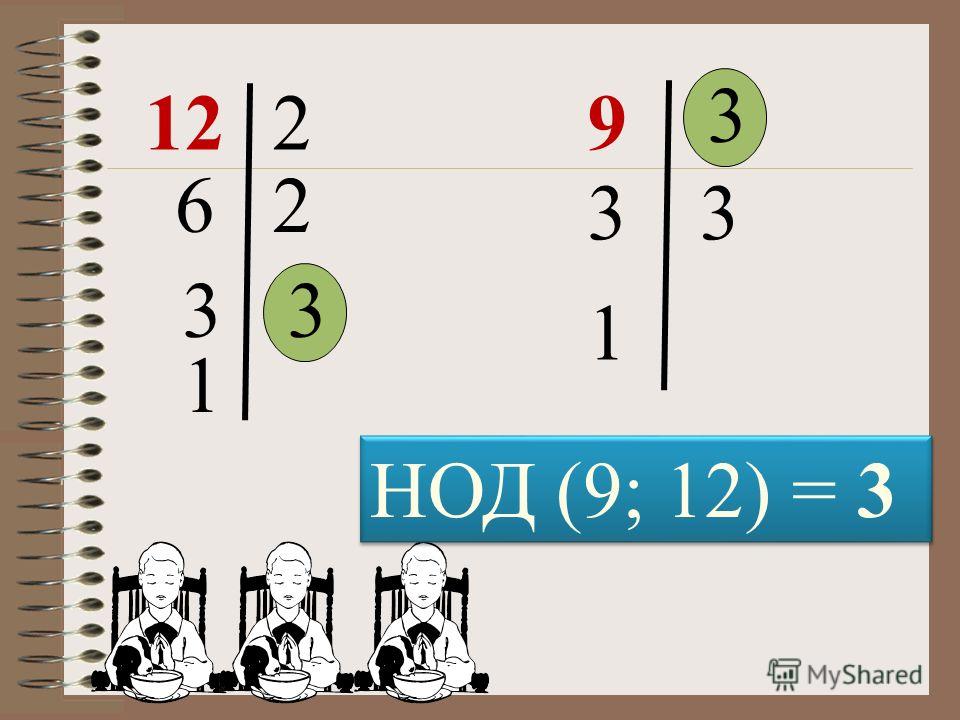
 Шейные лимфатические узлы. В: Брунетон Дж. Н., редактор. УЗИ шеи. Берлин: Springer-Verlag. 1987; с. 81 [Google Scholar]
Шейные лимфатические узлы. В: Брунетон Дж. Н., редактор. УЗИ шеи. Берлин: Springer-Verlag. 1987; с. 81 [Google Scholar] , Ван Каутерен М., Накамура Т. МРТ-микровизуализация доброкачественных и злокачественных узлов на шее. AJR Am J Рентгенол. 2006;186:749. [PubMed] [Google Scholar]
, Ван Каутерен М., Накамура Т. МРТ-микровизуализация доброкачественных и злокачественных узлов на шее. AJR Am J Рентгенол. 2006;186:749. [PubMed] [Google Scholar] Радиология. 1991;179:155. [PubMed] [Google Scholar]
Радиология. 1991;179:155. [PubMed] [Google Scholar] 1998; 26:383. [PubMed] [Google Scholar]
1998; 26:383. [PubMed] [Google Scholar] Клин Радиол. 1995;50:391. [PubMed] [Google Scholar]
Клин Радиол. 1995;50:391. [PubMed] [Google Scholar] Клин Радиол. 1996;51:186. [PubMed] [Google Scholar]
Клин Радиол. 1996;51:186. [PubMed] [Google Scholar] Ж Ларынгол Отол. 1999;113:993. [PubMed] [Google Scholar]
Ж Ларынгол Отол. 1999;113:993. [PubMed] [Google Scholar] Радиология. 1990;177:379. [PubMed] [Google Scholar]
Радиология. 1990;177:379. [PubMed] [Google Scholar] Сонографический вид и значение метастатических узлов шейки матки после лучевой терапии рака носоглотки. Клин Радиол. 1996; 51:698. [PubMed] [Google Scholar]
Сонографический вид и значение метастатических узлов шейки матки после лучевой терапии рака носоглотки. Клин Радиол. 1996; 51:698. [PubMed] [Google Scholar] Энергетическая допплерография нормальных шейных лимфатических узлов. J УЗИ Мед. 2000;19:511. [PubMed] [Google Scholar]
Энергетическая допплерография нормальных шейных лимфатических узлов. J УЗИ Мед. 2000;19:511. [PubMed] [Google Scholar] Рак. 1999;85:2485. [PubMed] [Академия Google]
Рак. 1999;85:2485. [PubMed] [Академия Google] Радиология. 1987; 165:233. [PubMed] [Google Scholar]
Радиология. 1987; 165:233. [PubMed] [Google Scholar] Клин Радиол. 2001; 56:111. [PubMed] [Google Scholar]
Клин Радиол. 2001; 56:111. [PubMed] [Google Scholar]
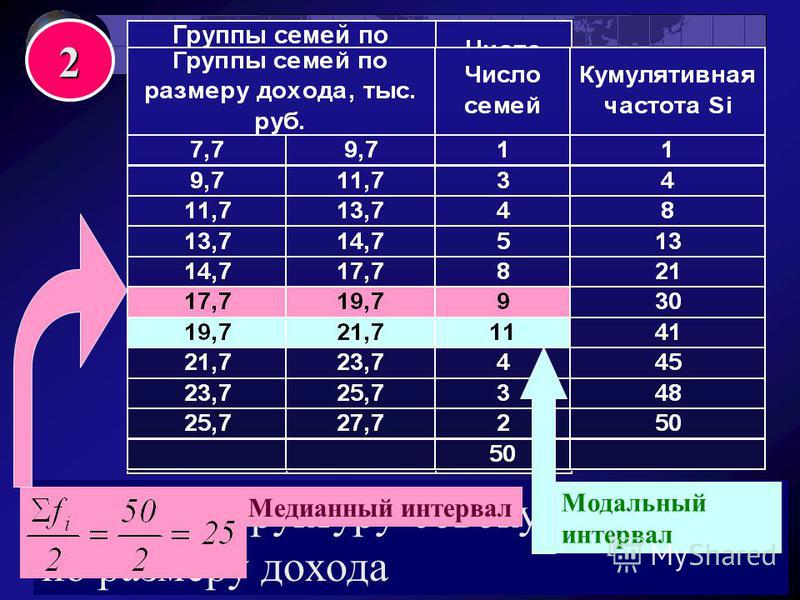

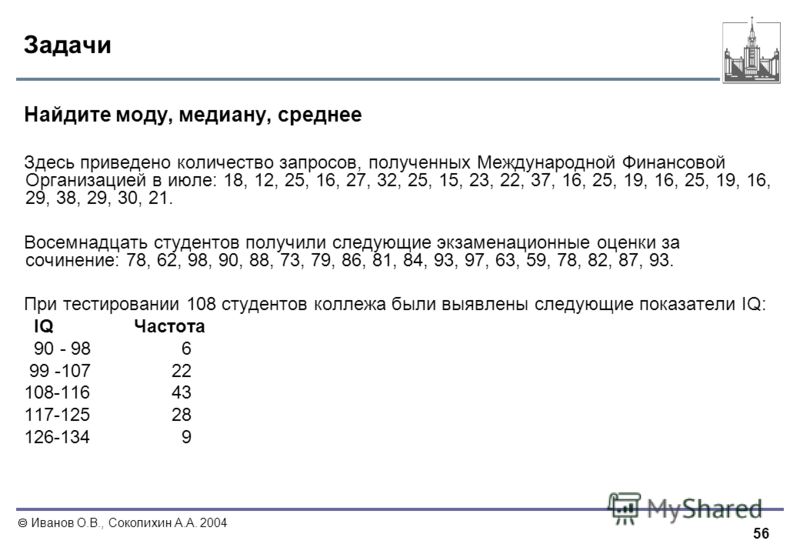
 И ориентируясь по накопленным частотам, легко
прийти к выводу, что эти варианты содержатся в интервале .
И ориентируясь по накопленным частотам, легко
прийти к выводу, что эти варианты содержатся в интервале .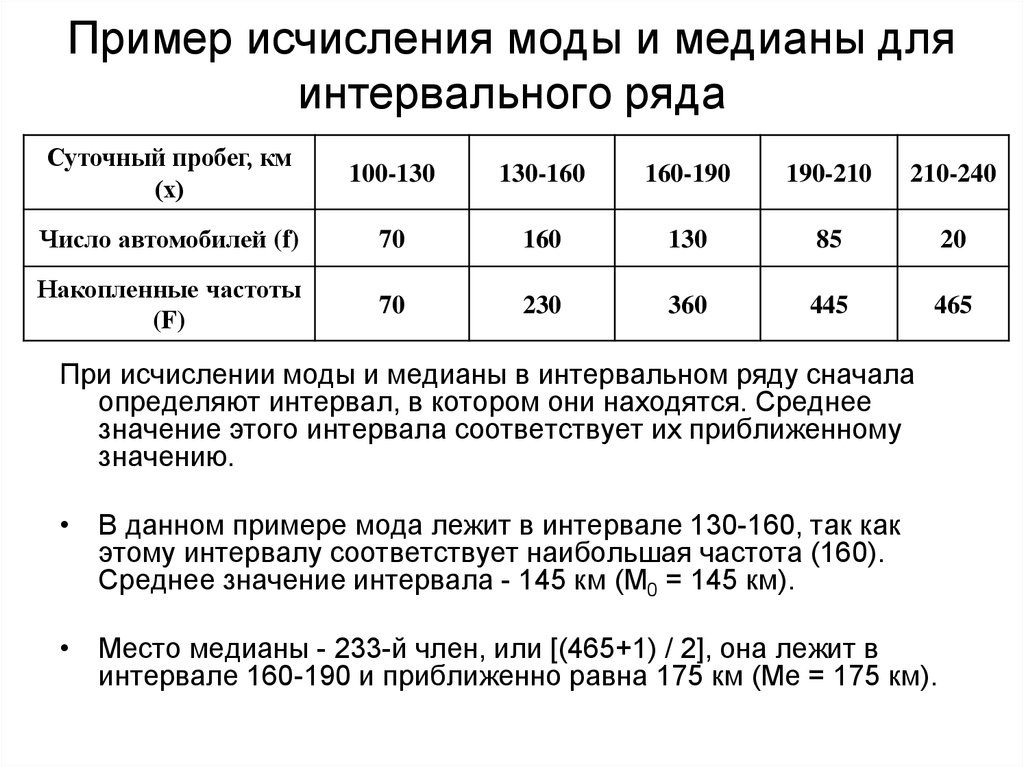 ед.
ед.

 Это говорит о неоднородности совокупности, возможно, представляющей собой сумму нескольких совокупностей с разными модами.
Это говорит о неоднородности совокупности, возможно, представляющей собой сумму нескольких совокупностей с разными модами.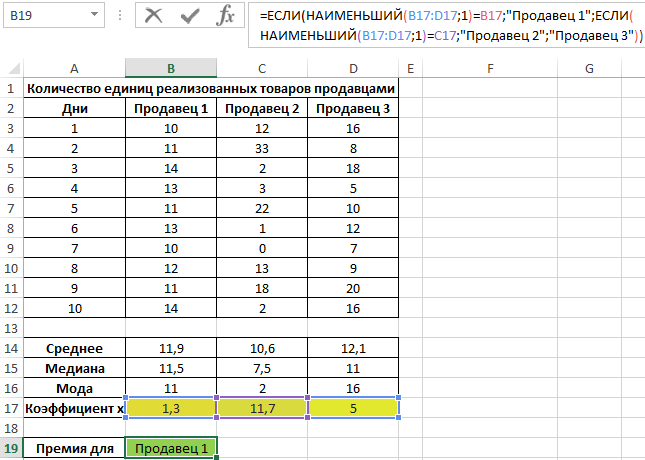
 5
5 Такова, например, медиана — величина варьирующего признака, делящая совокупность на две равные части по числу единиц совокупности.
Такова, например, медиана — величина варьирующего признака, делящая совокупность на две равные части по числу единиц совокупности.


 Вы нашли середину!
Вы нашли середину! Затем мы складываем эти два числа вместе.
Затем мы складываем эти два числа вместе.

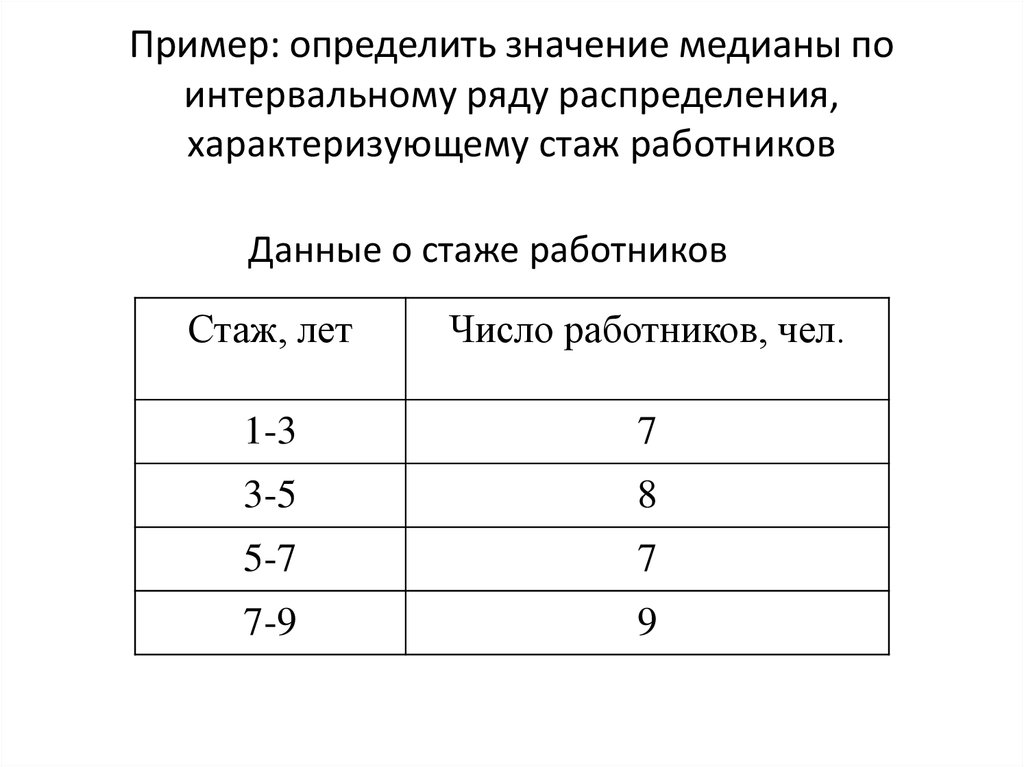

 Он убирает действительно высокие и низкие цифры, чтобы вы могли лучше понять, что делает большинство людей в этой компании.
Он убирает действительно высокие и низкие цифры, чтобы вы могли лучше понять, что делает большинство людей в этой компании.
 Эти значения используются для определения различных параметров данного набора данных. Мера центральной тенденции (среднее значение, медиана и мода) дает полезную информацию об изучаемых данных, они используются для изучения любого типа данных, таких как средняя заработная плата сотрудников в организации, средний возраст любого класса, количество людей. кто играет в крикет в спортивном клубе и т. д. Три показателя центральной тенденции:
Эти значения используются для определения различных параметров данного набора данных. Мера центральной тенденции (среднее значение, медиана и мода) дает полезную информацию об изучаемых данных, они используются для изучения любого типа данных, таких как средняя заработная плата сотрудников в организации, средний возраст любого класса, количество людей. кто играет в крикет в спортивном клубе и т. д. Три показателя центральной тенденции: Сортировка данных может производиться как по возрастанию, так и по убыванию. Медиана делит данные на две равные половины. Формула для медианы:
Сортировка данных может производиться как по возрастанию, так и по убыванию. Медиана делит данные на две равные половины. Формула для медианы: