Сколько формул в математике? – Обзоры Вики
Список. Формулы с 6 по 12 класс.
…
Список математических формул (для всех понятий)
| 2cosacosb Формула | 30-60-90 Формулы |
|---|---|
| Арктан Формула | Формула площади четырехугольника |
| Формулы площади | Формула площади круга |
| Площадь формулы Пентагона | Формула площади сектора круга |
| Площадь квадратной формулы | Площадь формулы трапеции |
Отсюда, Почему формулы используются в математике? Мы узнали, что математические формулы уравнения, которые показывают нам, как что-то решить. Мы используем их, чтобы помочь нам решить проблемы проще и быстрее. … Получив нашу формулу, мы сопоставляем буквы в формуле со значениями из задачи и подставляем эти значения.
Какова основная формула? 1. Формы. В Excel формула представляет собой выражение, которое работает со значениями в диапазоне клетки или ячейка. Например, =A1+A2+A3, который находит сумму диапазона значений от ячейки A1 до ячейки A3.
Например, =A1+A2+A3, который находит сумму диапазона значений от ячейки A1 до ячейки A3.
Дополнительно Какова лучшая математическая формула? 11 самых красивых математических уравнений
- Теорема Пифагора. …
- 1 = 0.999999999…. …
- Специальная теория относительности. …
- Уравнение Эйлера. …
- Уравнения Эйлера-Лагранжа и теорема Нётер. …
- Уравнение Каллана-Симанзика. …
- Уравнение минимальной поверхности. …
- Линия Эйлера. (Изображение предоставлено Патриком Ионом/Mathematical Reviews/AMS)
Что такое расчетная формула? Формулы исчисления в основном описывают скорость изменения функции для данного входного значения с использованием производная функции/формулы дифференцирования. Процесс нахождения производной любой заданной функции известен как дифференцирование.
Что такое пример формулы?
Формула — это определяемая пользователем инструкция для выполнения вычислений. Это выражение, которое может включать адреса ячеек, числа, арифметические операторы и круглые скобки. Он начинается с символа равенства (=), за которым следуют ссылки на ячейки и операторы. Например: =A2+B2*5-SUM(E3:E5)
Он начинается с символа равенства (=), за которым следуют ссылки на ячейки и операторы. Например: =A2+B2*5-SUM(E3:E5)
Что является примером формулы? Формула — это выражение, сообщающее компьютеру, какую математическую операцию следует выполнить над определенным значением. На картинке ниже пример Microsoft Формула Excel = СУММ (1 австралийский доллар: 3 австралийских доллара), который складывает сумму ячеек A1, A2 и A3. … В этой формуле СУММ является функцией формулы.
Какова формула 2ab? в2 — б2 =(аб)(а+б) (а+б)2 =a2 + 2аб + б.
Как вы делаете математические формулы?
Кто изобрел пи?
Пи, в математике, отношение длины окружности к ее диаметру. Символ π был изобретен Британский математик Уильям Джонс в 1706 году для представления отношения, а позже популяризировал швейцарский математик Леонард Эйлер.
Символ π был изобретен Британский математик Уильям Джонс в 1706 году для представления отношения, а позже популяризировал швейцарский математик Леонард Эйлер.
Что означает Е в математике? В статистике этот символ математическая константа примерно равна 2.71828183. Призма переключается на экспоненциальное представление, когда значения очень большие или очень маленькие. Например: 2.3e-5 означает 2.3 умножить на десять в степени минус пять, или 0.000023.
Является ли пи действительным числом?
Независимо от размера круга это отношение всегда будет равно пи. В десятичной форме значение пи составляет примерно 3.14. Но пи — иррациональное число, что означает, что его десятичная форма не заканчивается (например, 1/4 = 0.25) и не становится повторяющейся (например, 1/6 = 0.166666…). (Всего с 18 десятичными знаками число пи равно 3.141592653589793238.)
Для чего используется алгебра?
Где используется алгебра? Алгебра широко используется в формулы, когда мы не знаем хотя бы одно из чисел, или когда одно из чисел может измениться.
Что такое Dy в dy dx? d/dx — это операция, которая означает «взять производную по x», тогда как dy/dx указывает, что «производная у была взята по х».
Является ли алгебра исчислением? Является ли алгебра тем же, что и исчисление? Нет. Хотя они тесно связаны, они оба принадлежат к разным разделам математики. В то время как исчисление имеет дело с операциями над функциями и их производными, алгебра включает операции с числами и переменными.
Какая основная формула?
Формула выражение, которое вычисляет значения в ячейке или в диапазоне ячеек. Например, = A2 + A2 + A3 + A4 — это формула, которая складывает значения в ячейках с A2 по A4. Функция — это предопределенная формула, уже доступная в Excel.
Что такое математический пример? Пример математического выражения с переменной: 2х + 3. Все переменные должны иметь коэффициент, число, которое умножается на переменную. В выражении 2х + 3 коэффициент при х равен числу 2, а это означает 2 умноженное на х плюс 3.
Являются ли уравнения алгеброй?
Давай учить!
В алгебре уравнение можно определить как математическое выражение, состоящее из символа равенства между двумя алгебраическими выражениями, имеющими одинаковое значение. Самые простые и распространенные алгебраические уравнения в математике состоят из одной или нескольких переменных.
Кто изобрел алгебру?
Мухаммед ибн Муса аль-Хорезми был мусульманским математиком и астрономом IX века. Он известен как «отец алгебры», это слово происходит от названия его книги «Китаб аль-Джабр». Его новаторская работа предлагала практические ответы на вопросы распределения земли, правил наследования и распределения заработной платы.
Какова формула 4ab?
Ответ: Формула для 4ab: ( 4ab) =( a+b )²- ( ab )² .
ФОРМУЛА ПИКА — Математика в колледже
ФОРМУЛА ПИКА Площадь искомой фигуры можно найти по формуле: М – количество узлов на границе треугольника (на сторонах и вершинах) N – количество узлов внутри треугольника *Под «узлами» имеется ввиду пересечение линий. Найдём площадь треугольника: Отметим узлы: 1 клетка = 1 см M = 15 (обозначены красным) N = 34 (обозначены синим)
Ещё пример. Найдём площадь параллелограмма: Отметим узлы: M = 18 (обозначены красным) N = 20 (обозначены синим)
Найдём площадь трапеции: Отметим узлы: M = 24 (обозначены красным) N = 25 (обозначены синим)
Найдём площадь многоугольника: Отметим узлы: M = 14 (обозначены красным) N = 43 (обозначены синим) Понятно, что находить площадь трапеции, параллелограмма, треугольника проще и быстрее по соответствующим формулам площадей этих фигур. А вот когда дан многоугольник, у которого пять и более углов эта формула работает хорошо. Теперь взгляните на следующие фигуры: Это типовые фигуры, в заданиях стоит вопрос о нахождении их площади. Такие или подобные им будут на ЕГЭ. При помощи формулы Пика такие задачи решаются за минуту. Например, найдём площадь фигуры: Отметим узлы: M = 11 (обозначены красным) N = 5 (обозначены синим) Ответ: 9,5
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см. Ответ дайте в квадратных сантиметрах. Посмотреть решение
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см. Ответ дайте в квадратных сантиметрах. Посмотреть решение
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см. Посмотреть решение
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см. Ответ дайте в квадратных сантиметрах. Посмотреть решение
Конечно, можно и эти «микрофигурки» дробить на более простые фигуры (треугольники, трапеции). Способ решения выбирать вам. Рассмотрим подход оговоренный в статье «Площадь четырёхугольника. Универсальный способ». Найдём площадь фигуры: Опишем около неё прямоугольник: Из площади прямоугольника (в данном случае это квадрат) вычтем площади полученных простых фигур:
Ответ: 4,5 В будущем будем рассматривать задания на нахождение площади, связанные с окружностями построенными на листе в клетку, не пропустите!
|
Математическая формула: примеры, производная и доказательство
Допустим, вы хотите установить на пол вашей спальни деревянную поверхность, имеющую форму прямоугольника. Длина и ширина вашего этажа измеряются \(5\) метров на \(4\) метров. Учитывая эти размеры, есть ли способ определить, сколько деревянных панелей вам понадобится для покрытия пола?
Длина и ширина вашего этажа измеряются \(5\) метров на \(4\) метров. Учитывая эти размеры, есть ли способ определить, сколько деревянных панелей вам понадобится для покрытия пола?
Итак, поскольку у вас есть длина и ширина пола, вы можете просто использовать формулу площади прямоугольника, чтобы определить необходимое количество материала. Площадь прямоугольника определяется произведением его длины на ширину. В этом случае вам понадобится в общей сложности \(20\) квадратных метров деревянных панелей, чтобы покрыть пол. Это пример математической формулы.
В этой статье вы познакомитесь с математическими формулами и способами их выражения, чтобы использовать их для решения числовых задач.
Определение формулы в математике
Формула в математике — это полезный инструмент, используемый для определения решений с помощью заданного выражения. Зная общий рецепт, необходимый для решения конкретной проблемы, вы сможете воспроизвести тот же стиль работы, если столкнетесь с похожей ситуацией. Этот процесс осуществляется с помощью различных математических операций.
Этот процесс осуществляется с помощью различных математических операций.
Математическая формула — это правило в форме утверждения, выраженное в виде символов, помогающее легко решать задачи.
Формулы состоят из различных величин, соединенных знаком равенства. Они содержат переменные и иногда константы. Это означает, что если у вас есть значения определенных переменных в формуле, вы можете найти значение остальных переменных.
Пример математической формулы
Чтобы лучше понять, что такое математическая формула, давайте продемонстрируем ее на примере.
Допустим, прямоугольник — это участок земли, принадлежащий мистеру Паркеру. Он хочет превратить его в парк, куда дети со всего района могут приходить играть. Он хочет знать точные размеры этой земли, в частности, сумму всех длин и ширин. Это измерение известно как периметр.
Одним из способов измерения периметра прямоугольника выше является ручное измерение всего участка земли. Однако это можно сделать математически, если известны некоторые стороны. Если вы знаете, что длина равна \(100\) метрам, а ширина — \(55\) метрам, вы можете просто использовать математическую формулу, которая даст вам общий рецепт для вычисления периметра прямоугольника.
Однако это можно сделать математически, если известны некоторые стороны. Если вы знаете, что длина равна \(100\) метрам, а ширина — \(55\) метрам, вы можете просто использовать математическую формулу, которая даст вам общий рецепт для вычисления периметра прямоугольника.
Внимательно изучив свойства прямоугольника, вы заметите, что две противоположные стороны равны. Это означает, что если длина ниже составляет \(100\) метров, длина выше также будет \(100\) метров. По этому можно написать формулу нахождения его периметра. Пусть буква \(l\) представляет длину, а \(w\) представляет ширину:
\[ \text{Периметр прямоугольника} = l + l + w+w.\]
Далее это может быть упрощено добавлением подобных терминов
\[ \text{Периметр прямоугольника} = 2l + 2w.\]
Вы можете вынести \(2\), чтобы получить
\[ \text{Периметр прямоугольника} = 2(l + w).\]
Имея это как формулу для нахождения периметра прямоугольника, вы может заменить его числами, чтобы посмотреть, поможет ли это мистеру Паркеру эффективно решить его проблему.
\[ \begin{align} \text{Периметр прямоугольника } &= 2(l + w) \\ &= 2(100 + 55) \\ &= 2(155) \\ &= 310 \, м . \end{align}\]
Используя формулу, мистер Паркер может просто узнать периметр своего земельного участка, не измеряя его вручную.
В нескольких областях математики применяются разные формулы. Чтобы знать, где и как можно применять формулы, вы должны понимать проблему, с которой имеете дело, и знать, какие переменные являются значимыми.
Как написать математическую формулу
Как упоминалось ранее, формулы представляют собой уравнения или тождества. Они состоят из переменных и иногда констант. Фундаментальная задача написания формул состоит в том, чтобы знать, что представлять в качестве релевантной переменной.
Например, если вы хотите написать формулу для периметра прямоугольника, вы должны знать, что длина тесно связана с периметром. Вы можете взять пример того, как пишутся формулы.
Предположим, вы знаете, что \(3\) кошки едят столько же еды, сколько одна большая собака. Напишите формулу, чтобы определить объем пищи, который вам понадобится, чтобы накормить \(27\) кошек и \(10\) крупных собак в пересчете на количество имеющихся у вас собак.
Напишите формулу, чтобы определить объем пищи, который вам понадобится, чтобы накормить \(27\) кошек и \(10\) крупных собак в пересчете на количество имеющихся у вас собак.
Решение
Хорошо бы сначала решить, что вы пытаетесь сделать! Вы ищете, чтобы найти формулу для объема, учитывая количество кошек и количество собак. Итак, давайте дадим этим вещам некоторые переменные.
- \(c\) — количество кошек
- \(d\) — количество собак
- \(V\) — объем пищи
Вас просят найти формулу объема корма для \(27\) кошек и \(10\) собак. Что ты знаешь? Вы знаете, что \(3\) кошки едят столько же, сколько одна большая собака. Итак,
\[3c = 1d.\]
Вам нужна формула для \(27\) кошек и \(10\) собак, или, другими словами, формула для
\[ V = 27c + 10d,\ ]
но вы хотите это с точки зрения собак, а не собак и кошек! Что делать? Что ж, вы не воспользовались тем, что \(3c = d\). Вы можете сделать небольшой факторинг, чтобы получить
\[ \begin{align} V &=27c + 10d \\ &= 9(3c) + 10d, \end{align}\]
и затем подставить в \(3c = d\), чтобы получить
\[ \begin{align} V &=9(3c) + 10d \\ &= 9d+ 10d \\ &= 19d, \end{align}\]
, что является формулой количества пищи, которое вам нужно кормить \(27\) кошек и \(10\) крупных собак по количеству имеющихся у вас собак.
Наиболее важные математические формулы
Термин «самый важный» немного вводит в заблуждение, так как это действительно зависит от того, кого вы спрашиваете! Однако в этом разделе вы обсудите некоторые общие формулы, которые используются в математике.
Области фигур
Площадь фигуры определяется двумерной областью, ограниченной данной формой.
Concept | Formula |
Area of rectangle | Area = length \(\times\) width |
Area of parallelogram | Area = основание \(\times\) высота |
Площадь треугольника | Площадь = \( \dfrac{1}{2} \times\) основание \(\times\) высота |
Площадь круга | Площадь = \(\pi\times \ ) radius\(\times\) radius |
Объемы твердых тел
Объем твердого тела – это объем трехмерного пространства, занимаемого объектом, контейнером или замкнутой поверхностью.
Концепт | Формула |
Прямоугольник | Объем = длина \(\times\) основание\(\times\) высота |
Треугольная призма | 10102 Объем ={2 \fracd 90}{0} раз\) длина \(\раз\) основание\(\раз\) высота|
Цилиндр | Объем = \(\пи\раз\) радиус\(\раз\) радиус\(\ раз\) height |
Составная мера
Составные меры — это выражения, содержащие более одной величины.
Concept | Formula |
Speed | \( \text{Speed } = \dfrac{ \text{ Distance}}{\text{time}}\) |
Density | \( \text{Density } = \dfrac{ \text{ Mass}}{\text{ Volume}}\) |
Pressure | \( \ text{Давление} = \dfrac{ \text{ Сила}}{\text{Площадь}}\) |
Алгебра перезаписи формул
Полезно знать, как переписывать формулы, так как вам могут дать площадь прямоугольника и попросить найти его длину. Когда вы переписываете формулу, цель состоит в том, чтобы создать уравнение, эквивалентное формуле, но с отсутствующей переменной.
Когда вы переписываете формулу, цель состоит в том, чтобы создать уравнение, эквивалентное формуле, но с отсутствующей переменной.
Для этого используется основное правило — золотое правило манипулирования уравнениями. Он говорит, что делайте с одной стороной уравнения то, что вы делаете с другой. Это означает, что если манипуляция требует, чтобы вы добавили значения к одной части уравнения, сделайте то же самое добавление к левой части уравнения. Вот пример.
Если бы были даны значения массы и плотности, то какой была бы формула для объема?
Раствор
Формула, в которой присутствуют все указанные величины, является формулой плотности.
\[\text{Плотность } = \dfrac{ \text{ Масса}}{\text{ Объем}}\]
Чтобы найти формулу для объема, вам нужно сделать объем предметом уравнения. Это будет означать, что любая форма манипуляции на любой стороне уравнения потребует ее воспроизведения на другой стороне. Для этого вам сначала нужно будет умножить обе части уравнения на объем,
\[\text{Плотность }\times \text{ Объем } = \dfrac{ \text{ Масса}}{\text{ Объем}} \times \text{ Объем}\]
и затем отмените, чтобы получить
\[\text{Плотность }\times \text{ Объем } = \text{ Масса}. \]
\]
Теперь вы можете разделить обе части на Плотность
\[\dfrac{\text{Плотность }\times \text { Volume }}{\text{Density} } = \dfrac{\text{ Mass}}{\text{Density} }\]
и снова отмените, чтобы получить
\[\text{ Volume } = \dfrac{ \text{ Масса}}{\text{Плотность} }.\] 92\), а его ширина равна \(6\, см\).
Решение
Прежде всего, вы можете написать формулу для нахождения площади прямоугольника вниз:
\[A = lw.\]
Чтобы найти длину, вам придется сделать ее предметом уравнения. Это означает, что вам предстоит выполнить несколько манипуляций. То, что вы делаете на одной стороне, потребует того, чтобы это было сделано на другой. Чтобы изолировать длину в одной части уравнения, вам придется разделить обе части уравнения на ширину
\[ \frac{A}{w} = \frac{lw}{w}\]
и затем отмените, чтобы получить
\[ l = \frac{A}{w}.\]
Вы теперь есть формула для нахождения длины в этом сценарии. Вы можете найти решение проблемы, подставив в формулу:
\[ \begin{align} l &= \frac{A}{w}\\ &= \frac{42}{6} \ \ &= 7. \end{align}\]
\end{align}\]
Не забудьте единицы! Длина \(7\, см\).
Замена в формулах
Замена в формулах — это процесс замены переменной ее значением в формуле. В этом разделе использование формул становится чрезвычайно очевидным. При правильных значениях переменных можно найти неизвестные переменные.
Весь процесс подстановки в формулы заключается в замене букв (переменных) их заданными значениями. Вы возьмете множество примеров, чтобы увидеть, как можно подходить к различным типам возможных ситуаций.
Найдите \(z\), когда \(x=7\) в заданной формуле
\[z = x+2.\]
Решение
Все, что вам нужно сделать, это заменить \( x\) в формуле с \(7\), так как задача говорит, что \(x\) совпадает с \(7\).
\[ \begin{align} z &= x+2 \\ &= 7 + 2 \\ &= 9.\end{align}\]
Вот вам еще один пример!
Найти \(l\), когда \(m=5\) в данной формуле
\[ l = 7m.\]
Решение
число \(5\), указанное в задаче, тогда вы можете найти \(l\). Итак,
Итак,
\[ l = 7m.\]
Связь между \(7\) и \(m\) здесь есть умножение. В целом эту формулу можно записать как
\[l = 7 \cdot m,\]
или
\[l = 7(m).\]
Подставив \(5\) вместо \(m\), вы получите
\[ \begin{align} l &= 7(5) \\ &= 35.\end{align}\]
Математическая формула — ключевые выводы
- Математическая формула — это правило в форме утверждения, выраженное в виде символов, помогающее легко решать задачи.
- Формулы состоят из различных величин, соединенных знаком равенства.
- Фундаментальное правило, используемое для переписывания формул, — это золотое правило манипулирования уравнениями, которое гласит: делайте с одной стороной уравнения то, что делаете с другой.
- Подстановка в формулы — это процесс замены переменной ее значением в формуле.
терминология — В чем разница между уравнением и формулой?
спросил
Изменено 20 дней назад
Просмотрено 136 тысяч раз
$\begingroup$
Иногда уравнение и формула используются взаимозаменяемо, но мне интересно, есть ли разница.
Например, предположим, что мы можем рассчитать топливную экономичность автомобиля как:
миль на галлон = пройденное расстояние в милях / расход топлива в галлонах
Это уравнение или формула?
- терминология
- определение
$\endgroup$
2
$\begingroup$
Уравнение — это любое выражение со знаком равенства, поэтому ваш пример по определению является уравнением. Уравнения часто появляются в математике, потому что математики любят использовать знаки равенства.
Формула представляет собой набор инструкций для получения желаемого результата. К нематематическим примерам относятся такие вещи, как химические формулы (два Н и один О составляют Н3О) или формула кока-колы (которая представляет собой просто список ингредиентов). Вы можете возразить, что эти примеры не являются уравнениями в том смысле, что водород и кислород не «равны» воде, но вы можете использовать их для получения воды.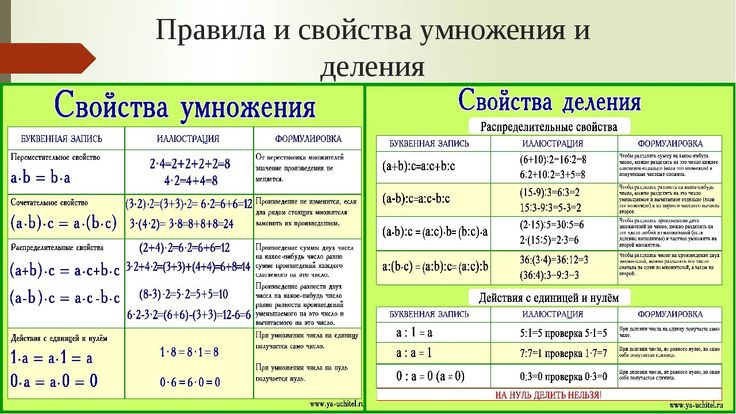 92$ можно рассматривать как формулу для нахождения длины стороны прямоугольного треугольника, но оказывается, что такая длина всегда равна комбинации двух других длин, так что мы можем выразить формула как уравнение. Основная идея заключается в том, что уравнение отражает не только ингредиенты формулы, но и взаимосвязь между различными ингредиентами.
92$ можно рассматривать как формулу для нахождения длины стороны прямоугольного треугольника, но оказывается, что такая длина всегда равна комбинации двух других длин, так что мы можем выразить формула как уравнение. Основная идея заключается в том, что уравнение отражает не только ингредиенты формулы, но и взаимосвязь между различными ингредиентами.
В вашем случае «миль на галлон = расстояние/галлоны» лучше всего понимать как «формулу в виде уравнения», что означает, что в данном случае эти два слова взаимозаменяемы.
$\endgroup$
3
$\begingroup$
Уравнение нужно решить, то есть есть неизвестные. Формула предназначена для вычисления, то есть вы заменяете в ней все переменные значениями и получаете значение формулы.
Ваш пример — формула для миль на галлон . Но это может стать уравнением, если дано миль на галлон и одно из других значений, а оставшееся значение ищется.
$\endgroup$
9
$\begingroup$
Я бы сказал, что уравнение — это что угодно, в котором есть знак равенства; формула — это уравнение вида $A={\rm\stuff}$, где $A$ не входит в число веществ в правой части.
$\endgroup$
1
$\begingroup$
Пожалуйста, проголосуйте против меня, если хотите, но я бы сказал, что эти слова на самом деле являются синонимами друг друга. Оба они выражают, что между некоторыми математическими выражениями существует некоторая основная связь.
$\endgroup$
6
$\begingroup$
Формула — это уравнение, показывающее взаимосвязь между двумя или более величинами. Это будут правила или инструкции, которые используются для демонстрации взаимосвязи между двумя или более величинами.
Это будут правила или инструкции, которые используются для демонстрации взаимосвязи между двумя или более величинами.
Уравнение — это задача, отображаемая с помощью цифр или символов, где где-то присутствует знак равенства (=); обычно ближе к концу уравнения. Если только это не отношение или деление.
$\endgroup$
$\begingroup$
Вы решаете уравнение, пока вычисляете формулу.
Между прочим, уравнение, которое содержит любые значения переменных, является тождеством.
$\endgroup$
$\begingroup$ 92$ и $f=ma$ являются «уравнениями», обычно не называемыми «формулами». Вы бы сказали не «формула силы», а «уравнение силы». Они могут иметь бесконечное количество решений. так что я бы сказал, что термины также взаимозаменяемы.
http://en.wikipedia.org/wiki/Force
$\endgroup$
$\begingroup$
Простой ответ исходит от https://www. bbc.co.uk/bitesize/guides/zwbq6yc/revision/1
bbc.co.uk/bitesize/guides/zwbq6yc/revision/1
Для вашего удобства краткое объяснение по ссылке: 9{\ circ} F $)
Уравнение :
- обычно имеет только одну переменную, хотя может встречаться более одного раза
- будет правильным только для определенных значений (например, $2x = 10$ верно только для $x = 5$)
- не всегда верно.
Хотя я предлагаю вам посмотреть на 92 $
$\endgroup$
$\begingroup$
В формуле все переменные могут быть выбраны произвольно. Уравнение допускает только частные значения непостоянной переменной/s.
$\endgroup$
$\begingroup$
TL;DR Я бы сказал, что это действительно зависит от контекста.
Что я помню в старшей/средней школе:
Нам давали задачи типа
Зная длину и площадь прямоугольника, найдите его ширину.
(Не совсем прямоугольник. Это, конечно, больше подходит для начальной школы. Может быть прямоугольной призмой или чем-то еще.)
‘Формула’ $A =wl$.
«Уравнение» — это то, что вы получите, если подставите заданные значения для $A$ и $l$. Итак, если у вас есть $A=10$ и $l=7$, тогда уравнение равно $10=7w$.
В то время я думал, что это очень придирчиво/субъективно/традиционно/контекстуально. Теперь я все еще делаю это, но у меня есть 10 000+ репутации и степени бакалавра и магистра, чтобы жаловаться на это.
По словам моих учителей средней школы, то, что вы предоставили, является формулой, но это в контексте заполнения пробелов уравнения и формулы в школе.
Заключение : Я бы сказал, что это действительно зависит от контекста. Если определить уравнение как утверждение со знаком равенства, то каждая формула со знаком равенства является уравнением. .. Кстати, в Википедии вроде бы нет неравенств, которые были бы формулами.
.. Кстати, в Википедии вроде бы нет неравенств, которые были бы формулами.
$\endgroup$
$\begingroup$
Мои определения будут сосредоточены на математике.
В контексте математики уравнение представляет собой математическое выражение, состоящее из чисел, переменных, операций и знака равенства, которому удовлетворяют некоторые конкретные значения желаемой переменной при заданных значениях других переменных в нем.
В контексте математики формула представляет собой уравнение, в котором желаемая переменная явно выражена в терминах (т. е. явная функция) другой переменной (переменных).
В вашем случае топливная экономичность автомобиля на галлон явно выражена с точки зрения пройденного расстояния и израсходованного топлива, т. е. соотношения расстояния и израсходованного топлива. Поэтому лучше всего использовать формулу .
ПРИМЕЧАНИЕ: В контексте математики каждая формула является уравнением, но уравнение не обязательно является формулой.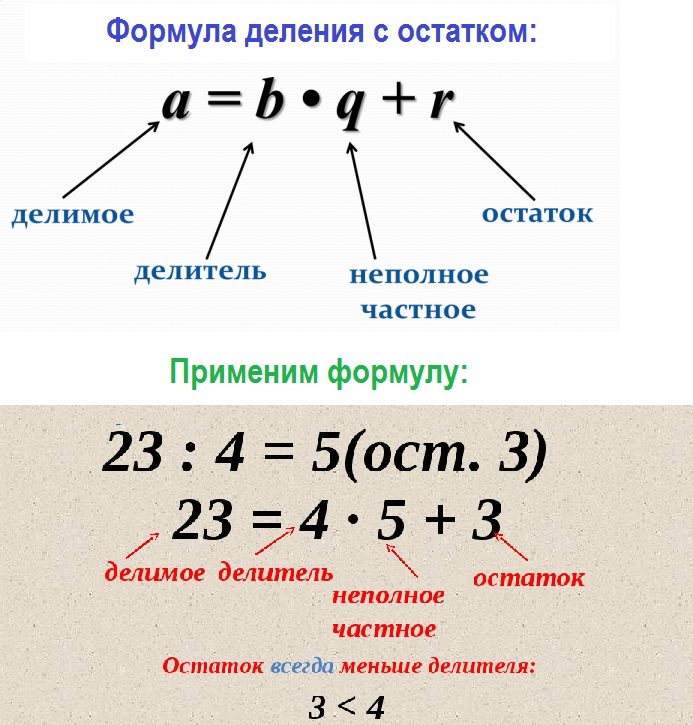
$\endgroup$
$\begingroup$
Один из способов ответить на этот вопрос был разработан на первом и втором курсах алгебры средней школы США.
В первом курсе в глоссарии формально изложены следующие определения.
уравнение : Оператор, образованный путем помещения знака равенства между двумя числовыми или переменными выражениями.
Например, $11-7=4$, $5x-1=9$ и $y+2=2+y$ являются уравнениями, поскольку все они удовлетворяют данному определению.
Следующее определение формулы также официально указано в глоссарии:
формула : Уравнение, устанавливающее правило отношения.
Вот две полезные формулы: $A=lw$, формула площади прямоугольника; $P=2l+2w$, формула периметра прямоугольника.
В то время как в начале второго курса следующее предложение резюмирует, что связь существует между двумя или более переменными:
Формула — это уравнение, которое устанавливает связь между двумя или более переменными.

 Но знайте, что можно это делать и таким образом.
Но знайте, что можно это делать и таким образом.  Ответ дайте в квадратных сантиметрах.
Ответ дайте в квадратных сантиметрах.
 Не торопите ребенка и не подсказывайте ему, но обязательно проверьте его ответы на правильность.
Не торопите ребенка и не подсказывайте ему, но обязательно проверьте его ответы на правильность. С помощью карточек можно составлять любые примеры на прибавление, отнимание, умножение, деление, а также выполнять сравнение чисел (используя знаки «больше», «меньше»).
С помощью карточек можно составлять любые примеры на прибавление, отнимание, умножение, деление, а также выполнять сравнение чисел (используя знаки «больше», «меньше»).  А. Как нет на свете без ножек столов, Как нет на свете без рожек козлов, Котов без усов и без панцирей раков, Так нет в арифметике действий без знаков!
А. Как нет на свете без ножек столов, Как нет на свете без рожек козлов, Котов без усов и без панцирей раков, Так нет в арифметике действий без знаков! Символы для арифметических операций сложения (плюс “+’’) и вычитания (минус “-‘’) встречаются настолько часто, что мы почти никогда не задумываемся о том, что они существовали не всегда. В самом деле, кто-то должен был изобрести эти символы (или по крайней мере другие, которые впоследствии превратилась в те, которые мы используем сегодня). Наверняка также прошло некоторое время, прежде чем данные символы стали общепринятыми. Существует мнение, что знаки «+» и «–» возникли в торговой практике. Виноторговец чёрточками отмечал, сколько мер вина он продал из бочки. Приливая в бочку новые запасы, он перечёркивал столько расходных чёрточек, сколько мер он восстановил. Так, якобы, произошли знаки сложения и вычитания в ХV веке. Относительно происхождения знака «+» существует и другое объяснение. Вместо «а + b» писали «а и b», по латыни «а et b». Так как слово «et» («и») приходилось писать очень часто, то его стали сокращать: писали сначала одну букву t, которая, в конце концов, превратилась в знак «+»
Символы для арифметических операций сложения (плюс “+’’) и вычитания (минус “-‘’) встречаются настолько часто, что мы почти никогда не задумываемся о том, что они существовали не всегда. В самом деле, кто-то должен был изобрести эти символы (или по крайней мере другие, которые впоследствии превратилась в те, которые мы используем сегодня). Наверняка также прошло некоторое время, прежде чем данные символы стали общепринятыми. Существует мнение, что знаки «+» и «–» возникли в торговой практике. Виноторговец чёрточками отмечал, сколько мер вина он продал из бочки. Приливая в бочку новые запасы, он перечёркивал столько расходных чёрточек, сколько мер он восстановил. Так, якобы, произошли знаки сложения и вычитания в ХV веке. Относительно происхождения знака «+» существует и другое объяснение. Вместо «а + b» писали «а и b», по латыни «а et b». Так как слово «et» («и») приходилось писать очень часто, то его стали сокращать: писали сначала одну букву t, которая, в конце концов, превратилась в знак «+» , которая была найдена в библиотеке Дрездена. В латинской рукописи того же времени (также из библиотеки Дрездена), есть оба символа: + и — . Известно, что Йоганн Видман рассматривал и комментировал обе эти рукописи. В 1489 году он издал в Лейпциге первую печатную книгу (Mercantile Arithmetic — “Коммерческая арифметика’’), в которой присутствовали оба знака + и — (см. рисунок). Тот факт, что Видман использовал эти символы как если бы они были общеизвестны, указывает на возможность их происхождения из торговли. Анонимная рукопись, написанная, видимо, примерно в то же время, также содержит эти же символы, и это обеспечило выход двух дополнительных книг, изданных в 1518 и 1525 годах.
, которая была найдена в библиотеке Дрездена. В латинской рукописи того же времени (также из библиотеки Дрездена), есть оба символа: + и — . Известно, что Йоганн Видман рассматривал и комментировал обе эти рукописи. В 1489 году он издал в Лейпциге первую печатную книгу (Mercantile Arithmetic — “Коммерческая арифметика’’), в которой присутствовали оба знака + и — (см. рисунок). Тот факт, что Видман использовал эти символы как если бы они были общеизвестны, указывает на возможность их происхождения из торговли. Анонимная рукопись, написанная, видимо, примерно в то же время, также содержит эти же символы, и это обеспечило выход двух дополнительных книг, изданных в 1518 и 1525 годах. “The Whetstone of Witte” математика из Оксфорда Роберта Рекорда, который также ввел знак равенства, который был гораздо длиннее, чем нынешний знак. В описании знаков плюс и минус Рекорд писал: “Часто используются другие два знака, первый из которых пишется «+» и обозначает больше, а второй «-» и обозначает меньше’’.
“The Whetstone of Witte” математика из Оксфорда Роберта Рекорда, который также ввел знак равенства, который был гораздо длиннее, чем нынешний знак. В описании знаков плюс и минус Рекорд писал: “Часто используются другие два знака, первый из которых пишется «+» и обозначает больше, а второй «-» и обозначает меньше’’.
 Название «множитель» упоминается в работах XI века. На протяжении тысячелетий действие деление не обозначали знаками. Арабы ввели для обозначения деления черту «/». Её перенял от арабов в XIII веке итальянский математик Фибоначчи. Он же первым употребил термин «частное». Знак двоеточия «:» для обозначения деления вошёл в употребление в конце XVII века. В России названия «делимое», «делитель», «частное» впервые ввёл Л.Ф. Магницкий в начале XVIII века. Знак умножения ввёл в 1631 году Уильям Отред (Англия) в виде косого крестика. До него использовали букву M. Позднее Лейбниц заменил крестик на точку (конец XVII века), чтобы не путать его с буквой x; до него такая символика встречалась у Региомонтана (XV век) и английского учёного Томаса Хэрриота (1560-1621).
Название «множитель» упоминается в работах XI века. На протяжении тысячелетий действие деление не обозначали знаками. Арабы ввели для обозначения деления черту «/». Её перенял от арабов в XIII веке итальянский математик Фибоначчи. Он же первым употребил термин «частное». Знак двоеточия «:» для обозначения деления вошёл в употребление в конце XVII века. В России названия «делимое», «делитель», «частное» впервые ввёл Л.Ф. Магницкий в начале XVIII века. Знак умножения ввёл в 1631 году Уильям Отред (Англия) в виде косого крестика. До него использовали букву M. Позднее Лейбниц заменил крестик на точку (конец XVII века), чтобы не путать его с буквой x; до него такая символика встречалась у Региомонтана (XV век) и английского учёного Томаса Хэрриота (1560-1621). В Англии и США распространение получил символ ÷ (обелюс), который предложили Йоханн Ран и Джон Пелл (John Pell) в середине XVII века.
В Англии и США распространение получил символ ÷ (обелюс), который предложили Йоханн Ран и Джон Пелл (John Pell) в середине XVII века. Версий его происхождения тоже несколько, все они интересны и заслуживают внимания.
Версий его происхождения тоже несколько, все они интересны и заслуживают внимания.  По сюжету, у игрока был помощник, верный пес, который помогал искать клады, защищал от разных монстров, отправлялся в разведку и в катакомбы. И конечно же обозначался пес знаком @.
По сюжету, у игрока был помощник, верный пес, который помогал искать клады, защищал от разных монстров, отправлялся в разведку и в катакомбы. И конечно же обозначался пес знаком @. В самом деле, кто-то должен был изобрести эти символы (или по крайней мере другие, которые впоследствии превратилась в те, которые мы используем сегодня). Наверняка также прошло некоторое время, прежде чем данные символы стали общепринятыми. Когда я начал изучать историю этих знаков, я обнаружил, к своему удивлению, что они появились вовсе не в глубокой древности. Многое из того, что нам известно, происходит из всеобъемлющего и впечатляющего исследования 1928–1929 гг., которое до сих пор остается непревзойденным. Это “История математических обозначений’’ швейцарско-американского историка математики Флориана Каджори (1859-1930).
В самом деле, кто-то должен был изобрести эти символы (или по крайней мере другие, которые впоследствии превратилась в те, которые мы используем сегодня). Наверняка также прошло некоторое время, прежде чем данные символы стали общепринятыми. Когда я начал изучать историю этих знаков, я обнаружил, к своему удивлению, что они появились вовсе не в глубокой древности. Многое из того, что нам известно, происходит из всеобъемлющего и впечатляющего исследования 1928–1929 гг., которое до сих пор остается непревзойденным. Это “История математических обозначений’’ швейцарско-американского историка математики Флориана Каджори (1859-1930). В конце пятнадцатого века французский математик Шике (1484 г.) и итальянский Пачоли (1494 г.) использовали “’’ или “’’ (обозначая “плюс’’) для сложения и “’’ или “’’ (обозначая “минус’’) для вычитания.
В конце пятнадцатого века французский математик Шике (1484 г.) и итальянский Пачоли (1494 г.) использовали “’’ или “’’ (обозначая “плюс’’) для сложения и “’’ или “’’ (обозначая “минус’’) для вычитания. , которая была найдена в библиотеке Дрездена. В латинской рукописи того же времени (также из библиотеки Дрездена), есть оба символа: и . Известно, что Йоганн Видман рассматривал и комментировал обе эти рукописи. В 1489 году он издал в Лейпциге первую печатную книгу (Mercantile Arithmetic — “Коммерческая арифметика’’), в которой присутствовали оба знака и (см. рисунок). Тот факт, что Видман использовал эти символы как если бы они были общеизвестны, указывает на возможность их происхождения из торговли. Анонимная рукопись, написанная, видимо, примерно в то же время, также содержит эти же символы, и это обеспечило выход двух дополнительных книг, изданных в 1518 и 1525 годах.
, которая была найдена в библиотеке Дрездена. В латинской рукописи того же времени (также из библиотеки Дрездена), есть оба символа: и . Известно, что Йоганн Видман рассматривал и комментировал обе эти рукописи. В 1489 году он издал в Лейпциге первую печатную книгу (Mercantile Arithmetic — “Коммерческая арифметика’’), в которой присутствовали оба знака и (см. рисунок). Тот факт, что Видман использовал эти символы как если бы они были общеизвестны, указывает на возможность их происхождения из торговли. Анонимная рукопись, написанная, видимо, примерно в то же время, также содержит эти же символы, и это обеспечило выход двух дополнительных книг, изданных в 1518 и 1525 годах. В описании знаков плюс и минус Рекорд писал: “Часто используются другие два знака, первый из которых пишется и обозначает больше, а второй и обозначает меньше’’.
В описании знаков плюс и минус Рекорд писал: “Часто используются другие два знака, первый из которых пишется и обозначает больше, а второй и обозначает меньше’’. В нескольких книгах семнадцатого века (например, у Декарта и Мерсенна) использованы две точки “∙ ∙’’ или три точки “∙ ∙ ∙’’ для обозначения вычитания.
В нескольких книгах семнадцатого века (например, у Декарта и Мерсенна) использованы две точки “∙ ∙’’ или три точки “∙ ∙ ∙’’ для обозначения вычитания. Ранее вместо запятой ставили иные символы — вертикальную черту: 3|62, или нуль в скобках: 3 (0) 62
Ранее вместо запятой ставили иные символы — вертикальную черту: 3|62, или нуль в скобках: 3 (0) 62 Позднее Лейбниц заменил крестик на точку (конец XVII века), чтобы не путать его с буквой x ; до него такая символика встречалась у Региомонтана (XV век) и английского учёного Томаса Хэрриота (1560—1621).
Позднее Лейбниц заменил крестик на точку (конец XVII века), чтобы не путать его с буквой x ; до него такая символика встречалась у Региомонтана (XV век) и английского учёного Томаса Хэрриота (1560—1621). Гюнтер в 1882 году.
Гюнтер в 1882 году.
 Английская и немецкая математические школы до конца XIX века предлагали иные обозначения: , но они не прижились.
Английская и немецкая математические школы до конца XIX века предлагали иные обозначения: , но они не прижились. Обычно при заимствовании названия из другого языка новое не изобретается, а просто копируется (так в русский язык пришли слова «почта» и «табак», а слова «водка» и «спутник» пересекли границу в обратном направлении). Но иногда исходное название может оказаться непроизносимым, неприличным или не соответствующим правилам языка. Видимо, это и произошло с символом @ — его официальное название «коммерческое эт» русскому уху кажется совершенно бессмысленным. Название должно быть таким, чтобы его хотелось запомнить и применять. В 1990-е годы, когда значок @ впервые пытались перевести на русский, существовало множество равноправных вариантов — «кракозябра», «закорючка», «лягушка», «ухо» и другие. Правда, в настоящее время они практически исчезли, а «собака» распространилась по всему Рунету и осталась, потому что любой язык стремится иметь только одно универсальное слово для обозначения чего бы то ни было. Остальные названия остаются маргинальными, хотя их может быть очень много. Например, в английском языке символ @ называют не только словами commercial at, но и mercantile symbol, commercial symbol, scroll, arobase, each, about и т.
Обычно при заимствовании названия из другого языка новое не изобретается, а просто копируется (так в русский язык пришли слова «почта» и «табак», а слова «водка» и «спутник» пересекли границу в обратном направлении). Но иногда исходное название может оказаться непроизносимым, неприличным или не соответствующим правилам языка. Видимо, это и произошло с символом @ — его официальное название «коммерческое эт» русскому уху кажется совершенно бессмысленным. Название должно быть таким, чтобы его хотелось запомнить и применять. В 1990-е годы, когда значок @ впервые пытались перевести на русский, существовало множество равноправных вариантов — «кракозябра», «закорючка», «лягушка», «ухо» и другие. Правда, в настоящее время они практически исчезли, а «собака» распространилась по всему Рунету и осталась, потому что любой язык стремится иметь только одно универсальное слово для обозначения чего бы то ни было. Остальные названия остаются маргинальными, хотя их может быть очень много. Например, в английском языке символ @ называют не только словами commercial at, но и mercantile symbol, commercial symbol, scroll, arobase, each, about и т. д. Откуда взялась ассоциация между главным компьютерным значком и другом человека? Для многих символ @ действительно напоминает свернувшуюся калачиком собаку. Существует экзотическая версия, что отрывистое произношение английского at может напомнить собачий лай. Однако гораздо более вероятная гипотеза связывает наш символ с очень старой компьютерной игрой Adventure. В ней нужно было путешествовать по лабиринту, сражаясь с разными малоприятными подземными тварями. Поскольку игра была текстовая, сам игрок, стены лабиринта, монстры и клады обозначались различными символами (скажем, стены были постоены из «!», «+» и «-»). Игрока в Adventure сопровождал пес, которого можно было посылать с разведывательными миссиями. Обозначался он символом @. Возможно, именно благодаря этой ныне забытой компьютерной игре в России укоренилось название «собака». В современном мире знак @ присутствует повсюду, особенно с того момента, как он стал неотъемлемой частью адреса электронной почты. Но этот символ задолго до компьютерной эры входил в раскладку стандартной американской пишущей машинки, а компьютерным стал лишь потому, что сравнительно мало использовался.
д. Откуда взялась ассоциация между главным компьютерным значком и другом человека? Для многих символ @ действительно напоминает свернувшуюся калачиком собаку. Существует экзотическая версия, что отрывистое произношение английского at может напомнить собачий лай. Однако гораздо более вероятная гипотеза связывает наш символ с очень старой компьютерной игрой Adventure. В ней нужно было путешествовать по лабиринту, сражаясь с разными малоприятными подземными тварями. Поскольку игра была текстовая, сам игрок, стены лабиринта, монстры и клады обозначались различными символами (скажем, стены были постоены из «!», «+» и «-»). Игрока в Adventure сопровождал пес, которого можно было посылать с разведывательными миссиями. Обозначался он символом @. Возможно, именно благодаря этой ныне забытой компьютерной игре в России укоренилось название «собака». В современном мире знак @ присутствует повсюду, особенно с того момента, как он стал неотъемлемой частью адреса электронной почты. Но этот символ задолго до компьютерной эры входил в раскладку стандартной американской пишущей машинки, а компьютерным стал лишь потому, что сравнительно мало использовался. Значок @ применяется в коммерческих расчетах — в значении «по цене» (at the rate). Скажем, 10 галлонов масла по цене в 3,95 доллара США за галлон будет кратко записываться: 10 gal of oil @ $3.95/gal. В англоязычных странах символ применяется и в науке в значении «при»: например, плотность 1,050 г/см при 15°C будет записана: 1.050 g/cm @ 15°C. Кроме того, знак @ полюбили и часто используют анархисты ввиду его сходства с их символом — «А в круге». Однако его изначальное происхождение окутано тайной. С точки зрения лингвиста Ульмана, символ @ был изобретен средневековыми монахами для сокращения латинского ad («на», «в», «в отношении» и так далее), что очень напоминает его нынешнее использование. Другое объяснение дает итальянский ученый Джорджо Стабиле — он обнаружил этот символ в записях флорентийского купца Франческо Лапи за 1536 год в значении «амфора»: например, цена одной @ вина. Интересно, что испанцы и португальцы называют символ в электронных письмах именно «амфорой» (arroba) — словом, которое французы, исказив, превратили в arobase.
Значок @ применяется в коммерческих расчетах — в значении «по цене» (at the rate). Скажем, 10 галлонов масла по цене в 3,95 доллара США за галлон будет кратко записываться: 10 gal of oil @ $3.95/gal. В англоязычных странах символ применяется и в науке в значении «при»: например, плотность 1,050 г/см при 15°C будет записана: 1.050 g/cm @ 15°C. Кроме того, знак @ полюбили и часто используют анархисты ввиду его сходства с их символом — «А в круге». Однако его изначальное происхождение окутано тайной. С точки зрения лингвиста Ульмана, символ @ был изобретен средневековыми монахами для сокращения латинского ad («на», «в», «в отношении» и так далее), что очень напоминает его нынешнее использование. Другое объяснение дает итальянский ученый Джорджо Стабиле — он обнаружил этот символ в записях флорентийского купца Франческо Лапи за 1536 год в значении «амфора»: например, цена одной @ вина. Интересно, что испанцы и португальцы называют символ в электронных письмах именно «амфорой» (arroba) — словом, которое французы, исказив, превратили в arobase. Впрочем, в разных странах существуют самые разные названия для символа @, чаще всего зоологические. Поляки называют его «обезьянкой», тайваньцы — «мышкой», греки — «уточкой», итальянцы и корейцы — «улиткой», венгры — «червячком», шведы и датчане — «слоновым хоботом», финны — «кошачьим хвостом» или «знаком мяу», а армяне, подобно нам, — «песиком». Есть гастрономические названия — «штрудель» в Израиле и «рольмопс» (сельдь под маринадом) в Чехии и Словакии. Кроме того, часто этот символ называют просто «скрюченным А», или «А с завитком», или, как сербы, «чокнутым А». Впрочем, самая удивительная из современных историй, связанных с символом @, произошла в Китае, где знак банально называется «А в круге». Несколько лет назад китайская пара дала такое имя новорожденному. Возможно, знак стали воспринимать как иероглиф, символизирующий технический прогресс, и решили, что он принесет счастье и успех юному обитателю Срединной державы.
Впрочем, в разных странах существуют самые разные названия для символа @, чаще всего зоологические. Поляки называют его «обезьянкой», тайваньцы — «мышкой», греки — «уточкой», итальянцы и корейцы — «улиткой», венгры — «червячком», шведы и датчане — «слоновым хоботом», финны — «кошачьим хвостом» или «знаком мяу», а армяне, подобно нам, — «песиком». Есть гастрономические названия — «штрудель» в Израиле и «рольмопс» (сельдь под маринадом) в Чехии и Словакии. Кроме того, часто этот символ называют просто «скрюченным А», или «А с завитком», или, как сербы, «чокнутым А». Впрочем, самая удивительная из современных историй, связанных с символом @, произошла в Китае, где знак банально называется «А в круге». Несколько лет назад китайская пара дала такое имя новорожденному. Возможно, знак стали воспринимать как иероглиф, символизирующий технический прогресс, и решили, что он принесет счастье и успех юному обитателю Срединной державы. Их можно использовать в различных типах уравнений, и они образуют универсальный язык математики, на который можно ссылаться в любое время. Учащиеся также могут научиться решать более сложные математические уравнения, интуитивно понимая значения символов, таких как число пи, римские цифры, деление, дроби и т. д.
Их можно использовать в различных типах уравнений, и они образуют универсальный язык математики, на который можно ссылаться в любое время. Учащиеся также могут научиться решать более сложные математические уравнения, интуитивно понимая значения символов, таких как число пи, римские цифры, деление, дроби и т. д. 

 15 ≠ Z
15 ≠ Z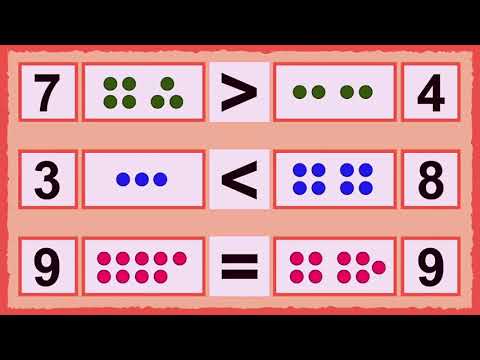

 Используя научно разработанные игры и курсы, созданные в сотрудничестве с ведущими преподавателями, наша программа повышает успеваемость и уверенность в своих математических способностях.
Используя научно разработанные игры и курсы, созданные в сотрудничестве с ведущими преподавателями, наша программа повышает успеваемость и уверенность в своих математических способностях.

 Узнать количество делителей, которые имеют числа, будет намного проще.
Узнать количество делителей, которые имеют числа, будет намного проще.
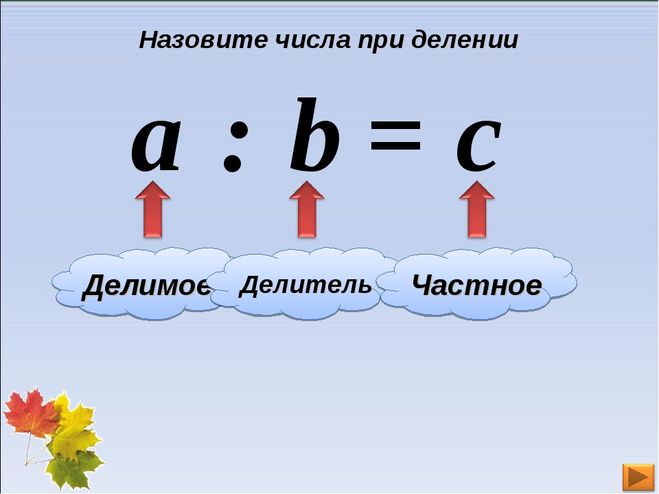 Можно провести разложение любого натурального числа, которое входит в заданное выражение им же, но представленном в ином виде. Для этого требуется изучить делители чисел. Они пригодятся в соответствующей операции.
Можно провести разложение любого натурального числа, которое входит в заданное выражение им же, но представленном в ином виде. Для этого требуется изучить делители чисел. Они пригодятся в соответствующей операции. Его легко освоить даже в начальных классах, после изучения таблицы умножения. Подходит для небольших «цифр». Когда дело доходит до больших значений, стоит воспользоваться иным методом:
Его легко освоить даже в начальных классах, после изучения таблицы умножения. Подходит для небольших «цифр». Когда дело доходит до больших значений, стоит воспользоваться иным методом:
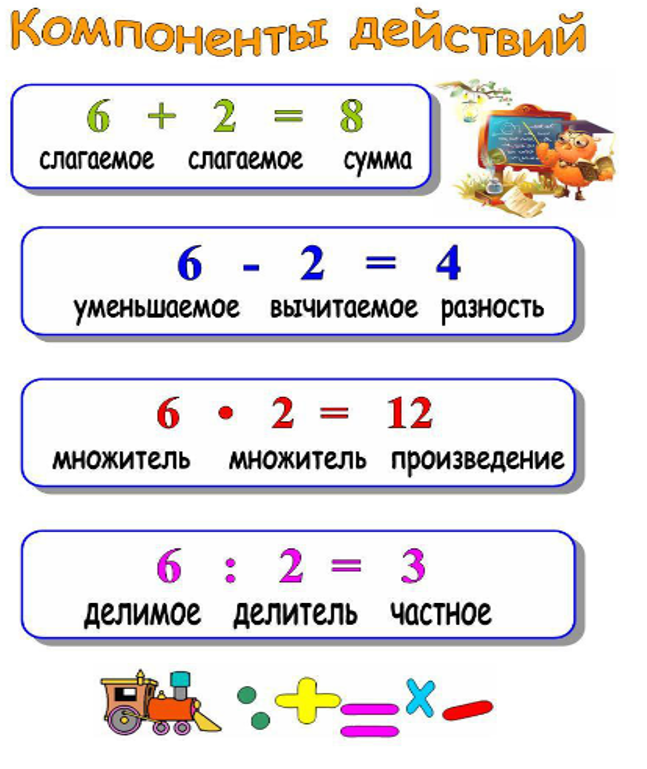

 В их число входят a, −a, 1 и −1.
В их число входят a, −a, 1 и −1.
 Таким образом, для любого натурального a положительный делитель b будет соответствовать условию 1≤b≤a. Важную роль здесь также играет наибольший общий делитель (НОД), о котором мы поговорим отдельно.
Таким образом, для любого натурального a положительный делитель b будет соответствовать условию 1≤b≤a. Важную роль здесь также играет наибольший общий делитель (НОД), о котором мы поговорим отдельно.
 — Аллан Слоан, Washington Post , 16 декабря 2022 г.
Дрейер начал урок с того, что написал пример оценки частного с двузначным числом 9.0011 делитель на доске и попросил учеников поднять руку и поделиться своими наблюдениями, включая возможные пути решения проблемы.
— Кливленд , 18 ноября 2022 г.
Например, для деления в длинное учащиеся использовали цветные карандаши, чтобы сопоставить штрихи делителя и в делимом.
— Алена Найден, Anchorage Daily News , 7 ноября 2022 г.
Используя этот новый делитель , ожидаемая продолжительность жизни будет уменьшаться на единицу каждый год.
— Джули Джейсон, Jd, Forbes , 7 марта 2022 г.
Текущий делитель промышленного индекса Доу-Джонса равен 0,1517.
— Аллан Слоан, Washington Post , 16 декабря 2022 г.
Дрейер начал урок с того, что написал пример оценки частного с двузначным числом 9.0011 делитель на доске и попросил учеников поднять руку и поделиться своими наблюдениями, включая возможные пути решения проблемы.
— Кливленд , 18 ноября 2022 г.
Например, для деления в длинное учащиеся использовали цветные карандаши, чтобы сопоставить штрихи делителя и в делимом.
— Алена Найден, Anchorage Daily News , 7 ноября 2022 г.
Используя этот новый делитель , ожидаемая продолжительность жизни будет уменьшаться на единицу каждый год.
— Джули Джейсон, Jd, Forbes , 7 марта 2022 г.
Текущий делитель промышленного индекса Доу-Джонса равен 0,1517. — Q.ai — Движение за личное богатство, Forbes , 9 октября 2022 г.
Дивидендная доходность в целом не изменится, но дивиденд на акцию может уменьшиться на те же делитель как раскол.
— Ли Клиффорд, Fortune , 10 марта 2022 г.
Дивидендная доходность в целом не изменится, но дивиденд на акцию может быть уменьшен на тот же делитель , что и дробление.
— Ли Клиффорд, Fortune , 10 марта 2022 г.
Дивидендная доходность в целом не изменится, но дивиденд на акцию может уменьшиться на те же делитель как раскол.
— Ли Клиффорд, Fortune , 10 марта 2022 г.
Узнать больше
— Q.ai — Движение за личное богатство, Forbes , 9 октября 2022 г.
Дивидендная доходность в целом не изменится, но дивиденд на акцию может уменьшиться на те же делитель как раскол.
— Ли Клиффорд, Fortune , 10 марта 2022 г.
Дивидендная доходность в целом не изменится, но дивиденд на акцию может быть уменьшен на тот же делитель , что и дробление.
— Ли Клиффорд, Fortune , 10 марта 2022 г.
Дивидендная доходность в целом не изменится, но дивиденд на акцию может уменьшиться на те же делитель как раскол.
— Ли Клиффорд, Fortune , 10 марта 2022 г.
Узнать больше Мнения, выраженные в примерах, не отражают точку зрения Merriam-Webster или ее редакторов. Отправьте нам отзыв.
Мнения, выраженные в примерах, не отражают точку зрения Merriam-Webster или ее редакторов. Отправьте нам отзыв. merriam-webster.com/dictionary/divisor. По состоянию на 30 января 2023 г.
merriam-webster.com/dictionary/divisor. По состоянию на 30 января 2023 г. com
com ..
..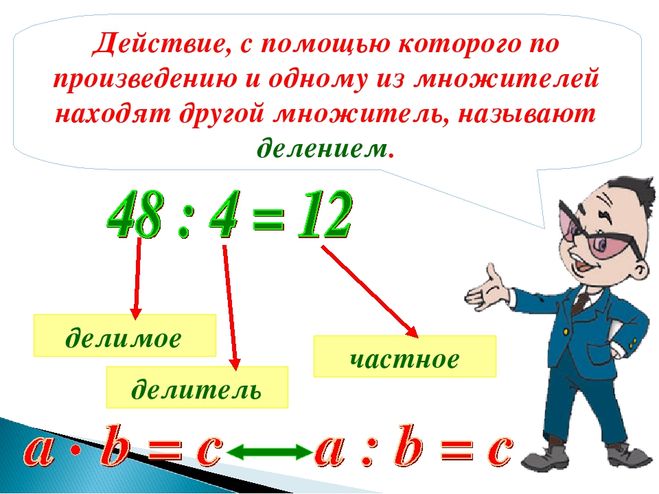 Например, 9является недостаточным числом, потому что правильными делителями 9 являются 1 и 3, которые в сумме дают 4, что меньше 9. Сравните с обильным числом, совершенным числом.
Например, 9является недостаточным числом, потому что правильными делителями 9 являются 1 и 3, которые в сумме дают 4, что меньше 9. Сравните с обильным числом, совершенным числом. Люди играют в бейсбол на ромбовидном поле.
Люди играют в бейсбол на ромбовидном поле. Аналитическая геометрия и линейная…
Аналитическая геометрия и линейная… ..
.. В. (ред.), Поспелов А.С. (ред.) Сборник задач по…
В. (ред.), Поспелов А.С. (ред.) Сборник задач по…

 Высшая школа.
Высшая школа. Краткие теоретические сведения, снабженные большим количеством разобранных примеров, позволяют использовать сборник для всех видов обучения.
Краткие теоретические сведения, снабженные большим количеством разобранных примеров, позволяют использовать сборник для всех видов обучения. ..
.. ..)
..) .. — СтудИзба
.. — СтудИзба ..
..

 ред. А.В.Ефимова и А.С.Поспелова.
ред. А.В.Ефимова и А.С.Поспелова. ..)
..)
 В., Поспелов А.С. (ред.))
В., Поспелов А.С. (ред.)) : Издательство Физико-математической литературы,
2001. — 288 с. — ISBN 5-94052-034-0 (Ч. 1).
: Издательство Физико-математической литературы,
2001. — 288 с. — ISBN 5-94052-034-0 (Ч. 1).
 Авторы посчитали также необходимым добавить один новый раздел
«Основы общей алгебры» и предложить цикл задач по тензорной
алгебре в разделе «Линейная алгебра» в первый,
«алгебраический» том Сборника. Это связано с тем, что круг
идей и методов общей алгебры все глубже проникает в наукоемкие
отрасли промышленности и, следовательно, становится
необходимой частью образования и подготовки специалистов по
инженерным специальностям.
Авторы посчитали также необходимым добавить один новый раздел
«Основы общей алгебры» и предложить цикл задач по тензорной
алгебре в разделе «Линейная алгебра» в первый,
«алгебраический» том Сборника. Это связано с тем, что круг
идей и методов общей алгебры все глубже проникает в наукоемкие
отрасли промышленности и, следовательно, становится
необходимой частью образования и подготовки специалистов по
инженерным специальностям. П.Демидовича помешала ему осуществить эту работу. Настоящий
«Сборник задач», подготовленный авторским коллективом, имеющим
большой педагогический опыт работы во втузах, — воплощение в
жизнь идеи Б.П.Демидовича.
П.Демидовича помешала ему осуществить эту работу. Настоящий
«Сборник задач», подготовленный авторским коллективом, имеющим
большой педагогический опыт работы во втузах, — воплощение в
жизнь идеи Б.П.Демидовича.
 Линейные операции над векторами.
2. Базис и координаты вектора.
3. Декартовы прямоугольные координаты точки. Простейшие задачи
аналитической геометрии.
4. Скалярное произведение векторов.
5. Векторное произведение векторов.
6. Смешанное произведение векторов.
Линейные операции над векторами.
2. Базис и координаты вектора.
3. Декартовы прямоугольные координаты точки. Простейшие задачи
аналитической геометрии.
4. Скалярное произведение векторов.
5. Векторное произведение векторов.
6. Смешанное произведение векторов. Определители
Определители
 Посетите mathnic.org для деталей.
Посетите mathnic.org для деталей. Эти инструменты подходят для любой учебной программы, направленной на углубление понимания учащимися математических концепций и развитие их способности применять эти знания для решения нестандартных задач.
Эти инструменты подходят для любой учебной программы, направленной на углубление понимания учащимися математических концепций и развитие их способности применять эти знания для решения нестандартных задач.
 09.20
09.20 OA.C.6 и MP.5.
Использует отношение между add…
OA.C.6 и MP.5.
Использует отношение между add… 07.14
07.14 NBT.A.1, 2.NBT.B.5 и MP.8.
Предлагает возможность т…
NBT.A.1, 2.NBT.B.5 и MP.8.
Предлагает возможность т… 10.13
10.13 NF.A.3d и MP.3
Представлены две дроби с одинаковым числом…
NF.A.3d и MP.3
Представлены две дроби с одинаковым числом… B.5,
Часть …
B.5,
Часть … 09.13
09.13

 dt
dt

 Решая
Решая

 для втузо:. в 2 т./ Н.С. Пискунов. –М.:Интеграл-Пресс, 2002.– Т. II. – 544 с.
для втузо:. в 2 т./ Н.С. Пискунов. –М.:Интеграл-Пресс, 2002.– Т. II. – 544 с. Бумага писчая Оперативный способ печати Гарнитура Times New Roman Усл. п.л. 9,5 уч-изд.л. 6,9 Тираж 250 экз. Заказ №___
Бумага писчая Оперативный способ печати Гарнитура Times New Roman Усл. п.л. 9,5 уч-изд.л. 6,9 Тираж 250 экз. Заказ №___
 или читать онлайн, а также в формате аудиокниг, которые можно также прослушать онлайн или скачать в формате mp3 бесплатно.
или читать онлайн, а также в формате аудиокниг, которые можно также прослушать онлайн или скачать в формате mp3 бесплатно. Предназначено студентам экономических специальностей, изучающих курс «Высшая математика» во втором семестре.
Предназначено студентам экономических специальностей, изучающих курс «Высшая математика» во втором семестре.
 Содержание соответствует программе раздела «Ряды» дисциплины «Математика», «Математический анализ». Тематика пособия отвечает требованиям образовательного стандарта. Кроме теоретической части курса в книге есть большое число примеров с разобранными решениями, задачи для самостоятельного решения, типовой расчет.
Содержание соответствует программе раздела «Ряды» дисциплины «Математика», «Математический анализ». Тематика пособия отвечает требованиям образовательного стандарта. Кроме теоретической части курса в книге есть большое число примеров с разобранными решениями, задачи для самостоятельного решения, типовой расчет. studmed.ru
studmed.ru n. Для таких бильярдов изучаются замкнутые траектории, которые ударяются о границу ровно m раз за период. С помощью теории Люстерника-Шнирельмана, в модификации Красносельского-Шварца, получена оценка снизу (n-2)(m-1)+2 на число различных таких траекторий, в случае простого m. Статью также можно скачать на arxiv.org.
n. Для таких бильярдов изучаются замкнутые траектории, которые ударяются о границу ровно m раз за период. С помощью теории Люстерника-Шнирельмана, в модификации Красносельского-Шварца, получена оценка снизу (n-2)(m-1)+2 на число различных таких траекторий, в случае простого m. Статью также можно скачать на arxiv.org. В нем отобраны и систематизир…
В нем отобраны и систематизир… Учебное пособие. Карасева Р.Б. — купить книгу с доставкой
Учебное пособие. Карасева Р.Б. — купить книгу с доставкой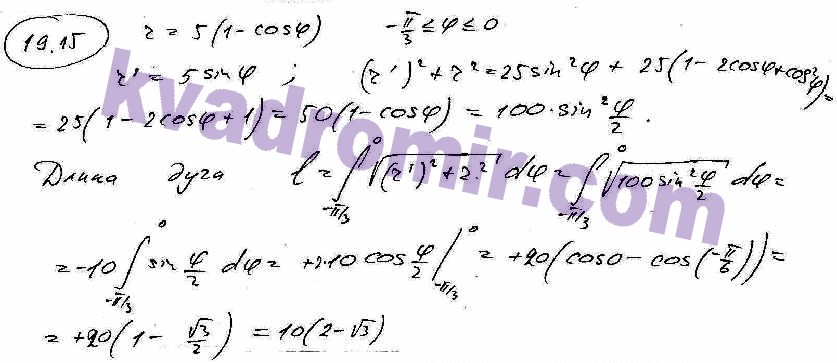 Н. — Кафедра высшей математики
Н. — Кафедра высшей математики Кармическая…
Кармическая… ..
..
 Что еще более важно, использование калькуляторов не отменяет необходимости для учащихся развивать навыки эффективных и точных методов вычислений в уме и с помощью карандаша и бумаги, а также делать разумные оценки. Акцент
и реализация являются критическими вопросами — когда и для каких целей следует использовать калькуляторы в классе начальной математики?
Что еще более важно, использование калькуляторов не отменяет необходимости для учащихся развивать навыки эффективных и точных методов вычислений в уме и с помощью карандаша и бумаги, а также делать разумные оценки. Акцент
и реализация являются критическими вопросами — когда и для каких целей следует использовать калькуляторы в классе начальной математики? Скорее, при правильном использовании калькуляторы играют ключевую роль в развитии у учащихся беглости с числами, операциями и навыками оценки. Кроме того, стратегическое использование калькуляторов способствует эффективному обучению.
среда, укрепляющая положительное отношение к математике (Ellington, 2003).
Скорее, при правильном использовании калькуляторы играют ключевую роль в развитии у учащихся беглости с числами, операциями и навыками оценки. Кроме того, стратегическое использование калькуляторов способствует эффективному обучению.
среда, укрепляющая положительное отношение к математике (Ellington, 2003).
 Во втором ответы вписываются по принципу чайнворда: последняя цифра примера является первой цифрой следующего примера.
Во втором ответы вписываются по принципу чайнворда: последняя цифра примера является первой цифрой следующего примера.

 В задании, изначально, необходимо не посчитать то, что нарисовано на картинке, а подумать, сколько чего было.
В задании, изначально, необходимо не посчитать то, что нарисовано на картинке, а подумать, сколько чего было.
 Проверьте, понимает ли он, что такое общий признак предмета: например — это дети, это — игрушки, это -мальчики и т. д.
Проверьте, понимает ли он, что такое общий признак предмета: например — это дети, это — игрушки, это -мальчики и т. д.
 com/pro_matem
com/pro_matem



 В течение первой недели в школе я прошу учеников поставить свою именную палатку в начале урока. Это значительно упростило изучение имен!
В течение первой недели в школе я прошу учеников поставить свою именную палатку в начале урока. Это значительно упростило изучение имен!

 Улов?
Улов? Учащиеся по очереди выбирают карточку для передачи хранителю правил.
Учащиеся по очереди выбирают карточку для передачи хранителю правил. Ученикам дается сетка из перемешанных чисел.
Ученикам дается сетка из перемешанных чисел. У вас есть два ведра. Одно ведро вмещает ровно пять галлонов. Другое ведро вмещает ровно три галлона. Как вы можете отмерить ровно четыре галлона воды в пятигаллонном ведре?
У вас есть два ведра. Одно ведро вмещает ровно пять галлонов. Другое ведро вмещает ровно три галлона. Как вы можете отмерить ровно четыре галлона воды в пятигаллонном ведре? Сможете ли вы сделать квадрат, используя ровно 1 часть? А если ровно 4 штуки? Наконец, сможете ли вы составить квадрат, используя ровно 5 частей?
Сможете ли вы сделать квадрат, используя ровно 1 часть? А если ровно 4 штуки? Наконец, сможете ли вы составить квадрат, используя ровно 5 частей? По мере того как плитки с числами достаются из мешка, учащиеся должны поместить числа в свой «поезд». Учащиеся зарабатывают баллы за размещение чисел в порядке возрастания.
По мере того как плитки с числами достаются из мешка, учащиеся должны поместить числа в свой «поезд». Учащиеся зарабатывают баллы за размещение чисел в порядке возрастания. Иногда они даже сами запускают игру!
Иногда они даже сами запускают игру!
 2.29. . 2.30. . 2.31. . 2.32. . 2.33. . 2.34. . 2.35. . 2.36. . 2.37. . 2.38. .
2.29. . 2.30. . 2.31. . 2.32. . 2.33. . 2.34. . 2.35. . 2.36. . 2.37. . 2.38. . 3.11. г) линейно зависима. 3.11. д) линейно зависима. 3.11. е) линейно независима. 3.12.
а) ранг 3, в
качестве базиса можно взять
В
этом базисе
. 3.12. б) ранг
3, в качестве базиса можно взять
В
этом базисе 3.12. в) ранг
2, в качестве базиса можно взять
В
этом базисе
, 3.12. г) ранг
3, в качестве базиса можно взять
В
этом базисе 3.13. а)
в качестве базиса можно взять В этом базисе
. 3.13. б) в качестве базиса можно взять В этом базисе
. 3.13. в) в качестве базиса можно взять В этом базисе
. 3.14. а) . 3.14. б) .
3.11. г) линейно зависима. 3.11. д) линейно зависима. 3.11. е) линейно независима. 3.12.
а) ранг 3, в
качестве базиса можно взять
В
этом базисе
. 3.12. б) ранг
3, в качестве базиса можно взять
В
этом базисе 3.12. в) ранг
2, в качестве базиса можно взять
В
этом базисе
, 3.12. г) ранг
3, в качестве базиса можно взять
В
этом базисе 3.13. а)
в качестве базиса можно взять В этом базисе
. 3.13. б) в качестве базиса можно взять В этом базисе
. 3.13. в) в качестве базиса можно взять В этом базисе
. 3.14. а) . 3.14. б) . г) -36. 3.18. д) -40. 3.18. е) -150. 3.18. ж) -10. 3.18. з) 5. 3.18. и) –720. 3.19. . 3.20. . 3.21. . 3.22. . 3.23. . 3.24. . 3.25. а) .
г) -36. 3.18. д) -40. 3.18. е) -150. 3.18. ж) -10. 3.18. з) 5. 3.18. и) –720. 3.19. . 3.20. . 3.21. . 3.22. . 3.23. . 3.24. . 3.25. а) . 4.1. г) ,
,
. 4.4. . 4.5. . 4.6. . 4.10. ,
. 4.11. ,
. 4.12. ,
.
4.1. г) ,
,
. 4.4. . 4.5. . 4.6. . 4.10. ,
. 4.11. ,
. 4.12. ,
. Площадь поверхности вращения для параметрически заданной линии
Площадь поверхности вращения для параметрически заданной линии Площадь его боковой поверхности: = 2ydl + dydl.
Площадь его боковой поверхности: = 2ydl + dydl. е. F = kx, где k — коэффициент пропорциональности. По условию задачи сила F = 100 Н растягивает пружину на x = 0,01 м; следовательно, 100 = k 0,01, откуда k = 10000; следовательно, F = 10000x.
е. F = kx, где k — коэффициент пропорциональности. По условию задачи сила F = 100 Н растягивает пружину на x = 0,01 м; следовательно, 100 = k 0,01, откуда k = 10000; следовательно, F = 10000x.
 Попробуем на нескольких примерах понять, как работает эта программа, проанализируем полученные с ее помощью решения и сравним эти решения с решениями, полученными другими методами.
Попробуем на нескольких примерах понять, как работает эта программа, проанализируем полученные с ее помощью решения и сравним эти решения с решениями, полученными другими методами. Кроме того, некоторые из полученных решений требуют дополнительных исследований.
Кроме того, некоторые из полученных решений требуют дополнительных исследований. Конечно, это далеко не исчерпывающий перечень наук, использующих интегральный метод для нахождения заданного значения при решении конкретной задачи, установления теоретических фактов.
Конечно, это далеко не исчерпывающий перечень наук, использующих интегральный метод для нахождения заданного значения при решении конкретной задачи, установления теоретических фактов.

 Найти площадь области, ограниченной кривой
Найти площадь области, ограниченной кривой





 И даже не понимают, что такое интегралы. Из технических средств вам понадобится микрокалькулятор. Да-да, ждем рутинных школьных расчетов. А еще лучше скачай мой полуавтоматический вычислитель для метода трапеций и метода Симпсона . Калькулятор написан в Excel и позволит сократить время решения и обработки задач в десятки раз. Видео руководство включено для чайников Excel! Кстати, первое видео с моим голосом.
И даже не понимают, что такое интегралы. Из технических средств вам понадобится микрокалькулятор. Да-да, ждем рутинных школьных расчетов. А еще лучше скачай мой полуавтоматический вычислитель для метода трапеций и метода Симпсона . Калькулятор написан в Excel и позволит сократить время решения и обработки задач в десятки раз. Видео руководство включено для чайников Excel! Кстати, первое видео с моим голосом. Под интегралом непрерывно на отрезке, а определенный интеграл численно равен заштрихованной площади. Да вот только одна загвоздка — интеграл не берется. И в таких случаях на помощь приходят численные методы. В этом случае задача возникает в двух постановках:
Под интегралом непрерывно на отрезке, а определенный интеграл численно равен заштрихованной площади. Да вот только одна загвоздка — интеграл не берется. И в таких случаях на помощь приходят численные методы. В этом случае задача возникает в двух постановках: Точнее, ответ 5,347 должен отличаться от истинного по модулю (в ту или иную сторону) не более чем на 0,001.
Точнее, ответ 5,347 должен отличаться от истинного по модулю (в ту или иную сторону) не более чем на 0,001.

 Это утверждение называется второй теоремой Хульдена или теоремой Паппа о центроиде.
Это утверждение называется второй теоремой Хульдена или теоремой Паппа о центроиде.

 Некоторые из них никогда не будут решены, ибо простые числа не поддаются никакой логике, не возможно определить закономерность их расположения на числовой оси, невозможно (или ограниченно возможно) описать их какими-либо общими формулами. Простые числа — камень преткновения всей математики.
Некоторые из них никогда не будут решены, ибо простые числа не поддаются никакой логике, не возможно определить закономерность их расположения на числовой оси, невозможно (или ограниченно возможно) описать их какими-либо общими формулами. Простые числа — камень преткновения всей математики. Они в основном имеют форму гипотез, которые предположительно верны, но нуждаются в доказательной базе. На данный момент известными списками математических проблем являются:
— Проблема Гильберта
— Проблемы Ландау
— Проблемы тысячелентия
— Проблема Смейла
Со временем… Читать далее
Они в основном имеют форму гипотез, которые предположительно верны, но нуждаются в доказательной базе. На данный момент известными списками математических проблем являются:
— Проблема Гильберта
— Проблемы Ландау
— Проблемы тысячелентия
— Проблема Смейла
Со временем… Читать далее Слухи о чудаковатых ученых сильно преувеличены. Люди, разбирающиеся в математике, ценятся не только потому, что они обладают специальными знаниями, а скорее потому, что умеют думать и анализировать.
Слухи о чудаковатых ученых сильно преувеличены. Люди, разбирающиеся в математике, ценятся не только потому, что они обладают специальными знаниями, а скорее потому, что умеют думать и анализировать. Особую роль математические результаты играют в мире IT. Технологические прорывы часто основаны на принципиально новых алгоритмах и теоремах, подчас из весьма абстрактных областей математики.
Особую роль математические результаты играют в мире IT. Технологические прорывы часто основаны на принципиально новых алгоритмах и теоремах, подчас из весьма абстрактных областей математики. Вопрос только в том, что с этой информацией делать: собранные груды данных человек или даже научный коллектив не сможет проанализировать за многие годы. Идея современного анализа данных в том, что компьютерные системы и реализованные на них алгоритмы сами работают с полученными массивами информации и выдают пользователю только окончательный результат — интересующую его статистику и те или иные обнаруженные закономерности. Это позволяет не только с математической строгостью подтвердить или опровергнуть гипотезы из гуманитарной сферы, но и обнаружить зависимости, которые были неизвестны специалистам. Математически подкованные гуманитарии тут необходимы — они могут поставить задачу, объяснить, что за данные планируется собирать и какого сорта характеристики нас будут интересовать.
Вопрос только в том, что с этой информацией делать: собранные груды данных человек или даже научный коллектив не сможет проанализировать за многие годы. Идея современного анализа данных в том, что компьютерные системы и реализованные на них алгоритмы сами работают с полученными массивами информации и выдают пользователю только окончательный результат — интересующую его статистику и те или иные обнаруженные закономерности. Это позволяет не только с математической строгостью подтвердить или опровергнуть гипотезы из гуманитарной сферы, но и обнаружить зависимости, которые были неизвестны специалистам. Математически подкованные гуманитарии тут необходимы — они могут поставить задачу, объяснить, что за данные планируется собирать и какого сорта характеристики нас будут интересовать. Тренировочные задания уже открыты на сайте — можно проверить свои силы.
Тренировочные задания уже открыты на сайте — можно проверить свои силы.
 Рамануджан прибыл в Англию в 1914 году, чтобы работать с Г.Х. Харди, теоретиком чисел из Кембриджского университета. Во время пребывания там он перенес тяжелую болезнь. (К сожалению, он умер вскоре после возвращения в Индию. Ему было всего 32 года.)
Рамануджан прибыл в Англию в 1914 году, чтобы работать с Г.Х. Харди, теоретиком чисел из Кембриджского университета. Во время пребывания там он перенес тяжелую болезнь. (К сожалению, он умер вскоре после возвращения в Индию. Ему было всего 32 года.) Havens спрашивает, когда 1729y 2 +1=x 2 имеет целочисленное решение как для x, так и для y, поэтому вы начинаете с перестановки уравнения так, чтобы 1 была сама по себе. И в вопросе Хейвенса, и в уравнении Пелла нам нужны не какие-то старые решения, а пары чисел x и y, которые удовлетворяют уравнению, где x и y — целые числа.
Havens спрашивает, когда 1729y 2 +1=x 2 имеет целочисленное решение как для x, так и для y, поэтому вы начинаете с перестановки уравнения так, чтобы 1 была сама по себе. И в вопросе Хейвенса, и в уравнении Пелла нам нужны не какие-то старые решения, а пары чисел x и y, которые удовлетворяют уравнению, где x и y — целые числа.
 Другими словами, числа, удовлетворяющие x 2 −Ny 2 =1 близки к числам, удовлетворяющим x 2 =Ny 2 или (x/y) 2 =N. Следовательно, поиск рационального числа x/y, квадрат которого близок к 1729, поможет вам найти числа x и y, которые удовлетворяют x 2 −1729y 2 =1.
Другими словами, числа, удовлетворяющие x 2 −Ny 2 =1 близки к числам, удовлетворяющим x 2 =Ny 2 или (x/y) 2 =N. Следовательно, поиск рационального числа x/y, квадрат которого близок к 1729, поможет вам найти числа x и y, которые удовлетворяют x 2 −1729y 2 =1.

 Задания требуют не только простого выполнения математических действий, но и смекалки, умения анализировать и просчитывать решение на несколько шагов вперед.
Задания требуют не только простого выполнения математических действий, но и смекалки, умения анализировать и просчитывать решение на несколько шагов вперед.
 И вот на финише трое: первым пришёл кузнечик, вторым — муравей, а третье место занял жук-навозник. Главный судья — уважаемый шмель — сел подписывать дипломы победителям, но не может вспомнить, как кого зовут!
И вот на финише трое: первым пришёл кузнечик, вторым — муравей, а третье место занял жук-навозник. Главный судья — уважаемый шмель — сел подписывать дипломы победителям, но не может вспомнить, как кого зовут! Пройдите сюжетную игру и решите три задачи на логику!
Пройдите сюжетную игру и решите три задачи на логику! Никакой скуки! Ни одно задание не повторяется!
Никакой скуки! Ни одно задание не повторяется!

 Мы понимаем, как важны учащимся 4 класса самоутверждение и высокая самооценка. Это поможет им в дальнейшей жизни увереннее чувствовать себя на уроках. Это одна из главных задач нашего проекта.
Мы понимаем, как важны учащимся 4 класса самоутверждение и высокая самооценка. Это поможет им в дальнейшей жизни увереннее чувствовать себя на уроках. Это одна из главных задач нашего проекта.
 Сколько кг груш собрали? Напишите число, которое получится в кг. Измените вопрос задачи так, чтобы решение было в два действия. Решите новую задачу и дайте ответ.
Сколько кг груш собрали? Напишите число, которое получится в кг. Измените вопрос задачи так, чтобы решение было в два действия. Решите новую задачу и дайте ответ.

 Это может быть «поворотный момент» с точки зрения ощущения успеха или разочарования в математике. Учащиеся узнают, что существует несколько способов решения математической задачи, и начнут применять то, что они изучают по математике, к реальным проблемам.
Это может быть «поворотный момент» с точки зрения ощущения успеха или разочарования в математике. Учащиеся узнают, что существует несколько способов решения математической задачи, и начнут применять то, что они изучают по математике, к реальным проблемам. Вы можете позволить своему ребенку вернуться и попрактиковаться в некоторых областях в предыдущем классе, которые нуждаются в укреплении.
Вы можете позволить своему ребенку вернуться и попрактиковаться в некоторых областях в предыдущем классе, которые нуждаются в укреплении.
 Округление чисел
Округление чисел Используйте частичные произведения и мысленное умножение в качестве стратегий.
Используйте частичные произведения и мысленное умножение в качестве стратегий.

 Решайте проблемы, требующие внесения сдачи на сумму до 100 долларов США.
Решайте проблемы, требующие внесения сдачи на сумму до 100 долларов США.

 (ребра, вершины и грани) Определите и создайте двухмерное представление трехцентовика.
(ребра, вершины и грани) Определите и создайте двухмерное представление трехцентовика.
 (чашка, пинта, кварта, галлон) Оцените и сравните вместимость.
(чашка, пинта, кварта, галлон) Оцените и сравните вместимость. Оцените и сравните емкость.
Оцените и сравните емкость.


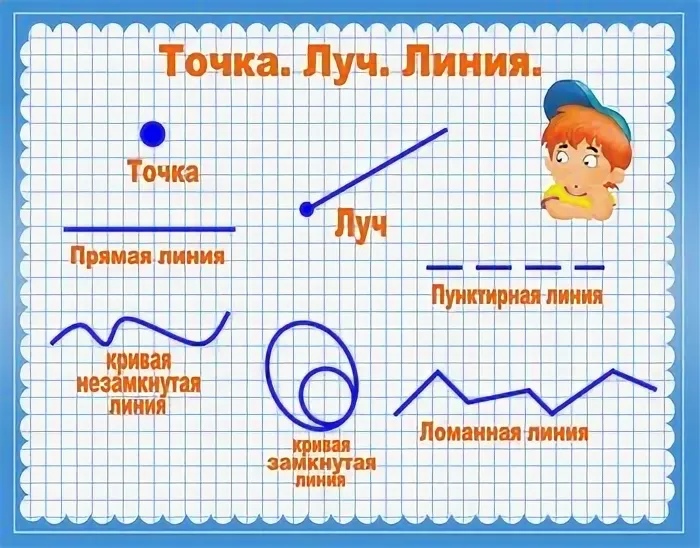
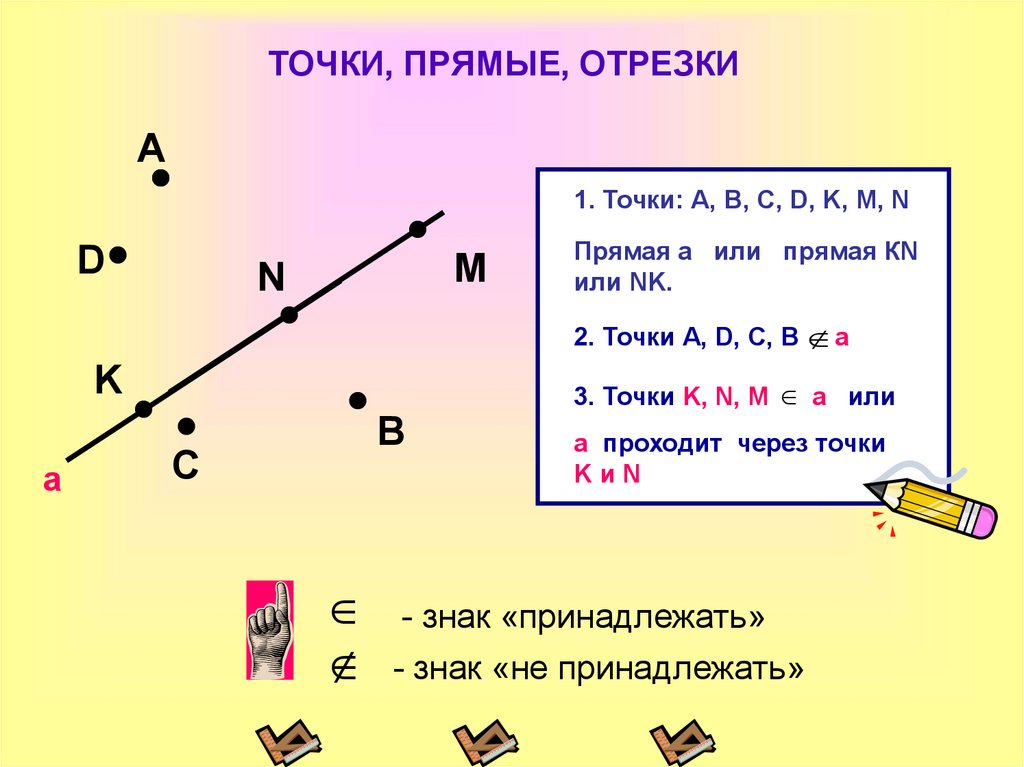
 Она обозначается заглавными литерами латинского алфавита (S, T, A и т. д. ) и предназначена для построения прямых (линий), отрезков, лучей, углов и прочих фигур.
Она обозначается заглавными литерами латинского алфавита (S, T, A и т. д. ) и предназначена для построения прямых (линий), отрезков, лучей, углов и прочих фигур. Если на луче отметить еще одну точку, получится отрезок (часть линии или луча, ограниченная с двух сторон). Его обозначение состоит из двух букв (АВ). В этом случае прямую можно обозначить также двумя литерами АВ (АБ). Следует отметить, что она также бывает и ломаной линией.
Если на луче отметить еще одну точку, получится отрезок (часть линии или луча, ограниченная с двух сторон). Его обозначение состоит из двух букв (АВ). В этом случае прямую можно обозначить также двумя литерами АВ (АБ). Следует отметить, что она также бывает и ломаной линией.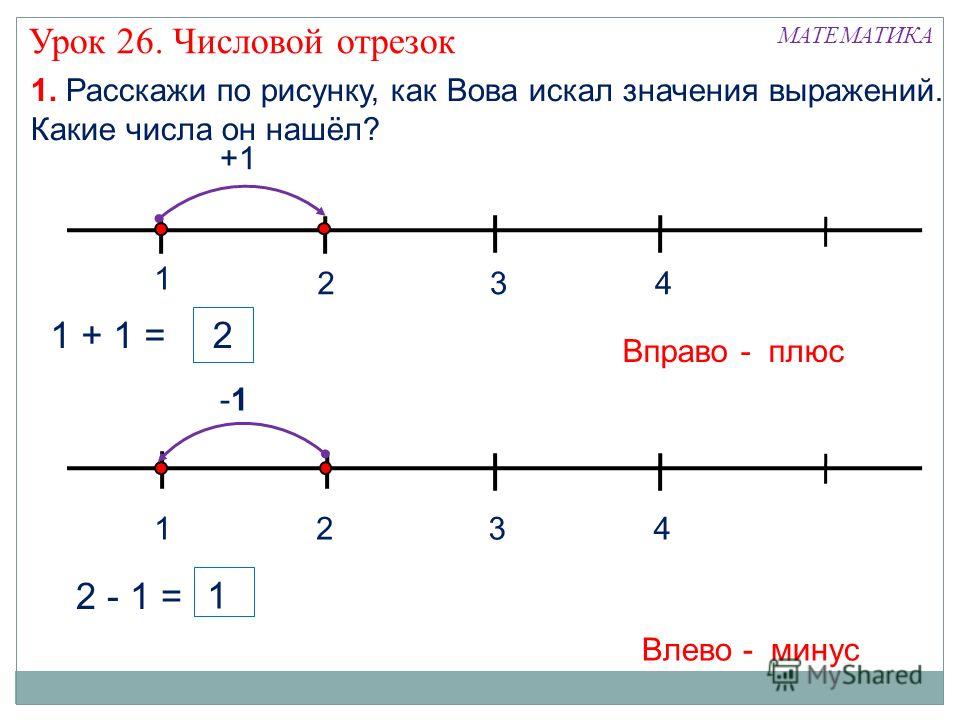
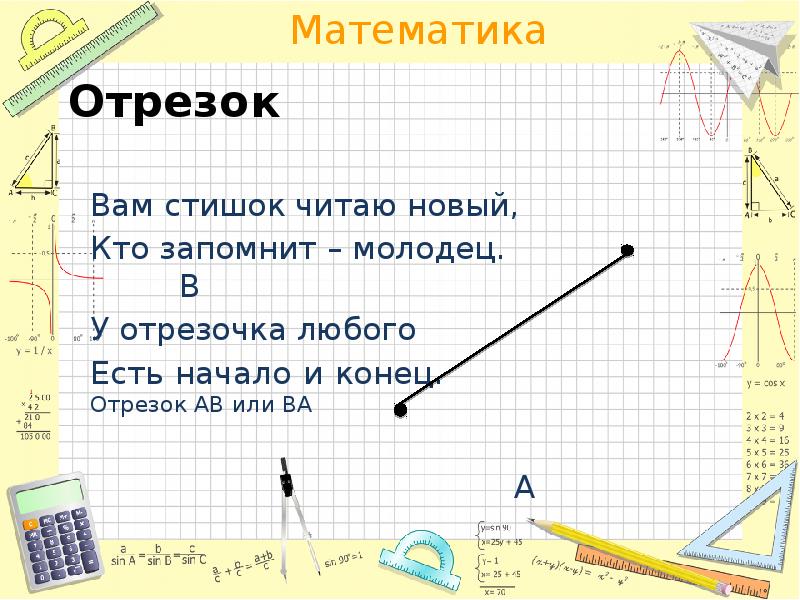
 Расположения линии зависит от k и m. В этом случае нужно разобрать некоторые свойства:
Расположения линии зависит от k и m. В этом случае нужно разобрать некоторые свойства: