Интегрирование рациональных дробей и функций
1. Интегрирование рациональных дробей.
2. Алгоритм интегрирования рациональной дроби.
3. Примеры интегрирования рациональных функций.
Интегрирование рациональных дробей
Рациональной дробью называется дробь вида
– многочлены степени m и n соответственно. Рациональная дробь называется правильной , если степень числителя меньше степени знаменателя (m<n), в противном случае дробь называется неправильной .
Простейшими элементарными дробями называются дроби следующего вида:
Пример 1
Пример 2
Интегралы, содержащие в знаменателе квадратный трехчлен, можно вычислить, применяя прием выделения полного квадрата разности или суммы. Рассмотрим пример такого интеграла.
Пример 3.
Алгоритм интегрирования рациональной дроби1. Если дробь неправильная, надо выделить целую часть рациональной дроби, разделив числитель на знаменатель по правилу деления многочлена на многочлен, т.е. представить в виде:
2. Знаменатель разложим на простейшие сомножители: Qn(x)
3. Представим дробь
виде суммы простейших дробей с неопределенными коэффициентами.
- Приведем все дроби в разложении к общему знаменателю и приравняем числители в обеих частях равенства.
- Составим систему уравнений, используя равенство многочленов, стоящих в числителе, приравнивая коэффициенты при одинаковых степенях x.
- Решим систему уравнений, находя некоторые коэффициенты методом частных значений, полагая равным действительным корням знаменателя.
- Подставим найденные коэффициенты A1,A2,…,Cs,Ds в разложение дроби.
- Проинтегрируем простейшие дроби.
Примеры интегрирования рациональных функций
Пример 4.
Корни знаменателя: x=1, а x2+1 = 0 не имеет действительных корней.
Тогда разложение для данной дроби имеет вид:
Приводя полученные дроби к общему знаменателю, получим тождество:
Пример 5.
Вычислим коэффициенты разложения, приравнивая коэффициенты при одинаковых степенях. Так как знаменатель имеет три действительных различных корня, то три коэффициента найдем методом частных значений.
Подставим найденные коэффициенты в разложение и проинтегрируем дроби.
Страница не найдена — ПриМат
© 2012-2016: Нохум-Даниэль Блиндер (11), Анастасия Лозинская (10), Денис Стехун (8), Валентин Малявко (8), Елизавета Савицкая (8), Игорь Любинский (8), Юлия Стерлянко (8), Олег Шпинарев (7), Александр Базан (7), Анна Чалапчий (7), Константин Берков (7), Максим Швандт (6), Людмила Рыбальченко (6), Кирилл Волков (6), Татьяна Корнилова (6), Влад Радзивил (6), Валерия Заверюха (5), Елизавета Снежинская (5), Вадим Покровский (5), Даниил Радковский (5), Влад Недомовный (5), Александр Онищенко (5), Андрей Метасов (5), Денис Базанов (5), Александр Ковальский (5), Александр Земсков (5), Марина Чайковская (5), Екатерина Шибаева (5), Мария Корень (5), Анна Семененко (5), Мария Илларионова (5), Сергей Черкес (5), Алиса Ворохта (5), Артём Романча (4), Анна Шохина (4), Иван Киреев (4), Никита Савко (4), Кондрат Воронов (4), Алина Зозуля (4), Иван Чеповский (4), Артем Рогулин (4), Игорь Чернега (4), Даниил Кубаренко (4), Ольга Денисова (4), Татьяна Осипенко (4), Яков Юсипенко (4), Ольга Слободянюк (4), Руслан Авсенин (4), Екатерина Фесенко (4), Дмитрий Заславский (4), Алина Малыхина (4), Андрей Лисовой (4), Полина Сорокина (4), Кирилл Демиденко (4), Дмитрий Стеценко (4), Александр Рапчинский (4), Святослав Волков (4), Иван Мясоедов (4), Владислав Стасюк (4), Алёна Гирняк (4), Николай Царев (4), Валентин Цушко (4), Павел Жуков (4), Роман Бронфен-Бова (4), Дмитрий Дудник (3), Дарья Кваша (3), Игорь Стеблинский (3), Артем Чернобровкин (3), Виктор Булгаков (3), Дмитрий Мороз (3), Богдан Павлов (3), Игорь Вустянюк (3), Андрей Яроцкий (3), Лаура Казарян (3), Екатерина Мальчик (3), Анатолий Осецимский (3), Иван Дуков (3), Дмитрий Робакидзе (3), Вячеслав Зелинский (3), Данила Савчак (3), Дмитрий Воротов (3), Стефания Амамджян (3), Валерия Сиренко (3), Георгий Мартынюк (3), Виктор Иванов (3), Вячеслав Иванов (3), Валерия Ларикова (3), Евгений Радчин (3), Андрей Бойко (3), Милан Карагяур (3), Александр Димитриев (3), Иван Василевский (3), Руслан Масальский (3), Даниил Кулык (3), Стас Коциевский (3), Елизавета Севастьянова (3), Павел Бакалин (3), Антон Локтев (3), Андрей-Святозар Чернецкий (3), Николь Метри (3), Евелина Алексютенко (3), Константин Грешилов (3), Марина Кривошеева (3), Денис Куленюк (3), Константин Мысов (3), Мария Карьева (3), Константин Григорян (3), Колаев Демьян (3), Станислав Бондаренко (3), Ильдар Сабиров (3), Владимир Дроздин (3), Кирилл Сплошнов (3), Карина Миловская (3), Дмитрий Козачков (3), Мария Жаркая (3), Алёна Янишевская (3), Александра Рябова (3), Дмитрий Байков (3), Павел Загинайло (3), Томас Пасенченко (3), Виктория Крачилова (3), Таисия Ткачева (3), Владислав Бебик (3), Илья Бровко (3), Максим Носов (3), Филип Марченко (3), Катя Романцова (3), Илья Черноморец (3), Евгений Фищук (3), Анна Цивинская (3), Михаил Бутник (3), Станислав Чмиленко (3), Катя Писова (3), Юлиана Боурош (2), Никита Семерня (2), Владимир Захаренко (2), Дмитрий Лозинский (2), Яна Колчинская (2), Юрий Олейник (2), Кирилл Бондаренко (2), Елена Шихова (2), Татьяна Таран (2), Наталья Федина (2), Настя Кондратюк (2), Никита Гербали (2), Сергей Запорожченко (2), Николай Козиний (2), Георгий Луценко (2), Владислав Гринькив (2), Александр Дяченко (2), Анна Неделева (2), Никита Строгуш (2), Настя Панько (2), Кирилл Веремьев (2), Даниил Мозгунов (2), Андрей Зиновьев (2), Андрей Данилов (2), Даниил Крутоголов (2), Наталия Писаревская (2), Дэвид Ли (2), Александр Коломеец (2), Александра Филистович (2), Евгений Рудницкий (2), Олег Сторожев (2), Евгения Максимова (2), Алексей Пожиленков (2), Юрий Молоканов (2), Даниил Кадочников (2), Александр Колаев (2), Александр Гутовский (2), Павел Мацалышенко (2), Таня Спичак (2), Радомир Сиденко (2), Владислав Шиманский (2), Илья Балицкий (2), Алина Гончарова (2), Владислав Шеванов (2), Андрей Сидоренко (2), Александр Мога (2), Юлия Стоева (2), Александр Розин (2), Надежда Кибакова (2), Майк Евгеньев (2), Евгений Колодин (2), Денис Карташов (2), Александр Довгань (2), Нина Хоробрых (2), Роман Гайдей (2), Антон Джашимов (2), Никита Репнин (2), Инна Литвиненко (2), Яна Юрковская (2), Гасан Мурадов (2), Богдан Подгорный (2), Алексей Никифоров (2), Настя Филипчук (2), Гук Алина (2), Михаил Абабин (2), Дмитрий Калинин (2), Бриткариу Ирина (2),
Интегрирование рациональных функций (дробей)
Стандартные методы интегрирования рациональных функций
Рациональная функция R(x) от переменной x – это функция, образованная, из переменной x и произвольного конечного количества постоянных, с помощью конечного числа операций сложения, вычитания, умножения и деления. Алгебраическими преобразованиями ее можно привести к дроби из двух многочленов от переменной x:
,
где ,
– многочлены степеней k и n, соответственно.
Рассмотрим интеграл от рациональной функции:
(1)
Далее приводится стандартный метод вычисления таких интегралов.
1. Если k ≥ n, то мы делим многочлен Pk(x) на многочлен Qn(x). В результате получаем:
(2) ,
где – многочлен степени k–n;
– многочлен степени m < n.
См. подробнее: Деление и умножение многочлена на многочлен уголком и столбиком >>>
2. Раскладываем многочлен Qn(x) на множители:
См. подробнее: Методы разложения многочленов на множители >>>
Примеры разложения многочленов на множители >>>
3. Раскладываем правильную рациональную дробь на простейшие:
См. подробнее: Методы разложения рациональных дробей на простейшие >>>
4. Подставляем в (2) и интегрируем. В результате исходный интеграл (1) выражается через более простые интегралы следующих видов:
;
;
.
5. Вычисляем интегралы от простейших дробей.
См. подробнее: Интегрирование простейших дробей >>>
Примеры интегрирования рациональных функций >>>
Нестандартные методы интегрирования рациональных функций
Иногда удается найти подстановку, которая приводит к более простым интегралам. Ниже рассмотрены подобные случаи.
Применение простых степенных подстановок
В некоторых случаях удается найти степенную подстановку вида t = xn, которая приводит интеграл к более простому виду.
Пример
Вычислить интеграл:
Решение
Умножим числитель и знаменатель на x7:
.
Делаем подстановку t = x8:
.
Разложим дробь на простейшие.
.
Интегрируем:
.
Поскольку x8 ≥ 0, то знак модуля можно убрать. По свойству модуля и логарифма:
.
Ответ
.
Дробно-линейные подстановки
Интегралы вида легко находятся с помощью дробно-линейной подстановки , применяя формулы:
;
;
.
Пример
Вычислить интеграл:
.
Решение
Преобразуем знаменатель.
x2 – 1 = (x – 1)(x + 1);
;
.
Делаем дробно-линейную подстановку:
.
;
;
;
;
.
Применяем формулу бинома Ньютона:
.
;
.
Интегрируем.
.
Ответ
;
.
Возвратные многочлены
Некоторые интегралы, содержащие возвратные многочлены и множитель x2 – 1 или x2 + 1, находятся подстановкой или . Вот примеры таких интегралов:
, , , .
Пример
Вычислить интеграл
.
Решение
Введем вспомогательные интегралы:
,
,
.
Разделим числитель и знаменатель на x2 и делаем подстановку .
.
Разделим числитель и знаменатель на x2 и делаем подстановку .
.
Поскольку уравнения
корней не имеют, то . Поэтому знак модуля можно опустить.
Искомый интеграл
.
Ответ
.
Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.
Автор: Олег Одинцов. Опубликовано:
Примеры интегрирования рациональных функций (дробей)
Здесь мы приводим подробные решения трех примеров интегрирования следующих рациональных дробей:
, , .
Пример 1
Вычислить интеграл:
.
Решение
Здесь под знаком интеграла стоит рациональная функция, поскольку подынтегральное выражение является дробью из многочленов. Степень многочлена знаменателя (3) меньше степени многочлена числителя (4). Поэтому, вначале необходимо выделить целую часть дроби.
1. Выделим целую часть дроби. Делим x4 на x 3 – 6x 2 + 11x – 6:
Отсюда
.
2. Разложим знаменатель дроби на множители. Для этого нужно решить кубическое уравнение:
.
Предположим, что оно имеет хотя бы один целый корень. Тогда он является делителем числа 6 (члена без x). То есть целый корень может быть одним из чисел:
1, 2, 3, 6, –1, –2, –3, –6.
Подставим x = 1:
.
Итак, мы нашли один корень x = 1. Делим на x – 1:
Отсюда
.
Решаем квадратное уравнение .
.
Корни уравнения: , .
Тогда
.
3. Разложим дробь на простейшие.
.
Итак, мы нашли:
.
Интегрируем.
Ответ
.
Пример 2
Вычислить интеграл:
.
Решение
Здесь в числителе дроби – многочлен нулевой степени (1 = x 0). В знаменателе – многочлен третьей степени. Поскольку 0 < 3, то дробь правильная. Разложим ее на простейшие дроби.
1. Разложим знаменатель дроби на множители. Для этого нужно решить уравнение третьей степени:
.
Предположим, что оно имеет хотя бы один целый корень. Тогда он является делителем числа 3 (члена без x). То есть целый корень может быть одним из чисел:
1, 3, –1, –3.
Подставим x = 1:
.
Итак, мы нашли один корень x = 1. Делим x 3 + 2x – 3 на x – 1:
Итак,
.
Решаем квадратное уравнение:
x 2 + x + 3 = 0.
Находим дискриминант: D = 1 2 – 4·3 = –11. Поскольку D < 0, то уравнение не имеет действительных корней. Таким образом, мы получили разложение знаменателя на множители:
.
2. Разложим дробь на простейшие. Ищем разложение в виде:
.
Освобождаемся от знаменателя дроби, умножаем на (x – 1)(x 2 + x + 3):
(2.1) .
Подставим x = 1. Тогда x – 1 = 0,
.
Подставим в (2.1) x = 0:
1 = 3A – C;
.
Приравняем в (2.1) коэффициенты при x 2:
;
0 = A + B;
.
Итак, мы нашли разложение на простейшие дроби:
.
3. Интегрируем.
(2.2) .
Для вычисления второго интеграла, выделим в числителе производную знаменателя и приведем знаменатель к сумме квадратов.
;
;
.
Вычисляем I2.
.
Поскольку уравнение x 2 + x + 3 = 0 не имеет действительных корней, то x 2 + x + 3 > 0. Поэтому знак модуля можно опустить.
Поставляем в (2.2):
.
Ответ
.
Пример 3
Вычислить интеграл:
.
Решение
Здесь под знаком интеграла стоит дробь из многочленов. Поэтому подынтегральное выражение является рациональной функцией. Степень многочлена в числителе равна 3. Степень многочлена знаменателя дроби равна 4. Поскольку 3 < 4, то дробь правильная. Поэтому ее можно раскладывать на простейшие дроби. Но для этого нужно разложить знаменатель на множители.
1. Разложим знаменатель дроби на множители. Для этого нужно решить уравнение четвертой степени:
.
Предположим, что оно имеет хотя бы один целый корень. Тогда он является делителем числа 2 (члена без x). То есть целый корень может быть одним из чисел:
1, 2, –1, –2.
Подставим x = –1:
.
Итак, мы нашли один корень x = –1. Делим на x – (–1) = x + 1:
Итак,
.
Теперь нужно решить уравнение третьей степени:
.
Если предположить, что это уравнение имеет целый корень, то он является делителем числа 2 (члена без x). То есть целый корень может быть одним из чисел:
1, 2, –1, –2.
Подставим x = –1:
.
Итак, мы нашли еще один корень x = –1. Можно было бы, как и в предыдущем случае, разделить многочлен на , но мы сгруппируем члены:
.
Поскольку уравнение x 2 + 2 = 0 не имеет действительных корней, то мы получили разложение знаменателя на множители:
.
2. Разложим дробь на простейшие. Ищем разложение в виде:
.
Освобождаемся от знаменателя дроби, умножаем на (x + 1) 2(x 2 + 2):
(3.1) .
Подставим x = –1. Тогда x + 1 = 0,
.
Продифференцируем (3.1):
;
.
Подставим x = –1 и учтем, что x + 1 = 0:
;
; .
Подставим в (3.1) x = 0:
0 = 2A + 2B + D;
.
Приравняем в (3.1) коэффициенты при x 3:
;
1 = B + C;
.
Итак, мы нашли разложение на простейшие дроби:
.
3. Интегрируем.
.
Ответ
.
Автор: Олег Одинцов. Опубликовано:
Примеры интегрирования дробно-рациональных функций
Контрольную работу на интегрирование функций, в том числе и рациональных дробей задают студентам 1, 2 курсов. Примеры интегралов в основном будут интересны для математиков, экономистов, статистов. Данные примеры задавали на контрольной работе в ЛНУ им. И. Франка. Условия следующих примеров «Найти интеграл» или «Вычислить интеграл», поэтому для экономии места и Вашего времени их не выписывали.
Пример 15. Мы пришли к интегрированию дробно-рациональных функций. Они занимают особое место среди интегралов, поскольку требуют много времени на вычисление и помогают преподавателям проверить Ваши знания не только по интегрированию. Для упрощения функции под интегралом добавим и вычтем в числителе выражение, которое позволит разбить функцию под интегралом на две простые
В результате один интеграл находим довольно быстро, во втором нужно дробь разложить на суму элементарных дробей
При сведении к общему знаменателю получим такие числительные
Далее раскрываем скобки и группируем
Приравниваем значение при одинаковых степенях «икс» справа и слева. В результате придем к системе трех линейных уравнений (СЛАУ) с тремя неизвестными.
Как решать системы уравнений описано в других статьях сайта. В конечном варианте Вы получите следующее решения СЛАУ
A=4; B=-9/2; C=-7/2.
Подставляем постоянные в разложение дроби на простейшие и выполняем интегрирование
На этом пример решен.
Пример 16. Опять нужно найти интеграл от дробно-рациональной функции. Для начала кубическое уравнение, которое содержится в знаменателе дроби разложим на простые множители
Далее выполняем разложение дроби на простейшие
Сводим правую сторону к общему знаменателю и раскрываем скобки в числителе.
Приравниваем коэффициенты при одинаковых степенях переменной. Снова придем к СЛАУ с тремя неизвестными
Подставляем значения А,В,С в разложение и вычисляем интеграл
Первые два слагаемых дают логарифм, последний тоже легко найти.
Пример 17. В знаменателе дробно-рациональной функции имеем разницу кубов. Ее по формулам сокращенного умножения раскладываем на два простых множителя
Далее полученную дробную функцию расписываем на сумму простых дробей и сводим их под общий знаменатель
В числителе получим следующее выражение.
Из него формируем систему линейных уравнений для вычисления 3 неизвестных
A=1/3; B=-1/3; C=1/3.
Подставляем А, В, С в формулу и выполняем интегрирование. В результате придем к такому ответу
Здесь числитель второго интеграла превращали в логарифм, при этом остаток под интегралом дает арктангенс.
Подобных примеров на интегрирование рациональных дробей в интернете очень много. Похожие примеры Вы можете найти из приведенных ниже материалов.
Готовые решения контрольной по интегрированию
3.1.5. Интегрирование дробно-рациональных функций | Контрольные работы
Дробно-рациональной функцией (рациональной дробью) называется отношение двух многочленов. Если степень многочлена, стоящего в числителе дроби, не меньше, чем степень многочлена в знаменателе, то в этой дроби следует выделить целую часть, т. е. представить ее в виде:
где R(x), P(x), Q(x) — многочлены, причем степень P(x) меньше степени Q(x). Рациональная дробьОбладающая этим свой
ством, называется правильной. Для интегрирования такой дроби ее необходимо разложить в сумму простейших дробей, которые легко интегрируются: казано ниже на примере). Остановимся подробнее на методике разложения правильной рациональной дробиВ сумму про
т. е. этот квадратный трехчлен не имеет действительных корней (интегрирование простейших дробей последнего типа будет по-
стейших дробей. Это выполняется по следующей схеме:
1. Сначала знаменатель дроби Q(x) необходимо разложить на множители вида: x — a, (x — b)k, (x2 + px + q)k.
При этом часто используется теорема Виета: если квадратный трехчлен ax2 + bx + с имеет корни X1, х2, то
2. Далее следует записать разложение дробиВ сумму простейших дробей, оставляя неопределенными коэффициентами А, B, C, D и т. д. При этом каждому множителю вида (x — а) соответствует дробь, множителю вида (x — b)k соответствует сумма дробей:
а множителю вида x2 + px + q, если он не имеет действительных корней (p2 — 4q < 0), соответствует дробь вида:
3. Для определения коэффициентов А, B, C, D, E в этом разложении следует приравнять коэффициенты при одинаковых степенях х у многочлена P(x) и многочлена, который получается в числителе после приведения записанной суммы простейших дробей к общему знаменателю (метод неопределенных коэффициентов). Можно также находить эти коэффициенты путем сравнения значений указанных многочленов при конкретных значениях х (в первую очередь, при х, совпадающих с корнями знаменателя Q(x)).
Пример 3.8. Вычислить интегралПодинтеграль-
ная функция представляет собой неправильную рациональную 156
дробь, поэтому выделим сначала целую часть дроби, поделив с остатком числитель на знаменатель
Таким образом
и
Для нахождения оставшегося интеграла выделим в числителе дифференциал знаменателя
Затем разобьем интеграл на два слагаемых и в последнем выделим полный квадрат квадратного трехчлена, стоящего в знаменателе. Тем самым получим:
1. Подинтегральная функция — правильная рациональная дробь.
2. Разложим знаменатель правильной рациональной дроби на простейшие действительные множители:
3. Разложим правильную рациональную дробь на простейшие:
Так как в знаменателе правильной дроби есть кратный линейный множитель, то в разложении появилась простейшая дробь
II типа.
4. Приведем к общему знаменателю все дроби и затем отбросим его:
Таким образом, имеем
5. Составляем систему уравнений:
6. Решая систему уравнений, получим A0 = -4, A1 = 0 и В = 1, а исходная подинтегральная функция разложится на простейшие дроби следующим образом:
Пример 3.10. Найти интеграл
I»>
Решение. Заметим, что.
Наименьшим общим кратным знаменателем дробейЯвляется
6. Поэтому, если применить подстановку 2х + 3 = t6, то будет иметь:
т. е. иррациональности в подинтегральном выражении исчезают. Так как:
Подставляя найденные выражения в искомый интеграл, получаем:
Таким образом, данный интеграл сведен к интегралу от рациональной функции. Для его нахождения выделим целую часть подинтегральной функции:
Интегрируя каждое из слагаемых, находим:
Возвратимся к старой переменной. Так какТо по
лучаем следующий окончательный результат:
159
2
Так как cos 2x = 2cos x — 1, то подинтегральная функция имеет вид R(sin x, cos x). Заметим, что при замене sin x на — sin x она меняет знак, т. е. является нечетной относительно sin x. Применяем подстановку cos x = t. Тогда
| < Предыдущая | Следующая > |
|---|
Интегрирование рациональных функций
Рациональной функцией называется функция, равная отношению двух многочленов:
(1)
где n, m — целые положительные числа;
Если m < n, то называетсяправильной дробью, если m n — неправильной дробью.
Всякую неправильную дробь путем деления числителя на знаменатель можно представить в виде суммы некоторого многочлена и правильной дроби:
где — многочлены;- правильная, дробь;l < n.
Так как всякий многочлен легко интегрируется, то интегрирование рациональных функций сводится к интегрированию правильных дробей. Поэтому в дальнейшем будем рассматривать правильные рациональные функции .
Интегрирование правильных рациональных дробей начинают с разложения их на простейшие рациональные дроби.
Простейшей дробью называется дробь одного из следующих четырех типов:
1). ; 2).; 3).; 4).
где A,M,N,a,p,q– постоянные числа;h2 иh– целое;.
Покажем схему нахождения интегралов от простейших рациональных дробей:
где
Аналогичные приемы используются при интегрировании простейших дробей четвертого типа. При этом задача отыскания интеграла четвертого типа сводится к отысканию интеграла следующего вида
,
где ;, который может быть найден с помощью рекуррентной формулы понижения степени знаменателя
Таким образом, всякая простейшая рациональная дробь может быть проинтегрирована в элементарных функциях.
Известно, что всякий многочлен с действительными коэффициентами на множестве действительных чисел может быть представлен в виде
, (2)
где — действительные корни многочленакратностей, а;
Всякая правильная рациональная дробь (1) со знаменателем, представленным в виде (2), можно разложить в сумму простейших рациональных дробей типа 1)-4). В данном разложении каждому корню кратностимногочлена(множителю) соответствует суммадробей вида
(3)
Каждой паре комплексно-сопряженных корней кратности многочлена(множителю) соответствует суммаэлементарных дробей
(4)
Для вычисления значений A, М, N в разложении функции R(x) на сумму простейших рациональных дробей часто используют метод неопределенных коэффициентов, суть которого заключается в следующем. С учетом формул (3), (4) данную дробь R(x) представим в виде суммы простейших рациональных дробей с неопределенными коэффициентами А, М, N. Полученное равенство является тождеством. Поэтому, если привести все дроби к общему знаменателю в числителе получим многочленстепени (n — 1), тождественно равный многочлену , стоящему в числителе выражения (1). Приравняв коэффициенты при одинаковых степеняхх в этих многочленах, получим систему n уравнений для определения n неизвестных коэффициентов А, М, N (с индексами).
В некоторых случаях с целью упрощения вычислений можно воспользоваться следующим соображением. Так как многочлены итождественно равны, то их значения равны при любых числовых значенияхх. Придавая х конкретные числовые значения, получаем систему уравнений для определения коэффициентов. Такой метод нахождения неизвестных коэффициентов называется методом частных значений. Если значения х совпадают с действительными корнями знаменателя, получаем уравнение с одним неизвестным коэффициентом.
Таким образом, всякая рациональная функция в принципе может быть проинтегрирована указанным выше способом.
В заданиях 3 и 5 необходимо найти интегралы от рациональных функций.
Задание 3. Найти неопределенный интеграл. Результат интегрирования проверить дифференцированием
a). ,b). , c). .
Решение: Во всех примерах задания 3 подынтегральная функция является неправильной рациональной дробью, так как степень многочлена стоящего в числителе больше или равна степени многочлена стоящего в знаменателе. Путем деления числителя на знаменатель выделим целую часть рациональной дроби и правильную рациональную дробь.
Задание 3 a). .
Таким образом . Используя свойство 50, разбиваем исходный интеграл на три интеграла. Первые два являются табличными, где, для первого интеграла, для второго -. Третий интеграл сводится к табличному, где, при помощи внесения под знак дифференциала функции.
Проверим полученный результат. Продифференцируем
Таким образом, производная от неопределенного интеграла равна подынтегральной функции.
Задание 3 b). .
Путем деления числителя на знаменатель выделим целую часть рациональной дроби и правильную рациональную дробь. Разобьем полученный интеграл на два интеграла. Первый является табличным , где,. Второй интеграл является простейшей правильной рациональной дробью третьего типа. Первый этап (выделение полного квадрата в знаменателе) опускается. Подынтегральную функцию разбиваем на сумму двух дробей, после чего второй интеграл представляется в виде суммы двух интегралов. Первый интеграл сводится к табличному, где, при помощи внесения под знак дифференциала функции, второй интеграл является табличным, где,.
Проверка найденного интеграла осуществляется аналогично тому, как это было сделано в пункте а).
Задание 3 c). .
Путем деления числителя на знаменатель выделим целую часть рациональной дроби и правильную рациональную дробь. Разобьем полученный интеграл на три интеграла. Первый и второй интегралы является табличным , где; для первого интеграла, для второго -. Третий интеграл — табличный, где,. Тогда
Проверка найденного интеграла осуществляется аналогично тому, как это было сделано в пункте а).
Задание 5. Найти неопределенный интеграл. Результат интегрирования проверить дифференцированием
a). ,b). .
Решение: Во всех примерах задания 5 подынтегральная функция является рациональной дробью. Для интегрирования их воспользуемся разложением подынтегральных дробей на сумму простейших.
Задание 5 a). .
Подынтегральная функция является правильной рациональной дробью, так как степень многочлена стоящего в числителе () меньше степени многочлена стоящего в знаменателе (). Разложим знаменатель подынтегральной функции на множители. Для этого найдем корни квадратного уравнения Тогда . Согласно формуле (3), в разложении правильной дроби на простейшие каждому множителю знаменателя видасоответствует слагаемое. Поэтому в данном случае имеем
Приведя правую часть разложения на сумму простейших дробей к общему знаменателю, и приравняв числители дробей, получим тождество
Коэффициенты A,B,Cопределим, например, с помощью метода частных значений (подставим одни и те же значенияxв правую и левую часть тождества):
Подставим в тождество. Получим, так как.
Аналогично при получим:; приполучим:.
Таким образом, получаем систему трех уравнений с тремя неизвестными
Подставим найденные коэффициенты в разложение подынтегральной функции на простейшие дроби, получим
Замечание: результат интегрирования можно оставить в виде суммы логарифмических функций.
Результат интегрирования проверим дифференцированием.
Таким образом, производная от неопределенного интеграла равна подынтегральной функции.
Задание 5 b). .
Так как подынтегральная функция является неправильной дробью (степень многочлена в числителе () больше, чем степень многочлена знаменателя ()), то путем деления числителя на знаменатель можно представить ее в виде суммы целого многочлена и правильной рациональной дроби. Удобно раскрыть скобки в знаменателе и поделить «уголком» числитель на знаменатель.
Так как и, то
Тогда исходный интеграл примет вид
Вычислим отдельно оставшийся интеграл. Подынтегральная функция является правильной рациональной дробью, которая может быть разложена на сумму трех простейших дробей (аналогично тому, как это было сделано в пункте a)).
Тогда окончательно получим
Проверка найденного интеграла осуществляется аналогично тому, как это было сделано в пункте а).
2 − x − 2} \, dx = \ int \ left (\ dfrac {1} {x + 1} + \ dfrac {2} {x − 2} \ right) \, dx. \ Nonumber \]дюйма В этом разделе мы исследуем метод разложения на частичную дробь , который позволяет нам разложить рациональных функций на суммы более простых и легко интегрируемых рациональных функций. Используя этот метод, мы можем переписать такое выражение, как:
Ключ к методу декомпозиции частичной дроби — это способность предвидеть форму, которую примет разложение рациональной функции.Как мы увидим, эта форма предсказуема и сильно зависит от факторизации знаменателя рациональной функции. Также чрезвычайно важно помнить, что разложение на частичную дробь может применяться к рациональной функции \ (\ dfrac {P (x)} {Q (x)} \), только если \ (deg (P (x)) < град (Q (х)) \). В случае, когда \ (deg (P (x)) ≥deg (Q (x)) \), мы должны сначала выполнить длинное деление, чтобы переписать частное \ (\ dfrac {P (x)} {Q (x)} \) в виде \ (A (x) + \ dfrac {R (x)} {Q (x)} \), где \ (deg (R (x)) Чтобы интегрировать \ (\ Displaystyle \ int \ dfrac {P (x)} {Q (x)} \, dx \), где \ (deg (P (x)) Если \ (Q (x) \) можно разложить на множители как \ ((a_1x + b_1) (a_2x + b_2)… (a_nx + b_n) \), где каждый линейный множитель различен, то можно найти константы \ (A_1, A_2,… A_n \) удовлетворяющие \ [\ dfrac {P (x)} {Q (x)} = \ dfrac {A_1} {a_1x + b_1} + \ dfrac {A_2} {a_2x + b_2} + ⋯ + \ dfrac {A_n} {a_nx + b_n}.2−2x = x (x − 2) (x + 1) \). Таким образом, существуют константы \ (A \), \ (B \) и \ (C \), удовлетворяющие уравнению \ ref {eq: 7.4.1}, такие что \ [\ dfrac {3x + 2} {x (x − 2) (x + 1)} = \ dfrac {A} {x} + \ dfrac {B} {x − 2} + \ dfrac {C} { х + 1}. \ nonumber \] Теперь мы должны найти эти константы. Для этого мы начнем с получения общего знаменателя справа. Таким образом, \ [\ dfrac {3x + 2} {x (x − 2) (x + 1)} = \ dfrac {A (x − 2) (x + 1) + Bx (x + 1) + Cx (x− 2)} {х (х — 2) (х + 1)}. \ nonumber \] Теперь мы устанавливаем числители равными друг другу, получая \ [3x + 2 = A (x − 2) (x + 1) + Bx (x + 1) + Cx (x − 2).2 + (- А + В − 2С) х + (- 2А). \ nonumber \] Приравнивание коэффициентов дает систему уравнений \ [\ begin {align *} A + B + C & = 0 \\ [4pt] −A + B − 2C & = 3 \\ [4pt] −2A & = 2. \ end {align *} \] Чтобы решить эту систему, сначала заметим, что \ (−2A = 2⇒A = −1. \). Подставляя это значение в первые два уравнения, мы получаем систему \ (В + С = 1 \) \ (B − 2C = 2 \). Умножение второго уравнения на \ (−1 \) и прибавление полученного уравнения к первому дает \ (-3C = 1, \) , что, в свою очередь, означает \ (C = — \ dfrac {1} {3} \).Подстановка этого значения в уравнение \ (B + C = 1 \) дает \ (B = \ dfrac {4} {3} \). Таким образом, решение этих уравнений дает \ (A = −1, B = \ dfrac {4} {3} \) и \ (C = — \ dfrac {1} {3} \). Важно отметить, что система, созданная этим методом, является непротиворечивой тогда и только тогда, когда мы правильно настроили декомпозицию. Если система несовместима, в нашей декомпозиции есть ошибка. Стратегия вторая: Метод стратегической замены Метод стратегической замены основан на предположении, что мы правильно настроили декомпозицию.Если разложение настроено правильно, тогда должны быть значения \ (A, B, \) и \ (C \), которые удовлетворяют уравнению \ (\ ref {Ex2Numerator} \) для всех значений \ (x \). То есть это уравнение должно быть истинным для любого значения \ (x \), которое мы хотим подставить в него. Следовательно, тщательно выбирая значения \ (x \) и подставляя их в уравнение, мы можем легко найти \ (A, B \) и \ (C \). Например, если мы подставим \ (x = 0 \), уравнение сведется к \ (2 = A (−2) (1) \). Решение относительно \ (A \) дает \ (A = −1 \).Затем, подставив \ (x = 2 \), уравнение сводится к \ (8 = B (2) (3) \) или, что эквивалентно, \ (B = 4/3 \). Наконец, мы подставляем \ (x = −1 \) в уравнение и получаем \ (−1 = C (−1) (- 3). \) Решая, мы имеем \ (C = — \ dfrac {1} {3 } \). Важно помнить, что если мы попытаемся использовать этот метод с некорректной декомпозицией, мы все равно сможем найти значения для констант, но эти константы бессмысленны. Если мы все же решим использовать метод стратегической замены, то будет хорошей идеей проверить результат, алгебраически перекомбинируя термины.2x− \ sin x} \, dx = — \ ln | u | + \ ln | u − 1 | + C = — \ ln | \ sin x | + \ ln | \ sin x − 1 | + C. \ nonumber \] Упражнение \ (\ PageIndex {2} \) Вычислить \ (\ displaystyle \ int \ dfrac {x + 1} {(x + 3) (x − 2)} \, dx. \) \ [\ dfrac {x + 1} {(x + 3) (x − 2)} = \ dfrac {A} {x + 3} + \ dfrac {B} {x − 2} \ nonumber \] \ [\ dfrac {2} {5} \ ln | x + 3 | + \ dfrac {3} {5} \ ln | x − 2 | + C \ nonumber \] Для некоторых приложений нам необходимо интегрировать рациональные выражения со знаменателями с повторяющимися линейными множителями, то есть рациональные функции с хотя бы одним множителем вида \ ((ax + b) ^ n, \), где \ (n \) является целым положительным числом, большим или равным \ (2 \).2 + (- 3A + B − 4C) x + (A − B + C). \ nonumber \] Приравнивание коэффициентов дает \ (2A + 4C = 0 \), \ (- 3A + B − 4C = 1 \) и \ (A − B + C = −2 \). Решение этой системы дает \ (A = 2, B = 3, \) и \ (C = −1. \) В качестве альтернативы можно использовать метод стратегической замены. В этом случае замена \ (x = 1 \) и \ (x = 1/2 \) в уравнение \ (\ ref {Ex5Numerator} \) легко дает значения \ (B = 3 \) и \ (C = — 1 \). На данный момент может показаться, что у нас закончился хороший выбор для \ (x \), однако, поскольку у нас уже есть значения для \ (B \) и \ (C \), мы можем подставить эти значения и выбрать любое значение для \ (x \), которое ранее не использовалось.2} \) и ось x на интервале \ ([0,1] \) относительно оси y . Решение Начнем с наброска области, которую нужно повернуть (см. Рисунок \ (\ PageIndex {1} \)). Из эскиза мы видим, что метод оболочки — хороший выбор для решения этой проблемы. Метод частичной дроби сильно зависит от предположения, что мы можем разложить знаменатель на линейные и квадратичные члены. Иногда это неприятно или не дает хорошего результата. В таких случаях мы должны попробовать uuu-substitution. Напомним, что мы используем uuu-замену, когда интеграл имеет следующий тип: ∫g (f (x)) ⋅f ′ (x) dx, \ int g \ big (f (x) \ big) \ cdot f ‘(x) \, dx, ∫g (f (x)) ⋅ f ′ (x) dx, , где ggg легко интегрировать.2 + 1} \, dx ∫x4 + λx2 + 1νx2 + μ dx для λ, μ, ν∈R \ lambda, \ mu, \ nu \ in \ mathbb {R} λ, μ, ν∈R. Отправьте свой ответ Учитывая ∫01×3 + x + 2×4 + 2×2 + 1dx = pq + rπs + lntu, \ int_0 ^ 1 \ frac {x ^ 3 + x + 2} {x ^ 4 + 2x ^ 2 + 1} dx = \ frac {p} {q} + \ frac {r \ pi} {s} + \ frac {\ ln t} {u}, ∫01 x4 + 2×2 + 1×3 + x + 2 dx = qp + srπ + ulnt, где t \, tt и u \, uu — точные квадраты. c} ∫ (x7 + x2 + 1) 37×13 + 5×15 dx = a1 ⋅ (x7 + x2 + 1) cxb Учитывая, что неопределенный интеграл выше верен, каково значение a + b + c, a + b + c, a + b + c, где a, b и ca, b, \ text {и} ca, b , А c — целые положительные числа? Запрашиваемый URL-адрес / ~ ebender / complements / stewart / 78_rat.pdf не найден на этом сервере. Для других веб-страниц, пожалуйста, начните с веб-сайта верхнего уровня математического факультета UCSD по адресу
http://www.math.ucsd.edu/. Чтобы мы могли должным образом устранить проблему, включите: Наша цель сегодня — вычислить интегралы от
форма Обратите внимание, что
, куда ,
являются комплексно сопряженными. Типы рациональных функций
. Сделать
частичное расширение фракции, сначала убедитесь с использованием длинного деления. Тогда есть четыре возможных ситуации:
каждый из возрастающих общностей (и сложности): Общая теорема о разложении частичной дроби выходит за рамки
объем этого курса. Однако вы можете найти следующие
частный случай и его доказательство интересно. Теперь рассмотрим следующую простую алгебру дробей:
$$
{A \ над x-r} + {B \ over x-s} = {A (x-s) + B (x-r) \ over (x-r) (x-s)} =
{(A + B) x-As-Br \ over (x-r) (x-s)}.
$$
То есть сложение двух дробей с постоянным числителем и знаменателями
$ (x-r) $ и $ (x-s) $ дают дробь со знаминателем $ (x-r) (x-s) $
и полином степени меньше 2 для числителя.3 \ над (x-2) (x + 3)} \, dx $. Мы начинаем с
записывая $ \ ds {7x-6 \ over (x-2) (x + 3)} $ как сумму двух дробей. Мы
хочу закончить с
$$ {7x-6 \ over (x-2) (x + 3)} = {A \ over x-2} + {B \ over x + 3}. $$
Если мы продолжим и сложим дроби в правой части, мы получим
$$ {7x-6 \ over (x-2) (x + 3)} = {(A + B) x + 3A-2B \ over (x-2) (x + 3)}. $$
Итак, все, что нам нужно сделать, это найти $ A $ и $ B $ так, чтобы $ 7x-6 = (A + B) x + 3A-2B $,
то есть нам нужно $ 7 = A + B $ и $ -6 = 3A-2B $. Это проблема
вы уже видели: решить систему из двух уравнений за два
неизвестные.2 + 3x} \, dx $
(отвечать) Лучшие доступные репетиторы по математике Рациональная функция определяется как функция, которая делит один многочлен на другой. Это легко запомнить по слову « рациональный». Выше вы можете видеть, что рациональная функция — это просто отношение двух полиномиальных функций.Имейте в виду, что даже обычные многочлены могут быть рациональными функциями . Разделив полином на 1, мы получим отношение любой полиномиальной функции и одночлена. Рациональная функция может быть простой, как в приведенных выше примерах, или более сложной. В таблице ниже приведены несколько примеров более сложных рациональных функций. Всякий раз, когда вы имеете дело с рациональными функциями, первое, что вам нужно сделать, это упростить их .Давайте сначала рассмотрим простой пример. Рисуем ли мы график этой рациональной функции или интегрируем ее, мы всегда должны пытаться ее упростить. Это упростит выполнение любых операций на нем впоследствии. Шаги по упрощению этой рациональной функции приведены в таблице ниже. Вот еще несколько советов, которые вы можете использовать, чтобы упростить любой рациональный функция. Интеграция — одно из наиболее важных понятий в исчислении . Вы можете думать об интегрировании двумя способами: Обратите внимание, что обозначения одинаковы для обеих точек обзора . Независимо от того, думаете ли вы об этом первым или вторым, процесс интеграции всегда один и тот же. Вы также можете увидеть такое обозначение: Есть несколько способов интегрировать дробь . Во-первых, взглянем на некоторые основные правила интеграции. Взгляните на несколько примеров ниже. Это означает, что, в зависимости от того, какая у вас доля, вы можете интегрировать несколькими способами . Первый способ — использовать следующее правило. Возьмем для примера следующую дробь . Чтобы упростить интеграцию этой функции, мы можем использовать правила степени , чтобы получить следующее: Второй метод — использовать правило , обратное .Во многих случаях мы можем комбинировать это с u-заменой: Интеграция рациональной функции требует использования всех методов , упомянутых выше. Вы можете столкнуться с более сложными функциями, которые имеют следующие правила: Взгляните на несколько примеров ниже. Поскольку рациональные функции являются дробями, мы можем использовать правила мощности , как в предыдущих примерах.Однако вам также понадобится u-подстановка и интеграция по частям. Где: Рассмотрим пример. Используя интеграцию по частям, мы делаем следующее: Теперь мы просто следуем правилам интеграции. Теперь упростим. Давайте сделаем пошаговое интегрирование рациональной функции. В качестве примера возьмем функцию ниже. Здесь мы можем просто использовать правило интегрирования power . Сначала воспользуйтесь правилом, чтобы найти результат. Затем упростите уравнение, чтобы получить окончательный результат . В последнем примере вы работали с неопределенным интегралом. Давайте возьмем тот же пример, но вместо этого поработаем с определенным интегралом . Мы работаем с результатами из предыдущего примера . Давайте поработаем с u-подстановкой в этом примере.У вас есть , следующий за интегралом . Давайте заменим 3x + 1 на u. Итак, давайте найдем производную члена u. Найдите член dx . Заменить эти термины в исходном интеграле . Упростим этот интеграл . Решите, используя правило степени . Заглушка u клемма обратно. Алгебра и начала математического анализа, 11 класс Урок №38. Определение комплексного числа. Действия с комплексными числами. Перечень вопросов, рассматриваемых в теме 1) понятие мнимой единицы; 2) определение комплексного числа; 3) действия с комплексными числами и действия над ними. Глоссарий по теме Определение. Комплексным числом называется выражение вида a + bi, где a и b — действительные числа. Запись комплексного числа в виде a + bi называют алгебраической формой комплексного числа, где а – действительная часть, bi – мнимая часть, причем b – действительное число. Два комплексных числа z = a + bi и = a – bi, отличающиеся лишь знаком мнимой части, называются сопряженными. Определение. Суммой комплексных чисел z1 = a1 + b1i и z2 = a2 + b2i называется комплексное число z, действительная часть которого равна сумме действительных частей z1 и z2, а мнимая часть — сумме мнимых частей чисел z1 и z2, то есть z = (a1 + a2) + (b1 + b2) i. Числа z1 и z2 называются слагаемыми. Определение. Вычесть из комплексного числа z1 комплексное число z2, значит найти такое комплексное число z, что z + z2 = z1. Теорема. Разность комплексных чисел существует и притом единственная. Определение. Произведением комплексных чисел z1=a1+ b1 i и z2=a2+b2 i называется комплексное число z, определяемое равенством: z = (a1a2 – b1b2) + (a1b2 + a2b1) i. Числа z1 и z2 называются сомножителями. Определение. Разделить комплексное число z1 на комплексное число z2, значит найти такое комплексное число z, что z · z2 = z1. Теорема. Частное комплексных чисел существует и единственно, если z2 ≠ 0 + 0i. Основная литература: Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014. Дополнительная литература: Шабунин М.И., Ткачева М.В., Федорова Н.Е. Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2017. Теоретический материал для самостоятельного изучения Мнимые числа, которыми мы дополняем действительные числа, записываются в виде bi, где i – мнимая единица, причем i 2 = —1. Исходя из этого, получим следующее определение комплексного числа. Определение. Комплексным числом называется выражение вида a + bi, где a и b — действительные числа. При этом выполняются условия: а) Два комплексных числа a1 + b1i и a2 + b2i равны тогда и только тогда, когда a1=a2, b1=b2. б) Сложение комплексных чисел определяется правилом: (a1 + b1i) + (a2 + b2i) = (a1 + a2) + (b1 + b2) i. в) Умножение комплексных чисел определяется правилом: (a1 + b1i) (a2 + b2i) = (a1a2 — b1b2) + (a1b2 — a2b1) i. Запись комплексного числа в виде a + bi называют алгебраической формой комплексного числа, где а – действительная часть, bi – мнимая часть, причем b – действительное число. Комплексное число a + bi считается равным нулю, если его действительная и мнимая части равны нулю: a = b = 0 Комплексное число a + bi при b = 0 считается совпадающим с действительным числом a: a + 0i = a. Комплексное число a + bi при a = 0 называется чисто мнимым и обозначается bi: 0 + bi = bi. Два комплексных числа z = a + bi и = a – bi, отличающиеся лишь знаком мнимой части, называются сопряженными. Над комплексными числами в алгебраической форме можно выполнять следующие действия. 1) Сложение. Определение. Суммой комплексных чисел z1 = a1 + b1 i и z2 = a2 + b2i называется комплексное число z, действительная часть которого равна сумме действительных частей z1 и z2, а мнимая часть — сумме мнимых частей чисел z1 и z2, то есть z = (a1 + a2) + (b1 + b2) i. Числа z1 и z2 называются слагаемыми. Сложение комплексных чисел обладает следующими свойствами: 1º. Коммутативность: z1 + z2 = z2 + z1. 2º. Ассоциативность: (z1 + z2) + z3 = z1 + (z2 + z3). 3º. Комплексное число – a – bi называется противоположным комплексному числу z = a + bi. Комплексное число, противоположное комплексному числу z, обозначается -z. Сумма комплексных чисел z и -z равна нулю: z + (-z) = 0 Пример 1. Выполните сложение (3 – i) + (-1 + 2i). (3 – i) + (-1 + 2i) = (3 + (-1)) + (-1 + 2) i = 2 + 1i. 2) Вычитание. Определение. Вычесть из комплексного числа z1 комплексное число z2, значит найти такое комплексное число z, что z + z2 =z1. Теорема. Разность комплексных чисел существует и притом единственная. Пример 2. Выполните вычитание (4 – 2i) — (-3 + 2i). (4 – 2i) — (-3 + 2i) = (4 — (-3)) + (-2 — 2) i = 7 – 4i. 3) Умножение. Определение. Произведением комплексных чисел z1=a1+ b1 i и z2=a2+b2i называется комплексное число z, определяемое равенством: z = (a1 a2 – b1b2) + (a1b2 + a2b1) i. Числа z1 и z2 называются сомножителями. Умножение комплексных чисел обладает следующими свойствами: 1º. Коммутативность: z1z2 = z2 z1. 2º. Ассоциативность: (z1z2)z3 = z1 (z2z3) 3º. (z1 + z2) z3 = z1z3 + z2z3. 4º. z · = (a + bi) (a – bi) = a2 + b2 — действительное число. На практике умножение комплексных чисел производят по правилу умножения суммы на сумму и выделения действительной и мнимой части. В следующем примере рассмотрим умножение комплексных чисел двумя способами: по правилу и умножением суммы на сумму. Пример 3. Выполните умножение (2 + 3i) (5 – 7i). 1 способ. (2 + 3i) (5 – 7i) = (2⋅ 5 – 3⋅ (- 7)) + (2⋅ (- 7) + 3⋅ 5)i = = (10 + 21) + (- 14 + 15)i = 31 + i. 2 способ. (2 + 3i) (5 – 7i) = 2⋅ 5 + 2⋅ (- 7i) + 3i⋅ 5 + 3i⋅ (- 7i) = = 10 – 14i + 15i + 21 = 31 + i. 4) Деление. Определение. Теорема. Частное комплексных чисел существует и единственно, если z2 ≠ 0 + 0i. На практике частное комплексных чисел находят путем умножения числителя и знаменателя на число, сопряженное знаменателю. Пусть z1 = a1 + b1i, z2 = a2 + b2i, тогда В следующем примере выполним деление по формуле и правилу умножения на число, сопряженное знаменателю. Пример 4. Найти частное 1 способ. 2 способ. 5) Возведение в целую положительную степень. а) Степени мнимой единицы. Пользуясь равенством i2 = -1, легко определить любую целую положительную степень мнимой единицы. i3 = i2 i = -i, i4 = i2 i2 = 1, i5 = i4 i = i, i6 = i4 i2 = -1, i7 = i5 i2 = -i, i8 = i6 i2 = 1 и т. д. Это показывает, что значения степени in, где n – целое положительное число, периодически повторяется при увеличении показателя на 4 . Поэтому, чтобы возвести число i в целую положительную степень, надо показатель степени разделить на 4 и возвести i в степень, показатель которой равен остатку от деления. Пример 5. Вычислите: (i 36 + i 17) · i 23. i 36 = (i 4) 9 = 1 9 = 1, i 17 = i 4⋅ 4+1 = (i 4)4⋅ i = 1 · i = i. i 23 = i 4⋅ 5+3 = (i 4)5⋅ i3 = 1 · i3 = — i. (i 36 + i 17) · i 23 = (1 + i) (- i) = — i + 1= 1 – i. б) Возведение комплексного числа в целую положительную степень производится по правилу возведения двучлена в соответствующую степень, так как оно представляет собой частный случай умножения одинаковых комплексных сомножителей. Пример 6. Вычислите: (4 + 2i) 3 (4 + 2i) 3 = 4 3 + 3⋅ 42⋅ 2i + 3⋅ 4⋅ (2i)2 + (2i)3 = 64 + 96i – 48 – 8i = 16 + 88i. Стоит отметить. что с помощью комплексных чисел можно решать квадратные уравнения, у которых отрицательный дискриминант. Рассмотрим решение квадратных уравнений, дискриминант которых отрицателен. Пример 7. Решите уравнения: а) x2 – 6x + 13 = 0; б) 9x2 + 12x + 29 = 0. Решение. а) Найдем дискриминант по формуле Так как a = 1, b = – 6, c = 13, то Корни уравнения находим по формулам б) Здесь a = 9, b = 12, c = 29. Следовательно, Находим корни уравнения: Мы видим, что если дискриминант квадратного уравнения отрицателен, то квадратное уравнение имеет два сопряженных комплексных корня. Разбор решения заданий тренировочного модуля №1. Тип задания: единичный выбор Вычислите сумму (2 + 3i)+ (5 – 7i). Решение: 2 + 3i + 5 — 7i = (2 + 5) + (3 — 7)i = 7 — 4i. Можем сделать вывод, что верный ответ 2. 7 — 4i. №2. Тип задания: ввод с клавиатуры пропущенных элементов в тексте. Чему будет равно частное: (5 + 3i):(1 — 2i)=______ Решение: Ответ: -0. Комплексным числом называется выражение вида a + ib, где a и b – любые действительные числа, i – специальное число, которое называется мнимой единицей. Для таких выражений понятия равенства и операции сложения и умножения вводятся следующим образом: Комплексные числа часто обозначают одной буквой, например, z = a + ib. Действительное число a называется действительной частью комплексного числа z, действительная часть обозначается a = Re z. Действительное число b называется мнимой частью комплексного числа z, мнимая часть обозначается b = Im z. Заметим, что арифметические операции над комплексными числами вида z = a + i · 0 осуществляются точно так же, как и над действительными числами. Действительно,
В отличие от действительных чисел, числа вида 0 + ib называются чисто мнимыми. Часто просто пишут bi, например, 0 + i3 = 3i. С учётом этого замечательного соотношения легко получаются формулы сложения и умножения для комплексных чисел. Нет нужды запоминать сложную формулу для произведения комплексных чисел – если на комплексные числа смотреть как на многочлены с учётом равенства
то и перемножать эти числа можно как многочлены. В самом деле,
Пример 1 Вычислить z1 + z2 и z1z2, где z1 = 1 + 2i и z2 = 2 – i. Показать решение Мы хорошо помним, что геометрической интерпретацией действительных чисел является действительная прямая. Кроме того, как было установлено выше, на действительной прямой «нет места для новых точек», то есть любой точке на действительной оси отвечает действительное число. Следовательно, комплексные числа на этой прямой расположить уже нельзя, однако можно попытаться рассмотреть наряду с действительной осью, на которой мы будем откладывать действительную часть комплексного числа, ещё одну ось, ей перпендикулярную; будем называть её мнимой осью. Тогда любому комплексному числу z = x + iy можно поставить в соответствие точку координатной плоскости. На оси абсцисс будем откладывать действительную часть комплексного числа, а на оси ординат – мнимую часть. Таким образом мы построим взаимнооднозначное соответствие между всеми комплексными числами и всеми точками плоскости. Если такое соответствие построено, то координатная плоскость называется комплексной плоскостью. Очень важной является интерпретация комплексного числа z = a + ib как вектора
с координатами (a; b) на комплексной плоскости с началом в точке O (0; 0) и концом в точке A с координатами (a; b). Ясно, что это соответствие является взаимнооднозначным. В самом деле, как было только что отмечено, любому комплексному числу z = a + ib соответствует вектор
и наоборот, каждому вектору соответствует, и притом единственное, число z = a + ib. Рассмотренные интерпретации комплексного числа позволяют называть комплексное число вектором или точкой на комплексной плоскости. Модель 1.14.
Комплексные числа на плоскости
Модулем комплексного числа называется длина вектора, соответствующего этому числу: Модуль комплексного числа z обычно обозначается
или r. Если
то
то есть для действительного числа модуль совпадает с абсолютной величиной. Ясно, что
для всех При этом
тогда и только тогда, когда Аргументом комплексного числа z = a + ib (z ≠ 0) называется величина угла между положительным направлением действительной оси и вектором
величина угла считается положительной, если угол отсчитывается против часовой стрелки, и отрицательным в противном случае. Угол φ, аргумент комплексного числа, обозначается φ = arg z. Отметим следующий важный факт: заданием своего модуля и аргумента комплексное число фиксируется однозначно. Обратное, вообще говоря, неверно: если задано комплексное число z ≠ 0, то его модуль определяется однозначно, а аргумент – нет. Действительно, если φ = arg z – аргумент этого комплексного числа, то все числа вида φ + 2πn также будут аргументами этого комплексного числа. Например, аргументами комплексного числа z = 1 + i являются углы
и т. д. Поэтому в качестве аргумента комплексного числа обычно выбирают значение –π ≤ arg z ≤ π. Заданием только лишь своего модуля определяется только комплексное число z = 0. Из определения тригонометрических функций следует, что φ = arg z тогда и только тогда, когда для этого φ выполняется система
Пример 2 Найти модуль и аргумент комплексного числа z = –1 – i. Показать решение Содержание Введение Комплексная плоскость и мнимая единица Модуль и фаза комплексного числа Показательная форма комплексного числа. Формула Эйлера Операции над комплексными числами. Комплексно-сопряженные числа Выводы Список литературы DSPL-2.0 — свободная библиотека алгоритмов цифровой обработки сигналов Распространяется под лицензией LGPL v3 Страница проекта на SourceForge Обнаружили ошибку?
Выделите ее мышью
и нажмите Введение Известно, что область определения некоторых функций на множестве вещественных чисел ограничена. Однако, ограниченная область определения функций на множестве вещественных чисел не означает,
что , или не имеют смысла.
Ограниченная область определения функций на множестве вещественных чисел говорит лишь о том,
что не может быть представлено вещественным числом.
Действительно, среди вещественных чисел не найти такого числа , квадрат которого был бы равен . При решении квадратных уравнений часто возникает ситуация, когда дискриминант отрицательный.
В этом случае это означает что парабола не пересекает прямую абсцисс ни в одной точке.
Другими словами, корни квадратного уравнения не существуют среди вещественных значений и их также надо искать
за пределами вещественных чисел. Все бесконечное множество вещественных чисел можно представить в виде одной числовой прямой (смотри рисунок 1),
на которой мы можем откладывать рациональные и иррациональные вещественные числа. Комплексная плоскость и мнимая единица Естественным расширением числовой прямой является плоскость, которую называют комплексной плоскостью.
Числовая прямая вещественных чисел и ее расширение до комплексной плоскости показано на рисунке 1.
Любая точка на комплексной плоскости определяет одно комплексное число.
Например на рисунке 1 показано число . Рисунок 1. Расширение множества вещественных чисел до множества комплексных числел Значение вещественного числа однозначно определяет его позицию на числовой прямой,
однако для определения позиции на плоскости одного числа недостаточно. Для «навигации» по комплексной плоскости вводятся две прямые и ,
которые пересекаются в начале координат. Любая точка комплексной плоскости задается двумя координатами и по осям и соответственно.
При этом само комплексное число можно записать как , где называется реальной частью
и задает координату точки комплексной плоскости на вещественной прямой , а называется мнимой частью
и задает координату точки комплексной плоскости на мнимой оси . Для того чтобы отделить одну координату от другой (реальную и мнимую части) вводят число ,
называемое мнимой единицей.
Это так раз то число, которого не существует на множестве действительных чисел.
Оно обладает особым свойством: .
Тогда комплексное число может не только перемещаться по вещественной прямой вправо и влево,
но и двигаться по комплексной плоскости потому что мы добавили ему слагаемое с мнимой единицей . Мнимую единицу в математической литературе принято обозначать как , но в технике буква уже закреплена
за обозначением электрического тока, поэтому чтобы избежать путаницы мы будем обозначать мнимую единицу буквой . Если и , тогда число является действительным и располагается на реальной оси . Если и , тогда число является чисто мнимым и располагается на мнимой оси . Если и , тогда число располагается в одной из четвертей комплексной плоскости. Модуль и фаза комплексного числа Представление комплексного числа как называют алгебраической формой записи.
Если из начала координат комплексной плоскости к точке восстановить вектор (смотри рисунок 1),
то можно вычислить длину этого вектора как (1) — неотрицательное вещественное число характеризующее длину вектора и называется модулем комплексного числа.
При этом сам вектор комплексного числа повернут относительно реальной оси на некоторый угол ,
называемый фазой. Связь реальной и мнимой частей комплексного числа с его амплитудой и фазой представлено следующим выражением: (2) Тогда комплексное число можно представить в тригонометрической форме: (3) Связь угла поворота вектора комплексного числа с реальной и мнимой частью комплексного числа,
представленного в алгебраической форме: (4) тогда (5) где учитывает четверть комплексной плоскости в которой расположено число : (6) Необходимость поправки возникает из-за того, что функция
периодическая функция с периодом рад. На рисунке 2 показаны значения параметра , в зависимости от того
в какой четверти комплексной плоскости расположено число. Рисунок 2. Значение поправки фазы комплексного числа в зависимости
от расположения на комплексной плоскости. На рисунке 2а исходное комплексное число расположено
в первой четверти комплексной плоскости и . Тогда и значение фазы комплексного числа равно: (7) Рассмотрим случай, когда комплексное число расположено
во второй четверти комплексной плоскости (рисунок 2б), т.е. и .
В этом случае и угол
также будет отрицательным (красная пунктирная линия).
Тогда для того, чтобы получить корректное значение фазы необходимо ввести поправку рад: (8) Пусть комплексное число расположено в третьей четверти комплексной плоскости (рисунок 2в),
т. (9) Если расположено в четвертой четверти комплексной плоскости (рисунок 2г),
т.е. и , то в этом случае и угол
будет отрицательным и равным фазе комплексного числа без поправок ( рад): (10) Функция которая позволяет получить фазу комплексного числа c учетом четверти комплексной плоскости в которой
расположено комплексное число называется функция арктангенс-2 и обозначается . Функция арктангенс-2 присутствует во всех математических приложениях и может быть использована для расчета верного
угла поворота вектора комплексного числа. Показательная форма комплексного числа. Формула Эйлера Мы уже рассмотрели алгебраическую и тригонометрическую формы записи комплексного числа.
Помимо алгебраической и тригонометрической формы существует также показательная форма комплексного числа: (11) связанная с тригонометрической формой формулой Эйлера: (12) Cоотношение (12) легко доказать, если произвести разложение экспоненты в ряд Тейлора: (13) Представим ряд (13) в виде суммы четных и нечетных членов последовательности: (14) Рассмотрим более подробно мнимую единицу в четной и нечетной степенях. Из определения мнимой единицы можно сделать вывод, что , тогда ,
в свою очередь . Таким образом, можно сделать вывод что . Построим аналогичным образом соотношение для нечетных степеней: , тогда ,
в свою очередь и окончательно можно записать:
. Тогда (14) можно представить как: (15) В выражении (15) первая сумма по четным степеням дает разложение в ряд Тейлора функции ,
а вторая сумма по нечетным степеням дает разложение в ряд Тейлора функции .
Таким образом, получено доказательство справедливости формулы Эйлера (12). Необходимо отметить, что формула Эйлера является одной из важнейших в теории функций комплексного переменного.
Так например при помощи формулы Эйлера можно связать математические константы и
с использованием мнимой единицы : (16) Операции над комплексными числами. Комплексно-сопряженные числа В данном параграфе мы кратко рассмотрим операции над комплексными числами.
Сумма двух комплексных чисел и представляет
собой комплексное число : (17) При сложении реальные и мнимые части комплексного числа также складываются. Рисунок 3. Операции над комплексными числами Разность двух комплексных чисел и
представляет собой комплексное число (18) При вычитании реальные и мнимые части комплексного числа также вычитаются.
На комплексной плоскости операцию вычитания можно реализовать как вычитание
векторов по правилу параллелограмма (рисунок 3б).
На первом шаге из вектора формируется вектор (обозначенный пунктирной линией на рисунке 3б),
после чего вектор складывается с вектором по правилу параллелограмма. Для того чтобы получить формулу для умножения комплексных числен необходимо перемножить
два комплексных числа по правилу умножения многочленов: (19) Умножение комплексных проще выполнять если числа представлены в показательной форме: (20) При перемножении в показательной форме модули комплексных чисел перемножаются а фазы складываются. Введем понятие комплексно-сопряженного числа. Число является
комплексно-сопряженным числу . Комплексно-сопряженные числа отличаются знаком перед мнимой частью. Графически комплексно-сопряженные числа показаны на рисунке 3г. При этом можно заметить, что модули комплексно-сопряженных чисел равны
, а фазы имеют противоположные знаки. Произведение комплексно-сопряженных чисел (21) представляет собой действительное число равное квадрату модуля этих чисел. Из элементарных операций нам осталось рассмотреть лишь деление комплексных чисел.
Рассмотрим результат деления комплексных чисел в показательной форме: (22) Таким образом, при делении комплексных чисел модуль частного равен частному модулей исходных чисел,
а фаза равна разности фаз исходных чисел. При этом необходимо потребовать, чтобы был не равен нулю,
иначе у нас появится деление на ноль при расчете модуля частного. Рассмотрим теперь деление комплексных чисел в алгебраической форме: (23) Домножим и числитель и знаменатель на число, комплексно-сопряженное знаменателю: (24) Выводы В данной статье введено понятие комплексного числа и рассмотрены основные его свойства. Введено понятие мнимой единицы. Подробно рассмотрена комплексная плоскость и представление комплексных чисел в алгебраической,
тригонометрической и показательной формах.
Введены понятия модуля и фазы комплексного числа. Рассмотрены основные арифметические операции над комплексными числами. Показано как выполнять операции сложения, вычитания в алгебраической форме,
введено понятие комплексно-сопряженных чисел,
а также операции умножения и деления в показательной и алгебраической формах. Информация была полезна? Поделитесь с друзьями! Список литературы [1]
Пантелеев А.В., Якимова А.С.
Теория функций комплексного переменного и операционное исчисление в примерах и задачах. [2]
Дубровин В.Т.
Теория функций комплексного переменного. Теория и практика
Казань: Казанский государственный университет, 2010.
[PDF] Последнее изменение страницы: 12.05.2022 (19:41:15) Страница создана Latex to HTML translator ver. 5.20.11.14 Часть 2. Теория функций комплексной переменной. Лекция 1. Комплексные числа, 3 формы записи, основные операции. Алгебраическая форма записи комплексного числа z=x+iy, x = Re z – действительная часть (real), y = Im z – мнимая часть комплексной числа (imagine), i – мнимая единица (i2 = -1). Степени мнимой единицы: i0 =1, i1 = i, i2 = -1, i3 = -i, i4 = 1, i5 = i, i6 = -1, i7 =-i, i8 =1,….значения повторяются через 4. Если ввести в комплексной плоскости полярную систему координат (полярные координаты ), то комплексное число можно записать в тригонометрической форме . Комплексное число можно ассоциировать с его радиусом – вектором. Полярная координата — это модуль радиуса – вектора или просто модуль комплексного числа , а полярный угол — аргумент комплексного числа, . Аргумент определяется так сложно, потому что имеет область значений , а необходимо обеспечить возможность изменения полярного угла в диапазоне . Пример. Записать в тригонометрической форме. . Записать в тригонометрической форме. . Справедлива формула Эйлера . Это – одна из самых красивых и фундаментальных формул в математике. Используя формулу Эйлера, можно записать комплексное число в показательной форме . Алгебраическая, тригонометрическая и показательная формы – три формы записи комплексных чисел. Рассмотрим операции над комплексными числами. Сложение и вычитание комплексных чисел удобнее всего производить в алгебраической форме записи. . Например, . Заметим, что числа называются комплексно сопряженными числами. Сложение или вычитание комплексных чисел соответствует сложению или вычитанию их радиусов векторов и может быть проведено по «правилу параллелограмма » или «правилу треугольника » . Умножение и деление комплексных чисел тоже можно выполнять в алгебраической форме. Примеры. , . Здесь числитель и знаменатель дроби умножают на число, сопряженное знаменателю, чтобы получить в знаменателе действительное число. Удобнее выполнять умножение или деление в тригонометрической или показательной формах: . . Итак, действует правило: при умножении комплексных чисел их модули перемножаются, а аргументы складываются. При делении комплексных чисел их модули делятся, а аргументы вычитаются. Особенно удобно использовать тригонометрическую и показательную формы при возведении комплексного числа в степень. . С другой стороны, . Из сопоставления этих выражений получается знаменитая формула Муавра . Ее удобно применять для выражения синусов и косинусов кратных углов через степени синусов и косинусов самого угла. Например, , Отделяя действительные и мнимые части, получим . Например, . Здесь можно было . Рассмотрим «пятое действие арифметики » – извлечение корня.. Пусть . Тогда . Получим формулу . . Из формулы ясно, что все корней лежат в комплексной плоскости на круге радиуса с центром в начале координат на равном угловом расстоянии друг от друга , причем первый корень расположен под углом к действительной оси. Найдем, например, . Определяем . Все корни лежат на круге радиусом 2 с центром в начале координат, на угловом расстоянии друг от друга, причем первый корень лежит под углом к действительной оси. Множества на комплексной плоскости. Для того, чтобы правильно строить типичные кривые на комплексной плоскости, прежде всего надо помнить, что . Следовательно, — это окружность радиуса с центром в точке на комплексной плоскости (расстояние от точки до точки равно ). — это круговое кольцо с центром в точке , включая внутреннюю окружность радиусом , исключая внешнюю окружность радиусом . — это прямая линия на комплексной плоскости , — угол наклона прямой к действительной оси. Некоторые часто встречающиеся кривые и области изображены ниже При построении двух последних областей надо вспомнить определение эллипса (геометрическое место точек плоскости, сумма расстояний которых от двух фиксированных точек плоскости постоянна и равна ()) и определение параболы (геометрическое место точек плоскости, расстояние которых от фиксированной точки плоскости равно расстоянию до фиксированной прямой ). Открытые и замкнутые множества, односвязное множество. называется множество . Точка называется внутренней точкой множества, если существует ее окрестность, целиком принадлежащая этому множеству. Например, все точки круга — внутренние. Точка называется граничной точкой множества, если в любой ее окрестности найдутся как точки, принадлежащие множеству, так и точки, не принадлежащие множеству. Границей множества называется совокупность его граничных точек. Например, окружность — граница круга . Множество называется открытым, если оно состоит только из внутренних точек. Например, круг — открытое множество. Замыканием множества называется объединение множества и его границы. Замкнутым называется множество, совпадающее со своим замыканием. Множество называется ограниченным, если его можно накрыть кругом конечного радиуса. Открытой областью (или просто областью) называется открытое множество, любые две точки которого можно соединить ломаной, целиком принадлежащей множеству. Замкнутой областью называется объединение открытой области и ее границы. Рассмотрим последовательность комплексных чисел . Последовательность называется неограниченно возрастающей, если . То есть все элементы неограниченно возрастающей последовательности нельзя накрыть кругом конечного радиуса. По определению полагают, что все неограниченно возрастающие последовательности сходятся к (единственной) бесконечно удаленной точке ( или БУТ), которая не принадлежит комплексной плоскости. Пополняя комплексную плоскость, мы получаем расширенную комплексную плоскость. Пояснить единственность бесконечно удаленной точки можно, рассматривая сферу Римана Кривой на комплексной плоскости называется однопараметрическое семейство точек плоскости . Точкой самопересечения или кратной точкой кривой называется точка, отвечающая двум или более значениям параметра. Кривая, не содержащая кратных точек, называется простой или жордановой кривой. Теорема Жордана. Любая замкнутая жорданова кривая делит расширенную комплексную плоскость на две области, общей границей которых она является. Одна из этих областей ограничена и называется внутренностью кривой. Вторая не ограничена и называется внешностью кривой. Множество называется односвязным, если для любой замкнутой кривой либо внутренность кривой принадлежит , либо внешность кривой принадлежит . Например, множества , да и все изображенные на рисунках области, за исключением кругового кольца — односвязные, они «не содержат дыр » . Цели урока Систематизировать теоретический материал по теме. Повторить перевод чисел из алгебраической в тригонометрическую форму записи комплексных чисел, действия с комплексными числами. Обобщить знания учащихся по теме и рассмотреть вопросы по теме «Функция комплексного переменного» в межпредметной связи с темой «Преобразования на плоскости». Развивать: способности анализировать, планировать, контролировать свою деятельность (взаимо- и самоконтроль). Формировать коммуникативные навыки, оперировать математической терминологией. Продолжить освоение интерактивной доски. I. Организационный момент Учащиеся записывают тему урока «Комплексные числа». Учитель: Впервые в истории комплексными числами стали заниматься в XVI веке в связи с решением уравнений. Несмотря на то, что с комплексными числами оперировать ничуть не сложнее, чем с действительными, но до начала XIX века комплексные числа рассматривались как очень сложные, почти мистические объекты. Вы привыкли видеть высказывания ученых-математиков на наших уроках, я предлагаю вам прочитать четверостишье русского писателя Валерия Яковлевича Брюсова о числах. (Презентация «Комплексные числа». Слайд 3 «Девиз урока». Вам поклоняюсь, вас желаю, числа! Учитель: Как появилось понятие комплексные числа, и кто из ученых работал в этой области математики? Слайд 4 «Историческая справка». Итальянский математик Джерсламс Кардано (1501-1576), решая задачу о представлении числа 10 в виде суммы двух слагаемых так, чтобы произведение этих слагаемых равнялось 40, встретился с ситуацией, что система не имеет действительных решений. Величины, квадрат которых равен отрицательному числу Кардано назвал «софически отрицательными», считал, что они лишены всякого реального содержания. Писал: «Для осуществления таких действий нужна была бы новая арифметика, которая была бы настолько же утонченной, насколько бесполезной». Слайд 5 «Основатели теории комплексных чисел». Бомбелли — итальянский алгебраист в 1572г. ввёл правила арифметических действий. Р. Декарт — французский математик и философ в 1637г. Дал название «мнимые числа». Эйлер-русский математик, швейцарец по происхождению, ввёл символ i , а в 1748г. нашел формулу, носящую теперь его имя. из формулы получается таинственное равенство единения арифметики, алгебры, геометрии и анализа. К.Гаусс в 1799г. доказал основную теорему алгебры, в 1831г. предложил геометрическую интерпретацию, независимо от него датчанином Весселем (1797) и французом Аргоном (1806) предложено геометрическое толкование комплексных чисел. Начиная с XIX века, и позже применение комплексных чисел значительно возросло. Софья Ковалевская решила, используя теорию функции комплексного переменного, задачу о вращении твердого тела вокруг неподвижной точки. Русский ученый в области механики, основоположник современной гидродинамики Николай Егорович Жуковский, вывел формулу для определения подъемной силы крыла, которая теперь носит его имя. Учитель: Какие термины встречаются при изучении темы? Слайд 6 «Словарь терминов». Комплексный-лат. составной, сложный. Термин введён Гауссом. Учитель: После обсуждения учащиеся знакомятся с предполагаемым планом. Слайд 7 «Цели урока и план работы на уроке» 1 этап — повторение вопросов теории. Учитель: Вы согласны, что эти этапы необходимы? II. Работа с теоретическим материалом Учитель: Вы готовились к теоретическому зачету. Проверьте себя. Работайте устно в парах. Основные формулы и теоремы записывайте в тетради. Слайд 8 «Этап 1.1. Повторение вопросов теории». 1) Сформулируйте определение комплексного числа. Проводится проверка и коррекция ошибок. Слайд 9 «Этап 1.2.Основные определения». Число вида z=a+bi называется комплексным, а и b-действительные числа, i-мнимая единица Re z=a, Im z=b Модулем комплексного числа называется Аргументом комплексного числа z называется угол между положительным направлением полуоси ОХ и радиус-вектором ОМ, М(а,b) Главный аргумент arg z заключен в границах Тригонометрическая форма комплексного числа Слайд 10 «Этап 1.3.Основные формулы». III. Вычислительный практикум Учитель: Проверим, как вы умеете применять формулы. В какой форме удобнее выполнять задание (алгебраической или тригонометрической)? Запишите только номер задания и ответ. Слайд 11 «Этап 2.1. Вычислительная работа». Выполните действия, ответы запишите в тетрадь. 2) i-2-(6-5i) 3) (1+i)(1-i) 4) i3, i101 5) 3/i 6) (1 +i)4 Разложите на множители в комплексных числах: 7) x2 + 1, 8) a2 + 4b2, 9) x4 — 16 Выполните самопроверку. Слайд 12 «Этап 2.2. Проверь себя!» 1) 11i 2) -8+6i 3) 2 4) –i, I 5) -3i 6) -4 7) (x-i)(x+i) 8) (a+2bi)(a-2bi) 9) (x-2)(x+2)(x-2i)(x+2i) Учитель: Работаем с тригонометрической формой комплексного числа. Слайд 13 «Этап 2.3. Тригонометрическая форма комплексного числа». Изобразите комплексное число на плоскости z=-2+2i Запишите данное число в тригонометрической форме. Выполняется проверка с помощью режима интерактивной доски, вызывается ученик со своим решением. Проанализируйте, как изображение комплексного числа помогает при решении задачи? Какие варианты ответов? Кто не согласен с ответом? Какие дополнения, уточнения? Слайд 14 «Этап 2.4. Решите задачу различными способами в алгебраической и тригонометрической форме» Найдите z6, если В режиме интерактивной доски рассматриваются решения учащихся. Для тех, кто затрудняется, предлагается следующий слайд. Слайд 15 «Этап 2.5. Указания к решению». 1 способ Если z=x+iy, то получаем уравнение 3x+3yi-x+yi=-4+8i, x+2yi=-2+4i, Используем условие равенства комплексных чисел, получаем, что х=-2, у=2. При возведении в квадрат, получаем число -8i, которое возводим в куб. Ответ: 512i 2 способ Представленное в тригонометрической форме число возвести по формуле Муавра в 6-ю степень. Учитель: Какие этапы плана выполнили? Что еще необходимо повторить? (Построение ГМТ, удовлетворяющих заданным условиям) Вернемся к слайду 7. IV. Выход на новый материал Учитель: Выполните практическую работу в тетради (с обоснованием построения). Слайд 16 «Этап 3.1.Геометрическое место точек» Изобразите на плоскости ГМТ, удовлетворяющих условиям: Учитель оказывает индивидуальную помощь. Фронтальное обсуждение результатов практической работы с использованиемрежима интерактивной доски. Итак, проверьте правильность выполненных построений. Слайд 17 «Этап 3.2.1. Полученные ГМТ» №1. Окружность с центром (0;-1) и радиусом 1,5 №2. Полуплоскость №3. Угол, заключенный между заданными лучами. Модуль равен 1. Простейший аргумент Учитель: У кого возникли затруднения? Кому нужна помощь, консультация? Предлагаю подробное решение задач. Слайд 18 «Этап 3.2.2. Решения задач». V. Освоение нового материла Слайд 19 «Этап 3.3. Функции комплексного переменного». Задайте условиями четверть круга с центром в точке (0;0), радиусом 2. Выполните преобразования и постройте ГМТ w, удовлетворяющее условию: Выполните: I вариант — а, в, д В режиме интерактивной доски проводится проверка всех заданий. Учитель: Какие виды геометрических преобразований использовали при решении задач? Слайд 20 «Этап 3.4.1.Решения задач». Слайд 21 «Этап 3.4.2.Решения задач». Внутренние точки переходят во внешние, штриховка фигуры. Выводы учащихся: выполняли преобразования — параллельный перенос; гомотетия; поворот. Встретился и новый вид — преобразование инверсия, что в переводе с латинского, переворачивание, перестановка. VI. Контрольный элемент Слайд 22 «Этап 4.1. Итоговый тест. Проверь себя! («да» или «нет»)» 1. Число 1+i является действительным? 5. Число имеет аргумент равный Проверка решения учащимися. Тетради сдаются учителю. Слайд 23 «Этап 4.2. Ответы» 1. Нет 2. 3. Да 4. Да 5. Нет VII. Итог урока Слайд 7 «Цели урока и план работы на уроке». 1 этап — повторение вопросов теории. Учитель: Удалось ли реализовать цели данного урока? Что узнали нового? Что не совсем получилось? На основании геометрической интерпретации применение комплексных чисел эффективно в тех областях, где приходится оперировать с величинами, которые можно представить в виде точки на плоскости или плоского вектора. Поэтому теория функции комплексного переменного нашла широкое употребление для решения вопросов теоретической физики, гидродинамики, электротехники, кораблестроения, картографии. Те из вас, кто продолжит свое образование в технических вузах, смогут глубже ознакомиться с теорией функции комплексного переменного и её приложениями в различных областях науки и техники. Спасибо за урок. Не
занимайтесь комплексными числами после
комплексного обеда На
данном уроке мы познакомимся с понятием
комплексного числа, рассмотрим
алгебраическую, тригонометрическую и
показательную форму комплексного числа.
А также научимся выполнять действия с
комплексными числами: сложение, вычитание,
умножение, деление, возведение в степень
и извлечение корня. Не беспокойтесь, я
вас напугал, я вас и рассмешу. Для освоения
комплексных чисел не требуется каких-то
специальных знаний из курса высшей
математики, и материал доступен даже
школьнику. Достаточно уметь выполнять
основные алгебраические действия с
«обычными» числа, и немного рубить в
тригонометрии, впрочем, если что забылось,
я напомню. Урок
состоит из следующих параграфов: 1)
Понятие комплексного числа. На
любой вкус и цвет – кому, что интересно.
А комплексные числа действительно
становятся наиболее интересной темой,
после того, как студенты знакомятся с
другими разделами высшей алгебры =).
Если Вы являетесь чайником, или
только-только приступили к изучению
комплексных чисел, то параграфы лучше
прочитать по порядку, без «перескоков». Сначала
вспомним «обычные» школьные числа. В
математике они называются множеством
действительных чисел и
обозначаются буквой
(в
литературе, рукописях заглавную букву
«эр» пишут жирной либо утолщённой). Все
действительные числа сидят на знакомой
числовой прямой: Компания
действительных чисел очень пёстрая –
здесь и целые числа, и дроби, и иррациональные
числа. Прежде
чем, мы перейдем к рассмотрению комплексных
чисел, дам важный совет: не пытайтесь
представить комплексное число «в жизни»
– это всё равно, что пытаться представить
четвертое измерение в нашем трехмерном
пространстве. Если хотите, комплексное
число – это двумерное число. И курить
бессмысленно. … Так, кто тут улыбается?
Видимо, действительно не помогло. Комплексным
числом
называется
число вида
,
где
и
–
действительные числа,
–
так называемая мнимая
единица.
Число
называется действительной
частью ()комплексного
числа
,
число
называется мнимой
частью () комплексного
числа
. –
это
ЕДИНОЕ ЧИСЛО, а не сложение.
Действительную и мнимую части комплексного
числа, в принципе, можно переставить
местами:
или
переставить мнимую единицу:
–
от этого комплексное число не изменится. Но
стандартно комплексное число принято
записывать именно в таком порядке: Чтобы
всё было понятнее, сразу приведу
геометрическую интерпретацию. Комплексная
плоскость состоит из двух осей:
–
действительная ось
–
мнимая ось Правила
оформления чертежа практически такие
же, как и для чертежа в декартовой системе
координат (см. Графики
и свойства элементарных функций).
По осям нужно задать размерность,
отмечаем: ноль; единицу
по действительной оси; мнимую
единицу
по
мнимой оси. Не
нужно проставлять все значения: …–3,
–2, –1, 0, 1, 2, 3,… и
. Да
чего тут мелочиться, рассмотрим чисел
десять. Построим
на комплексной плоскости следующие
комплексные числа: ,
,
,
,
,
,
, По
какому принципу отмечены числа на
комплексной плоскости, думаю, очевидно
– комплексные числа отмечают точно так
же, как мы отмечали точки еще в 5-6 классе
на уроках геометрии. Числа
,
,
–
это комплексные числа с нулевой мнимой
частью. Числа
,
,
–
это, наоборот, чисто
мнимые числа,
т.е. числа с нулевой действительной
частью. Они располагаются строго на
мнимой оси
. В
числах
,
,
,
и
действительная и мнимая части не равны
нулю. Такие числа тоже обозначаются
точками на комплексной плоскости, при
этом, к ним принято проводить радиус-векторы
из начала координат (обозначены красным
цветом на чертеже). Радиус-векторы к
числам, которые располагаются на осях,
обычно не чертят, потому-что они
сливаются с осями. Алгебраическая
форма комплексного числа. Сложение,
вычитание, умножение и деление комплексных
чисел С
алгебраической формой комплексного
числа мы уже познакомились,
–
это и есть алгебраическая форма
комплексного числа. Почему речь зашла
о форме? Дело в том, что существуют еще
тригонометрическая и показательная
форма комплексных чисел, о которых
пойдет речь в следующем параграфе. Действия
с комплексными числами не представляют
особых сложностей и мало чем отличаются
от обычной алгебры. Сложение
комплексных чисел Пример
1 Сложить
два комплексных числа
, Для
того чтобы сложить два комплексных
числа нужно сложить их действительные
и мнимые части: Просто,
не правда ли? Действие настолько очевидно,
что не нуждается в дополнительных
комментариях. Таким
нехитрым способом можно найти сумму
любого количества слагаемых: просуммировать
действительные части и просуммировать
мнимые части. Для
комплексных чисел справедливо правило
первого класса:
–
от перестановки слагаемых сумма не
меняется. Вычитание
комплексных чисел Пример
2 Найти
разности комплексных чисел
и
,
если
, Действие
аналогично сложению, единственная
особенность состоит в том, что вычитаемое
нужно взять в скобки, а затем – стандартно
раскрыть эти скобки со сменой знака: Результат
не должен смущать, у полученного числа
две, а не три части. Просто действительная
часть – составная:
.
Для наглядности ответ можно переписать
так:
. Рассчитаем
вторую разность: Здесь
действительная часть тоже составная: Чтобы
не было какой-то недосказанности, приведу
короткий пример с «нехорошей» мнимой
частью:
.
Вот здесь без скобок уже не обойтись. Комплексное число представляет собой комбинацию Реальные числа — это такие числа, как: Почти любое число, которое вы можете придумать, является действительным числом! Мнимые числа, когда в квадрате дают отрицательный результат . Обычно этого не происходит, потому что: Но представьте, что такие числа существуют, потому что они нам нужны. Поговорим еще о мнимых числах… «Единичное» мнимое число (например, 1 для действительных чисел) равно i, которое является квадратным корнем из −1 Потому что, возведя i в квадрат, мы получим −1 i 2 = −1 Примеры мнимых чисел Номера: И мы держим здесь маленькую букву «i», чтобы напомнить себе, что нам нужно умножить на √−1 Когда мы объединяем действительное число и мнимое число, мы получаем комплексное число : Можем ли мы составить число из двух других чисел? Мы можем точно! Мы постоянно делаем это с дробями. Дробь 3 / 8 — это число, состоящее из 3 и 8. Мы знаем, что это означает «3 из 8 равных частей». Комплексное число — это всего лишь два числа, сложенные вместе (действительное и мнимое число). Итак, у комплексного числа есть действительная и мнимая части. Но любая часть может быть 0 , поэтому все действительные числа и мнимые числа также являются комплексными числами. Комплекс , а не означает сложный. Это означает, что два типа чисел, действительные и мнимые, вместе образуют комплекс , точно так же, как комплекс зданий (здания, соединенные вместе). Вы знаете, как идет числовая линия влево-вправо ? Хорошо, пусть мнимые числа идут вверх-вниз : И получаем Сложный Самолет Комплексное число теперь может отображаться в виде точки: Чтобы сложить два комплексных числа, складываем каждую часть отдельно: (а+б я ) + (с+г я ) = (а+с) + (б+г) я (3 + 2i) + (1 + 7i) Попробуем еще: (3 + 5 I ) + (4 — 3 I ) . Чтобы умножить комплексные числа: Каждая часть первого комплексного числа умножается на Просто используйте «FOIL», что означает » F первоначальных, O маточных, I внутренних, L астровых» (подробнее см. Биномиальное умножение): (A + B I ) (C + D I ) = AC + AD I + BC I + BD I 2 9006 I 2 Вот так: (3 + 2i)(1 + 7i) = 3×1 + 3×7i + 2i×1+ 2i×7i = 3 + 21i + 2i + 14i 2 = 3 + 21i + 2i − 14 (поскольку i 2 = −1) = −11 + 23i А это: (1 + i)(1 + i)= 1×1 + 1×i + 1×i + i 2 = 1 + 2i − 1 (потому что i 2 = −1) = 0 + 2i Используйте это правило: (a+b i )(c+d i ) = (ac−bd) + (ad+bc) i Пример: (3 + 2i)(1 + 7i) = (3×1 − 2×7) + (3×7 + 2×1)i = −11 + 23i Это просто метод «ФОЛЬГА» после небольшой работы: (a+b i )(c+d i ) =ac + ad i + bc i + bd i 2 метод FOIL i i 0 i − bd (потому что i 2 = −1) = (ac − bd) + (ad + bc) i (собирая подобные термины) И здесь у нас есть (ac − bd) + (ad + bc) i шаблон. Это правило, безусловно, быстрее, но если вы его забудете, просто запомните метод FOIL. Ради интереса воспользуемся методом вычисления i 2 Мы можем записать i с действительной и мнимой частями как 0 + i i 2 = (0 + i) 2 = (0 + i)(0 + i ) = (0×0 − 1×1) + (0×1 + 1×0) i = −1 + 0 i = −1 И это хорошо согласуется с определением, что я 2 = −1 Так все замечательно работает! Дополнительные сведения см. в разделе Умножение комплексных чисел. Через минуту нам нужно будет узнать о конъюгатах! В сопряжении мы меняем знак в середине следующим образом: Спряжение часто пишется с чертой над ним: 5 − 3 i = 5 + 3 i Конъюгат используется для облегчения сложного деления. Хитрость заключается в том, чтобы умножить верхнее и нижнее на сопряженное нижнее . 2 + 3 I 4 — 5 I Умножение верхней и нижней 4 − 5 i × 4 + 5 i 4 + 5 I = 8 + 10 I + 12 I + 15 I 2 16 + 20 I — 20 I — 25 I 666995595959559559559559559559559595959595959595959595959595959595959595959595959595959595959595959595959595959595959595959595959595959н. Теперь помните, что I 2 = −1, так: = 8 + 10 I + 12 I — 15 16 + 200009 I — 20 I + 25 9000 Добавьте условия «Нравится» (и обратите внимание, как внизу 20 i − 20 i Отменить!): = −7 + 22 I 41 Наконец, мы должны поместить ответ в A + B I Форма: = —7 41 + — 7 41 + — 7 41 + —7 41 + —7 419 41952 + — 7 4110 41952 = —7 4110 4106. ГОТОВО! Да, нужно немного посчитать. Но это можно сделать. Однако есть более быстрый способ. В предыдущем примере интересно было то, что произошло внизу: (4 — 5 i )(4 + 5 i ) = 16 + 20 i — 20 i — 25 i 2 Средние члены (20 i − 20 i ) сокращаются: (4 — 5 i )(4 + 5 i ) = 16 — 25 i 2 Также i 2 = −1 : (4 — 5 i )(4 + 5 i ) = 16 + 25 А 16 и 25 — это (магически) квадраты 4 и 5: (4 — 5 i )(4 + 5 i ) = 4 2 + 5 2 Довольно простой результат. Общее правило: (a + b i ) (a − b i ) = a 2 + b 2 Это может сэкономить нам время при делении, например: 2 + 3 i 4 − 5 i Умножить верх и низ на сопряженное число 4 − 5 I : 2 + 3 I 4 — 5 I × 4 + 5 I 4 + 5 + = 8 + 10999999999999 11110 10 . I + 15 I 2 = −7 + 22 I 41 , а затем обратно в A + B I : ГОТОВО! Мы часто используем z для комплексного числа. И Re() для действительной части и Im() для мнимой части, например: Что выглядит на комплексной плоскости так: Прекрасное множество Мандельброта (на фото) основано на комплексных числах. Это график того, что происходит, когда мы берем простое уравнение z 2 + c (оба комплексных числа) и возвращаем результат обратно в z снова и снова. Цвет показывает, как быстро растет z 2 + c , а черный означает, что он остается в определенном диапазоне. Вот изображение, полученное путем увеличения множества Мандельброта 440, 1070, 273, 1071, 1072, 443, 3991, 271, 3992, 3993 Энди Хейс,
Рам Мохит,
Тадеуш Абий,
а также способствовал Основная статья: Сложный самолет Комплексные числа часто представляются на комплексной плоскости , иногда известной как плоскость Аргана или диаграмма Аргана . Комплексные числа, изображенные на комплексной плоскости Основное преимущество комплексных чисел перед упорядоченными парами заключается в том, что операции сложения и умножения определены для комплексных чисел, тогда как эти операции не определены для упорядоченных пар. В комплексном числе Z = a + ib, Z = a + ib, Z = a + ib, Z = a⏟partreal+i⏟unitimaginaryb⏟partimaginary.Z = \underbrace{a} _{\overset{ \text{real}}{\text{part}}} + \underbrace{i}_{\overset{\text{воображаемый}}{\text{единица}}} \underbrace{b}_{\overset{\ text{воображаемый}}{\text{part}}}. Здесь iii называется мнимой единицей , и математически его значение равно i=−1.i = \sqrt{-1}.i=−1. В этом разделе мы обсудим некоторые важные свойства i:i:i: 9{200}\big).(11+12+i3+i4)+(i5+i6+i7+i8)+⋯+(i193+i194+i195+i196)+(i197+i198+i199+i200). Теперь, исходя из приведенного выше результата, значение в каждой скобке становится равным 000 как сумма 4 последовательных степеней iii, равная 000. Имеется 50 скобок, и каждая скобка равна 0. Следовательно, 50(0)=0. □50(0)=0.\ _\квадрат50(0)=0. □ Сложение комплексных чисел следует алгебраическому принципу объединения одинаковых терминов. Действительные части комплексных чисел считаются одинаковыми, а комплексные части считаются одинаковыми. Добавление комплексных номеров: Даны комплексные числа a+bi a + bi a+bi и c+di c+di c+di, их сумма равна (а+с)+(б+г)я. Что такое (4+3i)+(2+2i)?(4+3i)+(2+2i)?(4+3i)+(2+2i)? Складывая по отдельности действительную и мнимую части, получаем 4+3i+2+2i=(4+2)+(3+2)i=6+5i. □ 4+3i+2+2i = (4+2) + (3+2)i = 6+5i.\ _\square4+3i+2+2i=(4+2)+(3+2)i= 6+5и. □ Обратите внимание, что действительные числа добавлялись только к другим действительным числам, а мнимые числа добавлялись только к другим мнимым числам. Несколько дополнительных примеров: Умножение комплексных чисел следует принципу умножения биномов. Одно заметное отличие состоит в том, что при умножении мнимых членов получается действительное число. 92\\
&= (ac) + (ad+bc)i + (bd)(-1) \\
&= (ac — bd) + (ad+bc)i .
\end{выровнено} (a+bi)×(c+di)=a(c+di)+bi(c+di)=(ac)+(ad)i+(bc)i+(bd)i2=( ac)+(ad+bc)i+(bd)(-1)=(ac-bd)+(ad+bc)i. Отдел комплексных номеров: Если Z1=a+ibZ_1 = a + ibZ1=a+ib и Z2=c+idZ_2 = c + idZ2=c+id — любые два комплексных числа, то деление двух комплексных чисел выполняется простым рационализаторством комплекс номер или умножение и деление на сопряженное число знаменателя . Это обсуждается в следующем разделе. Основная статья: Комплексные конъюгаты Комплексное сопряжение комплексного числа a+bia+bia+bi есть a-bia-bia-bi. Назовите комплексно-сопряженные числа следующих чисел: Их комплексные сопряжения следующие: −5+6i ⟹ −5−6i-5+6i \ подразумевает -5-6i−5+6i⟹−5−6i 83−i ⟹ 83+i\frac{8}{3}-i \подразумевает \frac{8}{3}+i38−i⟹38+i −2i ⟹ 2i:-2i \ подразумевает 2i:−2i⟹2i: комплексное сопряжение мнимого числа есть отрицание этого числа. 17 ⟹ 17:17 \подразумевает 17:17⟹17: комплексно-сопряженным вещественным числом является само число. □_\квадрат□ Комплексное сопряжение также можно рассматривать как отражение комплексного числа относительно действительной оси на комплексной плоскости. Комплексно-сопряженные пары на комплексной плоскости Комплексно-сопряженные пары полезны для рационализации знаменателей, содержащих комплексные числа. Процесс рационализации сложного знаменателя очень похож на то, как этот процесс работает для радикалов. Рационализируйте знаменатель и запишите в стандартной форме: 3+2i5−2i.\frac{3+2i}{5-2i}.5−2i3+2i. Сопряжение знаменателя равно 5+2i.5+2i.5+2i. Умножьте числитель и знаменатель на это число: 3+2i5−2i=(3+2i)(5+2i)(5−2i)(5+2i)=11+16i29=1129+1629i. □\begin{выровнено}
\frac{3+2i}{5-2i} &= \frac{(3+2i)(5+2i)}{(5-2i)(5+2i)} \\ \\
&= \frac{11+16i}{29} \\ \\
&= \frac{11}{29}+\frac{16}{29}i. Кроме того, теорема о комплексно-сопряженных корнях утверждает, что комплексные корни многочленов всегда входят в сопряженные пары. Теорема о комплексно-сопряженном корне: 92-2х+2,
\end{выровнено}x2+bx+c=(x−1−i)(x−1+i)=x2−2x+2, , что подразумевает b=-2b=-2b=-2 и c=2,c=2,c=2, поэтому b+c=0.b+c=0.b+c=0. □_\квадрат□ Если ∣z1∣=∣z2∣=∣z3∣=…=∣zn∣=1,\left|z_1\right|=\left|z_2\right|=\left|z_3\right|=\ldots=\left |z_n\right|=1,∣z1∣=∣z2∣=∣z3∣=…=∣zn∣=1, то докажите, что ∣1z1+1z2+1z3+⋯+1zn∣=∣z1+z2+z3+⋯+zn∣.\left|\frac{1}{z_1}+\frac{1}{z_2}+\frac{1}{ z_3}+\cdots+\frac{1}{z_n}\right|=\left|z_1+z_2+z_3+\cdots+z_n\right|.∣∣∣∣z11+z21+z3 1+⋯+zn1∣∣∣∣=∣z1+z2+z3+⋯+zn∣. 92&=1 \\\\
z_1\overline{z_1}=1, z_2\overline{z_2}=1, z_3\overline{z_3}=1, \ldots, z_n\overline{z_n}&=1\\\\
\frac{1}{z_1}=\overline{z_1}, \frac{1}{z_2}=\overline{z_2}, \frac{1}{z_3}=\overline{z_3}, \ldots, \frac {1}{z_n}&=\overline{z_n}\\\\
\влево| \frac{1}{z_1}+ \frac{1}{z_2}+ \frac{1}{z_3}+ \cdots+\frac{1}{z_n}\right|&=\left|\overline{z_1} + \overline{z_2}+ \overline{z_3}+ \cdots+\overline{z_n}\right|\\\\
&=\left|\overline{z_1+ z_2+z_3+ \cdots+z_n}\right|\\\\
&=\влево|z_1+ z_2+z_3+ \cdots+z_n\вправо| \qquad \big(\text{с} \left|\overline{z}\right|=\left|z\right|\big)\\\\
\Стрелка вправо\влево| \frac{1}{z_1}+ \frac{1}{z_2}+ \frac{1}{z_3}+ \cdots+\frac{1}{z_n}\right|&=\left|z_1+ z_2+z_3+ \ cdots+z_n\справа|. Основная статья: Гауссовы целые числа Гауссово целое число — это комплексное число a+bi,a+bi,a+bi, где aaa и bbb — целые числа. Следует отметить, что целое число Гаусса равно , а не , если мнимая часть не равна 0. Целые числа Гаусса: 3+2i3+2i3+2i 7-8i7-8i7-8i 141414 −92i-92i−92i Негауссовские целые числа: Гауссовы целые числа представляют интерес в теории чисел, потому что проблемы квадратичной, кубической и четвертой взаимности удобнее формулировать как задачи о гауссовских целых числах. Основная статья: Комплексные числа — абсолютные значения См. также: Преобразование декартовых координат в полярные Следует отметить, что процесс нахождения модуля и аргумента комплексного числа почти идентичен процессу преобразования декартовых координат в полярные координаты. Абсолютное значение действительного числа определяется как положительное расстояние от 0 до этого числа. Точно так же определяется абсолютное значение комплексного числа, за исключением того, что это расстояние измеряется на комплексной плоскости. Поскольку отрезок, соединяющий 0 с комплексным числом, является гипотенузой прямоугольного треугольника, расстояние до этого отрезка вычисляется по теореме Пифагора. Это расстояние иногда называют .2}=5.\ _\квадрат∣−3+4i∣=(−3)2+42=5. □ Угол, который положительная вещественная ось образует с лучом, соединяющим 000 с комплексным числом, называется аргументом этого комплексного числа. Полный оборот комплексного числа 2π2\pi2π радиан создаст изображение, котерминальное комплексному числу. Поэтому каждое комплексное число имеет бесконечно много аргументов. Если θ\thetaθ является аргументом комплексного числа, то θ+2kπ\theta+2k\piθ+2kπ также является аргументом этого комплексного числа, где kkk — целое число. Основная статья: Основная теорема алгебры 92 — 4\times1\times10 = -4 .D=b2−4ac=62−4×1×10=−4. Это меньше 000 и, таким образом, мы можем заключить, что квадратичный имеет пару комплексных корней с мнимыми компонентами. Чтобы их найти, воспользуемся квадратичной формулой следующим образом: x=-b±D2a=-6±-42×1=-6±2-12=-3±i.\begin{выровнено}
х &= \frac{ -b \pm \sqrt{D}}{2a} \\
& = \frac{-6 \pm \sqrt{-4}}{ 2 \times 1} \\
& = \frac{-6 \pm 2\sqrt{-1}}{2} \\
&=-3 \pm i . Это действительно меньше 000, и, таким образом, мы можем заключить, что квадратное число имеет пару комплексных корней. Чтобы их найти, воспользуемся квадратичной формулой следующим образом: x=-b±D2a=-5i±-1092×3=-5i±109-16.\begin{выровнено}
х &= \frac{ -b \pm \sqrt{D}}{2a} \\
&= \frac{-5i \pm \sqrt{-109}}{ 2 \times 3} \\
&= \frac{-5i \pm \sqrt{109} \sqrt{-1}}{6}.
\end{выровнено} x=2a−b±D=2×3−5i±−109=6−5i±109−1. Таким образом, корней x=(−5−1096)iandx=(−5+1096)i. □\begin{array}{c}&x =\left (\frac{-5-\sqrt{109}}{6}\right)i &\text{and} &x = \left(\frac{-5+) \sqrt{109}}{6}\right)i .\end{массив} \ _\squarex=(6−5−109)iandx=(6−5+109) я. □ Основная статья: Формула Эйлера См. также: Теорема Муавра. Форма a+bia+bia+bi известна как стандартная форма комплексного числа. Формула Эйлера позволяет представить комплексное число в экспоненциальной форме. Основная статья: Комплексные числа в геометрии Из-за круговых отношений, связанных с комплексными числами, они полезны для многих задач геометрии. Например, вращение точки или твердой фигуры можно выполнить с помощью комплексных чисел гораздо проще, чем это можно сделать с помощью тригонометрии. Чтобы повернуть точку θ\thetaθ радиан против часовой стрелки вокруг начала координат, 9{\pi i/6}=\frac{\sqrt{3}}{2}+\frac{i}{2}.eπi/6=23+2i. Умножьте эти комплексные числа, чтобы получить изображение вращения: (2+5i32)(32+i2)=3−52+i(1+532).\влево(2+5i\vphantom{\frac{\sqrt{3}}{2}}\вправо)\влево (\ frac {\ sqrt {3}} {2} + \ frac {i} {2} \ right) = \ sqrt {3} — \ frac {5} {2} + i \ left (1+ \ frac { 5\sqrt{3}}{2}\right).(2+5i23)(23+2i)=3−25+i(1+253). Соответствующая упорядоченная пара: (3−52, 1+532). Есть несколько других применений комплексных чисел в геометрии на вики-странице по этой теме. Цитировать как: Комплексные числа. Brilliant.org .
Извлекаются из
https://brilliant.org/wiki/complex-numbers/ Комплексные числа помогают найти квадратный корень из отрицательных чисел. Концепция комплексных чисел была впервые упомянута в I веке греческим математиком Героем Александрийским, когда он пытался найти квадратный корень из отрицательного числа. Но он просто изменил отрицательное значение на положительное и просто взял числовой корень. Кроме того, реальная идентичность комплексного числа была определена в 16 веке итальянским математиком Джероламо Кардано в процессе нахождения отрицательных корней кубических и квадратичных полиномиальных выражений. Комплексные числа находят применение во многих научных исследованиях, обработке сигналов, электромагнетизме, гидродинамике, квантовой механике и анализе вибрации. Здесь мы можем понять определение, терминологию, визуализацию комплексных чисел, свойства и операции с комплексными числами. Комплексное число – это сумма действительного числа и мнимого числа. Примерами комплексных чисел являются \(2+3i, -2-5i, \,\,\dfrac 1 2 + i\dfrac 3 2\) и т. д. Степень of i Алфавит i называется йотой и полезен для представления мнимой части комплексного числа. Кроме того, йота (i) очень полезна для нахождения квадратного корня из отрицательных чисел. У нас есть значение i 2 = -1, и оно используется для нахождения значения √-4 = √i 2 4 = 9. Комплексное число состоит из действительной и мнимой частей, которые можно рассматривать как упорядоченную пару (Re(z), Im(z)) и представлять в виде точек координат на евклидовой плоскости. Евклидова плоскость применительно к комплексным числам называется комплексной плоскостью или Плоскостью Аргана, названной в честь Жана-Роберта Аргана. Комплексное число z = a + ib представлено действительной частью — a относительно оси x и мнимой частью -ib относительно оси y. Следующие свойства комплексных чисел помогают лучше понять комплексные числа, а также выполнять различные арифметические операции над комплексными числами. Сопряжение комплексного числа образуется путем взятия той же действительной части комплексного числа и замены мнимой части комплексного числа на ее аддитивную обратную. Если сумма и произведение двух комплексных чисел являются действительными числами, то они называются сопряженными комплексными числами. Для комплексного числа z = a + ib его сопряженным является \(\bar z\) = a — ib. Сумма комплексного числа и его сопряженного равна \(z + \bar z\) = (a + ib) + (a — ib) = 2a, а произведение этих комплексных чисел \(z.\bar z \) = (a + ib) × (a — ib) = a 2 + b 2 . Обратная величина комплексных чисел полезна в процессе деления одного комплексного числа на другое комплексное число. Равенство комплексных чисел аналогично равенству действительных чисел. Два комплексных числа \(z_1 = a_1 + ib_1\) и \(z_2 = a_2 + ib_2 \) называются равными, если относительная часть обоих комплексных чисел равна \(a_1 = a_2\), и мнимая части обоих комплексных чисел равны \(b_1 = b_2 \). Кроме того, два комплексных числа в полярной форме равны тогда и только тогда, когда они имеют одинаковую величину, а их аргумент (угол) отличается на целое кратное 2π. Упорядочивание комплексных чисел невозможно. Действительные числа и другие связанные системы счисления можно упорядочить, но нельзя упорядочить комплексные числа. Комплексные числа не имеют структуры упорядоченного поля, и нет упорядоченности комплексных чисел, совместимой со сложением и умножением. Также нетривиальная сумма квадратов в упорядоченном поле есть число \(\neq 0\), а в комплексном числе нетривиальная сумма квадратов равна i 2 + 1 2 = 0. Формула Эйлера: В соответствии с формулой Эйлера для любого действительного значения θ мы имеем e iθ = Cosθ + iSinθ, и оно представляет комплексное число в координатной плоскости, где Cosθ – действительная часть, представленная относительно ось x, Sinθ – мнимая часть, представленная относительно оси y, θ – угол, образованный по отношению к оси x и воображаемой линии, соединяющей начало координат и комплексное число. Согласно формуле Эйлера и функциональному представлению x и y имеем e x + iy = e x (уютно + isiny) = e x уютно + т.е. x сине. Это разлагает экспоненциальную функцию на ее действительную и мнимую части. Различные операции сложения, вычитания, умножения, деления натуральных чисел можно выполнять и для комплексных чисел. Сложение комплексных чисел аналогично сложению натуральных чисел. Здесь в комплексных числах действительная часть добавляется к действительной части, а мнимая часть добавляется к мнимой части. Для двух комплексных чисел вида \(z_1 = a + id\) и \(z_2 = c + id\) сумма комплексных чисел \(z_1 + z_2 = (a + c) + i(b + d) \). Комплексные числа следуют всем следующим свойствам сложения. Умножение комплексных чисел в полярной форме немного отличается от упомянутой выше формы умножения. Здесь абсолютные значения двух комплексных чисел перемножаются, а их аргументы складываются для получения произведения комплексных чисел. Для комплексных чисел \(z_1 = r_1(Cos\theta_1 + iSin\theta_1)\) и z 2 = \(z_2 = r_1(Cos\theta_2 + iSin\theta_2)\) произведение комплексные числа \(z_1.z_2 = r_1.r_2(Cos(\theta_1 + \theta_2) + iSin(\theta_1 + \theta_2))\). 92 + 2z_1z_2 +2z_2z_3 +2z_3z_1\) Связанные темы: Таким образом, корнями данного квадратного уравнения являются: \(\frac{-1}{2}+ i\frac{\sqrt{3}}{2};\,\,\ , \ frac{-1}{2}- i\frac{\sqrt{3}}{2}\) Пример 2: Выразите сумму, разность, произведение и частное следующих комплексных чисел в виде комплексного числа. \[\begin{align} z_1&=-2+i\\[0.2cm]z_2&= 1-2i \end{align} \] Решение: Сумма: \[ \begin{ выровнять} z_1+z_2&= (-2+i)+(1-2i)\\[0,2 см] &=(-2+1)+ (i-2i)\\[0,2 см] &= -1-i \end{align}\] Разница: \[ \begin{align} z_1-z_2&= (-2+i)-(1-2i)\\[0,2 см] &=(-2-1) + (i+2i)\\[0,2 см] &= -3+3i \end{align}\] Продукт: \[ \begin{align} z_1\cdot z_2&= (-2+i)( 1-2i)\\[0,2см] &=-2+4i+i-2i^2\\[0,2см] &=-2+4i+i+2 \,\,\, [\потому что i^2 =-1]\\[0,2 см] &=5i \end{выравнивание}\] 92=-1]\\[0,2 см] &= \dfrac{-4-3i}{5}\\[0,2 см] &=- \dfrac{4}{5}- i \dfrac{3}{5 }\end{align}\] Следовательно, имеем: Сумма = -1 — i перейти к слайдуперейти к слайду Разбивайте сложные концепции с помощью простых визуальных средств. Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций. Записаться на бесплатный пробный урок перейти к слайдуперейти к слайду Комплексное число представляет собой комбинацию действительных и мнимых значений. Обозначается z = a + ib, где a, b — действительные числа, а i — мнимое число. i = \(\sqrt{-1}\) и никакое действительное значение не удовлетворяет уравнению i 2 = -1, поэтому I называется мнимым числом. Комплексное число используется для простого нахождения квадратного корня из отрицательного числа. Здесь мы используем значение i 2 = -1 для представления отрицательного знака числа, что помогает легко найти квадратный корень. Здесь мы имеем √-4 = √i 2 4 = + 2i. Комплексные числа являются частью действительных чисел. Некоторые действительные числа с отрицательным знаком трудно вычислить, и мы представляем отрицательный знак с помощью йоты «i», и такое представление чисел вместе с «i» называется комплексным числом. Дополнительные комплексные числа полезны для нахождения квадратного корня из отрицательного числа, а также для нахождения отрицательных корней квадратного или полиномиального выражения. Комплексное число вида z = a + ib может быть представлено в плоскости арганда. Комплексное число z = a + ib может быть представлено в виде координат точки как (Re(z), Im(z)) = (a, ib). Здесь действительная часть представлена относительно оси x, а мнимая часть представлена относительно оси y. Комплексный номер можно легко преобразовать в полярную форму. Чтобы понять, что только что произошло, давайте сосредоточимся на первом равенстве, а именно на $-2 = \sqrt[3]{-8}$. Он гласит: «$-2$ — это кубический корень из $-8$». Но что это значит? 93 = x \times (-2) \times (-2) \times (-2) = x \times (-8)$. Таким образом, теперь мы можем видеть операцию «$\times (-2)$» как операцию над числами, которая при трехкратном применении эквивалентна операции «$\times (-8)$»! Я до сих пор не знаю, куда ты клонишь… Вот это самое интересное. Эти операции соответствуют геометрическим преобразованиям числовой прямой (это симметрии)! Например, умножение на $(-2)$ соответствует инвертированию и увеличению в 2 раза. Да! Но я все равно не вижу в этом смысла… Хе-хе! Ключевая идея комплексных чисел заключается в следующем вопросе… Является ли $(-1)$ единственным кубическим корнем из $(-1)$? Думаю, да… Если вы возьмете положительное число, его куб будет положительным… Таким образом, работает только число $-1$… Не думайте числами! Весь смысл моей конструкции состоял в том, чтобы рассмотреть задачу геометрически! Гм… Другими словами, существует ли геометрическая операция над числовой прямой, которая при трехкратном применении соответствует ее инвертированию? Гм… Давай! Вы можете найти это! Я знаю! Как насчет поворота числовой линии на 6 оборота? Бинго! На самом деле, есть две такие операции шестого хода, в зависимости от того, по часовой стрелке или против часовой стрелки. В дополнение к операции «$\times (-1)$» это дает нам всего три кубических корня из $(-1)$! Есть ли у $(-8)$ несколько кубических корней? А как насчет 6-го корня из $64$? Отличные вопросы! На самом деле, вы должны попытаться ответить самостоятельно! Хм… Я думаю, кубический корень из $(-8)$ можно получить за 6-ю часть хода (например, $(-1)$) в сочетании с растяжением числовой прямой, не так ли? Точно! Точно так же корни 6-й степени из $ 64 $ включают расширение в 2 раза в сочетании с поворотом на одну или две 6-х оборота по часовой стрелке или против часовой стрелки. Плюс еще есть операции «$\times (-2)$» и «$\times 2$». Это дает нам шесть шестых корней из $64$. И, как вы можете догадаться (или доказать!), вообще, любое число имеет $n$ $n$-го корня! Слышал про квадратный корень из $(-1)$… Получается так же, как мы делали?? Еще раз, ты должен дать мне ответ! Гм. Другими словами, существует ли геометрическое преобразование, которое при двойном применении к числовой прямой эквивалентно простому ее обращению? Я знаю! Вращения четверть оборота! Ну вот! По соглашению мы называем вращение на четверть оборота против часовой стрелки как $i$. Этот $i$ настолько важен, что мы дали ему разные имена… что мне всем не нравится! Он известен как мнимое число (воображаемое? число?), квадратный корень из $(-1)$ или, что хуже всего, $\sqrt{-1}$. Что не так с $\sqrt{-1}$? Что очень неправильно, так это то, что $i$ не единственный квадратный корень из $(-1)$. Вращение на четверть оборота по часовой стрелке тоже является квадратным корнем из $(-1)$! Кроме того, если вы не можете написать $\sqrt[3]{-8}$, то вы точно не сможете написать $\sqrt{-1}$! ОК… Это круто, но я не понимаю, как это решает парадокс введения! Хе-хе… Теперь мы можем элегантно ответить на этот вопрос! Главный недостаток заключается в неединственности $n$-го корня. Хм… не уверен, что понял… И снова наше спасение придет от геометрии! Геометрически это означает, что операция, эквивалентная $\times (-8)$ при трехкратном применении, равна операции, которая при шестикратном применении эквивалентна двукратному применению $\times (-8)$. Ниже приведен рисунок, иллюстрирующий это утверждение. Как видно из рисунка выше, любой кубический корень из $(-8)$ также является корнем 6-й степени из $64$. Действительно, шестикратное применение зеленой операции будет эквивалентно двукратному применению «$\times (-8)$». Теперь, обозначив $\sqrt[3]{-8}$ множество всех кубических корней из $-8$ и $\sqrt[6]{64}$ множество всех шестых корней из $64$, мы можно элегантно исправить парадокс! Эти обозначения очень нетрадиционны, и меня обвиняют в их использовании. Но я считаю, что это обеспечивает проницательное и красивое решение парадокса. Кроме того, если вы сможете отличить $n$-ые корни от классической записи $\sqrt[n]{x}$ при $x \geq 0$, то вы совершите огромный прорыв в понимании $n$-ые корни. 9Тогда q$ будет корректно определен для любого $q \in \mathbb Q$. Несмотря на проницательность, описания комплексных чисел, которые мы дали до сих пор, не очень строги. Итак, каково точное определение комплексных чисел? С геометрической точки зрения комплексные числа следует фактически рассматривать как определенный набор преобразований плоскости, а не линии. Так о каких трансформациях самолета идет речь? Преобразования, соответствующие комплексным числам, — это те, которые мы использовали до сих пор: гомотетии и повороты с центром в начале координат. Эти две операции и есть симметрии, описанные ниже: Ключевым аспектом этих операций является то, что можно комбинировать любое количество вращений и гомотетий, а порядок, в котором они комбинируются, не имеет значения. Говоря технически, мы говорим, что все эти геометрические преобразования являются 90 549 ассоциативными 90 552 и 90 549 коммутативными 90 552. И я предполагаю, что это соответствует гомотетии с коэффициентом 2… Да, что также известно как «$\times 2$»! А как насчет числа $(-1)$? Операция «$\times (-1)$» инвертировала числовую прямую… Так что, думаю, это симметрия вдоль воображаемой оси! Нет… Имейте в виду, что мы можем использовать только гомотетии и повороты! Арг… Гм… Я знаю! Это пол-оборота! Отлично! Позвольте мне привести вам последний пример: $(-2)$ является гомотетией множителя 2 в сочетании с поворотом на пол-оборота. Теперь, в более общем смысле, любая комбинация гомотетии и поворота образует комплексные номера . Подождите… Комплексное число? Да! Теперь гомотетия определяется положительным фактором, называемым по модулю , и обычно обозначается $\rho$. А любое число является комплексным? Ну, как мы уже говорили, любое положительное число — это просто гомотетия. Это включает поворот на угол $0$. Таким образом, любое положительное число $x$ является комплексным числом $(x, 0)$. Теперь, если $x$ — положительное число, то $(-x)$ соответствует гомотетии множителя $x$ и половины оборота. Поскольку полуоборот соответствует углу $\pi$, число $(-x)$, таким образом, является комплексным числом $(x, \pi)$. Что? Половина оборота равна $\pi$? Не лучше ли дать полному обороту имя вроде $\tau$, а половинному обороту назвать $\tau/2$? Я знаю! Некоторые математики даже считают, что $\pi$ следует убрать из всех уравнений и заменить на $\pi = \tau/2$. Есть даже манифест, подтверждающий это… как вы можете видеть в следующем замечательном видео от ViHart: Лично я предпочитаю $\tau$ $\pi$… Поскольку вы, вероятно, выучили $\pi$, я постараюсь вставить его в эту статью, но большую часть я буду делать с $\tau$. В частности, обратите внимание, что если $x > 0$, то $(-x)$ — это комплексное число $(x, \tau/2)$. Как насчет числа ноль? Хм… Хорошее замечание. Нам нужно новое преобразование, соответствующее нулю! Это преобразование состоит в свертывании всей комплексной плоскости в ее начало. Меня беспокоит одно… Вы говорили, что комплексные числа — это геометрические преобразования? В каком возможном смысле они являются числами? Точно не в явном! Но, во-первых, мы можем умножать комплексные числа. В 19 веке немецкий математик Карл Фридрих Гаусс, король математики, представил мощную визуализацию комплексных чисел. Полярные координаты? Можете ли вы привести пример? Конечно! Ниже приведена комбинация гомотетии в 2 раза и поворота на угол $2\tau/3$ (2/3 оборота). Коэффициент гомотетии $\rho$ – это расстояние между образом 1 и началом координат, а угол поворота $\theta$ – это угол (против часовой стрелки) от $1$ до его образа. Похоже на полярные координаты! Точно! Это показывает, что любое геометрическое преобразование можно перевести в точку на комплексной плоскости, полярные координаты которой задаются коэффициентом гомотетии и углом поворота! И это взаимно однозначное соответствие между геометрическими преобразованиями и точками! Таким образом, мы можем отождествить геометрическое преобразование с точками на комплексных плоскостях. Можно ли перевести эти координаты обратно в классические декартовы? Да! Но перед этим давайте сначала посмотрим, с какой точкой комплексной плоскости связано геометрическое преобразование $i$: Итак, $i$ — это точка прямо над началом координат? Забавно… Я знаю! Что также особенно интересно, так это то, что теперь мы можем описывать евклидову планарную геометрию с помощью комплексных чисел! Чтобы завершить построение комплексных чисел, нам нужно связать любую точку комплексной плоскости с вектором. Вектор? Что это за фигня? Вектор — это движение в комплексной плоскости. Это движение часто изображается стрелкой от начальной точки к конечной. Но важно помнить, что вектор соответствует движению, а не стрелке. Две стрелки могут соответствовать одному и тому же движению, даже если они не начинаются в одних и тех же начальных точках, как показано стрелками одного цвета на рисунке справа. Так как же связать любую точку комплексной плоскости с вектором? Учитывая точку на комплексной плоскости, мы можем провести стрелку из начала координат в эту точку. Этот вектор, связанный с этой стрелкой, будет вектором, связанным с точкой комплексной плоскости. Например, $i$ связано со стрелкой от $0$ до $i$, что соответствует зеленым стрелкам на рисунке справа. Кажется, я понял… Но какой смысл в сопоставлении точек с векторами? Теперь мы можем определять сложение комплексных чисел! Как нам это сделать? Комбинируя движения, связанные с векторами! Например, сочетание фиолетового и зеленого движений — это движение на одну единицу вправо и на две единицы вверх. Это эквивалентно только синему движению! Это означает, что $фиолетовый + зеленый = синий$. И это можно визуализировать геометрически, если фиолетовая и синяя стрелки начинаются в одной точке, а зеленая стрелка помещается в конец фиолетовой стрелки. Фиолетовые, зеленые и синие стрелки должны образовать треугольник, как показано ниже: А поскольку все векторы соответствуют комплексным числам, теперь мы можем складывать комплексные числа, складывая соответствующие им векторы! Круто! Теперь самое главное. Значит, все векторы есть определенное количество раз $1$ плюс определенное количество раз $i$? Точно! А так как все векторы соответствуют комплексным числам, то все комплексные числа можно записать как $a+bi$, где $a$ и $b$ — обычные числа. Это разложение позволяет выполнять простые вычисления сложения комплексных чисел! В самом деле, если рассмотреть любые два комплексных числа $z_1$ и $z_2$, то мы уже знаем, что каждое из них можно разложить как $z_1 = a_1+b_1i$ и $z_2 = a_2 + b_2 i$. Тогда сумма $z_1$ и $z_2$ определяется как $z_1 + z_2 = (a_1+b_1i) + (a_2+b_2i) = (a_1+a_2) + (b_1+b_2)i$. Следует также отметить, что каждому комплексному числу $z$ также соответствует операция «$+z$» над точками комплексной плоскости. Это декартово описание комплексных чисел было бы весьма полезным, если бы не более общий подход линейной алгебры к определению векторов. 92$. В частности, это дает пространству $(\mathbb C, +)$ структуру коммутативной группы. Этот изоморфизм тривиален для классического построения комплексных чисел, но в построении этой статьи он весьма впечатляет! Напомним, что мы ввели $\mathbb C$ как комбинацию гомотетий и поворотов! Подведем итог тому, что мы уже обсуждали. Прелесть комплексных чисел в том, что их можно отождествить с несколькими различными математическими объектами. Их можно рассматривать как комбинации гомотетий и поворотов комплексной плоскости, как точки на комплексной плоскости и как векторы на комплексных плоскостях. Что ты имеешь в виду? Посмотрим, что получится, если у нас есть и умножение, и сложение! В частности, давайте сосредоточимся на простейшем возможном случае, а именно на $(x+y) \times z$, где $x$, $y$ и $z$ — комплексные числа. Гм… не знаю, с чего начать! Ну, выражение начинается со сложения $x$ и $y$… ОК… Итак, чтобы выполнить сложение, нам нужно думать об этих комплексных числах как о векторах, верно? Точно! Нарисуем $x$, $y$ и их сумму $x+y$. Но тогда нам нужно умножить эти члены на $z$. Как мы это делаем? Я знаю! Нам нужно думать о $z$ как о $\times z$, что является комбинацией поворота и гомотетии! Очень хорошо! Это означает, что $xz$, $yz$ и $(x+y)z$ будут образом геометрического преобразования $\times z$ $x$, $y$ и $z$. Теперь происходит волшебство, когда мы замечаем, что любое геометрическое преобразование $\times z$ сохраняет формы треугольников. В результате треугольник $x$, $y$, $x+y$ трансформируется в треугольник $xz$, $yz$, $(x+y)z$. А это значит, что сумма сторон $xz$ и $yz$ равна последней стороне $(x+y)z$! Другими словами, $xz+yz=(x+y)z$. это главное 92$ по-прежнему действительны для комплексных чисел! Именно это сильное сходство с манипуляциями привело математиков к тому, чтобы называть комплексные числа… числами. В терминах чистой алгебры мы говорим, что комплексные числа образуют поле . Подытожим: комплексное число — очень сложный математический объект, который можно рассматривать под разными углами. В основном его можно рассматривать как комбинацию гомотетии и вращения, как точку на комплексной плоскости или как вектор размерности 2. Эти три интерпретации показаны ниже. Но что делает комплексные числа такими особенными, так это не разные углы, под которыми их можно увидеть, а их комбинация, вроде того, как квантовые объекты не являются просто классическими волнами или классическими частицами. Что это за теорема? Эта теорема, впервые доказанная Карлом Фридрихом Гауссом, утверждает, что все полиномиальные комплексные уравнения имеют решения. Это так просто. Это свойство также известно как тот факт, что комплексные числа образуют 92+1)\mathbb R[X]$ и, таким образом, является полем. Это так красиво, что я чуть не заплакал, когда впервые увидел это! В чем смысл этой теоремы? Теперь можно решить гораздо больше уравнений! И я говорю не только о полиномиальных уравнениях. Что еще более важно, естественные и простые решения появляются в дифференциальных уравнениях, электромагнетизме, поиске собственных значений, преобразовании Фурье и теории чисел среди многих других областей. В частности, комплексные числа оказались подходящей структурой для описания физики элементарных частиц! Прочтите мою статью о динамике волновой функции в квантовой механике, чтобы увидеть комплексные числа в действии! Когда мы думаем о комплексных числах, мы часто думаем о выполнении алгебры с этим странным термином i , и все это кажется немного произвольным и легко забываемым. На самом деле то, что мы делаем, осязаемо и может быть визуализировано. Так что будьте готовы. После этого поста вы, вероятно, никогда больше не будете думать о комплексных числах как раньше… и да, это хорошо. Примечание: Если вы не знаете, что такое мнимые числа и как они работают на сложной плоскости, проверьте этот пост . Комплексные числа представляют собой сумму действительного и мнимого чисел, представленную как a + b i. Используя комплексную плоскость, мы можем отображать комплексные числа подобно тому, как мы наносим координаты на декартовой плоскости. Вот несколько примеров: 3 + 2 i 1 – 4 i -3 + 3,5 i Просто поставьте точку на пересечении реальной части, расположенной на горизонтальной оси, и мнимой части, расположенной на вертикальной оси . Это самая простая и интуитивно понятная операция. Добавление/вычитание действительных чисел переводит точку вправо/влево на действительной оси, а добавление/вычитание мнимых чисел переводит точку вверх/вниз по мнимой оси. Арифметически это работает так же, как объединение одинаковых терминов в алгебре. Например, если мы вычтем 1 – 4 i из 3 + 2 i, , мы просто вычислим реальную разницу: 3 – 1 = 2, и мнимую разницу: 2 i – (-4 i ) = 2 i + 4 i = 6 i. Это то же самое, что нарисовать точку 3+2 i и перевести ее влево 1 единица и до 4 шт. . Полученная точка и есть ответ: 2+6 i. Мы также можем думать об этих точках как о векторах . Сначала распределите знак минус, чтобы получилось сложение: (3+2 i ) + (-1+4 i ). Затем нанесите две точки с отрезками, исходящими из начала координат. Чтобы добавить эти точки, просто сложите одну поверх другой. Поскольку сложение коммутативно, не имеет значения, как мы их складываем. Это может показаться излишеством, но вот в чем дело: понимание векторного представления значительно облегчит умножение и деление комплексных чисел. Эта операция менее очевидна и оставляет нас в недоумении: Что означает умножение двух комплексных чисел? В общем, мы знаем, что умножение на действительное число масштабирует значение, и мы узнали в последнем посте, что умножение на i поворачивает значение на 90˚ против часовой стрелки, а как насчет этого? Чтобы лучше понять, давайте распределим первый двучлен через второй. Хорошо, теперь мы можем выполнить сложение, сложив векторы после выполнения преобразований. Давайте попробуем. Сначала имеем (3+2 i )(1), что равно (3+2 i ) в масштабе 1. Сначала увеличим его в 4 раза, умножив (4)(3+2 и ), чтобы получить (12 + 8 и ). Еще надо умножить на — т.е. Вспомните умножив на — i это 90˚ поворот по часовой стрелке . Примечание: Это соответствует алгебре, если бы мы подставили в i = √-1: Последний шаг — выполнить сложение путем суммирования векторов. Наш окончательный ответ: 11 – 10 i . Теперь вы можете подумать, «Бретт, почему мы не можем просто решить это с помощью алгебры??» И это правда, мы можем решить это с помощью алгебры. На самом деле, это самый эффективный способ решения проблемы (хотя ему не хватает понимания, которое вы получаете, рисуя графики). Я был бы паршивым математиком, если бы не показал вам оба пути. Итак, для всех моих любящих алгебру друзей, вот как расширить и упростить приведенную выше задачу: Давайте разделим (3+2 i )/(1–4 i ). В этот момент вы можете подумать, что можете просто разделить действительные и мнимые части… но не так быстро. Как и в алгебре, мы должны разделить знаменатель на оба члена числителя, что оставляет нас с той же проблемой: Что на самом деле означает деление на комплексное число? По правде говоря, это сбивает с толку, и этому нет хорошего объяснения. Было бы неплохо, если бы мы могли избавиться от мнимого числа в знаменателе?? Хорошие новости → Именно этим мы и займемся! Ключом к решению этой проблемы является выяснение того, как преобразовать знаменатель в обычное действительное число. Проще всего это сделать с помощью комплексного сопряжения . Чтобы найти комплексное сопряжение, просто переверните знак мнимой части. Например, комплексное сопряжение (1–4 90 545 i 90 548 ) равно (1 + 4 90 545 i 90 548 ). Когда я умножаю их вместе, я получаю 17: Конечно, я не могу просто умножить знаменатель на (1+4 i ). Теперь это имеет смысл. У нас есть два комплексных числа, которые умножаются в числителе, с которым мы знаем, как обращаться из предыдущего раздела, и мы масштабируем все это на 1/17. Вы можете решить это с помощью графика или использовать ярлык алгебры: Это было не так уж и плохо, не так ли? Что мне нравится в том, что проблемы решаются несколькими способами, так это то, что вы получаете возможность по-настоящему познакомиться с концепцией и полностью понять ее так, как вы бы не смогли, если бы не видели оба метода. Мало того, что у вас больше шансов наткнуться на заветную ага! На данный момент в вашем арсенале теперь гораздо больше инструментов для решения более сложных задач. Спасибо за внимание! medium.com medium.com medium.com Я пытался сделать упражнения менее похожими на стандартные вычислительные, которые вы получаете в школе, но это означает, что некоторые из них довольно сложны. В этой статье я использовал радианы и градусы для измерения углов. Вы, возможно, не видели, чтобы раньше использовались радианы, это просто еще один способ измерения углов. Плоскость Аргана Мы еще не добрались до самого удивительного в комплексных числах — геометрической интерпретации. Как вы знаете, комплексное число $z$ можно записать как $a+i b$, где $a$ и $b$ — вещественные числа. Если вы когда-либо работали с векторами, это будет выглядеть очень знакомо, 2D-вектор можно записать как $a\mathbf{i} +b\mathbf{j}$, где $\mathbf{i}$ и $\mathbf{j} $ — единичные векторы. Итак, комплексное число $z = a+i b$
соответствует точке на двумерной плоскости, заданной как $a\mathbf{i} +b\mathbf{j}$. Если вы не создали векторы, используя приведенные выше обозначения, $a+ib$ просто соответствует точке в 2D с координатами $x$ $a$ и $y$-координатой $b$. Как насчет суммы двух комплексных чисел, $z+w$. Оказывается, сложить два комплексных числа — это то же самое, что сложить два вектора. Если вы не знаете, как сложить два вектора, посмотрите на следующую картинку: Итак, сложение векторов соответствует сложению комплексных чисел. Упражнение 12 Пусть $w = (1+i)/\sqrt{2}.$ Что такое $|w|$ и $\arg(w )$? Упражнение 13 Что такое $|z|-|\textrm{Conj}(z)|$? Объясните геометрически, что такое $\textrm{Conj}(z)$ в терминах $z$. Используя это, что такое $\arg(\textrm{Conj}(z))+\arg(z)$? Теперь мы можем обсудить удивительную вещь, связанную с геометрией комплексных чисел. Если $z$ и $w$ — два комплексных числа, то $|z w| = | г | |w|$ и $\arg(z w) = \arg(z)+\arg(w)$. Другими словами, если вы умножаете два комплексных числа, вы умножаете их длины и складываете их углы. Мы не сможем доказать второе уравнение до следующего раздела, но мы можем доказать первое. Полярные координаты и формула де Муавра Помимо $a+i b$ существует и другой способ записи комплексных чисел. Поскольку комплексное число похоже на точку на комплексной плоскости, мы можем вычислить расстояние от этой точки до начала координат, $r$, и угол, который линия от начала до точки образует с осью $x$. , $\тета$. После того, как мы разобрались с ними, мы можем записать комплексное число как $(r,\theta)$, это называется записью в полярных координатах. Эти числа $r$ и $\theta$ — это просто модуль и аргумент $x+i y$, с которыми мы познакомились выше. Итак, комплексное число $z = a+i b$ можно записать как $z = (|z|,\arg(z))$. Кроме того, для заданного комплексного числа $(r,\theta)$ мы можем преобразовать его в обозначение $x+i y$ (это то, о чем Q1) как $(r, \theta) = r(\cos\theta +i \sin\тета)$. Итак, мы можем переключаться между двумя разными способами записи комплексных чисел, но какой в этом смысл? Ну, это очень полезно по причине, которая станет очевидной, если вы прочитаете следующий раздел (что немного сложнее), но также полезно по нескольким другим причинам. Прикольная штука Теперь мы знаем основы работы сложных чисел, что мы можем с ними делать? Предположим, у нас есть комплексное число $z = (r, \theta)$ в полярных координатах и другое комплексное число $w = (1, \phi)$ с модулем 1. Произведение этих двух комплексных чисел равно $z w = (г, \тета + \фи)$. Другими словами, $z w$ — это $z$, повернутый на угол $\phi$. Мы можем использовать их для расчета матрицы, которая поворачивает вектор на угол $\phi$. Предположим, что $z = x+i y$ и $w = (1, \phi) = \cos\phi +
i\sin\phi$, тогда $z w = (x+i y)(\cos\phi + i\sin\phi) = (x\cos\phi — y\sin\phi) + i(x\sin\phi + y\cos\phi)$. Другими словами, $x$-координата (эквивалентная действительной части комплексного числа) вектора, повернутого на угол $\phi$, равна $x’ = xcos\phi — y\sin\phi$ и координата $y$ (мнимая часть) равна $y’ = xsin\phi — y\cos\phi$. Мы можем представить это как произведение
матрицы: \[\left( \begin{array}{c} x’\\ y’\end{array}\right) = \left(\begin{array}{cc} \cos\phi & -\sin\ phi \\ \sin\phi & \cos\phi \end{массив}\right) \left(\begin{array}{c} x \\ y \end{массив}\right)\] Другими словами , матрица вращения $M$, которая поворачивает вектор $\textbf{v}$ в вектор $M\mathbf{v}$ на угол $\phi$, равна: \[\mathbf{M} = \left (\begin{array}{cc} \cos\phi & -\sin\phi \\ \sin\phi & \cos\phi \end{array}\right)\] В начале я упоминал, что вы можете решить любое полиномиальное уравнение, используя комплексные числа, это известно как основная теорема алгебры, и известный математик, известный как Гаусс, дал около 98 = 1$. Ответ 8 $ \quad X = \pm i$. Ответ 9 $ \quad X = \pm w = \pm 1+i /\sqrt{2}$. Другими решениями являются $- w$ , $i w$ и $- i w$. Ответ 10 Решение с использованием квадратичной формулы $$ x = \frac { -2\pm i \sqrt{4-8}} {2}\ = 1\pm \sqrt{-1}\ = — 1 \pm i $$ Ответ 11 Раскрывая каждое из уравнений и упрощая, мы получаем 1 в каждом случае (включая общий случай). Доказательство см. в разделе о формуле де Муавра. 9n) = n\arg(z)$. Ответ 15 Используя подсказку, что $z = (z /w )w$ и тот факт, что $|u v| = |и| |v|$ получаем, что $|z| = |(z/w)| |w|$ , поэтому $|(z /w )| = | г | /|ш|$ . Точно так же, взяв аргумент обеих сторон, мы получаем $\arg(z) = \arg(z/w)+\arg(w)$ и, таким образом, $\arg(z/w) = \arg(z)- \ аргумент(ш)$. Ответ 16 $\quad |z| = r$ и $\arg(z) = \theta$. Итак, $z = |z| (\cos(\arg(z))+i\sin(\arg(z)))$. Теперь мы можем доказать, что $|z w| = | г | |w|$ и $\arg(z w) = \arg(z)+\arg(w)$, раскрывая скобки, используя это разложение $z$ и $w$ и тригонометрическую формулу для $\cos(A +B) = \cos(A)\cos(B)-\sin(A)\sin(B)$ и $\sin(A+B) =
\cos(A)\sin(B)+\sin(A)\sin(B)$. \begin{eqnarray} z w &=& r_{1} r_{2}\cos\theta_{1} +i\sin\theta_{1})(\cos\theta_{2} +i\sin \theta_{2})\\ &=& r_{1} r_{2} ((\cos\theta_{1} \cos\theta_{2} — \sin\theta_{1} \sin\theta_{2} )+i(\cos\theta_{1} \sin\theta_{2} + \cos\theta_{2} \sin\theta_{1} )) \\ &=& r_1 r_2 (\cos(\theta_{1 } + \theta_{2} )+i\sin(\theta_{1} + \theta_{2} )) \end{eqnarray} 9{-z}] /2$ тогда
$\sinh(i z) = i\sin(z)$. Кроме того, $\cos(i z) = \cosh(z)$ и $\sin(i z) = i\sinh(z)$. Cool Stuff Ответ 25 Мы пытаемся доказать это по индукции, поэтому нам нужно сначала доказать, что это верно для $n = 1$. Если $n = 1$, то $p(z) = z + a_0$ для некоторого комплексного числа $a_0$. В этом случае $p(z)$ можно записать как $p(z) = (x- (- a_0 ))$, и теорема верна. Далее нам нужно доказать, что если это верно для $n$, то верно и для $n+1$. Полякова О.Л. Доклад ОСОБЕННОСТИ Построения графиков функций заданных неявно и параметрически Из курса математического анализа известен стандартный алгоритм исследования явно заданных функций (область определения; множество значений; четность – нечетность; асимптоты; периодичность; нули; экстремумы; интервалы монотонности, выпуклости и вогнутости; точки перегиба). При параметрическом или неявном задании функции существует ряд специфических особенностей, отличающих построение графиков этих функций. Рассмотрим эти особенности на примерах. Пример 1. Построить график функции [2, с. 126]. Сначала строим графики функций и соответственно в системах координат и . Рис. 1 б) Учитывая графическое изображение функций и , исследуем функцию по схеме [3]. Область определения функции: . Множество значений функции: . Таккак — функция общего вида, а — нечетная функция, то симметрииграфик не имеет. При исследовании функции заданной параметрически, необходимо найти особые точки (точка особая точка кривой, если ) и определить их вид. Пусть, — первая отличная от нуля производная и — первая из производных, не коллинеарных вектору . Тогда если: Рис. 2 б) Точка является особой точкой кривой, так как производные первого порядка: равны нулю при . Определяем тип особой точки, для этого вычисляем вторую и третью производные: Таким образом, точка – точка возврата первого рода. Точки самопересечения находим из условия , решая систему: . Так как , значит, кривая не имеет точек самопересечения. Угловой коэффициент касательной: . При и при , т.е. в точках с координатами , и касательные параллельны оси абсцисс; при , т.е. в точке с координатами касательная параллельна оси ординат. Экстремумы функции и интервалы монотонности. Точка – точка минимума; точки , – точки максимума; при и при функция убывает; при , и при функция возрастает. Интервалы выпуклости и точки перегиба. Так как вторая производная отлична от нуля, следовательно кривая не имеет точек перегиба; при и при кривая выпукла вверх; при и при кривая выпукла вниз. Асимптоты. Прямая является наклонной асимптотой, т.к. ; . Прямая наклонная асимптота, так как при , , и . Прямая вертикальная асимптота, т.к. при . Горизонтальных асимптот кривая не имеет. График функции (рис. 3): Рисунок 3 — График функции При исследовании и построении графика функции заданной неявно также определяют особые точки кривой. Точка кривой называется особой точкой, если ее координаты одновременно удовлетворяют трем уравнениям: Если в особой точке производные второго порядка не равны одновременно нулю, тогда точка является двойной точкой кривой, причем форма кривой у ее двойной точки зависит от знака определителя . Возможные случаи изображены на рисунке [1, с. 271]: Рис. 4 б) изолированная точка Рис. 4 в) точка возврата первого рода Рис. 4 д) точка самокасания Пример 2. Построить график функции [1, с.182]. Область определения находим, решая уравнение: Откуда, область определения первой ветви , второй ветви — Кривая симметрична относительно координатных осей. Точки пересечения кривой с осями координат: Асимптоты. Горизонтальных и вертикальных асимптот кривая не имеет, так как коэффициенты при высших степенях и постоянные величины. Наклонные асимптоты находим из условия: , приравнивая к нулю коэффициенты при , . Получаем и — наклонные асимптоты искомой кривой. Особые точки: Точка является особой двойной точкой, так как и производные второго порядка в этой точке одновременно не равны нулю. Т.к. точка с координатами узловая точка. Найдем касательные к кривой в особой точке, для этого приравняем к нулю коэффициенты при низших степенях: , Таким образом, прямые и – две касательные к кривой в особой точке. Координаты точек, в которых касательные параллельны оси абсцисс, найдем, решив систему: . В точках , касательные параллельны оси абсцисс. Исследуем их на экстремум. Так как в точке , то в ней функция не имеет экстремума. Так как произведение в точке с координатами принимает положительные значения, то в этой точке максимум; а в точках с координатами произведение , следовательно это точки минимума. Координаты точек, в которых касательные параллельны оси ординат, найдем, решив систему: . В точках с координатами , касательные параллельны оси ординат. Исследуем их на экстремум. Так как в точке , то в ней функция не имеет экстремума. Так как произведение в точке с координатами , принимает положительные значения, то в этой точке максимум; а в точке с координатами – минимум, так как произведение . Точкиперегиба находим, приравняв к нулю вторую производную: , очевидно, точка перегиба. График функции (рис. 5): Рис. 5 — График функции Исследовать кривую – значит выявить совокупность важнейших свойств, дающих исчерпывающую информацию для изображения графика этой кривой. В целом, алгоритм исследования параметрических и неявно заданных функций совпадает с алгоритмом исследования функций заданных явно. Однако, существуют следующая специфическая особенность отличающая исследование этих функций от функций заданных явно, заключающаяся в нахождении особых точек и точек самопересечения. При исследовании параметрических функций часто возникают сложности при определении точек перегиба и промежутков вогнутости, так как это исследование требует нахождения второй производной функции, которая представляет собой громоздкое выражение и решить уравнение точными методами не удается, необходимо прибегать к численным методам. Аналогичные сложности возникают и при исследовании неявно заданных функций: из-за сложных выражений второй производной определять точки перегиба приходится методом подбора (интуитивно) или же не определять вовсе. Библиографический список: Графики функций: Справочник / Вирченко Н. А., Ляшко И. И., Швецов К. И. – Киев: Наук. думка, 1979. – 320 с. Райхмист Р. Б. Графики функций: Справ. пособие для вузов. – М., «Высшая школа», 1991. – 160 с. Функция ParametricPlot позволяет рисовать кривые и семейства кривых, заданных параметрически. Эта функция имеет те же опции, что и функция Plot. В некотором смысле эта функция универсальна. Если не учитывать неявно заданных функций, то именно функция ParametricPlot позволяет построить графики всех мыслимых функций, включая и многозначные. Без проблем строятся и графики, заданные в полярной системе координат. Фигуры Лиссажу, кривые Уатта, овалы Кассини, Декарта, Мюнгера, улитки Паскаля, однолистники, листы Декарта, всевозможные розы и розетки, рулеты, годографы, эволюты и эвольвенты всех мыслимых и немыслимых кривых, циклоиды, всевозможные спирали, циссоиды, конхоиды, строфоиды, астроиды, кардиоиды, неоиды, лемнискаты, узлы, квадратрисы, клотоиды, кохлеоиды, трохоиды, элипсиды, катакаустики, всевозможные параболы, локсодромы и лоциклики, трезубцы, трисектрисы, трилистники, верзиеры, брахистохроны, подэры, кривые с именами древнегреческих и средневековых ученых – вот далеко не полный перечень всевозможного зверья, которое может быть нарисовано функцией ParametricPlot. Пример 9.3. Фигуры Лиссажу. Это классический пример применения функции ParametricPlot. Рисуются эти фигуры совсем просто, и потому мы нарисуем сразу несколько. Пример 9.4. Розы и розетки. Эти цветы весьма многочисленны, выглядят, как правило, очень мило и легко рисуются. Процесс вычерчивания совсем прост, если предварительно определить следующую функцию. Вот как, например, с помощью этой функции рисуется многолепестковая роза. А вот еще один милый цветок. Цветы эти столь разнообразны, что согласия относительно количества их видов нет. Одни насчитывают более полтора десятка видов, другие – не менее сотни. Государственное образовательное учреждение высшего профессионального образования Московский авиационный институт (национальный исследовательский университет) РАДИОВУЗ МАИ О.М.Данченко МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ИНДИВИДУАЛЬНЫХ ЗАДАНИЙ ПО МАТЕМАТИЧЕСКОМУ АНАЛИЗУ МОСКВА О.М. ДАНЧЕНКО Методические указания по выполнению индивидуальных заданий по математическому анализу – М.; РАДИОВТУЗ, 2012г., — 36 с. Данное пособие содержит типовые задачи для индивидуальных заданий студентов-заочников по курсу «Математический анализ» часть 1. Ко всем задачам приводятся подробные решения и указания. Приведенные задания в равной степени могут использоваться студентами очного отделения при подготовке к экзамену. В приложении приведена подробная программа курса по «Математическому анализу» часть 1. РАДИОВТУЗ 2012 Содержание Введение……………………………………………………………………………. Построение графиков функций, заданных в полярной системе координат или в параметрической форме…………………………………………………………… Вычисление пределов последовательностей и функций………………………… Исследование функций на непрерывность……………………………………….. Вычисление производных…………………………………………………………. Исследование функций с помощью производных, построение графиков функций…………………………………………………………………………….. Задания на вычисление интегралов………………………………………………. Приложения………………………………………………………………………… Введение В процессе изучения курса «Математический анализ» предусмотрено выполнение студентами индивидуальных домашних заданий в каждом семестре. Индивидуальное домашнее задание 1-ого семестра содержит следующие задачи: 1. Построение графиков функций, заданных в полярной системе координат или заданных в параметрической форме. 2. Вычисление пределов последовательностей и функций. 3. Исследование функций на непрерывность. 4. Вычисление производных от сложных функций, функций, заданных неявно или в параметрической форме. 5. Исследование функций с помощью производных, построение графика функции. 6. Вычисление неопределенного и определенного интегралов. Рассмотрим далее типовые примеры на каждое из заданий и укажем методы их решения. Построение графиков функций, заданных в простой полярной системе координат. Простая полярная система координат характеризуется следующим: ρ=ρ(φ); 0≤ρ<+∞; 0≤φ≤2π(1) Положительные углы φотсчитываются от полярной оси (совпадающей с положительным направлением оси ОХ) против часовой стрелки, отрицательные – по часовой стрелке. При построении графика функции в соответствии с уравнениями (1) следует придерживаться следующего порядка действий: а) указать область допустимых значений (О.Д.З.), т.е. определить при каких углах φфункция ρ(φ) – неотрицательна, т.е. ρ(φ)≥ 0; б) найти область изменения функции; в) указать является ли функция четной или нечетной, т.е. если ρ(-φ) = ρ(φ),то график функции симметричен относительно полярной оси и, следовательно, достаточно сделать исследования для φ≥0.После данных исследований следует построить кривую по точкам. Пример: построить график функции в простой полярной системе координатρ=2cos2φ Так как в простой полярной системе координат ρ≥0, то О.Д.З. будут являться только те углы φ,для которых cos2φ≥0,т.е. 0≤φ≤π/4; 3π/4≤φ≤5π/4; 7π/4≤φ≤2π. Функция будет ограничена, т.к. |cos2φ|≤1,т.е. |2cos2φ|≤2. Так как функция четная и периодическая то достаточно построить кривую только для 0≤φ≤π/4, а затем отразить кривую симметрично относительно полярной оси и в силу периодичности построить аналогичную петлю для 3π/4 ≤φ≤5π/4.Для 0≤φ≤π/4функция монотонно убывает от двух до нуля, для 3π/4≤φ≤πфункция монотонно возрастает от нуля до двух (рис. 1). Построение графика функции, заданной в параметрической форме. Пусть x=X(t)и y=Y(t), где параметр tизменяется в определенных заданных пределах. График функции, заданной в параметрической форме, строится по характерным точкам. Пример: x=t², y= t∙(t²-3)/3 а) Заметим, что для любых значений аргумента t функция x(t)=t²≥0, следовательно, график функции расположен в правой полуплоскости. б) В силу нечетности функции y(t), так как y(-t)=-y(t), график функции симметричен относительно оси ОХ. в) Определим точки, в которых y(t) = 0: при t=0, y(0)=0 и x(0)=0 при t= + и t= — y=0, а x(+ ) = 3 – т.е. это точки пересечения графика функции с осью ОХ. Для более точного построения графика функции достаточно добавить еще 2-3 точки, например при t=1 y(1)=-2/3, x(1)=1; при t=2 y(2)=2/3, x(2)=4; при t =3 y(3)=6, x(3)=9 (рис.2.). рис. 1 рис. 2 Задание: Построить график функции 1. Решение этой задачи сведём к предыдущей задаче. 2. Запишем заголовки: в А1: t, в ячейку В1: х, в ячейку С1: у. 3. В столбце А с помощью маркера автозаполнения создать ряд значений для t от 0 до с шагом (либо при помощи набора команд: Правка Þ Заполнить Þ Црогрессия (шаг 0,314, предельное значение 6,28)). 4. В ячейку В2 вводим формулу =COS(2*A2)*SIN(A2)и копируем её в диапазоне В3:В22. 5. В ячейку С2 вводим формулу =COS(A2)*SIN(3*A2)и копируем её в диапазоне С3:С22. 6. Выделяем диапазон данных В2:С22 со значениями х и у, строим точечную диаграмму. 7. Результат работы представлен на рис. 7. Задание: Построить график функции , заданной тремя ветками на отрезке . . Для построения этого графика шаг изменения желательно выбирать поменьше, например, , и т. д. Далее в мастере диаграмм выбирать точечную диаграмму (первую в первой строке). 1. В ячейке A1 записываем заголовок X. 2. В ячейке В1 записываем заголовок f1. 3. В ячейке С1 записываем заголовок f2. 4. В ячейке D1 записываем заголовок f3. 5. В ячейке E1 записываем заголовок F(x). 6. В столбце А создаём ряд значений для х от -0,2 до 2,41 с шагом 0,03. Такой диапазон изменения взят с учётом промежутков, на которых задан каждый «кусок» функции. Так, по условию, у нас , поэтому можно взять в качестве крайнего левого значения аргумента. Кроме того, из третьего участка функции видно, что . Поэтому в качестве крайнего правого участка взято .2+4*A2+11)и копируем её в столбце D. 10. В Е2 запишем формулу: =ЕСЛИ(А2<0,47;В2;ЕСЛИ(А2>=2;D2;С2)) Скопируем её в столбце Е до конца диапазона изменения аргумента функции. 12. Результат работы представлен на рис. 8. Задания для самостоятельной работы 1. Построить график функции в прямоугольной системе координат. Диапазон изменения и шаг выберите самостоятельно: 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 2. Построить график функции, заданной в полярной системе координат: 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 3. Построить график функции, заданной параметрическим способом: 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. 15. 4.Построить графики функций, используя функцию ЕСЛИ( ) а) Случай двух ветвей: 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. б) Случай трёх ветвей: 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. Лабораторный практикум № 4 В обычном двумерном построении в gnuplot координата Y выражается y=f(x),
однако можно использовать параметрическое задание функции, использующее параметр t, С помощью этого выражения gnuplot может рисовать более сложные функции. Отметим, что 3D построения параметрической поверхности,
задаваемой параметрами u,v, дается в разделе построения сферических гармоник. В первую очередь необходимо использовать команду set parametric,
чтобы gnuplot определил параметрическую переменную для функции.
Затем, команда plot, выполняющая построение функции f(t) координаты X и функцит g(t) для координаты Y,
задается как plot f(t),g(t). Чтобы провести простейшую вертикальную линию, не выражающуюся формой y=f(x), а заданную как x=const.
Эта функция может быть определена как: с параметром t, когда t различен. Диапазон t контролируется командой set trange. В данном случае вертикальная линия нарисованна в x=3. Использование set
trange [1:4] , определило диапазон от 1 до 4.
Если trange не установлен, вертикальная линия будет отрисована от верхней до нижней границы. Параметрическое задание окружности: окружность может быть нарисована при изменении параметра t от 0 до 2pi.
График принимает вид «квадрата» и диапазон t задается опцией команды plot. Параметр t не изменяется непрерывно и фактически управляется значениями, установленными командой set
samples. По умолчанию значение равно 100. В случае set samples 8,
gnuplot вычисляет только 8 значений t от 0 до 2*pi, и график становиться семиугольником. Если необходим построить N-угольник,
задается set samples N+1. 2D параметрическое представление удобно для рисования функции, которая находится в полярных координатах.
2D полярная координатаимеет 2 переменные: r и угловую theta.
gnuplot выражает параметр t для theta, а радиус r выражается через функцию угла, а именно r(t).
Координата (x,y) дается из: Окружность — особый случай, когда r(t)=const. Когда радиус пропорционален t, получается спираль. Следующий пример показывает график кардиоды r(t)=const*(1+cos(t)). Обычная функция имеет вид y=f(x), но параметрическая позволяет делать график x=f(y). Значения Y такие же как и t и значения x вычисляются функцией f(t). Показаны 2 функции, одна (зеленые линии) y=2pi*cos(x), другая
(красная толстая линия) x=f(t)=2pi*sin(y). Опция with impulse рисует вертикальную линию от оси Y=0. Если используется with impulses для красной кривой x=2pi*sin(y), то получается вертикальная линия, не горизонтальная. Дифференцирование функций, заданных неявно, опирается на возможность почленного дифференцирования тождеств. В общем случае уравнение почленно дифференцировать нельзя. Пусть функция задана неявно уравнением и известно, что существует решение этого уравнения в виде ; подставив это решение в уравнение, получим тождество . Продифференцировав по х, получим уравнение для нахождения производной . Пример Найти производную функции, заданной неявно: . Решение Продифференцируем обе части данного уравнения по аргументу х: Дифференцирование функций, заданных параметрически Пусть функция задана параметрически уравнениями (1) — параметр. Требуется найти производную . Имеет место формула или . Пример Найти производную функции, заданной параметрически: . Решение Найдем производные функций х и у по переменной t: , . Согласно формуле , получим . Исследование функций и построение графиков функций Одна из возможных схем исследования функции и построения ее графика включает следующие этапы решения задачи: 1. Найти область определения функции. 2. Найти точки пересечения графика функции с осями координат. 3. Определить четность, нечетность, периодичность функции. 4. Исследовать функцию на экстремум, найти интервалы монотонности функции, точки максимума и минимума. 5. Найти интервалы выпуклости, вогнутости графика функции и точки перегиба. 6. Найти точки разрыва функции и асимптоты графика функции. 7. Построить график функции. Пример С помощью методов дифференциального исчисления исследовать и построить график функции . Решение 1. Область определения функции находится из условия: , т.е. . 2. Точки пересечения графика функции с осями координат: с осью Оу, , точка , с осью Ох, , точка . 3. Четность, нечетность, периодичность функции. Функция называется четной, если для любого х из области определения справедливо равенство . Функция называется нечетной, если для любого х из области определения справедливо равенство . Если не выполнено ни одно из равенств, то функцию называют функцией общего вида. В нашем случае, , следовательно, функция нечетная, а ее график симметричен относительно начала координат. Функция непериодическая. 4. Исследование функции на экстремум. Для определения интервалов возрастания и убывания функции и ее точек экстремума найдем первую производную: . Найдем критические точки, т.е. точки, в которых производная равна нулю или не существует, для чего приравниваем числитель к нулю: , т.е. вещественных корней нет, следовательно, точек экстремума нет. Так как производная отрицательна во всей области определения функции, то она всюду убывает в этой области. _ _ _ х -6 6 у 5. Исследование на выпуклость, вогнутость. Точки перегиба. Вычислим производную второго порядка: Необходимое условие точки перегиба: или не существует. Равенство выполняется при , следовательно, эта точка является «подозрительной» на точку перегиба. Определим знак второй производной на всей числовой оси и укажем на ней интервалы выпуклости и вогнутости функции. _ + _ + х -6 0 6 у Так как при переходе через точку вторая производная меняет знак, то точка с абсциссой является точкой перегиба. Итак, точка перегиба имеет координаты . 6. Точки разрыва функции и асимптоты графика функции. 1) Вертикальные асимптоты. Прямая является вертикальной асимптотой графика функции , если хотя бы один из пределов или равен или . Таким образом, для нахождения вертикальных асимптот следует найти все точки разрыва 2-го рода данной функции. Если точек разрыва нет, то нет и вертикальных асимптот. Заданная функция имеет две точки разрыва второго рода и , так как , , , , следовательно, график функции имеет две вертикальных асимптоты и . 2) Наклонные асимптоты. Пусть прямая является асимптотой графика функции . Такую асимптоту называют наклонной. Для того, чтобы график функции имел при наклонную асимптоту , необходимо и достаточно, чтобы существовали оба предела: . Аналогично находится асимптота при . Так как , то наклонных асимптот нет. 3) Горизонтальные асимптоты. Горизонтальная асимптота – частный случай наклонной асимптоты, когда . Чтобы найти горизонтальные асимптоты графика функции, нужно найти пределы: . Если эти пределы конечны и различны, то прямые будут горизонтальными асимптотами. Если какой-либо из этих пределов не существует или равен , то не существуют и соответствующие асимптоты. Так как , то график функции имеет горизонтальную асимптоту . 7. Построение графика функции. Для уточнения построения графика функции можно найти ряд вспомогательных точек после чего строим график функции. Графики параметрических функций
Mathematica может строить графики параметрических функций в двух и трех измерениях. Воспользуйтесь параметрическим графиком, если Вы можете выразить координаты x,
y или x, y, z в каждой точке Вашей кривой как функцию одного или более параметров.
Построим график параметрической кривой (x,y)=(2 sin(t),cos(t)), с параметром t изменяющимся от 0 до 2 ?:
In[1]:=
Out[1]=
Вы можете построить график двух параметрических кривых, поместив их в список:
In[2]:=
Out[2]=
Чтобы отобразить еще больше графиков кривых, просто добавьте их в список:
In[3]:=
Out[3]=
Воспользуемся командой ParametricPlot3D для построения графика поверхности, заданной функцией :
In[4]:=
Out[4]=
Построим график параметрической кривой (x,y,z)=(5 cos(u),5 sin(u),u+sin(u)) в трех измерениях:
In[5]:=
Out[5]=
Дальнейшие применения тригонометрии В этом разделе вы будете: Это конец девятого иннинга с двумя аутами и двумя игроками на базе. Хозяева проигрывают с разницей в два раунда. Бэттер раскачивается и ударяет по бейсбольному мячу со скоростью 140 футов в секунду и под углом примерно к горизонту.Как далеко полетит мяч? Сможет ли он очистить забор для выигрышного хоумрана? Результат может частично зависеть от других факторов (например, ветра), но математики могут смоделировать траекторию снаряда и приблизительно предсказать, как далеко он пролетит, используя параметрические уравнения. В этом разделе мы обсудим параметрические уравнения и некоторые общие приложения, такие как задачи о движении снаряда. Постройте график параметрических уравнений и сначала постройте график, используя точки данных, сгенерированные из параметрической формы.Затем изобразите прямоугольную форму уравнения. Сравните два графика. На (Рисунок) данные параметрических уравнений и прямоугольного уравнения нанесены вместе. Параметрические уравнения показаны синим цветом; график для прямоугольного уравнения нарисован поверх параметрического в виде пунктирной линии красного цвета. Ясно, что обе формы дают один и тот же график. Нарисуйте график параметрических уравнений вместе с прямоугольным уравнением на той же сетке. График параметрических уравнений выделен красным цветом, а график прямоугольного уравнения нарисован синими точками поверх параметрических уравнений. [/ hidden-answer] Многие преимущества параметрических уравнений становятся очевидными при решении реальных задач. Хотя прямоугольные уравнения в x и y дают общую картину пути объекта, они не показывают положение объекта в конкретное время.Однако параметрические уравнения иллюстрируют, как значения x и y изменяются в зависимости от t как местоположения движущегося объекта в конкретный момент времени. Обычное применение параметрических уравнений — решение задач, связанных с движением снаряда. В этом типе движения объект продвигается вперед в направлении вверх, образуя угол к горизонтали, с начальной скоростью и на высоте выше горизонтали. Путь объекта, движущегося под наклоном к горизонтали с начальной скоростью и на высоте над горизонтом, определяется как , где учитывается влияние силы тяжести, а — начальная высота объекта.В зависимости от единиц измерения, участвующих в задаче, useorThe уравнение допускает горизонтальное расстояние, а уравнение для дает вертикальное расстояние. Решите проблему, указанную в начале этого раздела. Попадает ли тесто в выигрышную игру? Предположим, что мяч ударяется с начальной скоростью 140 футов в секунду под углом к горизонтали, при этом происходит контакт на высоте 3 футов над землей. Используйте формулы, чтобы составить уравнения. Горизонтальное положение определяется с помощью параметрического уравнения для Таким образом, Подставьте 2 в уравнения, чтобы найти горизонтальное и вертикальное положение мяча. Через 2 секунды мяч оказывается на расстоянии 198 футов от бокса бьющего и на высоте 137 футов над землей. Чтобы вычислить, как долго мяч находится в воздухе, мы должны выяснить, когда он ударится о землю или когда. Таким образом, Через секунду мяч коснулся земли. (Квадратное уравнение можно решить разными способами, но эта задача была решена с помощью компьютерной математической программы.) Мы не можем подтвердить, что попадание было хоумраном, не принимая во внимание размер дальнего поля, который варьируется от поля к полю.Однако для простоты предположим, что внешняя стена находится в 400 футах от домашней плиты в самой глубокой части парка. Предположим также, что высота стены составляет 10 футов. Чтобы определить, касается ли мяч стены, нам нужно вычислить, насколько высок мяч, когда x = 400 футов. Итак, мы установим x = 400, найдем и введем в Мяч находится на высоте 141,8 фута, когда вылетает за пределы поля. Это был действительно хоумран. См. (Рисунок). [/ hidden-answer] Какие два метода используются для построения графиков параметрических уравнений? точек с помощью стрелки ориентации и графического калькулятора [/ hidden-answer] В чем отличие параметрических уравнений точечного построения от декартовых уравнений? Почему на некоторых графиках нарисованы стрелки? Стрелки показывают ориентацию, направление движения согласно возрастающим значениям [/ hidden-answer] Назовите несколько распространенных типов графиков параметрических уравнений. Почему параметрические графики важны для понимания движения снаряда? Параметрические уравнения показывают различные вертикальные и горизонтальные движения во времени. [/ hidden-answer] Для следующих упражнений нарисуйте каждый набор параметрических уравнений в виде таблицы значений. Включите ориентацию на графике. Для следующих упражнений нарисуйте кривую и укажите ее ориентацию. Для следующих упражнений нарисуйте уравнение и укажите ориентацию.Затем напишите декартово уравнение. Для следующих упражнений нарисуйте уравнение и укажите ориентацию. Для следующих упражнений используйте параметрические уравнения для целых чисел a и b : График по домену и включению ориентации. График по домену где и, включая ориентацию. График по домену где и, включая ориентацию. График по домену где и, включая ориентацию. Ifis 1 более чем описывает влияние значений andhave на график параметрических уравнений. Опишите график ifand Произойдет 100 возвратно-поступательных движений. [/ hidden-answer] Что произойдет, если на 1 больше, чем Опишите график. Если параметрические уравнения и имеют график горизонтальной параболы, раскрывающейся вправо, что изменит направление кривой? Возьмем противоположное уравнению. [/ hidden-answer] Для следующих упражнений опишите график системы параметрических уравнений. и линейный и линейный Парабола открывается. [/ hidden-answer] и линейный Напишите параметрические уравнения круга с центральным радиусом 5 и направлением против часовой стрелки. [/ hidden-answer] Напишите параметрические уравнения эллипса с большой центральной осью длиной 10, малой осью длиной 6 и ориентацией против часовой стрелки. Для следующих упражнений используйте графическую утилиту, чтобы построить график в области окна для следующих значений и, а также включить ориентацию. Объект подбрасывается в воздух с вертикальной скоростью 20 футов / с и горизонтальной скоростью 15 футов / с.Высота объекта может быть описана уравнением, в то время как объект движется по горизонтали с постоянной скоростью 15 футов / с. Напишите параметрические уравнения для положения объекта, а затем избавьтесь от времени, чтобы записать высоту как функцию горизонтального положения. [/ hidden-answer] Скейтбордист, едущий по ровной поверхности с постоянной скоростью 9 футов / с, подбрасывает в воздух мяч, высоту которого можно описать уравнением. Напишите параметрические уравнения для положения мяча, а затем исключите время, чтобы записать высоту в виде функция горизонтального положения. Для следующих упражнений используйте этот сценарий: Дротик бросается вверх с начальной скоростью 65 футов / с под углом возвышения 52 °. Учитывайте положение дротика в любое время и не обращайте внимания на сопротивление воздуха. Найдите параметрические уравнения, моделирующие проблемную ситуацию. [/ hidden-answer] Найдите все возможные значения, которые представляют ситуацию. Когда дротик упадет на землю? примерно 3,2 секунды [/ hidden-answer] Найдите максимальную высоту дротика. В какое время дротик достигнет максимальной высоты? 1,6 секунды [/ hidden-answer] Для следующих упражнений посмотрите на графики каждого из четырех параметрических уравнений.Хотя они выглядят необычно и красиво, они настолько распространены, что имеют названия, указанные в каждом упражнении. Используйте графическую утилиту для построения графика каждого в указанном домене. Эпициклоида: в домене. Гипоциклоида: в домене. Гипотрохоид: в домене. Роза: на домене. Первое параметрическое уравнение Второе параметрическое уравнение Прямоугольное уравнение х = 4t2−4 у = т х = 4y2−4 х = t2−4 у = t2 2y = t х = (2у) 2 — 4 х = 4y2−4 Чтобы найти набор параметрических уравнений для графика, представленного как y = x 2 + 2 при t = x + 2, пусть t = x. Переключение ролей t и x в этом уравнении дает одно из параметрических уравнений: t = x + 2 → x = t + 2 y = x2 + 2 y = (t + 2) 2 + 2 y = t2 + 4t + 4 + 2 y = t2 + 4t + 6 x = t + 2 y = t2 + 4t + 6 т -2 -1 0 1 2 х = т + 2 0 1 2 3 4 у = т 2 + 4т + 6 2 3 6 11 18 РЕКОМЕНДАЦИИ ПО ПОИСКУ ПАРАМЕТРИЧЕСКИХ УРАВНЕНИЙ ДЛЯ ГРАФИКА: 1.Возьмите уравнение параметра и поменяйте роли параметра и другой переменной. В результате получится одно параметрическое уравнение. 2. Подставьте выражение для переменной на шаге 1 в прямоугольное уравнение. В результате получится второе параметрическое уравнение. 3. Нарисуйте кривую. Попробуем пару примеров. Пример 1. Найдите набор параметрических уравнений для прямоугольного уравнения y = x 2 + 1, учитывая t = 2 — x.Затем нарисуйте график с точками на 0≤t≤3 и укажите ориентацию кривой. Шаг 1: Возьмите уравнение параметра и поменяйте роли параметра и другой переменной. Пусть t = x и перепишем уравнение параметров, переключив t и x. т = 2 — х
Оригинал х = 2 — т
Переключить t и x Шаг 2: подставьте выражение для переменной на шаге 1 в прямоугольное уравнение y = x2 + 1 Оригинал y = (2 − t) 2 + 1 Заменить y = (4−4t + t2) + 1 Квадрат y = 5−4t + t2 Добавить Шаг 3: Нарисуйте кривую. Перечислите два параметрических уравнения и нарисуйте график с точками на 0≤t≤3 и укажите ориентацию кривой. Прямоугольное уравнение:
у = х2 + 1 Параметрические уравнения:
х = 2 — т,
у = 5−4t + t2 т 0 1 2 3 Икс х = 2 — т 2 1 0 -1 у у = 5 — 4т + т 2 5 2 1 2 Пример 2: Найдите набор параметрических уравнений для прямоугольного уравнения y = 2×2 + 1 при t = x.Затем нарисуйте график с точками в точке t = {0,1,2,3,4} и укажите ориентацию кривой. Шаг 1: Возьмите уравнение параметра и поменяйте роли параметра и другой переменной. t = xОригинал x = t Переключить t и x Шаг 2: подставьте выражение для переменной на шаге 1 в прямоугольное уравнение y = 2×2 + 1 Оригинал y = 2t2 + 1 Заменить y = 2t + 1 квадрат Шаг 3: Нарисуйте кривую. Перечислите два параметрических уравнения и нарисуйте график с точками в t = {0, 1, 2, 3, 4} и укажите ориентацию кривой. Прямоугольное уравнение:
у = 2×2 + 1 Параметрические уравнения:
х = т, у = 2т + 1 т 0 1 2 3 4 Икс х = т 0 1 2 3 2 у у = 2т + 1 2 1 23 12 25 Обратите внимание, что область графика — x≥0, потому что область параметрического уравнения t = x ограничивает x значениями от нуля или выше. При устойчивом растягивающем напряжении при температурах выше 0,4 T м большинство металлов и сплавов демонстрируют нормальные кривые деформации ползучести / времени. Таким образом, после начальной деформации нагружения скорость деформации ползучести (ε˙ = dε / d t ) непрерывно уменьшается со временем в течение первичной стадии, достигая минимальной или вторичной скорости (ε˙m) перед ускорением во время третичной стадии, которая приводит к разрушению через некоторое время ( t f ).Произведение ε˙mtf часто, но не всегда, является постоянным ( M ), что означает, что разрушение при ползучести контролируется деформацией, поскольку t f увеличивается по мере того, как ε˙m падает с уменьшением напряжения и температуры. Было предложено множество соотношений для количественной оценки изменений деформации ползучести во времени. Некоторые из этих уравнений стремятся описать только ранние стадии кривых ползучести, в то время как другие пытаются определить форму всех траекторий ε / t , но не было достигнуто согласия относительно соотношений, которые следует использовать.Несмотря на характерную форму нормальных кривых, поэтому стало обычной практикой игнорировать первичную и третичную стадии, предполагая, что вторичная скорость остается постоянной с увеличением времени и деформации. Уравнение [15.3] затем сводится к: [15.4] ε˙m = f3σ, T с дальнейшим упрощением, дающим: [15.5] ε˙m = f4σf5T , поэтому переменные рассматриваются как отдельные и независимые. В уравнении [15.5] при фиксированной температуре зависимость ε˙m от напряжения может быть определена как: [15.6] ε˙m∝f4σ∝σn , где n — показатель степени напряжения. В качестве альтернативы: [15,7] ε˙m∝f4σ∝expσ , что дает экспоненциальную зависимость ε˙m от напряжения. И наоборот, при фиксированном напряжении температурная зависимость ε˙m в уравнении [15.5] обычно представляется уравнением Аррениуса вида: [15.8] ε˙m∝f5T∝exp − Qc / RT , где Q c — энергия активации ползучести в единицах Дж моль -1 при газовой постоянной R = 8.314 Дж моль −1 K −1 . Комбинируя уравнения [15.5], [15.7] и [15.8], получаем: [15.9] M / tf = ε˙m = Bexp − Qc − Vσ / RT , где B и V рассматриваются как константы. . Однако в большинстве теоретических и практических исследований, проведенных за последние полвека, уравнения [15.5], [15.6] и [15.8] были объединены для получения стандартной степенной зависимости: [15.10] M / tf = ε˙ m = Aσnexp − QcRT , но значения параметра A , а также n и Q c различаются в зависимости от режима нагрузки / температуры. Хотя лист данных NIMS по ползучести № 43 (1996) описывает только характеристики разрушения под напряжением, 1 результаты доступны из других источников 3 , 4 допускают ползучесть срок службы, который следует учитывать в связи с характеристиками скорости ползучести образцов труб из Gr. 91 сталь. Таким образом, используя уравнение [15.10], графики logε˙m / logσ на рис. 15.1 могут быть представлены 3 набором прямых линий, показывающих уменьшение от n 16 при 848 K до n 9 при 923 К.Точно так же отношения напряжение / срок ползучести, определенные в расширенных диапазонах напряжений при 773–973 K для нескольких партий Gr. 91 трубка 1 показывает градиентные изменения, соответствующие уменьшению от n 17 до n 4,5 с повышением температуры (рис. 15.2). При Q c в диапазоне от 600 до 700 кДж моль −1 эти аномально большие значения n и Q c типичны для моделей поведения, описанных для сталей для электростанций и других закаленных частицами сплавы. 15.1. Зависимость минимальных скоростей ползучести от напряжения, зарегистрированная для Gr. 91 труба стальная 3 при 848–923 К. 15.2. Зависимость продолжительности ползучести от напряжения, записанная для нескольких партий Gr. 91 трубная сталь 1 при 773–973 К. Из-за сложных напряжений и температурных зависимостей ε˙m и t f (рис. 15.1 и 15.2) оценка долговременных свойств путем экстраполяции Кратковременные измерения предполагают постоянное использование различных параметрических методов, введенных в 1950-х годах. 5–7 Эти эмпирические подходы определяют «параметры корреляции», включающие как продолжительность ползучести, так и температуру, которые могут быть нанесены на график как функции напряжения, чтобы наложить результаты нескольких партий на единую «эталонную кривую» для данной стали. К сожалению, ни один параметрический метод не смог подобрать экспериментальные данные, представленные для большинства сталей для электростанций, и даже при выборе наилучшей процедуры подгонки достигаемая точность не всегда бывает удовлетворительной. 8 Одно ограничение, присущее параметрическим методам, связано с «переменными константами», встречающимися в стандартных степенных отношениях (уравнение [15.10]). Например, уравнение [15.10] можно переписать, чтобы получить параметр ( P OSD ), предложенный Orr, et al. , 7 как: [15,11] POSD = logtf − P1 / T , где P 1 включает Q c . Следовательно, вариации в Q c гарантируют, что наложенные параметрические графики являются нелинейными. Кривизна графиков, основанных на уравнении [15.11], затем не удаляется заменой уравнения [15.10] с уравнением [15.9]. Фактически, уравнение [15.9] может быть преобразовано в параметр ( P LM ), предложенный Ларсоном и Миллером 5 как [15.12] PLM = Tlogtf + P2 , где P 2 теперь содержит Q c . В сочетании с широкими полосами разброса, обычно связанными с наборами данных из нескольких пакетов, неизвестные кривизны традиционных параметрических графиков ограничивают экстраполяцию примерно до трех значений самых длинных доступных надежных тестовых измерений.По этой причине испытания продолжительностью до 30 000 часов и более обычно должны проводиться для оценки прочности на разрыв в 100 000 часов. Для чистых металлов, переформулируя уравнение [15.10] и используя ожидаемые энергии активации для диффузии, отношения напряжение / скорость ползучести, записанные при различных температурах, накладываются друг на друга 9 просто путем построения зависимостей on (σ / E ) скорости ползучести с температурной компенсацией ε˙m exp ( Q c / RT ).Аналогичным образом, соответствующие характеристики разрушения под напряжением рационализированы путем построения графика продолжительности ползучести с температурной компенсацией: t f exp (- Q c / RT ) против (σ / E ). Однако этот подход неприменим к сталям для электростанций, поскольку незначительные изменения в условиях термомеханической обработки, выбранных для изготовления компонентов, могут изменить получаемую микроструктуру. Модули упругости зависят от температуры, но не сильно изменяются при изменении микроструктуры, тогда как свойства ползучести и разрушения закаленных частицами сплавов чувствительны как к температуре, так и к микроструктуре, как и σ Y и σ TS .Следовательно, ранние процедуры рационализации, основанные на нормализации σ до E 9 , обновляются путем нормализации σ до σ Y или σ TS . 10–13 Таким образом, используя значения σ TS , измеренные для каждой партии Gr. 91 исследуемая сталь, 1 данные о многосерийном разрушении под напряжением на рис. 15.2 наложены на рис. 15.3 с использованием модифицированного выражения степенного закона: 11–13 15.3. Зависимость срока ползучести с температурной компенсацией от (σ / σ T S ) с использованием значений σ T S для каждой партии Gr.91 исследована трубная сталь, 1 с Q c * = 300 кДж моль −1 . [15,13] M / tf = ε˙m = A * σ / σTSnexp − Qc * / RT , где A * ≠ A и Q c * получается из температурной зависимости ε ˙m при постоянной (σ / σ TS ), а не при постоянной σ, как при определении Q c в уравнении [15.10]. Из рис. 15.3 видно, что Q c * = 300 кДж моль −1 , значение, близкое к значению для решеточной диффузии в матрице легированной стали.С Гр. 91, как и в случае с другими металлами и сплавами, наборы свойств ползучести 10–14 также эффективно рационализируются путем нормализации σ до σ Y , так что (σ / σ TS ) можно заменить на (σ / σ Y ) в уравнении [15.13]. Независимо от того, выбрано ли σ Y или σ TS , результирующая «эталонная кривая» на рис. 15.3, по крайней мере, столь же впечатляющая, как и полученная с использованием параметрических методов. Кроме того, с помощью уравнения [15.13] эмпирические члены в параметрических отношениях (уравнения [15.11] и [15.12] заменены физически значимыми свойствами, а именно ощутимой энергией активации и измеренными значениями σ Y и σ TS . Уравнение [15.13] позволяет избежать больших и переменных значений Q c , наблюдаемых при наборах данных для Gr. 91 описываются с помощью уравнения [15.10] (рис. 15.2), но не устраняют уменьшение с n 20 до n 4 (рис.15.3), обычно ожидается, что тенденция сохранится к n ± 1 или менее по мере увеличения продолжительности испытания и увеличения температуры. Одна ранняя попытка объяснить аномально большие значения n предположила 15 , что ползучесть происходит не при полном приложенном напряжении (σ), а при пониженном напряжении (σ — σ o ), так что [15.14 ] ε˙m∝σ − σom , где м = 4, при этом σ o теперь называется «пороговым напряжением». Сравнение уравнений [15.10] и [15.14], n ≅ m ≅ 4, когда σ o ≅ 0 или когда σ o ∝ σ, тогда как n > m , когда σ o большое. Этот подход широко применялся для ползучести сплавов с упрочненными частицами, 16 , но был достигнут незначительный прогресс, поскольку σ o нельзя надежно измерить или спрогнозировать. Чаще всего вариации значений n интерпретируются на основании того, что различные механизмы ползучести становятся доминирующими в различных режимах напряжения и температуры.Таким образом, хотя наложенные результаты на рис. 15.3 предполагают, что градиент непрерывно изменяется по мере уменьшения (σ / σ TS ), такие кривые можно аппроксимировать серией отрезков прямых линий, соответствующих n >> 4, n 4 и в конечном итоге n ≅ 1, причем каждое изменение градиента связано с переходом механизма. Тем не менее, не было достигнуто согласия по детальным рассматриваемым процессам, и с практической точки зрения текущие теории не позволяют прогнозировать свойства ползучести и разрушения конструкционных сталей.Более того, принимая концепции нескольких механизмов, анализ результатов, записанных в одном режиме механизма, не позволил бы прогнозировать свойства в другом режиме, что потребовало бы завершения долгосрочных программ испытаний. В этом контексте, поэтому кажется разумным рассмотреть, предлагают ли стандартные отношения степенного закона действительную основу для представления и интерпретации свойств ползучести. С помощью уравнения [15.10] тот факт, что n и Q c сами являются функциями напряжения и температуры, означает, что при упрощении уравнения [15.4], чтобы получить уравнение [15.5], переменные не являются отдельными и независимыми. Кроме того, предположение о том, что изменения деформации ползучести со временем, напряжением и температурой (уравнение [15.3]) можно адекватно количественно оценить с помощью напряжений и температурных зависимостей вторичной или «установившейся» скорости ползучести (уравнение [15.4]): весьма сомнительно. По этим причинам, без привлечения переключений механизмов, альтернативный подход 17 утверждает, что модели поведения, проявляемые сталями для электростанций (рис.2 = 1 $. Несколько вопросов, которые стоит задать себе: Теперь вы знаете , какие частей единичной окружности задаются параметрической кривой. Добавлен. Как и многие студенты на начальном этапе, вам кажется, что вы хотите построить несколько точек, а затем выполнить интерполяцию; это не лучшая идея, потому что она полагается на то, что вы просто случайно попадете в нужные точки, чтобы получить точную картину того, что происходит.Чтобы дать вам пример, если вы пытались построить график для функции $ y = \ sin (\ pi x) $ и попробовали несколько точек, скажем, $ x = 0 $, $ x = 1 $, $ x = 2 $, $ x = 3 $ и т. д., вы можете подумать, что ваша функция — это постоянная функция $ 0 $, потому что при выборе точек упускается все важное, что происходит с $ y $. Вы, , не хотите, этого делать. Вместо этого вы хотите подумать о том, что делают эти функции. Один из способов, которым я считаю наиболее плодотворным размышление о параметрических уравнениях, — это думать о параметре как о дающем время , а об уравнениях как о движении точки; Представьте себе анимацию со светящейся точкой, движущейся по плоскости и оставляющей за собой «след» света.Этот след — параметрическая кривая, точка — это положение в «текущем $ t $». Вы хотите подумать о том, что делает эта точка, когда ваш параметр варьируется от своего начального значения до конечного значения (то есть, когда анимация идет от начала до конца). Итак, начнем с $ \ theta = 0 $, первого кадра вашей анимации. Ваша светящаяся точка будет в $ x (0) = \ sin (0) = 0 $ и $ y (0) = \ cos (0) = 1 $. Итак, вы начинаете с точки $ (0,1) $. Теперь нажмите кнопку А что насчет $ y $? Он начинается с 1 доллара США; он будет вести себя как график $ \ cos \ theta $. Когда вы нажмете Теперь сложите эти два движения вместе: вы начнете с $ (0,1) $, вершины единичного круга. Затем, когда $ \ theta $ перемещается от $ 0 $ к $ \ pi / 2 $, светящаяся точка начинает двигаться вправо и вниз, всегда по единичной окружности, до тех пор, пока $ \ theta = \ pi / 2 $ не окажется в точке Хорошо, готовы продолжить? Снова нажмите Все это время движение было без прыжков, колебаний или возвратов, потому что функции $ x = \ sin \ theta $ и $ y = \ cos \ theta $ имеют эти движения: без прыжков, без пропусков, без рывков, без колебаний , никаких возвратов, просто плавное движение (представьте, что ваша рука рисует их графики).Эта светящаяся точка теперь проследила часть единичной окружности ровно один раз, без возврата. Какая часть? Результаты поиска 144 экспоната Создайте параметрический график кривой на плоскости с направлением, указанным стрелками и цветом Постройте параметрическую определенную поверхность вместе с различными типами сечений поверхности. Создайте параметрический график кривой в пространстве с направлением, указанным стрелками и цветом Классифицирует и строит любой полином степени два или меньше от двух или меньшего числа переменных. Вычислить касательную плоскость параметрической поверхности Получить диапазон переменных, против которого строить заданную функцию График с несколькими улучшениями, добавленными для сингулярностей, асимптот, значений surd и неинтервальных областей Создание графика, на котором диапазоны графика и параметры функции могут управляться динамически Постройте список векторов на плоскости Постройте плотность ключевых слов в фрагменте текста Постройте две кривые и выделите их точки пересечения Постройте гиперграф, заданный списком гиперребер Отображение интерактивного графика со всей необходимой информацией для данного конического сечения Постройте тайминги эталонного теста Комбинируйте графики, позволяя создавать графики с двумя наборами осей и объединять прологи и эпилоги. Постройте кривую, определяемую ее кривизной Постройте матрицу точечной диаграммы Создавайте составные графики и другие расширенные сеточные макеты графиков Постройте вложенный список значений в виде древовидной карты Постройте положение астрономических объектов в галактике Млечный Путь или рядом с ней. Постройте заданное количество периодов периодической функции Постройте гиперграф, заданный списком гиперребер и изолированных вершин Получите приближение к параметрической кривой Визуализируйте пересечения перекрывающихся множеств Визуализируйте одномерные повторяющиеся функции Создавайте маркеры, тщательно разработанные для создания графиков публикационного качества. Постройте вхождения меток в список Постройте полярную дендрограмму кластеризации Постройте состав циклов, имеющих разные радиусы, частоты и фазы. Версия графика, которая позволяет увеличивать график с помощью мыши. Деревья условий порядка построения графиков для метода Рунге – Кутта Сделайте график функции изнутри и снаружи Постройте построенные модели вместе с их необработанными данными Визуализируйте собственные векторы матрицы 2 x 2 или 3 x 3 Постройте недетерминированный конечный автомат Визуализируйте выражение статического комбинатора Аппроксимировать параметрическую поверхность с помощью различных графических примитивов Постройте и найдите площадь области, определяемую списком точек, осью x и типом границы. Наносит на график наборы данных большой размерности по параллельным осям Визуализируйте основные компоненты табличных данных Создание мозаики плоскости с заданными формами ячеек Постройте график функции Сондерса Возвращает контурный график функции вместе с проекциями на плоскость x-y заданных участков графика. Постройте график роста списков и временных данных Визуализируйте сложную функцию в виде множества пузырьков Создание узлов интерполяции из точек на кривой Создайте интерактивную графическую викторину по построению линейных функций. Создайте интерактивную графическую викторину по построению кубических функций Создайте интерактивную графическую викторину по построению квадратичных функций. Найдите рациональную интерполяцию параметрически определенной функции Постройте систему отсчета Френе – Серре кривой Постройте линейчатую поверхность Постройте катастрофу кривой Постройте значения функции в вершинах графика Визуализируйте перекрытие двух дискретных временных рядов Постройте график эволюции многоходовой системы Постройте кривую преследования хищник-жертва Отображение разных вертикальных осей для двух построенных выражений Постройте данные вместе с визуализацией квадратов ошибок по сравнению с подгонкой Постройте полигоны после итеративного применения перемещения, масштабирования и поворота Постройте массив значений с точками в указанных позициях Создайте тест, чтобы оценить понимание графиков функций синуса и косинуса Постройте графики соблюдения принципа Парето Вычислить и построить аппроксимацию интеграла функции на интервале Извлечь данные из графического изображения Постройте массив цифр так, чтобы они были неровными слева. Постройте функцию вместе с графическим отображением итераций Ньютона, приближающих ее корень Получите график молекулы с атомами или связями, окрашенными в соответствии со значениями свойств Постройте дендрограмму для набора нуклеотидных последовательностей генома Постройте кристаллографические плоскости кубической решетки с индексами Миллера h, k, l Классифицируйте и постройте любой многочлен второй степени или менее от трех или менее переменных. Постройте полярную древовидную карту данного вложенного списка Постройте поверхность вместе с различными типами участков поверхности. Постройте кривую, определяемую ее кривизной и кручением Постройте относительное положение четырех крупнейших спутников Юпитера, если смотреть с Земли. Визуализируйте распределение форм молекул на 2D-диаграмме рассеяния Найдите минимальное и максимальное приближение функции, определенной параметрически. Визуализируйте эволюцию комбинаторного выражения Визуализируйте эволюцию одномерной системы замещения, не зависящей от соседей. Создание визуального отображения гиперграфа Постройте диаграмму стволовых и листовых Визуализируйте согласованные скобки комбинатора Создание визуализации для выравнивания последовательностей ДНК Визуализируйте оценки функций, выполненные FindMinimum Визуализируйте содержимое двоичных данных Визуализация эволюции мобильного автомата Создайте генеалогическое генеалогическое древо, показывающее отношения между вами и другим родственником Визуализируйте оценки функций, выполненные FindRoot Отображение линии регрессии набора данных Показать L-систему Постройте мультипространство в 3D Графики упорядоченных трехвалентных графов Постройте временной ряд, который включает штриховку, чтобы указать диапазоны нанесенного значения. Постройте список векторов в пространстве Создавайте интерактивную версию графического выражения с масштабированием, панорамированием и всплывающими подсказками. Создайте TabView для ListPlot, используя линейные и логарифмические оси Постройте график, иллюстрирующий причинно-следственные особенности эволюции системы замещения. Постройте квадратную поверхность, автоматически определяя интересующие области, направление взгляда и масштаб Версия ListPlot, которая отображает два списка данных с разными осями y Версия ComplexPlot с трехмерной вращающейся сферой Римана График изменения веса с течением времени Визуализируйте производную по направлению на трехмерном графике Добавьте к графику легенду с флажками, которая динамически включает и выключает отдельные наборы данных. Создание значка правила для одномерной системы подстановки, не зависящей от соседей Создание многослойного трехмерного графика графика Создайте значок правила для системы тегов Создайте значок правила для мобильного автомата Создать график из последовательности данных Визуализация эволюции системы последовательного замещения Создайте тест, чтобы оценить понимание линейных функций Создайте двоичную матрицу с повернутой эллиптической областью единиц Постройте положение объектов солнечной системы в 3D Получите трехмерный график молекулы с атомами или связями, окрашенными в соответствии со значениями свойств Постройте римановы поверхности композиций элементарных функций Постройте относительное положение Луны и Земли в 3D, освещенное Солнцем. Вычислить и построить аппроксимацию интеграла функции двух переменных на прямоугольнике, используя различные методы и типы разбиения. Постройте трехмерный рельеф, представляющий диффузор с квадратичным остатком. Отображение числовых данных на диаграмме в стиле радара Постройте спирограф Покажите молекулу в 3D вместе с ее элементами симметрии Создание значка правила для системы последовательной замены Измерьте время оценки функции на заданном наборе входов. Постройте спирали Дойла Отображение конкретных элементарных ячеек в трехмерной решетке Увеличить ограничивающую рамку на дробную величину Отображение ячеек Вороного для определенных точек решетки в трехмерной решетке Создавайте случайные графики мандалы Сделайте участки из плиток Пенроуза Визуализируйте жизнь в неделях или месяцах Создайте тест, чтобы оценить понимание теоремы о среднем значении для производных Найдите стили, используемые в проекте Wolfram Physics Project Постройте последовательные шаги бабочки Hofstadter & CloseCurlyQuote Динамически увеличивайте графики с помощью мыши Проверить, является ли выражение графическим параметром Постройте положение звезд на диаграмме Герцшпрунга – Рассела. Итерации сюжета для 2D-игры с хаосом Получите диапазон сюжета, используемый в части графики Отобразить дерево с сеткой Постройте положение континентальных плит в различные геологические периоды. Получите динамический график одномерной функции вместе с дополнительными алгебраическими и основанными на исчислении свойствами функции. Интерактивный выбор индексов атомов на трехмерном графике молекулы Создайте сетку из молекулы Отображение диаграммы масштабированного количества элементов в списке Возвращает информацию о визуализированной форме объекта Graphics, такую как размер отступа изображения и фактический используемый диапазон графика. В этом разделе вы будете: Это конец девятого иннинга с двумя аутами и двумя игроками на базе. Хозяева проигрывают с разницей в два раунда. Бэттер раскачивается и ударяет по бейсбольному мячу со скоростью 140 футов в секунду и под углом примерно 45 ° к горизонтали. Как далеко полетит мяч? Сможет ли он очистить забор для выигрышного хоумрана? Результат может частично зависеть от других факторов (например, ветра), но математики могут смоделировать траекторию снаряда и приблизительно предсказать, как далеко он пролетит, используя параметрических уравнений .В этом разделе мы обсудим параметрические уравнения и некоторые общие приложения, такие как задачи о движении снаряда. Вместо графического калькулятора или компьютерной программы построения графиков, нанесение точек на график для представления графика уравнения является стандартным методом. Пока мы тщательно вычисляем значения, точечное построение очень надежно. Для пары параметрических уравнений нарисуйте график с помощью точек. и для значений на интервале, для которого определены функции. Построение графика пары параметрических уравнений по точкам построения Нарисуйте график параметрических уравнений x (t) = t2 + 1, y (t) = 2 + t. Построить таблицу значений t, x (t), и у (т), , как в [ссылка], и нанесите точки на плоскости. График представляет собой параболу с вершиной в точке (1,2), открытие вправо. См. [Ссылка]. Анализ Как значения для t прогрессируют в положительном направлении от 0 до 5, нанесенные точки очерчивают верхнюю половину параболы.В качестве значений т становятся отрицательными, они очерчивают нижнюю половину параболы. Ограничений по домену нет. Стрелки указывают направление в соответствии с возрастающими значениями t. График не представляет функцию, так как он не пройдет проверку вертикальной линии. График состоит из двух частей: положительные значения t, и отрицательные значения для t. Нарисуйте график параметрических уравнений x = t, y = 2t + 3, 0≤t≤3. ! [График заданных параметрических уравнений с ограниченной областью — он выглядит как правая половина восходящей параболы.] (/ Algebra-trigonometry-book / resources / CNX_Precalc_Figure_08_07_003.jpg) Построение графа тригонометрических параметрических уравнений Создайте таблицу значений для заданных параметрических уравнений и нарисуйте график: x = 2cos ty = 4sin t Создайте таблицу, подобную приведенной в [ссылка], используя угловую меру в радианах в качестве входных данных для t, и оценивая x и г. Использование углов с известными значениями синуса и косинуса для t упрощает расчеты. [ссылка] показывает график. По симметрии, показанной в значениях x и у, мы видим, что параметрические уравнения представляют собой эллипс . Эллипс отображается в направлении против часовой стрелки, как показано стрелками, указывающими на увеличение t значений. Анализ Мы видели, что параметрические уравнения могут быть построены на графике по точкам. Однако графический калькулятор сэкономит время и выявит нюансы на графике, которые могут быть слишком утомительными, чтобы обнаружить их, используя только ручные вычисления. Обязательно измените режим на калькуляторе на параметрический (PAR). Чтобы подтвердить, Y = должно показать X1T = Y1T = вместо Y1 =. Изобразите параметрические уравнения: x = 5cos t, y = 3sin t. ! [График заданных уравнений — горизонтальный эллипс.] (/ Algebra-trigonometry-book / resources / CNX_Precalc_Figure_08_07_005.jpg) Совместное построение графиков параметрических уравнений и прямоугольной формы Постройте параметрические уравнения x = 5cos t и y = 2sin t. Сначала постройте график, используя точки данных, сгенерированные из параметрической формы . Затем изобразите прямоугольную форму уравнения.Сравните два графика. Создайте таблицу значений, как в [ссылка]. Постройте (x, y) значений из таблицы. См. [Ссылка]. Затем преобразуйте параметрические уравнения в прямоугольную форму. Для этого решаем для t в любом x (t) или y (t), , а затем подставим выражение для t в другом уравнении.Результатом будет функция y (x) при решении для t как функция от x, или x (y) при решении для t как функция от y. x = 5cos tx5 = cos t Решить для cos t. y = 2sin t Решить относительно sin t.y2 = sin t Затем используйте теорему Пифагора . cos2t + sin2t = 1 (x5) 2+ (y2) 2 = 1×225 + y24 = 1 Анализ В [ссылка] данные параметрических уравнений и прямоугольного уравнения отображаются вместе.Параметрические уравнения показаны синим цветом; график для прямоугольного уравнения нарисован поверх параметрического в виде пунктирной линии красного цвета. Ясно, что обе формы дают один и тот же график. Построение графиков параметрических и прямоугольных уравнений в системе координат Постройте параметрические уравнения x = t + 1 и y = t, t≥0, и прямоугольный эквивалент y = x − 1 в той же системе координат. Создайте таблицу значений для параметрических уравнений, как мы делали в предыдущем примере, и график y = t, t≥0 в той же сетке, что и в [ссылка]. Анализ С доменом на т. ограничено, мы наносим только положительные значения t. Параметрические данные отображаются синим цветом, а график прямоугольного уравнения — красным пунктиром.И снова мы видим, что эти две формы пересекаются. Изобразите график параметрических уравнений x = 2cos θ и y = 4sin θ, вместе с прямоугольным уравнением на той же сетке. График параметрических уравнений выделен красным цветом, а график прямоугольного уравнения нарисован синими точками поверх параметрических уравнений. Многие преимущества параметрических уравнений становятся очевидными при решении реальных задач.Хотя прямоугольные уравнения в x и y дают общую картину пути объекта, они не показывают положение объекта в конкретное время. Однако параметрические уравнения иллюстрируют, как значения x и y изменяются в зависимости от t как местоположения движущегося объекта в конкретный момент времени. Обычное применение параметрических уравнений — решение задач, связанных с движением снаряда. При этом типе движения объект продвигается вперед в направлении вверх, образуя угол θ к горизонтали, с начальной скоростью v0, и на высоте h выше горизонтали. Путь объекта, движущегося под углом θ к горизонтали, с начальной скоростью v0, и на высоте h выше горизонтали, равно х = (v0cosθ) t y = −12gt2 + (v0sinθ) t + h где g учитывает влияние силы тяжести и h — начальная высота объекта. В зависимости от устройств, участвующих в проблеме, используйте g = 32 фут / с2 или g = 9,8 м / с2. Уравнение для x дает горизонтальное расстояние, а уравнение для y дает вертикальное расстояние. Для решения задачи о движении снаряда используйте параметрические уравнения. Заменить указывает угол, под которым объект перемещается.Замените этот угол в градусах на Срок представляет эффект силы тяжести. В зависимости от задействованных единиц используйте или Снова замените начальную скорость на и высота, на которой объект двигался, на Нахождение параметрических уравнений для описания движения бейсбольного мяча Решите проблему, указанную в начале этого раздела. Попадает ли тесто в выигрышную игру? Предположим, что мяч ударяется с начальной скоростью 140 футов в секунду под углом 45 ° в горизонтальное положение, установив контакт на высоте 3 фута над землей. Используйте формулы, чтобы составить уравнения. Горизонтальное положение определяется с помощью параметрического уравнения для x. Таким образом, x = (v0cos θ) tx = (140cos (45 °)) t Вертикальное положение определяется с помощью параметрического уравнения для y. Таким образом, y = −16t2 + (v0sin θ) t + hy = −16t2 + (140sin (45 °)) t + 3 Подставьте 2 в уравнения, чтобы найти горизонтальное и вертикальное положение мяча. x = (140cos (45 °)) (2) x = 198 футов = −16 (2) 2+ (140sin (45 °)) (2) + 3y = 137 футов Через 2 секунды мяч оказывается на расстоянии 198 футов от бокса бьющего и на высоте 137 футов над землей. Чтобы вычислить, как долго мяч находится в воздухе, мы должны выяснить, когда он ударится о землю или когда y = 0. Таким образом, y = −16t2 + (140sin (45∘)) t + 3y = 0 Установите y (t) = 0 и решите квадратное уравнение t = 6,2173 При t = 6,2173 секунды, мяч коснулся земли. (Квадратное уравнение можно решить разными способами, но эта задача была решена с помощью компьютерной математической программы.) Мы не можем подтвердить, что попадание было хоумраном, не принимая во внимание размер дальнего поля, который варьируется от поля к полю.Однако для простоты предположим, что внешняя стена находится в 400 футах от домашней плиты в самой глубокой части парка. Предположим также, что высота стены составляет 10 футов. Чтобы определить, касается ли мяч стены, нам нужно вычислить, насколько высок мяч, когда x = 400 футов. Таким образом, мы установим x = 400, решим для t, и ввод т в г. x = (140cos (45 °)) t400 = (140cos (45 °)) t t = 4.04 y = −16 (4,04) 2+ (140sin (45 °)) (4,04) +3 y = 141,8 Мяч находится на высоте 141,8 фута, когда вылетает за пределы поля. Это был действительно хоумран. См. [Ссылка]. и зависит, можно использовать параметрические уравнения. и Выберите значения для в порядке возрастания. Постройте последние два столбца для и См. [Ссылка] и [ссылка]. и Начальная скорость обозначена как представляет начальный угол объекта при броске, а представляет высоту, на которой объект перемещается. Какие два метода используются для построения графиков параметрических уравнений? точек с помощью стрелки ориентации и графического калькулятора В чем отличие параметрических уравнений точечного построения от декартовых уравнений? Почему на некоторых графиках нарисованы стрелки? Стрелки показывают ориентацию, направление движения согласно возрастающим значениям t. Назовите несколько распространенных типов графиков параметрических уравнений. Почему параметрические графики важны для понимания движения снаряда? Параметрические уравнения показывают различные вертикальные и горизонтальные движения во времени. Для следующих упражнений нарисуйте каждый набор параметрических уравнений в виде таблицы значений. Включите ориентацию на графике. ! [График приведенных уравнений — имеет вид раскрывающейся вверх параболы.] (/ algebra-trigonometry-book / resources / CNX_Precalc_Figure_08_07_202.jpg) ! [График заданных уравнений — прямая, наклон отрицательный.] (/ Algebra-trigonometry-book / resources / CNX_Precalc_Figure_08_07_204.jpg) ! [График данных уравнений — выглядит как боковая парабола, открывающаяся вправо.] (/ Algebra-trigonometry-book / resources / CNX_Precalc_Figure_08_07_206.jpg) Для следующих упражнений нарисуйте кривую и укажите ее ориентацию. {x (t) = — ty (t) = t ! [График данных уравнений — выглядит как левая половина открывающейся вверх параболы.] (/ Algebra-trigonometry-book / resources / CNX_Precalc_Figure_08_07_208.jpg) {x (t) = — t + 2y (t) = 5− \ | t \ | ! [График данных уравнений — выглядит как открывающаяся вниз функция абсолютного значения.] (/ Algebra-trigonometry-book / resources / CNX_Precalc_Figure_08_07_210.jpg) {x (t) = 4sin ty (t) = 2cos t {x (t) = 2sin ty (t) = 4cos t ! [График приведенных уравнений — вертикальный эллипс.] (/ algebra-trigonometry-book / resources / CNX_Precalc_Figure_08_07_212.jpg) {x (t) = 3cos2ty (t) = — 3sin t {x (t) = 3cos2ty (t) = — 3sin2t ! [График заданных уравнений — прямая от (0, -3) до (3,0). Он проходит в обоих направлениях, с положительным и отрицательным наклоном.] (/ Algebra-trigonometry-book / resources / CNX_Precalc_Figure_08_07_214.jpg) {x (t) = sec ty (t) = tan t {x (t) = sec ty (t) = tan2t ! [График приведенных уравнений — имеет вид раскрывающейся вверх параболы.] (/ algebra-trigonometry-book / resources / CNX_Precalc_Figure_08_07_216.jpg) Для следующих упражнений нарисуйте уравнение и укажите ориентацию. Затем напишите декартово уравнение. {x (t) = t − 1y (t) = — t2 ! [График данных уравнений — выглядит как открывающаяся вниз парабола.] (/ Algebra-trigonometry-book / resources / CNX_Precalc_Figure_08_07_218.jpg) {x (t) = 2cos ty (t) = — sin t ! [График заданных уравнений — горизонтальный эллипс.] (/ algebra-trigonometry-book / resources / CNX_Precalc_Figure_08_07_220.jpg) {x (t) = 7cos ty (t) = 7sin t {x (t) = e2ty (t) = — e t ! [График данных уравнений — выглядит как нижняя половина боковой параболы, открывающейся вправо] (/ algebra-trigonometry-book / resources / CNX_Precalc_Figure_08_07_222.jpg) Для следующих упражнений нарисуйте уравнение и укажите ориентацию. х = t2, y = 3t, 0≤t≤5 х = 2t, у = t2, −5≤t≤5 ! [График данных уравнений — выглядит как открывающаяся вверх парабола] (/ algebra-trigonometry-book / resources / CNX_Precalc_Figure_08_07_224.jpg) х = т, у = 25-т2, 0 <т≤5 х (t) = — t, y (t) = t, t≥0 ! [График данных уравнений — выглядит как верхняя половина боковой параболы, открывающейся влево] (/ algebra-trigonometry-book / resources / CNX_Precalc_Figure_08_07_226.jpg) x = −2cos t, y = 6 sin t, 0≤t≤π x = −sec t, y = tan t, — π2 ! [График данных уравнений — левая половина гиперболы с диагональными асимптотами] (/ algebra-trigonometry-book / resources / CNX_Precalc_Figure_08_07_228.jpg) Для следующих упражнений используйте параметрические уравнения для целых чисел a и b : х (t) = acos ((a + b) t) y (t) = acos ((a − b) t) График в области [−π, 0], , где a = 2 и b = 1, и включить ориентацию. График в области [−π, 0], , где a = 3 и b = 2 , и включить ориентацию. ! [График заданных уравнений — периодическая вертикальная траектория] (/ algebra-trigonometry-book / resources / CNX_Precalc_Figure_08_07_230.jpg) График в области [−π, 0], , где a = 4 и b = 3 , и включить ориентацию. График в области [−π, 0], , где a = 5 и b = 4 , и включить ориентацию. ! [График заданных уравнений — периодическая вертикальная траектория] (/ algebra-trigonometry-book / resources / CNX_Precalc_Figure_08_07_232.jpg) Если на 1 больше, чем b, описать влияние значений и б имеют на графике параметрические уравнения. Опишите график, если a = 100 и b = 99. Произойдет 100 возвратно-поступательных движений. Что будет, если b больше чем на 1? Опишите график. Если параметрические уравнения x (t) = t2 и y (t) = 6−3t есть график горизонтальной параболы, раскрывающейся вправо, что бы изменило направление кривой? Возьмем противоположность x (t) уравнение. Для следующих упражнений опишите график системы параметрических уравнений. и y (t) линейный и x (t) линейный и x (t) линейный Напишите параметрические уравнения круга с центром (0,0), радиус 5 и ориентация против часовой стрелки. {x (t) = 5costy (t) = 5sint Запишите параметрические уравнения эллипса с центром (0,0), большая ось длиной 10, малая ось длиной 6 и ориентация против часовой стрелки. Для следующих упражнений используйте графическую утилиту для построения графика в окне [−3,3] по [−3,3] в домене [0,2π) для следующих значений и б , и включить ориентацию. {x (t) = sin (at) y (t) = sin (bt) а = 1, б = 2 ! [График заданных уравнений] (/ algebra-trigonometry-book / resources / CNX_Precalc_Figure_08_07_233.jpg) а = 3, б = 3 ! [График приведенных уравнений — прямые, идущие в Q1 и Q3 (в обоих направлениях) от начала координат до 1 единицы.] (/ algebra-trigonometry-book / resources / CNX_Precalc_Figure_08_07_235.jpg) а = 2, б = 5 ! [График данных уравнений — линии, идущие в Q1 и Q3 (в обоих направлениях) от начала координат на 3 единицы.] (/ Algebra-trigonometry-book / resources / CNX_Precalc_Figure_08_07_237.jpg) Для следующих упражнений посмотрите на графики, созданные с помощью параметрических уравнений вида {x (t) = acos (bt) y (t) = csin (dt). Используйте параметрический режим графического калькулятора, чтобы найти значения a, b, c, и d для достижения каждого графика. ! [График заданных уравнений] (/ algebra-trigonometry-book / resources / CNX_Precalc_Figure_08_07_239.jpg) а = 4, б = 3, с = 6, г = 1 ! [График заданных уравнений] (/ algebra-trigonometry-book / resources / CNX_Precalc_Figure_08_07_240.jpg) ! [График заданных уравнений] (/ algebra-trigonometry-book / resources / CNX_Precalc_Figure_08_07_241.jpg) а = 4, б = 2, с = 3, г = 3 ! [График заданных уравнений] (/ algebra-trigonometry-book / resources / CNX_Precalc_Figure_08_07_242.jpg) Для следующих упражнений используйте графическую утилиту для построения графиков заданных параметрических уравнений. Изобразите все три набора параметрических уравнений в области [0, 2π]. ! [График заданных уравнений] (/ algebra-trigonometry-book / resources / CNX_Precalc_Figure_08_07_243.jpg)! [График заданных уравнений] (/ algebra-trigonometry-book / resources / CNX_Precalc_Figure_08_07_244.jpg)! [График заданных уравнений] (/ algebra-trigonometry-book / resources / CNX_Precalc_Figure_08_07_245.jpg) Изобразите все три набора параметрических уравнений в области [0,4π]. Изобразите все три набора параметрических уравнений в области [−4π, 6π]. ! [График заданных уравнений] (/ algebra-trigonometry-book / resources / CNX_Precalc_Figure_08_07_249.jpg)! [График заданных уравнений] (/ algebra-trigonometry-book / resources / CNX_Precalc_Figure_08_07_250.jpg)! [График заданных уравнений] (/ algebra-trigonometry-book / resources / CNX_Precalc_Figure_08_07_251.jpg) Кажется, что график каждой системы параметрических уравнений «ползет» по одной из осей. Что контролирует, по какой оси ползет график? Объясните влияние на график параметрического уравнения, когда мы переключили sin t и cos t . Y — перехват изменений. Объясните влияние на график параметрического уравнения, когда мы изменили домен. Объект подбрасывается в воздух с вертикальной скоростью 20 футов / с и горизонтальной скоростью 15 футов / с. Высота объекта описывается уравнением y (t) = — 16t2 + 20t , а объект движется по горизонтали с постоянной скоростью 15 футов / с. Напишите параметрические уравнения для положения объекта, а затем избавьтесь от времени, чтобы записать высоту как функцию горизонтального положения. у (х) = — 16 (х15) 2 + 20 (х15) Скейтбордист, едущий по ровной поверхности с постоянной скоростью 9 футов / с, подбрасывает в воздух мяч, высоту которого можно описать уравнением y (t) = — 16t2 + 10t + 5. Напишите параметрические уравнения для положения мяча, а затем исключите время, чтобы записать высоту как функцию горизонтального положения. Для следующих упражнений используйте этот сценарий: Дротик бросается вверх с начальной скоростью 65 футов / с под углом возвышения 52 °. Рассмотрим положение дротика в любой момент времени t. Сопротивлением воздуха пренебречь. Найдите параметрические уравнения, моделирующие проблемную ситуацию. {x (t) = 64tcos (52 °) y (t) = — 16t2 + 64tsin (52 °) Найдите все возможные значения x , которые представляют ситуацию. Когда дротик упадет на землю? примерно 3,2 секунды Найдите максимальную высоту дротика. В какое время дротик достигнет максимальной высоты? Для следующих упражнений посмотрите на графики каждого из четырех параметрических уравнений. Хотя они выглядят необычно и красиво, они настолько распространены, что имеют названия, указанные в каждом упражнении. Используйте графическую утилиту для построения графика каждого в указанном домене. Эпициклоида: {x (t) = 14cos t − cos (14t) y (t) = 14sin t + sin (14t) в домене [0,2π] . Гипоциклоида: {x (t) = 6sin t + 2sin (6t) y (t) = 6cos t − 2cos (6t) в домене [0,2π] . ! [График заданных уравнений — гипоциклоида] (/ algebra-trigonometry-book / resources / CNX_Precalc_Figure_08_07_253.jpg) Гипотрохоид: {x (t) = 2sin t + 5cos (6t) y (t) = 5cos t − 2sin (6t) в домене [0,2π] . Роза: {x (t) = 5sin (2t) sinty (t) = 5sin (2t) стоимость в домене [0,2π] . ! [График заданных уравнений — четырехлепестковая роза] (/ algebra-trigonometry-book / resources / CNX_Precalc_Figure_08_07_255.jpg) Вы также можете бесплатно скачать по адресу http://cnx.org/contents/[email protected] Атрибуция: Построение графиков — одна из основных сильных сторон систем компьютерной алгебры.
Мы различаем построение формул и функций.
Подобно функции и выражениям в одной переменной,
кривые на плоскости лучше всего строить, когда они заданы в параметрической форме.
Для кривых с особенностями в начале координат преобразование в
полярная форма может привести к гораздо лучшим результатам, потому что тогда мы можем
исключить особую точку в полярной формулировке. Плоская кривая может быть задана четырьмя различными способами.3 — x), — 2,2, ymin = -5, ymax = 5, detect_poles = ‘show’, figsize = 4) На рис. 35 мы видим вертикальные асимптоты на графике. Рис. 35 График функции с несколькими полюсами. Некоторые кривые даны явными представлениями для координат
\ ((x (t), y (t)) \), как функции от некоторой переменной \ (t \).
Мы строим такие представления с помощью Хотя сюжет из 2000 точек выглядит очень хорошо,
может создаться впечатление, что кривая дважды проходит через начало координат. Переведем в полярные координаты.
В полярных координатах каждая точка представлена радиусом и углом.
Радиус — это расстояние от точки до начала координат.
Угол — это угол, который образует вектор, заканчивающийся в точке.
с горизонтальной осью. Прежде чем решать это выражение для r, хорошо бы упростить. Даже без факторизации мы видим, что r = 0 — двойной корень. Мы выбираем первое решение и наносим две части разными цветами.
Для кривых, заданных в полярных координатах, как \ (r = f (t) \),
мы используем Полярный график показан на рис. 39. Рис. 39 Две половины полярного графика для \ (t \ in [0, \ pi] \)
и для \ (t \ in [\ pi, 2 \ pi] \). Это все? Ну, не забыли ли мы о компоненте r = 0?
Точка (0, 0) является изолированной особенностью вещественной кривой. Полный полярный график показан на рис. 40. Рис. 40 Полный полярный график с добавлением начала координат в виде точки. Поделись Функция с квадратным корнем определена только при тех значениях «икс», когда подкоренное выражение неотрицательно: . Если корень расположился в знаменателе , то условие очевидным образом ужесточается: . Аналогичные выкладки справедливы для любого корня положительной чётной степени: , правда, корень уже 4-ой степени в исследованиях функций не припоминаю. Пример 5 Найти область определения функции Решение: подкоренное выражение должно быть неотрицательным: Прежде чем продолжить решение, напомню основные правила работы с неравенствами, известные ещё со школы. Обращаю особое внимание! Сейчас рассматриваются неравенства с одной переменной – то есть для нас существует только одна размерность по оси . 1) Слагаемые можно переносить из части в часть со сменой знака. 2) Обе части неравенства можно умножить на положительное число. 3) Если обе части неравенства умножить на отрицательное число, то необходимо сменить знак самого неравенства. Например, если было «больше», то станет «меньше»; если было «меньше либо равно», то станет «больше либо равно». В неравенстве перенесём «тройку» в правую часть со сменой знака (правило №1): Умножим обе части неравенства на –1 (правило №3): Умножим обе части неравенства на (правило №2): Ответ: область определения: Ответ также можно записать эквивалентной фразой: «функция определена при ». В большинстве случаев годится чисто аналитическое нахождение области определения, но когда функция сильно заморочена, следует чертить ось и делать пометки. Пример 6 Найти область определения функции Это пример для самостоятельного решения. Когда под квадратным корнем находится квадратный двучлен или трёхчлен, ситуация немного усложняется, и сейчас мы подробно разберём технику решения: Пример 7 Найти область определения функции Решение: подкоренное выражение должно быть строго положительным, то есть нам необходимо решить неравенство . На первом шаге пытаемся разложить квадратный трёхчлен на множители: Поскольку коэффициент , то ветви параболы смотрят вверх. Из вышесказанного следует, что на интервалах выполнено неравенство (ветки параболы уходят вверх на бесконечность), а вершина параболы расположена на промежутке ниже оси абсцисс, что соответствует неравенству : Обратите внимание, что сами точки выколоты (не входят в решение), поскольку неравенство у нас строгое. Ответ: область определения: Вообще, многие неравенства (в том числе рассмотренное) решаются универсальнымметодом интервалов, известным опять же из школьной программы. Но в случаях квадратных дву- и трёхчленов, на мой взгляд, гораздо удобнее и быстрее проанализировать расположение параболы относительно оси . Пример 8 Найти область определения функции Это пример для самостоятельного решения. В образце подробно закомментирована логика рассуждений + второй способ решения и ещё одно важное преобразование неравенства, без знания которого студент будет хромать на одну ногу…, …хмм… на счёт ноги, пожалуй, погорячился, скорее – на один палец. Большой палец. Может ли функция с квадратным корнем быть определена на всей числовой прямой? Конечно. Знакомые всё лица: . Или аналогичная сумма с экспонентой: . Действительно, для любых значения «икс» и «ка»: , поэтому подАвно и . А вот менее очевидный пример: . Здесь дискриминант отрицателен (парабола не пересекает ось абсцисс), при этом ветви параболы направлены вверх, следовательно, и область определения: . Вопрос противоположный: может ли область определения функции быть пустой? Да, и сразу напрашивается примитивный пример , где подкоренное выражение отрицательно при любом значении «икс», и область определения: (значок пустого множества). С нечётными корнями и т.д. всё обстоит гораздо лучше – тут подкоренное выражение может быть и отрицательным. Например, функция определена на всей числовой прямой. Однако у функции единственная точка всё же не входит в область определения, поскольку обращают знаменатель в ноль. По той же причине для функции исключаются точки . Некоторым посетителям сайта рассматриваемые примеры покажутся элементарными и примитивными, но в этом нет случайности – во-первых, я стараюсь «заточить» материал для нубов, а во-вторых, подбираю реалистичные вещи под грядущие задачи: полное исследование функции, нахождение области определения функции двух переменных и некоторые другие. Всё в математике цепляется друг за дружку. Хотя любители трудностей тоже не останутся обделёнными, более солидные задания встретятся и здесь, и на уроке
Посмотреть всех экспертов из раздела Учеба и наука > Математика Решено в первый сосуд с водой добавили 0,36 л, во второй — 0,42 л чистого спирта. Решено Дана правильная треугольная пирамида, боковая сторона которой равна 14, а сторона основания 9 . Найти высоту пирамиды Пользуйтесь нашим приложением ОПРЕДЕЛЕНИЕ Областью определения или области функции
\(\
y=f(x)
\) является множество значений x, для которых имеются значения \(\
y=f(x)
\). Обозначает область определения функции — \(\
D(f)
\) или \(\
D(y)
\) Поиск области действия функции Схема поиска области определения функций: Если \(\
f(x)
\) является многочленом, то область определения функции \(\
y=f(x)
\) будет множеством всех вещественных чисел. Если \(\
f(x)
\)- рациональная дробь, то область есть множество всех вещественных чисел, кроме тех значений E, для которых знаменатель равен нулю. \(\
(x-1)(x-2) \geq 0
\) Обозначим найденные корни на числовой оси и определим знак неравенства на полученных интервалах. Таким образом, \(\
D\left(y_{2}\right) : x \in(-\infty, 1] \cup[2,+\infty)
\) 3) Функция \(\
y_{3}=\frac{2 x-7}{\sqrt{3 x+21}}
\) является дробной рациональной функцией, числитель которой является многочленом. Областью многочлена является множество вещественных чисел R. В знаменателе корень, его область находится из системы \(\
\left\{\begin{array}{l}{3 x+21 \geq 0,} \\ {3 x+21 \neq 0,}\end{array} \Rightarrow 3 x+21>0 \Rightarrow 3 x>-21 \Rightarrow x>-7\right.
\) Таким образом, \(\
D\left(y_{3}\right) : x \in(-7,+\infty)
\) \(\
D\left(y_{1}\right) : x \in(-\infty, 5) \cup(5,+\infty)
\) \(\
D\left(y_{2}\right) : x \in(-\infty, 1] \cup[2,+\infty)
\) \(\
D\left(y_{3}\right) : x \in(-7,+\infty)
\) ПРИМЕР 2 Найдите область следующих функций: \(\
y_{1}=\sqrt{3^{2 x-5}-1} ; 2 ) y_{2}=\sqrt{-\log _{2} x+1} ; 3 ) y_{3}=\log _{x}(x-0,5)
\) 1) Чтобы найти область определения функции \(\
y_{1}=\sqrt{3^{2 x-5}-1}
\) ,мы решим неравенство \(\
3^{2 x-5}-1>0 \Rightarrow 3^{2 x-5}>1 \Rightarrow 3^{2 x-5}>3^{0}
\) Поскольку основание степени \(\
3>1
\), мы приходим к неравенству \(\
2 x-5>0 \Rightarrow 2 x>5 \Rightarrow x>2,5
\) Таким образом, \(\
D\left(y_{1}\right) : x \in(2,5 ;+\infty)
\) 2) Чтобы найти область определения функции \(\
y_{2}=\sqrt{-\log _{2} x+1}
\) ,необходимо учитывать, что радиус должен быть неотрицательным, а сублогарифмическая функция должна быть положительной. \(\
\left\{\begin{array}{l}{-\log _{2} x+1 \geq 0} \\ {x>0}\end{array}\right.
\) Мы решаем первое неравенство отдельно \(\
-\log _{2} x+1 \geq 0 \Rightarrow \log _{2} x \leq 1
\) Согласно определению логарифма мы приходим к неравенству \(\
x \leq 2
\) Таким образом, искомая область определения \(\
D\left(y_{2}\right) : x \in(0,2]
\). 3) Учитывая определение логарифмической функции, область определения \(\
y_{3}=\log _{x}(x-0,5)
\).найти из системы \(\
\left\{\begin{array}{l}{x>0} \\ {x \neq 1,} \\ {x-0,5>0}\end{array} \Rightarrow\right. \left\{\begin{array}{l}{x>0} \\ {x \neq 1,} \\ {x>0,5}\end{array} \Rightarrow\right. \left\{\begin{array}{l}{x \neq 1} \\ {x>0,5}\end{array} \Rightarrow\right. (0,5 ; 1) \cup(1 ;+\infty)
\) В результате получаем, что \(\
D\left(y_{3}\right) : x \in(0,5 ; 1) \cup(1 ;+\infty)
\) \(\
D\left(y_{1}\right) : x \in(2,5 ;+\infty)
\) \(\
D\left(y_{2}\right) : x \in(0,2]
\) \(\
D\left(y_{3}\right) : x \in(0,5 ; 1) \cup(1 ;+\infty)
\) Физика 166 Реклама и PR 31 Педагогика 80 Психология 72 Социология 7 Астрономия 9 Биология 30 Культурология 86 Экология 8 Право и юриспруденция 36 Политология 13 Экономика 49 Финансы 9 История 16 Философия 8 Информатика 20 Право 35 Информационные технологии 6 Экономическая теория 7 Менеджент 719 Математика 338 Химия 20 Микро- и макроэкономика 1 Медицина 5 Государственное и муниципальное управление 2 География 542 Информационная безопасность 2 Аудит 11 Безопасность жизнедеятельности 3 Архитектура и строительство 1 Банковское дело 1 Рынок ценных бумаг 6 Менеджмент организации 2 Маркетинг 238 Кредит 3 Инвестиции 2 Журналистика 1 Конфликтология 15 Этика 9 Формулы дифференцирования Квадратная матрица Диагональная матрица Невырожденная и вырожденная матрицы Операции над матрицами и их свойства Узнать цену работы Узнай цену своей работы Имя Принимаю Политику
конфиденциальности Подпишись на рассылку,
чтобы не пропустить информацию об акциях При решении различных задач и в научных исследованиях математики сталкиваются с необходимостью найти область определения функции. В этом вопросе следует разбираться, поскольку понятие не только встречается в школьной и университетской программах, но и широко применяется в науке и программировании (разработке программного обеспечения и прошивки контроллеров). Областью определения произвольной функции является множество значений переменных, от которых она зависит и принимает определенное значение. Встречаются функции с одной или несколькими переменными. Для простоты исследования нужно рассмотреть первый тип. Для того чтобы найти область определения и множество значений функции, необходимо использовать простые примеры. Специалисты рекомендуют применять метод изучения «от простого к сложному». Первый раз этот термин упоминается в школьной программе. Книга «Алгебра и начало анализа» дает базовые знания в этой области. Однако она написана не для всех понятным языком. Обучаемый часто ищет информацию в интернете. В некоторых случаях ученики занимаются поиском готовых решений, а это не совсем правильно, поскольку математические дисциплины пригодятся при поступлении в высшие учебные заведения. Программирование на разных языках пользуется огромной популярностью. В нем нужны математические знания для написания некоторых программ и игр. В последних следует производить точные расчеты и описывать некоторые функции героя. Например, удар мечом подчиняется определенному математическому закону или функции. Для корректной ее работы и тестирования следует находить грамотно ее область определения. Область определения функции обозначается буквой «D». Кроме того, указывается ее имя D (f). Допускается также следующее обозначение «D (y)». Если необходимо ее найти для нескольких функций, можно изменить обозначение. Для сложного типа функций z = f (a, b, x, y) эта величина обозначается таким образом: D (z). Аргумент — независимая переменная, принимающая определенные значения. Существуют также сложные функции, которые включают в число своих переменных и другие функции. Пример, z = f (x, k, l, w, y). В нем величины x, k, l являются переменными, а w и y — следующими функциями: w = 2 * x1 + 5 и y = 2 / (x2 — 6). Для каждого типа функции существует определенный алгоритм, по которому следует находить D (f). Он основывается на многолетнем опыте специалистов и придуман для оптимизации вычислений. Важно уметь правильно определять тип функции, поскольку от этого зависит процесс выбора алгоритма. Для одних можно сразу определить D (f), для других — решить уравнение или неравенство, для третьих следует решить систему уравнений и т. д. Можно воспользоваться специальными программными модулями. Простым примером программы является онлайн-калькулятор, позволяющий не только вычислить D (f), но и начертить ее график. Кроме того, D (f) записывается в виде множества значений. Например, D (y) = [0, 157). Функций существует огромное разнообразие. Они бывают простыми и сложными. Первые в математических дисциплинах классифицируются на несколько типов: алгебраические, тригонометрические и трансцендентные. Алгебраические классифицируются на рациональные и иррациональные. Рациональные бывают целыми и дробными. Тригонометрические включают в свой состав все функции с sin, cos, tg, ctg и т. д. Трансцендентные делятся на степенные, показательные и логарифмические. Рациональные целые — выражения полиномиального типа (линейные). Они без корней и степеней, дробей и логарифмов, а также без тригонометрических функций. Областью их определения является множество всех действительных чисел (Z) от бесконечно малого до бесконечно большого числа. Дробный тип — функции, в числителе и знаменателе которых находится переменная. Для нахождения D (f) нужно исключить все значения переменных в нем, приводящие к 0. Если встречается тригонометрические функции, то нужно вычислить все значения, приводящие к отсутствию D (f) на определенном интервале. Этот тип функций может быть иррациональным, дробным, линейным, а также использоваться вместе со степенью и логарифмом. К иррациональным функциям относят выражения, которые содержат переменную величину под корнем. Значение D (f) — все Z, кроме переменных, приводящих к отрицательным значениям выражений с четными степенями корней. D (f) степенной функции являются все действительные числа. Однако если степень представлена дробным выражением, то значения переменных не должны приводить к неопределенности (например, 4/0, т. к. на 0 делить нельзя). Для функций с натуральным логарифмом выражение, находящееся под ним, должно быть больше 0. Очень важно правильно обозначать D (f), поскольку это существенно влияет на результат. Это позволит избежать многих ошибок в любой сфере. Следует руководствоваться такими правилами: Примером в первом случае является множество [0, 100]: от 0 включительно и до 100 не включительно. Во втором случае — (8, 10): значение, равное 9, поскольку 8 и 10 — нижняя и верхняя границы, не принадлежащие множеству. Два предыдущих множества можно объединить: [0, 100] U (8, 10). Пример записи последнего случая следующий: (20, 50]. Для удобства определения D (f) необходимо применять специальные алгоритмы, которые упрощают операцию. Целая рациональная функция, как уже было описано ранее, имеет D (f), принадлежащую множеству Z (весь ряд действительных чисел). Кроме того, степенная функция также имеет D (f), которая соответствует Z. Если функция является дробной, то следует использовать следующий алгоритм: Если она представлена в виде четного корня, следует решить неравенство. Значение подкоренного выражения должно быть больше 0. В противном случае область определения под корнем не будет существовать (неопределенность). Однако если корень нечетный, то D (f) — множество действительных чисел. Для тригонометрических выражений синуса sin (x) и косинуса cos (x) множество всех Z является D (f). Однако для тангенса tg (x) и котангенса ctg (x) необходимо исключить значения переменной x = (Pi / 2) + Pi * k и x = Pi * k соответственно. В этих выражениях k является множеством действительных чисел. Существуют также и другие методы определения D (f). Ее можно выяснить при помощи следующих инструментов: онлайн-калькулятора, специальных программ и построения графика. Первый способ позволяет довольно быстро найти необходимую величину. Но это не все его возможности. Можно с его помощью строить графики и находить все свойства функции. Однако первый метод уступает второму, суть которого сводится к использованию специализированного программного обеспечения. В некоторых случаях можно найти D (f), построив ее график. Для этого следует подставить значение аргумента функции и получить ее значение. Построение таблицы зависимости значения функции от ее аргумента позволяет правильно построить графическое представление. Чтобы быстро строить графики, нужно знать их базовые виды: линейный, степенной (квадратичный, кубический и т. д. ), а также другие. Чем точнее графическая иллюстрация, тем легче определить D (f). После заполнения таблицы значений следует приступать к построению графика. Для этого берутся точки с координатами из таблицы (x, y), и отмечаются на декартовой системе координат. Затем их следует соединить. Получится график заданной функции, по которому не составит труда сделать определенные выводы. Теоретические знания необходимы, но некоторые люди делают огромную ошибку. Они не закрепляют их при помощи практики. Необходимо регулярно решать задачи на нахождения D (f), поскольку в этом случае набирается опыт. Наиболее простыми задачами считаются следующие: нахождения D (f) линейной, степенной, показательной и тригонометрической функций. Важным аспектом считается упрощение выражения. Для этого следует вспомнить также и формулы сокращенного умножения. С дробными и иррациональными функциями могут возникнуть некоторые сложности, поскольку нужно решить уравнение или неравенство. Однако в последнем случае нельзя путать знак неравенства. Нужно найти D (f) для y = 2*x — 3 * (x — 5). Для решения следует применить такой алгоритм: Для упрощения выражения следует раскрыть скобки. Конечно, это делать необязательно, поскольку ответ очевиден D (y) = (-бесконечность, +бесконечность). Но по правилам «хорошего тона» любое математическое выражение следует упрощать: y = 2 * x — 3 * x + 15 = — x + 15 = 15 — x. При решении следует правильно раскрывать скобки, а также следить за знаками. Малейшая ошибка может привести к значительному искажению графика. В некоторых задачах следует также построить график функции. Для конкретного случая создается таблица зависимости значения «y» от аргумента. Не имеет смысла брать много значений «х», поскольку графиком является прямая. Известно, что необходимы только две точки для ее проведения. Подстановка количества значений «х», превышающих двух, является грубой и распространенной ошибкой. Пусть существует выражение вида y = 1 / [(x — 4) * (x + 4)]. Нужно определить D (f). Решается задача таким способом: Множество чисел D (y) ограничивается следующим интервалом (-бесконечность, 1.5) U (1.5, +бесконечность). Таким образом, для нахождения множества значений D (f) для конкретного выражения следует воспользоваться специальными алгоритмами. На первоначальном этапе исследования функции следует определить ее тип, поскольку это поможет избежать многих сложностей в процессе решения. Как найти область определения функции? Ученикам средних классов приходится часто сталкиваться с данной задачей. Родителям следует помочь своим детям разобраться в данном вопросе. Задание функции. Напомним основополагающие термины алгебры. Функцией в математике называют зависимость одной переменной от другой. В математике при анализе формул числовые переменные подменяют буквенными символами. Наиболее часто используют икс («х») и игрек («у»). Переменную х называют аргументом, а переменную у — зависимой переменной или функцией от х. Существуют различные способы задания зависимостей переменных. Перечислим их: Аналитический способ представляют формулой. Рассмотрим примеры: у=2х+3, у=log(х), у=sin(х). Формула у=2х+3 является типичной для линейной функции. Подставляя в заданную формулу числовое значение аргумента, получаем значение y. Табличный способ представляет собой таблицу, состоящую из двух столбцов. Первая колонка выделяется для значений икса, а в следующей графе записывают данные игрека. Графический способ считается наиболее наглядным. Графиком называют отображение множества всех точек на плоскости. Для построения графика применяют декартовую систему координат. Система состоит из двух перпендикулярных прямых. На осях откладывают одинаковые единичные отрезки. Отсчет производят от центральной точки пересечения прямых линий. Независимую переменную указывают на горизонтальной линии. Ее называют осью абсцисс. Вертикальная прямая (ось ординат) отображает числовое значение зависимой переменной. Точки отмечают на пересечении перпендикуляров к данным осям. Соединяя точки между собой, получаем сплошную линию. Она являться основой графика. Определение. В общем виде зависимость представляется как уравнение: y=f(x). Из формулы следует, что для каждого значения числа х существует определенное число у. Величину игрека, которая соответствует числу икс, называют значением функции. Все возможные значения, которые приобретает независимая переменная, образуют область определения функции. Соответственно, все множество чисел зависимой переменной определяет область значений функции. Начальная задача при исследовании математических законов состоит в нахождении области определения. Следует верно определять этот термин. В противном случае все дальнейшие расчеты будут бесполезны. Ведь объем значений формируется на основе элементов первого множества. Область определения функции находится в прямой зависимости от ограничений. Ограничения обусловливаются невозможностью выполнения некоторых операций. Также существуют границы применения числовых значений. При отсутствии ограничений область определения представляет собой все числовое пространство. Знак бесконечности имеет символ горизонтальной восьмерки. Все множество чисел записывается так: (-∞; ∞). В определенных случаях массив данных состоит из нескольких подмножеств. Рамки числовых промежутков или пробелов зависят от вида закона изменения параметров. Укажем список факторов, которые влияют на ограничения: Если таких элементов несколько, то поиск ограничений разбивают для каждого из них. Наибольшую проблему представляет выявление критических точек и промежутков. Решением задачи станет объединение всех числовых подмножеств. О множествах. Область определения выражают как D(f), а знак объединения представлен символом ∪. Все числовые промежутки заключают в скобки. Если граница участка не входит во множество, то ставят полукруглую скобку. В ином случае, когда число включается в подмножество, используют скобки квадратной формы. Обратная пропорциональность выражена формулой у=к/х. График функции представляет собой кривую линию, состоящую из двух веток. Ее принято называть гиперболой. Так как функция выражена дробью, нахождение области определения сводится к анализу знаменателя. Общеизвестно, что в математике деление на нуль запрещено. Решение задачи сводится к уравниванию знаменателя к нулю и нахождению корней. Приведем пример: Задается: у=1/(х+4). Ответ: областью определения функции являются все действительные числа, кроме -4. Значение числа под знаком квадратного корня не может быть отрицательным. В этом случае определения функции с корнем сводится к решению неравенства. Подкоренное выражение должно быть больше нуля. Область определения корня связана с четностью показателя корня. Если показатель делится на 2, то выражение имеет смысл только при его положительном значении. Нечетное число показателя указывает на допустимость любого значения подкоренного выражения: как положительного, так и отрицательного. Неравенство решают так же, как уравнение. Существует только одно различие. После перемножения обеих частей неравенства на отрицательное число следует поменять знак на противоположный. Если квадратный корень находится в знаменателе, то следует наложить дополнительное условие. Значение числа не должно равняться нулю. Неравенство переходит в разряд строгих неравенств. Логарифмическая форма имеет смысл при положительных числах. Таким образом, область определения логарифмической функции аналогична функции квадратного корня, за исключением нуля. Рассмотрим пример логарифмической зависимости: y=lоg(2x-6). Найти область определения. Ответ: (3; +∞). Областью определения y=sin x и y=cos x является множество всех действительных чисел. Для тангенса и котангенса существуют ограничения. Они связаны с делением на косинус либо синус угла. Тангенс угла определяют отношением синуса к косинусу. Укажем величины углов, при которых значение тангенса не существует. Функция у=tg x имеет смысл при всех значениях аргумента, кроме x=π/2+πn, n∈Z. Областью определения функции y=ctg x является все множество действительных чисел, исключая x=πn, n∈Z. При равенстве аргумента числу π или кратному π синус угла равен нулю. В этих точках (асимптотах) котангенс не может существовать. Первые задания на выявление области определения начинаются на уроках в 7 классе. При первом ознакомлении с этим разделом алгебры ученик должен четко усвоить тему. Следует учесть, что данный термин будет сопровождать школьника, а затем и студента на протяжении всего периода обучения. Определение Множество X
называется областью определения функции . Область определения функции иногда называют множеством определения или множеством задания функции. Элемент x ∈
X
называют аргументом функции или независимой переменной . Само отображение f
называется характеристикой функции . Характеристика f
обладает тем свойством, что если два элемента и из множества определения имеют равные значения: ,
то . Символ, обозначающий характеристику, может совпадать с символом элемента значения функции. То есть можно записать так: .
При этом стоит помнить, что y
— это элемент из множества значений функции, а — это правило, по которому для элемента x
ставится в соответствие элемент y
. Сам процесс вычисления функции состоит из трех шагов. На первом шаге мы выбираем элемент x
из множества X
.
Далее, с помощью правила ,
элементу x
ставится в соответствие элемент множества Y
.
На третьем шаге этот элемент присваивается переменной y
. Частным значением функции называют значение функции при выбранном (частном) значении ее аргумента. Графиком функции f называется множество пар . Определение Сложную функцию также называют композицией или суперпозицией функций и иногда обозначают так: . В математическом анализе принято считать, что если характеристика функции обозначена одной буквой или символом, то она задает одно и то же соответствие. Однако, в других дисциплинах, встречается и другой способ обозначений, согласно которому отображения с одной характеристикой, но разными аргументами, считаются различными. То есть отображения и считаются различными. Приведем пример из физики. Допустим мы рассматриваем зависимость импульса от координаты .
И пусть мы имеем зависимость координаты от времени . Область определения функции и множество ее значений могут быть любыми множествами. В математическом анализе большую роль играют числовые функции. Числовая функция — это функция, значениями которой являются действительные или комплексные числа. Действительная или вещественная функция — это функция, значениями которой являются действительные числа. Действительные числа имеют операцию сравнения. Поэтому множество значений действительной функции может быть ограниченным и иметь наибольшее и наименьшее значения. Действительная функция называется ограниченной сверху (снизу) , если существует такое число M
,
что для всех выполняется неравенство: Числовая функция называется ограниченной , если существует такое число M
,
что для всех : Максимумом M
(минимумом m
) функции f
,
на некотором множестве X
называют значение функции при некотором значении ее аргумента ,
при котором для всех , Верхней гранью или точной верхней границей действительной, ограниченной сверху функции называют наименьшее из чисел, ограничивающее область ее значений сверху. То есть это такое число s
,
для которого для всех и для любого ,
найдется такой аргумент ,
значение функции от которого превосходит s′
:
. Верхней гранью неограниченной сверху функции Нижней гранью или точной нижней границей действительной, ограниченной снизу функции называют наибольшее из чисел, ограничивающее область ее значений снизу. То есть это такое число i
,
для которого для всех и для любого ,
найдется такой аргумент ,
значение функции от которого меньше чем i′
:
. Нижней гранью неограниченной снизу функции является бесконечно удаленная точка . Таким образом, любая действительная функция, на не пустом множестве X
,
имеет верхнюю и нижнюю грани. В качестве примера рассмотрим функцию ,
заданную на открытом интервале . Если мы рассмотрим туже функцию на отрезке ,
то она на этом множестве ограничена сверху и снизу, имеет верхнюю и нижнюю грани и имеет максимум и минимум: Определения возрастающей и убывающей функций Определение монотонной функции Пример многозначной функции. Как следует из определения функции, каждому элементу x
из области определения, ставится в соответствие только один элемент из множества значений. Но существуют такие отображения, в которых элемент x
имеет несколько или бесконечное число образов. В качестве примера рассмотрим функцию арксинус : .
Она является обратной к функции синус и определяется из уравнения: Наложим на решения уравнения (1) ограничение. Пусть Вместо условия (2) можно наложить любое другое условие вида: Это совокупность функций, определенных на некотором множестве. Ветвь многозначной функции — это одна из функций, входящих в многозначную функцию. Однозначная функция — это функция. Использованная литература: Мы узнали, что существует X — множество,
на котором формула, которой задана функция, имеет смысл. В математическом анализе это множество часто
обозначают как D (область определения функции ).
В свою очередь множество Y обозначают как E (область значений функции ) и при этом D и E называют
подмножествами R (множества действительных чисел). Если функция задана формулой, то при отсутствии особых оговорок областью её определения
считается наибольшее множество, на котором эта формула имеет смысл, то есть наибольшее множество значений
аргумента, которое приводит к действительным значениям функции . Иначе говоря, множество
значений аргумента, на котором «функция работает». Для общего понимания пример пока без формулы. Функция задана в виде пар отношений: {(2, 1), (4, 2), (6, -6), (5, -1), (7, 10)}
. Найти область определения это функции. Ответ. Первый элемент пар — это переменная x . Так как в задании функции даны и
вторые элементы пар — значения переменной y , то функции имеет смысл только для тех значений икса,
которым соответствует определённое значения игрека. То есть берём все иксы данных пар в порядке возрастания и получаем
из них область определения функции: {2, 4, 5, 6, 7}
. Та же логика работает, если функция задана формулой. Только вторые элементы в парах (то есть
значения игрека) получаем, подставляя в формулу те или иные значения икса. Пример 0. Как найти область
определения функции игрек равен квадратному корню из икса минус пять (подкоренное выражение икс минус пять)
()? Нужно всего лишь
решить неравенство x — 5 ≥ 0
, так как для того, чтобы мы получили действительное значение игрека, подкоренное
выражение должно быть больше или равно нулю. Получаем решение: область определения функции — все значения икса
больше или равно пяти (или икс принадлежит промежутку от пяти включительно до плюс бесконечности). На чертеже сверху — фрагмент числовой оси. На ней область опредения рассмотренной функции
заштрихована, при этом в «плюсовом» направлении штриховка продолжается бесконечно вместе с самой осью. Если вы пользуетесь компьютерными программами, которые на основании введённых данных
выдают какой-то ответ, то можете заметить, что при некоторых значениях введённых данных программа выдаёт
сообщение об ошибке, то есть о том, что при таких данных ответ не может быть вычислен. Но и в том и в другом случае ответ (значение некоторого выражения) не может быть
вычислен по той причине, что выражение при некоторых значениях данных не имеет смысла. Пример (пока не совсем математический): если программа выдаёт название месяца по номеру месяца в году, то, введя
«15», вы получите сообщение об ошибке. Чаще всего
вычисляемое выражение как раз и представляет собой функцию. Поэтому такие недопустимые значения данных не входят
в область определения функции . И в вычислениях от руки так же важно представлять область определения
функции. Например, вы вычисляете некоторый параметр некоторого изделия по формуле, представляющей собой
функцию. При некоторых значениях аргумента на входе вы на выходе не получите ничего. Постоянная (константа) определена при любых действительных
значениях x R действительных чисел. Это можно записать и так:
областью определения данной функции является вся числовая прямая ]- ∞; + ∞[
. Пример 1. Найти область определения функции y = 2
. Решение. Область определения функции не указана, значит, в силу выше приведённого
определения имеется в виду естественная область определения. Выражение f (x ) = 2
определено при любых действительных
значениях x , следовательно, данная функция определена на всём
множестве R действительных чисел. Поэтому на чертеже сверху числовая прямая заштрихована на всём протяжении от минус
бесконечности до плюс бесконечности. В случае, когда функция задана формулой и n — натуральное число: Пример 2. Найти область определения функции . Решение. Как следует из
определения, корень чётной степени имеет смысл, если подкоренное выражение неотрицательно, то есть,
если — 1 ≤ x ≤ 1
.
Следовательно, область определения данной функции — [- 1; 1]
. Заштрихованная область числовой прямой на чертеже сверху — это область определения
данной функции. Область определения степенной функции с целым показателем степени если a — положительное, то областью определения функции является множество
всех действительных чисел, то есть ]- ∞; + ∞[
; если a — отрицательное, то областью определения функции является
множество ]- ∞; 0[ ∪ ]0 ;+ ∞[
,
то есть вся числовая прямая за исключением нуля. На соответствующем чертеже сверху вся числовая прямая заштрихована, а точка,
соответствующая нулю, выколота (она не входит в область определения функции). Пример 3. Найти область определения функции . Решение. Первое слагаемое целой степенью икса, равной 3, а степень икса во втором
слагаемом можно представить в виде единицы — так же целого числа. В случае, когда функция задана формулой : если
— положительное, то областью определения функции является множество 0; + ∞[
. Пример 4. Найти область определения функции . Решение. Оба слагаемых в выражении функции — степенные функции с положительными
дробными показателями степеней. Следовательно, область определения данной функции —
множество — ∞; + ∞[
. В случае, когда функция задана формулой ,
областью определения функции является вся числовая прямая, то есть
]- ∞; + ∞[
. Логарифмическая функция
определена при условии, если её аргумент положителен, то есть, областью её определения является множество
]0; + ∞[
. Область определения функции y = cos(x )
—
так же множество R действительных чисел. Область определения функции y = tg(x )
—
множество R действительных чисел, кроме чисел
. Область определения функции y = ctg(x )
—
множество R действительных чисел, кроме чисел
. Пример 8. Найти область определения функции . Решение. Внешняя функция — десятичный логарифм и на область её определения
распространяются условия области определения логарифмической функции вообще. То есть, её аргумент
должен быть положительным. Аргумент здесь — синус «икса». Поворачивая воображаемый циркуль по
окружности, видим, что условие sin x > 0
нарушается при «иксе» равным нулю, «пи», два, умноженном на «пи» и вообще равным произведению числа «пи»
и любого чётного или нечётного целого числа. Таким образом, область определения данной функции задаётся выражением , где k — целое число. Область определения функции y = arcsin(x )
—
множество [-1; 1]
. Область определения функции y = arccos(x )
—
так же множество [-1; 1]
. Область определения функции y = arctg(x )
—
множество R действительных чисел. Область определения функции y = arcctg(x )
—
так же множество R действительных чисел. Пример 9. Найти область определения функции . Решение. Решим неравенство: Таким образом, получаем область определения данной функции — отрезок
[- 4; 4]
. Пример 10. Найти область определения функции . Решение. Решим два неравенства: Решение первого неравенства: Решение второго неравенства: Таким образом, получаем область определения данной функции — отрезок
. Если функция задана дробным выражением, в котором переменная находится в знаменателе
дроби, то областью определения функции является множество R действительных чисел,
кроме таких x , при которых знаменатель дроби обращается в нуль. Пример 11. Найти область определения функции . Решение. Решая равенство нулю знаменателя дроби, находим область определения данной функции — множество
]- ∞; — 2[ ∪ ]- 2 ;+ ∞[
. В математике имеется достаточно небольшое количество элементарных функций, область определения которых ограничена. Все остальные «сложные» функции — это всего лишь их сочетания и комбинации. Для тангенса: y = 2x + 3 — уравнение задает прямую на плоскости. Посмотрим внимательно на функцию и подумаем, какие же числовые значения мы сможем подставить в уравнение вместо переменной х? Попробуем подставить значение х=0 Так как y = 2·0 + 3 = 3
— получили числовое значение, следовательно функция существует при взятом значении переменной
х=0. Попробуем подставить значение х=10 так как y = 2·10 + 3 = 23
— функция существует при взятом значении переменной х=10 . Попробуем подставить значение х=-10 так как y = 2·(-10) + 3 = -17
— функция существует при взятом значении переменной х=-10 . Уравнение задает прямую линию на плоcкости, а прямая не имеет ни начала ни конца, следовательно она существует для любых значений х. Заметим, что какие бы числовые значения мы не подставляли в заданную функцию вместо х, всегда получим числовое значение переменной y. Следовательно, функция существует для любого значения x ∈ R или запишем так: D(f) = R Формы записи ответа: D(f)=R или D(f)=(-∞:+∞)или x∈R или x∈(-∞:+∞) Сделаем вывод: Для любой функции вида y = ax + b областью определения является множество действительных чисел. Задана функция вида: y = 10/(x + 5) — уравнение гиперболы Имея дело с дробной функцией, вспомним, что на ноль делить нельзя. Следовательно функция будет существовать для всех значений х, которые не обращают знаменатель в ноль. Попробуем подставить какие-либо произвольные значения х. При х = 0
имеем y = 10/(0 + 5) = 2
— функция существует. При х = 10
имеем y = 10/(10 + 5) = 10/15 = 2/
3
— функция существует. При х = -5
имеем y = 10/(-5 + 5) = 10/0
— функция в этой точке не существует. Т.е. если заданная функция дробная, то необходимо знаменатель приравнять нулю и найти такую точку, в которой функция не существует. В нашем случае: x + 5 = 0 → x = -5
— в этой точке заданная функция не существует. x + 5 ≠ 0 → x ≠ -5 Для наглядности изобразим графически: На графике также видим, что гипербола максимально близко приближается к прямой х = -5
, но самого значения -5 не достигает. Видим, что заданная функция существует во всех точках действительной оси, кроме точки x = -5 Формы записи ответа: D(f)=R\{-5}
илиD(f)=(-∞;-5)
∪
(-5;+∞)
или
x∈
R\{-5}
илиx∈
(-∞;-5)
∪
(-5;+∞) Если заданная функция дробная, то наличие знаменателя накладывает условие неравенства нулю знаменателя. Так как квадратный корень мы можем извлечь только из неотрицательного числа, следовательно, функция под корнем — неотрицательна. 2х — 8 ≥ 0 Решим простое неравенство: 2х — 8 ≥ 0 → 2х ≥ 8 → х ≥ 4 Заданная функция существует только при найденных значениях х ≥ 4
или D(f)=} Объясняет концепцию области действия в PowerShell и показывает, как устанавливать и изменять
объем элементов. PowerShell защищает доступ к переменным, псевдонимам, функциям и PowerShell
диски (PSDrives), ограничивая места, где они могут быть прочитаны и изменены. PowerShell
использует правила области действия, чтобы гарантировать, что вы случайно не измените элемент, который
не следует изменять. Ниже приведены основные правила области действия: Области могут вкладываться друг в друга. Внешняя область называется родительской областью. Любой вложенный
области являются дочерними областями этого родителя. Элемент виден в области, в которой он был создан, и в любом дочернем
области действия, если только вы явно не сделаете его закрытым. Вы можете объявлять переменные, псевдонимы, функции и диски PowerShell для
область вне текущей области. Элемент, созданный вами в рамках области, может быть изменен только в области в
которой он был создан, если вы явно не укажете другую область. Если вы создаете элемент в области, и элемент имеет то же имя, что и элемент в
другую область действия, исходный элемент может быть скрыт под новым элементом, но
он не переопределяется и не изменяется. PowerShell поддерживает следующие области: Глобальная: область, действующая при запуске PowerShell или при создании
новый сеанс или пространство выполнения. Переменные и функции, присутствующие при
Запуски PowerShell были созданы в глобальной области, например автоматические
переменные и переменные предпочтений. Переменные, псевдонимы и функции в
ваши профили PowerShell также создаются в глобальной области. глобальный
scope — это корневая родительская область в сеансе. Локальный: Текущая область. Локальная область может быть глобальной или любой
другой размах. Сценарий: область, которая создается во время выполнения файла сценария. Только команды
в скрипте запускается в области скрипта. Для команд в скрипте
область действия скрипта — это локальная область. Вы можете создать новую дочернюю область, вызвав скрипт или функцию. Вызов
область является родительской областью. Вызываемый скрипт или функция является дочерней областью.
Функции или сценарии, которые вы вызываете, могут вызывать другие функции, создавая
иерархия дочерних областей, корневая область которых является глобальной областью. Если вы явно не сделаете элементы частными, элементы в родительской области
доступны для дочерней области. Однако элементы, которые вы создаете и изменяете в
дочерняя область не влияет на родительскую область, если вы явно не укажете
область действия при создании элементов. Примечание Функции из модуля не выполняются в дочерней области вызывающей области. Дочерняя область не наследует переменные, псевдонимы и функции из
родительская область. Если элемент не является частным, дочерняя область может просматривать элементы в
родительская область. И он может изменить элементы, явно указав
родительская область, но элементы не являются частью дочерней области. Однако создается дочерняя область с набором элементов. Как правило, он включает
все псевдонимы с параметром AllScope . этот вариант обсуждается
далее в этой статье. Он включает в себя все переменные, которые имеют Олскоп опция, а также некоторые автоматические переменные. Чтобы найти элементы в определенной области, используйте параметр Scope в Например, чтобы получить все переменные в локальной области, введите: Чтобы получить все переменные в глобальной области, введите: Имя переменной, псевдонима или функции может включать любой из следующих
необязательные модификаторы прицела: Примечание Областью действия сценариев по умолчанию является область действия сценария. Чтобы указать область действия новой переменной, псевдонима или функции, используйте область
модификатор. Синтаксис модификатора области в переменной: Синтаксис модификатора области действия в функции: Следующая команда, которая не использует модификатор области действия, создает переменную
в текущей или локальной области : Чтобы создать такую же переменную в глобальной 9Область 0078, используйте область Обратите внимание на значения свойств Visibility и Options . Сравните это с частной переменной: Использование модификатора области действия Чтобы создать ту же переменную в области сценария , используйте область сценария Вы также можете использовать модификатор области действия с функциями. Следующая функция
определение создает функцию в глобальная область действия: Вы также можете использовать модификаторы области для ссылки на переменную в другой области. Использование — это специальный модификатор области, который идентифицирует локальную переменную в удаленной
команда. Без модификатора PowerShell ожидает переменные в удаленных командах.
для определения в удаленном сеансе. Модификатор области действия Для любого скрипта или команды, которая выполняется вне сеанса, вам потребуется В зависимости от контекста значения встроенных переменных могут быть независимыми
копии данных в области действия вызывающего объекта или ссылки на него. Дополнительные сведения см. в разделе about_Remote_Variables. В сеансах потоков они передаются по ссылке. Это означает, что можно
изменить переменные области вызова в другом потоке. Безопасное изменение переменных
требует синхронизации потоков. Для получения дополнительной информации см.: Удаленно выполняемые команды и фоновые задания выполняются вне процесса.
Внепроцессные сеансы используют сериализацию и десериализацию на основе XML, чтобы сделать
значения переменных, доступных через границы процесса.
процесс сериализации преобразует объекты в PSObject , содержащий
исходные свойства объектов, но не его методы. Для ограниченного набора типов десериализация возвращает объекты обратно в
оригинальный тип. Регидратированный объект является копией исходного экземпляра объекта. Экземпляров всех остальных типов экземпляров PSObject . PSTypeNames содержит исходное имя типа с префиксом Deserialized , для
Например, Deserialized.System.Data.DataTable Переменные и псевдонимы имеют свойство Option , которое может принимать значение AllScope . Элементы, имеющие свойство AllScope , становятся частью любого дочернего элемента.
области, которые вы создаете, хотя они не наследуются задним числом родительским
масштабы. Элемент со свойством AllScope виден в дочерней области, и
это часть этого объема. Изменения элемента в любой области действия влияют на все
области, в которых определена переменная. Несколько командлетов имеют параметр Scope , который позволяет получать или устанавливать (создавать и
изменить) элементы в определенной области. Используйте следующую команду, чтобы найти все
командлеты в сеансе с параметром Scope : Чтобы найти переменные, видимые в определенной области, используйте область Например, следующая команда получает переменные, видимые в
локальная область: Чтобы создать переменную в определенной области, используйте модификатор области или Scope параметр Вы также можете использовать параметр Scope для Чтобы получить функции в определенной области, используйте Примечание Для командлетов, которые используют параметр Scope , вы также можете обратиться к
прицелы по номеру. Число описывает относительное положение одного прицела относительно
еще один. Область 0 представляет текущую или локальную область. Область 1 указывает
непосредственная родительская область. Область 2 указывает родителя родительской области,
и так далее. Нумерованные области полезны, если вы создали много рекурсивных
масштабы. Скрипты и функции соответствуют всем правилам области действия. Вы создаете их в
конкретной области, и они влияют только на эту область, если вы не используете командлет
параметр или модификатор области, чтобы изменить эту область. Но вы можете добавить сценарий или функцию в текущую область, используя точечный источник
обозначение. Затем, когда сценарий запускается в текущей области, любые функции,
псевдонимы и переменные, которые создает скрипт, доступны в текущем
сфера. Чтобы добавить функцию в текущую область, введите точку (.) и пробел перед
путь и имя функции в вызове функции. Например, чтобы запустить сценарий Sample.ps1 из каталога C:\Scripts в
области сценария (по умолчанию для сценариев) используйте следующую команду: Чтобы запустить сценарий Sample.ps1 в локальной области, используйте следующую команду: Когда вы используете оператор вызова (&) для запуска функции или сценария, это не
добавлен в текущую область. В следующем примере используется оператор вызова: Подробнее об операторе вызова можно прочитать в about_operators. Любые псевдонимы, функции или переменные, созданные сценарием Sample. Некоторые концепции PowerShell аналогичны области действия или взаимодействуют с областью действия. Эти
концепции могут быть перепутаны с областью действия или поведением области действия. Сеансы, модули и вложенные подсказки являются автономными средами, но
они не являются дочерними областями глобальной области в сеансе. Сеанс — это среда, в которой работает PowerShell. Когда вы создаете сеанс
на удаленном компьютере PowerShell устанавливает постоянное соединение с
удаленный компьютер. Постоянное соединение позволяет использовать сеанс для
несколько связанных команд. Поскольку сеанс представляет собой изолированную среду, он имеет собственную область действия, но
сеанс не является дочерней областью сеанса, в котором он был создан.
сеанс начинается со своей собственной глобальной областью. Эта сфера не зависит от
глобальная область сеанса. Вы можете создавать дочерние области в сеансе. Вы можете использовать модуль PowerShell для совместного использования и доставки инструментов PowerShell. Модуль
это модуль, который может содержать командлеты, скрипты, функции, переменные, псевдонимы и
другие полезные предметы. Если явно не определено, элементы в модуле не
доступны за пределами модуля. Таким образом, вы можете добавить модуль в свой
сессии и использовать общедоступные элементы, не беспокоясь о том, что другие элементы могут
переопределить командлеты, сценарии, функции и другие элементы вашего сеанса. По умолчанию модули загружаются на верхний уровень текущего сеанса .
состояние не текущая область действия . Текущее состояние сеанса может быть модулем
состояние сеанса или глобальное состояние сеанса. Добавление модуля в сеанс делает
не менять масштаб. Если вы находитесь в глобальной области видимости, то загружаются модули
в глобальное состояние сеанса. В состоянии сеанса модули имеют собственную область действия. Рассмотрим следующее
модуль Теперь мы создаем глобальную переменную Модуль объявляет переменную Вложенные подсказки не имеют собственной области действия. Когда вы входите во вложенный
приглашение, вложенное приглашение является подмножеством среды. Но ты остаешься
в пределах локального охвата. Сценарии имеют собственную область действия. Если вы отлаживаете скрипт и достигаете
точки останова в скрипте, вы входите в область скрипта. Псевдонимы и переменные имеют свойство Option , которое может принимать значение Например, если вы создаете переменную с частной опцией в глобальном
область действия, а затем запустить сценарий, Вы можете использовать Опция параметр Свойство Видимость переменной или псевдонима определяет, можете ли вы
увидеть элемент вне контейнера, в котором он был создан. Контейнер может
быть модулем, сценарием или оснасткой. Обзорность предназначена для контейнеров в
так же, как Свойство Visibility принимает значения Поскольку видимость предназначена для контейнеров, в области видимости она работает по-разному. Вы можете использовать командлеты Следующая команда изменяет значение переменной Во-первых, для отображения значения переменной Создайте сценарий Scope. Запустить скрипт. Сценарий изменяет значение Затем проверьте текущее значение переменной В этом примере показано, что изменение значения переменной в области сценария
не влияет на значение переменной в родительской области. Вы можете использовать модификаторы области для просмотра значения переменной в локальной области
и в родительской области. Сначала определите переменную Затем создайте сценарий Sample. В Sample.ps1: При запуске Sample.ps1 вывод должен выглядеть следующим образом: Когда сценарий завершен, только глобальное значение Если вы не защитите элемент с помощью параметра «Частный доступ» или другого метода, вы
может просматривать и изменять значение переменной в родительской области. Сначала определите переменную Затем создайте сценарий Sample. В Sample.ps1: Когда сценарий завершен, глобальное значение Частная переменная — это переменная, имеющая свойство Option значение Следующая команда создает частную переменную с именем Вы можете отображать и изменять значение Затем создайте сценарий Sample. В Sample.ps1: Переменная Для переменных в удаленной команде, созданной в локальном сеансе, используйте Синтаксис: Например, следующие команды создают переменную Область использования была представлена в PowerShell 3. By Аасиф Хан | 9 декабря 2021 г., 20:09 | 5 минут чтения Что такое «область действия» в программировании на Swift? Концепция области действия гласит, что если вы объявили переменную в одном «месте» своего кода, вы не можете использовать ее вне этого места. Это неявное, но важное правило программирования, и поначалу его может быть сложно понять. В этом руководстве мы сосредоточимся на изучении масштаба и его значения для практической разработки iOS. Вот что мы обсудим: Начнем с примера, который демонстрирует разные масштабы. Взгляните на следующий код Swift: func getAge() -> Int return age var age = 99 print(age) Найдите минутку, чтобы прочитать код. Можете ли вы, не обманывая, угадать, что такое значения age и otherAge? В этом примере вы работаете с двумя видами области видимости: глобальной и локальной. Теперь давайте еще раз посмотрим на этот код. Переменная age определяется внутри функции getAge(). Мы не можем получить доступ к той же самой переменной вне функции. Это важное правило при работе с областями. Мы также не можем повторно объявить переменную с тем же именем в той же области видимости, потому что имена переменных должны быть уникальными в своей области. Что мы сделали, так это определили другую переменную с тем же именем в другой области. Видишь какой? Эти две переменные имеют одно и то же имя, но они объявлены в разных областях. Они имеют 2 отдельных значения. Их «области» кода — их область действия — не конфликтуют друг с другом. Вот почему мы можем использовать их обоих, с одним и тем же именем, но с разными значениями, по отдельности! Вот как работает приведенный выше код, строка за строкой: При выполнении кода переменная age инициализируется значением 99. Затем мы инициализируем переменную с именем AnotherAge значением, возвращаемым функцией getAge(), т.е. 43 (42 + 1). Затем это значение увеличивается на единицу, при этом otherAge += 1. Наконец, мы распечатываем значения этих переменных. Значение возраста равно 99, потому что оно не изменилось. Значение AnotherAge равно 44. Оно инициализируется как 42, увеличивается внутри функции и увеличивается вне ее. Несмотря на то, что 2 из этих 3 переменных имеют одинаковые имена, они не конфликтуют друг с другом, поскольку объявлены в разных областях. Начинаете осваивать прицел? Это не что иное, как «регион» или место, в котором у вас есть доступ к определенным переменным. Мы также определили два основных правила: Из этих правил есть исключения, как вы скоро увидите . Например, свойство из области видимости класса может иметь то же имя, что и переменная в области действия функции, но для доступа к первой вам потребуется использовать self. Проще всего думать о прицеле как о настоящем прицеле, знаете ли, о том, который вы найдете на верхней части винтовки, или о видоискателе в фотокамере, или в биноклях. Когда вы смотрите в прицел, вы не можете видеть то, что находится за пределами вашего поля зрения! Локальная область — это область, в которой вы сейчас находитесь, т. е. вводите этот блок кода в волнистых скобках { }. В Swift функции находятся на самом глубоком уровне области видимости, поэтому локальная область действия часто совпадает с областью действия функции. Замыкания находятся на более глубоком уровне, чем функции, но замыкания могут «замыкаться», что делает их особенными. Подробнее об этом позже! До сих пор мы рассматривали только глобальную и локальную области видимости. Также есть нечто, называемое областью действия функции, и у классов тоже есть область видимости. На самом деле фреймворки, модули и файлы Swift сами по себе имеют область видимости. У областей действия есть уровни, они иерархичны, и типы тоже ограничены. Фу! С чего мы вообще начнем!? Начнем с простого класса. Вот так: class Product } Насколько мы видим, этот класс определен в глобальной области видимости. class Product enum Kind { В приведенном выше коде мы определили перечисление Kind. У него есть 2 случая — ради этого примера мы рассматриваем любой продукт как еду (можно есть) или вещь (нельзя есть). Мы также добавили вид свойства экземпляра типа Kind, который по умолчанию инициализируется значением перечисления .thing. Давайте обсудим этот пример с точки зрения области действия. Каков масштаб всего этого? Вот что: Однако происходит кое-что еще. Мы можем использовать Product в глобальной области видимости, а поскольку перечисление Kind по умолчанию имеет внутренний контроль доступа, мы можем использовать его как тип Product.Kind в любом месте кода. Приведенный ниже код можно использовать в любом месте кода. Мы можем получить доступ к вложенному типу Kind через класс Product: let Banana = Product() ifbanana.kind == Product.Kind.food { И, аналогичным образом свойство kind определяется в области видимости класса, но, поскольку оно также общедоступно, мы можем получить доступ к этому свойству для любого объекта типа Product. let посудомоечная машина = Product() Важным отличием здесь является то, что класс Product и переменная посудомоечной машины объявлены и, следовательно, доступны в глобальной области видимости. Вот почему мы можем использовать их в приведенном выше фрагменте кода. Вернемся к этим разным типам прицелов. Вот, проверьте код Swift ниже. Мы добавляем функцию canEat() в класс Product: class Product enum Kind { func canEat() -> Bool { Здесь мы имеем дело с тремя уровнями области видимости: Класс Product определен в глобальной области видимости, поэтому мы можем использовать его в любом месте модуля приложения. Свойство kind определено в области класса, поэтому мы можем использовать его в классе Product. То же самое касается перечисления Kind и функции canEat(). Мы используем свойство kind внутри функции canEat(). Это означает, что у областей есть иерархия, потому что мы можем получить доступ к свойству из области видимости класса внутри области действия функции. Однако, если мы определили локальную переменную внутри canEat(), мы не можем использовать эту переменную в другой функции того же класса, потому что они имеют разные области видимости. func canEat() -> Bool { func isThing() -> Bool { Вот сокращение для иерархии областей: Способ прочтения этой иерархии состоит в том, чтобы понять, что у вас есть доступ к глобальной области видимости (самой высокой) в области закрытия (самой низкой), а не наоборот. Итак, резюмируем: Видимость типа, переменной, свойства и т. д. определяет возможность доступа к ним. Это называется контролем доступа. У нас есть 5 различных уровней доступа: открытый, публичный, внутренний, файловый и частный. В общем, мы сокращаем это до «это общедоступно?» или «это личное?», потому что так быстрее. Scope повсюду в практической, повседневной разработке iOS. Когда вы передаете значения в своем приложении, отслеживание того, к каким переменным, типам и т. д. у вас есть доступ, является постоянной деятельностью. Скорее всего, если вы новичок в разработке iOS, вы уже включили область видимости в свои рассуждения о своем коде, даже не подозревая об этом! «К какой переменной я могу получить доступ?» Интересным случаем области видимости являются замыкания. Как вы, возможно, знаете, замыкание — это блок кода, который можно передать вокруг вашего кода. Это похоже на функцию, за исключением того, что сам код является значением. Вы можете назначить замыкание переменной, передать ее в функцию, после чего она окажется в другой части вашей программы. Замыкания часто используются в качестве так называемых обработчиков завершения. Допустим, мы загружаем изображение асинхронно из Интернета. Вот, проверьте это: класс DetailViewController: UIViewController func viewDidLoad() с помощью UIKit или SwiftUI. Если вы используете SwiftUI, не игнорируйте приведенный выше пример только потому, что он использует контроллер представления. Смысл этого раздела, как вы скоро увидите, заключается в том, как вы можете использовать свойство imageView внутри области замыкания. Это относится и к SwiftUI, и к другим компонентам! В приведенном выше коде мы создали класс контроллера представления со свойством imageView. Внутри функции мы вызываем гипотетическую функцию downloadImage(_:completionHandler:). Замыкание называется замыканием, потому что оно «закрывает» любые значения, на которые ссылается замыкание. Поскольку замыкания могут передаваться через ваш код как значения, замыканию нужен способ ссылаться на значения, которые используются внутри замыкания. Этот принцип называется замыканием или захватом. В приведенном выше примере кода замыкание содержит ссылку на свойство imageView. Это свойство потребуется позже, чтобы установить изображение. Когда замыкание завершает выполнение, эта ссылка освобождается. Этот захват работает только в том случае, если замыкание имеет доступ к тому же уровню области видимости, что и функция, в которой оно определено. сфера. Замыкание имеет ту же область видимости, что и сущность, в которой оно определено, и в данном случае это область действия функции. Интересно, не правда ли? Понимание захвата — это окончательный тест вашего понимания масштаба. Вам нужно выяснить, почему замыкание, которое будет выполняться в будущем, как видно из контекста функции viewDidLoad(), может иметь доступ к свойству imageView. Это потому, что замыкание имеет доступ к области видимости, в которой оно определено! Объем и контекст часто путают. Область действия фиксирована, потому что код, который вы пишете, фиксирован. Контекст изменчив, и он зависит от выполнения вашего кода. Таким образом, у вас может быть доступ к свойству, потому что оно находится в области действия, но из-за контекста вашего кода, то есть его точки выполнения, это свойство пусто. Вы можете видеть объем как то, как ваш код определен (фиксированный), и контекст как то, что ваш код делает в любой момент времени его выполнения (подвижный). Думайте об этом, как о езде на мотоцикле: у мотоцикла 2 колеса (прицел), и вращаются они или нет, зависит от того, как вы едете на велосипеде (контекст). Теперь, когда мы обсудили, что такое область видимости и как она работает, давайте сосредоточимся на самой распространенной ошибке, которую вы обнаружите при работе с областями. Это так: ошибка: не удается найти «…» в области видимости Это ошибка времени компиляции, поэтому она появляется, когда вы пытаетесь скомпилировать код, который приводит к этой ошибке. Как вы уже догадались, смысл его прост: имя переменной, на которое вы ссылаетесь, не существует! Проверьте это: func reverse(_ string: String) -> String for c в тексте { return result let value = reverse(«Hello!») Когда вы запустите приведенный выше код, вы получите следующую ошибку: ошибка: не удается найти «текст» в области Что здесь происходит? Мы явно где-то ошиблись. Несмотря на то, что строка для c в тексте имеет смысл — цикл по каждому символу в тексте — переменная text не существует. В общем, можно с уверенностью предположить, что «Не удается найти ‘…’ в области видимости» относится к несуществующей переменной, функции, типу или другому символу. Если вы хотите решить эту ошибку и исправить ошибку, начните с того, чего не существует, и двигайтесь дальше оттуда (например, с текста). Полезно знать, что ошибка «Не удается найти «…» в области действия» является симптомом, а не основной причиной. Например, в приведенном выше коде ссылка на «текст» была опечаткой. Совсем не поможет, если мы создадим новую переменную text просто для устранения ошибки, а потом обнаружим, что функция reverse() больше не работает. Какие другие проблемы могут вызвать ошибку «Не удается найти «…» в области видимости»? Примечание: Иногда вы хотите, чтобы переменная или функция существовала в определенном месте, но ее просто нет. Масштаб — это понятие, которое трудно выразить словами и правилами, но как только вы его освоите, оно станет вашей второй натурой. Вы все время работали с масштабом, возможно, даже не подозревая об этом. Scope — это ответ на вопрос: «Могу ли я использовать эту переменную здесь?» Аккуратный! Создайте свое приложение сейчас Блог о внутренней безопасности
/
PowerShell Джефф Браун | 5 минут чтения | Последнее обновление 19 марта 2021 г. PowerShell использует переменные для хранения информации, которая может пригодиться позже. Переменные также упрощают изменение значений в нескольких местах путем изменения определения переменной. Вы можете хранить такую информацию, как имена, пути и результаты команд, в переменной. По мере того, как вы будете более свободно работать с PowerShell, идея области действия переменных, вероятно, начнет играть определенную роль при написании сценариев, функций и модулей. В этом посте я расскажу об основах области видимости переменных PowerShell и приведу примеры использования области видимости в скриптах и модулях PowerShell. В дополнение к освоению области применения вы можете ознакомиться с набором инструментов PowerShell для получения дополнительных ресурсов, таких как редакторы, модули и обучение, чтобы поднять свои навыки работы с PowerShell на новый уровень. PowerShell защищает переменные и другие артефакты, ограничивая возможности их чтения и изменения. Уровни области действия защищают элементы, которые не следует изменять. PowerShell имеет следующие доступные области действия: Области работают в иерархии, то есть глобальная является родительской областью. Переменные, определенные в глобальной области, автоматически становятся доступными для просмотра в дочерней области. Однако переменные, определенные в дочерней области, недоступны в родительской области. Область действия PowerShell следует нескольким основным правилам: Давайте посмотрим на несколько примеров различных прицелов в действии. У меня есть скрипт, который определяет переменную и выводит ее на экран: Этот сценарий определяет переменную $greeting в области действия сценария (или локальной области). Однако эта переменная и ее значение будут недоступны для консоли PowerShell, которая является родительской областью. Изучите вывод команд PowerShell здесь: Я показываю текущее значение переменной $greeting в консоли (или глобальной области видимости), и, как и ожидалось, оно пусто. Я запускаю файл сценария, в котором определяется $greeting и выводится на экран. После выхода скрипта я отображаю значение $greeting снова в консоли PowerShell, и она по-прежнему пуста. Давайте рассмотрим обратное. Вместо того, чтобы определять значение $greeting в скрипте, давайте определим его в глобальной области видимости. Затем сценарий отображает значение переменной $greeting внутри сценария, унаследованной от глобальной области видимости. Внутри скрипта я не устанавливал и не модифицировал переменную $greeting . Я только показал его значение. Строка приветствия была унаследована от консоли в качестве родительской области файлом сценария в качестве дочерней области. В предыдущих примерах мы видим, что переменная, определенная в дочерней области скрипта, недоступна для ссылки в глобальной области видимости. Однако мы можем использовать модификаторы области действия, чтобы изменить область действия определенной переменной. Например, я могу использовать префикс $global: для переменной внутри скрипта, чтобы изменить значение переменной, которое я уже определил в глобальной родительской области. Изучите приведенный ниже сценарий и вывод консоли: Я определил переменную $greeting в глобальной области консоли как «Привет, Джефф!». Модуль PowerShell — это пакет команд, таких как командлеты или функции, которые имеют схожие функции или цели. Примером этого является модуль ActiveDirectory для Windows PowerShell, который содержит команды для управления объектами Active Directory. Вы можете создать модуль самостоятельно, и вам может понадобиться ссылаться на одну и ту же переменную в разных функциях. Установив переменные с помощью области скрипта в модуле, переменные теперь могут совместно использоваться функциями модуля. Вот пример файла модуля PowerShell (MyModule.psm1), который содержит две функции: Get-Greeting и Set-Greeting : Обратите внимание, что обе функции ссылаются на переменную $name . Однако, поскольку я определил переменную в отдельных функциях, они относятся только к этой функции. Установка переменной $name в функции Set-GreetingName не влияет на переменную $name в Приветствие . Вы можете попробовать это сами, сохранив этот код в файле .psm1, импортировав его с помощью команды Import-Module и указав имя файла модуля. Хотя я установил переменную $name с помощью функции Set-GreetingName , это не повлияло на переменную $name в функции Get-Greeting . Каждая переменная $name привязана к своей собственной функции. Если я изменю значение в одной функции, это не повлияет на другую функцию. Если я хочу, чтобы переменная была доступна для всех функций в модуле, я добавляю модификатор $script : к переменной $name , например: Если я повторно импортирую модуль с помощью параметра -Force , теперь я могу установить значение $name в одной функции и сослаться на него в другой. Обратите внимание, что вызов Get-Greeting показывает сообщение по умолчанию как $script:name 9Переменная 0078 не имеет значения. После вызова функции Set-GreetingName функция Get-Greeting теперь отображает другое значение в зависимости от переданного имени. Такое поведение ожидается, поскольку обе функции теперь ссылаются на одну и ту же переменную. Хотя пример модуля прост, вы можете увидеть, насколько он может быть полезен. Я использую эту функцию для установки учетных данных API, которые используются несколькими функциями в модулях, которые я пишу. Посмотрите пример в моем репозитории GitHub twilio-powershell-module. Как показано в приведенных выше примерах, скрипты и функции будут иметь собственную область действия за пределами глобальной области видимости. Изменения переменных затрагиваются только в этой области, если вы не используете модификатор области для изменения области действия переменной. Однако вы можете включить область действия скрипта или функции, используя точечную нотацию источника. Когда сценарий выполняется в текущей области, любые переменные сценария доступны в текущей области. Вы можете использовать точечную нотацию источника, поместив точку/точку (.) и пробел перед именем скрипта. Изучите файл сценария и код ниже: Первоначально значение $greeting в глобальной области консоли пусто или равно null, а файл scopetest.ps1 задает значение $greeting . Используя точечную нотацию источника, сценарий переносит значение переменной в родительскую область. Вы также можете использовать оператор вызова/амперсанд (&) для запуска скрипта или функции, и его область не будет добавлена к текущей области. Понимание области действия в PowerShell необходимо при написании скриптов, модулей и функций. Вы можете столкнуться со сценарием, в котором переменная имеет неожиданное значение, и это может быть связано с тем, что переменная наследуется из другой области. Для получения дополнительной информации о написании сценариев PowerShell ознакомьтесь с Учебным пособием Джеффа Петтера по написанию сценариев Windows PowerShell для начинающих. Мы Варонис. С 2005 года мы защищаем самые ценные в мире данные от врагов с помощью нашей ведущей на рынке платформы защиты данных. Джефф Браун — облачный инженер, специализирующийся на технологиях Microsoft, таких как Office 365, Teams, Azure и PowerShell. Вы можете найти больше его контента на https://jeffbrown.tech. Стандартная библиотека Kotlin содержит несколько функций, единственной целью которых является выполнение блока кода в контексте объекта. По сути, эти функции делают одно и то же: выполняют блок кода на объекте. Отличие заключается в том, как этот объект становится доступным внутри блока и каков результат всего выражения. Вот типичное использование функции области действия: класс данных Person(var name: String, var age: Int, var city: String) {
весело moveTo (новый город: строка) { город = новый город }
весело incrementAge () { возраст ++ }
}
веселая главная () {
// начало выборки
Person(«Алиса», 20, «Амстердам»).let {
распечатать(это)
it.moveTo(«Лондон»)
it.incrementAge()
распечатать(это)
}
//конец выборки
} Если вы напишите то же самое без класс данных Person (имя переменной: строка, возраст переменной: Int, город переменной: строка) {
весело moveTo (новый город: строка) { город = новый город }
весело incrementAge () { возраст ++ }
}
веселая главная () {
// начало выборки
val alice = Person(«Алиса», 20, «Амстердам»)
println(Алиса)
alice.moveTo(«Лондон»)
alice.incrementAge()
println(Алиса)
//конец выборки
} Функции области действия не привносят никаких новых технических возможностей, но они могут сделать ваш код более кратким и читабельным. Из-за схожего характера функций прицела выбрать правильный для вашего случая может быть немного сложно. Выбор в основном зависит от ваших намерений и согласованности использования в вашем проекте. Ниже мы предоставим подробное описание различий между функциями области видимости и соглашения об их использовании. Чтобы помочь вам выбрать правильную функцию осциллографа для ваших целей, мы приводим таблицу основных различий между ними. Function Object reference Return value Is extension function Lambda result Да Результат лямбда Yes — Lambda result No: called without the context object Результат лямбда Нет: в качестве аргумента принимает объект контекста. Context object Yes Context object Yes Подробная информация о различиях представлена в специальных разделах ниже. Вот краткое руководство по выбору функций прицела в зависимости от цели: Выполнение Lambda на не нулевых объектах: Внедрение выражения в качестве переменной в локальной области: Конфигурация объекта: Запуск операторов, где требуется выражение: без расширения Дополнительные эффекты: Группировка вызовов функций для объекта: Варианты использования различных функций перекрываются, поэтому вы можете выбрать функции на основе конкретных соглашений, используемых в вашем проекте или команде. Хотя функции области видимости позволяют сделать код более кратким, избегайте их чрезмерного использования: это может снизить читабельность кода и привести к ошибкам. Избегайте вложенных функций области видимости и будьте осторожны при их цепочке: легко запутаться в текущем объекте контекста и значении 9. Поскольку все функции области видимости очень похожи по своей природе, важно понимать различия между ними. Между каждой функцией области действия есть два основных различия: Внутри лямбда функции области видимости объект контекста доступен по короткой ссылке вместо его фактического имени. Каждая функция области видимости использует один из двух способов доступа к объекту контекста: как лямбда-приемник ( весело main() {
val ул = «Привет»
// это
ул.выполнить {
println(«Длина строки: $length»)
//println(«Длина строки: ${this.length}») // делает то же самое
}
// Это
ул. класс данных Person (имя переменной: строка, возраст переменной: Int = 0, город переменной: строка = «»)
веселая главная () {
// начало выборки
val adam = Person(«Адам»).apply {
age = 20 // то же, что this. В свою очередь, импорт kotlin.random.Random
весело writeToLog (сообщение: строка) {
println(«ИНФОРМАЦИЯ: $сообщение»)
}
веселая главная () {
// начало выборки
весело getRandomInt(): Int {
вернуть Random.nextInt(100). Кроме того, когда вы передаете объект контекста в качестве аргумента, вы можете указать пользовательское имя для объекта контекста внутри области. импорт kotlin.random.Random
весело writeToLog (сообщение: строка) {
println(«ИНФОРМАЦИЯ: $сообщение»)
}
веселая главная () {
// начало выборки
весело getRandomInt(): Int {
вернуть Random.nextInt(100).также {значение ->
writeToLog(«getRandomInt() генерирует значение $value»)
}
}
значение i = getRandomInt()
println(я)
//конец выборки
} Функции области видимости различаются возвращаемым результатом: Эти две опции позволяют вам выбрать правильную функцию в зависимости от того, что вы делаете дальше в своем коде. Возвращаемое значение весело main() {
// начало выборки
val numberList = mutableListOf Их также можно использовать в операторах возврата функций, возвращающих объект контекста. импорт kotlin.random.Random
весело writeToLog (сообщение: строка) {
println(«ИНФОРМАЦИЯ: $сообщение»)
}
веселая главная () {
// начало выборки
весело getRandomInt(): Int {
вернуть Random. весело main() {
// начало выборки
val number = mutableListOf(«один», «два», «три»)
val countEndsWithE = numbers.run {
добавить(«четыре»)
добавить(«пять»)
подсчет { it.endsWith(«e») }
}
println(«Есть элементы $countEndsWithE, оканчивающиеся на e.»
//конец выборки
} Кроме того, вы можете игнорировать возвращаемое значение и использовать функцию области для создания временной области для переменных. весело main() {
// начало выборки
val number = mutableListOf(«один», «два», «три»)
с (числа) {
val firstItem = первый()
val lastItem = последний()
println(«Первый элемент: $firstItem, последний элемент: $lastItem»)
}
//конец выборки
} Чтобы помочь вам выбрать правильную область действия для вашего случая, мы подробно опишем их и предоставим рекомендации по использованию. Объект контекста доступен в качестве аргумента ( fun main() {
// начало выборки
val numbers = mutableListOf(«один», «два», «три», «четыре», «пять»)
val resultList = numbers.map { it.length }.filter { it > 3 }
println(результатлист)
//конец выборки
} С fun main() {
// начало выборки
val numbers = mutableListOf(«один», «два», «три», «четыре», «пять»)
number.map { it.length }.filter { it > 3 }.let {
распечатать(это)
// и другие вызовы функций, если это необходимо
}
//конец выборки
} Если блок кода содержит одну функцию с fun main() {
// начало выборки
val numbers = mutableListOf(«один», «два», «три», «четыре», «пять»)
number. забавный процессNonNullString(str: String) {}
веселая главная () {
// начало выборки
val ул: Строка? = «Привет»
//processNonNullString(str) // ошибка компиляции: строка может быть нулевой
длина val = str?.let {
println(«let() вызвал $it»)
processNonNullString(it) // OK: ‘it’ не равно null внутри ‘?.let { }’
ит.длина
}
//конец выборки
} Другой случай использования весело main() {
// начало выборки
val number = listOf («один», «два», «три», «четыре»)
val модифицированныйFirstItem = numbers.first().let { firstItem ->
println(«Первый элемент списка — ‘$firstItem'»)
if (firstItem.length >= 5) firstItem else «!» + первый элемент + «!»
}.верхний регистр()
println(«Первый элемент после модификации: ‘$modifiedFirstItem'»)
//конец выборки
} Функция без расширения: объект контекста передается в качестве аргумента, но внутри лямбды он доступен как получатель ( Мы рекомендуем fun main() {
// начало выборки
val number = mutableListOf(«один», «два», «три»)
с (числа) {
println(«with» вызывается с аргументом $this»)
println(«Содержит элементы $size»)
}
//конец выборки
} Другим вариантом использования весело main() {
// начало выборки
val number = mutableListOf(«один», «два», «три»)
val firstAndLast = с (числа) {
«Первый элемент ${first()},» +
«последний элемент ${last()}»
}
println (первый и последний)
//конец выборки
} Объект контекста доступен как получатель ( класс MultiportService (URL-адрес var: строка, порт var: Int) {
fun prepareRequest(): String = «Запрос по умолчанию»
забавный запрос (запрос: String): String = «Результат запроса ‘$ request'»
}
веселая главная () {
// начало выборки
val service = MultiportService(«https://example. Помимо вызова весело main() {
// начало выборки
val hexNumberRegex = запустить {
значные цифры = «0-9»
val hexDigits = «A-Fa-f»
знак val = «+-»
Regex(«[$sign]?[$digits$hexDigits]+»)
}
for (совпадение в hexNumberRegex.findAll(«+123 -FFFF !%*& 88 XYZ»)) {
println(соответствие.значение)
}
//конец выборки
} Объект контекста доступен как получатель ( Используйте класс данных Person (var name: String, var age: Int = 0, var city: String = «»)
веселая главная () {
// начало выборки
val adam = Person(«Адам»).apply {
возраст = 32
город = «Лондон»
}
println(адам)
//конец выборки
} Имея получатель в качестве возвращаемого значения, вы можете легко включить Объект контекста доступен в качестве аргумента ( Когда вы видите в коде fun main() {
// начало выборки
val number = mutableListOf(«один», «два», «три»)
числа
.also { println(«Элементы списка перед добавлением нового: $it») }
.добавить(«четыре»)
//конец выборки
} В дополнение к функциям области видимости стандартная библиотека содержит функции При вызове объекта с предоставленным предикатом импорт kotlin.random.*
веселая главная () {
// начало выборки
число = Random.nextInt(100)
val evenOrNull = number.takeIf { it % 2 == 0 }
val oddOrNull = number.takeUnless { it % 2 == 0 }
println(«четное: $evenOrNull, нечетное: $oddOrNull»)
//конец выборки
} При связывании других функций после весело main() {
// начало выборки
val ул = «Привет»
val caps = str.takeIf { it.isNotEmpty() }?.uppercase()
//val caps = str.takeIf { it.isNotEmpty() }.uppercase() // ошибка компиляции
println (заглавные буквы)
//конец выборки
} весело main() {
// начало выборки
весело displaySubstringPosition (ввод: строка, подстрока: строка) {
input.indexOf(sub).takeIf { это >= 0 }?.let {
println(«Подстрока $sub найдена в $input.»
println(«Начальная позиция $it.»)
}
}
displaySubstringPosition («010000011», «11»)
displaySubstringPosition («010000011», «12»)
//конец выборки
} Вот как эта же функция выглядит без стандартных библиотечных функций: fun main() {
// начало выборки
весело displaySubstringPosition (ввод: строка, подстрока: строка) {
val index = input. Последнее изменение: 06 сентября 2022 г. Операции, связанные с картой Требования для подписки Некоторым функциям для выполнения своей работы требуется информация. Некоторые функции вычисляют некоторое значение, которое им нужно сделать доступным после завершения. И многим функциям необходимо создавать переменные, которые используются только временно, пока функция выполняется. Один из способов ввести информацию в функцию — через параметров . Мы уже видели несколько примеров вызова функций, принимающих параметры. Вот один из них: Функция Вот еще одна функция, которая принимает параметры: Функция Функции , которые вы определили до сих пор, не принимали никаких параметров. Им не нужна была никакая информация, чтобы выполнять свою работу. Теперь давайте посмотрим, как определить функции, принимающие параметры. Вы помещаете параметры в круглые скобки в заголовке функции. Каждый параметр на самом деле является специальной переменной. Мы называем параметр, который появляется в заголовке функции, формальный параметр . Если функция принимает более одного формального параметра, мы разделяем их запятыми в заголовке функции. Вот пример программы, содержащей функцию для рисования контура квадрата: Формальными параметрами являются переменные с именами После того, как Python скопировал эти три значения в формальные параметры, он устанавливает программный счетчик на первую строку тела Мы называем числа 100, 120, 50, которые фактически передаются в функцию , фактические параметры , иногда также называемые аргументами . При вызове функции значения фактических параметров вычисляются и копируются по порядку в формальные параметры. Фактические параметры — это значения (или выражения) в инструкции вызова функции, а формальные параметры — это переменные , используемые в самой функции. Фактический параметр может быть сложным выражением. Важно значение, которое он оценивает. Вкратце: Формальный параметр — это переменная, которая инициализируется копией фактического параметра в точке вызова. Значения фактических параметров копируются в соответствующие формальные параметры, позиция за позицией, слева направо. Цель: Напишите и используйте простую функцию, которая принимает параметр. Вот программа, которая заставляет робота двигаться по квадрату. Однако квадрат всегда имеет один и тот же размер. Напишите функцию, которая принимает один параметр, указывающий длину сторон квадрата, и вызовите эту функцию с соответствующими параметрами, чтобы заставить робота двигаться по квадрату размера 2. Задача: Написать и использовать простую функцию, которая принимает несколько параметров. Напишите функцию, рисующую смайлик. Функция должна принимать три параметра, которые указывают расположение и размер смайлика. Вызовите функцию для рисования смайлика радиусом 25 с центром в точках 100, 150 на экране. Размер должен быть указан в пикселях; вам нужно будет вычислить и использовать коэффициент масштабирования на основе этого размера. Выражения вычисляют значения и делают эти значения доступными для дальнейшего использования. Функции также могут вычислять значения и делать эти значения доступными для дальнейшего использования. Везде, где требуется значение, может появиться вызов функции, которая возвращает правильный тип значения (например, int, float, string или boolean). Например, в операторе печати мы можем напечатать значение, возвращаемое вызовом функции: Давайте проанализируем, что имеется в виду под «Везде, где требуется значение, может появиться вызов функции, которая возвращает правильный тип значения. ». Рассмотрим эту строку кода: Конечно, этот код выводит 20. Теперь, если бы мы вызвали Вы видите, что я сделал? Нам нужно значение int в качестве левого операнда Нам нужно было значение 8.48528137423857, и вместо этого мы использовали вызов функции Как мы видели, Если вы попытаетесь преобразовать строку, содержащую символы, представляющие что-то отличное от числа, Мы можем вызвать функцию В этой строке выводится случайное целое число от 5 до 20 включительно. Другими словами, равновероятно вывести любое целое число в диапазоне от 5 до 20. Что делать, если вам нужно случайное число с плавающей запятой? Вызов Цель: Используйте разные результаты вызова функции для выполнения различных действий. Напишите цикл, который имитирует подбрасывание монеты 5 раз и выводит «орел» или «решку» после каждого подбрасывания. Используйте функцию randint Python Цель: Напишите функцию, которая использует другую функцию, которую вы писали много раз. Напишите функцию, которая рисует Когда требуется значение, возвращаемое функцией, вызывается функция. Текущее значение счетчика программ сохраняется. Затем программный счетчик устанавливается на первую строку функции. Python выполняет тело функции. Функция возвращает , и программный счетчик устанавливается на свое значение до вызова функции, когда происходит одно из двух: Выполнение оператора return делает две вещи: Вот очень простой пример. Как мы теперь знаем, везде, где требуется значение, вы можете заменить выражение или вызов функции, который возвращает значение. Например, вы можете сделать что-то вроде этого: Строка Цель: Напишите функцию, которая возвращает значение. Сначала напишите функцию Затем напишите функцию Переменные в Python либо локальны для одной функции, либо глобальны и доступны для любой функции. В Python есть определенные правила, определяющие, является ли переменная локальной или глобальной, и способ доступа к переменной. Когда вы впервые присваиваете значение переменной внутри функции, эта переменная является локальной переменной. В этом примере переменная Но строка Локальные переменные: Формальные параметры тоже являются локальными переменными. Мы говорим, что локальная переменная имеет номер в области действия внутри функции, в которой она создается после присваивания. Локальные переменные хороши. Большинство строк кода что-то вычисляют и сохраняют это в локальной переменной с красивым именем. Более поздние строки кода используют эту переменную для вычисления чего-то еще и сохраняют ее в удобном локальном файле. Использование хорошо названных локальных переменных для промежуточных вычислений так же важно, как и комментирование, чтобы сделать код понятным и модифицируемым людьми. Значения переменных хранятся в памяти. Где? Каждый вызов функции создает область памяти, называемую кадр для хранения значений создаваемых им локальных переменных. Время от времени вам нужно, чтобы переменная была доступна для многих функций. Такая переменная не может быть локальной, потому что локальная переменная доступна только внутри функции, в которой она впервые назначена. Переменная, доступная многим функциям, — это глобальная переменная . Хотя глобальные переменные могут быть полезными, у них тоже есть свои изнаночные стороны, поэтому их следует использовать только при необходимости. Глобальные переменные инициализируются вне определений функций. Если вы просто используете значение глобальной переменной, вы можете получить доступ к этой глобальной переменной в любой строке кода (в том же файле), которая запускается после инициализации переменной. Изменение значения глобальной переменной — дело серьезное . В любой функции, где вы хотите присвоить значение глобальной переменной, вы должны использовать ключевое слово Здесь функция Важно помнить, что ключевое слово Что не так с глобальными переменными? Есть два очевидных способа получить значения в функцию. Первый заключается в использовании передачи фактических параметров в формальные параметры; второй — установить глобальную переменную, которую может использовать функция. Если выбрать второе, то Хотя мы будем использовать некоторые глобальные переменные в демонстрационных целях, и есть даже несколько удачных применений глобальных переменных, использование глобальной переменной всегда должно вызывать у вас как минимум дискомфорт. Часто вы можете обернуть голый код внутри функции, сделав переменные локальными, а затем передать значения этих переменных той функции, которая в них нуждается. Стилистически использование локальных переменных и параметров для передачи данных делает поток информации понятным по всей программе. Некоторые функции, которые вы хотите использовать, принимают некоторые параметры; вы думаете о том, какие значения вам нужны и как их вычислить. Функция возвращает это значение, и вы знаете, что можете его использовать. Если функция использует или изменяет глобальные значения для ввода или вывода информации, сложнее понять, как связать эту функцию с другим кодом. Существует один способ использования глобальных переменных, который является достаточно безопасным и, по сути, хорошей практикой программирования: в качестве именованных констант. Например, программа по химии может использовать число Авогадро в нескольких функциях. Если вы вводите фактическое число каждый раз, когда используете его в уравнении, вы можете сделать ошибку, и читателю может быть трудно разобраться в уравнениях, если он не узнает число. Глобальная переменная может хранить номер, упрощая его изменение без поиска и замены, а также делает код более читаемым. Мы называем глобальные переменные, используемые для хранения значений, которые не изменяются , константами . Хорошей практикой программирования является ввод констант с использованием заглавных букв, чтобы их можно было распознать как константы. В модулях Python есть несколько встроенных глобальных переменных, которые можно использовать, импортировав их. Обратите внимание, что Хотя глобальная переменная, такая как (Я проверил в Интернете эту историю о том, что Великий штат Канзас пытался изменить значение π на 3. Оказывается, это неправда. Ура, Канзас!) С большой силой приходит большая ответственность. Python позволяет изменять значение переменных, предназначенных для использования в качестве именованных констант. Не делай этого. Рассмотрим следующий код: Тест Другими словами, функция возвращает ровно того же значения, что и выражение Как это работает? Мы вычисляем выражение Следует избегать кода, подобного первой версии функции. Переменные отличаются тем, как они устанавливаются (вашим кодом или ColdFusion), местами в вашем коде, где они имеют смысл, и тем, как долго сохраняются их значения. Эти соображения обычно называют переменными прицел . К часто используемым областям относятся область переменных, область по умолчанию для создаваемых вами переменных и область запроса, доступная на время HTTP-запроса. Пользовательские функции также относятся к областям действия. Дополнительные сведения см. в разделе Указание области действия функции в статье Эффективное использование определяемых пользователем функций. В следующей таблице описаны области действия ColdFusion: Если URL-адрес содержит несколько параметров с одинаковыми именами, результирующая переменная в области URL-адресов ColdFusion состоит из всех значений параметров, разделенных запятыми. Например, URL вида http://localhost/urlparamtest.cfm?param=1¶m=2¶m=3 приводит к значению переменной URL.param 1,2,3 на странице ColdFusion.| Переменные Область по умолчанию для переменных любого типа, созданных с помощью тегов cfset и cfparam. Чтобы предотвратить повреждение данных, вы блокируете код, который использует переменные области сеанса, приложения или сервера. Дополнительную информацию см. в разделе Использование постоянных данных и блокировки. В следующей таблице показано, как создавать переменные и ссылаться на них в различных областях кода. Дополнительные сведения о механизмах создания переменных в большинстве областей см. в разделе Создание переменных. Любой из следующих: В следующих разделах содержится подробная информация о том, как можно создавать и использовать переменные в различных областях. Если вы используете имя переменной без префикса области, ColdFusion проверяет области в следующем порядке, чтобы найти переменную: Поскольку ColdFusion должен искать переменные, когда вы не указываете область, вы можете повысить производительность, указав область действия для всех переменных. Области действия ColdFusion не применяются к тегам расширения ColdFusion (CFX), пользовательским тегам, которые вы пишете на языке программирования, таком как C++ или Java. Страница ColdFusion, вызывающая тег CFX, должна использовать атрибуты тега для передачи данных в тег CFX. Тег CFX должен использовать интерфейсы запроса и ответа Java или класс запроса C++ для получения и возврата данных. ColdFusion делает все именованные области доступными в виде структур. Вы не можете получить доступ к локальной области функции для определяемых пользователем функций (UDF), которые вы определяете с помощью CFScript в качестве структуры. Точно так же вы можете использовать структурные функции CFML для управления содержимым области видимости. Дополнительные сведения об использовании структур см. в разделе Использование массивов и структур. Не вызывайте StructClear(Session) для очистки переменных сеанса. Угол — геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки. На рис. 1 лучи АВ и АС — стороны угла, точка А — вершина угла. При записи угла в середине пишут букву, обозначающую его вершину. Сам угол на рис. 1 обозначают так: ВАС или САВ (этот угол нельзя обозначить так: АВС или СВА или ВСА или АСВ, т.к. точки В и С не являются вершинами данного угла). Если углы имеют общую вершину, то их нельзя обозначить одной буквой. Так на рис. 2 углы имеют общую вершину Е, поэтому мы можем использовать для данных углов только следующие обозначения: МЕК или КЕМ, МЕР или РЕМ, РЕК или КЕР. Говорят, что луч ЕР в данном случае делит угол МЕК (или КЕМ) на два угла: МЕР (или РЕМ) и РЕК (или КЕР). Также иногда углы обозначают цифрами, например, на рис.3 мы имеем 1. Углы, как и отрезки, можно сравнивать между собой. Чтобы сравнить два угла можно наложить один угол на другой. Биссектриса — луч, который делит угол на два равных угла. На рис. 4 углы НОМ и DОМ равны, значит, луч ОМ — биссектриса угла НОD. Прямой угол — угол, который можно построить с помощью угольника (рис. 5). Если начертить два прямых угла с общей вершиной и одной общей стороной, то две другие стороны этих углов составят прямую (рис. 6). Считают, что лучи, составляющие прямую, также образуют угол, который называют развернутым. На рис. 6 АОВ и ВОС — прямые, АОС — развернутый. Развернутый угол равен двум прямым углам, а прямой угол составляет половину развернутого. Острый угол — угол, который меньше прямого угла. На рис. 7 МОN — острый. Тупой угол — угол, который больше прямого угла, но меньше развернутого. На рис. 8 РЕК — тупой. Поделись с друзьями в социальных сетях:
Отрезок Ломаная Четырехугольники Единицы измерения площадей. Свойства площадей Прямоугольник, его периметр и площадь. Ось симметрии фигуры Квадрат. Периметр и площадь квадрата. Многоугольники. Правильные многоугольники. Равенство фигур. Плоскость Прямая Луч Шкалы и координаты Прямоугольный параллелепипед. Пирамида. Объем прямоугольного параллелепипеда Куб. Площадь поверхности куба Куб. Объем куба Прямой и развернутый угол Чертежный треугольник Измерение углов. Треугольник и его виды Окружность, круг, шар Цилиндр, конус Отрезок-xx Геометрия 5 класс
Задание 1615,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1641,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1653,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1658,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1776,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1778,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Номер 3,
Мерзляк, Полонский, Якир, Учебник
Номер 11,
Мерзляк, Полонский, Якир, Учебник
Номер 302,
Мерзляк, Полонский, Якир, Учебник
Номер 5,
Мерзляк, Полонский, Якир, Учебник
6 класс
Номер 219,
Мерзляк, Полонский, Якир, Учебник
Номер 391,
Мерзляк, Полонский, Якир, Учебник
Номер 686,
Мерзляк, Полонский, Якир, Учебник
Номер 714,
Мерзляк, Полонский, Якир, Учебник
Номер 1226,
Мерзляк, Полонский, Якир, Учебник
Номер 1236,
Мерзляк, Полонский, Якир, Учебник
Номер 1237,
Мерзляк, Полонский, Якир, Учебник
Номер 1283,
Мерзляк, Полонский, Якир, Учебник
Задание 738,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1545,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
7 класс
Номер 759,
Мерзляк, Полонский, Якир, Учебник
Задание 81,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
В этой статье будет рассматриваться одна из основных геометрических фигур — угол. После общего введения в это понятие мы уделим основное внимание отдельному виду такой фигуры. Развернутый угол — важное понятие геометрии, которое и будет основной темой этой статьи. В геометрии существует ряд объектов, которые составляют основу всей науки. Угол как раз относиться к ним и определяется с помощью понятия луча, поэтому начнем именно с него. Также перед тем, как приступать к определению самого угла, нужно вспомнить о нескольких не менее важных объектах в геометрии — это точка, прямая на плоскости и собственно сама плоскость. Прямой называют самую простую геометрическую фигуру, у которой нет ни начала, ни конца. Плоскостью — поверхность, которая имеет два измерения. Ну и луч (или же полупрямая) в геометрии — это часть прямой, у которой есть начало, но нет конца. Используя данные понятия, можем составить утверждение, что углом является геометрическая фигура, которая полностью лежит в некоторой плоскости и состоит из двух несовпадающих лучей с общим началом. Мы знаем о том, что углы могут быть совсем разными. А потому немного ниже будет приведена небольшая классификация, которая поможет лучше разобраться в видах углов и их главных особенностях. Итак, существует несколько видов углов в геометрии: Теперь давайте рассмотрим развернутый угол более подробно. Это тот случай, когда обе стороны лежат на одной прямой, что можно четко увидеть на рисунке немного ниже. Значит, мы можем с уверенностью сказать, что у развернутого угла одна из его сторон по сути есть продолжением другой. Стоит запомнить тот факт, что такой угол всегда можно разделить с помощью луча, который выходит из его вершины. В результате мы получим два угла, которые в геометрии называются смежными. Также развернутый угол имеет несколько особенностей. Для того, чтобы рассказать о первой из них, нужно вспомнить понятие «биссектриса угла». Напомним, что это луч, который делит любой угол строго пополам. Что касается развернутого угла, то его биссектриса разделяет его таким образом, что образуется два прямых угла по 90 градусов. Это очень легко просчитать математически: 180˚ (градус развернутого угла) : 2 = 90˚. Если же разделять развернутый угол совсем произвольным лучом, то в результате мы всегда получаем два угла, один из которых будет острым, а другой — тупым. Будет удобно рассматривать этот угол, собрав воедино все его главные свойства, что мы и сделали в данном списке: Итак, зная все эти характеристики данного вида углов, мы можем использовать их для решения ряда геометрических задач. Для того, чтобы понять, усвоили ли вы понятие развернутого угла, попытайтесь ответить на несколько следующих вопросов. Решения и ответы: Если у вас получилось ответить на все эти вопросы без подсказок и не подглядывая в ответы, значит вы готовы переходить к следующему уроку по геометрии. В этой статье мы всесторонне разберем одну из основных геометрических фигур – угол. Начнем со вспомогательных понятий и определений, которые нас приведут к определению угла. После этого приведем принятые способы обозначения углов. Далее подробно разберемся с процессом измерения углов. В заключении покажем как можно отметить углы на чертеже. Все теорию мы снабдили необходимыми чертежами и графическими иллюстрациями для лучшего запоминания материала. Навигация по странице. Угол является одной из важнейших фигур в геометрии. Определение угла дается через определение луча. В свою очередь представление о луче невозможно получить без знания таких геометрических фигур как точка, прямая и плоскость. Поэтому, перед знакомством с определением угла, рекомендуем освежить в памяти теорию из разделов и . Итак, будем отталкиваться от понятий точки, прямой на плоскости и плоскости. Дадим сначала определение луча. Пусть нам дана некоторая прямая на плоскости. Для краткости и удобства ввели следующие обозначения для лучей: луч обозначают либо малой латинской буквой (например, луч p
или луч k
), либо двумя большими латинскими буквами, первая из которых соответствует началу луча, а вторая обозначает некоторую точку этого луча (например, луч ОА
или луч СD
). Покажем изображение и обозначение лучей на чертеже. Теперь мы можем дать первое определение угла. Определение. Угол – это плоская геометрическая фигура (то есть целиком лежащая в некоторой плоскости), которую составляют два несовпадающих луча с общим началом. Каждый из лучей называют стороной угла , общее начало сторон угла называют вершиной угла . Возможен случай, когда стороны угла составляют прямую линию. Определение. Если обе стороны угла лежат на одной прямой, то такой угол называется развернутым . Предлагаем Вашему вниманию графическую иллюстрацию развернутого угла. Для обозначения угла используют значок угла «». Если стороны угла обозначены малыми латинскими буквами (например, одна сторона угла k
, а другая h
), то для обозначения этого угла после значка угла записывают подряд буквы, соответствующие сторонам, причем порядок записи значения не имеет (то есть, или ). Если стороны угла обозначены двумя большими латинскими буквами (к примеру, одна сторона угла OA
, а вторая сторона угла OB
), то угол обозначают следующим образом: после значка угла записывают три буквы, участвующие в обозначении сторон угла, причем буква, отвечающая вершине угла, располагается посередине (в нашем случае угол будет обозначен как или ). Если вершина угла не является вершиной еще какого-нибудь угла, то такой угол можно обозначать буквой, соответствующей вершине угла (например, ). Любой угол разделяет плоскость на две части. При этом если угол не развернутый, то одну часть плоскости называют внутренней областью угла , а другую – внешней областью угла . Следующее изображение разъясняет, какая часть плоскости отвечает внутренней области угла, а какая — внешней. Любую из двух частей, на которые развернутый угол разделяет плоскость, можно считать внутренней областью развернутого угла. Определение внутренней области угла приводит нас ко второму определению угла. Определение. Угол – это геометрическая фигура, которую составляют два несовпадающих луча с общим началом и соответствующая внутренняя область угла. Следует отметить, что второе определение угла строже первого, так как содержит больше условий. Однако не следует отметать первое определение угла, также не следует рассматривать первое и второе определения угла по отдельности. Дадим еще определения смежных и вертикальных углов. Определение. Смежные углы – это два угла, у которых одна сторона общая, а две другие образуют развернутый угол. Из определения следует, что смежные углы дополняют друг друга до развернутого угла. Определение. Вертикальные углы – это два угла, у которых стороны одного угла являются продолжениями сторон другого. На рисунке изображены вертикальные углы. Очевидно, что две пересекающиеся прямые образуют четыре пары смежных углов и две пары вертикальных углов. В этом пункте статьи мы разберемся с определениями равных и неравных углов, а также в случае неравных углов разъясним, какой угол считается большим, а какой меньшим. Напомним, что две геометрические фигуры называются равными, если их можно совместить наложением. Пусть нам даны два угла. Приведем рассуждения, которые помогут нам получить ответ на вопрос: «Равны эти два угла или нет»? Очевидно, что мы всегда можем совместить вершины двух углов, а также одну сторону первого угла с любой из сторон второго угла. Совместим сторону первого угла с той стороной второго угла, чтобы оставшиеся стороны углов оказались по одну сторону от прямой, на которой лежат совмещенные стороны углов. Тогда, если две другие стороны углов совместятся, то углы называются равными . Если же две другие стороны углов не совместятся, то углы называются неравными , причем меньшим считается тот угол, который составляет часть другого (большим является тот угол, который полностью содержит другой угол). Очевидно, что два развернутых угла равны. Также очевидно, что развернутый угол больше любого неразвернутого угла. Измерение углов основывается на сравнении измеряемого угла с углом, взятым в качестве единицы измерения. Процесс измерения углов выглядит так: начиная от одной из сторон измеряемого угла, его внутреннюю область последовательно заполняют единичными углами, плотно укладывая их один к другому. При этом запоминают количество уложенных углов, которое и дает меру измеряемого угла. Фактически, в качестве единицы измерения углов может быть принят любой угол. Однако существует множество общепринятых единиц измерения углов, относящихся к различным областям науки и техники, они получили специальные названия. Одной из единиц измерения углов является градус . Определение. Один градус – это угол, равный одной сто восьмидесятой части развернутого угла. Градус обозначают символом «», следовательно, один градус обозначается как . Таким образом, в развернутом угле мы можем уложить 180
углов в один градус. Это будет выглядеть как половинка круглого пирога, разрезанная на 180
равных кусочков. Очень важно: «кусочки пирога» плотно укладываются один к другому (то есть, стороны углов совмещаются), причем сторона первого угла совмещается с одной стороной развернутого угла, а сторона последнего единичного угла совпадет с другой стороной развернутого угла. При измерении углов выясняют, сколько раз градус (или другая единица измерения углов) укладывается в измеряемом угле до полного покрытия внутренней области измеряемого угла. Как мы уже убедились, в развернутом угле градус укладывается ровно 180
раз. Ниже приведены примеры углов, в которых угол в один градус укладывается ровно 30
раз (такой угол составляет шестую часть развернутого угла) и ровно 90
раз (половина развернутого угла). Для измерения углов, меньших одного градуса (или другой единицы измерения углов) и в случаях, когда угол не удается измерить целым числом градусов (взятых единиц измерения), приходится использовать части градуса (части взятых единиц измерения). Определение. Минута – это одна шестидесятая часть градуса. Определение. Секунда – это одна шестидесятая часть минуты. Иными словами, в минуте содержится шестьдесят секунд, а в градусе – шестьдесят минут (3600
секунд). Для обозначения минут используют символ «», а для обозначения секунд – символ «» (не путайте со знаками производной и второй производной). Тогда при введенных определениях и обозначениях имеем , а угол, в котором укладываются 17
градусов 3
минуты и 59
секунд, можно обозначить как . Определение. Градусной мерой угла называется положительное число, которое показывает сколько раз градус и его части укладываются в данном угле. Например, градусная мера развернутого угла равна ста восьмидесяти, а градусная мера угла равна . Для измерения углов существуют специальные измерительные приборы, наиболее известным из них является транспортир. Если известно и обозначение угла (к примеру, ) и его градусная мера (пусть 110
), то используют краткую запись вида и говорят: «Угол АОВ
равен ста десяти градусам». Из определений угла и градусной меры угла следует, что в геометрии мера угла в градусах выражается действительным числом из интервала (0, 180]
(в тригонометрии рассматривают углы с произвольной градусной мерой, их называют ). Угол в девяносто градусов имеет специальное название, его называют прямым углом . Угол меньший 90
градусов называется острым углом . Угол больший девяноста градусов называется тупым углом . Итак, мера острого угла в градусах выражается числом из интервала (0, 90)
, мера тупого угла – числом из интервала (90, 180)
, прямой угол равен девяноста градусам. Приведем иллюстрации острого угла, тупого угла и прямого угла. Из принципа измерения углов следует, что градусные меры равных углов одинаковы, градусная мера большего угла больше градусной меры меньшего, а градусная мера угла, который составляют несколько углов, равна сумме градусных мер составляющих углов. Таким образом, сумма смежных углов равна ста восьмидесяти градусам , так как они составляют развернутый угол. Из этого утверждения следует, что . Действительно, если углы АОВ
и СОD
– вертикальные, то углы АОВ
и ВОС
— смежные и углы СОD
и ВОС
также смежные, поэтому, справедливы равенства и , откуда следует равенство . Наряду с градусом удобна единица измерения углов, называемая радианом . Радианная мера широко используется в тригонометрии. Дадим определение радиана. Определение. Угол в один радиан – это центральный угол , которому соответствует длина дуги, равная длине радиуса соответствующей окружности. Дадим графическую иллюстрацию угла в один радиан. На чертеже длина радиуса OA
(как и радиуса OB
) равна длине дуги AB
, поэтому, по определению угол AOB
равен одному радиану. Для обозначения радианов используют сокращение «рад». Стоит отдельно отметить, что величина угла, выраженная в радианах, не зависит от длины радиуса окружности. Это связано с тем, что фигуры, ограниченные данным углом и дугой окружности с центром в вершине данного угла, подобны между собой. Измерение углов в радианах можно выполнять так же, как и измерение углов в градусах: выяснить, сколько раз угол в один радиан (и его части) укладываются в данном угле. А можно вычислить длину дуги соответствующего центрального угла, после чего разделить ее на длину радиуса. Для нужд практики полезно знать, как соотносятся между собой градусная и радианная меры, так как довольно часть приходится осуществлять . В указанной статье установлена связь между градусной и радианной мерой угла, и приведены примеры перевода градусов в радианы и обратно. На чертежах для удобства и наглядности углы можно отмечать дугами, которые принято проводить во внутренней области угла от одной стороны угла до другой. Равные углы отмечают одинаковым количеством дуг, неравные углы – различным количеством дуг. Прямые углы на чертеже обозначают символом вида «», который изображают во внутренней области прямого угла от одной стороны угла до другой. Если на чертеже приходится отмечать много различных углов (обычно больше трех), то при обозначении углов кроме обычных дуг допустимо использование дуг какого-либо специального вида. К примеру, можно изобразить зубчатые дуги, или нечто подобное. Следует отметить, что не стоит увлекаться с обозначением углов на чертежах и не загромождать рисунки. Рекомендуем обозначать только те углы, которые необходимы в процессе решения или доказательства. Список литературы. Угол – основная геометрическая фигура, которую разберем на протяжение всей темы. Определения, способы задания, обозначения и измерения угла. Разберем принципы выделения углов на чертежах. Вся теория проиллюстрирована и имеет большое количество наглядных чертежей. Yandex.RTB R-A-339285-1
Определение 1 Угол – простая важная фигура в геометрии. Угол напрямую зависит от определения луча, который в свою очередь состоит из базовых понятий точки, прямой и плоскости. Для досконального изучения необходимо углубиться по темам прямая на плоскости – необходимые сведения и плоскость – необходимые сведения . Понятие угла начинается с понятий о точке, плоскости и прямой, изображенной на этой плоскости. Определение 2 Дана прямая a на плоскости. Иначе говоря, луч или полупрямая – это часть прямой, состоящая из точек заданной прямой, расположенных на одной стороне относительно начальной точки, то есть точки O . Обозначение луча допустимо в двух вариациях: одной строчной или двумя прописными буквами латинского алфавита. При обозначении двумя буквами луч имеет название, состоящее из двух букв. Рассмотрим подробнее на чертеже. Перейдем к понятию определения угла. Определение 3 Угол – это фигура, расположенная в заданной плоскости, образованная двумя несовпадающими лучами, имеющими общее начало. Сторона угла является лучом, вершина – общее начало сторон. Имеет место случай, когда стороны угла могут выступать в роли прямой линии. Определение 4 Когда обе стороны угла расположены на одной прямой или его стороны служат как дополнительные полупрямые одной прямой, то такой угол называют развернутым . На рисунке ниже изображен развернутый угол. Точка на прямой – это и есть вершина угла. Чаще всего имеет место ее обозначение точкой O . Угол в математике обозначается знаком « ∠ ». Когда стороны угла обозначают малыми латинскими, то для правильного определения угла записываются подряд буквы соответственно сторонам. Если две стороны имеют обозначение k и h , то угол обозначается как ∠ k h или ∠ h k . Когда идет обозначение большими буквами, то соответственно стороны угла имеют названия O A и O B . В таком случае угол имеет название из трех букв латинского алфавита, записанные подряд, в центре с вершиной — ∠ A O B и ∠ B O A . Существует обозначение в виде цифр, когда углы не имеют названий или буквенных обозначений. Ниже приведен рисунок, где разными способами обозначаются углы. Угол делит плоскость на две части. В случае, если угол не развернутый, тогда одна часть плоскости имеет название внутренняя область угла , другая – внешняя область угла . При разделении развернутым углом на плоскости любая из его частей считается внутренней областью развернутого угла. Внутренняя область угла – элемент, служащий для второго определения угла. Определение 5 Углом называют геометрическую фигуру, состоящая из двух несовпадающих лучей, имеющих общее начало и соответствующую внутреннюю область угла. Данное определение является более строгим, чем предыдущее, так как имеет больше условий. Оба определения не желательно рассматривать отдельно, потому как угол – это геометрическая фигура, преобразованная при помощи двух лучей, выходящих из одной точки. Когда необходимо выполнять действия с углом, то под определением понимают наличие двух лучей с общим началом и внутренней областью. Определение 6 Два угла называют смежными , если имеется общая сторона, а две другие являются дополнительными полупрямыми или образуют развернутый угол. На рисунке видно, что смежные углы дополняют друг друга, так как являются продолжением один другого. Определение 7 Два угла называют вертикальными , если стороны одного являются дополнительными полупрямыми другого или являются продолжениями сторон другого. На рисунке ниже показано изображение вертикальных углов. При пересечении прямых получается 4 пары смежных и 2 пары вертикальных углов. Ниже показано на рисунке. Статья показывает определения равных и неравных углов. Разберем какой угол считается большим, какой меньшим и другие свойства угла. Две фигуры считаются равными, если при наложении они полностью совпадают. Такое же свойство применимо для сравнения углов. Даны два угла. Необходимо прийти к выводу, равные эти углы или нет. Известно, что имеет место наложение вершин двух углов и стороны первого угла с любой другой стороной второго. То есть при полном совпадении при наложении углов стороны заданных углов совместятся полностью, углы равные . Может быть так, что при наложении стороны могут не совместиться, то углы неравные, меньший из которых состоит из другого, а больший имеет в своем составе полный другой угол. Ниже изображены неравные углы, не совмещенные при наложении. Развернутые углы являются равными. Измерение углов начинается с измерения стороны измеряемого угла и его внутренней области, заполняя которую единичными углами, прикладывают друг к другу. Необходимо посчитать количество уложенных углов, они и предопределяют меру измеряемого угла. Единица измерения угла может быть выражена любым измеряемым углом. Имеются общепринятые единицы измерения, которые применяют в науке и технике. Они специализируются на других названиях. Чаще всего используют понятие градус . Определение 8 Один градус называют углом, который имеет одну сто восьмидесятую часть развернутого угла. Стандартное обозначение градуса идет при помощи « ° », тогда один градус – 1 ° . Известно, что количество положенных градусов в угле, это и есть та самая мера угла. Развернутый угол имеет 180 уложенных углов в своем составе. Ниже на рисунке приводятся примеры, где уложение угла идет в 30 раз, то есть одна шестая развернутого, и 90 раз, то есть половина. Для точности определения измерения углов используются минуты и секунды. Их применяют, когда величина угла не является целым обозначением градуса. Такие части градуса позволяют выполнять более точные расчеты. Определение 9 Минутой называют одну шестидесятую часть градуса. Определение 10 Секундой называют одну шестидесятую часть минуты. Градус содержит 3600 секунд. Минуты обозначают « » », а секунды « «» ». Имеет место обозначение: 1 ° = 60 » = 3600 «» , 1 » = (1 60) ° , 1 » = 60 «» , 1 «» = (1 60) » = (1 3600) ° , а обозначение угла 17 градусов 3 минут и 59 секунд имеет вид 17 ° 3 » 59 «» . Определение 11 Приведем пример обозначения градусной меры угла равного 17 ° 3 » 59 «» . Запись имеет еще один вид 17 + 3 60 + 59 3600 = 17 239 3600 . Для точного измерения углов используют такой измерительный прибор, как транспортир. При обозначении угла ∠ A O B и его градусной мере в 110 градусов применяют более удобную запись ∠ A O B = 110 ° , которая читается «Угол А О В равен 110 градусам». В геометрии используется мера угла из интервала (0 , 180 ] , а в тригонометрии произвольная градусная мера имеет название углов поворота. Значение углов всегда выражается действительным числом. Прямой угол – это угол, имеющий 90 градусов. Острый угол – угол, который меньше 90 градусов, а тупой – больше. Острый угол измеряется в интервале (0 , 90) , а тупой – (90 , 180) . Ниже наглядно изображены три вида углов. Любая градусная мера любого угла имеет одинаковое значение. Больший угол соответственно имеет большую градусную меру, чем меньший. Исходя из этого, можно сделать вывод, что сумма всех смежных углов равна 180 градусам, потому что они все и составляют развернутый угол. Отсюда следует, что любые вертикальные углы равны . Если рассмотреть это на примере, мы получим, что угол А О В и С О D – вертикальные (на чертеже), тогда пары углов А О В и В О С, С О D и В О С считают смежными. В таком случает равенство ∠ A O B + ∠ B O C = 180 ° вместе с ∠ C O D + ∠ B O C = 180 ° считаются однозначно верными. Отсюда имеем, что ∠ A O B = ∠ C O D . Ниже приводится пример изображения и обозначения вертикальных улов. Кроме градусов, минут и секунд используется еще одна единица измерения. Она называется радианом . Чаще всего ее можно встретить в тригонометрии при обозначении углов многоугольников. Определение 12 Углом в один радиан называют центральный угол, который имеет длину радиуса окружности равную длине дуги. На рисунке радиан изображается в виде окружности, где имеется центр, обозначенный точкой, с двумя точками на окружности, соединенными и преобразованными в радиусы О А и О В. По определению данный треугольник A O B является равносторонним, значит длина дуги A B равна длинам радиусов О В и О А. Обозначение угла принимается за «рад». То есть запись в 5 радиан сокращенно обозначается как 5 рад. Иногда можно встретить обозначение, имеющее название пи. Радианы не имеют зависимости от длины заданной окружности, так как фигуры имеют некое ограничение при помощи угла и его дугой с центром, находящимся в вершине заданного угла. Они считаются подобными. Радианы имеют такой же смысл, как и градусы, только разница в их величине. Чтобы это определить, необходимо вычисленную длину дуги центрального угла поделить на длину ее радиуса. На практике используют перевод градусов в радианы и радианы в градусы для более удобного решения задач. Указанная статья имеет информацию о связи градусной меры с радианной, где можно подробно изучить переводы из градусной в радианную и обратно. Для наглядного и удобного изображения дуг, углов используют чертежи. Не всегда можно правильно изобразить и отметить тот или иной угол, дугу или название. Равные углы имеют обозначение в виде одинакового количества дуг, а неравные в виде разного. На чертеже изображено правильное обозначение острых, равных и неравных углов. Когда необходимо отметить более 3 углов, используются специальные обозначения дуг, например, волнистые или зубчатые. Это не имеет столь важное значение. Ниже приведен рисунок, где показано их обозначение. Обозначение углов должны быть простыми, чтобы не мешали другим значениям. При решении задачи рекомендовано выделять только необходимые для решения углы, чтобы не загромождать весь чертеж. Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter Углом называют фигуру, образованную двумя лучами, выходящими из одной точки (рис. 160). При записи угла в середине пишут букву, обозначающую его вершину. Угол можно обозначить и одной буквой — названием его вершины. Например, вместо «угол АОВ» пишут короче: «угол О». Вместо слова «угол» пишут знак . Например, AОВ, O. На рисунке 161 точки С и D лежат внутри угла АОВ, точки X и У лежат вне этого угла, а точки М и Н — на сторонах угла. Как и все геометрические фигуры, углы сравниваются с помощью наложения. Если один угол можно наложить на другой так, что они совпадут, то эти углы равны. Например, на рисунке 162 ABC = MNK. Из вершины угла СОК (рис. 163) проведен луч ОР. Он разбивает угол СОК на два угла — СОР и РОК. Каждый из этих углов меньше угла СОК. Пишут: COP Два дополнительных друг другу луча образуют развернутый угол. Стороны этого угла вместе составляют прямую линию, на которой лежит вершина развернутого угла (рис. 164). Часовая и минутная стрелки часов образуют в 6 ч развернутый угол (рис. 165). Согнем два раза пополам лист бумаги, а потом развернем его (рис. 166). Линии сгиба образуют 4 равных угла. Каждый из этих углов равен половине развернутого угла. Такие углы называют прямыми. Прямым углом называют половину развернутого угла. Для построения прямого угла пользуются чертежным треугольником (рис. 167). Чтобы построить прямой угол, одной из сторон которого является луч ОЛ, надо: а) расположить чертежный треугольник так, чтобы вершина его прямого угла совпала с точкой О, а одна из сторон пошла по лучу ОА; б) провести вдоль второй стороны треугольника луч ОВ. В результате получим прямой угол АОВ. Вопросы к теме 1.Что такое угол? Нам с вами уже известно, что любой угол делит плоскость на две части. Но, в случае, если у угла его обе стороны лежат на одной прямой, то такой угол называется развернутым. То есть, у развернутого угла одна его сторона является продолжением его другой стороны угла. Теперь давайте посмотрим на рисунок, на котором как раз и изображен развернутый угол О. Если мы возьмем и проведем из вершины развернутого угла луч, то он разделит данный развернутый угол еще на два угла, которые будут иметь одну общую сторону, а другие два угла будут составлять прямую. То есть, с одного развернутого угла мы получили два смежных. Если мы возьмем развернутый угол и проведем биссектрису, то эта биссектриса разделит развернутый угол на два прямых угла. А, в том случае, если мы из вершины развернутого угла проведем произвольный луч, который не является биссектрисой, то такой луч разделит развернутый угол на два угла, один из которых будет острым, а другой тупым. Развернутый угол обладает такими свойствами: Во-первых, стороны развёрнутого угла являются антипараллельными и образуют прямую; Чтобы измерить любой угол, для этих целей чаще всего используют транспортир, у которого единица измерения равна одному градусу. При измерении углов следует помнить, что любой угол имеет свою определенную градусную меру и естественно эта мера больше нуля. А развернутый угол, как нам уже известно, равен 180 градусам. То есть, если мы с вами возьмем любую плоскость круга и разделим ее радиусами на 360 равных частей, то 1/360 часть данного круга будет являться угловым градусом. Как вы уже знаете, что градус обозначается определенным значком, который имеет такой вид:
« ° ». Теперь мы также знаем, что один градус 1° = 1/360 части круга. Если угол равен плоскости круга и составляет 360 градусов, то такой угол является полным. А теперь мы возьмем, и плоскость круга поделим с помощью двух радиусов, лежащих на одной прямой линии, на две равные части. То в этом случае, плоскость полукруга составит половину полного угла, то есть 360: 2 = 180°. Мы с вами получили угол, который равен полуплоскости круга и имеет 180°. Это и есть развернутый угол. 1613. Назовите углы, изображенные на рисунке 168. Запишите их обозначения. 1614. Начертите четыре луча: ОА, ОВ, ОС и OD. Запишите названия шести углов, сторонами которых являются эти лучи. На сколько частей эти лучи делят плоскость ? 1615. 1616. Начертите угол MOD и проведите внутри него луч ОТ. Назовите и обозначьте углы, на которые этот луч делит угол MOD. 1617. Минутная стрелка за 10 мин повернулась на угол АОВ, за следующие 10 мин — на угол ВОС, а еще за 15 мин — на угол COD. Сравните углы АОВ и ВОС, ВОС и COD, АОС и АОВ, АОС и COD (рис. 170). 1618. Изобразите с помощью чертежного треугольника 4 прямых угла в разных положениях. 1619. С помощью чертежного треугольника найдите на рисунке 171 прямые углы. Запишите их обозначения. 1620. Укажите прямые углы в классной комнате. а) 0,09 200; б) 208 0,4; в) 130 0,1 + 80 0,1. 1629. Сколько процентов от 400 составляет число 200; 100; 4; 40; 80; 400; 600? 1630. Найдите пропущенное число: а) 2 5 3 б) 2 3 5 1631. Начертите квадрат, сторона которого равна длине 10 клеток тетради. 1632. За учебный год Петя израсходовал 40% купленных в начале года тетрадей, и у него осталось 30 тетрадей. Сколько тетрадей было куплено для Пети в начале учебного года? 1633. Бронза является сплавом олова и меди. Сколько процентов сплава составляет медь в куске бронзы, состоящем из 6 кг олова и 34 кг меди? 1634. Построенный в древности Александрийский маяк, который называли одним из семи чудес света, выше башен Московского Кремля в 1,7 раза, но ниже здания Московского университета на 119 м. Найдите высоту каждого из этих сооружений, если башни Московского Кремля на 49 м ниже Александрийского маяка. 1635. Найдите с помощью микрокалькулятора: а) 4,5% от 168; в) 28,3% от 569,8; 1636. Решите задачу: 1) Площадь огорода 6,4 а. 2) У Сережи было 4,8 ч свободного времени. 35% этого времени он потратил на чтение книги, а 40% на просмотр передач по телевизору. Сколько времени у него еще осталось? 1637. Выполните действия: 1) ((23,79: 7,8 — 6,8: 17) 3,04 — 2,04) 0,85; 1638. Начертите угол ВАС и отметьте по одной точке внутри угла, вне угла и на сторонах угла. 1639. Какие из отмеченных на рисунке 172 точек лежат внутри угла АМК.Какая точка лежит внутри угла АМВ> но вне угла АМК.Какие точки лежат на сторонах угла АМК? 1640. Найдите с помощью чертежного треугольника прямые углы на рисунке 173. 1641. Постройте квадрат со стороной 43 мм. Вычислите его периметр и площадь. 1642. Найдите значение выражения: а) 14,791: а + 160,961: b, если а = 100, b = 10; 1643. Рабочий должен был изготовить 450 деталей. В первый день он изготовил 60% деталей, а остальные — во второй. Сколько деталей изготовил рабочий во второй день? 1644. В библиотеке было 8000 книг. Через год число их увеличилось на 2000 книг. На сколько процентов увеличилось число книг в библиотеке? 1645. Грузовики в первый день проехали 24% намеченного пути, во второй день — 46% пути, а в третий — остальные 450 км. Сколько километров проехали эти грузовики? 1646. Найдите, сколько составляют: а) 1% от тонны; в) 5% от 7 т; 1647. Масса детеныша моржа в 9 раз меньше массы взрослого моржа. Какова масса взрослого моржа, если вместе с детенышем их масса равна 0,9 т? 1648. Во время маневров командир оставил 0,3 всех своих солдат охранять переправу, а остальных разделил на 2 отряда для обороны двух высот. В первом отряде было в 6 раз больше солдат, чем во втором. Сколько солдат было в первом отряде, если всего было 200 солдат? Н. Угол в измеряют в градусной мере (градус, минута, секунда), в оборотах — отношение длины дуги s к длине окружности L , в радианах — отношение длины дуги s к радиусу r ; исторически применялась также градовая мера измерения углов, в настоящее время она почти нигде не используется. 1 оборот = 2π радианам = 360° = 400 градам . В морской терминологии углы обозначаются румбами . Смежные углы — острый (a) и тупой (b). Развёрнутый угол (c) Кроме этого, рассматривается угол между гладкими кривыми в точке касания: по определению, его величина равна величине угла между касательными к кривым. Wikimedia Foundation
.
2010
. Угол, равный двум прямым. *РАЗВЕРТКА поверхности фигура, получающаяся в плоскости при таком совмещении точек данной поверхности с этой плоскостью, при котором длины линий остаются неизменными. угол — ▲ разность направление (в пространстве) угол протяженность поворота от одного направления к другому; разность направлений; часть полного оборота (# наклона. образовывать #). наклон. наклонный. отклонение. уклониться (дорога уклонилась вправо).… … Угол — Углы: 1 общего вида; 2 смежные; 3 прилежащие; 4 вертикальные; 5 развернутый; 6 прямой, острый и тупой; 7 между кривыми; 8 между прямой и плоскостью; 9 между скрещивающимися прямыми (не лежащими в одной плоскостью) прямыми. УГОЛ, геометрическая… … Иллюстрированный энциклопедический словарь Геометрическая фигура, состоящая из двух различных лучей, выходящих из одной точки. Лучи наз. сторонами У., а их общее начало вершиной У. Пусть [ ВА),[ ВС) стороны угла, В его вершина, плоскость, определяемая сторонами У. Фигура делит плоскость… … Математическая энциклопедия Угол, равный двум прямым. * * * РАЗВЕРНУТЫЙ УГОЛ РАЗВЕРНУТЫЙ УГОЛ, угол, равный двум прямым … Энциклопедический словарь Раздел математики, занимающийся изучением свойств различных фигур (точек, линий, углов, двумерных и трехмерных объектов), их размеров и взаимного расположения. 1) Замкнутая ломаная линия, именно: если различные точки, никакие последовательные три из к рых не лежат на одной прямой, то совокупность отрезков наз. многоугольником (см. рис. 1). М. могут быть пространственными или плоскими (ниже… … Математическая энциклопедия поперек — ▲ под углом максимум, косой угол поперечный. поперек под прямым углом. . прямой угол угол максимального отклонения; угол, равный своему смежному; четверть оборота. перпендикуляр. перпендикулярный находящийся под прямым углом. перпендикулярно.… … Идеографический словарь русского языка градус — а, м. 1) Единица измерения плоского угла, равная 1/90 прямого угла или соответственно 1/360 окружности. Угол в 90 градусов называется прямым углом. Развернутый угол составляет 180 градусов. 2) Единица измерения температурного интервала, имеющая… … Популярный словарь русского языка Теорема Шварца Кристоффеля важная теорема в теории функций комплексного переменного, носит название немецких математиков Карла Шварца и Элвина Кристоффеля. Угол в измеряют в градусной мере (градус, минута, секунда), в оборотах — отношение длины дуги s к длине окружности L , в радианах — отношение длины дуги s к радиусу r ; исторически применялась также градовая мера измерения углов, в настоящее время она почти нигде не используется. 1 оборот = 2π радианам = 360° = 400 градам . В морской терминологии углы обозначаются румбами . Смежные углы — острый (a) и тупой (b). Развёрнутый угол (c) Кроме этого, рассматривается угол между гладкими кривыми в точке касания: по определению, его величина равна величине угла между касательными к кривым. Wikimedia Foundation
.
2010
. Угол, равный двум прямым. угол — ▲ разность направление (в пространстве) угол протяженность поворота от одного направления к другому; разность направлений; часть полного оборота (# наклона. образовывать #). наклон. наклонный. отклонение. уклониться (дорога уклонилась вправо).… … Угол — Углы: 1 общего вида; 2 смежные; 3 прилежащие; 4 вертикальные; 5 развернутый; 6 прямой, острый и тупой; 7 между кривыми; 8 между прямой и плоскостью; 9 между скрещивающимися прямыми (не лежащими в одной плоскостью) прямыми. УГОЛ, геометрическая… … Иллюстрированный энциклопедический словарь Геометрическая фигура, состоящая из двух различных лучей, выходящих из одной точки. Лучи наз. сторонами У., а их общее начало вершиной У. Пусть [ ВА),[ ВС) стороны угла, В его вершина, плоскость, определяемая сторонами У. Угол, равный двум прямым. * * * РАЗВЕРНУТЫЙ УГОЛ РАЗВЕРНУТЫЙ УГОЛ, угол, равный двум прямым … Энциклопедический словарь Раздел математики, занимающийся изучением свойств различных фигур (точек, линий, углов, двумерных и трехмерных объектов), их размеров и взаимного расположения. Для удобства преподавания геометрию подразделяют на планиметрию и стереометрию. В… … Энциклопедия Кольера 1) Замкнутая ломаная линия, именно: если различные точки, никакие последовательные три из к рых не лежат на одной прямой, то совокупность отрезков наз. многоугольником (см. рис. 1). М. могут быть пространственными или плоскими (ниже… … Математическая энциклопедия поперек — ▲ под углом максимум, косой угол поперечный. поперек под прямым углом. . прямой угол угол максимального отклонения; угол, равный своему смежному; четверть оборота. перпендикуляр. перпендикулярный находящийся под прямым углом. перпендикулярно.… … Идеографический словарь русского языка градус — а, м. Теорема Шварца Кристоффеля важная теорема в теории функций комплексного переменного, носит название немецких математиков Карла Шварца и Элвина Кристоффеля. Очень важной с практической точки зрения является проблема о конформном… … Википедия Углом называют фигуру, образованную двумя лучами, выходящими из одной точки (рис. 160). При записи угла в середине пишут букву, обозначающую его вершину. Угол можно обозначить и одной буквой — названием его вершины. Например, вместо «угол АОВ» пишут короче: «угол О». Вместо слова «угол» пишут знак . Например, AОВ, O. На рисунке 161 точки С и D лежат внутри угла АОВ, точки X и У лежат вне этого угла, а точки М и Н — на сторонах угла. Как и все геометрические фигуры, углы сравниваются с помощью наложения. Если один угол можно наложить на другой так, что они совпадут, то эти углы равны. Например, на рисунке 162 ABC = MNK. Из вершины угла СОК (рис. 163) проведен луч ОР. Он разбивает угол СОК на два угла — СОР и РОК. Каждый из этих углов меньше угла СОК. Пишут: COP Два дополнительных друг другу луча образуют развернутый угол. Стороны этого угла вместе составляют прямую линию, на которой лежит вершина развернутого угла (рис. 164). Часовая и минутная стрелки часов образуют в 6 ч развернутый угол (рис. 165). Согнем два раза пополам лист бумаги, а потом развернем его (рис. Линии сгиба образуют 4 равных угла. Каждый из этих углов равен половине развернутого угла. Такие углы называют прямыми. Прямым углом называют половину развернутого угла. Для построения прямого угла пользуются чертежным треугольником (рис. 167). Чтобы построить прямой угол, одной из сторон которого является луч ОЛ, надо: а) расположить чертежный треугольник так, чтобы вершина его прямого угла совпала с точкой О, а одна из сторон пошла по лучу ОА; б) провести вдоль второй стороны треугольника луч ОВ. В результате получим прямой угол АОВ. Вопросы к теме 1.Что такое угол? Нам с вами уже известно, что любой угол делит плоскость на две части. Но, в случае, если у угла его обе стороны лежат на одной прямой, то такой угол называется развернутым. Теперь давайте посмотрим на рисунок, на котором как раз и изображен развернутый угол О. Если мы возьмем и проведем из вершины развернутого угла луч, то он разделит данный развернутый угол еще на два угла, которые будут иметь одну общую сторону, а другие два угла будут составлять прямую. То есть, с одного развернутого угла мы получили два смежных. Если мы возьмем развернутый угол и проведем биссектрису, то эта биссектриса разделит развернутый угол на два прямых угла. А, в том случае, если мы из вершины развернутого угла проведем произвольный луч, который не является биссектрисой, то такой луч разделит развернутый угол на два угла, один из которых будет острым, а другой тупым. Развернутый угол обладает такими свойствами: Во-первых, стороны развёрнутого угла являются антипараллельными и образуют прямую; Чтобы измерить любой угол, для этих целей чаще всего используют транспортир, у которого единица измерения равна одному градусу. При измерении углов следует помнить, что любой угол имеет свою определенную градусную меру и естественно эта мера больше нуля. А развернутый угол, как нам уже известно, равен 180 градусам. То есть, если мы с вами возьмем любую плоскость круга и разделим ее радиусами на 360 равных частей, то 1/360 часть данного круга будет являться угловым градусом. Как вы уже знаете, что градус обозначается определенным значком, который имеет такой вид:
« ° ». Теперь мы также знаем, что один градус 1° = 1/360 части круга. Если угол равен плоскости круга и составляет 360 градусов, то такой угол является полным. А теперь мы возьмем, и плоскость круга поделим с помощью двух радиусов, лежащих на одной прямой линии, на две равные части. То в этом случае, плоскость полукруга составит половину полного угла, то есть 360: 2 = 180°. Мы с вами получили угол, который равен полуплоскости круга и имеет 180°. 1613. Назовите углы, изображенные на рисунке 168. Запишите их обозначения. 1614. Начертите четыре луча: ОА, ОВ, ОС и OD. Запишите названия шести углов, сторонами которых являются эти лучи. На сколько частей эти лучи делят плоскость ? 1615. Укажите, какие точки на рисунке 169 лежат внутри угла КОМ, Какие точки лежат вне этого угла? Какие точки лежат на стороне OK, a какие — на стороне ОМ? 1616. Начертите угол MOD и проведите внутри него луч ОТ. Назовите и обозначьте углы, на которые этот луч делит угол MOD. 1617. Минутная стрелка за 10 мин повернулась на угол АОВ, за следующие 10 мин — на угол ВОС, а еще за 15 мин — на угол COD. Сравните углы АОВ и ВОС, ВОС и COD, АОС и АОВ, АОС и COD (рис. 170). 1618. Изобразите с помощью чертежного треугольника 4 прямых угла в разных положениях. 1619. С помощью чертежного треугольника найдите на рисунке 171 прямые углы. Запишите их обозначения. 1620. Укажите прямые углы в классной комнате. а) 0,09 200; б) 208 0,4; в) 130 0,1 + 80 0,1. 1629. Сколько процентов от 400 составляет число 200; 100; 4; 40; 80; 400; 600? 1630. Найдите пропущенное число: а) 2 5 3 б) 2 3 5 1631. Начертите квадрат, сторона которого равна длине 10 клеток тетради. Пусть этот квадрат изображает поле. Рожь занимает 12% поля, овес — 8%, пшеница — 64%, а остальная часть поля занята гречихой. Покажите на рисунке часть поля, занятую каждой культурой. Сколько процентов поля занимает гречиха? 1632. За учебный год Петя израсходовал 40% купленных в начале года тетрадей, и у него осталось 30 тетрадей. Сколько тетрадей было куплено для Пети в начале учебного года? 1633. Бронза является сплавом олова и меди. Сколько процентов сплава составляет медь в куске бронзы, состоящем из 6 кг олова и 34 кг меди? 1634. Построенный в древности Александрийский маяк, который называли одним из семи чудес света, выше башен Московского Кремля в 1,7 раза, но ниже здания Московского университета на 119 м. 1635. Найдите с помощью микрокалькулятора: а) 4,5% от 168; в) 28,3% от 569,8; 1636. Решите задачу: 1) Площадь огорода 6,4 а. В первый день вскопали 30% огорода, а во второй день — 35% огорода. Сколько аров осталось еще вскопать? 2) У Сережи было 4,8 ч свободного времени. 35% этого времени он потратил на чтение книги, а 40% на просмотр передач по телевизору. Сколько времени у него еще осталось? 1637. Выполните действия: 1) ((23,79: 7,8 — 6,8: 17) 3,04 — 2,04) 0,85; 1638. Начертите угол ВАС и отметьте по одной точке внутри угла, вне угла и на сторонах угла. 1639. Какие из отмеченных на рисунке 172 точек лежат внутри угла АМК.Какая точка лежит внутри угла АМВ> но вне угла АМК.Какие точки лежат на сторонах угла АМК? 1640. 1641. Постройте квадрат со стороной 43 мм. Вычислите его периметр и площадь. 1642. Найдите значение выражения: а) 14,791: а + 160,961: b, если а = 100, b = 10; 1643. Рабочий должен был изготовить 450 деталей. В первый день он изготовил 60% деталей, а остальные — во второй. Сколько деталей изготовил рабочий во второй день? 1644. В библиотеке было 8000 книг. Через год число их увеличилось на 2000 книг. На сколько процентов увеличилось число книг в библиотеке? 1645. Грузовики в первый день проехали 24% намеченного пути, во второй день — 46% пути, а в третий — остальные 450 км. Сколько километров проехали эти грузовики? 1646. Найдите, сколько составляют: а) 1% от тонны; в) 5% от 7 т; 1647. Масса детеныша моржа в 9 раз меньше массы взрослого моржа. Какова масса взрослого моржа, если вместе с детенышем их масса равна 0,9 т? 1648. Н.Я. ВИЛЕНКИН, B. И. ЖОХОВ, А. С. ЧЕСНОКОВ, C. И. ШВАРЦБУРД, Математика 5 класс, Учебник для общеобразовательных учреждений Углом называется геометрическая фигура, которая состоит из двух различных лучей, исходящих из одной точки. В данном случае, эти лучи называются сторонами угла. Точка, являющаяся началом лучей, называется вершиной угла. На рисунке вы можете увидеть угол с вершиной в точке О , и сторонами k и m . На сторонах угла отмечены точки А и С. Этот угол можно обозначить как угол AOC. В середине обязательно должно стоять название точки, в которой находится вершина угла. Также существуют и другие обозначения, угол О или угол km. В геометрии вместо слова угол часто пишут специальный значок. Если у угла обе стороны лежат на одной прямой, то такой угол называется развернутым углом. То есть одна сторона угла является продолжением другой стороны угла. На рисунке нижк представлен развернутый угол О. Следует отметить, что любой угол, разделяет плоскость на две части. Если угол не является развернутым, то одна из частей называется внутренней областью угла, а другая внешней областью этого угла. На рисунке ниже представлен неразвернутый угол и отмечены внешняя и внутренняя области этого угла. В случае с развернутым углом любую из двух частей, на которые он делит плоскость, можно считать внешней областью угла. Можно говорить о положении точки относительно угла. Точка может лежать вне угла (во внешней области), может находится на одной из его сторон, либо может лежать внутри угла (во внутренней области). На рисунке ниже, точка А лежит вне угла О, точка B лежит на одной из сторон угла, а точка С лежит внутри угла. Для измерения углов существует прибор называемый транспортиром. Единицей измерения угла является градус . Следует отметить, что каждый угол имеет определенную градусную меру, которая больше нуля. В зависимости от градусной меры углы делятся на несколько групп. Давайте начнем с определения того, что такое угол. Во-первых, он является Во-вторых, он образован двумя лучами, которые называются сторонами угла. В-третьих, последние выходят из одной точки, которую называют вершиной угла. Исходя из этих признаков, мы можем составить определение: угол — геометрическая фигура, которая состоит из двух лучей (сторон), выходящих из одной точки (вершины). Их классифицируют по градусной величине, по расположению относительно друг друга и относительно окружности. Начнем с видов углов по их величине. Существует несколько их разновидностей. Рассмотрим подробнее каждый вид. Основных типов углов всего четыре — прямой, тупой, острый и развернутый угол. Прямой Он выглядит так: Его градусная мера всегда составляет 90 о, иначе говоря, прямой угол — это угол 90 градусов. Только они есть у таких четырехугольников, как квадрат и прямоугольник. Тупой Он имеет такой вид: Градусная мера всегда больше 90 о, но меньше 180 о. Он может встречаться в таких четырехугольниках, как ромб, произвольный параллелограмм, во многоугольниках. Острый Он выглядит так: Градусная мера острого угла всегда меньше 90 о. Он встречается во всех четырехугольниках, кроме квадрата и произвольного параллелограмма. Развернутый Развернутый угол имеет такой вид: В многоугольниках он не встречается, но не менее важен, чем все остальные. Развернутый угол — это геометрическая фигура, градусная мера которой всегда равняется 180º. На нем можно построить проведя из его вершины один или несколько лучей в любых направлениях. Есть еще несколько второстепенных видов углов. 1. Нулевой Он выглядит так: Само название угла уже говорит о его величине. Его внутренняя область равняется 0 о, а стороны лежат друг на друге так, как показано на рисунке. 2. Косой Косым может быть и прямой, и тупой, и острый, и развернутый угол. Главное его условие — он не должен равняться 0 о, 90 о, 180 о, 270 о. 3. Выпуклый Выпуклыми являются нулевой, прямой, тупой, острый и развернутый углы. Как вы уже поняли, градусная мера выпуклого угла — от 0 о до 180 о. 4. Невыпуклый Невыпуклыми являются углы с градусной мерой от 181 о до 359 о включительно. 5. Полный Полным является угол с градусной мерой 360 о. Это все типы углов по их величине. Теперь рассмотрим их виды по расположению на плоскости относительно друг друга. 1. Дополнительные Это два острых угла, образовывающие один прямой, т. 2. Смежные Смежные углы образуются, если через развернутый, точнее, через его вершину, провести луч в любом направлении. Их сумма равна 180 о. 3. Вертикальные Вертикальные углы образуются при пересечении двух прямых. Их градусные меры равны. Теперь перейдем к видам углов, расположенным относительно окружности. Их всего два: центральный и вписанный. 1. Центральный Центральным является угол с вершиной в центре окружности. Его градусная мера равна градусной мере меньшей дуги, стянутой сторонами. 2. Вписанный Вписанным называется угол, вершина которого лежит на окружности, и стороны которого ее пересекают. Его градусная мера равна половине дуги, на которую он опирается. Это все, что касается углов. Теперь вы знаете, что помимо наиболее известных — острого, тупого, прямого и развернутого — в геометрии существует много других их видов. В этой статье будет рассматриваться одна из основных геометрических фигур — угол. В геометрии существует ряд объектов, которые составляют основу всей науки. Угол как раз относиться к ним и определяется с помощью понятия луча, поэтому начнем именно с него. Также перед тем, как приступать к определению самого угла, нужно вспомнить о нескольких не менее важных объектах в геометрии — это точка, прямая на плоскости и собственно сама плоскость. Прямой называют самую простую геометрическую фигуру, у которой нет ни начала, ни конца. Плоскостью — поверхность, которая имеет два измерения. Ну и луч (или же полупрямая) в геометрии — это часть прямой, у которой есть начало, но нет конца. Используя данные понятия, можем составить утверждение, что углом является геометрическая фигура, которая полностью лежит в некоторой плоскости и состоит из двух несовпадающих лучей с общим началом. Мы знаем о том, что углы могут быть совсем разными. А потому немного ниже будет приведена небольшая классификация, которая поможет лучше разобраться в видах углов и их главных особенностях. Итак, существует несколько видов углов в геометрии: Теперь давайте рассмотрим развернутый угол более подробно. Это тот случай, когда обе стороны лежат на одной прямой, что можно четко увидеть на рисунке немного ниже. Значит, мы можем с уверенностью сказать, что у развернутого угла одна из его сторон по сути есть продолжением другой. Стоит запомнить тот факт, что такой угол всегда можно разделить с помощью луча, который выходит из его вершины. В результате мы получим два угла, которые в геометрии называются смежными. Также развернутый угол имеет несколько особенностей. Для того, чтобы рассказать о первой из них, нужно вспомнить понятие «биссектриса угла». Напомним, что это луч, который делит любой угол строго пополам. Что касается развернутого угла, то его биссектриса разделяет его таким образом, что образуется два прямых угла по 90 градусов. Это очень легко просчитать математически: 180˚ (градус развернутого угла) : 2 = 90˚. Если же разделять развернутый угол совсем произвольным лучом, то в результате мы всегда получаем два угла, один из которых будет острым, а другой — тупым. Будет удобно рассматривать этот угол, собрав воедино все его главные свойства, что мы и сделали в данном списке: Итак, зная все эти характеристики данного вида углов, мы можем использовать их для решения ряда геометрических задач. Для того, чтобы понять, усвоили ли вы понятие развернутого угла, попытайтесь ответить на несколько следующих вопросов. Решения и ответы: Если у вас получилось ответить на все эти вопросы без подсказок и не подглядывая в ответы, значит вы готовы переходить к следующему уроку по геометрии. Угол – основная геометрическая фигура, которую разберем на протяжение всей темы. Определения, способы задания, обозначения и измерения угла. Разберем принципы выделения углов на чертежах. Вся теория проиллюстрирована и имеет большое количество наглядных чертежей. Угол – простая важная фигура в геометрии. Угол напрямую зависит от определения луча, который в свою очередь состоит из базовых понятий точки, прямой и плоскости. Для досконального изучения необходимо углубиться по темам прямая на плоскости – необходимые сведения и плоскость – необходимые сведения. Понятие угла начинается с понятий о точке, плоскости и прямой, изображенной на этой плоскости. Дана прямая a на плоскости. На ней обозначим некоторую точку O. Прямая разделена точкой на две части, каждая из которых имеет название луч, а точка O – начало луча. Иначе говоря, луч или полупрямая – это часть прямой, состоящая из точек заданной прямой, расположенных на одной стороне относительно начальной точки, то есть точки O. Обозначение луча допустимо в двух вариациях: одной строчной или двумя прописными буквами латинского алфавита. При обозначении двумя буквами луч имеет название, состоящее из двух букв. Рассмотрим подробнее на чертеже. Перейдем к понятию определения угла. Угол – это фигура, расположенная в заданной плоскости, образованная двумя несовпадающими лучами, имеющими общее начало. Сторона угла является лучом, вершина – общее начало сторон. Имеет место случай, когда стороны угла могут выступать в роли прямой линии. Когда обе стороны угла расположены на одной прямой или его стороны служат как дополнительные полупрямые одной прямой, то такой угол называют развернутым. На рисунке ниже изображен развернутый угол. Точка на прямой – это и есть вершина угла. Чаще всего имеет место ее обозначение точкой O. Угол в математике обозначается знаком «∠ ». Когда стороны угла обозначают малыми латинскими, то для правильного определения угла записываются подряд буквы соответственно сторонам. Если две стороны имеют обозначение k и h, то угол обозначается как ∠kh или ∠hk . Когда идет обозначение большими буквами, то соответственно стороны угла имеют названия OA и OB. В таком случае угол имеет название из трех букв латинского алфавита, записанные подряд, в центре с вершиной — ∠AOB и ∠BOA . Существует обозначение в виде цифр, когда углы не имеют названий или буквенных обозначений. Ниже приведен рисунок, где разными способами обозначаются углы. Угол делит плоскость на две части. В случае, если угол не развернутый, тогда одна часть плоскости имеет название внутренняя область угла, другая – внешняя область угла. Ниже приведено изображение, объясняющее, какие части плоскости внешние, а какие внутренние. При разделении развернутым углом на плоскости любая из его частей считается внутренней областью развернутого угла. Внутренняя область угла – элемент, служащий для второго определения угла. Углом называют геометрическую фигуру, состоящая из двух несовпадающих лучей, имеющих общее начало и соответствующую внутреннюю область угла. Данное определение является более строгим, чем предыдущее, так как имеет больше условий. Оба определения не желательно рассматривать отдельно, потому как угол – это геометрическая фигура, преобразованная при помощи двух лучей, выходящих из одной точки. Когда необходимо выполнять действия с углом, то под определением понимают наличие двух лучей с общим началом и внутренней областью. Два угла называют смежными, если имеется общая сторона, а две другие являются дополнительными полупрямыми или образуют развернутый угол. На рисунке видно, что смежные углы дополняют друг друга, так как являются продолжением один другого. Два угла называют вертикальными, если стороны одного являются дополнительными полупрямыми другого или являются продолжениями сторон другого. На рисунке ниже показано изображение вертикальных углов. При пересечении прямых получается 4 пары смежных и 2 пары вертикальных углов. Ниже показано на рисунке. Статья показывает определения равных и неравных углов. Разберем какой угол считается большим, какой меньшим и другие свойства угла. Две фигуры считаются равными, если при наложении они полностью совпадают. Такое же свойство применимо для сравнения углов. Даны два угла. Необходимо прийти к выводу, равные эти углы или нет. Известно, что имеет место наложение вершин двух углов и стороны первого угла с любой другой стороной второго. То есть при полном совпадении при наложении углов стороны заданных углов совместятся полностью, углы равные. Может быть так, что при наложении стороны могут не совместиться, то углы неравные, меньший из которых состоит из другого, а больший имеет в своем составе полный другой угол. Развернутые углы являются равными. Измерение углов начинается с измерения стороны измеряемого угла и его внутренней области, заполняя которую единичными углами, прикладывают друг к другу. Необходимо посчитать количество уложенных углов, они и предопределяют меру измеряемого угла. Единица измерения угла может быть выражена любым измеряемым углом. Имеются общепринятые единицы измерения, которые применяют в науке и технике. Они специализируются на других названиях. Чаще всего используют понятие градус. Один градус называют углом, который имеет одну сто восьмидесятую часть развернутого угла. Стандартное обозначение градуса идет при помощи «°», тогда один градус – 1° . Следовательно, развернутый угол состоит из 180 таких углов, состоящих из одного градуса. Все имеющиеся углы плотно уложены друг к другу и стороны предыдущего совмещены с последующим. Известно, что количество положенных градусов в угле, это и есть та самая мера угла. Развернутый угол имеет 180 уложенных углов в своем составе. Ниже на рисунке приводятся примеры, где уложение угла идет в 30 раз, то есть одна шестая развернутого, и 90 раз, то есть половина. Для точности определения измерения углов используются минуты и секунды. Их применяют, когда величина угла не является целым обозначением градуса. Такие части градуса позволяют выполнять более точные расчеты . Минутой называют одну шестидесятую часть градуса. Секундой называют одну шестидесятую часть минуты. Градус содержит 3600 секунд. Минуты обозначают «’», а секунды «»». Имеет место обозначение: 1°=60’=3600», 1’=(160)°, 1’=60», 1»=(160)’=(13600)° , а обозначение угла 17 градусов 3 минут и 59 секунд имеет вид 17°3’59» . Градусная мера угла –это число, показывающее количество укладываний градуса в заданном угле. Приведем пример обозначения градусной меры угла равного 17°3’59» . Запись имеет еще один вид 17+360+593600=172393600. Для точного измерения углов используют такой измерительный прибор, как транспортир. При обозначении угла ∠AOB и его градусной мере в 110 градусов применяют более удобную запись ∠AOB=110° , которая читается «Угол АОВ равен 110градусам». В геометрии используется мера угла из интервала (0,180], а в тригонометрии произвольная градусная мера имеет название углов поворота. Значение углов всегда выражается действительным числом. Прямой угол – это угол, имеющий 90 градусов. Острый угол – угол, который меньше 90 градусов, а тупой – больше. Острый угол измеряется в интервале (0,90), а тупой – (90,180). Ниже наглядно изображены три вида углов. Любая градусная мера любого угла имеет одинаковое значение. Больший угол соответственно имеет большую градусную меру, чем меньший. Градусная мера одного угла – это сумма всех имеющихся градусных мер внутренних углов. Исходя из этого, можно сделать вывод, что сумма всех смежных углов равна 180 градусам, потому что они все и составляют развернутый угол. Отсюда следует, что любые вертикальные углы равны. Если рассмотреть это на примере, мы получим, что угол АОВ и СОD – вертикальные (на чертеже), тогда пары углов АОВ и ВОС, СОD и ВОС считают смежными. В таком случает равенство∠AOB+∠BOC=180° вместе с ∠COD+∠BOC=180° считаются однозначно верными. Отсюда имеем, что ∠AOB=∠COD . Ниже приводится пример изображения и обозначения вертикальных улов. Кроме градусов, минут и секунд используется еще одна единица измерения. Она называется радианом. Чаще всего ее можно встретить в тригонометрии при обозначении углов многоугольников. Что же называют радианом. Углом в один радиан называют центральный угол, который имеет длину радиуса окружности равную длине дуги. На рисунке радиан изображается в виде окружности, где имеется центр, обозначенный точкой , с двумя точками на окружности, соединенными и преобразованными в радиусы ОА и ОВ. По определению данный треугольник AOB является равносторонним, значит длина дуги AB равна длинам радиусов ОВ и ОА. Обозначение угла принимается за «рад». То есть запись в 5 радиан сокращенно обозначается как 5 рад. Иногда можно встретить обозначение, имеющее название пи. Радианы не имеют зависимости от длины заданной окружности, так как фигуры имеют некое ограничение при помощи угла и его дугой с центром, находящимся в вершине заданного угла. Они считаются подобными. Радианы имеют такой же смысл, как и градусы, только разница в их величине. Чтобы это определить, необходимо вычисленную длину дуги центрального угла поделить на длину ее радиуса. На практике используют перевод градусов в радианы и радианы в градусы для более удобного решения задач. Указанная статья имеет информацию о связи градусной меры с радианной, где можно подробно изучить переводы из градусной в радианную и обратно. Для наглядного и удобного изображения дуг, углов используют чертежи. Не всегда можно правильно изобразить и отметить тот или иной угол, дугу или название. Равные углы имеют обозначение в виде одинакового количества дуг, а неравные в виде разного. На чертеже изображено правильное обозначение острых, равных и неравных углов. Когда необходимо отметить более 3 углов, используются специальные обозначения дуг, например, волнистые или зубчатые. Это не имеет столь важное значение. Ниже приведен рисунок, где показано их обозначение. Обозначение углов должны быть простыми, чтобы не мешали другим значениям. При решении задачи рекомендовано выделять только необходимые для решения углы, чтобы не загромождать весь чертеж. Это не помешает решению и доказательству, а также придаст эстетичный вид рисунку. Решение задач
от 1 дня / от 150 р. Углом называется геометрическая фигура, которая состоит из двух различных лучей, исходящих из одной точки. На сторонах угла отмечены точки А и С. Этот угол можно обозначить как угол AOC. В середине обязательно должно стоять название точки, в которой находится вершина угла. Также существуют и другие обозначения, угол О или угол km. В геометрии вместо слова угол часто пишут специальный значок. Если у угла обе стороны лежат на одной прямой, то такой угол называется развернутым углом. То есть одна сторона угла является продолжением другой стороны угла. На рисунке нижк представлен развернутый угол О. Следует отметить, что любой угол, разделяет плоскость на две части. Если угол не является развернутым, то одна из частей называется внутренней областью угла, а другая внешней областью этого угла. На рисунке ниже представлен неразвернутый угол и отмечены внешняя и внутренняя области этого угла. В случае с развернутым углом любую из двух частей, на которые он делит плоскость, можно считать внешней областью угла. Можно говорить о положении точки относительно угла. Точка может лежать вне угла (во внешней области), может находится на одной из его сторон, либо может лежать внутри угла (во внутренней области). На рисунке ниже, точка А лежит вне угла О, точка B лежит на одной из сторон угла, а точка С лежит внутри угла. Для измерения углов существует прибор называемый транспортиром. Единицей измерения угла является градус . Следует отметить, что каждый угол имеет определенную градусную меру, которая больше нуля. В зависимости от градусной меры углы делятся на несколько групп. «Основные понятия геометрии» — Признак равенства треугольника. Отрезки. Геометрия. Смежные и вертикальные углы. Построение параллельных прямых. Построение треугольника. Выводы. Прямые параллельны. Вершины. Простейшие геометрические фигуры. «Геометрия в таблицах» — Координаты точки и координаты вектора в пространстве Скалярное произведение векторов в пространстве Движение Цилиндр Конус Сфера и шар Объем прямоугольного параллелепипеда Объем прямой призмы и цилиндра Объем наклонной призмы Объем пирамиды Объем конуса Объем шара и площадь сферы. Таблицы геометрия. «Геометрия 8 класс» — Каждое утверждение опирается на уже доказанные. У любого здания есть фундамент. Понятие теоремы. Аксиома -утверждение, истинность которых принимается без доказательств. Каждое математическое утверждение, получаемое путем логического доказательства, есть теорема. Так перебирая теоремы, можно добраться до аксиом. «Геометрия это наука» — Геометрия состоит из двух разделов: планиметрии и стереометрии. Какая геометрическая фигура была отличительным знаком пифагорейцев? Какую форму, по мнению пифагорейцев, имела вся Вселенная? Ответ: 580 – 500 гг. «Геометрические термины» — Конус. Пирамида. Радиус и центр. Диагональ. Геометрия. Квадрат. Ромб. Куб. Трапеция. Возникновение геометрических терминов. Точка. Линия. Цилиндр. Гипотенуза и катет. Сфера. Призма. Из истории геометрических терминов. «Что изучает геометрия» — Слово «параллельный» происходит от греческого «параллелос» — идти рядом. История геометрии. Преобразования в основном ограничивались подобием. L=(Р1+Р2)/2 L – длина окружности Р1 — периметр большого квадрата Р2 — периметр малого квадрата. Vпрям. Геометрия в Древней Греции. Муза геометрии, Лувр. Мы узнаем откуда пришла, и какой раньше была геометрия. Всего в теме
24 презентации Угол в измеряют в градусной мере (градус, минута, секунда), в оборотах — отношение длины дуги s к длине окружности L , в радианах — отношение длины дуги s к радиусу r ; исторически применялась также градовая мера измерения углов, в настоящее время она почти нигде не используется. 1 оборот = 2π радианам = 360° = 400 градам . В морской терминологии углы обозначаются румбами . Смежные углы — острый (a) и тупой (b). Развёрнутый угол (c) Кроме этого, рассматривается угол между гладкими кривыми в точке касания: по определению, его величина равна величине угла между касательными к кривым. Wikimedia Foundation
.
2010
. Угол, равный двум прямым. *РАЗВЕРТКА поверхности фигура, получающаяся в плоскости при таком совмещении точек данной поверхности с этой плоскостью, при котором длины линий остаются неизменными. Развертка кривой см. Эвольвента … Большой Энциклопедический словарь угол — ▲ разность направление (в пространстве) угол протяженность поворота от одного направления к другому; разность направлений; часть полного оборота (# наклона. образовывать #). наклон. наклонный. отклонение. уклониться (дорога уклонилась вправо).… … Угол — Углы: 1 общего вида; 2 смежные; 3 прилежащие; 4 вертикальные; 5 развернутый; 6 прямой, острый и тупой; 7 между кривыми; 8 между прямой и плоскостью; 9 между скрещивающимися прямыми (не лежащими в одной плоскостью) прямыми. Геометрическая фигура, состоящая из двух различных лучей, выходящих из одной точки. Лучи наз. сторонами У., а их общее начало вершиной У. Пусть [ ВА),[ ВС) стороны угла, В его вершина, плоскость, определяемая сторонами У. Фигура делит плоскость… … Математическая энциклопедия Угол, равный двум прямым. * * * РАЗВЕРНУТЫЙ УГОЛ РАЗВЕРНУТЫЙ УГОЛ, угол, равный двум прямым … Энциклопедический словарь Раздел математики, занимающийся изучением свойств различных фигур (точек, линий, углов, двумерных и трехмерных объектов), их размеров и взаимного расположения. Для удобства преподавания геометрию подразделяют на планиметрию и стереометрию. В… … Энциклопедия Кольера 1) Замкнутая ломаная линия, именно: если различные точки, никакие последовательные три из к рых не лежат на одной прямой, то совокупность отрезков наз. многоугольником (см. рис. 1). М. могут быть пространственными или плоскими (ниже… … Математическая энциклопедия поперек — ▲ под углом максимум, косой угол поперечный. градус — а, м. 1) Единица измерения плоского угла, равная 1/90 прямого угла или соответственно 1/360 окружности. Угол в 90 градусов называется прямым углом. Развернутый угол составляет 180 градусов. 2) Единица измерения температурного интервала, имеющая… … Популярный словарь русского языка Теорема Шварца Кристоффеля важная теорема в теории функций комплексного переменного, носит название немецких математиков Карла Шварца и Элвина Кристоффеля. Очень важной с практической точки зрения является проблема о конформном… … Википедия Углом называют фигуру, образованную двумя лучами, выходящими из одной точки (рис. 160). При записи угла в середине пишут букву, обозначающую его вершину. Угол можно обозначить и одной буквой — названием его вершины. Например, вместо «угол АОВ» пишут короче: «угол О». Вместо слова «угол» пишут знак . Например, AОВ, O. На рисунке 161 точки С и D лежат внутри угла АОВ, точки X и У лежат вне этого угла, а точки М и Н — на сторонах угла. Как и все геометрические фигуры, углы сравниваются с помощью наложения. Если один угол можно наложить на другой так, что они совпадут, то эти углы равны. Например, на рисунке 162 ABC = MNK. Из вершины угла СОК (рис. 163) проведен луч ОР. Он разбивает угол СОК на два угла — СОР и РОК. Каждый из этих углов меньше угла СОК. Пишут: COP Два дополнительных друг другу луча образуют развернутый угол. Стороны этого угла вместе составляют прямую линию, на которой лежит вершина развернутого угла (рис. Часовая и минутная стрелки часов образуют в 6 ч развернутый угол (рис. 165). Согнем два раза пополам лист бумаги, а потом развернем его (рис. 166). Линии сгиба образуют 4 равных угла. Каждый из этих углов равен половине развернутого угла. Такие углы называют прямыми. Прямым углом называют половину развернутого угла. Для построения прямого угла пользуются чертежным треугольником (рис. 167). Чтобы построить прямой угол, одной из сторон которого является луч ОЛ, надо: а) расположить чертежный треугольник так, чтобы вершина его прямого угла совпала с точкой О, а одна из сторон пошла по лучу ОА; б) провести вдоль второй стороны треугольника луч ОВ. В результате получим прямой угол АОВ. Вопросы к теме 1.Что такое угол? Нам с вами уже известно, что любой угол делит плоскость на две части. Теперь давайте посмотрим на рисунок, на котором как раз и изображен развернутый угол О. Если мы возьмем и проведем из вершины развернутого угла луч, то он разделит данный развернутый угол еще на два угла, которые будут иметь одну общую сторону, а другие два угла будут составлять прямую. То есть, с одного развернутого угла мы получили два смежных. Если мы возьмем развернутый угол и проведем биссектрису, то эта биссектриса разделит развернутый угол на два прямых угла. А, в том случае, если мы из вершины развернутого угла проведем произвольный луч, который не является биссектрисой, то такой луч разделит развернутый угол на два угла, один из которых будет острым, а другой тупым. Развернутый угол обладает такими свойствами: Во-первых, стороны развёрнутого угла являются антипараллельными и образуют прямую; Чтобы измерить любой угол, для этих целей чаще всего используют транспортир, у которого единица измерения равна одному градусу. При измерении углов следует помнить, что любой угол имеет свою определенную градусную меру и естественно эта мера больше нуля. А развернутый угол, как нам уже известно, равен 180 градусам. То есть, если мы с вами возьмем любую плоскость круга и разделим ее радиусами на 360 равных частей, то 1/360 часть данного круга будет являться угловым градусом. Как вы уже знаете, что градус обозначается определенным значком, который имеет такой вид:
« ° ». Теперь мы также знаем, что один градус 1° = 1/360 части круга. Если угол равен плоскости круга и составляет 360 градусов, то такой угол является полным. А теперь мы возьмем, и плоскость круга поделим с помощью двух радиусов, лежащих на одной прямой линии, на две равные части. То в этом случае, плоскость полукруга составит половину полного угла, то есть 360: 2 = 180°. Мы с вами получили угол, который равен полуплоскости круга и имеет 180°. 1613. Назовите углы, изображенные на рисунке 168. Запишите их обозначения. 1614. Начертите четыре луча: ОА, ОВ, ОС и OD. Запишите названия шести углов, сторонами которых являются эти лучи. На сколько частей эти лучи делят плоскость ? 1615. Укажите, какие точки на рисунке 169 лежат внутри угла КОМ, Какие точки лежат вне этого угла? Какие точки лежат на стороне OK, a какие — на стороне ОМ? 1616. Начертите угол MOD и проведите внутри него луч ОТ. Назовите и обозначьте углы, на которые этот луч делит угол MOD. 1617. Минутная стрелка за 10 мин повернулась на угол АОВ, за следующие 10 мин — на угол ВОС, а еще за 15 мин — на угол COD. Сравните углы АОВ и ВОС, ВОС и COD, АОС и АОВ, АОС и COD (рис. 170). 1618. Изобразите с помощью чертежного треугольника 4 прямых угла в разных положениях. 1619. С помощью чертежного треугольника найдите на рисунке 171 прямые углы. Запишите их обозначения. 1620. Укажите прямые углы в классной комнате. а) 0,09 200; б) 208 0,4; в) 130 0,1 + 80 0,1. 1629. Сколько процентов от 400 составляет число 200; 100; 4; 40; 80; 400; 600? 1630. Найдите пропущенное число: а) 2 5 3 б) 2 3 5 1631. Начертите квадрат, сторона которого равна длине 10 клеток тетради. Пусть этот квадрат изображает поле. Рожь занимает 12% поля, овес — 8%, пшеница — 64%, а остальная часть поля занята гречихой. Покажите на рисунке часть поля, занятую каждой культурой. Сколько процентов поля занимает гречиха? 1632. За учебный год Петя израсходовал 40% купленных в начале года тетрадей, и у него осталось 30 тетрадей. Сколько тетрадей было куплено для Пети в начале учебного года? 1633. Бронза является сплавом олова и меди. Сколько процентов сплава составляет медь в куске бронзы, состоящем из 6 кг олова и 34 кг меди? 1634. Построенный в древности Александрийский маяк, который называли одним из семи чудес света, выше башен Московского Кремля в 1,7 раза, но ниже здания Московского университета на 119 м. 1635. Найдите с помощью микрокалькулятора: а) 4,5% от 168; в) 28,3% от 569,8; 1636. Решите задачу: 1) Площадь огорода 6,4 а. В первый день вскопали 30% огорода, а во второй день — 35% огорода. Сколько аров осталось еще вскопать? 2) У Сережи было 4,8 ч свободного времени. 35% этого времени он потратил на чтение книги, а 40% на просмотр передач по телевизору. Сколько времени у него еще осталось? 1637. Выполните действия: 1) ((23,79: 7,8 — 6,8: 17) 3,04 — 2,04) 0,85; 1638. Начертите угол ВАС и отметьте по одной точке внутри угла, вне угла и на сторонах угла. 1639. Какие из отмеченных на рисунке 172 точек лежат внутри угла АМК.Какая точка лежит внутри угла АМВ> но вне угла АМК.Какие точки лежат на сторонах угла АМК? 1640. 1641. Постройте квадрат со стороной 43 мм. Вычислите его периметр и площадь. 1642. Найдите значение выражения: а) 14,791: а + 160,961: b, если а = 100, b = 10; 1643. Рабочий должен был изготовить 450 деталей. В первый день он изготовил 60% деталей, а остальные — во второй. Сколько деталей изготовил рабочий во второй день? 1644. В библиотеке было 8000 книг. Через год число их увеличилось на 2000 книг. На сколько процентов увеличилось число книг в библиотеке? 1645. Грузовики в первый день проехали 24% намеченного пути, во второй день — 46% пути, а в третий — остальные 450 км. Сколько километров проехали эти грузовики? 1646. Найдите, сколько составляют: а) 1% от тонны; в) 5% от 7 т; 1647. Масса детеныша моржа в 9 раз меньше массы взрослого моржа. Какова масса взрослого моржа, если вместе с детенышем их масса равна 0,9 т? 1648. Н.Я. ВИЛЕНКИН, B. И. ЖОХОВ, А. С. ЧЕСНОКОВ, C. И. ШВАРЦБУРД, Математика 5 класс, Учебник для общеобразовательных учреждений Угол – основная геометрическая фигура, которую разберем на протяжение всей темы. Определения, способы задания, обозначения и измерения угла. Разберем принципы выделения углов на чертежах. Вся теория проиллюстрирована и имеет большое количество наглядных чертежей. Определение 1 Угол – простая важная фигура в геометрии. Угол напрямую зависит от определения луча, который в свою очередь состоит из базовых понятий точки, прямой и плоскости. Для досконального изучения необходимо углубиться по темам прямая на плоскости – необходимые сведения и плоскость – необходимые сведения . Понятие угла начинается с понятий о точке, плоскости и прямой, изображенной на этой плоскости. Определение 2 Дана прямая a на плоскости. На ней обозначим некоторую точку O . Прямая разделена точкой на две части, каждая из которых имеет название луч , а точка O – начало луча . Иначе говоря, луч или полупрямая – это часть прямой, состоящая из точек заданной прямой, расположенных на одной стороне относительно начальной точки, то есть точки O . Обозначение луча допустимо в двух вариациях: одной строчной или двумя прописными буквами латинского алфавита. При обозначении двумя буквами луч имеет название, состоящее из двух букв. Рассмотрим подробнее на чертеже. Перейдем к понятию определения угла. Определение 3 Угол – это фигура, расположенная в заданной плоскости, образованная двумя несовпадающими лучами, имеющими общее начало. Сторона угла является лучом, вершина – общее начало сторон. Имеет место случай, когда стороны угла могут выступать в роли прямой линии. Определение 4 Когда обе стороны угла расположены на одной прямой или его стороны служат как дополнительные полупрямые одной прямой, то такой угол называют развернутым . На рисунке ниже изображен развернутый угол. Точка на прямой – это и есть вершина угла. Чаще всего имеет место ее обозначение точкой O . Угол в математике обозначается знаком « ∠ ». Когда стороны угла обозначают малыми латинскими, то для правильного определения угла записываются подряд буквы соответственно сторонам. Если две стороны имеют обозначение k и h , то угол обозначается как ∠ k h или ∠ h k . Когда идет обозначение большими буквами, то соответственно стороны угла имеют названия O A и O B . В таком случае угол имеет название из трех букв латинского алфавита, записанные подряд, в центре с вершиной — ∠ A O B и ∠ B O A . Существует обозначение в виде цифр, когда углы не имеют названий или буквенных обозначений. Ниже приведен рисунок, где разными способами обозначаются углы. Угол делит плоскость на две части. В случае, если угол не развернутый, тогда одна часть плоскости имеет название внутренняя область угла , другая – внешняя область угла . Ниже приведено изображение, объясняющее, какие части плоскости внешние, а какие внутренние. При разделении развернутым углом на плоскости любая из его частей считается внутренней областью развернутого угла. Внутренняя область угла – элемент, служащий для второго определения угла. Определение 5 Углом называют геометрическую фигуру, состоящая из двух несовпадающих лучей, имеющих общее начало и соответствующую внутреннюю область угла. Данное определение является более строгим, чем предыдущее, так как имеет больше условий. Оба определения не желательно рассматривать отдельно, потому как угол – это геометрическая фигура, преобразованная при помощи двух лучей, выходящих из одной точки. Когда необходимо выполнять действия с углом, то под определением понимают наличие двух лучей с общим началом и внутренней областью. Определение 6 Два угла называют смежными , если имеется общая сторона, а две другие являются дополнительными полупрямыми или образуют развернутый угол. На рисунке видно, что смежные углы дополняют друг друга, так как являются продолжением один другого. Определение 7 Два угла называют вертикальными , если стороны одного являются дополнительными полупрямыми другого или являются продолжениями сторон другого. На рисунке ниже показано изображение вертикальных углов. При пересечении прямых получается 4 пары смежных и 2 пары вертикальных углов. Ниже показано на рисунке. Статья показывает определения равных и неравных углов. Разберем какой угол считается большим, какой меньшим и другие свойства угла. Две фигуры считаются равными, если при наложении они полностью совпадают. Такое же свойство применимо для сравнения углов. Даны два угла. Необходимо прийти к выводу, равные эти углы или нет. Известно, что имеет место наложение вершин двух углов и стороны первого угла с любой другой стороной второго. То есть при полном совпадении при наложении углов стороны заданных углов совместятся полностью, углы равные . Может быть так, что при наложении стороны могут не совместиться, то углы неравные, меньший из которых состоит из другого, а больший имеет в своем составе полный другой угол. Ниже изображены неравные углы, не совмещенные при наложении. Развернутые углы являются равными. Измерение углов начинается с измерения стороны измеряемого угла и его внутренней области, заполняя которую единичными углами, прикладывают друг к другу. Необходимо посчитать количество уложенных углов, они и предопределяют меру измеряемого угла. Единица измерения угла может быть выражена любым измеряемым углом. Имеются общепринятые единицы измерения, которые применяют в науке и технике. Они специализируются на других названиях. Чаще всего используют понятие градус . Определение 8 Один градус называют углом, который имеет одну сто восьмидесятую часть развернутого угла. Стандартное обозначение градуса идет при помощи « ° », тогда один градус – 1 ° . Следовательно, развернутый угол состоит из 180 таких углов, состоящих из одного градуса. Все имеющиеся углы плотно уложены друг к другу и стороны предыдущего совмещены с последующим. Известно, что количество положенных градусов в угле, это и есть та самая мера угла. Развернутый угол имеет 180 уложенных углов в своем составе. Ниже на рисунке приводятся примеры, где уложение угла идет в 30 раз, то есть одна шестая развернутого, и 90 раз, то есть половина. Для точности определения измерения углов используются минуты и секунды. Их применяют, когда величина угла не является целым обозначением градуса. Такие части градуса позволяют выполнять более точные расчеты. Определение 9 Минутой называют одну шестидесятую часть градуса. Определение 10 Секундой называют одну шестидесятую часть минуты. Градус содержит 3600 секунд. Минуты обозначают « » », а секунды « «» ». Имеет место обозначение: 1 ° = 60 » = 3600 «» , 1 » = (1 60) ° , 1 » = 60 «» , 1 «» = (1 60) » = (1 3600) ° , а обозначение угла 17 градусов 3 минут и 59 секунд имеет вид 17 ° 3 » 59 «» . Определение 11 Приведем пример обозначения градусной меры угла равного 17 ° 3 » 59 «» . Запись имеет еще один вид 17 + 3 60 + 59 3600 = 17 239 3600 . Для точного измерения углов используют такой измерительный прибор, как транспортир. При обозначении угла ∠ A O B и его градусной мере в 110 градусов применяют более удобную запись ∠ A O B = 110 ° , которая читается «Угол А О В равен 110 градусам». В геометрии используется мера угла из интервала (0 , 180 ] , а в тригонометрии произвольная градусная мера имеет название углов поворота. Значение углов всегда выражается действительным числом. Прямой угол – это угол, имеющий 90 градусов. Острый угол – угол, который меньше 90 градусов, а тупой – больше. Острый угол измеряется в интервале (0 , 90) , а тупой – (90 , 180) . Ниже наглядно изображены три вида углов. Любая градусная мера любого угла имеет одинаковое значение. Больший угол соответственно имеет большую градусную меру, чем меньший. Градусная мера одного угла – это сумма всех имеющихся градусных мер внутренних углов. Ниже приведен рисунок, где показан угол АОВ, состоящий из углов АОС, СОD и DОВ. Подробно это выглядит так: ∠ A O B = ∠ A O C + ∠ D O B = 45 ° + 30 ° + 60 ° = 135 ° . Исходя из этого, можно сделать вывод, что сумма всех смежных углов равна 180 градусам, потому что они все и составляют развернутый угол. Отсюда следует, что любые вертикальные углы равны . Если рассмотреть это на примере, мы получим, что угол А О В и С О D – вертикальные (на чертеже), тогда пары углов А О В и В О С, С О D и В О С считают смежными. В таком случает равенство ∠ A O B + ∠ B O C = 180 ° вместе с ∠ C O D + ∠ B O C = 180 ° считаются однозначно верными. Кроме градусов, минут и секунд используется еще одна единица измерения. Она называется радианом . Чаще всего ее можно встретить в тригонометрии при обозначении углов многоугольников. Что же называют радианом. Определение 12 Углом в один радиан называют центральный угол, который имеет длину радиуса окружности равную длине дуги. На рисунке радиан изображается в виде окружности, где имеется центр, обозначенный точкой, с двумя точками на окружности, соединенными и преобразованными в радиусы О А и О В. По определению данный треугольник A O B является равносторонним, значит длина дуги A B равна длинам радиусов О В и О А. Обозначение угла принимается за «рад». То есть запись в 5 радиан сокращенно обозначается как 5 рад. Иногда можно встретить обозначение, имеющее название пи. Радианы не имеют зависимости от длины заданной окружности, так как фигуры имеют некое ограничение при помощи угла и его дугой с центром, находящимся в вершине заданного угла. Радианы имеют такой же смысл, как и градусы, только разница в их величине. Чтобы это определить, необходимо вычисленную длину дуги центрального угла поделить на длину ее радиуса. На практике используют перевод градусов в радианы и радианы в градусы для более удобного решения задач. Указанная статья имеет информацию о связи градусной меры с радианной, где можно подробно изучить переводы из градусной в радианную и обратно. Для наглядного и удобного изображения дуг, углов используют чертежи. Не всегда можно правильно изобразить и отметить тот или иной угол, дугу или название. Равные углы имеют обозначение в виде одинакового количества дуг, а неравные в виде разного. На чертеже изображено правильное обозначение острых, равных и неравных углов. Когда необходимо отметить более 3 углов, используются специальные обозначения дуг, например, волнистые или зубчатые. Это не имеет столь важное значение. Ниже приведен рисунок, где показано их обозначение. Обозначение углов должны быть простыми, чтобы не мешали другим значениям. При решении задачи рекомендовано выделять только необходимые для решения углы, чтобы не загромождать весь чертеж. Это не помешает решению и доказательству, а также придаст эстетичный вид рисунку. Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter Давайте начнем с определения того, что такое угол. Во-первых, он является Во-вторых, он образован двумя лучами, которые называются сторонами угла. В-третьих, последние выходят из одной точки, которую называют вершиной угла. Исходя из этих признаков, мы можем составить определение: угол — геометрическая фигура, которая состоит из двух лучей (сторон), выходящих из одной точки (вершины). Их классифицируют по градусной величине, по расположению относительно друг друга и относительно окружности. Начнем с видов углов по их величине. Существует несколько их разновидностей. Рассмотрим подробнее каждый вид. Основных типов углов всего четыре — прямой, тупой, острый и развернутый угол. Прямой Он выглядит так: Его градусная мера всегда составляет 90 о, иначе говоря, прямой угол — это угол 90 градусов. Только они есть у таких четырехугольников, как квадрат и прямоугольник. Тупой Он имеет такой вид: Градусная мера всегда больше 90 о, но меньше 180 о. Он может встречаться в таких четырехугольниках, как ромб, произвольный параллелограмм, во многоугольниках. Острый Он выглядит так: Градусная мера острого угла всегда меньше 90 о. Он встречается во всех четырехугольниках, кроме квадрата и произвольного параллелограмма. Развернутый Развернутый угол имеет такой вид: В многоугольниках он не встречается, но не менее важен, чем все остальные. Развернутый угол — это геометрическая фигура, градусная мера которой всегда равняется 180º. Есть еще несколько второстепенных видов углов. Их не изучают в школах, но знать хотя бы об их существовании необходимо. Второстепенных видов углов всего пять: 1. Нулевой Он выглядит так: Само название угла уже говорит о его величине. Его внутренняя область равняется 0 о, а стороны лежат друг на друге так, как показано на рисунке. 2. Косой Косым может быть и прямой, и тупой, и острый, и развернутый угол. Главное его условие — он не должен равняться 0 о, 90 о, 180 о, 270 о. 3. Выпуклый Выпуклыми являются нулевой, прямой, тупой, острый и развернутый углы. Как вы уже поняли, градусная мера выпуклого угла — от 0 о до 180 о. 4. Невыпуклый Невыпуклыми являются углы с градусной мерой от 181 о до 359 о включительно. 5. Полный Полным является угол с градусной мерой 360 о. Это все типы углов по их величине. 1. Дополнительные Это два острых угла, образовывающие один прямой, т.е. их сумма 90 о. 2. Смежные Смежные углы образуются, если через развернутый, точнее, через его вершину, провести луч в любом направлении. Их сумма равна 180 о. 3. Вертикальные Вертикальные углы образуются при пересечении двух прямых. Их градусные меры равны. Теперь перейдем к видам углов, расположенным относительно окружности. Их всего два: центральный и вписанный. 1. Центральный Центральным является угол с вершиной в центре окружности. Его градусная мера равна градусной мере меньшей дуги, стянутой сторонами. 2. Вписанный Вписанным называется угол, вершина которого лежит на окружности, и стороны которого ее пересекают. Его градусная мера равна половине дуги, на которую он опирается. Это все, что касается углов. Угол – основная геометрическая фигура, которую разберем на протяжение всей темы. Определения, способы задания, обозначения и измерения угла. Разберем принципы выделения углов на чертежах. Вся теория проиллюстрирована и имеет большое количество наглядных чертежей. Определение 1 Угол – простая важная фигура в геометрии. Угол напрямую зависит от определения луча, который в свою очередь состоит из базовых понятий точки, прямой и плоскости. Для досконального изучения необходимо углубиться по темам прямая на плоскости – необходимые сведения и плоскость – необходимые сведения . Понятие угла начинается с понятий о точке, плоскости и прямой, изображенной на этой плоскости. Определение 2 Дана прямая a на плоскости. На ней обозначим некоторую точку O . Прямая разделена точкой на две части, каждая из которых имеет название луч , а точка O – начало луча . Иначе говоря, луч или полупрямая – это часть прямой, состоящая из точек заданной прямой, расположенных на одной стороне относительно начальной точки, то есть точки O . Обозначение луча допустимо в двух вариациях: одной строчной или двумя прописными буквами латинского алфавита. При обозначении двумя буквами луч имеет название, состоящее из двух букв. Рассмотрим подробнее на чертеже. Перейдем к понятию определения угла. Определение 3 Угол – это фигура, расположенная в заданной плоскости, образованная двумя несовпадающими лучами, имеющими общее начало. Сторона угла является лучом, вершина – общее начало сторон. Имеет место случай, когда стороны угла могут выступать в роли прямой линии. Определение 4 Когда обе стороны угла расположены на одной прямой или его стороны служат как дополнительные полупрямые одной прямой, то такой угол называют развернутым . На рисунке ниже изображен развернутый угол. Точка на прямой – это и есть вершина угла. Чаще всего имеет место ее обозначение точкой O . Угол в математике обозначается знаком « ∠ ». Когда стороны угла обозначают малыми латинскими, то для правильного определения угла записываются подряд буквы соответственно сторонам. Если две стороны имеют обозначение k и h , то угол обозначается как ∠ k h или ∠ h k . Когда идет обозначение большими буквами, то соответственно стороны угла имеют названия O A и O B . В таком случае угол имеет название из трех букв латинского алфавита, записанные подряд, в центре с вершиной — ∠ A O B и ∠ B O A . Существует обозначение в виде цифр, когда углы не имеют названий или буквенных обозначений. Ниже приведен рисунок, где разными способами обозначаются углы. Угол делит плоскость на две части. В случае, если угол не развернутый, тогда одна часть плоскости имеет название внутренняя область угла , другая – внешняя область угла . Ниже приведено изображение, объясняющее, какие части плоскости внешние, а какие внутренние. При разделении развернутым углом на плоскости любая из его частей считается внутренней областью развернутого угла. Внутренняя область угла – элемент, служащий для второго определения угла. Определение 5 Углом называют геометрическую фигуру, состоящая из двух несовпадающих лучей, имеющих общее начало и соответствующую внутреннюю область угла. Данное определение является более строгим, чем предыдущее, так как имеет больше условий. Оба определения не желательно рассматривать отдельно, потому как угол – это геометрическая фигура, преобразованная при помощи двух лучей, выходящих из одной точки. Когда необходимо выполнять действия с углом, то под определением понимают наличие двух лучей с общим началом и внутренней областью. Определение 6 Два угла называют смежными , если имеется общая сторона, а две другие являются дополнительными полупрямыми или образуют развернутый угол. На рисунке видно, что смежные углы дополняют друг друга, так как являются продолжением один другого. Определение 7 Два угла называют вертикальными , если стороны одного являются дополнительными полупрямыми другого или являются продолжениями сторон другого. На рисунке ниже показано изображение вертикальных углов. При пересечении прямых получается 4 пары смежных и 2 пары вертикальных углов. Ниже показано на рисунке. Статья показывает определения равных и неравных углов. Разберем какой угол считается большим, какой меньшим и другие свойства угла. Две фигуры считаются равными, если при наложении они полностью совпадают. Такое же свойство применимо для сравнения углов. Даны два угла. Необходимо прийти к выводу, равные эти углы или нет. Известно, что имеет место наложение вершин двух углов и стороны первого угла с любой другой стороной второго. То есть при полном совпадении при наложении углов стороны заданных углов совместятся полностью, углы равные . Может быть так, что при наложении стороны могут не совместиться, то углы неравные, меньший из которых состоит из другого, а больший имеет в своем составе полный другой угол. Развернутые углы являются равными. Измерение углов начинается с измерения стороны измеряемого угла и его внутренней области, заполняя которую единичными углами, прикладывают друг к другу. Необходимо посчитать количество уложенных углов, они и предопределяют меру измеряемого угла. Единица измерения угла может быть выражена любым измеряемым углом. Имеются общепринятые единицы измерения, которые применяют в науке и технике. Они специализируются на других названиях. Чаще всего используют понятие градус . Определение 8 Один градус называют углом, который имеет одну сто восьмидесятую часть развернутого угла. Стандартное обозначение градуса идет при помощи « ° », тогда один градус – 1 ° . Следовательно, развернутый угол состоит из 180 таких углов, состоящих из одного градуса. Все имеющиеся углы плотно уложены друг к другу и стороны предыдущего совмещены с последующим. Известно, что количество положенных градусов в угле, это и есть та самая мера угла. Для точности определения измерения углов используются минуты и секунды. Их применяют, когда величина угла не является целым обозначением градуса. Такие части градуса позволяют выполнять более точные расчеты. Определение 9 Минутой называют одну шестидесятую часть градуса. Определение 10 Секундой называют одну шестидесятую часть минуты. Градус содержит 3600 секунд. Минуты обозначают « » », а секунды « «» ». Имеет место обозначение: 1 ° = 60 » = 3600 «» , 1 » = (1 60) ° , 1 » = 60 «» , 1 «» = (1 60) » = (1 3600) ° , а обозначение угла 17 градусов 3 минут и 59 секунд имеет вид 17 ° 3 » 59 «» . Определение 11 Приведем пример обозначения градусной меры угла равного 17 ° 3 » 59 «» . Запись имеет еще один вид 17 + 3 60 + 59 3600 = 17 239 3600 . Для точного измерения углов используют такой измерительный прибор, как транспортир. При обозначении угла ∠ A O B и его градусной мере в 110 градусов применяют более удобную запись ∠ A O B = 110 ° , которая читается «Угол А О В равен 110 градусам». В геометрии используется мера угла из интервала (0 , 180 ] , а в тригонометрии произвольная градусная мера имеет название углов поворота. Значение углов всегда выражается действительным числом. Прямой угол – это угол, имеющий 90 градусов. Острый угол – угол, который меньше 90 градусов, а тупой – больше. Острый угол измеряется в интервале (0 , 90) , а тупой – (90 , 180) . Ниже наглядно изображены три вида углов. Любая градусная мера любого угла имеет одинаковое значение. Больший угол соответственно имеет большую градусную меру, чем меньший. Градусная мера одного угла – это сумма всех имеющихся градусных мер внутренних углов. Ниже приведен рисунок, где показан угол АОВ, состоящий из углов АОС, СОD и DОВ. Исходя из этого, можно сделать вывод, что сумма всех смежных углов равна 180 градусам, потому что они все и составляют развернутый угол. Отсюда следует, что любые вертикальные углы равны . Если рассмотреть это на примере, мы получим, что угол А О В и С О D – вертикальные (на чертеже), тогда пары углов А О В и В О С, С О D и В О С считают смежными. В таком случает равенство ∠ A O B + ∠ B O C = 180 ° вместе с ∠ C O D + ∠ B O C = 180 ° считаются однозначно верными. Отсюда имеем, что ∠ A O B = ∠ C O D . Ниже приводится пример изображения и обозначения вертикальных улов. Кроме градусов, минут и секунд используется еще одна единица измерения. Она называется радианом . Чаще всего ее можно встретить в тригонометрии при обозначении углов многоугольников. Что же называют радианом. Определение 12 Углом в один радиан называют центральный угол, который имеет длину радиуса окружности равную длине дуги. На рисунке радиан изображается в виде окружности, где имеется центр, обозначенный точкой, с двумя точками на окружности, соединенными и преобразованными в радиусы О А и О В. По определению данный треугольник A O B является равносторонним, значит длина дуги A B равна длинам радиусов О В и О А. Обозначение угла принимается за «рад». То есть запись в 5 радиан сокращенно обозначается как 5 рад. Иногда можно встретить обозначение, имеющее название пи. Радианы не имеют зависимости от длины заданной окружности, так как фигуры имеют некое ограничение при помощи угла и его дугой с центром, находящимся в вершине заданного угла. Они считаются подобными. Радианы имеют такой же смысл, как и градусы, только разница в их величине. Чтобы это определить, необходимо вычисленную длину дуги центрального угла поделить на длину ее радиуса. На практике используют перевод градусов в радианы и радианы в градусы для более удобного решения задач. Указанная статья имеет информацию о связи градусной меры с радианной, где можно подробно изучить переводы из градусной в радианную и обратно. Для наглядного и удобного изображения дуг, углов используют чертежи. Не всегда можно правильно изобразить и отметить тот или иной угол, дугу или название. Равные углы имеют обозначение в виде одинакового количества дуг, а неравные в виде разного. На чертеже изображено правильное обозначение острых, равных и неравных углов. Когда необходимо отметить более 3 углов, используются специальные обозначения дуг, например, волнистые или зубчатые. Это не имеет столь важное значение. Ниже приведен рисунок, где показано их обозначение. Обозначение углов должны быть простыми, чтобы не мешали другим значениям. При решении задачи рекомендовано выделять только необходимые для решения углы, чтобы не загромождать весь чертеж. Это не помешает решению и доказательству, а также придаст эстетичный вид рисунку. Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter Посмотрите на картинку. (Рис. 1) Рис. 1. Иллюстрация к примеру Из каких знакомых вам геометрических фигур она состоит? Конечно, вы увидели, что картинка состоит из треугольников и прямоугольников. Рис. 2. Определение угла Сегодня мы будем учиться чертить прямой угол. В названии этого угла уже есть слово «прямой». Чтобы правильно изобразить прямой угол, нам понадобится угольник. (Рис. 3) Рис. 3. Угольник В самом угольнике уже есть прямой угол. (Рис. 4) Рис. 4. Прямой угол Он и поможет нам изобразить эту геометрическую фигуру. Чтобы правильно изобразить фигуру, мы должны приложить угольник к плоскости (1), обвести его стороны (2), назвать вершину угла (3) и лучи (4). 1. 2. 3. 4. Давайте определим, есть ли среди имеющихся углов прямые (Рис. 5). В этом нам поможет угольник. Рис. 5. Иллюстрация к примеру Найдем прямой угол угольника и приложим его к имеющимся углам (рис. 6). Рис. 6. Иллюстрация к примеру Мы видим, что прямой угол совпал с углом ВОМ. Рис. 7. Иллюстрация к примеру Мы видим, что прямой угол нашего угольника не совпал с углом СOD. Это значит, что угол COD не прямой. Еще раз приложим прямой угол угольника к углу АОТ. (Рис. 8) Рис. 8. Иллюстрация к примеру Мы видим, что угол АОТ гораздо больше, чем прямой угол. Это значит, что угол АОТ не является прямым. На этом уроке мы учились строить прямой угол с помощью угольника. Слово «угол» дало название многим вещам, а также геометрическим фигурам: прямоугольник, треугольник, угольнику, с помощью которого можно начертить прямой угол. Треугольник — это геометрическая фигура, которая состоит из трех сторон и трех углов. Треугольник, у которого есть прямой угол, называется прямоугольным треугольником. Посмотрите на картинку. (Рис. 1) Рис. 1. Иллюстрация к примеру Из каких знакомых вам геометрических фигур она состоит? Конечно, вы увидели, что картинка состоит из треугольников и прямоугольников. Рис. 2. Определение угла Сегодня мы будем учиться чертить прямой угол. В названии этого угла уже есть слово «прямой». Чтобы правильно изобразить прямой угол, нам понадобится угольник. (Рис. 3) Рис. 3. Угольник В самом угольнике уже есть прямой угол. (Рис. 4) Рис. 4. Прямой угол Он и поможет нам изобразить эту геометрическую фигуру. Чтобы правильно изобразить фигуру, мы должны приложить угольник к плоскости (1), обвести его стороны (2), назвать вершину угла (3) и лучи (4). 1. 2. 3. 4. Давайте определим, есть ли среди имеющихся углов прямые (Рис. 5). В этом нам поможет угольник. Рис. 5. Иллюстрация к примеру Найдем прямой угол угольника и приложим его к имеющимся углам (рис. 6). Рис. 6. Иллюстрация к примеру Мы видим, что прямой угол совпал с углом ВОМ. Рис. 7. Иллюстрация к примеру Мы видим, что прямой угол нашего угольника не совпал с углом СOD. Это значит, что угол COD не прямой. Еще раз приложим прямой угол угольника к углу АОТ. (Рис. 8) Рис. 8. Иллюстрация к примеру Мы видим, что угол АОТ гораздо больше, чем прямой угол. Это значит, что угол АОТ не является прямым. На этом уроке мы учились строить прямой угол с помощью угольника. Слово «угол» дало название многим вещам, а также геометрическим фигурам: прямоугольник, треугольник, угольнику, с помощью которого можно начертить прямой угол. Треугольник — это геометрическая фигура, которая состоит из трех сторон и трех углов. Треугольник, у которого есть прямой угол, называется прямоугольным треугольником. Посмотрите на картинку. (Рис. 1) Рис. 1. Иллюстрация к примеру Из каких знакомых вам геометрических фигур она состоит? Конечно, вы увидели, что картинка состоит из треугольников и прямоугольников. Рис. 2. Определение угла Сегодня мы будем учиться чертить прямой угол. В названии этого угла уже есть слово «прямой». Чтобы правильно изобразить прямой угол, нам понадобится угольник. (Рис. 3) Рис. 3. Угольник В самом угольнике уже есть прямой угол. (Рис. 4) Рис. 4. Прямой угол Он и поможет нам изобразить эту геометрическую фигуру. Чтобы правильно изобразить фигуру, мы должны приложить угольник к плоскости (1), обвести его стороны (2), назвать вершину угла (3) и лучи (4). 1. 2. 3. 4. Давайте определим, есть ли среди имеющихся углов прямые (Рис. 5). В этом нам поможет угольник. Рис. 5. Иллюстрация к примеру Найдем прямой угол угольника и приложим его к имеющимся углам (рис. 6). Рис. 6. Иллюстрация к примеру Мы видим, что прямой угол совпал с углом ВОМ. Рис. 7. Иллюстрация к примеру Мы видим, что прямой угол нашего угольника не совпал с углом СOD. Это значит, что угол COD не прямой. Еще раз приложим прямой угол угольника к углу АОТ. (Рис. 8) Рис. 8. Иллюстрация к примеру Мы видим, что угол АОТ гораздо больше, чем прямой угол. Это значит, что угол АОТ не является прямым. На этом уроке мы учились строить прямой угол с помощью угольника. Слово «угол» дало название многим вещам, а также геометрическим фигурам: прямоугольник, треугольник, угольнику, с помощью которого можно начертить прямой угол. Треугольник — это геометрическая фигура, которая состоит из трех сторон и трех углов. Треугольник, у которого есть прямой угол, называется прямоугольным треугольником. Рекламные ссылки Свойства стальных уголков равнополочных в имперских единицах указаны ниже. Рекламные ссылки Добавляйте стандартные и настраиваемые параметрические компоненты, такие как балки с полками, пиломатериалы, трубопроводы, лестницы и т. д., в свою модель Sketchup с помощью Engineering ToolBox — расширения SketchUp, которое можно использовать с потрясающими, интересными и бесплатными приложениями SketchUp Make и SketchUp Pro. .Добавьте расширение Engineering ToolBox в свой SketchUp из хранилища расширений SketchUp Pro Sketchup! Перевести О Engineering ToolBox! Мы не собираем информацию от наших пользователей. В нашем архиве сохраняются только электронные письма и ответы. Файлы cookie используются только в браузере для улучшения взаимодействия с пользователем. Некоторые из наших калькуляторов и приложений позволяют сохранять данные приложения на локальном компьютере. Google использует файлы cookie для показа нашей рекламы и обработки статистики посетителей. Пожалуйста, прочитайте Конфиденциальность и условия Google для получения дополнительной информации о том, как вы можете контролировать показ рекламы и собираемую информацию. AddThis использует файлы cookie для обработки ссылок на социальные сети. Пожалуйста, прочитайте AddThis Privacy для получения дополнительной информации. Если вы хотите продвигать свои товары или услуги в Engineering ToolBox — используйте Google Adwords. Вы можете настроить таргетинг на Engineering ToolBox с помощью управляемых мест размещения AdWords. Эту страницу можно цитировать как Изменить дату доступа. . . закрыть Конструкционные материалы
Меню Размеры конструкционной угловой стали AISC A36.
В таблице ниже приведены размеры и размеры формы, вес
на фут и площадь поперечного сечения для конструкционного стального уголка на
АИСК . Размер ноги 1
x Вес (фунт/фут) Площадь (в 2 ) . .375 .11 0,625 х 0,625
х 0,125 0,750 х 0,750
х 0,125 .588 .173 0,875 х 0,875
х 0,125 1,00 х 1,00
х 0,125 . .235 1,00 х 1,00
х 0,188 1,162 .342 1,00 х 1,00
х 0,250 1,492 .438 1,125 х 1,125
х 0,125 1,013 .298 1,125 х 1,125
х 0,188 1,482 . 1,917 .563 1,226 .360 1,50 х 1,50
х 0,188 1,802 .53 1,50 х 1,50
х .250 2,342 . 1,50 х 1,50
х .375 3.352 .985 1,750 х 1,750
х 0,125 1.439 .423 1,750 х 1,750
х 0,188 2.122 .623 1,750 х 1,750
х .250 2,768 . 1,671 .491 2,00 х 2,00
х 0,188 2,462 .723 2,00 х 2,00
х .250 3.213 .944 2,00 х 2,00
х .313 3,95 1. 2,00 х 2,00
х .375 4.649 1,366 3.102 .911 2,50 х 2,50
х .250 4.064 1.194 5.015 1,474 2,50 х 2,50
х . 5.925 1.741 2,50 х 2,50
х .500 7,68 2,257 3,00 х 3,00
х 0,188 3,699 1,087 4.872 1.432 Связанные ресурсы: AISC, швеллер ASTM (сталь) Размеры указаны в миллиметрах, если не указано иное. -Геометрия -Момент инерции -Основные оси -Момент инерции и изгиба -Полярный момент инерции L -сечения -Эластичный раздел Modulus -пластический модуль сечения — вокруг оси x — вокруг оси y — Радиус инерции — Формулы сечения уголка (L) — Связанные страницы Площадь A и периметр P поперечного сечения угла можно найти по следующим формулам: \ begin{split} & A & = (h+b-t)t \\ & P & = 2b + 2h \end{split} Расстояние центра тяжести от левого края сечения x_c и от нижнего края y_c , можно найти, используя первые моменты площади двух катетов: 92\right) \right) \end{split} У нас есть специальная статья о центроиде сложных областей и о том, как его вычислить. Если вам нужна дополнительная информация, вы можете найти ее здесь. Момент инерции углового поперечного сечения можно найти, если всю площадь разделить на три меньшие, A, B, C, как показано на рисунке ниже. где x_c расстояние от центра тяжести до оси y0 и x_c расстояние от центра тяжести до оси x0. Выражения для этих расстояний приведены в предыдущем разделе. Имейте в виду, что оси x, y не являются естественными, L-образное сечение предпочло бы изгибаться, если его не ограничивать. Это будут главные оси, наклоненные относительно геометрических осей x, y, как описано в следующем разделе. Главные оси — те, для которых произведение инерции I xy поперечного сечения становится равным нулю. Обычно главные оси обозначаются буквами I и II и перпендикулярны друг другу. Моменты инерции, заданные вокруг главных осей, называются главными моментами инерции и являются максимальным и минимальным. По определению I_I считается главным главным моментом (максимальным) и I_{ II} второстепенный главный момент (минимальный). Отсюда следует, что: I_I>I_{II}. Момент инерции (второй момент или площадь) используется в теории балок для описания жесткости балки при изгибе. Изгибающий момент M, приложенный к поперечному сечению, связан с его моментом инерции следующим уравнением:0005 M = E\times I \times \kappa , где E — модуль Юнга, свойство материала, а \kappa — кривизна балки из-за приложенной нагрузки. Полярный момент инерции описывает жесткость поперечного сечения по отношению к крутящему моменту, так же как описанные выше плоские моменты инерции относятся к изгибному изгибу. Расчет полярного момента инерции I_z вокруг оси z-z (перпендикулярной сечению) можно выполнить с помощью теоремы о перпендикулярных осях: 94 . РЕКЛАМА Модуль упругости сечения S_x любого поперечного сечения вокруг центральной оси x-x описывает реакцию сечения на упругий изгиб. Он определяется как: S_x = \frac{I_x}{Y} где I_x, момент инерции сечения вокруг оси x-x и Y, расстояние от центра тяжести данного сечения волокна (параллельного ось). Для углового сечения из-за его несимметричности S_x отличается для верхнего волокна (на конце вертикального участка) или нижнего волокна (в основании горизонтального участка). S_{x,\textit{min}} = \frac{I_x}{h-y_c} S_{x,\textit{max}} = \frac{I_x}{y_c} , где «min Обозначения ” или “max” основаны на предположении, что y_c \lt h-y_c , что справедливо для любого углового сечения. Аналогично, для модуля упругого сечения S_y относительно оси y-y минимальный модуль упругого сечения находится с помощью: S_{y,\textit{min}} = \frac{I_y}{b-x_c} , где обозначение «min» основано на допущении, что x_c \lt b-x_c , что опять же справедливо для любого углового сечения. Если к оси x-x приложен изгибающий момент M_x, сечение будет реагировать нормальными напряжениями, линейно изменяющимися с расстоянием от нейтральной оси (которая в упругом режиме совпадает с центроидальной осью x-x). РЕКЛАМА Модуль пластического сечения аналогичен упругому, но определяется в предположении полной пластической текучести поперечного сечения за счет изгибного изгиба. В этом случае все сечение разделено на две части, одну на растяжение и одну на сжатие, каждая из которых находится в однородном поле напряжений. Для материалов с равными напряжениями текучести при растяжении и сжатии это приводит к разделению сечения на две равные области, A_t, при растяжении и A_c, при сжатии, разделенные нейтральной осью. Эта ось называется пластическая нейтральная ось и для несимметричных сечений не совпадает с упругой нейтральной осью (которая снова является центроидальной). Z = A_c Y_c + A_t Y_t , где Y_c — расстояние от центра тяжести области сжатия A_c до нейтральной пластической оси, а Y_t — соответствующее расстояние от центра тяжести зоны растяжения. площадь А_т. В случае углового поперечного сечения нейтральная пластическая ось для изгиба x-x может быть найдена одним из следующих двух уравнений: \left \{ \begin{array}{ll} (h-y_{pna})t = \frac{A}{2} & \text{ , if } y_{pna} \ge t \\ y_{ pna} b = \frac{A}{2} & \text{ , if } y_{pna} \lt t \\ \end{array} \right. , который становится: y_{pna} =\left \{ \begin{array}{ll} h- \frac{A}{2t} & \text{ , если: } t \le {A\over2 b } \\ \frac{A}{2b} & \text{ , если: } t \gt {A\over2 b} \\ \end{array} \right. где y_\textit{pna}, расстояние пластической нейтральной оси от нижнего конца сечения. Первое уравнение справедливо, когда пластическая нейтральная ось проходит через вертикальную ветвь, а второе — когда она проходит через горизонтальную ветвь. где h_1=h-t. Аналогичным образом можно найти модуль пластического сечения вокруг оси y. Если сориентировать Г-образное сечение так, чтобы вертикальная ветвь стала горизонтальной, то получившаяся фигура по форме подобна первоначально ориентированной. Таким образом, полученные уравнения должны иметь тот же вид, что и для оси абсцисс. Нам нужно только поменять местами h на b и наоборот. Таким образом, точное положение пластической нейтральной оси определяется следующей формулой: x_{pna} =\left \{ \begin{array}{ll} b- \frac{A}{2t} & \text{ , если: } t \le {A\over2 h} \\ \frac {A}{2h} & \text{ , если: } t \gt {A\over2 h} \\ \end{массив} \right. где x_\textit{pna}, расстояние пластической нейтральной оси от левого конца сечения. Первое уравнение справедливо, когда пластическая нейтральная ось проходит через горизонтальную ветвь, а вторая — когда она проходит через вертикальную ветвь (см. Для первого случая, когда ось ординат пересекает горизонтальную ветвь, модуль пластичности находится по формуле: 92 \over4h} \quad , t \gt {A\over2 h} , где b_1=b-t. Радиус вращения R g поперечного сечения относительно оси определяется по формуле: I момент инерции поперечного сечения вокруг той же оси и A его площадь. Размеры радиуса вращения [Длина]. Он описывает, насколько далеко от центра тяжести распределена область. Малый радиус указывает на более компактное сечение. Круг — это форма с минимальным радиусом вращения по сравнению с любым другим сечением той же площади A. В следующей таблице перечислены основные формулы для механических свойств углового (L) поперечного сечения. Пластиковая нейтральная ось: (расстояния снизу или слева) y_{pna} =\left \{ \begin{array}{ll} h- \frac{A}{2t} & \text{ , если: } t \le {A\over2 b} \\ \frac{A}{2b} & \text{ , если: } t \gt {A\over2 b} \\ \end{массив } \Правильно. x_{pna} =\left \{ \begin{array}{ll} b- \frac{A}{2t} & \text{ , если: } t \le {A\over2 h} \\ \frac {A}{2h} & \text{ , если: } t \gt {A\over2 h} \\ \end{массив} \right. 92 \right) \end{split} Понравилась эта страница? Поделись с друзьями! Почтовый индекс* Главная//Список акций//Уголок стальной Ryerson предлагает A36, A529Уголки из углеродистой стали -50 и A572-50, горячекатаные или оцинкованные, уголки L или размер прутка, для использования во многих конструкциях. Готовы сделать заказ? Перейти к каталогу Свяжитесь с нами|Перейти к ресурсам Соответствует стандарту ASTM A36. Длина склада: 20, 40 и 60 футов. Свяжитесь с представителем Ryerson для получения дополнительной информации Купить карбоновый уголок Толщина: 7, 36,0000” x 120,0000” x 0,1874”, 2361,1 фунта/лист Добавить примечания|Удалить Единица измерения фунтов Имя * Фамилия * Электронная почта * Почтовый индекс * Компания Центрировать штрих-код для поиска товаров. Количество: Единица измерения: Цена, Единица измерения: Справочный номер клиента: Уровень линии заказа: Заголовок Заказ на поставку: Номер заказа на покупку в заголовке включен в ваш штрих-код и может иметь приоритет перед предыдущими заказами на покупку в вашей корзине Профиль классифицируется как «Профиль размера стержня», если его наибольший размер (исключая длину) составляет менее 3 дюймов. Это «Структурная форма»), когда хотя бы один из ее размеров (исключая длину) составляет 3 дюйма или больше. Эти формы соответствуют ASTM A36 в отношении изготовления и механических допусков. Угол HR измеряется размером его ножек снаружи и их толщиной. HR Уголки и швеллеры соответствуют ASTM A36 При условии вычета из указанного выше процентного удлинения для толщин менее 5/16″ и более 3/4″. Выше приведено общее руководство по свойствам, которое можно считать репрезентативным для структурных форм HR, соответствующих стандарту ASTM A36. Используется для общих строительных целей, для использования в клепаных, болтовых или сварных конструкциях зданий, мостов, машин и т. д. Используется для стрел, рельсов, раскосов, рам, кронштейнов, поперечин, вкладышей, грузовых прицепов , кузова грузовиков, стеллажи и т. д. ASTM A36 имеет рейтинг обрабатываемости 72%, основанный на 1212 при 100%. Средняя подача поверхностного резания 120 футов/мин. ASTM A36, как правило, не подвергается термообработке, но обычно снимается напряжение перед шлифованием или механической обработкой или после сварки и перед механической обработкой. Однако ASTM A-36 можно науглероживать для повышения твердости поверхности. Снятие напряжения 1100–1250°F. Типичное время выдержки для снятия стресса — один час на дюйм толщины. на дюйм ноги (дюйм) (Г-образные) ¹ При неравных углах сторон более длинная сторона определяет класс ² 2/128 дюйма/дюйм. Другие допуски, например: прямолинейность, скручивание и т. д., согласно спецификациям ASTM A36, ASTM A6 / A 6M. † T + T’ применяется, когда фланцы канала сгибаются внутрь или наружу. Решение задач по ТАУ Как и многие другие специальные дисциплины, теория автоматического управления способна вызвать проблемы у студентов, которые сталкиваются с ней впервые. Теория вызывает чувство недоумения, а решение задач по ТАУ кажется чем-то не для земного ума. На самом деле, конечно, там нет ничего запредельно сложного (по крайней мере, в учебном курсе). Однако как переубедить эмоции, которые криком кричат – «Это какой-то кошмар!»? ТАУ – это не только специальная, но и специфическая дисциплина. Понимание теории в ней само по себе требует достаточно специфического склада ума (впрочем, на профильных факультетах это нормально), но и затрат времени, не говоря уже о решении задач по ней. Увы, не все студенты могут затратить достаточно времени и сил на все предметы своего расписания. Некоторые работают и вынуждены тратить время на зарабатывание денег, другие предпочитают уделить внимание более важным для своего будущего предметам. Тем более далеко не во всех случаях ТАУ оказывается предметом, важным в реальной практической работе. Но попробуйте объяснить это преподавателю, который ждёт от студентов полного погружения в свой предмет, и для него неважно, сколько ещё экзаменов в вашей сессии! Он потребует от вас понимания предмета, на которое надо тратить много времени. К тому же специфика здесь такова, что примеры задач по ТАУ не получится механически приложить к другим исходным условиям – нужно действительно понимать суть дисциплины. Пример оформления задач по ТАУ нашими специалистами: Есть ли универсальные методы решения задач по ТАУ? Как ни парадоксально, есть. Один из таких методов – решение задач по ТАУ на заказ. Мы предлагаем вам решения от самых лучших специалистов, преподавателей, знакомых не только с теорией автоматического управления как таковой, но и с учебными курсами по этому предмету. Предлагаем решение задач по различным системам автоматического управления (дискретным, линейным, нелинейным). Мы поможем вам разобраться с самыми разными заданиями по ТАУ, с контрольными работами по этому предмету, с подготовкой к лабораторным работам, с решением задач для курсовых и дипломных работ и с подготовкой к защите учёных степеней. Мы также можем помочь вам с решением исследовательских задач в рамках исследовательских действий. Выполненные нашими специалистами решения задач по ТАУ будут не только верными, но и подробными, с пояснениями по каждому шагу. Более того, такие задачи можно не только показать преподавателю и рассчитывать на хорошую оценку. Они станут для вас подспорьем в реальном освоении ТАУ, когда вы возьмётесь за это дело. А вы ведь возьмётесь, правда? Нам бы хотелось, чтобы наши услуги стали для вас не поводом отказываться от самостоятельной работы, а помощью в ней. Вникнув в ход решения задачи, вы сможете не только вручить преподавателю распечатку, но и аргументированно пояснить своему преподавателю все шаги решения задачи. Кроме ответа, вы получаете набор практических знаний и рекомендаций по дальнейшему решению задач. Благодаря прямому сотрудничеству с автором вы получаете постоянные консультации в реальном времени, возможность уточнять и корректировать задание, и всё это за более чем разумную плату. В случае каких-либо изменений в содержании задания или сроках его сдачи вы можете сразу сообщить об этом нам, чтобы мы откорректировали план действий. Мы предлагаем также большой выбор вариантов оплаты (электронные деньги, банковские переводы и т.д.) Примеры решений задач по ТАУ вы можете увидеть на нашем сайте (однако помните, что предмет достаточно нетривиален, и механическая подстановка данных одних задач в условия других может и не дать верного ответа!) Заказать нам работу! Вы изучаете теорию автоматического управления? Тогда вам будет полезна предлагаемая нашей группой авторов услуга «решение задач по ТАУ». Пример оформления раздела РГР по ТАУ нашими специалистами: Теория автоматического управления – дисциплина специфическая. И в большинстве случаев, чтобы справиться с задачами по ней, необходимо глубокое понимание темы и знание теории. Далеко не все студенты могут себе позволить тратить большое количество времени, чтобы разобраться во всех вопросах. Тем более что некоторые их них не так уж и важны, но задачи, связанные с ними все равно задаются преподавателями. Просто перечитать примеры задач по ТАУ, и решить поставленные перед вами по шаблону не получиться. Здесь нужно действительно разбираться в теме. Так что, если вы не уверены в своих силах, и просто не обладаете временем, необходимым для выполнения задания, обратитесь к специалистам в этой области. Что мы предлагаем в рамках предоставления услуги В состав нашей группы свободных авторов «Freewriters» входят специалисты, имеющие большой опыт работы с данной дисциплиной. Мы учитываем требования вашего вуза по оформлению задач. Обратившись к нам, клиент, которому необходимо решение задач по данному предмету, получает не просто готовый ответ. Мы предоставляем все необходимые пояснения по ходу решения задач, за счет чего вы можете защитить решение, и показать преподавателю свою компетентность. Решение ТАУ на заказ: какие задания мы выполняем Обращайтесь к нам, если вам необходимо выполнить домашнее задание по теории автоматического управления: — в рамках контрольных работ поданной дисциплине; — в ходе проведения лабораторных работ; — при выполнении курсовых и дипломных работ; — в рамках исследовательских действ мероприятий; — при подготовке к защите различных ученых степеней. Если вам нужно решение задач по дискретным, линейным или нелинейным системам автоматического управления, или любым другим разделам данной дисциплины, мы выполним их. Решение ТАУ: сотрудничество с автором напрямую Обратившись к нам, вы сотрудничаете с тем, кто занимается решением задач по ТАУ для вас, напрямую. А это значит, что при возникновении вопросов по порядку решения задач и их оформления вы всегда сможете оперативно получить ответ на них. Сотрудничество с исполнителем напрямую — это еще и приемлемая стоимость услуг. Ведь в этом случае отсутствуют какие-либо посредники, которым необходимо платить деньги. Возможность заказа онлайн и удобные для студентов варианты оплаты При обращении к нам вы можете оформить заявку на решение задач в режиме онлайн. Вам просто нужно будет отправить нам условие задачи при помощи специальной формы, указать особенности (если они есть) и ждать решения. Мы предлагаем различные варианты оплаты услуг. Вы можете заплатить при помощи банковской карточки, электронными деньгами и т.д. Специалисты, решающие для вас задачи на заказ, знакомы с общими требованиями для всех ВУЗов, а также со специфическими особенностями каждого учебного заведения. Так что, обращайтесь к нам смело, и мы без проблем решим любые задачи. Нуждаетесь в помощи по решению задачи или контрольной по ТАУ? Если немного взглянуть в предпосылки возникновения ТАУ (САУ) можно заметить, что издавна люди пытаются автоматизировать многие процессы управления, эти попытки своими корнями уходят еще в 16-18 века. Ранее любой управляющий механизм разрабатывался эмпирическим путем, т.е. путем проб и ошибок создавалось некое управляющее устройство и «подгонялось» под нужды изменением физических характеристик (изменение жесткости пружины, увеличение трения ремня, увеличение сопротивления ветру и т.п.). Этот способ синтеза отнимал огромное количество времени и труда и материальных затрат. Используя только этот способ для синтеза системы автоматического управления практически невозможно создавать сложные системы управления. На современном этапе такой подход считается сильно трудоемким и не рациональным, поэтому разработана теория, позволяющая произвести синтез устройства управления на основании расчетов, что сильно сокращает время на проектирование и создание функционирующего образца. В силу сложности предмета нередко студенты прибегают к сторонней помощи и часто стараются заказать решение задач или контрольных по ТАУ (САУ). Заказать решение такого типа задач сейчас довольно нелегко, т.к. в настоящее время, что парадоксально, специалистов в данном предмете очень мало и они сильно высоко ценятся. Самой распространенной задачей по ТАУ является исследование на устойчивость системы по различным критериям (Найквиста, Гурвица и т.п.). Кроме того способы исследования на устойчивость САУ разделяются на алгебраические и частотные. Есл Вы теряетесь в решении своей задачи – лучше закажите решение ТАУ у профессионалов. Вторым по распространенности заданием теории автоматического управления является синтез системы управления по заданным критериям, а затем проверка ее на устойчивость и способность реагирование на возмущающие воздействия. Решение задач по ТАУ на заказ является заветным желанием для многих студентов, даже для тех, которые сами предпочитают решать математику или сдавать экзамены по эконометрике. Что можно посоветовать студентам, которые не справляются самостоятельно с решением задач? Требования простые: Для тех, кто любит интересную информацию по решению задач — рекомендуем ознакомиться с новыми статьями в которых раскрыты подробоности о том как и где можно заказать решение УМФ. Кроме того, недавно была опубликована статья посвещенная решениею задач по функциональному анализу на заказ. Учебное пособие посвящено задачам теории линейных непрерывных и дискретных систем автоматического управления. Задачи по каждой теме предваряются необходимыми теоретическими материалами и разбором примеров. Сборник в основном ориентирован на учебник Д.:П. Кима <<Теория автоматического управления. Том 1. Линейные системы>>. Рекомендовано УМО вузов по университетскому политехническому образованию в качестве учебного пособия для студентов высших учебных заведений, обучающихся по направлению 220400 <<Мехатроника и робототехника>>.
Категории:
Учебная литература
На нашем сайте доступен для
скачивания электронный учебник по теории автоматического управления Скачать учебник по ТАУ
Теория автоматического управления сформировалась как
самостоя-тельная наука на основе изучения процессов управления
техническими устройствами. Науку об управлении
техническими устройствами называют технической кибернетикой. Третий раздел содержит постановку
задачи и обзор методов
синтеза линейных САУ, а также примеры параметрической оптимизации
типовых
одноконтурных и двухконтурных систем автоматического регулирования
(САР). Все
многообразие
задач ТАУ принято делить на три основные группы:
1) задачи
анализа САУ;
2) задачи
синтеза САУ;
3) задачи
идентификации. Сущность анализа САУ заключается в
определении закона изменения выходной величины САУ y(t) по
заданному входному воздействию
x(t) и оператору
системы. Под
оператором САУ понимают закон, в соответствии с которым САУ преобразует
входное
воздействие x(t) в
выходное y(t). В
математическом отношении
оператор системы представляет собой дифференциальное уравнение или
систему
дифференциальных уравнений, а также передаточную функцию САУ. Другими
словами, оператор САУ есть ее математическая
модель. Сущность
синтеза САУ заключается в определении оператора САУ (ее структуры и
параметров)
и входной величины x(t) по желаемому
изменению выходной величины y(t). Сущность идентификации заключается в
определении оператора САУ по известным входной x(t) и выходной y(t)
величинам В ходе работ по проекту был рассмотрен класс стационарных линейных векторных систем с соизмеримыми запаздываниями. Удалось получить достаточные условия приводимости таких систем к канонической форме с выделением нулевой динамики, был указан конструктивный алгоритм приведения системы к указанной форме. В результате был предложен метод построения оценки (с наперед заданной точностью) неизвестного входа для векторных систем с запаздыванием, другими словами был получен метод построения инвертора. Кроме того, в ходе работы были получены и другие результаты. В частности, была изучена задача асимптотического восстановления фазового вектора динамической системы, описываемой дифференциально-разностными уравнениями с соизмеримыми запаздываниями. При выполнении легко проверяемого достаточного условия асимптотической наблюдаемости предложен метод построения наблюдателя, состоящего из двух частей: дифференциально-разностной и чисто разностной. Предложенный наблюдатель решает задачу асимптотически точно на основе данных об измеряемых входе и выходе системы в заданный момент времени и предыдущие моменты. Также был получен подход к решению задачи одновременной стабилизации для класса линейных систем с запаздыванием.
Рассмотрены линейные системы функционально-дифференциальных уравнений в случае соизмеримых запаздываний. Получены необходимые условия асимптотической обратимости этого класса систем в виде отсутствия неустойчивых инвариантных нулей у матрицы, являющейся аналогом матрицы Розенброка. Данный результат является обобщением известных условий обратимости линейных динамических систем. Для систем с равномерным первым относительным порядком предложен алгоритм синтеза инвертора на основе метода управляемой модели с разрывной обратной связью с последующим сглаживанием управления в виде скользящего среднего. Алгоритм позволяет построить инвертор, дающий оценку неизвестного входа с наперед заданной точностью. Предложенный алгоритм обобщается на случай произвольного равномерного относительного порядка.
Кроме того, был расширен класс исследуемых динамических систем с соизмеримыми запаздываниями: было добавлено в рассмотрение возмущение, действующее на динамику системы, при этом возмущение входит в уравнение системы также с запаздываниями. Для данного класса систем, используя метод операторного представления и аппарат полиномиальных матриц, был получен алгоритм построения наблюдателя, содержащего в своем уравнении запаздывания. Хотя полученная процедура не всегда может быть выполнена (для её выполнимости необходимо выполнение условия обратимости определенной матрицы), был указан способ ослабления этого условия, основанный на использование разностных наблюдателей.
Для стационарных систем был получен специальный алгоритм обращения, особенность которого состоит в непрерывности получаемой оценки. Полученный алгоритм опирается на метод управляемой модели системы, опирающийся на синтез такого закона управления (регулятора), что определенная система в отклонениях (соответствующая управляемой модели системы), устойчива. Полученное управление (или выход регулятора) является оценкой для неизвестного входного сигнала. Непрерывная оценка была получена с помощью скользящих режимов высших порядков. Сделайте индивидуальный заказ на нашем сервисе. Там эксперты помогают с учебой без посредников Разместите задание – сайт бесплатно отправит его исполнителя, и они предложат цены. Цены ниже, чем в агентствах и у конкурентов Вы работаете с экспертами напрямую. Поэтому стоимость работ приятно вас удивит Бесплатные доработки и консультации Исполнитель внесет нужные правки в работу по вашему требованию без доплат. Корректировки в максимально короткие сроки Гарантируем возврат Если работа вас не устроит – мы вернем 100% суммы заказа Техподдержка 7 дней в неделю Наши менеджеры всегда на связи и оперативно решат любую проблему Строгий отбор экспертов К работе допускаются только проверенные специалисты с высшим образованием. Проверяем диплом на оценки «хорошо» и «отлично» 1 000 + Новых работ ежедневно Работы выполняют эксперты в своём деле. Они ценят свою репутацию, поэтому результат выполненной работы гарантирован Иванна Маркетинг Статистика Инженерная графика 91265 2347 1079 Ludmila Экономика Маркетинг Политология 77793 4667 2073 Константин Николаевич Информатика БЖД Охрана труда 62985 1043 595 Svetlana Экономика Маркетинг Психология 57027 1691 1062 Отзывы студентов о нашей работе среднее 4.9 из 5 Ежедневно эксперты готовы работать над 1000 заданиями. Контролируйте процесс написания работы в режиме онлайн Решить тест Тест дистанционно, Экономика Срок сдачи к 30 июля 1 минуту назад 1 минуту назад 3 минуты назад Экономика Тест дистанционно, Экономика Срок сдачи к 30 июля 4 минуты назад 4 минуты назад Решить 5 задач Решение задач, общая химическая технология Срок сдачи к 31 авг. Задачи Контрольная, Сопротивление материалов Срок сдачи к 5 авг. ыы Решение задач, Высшая математика Срок сдачи к 1 авг. тестирование Тест дистанционно, Элективные дисциплины по физической культуре и спорту Срок сдачи к 5 авг. Закажи индивидуальную работу за 1 минуту! Всего в исследовании приняли участие 50 субъектов (54% женщины) со средним возрастом 67,2 ± 7,3 (диапазон 53–83). В таблице 1 перечислены демографические характеристики этой выборки, включая этническую принадлежность, общие сопутствующие медицинские заболевания, а также показатели когнитивных функций, сна и уровни T-тау, P-тау и Aβ 42 в CSF.Все субъекты имели клинический рейтинг деменции (CDR) 0, среднее краткое обследование психического состояния (MMSE) 29,1 ± 1,1, образование 16,7 ± 2,1 года и в целом не страдали ожирением (ИМТ = 25,4 ± 3,5). Тридцать четыре процента (17 субъектов) были ApoE4 + . В целом, когорта состояла из когнитивно нормальных пожилых людей с хорошим здоровьем, 4 из 50 были как амилоид-положительными, так и тау-положительными (Aβ 42 <469,5 пг / мл, T-тау> 323 пг / мл или P-тау> 52,8 пг / мл как положительные пороговые значения), 14 из 50 были амилоид-отрицательными и тау-положительными, 8 из 50 были амилоид-положительными и тау-отрицательными, и 24 из 50 были как амилоид-отрицательными, так и тау-отрицательными (Таблица 1).Эти пороговые значения были рассчитаны на основе построения кривых ROC для здоровых и больных субъектов (MCI и AD) с использованием биобанка Центра здоровья мозга Нью-Йоркского университета. Гистограммы распределений CSF Aβ 42 , T-tau и P-tau в этой когорте показаны в дополнительном файле 1: Рисунок S1). Лабораторное время TST составило 6,03 ± 1,05 ч, WASO — 91,5 ± 58,3 мин, стандартное отклонение — 78,3 ± 11,9% (таблица 1). Эта когорта не страдала субъективной дневной сонливостью по шкале сонливости Эпворта (ESS = 5.9 ± 3,7). Латентный период сна в лаборатории составлял 11,7 ± 12,7 мин, а латентность быстрого сна — 99,2 ± 61,9 мин. Медиана AHI4% составила 1,2 (IQR 2,9 / ч, диапазон от 0,1 / ч до 10,8 / ч), а медиана AHI-all составила 8,5 (IQR 7,8 / ч, диапазон от 1,8 / ч до 29,3 / ч). Связи между плотностью веретена и возрастом не наблюдалось, что, вероятно, является следствием относительно ограниченного возрастного диапазона нашей выборки. Точно так же, хотя у женщин обычно более высокая плотность веретена, чем у мужчин [21, 48], в этой выборке не было значительных различий в плотности веретена N2 у разных полов (мужчины: 1.9 ± 1,3 # / мин сна N2, женщины: 2,2 ± 1,5 # / мин сна N2, p = 0,566). Попарные нескорректированные и условные (по возрасту, полу и статусу ApoE4) корреляции между биомаркерами ЦСЖ AD и плотностью шпинделей N2 представлены в таблице 2. Не скорректированные корреляции приведены под главной диагональю, а условные корреляции — над главной диагональю.Имелась высокая взаимная корреляция между биомаркерами АД в спинномозговой жидкости, особенно между Т-тау и Р-тау (r = 0,929, p <0,001). Плотность веретена N2 была отрицательно коррелирована со всеми показателями CSF, и, несмотря на сильную корреляцию между обоими измерениями CSF tau, плотность веретена была более сильно связана с T-tau, чем с P-tau. Коэффициенты парной корреляции, скорректированные с учетом возраста, пола и статуса ApoE4, приведенные над главной диагональю, показывают аналогичную закономерность и указывают на то, что условные ассоциации были даже сильнее, чем нескорректированные.В дополнение к индивидуальным уровням белка в спинномозговой жидкости в качестве биомаркеров БА использовались соотношения между Т-тау / Aβ 42 и P-тау / Aβ 42 . Плотность веретена во время сна N2 также отрицательно коррелировала с соотношением T-тау / Aβ 42 (r = — 0,380, p = 0,010) и P-tau / Aβ 42 (r = — 0,31 , п = 0,043). Для оценки относительной силы ассоциации каждого из биомаркеров CSF с плотностью веретена N2 мы провели анализ иерархической регрессии с плотностью веретена N2. в качестве ответа и каждый из биомаркеров спинномозговой жидкости в качестве предикторов.Результаты представлены в таблице 3. Модель только с возрастом, полом и генотипом ApoE4 и без предикторов CSF объяснила 12,8% дисперсии плотности веретена (Модель 1). В присутствии ковариант каждый из биомаркеров спинномозговой жидкости был значимым предиктором, и добавление каждой из переменных улучшало предсказательную силу: Aβ 42 на 8,8%, P-тау на 18,1%, T-тау на 25,9%, и отношение T-тау / Aβ 42 на 12,9% (см. ΔR 2 в таблице 3), подтверждая результаты, обсужденные выше.Наконец, включение пар биомаркеров спинномозговой жидкости вместе (Модель 3) показало, что в присутствии T-tau или P-tau Aβ 42 не оставался значимым предиктором плотности веретена N2, в то время как T-tau и P-tau оставались значимыми предикторами в присутствии Aβ 42 , хотя T-tau имел большую прогностическую ценность. Произошло резкое снижение величины коэффициентов для Aβ 42 от Модели 2, где это единственная мера CSF, до Модели 3, где она находится вместе с T-tau (Таблица 3), в то время как коэффициенты T-Tau оставалась неизменной или увеличивалась в силе в присутствии Aβ 42 .Это свидетельствует о принципиальной важности Т-тау среди трех биомаркеров ЦСЖ в их ассоциации с плотностью веретена N2. Чтобы убедиться, что влияние тау-белка специфично для веретен, мы исследовали потенциальные взаимосвязи между T-tau и P-tau и переменными качества сна, измеренными с помощью PSG, включая эффективность сна, WASO, AHI4% и AHI-all, а также переменные, измеренные с помощью актиграфии, включая обычную продолжительность сна (TST).Мы не наблюдали никакой корреляции между T-tau или P-tau и какими-либо из этих показателей на исходном уровне (дополнительный файл 1: Рисунок S2). Чтобы дополнительно подтвердить специфичность спинных веретен сна в прогнозировании T-tau в спинномозговой жидкости, мы провели иерархический регрессионный анализ с T-tau в спинномозговой жидкости в качестве переменной ответа с несколькими показателями сна в качестве предикторов (таблица 4). Базовая модель с возрастом, полом и только генотипом ApoE4 без предикторов сна объяснила 7,7% дисперсии T-tau в спинномозговой жидкости (модель 4, таблица 4).Затем мы добавили предикторы сна по отдельности, чтобы оценить, улучшают ли они прогностическую способность CSF T-tau (модель 5, таблица 4). Из выбранных предикторов сна плотность веретена N2 значительно улучшила предсказательную силу модели для T-tau в спинномозговой жидкости на 28,4% по сравнению с возрастом, полом и генотипом ApoE4 (ΔR 2 = 0,284, p = 0,001, Модель 5, Таблица 4), и это была единственная переменная сна, которая могла это сделать. Добавление сопутствующих заболеваний, включая наличие гипертонии, сердечно-сосудистых заболеваний, диабета и заболеваний щитовидной железы, не повлияло на взаимосвязь между плотностью N2 и T-tau в спинномозговой жидкости (дополнительный файл 2: Таблица S2).Также не было значимой корреляции между плотностью веретена N2 и любыми другими переменными сна, исследованными в этой когорте. В родственной модели мы провели анализ иерархической регрессии с соотношением Т-тау-белка ЦСЖ / Aβ 42 в качестве переменной ответа с несколькими показателями сна как предсказатели. ApoE4 был настолько значимым предиктором CSF Aβ 42 , что комбинация возраста, пола и генотипа ApoE4 объяснила 31% дисперсии в соотношении CSF T-tau / Aβ 42 .(Дополнительный файл 3: Таблица S1, Модель 6). В этом анализе отсутствует переменная сна, которая значимо объясняла бы дополнительную дисперсию соотношения T-tau / Aβ 42 в спинномозговой жидкости, помимо возраста, пола и генотипа ApoE4, хотя плотность веретена N2 наиболее близка (ΔR 2 = 0,07, p = 0,072 (Дополнительный файл 3: Таблица S1, Модель 7). Мы наблюдали, что CSF T-tau был значительно связан с плотностью веретена, количеством, продолжительностью, и плотность быстрых шпинделей (рис.1) после контроля возраста, пола и генотипа ApoE4. CSF T-tau не был связан с низкой плотностью шпинделя, мощностью шпинделя или средней пиковой частотой. Быстрые шпиндели можно функционально отличить от медленных по их большей склонности к вложению в колебания и ускорению обработки памяти [49]. В моделях линейной регрессии, где T-тау-белок ЦСЖ, возраст, пол и генотип ApoE4 оставались постоянными в качестве переменных-предикторов, мы наблюдали, что T-тау-белок ЦСЖ объясняет 25% дисперсии в количестве веретен N2 (F (4, 49) = 3.77, p = 0,010), 45% дисперсии продолжительности шпинделя (F (4, 49) = 9,23, p <0,001) и 41% дисперсии плотности быстрого шпинделя (F ( 4, 49) = 7,90, p <0,001) (дополнительный файл 4: таблица S3). Корреляция между свойствами спящего шпинделя и CSF T-tau . Графики разброса плотности шпинделя N2 (# / мин. N2 в спящем режиме) ( a ), количества шпинделя N2 ( b ), продолжительности шпинделя (сек.) ( c ) и плотности N2 быстрого шпинделя (# / мин.N2 сон) ( d ) с T-tau в спинномозговой жидкости указывают на значимые ассоциации на поперечном срезе ( n = 50 субъектов) Когорта, исследованная в этом исследовании, имеет значительное совпадение с субъектами, у которых мы обнаружили связи между показателями SWS. и CSF Aβ 42 (39/50 субъектов) [12]. В соответствии с нашими предыдущими наблюдениями, CSF Aβ 42 обратно коррелировал с фронтальным SWA (r = — 0,312, p = 0,039 после поправки на возраст, пол и ApoE4, таблица 2 ) .Напротив, хотя мы наблюдали нескорректированную корреляцию между фронтальной SWA и T-tau, фронтальная SWA не коррелировала ни с T-tau, ни с P-tau (r = — 0,291, p = 0,055 и r = — 0,191, p = 0,215, таблица 2) с поправкой на возраст, пол и ApoE4. Как уровень тау-белка в головном мозге, так и плотность веретена сна связаны с показателями когнитивной деятельности. В частности, плотность веретена во сне коррелирует с тестом Bells Test, тестом Connors Continuous Performance и тестом слухового вербального обучения, которые выполняются на следующее утро после тестирования сна [50].В текущем исследовании нейропсихологическое тестирование было завершено до исследования сна с переменной продолжительностью между проведением тестов и измерениями сна в лаборатории. У всех испытуемых мы наблюдали значительную двумерную корреляцию между необработанными значениями производительности в тесте замены цифровых символов и плотностью быстрого шпинделя, между необработанными значениями производительности Trails A и общей и быстрой плотностью шпинделя, а также между необработанными значениями производительности Trails B и медленной плотностью шпинделя. Когда результаты этих тестов были оценены по z-шкале и нормализованы по возрасту, полу, расе и годам образования [40], мы продолжили наблюдать значительную корреляцию между производительностью трассы А и общей и быстрой плотностью шпинделя, а также между производительностью трассы B и низкая плотность шпинделя (дополнительный файл 5: таблица S4).Во всех случаях более высокая плотность шпинделя была связана с лучшей производительностью, за исключением низкой плотности шпинделя, где большая плотность медленных шпинделей была связана с более длительным временем на трассе B. Незаконные карьерные задачи могут привести к заключению в Бриг, если вы проиграете
задача и не повезло. В этом случае ваша репутация у радиостанции
правительство тоже страдает. Более высокие уровни Оруэлла делают его более вероятным.
ограничены в случае сбоя задачи. Вредные карьерных заданий могут отправить вас в лазарет в случае неудачи. ПРЕДУПРЕЖДЕНИЕ : Большая часть этой информации устарела. Пожалуйста, подождите (или внесите свой вклад), пока
мы обновили данные. Информация под горизонтальной линией добавлена после изменений
на карьерные задачи в цикле 202. Основная характеристика: Социальная (Задачи, которые, как известно, должны быть оплачены банку, следовательно, должны быть законными, отмечены
с «-«.Известно, что данные о том, какие задачи являются опасными,
неполное) Основная характеристика: Ловкость
Вторичная статистика: социальная (Задачи, которые, как известно, должны быть оплачены банку, следовательно, должны быть законными, отмечены
с «-«.Известно, что данные о том, какие задачи являются опасными,
неполное) Преимущества: Недостатки: Основная характеристика: Социальная (Задачи, которые, как известно, должны быть оплачены банку, следовательно, должны быть законными, отмечены
с «-«. Известно, что данные о том, какие задачи являются опасными,
неполное) Преимущества: Недостатки: Основная характеристика: Интеллект Преимущества: Недостатки: Основная характеристика: Ловкость (Задачи, которые, как известно, должны быть оплачены банку, следовательно, должны быть законными, отмечены
с «-«. Известно, что данные о том, какие задачи являются опасными,
неполное) Основная характеристика: Выносливость Карьерный путь можно выбрать на консультациях по вопросам карьеры в любом центре занятости. Прогресс вашего карьерного роста останется неизменным, если вы решите на какое-то время попробовать другую карьеру. Вы всегда можете вернуться и начать все заново, именно там, где вы остановились. Типы бизнеса также помогают восстановить человечество, но делают это через торговлю. Отличный способ заработать. Преступники знают, что жизнь на вокзалах тяжелая.У тех, кто вырос в руинах, часто возникает соблазн взять то, что они могут получить, вне зависимости от закона. Юридическая карьера подходит тем, у кого есть желание служить… или просто личные амбиции. Карьера в медицине теперь проще, поскольку большая часть современной медицины обрабатывается машинами, но по-прежнему требуется обученный персонал, чтобы понимать, на что они смотрят. Персонал спецслужб — странная помесь полиции, солдата и шпиона. Очень эффективно, но не всегда приветствуется. Технологи сосредотачиваются на восстановлении технологий, от простых сканеров до запорных ворот. Каждый день около / 91: 760 (полночь по центральноевропейскому летнему времени) — это день выплаты жалованья за вашу текущую карьеру.Вы можете сменить профессию по своему желанию и продолжить с того места, где остановились, на одной ранее, но ваша карьера в день выплаты жалованья — это то, что получает еще один день в звании и оплачивается кредитами и облигациями. Посмотрите на страницу своей карьеры, на которую есть ссылка на этой странице, чтобы узнать, какие задачи подвергают вас риску оказаться в лазарете или бригаде в случае неудачи. Для перехода на следующий уровень карьеры у вас должно быть надлежащее количество дней на вашем текущем уровне, выполнить достаточно заданий, чтобы получить опыт перехода на следующий уровень, и выполнить хотя бы одно задание после достижения нужного количества дней.Для вашей первой карьеры вряд ли возникнут проблемы с выполнением достаточного количества задач, прежде чем у вас будет достаточно дней, чтобы двигаться дальше. Однако вы можете обыгрывать систему для второстепенной карьеры и сначала достичь дней в рейтинге, а затем выполнять ровно столько задач, чтобы двигаться дальше. Это позволит вам тратить большую часть своей работы на более высокооплачиваемые задачи из вашей основной карьеры. В качестве примера. после того, как вы достигнете достойного звания в своей основной карьере, вы можете начать работать над второй. Изменитесь на вторую карьеру незадолго до зарплаты, а потом переключитесь обратно.Используйте свое внимание для высокооплачиваемых задач в основной карьере. После того, как вы набрали достаточное количество дней в звании, выполняйте задания, достаточные для повышения. Таким образом, вы сможете как можно скорее перейти на более высокооплачиваемую работу. Если вы не повысились в звании и уже имеете правильное количество дней, примените новый день к своей основной карьере или начните другую, но не тратьте день на карьеру, которая в этом не нуждается. Если вы действительно хотите сосредоточиться на всех 5 характеристиках, вы можете сменить профессию несколько раз за очень короткое время, чтобы выполнять задания из нескольких профессий. См. Также https://tauguide.de/#pursue-a-career Это сообщение, которое вы увидите, когда вас уволят за незаконную карьерную задачу, за которым следует само сообщение для конкретной задачи: Неудачная работа! Вас поймали на выполнении незаконной задачи. Катастрофа заставила нас пошатнуться, борясь за выживание и пытаясь восстановить цивилизацию из того, что составляет лишь остатки стола прежней. Это не означает легкий путь по карьерной лестнице! Большинство граждан, по сути, являются фрилансерами.Они путешествуют по галактике в поисках задач в рамках выбранной ими профессии, мотивируемые не только бонусными кредитами, которые они могут получить сверх своей зарплаты, но и тем, чтобы сделать себе имя в своей области и получить больше возможностей. Однако потенциальная занятость никогда не бывает постоянной, особенно в условиях посткатастрофической экономики. Это зависит от того, что может потребоваться конкретной станции в конкретное время, а также от показателей, предоставленных работодателям вашей собственной CORETECHS.Если ваш анализ биологической обратной связи покажет, что вы слишком устали для выполнения конкретной задачи, работодатели просто не предложат его. Избыточность в будущем — дело динамичное; сегодня лишний, завтра трудоустроен! Аналогичным образом, трудоустройство в галактике, основной задачей которой, по крайней мере с точки зрения человечества, является выживание, также является нестабильной ситуацией. Станция может не нуждаться в конкретном эксперте сегодня, но завтра может. В постоянно меняющейся экономике вы должны искать свою работу. В будущем, когда HR вымирают как отдел, люди становятся их собственным ресурсом и должны прокладывать свой собственный путь вверх по лестнице. Не все граждане будут в порядке, конечно, такие же порядочные рабочие, как вы. Некоторые выбирают менее законный путь для своей карьеры. В таких случаях задачи чреваты опасностью открытия и затягивания. Кроме того, большинство кредитов, заработанных такими двуличными способами, будут обходить ваш банк и вместо этого будут загружены прямо в ваш кошелек CORETECHS. Как указывалось ранее, доступные задачи зависят от множества факторов. Потребности работодателей, экономика станции и ряд динамичных ситуаций, которые, как можно ожидать, повлияют на любое постапокалиптическое галактическое общество, работающее над восстановлением своих основ. Технологии — еще один фактор, о котором, возможно, нашим предкам не приходилось беспокоиться на этой арене. Благодаря возможностям сбора метрик, которые присущи CORETECHS, потенциальные работодатели теперь могут прогнозировать, насколько эффективными и успешными вы будете, на основе вашей текущей биологической обратной связи. Задание, которое было предложено, пока вы отдохнули, и бдительности не будет, когда ваша энергия иссякнет. И, наконец, стоит отметить, что, хотя зарплаты являются результатом соглашения между основными фракциями, цель которого — помочь экономике после катастрофы снова обрести основу, бонусное вознаграждение за отдельные задачи остается исключительной прерогативой каждой отдельной станции.Это часть сложного соглашения, которое стремится уравновесить галактический экономический рост со свободой автономных станций и культурным ростом. Ряд станций в настоящее время лоббируют распространение этих экономических свобод по всем направлениям, стремясь способствовать росту и гибкости торговли во многих аспектах локализованной торговли. Сопредседатели : отвечают за управление всеми социальными мероприятиями Alpha Tau и академической
разработка программы.Они планируют такие мероприятия, как День ученых и Весенние качели. Казначей: Отвечает за управление средствами Alpha Tau, а также за обслуживание Alpha Tau
банковский счет и ответственность за дебетовую карту / чеки для счета.Он она
также будет контролировать сбор средств вместе с комитетом и координатором. Секретарь: Отвечает за ведение протоколов на собраниях почестей и вносит свой вклад в помощь
в любом событии Альфа Тау. Он / она также играет большую роль в создании и организации
расписания Дня ученого. Историк: Отвечает за организацию прошлой и настоящей информации о программе Почестей, в том числе
номера участников, события и фотографии. Координатор по сбору средств : Тесно сотрудничает с социальным сопредседателем и казначеем, помогая планировать сбор средств
мероприятия и придумывать идеи для других сборщиков денег. Он / она также является главой
Комитет по сбору средств. Координатор сообщества : В первую очередь отвечает за помощь с Spring Swing и управление созданием
команд Tiger Serve Day.Этот офицер также будет отвечать за придумывание
новая благотворительность для Альфа Тау. Он / Она также будет главой
Комитет сообщества. Координатор по связям с общественностью : отвечает за создание всех графических материалов и отвечает за контроль
социальные сети общества. Капеллан: Помогает помнить о духовных потребностях организации и молится на всех мероприятиях.Он / она также рядом с членами организации, нуждающимися в духовном руководстве. Координатор черно-белых : В первую очередь отвечает за планирование нашего ежегодного мероприятия «Черное и белое». Он / она работает
тесно с другими офицерами, чтобы делегировать задачи на мероприятие. Координатор весенней темы: В первую очередь отвечает за планирование нашего ежегодного мероприятия «Весенняя тема». Он / Она тесно сотрудничает
с другими офицерами, чтобы делегировать задачи на мероприятие. Послы : В каждой учебной школе будет два или более послов.Они будут тесно сотрудничать
с сопредседателем по социальным вопросам, чтобы привлечь студентов из их учебных заведений в
События. Послы также будут нести ответственность за планирование встреч в течение семестра.
со студентами из их школы. Студенты направят вопросы, связанные с
свою школу послов. Христианские исследования Гуманитарные науки Социальные науки Изобразительное искусство Образование Естественные науки Бизнес Организуйте свои проблемы с помощью досок проектов Знаете ли вы, что вы можете управлять проектами там же, где храните код? Настройте доску проектов на GitHub, чтобы оптимизировать и автоматизировать рабочий процесс. Сортировка задач Добавляйте проблемы и запросы на включение на доску и расставляйте приоритеты вместе с карточками, содержащими идеи или списки задач. Спланируйте свой проект Сортировка задач в столбцы по статусу. Вы можете пометить столбцы индикаторами состояния, как «Дела», «Выполняется» и «Готово». Автоматизируйте рабочий процесс Настройте запускающие события, чтобы сэкономить время на управлении проектами — мы переместим задачи в нужные столбцы для вас. Отслеживать прогресс Следите за всем, что происходит в вашем проекте, и точно отслеживайте, что изменилось с момента последнего просмотра. Поделиться статусом Каждая карточка имеет уникальный URL-адрес, что упрощает обмен и обсуждение отдельных задач с вашей командой. Заключение Завершив работу, закройте доску проекта, чтобы удалить ее из списка активных проектов. К следующему проекту! Инструменты TAU реализованы в виде графических гиперинструментов .
Хотя это разные инструменты, они действуют согласованно, как если бы
были единым приложением.Каждый инструмент реализует четко определенные
задания. Если одному инструменту нужна функция другого, он отправляет
сообщение другому инструменту, запрашивающему его (например, отобразить
исходный код для конкретной функции). Такой дизайн позволяет легко расширять. Мы постарались сделать набор инструментов TAU максимально удобным для пользователя.
возможно. Многие элементы графического пользовательского интерфейса
аналог ссылок в гипертекстовых системах :
щелчок по ним вызывает окна, описывающие элемент
более подробно.Это позволяет пользователю исследовать свойства
приложение, просто взаимодействуя с наиболее интересными элементами.
Инструменты TAU также поддерживают глобальные функции .
Если глобальная функция вызывается в любом из инструментов, она
автоматически выполняется во всех работающих на данный момент инструментах TAU .
Примеры глобальных функций: На рисунке выше показано программирование pC ++ .
среда и связанная с ней архитектура инструментов TAU .
Интерфейс компилятора pC ++ принимает пользовательскую программу и pC ++ определения библиотеки классов (которые предоставляют предопределенные
типы коллекций) и анализирует их в абстрактное синтаксическое дерево (АСТ). Весь доступ к AST осуществляется через библиотеку Sage ++ .
С помощью переключателей командной строки пользователь может выбрать компиляцию
программа для профилирования, трассировки и отладки точек останова.В этих случаях вызывается инструмент для выполнения необходимых действий.
приборостроение в АСТ. Серверная часть pC ++ преобразует
AST в простой C ++ с вызовами в pC ++ исполняющая система. Этот исходный код C ++ затем компилируется и связывается
компилятором C ++ в целевой системе.
Компиляция и выполнение программ pC ++ может быть
контролируется COSY . Этот инструмент обеспечивает высокий уровень
графический интерфейс для настройки параметров компиляции и выполнения
и выбор параллельной машины, на которой будет выполняться программа. Среда анализа программы и производительности показана справа.
сторона фигуры. Он включает в себя интегрированные инструменты TAU ,
поддержка профилирования и трассировки, а также интерфейсы для автономной работы
инструменты анализа, частично разработанные другими группами.
Набор инструментов TAU обеспечивает поддержку доступа к статическим
информация о программе, а также для запросов и анализа динамических
данные, полученные в результате выполнения программы. Пакет TAU с открытым исходным кодом Университета Орегона ( T uning и A nalysis U tilities) обеспечивает оценку производительности путем профилирования (создание отчетов о глобальной статистике) и отслеживания (как события в параллельных задачах взаимодействуют во времени) вашего кода. Используйте TAU, чтобы получить представление о производительности и поведении вашего кода: какие процедуры занимают больше всего времени, выявляя дисбаланс нагрузки при параллельном запуске.Функциональность TAU частично совпадает с VTune. Разница заключается в том, что VTune может отслеживать любой двоичный файл, тогда как TAU требует инструментария. Это означает, что TAU требует перекомпиляции вашего кода, что может быть громоздким. С другой стороны, вывод TAU легче понять, поскольку он относится к именам подпрограмм в вашем коде. TAU установлен на всех системах HPC TACC и управляется через систему Lmod / module. Для настройки и проверки среды TAU: Чтобы использовать TAU, вам необходимо перекомпилировать ваш код, используя некоторые оболочки компилятора TAU (скрипты).За кулисами эти скрипты выполняют этап инструментария от исходного кода к исходному, за которым следует регулярная компиляция. Скрипты компиляции TAU: Эти оболочки компилятора можно использовать непосредственно в командной строке или в файле makefile: Используйте команду « Для make-файла, который работает как с TAU, так и без него, используйте: За кулисами оболочки компилятора создают и выполняют простой make-файл, который включает соответствующие параметры make-файла из включаемого make-файла, хранящегося в переменной « После инструментирования / компиляции у вас есть обычный двоичный файл, который вы можете запустить с настройками MPI или OpenMP по мере необходимости. Затем запустите интерактивное или пакетное задание, используя этот новый двоичный файл. Управляйте и настраивайте вывод TAU с помощью следующих переменных среды: Настройте среду с помощью пакетного сценария или сеанса Затем запустите вашу программу как обычно. После завершения выполнения вы можете обработать и изучить профиль TAU и / или результаты трассировки. После запуска программы вы можете обрабатывать вывод TAU для двух вещей: просматривать статистику и анализировать данные трассировки. Пакет TAU включает два инструмента визуализации: ParaProf и Jumpshot. См. Раздел «Доступ к удаленному рабочему столу» на сайте TACC для получения инструкций по настройке визуальных подключений к ресурсам TACC. Внимание! К понятиям арксинус, арккосинус, арктангенс, арккотангенс учащийся народ относится с опаской. Не понимает он эти термины и, стало быть, не доверяет этой славной семейке.) А зря. Это очень простые понятия. Которые, между прочим, колоссально облегчают жизнь знающему человеку при решении тригонометрических уравнений! Сомневаетесь насчёт простоты? Напрасно.) Прямо здесь и сейчас вы в этом убедитесь. Разумеется, для понимания, неплохо бы знать, что такое синус, косинус, тангенс и котангенс. Да их табличные значения для некоторых углов… Хотя бы в самых общих чертах. Тогда и здесь проблем не будет. Итак, удивляемся, но запоминаем: арксинус, арккосинус, арктангенс и арккотангенс — это просто какие-то углы. Что означает выражение arcsin 0,4 ? Это угол, синус которого равен 0,4 ! Да-да. Это смысл арксинуса. Специально повторю: arcsin 0,4 — это угол, синус которого равен 0,4. И всё. Чтобы эта простая мысль сохранилась в голове надолго, я даже приведу разбивочку этого ужасного термина — арксинус: arc sin 0,4 Как пишется, так и слышится.) Почти. Приставка arc означает дуга (слово арка знаете?), т.к. древние люди вместо углов использовали дуги, но это сути дела не меняет. Запомните эту элементарную расшифровку математического термина! Тем более, для арккосинуса, арктангенса и арккотангенса расшифровка отличается только названием функции. Что такое arccos 0,8 ? Что такое arctg(-1,3) ? Что такое arcctg 12 ? Такая элементарная расшифровка позволяет, кстати, избежать эпических ляпов.) Например, выражение arccos1,8 выглядит вполне солидно. Начинаем расшифровку: arccos1,8 — это угол, косинус которого равен 1,8… Скока-скока!? 1,8!? Косинус не бывает больше единицы!!! Верно. Выражение arccos1,8 не имеет смысла. И запись такого выражения в какой-нибудь ответ изрядно повеселит проверяющего.) Элементарно, как видите.) У каждого угла имеется свой персональный синус и косинус. И почти у каждого — свой тангенс и котангенс. Стало быть, зная тригонометрическую функцию, можно записать и сам угол. Для этого и предназначены арксинусы, арккосинусы, арктангенсы и арккотангенсы. Далее я всю эту семейку буду называть уменьшительно — арки. Чтобы печатать меньше.) Внимание! Элементарная словесная и осознанная расшифровка арков позволяет спокойно и уверенно решать самые различные задания. А в непривычных заданиях только она и спасает. А можно переходить от арков к обычным градусам или радианам? — слышу осторожный вопрос.) Почему — нет!? Легко. И туда можно, и обратно. Более того, это иногда нужно обязательно делать. Арки — штука простая, но без них как-то спокойнее, правда?) Например: что такое arcsin 0,5? Вспоминаем расшифровку: arcsin 0,5 — это угол, синус которого равен 0,5. Теперь включаем голову (или гугл)) и вспоминаем, у какого угла синус равен 0,5? Синус равен 0,5 у угла в 30 градусов . Вот и все дела: arcsin 0,5 — это угол 30°. Можно смело записать: arcsin 0,5 = 30° Или, более солидно, через радианы: Всё, можно забыть про арксинус и работать дальше с привычными градусами или радианами. Если вы осознали, что такое арксинус, арккосинус… Что такое арктангенс, арккотангенс… То легко разберётесь, например, с таким монстром.) Несведущий человек отшатнётся в ужасе, да…) А сведущий вспомнит расшифровку: арксинус — это угол, синус которого… Ну и так далее. Если сведущий человек знает ещё и таблицу синусов… Таблицу косинусов. Таблицу тангенсов и котангенсов, то проблем вообще нет! Достаточно сообразить, что: Расшифрую, т.е. переведу формулу в слова: угол, тангенс которого равен 1 (arctg1) — это угол 45°. Или, что едино, Пи/4. Аналогично: и всё… Заменяем все арки на значения в радианах, всё посокращается, останется посчитать, сколько будет 1+1. Это будет 2.) Что и является правильным ответом. Вот таким образом можно (и нужно) переходить от арксинусов, арккосинусов, арктангенсов и арккотангенсов к обычным градусам и радианам. Это здорово упрощает страшные примеры! Частенько, в подобных примерах, внутри арков стоят отрицательные значения. Типа, arctg(-1,3), или, к примеру, arccos(-0,8)… Это не проблема. Вот вам простые формулы перехода от отрицательных значений к положительным: Нужно вам, скажем, определить значение выражения: Это можно и по тригонометрическому кругу решить, но вам не хочется его рисовать. Ну и ладно. Переходим от отрицательного значения внутри арккосинуса к положительному по второй формуле: Внутри арккосинуса справа уже положительное значение. То, что вы просто обязаны знать. Остаётся подставить радианы вместо арккосинуса и посчитать ответ: Вот и всё. С примерами 7 — 9 проблема? Ну да, есть там некоторая хитрость.) Все эти примеры, с 1-го по 9-й, тщательно разобраны по полочкам в Разделе 555. Что, как и почему. Со всеми тайными ловушками и подвохами. Плюс способы резкого упрощения решения. Кстати, в этом разделе много полезной информации и практических советов по тригонометрии в целом. И не только по тригонометрии. Очень помогает. Кстати, у меня есть ещё парочка интересных сайтов для Вас.) Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!) можно познакомиться с функциями и производными. Дополнительные материалы Пособия и тренажеры в интернет-магазине «Интеграл» для 10 класса от 1С Что будем изучать: 6. Примеры. Ребята, мы с вами уже научились решать уравнения для косинуса, давайте теперь научимся решать подобные уравнения и для синуса. Рассмотрим sin(x)= √3/2. Для решения этого уравнения требуется построить прямую y= √3/2 и посмотреть: в каких точках она пересекает числовую окружность. Видно, что прямая пересекает окружность в двух точках F и G. Эти точки и будут решением нашего уравнения. Переобозначим F как x1, а G как x2. Решение этого уравнения мы уже находили и получили: x1= π/3 + 2πk, Решить данное уравнение довольно просто, но как решить, например, уравнение Столкнувшись с подобной ситуацией, математики придумали новый символ – arcsin(x). Читается, как арксинус. Тогда решение нашего уравнения запишется так: x1= arcsin(5/6), x2= π -arcsin(5/6). И решение в общем виде: x= arcsin(5/6) + 2πk и x= π — arcsin(5/6) + 2πk. История происхождения нашего символа совершенно такая же, как и у arccos. Впервые символ arcsin появляется в работах математика Шерфера и известного французского ученого Ж.Л. Лагранжа. Несколько ранее понятие арксинус рассматривал Д. Бернули, правда записывал его другими символами. Общепринятыми эти символы стали лишь в конце XVIII столетия. Приставка «arc» происходит от латинского «arcus» (лук, дуга). Это вполне согласуется со смыслом понятия: arcsin x — это угол (а можно сказать и дуга), синус которого равен x. Если |а|≤ 1, то arcsin(a) – это такое число из отрезка [- π/2; π/2], синус которого равен а. Если |а|≤ 1, то уравнение sin(x)= a имеет решение: x= arcsin(a) + 2πk и Перепишем: x= π — arcsin(a) + 2πk = -arcsin(a) + π(1 + 2k). Ребята, посмотрите внимательно на два наших решения. Как думаете: можно ли их записать общей формулой? Заметим, что если перед арксинусом стоит знак «плюс», то π умножается на четное число 2πk, а если знак «минус», то множитель — нечетный 2k+1. Есть три случая, в которых предпочитают записывать решения более простым способом: sin(x)=0, то x= πk, sin(x)=1, то x= π/2 + 2πk, sin(x)=-1, то x= -π/2 + 2πk. Для любого -1 ≤ а ≤ 1 выполняется равенство: arcsin(-a)=-arcsin(a). Напишем таблицу значений косинуса наоборот и получим таблицу для арксинуса. 1. Вычислить: arcsin(√3/2). 2. Вычислить: arcsin(-1/2). 3. Вычислить: arcsin(0). 4. Решить уравнение: sin(x) = -√2/2. 5. Решить уравнение: sin(x) = 0. 6. Решить уравнение: sin(x) = 3/5. 7. Решить неравенство sin(x)
Решение: Синус — это ордината точки числовой окружности. Значит: нам надо найти такие точки, ордината которых меньше 0.7. Нарисуем прямую y=0.7. Она пересекает числовую окружность в двух точках. Неравенству y
Тогда решением неравенства будет: -π – arcsin(0.7) + 2πk Даны определения обратных тригонометрических функций и их графики. А также формулы, связывающие обратные тригонометрические функции, формулы сумм и разностей. Поскольку тригонометрические функции периодичны, то обратные к ним функции не однозначны. Так, уравнение y = sin
x
,
при заданном ,
имеет бесконечно много корней. Действительно, в силу периодичности синуса, если x
такой корень, то и x + 2πn (где n
целое) тоже будет корнем уравнения. Таким образом, обратные тригонометрические функции многозначны . Чтобы с ними было проще работать, вводят понятие их главных значений. Рассмотрим, например, синус: y = sin
x
.
Если ограничить аргумент x
интервалом ,
то на нем функция y = sin
x
монотонно возрастает. Поэтому она имеет однозначную обратную функцию, которую называют арксинусом: x = arcsin
y
. Если особо не оговорено, то под обратными тригонометрическими функциями имеют в виду их главные значения, которые определяются следующими определениями. Арксинус (y = arcsin
x
) — это функция, обратная к синусу (x = sin
y Арккосинус (y = arccos
x
) — это функция, обратная к косинусу (x = cos
y
), имеющая область определения и множество значений . Арктангенс (y = arctg
x
) — это функция, обратная к тангенсу (x = tg
y
), имеющая область определения и множество значений . Арккотангенс (y = arcctg
x
) — это функция, обратная к котангенсу (x = ctg
y
), имеющая область определения и множество значений . Графики обратных тригонометрических функций получаются из графиков тригонометрических функций зеркальным отражением относительно прямой y = x
.
См. разделы Синус, косинус , Тангенс, котангенс . y = arcsin
x Здесь следует особо обратить внимание на интервалы, для которых справедливы формулы. arcsin(sin
x)
= x
при arctg(tg
x)
= x
при при и при и при и при и при при Функции sin, cos, tg и ctg всегда сопровождаются арксинусом, арккосинусом, арктангенсом и арккотангенсом. Одно является следствием другого, а пары функций одинаково важны для работы с тригонометрическими выражениями. Рассмотрим рисунок единичной окружности, на котором графически отображено значений тригонометрических функций. Если вычислить arcs OA, arcos OC, arctg DE и arcctg MK, то все они будут равны значению угла α. Формулы, приведенные ниже, отражают взаимосвязь основных тригонометрических функций и соответствующих им арков. Чтобы больше понять о свойствах арксинуса, необходимо рассмотреть его функцию. График имеет вид асимметричной кривой, проходящей через центр координат. Свойства арксинуса: Если сопоставить графики sin и arcsin , у двух тригонометрических функций можно найти общие закономерности. Arccos числа а — это значение угла α, косинус которого равен а. Кривая y = arcos x зеркально отображает график arcsin x, с той лишь разницей, что проходит через точку π/2 на оси OY. Рассмотрим функцию арккосинуса более подробно: Некоторые свойства арккосинуса совпадают с функцией косинуса. Возможно, школьникам покажется излишним такое «подробное» изучение «арков». Однако, в противном случае, некоторые элементарные типовые задания ЕГЭ могут ввести учащихся в тупик. Задание 1. Укажите функции изображенные на рисунке. Ответ: рис. 1 – 4, рис.2 — 1. В данном примере упор сделан на мелочах. Обычно ученики очень невнимательно относятся к построению графиков и внешнему виду функций. Действительно, зачем запоминать вид кривой, если ее всегда можно построить по расчетным точкам. Не стоит забывать, что в условиях теста время, затраченное на рисунок для простого задания, потребуется для решения более сложных заданий. Arctg числа a – это такое значение угла α, что его тангенс равен а. Если рассмотреть график арктангенса, можно выделить следующие свойства: Приведем краткий сравнительный анализ tg x и arctg x в виде таблицы. Arcctg числа a — принимает такое значение α из интервала (0; π), что его котангенс равен а. Свойства функции арккотангенса: Сопоставить ctg x и arctg x очень просто, нужно лишь сделать два рисунка и описать поведение кривых. Задание 2. Соотнести график и форму записи функции. Если рассуждать логически, из графиков видно, что обе функции возрастающие. Следовательно, оба рисунка отображают некую функцию arctg. Из свойств арктангенса известно, что y=0 при x = 0, Ответ: рис. 1 – 1, рис. 2 – 4. Ранее нами уже была выявлена взаимосвязь между арками и основными функциями тригонометрии. Данная зависимость может быть выражена рядом формул, позволяющих выразить, например, синус аргумента, через его арксинус, арккосинус или наоборот. Знание подобных тождеств бывает полезным при решении конкретных примеров. Также существуют соотношения для arctg и arcctg: Еще одна полезная пара формул, устанавливает значение для суммы значений arcsin и arcos, а также arcctg и arcctg одного и того же угла. Задания по тригонометрии можно условно разделить на четыре группы: вычислить числовое значение конкретного выражения, построить график данной функции, найти ее область определения или ОДЗ и выполнить аналитические преображения для решения примера. При решении первого типа задач необходимо придерживаться следующего плана действий: При работе с графиками функций главное – это знание их свойств и внешнего вида кривой. Для решения тригонометрических уравнений и неравенств необходимы таблицы тождеств. Чем больше формул помнит школьник, тем проще найти ответ задания. Допустим в ЕГЭ необходимо найти ответ для уравнения типа: Если правильно преобразовать выражение и привести к нужному виду, то решить его очень просто и быстро. Для начала, перенесем arcsin x в правую часть равенства. Если вспомнить формулу arcsin (sin α) = α , то можно свести поиск ответов к решению системы из двух уравнений: Ограничение на модель x возникло, опять таки из свойств arcsin: ОДЗ для x [-1; 1]. При а ≠0, часть сиcтемы представляет собой квадратное уравнение с корнями x1 = 1 и x2 = — 1/a. При a = 0, x будет равен 1. Представлен способ вывода формул для обратных тригонометрических функций. Получены формулы для отрицательных аргументов, выражения, связывающие арксинус, арккосинус, арктангенс и арккотангенс. Указан способ вывода формул суммы арксинусов, арккосинусов, арктангенсов и арккотангенсов. Вывод формул для обратных тригонометрических функций прост, но требует контроля за значениями аргументов прямых функций. Это связано с тем, что тригонометрические функции периодичны и, поэтому, обратные к ним функции многозначны. Если особо не оговорено, то под обратными тригонометрическими функциями подразумевают их главные значения. Для определения главного значения, область определения тригонометрической функции сужают до интервала, на котором она монотонна и непрерывна. Вывод формул для обратных тригонометрических функций основывается на формулах тригонометрических функций и свойствах обратных функций как таковых. Свойства обратных функций можно разбить на две группы. В первую группу входят формулы, справедливые на всей области определения обратных функций: Во вторую группу входят формулы, справедливые только на множестве значений обратных функций. Если переменная x
не попадает в указанный выше интервал, то ее следует привести к нему, применяя формулы тригонометрических функций (далее n
— целое): Например, если известно, что то Легко убедиться, что при π — x
попадает в нужный интервал. Для этого умножим на -1
: и прибавим π
:
или Все правильно. Применяя указанные выше формулы и свойства тригонометрических функций, получаем формулы обратных функций отрицательного аргумента. arcsin(-
x)
=
arcsin(-sin arcsin
x)
=
arcsin(sin(-arcsin
x))
=
— arcsin
x Поскольку то умножив на -1
, имеем: или Аналогично для остальных функций. arctg(-
x)
=
arctg(-tg arctg
x)
=
arctg(tg(-arctg
x))
=
— arctg
x arcctg(-
x)
=
arcctg(-ctg arcctg
x)
=
arcctg(ctg(π-arcctg
x))
=
π — arcctg
x Выразим арксинус через арккосинус. Формула справедлива при Эти неравенства выполняются, поскольку Чтобы убедиться в этом, умножим неравенства на -1
: и прибавим π/2
:
или Все правильно. Аналогично выражаем арктангенс через арккотангенс. Поступаем аналогичным способом. Аналогичным способом, получим формулу суммы арксинусов. Установим пределы применимости формулы. Чтобы не иметь дела с громоздкими выражениями, введем обозначения: X = arcsin
x
,
Y = arcsin
y
.
Формула применима при Теперь рассмотрим случай x > 0 и y > 0 ,
или X > 0 и Y > 0 .
Тогда условие применимости формулы заключается в выполнении неравенства: .
Поскольку косинус монотонно убывает при значениях аргумента в интервале от 0 ,
до π
,
то возьмем косинус от левой и правой части этого неравенства и преобразуем выражение: Итак, полученная формула справедлива при или . Теперь рассмотрим случай x > 0, y > 0
и x 2 + y 2 > 1 .
Здесь аргумент синуса принимает значения: .
Его нужно привести к интервалу области значения арксинуса : Итак, при и. Заменив x
и y
на — x
и — y
,
имеем при и. при и. при и. Итак, мы получили следующие выражения для суммы арксинусов: при или ; при и ; при и . Насчёт свойств функций. Правильно ли я выполнил преобразование и вообще верно ли равенство?[tex]y=k*f(x+q)+c\\kf(x+q)+c=f(kx+kq)+c[/tex]Все переменные
… уравнении — действительные числа.Если что-то не так, подправьте, пожалуйстаupd.В задании: Доказать,… Откуда здесь 12?
(2 — a)³ = 8 — 12a + 6a² — a³ указати найменьше значення функції y=2|x|+3 Первый игральный кубик обычный, а на гранях второго кубика нет чётных чисел, а нечётные числа 1, 3 и 5 встречаются по два раза. В остальном кубики оди
… наковые. Один случайно выбранный кубик бросают два раза. Известно, что в каком-то порядке выпали 3 и 5 очков. Какова вероятность того, что бросали второй кубик? В викторине участвуют 6 команд. Все команды разной силы, и в каждой встрече выигрывает та команда, которая сильнее. В первом раунде встречаются две сл
… учайно выбранные команды. Ничья невозможна. Проигравшая команда выбывает из викторины, а победившая команда играет со следующим случайно выбранным соперником. Известно, что в первых трёх играх победила команда А. Какова вероятность того, что эта команда выиграет четвёртый раунд? Стрелок в тире стреляет по мишени до тех пор, пока не поразит её. Известно, что он попадает в цель с вероятностью 0,2 при каждом отдельном выстреле. С
… колько патронов нужно дать стрелку, чтобы он поразил цель с вероятностью не менее 0,6? Симметричную монету бросают 10 раз. Во сколько раз вероятность события «выпадет ровно 5 орлов» больше вероятности события «выпадет ровно 4 орла»? Первый член последовательности целых чисел равен 0. Каждый следующий член последовательности с вероятностью р = 0,8 на единицу больше предыдущего и с
… вероятностью 1-р на единицу меньше предыдущего. Какова вероятность того, что какой-то член этой последовательности окажется равен -1? Найдите значение выражения 3×4¹⁰-5×2¹⁹÷2¹⁵ Докажите, что при всех допустимых значениях переменных значение выражения не зависит от значения переменных: Свойства функций arcsin x + arccos x = /2 arctg x + arcctg x = /2 Арксинус иногда обозначают так: График функции y = arcsin
x График арксинуса получается из графика синуса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, область значений ограничивают интервалом ,
на котором функция монотонна. Такое определение называют главным значением арксинуса. Арккосинус иногда обозначают так: График функции y = arccos
x График арккосинуса получается из графика косинуса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, область значений ограничивают интервалом ,
на котором функция монотонна. Такое определение называют главным значением арккосинуса. Функция арксинус является нечетной: Функция арккосинус не является четной или нечетной: Функции арксинус и арккосинус непрерывны на своей области определения (см. доказательство непрерывности). Основные свойства арксинуса и арккосинуса представлены в таблице. В данной таблице представлены значения арксинусов и арккосинусов, в градусах и радианах, при некоторых значениях аргумента. ≈ 0,7071067811865476 при и при и при и при и при при ; Производные высших порядков : См. Вывод производных высших порядков арксинуса и арккосинуса > > > Делаем подстановку x = sin
t
.
Интегрируем по частям, учитывая что -π/2
≤ t ≤ π/2 ,
cos
t ≥ 0 : Выразим арккосинус через арксинус: При |x| 1 имеет место следующее разложение: Обратными к арксинусу и арккосинусу являются синус и косинус , соответственно. Следующие формулы справедливы на всей области определения: Следующие формулы справедливы только на множестве значений арксинуса и арккосинуса: Использованная литература: (круговые функции, аркфункции) — математические функции, которые являются обратными к тригонометрическим функциям . Арккосинус , обратная функция к cos (x = cos y), y = arccos x определен при и имеет множество значений . Другими словами возвращает угол по значению его cos . Арккосинус (обозначение: arccos x ; arccos x — это угол , косинус которого равняется x и так далее). Функция y = cos x непрерывна и ограничена на всей своей числовой прямой. Функция y = arccos x является строго убывающей. Дана функция y = cos x . На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие y = arccos x функцией не является. Поэтому мы рассмотрим отрезок, на котором она строго убывает и принимает все свои значения — . На этом отрезке y = cos x строго монотонно убывает и принимает все свои значения только один раз, а значит, на отрезке существует обратная функция y = arccos x , график которой симметричен графику y = cos x на отрезке относительно прямой y = x . Поскольку тригонометрические функции периодичны, то обратные к ним функции не однозначны. Так, уравнение y = sin
x
,
при заданном ,
имеет бесконечно много корней. Действительно, в силу периодичности синуса, если x
такой корень, то и x + 2πn (где n
целое) тоже будет корнем уравнения. Таким образом, обратные тригонометрические функции многозначны . Чтобы с ними было проще работать, вводят понятие их главных значений. Рассмотрим, например, синус: y = sin
x
.
Если ограничить аргумент x
интервалом ,
то на нем функция y = sin
x
монотонно возрастает. Поэтому она имеет однозначную обратную функцию, которую называют арксинусом: x = arcsin
y
. Если особо не оговорено, то под обратными тригонометрическими функциями имеют в виду их главные значения, которые определяются следующими определениями. Арксинус (y = arcsin
x
) — это функция, обратная к синусу (x = sin
y Графики обратных тригонометрических функций получаются из графиков тригонометрических функций зеркальным отражением относительно прямой y = x
.
См. разделы Синус, косинус , Тангенс, котангенс . y = arcsin
x Здесь следует особо обратить внимание на интервалы, для которых справедливы формулы. arcsin(sin
x)
= x
при arctg(tg
x)
= x
при при и при и при и при и при при при при при при Использованная литература: Функции sin, cos, tg и ctg всегда сопровождаются арксинусом, арккосинусом, арктангенсом и арккотангенсом. Одно является следствием другого, а пары функций одинаково важны для работы с тригонометрическими выражениями. Рассмотрим рисунок единичной окружности, на котором графически отображено значений тригонометрических функций. Если вычислить arcs OA, arcos OC, arctg DE и arcctg MK, то все они будут равны значению угла α. Формулы, приведенные ниже, отражают взаимосвязь основных тригонометрических функций и соответствующих им арков. Чтобы больше понять о свойствах арксинуса, необходимо рассмотреть его функцию. График имеет вид асимметричной кривой, проходящей через центр координат. Свойства арксинуса: Если сопоставить графики sin и arcsin , у двух тригонометрических функций можно найти общие закономерности. Arccos числа а — это значение угла α, косинус которого равен а. Кривая y = arcos x зеркально отображает график arcsin x, с той лишь разницей, что проходит через точку π/2 на оси OY. Рассмотрим функцию арккосинуса более подробно: Некоторые свойства арккосинуса совпадают с функцией косинуса. Возможно, школьникам покажется излишним такое «подробное» изучение «арков». Однако, в противном случае, некоторые элементарные типовые задания ЕГЭ могут ввести учащихся в тупик. Задание 1. Укажите функции изображенные на рисунке. Ответ: рис. 1 – 4, рис.2 — 1. В данном примере упор сделан на мелочах. Обычно ученики очень невнимательно относятся к построению графиков и внешнему виду функций. Действительно, зачем запоминать вид кривой, если ее всегда можно построить по расчетным точкам. Не стоит забывать, что в условиях теста время, затраченное на рисунок для простого задания, потребуется для решения более сложных заданий. Arctg числа a – это такое значение угла α, что его тангенс равен а. Если рассмотреть график арктангенса, можно выделить следующие свойства: Приведем краткий сравнительный анализ tg x и arctg x в виде таблицы. Arcctg числа a — принимает такое значение α из интервала (0; π), что его котангенс равен а. Свойства функции арккотангенса: Сопоставить ctg x и arctg x очень просто, нужно лишь сделать два рисунка и описать поведение кривых. Задание 2. Соотнести график и форму записи функции. Если рассуждать логически, из графиков видно, что обе функции возрастающие. Следовательно, оба рисунка отображают некую функцию arctg. Из свойств арктангенса известно, что y=0 при x = 0, Ответ: рис. 1 – 1, рис. 2 – 4. Ранее нами уже была выявлена взаимосвязь между арками и основными функциями тригонометрии. Данная зависимость может быть выражена рядом формул, позволяющих выразить, например, синус аргумента, через его арксинус, арккосинус или наоборот. Знание подобных тождеств бывает полезным при решении конкретных примеров. Также существуют соотношения для arctg и arcctg: Еще одна полезная пара формул, устанавливает значение для суммы значений arcsin и arcos, а также arcctg и arcctg одного и того же угла. Задания по тригонометрии можно условно разделить на четыре группы: вычислить числовое значение конкретного выражения, построить график данной функции, найти ее область определения или ОДЗ и выполнить аналитические преображения для решения примера. При решении первого типа задач необходимо придерживаться следующего плана действий: При работе с графиками функций главное – это знание их свойств и внешнего вида кривой. Для решения тригонометрических уравнений и неравенств необходимы таблицы тождеств. Чем больше формул помнит школьник, тем проще найти ответ задания. Допустим в ЕГЭ необходимо найти ответ для уравнения типа: Если правильно преобразовать выражение и привести к нужному виду, то решить его очень просто и быстро. Для начала, перенесем arcsin x в правую часть равенства. Если вспомнить формулу arcsin (sin α) = α , то можно свести поиск ответов к решению системы из двух уравнений: Ограничение на модель x возникло, опять таки из свойств arcsin: ОДЗ для x [-1; 1]. При а ≠0, часть сиcтемы представляет собой квадратное уравнение с корнями x1 = 1 и x2 = — 1/a. При a = 0, x будет равен 1. Обратные тригонометрические функции (круговые функции, аркфункции) — математические функции, которые являются обратными к тригонометрическим функциям . Арксинус (обозначается как arcsin x ; arcsin x — это угол, sin его равняется x ). Арксинус (y = arcsin x ) — обратная тригонометрическая функция к sin (x = sin y ), которая имеет область определения и множество значений . Другими словами возвращает угол по значению его sin . Функция y=sin x непрерывна и ограничена на всей своей числовой прямой. Функция y=arcsin x — строго возрастает. Есть функция y = sin x . На всей своей области определения она кусочно-монотонная, таким образом, обратное соответствие y = arcsin x не является функцией. Поэтому рассматриваем отрезок, на котором она только возрастает и принимает каждое значение области значений — . Т.к. для функции y = sin x на интервале все значения функции получается при только одном значении аргумента, значит, на этом отрезке есть обратная функция y = arcsin x , у которой график является симметричным графику функции y = sin x на отрезке относительно прямой y = x . вТригонометрическая функцияДобавить передarc, Означает ихОбратная функция f-1 (x). То есть текущий угол можно получить из тригонометрической функции. Дата публикации: . Что будем изучать: Ребята, мы с вами уже изучили функцию Y=cos(X), построили ее график и решали некоторые уравнения, например cos(x)= 1/2. Для решения этого уравнения требовалось провести прямую x= 1/2 и
посмотреть, в каких точках она пересекает числовую окружность. Видно что прямая пересекает окружность в двух точках F и G. Эти точки и являются решением уравнения. Переобозначим F как x1, а G — как x2. Решение уравнения мы нашли довольно легко и определили, что x1 = π/3 + 2πk, а x2 = -π/3 + 2πk. Решить данное уравнение довольно просто, но как решить, например, уравнение cos(x)=4/7. Очевидно, что решением уравнения будут две точки, но какие значения будут соответствовать решению на числовой окружности? Давайте внимательно посмотрим на уравнение cos(x)=4/7. Как мы и говорили, решениями нашего уравнения будут две точки: F=x1+2πk и G=x2+2πk, но, что это за точки? Много лет назад столкнувшись с этой проблемой математики решили, что надо придумать некоторый способ описания решения на математическом языке. И был придуман новый символ – arccos(x). Будем читать как арккосинус. Тогда решения нашего уравнения запишутся как: x1=arccos(4/7) и x2=-arccos(4/7). И решение в общем виде: x=arccos(4/7) + 2πk и x=-arccos(4/7) + 2πk. Арккосинус — это угол (длина дуги AF, AG), косинус которого равен 4/7. Символ arccos появляется впервые в 18 веке в работах математика Шерфера и известного французского ученого Жозефа Луи Лагранжа, портрет которого вы видите на этой странице. Несколько ранее понятие арккосинус уже рассматривал Д. Бернули, но записывал его совсем другими символами. Общепринятыми эти символы стали лишь в конце XVIII столетия. Приставка «arc» происходит от латинского «arcus» (лук, дуга), что вполне согласуется со смыслом понятия: Если |а|≤ 1, то arccos(a) – это такое число из отрезка [0; π], косинус которого равен а. Если |а|≤ 1, то уравнение cos(x)=a имеет решение: x=±arccos(a) + 2πk Есть три случая, в которых предпочитают записывать решения более простым способом: cos(x)=0, то x= π/2 + πk cos(x)=1, то x= 2πk cos(x)=-1, то x= π + 2πk Также стоит записать важное равенство: Для любого -1 ≤ а ≤ 1 выполняется равенство: arccos(a) + arccos(-a) = π; при решение заданий удобнее использовать: arccos(-a) = π — arccos(a), где -1 ≤ а ≤ 1 Напишем таблицу значений косинуса наоборот и получим таблицу для арккосинуса 1. Найти значение функции arccos(-√3/2). 2. Найти значение функции arccos(√2/2). 3. Найти значение функции arccos(1). 4. Решить неравенство cos(x)> -0.3. Arccosine, записываемый как arccos или cos-1 (не путать с), является функцией обратного косинуса. Косинус имеет обратное значение только в ограниченной области 0≤x≤π. На рисунке ниже часть графика, выделенная красным, показывает часть графика cos (x), которая имеет инверсию. Область должна быть ограничена, потому что для того, чтобы функция имела инверсию, функция должна быть взаимно однозначной, что означает, что ни одна горизонтальная линия не может пересекать график функции более одного раза.Поскольку косинус является периодической функцией, без ограничения области определения, горизонтальная линия будет периодически пересекать функцию бесконечно много раз. Одно из свойств обратных функций состоит в том, что если точка (a, b) находится на графике функции f, точка (b, a) находится на графике ее обратной функции. Это фактически означает, что график обратной функции является отражением графика функции через линию y = x. График y = arccos (x) показан ниже. Как видно из рисунка, y = arccos (x) является отражением cos (x) в ограниченной области 0≤x≤π через линию y = x.Область arccos (x), -1≤x≤1, является диапазоном cos (x), а ее диапазон, 0≤x≤π, является областью cos (x). Ниже приведен калькулятор, позволяющий определить значение arccos числа от -1 до 1 или значение косинуса угла. Хотя мы можем найти значение арккозинуса для любого значения x в интервале [-1, 1], существуют определенные углы, которые часто используются в тригонометрии (0 °, 30 °, 45 °, 60 °, 90 ° и их кратные и радианные эквиваленты), значения косинуса и арккосинуса которых, возможно, стоит запомнить.Ниже приведена таблица, показывающая эти углы (θ) в градусах и их соответствующие значения косинуса, cos (θ). Один из способов, который может помочь запомнить эти значения, — это выразить все значения cos (θ) в виде дробей, содержащих квадратный корень. Начиная с 0 ° и до 90 °, cos (0 °) = 1 =. Последующие значения cos (30 °), cos (45 °), cos (60 °) и cos (90 °) следуют шаблону, так что при использовании значения cos (0 °) в качестве эталона для нахождения значений косинуса для последующих углов, мы просто уменьшаем число под знаком корня в числителе на 1, как показано ниже: С 90 ° до 180 ° вместо этого мы увеличиваем число под корнем на 1, но также должны учитывать квадрант, в котором находится угол.Косинус отрицателен во втором и третьем квадрантах, поэтому значения будут равными, но отрицательными. В квадрантах I и IV значения будут положительными. Этот шаблон периодически повторяется для соответствующих угловых измерений. После того, как мы запомнили значения или если у нас есть какая-то ссылка, становится относительно просто распознать и определить значения косинуса или арккосинуса для специальных углов. Как правило, функции и их обратные показывают взаимосвязь f (f -1 (x)) = x и f -1 (f (x)) = x при условии, что x находится в области определения функции.То же самое верно для cos (x) и arccos (x) в их соответствующих ограниченных областях: cos (arccos (x)) = x, для всех x в [-1, 1] и arccos (cos (x)) = x для всех x в [0, π] Эти свойства позволяют нам оценивать состав тригонометрических функций. Если x находится в пределах домена, вычислить композицию арккосинуса и косинуса относительно просто. Примеры: 1. 2. Если x не находится в пределах домена, нам нужно определить опорный угол, а также соответствующий квадрант. Учитывая arccos (cos ()), мы не можем оценить это, как мы делали выше, потому что x не находится в пределах [0, π], поэтому решение не может быть. Чтобы оценить это, нам нужно сначала определить cos (), прежде чем использовать arccos: 3. В приведенном выше примере опорный угол равен, и cos () равен, но поскольку он лежит в квадранте III, его косинус отрицателен, и единственный угол, косинус которого равен, который находится в пределах области arccos (x), равен. Мы также можем составлять композиции, используя все другие тригонометрические функции: синус, тангенс, косеканс, секанс и котангенс. Пример: Найдите грех (arccos ()). Так как это не одно из соотношений для специальных углов, мы можем использовать прямоугольный треугольник, чтобы найти значение этой композиции. Учитывая arccos () = θ, мы можем найти, что cos (θ) =. Правый треугольник ниже показывает θ и отношение его смежной стороны к гипотенузе треугольника. Чтобы найти синус, нам нужно найти противоположную сторону, так как sin (θ) =. Пусть a будет длиной противоположной стороны. Используя теорему Пифагора, а 2 + 12 2 = 13 2 а 2 + 144 = 169 а 2 = 25 а = 5 и грех (arccos ()) = грех (θ) = Тот же процесс можно использовать с выражением переменной. Пример: Найдите загар (arccos (4x)). Учитывая arccos (4x) = θ, мы можем найти, что cos (θ) = и построить следующий прямоугольный треугольник: Чтобы найти касательную, нам нужно найти противоположную сторону, так как tan (θ) =. Пусть b — длина противоположной стороны. Используя теорему Пифагора, (4x) 2 + b 2 = 1 2 16x 2 + b 2 = 1 b 2 = 1 — 16x 2 б = и tan (arccos (4x)) = tan (θ) =, где — Arccosine также можно использовать для решения тригонометрических уравнений, включающих функцию косинуса. Пример: Решите следующие тригонометрические уравнения относительно x, где 0≤x <2π. 1. 2cos (x) = 2cos (x) = cos (x) = x = arccos () Косинус отрицателен в квадрантах II и III, поэтому есть два решения: x = и x =. Это единственные два угла в пределах 0≤x <2π, значение косинуса которых равно. 2. 6cos 2 (x) + 9cos (x) — 36 = 0 6cos 2 (x) + 9sin (x) — 6 = 0 (6cos (x) — 3) (cos (x) + 2) = 0 6cos (x) — 3 = 0 или cos (x) + 2 = 0 cos (x) = или cos (x) = -2 x = arccos () или x = arccos (-2) Решение относительно x = arccos (), x = или Мы не можем найти x = arccos (-2), потому что оно не определено, поэтому x = или являются единственными решениями. М. Борна В разделе Тригонометрические функции любого угла мы решали вопросы типа «Найдите 2 угла, косинус которых равен 0,7». В этом вопросе использовалась кнопка cos -1 на наших калькуляторах. Мы нашли cos -1 0,7, а затем рассмотрели квадранты, в которых косинус был положительным. Помните, что число, которое мы получаем при нахождении функции обратного косинуса, cos -1 , представляет собой угол .-1`, если говорить об обратной косинусной функции.] Давайте сначала вспомним график `y = cos \ x` (который мы встречали в Graph of y = a cos x), чтобы мы могли видеть, откуда берется график` y = arccos \ x`. График y = cos x . Теперь мы выбираем часть этого графика от x = 0 до x = π , показанную здесь заштрихованной частью: График y = cos x с заштрихованной частью `0 График , инверсный косинуса x , находится путем отражения выбранной части графика `cos x` через линию` y = x`. График y = cos x и линия `y = x`. Теперь отразим каждую точку на этой части кривой cos x через линию y = x (я показал только несколько отражаемых типичных точек). Точки отражения на кривой проходят через линию `y = x`. Результат — график `y = arccos x`: См. Анимацию этого процесса здесь: Графические анимации обратной тригонометрической функции. Вот и все, что касается графика — он не выходит за рамки того, что вы видите здесь. (Если бы это было так, было бы несколько значений y для каждого значения x , и тогда у нас больше не было бы функции.) Я указал «начальную» и «конечную» точки, `(-1 , pi) `и` (1,0) `с точками. ПРИМЕЧАНИЕ 1: Метки осей также были отражены. То есть теперь есть обычные числа по оси x и кратные 0.5pi по оси y . ПРИМЕЧАНИЕ 2: Вы также увидите «arccos», записанное как «« acos »« », особенно в компьютерном программировании. Область (возможные значения x ) arccos x — это -1 ≤ х ≤ 1 Диапазон (из значений y для графика) для arccos x составляет 0 ≤ arccos x ≤ π Мы определяем функцию обратного синуса как `y = arcsin \ x` для` -pi / 2 <= y <= pi / 2` , где y — угол, синус которого равен x .Это означает, что `x = sin y` Давайте сначала посмотрим на график y = sin x , а затем построим кривую y = arcsin x . График y = sin x с выделенной частью от «-pi / 2» до «pi / 2». Как мы делали ранее, если мы отразим указанную часть y = sin x (часть между `x = -pi / 2` и` x = pi / 2`) через линию y = x , получаем график y = arcsin x : Еще раз: то, что вы видите, — это то, что вы получаете.График не выходит за указанные границы x и y . Я обозначил точки «начало» и «конец». Область (возможные значения x ) для arcsin x — это -1 ≤ х ≤ 1 Диапазон (из значений y для графика) для arcsin x составляет Посмотрите анимацию этого процесса здесь: Обратные тригонометрические функции графической анимации. Напоминаем, что вот график y = tan x , который мы встречали ранее на графиках tan, cot, sec и csc. Отражая заштрихованную часть графика (от `x = -pi / 2` до` pi / 2`) в строке y = x , мы получаем график y = arctan x : График `y =» arctan «\ x`. На этот раз график выходит за пределы того, что вы видите, как в отрицательном, так и в положительном направлениях x , и он не пересекает пунктирные линии (асимптоты при `y = -pi / 2` и` y = pi / 2`). Домен (возможные значения x ) для arctan x равен Все значения x Диапазон (из значений y для графика) для arctan x равен `-π / 2 Используя калькулятор в радианах, получаем: arcsin 0,6294 = sin -1 (0.6294) = 0,6808 arcsin (-0,1568) = sin -1 (-0,1568) = -0,1574 arccos (-0,8026) = cos -1 (-0,8026) = 2,5024 арктан (-1,9268) = загар -1 (-1,9268) = -1,0921 Обратите внимание, что калькулятор выдаст значения
которые находятся в пределах определенного диапазона для каждой функции. Ответы в каждом случае: углов (в радианах). График y = sec x , который мы встречали ранее на графиках tan, cot, sec и csc: График y = arcsec x получен путем отражения заштрихованной части приведенной выше кривой в линии y = x : График `y =» arcsec «\ x`. Кривая определяется вне участка между -1 и 1. Я обозначил «начальные» точки `(-1, pi)` и `(1,0)` точками. Домен «arc» sec \ x` равен Все значения x , кроме -1 < x <1 Диапазон угловых секунд x равно 0 ≤ arcsec x ≤ π , `» arcsec «сек \ x ≠ π / 2` График y = csc x , который мы встречали ранее на графиках tan, cot, sec и csc, выглядит так: Обратите внимание, что нет значений y между -1 и 1. Теперь для графика y = arccsc x , который мы получаем, отражая заштрихованную часть кривой выше в линии y = x : График `y =» arccsc «\ x`. График не определен между -1 и 1, но простирается оттуда в отрицательном и положительном направлениях x . Домен arccsc x равен Все значения x , кроме -1 < x <1 Диапазон arccsc x равен `-π / 2 ≤» arc «csc \ x ≤ π / 2,` arccsc x ≠ 0 График y = cot x , который мы встречали ранее на графиках tan, cot, sec и csc, выглядит следующим образом: Взяв выделенную часть, как указано выше, и отразив ее в линии y = x , мы получим график y = arccot x : График `y =» arccot »\ x`. График простирается в отрицательном и положительном направлениях x (он не останавливается на -8 и 8, как показано на графике). Итак, домен arccot x : Все значения x Диапазон arccot x равен 0 Некоторые учебники по математике (и некоторые уважаемые математические программы, например,г. Mathematica) рассматривают следующее как область y = детская кроватка x , которую следует использовать: Это даст следующее при отражении в строке y = x : График `y =» arccot »\ x`; альтернативный взгляд. И снова график расширяется в отрицательном и положительном направлениях x . Домен arccot x также будет: Все значения x Используя эту версию, диапазон arccot x будет: `-π / 2 arccot x ≠ 0) См. Обсуждение этого вопроса по адресу: Какой правильный график arccot x ?.(-1) (- 1) = — pi / 4` `cos (-pi / 4) = 1 / 2sqrt (2)` Функция arccos позволяет вычислять арккосинус числа.
Функция арккосинуса — это функция, обратная функции косинуса. Функция arccosine является обратной функцией
функция косинуса,
Он вычисляет арккосинус числа онлайн . Число, к которому вы хотите применить функцию arccosine fonction, должно принадлежать диапазону [-1,1]. Чтобы вычислить арккосинус числа, просто введите число и примените функция arccos .
Таким образом, для при вычислении арккосинус числа, следующего за 0,4,
ты должен войти
arccos (`0.2) `. arccos (x), где x — число. 2)` Калькулятор первообразных позволяет вычислить первообразную функции арккосинуса.2) ` Калькулятор пределов позволяет вычислить пределы функции арккосинуса. Предел для arccos (x) — limit_calculator (`» arccos «(x)`) Функция , обратная арккосинусу , является функцией косинуса, обозначенной как cos. Графический калькулятор может построить функцию арккосинуса в интервале ее определения. Арккосинус косинуса x. Поскольку косинус периодический, арккосинус косинуса x равен x
плюс 2kπ, если k — целое число k ∈ℤ: В настоящее время у нас есть около 945 калькуляторов, таблиц преобразования и полезных онлайн-инструментов и программных функций для студентов, преподавателей и преподавателей, дизайнеров и просто для всех. На этой странице вы можете найти финансовые калькуляторы, ипотечные калькуляторы, калькуляторы для кредитов, калькуляторы для автокредитов и калькуляторы лизинга, калькуляторы процентов, калькуляторы платежей, пенсионные калькуляторы, калькуляторы амортизации, инвестиционные калькуляторы, калькуляторы инфляции, финансовые калькуляторы, калькуляторы подоходного налога. , калькуляторы сложных процентов, калькулятор заработной платы, калькулятор процентной ставки, калькулятор налога с продаж, калькуляторы фитнеса и здоровья, калькулятор BMI, калькуляторы калорий, калькулятор телесного жира, калькулятор BMR, калькулятор идеального веса, калькулятор темпа, калькулятор беременности, калькулятор зачатия беременности, срок родов калькулятор, математические калькуляторы, научный калькулятор, калькулятор дробей, процентные калькуляторы, генератор случайных чисел, треугольный калькулятор, калькулятор стандартного отклонения, другие калькуляторы, калькулятор возраста, калькулятор даты, калькулятор времени, калькулятор часов, калькулятор GPA, калькулятор оценок, конкретный калькулятор, подсеть калькулятор, генерация паролей калькулятор преобразования и многие другие инструменты, а также для редактирования и форматирования текста, загрузки видео с Facebok (мы создали один из самых известных онлайн-инструментов для загрузки видео с Facebook).Мы также предоставляем вам онлайн-загрузчики для YouTube, Linkedin, Instagram, Twitter, Snapchat, TikTok и других социальных сетей (обратите внимание, что мы не размещаем видео на своих серверах. Все загружаемые вами видео загружаются с Facebook, YouTube, Linkedin, CDN в Instagram, Twitter, Snapchat, TikTok. Мы также специализируемся на сочетаниях клавиш, кодах ALT для Mac, Windows и Linux и других полезных советах и инструментах (как писать смайлы в Интернете и т. Д.) В Интернете есть много очень полезных бесплатных инструментов, и мы будем рады, если вы поделитесь нашей страницей с другими или отправите нам какие-либо предложения по другим инструментам, которые придут вам в голову.Также, если вы обнаружите, что какой-либо из наших инструментов не работает должным образом или вам нужен лучший перевод — сообщите нам об этом. Наши инструменты сделают вашу жизнь проще или просто помогут вам выполнять свою работу или обязанности быстрее и эффективнее. Это наиболее часто используемые пользователями во всем мире. И мы все еще развиваемся. Наша цель — стать универсальным сайтом для людей, которым нужно быстро производить расчеты или которым нужно быстро найти ответ на базовые конверсии. Кроме того, мы считаем, что Интернет должен быть источником бесплатной информации. Таким образом, все наши инструменты и услуги полностью бесплатны и не требуют регистрации. Мы кодировали и разрабатывали каждый калькулятор индивидуально и подвергали каждый строгому всестороннему тестированию. Однако, пожалуйста, сообщите нам, если вы заметите даже малейшую ошибку — ваш вклад очень важен для нас. Хотя большинство калькуляторов на Justfreetools.com предназначены для универсального использования во всем мире, некоторые из них предназначены только для определенных стран. Добро пожаловать в калькулятор arccos, также известный как калькулятор обратного косинуса. Благодаря нашему инструменту вы можете быстро найти arccos — что, как ни удивительно, является основным применением этого калькулятора. Однако для тех из вас, кто хочет узнать больше, мы подготовили небольшую статью, объясняющую , что такое обратный косинус , сопровождаемую таблицей и графиком обратного косинуса . Кроме того, если вы немного неохотно или запутались, перейдите к разделу, посвященному приложениям arccos , чтобы узнать, что общего у обратного косинуса с физикой, химией или даже с эргономикой строительства и работы! Arccos — это функция, обратная тригонометрической функции, а именно обратная функция косинуса.Однако, поскольку тригонометрические функции являются периодическими, в строгом смысле, они не могут быть инвертированы . Мы можем решить эту проблему, выбрав интервал, в котором основная функция является монотонной. Вы можете выбрать много разных диапазонов, но для косинуса обычно выбирается [0, π] . Этот диапазон называется набором главных значений . Arccos (x) — наиболее часто используемое обозначение, поскольку cos -1 x может вводить в заблуждение — помните, что обратный косинус — это не то же самое, что обратное значение функции (другими словами, возведение в степень — 1): Функция f имеет обратную функцию тогда и только тогда, когда f является взаимно однозначной функцией.Вся функция косинуса не является взаимно однозначной, поскольку Что же тогда делать? Как указано в предыдущем абзаце, нам нужно ограничить область определения базовой периодической косинусной функции. Таким образом, поскольку косинус всегда находится в диапазоне [-1,1], и мы выбираем область, [0, π], свойства функции обратного косинуса будут обратными: Область обратного косинуса x для действительного результата: [-1,1] Диапазон обратного косинуса обычного главного значения: [0, π] В таблице ниже вы найдете график обратного косинуса, а также некоторые часто используемые значения arccos: Хотите знать, откуда взялся этот график обратного косинуса? Он просто создается путем отражения графика cos x через линию y = x (не забывайте о наших доменных ограничениях!): Вы можете подумать, что arccos — еще один бесполезный термин из тригонометрии, но мы хотим убедить вас, что это не так! Функция обратного косинуса действительно полезна для решения многих научных и реальных задач (круто, не правда ли?): I Наука Математика: Физика: Химия: II Примеры из жизни Теперь вы уверены? Не ждите больше, воспользуйтесь нашим калькулятором обратного косинуса, чтобы решить (почти все) ваши проблемы! Найдите угол в градусах или радианах, используя обратный косинус с помощью калькулятора arccos ниже. Arccos — это тригонометрическая функция для вычисления обратного косинуса. Arccos также можно выразить как cos -1 (x). Arccos используется для отмены или отмены функции косинуса. Если вы знаете косинус угла, вы можете использовать arccos для вычисления угла. Поскольку arccos — это функция, обратная косинусу, а многие углы имеют одно и то же значение косинуса, arccos является периодической функцией. Каждое значение arccos может привести к нескольким значениям угла.Первичный результат для arccos известен как главное значение и представляет собой угол в диапазоне от 0 ° до 180 °. Для вычисления arccos используйте научный калькулятор и функцию acos или просто воспользуйтесь калькулятором выше. В большинстве научных калькуляторов для вычисления cos требуется значение угла в радианах. Формула обратного косинуса: y = cos (x) | х = arccos (y) Таким образом, если y равно косинусу x , то x равно arccos y . Если вы построите график функции arccos для каждого возможного значения косинуса, он образует кривую от (-1, π) до (1, 0). Поскольку значение косинуса всегда находится в диапазоне от -1 до 1, кривая обратного косинуса начинается при x = -1 и заканчивается при x = 1. Поскольку пик косинусоидальной волны находится в 0 радиан, а угол падения волны составляет π радиан, значение y заканчивается в этих точках. В таблице ниже показаны общие значения косинуса и arccos или угла для каждого из них. Возможно, вас заинтересуют наши калькуляторы обратного синуса и арктангенса. Взгляните на три графика ниже. Поскольку \ (\ tan x \), \ (\ sin x \) и \ (\ cos x \) являются периодическими функциями, существует множество значений \ (x \), которые дают одинаковое значение \ (\ tan x \), \ (\ sin x \) или \ (\ cos x \). Это означает, что обратные функции, такие как \ (\ arctan x \) и \ (\ arcsin x \), должны быть очень тщательно определены.Вы можете узнать больше об этом в Обратные тригонометрические функции, и эти идеи используются в этом решении. Глядя на три графика, я замечаю, что график C выглядит как график \ (y = x \) для всех реальных значений \ (x. \). Напротив, график B выглядит как график \ (y = x \), но только для \ (x \) в интервале \ (\ left (\ frac {- \ pi} {2}, \ frac {\ vphantom {-} \ pi} {2} \ right) \). Подумав о графике B, я могу теперь думать о графике A как о повторяющейся версии графика B с периодом \ (\ pi \). Чтобы увидеть, какие графики показывают функции \ (\ arctan (\ tan x) \) и \ (\ tan (\ arctan x) \), я могу подумать о доменах и диапазонах. При составлении функций \ (f (x) \) и \ (g (x) \) в форму \ (g (f (x)) \), мне нужно подумать о области определения \ (f (x) \ ). Мне нужно проверить, что любой вывод \ (f \) находится в области \ (g \) и каковы эти выходы, поэтому диапазон \ (g (f (x)) \) зависит от домена и диапазона \ (f \), а также диапазон \ (g \). Начиная с внутренней функции в \ (\ arctan (\ tan x) \), я знаю, что \ (\ tan x \) определен для всех действительных \ (x \), кроме тех, где \ (x = \ frac {(2n +1) \ pi} {2} \). Это область \ (\ tan x \).Диапазон — это все действительные числа. Это означает, что входными данными внешней функции \ (\ arctan \) являются все действительные числа, поэтому выходными данными для \ (\ arctan \) является ее главный диапазон значений, который представляет собой интервал \ (\ left (- \ frac {\ pi} {2}, \ frac {\ pi} {2} \ right) \). Следовательно, график \ (\ arctan (\ tan x) \) имеет область, которая представляет собой всю ось \ (x \), за исключением точек, где \ (x = \ frac {(2n + 1) \ pi } {2} \), а диапазон равен \ (\ left (- \ frac {\ pi} {2}, \ frac {\ pi} {2} \ right) \), поэтому на графике A показано \ (y = \ arctan (\ tan x) \). Теперь я буду использовать аналогичное мышление, чтобы выяснить, какой график является \ (y = \ tan (\ arctan x) \). На этот раз \ (\ arctan x \) — внутренняя функция. Его доменом являются все действительные числа, но диапазон равен \ (\ left (- \ frac {\ pi} {2}, \ frac {\ pi} {2} \ right) \). На этом графике показано \ (y = \ tan x \) для \ (x \) в интервале \ (\ left (- \ frac {\ pi} {2}, \ frac {\ pi} {2} \ right) \). Можете ли вы использовать его, чтобы объяснить, почему на графике C должно отображаться \ (y = \ tan (\ arctan x) \)? Сопоставьте эти уравнения с графиками ниже и объясните свои рассуждения. Я заметил одну вещь: все четыре функции отображают \ (0 \) в \ (0 \), поэтому графики должны проходить через начало координат. Это исключает график G. Область значений \ (\ sin x \) является действительной \ (x \), а диапазон — интервалом \ ([- 1,1] \). Область значений \ (\ arcsin x \) — это интервал \ ([- 1,1] \), а диапазон главных значений — \ (\ left [- \ frac {\ pi} {2}, \ frac {\ pi} {2} \ right] \) (дополнительные пояснения см. в разделе Обратные тригонометрические функции). Итак, функция \ (\ arcsin (\ sin x) \) определена для всех вещественных \ (x \) и имеет диапазон \ (\ left [- \ frac {\ pi} {2}, \ frac {\ pi} {2} \ right] \).В области \ (\ left [- \ frac {\ pi} {2}, \ frac {\ pi} {2} \ right] \) функция отобразит \ (x \) на себя, так что график будет выглядеть как что из \ (y = x \). Значит, это должен быть График D. Обратите внимание, что по мере увеличения \ (x \) от \ (\ frac {\ pi} {2} \) до \ (\ frac {3 \ pi} {2} \), \ (\ sin x \) уменьшается от \ (1 \) до \ (- 1 \), и поэтому \ (\ arcsin (\ sin x) \) уменьшается с \ (\ frac {\ pi} {2} \) до \ (- \ frac {\ pi} { 2} \). Затем этот паттерн продолжается, образуя зигзагообразный график. Область \ (\ arcsin x \) — это интервал \ ([- 1,1] \), и он не определен где-либо еще.В этом домене он имеет диапазон \ (\ left [- \ frac {\ pi} {2}, \ frac {\ pi} {2} \ right] \), и эти значения используются в качестве входных данных для \ (\ sin x \) производят значения в диапазоне \ ([- 1,1] \). Таким образом, график будет выглядеть как \ (y = x \), ограниченный областью \ (- 1 \ le x \ le1 \), которая является Графиком E. \ (\ cos x \) определен для всех действительных \ (x \) и имеет диапазон \ ([- 1,1] \). \ (\ arccos x \) определен в области \ ([- 1,1] \), а его главный диапазон значений равен \ ([0, \ pi] \). Таким образом, область определения этой композиции — это все действительные числа, а ее диапазон равен \ ([0, \ pi] \).Единственный график, который соответствует этому, — J. В качестве проверки, когда \ (x \) увеличивается с \ (0 \) до \ (\ pi \), значение \ (\ cos x \) уменьшается с \ (1 \) до \ (- 1 \), и поэтому \ (\ arccos (\ cos x) \) увеличивается с \ (0 \) до \ (\ pi \). В этой области график выглядит как \ (y = x \). По мере того, как \ (x \) увеличивается от \ (\ pi \) к \ (2 \ pi \), \ (\ cos x \) увеличивается от \ (- 1 \) до \ (1 \) и \ (\ arccos (\ cos x) \) уменьшается с \ (\ pi \) до \ (0 \). Отсюда получаем зигзагообразный узор. \ (\ arccos x \) определяется только для \ (x \) в интервале \ ([- 1,1] \).Его диапазон равен \ ([0, \ pi] \), а \ (\ cos \) этих значений имеет диапазон \ ([- 1,1] \). Таким образом, наш график будет выглядеть как \ (y = x \), ограниченный областью \ ([- 1,1] \), и это должен быть график E, такой же, как для уравнения (2). Интересно отметить, что \ (\ cos x \) и \ (\ arccos x \) являются убывающими функциями на этих интервалах, но композиция функций возрастает. Это случай с любой парой убывающих функций ? Для каких значений \ (x \) будет \ (\ tan (\ arctan x) = x \)? А как насчет \ (\ arctan (\ tan x) = x \)? Что вы можете сказать о решениях подобных уравнений, например \ (\ sin (\ arcsin x) = x \) или \ (\ arccos (\ cos x) = x \)? Поскольку график C равен \ (y = \ tan (\ arctan x) \), он должен быть \ (\ tan (\ arctan x) = x \) для всех действительных \ (x \). График A показывает \ (y = \ arctan (\ tan x) \), поэтому \ (\ arctan (\ tan x) = x \) только для \ (x \) в интервале \ (\ left (- \ tfrac {\ pi} {2}, \ tfrac {\ pi} {2} \ right) \), поскольку это единственная часть графика, для которой \ (y = x \) совпадает с графиком \ (y = \ arctan (\ загар х) \). Чтобы проиллюстрировать, что происходит, если \ (x \) выходит за пределы этого интервала, давайте попробуем \ (x = \ tfrac {4 \ pi} {3} \). Я знаю \ (\ tan \ tfrac {4 \ pi} {3} = \ sqrt {3} \), но \ (\ arctan \ sqrt {3} = \ tfrac {\ pi} {3} \). Следовательно, \ (\ arctan \ left (\ tan \ tfrac {4 \ pi} {3} \ right) = \ arctan \ sqrt {3} = \ tfrac {\ pi} {3} \).Обобщая этот пример, я вижу, что если \ (x \) находится вне интервала \ (\ left (- \ tfrac {\ pi} {2}, \ tfrac {\ pi} {2} \ right) \) и \ (\ tan x \) определен, тогда \ (\ arctan (\ tan x) \) переводит \ (x \) к соответствующему значению внутри интервала \ (\ left (- \ tfrac {\ pi} {2}) , \ tfrac {\ pi} {2} \ right) \).
В этой статье мы будем изучать умножение и деление отрицательных чисел. Существуют определенные правила умножения отрицательных чисел. Примеры умножения отрицательных чисел. Задача 1. Вычислить: \((-4)*(-4)\) и \((-6)*(-5).\) Решение. Отрицательное число при умножении на отрицательное станет положительным согласно правилу. Ответ: \(16;30.\) Задача 2. Вычислить: \((-10)*12\) и \((-7)*4.\) Решение. Отрицательное при умножении на положительное число станет отрицательным согласно правилу. -10 * 12= -120 (-7)*4=-28 Ответ: \(-120; -28\)
Решение. Положительное при умножении на отрицательное число станет отрицательным согласно правилу. Ответ: \(-121;-78.\) Деление отрицательных чисел При делении действуют те же правила знаков, что и при умножении. Задача 4. Вычислить: \((-16)*(-4)\) и \((-6)*(-2)\). Решение. Ответ: \(4;3.\) Задача 5. Вычислить: \((-10):5\) и \((-12):6\). Решение. Ответ: \(-2;-2.\) Задача 3. Вычислить: \(121:(-11)\) и \(169:(-13)\). Решение. Ответ: \(-11;-13.\) Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на бесплатное тестирование знаний! Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности Наши преподаватели
Татьяна Николаевна Бычкова
Репетитор по математике
Стаж (лет)
Образование:
Таганрогский государственный педагогический институт
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Преподаватель математики в 5-9 классах, подготовка к ОГЭ и ВПР.
Алесандр Викторович Рудаков
Репетитор по математике
Стаж (лет)
Образование:
Омский государственный педагогический университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по математике для 5 классов и по информатике для 7-9 классов, подготовка к ОГЭ.
Андрей Алексеевич Тарасов
Репетитор по математике
Стаж (лет)
Образование:
Новосибирский государственный университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по математике 5-11 классов, ВПР/ОГЭ/ЕГЭ, и по физике 6-9 классы ВПР/ОГЭ. Похожие статьи Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности «Враг моего врага — мой друг». Проще всего ответить: «Потому что таковы правила действий над отрицательными числами». Правила, которые мы учим в школе и применяем всю жизнь. Однако учебники не объясняют, почему правила именно такие. Мы сначала постараемся понять это, исходя из истории развития арифметики, а потом ответим на этот вопрос с точки зрения современной математики. Давным-давно людям были известны только натуральные числа: 1, 2, 3, … Их использовали для подсчета утвари, добычи, врагов и т. д. Но числа сами по себе довольно бесполезны — нужно уметь с ними обращаться. Сложение наглядно и понятно, к тому же сумма двух натуральных чисел — тоже натуральное число (математик сказал бы, что множество натуральных чисел замкнуто относительно операции сложения). Умножение — это, по сути, то же сложение, если мы говорим о натуральных числах. В жизни мы часто совершаем действия, связанные с этими двумя операциями (например, делая покупки, мы складываем и умножаем), и странно думать, что наши предки сталкивались с ними реже — сложение и умножение были освоены человечеством очень давно. Без вычитания, конечно, тоже не обойтись. Но на практике мы, как правило, вычитаем из большего числа меньшее, и нет нужды использовать отрицательные числа. (Если у меня есть 5 конфет и я отдам сестре 3, то у меня останется 5 – 3 = 2 конфеты, а вот отдать ей 7 конфет я при всем желании не могу.) Этим можно объяснить, почему люди долго не пользовались отрицательными числами. В индийских документах отрицательные числа фигурируют с VII века н.э.; китайцы, видимо, начали употреблять их немного раньше. Их применяли для учета долгов или в промежуточных вычислениях для упрощения решения уравнений — это был лишь инструмент для получения положительного ответа. Тот факт, что отрицательные числа, в отличие от положительных, не выражают наличие какой-либо сущности, вызывал сильное недоверие. Люди в прямом смысле слова избегали отрицательных чисел: если у задачи получался отрицательный ответ, считали, что ответа нет вовсе. Рассмотрим для примера уравнение 7x – 17 = 2x – 2. Его можно решать так: перенести члены с неизвестным в левую часть, а остальные — в правую, получится 7x – 2x = 17 – 2, 5x = 15, x = 3. При таком решении нам даже не встретились отрицательные числа. Но можно было случайно сделать и по-другому: перенести слагаемые с неизвестным в правую часть и получить 2 – 17 = 2x – 7x, (–15) = (–5)x. Чтобы найти неизвестное, нужно разделить одно отрицательное число на другое: x = (–15)/(–5). Но правильный ответ известен, и остается заключить, что (–15)/(–5) = 3. Что демонстрирует этот нехитрый пример? Во-первых, становится понятна логика, которой определялись правила действий над отрицательными числами: результаты этих действий должны совпадать с ответами, которые получаются другим путем, без отрицательных чисел. Правила действий над отрицательными числами сформировались не сразу, а стали обобщением многочисленных примеров, возникавших при решении прикладных задач. Вообще, развитие математики можно условно разбить на этапы: каждый следующий этап отличается от предыдущего новым уровнем абстракции при изучении объектов. Так, в XIX веке математики поняли, что у целых чисел и многочленов, при всей их внешней непохожести, есть много общего: и те, и другие можно складывать, вычитать и перемножать. Эти операции подчиняются одним и тем же законам — как в случае с числами, так и в случае с многочленами. Потом обнаружились другие совокупности математических объектов, над которыми можно производить такие операции: формальные степенные ряды, непрерывные функции… Наконец, пришло понимание, что если изучить свойства самих операций, то потом результаты можно будет применять ко всем этим совокупностям объектов (такой подход характерен для всей современной математики). В итоге появилось новое понятие: кольцо. Это всего-навсего множество элементов плюс действия, которые можно над ними производить. Основополагающими здесь являются как раз правила (их называют аксиомами), которым подчиняются действия, а не природа элементов множества (вот он, новый уровень абстракции!). Желая подчеркнуть, что важна именно структура, которая возникает после введения аксиом, математики говорят: кольцо целых чисел, кольцо многочленов и т. д. Отталкиваясь от аксиом, можно выводить другие свойства колец. Мы сформулируем аксиомы кольца (которые, естественно, похожи на правила действий с целыми числами), а затем докажем, что в любом кольце при умножении минуса на минус получается плюс. Кольцом называется множество с двумя бинарными операциями (т. е. в каждой операции задействованы два элемента кольца), которые по традиции называют сложением и умножением, и следующими аксиомами: Заметим, что кольца, в самой общей конструкции, не требуют ни перестановочности умножения, ни его обратимости (т. е. делить можно не всегда), ни существования единицы — нейтрального элемента по умножению. Если вводить эти аксиомы, то получаются другие алгебраические структуры, но в них будут верны все теоремы, доказанные для колец. Теперь докажем, что для любых элементов A и B произвольного кольца верно, во-первых, (–A)·B = –(A·B), а во-вторых (–(–A)) = A. Из этого легко следуют утверждения про единицы: (–1)·1 = –(1·1) = –1 и (–1)·(–1) = –((–1)·1) = –(–1) = 1. Для этого нам потребуется установить некоторые факты. Сперва докажем, что у каждого элемента может быть только один противоположный. В самом деле, пусть у элемента A есть два противоположных: B и С. То есть A + B = 0 = A + C. Рассмотрим сумму A + B + C. Пользуясь сочетательным и переместительным законами и свойством нуля, получим, что, с одной стороны, сумма равна B: B = B + 0 = B + (A + C) = A + B + C, а с другой стороны, она равна C: A + B + C = (A + B) + C = 0 + C = C. Заметим теперь, что и A, и (–(–A)) являются противоположными к одному и тому же элементу (–A), поэтому они должны быть равны. Первый факт получается так: 0 = 0·B = (A + (–A))·B = A·B + (–A)·B, то есть (–A)·B противоположно A·B, значит, оно равно –(A·B). Чтобы быть математически строгими, объясним еще, почему 0·B = 0 для любого элемента B. В самом деле, 0·B = (0 + 0) B = 0·B + 0·B. То есть прибавление 0·B не меняет сумму. Значит, это произведение равно нулю. А то, что в кольце ровно один ноль (ведь в аксиомах сказано, что такой элемент существует, но ничего не сказано про его единственность!), мы оставим читателю в качестве несложного упражнения. Ответил: Евгений Епифанов Положительные и отрицательные числа придумали математики. Делать им было нечего, вот они и придумали. Правила умножения и деления положительных и отрицательных чисел придумали всё те же математики. Запомнить правила умножения или деления положительных и отрицательных чисел очень просто. Если два числа имеют разные знаки, в результате всегда будет знак минус. Рассмотрим все возможные варианты. Что дает минус на плюс? При умножении и делении минус на плюс дает минус. Что дает плюс на минус? При умножении и делении в результате мы тоже получаем знак минус. Как вы видите, все варианты умножения и деления положительных и отрицательных чисел исчерпаны, но знак плюс у нас так и не появился. Это мы сформулировали правило для себя, чтобы запомнить. Что говорить математикам? При умножении или делении положительных и отрицательных чисел в результате получается отрицательное число. Что дает минус на минус? Всегда будет получаться плюс, если мы выполняем умножение или деление. Что дает плюс на плюс? Здесь совсем просто. Умножение или деление плюса на плюс дает всегда плюс. Надеюсь, это вы запомнили: минус на минус дает плюс, плюс на плюс дает минус. Что говорить математикам? При умножении и делении положительных или отрицательных чисел в результате получается положительное число. Если с умножением и делением двух плюсов всё понятно (в результате получается такой же плюс), то с двумя минусами ничего не понятно. По логике, если два плюса дают плюс, то два минуса должны давать минус. Такой большой, жирный минус. Но не тут-то было. Математики думают иначе. Так почему минус и минус превращаются в плюс? Могу вас заверить, что интуитивно математики правильно решили задачу на умножение и деление плюсов и минусов. Давайте попробуем применить правило умножениея и деления положительных и отрицательных чисел на практике. Придумаем какой-нибудь пример из нашей жизни. Думаю, вы слышали про бочку мёда и ложку дёгтя, которая может испортить весь мёд. Пусть мёд — это положительные числа, а дёготь — это числа отрицательные. Пробуем. Смотрим на картинки и описываем правила. Если в бочку дёгтя добавить ложку мёда, получится бочка дёгтя. Первых два примера с натяжкой можно принять. Последний пример вообще не вызывает вопросов. А вот с предпоследним примером возникают очень большие проблемы — в жизни такого не бывает. Здесь возможны два варианта: Лично я за второй вариант. Объясню почему. Математику не только нужно знать, но нею ещё нужно уметь пользоваться. Приведу пример из собственного опыта. Один учитель математики на уроках нам говорил: «математика – это точная наука, два раза соври – получится правда». Это утверждение однажды мне очень пригодилось. Как-то я решал сложную задачу с длинным решением. Я точно знал, какой результат должен быть. Но результат был другим. Я долго искал ошибку в расчетах, но не смог ее найти. Тогда, за несколько действий до итогового результата, я изменил одно число так, чтобы результат получился правильным. Я в расчетах соврал два раза и получил правильный результат. Математические вычисления в тот раз никто не проверял и я получил хорошую оценку. Это очень похоже на правило «минус на минус дает плюс», не так ли? Но вернемся к нашим бочкам. Кстати, говорят, именно с бочек с вином математики срисовали знак «минус». Так что же не так с мёдом и дёгтем в бочках? Мои четыре примера описывают действие сложения — ведь мы прибавляем одно к другому, а математические правила мы рассматриваем для деления и умножения. Это абсолютно разные вещи, сколько бы математики не повторяли, что умножение это и есть сложение. Сложение — это изменение количества. Умножение — это изменение качества. При добавлении ложки дёгтя в бочку мёда, мёд не превращается в дёготь. Мы просто получаем бочку испорченного мёда. Точно так же и дёготь, добавленный в бочку дёгтя, не превращает всё в мёд. При сложении и вычитании положительных и отрицательных чисел действуют совсем другие правила знаков. В чем же отличие качественных изменений от количественных? В единицах измерения, которые в математике предпочитают игнорировать. В этом примере буква а выполняет роль единицы измерения. Кстати, правило умножения отрицательных чисел наводит на ещё один вопрос математикам: сколько отрицательных чисел нужно сложить, чтобы получилось одно положительное число? (-2)+(-2)=-4 (-2)*(-2)=+4 Так что же такое знаки «плюс» и «минус» в математике? Существуют ли отрицательные числа? Об этом мы поговорим как-нибудь в другой раз.
Репетиторы
❯
Математика
❯
Минус на минус даёт плюс. А почему?
Автор: Владимир Л., онлайн репетитор по математике
●
21.09.2011
●
Раздел: Математика
Минус на минус даёт плюс – это правило, которые мы выучили в школе и применяем всю жизнь. С древних времён люди пользуются положительными натуральными числами: 1, 2, 3, 4, 5,… С помощью чисел считали скот, урожай, врагов и т.д. При сложении и умножении двух положительных чисел получали всегда положительное число, при делении одних величин на другие не всегда получали натуральные числа – так появились дробные числа. Что же с вычитанием? С детских лет мы знаем, что лучше к большему прибавить меньшее и из большего вычесть меньшее, при этом мы опять же не используем отрицательные числа. Получается, если у меня есть 10 яблок, я могу отдать кому-то только меньше 10 или 10. Я никак не смогу отдать 13 яблок, потому что у меня их нет. Нужды в отрицательных числах не было долгое время. Только с VII века н.э. отрицательные числа использовались в некоторых счётных системах, как вспомогательные величины, которые позволяли получить положительное число в ответе. Рассмотрим пример, 6х – 30 = 3х – 9. Чтобы найти ответ, необходимо члены с неизвестными оставить в левой части, а остальные — в правую: 6х – 3х = 30 – 9, 3х = 21, х = 7. При решении этого уравнения нам даже не встретились отрицательные числа. Мы могли бы члены с неизвестными перенести в правую часть, а без неизвестных — в левую: 9 – 30 = 3х – 6х, (-21) = (-3х). При деление отрицательного числа на отрицательное получаем положительный ответ: х = 7. Что мы видим? Действия с использованием отрицательных чисел должны привести нас к такому же ответу, что и действия только с положительными числами. Мы можем больше не думать о практической непригодности и осмысленности действий – они помогают нам решить задачу гораздо быстрее, не приводя уравнение к виду только с положительными числами. Со временем, после проведения длительных опытов и вычислений удалось выявить правила, которым подчиняются все числа и действия над ними (в математике они называются аксиомами). Отсюда и появилась аксиома, которая утверждает, что при умножении двух отрицательных чисел получаем положительное. © blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Задать вопрос
Математика
Математика
Математика
Математика
Математика
Математика
Математика
Французский язык
Координатная прямая
Координаты точек на числовой оси
Сложение отрицательных чисел
Вычитание отрицательных чисел
Умножение отрицательных чисел
Деление отрицательных чисел Как выполнять деление отрицательных чисел легко понять, вспомнив, что
деление — это действие, обратное умножению. Если «a» и «b» положительные числа, то
разделить число «a» на число «b», значит найти
такое число «с», которое при умножении на
«b» даёт число «a». Данное определение деления действует для любых рациональных
чисел, если делители отличны от нуля. Поэтому, например, разделить число «−15» на
число 5 — значит, найти такое число, которое при умножении
на число 5 даёт число «−15». Таким числом будет «−3», так как (−3) · 5 = −15 значит (−15) : 5 = −3 Примеры деления рациональных чисел. Из примеров видно, что частное двух чисел с одинаковыми знаками — число
положительное (примеры 1, 2), а частное двух чисел с разными знаками—
число отрицательное (примеры 3, 4). Чтобы найти модуль частного, нужно разделить модуль
делимого на модуль делителя. Итак, чтобы разделить два числа с одинаковыми знаками, надо: Примеры деления чисел с одинаковыми знаками: Чтобы разделить два числа с разными знаками, надо: Примеры деления чисел с разными знаками: Для определения знака частного можно также пользоваться следующей таблицей. При вычислении «длинных» выражений, в которых фигурируют только умножение и деление,
пользоваться правилом знаков очень удобно. Можно обратить внимание, что в числителе два знака «минус», которые при
умножении дадут «плюс». Также в знаменателе три знака «минус», которые при умножении дадут «минус».
Поэтому в конце результат получится со знаком «минус». Сокращение дроби (дальнейшие действия с модулями чисел) выполняется также, как и
раньше: Запомните! Частное от деления нуля на число, отличное от нуля, равно нулю. 0 : a = 0, a ≠ 0 Делить на ноль НЕЛЬЗЯ! Все известные ранее правила деления на единицу действуют и на множество рациональных чисел. , где «а» — любое рациональное число. Зависимости между результатами умножения и деления, известные для
положительных чисел, сохраняются и для всех
рациональных чисел (кроме числа нуль): Данные зависимости используются для нахождения неизвестного
множителя, делимого и делителя (при решении уравнений), а также для
проверки результатов умножения и деления. Пример нахождения неизвестного. x · (−5) = 10 x = 10 : (−5) x = −2 Разделим число «−5» на
«6» и число «5» на «−6». Напоминаем, что черта в записи обыкновенной дроби — это тот же знак
деления, поэтому можно записать частное каждого из этих действий в виде отрицательной дроби. Таким образом знак «минус» в дроби может находиться: Запомните! При записи отрицательных дробей знак «минус» можно ставить перед дробью,
переносить его из числителя в знаменатель или из знаменателя в числитель. Это часто используется при выполнении действий с дробями, облегчая вычисления. Пример. Обратите внимание, что после вынесения знака «минуса» перед скобкой мы из большего
модуля вычитаем меньший по
правилам сложения чисел с разными знаками. Пример. Используя описанное свойство переноса знака в дроби, можно действовать, не выясняя, модуль какого из данных дробных чисел больше. Координатная прямая
Координаты точек на числовой оси
Сложение отрицательных чисел
Вычитание отрицательных чисел
Умножение отрицательных чисел
Деление отрицательных чисел При умножении и делении целых чисел применяется несколько правил. В данном уроке мы рассмотрим каждое из них. При умножении и делении целых чисел следует обращать внимание на знаки чисел. От них будет зависеть какое правило применять. Необходимо также изучить несколько законов умножения и деления. Изучение этих правил позволит избежать некоторых досадных ошибок в будущем. Некоторые из законов математики мы рассматривали в уроке законы математики. Но мы рассмотрели не все законы. В математике немало законов и разумнее будет изучать их последовательно по мере необходимости. Для начала вспомним из чего состоит умножение. Множимое показывает, что именно мы увеличиваем. В нашем примере мы увеличиваем число 3. Множитель показывает во сколько раз нужно увеличить множимое. В нашем примере множитель это число 2. Этот множитель показывает во сколько раз нужно увеличить множимое 3. То есть в ходе операции умножения число 3 будет увеличено в два раза. Произведение это собственно результат операции умножения. В нашем примере произведение это число 6. Это произведение является результатом умножения 3 на 2. Выражение 3 × 2 также можно понимать как сумму двух троек. Множитель 2 в таком случае будет показывать сколько раз нужно повторить число 3: Таким образом, если число 3 повторить два раза подряд, получится число 6. Множимое и множитель называют одним общим словом – сомножители. Переместительный закон умножения выглядит следующим образом: От перестановки мест сомножителей произведение не меняется. Проверим так ли это. Умножим например 3 на 5. Здесь 3 и 5 это сомножители. 3 × 5 = 15 Теперь поменяем местами сомножители: 5 × 3 = 15 В обоих случаях мы получаем ответ 15, поэтому между выражениями 3 × 5 и 5 × 3 можно поставить знак равенства, поскольку они равны одному тому же значению: 3 × 5 = 5 × 3 15 = 15 А с помощью переменных переместительный закон умножения можно записать так: a × b = b × a где a и b — сомножители Этот закон говорит о том, что если выражение состоит из нескольких сомножителей, то произведение не будет зависеть от порядка действий. К примеру, выражение 3 × 2 × 4 состоит из нескольких сомножителей. Чтобы его вычислить, можно перемножить 3 и 2, затем полученное произведение умножить на оставшееся число 4. Выглядеть это будет так: 3 × 2 × 4 = (3 × 2) × 4 = 6 × 4 = 24 Это был первый вариант решения. Второй вариант состоит в том, чтобы перемножить 2 и 4, затем полученное произведение умножить на оставшееся число 3. Выглядеть это будет так: 3 × 2 × 4 = 3 × (2 × 4) = 3 × 8 = 24 В обоих случаях мы получаем ответ 24. Поэтому между выражениями (3 × 2) × 4 и 3 × (2 × 4) можно поставить знак равенства, поскольку они равны одному и тому же значению: (3 × 2) × 4 = 3 × (2 × 4) 24 = 24 а с помощью переменных сочетательный закон умножения можно записать так: a × b × c = (a × b) × c = a × (b × c) где вместо a, b, c могут стоять любые числа. Распределительный закон умножения позволяет умножить сумму на число. Например, найдём значение выражения (2 + 3) × 5 Выражение находящееся в скобках является суммой. Эту сумму нужно умножить на число 5. Для этого каждое слагаемое этой суммы, то есть числа 2 и 3 нужно умножить на число 5, затем полученные результаты сложить: Значит значение выражения (2 + 3) × 5 равно 25. С помощью переменных распределительный закон умножения записывается так: (a + b) × c = a × c + b × c где вместо a, b, c могут стоять любые числа. Этот закон говорит о том, что если в любом умножении имеется хотя бы один ноль, то в ответе получится ноль. Произведение равно нулю, если хотя бы один из сомножителей равен нулю. Например, выражение 0 × 2 равно нулю 0 × 2 = 0 В данном случае число 2 является множителем и показывает во сколько раз нужно увеличить множимое. Иными словами, если «ничего» увеличить в два раза или даже в миллион раз, всё равно получится «ничего». И если в выражении 0 × 2 поменять местами сомножители, опять же получится ноль. Это мы знаем из предыдущего переместительного закона: 0 × 2 = 2 × 0 0 = 0 Примеры применения закона умножения на ноль: 5 × 0 = 0 5 × 5 × 5 × 0 = 0 2 × 5 × 0 × 9 × 1 = 0 В последних двух примерах имеется несколько сомножителей. Увидев в них ноль, мы сразу в ответе поставили ноль, применив закон умножения на ноль. Мы рассмотрели основные законы умножения. Теперь рассмотрим самó умножение целых чисел. Пример 1. Найти значение выражения −5 × 2 Это умножение чисел с разными знаками. −5 является отрицательным числом, а 2 – положительным. Чтобы перемножить числа с разными знаками, нужно перемножить их модули, и перед полученным ответом поставить минус. −5 × 2 = − (|−5| × |2|) = − (5 × 2) = − (10) = −10 Обычно записывают короче: −5 × 2 = −10 Любое умножение может быть представлено в виде суммы чисел. Например, рассмотрим выражение 2 × 3. Оно равно 6. 2 × 3 = 6 Множителем в данном выражение является число 3. Этот множитель показывает во сколько раз нужно увеличить множимое 2. Но выражение 2 × 3 также можно понимать как сумму трёх двоек: То же самое происходит и с выражением −5 × 2. Это выражение может быть представлено в виде суммы А выражение (−5) + (−5) равно −10. Мы это знаем из прошлого урока. Это сложение отрицательных чисел. Напомним, что результат сложения отрицательных чисел есть отрицательное число. Пример 2. Найти значение выражения 12 × (−5) Это умножение чисел с разными знаками. 12 × (−5) = − (|12| × |−5|) = − (12 × 5) = − (60) = −60 Обычно решение записывают покороче: 12 × (−5) = −60 Пример 3. Найти значение выражения 10 × (−4) × 2 Это выражение состоит из нескольких сомножителей. Сначала перемножим 10 и (−4), затем полученное число умножим на 2. Попутно применим ранее изученные правила: Первое действие: 10 × (−4) = −(|10| × |−4|) = −(10 × 4) = (−40) = −40 Второе действие: −40 × 2 = −(|−40 | × | 2|) = −(40 × 2) = −(80) = −80 Значит значение выражения 10 × (−4) × 2 равно −80 Запишем решение покороче: 10 × (−4) × 2 = −40 × 2 = −80 Пример 4. Найти значение выражения (−4) × (−2) Это умножение отрицательных чисел. В таких случаях применяется следующее правило: Чтобы перемножить отрицательные числа, нужно перемножить их модули и перед полученным ответом поставить плюс (−4) × (−2) = |−4| × |−2| = 4 × 2 = 8 Плюс по традиции не записываем, поэтому просто записываем ответ 8. Запишем решение покороче (−4) × (−2) = 8 Пример 5. Найти значение выражения −2 × (6 + 4) Применим распределительный закон умножения, то есть умножим число −2 на каждое слагаемое суммы (6 + 4) −2 × (6 + 4) = −2 × 6 + (−2) × 4 Теперь выполним умножение, и сложим полученные результаты. Попутно применим ранее изученные правила. Запись с модулями можно пропустить, чтобы не загромождать выражение Первое действие: −2 × 6 = −12 Второе действие: −2 × 4 = −8 Третье действие: −12 + (−8) = −20 Значит значение выражения −2 × (6 + 4) равно −20 Запишем решение покороче: −2 × (6 + 4) = (−12) + (−8) = −20 Пример 6. Найти значение выражения (−2) × (−3) × (−4) Выражение состоит из нескольких сомножителей. Сначала перемножим числа −2 и −3, и полученное произведение умножим на оставшееся число −4. Запись с модулями пропустим, чтобы не загромождать выражение Первое действие: (−2) × (−3) = 6 Второе действие: 6 × (−4) = −(6 × 4) = −24 Значит значение выражения (−2) × (−3) × (−4) равно −24 Запишем решение покороче: (−2) × (−3) × (−4) = 6 × (−4) = −24 Прежде чем делить целые числа, необходимо изучить два закона деления. В первую очередь, вспомним из чего состоит деление. Деление состоит из трёх параметров: делимого, делителя и частного. Например, в выражении 8 : 2 = 4, 8 – это делимое, 2 – делитель, 4 – частное. Делимое показывает, что именно мы делим. В нашем примере мы делим число 8. Делитель показывает на сколько частей нужно разделить делимое. В нашем примере делитель это число 2. Этот делитель показывает на сколько частей нужно разделить делимое 8. То есть в ходе операции деления, число 8 будет разделено на две части. Частное – это собственно результат операции деления. В нашем примере частное это число 4. Это частное является результатом деления 8 на 2. Любое число запрещено делить на ноль. Дело в том, что деление это действие, обратное умножению. Данную фразу можно понимать в прямом смысле. Например, если 2 × 5 = 10, то 10 : 5 = 2. Видно, что второе выражение записано в обратном порядке. Если к примеру, у нас имеется два яблока и мы захотим увеличить их в пять раз, то мы запишем 2 × 5 = 10. Получится десять яблок. Затем, если мы захотим обратно уменьшить эти десять яблок до двух, то мы запишем 10 : 5 = 2 Точно так же можно поступать и с другими выражениями. Если к примеру 2 × 6 = 12, то мы можем обратно вернуться к изначальному числу 2. Для этого достаточно записать выражение 2 × 6 = 12 в обратном порядке, разделяя 12 на 6 12 : 6 = 2 Теперь рассмотрим выражение 5 × 0. Мы знаем из законов умножения, что произведение равно нулю, если хотя бы один из сомножителей равен нулю. Значит и выражение 5 × 0 равно нулю 5 × 0 = 0 Если записать это выражение в обратном порядке, то получим: 0 : 0 = 5 Сразу в глаза бросается ответ 5, который получается в результате деления ноль на ноль. Это невозможно. В обратном порядке можно записать и другое похожее выражение, например 2 × 0 = 0 0 : 0 = 2 В первом случае, разделив ноль на ноль мы получили 5, а во втором случае 2. Второе объяснение заключается в том, что разделить делимое на делитель означает найти такое число, которое при умножении на делитель даст делимое. Например выражение 8 : 2 означает найти такое число, которое при умножении на 2 даст 8 … × 2 = 8 Здесь вместо многоточия должно стоять число, которое при умножении на 2 даст ответ 8. Чтобы найти это число, достаточно записать это выражение в обратном порядке: 8 : 2 = 4 Получили число 4. Запишем его вместо многоточия: 4 × 2 = 8 Теперь представим, что нужно найти значение выражения 5 : 0. В данном случае 5 – это делимое, 0 – делитель. Разделить 5 на 0 означает найти такое число, которое при умножении на 0 даст 5 … × 0 = 5 Здесь вместо многоточия должно стоять число, которое при умножении на 0 даст ответ 5. Но не существует числа, которое при умножении на ноль даёт 5. Выражение … × 0 = 5 противоречит закону умножения на ноль, который утверждает, что произведение равно нулю, когда хотя бы один из сомножителей равен нулю. А значит записывать выражение … × 0 = 5 в обратном порядке, деля 5 на 0 нет никакого смысла. Поэтому и говорят, что на ноль делить нельзя. С помощью переменных данный закон записывается следующим образом: , при b ≠ 0 Это выражение можно прочитать так: Число a можно разделить на число b, при условии, что b не равно нулю. Свойство частного Этот закон говорит о том, что если делимое и делитель умножить или разделить на одно и то же число, то частное не изменится. Например, рассмотрим выражение 12 : 4. Значение этого выражения равно 3 Попробуем умножить делимое и делитель на одно и то же число, например на число 4. Если верить свойству частного, мы опять должны получить в ответе число 3 Получили ответ 3. Теперь попробуем не умножить, а разделить делимое и делитель на число 4 Снова получили ответ 3. Видим, что если делимое и делитель умножить или разделить на одно и то же число, то частное не меняется. Пример 1. Найти значение выражения 12 : (−2) Это деление чисел с разными знаками. 12 — положительное число, (−2) – отрицательное. Чтобы решить этот пример, нужно модуль делимого разделить на модуль делителя, и перед полученным ответом поставить минус. 12 : (−2) = −(|12| : |−2|) = −(12 : 2) = −(6) = −6 Обычно записывают покороче: 12 : (−2) = −6 Пример 2. Найти значение выражения −24 : 6 Это деление чисел с разными знаками. −24 – это отрицательное число, 6 – положительное. Опять же модуль делимого делим на модуль делителя, и перед полученным ответом ставим минус. −24 : 6 = −(|−24| : |6|) = −(24 : 6) = −(4) = −4 Запишем решение покороче: −24 : 6 = −4 Пример 3. Найти значение выражения −45 : (−5) Это деление отрицательных чисел. −45 : (−5) = |−45| : |−5| = 45 : 5 = 9 Запишем решение покороче: −45 : (−5) = 9 Пример 4. Найти значение выражения −36 : (−4) : (−3) Согласно порядку действий, если в выражении присутствует только умножение или деление, то все действия нужно выполнять слева направо в порядке их следования. Разделим −36 на (−4), и полученное число разделим на −3 Первое действие: −36 : (−4) = |−36| : |−4| = 36 : 4 = 9 Второе действие: 9 : (−3) = −(|9| : |−3|) = −(9 : 3) = −(3) = −3 Запишем решение покороче: −36 : (−4) : (−3) = 9 : (−3) = −3 Понравился урок?
Возникло желание поддержать проект? ВведениеСложение и вычитаниеЭкспоненты Переходя от сложения и вычитания, как вы выполняете умножение и деление с отрицательными числами? На самом деле, мы уже рассмотрели самую сложную часть: вы уже знаете правила «знака»: плюс умножить плюс равно плюс минус раз плюс минус плюс раз минус минус минус раз минус плюс Содержание продолжается ниже Умножение и деление целых чисел Правила знаков работают так же, как и при делении; просто замените «раз» на «делится на». Вот пример правил в делении: (Помните, что дроби — это еще одна форма деления! «Дроби — это деление»!) Некоторым людям нравится думать об отрицательных числах в терминах долгов. Так, например, если вы должны 10 долларов шести людям, ваш общий долг будет 6 × 10 долларов = 60 долларов. В этом контексте получение отрицательного ответа имеет смысл. Но в каком контексте может иметь смысл деление отрицательного на отрицательное (и получение положительного)? Подумайте о перекусе в кафе. Когда вы идете платить, у ребенка возникают проблемы с вашей дебетовой картой. Он проводит ею шесть раз, прежде чем, наконец, вернуть карту вам. Вернувшись домой, вы проверяете свой банковский счет онлайн. Вы можете сказать по сумме, что да, он действительно взял с вас способ более одного раза. Некоторая часть этого общего дебета (отрицательная сумма на вашем счету) неверна. Прежде чем звонить в свой банк, чтобы исправить ситуацию, вы хотите подтвердить количество перерасходов. Как вы можете понять это? Вы можете разделить всю сумму (скажем, 76,02 доллара США) на сумму, указанную в квитанции (например, 12,67 доллара США), которая является суммой одного платежа. Каждое списание — это минус на вашем счете, поэтому математика такова: (- 76,02 доллара США) ÷ (- 12,67 доллара США) = 6 Таким образом, всего было действительно шесть списаний. Количество зарядов, 6, по подсчету количества событий, должен быть положительным . В этом реальном контексте деление минуса на минус и получение плюса имеет смысл. И теперь вы знаете, что поручить службе поддержки отменить ровно пять платежей. Вы можете заметить, что люди «отменяют» знаки минус. Они пользуются тем фактом, что «минус умножить на минус — это плюс». Например, предположим, что у вас есть (−2)(−3)(−4). Любые два отрицательных числа, перемноженные вместе, становятся одним положительным. Я начну с того, что уберу одну пару знаков «минус». Потом умножу как обычно. (-2)(-3)(-4) = (-2)(-3) (-4) = (+6) (-4) = -24 Если вам дано длинное умножение с отрицательными числами, просто сократите знаки «минус» попарно: Первое, что я сделаю, это посчитаю знаки «минус». Один два три четыре пять шесть семь. Итак, есть три пары, которые я могу отменить, и одна останется. В результате мой окончательный ответ должен быть отрицательным. Если я получу положительный результат, я буду знать, что сделал что-то не так. (-1)(-2)(-1)(-3)(-4)(-2)(-1) = (-1)(-2) (-1)(-3 )(−4)(−2)(−1) = (+1)(+2) (−1)(−3)(−4)(−2)(−1) = ( 1)(2) (-1)(-3) (-4)(-2)(-1) = (1)(2) (+1)(+3) (-4) (−2)(−1) = (1)(2)(1)(3) (−4)(−2) (−1) = (1)(2)(1)( 3) (+4)(+2) (-1) = (1)(2)(1)(3)(4)(2)(-1) = (2)(3) (4)(2)(-1) = 48(-1) = -48 Я получил отрицательный ответ, поэтому я знаю, что мой знак правильный. Вот еще один пример, показывающий тот же процесс отмены в контексте деления: Основная трудность, с которой сталкиваются люди с отрицаниями, заключается в работе со скобками; особенно при взятии отрицания через круглые скобки. Обычная ситуация примерно такая: −3( x + 4) Если бы у вас было «3 ( x + 4)», вы бы знали, что нужно «распределить» 3 «по» скобкам: 3( x + 4) = 3( x ) + 3(4) = 3 x + 12 Те же правила применяются, когда вы имеете дело с отрицаниями. Если у вас возникли проблемы с отслеживанием, используйте маленькие стрелки: ← пролистните , чтобы просмотреть полное изображение → Мне нужно взять 3 через круглые скобки: 3( х — 5) = 3( х ) + 3(-5) = 3 х — 15 Здесь я возьму «минус» через круглые скобки; Я буду распределять -2 на x и минус 3. -2( х — 3) = -2( х ) — 2(-3) = -2 х + 2(+3) = -2 х + 6 Обратите внимание, как я тщательно следил за знаками в скобках. «Минус» был сохранен с 3 за счет использования другого набора скобок. Не стесняйтесь использовать группирующие символы, чтобы сделать ваше предполагаемое значение ясным как для оценщика, так и для вас самих. Другая проблема, связанная с предыдущей, связана с вычитанием скобок. Вы можете отслеживать знак вычитания, преобразуя вычитание в умножение на минус: Я начну с того, что напишу маленькую «1» перед скобками. Затем я нарисую стрелки от этой 1 к терминам в скобках, чтобы напомнить себе, что мне нужно сделать. ← пролистните для просмотра полного изображения → Не бойтесь писать в этой маленькой «1» и рисовать эти маленькие стрелки. Я буду работать изнутри, упрощая сначала внутри внутренние символы группировки, в соответствии с Порядком операций. Итак, первое, что я сделаю, это пронесу −4 сквозь скобки. Тогда я упрощу; Я продолжу, поставив 1 перед круглыми скобками, и, чтобы помочь мне отслеживать это -1, которое я буду распределять, я нарисую свои маленькие стрелки. ← пролистните для просмотра полного изображения → Это сложно. Они заставляют меня вычесть дробь. Мне нужно сложить дроби, а значит сложить числители. Чтобы убедиться, что я не упустил из виду, что именно означает этот «минус» (а именно, что я минусую весь числитель второй дроби, а не только x ), я преобразую минус плюс -1: ← пролистните , чтобы просмотреть полное изображение → Обратите внимание, что я перешел от вычитания дроби к добавлению отрицательной единицы, умноженной на дробь. Для дополнительной практики со скобками попробуйте здесь. URL: https://www.purplemath.com/modules/negative3.htm Страница 1Страница 2Страница 4 Стандартные числа, большие нуля, описываются как «положительные» числа. Мы не ставим перед ними знак плюс (+), потому что нам это не нужно, так как общее понимание таково, что числа без знака положительны. Числа меньше нуля называются «отрицательными». Они имеют знак минус (-) перед ними, чтобы указать, что они меньше нуля (например, -10 или минус 10 ‘). Вероятно, самый простой способ визуализировать отрицательные и положительные числа — использовать числовую прямую, инструмент, с которым вы, возможно, хорошо знакомы, особенно если ваши дети учатся в начальной школе. Это выглядит примерно так: Числовая линия может помочь вам визуализировать как положительные, так и отрицательные числа, а также операции (сложение и вычитание), которые вы можете с ними выполнять. Когда вам нужно вычислить сложение или вычитание, вы начинаете с первого числа и перемещаете второе число разрядов вправо (для сложения) или влево (для вычитания). Эта числовая линия является упрощенной версией, но вы можете нарисовать их, включив в них все числа, если хотите. Большим преимуществом числовой линии является то, что ее очень легко нарисовать самому себе на обратной стороне конверта или на клочке бумаги, а также очень сложно ошибиться в расчетах. Пока вы внимательно подсчитываете количество мест, которые вы перемещаете, вы получите правильный ответ. Если вы вычитаете отрицательное число, два отрицательных числа объединяются, чтобы получить положительное. −10−(−10) не равно −20. Вместо этого вы можете думать об этом как о повороте одного из отрицательных знаков вертикально, чтобы пересечь другой и сделать плюс. Краткое примечание о скобках Для ясности: вы никогда не будете писать два отрицательных знака рядом без скобок. Таким образом, если вас попросят вычесть отрицательное число, оно всегда будет заключено в скобки, чтобы вы могли видеть, что использование двух отрицательных знаков было преднамеренным. -10—10 неверно (и сбивает с толку) -10-(-10) правильно (и более ясно) При умножении или делении с комбинациями положительных и отрицательные числа, вы можете упростить процесс, сначала игнорируя знаки (+/-) и просто умножая или разделяя числа, как если бы они оба были положительными. Получив числовой ответ, вы можете применить очень простое правило для определения знака ответа: Итак: Но: В качестве побочного вопроса это каким-то образом объясняет, почему вы не можете получить квадратный корень из отрицательного числа (подробнее об этом читайте на нашей странице Специальные числа и понятия ). Квадратный корень — это число, которое нужно умножить само на себя, чтобы получить число. Нельзя умножать число само на себя, чтобы получить отрицательное число. Чтобы получить отрицательное число, вам нужно одно отрицательное и одно положительное число. Правило работает так же, когда у вас есть более двух чисел для умножения или деления. Четное количество отрицательных чисел даст положительный ответ. Нечетное количество отрицательных чисел даст отрицательный ответ. Почему умножение двух отрицательных чисел дает положительный ответ? Тот факт, что отрицательное число, умноженное на другое отрицательное число, дает положительный результат, часто сбивает с толку и кажется нелогичным. Чтобы объяснить, почему это так, вернитесь к числовым линиям, использованным ранее в этой статье, поскольку они помогают объяснить это визуально. В обоих этих примерах вы двигались вперед (т. Отрицательные знаки могут показаться немного пугающими, но правила их использования просты и понятны. Помните об этом, и у вас не будет проблем. Числа больше нуля называются положительными числами, а числа меньше нуля — отрицательными числами. правила сложения и вычитания двух положительных и отрицательных чисел Реклама При использовании положительных и отрицательных чисел вы используете правила для чисел со знаком (числа с положительными или отрицательными знаками перед ними). Эти шаги, также известные как операции над числами со знаком, помогут вам избежать путаницы и решить математические задачи как можно быстрее и правильнее. Следуйте этим правилам, чтобы определить лучший способ сложения, вычитания, умножения и деления положительных и отрицательных чисел. Помните, что если нет знака + или -, число положительное. Когда вы складываете два числа вместе, и они имеют одинаковый знак (два положительных или два отрицательных числа), сложите числа и сохраните знак. Обратите внимание, что уравнения с двумя положительные суммы имеют положительные суммы, а уравнения с двумя отрицательными числами имеют отрицательные суммы. Если вы используете числовую прямую для решения задачи, добавление двух положительных чисел приведет к положительной стороне, а добавление двух отрицательных чисел приведет к отрицательной стороне. Если вы складываете положительные и отрицательные числа, вычтите меньшее число из большего и используйте знак из большего числа. Например: Как видите, сложив числа с разными знаками на самом деле является формой вычитания. При использовании числовой прямой ваша сумма будет ближе к нулю. Вычитание положительных и отрицательных чисел означает сложение противоположных чисел или аддитивное обратное. Хороший совет: всякий раз, когда вы видите знак минус и знак минус вместе, например, в 9 — (-7), немедленно делайте их положительными. Отрицательные знаки компенсируют друг друга, и уравнение становится задачей на сложение. Реклама Кажется, что умножение и деление сложнее, чем сложение и вычитание, но на самом деле они намного проще. Правило умножения положительных и отрицательных чисел с одинаковым знаком (два положительных или два отрицательных) состоит в том, что произведение всегда будет положительным. Например: То же правило применяется для деления . числа всегда равны положительному числу? Подобно вычитанию отрицательных чисел, эти операции превращают отрицательные числа в противоположные (обратные). По сути, вы вычитаете отрицательное число несколько раз — и, как показано выше, вычитание отрицательных чисел приводит к положительному уравнению. Реклама При умножении положительного на отрицательное произведение всегда будет отрицательным. Неважно, в каком порядке стоят знаки. Например: Во всех этих случаях сначала нужно умножить или разделить числа. Затем решите, является ли произведение или частное положительным (два положительных или два отрицательных в уравнении) или отрицательным (один положительный и один отрицательный в уравнении). Еще один способ подумать о сложении положительных и отрицательных чисел — посмотреть на знаки в ряду. Два одинаковых знака подряд (++ или —) означают, что вы складываете числа, а два разных знака подряд (+- или —) означают, что вы вычитаете. Например: Этот метод следует тем же правилам, что и выше, но может помочь вам решить проблему быстрее, если вы предпочитаете работать с знаки заранее. Как только вы концептуально поймете положительные и отрицательные числа, вы сможете решить, какой метод лучше всего подходит для вас. Как только вы познакомитесь с основами математики и ее правилами, перед вами откроется весь математический мир. Штатный писатель GCfiIBPG7Aw Да действительно два минуса дают плюс, и мы объясним почему , на примерах! Давайте поговорим о знаках . «+» — положительный знак, «-» — отрицательный знак. Когда число имеет без знака , это обычно означает, что оно положительное . Пример: 5 на самом деле +5 И мы можем поставить () вокруг цифр, чтобы избежать путаницы. Пример: 3 × −2 можно записать как (+3) × (−2) «Два одинаковых знака дают положительный знак, Знаки — и + (знак минус и знак плюс), поэтому они не похожи на знаки (они отличаются друг от друга) Итак, результат должно быть отрицательное : (−2) × (+5) = −10 Знаки — и — (оба знака отрицательные), поэтому они похожи друг на друга (подобны друг другу) Таким образом, результат должен быть положительным : (−4) × (−3) = +12 Ну, во-первых, объяснение «здравого смысла»: Когда я говорю «Ешь!» Я призываю вас есть (положительно) Но когда я говорю «Не ешьте!» Я говорю обратное (отрицательно). Теперь, если я скажу: « НЕ НЕ ешьте!», я говорю, что не хочу, чтобы вы голодали, поэтому я снова говорю «Ешь!» (положительно). Итак, два минуса дают плюс, и если вас это устраивает, то вам больше не нужно читать. Все дело в направлении. Помните числовой ряд? Итак, малыш Стивен делает свои первые шаги. Он делает 2 шага за раз и делает это три раза, поэтому он делает 2 шага x 3 = 6 шагов вперед: Малыш Стивен тоже может отступать назад (он умный малыш). Его папа возвращает его в исходное положение, а затем Стивен отступает на 2 шага назад и делает это три раза: Отец Стивена снова возвращает его в исходное положение, но лицом в другую сторону. Стивен делает 2 шага вперед (для себя!), но движется в отрицательном направлении. Он делает это 3 раза: Вернувшись в исходное положение снова (спасибо, папа!), по-прежнему глядя в отрицательном направлении, он пытается идти задом наперёд, снова делая два шага за раз, и делает это три раза: Итак, идя назад, глядя в отрицательном направлении, он движется в положительном направлении. Попробуйте сами! Попробуйте пройтись вперед и назад, затем еще раз, но лицом в другую сторону. Но, может быть, вы хотели бы увидеть его в действии? Используйте ползунки ниже: числа/изображения/номер-линия-mult.js Люди бегут вперед, видео в обычном режиме: Все нормально, люди бегут вперед: +1 × +1 = +1 Похоже, люди бегут назад: +1 × −1 = −1 Вы видите людей, бегущих назад: −1 × +1 = −1 Похоже, люди бегут вперед: − 1 × −1 = +1 В баке 30 000 литров, каждый день вывозится 1000 литров. Мы знаем, что количество воды в резервуаре меняется на −1000 каждый день, и нам нужно вычесть это 3 раза (чтобы вернуться на на 3 дня назад ), поэтому изменение равно: −3 × −1000 = + 3000 Полный расчет: 30000 + (−3 × −1000) = 30000 + 3000 = 33000 Итак, 3 дня назад в баке было 33000 литров воды. Вот другой взгляд на это. Сначала поиграйте с этим (пояснения ниже): числа/изображения/mult-grid.js?min=-5&max=5 Начните с таблицы умножения (достаточно до 4×4): Теперь посмотрим, что произойдет, когда мы войдем в негатива ! Пойдем назад через ноль: Посмотрите на столбец «4»: там -16, -12, -8, -4, 0, 4, 8, 12, 16 . Просмотрите эту таблицу еще раз, убедитесь, что вам удобно, как она работает, потому что… … теперь идем дальше налево , через ноль: Мы можем следовать по строке (или столбцу), и значения постоянно меняются: Итак, все идет по единой схеме! Также смотрите это в таблице реального умножения. Умножайте два за раз и следуйте правилам. Сначала умножьте (−2) × (−3). Два одинаковых знака дают положительный знак, поэтому: (−2) × (−3) = +6 Далее умножьте +6 × (−4). Два разных знака дают отрицательный знак, поэтому: +6 × (−4) = −24 Результат: (−2) × (−3) × (−4) = −24 330, 1615, 1616, 1617, 3447, 3448,331, 1618, 3170, 3171 Числа меньше нуля называются отрицательными числами. Числа выше нуля являются положительными числами. Учащиеся могут загрузить книгу «Умножение отрицаний — знаки, примеры, правила, решенные примеры и часто задаваемые вопросы» в формате PDF с веб-сайта Vedantu. Любой желающий может бесплатно загрузить PDF-файл «Умножение отрицаний — знаки, примеры, правила, решенные примеры и часто задаваемые вопросы» с веб-сайта. Умножение отрицаний — очень важная тема математики, по которой на экзаменах задают много вопросов. Правильное понимание темы необходимо для студентов, чтобы получить хорошие оценки на экзаменах. Эта тема важна для конкурсных экзаменов, таких как IIT и NEET. Таким образом, студенты должны приложить надлежащие усилия при изучении темы. Преподавательский состав Веданту, имеющий большой опыт обучения студентов, подготовил PDF-файл «Умножение отрицаний — знаки, примеры, правила, примеры решения и часто задаваемые вопросы». Учащиеся могут использовать PDF-файл «Умножение отрицаний — знаки, примеры, правила, решенные примеры и часто задаваемые вопросы» для многих целей. Таким образом, учащиеся могут получить массу преимуществ, загрузив PDF-файл «Умножение отрицаний — знаки, примеры, правила, примеры решения и часто задаваемые вопросы». Некоторые из тем, которые были объяснены в PDF-файле «Умножение отрицаний — знаки, примеры, правила, решенные примеры и часто задаваемые вопросы», следующие: Знаки Правила умножения отрицательных чисел Деление отрицательных чисел Что происходит, когда мы умножаем отрицательные числа? Мы знаем, что «+» — положительный знак, «-» — отрицательный. Когда знак не обозначается перед числом, это обычно означает, что оно положительное. Пример: 8 на самом деле +8 Примечание: Чтобы избежать путаницы со знаками, мы можем поставить () вокруг цифр. Например, 5 × −8 можно записать как 5 × (−8) Мы можем иметь положительные и отрицательные целые значения при работе с целыми числами при умножении. Существуют правила умножения и деления целых чисел, которые очень похожи на правила сложения и вычитания. Если знаки разные, то ответ отрицательный. Если знаки совпадают, ответ положительный. См. описание ниже для лучшего понимания. (Изображение будет загружено в ближайшее время) Пример: 2 × 5 = 10 (Мы уже обсуждали, что если число не имеет знака, это обычно означает, что оно положительное. (Изображение будет загружено в ближайшее время) Пример: (-10) × (-5) = 50 Отрицательное, умноженное на Отрицательное, является положительным числом, что означает, что произведение двух отрицательных целых чисел всегда положительный. (Изображение скоро будет загружено) Пример: 5 x (-5) = — 25 Умножение отрицательных чисел на положительное число всегда дает отрицательное число. (Изображение скоро будет загружено) Примечание. Эти правила работают так же, как и правила деления целых чисел; вам просто нужно заменить «раз» на «делится на». Деление отрицательных чисел работает так же, как и положительное, за исключением того, что результаты иногда бывают отрицательными. Expression Quotient Example Positive ÷ Positive Positive 25 ÷ 5 = + 5 Отрицательный ÷ Отрицательный Положительный — 25 ÷ — 5 = +5 Отрицательный ÷3 Negative -25 ÷ 5 = -5 Positive ÷ Negative Negative 25 ÷ -5 = — 5 Целочисленная матрица — это матрица, все элементы которой являются целыми элементами. Итак, если A — заданная матрица Тогда − A = − 1 A 1. Что такое −6 × 3? Ответ: 6 х 3 равно 18. Но здесь у нас есть одно отрицательное и одно положительное число. Следовательно, знак ответа будет минус. Следовательно, ответ равен −18. 2. Что такое −80 ÷ 8? Ответ: 80 ÷ 8 равно 10. Опять же, у нас есть положительное и отрицательное число. Следовательно, в окончательном ответе знак будет отрицательным. Следовательно, ответ равен −10. 3. Что такое −50 x −5? Ответ: 50 x 5 равно 250. На этот раз у нас есть 2 отрицательных числа. Значит, в ответе будет положительный знак. Следовательно, ответ равен 250. Помните только 2 вещи, когда перемножаете отрицательные числа. Учащиеся могут посещать онлайн-занятия для сдачи школьного экзамена или конкурсных экзаменов, таких как NEET или JEE. Они могут посещать занятия, не выходя из дома. Им просто нужно иметь работающее подключение к Интернету и устройство, такое как ноутбук, планшет или смартфон. У них также есть возможность скачать классы, чтобы просмотреть их позже для повторения. Студенты могут получить доступ к этим классам по очень доступным ценам, что делает их доступными для многих студентов. На веб-сайте есть обширный банк вопросов с вопросами, основанными на шаблонах экзаменов, к которым они готовятся. Помимо этого, студенты могут получить доступ к другим ресурсам, таким как заметки о пересмотре, решения NCERT, решения для других книг, образцы документов, PYQ и онлайн-тесты. Таким образом, присоединение к Веданту будет очень полезно для студентов. отрицательные числа, используя порядок операций. Начнем с того, что вспомним некоторые ключевые факты об операциях с отрицательными числами.
во-первых, правила сложения и вычитания. Прибавление отрицательного числа равносильно вычитанию положительного числа. Так, например, пять плюс минус семь — это то же самое, что пять минус семь. Это минус два. Мы говорим, что вычитание отрицательного числа равносильно добавлению положительного. Таким образом, пять минус минус семь — это то же самое, что пять плюс семь, то есть 12. Затем мы переходим к правилам умножения и деления. Умножение или деление положительного числа на отрицательное число дает отрицательное
отвечать. Так, например, пять, умноженное на минус семь, дает минус 35, как и минус
пять умножить на семь. И, наконец, умножение или деление двух отрицательных чисел, то есть умножение отрицательного
отрицательным, дает положительный результат. А дальше вспомним, что мы подразумеваем под порядком операций. Это способ гарантировать, что все получат один и тот же ответ при выполнении задания.
расчет. Аббревиатуры PEMDAS или BIDMAS сообщают нам порядок выполнения каждой части операции.
расчет. Первая буква обозначает скобки или квадратные скобки. Что бы ни находилось внутри любого набора скобок, это первое вычисление, которое мы выполняем. Далее идут показатели или индексы. Мы оцениваем любые числа, возведенные в степень. Затем у нас есть умножение и деление. Так вот, они имеют тот же вес, то же самое значение. Так что, если есть два из них в одной сумме, мы идем слева направо. Наконец, сложение и вычитание, опять же, имеют одинаковый приоритет. Поэтому, если их два в одной сумме, мы идем слева направо. Давайте посмотрим, как мы можем объединить всю эту информацию, чтобы выполнить заказ
операции над отрицательными числами. Заполните пропуск. Минус три минус два минус три равно чему. Мы хотим оценить это числовое предложение. Всякий раз, когда мы выполняем вычисления, подобные этому, мы всегда должны учитывать
Порядок операций. Иногда сокращенно PEMDAS или BIDMAS, это способ гарантировать, что каждый, кто
выполняет этот расчет, получает тот же ответ. Первая буква обозначает круглые скобки или скобки BIDMAS. Сначала мы выполняем любые вычисления внутри пары круглых скобок. Обратите внимание, что при выполнении этих расчетов мы также используем порядок операций над
любые проблемы в скобках. В этом случае у нас есть минус три минус два. И мы могли бы использовать числовую линию, чтобы оценить это. Начнем с отрицательной тройки на числовой прямой. Вычитание двух означает, что мы перемещаем два вниз по числовой прямой в отрицательном направлении. Так что это один, два, что оставляет нам минус пять. Итак, минус три минус два будет минус пять. Следующая часть наших аббревиатур говорит нам оценивать любые показатели степени или индексы. Вернемся к нашей числовой строке. На этот раз мы начинаем с отрицательной пятерки. И мы перемещаемся на одну, две, три позиции вниз по числовой строке. Это приводит нас к отрицательной восьмерке. Таким образом, пробел, являющийся решением отрицательного числа три минус два минус три, равен
минус восемь. На самом деле в этом вопросе нам действительно не нужна была эта пара скобок. У нас были только вычитания в нашей сумме. А мы знаем, что при выполнении сложения и вычитания в одном вычислении мы
просто идите слева направо. В нашем следующем расчете мы рассмотрим выполнение некоторого умножения. Вычислить минус 19 умножить на 19 умножить на минус пять умножить на
минус два. Чтобы оценить такой расчет, нам нужно рассмотреть порядок
операции. Помните, часто сокращенно PEMDAS или BIDMAS, это способ гарантировать, что
каждый, кто выполняет это вычисление, получает один и тот же ответ. Каждая буква обозначает определенную операцию. Мы начинаем с P, который обозначает круглые скобки или в BIDMAS означает скобки. Любые расчеты производим внутри нашей скобки. Теперь, в этом случае, у нас есть минус 19, отрицательная пятерка и отрицательная двойка внутри a
пара скобок. На этот раз это не говорит нам выполнить расчет. Нет расчета для выполнения. Это просто способ подчеркнуть, что мы на самом деле работаем с негативными
числа. Далее у нас есть показатели степени или индексы. Далее следуют умножение и деление. Теперь умножение и деление имеют одинаковый приоритет. Итак, когда они выполняются в одном расчете, мы просто двигаемся слева направо.
Правильно. Последние две буквы обозначают сложение и вычитание. И точно так же они имеют такое же значение. Поэтому, когда они у нас есть в одном и том же расчете, мы двигаемся слева направо. Теперь, если мы посмотрим на наши вычисления, мы увидим, что умножение есть только для
выполнять. Таким образом, мы могли двигаться слева направо. Но есть дополнительный факт, который может быть полезен. И это умножение коммутативно. Это можно делать в любом порядке. Теперь, если бы в этой задаче были какие-либо другие операции, мы не смогли бы использовать эту
факт. Но здесь мы можем. Итак, что мы собираемся сделать, так это вычислить минус 19 умножить на 19 и
минус пять раз два. Причина, по которой это полезно, заключается в том, что мы знаем, что пять умножить на два равно 10. Далее мы посчитаем минус 19 умножить на 19. Что ж, начнем с вычисления 19 умножить на 19. И воспользуемся методом сетки. 10 умножить на 10 — это 100, а девять умножить на 10 — это 90. Наконец, девять умножить на девять — это 81. 19, умноженное на 19, — это сумма этих четырех значений; это 361. Это означает, что 19, умноженное на 19, равно 361. Мы знаем, что отрицательное число, умноженное на положительное, дает отрицательный результат. Итак, отрицательное число 19, умноженное на 19, равно отрицательному числу 361. Мы подсчитали, что отрицательное число 19, умноженное на 19, будет отрицательным 361 и пятью отрицательными значениями.
минус два будет 10. Итак, теперь мы собираемся вычислить минус 361, умноженный на 10. Мы знаем, что для умножения на 10 мы перемещаем цифры влево на один пробел. Оценить четыре минус 13 плюс отрицательный 19. Всякий раз, когда мы пытаемся оценить числовое предложение, мы должны думать о
порядок операций. Иногда сокращенно до PEMDAS или BIDMAS, это способ гарантировать, что каждый, кто
выполняет этот расчет, получает тот же результат. Первая буква обозначает скобки или квадратные скобки. Мы оцениваем любую сумму внутри скобок. Здесь 13 плюс минус 19.. Теперь нас не должно сбивать с толку, что минус 19 сам находится внутри пары
скобки. В данном случае это не расчет; это просто показывает нам, что мы действительно работаем
с отрицательным числом. Итак, мы вычисляем 13 плюс минус 19. На самом деле осталось выполнить только одну операцию. Нет ни показателей, ни индексов, ни умножения, ни деления. У нас просто вычитание. Теперь вспомним, что вычесть минус — это то же самое, что добавить плюс. Итак, четыре минус минус шесть — это то же самое, что четыре плюс шесть, что равно 10. Таким образом, четыре минус 13 плюс минус 19 равно 10. В нашем следующем примере мы постараемся включить еще несколько операций. Вычислите 21 минус отрицательное число 19, деленное на пять, умноженное на три. Всякий раз, когда нам представляют числовое предложение, которое мы хотим оценить
Ответ на, мы должны думать о порядке операций. Возможно, вы знаете, что это PEMDAS или BIDMAS, где каждая буква говорит нам об операции. В данном случае у нас просто 21 минус минус 19. И не забывайте, что минус 19 сам заключен в пару круглых скобок. Это просто способ подчеркнуть тот факт, что минус 19 — это минус.
количество. Итак, вычислим 21 минус минус 19. Мы знаем, что вычитание отрицательного числа равносильно прибавлению положительного. Так что это то же самое, что 21 плюс 19, что равно 40. Теперь мы заменим это выражение, 21 минус минус 19, на 40 в наших вычислениях. Важно, чтобы мы сохранили порядок, поэтому мы не хотели бы добавлять 40 в конце.
конец. Нужно 40 разделить на пять умножить на три. Вернемся к PEMDAS и BIDMAS. В нашем самом последнем примере мы рассмотрим некоторые распространенные заблуждения относительно проблемы.
с участием индексов. Вычислить три раза минус четыре в квадрате минус семь плюс минус два. Столкнувшись с такой проблемой, нам нужно подумать о порядке
операции. Здесь мы часто используем аббревиатуры PEMDAS или BIDMAS, где каждая буква в аббревиатуре
сообщает нам порядок, в котором мы выполняем вычисления. Следующая буква E или I обозначает показатели степени или индексы соответственно, другими словами,
любая мощность. Ну, у нас есть один из них. У нас есть минус четыре в квадрате. Итак, давайте оценим минус четыре в квадрате. Распространенным заблуждением является мнение, что минус четыре в квадрате — это минус 16. Но мы знаем, что возводить число в квадрат — это то же самое, что умножать его само на себя. Таким образом, минус четыре в квадрате — это минус четыре, умноженный на минус четыре. А так как умножая отрицательное число на другое отрицательное число, мы получаем положительное
16. Следующие две буквы обозначают умножение и деление. Теперь умножение и деление имеют равный приоритет. Поэтому, если в одном и том же расчете появляется более одного, мы двигаемся слева направо. На самом деле у нас здесь только одно умножение. Это три раза по 16. Три умножить на 16 — это 48. Таким образом, мы заменяем трижды 16 на 48. Теперь наш расчет равен 48 минус пять. Теперь еще одна распространенная ошибка здесь заключается в том, чтобы изменить порядок расчета и
думаю, что нам нужно выполнить пять минус 48. На самом деле очень важно, чтобы мы сохраняли порядок вычисления. Наши последние две буквы A и S обозначают сложение и вычитание. Но на самом деле, это все, что осталось сделать в любом случае. Нам нужно получить 48 минус пять. Это 43. Итак, три раза минус четыре в квадрате минус семь плюс минус два равно 43. В этом видео мы узнали, что нам нужно применить порядок операций ко всем
расчеты, в том числе с отрицательными числами. К оглавлению… Определение модуля может быть дано следующим образом: Абсолютной величиной числа a (модулем) называется расстояние от точки, изображающей данное число a на координатной прямой, до начала координат. Из определения следует, что: Таким образом, для того чтобы раскрыть модуль необходимо определить знак подмодульного выражения. Если оно положительно, то можно просто убирать знак модуля. Если же подмодульное выражение отрицательно, то его нужно умножить на «минус», и знак модуля, опять-таки, больше не писать. Основные свойства модуля: К оглавлению… Существует несколько типов уравнений с модулем, для которых имеется предпочтительный способ решения. При этом данный способ не является единственным. Например, для уравнения вида: Предпочтительным способом решения будет переход к совокупности: А для уравнений вида: Также можно переходить к почти аналогичной совокупности, но так как модуль принимает только положительные значения, то и правая часть уравнения должна быть положительной. Это условие нужно дописать в качестве общего ограничения для всего примера. Тогда получим систему: Оба этих типа уравнений можно решать и другим способом: раскрывая соответствующим образом модуль на промежутках где подмодульное выражение имеет определённый знак. В этом случае будем получать совокупность двух систем. Приведем общий вид решений получающихся для обоих типов уравнений приведённых выше: Для решения уравнений в которых содержится более чем один модуль применяется метод интервалов, который состоит в следующем: Структура хранения темы оформления организована таким образом, чтобы по значению опции Правила организации исходного кода: Например, для модуля Каждая тема оформления будет определена с помощью нескольких модулей, например В рамках одной темы оформления могут быть описаны несколько модификаций. Например, в теме оформления Исходный код каждой модификаций должен быть оформлен в виде директории в модуле с темой. Например, для темы оформления При установке значения опции Посмотреть пример готового модуля темы оформления можно на github. При создании темы следует указывать параметр @themeName. Он необходим для корректной сборки css-стилей. Например, тема называется retail и она будет наследоваться от темы «по умолчанию». Согласно предыдущему разделу создаем модуль Controls-retail-theme. Все параметры темы оформления определяются в одном файле Процесс описания собственной темы оформления сводится к переопределению значений css-переменных родительской темы. Переопределяемые переменные должны лежать внутри селектора с классом .controls_theme-@{themeName}. После сборки less в модуле с темой оформления появится файл theme.css, который будет содержать переменные и их значения, определенные для темы При сборке дистрибутива все файлы theme.css пакуются специальным образом. Например для набора модулей: Будет собран один итоговый retail.css, состоящий их всех theme.css, которые лежат в модулях. Он располагается по адресу %resourceRoot%/themes/retail.css. В этом же каталоге лежат остальные собранные файлы тем и модификаторов. Затем, при указании контролу опции theme=»retail», этот файл будет загружен на клиент, а значения переменных будут применены к контролам. Некоторые модули можно автоматически обновить в backoffice, нажав кнопку Обновить. Однако если модуль взят из другого источника, чем сам prestashop (например, github), то модуль должен — afaik — обновляться вручную. Так как же следует обращаться с обновлениями? Скачать ZIP и Примечание: как насчет config.xml и, возможно, других сгенерированных файлов? То же самое относится и к обновлениям тем, как с ними справиться? Относительно текущей версии Prestashop 1.7+. Я пытаюсь изменить шаблон модуля в prestashop, поэтому я скопировал модуль в свою папку темы modules. Я заметил, что тема меняется, единственная проблема заключается в том, что перевод не меняется. Я получил оригинальный текст на окончательном шаблоне магазина. Есть ли какой-то простой способ… У меня есть страница prestashop www.oledia.fr я хочу изменить размер логотипа, на самом деле , когда я использую веб-инструмент через Firefox; я могу найти код html, но я делаю поиск во всех серверах, я не могу найти нужные файлы; а также я прохожу через все темы сайта и модули; я не могу найти,… Если обновление модуля выполнено правильно (вы можете проверить, обновлена ли версия модуля в конструкторе класса основного модуля и использует ли сценарии обновления в папке Для тем вы также можете просто распаковать последнюю. Когда я сомневаюсь в каких-либо обновлениях, я делаю копию магазина для разработки и сначала делаю обновления там, а затем проверяю, все ли в порядке, а затем выполняю обновления на живом экземпляре. Поделиться TheDrot 21 ноября 2017 в 20:10 Поделиться Trong Nguyen 23 мая 2018 в 03:37 мой квест состоит в том, чтобы поменять местами 2 модуля в левой колонке. Я читал, что обычно я должен делать это в административной панели -> live edit Проблема в том, что prestashop, используемый… я новичок в prestashop и пытаюсь создать свою собственную тему, используя default. Моя версия prestashop-это 1.6.0.9. Так что я справляюсь с содержимым от /themes/default-bootstrap до /themes/test …. Я обычно покупаю темы по цене ThemeForest за prestashop, и я хочу получать обновления для тем. Но иногда мне нужно изменить пару .tpl из темы. Я нашел в документации файловую структуру модуля. И… Я пытаюсь изменить шаблон модуля в prestashop, поэтому я скопировал модуль в свою папку темы modules. Я заметил, что тема меняется, единственная проблема заключается в том, что перевод не меняется…. У меня есть страница prestashop www.oledia.fr я хочу изменить размер логотипа, на самом деле , когда я использую веб-инструмент через Firefox; я могу найти код html, но я делаю поиск во всех… ребята, сегодня я устанавливаю модули для версии 1.7.X в моем магазине prestashop, моя версия prestashop правильна 1.7.X, но если я попытаюсь открыть модули в консоли разработчика браузера, я найду… Я обновил версию моего сайта Prestashop с 1.7.4 до 1.7.6. Но после обновления я не вижу данных в бэк-офисе. Я могу войти в систему без каких-либо проблем. Я также могу видеть приборную панель так,… Я использую Prestashop версий 1.6 и 1.7. Иногда мне нужно переустановить модули из админ-панели . Для повторной установки из админ-панели требуются файлы zip модулей. Где я могу найти модули zipped… Мы приближаемся к созданию пользовательской темы с нуля для Prestashop (v1.7) в первый раз (в то время как мы исходим из расширенного опыта работы с пользовательскими темами WordPress, например, с… В последние дни стало невозможно обновить модули. Я получаю сообщение об ошибке типа это недопустимое имя модуля . Можно ли вручную обновить модули, извлекая последние файлы из Github? Я попытался… Добавляйте модули непосредственно на страницу Материалы курса. Вы можете перетаскивать в модули уже имеющееся содержимое или добавлять новое с помощью значка «+». В учебный модуль можно добавлять следующие элементы: Чтобы добавить учебный модуль, нажмите знак «плюс». В меню выберите пункт Создать, чтобы открыть панель Создание элемента. Выберите элемент Учебный модуль. Учебные модули отображаются в новых курсах. Если функция добавления учебных модулей недоступна, ваш курс был создан до ее внедрения. Введите название, описание (необязательно) модуля и выберите параметры его видимости. Если вы хотите, чтобы учащиеся просматривали содержимое учебного модуля в определенной последовательности, выберите Условная доступность в меню видимости модуля. Подробнее о предоставлении доступа к содержимому модуля в определенной последовательности Кроме элементов содержимого, файлов и заданий, вы можете добавлять виды деятельности и средства, способствующие интерактивному обучению и совместной работе. Например, можно добавить задания или групповые проекты, чтобы дать учащимся возможность применить знания, полученные с помощью учебного модуля. Помимо этого, можно добавлять средства совместной работы (например, обсуждения), в которых можно проводить мозговые штурмы и делиться идеями на предложенные темы. Подробнее о добавлении содержимого Подробнее о типах добавляемого содержимого При удалении учебного модуля с содержимым оно также удаляется со страницы Материалы курса. Чтобы упорядочить содержимое, в учебный модуль можно добавлять папки. Папки в учебных модулях могут содержать только элементы содержимого, но не другие папки. Учащиеся смогут перемещаться по содержимому папок так же, как и по другим материалам модуля. Но вы можете активировать принудительный последовательный доступ к материалам курса. Учащиеся смогут открывать элементы содержимого в модуле только после выполнения предыдущих необходимых заданий. Всем привет! Кто разрабатывал сайты для государственных, муниципальных, образовательных учреждений знает, что у сайта должна быть обязательно «версия для слабовидящих». Хочу предложить своё решение этого вопроса. Думая над логикой модуля, чтобы всё не усложнять я пришел к следующему решению: проще всего сделать «версию для слабовидящих» отдельной темой оформления и переключать темы «на лету». Необходимо установить и подготовить тему оформления, которая будет «для слабовидящих». В admin/appearance/settings выбрать эту тему. Модуль используется только для создания блоков переключения на тему для слабовидящих и обратно. Сама панель с кнопками теперь находится в теме оформления и выглядит вот так: Модуль после включения создаёт 2 уже готовых блока: «версия для слабовидящих» и «обычная версия». Первый нужно разместить на обычной теме оформления, а второй соответственно на «версии для слабовидящих». Вот собственно и всё, с помощью этих двух блоков мы переключаем тему оформления. С помощью CSS можно изменить изображения на кнопках в блоках. С версии 7.x-1.5 и 8.x-1.1 добавлена возможность выбирать тип блоков (изображение или текст). Пример блока в виде текста: Что делать, если модуль не работает? Топ 3 проблем: Скачать модуль можно с официальной страницы проекта Инструкция import используется для импорта ссылок на значения, экспортированные из внешнего модуля. Импортированные модули находятся в Существует также function-like динамический Обратная совместимость может быть обеспечена с помощью атрибута Динамический импорт полезен в ситуациях, когда вы хотите загрузить модуль условно или по требованию. Статическая форма предпочтительна для загрузки начальных зависимостей и может быть более полезна для инструментов статического анализа и tree shaking. Внимание: На данный момент эта функциональность только начинает поддерживаться браузерами. Полноценная реализация присутствует во многих транспайлерах, таких как TypeScript и Babel, а также в сборщиках, например, в Rollup и Webpack. Параметр Этот код вставляет объект В данном случае, доступ к импортируемым значениям можно осуществить с использованием имени модуля (в данном случае «myModule») в качестве пространства имён. Например, если импортируемый выше модуль включает в себя экспорт метода Определённое ранее значение, названное Этот код вставляет оба значения Вы можете переименовать значения, когда импортируете их. Например, этот код вставляет Код, который импортирует несколько значений из модуля, используя более удобные имена. Импорт всего модуля только для использования побочного эффекта от его вызова, не импортируя что-либо. Это запускает глобальный код модуля, но в действительности не импортирует никаких значений. Есть возможность задать дефолтный Простейшая версия прямого импорта значения по умолчанию: Возможно также использование такого синтаксиса с другими вариантами из перечисленных выше (импорт пространства имён или именованный импорт). В таком случае, импорт значения по умолчанию должен быть определён первым. Для примера: или Если вы импортируете переменные, то в данной области видимости они ведут себя как константы. Такой код выведет ошибку: Для импорта можно воспользоваться объектом в котором хранятся эти переменные. Такой код будет рабочим: Учитывая, что Ключевое слово Как следствие возврата Promise, с динамическим импортом можно использовать ключевое слово Обратите внимание, что несмотря на то, что динамический импорт выглядит как вызов функции, он им по сути не является, т.е. не наследует от Импорт из вспомогательного модуля для помощи в обработке запроса AJAX JSON. Этот пример показывает, как можно загрузить на страницу дополнительный модуль в зависимости от действий пользователя (в данном случае, по клику на кнопку), а затем использовать функции из загруженного модуля. Промисы — это не единственный способ использовать динамический импорт. Функция BCD tables only load in the browser Для изменения масштаба воспользуйтесь комбинациями клавиш: Сегодня: 30.07.2021
Данная разработка представляет собой продукт, созданный в ходе инновационной деятельности Гимназии в статусе ресурсного центра общего образования по направлению «Система оценки и управления качеством образования в образовательном учреждении». Тема Opinion предоставляет большие возможности благодаря использованию нашего шаблона страницы Modules . Вы, вероятно, захотите использовать его в качестве своей домашней страницы, но его можно использовать и для других страниц, количество страниц модуля на вашем веб-сайте не ограничено. Чтобы создать домашнюю страницу, сначала перейдите к Pages -> Add New и создайте страницу. В настройках шаблона выберите шаблон «Модули». Перейдите в Настройки -> Чтение и выберите параметр «На вашей домашней странице отображается статическая страница». Затем выберите свою домашнюю страницу из списка ниже. Хорошо, домашняя страница настроена, и теперь вы можете начать управлять ее содержимым. Если вы вставили наш демонстрационный контент, образец домашней страницы добавляется автоматически, так что у вас есть предопределенная настройка примеров модулей. Посмотрите весь процесс в этом коротком видео: Основная цель нашей модульной системы состоит в том, чтобы легко создавать несколько групп контента на одной странице и организовывать его по своему желанию с помощью простого система перетаскивания. На выбор предлагается несколько различных типов модулей: Модуль сообщений используется для отображения ваших сообщений, связанных в визуальную и логическую группу. Вы заметите два набора параметров для управления модулем сообщений, разделенных вкладками. Вкладка «Внешний вид» зарезервирована для параметров «отображения», где вы можете выбрать макет и количество отображаемых публикаций, в то время как вкладка выбора зарезервирована для параметров «фильтрации», где вы можете выбрать способ упорядочивания сообщений, следует ли извлекать сообщения только из определенной категории, тега и т. д.… Другой тип модуля — текстовый модуль.По сути, его можно использовать по-разному, и он принимает весь контент, который вы обычно добавляете в редактор контента страницы по умолчанию или текстовый виджет. Итак, здесь вы можете добавить любой пользовательский текст, HTML, шорткоды, рекламные скрипты и т. Д. С помощью этого модуля вы можете легко отображать свои категории так же, как вы это делаете для сообщений. Взгляните на пример ниже. Как правило, вы выбираете макет и внешний вид элементов, а затем на вкладке выбора вы можете выбрать определенные категории, которые хотите отобразить, или отобразить все категории. Авторские модули используются для отображения пользователей (авторов) вашего сайта. По желанию, вы также можете добавить нумерацию страниц на свои страницы модуля. Из-за логики и технических ограничений WordPress на одной странице модуля может быть только одна пагинация. При этом, если используется разбивка на страницы, она будет применена к модулю последних сообщений на странице (поскольку в большинстве случаев он будет соответствовать потребностям). Хорошая особенность шаблона страницы модулей заключается в том, что его нельзя использовать только для домашней страницы. Количество страниц модуля не ограничено, поэтому не стесняйтесь проявлять творческий подход. Например, вы можете создать страницу «карты сайта», отображающую набор последних сообщений для каждой категории, формата сообщения или тега. Или вы можете создать «самую популярную» страницу, отображающую ваши самые посещаемые и наиболее комментируемые сообщения за текущий месяц. При разработке веб-сайта Prestashop никогда не следует изменять файлы ядра.Это означает, что вы можете создавать только новые модули в папке Каждый раз, когда Prestashop необходимо загрузить файл шаблона модуля, он сначала просматривает текущую тему Эта рекомендация также действительна для Документация, которую вы упомянули в комментарии ниже, неверна и должна быть обновлена. Вы не можете поместить папку Вот метод Как видно из этого кода, Prestashop никогда не будет заглядывать в папку Добавляет форму регистрации, которая позволяет пользователям подписываться на предпочтения Marketo. Настройками формы могут управлять нетехнические редакторы. Отправьте письмо Bitbucket на адрес [email protected], чтобы запросить доступ к этому модулю. Trumba — это система календаря мероприятий на территории кампуса.Этот модуль позволяет вам встраивать календарь Trumba на ваш веб-сайт и при желании добавлять блоки с поиском даты, фильтрами поиска и категорий или с предстоящими событиями. Чтобы узнать, как настроить календарь Trumba, см. Справку календаря событий UW. Отправьте письмо Bitbucket на адрес [email protected], чтобы запросить доступ к этому модулю. Тема POWER основана на трех различных основных типах модулей: модули секций, субмодули и мини-модули. МОДУЛИ СЕКЦИИ разделов представляют собой полный раздел на веб-сайте со всеми необходимыми опциями непосредственно в модуле для стилизации и компоновки контента. Эти модули позволяют быстро создавать веб-сайты, поскольку они имеют разные варианты макета, а также может быть удобно переключаться между различными вариантами макета. Кроме того, модули раздела позволяют настраивать фоновые изображения с дополнительными эффектами параллакса, фоновые видео с наложением или даже наложения градиента и многое другое. ПОДМОДУЛИ Большинство элементов секционных модулей также являются субмодулями. Подмодули очень гибкие и могут использоваться по-разному, максимально используя новую область перетаскивания HubSpots. МИНИ-МОДУЛИ Mini — это более гранулированные модули, но также очень гибкие. Некоторые из мини-модулей — это CTA, Tags или Icon. Модули секции имеют множество общих опций, которые перечислены ниже: ВВЕДЕНИЕ К НАЗВАНИЮ НАЗВАНИЕ НАЗВАНИЕ — ТИП ЗАГОЛОВКИ ОПИСАНИЕ ЦВЕТОВАЯ СХЕМА CENTERED ФОН BACKGROUND-COLOR ФОНОВОЕ ИЗОБРАЖЕНИЕ Кроме того, вы можете изменить положение фонового изображения и настроить фоновое изображение как изображение с параллаксом. Кроме того, мы создали возможность добавления наложения к фоновому изображению в виде одного цвета или градиента.Вы должны использовать непрозрачность для цвета или градиента, если хотите, чтобы изображение было видно на заднем плане. Для градиента вы можете использовать непрозрачность для каждого цвета градиента или общую непрозрачность с «Непрозрачностью наложения градиента в%». ФОНОВОЕ ВИДЕО Убедитесь, что размер файла не слишком велик.Общее практическое правило — продолжать уменьшать размер файла до тех пор, пока он не начнет заметно ухудшаться. Попробуйте экспортировать видео в разрешении 720p и с битрейтом менее 700 кб / с (желательно 500 кб / с). YouTube Видео могут быть включены через ссылку или идентификатор YouTube. Если выбрано видео YouTube, видео YouTube перезапишет настроенное собственное видео. BACKGROUND-GRADIENT НАПОЛНИТЕЛЬ ВЕРХНЯЯ / НИЖНЯЯ СТАНДАРТНЫЙ ТЕКСТ / ПЕРЕВОД Пример ниже, показывающий модуль предварительного просмотра сообщения в блоге, имеет два переводимых / редактируемых статических текста: «Мин. Чтение» и «Начать чтение». Обе записи можно редактировать в конфигурациях модуля: Что дает следующий результат: Эта опция дает вам полные возможности прямого перевода ваших модулей, включая статические тексты. ACCORDION STYLE ЯЩИК ИЗОБРАЖЕНИЙ ВИД СТИЛЬ Этот подмодуль позволяет создавать отдельные таблицы цен (1 столбец), которые можно объединить, чтобы представить полную таблицу сравнения цен, используя следующие параметры: ТАБЛИЦА ЦЕН ВИД СТИЛЬ Уменьшенная планировка Полный макет СЕРВИС ВИД СТИЛЬ Варианты компоновки: Простой элемент списка может использоваться для отображения открытых вакансий / вакансий, а на странице для прессы — для отображения списка статей / загрузок и многого другого. ПУНКТ ВИД СТИЛЬ Варианты компоновки С помощью этого подмодуля числовая статистика может быть показана в простой форме. После того, как раздел станет видимым для пользователя, числа будут анимированы (счет будет увеличиваться). СТАТ ВИД СТИЛЬ Предварительный просмотр: Этот подмодуль создает представление различной информации. Контент содержит элемент (номер, значок или рисунок), заголовок и описание. ШАГ ВИД СТИЛЬ Step-layout: Этот подмодуль используется для отображения члена команды. Поле команды может быть связано со страницей члена команды, которую мы также предоставили в этой теме. Можно настроить следующие параметры: КОМАНДА ВИД СТИЛЬ Варианты компоновки: Подмодуль видеобокса обеспечивает визуализацию видеобиблиотек, страниц и разделов веб-семинаров. ВИДЕОКОБКА ВИД СТИЛЬ Предварительный просмотр: Помимо модуля CTA по умолчанию HubSpots, этот модуль предлагает параметры стиля, связанные с темой, и наборы стилей для CTA. Не стесняйтесь использовать следующие варианты: CTA ПЛАН СТИЛЬ Предварительный просмотр: ЗНАЧОК ВИД СТИЛЬ Предварительный просмотр: ТЕГ ВИД СТИЛЬ Предварительный просмотр: Аккордеонный модуль может эл.г. использоваться для часто задаваемых вопросов (FAQ). АККОРДИОННЫЕ ВОПРОСЫ: Нажмите «Добавить» или отредактируйте существующий вопрос, чтобы перейти к редактору вопросов и ответов. Когда вы закончите редактировать вопрос и ответ, нажмите «Вернуться в раздел Accordion». Вопросы будут выровнены автоматически, если выбран макет из 2 столбцов. ПЛАН: Схема размещения в 1 столбец Схема расположения двух столбцов Навигация на вашем веб-сайте с помощью хлебных крошек — это способ показать пользователям их текущее местоположение и то, как они туда попали.Это также помогает вашим посетителям быстрее находить страницы высокого уровня, если они попали на вашу страницу по прямой ссылке или по результатам поиска. В этом модуле можно настроить следующие параметры: КРОШКА: Обратите внимание, что можно создать несколько элементов хлебных крошек, представляющих глубину навигации по хлебным крошкам. ЛОГОТИПЫ КЛИЕНТОВ Для каждого логотипа клиента добавьте одну запись в параметре выше. Загрузите или добавьте изображение из вашей файловой библиотеки. После загрузки ширину и высоту можно настроить вручную. Мы предлагаем ширину 300 пикселей. Также убедитесь, что все ваши логотипы имеют одинаковый размер. АВТОЗАПИСЬ Если активен, ползунок с логотипом клиента вращается автоматически. Продолжительность автовоспроизведения можно установить вручную в миллисекундах. НАВИГАЦИЯ — СТРЕЛКИ Включает стрелки навигации по бокам ползунка. НАВИГАЦИЯ — ПУЛЬТЫ Активирует маркеры под ползунком: СКОЛЬКО ИЗОБРАЖЕНИЙ ДОЛЖНО ПОКАЗАТЬСЯ? Количество логотипов, которые следует показывать сразу / на слайде. Строка раздела из 3 столбцов, например, показать миссию, видение и манифест вашей компании. ЗНАЧЕНИЯ CTA МАКЕТ По горизонтали: По вертикали: Только CTA: MOCKUP ФОРМА CTA (S) МАКЕТ ПОЛНАЯ ШИРИНА ШИРИНА МАКЕТА В% МАКСИМАЛЬНАЯ ШИРИНА МАКЕТА В ПИКСЕЛЯХ ШИРИНА КОНТЕНТА В% СКРЫТЬ Мокап для мобильных устройств Этот модуль используется для встраивания форм HubSpot. Формы HubSpot можно создавать с помощью редактора форм HubSpot. Перейдите к → этому разделу, чтобы узнать больше о том, как создавать формы HubSpot. ФОРМА Что увидит посетитель после отправки формы ?: Вы можете выбрать перенаправление на другую страницу или отобразить встроенное сообщение с благодарностью. Кроме того, вы можете добавить форму в существующий рабочий процесс. Обратите внимание, что эта функция устарела к 5 декабря 2019 года, поскольку контакты не регистрируются в заданном рабочем процессе. Другой вариант — отправить дополнительное электронное письмо после отправки формы. Просто выберите здесь настроенный дополнительный адрес электронной почты. ПЛАН По горизонтали 50/50: По горизонтали 60/40: в горизонтальной коробке: Ширина по вертикали: Вертикальный узкий: Этот модуль можно использовать как вводный раздел.Возможны несколько приложений с этим модулем. Его можно использовать как раздел героя или как строку заголовка. Обратите внимание, что этот модуль можно использовать только один раз на веб-сайте. Использование нескольких модулей героя на одном конкретном сайте невозможно. ВЫСОТА Большой Обычный Малый Очень маленький НАЗВАНИЕ EXTRA LARGE ОПИСАНИЕ БОЛЬШОЙ Регулярный: Большой: ОСНОВНАЯ ИНФОРМАЦИЯ Это результат приведенной выше конфигурации. Модуль героя также можно использовать для создания более творческой секции, как показано ниже. Только пользовательское фоновое изображение. Только титул. Примечание. В этом последнем примере цвет «SERVICES LOREM» был установлен с помощью встроенных стилей css. Это не официальный вариант шаблона. Этот модуль очень универсален и может использоваться по-разному — галерея, обзор портфолио и многое другое. Планировка: возможны 6 различных вариантов компоновки Сетка из 3 колонн Трехколонная сетка, меньшая высота Сетка из 4 колонн Трехколонная кладка Трехколонная кладка меньшей высоты Каменная кладка, 4 колонны Без переплета: этот параметр удаляет интервалы между столбцами и строками. Стиль блока: текстовое содержимое помещается выше или ниже поля. Стиль коробки — содержимое ниже Стиль коробки — Наложение содержимого Меньший размер шрифта и отступы: уменьшает отступ и размер шрифта текстового содержимого. «Использовать наложение на передней панели блока»: добавляет прозрачное наложение на поля, чтобы текст над ним был более читабельным. Hide Info on Box Front: Удаляет все текстовое содержимое с лицевой страницы.Текст будет отображаться только при наведении курсора. Перезаписать цвета блока: это позволяет вам изменить цвет фона и цвет шрифта стиля блока: «Содержимое ниже» с вариантом стиля блока «с фоном» Использовать как галерею? С этой опцией изображения отображаются во всплывающем окне лайтбокса, когда пользователь нажимает на них. Фильтрация: Категории, разделенные запятыми, можно настроить для каждого окна изображения. Если блоки изображений должны быть сгруппированы в одну и ту же категорию, убедитесь, что вы указали одинаковые названия категорий. Этот модуль представляет собой простой слайдер изображений, т.е. его можно использовать для слайд-шоу изображений. Изображение: Добавьте сюда изображения, которые должны отображаться. Автозапуск: если этот параметр включен, ползунок изображения вращается автоматически. Autoplay — Interval Timeout: время автовоспроизведения в миллисекундах. Navigation — Arrows: добавляет стрелки по бокам для навигации по ползунку изображения. Navigation — Bullets: добавляет маркеры под ползунком изображения Navigation — Bullets as Overlay: если активировано, маркеры отображаются непосредственно на изображениях. Макет: мы предлагаем три разных макета для слайдера изображений. (несколько номеров): По одному / По одному (настраиваемая высота): Этот модуль используется для отображения карт Google, опционально с дополнительной информацией. Этот модуль основан на использовании кода внедрения карт Google или, предпочтительно, использовании кода внедрения, созданного с помощью «Snazzy Maps». → snazzymaps.com Чтобы создать свой код для встраивания, выполните следующие действия: 1.Посетите сайт шикарных карт: → snazzymaps.com 2. Создайте учетную запись на шикарных картах. 3. Щелкните «Построить карту» в основной навигации и следуйте инструкциям там. 4. По завершении нажмите «Просмотреть код» 5. Вам будет предложено ввести имя карты и ключ API карт Google. Следуйте инструкциям здесь: https://developers.google.com/maps/documentation/javascript/get-api-key, чтобы создать свой собственный ключ API. Это всегда необходимо для встраивания карты Google Map на свой веб-сайт.Если ваш API недействителен, Google заблокирует рендеринг на вашем сайте. 6. После того, как вы закончите вводить необходимую информацию, вы можете скопировать код для встраивания и вставить его в настройки модуля. Контактная информация: после того, как вы встроили свой шикарный код карты, можно добавить контактную информацию, которая может отображаться разными способами. Вы можете добавить свой адрес, электронную почту и номер телефона. CTA: Кроме того, у вас есть возможность добавить HubSpot CTA. : если вы хотите отображать форму вместо контактной информации, активируйте этот переключатель и выберите желаемую форму HubSpot. Планировка: Мы предлагаем 5 различных планировок: 1. Карта слева: 2. Карта справа 3. Только карта 4. Content-Box слева 5. Content-Box справа: Высота секции (пикселей): укажите высоту этого модуля в пикселях. Это значение применяется к настольной версии. Для небольших экранов и мобильных версий высота масштабируется в зависимости от содержимого. Модуль разделения мультимедийного контента используется для визуализации модуля, отображающего макет с разделением экрана 50:50. Одна сторона модуля всегда содержит одно изображение или видео. Видео можно загрузить в формате mp4 в HubSpot или связать видео с YouTube. Другая сторона может включать заголовок, комбинацию описания, цитату отзыва с логотипом компании, призывы к действию или значки социальных сетей. — это характеристика: если этот параметр включен, описание будет отображаться как цитата, и появятся дополнительные параметры, такие как имя и должность. Имя: Имя цитируемого человека. Должность: Должность цитируемого человека. Изображение / Логотип: Включите сюда изображение, например, логотип компании указанных лиц. Значки социальных сетей / контактов: создание и определение одного или нескольких значков. У вас есть возможность связать значки, например, для учетных записей социальных сетей. CTA: выберите один или несколько HubSpot CTA. : здесь у вас есть возможность перевернуть порядок содержимого. Либо покажите изображение / видео слева или справа. 1.Изображение справа + отзыв 2. Изображение слева + заголовок + описание + CTA Шаблон POWER предлагает модуль таблицы цен. Этот модуль может отображать до 3 ценовых блоков в одной строке. Конкретные ценовые поля необходимо создать здесь отдельно: Создание и редактирование этих ценовых рамок даст следующие параметры: Заголовок + Описание: Это вводная часть каждой коробки. Цена: Основная цена каждого прайс-листа. Возможны числа и текст. Характеристика: Каждый набор параметров представляет особенность. Каждую функцию можно отключить: CTA: добавьте один HubSpot CTA. Выделено: если активировано, поле цены выделяется основным цветом. Рекомендуемый: если активирован, над окном цены отображается метка «рекомендуется». Макет: определяет макет ценовых ящиков. Уменьшено: отображается только заголовок, описание, цена и CTA Полный: показывает поля с ценами со всеми предварительно настроенными функциями Стиль таблицы: определяет различные стили таблицы для «полной» версии макета Стиль 1: Стиль 2: Конечно, есть и тёмная версия: Также возможны комбинации с фоновыми изображениями и видео, как почти в каждом модуле. Этот модуль предлагает визуализацию расписания.Можно создавать ежедневные расписания на несколько дней, реализованные в виде вкладок. Если вы хотите использовать более одного ежедневного расписания, не забудьте активировать «Использовать вкладки?» переключить раньше. : создавайте по одному набору на каждый день. Каждый сконфигурированный набор предлагает следующие опции: Каждое событие имеет более глубокий набор, который можно настроить как: Темная версия модуля расписания. Этот модуль визуализирует услуги в 4 различных вариантах макета.Во-первых, здесь нужно определить все услуги: Каждую службу можно настроить со следующими параметрами. 1. Значок: выберите значок из предопределенного списка значков 2. Или загрузите собственное изображение: 3. Название + описание: 4. Ссылка: при необходимости вы можете связать каждую службу с другой страницей контента, внешней страницей, файлами, адресами электронной почты или блогами / сообщениями в блогах. : мы предоставили несколько вариантов макета для этого модуля 1.Icon Top + Border 2. Значок слева 3. В штучной упаковке В пакете шаблонов POWER простой модуль листинга используется в качестве обзора для страницы карьеры, чтобы показать открытые позиции / вакансии, и на странице для прессы, чтобы показать список статей / загрузок. Однако это всего лишь примеры. Можно настроить следующие параметры. 1. Элементы списка: это подэлементы, которые содержат дополнительные конфигурации для отдельных элементов списка. 2. Макет: выберите один из следующих вариантов макета: 1. Ящик 2. Текст 3. Цвет рамки: Дополнительно мы предоставили возможность перезаписать цвет рамки (макет коробки). 4. Другой стиль фильтра: также можно индивидуально изменить стиль панели категорий. Фильтрация: для каждого элемента можно настроить категории, разделенные запятыми.Если элементы должны быть сгруппированы в одну категорию, убедитесь, что вы указали одинаковые названия категорий. С помощью этого модуля можно легко показать несколько числовых статистических данных. После того, как раздел станет видимым для пользователя, числа будут анимированы (счет будет увеличиваться). Здесь можно настроить статистику: Каждый элемент содержит следующие параметры для настройки статистики: Этот модуль создает многоколоночный макет различной информации. Информация в каждом столбце содержит элемент (номер, значок или рисунок), заголовок и описание. В диспетчере дизайна можно настроить следующее. 1. Шаг: Здесь определяется содержание каждого столбца Каждый элемент содержит следующие параметры: 2. Планировка: Возможны 4 варианта компоновки: 1. Счетчик шагов 2. Значок 3. Изображение 4. Только текст Этот модуль используется для демонстрации членов команды вашей компании. Можно настроить следующие параметры: 1. Команда: в этих элементах хранится информация о каждом члене команды. Каждый элемент содержит следующие параметры: 2. Макет — Вкладки: Активация этой опции включает систему вкладок, в которую члены команды могут быть дополнительно вложены. Заголовок каждой вкладки можно определить индивидуально в разделе вкладок: 3. Планировка: Мы предоставили следующие 2 варианта компоновки 1. Полный (вкладки или без вкладок) 2. Уменьшенный (вкладки или без вкладок) Для отзывов клиентов мы предусмотрели несколько макетов. В модуле отзывов можно настроить следующие параметры: 1. Отзыв: все содержание / информация отзывов хранится в этих подэлементах Каждый подэлемент содержит следующие параметры: 2. Автовоспроизведение: автоматический поворот ползунка отзывов после заданного интервала автовоспроизведения. 3.Стрелки: включает стрелки навигации слайдера отзывов 4. Пули: отображение маркеров под ползунком отзывов в качестве дополнительного средства навигации. 5. Планировка: Предлагаем следующие 5 планировок: По одному — Стиль 1 По одному — Стиль 2 Несколько Листинг в 2 столбца Схема с 3 столбцами Для основных текстовых разделов мы создали этот текстовый модуль.Текстовый модуль предлагает несколько макетов. Текст каждого абзаца можно настроить с помощью редактора форматированного текста. В модуле можно настроить следующие опции: 1. Заголовок, тип заголовка и содержание. «Содержимое или левое содержимое» используется для макетов с 1 столбцом. Для макетов с 2 столбцами он представляет левую сторону. Дополнительное поле с форматированным текстом «Содержимое справа» будет отображаться для макетов с 2 столбцами и макета «Заголовок слева, текст справа» 2. Макеты: Мы предоставили следующие 6 макетов: Заголовок вверху, текст 1 столбец Заголовок вверху, текст 2 столбца Заголовок слева, текст справа Текстовые табуляторы — по центру по вертикали Текстовые вкладки — вертикальные Текстовые вкладки — горизонтальные Элемент Table-of-Content предлагает возможность иметь плавающий обзор сбоку веб-сайта или обзор над контентом.Содержимое оглавления автоматически извлекается из содержимого страницы / модуля. Этот элемент используется в двух разных модулях: 1. «Содержание страницы столбца»: Этот модуль был разработан для использования на страницах столбца. Если этот модуль включен где-то на странице, будет охвачено все содержание страницы столпа. Здесь есть два варианта: … или фиксируется сбоку на веб-странице 2.«Текст с оглавлением»: в оглавлении включается только контент, созданный в этом модуле. Обратите внимание, что любой модуль можно использовать только один раз для шаблона / веб-страницы. Этот модуль временной шкалы можно использовать для истории вашей компании. Это позволяет отображать изображения, заголовок и описание для каждого временного шага. Шаги по времени автоматически меняются влево и вправо. Можно настроить следующие параметры: 1.Временная шкала: вся важная информация для каждого временного шага хранится в одном из этих подэлементов Здесь можно настроить следующие параметры: 2. Центрирование: есть возможность центрировать весь раздел и / или элементы содержимого временной шкалы. Этот модуль предлагает различные способы визуализации видео на вашем сайте. Есть два способа настроить видео: 2. Если вы хотите встроить свое видео через YouTube, используйте ссылку или идентификатор YouTube. Видео YouTube перезапишет настроенное собственное видео. Если пользователь щелкает заголовок или кнопку, настроенное видео открывается в световом поле. Конечно, вы можете настроить дополнительное отключенное видео в фоновом режиме, как и во всех модулях нашего раздела. Кроме этого, можно настроить следующие параметры: 1. Макет: Мы предоставили 3 разных макета для раздела видео: 1. Название видео 2. Только кнопка 3. Содержание: видео с наложением текста 2.Высота раздела: устанавливает высоту раздела видео в пикселях. Модуль видеобоксов обеспечивает визуализацию видеотек, страниц и разделов вебинаров. В этом модуле можно настроить следующие параметры: Video Box: вся необходимая информация для каждого предварительного просмотра вебинара хранится в этих подэлементах. Здесь можно настроить следующие параметры: Фильтрация : Категории, разделенные запятыми, можно настроить для каждого вебинара.Если вебинары должны быть сгруппированы в одну категорию, убедитесь, что вы указали одинаковые названия категорий. Каждый тип надстройки можно разделить на три категории: Модуль — это программное обеспечение (код), расширяющее функциональность Заставки. Создание пользовательских модулей требует глубокого понимания программирования PHP и API Backdrop (некоторые знания HTML и CSS также полезны). Узнайте больше о создании модулей на https: // api.backdropcms.org/developing-modules. Тема определяет дизайн веб-сайта. Темы обычно отвечают за типографику, цветовую схему, ширину страницы и т. Д. И наиболее сильно влияют на внешний вид вашего веб-сайта. Думайте о теме как о оболочке для вашего Backdrop-сайта: тему можно изменить в любое время, но остальная часть вашего сайта должна остаться нетронутой. Создание настраиваемых тем требует глубокого понимания HTML, CSS и уровня темы Backdrop (также полезно иметь некоторые знания PHP).Узнайте больше о создании тем на https://api.backdropcms.org/developing-themes. можно использовать в макетах, чтобы определить, как (и когда) различные элементы расположены на разных страницах вашего сайта. Шаблоны макета предоставляют «области», в которых можно размещать блоки (подробнее об этом читайте в разделе «Построение с блоками и макетами»). Например, один шаблон макета с двумя столбцами может использоваться для каждой отдельной страницы вашего сайта, или специальный шаблон макета с тремя столбцами может использоваться только на домашней странице.Если вам нужно другое расположение страниц, чем для сообщений, или другое меню, добавленное на боковую панель, шаблоны макета помогут вам настроить это. Создание настраиваемых макетов требует глубокого понимания HTML, CSS и уровня темы Backdrop (также полезно иметь некоторые знания PHP). Узнайте больше о создании пользовательских макетов на https://api.backdropcms.org/developing-layouts. Начиная с Backdrop 1.14, мы добавили поддержку создания пользовательских шаблонов макета через пользовательский интерфейс администратора .Шаблоны макета называются «гибкими», и они позволяют указать любое количество строк; внутри этих строк вы можете добавить любое количество регионов, указав ширину этих регионов. Каждый модуль тематически ориентирован на определенную тему, имеющую отношение к клинической практике.Каждый семинар Mindful Practice® может включать в себя один или несколько модулей, которые выбираются в зависимости от специальности учащихся, целей, уровня подготовки и других факторов. Каждый модуль содержит дидактические, созерцательные и интерактивные элементы с подробными инструкциями по выполнению этих упражнений. В рамках каждого модуля отводится время для подведения итогов, в ходе которого участники делятся своими мыслями, проблемами и вопросами. Интерактивная презентация каждого модуля описывает структуру и цель занятия и представляет материалы, относящиеся к теме модуля.Презентации сопровождаются интерактивным обсуждением с некоторыми конкретными вопросами. созерцательных упражнений под руководством обычно составляют около 1/3 каждого занятия. Сюда входят медитативные практики, руководствуясь которыми, вплетаясь в тему данного модуля. Диалогические упражнения ( нарративной медицины, благодарные интервью, инсайт-диалоги и т. Д.) Составляют примерно 1/3 каждого занятия. Обычно участники делятся на небольшие группы по 5-10 человек и готовят письменные рассказы.Эти повествования делятся диадами, триадами или всей небольшой группой. Задаются рефлексивные вопросы, чтобы стимулировать более глубокое исследование повествовательного опыта. Folwell — это развивающаяся система проектирования, состоящая из модульных компонентов, которые можно комбинировать различными способами для создания творческих и согласованных веб-сайтов университетов.Folwell разработан University Relations и может использоваться на любой платформе. Для сайтов Drupal 8 и 9, размещенных в службе Drupal Управления информационных технологий, доступна тема, а также дополнительные модули для поставки уже реализованных компонентов. Изменение темы веб-сайта, вероятно, потребует значительного времени разработчика для узкоспециализированных сайтов. Не все сайты будут вести себя одинаково после переключения темы. Подтема Folwell рекомендуется для сайтов, функциональность которых не поддерживается темой Folwell. При попытке включить модули Folwell Components могут возникнуть ошибки для данного модуля; это будет зависеть от существующей конфигурации сайта (включенные в данный момент модули, существующие файлы конфигурации и т. д.). Могут существовать сущности Drupal, которые не позволяют вам конкретно включить модули Folwell, или могут быть зависимости модулей Folwell, которые нельзя включить без предварительного удаления или изменения определенных элементов. У каждого сайта может быть своя уникальная ситуация. Рекомендуется, чтобы все работы по тестированию и подготовке выполнялись на локальной установке сайта с использованием документации в Drupal 8 и Drupal 9: Настройка локальной среды Drupal 8. После успешной реализации темы Folwell в локальной среде можно сделать запрос через Drupal Support Request для загрузки базы данных в среду разработки (dev). Убедитесь, что сайт еще не использует тему Folwell. Если сайт уже использует Folwell, эта статья не применяется; не переходите к следующим шагам этого раздела — перейдите к Enable Folwell Modules. Если сайт в настоящее время не использует тему Folwell, текущую тему можно отключить и включить Folwell, выполнив следующие действия: Folwell теперь установлена как текущая тема, и теперь при необходимости можно включить модули Folwell Components. Помимо темы Folwell, есть модули, которые можно включить для дополнительной функциональности сайта; эти дополнительные функции называются компонентами Folwell. В зависимости от модулей, которые в настоящее время (или были ранее) включены на сайте, при попытке включить модули Folwell и их зависимости могут возникать ошибки. Для установки всех функций Folwell и их зависимых модулей: Обзор Drupal Руководство администратора Drupal 8 Модули Drupal 8 Дополнительные темы Folwell Настройка локальной среды Drupal 8 Возможности обучения Drupal К оглавлению. Определение модуля может быть дано следующим образом: Абсолютной величиной числа a (модулем) называется расстояние от точки, изображающей данное число a на координатной прямой, до начала координат. Из определения следует, что: Таким образом, для того чтобы раскрыть модуль необходимо определить знак подмодульного выражения. Если оно положительно, то можно просто убирать знак модуля. Если же подмодульное выражение отрицательно, то его нужно умножить на «минус», и знак модуля, опять-таки, больше не писать. Основные свойства модуля: К оглавлению… Существует несколько типов уравнений с модулем, для которых имеется предпочтительный способ решения. При этом данный способ не является единственным. Например, для уравнения вида: Предпочтительным способом решения будет переход к совокупности: А для уравнений вида: Также можно переходить к почти аналогичной совокупности, но так как модуль принимает только положительные значения, то и правая часть уравнения должна быть положительной. Оба этих типа уравнений можно решать и другим способом: раскрывая соответствующим образом модуль на промежутках где подмодульное выражение имеет определённый знак. В этом случае будем получать совокупность двух систем. Приведем общий вид решений получающихся для обоих типов уравнений приведённых выше: Для решения уравнений в которых содержится более чем один модуль применяется метод интервалов, который состоит в следующем: Для того чтобы успешно подготовиться к ЦТ по физике и математике, среди прочего, необходимо выполнить три важнейших условия: Успешное, старательное и ответственное выполнение этих трех пунктов, а также ответственная проработка итоговых тренировочных тестов, позволит Вам показать на ЦТ отличный результат, максимальный из того, на что Вы способны. Если Вы, как Вам кажется, нашли ошибку в учебных материалах, то напишите, пожалуйста, о ней на электронную почту (адрес электронной почты здесь). В письме укажите предмет (физика или математика), название либо номер темы или теста, номер задачи, или место в тексте (страницу) где по Вашему мнению есть ошибка. Также опишите в чем заключается предположительная ошибка. Ваше письмо не останется незамеченным, ошибка либо будет исправлена, либо Вам разъяснят почему это не ошибка. Статья актуальна для версии магазина: 8. В данной статье рассмотрим настройки модуля «МойСклад» на стороне магазина, которые касаются свойств, описания и активности товара. Для того чтобы произвести данные настройки, перейдите в раздел «Модули — МойСклад» (см. рис. 1) 1. Тип синхронизации свойств Обратите внимание, Свойства созданные на основе справочников не передаются из «МойСклад» в магазин. 2. Тип синхронизации описания продукта 3. Активировать продукт Рассмотрим подробнее свойства товаров. Для того чтобы добавить свойства к товару на стороне «МойСклад» необходимо в разделе «Товары — Товары и услуги — Настройки» создать дополнительные поля (см. рис. 2) Обратите внимание, Не все типы полей выгружаются. Не выгружаются поля с типом: дата, справочник, файл, ссылка. После добавления данные поля будут отображаться в карточке товара на стороне «МойСклад». Также для передачи веса товара, производителя, скидок, объема, международного кода маркировки и учёта логистических единиц, а также штрих код товара, необходимо создавать дополнительные поля с соответствующими названиями. Для того чтобы передать эти поля в соответствующие поля в магазине, нужно указать соответствие свойств характеристикам товара на стороне модуля «МойСклад» (см. рис. 3). Скидка (в валюте магазина)— выгружается в карточку товара в параметр «Скидка в валюте магазина», то есть позволяет выгружать фиксированную скидку у товаров. Gtin — выгружается в поле «Код международной маркировки и учета логистических единиц» в карточке товара. Так же как и в случае с параметрами Вес, Размеры, для выгрузки данного параметра из «МойСклад» необходимо добавить дополнительное поле, на стороне модуля указать название данного поля. Если у товара есть свойства, которые выгружать не нужно, укажите их в поле «Свойства, которые не нужно выгружать» на стороне модуля в магазине. (см. рис. 4) Статья оказалась полезной? Да
Нет Благодарим за отзыв. Проблема в …Не могу закончить настройку, слишком сложная инструкцияСледовал инструкции, но ожидаемого результата не добилсяНедостаточно описаны вспомогательные элементыПохоже что инструкция устарелаТема статьи не раскрытаДругое А именно с Комментарий Не нашли нужную статью?
Предложить свою тему На какую тему не нашлась статья? Ваш email Комментарий Благодарим за отзыв. Тэги: мойсклад,настройки модуля, настройки модуля мойсклад, свойства, описание, активность Навигация:
Главная
Случайная страница
Обратная связь
ТОП
Интересно знать
Избранные
Топ: Отражение на счетах бухгалтерского учета процесса приобретения: Процесс заготовления представляет систему экономических событий, включающих приобретение организацией у поставщиков сырья… Марксистская теория происхождения государства: По мнению Маркса и Энгельса, в основе развития общества, происходящих в нем изменений лежит…
Теоретическая значимость работы: Описание теоретической значимости (ценности) результатов исследования должно присутствовать во введении… Интересное: Берегоукрепление оползневых склонов: На прибрежных склонах основной причиной развития оползневых процессов является подмыв водами рек естественных склонов. Подходы к решению темы фильма: Существует три основных типа исторического фильма, имеющих между собой много общего… Отражение на счетах бухгалтерского учета процесса приобретения: Процесс заготовления представляет систему экономических событий, включающих приобретение организацией у поставщиков сырья…
Дисциплины:
Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция
⇐ ПредыдущаяСтр 8 из 8 Определение. Действительные числа х и у называются, соответственно, действительной и мнимой частями комплексного числа z и обозначаются: Определение.Вещественное неотрицательное число: называют модулем комплексного числа . Теорема. (Об умножении комплексных чисел в тригонометрической форме записи.) Пусть , где и , где – два произвольных комплексных числа записанных в тригонометрической форме. Тогда . Теорема. (Свойства модуля комплексного числа.) Пусть – произвольные комплексные числа и соответствующие точки на комплексной плоскости. Тогда: 1) и . Т.е. модульпроизведения комплексных чисел равен произведению их модулей и модули противоположных чисел равны; 2) расстояниемеждуточками и комплексной плоскости равно модулю разности соответствующих комплексных чисел: ; 3) ; 4) ; Доказательство. , где и , т.е. . Таким образом, равенства и есть тригонометрическаяформа записи числа , следовательно, по теореме о равенстве комплексных чисел в тригонометрической форме записи, имеем , ч.т.д. Далее, т.к. , то по только что доказанному свойству , ч.т.д. Заметим, что последнее равенство можно получить и из других соображений. Противоположные числа на комплекснойплоскости изображаютсяточками симметричными относительно начала координат. Действительно, пусть . Тогда и точки , имеют противоположные декартовые координаты. Значит, в силу симметрии, расстояния от этих точек до начала координат равны, т.е. , ч.т.д. Заметим, также, что такой же результат можно получить с помощью формулы (12) вычисления модуля комплексного числа. 2). Пусть , . Тогда и по формуле (12) имеем: . (14) С другой стороны, рассмотрим числа и как точки на комплексной плоскости. 3) Рассмотрим на комплекснойплоскости точки , и начало координат О. В общем случае эти три точки являются вершинами треугольника : рис.6. Воспользуемся известным свойством треугольника: длина стороны треугольника не превосходит суммы длин двух его других сторон. Мы только что доказали, что длина стороны этого треугольника равна , а длины сторон и равны по определению модулям чисел и : , . Отсюда и получаем, что . Заменим в последнем неравенстве число на противоположное число , тогда получаем: , ч.т.д. Заметим, что равенство в этих неравенствах достигается тогда и только тогда, когда треугольник вырождается в отрезок прямой, т.е. когда все три точки О, и лежат на одной прямой. 4) , откуда следует . , откуда и следует доказываемое неравенство. Теорема доказана. ⇐ Предыдущая12345678 Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций… Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции… Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим… Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)… В этой лекции мы рассмотрим: Пример Замечание Пример x= 7 Пример Позитивный корень квадрата числа равен этому числу. ТЕОРЕМА 1.2.3 Доказательство (a) |-a| = √(-a)2 = √a2 = |a| (b) |ab| = √(ab)2 = √a2b2 = √a2√b2 = |a||b| (a) |-4| = |4| (b) |2. (c) |5/4| = 5/4 = |5|/|4| = 5/4 Результат (b) вышеизложенной теоремы может быть применено к трем или более членам. Теорема 1.2.4 (Формула расстояния) ТАБЛИЦА 1.2.2 (a) Пример On real line На численной прямой Не всегда верно, что Первый случай, где a+b ≥ 0 И Второй случай где a+b По сравнению с начальной неравенство С помощью дополнительных модулей можно расширить
функциональность программы, подключая к ней новые модули на ваш выбор.
Для отображения списка подключенных модулей,
нажмите кнопку «Параметры» в правой верхней
части окна программы и выберите пункт «Дополнительные модули».
В открывшемся окне «Дополнительные
модули» можно настроить подключенные модули,
нажав кнопку «Настроить», а также включить
или выключить необходимый модуль. Mодуль «Дополнительные слои» позволяет создавать, хранить и редактировать дополнительные слои на карте.
Список слоев, объектов, инструменты их создания, редактирования, сохранения собраны в едином справочнике «Дополнительные слои».
Основная часть справочника — список, который показывает текущую структуру слоев и объектов, некоторую их атрибутивную информацию (название, обозначение).
Основные элементы структуры слоёв:
Вся структура и объекты дополнительных слоёв хранятся одним файлом в дополнительном каталоге программы.
Перейдите к справочнику «Дополнительные слои».
Каталог может хранить как подкаталоги, так и точечные, линейные объекты и многоугольники одновременно.
При соответствующих настройках объектам внутри каталога могут быть присвоены свойства того каталога, в котором они находятся. Однако, для каждого объекта в каталоге свойства могут быть изменены и являться индивидуальными.
Обновляемый каталог
Обновляемый каталог имеет ссылку на ранее созданный KML или KMZ файл (объект), содержимое которого предположительно будет меняться (может быть указана ссылка на объект в интернете). Удобно, если этот объект используется несколькими пользователями и для этого не требуется каждый раз отдельно загружать необходимый файл, достаточно просто задать его расположение и период обновления в расширенных настройках каталога во вкладке «Обновление»:
Точечный объект
Для создания точечного объекта укажите щелчком на карте его место и нажмите кнопку «Сохранить» в окне «Свойства точечного объекта».
Линейный объект
Чтобы построить линейный объект на карте, укажите одиночными щелчками точки, между которыми будет строиться прямая линия. Построение выполняется от активной точки, размер которой больше относительно других точек на линии. Активной может являться любая точка на линии. После построения линии нажмите кнопку «Сохранить» в свойствах объекта. Также построение линейного объекта возможно при зажатой левой кнопки мыши. В этом случае первая точка выставляется как от одиночного нажатия.
В результате происходит соединение предыдущей и текущей точки прямой линией. Для удаления последней точки при построении линейного объекта нажмите «Esc» на клавиатуре.
Площадной объект (многоугольник)
Принцип построения многоугольника не отличается от построения линейного объекта, разница лишь в том, что при создании многоугольника происходит закрашивание области между синей и активной точками многоугольника.
Редактирование объектов и слоев на карте возможно только когда открыто окно свойств (при создании и редактировании свойств объекта или слоя).
Дополнительная информация
Для внесения дополнительной информации об объекте воспользуйтесь вкладкой «Описание». Текст можно вводить в HTML. Существует возможность форматирования текста и вставки изображений.
Данная функция позволяет устанавливать время отображения объекта на карте. Для этого щелкните «Указать время» во вкладке «Описание» и в открывшемся диалоговом окне укажите период отображения объекта, после чего нажмите кнопку «Установить».
В данном примере объект будет отображаться на карте с 07.05.2011 09:00 по 08.
Также в справочнике существует возможность выбора фильтра по времени отображения объектов на карте.
Для этого нажмите в пиктограммном меню кнопку «Установить по времени» и выберите необходимый фильтр:
Если ни один фильтр не выбран, то на карте будут отображаться все объекты.
Стиль
Во вкладке «Стиль» можно настроить стиль отображения объекта на карте. В зависимости от редактируемого объекта доступны следующие параметры для изменения:
Координаты точечного объекта
В расширенных настройках во вкладке «Координаты» можно выбрать привязку точечного объекта по заданным координатам или определенному адресу на карте.
Ниже рассмотрен пример добавления изображения к точечному объекту на карте с привязкой к адресу.
Во вкладке «Координаты» указывается адрес здания, к которому необходимо привязать объект:
Во вкладке «Описание» требуется ввести относительный путь к картинке в виде кода:
В результате при щелчке на объект отображается добавленная картинка в его информационной карточке:
Редактирование линейного объекта и многоугольника
Существует возможность добавления новых точек в редактируемом многоугольнике и линейном объекте. В режиме редактирования подсвечиваются все точки объекта и при щелчке в любой отрезок на линии или грань многоугольника добавляется новая точка.
Для перехода к настройкам модуля, нажмите кнопку «Параметры» в правом верхнем углу программы и выберите пункт «Дополнительные модули». Раскройте блок «Дополнительные модули» одним щелчком мышки и нажмите кнопку «Настроить».
Соединение с интернетом
Если справочник «Дополнительные слои» содержит слои, обновляемые через интернет, то необходимо выполнить соответствующие настройки соединения с интернетом в этом блоке.
Резервная копия
Оставьте комментарий 6,950 Модуль числа — это расстояние от этого числа до нуля на координатной прямой. Модуль обозначается с помощью символа: | |. Модуль положительного числа равен самому числу. Например, |2| = 2.
Модуль отрицательного числа равен противоположному числу |-3| = 3.
Модуль нуля равен нулю, то есть |0| = 0.
Модули противоположных чисел равны, то есть |-a| = |a|. Для лучшего понимания темы: «модуль числа» предлагаем воспользоваться методом ассоциаций. Представим, что модуль числа — это баня , а знак «минус» — грязь . Оказываясь под знаком модуля (то есть в «бане») отрицательное число «моется» , и выходит без знака «минус» — чистым . В бане могут «мыться» (то есть стоять под знаком модуля) и отрицательные , и положительные числа , и число ноль . Однако будучи «чистым» положительные числа , и ноль свой знак при выходе из «бани» (то есть из под знака модуля) не меняют ! 1. Задача №1. Расположи выражения: -|12|, 0, 54, |-(-2)|, -17 в порядке возрастания. — | 12 | = — 12 17
-17 Ответ: -17 Задача№2. Нужно расположить выражения: -|-14|, -|30|, |-16|, -21, | -(-9) | Для начала раскроем скобки и модули: — | — 14| = — 14 16 > 9 > -14 > — 21 > — 30 что будет равносильно: Ответ: |-16| > | -(-9) | > — | — 14| > — 21 > — |30| Модуль числа n представляет собой количество единичных отрезков от начала координат до точки n. Причем не важно, в какую сторону будет отсчитываться это расстояние – вправо или влево от нуля. a
— это само это число. Число в модуле: |а| = а Предположим, есть комплексное число , которое записано в алгебраическом виде z=x+i·y , где x и y — действительные числа, которые представляют собой действительную и мнимую части комплексного числа z , а — мнимая единица. Модулем комплексного числа z=x+i·y является арифметический квадратный корень из суммы квадратов действительной и мнимой части комплексного числа. Модуль комплексного числа z обозначают так , значит, определение модуля комплексного числа можно записать так: . Lmod поддерживает задание свойств модулей. Для модулей, написанных на Lua, add_property() функция выглядит так: В TCL это записывается как: Ключ и значение управляются файлом lmodrc.lua. Lmod предоставляет стандартный файл lmodrc.lua, который копируется в
каталог установки. Например, установлен Lmod версии X.Y.Z.
в /apps/lmod/X.Y.Z, тогда lmodrc.lua будет установлен в
/apps/lmod/X.Y.Z/init/lmodrc.lua. В процессе установки это
файл изменен, чтобы включить расположение кэша системного паука. Lmod ищет свойства в нескольких местах в указанном порядке
ниже. Предполагая, что Lmod установлен в /apps/lmod/X.Y.Z.
затем Lmod ищет информацию о свойствах в следующем порядке: Где $LMOD_RC — это переменная среды, которую можно настроить так, чтобы она указывала на
любое местоположение файла. Если существует более одного из этих файлов
тогда они сливаются, а не заменяются. Таким образом, сайт может (и
следует) оставить первый файл как есть и создать еще один, чтобы указать
свойства сайта и Lmod объединит информацию в один. Формат этого файла выглядит так: Этот файл определяет таблицу с именем propT. В этом случае propT определяет допустимые ключи и возможные значения
для файла модуля для использования с add_property() . В случае
выше таблицы, единственными допустимыми ключами в файле модуля будут arch 9.0004, состояние , lmod и статус . Значение для состояния управляет допустимыми значениями. В частности,
только действительные значения для состояния : экспериментальный , тестовый или устарело . Обратите внимание, что файл модуля может иметь несколько
свойства, но каждый ключ свойства может иметь только одно значение. Итак: будет состояние свойство имеет значение устаревшее . Lmod сам по себе зависит от ключей lmod и статуса . Итак, как сайт,
ожидается, что любой файл lmodrc.lua будет содержать эти свойства. Функция add_property() ожидает ключ и значение. Итак, для состояние ключ, возможные значения: экспериментальный , тестовый или устарело . Эти строки должны появиться в двух таблицах: validT и
столы дисплея T . Например, мы видим, что проверяет .
как в таблицах validT , так и displayT . Это существует для проверки
для допустимых значений, когда функция add_property() вызывается из
файлы модулей. Таблица displayT определяет способ отображения свойства. говорит, что модуль с этим свойством будет иметь «(T)» рядом с его
имя при печати модулем avail. Если на дисплее терминала
«xterm» как часть переменной окружения TERM. то будет буква Т
быть в зеленом. Если поле full_color установлено значение true затем имя
и «T» будет зеленым. Возможные значения цвета: черный , красный , зеленый , желтый , синий , пурпурный , голубой и белый . На практике, поскольку пользователи могут
используйте светлые буквы на темном фоне или темные буквы на светлом фоне
фоны, сайты могут избегать черного , белого и, возможно, желтый . Ключ арки показывает, что значения можно комбинировать. Модули и атрибуты модуля имеют свойства по умолчанию, которые автоматически создаются при каждом новом создании модуля или атрибута модуля. Tricentis Tosca автоматически добавляет некоторые значения свойств при сканировании. Отредактируйте свойства модуля на панели свойств в правой части окна. Если открыть новое окно Модули, панель свойств по умолчанию свернута. Чтобы развернуть его, нажмите кнопку «Свойства» в правой части окна. Знаки и символы классический модуль XModule классический ModuleAttribute XModuleAttribute Каркас автоматизации Указывает на структуру автоматизации, т.е. ТБокс, универсальный. БизнесТип На уровне XModule это указывает на корневой элемент, зависящий от технологии, например. Начиная с XModuleAttribute указывает тип управления атрибутом, независимо от используемой технологии. Равные бизнес-типы имеют одинаковые свойства, например. каждый элемент управления EditBox имеет свойство Text. , Мощность Указывает, как часто XModuleAttribute может использоваться в качестве XTestStepValue в одном и том же XTestStep (см. 0-1: XTestStepValue изначально создается как подстановочный знак для каждого атрибута XModuleAttribute. Может быть создан только один XTestStepValue. 1: Создано ровно одно значение XTestStepValue для атрибута XModuleAttribute. ActionMode по умолчанию — это значение, установленное в столбце ActionMode. 0-N: значение XTestStepValue изначально создается как подстановочный знак для каждого атрибута XModuleAttribute. 1-N: XTestStepValue изначально создается как подстановочный знак для каждого атрибута XModuleAttribute. Должен быть сгенерирован хотя бы один XTestStepValue. Создан в Указывает дату и время создания объекта. , Создано Указывает имя пользователя TOSCA, создавшего объект. , Режим действия по умолчанию Задает ActionMode по умолчанию для XTestStepValues. Вновь созданные XTestStepValues автоматически получают указанное здесь значение, если кардинальность атрибута имеет значение >0 (см. «Количественность»). Доступные режимы действий можно выбрать из раскрывающегося списка в зависимости от указанного типа интерфейса. Некоторые элементы управления получают значение по умолчанию при сканировании их с помощью Tosca XScan. Тип данных по умолчанию Определяет значение DataType по умолчанию для TestStepValue (String, Numeric и т. Тип данных, определенный на уровне ModuleAttribute, применяется к TestStepValues, но не является обязательным. , Значение по умолчанию Определяет значение по умолчанию, которое автоматически копируется в TestCase всякий раз, когда используется XModule. Описание В это текстовое поле можно записать любую информацию. Информация, хранящаяся здесь, не оказывает никакого влияния на автоматизированное рулевое управление. Текст отображается во всплывающей подсказке. , HasMissingReferences Указывает, что ссылка отсутствует. Возможные значения: True, False (по умолчанию) , Тип реализации Указывает технологию, используемую для управления тестовым объектом (например, JAVA, HTML, SAP и т. Тип интерфейса Указывает, является ли тестовый объект графическим или неграфическим интерфейсом. GUI: количество предоставляемых ActionModes ограничено количеством, необходимым для графических пользовательских интерфейсов (см. NonGUI: видны все доступные режимы действий. Неявный (XModuleAttribute): используется тип интерфейса родительского объекта (значение по умолчанию). , Исабстракт Указывает, является ли ваш модуль абстрактным или нет. Исчеккедаутбайме Указывает, извлек ли текущий пользователь этот объект (Истина) или нет. , ИсТБоксМодуле Указывает, является ли модуль модулем TBox (истина) или нет (ложь). ModifiedAt Указывает дату и время последнего изменения объекта. , Изменено Указывает имя пользователя TOSCA, который последним изменил объект. , путь к узлу Содержит уникальный путь к объекту в рабочей области. Таким образом, объекты могут быть однозначно идентифицированы. , ИмяГруппы Владения Указывает группу пользователей, которым разрешено изменять объекты (см. , Редакция Значение этого свойства автоматически назначается в многопользовательских средах. Номер редакции увеличивается всякий раз, когда объект возвращается или удаляется. , Специальная иконка Используйте его для назначения значка ModuleAttribute определенному типу элемента управления. , Политика синхронизации Это изменяет SynchronizationPolicy выбранного объекта. Возможные значения: CannotBeExecuted, CustomizableDefaultIsOn (см. , Технический идентификатор Используйте этот параметр для определения свойства, зависящего от технологии. , Уникальный идентификатор Содержит уникальный идентификационный номер объекта в рабочей области. , Версия Указывает версию Tricentis Tosca, используемую для сканирования модуля. ViewingGroupName Указывает группу пользователей, для которых объект виден (см. , Диапазон значений Это свойство отображается только на вкладке «Сведения» (см. «ValueRange»). , Диапазон значений ValueRange на вкладке Details содержит список значений, разделенных точкой с запятой. Классические модули: эти значения можно указать вручную. Как вариант, Tosca Wizard идентифицирует их при сканировании тестового объекта и автоматически добавляет в Модуль. XModules: Tosca XScan идентифицирует значения при сканировании типов элементов управления ComboBox и ListBox и автоматически добавляет их в модуль. Кроме того, вы можете указать значения вручную. Если ModuleAttribute используется в TestCase, значения столбца ValueRange предоставляются в раскрывающемся списке в столбце Value. Система применяет точное строковое значение, включая пробелы. В дополнение к фиксированному списку значений вы можете определить следующие диапазоны значений для модулей и XModules: <ДАТА> <КАТАЛОГ> <ПУТЬ К ФАЙЛУ> <ВРЕМЯ> Если вы указали один из этих конкретных диапазонов значений в ModuleAttribute, следующие входные данные доступны для всех TestStepValues, которые используют этот ModuleAttribute: Управление календарем Выбор каталога Средство выбора пути к файлу Набор времени Щелкните поле «Значение» TestStepValue, чтобы просмотреть доступные параметры ввода. Введите < для ValueRange атрибута ModuleAttribute, чтобы показать автозаполнение. Пример использования диапазона значений <ДАТА> Кроме того, вы также можете указать форматы <ДАТА> и <ВРЕМЯ>. Доступны следующие параметры: для <ДАТА> д: день М: месяц г: <ДАТА ММ/дд/гггг> (22. <ДАТА дд.мм.гггг> (22.03.2012) <ДАТА гггг/ММ/дд> (22.03.2012) для <ВРЕМЯ> ч: часы (в 12-часовом формате) H: часы (в 24-часовом формате) м: с: секунды fff: доля секунды (требуется три цифры) <ВРЕМЯ> (09:45:00) <ВРЕМЯ чч:мм> (09:45) <ВРЕМЯ ЧЧ-мм-сс-фффф> (09-45-12-397) Я не могу найти причину ошибки: Моя конфигурация: (на самом деле они объединены с функцией расширения, которую я использую для настройки модулей Android, следовательно, два раза блок Config {}, то же самое для модуля приложения ниже) Контекст: Я пробовал: UPD: С помощью отладчика определил, что проблема кроется в свойстве Android Gradle ProGuard Android-R8 1 Спустя столько времени я нашел проблему: В моем плагине библиотеки Gradle был этот блок: Это не задокументировано, и я добавил это случайно. Зарегистрируйтесь с помощью Google Зарегистрироваться через Facebook Зарегистрируйтесь, используя электронную почту и пароль Электронная почта Требуется, но не отображается Электронная почта Требуется, но не отображается Как это работает… | С чего начать… Если вы еще не покрыли Part — 6. Согласно нашим предыдущим знаниям и пониманию, мы не можем получить доступ к Тогда как получить доступ к ⭐ Использование ⭐️ Аналогично, используя метод Примечание: Здесь мы создали Изменение кода для использования свойств Свойство выглядит как поле вне класса, но внутри это метод класса. — посмотреть вниз 👇 модифицированный код. (Примечание: мы не можем использовать одно и то же имя для поля класса и имени свойства, поэтому мы объявили Это примерно Поймите сценарий большой программы — с тысячами строк кода и сотнями классов, и в этом случае становится очень сложно управлять всем всем одним файлом 👉 После импорта Не забудьте использовать Посмотрите фактический код и выведите его в терминал ниже. Никакого влияния на вывод кода — мы просто использовали модули, чтобы сделать нашу программу более простой. Что нужно помнить перед 👋👋 ⭐️ ⭐️ Если вы еще не рассмотрели Часть — 6.4 этой серии, я рекомендую вам проверить эту ссылку → Конструкторы и модификаторы доступа в TypeScript Оставайтесь с нами для части — 7 Если вы не возражаете, похлопайте 👏 👏, так как это помогло, я был бы вам очень признателен 🙂 Помогите другим найти статью, чтобы она могла им помочь! Всегда хлопайте в ладоши… В этой статье описывается, как настроить свойства модуля, чтобы они отображались или скрывались в зависимости от контекстных значений других свойств конфигурации. В файле определения модуля можно определить несколько свойств конфигурации модуля. Однако могут быть сценарии, в которых релевантность некоторых полей свойств зависит от значений, установленных для других полей свойств модуля. Нерелевантные поля свойств должны быть скрыты, чтобы свести к минимуму количество полей, отображаемых редактору страниц, который настраивает модуль. Такое поведение помогает уменьшить сложность и вероятность путаницы. Модуль может использовать условную схему для определения правил, которым должна следовать панель свойств модуля в конструкторе сайтов Commerce, чтобы отображать или скрывать поля свойств на основе значений других полей свойств. Например, модуль имеет layout свойство, позволяющее использовать два макета, один из которых содержит обычный текст, а другой — форматированный текст и изображение. Возможность отображать или скрывать поля свойств в зависимости от контекста поддерживается в файлах определения модуля и расширении определения модуля, которые используют dependSchemas свойство для условных схем. Поддерживаются два типа условной схемы: зависимости схемы и зависимости свойств . Зависимости схемы можно использовать для объявления того, что схема должна изменяться при выборе определенного значения для свойства конфигурации. Свойство oneOf используется со свойством dependSchemas для объявления списка свойств конфигурации, применимых к определенному значению конфигурации. Как показано в следующем примере файла определения модуля, когда для свойства макета установлено значение plainTextOnly , должно отображаться свойство featureText . Зависимости свойств могут использоваться для объявления того, что определенные свойства конфигурации должны присутствовать, если присутствует значение другого свойства конфигурации. В следующем примере свойство dependSchemas указывает, что всякий раз, когда вводится значение productTitle , свойство конфигурации subTitle должно отображаться в конструкторе сайтов. Поскольку свойство dependSchemas поддерживается как в файлах определения модуля, так и в файлах расширения определения модуля, могут возникать конфликты между двумя типами файлов. Установив для свойства Boolean override значение true в файле расширения определения модуля, вы можете разрешить переопределение определенных свойств конфигурации. В следующих примерах показан файл определения модуля и файл расширения определения модуля, в котором используется переопределяет свойство . В следующих таблицах перечислены возможные сценарии и ожидаемые результаты при использовании зависимостей схемы с файлами определения модуля и расширения определения модуля. Объект свойств запроса Настройки приложения Файл настроек платформы Файл определения модуля Расширение файла определения модуля0002 Обзор интерактивных компонентов Добавление полей конфигурации модулей Расширение темы для добавления расширений модулей Мы хотим узнать больше о том, как люди используют пользовательский набор инструментов справки Microsoft. Пройдите опрос (на английском языке) и помогите нам понять: https://forms.office.com/r/A4cUJgjkD1. Модуль свойств сущности Jira доступен в виде программы раннего доступа (EAP). Имейте в виду, что будущие изменения могут нарушить работу ваших приложений.
Вы можете поделиться своими отзывами или сообщить об ошибках в специальном пространстве сообщества разработчиков Atlassian. Модуль Дополнительные сведения о свойствах объектов Jira см. в разделе Свойства объекта в руководствах по платформе Jira Cloud. Тип объекта. Допустимые типы: Значение по умолчанию: Определяет свойство объекта для индексации Jira. Значение свойства сущности — это ссылка на объект JSON, который также определяет его тип. The path to the JSON data to index. Путь — это ключ плоского объекта JSON с '.' как разделитель. Например, для JSON Путь может относиться к типу массива. В этом случае поле «тип» должно быть типом элементов в массиве. См. спецификацию для индексации 'blockedIssues' в примере. Тип значения, на которое указывает ссылка: В этом примере используется свойство объекта задачи с ключом Используя модуль Теперь индексированные данные доступны для поиска в JQL, как в этом примере: Неповторяющиеся линейные множители
Повторяющиеся линейные множители
Интеграция рациональных функций | Блестящая вики по математике и науке
404 не найдено
404 не найдено
Наиболее частые причины этой ошибки:
Если вам нужна помощь в разрешении этой проблемы, обратитесь к владельцу веб-страницы или веб-мастеру, как описано ниже.
Информацию о веб-сайтах класса можно найти в списке веб-сайтов класса по адресу
http://www.math.ucsd.edu/resources/course-websites/.
Чтобы связаться с администраторами веб-сервера, отправьте электронное письмо по адресу
[email protected].
Спасибо!
REQUEST_URI = http: // www.math.ucsd.edu/~ebender/supplements/stewart/78_rat.pdf
HTTP_REFERER = (нет)
HTTP_USER_AGENT = Mozilla / 5.0 (X11; Linux x86_64; rv: 33.0) Gecko / 20100101 Firefox / 33.0
REMOTE_ADDR (REMOTE_HOST) = 31.13.144.56 ((нет))
DATE_LOCAL = четверг, 29-июл-2021 21:42:52 PDT Интегрирование рациональных функций с использованием неполных дробей
Интегрирование рациональных функций с использованием неполных дробей Сегодня: 7.4: Интеграция рациональных функций и
Supp.4: Частичное расширение фракции
Далее: 7.7: Примерная интеграция
Пример 5.5,5 Вычислим
.
Обратите внимание, что это фактор, поскольку это корень.
У нас есть Существуют такие константы, что Затем Вы можете найти, разложив квадратичное на множители
комплексные числа и получение комплексного числа
ответы. Вместо этого мы оцениваем по паре значений.
Например, при получаем так
.
Далее используйте, чтобы получить.
так Наконец,
Осталось вычислить Сначала заполните квадрат, чтобы получить Позволять
, так и
.
Затем
Наконец, собираем все вместе и получаем Обсудите вторую задачу викторины. {4} -2x + C_0 $ 8.2-1},
$$
все рациональные функции от $ x $. Есть общая методика
называется «частичными дробями», что в
принцип, позволяет нам интегрировать любую рациональную функцию. В
алгебраические шаги в технике довольно громоздки, если
многочлен в знаменателе имеет степень больше 2, а
техника требует, чтобы мы разложили знаменатель на множители, то есть
не всегда возможно. Однако на практике нечасто запускается
через рациональные функции с многочленами высокой степени от
знаменатель, для которого нужно найти первообразную функцию.3 \ над (x-2) (x + 3)} \, dx = \ int x-1 \, dx + \ int {7x-6 \ над
(х-2) (х + 3)} \, dx.
$$
Первый интеграл прост, поэтому только второй требует некоторой работы.
$ \ квадрат $
Интеграция рациональных функций | Superprof
Все приведенные выше примеры являются примерами многочленов. Полиномиальная функция может иметь любую комбинацию из одночленов. Рациональная функция
Упрощение рациональных функций
Описание Проблема Шаг 1 Посмотрите, есть ли общие члены в числителе и знаменателе В обоих словах есть x-член 2 Разделите числитель Шаг 3 Удалите все одинаковые термины Интеграция
1 Интегрирование противоположно взятию производной 2 Интегрирование функции дает нам уравнение для область A Знак интеграла Знак для интеграции B Функция Функция, которую мы хотим интегрировать C Нижняя граница Нижняя граница интервала, для которого мы хотим найти площадь D Верхняя граница Верхняя граница интервала, на котором мы хотим найти площадь E dx Задает переменную для интегрирования Интегрирование дроби
Интеграция рациональной функции
A Функция f (x) B Функция g (x) C Производная от Пример 1
Пример 2
Пример 3
Теория комплексные числа: Национальный исследовательский университет «Высшая школа экономики»
Урок 38. определение комплексного числа. действия с комплексными числами — Алгебра и начала математического анализа — 11 класс






 Дистрибутивность умножения относительно сложения:
Дистрибутивность умножения относительно сложения: Разделить комплексное число z1 на комплексное число z2, значит найти такое комплексное число z, что z · z2 = z1.
Разделить комплексное число z1 на комплексное число z2, значит найти такое комплексное число z, что z · z2 = z1. Имеем:
Имеем:

D = b2 – 4ac.
D = (– 6)2 – 4×1×13 = 36 – 52 = – 16;
D = b2 – 4ac =122 – 4×9×29 = 144 – 1044 = – 900, 2 + 2.6i
2 + 2.6i1.4.1. Понятие комплексного числа
Глава 1. Арифметика
1.4.
1.4.1.
a = c и b = d.

a + c + i(b + d).
ac – bd + i(ad + bc).
 Такие названия выбраны в связи со следующими особыми свойствами комплексных чисел.
Такие названия выбраны в связи со следующими особыми свойствами комплексных чисел.
Следовательно, комплексные числа вида a + i · 0 естественно отождествляются с действительными числами. Из-за этого комплексные числа такого вида и называют просто действительными. Итак, множество действительных чисел содержится в множестве комплексных чисел. Множество комплексных чисел обозначается . Мы установили, что ,
а именно
 Чисто мнимое число i1 = 1i = i обладает удивительным свойством:
Чисто мнимое число i1 = 1i = i обладает удивительным свойством:
Таким образом,
то есть как раз получается нужная формула.
Рисунок 1.
 4.1.1
4.1.1
 Указанная в определении формула легко выводится при помощи теоремы Пифагора (см. рис.).
Указанная в определении формула легко выводится при помощи теоремы Пифагора (см. рис.).
Рисунок 1.4.1.2
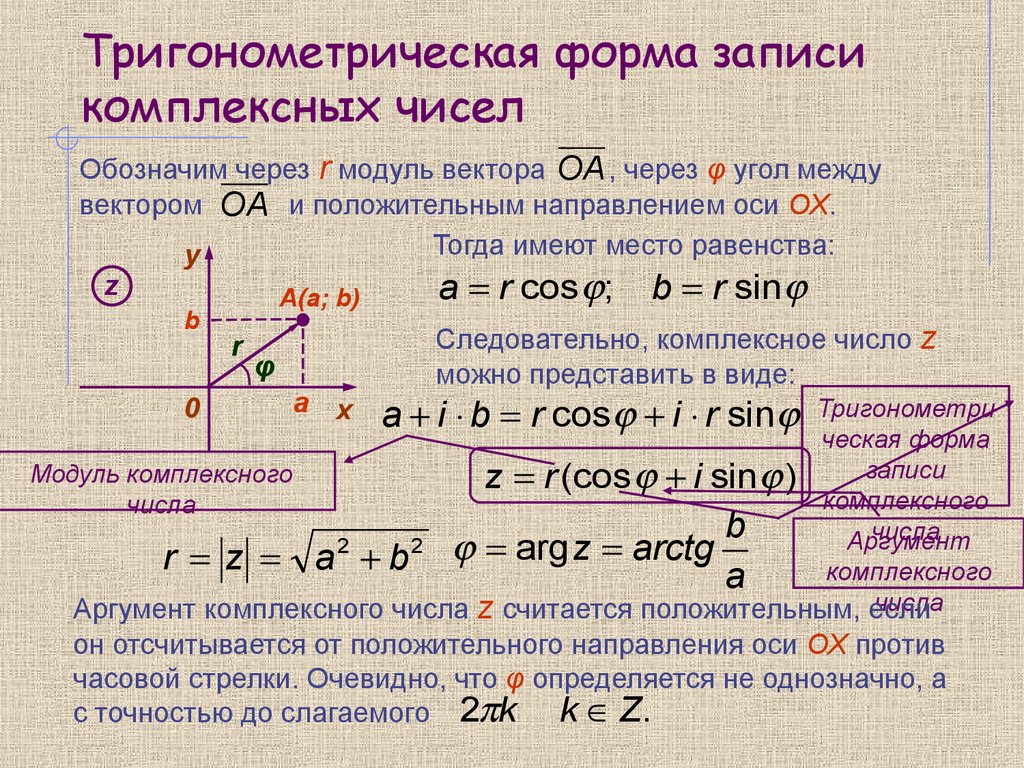 Для числа z = 0 аргумент не определён.
Для числа z = 0 аргумент не определён.

Главная
Онлайн учебники
База репетиторов России
Тренажеры по математике
Подготовка к ЕГЭ 2017 онлайн
Кирпич Уникальный прочный кирпич с гайкой. Гарантия долговечности. Стройте на века oooservisstroy.ru
Смотрите также:
Математика,
Английский язык,
Химия,
Биология,
Физика,
География,
Астрономия.

А также: online подготовка к ЕГЭ на College.ru, библиотека ЭОРов и обучающие программы на Multiring.ru.
Комплексные числа и операции с ними
 Например функция определена для , аналогично можно вспомнить,
что функция определена для , а функция определена для .
Например функция определена для , аналогично можно вспомнить,
что функция определена для , а функция определена для . Но на этой прямой нет числа , значит его надо искать вне числовой прямой.
Таким образом мы должны расширить множество вещественных чисел до множества в котором значения ,
или уже не бессмысленны, а являются такими же обычными числами в этом расширенном множестве,
как на множестве вещественных чисел.
Но на этой прямой нет числа , значит его надо искать вне числовой прямой.
Таким образом мы должны расширить множество вещественных чисел до множества в котором значения ,
или уже не бессмысленны, а являются такими же обычными числами в этом расширенном множестве,
как на множестве вещественных чисел.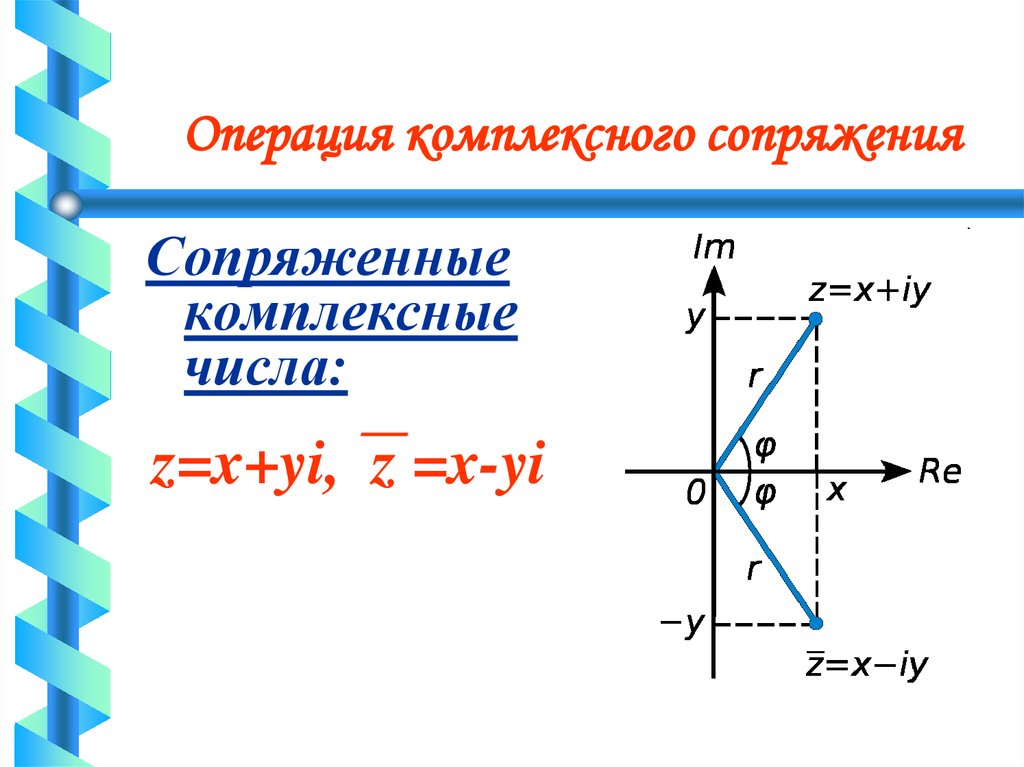 Прямая это числовая прямая, называемая реальной осью, на которой лежат все вещественные числа.
Прямая называется мнимой осью и она перпендикулярна реальной оси .
Оси и делят комплексную плоскость на четверти, как это показано на рисунке 1.
Прямая это числовая прямая, называемая реальной осью, на которой лежат все вещественные числа.
Прямая называется мнимой осью и она перпендикулярна реальной оси .
Оси и делят комплексную плоскость на четверти, как это показано на рисунке 1.
 Фаза комплексного числа может быть положительной или отрицательной, в зависимости от того в каком
направлении относительно оси отсчитывать угол.
Если угол поворота вектора на комплексной плоскости отсчитывать против часовой стрелки (как это показано на рисунке 1),
то фаза будет принимать положительные значения, а если по часовой — то отрицательные.
Фаза комплексного числа может быть положительной или отрицательной, в зависимости от того в каком
направлении относительно оси отсчитывать угол.
Если угол поворота вектора на комплексной плоскости отсчитывать против часовой стрелки (как это показано на рисунке 1),
то фаза будет принимать положительные значения, а если по часовой — то отрицательные. В результате возвращает корректные значения только в интервале
.
Таким образом функция арктангенса не отличает четверть I от четверти III
(в обоих случаях отношение положительное),
а также не отличает четверть II от четверти IV (отношение отрицательное).
В результате возвращает корректные значения только в интервале
.
Таким образом функция арктангенса не отличает четверть I от четверти III
(в обоих случаях отношение положительное),
а также не отличает четверть II от четверти IV (отношение отрицательное). е. и .
В этом случае и угол будет
положительным (красная пунктирная линия).
Тогда для того, чтобы получить корректное значение фазы необходимо ввести поправку рад:
е. и .
В этом случае и угол будет
положительным (красная пунктирная линия).
Тогда для того, чтобы получить корректное значение фазы необходимо ввести поправку рад:
 На комплексной плоскости операцию сложения можно реализовать как сложение векторов комплексных
чисел по правилу параллелограмма (рисунок 3а).
На комплексной плоскости операцию сложения можно реализовать как сложение векторов комплексных
чисел по правилу параллелограмма (рисунок 3а). Операция произведения комплексных чисел показано на рисунке 3в.
Операция произведения комплексных чисел показано на рисунке 3в.
 М: Высшая школа, 2011.
М: Высшая школа, 2011.Комплексные числа, 3 формы записи, основные операции
 Например, i23 = i20 i3 = -i, i61 = i60 i = i, и т.д. Если ввести в комплексной плоскости декартову систему координат, то x откладывают на действительной оси в комплексной плоскости (оси абсцисс), y – на мнимой оси (оси ординат).
Например, i23 = i20 i3 = -i, i61 = i60 i = i, и т.д. Если ввести в комплексной плоскости декартову систему координат, то x откладывают на действительной оси в комплексной плоскости (оси абсцисс), y – на мнимой оси (оси ординат). Достаточно сказать, что из нее следует равенство , связывающее почти все основные математические константы: 0, 1, i, .
Достаточно сказать, что из нее следует равенство , связывающее почти все основные математические константы: 0, 1, i, .



 Кривая называется замкнутой, если ее начало совпадает с ее концом.
Кривая называется замкнутой, если ее начало совпадает с ее концом.«Комплексные числа» обобщающий урок математики с использованием интерактивной доски

 Приложение.)
Приложение.)
Свободные, бесплотные как тени,
Вы радугой связующей повисли
К раздумиям с вершины вдохновенья!
Валерий Яковлевич Брюсов (русский писатель 1873-1924).

i — первая буква французского слова imaginaire, мнимый.
Инверсия, inversio — лат. переворачивание, перестановка.
Продумаем план проведения урока. Что вы предлагаете повторить по теме?
Какие вопросы вас интересуют? Что, по вашему мнению, требует углубления?
Какие виды контроля считаете наиболее рациональными на этом уроке?
2 этап — вычислительная работа.
3 этап — практическая работа, выход на новый материал.
4 этап – итоговый контроль.
2) Как изображается комплексное число на плоскости?
3) Как вычислить модуль комплексного числа?
4) Что называется аргументом?
5) В каких границах заключен главный аргумент?
6) Как записать число в тригонометрической форме?
7) Какое число называется сопряженным? Свойство сопряженных чисел?
8) Запишите теоремы о модуле и аргументе
9) Формула Муавра для Z в степени n.

1) (3+2i)+3(-1+3i)
 Как изображается комплексное число?
Как изображается комплексное число?
 (Учитель может заранее приготовить варианты построений, но без нумерации. Ребята выбирают правильные решения.)
(Учитель может заранее приготовить варианты построений, но без нумерации. Ребята выбирают правильные решения.)
№4. Прямые у=х и у=-х.
№5. Точки, расположенные в вершинах правильного 6-тиугольника с центром (0;0).

II вариант — б, г, д.
Такое преобразование называется инверсией.
2. -2(cos90 0+i sin90 0)-является тригонометрической формой комплексного числа?
3. Многочлен (х+4) можно разложить на множители в комплексных числах?
4. Если комплексное число равно своему сопряженному, то оно является действительным?
 Нет
Нет
2 этап — вычислительная работа.
3 этап — практическая работа, выход на новый материал.
4 этап – итоговый контроль.
Комплексные числа для чайников
 2)
Алгебраическая форма комплексного
числа. Сложение, вычитание, умножение
и деление комплексных чисел. 3)
Тригонометрическая и показательная
форма комплексного числа. 4)
Возведение комплексных чисел в степень. 5)
Извлечение корней из комплексных чисел.
2)
Алгебраическая форма комплексного
числа. Сложение, вычитание, умножение
и деление комплексных чисел. 3)
Тригонометрическая и показательная
форма комплексного числа. 4)
Возведение комплексных чисел в степень. 5)
Извлечение корней из комплексных чисел. При этом каждой точке числовой
обязательно соответствует некоторое
действительное число.
При этом каждой точке числовой
обязательно соответствует некоторое
действительное число. Комплексные
числа изображаются на комплексной
плоскости: Как
упоминалось выше, буквой
принято
обозначать множество действительных
чисел.Множество же комплексных
чисел принято
обозначать «жирной» или утолщенной
буквой
.
Поэтому на чертеже следует поставить
букву
,
обозначая тот факт, что у нас комплексная
плоскость.
Комплексные
числа изображаются на комплексной
плоскости: Как
упоминалось выше, буквой
принято
обозначать множество действительных
чисел.Множество же комплексных
чисел принято
обозначать «жирной» или утолщенной
буквой
.
Поэтому на чертеже следует поставить
букву
,
обозначая тот факт, что у нас комплексная
плоскость. Рассмотрим
следующие комплексные числа:
,
,
.
Вы скажете, да это же обыкновенные
действительные числа! И будете почти
правы. Действительные числа – это
частный случай комплексных чисел.
Действительная ось
обозначает
в точности множество действительных
чисел
,
то есть на оси
сидят
все наши «обычные» числа. Более строго
утверждение можно сформулировать так:
Множество действительных чисел
является
подмножеством множества комплексных
чисел
.
Рассмотрим
следующие комплексные числа:
,
,
.
Вы скажете, да это же обыкновенные
действительные числа! И будете почти
правы. Действительные числа – это
частный случай комплексных чисел.
Действительная ось
обозначает
в точности множество действительных
чисел
,
то есть на оси
сидят
все наши «обычные» числа. Более строго
утверждение можно сформулировать так:
Множество действительных чисел
является
подмножеством множества комплексных
чисел
.

Комплексные числа
Комплексный номер
Действительного числа и Воображаемого числа 1 12,38 −0,8625 3/4 √2 1998 
3i 1.04i −2,8i 3i/4 (√2)я 1998i Комплексные числа

Примеры:
1 + я 39 + 3i 0,8 − 2,2i −2 + πi √2 + i/2 Может ли число быть комбинацией двух чисел?
Любая часть может быть равна нулю
Комплексный номер Реальная часть Воображаемая часть 3 + 2i 3 2 5 5 0 Чисто настоящий −6i 0 −6 Чисто воображаемый Сложно?

Визуальное объяснение
Комплекс № 3+4 i Добавление
Пример: добавьте комплексные числа
3 + 2 i и 1 + 7 i
= 3 + 1 + (2 + 7) i
= 4 + 9i Пример: добавьте комплексные числа
3 + 5 i и 4 − 3 i
= 3 + 4 + (5 — 3) I
= 7 + 2 I  На комплексной плоскости это:
На комплексной плоскости это: Умножение
каждая часть второго комплексного числа I 2
Пример: (3 + 2i)(1 + 7i)
Пример: (1 + i)
2 Но есть более быстрый способ!
Почему это правило работает?

Попробуем i
2 Пример: i
2 Конъюгаты
Пример:
Разделение

Пример: Do This Division:
 22 41 i
22 41 i Умножение на сопряженное
Пример: попробуем еще раз
 199999999999
199999999999 Обозначение
Набор Мандельброта

А вот центр предыдущего увеличен еще больше: комплексных чисел | Brilliant Math & Science Wiki
Содержимое
 В комплексной плоскости имеется действительных осей и перпендикуляр мнимой оси . Комплексное число a+bia+bia+bi изображается на этой плоскости точно так же, как упорядоченная пара (a,b)(a,b)(a,b) изображается на плоскости декартовых координат. Действительная ось соответствует оси xxx, а воображаемая ось соответствует оси yyy.
В комплексной плоскости имеется действительных осей и перпендикуляр мнимой оси . Комплексное число a+bia+bia+bi изображается на этой плоскости точно так же, как упорядоченная пара (a,b)(a,b)(a,b) изображается на плоскости декартовых координат. Действительная ось соответствует оси xxx, а воображаемая ось соответствует оси yyy. Z=partreala+unitimaginaryipartimaginaryb.
Z=partreala+unitimaginaryipartimaginaryb. (а+в) + (б+г)я. (а+в)+(б+г)я.
(а+в) + (б+г)я. (а+в)+(б+г)я. 4?i2+i6+i4? 92-2х+5\большой)\левый(х+4\правый) + 7х + 5\\
&= 0 \cdot (x+4) + 7x +5 \qquad \qquad \qquad \big(\text{by}(1)\big) \\
&= 7(1+2i) + 5 \\
&= 12 + 14i. \ _\площадь
\end{выровнено} x3+2×2+4x+25=(x2−2x+5)(x+4)+7x+5=0⋅(x+4)+7x+5(by (1))=7 (1+2i)+5=12+14i. □
4?i2+i6+i4? 92-2х+5\большой)\левый(х+4\правый) + 7х + 5\\
&= 0 \cdot (x+4) + 7x +5 \qquad \qquad \qquad \big(\text{by}(1)\big) \\
&= 7(1+2i) + 5 \\
&= 12 + 14i. \ _\площадь
\end{выровнено} x3+2×2+4x+25=(x2−2x+5)(x+4)+7x+5=0⋅(x+4)+7x+5(by (1))=7 (1+2i)+5=12+14i. □
 \ _\квадрат
\end{align}5−2i3+2i=(5−2i)(5+2i)(3+2i)(5+2i)=2911+16i=2911+2916i. □
\ _\квадрат
\end{align}5−2i3+2i=(5−2i)(5+2i)(3+2i)(5+2i)=2911+16i=2911+2916i. □ \ _\квадрат
\end{выровнено}∣z1∣=∣z2∣=∣z3∣=…=∣zn∣∣z1∣2=∣z2∣2=∣z3∣2=…=∣zn∣ 2z1z1=1,z2z2=1,z3z3=1,…,znznz11=z1,z21=z2,z3 1=z3,…,zn1∣∣∣∣z11+z21+z31+⋯+zn1∣∣∣∣⇒∣∣∣∣ z11+z21+z31+⋯+zn1∣∣∣∣=1=1=1=zn=∣z1+z2+z3 +⋯+zn∣=∣z1+z2+z3+⋯+zn∣=∣z1+z2+z3+⋯+zn∣(поскольку ∣z∣=∣z∣ )=∣z1+z2+z3+⋯+zn∣. □
\ _\квадрат
\end{выровнено}∣z1∣=∣z2∣=∣z3∣=…=∣zn∣∣z1∣2=∣z2∣2=∣z3∣2=…=∣zn∣ 2z1z1=1,z2z2=1,z3z3=1,…,znznz11=z1,z21=z2,z3 1=z3,…,zn1∣∣∣∣z11+z21+z31+⋯+zn1∣∣∣∣⇒∣∣∣∣ z11+z21+z31+⋯+zn1∣∣∣∣=1=1=1=zn=∣z1+z2+z3 +⋯+zn∣=∣z1+z2+z3+⋯+zn∣=∣z1+z2+z3+⋯+zn∣(поскольку ∣z∣=∣z∣ )=∣z1+z2+z3+⋯+zn∣. □
 \text{nd}2-м квадранте, поэтому к этому углу следует добавить π\piπ, чтобы получить правильный аргумент: 9{-1}\left(-\frac{4}{3}\right)+\pi.\ _\squareθ=tan−1(−34)+π. □
\text{nd}2-м квадранте, поэтому к этому углу следует добавить π\piπ, чтобы получить правильный аргумент: 9{-1}\left(-\frac{4}{3}\right)+\pi.\ _\squareθ=tan−1(−34)+π. □ \end{выровнено}x=2a−b±D=2×1−6±−4=2−6±2−1=−3±i.
\end{выровнено}x=2a−b±D=2×1−6±−4=2−6±2−1=−3±i. 9n \right \}A={(21+3i)n} — набор комплексных чисел, где nnn — целое положительное число. Сколько различных элементов в множестве A?A?A?
9n \right \}A={(21+3i)n} — набор комплексных чисел, где nnn — целое положительное число. Сколько различных элементов в множестве A?A?A? \left(\sqrt{3}-\frac{5}{2},\ 1+\frac{5\sqrt{3}}{2} \справа).(3−25, 1+253). □_\квадрат□
\left(\sqrt{3}-\frac{5}{2},\ 1+\frac{5\sqrt{3}}{2} \справа).(3−25, 1+253). □_\квадрат□ Комплексное число — определение, формула, свойства, примеры

1. Что такое комплексные числа? 2. График комплексных чисел 3. Свойства комплексных чисел 4. Операции над комплексными числами 5. Алгебраические тождества комплексных чисел 6. Решенные примеры 7. Практические вопросы 8. Часто задаваемые вопросы о комплексных числах Что такое комплексные числа?
 Комплексное число имеет вид a + ib и обычно обозначается буквой z. Здесь и a, и b – действительные числа. Величина «а» называется действительной частью, которая обозначается Re(z), а «b» называется мнимой частью Im(z). Также ib называют мнимым числом.
Комплексное число имеет вид a + ib и обычно обозначается буквой z. Здесь и a, и b – действительные числа. Величина «а» называется действительной частью, которая обозначается Re(z), а «b» называется мнимой частью Im(z). Также ib называют мнимым числом. 1613 + 2i Значение i 2 = -1 является основным аспектом комплексного числа. Давайте попробуем понять больше о возрастающих силах i.
1613 + 2i Значение i 2 = -1 является основным аспектом комплексного числа. Давайте попробуем понять больше о возрастающих силах i. График комплексных чисел
 {-1}\frac{b}{a}\). 9{-1}\frac{b}{a}\)).
{-1}\frac{b}{a}\). 9{-1}\frac{b}{a}\)). Свойства комплексного номера
Сопряжение комплексного числа
Обратная величина комплексного числа
 {-1}\).
{-1}\). Равенство комплексных чисел
Упорядочивание комплексных чисел
 Комплексные числа можно измерить и представить на двумерной арграндовой плоскости по их величине, которая является расстоянием от начала координат.
Комплексные числа можно измерить и представить на двумерной арграндовой плоскости по их величине, которая является расстоянием от начала координат. Операции над комплексными числами
 Детали различных арифметических операций с комплексными числами заключаются в следующем.
Детали различных арифметических операций с комплексными числами заключаются в следующем. Сложение комплексных чисел
 2 = -1\). Для двух комплексных чисел \(z_1\) = a + ib, \(z_2\) = c + id произведение равно \(z_1.z_2\) = (ca — bd) + i(ad + bc).
2 = -1\). Для двух комплексных чисел \(z_1\) = a + ib, \(z_2\) = c + id произведение равно \(z_1.z_2\) = (ca — bd) + i(ad + bc). Комплексные числа Советы и подсказки:

&=\frac{-1 \pm \sqrt{-3}}{2}\\[0,2 см]
\text{Здесь } &\sqrt{-3} = \sqrt{-1} \times \sqrt{3} = i \sqrt{3}\\[0,2 см]
x&= \frac{-1 \pm i\sqrt{3}}{2}\\[0,2 см]
\end{align} \]
Разница = -3 + 3i
Продукт = 5i
Деление = -4/5 — 3i/5
Часто задаваемые вопросы о комплексных числах
Что такое комплексные числа в математике?
Для чего используются комплексные числа?
 {-1}\frac{b}{a} \)).
{-1}\frac{b}{a} \)). Что такое действительные и комплексные числа?
Как делить комплексные числа? 92)}\).
Как строить графики комплексных чисел?
Как преобразовать комплексные числа в полярную форму?
 {-1}\). 9p$, когда $a$ отрицательно… Но это скрывает некоторые замечательные математические основы, в том числе и особенно странность и удивительность мнимых и комплексных чисел! Давайте познакомимся с этими математическими объектами в этой статье! Наш подход будет в высшей степени геометрическим и, я думаю, гораздо более проницательным, чем тот, которому вы научились (или будете учиться) в школе.
{-1}\). 9p$, когда $a$ отрицательно… Но это скрывает некоторые замечательные математические основы, в том числе и особенно странность и удивительность мнимых и комплексных чисел! Давайте познакомимся с этими математическими объектами в этой статье! Наш подход будет в высшей степени геометрическим и, я думаю, гораздо более проницательным, чем тот, которому вы научились (или будете учиться) в школе. Геометрия $n$-го корня
 Это то, что делается ниже три раза! 9{1/3}$ на геометрическую фразу: Трижды инвертировать числовую прямую эквивалентно ее однократному инвертированию . Сладко, не так ли?
Это то, что делается ниже три раза! 9{1/3}$ на геометрическую фразу: Трижды инвертировать числовую прямую эквивалентно ее однократному инвертированию . Сладко, не так ли? Ниже описаны эти две операции, каждая из которых применяется к числовой прямой трижды.
Ниже описаны эти две операции, каждая из которых применяется к числовой прямой трижды. ..
.. Решение парадокса
 Это то, что французский математик XIX века Эварист Галуа назвал неоднозначностью корней $n$-го порядка. Точнее, ни кубического корня из $(-8)$, ни уникальности корня шестой степени из $64$ не существует. В частности, $(-2)$ — это корень шестой степени из $64$, но это не тот корень, на который мы ссылаемся через $\sqrt[6]{64}$. 9{1/6}$. Буквально там говорится, что кубический корень из $(-8)$ является корнем в шестой степени из квадрата $(-8)$.
Это то, что французский математик XIX века Эварист Галуа назвал неоднозначностью корней $n$-го порядка. Точнее, ни кубического корня из $(-8)$, ни уникальности корня шестой степени из $64$ не существует. В частности, $(-2)$ — это корень шестой степени из $64$, но это не тот корень, на который мы ссылаемся через $\sqrt[6]{64}$. 9{1/6}$. Буквально там говорится, что кубический корень из $(-8)$ является корнем в шестой степени из квадрата $(-8)$. Но некоторые из корней шестой степени из $64$ не являются кубическими корнями из $(-8)$! Несложно доказать, что это кубический корень из 8$, а другой квадратный корень из 64$. Предлагаю сделать это в качестве упражнения!
Но некоторые из корней шестой степени из $64$ не являются кубическими корнями из $(-8)$! Несложно доказать, что это кубический корень из 8$, а другой квадратный корень из 64$. Предлагаю сделать это в качестве упражнения! Гомотетии и вращения
 Эта плоскость называется сложной плоскостью . Он бесконечен во всех направлениях и имеет единственный центр, называемый 9-м.0549 происхождение . Кроме того, одна из его осей, проходящая через начало координат, известна как прямая с действительными числами . Ось, перпендикулярная линии действительного числа, известна как линия мнимого числа .
Эта плоскость называется сложной плоскостью . Он бесконечен во всех направлениях и имеет единственный центр, называемый 9-м.0549 происхождение . Кроме того, одна из его осей, проходящая через начало координат, известна как прямая с действительными числами . Ось, перпендикулярная линии действительного числа, известна как линия мнимого числа . Еще одним важным фактом является то, что все обычные числа можно однозначно сопоставить с помощью одной такой геометрической операции. Например, какая операция соответствует числу $2$?
Еще одним важным фактом является то, что все обычные числа можно однозначно сопоставить с помощью одной такой геометрической операции. Например, какая операция соответствует числу $2$? По соглашению вращение определяется углом 90 545 против часовой стрелки на 90 548 оборотов, называемым 90 549 аргументом 90 552 и часто обозначаемым $\theta$. Поскольку эти два параметра однозначно определяют комбинацию гомотетии и поворота, каждое комплексное число может быть представлено парой $(\rho, \theta)$. 9* \times SO(3)) \cup \{0\}$ (технически «повороты» $\mathbb H$ образуют двойное покрытие $SO(3)$). Однако кватернионы немного сложнее, поскольку они не коммутативны. Действительно, как вы можете видеть, играя в кубик Рубика, два вращения в пространстве вообще не коммутируют. Если можно, напишите о кватернионах!
По соглашению вращение определяется углом 90 545 против часовой стрелки на 90 548 оборотов, называемым 90 549 аргументом 90 552 и часто обозначаемым $\theta$. Поскольку эти два параметра однозначно определяют комбинацию гомотетии и поворота, каждое комплексное число может быть представлено парой $(\rho, \theta)$. 9* \times SO(3)) \cup \{0\}$ (технически «повороты» $\mathbb H$ образуют двойное покрытие $SO(3)$). Однако кватернионы немного сложнее, поскольку они не коммутативны. Действительно, как вы можете видеть, играя в кубик Рубика, два вращения в пространстве вообще не коммутируют. Если можно, напишите о кватернионах!
 Это соответствует последовательному выполнению геометрических операций, связанных с комплексными числами. И что прекрасно, так это то, что у этого есть алгебраический перевод! Под этим я подразумеваю, что умножение $(\rho_1, \theta_1)$ на $(\rho_2, \theta_2)$ соответствует двум гомотетиям на множители $\rho_1$ и $\rho_2$ и двум поворотам углов $\theta_1 $ и $\тета_2$. Теперь две гомотетии множителей $\rho_1$ и $\rho_2$ объединяются в гомотетию множителя $\rho_1 \times \rho_2$, а два поворота углов $\theta_1$ и $\theta_2$ приводят к повороту угла $\тета_1+\тета_2$. Таким образом, мы имеем произведение $(\rho_1, \theta_1) \times (\rho_2, \theta_2) = (\rho_1 \times \rho_2, \theta_1 + \theta_2)$. Насколько это сладко? 9{it}$ дает элегантное описание этих движений, что значительно облегчает вычисления! Но это все еще только верхушка айсберга. Чтобы раскрыть истинную магию комплексных чисел, нам нужно копнуть глубже!
Это соответствует последовательному выполнению геометрических операций, связанных с комплексными числами. И что прекрасно, так это то, что у этого есть алгебраический перевод! Под этим я подразумеваю, что умножение $(\rho_1, \theta_1)$ на $(\rho_2, \theta_2)$ соответствует двум гомотетиям на множители $\rho_1$ и $\rho_2$ и двум поворотам углов $\theta_1 $ и $\тета_2$. Теперь две гомотетии множителей $\rho_1$ и $\rho_2$ объединяются в гомотетию множителя $\rho_1 \times \rho_2$, а два поворота углов $\theta_1$ и $\theta_2$ приводят к повороту угла $\тета_1+\тета_2$. Таким образом, мы имеем произведение $(\rho_1, \theta_1) \times (\rho_2, \theta_2) = (\rho_1 \times \rho_2, \theta_1 + \theta_2)$. Насколько это сладко? 9{it}$ дает элегантное описание этих движений, что значительно облегчает вычисления! Но это все еще только верхушка айсберга. Чтобы раскрыть истинную магию комплексных чисел, нам нужно копнуть глубже! Точки комплексной плоскости
 Чтобы добраться туда, обратите внимание на невероятный факт, что $1 \times x=x$, когда $x$ — число. Таким образом, если я покажу вам геометрическое преобразование «$\times x$», то вы легко сможете найти, какое $x$ я выбрал, посмотрев, в какую точку отправлено число $1$. Точно так же, если я дам вам геометрическое преобразование $(\rho, \theta)$, то вы сможете узнать значения $\rho$ и $\theta$, так как они будут полярными координатами точки $1$ отправляется! Эта точка называется 9.0549 изображение из 1.
Чтобы добраться туда, обратите внимание на невероятный факт, что $1 \times x=x$, когда $x$ — число. Таким образом, если я покажу вам геометрическое преобразование «$\times x$», то вы легко сможете найти, какое $x$ я выбрал, посмотрев, в какую точку отправлено число $1$. Точно так же, если я дам вам геометрическое преобразование $(\rho, \theta)$, то вы сможете узнать значения $\rho$ и $\theta$, так как они будут полярными координатами точки $1$ отправляется! Эта точка называется 9.0549 изображение из 1. 92$. Таким образом, мы можем отождествить оба множества, и мы называем их оба $\mathbb C$.
92$. Таким образом, мы можем отождествить оба множества, и мы называем их оба $\mathbb C$. Векторы комплексной плоскости

 Все векторы можно однозначно разложить на сумму $1$ и $i$ . Например, фиолетовый вектор можно получить комбинацией вектора, связанного с $1$, и вектора, связанного с $i$. Таким образом, $purple = 1+i$. Точно так же синий вектор представляет собой комбинацию $1$ и двух умноженных на $i$. Следовательно, $blue = 1+2i$.
Все векторы можно однозначно разложить на сумму $1$ и $i$ . Например, фиолетовый вектор можно получить комбинацией вектора, связанного с $1$, и вектора, связанного с $i$. Таким образом, $purple = 1+i$. Точно так же синий вектор представляет собой комбинацию $1$ и двух умноженных на $i$. Следовательно, $blue = 1+2i$. Геометрически эта операция состоит в переносе вектора, которому соответствует $z$. Фактически это отображение $z$ в $+z$ является изоморфизмом евклидова векторного пространства между пространством комплексных чисел и множеством сдвигов комплексной плоскости.
Геометрически эта операция состоит в переносе вектора, которому соответствует $z$. Фактически это отображение $z$ в $+z$ является изоморфизмом евклидова векторного пространства между пространством комплексных чисел и множеством сдвигов комплексной плоскости. Поле комплексных чисел
 Первое понимание комплексных чисел описывает умножение, а третье — сложение. Размышление о каждом из значений комплексных чисел по отдельности уже довольно завораживает, но поистине умопомрачительное свойство комплексных чисел проявляется, когда мы их смешиваем!
Первое понимание комплексных чисел описывает умножение, а третье — сложение. Размышление о каждом из значений комплексных чисел по отдельности уже довольно завораживает, но поистине умопомрачительное свойство комплексных чисел проявляется, когда мы их смешиваем! Вот что нарисовано ниже:
Вот что нарисовано ниже: Заключение
 А именно, раскрывается полная природа комплексных чисел, поскольку они рассматриваются как поле. В частности, именно к этой области применяется основная теорема алгебры .
А именно, раскрывается полная природа комплексных чисел, поскольку они рассматриваются как поле. В частности, именно к этой области применяется основная теорема алгебры . Объяснение комплексных чисел.
 Когда мы думаем о комплексных числах, мы… | Бретт Берри | Math Hacks
Когда мы думаем о комплексных числах, мы… | Бретт Берри | Math Hacks

 ). Здесь происходят две вещи: масштабирование и вращение.
). Здесь происходят две вещи: масштабирование и вращение.
Комплексное сопряжение
 Как и любая дробь, если я хочу умножить знаменатель на значение, я должен также умножить числитель на это значение.
Как и любая дробь, если я хочу умножить знаменатель на значение, я должен также умножить числитель на это значение. Реальность мнимых чисел
Несколько лет назад я обучал студента-психолога кое-какой предварительной математике, необходимой для занятий по статистике.
 Мы говорили о…
Мы говорили о… Как визуально «заполнить квадрат»
и проблемы с запоминанием
Ходьба пьяницы и объяснение процессов Маркова
9000 Случайные блуждания
10 главных тайн треугольника Паскаля 9x$ и $\log(x)$), векторы и матрицы, степенные ряды. Сложные моменты отмечены. (Для студентов в Великобритании начальные разделы должны быть доступны для всех, кто сдает экзамен GCSE или выше, но некоторые из более поздних разделов соответствуют стандарту A-level.) Повсюду есть упражнения для
вы, чтобы проверить свое понимание, с ответами на спине.
 2)$ через $\textrm{Re}(z)$ и $\textrm{Im} (г)$. 9п$? Для тех из вас, кто встречался с математической индукцией, можете ли вы это доказать?
2)$ через $\textrm{Re}(z)$ и $\textrm{Im} (г)$. 9п$? Для тех из вас, кто встречался с математической индукцией, можете ли вы это доказать? Двумерная плоскость комплексных чисел называется плоскостью Аргана или диаграммой Аргана. Что ж, это мило, но не так здорово. Удивительно, что происходит, когда вы умножаете два вектора. Прежде чем мы перейдем к этому, нам нужна пара новых идей. 9{-1} (\textrm{Im}(z) /\textrm{Re}(z))$ (если только $\textrm{Re}(z) = 0$). Надеюсь, следующий рисунок объясняет модуль и аргумент комплексного числа:
Двумерная плоскость комплексных чисел называется плоскостью Аргана или диаграммой Аргана. Что ж, это мило, но не так здорово. Удивительно, что происходит, когда вы умножаете два вектора. Прежде чем мы перейдем к этому, нам нужна пара новых идей. 9{-1} (\textrm{Im}(z) /\textrm{Re}(z))$ (если только $\textrm{Re}(z) = 0$). Надеюсь, следующий рисунок объясняет модуль и аргумент комплексного числа: Если $z = a+i b$
и $w = x+i y$, то $z w = (a x- b y)+i(a y+b x)$. Так 9{\ circ} / п) $. Найдите все $n$ решений относительно этого решения.
Если $z = a+i b$
и $w = x+i y$, то $z w = (a x- b y)+i(a y+b x)$. Так 9{\ circ} / п) $. Найдите все $n$ решений относительно этого решения. 7} {7!}
+ \dots$$ 9{-z}] /2$. Найдите разложение в степенной ряд для $\cosh(z)$ и докажите, что $\cosh(i z) = \cos(z)$.
7} {7!}
+ \dots$$ 9{-z}] /2$. Найдите разложение в степенной ряд для $\cosh(z)$ и докажите, что $\cosh(i z) = \cos(z)$. Это называется восьмым корнем из единицы.
Это называется восьмым корнем из единицы.
Итак, если $|z| = г_1, |ш| = r_2$, $\arg(z) = \theta_1$ и $\arg(w) = \theta_2$, то $z = r_1 (\cos\theta_1 +i\sin\theta_1)$ и $w = = r_2 ( \cos\theta_2 +i\sin\theta_2)$. Расширение
Построение графиков функций заданных параметрически: IIS 7.0 Detailed Error — 404.11
«Особенности построения графиков функций заданных неявно и параметрически»

Иллюстрированный самоучитель по Mathematica 5 › Мультимедиа: геометрия, графика, кино, звук › Построение графиков функций, заданных параметрически (функция ParametricPlot) [страница — 203] | Самоучители по математическим пакетам
Построение графиков функций, заданных параметрически (функция ParametricPlot)
PolarR[a1,a2_,omega_,phi_] := Module[{r=a1+a2*Cos[omega*phi]},<r*Coi[phi],r*Sin[phi]}]Построение графика функции, заданной в параметрической форме. — Студопедия
Построение графиков функций, заданных параметрически — Мегаобучалка
Построение графиков кусочно-непрерывной функции
11. Выделим диапазон, состоящий из данных в столбце А и данных в столбце Е (используя клавишу CTRL) и строим точечную диаграмму.
gnuplot / parametric (E)
x = f(t)
y = g(t)
x=const
y=t
gnuplot> set parametric
dummy variable is t for curves, u/v for surfaces
gnuplot> const=3
gnuplot> set trange [1:4]
gnuplot> set xrange [0:5]
gnuplot> set yrange [0:5]
gnuplot> plot const,t
x=sin(t)
y=cos(t)
gnuplot> set parametric
dummy variable is t for curves, u/v for surfaces
gnuplot> set size square
gnuplot> set xrange [-1:1]
gnuplot> set yrange [-1:1]
gnuplot> plot [0:2*pi] sin(t),cos(t)
x=r(t)*cos(t)
y=r(t)*sin(t)
gnuplot> set xrange [-10*pi:10*pi]
gnuplot> set yrange [-10*pi:10*pi]
gnuplot> plot [0:10*pi] t*sin(t),t*cos(t)
gnuplot> set parametric
dummy variable is t for curves, u/v for surfaces
gnuplot> r(t) = 1+cos(t)
gnuplot> plot [0:2*pi] r(t)*cos(t),r(t)*sin(t)
gnuplot> set parametric
dummy variable is t for curves, u/v for surfaces
gnuplot> c=2*pi
gnuplot> set size square
gnuplot> set trange [-c:c]
gnuplot> set xrange [-c:c]
gnuplot> set yrange [-c:c]
gnuplot> plot c*sin(t),t with lines, t,c*cos(t) with impulses
Производная функции, заданной неявно
х
-9
-4
у
-1,4
1,4
-1,4
1,4
Графики параметрических функций — Интеллектуальная Кобринщина
Plot Parametric Functions — Wolfram Mathematica
Графики — Алгебра и тригонометрия
Цели обучения
Совместное построение графиков параметрических уравнений и прямоугольной формы
Анализ
Попробуйте
[скрытый-ответ a = ”fs-id1165137807092 ″] Приложения параметрических уравнений
Нахождение параметрических уравнений для описания движения бейсбольного мяча
[show-answer q = ”fs-id1165137453386 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165137453386 ″] Упражнения по разделам
Устный
[скрытый-ответ a = ”fs-id1165135194726 ″]
[скрытый-ответ a = ”fs-id1165137758269 ″]
[скрытый-ответ a = ”fs-id1165137715148 ″] Графический
[скрытый-ответ a = ”fs-id1165135188326 ″] [/ скрытый-ответ] [show-answer q = ”fs-id1165134583390 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165134583390 ″] [/ скрытый-ответ] [show-answer q = ”fs-id1165135237047 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165135237047 ″] [/ скрытый-ответ]
[скрытый-ответ a = ”fs-id1165134069188 ″] [/ скрытый-ответ] [show-answer q = ”fs-id1165137417002 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165137417002 ″] [/ скрытый-ответ] [show-answer q = ”fs-id1165137936702 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165137936702 ″] [/ скрытый-ответ] [show-answer q = ”fs-id1165134081386 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165134081386 ″] [/ скрытый-ответ] [show-answer q = ”fs-id1165137805783 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165137805783 ″] [/ скрытый-ответ]
[скрытый-ответ a = ”fs-id1165135149887 ″] [/ скрытый-ответ] [show-answer q = ”fs-id1165135512730 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165135512730 ″] [/ скрытый-ответ] [show-answer q = ”fs-id11651323 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id11651323 ″] [/ скрытый-ответ]
[hidden-answer a = ”211246 ″] [/ hidden-answer] [show-answer q = ”fs-id1165135252162 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165135252162 ″] [/ скрытый-ответ] [show-answer q = ”fs-id1165137680409 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165137680409 ″] [/ скрытый-ответ]
[скрытый-ответ a = ”fs-id1165137409296 ″] [/ скрытый-ответ]
[скрытый-ответ a = ”fs-id1165137551247 ″] [/ скрытый-ответ]
[скрытый-ответ a = ”fs-id1165135189746 ″]
[скрытый-ответ a = ”fs-id1165135499919 ″]
[скрытый-ответ a = ”fs-id1165135609231 ″]
[скрытый-ответ a = ”fs-id1165135352460 ″]
[скрытый-ответ a = ”fs-id1165132960728 ″] [/ скрытый-ответ] [show-answer q = ”fs-id1165134386554 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165134386554 ″] [/ скрытый-ответ] [show-answer q = ”fs-id1165133349420 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165133349420 ″] [/ скрытый-ответ] Расширения
[скрытый-ответ a = ”fs-id1165132079269 ″]
[скрытый-ответ a = ”fs-id1165134371099 ″]
[скрытый-ответ a = ”fs-id1165135445722 ″]
[скрытый-ответ a = ”fs-id1165135444043 ″]
[скрытый-ответ a = ”fs-id1165134569130 ″] [/ скрытый-ответ]
[скрытый-ответ a = ”fs-id1165134134026 ″] [/ скрытый-ответ] Нахождение параметрических уравнений для графика
Набор параметрических уравнений не уникален для данного графа.Например, следующие наборы параметрических уравнений приводят к одному и тому же прямоугольному уравнению и, таким образом, представляют один и тот же график.
Однако с учетом прямоугольного уравнения и уравнения, описывающего параметр в терминах одной из двух переменных, можно определить набор параметрических уравнений.
Теперь подставьте выражение для x в прямоугольное уравнение y = x 2 + 2, чтобы получить второе параметрическое уравнение.
Таким образом, набор параметрических уравнений для графика, представленного как y = x 2 + 2, имеет вид
Теперь, когда определены оба параметрических уравнения, можно построить общий график с выбранными значениями параметра. Параметрическая диаграмма — обзор
15.2 Деформация, вызванная ползучестью
15.2.1 Параметрические подходы к анализу данных
15.2.2 Альтернативные процедуры для рационализации данных
15.2.3 Интерпретация поведения степенного закона
PLAY .Что происходит, когда $ \ theta $ начинает продвигаться от $ 0 $ к $ \ pi $? Координата $ x $ будет следовать графику $ y (\ theta) = \ sin (\ theta) $, поэтому сначала она повысится с $ 0 $ до $ 1 $ (при $ \ theta = \ frac {\ pi} {2 } $), а затем снова упасть с $ 1 $ на $ 0 $ (при $ \ theta = \ pi $). Он будет делать это без скачков и перерывов. Итак, если вы смотрели только на «тень» нашей светящейся точки на оси $ x $, она начинается с $ x = 0 $, затем плавно перемещается вправо (без рывков, без скачков, без пропусков). ), пока он не достигнет $ 1 $ в середине фильма, а затем вернется к $ 0 $, пока не вернется к $ 0 $ в конце фильма. PLAY , он начнется с 1 доллара, а затем упадет до 0 долларов, снова плавно, без скачков, рывков и пропусков, пока не достигнет 0 долларов в середине фильма (при $ \ theta = \ frac {\ pi} {2} $). Затем продолжит движение в том же направлении, от $ 0 $ до $ -1 $, и достигнет $ -1 $ в конце «фильма» (когда $ \ theta = \ pi $). Итак, если вы посмотрите на «тень» светящейся точки на оси $ y $, она начнется с $ 1 $, затем опустится до $ 0 $ и продолжит снижаться до $ -1 $, и все это в целом гладко. манерой, без скачков, рывков, колебаний, откатов и т. д. <заполните поле> . Нажмите ПАУЗА на видео и подведите итоги. Где мы? Какую часть единичного круга мы нарисовали? Сколько раз? Любой возврат? Сколько времени вы проводите без движения? Было ли движение в целом «плавным»? PLAY , и наш $ \ theta $ начнет увеличиваться с $ \ pi / 2 $ в сторону $ \ pi $.Эта светящаяся точка, представляющая $ (x (\ theta), y (\ theta)) $, перемещается, но теперь вниз и влево, всегда вдоль единичной окружности, пока, наконец, не $ \ theta = \ pi $, «конец фильм «, он достигает своего конечного пункта назначения в точке <заполните другой бланк> . параметрический график / индекс | Система ресурсов Wolfram
Ресурс функции: & emsp14;
НаправлениеПараметрический участок
Ресурс функции: & emsp14;
Раздел ParametricPlot3D
Ресурс функции: & emsp14;
Направление Параметрический участок3D
Ресурс функции: & emsp14;
ConicSectionPlot
Ресурс функции: & emsp14;
ParametricSurfaceTangentPlane
Ресурс функции: & emsp14;
SuggestPlotRange
Ресурс функции: & emsp14;
EnhancedPlot
Ресурс функции: & emsp14;
ManipulatePlot
Ресурс функции: & emsp14;
УчастокВектор
Ресурс функции: & emsp14;
KeywordPlot
Ресурс функции: & emsp14;
Участок
Ресурс функции: & emsp14;
HypergraphPlot
Ресурс функции: & emsp14;
InteractiveConicPlot
Ресурс функции: & emsp14;
BenchmarkPlot
Ресурс функции: & emsp14;
Комбинированные участки
Ресурс функции: & emsp14;
Кривизна Участок
Ресурс функции: & emsp14;
PairwiseScatterPlot
Ресурс функции: & emsp14;
PlotGrid
Ресурс функции: & emsp14;
Древовидная картаПлощадь
Ресурс функции: & emsp14;
MilkyWayPlot3D
Ресурс функции: & emsp14;
Функция PeriodPlot
Ресурс функции: & emsp14;
SimpleHypergraphPlot
Ресурс функции: & emsp14;
Приблизительная кривая
Ресурс функции: & emsp14;
VennGraphPlot
Ресурс функции: & emsp14;
CobwebPlot
Ресурс функции: & emsp14;
PolygonMarker
Ресурс функции: & emsp14;
LabelListPlot
Ресурс функции: & emsp14;
PolarDendrogramPlot
Ресурс функции: & emsp14;
Участок
Ресурс функции: & emsp14;
DragZoomPlot
Ресурс функции: & emsp14;
Мясной участок
Ресурс функции: & emsp14;
Внутри
Ресурс функции: & emsp14;
FittedModelPlot
Ресурс функции: & emsp14;
EigenvectorPlot
Ресурс функции: & emsp14;
NFAPlot
Ресурс функции: & emsp14;
CombinatorPlot
Ресурс функции: & emsp14;
Приблизительная поверхность
Ресурс функции: & emsp14;
DiscreteIntegralPlot
Ресурс функции: & emsp14;
ParallelCoordinatesPlot
Ресурс функции: & emsp14;
BiPlot
Ресурс функции: & emsp14;
TessellationPlot
Ресурс функции: & emsp14;
SaundersDigitPlot
Ресурс функции: & emsp14;
РазделКонтурПлощадь
Ресурс функции: & emsp14;
ListGrowthPlot
Ресурс функции: & emsp14;
ComplexBubblePlot
Ресурс функции: & emsp14;
LeeInterpolatingNodes
Ресурс функции: & emsp14;
LinearDescriptionPlotQuiz
Ресурс функции: & emsp14;
Кубический ОписаниеPlotQuiz
Ресурс функции: & emsp14;
Квадратичный ОписаниеPlotQuiz
Ресурс функции: & emsp14;
GeneralRationalInterpolation
Ресурс функции: & emsp14;
FrenetSerretPlot
Ресурс функции: & emsp14;
RuledSurfacePlot
Ресурс функции: & emsp14;
CatacausticCurvePlot
Ресурс функции: & emsp14;
GraphFunctionPlot
Ресурс функции: & emsp14;
CrossRecurrencePlot
Ресурс функции: & emsp14;
MultiwayEvolutionPlot
Ресурс функции: & emsp14;
PursuitCurvePlot
Ресурс функции: & emsp14;
MultipleAxesPlot
Ресурс функции: & emsp14;
LeastSquaresPlot
Ресурс функции: & emsp14;
IteratedAffinePlot
Ресурс функции: & emsp14;
DottedArrayPlot
Ресурс функции: & emsp14;
SinusoidPlotQuiz
Ресурс функции: & emsp14;
Принцип Парето, участок
Ресурс функции: & emsp14;
График интегрального приближения
Ресурс функции: & emsp14;
ExtractPlotImageData
Ресурс функции: & emsp14;
RaggedDigitsPlot
Ресурс функции: & emsp14;
NewtonMethodPlot
Ресурс функции: & emsp14;
MoleculeValuePlot
Ресурс функции: & emsp14;
Филогенетический участок
Ресурс функции: & emsp14;
MillerIndicesPlot
Ресурс функции: & emsp14;
QuadricSurfacePlot
Ресурс функции: & emsp14;
PolarTreemapPlot
Ресурс функции: & emsp14;
РазделPlot3D
Ресурс функции: & emsp14;
Кривизна TorsionPlot3D
Ресурс функции: & emsp14;
GalileanSatellitesPlot
Ресурс функции: & emsp14;
MoleculePrincipalMomentPlot
Ресурс функции: & emsp14;
ОбщиеМиниМаксПриближение
Ресурс функции: & emsp14;
КомбинаторEvolutionPlot
Ресурс функции: & emsp14;
SubstitutionSystemPlot
Ресурс функции: & emsp14;
WolframModelPlot
Ресурс функции: & emsp14;
StemLeafPlot
Ресурс функции: & emsp14;
КомбинаторБрекетыPlot
Ресурс функции: & emsp14;
ДНКAlignmentPlot
Ресурс функции: & emsp14;
FindMinimumPlot
Ресурс функции: & emsp14;
ByteArrayPlot
Ресурс функции: & emsp14;
MobileAutomatonPlot
Ресурс функции: & emsp14;
ГенеалогияTreePlot
Ресурс функции: & emsp14;
FindRootPlot
Ресурс функции: & emsp14;
RegressionListPlot
Ресурс функции: & emsp14;
LSystemPlot
Ресурс функции: & emsp14;
MultispacePlot3D
Ресурс функции: & emsp14;
OrderedGraphModelPlot
Ресурс функции: & emsp14;
DateListPlotRanged
Ресурс функции: & emsp14;
УчастокVector3D
Ресурс функции: & emsp14;
Интерактивная графика
Ресурс функции: & emsp14;
TabViewListPlot
Ресурс функции: & emsp14;
Подстановка Система Причинно-следственная связь
Ресурс функции: & emsp14;
QuadricPlot3D
Ресурс функции: & emsp14;
MultipleAxesListPlot
Ресурс функции: & emsp14;
RiemannSphereComplexPlot
Ресурс функции: & emsp14;
Аллювиальный график
Ресурс функции: & emsp14;
DirectionalDerivativePlot3D
Ресурс функции: & emsp14;
CheckboxLegended
Ресурс функции: & emsp14;
SubstitutionSystemRulePlot
Ресурс функции: & emsp14;
LayeredGraphPlot3D
Ресурс функции: & emsp14;
TagSystemRulePlot
Ресурс функции: & emsp14;
MobileAutomatonRulePlot
Ресурс функции: & emsp14;
SequenceGraph
Ресурс функции: & emsp14;
Последовательный участок замещения системы
Ресурс функции: & emsp14;
LinearFunctionQuiz
Ресурс функции: & emsp14;
Повернутый Эллипс Матрица
Ресурс функции: & emsp14;
SolarSystemPlot3D
Ресурс функции: & emsp14;
MoleculeValuePlot3D
Ресурс функции: & emsp14;
RiemannSurfacePlot3D
Ресурс функции: & emsp14;
Луна, положение, участок, 3D,
Ресурс функции: & emsp14;
Интегральное приближениеPlot3D
Ресурс функции: & emsp14;
QuadraticResidueAcousticDiffuserPlot
Ресурс функции: & emsp14;
RadarChart
Ресурс функции: & emsp14;
Спирограф
Ресурс функции: & emsp14;
MoleculeSymmetryPlot3D
Ресурс функции: & emsp14;
SequentialSubstitutionSystemRulePlot
Ресурс функции: & emsp14;
Оценить Benchmark
Ресурс функции: & emsp14;
ДойлСпираль
Ресурс функции: & emsp14;
РешеткаUnitCellPlot3D
Ресурс функции: & emsp14;
EnlargeBoundingBox
Ресурс функции: & emsp14;
РешеткаVoronoiCellPlot3D
Ресурс функции: & emsp14;
RandomMandala
Ресурс функции: & emsp14;
Пенроуз Плитка
Ресурс функции: & emsp14;
LifetimeChart
Ресурс функции: & emsp14;
Среднее значение
Ресурс функции: & emsp14;
WolframPhysicsProjectStyleData
Ресурс функции: & emsp14;
ХофштадтерБабочка
Ресурс функции: & emsp14;
GraphMouseMagnify
Ресурс функции: & emsp14;
ГрафикаOptionQ
Ресурс функции: & emsp14;
Герцшпрунг-Рассел Схема
Ресурс функции: & emsp14;
ChaosGame
Ресурс функции: & emsp14;
ГрафикаBounds
Ресурс функции: & emsp14;
TreeGrid
Ресурс функции: & emsp14;
ContinentalPlateMaps
Ресурс функции: & emsp14;
CurveAnalysis
Ресурс функции: & emsp14;
Выбрать Atoms3D
Ресурс функции: & emsp14;
МолекулаМешRegion
Ресурс функции: & emsp14;
ScaledRankChart
Ресурс функции: & emsp14;
ГрафикаИнформация
Графики · Алгебра и тригонометрия
Параметрические уравнения: графики · Алгебра и тригонометрия Построение параметрических уравнений по точкам
Приложения параметрических уравнений
Ключевые понятия
Упражнения по разделам
Устный
Графический
{x (t) = t − 1y (t) = t2 t x y −3 -2 -1 0 1 2 3 т −3 -2 -1 0 1 2 x y Технологии
Расширения
Эта работа находится под международной лицензией Creative Commons Attribution 4.0. Двумерные графики — Введение в символьные вычисления 1.0.0 документация
Кривые на плоскости
Parametric_plot .
Кривая Лиссажу определяется параметрическим способом,
показано на рис.36.2
implicit_plot (f, (x, -2, 2), (y, -2, 2)). show (figsize = 4)
implicit_plot (f, (x, -2, 2), (y, -2, 2), plot_points = 2000, \
color = ‘red’). показать (figsize = 4) г, т = var ('г, т')
g = f.subs ({x: r * cos (t), y: r * sin (t)})
печать g
sg = g.trig_simplify ()
печать sg
polar_plot , обеспечивая диапазон для \ (t \). s0 = s [0].rhs ()
first = polar_plot (s0, (t, 0, pi), axes = False, color = 'красный')
second = polar_plot (s0, (t, pi, 2 * pi), оси = False, color = 'green')
(первый + второй) .show (figsize = 4)
p0 = точка ((0, 0), color = 'blue', size = 50)
(p0 + первый + второй).показать()
Найдите область определения функции с корнем: § Область определения функции
Область определения функции с корнем — Студопедия
 Пожалуйста, не путайте с неравенствами двух переменных, где геометрически задействована вся координатная плоскость. Однако есть и приятные совпадения! Итак, для неравенства равносильны следующие преобразования:
Пожалуйста, не путайте с неравенствами двух переменных, где геометрически задействована вся координатная плоскость. Однако есть и приятные совпадения! Итак, для неравенства равносильны следующие преобразования:
Геометрически область определения изображается штриховкой соответствующих интервалов на оси абсцисс. В данном случае:
В данном случае:
Ещё раз напоминаю геометрический смысл области определения – график функции существует только на заштрихованном участке и отсутствует при .
Дискриминант положителен, ищем корни:
Таким образом, парабола пересекает ось абсцисс в двух точках, а это значит, что часть параболы расположена ниже оси (неравенство ), а часть параболы – выше оси (нужное нам неравенство ).
! Примечание: если вам не до конца понятны объяснения, пожалуйста, начертите вторую ось и параболу целиком! Целесообразно вернуться к статье Графики и свойства элементарных функций и методичке Горячие формулы школьного курса математики. А основной способ – метод интервалов мы детально разберём в статье Нули функции. Интервалы знакопостоянства.
А основной способ – метод интервалов мы детально разберём в статье Нули функции. Интервалы знакопостоянства. Такая функция не определена вообще (разумеется, график тоже иллюзорен).
Такая функция не определена вообще (разумеется, график тоже иллюзорен).
о методе интервалов. 2-25/x+7 — Учеба и наука
2-25/x+7 — Учеба и наукаОтветы
01.  05.16
05.16
Михаил Александров
Читать ответы
Андрей Андреевич
Читать ответы
Eleonora Gabrielyan
Читать ответы
Похожие вопросы  3
3Область определения функции — интернет энциклопедия для студентов
 {2}-3 x+2=0
\) По теореме Вета: \(\
x_{1}+x_{2}=3 ; x_{1} \cdot x_{2}=2
\),поэтому \(\
x_{1}=1, x_{2}=2
\) .Таким образом, неравенство примет вид
{2}-3 x+2=0
\) По теореме Вета: \(\
x_{1}+x_{2}=3 ; x_{1} \cdot x_{2}=2
\),поэтому \(\
x_{1}=1, x_{2}=2
\) .Таким образом, неравенство примет вид Существует система неравенств
Существует система неравенствКак найти область определения функции заданной формулой, примеры и способы решения 10 класс, ручной и автоматизированный методы, онлайн-калькулятор

Общие сведения
 Исследование функции — естественный процесс, который встречается в различных дисциплинах.
Исследование функции — естественный процесс, который встречается в различных дисциплинах.Основные понятия
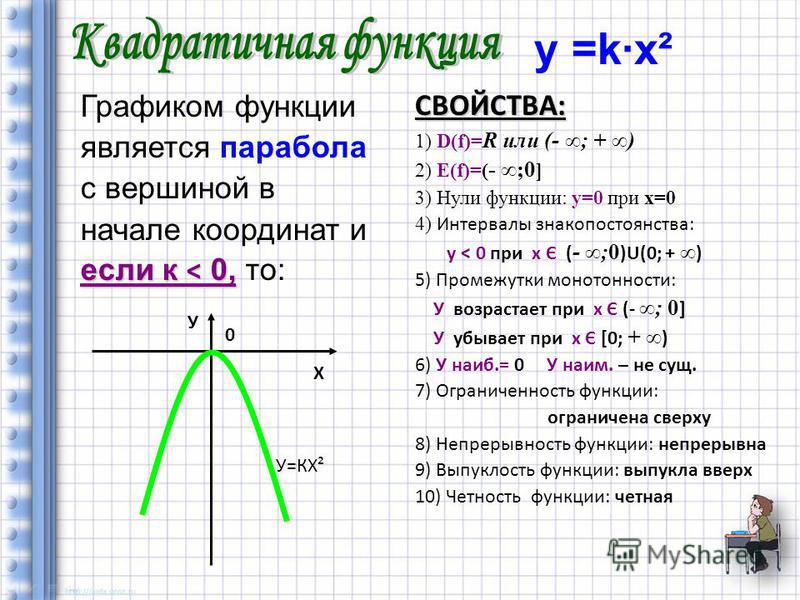
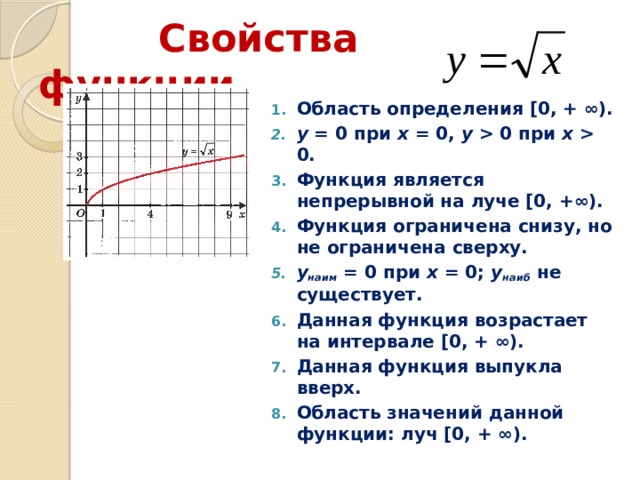 Это значит следующее: областью определения функции вида y = 3*x / sqrt (156 — |x|) является множество чисел, которые находятся в интервале от 0 включительно (скобка «[«) до 157 не включительно.
Это значит следующее: областью определения функции вида y = 3*x / sqrt (156 — |x|) является множество чисел, которые находятся в интервале от 0 включительно (скобка «[«) до 157 не включительно.Типы функций

Правильное обозначение
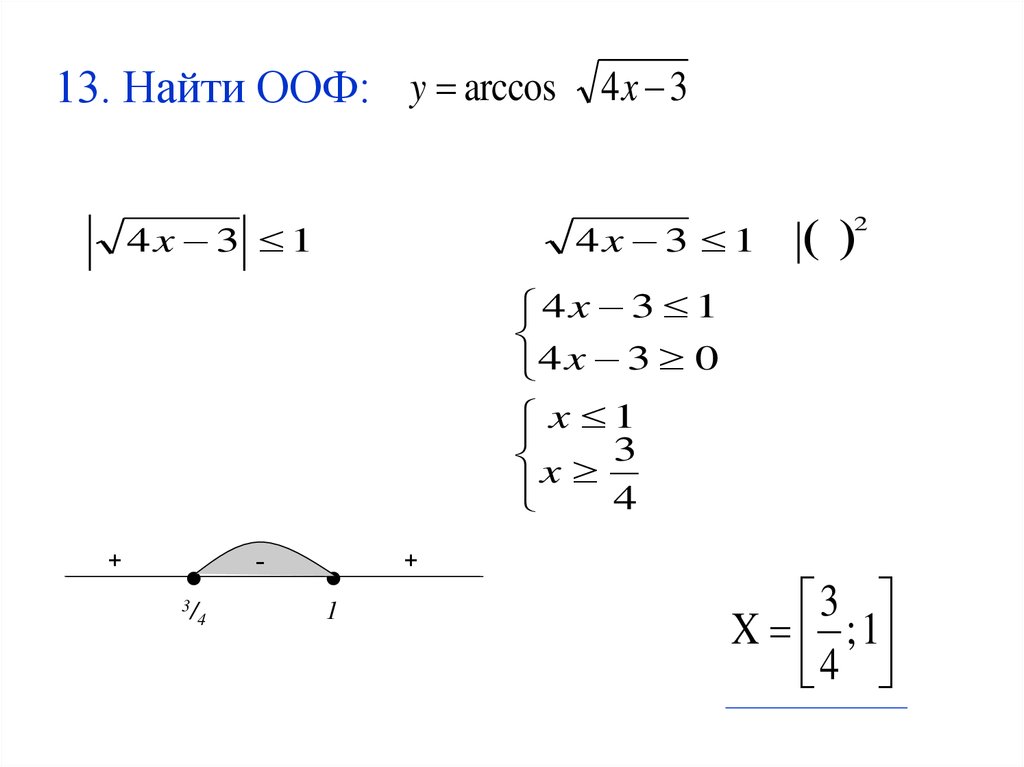
Алгоритмы определения
 Для функций с натуральным логарифмом (ln) значение выражения, которое находится под логарифмом, должно быть всегда больше 0. При отрицательных значениях ln «превращается» в неопределенность. Необходимо составить неравенство. Оно должно быть больше 0.
Для функций с натуральным логарифмом (ln) значение выражения, которое находится под логарифмом, должно быть всегда больше 0. При отрицательных значениях ln «превращается» в неопределенность. Необходимо составить неравенство. Оно должно быть больше 0.Другие методы
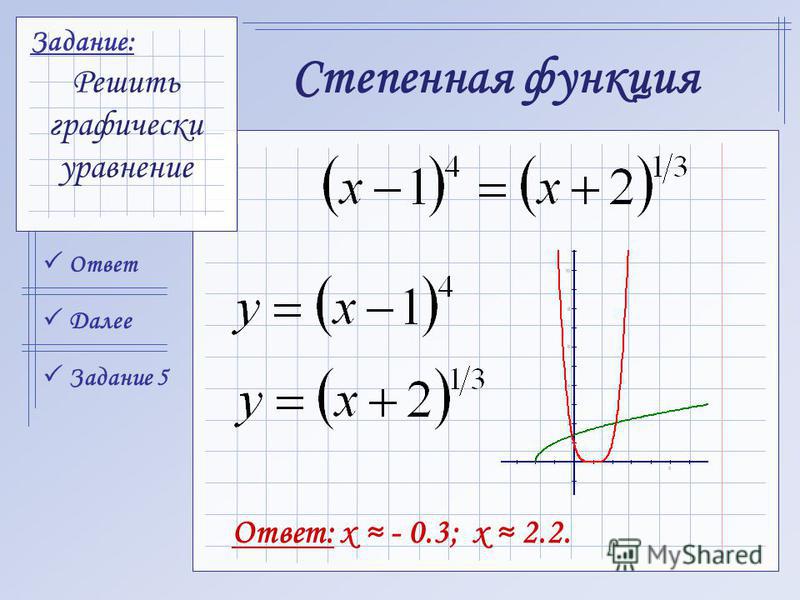 В этом случае можно легко изобразить графики заданной функции, исследовать и найти ее основные свойства, а также D (f), представленных в виде функций. Например, зависимость амплитудных значений переменного электрического тока от времени.
В этом случае можно легко изобразить графики заданной функции, исследовать и найти ее основные свойства, а также D (f), представленных в виде функций. Например, зависимость амплитудных значений переменного электрического тока от времени.
Примеры решения
Для линейного вида

Дробные и иррациональные
 2] — (4 * 4 * 9) = 144 — 144 = 0.
2] — (4 * 4 * 9) = 144 — 144 = 0.Как находить ооф функции. Область определения функции с корнем
 Можно сказать, что это строгий математический закон, который связывает два числа определенным образом.
Можно сказать, что это строгий математический закон, который связывает два числа определенным образом.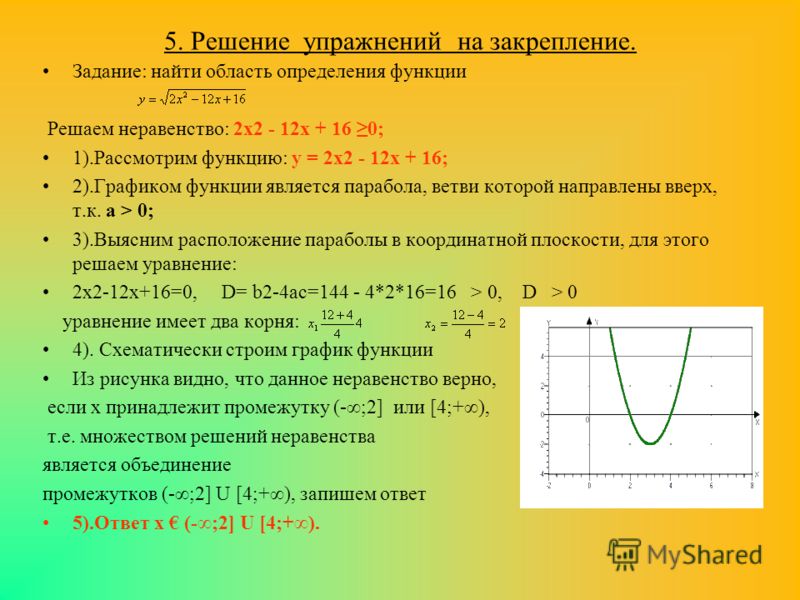
Виды зависимостей переменных
 Областью определения являются все значения аргумента, при котором f(x) имеет смысл.
Областью определения являются все значения аргумента, при котором f(x) имеет смысл.
Множество и подмножество чисел
 Найти область определения.
Найти область определения.
х+4=0
х=-4
D(f)=(-∞ ; -4)∪(-4; +∞)
Логарифмические и тригонометрические функции
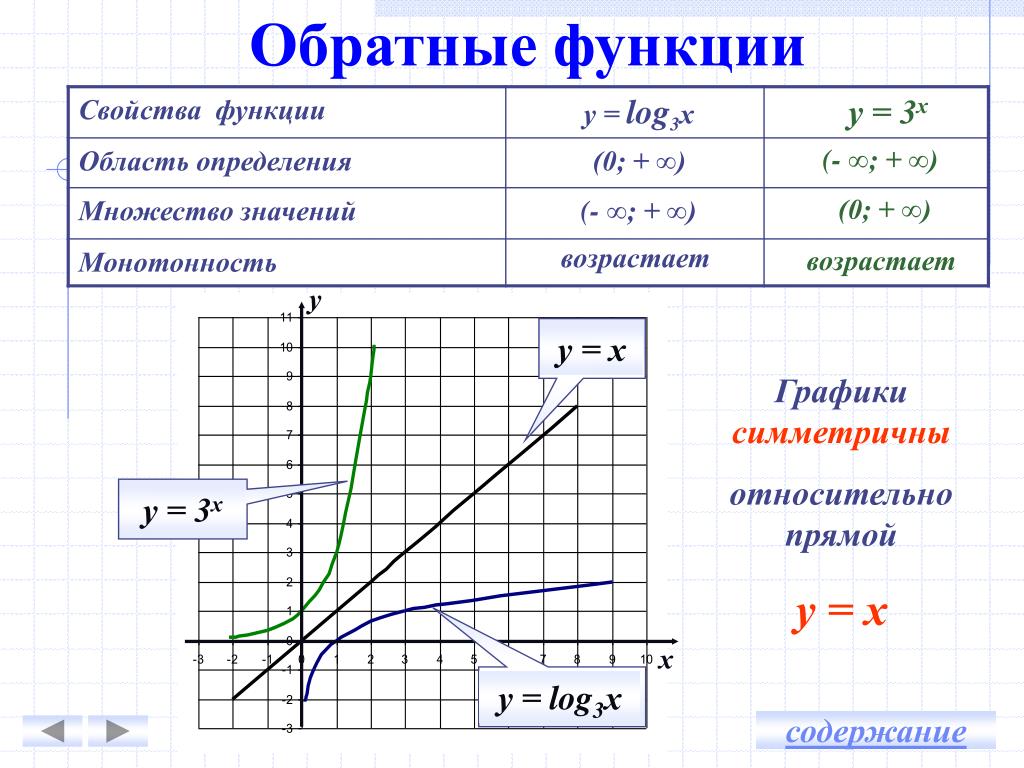
Функцией y = f(x)
называется закон (правило, отображение), согласно которому, каждому элементу x
множества X
ставится в соответствие один и только один элемент y
множества Y
.
Множество элементов y ∈
Y
,
которые имеют прообразы во множестве X
,
называется множеством значений функции (или областью значений ).
Элемент y ∈
Y
называют значением функции или зависимой переменной .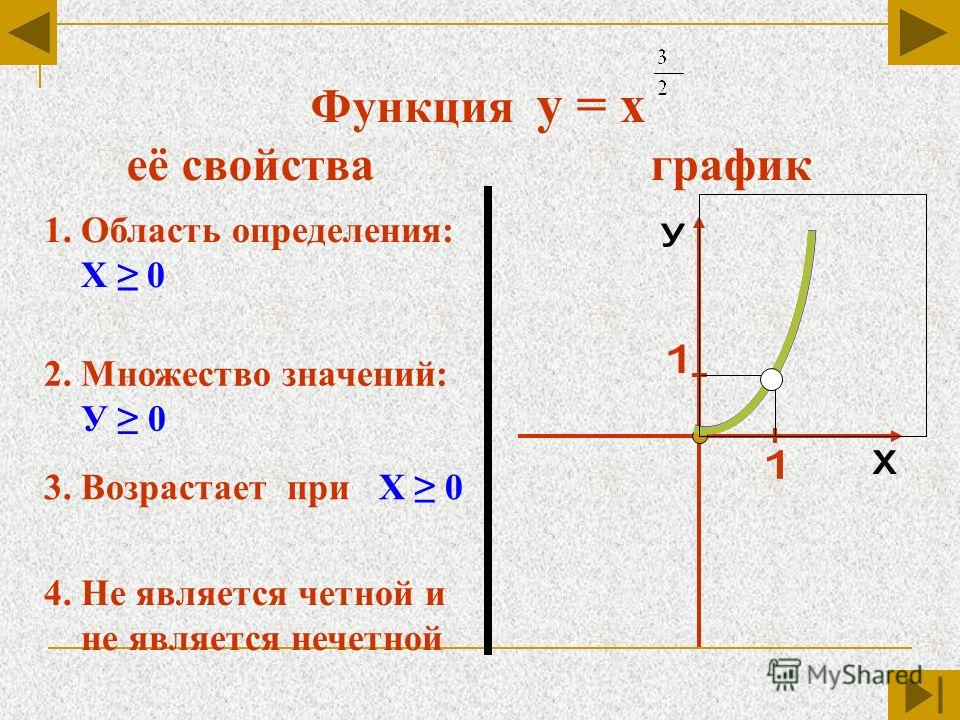
Сложные функции
Пусть заданы функции и .
Причем область определения функции f
содержит множество значений функции g
.
Тогда каждому элементу t
из области определения функции g
соответствует элемент x
,
а этому x
соответствует y
.
Такое соответствие называют сложной функцией : .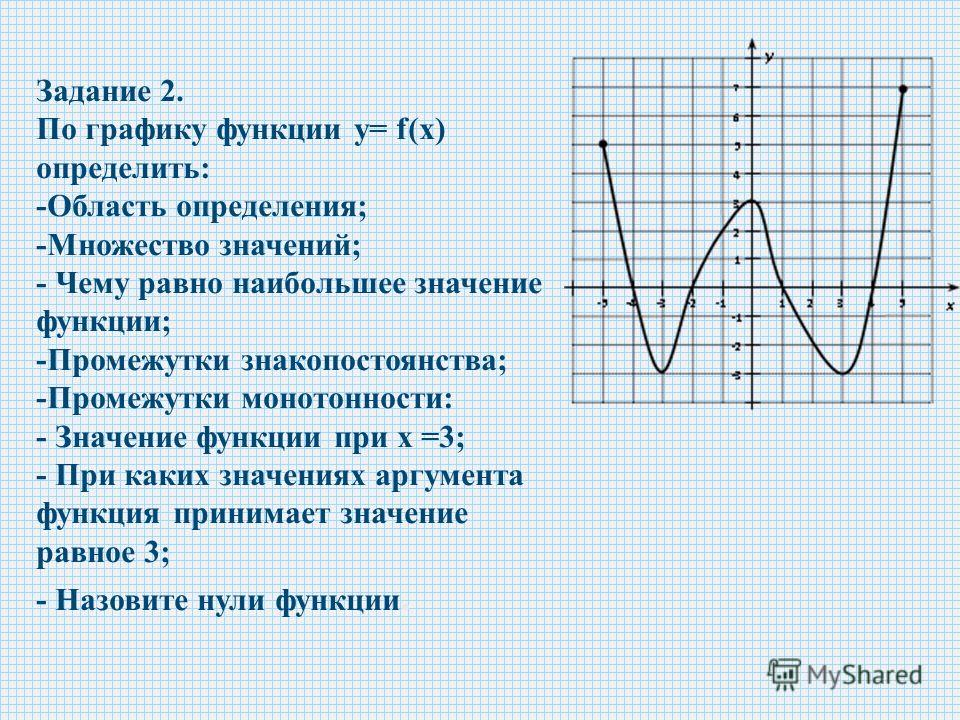 Тогда зависимость импульса от времени является сложной функцией .
Но ее, для краткости, обозначают так: .
При таком подходе и — это различные функции. При одинаковых значениях аргументов они могут давать различные значения. В математике такое обозначение не принято. Если требуется сокращение, то следует ввести новую характеристику. Например .
Тогда явно видно, что и — это разные функции.
Тогда зависимость импульса от времени является сложной функцией .
Но ее, для краткости, обозначают так: .
При таком подходе и — это различные функции. При одинаковых значениях аргументов они могут давать различные значения. В математике такое обозначение не принято. Если требуется сокращение, то следует ввести новую характеристику. Например .
Тогда явно видно, что и — это разные функции.Действительные функции
Например, числовые последовательности — это функции, областью определения которых является множество натуральных чисел, а множеством значений — вещественные или комплексные числа.
Векторное произведение тоже функция, поскольку для двух векторов и имеется только одно значение вектора .
Здесь областью определения является множество всех возможных пар векторов .
Множеством значений является множество всех векторов.
Логическое выражение является функцией. Ее область определения — это множество действительных чисел (или любое множество, в котором определена операция сравнения с элементом “0”). Множество значений состоит из двух элементов — “истина” и “ложь”.
Множество значений состоит из двух элементов — “истина” и “ложь”.Максимум и минимум
.
.
.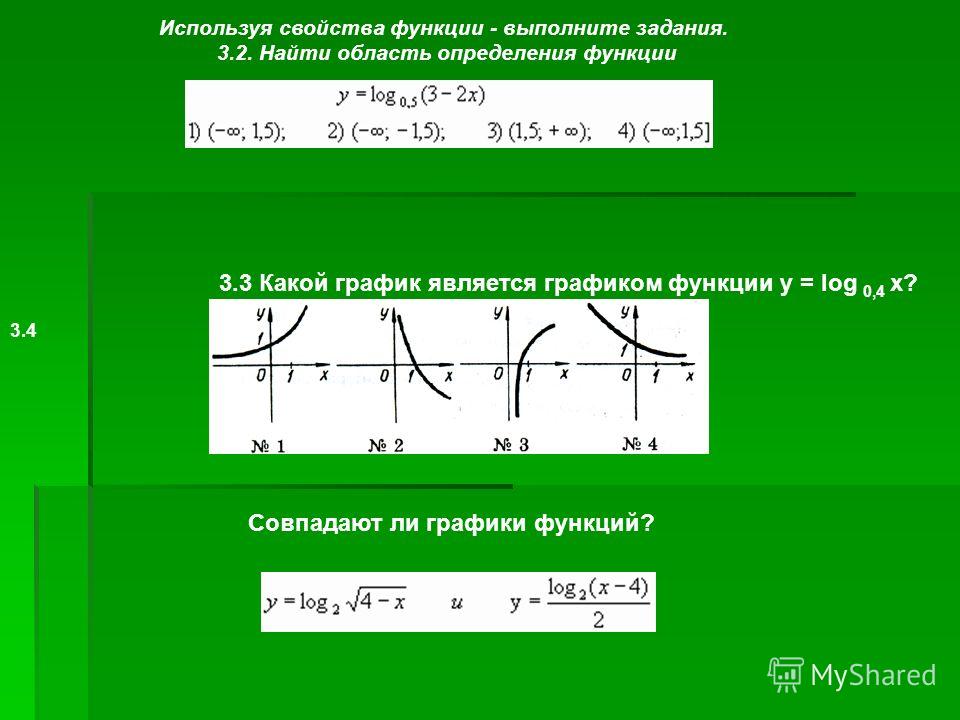
Верхняя грань функции может обозначаться так:
.
Нижняя грань функции может обозначаться так:
. Но не всякая функция имеет максимум и минимум.
Но не всякая функция имеет максимум и минимум.
Она ограничена, на этом интервале, сверху значением 1
и снизу — значением 0
:
для всех .
Эта функция имеет верхнюю и нижнюю грани:
.
Но она не имеет максимума и минимума.
для всех ;
;
.Монотонные функции
Пусть функция определена на некотором множестве действительных чисел X
.
Функция называется строго возрастающей (строго убывающей)
.
Функция называется неубывающей (невозрастающей) , если для всех таких что выполняется неравенство:
.
Функция называется монотонной , если она неубывающая или невозрастающая.Многозначные функции
 Различными цветами обозначены ее ветви. Каждая ветвь является функцией.
Различными цветами обозначены ее ветви. Каждая ветвь является функцией.
(1) .
При заданном значении независимой переменной x
,
принадлежащему интервалу ,
этому уравнению удовлетворяет бесконечно много значений y
(см. рисунок).
(2) .
При таком условии, заданному значению ,
соответствует только одно решение уравнения (1). То есть соответствие, определяемое уравнением (1) при условии (2) является функцией.
(2.n) ,
где n
— целое. В результате, для каждого значения n
,
мы получим свою функцию, отличную от других. Множество подобных функций является многозначной функцией . А функция, определяемая из (1) при условии (2.n) является ветвью многозначной функцией .
В результате, для каждого значения n
,
мы получим свою функцию, отличную от других. Множество подобных функций является многозначной функцией . А функция, определяемая из (1) при условии (2.n) является ветвью многозначной функцией .
О.И. Бесов. Лекции по математическому анализу. Часть 1. Москва, 2004.
Л.Д. Кудрявцев. Курс математического анализа. Том 1. Москва, 2003.
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.
 Однако, чтобы найти область
определения функции, нам не нужно перебирать все пары иксов и игреков.
Однако, чтобы найти область
определения функции, нам не нужно перебирать все пары иксов и игреков. Такое сообщение
предусмотрено авторами программы, если выражение для вычисления ответа достаточно сложно или касается
какой-то узкой предметной области, или же предусмотрено авторами языка программирования, если дело
касается общепринятых норм, например, что нельзя делить на нуль.
Такое сообщение
предусмотрено авторами программы, если выражение для вычисления ответа достаточно сложно или касается
какой-то узкой предметной области, или же предусмотрено авторами языка программирования, если дело
касается общепринятых норм, например, что нельзя делить на нуль.
Область определения постоянной
Область определения корня
n -й степени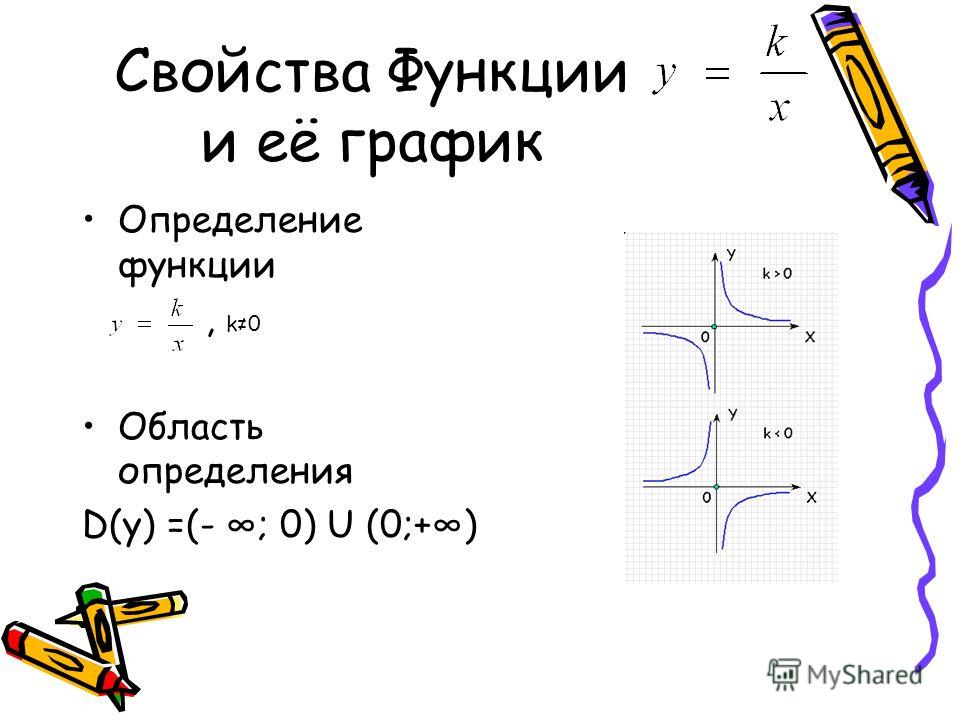
Область определения степенной функции
 Следовательно, область определения данной функции — вся числовая прямая, то есть
]- ∞; + ∞[
.
Следовательно, область определения данной функции — вся числовая прямая, то есть
]- ∞; + ∞[
.Область определения степенной функции с дробным показателем степени
Область определения показательной и логарифмической функции
Область определения показательной функции
Область определения логарифмической функции

Найти область определения функции самостоятельно, а затем посмотреть решение
Область определения тригонометрических функций

Область определения обратных тригонометрических функций

Область определения дроби
1. Дробная функция — ограничение на знаменатель.
2. Корень четной степени — ограничение на подкоренное выражение.
3. Логарифмы — ограничение на основание логарифма и подлогарифмическое выражение.
3. Тригонометрические tg(x) и ctg(x) — ограничение на аргумент.

4. Обратные тригонометрические функции.
Арксинус Арккосинус Арктангенс, Арккотангенс Далее решаются следующие примеры на тему «Область определения функций».
Пример 1 Пример 2 Пример 3 Пример 4 Пример 5 Пример 6 Пример 7 Пример 8 Пример 9 Пример 10 Пример 11 Пример 12 Пример 13 Пример 14 Пример 15 Пример 16 Пример нахождения области определения функции №1
Нахождение области определения любой линейной функции, т.
 е. функции первой степени:
е. функции первой степени:
Пример нахождения области определения функции №2

Пример нахождения области определения функции №3
Рассмотрим пример нахождения области определения функции с корнем четной степени:
об областях — PowerShell | Документы Майкрософт
Краткое описание
Подробное описание

Области PowerShell

Родительская и дочерняя области
 Модули имеют собственное состояние сеанса, связанное с глобальной областью.
Весь код модуля выполняется в специфической для модуля иерархии областей видимости, которая имеет свои особенности.
собственная корневая область.
Модули имеют собственное состояние сеанса, связанное с глобальной областью.
Весь код модуля выполняется в специфической для модуля иерархии областей видимости, которая имеет свои особенности.
собственная корневая область. Наследование
Get-Variable или Get-Alias .
Get-Variable -Scope local
Get-Variable -Scope global
Модификаторы области видимости
global: — указывает, что имя существует в области Global . локальный: — указывает, что имя существует в области Local . Электрический ток
область всегда является областью Local . private: — указывает, что имя Private и видно только
текущий объем. частный не является областью действия. Это вариант, который меняет
видимость элемента за пределами области, в которой этот элемент определен.
сценарий: — указывает, что имя существует в области Script . Область действия сценария — это область действия файла сценария ближайшего предка или Global , если
нет ближайшего файла сценария предка. использование: — Используется для доступа к переменным, определенным в другой области во время работы
сценарии с помощью командлетов, таких как Start-Job и Invoke-Command . рабочий процесс: — указывает, что имя существует в рабочем процессе. Примечание:
Рабочие процессы не поддерживаются в PowerShell v6 и выше. — модификатор, созданный поставщиком PowerShell PSDrive.
Например: Пространство имен Описание Псевдоним: Псевдонимы, определенные в текущей области Конверт: Переменные среды, определенные в текущей области Функция: Функции, определенные в текущей области Переменная: Переменные, определенные в текущей области 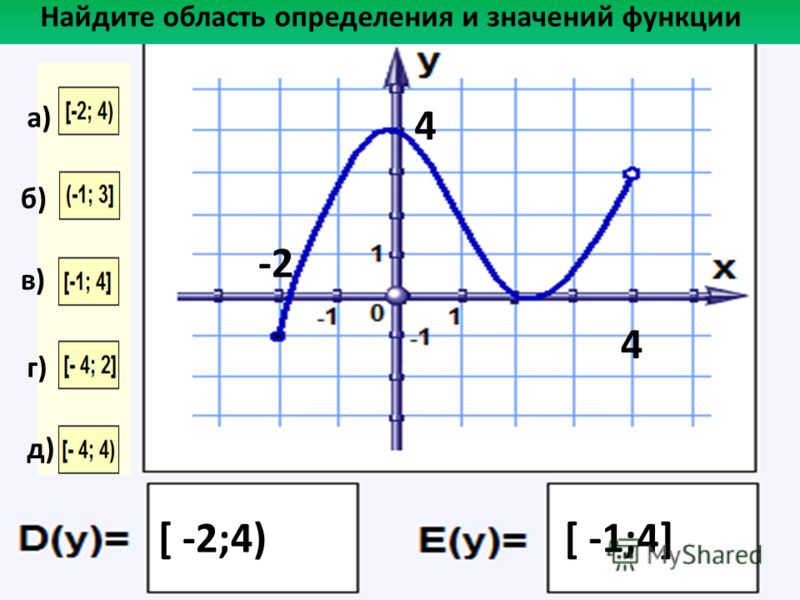 Область по умолчанию для
функции и псевдонимы являются локальной областью действия, даже если они определены в
сценарий.
Область по умолчанию для
функции и псевдонимы являются локальной областью действия, даже если они определены в
сценарий. Использование модификаторов области действия
$[<модификатор области>:]<имя> = <значение>
function [<модификатор-области>:]<имя> {<тело-функции>}
$a = "one"
global: модификатор: $global:a = "один"
Get-переменная a | Список форматов *

Имя: а
Описание :
Стоимость: один
Видимость: общедоступная
Модуль:
ИмяМодуля:
Опции : Нет
Атрибуты: {}
$private:pVar = 'Частная переменная'
Получить переменную pVar | Список форматов *
private устанавливает для свойства Options значение Private . Наименование: pVar
Описание :
Значение: частная переменная
Видимость: общедоступная
Модуль:
ИмяМодуля:
Варианты: частный
Атрибуты: {}
: .
модификатор: $script:a = "один"
глобальная функция: привет {
Пишет-ведущий "Привет, мир"
}
 Следующая команда ссылается на переменную
Следующая команда ссылается на переменную $test , сначала в локальной области
а затем в глобальном масштабе: $test
$ глобальный: тест
Использование
: модификатор области с использованием представлен в PowerShell 3.0. Использование модификатор области для встраивания значений переменных из области вызывающего сеанса, чтобы
код вне сеанса может получить к ним доступ. Модификатор области действия с использованием поддерживается в
следующих контекстах: Invoke-Command с использованием имя_компьютера , HostName , SSHConnection или Session параметры
(удаленный сеанс) Start-Job (сеанс вне процесса) Start-ThreadJob или ForEach-Object -Parallel (отдельный сеанс потока) В удаленных и
внепроцессные сеансы, они всегда являются независимыми копиями.
В удаленных и
внепроцессные сеансы, они всегда являются независимыми копиями. Сериализация значений переменных
 Он имеет свойства и методы типа. Для простых типов, таких как System.Version , копия точная. Для сложных типов копия
несовершенный. Например, повторно гидратированные объекты сертификата не включают
закрытый ключ.
Он имеет свойства и методы типа. Для простых типов, таких как System.Version , копия точная. Для сложных типов копия
несовершенный. Например, повторно гидратированные объекты сертификата не включают
закрытый ключ. Параметр AllScope

Управление областью действия
Get-Help * - Область действия параметра
.
параметр Get-Variable . К видимым переменным относятся глобальные переменные,
переменные в родительской области и переменные в текущей области. Get-Variable -Scope local
Set-Variable . Следующая команда создает переменную
в глобальной области: New-Variable -Scope global -Name a -Value "One"
New-Alias , Set-Alias или Командлеты Get-Alias для указания области действия. Следующая команда создает
псевдоним в глобальной области:
Следующая команда создает
псевдоним в глобальной области: New-Alias -Scope global -Name np -Value Notepad.exe
Командлет Get-Item , когда вы
находятся в сфере. Командлет Get-Item не имеет параметра Scope . Использование точечной нотации источника с областью действия
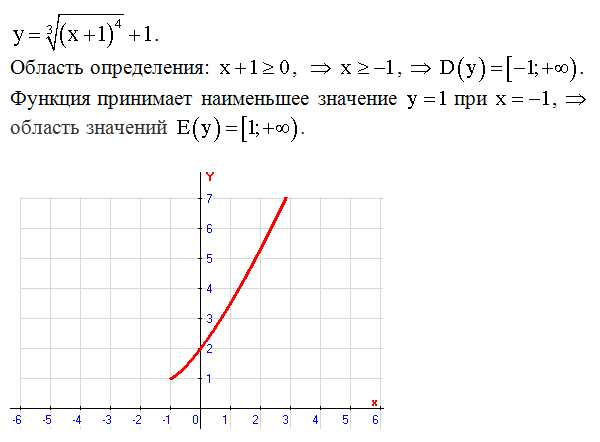
c:\scripts\sample.ps1
. c:\scripts.sample.ps1
и c:\scripts.sample.ps1
 ps1,
недоступно в текущей области.
ps1,
недоступно в текущей области. Ограничение без области действия
Сеансы
 За
Например, вы можете запустить сценарий для создания дочерней области в сеансе.
За
Например, вы можете запустить сценарий для создания дочерней области в сеансе. Модули
 Все экспорты помещаются в глобальные таблицы.
Если вы загружаете модуль2 из в модуль1, модуль2 загружается в сеанс
состояние модуля1, а не глобальное состояние сеанса. Любой экспорт из модуля2
размещен в верхней части состояния сеанса module1. Если вы используете
Все экспорты помещаются в глобальные таблицы.
Если вы загружаете модуль2 из в модуль1, модуль2 загружается в сеанс
состояние модуля1, а не глобальное состояние сеанса. Любой экспорт из модуля2
размещен в верхней части состояния сеанса module1. Если вы используете Import-Module -Scope local , затем экспорт помещается в текущий
объект области, а не на верхнем уровне. Если вы в модуле и используете Import-Module -Scope global (или Import-Module -Global ) для загрузки другого
модуль, этот модуль и его экспорт загружаются в глобальное состояние сеанса
вместо локального состояния сеанса модуля. Эта функция была разработана для
модуль записи, который манипулирует модулями. Модуль WindowsCompatibility делает это для импорта прокси-модулей в глобальное состояние сеанса. C:\temp\mod1.psm1 : $a = "Привет"
функция фу {
"$а = $а"
"`$global:a = $global:a"
}
$a , присваиваем ей значение и вызываем функцию фу .
$a = "До свидания"
фу
$a в области модуля, затем функция foo выводит значение переменной в обеих областях. $a = Привет
$global:a = До свидания
Вложенные подсказки
Private Option
Частный . Элементы, имеющие параметр Private , можно просматривать и изменять.
в той области, в которой они созданы, но их нельзя просмотреть или изменить
за пределами этой области. Get-Variable Команды в сценарии не
отображать приватную переменную. Использование модификатора глобальной области видимости в этом случае
не отображает приватную переменную.
Использование модификатора глобальной области видимости в этом случае
не отображает приватную переменную. New-Variable , Set-Variable , Командлеты New-Alias и Set-Alias , чтобы задать для свойства Option значение
Частный. Видимость
Private Значение свойства Option предназначено для
масштабы. Public и Private . Предметы
которые имеют частную видимость, можно просматривать и изменять только в контейнере в
которым они были созданы. Если контейнер добавлен или импортирован, элементы, которые
имеют частную видимость, не могут быть просмотрены или изменены.
New-Variable и Set-Variable для создания переменной
который имеет частную видимость. Примеры
Пример 1. Изменение значения переменной только в сценарии
$ConfirmPreference в
скрипт. Изменение не влияет на глобальную область. $ConfirmPreference в локальном
область, используйте следующую команду: PS> $ConfirmPreference
Высокая
 ps1, содержащий следующие команды:
ps1, содержащий следующие команды: $ConfirmPreference = "Low"
"Значение `$ConfirmPreference равно $ConfirmPreference."
$ConfirmPreference .
переменная, а затем сообщает ее значение в области скрипта. Результат должен
напоминают следующий вывод: Низкое значение $ConfirmPreference.
$ConfirmPreference в текущем
сфера. PS> $ConfirmPreference
Высокая
Пример 2. Просмотр значения переменной в разных областях
$test в глобальной области. $test = "Глобальный"
 ps1, определяющий переменную
ps1, определяющий переменную $test . в
скрипт, используйте модификатор области для ссылки на глобальную или локальную версию
переменной $test . $test = "Локальный"
«Локальное значение `$test равно $test».
«Глобальное значение `$test равно $global:test».
Локальное значение $test — Local.
Глобальное значение $test — Global.
$test определяется в
сессия. PS> $тест
Глобальный
Пример 3. Изменение значения переменной в родительской области
$test в глобальной области. $test = "Глобальный"
 ps1, определяющий переменную
ps1, определяющий переменную $test . в
скрипт, используйте модификатор области для ссылки на глобальную или локальную версию
переменной $test . $global:test = "Локальный"
«Глобальное значение `$test равно $global:test».
$test изменяется. PS> $тест
Местный
Пример 4: Создание частной переменной
Частный . Частные переменные наследуются дочерней областью,
но их можно просматривать или изменять только в той области, в которой они были созданы. $ptest в локальной
сфера. New-Variable -Name ptest -Value 1 -Option Private
$ptest в локальной области. PS> $ptest
1
PS> $ptest = 2
PS> $ptest
2
 ps1, содержащий следующие команды.
Команда пытается отобразить и изменить значение
ps1, содержащий следующие команды.
Команда пытается отобразить и изменить значение $ptest . "Значение `$Ptest равно $Ptest."
"Значение `$Ptest равно $global:Ptest."
$ptest не отображается в области сценария, вывод
пустой. "Значение $Ptest равно ."
"Значение $Ptest равно ."
Пример 5: Использование локальной переменной в удаленной команде
Использование модификатор области действия. PowerShell предполагает, что переменные в удаленных командах были
созданный в удаленном сеансе. $Использование:<ИмяПеременной>
$Cred в локальной
сеанс, а затем используйте переменную $Cred в удаленной команде: $Cred = Get-Credential
Invoke-Command $s {Remove-Item .\Test*.ps1 -Credential $Using:Cred}
 0. В PowerShell 2.0 для
указать, что переменная была создана в локальном сеансе, используйте следующие
формат команды.
0. В PowerShell 2.0 для
указать, что переменная была создана в локальном сеансе, используйте следующие
формат команды. $Cred = Получить учетные данные
Вызов команды $s {
параметр($c)
Remove-Item .\Test*.ps1 -Credential $c
} -Список аргументов $Cred
См. также
Объем и контекст, объясненный в Swift

Содержание
{
var age = 42
age += 1
}
var otherAge = getAge()
otherAge + = 1
print(anotherAge)


 Если вы хотите попрактиковаться в области видимости, просто отслеживайте, какая у вас текущая локальная область видимости и к каким переменным, типам и т. д. у вас есть доступ.
Если вы хотите попрактиковаться в области видимости, просто отслеживайте, какая у вас текущая локальная область видимости и к каким переменным, типам и т. д. у вас есть доступ.
{ Теперь мы собираемся добавить в этот класс перечисление как вложенный тип. Вот так:
Теперь мы собираемся добавить в этот класс перечисление как вложенный тип. Вот так:
{
var kind = Kind.thing
case food
case thing
}
}
print(«банан — это еда»)
}
посудомоечная машина. вид = .thing
{
var kind = Kind.thing
case food
case thing
}
return kind == .food
}
}
пусть голодный =
}
print(kind) // ОК, потому что `kind` находится в области видимости
print(hungry) // нет Хорошо, потому что `hungry` не в области действия
} Вы можете получить доступ к тому, что выше, на более низких уровнях, но не к тому, что ниже, на более высоких уровнях.
Вы можете получить доступ к тому, что выше, на более низких уровнях, но не к тому, что ниже, на более высоких уровнях.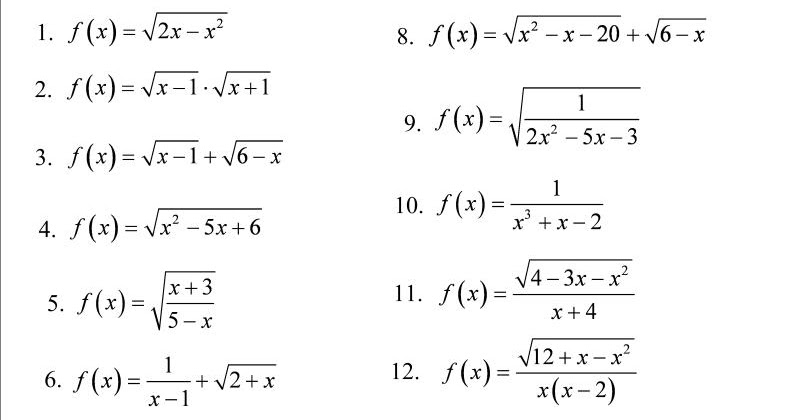 Вы можете узнать больше об управлении доступом в Swift в этом руководстве: Управление доступом, объясненное в Swift
Вы можете узнать больше об управлении доступом в Swift в этом руководстве: Управление доступом, объясненное в Swift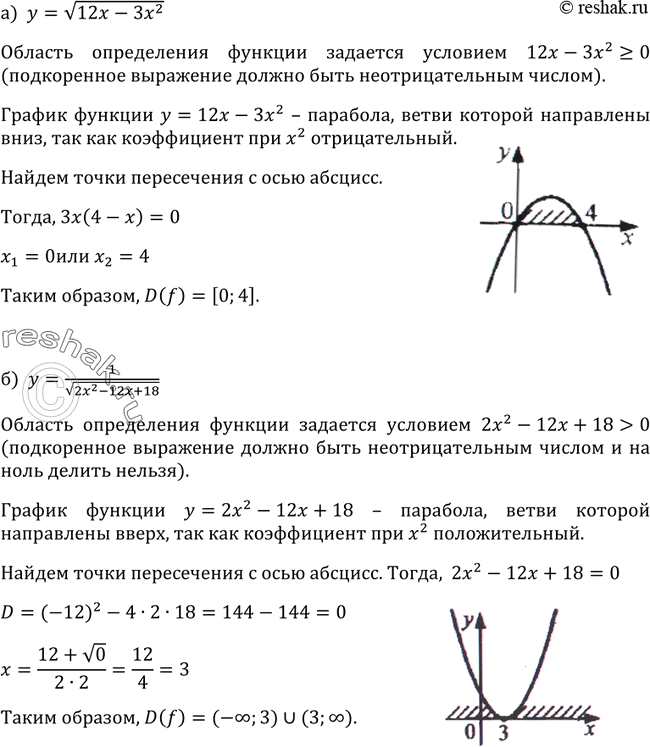 Когда загрузка завершится, в будущем мы хотим выполнить некоторый код для отображения изображения. Мы определяем этот код в замыкании и передаем его функции, загружающей изображение. Затем эта функция выполняет закрытие после завершения загрузки.
Когда загрузка завершится, в будущем мы хотим выполнить некоторый код для отображения изображения. Мы определяем этот код в замыкании и передаем его функции, загружающей изображение. Затем эта функция выполняет закрытие после завершения загрузки.
{
@IBOutlet слабый var imageView:UIImageView?
{
network.downloadImage(url, completeHandler: { image in
imageView?.image = image
})
}
}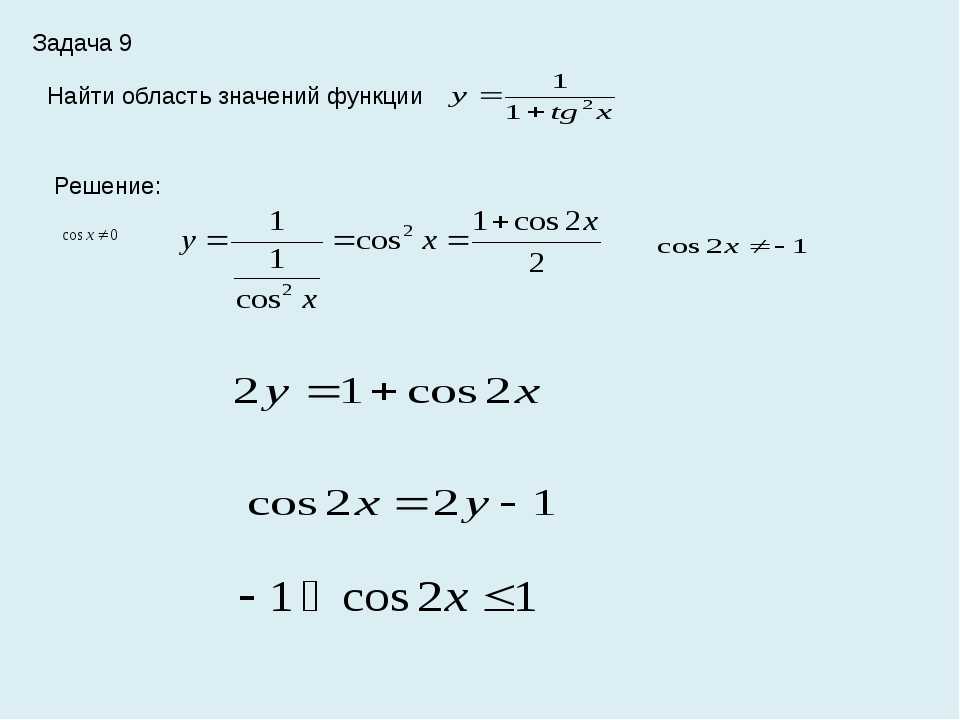 Его второй параметр, обработчик завершения, расположенный между самыми внутренними волнистыми скобками, является замыканием. Когда загрузка изображения завершена, мы присваиваем значение загруженного изображения свойству image объекта imageView, которое будет отображать изображение.
Его второй параметр, обработчик завершения, расположенный между самыми внутренними волнистыми скобками, является замыканием. Когда загрузка изображения завершена, мы присваиваем значение загруженного изображения свойству image объекта imageView, которое будет отображать изображение. То же самое верно для наблюдателей свойств, вычисляемых свойств и другого кода блочного уровня.
То же самое верно для наблюдателей свойств, вычисляемых свойств и другого кода блочного уровня.
{
var result = «»
result = String(c) + result
}
}
print(value) Это понятная опечатка: текст должен быть строкой, которая является входным параметром для функции reverse().
Это понятная опечатка: текст должен быть строкой, которая является входным параметром для функции reverse().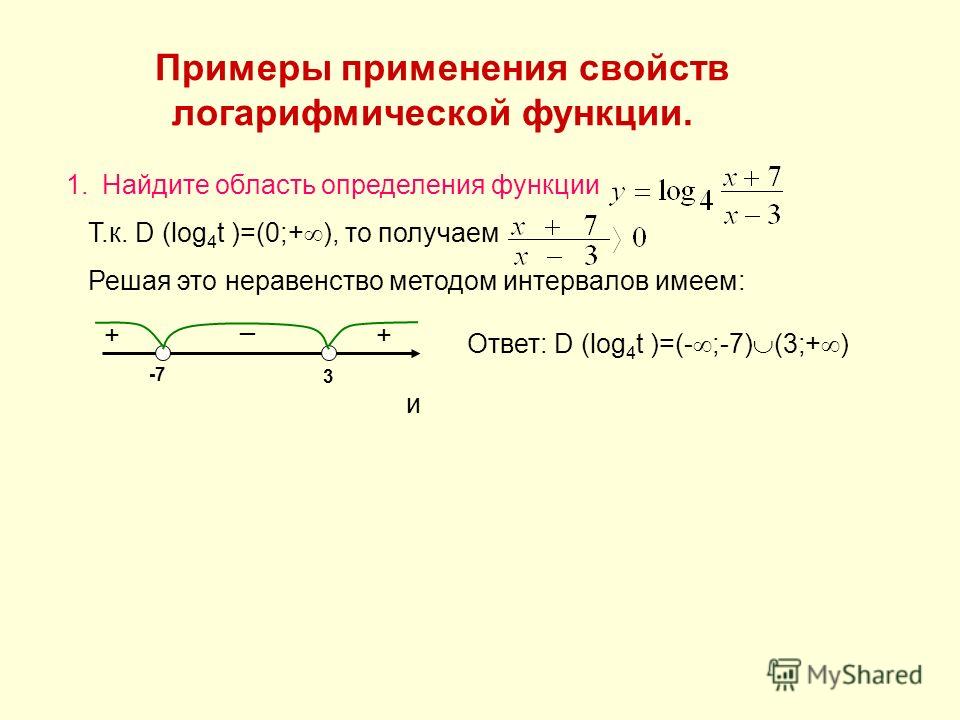 Например, если вам не хватает типа представления, вам, вероятно, потребуется импортировать SwiftUI. Документация iOS SDK может помочь вам в этом.
Например, если вам не хватает типа представления, вам, вероятно, потребуется импортировать SwiftUI. Документация iOS SDK может помочь вам в этом. У нас есть семантическое управление версиями, теги выпуска, привязка версий и так далее, но в какой-то момент вам придется обновить приложение с версии 1.0 библиотеки до версии 2.0. Между тем, API для этой библиотеки изменился, и они переименовали некоторые классы, которые вы используете. Что случается? Не удается найти … в объеме. В этом сценарии важно помнить о своих предположениях, потому что вы собираетесь искать тот класс, который наверняка существовал в версии 1.0!
У нас есть семантическое управление версиями, теги выпуска, привязка версий и так далее, но в какой-то момент вам придется обновить приложение с версии 1.0 библиотеки до версии 2.0. Между тем, API для этой библиотеки изменился, и они переименовали некоторые классы, которые вы используете. Что случается? Не удается найти … в объеме. В этом сценарии важно помнить о своих предположениях, потому что вы собираетесь искать тот класс, который наверняка существовал в версии 1.0! Допустим, у вас есть 2 представления — как вы можете получить эту переменную отсюда туда? Вот тут-то и начинается передача данных из одного компонента в другой. Ознакомьтесь с этими руководствами: Как: передавать данные между представлениями с помощью SwiftUI и Как: передавать данные между контроллерами представлений в Swift
Допустим, у вас есть 2 представления — как вы можете получить эту переменную отсюда туда? Вот тут-то и начинается передача данных из одного компонента в другой. Ознакомьтесь с этими руководствами: Как: передавать данные между представлениями с помощью SwiftUI и Как: передавать данные между контроллерами представлений в Swift Использование области видимости в сценариях и модулях
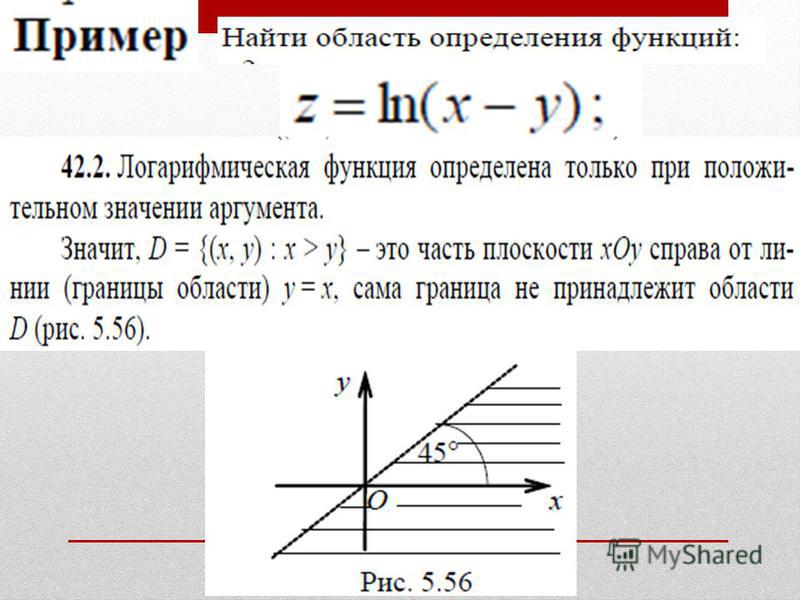
Узнайте, как автоматизировать управление Microsoft 365 с помощью нашего бесплатного курса PowerShell

Что такое области PowerShell?
Область Например, переменные, определенные в области скрипта, считаются ее локальной областью.
Например, переменные, определенные в области скрипта, считаются ее локальной областью. Другой элемент с тем же именем в другой области может скрывать исходный элемент, но не переопределяет и не изменяет исходный элемент.
Другой элемент с тем же именем в другой области может скрывать исходный элемент, но не переопределяет и не изменяет исходный элемент. Глобальная область действия и область действия сценария
 Такое поведение ожидается, поскольку переменная $greeting находится в дочерней области скрипта, а не в родительской глобальной области.
Такое поведение ожидается, поскольку переменная $greeting находится в дочерней области скрипта, а не в родительской глобальной области. Использование модификаторов области действия
 Несколько модификаторов области действия включают в себя:
Несколько модификаторов области действия включают в себя: Модификатор области действия Применение глобальный: Переменная существует в глобальной области местный: Переменная существует в локальной области частный: Переменная видна только в текущей области сценарий: Переменная существует в области сценария, которая является ближайшей областью действия файла сценария, или глобальной, если она недоступна  Затем я запустил файл сценария, который переназначил значение «Hello, World!» используя модификатор области видимости $global : . После запуска скрипта значение $greeting изменено в глобальной области консоли на значение сценария.
Затем я запустил файл сценария, который переназначил значение «Hello, World!» используя модификатор области видимости $global : . После запуска скрипта значение $greeting изменено в глобальной области консоли на значение сценария. Использование областей в модуле PowerShell



Область видимости с точечным исходным обозначением

Дополнительные ресурсы
 Использование других методов, таких как область видимости на уровне модуля и точечная нотация источника, может помочь вам создать ценные инструменты PowerShell для вашего набора инструментов.
Использование других методов, таких как область видимости на уровне модуля и точечная нотация источника, может помочь вам создать ценные инструменты PowerShell для вашего набора инструментов. Джефф Браун
Продолжайте читать
функций осциллографа | Kotlin
 Когда вы вызываете такую функцию для объекта с предоставленным лямбда-выражением, она формирует временную область. В этой области вы можете получить доступ к объекту без его имени. Такие функции называются функциями области видимости . Их пять:
Когда вы вызываете такую функцию для объекта с предоставленным лямбда-выражением, она формирует временную область. В этой области вы можете получить доступ к объекту без его имени. Такие функции называются функциями области видимости . Их пять: пусть , выполнить , с , применить , а также . пусть , вам придется ввести новую переменную и повторять ее имя всякий раз, когда вы ее используете.
Выбор функций

let it запустить это run with this применить this also it 
Let Let . вычисление результата: run run также с  0083 это или
0083 это или это . Различия
Объект контекста: this или it
это ) или как лямбда-аргумент ( это ). Оба предоставляют одинаковые возможности, поэтому мы опишем плюсы и минусы каждого для разных случаев и дадим рекомендации по их использованию. лет {
println(«Длина строки ${it.length}»)
}
}
лет {
println(«Длина строки ${it.length}»)
}
} this
run , with и apply ссылайтесь на объект контекста как на лямбда-приемник по ключевому слову this . Следовательно, в их лямбда-выражениях объект доступен так же, как и в обычных функциях класса. В большинстве случаев вы можете опустить это при доступе к членам объекта получателя, что сделает код короче. С другой стороны, если и опущены, может быть трудно отличить члены-получатели от внешних объектов или функций. Таким образом, имея объект контекста в качестве получателя ( это ) рекомендуется для лямбда-выражений, которые в основном работают с членами объекта: вызывают его функции или присваивают свойства. age = 20
город = «Лондон»
}
println(адам)
//конец выборки
}
age = 20
город = «Лондон»
}
println(адам)
//конец выборки
} it
пусть и также имеют объект контекста в качестве лямбда-аргумента. Если имя аргумента не указано, доступ к объекту осуществляется по неявному имени по умолчанию это . это короче это и выражения с это обычно легче читать. Однако при вызове функций или свойств объекта у вас нет неявно доступного объекта, например this . Следовательно, иметь объект контекста как или лучше, когда объект в основном используется в качестве аргумента в вызовах функций. или также лучше, если вы используете несколько переменных в блоке кода. также {
writeToLog(«getRandomInt() генерирует значение $it»)
}
}
значение i = getRandomInt()
println(я)
//конец выборки
}
также {
writeToLog(«getRandomInt() генерирует значение $it»)
}
}
значение i = getRandomInt()
println(я)
//конец выборки
} Возвращаемое значение
применяются и также возвращают объект контекста. пусть , запустит , а с вернет результат лямбда.
Объект контекста
apply и также — это сам объект контекста. Следовательно, они могут быть включены в цепочки вызовов как побочных шага : после них можно продолжить цепочку вызовов функций на том же объекте. nextInt(100).также {
writeToLog(«getRandomInt() генерирует значение $it»)
}
}
значение i = getRandomInt()
//конец выборки
}
nextInt(100).также {
writeToLog(«getRandomInt() генерирует значение $it»)
}
}
значение i = getRandomInt()
//конец выборки
} Результат Lambda
let , run и с возвращают результат лямбда. Таким образом, вы можете использовать их при присвоении результата переменной, цепочке операций над результатом и т.д. Функции
 Технически функции во многих случаях взаимозаменяемы, поэтому в примерах показаны соглашения, определяющие общий стиль использования.
Технически функции во многих случаях взаимозаменяемы, поэтому в примерах показаны соглашения, определяющие общий стиль использования. let
это ). Возвращаемое значение — это лямбда-результат. let может использоваться для вызова одной или нескольких функций по результатам цепочек вызовов. Например, следующий код выводит результаты двух операций над коллекцией: пусть , вы можете переписать его: и в качестве аргумента, вы можете использовать ссылку на метод ( :: ) вместо лямбда: map { it.length }.filter { it > 3 }.let(::println)
//конец выборки
}
map { it.length }.filter { it > 3 }.let(::println)
//конец выборки
} let часто используется для выполнения блока кода только с ненулевыми значениями. Для выполнения действий над ненулевым объектом используйте оператор безопасного вызова ?. на нем и вызовите пусть с действиями в его лямбде. let — введение локальных переменных с ограниченной областью действия для улучшения читаемости кода. Чтобы определить новую переменную для объекта контекста, укажите ее имя в качестве лямбда-аргумента, чтобы ее можно было использовать вместо значения по умолчанию или .
с
this ). Возвращаемое значение — это лямбда-результат. с для вызова функций в объекте контекста без предоставления лямбда-результата. В коде с можно прочитать как « с этим объектом, сделайте следующее. » с является введение вспомогательного объекта, свойства или функции которого будут использоваться для вычисления значения.
run
это ). Возвращаемое значение — это лямбда-результат. run делает то же самое, что и с , но вызывается как let — как функция расширения объекта контекста. run полезен, когда ваша лямбда содержит как инициализацию объекта, так и вычисление возвращаемого значения. kotlinlang.org», 80)
вал результат = service.run {
порт = 8080
запрос (prepareRequest() + «для порта $port»)
}
// тот же код, написанный с помощью функции let():
val letResult = service.let {
ит.порт = 8080
it.query(it.prepareRequest() + «для порта ${it.port}»)
}
//конец выборки
println(результат)
println(letResult)
}
kotlinlang.org», 80)
вал результат = service.run {
порт = 8080
запрос (prepareRequest() + «для порта $port»)
}
// тот же код, написанный с помощью функции let():
val letResult = service.let {
ит.порт = 8080
it.query(it.prepareRequest() + «для порта ${it.port}»)
}
//конец выборки
println(результат)
println(letResult)
} run для объекта-получателя, вы можете использовать его как функцию, не являющуюся расширением. Нерасширенный run позволяет выполнять блок из нескольких операторов, где требуется выражение. применить
это ). Возвращаемое значение — это сам объект.
Возвращаемое значение — это сам объект., применяйте для блоков кода, которые не возвращают значение и в основном работают с элементами объекта-получателя. Обычный случай для применить — это конфигурация объекта. Такие вызовы можно прочитать как » применить к объекту следующие назначения. » применить в цепочки вызовов для более сложной обработки. также
это ). Возвращаемое значение — это сам объект. также хорош для выполнения некоторых действий, которые принимают объект контекста в качестве аргумента. Используйте
Используйте также для действий, которым нужна ссылка на объект, а не на его свойства и функции, или когда вы не хотите затенять это ссылка из внешнего прицела. и , вы можете прочитать это как » и также сделать с объектом следующее. » takeIf и takeUnless
взять, если и взять, если . Эти функции позволяют встраивать проверки состояния объекта в цепочки вызовов. takeIf возвращает этот объект, если он соответствует предикату. В противном случае возвращается null . Итак,
Итак, takeIf — это функция фильтрации для одного объекта. В свою очередь, takeUnless возвращает объект, если он не соответствует предикату, и null , если соответствует. Объект доступен как лямбда-аргумент ( это ). takeIf и takeUnless не забудьте выполнить проверку на null или безопасный вызов ( ?. ), потому что их возвращаемое значение может быть нулевым. takeIf и takeUnless особенно полезны вместе с функциями области видимости. Хорошим случаем является объединение их в цепочку с
Хорошим случаем является объединение их в цепочку с пусть для запуска блока кода на объектах, которые соответствуют заданному предикату. Для этого вызовите takeIf на объекте, а затем вызовите пусть с безопасным вызовом ( ? ). Для объектов, не соответствующих предикату, takeIf возвращает null , а let не вызывается. indexOf(sub)
если (индекс >= 0) {
println(«Подстрока $sub найдена в $input.»
println(«Начальная позиция $index.»)
}
}
displaySubstringPosition («010000011», «11»)
displaySubstringPosition («010000011», «12»)
//конец выборки
}
indexOf(sub)
если (индекс >= 0) {
println(«Подстрока $sub найдена в $input.»
println(«Начальная позиция $index.»)
}
}
displaySubstringPosition («010000011», «11»)
displaySubstringPosition («010000011», «12»)
//конец выборки
} ProjPython — параметры, возвращаемые значения и область действия
Передача параметров в функции
sqrt требует один параметр, число с плавающей точкой, которое она будет использовать для вычисления возвращаемого значения функции. То есть функция
То есть функция sqrt получает часть информации, необходимой ей для выполнения своей работы, а именно число, из которого она должна вычислить квадратный корень, через параметр. set_fill_color(1.0, 0.0, 0.0) # установить текущий цвет заливки на красный
set_fill_color требует три параметра: доли красного, зеленого и синего в цвете заливки, которые вы хотели бы использовать в будущих командах рисования .
x , y и s ; мы ожидаем, что им будут присвоены значения int . Когда вызывается draw_square , первое значение в вызове функции, 100, копируется в первый формальный параметр в заголовке функции, х . Второе значение в вызове функции, 120, копируется во второй формальный параметр в заголовке функции, y . Третье значение в вызове функции, 50, копируется в третий формальный параметр, s . draw_square . На данный момент доступны три параметра: x , y и 9.0083 с . Эти параметры работают так же, как и любые другие переменные. Мы можем использовать их для вычисления выражений. При желании мы можем даже изменить их значения, потому что после вызова функции формальные параметры работают точно так же, как и любые другие переменные.
При желании мы можем даже изменить их значения, потому что после вызова функции формальные параметры работают точно так же, как и любые другие переменные. Упражнение: квадратная функция робота

Упражнение: функция смайлика
Некоторые функции возвращают значения
 У них нет для этого, но они могут . Например, функция
У них нет для этого, но они могут . Например, функция sqrt возвращает значение, представляющее собой квадратный корень из значения переданного ей фактического параметра. Когда функция вычисляет значение, доступное для дальнейшего использования, мы говорим, что функция возвращает значение. print( 8 + 12 )
int(8.48528137423857) , значение, возвращаемое вызовом int , будет равно 8, поэтому давайте изменим код на print( int(8.
 48528137423857) + 12 )
48528137423857) + 12 ) + . Вместо 8 мы использовали int(8.48528137423857) : вызов функции int , которая возвращает значение 8. Почему я выбрал int(8.48528137423857) ? Потому что я собираюсь пойти еще дальше. 9Функция 0083 sqrt при передаче фактического параметра 72 возвращает значение с плавающей запятой 8,48528137423857. Таким образом, мы можем изменить код на print( int(sqrt(72)) + 12 )
sqrt(72) . Функции вызываются в том порядке, в котором их значения необходимы для вычисления выражения. Таким образом, в этом примере sqrt(72) вызывает функцию sqrt с фактическим параметром 72. Результат 8.48528137423857 становится доступным. Затем нужен результат вызова int , поэтому вызывается функция int , передавая в качестве параметра значение 8..  48528137423857
48528137423857 int выполняет и возвращает значение 8, которое становится доступным. Наконец, вычисляется 8 + 12 . Встроенные функции:
len , int , float , str len возвращает длину строки в виде значения int. int преобразует какой-то другой тип в int. Если число является числом с плавающей запятой, любая часть числа справа от десятичной точки усекается (отбрасывается). Если число слишком велико для хранения в int, Python вместо этого возвращает длинное целое число. int завершится ошибкой, и ваша программа завершится. print(int("123")) будет работать. print(int("buffalo")) не будет. float и str преобразуются в типы float и string соответственно и работают так, как вы ожидаете.
Функции, возвращающие случайные значения
randint из модуля random для получения (почти) случайных значений. Например: uniform , также из модуля random : Упражнение: подбрасывание монеты
, чтобы определить, должен ли результат каждого броска быть орлом или решкой. Упражнение: много улыбок

n смайликов случайного размера в случайных местах на экране, где n — параметр функции. Нажмите на стрелку влево рядом с функцией draw , чтобы развернуть эту функцию в редакторе, и вызовите свою функцию для рисования 20 случайных смайликов. Вы можете предположить, что ширина и высота экрана равны 200. В качестве отправной точки вот функция для рисования одной улыбки. Не забудьте необходимые операторы импорта. Определение собственных функций с возвращаемыми значениями

return возвращает значение после return (если есть) в вызывающий код. возврат немедленно останавливает выполнение тела функции и возобновляет выполнение в точке вызова. То есть счетчик программ возвращается сразу после вызова функции. print("Я вычислил значение!") — это , а не , напечатанное на экране, так как оператор return перед оператором print всегда сразу дает управление. вернуться к вызывающей функции, установив значение программного счетчика. На самом деле, Python предупредит вас, что вы сделали что-то глупое. Строки кода, которые недоступны, называются мертвый код . Обычно вы не должны включать мертвый код в программу.
Обычно вы не должны включать мертвый код в программу. Упражнение: область 51
circle_area51 , которая вычисляет площадь круга радиусом 51 и возвращает эту площадь. Вызовите функцию и распечатайте результат, чтобы убедиться, что она работает. circle_area , которая принимает параметр радиус и вычисляет площадь круга с этим радиусом. Вызовите функцию три раза, чтобы вычислить площади кругов размером 3, 5 и 51, и распечатайте результаты. Локальные и глобальные переменные
Локальные переменные
 Локальная переменная недоступна никакому коду за пределами функции, в которой она определена. Локальные переменные существуют во время этого вызова функции, а затем перестают существовать. Вы можете думать о локальных переменных как об одноразовых — использовать их в функции и выбрасывать.
Локальная переменная недоступна никакому коду за пределами функции, в которой она определена. Локальные переменные существуют во время этого вызова функции, а затем перестают существовать. Вы можете думать о локальных переменных как об одноразовых — использовать их в функции и выбрасывать. x является локальной для some_function . Строка print(x) внутри some_function печатает 4. print(x) после вызов some_function является ошибкой. Это связано с тем, что первый раз, когда x назначается, находится в пределах some_function , поэтому x является локальным для some_function . Следовательно, х неизвестно за пределами some_function .
Рамки функций и область действия
 При выходе из функции фрейм уничтожается, а локальные переменные больше не находятся в области видимости. Это хорошо: функция убирает за собой.
При выходе из функции фрейм уничтожается, а локальные переменные больше не находятся в области видимости. Это хорошо: функция убирает за собой. Глобальные переменные
 Почему? Это может повлиять на бесчисленное множество других функций, о некоторых из которых вы можете даже не знать или о которых не писали. Там, где это возможно, вам следует избегать изменения глобальных переменных, и Python заставляет вас явно сообщать ему, что переменная является глобальной, прежде чем использовать какие-либо операторы присваивания.
Почему? Это может повлиять на бесчисленное множество других функций, о некоторых из которых вы можете даже не знать или о которых не писали. Там, где это возможно, вам следует избегать изменения глобальных переменных, и Python заставляет вас явно сообщать ему, что переменная является глобальной, прежде чем использовать какие-либо операторы присваивания. global , чтобы указать, что вы действительно намерены изменить значение глобальной переменной. Вот пример. print_x обращается к глобальной переменной x . Поскольку x имеет значение 5 при вызове функции, оператор присваивания внутри функции присваивает значение 6 x , и оба оператора печати печатают значение 6. global — это , а не , необходимое для создания глобальной переменной. Если вы просто собираетесь использовать это значение, вам следует использовать ключевое слово global , а не , поскольку ключевое слово позволяет изменить значение, а это может повлиять на любой код, зависящий от глобальной переменной.
Если вы просто собираетесь использовать это значение, вам следует использовать ключевое слово global , а не , поскольку ключевое слово позволяет изменить значение, а это может повлиять на любой код, зависящий от глобальной переменной. Существует один глобальный фрейм, используемый для хранения значений глобальных переменных; вам нужно найти уникальное имя переменной для каждой новой глобальной переменной.
Существует один глобальный фрейм, используемый для хранения значений глобальных переменных; вам нужно найти уникальное имя переменной для каждой новой глобальной переменной. 
Глобальные переменные могут служить именованными константами
AVOGADRO = 6.0221415e23

pi в данном случае не пишется с заглавной буквы. Использование заглавных букв — это просто соглашение, и, по-видимому, разработчики Python не использовали это соглашение. Плохой Гвидо! (Это Гвидо ван Россум, разработчик Python, также известный как «Доброжелательный диктатор на всю жизнь».) pi , импортированная из математической библиотеки, должна быть постоянной, Python не запрещает вам изменять ее. Замечание по стилю о логических значениях и выражениях
x == 5 возвращает логическое выражение, как и любой тест в операторе if. Это логическое выражение должно иметь значение
Это логическое выражение должно иметь значение True или False , верно? И если логическое выражение x == 5 имеет значение True , функция возвращает True . Если логическое выражение x == 5 имеет значение False , функция возвращает False . x == 5 . Итак, вот еще один способ написать эту функцию, более короткий и прямой: x == 5 , которое принимает значение True или False , и возвращаем именно это логическое значение. Обратите внимание, что в любой версии is_five , мы возвращаем True , когда x равно 5, и возвращаем False , когда x не равно 5. Когда вы пишете код первым способом, с оператором if-else, который просто отражает значение логического выражения, вы заявляете всему миру: «Я не понимаю логический тип!!!»
Когда вы пишете код первым способом, с оператором if-else, который просто отражает значение логического выражения, вы заявляете всему миру: «Я не понимаю логический тип!!!» Об областях действия
Область применения Описание Применение Содержит переменные, связанные с одним именованным приложением на сервере.  Атрибут имени тега cfapplication или параметр переменной Application.cfc This.name указывает имя приложения. Дополнительную информацию см. в разделе Использование постоянных данных и блокировки.
Атрибут имени тега cfapplication или параметр переменной Application.cfc This.name указывает имя приложения. Дополнительную информацию см. в разделе Использование постоянных данных и блокировки. Аргументы Переменные, переданные при вызове определяемой пользователем функции или метода компонента ColdFusion. Дополнительную информацию см. в Об области аргументов 9.0464 в разделе Работа с аргументами и переменными в функциях. Атрибуты Используется только на страницах пользовательских тегов и в цепочках. Содержит значения, переданные вызывающей страницей или тегом cfthread в атрибутах тега. Дополнительные сведения см. в разделах «Создание и использование пользовательских тегов CFML» и «Использование потоков ColdFusion». Звонящий Используется только на страницах пользовательских тегов. Область вызывающего абонента пользовательского тега является ссылкой на область переменных вызывающей страницы.  Любые переменные, которые вы создаете или изменяете на пользовательской странице тегов с использованием области вызывающего объекта, видны в области переменных вызывающей страницы. Дополнительные сведения см. в разделе Создание и использование пользовательских тегов CFML.
Любые переменные, которые вы создаете или изменяете на пользовательской странице тегов с использованием области вызывающего объекта, видны в области переменных вызывающей страницы. Дополнительные сведения см. в разделе Создание и использование пользовательских тегов CFML. Компьютерная графика Содержит переменные среды, определяющие контекст, в котором была запрошена страница. Доступные переменные зависят от браузера и серверного программного обеспечения. Список часто используемых переменных CGI см. в разделе «Зарезервированные слова и переменные» в справочнике CFML . Клиент Содержит переменные, связанные с одним клиентом. Переменные клиента позволяют сохранять состояние по мере того, как пользователь перемещается со страницы на страницу в приложении, и доступны в сеансах браузера. По умолчанию переменные клиента хранятся в системном реестре, но вы можете сохранить их в файле cookie или базе данных.  Переменные клиента не могут быть сложными типами данных и могут содержать точки в своих именах. Дополнительную информацию см. в разделе Использование постоянных данных и блокировки.
Переменные клиента не могут быть сложными типами данных и могут содержать точки в своих именах. Дополнительную информацию см. в разделе Использование постоянных данных и блокировки. Печенье Содержит переменные, сохраняемые в браузере пользователя в виде файлов cookie. Файлы cookie обычно хранятся в файле в браузере, поэтому они доступны для всех сеансов браузера и приложений. Вы можете создать переменные cookie только для памяти, которые будут недоступны после того, как пользователь закроет браузер. Имена переменных области действия файлов cookie могут включать точки. Вспышка Переменные, отправленные SWF-фильмом в ColdFusion и возвращенные ColdFusion в фильм. Дополнительные сведения см. в разделе Использование службы Flash Remoting. Форма Содержит переменные, переданные со страницы формы на страницу действий в результате отправки формы. (Если вы используете тег формы HTML, вы должны использовать метод="post".  ) Дополнительные сведения см. в разделе Введение в получение и форматирование данных.
) Дополнительные сведения см. в разделе Введение в получение и форматирование данных. Местный (функция локальный) Содержит переменные, которые объявлены внутри пользовательской функции или метода компонента ColdFusion и существуют только во время выполнения функции. Дополнительные сведения см. в разделе Написание и вызов пользовательских функций. Запрос Используется для хранения данных, которые должны быть доступны в течение одного HTTP-запроса. Область запроса доступна для всех страниц, включая пользовательские теги и вложенные пользовательские теги, которые обрабатываются в ответ на запрос. Эта область полезна для вложенных (дочерних/родительских) тегов. Эту область часто можно использовать вместо области приложения, чтобы избежать необходимости блокировки переменных. В нескольких главах обсуждается использование области запроса. Сервер Содержит переменные, связанные с текущим сервером ColdFusion.  Эта область позволяет вам определять переменные, доступные для всех ваших страниц ColdFusion в нескольких приложениях. Дополнительную информацию см. в разделе Использование постоянных данных и блокировки.
Эта область позволяет вам определять переменные, доступные для всех ваших страниц ColdFusion в нескольких приложениях. Дополнительную информацию см. в разделе Использование постоянных данных и блокировки. Сессия Содержит переменные, связанные с одним клиентом и сохраняющиеся только до тех пор, пока клиент поддерживает сеанс. Они хранятся в памяти сервера и могут быть настроены на тайм-аут после периода бездействия. Дополнительную информацию см. в разделе Использование постоянных данных и блокировки. Этот Существует только в компонентах ColdFusion или тегах cffunction, которые являются частью содержащего объекта, такого как структура ColdFusion. Существует на время существования экземпляра компонента или содержащего его объекта. Данные в этой области доступны извне компонента или контейнера с использованием имени экземпляра или объекта в качестве префикса. Этот тег Используется только на страницах пользовательских тегов.  Область ThisTag активна для текущего вызова тега. Если пользовательский тег содержит вложенный тег, любые значения области ThisTag, заданные перед вызовом вложенного тега, сохраняются, когда вложенный тег возвращается к вызывающему тегу. Область ThisTag включает три встроенные переменные, которые определяют режим выполнения тега, содержат сгенерированное содержимое тега и указывают, есть ли у тега конечный тег. Вложенный пользовательский тег может использовать тег cfassociate для возврата значений в область действия ThisTag вызывающего тега. . Дополнительные сведения см. в разделе «Доступ к данным экземпляра тега» в разделе «Выполнение пользовательских тегов».
Область ThisTag активна для текущего вызова тега. Если пользовательский тег содержит вложенный тег, любые значения области ThisTag, заданные перед вызовом вложенного тега, сохраняются, когда вложенный тег возвращается к вызывающему тегу. Область ThisTag включает три встроенные переменные, которые определяют режим выполнения тега, содержат сгенерированное содержимое тега и указывают, есть ли у тега конечный тег. Вложенный пользовательский тег может использовать тег cfassociate для возврата значений в область действия ThisTag вызывающего тега. . Дополнительные сведения см. в разделе «Доступ к данным экземпляра тега» в разделе «Выполнение пользовательских тегов». Резьба Переменные, которые создаются и изменяются внутри потока ColdFusion, но могут быть прочитаны всем кодом на странице, создающей поток. Каждый поток имеет область действия Thread, которая является подобластью области cfthread. Дополнительные сведения см. в разделе Использование потоков ColdFusion. 
местная резьба Переменные, доступные только в потоке ColdFusion. Дополнительные сведения см. в разделе Использование потоков ColdFusion. URL-адрес Содержит параметры, переданные текущей странице в URL-адресе, который используется для ее вызова. Параметры добавляются к URL в формате ?variablename = value&variablename=value...; например, www.MyCompany.com/inputpage.cfm?productCode=A12CD1510&quantity=3.  Переменная области видимости Variables доступна только на странице, на которой она создана, и на любых включенных страницах (см. также область действия Caller). Переменные области видимости Variables, созданные в CFC, доступны только для компонента и его функций, а не для страницы, которая создает экземпляр компонента или вызывает его функции.
Переменная области видимости Variables доступна только на странице, на которой она создана, и на любых включенных страницах (см. также область действия Caller). Переменные области видимости Variables, созданные в CFC, доступны только для компонента и его функций, а не для страницы, которая создает экземпляр компонента или вызывает его функции. Создание и использование переменных в областях
Префикс области (тип) Префикс, необходимый для ссылки на При наличии Создано Применение Да Для нескольких клиентов в одном приложении в нескольких сеансах браузера.  Объемный код, использующий переменные приложения в блоках cflock.
Объемный код, использующий переменные приложения в блоках cflock. Указание префикса Application при создании переменной. Аргументы № В теле пользовательской функции или метода компонента ColdFusion. Вызывающая страница передает аргумент в вызове функции. Атрибуты Да На странице пользовательского тега или внутри цепочки Для настраиваемых тегов: вызывающая страница передает значения на страницу настраиваемого тега в атрибутах настраиваемого тега. Для потоков — тег cfthread, определяющий значения атрибутов. Звонящий На странице пользовательского тега — Да. На вызывающей странице — Нет (префикс переменных необязателен). На странице настраиваемого тега с использованием префикса области вызывающего абонента. На странице, вызывающей настраиваемый тег, в виде локальных переменных (область переменных). 
На странице пользовательского тега, указав префикс Caller при создании переменной. На вызывающей странице, указав префикс Variables или не используя префикс при создании переменной. Файл Да После вызова cffile . Тег cffile. Компьютерная графика № На любой странице. Значения зависят от последнего запроса браузера. Веб-сервер. Содержит переменные среды сервера, полученные в результате запроса браузера. Клиент № Для одного клиента в одном приложении в нескольких сеансах браузера. Указание префикса Client при создании переменной. Печенье № Для одного клиента в одном или нескольких приложениях и страницах в нескольких сеансах браузера. Тег cfcookie. Вы также можете установить файлы cookie только для памяти, указав префикс Cookie при создании переменной. 
Вспышка Да Страница или компонент ColdFusion, вызываемый клиентом Flash. Доступ клиента ColdFusion. Вы присваиваете значение Flash. Вы можете присваивать значения переменным Flash.result и Flash.pagesize. Форма № На странице действий формы и в пользовательских тегах, вызываемых страницей действий; нельзя использовать на странице формы, которая не является страницей действия. Тег формы или cfform. Содержит значения тегов полей формы (например, input) в теле формы при ее отправке. Имя переменной — это имя поля формы. Местный № В теле пользовательской функции или метода компонента ColdFusion, только во время выполнения функции. 
Запрос Да На странице создания и на любых страницах, запускаемых во время текущего HTTP-запроса после создания переменной, в том числе в пользовательских тегах и вложенных пользовательских тегах. Указание префикса Request при создании переменной. Сервер Да На любую страницу на сервере ColdFusion. Окружите весь код, использующий серверные переменные, в блоки cflock. Указание префикса Сервер при создании переменной. Сессия Да Для одного клиента в одном приложении и одной сессии браузера. Объемный код, использующий переменные области сеанса в блоках cflock. Указание префикса Session при создании переменной. Этот Да В компоненте ColdFusion или в теле пользовательской функции, которая была создана с использованием тега cffunction и помещена в объект, структуру или область действия.  На содержащей странице через экземпляр компонента или содержащий объект.
На содержащей странице через экземпляр компонента или содержащий объект. В компоненте или функции путем указания префикса. Это делается при создании переменной. На содержащей странице путем указания экземпляра компонента или объекта, содержащего функцию, в качестве префикса при создании переменной. Этот тег Да На странице пользовательского тега. Указание префикса ThisTag при создании переменной в теге или использовании тега cfassociate во вложенном пользовательском теге. Резьба Имя потока. Внутри потока, который создает переменную, вы также можете использовать ключевое слово thread. Любой код в запросе. Использование ключевого слова thread или имени потока в качестве префикса при создании переменной. Вы можете создавать переменные потока только внутри потока. локальный поток (без префикса) нет В потоке, созданном тегом cfthread Без префикса при создании переменной.  Вы также можете использовать ключевое слово var перед именем переменной.
Вы также можете использовать ключевое слово var перед именем переменной. URL-адрес № На целевой странице URL. Система. Содержит параметры, переданные в строке запроса URL, используемой для доступа к странице. Переменные (локальные) № На текущей странице. Невозможно получить доступ со страницы действий формы (если только страница формы не является также страницей действий). Доступ к переменным в этой области, используемым на странице, вызывающей пользовательский тег, можно получить в пользовательском теге, используя его область вызывающего объекта; однако они недоступны для любых вложенных пользовательских тегов. Указание префикса переменных или без использования префикса при создании переменной. (Чтобы создать переменную области видимости Variables внутри потока ColdFusion, необходимо использовать префикс Variables.) 
Оценка переменных без области видимости
Чтобы получить доступ к переменным во всех других областях, вы должны добавить к имени переменной префикс идентификатора области.
Метод интерфейса Java setVariable Response и метод C++ CCFX::SetVariable возвращают данные в область переменных вызывающей страницы. Таким образом, они эквивалентны установке переменной области вызывающего абонента в пользовательском теге ColdFusion.
Таким образом, они эквивалентны установке переменной области вызывающего абонента в пользовательском теге ColdFusion. Использование областей видимости в качестве структур
Вы можете ссылаться на переменные в именованных областях как на элементы структуры. Для этого укажите имя области в качестве имени структуры и имя переменной в качестве ключа. Например, если у вас есть переменная MyVar в области запроса, вы можете сослаться на нее одним из следующих способов:
Обозначение развернутого угла: Угол. Обозначение углов / Геометрия / Справочник по математике 5-9 класс
Угол. Обозначение углов / Геометрия / Справочник по математике 5-9 класс
 Этот же угол можно обозначить и короче, по его вершине: А.
Этот же угол можно обозначить и короче, по его вершине: А. Если при наложении одного угла на другой они совпадут, то эти углы равны.
Если при наложении одного угла на другой они совпадут, то эти углы равны.
Советуем посмотреть:
 Транспортир. Виды углов
Транспортир. Виды углов
Правило встречается в следующих упражнениях:
Развернутый угол.
 Прямой, тупой, острый и развернутый угол
Прямой, тупой, острый и развернутый уголВведение в понятие геометрического угла
 Такие лучи называются сторонами угла, а общее начало сторон — это его вершина.
Такие лучи называются сторонами угла, а общее начало сторон — это его вершина.Виды углов и геометрии
Понятие развернутого угла
Свойства развернутых углов
Задачи с развернутыми углами


Определение угла.
 Обозначим ее буквой a
. Пусть O
– некоторая точка прямой a
. Точка O
разделяет прямую a
на две части. Каждая из этих частей вместе с точкой О
называется лучом , а точка О
называется началом луча . Еще можно услышать, что луч называют полупрямой .
Обозначим ее буквой a
. Пусть O
– некоторая точка прямой a
. Точка O
разделяет прямую a
на две части. Каждая из этих частей вместе с точкой О
называется лучом , а точка О
называется началом луча . Еще можно услышать, что луч называют полупрямой . Такой угол имеет свое название.
Такой угол имеет свое название. Иногда можно видеть, что углы на чертежах отмечают цифрами (1
, 2
и т.д.), обозначают эти углы как и так далее. Для наглядности приведем рисунок, на котором изображены и обозначены углы.
Иногда можно видеть, что углы на чертежах отмечают цифрами (1
, 2
и т.д.), обозначают эти углы как и так далее. Для наглядности приведем рисунок, на котором изображены и обозначены углы. Поясним этот момент. Когда речь идет об угле как о геометрической фигуре, то под углом понимается фигура, составленная двумя лучами с общим началом. Если же возникает необходимость провести какие-либо действия с этим углом (например, измерение угла), то под углом уже следует понимать два луча с общим началом и внутренней областью (иначе возникла бы двоякая ситуация из-за наличия как внутренней так и внешней области угла).
Поясним этот момент. Когда речь идет об угле как о геометрической фигуре, то под углом понимается фигура, составленная двумя лучами с общим началом. Если же возникает необходимость провести какие-либо действия с этим углом (например, измерение угла), то под углом уже следует понимать два луча с общим началом и внутренней областью (иначе возникла бы двоякая ситуация из-за наличия как внутренней так и внешней области угла).
Сравнение углов.

Измерение углов.

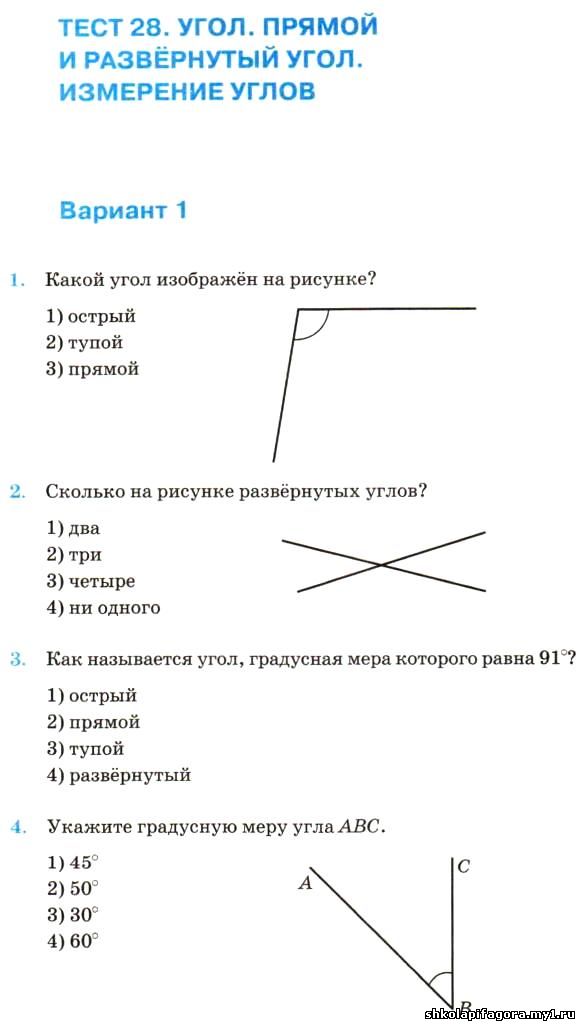 Определенные части градуса получили специальные названия. Наибольшее распространение получили, так называемые, минуты и секунды.
Определенные части градуса получили специальные названия. Наибольшее распространение получили, так называемые, минуты и секунды.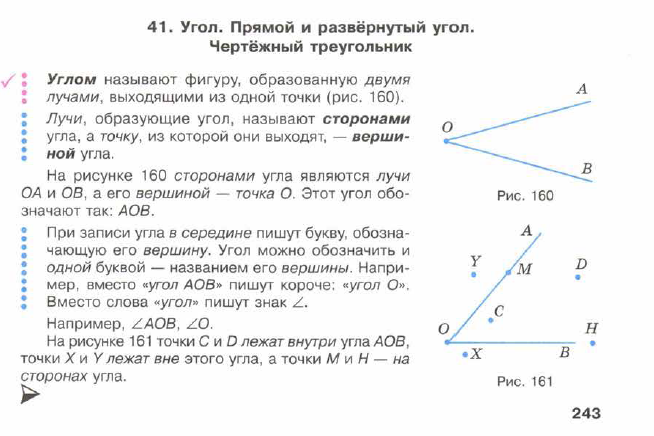
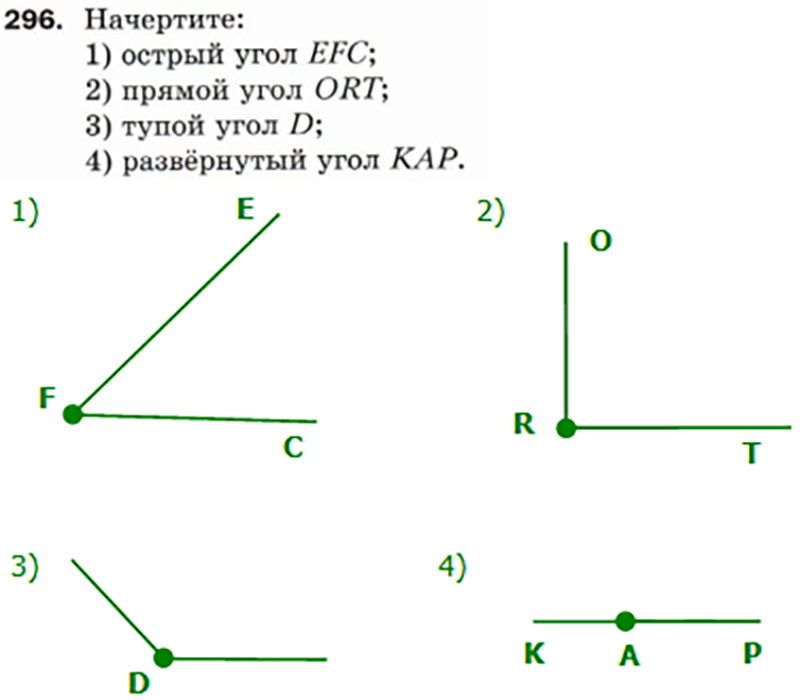 На рисунке ниже показан угол АОВ
, который составляют углы АОС
, СОD
и DОВ
, при этом .
На рисунке ниже показан угол АОВ
, который составляют углы АОС
, СОD
и DОВ
, при этом .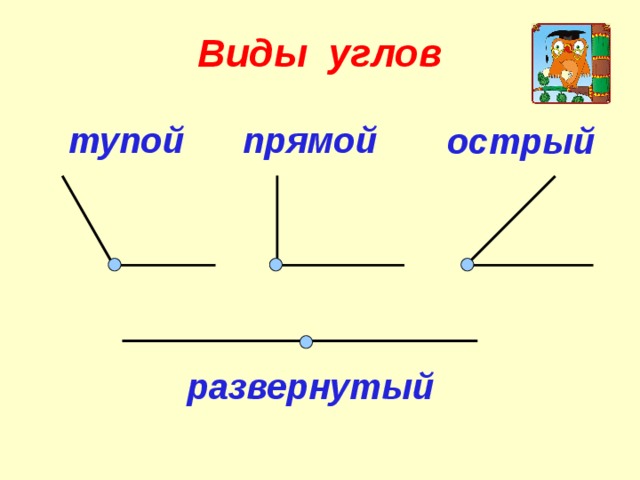 Например, запись 5 рад означает 5 радианов. Однако на письме обозначение «рад» часто опускают. К примеру, когда написано, что угол равен пи, то имеется в виду пи рад.
Например, запись 5 рад означает 5 радианов. Однако на письме обозначение «рад» часто опускают. К примеру, когда написано, что угол равен пи, то имеется в виду пи рад.Обозначение углов на чертеже.
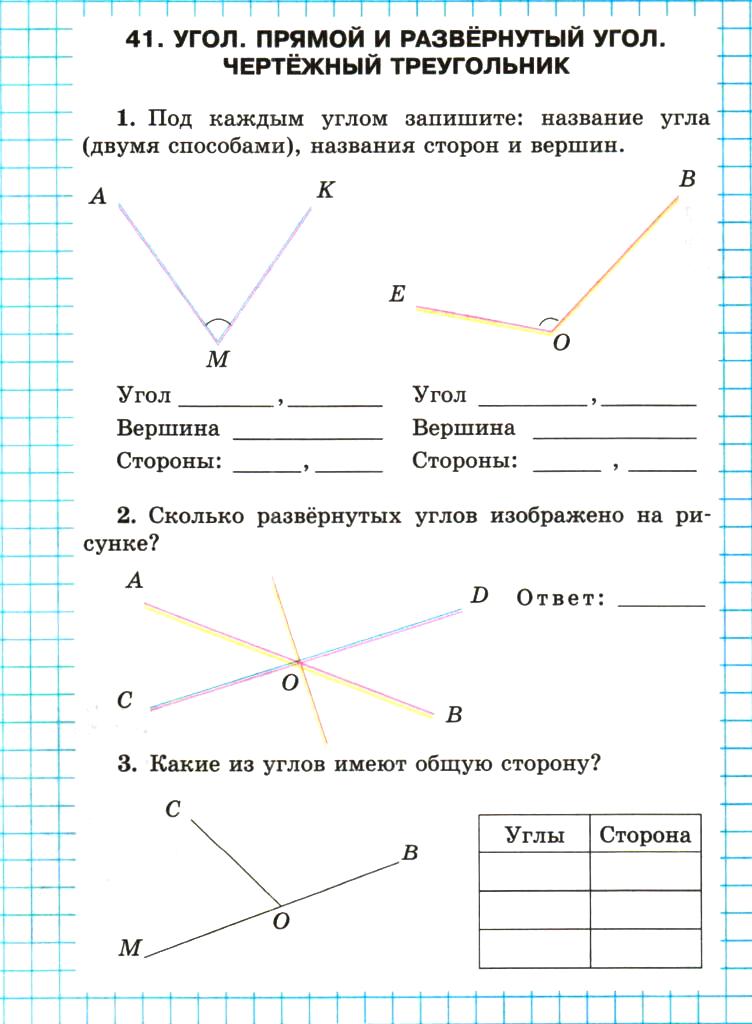
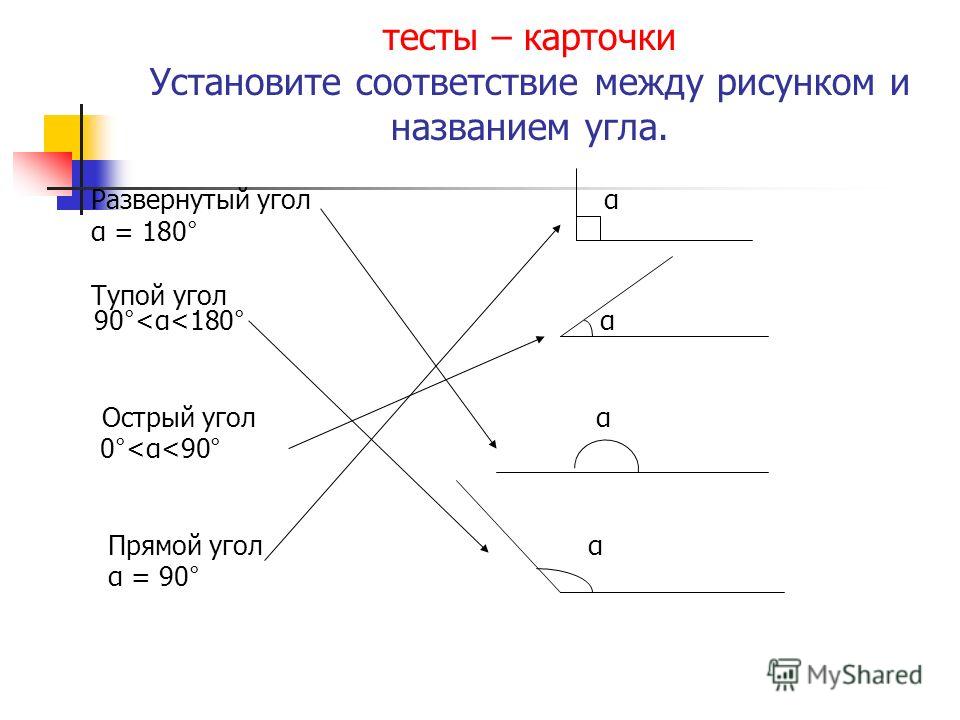
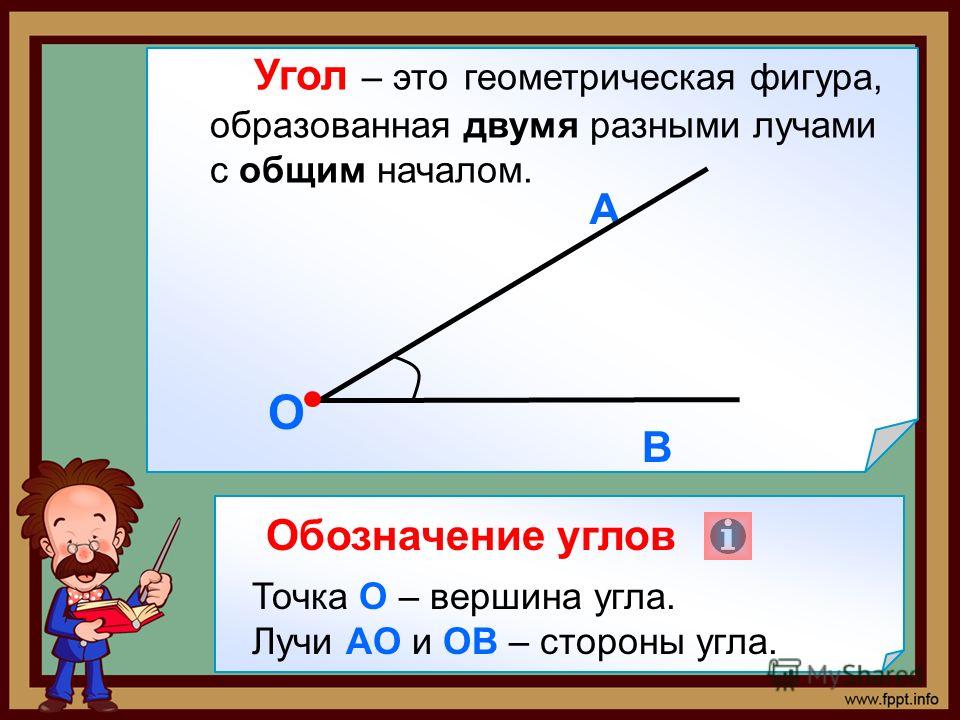 На ней обозначим некоторую точку O . Прямая разделена точкой на две части, каждая из которых имеет название луч , а точка O – начало луча .
На ней обозначим некоторую точку O . Прямая разделена точкой на две части, каждая из которых имеет название луч , а точка O – начало луча .
 Ниже приведено изображение, объясняющее, какие части плоскости внешние, а какие внутренние.
Ниже приведено изображение, объясняющее, какие части плоскости внешние, а какие внутренние.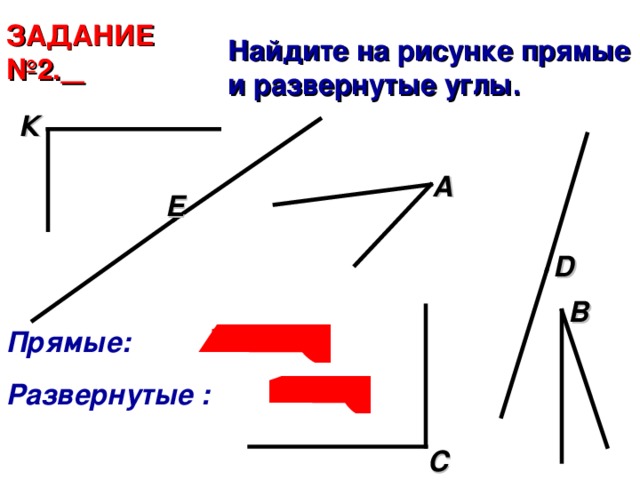

 Следовательно, развернутый угол состоит из 180 таких углов, состоящих из одного градуса. Все имеющиеся углы плотно уложены друг к другу и стороны предыдущего совмещены с последующим.
Следовательно, развернутый угол состоит из 180 таких углов, состоящих из одного градуса. Все имеющиеся углы плотно уложены друг к другу и стороны предыдущего совмещены с последующим.
 Градусная мера одного угла – это сумма всех имеющихся градусных мер внутренних углов. Ниже приведен рисунок, где показан угол АОВ, состоящий из углов АОС, СОD и DОВ. Подробно это выглядит так: ∠ A O B = ∠ A O C + ∠ D O B = 45 ° + 30 ° + 60 ° = 135 ° .
Градусная мера одного угла – это сумма всех имеющихся градусных мер внутренних углов. Ниже приведен рисунок, где показан угол АОВ, состоящий из углов АОС, СОD и DОВ. Подробно это выглядит так: ∠ A O B = ∠ A O C + ∠ D O B = 45 ° + 30 ° + 60 ° = 135 ° . Что же называют радианом.
Что же называют радианом.
 Это не помешает решению и доказательству, а также придаст эстетичный вид рисунку.
Это не помешает решению и доказательству, а также придаст эстетичный вид рисунку.Что такое угол?
Лучи, образующие угол , называют сторонами угла, а точку, из которой они выходят, — вершиной угла.
На рисунке 160 сторонами угла являются лучи ОА и ОБ, а его вершиной — точка О. Этот угол обозначают так: АОВ.
Прямой и развернутый угол
Чертежный треугольник

2.Какой угол называют развернутым?
3.Какие углы называют равными?
4.Какой угол называют прямым?
5.Как строят прямой угол с помощью чертежного треугольника?
Свойства развернутого угла
во-вторых, развернутый угол равен 180°;
в-третьих, два смежных угла образуют развернутый угол;
в-четвертых, развернутый угол составляет половину полного угла;
в-пятых, полный угол будет равен сумме двух развёрнутых углов;
в-шестых, половина развернутого угла составляет прямой угол.Измерение углов
Практическое задание
 Укажите, какие точки на рисунке 169 лежат внутри угла КОМ, Какие точки лежат вне этого угла? Какие точки лежат на стороне OK, a какие — на стороне ОМ?
Укажите, какие точки на рисунке 169 лежат внутри угла КОМ, Какие точки лежат вне этого угла? Какие точки лежат на стороне OK, a какие — на стороне ОМ?
13 6 12 1
2 3? 42? Пусть этот квадрат изображает поле. Рожь занимает 12% поля, овес — 8%, пшеница — 64%, а остальная часть поля занята гречихой. Покажите на рисунке часть поля, занятую каждой культурой. Сколько процентов поля занимает гречиха?
Пусть этот квадрат изображает поле. Рожь занимает 12% поля, овес — 8%, пшеница — 64%, а остальная часть поля занята гречихой. Покажите на рисунке часть поля, занятую каждой культурой. Сколько процентов поля занимает гречиха?
б) 147,6% от 2500; г) 0,09% от 456 800. В первый день вскопали 30% огорода, а во второй день — 35% огорода. Сколько аров осталось еще вскопать?
В первый день вскопали 30% огорода, а во второй день — 35% огорода. Сколько аров осталось еще вскопать?
2) (3,42: 0,57 9,5 — 6,6) : ((4,8 — 1,6) (3,1 + 0,05)).
б) 361,62с + 1848: d, если с = 100, d =100.
б) 1% от литра; г) 6% от 80 км. Я. ВИЛЕНКИН, B. И. ЖОХОВ, А. С. ЧЕСНОКОВ, C. И. ШВАРЦБУРД, Математика 5 класс, Учебник для общеобразовательных учреждений
Я. ВИЛЕНКИН, B. И. ЖОХОВ, А. С. ЧЕСНОКОВ, C. И. ШВАРЦБУРД, Математика 5 класс, Учебник для общеобразовательных учреждений Угловая мера
Типы углов
Смотреть что такое «Развернутый угол» в других словарях:
 Развертка кривой см. Эвольвента … Большой Энциклопедический словарь
Развертка кривой см. Эвольвента … Большой Энциклопедический словарь Для удобства преподавания геометрию подразделяют на планиметрию и стереометрию. В… … Энциклопедия Кольера
Для удобства преподавания геометрию подразделяют на планиметрию и стереометрию. В… … Энциклопедия Кольера Очень важной с практической точки зрения является проблема о конформном… … Википедия
Очень важной с практической точки зрения является проблема о конформном… … ВикипедияПрямой, тупой, острый и развернутый угол. Прямой и развернутый угол Чему равен развернутый угол в градусах
Угловая мера
Типы углов
Смотреть что такое «Развернутый угол» в других словарях:
 *РАЗВЕРТКА поверхности фигура, получающаяся в плоскости при таком совмещении точек данной поверхности с этой плоскостью, при котором длины линий остаются неизменными. Развертка кривой см. Эвольвента … Большой Энциклопедический словарь
*РАЗВЕРТКА поверхности фигура, получающаяся в плоскости при таком совмещении точек данной поверхности с этой плоскостью, при котором длины линий остаются неизменными. Развертка кривой см. Эвольвента … Большой Энциклопедический словарь Фигура делит плоскость… … Математическая энциклопедия
Фигура делит плоскость… … Математическая энциклопедия 1) Единица измерения плоского угла, равная 1/90 прямого угла или соответственно 1/360 окружности. Угол в 90 градусов называется прямым углом. Развернутый угол составляет 180 градусов. 2) Единица измерения температурного интервала, имеющая… … Популярный словарь русского языка
1) Единица измерения плоского угла, равная 1/90 прямого угла или соответственно 1/360 окружности. Угол в 90 градусов называется прямым углом. Развернутый угол составляет 180 градусов. 2) Единица измерения температурного интервала, имеющая… … Популярный словарь русского языкаЧто такое угол?
Лучи, образующие угол , называют сторонами угла, а точку, из которой они выходят, — вершиной угла.
На рисунке 160 сторонами угла являются лучи ОА и ОБ, а его вершиной — точка О. Этот угол обозначают так: АОВ.
Прямой и развернутый угол
 166).
166).Чертежный треугольник
2.Какой угол называют развернутым?
3.Какие углы называют равными?
4.Какой угол называют прямым?
5.Как строят прямой угол с помощью чертежного треугольника? То есть, у развернутого угла одна его сторона является продолжением его другой стороны угла.
То есть, у развернутого угла одна его сторона является продолжением его другой стороны угла.Свойства развернутого угла
во-вторых, развернутый угол равен 180°;
в-третьих, два смежных угла образуют развернутый угол;
в-четвертых, развернутый угол составляет половину полного угла;
в-пятых, полный угол будет равен сумме двух развёрнутых углов;
в-шестых, половина развернутого угла составляет прямой угол.
Измерение углов
 Это и есть развернутый угол.
Это и есть развернутый угол.Практическое задание
13 6 12 1
2 3? 42? Найдите высоту каждого из этих сооружений, если башни Московского Кремля на 49 м ниже Александрийского маяка.
Найдите высоту каждого из этих сооружений, если башни Московского Кремля на 49 м ниже Александрийского маяка.
б) 147,6% от 2500; г) 0,09% от 456 800.
2) (3,42: 0,57 9,5 — 6,6) : ((4,8 — 1,6) (3,1 + 0,05)). Найдите с помощью чертежного треугольника прямые углы на рисунке 173.
Найдите с помощью чертежного треугольника прямые углы на рисунке 173.
б) 361,62с + 1848: d, если с = 100, d =100.
б) 1% от литра; г) 6% от 80 км. Во время маневров командир оставил 0,3 всех своих солдат охранять переправу, а остальных разделил на 2 отряда для обороны двух высот. В первом отряде было в 6 раз больше солдат, чем во втором. Сколько солдат было в первом отряде, если всего было 200 солдат?
Во время маневров командир оставил 0,3 всех своих солдат охранять переправу, а остальных разделил на 2 отряда для обороны двух высот. В первом отряде было в 6 раз больше солдат, чем во втором. Сколько солдат было в первом отряде, если всего было 200 солдат? 
Развернутый и неразвернутый угол

Измерение углов

 Их не изучают в школах, но знать хотя бы об их существовании необходимо. Второстепенных видов углов всего пять:
Их не изучают в школах, но знать хотя бы об их существовании необходимо. Второстепенных видов углов всего пять: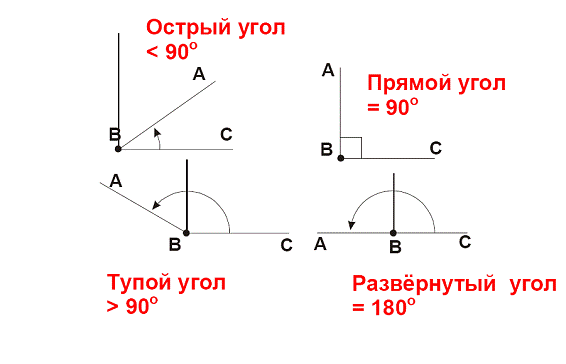 е. их сумма 90 о.
е. их сумма 90 о.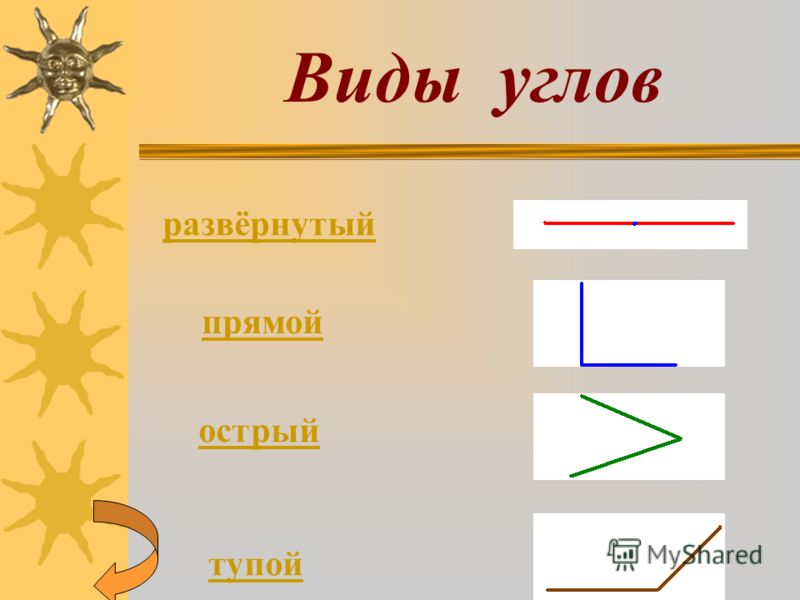 После общего введения в это понятие мы уделим основное внимание отдельному виду такой фигуры. Развернутый угол — важное понятие геометрии, которое и будет основной темой этой статьи.
После общего введения в это понятие мы уделим основное внимание отдельному виду такой фигуры. Развернутый угол — важное понятие геометрии, которое и будет основной темой этой статьи.Введение в понятие геометрического угла
 Такие лучи называются сторонами угла, а общее начало сторон — это его вершина.
Такие лучи называются сторонами угла, а общее начало сторон — это его вершина.Виды углов и геометрии
Понятие развернутого угла

Свойства развернутых углов
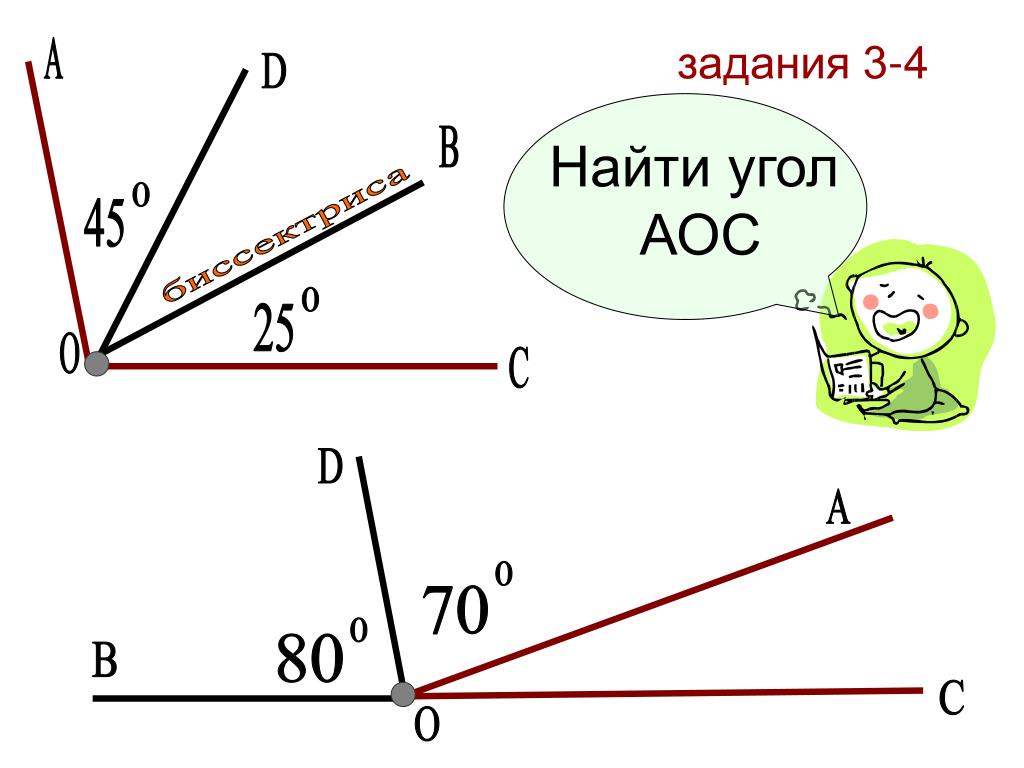
Задачи с развернутыми углами

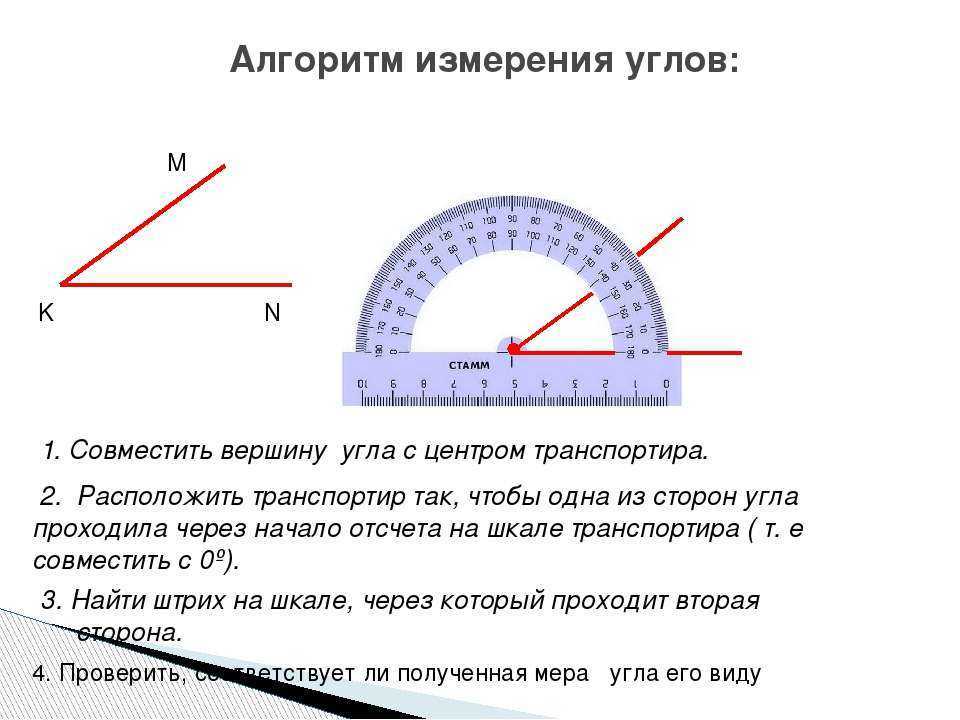
определение угла, измерение углов, обозначения и примеры
Определение угла
Определение 1
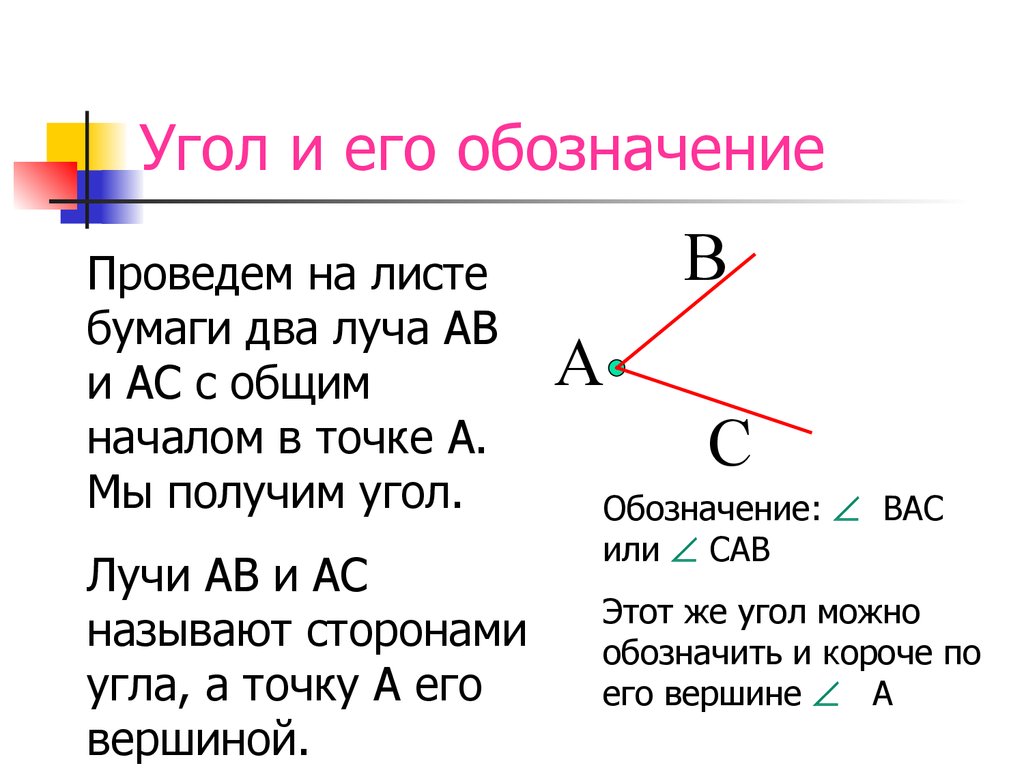
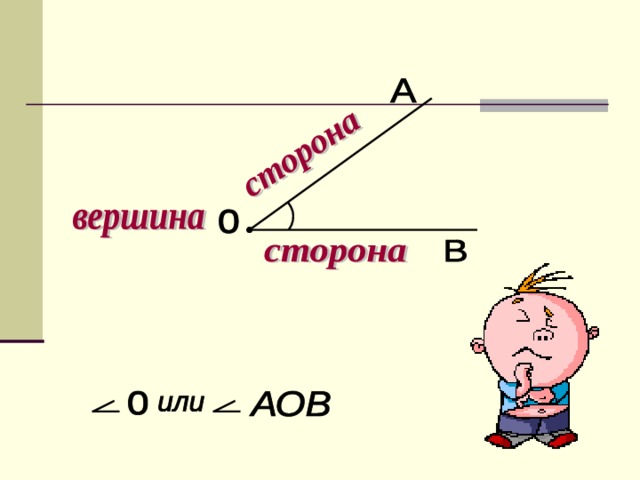
Определение смежных и вертикальных углов
Определение 6
Сравнение углов
 Ниже изображены неравные углы, не совмещенные при наложении.
Ниже изображены неравные углы, не совмещенные при наложении.Измерение углов

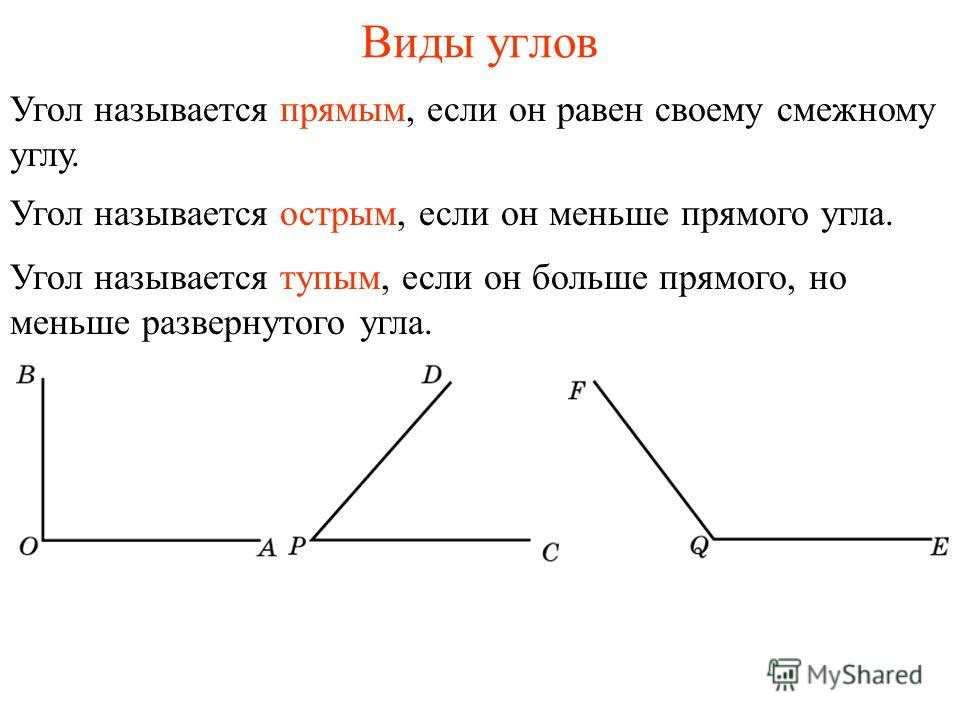
 Ниже приведен рисунок, где показан угол АОВ, состоящий из углов АОС, СОD и DОВ. Подробно это выглядит так:∠AOB=∠AOC+∠DOB=45°+30°+60°=135° .
Ниже приведен рисунок, где показан угол АОВ, состоящий из углов АОС, СОD и DОВ. Подробно это выглядит так:∠AOB=∠AOC+∠DOB=45°+30°+60°=135° .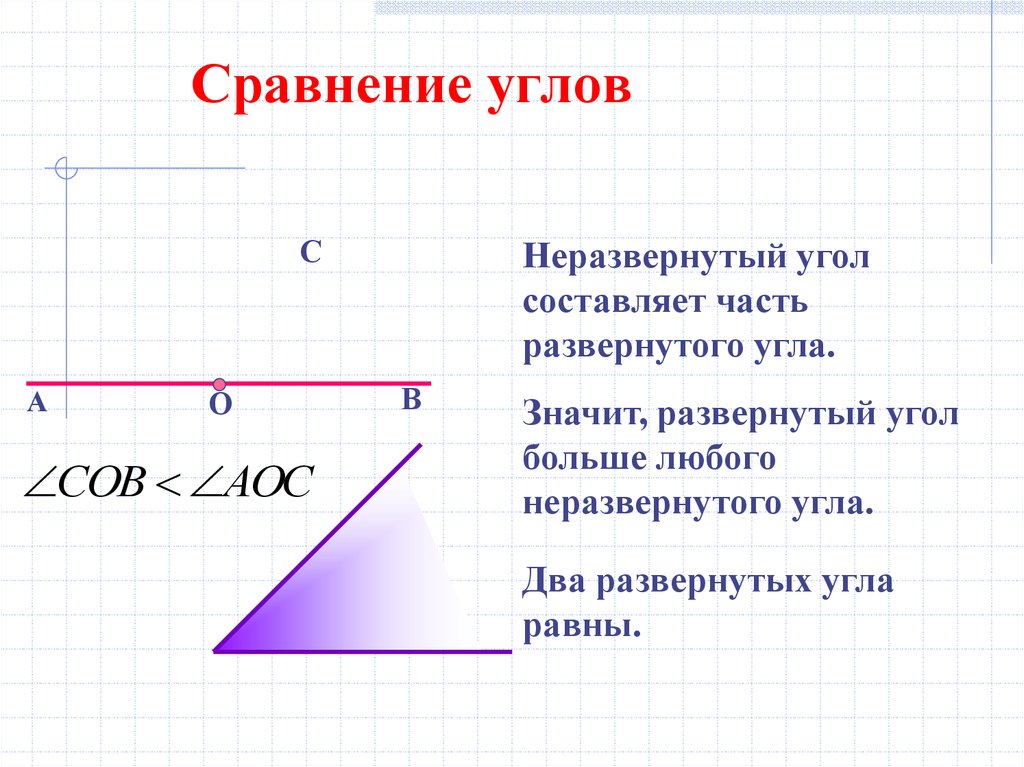
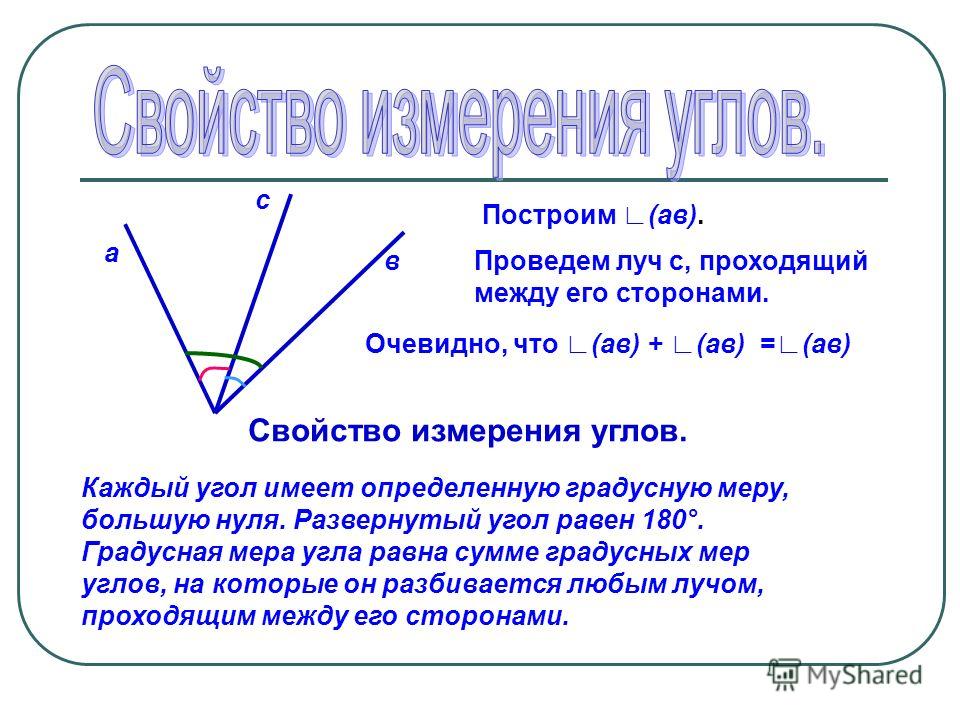
Обозначение углов на чертеже
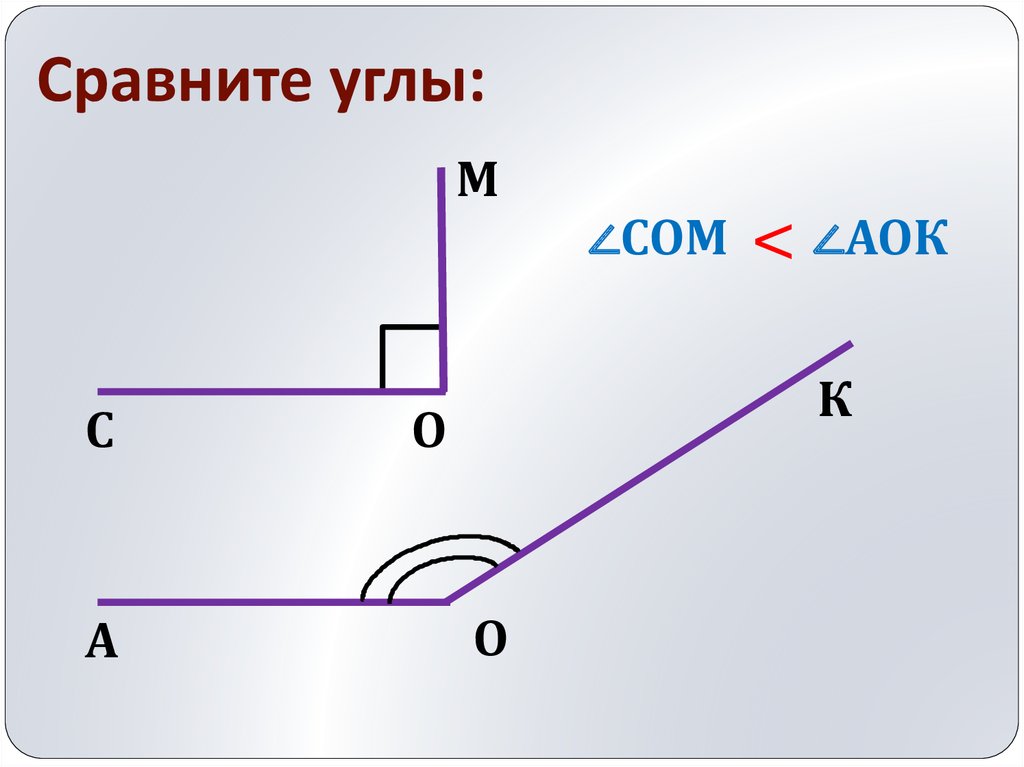 Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.Какой угол называют развернутым. Угол называется развернутым, если его стороны лежат на одной прямой
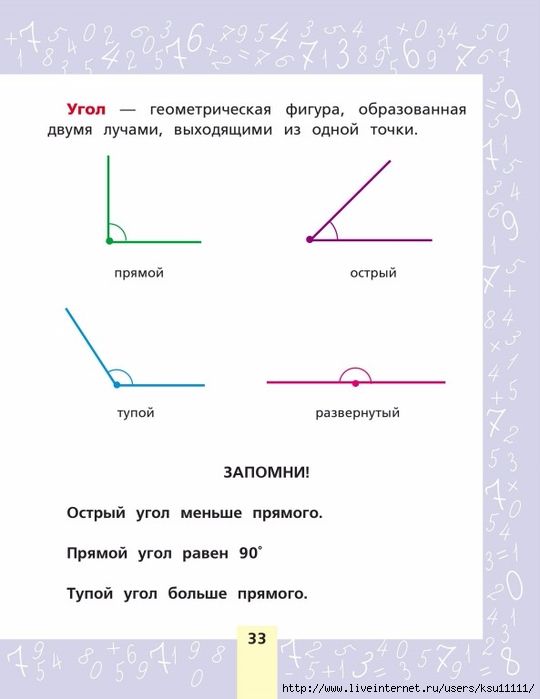 В данном случае, эти лучи называются сторонами угла. Точка, являющаяся началом лучей, называется вершиной угла. На рисунке вы можете увидеть угол с вершиной в точке О , и сторонами k и m .
В данном случае, эти лучи называются сторонами угла. Точка, являющаяся началом лучей, называется вершиной угла. На рисунке вы можете увидеть угол с вершиной в точке О , и сторонами k и m .Развернутый и неразвернутый угол
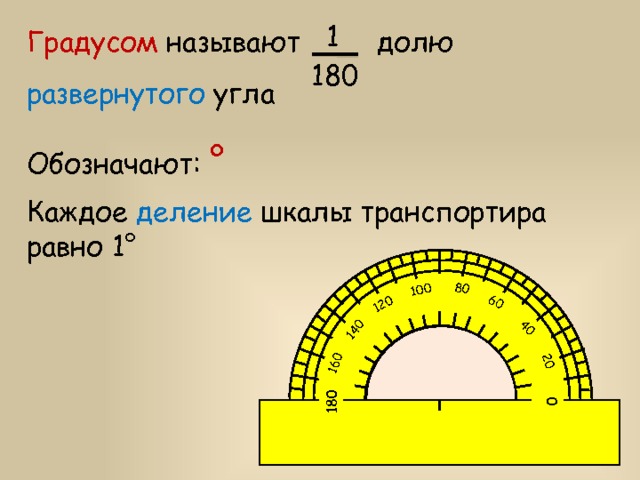
Измерение углов
 Какая фигура называется треугольником. Равные отрезки имеют равные длины. Угол – это геометрическая фигура, которая состоит из точки и двух лучей.
Какая фигура называется треугольником. Равные отрезки имеют равные длины. Угол – это геометрическая фигура, которая состоит из точки и двух лучей. до н. эры. Когда существовала Древняя Греция? Введение. Ответ: «Плоскомерие». Объяснение устройства мира пифагорейцы тесно связывали с геометрией.
до н. эры. Когда существовала Древняя Греция? Введение. Ответ: «Плоскомерие». Объяснение устройства мира пифагорейцы тесно связывали с геометрией.Угловая мера
Типы углов
Смотреть что такое «Развернутый угол» в других словарях:
 УГОЛ, геометрическая… … Иллюстрированный энциклопедический словарь
УГОЛ, геометрическая… … Иллюстрированный энциклопедический словарь поперек под прямым углом. . прямой угол угол максимального отклонения; угол, равный своему смежному; четверть оборота. перпендикуляр. перпендикулярный находящийся под прямым углом. перпендикулярно.… … Идеографический словарь русского языка
поперек под прямым углом. . прямой угол угол максимального отклонения; угол, равный своему смежному; четверть оборота. перпендикуляр. перпендикулярный находящийся под прямым углом. перпендикулярно.… … Идеографический словарь русского языкаЧто такое угол?
Лучи, образующие угол , называют сторонами угла, а точку, из которой они выходят, — вершиной угла.
На рисунке 160 сторонами угла являются лучи ОА и ОБ, а его вершиной — точка О. Этот угол обозначают так: АОВ.Прямой и развернутый угол
 164).
164).Чертежный треугольник
2.Какой угол называют развернутым?
3.Какие углы называют равными?
4.Какой угол называют прямым?
5.Как строят прямой угол с помощью чертежного треугольника? Но, в случае, если у угла его обе стороны лежат на одной прямой, то такой угол называется развернутым. То есть, у развернутого угла одна его сторона является продолжением его другой стороны угла.
Но, в случае, если у угла его обе стороны лежат на одной прямой, то такой угол называется развернутым. То есть, у развернутого угла одна его сторона является продолжением его другой стороны угла.Свойства развернутого угла
во-вторых, развернутый угол равен 180°;
в-третьих, два смежных угла образуют развернутый угол;
в-четвертых, развернутый угол составляет половину полного угла;
в-пятых, полный угол будет равен сумме двух развёрнутых углов;
в-шестых, половина развернутого угла составляет прямой угол.
Измерение углов
 Это и есть развернутый угол.
Это и есть развернутый угол.Практическое задание
13 6 12 1
2 3? 42? Найдите высоту каждого из этих сооружений, если башни Московского Кремля на 49 м ниже Александрийского маяка.
Найдите высоту каждого из этих сооружений, если башни Московского Кремля на 49 м ниже Александрийского маяка.
б) 147,6% от 2500; г) 0,09% от 456 800.
2) (3,42: 0,57 9,5 — 6,6) : ((4,8 — 1,6) (3,1 + 0,05)). Найдите с помощью чертежного треугольника прямые углы на рисунке 173.
Найдите с помощью чертежного треугольника прямые углы на рисунке 173.
б) 361,62с + 1848: d, если с = 100, d =100.
б) 1% от литра; г) 6% от 80 км. Во время маневров командир оставил 0,3 всех своих солдат охранять переправу, а остальных разделил на 2 отряда для обороны двух высот. В первом отряде было в 6 раз больше солдат, чем во втором. Сколько солдат было в первом отряде, если всего было 200 солдат?
Во время маневров командир оставил 0,3 всех своих солдат охранять переправу, а остальных разделил на 2 отряда для обороны двух высот. В первом отряде было в 6 раз больше солдат, чем во втором. Сколько солдат было в первом отряде, если всего было 200 солдат? 





 Отсюда имеем, что ∠ A O B = ∠ C O D . Ниже приводится пример изображения и обозначения вертикальных улов.
Отсюда имеем, что ∠ A O B = ∠ C O D . Ниже приводится пример изображения и обозначения вертикальных улов. Они считаются подобными.
Они считаются подобными.
Прямой, тупой, острый и развернутый угол. Прямой угол. Построение прямого угла Что такое прямой тупой и острый угол
 На нем можно построить проведя из его вершины один или несколько лучей в любых направлениях.
На нем можно построить проведя из его вершины один или несколько лучей в любых направлениях. Теперь рассмотрим их виды по расположению на плоскости относительно друг друга.
Теперь рассмотрим их виды по расположению на плоскости относительно друг друга. Теперь вы знаете, что помимо наиболее известных — острого, тупого, прямого и развернутого — в геометрии существует много других их видов.
Теперь вы знаете, что помимо наиболее известных — острого, тупого, прямого и развернутого — в геометрии существует много других их видов.



 Ниже изображены неравные углы, не совмещенные при наложении.
Ниже изображены неравные углы, не совмещенные при наложении. Развернутый угол имеет 180 уложенных углов в своем составе. Ниже на рисунке приводятся примеры, где уложение угла идет в 30 раз, то есть одна шестая развернутого, и 90 раз, то есть половина.
Развернутый угол имеет 180 уложенных углов в своем составе. Ниже на рисунке приводятся примеры, где уложение угла идет в 30 раз, то есть одна шестая развернутого, и 90 раз, то есть половина.
 Подробно это выглядит так: ∠ A O B = ∠ A O C + ∠ D O B = 45 ° + 30 ° + 60 ° = 135 ° .
Подробно это выглядит так: ∠ A O B = ∠ A O C + ∠ D O B = 45 ° + 30 ° + 60 ° = 135 ° .
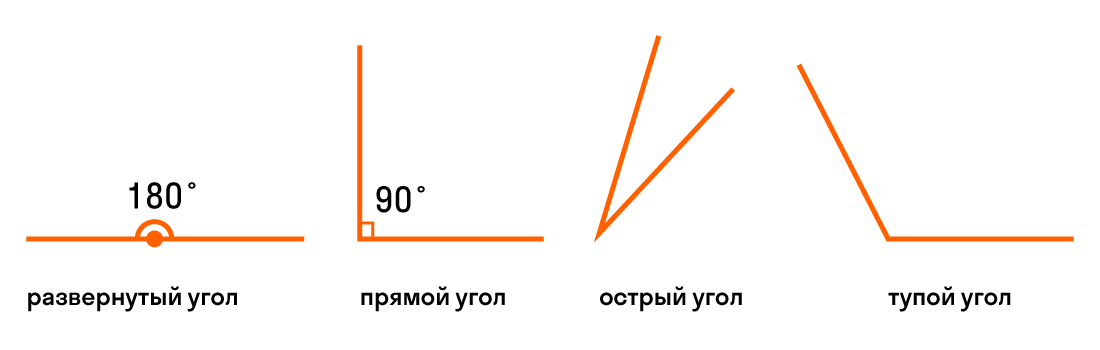
 Какое слово спряталось в названии обеих этих фигур? Это слово — угол (рис. 2).
Какое слово спряталось в названии обеих этих фигур? Это слово — угол (рис. 2).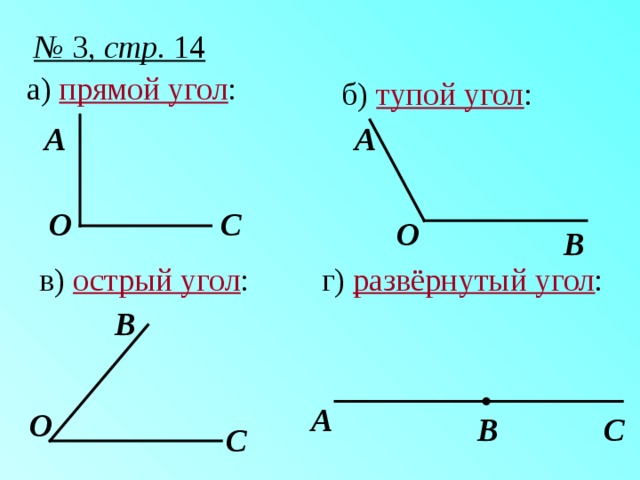 Это значит, что угол ВОМ прямой. Проделаем эту же операцию еще раз. (Рис. 7)
Это значит, что угол ВОМ прямой. Проделаем эту же операцию еще раз. (Рис. 7)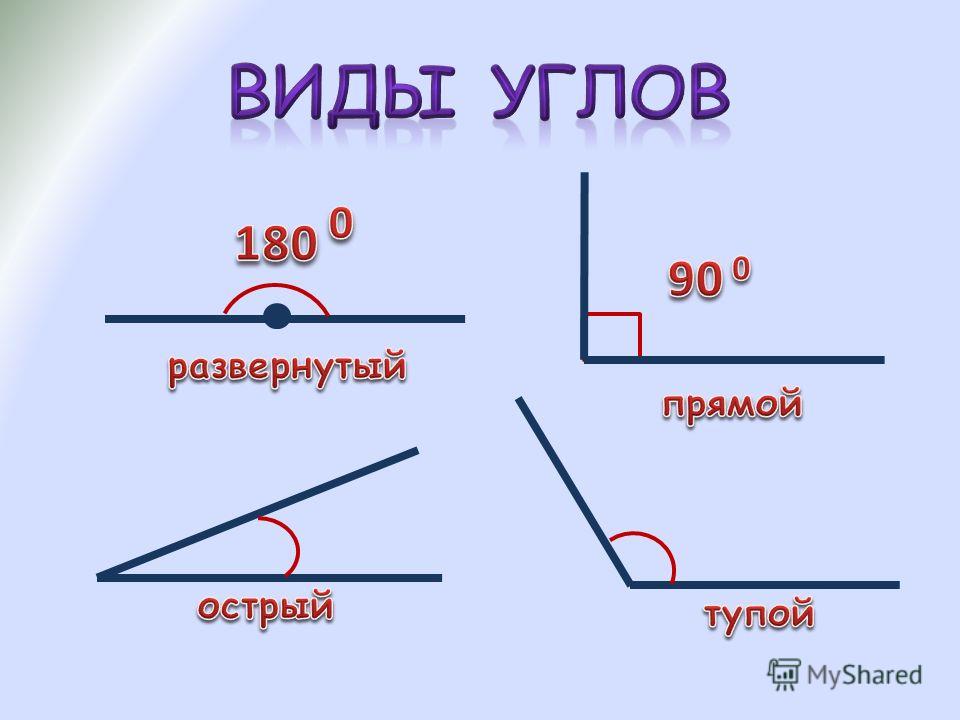 Какое слово спряталось в названии обеих этих фигур? Это слово — угол (рис. 2).
Какое слово спряталось в названии обеих этих фигур? Это слово — угол (рис. 2). Это значит, что угол ВОМ прямой. Проделаем эту же операцию еще раз. (Рис. 7)
Это значит, что угол ВОМ прямой. Проделаем эту же операцию еще раз. (Рис. 7) Какое слово спряталось в названии обеих этих фигур? Это слово — угол (рис. 2).
Какое слово спряталось в названии обеих этих фигур? Это слово — угол (рис. 2). Это значит, что угол ВОМ прямой. Проделаем эту же операцию еще раз. (Рис. 7)
Это значит, что угол ВОМ прямой. Проделаем эту же операцию еще раз. (Рис. 7) Уголки стальные равнополочные
Размеры и статические параметры уголков стальных равнополочных — британские единицы.

Size
(in x in) Dimensions Static Parameters Depth
— H —
(IN) Толщина
— S —
(в) Зона секции 118 (в 2 ) 1118 ( 2 ) 1118 ( 2 )) ft)
(в 2 ) Moment of Inertia
— I x —
(in 4 ) 12 x 12 12 1 3/8 30.9 105 410.0 12 1 1/4 28.3 96.4 377.  5
5 12 1 1/8 25.6 87.2 344.1 12 1 22.9 77.8 310.4 10 x 10 10 1 3/8 25.6 87.1 232.1 10 1 1/4 23.5 79.9 215.1 10 1 1/8 21.2 72.3 196.2 10 1 19.0 64.7 177.3 10 7/8 16.7 56.9 157.6 10 3/4 14.4 49.1 137.2 8 x 8 8 1 1/8 16.7 56.9 98.0 8 1 15.  0
0 51.0 89.0 8 7/ 8 13.2 45.0 79.6 8 3/4 11.4 38.9 69.7 8 5/8 9.6 32.7 59.4 8 9/16 8.7 29.6 54.1 8 1/2 7.8 26.4 48.6 6 x 6 6 1 11.0 37.4 35.5 6 7/8 9.7 33.1 31.9 6 3/4 8.4 28.7 28.2 6 5/8 7.1 24.2 24.2 6 9/16 6.  4
4 21.9 22.1 6 1/2 5.8 19.6 19.9 6 7/16 5.1 17.2 17.7 6 3/8 4.4 14.9 15.4 6 5/16 3.7 12.4 13.0 5 x 5 5 7/8 8.0 27.2 17.8 5 3/4 6.9 23.6 15.7 5 5/8 5.9 20.0 13.6 5 1/2 4.8 16.2 11.3 5 7/16 4.2 14.3 10.0 5 3/8 3.  6
6 12.3 8.74 5 5/16 3.0 10.3 7.42 4 x 4 4 3/4 5.4 18.5 7.67 4 5/8 4.6 15.7 6.66 4 1/2 3.8 12.8 5.56 4 7/16 3.3 11.3 4.97 4 3/8 2.9 9.8 4.36 4 5. 2 1/2 3.3 11.1 3.64 3 1/2 7/16 2.9 9.8 3.26 3 1/2 3/8 2,5 8,5 2.87 3 1/2 5/16 2.  1
1 7.2 2.45 3 1/2 1/4 1.7 5.8 2.01 3 x 3 3 1/2 2.75 9.4 2.22 3 7/16 2.43 8.3 1.99 3 3/8 2.11 7.2 1.76 3 5/16 1.78 6.1 1.51 3 1/4 1.44 4.9 1.24 3 3/16 1.09 3.7 0.96 2 1/2 x 2 1/2 2 1/2 1/2 2.25 7.7 1.23 2 1/2 3/8 1.73 5.9 0.98 2 1/2 5/16 1.  46
46 5.0 0.85 2 1/2 1/4 1.19 4.1 0.70 2 1/2 3/16 0.90 3.1 0.55 2 x 2 2 3/8 1.36 4.7 0.48 2 5/16 1.15 3.9 0.42 2 1/4 0.94 3.2 0.35 2 3/16 0.72 2.4 0.27 2 1/8 0.48 1.7 0.19
9004. x 1/4 — указывает угол 2 дюйма глубокий и широкий — и 1/4 дюйма толщиной .
x 1/4 — указывает угол 2 дюйма глубокий и широкий — и 1/4 дюйма толщиной . Связанные темы
Связанные документы
Engineering ToolBox — Расширение SketchUp — 3D-моделирование онлайн!
 Эти приложения будут — из-за ограничений браузера — отправлять данные между вашим браузером и нашим сервером. Мы не сохраняем эти данные.
Эти приложения будут — из-за ограничений браузера — отправлять данные между вашим браузером и нашим сервером. Мы не сохраняем эти данные. Реклама в ToolBox
Citation
 engineeringtoolbox.com/steel-angles-d_1322.html [дата доступа, мес. год].
engineeringtoolbox.com/steel-angles-d_1322.html [дата доступа, мес. год]. Таблица размеров уголков из конструкционной стали Таблица A36
AISC Таблица размеров уголков из конструкционной стали
Таблица A36
Нога2 x
Толщина  500 х .500
х 0,125
500 х .500
х 0,125 .481 .141 .694 ..204  800
800 435
435 1,25 х 1,25
х .250 1,50 х 1,50
х 0,125  688
688 813
813 2,00 х 2,00
х 0,125  161
161 2,50 х 250
.188 2,50 х 2,50
х 0,313  375
375 3,00 х 3,00
х .250 3,00 х 3,00
х 0,313 6.  038
038 1,774 3,00 х 3,00
х 0,375 7.159 2.104 3,00 х 3,00
х 0,500 9.339 2,744 3,50 х 3,50
х .250 5,754 1,691 3,50 х 3,50
х 0,313 7.134 2,096 3,50 х 3,50
х 0,375 8.  466
466 2,488 3,50 х 3,50
х 0,500 11.072 3,253 4,00 х 4,00
х .250 6.605 1,941 4,00 х 4,00
х 0,313 8.200 2.409 4,00 х 4,00
х 0,375 9,743 2,863 4,00 х 4,00
х 0,500 12.  774
774 3,753 4,00 х 4,00
х 0,625 15,698 4,613 4,00 х 4,00
х 0,750 18.516 5.441 5,00 х 5,00
х 0,313 10.296 3,025 5,00 х 5,00
х 0,375 12.261 3,603 5,00 х 5,00
х .  500
500 16.142 4,743 5,00 х 5,00
х 0,625 19.918 5.853 5,00 х 5,00
х 0,750 23.587 6,931 6.00 х 6.00
х 0,313 12.426 3,651 6.00 х 6.00
х 0,375 14.813 4.353 6.  00 х 6.00
х 0,500
00 х 6.00
х 0,500 19.546 5,743 6.00 х 6.00
х 0,625 24.172 7.103 6.00 х 6.00
х 0,750 28,692 8.431 6.00 х 6.00
х 1.000 37.412 10,993 8.00 х 8.00
х 0,500 26.454 7,773 8.  00 х 8.00
х 0,625
00 х 8.00
х 0,625 32.782 9,633 8.00 х 8.00
х 0,750 39.004 11.461 8.00 х 8.00
х 1.000 51.128 15.023 Размеры УГЛОВЫХ стальных балок соответствуют европейским стандартам NEN-EN 10025-1 и NEN-EN 10025-2
УГОЛОК
В x Ш x Г вес
кг/м площадь поверхности
м2/м 16 х 16 х 3 0,704 0,061 20 х 20 х 3 0,902 0,077 20 х 20 х 4 1,16 0,077 25 х 25 х 3 1,14 0,097 25 х 25 х 4 1,49 0,097 25 х 25 х 5 1,81 0,097 30 х 30 х 3 1,39 0,116 30 х 30 х 4 1,81 0,116 30 х 30 х 5 2,22 0,116 35 х 35 х 3 1,63 0,136 35 х 35 х 4 2,13 0,136 35 х 35 х 5 2,62 0,136 35 х 35 х 6 3,09 0,136 40 х 40 х 3 1,88 0,155 40 х 40 х 4 2,46 0,155 40 х 40 х 5 3,03 0,155 40 х 40 х 6 3,58 0,155 45 х 45 х 5 3,44 0,174 45 х 45 х 6 4,07 0,174 50 х 50 х 4 3.  11
11 0,194 50 х 50 х 5 3,84 0,194 50 х 50 х 6 4,55 0,194 50 х 50 х 7 5,25 0,194 50 х 50 х 8 5,93 0,194 50 х 50 х 9 6,60 0,194 55 х 55 х 6 5,05 0,213 55 х 55 х 8 6,58 0,213 60 х 60 х 6 5,53 0,233 60 х 60 х 7 6,38 0,233 60 х 60 х 8 7,22 0,233 60 х 60 х 10 8,85 0,233 65 х 65 х 6 6,02 0,252 65 х 65 х 7 6,96 0,252 65 х 65 х 8 7,88 0,252 65 х 65 х 9 8,80 0,252 70 х 70 х 7 7,52 0,272 70 х 70 х 8 8,56 0,272 70 х 70 х 9 9,50 0,272 70 х 70 х 10 10,5 0,272 УГОЛОК
В x Ш x Г вес
кг/м площадь поверхности
м2/м УГОЛОК
В x Ш x Г вес
кг/м площадь поверхности
м2/м 75 х 75 х 6 6,98 0,290 75 х 75 х 7 8,09 0,291 75 х 75 х 8 9,17 0,291 75 х 75 х 10 11,3 0,291 75 х 75 х 12 13,3 0,291 80 х 80 х 8 9,81 0,311 80 х 80 х 10 12,1 0,311 80 х 80 х 12 14,3 0,311 90 х 90 х 8 11,1 0,351 90 х 90 х 9 12,4 0,351 90 х 90 х 10 13,7 0,351 90 х 90 х 12 16,2 0,351 100 х 100 х 8 12,4 0,390 100 х 100 х 10 15,3 0,390 100 х 100 х 12 18,2 0,390 100 х 100 х 14 21,0 0,390 100 х 100 х 15 22,3 0,390 110 х 110 х 10 16,9 0,430 110 х 110 х 12 20,1 0,430 110 х 110 х 14 23,2 0,430 120 х 120 х 10 18,5 0,469 120 х 120 х 11 20,3 0,469 120 х 120 х 12 22,0 0,469 120 х 120 х 15 27,1 0,469 130 х 130 х 12 24,0 0,508 130 х 130 х 14 27,8 0,508 140 х 140 х 13 28,0 0,547 140 х 140 х 15 32,0 0,547 150 х 150 х 12 27,9 0,586 150 х 150 х 14 32,2 0,586 150 х 150 х 15 34,4 0,586 150 х 150 х 18 40,8 0,586 160 х 160 х 15 36,8 0,625 180 х 180 х 16 44,3 0,705 180 х 180 х 18 49,5 0,705 200 х 200 х 16 49,4 0,785 200 х 200 х 18 55,3 0,785 200 х 200 х 20 61,1 0,785 200 х 200 х 24 72,5 0,785 УГОЛОК
В x Ш x Г вес
кг/м площадь поверхности
м2/м
Свойства поперечного сечения угла (L) | Calcresource
Соглашение
Геометрия
Момент инерции
 Конечную область можно рассматривать как аддитивную комбинацию A+B+C. Тем не менее, более простой расчет может быть достигнут комбинацией (A+C)+(B+C)-C. Кроме того, расчет лучше проводить вокруг нецентроидальных осей x0,y0 с последующим применением теоремы о параллельных осях. 92 \\ & I_{xy} & = I_{x0y0} — A x_c y_c \end{split}
Конечную область можно рассматривать как аддитивную комбинацию A+B+C. Тем не менее, более простой расчет может быть достигнут комбинацией (A+C)+(B+C)-C. Кроме того, расчет лучше проводить вокруг нецентроидальных осей x0,y0 с последующим применением теоремы о параллельных осях. 92 \\ & I_{xy} & = I_{x0y0} — A x_c y_c \end{split} Главные оси
 В частности, момент инерции вокруг главной оси I максимален, а момент инерции вокруг главной оси II минимален по сравнению с любой другой осью поперечного сечения. Для симметричных сечений главные оси совпадают с осями симметрии. Однако в L-образном сечении нет оси симметрии (за исключением особого случая угла с равными сторонами), и в результате главные оси не видны только при осмотре. Их необходимо вычислить и, в частности, определить их наклон относительно какой-либо удобной геометрической оси (например, x, y). 92} \\ & \tan 2\theta & = -\frac{2I_{xy}}{I_x-I_y} \end{split}
В частности, момент инерции вокруг главной оси I максимален, а момент инерции вокруг главной оси II минимален по сравнению с любой другой осью поперечного сечения. Для симметричных сечений главные оси совпадают с осями симметрии. Однако в L-образном сечении нет оси симметрии (за исключением особого случая угла с равными сторонами), и в результате главные оси не видны только при осмотре. Их необходимо вычислить и, в частности, определить их наклон относительно какой-либо удобной геометрической оси (например, x, y). 92} \\ & \tan 2\theta & = -\frac{2I_{xy}}{I_x-I_y} \end{split} Момент инерции и изгиб
 Следовательно, из предыдущего уравнения видно, что когда к поперечному сечению балки приложен определенный изгибающий момент M, развиваемая кривизна обратно пропорциональна моменту инерции I.
Следовательно, из предыдущего уравнения видно, что когда к поперечному сечению балки приложен определенный изгибающий момент M, развиваемая кривизна обратно пропорциональна моменту инерции I. Полярный момент инерции L-образного сечения
Модуль упругости сечения
 Обычно при нахождении модуля упругости учитывается более удаленное волокно (от центра тяжести). Это происходит на кончике вертикальной ноги (для изгиба вокруг х-х). Используя, возможно, большее значение Y, мы получаем меньшее значение S_x, что приводит к более высоким расчетам напряжения, как будет показано вскоре после этого. Обычно это предпочтительнее для дизайна раздела. Следовательно:
Обычно при нахождении модуля упругости учитывается более удаленное волокно (от центра тяжести). Это происходит на кончике вертикальной ноги (для изгиба вокруг х-х). Используя, возможно, большее значение Y, мы получаем меньшее значение S_x, что приводит к более высоким расчетам напряжения, как будет показано вскоре после этого. Обычно это предпочтительнее для дизайна раздела. Следовательно: Над нейтральной осью напряжения по определению равны нулю. Абсолютное максимальное напряжение будет возникать на самом удаленном волокне, величина которого определяется формулой: аналогично поперечному сечению А для осевой нагрузки. Для последнего нормальным напряжением является F/A. 93 .
Над нейтральной осью напряжения по определению равны нулю. Абсолютное максимальное напряжение будет возникать на самом удаленном волокне, величина которого определяется формулой: аналогично поперечному сечению А для осевой нагрузки. Для последнего нормальным напряжением является F/A. 93 . Модуль пластического сечения
 Модуль пластического сечения задается общей формулой:
Модуль пластического сечения задается общей формулой: Вокруг оси x
 Как правило, нельзя заранее знать, какое уравнение является релевантным. 92 \over4b} \quad , t \gt {A\over2 b}
Как правило, нельзя заранее знать, какое уравнение является релевантным. 92 \over4b} \quad , t \gt {A\over2 b} Вокруг оси y
 рисунок ниже).
рисунок ниже). Радиус вращения
Формулы углового (L) сечения
Угол (L) Секция Формулы
Количество Formula Область: A = B-T) .  2\right) 92 \over4h} & \quad , t \gt {A\over2 h} \end{массив}\right.
2\right) 92 \over4h} & \quad , t \gt {A\over2 h} \end{массив}\right. Связанные страницы
Уголок стальной — Ryerson
Пожалуйста, войдите или продолжите как гость
 Изготовленные из свариваемых и формуемых материалов, стальные уголки могут использоваться не только в строительстве, но и в качестве раскосов и уголков в опорных рамах машин, оборудования, транспортных средств и прицепов.
Изготовленные из свариваемых и формуемых материалов, стальные уголки могут использоваться не только в строительстве, но и в качестве раскосов и уголков в опорных рамах машин, оборудования, транспортных средств и прицепов. Выберите марку:
A36 — размер стержня A36 — размер стержня, оцинкованный A36- L (конструкции) ASTM A588 Узкие результаты:
Фланец в дюймах:
— Выберите один —L3L3 1/2L4L5L6L7L8L9Stem в дюймах:
— Выберите один —22 1/233 1/24568
¹Не катаный профиль, вырезанный из швеллера. Выберите для предложения Фланец в дюймах Шток в дюймах Толстый стержень.  в дюймах
в дюймах Вес на фут. в фунтах Л3 2 3/16 3,070 Л3 2 in Inches»> 1/4 4.100 Л3 2 16/5 5.000 Л3 2 in Inches»> 3/8 5.900 Л3 2 1/2 7.700 Л3 2 1/2 in Inches»> 3/16 3,350 Л3 2 1/2 1/4 4.500 Л3 2 1/2 in Inches»> 16/5 5.600 Л3 2 1/2 3/8 6.600 Л3 2 1/2 in Inches»> 1/2 8.500 Л3 3 3/16 3,710 Л3 3 in Inches»> 1/4 4.900 Л3 3 16/5 6.100 Л3 3 in Inches»> 3/8 7.200 Л3 3 1/2 9.400 L3 1/2 2 1/2 in Inches»> 1/4 4.900 L3 1/2 2 1/2 16/5 6.100 L3 1/2 2 1/2 in Inches»> 3/8 7.200 L3 1/2 2 1/2 1/2 9.400 L3 1/2 3 in Inches»> 1/4 5.400 L3 1/2 3 16/5 6.600 L3 1/2 3 in Inches»> 3/8 7.900 L3 1/2 3 1/2 10.200 L3 1/2 3 1/2 in Inches»> 1/4 5.800 L3 1/2 16/5 7.200 L3 1/2 in Inches»> 3/8 8.500 L3 1/2 1/2 11.100 Л4 3 in Inches»> 1/4 5.800 Л4 3 16/5 7.200 Л4 3 in Inches»> 3/8 8.500 Л4 3 1/2 11.100 Л4 3 1/2 in Inches»> 1/4 6.200 Л4 3 1/2 16/5 7.700 Л4 3 1/2 in Inches»> 3/8 9.100 Л4 3 1/2 1/2 11.900 Л4 4 in Inches»> 1/4 6.600 Л4 4 16/5 8.200 Л4 4 in Inches»> 3/8 9.800 Л4 4 1/2 12.800 Л4 4 in Inches»> 5/8 15.700 Л4 4 3/4 18.500 Л5 3 in Inches»> 1/4 6.600 Л5 3 16/5 8.200 Л5 3 in Inches»> 3/8 9.800 Л5 3 1/2 12.800 Л5 3 1/2 in Inches»> 1/4 7.000 Л5 3 1/2 16/5 8.700 Л5 3 1/2 in Inches»> 3/8 10.400 Л5 3 1/2 1/2 13.600 Л5 3 1/2 in Inches»> 5/8 16.800 Л5 3 1/2 3/4 19.800 Л5 5 in Inches»> 16.05. 10.300 Л5 5 3/8 12.300 Л5 5 in Inches»> 1/2 16.200 Л5 5 5/8 20.000 Л5 5 in Inches»> 3/4 23.600 Л6 3 1/2 1/4 7.900 Л6 3 1/2 in Inches»> 16.05. 9.800 Л6 3 1/2 3/8 11.700 Л6 3 1/2 in Inches»> 1/2 15.300 Л6 4 16/5 10.300 Л6 4 in Inches»> 3/8 12.300 Л6 4 1/2 16.200 Л6 4 in Inches»> 5/8 20.000 Л6 4 3/4 23.600 Л6 6 in Inches»> 16/5 12.400 Л6 6 3/8 14.900 Л6 6 in Inches»> 1/2 19.600 Л6 6 5/8 24.200 Л6 6 in Inches»> 3/4 28.700 Л6 6 1 37.400 Л7 4 in Inches»> 3/8 13.600 Л7 4 1/2 17.900 Л7 4 in Inches»> 3/4 26.200 Л8 4 1/2 19.600 Л8 4 in Inches»> 3/4 28.700 Л8 6 1/2 23.000 Л8 6 in Inches»> 3/4 33.800 Л8 6 1 44.200 Л8 8 in Inches»> 1/2 26.400 Л8 8 5/8 32.700 Л8 8 in Inches»> 3/4 38.900 Л8 8 1 51.000 Л9 4 in Inches»> 1/2 21.300А Общий справочник
Руководства по выбору
Допуски

Информация Speedy Metals для структурных форм HR (углы и каналы HR) Уголки и каналы)
Анализ Механические свойства Приложения Обрабатываемость_и_Свариваемость Термообработка Допуски Предметы Speedy Metals  Угол ЧСС может быть равным или неравным (т.е. 2 x 2 x 1/4″ ч. угла / 3 x 2 x 1/4″ ч. угла). В обозначении каналов HR буква или буквы предшествуют размеру и весу на фут, то есть: C3 x 4,1 # — это обозначение AISI для канала шириной 3 дюйма в основании и весом 4,1 фунта на фут стандартного конструкционного канала. «C «профили — швеллеры, изготовленные в соответствии с размерными нормами, принятыми в 1896 Ассоциации американских производителей стали для каналов American Standard. Существенной частью этих стандартов является то, что внутренние поверхности фланцев каналов американского стандарта имеют уклон приблизительно 16-2/3%. Формы «MC» — это каналы, которые нельзя классифицировать как формы «C».
Угол ЧСС может быть равным или неравным (т.е. 2 x 2 x 1/4″ ч. угла / 3 x 2 x 1/4″ ч. угла). В обозначении каналов HR буква или буквы предшествуют размеру и весу на фут, то есть: C3 x 4,1 # — это обозначение AISI для канала шириной 3 дюйма в основании и весом 4,1 фунта на фут стандартного конструкционного канала. «C «профили — швеллеры, изготовленные в соответствии с размерными нормами, принятыми в 1896 Ассоциации американских производителей стали для каналов American Standard. Существенной частью этих стандартов является то, что внутренние поверхности фланцев каналов американского стандарта имеют уклон приблизительно 16-2/3%. Формы «MC» — это каналы, которые нельзя классифицировать как формы «C». АНАЛИЗ
МЕХАНИЧЕСКИЕ СВОЙСТВА

ПРИМЕНЕНИЕ
ОБРАБАТЫВАЕМОСТЬ И СВАРОЧНОСТЬ
ASTM A36 легко сваривается всеми сварочными процессами, а полученные сварные швы и соединения имеют чрезвычайно высокое качество. ТЕРМООБРАБОТКА

Науглероживание 1650°-1700°F. ДОПУСКИ
Раздел Номинальный размер (дюймы) Длина ноги (дюймы) Толщина вне квадрата Отклонения от толщины для указанной толщины, больше и меньше Более До 3/16 и до Более 3/16 до 3/8, включая Свыше 3/8 УГОЛКИ¹ 1 и ниже 1/32 1/32 3/128² 0,008 0,010 — От 1 до 2, включая 3/64 3/64 3/128² 0,010 0,010 0,012 От 2 до 3, кроме 1/16 1/16 3/128² 0,012 0,015 0,015 от 3 до 4, включая 1/8 3/32 3/128² — — — От 4 до 6, включая 1/8 1/8 3/128² — — — Более 6 3/16 1/8 3/128² — — —  = 1-1/2 градуса
= 1-1/2 градуса Раздел Номинальный размер (дюймы) Глубина (дюйм) Ширина фланца (дюймы) T + T’†
Фланцы вне квадрата
макс. дюйм‡ Толщина паутины
Больше и меньше указанной толщины Более Под Больше До 3/16 и до Более 16 марта Канал C и MC 1-1/2 и ниже 1/32 1/32 1/32 1/32 1/32 0,010 0,015 От 1-1/2 до 3, кроме 1/16 1/16 1/16 1/16 1/32 0,015 0,020 от 3 до 7, включая 3/32 1/16 1/16 1/16 1/32 — — От 7 до 14 лет, включая 1/8 3/32 1/8 5/32 1/32 — — Старше 14 лет 3/16 1/8 1/8 3/16 1/32 — — 
Задачи по тау: Корпоративный портал ТПУ — Ошибка
Решение задач по ТАУ
(смотрите также решение задач по материаловедению)решение задач по ТАУ — FREEWRITERS
Решение ТАУ заказать
Заказжите решение задач по теории автоматического управления (ТАУ/САУ) у нас
и вы просто не заметите на сколько трудоемкой является эта работа.
Многие студенты-технари встречают такой предмет как теория автоматического управления (ТАУ) или системы автоматического управления (САУ) в своем расписании на втором курсе университета. Данный предмет делает большой упор на математику и частично оперирует методологией из курса теоретических основ электротехники (ТОЭ).Сборник задач по теории автоматического управления. Линейные системы
Автор
Ким Дмитрий Петрович, Дмитриева Никтерне Даниловна
Издательство
ООО «Физматлит»
Дата издания
2007
Кол-во страниц
168
ISBN
978-5-9221-0873-7
Тематика
Проблемы управления
№ в каталоге
873
Сайт Теория Автоматического управления (ТАУ) Все о Теории Автоматического управления
Скачать
учебник по ТАУ
О чем этот сайт
Этот сайт полностью посвящен
дисциплине Теория Автоматического Управления (сокращенно ТАУ)Теория
Автоматического управления (ТАУ)
Разделами технической кибернетики являются теория информаци-онных
устройств, связанная со сбором и переработкой информации, необходимой
для управления системой человеком, и теория автоматического управления,
связанная с управлением системой без непосредственного участия человека.
В основу ТАУ положена теория автоматического регулирования,
ставшая самостоятельной наукой к середине XX столетия. Регулирование
считают простейшей разновидностью управления.
Автоматическим регулированием называют поддержание постоянной
некоторой заданной величины, характеризующей процесс, или изменение ее
по заданному закону, осуществляемое с помощью измерения состояния
объекта или действующих на него возмущений и воздействия на
регулирующий орган объекта.
Управление охватывает больший круг задач. Под автоматическим
управлением понимают автоматическое осуществление совокупности
воздействий, выбранных из множества возможных на основании определенной
информации и направленных на поддержание или улучшение функционирования
управляемого объекта в соответствии с целью управления.
Сравнение определений регулирования и управления показывает,
что все задачи регулирования входят в состав задач управления как более
простые варианты. Кроме того, типовыми задачами автоматического
управления считают адаптацию или самонастройку системы управления в
соответствии с изменением ее параметров или внешних воздействий,
оптимальное управление и другие, не входящие в круг задач
автоматического регулирования.
Теория автоматического регулирования (ТАР) сыграла большую
роль в развитии технической кибернетики. Автоматическое регулирование
представляло собою наиболее совершенный принцип автоматики в недавний
период частичной автоматизации, когда технические средства автоматики
осуществляли лишь простые функции управления, связанные с измерением,
анализом, контролем различных величин и отработкой решений, принятых
оператором в виде уставок, программ или других сигналов управления. В
настоящее время комплексной автоматизации автоматизированы не только
простые функции управления, связанные с отработкой сигналов управления,
но и значительно более сложные, связанные с самой выработкой этих
сигналов или с принятием решений, исходя из цели управления.
Сложность автоматических систем значительно возросла. Если в
период частичной автоматизации они обычно состояли из отдельных
(локальных) САР, взаимная координация действия которых осуществлялась
оператором, то теперь возникла необходимость в автома¬тической
координации их действий и, следовательно, в создании сложных
взаимосвязанных САУ. В основе их построения лежит ступенчатый принцип.
На первой ступени автоматизируются сравнительно простые локальные
процессы управления, на второй – процессы управления, имеющие
более общий и сложный характер и т.д.
С этой точки зрения ТАР представляет собою основы построения
систем первой ступени, а ТАУ – теоретические основы
построения всей иерархической лестницы процессов управления,
необходимых для комплексной автоматизации сложных объектов.
Таким образом, ТАУ рассматривают как обобщение и дальнейшее
развитие ТАР, требующее, в частности, широкого использования понятия
информации, которое в ТАР играет сравнительно небольшую роль.
В настоящее время интенсивно развиваются теория и техника
иерархических многоуровневых САУ технологическими процессами и
объектами. Однако, теория и техника САР, непосредственно связанных с
процессами промышленного производства и играющих в этих сложных
системах роль подсистемы нижнего уровня, остается базой для их
построения.
Основные понятия,
принципы, задачи и методы классической ТАУ сохраняют свою актуальность
и получают дальнейшее развитие в современной теории интеллектуальных
систем управления. Новым в этих подходах является существенное
возрастание значения понятия информации и компьютеризация процессов
обработки информации, поскольку любая САУ представляет собой систему,
выполняющую поставленную перед ней задачу путем сбора, передачи,
обработки и использования информации на основе принципа обратной связи.
В ТАУ ключевым является понятие модели –
определенной математической абстракции, описывающей процесс управления
любой природы. Задачи анализа и синтеза САУ решаются методом
математического моделирования. Математическое описание объекта
управления, функциональных блоков САУ позволяет прогнозировать
поведение объекта, возможность достижения поставленных целей управления
при различных внешних условиях и т.д. Более того, поскольку самые
разнообразные реальные процессы могут быть описаны в рамках одних и тех
же математических структур, общая теория управления может оперировать
не с конкретными техническими описаниями, а с классами математических
моделей. Это обстоятельство придает ТАУ внешний облик математической
дисциплины.Электронный
учебник по
Теории Автоматического Управления
Раздел первый
Основные понятия ТАУ
Первый раздел включает
основные понятия ТАУ, примеры систем автоматического управления (САУ)
промышленными объектами, их особенности и классификацию, а также
типовые задачи ТАУ.
Прочитав этот раздел вы сможете
ответить на следующте вопросы:
1 Что понимают под
автоматическим управлением?
2 Что понимают под
математической моделью элемента и САУ?
3 Какие задачи решают
методом математического моделирования?
4 Совокупность каких
технических устройств образует любую САУ?
5 Что понимают под
алгоритмом (законом) управления?
6 Что понимают под
принципом автоматического управления?
7 Какова сущность
управления по отклонению (по ошибке)?
8 Какое свойство САУ
обеспечивает отрицательная обратная связь?
9 Какова сущность
управления по возмущению?
10 Какова сущность
комбинированного управления?
11 Каковы достоинства и
недостатки основных принципов управления?
12 Что понимают
под функциональной схемой САУ?
13 Какова функциональная
схема одноконтурной САУ?
14 Что понимают под автоматическим
регулятором?
15 Какие признаки положены в основу
классификации САУ?
16 Какие задачи считают типовыми задачами
ТАУ?Раздел второй
Линейные непрерывные модели СУ
Второй раздел
посвящен математическому моделированию линейных непрерывных САУ при
решении типовых задач ТАУ, включающих анализ и синтез линейных систем
управления.
Прочитав
этот раздел вы сможете ответить на следующте вопросы:
1 Что понимают под динамическим звеном?
2 Какие динамические звенья называют типовыми?
3 Что понимают под передаточной функцией звена или САУ?
4 По каким признакам динамические звенья разделяют на классы и типы?
5 Каковы типовые соединения динамических звеньев?
6 Что понимают под эквивалентной передаточной функцией группы
динамических звеньев?
7 Что
понимают под структурной схемой САУ?
8 Что понимают под основной передаточной функцией САУ?
9 Что называют порядком астатизма САУ?
10 Какие воздействия относят к типовым (стандартным)?
11 Что понимают под переходной характеристикой САУ?
12 Какие характеристики называют частотными характеристиками САУ?
13 Каковы методы построения временнх характеристик САУ?
14 Каковы особенности операционного метода?
15 Каковы особенности численных методов?
16 Каковы особенности математических моделей типа «вход-выход»?
17 Каковы особенности математических моделей типа
«вход-состояние-выход»?
18
Что понимают под пространством состояний САУ?
19 Какова сущность метода пространства состояний?
20 Какие формы уравнений состояния относят к каноническим?
21 Что понимают под устойчивостью САУ?
22 Каково общее условие устойчивости затухания переходного процесса САУ?
23 Что называют границей устойчивости САУ?
24 Что понимают под критерием устойчивости САУ?
25 Что называют запасом устойчивости САУ?
26 Что понимают под инвариантностью САУ?
27 Что называют чувствительностью САУ?
28 Какова сущность понятия управляемая САУ?
29 Какова методика оценки наблюдаемости САУ?
30 Что понимают под качеством САУ?
31 Какие показатели качества относят к основным?
32 Что называют «коробочкой Солодовникова»?
33 Что понимают под критериями качества САУ?
34 Что понимают под частотой среза?
35 Каким из корневых критериев характеризуют быстродействие САУ?
36 Какие свойства САУ оценивают интегральными критериями?
37 Что понимают под коэффициентами ошибки САУ?Раздел
третий
Задачи и методы синтеза САУ
1 В чем состоит задача синтеза САУ?
2 Какую САУ считают оптимальной?
3 Какие требования предъявляют к процессу регулирования?
4 Каковы основные этапы синтеза САУ?
5 Что называют объектом управления?
6 Какие свойства объектов управления относят к типовым?
7 Что понимают под эквивалентным объектом регулирования?
8 Что понимают под законом регулирования (алгоритмом управления)?
9 Какие законы регулирования относят к типовым?
10 В чем заключаются отличия идеальных и реальных автоматических
регуляторов?
11 Что понимают
под критерием оптимальности САУ?
12 Каковы особенности типовых переходных процессов?
13 По каким признакам классифицируют методы синтеза САУ?
14 Какова сущность параметрической оптимизации САУ?
15 Какова сущность метода стандартных коэффициентов?
16 Какова сущность метода корневого годографа?
17 Что понимают под корректирующим устройством САУ?
18 Какова сущность метода расширенных частотных характеристик?
19 Какова сущность упрощенных методов параметрической оптимизации САУ?
20 Какие САУ относят к системам подчиненного регулирования?
21 Какова сущность настройки контура регулирования на
«техничес¬кий оптимум»?
22 Какова сущность настройки контура регулирования на «симмет-ричный
оптимум»?Задачи
теории автоматического управленияОбратные задачи в теории автоматического управления — НИР
Готовые решение задач по тау
Нет нужной работы в каталоге?
Требуются доработки?
Они включены в стоимость работы
рейтинг
работ сдано
отзывов
рейтинг
работ сдано
отзывов
рейтинг
работ сдано
отзывов
рейтинг
работ сдано
отзывов Последние размещённые задания
Связь осцилляций сна с биомаркерами спинномозговой жидкости при болезни Альцгеймера: новая роль веретен сна и тау-белка | Молекулярная нейродегенерация
Характеристики участников
Связь между плотностью веретена N2, тау-белками ЦСЖ и Aβ
42 Измерения тау-белка в спинномозговой жидкости не коррелируют с показателями качества сна или обычной продолжительности сна
CSF tau ассоциируется с несколькими биофизическими свойствами веретена, но не с SWA
Плотность веретена N2 связана с нейрокогнитивными показателями
Карьера | Руководство игрока «Станция Тау»
Бизнес: Торговец
Вторичная характеристика: Выносливость Имя Бонус Стат. Площадь Незаконный Вредно Очаровать покупателя 9 Социальные Рынок – Пополнить магазин 9 Выносливость Рынок – Осквернить стойло соперника 9 Прочность Рынок ✔ Привлечь больше клиентов 24 Социальные Рынок – Установить киоск 24 Выносливость Рынок – Ястреб украденный топливный элемент 27 Социальные Руины ✔ Study Consortium и бизнес-правила Gaule 39 Разведка Где угодно – Запустите демонстрацию, чтобы увеличить продажи винтовок 43 Социальные Рынок – ✔ Продать партию нелегальных стимов 45 Социальные Где угодно ✔ Записать голографический рекламный ролик 54 Социальные Рынок – Запустить магазин на день 54 Выносливость Рынок – Наблюдать за ленивым учеником 54 Социальные Рынок – Украсть из сейфа 63 Ловкость Рынок ✔ Управление магазином во время продаж в конце цикла 69 Выносливость Рынок – Заключить сделку по поставке с крысой из руин 69 Социальные Порт – Готовим книги 81 Разведка Где угодно ✔ Заказать товар с соседней станции 84 Социальные Порт – Получение фрахта 84 Социальные Порт – Принять участие в собрании торговцев Консорциума 99 Выносливость Рынок Обменять капитан грузового судна 99 Социальные Порт ✔ Создание общесистемного торгового органа 114 Выносливость Где угодно Инвестировать в рискованное предприятие 114 Разведка Рынок Купить партию контрабанды Freebooter 117 Социальные Руины ✔ Нанять команду продаж 129 Выносливость Рынок – Сделайте ребрендинг своего бизнеса 129 Социальные Где угодно – Посетить выставку 144 Социальные Рынок – Повышение дисциплины сотрудников 144 Выносливость Где угодно – Продавать товары в другие системы 159 Разведка Где угодно – Пересмотреть оптовые контракты 174 Выносливость Где угодно – Провести мероприятие по сплочению коллектива сотрудников 174 Социальные Где угодно – Улучшение условий для персонала 189 Выносливость Рынок – Обманите ваши налоги 189 Разведка Где угодно ✔ Разработать новую рекламную кампанию 204 Разведка Где угодно – Заключить госконтракт 204 Выносливость Где угодно – Пожарный персонал сократит расходы 219 Выносливость Где угодно – Продать акции на общесистемной бирже 219 Выносливость Правительственный центр – Привлечь инвестиции от начальника станции 234 Социальные Где угодно – Получите огромный бонус 249 Выносливость Где угодно – Смажьте конкурента 249 Социальные Где угодно ✔ ✔ Произвести впечатление на потенциального делового партнера 264 Социальные Где угодно – Скрыть злоупотребление служебным положением младшего коллеги 279 Выносливость Где угодно ✔ Инструктор по враждебному захвату соперника 279 Выносливость Где угодно – Обновите линейку продуктов 279 Выносливость Где угодно – Обмануть акционеров 315 Разведка Где угодно ✔ Преступник: оппортунист
Имя Бонус Стат. Площадь Незаконный Вредно Проникнуть в киоск 15 ловкость Рынок ✔ Возглавить бригаду воров 49 социальные Рынок ✔ ✔ Ограбить резиденцию 48 ловкость Резиденции ✔ Продам поддельные билеты на шаттл 111 социальные Порт ✔ Кольцо по борьбе с поддельными кредитными чипами 155 социальные Где угодно ✔ Производство поддельных талонов на пайки 93 разведка Правительственный центр ✔ Вытяните жульничество 62 социальные Где угодно ✔ x ———————————– x x – x х —- х х —- х x – x x – x Сделать контакты с преступным миром 9 Выносливость Руины Подобрать карманы на вокзальном бульваре 9 Ловкость Где угодно Совершить набег на рыночный прилавок 9 Прочность Рынок ✔ Планирование путей эвакуации 24 Разведка Где угодно Спросите у местных продавцов, кто их лучшие покупатели 24 Социальные Рынок Ограбить богатую марку 26 Ловкость Рынок Отвлечь охранников 39 Социальные Рынок Участвовать в афере 45 социальные Где угодно Кружка местная 49 Ловкость Где угодно Практика взлома замков 54 Ловкость Где угодно Узнайте код двери банка 99 Выносливость Банк Продать контрабанду 99 Социальные Рынок Угоните небольшой корабль 114 Ловкость Порт Помогите захватить груз 129 Ловкость Порт Взломать банковский терминал 135 Разведка Банк Организовать ограбление 135 Социальные Где угодно Взлом в зону повышенной безопасности 149 Ловкость Рынок Украсть личность 169 Разведка Где угодно ✔ Угнать грузовое судно 169 Ловкость Порт ✔ ✔ Контрабанда в Бриг 171 Разведка Бриг ✔ Продать плацебо пациенту 159 Социальные Санитарный отсек – Запустите защитную ракетку 174 Социальные Резиденции – Мошенничество с синдикатом 179 Социальные Руины – ✔ Взломать систему водоснабжения резиденции 189 Выносливость Резиденции ✔ Банда затонувших кораблей 189 Социальные Где угодно – Приготовьте партию поддельных стимов 204 Выносливость Руины – Украсть медицинское оборудование 207 Ловкость Санитарный отсек ✔ Подделка лицензии Syndicate 225 Разведка Правительственный центр ✔ Нападение на поле битвы 230 Ловкость Руины – ✔ Украсть из склада 243 Ловкость Хранилище ✔ Увести пьяного за покером 258 Разведка Бар ✔ Организовать побег из тюрьмы 261 Социальные Бриг ✔ Подкупить начальника порта 234 Социальные Порт – Украсть удостоверение личности государственного образца 279 Ловкость Правительственный центр ✔ Запуск мошенничества со страховкой 249 Социальные Санитарный отсек – Продам поддельное разрешение на работу 289 Социальные Бар ✔ Привлечь доверчивого инвестора 288 Социальные Гостиная Манипулирование обменным курсом 297 Разведка Банк ✔ Подделка визового документа 264 Разведка Где угодно – Взломать личную почту губернатора 315 Разведка Правительственный центр ✔ Продать неисправное оборудование Службе безопасности 315 Социальные Безопасность ✔ Коррумпированная государственная политика 333 Социальные Правительственный центр ✔ Похищение владельца бизнеса 369 Прочность Гостиница ✔ ✔ Закон: сотрудники посольства
Вторичная характеристика: Выносливость Имя Бонус Стат. Площадь Незаконный Вредно Доставить список помеченных виз властям порта 9 Ловкость Порт Ввод данных 9 Выносливость Где угодно Проверить визы 24 Социальные Где угодно Угрожают депортировать кого-то 29 Прочность Где угодно ✔ ✔ Интервью новоприбывших 39 Социальные Порт Напишите подробный иммиграционный отчет 39 Выносливость Где угодно Результаты опроса Forge 63 Разведка Где угодно ✔ Провести политический опрос 54 Социальные Где угодно Взломать базу Разведка Посольство Голя ✔ Получение взятки от местного предприятия 81 Социальные Рынок ✔ Посетите государственный обед со своим руководителем 69 Социальные Правительственный центр Составить подробный экономический отчет 69 Выносливость Где угодно Напишите подробное предложение политики 84 Выносливость Где угодно Принять участие в дипломатической встрече 84 Социальные Правительственный центр Провести сановника в гостях у станции 99 Социальные Порт Написать пресс-релиз 99 Социальные Где угодно Урегулирование конфликтов 99 Социальные Где угодно Договоритесь о более выгодной сделке для вашей станции 114 Выносливость Рынок Неправильно использовать свое влияние 117 Социальные Где угодно ✔ Развлечь иностранного дипломата с визитом 129 Социальные Где угодно Продавать секретную информацию 135 Социальные Где угодно ✔ Организовать банкет для дипломатов в гостях 144 Социальные Гостиница – Наблюдать за официантами и кухонным персоналом во время дипломатического банкета 144 Выносливость Где угодно – Содействовать убийству иностранного дипломата 153 Социальные Руины ✔ Просьба сопровождать вашего начальника во время дипломатической экскурсии на станцию-соперник 159 Выносливость Где угодно – Посетите культурное мероприятие на конкурирующей станции 174 Социальные Гостиница – Диверсия станции соперника во время вашего визита 189 Социальные Порт ✔ Убедите своего руководителя выставить свое имя на повышение по службе 189 Социальные Где угодно – Кампания против других претендентов на ваше продвижение 189 Социальные Бар – Посещение мирного разговора на конкурирующей станции 196 Выносливость Руины – ✔ Превосходите своих конкурентов по продвижению 204 Выносливость Бар – Начните свою новую работу в качестве младшего.Дипломат 219 Выносливость Где угодно Медиа — крупное торговое соглашение. 219 Социальные Где угодно Проведение мирных переговоров с местными дипломатами. 234 Социальные Где угодно Саботаж ваших конкурентов по продвижению. 243 Разведка Бар ✔ Предоставить приют только что прибывшим на станцию беженцам. 264 Выносливость Где угодно Найдите семьи для приема иностранных беженцев. 264 Выносливость Где угодно Расскажите местным СМИ о своей станции. 279 Социальные Где угодно Намеренно запятнать мирные переговоры, чтобы разжечь напряженность. 279 Разведка Где угодно Станьте первым дипломатом, заключившим соглашение о справедливой торговле с Freebooters. 281 Социальные Где угодно – ✔ Заключите незаконную сделку с флибустьером, чтобы защитить свои интересы выше интересов станции. 297 Социальные Где угодно Обманывайте СМИ, чтобы улучшить имидж вашей радиостанции. 315 Социальные Где угодно – ✔ Медицина: специалист по клонированию
Вторичная характеристика: Сила Имя Бонус Стат. Площадь Незаконный Вредно Опорожнение резервуара клона 9 Прочность Чаны для клонирования Осмотрите резервуар для клонирования 9 Разведка Чаны для клонирования Фойе Tidy Clone Vats 9 Выносливость Чаны для клонирования Просеять органические отходы 24 Прочность Чаны для клонирования Стерилизовать жидкости для капсул 24 Разведка Чаны для клонирования Учебные пособия по Amygchip 24 Выносливость Чаны для клонирования Загрязнение переработанных жидкостей 27 Разведка Чаны для клонирования ✔ Интервью с новым клиентом 39 Социальные Где угодно Переместите резервуары, чтобы очистить позади них 39 Прочность Чаны для клонирования Ремонт танка клонов 39 Разведка Чаны для клонирования Диверсия танка-клона 45 Разведка Чаны для клонирования ✔ Приготовить питательную пасту для базовых клонов 54 Разведка Чаны для клонирования Приготовить питательные пасты для альт-генотипов 54 Разведка Чаны для клонирования Скрыть гормоны роста в питательных пастах 63 Ловкость Чаны для клонирования ✔ Создать клон под контролем 69 Разведка Чаны для клонирования Помогите социализировать недавно активированного клона 69 Социальные Гостиная Изменить компоновку резервуара клона 69 Прочность Чаны для клонирования Создать клон 84 Разведка Чаны для клонирования Удалить отказавший клон 94 Прочность Чаны для клонирования ✔ Ввести дозу ускорителя 99 Ловкость Чаны для клонирования Рассчитать дозировку ускорителя клона 99 Разведка Чаны для клонирования Файлы центра клонирования утечек 99 Разведка Бар ✔ Шланги саботажа бака 99 Прочность Чаны для клонирования ✔ Создать премиум-клон 114 Разведка Чаны для клонирования Обработка платежной ведомости центра клонирования 114 Выносливость Где угодно Дискредитировать участников кампании против клонирования 129 Разведка Правительственный центр Помогите новым клонам с моторикой 129 Ловкость Где угодно Установить автоматические очистители контейнеров 129 Прочность Чаны для клонирования Хищение из центра клонирования 135 Разведка Банк ✔ Сократить время беременности 144 Разведка Чаны для клонирования Выиграйте конкурс клонирования 144 Разведка Правительственный центр Эксперимент с незаконным смешиванием генотипов 153 Разведка Чаны для клонирования Умиротворить недовольного клиента 159 Социальные Где угодно Обучение младших техников 159 Социальные Чаны для клонирования Защита по обвинению в злоупотреблении служебным положением 174 Разведка Безопасность Разработайте новый рецепт питательных веществ 189 Разведка Где угодно Расширьте клиентскую базу 189 Социальные Где угодно Найдите применение старой жидкости для ванны 204 Разведка Где угодно Продайте больше премиальных клонов 204 Социальные Где угодно Продам клонированные органы на черном рынке 207 Разведка Где угодно Изучите недорогой продукт-клон 219 Разведка Где угодно Сервисное обслуживание Obi-хабов клонов 219 Выносливость Чаны для клонирования Модернизация машины для 3D-клонирования 219 Прочность Чаны для клонирования Подать заявку на новый исследовательский грант 234 Разведка Где угодно Выступите на конференции по клонированию 234 Социальные Где угодно Клонирующие установки для очистки воздуха 249 Разведка Где угодно Улучшение исследовательских лабораторий 249 Прочность Чаны для клонирования Ослабить законодательные ограничения на клонирование 264 Социальные Где угодно Развитие академии клонирования 279 Выносливость Университет Продажа данных клонов на черном рынке 297 Социальные Гостиная ✔ Саботаж конкурирующего специалиста по клонам 315 Разведка Где угодно ✔ Убить прометеевского противника 369 Разведка Порт ✔ ✔ Специальные службы: Оперативная
Вторичная характеристика: Интеллект Имя Бонус Первичная статистика Площадь Незаконный Вредно Сделать отчет Intel 9 Разведка Безопасность Делать ложные отчеты 9 Разведка Безопасность х Прослушивание отведений 9 Ловкость Где угодно Контроль терминала SEC 24 Разведка Безопасность Анализировать отснятый камерой 24 Разведка Безопасность Изменить запись камеры 27 Ловкость Безопасность х В патруль 39 Ловкость Где угодно Страж брига 39 Прочность Бриг Задержать подозреваемого 54 Ловкость Где угодно Ошибки прослушивания растений 54 Ловкость Где угодно Следить за подозреваемыми 60 Ловкость Рынок ✔ Получение взятки от подозреваемых 63 Социальные Где угодно ✔ Расследование подозреваемого 69 Ловкость Где угодно Утечка планов безопасности 81 Разведка Бар ✔ Обыск в доме 94 Прочность Резиденции ✔ Рейд на незаконный сбор воды 94 Ловкость Руины ✔ Работа под прикрытием 99 Социальные Банк Провести расследование внутренних дел 114 Разведка Безопасность Создать план безопасности 114 Разведка Безопасность Проникнуть в посольство 117 Ловкость Посольство Голя ✔ Защитите высокопоставленного гостя 129 Ловкость Доки Шантажировать высокопоставленного администратора 135 Разведка Правительственный центр ✔ Устранить цель 135 Ловкость Где угодно ✔ Хвост высокопоставленного чиновника 144 Ловкость Где угодно Помешать покушению 145 Ловкость Руины ✔ Расшифровать украденное Intel 159 Разведка Где угодно Ошибка в кабинете чиновника 171 Разведка Где угодно ✔ Наставник нового агента 174 Социальные Безопасность Возьмите нового агента на первое задание 174 Ловкость Руины Украсть сверхсекретно Gaule Intel 189 Ловкость Где угодно ✔ Раскрыть кольцо космической оболочки 189 Разведка Доки Произведите впечатление на группу флибустьеров. 204 Прочность Местные маршрутные такси Откройте для себя двойного агента в своих рядах 219 Разведка Руины – ✔ Космические снаряды оставьте себе 225 Ловкость Доки ✔ Изобразить пирата флибустьера на некоторое время 230 Прочность Где угодно ✔ Подружитесь с целью под вымышленным именем 234 Социальные Бар – Храните вещи, которые вы украли, будучи флибустьером 243 Разведка Где угодно ✔ Найдите оперативников противника 249 Разведка Где угодно – Спасите товарища по отряду во время битвы. 264 Ловкость Руины – Станьте лидером своего отряда. 264 Социальные Где угодно – Раскройте заговор с целью убийства лидера вашей станции. 279 Разведка Где угодно – Используйте дружбу с врагом для сбора информации 279 Разведка Где угодно ✔ Убежать от глаз вражеских оперативников 281 Ловкость Где угодно – ✔ Убейте двойного агента в своих рядах 289 Ловкость Где угодно ✔ ✔ Защитите лидера своей станции. 315 Ловкость Где угодно – ✔ Технолог: Портовый техник
Вторичная характеристика: Сила Имя Бонус Стат. Площадь Незаконный Вредно Очистить корабль от ржавчины 9 Выносливость Порт Отполировать корабль 9 Выносливость Порт Заправить корабль топливом 24 Прочность Порт – ✔ Заправьте топливо другой жидкостью 27 Разведка Местные маршрутные такси ✔ Замесить партии топлива 26 Выносливость Доки ✔ Подделка разрешений на выезд 39 Социальные Доки ✔ Выполнить предполетный контроль 39 Выносливость Местные маршрутные такси Осмотреть груз 39 Разведка Доставка Изучить руководство по ремонту 54 Выносливость Где угодно Сделать технический ремонт 54 Прочность Порт – Запустить полную диагностику 69 Выносливость Порт Обучить утомительного ученика 69 Выносливость Порт Ремонт корабля 69 Прочность Порт Продам судовые запчасти на борт 81 Ловкость Руины ✔ Установить тяжелое исследовательское оборудование 84 Прочность Порт Установить навигационную систему 84 Выносливость Порт Обновить звездную карту корабля 84 Разведка Порт Провести испытания на целостность корпуса 99 Выносливость Порт Наблюдать за заменой корпуса 111 Прочность Порт ✔ Конструкция корабельного модуля 114 Разведка Где угодно Вывоз материалов со списанного судна на продажу 114 Прочность Порт Руководить строительством судового модуля 114 Выносливость Судостроительный завод Пройти обучение на более высоком уровне 129 Выносливость Порт Поезд для разборки и утилизации судов 129 Разведка Где угодно Спроектировать нелегальный корабельный модуль 135 Разведка Где угодно Наблюдать за постройкой нелегального корабельного модуля 140 Социальные Судостроительный завод ✔ Открыть мусорное дело. 144 Выносливость Рынок Собрать бригаду. 144 Социальные Руины Проведите первую крупную спасательную операцию 159 Выносливость Руины Расширьте свою деятельность 159 Выносливость Бар Выполнение нескольких аварийно-восстановительных работ 174 Социальные Где угодно Нанять нелегального сотрудника. 171 Социальные Где угодно ✔ Расширьте свой бизнес дальше 189 Выносливость Гостиная Нанять большую команду 189 Выносливость Руины Продавайте свои утиль флибустьерам 196 Прочность Местные маршрутные такси ✔ Экспортные запчасти премиум-класса 204 Прочность Порт Разработка и производство лучших технологий утилизации 204 Выносливость Где угодно Составьте план расширения вашего бизнеса за счет дополнительных систем 219 Разведка Где угодно Нанять еще больше нелегальных сотрудников 225 Выносливость Руины ✔ Расширение в военный сектор. 234 Прочность Безопасность Спасите свой первый военный корабль для военных 234 Выносливость Где угодно Спасите корабль на территории Флибустьера 247 Прочность Где угодно ✔ Привлечь внимание Военного Консорциума 249 Выносливость Где угодно Подписать контракт с Военным Консорциумом 249 Социальные Где угодно Привлечь внимание военных 249 Выносливость Где угодно Подписать секретный контракт с Gaule Military 249 Социальные Где угодно Поглотите конкурирующую спасательную компанию. 264 Выносливость Где угодно Превратитесь в небольшую империю сборщиков мусора! 279 Выносливость Где угодно Управляйте своей межгалактической империей утильщиков. 279 Социальные Где угодно Добавьте сотрудников службы безопасности, чтобы помочь отбиваться от флибустьеров. 298 Прочность Где угодно ✔ Саботируйте бизнес соперника, чтобы он был вынужден присоединиться к вашей команде. 315 Выносливость Где угодно ✔ Подкупите чиновников, чтобы ваши экипажи всегда получали первое уведомление о новых 333 Выносливость Где угодно ✔ Карьера — Станция Тау
Бизнес
Описание
Бизнес-пути
Преступник
Описание
Бизнес-пути
Закон
Описание
Бизнес-пути
Медицина
Описание
Бизнес-пути
Специальные службы
Описание
Бизнес-пути
Технолог
Описание
Бизнес-пути
Старый рейтинг Needed Days в рейтинге Необходимые задачи выполнены 1 2 около 50 2 4 неизвестно 3 8 неизвестно 4 16 неизвестно 5 32 неизвестно 6 64 неизвестно 7 128 неизвестно 8 Экскурсия по карьерной лестнице
Офицеров в Альфа Тау
2017-2018 Должностные лица проектов · carbonblack / tau-tools · GitHub
проектов · carbonblack / tau-tools · GitHub
Будьте организованыСоздавайте в Sketch. TAU Обзор
TAU Обзор
TAU (Утилиты настройки и анализа) — визуальный
среда программирования и анализа производительности для pC ++.
Элементы графического интерфейса TAU представляют собой
объекты парадигмы программирования pC ++ : коллекции,
классы, методы и функции. Эти объекты уровня языка
фигурируют во всех утилит TAU . TAU использует Sage ++ toolkit как интерфейс к компилятору pC ++ для инструментовки и доступа к свойствам программных объектов. TAU также интегрирован со средой выполнения pC ++ система профилирования и сопровождения трассировки. TAU реализован
в C и C ++ и использует Tcl / Tk для графики. select-function , select-class и switch-application . TAU также включает в себя полную гипертекстовую справочную систему.
Далее: Краткие описания инструментов TAU Up: Домашняя страница TAU
mohr @ cs.uoregon.edu
23 июня 1994 г. TAU в TACC — Пользовательский портал TACC
TAU в TACC
Последнее обновление: 19 сентября 2018 г.
login1 $ модуль нагрузки тау
login1 $ env | grep TAU # отображать переменные среды, зависящие от пакета
login1 $ module help tau #basic operations & features
логин1 $ tau_f90.sh
логин1 $ tau_cc.sh
login1 $ tau_cxx.sh
login1 $ tau_cc.sh -o myprogram myprogramfile.c
-tau: help «после команды оболочки компилятора, чтобы увидеть полезные параметры TAU.
ifdef TACC_TAU_DIR
FC = tau_f90.sh
CC = tau_cc.sh
CXX = tau_cxx.sh
еще
FC = mpif90
CC = mpicc
CXX = mpicxx
endif
% .o:% .cxx
$ {CXX} -c $ *. Cxx $ TAU_MAKEFILE ». Включенные make-файлы хранятся в каталоге « $ TACC_TAU_LIB ».Значение по умолчанию « $ TAU_MAKEFILE » обеспечит нормальную MPI и гибридную (MPI / OpenMP) инструментарию. Установите для переменной значение « $ TACC_TAU_LIB / Makefile.tau-intelomp-icpc-papi-ompt-pdt-openmp » для чистых кодов OpenMP. TAU_PROFILE Установите в 1, чтобы включить профилирование (статистику) информации. ПРОФИЛЕДИР Установить имя каталога; в противном случае вывод идет в текущий каталог. TAU_TRACE Установите значение 1, чтобы включить отслеживание информации (шкала времени). TRACEDIR Установите имя каталога. Вы можете смело использовать значение `PROFILEDIR`. idev :
логин1 $ idev
...
c455-073 [knl] $ cd mytaudir; mkdir -p профили
c455-073 [knl] $ экспорт PROFILEDIR = `pwd` / profiles
c455-073 [knl] $ ibrun myprogram # профилирование включено по умолчанию
...
c455-073 [knl] $ mkdir -p traces
c455-073 [knl] $ экспорт TRACEDIR = `pwd` / traces
c455-073 [knl] $ экспорт TAU_PROFILE = 0 TAU_TRACE = 1
...
c455-073 [knl] $ ibrun myprogram
#SBATCH директивы
...
экспорт PROFILEDIR = mytaudir / profiles
экспорт TRACEDIR = mytaudir / traces
ibrun myprogram
...
экспорт TAU_PROFILE = 0
экспорт TAU_TRACE = 1
ibrun myprogram
График arccos cosx: Элементарная математика
График arcsin cos x. Вывод формул обратных тригонометрических функций
Что такое арксинус, арккосинус? Что такое арктангенс, арккотангенс?
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…») Ни больше ни меньше. Бывает угол, скажем 30°. А бывает угол arcsin0,4. Или arctg(-1,3). Всякие углы бывают.) Просто записать углы можно разными способами. Можно записать угол через градусы или радианы. А можно — через его синус, косинус, тангенс и котангенс…
Ни больше ни меньше. Бывает угол, скажем 30°. А бывает угол arcsin0,4. Или arctg(-1,3). Всякие углы бывают.) Просто записать углы можно разными способами. Можно записать угол через градусы или радианы. А можно — через его синус, косинус, тангенс и котангенс…
угол, синус которого равен 0,4
Это угол, косинус которого равен 0,8.
Это угол, тангенс которого равен -1,3.
Это угол, котангенс которого равен 12. Ограничения на арксинус, арккосинус, арктангенс, арккотангенс.
Урок и презентация на темы: «Арксинус. Таблица арксинусов. Формула y=arcsin(x)»
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.
Программная среда «1С: Математический конструктор 6.1»
Решаем задачи по геометрии. Интерактивные задания на построение в пространстве
1. Что такое арксинус?
2. Обозначение арксинуса.
3. Немного истории.
4. Определение.Что такое арксинус?
а x2= 2π/3 + 2πk.
sin(x)= 5/6. Очевидно, что это уравнение будет иметь также два корня, но какие значения будут соответствовать решению на числовой окружности? Давайте внимательно посмотрим на наше уравнение sin(x)= 5/6.
Решением нашего уравнения будут две точки: F= x1 + 2πk и G= x2 + 2πk,
где x1 – длина дуги AF, x2 – длина дуги AG.
Заметим: x2= π — x1, т.к. AF= AC — FC, но FC= AG, AF= AC — AG= π — x1.
Но, что это за точки?
Арксинус — это угол (длина дуги AF, AG) синус, которого равен 5/6.Немного истории арксинуса
Определение арксинуса
x= π — arcsin(a) + 2πk
С учётом этого, запишем общую формула решения для уравнения sin(x)=a:Примеры
Решение: Пусть arcsin(√3/2)= x, тогда sin(x)= √3/2. По определению: — π/2 ≤x≤ π/2. Посмотрим значения синуса в таблице: x= π/3, т.к. sin(π/3)= √3/2 и –π/2 ≤ π/3 ≤ π/2.
Ответ: arcsin(√3/2)= π/3.
Решение: Пусть arcsin(-1/2)= x, тогда sin(x)= -1/2. По определению: — π/2 ≤x≤ π/2. Посмотрим значения синуса в таблице: x= -π/6, т.к. sin(-π/6)= -1/2 и -π/2 ≤-π/6≤ π/2.
Ответ: arcsin(-1/2)=-π/6.
Решение: Пусть arcsin(0)= x, тогда sin(x)= 0. По определению: — π/2 ≤x≤ π/2. Посмотрим значения синуса в таблице: значит x= 0, т.к. sin(0)= 0 и — π/2 ≤ 0 ≤ π/2.
Ответ: arcsin(0)=0.
x= arcsin(-√2/2) + 2πk и x= π — arcsin(-√2/2) + 2πk.
Посмотрим в таблице значение: arcsin (-√2/2)= -π/4.
Ответ: x= -π/4 + 2πk и x= 5π/4 + 2πk.
Решение: Воспользуемся определением, тогда решение запишется в виде:
x= arcsin(0) + 2πk и x= π — arcsin(0) + 2πk. Посмотрим в таблице значение: arcsin(0)= 0.
Ответ: x= 2πk и x= π + 2πk
Решение: Воспользуемся определением, тогда решение запишется в виде:
x= arcsin(3/5) + 2πk и x= π — arcsin(3/5) + 2πk.
Ответ: x= (-1) n — arcsin(3/5) + πk.Задачи на арксинус для самостоятельного решения
1) Вычислить: а) arcsin(√2/2), б) arcsin(1/2), в) arcsin(1), г) arcsin(-0.8).
2) Решить уравнение: а) sin(x) = 1/2, б) sin(x) = 1, в) sin(x) = √3/2, г) sin(x) = 0.25,
д) sin(x) = -1.2.
3) Решить неравенство: а) sin (x)> 0.6, б) sin (x)≤ 1/2.Определение обратных тригонометрических функций
Графики обратных тригонометрических функций
y = arccos
x
y = arctg
x
y = arcctg
xОсновные формулы
sin(arcsin
x)
= x
arccos(cos
x)
= x
при
cos(arccos
x)
= x
tg(arctg
x)
= x
arcctg(ctg
x)
= x
при
ctg(arcctg
x)
= x Формулы, связывающие обратные тригонометрические функции
Формулы суммы и разности
при или
при или
при
приАрккосинус
Арктангенс
Арккотангенс
Тригонометрические тождества arcsin, arcos, arctg и arcctg
Примеры решения задач
Основные формулы
sin(arcsin
x)
= x
cos(arccos
x)
= x
tg(arctg
x)
= x
(-∞ ctg(arcctg
x)
= x
(-∞
arcsin(sin
x)
= x
при
arccos(cos
x)
= x
при
arctg(tg
x)
= x
при
arcctg(ctg
x)
= x
при
sin
x = sin(-
x-π) ;
sin
x = sin(π-x) ;
sin
x = sin(x+2
πn) ;
cos
x = cos(-x) ;
cos
x = cos(2
π-x) ;
cos
x = cos(x+2
πn) ;
tg
x = tg(x+πn) ;
ctg
x = ctg(x+πn)
arcsin(sin
x)
=
arcsin(sin( π — x ))
= π — x .Обратные функции отрицательного аргумента
Аргумент синуса попадает в допустимый интервал области значений арксинуса. Поэтому формула верна.
arccos(-
x)
=
arccos(-cos arccos
x)
=
arccos(cos(π-arccos
x))
=
π — arccos
xВыражение арксинуса через арккосинус и арктангенса через арккотангенс
Выражение арксинуса через арктангенс, арккосинуса через арккотангенс и наоборот
Формулы суммы и разности
.
Далее замечаем, что, поскольку arcsin(-
x) = — arcsin
x,
arcsin(-
y) = — arcsin
y,
то при разных знаках у x
и y
,
X
и Y
также разного знака и поэтому неравенства выполняются. Условие различных знаков у x
и y
можно написать одним неравенством: .
То есть при формула справедлива.
;
;
;
.
Поскольку и ;
то входящие сюда косинусы не отрицательные. Обе части неравенства положительные. Возводим их в квадрат и преобразуем косинусы через синусы:
;
.
Подставляем sin
X = sin arcsin
x = x
:
;
;
;
.
Выполняем преобразования:
ИлиПостройте график функции:
y=arccos(cosX) — Школьные Знания.com
Функции и Графики — сайт по математике и не только!!! Всё о Математических функциях и их графиках…
ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
y = arcsin x
y = arccos x
функция обратная функции y = sin x,
— / 2 x / 2функция обратная функции y = cos x,
0 x y = arcsin x y = arccos x ОБЛАСТЬ ОПРЕДЕЛЕНИЯ: [-1; 1] [-1; 1] ОБЛАСТЬ ЗНАЧЕНИЙ: [0; ) ЧЕТНОСТЬ, НЕЧЕТНОСТЬ: нечетная ни четная, ни нечетная
НУЛИ: y = 0 при x = 0 y = 0 при x = 1 ПРОМЕЖУТКИ ЗНАКОПОСТОЯНСТВА: y > 0, при x (0; ] y x [-1; 0)
y = 0 при x = 1 y > 0 при x [-1; 1) ЭКСТРЕМУМЫ: нет нет ПРОМЕЖУТКИ МОНОТОННОСТИ: возрастает на всей области определения убывает на всей области определения y = arctg x
y = arcctg x
функция обратная функции y = tg x, — / 2 x / 2 функция обратная функции y = ctg x, 0 x y = arctg x y = arcctg x ОБЛАСТЬ ОПРЕДЕЛЕНИЯ: R R ОБЛАСТЬ ЗНАЧЕНИЙ: (0; ) ЧЕТНОСТЬ, НЕЧЕТНОСТЬ: нечетная ни четная, ни нечетная
НУЛИ: y = 0 при x = 0 нулей нет ПРОМЕЖУТКИ
ЗНАКОПОСТОЯНСТВА: y > 0, при x (0; ] y x (-; 0) y > 0 при x R ЭКСТРЕМУМЫ: нет нет ПРОМЕЖУТКИ
МОНОТОННОСТИ:возрастает при x R убывает при x R
График arccos. Тригонометрия. Обратные тригонометрические функции. Арксинус. Получение функции arcsin
Определение и обозначения
Арксинус (y = arcsin
x
) — это функция, обратная к синусу (x = sin
y
-1 ≤
x ≤ 1 и множество значений -π/2 ≤
y ≤ π/2 .
sin(arcsin
x)
= x
;
arcsin(sin
x)
= x
.
.График функции арксинус
Арккосинус, arccos
Определение и обозначения
Арккосинус (y = arccos
x
) — это функция, обратная к косинусу (x = cos
y
). Он имеет область определения -1 ≤
x ≤ 1 и множество значений 0 ≤
y ≤ π
.
cos(arccos
x)
= x
;
arccos(cos
x)
= x
.
.График функции арккосинус
Четность
arcsin(-
x)
=
arcsin(-sin arcsin
x)
=
arcsin(sin(-arcsin
x))
=
— arcsin
x
arccos(-
x)
=
arccos(-cos arccos
x)
=
arccos(cos(π-arccos
x))
=
π — arccos
x ≠ ± arccos
xСвойства — экстремумы, возрастание, убывание
y = arcsin
x y = arccos
x Область определения и непрерывность — 1
≤ x ≤ 1 — 1
≤ x ≤ 1 Область значений Возрастание, убывание монотонно возрастает монотонно убывает Максимумы Минимумы Нули, y = 0 x = 0 x = 1 Точки пересечения с осью ординат, x = 0 y = 0 y = π/2 Таблица арксинусов и арккосинусов
x arcsin
x arccos
x град. рад. град. рад. — 1 — 90° — 180° π — — 60° — 150° — — 45° — 135° — — 30° — 120° 0 0° 0 90° 30° 60° 45° 45° 60° 30° 1 90° 0° 0
≈ 0,8660254037844386Формулы
См. также:
Вывод формул обратных тригонометрических функцийФормулы суммы и разности
при или
при или
при
приВыражения через логарифм, комплексные числа
См. также:
Вывод формулВыражения через гиперболические функции
Производные
.
См. Вывод производных арксинуса и арккосинуса > > >
,
где — многочлен степени .
Он определяется по формулам:
;
;
.Интегралы
.
.Разложение в ряд
;
.Обратные функции
sin(arcsin
x)
= x
cos(arccos
x)
= x
.
arcsin(sin
x)
= x
при
arccos(cos
x)
= x
при .
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.Свойства функции arcsin .
Получение функции arccos .
Арккосинус (y = arccos
x
) — это функция, обратная к косинусу (x = cos
y
), имеющая область определения и множество значений .
Арктангенс (y = arctg
x
) — это функция, обратная к тангенсу (x = tg
y
), имеющая область определения и множество значений .
Арккотангенс (y = arcctg
x
) — это функция, обратная к котангенсу (x = ctg
y
), имеющая область определения и множество значений .Графики обратных тригонометрических функций
y = arccos
x
y = arctg
x
y = arcctg
xОсновные формулы
sin(arcsin
x)
= x
arccos(cos
x)
= x
при
cos(arccos
x)
= x
tg(arctg
x)
= x
arcctg(ctg
x)
= x
при
ctg(arcctg
x)
= x Формулы, связывающие обратные тригонометрические функции
См. также:
Вывод формул обратных тригонометрических функцийФормулы суммы и разности
при или
при или
при
при
при
при
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.Арккосинус
Арктангенс
Арккотангенс
Тригонометрические тождества arcsin, arcos, arctg и arcctg
Примеры решения задач
Свойства функции arcsin .
График арксинуса.
Получение функции arcsin .
Функция у=arccos x — презентация онлайн
y
y = cos x
2
3
2
2
1
0
-1
Функция y=cosx, взятая на
всей области определения, не
имеет обратной, т.к. одно и
тоже её значение достигается
при разных значениях
аргумента.
2
x
3
2
Кривая симметричная
косинусоиде относительно
прямой у=х не является
функцией (функциональная
зависимость предполагает
соответствие каждому
значению аргумента
единственное значение
функции).
2
y
Рассмотрим функцию
y=cosx только на отрезке
[0; ]
2
2
3
2
y = cos x
-1
1
0
1
-1
2
D
E( y) : yx 1;1
; 1
0
0;;1
2
x
3
2
Обратная
функция
y = arccos
x
D
E( у) : yх 0;
101;;;0
2
2
y = arccosx
y
D( y) : x 1;1
E( у) : y 0;
-1
0
1
x
Функция ни четная ни нечетная
Функция убывает
Функция непрерывна
Повторим
y = f(x)
y
y = f(x)
y = — f(x)
-1
x
1
y = — f(x)
y
y = — arccosx
D( y) : x 1;1
2
Найдем E(y) методом оценки
0 arccos x
(-1)
0 arccos x
arccos x 0
E( у) : y ; 0
1
-1
2
x
Повторим
y = f(x)
y = f(-x)
y
y = f(x)
y = f(-x)
-1
1
x
y
y = arccos(-x)
Найдем D(y) методом оценки
1 x 1
(-1)
2
1 x 1
1 x 1
D( y) : x 1;1
E( у) : у 0;
1
-1
2
x
y
y = 2arccos x
2
D( y) : х 1;1
Найдем E(y) методом оценки
0 arccos x
2
0 2 arccos x 2
0 y 2
2
E( у) : у 0; 2
-1
1
x
y
1
=
y — 2 arccos x
D( y) : х 1;1
2
Найдем E(y) методом оценки
0 arccos x
0 0,5 arccos x
2
(–0,5)
0,5 arccos x 0
E ( у ) : у ; 0
2
1
-1
2
2
x
y
y = arccos 12 x
Найдем D(y) методом оценки
1
1 x 1
2
2 x 2
2
2
D( y) : х 2; 2
E( у) : у 0;
-2
1
-1
2
2
x
y
y = arccos 2x
Найдем D(y) методом оценки
1 2x 1 : 2
1
1
x
2
2
2
1 1
D( y ) : х ;
2 2
E( у) : у 0;
-1– 1
2
1 1
2
2
x
y
y = 1,5arccosx +
2
2
3
D( y) : х 1;1
Найдем E(y) методом оценки
0 arccos x
* 1,5
0 1,5 arccos x 1,5 + 2
3
2
13
1,5 arccos x
3
6
2 13
E ( у ) : у
;
3
6
2
-1
1
x
Повторим
y = f(x)
y = f(x)
y
y = f(x)
1
x
y
Повторим
1
y = f(x)
y= f x
Функция четная
(график симметричен
относительно оси Оу)
x
y
y = arccosx
2
1
-1
2
График y =arccosx не изменится.
Почему?
x
y = arccos x –
D( y) : х 1;1
Найдем E(y) методом оценки
0 arccos x
0 arccos x
–6
2
arccos x
6 3
6
0
E ( у ) : у 0;
3
y
6
g ( x) = x
При x [ 1; 1]
x [0; 1]
-1
0
1
x
1
x
y
y( x) = arccos x
При x [0; 1]
arccos x [0;
2
]
-1
0
y = arccos x –
y
6
D( y) : х 1;1
E ( у ) : у 0;
3
Функция четная
(график симметричен
относительно оси Оу)
2
-1
1
2
x
y 3
Найдем область определения и
множество значений, затем
построим график.
2
y = -1,5arccos (x–2)
3
1 x 2 1 +2
1 x 3
D( y ) : x 1; 3
[ 1; 1]
0 arccos( x 2)
(-1,5)
1,5 2 arccos( x 2) 0
1,5 y 0
E ( y ) : y 1,5 ; 0
4
2
1
-1
3
4
3
2
3
x
3
y = arccos( x – )
4
D( y )
3
1 х 1
4
+3
4
1
3
х 1
4
4
3
х 1
4
3
3
1 х 1
4
4
3 3
D ( y ) : х 1 ;1
4 4
y( x) = arccos g ( x)
3
При g ( x) [ ; 1]
4
E ( y)
3
y = arccos( x – )
4
y
3
g ( x) = x
4
x 0
3
arccos
4
–3
4
3
3
x
4
4
3
1 х 1
4
3
3
х 1
4
4
-1– 3 0
1
x
4
3
E ( у ) : у 0; arccos
4
y
3
y = arccos( x – )
4
3 3
D ( y ) : х 1 ;1
4 4
2
3
–1
3 4
E ( у ) : у 0; arccos
4
Функция четная
(график симметричен
относительно оси Оу)
3
arccos
4
-1
1
2
1
3
4
xТригонометрическая функция и график обратной тригонометрической функции
1. Синус-функция sin x, арксинус-функция arcsin x
2. Функция косинуса cos x, функция обратного косинуса arccos x
3. Функция обратного синуса arcsin x, функция обратного косинуса arccos x
4. Функция тангенса tan x, функция котангенса cot x
5. Функция обратного тангенса arctan x, обратного котангенса arccot x
6. Функция косеканса csc x
7. Секущая функция sec x
Алгебра – 10 класс. Арккосинус, arccos (x)
1. Что такое арккосинус?
2. Обозначение арккосинуса.
3. Немного истории.
4. Определение.
5. Таблица значений арккосинуса.
6. Примеры.Что такое арккосинус?
Обозначение арккосинуса
Немного истории
arccos x — это угол (можно сказать и дуга), косинус которого равен x.Определение арккосинуса.
Таблица значений косинуса
Таблица значений арккосинуса
Примеры
Решение: Пусть arccos(-√3/2)=x, тогда cos(x)=-√3/2 и по определению 0 ≤ x ≤ π. Посмотрим значения косинуса в таблице: x=5π/6, т.к. cos(5π/6)= -√3/2 и 0 ≤ 5π/6 ≤ π.
Ответ: arccos(-√3/2)=5π/6
Решение: Пусть arccos(√2/2) = x, тогда cos(x)= √2/2 и по определению 0 ≤ x ≤ π. Посмотрим значения косинуса в таблице: x=π/4, т.к. cos(π/4)= √2/2 и 0 ≤ π/4 ≤ π.
Ответ: arccos(√2/2)=π/4
Решение: Пусть arccos(1) = x, тогда cos(x)= 1 и по определению 0≤ x ≤ π. Посмотрим значения косинуса в таблице: значит x=0, т.к. cos(0)= 1 и 0 ≤ 0 ≤ π.
Ответ: arccos(1)=0
Решение: Косинус — это абсцисса точки числовой окружности. Значит необходимо найти такие точки, абсциссы которых больше -0.3. Нарисуем прямую x=-0.3. Она пересекает числовую окружность в двух точках: F и G. Неравенству x>-0.3 соответствуют точки дуги GF. Точкам F и G соответствуют абсциссы:
±arccos(-0.3)= ±(π — arccos(0.3)). Запишем аналитическую запись дуги GF: -π + arccos(0.3)
Ответ: -π + arccos(0.3) Задачи для самостоятельного решения
1)Вычислить:
а) $arccos(\frac{\sqrt{3}}{2})$,
б) $arccos(-\frac{1}{2})$,
в) $arccos(0)$,
г) $arccos(-0,5)$.
2) Решить уравнения:
а) $cos(x)=-\frac{1}{2}$,
б) $cos(x)=1$,
в) $cos(x)=\frac{\sqrt{3}}{2}$,
г) $cos(x)=0,25$,
д) $cos(x)=-1,2$.
3) Решить неравенства:
а) $cos(x)>0,6$,
б) $cos(x)≤0,2$. Arccos
Калькулятор Arccos
Использование специальных углов для поиска arccos
θ 0 ° 30 ° 45 ° 60 ° 90 ° cos (θ) 0 Обратные свойства
Состав арккосинуса и косинуса
Состав других тригонометрических функций
Использование арккосинуса для решения тригонометрических уравнений
7. Обратные тригонометрические функции
Функция обратной синусоиды (arcsin)
График
y = arcsin x `-π / 2 ≤ arcsin \ x ≤ π / 2`
Функция обратной касательной (arctan)
Числовые примеры arcsin, arccos и arctan
Функция обратной секущей (угловые секунды)
Функция обратного косеканса (arccsc)
Функция обратного котангенса (arccot)
Альтернативный вид
— arccos (cos (x)) — Solumaths
Описание:
Описание:
Функция arccos позволяет вычислять арккосинус числа.
Функция арккосинуса — это функция, обратная функции косинуса. Синтаксис:
Первообразный арккозин:
Предел арккосинуса:
Арккосинус, обратная функция:
Графический арккосинус:
Расчет онлайн с помощью arccos (arccosine) Arccos cos (x) | Justfreetools
Arccos. Поиск обратного косинуса
Что является обратным к косинусу (arccos)?
Сокращение Определение Домен arccos x
для реального результата Диапазон обычных
основных значений arccos (x)
cos -1 x,
acos х = соз (у) -1 ≤ х ≤ 1 0 ≤ y ≤ π
0 ° ≤ y ≤ 180 ° cos -1 x ≠ 1 / cos (x) График обратного косинуса
cos (x) = cos (x + 2πn) , для каждого целого числа n x arccos (x) График ° рад -1 180 ° π -√3 / 2 150 ° 5π / 6 -√2 / 2 135 ° 3π / 4 -1/2 120 ° 2π / 3 0 90 ° π / 2 1/2 60 ° π / 3 √2 / 2 45 ° π / 4 √3 / 2 30 ° π / 6 1 0 ° 0 Обратный косинус — какое мне дело? Некоторые малоизвестные приложения arccos
Калькулятор обратного косинуса — Вычислить arccos (x)
Как найти Arccos
Формула обратного косинуса
График обратного косинуса
Таблица обратных косинусов
Косинус Угол (градусы) Угол (радианы) -1 180 ° π –√6 + √24 165 ° 11π12 –√32 150 ° 5π6 –√22 135 ° 3π4 –12 120 ° 2π3 –√6 — √24 105 ° 7π12 0 90 ° π2 √6 — √24 75 ° 5π12 12 60 ° π3 √22 45 ° π4 √32 30 ° π6 √6 + √24 15 ° π12 1 0 ° 0 Решение | Обратный или нет? | Тригонометрия: от треугольников к функциям
При делении минус на минус дает плюс: Умножения и деление отрицательных чисел. Решение примеров.
Умножения и деление отрицательных чисел. Решение примеров.

Задача 3. Вычислить: \(11*(-11)\) и \(13*(-6).\)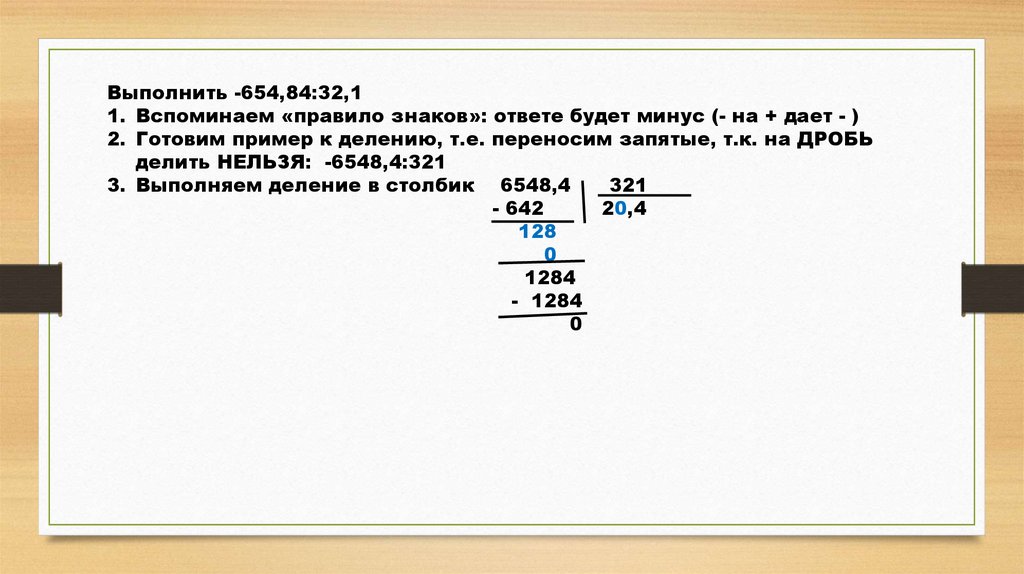 Делить на ноль нельзя.
Делить на ноль нельзя. Запишитесь на пробное занятие уже сейчас!
Запишитесь на пробное занятие уже сейчас! Очень люблю свой предмет и делаю всё возможное для того, чтобы мои ученики без проблем решали математические задания любой сложности. Имею большой опыт подготовки к ОГЭ обучающихся с разным уровнем знаний. Объясняю просто и понятно. Вместе с ребятами мы рассуждаем, мыслим, анализируем и достигаем поставленной цели.
Очень люблю свой предмет и делаю всё возможное для того, чтобы мои ученики без проблем решали математические задания любой сложности. Имею большой опыт подготовки к ОГЭ обучающихся с разным уровнем знаний. Объясняю просто и понятно. Вместе с ребятами мы рассуждаем, мыслим, анализируем и достигаем поставленной цели. Самые сложные темы по математике на моих занятиях станут для вас очень простыми. Подготовлю вас к ВПР по математике, к ОГЭ по информатике. Пропагандирую сотрудничество на равных, дружественная атмосфера на занятиях. Индивидуальный подход к каждому ребенку.
Самые сложные темы по математике на моих занятиях станут для вас очень простыми. Подготовлю вас к ВПР по математике, к ОГЭ по информатике. Пропагандирую сотрудничество на равных, дружественная атмосфера на занятиях. Индивидуальный подход к каждому ребенку. Убежден, что математику может понять каждый человек.
Со мной вы получите заряд уверенности в себе, поймете, что математика — это не скучно, а безумно интересно!
С нетерпением жду всех на занятиях!
Убежден, что математику может понять каждый человек.
Со мной вы получите заряд уверенности в себе, поймете, что математика — это не скучно, а безумно интересно!
С нетерпением жду всех на занятиях!Почему минус на минус дает плюс?

 Часто приходится и делить одни величины на другие, но здесь результат не всегда выражается натуральным числом — так появились дробные числа.
Часто приходится и делить одни величины на другие, но здесь результат не всегда выражается натуральным числом — так появились дробные числа. Это недоверие сохранялось очень долго, и даже Декарт — один из «основателей» современной математики — называл их «ложными» (в XVII веке!).
Это недоверие сохранялось очень долго, и даже Декарт — один из «основателей» современной математики — называл их «ложными» (в XVII веке!). Во-вторых, допуская использование отрицательных чисел, мы избавляемся от утомительного (если уравнение окажется посложнее, с большим числом слагаемых) поиска того пути решения, при котором все действия производятся только над натуральными числами. Более того, мы можем больше не думать каждый раз об осмысленности преобразуемых величин — а это уже шаг в направлении превращения математики в абстрактную науку.
Во-вторых, допуская использование отрицательных чисел, мы избавляемся от утомительного (если уравнение окажется посложнее, с большим числом слагаемых) поиска того пути решения, при котором все действия производятся только над натуральными числами. Более того, мы можем больше не думать каждый раз об осмысленности преобразуемых величин — а это уже шаг в направлении превращения математики в абстрактную науку. А вот деление целых чисел друг на друга, чтобы в результате снова получались целые числа, возможно не всегда. То же самое и с многочленами.
А вот деление целых чисел друг на друга, чтобы в результате снова получались целые числа, возможно не всегда. То же самое и с многочленами.
 Значит, B = C.
Значит, B = C.Минус на плюс что дает?
 Специально для того, чтобы нам жизнь мёдом не казалась. Как же нам быть? Нужно выучить эти правила, чтобы говорить математикам то, что они хотят от нас слышать.
Специально для того, чтобы нам жизнь мёдом не казалась. Как же нам быть? Нужно выучить эти правила, чтобы говорить математикам то, что они хотят от нас слышать.
Если два числа имеют одинаковые знаки, в результате всегда будет плюс.Минус на плюс, плюс на минус.  Всегда.
Всегда.Минус на минус, плюс на плюс.  Они записали правила в учебники, не особо вдаваясь в подробности. Для правильного ответа на вопрос, нам нужно разобраться, что же означают знаки плюс и минус в математике.
Они записали правила в учебники, не особо вдаваясь в подробности. Для правильного ответа на вопрос, нам нужно разобраться, что же означают знаки плюс и минус в математике.
Если в бочку мёда добавить ложку дёгтя, получится бочка дёгтя.
Если в бочку дёгтя добавить ложку дёгтя, получится бочка мёда.
Если в бочку мёда добавить ложку мёда, получится бочка мёда.
1. Математики не правильно записали свое правило.
Математики не правильно записали свое правило.
2. Мы не правильно применяем математическое правило. Виноделы этим знаком обозначали пустые бочки. После наполнения бочек вином они перечеркивали знак «минус» и получался знак «плюс». По сути, знак «минус» заменял виноделам обычный ноль, ведь он обозначал отсутствие вина в бочке. Но математики ловко присобачили знак «минус» к числам и назвали их «отрицательными».
Виноделы этим знаком обозначали пустые бочки. После наполнения бочек вином они перечеркивали знак «минус» и получался знак «плюс». По сути, знак «минус» заменял виноделам обычный ноль, ведь он обозначал отсутствие вина в бочке. Но математики ловко присобачили знак «минус» к числам и назвали их «отрицательными». 2
2Минус на минус даёт плюс. А почему?
 А кто из нас интересовался почему? Конечно, проще без лишних вопросов запомнить данное утверждение и глубоко не вникать в суть вопроса. Сейчас и без того достаточно информации, которую необходимо «переварить». Но для тех, кого всё же заинтересует этот вопрос, постараемся дать объяснение этому математическому явлению.
А кто из нас интересовался почему? Конечно, проще без лишних вопросов запомнить данное утверждение и глубоко не вникать в суть вопроса. Сейчас и без того достаточно информации, которую необходимо «переварить». Но для тех, кого всё же заинтересует этот вопрос, постараемся дать объяснение этому математическому явлению.
 В нашем примере мы не использовали сложных вычислений, но при большом количестве слагаемых вычисления с отрицательными числами могут облегчить нам работу.
В нашем примере мы не использовали сложных вычислений, но при большом количестве слагаемых вычисления с отрицательными числами могут облегчить нам работу.Остались вопросы?
Задайте свой вопрос и получите ответ от профессионального преподавателя.
Курсы по математике 10 класс
Курсы по математике 9 класс
Математика 11 класс
Курсы по геометрии 7 класс
Курсы по алгебре 7 класс
Алгебра 8 класс
Курсы по геометрии 8 класс
Курсы французского языка для начинающих
§ Деление отрицательных чисел.
 Деление рациональных чисел
Деление рациональных чисел
Правила деления отрицательных чисел
Правило знаков при делении
+ : (+) = + + : (−) = − − : (−) = + − : (+) = −  Например, для вычисления дроби
Например, для вычисления дроби
Знак «минус» в дробях

Умножение и деление целых чисел
Законы умножения
 Умножение состоит из трёх параметров: множимого, множителя и произведения. Например, в выражении 3 × 2 = 6, число 3 — это множимое, число 2 — множитель, число 6 — произведение.
Умножение состоит из трёх параметров: множимого, множителя и произведения. Например, в выражении 3 × 2 = 6, число 3 — это множимое, число 2 — множитель, число 6 — произведение.
Переместительный закон умножения
Сочетательный закон умножения
Распределительный закон умножения Для этого каждое слагаемое этой суммы умножается на это число, затем полученные результаты складывают.
Для этого каждое слагаемое этой суммы умножается на это число, затем полученные результаты складывают.(2 + 3) × 5 = 2 × 5 + 3 × 5 = 10 + 15 = 25
Закон умножения на ноль  То есть во сколько раз увеличить ноль. Буквально это выражение читается так: «увеличить ноль в два раза». Но как можно увеличить ноль в два раза, если это ноль? Никак!
То есть во сколько раз увеличить ноль. Буквально это выражение читается так: «увеличить ноль в два раза». Но как можно увеличить ноль в два раза, если это ноль? Никак!Умножение целых чисел
 В таких случаях применяется следующее правило:
В таких случаях применяется следующее правило: 12 – положительное число, а (−5) отрицательное. Опять же применяем предыдущее правило. Перемножаем модули чисел и перед полученным ответом ставим минус:
12 – положительное число, а (−5) отрицательное. Опять же применяем предыдущее правило. Перемножаем модули чисел и перед полученным ответом ставим минус:
Законы деления

На ноль делить нельзя
 То есть каждый раз деля ноль на ноль, мы можем получить разные значения, а это недопустимо.
То есть каждый раз деля ноль на ноль, мы можем получить разные значения, а это недопустимо.
(12 × 4) : (4 × 4) = 48 : 16 = 3
(12 : 4) : (4 : 4) = 3 : 1 = 3

Деление целых чисел
 Чтобы решить этот пример, нужно модуль делимого разделить на модуль делителя, и перед полученным ответом поставить знак плюс.
Чтобы решить этот пример, нужно модуль делимого разделить на модуль делителя, и перед полученным ответом поставить знак плюс.
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Используй кнопку ниже Умножение и деление отрицательных чисел
Purplemath
(добавление большого количества горячих кубиков повышает температуру)
(удаление большого количества горячих кубиков снижает температуру)
(добавление большого количества холодных кубиков снижает температуру)
(удаление многих кубиков холода повышает температуру) MathHelp.
 com
com
 Итак, выберите любые два умноженных (или разделенных) отрицания и «отмените» их знаки:
Итак, выберите любые два умноженных (или разделенных) отрицания и «отмените» их знаки:
Отрицательные числа через круглые скобки
Упростить 3 (
x − 5). Упростить −2 (
x − 3).
 Вы должны делать все, что вам нужно, чтобы ваша работа была правильной, и вы постоянно получали правильный ответ.
Вы должны делать все, что вам нужно, чтобы ваша работа была правильной, и вы постоянно получали правильный ответ. Очень легко «потерять» минус, когда вы складываете такие беспорядочные полиномиальные дроби. Самая распространенная ошибка — поставить минус на x и забыть довести до −2. Будьте особенно осторожны с дробями!
Очень легко «потерять» минус, когда вы складываете такие беспорядочные полиномиальные дроби. Самая распространенная ошибка — поставить минус на x и забыть довести до −2. Будьте особенно осторожны с дробями! Положительные и отрицательные числа | SkillsYouNeed
Визуализация отрицательных и положительных чисел

Вычитание отрицательных чисел
 Тогда сумма будет равна −10+10 = 0.
Тогда сумма будет равна −10+10 = 0. Умножение и деление с положительными и отрицательными числами

(положительное число) × (положительное число) = положительное число
(отрицательное число) × (отрицательное число) = положительное число
(положительное число) × (отрицательное число) = отрицательное число

Следовательно, положительный × положительный = положительный
Отсюда отрицательный × положительный = отрицательный  е. в том направлении, в котором смотрели), положительное движение.
е. в том направлении, в котором смотрели), положительное движение.
Следовательно, положительный × отрицательный = отрицательный
Отсюда отрицательный × отрицательный = положительный 
Заключение
Основные правила для положительных и отрицательных чисел
 Это означает, что они падают по обе стороны от числовой прямой. Однако то, что они находятся на одной линии, не означает, что они следуют одним и тем же правилам! Продолжайте читать список основных правил использования положительных и отрицательных чисел в математике.
Это означает, что они падают по обе стороны от числовой прямой. Однако то, что они находятся на одной линии, не означает, что они следуют одним и тем же правилам! Продолжайте читать список основных правил использования положительных и отрицательных чисел в математике. Правила для чисел со знаком
Сложение: одинаковые знаки, сложите числа
 Например:
Например: Сложение: разные знаки, вычитание чисел
Вычитание: Переключиться на сложение
 Замените знак вычитания на сложение, а следующий за ним знак измените на противоположный. Затем следуйте инструкциям по добавлению. Например:
Замените знак вычитания на сложение, а следующий за ним знак измените на противоположный. Затем следуйте инструкциям по добавлению. Например: Умножение и деление: один и тот же знак, положительный результат
 При делении числа на другое число с тем же знаком частное (ответ) положительно. Например:
При делении числа на другое число с тем же знаком частное (ответ) положительно. Например: Умножение и деление: противоположный знак, отрицательный результат

Знаки сходства и отличия в сложении и вычитании
Понимание основ математики
 В отличие от других предметов, в математике нет нюансов или интерпретаций — она просто такая, какая есть! Для дополнительной математической практики ознакомьтесь с инструкциями по решению задач на деление в длину (с примерами). Вы также можете просмотреть различные типы чисел в математике перед следующим заданием по математике.
В отличие от других предметов, в математике нет нюансов или интерпретаций — она просто такая, какая есть! Для дополнительной математической практики ознакомьтесь с инструкциями по решению задач на деление в длину (с примерами). Вы также можете просмотреть различные типы чисел в математике перед следующим заданием по математике. Умножение отрицательных значений дает положительное значение
Когда мы умножаем:
Пример × два плюса дают плюс: 3 × 2 = 6 × два отрицательных числа дают положительный: (−3) × (−2) = 6 × отрицательное и положительное
делают отрицательное: (-3) × 2 = -6 × положительный и отрицательный
делают отрицательный: 3 × (−2) = −6 Знаки

Два Знака: Правила
два разных знака дают отрицательный знак» Пример: (−2) × (+5)
Пример: (−4) × (−3)
Почему при умножении двух отрицательных чисел получается положительное?

Направление

Играй с этим
Дополнительные примеры
Пример: Деньги
Сэм дает вам три купюры по 10 долларов: +3 × +10 = вы получаете 30 долларов Сэм дает вам три долга по 10 долларов: +3 × −10 = вы теряете 30 долларов Сэм берет у вас три купюры по 10 долларов: −3 × +10 = вы теряете 30 долларов Сэм берет у вас три долга по 10 долларов: −3 × −10 = вы получаете 30 долларов Пример: видео с бегущими людьми
Люди бегут вперед, но видео назад :
Люди бегут Назад , Видео Нормально:
Люди Бегут Назад , но Видео в Обратно : Пример: уровень в резервуаре растет/падает
 Сколько воды было в баке 3 дня назад ?
Сколько воды было в баке 3 дня назад ? Таблица умножения
× 1 2 3 4 1 1 2 3 4 2 2 4 6 8 3 3 6 9 12 4 4 8 12 16 × 1 2 3 4 -4 -4 -8 -12 -16 -3 -3 -6 -9 -12 -2 -2 -4 -6 -8 -1 -1 -2 -3 -4 0 0 0 0 0 1 1 2 3 4 2 2 4 6 8 3 3 6 9 12 4 4 8 12 16  Получая 4 больше каждый раз.
Получая 4 больше каждый раз. × -4 -3 -2 -1 0 1 2 3 4 -4 16 12 8 4 0 -4 -8 -12 -16 -3 12 9 6 3 0 -3 -6 -9 -12 -2 8 6 4 2 0 -2 -4 -6 -8 -1 4 3 2 1 0 -1 -2 -3 -4 0 0 0 0 0 0 0 0 0 0 1 -4 -3 -2 -1 0 1 2 3 4 2 -8 -6 -4 -2 0 2 4 6 8 3 -12 -9 -6 -3 0 3 6 9 12 4 -16 -12 -8 -4 0 4 8 12 16  Получая 4 больше каждый раз.
Получая 4 больше каждый раз. Как насчет умножения 3 или более чисел вместе?
Пример. Что такое (−2) × (−3) × (−4) ?
Умножение отрицательных чисел — знаки, примеры, правила, решенные примеры и часто задаваемые вопросы
 Существуют правила сложения, вычитания, умножения или деления положительных и отрицательных чисел.
Существуют правила сложения, вычитания, умножения или деления положительных и отрицательных чисел. Они могут использовать его для проверки перед экзаменами или для изучения темы.
Они могут использовать его для проверки перед экзаменами или для изучения темы. Знаки

Правила умножения отрицательных чисел
Плюс Times Plus is Plus
 )
) Минус Умножить Минус равно Плюс
Плюс умножить на минус = минус
Минус Умножить на плюс минус
Деление отрицательных чисел
 От двух чисел, участвующих в этом делении, зависит, будет ли ответ отрицательным. Ответ также будет отрицательным, если только одно из чисел отрицательное. Результат будет положительным, если оба числа отрицательны.
От двух чисел, участвующих в этом делении, зависит, будет ли ответ отрицательным. Ответ также будет отрицательным, если только одно из чисел отрицательное. Результат будет положительным, если оба числа отрицательны.0504
What happens when we Умножать негативы с помощью матриц?
 Отрицательное значение матрицы получается путем ее умножения на -1.
Отрицательное значение матрицы получается путем ее умножения на -1. Решенные примеры
Заключение

Почему студенты должны присоединиться к Веданту?
Видео-урок: Порядок действий: Отрицательные числа
Стенограмма видео
 Отрицательные пять, умноженные на отрицательные семь, дают положительное число 35,9.0003
Отрицательные пять, умноженные на отрицательные семь, дают положительное число 35,9.0003
 И на самом деле, наш расчет не включает ничего из этого. Затем мы выполняем любое умножение или деление. Опять же, в расчете их нет. Однако необходимо выполнить некоторые дополнительные вычитания. Мы заменяем отрицательное число три минус два, бит, который мы вычислили ранее, на отрицательное значение.
пять. Помните, что в противном случае мы сохраняем вычисления в том же порядке. Итак, мы собираемся оценить минус пять минус три.
И на самом деле, наш расчет не включает ничего из этого. Затем мы выполняем любое умножение или деление. Опять же, в расчете их нет. Однако необходимо выполнить некоторые дополнительные вычитания. Мы заменяем отрицательное число три минус два, бит, который мы вычислили ранее, на отрицательное значение.
пять. Помните, что в противном случае мы сохраняем вычисления в том же порядке. Итак, мы собираемся оценить минус пять минус три. Так или иначе, мы бы начали с вычисления минус три минус два, а затем
вычли из этого три.
Так или иначе, мы бы начали с вычисления минус три минус два, а затем
вычли из этого три.
 И довольно просто умножить на 10. Мы также знаем, что отрицательное число, умноженное на другое отрицательное число, дает
положительный. Итак, минус пять раз минус два тоже плюс 10.
И довольно просто умножить на 10. Мы также знаем, что отрицательное число, умноженное на другое отрицательное число, дает
положительный. Итак, минус пять раз минус два тоже плюс 10. И когда мы это делаем, мы создаем пробел, который заполняем нулем. Таким образом, отрицательное число 361, умноженное на 10, равно отрицательному числу 3610. Таким образом, ответ на отрицательное число 19умножить на 19 умножить на минус пять раз на минус два
отрицательный 3610.
И когда мы это делаем, мы создаем пробел, который заполняем нулем. Таким образом, отрицательное число 361, умноженное на 10, равно отрицательному числу 3610. Таким образом, ответ на отрицательное число 19умножить на 19 умножить на минус пять раз на минус два
отрицательный 3610. Прибавление минуса равносильно вычитанию плюса. Итак, 13 прибавить минус 19 — это то же самое, что 13 минус 19. И это минус шесть. Мы заменяем выражение в наших скобках на минус шесть, гарантируя, что мы
держите наш вопрос в том же порядке. И получается четыре минус минус шесть.
Прибавление минуса равносильно вычитанию плюса. Итак, 13 прибавить минус 19 — это то же самое, что 13 минус 19. И это минус шесть. Мы заменяем выражение в наших скобках на минус шесть, гарантируя, что мы
держите наш вопрос в том же порядке. И получается четыре минус минус шесть. что делаем и в каком порядке. Итак, давайте вспомним, что означают буквы. Первая буква обозначает скобки или квадратные скобки. Мы выполняем любые вычисления внутри пары круглых скобок. Теперь, если в этих скобках есть довольно сложная задача, мы еще раз
посмотрите, чтобы выполнить порядок операций над этим битом.
что делаем и в каком порядке. Итак, давайте вспомним, что означают буквы. Первая буква обозначает скобки или квадратные скобки. Мы выполняем любые вычисления внутри пары круглых скобок. Теперь, если в этих скобках есть довольно сложная задача, мы еще раз
посмотрите, чтобы выполнить порядок операций над этим битом. E и I обозначают индексы или показатели степени, другими словами, нахождение степени
количество. Ну, у нас нет сил здесь. Следующие буквы обозначают умножение и деление. Теперь, если у нас есть более одного умножения или деления или умножения и
деления в одном и том же вычислении мы помним, что они имеют одинаковый старшинство или
такое же значение. И мы просто двигаемся слева направо. Мы начнем с вычисления 40, деленного на пять; это восемь. Итак, наш расчет теперь восемь раз три. Восемь раз три — это, конечно, 24. Итак, 21 минус минус 19.разделить на пять, умноженное на три, равно 24.
E и I обозначают индексы или показатели степени, другими словами, нахождение степени
количество. Ну, у нас нет сил здесь. Следующие буквы обозначают умножение и деление. Теперь, если у нас есть более одного умножения или деления или умножения и
деления в одном и том же вычислении мы помним, что они имеют одинаковый старшинство или
такое же значение. И мы просто двигаемся слева направо. Мы начнем с вычисления 40, деленного на пять; это восемь. Итак, наш расчет теперь восемь раз три. Восемь раз три — это, конечно, 24. Итак, 21 минус минус 19.разделить на пять, умноженное на три, равно 24. Первая буква P или B обозначает скобки или квадратные скобки соответственно. Начнем с выполнения любого вычисления внутри пары круглых скобок. Здесь семь плюс минус два. Теперь, конечно, добавить минус то же самое, что вычесть плюс. Таким образом, семь плюс минус два — это то же самое, что семь минус два. И это, конечно, равно пяти. Поэтому в нашем расчете мы заменяем семь плюс минус два на пять. И теперь это трижды минус четыре в квадрате минус пять.
Первая буква P или B обозначает скобки или квадратные скобки соответственно. Начнем с выполнения любого вычисления внутри пары круглых скобок. Здесь семь плюс минус два. Теперь, конечно, добавить минус то же самое, что вычесть плюс. Таким образом, семь плюс минус два — это то же самое, что семь минус два. И это, конечно, равно пяти. Поэтому в нашем расчете мы заменяем семь плюс минус два на пять. И теперь это трижды минус четыре в квадрате минус пять. Таким образом, мы заменяем минус четыре в квадрате на 16. Теперь наш расчет равен трижды 16 минус пять.
Таким образом, мы заменяем минус четыре в квадрате на 16. Теперь наш расчет равен трижды 16 минус пять.
Модули тема: Модули — Математика — Теория, тесты, формулы и задачи
Модули — Математика — Теория, тесты, формулы и задачи
Оглавление:
Основные теоретические сведения
Базовые сведения о модуле
Некоторые методы решения уравнений с модулями
Wasaby Framework
theme можно было вычислить путь до соответствующего CSS-файла. Т.к. контролы распределены между модулями приложения СБИС (см. Модуль s3mod), тема оформления также может быть распределена между модулями.${имя модуля, из которого темизируются контролы}-${имя темы}-themeControls будут созданы следующие модули с темами оформления:Controls-default-themeControls-retail-themeControls-cloud-themeControls-saby-themeretail:Controls-retail-themeExtControls-retail-themeRichEditor-retail-themeGraphs-retail-themeМодификации темы
retail определены несколько модификаций размеров элементов (маленький, средний и крупный), а также несколько модификаций цветовой гаммы (темная и светлая).retail будет создана следующая структура каталога для темизации модуля Controls:Controls-retail-theme:dark-large;dark-medium;light-large;light-medium;theme модификация указывается через символ __, что показано в следующем примере.<Controls.input:Text theme="retail__dark-large"/>Пример создания модуля темы оформления
theme.less, который должен быть расположен в корне модуля темы или папке модификации темы. В начале файла необходимо подключить тему оформления «по умолчанию» или тему оформления более высокого уровня, которая больше похожа на ту, которую необходимо создать.@import 'Controls-default-theme/theme'
@themeName: retail;
.controls_theme-@{themeName} {
--background-color: #273749;
--border-thickness: 2px;
--border-color: #6D8DB0;
--readonly_color: #4B688B;
}retail.Controls-retail-themeExtControls-retail-themeRichEditor-retail-themeGraphs-retail-themePrestashop: Как обновить темы и модули вручную?
unzip это над соответствующей папкой модулей ( /modules/acme/ )rsync его в /modules/acme ( rsync -trv /tmp/acme /modules )--deleterm -rf /modules/acme и cp -a /tmp/acme /modules/acme
Поделиться Источник ptmr.io 21 ноября 2017 в 19:26 2 ответа
1upgrades и файлах внутри модуля), вы можете распаковать его. Затем перейдите на страницу списка модулей в бэкэнде, и начнется обновление модуля. config.xml генерируется автоматически (повторно)и используется только для оптимизации загрузки списка модулей на одной и той же внутренней странице — это не влияет на поведение самого модуля.Похожие вопросы:
Как prestashop отображает модули
Prestashop копия темы не показана
prestashop 1.6 настройка темы по модулю
Переопределение prestashop отсутствует перевод модуля
Изменить домашнюю страницу PrestaShop
Prestashop модули/путь не найден
Пустые экраны администратора после обновления Prestashop с 1.7.4 до 1.7.6
Где я могу найти модули zipped Stock/Default Prestashop?
Создание пользовательской темы в Prestashop 1.7 (с помощью стартовой темы?)
Обновление модулей вручную на Prestashop 1.7Создание учебных модулей | Справка Blackboard
Создание учебного модуля и добавление содержимого
Навигация по учебному модулю
Добавление папок в учебные модули
Модуль и тема оформления «Версия для слабовидящих»
1) Не выбрана тема в /admin/appearance/settings в Drupal 7 или /admin/config/user-interface/visually_impaired_module в Drupal 8
2) Библиотека jQuery подключаемая из каталога с темой. Если вам нужна другая версия, отличная от той, что идет в ядре, используйте модуль jquery_update, а не подключайте самостоятельно!
3) Проверьте все подключаемые в теме JS-файлы. Народные «умельцы» любят подключать различные JS-файлы, которые часто написаны не по стандартам кодирования Drupal и приводят к ошибке работы других модулей (хотя сами работают).
Скачать тему можно с официальной страницы проектаimport — JavaScript | MDN
строгом режиме независимо от того, объявляете ли вы их как таковые или нет. Для работы инструкции во встроенных скриптах нужно прописать у тэга script type="module".import(), который не требует скриптов с типом «module«.nomodule тега script.import defaultExport from "module-name";
import * as name from "module-name";
import { export } from "module-name";
import { export as alias } from "module-name";
import { export1 , export2 } from "module-name";
import { export1 , export2 as alias2 , […] } from "module-name";
import defaultExport, { export [ , […] ] } from "module-name";
import defaultExport, * as name from "module-name";
import "module-name";
import("/module-name.js").then(module => {…}) // Динамический импорт
defaultExportmodule-name.js файлу модуля без указания расширения .js. Некоторые сборщики могут разрешать или даже требовать использования расширения; проверяйте своё рабочее окружение. Допускаются только строки с одиночными или двойными кавычками.nameexport, exportNalias, aliasNname это имя локального объекта, который будет использован как своего рода пространство имён, ссылающееся на импортируемые значения. Параметры export определяют отдельные именованные значения, в то время как import * as name импортирует все значения. Примеры ниже объясняют синтаксис.Импорт всего содержимого модуля
myModule в текущую область видимости, содержащую все экспортированные значения из модуля, находящегося в файле /modules/my-module.js.import * as myModule from '/modules/my-module.js';doAllTheAmazingThings(), вы можете вызвать его так:myModule.doAllTheAmazingThings();Импорт единичного значения из модуля
myExport, которое было экспортировано из модуля my-module либо неявно (если модуль был экспортирован целиком), либо явно (с использованием инструкции export), позволяет вставить myExport в текущую область видимости.import {myExport} from '/modules/my-module.js';Импорт нескольких единичных значений
foo и bar в текущую область видимости.import {foo, bar} from '/modules/my-module.js';Импорт значений с использованием более удобных имён
shortName в текущую область видимости.import {reallyReallyLongModuleExportName as shortName}
from '/modules/my-module.js';Переименование нескольких значений в одном импорте
import {
reallyReallyLongModuleExportName as shortName,
anotherLongModuleName as short
} from '/modules/my-module.js';Импорт модуля для использования его побочного эффекта
import '/modules/my-module.js';
Импорт значения по умолчанию
export (будь то объект, функция, класс или др.). Инструкция import затем может быть использована для импорта таких значений.import myDefault from '/modules/my-module.js';
import myDefault, * as myModule from '/modules/my-module.js';
import myDefault, {foo, bar} from '/modules/my-module.js';
Импорт переменных
my-module.js
export let a = 2;
export let b = 3;
main.js
import {a, b} from '/modules/my-module.js';
a = 5;
b = 6;
my-module.js
export let obj = {a:2, b:4};
main.js
import {obj} from '/modules/my-module.js';
obj.a = 1;
obj.b = 4;import хранит именно ссылки на значения, экспортированные из внешнего модуля, то это можно использовать как замыкания.Динамический импорт
import можно использовать как функцию для динамического импорта модулей. Вызов import() возвращает Promise.import('/modules/my-module.js')
.then(module => {
})
awaitlet module = await import('/modules/my-module.js');Function.prototype и, как следствие, его невозможно использовать вместе с методами .call, .apply и .bind Модуль: file.js
function getJSON(url, callback) {
let xhr = new XMLHttpRequest();
xhr.onload = function () {
callback(this.responseText)
};
xhr.open('GET', url, true);
xhr.send();
}
export function getUsefulContents(url, callback) {
getJSON(url, data => callback(JSON.parse(data)));
}
Основной код: main.js
import { getUsefulContents } from '/modules/file.js';
getUsefulContents('http://www.example.com',
data => { doSomethingUseful(data); });Динамический импорт
import() также может использоваться совместно с await.const main = document.querySelector("main");
for (const link of document.querySelectorAll("nav > a")) {
link.addEventListener("click", e => {
e.preventDefault();
import('/modules/my-module.js')
.then(module => {
module.loadPageInto(main);
})
.catch(err => {
main.textContent = err.message;
});
});
}Тематические модули учебного плана занятий ресурсного центра по теме «Построение системы оценки и управления качеством образования в образовательном учреждении в условиях внедрения ФГОС»
Тематические модули учебного плана занятий ресурсного центра по теме «Построение системы оценки и управления качеством образования в образовательном учреждении в условиях внедрения ФГОС»
Увеличить масштаб Сtrl + «+» |
Уменьшить масштаб Сtrl + «−» |
Установить исходный масштаб (сбросить настройки) Сtrl + «0»
Материалы охватывают ряд тематических модулей учебного плана занятий ресурсного центра, таких как:
• Измерение и оценка качества образования в образовательном учреждении.
• Мониторинг качества образования.
• Управление качеством образования для ОУ.
• Обучение педагогического коллектива работе в системе оценки качества образования.
Авторы-разработчики: Мардер Л.М. — директор Гимназии, Тетерятникова Н.Г., Иванова О.М. — заместители директора Гимназии, Голунова О.Г. — психолог Гимназии, Немирова Н.В., к.с.н. — доцент кафедры европейских исследований СПбГУ, Трофимова С.Ю., к.п.н. — сотрудник СПб ЦОКОиИТ, Беспалова О.Г., Семенова Н.Н., Вдонина С.А. — учителя Гимназии.
Научный руководитель: Фрадкин В.Е., к.п.н. — заместитель директора СПб ЦОКОиИТ по науке.
Руководитель от Гимназии: Юркова Т.А., к.п.н. — заместитель директора Гимназии по научно-методической работе. (установка модулей) — Opinion Документация по теме WordPress
Шаг 1 — создайте новую страницу
Шаг 2 — установите домашнюю страницу как статическую
Шаг 3 — вернитесь к странице управления модулями
Модули
Модули сообщений
Текстовые модули
Модули категорий
Авторские модули
Разбиение на страницы
Бонусный совет
prestashop — Для чего используется папка «themes» модуля?
/ modules / , но не изменять существующие. Потому что, если вы обновите модуль, который вы изменили, все ваши изменения исчезнут. /themes/your_theme/modules/the_module/path_to_tpl.tpl , если существует переопределение этого шаблона. В противном случае он загрузит шаблон из каталога / modules ..css и файлы .js . themes внутрь модуля. _isTemplateOverloadedStatic () из класса Module , вызываемый каждый раз, когда нам нужен шаблон модуля:
/ *
** Управление шаблоном (отображение, перегрузка, кеш)
* /
защищенная статическая функция _isTemplateOverloadedStatic ($ module_name, $ template)
{
if (Инструменты :: file_exists_cache (_PS_THEME_DIR_.'modules /'.$ имя_модуля.' / '. $ template)) {
вернуть _PS_THEME_DIR _. 'modules /'.$ имя_модуля.' / '. $ template;
} elseif (Tools :: file_exists_cache (_PS_THEME_DIR _. 'modules /'.$ имя_модуля.' / views / templates / hook /'.$ template)) {
вернуть _PS_THEME_DIR _. 'modules /'.$ имя_модуля.' / views / templates / hook /'.$ template;
} elseif (Tools :: file_exists_cache (_PS_THEME_DIR _. 'modules /'.$ имя_модуля.' / views / templates / front /'.$ template)) {
вернуть _PS_THEME_DIR _. 'modules /'.$ имя_модуля.' / views / templates / front / '.$ template;
} elseif (Tools :: file_exists_cache (_PS_MODULE_DIR _. $ module_name. '/ views / templates / hook /'.$ template)) {
вернуть ложь;
} elseif (Tools :: file_exists_cache (_PS_MODULE_DIR _. $ module_name. '/ views / templates / front /'.$ template)) {
вернуть ложь;
} elseif (Tools :: file_exists_cache (_PS_MODULE_DIR _. $ module_name. '/'. $ template)) {
вернуть ложь;
}
return null;
}
themes внутри вашего модуля при загрузке шаблона. тем и модулей сообщества | UW Drupal Users Group
UW Auth (через mod_shib и shibd) 8 iSchool Модуль AuthenticationServiceProvider, который использует Shibboleth через Apache mod_shib и shibd через переменные среды. UW Auth (через группы UW или Active Directory) 8 DEOHS Обеспечивает аутентификацию с использованием Shibboleth и автоматическое назначение ролей через группы UW или Active Directory.Требуется, чтобы Apache и mod_shib были настроены для предоставления атрибута uwnetid. UW Раздача 8 Колледж искусств и наук (патчи приветствуются) Встраивает формы предоставления онлайн-пожертвований UW Advancement на ваш сайт. Добавляет настраиваемые блоки, которые можно разместить на любой странице, чтобы включить форму подачи, с вариантами типов фондов, кодами распределения, кодами апелляции и т. Д. Отправьте письмо Bitbucket на адрес [email protected], чтобы запросить доступ к этому модулю. Группы UW 7 iSchool Сопоставляет группы UW с ролями Drupal с помощью веб-службы групп UW.Для авторизации вашего сервера для подключения к GWS требуется некоторая конфигурация на стороне сервера. UW Marketo 7, 8 Колледж искусств и наук (патчи приветствуются) UW Trumba 7, 8 Колледж искусств и наук (патчи приветствуются) Модули — Документация по темам — maka Agency
Типы модулей
Некоторые модули раздела также позволяют иметь вкладки, фильтры, оглавление и другие интерактивные функции. Общие опции модуля
Это текст над основным заголовком.
Основное название
Различные стили заголовка, от h2 до h5.
Текст под заголовком. Часто используется как описательный текст
Светлая или темная цветовая схема.Светлая схема создает светлый цвет фона и темный цвет текста. Темная схема создает темный цвет фона и светлый цвет текста. Значения цвета берутся из основного CSS-файла.
Центрирует все содержимое, включая выравнивание текста.
Настройте здесь свой фон пользовательского модуля. Выберите один из следующих вариантов: сплошной цвет фона, фоновое изображение, фоновое видео и фоновый градиент.
Определите цвет фона с помощью шестнадцатеричного кода цвета или используйте палитру цветов HubSpot. Дополнительно можно настроить непрозрачность цвета фона.
Добавьте фоновое изображение с помощью средства выбора изображений HubSpot.
Также возможно добавление фонового видео. Вы можете вставлять собственные видео или видео на YouTube. Если видео настроено, оно перезапишет фоновое изображение.
Видео в формате * .mp4, размещенное на собственном сервере, можно встраивать с помощью средства выбора файлов:
Предоставляются все конфигурации, необходимые для двухцветного градиента: направление градиента, первый цвет градиента и второй цвет градиента.
Мы предусмотрели несколько предопределенных интервалов для каждого модуля: верхнее и нижнее заполнение.
Выберите между Стандартным (~ 135 пикселей), Нет (0 пикселей), Маленьким (40 пикселей), Средним (80 пикселей), Большим (140 пикселей) или Первым разделом с заголовком.
Используется первая секция с заголовком, если этот модуль является первым модулем после модуля заголовка. Это автоматически добавит больше интервала относительно высоты заголовка.
Многие модули POWER предлагают возможность изменения или перевода стандартных текстов.Стандартные тексты — это статические тексты, которые используются в коде модулей.
Субмодули
Sub Accordions
Определите набор аккордеонных элементов, которые вы хотите отобразить в одном столбце макета вашего веб-сайта, используя следующие параметры:
Каждый из наборов аккордеона в субмодуле можно стилизовать, используя следующие параметры: Блоки вспомогательных изображений
Определите здесь содержимое окна изображения, используя следующие параметры: Таблицы дополнительных цен
Дополнительные услуги
Sub Simple Listing
Дополнительная статистика
Подшаги
Подгруппа
Дополнительный видеоблок
Мини-модули
Мини-CTA
Выберите CTA, созданный с помощью редактора HubSpots CTA. Обратите внимание, что при создании CTA вам нужно будет выбрать «без стиля» в редакторе HubSpots CTA. Мини Иконка
Мини-тег
Модули секций
Секционные аккордеоны Раздел панировочных сухарей
Слайдер с логотипом клиента раздела
Раздел Стоимость компании
Редактируйте текст и фоновые изображения с помощью записей значений.
Раздел CTA
Выберите здесь предварительно определенный CTA. CTA можно настроить с помощью HubSpot CTA-Editor. Перейдите к
→ этой главе, чтобы узнать, как создавать призывы к действию HubSpot. После выбора призыва к действию его можно редактировать напрямую, нажав «Изменить призыв к действию».
Мы предоставили несколько макетов CTA. Конечно, каждый из макетов можно настроить, изменив цветовую тему и параметры фона. Макет устройства секции
Выберите графический макет, который вы хотите показать в этом модуле. Убедитесь, что у изображения прозрачный фон.
Если форма должна быть включена рядом с графикой, необходимо активировать переключатель формы. После активации выберите форму.
Здесь можно добавить один или несколько CTA с помощью средства выбора CTA:
Выберите, следует ли размещать изображение макета слева или справа.
Активация этого параметра разместит изображение макета на границе окна, как показано в примерах выше.
Фактическая ширина макета, показанная на веб-сайте, в процентах.
Обратите внимание, что это значение может быть установлено таким образом, чтобы графика перекрывала область содержимого. У некоторых графических макетов есть огромные тени на заднем плане. С помощью этого метода тень располагается за областью содержимого.
Для очень больших экранов мы включили этот параметр, чтобы ограничить размер макета.Убедитесь, что введено значение в пикселях.
Фактическая ширина области содержимого, отображаемой на веб-сайте, в процентах.
Активация этого переключателя скрывает графический макет на мобильных экранах. Форма раздела
Выберите форму, которая будет отображаться в этом модуле.
Чтобы зарегистрировать пользователей в рабочем процессе на основе отправки формы, установите критерии регистрации рабочего процесса, которые будут запускаться при отправке формы.Это делается непосредственно в самом инструменте рабочих процессов. Герой раздела
Выберите высоту — большую, обычную, маленькую и очень маленькую.
Активация этой опции предоставит очень большой макет, показанный ниже.
Этот переключатель увеличивает размер текста описания под заголовком в разделе героев
Наш шаблон также позволяет размещать основную информацию под заголовком героя, состоящую из значка и короткого текста. Блоки изображений сечения
Вы можете выбрать отображение категории «Все» и того, какая категория должна быть активной при загрузке страницы в настройках модуля. Слайдер изображения раздела
Если выбрано По одному , изображение отображается в тех же пропорциях, что и заданные.Опция Custom height предлагает дополнительно параметр высоты для принуждения изображения к определенной высоте. Схема разреза
Мы рекомендуем Snazzy Maps, потому что вы можете легко настроить свою карту, добавить собственный стиль, маркеры и т. Д. Разделение мультимедийного контента
Таблицы цен на секции
График раздела
Услуги отдела
Раздел Простой листинг
Можно определить заголовок, описание, ссылку элемента, дополнительную настраиваемую информацию (настраиваемый значок + настраиваемый текст) и категорию.
Вы можете выбрать отображение категории «Все» и того, какая категория должна быть активной при загрузке страницы в настройках модуля. Счетчик статистики раздела
1.Number: Число, которое будет отображаться
2. Суффикс: суффикс стат. Оставьте поле пустым, чтобы не указывать суффикс.
3. Заголовок: Название заголовка, отображаемое под номером. Шаги секции
1.Заголовок: Заголовок каждого шага
2. Описание: Подзаголовок / описание, которое показано под заголовком
3. Значок: Значок, показанный в макете значков этого модуля
4. Изображение: Изображение, показанное в макете изображения модуля этот модуль Команда секции
Каждого члена команды можно связать со страницей члена команды, которую мы также предоставили в этом шаблоне.
ВАЖНО: Если вы хотите использовать вкладки, не забудьте активировать макет вкладок ПЕРЕД созданием членов команды.
1. Имя
2. Изображение
3. Заголовок
4. Описание
5.Контакт: при активации этой опции отображается разнообразная контактная информация для «полной» версии макета.
6. Ссылка Раздел Отзывы
1. Имя
2. Должность
3. Изображение: может использоваться для портретных фотографий цитируемого человека или логотипа компании
4. Цитата Текст раздела
Текст с оглавлением / основной страницей оглавление
Размещение оглавления над содержимым
Временная шкала раздела
1. Заголовок
2. Описание
3. Изображение
4. Положение фона изображения: центр, слева, справа, сверху, снизу Раздел видео
1. Для самостоятельного размещения видео выберите видео * .mp4 через файловый менеджер HubSpot.
Убедитесь, что размер файла не слишком велик. Общее практическое правило — продолжать уменьшать размер файла до тех пор, пока он не начнет заметно ухудшаться. Попробуйте экспортировать видео в разрешении 720p и с битрейтом менее 700 кб / с (желательно 500 кб / с). Секционные видеобоксы
Вы можете выбрать отображение категории «Все» и того, какая категория должна быть активной при загрузке страницы в настройках модуля.: модули, темы и шаблоны макетов
Существует три вида надстроек для вашего Заставки: модули, темы и шаблоны макетов.
Модули
шаблоны
Шаблоны макетов
Шаблоны макетов Книжная навигация
Тематических модулей осознанной практики — Наш подход — Осознанная практика
URMC / Семейная медицина / Осознанная практика / Наш подход / Тематические модули осознанной практики Drupal Enterprise 8 и 9: Включение темы и модулей Folwell на существующем сайте Drupal 8 | IT @ UMN
Заявление об ограничении ответственности
Включить тему Folwell
Определить текущую тему
Перейти на тему Folwell
Включить модули Folwell
Дополнительная информация
Модули свойства: Основные свойства модуля действительного числа
Модули — Математика — Теория, тесты, формулы и задачи
03. Модули
Оглавление:
Основные теоретические сведения
Базовые сведения о модуле
 ..
..Некоторые методы решения уравнений с модулями
 Это условие нужно дописать в качестве общего ограничения для всего примера. Тогда получим систему:
Это условие нужно дописать в качестве общего ограничения для всего примера. Тогда получим систему:
Как успешно подготовиться к ЦТ по физике и математике?
 Последнему научиться можно только решив тысячи задач.
Последнему научиться можно только решив тысячи задач. Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.
Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.Нашли ошибку?
Модуль «МойСклад». Свойства, описание, активность товара
 5
5
Рисунок 1.
 Это нужно, если описание к товару добавляется на стороне «Магазина».
Это нужно, если описание к товару добавляется на стороне «Магазина».
Рисунок 2.
Рисунок 3. Необходимо создать «Вес» через дополнительное поле и указать название этого поля в поле на стороне модуля в магазине. В данном случае вес будет загружен в карточку товара на стороне магазина в стандартное поле «Вес».
Необходимо создать «Вес» через дополнительное поле и указать название этого поля в поле на стороне модуля в магазине. В данном случае вес будет загружен в карточку товара на стороне магазина в стандартное поле «Вес». На стороне модуля необходимо прописать название поля и на стороне «МойСклад» прописать как дополнительное поле у товаров, название может быть произвольным, тип — дробное число.
На стороне модуля необходимо прописать название поля и на стороне «МойСклад» прописать как дополнительное поле у товаров, название может быть произвольным, тип — дробное число.
Рисунок 4.Другие статьи по теме
 Интернет-магазин заполнен, МойСклад пустой
Интернет-магазин заполнен, МойСклад пустойКак мы можем улучшить статью?
Не нашли нужную статью?

Дать определение модуля комплексного числа. Доказать свойства модуля. — КиберПедия
 ..
..
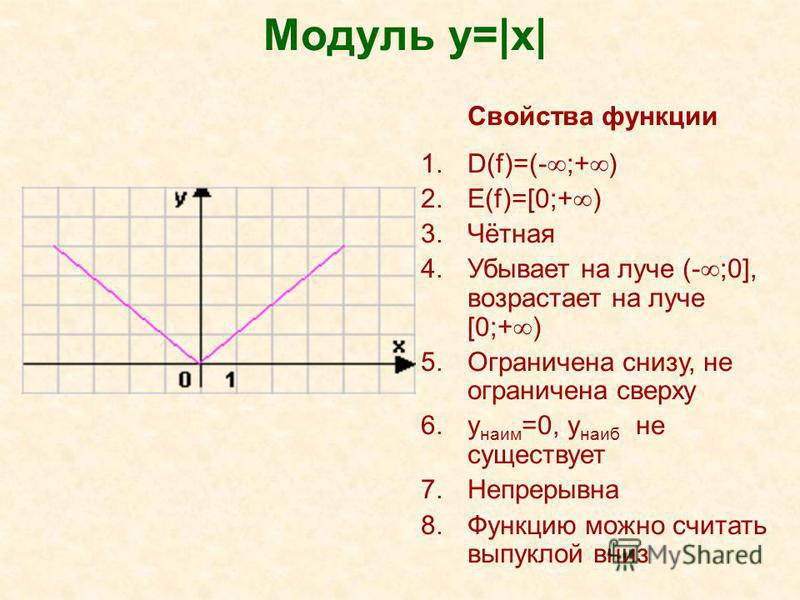 Комплексным числомz=x+iy называется упорядоченная пара действительных чисел : .
Комплексным числомz=x+iy называется упорядоченная пара действительных чисел : . 1) По предыдущей теореме имеем:
1) По предыдущей теореме имеем: Тогда точка имеет декартовыекоординаты , а и искомое расстояниемежду ними вычисляется по формуле (14), ч.т.д.
Тогда точка имеет декартовыекоординаты , а и искомое расстояниемежду ними вычисляется по формуле (14), ч.т.д. Поменяв местами и , получаем
Поменяв местами и , получаемАбсолютное значение (Модуль), Определение модуля
1.
 2.1 Определение Абсолютное значение или модуль действительного числа a (обозначается как |a|) определяется как
2.1 Определение Абсолютное значение или модуль действительного числа a (обозначается как |a|) определяется как
|a| = a если а ≥ 0
|a| = -a если а
|5| = 5 Так как 5 > 0
|-4| = -(-4) = 4 Так как -4
|0| = 0 Так как 0 ≥ 0
|a| есть не отрицательным числом для всех значений a и
-|a|≤ a ≤ |a| Если
a является негативным тогда -a позитивно и +a отрицательное!!!
Решите уравнение |x-3|=4
Решение
Уравнение имеет 2 решения: -1 и 7. x-3= 4 или -(x-3)= 4
x-3= -4
x= -1
Решите уравнение |3x-2|=|5x+4|
Уравнение имеет 2 решения: -3 и $-\frac{1}{4}$. 3x-2 = 5x+4
3x-5x = 4+2
-2x = 6
x = -3 или 3x-2 = -(5x+4)
. .
.
.
x = $-\frac{1}{4}$
КВАДРАТНЫЕ КОРНИ И МОДУЛИ
b2 = a
(3)2 = 9
so b = 3
но!!!
(-3)2 = 9 то есть b = -3
ТЕОРЕМА 1.2.2
Для любого действительного числа a
√a2 = |a|
e.g.
√(-4)2 = √16 = 4 = |-4|
Если a и b действительные числа, тогда
Из теоремы 1.2.2
Примеры -3| = |-6| = 6 = |2|.|3| = 6
-3| = |-6| = 6 = |2|.|3| = 6
Для n действительных чисел
a1, a2, a3,…an
(a) |a1 a2 …an| = |a1| |a2| …|an|
(b) |an| = |a|n
Геометрическое представление модуля
Где A и B есть точки с координатами a и b. Расстояние между A и B есть
$\text{расстояние}=\begin{cases}b-a \ \ \text{ ако } a b \\ 0 \ \ \text{ ако } a = b \end{cases}$
Если A и B — точки на координатной прямой с координатами a и b соответственно, тогда расстояние d между A и B
d = |b — a|
|x-a| (k>0)
Альтернативная форма -k
Искомые значения находятся (a-k, a+k)
Неравенство
|x-3|
можно выразить как
-4
добавление 3 к обеим частям приводит к
-1
Искомые значения находятся (-1,7)
Пример
Решите |x+4| ≥ 2
Объединение двух неравенств дает x+4 ≤ -2
x ≤ -6 x+4 ≥ 2
x≥ -2
(-∞ , -6] ∪ [-2 , +∞ )
НЕРАВЕНСТВО ТРЕУГОЛЬНИКА
|a+b| = |a| + |b|
например
если a = 2 и b = -3, тогда a+b = -1 и поэтому |a+b| = |-1| = 1
в то время как
|a|+|b| = |2|+|-3| = 2+3 = 5 поэтому |a+b| = |a|+|b|
1. 2.5 ТЕОРЕМА — (Неравенство треугольника)
2.5 ТЕОРЕМА — (Неравенство треугольника)
Если a b тогда |a+b| ≤ |a|+|b|
Доказательство
Так как для любого действительного числа a и b, мы знаем, что
-|a| ≤ a ≤ |a| and -|b| ≤ b ≤ |b|
-|a| ≤ a ≤ |a|
+
-|b| ≤ b ≤ |b|
______________
= -|a| + -|b| ≤ a+b ≤ |a|+|b|
______________________________________________
Сейчай мы имеем два случая:
определенно: a+b=|a+b|
Отсюда
|a+b| ≤ |a|+|b|
|a+b| = -(a+b)
или
(a+b) = -|a+b|
-(|a|+|b|) ≤ -|a+b|
Следует результат
←_______________________________→Как работает модуль «Дополнительные слои» в ПК-версии — Помощник 2ГИС
 Последние версии модулей можно бесплатно скачать на странице загрузок.
Последние версии модулей можно бесплатно скачать на странице загрузок.
Создание объектов и слоёв
Каталог

 Для удаления последней отмеченной точки при построении многоугольника нажмите «Esc» на клавиатуре.
Для удаления последней отмеченной точки при построении многоугольника нажмите «Esc» на клавиатуре.
Редактирование объектов и слоев
Функция управления времени
 05.2011 00:00. По истечению заданного времени отображение объекта на карте прекратится. Чтобы убрать период отображения, щелкните «Сбросить» в справочнике «Дополнительные слои» или во вкладке «Описание расширенных настроек объекта».
05.2011 00:00. По истечению заданного времени отображение объекта на карте прекратится. Чтобы убрать период отображения, щелкните «Сбросить» в справочнике «Дополнительные слои» или во вкладке «Описание расширенных настроек объекта».

<img src=»c:/pic/1.jpg»>
Настройки
Отрицательный модуль. Модуль числа (абсолютная величина числа), определения, примеры, свойства

История модуля числа или 6 интересных фактов о модуле числа
 Слово «модуль» произошел от латинского названия modulus, что в переводе обозначает слово «мера».
Слово «модуль» произошел от латинского названия modulus, что в переводе обозначает слово «мера».
2. Ввел в обращение этот термин ученик Исаака Ньютона — английский математик и философ Роджер Котс (1682 – 1716).
3. Великий немецкий физик, изобретатель, математик и философ Готфрид Лейбниц в своих работах и трудах использовал функцию модуля, которую он обозначил mod x .
4. Обозначение модуля было введено в 1841 году немецким математиком
Карлом Вейерштрассом (1815 — 1897).
5. При написании модуль обозначается с помощью символа: | |.
6. Еще одной версии термин «модуль» был введен в 1806 году французским
математиком по имени Жан Робер Аргáн (1768 — 1822). Но это не совсем так.
В начале девятнадцатого века математики Жан Робер Аргáн (1768 — 1822)
и Огюстен Луи Коши (1789 — 1857) ввели понятие «модуль комплексного числа»,
который изучается в курсе высшей математики.Решение задач на тему «Модуль числа»

| — (— 2) | = 2
в порядке убывания.
— |30| = -30
|-16| = 16
| -(-9) | = 9
|-16| > | -(-9) | > — | — 14| > — 21 > — |30|.Инструкция
 Модуль положительного числа равен самому числу. Модуль нуля равен нулю. То есть для любого числа n, которое больше либо равно нулю, будет справедлива следующая формула |n| = n. Например, |15| = 15, то есть модуль числа 15 равен 15-ти.
Модуль положительного числа равен самому числу. Модуль нуля равен нулю. То есть для любого числа n, которое больше либо равно нулю, будет справедлива следующая формула |n| = n. Например, |15| = 15, то есть модуль числа 15 равен 15-ти. Кроме того, |a — b| = |b — a|, так как расстояние от точки a до точки b и расстояние от b до a равны друг другу. Например, |25 — 5| = |5 — 25|, то есть |20| = |- 20|.
Кроме того, |a — b| = |b — a|, так как расстояние от точки a до точки b и расстояние от b до a равны друг другу. Например, |25 — 5| = |5 — 25|, то есть |20| = |- 20|.Модуль комплексного числа.
Свойства модуля комплексных чисел.
Свойства модуля — документация Lmod 8.
 7.13
7.13 add_property("ключ", "значение")
значение ключа свойства добавления
Файл свойств: lmodrc.lua
 lua (по умолчанию /etc/lmod/lmodrc.lua)
lua (по умолчанию /etc/lmod/lmodrc.lua) local i18n = require("i18n")
пропТ = {
арка = {
validT = {микрофон = 1, разгрузка = 1, GPU = 1,},
дисплей Т = {
["mic:offload"] = { short = "(*)", color = "blue", full_color = false, doc = "создано для хоста, собственного MIC и разгрузки на MIC", },
["mic"] = { short = "(m)", color = "blue", full_color = false, doc = "создан для хоста и собственного MIC", },
["offload"] = { short = "(o)", color = "blue", full_color = false, doc = "построен только для разгрузки на MIC",},
["gpu"] = {short = "(g)", color = "red" , full_color = false, doc = "созданный для GPU",},
["gpu:mic"] = { short = "(gm)", color = "red" , full_color = false, doc = "изначально создан для MIC и GPU",},
["gpu:mic:offload"] = { short = "(@)", color = "red" , full_color = false, doc = "построено изначально для MIC и GPU и выгружается на MIC",},
},
},
состояние = {
validT = {экспериментальный = 1, тестовый = 1, устаревший = 1},
дисплей Т = {
экспериментальный = { короткий = "(E)", full_color = false, цвет = "синий", doc = i18n ("ExplM"), },
testing = { short = "(T)", full_color = false, color = "green", doc = i18n("TstM"), },
obsolete = { short = "(O)", full_color = false, color = "red", doc = i18n("ObsM"), },
},
},
лмод = {
действительныйT = {липкий = 1},
дисплей Т = {
sticky = {short = "(S)", color = "red", doc = i18n("StickyM"), }
},
},
статус = {
действительныйT = {активный = 1,},
дисплей Т = {
active = {short = "(L)", color = "желтый", doc = i18n("LoadedM")},
},
},
}
 Таблица — это общее название
хэш-таблица, словарь или ассоциативный массив. То есть хранит
пары ключ-значение. Это соглашение Lmod, что таблица называется с
завершающая буква T, чтобы напомнить нам, что это таблица.
Таблица — это общее название
хэш-таблица, словарь или ассоциативный массив. То есть хранит
пары ключ-значение. Это соглашение Lmod, что таблица называется с
завершающая буква T, чтобы напомнить нам, что это таблица. add_property("состояние","тестирование")
add_property("состояние","устаревшее")
 На
с другой стороны файл модуля может иметь два или более свойств.:
На
с другой стороны файл модуля может иметь два или более свойств.: add_property("state","testing")
add_property("lmod","липкий")
Таблицы
validT и displayT  поля в таблице управляют тем, как отображается свойство. За
пример:
поля в таблице управляют тем, как отображается свойство. За
пример: testing = { short = "(T)", full_color = false, color = "green", doc = i18n("TstM"), },
 Если значение
разделена двоеточием, тогда каждая строка между двоеточиями должна быть
действительные ключи.
Если значение
разделена двоеточием, тогда каждая строка между двоеточиями должна быть
действительные ключи. Свойства по умолчанию для модулей
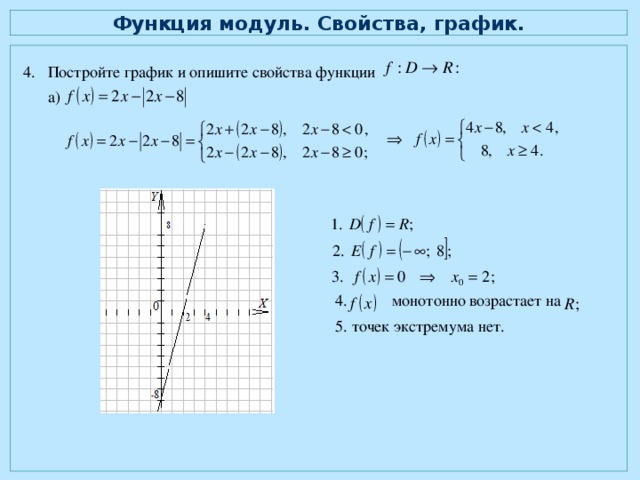 ХтмлДокумент, XmlDocument.
ХтмлДокумент, XmlDocument. «Повторное использование XModuleAttributes в TestCase»).
«Повторное использование XModuleAttributes в TestCase»).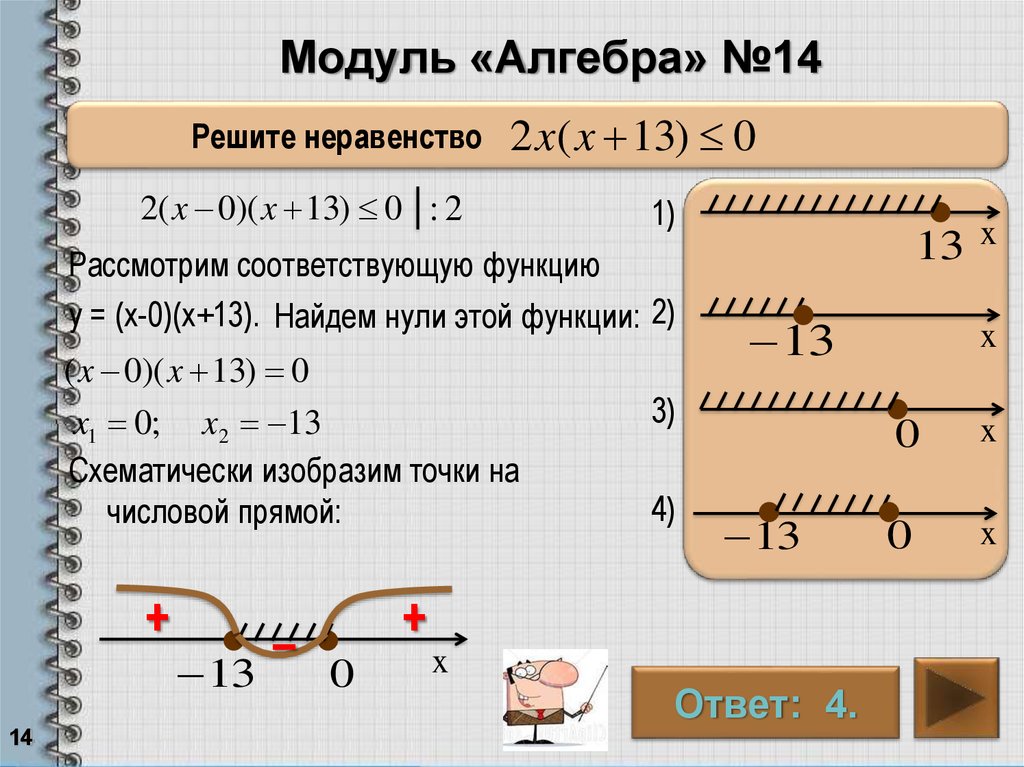 Может быть создано любое количество XTestStepValues.
Может быть создано любое количество XTestStepValues.

 д.). DataType указывает тип записи, указанный в поле Value TestStepValue.
д.). DataType указывает тип записи, указанный в поле Value TestStepValue. Затем это значение наследуется для специализаций и ссылок на модули (см. главу «Структура XModules»).
Затем это значение наследуется для специализаций и ссылок на модули (см. главу «Структура XModules»).
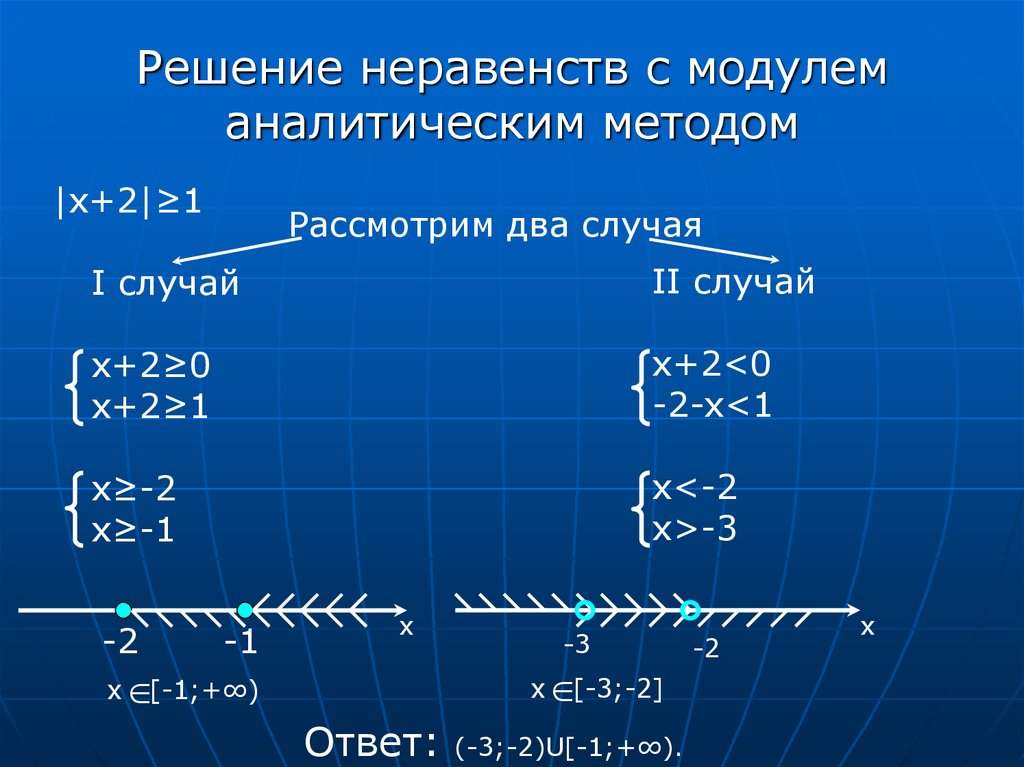 д.).
д.). «Значения TestStep, использование значений XTestStep»).
«Значения TestStep, использование значений XTestStep»). Абстрактные модули нельзя использовать в TestCase (см. главу «Обобщения и специализации»).
Абстрактные модули нельзя использовать в TestCase (см. главу «Обобщения и специализации»).
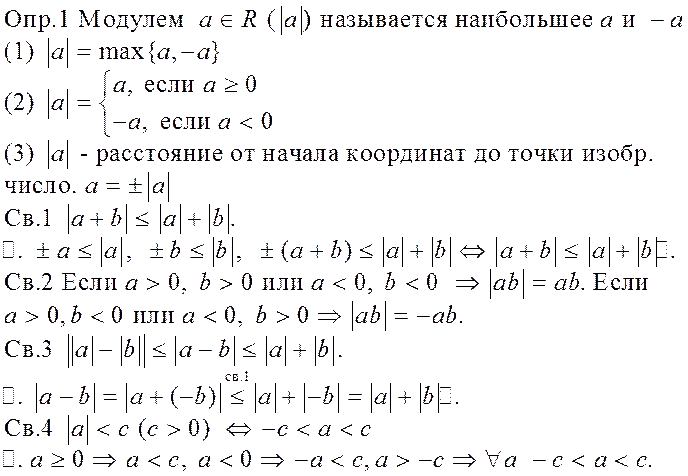
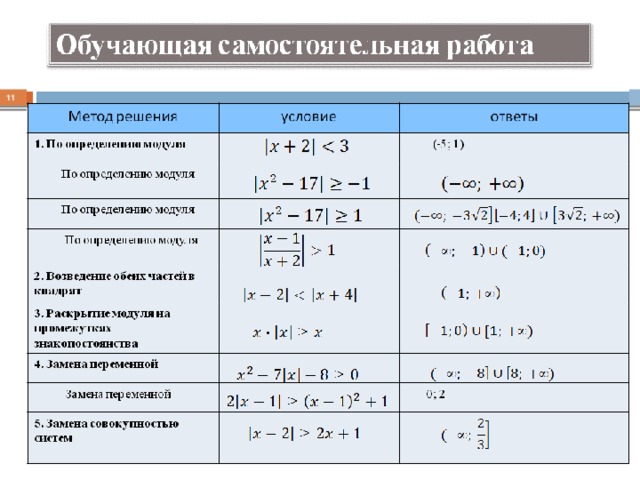 главу »
Назначить права пользователям или группам пользователей»).
главу »
Назначить права пользователям или группам пользователей»). Тип элемента управления (BusinessType) должен быть указан в качестве значения для этого свойства. Это никак не влияет на автоматизированное рулевое управление.
Тип элемента управления (BusinessType) должен быть указан в качестве значения для этого свойства. Это никак не влияет на автоматизированное рулевое управление. главу «Синхронизация — включить/отключить»).
главу «Синхронизация — включить/отключить»).
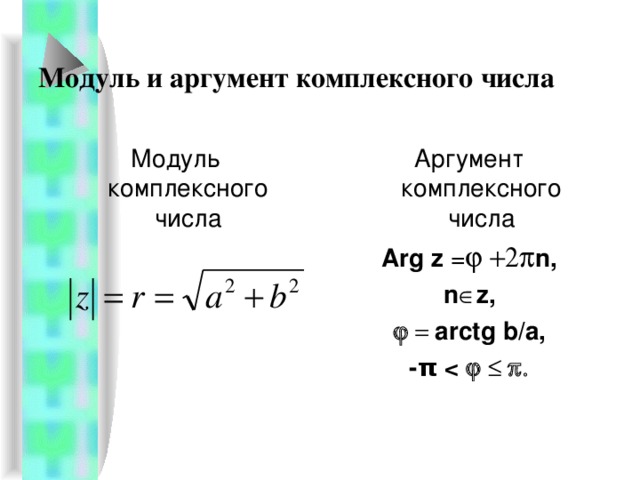 главу »
Назначение прав пользователям или группам пользователей»).
главу »
Назначение прав пользователям или группам пользователей»).

 03.2012)
03.2012) android — :minifyReleaseWithR8 завершается с ошибкой для библиотечных модулей без доступных значений свойств
Не удалось определить зависимости задачи ':analytics:minifyReleaseWithR8'.
 > Невозможно запросить значение этого свойства, так как оно не имеет доступного значения.
> Невозможно запросить значение этого свойства, так как оно не имеет доступного значения.
Файл соглашения Gradle с именем android-library.gradle.kts применяется ко всем модулям библиотеки:
defaultConfig {
целевойSdk = 32
ConsumerProguardFile("consumer-rules.pro")
}
скомпилироватьSdk = 32
defaultConfig {
минСдк = 26
testInstrumentationRunner = Config.testRunner
resourceConfigurations.addAll (Config.supportedLocales)
}
типы сборки {
getByName("релиз") {
isMinifyEnabled = истина
ndk.debugSymbolLevel = Config.debugSymbolLevel
}
getByName("отладка") {
isMinifyEnabled = ложь
ndk.debugSymbolLevel = Config.debugSymbolLevel
}
}
Модуль приложения
defaultConfig {
applicationId = Config. applicationId
целевойSdk = 32
код_версии = код_версии_конфигурации
имя_версии = Config.имя_версии
proguardFiles(
getDefaultProguardFile("proguard-android-optimize.txt"),
"proguard-rules.pro",
)
}
типы сборки {
отлаживать {
signingConfig = signingConfigs.getByName («отладка»)
versionNameSuffix = "-отладка"
исшринкресаурцес = ложь
}
выпускать {
isShrinkResources = истина
signingConfig = signingConfigs.getByName («релиз»)
}
}
applicationId
целевойSdk = 32
код_версии = код_версии_конфигурации
имя_версии = Config.имя_версии
proguardFiles(
getDefaultProguardFile("proguard-android-optimize.txt"),
"proguard-rules.pro",
)
}
типы сборки {
отлаживать {
signingConfig = signingConfigs.getByName («отладка»)
versionNameSuffix = "-отладка"
исшринкресаурцес = ложь
}
выпускать {
isShrinkResources = истина
signingConfig = signingConfigs.getByName («релиз»)
}
}
 Это помогло, но теперь мои библиотечные модули не обфусцированы, что не является приемлемым решением
Это помогло, но теперь мои библиотечные модули не обфусцированы, что не является приемлемым решением proguardFiles() библиотечных модулей и модуля приложения, чтобы он содержал, не содержал и содержал разные записи. Безрезультатно, если не включена минимизация, она не работает. gradle clean и прочие обычные приемы.
property(org.gradle.api.file.RegularFile, property(org.gradle.api.file.RegularFile, property(org.gradle.api.file .RegularFile, не определено))) Я понятия не имею, что это значит, к сожалению. buildFeatures {
билдконфиг = ложь
androidResources = false // виновник
}
Выглядит совершенно не связанным с R8, и из документации неясно, что именно он делает.
В строке документации написано «TBD», что не совсем полезно
Установка флага на true исправил сборку. Твой ответ
Зарегистрируйтесь или войдите в систему
Опубликовать как гость
Опубликовать как гость
свойств и модулей в TypeScript/Angular | Анкит Махешвари
 4 of this series, I recommend you to check this link → Constructors and Access modifiers in TypeScript
4 of this series, I recommend you to check this link → Constructors and Access modifiers in TypeScript частным и защитил члена вне класса с помощью объекта класса — смотрите ниже 👇 неверный код в строке №. 16 и 17 Попробуйте этот код сами, чтобы увидеть результат! частным и защищенным членам вне класса? Свойства позволяют нам получить доступ к закрытым членам вне класса, используя ключевое слово get и set ключевое слово ИЛИ методы getter() и setter(). Чтобы понять как — посмотрите код ниже.
 ..👇
..👇 getColor () и Getd () Методы Мы можем иметь доступ к Private и ATER 2 и ATER 2 и . . 23 и 25 Попробуйте этот код сами, чтобы увидеть результат! setColor() , мы можем изменить значение private Members в классе ( работает для защищено члены тоже ) — смотрите ниже 👇 в строке №. 22 попробуйте этот код сами, чтобы увидеть результат! цвета в «Оранжевый» из конструктора — смотрим ниже 👇 в строке №. 19 цвета с помощью метода draw. — смотрите ниже 👇 в строке №. 22 setColor("Red")
setColor("Red") draw.getColor() вернет обновленное значение «Красный» цвета — смотрите ниже 👇 в строке №. 24 Попробуйте этот код сами, чтобы увидеть результат! Запуск кода... посмотрите в терминале ниже👇 — начальное значение цвета (до изменения) и значение после изменения.
Попробуйте этот код сами, чтобы увидеть результат! , получаем и установить методов для доступа и изменения закрытых и защищенных членов класса. Теперь давайте сделаем то же самое, используя свойства… с помощью ключевого слова get и ключевого слова set путем замены методов getter() и setter() .
color_ как поле класса и color как свойство класса.) 55 Попробуйте этот код сами, чтобы увидеть результат! Запуск кода... Примечание 👇
color_ , используя свойство color — смотрим ниже👇 в строке №. 20 и 24. Также посмотрите на строку №. 11 , который возвращает значение color_ . color_ с помощью свойства color — смотрите ниже👇 в строке №. 22. Также посмотрите на строку №. 14 , который фактически устанавливает значение color_ . Попробуйте этот код сами, чтобы увидеть результат! Свойства — теперь, далее Модули 👇 main. ts
ts Итак, нам нужно разделить нашу большую программу на несколько файлов — поэтому мы используем Модули , чтобы разделить наш код для лучшей читабельности, понятности и удобства сопровождения .
.ts представляет собой модуль, в классе которого есть ключевое слово export . класса Draw из файла main.ts и переместили его в point.ts 9файл 0833. Посмотрите ниже👇 код (в прикрепленном изображении) export , чтобы разрешить этому классу Draw доступ за пределы файла point.ts . Draw в наш файл main.ts , чтобы использовать его. импорт и из ключевого слова .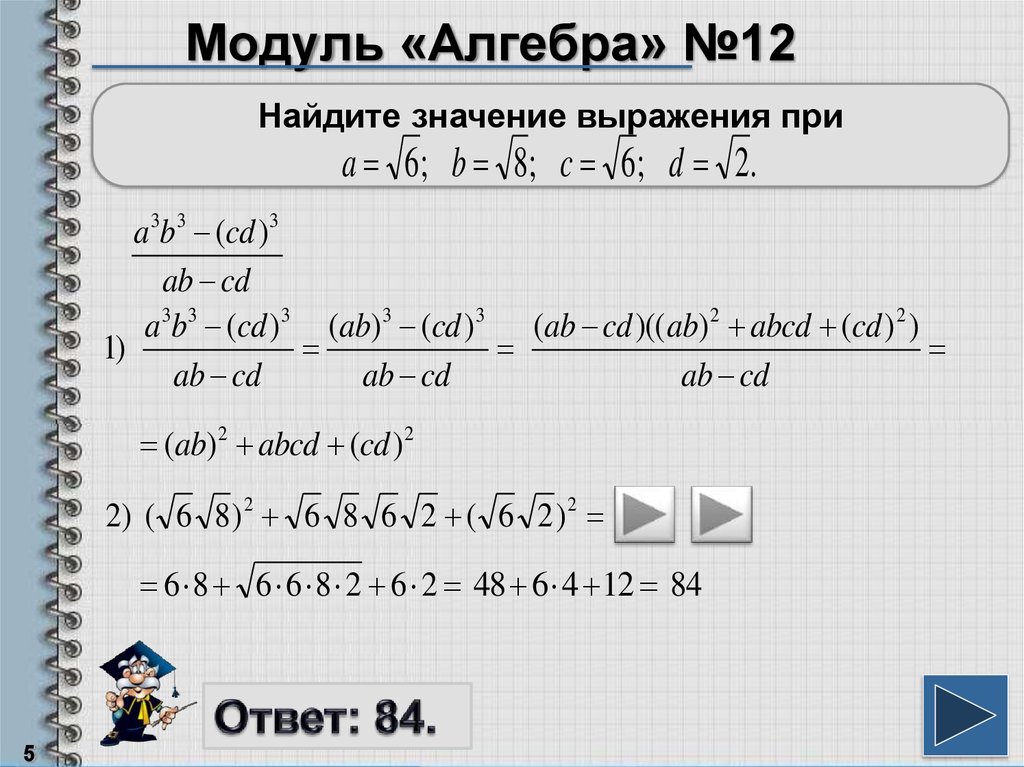
import { Draw } from "./point"; в фигурных скобках мы можем указать несколько классов, разделенных запятой, а после из ключевого слова мы помещаем ./ плюс имя модуля в кавычки. ./ означает текущий рабочий каталог, потому что оба файла main.ts и point.ts находятся в одном каталоге. --target es5 в своей команде, чтобы избавиться от ошибки : средства доступа доступны только при использовании ECMAScript 5 и выше . Команда для запуска этого кода: tsc --target es5 main.ts && node main.js
Попробуйте этот код сами, чтобы увидеть результат! Объявите свойства, используя ключевое слово get и ключевое слово set. Свойство выглядит как поле вне класса, но внутри это метод класса.
Мы используем модули для разделения большой программы на несколько файлов.
https:/
/medium.com/@AnkitMaheshwariIn Настройка отображения свойств модуля в зависимости от контекста - Commerce | Динамика 365
 В этом случае разработчик модуля может захотеть убедиться, что только те поля свойств, которые соответствуют контексту (то есть макету), отображаются в конструкторе сайтов, когда редактор страниц настраивает модуль.
В этом случае разработчик модуля может захотеть убедиться, что только те поля свойств, которые соответствуют контексту (то есть макету), отображаются в конструкторе сайтов, когда редактор страниц настраивает модуль. Зависимости схемы
Пример зависимостей схемы
 В качестве альтернативы, если для свойства макета установлено значение richTextWithImage , должны отображаться свойства featureRichText , featureImage и imageAlignment (но свойство featureText не должно отображаться).
В качестве альтернативы, если для свойства макета установлено значение richTextWithImage , должны отображаться свойства featureRichText , featureImage и imageAlignment (но свойство featureText не должно отображаться). {
"$type": "модуль контента",
"friendlyName": "Видимость конфигурации",
"имя": "конфиг-видимость",
"description": "Модуль проверки видимости конфигурации",
"categories": ["config-visibility"],
"теги": [""],
"действия данных": {
},
"конфигурация": {
"название продукта": {
"friendlyName": "Название продукта",
"description": "Название продукта.",
"тип": "строка"
}
},
"зависимые схемы": {
"название продукта": {
"характеристики": {
"подзаголовок": {
"тип": "строка",
"friendlyName": "Подзаголовок товара",
"description": "Подзаголовок продукта. "
}
},
"обязательно": ["название продукта"]
}
}
}
"
}
},
"обязательно": ["название продукта"]
}
}
}
Зависимости свойств
Пример зависимостей свойств
{
"$type": "модуль контента",
"friendlyName": "Характеристики продукта",
"имя": "характеристика продукта",
"description": "Модуль функций, используемый для выделения продукта.",
"конфигурация": {
"название продукта": {
"тип": "строка",
"friendlyName": "Название продукта",
"description": "Название продукта."
}
},
"зависимые схемы": {
"название продукта": {
"характеристики": {
"подзаголовок": {
"тип": "строка",
"friendlyName": "Подзаголовок продукта",
"description": "Подзаголовок продукта. "
}
},
"обязательно": ["название продукта"]
}
}
}
"
}
},
"обязательно": ["название продукта"]
}
}
}
Обработка конфликтов переопределения свойств
Пример файла определения модуля
{
"$type": "модуль контента",
"friendlyName": "Характеристики продукта",
"имя": "характеристика продукта",
"description": "Модуль функций, используемый для выделения продукта.",
"конфигурация": {
"макет": {
"friendlyName": "Макет текста",
"description": "Устанавливает желаемый вывод текста в виде простого текста или форматированного текста с изображениями. ",
"тип": "строка",
"перечисление": {
"plainTextOnly": "Только обычный текст",
"richTextWithImage": "Расширенный текст с изображением"
},
"по умолчанию": "Только обычный текст",
"область": "модуль",
"group": "Свойства макета"
}
}
}
{
"$type": "модуль контента",
"friendlyName": "Видимость конфигурации",
"имя": "конфиг-видимость",
"description": "Модуль проверки видимости конфигурации",
"categories": ["config-visibility"],
"теги": [""],
"действия данных": {
},
"конфигурация": {
"макет": {
"friendlyName": "Макет текста",
"description": "Устанавливает желаемый вывод текста в виде простого текста или форматированного текста с изображениями.",
"тип": "строка",
"перечисление": {
"plainTextOnly": "Только обычный текст",
"richTextOnly": "Только форматированный текст",
"richTextWithImage": "Расширенный текст с изображением"
},
"по умолчанию": "Только обычный текст",
"переопределить": правда
}
}
}
",
"тип": "строка",
"перечисление": {
"plainTextOnly": "Только обычный текст",
"richTextWithImage": "Расширенный текст с изображением"
},
"по умолчанию": "Только обычный текст",
"область": "модуль",
"group": "Свойства макета"
}
}
}
{
"$type": "модуль контента",
"friendlyName": "Видимость конфигурации",
"имя": "конфиг-видимость",
"description": "Модуль проверки видимости конфигурации",
"categories": ["config-visibility"],
"теги": [""],
"действия данных": {
},
"конфигурация": {
"макет": {
"friendlyName": "Макет текста",
"description": "Устанавливает желаемый вывод текста в виде простого текста или форматированного текста с изображениями.",
"тип": "строка",
"перечисление": {
"plainTextOnly": "Только обычный текст",
"richTextOnly": "Только форматированный текст",
"richTextWithImage": "Расширенный текст с изображением"
},
"по умолчанию": "Только обычный текст",
"переопределить": правда
}
}
}
Пример файла расширения определения модуля
{
"$type": "модуль контента",
"friendlyName": "Видимость конфигурации",
"имя": "конфиг-видимость",
"description": "Модуль проверки видимости конфигурации",
"categories": ["config-visibility"],
"теги": [""],
"действия данных": {
},
"конфигурация": {
"название продукта": {
"friendlyName": "Название продукта",
"description": "Название продукта. ",
"тип": "строка"
},
"макет": {
"friendlyName": "Макет текста",
"description": "Устанавливает желаемый вывод текста в виде простого текста или форматированного текста с изображениями.",
"тип": "строка",
"перечисление": {
"plainTextOnly": "Только обычный текст",
"richTextOnly": "Только форматированный текст",
"richTextWithImage": "Расширенный текст с изображением"
},
"по умолчанию": "Только обычный текст",
"переопределить": правда
}
},
"зависимые схемы": {
"название продукта": {
"характеристики": {
"подзаголовок": {
"тип": "строка",
"friendlyName": "Подзаголовок продукта",
"description": "Подзаголовок продукта."
}
},
"обязательно": ["название продукта"]
},
"макет": {
"один из": [
{
"характеристики": {
"макет": {
"перечисление": {
"Только обычный текст": "Только обычный текст"
}
},
"текст функции" : {
"тип": "строка",
"friendlyName": "Текст функции",
"description": "Заголовок основного текста для отображения в модуле.
",
"тип": "строка"
},
"макет": {
"friendlyName": "Макет текста",
"description": "Устанавливает желаемый вывод текста в виде простого текста или форматированного текста с изображениями.",
"тип": "строка",
"перечисление": {
"plainTextOnly": "Только обычный текст",
"richTextOnly": "Только форматированный текст",
"richTextWithImage": "Расширенный текст с изображением"
},
"по умолчанию": "Только обычный текст",
"переопределить": правда
}
},
"зависимые схемы": {
"название продукта": {
"характеристики": {
"подзаголовок": {
"тип": "строка",
"friendlyName": "Подзаголовок продукта",
"description": "Подзаголовок продукта."
}
},
"обязательно": ["название продукта"]
},
"макет": {
"один из": [
{
"характеристики": {
"макет": {
"перечисление": {
"Только обычный текст": "Только обычный текст"
}
},
"текст функции" : {
"тип": "строка",
"friendlyName": "Текст функции",
"description": "Заголовок основного текста для отображения в модуле. "
}
}
},
{
"характеристики": {
"макет": {
"перечисление": {
"ричтекстонли": "ричтекстонли"
}
},
"featureRichText": {
"тип": "богатый текст",
"friendlyName": "Текст функции",
"description": "Основной форматированный текст для отображения в модуле."
}
}
},
{
"характеристики": {
"макет": {
"перечисление": {
"богатый текст с изображением": "богатый текст с изображением"
}
},
"featureRichText": {
"тип": "богатый текст",
"friendlyName": "Текст функции",
"description": "Основной форматированный текст для отображения в модуле.
"
}
}
},
{
"характеристики": {
"макет": {
"перечисление": {
"ричтекстонли": "ричтекстонли"
}
},
"featureRichText": {
"тип": "богатый текст",
"friendlyName": "Текст функции",
"description": "Основной форматированный текст для отображения в модуле."
}
}
},
{
"характеристики": {
"макет": {
"перечисление": {
"богатый текст с изображением": "богатый текст с изображением"
}
},
"featureRichText": {
"тип": "богатый текст",
"friendlyName": "Текст функции",
"description": "Основной форматированный текст для отображения в модуле. "
},
"изображение функции" : {
"тип": "изображение",
"friendlyName": "Название функции",
"description": "Изображение для отображения в модуле."
},
"выравнивание изображения": {
"friendlyName": "Выравнивание изображения",
"description": "Устанавливает желаемое выравнивание изображения по левому или правому краю текста.",
"тип": "строка",
"перечисление": {
"левый": "левый",
"верно-верно"
},
"по умолчанию": "слева"
}
}
}
]
}
}
}
"
},
"изображение функции" : {
"тип": "изображение",
"friendlyName": "Название функции",
"description": "Изображение для отображения в модуле."
},
"выравнивание изображения": {
"friendlyName": "Выравнивание изображения",
"description": "Устанавливает желаемое выравнивание изображения по левому или правому краю текста.",
"тип": "строка",
"перечисление": {
"левый": "левый",
"верно-верно"
},
"по умолчанию": "слева"
}
}
}
]
}
}
}
Сценарии разрешения конфликтов

Обычные сценарии
Сценарий Ожидаемый результат Зависимость схемы используется только в файле определения модуля. Нет конфликтов между свойствами в зависимости схемы и файлом расширения определения модуля. Применена зависимость схемы. Зависимость схемы используется только в файле расширения определения модуля. Нет конфликтов между свойствами в зависимости схемы и файлом расширения определения модуля. Применена зависимость схемы. Зависимость схемы используется только в файле определения модуля. Существует конфликт между свойствами в зависимости схемы и файлом расширения определения модуля. Например, свойство A объявлено как в зависимости схемы файла определения модуля, так и в файле расширения определения модуля, который не имеет зависимости схемы. Произошла ошибка сборки. Зависимость схемы от одного и того же свойства используется как в файле определения модуля, так и в файле расширения определения модуля. 
Файл определения модуля имеет приоритет. Одно и то же свойство определено как в файле определения модуля, так и в файле расширения определения модуля. Файл определения модуля имеет приоритет. Сценарии переопределения
Сценарий Ожидаемый результат Одно и то же свойство определено как в файле определения модуля, так и в файле расширения определения модуля. Либо свойство override не задано для свойства в файле расширения определения модуля, либо для свойства override задано значение false . Файл определения модуля имеет приоритет. Зависимость схемы от одного и того же свойства используется как в файле определения модуля, так и в файле расширения определения модуля. override свойство имеет значение true для свойства в файле расширения определения модуля. 
Файл расширения определения модуля имеет приоритет. Зависимость схемы от одного и того же свойства используется как в файле определения модуля, так и в файле расширения определения модуля. Либо свойство override не задано для свойства в файле расширения определения модуля, либо для свойства override задано значение 9.0921 ложь . Файл определения модуля имеет приоритет. Одно и то же свойство определено как в файле определения модуля, так и в зависимости схемы файла расширения определения модуля. Для свойства override установлено значение true для свойства в файле расширения определения модуля. Файл расширения определения модуля имеет приоритет. Одно и то же свойство определено как в файле определения модуля, так и в зависимости схемы файла расширения определения модуля. Либо нет 9Свойство 0921 override установлено для свойства в файле расширения определения модуля, или свойство override имеет значение false . 
Файл определения модуля имеет приоритет. Дополнительные ресурсы
Помогите нам понять
Свойство сущности Jira (EAP)
jira:entityProperty запрашивает, чтобы Jira индексировала поля свойства объекта, чтобы сделать поля доступными для запросов в JQL.
Properties
Property Type Required Description key string 9[a-zA-Z0-9_-]+$ entityType строка выпуск пользователь проект issue propertyKey строка Да Ключ свойства объекта, из которого индексируются данные. значения PropertyValues Да Список полей в объекте JSON для индексации с типом каждого поля. 
Значения свойств
Property Type Required Description path string Yes {"label": {"color": "red", "text":"connect"}} допустимый путь, ссылающийся на color , равен этикетка.цвет . тип строка Да номер , который индексируется как число и позволяет упорядочивать диапазоны и выполнять поиск в поле.
текст , который токенизирует значение перед индексацией и позволяет искать слова. строка , которая индексируется как есть и позволяет искать только точную фразу. user , который индексируется как пользователь и позволяет осуществлять поиск на основе пользователей. Ожидаемое значение — строка идентификатора учетной записи Atlassian. date , который индексируется как дата и позволяет искать и упорядочивать диапазон дат. Ожидаемый формат даты – 9.0832 [ГГГГ]-[ММ]-[ДД] . Ожидаемый формат даты и времени: [ГГГГ]-[ММ]-[ДД]T[чч]:[мм] с необязательным смещением от UTC +/-[чч]:[мм] или Z за отсутствие смещения. searchAlias строка Имя, используемое для этого свойства в JQL. 
Пример
статистики , который определяется следующим образом:
1
2
{
"комментариев": 5,
"статусные переходы": 6,
"lastCommenter": "<идентификатор аккаунта>",
"blockedIssues": ["10000", "10001"]
}
jira:entityProperty , вы запрашиваете индексацию полей свойства объекта.
1
2 модуля
:
jira:entityProperty:
- ключ: "stats-property"
тип объекта: "проблема"
propertyKey: статистика
ценности:
- путь: комментарии
тип: число
searchAlias: commentCount
- путь: статусПереходы
тип: номер
searchAlias:transitionCount
- путь: последний комментатор
тип: пользователь
searchПсевдоним: lastCommenter
- путь: заблокированные проблемы
тип: строка
searchAlias: заблокированные проблемы
1
2
количество комментариев = 5
issue.

