Онлайн-калькулятор рабочих и календарных дней между двумя датам — Контур.Экстерн
Вы сможете посчитать:
- сколько календарных дней прошло между двумя заданными датами;
- сколько рабочих дней и часов в заданном вами периоде;
- сколько выходных дней было в заданном вами периоде.
Сдавайте электронную отчетность через интернет. Сервис Экстерн дарит вам 3 месяца бесплатно!
Как работать с калькулятором дней между двумя датами
Вам понадобятся всего два значения. В соответствующих полях калькулятора нужно указать дату начала и конца периода — день, месяц и год. Просто кликните по нужной ячейке левой клавишей мыши и выберите из списка нужный вариант.
Также следует задать количество рабочих часов в день. Например, у офисных работников стандартный рабочий день составляет 8 часов, а на производстве рабочая смена может длиться 10 часов. По умолчанию в калькуляторе указано 8 рабочих часов в сутки.
После того как вы введете в поля калькулятора нужные значения, справа отразится полный расчет. В нем вы увидите количество календарных и рабочих дней, а также количество рабочих часов согласно заданным параметрам.
Пример. Директор ООО «Мечта» дал поручение главному бухгалтеру: рассчитать количество отработанных часов в IV квартале 2018 года. Все работники фирмы в этот период работали по графику, в отпуска не ходили. Главбух открыл онлайн-калькулятор и ввел следующие данные:
Начальная дата — 01.10.2018
Конечная дата — 31.12.2018
Поле «Количество рабочих часов» главбух оставил без изменений.
Калькулятор автоматически произвел расчет и выдал такие цифры:
- календарных дней — 92;
- рабочих дней — 65;
- рабочих часов — 520.
Калькулятор учитывает и сокращенные дни. Например, 02.11.2018 был сокращенный на один час день, и вместо 521 дней калькулятор выдал 520 дней (64 х 8 — 1).
Сдавайте электронную отчетность через интернет. Сервис Экстерн дарит вам 3 месяца бесплатно!
Срок выплаты по ОСАГО
Водители транспортных средств, в случае ДТП, рассчитывают на возмещение от страховщика по ОСАГО. Каждая страховая организация в отведенные сроки обязана выплатить определенную сумму своему клиенту. Но компании редко укладываются в назначенный период. Чаще всего они под разными предлогами затягивают выплаты.
Чтобы минимизировать претензии страховщика, рекомендуется придерживаться некоторых правил:
- В случае аварии сразу же сообщить в полицию и страховое агентство.
- До приезда представителей нельзя выполнять каких-либо манипуляций с транспортным средством (перемещать авто, поврежденные вещи и так далее).
- Заполнить форму извещения о ДТП совместно с другим участником аварии.
- Узнать персональные данные другой стороны, его страховую компанию.
- Взять справку и протокол у инспектора ГИБДД.
- Собрать необходимые документы: с места аварии, на авто, реквизиты счета, копию доверенности на транспорт.
- Отнести бумаги в фирму.
Страховая фирма рассматривает каждый отдельный случай и по результатам выносит решение. Надежная, добросовестная организация переводит установленную сумму на счет пострадавшей стороны на протяжении двух недель.
Срок выплаты по ОСАГО по закону
Согласно закону «Об ОСАГО», период денежной компенсации составляет 20 календарных дней. Отсчет периода данного для возмещения ущерба начинается с числа, когда было оформлено заявление в организации. Дата аварии хоть и прописывается, но началом отсчета по закону РФ не является. Обращаться в страховую следует на протяжении 5 дней, после произошедшего ДТП.
Также важным фактором, который обязательно влияет на продолжительность периода возмещения, является количество праздников (нерабочих дней). К таким датам, например, относятся: 1, 7 января, 9 мая, 8 марта и так далее. Подобные праздничные дни увеличивают время перечислений по полису.
Ответственность за нарушение периода выплат страховщиком также регулируется законом. За каждый день просрочки компания обязана платить неустойку в размере от ставки рефинансирования Центробанком на день, когда компенсация обязана была быть.
Но не всегда аварии заканчиваются только повреждением автомобиля. Не редки случаи значительных травм водителей. Если участники аварии получили серьезные повреждения и находятся на стационарном лечении, они естественно не смогут вовремя обратиться с заявлением. Но долгое пребывание в медицинском учреждении, может негативно повлиять на сроки выплаты по полису. В такой ситуации пострадавший возмещение получит, но по заниженной оценке ущерба.
В подобном варианте поврежденное авто оценивается независимым экспертом, и претензия с отчетом передается собственником транспорта в страховое учреждение. Ответ на претензию, как правило, отрицательный. То есть решать вопрос потребуется через суд. Срок давности по иску в данном случае — три года. Период отсчитывается от даты, которая отмечена в заявлении.
Срок выплаты по ОСАГО на практике
В реальности на получение компенсации может уйти около года и больше. Не редко страховщик пытается занизить сумму ущерба, дело передается в суд, назначается независимая экспертиза. Все длится долго и требует изрядной доли терпения пострадавшего.
По статистике, чаще всего перечисление финансовых средств затягивают малоизвестные страховые организации. В некоторых случаях выплачивать возмещение не хотят из-за неблагоприятного материального положения фирмы. В этом варианте, если, например, фирму лишили лицензии, можно получить компенсацию через Российский Союз Автостраховщиков. Бывают ситуации, когда денег приходится ждать годами.
Крупные компании затягивают возмещение редко, но они очень часто стараются значительно занизить сумму ущерба, рассчитывая, что потерпевший не будет добиваться изменения суммы через суд.
Можно ли ускорить выплаты по ОСАГО?
Понятие «ускорить» предполагает лишь компенсацию без задержек. Ранее установленного срока ни одна организация производить возмещение не будет.
Поэтому, чтобы деньги были перечислены вовремя, следует придерживаться таких правил:
- Форму 11, полученную в компании, надо лично отвезти в ГИБДД и самому же забрать бумаги в инспекции.
- Необходимо скопировать весь комплект документов, которые подаются в страховую фирму.
- В случае, когда есть сомнения, что экспертиза не будет проведена верно, лучше отказаться от услуг специалиста агентства, и выбрать своего эксперта. А чтобы в суде компания не оспорила результаты экспертизы, следует сообщить о ней заранее заказным письмом с уведомлением.
- Почаще звоните страховщику, который принял документы и занимается вашим делом.
- Когда деньги вовремя не были перечислены, обращайтесь в судовой орган, уведомив об этом организацию. Бывают ситуации, когда, чем раньше начнется разбирательство, тем больший шанс на быстрое разрешение дела.
Надо также отметить, что некоторые организации с целью предупреждения мошенничества, перечисляют деньги напрямую в авторемонтную мастерскую, где будет восстанавливаться пострадавший автомобиль. Такая услуга очень удобна, так как не нужно будет спорить из-за суммы и сроков выплаты, искать того, кто отремонтирует транспорт.
На подготовку градостроительной документации уйдёт на 50 дней меньше
В поправках речь идёт о сокращении сроков внесения изменений в Правила землепользования и застройки (ПЗЗ), а также подготовки документации по планировке территории. Например, с 30 до 25 дней уменьшено время, отпущенное градостроительной комиссии, чтобы рассмотреть предложение о корректировке ПЗЗ и выдать заключение. На принятие решения о внесении изменений главе местной администрации тоже дают 25 дней.
Кроме того, установлен срок подготовки разрешения на отклонение от предельных параметров разрешённого строительства и реконструкции – 15 рабочих дней. Но этот документ всё ещё подлежит рассмотрению на общественных обсуждениях или публичных слушаниях. По их результатам комиссия должна дать добро или отказать заявителю тоже за 15 дней. С 20 до 15 рабочих дней сокращён срок согласования документации по планировке территории для различных бюджетных объектов.
Когда документацию по планировке территории проверяют и утверждают федеральные органы исполнительной власти, им тоже придётся уложиться не в 30, а в 15 дней. До 15 дней урезаны сроки согласования документации по планировке территории земель лесного фонда и время на оценку проекта планировки при изъятии участков для государственных или муниципальных нужд. Главам поселений или городских округов дают только 15 дней на согласование документации по планировке территорий при размещении объектов федерального, регионального или местного значения. Если они в этот срок не уложатся, документ считается одобренным.
Кроме того, Правительство РФ получает право указывать, какие из процедур в сфере строительства должны осуществляться исключительно в электронной форме и устанавливать такой порядок.
Вносятся изменения и в закон «Об объектах культурного наследия». Например, устанавливаются сроки рассмотрения Минкультом проекта Генплана исторических поселений федерального значения – не более 20 календарных дней. А проект Правил землепользования и застройки он должен рассмотреть за семь рабочих дней. Местному органу охраны тоже даётся семь дней на рассмотрение Генплана исторических поселений регионального значения и на согласование ПЗЗ.
Строители часто недоумевали, почему власти, желая сократить сроки реализации проектов, говорят только о времени оформления разрешения на строительство. Между тем разработку и согласование проектов планировки территорий застройщики называли одной из самых длительных процедур, которая может занимать не один год. Возможно, теперь ситуация упростится, хотя большинство поправок направлены на упрощение строительства бюджетных и линейных объектов. Впрочем, помимо градостроительной документации на сроки влияют и другие проблемы, например, с монополистами: получение техусловий для подключения к сетям, проверка их выполнения, получение актов и допусков также могут занимать по несколько месяцев.
| График зачетно-экзаменационных сессий2020-21 учебный год *по состоянию на 10.09.2020 г. НАПРАВЛЕНИЕ 38.03.01 ЭКОНОМИКА
НАПРАВЛЕНИЕ 38.03.02 МЕНЕДЖМЕНТ
НАПРАВЛЕНИЕ 09.03.03 ПРИКЛАДНАЯ ИНФОРМАТИКА
НАПРАВЛЕНИЕ 05.03.06 ЭКОЛОГИЯ И ПРИРОДОПОЛЬЗОВАНИЕ
НАПРАВЛЕНИЕ 05.03.05 ПРИКЛАДНАЯ ГИДРОМЕТЕОРОЛОГИЯ
|
Производственный календарь 2021: графика выходных и праздников на 2021 год
В 2021 выходные и праздничные дни отмечаются в привычные даты, но есть несколько нововведений. В 2021 году 365 календарных дней, при этом рабочих — 243, праздничных, выходных и нерабочих — 122. Всего получилось шесть праздничных периодов.
В 2021 году предусмотрен перенос следующих выходных дней:
- с субботы 2 января на пятницу 5 ноября;
- с воскресенья 3 января на пятницу 31 декабря;
- с субботы 20 февраля на понедельник 22 февраля.
Январь
Новогодние каникулы продлились с 1 по 10 января 2021 года (десять дней — с пятницы по воскресенье).
Февраль
Во второй половине февраля россиян ждала единственная в течение года шестидневная рабочая неделя. Нерабочую субботу, 20 февраля, перенесли на понедельник, 22 февраля. Россияне отдыхали на День защитника Отечества три выходных подряд: с 21 по 23 февраля.
Март
В Международный женский день россиян ждали сразу три нерабочих дня — с 6 по 8 марта. После обычных выходных 6–7 марта россияне получили еще один день отдыха.
Май
Первоначально на майские праздники россияне планировали отдыхать в промежутки с 1 по 3 мая и с 8 по 10 мая. 23 апреля президент РФ Владимир Путин подписал указ о нерабочих днях между майскими праздниками в 2021 году. Таким образом, период отдыха продлится с 1 по 10 мая включительно.
Июнь
В июне мы отдыхаем на День России три дня, с субботы по понедельник, с 12 по 14 июня. 12 июня в 2021 году приходится на субботу, и выходным станет ближайший понедельник — 14 июня.
Ноябрь
День народного единства отмечается 4 ноября. В 2021 году праздник выпадает на четверг. Пятница, 5 ноября, также станет нерабочим днем за счет переноса выходного с 2 января 2021 года. Россиян ждут сразу четыре нерабочих дня — с 4 по 7 ноября.
Декабрь
Последний день 2021 года, пятница, 31 декабря, будет нерабочим днем.
Услуга | Примечание | Размер платы, взимаемой с заявителя при предоставлении услуги | Реквизиты |
Срок оказания услуги |
Бесплатное предоставление земельных участков в собственность отдельным категориям граждан для целей индивидуального жилищного строительства | с.Чемал, с.Чепош, с. Кош-Агач, с.Усть-Кокса, г.Горно-Алтайск, с.Шебалино, с.Турочак, с.Майма |
|
| 30 календарных дней |
с. Усть-Кан |
|
| 45 календарных дней | |
Предоставление земельных участков в собственность бесплатно отдельным категориям граждан для целей индивидуального жилищного строительства | с.Шебалино, с.Улаган |
|
| 30 календарных дней |
Постановка на учет и предоставление отдельным категориям граждан Российской Федерации земельных участков для индивидуального жилищного строительства без проведения торгов из земель государственной или муниципальной собственности | с.Майма, с.Соузга, с.Бирюля, с.Манжерок, с.Кызыл-Озек |
|
| 30 календарных дней |
Бесплатное предоставление земельных участков в собственность отдельным категориям граждан без проведения торгов | г.Горно-Алтайск |
|
| 30 календарных дней |
Предоставление прав на участки, находящиеся в государственной собственности, на которых расположены здания, строения, сооружения | г. Горно-Алтайск, с.Чоя |
|
| 30 календарных дней |
Предоставление земельных участков, находящихся в государственной или муниципальной собственности, гражданам для индивидуального жилищного строительства, ведения личного подсобного хозяйства в границах населённого пункта, садоводства, дачного хозяйства, гражданам и крестьянским (фермерским) хозяйствам его деятельности | с.Чоя |
|
| 30 календарных дней |
Предоставление прав на земельные участки, которые находятся в муниципальной собственности или гос. собственность на которых не разграничена, на которых расположены здания, строения, сооружения | с.Шебалино, с.Черга, с.Чемал, с.Улаган, с.Турочак, с.Чемал, с.Онгудай |
|
| 30 календарных дней |
Предоставление юридическим и физическим лицам в постоянное (бессрочное пользование), в безвозмездное пользование, аренду, собственность земельных участков из земель государственной и муниципальной собственности | с.Майма, с.Усть-Кан, с.Турочак |
|
| 30 календарных дней |
с.Онгудай |
|
| 30 рабочих дней | |
Предоставление в собственность, постоянное (бессрочное пользование), в безвозмездное пользование, аренду земельных участков из состава земель, находящихся в собственности муниципального образования, юридическим лицам и гражданам | с.Кош-Агач |
|
| 30 календарных дней |
Заключение договора безвозмездного пользования в отношении земельного участка из земель, находящихся в государственной или муниципальной собственности | с.Чоя |
|
| 30 календарных дней |
Заключение договоров аренды земельных участков, находящихся в муниципальной собственности, или земельных участков, государственная собственность на которые не разграничена, на новый срок | г.Горно-Алтайск |
|
| 30 календарных дней |
Предоставление уведомления о наличии и отсутствии задолженности по арендной плате | г.Горно-Алтайск, с.Шебалино, с.Усть-Кан, с.Усть-Кокса, с.Онгудай, с. Майма |
|
| 7 рабочих дней |
Выдача выписки из реестра муниципальной собственности | с.Майма, с.Шебалино, |
|
| 10 календарных дней |
с.Усть-Кан |
|
| 5 рабочих дней | |
с.Турочак |
|
| 30 календарных дней | |
Предоставление сведений из реестра муниципальной собственности | с.Шебалино |
|
| 10 календарных дней |
с.Чемал |
|
| 5 рабочих дней | |
Выдача выписки из реестра муниципального имущества | с.Онгудай, г.Горно-Алтайск |
|
| 10 календарных дней |
с. Кош Агач, |
|
| 5 рабочих дней | |
с.Чемал |
|
| 10 календарных дней | |
Предоставление сведений об объектах имущества, включенных в перечень муниципального имущества, предназначенного для предоставления во владения и (или) пользования субъектам малого и среднего предпринимательства | г.Горно-Алтайск |
|
| 15 календарных дней |
с.Чоя |
|
| 10 рабочих дней | |
Заключение соглашений о перераспределении земель и (или) земельных участков, находящихся в муниципальной собственности, или земель и (или) земельных участков, государственная собственность на которые не разграничена, земельных участков, находящихся в частной собственности | г.Горно-Алтайск |
|
| 90 календарных дней |
Выдача разрешения на строительство | г.Горно-Алтайск, с.Майма, с.Чемал, с.Улаган, с.Онгудай, Кош-Агач, с.Турочак |
|
| 5 рабочих дней |
с.Шебалино |
|
| 6 рабочих дней | |
с.Усть-Кан |
|
| 10 календарных дней | |
с.Чоя |
|
| 30 календарных дней | |
с.Усть-Кокса |
|
| 15 рабочих дней | |
Предоставление разрешения на строительство | с.Турочак |
|
| 5 рабочих дней |
с.Чоя |
|
| 30 календарных дней | |
Внесение изменений в разрешения на строительство (реконструкцию) объектов капитального строительства | г. Горно-Алтайск |
|
| 5 рабочих дней |
с.Шебалино |
|
| 10 рабочих дней | |
с.Майма |
|
| 7 рабочих дней | |
Внесение изменений в разрешение на строительство | с.Чоя |
|
| 5 рабочих дней |
Выдача разрешения на ввод объектов в эксплуатацию | г.Горно-Алтайск, с.Шебалино, с.Усть-Кан, |
|
| 10 рабочих дней |
с.Усть-Кокса |
|
| 6 рабочих дней | |
с.Майма, с.Чемал, с.Улаган, с.Онгудай, с.Турочак |
|
| 5 рабочих дней | |
Выдача разрешений на ввод объектов в эксплуатацию при осуществлении строительства, реконструкции, капитального ремонта объектов капитального строительства, расположенных на территории муниципального образования | с.Кош-Агач |
|
| 5 рабочих дней |
Предоставление разрешения на ввод объекта в эксплуатацию | с.Чоя, с.Турочак |
|
| 5 рабочих дней |
Выдача градостроительного плана земельного участка | г.Горно-Алтайск, с.Усть-Кан, с.Усть-Кокса, с.Улаган, |
|
| 30 календарных дней
|
с.Кош-Агач, с. Джазатор |
|
| 15 календарных дней | |
с.Улаган, |
|
| 14 календарных дней | |
с.Шебалино |
|
| 15 рабочих дней | |
с.Майма, с.Чемал, с.Чемал, с.Онгудай |
|
| 14 рабочих дней | |
с.Усть-Кан |
|
| 30 рабочих дней | |
Предоставление градостроительного плана земельного участка | с.Турочак |
|
| 14 рабочих дней |
с.Чоя |
|
| 14 рабочих дней | |
Прием документов, необходимых для согласования перепланировки и (или) переустройства жилого (нежилого) помещения, а также выдача соответствующих решений о согласовании или об отказе | с.Шебалино |
|
| 30 календарных дней |
Выдача разрешения на продление (прекращение) действия разрешений на строительство (реконструкцию) объектов капитального строительства | г. Горно-Алтайск |
|
| 5 рабочих дней |
Продление срока действия ранее выданного разрешения на строительство | с. Майма |
|
| 7 рабочих дней |
Продление срока действия разрешения на строительство | с.Шебалино |
|
| 10 рабочих дней |
с.Чоя |
|
| 30 календарных дней | |
Предоставление разрешения на условно разрешенный вид использования земельного участка или объекта капитального строительства | г.Горно-Алтайск |
|
| 60 календарных дней |
Предоставление согласия на перевод земельного участка из одной категории в другую, за исключением земель, находящихся в федеральной собственности | с.Чемал, с.Чепош |
|
| 30 календарных дней |
Отнесение земель к категориям, перевод земельного участка из одной категории в другую | с.Майма |
|
| 70 календарных дней |
Присвоение, изменение и аннулирование адресов | г.Горно-Алтайск |
|
| 18 рабочих дней |
Предоставление сведений, содержащихся в адресном реестре МО «Шебалинское сельское поселение» | с. Шебалино |
|
| 5 рабочих дней |
Присвоение адреса объекту недвижимости | с. Чемал, с.Чепош |
|
| 30 календарных дней |
Принятие решения об утверждении схемы расположения земельного участка на кадастровом плане территории | с.Чоя |
|
| 20 календарных дней |
Предоставление разрешения на осуществления земляных работ | с.Шебалино |
|
| I-этап 5 рабочих дней, II-этап 7 рабочих дней |
Предоставление решения о согласовании архитектурно-градостроительного облика | с.Шебалино |
|
| 30 календарных дней |
Передача материалов для размещения в информационной системе обеспечения градостроительной деятельности | с.Шебалино |
|
| 14 календарных дней |
Принятие решения о подготовке документации по планировке территории | с.Шебалино, с.Майма |
|
| 1 месяц |
Утверждение документации по планировке территории | с.Шебалино |
|
|
|
Утверждение документации по планировке территории (проектов планировки и проектов межевания) на территории муниципального образования «Майминский район» | с.Майма |
|
| 1 месяц |
Допуск заявителя к участию в аукционе на право заключить договор о развитии застроенной территории | с.Шебалино |
|
| За 5 дней до начала аукциона |
Выдача архивных справок | с.Чемал, с.Чепош |
|
| 10 рабочих дней |
Предоставление справок, выписки из похозяйственной книги (кроме архивных) | с.Майма, с.Соузга, с.Бирюля, с.Манжерок, с.Кызыл-Озек |
|
| 5 рабочих дней |
Выдача выписок из похозяйственной книги | с.Шебалино |
|
| 2 рабочих дня |
Выдача акта освидетельствования проведения основных работ по строительству (реконструкции) объекта индивидуального жилищного строительства, осуществляемому с привлечением средств материнского (семейного) капитала | с.Чемал, г.Горно-Алтайск |
|
| 5 рабочих дней |
с.Усть-Кан, |
|
| 10 рабочих дней | |
с.Шебалино, с.Усть-Кокса |
|
| 10 рабочих дней | |
Признание молодых семей нуждающимися в жилых помещениях и участниками подпрограммы «Обеспечение жильем молодых семей ФЦП «Жилище» на 2015-2020 годы | с.Кош-Агач |
|
| 10 календарных дней |
Направление уведомления о соответствии построенных или реконструированных объекта индивидуального жилищного строительства или садового дома требованиям законодательства о градостроительной деятельности | с.Иогач, г.Горно-Алтайск, с.Шебалино |
|
| 6 рабочих дней |
с.Турочак, с. Кебезень, |
|
| 5 рабочих дней | |
Предоставление уведомления о соответствии построенных или реконструированных объекта индивидуального жилищного строительства или садового дома установленным параметрам допустимости размещения объекта индивидуального жилищного строительства или садового дома на земельном участке | с.Чоя |
|
| 20 рабочих дней |
Перевод земель или земельных участков из одной категории в другую категорию до разграничения государственной собственности на землю | с.Чоя |
|
| 20 рабочих дней |
Уведомление об изменении параметров планируемого строительства или реконструкции объекта индивидуального жилищного строительства или садового дома | с.Шебалино |
|
| 6 рабочих дней |
Поликлиника №1 города-курорта Кисловодска — Порядок и сроки госпитализации
Порядок и сроки госпитализации
Выдержка из Приложения 3 к Территориальной программе государственных гарантий бесплатного оказания гражданам медицинской помощи на территории Ставропольского края
V. Сроки ожидания медицинской помощи, оказываемой в плановой
форме, в том числе сроки ожидания оказания медицинской
помощи в стационарных условиях, проведения отдельных
диагностических обследований, а также консультаций
врачей-специалистов
27. Плановая медицинская помощь предоставляется в порядке очередности в пределах установленного настоящими Порядком и условиями срока ожидания оказания медицинской помощи.
28. Срок ожидания проведения консультаций врачей-специалистов при оказании первичной специализированной медико-санитарной помощи в плановой форме составляет не более 14 календарных дней со дня обращения пациента в медицинскую организацию Ставропольского края, для детей-сирот и детей, оставшихся без попечения родителей, — не более 10 календарных дней со дня обращения пациента в медицинскую организацию Ставропольского края.
Срок ожидания приема врачами-терапевтами участковыми, врачами общей практики (семейными врачами), врачами-педиатрами участковыми составляет не более 24 часов с момента обращения пациента в медицинскую организацию Ставропольского края.
Срок ожидания проведения диагностических инструментальных (рентгенографических исследований, включая маммографию, функциональной диагностики, ультразвуковых исследований) и лабораторных исследований при оказании первичной медико-санитарной помощи в плановой форме составляет не более 14 календарных дней со дня назначения, для детей-сирот и детей, оставшихся без попечения родителей, — не более 10 календарных дней со дня назначения.
Срок ожидания проведения компьютерной томографии (включая однофотонную эмиссионную компьютерную томографию), магнитнорезонансной томографии и ангиографии при оказании первичной медикосанитарной помощи в плановой форме составляет не более 30 календарных дней со дня назначения, для детей-сирот и детей, оставшихся без попечения родителей, — не более 20 календарных дней со дня назначения.
Срок ожидания оказания специализированной (за исключением высокотехнологичной) медицинской помощи в плановой форме составляет не более 30 календарных дней со дня выдачи лечащим врачом направления на госпитализацию (при условии обращения пациента за госпитализацией в рекомендуемые лечащим врачом сроки), для детей-сирот и детей, оставшихся без попечения родителей, — не более 20 календарных дней со дня выдачи лечащим врачом направления на госпитализацию (при условии обращения пациента за госпитализацией в рекомендуемые лечащим врачом сроки).
29. Направление пациента на плановую госпитализацию осуществляется лечащим врачом в соответствии с клиническими показаниями, требующими госпитального режима, активной терапии и круглосуточного наблюдения врача, при этом согласовывается дата плановой госпитализации. Направление на госпитализацию выдается по установленному образцу и регистрируется в едином информационном ресурсе Ставропольского края, реализованном в режиме онлайн, предназначенном для информационного сопровождения застрахованных лиц при организации оказания им медицинской помощи страховыми медицинскими организациями Ставропольского края.
В медицинских организациях Ставропольского края, оказывающих специализированную медицинскую помощь в стационарных условиях и в условиях дневного стационара, ведется лист ожидания оказания специализированной медицинской помощи в плановой форме и осуществляется информирование граждан в доступной форме, в том числе с использованием информационно-телекоммуникационной сети «Интернет», о сроках ожидания оказания специализированной медицинской помощи с учетом требований законодательства Российской Федерации о персональных данных.
20 дней с сегодняшнего дня | WikiDates.org
Среда, 18 августа 2021 г.
Какая дата через 20 дней после сегодняшнего дня?
| Календарь на август 2021 года | ||||||||
| № | Вс | Пн | Вт | Ср | Чт | Пт | Сб | |
| 31 | 1 | 2 | 3 | 4 | 5 | 5 | 7 | |
| 32 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | |
| 33 | 15 | 16 | 17 | 19 | 20 | 21 | ||
| 34 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | |
| 35 | 29 | 30 | ||||||
• Сегодня четверг, 29 июля 2021 г.
• Через 20 дней (14 рабочих дней) будет среда, 18 августа 2021 г. .
• 18 августа 2021 года — среда.
• Это 230-й день в году и 33-я неделя в году (неделя начинается с воскресенья).
• В августе 2021 года 31 день.
• 2021 год не високосный, поэтому в этом году 365 дней.
Какая дата 20 рабочих дней с сегодняшнего дня?
Четверг, 26 августа 2021 г.
| Календарь на август 2021 года | ||||||||||||||
| № | Вс | Пн | Вт | Ср | Чт | Пт | Сб | |||||||
| 31 | 1 | 2 | 3 | 4 | 5 | 7 | 00000000000000032 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 33 | 15 | 16 | 17 | 18 | 19 | 21 | ||||||||
| 34 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | |||||||
| 35 | 29 | 30 | 31 | |||||||||||
Калькулятор даты судебного заседания доступен для помощи в проверке расчета количества судебных дней с заданной даты. Судебные дни не включают выходные и праздничные дни. Верховный суд Лос-Анджелеса и округ Лос-Анджелес считают, что Калькулятор даты суда точно рассчитывает эту информацию.Однако информация, полученная с помощью калькулятора даты суда, не является официальным расчетом суда и не может использоваться в качестве доказательства. Любой пользователь Калькулятора даты суда информируется о том, что он использует и полагается на информацию, полученную без каких-либо гарантий, и что в этой информации могут быть ошибки или упущения. В той мере, в какой это разрешено применимым законодательством, Верховный суд Лос-Анджелеса отказывается от всех гарантий, включая, помимо прочего, любые подразумеваемые гарантии товарной пригодности, точности и пригодности для конкретной цели, а также ненарушения прав.Пользователь признает и соглашается с тем, что ни Верховный суд Лос-Анджелеса, ни округ Лос-Анджелес не несут никакой ответственности за точность или достоверность предоставленной информации. Календарь судебных дат рассчитывает даты с января 2006 года по декабрь 2025 года. Чтобы начать, щелкните дату начала справа (по умолчанию — текущая дата).Затем введите количество дней суда, прошедших или будущих, для расчета и нажмите кнопку «Рассчитать». Чтобы рассчитать «прошедшие» дни в суде, поставьте перед числом знак минус. |
Годовая система нумерации
Годовая система нумерацииКак AZMET обозначает дни и часы
Файлы исходных данных AZMET используют систему нумерации дней года (DOY).Это общий формат, используемый в данных исследований и военными. Система дня года игнорирует существование месяцев и чисел. каждый день года подряд.
В обычные годы мы нумеруем каждый день года от 1 до 365 В високосные годы мы добавляем «високосный день» (29 февраля), в 60-й день года, таким образом смещая остальную часть года «вниз» на один день. Система «День года» используется как в файлах данных по дням, так и по часам.
Примечание:
Есть и другие агентства по сбору данных о погоде, которые используют разные
форматы календаря для своих данных.Они установили продолжительность всех лет на 366
дней. Их «високосный день» (29 февраля; 60 DOY) оставлен пустым (нули или нулевые значения данных)
для невисокосных лет. В високосные годы позиция високосного дня действительно содержит данные.
AZMET не использует этот метод. Наши годы различаются по длине.
AZMET использует 24-часовой формат.
Нумеруем каждый час дня от 1 до 24.
Очевидно, это используется в файлах почасовых данных.
[Мы не используем «цифровые часы» с двоеточием (например, с 1:00 до 24:00).
Мы также не используем формат от 100 до 2400.]
Все данные AZMET собираются, хранятся и представляются в
местного времени «Аризона», которое находится в часовом поясе «Mountain Standard».
В Аризоне не действует переход на летнее время.
Следовательно, время, указанное в файлах данных AZMET,
всегда на семь часов отстает от всемирного координированного времени (UTC)
(также известное как: среднее время по Гринвичу; время зулусов).
Ниже приведены несколько таблиц и списков, чтобы помочь вам в визуализации системы дня года: В этой первой таблице числа дней года сгруппированы по месяцам: День года по месяцам ======================================= Обычный год Високосный год -------------- --------------- 1–31 января 1–31 января 32–59 февраля 32–60 февраля 60-90 марта 61-91 марта 91 - 120 апр. 92 - 121 апр. 121 - 151 май, 122 - 152 мая 152 - 181 июн. 153 - 182 июн. Июл 182 - 212 июл 183 - 213 213 - 243 августа - 214 - 244 августа 244 - 273 сен 245 - 274 Октябрь 274 - 304 окт 275 - 305 305–334 ноя 306–335 Декабрь 335 - 365 декабрь 336 - 366В этой второй календарной таблице Верхнее число в каждом поле представляет собой обычный календарный день месяца.Нижнее число в каждом поле представляет день года (DOY).
Январь + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + - - + --- + --- + --- + --- + --- + --- + | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + - - + --- + --- + --- + --- + --- + --- + | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | | | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | | + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + - - + --- + --- + --- + --- + --- + --- + Февраль + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + - - + --- + --- + --- + --- + --- + --- + | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | + --- + --- + --- + --- + --- + --- + --- + --- + --- + ****** - + --- + - - + --- + --- + --- + --- + --- + --- + | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 * 29 * ПРИМЕЧАНИЕ. В високосные годы прибавляйте 1 | | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 * 60 * на каждый день года после 29 февраля | + --- + --- + --- + --- + --- + --- + --- + --- + --- + ****** - + --- + - - + --- + --- + --- + --- + --- + --- + Март + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + - - + --- + --- + --- + --- + --- + --- + | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + - - + --- + --- + --- + --- + --- + --- + | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | Добавить 1 к DOY | | 79 | 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | в високосные годы.| + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + - - + --- + --- + --- + --- + --- + --- + апреля + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + - - + --- + --- + --- + --- + --- + --- + | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 | 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + - - + --- + --- + --- + --- + --- + --- + | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | Добавить 1 к DOY | | 110 | 111 | 112 | 113 | 114 | 115 | 116 | 117 | 118 | 119 | 120 | в високосные годы.| + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + ----- -------------------------- + Май + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + - - + --- + --- + --- + --- + --- + --- + | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | | 121 | 122 | 123 | 124 | 125 | 126 | 127 | 128 | 129 | 130 | 131 | 132 | 133 | 134 | 135 | 136 | 137 | 138 | 139 | + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + - - + --- + --- + --- + --- + --- + --- + | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | Добавить 1 к DOY | | 140 | 141 | 142 | 143 | 144 | 145 | 146 | 147 | 148 | 149 | 150 | 151 | в високосные годы.| + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + - - + --- + --- + --- + --- + --- + --- + июнь + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + - - + --- + --- + --- + --- + --- + --- + | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | | 152 | 153 | 154 | 155 | 156 | 157 | 158 | 159 | 160 | 161 | 162 | 163 | 164 | 165 | 166 | 167 | 168 | 169 | 170 | + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + - - + --- + --- + --- + --- + --- + --- + | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | Добавить 1 к DOY | | 171 | 172 | 173 | 174 | 175 | 176 | 177 | 178 | 179 | 180 | 181 | в високосные годы.| + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + - - + --- + --- + --- + --- + --- + --- + июль + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + - - + --- + --- + --- + --- + --- + --- + | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | | 182 | 183 | 184 | 185 | 186 | 187 | 188 | 189 | 190 | 191 | 192 | 193 | 194 | 195 | 196 | 197 | 198 | 199 | 200 | + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + - - + --- + --- + --- + --- + --- + --- + | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | Добавить 1 к DOY | | 201 | 202 | 203 | 204 | 205 | 206 | 207 | 208 | 209 | 210 | 211 | 212 | в високосные годы.| + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + - - + --- + --- + --- + --- + --- + --- + август + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + - - + --- + --- + --- + --- + --- + --- + | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | | 213 | 214 | 215 | 216 | 217 | 218 | 219 | 220 | 221 | 222 | 223 | 224 | 225 | 226 | 227 | 228 | 229 | 230 | 231 | + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + - - + --- + --- + --- + --- + --- + --- + | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | Добавить 1 к DOY | | 232 | 233 | 234 | 235 | 236 | 237 | 238 | 239 | 240 | 241 | 242 | 243 | в високосные годы.| + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + - -------------------------- + сентябрь + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + - - + --- + --- + --- + --- + --- + --- + | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | | 244 | 245 | 246 | 247 | 248 | 249 | 250 | 251 | 252 | 253 | 254 | 255 | 256 | 257 | 258 | 259 | 260 | 261 | 262 | + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + - - + --- + --- + --- + --- + --- + --- + | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | Добавить 1 к DOY | | 263 | 264 | 265 | 266 | 267 | 268 | 269 | 270 | 271 | 272 | 273 | в високосные годы.| + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + - - + --- + --- + --- + --- + --- + --- + Октябрь + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + - - + --- + --- + --- + --- + --- + --- + | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | | 274 | 275 | 276 | 277 | 278 | 279 | 280 | 281 | 282 | 283 | 284 | 285 | 286 | 287 | 288 | 289 | 290 | 291 | 292 | + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + - - + --- + --- + --- + --- + --- + --- + | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | Добавить 1 к DOY | | 293 | 294 | 295 | 296 | 297 | 298 | 299 | 300 | 301 | 302 | 303 | 304 | в високосные годы.| + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + - - + --- + --- + --- + --- + --- + --- + Ноябрь + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + - - + --- + --- + --- + --- + --- + --- + | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | | 305 | 306 | 307 | 308 | 309 | 310 | 311 | 312 | 313 | 314 | 315 | 316 | 317 | 318 | 319 | 320 | 321 | 322 | 323 | + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + - - + --- + --- + --- + --- + --- + --- + | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | Добавить 1 к DOY | | 324 | 325 | 326 | 327 | 328 | 329 | 330 | 331 | 332 | 333 | 334 | в високосные годы.| + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + - - + --- + --- + --- + --- + --- + --- + Декабрь + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + - - + --- + --- + --- + --- + --- + --- + | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | | 335 | 336 | 337 | 338 | 339 | 340 | 341 | 342 | 343 | 344 | 345 | 346 | 347 | 348 | 349 | 350 | 351 | 352 | 353 | + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + - - + --- + --- + --- + --- + --- + --- + | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | Добавить 1 к DOY | | 354 | 355 | 356 | 357 | 358 | 359 | 360 | 361 | 362 | 363 | 364 | 365 | в високосные годы.| + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + --- + - -------------------------- + Джулианский нормальный прыжок День Год Год ----- ------ ------ 1 = 1 января 1 января 2 = 2 января 2 января 3 = 3 января 3 января 4 = 4 января 4 января 5 = 5 января, 5 января 6 = 6 января, 6 января 7 = 7 января, 7 января 8 = 8 января 8 января 9 = 9 января, 9 января 10 = 10 января 10 января 11 = 11 января, 11 января 12 = 12 января, 12 января 13 = 13 января 13 января 14 = 14 января, 14 января 15 = 15 января, 15 января 16 = 16 января, 16 января 17 = 17 января, 17 января 18 = 18 января, 18 января 19 = 19 января 19 января 20 = 20 января 20 января 21 = 21 января, 21 января 22 = 22 января 22 января 23 = 23 января, 23 января 24 = 24 января, 24 января 25 = 25 января 25 января 26 = 26 января, 26 января 27 = 27 января, 27 января 28 = 28 января, 28 января 29 = 29 января 29 января 30 = 30 января 30 января 31 = 31 января 31 января 32 = 1 февраля 1 февраля 33 = 2 февраля 2 февраля 34 = 3 февраля 3 февраля 35 = 4 февраля 4 февраля 36 = 5 февраля 5 февраля 37 = 6 февраля, 6 февраля 38 = 7 февраля, 7 февраля 39 = 8 февраля 8 февраля 40 = 9 февраля, 9 февраля 41 = 10 февраля 10 февраля 42 = 11 февраля 11 февраля 43 = 12 февраля, 12 февраля 44 = 13 февраля 13 февраля 45 = 14 февраля 14 февраля 46 = 15 февраля, 15 февраля 47 = 16 февраля 16 февраля 48 = 17 февраля 17 февраля 49 = 18 февраля 18 февраля 50 = 19 февраля 19 февраля 51 = 20 февраля 20 февраля 52 = 21 февраля 21 февраля 53 = 22 февраля 22 февраля 54 = 23 февраля 23 февраля 55 = 24 февраля 24 февраля 56 = 25 февраля 25 февраля 57 = 26 февраля 26 февраля 58 = 27 февраля 27 февраля 59 = 28 февраля 28 февраля 60 = 1 марта 29 февраля 61 = 2 марта 1 марта 62 = 3 марта 2 марта 63 = 4 марта 3 марта 64 = 5 марта 4 марта 65 = 6 марта 5 марта 66 = 7 марта 6 марта 67 = 8 марта 7 марта 68 = 9 марта 8 марта 69 = 10 марта 9 марта 70 = 11 марта 10 марта 71 = 12 марта 11 марта 72 = 13 марта 12 марта 73 = 14 марта 13 марта 74 = 15 марта 14 марта 75 = 16 марта 15 марта 76 = 17 марта 16 марта 77 = 18 марта 17 марта 78 = 19 марта 18 марта 79 = 20 марта 19 марта 80 = 21 марта 20 марта 81 = 22 марта 21 марта 82 = 23 марта 22 марта 83 = 24 марта 23 марта 84 = 25 марта 24 марта 85 = 26 марта 25 марта 86 = 27 марта 26 марта 87 = 28 марта 27 марта 88 = 29 марта 28 марта 89 = 30 марта 29 марта 90 = 31 марта 30 марта 91 = 1 апреля 31 марта 92 = 2 апреля 1 апреля 93 = 3 апреля 2 апреля 94 = 4 апреля 3 апреля 95 = 5 апреля 4 апреля 96 = 6 апреля 5 апреля 97 = 7 апреля 6 апреля 98 = 8 апреля 7 апреля 99 = 9 апреля 8 апреля 100 = 10 апреля 9 апреля 101 = 11 апреля 10 апреля 102 = 12 апреля 11 апреля 103 = 13 апреля 12 апреля 104 = 14 апреля 13 апреля 105 = 15 апреля 14 апреля 106 = 16 апреля 15 апреля 107 = 17 апреля 16 апреля 108 = 18 апреля 17 апреля 109 = 19 апреля 18 апреля 110 = 20 апреля 19 апреля 111 = 21 апреля 20 апреля 112 = 22 апреля 21 апреля 113 = 23 апреля 22 апреля 114 = 24 апреля 23 апреля 115 = 25 апреля 24 апреля 116 = 26 апреля 25 апреля 117 = 27 апреля 26 апреля 118 = 28 апреля 27 апреля 119 = 29 апреля 28 апреля 120 = 30 апреля 29 апреля 121 = 1 мая 30 апреля 122 = 2 мая 1 мая 123 = 3 мая 2 мая 124 = 4 мая 3 мая 125 = 5 мая 4 мая 126 = 6 мая 5 мая 127 = 7 мая 6 мая 128 = 8 мая 7 мая 129 = 9 мая 8 мая 130 = 10 мая 9 мая 131 = 11 мая 10 мая 132 = 12 мая 11 мая 133 = 13 мая 12 мая 134 = 14 мая 13 мая 135 = 15 мая 14 мая 136 = 16 мая 15 мая 137 = 17 мая 16 мая 138 = 18 мая 17 мая 139 = 19 мая 18 мая 140 = 20 мая 19 мая 141 = 21 мая 20 мая 142 = 22 мая 21 мая 143 = 23 мая 22 мая 144 = 24 мая 23 мая 145 = 25 мая 24 мая 146 = 26 мая 25 мая 147 = 27 мая 26 мая 148 = 28 мая 27 мая 149 = 29 мая 28 мая 150 = 30 мая 29 мая 151 = 31 мая 30 мая 152 = 1 июня 31 мая 153 = 2 июня 1 июня 154 = 3 июня 2 июня 155 = 4 июня 3 июня 156 = 5 июня, 4 июня 157 = 6 июня, 5 июня 158 = 7 июня, 6 июня 159 = 8 июня 7 июня 160 = 9 июня 8 июня 161 = 10 июня, 9 июня 162 = 11 июня 10 июня 163 = 12 июня 11 июня 164 = 13 июня, 12 июня 165 = 14 июня 13 июня 166 = 15 июня 14 июня 167 = 16 июня 15 июня 168 = 17 июня 16 июня 169 = 18 июня 17 июня 170 = 19 июня 18 июня 171 = 20 июня 19 июня 172 = 21 июня 20 июня 173 = 22 июня 21 июня 174 = 23 июня 22 июня 175 = 24 июня 23 июня 176 = 25 июня 24 июня 177 = 26 июня 25 июня 178 = 27 июня 26 июня 179 = 28 июня 27 июня 180 = 29 июня 28 июня 181 = 30 июня 29 июня 182 = 1 июля, 30 июня 183 = 2 июля, 1 июля 184 = 3 июля 2 июля 185 = 4 июля 3 июля 186 = 5 июля, 4 июля 187 = 6 июля, 5 июля 188 = 7 июля, 6 июля 189 = 8 июля, 7 июля 190 = 9 июля 8 июля 191 = 10 июля, 9 июля 192 = 11 июля 10 июля 193 = 12 июля 11 июля 194 = 13 июля, 12 июля 195 = 14 июля 13 июля 196 = 15 июля 14 июля 197 = 16 июля 15 июля 198 = 17 июля, 16 июля 199 = 18 июля 17 июля 200 = 19 июля 18 июля 201 = 20 июля 19 июля 202 = 21 июля 20 июля 203 = 22 июля, 21 июля 204 = 23 июля 22 июля 205 = 24 июля 23 июля 206 = 25 июля, 24 июля 207 = 26 июля 25 июля 208 = 27 июля, 26 июля 209 = 28 июля, 27 июля 210 = 29 июля 28 июля 211 = 30 июля 29 июля 212 = 31 июля 30 июля 213 = 1 августа 31 июля 214 = 2 августа 1 августа 215 = 3 августа 2 августа 216 = 4 августа 3 августа 217 = 5 августа, 4 августа 218 = 6 августа 5 августа 219 = 7 августа, 6 августа 220 = 8 августа 7 августа 221 = 9 августа 8 августа 222 = 10 августа 9 августа 223 = 11 августа 10 августа 224 = 12 августа 11 августа 225 = 13 августа 12 августа 226 = 14 августа 13 августа 227 = 15 августа 14 августа 228 = 16 августа 15 августа 229 = 17 августа 16 августа 230 = 18 августа 17 августа 231 = 19 августа 18 августа 232 = 20 августа 19 августа 233 = 21 августа 20 августа 234 = 22 августа 21 августа 235 = 23 августа 22 августа 236 = 24 августа 23 августа 237 = 25 августа 24 августа 238 = 26 августа 25 августа 239 = 27 августа 26 августа 240 = 28 августа 27 августа 241 = 29 августа 28 августа 242 = 30 августа 29 августа 243 = 31 августа 30 августа 244 = 1 сентября 31 августа 245 = 2 сентября 1 сентября 246 = 3 сентября 2 сентября 247 = 4 сентября 3 сентября 248 = 5 сентября 4 сентября 249 = 6 сентября, 5 сентября 250 = 7 сентября, 6 сентября 251 = 8 сентября, 7 сентября 252 = 9 сентября 8 сентября 253 = 10 сентября, 9 сентября 254 = 11 сентября 10 сентября 255 = 12 сентября 11 сентября 256 = 13 сентября 12 сентября 257 = 14 сентября 13 сентября 258 = 15 сентября 14 сентября 259 = 16 сентября 15 сентября 260 = 17 сентября 16 сентября 261 = 18 сентября, 17 сентября 262 = 19 сентября 18 сентября 263 = 20 сентября, 19 сентября 264 = 21 сентября 20 сентября 265 = 22 сентября 21 сентября 266 = 23 сентября 22 сентября 267 = 24 сентября 23 сентября 268 = 25 сентября 24 сентября 269 = 26 сентября 25 сентября 270 = 27 сентября 26 сентября 271 = 28 сентября, 27 сентября 272 = 29 сентября 28 сентября 273 = 30 сентября 29 сентября 274 = 1 октября, 30 сентября 275 = 2 октября 1 октября 276 = 3 октября 2 октября 277 = 4 октября, 3 октября 278 = 5 октября, 4 октября 279 = 6 октября, 5 октября 280 = 7 октября, 6 октября 281 = 8 октября, 7 октября 282 = 9 октября, 8 октября 283 = 10 октября, 9 октября 284 = 11 октября, 10 октября 285 = 12 октября, 11 октября 286 = 13 октября, 12 октября 287 = 14 октября, 13 октября 288 = 15 октября, 14 октября 289 = 16 октября, 15 октября 290 = 17 октября, 16 октября 291 = 18 октября, 17 октября 292 = 19 октября, 18 октября 293 = 20 октября, 19 октября 294 = 21 октября 20 октября 295 = 22 октября, 21 октября 296 = 23 октября 22 октября 297 = 24 октября, 23 октября 298 = 25 октября, 24 октября 299 = 26 октября, 25 октября 300 = 27 октября, 26 октября 301 = 28 октября, 27 октября 302 = 29 октября, 28 октября 303 = 30 октября, 29 октября 304 = 31 октября, 30 октября 305 = 1 ноября, 31 октября 306 = 2 ноября, 1 ноября 307 = 3 ноября, 2 ноября 308 = 4 ноября, 3 ноября 309 = 5 ноября, 4 ноября 310 = 6 ноября, 5 ноября 311 = 7 ноября, 6 ноября 312 = 8 ноября, 7 ноября 313 = 9 ноября, 8 ноября 314 = 10 ноября, 9 ноября 315 = 11 ноября 10 ноября 316 = 12 ноября, 11 ноября 317 = 13 ноября, 12 ноября 318 = 14 ноября, 13 ноября 319 = 15 ноября, 14 ноября 320 = 16 ноября, 15 ноября 321 = 17 ноября, 16 ноября 322 = 18 ноября, 17 ноября 323 = 19 ноября, 18 ноября 324 = 20 ноября, 19 ноября 325 = 21 ноября 20 ноября 326 = 22 ноября, 21 ноября 327 = 23 ноября 22 ноября 328 = 24 ноября, 23 ноября 329 = 25 ноября, 24 ноября 330 = 26 ноября 25 ноября 331 = 27 ноября, 26 ноября 332 = 28 ноября, 27 ноября 333 = 29 ноября, 28 ноября 334 = 30 ноября, 29 ноября 335 = 1 декабря, 30 ноября 336 = 2 декабря 1 декабря 337 = 3 декабря 2 декабря 338 = 4 декабря 3 декабря 339 = 5 декабря, 4 декабря 340 = 6 декабря 5 декабря 341 = 7 декабря, 6 декабря 342 = 8 декабря, 7 декабря 343 = 9 декабря 8 декабря 344 = 10 декабря 9 декабря 345 = 11 декабря 10 декабря 346 = 12 декабря 11 декабря 347 = 13 декабря 12 декабря 348 = 14 декабря 13 декабря 349 = 15 декабря 14 декабря 350 = 16 декабря 15 декабря 351 = 17 декабря 16 декабря 352 = 18 декабря 17 декабря 353 = 19 декабря 18 декабря 354 = 20 декабря 19 декабря 355 = 21 декабря 20 декабря 356 = 22 декабря 21 декабря 357 = 23 декабря 22 декабря 358 = 24 декабря 23 декабря 359 = 25 декабря 24 декабря 360 = 26 декабря 25 декабря 361 = 27 декабря 26 декабря 362 = 28 декабря 27 декабря 363 = 29 декабря 28 декабря 364 = 30 декабря 29 декабря 365 = 31 декабря 30 декабря 366 = 31 декабря День года по месяцам ======================================= Обычный год Високосный год -------------- --------------- 1–31 января 1–31 января 32–59 февраля 32–60 февраля 60-90 марта 61-91 марта 91 - 120 апр. 92 - 121 апр. 121 - 151 май, 122 - 152 мая 152 - 181 июн. 153 - 182 июн. Июл 182 - 212 июл 183 - 213 213 - 243 августа - 214 - 244 августа 244 - 273 сен 245 - 274 Октябрь 274 - 304 окт 275 - 305 305–334 ноя 306–335 Декабрь 335 - 365 декабрь 336 - 366 Последние високосные годы: прошлые и будущие високосные годы ============================ ====================== ============ 1987 1896 1936 1972 2008 * 1988 - Високосный год 1904 1940 1976 2012 2012 1989 1908 1944 1980 2016 1990 1912 1948 1984 2020 1991 1916 1952 1988 2024 * 1992 - Високосный год 1920 1956 1992 2028 1993 1924 1960 1996 2032 1994 1928 1964 2000 2036 1995 1932 1968 2004 2040 * 1996 - високосный год 1997 г. 1998 г. 1999 г. * 2000 - Високосный год (Практическое правило: високосные годы = U.S. Годы президентских выборов) Официальные правила високосного года: Если год делится на 4 без остатка, это високосный год. Примеры: 1996/4 = 499, следовательно, это високосный год. 1997/4 = 499,25, следовательно, это не високосный год. Первое исключение: Из тех лет, которые делятся на 4 без остатка, если год также делится на 100 без остатка, это НЕ високосный год. Пример: 1900/4 = 475. 1900/100 = 19, следовательно, это НЕ високосный год. Второе исключение: Из тех лет, которые без остатка делятся на 4 и 100, если год также делится на 400 без остатка, это високосный год.Пример: 2000/4 = 500 2000/100 = 20 2000/400 = 5, следовательно, это високосный год. 1900/400 = 4,75, следовательно, это НЕ високосный год. Юлианский календарь был разработан Юлием Цезарем и египтянином. астроном Сосигенес в 46 г. до н. э. Они стремились создать 12 месячный календарь, основанный на солнечном году; время, необходимое для Земля совершит один полный оборот вокруг Солнца, что составляет 365,2422 дня. (До этого римляне и большинство других цивилизаций использовали лунный или лунно-солнечный гибридный календарь; только в Египте был строго солнечный календарь.) Они устанавливают нормальный год равным 365 дням, а затем назначают каждый четвертый год. год (високосный) должен иметь 366 дней. Это было сделано для исправления частичного .2422 день, который отсутствовал в текущем году и в каждом из предыдущие три года. Для этого они включили «равномерно делится на 4 'в их календаре. Юлианский календарь был принят Никейским собором в 325 году нашей эры. Однако к 1582 году нашей эры количество прошлых високосных лет изменилось. (0,2422 умножить на 4 года =.9688 день, а не 1 день) а по юлианскому календарю на орбите Земли увеличилось на 10 дней положение вокруг солнца. Если не отметить, Пасха в конечном итоге происходят летом. Чтобы исправить это, Папа Григорий XIII бросил 10 дней. с 1582 г. и ввел в действие первое и второе исключения ('делимые без остатка на 100 и на 400 '), как описано выше. Первое исключение исключает високосный год каждые 100 лет. Используя только первое исключение, календарь через несколько столетий будет немного недокорректирован.То есть он не соответствовал бы истинному орбитальному положению Земли. Понимая это, математики Папы добавили второе исключение. который включает високосный год каждые 400 лет (1600, 2000, 2400 и т. д.). Эти правила не полностью корректируют календарь до идеальных 365,2422 дней. в год; к 5000 году нашей эры он получит 1 день и еще один потребуется регулировка. Раздел «Календарь» любого хорошего Альманаха проверит эти правила относительно високосных лет ----- ВРЕМЯ: Все данные AZMET собираются, хранятся и представляются в местное время «Аризона», которое находится в часовом поясе «Mountain Standard».В Аризоне не действует переход на летнее время. Следовательно, время, указанное в файлах данных AZMET, является всегда на семь часов отстает от всемирного координированного времени (UTC) (также известное как: среднее время по Гринвичу; время зулусов).
UTC Аризона Аризона 12 часов
------ ------- -------------
8:00 1:00 1:00 утра
9:00 2:00 2:00 утра
10:00 3:00 3:00 утра
11:00 4:00 4:00 утра
12:00 5:00 5:00 утра
13:00 6:00 6:00 утра
14:00 7:00 7:00
15:00 8:00 8:00
16:00 9:00 9:00 утра
17:00 10:00 10:00
18:00 11:00 11:00
19:00 12:00 12:00 утра
20:00 13:00 13:00
21:00 14:00 14:00
22:00 15:00 15:00
23:00 16:00 16:00
24:00 17:00 17:00
13:00 18:00 18:00
14:00 19:00 19:00
15:00 20:00 20:00
16:00 21:00 21:00
17:00 22:00 22:00
18:00 23:00 23:00
19:00 24:00 12:00
| 2020 | |
| 3 июля | Праздник Дня независимости — Школы и офисы закрыты |
| 31 июля | Курбан-байрам * |
| 17-19 августа | Дней профессиональной службы для новых учителей |
| 20-28 августа | Дней профессиональной службы для всех учителей |
| 26 августа | Профессиональное развитие |
| 28 августа | Ориентация для студентов / Пробный виртуальный день класса (все студенты) |
| 31 августа | Первый день в школе для всех учеников |
| 7 сентября | Праздник Дня труда — школы и офисы закрыты |
| 19-20 сентября | Рош ха-Шана * |
| 25 сентября | Повышение квалификации — закрытые школы для учащихся |
| 28 сентября | Праздник Йом Киппур * — Школы и офисы закрыты |
| 12 октября | День коренных американцев и конференции родителей и учителей — школы закрыты для учащихся |
| 16 октября | Повышение квалификации — школы, закрытые для учащихся |
| 3 ноября | День выборов — Закрытые школы и офисы |
| 5 ноября | Конец 1 квартала (44 дня) |
| 6 ноября | Профессиональный день учителей — 2 часа.Досрочное увольнение студентов |
| 14 ноября | Дивали * |
| 25-27 ноября | Праздники Дня благодарения — школы и офисы закрыты |
| 11 декабря | Повышение квалификации — школы, закрытые для учащихся |
| 24-31 декабря | Зимние каникулы и рождественские каникулы — школы и офисы закрыты |
| 2021 | |
| 1 января | Зимние каникулы и новогодние каникулы — школы и офисы закрыты |
| 18 января | Мартин Л.День короля-младшего — школы и офисы закрыты |
| 27 января | Конец второго квартала (46 дней) |
| 28 января | Профессиональный день учителей — 2 часа. Досрочное увольнение студентов |
| 15 февраля | Праздник в День президентов — школы и офисы закрыты |
| 16 февраля | Встречи родителей и учителей — 2-час. Отсроченное открытие для студентов |
| 28 марта — 4 апреля | Пасха |
| 29 марта — 1 апреля | Весенние каникулы — школы закрыты для учащихся и учителей |
| 2 и 5 апреля | Весенние каникулы и пасхальные каникулы — школы и офисы закрыты |
| 9 апреля | Конец третьего квартала (45 дней) |
| 12 апреля | Профессиональный день учителей — 2 часа.Досрочное увольнение студентов |
| 13 апреля | Первый день Рамадана |
| 11 мая | Последний день Рамадана |
| 13 мая | Праздник Ид аль-Фитр * — школы и офисы закрыты |
| 31 мая | День поминовения — школы и офисы закрыты |
| 14 июня | 2-часовой. Досрочное увольнение студентов 1 |
| 15 июня | Последний день для студентов 1 и конец четвертой четверти (45 дней) — 2-час.Досрочное увольнение студентов |
| 16 июня | Последний день учителя 1 |
| 16–18 сентября | Среда – пятница | Полностью удаленные неполные школьные дни для учащихся. |
| 21 сентября | Понедельник | Очное обучение начинается для учащихся 3K, Pre-K и всех учащихся округа 75 |
| 28 сентября | Понедельник | Йом Кипур, школы закрыты |
| 29 сентября | Вторник | Очное обучение начинается для всех учеников начальной школы (K-12, K-5, K-8, K-2 и K-3 школы) |
| 1 октября | Четверг | Очное обучение начинается в средней школе, средней школе, средних школах, переходных школах, образовательных учреждениях для взрослых и вечерних школах. |
| 12 октября | Понедельник | День Колумба, школы закрыты |
| 3 ноября | Вторник | День выборов, полностью дистанционное обучение для всех учащихся |
| 4 ноября | ноябряСреда | Вечерние конференции родителей и учителей для начальных школ и школ K – 8. |
| 5 ноября | Четверг | Дневные конференции родителей и учителей для начальных школ и школ K – 8; учеников этих школ увольняют на три часа раньше. |
| 11 ноября | Среда | День ветеранов, школы закрыты |
| 12 ноября | Четверг | Вечерние конференции родителей и учителей для средних школ, K – 12 и 6–12 школ. |
| 13 ноября | Пятница | Дневные конференции родителей и учителей для средних школ, школ K – 12 и школ 6–12; учеников этих школ увольняют на три часа раньше. |
| 18 ноября | Среда | Вечерние родительские собрания для учащихся средних школ и школьных программ Округа 75. |
| 19 ноября | Четверг | Дневные конференции для учащихся средних школ и школьных программ Округа 75; учеников этих школ увольняют на три часа раньше. |
| 26–27 ноября | Четверг – пятница | Перерыв на День благодарения, школы закрыты |
| 24 декабря – 1 января | Четверг – следующая пятница | Зимние каникулы, школы закрыты |
| 18 января | Понедельник | Преподобный д-р Мартин Лютер Кинг-младшийДень, школы закрыты |
| 1 февраля | Понедельник | День профессионального развития для 9–12 и 6–12 школ только в округах 1–32; ученики этих школ не посещают. Посещают учащиеся школ и программ K – 5, K – 6, 6–8, K – 12 и D75. |
| 12 февраля | Пятница | Лунный Новый год, школы закрыты |
| 15–19 февраля | Понедельник – пятница | Зимние каникулы (включая День президентов и День рождения Линкольна), школы закрыто |
| 3 марта | Среда | Вечерние конференции родителей и учителей для начальных школ и школ K – 8. |
| 4 марта | Четверг | Дневные конференции родителей и учителей для начальных школ и школ K – 8; учеников этих школ увольняют на три часа раньше. |
| 10 марта | Среда | Вечерние конференции родителей и учителей для средних школ и школ и программ округа 75. |
| 11 марта | Четверг | Дневные конференции родителей и учителей для средних школ и школ и программ округа 75; учеников этих школ увольняют на три часа раньше. |
| 18 марта | Четверг | Вечерние родительские собрания для старшеклассников, школ K – 12 и 6–12. |
| 19 марта | Пятница | Дневные конференции родителей и учителей для средних школ, школ K – 12 и школ 6–12; учеников этих школ увольняют на три часа раньше. |
| 29 марта — 2 апреля | Понедельник – пятница | Весенние каникулы, школы закрыты |
| 13 мая | Четверг | Ид аль-Фитр, школы закрыты |
| 31 мая | Понедельник | День памяти, школы закрыты |
| 3 июня | Четверг | Юбилейный день.День канцлерской конференции по развитию персонала. Студенты не посещают занятия. |
| 8 июня | Вторник | Канцелярский день только для школ и программ K – 5, K – 6, 6–8, K – 12 и D75; ученики этих школ не посещают. Посещают учеников 9–12 и 6–12 школ в округах 1–32. |
| 25 июня | Пятница | Последний день в школе для всех учащихся. |
| Дом Контентные каналы: Основные праздники Рождество Праздничный день
Рецепты Как для создания особых дней «Национальный»
Определение дней | Ежедневный праздничный календарь Major 2020Есть много ежедневных праздников и особых дней, по одному или нескольким на каждый день. день года.Вот некоторые из основных ежедневных праздничных событий по месяцам. Обязательно отметьте их в своем календаре и отметьте каждого, большого или небольшой. Major 2020 Праздники: Дополнительная информация Скоро будет! Следите за новостями на 2021 год ежедневно по выходным месяцам. Holiday Insights , где каждый день в году — это праздник, странный или дурацкий день, религиозный праздник или особое событие.Присоединяйтесь к нам в ежедневное веселье в календаре каждый день год. Знаете ли вы? Есть буквально тысячи ежедневных праздников,
особые события и памятные даты. Их больше одного на каждый день в году.
Многие из этих праздников новы. Регулярно создаются новые праздники. В отпуске
Insights, мы прилагаем большие усилия, чтобы тщательно исследовать и задокументировать детали каждого из них,
максимально полно и точно. Зачёт по теме «Лексика и культура речи» (тест) 6 класс Вариант I. 1. Какое утверждение является неверным? А. Лексикология – раздел науки о языке, изучающий лексическое значение слова, употребление и происхождение слов. Б. Многозначные слова имеют несколько лексических значений. В. Все слова, помимо прямого значения, имеют переносное значение. Г. Омонимы – это слова одной и той же части речи, одинаковые по звучанию и написанию, но разные по лексическому значению. 2. Слова одной и той же части речи с противоположным лексическим значением называются: А. Антонимами. Б. Синонимами. В. Омонимами. 3. Слова, употребляемые жителями той или иной области, называются: А. Профессиональными. Б. Диалектными. В. Устаревшими. 4. Фразеологизмы – это: А. Слова, вошедшие в русский язык из других языков. Б. Устойчивые сочетания слов. В. Новые слова, возникшие в языке. 5. Какую букву нужно вставить? А Б В Г Пос..деть к старости е е и и Пол. Прим..рять друзей е и и е 6. Какая из данных пар слов не является антонимами? А. Болезнь-хворь. В. Трудолюбие-лень. Б. Чистовик-черновик. Г. Открытое-сокровенное. 7. Какая из данных пар слов не является синонимами? А. Истина-правда. В. Свобода-воля. Б. Добро-зло. Г. Запущенность-заброшенность. 8. В каком предложении есть фразеологизм. А. По вечерам бабушка рассказывала внуку сказки. Б. Алешка набрал в рот воды и раздул щеки. В. Г. На арене цирка заяц ходил на задних лапках. 9. Найдите сочетания слов, употребленные в переносном значении. А. Сухие листья трепетали на ветках. Б. Тишину нарушал треск сухой ветки под ногой. В. Спокойно дремлет лес над тихими полями. Г. Крики диких уток отдавались в дальнем озере. 10. Значение какого слова определено неверно? А. Колорит – сочетание красок, цветов в картине. Б. Фразеология – раздел науки о языке, изучающий способы построения фраз. В. Жалюзи – шторы из пластинок, навешиваемые на окна. Г. Филолог – ученый, занимающийся изучением языка и литературы. Вариант II. 1. Какое утверждение является неверным? А. Лексика изучает слово с точки зрения его смыслового значения. Б. Однозначные слова имеют только одно лексическое значение. В. Синонимами могут быть слова различных частей речи. Г. Метафора – средство выразительности языка, основанное на уподоблении одного предмета или явления другому по сходству или контрасту. 2. Слова одной и той же части речи, обозначающие одно и то же, но отличающиеся оттенками лексического значения и употреблением в речи, называются: А. Омонимами. Б. Синонимами. В. Антонимами. 3. Слова, вышедшие из активного повседневного употребления, называются: А. Б. Устаревшими. В. Профессиональными 4. Фразеологизмы – это: А. Устойчивые сочетания слов. Б. Слова, вошедшие в русский язык из других языков. В. Новые слова, возникшие в языке. 5. Какую букву нужно вставить? А Б В Г пос..деть рядом и и е е пол..скать белье о а о а прим..рять платье е е и и 6. Какая из данных пар слов не является антонимами? А. Доброта – жадность. В. Свет – тень. Б. 7. Какая из данных пар слов не является синонимами? А. Прозрачный – чистый. Б. Произведение – творение. В. Убирать – уборка Г. Размашистый – широкий. 8. В каком предложении есть фразеологизм. А. В этом году уродилось много грибов, так что за ними далеко ходить не надо. Б. Машина дала задний ход и остановилась. В. Надо внимательнее слушать объяснение учителя, а не хлопать ушами. Г. Свинья села в лужу прямо посредине двора. 9. Найдите сочетание слов, употребленное в переносном значении. А. Падая, лист крутится в воздухе. Б. В тени молодых березок разостлали ковер. В. Колокольчик хохочет до слез. Г. Сквозь зеленые ветки берез просвечивало солнце. 10. Значение какого слова определено неверно? А. Гамма – последовательный ряд музыкальных звуков. Б. Эстамп – оттиск, отпечаток картины на бумаге ( на камне, металле, дереве) с печатной формы. В. Яхтсмен – человек, строящий яхты. Г. Сентиментальный (человек) – излишне чувствительный. Происшествия
1957 Поделиться Следственный комитет сообщил, что глава ведомства Александр Бастрыкин поручил возбудить уголовное дело по факту пожара на подмосковном складе Ozon. В пресс-службе ведомства заявили, что ход и результаты расследования будут поставлены на контроль в центральном аппарате СК. По последним данным, площадь пожара на складе в Истринском округе достигла 50 тысяч квадратных метров, огонь приближается к размещенным неподалеку цистернам ГСМ. По оценкам местных властей, здание склада спасти уже не удастся. На месте работает пожарная авиация, направлен пожарный поезд. Информагентства со ссылкой на источники сообщают о гибели одного человека, без вести пропавшим числится еще один сотрудник склада. Также сообщается о 13 пострадавших. При этом в МЧС заявили, что у ведомства пока нет сведений о жертвах, официально подтвержден список пострадавших из 11 человек, двое госпитализированы. По сообщениям источников, основной версией произошедшего считается поджог. Смотрите фотогалерею по теме Подписаться Авторы: МЧС
Подмосковье — Московская область
Пожар Что почитать:Ещё материалы 12900 Елена Одинцова Фото
12600 Ирина Стафеева 3276 Белобородько Мария Фото
2748 Сэсэг Жигжитова Фото
2466 Юрий Асадулин 2278 Роксана Родионова В регионах:Ещё материалы В данной статье описано использование агрегатной функции для суммирования данных в результатах запроса.
Общее представление о способах суммирования данных
Подготовка примера данных
Суммирования данных с помощью строки итогов
Вычисление общих итогов с помощью запроса
Вычисление итогов по группе с помощью итогового запроса
Суммирование данных из нескольких групп с помощью перекрестного запроса
Справочные сведения об агрегатных функциях
Просуммировать числовой столбец в запросе можно с помощью агрегатной функции. Кроме того, в Access предусмотрено несколько способов добавления функции Sum и других агрегатных функций в запрос. Вы можете: Открыть запрос в режиме таблицы и добавить строку итогов. Строка итогов — возможность Access, позволяющая использовать агрегатные функции в одном или нескольких столбцах в результатах запроса без необходимости изменять его структуру. Создать итоговый запрос. Итоговый запрос вычисляет промежуточные итоги для групп записей, а строка итогов — общие итоги для одного или нескольких столбцов (полей) данных. Например, если вы хотите вычислить промежуточную сумму всех продаж по городам или по кварталам, следует использовать итоговый запрос для группировки записей по нужной категории, а затем просуммировать все объемы продаж. Создать перекрестный запрос. Перекрестный запрос — это особый тип запросов, отображающий результаты в сетке, напоминающей лист Excel. Перекрестные запросы суммируют значения и затем группируют их по двум наборам фактов — вдоль боковой стороны (заголовки строк) и в верхней части (заголовки столбцов). Например, вы можете использовать перекрестный запрос для отображения итоговых значений продаж для каждого города за последние три года, как показано в таблице:
Город
2003
2004
2005
Краснодар
254 556 372 455 467 892
Санкт-Петербург
478 021 372 987 276 399
Москва
572 997 684 374 792 571
. … … … Примечание: Ниже в разделах этой статьи подробно описано применение функции Sum, однако следует помнить, что вы можете использовать другие агрегатные функции в строках итогов и запросах. Дополнительные сведения об использовании других агрегатных функций см. ниже в разделе Справочные сведения об агрегатных функциях. Дополнительные сведения о способах использования других агрегатных функций см. в разделе Отображение итогов по столбцу в таблице. В следующих разделах описано, как добавить строку итогов, использовать итоговый запрос для суммирования данных и перекрестный запрос, вычисляющий промежуточные итоги по группам и интервалам времени. Общие сведения о типах данных см. в статье Изменение типа данных для поля.
К началу страницы
В инструкциях этой статьи приводятся таблицы с примерами данных. Они помогают понять, как работают агрегатные функции. Вы можете добавить примеры таблиц в новую или существующую базу данных. Сделать это в Access можно несколькими способами. Вы можете ввести данные вручную, скопировать каждую таблицу в редактор электронных таблиц (такой как Excel) и импортировать листы в Access или же вставить данные в текстовый редактор, например Блокнот, и импортировать их из созданных текстовых файлов. В пошаговых инструкциях этого раздела объясняется, как вводить данные вручную на пустой лист, а также как копировать примеры таблиц в редактор электронных таблиц и затем импортировать их в Access. Дополнительные сведения о создании и импорте текстовых данных см. в статье Импорт данных или связывание с данными текстового файла. В пошаговых инструкциях в этой статье используются приведенные ниже таблицы. Создайте пример данных на их основе: Таблица «Категории»
Категория
Куклы Игры и головоломки Картины и рамы Видеоигры DVD-диски и фильмы Модели для сборки, хобби Спортивное снаряжение Таблицы «Товары»
Наименование товара
Цена
Категория
Фигурка программиста 12,95 ₽ Куклы Эксперименты с C# (игра для всей семьи) 15,85 ₽ Игры и головоломки Схема реляционной базы данных 22,50 ₽ Картины и рамы Волшебная микросхема (500 деталей) 32,65 ₽ Игры и головоломки Access! Игра! 22,95 ₽ Игры и головоломки Компьютерные маньяки и мифические животные 78,50 ₽ Видеоигры Упражнение для компьютерных мониторов! DVD-диск! 14,88 ₽ DVD-диски и фильмы Неуловимая летающая пицца 36,75 ₽ Спортивное снаряжение Внешний дисковод гибких дисков 5. 65,00 ₽ Модели для сборки, хобби Недвижущаяся фигурка бюрократа 78,88 ₽ Куклы Тьма 53,33 ₽ Видеоигры Собери клавиатуру 77,95 ₽ Модели для сборки, хобби Таблица Заказы
Дата заказа
Дата отгрузки
Город назначения
Стоимость доставки
14. 15.11.2005 Москва 55,00 ₽ 14.11.2005 15.11.2005 Санкт-Петербург 76,00 ₽ 16.11.2005 17.11.2005 Санкт-Петербург 87,00 ₽ 17. 18.11.2005 Москва 43,00 ₽ 17.11.2005 18.11.2005 Краснодар 105,00 ₽ 17.11.2005 18.11.2005 Новосибирск 112,00 ₽ 18. 19.11.2005 Иркутск 215,00 ₽ 19.11.2005 20.11.2005 Владивосток 525,00 ₽ 20.11.2005 21.11.2005 Иркутск 198,00 ₽ 20. 21.11.2005 Краснодар 187,00 ₽ 21.11.2005 22.11.2005 Санкт-Петербург 81,00 ₽ 23.11.2005 24.11.2005 Москва 92,00 ₽ Таблица Сведения о заказах
Идентификатор заказа
Наименование товара
Код товара
Цена за единицу
Количество
Скидка
1 Собери клавиатуру 12 77,95 ₽ 9 5% 1 Недвижущаяся фигурка бюрократа 2 78,88 ₽ 4 7,5% 2 Упражнение для компьютерных мониторов! DVD-диск! 7 14,88 ₽ 6 4% 2 Волшебная микросхема 4 32,65 ₽ 8 0 2 Компьютерные маньяки и мифические животные 6 78,50 ₽ 4 0 3 Access! Игра! 5 22,95 ₽ 5 15% 4 Фигурка программиста 1 12,95 ₽ 2 6% 4 Неуловимая летающая пицца 8 36,75 ₽ 8 4% 5 Внешний дисковод гибких дисков 5. 9 65,00 ₽ 4 10% 6 Схема реляционной базы данных 3 22,50 ₽ 12 6,5% 7 Тьма 11 53,33 ₽ 6 8% 7 Схема реляционной базы данных 3 22,50 ₽ 4 9% Примечание: Помните, что в типичной базе данных таблица «Сведения о заказах» будет содержать только поле «Код товара» (без поля «Наименование товара»). на вкладке Создание в группе Таблицы нажмите кнопку Таблица. Access добавит в базу данных новую пустую таблицу. Примечание: Эту операцию следует выполнять только при необходимости добавить таблицу в базу данных. При открытии новой пустой базы данных это действие не требуется. Дважды щелкните первую ячейку в строке заголовков и введите имя поля из примера таблицы. По умолчанию в Access пустые поля обозначаются надписью Добавить поле в строке заголовков:
С помощью клавиш со стрелками перейдите в следующую пустую ячейку заголовка и введите имя второго поля (чтобы перейти в другую ячейку, можно также нажать клавишу TAB или щелкнуть эту ячейку два раза). Повторите эти действия, чтобы ввести имена всех полей. Введите данные в пример таблицы. По мере ввода данных Access определяет их тип для каждого поля. Если вы плохо знакомы с реляционными базами данных, для каждого поля таблицы следует задать конкретный тип данных, например «Число», «Текст» или «Дата/время». Это обеспечивает точный ввод данных и помогает предотвратить ошибки, например использование цифр номера телефона в вычислениях. Для этих примеров таблиц можно определить тип данных автоматически. Завершив ввод данных, нажмите кнопку Сохранить.
(Сочетание клавиш: нажмите CTRL+S.) Откроется диалоговое окно Сохранение документа. В поле Имя таблицы введите имя примера таблицы и нажмите кнопку ОК. Следует использовать указанные имена таблиц, потому что они применяются в запросах, приведенных в пошаговых инструкциях. Повторяйте эти шаги, пока не создадите каждый из примеров таблиц, приведенных в начале этого раздела. Если вы не хотите вводить данные вручную, можно выполнить указанные ниже действия для копирования информации в файл электронной таблицы, а затем импортировать данные из него в Access. Запустите редактор электронных таблиц и создайте пустой файл. Если вы используете Excel, по умолчанию создается пустая книга. Скопируйте первый пример таблицы и вставьте его на первый лист, начиная с первой ячейки. Присвойте листу имя с помощью функций редактора электронных таблиц. Оно должно совпадать с именем примера таблицы. Например, если пример называется Категории, присвойте листу это же имя. Повторяйте шаги 2 и 3, чтобы скопировать каждый пример таблицы на пустой лист и переименовать этот лист. Примечание: К файлу электронной таблицы может понадобиться добавить листы. Сведения о том, как сделать это, см. в справке редактора электронных таблиц. Сохраните книгу в нужной папке на компьютере или в сети и переходите к следующей процедуре. На вкладке Внешние данные в группе Импорт щелкните Excel. -или- Нажмите кнопку Дополнительно, а затем выберите редактор электронных таблиц из списка. Откроется диалоговое окно Внешние данные — лист <имя программы>. Нажмите кнопку Обзор, откройте файл электронной таблицы, созданный на предыдущих этапах, и нажмите кнопку ОК. Откроется окно мастера импорта электронных таблиц. По умолчанию мастер выбирает первый лист в книге (в этом примере — лист Клиенты), и данные из этого листа появляются в нижней части страницы мастера. Нажмите кнопку Далее. На следующей странице мастера выберите Первая строка содержит названия столбцов, а затем нажмите кнопку Далее. Если нужно, вы можете изменить имена полей и типы данных или пропустить некоторые поля, воспользовавшись текстовыми полями и списками в группе Параметры поля. В противном случае нажмите кнопку Далее. Оставьте параметр автоматически создать ключ выбранным и нажмите кнопку Далее. По умолчанию Access использует имя листа для новой таблицы. Оставьте это имя или введите другое, а затем нажмите кнопку Готово. Повторите шаги с 1 по 7 для каждого листа книги Excel, чтобы создать для него таблицу. Примечание: При импорте листов Access автоматически добавляет в каждую таблицу столбец первичного ключа и по умолчанию присваивает ему имя «Код» и тип данных «Счетчик». В этом разделе даны инструкции по переименованию полей первичного ключа. Это позволяет четко определить все поля в запросе. В области навигации щелкните правой кнопкой мыши каждую таблицу, созданную на предыдущем шаге, и выберите команду Конструктор. Для каждой таблицы найдите поле первичного ключа. По умолчанию Access присваивает каждому полю имя Код. В столбце Имя поля каждого поля первичного ключа добавьте имя таблицы. Например, можно переименовать поле «ИД» в таблице «Категории» в «ИД категории», а поле таблицы «Заказы» — в «ИД заказа». В таблице «Сведения о заказе» переименуем поле в «Подробный ИД». В таблице «Товары» переименуем поле в «ИД товара». Сохраните изменения. В последующих ссылках на примеры таблиц в данной статье указываются поля первичного ключа, переименованные, как описано выше.
К началу страницы
Чтобы добавить в запрос строку итогов, откройте его в режиме таблицы, добавьте строку, а затем выберите нужную агрегатную функцию, например Sum, Min, Max или Avg. На вкладке Создать в группе Другое нажмите кнопку Конструктор запросов. Дважды щелкните таблицу или таблицы, которые вы хотите использовать в запросе. Выбранные таблицы отображаются в виде окон в верхней части конструктора запросов. Дважды щелкните поля таблицы, которые вы хотите использовать в запросе. Можно включить поля, содержащие описательные данные, например имена и описания, но следует обязательно добавить поле, содержащее числовые или денежные значения. Каждое поле отображается в ячейке в бланке запроса. Нажмите кнопку Выполнить для выполнения запроса. Результаты запроса будут отображены в режиме таблицы. При необходимости переключитесь в Конструктор и скорректируйте запрос. Для этого щелкните правой кнопкой мыши вкладку документа для запроса и выберите команду Конструктор. Сохраните запрос. Убедитесь в том, что запрос открыт в режиме таблицы. Для этого щелкните правой кнопкой мыши вкладку документа для запроса и выберите команду Режим таблицы. -или- Дважды щелкните запрос в области навигации. Запрос будет выполнен, а его результаты будут загружены в таблицу. На вкладке Главная в группе Записи нажмите кнопку Итоги. В таблице появится новая строка Итог. В строке Итог щелкните ячейку в поле, по которому вы хотите вычислить сумму, и выберите в списке функцию Sum. Дополнительные сведения об использовании строки итогов см. в разделе Отображение итогов по столбцу в таблице.
К началу страницы
Общие итоги — это сумма по всем значениям столбца. Можно вычислять нескольких типов общих итогов, включая: Простой общий итог, суммирующий значения одного столбца. Например, можно вычислить общую стоимость доставки. Вычисляемый общий итог, суммирующий значения нескольких столбцов. Например, можно вычислить суммы продаж путем умножения цены нескольких товаров на число заказанных товаров, а затем просуммировав результирующие значения. Общий итог за исключением нескольких записей. Например, можно вычислить сумму продаж только по последней пятнице. В следующих разделах описано, как вычислить каждый из типов общих итогов. В инструкциях используются таблицы «Заказы» и «Сведения о заказах».
Таблица «Заказы»
Идентификатор заказа
Дата заказа
Дата отгрузки
Город назначения
Стоимость доставки
1 14. 15.11.2005 Москва 55,00 ₽ 2 14.11.2005 15.11.2005 Санкт-Петербург 76,00 ₽ 3 16.11.2005 17. Санкт-Петербург 87,00 ₽ 4 17.11.2005 18.11.2005 Москва 43,00 ₽ 5 17.11.2005 18.11.2005 Краснодар 105,00 ₽ 6 17. 18.11.2005 Новосибирск 112,00 ₽ 7 18.11.2005 19.11.2005 Иркутск 215,00 ₽ 8 19.11.2005 20. Владивосток 525,00 ₽ 9 20.11.2005 21.11.2005 Иркутск 198,00 ₽ 10 20.11.2005 21.11.2005 Краснодар 187,00 ₽ 11 21. 22.11.2005 Санкт-Петербург 81,00 ₽ 12 23.11.2005 24.11.2005 Москва 92,00 ₽
Таблица «Сведения о заказах»
Код сведений
Идентификатор заказа
Наименование товара
Код товара
Цена за единицу
Количество
Скидка
1 1 Собери клавиатуру 12 77,95 ₽ 9 0,05 2 1 Недвижущаяся фигурка бюрократа 2 78,88 ₽ 4 0,075 3 2 Упражнение для компьютерных мониторов! DVD-диск! 7 14,88 ₽ 6 0,04 4 2 Волшебная микросхема 4 32,65 ₽ 8 0,00 5 2 Компьютерные маньяки и мифические животные 6 78,50 ₽ 4 0,00 6 3 Access! Игра! 5 22,95 ₽ 5 0,15 7 4 Фигурка программиста 1 12,95 ₽ 2 0,06 8 4 Неуловимая летающая пицца 8 36,75 ₽ 8 0,04 9 5 Внешний дисковод гибких дисков 5. 9 65,00 ₽ 4 0,10 10 6 Схема реляционной базы данных 3 22,50 ₽ 12 0,065 11 7 Тьма 11 53,33 ₽ 6 0,08 12 7 Схема реляционной базы данных 3 22,50 ₽ 4 0,09 На вкладке Создать в группе Другое нажмите кнопку Конструктор запросов. Дважды щелкните таблицу, которую вы хотите использовать в запросе. При использовании примера данных нужно дважды щелкнуть таблицу «Заказы». Таблица появится в окне в верхней части конструктора запросов. Дважды щелкните поле, для которого вы хотите найти сумму. Убедитесь, что поле имеет тип данных «Число» или «Денежный». При попытке суммировать значения в нечисловых полях, например в текстовом поле, Access выводит сообщение об ошибке Несоответствие типов данных в выражении условия отбора. Если вы используете пример данных, дважды щелкните столбец «Стоимость доставки». Вы можете добавить дополнительные числовые поля, если хотите вычислить для них общие итоги. Итоговый запрос может вычислять общие итоги для нескольких столбцов. На вкладке Конструктор в группе Показать или скрыть нажмите кнопку Итоги. В бланке появится строка Итог, а в ячейке столбца «Стоимость доставки» будет указано Группировка. Измените значение в ячейке строки Итог строки на Sum. Чтобы выполнить запрос и отобразить результаты в режиме таблицы, нажмите кнопку Выполнить . Совет: Обратите внимание, что Access добавит «СуммаOf» в начало имени поля, которое вы суммируете. Чтобы изменить заголовок столбца на более осмысленный, например «Всего доставки», переключиться обратно в конструктор и щелкните в строке «Поле» столбца «Стоимость доставки» в сетке конструктора. Поместите курсор рядом с искомой стоимостью доставки и введите слова Total Shippingи двоеточие, например: Total Shipping: Shipping Fee. При необходимости вы можете сохранить запрос и закрыть его. На вкладке Создать в группе Другое нажмите кнопку Конструктор запросов. Дважды щелкните таблицы «Заказы» и «Сведения о заказах». Добавьте поле «Дата заказа» из таблицы «Заказы» в первый столбец на бланке запроса. В строке Условие отбора первого столбца введите Date() -1. Это выражение исключает записи с текущей датой из вычисляемого итогового значения. Затем создайте столбец, который вычисляет объем продаж по каждой транзакции. Введите в строку Поле второго столбца на бланке следующее выражение:
Общее значение продаж: (1-[Сведения о заказах].[Скидка]/100)*([Сведения о заказах].[Цена за единицу]*[Сведения о заказах].[Количество])
Убедитесь, что выражение ссылается на поля с типами данных «Число» или «Денежный». Если оно ссылается на поля с другими типами данных, то при попытке выполнения запроса появится сообщение Несоответствие типов данных в выражении условия отбора. На вкладке Конструктор в группе Показать или скрыть нажмите кнопку Итоги. В бланке появится строка Итог, а в первом и втором столбцах будет указано Группировка. Во втором столбце измените значение в ячейке строки Итог строки на Sum. Функция Sum суммирует отдельные показатели продаж. Чтобы выполнить запрос и отобразить результаты в режиме таблицы, нажмите кнопку Выполнить . Сохраните запрос с именем Продажи за день. Примечание: При следующем открытии запроса в Конструкторе можно заметить небольшие изменения в значениях, указанных для строк Поле и Итог в столбце «Общее значение продаж». Выражение заключено в функцию Sum, а в строке Итог выводится Выражение вместо функции Sum. Например, если вы использовали пример данных и создали запрос, как показано выше, будет отображено:
Общее значение продаж: Sum((1-[Сведения о заказах].Скидка/100)*([Сведения о заказах].Цена*[Сведения о заказах].Количество))
К началу страницы
В этом разделе описано, как создать итоговый запрос для вычисления промежуточных итогов по группам данных. Помните, что по умолчанию итоговый запрос может включать только поле или поля, содержащие данные, по которым выполняется группировка, например поле «Категории», а также поля со значениями, которые вы хотите просуммировать, например поле «Продажи». Итоговые запросы не могут включать другие поля, описывающие значения внутри категории. В этом разделе описано, как создавать итоговые запросы и запросы на выборку, если требуется определить объем продаж для каждого товара. В качестве примера используются следующие таблицы:
Таблицы «Товары»
Код товара
Наименование товара
Цена
Категория
1 Фигурка программиста 12,95 ₽ Куклы 2 Эксперименты с C# (игра для всей семьи) 15,85 ₽ Игры и головоломки 3 Схема реляционной базы данных 22,50 ₽ Картины и рамы 4 Волшебная микросхема (500 деталей) 32,65 ₽ Картины и рамы 5 Access! Игра! 22,95 ₽ Игры и головоломки 6 Компьютерные маньяки и мифические животные 78,50 ₽ Видеоигры 7 Упражнение для компьютерных мониторов! DVD-диск! 14,88 ₽ DVD-диски и фильмы 8 Неуловимая летающая пицца 36,75 ₽ Спортивное снаряжение 9 Внешний дисковод гибких дисков 5. 65,00 ₽ Модели для сборки, хобби 10 Недвижущаяся фигурка бюрократа 78,88 ₽ Куклы 11 Тьма 53,33 ₽ Видеоигры 12 Собери клавиатуру 77,95 ₽ Модели для сборки, хобби
Таблица «Сведения о заказах»
Код сведений
Идентификатор заказа
Наименование товара
Код товара
Цена за единицу
Количество
Скидка
1 1 Собери клавиатуру 12 77,95 ₽ 9 5% 2 1 Недвижущаяся фигурка бюрократа 2 78,88 ₽ 4 7,5% 3 2 Упражнение для компьютерных мониторов! DVD-диск! 7 14,88 ₽ 6 4% 4 2 Волшебная микросхема 4 32,65 ₽ 8 0 5 2 Компьютерные маньяки и мифические животные 6 78,50 ₽ 4 0 6 3 Access! Игра! 5 22,95 ₽ 5 15% 7 4 Фигурка программиста 1 12,95 ₽ 2 6% 8 4 Неуловимая летающая пицца 8 36,75 ₽ 8 4% 9 5 Внешний дисковод гибких дисков 5. 9 65,00 ₽ 4 10% 10 6 Схема реляционной базы данных 3 22,50 ₽ 12 6,5% 11 7 Тьма 11 53,33 ₽ 6 8% 12 7 Схема реляционной базы данных 3 22,50 ₽ 4 9% Следующие действия также предполагают наличие отношения «один-ко-многим» между полями «Код товара» в таблицах «Заказы» и «Сведения о заказах» с таблицей «Заказы» на стороне «один» данного отношения. На вкладке Создать в группе Другое нажмите кнопку Конструктор запросов. Выберите нужные таблицы и нажмите кнопку «Добавить». Таблица появится в виде окна в верхней части конструктора запросов. При использовании примеров таблиц, указанных выше, добавьте таблицы «Товары» и «Сведения о заказах». Дважды щелкните поля таблицы, которые вы хотите использовать в запросе. Как правило, в запрос добавляются только поле группы и поле значений. Однако вместо поля значения можно использовать вычисление — в следующих действиях объясняется, как это сделать. Добавьте поле «Категория» из таблицы «Товары» в бланк запроса. Создайте столбец, вычисляющий объемы продаж для каждой транзакции, введя во второй столбец бланка запроса следующее выражение:
Общее значение продаж: (1-[Сведения о заказах].[Скидка]/100)*([Сведения о заказах].[Цена за единицу]*[Сведения о заказах].[Количество])
Убедитесь, что поля, на которые ссылается выражение, имеют типы данных «Число» или «Денежный». На вкладке Конструктор в группе Показать или скрыть нажмите кнопку Итоги. В бланке появится строка Итог, в первом и втором столбцах которой будет указано Группировка. Во втором столбце измените значение в строке Итог строки на Sum. Функция Sum суммирует отдельные показатели продаж. Чтобы выполнить запрос и отобразить результаты в режиме таблицы, нажмите кнопку Выполнить . Оставьте запрос открытым, чтобы использовать его в следующем разделе. Использование условий в итоговом запросе Запрос, созданный в предыдущем разделе, включает все записи в базовых таблицах. Он не исключает никакие заказы при вычислении итогов и отображает итоги для всех категорий. Если вам нужно исключить некоторые записи, можно добавить условия в запрос. Например, вы можете пропустить транзакции с суммой менее 100 ₽ или вычислить итоги только по некоторым категориям товаров. В этом разделе описано использование трех типов условий:
Условия, игнорирующие некоторые группы при вычислении итогов. Например, можно вычислить итоги только для категорий товаров «Видеоигры», «Картины и рамы» и «Спортивное снаряжение».
Условия, скрывающие некоторые итоговые значения после их вычисления. Например, можно отобразить только итоговые значения свыше 150 000 ₽.
Условия, исключающие некоторые записи при вычислении итогового значения. Например, можно исключить отдельные транзакции, в которых значение (Цена за единицу * Количество) меньше 100 ₽. На примере следующих действий объясняется, как добавить условия одно за другим и как это повлияет на результаты запроса. Добавление условий в запрос Откройте запрос из предыдущего раздела в Конструкторе. Для этого щелкните правой кнопкой мыши вкладку документа для запроса и выберите команду Конструктор. -или- Щелкните правой кнопкой мыши запрос в области навигации и выберите Конструктор. В строке Условия отбора столбца «Код категории» введите =Куклы Or Спортивное снаряжение or Картины и рамы. Чтобы выполнить запрос и отобразить результаты в режиме таблицы, нажмите кнопку Выполнить . Вернитесь в Конструктор и в строке Условия отбора столбца «Общее значение продаж» введите >100. Выполните запрос, чтобы просмотреть результаты, а затем переключитесь в Конструктор. Теперь добавьте условия для исключения отдельных транзакций, сумма которых меньше 100 ₽. Для этого необходимо добавить еще один столбец. Примечание: Невозможно указать третье условие для столбца «Общее значение продаж». Любое условие, указанное для этого столбца, будет применено к итоговому значению, а не к отдельным значениям. Скопируйте выражение из второго столбца в третий столбец. В строке Итог нового столбца выберите Условие, а в строке Условия отбора введите >20. Выполните запрос, чтобы просмотреть результаты, а затем сохраните его. Примечание: При следующем открытии запроса в Конструкторе можно заметить небольшие изменения в бланке. Во втором столбце выражение в строке Поле будет заключено в функцию Sum, а в строке Итоги будет указано Выражение вместо функции Sum.
Общее значение продаж: Sum((1-[Сведения о заказах].Скидка/100)*([Сведения о заказах].Цена*[
Сведения о заказах].Количество))
Будет также отображен четвертый столбец. Этот столбец — копия второго столбца, но условия, заданные во втором столбце, на самом деле отображаются как часть нового столбца.
К началу страницы
Перекрестный запрос — это особый тип запросов, отображающий результаты в сетке, напоминающей лист Excel. Перекрестные запросы суммируют значения и затем группируют их по двум наборам фактов — один набор вдоль боковой стороны (заголовки строк) и второй набор вдоль верхней части (заголовки столбцов).
Помните, что перекрестный запрос не всегда заполняет все поля в наборе результатов, потому что таблицы, используемые в запросе, не всегда содержат значения для всех возможных точек данных. При создании перекрестного запроса обычно включаются данные из нескольких таблиц, и всегда включаются три типа данных: данные, используемые в качестве заголовков строк, данные, используемые в качестве заголовков столбцов и значения, которые вы хотите просуммировать или с которыми необходимо произвести другие вычисления. Инструкции в данном разделе предполагают использование следующих примеров таблиц:
Таблица «Заказы»
Дата заказа
Дата отгрузки
Город назначения
Стоимость доставки
14. 15.11.2005 Москва 55,00 ₽ 14.11.2005 15.11.2005 Санкт-Петербург 76,00 ₽ 16.11.2005 17.11.2005 Санкт-Петербург 87,00 ₽ 17. 18.11.2005 Москва 43,00 ₽ 17.11.2005 18.11.2005 Краснодар 105,00 ₽ 17.11.2005 18.11.2005 Новосибирск 112,00 ₽ 18. 19.11.2005 Иркутск 215,00 ₽ 19.11.2005 20.11.2005 Владивосток 525,00 ₽ 20.11.2005 21.11.2005 Иркутск 198,00 ₽ 20. 21.11.2005 Краснодар 187,00 ₽ 21.11.2005 22.11.2005 Санкт-Петербург 81,00 ₽ 23.11.2005 24.11.2005 Москва 92,00 ₽
Таблица «Сведения о заказах»
Идентификатор заказа
Наименование товара
Код товара
Цена за единицу
Количество
Скидка
1 Собери клавиатуру 12 77,95 ₽ 9 5% 1 Недвижущаяся фигурка бюрократа 2 78,88 ₽ 4 7,5% 2 Упражнение для компьютерных мониторов! DVD-диск! 7 14,88 ₽ 6 4% 2 Волшебная микросхема 4 32,65 ₽ 8 0 2 Компьютерные маньяки и мифические животные 6 78,50 ₽ 4 0 3 Access! Игра! 5 22,95 ₽ 5 15% 4 Фигурка программиста 1 12,95 ₽ 2 6% 4 Неуловимая летающая пицца 8 36,75 ₽ 8 4% 5 Внешний дисковод гибких дисков 5. 9 65,00 ₽ 4 10% 6 Схема реляционной базы данных 3 22,50 ₽ 12 6,5% 7 Тьма 11 53,33 ₽ 6 8% 7 Схема реляционной базы данных 3 22,50 ₽ 4 9% Ниже объясняется, как создавать перекрестный запрос, группирующий итоги продаж по городам. На вкладке Создать в группе Другое нажмите кнопку Конструктор запросов. Дважды щелкните таблицы, которые вы хотите использовать в запросе. Таблица появится в виде окна в верхней части конструктора запросов. При использовании примеров таблиц дважды щелкните таблицы «Заказы» и «Сведения о заказах». Дважды щелкните поля, которые вы хотите использовать в запросе. Каждое имя поля появится в пустой ячейке в строке Поле на бланке. При использовании примеров таблиц добавьте поля «Город назначения» и «Дата отгрузки» из таблицы «Заказы». В следующую пустую ячейку строки Поле скопируйте и вставьте или введите следующее выражение: Итоги продаж: Sum(CCur([Сведения о заказах].[Цена за едницу]*[Количество]*(1-[Скидка])/100)*100) На вкладке Конструктор в группе Тип запроса щелкните элемент Перекрестная таблица. В бланке запроса будут отображены строки Итог и Перекрестный. Щелкните ячейку в строке Итог в поле «Город назначения» и выберите Группировка. Выполните те же действия для поля «Дата отгрузки». Измените значение в ячейке Итоги поля «Итоги продаж» на Выражение. В строке Перекрестный присвойте ячейке в поле «Город назначения» значение Заголовки строк, полю «Дата отгрузки» — значение Заголовки столбцов, а полю «Итоги продаж» — Значение. На вкладке Конструктор в группе Результаты нажмите кнопку Выполнить. Результаты запроса будут отображены в режиме таблицы.
К началу страницы
В следующей таблице перечислены и отписаны агрегатные функции Access, которые можно использовать в строке итогов и в запросах. Помните, что в Access предусмотрено больше агрегатных функций для запросов, чем для строки итогов. Кроме того, при работе с проектом Access (внешней базой данных Access, которая подключается к базе данных Microsoft SQL Server) можно использовать расширенный набор агрегатных функций, предоставляемый SQL Server. Дополнительные сведения о них см. в электронной документации Microsoft SQL Server.
Функция
Описание
Поддерживаемые
типы данных
Average Вычисляет среднее значение для столбца. «Число», «Денежный», «Дата/время» Count Подсчитывает число элементов в столбце. Все типы данных, за исключением сложных повторяющихся скалярных данных, таких как столбец многозначных списков. Дополнительные сведения о списках, которые могут быть многоценными, см. в руководстве по полям, которые могут быть многоценными, а также к созданию или удалите многофаентное поле. Максимум Возвращает элемент, имеющий наибольшее значение. «Число», «Денежный», «Дата/время» Minimum Возвращает элемент, имеющий наименьшее значение. Для текстовых данных наибольшим будет первое по алфавиту значение, причем Access не учитывает регистр. Функция игнорирует пустые значения. «Число», «Денежный», «Дата/время» Standard Deviation Показывает, насколько значения отклоняются от среднего. Дополнительные сведения об этой функции см. «Число», «Денежный» Sum Суммирует элементы в столбце. Подходит только для числовых и денежных данных. «Число», «Денежный» Variance Вычисляет статистическую дисперсию для всех значений в столбце. Подходит только для числовых и денежных данных. Если таблица содержит менее двух строк, Access возвращает пустое значение. Дополнительные сведения о функциях для расчета дисперсии см. в разделе Отображение итогов по столбцу в таблице. «Число», «Денежный»
К началу страницы
Я трижды переезжала из квартиры в квартиру и знаю, как непросто разбирать горы мебели и коробки с вещами. Полина Калмыкова переезжает с комфортом Профиль автора Поэтому пришлось разобраться, как работают сервисы временного хранения — это такие цивилизованные аналоги гаражу. В них можно оставить коробки с вещами не первой необходимости, чтобы они не мешали во время перестановок. Или бытовую технику или мебель, которая оказалась лишней при переезде, но в перспективе еще пригодится. В этом материале — склады и службы доставки, которые не подведут. Сохраните статью в закладки на случай, если у вас в квартире окажется больше вещей, чем нужно. Сколько стоит: от 900 Р в месяц Условия. «Хоумсклад» — одна из самых крупных сетей хранения в Москве: сейчас у компании шесть складов в разных районах города. Цены и размеры ячеек зависят от конкретного склада. В основном за месячную аренду квадратного метра просят 1500—1900 Р, но так только в теплых складах с постоянной температурой воздуха +18 °C. Если хотите сэкономить, арендуйте уличные контейнеры от 900 Р в месяц за квадратный метр. Правда, это не финальная цена: к стоимости аренды добавится страховой депозит в размере месячной платы — потом его можно вернуть или засчитать в оплату последнего месяца аренды. Доступ в помещения складов круглосуточный, а вот к уличным контейнерам ночью не пустят. У охраны и сотрудников склада ключей от ячеек нет: попасть в бокс может или арендатор, или его доверенный человек, о котором предупреждена администрация. Сколько стоит: от 1956 Р в месяц Условия. «Складовка» — еще одна компания с большим количеством филиалов: можно выбрать один из девяти складов в разных районах города. Правда, почти все они находятся неподалеку от Мкада. Чтобы рассчитать, какой объем бокса понадобится, на сайте есть удобный калькулятор: он умеет переводить в квадратные метры количество коробок или громоздкую мебель. Большая часть складов находится в закрытых теплых помещениях: зимой температура не опускается ниже +12 °C. Но для клиентов, которым нужно хранить что-то морозоустойчивое, есть экспериментальные уличные боксы. Попасть на склад можно по индивидуальному пин-коду в любое время суток. Если помимо арендатора заходить в бокс нужно будет кому-то другому, его потребуется отдельно вписать в договор. Сколько стоит: от 1700 Р в месяц Условия. «Сити-бокс» выделяется своим вниманием к безопасности хранилища: компания предусмотрела восемь степеней защиты, которые не дадут посторонним добраться до вещей клиентов. Склады спроектированы так, чтобы автомобиль с вещами мог подъехать как можно ближе к ячейке, а довезти коробки до финальной точки помогут тележки и подъемники. Все упаковочные материалы — коробки, скотчи, вакуумные пакеты, пленки и наполнители — можно купить в «Сити-боксе», а стеллажи и пластиковые контейнеры придется взять у компании в аренду. Сколько стоит: от 1275 Р в месяц Условия. «Хранилище» — идеальный вариант для клиентов, которые хотят контролировать состояние вещей самостоятельно: за 1000 Р в месяц сотрудники склада установят камеру в бокс, которая будет показывать видео арендатору в прямом эфире. В остальном условия стандартные: посещать склад можно круглосуточно, но только арендатору, а на любого другого человека нужно оформлять доверенность. Оплата помесячная, причем для заключения договора нужно внести страховой депозит — 100% от арендной платы за месяц. Сколько стоит: от 672 Р в месяц Условия. «Кладовкин» — более технологичная версия складов с индивидуальными ячейками: на сайте можно посмотреть адреса помещений, режим температуры и влажности в каждом из них, а еще увидеть, какие боксы свободны, и сразу забронировать понравившийся. Попасть в хранилище можно по индивидуальному пин-коду в любое время суток: склад работает без выходных и перерывов. Для клиентов, которые хотят убедиться в удобстве и безопасности склада своими глазами, предусмотрен гостевой режим. По запросу сервис предоставляет одноразовый код доступа к любому свободному боксу, воспользоваться им можно в течение недели. Ячейки отличаются друг от друга размерами и конфигурацией: можно подобрать идеальное помещение для длинных лыж или громоздкого компьютера. На некоторых складах контейнеры стоят таким образом, чтобы прямо к ним можно было подъехать на машине и не мучиться с транспортировкой тяжелых или громоздких вещей с парковки до бокса. Чтобы заключить договор, клиенту потребуется оплатить услуги склада и оставить страховой депозит — 50% от размера ежемесячного платежа. Сколько стоит: от 1283 Р в месяц Условия. «Альфасклад» тоже предлагает клиентам онлайн-бронирование: можно заранее увидеть все свободные боксы и ячейки во всех филиалах и забронировать самую удобную — например, узкую, но высокую, чтобы хранить велосипед. Определиться с объемом бокса поможет калькулятор: туда включена не только мебель, но и другие повседневные вещи — от пианино до детской коляски. А тем, кто планирует использовать склад в коммерческих целях, подойдут другие единицы измерения: коробки и палеты. Время посещения боксов зависит от склада. В большинстве филиалов клиент может приходить в бокс круглосуточно, но в помещении на Звенигородском шоссе ночной доступ закрыт: зайти на склад можно только с 08:00 до 20:30. Как грамотно потратить и сэкономить Рассказываем в нашей рассылке дважды в неделю. Подпишитесь, чтобы совладать с бюджетом Сколько стоит: от 2000 Р в месяц Условия. В «Кладовой № 1» нет маленьких ячеек: все боксы — это отдельно огороженные комнаты разной площади с высокими потолками. Зато компания предлагает одни из самых вместительных складских помещений — до 100 м²: это вряд ли пригодится обычной семье, которая переезжает из двушки в трешку, но может быть удобно владельцам интернет-магазинов. За каждый квадратный метр компания попросит 1000 Р в месяц. Это все: страховой депозит или другие дополнительные траты договором не предусмотрены. Посещать склад можно в любое время: но если клиент хочет попасть в свою ячейку раньше 9 утра и позже 9 вечера, об этом нужно заранее предупредить администрацию. Ключи от ячейки находятся только у арендатора: сотрудники компании не смогут попасть в бокс без согласования с клиентом. Сколько стоит: от 450 Р в месяц Условия. Safebox — практически такой же минималистичный сервис, как и «Кладовая № 1»: компания сдает помещения в аренду и продает необходимые упаковочные материалы, но никаких других дополнительных услуг не оказывает. Правда, к стоимости аренды все-таки добавляется депозит: его размер зависит от размера бокса. Главное преимущество — можно занять совсем маленькую ячейку. Это удобно, если нужно хранить документы или другие компактные вещи. Минимальный срок аренды в Safebox тоже один из самых коротких: вещи можно оставить всего на одну неделю. Доступ на склад — в любое время суток, а чтобы охрана пустила на склад кого-то кроме самого арендатора, потребуется доверенность. Сколько стоит: от 450 Р в месяц Условия. «Инбокс» предлагает два типа хранилищ: теплые склады и морские контейнеры, которые стоят на улице. Контейнеры стоят дешевле, но подойдут не для всех вещей: одежда, книги и мебель могут пострадать от перепадов температуры и влажности. А еще контейнеры можно снять только целиком — если вещей немного, платить за лишнюю площадь может быть невыгодно. Платить нужно только за аренду склада: компания не берет страховой депозит, а вместо этого работает по предоплатной системе. Тарификация посуточная: минимальный срок аренды — 7 дней, а после этого можно платить только за те дни, когда вещи реально находились в боксе, и не переплачивать за полный месяц. Сколько стоит: от 400 Р в сутки и 2750 Р в месяц Условия. «Мобиус» предлагает клиентам особенную систему хранения: в мобильных контейнерах, которые можно загрузить прямо перед домом, а потом в закрытом виде привезти на склад. Когда вещи понадобятся обратно, процедура погрузки-разгрузки пройдет также быстро: грузовик просто привезет контейнер к дому и вернет его в компанию уже пустым. Цена на хранение зависит от размера контейнера и площадки, на которой он будет стоять. У «Мобиуса» небольшой выбор доступных объемов: 5,10 м³, 8,57 м³, 11,83 м³ и 15,91 м³. Зато можно не переплачивать за поддержание тепла, если вещи в контейнере не требуют особых условий: хранение на открытой площадке стоит дешевле. Для тех, кому нужно сохранить только шины до следующего сезона, у «Мобиуса» есть специальное предложение: можно не арендовать для этого целый склад, а оставить резину в общем контейнере — от 1800 Р за хранение комплекта в течение полугода. Сколько стоит: от 499 Р в месяц Условия. Другие склады предлагают сервис под ключ как дополнительную услугу, а «Чердак» сделал ее базовым вариантом. Клиент не может прийти на склад или арендовать ячейку: только вызвать грузчиков — и передать им вещи, которые сотрудники сервиса упакуют в подходящие коробки, а потом отвезут на склад. На складе вещи погрузят на палеты и поставят на общие полки, а чтобы не запутаться, где чьи коробки, их промаркируют персональными штрихкодами. Эти же штрихкоды клиент увидит в личном кабинете: если ему понадобится срочно достать с полок какую-то вещь, ее возврат можно будет заказать в один клик. Вещи, которые требуют специальных условий, хранят соответствующе: мотоциклы накрывают чехлами, а лыжи, велосипеды и сноуборды устанавливают в специальные крепления. За счет того, что вещи на складе стоят на общих полках, клиентам не приходится переплачивать за воздух: деньги берут только за тот объем, который занимают вещи. Доставка и сбор вещей оплачиваются отдельно: 990 Р за 1 м³. Чтобы сэкономить, можно сдавать и забирать коробки в терминале самовывоза: это бесплатно. Сколько стоит: от 149 Р в месяц Условия. «Кьюби» работает по той же схеме, что и «Чердак»: клиенты не складывают вещи в ячейки, а передают сотрудникам сервиса, которые размещают их на общих полках. Тарифы сервиса делятся на две большие группы: можно сдавать вещи поштучно и платить за каждый предмет отдельно, а можно выбрать объем, который они займут, и оплачивать его. Для мелких вещей компания бесплатно предоставляет пластиковые контейнеры — их наполняет клиент, а габаритные предметы уже упаковывают грузчики «Кьюби». Первый вывоз вещей бесплатный, а дальше зависит от тарифа: поштучный вывоз стоит от 250 Р, час работы грузчиков-упаковщиков — 1500 Р. Вернуть вещи можно бесплатно: два раза в месяц, если клиент выбрал оплату за объем, и всегда, если вещи хранятся поштучно. Помимо хранения «Кьюби» может вывезти и сдать на благотворительность ненужные вещи — их передадут фонду «Второе дыхание», а еще выставить вещи на перепродажу. Представим, что у нас есть комплект шин, для которых места в квартире нет. Их нужно куда-то сплавить на полгода. Таблица ниже покажет, где будет выгоднее хранить эти шины, если нет свободного гаража или кладовки. Хоумсклад Депозит ✅ Бронирование онлайн ❌ Уличные контейнеры ✅ Упаковка и доставка ✅ Хранение шин на полгода 9024 Р Складовка Депозит ✅ Бронирование онлайн ❌ Уличные контейнеры ✅ Упаковка и доставка ✅ Хранение шин на полгода 10 430 Р Сити-бокс Депозит ❌ Бронирование онлайн ❌ Уличные контейнеры ❌ Упаковка и доставка ✅ Хранение шин на полгода 10 200 Р Хранилище Депозит ✅ Бронирование онлайн ❌ Уличные контейнеры ❌ Упаковка и доставка ✅ Хранение шин на полгода 6885 Р Кладовкин Депозит ✅ Бронирование онлайн ✅ Уличные контейнеры ❌ Упаковка и доставка ✅ Хранение шин на полгода 7800 Р Альфасклад Депозит ✅ Бронирование онлайн ✅ Уличные контейнеры ❌ Упаковка и доставка ✅ Хранение шин на полгода 2100 Р Кладовая № 1 Депозит ❌ Бронирование онлайн ❌ Уличные контейнеры ❌ Упаковка и доставка ❌ Хранение шин на полгода 12 000 Р Safebox Депозит ✅ Бронирование онлайн ✅ Уличные контейнеры ❌ Упаковка и доставка ❌ Хранение шин на полгода 5850 Р Инбокс Депозит ❌ Бронирование онлайн ❌ Уличные контейнеры ✅ Упаковка и доставка ✅ Хранение шин на полгода 7200 Р Мобиус Депозит ❌ Бронирование онлайн ❌ Уличные контейнеры ✅ Упаковка и доставка ✅ Хранение шин на полгода 3360 Р Чердак Депозит ❌ Бронирование онлайн ✅ Уличные контейнеры ❌ Упаковка и доставка ✅ Хранение шин на полгода 2994 Р Депозит ❌ Бронирование онлайн ✅ Уличные контейнеры ❌ Упаковка и доставка ✅ Хранение шин на полгода 2994 Р Москва Ваш город: Москва ПартнерамДля СМИ Рус
Eng Неделя С 1 октября 2021 года актуальные материалы по финансовой грамотности читайте на сайте МОИФИНАНСЫ.РФ В этом разделе вы можете ознакомиться с материалами, созданными в рамках совместного проекта Минфина России и Всемирного банка в период с 2010 по 2020 год. Страница, которую вы запросили, отсутствует на нашем сайте. Возможно, вы ошиблись при наборе адреса или перешли по неверной ссылке. — Федеральный методический центр по финансовой грамотности системы общего и среднего профессионального образования — Федеральный сетевой методический центр повышения квалификации преподавателей вузов и развития программ повышения финансовой грамотности студентов — Федеральный консультационно-методический центр по повышению финансовой грамотности взрослого населения — Родителям — Педагогам — Исследователям — Детям и молодежи — Финансовым институтам — Взрослым — Пенсионерам — Для участников проекта — Описание — Итоговый релиз — Публикации в СМИ — ТВ сюжеты — Медиагалерея — Учебно-методические материалы для учащихся 2-3 классов — Методические материалы для учащихся 4 классов — Методические материалы для учащихся 5–7 классов — Методические материалы для учащихся 8–9 классов — Методические материалы для учащихся 10–11 классов — Учебно-методические материалы для учащихся 10–11 классов социально-экономического профиля — Учебно-методические материалы для студентов среднего профессионального образования — Учебно-методические материалы для воспитанников организаций для детей-сирот и детей, оставшихся без попечения родителей — Студентам и молодым специалистам — Подборка материалов для взрослых — Для пенсионеров и граждан предпенсионного возраста — Информация о COVID-19 Терминал сбора данных Zebra WT-40 со сканером-кольцом. На протяжении нескольких лет мы очень быстро открывали магазины и росли. Закончилось это тем, что сейчас наши склады принимают и отправляют порядка 20 тысяч паллет в день. Естественно, сегодня у нас уже больше складов: два больших в Москве — 100 и 140 тысяч квадратных метров, но есть и небольшие в других городах. Каждая сэкономленная секунда в процессах приёмки, сборки или отправки товара в таких масштабах — это возможность сберечь время на операции. А ещё это огромная экономия. Именно поэтому два главных множителя эффективности — это продуманный алгоритм действий (процесс) и настроенные ИТ-системы. Желательно «как часы», но «работающие чуть менее, чем идеально» тоже вполне подойдёт. Всё же мы в реальном мире. История началась шесть лет назад, когда мы присмотрелись к тому, как именно поставщики разгружают фуры у нас на складе. Это было настолько нелогично, но привычно, что сотрудники даже не замечали неоптимальности процесса.
Как мы уже говорили, наша компания на тот момент (как, в принципе, и сейчас) стремилась открыть много магазинов, поэтому пришлось оптимизировать складские процессы для увеличения пропускной способности (больше товаров за меньшее количество времени). Это непростая задача, и решить её, просто увеличив персонал, было нельзя хотя бы потому, что все эти люди будут друг другу мешать. Таким образом, мы начали думать о внедрении информационной системы WMS (warehouse management system). Как и полагается, мы начали с описания целевых складских процессов и уже в самом начале обнаружили непаханое поле для улучшений в процессе приёмки товара. Нужно было отработать процессы на одном из складов, чтобы потом накатить их на остальные. Приёмка — это одна из первых больших операций на складе. Она бывает нескольких типов: когда мы просто пересчитываем количество грузовых мест и когда нам необходимо, помимо этого, посчитать, сколько и каких артикулов лежит на каждой паллете. Большая часть товаров у нас проходит по потоку кросс-докинг. Это когда товары приезжают на склад от поставщика, а склад выступает в роли роутера и старается тут же переотправить их на конечного получателя (магазин). Есть и другие потоки, например, когда склад выступает в роли кэша или в роли накопителя (нужно положить поставку в сток, разделить на части и постепенно вывозить в магазины). Наверное, про работу со стоком лучше расскажут мои коллеги, которые занимаются математическими моделями оптимизации остатков. Но тут сюрприз! Проблемы стали возникать чисто на ручных операциях. Процесс выглядел так: грузовик приезжал, водитель менялся документами с администратором склада, администратор понимал, что там приехало и куда его отправить, потом направлял грузчика забирать товар. Какие были потери? Их было море. Во-первых, работники склада получали бумажные документы. Они ориентировались и принимали решения, что делать с поставкой, по ним. Во-вторых, они считали паллеты вручную и в этих же товарных накладных отмечали количество. Потом заполненные бланки приёмки относились к компьютеру, где данные забивались в XLS-файл. Данные из этого файла затем импортировались в ERP, и только тогда наше ИТ-ядро по факту видело товар. Мы имели очень мало метаданных о заказе вроде времени прибытия транспорта, либо эти данные были неточными. Первое, что мы сделали, — это начали автоматизировать сами склады так, чтобы у них появилась поддержка процессов (понадобилось поставить кучу софта, железа наподобие мобильных сканеров штрихкодов, развернуть инфраструктуру для всего этого). Стало так:
В старом процессе паллеты перемещались зачастую в специальную буферную зону, где уже с ними работали: считали, регистрировали брак и так далее. Нужно было это для того, чтобы освободить док для следующей машины. Сейчас все процессы настроены так, что эта буферная зона просто не нужна. Есть выборочные пересчёты (один из примеров — процесс выборочного внутритарного пересчёта для кросс-докинга на складе, реализованный в проекте «Светофор»), но большая часть товара обрабатывается сразу по факту приёмки и именно из дока едет на оптимальное место на складе или сразу в другой док для погрузки, если транспорт на отгрузку со склада уже прибыл.
Дальше, если это не кросс-докинг (и товар уже не уехал в буфер перед отправкой или прямо в док), то его нужно положить в сток на хранение. Нужно определить, куда этот товар пойдёт, в какую ячейку хранения. В старом процессе нужно было зрительно определить, в какой зоне мы храним товары данного типа, и потом выбрать там место и отвезти, положить, записать, что положили. Сейчас у нас настроены маршруты размещения по каждому товару по топологии. Мы знаем, какой товар в какую зону и в какую ячейку должен попасть, знаем, сколько ячеек занять дополнительно рядом, если это негабарит. Человек подходит к паллете и сканирует её SSCC с помощью ТСД. Сканер показывает: «Вези в А101-0001-002». На этом первая часть работы с товаром заканчивается. Дальше магазин готов забирать его со склада. И это порождает следующий процесс, про который лучше расскажут коллеги из отдела снабжения. Итак, в системе сток обновляется в момент приёмки заказа. А запас ячейки — в момент постановки паллеты в неё. То есть мы всегда знаем, сколько товара есть на складе итого и где какой лежит конкретно. Очень много потоков работает напрямую в хабы (региональные перевалочные склады), потому что у нас много местных поставщиков в каждом регионе. Те же кондиционеры из Воронежа удобнее ставить не на федеральный склад, а сразу в хабы на местах, если это быстрее. Обратные потоки брака тоже слегка оптимизированы: если товар на кросс-докинге, то поставщик может забрать его со склада в Москве. Если брак вскрылся уже после открытия транспортной упаковки (и снаружи это было непонятно, то есть он появился не по вине транспортников), то есть зоны возврата в каждом магазине. Ещё один процесс, который сейчас нуждается в оптимизации, — это обработка непроданных сезонных товаров. Дело в том, что у нас есть два важных сезона: Новый год и время сада-огорода. То есть в январе мы получаем на РЦ нереализованные искусственные ёлки и гирлянды, а к зиме — газонокосилки и другие сезонные товары, которые нужно сохранить, если они выдержат ещё год. По идее, нужно распродавать их полностью в конце сезона либо отдавать кому-то ещё, а не тащить обратно на склад — вот это та часть, куда у нас ещё не дошли руки. За пять лет мы сократили время приёмки товара (разгрузку машины) в четыре раза и ускорили ряд других процессов, что в общей сложности улучшило оборачиваемость кросс-докинга чуть больше, чем вдвое. Наша задача — оптимизация, чтобы снизить запас и не «замораживать» деньги на складе. И дали возможность магазинам получать нужный товар чуть более вовремя. По складским процессам большие улучшения заключались в том, чтобы автоматизировать то, что раньше было бумагой, избавиться от лишних этапов в процессе за счёт оборудования и правильно настроенных процессов и соединить все ИТ-системы компании в единое целое, чтобы заказ из ERP (например, в магазине чего-то не хватает на третьей полке слева) в конечном итоге превращался в конкретные действия в системе складского хранения, заказа транспорта и так далее. Сейчас оптимизация больше касается тех процессов, до которых мы ещё не добирались, и математики прогнозирования. То есть эпоха бурного внедрения закончилась, мы сделали те 30 % работы, которые дали 60 % результата, и дальше надо постепенно покрывать всё остальное. Либо двигаться на другие участки, если там можно сделать больше. Ну и если считать в спасённых деревьях, то переход поставщиков на EDI-порталы тоже очень много дал. Сейчас практически все поставщики не звонят и не общаются с менеджером, а сами в личном кабинете смотрят заказы, подтверждают их и везут товар. За пять лет у нас стало в четыре раза больше магазинов, в три раза больше различных документов, и, если бы не было EDI, у нас было бы в три раза больше бухгалтеров. Мы не останавливаемся на достигнутом и продолжаем подключать к EDI новые сообщения, новых поставщиков к электронному документообороту. В прошлом году мы открыли крупнейший распределительный центр в Европе — 140 тыс. кв. м — и взялись за его механизацию. Об этом я расскажу в другой статье. Первое, что я вижу на складе Amazon в Суонси, — это упаковка собачьих подгузников. Второй — массивный розовый пластиковый фаллоимитатор. Но с другой стороны, на его британском веб-сайте есть более 100 миллионов товаров: если вы можете себе это представить, Amazon продает их. И если вы не можете себе этого представить, что ж, Amazon тоже это продает. Тратить 10,5 часов в день, выбирая товары с полок, означает созерцать самые темные уголки наших потребительских желаний, самые дикие уголки вещей, вещи, которые можно купить за деньги: браслет с подвесками One Direction, комбинезон для собаки, когтеточка для кошек, разработанная выглядеть как пластинка ди-джея, нож для бананов, фальшивая веточка. Я работаю в основном в крупногабаритном «неперевозимом» отделе, где продаются корма для диабетических собак, биоорганические вегетарианские корма для собак и корма для собак с ожирением; 52-дюймовые телевизоры и шесть упаковок воды, доставленные с Фиджи, и негабаритные секс-игрушки — 18-дюймовые двойные донги (секс-игрушки обычного размера находятся на полках в разделе сортируемых товаров). На второй день менеджер говорит нам, что только мы собрали и упаковали 155 000 товаров за последние 24 часа. Завтра, 2 декабря, в самый загруженный день онлайн-покупок в году, эта цифра приблизится к 450 000. И это только один из восьми складов по всей стране. В прошлом году Amazon принял 3,5 млн заказов за один день. Рождество — это ее Вьетнам — испытание ее корпоративного характера и своего рода вызов, который заставил бы даже самого опытного менеджера по поставкам сломаться и заплакать. За последние две недели компания наняла дополнительно 15 000 сотрудников агентства в Великобритании. И он рассчитывает удвоить количество складов в Великобритании в ближайшие три года. Компания рассчитывает продолжить рост, сделавший ее одной из самых мощных транснациональных корпораций на планете. Прямо сейчас в Суонси четыре смены будут работать по крайней мере 50 часов в неделю, вручную собирая и упаковывая каждый предмет, или, как написала Daily Mail в статье несколько недель назад, быть «Amazon’s эльфы» в «гроте Санты 21 века». Если бы Санта платил своим временным эльфам минимальную заработную плату, одновременно подгоняя их к пределам директивы ЕС о рабочем времени и увольняя их, если они берут три больничных в любой трехмесячный период, это было бы подходящим сравнение. Вероятно, разумно предположить, что уклонение от уплаты налогов не является «конституционно» частью бизнес-модели Санта-Клауса, как утверждает Брэд Стоун, автор новой книги об Amazon, Магазин всего: Джефф Безос и эпоха Amazon , говорит мне, что это в случае с Amazon. Санта также не пытается запугивать своих конкурентов, в чем его обвиняет Марк Константин, основатель косметической компании Lush, который на прошлой неделе подал на Amazon в суд. Дед Мороз не был вызван в Счетный комитет палаты общин, и депутаты назвали его «аморальным». В течение недели я был амазонским эльфом: временным работником, получившим работу через агентство по трудоустройству Суонси — хотя оказалось, что я был не единственным журналистом, которому пришла в голову эта идея. Но кто же тогда не щелкал что-нибудь по рассеянности в праздную минуту на работе, или при просмотре телека в пижаме, и, как маленькое чудо современной жизни, не получал знакомый коричневый картонный пакет, падающий на ваш коврик через день. В конце моего первого дня я вхожу в свою учетную запись Amazon. Я вышел из дома моей мамы за пределами Кардиффа в 6:45 утра и вернулся в 19:30, и мне нужен блистерный пластырь Compeed для пальцев ног, и я не могу сделать это перед работой, и я не могу сделать это после работы. Мой палец зависает над опцией «добавить в корзину», но вместо этого я смотрю на свою историю Amazon. Я сделал свою первую покупку, The Rough Guide to Italy , в феврале 2000 года и помню, что купил его для статьи, которую я написал о бронировании отпуска в Интернете. Но ведь это феноменальная операция. А работать в — и мне трудно напечатать эти слова, не испытывая припадка иронии — «центр выполнения» должен быть крошечным винтиком в огромной глобальной машине распределения. Это промышленный процесс в действительно массовом масштабе, который стал возможен благодаря новым технологиям. Место может выглядеть так, как будто оно было заполнено в 2 часа ночи пьяным заполнителем полок: на типичной полке может быть набор бритвенных лезвий, упаковка презервативов и DVD My Little Pony . И все же все систематизировано, потому что так должно быть. Именно здесь, когда настоящие люди сталкиваются с бизнес-требованиями одной из самых передовых технологических компаний на планете, все становится грязным. Это система, включающая в себя такие несистематические вещи, как надежды и страхи, планы на будущее, детей и жизни. А в местах с высоким уровнем безработицы и низкими экономическими возможностями, где Amazon намеренно размещает свои распределительные центры — компания получила 8,8 млн фунтов стерлингов в виде грантов от правительства Уэльса на размещение здесь склада, — отчаяние просачивается по краям. На собеседовании — заполнении анкет, тестировании на наркотики и алкоголь, общей проверке умений читать в местном агентстве по трудоустройству — нам показывают видео. Объясняется процесс и берутся интервью у некоторых людей. Нам сказали, что после Рождества Amazon будет брать людей на постоянной основе, и если вы будете усердно работать, вы можете стать одним из них. В районе Суонси/Нит/Порт-Талбот, области, все еще страдающей от ударов британского постиндустриального упадка, это сильные слова, хотя все начинает довольно быстро распутываться. Есть четыре агентства, которые предоставили персонал на склад, и их представители работают за столами на складском этаже. Переходя с одной тренировки на другую, я спрашиваю одного из них, сколько постоянных сотрудников работает на складе, но он меня ослышался и отвечает совсем на другой вопрос: «Ну, очевидно, не всех возьмут. Вы только посмотрите на цифры. Честно говоря, агентства должны говорить это только для того, чтобы заставить людей пройти через дверь». Так и есть. А еще есть «Лес», один из наших тренеров. У него есть специальный цветной ремешок, который показывает, что он «посол» Amazon, и другой, на котором написано, что он оказывает первую помощь. «Они развешивают эти синие значки перед вами», — говорит Билл Вулкок, бывший сотрудник центра выполнения заказов Amazon в Ругли, Стаффордшир. «Если у вас есть синий значок, у вас есть лучшая заработная плата, соответствующие права. Вы можете работать вместе с кем-то на той же работе, но они стабильны, а вы просто пушечное мясо. Почему тебе не дали нормальную работу, спрашиваю я Леса, и он пожимает головой, но в других местах люди бормочут: это друзья менеджеров получают работу. Это HR выбирает имена наугад. Это какая-то черная магия, которую никто не понимает. Уходя со смены в огромной волне оранжевых светоотражающих жилетов, я болтаю с другим мужчиной лет шестидесяти. По его словам, он работал на шахте Юнити недалеко от Нита, пока месяц назад его не уволили во второй раз за два года. На прошлое Рождество он тоже работал в Amazon. «И они просто отпустили меня сразу после этого, без предупреждения или чего-то еще. Когда я задал вопрос Amazon, он ответил: «Небольшое количество сезонных сотрудников работает с нами в течение длительного периода времени, и мы стремимся сохранить этих людей, чтобы мы могли предоставить им постоянную роль, когда один становится доступным. В 2013 году мы смогли создать 2300 постоянных рабочих мест для сезонных сотрудников, воспользовавшись сезонностью Рождества, чтобы найти отличных постоянных сотрудников, но, к сожалению, мы просто не можем удержать 15 000 сезонных сотрудников». А вот что Amazon говорит о своей политике в отношении болезней: «Amazon — это компания, которая развивается, и мы предлагаем высокий уровень безопасности для всех наших сотрудников. Как и многие компании, мы используем систему учета посещаемости сотрудников. и проверять все личные обстоятельства в отношении любых проблем с посещаемостью, и мы не будем увольнять кого-либо по причине болезни Текущие системы, используемые для учета посещаемости сотрудников, являются справедливыми и предсказуемыми и привели к увольнению 11 постоянных сотрудников из более чем 5000 постоянных сотрудников. Стоит отметить, что агентские работники не являются сотрудниками Amazon. Без сомнения, это тяжелая физическая работа. Документальный фильм Panorama был посвящен милям, которые прошел Адам, волдырям, которые он получил, нелепым целям и тому факту, что за вами каждую секунду каждую смену следит оруэлловская трубка. Как работнику агентства, вам платят 19 пенсов в час сверх минимальной заработной платы — 6,50 фунтов стерлингов — и смены длятся 10,5 часов. Но многие работы связаны с тяжелым физическим трудом. Это не то, что беспокоит людей. Почти все остаются стойкими перед лицом физического дискомфорта и истощения. И они валлийцы: теплота и дружелюбие исходят почти от всех, кто там работает. Лидер моей группы не корпоративный дроид. Он начал с цеха, звучит как Ричард Бертон и мягко подбадривает. И все еще. «Я работал везде», — говорит мне водитель погрузчика. «И это самое худшее. Они платят дерьмо, потому что могут. Потому что другой работы там нет. Несправедливость, у которой нет выхода. После документального фильма Би-би-си Хайвел Фрэнсис, член парламента от Аберавона, на прошлой неделе сумел добиться встречи с директором по общественной политике Amazon, встречи, которую он пытался добиться в течение многих лет. Он не хочет говорить о жалобах, которые он услышал от своих избирателей, но говорит, что «завод является исключительным в этом районе тем, что на нем нет представительства профсоюза. Это был долгий путь, чтобы даже добраться туда и узнать, что происходит». Это была черная дыра, где отсутствие каких-либо проверок его мощности оставило ощущение, что все сделано до мелочей — от самой дешевой из дешевых пластиковых защитных ботинок, на замену которых, кажется, большинство сотрудников с большим стажем работы тратят собственные деньги. Работать в Amazon — значит проводить дни на острие потребительства. Чтобы засвидетельствовать нашу жажду вещей. Материалы этого года включают в себя огромное количество Xbox и Kindle, а также кулинарную книгу Джейми Оливера этого сезона, «Сохранить с Джейми » (хотите сэкономить с Джейми? Не покупайте его дерьмовую книгу) и « пирогов и пудингов» Пола Голливуда и . Рик Стайн Индия . Кулинарные книги знаменитых поваров приводят меня в ярость. Они даже не удосуживаются вынуть их из коробок. Рождественский адвент-календарь куклы Барби, однако, меня чуть не сломил. Я хожу туда-сюда в секцию F, где разрезаю коробку, беру еще один адвент-календарь Барби, распаковываю коробку и кладу ее в мусорную кучу, кладу календарь, который был доставлен из Китая, передан из контейнерного порта в стороннего дистрибьютора, а оттуда на склад Amazon, на мою тележку и передать ее упаковщикам, где она будет переупакована в другую коробку и, наконец, достигнет своего конечного пункта назначения: радости в сердце маленького ребенка. Нам нужны дешевые вещи. И мы хотим заказать его с наших кресел. И мы хотим, чтобы его доставили к нашим дверям. И именно Amazon придумал, как это сделать. Со временем, как у закоренелого наркомана, моя привычка к Amazon увеличилась. В 2002 году я заказал свой первый некнижный товар, видео This Life серии 1; в 2005 году мой первый продукт не от Amazon, подержанная копия биографии Патрисии Хайсмит; а в 2008 году я начал делать онлайн-эквивалент внутривенных инъекций, когда купил на сайте телевизор. «Мы самая клиентоориентированная компания на земле», — говорят нам на вступительном брифинге, незадолго до того, как нам объясняют, что если мы опоздаем, то получим полбалла, а после трех из них мы вылетаем. Я вырос в Южном Уэльсе и своими глазами видел, как рецессия 1980-х нанесла жестокий удар по всему, включая мою собственную большую семью. Я всегда знал, что между очень разными жизнями есть лишь тонкий кусочек удачи. Но тогда мой дедушка работал на складе в Суонси. В моем случае между мной и жизнью амазонки на самом деле всего лишь кусочек удачи. У меня есть много времени, чтобы подумать об этом в течение моего 10,5-часового рабочего дня. В клубе рабочих Neath вниз по дороге один из сотрудников сказал мне, что Amazon является «работодателем последней надежды». Это место, где вы получаете работу, если вы не можете найти работу где-либо еще. И это так душераздирающе. Чем вы занимались раньше, спрашиваю я людей. И они говорят, что они строители, менеджеры гостиничного бизнеса, выпускники отдела маркетинга, специалисты по информационным технологиям, плотники, электрики. У них был собственный бизнес, и их уволили. Amazon не несет ответственности за экономику в целом, но именно экономика в целом делает модель Amazon такой пугающей. Под угрозой оказываются не только приятные приятные рабочие места, такие как работа в книжном магазине, как Хью Грант в Notting Hill , или в музыкальном магазине, как герой в High Fidelity Ника Хорнби, или работы, которые побывали в Borders, Woolworths, Jessops и HMV, да и во всем остальном тоже. На очереди все: работа в обувном отделе в John Lewis, или за кассой в Tesco, или работа с персоналом, или аудит их счетов, или создание их веб-сайтов, или написание их корпоративных журналов. Торговый центр Суонси дальше по дороге уже превратился в катастрофу; пустырь благотворительных магазинов и то, что Сара Риз из книжного магазина Cover to Cover называет «второсортным Debenhams и третьесортным Marks and Spencer». «Люди знают об их методах работы, и все курьеры их ненавидят, но помнят ли люди об этом, когда щелкают? Наверное, нет. Мы пытаемся убить их добротой», — говорит она. «Джинна обратно в бутылку не посадишь». Но тогда больше нечем их убивать. Часто для нее дешевле заказывать книги на Amazon, чем через своего дистрибьютора. «Мы открыто говорим об этом и рассказываем людям, но у нас просто нет возможности конкурировать с ними по цене». Аппетитам Amazon нет конца. «Он расширяется во всех мыслимых направлениях, — говорит мне Брэд Стоун. «Вот почему я назвал свою книгу Магазин всего . Их стремление продать все. У них уже есть свои цифровые услуги и свои корпоративные услуги. Они только начали продавать искусство. Одежда все еще очень незрелая и настроена на расширение. Продовольственные товары — следующая большая вещь. После этого они идут очень активно, потому что это сократит расходы в других местах. Если они смогут запустить свои собственные грузовики в крупных городских районах, они смогут сократить расходы на сторонних грузоотправителей». Наша страсть к дешевым товарам со скидкой, доставляемым к нашим дверям быстро и эффективно, имеет свою цену. Мы просто еще не поняли, что это такое. Это, конечно, налоги, которые оплачивают дороги, по которым ездят грузовики Amazon, и школы, в которых учатся ее сотрудники, и больницы, в которых рождаются их дети и им латают артерии, и в которых, когда-нибудь о них можно будет позаботиться, когда они предстанут перед смертью. Налоги, которые платят все ее работники, и которые, как выяснилось в 2012 году, она, как правило, не платит. Брэд Стоун сказал мне, что уклонение от уплаты налогов заложено в ДНК компании. С самого начала он был «конституционно ориентирован на обеспечение всех возможных преимуществ для своих клиентов, установление максимально низких цен, использование всех известных налоговых лазеек или создание новых». Это то, над чем Марк Константин, соучредитель косметики Lush, долго размышлял. Он отказывается продавать через Amazon, но это не помешало Amazon использовать имя Lush для направления покупателей на свой сайт, где предлагались альтернативные продукты, которые могли бы им понравиться. «Это способ заставить бизнес пользоваться их услугами. И мы отказались. На этой неделе мы обратились в Верховный суд, чтобы подать на них в суд за нарушение прав на товарный знак. На данный момент защита нашего бизнеса обошлась нам в полмиллиона фунтов стерлингов. Большинство компаний просто не могут себе этого позволить. Но мы сделали это, потому что это вопрос принципа. Они продолжают принуждать вас к действию, но у них нет жизнеспособной бизнес-модели. Единственный способ, которым они могут себе это позволить, это неуплаты налогов.Если бы им пришлось вести себя более традиционно, им пришлось бы бороться9.0003 «Это форма пиратского капитализма. Они врываются в страны людей, вывозят деньги и сбрасывают их в удобном порту. Это не бизнес в традиционном смысле. Это уродливый возврат к форме эксплуататорского капитализм, который был у нас столетие назад, и мы как общество решили уйти от него». В Суонси я некоторое время болтаю с кем-то, чье имя не Мартин. Сегодня суббота, светит солнце, и на складе стало тихо. Это зеркальное отражение того, что происходит в цеху. «Они берут огромные субсидии от государства и не возвращают их», — говорит Мартин Смит из профсоюза GMB. «Их аргумент состоит в том, что они создают рабочие места, но то, что они делают, вытесняет и заменяет другие рабочие места. Лучшие рабочие места. А магазины на центральных улицах, как правило, платят налоги. льготы, позволяющие людям выжить. Когда компании платят минимальную заработную плату, они фактически субсидируются налогоплательщиком». Вернувшись в Суонси, в последний перерыв моего последнего дня, я сижу и болтаю с Питом и Сьюзен из Рондды и Сэмми, просителем убежища из Судана. Сьюзен по-прежнему хочет найти постоянную работу, но сомневается, что это произойдет. Мусорная работа всегда была. Ян Бринкли, директор Work Foundation, называет методы трудоустройства Amazon «старым вином в новых бутылках». Рестораны и кебабные делают то же самое в течение многих лет. Но Amazon — это не шашлычная. Это будущее. Что может быть, а может и не быть тем, о чем нужно подумать, когда вы нажимаете «добавить в корзину». Рынки США Загрузка…
ЧАС
М
С
В новостях Кэрол Кадуоллдр, Хранитель 2013-12-01T16:48:00Z Скачать приложение Но с другой стороны, на его британском веб-сайте есть более 100 миллионов товаров: если вы можете себе это представить, Amazon продает их. И если вы не можете себе этого представить, что ж, Amazon тоже это продает. Тратить 10,5 часов в день, выбирая товары с полок, означает созерцать самые темные уголки наших потребительских желаний, самые дикие уголки вещей, вещи, которые можно купить за деньги: браслет с подвесками One Direction, комбинезон для собаки, когтеточка для кошек, разработанная выглядеть как пластинка ди-джея, нож для бананов, фальшивая веточка. Я работаю в основном в крупногабаритном «неперевозимом» отделе, где продаются корма для диабетических собак, биоорганические вегетарианские корма для собак и корма для собак с ожирением; 52-дюймовые телевизоры и шесть упаковок воды, доставленные с Фиджи, и негабаритные секс-игрушки — 18-дюймовые двойные донги (секс-игрушки обычного размера находятся на полках в разделе сортируемых товаров). На второй день менеджер говорит нам, что только мы собрали и упаковали 155 000 товаров за последние 24 часа. Завтра, 2 декабря, в самый загруженный день онлайн-покупок в году, эта цифра приблизится к 450 000. И это только один из восьми складов по всей стране. В прошлом году Amazon принял 3,5 млн заказов за один день. Рождество — это ее Вьетнам — испытание ее корпоративного характера и своего рода вызов, который заставил бы даже самого опытного менеджера по поставкам сломаться и заплакать. За последние две недели компания наняла дополнительно 15 000 сотрудников агентства в Великобритании. И он рассчитывает удвоить количество складов в Великобритании в ближайшие три года. Компания рассчитывает продолжить рост, сделавший ее одной из самых мощных транснациональных корпораций на планете. Прямо сейчас в Суонси четыре смены будут работать по крайней мере 50 часов в неделю, вручную собирая и упаковывая каждый предмет, или, как написала Daily Mail в статье несколько недель назад, быть «Amazon’s эльфы» в «гроте Санты 21 века». Если бы Санта платил своим временным эльфам минимальную заработную плату, одновременно подгоняя их к пределам директивы ЕС о рабочем времени и увольняя их, если они берут три больничных в любой трехмесячный период, это было бы подходящим сравнение. Вероятно, разумно предположить, что уклонение от уплаты налогов не является «конституционно» частью бизнес-модели Санта-Клауса, как утверждает Брэд Стоун, автор новой книги об Amazon, Магазин всего: Джефф Безос и эпоха Amazon , говорит мне, что это в случае с Amazon. Санта также не пытается запугивать своих конкурентов, в чем его обвиняет Марк Константин, основатель косметической компании Lush, который на прошлой неделе подал на Amazon в суд. Дед Мороз не был вызван в Счетный комитет палаты общин, и депутаты назвали его «аморальным». В течение недели я был амазонским эльфом: временным работником, получившим работу через агентство по трудоустройству Суонси — хотя оказалось, что я был не единственным журналистом, которому пришла в голову эта идея. Но кто же тогда не щелкал что-нибудь по рассеянности в праздную минуту на работе, или при просмотре телека в пижаме, и, как маленькое чудо современной жизни, не получал знакомый коричневый картонный пакет, падающий на ваш коврик через день. В конце моего первого дня я вхожу в свою учетную запись Amazon. Я вышел из дома моей мамы за пределами Кардиффа в 6:45 утра и вернулся в 19:30, и мне нужен блистерный пластырь Compeed для пальцев ног, и я не могу сделать это перед работой, и я не могу сделать это после работы. Мой палец зависает над опцией «добавить в корзину», но вместо этого я смотрю на свою историю Amazon. Я сделал свою первую покупку, The Rough Guide to Italy , в феврале 2000 года и помню, что купил его для статьи, которую я написал о бронировании отпуска в Интернете. Но ведь это феноменальная операция. А работать в — и мне трудно напечатать эти слова, не испытывая припадка иронии — «центр выполнения» должен быть крошечным винтиком в огромной глобальной машине распределения. Это промышленный процесс в действительно массовом масштабе, который стал возможен благодаря новым технологиям. Место может выглядеть так, как будто оно было заполнено в 2 часа ночи пьяным заполнителем полок: на типичной полке может быть набор бритвенных лезвий, упаковка презервативов и DVD My Little Pony . И все же все систематизировано, потому что так должно быть. Именно здесь, когда настоящие люди сталкиваются с бизнес-требованиями одной из самых передовых технологических компаний на планете, все становится грязным. Это система, включающая в себя такие несистематические вещи, как надежды и страхи, планы на будущее, детей и жизни. А в местах с высоким уровнем безработицы и низкими экономическими возможностями, где Amazon намеренно размещает свои распределительные центры — компания получила 8,8 млн фунтов стерлингов в виде грантов от правительства Уэльса на размещение здесь склада, — отчаяние просачивается по краям. На собеседовании — заполнении анкет, тестировании на наркотики и алкоголь, общей проверке умений читать в местном агентстве по трудоустройству — нам показывают видео. Объясняется процесс и берутся интервью у некоторых людей. Нам сказали, что после Рождества Amazon будет брать людей на постоянной основе, и если вы будете усердно работать, вы можете стать одним из них. В районе Суонси/Нит/Порт-Талбот, области, все еще страдающей от ударов британского постиндустриального упадка, это сильные слова, хотя все начинает довольно быстро распутываться. Есть четыре агентства, которые предоставили персонал на склад, и их представители работают за столами на складском этаже. Переходя с одной тренировки на другую, я спрашиваю одного из них, сколько постоянных сотрудников работает на складе, но он меня ослышался и отвечает совсем на другой вопрос: «Ну, очевидно, не всех возьмут. Вы только посмотрите на цифры. Честно говоря, агентства должны говорить это только для того, чтобы заставить людей пройти через дверь». Так и есть. А еще есть «Лес», один из наших тренеров. У него есть специальный цветной ремешок, который показывает, что он «посол» Amazon, и другой, на котором написано, что он оказывает первую помощь. Он проработал на складе больше года, и в течение недели я вижу, как он мчится по цеху со скоростью как минимум вдвое превышающей мою. «Они развешивают эти синие значки перед вами», — говорит Билл Вулкок, бывший сотрудник центра выполнения заказов Amazon в Ругли, Стаффордшир. «Если у вас есть синий значок, у вас есть лучшая заработная плата, соответствующие права. Вы можете работать вместе с кем-то на той же работе, но они стабильны, а вы просто пушечное мясо. Я работал там с сентября 2011 года по февраль 2012 года и далее. В канун Рождества у выхода стоял представитель агентства с блокнотом и говорил: «Вы вернулись после Рождества. Почему тебе не дали нормальную работу, спрашиваю я Леса, и он пожимает головой, но в других местах люди бормочут: это друзья менеджеров получают работу. Это HR выбирает имена наугад. Это какая-то черная магия, которую никто не понимает. Уходя со смены в огромной волне оранжевых светоотражающих жилетов, я болтаю с другим мужчиной лет шестидесяти. По его словам, он работал на шахте Юнити недалеко от Нита, пока месяц назад его не уволили во второй раз за два года. На прошлое Рождество он тоже работал в Amazon. «И они просто отпустили меня сразу после этого, без предупреждения или чего-то еще. И я не мог работать больше! Я выработал свои носки!» Когда я задал вопрос Amazon, он ответил: «Небольшое количество сезонных сотрудников работает с нами в течение длительного периода времени, и мы стремимся сохранить этих людей, чтобы мы могли предоставить им постоянную роль, когда один становится доступным. А вот что Amazon говорит о своей политике в отношении болезней: «Amazon — это компания, которая развивается, и мы предлагаем высокий уровень безопасности для всех наших сотрудников. Как и многие компании, мы используем систему учета посещаемости сотрудников. и проверять все личные обстоятельства в отношении любых проблем с посещаемостью, и мы не будем увольнять кого-либо по причине болезни Текущие системы, используемые для учета посещаемости сотрудников, являются справедливыми и предсказуемыми и привели к увольнению 11 постоянных сотрудников из более чем 5000 постоянных сотрудников. сотрудников в 2013 году». Стоит отметить, что агентские работники не являются сотрудниками Amazon. Без сомнения, это тяжелая физическая работа. «Я работал везде», — говорит мне водитель погрузчика. «И это самое худшее. Они платят дерьмо, потому что могут. Потому что другой работы там нет. Поверьте мне, я знаю, я пытался. На моей последней работе я работал за 12 фунтов в час. Я получаю 8 фунтов». час здесь. Раньше я работал в Sony, и они были строгими, но справедливыми. Несправедливость, у которой нет выхода. После документального фильма Би-би-си Хайвел Фрэнсис, член парламента от Аберавона, на прошлой неделе сумел добиться встречи с директором по общественной политике Amazon, встречи, которую он пытался добиться в течение многих лет. Он не хочет говорить о жалобах, которые он услышал от своих избирателей, но говорит, что «завод является исключительным в этом районе тем, что на нем нет представительства профсоюза. Это был долгий путь, чтобы даже добраться туда и узнать, что происходит». Это была черная дыра, где отсутствие каких-либо проверок его мощности оставило ощущение, что все сделано до мелочей — от самой дешевой из дешевых пластиковых защитных ботинок, на замену которых, кажется, большинство сотрудников с большим стажем работы тратят собственные деньги. с чем-то, в чем они могут ходить, к политике увольнения, если вы больны, к 15-минутному перерыву, который начинается, где бы вы ни оказались на складе. Работать в Amazon — значит проводить дни на острие потребительства. Чтобы засвидетельствовать нашу жажду вещей. Материалы этого года включают в себя огромное количество Xbox и Kindle, а также кулинарную книгу Джейми Оливера этого сезона, «Сохранить с Джейми » (хотите сэкономить с Джейми? Не покупайте его дерьмовую книгу) и « пирогов и пудингов» Пола Голливуда и . Рик Стайн Индия . Кулинарные книги знаменитых поваров приводят меня в ярость. Они даже не удосуживаются вынуть их из коробок. Они лежат огромными кучками размером с гору европейского масла в конце прохода. Приготовьте яйцо по телевизору, и это все равно, что получить лицензию на печать денег на всю вечность. Рождественский адвент-календарь куклы Барби, однако, меня чуть не сломил. Я хожу туда-сюда в секцию F, где разрезаю коробку, беру еще один адвент-календарь Барби, распаковываю коробку и кладу ее в мусорную кучу, кладу календарь, который был доставлен из Китая, передан из контейнерного порта в стороннего дистрибьютора, а оттуда на склад Amazon, на мою тележку и передать ее упаковщикам, где она будет переупакована в другую коробку и, наконец, достигнет своего конечного пункта назначения: радости в сердце маленького ребенка. Потому что ничто так не отражает волшебство Рождества, как фотография надувной блондинки с несколькими сумками для покупок. Нам нужны дешевые вещи. И мы хотим заказать его с наших кресел. И мы хотим, чтобы его доставили к нашим дверям. И именно Amazon придумал, как это сделать. Со временем, как у закоренелого наркомана, моя привычка к Amazon увеличилась. В 2002 году я заказал свой первый некнижный товар, видео This Life серии 1; в 2005 году мой первый продукт не от Amazon, подержанная копия биографии Патрисии Хайсмит; а в 2008 году я начал делать онлайн-эквивалент внутривенных инъекций, когда купил на сайте телевизор. «Мы самая клиентоориентированная компания на земле», — говорят нам на вступительном брифинге, незадолго до того, как нам объясняют, что если мы опоздаем, то получим полбалла, а после трех из них мы вылетаем. Что такое опоздание, спрашиваю я. «Одну минутку», — говорят мне. Я вырос в Южном Уэльсе и своими глазами видел, как рецессия 1980-х нанесла жестокий удар по всему, включая мою собственную большую семью. В клубе рабочих Neath вниз по дороге один из сотрудников сказал мне, что Amazon является «работодателем последней надежды». Это место, где вы получаете работу, если вы не можете найти работу где-либо еще. И это так душераздирающе. Чем вы занимались раньше, спрашиваю я людей. И они говорят, что они строители, менеджеры гостиничного бизнеса, выпускники отдела маркетинга, специалисты по информационным технологиям, плотники, электрики. У них был собственный бизнес, и их уволили. Или бизнес разорился. Или у них был инсульт. Или их контракт закончился. Это люди, имевшие квалифицированную работу, или профессиональную работу, или просто более высокооплачиваемую работу. А теперь они работают на Amazon, получая минимальную заработную плату, и большинство из них благодарны за это. Amazon не несет ответственности за экономику в целом, но именно экономика в целом делает модель Amazon такой пугающей. Под угрозой оказываются не только приятные приятные рабочие места, такие как работа в книжном магазине, как Хью Грант в Notting Hill , или в музыкальном магазине, как герой в High Fidelity Ника Хорнби, или работы, которые побывали в Borders, Woolworths, Jessops и HMV, да и во всем остальном тоже. На очереди все: работа в обувном отделе в John Lewis, или за кассой в Tesco, или работа с персоналом, или аудит их счетов, или создание их веб-сайтов, или написание их корпоративных журналов. Торговый центр Суонси дальше по дороге уже превратился в катастрофу; пустырь благотворительных магазинов и то, что Сара Риз из книжного магазина Cover to Cover называет «второсортным Debenhams и третьесортным Marks and Spencer». «Люди знают об их методах работы, и все курьеры их ненавидят, но помнят ли люди об этом, когда щелкают? Наверное, нет. Мы пытаемся убить их добротой», — говорит она. Аппетитам Amazon нет конца. «Он расширяется во всех мыслимых направлениях, — говорит мне Брэд Стоун. «Вот почему я назвал свою книгу Магазин всего . Их стремление продать все. У них уже есть свои цифровые услуги и свои корпоративные услуги. Они только начали продавать искусство. Одежда все еще очень незрелая и настроена на расширение. Продовольственные товары — следующая большая вещь. После этого они идут очень активно, потому что это сократит расходы в других местах. Если они смогут запустить свои собственные грузовики в крупных городских районах, они смогут сократить расходы на сторонних грузоотправителей». Я подозреваю, что они будут приобретать», — говорит он. И везде это убивает рабочие места. Согласно исследованию, проведенному компанией ILSR, в магазинах работает 47 человек на каждые 10 миллионов долларов продаж. Наша страсть к дешевым товарам со скидкой, доставляемым к нашим дверям быстро и эффективно, имеет свою цену. Мы просто еще не поняли, что это такое. Это, конечно, налоги, которые оплачивают дороги, по которым ездят грузовики Amazon, и школы, в которых учатся ее сотрудники, и больницы, в которых рождаются их дети и им латают артерии, и в которых, когда-нибудь о них можно будет позаботиться, когда они предстанут перед смертью. Налоги, которые платят все ее работники, и которые, как выяснилось в 2012 году, она, как правило, не платит. При продажах в Великобритании в размере 4,2 млрд фунтов стерлингов в 2012 году компания заплатила 3,2 млн фунтов стерлингов корпоративного налога. Брэд Стоун сказал мне, что уклонение от уплаты налогов заложено в ДНК компании. С самого начала он был «конституционно ориентирован на обеспечение всех возможных преимуществ для своих клиентов, установление максимально низких цен, использование всех известных налоговых лазеек или создание новых». Это то, над чем Марк Константин, соучредитель косметики Lush, долго размышлял. Он отказывается продавать через Amazon, но это не помешало Amazon использовать имя Lush для направления покупателей на свой сайт, где предлагались альтернативные продукты, которые могли бы им понравиться. «Это способ заставить бизнес пользоваться их услугами. И мы отказались. На этой неделе мы обратились в Верховный суд, чтобы подать на них в суд за нарушение прав на товарный знак. «Это форма пиратского капитализма. Они врываются в страны людей, вывозят деньги и сбрасывают их в удобном порту. Это не бизнес в традиционном смысле. Это уродливый возврат к форме эксплуататорского капитализм, который был у нас столетие назад, и мы как общество решили уйти от него». В Суонси я некоторое время болтаю с кем-то, чье имя не Мартин. Сегодня суббота, светит солнце, и на складе стало тихо. Нам сказали перестать собирать. Заказы были отключены как кран. «Это погода, — говорит он. «Когда идет дождь, он может внезапно сойти с ума». Мы убираем коробки, и встает вопрос о налогах. Это зеркальное отражение того, что происходит в цеху. Точно так же, как Amazon подорвала 200-летние права рабочих, используя агентства, и сделала большую часть своих работников бесправными, точно так же она провернула тот же трюк с корпоративной ответственностью. «Они берут огромные субсидии от государства и не возвращают их», — говорит Мартин Смит из профсоюза GMB. «Их аргумент состоит в том, что они создают рабочие места, но то, что они делают, вытесняет и заменяет другие рабочие места. Лучшие рабочие места. А магазины на центральных улицах, как правило, платят налоги. льготы, позволяющие людям выжить. Когда компании платят минимальную заработную плату, они фактически субсидируются налогоплательщиком». Вернувшись в Суонси, в последний перерыв моего последнего дня, я сижу и болтаю с Питом и Сьюзен из Рондды и Сэмми, просителем убежища из Судана. Сьюзен по-прежнему хочет найти постоянную работу, но сомневается, что это произойдет. Ее лодыжка все еще опухла. Ее рейтинг выбора был низким. Нам сказали, что на следующей неделе количество рабочих часов увеличится на час в день и будет добавлен дополнительный день обязательной сверхурочной работы. Мусорная работа всегда была. Ян Бринкли, директор Work Foundation, называет методы трудоустройства Amazon «старым вином в новых бутылках». Рестораны и кебабные делают то же самое в течение многих лет. Но Amazon — это не шашлычная. Это будущее. Что может быть, а может и не быть тем, о чем нужно подумать, когда вы нажимаете «добавить в корзину». Первоначально эта статья была опубликована на сайте guardian.co.uk Подпишитесь на уведомления от Insider! Будьте в курсе того, что вы хотите знать. Подписаться на push-уведомления Продолжай читать На стол губернатора попал законопроект, направленный на защиту работников складов в Калифорнии от неправомерных систем квот. Законопроект 701 Ассамблеи, недавно получивший одобрение в Ассамблее и Сенате, был подготовлен женщиной-ассамблеей Лореной Гонсалес, штат Сан-Диего. Если закон будет принят, он станет первым в стране законом, обязывающим компании раскрывать требования к производительности и показатели скорости работы, которые они устанавливают для сотрудников. Он запрещает увольнять рабочих за невыполнение нормы, которая мешает им пользоваться туалетом или делать перерывы на отдых, а работодателям запрещается наказывать сотрудников склада за то, что они «не работают», когда они соблюдают законы о здоровье и безопасности. В законе конкретно не упоминается Amazon, но сторонники и противники законопроекта говорят, что базирующийся в Сиэтле гигант электронной коммерции явно является главной целью для правил. «Amazon заставляет работников рисковать своим телом для доставки на следующий день, в то время как они не могут даже пользоваться туалетом, не опасаясь возмездия», — говорится в заявлении Гонсалеса. Связаться с представителями Amazon для комментариев не удалось, несмотря на неоднократные попытки. В интервью The Guardian в феврале 2020 года представитель Amazon сказал: «Как и у большинства компаний, у нас есть ожидания по производительности для каждого амазонца, и мы измеряем фактическую производительность по сравнению с этими ожиданиями». Калифорнийская ассоциация розничных продавцов выступает против AB 701, заявляя, что эта мера затрагивает слишком много компаний, хотя мера явно нацелена на Amazon. «Если вы забросите эту огромную сеть, чтобы преследовать одну компанию, будут непредвиденные последствия», — сказала президент ассоциации Рэйчел Мишлен. Michelin заявила, что законопроект повлияет на распределительные центры в нескольких отраслях и повысит стоимость жизни для калифорнийцев, убьет хорошо оплачиваемые рабочие места и нанесет ущерб хрупкой цепочке поставок в регионе. Пятьдесят организаций, от розничных продавцов и производителей продуктов питания до производителей автозапчастей и этнических торговых палат, выступают против AB 701. Они объединены через noonab701.org. Быстрый всплеск покупок в электронной коммерции вызвал бешеный ажиотаж на складах в Южной Калифорнии, и эта тенденция усугубляется тем, что опасающиеся пандемии потребители не хотят делать покупки в обычных магазинах. Поток потребительских товаров, прибывающих из Азии через порты Лос-Анджелеса и Лонг-Бич, также способствовал росту складских помещений, особенно во Внутренней Империи. Данные Digital Commerce 360 показывают, что в 2020 году потребители потратили 791,70 млрд долларов в Интернете у американских розничных продавцов, что на 32,4% больше, чем 598,02 млрд долларов в предыдущем году. Расходы на электронную коммерцию составили почти 20 % от общего объема розничных продаж в прошлом году по сравнению с 15,8 % в 2019 году. условий работы на складах Amazon. «Работники сообщили, что чрезмерные квоты Amazon делают невозможным выполнение работы и безопасный расчет», — говорится в отчете. «Большинство опрошенных работников сообщили, что испытывают постоянный стресс, пытаясь не отставать». Один работник склада, участвовавший в исследовании, утверждает, что для того, чтобы «делать ставки» или поддерживать ожидаемый Amazon темп движения товаров, ей необходимо сканировать не менее 200 товаров в час, независимо от их размера. Если она останавливает сканирование более чем на шесть минут — время, которое может потребоваться, например, для упаковки и сканирования более крупного предмета — сканирующее устройство Amazon подает сигнал тревоги, указывающий на то, что она потратила слишком много «нерабочего времени». В отчете говорится, что когда работники превышают лимит нерабочего времени, установленный Amazon, или не выполняют норму, они предположительно подвергаются проверке, выписке или увольнению. Информационный бюллетень, прилагаемый к отчету, показывает, что работникам склада Amazon разрешено всего шесть минут «отгула» в день, не считая 30-минутного обеденного перерыва. Сотрудники говорят, что ближайший туалет на огромных складах компании часто находится более чем в шести минутах от их рабочего места. «Расценки на работу Amazon диктуют опасный темп работы, который приводит к травмам», — говорится в отчете. «Исследования показывают, что быстрый темп работы связан с рядом последствий для здоровья, включая боль в шее и плечах, симптомы в мышцах или суставах и заболевания спины». Шестьдесят семь процентов работников Amazon, опрошенных для исследования, сообщили о получении травм в результате работы в Amazon, а 75% заявили, что их требуемая скорость работы либо «всегда», либо «часто» слишком высока для работы в безопасном темпе. Гонсалес сказал, что AB 701 позволит работникам иметь право голоса на своем рабочем месте, «даже когда их начальником является алгоритм». В соответствии с AB 701 работники склада, считающие квоты небезопасными, имеют право на 90-дневный доступ к своим личным показателям скорости работы и описаниям квот для лучшего документирования нарушений. Если работник подвергается дисциплинарному взысканию в течение 90 дней после запроса данных или подачи жалобы своему работодателю или государственному органу на небезопасную квоту, AB 701 создает презумпцию того, что действие было репрессивным. American LUMP Орландо, Флорида 32824 Опубликовано сегодня Подать заявку на эту вакансию Мы являемся растущей общенациональной компанией по управлению складами. Описание работы: Shift- 1-й Mon-Fri 6 утра (12:00 до 14:00) Плата- $ 140337 $ 1403337 7777 $ 1403337 77777 $ 140337 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 7 9000 2 9000. Сохранить эту работу
Подать заявку Медицинский центр Милосердия — Сидар-Рапидс
Сидар-Рапидс, ИА 52403 Сегодня Эта должность поддерживает философию Mercy, ориентированную на пациента, путем предоставления непосредственного ухода за пациентами и поддержки пациентов с поведенческими проблемами. Юнайтед Эйрлайнз Инк.
Чикаго, Иллинойс 60601 Сегодня Никогда не было более захватывающего времени, чтобы присоединиться к United Airlines. Мы были на пути к тому, чтобы стать лучшей авиакомпанией в истории авиации. Наша общая цель Объединять людей, объединять Реабилитационная больница Реюньон Дублин Сегодня Получайте оплату за поездки!!! Nobis Rehabilitation Partners ищет путешествующих медсестер для работы между нашими многочисленными стационарными реабилитационными больницами по всей территории Соединенных Штатов. Армия Спасения — Юго-Западная дивизия Сегодня РАСПОЛОЖЕНИЕ: Альбукерке, Нью-Мексико. АРПСТАТУС: Полная/почасовая ЗАЯВЛЕНИЕ О МИССИИ: Армия Спасения, международное движение, является евангельской частью всемирной христианской церкви. Его сообщение основано на Системы SambaNova
Пало-Альто, Калифорния Сегодня Программа возвращения к работе Path Forward в SambaNova представляет собой 12-недельное оплачиваемое возвращение для опытных специалистов, возвращающихся на работу после отпуска по уходу. Программа открыта до Allstate Sales & Leasing Corp.
Сент-Луис Парк, MN 55426 Сегодня Allstate Peterbilt Group занимается обслуживанием грузовых автомобилей средней и большой грузоподъемности и прицепов на Среднем Западе. С начала процесса покупки автомобиля через Лития Моторс, Инк. Дилер: L0341 Тампа Хонда Тампа Хонда Надежный. Мотивированный. Подотчетный. Эти слова описывают вас? Если это так, подайте заявку на вакансию нашего водителя по запчастям и начните свою карьеру.
Город Гринвилл, Северная Каролина Сегодня Целью этой должности является поддержание содержания и чистоты городских зданий и территорий для обеспечения надежной работы и безопасной рабочей среды. Имя пользователя Пароль Запомните меня Забыли пароль? Закон о справедливых трудовых стандартах (FLSA) гарантирует ряд прав, в первую очередь направленных на обеспечение того, чтобы работники получали справедливую оплату за отработанное время. Работодатели должны платить всем застрахованным работникам не меньше минимальной заработной платы, которая в настоящее время установлена на уровне 7,25 долларов в час. В некоторых штатах установлена минимальная заработная плата, превышающая федеральную, и вы имеете право на более высокую ставку, если она разрешена в вашем штате. Работодатели, не подпадающие под действие FLSA, такие как владельцы мелких ферм, обязаны платить всем работникам минимальную заработную плату штата. (Для получения информации о законе о минимальной заработной плате в вашем штате см. Законы о заработной плате и рабочем времени в зависимости от штата.) FLSA не требует какой-либо конкретной системы оплаты, поэтому работодатели могут основывать оплату на рабочем времени, сдельной ставке или каком-либо другом измерении. Однако во всех случаях заработная плата работника, деленная на количество отработанных часов в течение платежного периода, должна равняться минимальной заработной плате или превышать ее. Некоторых работодателей либо смущают нюансы и исключения из закона о заработной плате и рабочем времени, либо они изменяют правила в угоду своему карману. • Ежечасно. Почасовым работникам должна выплачиваться минимальная заработная плата за все отработанные часы. Ваш работодатель не может брать среднюю заработную плату или платить вам меньше минимальной заработной платы за одни отработанные часы и больше за другие. • Фиксированная ставка или оклад. Работники, получающие фиксированную ставку, могут проверить свою заработную плату, разделив сумму, которую они получают за расчетный период, на количество отработанных часов. Полученная средняя должна быть не ниже минимальной заработной платы. • Комиссионные и сдельные расценки. Ваша общая заработная плата, разделенная на количество отработанных часов, должна в среднем составлять не менее минимальной почасовой ставки. В соответствии с FLSA, оплата, которую вы получаете, должна быть в виде наличных денег или чего-то, что может быть легко конвертировано в наличные или другие законные формы компенсации, такие как питание и проживание. Ни раздел о минимальной заработной плате, ни какая-либо другая часть FLSA не требуют от работодателей выплаты работникам за отгулы, такие как отпуск, праздники или больничные. Хотя большинство работодателей каждый год предоставляют работникам, занятым полный рабочий день, оплачиваемый отпуск, FLSA покрывает оплату только времени, проведенного на работе. Однако законы некоторых штатов требуют, чтобы сотрудники получали оплачиваемый отпуск для работы в качестве присяжного, голосования, отпуска по семейным обстоятельствам и отпуска по болезни. Некоторые штаты и местные органы власти требуют, чтобы работники оплачивались за больничные или определенные виды отпуска по семейным обстоятельствам либо работодателем, либо из государственного фонда. Когда сотрудники регулярно получают минимальную сумму чаевых в рамках своей работы — обычно от 20 до 30 долларов в месяц, как установлено законом штата, — их работодатели могут платить меньше минимальной заработной платы и кредитовать полученные чаевые. против требования минимальной заработной платы. Однако почасовая заработная плата работника плюс чаевые, которые фактически зарабатывает работник, должны в сумме составлять как минимум минимальную заработную плату, иначе работодатель должен компенсировать разницу. (Дополнительную информацию см. в разделах Чаевые, Объединение чаевых и Баллы чаевых: что нужно знать сотрудникам сферы обслуживания.) Когда люди получают комиссионные за продажи, эти комиссионные могут заменить заработную плату. ПРИМЕР: Джулия, продавец в магазине электроники, получает процент от долларового объема продаж, которые она совершает. В течение одной медленной недели она получала в среднем всего 2 доллара комиссионных в час. В соответствии с FLSA ее работодатель должен платить ей дополнительную сумму за каждый час, который она отработала в течение первых 40 часов этой недели, чтобы равняться минимальной заработной плате, и больше за любые сверхурочные часы. Мужчины и женщины, выполняющие одну и ту же работу или работу, требующую равных навыков и ответственности, должны получать компенсацию в виде равной заработной платы и пособий в соответствии с поправкой 1963 года к Закону о равной оплате труда, которая называется Законом о равной оплате труда. (29 U.S.C. § 206.) Однако имейте в виду, что некоторые схемы оплаты, которые на первый взгляд могут показаться дискриминационными, на самом деле не нарушают Закон о равной оплате труда. • системах стажа • системы заслуг • системы измерения заработка по количеству или качеству продукции, такие как поштучное распределение товаров, или • любой фактор, кроме пола, например, разница в заработной плате, возникающая из-за неравной начальной заработной платы, основанной на различиях в уровни опыта. Хотя Закон о равной оплате труда в основном распространяется на тех же работодателей и работников, что и остальная часть FLSA, есть одно важное отличие: Закон о равной оплате труда также защищает от дискриминационных механизмов оплаты труда руководящих, административных и профессиональных сотрудников, включая администраторов и учителей. в начальных и средних школах. FLSA не ограничивает количество часов, которые сотрудник может отработать в неделю, за исключением случаев, когда сотрудник является несовершеннолетним. В дополнение к Положения FLSA о сверхурочной работе, законы ряда штатов также определяют, как и когда должна оплачиваться сверхурочная работа. В некоторых штатах сверхурочная работа измеряется ежедневно, а не еженедельно. В этих штатах работники, работающие более восьми часов в день, как правило, имеют право на сверхурочную работу, даже если они работают в общей сложности 40 или менее часов в неделю. (Чтобы узнать правила вашего штата о сверхурочной работе, выберите его из списка в разделе «Законы о заработной плате и рабочем времени по штатам».) Математика проста, если вам платят по часам. ПРИМЕР: Рэймонд работает в компании по доставке программного обеспечения с зарплатой 8 долларов в час. Джоди, вице-президент компании по доставке программного обеспечения, а также начальник Рэймонда, тоже работала 50 часов в ту же неделю. Поскольку Джоди имеет квалификацию руководителя и освобождена от FLSA, она не имеет права на оплату сверхурочных, но получает свою обычную еженедельную зарплату. Законодательство FLSA не требует, чтобы работники получали оплату за сверхурочную работу только потому, что они работали более восьми часов в день (хотя в некоторых штатах это требуется). Также нет ничего, что требовало бы от работника оплаты сверхурочной работы на месте. В соответствии с FLSA работодателю разрешается рассчитывать и оплачивать сверхурочные по неделям, что может быть любым 168-часовым периодом, состоящим из семи последовательных 24-часовых периодов. Обычай, а не закон определяет, что рабочая неделя начинается в понедельник. Кроме того, из-за характера выполняемой работы здравый смысл и закон диктуют, что некоторые рабочие места освобождаются от требований FLSA по оплате сверхурочных. К наиболее распространенным из этих должностей относятся: • наемные работники предприятий розничной торговли или сферы обслуживания • рабочие некоторых автомобилей, грузовиков, прицепов, сельскохозяйственных орудий, лодок или самолетов • работники железнодорожных и авиаперевозчиков, водители такси, некоторые работники автотранспортных перевозчиков, моряки и женщины на американских судах, работники местных служб доставки • дикторы, редакторы новостей и главные инженеры малых внегородских радиостанций • работники домашней прислуги, проживающие в домах своих работодателей • работники кинотеатров и • сельскохозяйственные рабочие. И, наконец, некоторые сотрудники могут быть частично освобождены от требований Закона об оплате сверхурочной работы. Наиболее распространенным представителем этого гибридного типа является сотрудник, работающий в больнице или учреждении интернатного типа, который соглашается отработать 14-дневный рабочий период. Тем не менее, эти сотрудники должны получать надбавку за сверхурочную работу за все часы, отработанные более восьми часов в день или 80 часов в течение 14-дневного рабочего периода, в зависимости от того, какое из этих часов больше. СОВЕТ Это бонус или дубинка? Некоторые работодатели пытались обойти требования по оплате сверхурочной работы, называя часть полученной оплаты премией. На самом деле бонусы имеют строгое юридическое определение и предназначены только для денег, выплачиваемых в дополнение к заработной плате за дополнительные усилия, которые вы приложили на работе, в качестве вознаграждения за верную службу или в качестве подарка. Люди, которые работают по сдельным расценкам и комиссионным, а не по часам, имеют более сложную задачу при расчете своих ставок заработной платы. Для сдельных рабочих обычная ставка заработной платы может быть рассчитана путем усреднения почасовой сдельной заработной платы за неделю. Расчет сверхурочной работы немного сложнее. Работники имеют право на дополнительную половину обычной ставки заработной платы за каждый час, отработанный свыше 40, плюс полную сдельную заработную плату. ПРИМЕР: Макс работает сборщиком на копировальной фабрике, ему платят 75 центов за каждую установленную им крышку копировального аппарата. Одну неделю он работал 40 часов и установил 400 крышек, поэтому его обычная ставка оплаты за эту неделю составляла 7,50 долларов в час (400 x 0,75, деленное на 40). Для определения оплаты Макса за сверхурочную работу можно использовать один из двух вариантов: • Увеличить сдельную ставку на 50% в часы сверхурочной работы. Например, работодатель Макса мог поднять его сдельную ставку до 1,13 доллара за крышку копировального аппарата (150% от 0,75 доллара) за сверхурочные часы. • Оценить среднюю почасовую заработную плату, а затем использовать эту расчетную среднюю для расчета сверхурочной работы. Имейте в виду, что если Министерство труда США расследует законность вашей ставки заработной платы, оно может потребовать доказательства того, что любые оценки, использованные для расчета вашей заработной платы, соответствуют сдельной оплате, которую вы фактически зарабатывали в течение значительного времени — обычно несколько месяцев. . Методы расчета и выплаты комиссий сильно различаются. Если у вас есть вопросы о том, соблюдает ли ваш работодатель законы о заработной плате в отношении сдельных ставок и комиссионных, позвоните или посетите ближайший офис отдела заработной платы и рабочего времени Департамента труда. Если вы регулярно работаете за чаевые, получаемые вами чаевые не учитываются как часть вашей обычной ставки оплаты при расчете оплаты за сверхурочную работу. Учитывается только заработная плата, которую ваш работодатель согласился платить вам; в большинстве случаев, когда люди работают за чаевые, это федеральная минимальная заработная плата. Конечно, чаевые, которые вы получаете сверх минимальной суммы заработной платы, по-прежнему облагаются налогом как доход. ПРИМЕР: Лиза работает официанткой за зарплату плюс чаевые. Поскольку она получает значительную сумму в виде чаевых, ее работодателю разрешено производить зачет — минимальный почасовой лимит, установленный законом для сотрудников, получающих чаевые. Тем не менее, ее обычная ставка оплаты за сверхурочную работу в соответствии со стандартами FLSA по-прежнему составляет минимальную заработную плату. За одну неделю Лиза отработала 41 час — один час сверхурочно. Если ваша работа связана с различными видами работ, для которых установлены разные шкалы заработной платы, вы должны рассчитать свою обычную ставку оплаты для каждой категории работы, а затем применить соответствующую ставку ко всем сверхурочным часам. Шкала оплаты, которая применяется к типу работы, которую вы выполняли в сверхурочные часы, — это та, на основе которой вы рассчитываете правило полутора часов. ПРИМЕР: Мэтт работает в компании, которая управляет большим жилым комплексом. За работу по благоустройству ему платят 8 долларов в час. Когда он работает охранником в частной службе безопасности комплекса, Мэтт получает 10 долларов в час. Для расчета заработной платы его рабочая неделя начинается в понедельник. В течение одной весенней недели он работал восемь часов в день, с понедельника по пятницу, в общей сложности 40 часов с командой ландшафтных дизайнеров. Поскольку правила оплаты сверхурочной работы FLSA вступают в силу только после того, как сотрудник отработает 40 часов в неделю, восемь сверхурочных часов, которые Мэтт отработал в службе безопасности, соответствовали ставке патрулирования службы безопасности в размере 10 долларов в час. Его оплата сверхурочных за эту неделю составляет 120 долларов (10 долларов x 8 x 1 В первые мрачные дни пандемии, когда работник Amazon по имени Кристиан Смоллс запланировал небольшую паническую забастовку из-за безопасности условиях в единственном фулфилмент-центре ритейлера в Нью-Йорке, компания незаметно мобилизовалась.0003 Amazon сформировала группу реагирования, включающую 10 отделов, в том числе Глобальную разведывательную программу, группу безопасности, в которой работают многие ветераны вооруженных сил. В конце концов, было больше руководителей, в том числе 11 вице-президентов, которые были предупреждены о протесте, чем рабочих, которые его посетили. Главный юрисконсульт Amazon, охарактеризовав г-на Смоллса как «неумного или красноречивого», в электронном письме, ошибочно разосланном более чем 1000 человек, рекомендовал сделать его «лицом» усилий по организации рабочих. Компания уволила мистера Смоллса, заявив, что он нарушил правила карантина, придя на забастовку. Увольняя и очерняя его, компания полагалась на жесткую тактику, которая привела ее к доминированию на рынке. Но в пятницу он выиграл первое успешное объединение в профсоюзы на любом складе Amazon в Соединенных Штатах, что стало одной из самых значительных трудовых побед за поколение. Реакция компании на его крошечный первоначальный протест может преследовать ее долгие годы. Мистер Смоллс и его лучший друг со склада Деррик Палмер нацелились на объединение в профсоюз после того, как его выгнали. Наряду с растущим кругом коллег — и отсутствием членства в национальной организации труда — эти двое мужчин провели последние 11 месяцев, выступая против Amazon, чьи 1,1 миллиона сотрудников в Соединенных Штатах делают его вторым по величине частным работодателем в стране. На автобусной остановке возле склада, месте на Статен-Айленде, известном как JFK8, они развели костры, чтобы согреть коллег, ожидающих рассвета, чтобы вернуться домой. Они снимали видео в TikTok, чтобы охватить рабочих по всему городу. Г-н Палмер привез на площадку домашнюю выпечку зити; другие продавали блинчики с мясом и западноафриканские блюда из риса, чтобы привлечь рабочих-иммигрантов. Они установили таблички с надписью «Бесплатная травка и еда». По словам г-на Смоллса, профсоюз потратил в общей сложности 120 000 долларов, собранных через GoFundMe. «Мы начали это с нуля, с двумя столами, двумя стульями и палаткой», — вспоминал он. Голосование за объединение в профсоюзы отражает эпоху роста власти рабочих. В последние месяцы ряд магазинов Starbucks также проголосовали за организацию. Но JFK8 с 8000 сотрудников — один из фирменных складов Amazon, его самый важный путь к самому важному рынку. Image Amazon годами боролась с профсоюзами, считая это серьезной угрозой для своей бизнес-модели. Его способность доставлять посылки потребителям основана на обширной цепочке ручного труда, который контролируется с точностью до секунды. Никто не знает, что произойдет, если вновь организованные рабочие попытаются изменить эту модель или нарушить работу по номеру , или если их союз будет воспроизведен среди более чем 1000 центров выполнения Amazon и других объектов по всей стране. При всех недостатках «Давида против Голиафа» организаторы Стейтен-Айленда имели культурный момент на своей стороне. Их поддержали ужесточение рынка труда, расплата за то, что работодатели должны своим работникам, и Национальный совет по трудовым отношениям, получивший смелость при президенте Байдене, который принял ключевое решение в их пользу. Доморощенная малобюджетная инициатива их независимого профсоюза Amazon превзошла по эффективности традиционных организаторов профсоюзов, которым не удалось объединить Amazon извне, совсем недавно в Бессемере, штат Алабама 9.0003 «Я думаю, что это встряхнет рабочее движение и перевернет ортодоксию с ног на голову», — сказала Жюстин Медина, упаковщик коробок и профсоюзный организатор JFK8, которая вместе с восторженной толпой ждала в Бруклине результатов голосования. Будущее американских усилий по объединению в профсоюзы «не может быть связано с тем, что люди придут извне с планом организации, которому люди должны следовать», — сказала Сара Нельсон, глава профсоюза бортпроводников, в интервью. Теперь и зарождающийся профсоюз JFK8, и Amazon сталкиваются с неотложными вопросами. Профсоюз, не имеющий традиционной инфраструктуры, опыта или руководства, скорее всего, столкнется с судебной тяжбой из-за голосования и переговоров по контракту. Компании, которая не ответила на запрос о комментариях для этой статьи, придется решить, стоит ли пересмотреть некоторые из своих тактик и устранить скрытую неудовлетворенность рабочей силой, которая нанесла ей такое сокрушительное поражение. «Amazon хотел сделать меня лицом всей профсоюзной кампании против них», — написал г-н Смоллс в твиттере в пятницу, выглядя неустрашимым перед предстоящей задачей. «Ну вот!» Когда в 2018 году Amazon открыл обширный сайт JFK8, компания одновременно и привлекала, и опасалась Нью-Йорка, самого важного потребительского рынка Америки. Созданный Союз розничных, оптовых и универмагов объявил о смелой цели: превратить JFK8 в первый организованный склад Amazon в стране. Вскоре Amazon отказался от широко разрекламированного плана по открытию второй штаб-квартиры в городе, поскольку нарастала негативная реакция на государственные субсидии, которые она получит, и ее история противодействия профсоюзам. Но разговоры об организации JFK8 ни к чему не привели. В рабочих кругах многие считали, что оборот Amazon слишком высок, а ее тактика слишком воинственна, чтобы профсоюз мог добиться успеха. Когда в марте 2020 года в JFK8 были подтверждены первые случаи заражения коронавирусом, г-н Палмер и г-н Смоллс обратились к менеджерам с проблемами безопасности. Сотрудники все больше беспокоились о росте заболеваемости и считали, что Amazon не уведомляет их своевременно о делах, о чем менеджеры задокументировали в недавно опубликованных судебных протоколах. Но Amazon отказал в приостановке операций, заявив, что принял «крайние меры» для обеспечения безопасности работников. Пандемия превратила JFK8 в спасательный круг для города, где круглосуточные смены и парк грузовиков доставляли припасы, когда он был заблокирован. После увольнения, клеветы главного адвоката на мистера Смоллса — полные извинения пришли только позже — и увольнения еще одного протестующего двое друзей решили действовать. Мистер Смоллс был откровенен, мистер Палмер обдуманно. Они оба были темнокожими мужчинами из Нью-Джерси и одного возраста (31 тогда, 33 сейчас). Оба бросили местный колледж, гордились высокими баллами по показателям производительности Amazon и когда-то надеялись подняться в компании. Теперь у них появились новые планы. Мистер Палмер будет продолжать работать в JFK8, чтобы лучше изменить его изнутри. В начале 2021 года они отправились на другой склад Amazon. К апрелю рабочие Бессемера отвергли профсоюз более чем 2 к 1. Г-н Палмер и г-н Смоллс объявили о своем намерении организовать JFK8, но мало кто воспринял их всерьез. Почему они должны побеждать, когда более обеспеченные и более опытные оперативники потерпели поражение? Когда они приступили к своей первой задаче — сбору тысяч подписей рабочих для проведения голосования по объединению в профсоюзы — в модели занятости Amazon стали очевидны трещины. JFK8 предложил работу работникам, уволенным из других отраслей во время пандемии. Чернокожие сотрудники JFK8 почти на 50% чаще были уволены, чем их белые коллеги, согласно внутреннему документу. Еще до того, как пандемия перевернула работу, склады Amazon имели поразительный годовой оборот в 150 процентов. Когда мистер Палмер и мистер Смоллс подошли к рабочим на автобусной остановке, тон Amazon по отношению к своим сотрудникам стал меняться. Джефф Безос, основатель компании, передал роль генерального директора Энди Джасси, и компания повысила заработную плату и добавила к своим руководящим принципам цель стать «лучшим работодателем Земли». Он обязался выслушать жалобы и улучшить условия труда. В других случаях это было спорным. В широко разрекламированном Twitter-аккаунте об организации Бессемера Amazon настолько пренебрежительно отозвалась о работниках, которые не могут ходить в туалет и вынуждены мочиться в бутылки, что ей пришлось принести извинения. В мае в JFK8 антипрофсоюзный консультант назвал большинство чернокожих профсоюзных организаторов «головорезами», согласно жалобе, поданной против Amazon N.L.R.B. Продавец отрицал этот эпизод. А в ноябре агентство по труду заявило, что Amazon продемонстрировала «вопиющее неуважение» к закону и отменила результаты бессемеровского складского голосования, заказав еще одно. Той осенью, после нескольких месяцев сбора поддержки, нью-йоркские профсоюзные организаторы поставили более 2000 подписей в совет по труду, но они были отклонены из-за того, что они не соответствуют минимуму, необходимому для проведения выборов. Г-н Смоллс сказал, что Amazon представила совету директоров данные о заработной плате, указывающие на то, что компания считает, что половина людей, подписавших карты, больше не работают на складе. «После всех этих месяцев напряженной работы казалось, что импульс пропал», — вспоминал г-н Палмер в интервью. Между работой по сменам и организацией работы в JFK8 в свободное от работы время он месяцами проводил вдали от склада едва ли день. Некоторые из сотрудников, к которым он обращался, скептически относились к профсоюзам или взносам или просто были благодарны Amazon за медицинское обслуживание и зарплату, которая в JFK8 начинается с 18 долларов в час. Другие казались слишком измученными и настороженными, чтобы даже вступать в бой. Чтобы двигаться дальше, профсоюзные лидеры размещали видео TikTok, устраивали сморы на открытом воздухе и подпевали хип-хопу и Марвину Гэю. Когда рабочие сталкивались с семейными кризисами, многообещающий профсоюз молился. Один уволенный сотрудник стал бездомным, и группа организовала кампанию по сбору средств. Помогло их почти постоянное присутствие на складе. «Чем комфортнее они чувствуют себя у нас, тем больше они начинают нам открываться», — сказал г-н Палмер о других работниках. Некоторые сторонники профсоюзов устроились на работу в JFK8 специально, чтобы помочь организационным усилиям, по словам г-жи Медины, которая была среди них. Amazon противодействовала всей силой своего антипрофсоюзного аппарата. Он отслеживал социальные сети организаторов, демонстрацию судебных документов, забрасывал рабочих текстовыми сообщениями и устилал склад табличками с надписью «Голосуйте НЕТ» или с утверждениями, что профсоюзные лидеры были посторонними. «Профсоюз Amazon никогда не заключал контракты», — говорилось в одной из презентаций. Взносы будут дорогими, продолжал он, а у профсоюза «нет опыта управления такой огромной суммой денег». Андро Перес, 35 лет, работает на небольшом складе Amazon возле JFK8, где в этом месяце запланировано еще одно голосование профсоюза. По его словам, он склоняется к тому, чтобы проголосовать за, потому что на обязательных собраниях Amazon в основном критиковались профсоюзы. Он бы предпочел, чтобы его работодатель ответил на вопрос: «Что вы могли бы сделать лучше?» Организаторы JFK8 сопротивлялись, подав десятки жалоб в NLRB. К Рождеству организаторы добились крупной юридической победы. Amazon согласилась на общенациональное соглашение, одно из крупнейших в истории агентства, в котором говорилось, что рабочие могут оставаться в зданиях, чтобы организоваться, когда они не работают. При этом организаторы перенесли свои обеды в помещения, предоставив им больше доступа и легитимности. Тетя мистера Смоллса приготовила домашнюю пищу для души: макароны с сыром, засахаренный ямс, листовую капусту и запеченную курицу. «Что вы делаете, так это создаете сообщество рабочих, которого у Amazon никогда не было», — сказал Сет Гольдштейн, юрист, который бесплатно представлял организаторов. Однажды в феврале этого года мистер Смоллс принес обед в комнату отдыха, когда Амазон позвонил в полицию, заявив, что он нарушил границы. 41-летняя Кэтлин Лехуез, проработавшая в Amazon в течение девяти лет, сказала, что не является «фанаткой профсоюза», но голосовала за организационные усилия, направленные на то, чтобы отправить сообщение компании, которая, по ее мнению, потеряла связь с работниками. «Человечности в Amazon больше нет, — сказала она в интервью. За несколько недель до подсчета голосов Amazon, которая постоянно заявляла, что ее работникам лучше всего подходят прямые отношения с компанией, заложила основу для потенциальных проблем с выборами, утверждая в юридических документах, что совет по труду отказался от « нейтралитет своей должности» в пользу союза. В пятницу утром в офисе агентства в Бруклине мистер Смоллс в ярко-красной уличной одежде сидел рядом с юристом Amazon и просматривал каждый бюллетень. Его колено дрожало при представлении каждого голоса. Автор: Bill4iam
Лейкоцитарная формула – процентное соотношение различных форм лейкоцитов в сыворотке крови и подсчет их числа в единице объема.9/л (10 в ст. 9/л). Какой биоматериал можно использовать для исследования? Венозную, капиллярную кровь. Как правильно подготовиться к исследованию? Общая информация об исследовании Лейкоциты, как и другие клетки крови, образуются в костном мозге. Основная их функция – борьба с инфекцией, а также ответ на повреждение тканей. В отличие от эритроцитов, популяция которых является однородной, лейкоциты делятся на 5 типов, отличающихся по внешнему виду и выполняемым функциям: нейтрофилы, лимфоциты, моноциты, эозинофилы, базофилы. Лейкоциты образуются из стволовых клеток костного мозга. Они живут недолго, поэтому происходит их постоянное обновление. Продукция лейкоцитов в костном мозге возрастает в ответ на любое повреждение тканей, это часть нормального воспалительного ответа. Разные типы лейкоцитов имеют несколько разные функции, однако они способны к координированным взаимодействиям путем «общения» с использованием определенных веществ – цитокинов. Долгое время лейкоцитарную формулу высчитывали вручную, однако современные анализаторы позволяют гораздо точнее проводить исследование в автоматическом режиме (врач смотрит 100-200 клеток, анализатор – несколько тысяч). Если анализатором определяются атипичные формы клеток либо выявляются значительные отклонения от референсных значений, то лейкоцитарная формула дополняется микроскопическим исследованием мазка крови, который позволяет диагностировать некоторые заболевания, такие как, например, инфекционный мононуклеоз, определить степень тяжести инфекционного процесса, описать тип выявленных атипичных клеток при лейкозе. Нейтрофилы – наиболее многочисленные из лейкоцитов – первыми начинают бороться с инфекцией и первыми появляются в месте повреждения тканей. Нейтрофилы имеют ядро, разделенное на несколько сегментов, поэтому их еще называют сегментоядерными нейтрофилами или полиморфноядерными лейкоцитами. Эти названия, однако, относятся только к зрелым нейтрофилам. Созревающие формы (юные, палочкоядерные) содержат цельное ядро. В очаге инфекции нейтрофилы окружают бактерии и ликвидируют их путем фагоцитоза. Лимфоциты – одно из важнейших звеньев иммунной системы, они имеют большое значение в уничтожении вирусов и борьбе с хронической инфекцией. Существует два вида лимфоцитов – Т и В (в лейкоцитарной формуле подсчета видов лейкоцитов по отдельности нет). B-лимфоциты вырабатывают антитела – специальные белки, которые связываются с чужеродными белками (антигенами), находящимися на поверхности вирусов, бактерий, грибов, простейших. Окруженные антителами клетки, содержащие антигены, доступны для нейтрофилов и моноцитов, которые убивают их. Т-лимфоциты способны разрушать зараженные клетки и препятствовать распространению инфекции. Также они распознают и уничтожают раковые клетки. Моноцитов в организме не очень много, однако они осуществляют крайне важную функцию. После непродолжительной циркуляции в кровяном русле (20-40 часов) они перемещаются в ткани, где превращаются в макрофаги. Макрофаги способны уничтожать клетки, так же как нейтрофилы, и держать на своей поверхности чужеродные белки, на которые реагируют лимфоциты. Они играют роль в поддержании воспаления при некоторых хронических воспалительных заболеваниях, таких как ревматоидный артрит. Эозинофилов в крови содержится небольшое количество, они тоже способны к фагоцитозу, однако в основном играют другую роль – борются с паразитами, а также принимают активное участие в аллергических реакциях. Базофилов в крови также немного. Они перемещаются в ткани, где превращаются в тучные клетки. Когда они активируются, из них выделяется гистамин, обусловливающий симптомы аллергии (зуд, жжение, покраснение). Для чего используется исследование? Когда назначается исследование? Что означают результаты? Лейкоцитарная формула обычно интерпретируется в зависимости от общего количества лейкоцитов.9/л |
Нейтрофилы, %
|
Возраст |
Референсные значения |
|
Меньше 1 года |
16 — 45 % |
|
1-2 года |
28 — 48 % |
|
2-4 года |
32 — 55 % |
|
4-6 лет |
32 — 58 % |
|
6-8 лет |
38 — 60 % |
|
8-10 лет |
41 — 60 % |
|
10-16 лет |
43 — 60 % |
|
Больше 16 лет |
47 — 72 % |
Чаще всего уровень нейтрофилов повышен при острых бактериальных и грибковых инфекциях. Иногда в ответ на инфекцию продукция нейтрофилов увеличивается столь значительно, что в кровяное русло выходят незрелые формы нейтрофилов, увеличивается количество палочкоядерных. Это называется сдвигом лейкоцитарной формулы влево и свидетельствует об активности ответа костного мозга на инфекцию.
Встречается и сдвиг лейкоцитарной формулы вправо, когда количество палочкоядерных форм уменьшается и увеличивается количество сегментоядерных. Так бывает при мегалобластных анемиях, заболеваниях печени и почек.
Другие причины повышения уровня нейтрофилов:
- системные воспалительные заболевания, панкреатит, инфаркт миокарда, ожоги (как реакция на повреждение тканей),
- онкологические заболевания костного мозга.
Количество нейтрофилов может уменьшаться при:
- массивных бактериальных инфекциях и сепсисе, в случаях когда костный мозг не успевает воспроизводить достаточно нейтрофилов,
- вирусных инфекциях (гриппе, кори, гепатите В),
- апластической анемии (состоянии, при котором угнетена работа костного мозга), B12-дефицитной анемии,
- онкологических заболеваниях костного мозга и метастазах других опухолей в костный мозг.9/л
Лимфоциты, %
|
Возраст |
Референсные значения |
|
Меньше 1 года |
45 — 75 % |
|
1-2 года |
37 — 60 % |
|
2-4 года |
33 — 55 % |
|
4-6 лет |
33 — 50 % |
|
6-8 лет |
30 — 50 % |
|
8-10 лет |
30 — 46 % |
|
10-16 лет |
30 — 45 % |
|
Больше 16 лет |
19 — 37 % |
Причины повышенного уровня лимфоцитов:
- инфекционный мононуклеоз и другие вирусные инфекции (цитомегаловирус, краснуха, ветряная оспа, токсоплазмоз),
- некоторые бактериальные инфекции (туберкулез, коклюш),
- онкологические заболевания костного мозга (хронический лимфолейкоз) и лимфоузлов (неходжкинская лимфома).9/л
Моноциты, %
Возраст
Референсные значения
Меньше 1 года
4 — 10 %
1 — 2 года
3 — 10 %
Больше 2 лет
3 — 12 %
Причины повышения уровня моноцитов:
- острые бактериальные инфекции,
- туберкулез,
- подострый бактериальный эндокардит,
- сифилис,
- онкологические заболевания костного мозга и лимфоузлов,
- рак желудка, молочных желез, яичников,
- заболевания соединительной ткани,
- саркоидоз.9/л
Эозинофилы, %
Возраст
Референсные значения
Меньше 1 года
1 — 6 %
1 — 2 года
1 — 7 %
2 — 4 года
1 — 6 %
Больше 4 лет
1 — 5 %
Наиболее распространенные причины повышения уровня эозинофилов:
- аллергические заболевания (бронхиальная астма, сенная лихорадка, пищевая аллергия, экзема),
- заражение паразитическими червями,
- аллергическая реакция на лекарственные препараты (антибиотики, аллопуринол, гепарин, пропранолол и др.9/л.
Базофилы, %: 0 — 1,2 %.
Увеличение содержания базофилов встречается редко: при онкологических заболеваниях костного мозга и лимфоузлов, истинной полицитемии, аллергических заболеваниях.
Уменьшаться количество базофилов может при острой фазе инфекции, гипертиреозе, длительной терапии кортикостероидами (преднизолоном).
Скачать пример результатаТакже рекомендуется
Кто назначает исследование?
Врач общей практики, терапевт, педиатр, хирург, инфекционист, гематолог, гинеколог, уролог.
«Необычные способы умножения» 8 класс
Муниципальное общеобразовательное учреждение
«Лаголовская общеобразовательная школа»
ИССЛЕДОВАТЕЛЬСКАЯ РАБОТА
ПО МАТЕМАТИКЕ НА ТЕМУ:
«НЕОБЫЧНЫЕ СПОСОБЫ УМНОЖЕНИЯ».
Выполнила: Кубринская Анастасия
Ученица 8 «Б» класса
Руководитель: Кондратьева Людмила Алексеевна
Учитель математики
.
2016-2017 уч. год
Оглавление.
Вступление
Основная часть. Необычные способы умножения:
Актуальность темы
Историческая справка
Умножение на пальцах
Умножение на 9
Русский крестьянский способ
Умножение методом Ферроля
Линейный (японский) способ
Итальянский способ – способ решетки
Индийский способ умножения
Практическая часть
Заключение
Список литературы
I. Вступление.
Человеку в повседневной жизни невозможно обойтись без вычислений. Поэтому на уроках математики, нас в первую очередь учат выполнять действия над числами, то есть считать. Умножаем, делим, складываем и вычитаем мы привычными для всех способами, которые изучаются в школе.
Постоянное применение современной вычислительной техники приводит к тому, что учащиеся затрудняются производить какие-либо расчеты, не имея в своем распоряжении таблиц или счетной машины. Знание упрощенных приемов вычислений дает возможность не только быстро производить простые расчеты в уме, но и контролировать, оценивать, находить и исправлять ошибки в результате механизированных вычислений. Кроме того, освоение вычислительных навыков развивает память, повышает уровень математической культуры мышления, помогает полноценно усваивать предметы физико-математического цикла.
Цель работы:
Познакомиться с необычными приемами умножения;
Расширить знания по различным приемам умножения;
Научиться выполнять действия с натуральными числами, используя необычные способы умножения.
Задачи:
Изучение источников, в которых встречаются необычные способы умножения;
Поиск нестандартных оригинальных решений;
Изучение выбранных способов умножения натуральных чисел;
Описание и освоение быстрых способов умножения;
Сравнение и выявление преимуществ и недостатков;
Выбрать для себя самые интересные или более легкие и использовать их при счете.
II. Основная часть. Необычные способы умножения.
2.1. Актуальность темы
В современной жизни каждому человеку часто приходится выполнять огромное количество расчётов и вычислений. Основополагающим элементом вычислительной культуры являются сознательные и прочные вычислительные навыки.
Проблема формирования вычислительной культуры актуальна для всего школьного курса математики, начиная с начальных классов, и требует не простого овладения вычислительными навыками, а использования их в различных ситуациях.
Владение вычислительными умениями и навыками имеет большое значение для усвоения изучаемого материала, позволяет воспитывать ценные трудовые качества: ответственное отношение к своей работе, умение обнаруживать и исправлять допущенные в работе ошибки, аккуратное исполнение задания, творческое отношение к труду.
2.2. Историческая справка
В истории математики известно около 30 общих способов умножения, отличающихся либо схемой записи, либо самим ходом вычисления.
Индусы, с давних времен знавшие десятичную систему счисления, предпочитали устный счет письменному. Они изобрели несколько способов быстрого умножения. Позже из заимствовали арабы, а от них эти способы перешли к европейцам. Те, однако, ими не ограничились и разработали новые, в частности тот, что изучается в школе – умножение столбиком. Этот способ известен с начала XV века, в следующем столетии он прочно вошел в употребление у математиков, а сегодня им пользуются повсеместно. Но является ли умножение столбиком лучшим способом осуществления этого арифметического действия? На самом деле существуют и другие, в наше время забытые способы умножения, ничуть не хуже
2.3. Умножение на пальцах.
Древнерусский способ умножения на пальцах является одним из наиболее употребительных методов, которым успешно пользовались на протяжении многих столетий российские купцы. Они научились умножать на пальцах однозначные числа от 6 до 9. При этом достаточно было владеть начальными навыками пальцевого счета “единицами”, “парами”, “тройками”, “четверками”, “пятерками” и “десятками”. Пальцы рук здесь служили вспомогательным вычислительным устройством.
Для этого на одной руке вытягивали столько пальцев, на сколько первый множитель превосходит число 5, а на второй делали то же самое для второго множителя. Остальные пальцы загибали. Потом бралось число (суммарное) вытянутых пальцев и умножалось на 10, далее перемножались числа, показывавшие, сколько загнуто пальцев на руках, а результаты складывались.
Например, умножим 7 на 8. В рассмотренном примере будет загнуто 2 и 3 пальца. Если сложить количества загнутых пальцев (2+3=5) и перемножить количества не загнутых (2•3=6), то получатся соответственно числа десятков и единиц искомого произведения 56 . Так можно вычислять произведение любых однозначных чисел, больше 5.
2.4. Умножение на 9.
Умножение для числа 9 — 9·1, 9·2 … 9·10 — легче выветривается из памяти и труднее пересчитывается вручную методом сложения, однако именно для числа 9 умножение легко воспроизводится «на пальцах». Растопырьте пальцы на обеих руках и поверните руки ладонями от себя. Мысленно присвойте пальцам последовательно числа от 1 до 10, начиная с мизинца левой руки и заканчивая мизинцем правой руки (это изображено на рисунке).
Допустим, хотим умножить 9 на 6. Загибаем палец с номером, равным числу, на которое мы будем умножать девятку. В нашем примере нужно загнуть палец с номером 6. Количество пальцев слева от загнутого пальца показывает нам количество десятков в ответе, количество пальцев справа — количество единиц. Слева у нас 5 пальцев не загнуто, справа — 4 пальца. Таким образом, 9·6=54. Ниже на рисунке детально показан весь принцип «вычисления».
Еще пример: нужно вычислить 9·8=?. По ходу дела скажем, что в качестве «счетной машинки» не обязательно могут выступать пальцы рук. Возьмите, к примеру, 10 клеточек в тетради. Зачеркиваем 8-ю клеточку. Слева осталось 7 клеточек, справа — 2 клеточки. Значит 9·8=72. Все очень просто.
7 клеток 2 клетки.
2.5. Русский крестьянский способ умножения
Самым, на мой взгляд, «родным» и легким способом умножения является способ, который употребляли русские крестьяне. Этот прием вообще не требует знания таблицы умножения дальше числа 2. Сущность его в том, что умножение любых двух чисел сводится к ряду последовательных делений одного числа пополам при одновременном удвоении другого числа. Деление пополам продолжают до тех пор, пока в частном не получится 1, параллельно удваивая другое число. Последнее удвоенное число и дает искомый результат.
В случае нечетного числа надо откинуть единицу и делить остаток пополам; но зато к последнему числу правого столбца нужно будет прибавить все те числа этого столбца, которые стоят против нечетных чисел левого столбца: сумма и будет искомым произведением
37……….32
74……….16
148……….8
296……….4
592……….2
1184……….1
Произведение всех пар соответственных чисел одинаковое, поэтому
37 ∙ 32 = 1184 ∙ 1 = 1184
В случае, когда одно из чисел нечетное или оба числа нечетные, поступаем следующим образом:
24 ∙ 17
24 ∙ 16 =
= 48 ∙ 8 =
= 96 ∙ 4 =
= 192 ∙ 2 =
=384 ∙ 1 = 384
24 ∙ 17 = 24∙(16+1)=24 ∙ 16 + 24 = 384 + 24 = 408
2.6. Умножение методом Ферроля
Индусы этот метод называют молниеносным, греки – «хиазм», итальянцы же называют – per crocetta, что означает накрест. Известно и другое его название – метод Фурье.
Для умножения единиц произведения переумножения перемножают единицы множителей, для получения десятков, умножают десятки одного на единицы другого и наоборот и результаты складывают, для получения сотен перемножают десятки. Методом Ферроля легко перемножать устно двухзначные числа от 10 до 20.
Например: 12х14= 1 6 8
2х4=8
1х4+1х2=6
1х1=1
2.7. Линейный (японский) способ
Допустим нам надо умножить 32х21.
На листе бумаги поочередно рисуем линии, количество которых определяется из данного примера.
Сначала число 32, рисуем 3 красные горизонтальные линии и чуть ниже 2 синие горизонтальные линии.
Число 21, рисуем линии перпендикулярные горизонтальным 2 зеленые и 1 малиновая. Затем считаем количество точек пересечения в каждой из трех областей (на рисунке области показаны в виде окружностей). Итак, в первой области (области сотен) – 6 точек. Во второй области (области десятков) – 7 точек, в третьей (область единиц) – 2 точки. Следовательно ответ: 672
Рассмотрим еще один пример. Те области где количество точек получилось в виде однозначного числа сложности не вызывают. Поэтому начнем разбирать сразу треть область где 16 точек пересечения, от 16 в этой области оставляем только последнюю цифру т.е. 6, все остальное, а значит это цифра 1 переносим в соседнюю область справа налево, следовательно, в третьей области осталось число 6, а второй области к имеющимся 9 точкам надо добавить перенесенную единицу. Следовательно во второй области 10 точек, а это двухзначное число, значит в этой области мы оставляем ноль, а единицу переносим в первую область, где есть уже 4 точки (4+1=5). Составим ответ 50676.
2.8. Итальянский способ – способ решетки
В Италии, а также во многих странах Востока, этот способ приобрел большую известность.
Например,
умножим 6827 на 345.
Вычерчиваем квадратную сетку и пишем одно из чисел над колонками, а второе по высоте.
Умножаем число каждого ряда последовательно на числа каждой колонки. Т.е 6х3=18, записываем 1 и 8
8х3=24, записываем 2 и 4
2х3=6, записываем 0 и 6, если при умножении получается однозначное число, то мы сверху пишем ноль, а снизу это однозначное число.
7х3=21, записываем 2 и 1
Заполняем всю сетку и складываем числа, следуя диагональным полосам. Начинаем складывать справа налево. Если сумма одной диагонали содержит десятки, то прибавляем их к единицам следующей диагонали.
0+5=5
8+3=11
1+2+8+1=12 , 12+1=13
2+6+0+2+4+0=14, 14+1=15
0+4+3+4+3=14, 14+1=15
2+8+2=12,12+1=13
1+0=1,1+1= 2
Ответ: 2 355 315
2.9. Индийский способ умножения.
Самый ценный вклад в сокровищницу математических знаний был совершен в Индии. Индусы предложили употребляемый нами способ записи чисел при помощи десяти знаков: 1, 2, 3, 4, 5, 6, 7, 8, 9, 0.
Основа этого способа заключается в идее, что одна и та же цифра обозначает единицы, десятки, сотни или тысячи, в зависимости от того, какое место эта цифра занимает. Занимаемое место, в случае отсутствия каких – нибудь разрядов, определяется нулями, приписываемыми к цифрам.
Индусы отлично считали. Они придумали очень простой способ умножения. Они умножение выполняли, начиная со старшего разряда, и записывали неполные произведения как раз над множимым, поразрядно. При этом сразу был виден старший разряд полного произведения и, кроме того, исключался пропуск какой-либо цифры. Знак умножения еще не был известен, поэтому между множителями они оставляли небольшое расстояние. Например, умножим их способом 537 на 6:
Однако, существует еще один способ, который использовали индусы в Древней Индии.
Для умножения, например, 793 на 92 напишем одно число как множимое и под ним другое как множитель. Чтобы легче ориентироваться, можно использовать сетку (А) как образец.
Теперь умножаем левую цифру множителя на каждую цифру множимого. Полученные произведения пишем в сетку (Б).
Повторим весь процесс с другими цифрами множителя, следуя тем же правилам (С).
IV.Практическая часть
Умножение на пальцах
Выполните умножение данным способом:
9 х 8=72
6 х 9=36
8 х 8=64
Умножение на 9 на пальцах
Выполните умножение данным способом
7 х 9 = 63
6 х 9 = 54
9 х 9 = 81
Русский крестьянский способ
Выполните умножение данным способом
25 х 128 = 3200
47 х 64 = 3008
13 х 256 = 3328
47 х 24 = 1128
26 х 48 = 1248
56 х 72 = 4032
Способ Ферроля
Выполните умножение данным способом
11 х 19 = 209
12 х 13 = 156
16 х 18 = 288
17 х 15 = 255
19 х 14 = 266
Линейный (японский) способ
Выполните умножение данным способом
31 Х 45 = 1395
24 х 67 = 1608
29 х 33 = 957
341 х 913 = 311333
152 х 421 = 63992
178 х 432 = 76896
Итальянский способ – способ решетки
Выполните умножение данным способом
4986 х 965 = 4811490
17893 х 357 = 6381801
4328 х 6943 = 30049304
Индийский способ
Выполните умножение данным способом
486 х 17 = 8262
369 х 85 = 31365
784 х 63 = 49392
951 х 96 = 91296
654 х 38 = 24852
V. Заключение.
Научившись считать всеми представленными способами, мы пришли к выводу: что самые простые способы это те, которые мы изучаем в школе, может быть они для нас более привычны.
Из всех найденных нами необычных способов счета более интересным показался способ «решетчатого умножения».
Самым простым нам показался метод «удвоения и раздвоения», который использовали русские крестьяне. Его хорошо использовать при умножении не слишком больших чисел (очень удобно его использовать при умножении двузначных чисел).
Мы думаем, что и наш способ умножения в столбик не является совершенным и можно придумать еще более быстрые и более надежные способы.
VI.Литература
Депман И. «Рассказы о математике». – Ленинград.: Просвещение, 1954. – 140 с.
Корнеев А.А. Феномен русского умножения. История. http://numbernautics.ru/
Олехник С. Н., Нестеренко Ю. В., Потапов М. К. «Старинные занимательные задачи». – М.: Наука. Главная редакция физико-математической литературы, 1985. – 160 с.
Перельман Я.И. Быстрый счет. Тридцать простых приемов устного счета. Л., 1941 — 12 с.
Перельман Я.И. Занимательная арифметика. М.Русанова,1994—205с.
Энциклопедия «Я познаю мир. Математика». – М.: Астрель Ермак, 2004.
Энциклопедия для детей. «Математика». – М.: Аванта +, 2003. –
Интернет ресурсы http://nsportal.ru
Интернет ресурсы http://www.bugaga.ru
Энтузиаст протестировал новые китайские процессоры Loongson 3A5000
Энтузиаст состоит в различных чатах в Telegram и как-то недавно наткнулся на канал по процессорам Loongson и ему удалось провести различные тесты данного процессора.
Сперва рассмотрим характеристики процессора Loongson 3A5000 и его предыдущую модель Loongson 3A4000.
Характеристики процессоров Loongson 3A5000 и Loongson 3A4000:
Были проведены следующие тесты:
- 7zip встроенный бенчмарк
- Dhrystone, Whetsone
- Coremark
- Scimark 2
- Mp MFLOPS
- Stream
- Готовые результаты в SPEC 2006 (1 поток)
Сразу переходим к результатам, но детали тестов смотрите далее.
Результаты
По результатам можно сделать вывод, что процессор примерно сравним с процессором Core i7 4700 HQ и немного не дотягивает (~30%, но 4 потока против 8 HT потоков и частота 2.5 ГГц против 3.4 ГГц) до Core i7-2600, хотя обгоняет его по GFLops’ам.
Немного об архитектуре LoongArch
Loongson 3A5000 — процессор на основе сильно переработанной RISC архитектуре MIPS64, часть ненужных команд MIPS64 была удалена и добавлено большое число расширений (SIMD, шифрование, бинарная трансляция, виртуализация), всего порядка 2000+ инструкций.
Loongson 3A5000 (LS3A5000)
Loongson 3A5000 — процессор на основе 64 разрядной RISC сильно переработанной архитектуре MIPS64 (loongarch64), имеет 4 ядра, которые работают на частоте 2.5 ГГц.
Architecture: loongarch64 Byte Order: Little Endian CPU(s): 4 On-line CPU(s) list: 0-3 Thread(s) per core: 1 Core(s) per socket: 4 Socket(s): 1 NUMA node(s): 1 Model name: Loongson-3A5000 CPU max MHz: 2500.0000 CPU min MHz: 225.0000 BogoMIPS: 4992.00 L1d cache: 64K L1i cache: 64K L2 cache: 256K L3 cache: 16384K NUMA node0 CPU(s): 0-3Особенности процессора Loongson 3A5000:
- 64 битная архитектура loongarch64
- 128 битные SIMD расширения Loongson SIMD EXtension (LSX)
- 256 битные SIMD расширения Loongson Advanced SIMD EXtension (LASX)
- Внеочередное исполнение
- Предсказание ветвлений
- Поддержка виртуализации (LVZ)
- Поддержка бинарной трансляции (LBT) архитектур MIPS, ARM, x86
- 4 АЛУ
- 2 SIMD блока
- Кеши
- 64 КБ L1 кэш команд на ядро
- 64 КБ L1 кэш данных на ядро
- 256 КБ L2 кэш на ядро
- 16 МБ L3 кэш
Разбираем результаты
Dhrystone
Dhrystone достаточно древний тест 80х годов, написан на C. Тестирует целочисленную арифметику и работу со строками. Результаты измеряются в Dhrystone/s и DMIPS. (DMIPS = Dhrystone/s делить на 1757).
Вывод теста Dhrystone########################################## Dhrystone Benchmark, Version 2.1 (Language: C or C++) Optimisation loongarch64 loongarch64 optimized Register option not selected 10000 runs 0.00 seconds 100000 runs 0.00 seconds 1000000 runs 0.03 seconds 10000000 runs 0.32 seconds 20000000 runs 0.63 seconds 40000000 runs 1.27 seconds 80000000 runs 2.53 seconds Final values (* implementation-dependent): Int_Glob: O.K. 5 Bool_Glob: O.K. 1 Ch_1_Glob: O.K. A Ch_2_Glob: O.K. B Arr_1_Glob[8]: O.K. 7 Arr_2_Glob8/7: O.K. 80000010 Ptr_Glob-> Ptr_Comp: * 753386704 Discr: O.K. 0 Enum_Comp: O.K. 2 Int_Comp: O.K. 17 Str_Comp: O.K. DHRYSTONE PROGRAM, SOME STRING Next_Ptr_Glob-> Ptr_Comp: * 753386704 same as above Discr: O.K. 0 Enum_Comp: O.K. 1 Int_Comp: O.K. 18 Str_Comp: O.K. DHRYSTONE PROGRAM, SOME STRING Int_1_Loc: O.K. 5 Int_2_Loc: O.K. 13 Int_3_Loc: O.K. 7 Enum_Loc: O.K. 1 Str_1_Loc: O.K. DHRYSTONE PROGRAM, 1'ST STRING Str_2_Loc: O.K. DHRYSTONE PROGRAM, 2'ND STRING Nanoseconds one Dhrystone run: 31.68 Dhrystones per Second: 31560942 VAX MIPS rating = 17962.97Whetstone
Тестирует арифметику с плавающей/фиксированной запятой, математические функции, ветвления, вызовов функций, присваиваний, работы с числами с фиксированной запятой, ветвлений. Результаты измеряются в MMIPS.
Вывод теста Whetstone########################################## Single Precision C Whetstone Benchmark loongarch64 loongarch64 optimized, Sat Jul 24 21:37:34 2021 Calibrate 0.00 Seconds 1 Passes (x 100) 0.01 Seconds 5 Passes (x 100) 0.06 Seconds 25 Passes (x 100) 0.31 Seconds 125 Passes (x 100) 1.57 Seconds 625 Passes (x 100) 7.83 Seconds 3125 Passes (x 100) Use 3989 passes (x 100) Single Precision C/C++ Whetstone Benchmark Loop content Result MFLOPS MOPS Seconds N1 floating point -1.12367534637451172 929.727 0.082 N2 floating point -1.12167274951934814 1370.698 0.391 N3 if then else 1.00000000000000000 0.000 0.000 N4 fixed point 12.00000000000000000 32371.396 0.039 N5 sin,cos etc. 0.49911010265350342 99.825 3.325 N6 floating point 0.99999982118606567 599.758 3.588 N7 assignments 3.00000000000000000 3747.925 0.197 N8 exp,sqrt etc. 0.75110864639282227 62.452 2.376 MWIPS 3990.075 9.997Современный тест, который должен заменить Dhrystone и Whetstone. Написан на C. Считает различные массивы, матрицы, сортировка массивов и т. д. Предназначался для запуска на всём: от микроконтроллеров до мощных процессоров.
Вывод однопоточного теста Coremark2K performance run parameters for coremark. CoreMark Size : 666 Total ticks : 14503 Total time (secs): 14.503000 Iterations/Sec : 13790.250293 Iterations : 200000 Compiler version : GCC8.3.0 Compiler flags : -Ofast -DPERFORMANCE_RUN=1 -DUSE_FORK=1 -lrt Memory location : Please put data memory location here (e.g. code in flash, data on heap etc) seedcrc : 0xe9f5 [0]crclist : 0xe714 [0]crcmatrix : 0x1fd7 [0]crcstate : 0x8e3a [0]crcfinal : 0x4983 Correct operation validated. See README.md for run and reporting rules. CoreMark 1.0 : 13790.250293 / GCC8.3.0 -Ofast -DPERFORMANCE_RUN=1 -DUSE_FORK=1 -lrt / Heap
Вывод многопоточного теста Coremark2K performance run parameters for coremark. CoreMark Size : 666 Total ticks : 14623 Total time (secs): 14.623000 Iterations/Sec : 54708.336183 Iterations : 800000 Compiler version : GCC8.3.0 Compiler flags : -Ofast -march=native -DPERFORMANCE_RUN=1 -DUSE_FORK=1 -lrt Parallel Fork : 4 Memory location : Please put data memory location here (e.g. code in flash, data on heap etc) seedcrc : 0xe9f5 [0]crclist : 0xe714 [1]crclist : 0xe714 [2]crclist : 0xe714 [3]crclist : 0xe714 [0]crcmatrix : 0x1fd7 [1]crcmatrix : 0x1fd7 [2]crcmatrix : 0x1fd7 [3]crcmatrix : 0x1fd7 [0]crcstate : 0x8e3a [1]crcstate : 0x8e3a [2]crcstate : 0x8e3a [3]crcstate : 0x8e3a [0]crcfinal : 0x4983 [1]crcfinal : 0x4983 [2]crcfinal : 0x4983 [3]crcfinal : 0x4983 Correct operation validated. See README.md for run and reporting rules. CoreMark 1.0 : 54708.336183 / GCC8.3.0 -Ofast -march=native -DPERFORMANCE_RUN=1 -DUSE_FORK=1 -lrt / Heap / 4:ForkMP MFLOPS
Выполняет операции с плавающей запятой на векторах.
Вывод теста MP-MFLOPSMP-MFLOPS Compiled for loongarch64 Sat Jul 24 20:52:23 2021 FPU Add & Multiply using 1, 2, 4 and 8 Threads 2 Ops/Word 32 Ops/Word KB 12.8 128 12800 12.8 128 12800 MFLOPS 1T 18882 12721 10789 26652 26031 25988 2T 32784 37675 21228 51444 54126 51909 4T 51385 70939 40023 94571 107173 102566 8T 41463 66280 42473 84137 105576 103068 Results x 100000, 0 indicates ERRORS 1T 76406 97075 99969 0 0 99951 2T 76406 97075 99969 0 0 99951 4T 76406 97075 99969 0 0 99951 8T 76406 97075 99969 0 0 99951 End of test Sat Jul 24 20:52:23 20217zip
Встроенный тест архиватора 7z.
Запускается так:
7z b
Вывод теста 7z7-Zip (a) 16.02 : Copyright (c) 1999-2016 Igor Pavlov : 2016-05-21 p7zip Version 16.02 (locale=zh_CN.UTF-8,Utf16=on,HugeFiles=on,64 bits,4 CPUs LE) LE CPU Freq: 64000000 - - - - - - - - RAM size: 16165 MB, # CPU hardware threads: 4 RAM usage: 882 MB, # Benchmark threads: 4 Compressing | Decompressing Dict Speed Usage R/U Rating | Speed Usage R/U Rating KiB/s % MIPS MIPS | KiB/s % MIPS MIPS 22: 11279 327 3352 10973 | 130124 396 2803 11102 23: 10681 325 3346 10883 | 127682 393 2810 11048 24: 11183 353 3406 12025 | 126626 395 2815 11116 25: 11099 360 3525 12673 | 124248 394 2805 11058 ---------------------------------- | ------------------------------ Avr: 341 3407 11638 | 395 2808 11081 Tot: 368 3108 11360STREAM
Тест производительности ОЗУ.
Вывод теста STREAMFunction Best Rate MB/s Avg time Min time Max time Copy: 16748.3 0.009969 0.009553 0.010576 Scale: 18735.0 0.009437 0.008540 0.010660 Add: 16333.2 0.015492 0.014694 0.016449 Triad: 17796.0 0.014789 0.013486 0.015294Версия компилятора, ядра Linux
Ядро Linux:
Linux 4.19.167-rc5.lnd.1-loongson-3 #1 SMP Sat Apr 17 07:32:32 UTC 2021 loongarch64 loongarch64 loongarch64 GNU/LinuxВерсия компилятора:
gcc version 8.3.0 (Debian 8.3.0-6.lnd.vec.20).Выводы
Loongson 3A5000 вышел достаточно неплохим процессором, который уже сейчас может применяться в различных десктопных решениях, а процессоры с низкими частотами могут применяться в ноутбуках (с TDP порядка 30 Вт.)
Очень хотелось бы попробовать в работе такие компьютеры, а учитывая то, что они поддерживают видеокарты от AMD, то можно запускать и игры с открытым исходным кодом. Будем надеяться, что такие процессоры получат широкое применение.Другие результаты для сравнения:
Картинка
Ссылки
16-кратная таблица — выучить таблицу из 16
Таблица умножения на 16 — это таблица умножения, которая создается путем умножения числа 16 на разные целые числа. Переход от подсчета пальцев к ментальной арифметике начинается с обучения таблицам умножения. В этом мини-уроке вы найдете таблицу умножения на 16, то есть умножение 16 на различные целые числа, а также некоторые приемы для запоминания таблицы.
16-кратная таблица:
Таблица умножения 16
- Изучение таблицы умножения на 16 в годы обучения помогает студентам решать длинные задачи, связанные с умножением и делением. Таблица умножения
- на 16 помогает визуализировать шаблоны умножения и применять их в реальных сценариях.
Для быстрых вычислений просмотрите таблицу 16 умножения , которая приведена ниже.
16-кратная таблица
>> Скачать 16-кратную таблицу16-кратная таблица до 10 16 × 1 = 16 16 × 6 = 96 16 × 2 = 32 16 × 7 = 112 16 × 3 = 48 16 × 8 = 128 16 × 4 = 64 16 × 9 = 144 16 × 5 = 80 16 × 10 = 160 Советы для таблицы 16 раз
1. 16 не имеет никаких правил, которые упрощают запоминание таблицы умножения 16, но есть образец для каждых пяти кратных шестнадцати: 16, 32, 48, 64, 80, 96, 112, 128, 144, 160.
2. Последняя цифра этих кратных чисел всегда повторяется, что означает, что учащиеся могут запомнить эти цифры, чтобы помочь им с таблицей умножения на 16.
Другой способ запомнить таблицу от 16 до 10:
Как вы можете заметить на изображении выше, цифры, которые сначала стоят на месте единицы, записываются в последовательности 8, 6, 4, 2, 0 во всех 4 рядах двух видимых сеток.Вместо разряда десятков напишите все числа и повторите каждое число, кратное 4. Следовательно, повторяются 4, 8 и 12. Каждое альтернативное число после 16 обведено в кружок, и числа представляют собой таблицу умножения на 16.
Стол от 16 до 20
Мы получили первые десять чисел, кратных 16. Давайте оценим таблицу от 16 до 20.
16 × 11 = 176 16 × 16 = 256 16 × 12 = 192 16 × 17 = 272 16 × 13 = 208 16 × 18 = 288 16 × 14 = 224 16 × 19 = 304 16 × 15 = 240 16 × 20 = 320 8 раз, что равно 16?
Онлайн калькуляторы> Математические калькуляторы
8 умножить на 2 равно 16, потому что 16/8 = 2.Ниже приведена таблица умножения 8, в которой 8 умножается от 1 до 25.
В 9 раз больше, что равно 98 x 1 = 8 8 x 2 = 16 8 x 3 = 24 8 x 4 = 32 8 x 5 = 40 8 x 6 = 48 8 x 7 = 56 8 x 8 = 64 8 x 9 = 72 8 x 10 = 80 8 х 11 = 88 8 х 12 = 96 8 х 13 = 104 8 х 14 = 112 8 х 15 = 120 8 х 16 = 128 8 х 17 = 136 8 х 18 = 144 8 x 19 = 152 8 x 20 = 160 8 x 21 = 168 8 х 22 = 176 8 x 23 = 184 8 х 24 = 192 8 x 25 = 200
, в 8 раз больше, что равно 24
Электрические калькуляторы
Калькуляторы недвижимости
Бухгалтерские калькуляторы
Бизнес-калькуляторы
Строительные калькуляторы
Спортивные калькуляторыФинансовые калькуляторы
Калькулятор сложных процентов
Ипотечный калькулятор
Сколько дома я могу себе позволить
Кредитный калькулятор
Фондовый калькулятор
Инвестиционный калькулятор
Пенсионный калькулятор
401k Калькулятор
Калькулятор комиссионных сборов eBay
PayPal калькулятор комиссионных
Etsy30 Комиссия наценка TV
Калькулятор LTV
Калькулятор аннуитета
Сколько я зарабатываю в годуМатематические калькуляторы
Смешанное число в десятичном формате
Ratio Simplifier
Percentage CalculatorHealth Calculators
BMI Calculator
Weight Loss Calculator CMConversion 901 and Feet 901 MM в дюймах
Другое
Сколько мне лет
Выбор случайных имен
Генератор случайных чиселСумма чисел, умноженных на 8 и 19, составляет не менее 16
Тимоти С.ответил • 05.01.20
Опытный репетитор по математике и естественным наукам из Калифорнийского университета в Дэвисе
скажем, число x
8x + 19 ≥ 16
8x ≥ -3
x ≥ -3/8
Все еще ищете помощь? Получите правильный ответ быстро.
ИЛИ
Найдите онлайн-репетитора сейчасВыберите эксперта и познакомьтесь онлайн.Никаких пакетов или подписок, платите только за необходимое время.
¢ € £ ¥ ‰ µ · • § ¶ SS ‹ › « » < > ≤ ≥ — — ¯ ‾ ¤ ¦ ¨ ¡ ¿ ˆ ˜ ° — ± ÷ ⁄ × ƒ ∫ ∑ ∞ √ ∼ ≅ ≈ ≠ ≡ ∈ ∉ ∋ ∏ ∧ ∨ ¬ ∩ ∪ ∂ ∀ ∃ ∅ ∇ * ∝ ∠ ´ ¸ ª º † ‡ А Á Â Ã Ä Å Æ Ç È É Ê Ë Я Я Я Я Ð Ñ Ò Ó Ô Õ Ö Ø Œ Š Ù Ú Û Ü Ý Ÿ Þ à á â ã ä å æ ç è é ê ë я я я я ð ñ ò ó ô х ö ø œ š ù ú û ü ý þ ÿ Α Β Γ Δ Ε Ζ Η Θ Ι Κ Λ Μ Ν Ξ Ο Π Ρ Σ Τ Υ Φ Χ Ψ Ω α β γ δ ε ζ η θ ι κ λ μ ν ξ ο π ρ ς σ τ υ φ χ ψ ω ℵ ϖ ℜ ϒ ℘ ℑ ← ↑ → ↓ ↔ ↵ ⇐ ⇑ ⇒ ⇓ ⇔ ∴ ⊂ ⊃ ⊄ ⊆ ⊇ ⊕ ⊗ ⊥ ⋅ ⌈ ⌉ ⌊ ⌋ 〈 〉 ◊Как вводить доли часа в табели учета рабочего времени в Small Business Accounting, Accounting Professional и Accounting Express
ВВЕДЕНИЕ
В этой статье описывается, как вводить доли часа в табели учета рабочего времени в Microsoft Office Small Business Accounting, Microsoft Office Accounting Professional и Microsoft Office Accounting Express.
Дополнительная информация
При вводе количества часов, проработанных сотрудником в табеле учета рабочего времени, необходимо ввести минуты как доли часа. Например, если сотрудник проработал 1 час 20 минут, введите 1,333 в поле Продолжительность (часы) . На следующей диаграмме показано, как минуты преобразуются в доли часа путем деления количества минут на 60.
Минут
Доля часа
0
0.000
1
0,017
2
0,033
3
0.050
4
0,067
5
0,083
6
0.100
7
0,117
8
0,133
9
0.150
10
0,167
11
0,183
12
0.200
13
0,217
14
0,233
15
0.250
16
0,267
17
0,283
18
0.300
19
0,317
20
0,333
21
0.350
22
0,367
23
0,383
24
0.400
25
0,417
26
0,433
27
0.450
28
0,467
29
0,483
30
0.500
31
0,517
32
0,533
33
0.550
34
0,567
35
0,583
36
0.600
37
0,617
38
0,633
39
0.650
40
0,667
41
0,683
42
0.700
43
0,717
44
0,733
45
0.750
46
0,767
47
0,783
48
0.800
49
0,817
50
0,833
51
0.850
52
0,867
53
0,883
54
0.900
55
0,917
56
0,933
57
0.950
58
0,967
59
0,983
60
1.000
8 человек погибли в результате стрельбы в 3 спа-центрах Атланты
АТЛАНТА —Мужчина, обвиняемый в убийстве восьми человек, в том числе шести женщин азиатского происхождения, в ряде спа-салонов Атланты сообщил властям, что у него «сексуальный контакт». зависимость »и хотел избавиться от соблазна, который представляли заведения.
В среду власти заявили, что нападения «не похоже» были мотивированы расовой принадлежностью. Но правозащитные группы подчеркнули, что нельзя игнорировать более широкий контекст недавнего всплеска преступлений на почве ненависти и преследований, направленных против американцев азиатского происхождения, и начальник полиции Атланты Родни Брайант предупредил, что расследование все еще находится на начальной стадии.
Для записи:
, 5:15, 17 марта 2021 г. В предыдущей версии этой истории Фрэнк Рейнольдс был неверно идентифицирован. Он шериф округа Чероки, а не Крисп.
Роберт Аарон Лонг, 21 год, из Вудстока, штат Джорджия, был арестован вечером во вторник в округе Крисп, примерно в 150 милях к югу от Атланты, после стрельбы в спа-салоне в Акворте, штат Джорджия, и в двух спа-салонах Атланты, где работают многие из сотрудников. Азиатский. Атаки подогревали опасения, что жертвы стали жертвами из-за их расы.
В среду власти заявили, что Лонг , , который был схвачен после того, как его родители обратились к властям, признал, что совершил нападение. На вопрос, была ли стрельба мотивирована расовыми мотивами, шериф округа Чероки Фрэнк Рейнольдс сказал, что «мы считаем, что он часто бывал в этих местах в прошлом и, возможно, набрасывался», но этот расизм «не был мотивом».
«У него есть проблемы, потенциально сексуальная зависимость», — сказал Рейнольдс репортерам. «Мы все еще на раннем этапе, нам еще многое предстоит обработать.”
Брайант добавил, что еще слишком рано говорить о том, была ли раса составной частью атак.
«Мы все еще находимся в начале этого расследования, поэтому мы не можем сделать это определение в настоящий момент», — сказал Брайант. «Впереди еще много работы».
Власти заявили, что Лонг направлялся во Флориду, чтобы совершить там аналогичные атаки. Капитан шерифа округа Чероки Джей Бейкер сказал, что курорты были «искушением» для Лонга.
«Для него это искушение, которое он хотел устранить, — сказал Бейкер.«Эти места, он видит в них выход для себя — то, чего он не должен делать, проблема с порно — и что он пытался избавиться от этого искушения».
По крайней мере четверо из убитых были корейского происхождения.
В среду офис шерифа округа Чероки обнародовал имена погибших жертв первой стрельбы: Делайна Эшли Яун, 33 года, из Акворта, Пол Андре Михельс, 54 года, из Атланты, Сяоцзе Ян, 49 лет, из Кеннесо, и Даою. Фэн, 44 года, адрес неизвестен.Пятая жертва, 30-летний Эльсиас Р. Эрнандес-Ортис из Акворта, была ранена.
Полицейское управление Атланты заявило, что жертвы инцидентов, произошедших в городе Атланта , еще не были идентифицированы, а уведомление о ближайших родственниках не было подтверждено судмедэкспертом округа Фултон.
«Мы убиты горем этими актами насилия», — говорится в заявлении Стефани Чо, исполнительного директора организации «Американцы азиатского происхождения, продвигающей правосудие».«Шесть азиатских женщин погибли. Пришло время держать жертв и их семьи в наших сердцах и в нашем свете ».В среду утром Лонг был доставлен в центр заключения для взрослых округа Чероки утром в среду. Управление шерифа округа Чероки заявило, что ему было предъявлено обвинение по четырем пунктам обвинения в убийстве и одному пункту обвинения в нападении при отягчающих обстоятельствах без залога.
Выпускник 2017 года средней школы Секвойя в Кантоне, штат Джорджия, Лонг, принадлежал к Первой баптистской церкви Crabapple в Милтоне и описал свои интересы в Instagram как «пицца, оружие, барабаны, музыка, семья и Бог», — сообщает Daily Beast. .В среду утром веб-сайт церкви и страница в Facebook перестали быть общедоступными. Его пастор не ответил на просьбу о комментарии.
Атаки начались около 17:00. Во вторник, когда Бейкер сообщил Associated Press, когда во время сеанса азиатского массажа Янга в торговом центре в Акворте, примерно в 25 милях к северо-западу от центра Атланты, были застрелены пять человек. Четыре человека погибли и один получил ранения.
На месте происшествия никого не задержали, но видеозаписи наблюдения запечатлели подозреваемого и черный Hyundai Tucson 2007 года выпуска.
Менее чем через 50 минут полицейские Атланты отреагировали на сообщение об ограблении примерно в 25 милях к югу от Gold Spa на северо-востоке Атланты, где они обнаружили трех женщин, которые были смертельно ранены. Когда офицеры отреагировали на место происшествия, они получили сообщение о выстрелах в спа-центр ароматерапии через дорогу. Внутри этого предприятия они обнаружили тело еще одной застреленной женщины.
В 20:00 Рейнольдс предупредил дорожный патруль и управление шерифа округа Крисп, примерно в 150 милях к югу, о том, что подозреваемый направлялся на юг по межштатной автомагистрали 75 на черном Hyundai Tucson 2007 года выпуска.
Hyundai был замечен около 8:30, и военнослужащий штата выполнил маневр, в результате которого автомобиль вышел из-под контроля, сказал шериф округа Крисп Билли Хэнкок. Лонг был взят под стражу без происшествий и доставлен в тюрьму округа Крисп.
Опасаясь, что курорты города распространились, полиция Атланты заявила, что командиры в районе, где произошли убийства, усилили патрулирование и направили офицеров для проверки аналогичных предприятий поблизости.
В заявлении национальной коалиции STOP AAPI Hate, направленной против антиазиатской ненависти в условиях пандемии, стрельба была названа «невыразимой трагедией — в первую очередь для семей жертв, но также и для сообщества AAPI, — которое пошатнулось. от высокого уровня расовой дискриминации.”
Группа заявила, что, даже не зная мотивов подозреваемого, «прямо сейчас в азиатско-американском сообществе существует много страха и боли, с которыми необходимо бороться».
За последний год города США зафиксировали рост агрессии против американцев азиатского происхождения. В ходе опроса полицейских управлений в 16 крупных городах Центр изучения ненависти и экстремизма штата Калифорния Сан-Бернардино обнаружил в общей сложности 122 преступления на почве ненависти к Азии в 2020 году — на 149% больше, чем в 2019 году.
«То, что убитые вчера азиатские женщины работали на очень уязвимых и низкооплачиваемых работах во время продолжающейся пандемии, прямо говорит о совокупных последствиях женоненавистничества, структурного насилия и превосходства белых», — сказала Фи Нгуен, директор по судебным процессам в Asian Americans Advancing Justice. Атланта.
Группа добавила, что «в то время как антиазиатское насилие пронизано всей историей нашей страны, безжалостное обвинение со стороны администрации Трампа в адрес азиатов за продолжающуюся пандемию COVID-19 увеличило количество случаев ненависти и насилия в отношении американцев азиатского происхождения по всей стране.”
Министерство иностранных дел Южной Кореи заявило в среду, что его дипломаты в Атланте подтвердили полиции, что четверо из погибших были женщинами корейского происхождения. Министерство заявило, что офис его генерального консульства в Атланте пытается подтвердить национальность женщин.
«Мы в ужасе от этого насилия, которому нет места ни в Америке, ни где-либо еще, если на то пошло», — сказал госсекретарь Энтони Блинкен в Сеуле, где он встретился в среду с высокопоставленными официальными лицами Южной Кореи.«И я хочу выразить наши глубочайшие соболезнования семьям и друзьям погибших, а также всем членам корейской общины, которые потрясены и глубоко встревожены этим инцидентом. Мы тоже, и мы будем отстаивать право наших соотечественников-американцев и корейских американцев на безопасность, на достойное и уважительное обращение ».
Пресс-секретарь Белого дома Джен Псаки заявила, что президент Байден был проинформирован об «ужасающих перестрелках» и что официальные лица администрации поддерживали контакт с мэрией Атланты и ФБР.
Первая леди Джилл Байден упомянула стрельбу во время посещения школы в Конкорде, штат Нью-Хэмпшир: «Я хочу начать с того, что скажу кое-что непосредственно семьям жертв стрельбы в Атланте прошлой ночью. Мое сердце с тобой. И я надеюсь, что все американцы присоединятся ко мне в молитве за всех, кого коснулась эта бессмысленная трагедия ».
В северо-западном пригороде Атланты Young’s Asian Massage — это небольшой бизнес, расположенный в торговом центре, между салоном красоты и бутиком, в разнообразном районе через дорогу от такерии, карникерии и панадерии.
Стрельба в 25 милях к югу от района Бакхед в Атланте произошла на участке Пьемонт-роуд, широко известном в городе своими массажными кабинетами и развлекательными клубами для взрослых. На своем веб-сайте Gold Spa предлагает массаж глубоких тканей и шведский массаж от «международного» персонала. Aromatherapy Spa описывает себя как «азиатский латиноамериканский массажный спа».
По словам представителя ФБР Кевина Роусона, ФБР помогает местным агентствам в расследовании стрельбы.
Штатные авторы Times Трейси Уилкинсон и Крис Мегериан в Вашингтоне и Associated Press внесли свой вклад в этот отчет.
Границы | 8:30 утра еще слишком рано, чтобы идти в школу? Начало занятий в 10:00 утра улучшает здоровье и успеваемость учащихся 13–16 лет
Введение
Несмотря на общепринятые естественные сдвиги в сторону более позднего бодрствования и сна, которые происходят в подростковом возрасте, в большинстве школ сохраняется раннее время начала занятий.В настоящее время время начала занятий в школе не корректируется с учетом перехода на более позднее время бодрствования и сна, которое происходит естественным образом в подростковом возрасте. Это несоответствие между биологией подростков и общепринятой практикой раннего поступления в школу приводит к систематическому сокращению количества времени, доступного подросткам для сна, и, как следствие, к хроническому дефициту сна. Центры по контролю и профилактике заболеваний и Американская академия педиатрии (2014) заявили, что раннее начало обучения в школе связано с повышенным риском ожирения, депрессии и употребления наркотиков, а также с более низкой успеваемостью (Owens et al., 2014; Wheaton et al., 2015). Их рекомендация открывать средние и старшие школы не ранее 8:30 теперь поддержана Американской медицинской ассоциацией (2016). Почти во всех исследованиях на сегодняшний день, хотя время начала занятий в школе было позже, чем раньше, сохранялось время начала 9:00 или раньше (Kirkby et al., 2011). Одно исследование в Новой Зеландии сообщило об улучшении сна у 17-18-летних студентов, когда время начала было перенесено с 9:00 на 10:30, по сравнению с более молодыми контрольными, которые оставались в 9:00 a.м. (Borlase et al., 2013). Недавнее исследование оптимального времени для когнитивной деятельности учащихся в возрасте 18–19 лет показало, что оптимальным было гораздо более позднее время, особенно после 11 часов утра или 12 часов дня (Evans et al., 2017).
Доказательства повышенного риска для здоровья, связанного с ранним началом школьного обучения, являются существенными и демонстрируются с помощью различных исследовательских методологий (Hansen et al., 2005; Millman, 2005; Basch et al., 2014; de Souza and Hidalgo, 2014). Основные биологические факторы также хорошо известны.Подросткам требуется от 8 до 10 часов сна в сутки для полноценного здоровья и успеваемости в зависимости от возраста и индивидуальных различий, но большинству из них требуется гораздо меньше сна (Iglowstein et al., 2003; Foster et al., 2013; Hirshkowitz et al. ., 2015). Биологические изменения суточных суточных часов в подростковом возрасте задерживают наступление времени бодрствования и сна, и этот сдвиг не меняется до раннего взросления (Roenneberg et al., 2004). Кроме того, гомеостатическая регуляция давления для сна нарастает медленнее, и требуется больше времени для достижения критического порога, необходимого для засыпания (Carskadon, 2011).Ограничение сна у подростков явно связано с ранним началом школьного обучения, поскольку в неурочные дни подростки просыпаются на два или более часа позже (Roenneberg et al., 2007), что, по-видимому, не существенно зависит от культурных факторов (Gradisar et al., 2011). ; Foster et al., 2013).
Более позднее время начала занятий в школе способствует улучшению сна, здоровья и обучения подростков (Curcio et al., 2006; Carskadon, 2011; Lufi et al., 2011). Имеются веские доказательства того, что более позднее время начала обучения благоприятно сказывается на успеваемости даже на ранних стадиях полового созревания, и это положительное влияние сохраняется и в позднем подростковом возрасте (Carrell et al., 2011; Эдвардс, 2012; Meltzer et al., 2014). Более позднее время начала связано с улучшением сна, которое продолжается в годы после внедрения (Borlase et al., 2013; Wahlstrom et al., 2014). Более позднее время начала занятий также снижает количество дорожно-транспортных происшествий среди студентов (Danner and Phillips, 2008) и снижает количество сообщений о депрессии (Kirkby et al., 2011).
Принцип, согласно которому время начала занятий для подростков должно быть позже, чем в настоящее время является нормой в американских школах (около 8:00 утра до вечера).м.) в настоящее время получили широкое распространение. В настоящее время необходимы исследования для более точной синхронизации времени начала занятий в школе с биологией подростков, принимая во внимание возрастающее влияние изменений циркадных ритмов в подростковом возрасте (Shekleton et al., 2013; Kelley et al., 2015). Хотя данные о начале обучения в средней и старшей школе в 8:30 или позже положительны, эта рекомендация основана на доказательствах, ограниченных исследованиями, в которых школьное время переносится не позднее 9:00 или часто раньше, оставляя вопрос без ответа. о том, насколько поздним должно быть время начала занятий в школе.Чтобы изучить влияние гораздо более позднего начала занятий в школе, мы изучили влияние времени начала занятий в 10 часов утра (что представляет собой задержку на 1:10 ч по сравнению с 8:50 утра) на показатели заболеваемости среди 13–16 летних. старшеклассники и успеваемость от 14 до 16 лет.
Участники и методы
Определение времени начала
В свете существовавших на тот момент данных о времени начала занятий, ведущий исследователь настоящего исследования (ПК) разработал и направил полевой эксперимент для реализации и оценки эффективности гораздо более позднего времени начала занятий в школе.Схема кратко изложена в таблице 1, столбцы 1, 2 и 4 (см. Раздел «Результаты»). Школа была смешанной, финансируемой государством, для учеников от 13 до 18 лет. В начале исследования успеваемость школьников была значительно ниже средней по стране. Школа находилась в городском районе с населением 0,7 миллиона человек, в регионе Англии, где успеваемость была ниже, чем в среднем по стране.
Таблица 1 . Влияние экспериментального лечения (10:00 начало занятий в школе) на пропуски занятий по болезни.
В школе не было дополнительного финансирования, выборочного зачисления или других образовательных мероприятий во время исследования. Школа действовала в рамках Innovation Trust, благотворительного фонда по улучшению школ в партнерстве с ведущими учеными (см. Раздел «Благодарности»). При работе с этой группой экспертов было рассмотрено более позднее время начала с акцентом на определение времени начала занятий для подростков 13–18 лет. Первоначальное тестирование успеваемости учащихся в 10:00 и 14:00, добровольные исследования хронотипа и уровни телесного жира учащихся привели к выводу, что должен быть основной период времени для всех учащихся с 11:00 до 15:00 с дополнительным обучением. время до (для утренних / средних хронотипов) и после (для вечерних хронотипов) (Sussman, 2009).Это казалось слишком радикальным изменением, и в сочетании с текущим решением Национальной службы здравоохранения о том, что школы не могут по закону хранить какие-либо данные о психическом здоровье учащихся в возрасте 16 лет и младше, включая данные о сне и жировой ткани, привело к ограничению возрастного диапазона 13–16 лет. и с использованием только существующих национальных показателей здоровья и успеваемости. Поэтому анализ соответствующих исследований сна и циркадной нейробиологии, указывающих на то, что время начала 10: 00–10: 30 утра, будет уместным в возрасте 16 лет (Kelley et al., 2015). Этот процесс привел к окончательному выбору 10:00 утра в качестве времени начала занятий в школе, что составляет 1 час 10 минут задержки по сравнению с традиционным временем начала 8:50, которое использовалось в то время.
Двухлетний процесс изменения времени начала был этически одобрен как The Innovation Trust, благотворительным образовательным исследовательским фондом, связанным со школой, так и Руководящим советом школы на том основании, что учащиеся не будут подвергаться дополнительным опросам, тестам или мерам. кроме более позднего времени начала. Была проведена юридически обязательная консультация с родителями, учениками, учителями и другими людьми.Это вызвало ряд проблем, включая транспорт до школы. В отличие от американских школ, городские школы в Англии, как правило, не предоставляют транспорт для всех учащихся, и существующая транспортная инфраструктура сделала это относительно незначительной проблемой. Школа уже поддержала часы работы родителей и транспорт, открыв их на 1 час раньше и на 1 час после школы (включая спортивные и клубные возможности). Поэтому с небольшими изменениями все время в школе было просто перенесено на час и 10 минут позже. Хотя родители поддержали изменения, наблюдалось сопротивление со стороны местных администраторов образования, явление, отмеченное в других исследованиях (Wahlstrom et al., 2014). Проблемы, поднятые во время консультации, хотя часто и были обоснованными, были рассмотрены по мере возможности, но считались второстепенными по отношению к raison d’etre для школ — помочь здоровым детям реализовать свой академический потенциал.
После утверждения изменения в 2010 г. был проведен 6-недельный пробный запуск с началом в 10:00, после того как были завершены все ежегодные экзамены и студенты, сдающие экзамены, ушли, но до начала нового учебного года. В ходе судебного разбирательства все связанные запланированные мероприятия были перенесены на 10:00 a.м. начните с транспорта в школу и обратно, семейных мероприятий, школьных клубов и мероприятий. Сообщалось также о некоторых дополнительных и неожиданных преимуществах: время в пути позволяло избежать часа пик и считалось более безопасным; а некоторые сотрудники могли забирать своих детей в начальную школу утром.
Через 2 года с временем начала в 10 часов утра, естественный эксперимент был произведен сменой местных администраторов образования, которые восстановили раннее начало, используемое во всех местных школах.Следовательно, время начала занятий в школе для детей в возрасте от 13 до 16 лет было изменено обратно на 8:50 утра из-за этих изменений политики, а не части плана исследования; однако мы воспользовались этим естественным экспериментом.
Вмешательство и сбор данных
В этом наблюдательном исследовании использовался план «до-после-до» (A-B-A). Время начала занятий в школе изменилось следующим образом за 4 года: в 0-м классе начало занятий в 8:50; 1-й и 2-й классы начинались в 10 часов утра; и у 3-го класса было начало 8:50 утра. За эти четыре академических года (сентябрь 2010 г. — август 2014 г.) были собраны национальные данные и данные школ о заболеваниях и успеваемости 2049 учащихся в возрасте 13–16 лет.
данных об образовании по английскому языку собираются на национальном уровне для каждой школы, и эти данные для всех школ публикуются Управлением национальной статистики Великобритании (2016). Для оценки влияния изменения времени использовались две переменные: отсутствие учащегося из-за болезни и общая успеваемость учащегося. Английские школы обязаны отличать отсутствие (не в школе по какой-либо причине) от отсутствия по болезни (что составляет ~ 60% всех пропусков в зависимости от года). Пропуски по болезни регистрируются для каждого учащегося на каждой утренней и дневной сессии, поэтому в качестве показателя болезни здесь использовалось количество пропущенных из-за болезни занятий на ученика в год.Этот показатель дает более точный показатель заболеваемости, чем количество простых прогулов (Департамент образования, 2016).
В то время ключевым показателем академической успеваемости учащихся были экзамены на аттестат зрелости (GCSE), сдаваемые в конце обязательного школьного образования в 16 лет. Хорошая успеваемость в 16 лет определялась как достижение пяти или более оценок GCSE. C или выше по английскому языку, математике и как минимум по трем другим предметам. Показателем успеваемости в школе был процент учащихся, достигших хорошей успеваемости.
Кроме того, Fisher Family Trust разработала национальную систему анализа добавленной стоимости отдельных учащихся и потенциальных достижений школы в оценках GCSE и хорошей успеваемости для всех учащихся и школ в Англии. Поскольку предыдущие способности когорт учащихся могут варьироваться от года к году, эффективность школ может меняться, и поэтому был проведен второй анализ успеваемости, основанный на этих прогнозах добавленной стоимости (Visscher and Coe, 2003; Koedel et al., 2015). Прогнозируемые результаты были основаны на предыдущих достижениях студентов в национальных тестах.Считается, что школы, в которых процентная хорошая успеваемость превышает прогнозируемый, имеют дополнительную ценность, выраженную в виде процента хорошей успеваемости по сравнению с прогнозируемыми результатами (с отрицательными результатами для школ ниже прогнозов). Например, если учащиеся достигли в среднем на 4% более высокой успеваемости, это будет иметь оценку добавленной стоимости + 4%. Эти два национальных показателя фактической и прогнозируемой успеваемости в школе использовались в нашем анализе.
Анализы
Национальные данные были использованы для анализа болезни и работоспособности.По возможности, для оценки стандартных отклонений использовались национальные данные. Кроме того, был создан набор данных из 2 880 аналогичных школ, где «похожие» были определены как финансируемые государством школы с учащимися от 13 до 16 лет в когортах> 100 и с отчетными данными экзаменов за период 2010–2014 гг. Используемые наборы данных представляют собой данные на уровне школ, опубликованные Управлением национальной статистики Великобритании и другими источниками, как указано (Управление национальной статистики Великобритании, 2016). Данные о достижениях имеют ограничения из-за политики и практики публикации.Ограничения политики включают решение об исключении школ, становящихся академиями (аналогично чартерным школам) из национальных данных, изменения экзаменов и данных, представленных в течение 4 лет.
Анализ данных о заболеваниях и производительности за этот период привел к представлению как исходных баллов, так и баллов, скорректированных с учетом национальных различий. Что касается национальных тенденций в заболеваемости и производительности, для оценки значимости использовались тесты T , а также d и h Коэна для оценки величины эффекта с учетом критики Хэтти образовательных мер для определения воздействия вмешательств (Hattie, 2008).Критика Хэтти исследований в области образования, основанная на синтезе более 800 метаанализов повышения успеваемости, подняла вопросы об анализе и значении образовательных данных. В частности, он утверждал, что более сложные статистические методы, большое количество предметов, обычно доступных в исследованиях в области образования, и другие факторы означают, что величина эффекта должна быть> 0,5 в отдельных исследованиях. Хэтти перечисляет 138 величин эффекта, обнаруженных в метаанализе значительных образовательных вмешательств за последние 20 лет, показывая, что у 20 самых высоких вмешательств величина эффекта варьировалась от 0.61 к 1,44. Обеспокоенность Хэтти по поводу образовательных исследований и размеров эффекта разделяют и другие (Snow, 2015; Church et al., 2017). В иллюстративных целях также были проанализированы затраты / выгоды от образовательных реформ в Англии и Нью-Йорке, направленных на повышение успеваемости.
Результаты
Показатели пропусков занятий по болезни среди учащихся в возрасте 13–16 лет были ниже с 10 часами утра (см. Таблицу 1 и Рисунок 1).
Рисунок 1 . Пропуски занятий по болезни, отличия от среднего показателя по стране.
В 0-м классе для базовой когорты учащихся в возрасте 13–16 лет, у которых время начала 8:50 в течение обоих лет обучения в целевой школе, среднее количество пропусков занятий по болезни составило 15,4 по сравнению с 11,5 по стране ( Год 0 «Полевая контрольная группа» в таблице 1, сравните столбец 6 для целевой школы с столбцом 5 для национального ориентира). Это разница в 3,9 пропуска, которая статистически значима при p <0,0005 (столбец 7). Более того, он большой: показатель в целевой школе был на 34% выше, чем в национальном эталоне (столбец 8).
Ситуация резко изменилась в течение 1-го года («Группа полевого лечения №1» в Таблице 1), первого года с экспериментальным началом лечения в 10 часов утра. Среднее количество пропусков в целевой школе снизилось с 15,4 до 11,3, то есть на 4,1 пропусков (столбец 6, сравните год 0 и год 1). Разрыв между целевым показателем пропусков в школе и национальным эталонным показателем сократился на 3,3 пропуска до 0,6 (1 год, столбец 7). Это сокращение составляет 31% -ное сокращение разрыва между целевой школой и национальным эталоном (год 1, столбец 10), снижение, которое является статистически значимым при p <0.0005. d Коэна для изменения составляет 0,58, что делает размер эффекта в диапазоне от среднего до большого. Из-за этого сниженного уровня пропусков у целевой школы осталось всего 0,6 пропуска по сравнению с национальным эталоном, разница настолько мала, что не является статистически значимой ( p > 0,05, столбец 7).
Суть полевого эксперимента — 2-й год, когда начало второго полного года в 10 часов утра (курсы GCSE целевой школы длятся 2 года с экзаменами на протяжении всего). Пропуски в целевой школе снизились со среднего 11 баллов.3 до среднего 7,9 (столбец 6), снижение на 3,4 пропуска. Это привело к тому, что показатель пропусков занятий в целевой школе оказался значительно ниже национального эталона (столбец 7). Этот сдвиг от немного выше национального эталона в 1-м году до значительно ниже национального эталона во 2-м году имеет коэффициент Коэна 0,48, средний размер эффекта.
Наиболее важное сравнение проводится между 2-м годом, когда начало работы в 10 часов утра было вторым полным годом, и годом 0, в котором учащиеся были на старте 8:50 в течение как минимум 2 лет.Среднее количество пропусков снизилось полностью на 7,5 (столбец 6, год 2 по сравнению с годом 0). Разрыв между целевым показателем школьного образования и национальным ориентиром сократился на 55%, составив 4,8 пропуска занятий. Это изменение статистически значимо при p <0,0005. Коэффициент Коэна для изменения равен 1,07, что является большой величиной эффекта.
Таким образом, полевой эксперимент по-разному демонстрирует, что экспериментальное лечение связано со снижением количества абсансов, которое является большим и статистически значимым не только по сравнению с контрольной группой, но и по сравнению с национальным эталоном.Эта закономерность видна на Рисунке 1.
Далее идет естественный эксперимент, когда время начала в целевой школе вернулось к 8:50 в 3-м классе из-за изменения в политике, которая передала контроль над целевой школой местным органам управления образованием, которые установили единое время раннего начала для всех сопоставимых школ . Среднее количество отсутствующих на работе повысилось до 11,2, что значительно выше уровня предыдущего года (столбец 6). Это на 20% выше национального ориентира, что явно контрастирует с показателем предыдущего года на 10% ниже эталона (столбец 8).С поправкой на ежегодные изменения в национальном уровне пропусков занятий, разрыв между целевой школой и страной увеличился до 2,8 пропусков в год, что на 30% больше (столбцы 11 и 12). Это изменение статистически значимо при p <0,0005 и имеет коэффициент Коэна 0,47, средний размер эффекта.
В целом, для прогулов полевой эксперимент показывает, что переход на 10 часов утра снизил количество прогулов по болезни более чем на 50 процентов по сравнению с общенациональными показателями, что является большим и статистически значимым снижением.Естественный эксперимент показывает, что возвращение к началу 8:50 вызвало уже в первый год обучения статистически значимое увеличение количества прогулов среднего размера. Эти данные согласуются с дозозависимым ответом на начало 10:00.
В нулевом классе целевой школы («Полевая контрольная группа» в таблице 2) в базовой когорте учащихся, у которых время начала 8:50 в течение обоих лет обучения, процент успешно сдавших экзамены GCSE составил 34 по сравнению с 56.2 на национальном уровне (столбцы 5 и 6). Это огромная разница в 22 процентных пункта, статистически значимая при p <0,0005 (столбец 7). Эта разница составляет 40% от национального базового уровня (столбец 8), что указывает на то, что целевая школа имеет очень низкий уровень успеваемости. Что касается добавленной стоимости, фактический процент успешных учеников был на 5 процентных пунктов ниже, чем оценка FFT для школы, основанная на прошлой успеваемости когорты (столбец 9), что показывает отрицательную добавленную стоимость.В целом, в 0-м классе целевой школы картина успеваемости была мрачной.
Таблица 2 . Влияние экспериментального лечения (начало занятий в 10 часов утра) на успеваемость.
Ситуация резко изменилась в течение 1-го года, первого года экспериментального лечения в 10 часов утра. Фактический процент академически успешных студентов вырос на 19 процентных пунктов до 53 (столбец 6, сравните курс 0 и год 1). Разрыв между целевой школой и национальным эталоном в 1-м классе настолько мал, что он не является статистически значимым (1-й год, столбец 7).Между 0 и 1 годом разрыв между целевым показателем успеваемости в школе и национальным эталоном сократился с 22 до 5 (1 год, столбец 7), сокращение на 17 процентных пунктов, что является статистически значимым при p <0,0005. Добавленная стоимость школы также выросла: фактическая добавленная стоимость школы на 4 процентных пункта больше, чем прогноз FFT, что на 9 процентных пунктов больше, чем в нулевом классе. Это составляет 15% от национального базового уровня и является статистически значимым на уровне . р <0.0005.
Суть полевого эксперимента — это сравнение 2-го и 0-го классов. Здесь снова есть обширные доказательства положительного влияния начала занятий в 10 часов утра на успеваемость учащихся. Успех учащихся во 2-м классе составляет 52% по сравнению с 34% для 0-го года (столбец 6), прирост значительный при p = 0,001 и среднего размера, с H Коэна 0,37. Между 0 и 2 годом разрыв между целевым показателем успеваемости в школе и национальным эталоном сократился с 22 до 7 лет (2 год, столбец 7).Фактический успех учащихся во 2-м классе превышает прогноз БПФ на 7 процентных пунктов (столбец 10). Действительно, добавленная стоимость школы увеличилась на 12 процентных пунктов, статистически значимый прирост при p <0,0005 (столбец 13) и составляет 20% от национального эталона.
Таким образом, полевой эксперимент демонстрирует множеством способов, что экспериментальное лечение связано со статистически значимым и существенным увеличением производительности не только по сравнению с контрольной группой, но и по сравнению с национальным эталоном.
Затем, в естественном эксперименте в 3-м классе, время начала занятий в школе изменилось с 10 до 8:50. Показатель успешности учащихся немного снизился до 51 (3-й год, столбец 6) по сравнению с национальным эталоном 60, что дает целевая школа дефицит в 9 процентных пунктов, что является статистически значимым при p = 0,014 (столбец 7). Добавленная стоимость школы сократилась на 4 процентных пункта, что составляет 7% от национального базового уровня (столбец 14).
Таким образом, даже если эти студенты прошли первый год своего 2-летнего курса с 10 а.м. Начало, возвращение к 8:50 утра для начала второго года обучения связано со снижением успеваемости по сравнению с национальным базовым уровнем и со снижением добавленной стоимости школы.
Полная картина объединенных результатов полевого эксперимента и естественного эксперимента ясна на рисунке 2.
Рисунок 2 . Успех в учебе: добавленная стоимость целевой школой.
В первом классе успеваемость учащихся в целевой школе была на 5 процентных пунктов ниже, чем можно было бы ожидать с учетом предыдущей успеваемости учащихся (БПФ).Затем начался полевой эксперимент. Введение 10 часов утра в середине курса когорты 1-го класса подняло добавленную стоимость школы на 9 процентных пунктов выше ожидаемого процента успеха. Далее наблюдалось небольшое увеличение добавленной стоимости на 12 процентных пунктов во втором году обучения для когорты, у которой оба года обучения началось в 10 часов утра. На этом полевой эксперимент закончился. Затем в естественном эксперименте время начала было изменено на 8:50, поэтому учащиеся в когорте 3-го класса имели первый год своего курса с 10 а.м. старт и второй год их курса со стартом 8:50. Добавленная стоимость по-прежнему была положительной для этой когорты, но упала на 4 процентных пункта по сравнению с предыдущей когортой, у которой 2 года начинались в 10 часов утра.
Обсуждение
На основании этого исследования перенос времени начала занятий в школе на более позднее, чтобы оно лучше соответствовало подростковому сну и моделям хронотипа, является практичным и полезным. После перехода на 10:00 часов начала занятий в школе количество пропусков занятий по болезни среди учащихся в возрасте 13–16 лет снизилось, а успеваемость учащихся в возрасте 14–16 лет значительно улучшилась.Когда время начала занятий было возвращено к 8:50 утра, эти льготы были отменены. Эти результаты показывают, что общая политическая рекомендация начинать обучение в средней школе не ранее 08:30, хотя и полезна, не должна рассматриваться как оправдание, исключающее рассмотрение гораздо более позднего времени начала занятий. Поскольку 8:50 утра уже будет считаться подходящим с учетом рекомендации 8:30 утра, это исследование показывает, что дальнейшие улучшения могут быть сделаны, когда время начала намного позже, в данном случае 10:00 утра.м.
Данные о пропуске занятий из-за заболеваемости подтверждают прямую выгоду от более позднего начала занятий в школе для здоровья учащихся. Дифференциация в регистрации отсутствия и отсутствия по болезни в Англии предлагает более точную оценку болезни и большой набор национальных данных. После начала 10:00 утра заболеваемость снизилась на второй год более чем на 50%. С возвращением 8:50 утра эти льготы были отменены, и заболеваемость увеличилась на 30%. Учебная успеваемость учащихся в возрасте 14–16 лет также улучшилась с 10:00 a.м. Начало. Особенно полезно было иметь более позднее время начала на 2 года; показывающий прирост добавленной стоимости на 12 процентных пунктов, который является статистически значимым при p <0,0005 и составляет 20% от национального эталона. Нет оснований полагать, что эти результаты отражают изменения мотивации. Учащиеся готовились к выпускным национальным экзаменам, которые определяют их право на продолжение обучения и, в конечном итоге, поступление в колледж или университет или их конкурентоспособность на рынке труда.Это были не тесты, связанные с учебой, а настоящие, разовые экзамены, которые имеют большое влияние на будущее детей и, следовательно, будут в равной степени мотивированы. Хотя существует несколько возможных объяснений низкой успеваемости учащихся в регионах с таким же низким социально-экономическим статусом, возможное влияние ограничения сна, связанного с ранним началом обучения в школе, редко рассматривается.
Одно из возражений против изменения времени начала занятий в школе заключается в том, что это изменение непрактично и не может преодолеть другие препятствия, такие как расписание автобусов или расписание спортивных программ.В то время как английская правовая база делает переход на более позднее время начала формальным процессом, который может предпринять любая школа (и, следовательно, более практичным, чем в некоторых других странах), перенос всех расписаний этой школы позже не вызвал практических трудностей. Выбирая время начала в 10 часов утра, школа стремилась обеспечить льготы для как можно большей части детей, учитывая межиндивидуальный разброс фазовых задержек, которые испытывают дети, означает, что некоторые существенно задержанные дети все равно будут просыпаться слишком рано в своем циркадном цикле ( Iglowstein et al., 2003; Келли и др., 2015). Даже более позднее время начала может решить эту проблему, но 10 часов утра считались разумным компромиссом между максимизацией биологических преимуществ для большинства детей при сохранении практичности. Национальная рекомендация США о том, что средние и средние школы должны начинаться после 8:30 утра, является явно оправданным положительным шагом, хотя данные этого исследования предполагают гораздо более позднее начало в 10:00 — даже при замене начала школы позже 8:30 Я рекомендую — приносит дополнительные преимущества.Недавнее исследование студентов университетов в возрасте 18–19 лет показало, что более позднее время начала занятий (после 11 часов утра или 12 часов дня) было оптимальным, а для старшеклассников 17–18 лет — намного позже, чем 8:30 утра. Исследование также показало, что использование фиксированного времени для всех учащихся поставит в невыгодное положение один или несколько хронотипов, в частности вечерних хронотипов, если начало занятий было ранним (Kelley et al., 2015; Evans et al., 2017). Таким образом, даже с учетом преимуществ, которые дает использование времени бодрствования в 10 часов утра для всех учащихся, этот подход не учитывает более широкие вариации времени бодрствования для разных хронотипов.
Ограничения в этом исследовании включают небольшие размеры выборки по некоторым параметрам, акцент в основном на болезни и невозможность измерить продолжительность сна учащихся. Хотя другие исследования показали улучшение сна после менее значительных вмешательств, некоторые отслеживали улучшения сна в течение 4 лет и обнаружили, что улучшения сохраняются (Borlase et al., 2013; Wahlstrom et al., 2014). Местоположение английского языка и показатели академической успеваемости трудно контекстуализировать с предыдущими исследованиями с использованием U.S. данные об испытаниях и выпуске по всему штату. Мы считаем, что общенациональные данные о болезнях по каждой школе, ориентированные на учащихся среднего подросткового возраста и время начала в 10:00 утра, являются уникальными в этой области исследований. Необходимо более подробное и подробное изучение школьных занятий после 9:00 утра, в том числе тех, которые начинаются после 10:00. Существуют предварительные доказательства того, что такие изменения могут иметь преимущества, особенно для старшеклассников (Carrell et al., 2011). .
Улучшение успеваемости на уровне школы в этом исследовании, если оно будет более широко воспроизведено, должно быть изучено с экономической и образовательной точек зрения.Например, расходы на сокращение разрыва в уровне владения английским языком между богатыми и бедными учениками достигли более одного миллиарда фунтов в период с 2010 по 2015 год, но при этом оказали относительно небольшое влияние по сравнению с доходами, полученными после изменения времени начала занятий в 10 часов утра в этом исследовании. Переход на более мелкие школы в ключевых городах США, таких как Нью-Йорк, был тщательно изучен после дополнительных затрат в размере более миллиарда долларов на повышение успеваемости (Schneider et al., 2007; Stiefel et al., 2015).Другие изменения в образовательной политике, в том числе создание новых типов школ, таких как чартерные, академические и научные, технологические, инженерные и математические (STEM) школы, увеличение продолжительности школьных занятий, изменение учебной программы и тестов или «Ни одного отстающего ребенка» также затрат, но минимальное влияние и небольшая научная строгость при оценке их воздействия. Напротив, переход на более позднее время начала является очень рентабельным вмешательством для повышения образовательных стандартов при значительной научной поддержке (Jacob and Rockoff, 2011; Snow, 2015; Hafner et al., 2017).
Ключевой вывод этого исследования — сокращение пропусков занятий по болезни более чем на 50% по сравнению с общенациональными показателями (таблица 1, столбцы 12 и 13). Это огромное изменение является как практически важным, так и очень значимым статистически ( p <0,0005 и d Коэна для изменения составляет 1,07, большая величина эффекта). Более широкое влияние более поздних стартов на конкретные аспекты здоровья подростков, такие как продолжительность и качество сна, психическое здоровье и социальное развитие, не оценивалось, хотя другие исследования показали потенциальное воздействие (de Souza and Hidalgo, 2014; Meltzer et al., 2014; Мингес и Редекер, 2016). Дополнительное исследование более поздних стартов должно измерить как фактический режим сна, так и оптимальное время успеваемости для отдельных учащихся. Наиболее важной областью для дальнейших исследований может быть влияние более поздних запусков на развитие социального поведения и психическое здоровье. Например, ежедневное недосыпание на два или более часов в день, вызванное ранним началом школы (которое невозможно восстановить с помощью 10 или более дополнительных часов сна по выходным), может подвергнуть людей с генетической предрасположенностью к психическим заболеваниям большему риску учитывая, что была установлена прямая связь между сном продолжительностью <6 часов и экспрессией генов (Möller-Levet et al., 2013). Депривация сна также связана с тем, что подростки менее восприимчивы к человеческим эмоциям (van der Helm et al., 2010; Guadagni et al., 2014), в период большей чувствительности к социокультурным сигналам (Blakemore and Mills, 2014) и связанным с этим. развитие мозга в подростковом возрасте. Эти взаимосвязанные факторы значительного недосыпания, генетической предрасположенности, высокой распространенности начала психических заболеваний в подростковом возрасте для ряда расстройств (Schmitt et al., 2014) и в меньшей степени восприятия социокультурных сигналов могут влиять на уровни умственного развития. болезни и эмоциональные расстройства в подростковом возрасте (Wulff et al., 2010, 2012).
Использование основанного на исследованиях подхода к определению времени начала занятий в школе для учащихся 13–16 лет привело к введению времени начала занятий в 10 часов утра. Это более позднее время начала обучения имело существенное преимущество для показателей заболеваемости и успеваемости. Основанный на исследованиях подход к времени начала занятий в школе явно воспроизводится в разных контекстах, культурах и странах. Что еще более важно, стратегия начала занятий в школе после 9:00 — это стратегия с небольшими затратами и множеством потенциальных выгод, которые начинают накапливаться буквально в мгновение ока.Применение исследований сна таким образом демонстрирует мощное влияние на общество и отдельных людей изменений в политике, основанных на фактических данных.
Заявление об этикеИнновационный фонд и руководство школы одобрили изменение времени начала занятий в соответствии с английским законодательством об образовании. Родители и ученики были проконсультированы во время изменения в соответствии с требованиями закона.
Авторские взносы
PK, SL и JK: дизайн исследования; JK и ME: анализ данных; PK, SL, JK и ME: написание и критический обзор рукописи.
Финансирование
Эта работа финансировалась Science + Technology in Learning (Премия № 1/2017).
Заявление о конфликте интересов
SL имела ряд коммерческих интересов за последние 12 месяцев (2016-17). Ни одно из них не имеет прямого отношения к исследованию или теме, описанной в этом документе, но в интересах полного раскрытия информации они изложены ниже. SL получила консультационные услуги от Atlanta Falcons, Atlanta Hawks, BHP Billiton и Slingshot Insights; имеет текущие консалтинговые контракты с Akili Interactive; Решения для сна для потребителей; ООО «Делос Ливинг»; ООО «Науки об экологическом освещении»; Headwaters Inc.; Hintsa Performance AG; Легкий познавательный; Умственная тренировка; OpTerra Energy Services Inc .; Pegasus Capital Advisors LP; PlanLED; и Wyle Integrated Science and Engineering; получил неограниченное количество подарков оборудования от Biological Illuminations LLC, Bionetics Corporation и F. Lux Software LLC; гонорары от Oxford University Press; и работал оплачиваемым экспертом по судебным разбирательствам, связанным со светом, сном и здоровьем. Он имеет патент Гарвардского университета и Бригама и женской больницы на «Системы и методы определения и / или контроля качества сна.Он является руководителем программы CRC по предупреждению, безопасности и продуктивности, Австралия.
Другие авторы заявляют, что исследование проводилось при отсутствии каких-либо коммерческих или финансовых отношений, которые могли бы быть истолкованы как потенциальный конфликт интересов.
Благодарности
Авторы хотели бы поблагодарить профессоров Дэвида Рейнольдса, Рассела Фостера и Дэниела Мейджса за их вклад в размышления об изменении времени начала на основе исследований сна, а также Дэвида Рейнольдса в качестве председателя Innovation Trust.
Сноски
Список литературы
Американская академия педиатрии (2014). Рабочая группа по подростковому сну: время начала занятий для подростков. Педиатрия 134, 642–649. DOI: 10.1542 / peds.2014-1697
CrossRef Полный текст
Basch, C.E., Basch, C.H., Ruggles, K.V, and Rajan, S. (2014). Распространенность продолжительности сна в течение средней школьной ночи среди 4 репрезентативных на национальном уровне последовательных выборок американских школьников, 2007–2013 гг. Пред. Хронический Диск . 11: E216. DOI: 10.5888 / pcd11.140383
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Блейкмор, С. Дж., И Миллс, К. Л. (2014). Является ли отрочество чувствительным периодом для социокультурной обработки? Annu. Rev. Psychol. 65, 187–207. DOI: 10.1146 / annurev-Psy-010213-115202
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Борлас, Б. Дж., Гандер, П. Х., Гибсон, Р. Х. (2013). Влияние времени начала занятий в школе и использования технологий на сон подростков: 1999–2008 гг. Sleep Biol. Ритмы 11, 46–54. DOI: 10.1111 / sbr.12003
CrossRef Полный текст | Google Scholar
Каррелл С. Э., Магакян Т. и Уэст Дж. Э. (2011). А от Зззза? Причинное влияние времени начала обучения в школе на успеваемость подростков. Am. Экон. J . 3, 62–81. DOI: 10.1257 / pol.3.3.62
CrossRef Полный текст
Церкви, Р., Доммет, Э. и Девоншир, И. (2017). Нейробиология для учителей: применение данных исследований мозга .Лондон: Издательство Crown House.
Google Scholar
Даннер Ф. и Филлипс Б. (2008). Подростковый сон, время начала занятий в школе и подростковые автомобильные аварии. J. Clin. Sleep Med. 4, 533–535.
PubMed Аннотация | Google Scholar
де Соуза, К. М., и Идальго, М. П. (2014). Середина сна в школьные дни связана с депрессией у подростков. Chronobiol. Int. 31, 199–205. DOI: 10.3109 / 07420528.2013.838575
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Департамент образования (2016). Отсутствие учащихся в школах в Англии: осень 2015 г. и весна 2016 г. Лондон, Великобритания: Департамент образования, SFR 51/2016.
Эдвардс, Ф. (2012). Рано вставать? Влияние времени начала дня на успеваемость. Экон. Educ. Ред. . 31, 970–983. DOI: 10.1016 / j.econedurev.2012.07.006
CrossRef Полный текст | Google Scholar
Эванс, М. Д. Р., Келли, П., и Келли, Дж. (2017). Определение наилучшего времени для когнитивного функционирования с использованием новых методов: сопоставление университетского времени с хронотипами бакалавриата. Фронт. Гм. Neurosci. 11: 188. DOI: 10.3389 / fnhum.2017.00188
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Фостер, Р. Г., Пирсон, С. Н., Вульф, К., Виннебек, Э., Веттер, К., и Роеннеберг, Т. (2013). Нарушение сна и циркадных ритмов при смене часовых поясов и психических заболеваниях. Prog. Мол. Биол. Пер. Sci . 119, 325–346. DOI: 10.1016 / B978-0-12-396971-2.00011-7
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Градисар, М., Гарднер, Г., Дохнт, Х. (2011). Последние мировые образцы сна и проблемы в подростковом возрасте: обзор и метаанализ возраста, региона и сна. Sleep Med. 12, 110–118. DOI: 10.1016 / j.sleep.2010.11.008
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Хансен, М., Янссен, И., Шифф, А., Зи, П. К. и Дубокович, М. Л. (2005). Влияние школьного распорядка дня на сон подростков. Педиатрия 115, 1555–1561. DOI: 10.1542 / пед.2004-1649
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Хэтти, Дж. (2008). Видимое обучение: синтез более 800 метаанализов, относящихся к достижению . Лондон: Рутледж.
Google Scholar
Хиршковиц М., Уитон К., Альберт С. М., Алесси К., Бруни О., Дон Карлос Л. и др. (2015). Обновленные рекомендации Национального фонда сна по продолжительности сна: Заключительный отчет. Здоровье сна 1, 233–243. DOI: 10.1016 / j.слей.2015.10.004
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Игловштейн, И., Дженни, О. Г., Молинари, Л., и Ларго, Р. Х. (2003). Продолжительность сна от младенчества до подросткового возраста: контрольные значения и тенденции поколений. Педиатрия 111, 302–307.
PubMed Аннотация | Google Scholar
Джейкоб Б. А. и Рокофф Дж. Э. (2011). Организация школ для повышения успеваемости учащихся: время начала занятий, конфигурации оценок и назначения учителей. Вашингтон, округ Колумбия: Документ для обсуждения проекта Брукингс / Гамильтон, 2011-08 гг.
Google Scholar
Келли П., Локли С. В., Фостер Р. Г. и Келли Дж. (2015). Синхронизация образования с подростковой биологией: «дай подросткам поспать, пойди в школу позже». ЖЖ. Медиа Технол . 40, 210–226. DOI: 10.1080 / 17439884.2014.942666
CrossRef Полный текст | Google Scholar
Киркби, М., Магги, С., и Д’Анджиулли, А. (2011). Время начала занятий в школе и цикл бодрствования и сна подростков: обзор и критическая оценка имеющихся данных. Educ. Res. 40, 56–61. DOI: 10.3102 / 0013189X11402323
CrossRef Полный текст | Google Scholar
Кёдел К., Михали К. и Рокофф Дж. Э. (2015). Моделирование с добавленной стоимостью: обзор. Экон. Educ. Ред. 47, 180–195. DOI: 10.1016 / j.econedurev.2015.01.006
CrossRef Полный текст | Google Scholar
Луфи Д., Цищинский О. и Хадар С. (2011). Задержка начала занятий в школе на один час: некоторые эффекты на уровне внимания у подростков. J. Clin. Sleep Med. 7, 137–143.
Google Scholar
Мельцер, Л. Дж., Шахид, К., Амблер, Д. (2014). Начинайте позже, спите позже: время начала занятий и подростковый сон в домашней школе по сравнению с учащимися государственных / частных школ. Behav. Сон Мед . 14: 140. DOI: 10.1080 / 15402002.2014.963584
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Миллман, Р. П. (2005). Чрезмерная сонливость у подростков и молодых людей: причины, последствия и стратегии лечения. Педиатрия 115, 1774–1786. DOI: 10.1542 / peds.2005-0772
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Мингес, К. Э., Редекер, Н. С. (2016). Позднее время начала занятий в школе и подростковый сон: систематический обзор экспериментальных данных. Sleep Med. Rev. 28, 82–91. DOI: 10.1016 / j.smrv.2015.06.002
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Мёллер-Левет, К.С., Арчер, С.Н., Букка, Г., Лэнг, Э.E., Slak, A., Kabiljo, R., et al. (2013). Влияние недостаточного сна на циркадную ритмичность и амплитуду экспрессии транскриптома крови человека. Proc. Natl. Soc. Sci. США 110, E1132 – E1141. DOI: 10.1073 / pnas.1217154110
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Оуэнс, Д., Дробнич, Д., Бейлор, А., и Левин, Д. (2014). Изменение времени начала занятий в школе: углубленное изучение школьных округов США. Mind Brain Educ. 8, 182–213. DOI: 10,1111 / mbe.12059
CrossRef Полный текст | Google Scholar
Роеннеберг, Т., Куэнле, Т., Джуда, М., Кантерманн, Т., Аллебрандт, К., Гордин, М., и др. (2007). Эпидемиология циркадных часов человека. Sleep Med. Rev. 11, 429–438. DOI: 10.1016 / j.smrv.2007.07.005
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Roenneberg, T., Kuehnle, T., Pramstaller, P. P., Ricken, J., Havel, M., Guth, A., et al. (2004).Маркер окончания подросткового возраста. Curr. Биол. 14, R1038 – R1039. DOI: 10.1016 / j.cub.2004.11.039
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Шмитт, Дж. Э., Нил, М. К., Фассасси, Б., Перес, Дж., Ленрут, Р. К., Уэллс, Э. М. и др. (2014). Динамическая роль генетики в формировании коркового паттерна в детстве и подростковом возрасте. Proc. Natl. Акад. Sci. США 111, 6774–6779. DOI: 10.1073 / pnas.1311630111
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Шнайдер, Б., Wyse, A.E., и Keesler, V. (2007). «Разве маленький действительно лучше? Проверка некоторых предположений о размере средней школы », в Brooking Papers on Education Evaluation Policy , ред. Т. Лавлесс и Ф. М. Хесс (Вашингтон, округ Колумбия: Институт Брукингса), 15–47.
Google Scholar
Шеклтон, Дж. А., Раджаратнам, С. М., Гули, Дж. Дж., Ван Рин, Э., Чейслер, К. А., и Локли, С. В. (2013). Улучшение нейроповеденческих характеристик в зоне поддержания бодрствования. J. Clin. Сон Мед .9: 353. DOI: 10.5664 / jcsm.2588
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Сноу, К. Э. (2015). 2014 г. Отличная лекция фонда Уоллеса: строгость и реализм: педагогическая наука в реальном мире. Educ. Res. 44, 460–466. DOI: 10.3102 / 0013189X15619166
CrossRef Полный текст | Google Scholar
Штифель Л., Шварц А. Э. и Висвалл М. (2015). Поднимает ли реформа малой средней школы городские районы? Свидетельства из Нью-Йорка. Educ. Res . 44, 161–172. DOI: 10.3102 / 0013189X15579187
CrossRef Полный текст | Google Scholar
Сассман, А. (2009). Британская радиовещательная корпорация (BBC), Horizon Series 2008-2009, Эпизод 11, Тайная жизнь ваших Bodyclock.
Управление национальной статистики Великобритании (2016). Выпуски данных GCSE за 2010–2015 гг. . Доступно в Интернете по адресу: https://www.ons.gov.uk/ (по состоянию на ноябрь 2017 г.).
Вишер, А. Дж., И Коу, Р.(2003). Системы обратной связи по успеваемости в школе: концептуализация, анализ и рефлексия. Sch. Эффект. Sch. Improv. 14, 321–349. DOI: 10.1076 / sesi.14.3.321.15842
CrossRef Полный текст | Google Scholar
Уолстрем, К., Дретцке, Б., Гордон, М., Петерсон, К., Эдвардс, К., и Гдула, Дж. (2014). Изучение влияния более позднего начала обучения в школе на здоровье и академическую успеваемость учащихся старших классов: исследование с нескольких площадок . Carei; Сент-Пол, Миннесота: Университет Миннесоты.
Google Scholar
Уитон А.Г., Ферро Г.А. и Крофт Дж. Б. (2015). Время начала занятий для учащихся средних и старших классов — США, 2011–2012 учебный год. MMWR Morb. Смертный. Wkly. Rep . 64, 809–813. DOI: 10.15585 / mmwr.mm6430a1
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Вульф, К., Дейк, Д. Дж., Миддлтон, Б., Фостер, Р. Г., и Джойс, Э. М. (2012). Нарушение сна и циркадного ритма при шизофрении. Brit. J. Psychiatry 200, 308–316. DOI: 10.1192 / bjp.bp.111.096321
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Вульф К., Гатти С., Веттштейн Дж. Г. и Фостер Р. Г. (2010). Нарушение сна и циркадных ритмов при психических и нейродегенеративных заболеваниях. Nat. Ред. Neurosci . 11, 589–599. DOI: 10.1038 / nrn2868
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Объяснение 4 различных типов — Клиника Кливленда
Если вы думали, что пост предназначен только для религиозных целей, подумайте еще раз.Новое явление в мире похудания, называемое прерывистым голоданием (IF), становится популярной тенденцией для здоровья и фитнеса.
Клиника Кливленда — некоммерческий академический медицинский центр. Реклама на нашем сайте помогает поддерживать нашу миссию. Мы не поддерживаем продукты или услуги, не принадлежащие Cleveland Clinic. Политика
Во время IF вы чередуете периоды приема пищи и голодание. Этот тип питания часто описывается как «шаблоны» или «циклы» голодание.
Есть несколько эффективных подходов к IF, но все они вплоть до личных предпочтений.
«Если вы хотите попробовать IF, будьте готовы выяснить, что лучше всего подходит для вас», — говорит зарегистрированный диетолог Анна Тейлор, MS, RD, LD, CDE. «Сначала может потребоваться метод проб и ошибок».
Некоторым людям легко голодать в течение 16 часов и ограничивать прием пищи только восемью часами дня, например, с 9 утра до 5 вечера, в то время как другим трудно и им нужно сократить период голодания, объясняет Тейлор.
Но полезно ли вам прерывистое голодание?
Пока некоторые исследования показал преимущества IF, такие как потеря веса, более низкая кровяное давление и улучшенное метаболическое здоровье, требуются дополнительные исследования все еще необходимо, особенно в отношении долгосрочных результатов ИФ. Также есть аспект устойчивости. Строгое ограничение калорий или длительный отказ от еды периоды за раз не для всех. Некоторые исследования даже показывает, что те, кто соблюдают периодическое голодание, обычно его не соблюдают по сравнению с теми, кто пытается похудеть на более традиционных диетах.
Тем не менее, IF было показано, что это эффективная форма потери веса. — но есть и другие варианты, такие как сбалансированное питание в сочетании с упражнение. Одно исследование предполагает, что IF не более эффективен для поддержки потери веса или улучшения сахара в крови, чем другие хорошо сбалансированные подходы.
«Потеря веса никогда не бывает универсальной», — говорит Тейлор. «IF может быть устойчивым для некоторых людей, в то время как другие считают, что просто не для них «.
Если вы хотите попробовать IF, вам сначала нужно выяснить, как вы собираетесь включить этот стиль питания в свою жизнь, особенно когда речь идет о таких вещах, как общественные мероприятия и поддержание активности, советует она.
Готовы изучить ваши варианты? Здесь Тейлор объясняет некоторые из самых популярных методов IF.
1. Метод дважды в неделю — 5: 2
Этот подход к IF фокусируется на ограничении ваши калории на уровне 500 два дня в неделю. В остальные пять дней неделю вы придерживаетесь здорового и нормального питания.
В разгрузочные дни этот подход обычно включает в себя прием пищи на 200 и 300 калорий. Важно сосредоточиться на продуктах с высоким содержанием клетчатки и белка, чтобы насытиться, но при этом сохранять низкое количество калорий во время голодания.
Вы можете выбрать любой из двух разгрузочных дней (например, вторник и четверг), если между ними есть не постный день. Обязательно ешьте столько же, сколько обычно в не постные дни.
2. Альтернативное дневное голодание
Этот вариант предполагает «модифицированное» голодание через день. Например, ограничьте количество калорий в дни голодания до 500 — или около 25% от вашего обычного потребления. В не разгрузочные дни возобновите обычную здоровую диету. (Существуют также строгие вариации этого подхода, которые включают потребление 0 калорий через день вместо 500.)
Интересное примечание: одно исследование показало, что у людей, которые следовали этой схеме ПФ в течение шести месяцев, значительно повысился уровень ЛПНП (или плохого) холестерина еще после шести месяцев отказа от диеты.
3. Еда с ограничением по времени (пример: метод 16/8 или 14/10)
В этом варианте вы установили окна голодания и приема пищи. Например, вы голодаете 16 часов в день и можете есть только восемь часов в день.
Поскольку большинство людей постятся уже во время сна, этот метод популярен.Это удобно, поскольку вы продлеваете ночное голодание, пропуская завтрак и не ешьте до обеда. Некоторые из наиболее распространенных способов?
- Метод 16/8: Еда только с 11:00 до 19:00. или полдень и 20:00
- 14/10 метод: Еда только с 10 до 20 часов.
Этот метод IF можно повторять сколько угодно часто или даже один или два раза в неделю — независимо от ваших личных предпочтений.
Поиск правильных периодов приема пищи и голодания для этого метода может занять несколько дней, особенно если вы очень активны или просыпаетесь голодным к завтраку.
«Эта форма голодания — более безопасный вариант для многих людей, которые хотят попробовать IF в первый раз», — говорит Тейлор.
4. 24-часовой пост (или метод «есть: стоп: есть»)
Этот метод предполагает полное голодание в течение полных 24 часов. Часто это делается один или два раза в неделю. Большинство людей постятся с завтрака до завтрака или с обеда до обеда. У этой версии IF могут быть очень сильные побочные эффекты, такие как утомляемость, головные боли, раздражительность, голод и упадок сил.
Если вы будете следовать этому методу, вы должны вернуться к нормальному здоровому питанию в не разгрузочные дни.
Прерывистое голодание — не волшебная пилюля
Соблюдаете ли вы IF, кето, низкоуглеводную, высокобелковую, вегетарианскую или средиземноморскую диету — вы называете это — все зависит от качества ваших калорий и того, сколько вы потребляете.
Итог с ЕСЛИ? Несмотря на то, что жюри еще не принято, а долгосрочные эффекты все еще изучаются, очень важно придерживаться здоровой, хорошо сбалансированной диеты, следуя IF.
«Нельзя есть нездоровую пищу и лишние калории в непосточные дни и рассчитывать на похудание», — говорит Тейлор.
Побочные эффекты и риски
Прерывистое голодание небезопасно для некоторых людей, включая беременных женщин, детей, людей с риском гипогликемии или людей с определенными хроническими заболеваниями.
«Если вы подвержены риску расстройства пищевого поведения, вам не следует пытаться соблюдать какую-либо диетическую диету», — советует Тейлор. «IF также, как известно, увеличивает вероятность переедания у некоторых людей из-за ограничения.”
Если вы хотите попробовать IF, вы также должны знать о некоторых не очень приятных побочных эффектах. IF может быть связан с раздражительностью, низкой энергией, постоянным голодом, температурной чувствительностью и плохой работой и активностью.


 .скать ребенка а а о о
.скать ребенка а а о о Нашлись люди неробкого десятка, которые не теряли присутствие духа.
Нашлись люди неробкого десятка, которые не теряли присутствие духа.
 Заимствованными.
Заимствованными. Настоящее – истинное. Г. Правдивый – лживый.
Настоящее – истинное. Г. Правдивый – лживый. 
 Статья УК РФ пока не названа.
Статья УК РФ пока не названа. ФОТО
ФОТО В ней также кратко описывается использование других агрегатных функций, например COUNT и AVG, для подсчета или вычисления средних значений в результирующем наборе записей. Кроме того, в этой статье рассматривается использование строки итогов — возможности Access, позволяющий суммировать данные без изменения структуры запросов.
В ней также кратко описывается использование других агрегатных функций, например COUNT и AVG, для подсчета или вычисления средних значений в результирующем наборе записей. Кроме того, в этой статье рассматривается использование строки итогов — возможности Access, позволяющий суммировать данные без изменения структуры запросов. Агрегатные функции выполняют вычисления со столбцами данных и возвращают единственное значение. В Access существует множество агрегатных функций, включая Sum, Count, Avg (для вычисления среднего значения), Min и Max. Суммирование данных производится путем добавления в запрос функции Sum, подсчет данных — путем использования функции Count и т. д.
Агрегатные функции выполняют вычисления со столбцами данных и возвращают единственное значение. В Access существует множество агрегатных функций, включая Sum, Count, Avg (для вычисления среднего значения), Min и Max. Суммирование данных производится путем добавления в запрос функции Sum, подсчет данных — путем использования функции Count и т. д. ..
..
 Помните, что многие агрегатные функции работают только с данными в полях, имеющих определенный тип данных. Например, функция SUM работает только с типами данных «Число», «Действительное» и «Денежный». Дополнительные сведения о типах данных, требуемых для каждой функции, см. ниже в разделе Справочные сведения об агрегатных функциях.
Помните, что многие агрегатные функции работают только с данными в полях, имеющих определенный тип данных. Например, функция SUM работает только с типами данных «Число», «Действительное» и «Денежный». Дополнительные сведения о типах данных, требуемых для каждой функции, см. ниже в разделе Справочные сведения об агрегатных функциях.
 25» (масштаб 1:4)
25» (масштаб 1:4) 11.2005
11.2005 11.2005
11.2005 11.2005
11.2005 11.2005
11.2005 25» (масштаб 1:4)
25» (масштаб 1:4) В данном примере поле «Наименование товара» используется для упрощения восприятия данных.
В данном примере поле «Наименование товара» используется для упрощения восприятия данных.



 В этом разделе объясняется, как создать простой запрос на выборку и добавить строку итогов. Не обязательно использовать примеры таблиц, представленные в предыдущем разделе.
В этом разделе объясняется, как создать простой запрос на выборку и добавить строку итогов. Не обязательно использовать примеры таблиц, представленные в предыдущем разделе. После этого можно изменить запрос, добавив или удалив поля таблицы. Чтобы удалить поле, выберите столбец в бланке запроса и нажмите клавишу DELETE.
После этого можно изменить запрос, добавив или удалив поля таблицы. Чтобы удалить поле, выберите столбец в бланке запроса и нажмите клавишу DELETE. 11.2005
11.2005 11.2005
11.2005 11.2005
11.2005 11.2005
11.2005 11.2005
11.2005 25» (масштаб 1:4)
25» (масштаб 1:4)


 Если вы хотите отобразить эти описательные данные, создайте второй запрос на выборку, объединяющий поля из итогового запроса с полями, содержащими дополнительные данные.
Если вы хотите отобразить эти описательные данные, создайте второй запрос на выборку, объединяющий поля из итогового запроса с полями, содержащими дополнительные данные. 25» (масштаб 1:4)
25» (масштаб 1:4) 25» (масштаб 1:4)
25» (масштаб 1:4)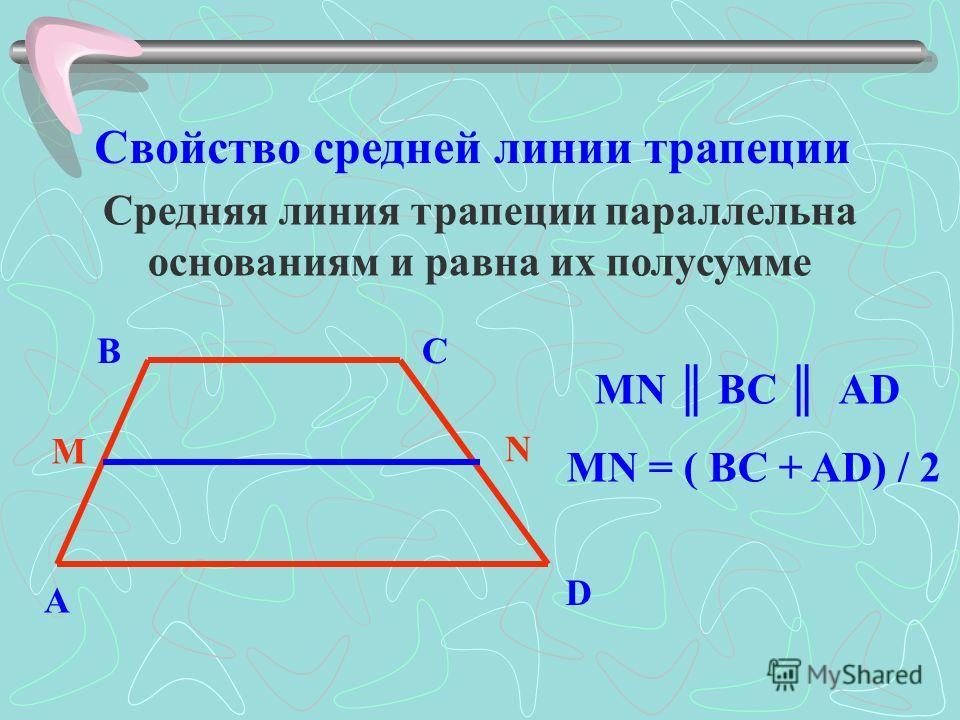 Точка пересечения диагоналей трапеции и середины оснований лежат на одной прямой.
Точка пересечения диагоналей трапеции и середины оснований лежат на одной прямой. Формулы длины основ через боковые стороны и углы при нижнем основании:
Формулы длины основ через боковые стороны и углы при нижнем основании: Формула высоты через сторону и прилегающий угол при основании:
Формула высоты через сторону и прилегающий угол при основании:
 Формулы диагоналей по теореме косинусов:
Формулы диагоналей по теореме косинусов: Формула площади через основания и высоту:
Формула площади через основания и высоту:

 Формула радиуса вписанной окружности через высоту:
Формула радиуса вписанной окружности через высоту:



 Сумма квадратов диагоналей трапеции равна сумме квадратов боковых сторон плюс удвоенное произведение ее оснований. Данное свойство диагоналей трапеции может быть доказано как отдельная теорема
Сумма квадратов диагоналей трапеции равна сумме квадратов боковых сторон плюс удвоенное произведение ее оснований. Данное свойство диагоналей трапеции может быть доказано как отдельная теорема В данном уроке приведено решение задач по геометрии о трапециях. Если Вы не нашли решение задачи по геометрии, интересующего Вас типа — задайте вопрос на форуме.
В данном уроке приведено решение задач по геометрии о трапециях. Если Вы не нашли решение задачи по геометрии, интересующего Вас типа — задайте вопрос на форуме.

 Получим:
Получим:

 Найдите площадь
Найдите площадь Найдите высоту трапеции.(24)
Найдите высоту трапеции.(24)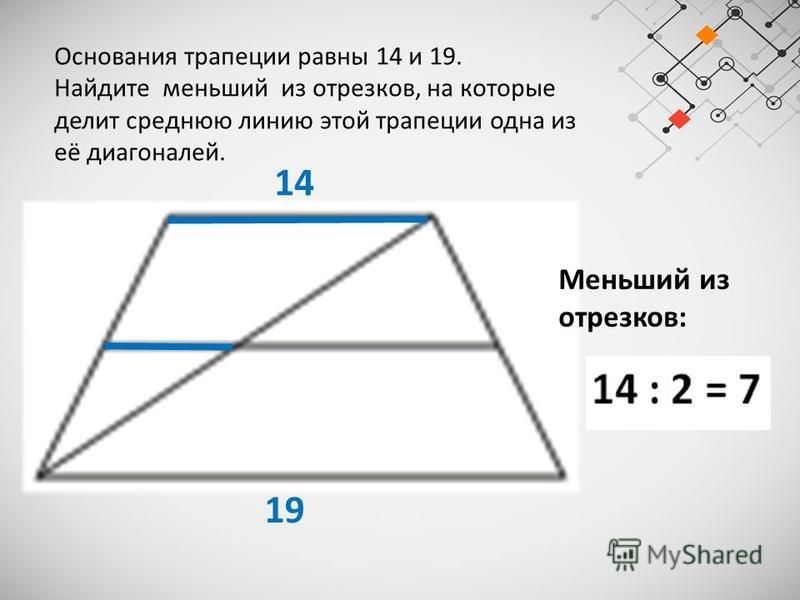 (24)
(24)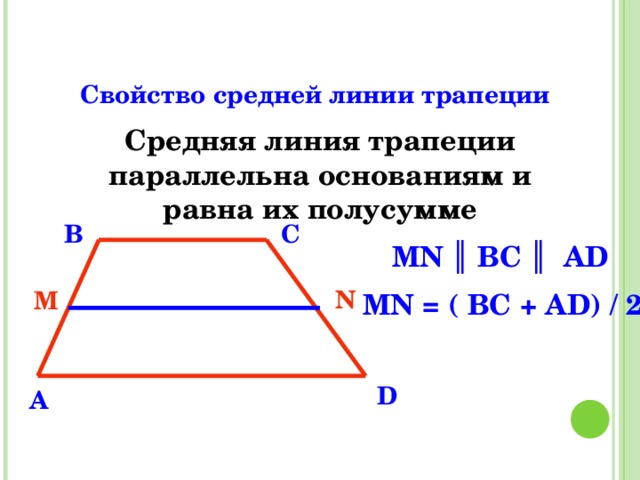 Найдите основание АВ.
Найдите основание АВ.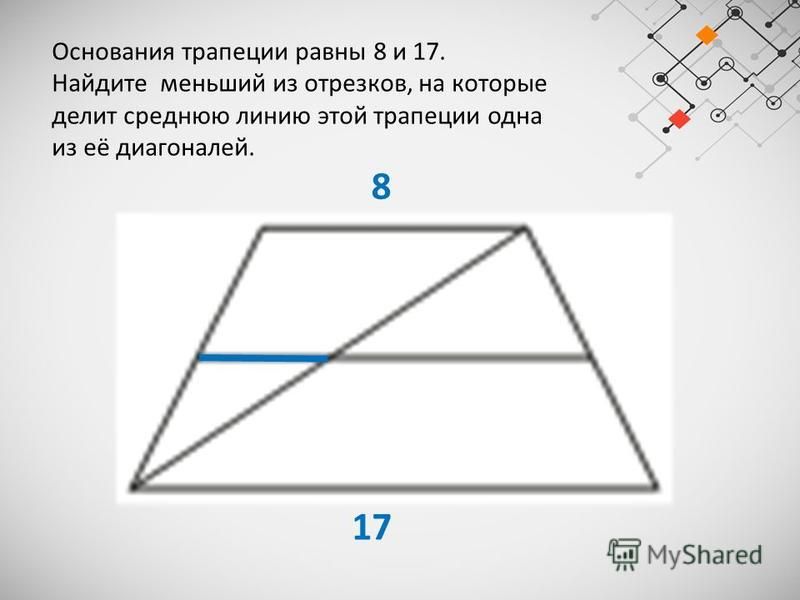 Найдите стороны параллелограмма , если его периметр равен 60см. (12и 18)
Найдите стороны параллелограмма , если его периметр равен 60см. (12и 18) Найдите биссектрису угла при основании. (6)
Найдите биссектрису угла при основании. (6) (16и9)
(16и9)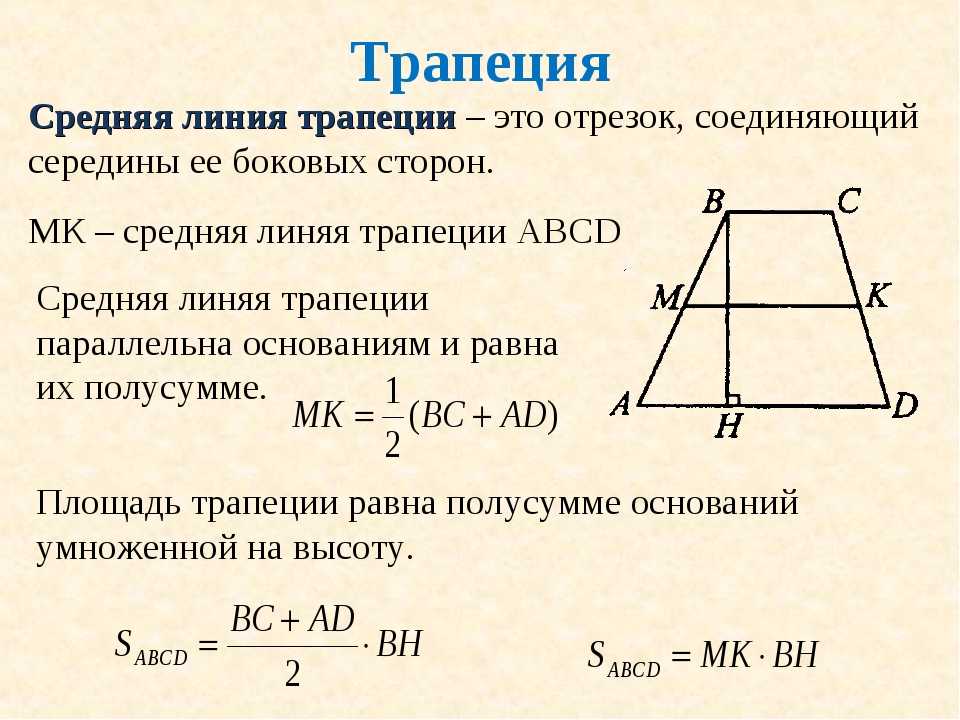 (28)
(28)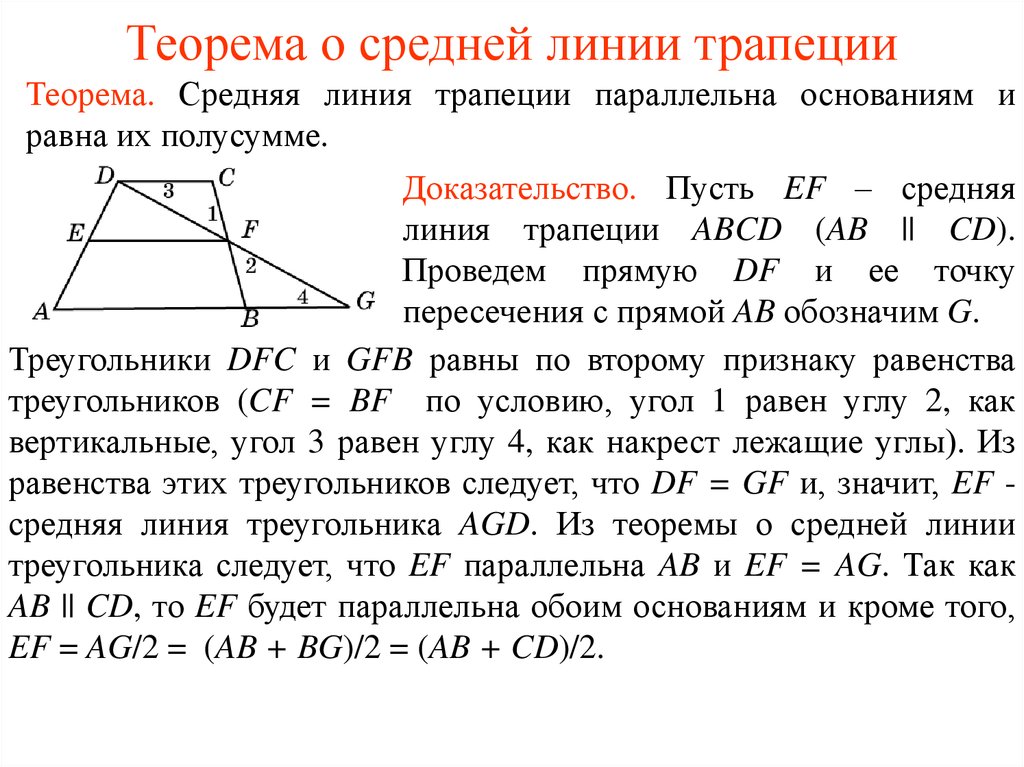 Найдите площадь трапеции. (20)
Найдите площадь трапеции. (20) Точки А,В,С лежат на окружности. Найдите хорду АС , если угол АВС=300, а диаметр окружности равен 10см. (5)
Точки А,В,С лежат на окружности. Найдите хорду АС , если угол АВС=300, а диаметр окружности равен 10см. (5) (4. 5/4√41)
(4. 5/4√41)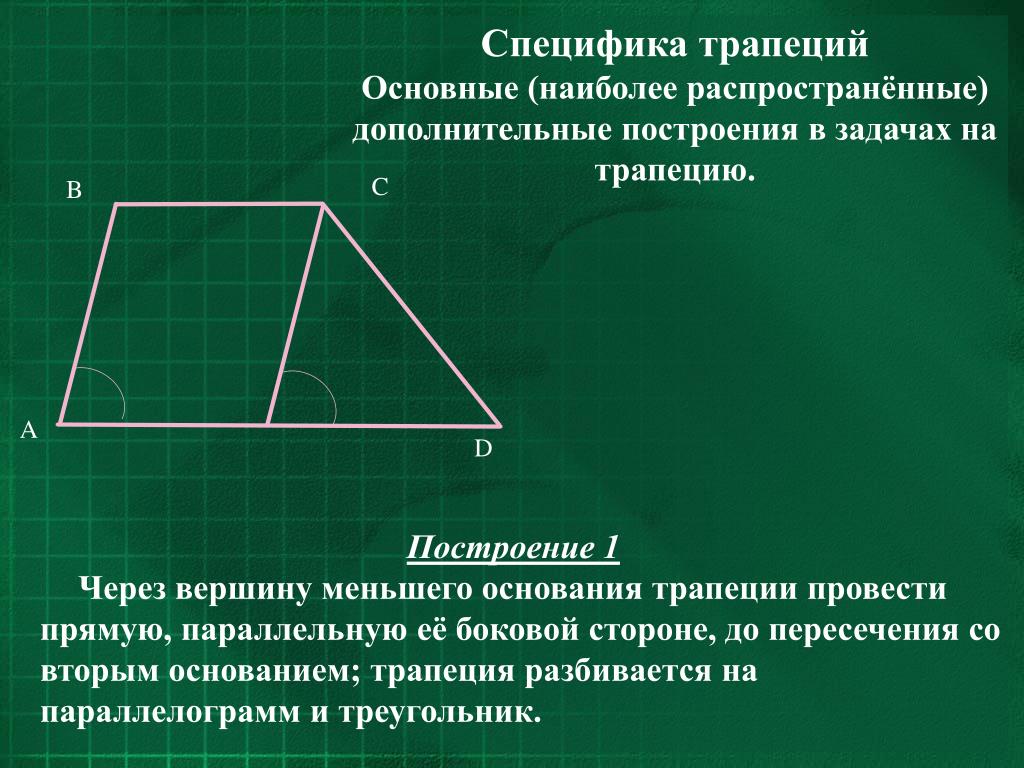 Четырехугольник АВСД со сторонами АВ=4см, ВС=2см, СД=6см , описан около окружности радиуса 5см. Найдите площадь четырехугольника. (50)
Четырехугольник АВСД со сторонами АВ=4см, ВС=2см, СД=6см , описан около окружности радиуса 5см. Найдите площадь четырехугольника. (50)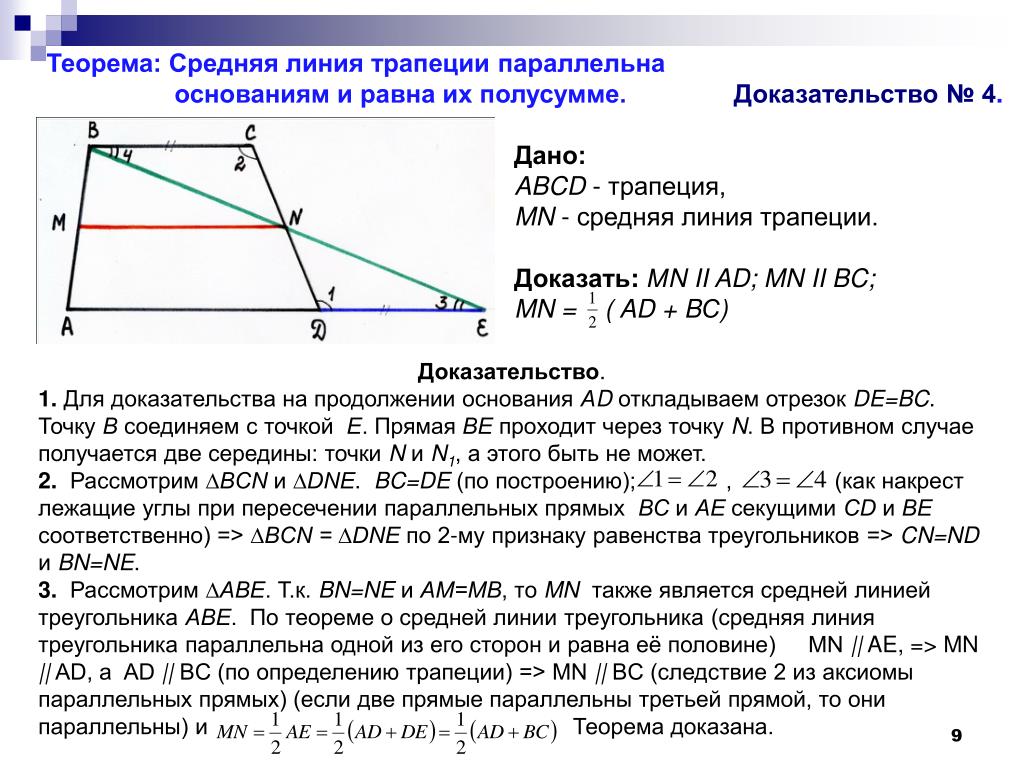 .. пучок света в шумах …» — пьеса Хуго Балля и ее постановки | Лектор: Юлиана Каминская | Организатор: Лекторий Cultura
Смотрите это видео на Лекториуме: https://www.lektorium.tv/lecture/29584
Подписывайтесь на канал: https://www.lektorium.tv/ZJA
Следите за новостями:
https://vk.com/openlektorium
https://www.facebook.com/openlektorium
.. пучок света в шумах …» — пьеса Хуго Балля и ее постановки | Лектор: Юлиана Каминская | Организатор: Лекторий Cultura
Смотрите это видео на Лекториуме: https://www.lektorium.tv/lecture/29584
Подписывайтесь на канал: https://www.lektorium.tv/ZJA
Следите за новостями:
https://vk.com/openlektorium
https://www.facebook.com/openlektorium Проект IoT принят в качестве приоритетного на государственном уровне в ЕС (www.internet-of-things.eu) и Китае, является ключевым для…
Проект IoT принят в качестве приоритетного на государственном уровне в ЕС (www.internet-of-things.eu) и Китае, является ключевым для…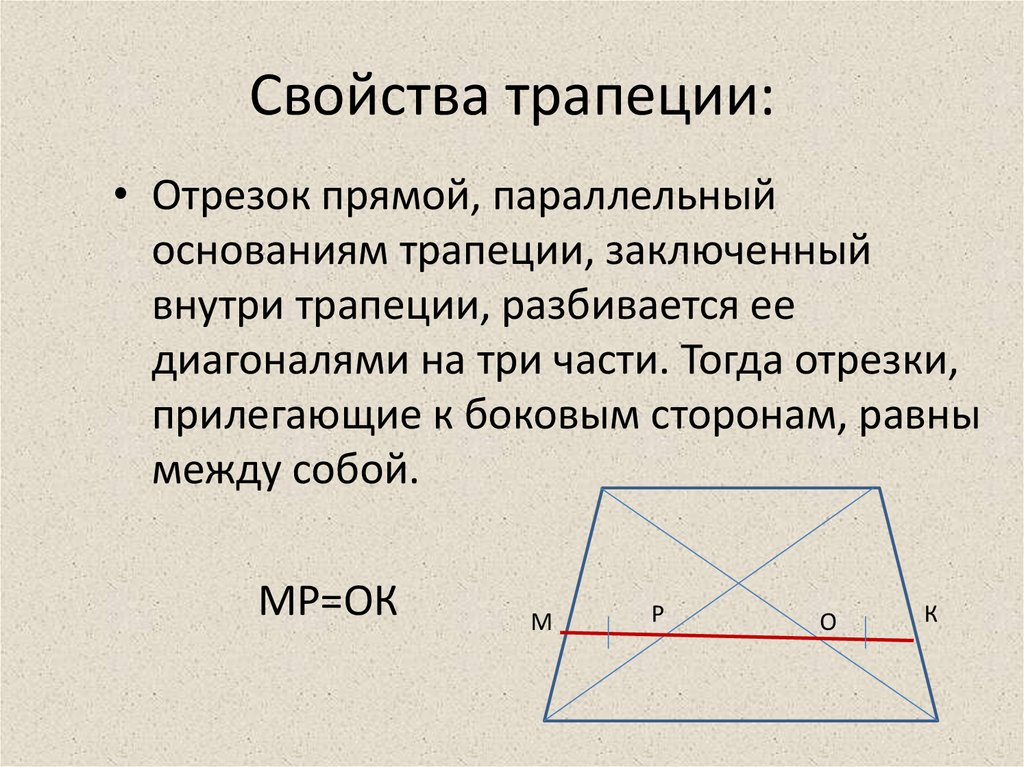 lektorium.tv/lecture/15202
Подписывайтесь на канал: https://www.lektorium.tv/ZJA
Следите…
lektorium.tv/lecture/15202
Подписывайтесь на канал: https://www.lektorium.tv/ZJA
Следите… Л.Чебышева
Смотрите это видео на Лекториуме: https://www.lektorium.tv/lecture/27887
Подписывайтесь на канал: https://www.lektorium.tv/ZJA
Следите за новостями:…
Л.Чебышева
Смотрите это видео на Лекториуме: https://www.lektorium.tv/lecture/27887
Подписывайтесь на канал: https://www.lektorium.tv/ZJA
Следите за новостями:… Лектор: Молчанов Евгений Геннадьевич, преподаватель кафедры высшей математики и кафедры математических основ управления МФТИ, лауреат конкурса Фонда «Династия» в номинации «Молодой учитель», а также многократный призер…
Лектор: Молчанов Евгений Геннадьевич, преподаватель кафедры высшей математики и кафедры математических основ управления МФТИ, лауреат конкурса Фонда «Династия» в номинации «Молодой учитель», а также многократный призер…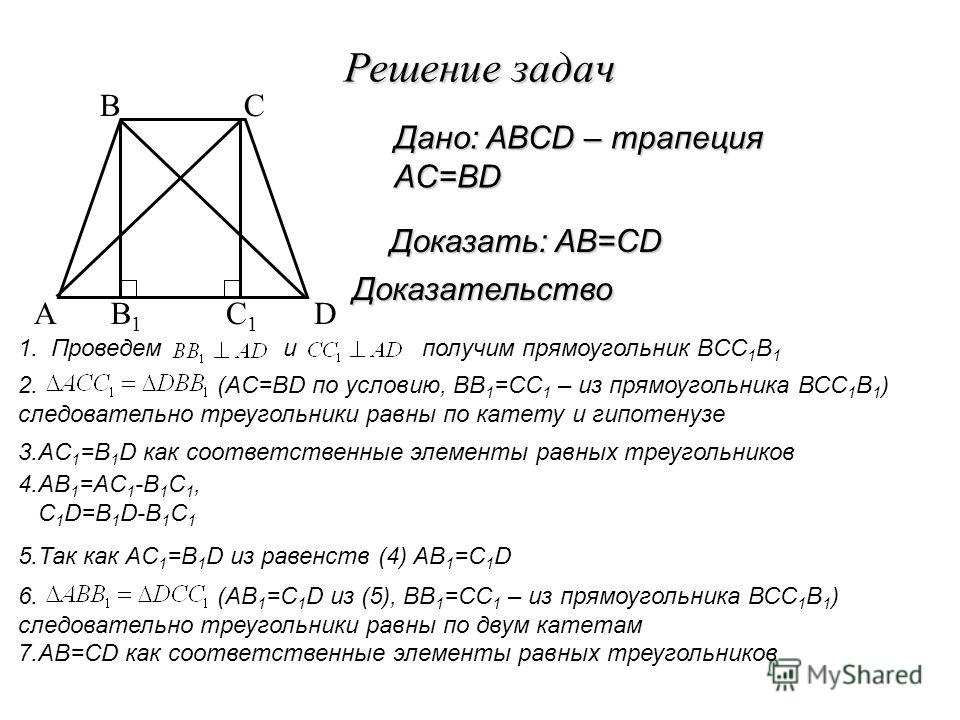 Лектор: Молчанов Евгений Геннадьевич, преподаватель кафедры высшей математики и кафедры математических основ управления МФТИ, лауреат конкурса Фонда «Династия» в номинации «Молодой учитель», а также…
Лектор: Молчанов Евгений Геннадьевич, преподаватель кафедры высшей математики и кафедры математических основ управления МФТИ, лауреат конкурса Фонда «Династия» в номинации «Молодой учитель», а также…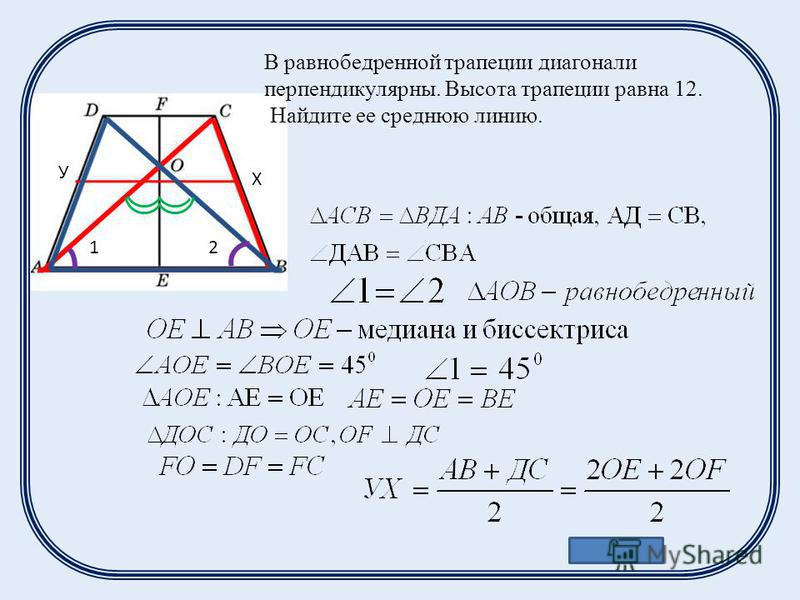

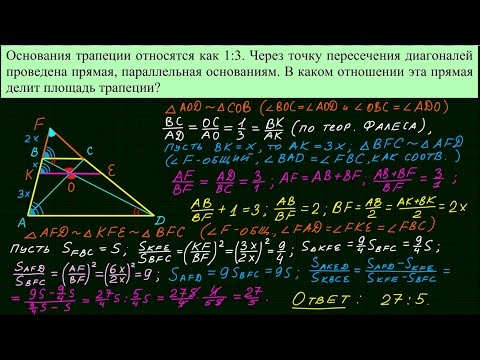



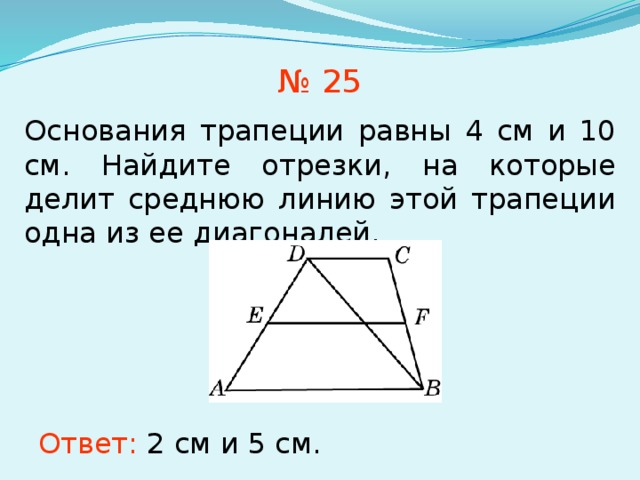
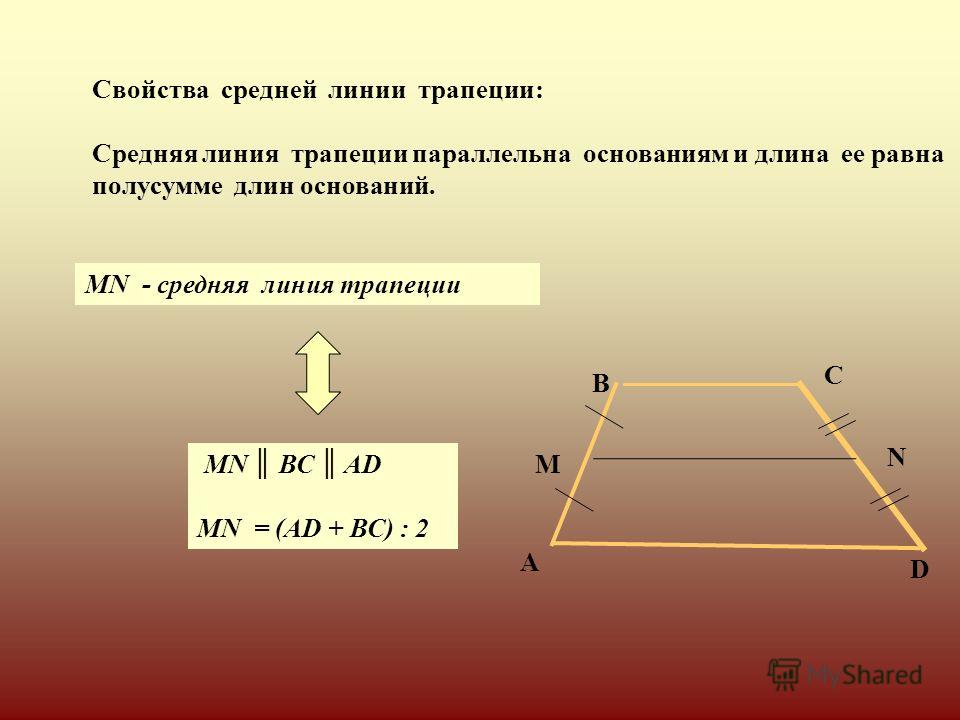 Действительно, из трапеции BB 3 A 3 A 5 мы видим, что BB 4 = B 4 B 3 . Таким же образом, из трапеции B 4 B 2 A 2 A 4 получаем B 4 B 3 = B 3 B 2
Действительно, из трапеции BB 3 A 3 A 5 мы видим, что BB 4 = B 4 B 3 . Таким же образом, из трапеции B 4 B 2 A 2 A 4 получаем B 4 B 3 = B 3 B 2

 Этот центральный четырёхугольник является параллелограммом Вариньона.
Этот центральный четырёхугольник является параллелограммом Вариньона.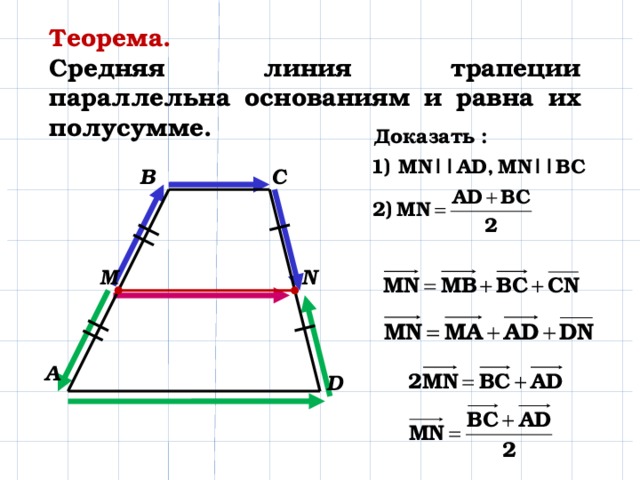



 В задачах для самостоятельного решения имеется именно такая задача. Только в ней не сказано, что отрезок соединяющий середины диагоналей лежит на средней линии. Рассмотрим задачи:
В задачах для самостоятельного решения имеется именно такая задача. Только в ней не сказано, что отрезок соединяющий середины диагоналей лежит на средней линии. Рассмотрим задачи: Третий отрезок равен меньшему основанию, так как при построении указанных высот образуется прямоугольник, а в прямоугольнике противолежащие стороны равны. В данной задаче:
Третий отрезок равен меньшему основанию, так как при построении указанных высот образуется прямоугольник, а в прямоугольнике противолежащие стороны равны. В данной задаче:
 Тут небольшой тупик возникает… Как зная высоту, в данном случае, вычислить основания? А ни как! Таких трапеций с фиксированной высотой и диагоналями пересекающимися по углом 90 градусов можно построить множество. Как быть?
Тут небольшой тупик возникает… Как зная высоту, в данном случае, вычислить основания? А ни как! Таких трапеций с фиксированной высотой и диагоналями пересекающимися по углом 90 градусов можно построить множество. Как быть? Построена она на листе в клетку и требуется найти среднюю линию, сторона клетки обычно равна 1, но может быть другая величина.
Построена она на листе в клетку и требуется найти среднюю линию, сторона клетки обычно равна 1, но может быть другая величина.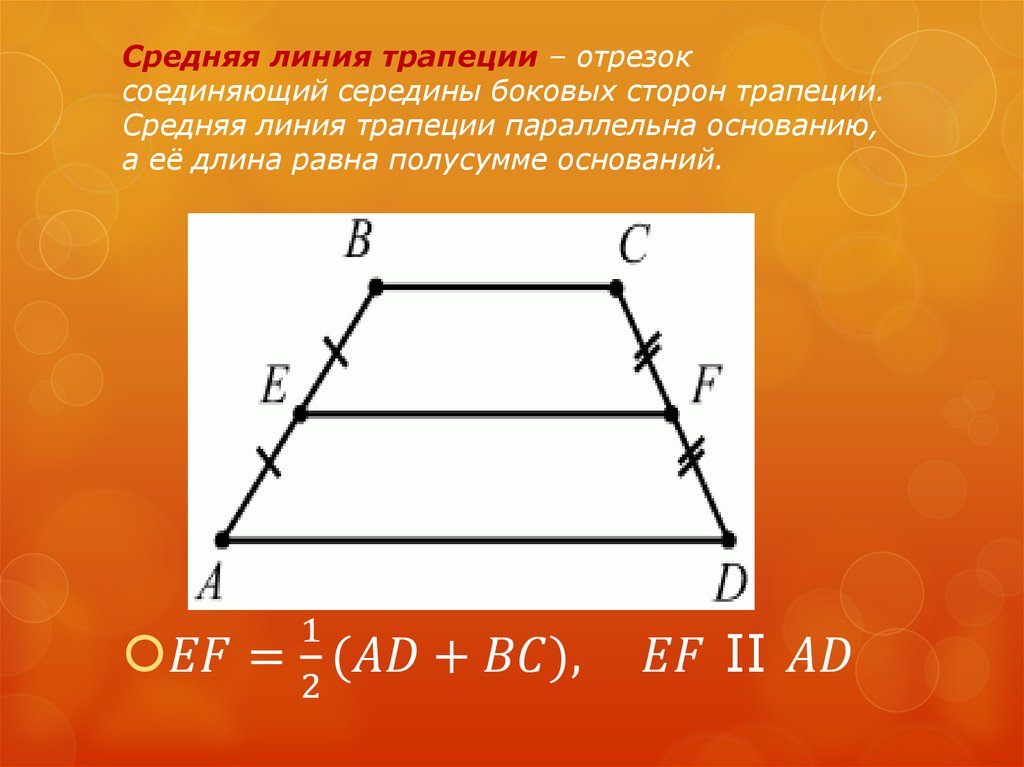
 Согласно свойству средней линией треугольника ABQ
Согласно свойству средней линией треугольника ABQ
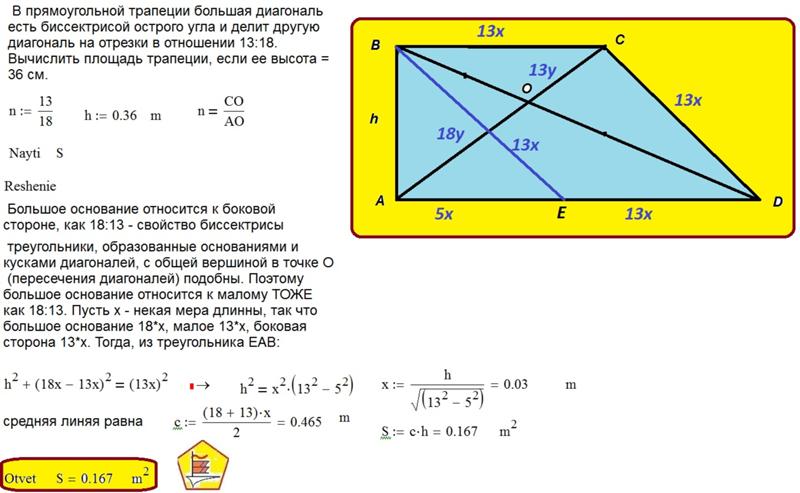


 При этом:
При этом:

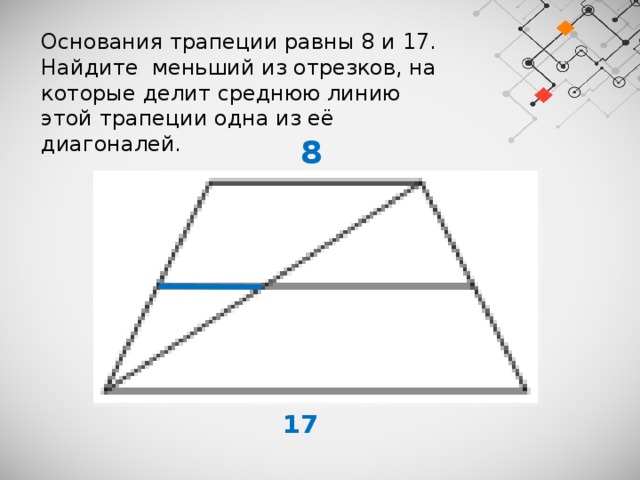 Поскольку трапеция неравнобокая — то обозначим
Поскольку трапеция неравнобокая — то обозначим

 Средние линии второго рода
Средние линии второго рода

 Так, если продолжить боковые стороны АК и МЕ в направлении меньшего основания, то рано или поздно они пересекутся к некоторой точке. Дальше, через середины оснований трапеции проведем прямую. Она пересекает основания в точках Х и Т.
Так, если продолжить боковые стороны АК и МЕ в направлении меньшего основания, то рано или поздно они пересекутся к некоторой точке. Дальше, через середины оснований трапеции проведем прямую. Она пересекает основания в точках Х и Т.

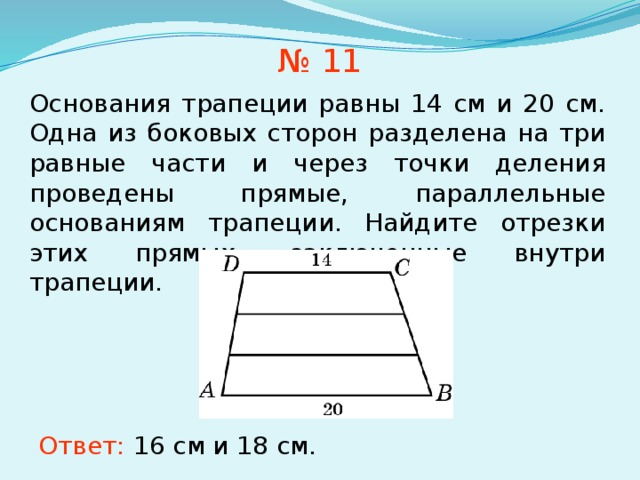
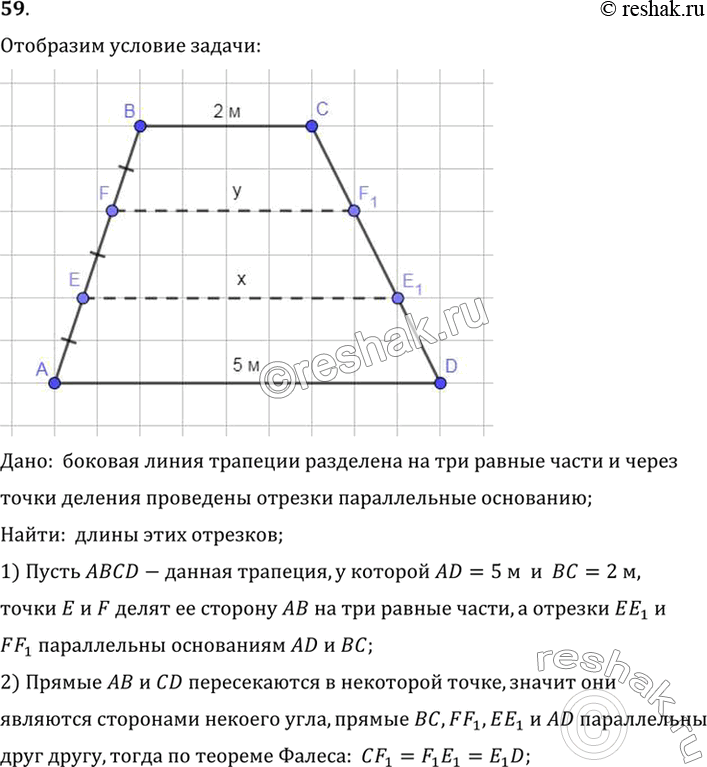 Так и поймете быстрее, и запомните лучше.
Так и поймете быстрее, и запомните лучше. Радиус можно найти через отношение стороны треугольника к синусу противолежащего угла, умноженному на два. Например, R = АЕ/2*sinАМЕ
Радиус можно найти через отношение стороны треугольника к синусу противолежащего угла, умноженному на два. Например, R = АЕ/2*sinАМЕ
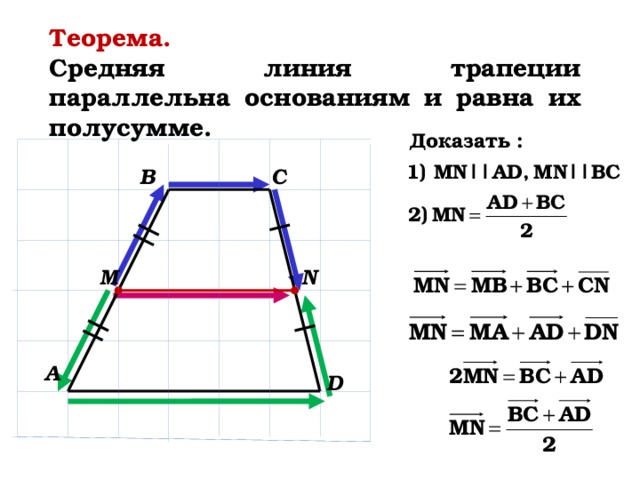 Это позволяет вычислять площадь прямоугольной трапеции (общая формула S = (a + b) * h/2
Это позволяет вычислять площадь прямоугольной трапеции (общая формула S = (a + b) * h/2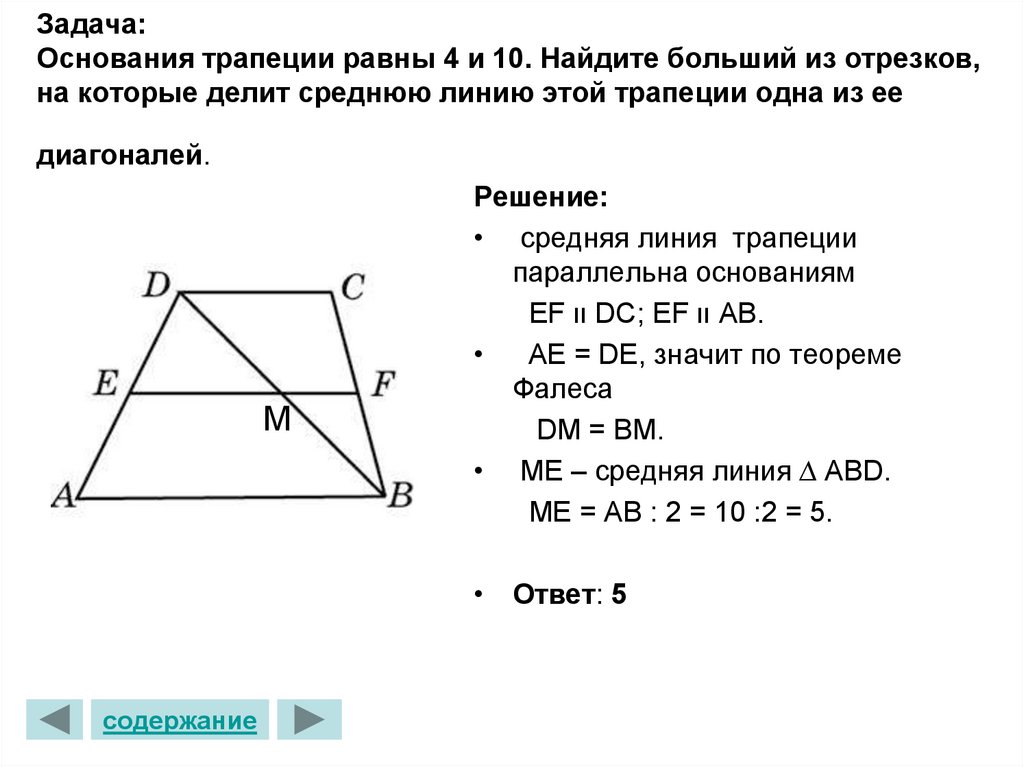 Получим параллелограмм КМХЕ (основание – МХ || КЕ и КМ || ЕХ).
Получим параллелограмм КМХЕ (основание – МХ || КЕ и КМ || ЕХ). Поэтому КН = ½АВ = 4 см.
Поэтому КН = ½АВ = 4 см. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
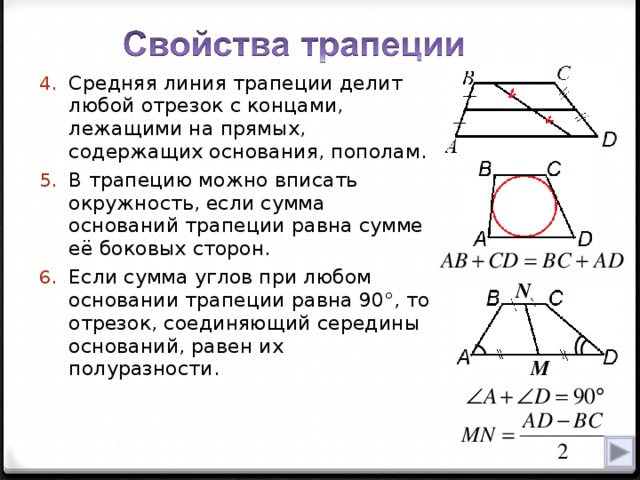
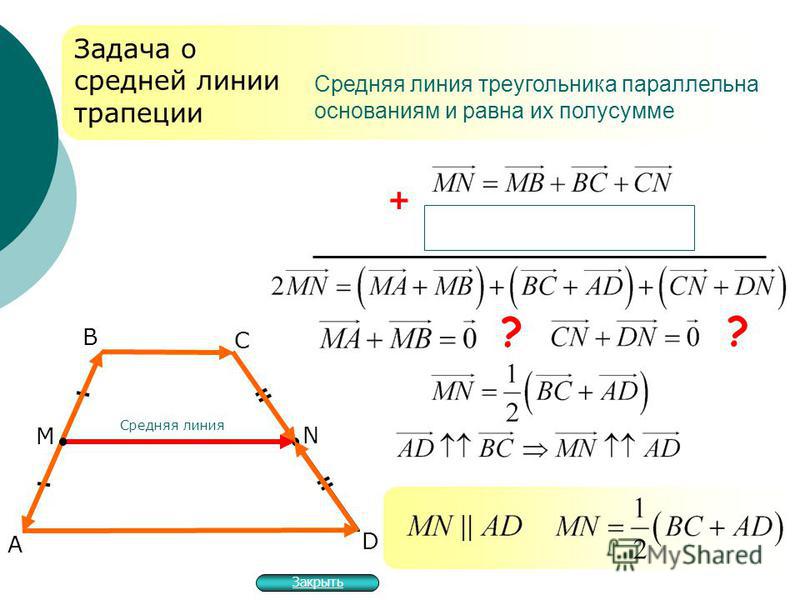

 2
2 (Только чтоб понятно было) — Знания.site
(Только чтоб понятно было) — Знания.site Омонимами.
Омонимами. .рять друзей е и и е
.рять друзей е и и е
 Лексика изучает слово с точки зрения его смыслового значения.
Лексика изучает слово с точки зрения его смыслового значения. Профессиональными
Профессиональными Какая из данных пар слов не является синонимами?
Какая из данных пар слов не является синонимами? Колокольчик хохочет до слез.
Колокольчик хохочет до слез. Найди значение выражения:
Найди значение выражения: Найди значение выражения:
Найди значение выражения:
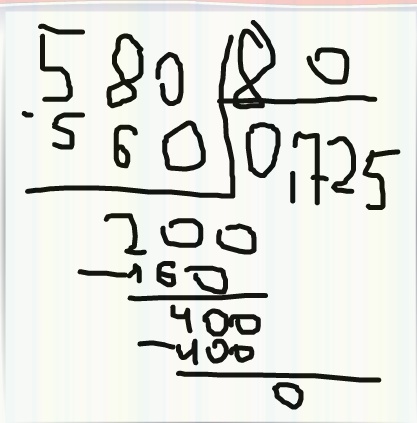 Какова длина ¼ части ленты?
Какова длина ¼ части ленты?
 Сколько километров он пролетит за четверть часа?
Сколько километров он пролетит за четверть часа? Сколько лет живёт хвоя сосны?
Сколько лет живёт хвоя сосны?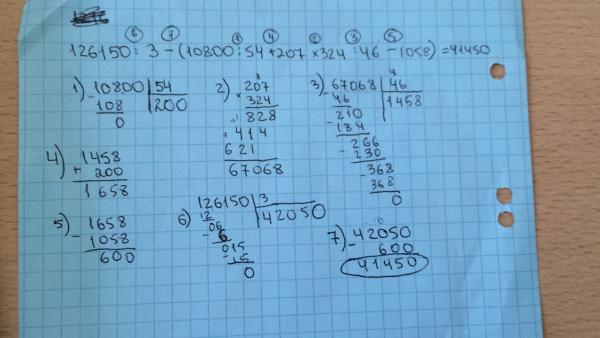 Сколько лет живёт заяц?
Сколько лет живёт заяц?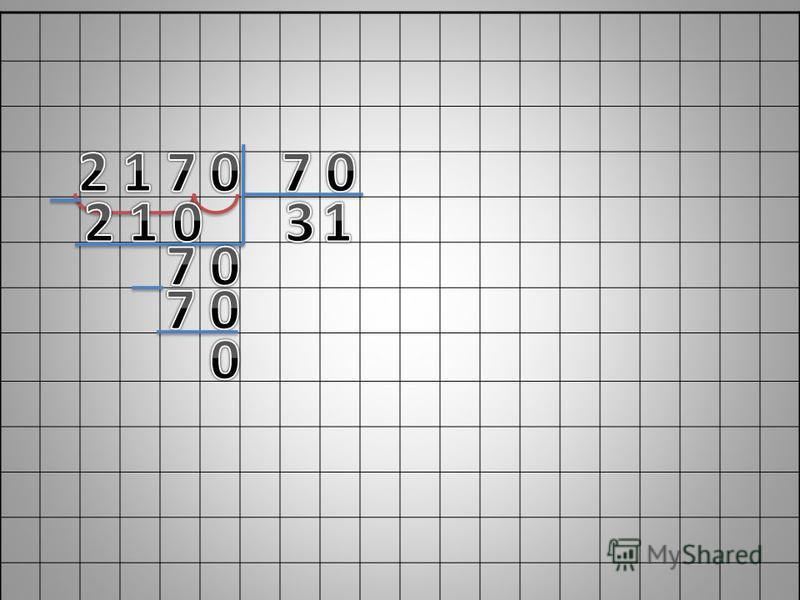 )
) Задание 231.
Задание 231.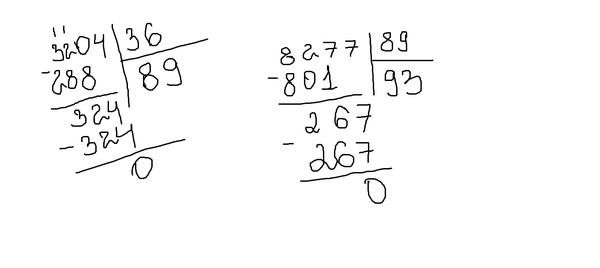 Задание 237.
Задание 237.
 Нарисуйте пути, по которым катера должны прийти к своим причалам, но так, чтобы эти пути не пересекались.
Нарисуйте пути, по которым катера должны прийти к своим причалам, но так, чтобы эти пути не пересекались. Поупражняемся в вычислениях.
Поупражняемся в вычислениях. Задание 237.
Задание 237.
 Перенести в делимом и делителе запятую вправо на столько цифр, сколько их после запятой в делителе;
Перенести в делимом и делителе запятую вправо на столько цифр, сколько их после запятой в делителе;

 \]
\] y=3} \end{array} \right.\]
y=3} \end{array} \right.\] Методы решения систем уравнений.
Методы решения систем уравнений. Решить систему методом сложения: \(\begin{equation*} \begin{cases} x-y-4=0 \\ 3x+y-8=0 \end{cases} \end{equation*}\).
Решить систему методом сложения: \(\begin{equation*} \begin{cases} x-y-4=0 \\ 3x+y-8=0 \end{cases} \end{equation*}\).
 Подготовка к ОГЭ. Учитель высшей категории. Стаж работы 30 лет.
Мои занятия будут способствовать качественному усвоению знаний, привитию интереса к науке. На своих уроках совмещаю традиционные и инновационные методы обучения. Большое внимание уделяю выработке практических навыков и умений.
Учащиеся, сдававшие ОГЭ по химии, показали хорошие и отличные результаты.
Регулярно повышаю свой уровень образования, занимаясь на курсах переподготовки. Принимала участие в обсуждении следующих вопросов:
1. «Формирование профессиональной компетентности учителя»
2. «Реализация требований обновлённых ФГОС в работе учителя химии и биологии»
3. «Методология и технологии цифровых образовательных технологий в образовательном процессе»
Подготовка к ОГЭ. Учитель высшей категории. Стаж работы 30 лет.
Мои занятия будут способствовать качественному усвоению знаний, привитию интереса к науке. На своих уроках совмещаю традиционные и инновационные методы обучения. Большое внимание уделяю выработке практических навыков и умений.
Учащиеся, сдававшие ОГЭ по химии, показали хорошие и отличные результаты.
Регулярно повышаю свой уровень образования, занимаясь на курсах переподготовки. Принимала участие в обсуждении следующих вопросов:
1. «Формирование профессиональной компетентности учителя»
2. «Реализация требований обновлённых ФГОС в работе учителя химии и биологии»
3. «Методология и технологии цифровых образовательных технологий в образовательном процессе»
 Люблю математику за то, что она воспитывает человека, приучая его к точности , учит логично мыслить, и в какой-то степени она способна привести ум в порядок. В своей работе использую не только традиционные формы и методы преподавания математики, но и новые современные технологии. Моя цель прежде всего, усилить мотивацию ребенка к познанию окружающего мира, продемонстрировать ему, что занятия математикой – это не получение отвлеченных от жизни знаний, а необходимая подготовка к жизни, поиск полезной информации и навыки ее применения в реальной жизни. Учитель пения, музыки.
Люблю математику за то, что она воспитывает человека, приучая его к точности , учит логично мыслить, и в какой-то степени она способна привести ум в порядок. В своей работе использую не только традиционные формы и методы преподавания математики, но и новые современные технологии. Моя цель прежде всего, усилить мотивацию ребенка к познанию окружающего мира, продемонстрировать ему, что занятия математикой – это не получение отвлеченных от жизни знаний, а необходимая подготовка к жизни, поиск полезной информации и навыки ее применения в реальной жизни. Учитель пения, музыки. Подготовка к ОГЭ, ЕГЭ, ВПР и олимпиадам. Средний балл подготовки к ЕГЭ у моих учеников выше 70 баллов и нет тех, кто не сдал. Жду на занятиях.
Подготовка к ОГЭ, ЕГЭ, ВПР и олимпиадам. Средний балл подготовки к ЕГЭ у моих учеников выше 70 баллов и нет тех, кто не сдал. Жду на занятиях. Алгебра 9 класс ФГОС
Алгебра 9 класс ФГОС А если подставим x=3
и y=3,
то получим верное числовое равенство.
А если подставим x=3
и y=3,
то получим верное числовое равенство.

 е. алгебраическое выражение, составленное из чисел и переменных с помощью операций сложения, вычитания, умножения, деления и возведения в натуральную степень).
е. алгебраическое выражение, составленное из чисел и переменных с помощью операций сложения, вычитания, умножения, деления и возведения в натуральную степень).


 Решить систему уравнений – это значит найти все ее решения или установить, что решений нет.
Решить систему уравнений – это значит найти все ее решения или установить, что решений нет. 5).
5). учреждений / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, И. Е. Феоктистов. — 7-е изд., испр. и доп. — М.: Мнемозина, 2008.
учреждений / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, И. Е. Феоктистов. — 7-е изд., испр. и доп. — М.: Мнемозина, 2008. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М. : Мнемозина, 2002.-143 с.: ил. № 90 – 94, 103, 104.
Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М. : Мнемозина, 2002.-143 с.: ил. № 90 – 94, 103, 104.

 Поэтому уравнение (3) равносильно уравнению(1).
Поэтому уравнение (3) равносильно уравнению(1). Такие уравнения называют линейными уравнениями с двумя переменными.
Такие уравнения называют линейными уравнениями с двумя переменными. Рассмотрим, например, уравнение . Его решениями служат все пары чисел (х ; у), в которых x = 6, а у — любое число. Изобразив эти пары точками, получим прямую, параллельную оси ординат (рис. 59).
Рассмотрим, например, уравнение . Его решениями служат все пары чисел (х ; у), в которых x = 6, а у — любое число. Изобразив эти пары точками, получим прямую, параллельную оси ординат (рис. 59). Найдем координаты двух каких-либо точек прямой:
Найдем координаты двух каких-либо точек прямой: Недостаточно внимания уделено методам решения заданий типа «Решить уравнение в натуральных или целых числах». Известно, что материалы ЕГЭ и билеты вступительных экзаменов часто содержат такие упражнения.
Недостаточно внимания уделено методам решения заданий типа «Решить уравнение в натуральных или целых числах». Известно, что материалы ЕГЭ и билеты вступительных экзаменов часто содержат такие упражнения.


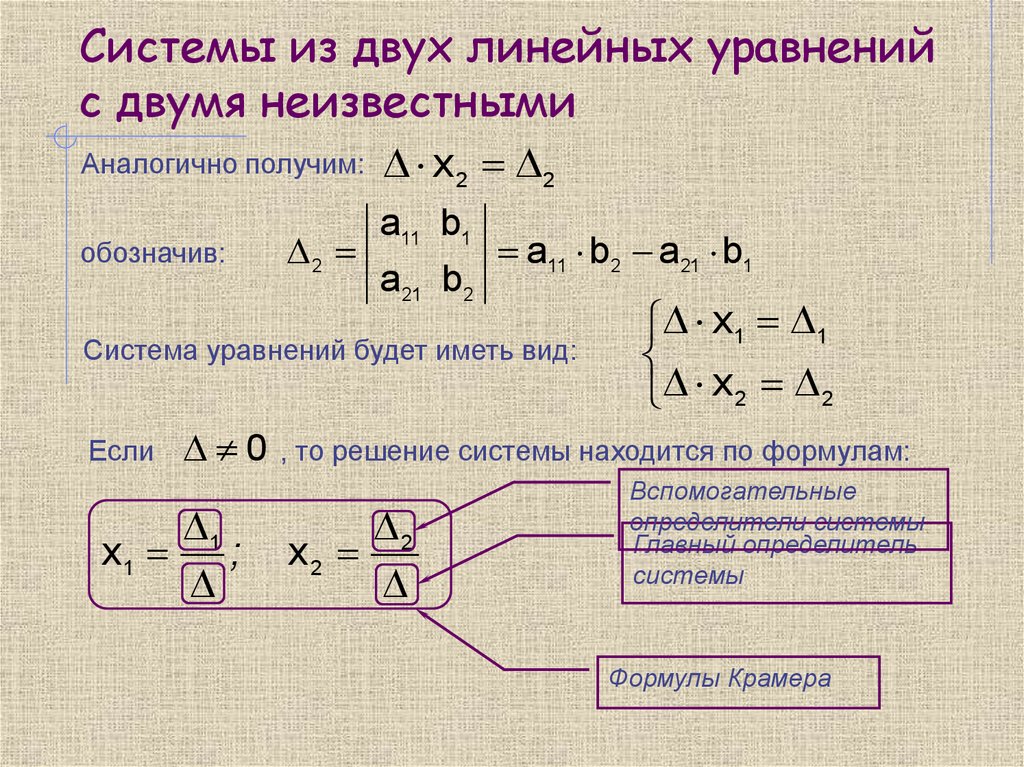 Целые корни ищем среди делителей числа 36.
Целые корни ищем среди делителей числа 36.  Целые корни ищем среди делителей числа 6.
Целые корни ищем среди делителей числа 6.  Целые корни ищем среди делителей числа 24.
Целые корни ищем среди делителей числа 24.  (Ь Н Ы)
(Ь Н Ы) Привести квадратное уравнение к общему виду:
Привести квадратное уравнение к общему виду:  Уравнение становиться линейным.
Уравнение становиться линейным. Решение квадратного уравнения с комплексными корнями.
Решение квадратного уравнения с комплексными корнями. 
 Пояснение:
Пояснение:
 Поскольку вес коробки плюс вес одного предмета составляет 6 фунтов, это можно представить уравнением
Поскольку вес коробки плюс вес одного предмета составляет 6 фунтов, это можно представить уравнением
 Хотя решить эту систему довольно легко, все же есть немало интересных концепций и идей, которые возникают, когда мы глубоко задумываемся о процессе. Эти концепции и идеи играют большую роль, когда мы позже рассмотрим более общие системы линейных уравнений.
Хотя решить эту систему довольно легко, все же есть немало интересных концепций и идей, которые возникают, когда мы глубоко задумываемся о процессе. Эти концепции и идеи играют большую роль, когда мы позже рассмотрим более общие системы линейных уравнений.
 \begin{выровнено}
\text{Уравнение 1: }x-2y &= 6 \\
\text{Уравнение 2: }3x+y &= 4.
\end{выровнено}
Уравнение 1: x−2yУравнение 2: 3x+y=6=4.
\begin{выровнено}
\text{Уравнение 1: }x-2y &= 6 \\
\text{Уравнение 2: }3x+y &= 4.
\end{выровнено}
Уравнение 1: x−2yУравнение 2: 3x+y=6=4. (2,-2).(2,−2).
(2,-2).(2,−2). \frac{a}{b}\neq \frac{c}{d} \ подразумевает ad-bc\neq 0.ba=dc⟹ad-bc =0.
\frac{a}{b}\neq \frac{c}{d} \ подразумевает ad-bc\neq 0.ba=dc⟹ad-bc =0. (Геометрически говоря, две «случайные» прямые почти всегда не будут параллельны и, следовательно, будут пересекаться ровно в одной точке.) Эта интуиция также будет сопровождать нас, когда мы будем исследовать более крупные системы уравнений.
(Геометрически говоря, две «случайные» прямые почти всегда не будут параллельны и, следовательно, будут пересекаться ровно в одной точке.) Эта интуиция также будет сопровождать нас, когда мы будем исследовать более крупные системы уравнений.

 Решите уравнение $latex -3x+5y=-6$ для x .
Решите уравнение $latex -3x+5y=-6$ для x .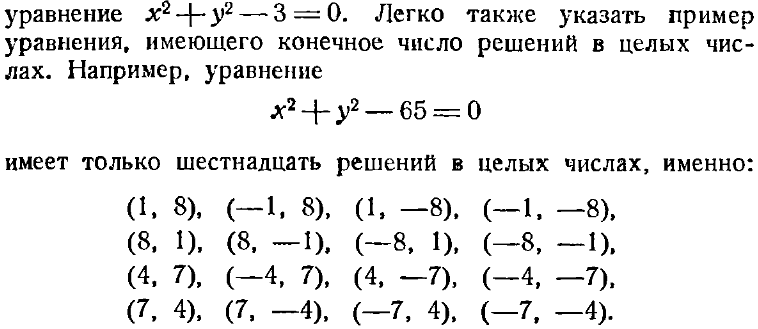 Решите уравнение $latex 3x+2 -4x+5)=3y+6$ для y .
Решите уравнение $latex 3x+2 -4x+5)=3y+6$ для y . Неравенство строгое, поэтому само значение \(-1\) «выкалываем» и в ответ не берем
Неравенство строгое, поэтому само значение \(-1\) «выкалываем» и в ответ не берем Причем оно будет верным при любом иксе, ведь он никак не влияет на получившееся неравенство. Значит, любое значение икса будет решением
Причем оно будет верным при любом иксе, ведь он никак не влияет на получившееся неравенство. Значит, любое значение икса будет решением И оно будет неверным при любом иксе, ведь он никак не влияет на получившееся неравенство. Значит, любое значение икса решением не будет.
И оно будет неверным при любом иксе, ведь он никак не влияет на получившееся неравенство. Значит, любое значение икса решением не будет.

 Поскольку разработал и активно внедрял символический язык алгебры – те самые, привычные нам «иксы и игреки».
Поскольку разработал и активно внедрял символический язык алгебры – те самые, привычные нам «иксы и игреки».
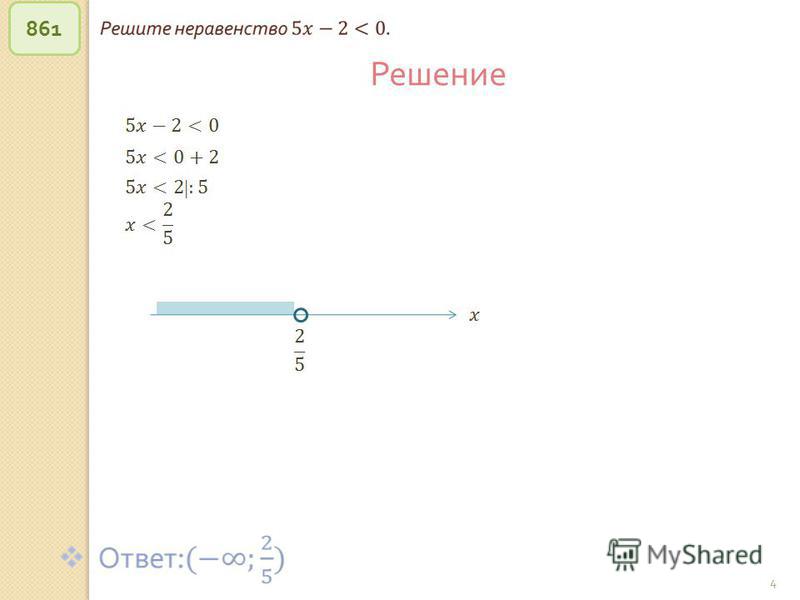

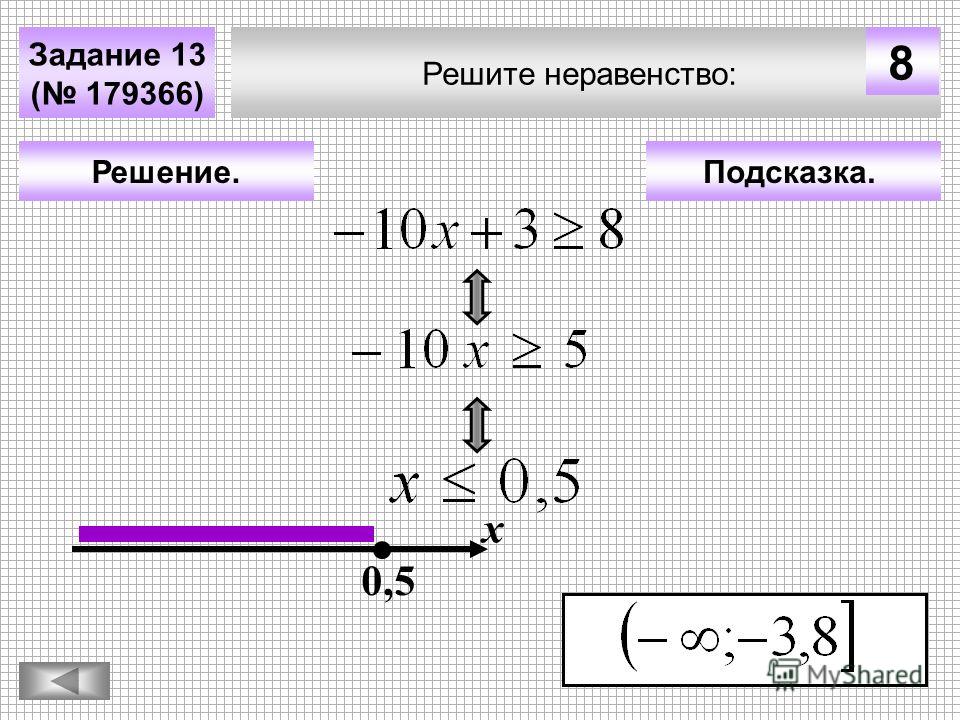 Построим графики этих уравнений и найдем координаты точки пересечения (рис.3).
Построим графики этих уравнений и найдем координаты точки пересечения (рис.3). 

 Подбирая значения х, можно найти еще несколько частных решений.
Подбирая значения х, можно найти еще несколько частных решений.

 Это положительно-направленный луч.
Это положительно-направленный луч.
 {2}-8\) — есть переменная во второй степени, это
{2}-8\) — есть переменная во второй степени, это
 Например, \(x-2>x\) не будет верным никогда, ведь слева из икса вычитают двойку, а справа – нет. Значит, слева всегда будет меньше, а не больше.
Например, \(x-2>x\) не будет верным никогда, ведь слева из икса вычитают двойку, а справа – нет. Значит, слева всегда будет меньше, а не больше. И оно будет неверным при любом иксе, ведь он никак не влияет на получившееся неравенство. Значит, любое значение икса решением не будет.
И оно будет неверным при любом иксе, ведь он никак не влияет на получившееся неравенство. Значит, любое значение икса решением не будет.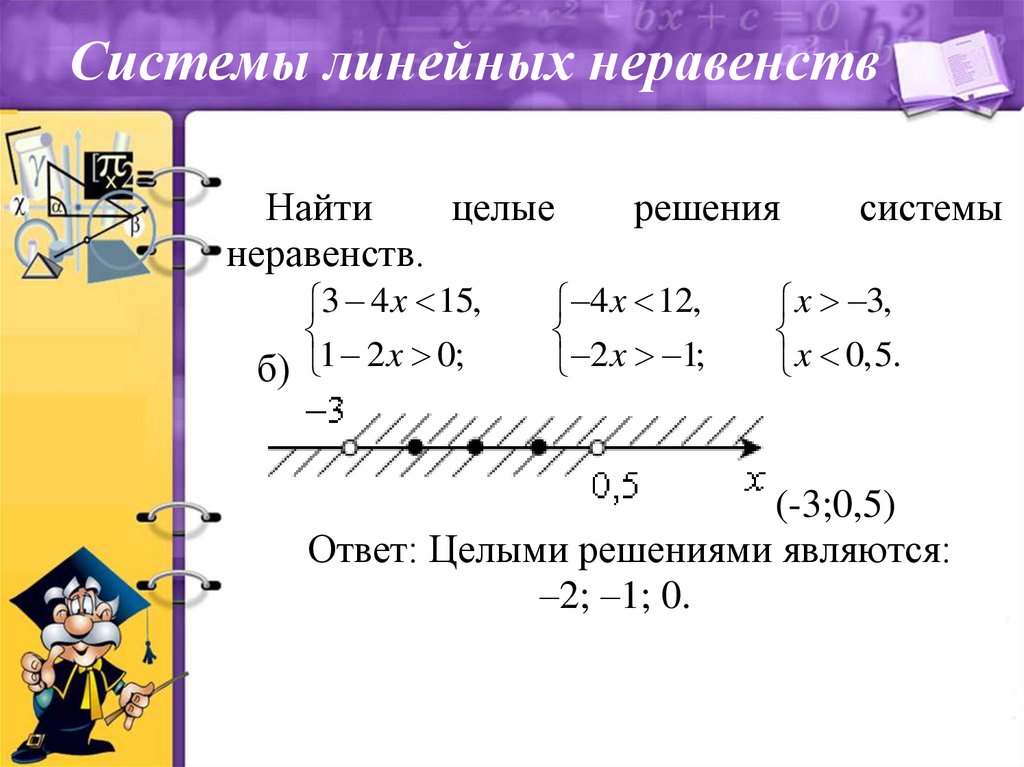 д.
д. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.

 Указать множество решений данного неравенства, записав ответ:
Указать множество решений данного неравенства, записав ответ:
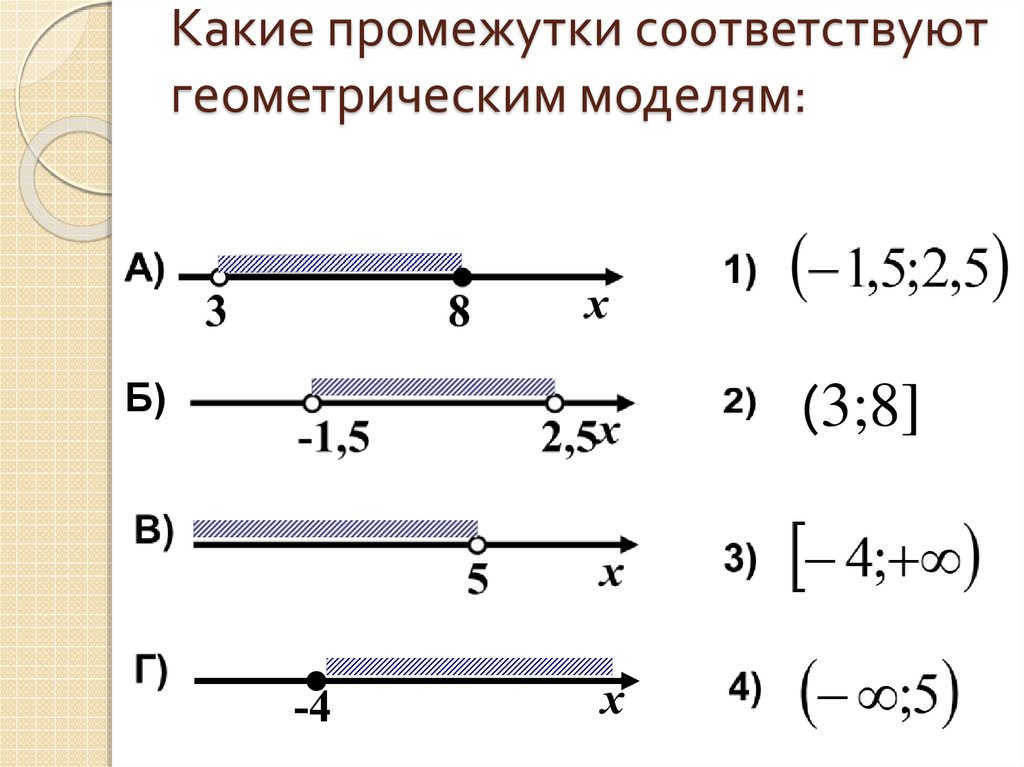
 И. Маркушевич
И. Маркушевич  Эти действия знакомы всем. Но, что характерно, косяки в этих действиях — и есть основная ошибка в решении неравенств, да… Стало быть, надо повторить эти действия. Называются эти действия вот как:
Эти действия знакомы всем. Но, что характерно, косяки в этих действиях — и есть основная ошибка в решении неравенств, да… Стало быть, надо повторить эти действия. Называются эти действия вот как: Поэтому я выделяю их красным цветом:
Поэтому я выделяю их красным цветом: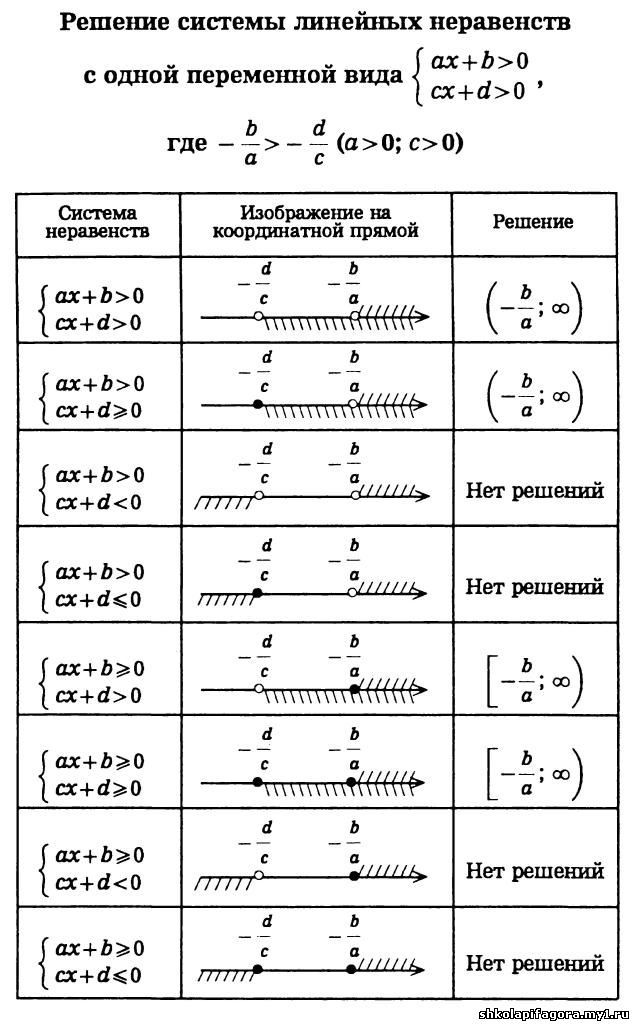 ) Полное враньё! Обман народа! Но стоит изменить знак неравенства на противоположный, как всё становится на свои места:
) Полное враньё! Обман народа! Но стоит изменить знак неравенства на противоположный, как всё становится на свои места: А теперь можно переходить к конкретным видам.
А теперь можно переходить к конкретным видам. Меньше же… И ноль годится, и -17, и 0,34… Да все числа, которые меньше двух — годятся! И даже 1,9999…. Хоть чуть чуть, да меньше!
Меньше же… И ноль годится, и -17, и 0,34… Да все числа, которые меньше двух — годятся! И даже 1,9999…. Хоть чуть чуть, да меньше!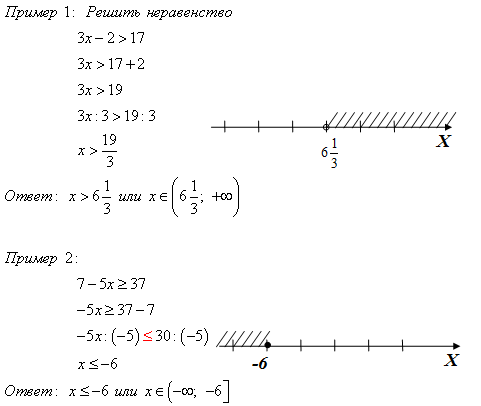 На этот раз я отмечаю область подходящих значений икса дужкой (от слова дуга ), а не штриховкой. Наводим курсор на рисунок и видим эту дужку.
На этот раз я отмечаю область подходящих значений икса дужкой (от слова дуга ), а не штриховкой. Наводим курсор на рисунок и видим эту дужку. Вполне логично. Икс может быть любым числом из всех возможных чисел от минус бесконечности до двух. Двойкой икс быть не может, о чём нам и говорит слово «не включая».
Вполне логично. Икс может быть любым числом из всех возможных чисел от минус бесконечности до двух. Двойкой икс быть не может, о чём нам и говорит слово «не включая».  Мы с этим в соответствующих темах разберёмся.
Мы с этим в соответствующих темах разберёмся. Пишите, какую хотите. Едем дальше.
Пишите, какую хотите. Едем дальше.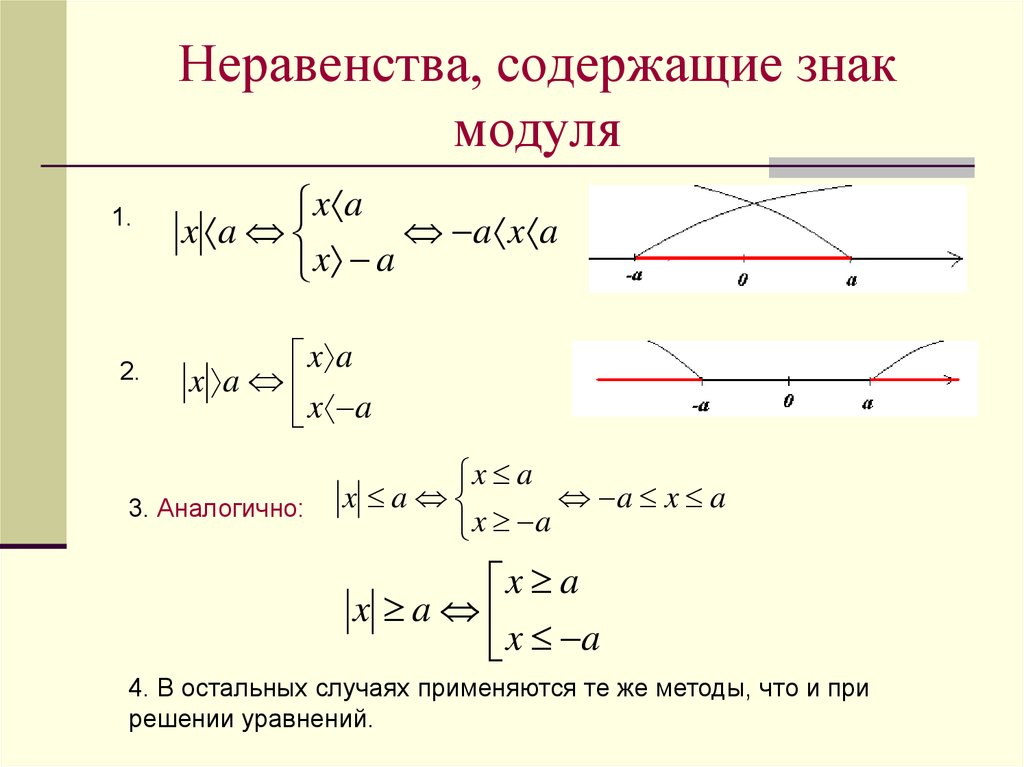 У тех, кто уравнения на автомате решает. А тем, кто уравнения не решает, неравенства, собственно, ни к чему…) Ещё пример популярного задания:
У тех, кто уравнения на автомате решает. А тем, кто уравнения не решает, неравенства, собственно, ни к чему…) Ещё пример популярного задания: Можно найти ещё число, меньше -5, но больше -6? Можно, например -5,5… Стоп! Нам сказано целое решение! Не катит -5,5! А минус шесть? Э-э-э! Неравенство строгое, минус 6 никак не меньше минус 6!
Можно найти ещё число, меньше -5, но больше -6? Можно, например -5,5… Стоп! Нам сказано целое решение! Не катит -5,5! А минус шесть? Э-э-э! Неравенство строгое, минус 6 никак не меньше минус 6!
 )
) 


 3) оба точечных множества, составляющих последнюю систему, получаем ответ примера
3) оба точечных множества, составляющих последнюю систему, получаем ответ примера
 Запись -3
Двойные неравенства могут быть решены с использованием принципов прибавления и умножения неравенств.
Запись -3
Двойные неравенства могут быть решены с использованием принципов прибавления и умножения неравенств.
 {5x-2}\)
{5x-2}\) .. И как же нам найти все возможные решения? Для этого используют Для нашего случая имеем:
.. И как же нам найти все возможные решения? Для этого используют Для нашего случая имеем: И на какое бы положительное число мы не умножали – всегда будем получать верное неравенство. А теперь попробуем умножить на отрицательное число, например, минус тройку:
И на какое бы положительное число мы не умножали – всегда будем получать верное неравенство. А теперь попробуем умножить на отрицательное число, например, минус тройку: Неравенство , поэтому само значение \(-1\) «выкалываем» и в ответ не берем
Неравенство , поэтому само значение \(-1\) «выкалываем» и в ответ не берем Таким образом, имеем второе требование на икс:
Таким образом, имеем второе требование на икс:

 Причем, когда a является положительным, то знак остается, когда a – отрицательное, меняется на противоположный.
Причем, когда a является положительным, то знак остается, когда a – отрицательное, меняется на противоположный.
 Оно является неверным. То есть 0 · x − 12 , 7 ≥ 0 не имеет решений.
Оно является неверным. То есть 0 · x − 12 , 7 ≥ 0 не имеет решений.
 Получаем, что − 3 · x = − 12 , x = 4 . Необходимо изобразить координатную прямую, где отмечаем точку 4 . Она будет выколотой, так как неравенство является строгим. Рассмотрим чертеж, приведенный ниже.
Получаем, что − 3 · x = − 12 , x = 4 . Необходимо изобразить координатную прямую, где отмечаем точку 4 . Она будет выколотой, так как неравенство является строгим. Рассмотрим чертеж, приведенный ниже. Для этого изобразим график линейной функции y = 0 , 5 · x − 1 , приведенный ниже.
Для этого изобразим график линейной функции y = 0 , 5 · x − 1 , приведенный ниже.
 Тогда прямая будет параллельна О х или совпадающей при b = 0 . Эти случаю показывают, что неравенство может не иметь решений, либо решением может быть любое число.
Тогда прямая будет параллельна О х или совпадающей при b = 0 . Эти случаю показывают, что неравенство может не иметь решений, либо решением может быть любое число.


 2+3=0$
2+3=0$ е. находить те значения переменной, при которых уравнение обращается в верное числовое равенство. Точно так же свойства числовых неравенств помогут нам решать неравенства с переменной, т. е. находить те значения переменной, при которых неравенство с переменной обращается в верное числовое неравенство. Каждое такое значение переменной называют обычно решением неравенства с переменной.
е. находить те значения переменной, при которых уравнение обращается в верное числовое равенство. Точно так же свойства числовых неравенств помогут нам решать неравенства с переменной, т. е. находить те значения переменной, при которых неравенство с переменной обращается в верное числовое неравенство. Каждое такое значение переменной называют обычно решением неравенства с переменной. Подставив вместо х значение 2,5, получим 2 — 2,5 + 5 < 7, т. е. 10 < 7 — неверное неравенство. Значит, х = 2,5 не является решением неравенства.
Подставив вместо х значение 2,5, получим 2 — 2,5 + 5 < 7, т. е. 10 < 7 — неверное неравенство. Значит, х = 2,5 не является решением неравенства.
 Обе части неравенства можно умножить или разделить на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный.
Обе части неравенства можно умножить или разделить на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный.