Mathway | Популярные задачи
| 1 | Оценить с использованием заданного значения | квадратный корень из 50 | |
| 2 | Оценить с использованием заданного значения | квадратный корень из 45 | |
| 3 | Вычислить | 5+5 | |
| 4 | Вычислить | 7*7 | |
| 5 | Разложить на простые множители | 24 | |
| 6 | Преобразовать в смешанную дробь | 52/6 | |
| 7 | Преобразовать в смешанную дробь | 93/8 | |
| 8 | Преобразовать в смешанную дробь | 34/5 | |
| 9 | График | y=x+1 | |
| 10 | Оценить с использованием заданного значения | квадратный корень из 128 | |
| 11 | Найти площадь поверхности | сфера (3) | |
| 12 | Вычислить | 54-6÷2+6 | |
| 13 | График | y=-2x | |
| 14 | Вычислить | 8*8 | |
| 15 | Преобразовать в десятичную форму | 5/9 | |
| 16 | Оценить с использованием заданного значения | квадратный корень из 180 | |
| 17 | График | y=2 | |
| 18 | Преобразовать в смешанную дробь | 7/8 | |
| 19 | Вычислить | 9*9 | |
| 20 | Risolvere per C | C=5/9*(F-32) | |
| 21 | Упростить | 1/3+1 1/12 | |
| 22 | График | y=x+4 | |
| 23 | График | y=-3 | |
| 24 | График | x+y=3 | |
| 25 | График | x=5 | |
| 26 | Вычислить | 6*6 | |
| 27 | Вычислить | 2*2 | |
| 28 | Вычислить | 4*4 | |
| 29 | Вычислить | 1/2+(2/3)÷(3/4)-(4/5*5/6) | |
| 30 | Вычислить | 1/3+13/12 | |
| 31 | Вычислить | 5*5 | |
| 32 | Risolvere per d | 2d=5v(o)-vr | |
| 33 | Преобразовать в смешанную дробь | 3/7 | |
| 34 | График | y=-2 | |
| 35 | Определить наклон | y=6 | |
| 36 | Перевести в процентное соотношение | 9 | |
| 37 | График | y=2x+2 | |
| 38 | График | y=2x-4 | |
| 39 | График | x=-3 | |
| 40 | Решить, используя свойство квадратного корня | x^2+5x+6=0 | |
| 41 | Преобразовать в смешанную дробь | 1/6 | |
| 42 | Преобразовать в десятичную форму | 9% | |
| 43 | Risolvere per n | 12n-24=14n+28 | |
| 44 | Вычислить | 16*4 | |
| 45 | Упростить | кубический корень из 125 | |
| 46 | Преобразовать в упрощенную дробь | 43% | |
| 47 | График | x=1 | |
| 48 | График | y=6 | |
| 49 | График | y=-7 | |
| 50 | График | y=4x+2 | |
| 51 | Определить наклон | y=7 | |
| 52 | График | y=3x+4 | |
| 53 | График | y=x+5 | |
| 54 | График | 3x+2y=6 | |
| 55 | Решить, используя свойство квадратного корня | x^2-5x+6=0 | |
| 56 | Решить, используя свойство квадратного корня | x^2-6x+5=0 | |
| 57 | Решить, используя свойство квадратного корня | x^2-9=0 | |
| 58 | Оценить с использованием заданного значения | квадратный корень из 192 | |
| 59 | Оценить с использованием заданного значения | квадратный корень из 25/36 | |
| 60 | Разложить на простые множители | 14 | |
| 61 | Преобразовать в смешанную дробь | 7/10 | |
| 62 | Risolvere per a | (-5a)/2=75 | |
| 63 | Упростить | x | |
| 64 | Вычислить | 6*4 | |
| 65 | Вычислить | 6+6 | |
| 66 | Вычислить | -3-5 | |
| 67 | Вычислить | -2-2 | |
| 68 | Упростить | квадратный корень из 1 | |
| 69 | Упростить | квадратный корень из 4 | |
| 70 | Найти обратную величину | 1/3 | |
| 71 | Преобразовать в смешанную дробь | 11/20 | |
| 72 | Преобразовать в смешанную дробь | 7/9 | |
| 73 | Найти НОК | 11 , 13 , 5 , 15 , 14 | , , , , |
| 74 | Решить, используя свойство квадратного корня | x^2-3x-10=0 | |
| 75 | Решить, используя свойство квадратного корня | x^2+2x-8=0 | |
| 76 | График | 3x+4y=12 | |
| 77 | График | 3x-2y=6 | |
| 78 | График | y=-x-2 | |
| 79 | График | y=3x+7 | |
| 80 | Определить, является ли полиномом | 2x+2 | |
| 81 | График | y=2x-6 | |
| 82 | График | y=2x-7 | |
| 83 | График | y=2x-2 | |
| 84 | График | y=-2x+1 | |
| 85 | График | y=-3x+4 | |
| 86 | График | y=-3x+2 | |
| 87 | График | y=x-4 | |
| 88 | Вычислить | (4/3)÷(7/2) | |
| 89 | График | 2x-3y=6 | |
| 90 | График | x+2y=4 | |
| 91 | График | x=7 | |
| 92 | График | x-y=5 | |
| 93 | Решить, используя свойство квадратного корня | x^2+3x-10=0 | |
| 94 | Решить, используя свойство квадратного корня | x^2-2x-3=0 | |
| 95 | Найти площадь поверхности | конус (12)(9) | |
| 96 | Преобразовать в смешанную дробь | 3/10 | |
| 97 | Преобразовать в смешанную дробь | 7/20 | |
| 98 | Преобразовать в смешанную дробь | 2/8 | |
| 99 | Risolvere per w | V=lwh | |
| 100 | Упростить | 6/(5m)+3/(7m^2) | |
Как рассчитать медиану выборки?
Как рассчитать медиану выборки?
mediāna «середина») набора чисел — число, которое находится в середине этого набора, если его упорядочить по возрастанию. Таким образом, медиана — это такое число, что половина из элементов набора больше него, а другая половина меньше (строго говоря, это верно только если все элементы набора различны).
Таким образом, медиана — это такое число, что половина из элементов набора больше него, а другая половина меньше (строго говоря, это верно только если все элементы набора различны).
Что такое медиана и мода?
Мода (Mo) представляет собой значение изучаемого признака, повторяющееся с наибольшей частотой, т. … мода – значение признака, встречающееся чаще всего. Медианой (Me) называется значение признака, приходящееся на середину ранжированной (упорядоченной) совокупности, т.
Как найти медианное значение?
Онлайн калькулятор для нахождения медианы ряда чисел. Медианой (серединой) набора чисел называется число стоящее посередине упорядоченного по возрастанию ряда чисел. Если количество чисел в ряду чётное, то медианой ряда является полусумма двух стоящих посередине чисел.
Что такое медиана и ее свойства?
Медианой треугольника называют отрезок, соединяющий вершину треугольника с серединой противоположной стороны (рис 1). Поскольку в каждом треугольнике имеется три вершины, то в каждом треугольнике можно провести три медианы. … Медиана треугольника делит его на два треугольника равной площади (равновеликих треугольника).
Поскольку в каждом треугольнике имеется три вершины, то в каждом треугольнике можно провести три медианы. … Медиана треугольника делит его на два треугольника равной площади (равновеликих треугольника).
Что такое медиана в массиве?
Медиана массива. … такое значение, которое после сортировки массива A[1…n] будет равно: элементу A[n / 2 + 1], при нечетном n и (A[n / 2] + A[n / 2 + 1]) / 2.
Как найти длину медианы?
Длина медианы треугольника е. медиана треугольника равняется половине корня квадратного из удвоенной суммы квадратов двух сторон минус квадрат третьей стороны.
Как медиана делит угол?
Так давайте разбираться. На самом деле, медиана — это такой отрезок, который проведён из вершины к противоположной стороне, деля её при этом на два одинаковых отрезка. Как Вы можете увидеть, то медиана делит не угол пополам, а сторону, к которой проведена. А угол пополам будет делить биссектриса.
В каком отношении медианы делятся точкой пересечения?
Основное свойство Все три медианы треугольника пересекаются в одной точке, которая называется центроидом или центром тяжести треугольника, и делятся этой точкой на две части в отношении 2:1, считая от вершины.
В каком отношении делятся медианы равностороннего треугольника?
Вспоминаем, что медианы точкой пересечения делятся в отношении 2:1, считая от вершины.
Как вывести формулу медианы треугольника?
Длина медианы, проведенной к стороне треугольника равна половине корня квадратного из удвоенного произведения суммы квадратов двух других сторон минус квадрат этой стороны.
Что такое медиана в прямоугольном треугольнике?
Медиана прямоугольного треугольника, проведённая из вершины прямого угла, равна половине гипотенузы. Признак прямоугольного треугольника: Если в треугольнике медиана равна половине стороны, к которой она проведена, то такой треугольник является прямоугольным.
Чему равен катет лежащий против угла в 30 градусов?
Катет, лежащий против угла 30 градусов, равен половине гипотенузы.
Как найти медиану равностороннего треугольника?
Найти медиану биссектрису высоту равностороннего треугольника
- Формула для вычисления высоты = биссектрисы = медианы.
- В равностороннем треугольнике: все высоты, биссектрисы и медианы, равны. …
- L — высота=биссектриса=медиана
- a — сторона треугольника
Как доказать что треугольник прямоугольный по сторонам?
Так вот, прямоугольный треугольник обладает такими свойствами:
- Сумма квадратов катетов прямоугольного треугольника равна квадрату его гипотенузы
- Медиана прямоугольного треугольника равна половины гипотенузы
- сумма двух острых углов прямоугольного треугольника равна 90 градусов
Как узнать Остроугольный ли треугольник по сторонам?
Если квадрат наибольшей стороны меньше суммы квадратов двух других сторон: с² треугольник остроугольный. Если квадрат наибольшей стороны больше суммы квадратов двух других сторон: с² > a²+b² – треугольник тупоугольный.
Если квадрат наибольшей стороны больше суммы квадратов двух других сторон: с² > a²+b² – треугольник тупоугольный.
Как определить вид треугольника по его сторонам?
Поскольку всего три стороны, то можно составить три варианта сложения двух сторон: a + b , b + c , a + c . Первую сумму сравниваем с оставшейся стороной , вторую — с a и третью — с b . Если хотя бы в одном случае сумма окажется не больше третьей стороны, то делается вывод, что треугольник не существует.
Как определить прямоугольный треугольник или нет?
Прямоуго́льный треуго́льник — это треугольник, в котором один угол прямой (то есть 90 градусов). Соотношения между сторонами и углами прямоугольного треугольника лежат в основе тригонометрии.
Как отличить остроугольный треугольник от Тупоугольного?
Остроугольный треугольник — это треугольник, у которого все углы острые. Прямоугольный треугольник — это треугольник, у которого есть прямой угол. Тупоугольный треугольник — треугольник, все стороны которого есть тупой угол.
Тупоугольный треугольник — треугольник, все стороны которого есть тупой угол.
Как найти высоту в прямоугольном треугольнике?
Примеры решения задач
| Задание | В прямоугольном треугольнике катеты равны см и см. Найти высоту , опущенную на гипотенузу . |
|---|
| Решение | Пусть катет см, а см (рис. 2). Тогда по теореме Пифагора гипотенуза см Площадь прямоугольного треугольника равна половине произведения катетов, т.е. Высоту найдем по формуле |
| Ответ | см |
Как найти катет зная катет и угол?
Катет прямоугольного треугольника равен его гипотенузе, умноженной на синус противолежащего или на косинус прилежащего к этому катету угла. Катет равен другому катету, умноженному на тангенс противолежащего или котангенс прилежащего к первому катету угла.
Как найти длины катетов?
Она лежит напротив прямого угла. Длина гипотенузы может быть найдена различными способами. Если известна длина обоих катетов, то ее размер вычисляется по теореме Пифагора: сумма квадратов двух катетов равняется квадрату гипотенузы. К примеру: катет a = 3 см, катет b = 4 см.
Длина гипотенузы может быть найдена различными способами. Если известна длина обоих катетов, то ее размер вычисляется по теореме Пифагора: сумма квадратов двух катетов равняется квадрату гипотенузы. К примеру: катет a = 3 см, катет b = 4 см.
Как найти гипотенузу зная катет и угол между ними?
Найти можно через тригонометрическую функцию Sin или Cos угла. Так как Sin = противолежащий катет/гипотенуза, а Cos = прилежащий катет/гипотенуза, то если известный угол прилежащий к катету гипотенуза = 3/Cos40 = 3.
Как найти длину гипотенузы зная угол и катет?
Формула: sin=a/c, где а – катет, лежащий против данного угла, а с – гипотенуза. Далее преобразуем формулу и получаем: a=sin*c. Пример. Гипотенуза равна 10 см, угол А равен 30 градусов.
Как найти гипотенузу в прямоугольном треугольнике?
Гипотенуза (греч. ὑποτείνουσα, натянутая) — самая длинная сторона прямоугольного треугольника, противоположная прямому углу. Длина гипотенузы прямоугольного треугольника может быть найдена с помощью теоремы Пифагора: Квадрат длины гипотенузы равен сумме квадратов длин катетов.
Длина гипотенузы прямоугольного треугольника может быть найдена с помощью теоремы Пифагора: Квадрат длины гипотенузы равен сумме квадратов длин катетов.
Как найти гипотенузу в равнобедренном треугольнике?
Найти ее можно как квадратный корень из удвоенного произведения квадрата катета – это следствие из теоремы Пифагора и равенства катетов, как боковых сторон равнобедренного треугольника.
Как найти синус угла?
Чтобы найти синус и косинус угла в прямоугольном треугольнике, нужно вспомнить определения. Синус угла равен отношению противоположного катета к гипотенузе. Косинус угла равен отношению прилежащего катета к гипотенузе.
Среднее арифметическое чисел. Мода. Медиана. Размах ряда чисел – онлайн-тренажер для подготовки к ЕНТ, итоговой аттестации и ВОУД
Запомнить
Восстановить пароль
Регистрация
Конспект
Среднее арифметическое нескольких величин – это отношение суммы величин к их количеству.
Правило. Чтобы вычислить среднее арифметическое нескольких чисел, нужно взять сумму этих чисел и разделить все на количество слагаемых. Частное и будет средним арифметическим этих чисел.
Например: найдем среднее арифметическое чисел 2; 6; 9; 15.
У нас четыре числа, значит надо их сумму разделить на четыре. Это и будет среднее арифметическое данных чисел: (2 + 6 + 9 + 15) : 4 = 8.
Размах ряда чисел – это разность между наибольшим и наименьшим из этих чисел.
Например: найдем размах чисел 2; 5; 8; 12; 33.
Наибольшее число здесь – 33, наименьшее – 2. Значит, размах составляет 31, т. е.: 33 – 2 = 31.
Мода ряда чисел – это число, которое встречается в данном ряду чаще других.
Например: найдем моду ряда чисел 1; 7; 3; 8; 7; 12; 22; 7; 11; 22; 8.
Чаще всего в этом ряде чисел встречается число 7 (3 раза). Оно и является модой данного ряда чисел.
Медианой упорядоченного ряда чисел с нечетным числом членов называется число, записанное посередине, а медианой упорядоченного ряда чисел с четным числом членов называется среднее арифметическое двух чисел, записанных посередине.
Медианой произвольного ряда чисел называется медиана соответствующего упорядоченного ряда.
Например: в ряде чисел 2; 5; 9; 15; 21 медианой является число 9, находящееся посередине.
Найдем медиану в ряде чисел 4; 5; 7; 11; 13; 19.
Здесь четное количество чисел (6). Поэтому ищем не одно, а два числа, записанных посередине. Это числа 7 и 11. Находим среднее арифметическое этих чисел: (7 + 11) : 2 = 9. Число 9 является медианой данного ряда чисел.
Вопросы
В институте сдавали зачет по высшей математике. В группе было 10 человек, и они получили соответствующие оценки: 3; 5; 5; 4; 4; 4; 3; 2; 4; 5.
Какую оценку получали чаще всего? Каков средний балл сдавшей зачет группы?
Дан ряд чисел: 175; 172; 179; 171; 174; 170; 172; 169.
Найдите медиану и размах ряда.
Дан ряд чисел: 175; 172; 179; 171; 174; 170; 172; 169.
Найдите моду ряда и среднее арифметическое ряда.
Имеются следующие данные о месячной заработной плате пяти рабочих (тг): 126000; 138000; 132000; 141000; 150000.
Найдите среднюю заработную плату.
Магазин продает 8 видов булочек по следующим ценам: 31; 22; 24; 27; 30; 36; 19; 27.
Найдите разность среднего арифметического и медианы этого набора.
Найдите объем и медиану числового ряда.
9; 7; 1; 1; 11; 5; 1.
Товарные запасы хлопчатобумажных тканей в магазине за первое полугодие составили (тыс. тг) на начало каждого месяца:
тг) на начало каждого месяца:
| I |
II |
III |
IV |
V |
VI |
VII |
|---|
| 37 |
34 |
35 |
32 |
36 |
33 |
38 |
|---|
Определите средний товарный запас хлопчатобумажных тканей за первое полугодие.
Провели несколько измерений случайной величины: 2,5; 2,2; 2; 2,4; 2,9; 1,8.
Найдите среднее арифметическое этого набора чисел.
Провели несколько измерений случайной величины: 6; 18; 17; 14; 4; 22.
Найдите медиану этого набора чисел.
Провели несколько измерений случайной величины:
800; 3200; 2000; 2600; 2900; 2000. Найдите моду этого набора чисел.
-
Магазин продает 8 видов хлеба по следующим ценам: 60, 75, 80, 85, 90, 100, 110, 120 тенге.
Найдите разность среднего арифметического и медианы этого набора.
-
Дан числовой ряд: 1; 7; 3; 8; 7; 12; 22; 7; 11; 22; 7,8.
Найдите среднее арифметическое, размах и моду.
Сообщить об ошибке
Инструмент для работы с графами онлайн
Визуализация графа, поиск кратчайшего пути и многое другое. В разделе Справка вы найдете обучающие видео.
В разделе Справка вы найдете обучающие видео.
Graph
Создание алгоритмы
Вставьте ваш алгоритм ниже и нажмите «Выполнить»
Задайте матрицу смежности. Используйте запятую «,» в качестве разделителя
Для мультиграфа матрица содержит значения минимальных дуг между вершинами.
Мартрица имеет неправильный формат. Используйте запятую «,» в качестве разделителя. Матрица должна иметь одинаковое количество столбцов и строк.
Задайте матрицу инцидентности. Используйте запятую «,» в качестве разделителя
Мартрица имеет неправильный формат. Используйте запятую «,» в качестве разделителя.
Ваш алгоритм отправлен на модерацию и в случае успеха он будет добавлен на сайт.
Ошибка создания графа. Матрица смежности имеет неправильный формат. Нажимте кнопку «исправить матрицу» чтобы исправить матрицу или кнопку «справка» чтобы открыть справку о формате матрицы
Нажимте кнопку «исправить матрицу» чтобы исправить матрицу или кнопку «справка» чтобы открыть справку о формате матрицы
Ошибка создания графа. Матрица инцидентности имеет неправильный формат. Нажимте кнопку «исправить матрицу» чтобы исправить матрицу или кнопку «справка» чтобы открыть справку о формате матрицы
Какие функции нам добавить в первую очередь?
Пожалуйста, напишите, какого алгоритма вам не хватает. Поддержвать проект.
Сервис уже поддерживает следущий функционал: Поиск пути алгоритмом Дейкстры, матрицу смежности, матрицу инцидентности.
Прозрачность
Выделите и перемещайте объекты или перемещайте рабочую область.
Перемещайте курсор для перемещения объекта
Выделите и перемещайте объекты или перемещайте рабочую область.
Перемещайте курсор для перемещения объекта
Кликните на рабочую область, чтобы добавить вершину. Нумерация вершин
Выделите первую вершину для создания дуги
Выделите вторую вершину, которую хотите соединить
Выделите вершину, из которой хотите найти кратчайших путь
Выделите конечную вершину кратчайшего пути
Расстояние между вершинами %d
Пути не существует
Кликните по объекту, который хотите удалить
Добавить ребро
Ориентированную
Неориентированную
Матрица смежности
Сохранить
Отмена
Мин. расстояние =
Матрица инцидентности
Сохранение графа
закрыть
Число компонентов связности графа равно
Число слабо связных компонентов равно
Что вы думаете о сайте?
Имя (email для ответа)
Написать
Отправить
Напишите нам
исправить матрицу
справка
Матрица имеет неправильный формат
Сохранение изображения графа
Полный отчёт
Краткий отчёт
Граф не содержит Эйлеров цикл
Граф содержит Эйлеров цикл
Обработка. ..
..
Добавить вершину
Переименовать вершину
Переименовать
ru
Изменить вес
ненагруженный
Групповое переименование
Опрос
Рекомендовать алгоритмы
Граф не содержит Эйлерову цепь
Граф содержит Эйлерову цепь
Граф минимальных расстояний.
Нажмите для сохранения
Показать матрицу расстояний
Матрица расстояний
Выделите исток максимального потока
Выделите сток максимального потока
Максимальный поток из %2 в %3 равен %1
Поток из %1 в %2 не существует
Исток
Сток
Граф не содержит Гамильтонов цикл
Граф содержит Гамильтонов цикл
Граф не содержит Гамильтонову цепь
Граф содержит Гамильтонову цепь
Выбирете начальную вершину обхода
Порядок обхода:
Изгиб дуги
Отменить
Сохранить граф
По умолчанию
Стиль отрисовки вершины
Стиль отрисовки дуги
Цвет фона
Мультиграф не поддерживает все алгоритмы
ненагруженный
Выделите несколько объектов используя Cmd⌘.
Выделите несколько объектов используя Ctrl.
Перемещайте группу.
Копировать
Удалить
Поиск в ширину
Раскраска графа
Найти компоненты связности
Поиск в глубину
Найти Эйлеров цикл
Найти Эйлерову цепь
Алгоритм Флойда — Уоршелла
Упорядочить граф
Найти Гамильтонов цикл
Найти Гамильтонову цепь
Поиск максимального потока
Поиск минимального остовного дерева
Визуализация на основе весов
Поиск радиуса и диаметра графа
Поиск кратчайший путь алгоритмом Дейкстры
Рассчитать степень вершин
Вес минимального остовного дерева равен
Мы игнорировали ориентацию дуг при рассчете.
Граф не является связным
Выделите первый граф для проверки на изоморфизм. Кликните по любой вершине графа
Выделите второй граф для проверки на изоморфизм. Кликните по любой вершине графа
Кликните по любой вершине графа
Выделите граф, которому должны быть изоморфны подграфов. Кликните по любой вершине графа
Выделите граф в котором необходимо найти изоморфные подграфы. Кликните по любой вершине графа
Графы изоморфны
Графы не изоморфны
Количество изоморфных подграфов равно
Граф не содержит изоморфных подграфов
Поиск изоморфных подграфов
Изоморфных подграф №
Для использования алгоритма необходимо создать хотя бы 2 не связных графа
Проверка изоморфности графов
Граф не является связным
Граф содержит только одну вершину
Радиус графа
Диаметр графа
Центральная
Периферийная
Максимальная степень вершин графа равна
Найденное количество цветов
Готово
Действия
Стиль обычной дуги
Стиль выделенной дуги
Стиль обычной вершины
Стиль выделенной вершины
Поиск всех путей
Количество путей из
в
равно
Путь №
Выделите конечную вершину
Выделите начальную вершину
Найти все кратчайшие пути от вершины
Расстояние от
Путь до
Поиск самого длинного пути
Длина самого длинного пути ровна
Особые действия
Поменять направление всех дуг
Сделать все дуги неориентированными
Сделать все дуги ориентированными
Структурные средние — мода, медиана, квартиль, дециль.

Решение задач и контрольных работ по статистике онлайн
Краткая теория
Наиболее широкое применение в статистике имеют структурные
средние, к числу которых относятся мода и медиана (непараметрические средние).
Мода — величина признака (варианта), которая
встречается в ряду распределения с наибольшей частотой (весом). К моде (Мо)
прибегают для выявления величины признака, имеющей наибольшее распространение
(цена на рынке, по которой было совершено наибольшее число продаж данного
товара, номер обуви, который пользуется наибольшим спросом у покупателей и т.
д.). Мода используется только в совокупностях большой численности. В дискретном
ряду мода находится как варианта, имеющая наибольшую частоту. В интервальном
ряду сначала находится модальный интервал, то есть интервал, обладающий наибольшей частотой, а
затем – приближенное значение модальной величины признака по формуле:
– нижняя граница модального интервала
— величина модального интервала
– частота интервала, предшествующего
модальному
– частота модального интервала
– частота интервала, следующего за модальным
Квантили -
величины, разделяющие совокупность на определенной количество равных по
численности элементов частей. Самый известный квантиль – медиана, делящая совокупность на две равные части. Кроме медианы часто используются квартили, делящие ранжированный ряд на 4 равные части, децили -10 частей и перцентили — на 100
частей.
Самый известный квантиль – медиана, делящая совокупность на две равные части. Кроме медианы часто используются квартили, делящие ранжированный ряд на 4 равные части, децили -10 частей и перцентили — на 100
частей.
Медиана -
величина признака у единицы, находящейся в середине ранжированного
(упорядоченного) ряда. Если ряд распределения представлен конкретными
значениями признака, то медиана (Me) находится как
серединное значение признака.
Если ряд распределения дискретный, то медиана находится как
серединное значение признака (например, если число значений нечетное – 45, то
соответствует 23 значению признака в ряду
значений, расположенных в порядке возрастания, если число значений четное – 44,
то медиана соответствует полусумме 22 и 23 значений
признака).
Если ряд распределения интервальный, то первоначально
находят медианный интервал, который содержит единицу, находящуюся в середине
ранжированного ряда. Для определения этого интервала сумму частот
делят пополам и на основании последовательного накопления (суммирования)
частот интервалов, начиная с первого, находят интервал, где расположена
медиана. Значение медианы в интервальном ряду вычисляют по формуле:
Для определения этого интервала сумму частот
делят пополам и на основании последовательного накопления (суммирования)
частот интервалов, начиная с первого, находят интервал, где расположена
медиана. Значение медианы в интервальном ряду вычисляют по формуле:
— нижняя граница медианного интервала
— величина медианного интервала
— сумма
частот ряда
– сумма накопленных частот в интервалах,
предшествующих медианному
– частота медианного интервала
Квартили — это значения
признака в ранжированном ряду, выбранные таким образом, что 25% единиц
совокупности будут меньше величины
, 25% единиц будут заключены между
и
; 25% -
между
и
,
остальные 25% превосходят
. Квартили определяются по формулам,
аналогичным формуле для расчета медианы. Для интервального ряда:
Для интервального ряда:
Децилем
называется структурная переменная, делящая распределение на 10 равных частей по
числу единиц в совокупности. Децилей 9, а децильных
групп 10. Децили определяются по формулам, аналогичным формуле для расчета
медианы и квартилей.
В целом общая формула для расчета квантилей в интервальном
ряду такова:
– порядковый номер квантиля
– размерность квантиля (на сколько частей эти
квартили делят совокупность)
– нижняя граница квантильного
интервала
– ширина квантильного
интервала
— накопленная частота предквантильного
интервала
Для дискретного ряда номер квантиля можно
найти по формуле:
Примеры решения задач
Задача 1
(дискретный ранжированный ряд)
В
результате исследований установлен среднемесячный доход жильцов одного
подъезда:
|
1. 5 5
|
1.8
|
2
|
2.5
|
2.8
|
2.8
|
2.8
|
3.0
|
3.6
|
3.8
|
|
3.9
|
4
|
5.8
|
5.9
|
6
|
6
|
6
|
6.8
|
7
|
7
|
Определите:
Модальный
и медианный доход, квартили и децили дохода.
Решение
Имеем уже ранжированный ряд — значения дохода жильцов распределены по возрастанию.
Мода
— наиболее часто встречающееся значение. В данном случае имеем ряд с двумя
модами.
и
Медиана
— такое значение признака, которое делит упорядоченное множество данных
пополам.
Квартили
— значения признака в ранжированном ряду, выбранные таким образом, что 25%
единиц совокупности будут меньше величины
; 25% единиц будут
заключены между
и
; 25% — между
и
; остальные 25%
превосходят
.
Дицили делят ряд на 10 равных частей:
Если не находите примера, аналогичного вашему, если сами не успеваете выполнить работу, если впереди экзамен по предмету и нужна помощь — свяжитесь со мной:
ВКонтакте
WhatsApp
Telegram
Я буду работать с вами, над вашей проблемой, пока она не решится.
Задача 2
(интервальный ряд)
Для
определения среднего размера вклада в кредитном учреждении были получены
следующие данные:
|
Размер вклада, тыс.р.
|
до 10.0
|
10.0-16.0
|
16.0-22.0
|
22.0-28.0
|
28.0-34.0
|
Свыше 34.0
|
|
Удельный вес
вкладов, %
|
5.0
|
8.0
|
15.0
|
22.0
|
30.0
|
20.0
|
Рассчитайте
структурные средние (моду, медиану,
квартили).
Решение
Вычислим моду размера вклада:
Мода — варианта, которой соответствует наибольшая частота.
Мода вычисляется по формуле:
-
начало модального интервала
-
величина интервала
-
частота модального интервала
-
частота интервала, предшествующего модальному
-
частота интервала, следующего за модальным
Таким образом, наибольшее
количество вкладов имеют размер 30,7 тыс.р.
Медиана — варианта, находящаяся в середине ряда распределения.
Расчет медианы производится по формуле:
-начало
(нижняя граница) медианного интервала
-величина интервала
-сумма всех частот ряда
-частота медианного интервала
-сумма накопленных частот вариантов до
медианного
Таким образом, половина вкладов имеет размер до 28 тыс. р.,
другая половина — более 28 тыс.р.
р.,
другая половина — более 28 тыс.р.
Вычислим квартили:
Таким
образом 25% вкладов меньше 20,8 тыс.р., 25% вкладов
лежат в интервале от 20,8 тыс.р. до 28 тыс.р., 25% лежат в интервале от 28 тыс.р.
до 33 тыс.р., 25% больше величины в 33 тыс.р.
Задача 3
Постройте
графики для вариационного ряда. На графике покажите моду, медиану, среднюю, квартили.
|
Возраст детей (лет)
|
Число детей (доли)
|
|
0-3
|
0.15
|
|
3-6
|
0.2
|
|
6-9
|
0.4
|
|
9-12
|
0. 2 2
|
|
12-15
|
0.05
|
Решение
Вычислим
среднюю
: Для этого просуммируем
произведения середин интервалов и соответствующих частот, и полученную сумму
разделим на сумму частот.
Вычисление моды интервального ряда на графике
Построим
гистограмму.
Мода определяется по
гистограмме распределения. Для этого выбирается самый высокий прямоугольник,
который в данном случае является модальным. Затем правую вершину модального
прямоугольника соединяют с правым верхним углом предыдущего прямоугольника. А
левую вершину модального прямоугольника – с левым верхним углом последующего
прямоугольника. Далее из точки их пересечения опускают перпендикуляр на ось
абсцисс.
Абсцисса точки пересечения
этих прямых и будет модой распределения
Гистограмма
По
гистограмме получаем, что
Вычисление медианы и квартилей интервального ряда на графике
Построим
кумулятивную кривую частот (график накопленных частот)
|
|
0-3
|
3-6
|
6-9
|
9-12
|
12-15
|
|
|
0. 15 15
|
0.35
|
0.75
|
0.95
|
1
|
Кумулятивная кривая частот
На получившимся графике
накопленных частот из последней получившейся точки (в нашем примере) проведем
линию перпендикулярную к оси
она так же
является максимальной высотой. Поделим ее на 4 части. Через полученные точки
строим параллельную оси
линии которая должна пересекать высоту к оси
и кумуляту. От
места пересечения кумуляты опускаем перпендикуляры. Получившиеся точки есть квартили
и медиана (квартиль при
).
Вывод к задаче
Таким образом
средний возраст детей 6,9 лет. Наибольшее количество детей имеют возраст 7,5
лет. Четверть детей младше 4,5 лет, а самая старшая четверть детей старше 9,1
лет. Половина детей имеет возраст менее 7,3 лет, другая половина – более 7,3
лет.
Половина детей имеет возраст менее 7,3 лет, другая половина – более 7,3
лет.
Новые приключения медианы йодурии | Герасимов
С начала 1990-х почти до конца нулевых годов отечественная тиреоидология развивалась под знаком “медианы йодурии”. Появление доступных методик, таких как определение концентрации йода в моче (КЙМ) и оценка объема щитовидной железы (ЩЖ) с помощью ультразвукового сканирования (УЗИ), помноженное на бескрайние просторы России, открыло невозделанное поле для эпидемиологических исследований. Аналогичные процессы происходили и в других частях света, и, применяя марксистскую терминологию, происходящее в то время можно было бы назвать “первоначальным накоплением капитала”, если под капиталом понимать новые знания о природе и распространенности йодного дефицита.
Опять же в силу бескрайности просторов Россия остается одной из немногих стран в мире, в которых в течение последних 25 лет не было проведено общенационального исследования распространенности йодного дефицита. Вместо этого во многих регионах страны были выполнены (иногда неоднократно) автономные проекты, включающие исследование КЙМ у школьников (реже – у других групп населения) с расчетом медианной КЙМ (мКЙМ) или, просто говоря, “медианы йодурии”. Несмотря на недостатки такого подхода (отсутствие единых критериев выбора кластеров и целевых групп населения), уже к началу нулевых годов исследования были проведены во всех федеральных округах и большинстве крупных регионов и показали, что практически на всей территории Российской Федерации потребление йода было недостаточным [1]. Снижение мКЙМ выявили даже там, где его меньше всего ожидали, – на берегу Черного моря и у жителей острова Сахалин, за исключением небольшой популяции корейцев, традиционно использующих в питании много морепродуктов и морских водорослей.
Вместо этого во многих регионах страны были выполнены (иногда неоднократно) автономные проекты, включающие исследование КЙМ у школьников (реже – у других групп населения) с расчетом медианной КЙМ (мКЙМ) или, просто говоря, “медианы йодурии”. Несмотря на недостатки такого подхода (отсутствие единых критериев выбора кластеров и целевых групп населения), уже к началу нулевых годов исследования были проведены во всех федеральных округах и большинстве крупных регионов и показали, что практически на всей территории Российской Федерации потребление йода было недостаточным [1]. Снижение мКЙМ выявили даже там, где его меньше всего ожидали, – на берегу Черного моря и у жителей острова Сахалин, за исключением небольшой популяции корейцев, традиционно использующих в питании много морепродуктов и морских водорослей.
Наиболее тяжелый йодный дефицит был выявлен в Туве, где среди воспитанников интернатов и домов ребенка были обнаружены недавние случаи йододефицитного кретинизма, а мКЙМ была ниже 20 мкг/л. В отличие от ряда других стран (например, Китая) только в одном населенном пункте России (г. Туринске Свердловской области) был выявлен природный избыток йода в питьевой воде, а мКЙМ у школьников составила 719 мкг/л, что было примерно в 6 раз выше, чем в соседнем городе [2].
В отличие от ряда других стран (например, Китая) только в одном населенном пункте России (г. Туринске Свердловской области) был выявлен природный избыток йода в питьевой воде, а мКЙМ у школьников составила 719 мкг/л, что было примерно в 6 раз выше, чем в соседнем городе [2].
Не обошлось и без “перегибов на местах”, что понудило тогдашнего научного редактора журнала “Проблемы эндокринологии” профессора В. Фадеева еще в 2003 г. открыть дискуссию на сайте “Тиронет”1 под названием “Медиана йодурии от измученного редактора” и начать ее словами: “Люди, опомнитесь!!!” Возможно, что нервный срыв был вызван чтением подобного рода текста: “Продолжающееся воздействие антропоэкологического напряжения может закончиться переходом нейроэндокринных гомеостатических систем организма на новый биоэнергетический уровень, который выражается в изменении состояния здоровья, характеризующегося как преморбидное состояние или хронизация негативных процессов” [3].
Также возникли сложности с интерпретацией выявленных в процессе эпидемиологических исследований расхождений степени выраженности йодного дефицита по показателям мКЙМ по отношению к частоте зоба по данным УЗИ. Часто получалось, что мКЙМ у школьников на фоне проводимых профилактических мероприятий возрастала до оптимальных показателей, в то время как частота зоба если и снижалась, то ненамного и оставалась выше эндемического порога в 5%.
Часто получалось, что мКЙМ у школьников на фоне проводимых профилактических мероприятий возрастала до оптимальных показателей, в то время как частота зоба если и снижалась, то ненамного и оставалась выше эндемического порога в 5%.
В статьях весьма авторитетных специалистов стали появляться утверждения, что “проведение йодной профилактики снижает напряженность зобной эндемии, но не ликвидирует ее полностью”. Что существуют некие таинственные “экопатогены”, которые “крайне неблагоприятно влияют на функцию щитовидной железы и тем самым способствуют формированию зоба”, “а в генезе зоба в большинстве регионов России в настоящее время помимо дефицита йода существенную роль играют и другие зобогенные факторы, в основном экопатогены”. При этом “в тех случаях, когда в генезе зоба ведущую роль играют экопатогены, а не дефицит йода, лечение йодсодержащими препаратами неэффективно”. В ответ я посвятил пару статей разбору этих явных и надуманных проблем [4, 5].
Нельзя не признать, что ранние руководства помониторингу йодного дефицита, выпущенные под эгидой ВОЗ, ЮНИСЕФ и Глобальной сети по йоду2 (ГСЙ), перечисляли индикаторы оценки йодного дефицита, как говорится, “через запятую”, не оценивая приоритетность и информативность тех или иных методов. У некоторых исследователей даже возникало впечатление, что для исследования йодного статуса населения необходимо применять всю батарею индикаторов (частоту зоба, экскрецию йода с мочой, уровень тиреоглобулина в крови и частоту повышения более 3% уровней неонатального тиреотропного гормона (ТТГ) свыше 5 мИЕ/л). Только в самой последней редакции руководства ВОЗ, ЮНИСЕФ и ГСЙ [6], выпущенной в 2007 г., приоритетным и наиболее информативным методом оценки текущего статуса йодной обеспеченности населения было названо определение йода в моче.
У некоторых исследователей даже возникало впечатление, что для исследования йодного статуса населения необходимо применять всю батарею индикаторов (частоту зоба, экскрецию йода с мочой, уровень тиреоглобулина в крови и частоту повышения более 3% уровней неонатального тиреотропного гормона (ТТГ) свыше 5 мИЕ/л). Только в самой последней редакции руководства ВОЗ, ЮНИСЕФ и ГСЙ [6], выпущенной в 2007 г., приоритетным и наиболее информативным методом оценки текущего статуса йодной обеспеченности населения было названо определение йода в моче.
Однако с момента выпуска руководства [6] прошло более 10 лет, и возникла необходимость дать обновленные рекомендации, основанные на опыте и ошибках последних 10–15 лет. У читателя не должно возникнуть впечатления, что проблемы с “медианой йодурии” возникали только в российских исследованиях; они, увы, носили массовый характер. Поэтому в ЮНИСЕФ было проведено техническое консультативное совещание по мониторингу программ йодирования соли, по результатам которого были подготовлены рекомендации [7], опубликованные в 2018 г. С любезного согласия д-ра Р. Купки, советника по микронутриентам штаб-квартиры ЮНИСЕФ в Нью-Йорке, наш журнал опубликовал в этом номере перевод данных рекомендаций с небольшой редакторской адаптацией [8].
С любезного согласия д-ра Р. Купки, советника по микронутриентам штаб-квартиры ЮНИСЕФ в Нью-Йорке, наш журнал опубликовал в этом номере перевод данных рекомендаций с небольшой редакторской адаптацией [8].
Естественно, в этой колонке я не буду пересказывать содержание рекомендаций, но попытаюсь остановиться на некоторых моментах, наиболее, на мой взгляд, интересных для читателей тиреоидологического журнала.
Начну с того, чему в рекомендациях уделено всего несколько строчек, но что может быть важным для эндокринологов, которые в России являются наиболее преданными сторонниками программ йодной профилактики. А сказано там буквально следующее: оценка распространенности зоба (с использованием УЗИ, а тем более пальпации) в эпидемиологических исследованиях не является надежным индикатором статуса йодного потребления. При этом показатели объема ЩЖ и распространенности зоба оказались нечувствительными к быстрым изменениям уровня потребления йода3. Также имела место существенная субъективность при оценке зобов небольшого размера даже при использовании УЗИ. Все это не новости. Новость в том, что впервые четко сформулирована рекомендация прекратить исследование распространенности зоба при рутинных обследованиях статуса йодной обеспеченности населения, отдавая предпочтение анализу показателей мКЙМ, являющейся наилучшим индикатором потребления йода с питанием.
Все это не новости. Новость в том, что впервые четко сформулирована рекомендация прекратить исследование распространенности зоба при рутинных обследованиях статуса йодной обеспеченности населения, отдавая предпочтение анализу показателей мКЙМ, являющейся наилучшим индикатором потребления йода с питанием.
Ни в коем случае нельзя понимать эту рекомендацию как запрет ученым изучать состояние ЩЖ при различном йодном статусе населения. Речь идет именно о рутинных исследованиях, проводимых в странах и регионах с определенными интервалами для мониторинга программ йодной профилактики.
В новых рекомендациях [7] впервые четко указано, что обследования на базе школ для оценки статуса йодной обеспеченности населения имеют определенные ограничения по дизайну. Выбор школьников как целевой группы был обусловлен в первую очередь относительной простотой сбора материала (образцов соли и мочи для определения йода) в учебных заведениях по сравнению с домохозяйствами. Показатели мКЙМ у школьников достаточно точно отражают степень обеспеченности йодом общей популяции (general population), но не беременных и кормящих женщин, потребность в йоде у которых повышена.
Например, в принятой к публикации в следующем номере журнала статье из Беларуси показано, что мКЙМ у школьников (общенациональная когорта из 873 детей) составляла 191 мкг/л, ровно посередине диапазона от 100 до 300 мкг/л, что свидетельствует об оптимальном уровне йодной обеспеченности общей популяции. Вместе с тем мКЙМ у беременных женщин (121 мкг/л; общенациональная когорта из 700 женщин) указывает на неадекватный статус йодной обеспеченности: оптимальный диапазон составляет 150–250 мкг/л [9]. Это нередкая ситуация: две трети европейских стран, в которых были проведены обследования, сообщили о неадекватном йодном обеспечении беременных. При этом мКЙМ могла быть оптимальной в общей популяции [10].
Школьные обследования также могут неточно отражать йодный статус всего населения в странах или регионах, где действуют широкомасштабные программы школьного питания (с использованием йодированной соли или иных йодных добавок). Это имеет прямое отношение к России: при скудости профилактических мер для преодоления йодной недостаточности именно школьники чаще всего получают обогащенные йодом хлеб и другие продукты в рамках программ питания организованных коллективов. И если в уездном городе N мКЙМ у школьников оптимальная, это может не отражать статус йодной обеспеченности у остальных обывателей, не охваченных заботой государства российского.
И если в уездном городе N мКЙМ у школьников оптимальная, это может не отражать статус йодной обеспеченности у остальных обывателей, не охваченных заботой государства российского.
Новые рекомендации [7] также расширяют диапазон мКЙМ, указывающий на адекватное потребление йода у школьников, с 100–199 до 100–299 мкг/л. При этом осталась неизменной интерпретация мКЙМ более 300 мкг/л как “избыточное” потребление йода у школьников. Согласно прежнему руководству [6], существовал отдельный диапазон мКЙМ от 200 до 299 мкг/л, именованный как “более чем адекватное” потребление йода. Это вызывало вопросы и недоумение: чем “более чем адекватное” потребление йода отличается от “избыточного”? Ответ дало большое многонациональное исследование функции щитовидной железы у детей в зависимости от величины потребления йода, поведенное в 2013 г. Оно показало отсутствие дисфункции щитовидной железы у школьников при мКЙМ в диапазоне 100–299 мкг/л [11].
Нужно иметь в виду, что, по мнению составителей новых рекомендаций [7], расширение адекватного диапазона мКЙМ у школьников не должно распространяться на женщин репродуктивного возраста и вообще взрослых лиц. По мнению ведущих специалистов4 , диапазоны мКЙМ у детей в целом должны с определенной осторожностью распространяться на взрослых лиц, нормативы для которых пока еще не разработаны.
По мнению ведущих специалистов4 , диапазоны мКЙМ у детей в целом должны с определенной осторожностью распространяться на взрослых лиц, нормативы для которых пока еще не разработаны.
Таким образом, мКЙМ является наилучшим индикатором статуса йодной обеспеченности населения, а мКЙМ у школьников в диапазоне от 100 до 299 мкг/л указывает на отсутствие дефицита йода в общей популяции. Типичной ошибкой, указанной в рекомендациях [7], является представление о том, что лица с КЙМ <100 мкг/л имеют дефицит йода. Потребление йода с питанием и, следовательно, КЙМ являются очень вариабельными изо дня в день (особенно при анализе уровня йода в разовой порции мочи). Даже у лиц, среднее потребление йода у которых достаточно для поддержания нормальной функции ЩЖ, могут случаться отдельные дни и часы, когда КЙМ снижается до <100 мкг/л. В результате в популяциях с адекватным потреблением йода всегда будут встречаться показатели КЙМ <100 мкг/л. Вместе с тем эти показатели не являются индикативными для оценки распространенности дефицита йода среди населения. Об этом писали уже не раз, но ошибки в интерпретации данных носили массовый характер.
Об этом писали уже не раз, но ошибки в интерпретации данных носили массовый характер.
Отчасти такая трактовка данных объясняется тем, что бюрократам в органах здравоохранения (не исключая ВОЗ!) не очень понятна суть “медианы йодурии”. Им нужны конкретные цифры “больных” и “здоровых”. Когда в качестве основного индикатора для оценки выраженности йодного дефицита использовалась заболеваемость или распространенность зоба, то все было в порядке. А как интерпретировать “медиану йодурии”? Вот и стали “больными” считать тех, у кого КЙМ при эпидемиологических исследованиях была <100 мкг/л.
Например, мКЙМ в 122 мкг/л, полученная при обследовании общенациональной репрезентативной когорты школьников в Швейцарии, указывает на отсутствие йодного дефицита в общей популяции этой замечательной страны. Неправильно интерпретировать долю образцов мочи с уровнем йода <100 мкг/л (в приведенном выше примере таковых было 40%) как процент населения с йодным дефицитом. В равной мере 10% школьников с мКЙМ ≥300 мкг/л нельзя интерпретировать как долю населения, якобы имеющего избыточное потребление йода.
Следует сказать, что в настоящее время ведется активный поиск новых методических подходов к тому, как использовать показатели КЙМ для определения доли лиц в популяции с дефицитом и избытком йода. В двух больших обследованиях, проведенных в Армении и Грузии в 2016–2017 гг., были впервые использованы оригинальные подходы для расчета не только мКЙМ, но и суточных показателей поступления йода с питанием, что позволяло вычислить долю лиц с низким и высоким потреблением йода [12]. Но эта тема выходит за рамки настоящей публикации и требует отдельного разговора.
В начале этой колонки я предположил, что эра “медианы йодурии” в отечественной тиреоидологии закончилась в конце нулевых годов. А после наступил естественный спад интереса к проблеме. Какой смысл повторных обследований йодной обеспеченности населения, если профилактические мероприятия в основном носят формальный характер? Определенным разочарованием была неспособность правительственных органов и Государственной Думы в течение уже более 15 лет принять закон, регулирующий (даже в ограниченном масштабе) обязательное йодирование соли.
В недавно опубликованной статье [13] сотрудники НМИЦ эндокринологии Минздрава России проанализировали показатели заболеваемости и распространенности отдельных форм йододефицитных заболеваний у детей (0–14 лет), подростков (15–17 лет) и взрослых лиц (старше 18 лет) за период с 2009 по 2015 г.
Результаты были вполне ожидаемыми: заболеваемость эндемическим и другими формами нетоксического зоба детей за изученный период возросла с 41,4 до 44,2 случаев, а взрослых – с 910,5 до 978,4 случаев на 100 тыс. населения. При этом заболеваемость зобом у подростков несколько снизилась (может быть, сказался эффект использования йодированной соли в школьном питании?). Также был отмечен существенный рост заболеваемости и распространенности субклинического гипотиреоза во всех возрастных группах. Даже признавая несовершенство приведенной выше статистики, рассчитанной по данным обращаемости населения в медицинские учреждения, можно сделать вывод о фактическом провале системы профилактики йодного дефицита в стране.
Скажу прямо: сегодня я не вижу необходимости возобновления широкомасштабных полевых эпидемиологических исследований статуса йодной обеспеченности населения России (как на национальном, так и региональном уровне). Вернуться к “медиане йодурии” можно только после того, как будут приняты законодательные акты, регламентирующие эффективные мероприятия по использованию йодированной соли в хлебопекарной промышленности, общественном питании и повышению ее доступности в розничной торговле.
Но и сидеть сложа руки тоже неправильно: нужно внедрять методы оценки, практически не требующие дополнительных затрат. Например, одним из перспективных индикаторов оценки статуса йодной обеспеченности является частота повышения уровня неонатального ТТГ свыше 5 мМЕ/л. Согласно руководству [6], при оптимальном статусе йодной обеспеченности частота случаев увеличения ТТГ свыше 5 мМЕ/л не должна превышать 3%.
За последние годы в России была создана эффективная система скрининга новорожденных на врожденный гипотиреоз (ВГ). В 2015 г. такой скрининг проводился в 85 субъектах Федерации, а доля охвата новорожденных скринингом составила 99,1% [14]. Учитывая то, что все лаборатории уже имеют базы данных по уровню ТТГ у новорожденных, на мой взгляд, не должно возникнуть существенных проблем с расчетом процентной доли уровней ТТГ в крови свыше 5 мМЕ/л. По крайней мере, такие наблюдения в течение уже более 20 лет проводят в Тюменской области. И за этот период времени частота неонатального ТТГ снизилась с 44% в 1993 г. до 5,0–5,4% в 2013–2015 гг. [15].
В 2015 г. такой скрининг проводился в 85 субъектах Федерации, а доля охвата новорожденных скринингом составила 99,1% [14]. Учитывая то, что все лаборатории уже имеют базы данных по уровню ТТГ у новорожденных, на мой взгляд, не должно возникнуть существенных проблем с расчетом процентной доли уровней ТТГ в крови свыше 5 мМЕ/л. По крайней мере, такие наблюдения в течение уже более 20 лет проводят в Тюменской области. И за этот период времени частота неонатального ТТГ снизилась с 44% в 1993 г. до 5,0–5,4% в 2013–2015 гг. [15].
Однако использование данных скрининга ВГ для целей мониторинга йодной обеспеченности имеет свои ограничения. Хотя неонатальный ТТГ полезен для выявления умеренной и тяжелой степени дефицита йода, его следует с осторожностью рекомендовать для оценки в регионах с оптимальным йодным обеспечением и при легком йодном дефиците. В статье из Грузии, опубликованной в этом же номере [16] , было показано, что частота повышения уровня ТТГ >5 мМЕ/л у новорожденных уменьшилась с 4,46% в 2009 г. до 3,5% в 2015 г. Однако только в г. Тбилиси частота ТТГ >5 мМЕ/л была ниже 3% – уровня отсечения для адекватного обеспечения питания йодом. В других регионах страны (Западная и Восточная Грузия) частота ТТГ >5 мМЕ/л составляла 3,8 и 4,4% соответственно, что можно было бы ошибочно интерпретировать как легкий дефицит йода. На самом деле, по данным общенационального репрезентативного обследования, проведенного в 2017 г., мКЙМ у беременных женщин составляла 211 мкг/л, а у школьников – 298 мкг/л [12].
до 3,5% в 2015 г. Однако только в г. Тбилиси частота ТТГ >5 мМЕ/л была ниже 3% – уровня отсечения для адекватного обеспечения питания йодом. В других регионах страны (Западная и Восточная Грузия) частота ТТГ >5 мМЕ/л составляла 3,8 и 4,4% соответственно, что можно было бы ошибочно интерпретировать как легкий дефицит йода. На самом деле, по данным общенационального репрезентативного обследования, проведенного в 2017 г., мКЙМ у беременных женщин составляла 211 мкг/л, а у школьников – 298 мкг/л [12].
Возможной причиной повышения частоты ТТГ >5 мМЕ/л было то, что в национальную когорту новорожденных в Грузии входили недоношенные дети. Кроме того, у какой-то части детей кровь для анализа ТТГ собрали вне рекомендованного периода (2–5 дней после родов) из-за быстрой выписки родильниц из медицинского учреждения. Исключение из общей когорты упомянутых групп новорожденных, у которых чаще встречается транзиторная гипертиротропинемия, по данным пока не опубликованного исследования, проведенного в Армении, снижало частоту ТТГ >5 мМЕ/л до менее 3%5. Следует добавить, что в Армении уже пару десятилетий тому назад достигнуто устойчивое оптимальное потребление йода всем населением с мКЙМ 242 мкг/л у школьников, 226 мкг/л у беременных [17].
Следует добавить, что в Армении уже пару десятилетий тому назад достигнуто устойчивое оптимальное потребление йода всем населением с мКЙМ 242 мкг/л у школьников, 226 мкг/л у беременных [17].
Завершая свою уже непомерно растянувшуюся колонку, скажу, что “медиана йодурии” стала теперь главным действующим лицом мониторинга программ йодной профилактики и приключения ее только начинаются.
Примечания:
- https://forums.rusmedserv.com/showthread.php?t=4654
- До переименования в 2012 г. – Международный совет по контролю за йододефицитными заболеваниями (ICCIDD).
- Именно этот реальный феномен, по всей видимости, стал причиной мифа об “экопатогенах”.
- М. Zimmermann – персональное сообщение (2017).
- Hutchings – персональное сообщение (2018).
1. Герасимов Г.А., Фадеев В.В., Свириденко Н.Ю., и др. Йододефицитные заболевания в России. Простое решение сложной проблемы. – М.: Адамантъ, 2002. [Gerasimov GA, Fadeev VV, Sviridenko NY, et al. Yododefitsitnye zabolevaniya v Rossii. Prostoe reshenie slozhnoy problemy. Moscow: Adamant; 2002. (In Russ.)]
Yododefitsitnye zabolevaniya v Rossii. Prostoe reshenie slozhnoy problemy. Moscow: Adamant; 2002. (In Russ.)]
2. Кияев А.В., Платонова Н.М., Абдулхабирова Ф.Х., и др. Влияние избыточного потребления йода на функциональное состояние щитовидной железы и спектр ее патологии у жителей г. Туринска, Свердловской области. // Клиническая и экспериментальная тиреоидология. – 2015. – Т. 11. – №1. – С. 43-49. [Kiyaev AV, Platonova NM, Abdulhabirova FM, et al. Influence of excessive iodine intake on the thyroid function and spectrum of thyroid abnormalities in population of Turinsk, Sverdlovsk Region, of Russia. Clinical and experimental thyroidology. 2015;11(1):43-49. (In Russ.)] doi: 10.14341/ket2015143-49.
3. Андрюков Б.Г., Кику П.Ф., Семенова В.В. Гигиеническая оценка влияния факторов среды обитания Приморского края на заболеваемость щитовидной железы. // Гигиена и санитария. – 2005. – №4. – C. 6-9. [Andryukov BG, Kiku PF, Semenova VV. Hygienic assessment of the impact of environmental factors of the Primorye Territory on the incidence of thyroid diseases. Gig Sanit. 2005;(4):6-9. (In Russ.)]
Gig Sanit. 2005;(4):6-9. (In Russ.)]
4. Герасимов Г.А. Отзыв на дискуссионную статью Э.П. Касаткиной “Диффузный нетоксический зоб. Вопросы классификации и терминологии”. // Проблемы эндокринологии. – 2001. – Т. 47. – №6. – С. 12-15. [Gerasimov GA. Otzyv na diskussionnuyu stat’yu E.P. Kasatkinoy “Diffuznyy netoksicheskiy zob. Voprosy klassifikatsii i terminologii”. Problems of endocrinology. 2001;47(6):12-15. (In Russ.)]
5. Герасимов Г.А. Куда катится колесо, или вновь о простом решении сложной проблемы. // Клиническая и экспериментальная тиреоидология. – 2006. – Т. 2. – №4. – С. 4-7. [Gerasimov GA. Where does the wheel roll or again about simple solution of the difficult problem. Clinical and experimental thyroidology. 2006;2(4):4-7. (In Russ.)]
6. World Health Organization. Assessment of iodine deficiency disorders and monitoring their elimination: a guide for programme managers. Geneva: WHO; 2007.
7. UNICEF. Guidance of the monitoring of salt iodization programmes and determination of population iodine status [Internet]. UNICEF, 2018 [cited 2018 Jul 22]. Avaliable from: https://www.unicef.org/nutrition/files/Monitoring-of-Salt-Iodization.pdf
UNICEF, 2018 [cited 2018 Jul 22]. Avaliable from: https://www.unicef.org/nutrition/files/Monitoring-of-Salt-Iodization.pdf
8. ЮНИСЕФ; Глобальная сеть по йоду. Рекомендации по мониторингу программ йодирования соли и оценке статуса йодной обеспеченности населения (русскоязычная версия) // Клиническая и экспериментальная тиреоидология. – 2018. – Т. 14. – №2. – C. 100-112 [UNICEF; IGN. Guidance on the monitoring of salt iodization programmes and determination of population iodine status: Russian language version. Clinical and experimental thyroidology. 2018;14(2):100-112 (In Russ.)] doi: 10.14341/ket9734.
9. Мохорт Т.В., Петренко С.В., Леушев Б.Ю., и др. Оценка йодного обеспечения детей школьного возраста и беременных женщин в Республике Беларусь в 2017–2018 годах. // Клиническая и экспериментальная тиреоидология. – 2018. – Т. 14. – №3. (в печати). [Mokhort TV, Petrenko SV, Leushev BY, et al. Assessment of iodine provision of school-age children and pregnant women in the Republic of Belarus in 2017–2018. Clinical and experimental thyroidology. 2018;14(3) (in press). (In Russ.)] doi: 10.14341/ket9732.
Clinical and experimental thyroidology. 2018;14(3) (in press). (In Russ.)] doi: 10.14341/ket9732.
10. Zimmermann MB, Gizak M, Abbott K, et al. Iodine deficiency in pregnant women in Europe. Lancet Diabetes Endocrinol. 2015;3(9):672-674. doi: 10.1016/s2213-8587(15)00263-6.
11. Zimmermann MB, Aeberli I, Andersson M, et al. Thyroglobulin is a sensitive measure of both deficient and excess iodine intakes in children and indicates no adverse effects on thyroid function in the UIC range of 100-299 mug/L: a UNICEF/ICCIDD study group report. J Clin Endocrinol Metab. 2013;98(3):1271-1280. doi: 10.1210/jc.2012-3952.
12. Gerasimov G, Sturua L, Ugulava T, van der Haar F. Georgia celebrates optimal iodine nutrition. IDD Newsletter. 2018;46(1):2-4.
13. Трошина Е.А., Платонова Н.М., Панфилова Е.А., Панфилов К.О. Аналитический обзор по результатам мониторинга основных эпидемиологических характеристик йододефицитных заболеваний у населения Российской Федерации за период 2009–2015 гг. // Проблемы эндокринологии. – 2018. – Т. 64. – №1. – С. 21-37. [Troshina EA, Platonova NM, Panfilova EA, Panfilov KO. The analytical review of monitoring of the basic epidemiological characteristics of iodine deficiency disorders among the population of the Russian Federation for the period 2009–2015. Problems of endocrinology. 2018;64(1): 21-37. (In Russ.)] doi: 10.14341/probl9308.
// Проблемы эндокринологии. – 2018. – Т. 64. – №1. – С. 21-37. [Troshina EA, Platonova NM, Panfilova EA, Panfilov KO. The analytical review of monitoring of the basic epidemiological characteristics of iodine deficiency disorders among the population of the Russian Federation for the period 2009–2015. Problems of endocrinology. 2018;64(1): 21-37. (In Russ.)] doi: 10.14341/probl9308.
14. Дедов И.И., Безлепкина О.Б., Вадина Т.А., и др. Скрининг на врожденный гипотиреоз в Российской Федерации. // Проблемы эндокринологии. – 2018. – Т. 64. – №1. – С. 14-20. [Dedov II, Bezlepkina OB, Vadina TA., et al. Screening for congenital hypothyroidism in the Russian Federation. Problems of endocrinology. 2018;64(1):14-20. (In Russ.)] doi: 10.14341/probl8752.
15. Суплотова Л.А., Макарова О.Б., Ковальжина Л.С., Шарухо Г.В. Профилактика йодного дефицита в Тюменской области: успех или неудача? // Клиническая и экспериментальная тиреоидология. – 2015. – Т. 11. – №3. – C. 39-46. [Suplotova LA, Makarova OB, Kovalzhina LS, Sharuho GV. Prevention of iodine deficiency in the Tyumen region: success or failure? Clinical and experimental thyroidology. 2015;11(3):39-46. (In Russ.)] doi: 10.14341/ket2015339-46.
Prevention of iodine deficiency in the Tyumen region: success or failure? Clinical and experimental thyroidology. 2015;11(3):39-46. (In Russ.)] doi: 10.14341/ket2015339-46.
16. Barnabishvilli N, Gerasimov G, Azikuri T. The results of neonatal TSH screening do not agree with indicators of the optimal iodine status of pregnant women in the Republic of Georgia. Clinical and experimental thyroidology. 2018;14(2):81-85. doi: 10.14341/ket9777.
17. Hutchings N, Gerasimov G. Salt iodization in Armenia: a model for sustained success. IDD Newsletter. 2017;45(4):2-4.
Калькулятор среднего, медианы, моды, диапазона
Для расчета укажите числа, разделенные запятой.
| 10, 2, 38, 23, 38, 23, 21 |
Калькулятор статистики | Калькулятор стандартного отклонения | Калькулятор размера выборки
Среднее
Слово среднее, которое является омонимом для нескольких других слов в английском языке, также неоднозначно даже в области математики. В зависимости от контекста, будь то математический или статистический, значение «среднего» меняется. В простейшем математическом определении наборов данных в качестве среднего используется среднее арифметическое, также называемое математическим ожиданием или средним значением. В этой форме среднее относится к промежуточному значению между дискретным набором чисел, а именно к сумме всех значений в наборе данных, деленной на общее количество значений. Уравнение для расчета среднего арифметического практически идентично уравнению для расчета статистических концепций генеральной совокупности и выборочного среднего, с небольшими различиями в используемых переменных:
В зависимости от контекста, будь то математический или статистический, значение «среднего» меняется. В простейшем математическом определении наборов данных в качестве среднего используется среднее арифметическое, также называемое математическим ожиданием или средним значением. В этой форме среднее относится к промежуточному значению между дискретным набором чисел, а именно к сумме всех значений в наборе данных, деленной на общее количество значений. Уравнение для расчета среднего арифметического практически идентично уравнению для расчета статистических концепций генеральной совокупности и выборочного среднего, с небольшими различиями в используемых переменных:
Среднее значение часто обозначается как x̄ , произносится как «x bar», и даже в других случаях, когда переменная не равна x , штриховое обозначение является обычным индикатором некоторой формы среднего значения. В конкретном случае среднего значения совокупности вместо использования переменной x̄ используется греческий символ мю или μ . Точно так же или, скорее, сбивает с толку, выборочное среднее в статистике часто обозначается с большой буквы X̄ . Учитывая набор данных 10, 2, 38, 23, 38, 23, 21, суммирование выше дает:
Точно так же или, скорее, сбивает с толку, выборочное среднее в статистике часто обозначается с большой буквы X̄ . Учитывая набор данных 10, 2, 38, 23, 38, 23, 21, суммирование выше дает:
| 10 + 2 + 38 + 23 + 38 + 23 + 21 | | | 7 |
8 | = | | = 22,143 |
Как упоминалось ранее, это одно из самых простых определений среднего, а некоторые другие включают взвешенное среднее арифметическое (которое отличается только тем, что одни значения в наборе данных вносят больший вклад, чем другие) и среднее геометрическое. Правильное понимание данных ситуаций и контекстов часто может предоставить человеку инструменты, необходимые для определения того, какой статистически значимый метод использовать. В общем, среднее значение, медиана, мода и диапазон в идеале должны быть рассчитаны и проанализированы для данной выборки или набора данных, поскольку они объясняют различные аспекты данных и, если их рассматривать отдельно, могут привести к искажению данных, как это будет продемонстрировано в следующих разделах.
Медиана
Статистическая концепция медианы — это значение, которое делит выборку данных, совокупность или распределение вероятностей на две половины. Поиск медианы по существу включает в себя поиск значения в выборке данных, которая имеет физическое расположение между остальными числами. Обратите внимание, что при вычислении медианы конечного списка чисел важен порядок выборок данных. Обычно значения перечислены в порядке возрастания, но нет реальной причины, по которой перечисление значений в порядке убывания приведет к другим результатам. В случае, когда общее количество значений в выборке данных нечетное, медиана — это просто число в середине списка всех значений. Если выборка данных содержит четное количество значений, медиана представляет собой среднее значение двух средних значений. Хотя это может сбивать с толку, просто помните, что хотя медиана иногда требует вычисления среднего значения, когда возникает этот случай, оно будет включать только два средних значения, тогда как среднее значение включает все значения в выборке данных. В нечетных случаях, когда есть только две выборки данных или есть четное количество выборок, где все значения одинаковы, среднее значение и медиана будут одинаковыми. При том же наборе данных, что и раньше, медиана будет получена следующим образом:
В нечетных случаях, когда есть только две выборки данных или есть четное количество выборок, где все значения одинаковы, среднее значение и медиана будут одинаковыми. При том же наборе данных, что и раньше, медиана будет получена следующим образом:
2,10,21, 23 ,23,38,38
После перечисления данных в порядке возрастания и определения нечетного числа значений становится ясно, что 23 является медианой для данного случая. Если бы к набору данных было добавлено другое значение:
2,10,21, 23 , 23 ,38,38,1027892
Поскольку число значений четное, медиана будет средней два средних числа, в данном случае 23 и 23, среднее значение которых равно 23. Обратите внимание, что в этом конкретном наборе данных добавлен выброс (значение, выходящее далеко за пределы ожидаемого диапазона значений), значение 1,027,892, не оказывает реального влияния на набор данных. Однако если для этого набора данных вычислить среднее значение, результатом будет 128 505,875. Это значение явно не является хорошим представлением семи других значений в наборе данных, которые намного меньше и ближе по значению, чем среднее значение и выброс. Это главное преимущество использования медианы при описании статистических данных по сравнению со средним значением. Хотя оба, а также другие статистические значения должны рассчитываться при описании данных, если можно использовать только одно из них, медиана может обеспечить лучшую оценку типичного значения в заданном наборе данных, когда между значениями существуют чрезвычайно большие различия.
Это значение явно не является хорошим представлением семи других значений в наборе данных, которые намного меньше и ближе по значению, чем среднее значение и выброс. Это главное преимущество использования медианы при описании статистических данных по сравнению со средним значением. Хотя оба, а также другие статистические значения должны рассчитываться при описании данных, если можно использовать только одно из них, медиана может обеспечить лучшую оценку типичного значения в заданном наборе данных, когда между значениями существуют чрезвычайно большие различия.
Режим
В статистике режим — это значение в наборе данных, имеющее наибольшее количество повторений. Набор данных может быть мультимодальным, то есть иметь более одного режима. Например:
2,10,21,23,23,38,38
И 23, и 38 появляются дважды каждое, что делает их оба модами для набора данных выше.
Подобно среднему и медиане, мода используется как способ выражения информации о случайных величинах и популяциях. Однако, в отличие от среднего и медианы, мода — это понятие, которое можно применять к нечисловым значениям, таким как марка тортильи, которую чаще всего покупают в продуктовом магазине. Например, при сравнении брендов Tostitos, Mission и XOCHiTL, если обнаружится, что при продаже чипсов из тортильи XOCHITL является модой и продается в соотношении 3: 2: 1 по сравнению с чипсами из тортильи марок Tostitos и Mission соответственно, соотношение может быть использовано для определения того, сколько мешков каждой марки необходимо хранить. В случае, если за определенный период продается 24 пакета чипсов из тортильи, в магазине будет 12 пакетов чипсов XOCHITL, 8 пакетов Tostitos и 4 пакета Mission при использовании режима. Если, однако, магазин просто использовал среднее значение и продал по 8 пакетов каждого, он потенциально мог бы потерять 4 продажи, если бы покупатель хотел только чипсы XOCHiTL, а не какой-либо другой бренд. Как видно из этого примера, важно учитывать всевозможные статистические значения при попытке сделать выводы о любой выборке данных.
Однако, в отличие от среднего и медианы, мода — это понятие, которое можно применять к нечисловым значениям, таким как марка тортильи, которую чаще всего покупают в продуктовом магазине. Например, при сравнении брендов Tostitos, Mission и XOCHiTL, если обнаружится, что при продаже чипсов из тортильи XOCHITL является модой и продается в соотношении 3: 2: 1 по сравнению с чипсами из тортильи марок Tostitos и Mission соответственно, соотношение может быть использовано для определения того, сколько мешков каждой марки необходимо хранить. В случае, если за определенный период продается 24 пакета чипсов из тортильи, в магазине будет 12 пакетов чипсов XOCHITL, 8 пакетов Tostitos и 4 пакета Mission при использовании режима. Если, однако, магазин просто использовал среднее значение и продал по 8 пакетов каждого, он потенциально мог бы потерять 4 продажи, если бы покупатель хотел только чипсы XOCHiTL, а не какой-либо другой бренд. Как видно из этого примера, важно учитывать всевозможные статистические значения при попытке сделать выводы о любой выборке данных.
Диапазон
Диапазон набора данных в статистике — это разница между наибольшим и наименьшим значениями. Хотя диапазон имеет разные значения в разных областях статистики и математики, это его самое основное определение, которое используется в предоставленном калькуляторе. Используя тот же пример:
2,10,21,23,23,38,38
38 — 2 = 36
Диапазон в этом примере равен 36. Как и в среднем, на диапазон могут существенно влиять очень большие или маленькие значения. Используя тот же пример, что и ранее:
2,10,21, 23 , 23 ,38,38,1027892
Диапазон в этом случае будет 1 027 890 по сравнению с 36 в предыдущем случае. Таким образом, важно тщательно анализировать наборы данных, чтобы гарантировать учет выбросов.
Калькулятор средней медианной моды с простым пошаговым решением
Калькулятор средней медианной моды
Значения данных (разделенные запятыми, максимум 50 значений): *
298,107,237,115,114,192,130,102,150,250,298
Решение:
Среднее значение:
Среднее значение набора данных обычно называют средним. Вы найдете среднее значение, взяв сумму всех значений данных и разделив эту сумму на общее количество значений данных. Формула среднего значения населения
$$ \mu = \frac{{\sum}x}{N} $$
Формула среднего значения выборки:
$$ \bar{x} = \frac{{\sum}x}{n} $$
Обе эти формулы используют один и тот же математический процесс: найдите сумму значений данных и разделите на общее количество. Для значений данных, введенных выше, решение:
$$ \frac{2730}{14} = 195$$
Вы найдете среднее значение, взяв сумму всех значений данных и разделив эту сумму на общее количество значений данных. Формула среднего значения населения
$$ \mu = \frac{{\sum}x}{N} $$
Формула среднего значения выборки:
$$ \bar{x} = \frac{{\sum}x}{n} $$
Обе эти формулы используют один и тот же математический процесс: найдите сумму значений данных и разделите на общее количество. Для значений данных, введенных выше, решение:
$$ \frac{2730}{14} = 195$$
Медиана:
Медиана набора данных находится путем упорядочивания набора данных по возрастанию и определения среднего числа. Если в наборе данных имеется нечетное количество значений данных, медиана представляет собой одно число. Если в наборе данных имеется четное количество значений данных, медиана представляет собой среднее значение двух средних чисел. Сортируя набор данных для введенных выше значений, мы имеем:
$$
102, 107, 114, 115, 130, 150, 192, 207, 219, 237, 263, 298, 298, 298 $$
Так как в этом наборе данных четное число значений данных, есть два средних числа. При 14 значениях данных средние числа — это значения данных в позициях 7 и 8. Это 192 и 207. Медиана — это среднее этих чисел. У нас есть $$ {\frac{192 + 207}{2}} $$
Следовательно, медиана
$$ 199,5 $$
При 14 значениях данных средние числа — это значения данных в позициях 7 и 8. Это 192 и 207. Медиана — это среднее этих чисел. У нас есть $$ {\frac{192 + 207}{2}} $$
Следовательно, медиана
$$ 199,5 $$
Режим:
Режим — это число, которое появляется чаще всего. Набор данных может иметь несколько режимов. Если он имеет две моды, набор данных называется бимодальным. Если все значения данных имеют одинаковую частоту, все значения данных являются модами. Здесь режим(ы) равен/являются
Калькулятор среднего значения средней моды находит меры центральной тенденции. Сначала калькулятор даст вам ответ, а затем предложит пошаговое решение , чтобы вы могли легко научиться решать задачу самостоятельно. Среднее значение — это среднее значение набора чисел. Медиана — это среднее число/числа, расположенные в числовом порядке. Наконец, мода — это число, которое появляется чаще всего.
После того, как вы закончите расчет показателей центральной тенденции, взгляните на Калькулятор диапазона, дисперсии и стандартного отклонения. Статистика никогда не была проще … Вы ПОЛУЧИЛИ это!
Статистика никогда не была проще … Вы ПОЛУЧИЛИ это!
Среднее значение, медиана и мода являются показателями центральной тенденции в статистике. Другими словами, это числа, которые мы используем для измерения и описания центра распределения. Когда студенты начинают изучать распределения на курсах статистики, преподаватели и учебники преподают среднее значение, медиану и моду в качестве одних из первых тем курса. Даже учителя начальной школы знакомят своих учеников с мерами центральной тенденции, поэтому учащиеся начальной школы также могут использовать калькулятор среднего медианного режима. Здесь мы рассмотрим, как найти среднюю медиану и моду вручную. Затем вы можете использовать калькулятор среднего медианного режима, чтобы проверить свою работу.
Как найти среднее
Среднее значение обычно известно как среднее набора чисел. Большинство учащихся хорошо знакомы со средними показателями и часто используют их для определения своей успеваемости в классе. Как найти среднее значение в математике? Мы находим среднее значение, складывая все числа набора данных, а затем разделяя их на общее количество значений.
Как найти среднее значение в математике? Мы находим среднее значение, складывая все числа набора данных, а затем разделяя их на общее количество значений.
$$ \text{mean} = \frac{\sum{\text{значения данных}}}{\text{total}} $$
В математике мы используем символ суммирования $\sum$, чтобы обратите внимание, что мы должны сложить все числа вместе.
Если вы изучаете статистику AP, статистику на уровне колледжа или что-то еще, выходящее за рамки математики средней школы, вы будете использовать специальные символы для обозначения среднего значения. Символически, вы обозначите совокупность как «mu» $\mu$ и обозначите размер совокупности как N. Вы обозначите среднюю выборку как «x-bar» $\bar{x}$, и вы обозначите размер выборки на n. Формула среднего значения генеральной совокупности:
$$ \mu = \frac{\sum{x}}{N} $$
Формула выборочного среднего:
$$ \bar{x} = \frac{\sum {x}}{n} $$
В каждой из этих формул x представляет каждое из чисел в наборе данных. Итак, $\sum{x}$ — это сумма всех значений данных.
Итак, $\sum{x}$ — это сумма всех значений данных.
Вот как найти среднее значение в наборе данных 3, 5, 9, 15, 17. Среднее значение генеральной совокупности равно
$$ \mu = \frac{3 + 5 + 9 + 15+ 17}{5} $$
$$ \mu = \frac{49}{5} = 9,8 $$
Вы можете использовать приведенный выше калькулятор среднего среднего режима и ввести значения 3, 5, 9,15, 17, чтобы убедиться, что среднее 9.8.
Как найти медиану?
Что означает медиана в математике? Когда вы упорядочиваете все числа в наборе данных в порядке возрастания, медиана — это число, которое попадает точно посередине. Если есть два числа, которые находятся посередине, медиана является средним значением этих двух чисел.
3, 5, 9, 15, 17
Медиана приведенного выше набора данных равна 9. 9 – это число в середине.
Теперь рассмотрим следующий набор данных:
3, 5, 9, 15, 17, 20
Как найти медиану в этом случае? Здесь нам нужно найти медиану четных чисел. Для этого мы берем среднее из двух средних чисел. Медиана этого набора данных представляет собой среднее значение 9и 15. То есть
Медиана этого набора данных представляет собой среднее значение 9и 15. То есть
$$ \frac{9 + 15}{2} = 12 $$
Теперь используйте Калькулятор средней средней моды выше, чтобы проверить, что медиана теперь равна 12.
Что такое мода?
Что означает режим в математике? При описании набора данных частота значения данных — это количество раз, когда это значение встречается. Значение данных с наибольшей частотой или то, которое встречается чаще всего, является режимом. Набор данных может иметь две моды, если два числа имеют одинаковую максимальную частоту. Мы говорим, что распределение бимодальное, если оно имеет две моды. Иногда, если есть более двух чисел с наибольшей частотой, мы будем говорить, что набор данных не имеет моды. Однако с помощью приведенного выше калькулятора среднего среднего режима найденный режим будет включать все числа с наибольшей частотой.
В наборе данных 3, 5, 9, 15, 17, 9 какой режим? Значение данных 9 имеет частоту 2, в то время как все остальные числа имеют частоту 1. 9 имеет наибольшую частоту и, следовательно, 9 является модой. Вы можете использовать Калькулятор средней средней моды выше, чтобы убедиться, что мода равна 9.
9 имеет наибольшую частоту и, следовательно, 9 является модой. Вы можете использовать Калькулятор средней средней моды выше, чтобы убедиться, что мода равна 9.
Вот несколько примеров средней медианы и моды в статистике.
Пример 1. Найдите среднее значение
Найдите среднее значение генеральной совокупности для набора данных: 85, 78, 92, 65
Решение:
Так как задача требует найти среднее значение генеральной совокупности, правильным символом для среднего является $ \mu $. Формула средней генеральной совокупности:
$$ \mu = \frac{85 + 78 + 92 + 65}{4} $$
$$ \mu = \frac{ 320}{4} = 80$$
Следовательно , среднее значение генеральной совокупности, $ \mu $, равно 80.
Вы можете вырезать и вставить этот набор данных в приведенный выше калькулятор режима среднего среднего и убедиться, что среднее значение равно 80.
Пример 2: найти медиану
Найти медиана для следующего набора данных:
72, 75, 77, 80, 81, 81, 84, 86, 87, 88, 89, 91, 93, 94, 94, 94, 97, 99, 100
Медиана — это среднее число. Поскольку в этом наборе данных 19 значений данных, среднее число — это число на 10-й позиции. То есть 88. Медиана равна 88.
Поскольку в этом наборе данных 19 значений данных, среднее число — это число на 10-й позиции. То есть 88. Медиана равна 88.
Давайте добавим еще одно значение данных в начало набора данных, чтобы получить в общей сложности 20 значений данных. Мы включим 71.
71, 72, 75, 77, 80, 81, 81, 84, 86, 87, 88, 89, 91, 93, 94, 94, 94, 97, 99, 100
Поскольку существует четный набор значений данных, медиана является средним значением двух средних чисел. При 20 значениях данных два средних значения находятся на позициях 10 и 11. Эти два числа равны 87 и 88. Среднее значение 87 и 88 равно:
$$ \text{median} = \frac{87 + 88}{ 2} $$
$$ \text{медиана} = 87,5 $$
Следовательно, медиана этого набора данных равна 87,5.
Вы можете вырезать и вставить этот набор данных в Калькулятор среднего среднего режима выше и убедиться, что медиана равна 87,5.
Пример 3. Определение режима
71, 72, 75, 77, 80, 81, 81, 84, 86, 87, 88, 89, 91, 93, 94, 94, 94, 97, 99, 100
Режим — это значение данных, которое появляется чаще всего. Это значение данных с наибольшей частотой. В этом наборе данных значение данных 94 имеет частоту 3, что больше, чем частота любого другого значения данных. Таким образом, режим равен 94.
Это значение данных с наибольшей частотой. В этом наборе данных значение данных 94 имеет частоту 3, что больше, чем частота любого другого значения данных. Таким образом, режим равен 94.
Вы можете вырезать и вставить этот набор данных в калькулятор среднего среднего режима выше и убедиться, что режим равен 9.4.
Найдите среднее значение с дополнительной оценкой выброса
Когда мы вычисляем среднее значение, мы обнаруживаем, что выброс сильно влияет на ответ. Выброс в наборе данных — это значение, которое намного меньше или намного больше, чем все остальные значения. Рассмотрим пример тестовых оценок. Предположим, что значения данных в Примере 1 выше представляют 4 оценки за тест.
85, 78, 92, 65
Мы обнаружили, что среднее значение этого набора данных равно 80. Теперь рассмотрим 5-ю оценку теста, равную 20. Мы считаем 20 выбросом, потому что он намного меньше, чем остальная часть теста. оценки.
85, 78, 92, 65, 20
Итак, что теперь значит?
$$ \mu = \frac{85 + 78 + 92 + 65 + 20}{5} $$
$$ \mu = \frac{ 340}{5} = 68 $$
Следовательно, новый среднее значение равно 68. Среднее значение, которое изменяется с 80 до 68, представляет собой большую разницу. Значение выброса 20 сильно влияет на среднее значение. Считаете ли вы, что оценка 68 представляет собой типичное значение в этом наборе данных?
Среднее значение, которое изменяется с 80 до 68, представляет собой большую разницу. Значение выброса 20 сильно влияет на среднее значение. Считаете ли вы, что оценка 68 представляет собой типичное значение в этом наборе данных?
Найдите медиану с дополнительной оценкой выброса
Если бы мы упорядочили исходные 4 оценки за тест и нашли медиану, мы бы вычислили ее как среднее между 78 и 85.
65, 78, 85, 92
$$ \text{медиана} = \frac{78 + 85}{2} $$
$$ \text{медиана} = \frac{163}{2} = 81,5 $$
Таким образом, медиана исходных 4 тестовых оценок равна 81,5.
Теперь давайте включим в набор данных пятую тестовую оценку 20 и найдем новую медиану. Итак, теперь наш набор данных равен
20, 65, 78, 85, 92
При нечетном числе значений данных медиана является средним числом. Здесь это значение равно 78. Итак, новая медиана с включенным выбросом – 78.
Что это значит? Среднее значение и медиана исходного набора данных были соответственно 80 и 81,5. Но когда мы включили выброс в набор данных, среднее значение и медиана стали равными 68 и 78. Хотя среднее значение уменьшилось на 12 пунктов с включенным выбросом, медиана уменьшилась на 3,5 пункта. Мы видим, что выброс сильно влияет на среднее значение, но лишь незначительно влияет на медиану. Поэтому мы говорим, что медиана более точно описывает типичную тестовую оценку, потому что она более устойчива (не так подвержена влиянию) к любым выбросам в наборе данных.
Но когда мы включили выброс в набор данных, среднее значение и медиана стали равными 68 и 78. Хотя среднее значение уменьшилось на 12 пунктов с включенным выбросом, медиана уменьшилась на 3,5 пункта. Мы видим, что выброс сильно влияет на среднее значение, но лишь незначительно влияет на медиану. Поэтому мы говорим, что медиана более точно описывает типичную тестовую оценку, потому что она более устойчива (не так подвержена влиянию) к любым выбросам в наборе данных.
Для нормального колоколообразного распределения
Среднее значение, медиана и мода находятся примерно в центре нормального колоколообразного распределения. Следовательно, мы можем оценить, что все они имеют одинаковое значение.
Средняя медиана и мода имеют одно и то же значение при нормальном распределении в форме колокола.
Вот пример набора данных с одинаковыми средним значением, медианой и модой. Вы можете убедиться, что меры центральной тенденции одинаковы, вставив этот набор данных в Калькулятор среднего среднего режима.
1, 2, 2, 3, 3, 3, 4, 4, 4, 4, 5, 5, 5, 5, 5, 6, 6, 6, 6, 7, 7, 7, 8, 8, 9
Для распределений с асимметрией влево или с отрицательной асимметрией
В распределениях с асимметрией влево или с отрицательной асимметрией в левой части распределения имеются низкие оценки, потенциально являющиеся выбросами, и они вытягивают левый хвост влево. Как мы видели в приведенном выше примере, выбросы сильно влияют на среднее значение, в то время как выбросы незначительно влияют на медиану. В режиме остается значение данных с наибольшей частотой. Следовательно, выбросы не влияют на моду.
Если мы посмотрим на изображение асимметричного левого распределения, мы поместим среднее значение в крайнее левое положение. Затем мы помещаем медиану в положение где-то посередине среднего значения и моды. Наконец, мы помещаем режим в позицию, где мы видим самый высокий пик графика, потому что это значение наибольшей частоты. Это наглядный пример того, как на среднее значение больше всего влияют выбросы, на медиану выбросы влияют незначительно, а на моду выбросы не влияют. Следовательно, порядок трех значений по горизонтальной оси следующий: среднее, затем медиана, затем мода.
Следовательно, порядок трех значений по горизонтальной оси следующий: среднее, затем медиана, затем мода.
Положение средней медианы и моды на смещенном влево распределении. Среднее вытягивается влево в сторону перекошенного хвоста.
Для распределений с перекосом вправо или с положительным перекосом
Когда распределение скошено вправо или скошено положительно, в правой части распределения есть высокие баллы, потенциально выбросы, перетаскивающие правый конец вправо. Как и в случае с асимметричным левым распределением, выбросы сильно влияют на среднее значение, а на медиану — незначительно. На режим не влияют выбросы.
Если мы посмотрим на изображение асимметричного распределения вправо, то среднее значение будет расположено дальше всего вправо. Это значение тянется в направлении перекошенного хвоста. Поскольку выбросы в правом хвосте лишь незначительно влияют на медиану, она будет располагаться где-то посередине среднего значения и моды. И снова мода будет располагаться на самом высоком пике графика, в положении наибольшей частоты. Следовательно, порядок трех значений по горизонтальной оси — мода, медиана и среднее значение.
Следовательно, порядок трех значений по горизонтальной оси — мода, медиана и среднее значение.
Положение средней медианы и моды на асимметричном правом распределении. Среднее вытягивается вправо в сторону перекошенного хвоста.
Приведенный выше калькулятор средней медианной моды поможет вам рассчитать три показателя центральной тенденции. Следующим шагом является развитие понимания мер изменчивости. Существуют три меры изменчивости: диапазон, дисперсия и стандартное отклонение. Из них стандартное отклонение будет широко представлено в курсе статистики на уровне колледжа.
Калькулятор размаха, дисперсии и стандартного отклонения — лучший онлайн-ресурс для обучения вычислению трех показателей изменчивости вручную. Он дает четкие шаги о том, как решить проблему самостоятельно. Чтобы лучше понять меры изменчивости, см. «Определение дисперсии и стандартного отклонения» и «Как найти стандартное отклонение и дисперсию».
Поиск диапазона и расчет среднего числа в наборе
Расчет среднего и диапазона
Математическое определение
- Среднее значение
- Среднее значение всех данных в наборе.

- Медиана
- Значение в наборе, наиболее близкое к середине диапазона.
- Режим
- Значение, которое чаще всего встречается в наборе данных.
- Диапазон
- Разница между наибольшими и наименьшими данными в наборе данных.
Пример расчета
Расчет среднего значения, медианы, моды и диапазона для 3, 19, 9, 7, 27, 4, 8, 15, 3, 11.
Как найти среднее значение (или среднее значение)
Чтобы вычислить среднее значение, сложите числа: 3+3+4+7+8 +9+11+15+19+27=106, затем разделите его на количество точек данных 106/10=10,6.
Как найти медиану
В порядке возрастания числа 3, 3, 4, 7, 8, 9, 11, 15, 19, 27. Всего имеется 10 чисел, поэтому 5-е и 6-е числа используются для вычислить медиану. (8+9)/2 = 8,5
Если бы в ряду было 9 чисел, а не 10, вы бы взяли 5-е число и не нужно было бы усреднять 2 средних числа. Два средних числа нужно усреднять только в том случае, если набор данных содержит четное количество точек данных.
Как найти режим
Единственное число, которое появляется несколько раз, это 3, так что это режим.
Как найти диапазон
Чтобы вычислить диапазон, вычтите наименьшее число из наибольшего числа 27-3=24.
Среднее значение, медиана и мода: тренды данных, обнаружение аномалий и использование в спорте знать, если мы
иметь хорошую оценку. Когда дело доходит до покупки дорогих товаров, мы часто спрашиваем
средняя цена для поиска лучших предложений.
Это всего лишь несколько примеров того, как средние значения используются в
реальная жизнь.
В этом разделе вы узнаете о различных типах средних показателей, о том, как они рассчитываются и применяются в различных областях, особенно в спорте.
Что означает термин «средний»?
Когда люди описывают «среднее» группы чисел, они часто ссылаются на среднее арифметическое. Это один из 3 различных типов среднего, включая медиану и моду.
Говоря языком разговора, большинство людей просто говорят «средний», когда
они действительно имеют в виду среднее значение. Арифметика означает и среднее
слова-синонимы, которые используются взаимозаменяемо, согласно Dictionary.com.
Арифметика означает и среднее
слова-синонимы, которые используются взаимозаменяемо, согласно Dictionary.com.
Рассчитывается путем сложения чисел в наборе и деления на общее число в наборе — так поступает большинство людей, когда находят среднее значение. См. пример ниже.
Среднее
Набор: 8, 12, 9, 7, 13, 10
Среднее = (8 + 12 + 9+ 7 + 13 + 10) / 6
= 59 / 6
= 9,83
Среднее или среднее арифметическое в этом примере равно 9,83 .
Медиана
Медиана , с другой стороны, является другим типом
среднее, представляющее среднее число в упорядоченной последовательности чисел. Этот
работает, упорядочивая последовательность чисел (в порядке возрастания), а затем определяя
число, которое находится в середине набора. См. пример ниже.
Средняя медиана
Набор: 22, 26, 29, 33, 39 , 40, 42, 47, 53
В этом примере 39 является медианой или средним значением в наборе.
Режим
Режим в основном является наиболее частым значением, которое
повторяется в наборе значений. Например, если в вашем наборе есть 21, 9, 14, 3,
11, 33, 5, 9, 16, 21, 5, 9, какой режим?
Ответ 9, потому что это значение повторяется 3 раза.
В статистике среднее, медиана и мода — все термины, используемые для
измерить центральную тенденцию в выборке данных. Это иллюстрируется обычным
график распределения ниже.
График нормального распределения используется для визуализации стандартного отклонения при анализе данных. Распределение статистических данных показывает, как часто встречаются значения в наборе данных.
На приведенном выше графике проценты представляют количество значений, попадающих в каждый раздел. Выделенные проценты в основном показывают, какая часть данных находится близко к середине графика.
Какая связь между средним, медианой и модой?
На первый взгляд может показаться, что связи нет
между средним, медианой и модой. Но есть эмпирический
отношения, которые существуют при измерении центра набора данных.
Но есть эмпирический
отношения, которые существуют при измерении центра набора данных.
Математики заметили, что обычно
разница между медианой и модой, а это разница в 3 раза
между средним и медианой.
Эмпирическая взаимосвязь выражается следующей формулой:
Среднее – Мода = 3 (Среднее – Медиана)
Давайте рассмотрим пример данных о населении, основанных на 50 штатах.
Например, среднее значение населения составляет 7 миллионов, а медиана 4,8.
млн и режим 1,5 млн.
- Среднее = 7 миллионов
- Медиана = 4,8 миллиона
- Мода = 1,5 миллиона
Среднее – Мода = 3 (Среднее – Медиана)
7 миллионов – 1,5 миллиона = 3(7 миллионов – 4,8 миллионов)
5,5 миллионов = 3(2,2)
5,5 миллион = 6,6 миллиона
Обратите внимание: Профессор математики Кортни Тейлор, доктор философии. заявил, что это не точное соотношение. Когда вы делаете расчеты, цифры не всегда точны. Но соответствующие цифры будут относительно близки.
Асимметричные или искаженные данные
Согласно Microeconomicsnotes.com, когда значения среднего, медианы и моды не
равны, то распределение асимметрично или асимметрично. Степень асимметрии
представляет степень, в которой набор данных отличается от нормального распределения.
Когда среднее значение больше, чем
медиана, а медиана больше моды (Среднее > Медиана > Мода),
является положительно асимметричным распределением . Он описывается как «перекошенный к
вправо», потому что длинный конец кривой направлен вправо.
На примере графика ниже медиана и мода расположены слева от среднего.
С другой стороны, в отрицательном
асимметричное распределение, среднее меньше медианы, а медиана меньше
чем мода (среднее < медиана < мода). Длиннохвостовой конец направлен к
левая сторона графика.
На приведенном ниже графике показаны медиана и мода, расположенные справа от среднего значения.
Отличие среднего от медианы: устойчивые числовые сводки
В наборе данных, когда среднее значение велико, читатель может предположить
медиана также будет высокой. Однако это не всегда следует.
Однако это не всегда следует.
Разница между средним значением и медианой становится очевидной, когда
набор данных имеет выдающееся несоизмеримое значение. Эта ситуация привлекает внимание
концепция стойкости
числовые сводки. Устойчивая статистика представляет собой числовую сводку, в которой
крайние значения не оказывают существенного влияния на его стоимость.
Давайте продемонстрируем это, показав, как присутствие Билла Гейтса влияет на среднее и медианное богатство, когда он входит в комнату.
Например, 10 человек обедают в ресторане. Назовем его набором А. В таблице ниже показаны их доходы от самого низкого до самого высокого.
Общий доход людей в ресторане составляет 506 000 долларов США,
со средним доходом 50 600 долларов.
Поскольку в наборе 10 человек, для получения медианы мы
необходимо добавить значения 5 th и 6 th (Kat and Luigi’s
годовой доход) и разделите на 2.
Медиана = (46 000 + 49 000) / 2 = 95000/2
= 47 500
Средний доход группы составляет 47 500 долларов.
Диапазон представляет собой разницу между наименьшим доходом
(Раффи) и самый высокий доход (Джон), который составляет 46 000 долларов.
Установить годовой доход
Теперь, если Джон выйдет из ресторана и войдет Билл Гейтс,
как это повлияет на статистику годового дохода группы? Давайте назовем эту следующую группу
набор B.
По данным Forbes, Билл Гейтс
составил $90 млрд с 2017 по 2018 год.
Set B Годовой доход
С Биллом Гейтсом общий доход теперь составляет 90 миллиардов долларов плюс
низкий доход людей в ресторане. Средний доход и диапазон
группы сейчас слишком высока.
Однако медиана
остается прежним и составляет около 47 500 долларов.
Медиана показывает, что она лучше отражает фактическое состояние людей.
финансовый статус. Точно так же мы можем сказать, что Билл Гейтс является исключением с годовым
доход, исчисляемый миллиардами.
Этот пример показывает, что среднее значение и диапазон не являются устойчивыми
до крайних значений. В то время как медиана, как численное обобщение, обычно показывает
сопротивление.
Что это нам говорит? Наличие экстремальных значений или выбросов указывает на то, что распределение асимметрично. Экстремальные значения обычно смещают среднее значение в сторону хвоста.
Значение выявления асимметрии
Наблюдение асимметрии на графике дает аналитикам более четкое представление
тенденции набора данных. Например, если вы собрали данные о 500 студентах, которые
сдавали Scholastic Assessment Test, вы хотели бы знать тенденцию оценки.
Если вы нанесете данные на график, вы поймете, что это положительно
перекошено, если имеется несколько высоких результатов и большинство значений сгруппированы
к нижней стороне шкалы. Если баллы стремятся в большую сторону
шкалы, с несколькими низкими баллами , распределение отрицательное
перекошенный.
В финансах инвесторы обращают внимание на асимметрию при анализе
обратная раздача. Это важно, потому что позволяет им увидеть
крайние диапазоны данных вместо того, чтобы просто сосредоточиться на средних значениях.
Распределение показывает асимметрию (степень асимметрии) или эксцесс
когда доходность падает на 90 140 за пределы 90 143 нормального распределения. Меры эксцесса
выбросы в любом хвосте асимметричного графа. Он вычисляет степень
график имеет пик по сравнению с нормальным распределением.
Как это помогает инвесторам? Наблюдение за асимметрией или эксцессом помогает аналитикам прогнозировать риски, возникающие при сравнении модели с нормальным распределением с набором данных с тенденцией к более высокому стандартному отклонению. Риск определяется путем расчета того, насколько числа далеки от нормального распределения.
Как определить аномалии данных
В статистике выбросы
или аномалии — это необычные наблюдения, не принадлежащие определенной популяции.
При размещении на графике это точки, которые падают далеко
из значений набора данных. Исследователи обычно находят выбросы на основе больших, хорошо структурированных данных.
данные.
Насколько отличным должно быть значение, чтобы оно считалось выбросом?
Чтобы определить это, можно использовать межквартильный
диапазон (IQR).
IQR описывается как сводка из 5 чисел, которая содержит:
- Минимальное значение набора данных
- Первый квартиль (Q 1 ) – Что такое четверть
пути через последовательность набора данных
- Медиана
- Третий квартиль (Q 3 ) Который
три четверти последовательности всех данных
- Максимальное значение набора данных
Межквартильный размах (IQR) также похож на размах, но
считается менее чувствительным к экстремальным значениям (устойчивая статистика). Найти
это, вы должны взять первый
квартиль и вычесть третий квартиль. Это показывает, как данные распространяются
вокруг медианы.
IQR = Q 3 – Q 1
Обнаружение выбросов с использованием IQR
Практически все наборы данных могут быть описаны с помощью 5
сводка по номеру. Вот как вы можете использовать IQR для поиска выбросов:
- Вычислите межквартильный размах для набора данных
- Умножьте IQR на 1,5
- Добавьте IQR x 1,5 к третьему квартилю. правило: Любое значение больше этого является выбросом.
- Вычтите IQR x 1,5 из первого квартиля. правило: Любое значение меньше этого является выбросом.
Вот пример. Предположим, вы нашли выброс для следующего набора данных:
1, 5, 6, 6, 9, 10, 10, 11, 12, 13, 18
5 сводка чисел:
- Минимальное значение = 1
- Q 1 = 6
- Медиана = 10
- Q 3 = 12
- Максимальное значение = 18
IQR = Q 3 — Q 10002 — Q 3 — Q 10002 — Q 3 — Q 19058. х 1,5 = ?
х 1,5 = ?
6 x 1,5 = 9
9 + Q 3 = ?
9 + 12 = 21 (любое значение больше 21 является выбросом)
6 – Q 1 = ?
6 – 9 = -3 ( любое значение меньше -3 является выбросом)
Пока в наборе нет значений меньше -3 или больше 21. Хотя максимальное значение 18 на 5 пунктов больше, чем 13, оно не считается выбросом для этого набора данных.
Использование средних статистических данных в спортивной аналитике
В спорте
аналитика, исследователи собирают статистику для измерения потенциала и
способностей профессиональных спортсменов.
Согласно конкурентному преимуществу
Athletic Performance Center, показатели спортивных результатов имеют отношение к
общее спортивное развитие. Чтобы добиться успеха в любой спортивной сфере, люди
должны достичь определенного уровня атлетизма, чтобы соревноваться на продвинутом уровне.
Фактически, многие профессиональные спортивные команды консультируются
статистики, чтобы помочь спортсменам отслеживать свои конкурентные преимущества. Это руководство
их в улучшении их силовых и кондиционных процедур.
Это руководство
их в улучшении их силовых и кондиционных процедур.
Отслеживание показателей эффективности помогает спортсменам выполнять 4 важных
вещи:
- Помогает им узнать свой текущий уровень или базовый уровень.
- Как только они улучшаются, это позволяет им конкурировать на
более высокий спортивный уровень.
- Позволяет спортсменам определять индивидуальные тренировки
потребности.
- Помогает снизить риск получения травм.
Рейтинг популярных видов спорта
Средний показатель
(BA) — это показатель производительности, используемый в бейсболе, крикете и софтболе. Это
измеряет количество средних пробежек, которые игрок может набрать, прежде чем выйти из игры.
Это старейший измерительный прибор, которым измеряют тесто.
успех. Более высокий BA означает, что у отбивающего больше шансов набрать очки без
выход.
БА рассчитывается путем деления количества попаданий игрока на его
общее количество летучих мышей для значения от 0,000 до 1,000.
Согласно веб-сайту Высшей лиги бейсбола,
BA всей лиги в последние годы оставался около 0,260. Для лучших отбивающих в игре,
они могут превышать 0,300.
Тем не менее, некоторые выдающиеся спортсмены бьют выше 0,400, что составляет 4 попадания на каждые 10 ударов летучими мышами. MLB заявляет, что нет
игрок делал это на протяжении всего сезона со времен Теда Уильямса.
(0,406) из Бостон Ред Сокс в 1941.
В сезоне 1994 года, сокращенном забастовкой, Тони Гвинн был близок к тому, чтобы забить 400 мячей, забив 394 мяча при 164 попаданиях из 419 мячей в 110 играх.
Вот таблица игроков Главной лиги бейсбольной лиги, в которой показаны средние показатели лидеров регулярного сезона с 1985 по 2019 год:
В баскетболе процент бросков с игры (FG) используется для измерения того, насколько эффективно команда забивает мяч во время игры.
FG учитывает все удары, сделанные игроком. Однако он не включает штрафные броски, которые измеряются независимо как процент штрафных бросков.
Формула FG – это количество успешных выстрелов, разделенное на
по общему количеству попыток выстрела.
FG 0,500 или 50% и выше обычно считается хорошим
процент. Согласно Баскетболу
Справка, активным игроком с самым высоким процентом в настоящее время является ДеАндре.
Иордания с 66,96%.
Известные баскетболисты, такие как Майкл Джордан, имеют FG 49,69% с рейтингом 151, в то время как Леброн Джеймс занимает 111 место с 50,42%. Зал славы, такой как Карим Абдул-Джаббар, занимает 14-е место с 55,9.5%, а Мэджик Джонсон занимает 64-е место с 51,97%.
Basketball Reference определил 4 фактора, которые помогают командам выигрывать игры:
- Удары (40%)
- Перехваты (25%)
- Подборы (20%)
- Штрафные броски (15%)
4, стрельба является наиболее важным фактором, за которым следуют потери, подборы и штрафные броски. Однако другие утверждают, что помимо эффективного процента попаданий с игры, игра выигрывается при наличии надежной стратегии защиты.
Ниже представлена таблица игроков НБА с самым высоким процентом попаданий с игры.
Активные игроки выделены полужирным шрифтом .
* Указывает на члена Зала Славы
Многие лидеры по проценту бросков с игры — большие мужчины, которые склонны к данкам и броскам с высокой процентной вероятностью ближних бросков. В последние годы более широкое распространение получил трехочковый бросок. Оценка отличной универсальной стрельбы — 50-40-90, где игрок имеет 50% FG, 40% с трехочковой дистанции и 90% с линии штрафного броска.
Практический результат
Существует три типа средних значений, и это среднее,
медиана и мода. Из трех наиболее часто используемым является арифметический
иметь в виду. Он определяется путем сложения всех значений в наборе и деления его на
общее количество факторов.
Вычисление среднего, медианы и моды позволяет исследователям
нормальное распределение или асимметрия на графике. В финансах инвесторы используют это, чтобы
измерить риск распределения прибыли. Чтобы обнаружить статистические выбросы, аналитики
используйте межквартильный диапазон.
Чтобы обнаружить статистические выбросы, аналитики
используйте межквартильный диапазон.
Вычисление средних значений особенно важно в спорте
аналитика. Он используется для установления ориентиров и улучшения спортивных результатов. Метрики
помочь спортсменам упорядочить силовые и кондиционные программы, а также избежать
травмы.
Об авторе
Корин — страстный исследователь и автор финансовых тем, изучающих экономические тенденции, их влияние на население, а также способы помочь потребителям принимать более разумные финансовые решения. Другие ее тематические статьи можно прочитать на Inquirer.net и Manileno.com. Она имеет степень магистра творческого письма Филиппинского университета, одного из ведущих учебных заведений мира, и степень бакалавра коммуникативных искусств Колледжа Мириам.
Когда сомневаетесь, автосумма 😉
Калькулятор диапазона среднего среднего режима
Калькулятор диапазона среднего среднего режима представляет собой интеллектуальный инструмент, который позволяет вам вычислять средний режим среднего значения и диапазон для заданного набора данных. Читайте дальше, чтобы выполнить определенные расчеты набора данных с помощью нашего калькулятора среднего среднего режима!
Читайте дальше, чтобы выполнить определенные расчеты набора данных с помощью нашего калькулятора среднего среднего режима!
Обзор! В статистике центральная тенденция (или мера центральной тенденции) называется центральным или типичным значением для распределения вероятностей. Говорят, что наиболее распространенными мерами центральной тенденции являются среднее арифметическое, медиана и мода.
Вы можете воспользоваться приведенным выше калькулятором среднего значения средней моды, чтобы найти меры центральной тенденции (среднее значение, медиана, мода). Этот калькулятор центральной тенденции не только помогает найти медиану средней моды, но также помогает рассчитать диапазон набора данных.
Что ж, перейдем к делу, просто прочитайте эту статью, чтобы узнать, как вычислить диапазон средней средней моды, что такое средняя медиана и мода (центральная тенденция) и диапазон, как найти среднее значение набора данных, медиана, режим и диапазон заданного набора данных и многое другое, что вам нужно знать!
Итак, начнем с термина «Среднее»
Что такое среднее значение в математике? Проще говоря, «среднее» — это среднее значение всех данных в наборе.
Математически «среднее» — это своего рода среднее значение, которое находят путем деления суммы набора чисел на количество чисел в наборе данных. Помните, что «среднее» — это не единственный вид среднего, это то, о чем думает большинство людей, рассматривая среднее значение. Вы можете использовать средства для нескольких видов полезных целей в своей повседневной жизни, в том числе от расчета времени, необходимого вам, чтобы добраться домой с работы, до расчета суммы, которую вы тратите в среднем за неделю.
Формула для среднего (арифметическая):
μ = ∑X / N
или
Среднее = сумма членов/число членов
Где;
- μ представляет собой среднее значение генеральной совокупности (ну, вместо этого вы можете использовать букву M для обозначения среднего значения выборки, но помните, что расчет такой же)
- ∑X означает сумму всех чисел
- N упоминается как общее количество номеров
Как рассчитать среднее значение (вручную): Да, найти среднее значение для данного набора данных довольно просто, все, что вам нужно, чтобы выполнить указанные шаги, чтобы рассчитать среднее значение: давайте посмотрим на примере:
- Прежде всего необходимо определить набор значений, которые необходимо усреднить.
 Такие числа могут быть большими или маленькими, и даже их может быть сколько угодно. Помните, что вы должны использовать реальные числа, а не переменные
Такие числа могут быть большими или маленькими, и даже их может быть сколько угодно. Помните, что вы должны использовать реальные числа, а не переменные
Например: 2, 3, 4, 5, 6.
- Вы должны сложить свои значения вместе, чтобы найти сумму. Кроме того, для этого можно просто использовать калькулятор вручную или приложение для работы с электронными таблицами
.
Например: 2 + 3 + 4+ 5+ 6 = 20
- Теперь вам нужно подсчитать количество значений в вашей группе. Вы должны посчитать все сложенные числа. Помните, что идентичные значения все равно должны учитываться, то есть, если в вашем наборе данных есть значения, которые повторяются, каждое из них по-прежнему учитывается при расчете вашей суммы. При подсчете количества значений не учитывайте сумму (ответ) всех сложенных чисел!
Пример: 2, 3, 4, 5, а также 6 дают в общей сложности пять значений.
- Наконец, вам нужно разделить сумму набора на количество значений.
 Результат называется медовухой (тип среднего) вашего набора. Да, это означает, что если каждое число в вашем наборе имеет среднее значение, то в сумме они будут равны
Результат называется медовухой (тип среднего) вашего набора. Да, это означает, что если каждое число в вашем наборе имеет среднее значение, то в сумме они будут равны .
Пример: 20/5 = 4. Таким образом, 4 называется средним числом. Кроме того, вы можете проверить свои расчеты, просто умножив среднее значение на количество значений в наборе. В этом случае вы должны умножить 4 (среднее) на 5 (количество значений в наборе), и ваш результат будет 20 (4 × 5 = 20).
Кроме того, вы можете использовать приведенный выше калькулятор среднего для расчета среднего значения для заданного набора данных. Читайте дальше, чтобы узнать об этом умном калькуляторе среднего (среднего)!
О калькуляторе среднего: Этот калькулятор среднего поможет вам вычислить среднее (среднее) для заданного набора данных. Неважно, получены ли данные из популяции или из выборки, так как это действительно не влияет на расчет среднего значения. Вы можете попробовать приведенный выше калькулятор среднего среднего диапазона мод, чтобы вычислить среднее (среднее), медиану, моду и диапазон вместе с различными параметрами для заданного набора данных n.
Как найти среднее значение с помощью калькулятора среднего значения: Калькулятор центральной тенденции очень прост в использовании. Все, что вам нужно сделать, это выполнить указанные шаги, чтобы вычислить среднее значение для заданного набора данных.
Ввод: - Все, что вам нужно, чтобы ввести набор данных в специальное поле этого среднего калькулятора
Вывод: После того, как вы ввели набор данных, для которого вы хотите найти среднее значение (среднее), просто нажмите кнопку расчета калькулятора режима среднего значения, инструмент покажет вам:
- Среднее (среднее)
- Медиана (средняя)
- Режим (наиболее распространенный)
- Диапазон (самый большой – самый маленький)
- Среднее геометрическое
- По возрастанию
- По убыванию
- Четные числа
- Нечетные числа
- Сумма чисел
- Максимальное количество
- Количество (общее количество)
- Столбчатая диаграмма заданного набора данных
Теперь давайте начнем с определения медианы в математике!
Что такое медиана в математике? Медиана называется средним значением в заданном наборе данных или представляет собой простую меру центральной тенденции. Когда вы ищете медиану в заданном наборе данных, который имеет нечетное количество общих чисел, процесс вычисления медианы слишком прост. Без сомнения, вычисление медианы в наборе данных с четным общим числом немного сложнее. Вы можете попробовать наш калькулятор медианы и использовать приведенную ниже формулу медианы для расчета медианы.
Когда вы ищете медиану в заданном наборе данных, который имеет нечетное количество общих чисел, процесс вычисления медианы слишком прост. Без сомнения, вычисление медианы в наборе данных с четным общим числом немного сложнее. Вы можете попробовать наш калькулятор медианы и использовать приведенную ниже формулу медианы для расчета медианы.
Формула для медианы:
Для расчета медианы будет учитываться эта формула:
Формула
Или
Медиана = среднее значение заданного набора данных
Чтобы найти медиану легко и успешно, проведите пальцем по экрану вниз!
Как вычислить медиану в нечетном наборе чисел: - Прежде всего, вы должны отсортировать числа в наборе данных от меньшего к большему. Если они зашифрованы, то вы должны выстроить их в ряд, начиная с наименьшего числа и заканчивая наибольшим числом. Если набор данных включает 5, 3, 1, 7, 2, то это будет как 1, 2, 3, 5, 7
- Теперь вам нужно найти число, которое находится ровно посередине заданного набора данных.
 Таким образом, ясно, что перед медианным числом стоит столько же чисел, сколько и за ним. Что ж, начните считать их, чтобы убедиться, что
Таким образом, ясно, что перед медианным числом стоит столько же чисел, сколько и за ним. Что ж, начните считать их, чтобы убедиться, что
Давайте посмотрим на этот набор данных 1, 2, 3, 5, 7 — вы можете видеть, что перед 3 стоят два числа, а также два числа позади него. Он показывает, что 3 — это число, которое находится ровно посередине
- Итак, медиана 1, 2, 3, 5, 7 равна 3. Помните, что медиана набора данных с нечетными номерами — это всегда число в сам набор данных. Имейте в виду, что медиана никогда не является числом, которого нет в последовательности.
Как вычислить медиану в четном наборе чисел: Например; четный набор чисел: 2, 3, 1, 4
- Прежде всего, вы должны отсортировать свой набор чисел от меньшего к большему. Итак, снова используйте тот же первый шаг, что и упомянутый выше. Помните, что четный набор чисел будет иметь два числа точно посередине. Если набор данных включает 2, 3, 1, 4, то это будет 1, 2, 3, 4
- Теперь вам нужно найти среднее значение двух чисел в середине.
 Вы можете видеть, что 2 и 3 находятся посередине, поэтому здесь вам следует добавить 2 и 3, а затем просто разделить сумму на 2. Используйте приведенную выше формулу для нахождения среднего значения двух чисел (сумма двух средних числа) / 2
Вы можете видеть, что 2 и 3 находятся посередине, поэтому здесь вам следует добавить 2 и 3, а затем просто разделить сумму на 2. Используйте приведенную выше формулу для нахождения среднего значения двух чисел (сумма двух средних числа) / 2 - Итак, медиана этого набора данных с четным количеством чисел равна 2 ½. Итак, ясно, что медиана в четном наборе чисел не обязательно должна быть числом в самом наборе данных
.
О калькуляторе медианы: Наш калькулятор медианы — это интеллектуальный инструмент, который эффективно работает как средство поиска медианы. Проще говоря, калькулятор медианы поможет вам найти медиану из заданного набора данных. Читайте дальше, чтобы узнать, что вам нужно сделать, чтобы найти медиану!
Как найти медиану с помощью Калькулятора медианы: Вышеупомянутый искатель медианы имеет простой и удобный интерфейс, все, что вам нужно выполнить, чтобы найти значения медианы из заданного набора данных:
Ввод: - Все, что вам нужно, чтобы ввести набор данных в специальное поле вышеуказанного калькулятора медианы
Вывод: - После того, как вы ввели набор данных, просто нажмите кнопку расчета — средство поиска медианы покажет вам медианное значение для заданного набора данных вместе со средним значением, режимом, диапазоном и другими статистическими данными
Теперь давайте узнаем определение режима в математике, как рассчитать режим набора данных вручную, пример расчета режима, калькулятор режима и многое другое.
Проведите вниз!
Что такое режим в математике? В режиме простого слова это значение, которое чаще всего встречается в наборе данных. Более конкретно, мода чисел — это число, которое чаще всего встречается в наборе данных. Помните, что набор данных не обязательно должен иметь только одну моду. Но когда два или более значения «связаны» как наиболее распространенные, можно сказать, что набор данных является бимодальным или мультимодальным соответственно. Другими словами, все наиболее распространенные числа являются модами множества. Просто попробуйте приведенный выше калькулятор среднего значения и моды, чтобы найти моду вместе с различными параметрами статистики.
Что ж, если вы хотите рассчитать режим чисел или режим (ы) набора данных, выполните указанные шаги.
Формула для режима:
Режим = наиболее повторяющийся элемент в наборе . Далее, вы должны подсчитать, сколько каждого числа. Число, которое появляется чаще всего, называется модусом чисел.
Давайте посмотрим на пример:
3, 7, 5, 13, 20, 23, 39, 23, 40, 23, 14, 12, 56, 23, 29
По порядку:
3, 5, 7, 12, 13 , 14, 20, 23, 23, 23, 23, 29, 39, 40, 56
По порядку становится легко увидеть, какие числа появляются чаще всего.
В этом примере режим чисел 23.
Другой пример режима:
{19, 8, 29, 35, 19, 28, 15}
Сначала расположите их по порядку:
{8 , 15, 19, 19, 28, 29, 35}
Здесь, 19это режим, поскольку он появляется дважды, а все остальные появляются только один раз.
Итак, как насчет более чем одного режима: У нас может быть более одного режима.
Да, иногда у нас может быть более одного режима.
Например:
{1, 3, 3, 3, 4, 4, 6, 6, 6, 9}
Пример: {1, 3, 3, 3, 4, 4, 6, 6, 6 , 9}
Здесь вы можете видеть, что 3 встречается три раза, как и 6.
Итак, это означает, что есть два режима, т.е. 3 и 6
Помните, что:
- Если ваш набор данных имеет два режима, то говорят, что он «бимодальный»
- Если ваш набор данных имеет более двух режимов, то он называется «мультимодальным»
Итак, подробнее о калькуляторе режимов!
О калькуляторе режимов: Калькулятор режимов — это интеллектуальный инструмент, который поможет вам вычислить значение режима набора чисел. Это означает, что этот калькулятор работает как средство поиска мод, которое помогает вам найти число, которое чаще всего встречается в наборе данных. Если набор данных имеет несколько режимов, лучше всего их найти с помощью калькулятора режимов.
Это означает, что этот калькулятор работает как средство поиска мод, которое помогает вам найти число, которое чаще всего встречается в наборе данных. Если набор данных имеет несколько режимов, лучше всего их найти с помощью калькулятора режимов.
Как найти моду набора данных с помощью этого калькулятора мод: Наш искатель мод довольно прост в использовании, все, что вам нужно, чтобы придерживаться заданных шагов, чтобы найти моду заданного набора данных в математике.
Ввод:
- Вы должны ввести набор данных, для которого вы хотите найти режим
Вывод: - После того, как набор данных введен в указанное поле, нажмите кнопку расчета, этот калькулятор режимов покажет вам режим (наиболее распространенный), медиану, среднее значение, диапазон и определенные параметры для данного набора данных. .
Итак, читайте дальше, чтобы узнать определение диапазона в математике, пример расчета диапазона, как найти диапазон с помощью простого калькулятора диапазона и многое другое!
Что такое диапазон в математике? Математически диапазоном набора данных называется разница между наибольшим и наименьшим значением в наборе. Если вы хотите найти диапазон набора данных, вам следует упорядочить набор чисел от наименьшего к наибольшему, а затем вы должны вычесть наименьшее значение из наибольшего значения. Итак, давайте взглянем на приведенные шаги, и если вы хотите мгновенно найти диапазон чисел, просто попробуйте наш калькулятор диапазона среднего среднего режима.
Если вы хотите найти диапазон набора данных, вам следует упорядочить набор чисел от наименьшего к наибольшему, а затем вы должны вычесть наименьшее значение из наибольшего значения. Итак, давайте взглянем на приведенные шаги, и если вы хотите мгновенно найти диапазон чисел, просто попробуйте наш калькулятор диапазона среднего среднего режима.
Формула диапазона в математике:
Диапазон = наибольшее значение – наименьшее значение
Как вычислить диапазон чисел или набор данных: Например:
Допустим, набор данных содержит следующие числа:
{7, 8, 65, 8, 4, 7}.
- Прежде всего, вы должны расположить набор чисел в порядке от меньшего к большему. Ну вот как выглядит ваш набор данных: {4, 7, 7, 8, 8, 65}
- Теперь вы должны определить наименьшее и наибольшее число в наборе данных, в этом наборе данных наименьшее число равно 4, а наибольшее число равно 65
- Затем нужно вычесть наименьшее число из наибольшего.
 Наименьшее число 4, а наибольшее число 65, значит 65 — 4 = 61
Наименьшее число 4, а наибольшее число 65, значит 65 — 4 = 61 - Итак, диапазон этого конкретного набора данных составляет 61
О калькуляторе диапазона: Калькулятор диапазона работает эффективно как дальномер, который помогает вам вычислить диапазон чисел из заданного набора данных. В частности, калькулятор диапазона, который поможет вам найти разницу между наибольшим и наименьшим значением в наборе данных.
Как найти диапазон с помощью калькулятора диапазона: Да, расчет диапазона с помощью калькулятора становится довольно простым, вы просто выполняете указанные шаги, чтобы мгновенно найти диапазон заданного набора данных:
Ввод: - Все, что вам нужно, чтобы ввести свой набор данных в специальное поле дальномера
Вывод: - После этого просто нажмите кнопку расчета, калькулятор диапазона мгновенно покажет вам значение диапазона набора данных, среднее значение, моду, медиану вместе с различными параметрами, которые вам нужно знать!
Часто задаваемые вопросы (среднее значение, медиана, мода и диапазон): Как найти среднюю медианную моду и диапазон? Чтобы найти это:
- Вы должны сложить все значения вашего набора данных и разделить на количество сложений, полученное значение называется средним значением набора данных
- Медиана называется средним числом набора данных в порядке от наименьшего к наибольшему
- Модой называется число, которое чаще всего встречается в вашем наборе данных
- Диапазон называется разницей между самым высоким и самым низким значениями в вашем наборе данных
Если вы не хотите зацикливаться на этих ручных вычислениях, просто введите свой набор данных в калькулятор диапазона среднего среднего режима и рассчитайте все за один раз!
Что делать, если в наборе данных нет моды? Режим набора данных указывает на число, которое встречается чаще всего. Если в вашем наборе данных нет числа, которое встречается чаще, чем любое другое, то это называется отсутствием режима для набора данных. Также возможно, что набор данных имеет более одного режима.
Если в вашем наборе данных нет числа, которое встречается чаще, чем любое другое, то это называется отсутствием режима для набора данных. Также возможно, что набор данных имеет более одного режима.
Может ли 0 быть режимом? Предположим, что ваш набор данных:
8, 0, -3, 4, 12, 0, 5, -1, 0
Теперь, упорядочив набор данных от меньшего к большему, вы получите:
8, -3, -1, 0, 0, 0, 4, 5, 12
В этом наборе данных значение моды равно 0. во внимание, чтобы найти среднее (среднее) и диапазон вместе с медианой и модой для данного набора данных.
Ссылки: Из Википедии, свободной энциклопедии – Среднее (среднее) – Типы среднего – Среднее вероятностного распределения – Взвешенное арифметическое среднее – Среднее значение функции – также найдите моду, медиану, диапазон от источника из Википедии
Из источника wikihow – как найти медиану набора чисел – Найти медиану в нечетном и четном наборе чисел – Соавтор: Штатный редактор wikiHow
Из источника исследования – Как рассчитать среднее значение, медиану, моду и диапазон — меры центральной тенденции — и узнать больше обо всем!
Из авторизованного источника пурпурной математики — примеры среднего, медианы, моды и диапазона — узнайте больше о показателях центральной тенденции, диапазоне и различных параметрах
Калькулятор среднего, медианы, моды и диапазона
Среднее значение, медиана, мода и диапазон являются одними из важных понятий статистики.

Все мы знаем, что статистика — это предмет, который целиком занимается данными или числами, их упорядочиванием и изучением. Когда у нас есть много данных, которые нужно изучить или проанализировать, важно иметь определенные параметры, которые сделают наше исследование лучше.
Что подразумевает Центральная Тенденция?
Прежде чем перейти к знаниям о среднем значении, медиане и моде, нам нужно получить представление о термине, который очень важен для этих трех терминов — Центральная тенденция.
- Центральная тенденция — это статистический термин, представляющий центральную точку данного набора данных.
- Указывает, куда попадает большинство значений данного распределения данных.
- Центральную тенденцию можно представить как точку, вокруг которой группируются все значения заданного набора данных.

Теперь среднее значение, медиана, мода и диапазон являются такими центральными тенденциями, которые дают общее представление о данных данного набора данных. Каждый из них имеет свою методику расчета, и каждый из них передает различную картину данного набора данных. Давайте поймем это лучше, когда мы будем двигаться дальше.
Среднее
Это всем нам более знакомо. Нас использовали для расчета среднего значения заданного набора значений, и это среднее значение в статистике называется средним.
Среднее значение = Сумма всех значений или чисел в наборе данных, деленная на общее количество элементов в наборе данных.
Медиана
Данный набор данных может содержать значения из разных диапазонов. Их можно расположить таким образом, чтобы они располагались либо в порядке возрастания, либо в порядке убывания.
Когда вы упорядочиваете заданный набор данных либо в порядке возрастания, либо в порядке убывания, самое среднее значение является медианой данного набора данных.
Медиана = самый средний член данного набора данных, когда его значения расположены либо в возрастающем, либо в убывающем порядке.
Примечание. Если общее количество терминов четное, то среднее двух средних чисел является медианой данного набора данных.
Режим
В заданном наборе данных может быть много значений, которые повторяются или встречаются много раз в наборе данных. Такое число или значение, которое повторяется наибольшее количество раз в заданном наборе данных, называется его модой.
Режим = Значение или элемент, который повторяется наибольшее количество раз в заданном наборе данных.
Диапазон
Это разница между наибольшим и наименьшим значением заданного набора данных.
Диапазон = наибольшее значение – наименьшее значение
Пример
Рассмотрим пример данных, как показано ниже: 2, 5, 3, 6, 2, 6, 7, 9, 1.
Для этого набора данных значения средней медианы и моды следующие:
Среднее = (2 + 5 + 3 + 6 + 2 + 6 + 7 + 9 + 1) / 9 = 45 / 10 = 4,5
Медиана = Среднее значение (1,2,2,3,5,6,6,7,9) = 5
Mode = Наиболее повторяющиеся значения (1, 2, 2, 3, 5, 6, 6, 7, 9) = ( 2, 6 )
Диапазон = (наибольшее значение) 9 – (наименьшее значение) 1 = 8
Примечание. Те же расчеты остаются в силе, даже если значения в данном наборе данных представлены дробями или десятичными значениями. Нужна помощь по дробям или десятичным значениям? Проверьте наш онлайн-калькулятор дробей бесплатно.
Те же расчеты остаются в силе, даже если значения в данном наборе данных представлены дробями или десятичными значениями. Нужна помощь по дробям или десятичным значениям? Проверьте наш онлайн-калькулятор дробей бесплатно.
Математика — это не числа, уравнения, вычисления или алгоритмы; это о понимании. – Уильям Пол Терстон
Практическое применение среднего, медианы, моды и диапазона
Эти основные тенденции находят применение во многих статистических вычислениях. Например, в режиме реального времени рассмотрим центр обработки данных. Он содержит много оборудования, такого как серверы, охлаждающее оборудование, вентиляторы и т. д., которые потребляют электроэнергию. Датчики и интеллектуальные блоки питания используют эти основные тенденции для оценки различных статистических данных о мощности, потребляемой в данной стойке серверов и другого электрооборудования в центре обработки данных.
Кстати, знаете ли вы различные аспекты, которые учитываются при расчете стоимости электроэнергии? Проверьте их на нашем бесплатном онлайн-калькуляторе стоимости электроэнергии.
Как пользоваться калькулятором среднего, медианы, режима и диапазона CalculatorHut?
Этот бесплатный онлайн-калькулятор среднего, медианы, моды и диапазона от CalculatorHut позволяет вычислять эти значения для заданного набора данных. Вы можете ввести значения имеющегося у вас набора данных и очень легко рассчитать эти центральные тенденции.
Вы можете разместить это в виде виджета в своем блоге или на веб-сайте и сообщать читателям, сколько их устройство будет отображаться в ежемесячном счете за электроэнергию. Напишите нам по адресу [email protected], чтобы получить бесплатный настраиваемый виджет.
CalculatorHut также имеет свое приложение с более чем 100 калькуляторами на различные темы — калькуляторы здоровья, финансовые калькуляторы, калькуляторы транспортных средств, математические калькуляторы, калькуляторы физики, калькуляторы химии и многие другие. Загрузите наше бесплатное приложение и носите мир вычислений в своем кармане.
Дайте нам знать, если вы хотите, чтобы мы добавили любой другой калькулятор в наш ассортимент. Мы будем рады служить вам. Удачных расчетов!!
Мы будем рады служить вам. Удачных расчетов!!
В реальной жизни не будь подлым! Будь медианой или модой!!
Калькулятор статистического среднего значения для среднего, медианы, моды и диапазона
Пример набора данных
Чтобы показать, как вычислять среднее значение, медиану, моду и диапазон, я буду использовать следующий набор данных:
36, 3, 8, 12, 15, 18, 22, 34, 8, 25, 17, 13, 23
Как вычислить среднее значение?
Среднее — это среднее всех чисел в наборе данных. Чтобы вычислить среднее значение набора чисел, вы складываете все числа вместе, а затем делите эту сумму на количество элементов в наборе.
| Набор данных: 36, 3, 8, 12, 15, 18, 22, 34, 8, 25, 17, 13, 23 36 + 3 + 8 + 12 + 15 + 18 + 22 + 34 + 8 + 25 + 17 + 13 + 23) ÷ 13 |
| Среднее значение = 234 ÷ 13 |
| Среднее значение = 18 |
Как вычислить медиану?
Медиана — это среднее число в наборе данных после сортировки набора данных от меньшего к большему. Чтобы вычислить медиану набора данных, вы подсчитываете количество элементов, а затем сортируете элементы от меньшего к большему. Далее, для нечетного числа элементов вы добавляете 1 к количеству элементов, а затем делите на 2, чтобы получить положение среднего числа. Из нашего примера набора данных медиана — это 7-е число в отсортированном списке, то есть число 17.
Чтобы вычислить медиану набора данных, вы подсчитываете количество элементов, а затем сортируете элементы от меньшего к большему. Далее, для нечетного числа элементов вы добавляете 1 к количеству элементов, а затем делите на 2, чтобы получить положение среднего числа. Из нашего примера набора данных медиана — это 7-е число в отсортированном списке, то есть число 17.
| Набор данных с нечетными номерами: 36, 3, 8, 12, 15, 18, 22, 34, 8, 25, 17, 13, 23 |
Количество элементов в наборе 171 81| Средняя позиция = ((count + 1) ÷ 2) | |
| Средняя позиция = ((13 + 1) ÷ 2) |
| Средняя позиция = (14 ÷ 2) |
| Средняя позиция = 7 0 7 7 |
| Количество | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| Data Set | 3 | 8 | 8 | 12 | 13 | 15 | 17 | 18 | 22 | 23 | 25 | 34 | 36 |
| Median = 17 (7th number in sorted data set) |
Note that for an даже числа элементов, вы найдете среднее из двух средних чисел. Первая средняя позиция будет равна количеству элементов, разделенному на 2 минус 1. Вторая средняя позиция будет первой средней позицией плюс 1. Затем вы сложите два средних числа вместе и разделите на 2, чтобы найти среднее значение. Из нашего исправленного примера набора данных это дает вам среднее значение 16, что является средним значением 6-го и 7-го элементов (15 и 17).
Первая средняя позиция будет равна количеству элементов, разделенному на 2 минус 1. Вторая средняя позиция будет первой средней позицией плюс 1. Затем вы сложите два средних числа вместе и разделите на 2, чтобы найти среднее значение. Из нашего исправленного примера набора данных это дает вам среднее значение 16, что является средним значением 6-го и 7-го элементов (15 и 17).
| Четный набор данных: 36, 3, 8, 12, 15, 18, 22, 34, 8, 25, 17, 13 |
| Количество элементов в наборе 12 |
| 1-я средняя позиция = (число ÷ 2) — 1 |
| 1-я средняя позиция = (12 ÷ 2) — 1 = 1-я средняя позиция |
9000 = 15| 2 -я средняя позиция = 1 -я средняя позиция + 1 |
| 2 -я средняя позиция = 6 + 1 = 7 |
| 2 -е среднее число = 17 |
| Среднее число средних чисел = (15 + 17 = 17 |
. ) ÷ 2 = 16 ) ÷ 2 = 16 |
| Count | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Data Set | 3 | 8 | 8 | 12 | 13 | 15 | 17 | 18 | 22 | 25 | 34 | 36 |
| Медиана = 16 (среднее значение 15 и 17) |
Как рассчитать моду?
Режим — это число в наборе данных, которое наиболее часто повторяется в наборе. Чтобы найти режим, вы просто подсчитываете, сколько раз каждое уникальное число появляется в наборе данных. Число, которое появляется чаще всего, является режимом. В нашем примере набора данных чаще всего встречается число 8. Следовательно, мода набора данных — 8.
| Набор данных: 36, 3, 8, 12, 15, 18, 22, 34, 8, 25, 17, 13, 23, |
| Сортированный набор данных | 3 | 8 | 3 | 8 | | 8 | 12 | 13 | 15 | 17 | 18 | 22 | 23 | 25 | 34 | 36 |
| Mode = 8 (8 appears the most often) |
Обратите внимание, что набор данных может иметь более 1 режима. Например, если бы приведенный выше набор данных включал еще 3, то набор имел бы две моды: 3 и 8. Набор данных, имеющий две моды, называется 9.0140 бимодальный набор , тогда как набор данных, имеющий более двух режимов, называется мультимодальным набором .
Как рассчитать диапазон?
Диапазон — это разница между наибольшим числом в наборе и наименьшим числом в наборе. Чтобы найти диапазон, вы сортируете диапазон от меньшего к большему, чтобы определить минимальное и максимальное значения. Затем вы вычитаете минимальное значение из максимального значения, чтобы найти диапазон. В нашем примере минимальное значение равно 3, а максимальное — 36, что дает диапазон 33 (36 — 3).
Чтобы найти диапазон, вы сортируете диапазон от меньшего к большему, чтобы определить минимальное и максимальное значения. Затем вы вычитаете минимальное значение из максимального значения, чтобы найти диапазон. В нашем примере минимальное значение равно 3, а максимальное — 36, что дает диапазон 33 (36 — 3).
| Набор данных: 36, 3, 8, 12, 15, 18, 22, 34, 8, 25, 17, 13, 23 |
| Сортируемые данные | 3 9003 | 8 80007 | 3 | | 8. | 8 | 12 | 13 | 15 | 17 | 18 | 22 | 23 | 25 | 34 | 36 |
9000 36 | 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 36 9000 |
9000 9000 9000 9000 9000 9000 9000 9000 9000
. “Методы решения уравнений четвертой степени”Муниципальное бюджетное общеобразовательное учреждение средняя общеобразовательная школа №1 г. Южи Ивановской области Педагогический проект по теме: “Методы решения уравнений четвертой степени” Выполнила Чурина Елена Вениаминовна, учитель математики первой квалификационной категории Г. Южа 2021 год Содержание Актуальность Цель и задачи работы:……………………………… 1. Исторические сведения об уравнениях четвёртой степени……стр. 2. Определение уравнения 4 степени………………………….стр. 3. Способы решения уравнений 4 степени……………………………стр. 3.1. Схема метода Феррари……………………….стр. 3.2. Разложение на множители. Кубическая резольвента……………стр. 3.3. Теорема Виета для уравнения 4 степени……………………..стр. 3.4. Решение уравнений 4 степени по схеме Горнера……………………стр. 4.Решение некоторых уравнений 4 степени……………………………стр. 4.1. Решение биквадратного уравнения………………………………стр. 4.2. Решение уравнения способом группировки………………….стр. 4.3. Решение уравнения по свободному члену……………………стр. 4.4. Графический метод………………………………………..стр. 4.5. Применение формул сокращенного умножения. Выделение полного квадрата………………………………………………..стр. 5. Исследование………………………………………………стр. 6. Выводы 7. Заключение 8. Тренировочные задания для отработки различных способов решения уравнений высших степеней……………………………………………стр. Список литературы Актуальность Как все знают, в математике одна из важнейших вещей — это уравнения. Чаще всего решаются линейные либо квадратные уравнения, но не мало важны уравнения 4 степени, которые решить сможет не каждый учащийся 9 класса. Чтобы решать такие уравнения было проще, нужно выбрать тот способ, который тебе более понятен. Задания с уравнениями высших степеней есть в контрольных измерительных материалах при проведении государственной итоговой аттестации. Значит, ученики должны уметь решать уравнения не только 2 степени, но и выше. А это умеет делать далеко не каждый. Цель работы: узнать и разобрать методы решения уравнений высших степеней. Задачи: Изучить литературу по истории приемов решения уравнений 4-й стпени Обобщить накопленные знания об уравнениях4-й степени и способах их решения. Сделать выводы. Разработать дидактический материал для проведения практикума по решению уравнений 4-й степени с использованием новых приемов в помощь ученикам, увлеченным математикой и учителям, ведущим факультативные занятия. Проблемный вопрос: существуют ли кроме общепринятых приемов решения квадратных уравнений другие, которые позволяют быстро и рационально решать уравнения 4-й степени? Гипотеза: существует универсальный способ для решения всех видов уравнений 4-степеней. Объект исследования: уравнения 4-й степени Предмет изучения: методы и приемы решениях уравнений 4-й степени, в том числе 1.Исторические сведения об уравнениях четвёртой степени Решение уравнений высших степеней – история полная драматизма, разочарования и радости открытия. В течение почти 700 лет математики разных стран пытались найти приёмы решения уравнений третьей, четвёртой и более высоких степеней. Необходимость решать уравнения не только первой, но и второй и высших степеней ещё в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земельными работами военного характера, а также с развитием астрономии и самой математики. Квадратные уравнения умели решать около 2000 лет до нашей эры вавилоняне. Однако уже при решении уравнений третей степени математики столкнулись с большими трудностями. История открытия способа решения кубических уравнений полна тайн, так как в древности учёные часто на открытых диспутах соревновались в решении трудных задач. От исхода этих состязаний зависела их научная репутация и материальное благополучие. Тот, кто первым овладел решением кубических уравнений, мог легко победить своих соперников давая им задачи, сводящиеся к кубическим уравнениям. Поэтому способы решения уравнения тщательно скрывались. Историки полагают, что первым нашёл способ решения кубических уравнений известный итальянский алгебраист Специна дель Ферро (1465-1576), но впервые опубликовал общую формулу решения кубических уравнений итальянский математик Джераламо Кордано (1501-1576г.). Эта формула носит теперь название формулы Кордано, хотя предполагают, что эту формулу ему передал итальянский математик Николо Тарталья ( 1500-1557). С именами этих же математиков связано открытие способов решения уравнений четвёртой степени. В дальнейшем математики активно пытались найти формулы вычисления корней уравнений пятой и более степени. И только почти через три столетия впервые итальянский учёный Паоло Руффини (1765-1822), а затем норвежский математик Нильс Хенрих Абель (1802-1829г.) доказали, что не существует формулы, выражающей корни любого целого уравнения пятой степени через конечное число алгебраических операций над его коэффициентами. Да и найденные формулы вычисления корней для уравнений третьей и четвёртой степени столь сложны, что ими практически не пользуются. Поэтому в современной математике разработаны методы, позволяющие находить с любой степенью точности приближенные значения корней уравнений. Использование компьютеров значительно облегчают эту работу. 2. Определение уравнения 4 степени Уравнение четвёртой степени —алгебраическое уравнение вида: , при этом a≠0 и где a,b,c,d,e- любые числа. Четвёртая степень для алгебраических уравнений является наивысшей, при которой существует аналитическое решение в радикалах в общем виде (то есть при любых значениях коэффициентов). 3. Способы решения уравнений 4 степени. 3.1 Схема метода Феррари a0x4 + a1x3 + a2x2 + a3x + a4 = 0, | (1) |
где a0, a1, a2, a3, a4 – произвольные вещественные числа, причем Метод Феррари состоит из двух этапов. На первом этапе уравнения вида (1) приводятся к уравнениям четвертой степени, у которых отсутствует член с третьей степенью неизвестного. На втором этапе полученные уравнения решаются при помощи разложения на множители, однако для того, чтобы найти требуемое разложение на множители, приходится решать кубические уравнения. Приведение уравнений 4-ой степени Разделим уравнение (1) на старший коэффициент a0 . Тогда оно примет вид x4 + ax3 + bx2 + cx + d = 0, | (2) |
где a, b, c, d – произвольные вещественные числа. Сделаем в уравнении (2) замену где y – новая переменная. Тогда, поскольку то уравнение (2) принимает вид Если ввести обозначения то уравнение (4) примет вид y4 + py2 + qy + r = 0, | (5) |
где p, q, r – вещественные числа. Первый этап метода Феррари завершён. 3.2.Разложение на множители. Кубическая резольвента Добавив и вычитая в левой части уравнения (5) выражение 2sy2 + s2, где s – некоторое число, которое мы определим чуть позже, из (5) получим Следовательно, уравнение (5) принимает вид Если теперь выбрать число s так, чтобы оно являлось каким-нибудь решением уравнения то уравнение (6) примет вид Избавляясь от знаменателя, уравнение (7) можно переписать в виде или, раскрыв скобки, — в виде Полученное кубическое уравнение (9), эквивалентное уравнению (7), называют кубической резольвентой уравнения 4-ой степени (5). Если какое-нибудь решение кубической резольвенты (9) найдено, то уравнение (8) можно решить, разложив его левую часть на множители с помощью формулы сокращенного умножения «Разность квадратов». Действительно, Таким образом, для решения уравнения (8) остаётся решить квадратное уравнение а также квадратное уравнение Вывод метода Феррари завершен. Пример решения уравнения 4-ой степени Пример. Решить уравнение x4 + 4×3 – 4×2 – 20x – 5 = 0. | (12) |
Решение. В соответствии с (3) сделаем в уравнении (12) замену Поскольку x4 + 4×3 – 4×2 – 20x – 5 = (y – 1)4 + 4(y – 1)3 – 4(y – 1)2 – 20(y – 1)– 5 =
= y4 – 4y3 + 6y2 – 4y + 1 + 4y3 – 12y2 + 12y – 4 – 4y2 + 8y – 4 – 20y + 20 – 5 =
= y4 – 10y2 – 4y + 8, то в результате замены (13) уравнение (12) принимает вид y4 – 10y2 – 4y + 8 = 0. | (14) |
В соответствии с (5) для коэффициентов уравнения (14) справедливы равенства p = – 10, q = – 4, r = 8. | (15) |
В силу (9) и (15) кубической резольвентой для уравнения (14) служит уравнение 2s3 + 10s2 – 16s – 84 = 0, которое при сокращении на 2 принимает вид: s3 + 5s2 – 8s – 42 = 0. | (16) |
Проверяя, какой из делителей свободного члена уравнения (16) является целым корнем этого уравнения, находим, что целым корнем кубической резольвенты является число Подставляя значения (15) и (17) в формулу (10), получаем уравнение y2 – 2y – 4 = 0, корни которого имеют вид: Подставляя значения (15) и (17) в формулу (11), получаем уравнение y2 + 2y – 2 = 0, корни которого имеют вид: В завершение, воспользовавшись формулой (13), из (18) и (19) находим корни уравнения (12): Ответ. Но эти способы очень сложны. Рассмотрю более простые способы, с помощью которых можно решить некоторые уравнения 4-й четверти. 3.3Теорема Виета для уравнения четвёртой степени Корни уравнения четвёртой степени {\displaystyle x_{1},\,x_{2},\,x_{3},\,x_{4}} связаны с коэффициентами {\displaystyle a,\,b,\,c,\,d,\,e}следующим образом: {\displaystyle x_{1}+x_{2}+x_{3}+x_{4}=-{\frac {b}{a}},} 3.4.Решение уравнений четвертой степени по схеме Горнера 2x4 + 5x3 — 11x2 — 20x + 12 = 0 Для начала нужно методом подбора найти один корень. Обычно он является делителем свободного члена. В данном случае делителями числа 12 являются ±1, ±2, ±3, ±4, ±6, ±12. Начнем их подставлять по-очереди: 1: 2 + 5 — 11 — 20 + 12 = -12 ⇒ число 1 не является корнем многочлена -1: 2 — 5 — 11 + 20 + 12 = 18 ⇒ число -1 не является корнем многочлена 2: 2 ∙ 16 + 5 ∙ 8 — 11 ∙ 4 — 20 ∙ 2 + 12 = 0 ⇒ число 2 является корнем многочлена Мы нашли 1 из корней многочлена. Корнем многочлена является 2, а значит исходный многочлен должен делиться на x — 2. Для того, чтобы выполнить деление многочленов, воспользуемся схемой Горнера: В верхней строке выставляются коэффициенты исходного многочлена. В первой ячейке второй строки ставится найденный нами корень 2. Во второй строке пишутся коэффициенты многочлена, который получится в результате деления. Они считаются так: | Во вторую ячейку второй строки запишем число 2, просто перенеся его из соответствующей ячейки первой строки. | | 2 ∙ 2 + 5 = 9 | | 2 ∙ 9 — 11 = 7 | | 2 ∙ 7 — 20 = -6 | | 2 ∙ (-6) + 12 = 0 | | |
Последнее число — это остаток от деления. Если он равен 0, значит мы все верно посчитали. Таким образом, мы исходный многочлен разложили на множители и переходим к уравнению. (х-2)(2х3+9х2+7х-6)=0 Многочлен, являющийся вторым множителем попробуем разложить на множители подобным образом. Отыщем опять делители свободного члена. В данном случае делителями числа -6: ±1, ±2, ±3, ±4, ±6. Число -2 является корнем многочлена. Напишем найденный корень в схему Горнера и начнем заполнять ячейки: Во вторую ячейку третьей строки запишем число 2, просто перенеся его из соответствующей ячейки второй строки. | -2 ∙ 2 + 9 = 5 | -2 ∙ 5 + 7 = -3 | -2 ∙ (-3) — 6 = 0 |
Таким образом, мы исходный многочлен разложили на множители и переходим к уравнению.{2}-4ac}}}{2a}}}.}
Пример. Решить уравнение Замена из этого следует, что уравнение имеет два корня. Обратная замена т.е. невозможно Ответ: . 4.2. Решение уравнения способом группировки Способом группировки можно решить уравнение 4 степени. Чтобы разложить уравнение на множители, надо сгруппировать слагаемые по парам. Мы должны сгруппировать слагаемые по парам таким образом, чтобы при вынесении общего множителя за скобки у слагаемых был одинаковый множитель. Решим на примере. 2х4-5х3+2х2-5х=0 (2х4-5х3)+( 2х2-5х)=0 х3(2х-5)+х(2х-5)=0 (2х-5)(х3-х)=0 х(2х-5)(х2-1)=0 х(2х-5)(х-1)(х+1)=0 х=0 или 2х-5=0 или х-1=0 или х+1=0 х1=0 х2=2,5 х3=1 х4=-1 4.3. Решение уравнения по свободному члену Любое уравнение вида можно свести к приведенному уравнению той же степени, домножив обе его части на и выполнив замену переменной вида :
Полученные коэффициенты тоже будут целыми. Таким образом, будем решать приведенное уравнение степени n с целыми коэффициентами вида . Алгоритм решения. Находим целые корни уравнения. Целые корни уравнения , i=1, 2, …, m (m – количество целых корней уравнения) находятся среди делителей свободного члена . То есть, первым делом выписываем делители свободного члена и подставляем их по очереди в исходное равенство для проверки. Перебираем их по очереди, пока не получим тождество. Как только тождество получено, то первый целый корень уравнения найден и уравнение предстает в виде , где — корень уравнения, а — частное от деления на . Продолжаем подставлять выписанные ранее делители в уравнение , начиная с (так как корни могут повторяться). Как только получаем тождество, то корень найден и уравнение предстает в виде , где — частное от деления на . И так продолжаем перебор делителей, начиная с . В итоге найдем все m целых корней уравнения и оно представится в виде , где — многочлен степени n-m. Весь этот процесс удобно проводить по схеме Горнера. Дробных корней приведенное уравнение с целыми коэффициентами иметь не может. Находим оставшиеся корни (иррациональные и/или комплексные) из уравнения любым способом. Решить уравнение . Во-первых, найдем все целые корни данного уравнения. Свободным членом является -3. Его делителями являются числа 1, -1, 3 и -3. Будем подставлять их по очереди в исходное равенство до получения тождества. При х=1 имеем . То есть х=1 является корнем уравнения. Разделим многочлен на (х-1) столбиком:
Следовательно, . Продолжим перебор делителей, но уже для равенства :
При х = -1 получили верное равенство, следовательно, -1 является корнем уравнения. Разделим на (х+1) столбиком:
Таким образом,
Продолжаем перебор делителей для равенства , начиная с х = -1:
Получили неверные равенства, следовательно, целых корней уравнение больше не имеет. Оставшиеся корни исходного уравнения являются корнями квадратного трехчлена . , то есть, действительных корней трехчлен не имеет, но имеет пару комплексно сопряженных. 4.4.Графический метод. Иногда полезно рассмотреть эскизы графиков функций у=ƒ(x) и у=g(x), входящих в уравнение ƒ(x) = g(x). Это может помочь выяснить: 1) на какие множества надо разбить числовую ось, чтобы на каждом из этих множеств использовать свой способ решения; 2) наличие или отсутствие корней, их количество. Пример: (материал взят из ОГЭ 2016г.) x4=(3x-10)2 Решение №3: x4=(3x-10)2 1) Рассмотрим две функции: у = х4 и у =(3х-10)2. 2) Построим график функции у = х4 — график парабола ветви направлены вверх. 3) Построим график линейной функции у = (3х-10)2. Это парабола ветви, которой направлены вверх. 4) В данном примере наглядно видна только одна точка пересечения В(2;16) (см. приложение рис.3), хотя очевидно, что графики пересекаются еще в одной точке (т.е. имеется еще одно решение). Как видим, что графический способ в данном случае не удобен, так как ограниченный размер листа тетради не позволяет увидеть все точки пересечения. Графическое решение уравнения- наглядный способ, он хорош при необходимости определения наличия или отсутствия корней и их количества. 4.5. Применение формул сокращенного умножения. Выделение полного квадрата. Этот метод основан на использовании формул: а2-b2=(а-b)(а+b)a2+2ab+b2=(a+b)2a2−2ab+b2=(a−b)2 а3+b3=(а+b)(а2-аb+b2)а3-b3=(а-b)(а2+аb+b2)(а+b)3=а3+3а2b+3аb2+b3 (а-b)3= а3-3а2b+3аb2-b3, Пример: х4=(3х-10)2 Способ 1: Используем формулу сокращенного умножения х4-(3х-10)2=0 (х2-3х+10)(х2+3х-10)=0 х2-3х+10=0 или х2+3х-10=0 D=9-40=-31 D=9+40=49 корней нет х1=-5, х2=2. Ответ: х1=-2, х2=5. 6. Выводы: 1. Уравнения высших степеней решали еще более 500 тыс. лет назад. 2. Есть много способов решения уравнений 4-й степеней. Некоторые из них довольно сложные, а некоторые помогут быстро решить задания на ОГЭ. 3. Уравнения 4-й степеней играют немалую роль в развитии математики. Лишь немногие из учащихся умеют решать такие уравнения. Эти методы решения уравнений высших степеней непросты в применении, но они всё равно могут заинтересовать увлекающихся математикой учеников. 7. Заключение В данной работе рассмотрены способы решения уравнений 4-й степени. А также рассмотрены приёмы решения уравнений 4-й степени, которые позволяют быстрее и проще решить такие уравнения. Данные приёмы решения заслуживают внимания, поскольку каждые из них интересны и уникальны. Овладение данными приёмами поможет экономить время и эффективно решать уравнения. Потребность в быстром и упрощенном решении обусловлена применением этих навыком на экзаменах. Таким образом, цель работы — узнать и разобрать методы решения уравнений высших степеней- достигнуты. Гипотеза доказана, существует универсальный способ решения уравнений 4-й степени. Это способ Феррари. Источники: Алгебра. 9 класс:учебник для общеобразовательных организаций / А45 Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; Под редакцией С. А. Теляковского. – 4-е издание – М.: Просвещение, 2017. – 287 с.: ил. – ISBN 978-5-09-046396-6. . М.Л. Галицкий, А.М. Гольдман, Л.М. Звавич «Сборник задач по алгебре для 8-9 классов». Учебное пособие для учащихся школ и классов с углубленным изучением математики -Москва «Просвещение», 1999. В.В. Бардушкин, И.Б. Кожухов, А.А. Прокофьев, А.М. Ревякин,
А.М. Терещенко «Письменный вступительный экзамен по математике» — Москва «Лист», 1998. Н.В. Бурмистрова, Н.Г. Старостенкова «Функции и их графики». Учебное пособие — Саратов «Лицей», 2003. М.А.Еремин «Уравнения высших степеней» — Арзамас, 2003. А.Г.Курош «Алгебраические уравнения произвольных степеней» — М.:Наука, 1975. Л.М.Лоповок «1000 проблемных задач по математике» — М.: Просвящение, 1995. И.Р.Шафаревич «Популярные лекции по математике. О решении уравнений высших степеней» Вып.15 – М.: Наука, 1954. 10.https://zaochnik.com/spravochnik/matematika/systems/reshenie-uravnenij-vysshih-stepenej/ 11. http://www.cleverstudents.ru/equations/equations_of_higher_degree.html 12. https://ru.wikipedia.org/wiki/Уравнение_четвёртой_степени Приложение 1 Тренировочные задания для отработки различных способов решения уравнений 4-й степени. №1 Решите уравнения способом замены: , б) X4-2×2-8=0, в) x4-8×2-9=0, г) x4-7×2+12=0, д) 3×4-13×2+4=0, е) 2×4-19×2+9=0, ж) 3×4-13×2+4=0, з) (x2+4x)(x2+4x-17)=60=0, и) (x2-5x)(x2-5x+10)+24=0, к)(x2-3x)2-2(x2-3x)=8, л) (x2+x)2-11(x2+x)=12, 1 м) ()+10=0, н) ()=3; о) №2 Решите уравнения, раскладывая левую часть на множители способом группировки: а) 2×4-5×3+2×2-5x=0, б) 6×4-3×3+12×2-6x=0, в) 2×4+3×3-8×2-12x=0, г) 2×4-5×3-18×2+45x=0. №3 Решите уравнения по свободному члену
а) 2×4 – 3×3 – 7×2 –15x + 50 =0 б)х4-4х2 +3х+2=0 в) х4+2х3-7х2 -8х+12=0 №4 Решить уравнения, применения формулы сокращенного умножения а) б). Уравнения четвертой степени, стр.6 — TopRef.ruУравнения
четвертой степени Метод решения уравнений четвертой
степени нашел в XVI
в. Лудовико Феррари, ученик Джероламо
Кардано. Он так и называется – метод Феррари. Как
и при решении кубического и квадратного
уравнений, в уравнении четвертой степени можно
избавиться от члена подстановкой
.
Поэтому будем считать, что коэффициент
при кубе неизвестного равен нулю: . Идея
Феррари состояла в том, чтобы представить
уравнение в виде
,
где левая часть – квадрат выражения
,
а правая часть – квадрат линейного
уравнения от
,
коэффициенты которого зависят от
.
После этого останется решить два
квадратных уравнения: и
.
Конечно, такое представление возможно
только при специальном выборе параметра
.
Удобно взять в виде
,
тогда уравнение перепишется так: . (15) Правая
часть этого уравнения – квадратный
трехчлен от
.
Полным квадратом он будет тогда, когда
его дискриминант равен нулю, т.е. ,
или . Это
уравнение называется резольвентным (т.е. «разрешающим»).
Относительно оно кубическое, и формула Кардано
позволяет найти какой-нибудь его корень
.
При правая часть уравнения (15) принимает
вид , а
само уравнение сводится к двум квадратным: . Их
корни и дают все решения исходного
уравнения. Решим
для примера уравнение . Здесь
удобнее будет воспользоваться не
готовыми формулами, а самой идеей
решения. Перепишем уравнение в виде и
добавим к обеим частям выражение
,
чтобы в левой части образовался полный
квадрат: . Теперь
приравняем к нулю дискриминант правой
части уравнения: , или,
после упрощения, . Один
из корней полученного уравнения можно
угадать, перебрав делители свободного
члена:
.
После подстановки этого значения получим
уравнение , откуда
.
Корни образовавшихся квадратных
уравнений — и
.
Разумеется, в общем случае могут
получиться и комплексные корни. Решение
Декарта-Эйлера подстановкой приводится к «неполному» виду . (16) Корни
,
,
, «неполного» уравнения четвертой
степени (16) равны одному из выражений , в
которых сочетания знаков выбираются
так, чтобы удовлетворялось условие , причем
, и — корни кубичного уравнения . Уравнения
высоких степеней Разрешимость в радикалах Формула корней квадратного
уравнения известна с незапамятных
времен, а в XVI
в. итальянские алгебраисты решили в
радикалах уравнения третьей и четвертой
степеней. Таким образом, было установлено,
что корни любого уравнения не выше
четвертой степени выражаются через
коэффициенты уравнения формулой, в
которой используются только четыре
арифметические операции (сложение,
вычитание, умножение, деление) и извлечение
корней степени, не превышающей степень
уравнения. Более того, все уравнения
данной степени ()
можно «обслужить» одной общей
формулой. При подстановке в нее
коэффициентов уравнения получим все
корни – и действительные, и комплексные. После
этого естественно возник вопрос: а есть
ли похожие общие формулы для решения
уравнений пятой степени и выше
Ответ на него смог найти норвежский
математик Нильс Хенрик Абель в начале
XIX
в. Чуть раньше этот результат был указан,
но недостаточно обоснован итальянцем
Паоло Руффини. Теорема Абеля-Руффини
звучит так: Общее уравнение степени при неразрешимо в радикалах. Таким образом, общей формулы,
применимой ко всем уравнениям данной
степени ,
не существует. Однако это не значит, что
невозможно решить в радикалах те или
иные частные виды уравнений высоких
степеней. Сам Абель нашел такое решение
для широкого класса уравнений произвольно
высокой степени – так называемых
абелевых уравнений. Теорема Абеля-Руффини
не исключает даже и того, что корни
каждого конкретного алгебраического
уравнения можно записать через его
коэффициенты с помощью знаков
арифметических операций и радикалов,
в частности, что любое алгебраическое
число, т.е. корень уравнения вида ,
, с
целыми коэффициентами, можно выразить
в радикалах через рациональные числа.
На самом деле такое выражение существует
далеко не всегда. Это следует из теоремы
разрешимости алгебраических уравнений,
построенной выдающимся французским
математиком Эваристом Галуа в его
«Мемуаре об условиях разрешимости
уравнений в радикалах» (1832 г.; опубликован
в 1846 г.). Подчеркнем,
что в прикладных задачах нас интересует
только приближенные значения корней
уравнения. Поэтому его разрешимость в
радикалах здесь обычно роли не играет.
Имеются специальные вычислительные
методы, позволяющие найти корни любого
уравнения с любой наперед заданной
точностью, ничуть не меньшей, чем дают
вычисления по готовым формулам. Решения уравнений четвёртой степени — Журнал Ольги Арефьевой — LiveJournalУ меня папа увлекается шахматами, шашками и математикой. У него инженерное образование. Его зовут Арефьев Виктор Андреевич, и ему сейчас 78 лет. Давно мне говорил, что написал математическую статью, но не знает, как набрать ее на компе (из-за формул). Зрение не очень, с компьютером несколько «на вы». Но со скайпом, вайбером, почтой, а также шахматными и шашечными играми онлайн — управляется. Статью он написал, только не знает, куда и кому ее послать, чтобы прочитали. Мой друг постарался и помог набрать текст с рукописного черновика. Это была эпопея, но теперь наконец все готово. Пожалуйста, если среди вас есть кто-то, кто разбирается, почитайте и отзовитесь, вдруг вам есть, что сказать в ответ. И, если можно, затегайте тех, кто еще может статью почитать и подсказать, где ее можно опубликовать в сообществах или на сайтах для интересующихся математикой. Я в математических задачах ничего не понимаю. При всей широте моих увлечений точные науки в них не вошли. Папе нужна связь с теми, кому это интересно и понятно, и с кем можно иногда виртуально общаться и получать обратную связь. Пока выложили на моем сайте.
Вот, что папа пишет:
«Уравнение Феррари давно известно, разложение на два квадратных уравнения тоже, сопряжённые числа тоже, но здесь приведено новое их применение для вывода решения Феррари. Я про это ничего не нашёл, хоть искал». Итак, в этой статье (идите по ссылке) I. Новый вывод метода Феррари решения уравнения четвёртой степени.
II. Решение уравнения четвёртой степени методом сопряжённых чисел.
III. Метод Декарта-Эйлера решения уравнения четвёртой степени.
IV. Сравнение методов на примере. И еще пишет:
«Я отдохнул от писанины и теперь решаю, с чего начать: 1. Законы Кеплера в теории двух тел с применением комплексного счисления. 2. Квадрат суммы двустороннего ряда равен сумме квадратов без удвоенных произведений. 3. Пирамиды для мертвых и для живых (заряды у молекулы воды расположены в вершинах тетраэдра и это даёт ей все важные для жизни свойства). 4. Свойства пространства с точки зрения физического вакуума — электрические, магнитные и гравитационные. 5. Разбор решения уравнения 5 степени Сергея Зайкова и опровержение альтернативного метода Валентина Подвысоцкого. 6. Решение интеграла от рациональной дроби любой степени в общем виде. 7. Решённые и нерешенные алгебраические ряды. Новые решения Базельской проблемы. 8. Суммирование рядов по методу Архимеда и определение погрешности при этом по треугольнику Паскаля. 9. Этюд Д.Кларка в шашках (1873г.) и его углубление. Углубление этюдов А.Врагова (1914г.) и И. Бленкаара (1894 г.). 10. Три дамки против дамки с тремя простыми — решение всех 36 вариантов».
Лекция по теме «Уравнения высших степеней. Методы их решения». 9-й классОсновные цели: - Закрепить понятие целого рационального уравнения -й степени.
- Сформулировать основные методы решения уравнений высших степеней (n >
3).
- Обучить основным методам решения уравнений высших степеней.
- Научить по виду уравнения определять наиболее эффективный способ его
решения.
Формы, методы и педагогические приемы, которые используются учителем на
уроке: - Лекционно-семинарская система обучения (лекции – объяснение нового
материала, семинары – решение задач).
- Информационно-коммуникационные технологии (фронтальный опрос, устная
работа с классом).
- Дифференцированное обучение, групповые и индивидуальные формы.
- Использование исследовательского метода в обучении, направленного на
развитие математического аппарата и мыслительных способностей каждого
конкретного ученика.
- Печатный материал – индивидуальный краткий конспект урока (основные
понятия, формулы, утверждения, материал лекций сжато в виде схем или таблиц).
План урока: - Организационный момент.
Цель этапа: включить учащихся в учебную деятельность, определить
содержательные рамки урока.
- Актуализация знаний учащихся.
Цель этапа: актуализировать знания учащихся по изученным ранее смежным темам
- Изучение новой темы (лекция). Цель этапа: сформулировать основные методы
решения уравнений высших степеней (n > 3)
- Подведение итогов.
Цель этапа: еще раз выделить ключевые моменты в материале, изученном на
уроке.
- Домашнее задание.
Цель этапа: сформулировать домашнее задание для учащихся.
Конспект урока
1. Организационный момент. Формулировка темы урока: “Уравнения высших степеней. Методы их решения”.
2. Актуализация знаний учащихся. Теоретический опрос – беседа. Повторение некоторых ранее изученных сведений
из теории. Учащиеся формулируют основные определения и дают формулировки
необходимых теорем. Приводят примеры, демонстрируя уровень полученных ранее
знаний. - Понятие уравнения с одной переменной.
- Понятие корня уравнения, решения уравнения.
- Понятие линейного уравнения с одной переменной, понятие квадратного
уравнения с одной переменной.
- Понятие равносильности уравнений, уравнения-следствия (понятие
посторонних корней), переход не по следствию (случай потери корней).
- Понятие целого рационального выражения с одной переменной.
- Понятие целого рационального уравнения n-й степени. Стандартный
вид целого рационального уравнения. Приведенное целое рациональное уравнение.
- Переход к совокупности уравнений более низких степеней путем разложения
исходного уравнения на множители.
- Понятие многочлена n-й степени от x. Теорема Безу.
Следствия из теоремы Безу. Теоремы о корнях (Z-корни и Q-корни)
целого рационального уравнения с целыми коэффициентами (соответственно
приведенного и неприведенного).
- Схема Горнера.
3. Изучение новой темы. Будем рассматривать целое рациональное уравнение n-й степени
стандартного вида с одной неизвестной переменной x : Pn(x) = 0
, где Pn(x) = anxn + an-1xn-1
+ a1x + a0 – многочлен n-й степени от x,
an≠ 0. Если an
= 1 то такое уравнение называют приведенным целым рациональным уравнением
n-й степени. Рассмотрим такие уравнения при различных значениях n
и перечислим основные методы их решения. n = 1 – линейное уравнение. n = 2 – квадратное уравнение. Формула дискриминанта. Формула
для вычисления корней. Теорема Виета. Выделение полного квадрата. n = 3 – кубическое уравнение. Метод группировки. Пример: x3 – 4x2 – x + 4 = 0
(x – 4)(x2– 1) = 0
x1 = 4 , x2 = 1, x3 = -1.
Возвратное кубическое уравнение вида ax3 + bx2
+ bx + a = 0. Решаем, объединяя члены с одинаковыми
коэффициентами. Пример: x3 – 5x2 – 5x + 1 = 0
(x + 1)(x2 – 6x + 1) = 0
x1 = -1, x2 = 3 + 2,
x3 = 3 – 2.
Уравнение с целыми коэффициентами. Подбор Z-корней на основании теоремы.
Схема Горнера. При применении этого метода необходимо сделать акцент на том, что
перебор в данном случае конечный, и корни мы подбираем по определенному
алгоритму в соответствии с теоремой о Z-корнях приведенного целого
рационального уравнения с целыми коэффициентами. Пример: x3 – 9x2 + 23x – 15 = 0.
Уравнение приведенное. Выпишем делители свободного члена {+1; +3;
+5; +15}. Применим схему Горнера:
|
x3 |
x2 |
x1 |
x0 |
вывод |
|
1 |
-9 |
23 |
-15 |
|
| 1 |
1 |
1 х 1 – 9 = -8 |
1 х (-8) + 23 = 15 |
1 х 15 – 15 = 0 |
1 – корень |
|
x2 |
x1 |
x0 |
|
|
Получаем
(x – 1)(x2 – 8x + 15) = 0
x1 = 1, x2 = 3, x3 = 5.
Уравнение с целыми коэффициентами. Подбор Q-корней на основании теоремы.
Схема Горнера. При применении этого метода необходимо сделать акцент на том, что
перебор в данном случае конечный и корни мы подбираем по определенному алгоритму
в соответствии с теоремой о Q-корнях неприведенного целого рационального
уравнения с целыми коэффициентами. Пример: 9x3 + 27x2 – x – 3 = 0.
Уравнение неприведенное. Выпишем делители свободного члена {+1; +3}.
Выпишем делители коэффициента при старшей степени неизвестного. {+1; +3;
+9} Следовательно, корни будем искать среди значений {+1; +;
+;
+3}. Применим схему Горнера:
|
x3 |
x2 |
x1 |
x0 |
вывод |
|
9 |
27 |
-1 |
-3 |
|
| 1 |
9 |
1 x 9 + 27 = 36 |
1 x 36 – 1 = 35 |
1 x 35 – 3 = 32 ≠ 0 |
1 – не корень |
| -1 |
9 |
-1 x 9 + 27 = 18 |
-1 x 18 – 1 = -19 |
-1 x (-19) – 3 = 16 ≠
0 |
-1 – не корень |
|
|
9 |
x 9 + 27 = 30 |
x 30 – 1 = 9 |
x 9 – 3 = 0 |
корень |
|
x2 |
x1 |
x0 |
|
|
Получаем
(x –
)(9x2
+ 30x + 9) = 0
x1 =
,
x2 = —
, x3 = -3. Для удобства подсчета при подборе Q-корней бывает удобно сделать
замену переменной, перейти к приведенному уравнению и подбирать Z-корни.
- Если свободный член равен 1
.
- Если можно воспользоваться заменой вида y = kx
.
Формула Кардано. Существует универсальный метод решения кубических
уравнений – это формула Кардано. Эту формулу связывают с именами итальянских
математиков Джероламо Кардано (1501–1576), Николо Тарталья (1500–1557), Сципиона
дель Ферро (1465–1526). Эта формула лежит за рамками нашего курса. n = 4 – уравнение четвертой степени. Метод группировки. Пример: x4 + 2x3 + 5x2
+ 4x – 12 = 0
(x4 + 2x3) + (5x2 + 10x)
– (6x + 12 ) = 0
(x + 2)(x3 + 5x – 6) = 0
(x + 2)(x – 1)(x2 + x + 6) = 0
x1 = -2, x2 = 1.
Метод замены переменной. - Биквадратное уравнение вида ax4 + bx2
+ с = 0.
Пример: x4 + 5x2
– 36 = 0. Замена y = x2. Отсюда y1 =
4, y2 = -9. Поэтому x1,2 = +2 .
- Возвратное уравнение четвертой степени вида ax4 +
bx3 + cx2 + bx + a = 0.
Решаем, объединяя члены с одинаковыми коэффициентами, путем замены вида
- Обобщенное возвратное уравнение четвертой степени вида ax4
+ bx3 + cx2 – bx + a = 0.
- Обобщенное возвратное уравнение четвертой степени вида ax4
+ bx3 + cx2 + kbx
+ k2a = 0.
- Замена общего вида. Некоторые стандартные замены.
Пример 1:
Пример 3. Замена общего вида (вытекает из вида конкретного
уравнения).
Уравнение с целыми коэффициентами. Подбор Z-корней на основании теоремы.
Схема Горнера. Алгоритм аналогичен рассмотренному выше для n = 3.
Уравнение с целыми коэффициентами. Подбор Q-корней на основании
теоремы. Схема Горнера. Алгоритм аналогичен рассмотренному выше для n =
3.
Формула общего вида. Существует универсальный метод решения уравнений
четвертой степени. Эту формулу связывают с именем Людовико Феррари (1522–1565).
Эта формула лежит за рамками нашего курса. n > 5 – уравнения пятой и более высоких степеней. Уравнение с целыми коэффициентами. Подбор Z-корней на основании теоремы.
Схема Горнера. Алгоритм аналогичен рассмотренному выше для n = 3.
Уравнение с целыми коэффициентами. Подбор Q-корней на основании
теоремы. Схема Горнера. Алгоритм аналогичен рассмотренному выше для n =
3.
Симметрические уравнения. Любое возвратное уравнение нечетной степени
имеет корень x = -1 и после разложения его на множители получаем, что
один сомножитель имеет вид (x + 1), а второй сомножитель – возвратное
уравнение четной степени (его степень на единицу меньше, чем степень исходного
уравнения). Любое возвратное уравнение четной степени вместе с корнем вида x
= φ содержит и корень вида
.
Используя эти утверждения, решаем задачу, понижая степень исследуемого уравнения.
Метод замены переменной. Использование однородности.
Не существует формулы общего вида для решения целых уравнений пятой
степени (это показали итальянский математик Паоло Руффини (1765–1822) и
норвежский математик Нильс Хенрик Абель (1802–1829)) и более высоких степеней (это
показал французский математик Эварист Галуа (1811–1832)). - Напомним еще раз, что на практике возможно использование комбинации
перечисленных выше методов. Удобно переходить к совокупности уравнений более
низких степеней путем разложения исходного уравнения на множители.
- За рамками нашего сегодняшнего обсуждения остались широко используемые
на практике графические методы решения уравнений и методы
приближенного решения уравнений высших степеней.
- Бывают ситуации, когда у уравнения нет R-корней.
Тогда решение
сводится к тому, чтобы показать, что уравнение корней не имеет. Для
доказательства анализируем поведение рассматриваемых функций на промежутках
монотонности. Пример: уравнение x8 – x3
+ 1 = 0 не имеет корней.
- Использование свойства монотонности функций
. Бывают ситуации, когда
использование различных свойств функций позволяет упростить поставленную
задачу.
Пример 1: уравнение x5 + 3x – 4 = 0 имеет
один корень x = 1. По свойству монотонности анализируемых функций
других корней нет.
Пример 2: уравнение x4 + (x – 1)4
= 97 имеет корни x1 = -2 и x2 = 3.
Проанализировав поведение соответствующих функций на промежутках
монотонности, заключаем, что других корней нет.
4. Подведение итогов. Резюме: Теперь мы овладели основными методами решения различных уравнений
высших степеней (для n > 3).
Наша задача научиться эффективно использовать перечисленные выше алгоритмы. В
зависимости от вида уравнения мы должны будем научиться определять, какой способ
решения в данном случае является наиболее эффективным, а также правильно
применять выбранный метод.
5. Домашнее задание. [1]: п.7, стр. 164–174, №№ 33–36,
39–44, 46,47. [4]: №№ 9.1–9.4, 9.6–9.8, 9.12,
9.14–9.16, 9.24–9.27. Возможные темы докладов или рефератов по данной тематике: - Формула Кардано
- Графический метод решения уравнений. Примеры решения.
- Методы приближенного решения уравнений.
Анализ усвоения материала и интереса учащихся к теме: Опыт показывает, что интерес учащихся в первую очередь вызывает возможность
подбора Z-корней и Q-корней уравнений при помощи достаточно
простого алгоритма с использованием схемы Горнера. Также учащиеся интересуются
различными стандартными типами замены переменных, которые позволяют существенно
упрощать вид задачи. Особый интерес обычно вызывают графические методы решения.
В этом случае дополнительно можно разобрать задачи на графический метод решения
уравнений; обсудить общий вид графика для многочлена 3, 4, 5 степени;
проанализировать, как связано число корней уравнений 3, 4, 5 степени с видом
соответствующего графика. Ниже приведен список книг, в которых можно найти
дополнительную информацию по данной тематике. Список литературы: - Виленкин Н.Я. и др. “Алгебра. Учебник для учащихся 9 классов с
углубленным изучением математики” – М., Просвещение, 2007 – 367 с.
- Виленкин Н.Я., Шибасов Л.П., Шибасова З.Ф. “За страницами
учебника математики. Арифметика. Алгебра. 10-11 класс” – М., Просвещение,
2008 – 192 с.
- Выгодский М.Я. “Справочник по математике” – М., АСТ, 2010 – 1055
с.
- Галицкий М.Л. “Сборник задач по алгебре. Учебное пособие для 8-9
классов с углубленным изучением математики” – М., Просвещение, 2008 – 301 с.
- Звавич Л.И. и др. “Алгебра и начала анализа. 8–11
кл. Пособие для школ и классов с углубленным изучением математики” – М.,
Дрофа, 1999 – 352 с.
- Звавич Л.И., Аверьянов Д.И., Пигарев Б.П., Трушанина Т.Н.
“Задания по математике для подготовки к письменному экзамену в 9 классе” –
М., Просвещение, 2007 – 112 с.
- Иванов А.А., Иванов А.П. “Тематические тесты для систематизации
знаний по математике” ч.1 – М., Физматкнига, 2006 – 176 с.
- Иванов А.А., Иванов А.П. “Тематические тесты для систематизации
знаний по математике” ч.2 – М., Физматкнига, 2006 – 176 с.
- Иванов А.П. “Тесты и контрольные работы по математике. Учебное
пособие”. – М., Физматкнига, 2008 – 304 с.
- Лейбсон К.Л. “Сборник практических заданий по математике. Часть
2–9 класс” – М., МЦНМО, 2009 – 184 с.
- Макарычев Ю.Н., Миндюк Н.Г. “Алгебра. Дополнительные главы к
школьному учебнику 9 класса. Учебное пособие для учащихся школ и классов с
углубленным изучением математики.” – М., Просвещение, 2006 – 224 с.
- Мордкович А.Г. “Алгебра. Углубленное изучение. 8 класс. Учебник”
– М., Мнемозина, 2006 – 296 с.
- Савин А.П. “Энциклопедический словарь юного математика” – М.,
Педагогика, 1985 – 352 с.
- Сурвилло Г.С., Симонов А.С. “Дидактические материалы по алгебре
для 9 класса с углубленным изучением математики” – М., Просвещение, 2006 –
95 с.
- Чулков П.В. “Уравнения и неравенства в школьном курсе математик.
Лекции 1–4” – М., Первое сентября, 2006 – 88 с.
- Чулков П.В. “Уравнения и неравенства в школьном курсе математик.
Лекции 5–8” – М., Первое сентября, 2009 – 84 с.
Внеклассный урок — Уравнение с одной переменной. Корень уравнения. Уравнения n-й степени. Уравнение с одной переменной.Уравнение с одной переменной. Корень уравнения. Уравнения n-й степени Уравнение – это равенство, содержащее переменную, обозначенную буквой. Корень уравнения (или решение уравнения) – это такое значение переменной, при котором уравнение превращается в верное равенство. Пример: решим уравнение (то есть найдем корень уравнения): 4x – 15 = x + 15 Итак:
4х – х = 15 + 15
3х = 30
х = 30 : 3
х = 10 Результат: уравнение имеет один корень – число 10. Уравнение может иметь и два, три, четыре и более корней. Например, уравнение (х-4)(х-5)(х-6) = 0 имеет три корня: 4, 5 и 6. Уравнение может вовсе не иметь корней. Например, уравнение х+2=х не имеет корней, т.к. при любом значении х равенство невозможно. Равносильность уравнений. Два уравнения являются равносильными, если они имеют одинаковые корни либо если оба уравнения не имеют корней. Пример1: Уравнения х + 3 = 5 и 3х – 1 = 5 равносильны, так как в обоих уравнениях х=2. Пример 2: Уравнения х4 + 2 = 1 и х2 + 5 = 0 равносильны, так как оба уравнения не имеют корней. Целое уравнение с одной переменной Целое уравнение с одной переменной – это уравнение, левая и правая части которого являются целыми выражениями (о целых выражениях см.раздел «Рациональные выражения»). Уравнение с одной переменной может быть записано в виде P(x) = 0, где P(x) – многочлен стандартного вида. Например:
y2 + 3y – 6 = 0
(здесь P(x) представлен в виде многочлена y2 + 3y – 6). В таком уравнении степень многочлена называют степенью уравнения. В нашем примере представлено уравнение второй степени (так как в нем многочлен второй степени). Уравнение первой степени. Уравнение первой степени можно привести к виду: ax + b = 0, где x – переменная, a и b – некоторые числа, причем a ≠ 0. Отсюда легко вывести значение x: b
x = – —
a Это значение x является корнем уравнения. Уравнения первой степени имеют один корень. Уравнение второй степени. Уравнение второй степени можно привести к виду: ax2 + bx + c = 0, где x – переменная, a, b, c – некоторые числа, причем a ≠ 0. Число корней уравнения второй степени зависит от дискриминанта: — если D > 0, то уравнение имеет два корня; — если D = 0, то уравнение имеет один корень; — если D < 0, то уравнение корней не имеет. Уравнение второй степени может иметь не более двух корней. (о том, что такое дискриминант и как находить корни уравнения, см.разделы «Формулы корней квадратного уравнения. Дискриминант» и «Другой способ решения квадратного уравнения»). Уравнение третьей степени. Уравнение третьей степени можно привести к виду: ax3 + bx2 + cx + d = 0, где x – переменная, a, b, c, d – некоторые числа, причем a ≠ 0. Уравнение третьей степени может иметь не более трех корней. Уравнение четвертой степени. Уравнение четвертой степени можно привести к виду: ax4 + bx3 + cx2 + dx + e = 0, где x – переменная, a, b, c, d, e – некоторые числа, причем a ≠ 0. Уравнение третьей степени может иметь не более четырех корней. Обобщение: 1) уравнение пятой, шестой и т.д. степеней можно легко вывести самостоятельно, следуя приведенной выше схеме; 2) уравнение n-й степени может иметь не более n корней. Пример 1: Решим уравнение x3 – 8x2 – x + 8 = 0. Мы видим, что это уравнение третьей степени. Значит, у него может быть от нуля до трех корней.
Найдем их и тем самым решим уравнение.
Разложим левую часть уравнения на множители: x2(x – 8) – (x – 8) = 0. Применим правило разложения многочлена способом группировки его членов. Для этого поставим перед вторыми скобками число 1: x2(x – 8) – 1(x – 8) = 0. Теперь сгруппируем многочлены x2 и –1, являющиеся множителями многочлена x–8.
Получим две группы многочленов: (x2 –1) и (x – 8). Следовательно, наше уравнение примет новый вид: (x – 8)(x2 – 1) = 0. Здесь выражение x2 – 1 можно представить в виде x2 – 12.
А значит, можем применить формулу сокращенного умножения: x2 – 12 = (x – 1)(x + 1).
Подставим в наше уравнение это выражение и получим: (x – 8)(x – 1)(x + 1) = 0. Дальше все просто. При x – 8 = 0 всё уравнение тоже равно нулю.
И так – в случае и с двумя остальными выражениями x – 1 и x + 1. Таким образом: x – 8 = 0 x – 1 = 0 x + 1 = 0 Осталось найти корни нашего уравнения: x1 = 0 + 8 = 8 x2 = 0 + 1 = 1 x3 = 0 – 1 = –1. Уравнение решено. Оно имеет три корня: 8, 1 и –1. Пример 2: Решим уравнение (x2 – 5x + 4)(x2 – 5x +6) = 120. Это уравнение сложнее. Но его можно упростить оригинальным образом – методом введения новой переменной.
В нашем уравнении дважды встречается выражение x2 – 5x.
Мы можем обозначить его переменной y. То есть представим, что x2 – 5x = y. Тогда наше уравнение обретает более простой вид: (y + 4)(y + 6) = 120. Раскроем скобки: y2 + 4y + 6y + 24 = 120 y2 + 10y + 24 = 120 Приравняем уравнение к нулю: y2 + 10y + 24 – 120 = 0 y2 + 10y – 96 = 0 Мы получили обычное квадратное уравнение. Найдем его корни. Нет необходимости производить расчеты: о том, как решать подобные уравнения, подробно написано в разделах «Квадратные уравнения» и «Формулы корней квадратного уравнения. Дискриминант». Здесь же мы сразу выведем результат. Квадратное уравнение y2 + 10y – 96 = 0 имеет два корня: y1 = -16 y2 = 6 Буквой y мы заменили выражение x2 – 5x. А значит, мы уже можем подставить значения y и найти корни заданного уравнения, тем самым решив задачу: 1) Сначала применяем значение y1 = –16: x2 – 5x = –16 Чтобы решить это уравнение, превращаем его в квадратное уравнение: x2 – 5x + 16 = 0 Решив его, мы обнаружим, что оно не имеет корней. 2) Теперь применяем значение y2 = 6: x2 – 5x = 6 x2 – 5x – 6 = 0 Решив это квадратное уравнение, мы увидим, что у него два корня: x1 = –1 x2 = 6. Уравнение решено. Оно имеет два корня: –1 и 6. Метод введения новой переменной позволяет легко решать уравнения четвертой степени, которые являются квадратными относительно x2 (такие уравнения называют биквадратными). Показательные уравнения — как решать? Примеры, свойства и определениеОпределение показательного уравненияПоказательными называются уравнения с показательной функцией f(x) = aх. Другими словами, неизвестная переменная в них может содержаться как в основании степени, так и в ее показателе. Простейшее уравнение такого вида: aх = b, где a > 0, a ≠ 1. |
Конечно, далеко не все задачи выглядят так просто, некоторые из них включают тригонометрические, логарифмические и другие конструкции. Но для решения даже простых показательных уравнений нужно вспомнить из курса алгебры за 6–7 класс следующие темы: Если что-то успело забыться, советуем повторить эти темы перед тем, как читать дальнейший материал. С точки зрения геометрии показательной функцией называют такую: y = ax, где a > 0 и a ≠ 1. У нее есть одно важное для решения показательных уравнений свойство — это монотонность. При a > 1 такая функция непрерывно возрастает, а при a < 1 (но больше 0) — непрерывно убывает. Это хорошо видно на рисунке ниже. Важно знать Показательная функция не может быть отрицательным числом, т. е. выражение у = ax при а ≤ 0 корней не имеет. Иногда в результате решения будет получаться несколько вариантов ответа, и в таком случае мы должны выбрать тот корень, при котором показательная функция больше нуля. Свойства степенейМы недаром просили повторить свойства степенной функции — на них будет основано решение большей части примеров. Держите небольшую шпаргалку по формулам, которые помогут упрощать сложные показательные уравнения. am x an | am+n | am:an | am-n | (a x b)n | an x bn | (a : b)n | an : bn | (an)m | an x m | a-n | 1/an | (a/b)-n | (b/a)n | n√a | a1/n |
Как видите, ничего нового здесь нет, все это проходят в 6–7 классе. Методы решения показательных уравненийСамые короткие и простые показательные уравнения решаются с помощью элементарной математики. Например: 4х = 64. Требуется найти, в какую степень нужно возвести 4, чтобы получить 64. 4 × 4 × 4 = 64 43 = 64 Х = 3 Но как решать показательные уравнения вот такого вида: 3√128= 42х? Нужно немного повозиться с преобразованием этого выражения. Например, сделать так, чтобы либо основания, либо степенные показатели стали одинаковы. Для этого мы можем разложить 128 и 4. Вы ведь заметили, что у них есть общий множитель? Правильно, это 2. 3√128= 42х 3√27= (22)2x 27/3 = 24х Теперь в нашем уравнении появились одинаковые основания, а значит, мы можем приравнять и степени. 4х = 7/3 х = 7/12 В данном случае мы используем один из алгоритмов решения показательных уравнений — привели обе части равенства к одинаковым основаниям. Дальше рассмотрим и другие методы. Приведение к одинаковому основаниюВесомую часть уравнений вида ах = b (при а и b 0) можно решить, превратив b в определенную степень числа a. Именно это мы сделали в примере выше, получив одинаковые основания. Главная трудность в том, чтобы найти у этих чисел общий множитель. Если у нас есть одинаковые основания, но разные показатели степени, то при умножении чисел степени складываются, а при делении — вычитаются. |
Пример 1Рассмотрим еще одно показательное уравнение с корнем. (1/642)-х = √1/8 Мы знаем, что у 64 и 8 есть общий множитель — это 2. Попробуем использовать это, и тогда 642 = 212, а 8 = 23. (1/212)-х = √1/23 1/2-12х = 1/22/3 (1/2)-12х = (1/2)3/2 -12х = 3/2 х = -1/8 Пример 2В этом примере показательного уравнения нужно будет отдельно преобразовать каждую составляющую. (0,5)х2 × 4х+1 = 64-1 Найдем общее основание показательных функций: 0,5 = 1/2 = 2-1 4 = 22 64 = 26 В результате у нас получается: (2-1)х2 × (22)х+1 = (26)-1 2-х2 × 22х+2 = 2-6 2-х2+2х+2 = 2-6 -х2 + 2х + 2 = -6 х2— 2х — 8 = 0 Здесь у нас будет два корня: -2 и 4. Приведение к одинаковой степениНе все показательные уравнения с разными основаниями можно решить предыдущим способом. Иногда проще преобразовать не основания, а показатели степени. Правда, пользоваться этим методом есть смысл только в том случае, когда мы имеем дело с умножением или делением. При умножении чисел с разными основаниями, но одинаковыми степенными показателями можно перемножить только основания (степень останется прежней): axbx = (ab)x. |
Пример52х-4 = 492-х Общих множителей у левой и правой части уравнения нет и привести их к одинаковому основанию достаточно трудно. Поэтому стоит поработать с показателями степеней: 52х-4 = 492-х 52х-4 = 74-2х 52х-4 = (1/7)2х-4 352х-4 = 1 2х — 4 = 0 х = 2 Пример 22х-2 = 52-х Нам нужно привести обе части уравнения к одинаковым степенным показателям, и для этого вначале попробуем преобразовать правую часть, используя свойство степенных функций. 2х-2 = 1/5х-2 Теперь умножим обе части на 52-х и придем к уравнению: 2х-2 × 52-х = 1 10х-2 = 1 10х-2 = 100 х — 2 = 0 х = 2 Замена переменнойЭтот способ решения показательных уравнений понадобится тем, кто не боится по-настоящему трудных задач. Ведь с помощью ввода новой переменной можно упростить даже самое сложное выражение. Его суть проста: мы заменяем «трудную» переменную на более простую и решаем уравнение, а после производим обратную замену. Главное — определить, какую именно переменную стоит заменить. Пример4x— 2x+1— 8 = 0 Очевидно, что в этом уравнении показательные функции легко привести к общему основанию: 4х = 22х, а 2х+1 = 2 × 2х. 22х — 2 × 2х — 8 = 0 Что-то напоминает. 🤔 Если бы из этого выражения можно было волшебным образом убрать 2х, получилось бы обычное квадратное уравнение. Поэтому мы обозначим 2х новой переменной — допустим, y. Если 2х = y, получается: у2— 2у — 8 = 0. У такого уравнения есть два корня: у1 = 4, у2 = -2. Проведем обратную замену: 2х = 4, 2х = -2. Но мы знаем, что показательная функция в любом случае не может быть отрицательным числом, а значит, 2х = -2 корней не имеет. Следовательно, 2х = 4. х = 2. Пример 225х — 6 × 5х + 5 = 0 Если присмотреться к этому выражению, становится понятно, что у него много общего с квадратным уравнением. Введем новую переменную: 5х = у. у2 — 6у + 5 = 0 Корни такого уравнения: 1 и 5. Выполним обратную замену: 5х = 1, значит х = 0. 5х = 5, значит х = 1. Выделение устойчивого выраженияВ предыдущих примерах мы преобразовывали разные виды показательных уравнений путем разложения многочленов на множители, потому что хотели найти способ решения — получить одинаковые основания или выделить переменную, которую можно заменить. Так вот, когда мы выносим некий множитель за скобку или заменяем переменную, пытаясь упростить уравнение — это действие по сути и является выделением устойчивого выражения. Устойчивое выражение — это некий многочлен, содержащий переменную, который в скрытом виде присутствует во всех показательных функциях уравнения. Его можно вынести за скобки или обозначить новой переменной, чтобы упростить уравнение. |
Хорошая новость: так или иначе устойчивое выражение можно найти почти в любом трудном уравнении. Проблема только в том, чтобы научиться верно определять такое выражение, а этот навык появляется лишь с опытом. Пример 13х+1 + 3х — 3х-2 = 35 В данном случае в качестве устойчивого выражения удобно взять 3х-2 как степень с наименьшим показателем. В итоге мы получим: 3х-2(33 + 32 — 1) = 35 3х-2 × 35 = 35 3х-2 = 1 Поскольку 1 равняется любое число в нулевой степени, мы можем записать: 3х-2 = 30 х — 2 = 0 х = 2 Пример 25 × 3-3х+1 + 3-3х+2 = 24 Для начала мы попробуем в левой части уравнения получить одинаковую степень: 3-3х+2 = 3-3х+1+1 = 3 × 3-3х+1. Теперь у нас есть устойчивое выражение 3-3х+1, которое можно вынести за скобки, чтобы получить более простое уравнение: 3-3х+1(5+3) = 24 8 × 3-3х+1 = 24 3-3х+1 = 31 -3х + 1 = 1 х = 0 Схема (метод) Горнера. Примеры. Решение уравнений четвертой степениРЕШЕНИЕ УРАВНЕНИЙ 4-ОЙ СТЕПЕНИ ПО СХЕМЕ ГОРНЕРА2x4 + 5x3 — 11x2 — 20x + 12 = 0 Для начала нужно методом подбора найти один корень. Обычно он является делителем свободного члена. В данном случае делителями числа 12 являются ±1, ±2, ±3, ±4, ±6, ±12. Начнем их подставлять по-очереди: 1: 2 + 5 — 11 — 20 + 12 = -12 ⇒ число 1 не является корнем многочлена -1: 2 — 5 — 11 + 20 + 12 = 18 ⇒ число -1 не является корнем многочлена 2: 2 ∙ 16 + 5 ∙ 8 — 11 ∙ 4 — 20 ∙ 2 + 12 = 0 ⇒ число 2 является корнем многочлена Мы нашли 1 из корней многочлена. Корнем многочлена является 2, а значит исходный многочлен должен делиться на x — 2. Для того, чтобы выполнить деление многочленов, воспользуемся схемой Горнера: В верхней строке выставляются коэффициенты исходного многочлена. В первой ячейке второй строки ставится найденный нами корень 2. Во второй строке пишутся коэффициенты многочлена, который получится в результате деления. Они считаются так: | Во вторую ячейку второй строки запишем число 2, просто перенеся его из соответствующей ячейки первой строки. | | 2 ∙ 2 + 5 = 9 | | 2 ∙ 9 — 11 = 7 | | 2 ∙ 7 — 20 = -6 | | 2 ∙ (-6) + 12 = 0 |
Последнее число — это остаток от деления. Если он равен 0, значит мы все верно посчитали. Таким образом мы исходный многочлен разложили на множители: 2x4 + 5x3 — 11x2 — 20x + 12 = (x — 2)(2x3 + 9x2 + 7x — 6) Но это еще не конец. Можно попробовать разложить таким же способом многочлен 2x3 + 9x2 + 7x — 6. Опять ищем корень среди делителей свободного члена. Делителями числа -6 являются ±1, ±2, ±3, ±6. 1: 2 + 9 + 7 — 6 = 12 ⇒ число 1 не является корнем многочлена -1: -2 + 9 — 7 — 6 = -6 ⇒ число -1 не является корнем многочлена 2: 2 ∙ 8 + 9 ∙ 4 + 7 ∙ 2 — 6 = 60 ⇒ число 2 не является корнем многочлена -2: 2 ∙ (-8) + 9 ∙ 4 + 7 ∙ (-2) — 6 = 0 ⇒ число -2 является корнем многочлена Напишем найденный корень в нашу схему Горнера и начнем заполнять пустые ячейки: | Во вторую ячейку третьей строки запишем число 2, просто перенеся его из соответствующей ячейки второй строки. | | -2 ∙ 2 + 9 = 5 | | -2 ∙ 5 + 7 = -3 | | -2 ∙ (-3) — 6 = 0 |
Таким образом мы исходный многочлен разложили на множители: 2x4 + 5x3 — 11x2 — 20x + 12 = (x — 2)(x + 2)(2x2 + 5x — 3) Многочлен 2x2 + 5x — 3 тоже можно разложить на множители. Для этого можно решить квадратное уравнение через дискриминант, а можно поискать корень среди делителей числа -3. Так или иначе, мы придем к выводу, что корнем этого многочлена является число -3 | 2 | 5 | -11 | -20 | 12 | | 2 | 2 | 9 | 7 | -6 | 0 | | -2 | 2 | 5 | -3 | 0 | | | -3 | 2 | | | | |
| Во вторую ячейку четвертой строки запишем число 2, просто перенеся его из соответствующей ячейки третьей строки. | | 2 | 5 | -11 | -20 | 12 | | 2 | 2 | 9 | 7 | -6 | 0 | | -2 | 2 | 5 | -3 | 0 | | | -3 | 2 | -1 | | | |
| -3 ∙ 2 + 5 = -1 | | 2 | 5 | -11 | -20 | 12 | | 2 | 2 | 9 | 7 | -6 | 0 | | -2 | 2 | 5 | -3 | 0 | | | -3 | 2 | -1 | 0 | | |
| -3 ∙ (-1) — 3 = 0 |
Таким образом мы исходный многочлен разложили на линейные множители: 2x4 + 5x3 — 11x2 — 20x + 12 = (x — 2)(x + 2)(x + 3)(2x — 1) А корнями уравнения являются: x = ±2; 3; 0.5 предварительное вычисление алгебры — Есть ли общая формула для решения уравнений 4-й степени (квартики)? Конечно, есть, но это некрасиво, сложно и не стоит запоминать. Люди знают об этом и цитировали или цитировали это для вас, но на самом деле они никогда бы не использовали это. Если вам нужно что-то действительно полезное для решений с ручкой и бумагой, вы можете понять фактическую теорию, лежащую в основе решения. Ниже я приведу один метод. Формула Quartic — это лишь конечный результат этой методологии, записанный в терминах исходных коэффициентов.Из-за этого метод намного легче запомнить, чем формулу, поэтому меня раздражает, когда люди цитируют только формулу и говорят вам: «Не беспокойтесь, используйте компьютер». Решение с ручкой и бумагой не сложно, это просто требует времени. Понимание того, как это делается, даже если вы никогда не используете его, расширяет ваш мозг и ваше понимание, позволяет реализовать его в программировании и позволяет воссоздавать его всякий раз, когда это может вам понадобиться, вместо чрезмерной зависимости от компьютеров, которые всегда будут рядом. ты, что, на мой взгляд, плохой математик. Есть три метода решения квартиков, которые я знаю и знаю: - Квадратичная факторизация Декарта
- Метод Эйлера
- Метод Феррари
Если кто-нибудь знает больше, дайте мне знать. Метод Феррари — исторически первый метод, открытый. Метод Эйлера очень похож на метод Кардано для кубических фигур и, вероятно, был смоделирован на основе того же подхода. Но я неравнодушен к технике квадратичной факторизации Декарта.Это относительно простой процесс, который я буду использовать ниже. Если вы хотите увидеть, как работают другие, дайте мне знать. Все вышеперечисленные методы начинаются одинаково: депрессия (удаление члена степени $ n-1 $, в данном случае кубического члена) и нормализация (доведение коэффициента опережения до 1, т. Е. Превращение полинома в однозначное число). Они все заканчивают примерно одним и тем же местом: решением кубического уравнения. Так что к этому нужно быть готовым. Я рекомендую вам освежить в памяти это; Я не буду объяснять здесь решение кубики, а буду ссылаться только на нее.2 + qz + r = 0 \; \; \; \; \; \; \; \; \; \; \; \; (1) $$ Для некоторых $ p, q, r \ in \ mathbb {R} $. Это не влияет на корневые позиции; все, что сделал коэффициент опережения, — увеличил ненулевые значения. Абсолютно без потери общности по нулям. Все эти константы, $ p, q, r $, могут быть вычислены из исходных коэффициентов, $ a, b, c, d, e $. Кубического члена по-прежнему нет, и теперь нет и коэффициента опережения. Интересно отметить, что случилось с многочленом.Мы начали с 5 произвольных констант и сократили их до 3, нормализовав шаг и убрав кубический член. Изначально у нас были произвольные значения $ a, b, c, d, e \ in \ mathbb {R} $, а теперь у нас есть произвольные значения $ p, q, r \ in \ mathbb {R} $. Хотя последние три вычисляются из исходных пяти, они имеют произвольные значения и нет потери общности. Это значительное упрощение проблемы. Отсутствие кубического члена окажется жизненно важным. До сих пор все было просто настройкой: запись многочлена в сокращенной монической форме.Напомним, что все методы четвертой степени достигают по крайней мере этого. Далее мы реализуем метод факторизации Декарта.
Метод факторизации Декарта Мы должны предполагать, что все коэффициенты действительны, $ p, q, r \ in \ mathbb {R} $. 2 } $$ Таким образом, мы, по сути, сократились до $ m $ как последнее неизвестное.2 = 0 $$ И, по сути, мы закончили. У нас остается кубический многочлен от $ w $ , который разрешим с помощью собственных методов. Приемы, о которых, как я полагаю, вы уже знаете, если пытаетесь решить квартики. Как и в случае с квартиками, как вы уже знаете, существуют кубические формулы, но я рекомендую изучить методы, лежащие в их основе. Если вам нужна помощь с кубиками, я рекомендую метод Кардано (исходное решение) или тригонометрическое решение Виета (я предпочитаю).Также есть Completing the Cube, хорошее доказательство концепции, но я бы никогда его не использовал. Смело задавайте по кубику отдельный вопрос и я с радостью отвечу. Дело в том, что задача свелась с поиска корней квартики к задаче поиска корней кубики. Проблема попроще! Обычно так бывает. Все методы нахождения корня четвертой степени требуют сначала нахождения корней кубической, очевидной или нет. Так же, как поиск корней кубики требует решения квадратичной.2 — mz + \ frac {r} {n}) = 0 $. Еще не сделано. Теперь каждый из этих квадратичных множителей должен быть решен с помощью формулы квадратиков, и у вас есть решения в $ z $. Это решает депрессивную моническую квартику, с которой мы начали метод квадратичной факторизации Декарта.
Наконец Не забывайте об исходной квартике, которая была у нас в самом начале, до депрессии и нормализации. Мы ввели горизонтальный сдвиг на $ x = z- \ frac {b} {4a} $. Выполнение этого последнего бита решит исходную квартику в терминах $ x $, что и является решением, которое вы хотите. Когда все будет готово, вы придете к набору решений. Обязательно проверьте свои ответы. У вас могут быть избыточные или лишние решения. Некоторые избыточные решения могут быть записаны очень разными алгебраическими способами, но будут представлять одно и то же числовое значение. Если вы выразите окончательный ответ $ x $ в терминах исходных $ a, b, c, d, e $, у вас будут точно такие же «формулы четвертой степени», которые вас цитируют другие люди. Выражение, конечно, будет немного отличаться в зависимости от того, какой из методов четвертой степени вы используете.
Проблемы Если вас беспокоит предположение, что коэффициенты $ p, q, r $ действительны, не стоит. Все это означает, что $ a, b, c, d, e $ реальны, что обычно является хорошим предположением. Фактически, мы можем обобщить. Значения $ p, q, r $ можно сделать сложными, подразумевая только то, что исходная квартика имеет комплекс $ a, b, c, d, e $. Это также означает, что вам придется решать кубику с комплексными коэффициентами. Это выполнимо, и математика по-прежнему работает нормально. (PDF) Классический новый метод решения уравнений четвертой степени Прикладная и вычислительная математика, 2013, 2 (2): 24-27 27 ii N 5622.06624.0,5622.06624.0 67.1398688.0,32.408688.0 3 + −− → ∠ − ∠ = Выбираются корни, удовлетворяющие уравнению (18): 3247.1 1 = N iN 5619.06224.0 2 −− = 5622.06624.0 3 + — = N iN 8749.03210.0,8749.03210.0 41 9000− + iiN 8749.03210.0,8749.03210.0 42 −− + = 15095.1,15095.1 43 — = N Выбраны ответы, удовлетворяющие уравнению (16): 7929.1 1 — = x ix ix x 75.11510.1 75.11510.1 5089.0 4 3 2 — = + = Используя второй метод, мы проверяем следующий пример . 5. Выводы Самым важным моментом во всех методах решения уравнения четвертой степени является сложность этих решений. Чтобы доказать эффективность и простоту предложенного метода , в четвертом разделе статьи приведен пример квартики, который решается с помощью предложенного инициированного метода. Ссылки [1] «Простой метод решения уравнений четвертой степени» Амир Фати, Пуйя Мобадерсани, Рахим Фатхи, Австралийский журнал Основные и прикладные науки, 6 (6): 331-336, 2012, ISSN 1991-8178. [2] Кардано, Джироламо, (перевод Т. Ричарда Витмера), Ars Magna или правила алгебры, Довер, Нью-Йорк, штат Нью-Йорк, 1993. [3] Фосетт, ВМ «Геометрическая интерпретация Решение общего многочлена четвертой степени ». Амер. Математика. Ежемесячно 103, 51-57, 1996. [4] Gellert, W .; Gottwald, S .; Hellwich, M .; Kästner, H .; и Künstner, H. (Eds.). ВНР Краткая энциклопедия Математика, 2-е изд.Нью-Йорк: Ван Ностранд Рейнхольд, 1989. [5] Хазевинкель М. (Управляющий ред.). Энциклопедия Математика: обновленный и аннотированный перевод советской «Математической энциклопедии ». Дордрехт, Нидерланды: Рейдел, 1988. [6] MathPages. «Преобразование квартиков в кубики». http://www.mathpages.com/home/kmath396.htm. [7] Смит Д. Э. Справочник по математике. Нью-Йорк: Дувр, 1994. [8] ван дер Варден, Б. Л. §64 по алгебре, т. 1. Нью-Йорк: Springer-Verlag, 1993. [9] Бейер, У. Х. Стандартные математические таблицы CRC, 28-е изд. Бока-Ратон, Флорида: CRC Press, стр. 12, 1987а. [10] Бейер, У. Х. Справочник по математическим наукам, 6-е изд. Бока-Ратон, Флорида: CRC Press, 1987b. [11] Биркгоф, Г., Мак Лейн, С. Обзор современной алгебры, 5-е изд. Нью-Йорк: Macmillan, стр.107-108, 1996. [12] Borwein, P. and Erdélyi, T. «Quartic Equations». §1.1.E.1e в полиномах и полиномиальных неравенствах. Нью-Йорк: Springer-Verlag, p. 4, 1995. [13] Бойер, К. Б., Мерцбах, У. С. История математики, 2-е изд. New York: Wiley, pp. 286-287, 1991. [14] И. Стюарт, «Теория Галуа», изд: Chapman & Hall / CRC Mathematics, 2004. [15] JJ O’Connor and Э.Ф. Робертсон, «Лодовико Феррари», в Архив истории математики MacTutor, изд. Школа математики и статистики, Университет Сент-Эндрюс Шотландия. [16] ЛЕГКИЙ ВЗГЛЯД НА КУБИЧЕСКУЮ ФОРМУЛУ. Томас Дж. Ослер. Математический факультет, Университет Роуэн, Глассборо, штат Нью-Джерси, 08028. Решение уравнений Полиномиальные уравнения 4-й степени Калькулятор позволяет вычислять корни любого многочлена четвертой степени. Коэффициенты могут быть как действительными, так и комплексными числами. Использовалась некая методика, которая нигде не описана и не отсортирована. Формулы Феррари использовать не стал — не интересно. Несмотря на свой путь, вы все равно утыкаетесь в задаче решения вспомогательного уравнения третьей степени, так называемой кубической резольвенты. И скорее всего избежать этого никак не получится. Но дальше все идет по другому. По любому из значений корня резольвенты, вычисляем три вспомогательных параметра. Зная эти три параметра, мы легко можем найти все четыре корня исходного уравнения. Есть только один нюанс, с которым столкнулись предшественники, мне иногда приходится некоторым определять знак + или тоже — для одного вспомогательного параметра. Теперь в виде формул Замена подстановки получаем так называемый заданный многочлен Ищем решение этого уравнения в виде сумм двух функций Три вспомогательных параметра связаны с коэффициентами данного полинома следующими соотношениями Выражая любой из вспомогательных параметров получаем, в том или ином виде кубическая резольвента Например, если мы выразим F2 Это кубическое уравнение, подстановка которого превращается в классическую кубическую резольвенту. Теперь о нюансе, о котором говорили ранее. Какой знак использовать при вычислении корней? Критерий получается очень простой. Берем любой корень резольвенты и сравниваем его , если это условие истинно, ставится + (плюс), если условие некорректно — (минус) Далее все эти параметры подставляются в формулу также определены корни уравнения 4 степени. Еще хотелось бы поговорить о критерии.Вдумчивый читатель спросит: «А что, если какой-то корень резольвенты является комплексным числом? Каков в данном случае критерий?» Наилучшим образом, я рассчитывал на подстановку корня в исходное уравнение. Для этого существует легкий алогритический способ, описанный в статье Значение производной многочлена по методу Хорнера. Если адрес выражения равен нулю, то есть истина, то знак не меняется. Если иначе то знак ставим минус. Теперь можно легко и быстро решать сложные уравнения 4 степени.Вы не найдете его в онлайн-сервисах. Попробуйте решить уравнение Один из корней равен Кто считает, что действительной частью можно пренебречь и отвергнуть как «почти нулевую», глубоко заблуждается. Отказавшись от него, мы будем иметь значение функции, а не ноль. И только с учетом «такой маленькой» действительной части уравнение стать идентичным. Поэтому точность расчетов очень важна. Если вдруг заметили ошибку в расчетах (а вдруг?) Просьба сообщить.Но я надеюсь, что этого не произойдет. Несколько примеров: Решение уравнения четвертой степени одной переменной Решение уравнения четвертой степени одной переменной 0 Предисловие В процессе обучения необходимо решить квадратное уравнение одной переменной.
Поскольку у него неизвестные параметры, я хотел использовать MATLAB для решения его аналитического решения и записать его на C ++ для расчета. Позже выяснилось, что решение было слишком долгим.
Если вы поместите его непосредственно в C ++, на решение в реальном времени уйдет даже больше времени, чем на решение унарного уравнения четвертой степени. Итак, найдите другой способ узнать, как решить унарное уравнение четвертой степени. 1. Метод 1 Метод Феррари, который также является самым простым способом попасть в Google. Я перестал смотреть на принцип временных ограничений и пошел прямо выяснять. Так совпало, что код есть в энциклопедии. Ссылка. Феррари.cpp #include
#include
#include <комплекс>
#include
std :: complex sqrtn (const std :: complex & x, double n)
{
двойное r = гипотеза (x.real (), x.imag ());
если (г> 0,0)
{
double a = atan2 (x.imag (), x.real ());
n = 1,0 / n;
r = pow (r, n);
а * = п;
return std :: complex (r * cos (a), r * sin (a));
}
return std :: complex <двойной> ();
}
std :: complex Ferrari (std :: complex x [4]
, std :: complex <двойной> a
, std :: complex <двойной> b
, std :: complex <двойной> c
, std :: complex <двойной> d
, std :: complex <двойной> e)
{
а = 1.0 / а;
б * = а;
с * = а;
д * = а;
е * = а;
std :: complex P = (c * c + 12.0 * e - 3.0 * b * d) / 9.0;
std :: complex Q = (27.0 * d * d + 2.0 * c * c * c + 27.0 * b * b * e - 72.0 * c * e - 9.0 * b * c * d) / 54.0;
std :: complex D = sqrtn (Q * Q - P * P * P, 2.0);
std :: complex <двойной> u = Q + D;
std :: complex <двойной> v = Q - D;
if (v.real () * v.real () + v.imag () * v.imag ()> u.real () * u.real () + u.imag () * u.imag ())
{
u = sqrtn (v, 3.0);
}
еще
{
u = sqrtn (u, 3,0);
}
std :: complex <двойной> y;
если (u.real () * u.real () + u.imag () * u.imag ()> 0,0)
{
v = P / u;
std :: complex o1 (-0,5, + 0,86602540378443864676372317075294);
std :: complex o2 (-0,5, -0,86602540378443864676372317075294);
std :: complex <двойной> & yMax = x [0];
двойной m2 = 0,0;
двойной m2Max = 0,0;
int iMax = -1;
для (int i = 0; i <3; ++ i)
{
у = и + v + с / 3.0;
u * = o1;
v * = o2;
а = b * b + 4,0 * (y - c);
m2 = a.real () * a.real () + a.imag () * a.imag ();
если (0 == я || m2Max m = sqrtn (b * b + 4.0 * (y - c), 2.0);
если (m.real () * m.real () + m.imag () * m.imag ()> = DBL_MIN)
{
std :: complex <двойной> n = (b * y - 2.0 * г) / м;
а = sqrtn ((b + m) * (b + m) - 8,0 * (y + n), 2,0);
х [0] = (- (b + m) + a) / 4,0;
х [1] = (- (b + m) - a) / 4,0;
a = sqrtn ((b - m) * (b - m) - 8,0 * (y - n), 2,0);
х [2] = (- (b - m) + a) / 4,0;
х [3] = (- (b - m) - a) / 4,0;
}
еще
{
a = sqrtn (b * b - 8,0 * y, 2,0);
х [0] =
х [1] = (-b + a) / 4,0;
х [2] =
х [3] = (-b - a) / 4,0;
}
вернуть x [4];
}
int main ()
{
std :: complex <двойной> x [4];
х [4] = Феррари (х, 1,2,3,4,5);
std :: cout << "root1:" << x [0] << std :: endl << "root2:" << x [1] << std :: endl << "root3:" << x [ 2] << std :: endl << "root4:" << x [3] << std :: endl;
вернуть истину;
}
Тестовый коэффициент: 1, 2, 3, 4, 5
Убедитесь, что результат верен, используйте Matlab для проверки: p = [1 2 3 4 5];
x = корни (p)
Результаты согласуются, ОК.{n-2} + \ cdots + c_1x + c_0
P (x) = xn + cn − 1 xn − 1 + cn − 2 xn − 2 + ⋯ + c1 x + c0
Сопутствующая матрица: M Икс знак равно [ 0 0 . . . 0 - c 0 1 0 . . . 0 - c 1 0 1 . . . 0 - c 2 . . . . . . . . . . . . . . . 0 0 . . . 1 - c п - 1 ] M_x = \ left [\ begin {array} {ccccc} 0 & {0} & {...} & {0} & {-c_0} \\ 1 & 0 & {...} & {0} & {- c_1} \\ {0} & {1} & {...} & {0} & {-c_2} \\ {...} & {...} & {...} & {...} & {...} \\ {0} & {0} & {...} & {1} & {-c_ {n-1}} \ end {array} \ right]
Mx = ⎣⎢⎢⎢⎢⎡ 010 ... 0 001 ... 0 ............... 000 ... 1 −c0 −c1 −c2 ...− cn − 1 ⎦⎥⎥⎥⎥⎤
Характерное значение п ( Икс ) Р (х)
P (x) Корни. Итак, используйте Eigen, чтобы решить многочлен: #include
#include
#include <Собственный / плотный>
используя пространство имен std;
int main (int argc, char ** argv)
{
Eigen :: Matrix matrix_44;
Eigen :: Matrix <комплексный , Eigen :: Dynamic, Eigen :: Dynamic> matrix_eigenvalues;
matrix_44 << 0, 0, 0, -5,
1, 0, 0, -4,
0, 1, 0, -3,
0, 0, 1, -2;
std :: cout << "matrix_44:" << std :: endl << matrix_44 << std :: endl << std :: endl;
матрица_собственные значения = матрица_44.собственные значения ();
std :: cout << "matrix_eigenvalues:" << std :: endl << matrix_eigenvalues << std :: endl;
возврат 0;
}
Результат такой же, как и выше: 3. Заключение Чем глубже математика, тем меньше сложность кода! ! почему мы не можем решать полиномиальные уравнения выше четвертой степени? : managelikeimfive Вот версия, которая безопасна (умная) 5-летней давности. Ведь они знают о многочленах. Учитывая многочлен, мы, конечно, хотели бы его решить. Для степени 1,2,3,4 у нас есть формул в терминах радикалов , то есть они могут использовать +, -, x, /, как обычно, и брать корни n-й степени (радикалы), и все. Теперь у многих многочленов есть решения, которые не находятся внутри обычных чисел (те, которые могут быть записаны в виде дробей, рациональные числа ). Попробуйте X 2 + 1 = 0. Нет решения! Итак, мы можем представить, что делаем нашу систему счисления больше, чтобы включить этих чисел.Это возможно! И самая маленькая такая система счисления называется полем разбиения полинома. Он «разбивает» многочлен на множители. (потому что вы, умный пятилетний ребенок, знаете о соответствии факторов и решений.) Теперь эта система счисления (или просто поле для краткости) является наименьшей, которая имеет решения для нашего многочлена, но содержит ли она другие системы счисления ? Насколько большим нам нужно было сделать поле? Француз Эварист Галуа сумел доказать, что существует структура, называемая группой , в которой есть элементы, и эти элементы в ней соединяются одно в одно с полями, содержащимися в нашем поле расщепления. Не знаю, кто это заметил, но какой-то чувак, у которого, должно быть, был гигантский мозг, кое-что заметил. Эти группы обладали особым свойством, когда решения в поле расщепления можно было записать в терминах радикалов. Это особое свойство известно как растворимость , но это hella Technical , поэтому я больше не буду о нем говорить. Еще одна вещь, группа, которую люди называют A_5, - это , а не . Итак, вот где мы находимся прямо сейчас: нам может быть дан многочлен, и мы можем построить новую систему счисления (его поле расщепления), в которой он имеет решения.С этим полем связана группа, которая описывает, какие другие поля оно содержит, и если эта группа разрешима, то решения могут быть записаны в радикалах. Итак, вы должны знать, что нас ждет: если мы не можем записать решения некоторого полинома 5-й степени в радикалах, у него должно быть поле расщепления, группа которого равна , не разрешима . Именно это и происходит. Некоторые полиномы 5-й степени имеют группу A_5, которая неразрешима! Итак, некоторые многочлены 5-й степени не могут иметь хорошо записанные решения. Теперь, конечно, если некоторые не могут быть написаны таким образом, это мешает нам использовать уравнение. Какую бы формулу вы ни записали, есть некоторые квинтики, которые она не решит, потому что ее решения - это числа, которые просто невозможно записать таким образом ! Edit Итак, чтобы объяснить 5-летнему ребенку, мы скрываем, что в основном представляет собой все мясо, в котором разрешимые группы соответствуют полям разбиения, в которых решения могут быть записаны в радикалах. Что там происходит? Что ж, группа описывает для нас подполя в поле разделения, и это фактически кодирует в каком-то смысле, как числа в больших полях строятся в терминах чисел в меньших полях.Разрешаемые группы означают, что мы «красиво» строим числа, так что корни можно записать в терминах радикалов. Как найти пример полинома четвертой степени математического класса 11 CBSE Подсказка: В приведенном выше вопросе нас просят найти многочлен четвертой степени, не имеющий действительных корней. Это означает, что корни мнимые. Чтобы найти многочлен, выберите любую сопряженную пару мнимых чисел. Тогда, просто перемножив их, мы получим требуемую четвертую степень полиномиального уравнения. Полный пошаговый ответ:
Теперь мы должны найти биквадратные многочлены, предполагая два мнимых корня с их сопряженными, поскольку у него нет реальных корней, поэтому корни биквадратного многочлена будут мнимыми.
Мы случайным образом возьмем любые комплексные числа с их сопряженными, так как мнимые корни всегда встречаются парами.
Следовательно, чтобы найти пример полиномиального уравнения четвертой степени, не имеющего действительных нулей или имеющего только мнимые корни, мы будем считать корнями \ [1 \ pm i \] и \ [2 \ pm i \].{2}} - 18x + 10 \]. Примечание: Другой метод решения вопроса заключается в том, что мы можем начать с любого квадратного уравнения, которое имеет положительный ведущий коэффициент или дискриминантное значение этого квадратного уравнения меньше нуля, а затем постоянно увеличивать постоянный член до значения где он больше не пересекает ось абсцисс. Решая приведенное выше уравнение, не забывайте брать мнимые корни в сопряженных парах.
Как решать уравнения четвертой степени Освоив приемы решения в случае работы с квадратными уравнениями, студенты сталкиваются с необходимостью повышения квалификации.Однако этот переход не всегда кажется простым, и требование найти корни в уравнении четвертой степени иногда становится невыполнимой задачей. Инструкция по эксплуатации 1 Примените формулу Виета, которая устанавливает связь между корнями уравнения четвертой степени и его коэффициентами. Согласно его положениям, сумма корней дает значение, равное отношению первого коэффициента ко второму, взятому с противоположным знаком.Порядок нумерации совпадает с убывающими степенями: первая соответствует максимальной степени, четвертая - минимальной. Сумма попарных произведений корней - это отношение третьего коэффициента к первому. Соответственно, количество произведений x1x3x4, x1x3x4, x1x4x4, x2x4 является значением, равным противоположному результату деления четвертого коэффициента на первый. А умножив все четыре корня, вы получите число, равное отношению свободного члена уравнения к коэффициенту, обращенному к переменной в максимальной степени.Скомпилированные таким образом четыре уравнения дают вам систему с четырьмя неизвестными, для которой достаточно базовых навыков. 2 Проверьте, принадлежит ли ваше выражение к одному из типов уравнений четвертой степени, которые называются «легко решаемыми»: биквадратичным или возвратным. Превратите первое в квадратное уравнение, изменив параметры и обозначив квадрат неизвестной другой переменной. Дифференциальные уравнения определение, типы ДУ, теория, как решать ДУ первого и второго порядка, методы и примеры подробных решений, онлайн-калькулятор Многих людей, хоть как-то изучавших курс высшей математики в учебном заведении, приводит в ужас словосочетание «дифференциальные уравнения». Согласно строгому научному определению в книгах – так именуются математические выражения, где в состав входят функция, ее производная или параметр. Имеется достаточно большое количество типов этих равенств, рассмотрим подходы к их решению так, чтобы они были понятны даже для «чайников». Дифференциальные уравнения первого порядка Обыкновенное диффуравнение (ДУ) 1-го порядка задается относительно некой функции, имеющей вид у(х): F(x,y(x),y´(x)) = 0, здесь, F(x,y,y’) – это функция, задающаяся для трех аргументов (в этом примере для х, у и у’).Таково строгое математическое определение ДУ. Для примера можно привести следующее уравнение: xy'(x) — y(x)2 = 0 функция вида F(x,y,p) = xp — y2 Простейшие ДУ первого порядка Общепринятый механизм нахождения решения таких выражений (чаще всего похожи на y’ = f(x)) – это интегрирование левой и правой части такого уравнения на заданном промежутке Х. После интегрирования получим такое выражение: ∫ y’dx = ∫ f(x)dx Воспользовавшись свойствами, которые относятся к интегральным выражениям, упростим выражение до вида: y = F(x) + N здесь, F(x) – это первообразная от функции f(x) на заданном интервале Х, а N – случайным образом выбранная константа. Задача №1 Необходимо определить все возможные варианты решения диффуравнения, имеющего вид Последовательно рассмотрим решение. Представленное диффуравнение может иметь смысл только при действительных значениях параметра х. Примем условие, что x ≠ 0, тогда выражение легко преобразовывается в следующее: Если же, напротив, принять, что х = 0, то выражение приобретет следующий вид, характерный для любых функций y’, удовлетворяющих данному условию: Можно заключить, что решением при справедливости условия х = 0 будет любая функция у, найденная, когда аргумент равен нулю. Остается только проинтегрировать полученное диффуравнение: Данное выражение – это решение для приведенного диффуравнения. ДУ с разделяющимися переменными Среди дифуров 1-го порядка можно выделить такие, где все переменные х и у можно преобразовать так, что они окажутся по разные стороны от знака равенства. Соответственно уравнения, где путем преобразований это возможно сделать, называются диффуравнениями с разделяющимися переменными. Их общий вид следующий: После проведения нескольких преобразований, это выражение может быть сведено к следующему виду: При составлении преобразований необходимо внимательно разделять переменные, не допуская, чтобы функции обращались в ноль, иначе возможна потеря некоторых значений. Задача №2 Рассмотрим обыкновенный пример. Необходимо определить все возможные решения диффуравнения y’ = y(x2 + ex) Как решать? В первую очередь проводим разделение переменных в разные части уравнения: Данные преобразования справедливы, если у ≠ 0. Если рассмотреть вариант решения при нулевом показателе функции, то можно заметить ,что Это означает, что y = 0 – одно из возможных решений задачи. Рассмотрим другие варианты решений, для чего произведем интегрирование диффуравнения: Финальная часть преобразований будет вторым решением диффуравнения. Останется только потенциировать это выражение, чтобы привести его к более явному виду: Правильными решениями, в результате преобразований, будут: Кроме того, можно воспользоваться онлайн системой для нахождения ответа. Подробные объяснения даны в решебниках Филиппова и Понтрягина. Линейные неоднородные ДУ первого порядка Линейные неоднородные уравнения – это такие выражения, которые можно записать в формате y’ + b(x)y = f(x), при этом функции b(x) и f(x) – непрерывные. Основной принцип при нахождении решения сводится к следующим шагам: Первым делом для уравнения необходимо произвести поиск решения, которое бы соответствовало линейному однородному диффуравнению. Затем необходимо варьировать произвольной постоянной, производя ее замену на функцию. На финальном этапе функция подставляется в первоначальное уравнение, откуда, решая ДУ, получается ответ. Задача №3 Рассмотрим применение методики решения на примере. Необходимо найти решение дифференциального уравнения вида Решение заключается в следующем. Первоначально примем, что y = m∗n, следовательно, получается: На следующем этапе нужно определить, что такое m (оно обязательно не должно быть равным нулю), при котором все выражение внутри скобок будет равно нулю. Получаем дополнительное дифференциальное уравнение: Теперь необходимо принять одно из частных решений n = x2 + 1, которое соответствует равенству С2 — С1=0. Выполняем оставшиеся преобразования: Вполне очевидно, что ответом на условие задачи будет функция: Задача Коши для ДУ При рассмотрении решения практически любого диффуравнения, имеющего вид F(m,n,n’) = 0, становится очевидно, что это бесконечно большое количество решений (это следствие самого возникновения диффуравнения). На данном этапе математики сталкиваются с вопросом о выборе конкретного решения и способе его выделения из множества.Иными словами, если представить решения в виде бесконечного множества интегральных кривых, то необходимо найти среди них нужную. Чтобы это сделать, необходимо рассмотреть плоскость Xoy, где должна быть задана некая точка D0, имеющая координаты (x0, y0) – именно через них и должна пройти интегральная кривая, чтобы стать искомым ответом. Когда мы с самого начала задаем точку D0(x0, y0) – это означает, задание начального условия y(x0) = y0. Диффуравнение, для которого определено начальное условие в представленном формате, называется уравнением с заданной задачей Коши. Диффуравнение, для которого определено начальное условие в представленном формате, называется уравнением с заданной задачей Коши.
Задача №4 Рассмотрим примеры с объяснениями. Необходимо определить решения задачи Коши вида: Ход решения строится в три этапа. На первом этапе решаем диффуравнение y’ = xy2 стандартным методом. Его решение приводить не будем, приведем только ответ: Производим подстановку начального значения (х = 0, у = 1) в решение и находим значение С: Производим подстановку полученного значения в ответ диффуравнения и получаем одно из частных решений: Полученная функция – ответ на задачу Коши в этом примере. Дифференциальные уравнения Бернулли ДУ Бернулли обычно представлено в следующем виде: y’ + b(x)y = c(x)yn Обязательное условие, что функции b(x) и c(x) – являются непрерывными.
Задача №5 Рассмотрим общее решение данного типа на примере. Необходимо выполнить поиск всех возможных решений уравнения: Во время оценки уравнения в нем можно идентифицировать ДУ Бернулли с параметром ½. Оно легко сводится к линейному ДУ, для этого достаточно заменить выражения: Находим производную: Выполним деление по начальному уравнению Бернулли на и выполним необходимые преобразования: Произведем замену параметра х на параметр у: Теперь вычисляем интегрирующий модуль для данной функции, он будет равен: Теперь производим ряд преобразований для вычисления решения диффуравнения: Переписываем полученную функцию в неявном виде и получаем ответ: Дифференциальные уравнения второго порядка Отличить ДУ 2-го порядка от таковых 1-го порядка достаточно просто – в их составе присутствует вторая производная (y’’) и не содержится производных более высокого уровня. Общий вид таких уравнений таков: F(m,n,n’,n») = 0 Линейные однородные ДУ второго порядка с постоянными коэффициентами Определение линейных дифференциальных однородных уравнений 2-го порядка крайне просто – они имеют вид: y» + ry’ + k = 0 При это важным условием теории является причисление r и k к действительным числам. Задача №6 Рассмотрим решение однородных диффуравнений 2-го порядка с постоянными коэффициентами на примере. Найти решение диффуравнения 2-го порядка вида: Во всех таких случаях начинаем с поиска характеристического уравнения: Методы решения данного уравнения достаточно простые, можно воспользоваться калькулятором или быстро решить на листочке, поэтому их приводить не будем, запишем лишь корни – 1, 5. Поскольку это все действительные, неодинаковые числа, то можно записать функцию-решение в следующем виде: Линейные неоднородные ДУ второго порядка с постоянными коэффициентами Общий вид неоднородных диффуравнений второго порядка легко определить по представленному образцу: y» + ry’ + ky = f(x) Переменные r и k должны быть вещественными и постоянными числами. Задача №7 Рассмотрим подробное решение. Необходимо определить все решения для уравнения y» + y = cos x. На первом этапе находим в составе неоднородного уравнения его однородную часть – это будет y» — y = 0. Для него уже выполняем поиск характеристического уравнения – оно будет иметь вид k2 + 1 = 0. Корнями для данного характеристического уравнения являются k1 = -i и k2 = i. Исходя из этого записываем решение для однородного уравнения: Из-за отсутствия параметра с производной первого порядка также будет справедливо записать: Теперь остается только подставить найденные выражения: Частное и общее решение для уравнения можно записать: Дифференциальные уравнения высших порядков Дифференциальные однородные уравнения высших порядков легко отличить, если они совпадают со следующим видом: Для неоднородных справедлив другой формат: Для выбора корректного пути решения ДУ, необходимо четко и правильно определить его тип. Для этого необходимо решить уравнение относительно его производной и проверить, возможно ли разложение функции на множители. После этого достаточно сравнить с одним из типов, приведенным в данной статье. Порядок дифференциального уравнения и его решения, задача КошиОбыкновенным дифференциальным уравнением называется уравнение, связывающее независимую переменную,
неизвестную функцию этой переменной и её производные (или дифференциалы) различных порядков. Порядком дифференциального уравнения называется порядок старшей производной, содержащейся в нём. Кроме обыкновенных изучаются также дифференциальные уравнения с частными производными. Это уравнения,
связывающие независимые переменные ,
неизвестную функцию этих переменных и её частные производные по тем же переменным. Но мы будем рассматривать только обыкновенные дифференциальные уравнения и поэтому будем для краткости опускать слово «обыкновенные». Это уравнения,
связывающие независимые переменные ,
неизвестную функцию этих переменных и её частные производные по тем же переменным. Но мы будем рассматривать только обыкновенные дифференциальные уравнения и поэтому будем для краткости опускать слово «обыкновенные». Примеры дифференциальных уравнений: (1) ; (2) ; (3) ; (4) ; (5) . Уравнение (1) — четвёртого порядка, уравнение (2) — третьего порядка, уравнения (3) и (4) — второго
порядка, уравнение (5) — первого порядка. Дифференциальное уравнение n-го порядка не обязательно должно содержать явно функцию, все
её производные от первого до n-го порядка и независимую переменную. В нём могут не содержаться явно производные
некоторых порядков, функция, независимая переменная. Например, в уравнении (1) явно нет производных третьего и второго порядков, а также функции;
в уравнении (2) — производной второго порядка и функции; в уравнении (4) — независимой переменной; в уравнении (5) — функции. Только в уравнении (3) содержатся явно все производные, функция и независимая переменная. Только в уравнении (3) содержатся явно все производные, функция и независимая переменная. Решением дифференциального уравнения называется всякая функция y = f(x), при
подстановке которой в уравнение оно обращается в тождество. Процесс нахождения решения дифференциального уравнения называется его интегрированием. Пример 1. Найти решение дифференциального уравнения . Решение. Запишем данное уравнение в виде .
Решение состоит в нахождении функции по её производной. Изначальная функция, как известно из интегрального исчисления, есть
первообразная для , т. е. . Это и есть решение данного дифференциального уравнения. Меняя в нём C, будем получать
различные решения. Мы выяснили, что существует бесконечное множество решений дифференциального уравнения первого порядка. Общим решением дифференциального уравнения n-го порядка называется его решение, выраженное
явно относительно неизвестной функции и содержащее n независимых произвольных постоянных, т. е. е. Решение дифференциального уравнения в примере 1 является общим. Частным решением дифференциального уравнения называется такое его решение, в котором
произвольным постоянным придаются конкретные числовые значения. Пример 2. Найти общее решение дифференциального уравнения
и частное решение при . Решение. Проинтегрируем обе части уравнения такое число раз, которому равен порядок дифференциального уравнения. , , . В результате мы получили общее решение — данного дифференциального уравнения третьего порядка. Теперь найдём частное решение при указанных условиях. Для этого подставим вместо произвольных коэффициентов
их значения и получим . Если кроме дифференциального уравнения задано начальное условие в виде ,
то такая задача называется задачей Коши. В общее решение уравнения подставляют значения и
и находят значение произвольной постоянной C,
а затем частное решение уравнения при найденном значении C. Это и есть решение задачи Коши. В общее решение уравнения подставляют значения и
и находят значение произвольной постоянной C,
а затем частное решение уравнения при найденном значении C. Это и есть решение задачи Коши. Нет времени вникать в решение? Можно заказать работу! Пример 3. Решить задачу Коши для дифференциального уравнения из примера 1
при условии . Решение. Подставим в общее решение
значения из начального условия y = 3, x = 1. Получаем . Записываем решение задачи Коши для данного дифференциального уравнения первого порядка: . При решении дифференциальных уравнений, даже самых простых, требуются хорошие навыки интегрирования
и взятия производных, в том числе сложных функций. Это видно на следующем примере. Пример 4. Найти общее решение дифференциального уравнения . Решение. Уравнение записано в такой форме, что можно сразу же интегрировать обе его части. . Применяем метод интегрирования заменой переменной (подстановкой). Пусть ,
тогда . Требуется взять dx и теперь — внимание — делаем это по правилам дифференцирования сложной
функции, так как x и есть сложная функция («яблоко» — извлечение квадратного корня или, что то же самое — возведение в степень
«одна вторая», а «фарш» — самое выражение под корнем): Находим интеграл: Возвращаясь к переменной x, получаем: . Это и есть общее решение данного дифференциального уравнения первой степени. Не только навыки из предыдущих разделов высшей математики потребуются в решении дифференциальных
уравнений, но и навыки из элементарной, то есть школьной математики. Как уже говорилось, в дифференциальном уравнении любого порядка может и не быть
независимой переменной, то есть, переменной x. Помогут решить эту проблему не забытые (впрочем, у кого как) со
школьной скамьи знания о пропорции. Таков следующий пример. Таков следующий пример. Пример 5. Найти общее решение дифференциального уравнения . Решение. Как видим, переменная x в уравнении отсутствует. Вспоминаем из курса дифференциального
исчисления, что производная может быть записана также в виде .
В результате уравнение приобретает вид , то есть, в нём в некотором виде появился x. Теперь вспомнаем одно из свойств пропорции: из пропорции
выткают следующие пропорции: , то есть в пропорции можно менять местами крайние и средние члены или те и другие одновременно. Применяя это свойство, преобразуем уравнение к виду , после чего интегрируем обе части уравнения: . Оба интеграла — табличные, находим их: и получаем решение данного дифференциалного уравнения первого порядка: . Эта статья представила необходимый минимум сведений о дифференциальных уравнениях и их решениях и
должна помочь вам уверенно и увлечённо перейти к изучению различных видов дифференциальных уравнений. К началу страницы Пройти тест по теме Дифференциальные уравнения Всё по теме «Дифференциальные уравнения» Порядок дифференциального уравнения и его решения, задача Коши Дифференциальные уравнения с разделяющимися переменными Однородные дифференциальные уравнения первого порядка Линейные дифференциальные уравнения первого порядка Дифференциальные уравнения Бернулли Дифференциальные уравнения в полных дифференциалах Дифференциальные уравнения второго порядка, допускающие понижение порядка Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами Поделиться с друзьями Дифференциальные уравнения второго порядка — онлайн справочник для студентов ОПРЕДЕЛЕНИЕ Дифференциальным уравнением второго порядка называется уравнение вида
\(\
F\left(x ; y ; y^{\prime} ; y^{\prime \prime}\right)=0
\) ПРИМЕР Задание Найти общий интеграл дифференциального уравнения второго порядка \(\
y^{\prime \prime}+x=0
\) Решение Перепишем заданное уравнение в виде:
\(\
y^{\prime \prime}=-x
\) Дважды проинтегрируем. {-3 x}
\) {-3 x}
\) Физика 166 Реклама и PR 31 Педагогика 80 Психология 72 Социология 7 Астрономия 9 Биология 30 Культурология 86 Экология 8 Право и юриспруденция 36 Политология 13 Экономика 49 Финансы 9 История 16 Философия 8 Информатика 20 Право 35 Информационные технологии 6 Экономическая теория 7 Менеджент 719 Математика 338 Химия 20 Микро- и макроэкономика 1 Медицина 5 Государственное и муниципальное управление 2 География 542 Информационная безопасность 2 Аудит 11 Безопасность жизнедеятельности 3 Архитектура и строительство 1 Банковское дело 1 Рынок ценных бумаг 6 Менеджмент организации 2 Маркетинг 238 Кредит 3 Инвестиции 2 Журналистика 1 Конфликтология 15 Этика 9 Формулы дифференцирования Дифференциальные уравнения первого порядка Решение дифференциальных уравнений Производная сложной функции Производная показательной функции Узнать цену работы Узнай цену своей работы Имя Выбрать тип работыЧасть дипломаДипломнаяКурсоваяКонтрольнаяРешение задачРефератНаучно — исследовательскаяОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерскаяНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация в ВАКПубликация в ScopusДиплом MBAПовышение оригинальностиКопирайтингДругое Принимаю Политику
конфиденциальности Подпишись на рассылку,
чтобы не пропустить информацию об акциях Линейные дифференциальные уравнения второго порядка. Решение задач и контрольных работ по высшей математике онлайн
- Определение
- Однородные дифференциальные линейные уравнения второго порядка
- Неоднородные дифференциальные линейные уравнения второго порядка
- Методы решения других видов дифференциальных уравнений
- Дифференциальные уравнения — основные понятия
- Дифференциальные уравнения первого порядка с разделяющимися переменными
- Однородные дифференциальные уравнения первого порядка
- Линейные дифференциальные уравнения первого порядка. Уравнение Бернулли
- Дифференциальные уравнения в полных дифференциалах
- Дифференциальные уравнения высших порядков
- Системы дифференциальных уравнений
Определение
Уравнение
(*) где
и
– непрерывные
функция в интервале
называется
неоднородным линейным дифференциальным уравнение второго порядка, функции
и
– его
коэффицинентами. Если
в
этом интервале, то уравнение принимает вид: Если
в
этом интервале, то уравнение принимает вид:
(**) и называется однородным
линейным дифференциальным уравнением второго порядка. Если уравнение (**) имеет
те же коэффициенты
и
, как уравнение (*), то оно называется
однородным уравнением, соответствующим неоднородному уравнению (*).
Однородные дифференциальные линейные уравнения второго порядка
Пусть в линейном уравнении
и
— постоянные
действительные числа. Частное решение уравнения
будем искать в виде функции
, где
– действительное
или комплексное число, подлежащее определению. Дифференцируя по
, получаем:
Подставляя в исходное дифуравнение, получаем:
Отсюда, учитывая, что
, имеем:
Это уравнение называется
характеристическим уравнением однородного линейного дифуравнения. Характеристическое уравнение и дает
возможность найти
. Это уравнение второй степени, поэтому
имеет два корня. Обозначим их через
и
. Возможны три случая: Характеристическое уравнение и дает
возможность найти
. Это уравнение второй степени, поэтому
имеет два корня. Обозначим их через
и
. Возможны три случая: Корни действительные и разные
В этом случае общее решение уравнения:
Пример 1
Решение Характеристическое уравнение имеет вид:
Решение характеристического уравнения:
Общее решение исходного дифуравнения:
Корни действительные и равные
В этом случае общее решение уравнения:
Пример 2
Решение Если не находите примера, аналогичного вашему, если сами не успеваете выполнить работу, если впереди экзамен по предмету и нужна помощь — свяжитесь со мной: ВКонтакте
WhatsApp
Telegram Я буду работать с вами, над вашей проблемой, пока она не решится. Характеристическое уравнение имеет вид:
Решение характеристического уравнения:
Общее решение исходного дифуравнения:
Корни комплексные
В этом случае общее решение уравнения:
Пример 3
Решение Характеристическое уравнение имеет вид:
Решение характеристического уравнения:
Общее решение исходного дифуравнения:
Неоднородные дифференциальные линейные уравнения второго порядка
Рассмотрим теперь решение некоторых
типов линейного неоднородного уравнения второго порядка с постоянными
коэффициентами
где
и
– постоянные
действительные числа,
– известная непрерывная
функция в интервале
. Для нахождения общего решения такого
дифференциального уравнения необходимо знать общее решение соответствующего
однородного дифференциального уравнения
и частное
решение
. Рассмотрим
некоторые случаи: Рассмотрим
некоторые случаи: Правая часть дифференциального уравнения имеет вид:
Частное решение дифференциального
уравнения ищем также в форме квадратного трехчлена:
Подставляя
и
в исходное
дифференциальное уравнение, получим тождество, откуда находим коэффициенты. Если нуль – однократный корень
характеристического уравнения, то
Если нуль – двухкратный корень
характеристического уравнения, то
Аналогично обстоит дело, если
– многочлен
произвольной степени
Пример 4
Решение Решим соответствующее однородное уравнение. Характеристическое уравнение:
Общее решение однородного уравнения:
Найдем частное решение неоднородного
дифуравнения:
Подставляя найденные производные в исходное дифуравнение, получаем:
Искомое частное решение:
Общее решение исходного дифуравнения:
Правая часть дифференциального уравнения имеет вид:
Частное решение ищем в виде
, где
– неопределенный
коэффициент. Подставляя
и
в исходное
дифференциальное уравнение, получим тождество, откуда находим коэффициент. Если
– корень
характеристического уравнения, то частное решение исходного дифференциального
уравнения ищем в виде
, когда
– однократный
корень, и
, когда
– двукратный
корень.
Пример 5
Решение Характеристическое
уравнение:
Общее
решение соответствующего однородного дифференциального уравнения:
Найдем
частное решение соответствующего неоднородного дифференциального уравнения:
Подставляя
в исходное дифуравнение, получаем:
Общее
решение дифуравнения:
Правая часть дифференциального уравнения имеет вид:
В этом случае частное решение
ищем в форме тригонометрического двучлена:
где
и
– неопределенные коэффициенты
Подставляя
и
в исходное
дифференциальное уравнение, получим тождество, откуда находим коэффициенты. Эти уравнения определяют коэффициенты
и
кроме случая, когда
(или когда
– корни характеристического уравнения). В
последнем случае частное решение дифференциального уравнения ищем в виде:
Пример 6
Решение Характеристическое
уравнение:
Общее
решение соответствующего однородного дифуравнения:
Найдем
частное решение неоднородного дифуравнения
Подставляя
в исходное дифуравнение, получаем:
Общее
решение исходного дифуравнения:
Дифференциальные уравнения — Математика — Смотреть онлайн видео уроки для начинающих бесплатно!
В категории Дифференциальные уравнения собраны бесплатные онлайн видео уроки по этой теме. Дифференциальное уравнение (ДУ) – это уравнение, которое связывает значение некоторой неизвестной функции в некоторой точке со значением производных этой функции различных порядков в той же точке. В состав ДУ входит неизвестная функция под знаком производной или дифференциала. Обыкновенное дифференциальное уравнение (ОДУ) – имеет неизвестную функцию с одной переменной. Уравнение частными производными (УРЧП) — неизвестная функция зависит от многих переменных. Стохастическое дифференциальное уравнение (СДУ) — включающее случайные процессы. Изучение дифференциальных уравнений по видео урокам будет полезно как для начинающих, так и для более опытных математиков. Видеоуроки из рубрики Дифференциальные уравнения Вы можете смотреть бесплатно в любое удобное время. К некоторым видео урокам по дифференциальным уравнениям приложены дополнительные материалы, которые можно скачать. Приятного Вам обучения! Дифференциальное уравнение (ДУ) – это уравнение, которое связывает значение некоторой неизвестной функции в некоторой точке со значением производных этой функции различных порядков в той же точке. В состав ДУ входит неизвестная функция под знаком производной или дифференциала. Обыкновенное дифференциальное уравнение (ОДУ) – имеет неизвестную функцию с одной переменной. Уравнение частными производными (УРЧП) — неизвестная функция зависит от многих переменных. Стохастическое дифференциальное уравнение (СДУ) — включающее случайные процессы. Изучение дифференциальных уравнений по видео урокам будет полезно как для начинающих, так и для более опытных математиков. Видеоуроки из рубрики Дифференциальные уравнения Вы можете смотреть бесплатно в любое удобное время. К некоторым видео урокам по дифференциальным уравнениям приложены дополнительные материалы, которые можно скачать. Приятного Вам обучения!
Новые · Лучшие · Популярные
Смотреть урок онлайн Геометрический смысл дифференциального уравненияВ этом видео рассказывается о геометрическом смысле дифференциального уравнения. Здесь приводится доказательство и формулировка геометрического смысла дифференциального уравнения как уравнения, которое определяет в некоторой области поле направлений, совпадающее с касательными к графикам решений этого уравнения — интегральными кривыми. Это позволяет, не решая дифференциального уравнения, строить графики его решений. На данном занятии также рассматривается пример, в котором требуется приближенно… Здесь приводится доказательство и формулировка геометрического смысла дифференциального уравнения как уравнения, которое определяет в некоторой области поле направлений, совпадающее с касательными к графикам решений этого уравнения — интегральными кривыми. Это позволяет, не решая дифференциального уравнения, строить графики его решений. На данном занятии также рассматривается пример, в котором требуется приближенно… Смотреть урок онлайн Интегрирующий множительВ этом онлайн уроке рассказывается о том, что такое интегрирующий множитель и как с его помощью можно решать уравнения. Существует такая функция, при умножении на которую обеих частей исходного уравнения, это уравнение становится уравнением в полных дифференциалах. Такую функцию называют интегрирующим множителем. Здесь будет рассматриваться уравнение общий вида, которое не является уравнением в полных дифференциалах. При нахождении интегрирующего множителя часто используют частные случаи. .. .. Смотреть урок онлайн Решение дифференциального уравнения второго порядка. Часть 2В этом видео рассказывается о том, как решать дифференциальные уравнения второго порядка, которые не содержат независимую переменную x. Здесь предложена схема, позволяющая понизить порядок и решить уравнение такого вида. Первым шагом, производную искомой функции y заменяют на некоторую функцию p, которая зависит от переменной y. Затем выполняется дифференцирование обеих частей по переменной x, чтобы получить выражение для второй производной функции y. Третьим шагом идет подстановка выражения, в… Смотреть урок онлайн Понижение порядка дифференциального уравнения. Часть 1Урок «Понижение порядка дифференциального уравнения. Часть 1» посвящен вопросу о том, как выполняется понижение порядка дифференциального уравнения. Здесь будет рассмотрено уравнение второго порядка, в котором не содержится искомой функции y. Решить его можно с помощью соответствующей замены переменной, в результате которого происходит преобразование исходного уравнения к уравнению первого порядка. Такое преобразование называется понижение порядка. На этом занятии дана схема последовательная… Решить его можно с помощью соответствующей замены переменной, в результате которого происходит преобразование исходного уравнения к уравнению первого порядка. Такое преобразование называется понижение порядка. На этом занятии дана схема последовательная… Смотреть урок онлайн Дифференциальные уравнения второго порядка, примеры, решениеВидео «Дифференциальные уравнения второго порядка, примеры, решение» посвящено вопросу о том, что собой представляют линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами и как они решаются. Здесь вы узнаете, какой общий вид имеет такое уравнение и его упрощенный вид. Очень важно уметь их решать, т.к. к ним сводится большое количество задач математики, механики, электротехники и некоторых других наук. С помощью линейных уравнений описываются всевозможные… Смотреть урок онлайн Уравнение в полных дифференциалах, примеры, решениеВ этом видео уроке рассказывается о том, что собой представляют дифференциальные уравнение в полных дифференциалах и как они решаются. В первой части занятия будет сформулировано определение, какое дифференциальное уравнение первого порядка, выраженное через дифференциалы своих переменных, называется уравнением в полных дифференциалах. Здесь вы также научитесь определять, является ли заданное уравнение, уравнением в полных дифференциалах. В данном видео уроке кроме теоретического материала… В первой части занятия будет сформулировано определение, какое дифференциальное уравнение первого порядка, выраженное через дифференциалы своих переменных, называется уравнением в полных дифференциалах. Здесь вы также научитесь определять, является ли заданное уравнение, уравнением в полных дифференциалах. В данном видео уроке кроме теоретического материала… Смотреть урок онлайн Линейные дифференциальные уравнения первого порядка, примеры, решениеОнлайн урок «Линейные дифференциальные уравнения первого порядка, примеры, решение» посвящен вопросу о том, что такое линейные дифференциальные уравнения и как они решаются. Начинается занятие с формулировки общего определения и разбора структуры такого уравнения. Здесь вы также узнаете, в каком случае уравнение называется однородным. Одним из наиболее эффективных методов решения линейных уравнений является метод Бернулли, алгоритм применения которого будет подробно рассмотрен. В этом видео… В этом видео… Смотреть урок онлайн Однородные дифференциальные уравнения первого порядка, решениеЭто видео посвящено вопросу о том, что собой представляют однородные дифференциальные уравнения первого порядка, а также как выполнять их решение на конкретном примере. Начинается урок с формулировки определения однородной функции. В качестве примера используется однородная функция второго порядка. После этого будет сформулировано определение однородного дифференциального уравнения и предоставлен набор формул, позволяющих свести такое уравнение к уравнению с разделяющимися переменными. В… Смотреть урок онлайн Дифференциальные уравнения с разделяющимися переменными. Часть 2В этом онлайн уроке рассказывается о дифференциальных уравнениях с разделяющимися переменными. Такие уравнения могут быть представлены в форме, когда в них входит не производная, а дифференциалы. При такой записи говорят, что дифференциальное уравнение представлено в симметричной форме. При этом переменные x и y равноправны, и каждую из них можно рассматривать как функцию другой. На этом занятии рассказывается, как решать такие уравнения. Решение производится путем преобразования исходного… При такой записи говорят, что дифференциальное уравнение представлено в симметричной форме. При этом переменные x и y равноправны, и каждую из них можно рассматривать как функцию другой. На этом занятии рассказывается, как решать такие уравнения. Решение производится путем преобразования исходного… Смотреть урок онлайн Дифференциальные уравнения с разделяющимися переменными. Часть 1Видео урок «Дифференциальные уравнения с разделяющимися переменными. Часть 1» посвящен вопросу о решении таких уравнений. Здесь дается определение дифференциальные уравнения первого порядка с разделяющимися переменными. Очень важно уметь решать такие уравнения, потому, что к ним сводится достаточно большое число уравнений других типов. Ход решения исходного уравнения идет через преобразования его к уравнению с разделенными переменными, решение которого можно получить с помощью интегрирования…
1 2
Если у Вас есть качественные видео уроки, которых нет на нашем сайте, то Вы можете добавить их в нашу коллекцию. Для этого Вам необходимо загрузить их на видеохостинг (например, YouTube) и добавить код видео в форму добавления уроков. Возможность добавлять свои материалы доступна только для зарегистрированных пользователей. Для этого Вам необходимо загрузить их на видеохостинг (например, YouTube) и добавить код видео в форму добавления уроков. Возможность добавлять свои материалы доступна только для зарегистрированных пользователей.
Дифференциальные уравнения — онлайн калькулятор.Как известно, теория обыкновенных дифференциальных уравнений начала развиваться в XVII веке одновременно с возникновением дифференциального и интегрального исчисления. Можно сказать, что необходимость решать дифференциальные уравнения для нужд механики, то есть находить траектории движений, явилась толчком для создания Ньютоном нового исчисления. Законы Ньютона позволяют строить математическую модель механического движения, которая обычно представляет собой дифференциальное уравнение. Рассмотрим, например, подробнее такую задачу. С некоторой высоты сброшено тело массой m. Требуется установить закон изменения скорости падения тела v(t), если на него действует сила сопротивления воздуха, пропорциональная скорости (коэффициент пропорциональности k). По II закону Ньютона где – ускорение движущегося тела, – сумма сил, действующих на тело – силы тяжести и силы сопротивления воздуха. Таким образом, имеем уравнение, связывающее искомую функцию v(t) и ее производную По II закону Ньютона где – ускорение движущегося тела, – сумма сил, действующих на тело – силы тяжести и силы сопротивления воздуха. Таким образом, имеем уравнение, связывающее искомую функцию v(t) и ее производную т. е. дифференциальное уравнение. В настоящее время теория дифференциальных уравнений является одним из самых больших разделов современной математики. Ее разработкой занимались крупнейшие ученые XVIII века, такие как Ж. Даламбер, Ж. Л. Лагранж, А. Клеро и др. Наибольшую роль в развитии этой теории сыграли труды Л. Эйлера. В первых двух томах его «Интегрального исчисления» содержится немало классических примеров интегрирования дифференциальных уравнений, в том числе и решения линейного однородного уравнения любого порядка с постоянными коэффициентами. Отметим, что изучение обыкновенных дифференциальных уравнений (ОДУ) на младших курсах обычно остается на уровне открытий XVIII века, и заключается в освоении приемов интегрирования лишь хорошо изученных типов уравнений и некоторых экзотических случаев, ибо «точно» интегрируемые уравнения – это исключительная редкость во множестве возможных уравнений. Переходя к реальным объектам исследования, студенты, инженеры и аспиранты сталкиваются с более сложными моделями и их математической реализацией. Даже в кругах исследователей – «чистых математиков» довольно долго интегрирование уравнений в квадратурах, теоретико-групповой подход к уравнениям считались тупиковой ветвью в науке. Тем не менее, теория обыкновенных дифференциальных уравнений является базой для уравнений математической физики и, кроме того, развитие современной физики показало, что именно те самые редкие и хорошо изученные случаи и представляют наибольший физический интерес. А успехи, достигнутые в ряде разделов математики – в алгебраической топологии, дифференциальной геометрии и коммутативной алгебре, позволяют надеяться на то, что общая теория уравнений с частными производными будет построена. Переходя к реальным объектам исследования, студенты, инженеры и аспиранты сталкиваются с более сложными моделями и их математической реализацией. Даже в кругах исследователей – «чистых математиков» довольно долго интегрирование уравнений в квадратурах, теоретико-групповой подход к уравнениям считались тупиковой ветвью в науке. Тем не менее, теория обыкновенных дифференциальных уравнений является базой для уравнений математической физики и, кроме того, развитие современной физики показало, что именно те самые редкие и хорошо изученные случаи и представляют наибольший физический интерес. А успехи, достигнутые в ряде разделов математики – в алгебраической топологии, дифференциальной геометрии и коммутативной алгебре, позволяют надеяться на то, что общая теория уравнений с частными производными будет построена. В математике и физике часто встречаются задачи, для решения которых требуется решить уравнение, содержащее не только неизвестную функцию и ее аргумент, но и производную неизвестной функции. Уравнение вида связывающее независимую переменную x, искомую функцию и ее производные ) , называется обыкновенным дифференциальным уравнением. Порядок старшей производной, входящей в дифференциальное уравнение, называется порядком дифференциального уравнения. Например, уравнения будут дифференциальными уравнениями первого порядка; уравнения будут дифференциальными уравнениями второго порядка; уравнение имеет третий порядок. Функция называется решением дифференциального уравнения на интервале (a,b) если при ее подстановке в это уравнение получается тождество, справедливое для всех x из интервала (a, b) Например, функция является решением дифференциального уравнения ; функция будет решением уравнения в интервале (-1;1) . Чтобы это проверить, достаточно подставить функцию в соответствующее уравнение. Уравнение задающее в неявном виде решение дифференциального уравнения, называется интегралом дифференциального уравнения. График решения (интеграла) дифференциального уравнения называется интегральной кривой. График решения (интеграла) дифференциального уравнения называется интегральной кривой. Так же если вы затрудняетесь в решении дифференциального уравнения, всегда можно воспользоваться онлайн калькулятором Процесс нахождения решений дифференциального уравнения называется интегрированием дифференциального уравнения. Это название не случайно, так как нахождение решений обычно связано с процессом интегрирования. Поскольку процесс интегрирования функции приводит к появлению множества функций, то и решений любое дифференциальное уравнение тоже будет иметь множество. Основной задачей теории дифференциальных уравнений является отыскание всех решений данного дифференциального уравнения в заданной области (в явной или неявной форме). Дифференциальное уравнение называется интегрируемым в квадратурах, если все его решения могут быть получены в результате конечной последовательности элементарных действий над известными функциями и интегрированием этих функций. Таких уравнений сравнительно немного. В нашем курсе мы рассмотрим основные типы дифференциальных уравнений, интегрируемых в квадратурах. Таких уравнений сравнительно немного. В нашем курсе мы рассмотрим основные типы дифференциальных уравнений, интегрируемых в квадратурах. В математике рассматриваются также уравнения, которые связывают искомую функцию нескольких переменных, ее аргументы и частные производные. Такие уравнения называются дифференциальными уравнениями в частных производных. Их интегрирование представляет собой значительно более сложную задачу, чем интегрирование обыкновенных дифференциальных уравнений. Позднее мы познакомимся с одним типом дифференциальных уравнений в частных производных. Калькулятор дифференциальных уравнений второго порядка + онлайн-решатель с бесплатными шагами Калькулятор дифференциальных уравнений второго порядка используется для нахождения начального решения линейных дифференциальных уравнений второго порядка. Дифференциальное уравнение второго порядка имеет вид: M(x) и N(x) являются непрерывными функциями x . 9{ αx } \ [ \ c_{1} \ cos( βx) + c_{2} \ sin( βx) \ ] \] 9{ αx } \ [ \ c_{1} \ cos( βx) + c_{2} \ sin( βx) \ ] \] Условия начального значения y(0) и y´(0) указаны пользователем определить значения c1 и c2 в общем решении. Что такое калькулятор дифференциальных уравнений второго порядка? Калькулятор дифференциальных уравнений второго порядка — это онлайн-инструмент, который используется для расчета начального решения однородного или неоднородного линейного дифференциального уравнения второго порядка. Как пользоваться калькулятором дифференциальных уравнений второго порядка Чтобы использовать калькулятор дифференциальных уравнений второго порядка, выполните следующие действия. Шаг 1 Сначала пользователь должен ввести уравнение линейного дифференциала второго порядка в окне ввода калькулятора. Уравнение имеет вид: L(x)y´´ + M(x)y´ + N(x) = H(x) Здесь L(x) , M(x) , и N(x) может быть непрерывным функциями или постоянными в зависимости от пользователя. Функция ‘H(x)’ может быть равна нулю или быть непрерывной функцией. Шаг 2 Теперь пользователь должен ввести начальных значений для дифференциального уравнения второго порядка. Их следует вводить в блоки с метками «y(0)» и «y´(0)» . Здесь y(0) — это значение y при x=0 . Значение y´(0) получается из первой производной от y и помещения x=0 в функцию первой производной. Вывод Калькулятор отображает вывод в следующих окнах. Ввод Окно ввода калькулятора показывает ввод дифференциального уравнения , введенного пользователем. Он также отображает условия начального значения y(0) и y´(0) . Результат Окно Результат показывает решение с начальным значением , полученное из общего решения дифференциального уравнения. Решение представляет собой функцию x относительно y . Решение представляет собой функцию x относительно y . Автономное уравнение В этом окне калькулятор отображает автономную форму дифференциального уравнения второго порядка. Это выражается сохранением y´´ в левой части уравнения. Классификация ОДУ ODE означает Обыкновенное дифференциальное уравнение . Калькулятор отображает классификацию дифференциальных уравнений, введенных пользователем в этом окне. Альтернативная форма Калькулятор показывает альтернативную форму входного дифференциального уравнения в этом окне. Графики решения Калькулятор также отображает в этом окне график решения решения дифференциального уравнения. Решенные примеры Следующий пример решается с помощью калькулятора дифференциальных уравнений второго порядка. Пример 1 Найдите общее решение приведенного ниже дифференциального уравнения второго порядка: 0) = 4 y´(0) = 6 Решение Пользователь должен сначала ввести коэффициентов заданного дифференциального уравнения второго порядка в окне ввода калькулятора. Коэффициенты y´´ , y´ и y равны 1 , 4 и 0 соответственно. Коэффициенты y´´ , y´ и y равны 1 , 4 и 0 соответственно. Уравнение является однородным, так как правая часть уравнения равна 0 . После ввода уравнения пользователь должен теперь ввести начальные условия , как показано в примере. Теперь пользователь должен « 9{- \ 4x} }{ 2 } \] Калькулятор отображает Автономное уравнение следующим образом: y´´(x) = – 4y´(x) Классификация ОДУ входного уравнения является линейным обыкновенным дифференциальным уравнением второго порядка. Альтернативная форма , выдаваемая калькулятором: Калькулятор также отображает график решения , как показано на рисунке 1. Рисунок 1 Все изображения созданы с помощью Geogebra. Список математических калькуляторов Дифференциальные уравнения — DE второго порядка Показать мобильное уведомление Показать все примечания Скрыть все примечания Уведомление для мобильных устройств Похоже, вы используете устройство с «узкой» шириной экрана ( т. е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана. В предыдущей главе мы рассмотрели дифференциальные уравнения первого порядка. {2} + br + c = 0\) — вещественные различные корни. 9{2} + br + c = 0\), повторяются, т. е. двойных, корней. Мы будем использовать понижение порядка, чтобы получить второе решение, необходимое для получения общего решения в этом случае. {2} + br + c = 0\) — вещественные различные корни. 9{2} + br + c = 0\), повторяются, т. е. двойных, корней. Мы будем использовать понижение порядка, чтобы получить второе решение, необходимое для получения общего решения в этом случае. Снижение порядка – В этом разделе мы кратко рассмотрим тему уменьшения порядка. Это будет один из немногих случаев в этой главе, когда будет рассмотрено дифференциальное уравнение с непостоянными коэффициентами. Фундаментальные наборы решений. В этом разделе мы рассмотрим некоторые теории решения дифференциальных уравнений второго порядка. Мы определяем фундаментальные наборы решений и обсуждаем, как их можно использовать для получения общего решения однородного дифференциального уравнения второго порядка. Мы также определим вронскиан и покажем, как его можно использовать, чтобы определить, является ли пара решений фундаментальным набором решений. Подробнее о вронскиане. В этом разделе мы рассмотрим, как можно использовать вронскиан, введенный в предыдущем разделе, для определения того, являются ли две функции линейно независимыми или линейно зависимыми. Мы также дадим и альтернативный метод нахождения вронскиана. Мы также дадим и альтернативный метод нахождения вронскиана. Неоднородные дифференциальные уравнения. В этом разделе мы обсудим основы решения неоднородных дифференциальных уравнений. Определим дополнительное и частное решение и приведем форму общего решения неоднородного дифференциального уравнения. Неопределенные коэффициенты. В этом разделе мы вводим метод неопределенных коэффициентов для нахождения конкретных решений неоднородного дифференциального уравнения. Мы работаем с большим количеством примеров, иллюстрирующих множество рекомендаций по первоначальному предположению о форме конкретного решения, необходимого для метода. Изменение параметров. В этом разделе мы вводим метод изменения параметров для нахождения частных решений неоднородного дифференциального уравнения. Мы даем подробное рассмотрение метода, а также выводим формулу, по которой можно найти частные решения. Механические вибрации. В этом разделе мы рассмотрим механические вибрации. В частности, мы будем моделировать объект, соединенный с пружиной и движущийся вверх и вниз. Мы также допускаем введение в систему демпфера и действия общих внешних сил на объект. Также обратите внимание, что, хотя в этом разделе мы приводим примеры механических вибраций, простое изменение обозначений (и соответствующее изменение в том, что представляют величины) может перенести это практически в любую другую область техники. Мы также допускаем введение в систему демпфера и действия общих внешних сил на объект. Также обратите внимание, что, хотя в этом разделе мы приводим примеры механических вибраций, простое изменение обозначений (и соответствующее изменение в том, что представляют величины) может перенести это практически в любую другую область техники. Дифференциальные уравнения второго порядка Здесь мы учимся решать уравнения такого типа: d 2 y dx 2 + p dy dx + 900 = 0 Дифференциальное уравнение Дифференциальное уравнение — это уравнение с функцией и одной или несколькими ее производными:
Пример: уравнение с функцией y и ее
производная dy дх Заказ Орден является высшей производной (это первая производная? вторая производная? и т.д.): Пример: dy dx + y 2 = 5x Имеет только первую производную dy dx , так что «9005 порядок» Пример: d 2 y dx 2 + xy = sin(x) Вторая производная d 2 y dx 2 , то есть «Второй порядок» или «Порядок 2» Example: d 3 y dx 3 + x dy dx + y = e x This has a third derivative d 3 y dx 3 который превосходит dy dx , то есть «Третий порядок» или «Порядок 3» Прежде чем приступать к дифференциальным уравнениям второго порядка, убедитесь, что вы знакомы с различными методами решения дифференциальных уравнений первого порядка. Дифференциальные уравнения второго порядка Мы можем решить дифференциальное уравнение второго порядка типа:
= f(x) , где P(x), Q(x) и f(x) являются функциями от x, используя: Неопределенные коэффициенты, которые работают только тогда, когда f(x) является полиномом, экспонентой, синусоидой, косинус или их линейная комбинация. Изменение параметров, которое немного сложнее, но работает с более широким набором функций. Но здесь мы начнем с изучения случая, когда f(x) = 0 (это делает его «однородным»): d 2 y dx 2 + P(x) dy dx + Q(x)y
= 0 , а также где функции P(X) и Q(x) являются константами p и q : d 2 y dx 2 + p dy dx + qy = 0 Давайте научимся их решать! e на помощь Мы собираемся использовать специальное свойство производной экспоненциальной функции: В любой точке наклон (производная) e x равен значению e x : И когда мы вводим значение «r» вот так: f(x) = e rx Находим: - первая производная равна f'(x) = re rx
- вторая производная равна f»(x) = r 2 e rx
Другими словами, первая и вторая производные f(x) кратны f(x) Это нам очень поможет! Пример 1: Решение D 2 Y DX 2 + DY DX — 6y = 0 LET Y = E RX — 6y = 0 LET Y = E RX — 6y = 0 Let Y = E RX — 6Y = 0 LET Y = E RX — 6Y = 0 итак получаем: - dy dx = re rx
- d 2 y dx 2 = r 2 e rx
Замените их в уравнение выше: R 2 E RX + RE RX — 6E RX = 0 Упрощение: E RX 9 09 09 9099 9099 9099 9099 9099 9099 ( E RX 909. ) = 0 ) = 0 r 2 + r − 6 = 0 Мы свели дифференциальное уравнение к обыкновенному квадратному уравнению! Это квадратное уравнение получило специальное название характеристическое уравнение . Мы можем разложить это на: (r − 2)(r + 3) = 0 Итак, r = 2 или −3 Итак, у нас есть два решения: y = e 2x y = e −3x Но это не окончательный ответ, потому что мы можем комбинировать различные кратных из этих двух ответов, чтобы получить более общее решение: y = Ae 2x + Be −3x Проверить Давайте проверим этот ответ. First take derivatives: y = Ae 2x + Be −3x dy dx = 2Ae 2x − 3Be −3x d 2 y dx 2 = 4Ae 2x + 9Be −3x Теперь подставим в исходное уравнение: d 2 y dx 2 + dy dx − 6y = 0 (4Ae 2x + 9Be −3x ) + (2Ae 2x − 3Be − 3x ) − 6(Ae 2x + Be −3x ) = 0 4Ae 2x + 9Be −3x + 2Ae 2x − 3Be −3x − 6Ae 2x − 6Be −3x = 0 4Ae 2x + 2Ae 2x − 6Ae 2x + 9Be −3x − 3Be −3x − 6Be −3x = 0 0 = 0 Сработало! Так вообще этот метод работает? Ну и да и нет. Ответ на этот вопрос зависит от констант p и q . Ответ на этот вопрос зависит от констант p и q . С y = e rx как решение дифференциального уравнения: d 2 y dx 2 + p dy dx + qy = 0 получаем: r 2 e rx + pre rx + qe rx = 0 e rx (r 2 + pr + q) = 0 г 2 + пр + кв = 0 Это квадратное уравнение, и может быть три типа ответа: - два действительных корня
- один действительный корень (т.е. оба действительных корня одинаковы)
- два сложных корня
Как мы решаем это зависит от типа! Мы можем легко определить тип, вычислив дискриминант p 2 − 4q . Когда будет - положительный получаем два действительных корня
- ноль получаем один реальный корень
- минус получаем два комплексных корня
Два действительных корня Когда дискриминант p 2 − 4q равен положительному , мы можем перейти прямо к дифференциальному уравнению д 2 y dx 2 + p dy dx + qy = 0 через «характеристическое уравнение»: г 2 + пр + кв = 0 к общему решению с двумя действительными корнями r 1 и r 2 : y = Ae r 1 x + Be r 2 x Пример 2: Решить d 2 y DX 2 — 9 DY DX + 20y = 0 Характерное уравнение:
R 2 — + 20000 2 : 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 — . 4)(r − 5) = 0 4)(r − 5) = 0 r = 4 или 5 Итак, общее решение нашего дифференциального уравнения: y = Ae 4x + Be 5x А вот некоторые примерные значения: Пример 3: Решить 6 D 2 Y DX 2 + 5 DY DX — 6Y = 0 Уравнение характерного. Фактор: (3R — 2) (2R + 3) = 0 R = 2 3 или — 3 2 Таким образом у = Ае ( 2 3 х) + Be ( −3 2 х) Пример 4: Решение D 2 Y DX 2 — 6 DY DX — Y = 0 . 6r — 1 = 0 Это не просто факторизовать, поэтому мы используем формулу квадратного уравнения:0005 с a = 9, b = −6 и c = −1 x = −(−6) ± √((−6) 2 − 4×9×(−1)) 2× 9 x = 6 ± √(36+ 36) 18 x = 6 ± 6√2 18 x = 1 ± √2 3 So the общее решение дифференциального уравнения: y = Ae ( 1 + √2 3 )x + Be ( 1 − √2 3 )x Один реальный корень Когда дискриминант p 2 − 4q равен нулю , мы получаем один действительный корень (т. е. оба действительных корня равны). е. оба действительных корня равны). Вот несколько примеров: Пример 5: Решение D 2 Y DX 2 — 10 DY DX + 25Y = 0 . + 25 = 0 Фактор: (r — 5) (r — 5) = 0 r = 5 , поэтому мы имеем одно решение: y = E 5x НО когда e 5x это решение, то xe 5x это тоже решение! Почему? Я могу показать вам: y = xe 5x
dy dx = e 5x + 5xe 5x d 2 y dx 2 = 5e 5x + 5e 5x + 25xe 5x So d 2 y dx 2 − 10 dy dx + 25y = 5e 5x + 5e 5x + 25xe 5x − 10(e 5x + 5xe 5x ) + 25xe 5x = (5e 5x + 5e 5x − 10e 5x ) + (25xe 5x − 50xe 5x + 25xe 5x ) = 0 So, in this case our solution is: y = Ae 5x + Bxe 5x Как это работает в общем случае? При y = xe rx получаем производные: - dy dx = e rx + rxe rx
- д 2 у дх 2 = re rx + re rx + r 2 xe rx
Так d 2 y dx 2 + p dy dx + qy = (re rx + re rx + r 2 xe rx ) + p( e rx + rxe rx ) + q( 0 9 0 0 9 0 9 0 ) = e rx (r + r + r 2 x + p + prx + qx) = e rx (2r + p + x(r 2 + pr + q)) = e rx (2r + p), потому что мы уже знаем, что r 2 + pr + q = 0 А когда r 2 + pr + q имеет повторяющийся корень, то r = −p 2 и 2r + p = 0 Таким образом, если r является повторяющимся корнем характеристического уравнения, то общее решение равно . у = Ae rx + Bxe rx Давайте попробуем другой пример, чтобы увидеть, как быстро мы можем получить решение: Пример 6: Решение 4 D 2 Y DX 2 + 4 DY DX + Y = 0,00005 . 4r + 1 = 0 Тогда: (2r + 1) 2 = 0 r = − 1 2 Итак, решение дифференциального уравнения0005 y = Ae (−½)x + Bxe (−½)x Сложные корни Когда дискриминант p 2 − 4q равен отрицательному , мы получаем комплексные корни. Давайте попробуем пример, который поможет нам понять, как сделать этот тип: Пример 7: Решение D 2 Y DX 2 — 4 DY DX + 13y = 0 .0425 r 2 − 4r + 13 = 0 Это не множит, поэтому мы используем формулу квадратного уравнения: с a = 1, b = −4 и c = 13 x = −(−4) ± √((−4) 2 − 4×1×13) 2×1 x = 4 ± √(16− 52) 2 x = 4 ± √(−36) 2 x = 9 ± 6i0360 2 x = 2 ± 3i Если мы будем следовать методу, используемому для двух действительных корней, то мы можем попробовать решить: y = Ae (2+3i)x + Be (2− 3i)x
Мы можем упростить это, так как e 2x является общим делителем: y = e 2x ( Ae 3ix + Be −3ix ) 9002 мы еще не закончили . .. ! .. ! Формула Эйлера говорит нам, что: e ix = cos(x) + i sin(x) Итак, теперь мы можем пойти по совершенно новому пути, чтобы (в конечном счете) сделать вещи проще. Глядя только на часть «A плюс B»: Ae 3ix + Be −3ix A(cos(3x) + i sin(3x)) + B(cos(−3x) + i sin(−3x)) Acos(3x) + Bcos(−3x) + i(Asin(3x) + Bsin(−3x)) Теперь применим тригонометрические тождества: cos(−θ)=cos(θ) и sin(−θ)=−sin(θ): Acos(3x) + Bcos(3x) + i(Asin(3x) − Bsin(3x) (A+B)cos(3x) + i(A−B)sin(3x) Заменить A+B на C и A−B на D: Ccos(3x) + iDsin(3x) И мы получаем решение:
y = e 2x ( Ccos(3x) + iDsin(3x) ) Проверить У нас есть наш ответ, но, возможно, нам следует проверить, действительно ли он удовлетворяет исходному уравнение: y = e 2x ( Ccos(3x) + iDsin(3x) ) dy dx = e 2x ( -3Csin(9x)+2xiDcos)0408 2x ( Ccos(3x)+iDsin(3x) ) d 2 y dx 2 = e 2x 9x (-(6C+9i) 6iD)cos(3x)) + 2e 2x (2C+3iD)cos(3x) + (−3C+2iD)sin(3x) ) Замена: d 2 y 8dx2904 − 4 dy dx + 13y = e 2x ( −(6C+9iD)sin(3x) + (−9C+6iD)cos(3x)) + 2e 2x (2C+3iD) cos(3x) + (−3C+2iD)sin(3x)) − 4( e 2x (-3Csin(3x)+3iDcos(3x)) + 2e 2x (Ccos(3x)+iDsin(3x)) ) + 13( e 2x (Ccos(3x) + iDsin(3x)) )
. .. эй, почему бы ВАМ не попробовать сложить все члены, чтобы увидеть, равны ли они нулю … если нет, пожалуйста, дайте мне знать, хорошо? .. эй, почему бы ВАМ не попробовать сложить все члены, чтобы увидеть, равны ли они нулю … если нет, пожалуйста, дайте мне знать, хорошо? Как это обобщить? Обычно, когда мы решаем характеристическое уравнение с комплексными корнями, мы получаем два решения r 1 = v + wi и r 2 = v − wi Таким образом, общее решение дифференциального уравнения равно . y = e vx (Ccos(wx) + iDsin(wx)) Пример 8: Решение D 2 Y DX 2 — 6 DY DX + 25Y = 0 . + 25 = 0 Используйте формулу квадратного уравнения: x = −b ± √(b 2 − 4ac) 2a с a = 1, b = −6 и c = 25 x = −(−6) ± √((−6) 2 − 4×1× 25) 2 × 1 x = 6 ± √ (36- 100) 2 x = 6 ± √ (-64) 2 x = 6 ± x = 6 ± 8603 x = 6 ± 8603 2 x = 6 ± 8603 2 x = 6. 2 2 x = 3 ± 4i И получаем решение:
y = e 3x (Ccos(4x) + iDsin(4x)) Пример 9: Решение 9 D 2 Y DX 2 + 12 DY DX + 29Y = 0 Активные характеристики. + 29 = 0 Используйте формулу квадратного уравнения: x = −b ± √(b 2 − 4ac) 2a при a = 1 9 и c0 = 2 0 9, b0 = 2 9, b х = -12 ± √(12 2 — 4×9×29) 2 × x = −12 ± √ (144– 1044) 18 x = −12 ± –1359 ± 18 x = –1360 18 x = –1360 18 x = –13609 18 х = − 2 3 ± 5 3 i And we get the solution:
y = e (− 2 3 )x (Ccos( 5 3 x) + iDsin( 5 3 х)) Резюме Решить линейное дифференциальное уравнение второго порядка вида d 2 y dx 2 + p dy dx + qy = 0 где p и q константы, надо найти корни характеристического уравнения г 2 + пр + кв = 0 Есть три случая, в зависимости от дискриминанта p 2 — 4q . Когда будет Когда будет положительный получаем два действительных корня, и решение y = Ae r 1 x + Be r 2 x ноль получаем один действительный корень, а решение у = Ae rx + Bxe rx отрицательное получаем два комплексных корня r 1 = v + wi и r 2 = v − wi , и решение у = е vx (Ccos(wx) + iDsin(wx)) 9479, 9480, 9481, 9482, 9483, 9484, 9485, 9486, 9487, 9488 Решение однородных дифференциальных уравнений второго порядка — Криста Кинг Математика Однородные дифференциальные уравнения равны 0 Однородные дифференциальные уравнения второго порядка имеют вид ???ay»+by’+cy=0??? Дифференциальное уравнение является уравнением второго порядка, поскольку оно включает вторую производную от ???y???. Оно однородно, потому что правая часть равна ???0???. Если правая часть уравнения отлична от нуля, дифференциальное уравнение называется неоднородным. Оно однородно, потому что правая часть равна ???0???. Если правая часть уравнения отлична от нуля, дифференциальное уравнение называется неоднородным. Привет! Я Криста. Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее. Первое, что мы хотим узнать об однородных дифференциальных уравнениях второго порядка, это то, как находить их общие решения. Формула, которую мы будем использовать для общего решения, будет зависеть от типов корней, которые мы найдем для дифференциального уравнения. Чтобы найти корни, мы сначала сделаем замену для функции ???y??? через переменную ???r???. Мне нравится говорить, что количество «решеток» на ???y??? равен показателю степени, который вы ставите перед ???r???. Другими словами 92+бр+с=0??? После подстановки у нас есть стандартная форма квадратного уравнения, и мы можем факторизовать левую часть, чтобы найти корни уравнения. Константы ???c_1??? и ???c_2??? остаются в общем решении. Позже мы узнаем, как решать начальные задачи для однородных дифференциальных уравнений второго порядка, в которых нам будут предоставлены начальные условия, которые позволят нам найти константы и найти частное решение для дифференциального уравнения. Позже мы узнаем, как решать начальные задачи для однородных дифференциальных уравнений второго порядка, в которых нам будут предоставлены начальные условия, которые позволят нам найти константы и найти частное решение для дифференциального уравнения. Примеры нахождения общего решения однородного дифференциального уравнения второго порядка, имеющего различные вещественные корни Пройти курс Хотите узнать больше о дифференциальных уравнениях? У меня есть пошаговый курс для этого. 🙂 Нахождение общего решения дифференциального уравнения с различными вещественными корнями 9{-3x}??? Это общее решение дифференциального уравнения. Дифференциальное уравнение является уравнением второго порядка, поскольку оно включает вторую производную от y. Он однороден, потому что правая часть равна 0, .  Общее решение дифференциального уравнения с одинаковыми действительными корнями Пример Найдите общее решение. ???y»+6y’+9y=0??? Если заменить ???y??? в пересчете на ???r??? получаем 92-4(1)(17)}}{2(1)}??? ???r=\frac{-2\pm\sqrt{4-68}}{2}??? ???r=\frac{-2\pm\sqrt{-64}}{2}??? ???r=\frac{-2\pm\sqrt{(64)(-1)}}{2}??? ???r=\frac{-2\pm8\sqrt{-1}}{2}??? Так как мнимое число ???i??? определяется как ???i=\sqrt{-1}???, мы получаем ???r=\frac{-2\pm8i}{2}??? ???r=-1\pm4i??? Корни — это два комплексных числа, которые являются сопряженными друг с другом, поэтому это комплексно-сопряженные корни. Это означает, что мы будем использовать формулу общего решения для комплексно-сопряженных корней. Сопоставление этих корней с ???r=\alpha\pm{\beta}i??? говорит нам, что ???\alpha=-1??? и ???\бета=4???, так что мы получаем 9{-x}\left[c_1\cos{(4x)}+c_2\sin{(4x)}\right]??? Это общее решение дифференциального уравнения. Получите доступ к полному курсу «Дифференциальные уравнения» Изучение математикиКриста Кинг математика, изучение онлайн, онлайн-курс, онлайн-математика, дифференциальные уравнения, однородные уравнения, однородные дифференциальные уравнения, второй порядок, уравнения второго порядка, дифференциальные уравнения второго порядка, однородные уравнения второго порядка уравнения, различные действительные корни, действительные корни, равные действительные корни, комплексно-сопряженные корни, общее решение 0 лайков Уникальность и существование дифференциальных уравнений второго порядка Уникальность и существование для второго порядка
Дифференциальные уравнения Напомним, что для линейного дифференциального уравнения первого порядка y’ + p(t)y
= g(t) y(t 0 )
= у 0 , если p(t) и g(t)
непрерывна на [a,b], то существует единственная
решение на отрезке [a,b]. Мы можем задать те же вопросы о линейном дифференциале второго порядка
уравнения. Сначала нам нужно сделать несколько замечаний. Во-первых, это
для дифференциального уравнения второго порядка недостаточно указать начальное
должность. Мы также должны иметь начальную скорость. Один из способов
убедить себя в том, что, поскольку нам нужно обратить две производные, две
будут введены константы интегрирования, следовательно, две части информации
необходимо найти для определения констант. Второй комментарий относится к обозначениям. Пусть y» + p(t)y’
+ q(t)y = g(t) — линейное дифференциальное уравнение второго порядка. Затем мы вызываем
оператор Л(г)
= y» + p(t)y’ + q(t)y соответствующий линейный
оператор . Таким образом, мы хотим найти решения уравнения Л(г)
= g(t) y(t 0 )
= у 0 у'(t 0 ) = у’ 0 Мы сформулируем следующую теорему без доказательства. Доказательство хорошо
выше уровня этого курса. Доказательство хорошо
выше уровня этого курса. Теорема: Существование и
Уникальность Пусть p(t), q(t),
и g(t) непрерывна на [a,b],
тогда дифференциальное уравнение y» + p(t)y’ + q(t)y = g(t)
у(т 0 ) = y 0 y'(t 0 )
= у’ 0 имеет уникальное решение, определенное для всех
т в [а, б]. |
Пример Найдите наибольший интервал, где (т 2 — 1)y» + 3ty’ + стоимость t y = e t у(0) = 4, у'(0) = 5 гарантированно имеет уникальное решение. Раствор Мы сначала приводим его в стандартную форму y» + 3t/(t 2 — 1)y’ + (cost t)/(t 2 — 1) y = e t /(t 2 — 1) у(0) = 4, у'(0)
= 5 p, q и g
все непрерывны, кроме момента t = -1
и t = 1. Теорема говорит нам
что существует единственное решение на [-1,1]. Теорема говорит нам
что существует единственное решение на [-1,1]. Однородные линейные дифференциальные уравнения второго порядка Далее мы будем исследовать решения однородных дифференциальных
уравнения. Рассмотрим однородное линейное дифференциальное уравнение L(y) = 0 У нас есть следующая теорема | Теорема Пусть L(y) =
0 — однородное линейное дифференциальное уравнение второго порядка и
пусть у 1 и у 2 быть два решения. Тогда с 1 г 1 + c 2 y 2 также является решением для любой пары или
константы c 1 и c 2 . |
Используя терминологию линейной алгебры, мы знаем, что L является линейным
преобразование векторного пространства дифференцируемых функций в
сам. Теорема напоминает нам, что ядро линейного преобразования
является векторным подпространством. Теорема напоминает нам, что ядро линейного преобразования
является векторным подпространством. Доказательство L(c 1 y 1 + c 2 y 2 ) = (c 1 y 1 + c 2 y 2 )»
+ p(t)(c 1 y 1 + c 2 y 2 )’ + q(t)(c 1 y 1 + с 2 у 2 ) = c 1 y 1 »
+ c 2 y 2 » + p(t)c 1 y 1 ‘ + p(t)c 2 г 2 ‘
+ q(t)c 1 y 1 + q(t)c 2 y 2 = c 1 y 1 »
+ p(t)c 1 y 1 ‘ + q(t)c 1 y 1 + q(t)c 2 y 2 »
+ p(t)c 2 y 2 ‘ + q(t)c 2 y 2 = с 1 (у 1 »
+ p(t)y 1 ‘ + q(t)y 1 ) + c 2 (у 2 » +
p(t)y 2 ‘ + q(t)y 2 ) = c 1 L(y 1 )
+ c 2 L(y 2 ) = 0 + 0 = 0, Далее исследуем начальные условия. Если мы найдем генерала
решения однородной системы, можно ли выбрать такие константы, что
решение удовлетворяет начальным условиям? То есть можем ли мы найти c 1 и c 2 такие, что Если мы найдем генерала
решения однородной системы, можно ли выбрать такие константы, что
решение удовлетворяет начальным условиям? То есть можем ли мы найти c 1 и c 2 такие, что c 1 y 1 (t 0 )
+ c 2 y 2 (t 0 ) = y 0 c 1 y 1 ‘(t 0 )
+ c 2 y 2 ‘(t 0 ) = y 0 ‘ Мы можем поместить это в матричное уравнение Это имеет единственное решение тогда и только тогда, когда определитель матрицы равен
не ноль. Этот определитель называется числом 9.0581 Вронскиан . Это доказывает следующую теорему | Теорема Пусть л(г) =
0 y(t 0 )
= y 0 y'(t 0 )
= у’ 0 быть однородным
линейное дифференциальное уравнение второго порядка и пусть y 1 и y 2 — два общих решения
(Нет начального значения. Тогда если вронскиан Тогда если вронскиан у 1 у 2 ‘ — у 1 ‘ у 2 отлично от нуля, существует решение начального значения
задача формы y = c 1 y 1 + c 2 y 2 |
Пример Рассмотрим дифференциальное уравнение у» + 2у’ —
8 лет = 0 Легко проверить, что общее решение дается числом . г
= c 1 e 2t + c 2 e -4t Вронскиан из г 1 = e 2t y 2 = e -4t задается e 2t (-4e -4t )
— (2е 2т )e -4t = -4e -2t — 2e -2t = -6e -2t Который никогда не равен нулю. Мы можем заключить, что любая задача с начальными значениями
будет иметь единственное решение вида г
= c 1 e 2t + c 2 e -4t
Назад
на домашнюю страницу линейных дифференциальных уравнений второго порядка Назад
на главную страницу дифференциальных уравнений Назад к математике
Домашняя страница отдела электронная почта Вопросы и предложения Дифференциальные уравнения второго порядка Возраст от 16 до 18 лет Статья Майкла Грейлинга Опубликовано в 2014 г. Пересмотрено в 2019 г. по первой производной, но и по высшим. Естественно, дифференциальные уравнения более высокого порядка возникают в STEP и других экзаменах по высшей математике. Для чего-то большего, чем вторая производная, вопрос почти наверняка будет вести вас через какое-то конкретное
трюк, очень специфичный для рассматриваемой проблемы. Однако для дифференциальных уравнений второго порядка вам нужно знать, как их решать в целом. К счастью, применяемая техника проста, и эта статья проведет вас через все, что вам нужно знать, а также с полезным примером! 92} + b \frac{dy}{dt}+cy=0.\) Пересмотрено в 2019 г. по первой производной, но и по высшим. Естественно, дифференциальные уравнения более высокого порядка возникают в STEP и других экзаменах по высшей математике. Для чего-то большего, чем вторая производная, вопрос почти наверняка будет вести вас через какое-то конкретное
трюк, очень специфичный для рассматриваемой проблемы. Однако для дифференциальных уравнений второго порядка вам нужно знать, как их решать в целом. К счастью, применяемая техника проста, и эта статья проведет вас через все, что вам нужно знать, а также с полезным примером! 92} + b \frac{dy}{dt}+cy=0.\) Здесь \(a\), \(b\) и \(c\) — просто константы. В общем случае коэффициенты рядом с нашими производными могут быть непостоянными, но, к счастью, вам не нужно беспокоиться о том, как подходить к таким задачам, как эта, в целом для STEP. Теперь наш подход к решению уравнения вышеуказанного типа прост: мы угадываем решение. Конечно, это обоснованная догадка, за которой стоит много математических расчетов, но, по сути, она сводится к попытке найти решение в форме \(y=e^{\lambda t}\). Здесь \(\lambda\) просто неизвестная константа, и наша цель состоит в том, чтобы найти \(\lambda\), для которого решение этого типа
удовлетворяет дифференциальному уравнению. Теперь наше предположение подразумевает, что: 9{rt} (A \cos st+B \sin st ).\) Здесь \(\lambda\) просто неизвестная константа, и наша цель состоит в том, чтобы найти \(\lambda\), для которого решение этого типа
удовлетворяет дифференциальному уравнению. Теперь наше предположение подразумевает, что: 9{rt} (A \cos st+B \sin st ).\) Таким образом, эти три формулы, которые мы получили, — это все, что нам нужно запомнить! Для любого однородного дифференциального уравнения второго порядка с постоянными коэффициентами мы просто переходим к вспомогательному уравнению, находим наше (\lambda\), записываем подразумеваемое решение для \(y\), а затем используем начальные условия, чтобы помочь нам найти константы, если требуется.
Неоднородные дифференциальные уравнения второго порядка Одним из дополнений к вышеизложенному, которое мы должны решить, является случай, когда RHS в нашем DE не равен нулю, т.е. когда мы имеем: 92} + b \frac{dy_p}{dt}+cy_p=f(t).\) Может показаться, что мы бесконечно усложнили задачу, но на самом деле это не так. Теперь должно быть ясно, что \(y_c\) находится из однородного случая, который мы рассмотрели выше; так что все, что нам нужно, чтобы найти это наше вспомогательное уравнение. Для \(y_p\) мы снова используем угадывание решения, но наше точное предположение зависит от f. К счастью, есть лишь небольшой список стандартных предположений, которые вам нужно
запомнить: Теперь должно быть ясно, что \(y_c\) находится из однородного случая, который мы рассмотрели выше; так что все, что нам нужно, чтобы найти это наше вспомогательное уравнение. Для \(y_p\) мы снова используем угадывание решения, но наше точное предположение зависит от f. К счастью, есть лишь небольшой список стандартных предположений, которые вам нужно
запомнить: | \(f(t)\) 9259{n-1}+…+Z\) |
|---|
| \(\cos \alpha t\) или \(\sin \alpha t\) | \(P\cos\alpha t + Q\sin\alpha t\) |
Чтобы найти константы, присутствующие в \(y_p\) выше, нам просто нужно дважды продифференцировать и подставить в его дифференциальное уравнение. Наконец, вооружившись \(y_c\) и \(y_p\), мы получаем общее решение для \(y\) и можем использовать начальные условия для нахождения констант в \(y_c\), если нам это нужно. Пример Чтобы поместить все это в контекст, давайте сами проработаем особенно сложный случай. | 
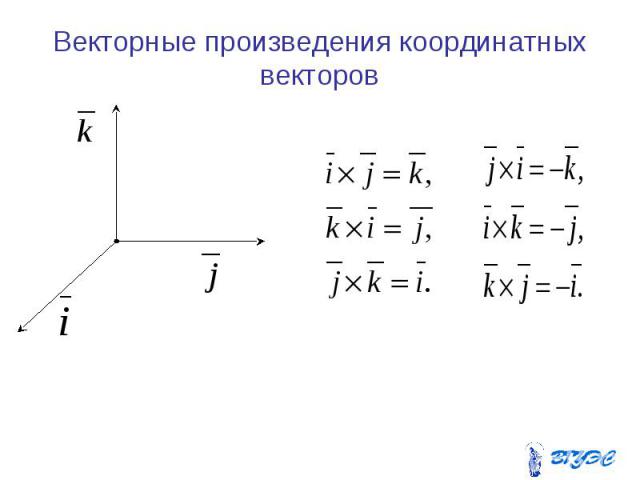 Найти векторное произведение векторов a = {1; 2; 3} и b = {2; 1; -2}.
Найти векторное произведение векторов a = {1; 2; 3} и b = {2; 1; -2}.
 5√2
5√2
 Элементы высшей алгебры
Элементы высшей алгебры  Обозначая их через x E ,y E , z E получим, что
Обозначая их через x E ,y E , z E получим, что
 Следовательно имеем матричное уравнение
Следовательно имеем матричное уравнение Из строки 3 вычитаем
первую строку, умноженную на 4. Из строки
4 вычитаем первую строку, получаем
матрицу:
Из строки 3 вычитаем
первую строку, умноженную на 4. Из строки
4 вычитаем первую строку, получаем
матрицу:
 Подставив в (4) координаты найденной
точки К и
угловой коэффициент
, получим
Подставив в (4) координаты найденной
точки К и
угловой коэффициент
, получим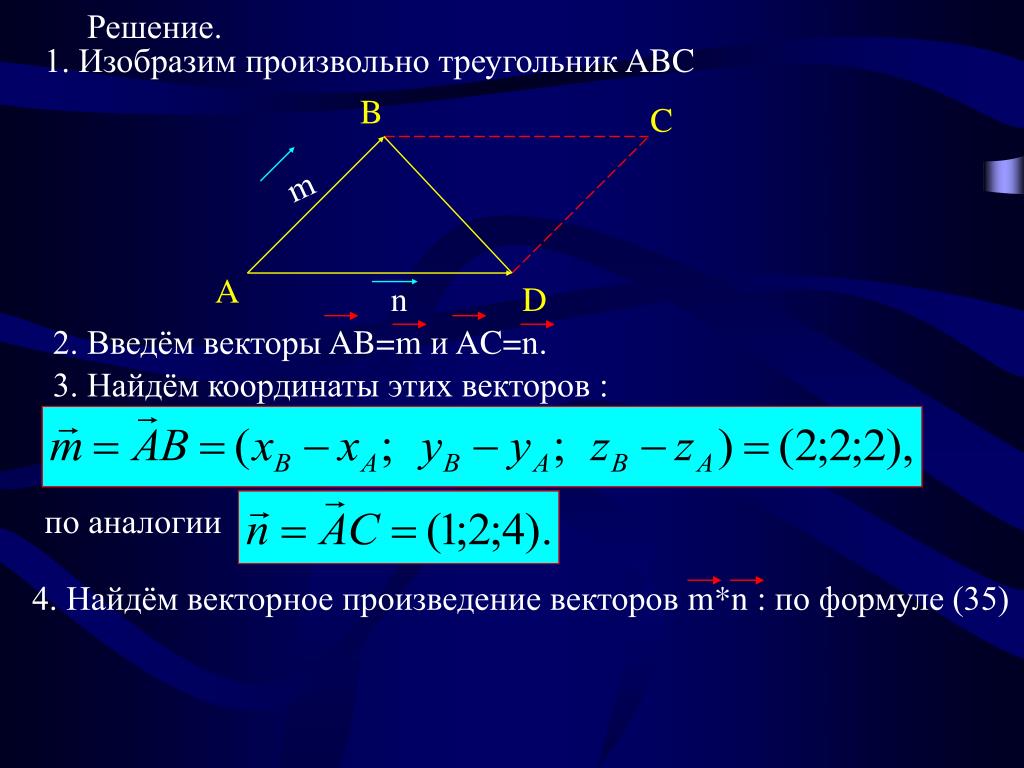

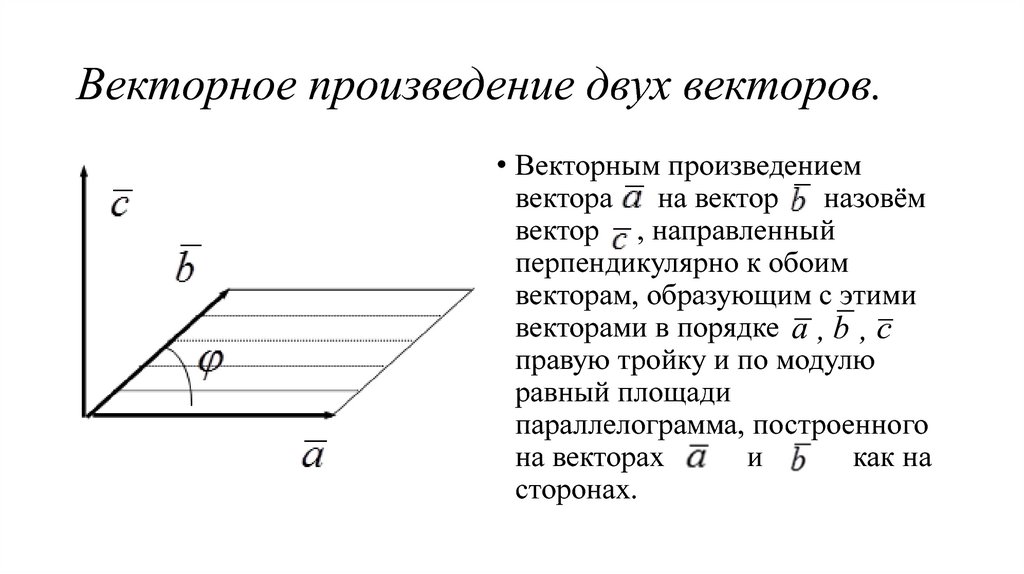 Это не так. В данном разделе высшей математики вообще мало дров, разве что на Буратино хватит. На самом деле материал очень распространенный и простой – вряд ли сложнее, чем то же скалярное произведение , даже типовых задач поменьше будет. Главное в аналитической геометрии, как многие убедятся или уже убедились, НЕ ОШИБАТЬСЯ В ВЫЧИСЛЕНИЯХ. Повторяйте как заклинание, и будет вам счастье =)
Это не так. В данном разделе высшей математики вообще мало дров, разве что на Буратино хватит. На самом деле материал очень распространенный и простой – вряд ли сложнее, чем то же скалярное произведение , даже типовых задач поменьше будет. Главное в аналитической геометрии, как многие убедятся или уже убедились, НЕ ОШИБАТЬСЯ В ВЫЧИСЛЕНИЯХ. Повторяйте как заклинание, и будет вам счастье =) Почему? Такими уж родились данные действия – векторное и смешанное произведение векторов определены и работают в трёхмерном пространстве. Уже проще!
Почему? Такими уж родились данные действия – векторное и смешанное произведение векторов определены и работают в трёхмерном пространстве. Уже проще!
 То есть, справедливо равенство .
То есть, справедливо равенство .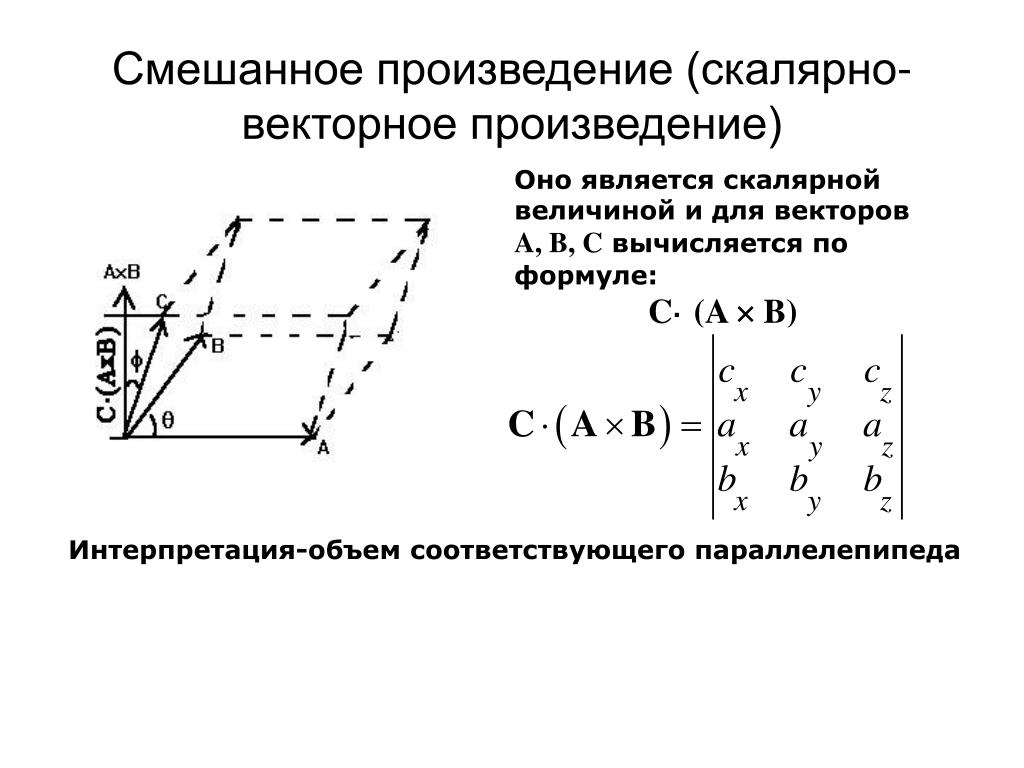 Следовательно, площадь треугольника, построенного на векторах (красная штриховка), можно найти по формуле:
Следовательно, площадь треугольника, построенного на векторах (красная штриховка), можно найти по формуле: Это тоже правоориентированный базис. Возможно, у вас возник вопрос: а какой базис имеет левую ориентацию? «Присвойте» тем же пальцам левой руки векторы , и полУчите левый базис и левую ориентацию пространства (в этом случае большой палец расположится по направлению нижнего вектора) . Образно говоря, данные базисы «закручивают» или ориентируют пространство в разные стороны. И это понятие не следует считать чем-то надуманным или абстрактным – так, например, ориентацию пространства меняет самое обычное зеркало, и если «вытащить отражённый объект из зазеркалья», то его в общем случае не удастся совместить с «оригиналом». Кстати, поднесите к зеркалу три пальца и проанализируйте отражение;-)
Это тоже правоориентированный базис. Возможно, у вас возник вопрос: а какой базис имеет левую ориентацию? «Присвойте» тем же пальцам левой руки векторы , и полУчите левый базис и левую ориентацию пространства (в этом случае большой палец расположится по направлению нижнего вектора) . Образно говоря, данные базисы «закручивают» или ориентируют пространство в разные стороны. И это понятие не следует считать чем-то надуманным или абстрактным – так, например, ориентацию пространства меняет самое обычное зеркало, и если «вытащить отражённый объект из зазеркалья», то его в общем случае не удастся совместить с «оригиналом». Кстати, поднесите к зеркалу три пальца и проанализируйте отражение;-) Если векторы коллинеарны, то их можно расположить на одной прямой и наш параллелограмм тоже «складывается» в одну прямую. Площадь такого, как говорят математики, вырожденного параллелограмма равна нулю. Это же следует и из формулы – синус нуля или 180-ти градусов равен нулю, а значит, и площадь нулевая
Если векторы коллинеарны, то их можно расположить на одной прямой и наш параллелограмм тоже «складывается» в одну прямую. Площадь такого, как говорят математики, вырожденного параллелограмма равна нулю. Это же следует и из формулы – синус нуля или 180-ти градусов равен нулю, а значит, и площадь нулевая Потому что оформление решений будет отличаться!
Потому что оформление решений будет отличаться! Этот момент всегда нужно держать на контроле, решая любую задачу по высшей математике, да и по другим предметам тоже.
Этот момент всегда нужно держать на контроле, решая любую задачу по высшей математике, да и по другим предметам тоже. Поэтому пусть будет.
Поэтому пусть будет. Загвоздка состоит в том, что векторы «цэ» и «дэ» сами представлены в виде сумм векторов. Алгоритм здесь стандартен и чем-то напоминает примеры № 3 и 4 урока Скалярное произведение векторов . Решение для ясности разобьём на три этапа:
Загвоздка состоит в том, что векторы «цэ» и «дэ» сами представлены в виде сумм векторов. Алгоритм здесь стандартен и чем-то напоминает примеры № 3 и 4 урока Скалярное произведение векторов . Решение для ясности разобьём на три этапа: Данное действие напоминает Пример 3:
Данное действие напоминает Пример 3:

 Мы дадим необходимые определения, запишем формулу для нахождения координат векторного произведения, перечислим и обоснуем его свойства. После этого остановимся на геометрическом смысле векторного произведения двух векторов и рассмотрим решения различных характерных примеров.
Мы дадим необходимые определения, запишем формулу для нахождения координат векторного произведения, перечислим и обоснуем его свойства. После этого остановимся на геометрическом смысле векторного произведения двух векторов и рассмотрим решения различных характерных примеров.
 Более того, эти два определения векторного произведения эквивалентны. Доказательство этого факта можете посмотреть в книге, указанной в конце статьи.
Более того, эти два определения векторного произведения эквивалентны. Доказательство этого факта можете посмотреть в книге, указанной в конце статьи.

 Найдем его
Найдем его

 2} = \sqrt{1878} ≈ 43, 34$.
2} = \sqrt{1878} ≈ 43, 34$. 2} = 5\sqrt{2}$.
2} = 5\sqrt{2}$.

 Итак,
Итак, 157), то модуль момента равняется произведению основания на высоту т. е. силе, умноженной на расстояние от точки О до прямой, вдоль которой действует сила.
157), то модуль момента равняется произведению основания на высоту т. е. силе, умноженной на расстояние от точки О до прямой, вдоль которой действует сила. j
;
j
;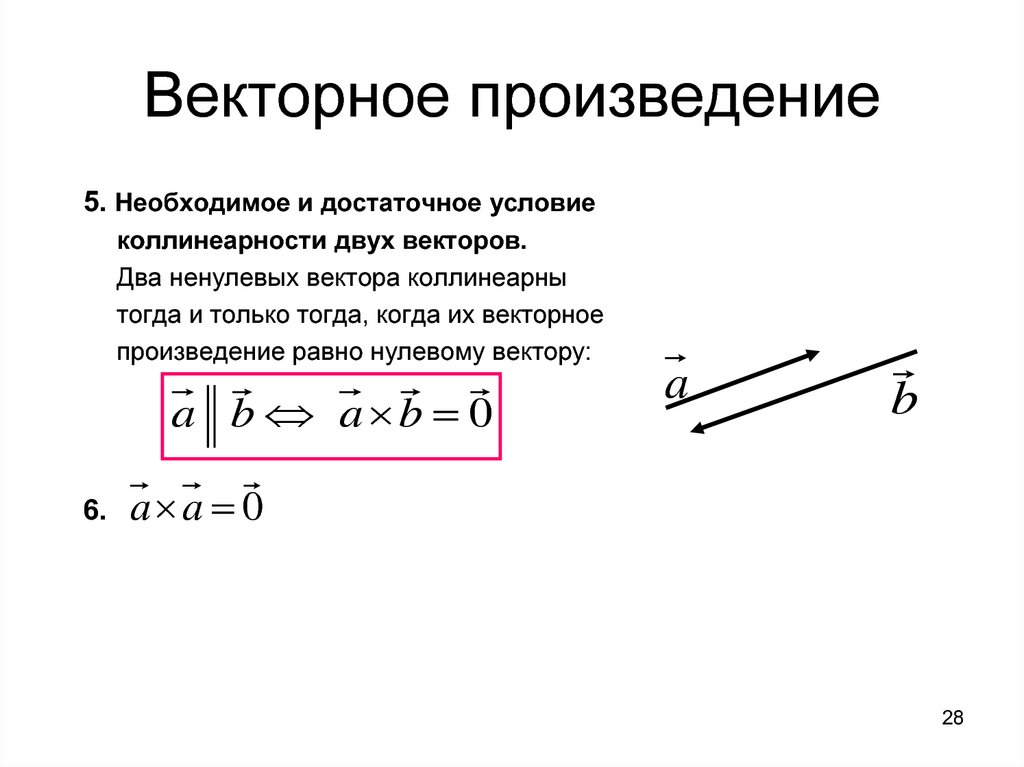 Аналогично доказывается при
l
Аналогично доказывается при
l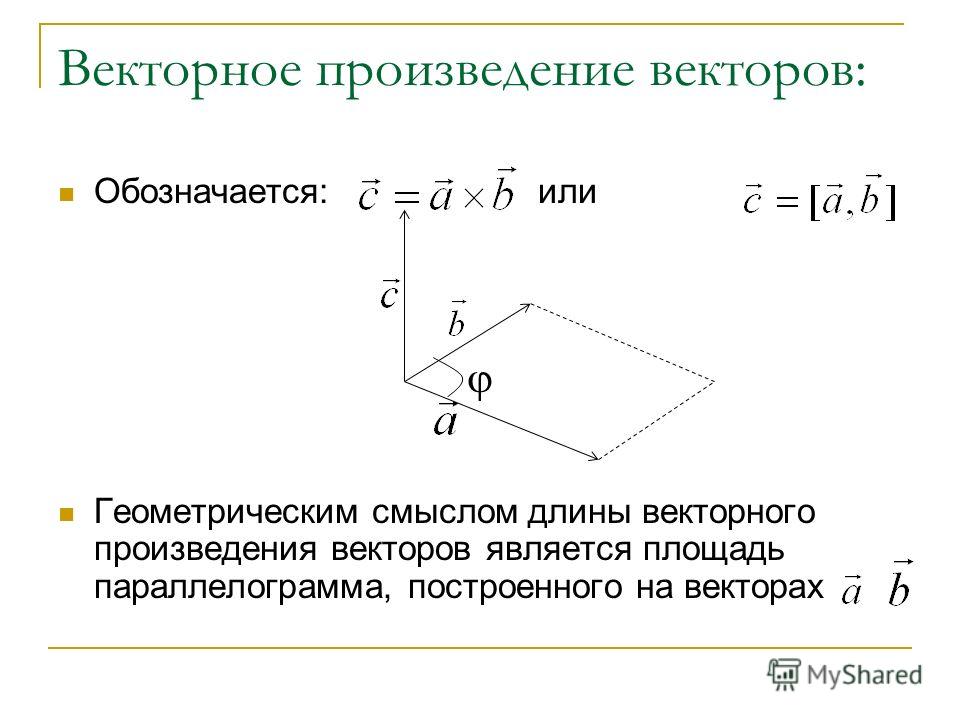 1) соответствует разложению
определителя третьего порядка по элементам первой строки.Равенство (7.2) легко
запоминается.
1) соответствует разложению
определителя третьего порядка по элементам первой строки.Равенство (7.2) легко
запоминается.
 Повторяйте как заклинание, и будет вам счастье =)
Повторяйте как заклинание, и будет вам счастье =)
 Случай коллинеарных векторов будет уместно рассмотреть чуть позже.
Случай коллинеарных векторов будет уместно рассмотреть чуть позже. Поэтому, исходя из вышесказанного, справедлива формула вычисления ДЛИНЫ векторного произведения:
Поэтому, исходя из вышесказанного, справедлива формула вычисления ДЛИНЫ векторного произведения: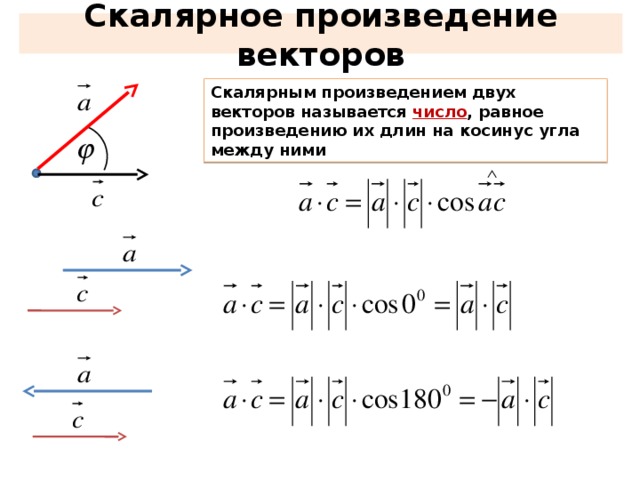 Объяснять буду на пальцах вашей правой руки . Мысленно совместите указательный палец с вектором и средний палец с вектором . Безымянный палец и мизинец прижмите к ладони. В результате большой палец – векторное произведение будет смотреть вверх. Это и есть правоориентированный базис (на рисунке именно он). Теперь поменяйте векторы (указательный и средний пальцы ) местами, в результате большой палец развернётся, и векторное произведение уже будет смотреть вниз. Это тоже правоориентированный базис. Возможно, у вас возник вопрос: а какой базис имеет левую ориентацию? «Присвойте» тем же пальцам левой руки векторы , и полУчите левый базис и левую ориентацию пространства (в этом случае большой палец расположится по направлению нижнего вектора) . Образно говоря, данные базисы «закручивают» или ориентируют пространство в разные стороны. И это понятие не следует считать чем-то надуманным или абстрактным – так, например, ориентацию пространства меняет самое обычное зеркало, и если «вытащить отражённый объект из зазеркалья», то его в общем случае не удастся совместить с «оригиналом».
Объяснять буду на пальцах вашей правой руки . Мысленно совместите указательный палец с вектором и средний палец с вектором . Безымянный палец и мизинец прижмите к ладони. В результате большой палец – векторное произведение будет смотреть вверх. Это и есть правоориентированный базис (на рисунке именно он). Теперь поменяйте векторы (указательный и средний пальцы ) местами, в результате большой палец развернётся, и векторное произведение уже будет смотреть вниз. Это тоже правоориентированный базис. Возможно, у вас возник вопрос: а какой базис имеет левую ориентацию? «Присвойте» тем же пальцам левой руки векторы , и полУчите левый базис и левую ориентацию пространства (в этом случае большой палец расположится по направлению нижнего вектора) . Образно говоря, данные базисы «закручивают» или ориентируют пространство в разные стороны. И это понятие не следует считать чем-то надуманным или абстрактным – так, например, ориентацию пространства меняет самое обычное зеркало, и если «вытащить отражённый объект из зазеркалья», то его в общем случае не удастся совместить с «оригиналом». Кстати, поднесите к зеркалу три пальца и проанализируйте отражение;-)
Кстати, поднесите к зеркалу три пальца и проанализируйте отражение;-)



 О длинах пока ни слова!
О длинах пока ни слова! Посмотрим, насколько вы были внимательны при изучении предыдущих примеров;-)
Посмотрим, насколько вы были внимательны при изучении предыдущих примеров;-)
 В учебной литературе оформление может быть несколько другим, я привык обозначать смешанное произведение через , а результат вычислений буквой «пэ».
В учебной литературе оформление может быть несколько другим, я привык обозначать смешанное произведение через , а результат вычислений буквой «пэ». После этого остановимся на геометрическом смысле векторного произведения двух векторов и рассмотрим решения различных характерных примеров.
После этого остановимся на геометрическом смысле векторного произведения двух векторов и рассмотрим решения различных характерных примеров.
 Более того, эти два определения векторного произведения эквивалентны. Доказательство этого факта можете посмотреть в книге, указанной в конце статьи.
Более того, эти два определения векторного произведения эквивалентны. Доказательство этого факта можете посмотреть в книге, указанной в конце статьи.

 Найдем его
Найдем его
 Это следует из правила, по которому выполняется операция умножения скаляра на вектор .
Это следует из правила, по которому выполняется операция умножения скаляра на вектор . Тем не менее, изменять традиции мы не станем и в дальнейшем будем считать, что декартова и прямоугольная (ортогональная) системы координат — это одно и то же.
Тем не менее, изменять традиции мы не станем и в дальнейшем будем считать, что декартова и прямоугольная (ортогональная) системы координат — это одно и то же. Так вот, если сама система координат неподвижна, а изменение координат движущегося объекта отслеживается в этой неподвижной системе, то обычно оси обозначают X, Y, Z, а их орты соответственно i , j , k .
Так вот, если сама система координат неподвижна, а изменение координат движущегося объекта отслеживается в этой неподвижной системе, то обычно оси обозначают X, Y, Z, а их орты соответственно i , j , k . Орт этой оси обозначают уже не j , а n . Третья ось (бывшая Z) перпендикулярна двум предыдущим. Это — бинормаль с ортом b (рис. 12, справа). Кстати, в этом случае такую прямоугольную систему координат часто называют «естественной» или натуральной.
Орт этой оси обозначают уже не j , а n . Третья ось (бывшая Z) перпендикулярна двум предыдущим. Это — бинормаль с ортом b (рис. 12, справа). Кстати, в этом случае такую прямоугольную систему координат часто называют «естественной» или натуральной. 1).
1).
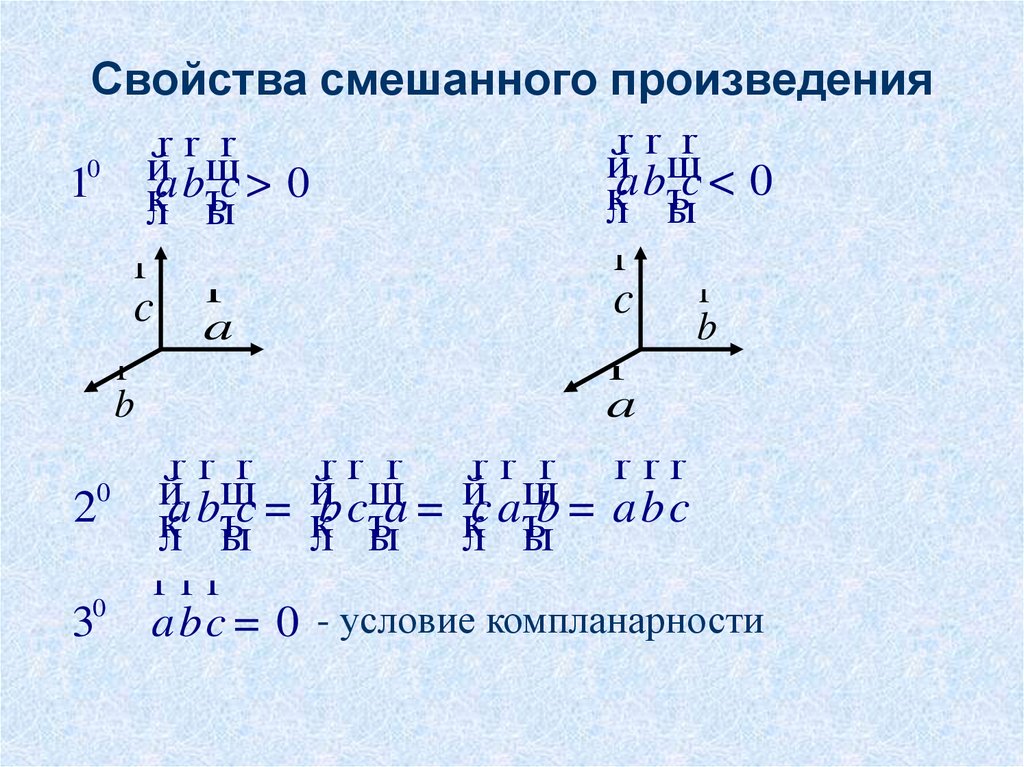 Найти векторное произведение векторов a = {1; 2; 3} и b = {2; 1; -2}.
Найти векторное произведение векторов a = {1; 2; 3} и b = {2; 1; -2}. 5√2.
5√2. 1).
1).


 к. определитель матрицы равен нулю,
то векторы линейно зависимы, следовательно
они компланарны.
к. определитель матрицы равен нулю,
то векторы линейно зависимы, следовательно
они компланарны. Я надеюсь изучить его немного лучше, чтобы не забыть, как вычислять якобиан при работе с поверхностными интегралами, где теорема о дивергенции неприменима.
Я надеюсь изучить его немного лучше, чтобы не забыть, как вычислять якобиан при работе с поверхностными интегралами, где теорема о дивергенции неприменима. 2} = |a_1b_2|$, очевидно. Но у параллелограмма есть основание $|a_1|$ и высота $|b_2|$, а это значит, что площадь параллелограмма задается точно таким же выражением.
2} = |a_1b_2|$, очевидно. Но у параллелограмма есть основание $|a_1|$ и высота $|b_2|$, а это значит, что площадь параллелограмма задается точно таким же выражением. Используя простую тригонометрию, пусть высотой параллелограмма будет буква X
Используя простую тригонометрию, пусть высотой параллелограмма будет буква X Остается заметить, что $\times_1, \times_2$ совпадают на базисных векторах $\bf{i}, \bf{j}, \bf{k}$, а значит, как и ожидалось, $\times_1 = \times_2$ .
Остается заметить, что $\times_1, \times_2$ совпадают на базисных векторах $\bf{i}, \bf{j}, \bf{k}$, а значит, как и ожидалось, $\times_1 = \times_2$ .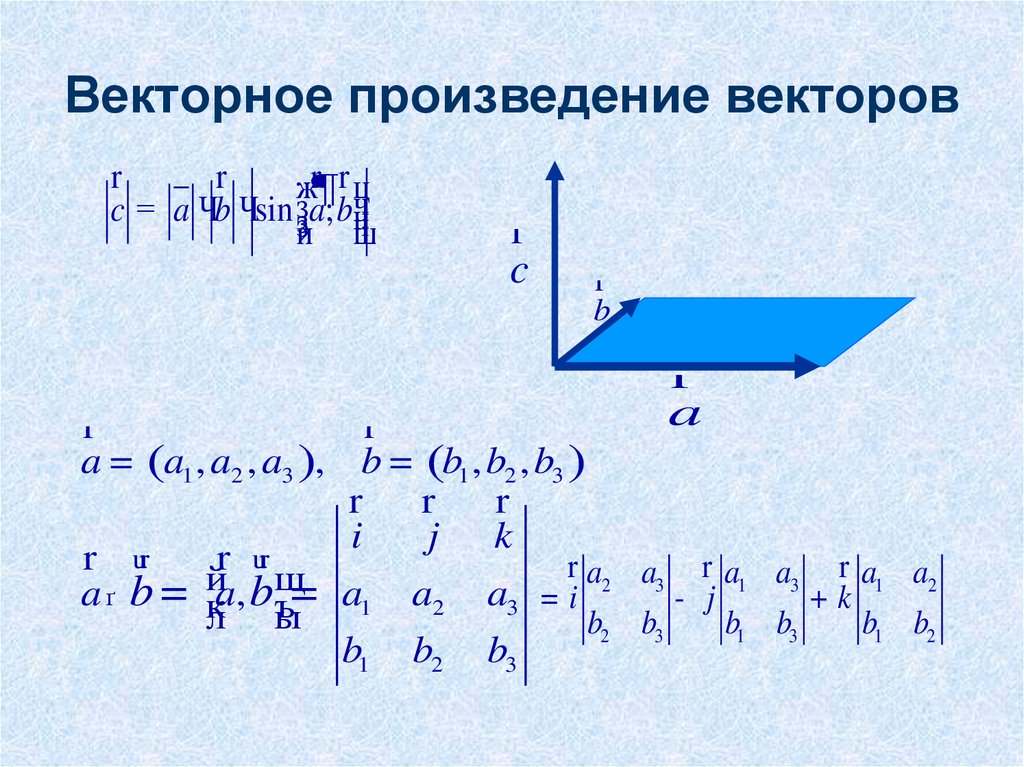


 е. замена $(x_2,y_2)$ на $(x_2+cx_1,y_2+cy_1)$ не меняет ни площадь, ни векторное произведение (дополнительные члены отменить)
е. замена $(x_2,y_2)$ на $(x_2+cx_1,y_2+cy_1)$ не меняет ни площадь, ни векторное произведение (дополнительные члены отменить)
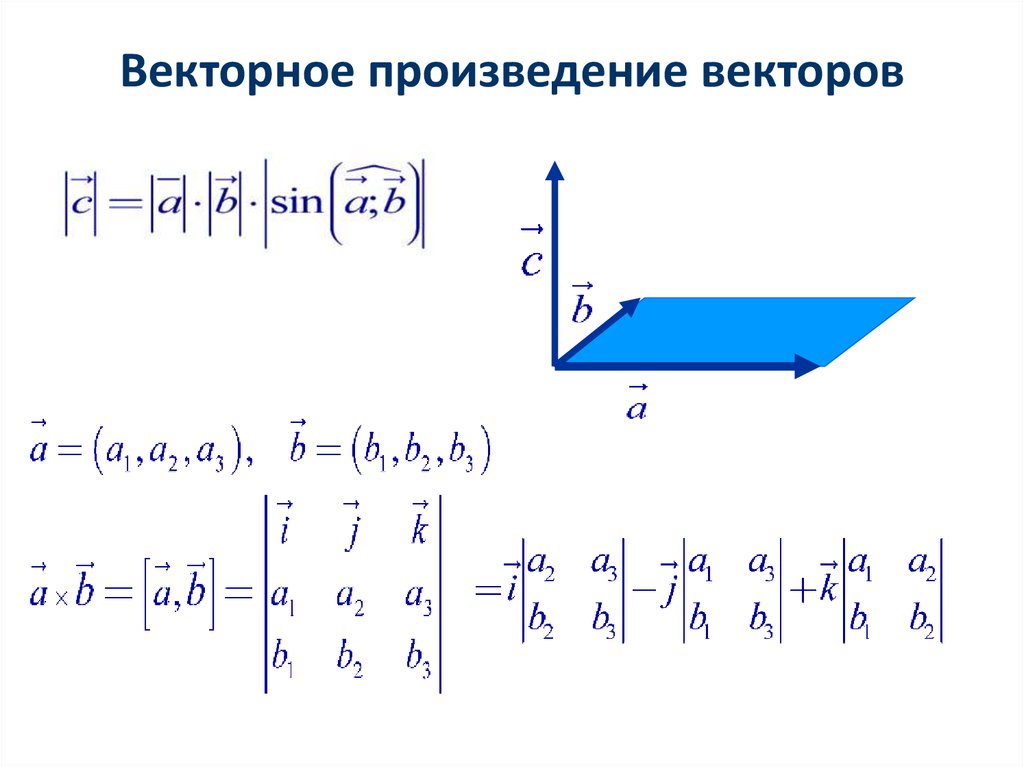

3: Если q угол, образованный u и v , то
 Действительно, имеем следующее:
Действительно, имеем следующее:Таким образом, их векторное произведение равно
 Перекрестное произведение обозначается знаком умножения (x) между двумя векторами. Это бинарная векторная операция, определенная в трехмерной системе. Перекрестное произведение двух векторов — это третий вектор, перпендикулярный двум исходным векторам. Его величина определяется площадью параллелограмма между ними, а его направление можно определить по правилу большого пальца правой руки. Перекрестное произведение двух векторов также известно как векторное произведение, поскольку результирующая перекрестного произведения векторов является векторной величиной. Здесь мы узнаем больше о векторном произведении двух векторов.
Перекрестное произведение обозначается знаком умножения (x) между двумя векторами. Это бинарная векторная операция, определенная в трехмерной системе. Перекрестное произведение двух векторов — это третий вектор, перпендикулярный двум исходным векторам. Его величина определяется площадью параллелограмма между ними, а его направление можно определить по правилу большого пальца правой руки. Перекрестное произведение двух векторов также известно как векторное произведение, поскольку результирующая перекрестного произведения векторов является векторной величиной. Здесь мы узнаем больше о векторном произведении двух векторов.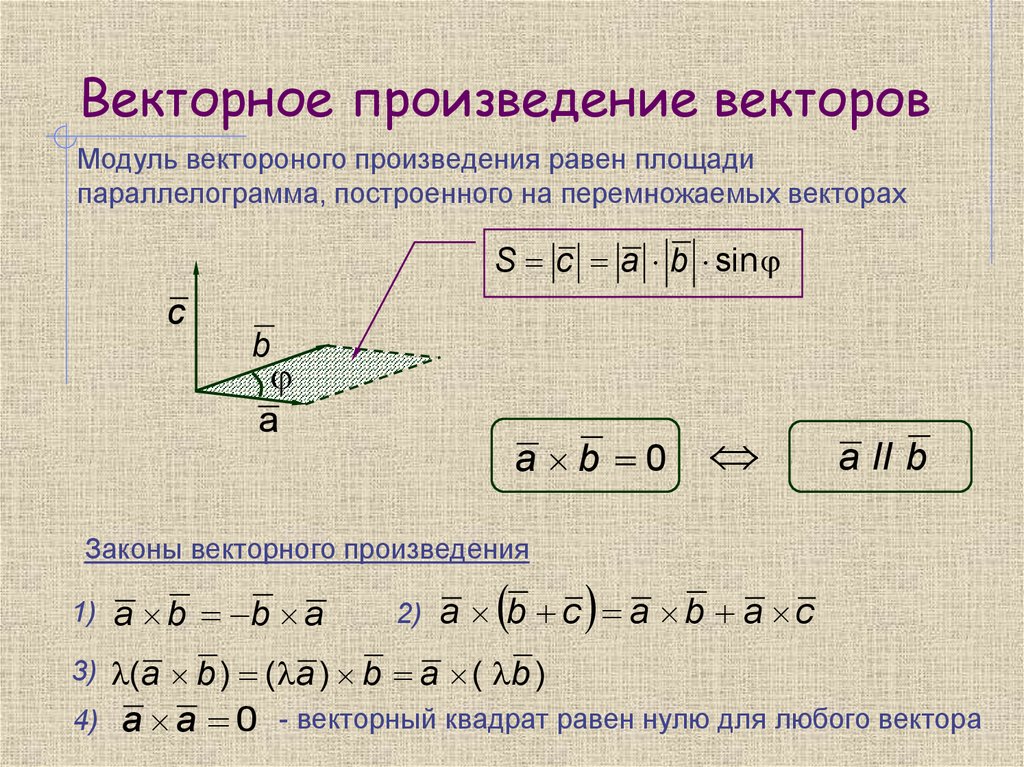
 Он представлен:
Он представлен: 
 Перекрестное произведение двух векторов определяется формулой:
Перекрестное произведение двух векторов определяется формулой:

 Результатом тройного перекрестного произведения является вектор. Равнодействующий вектора тройного пересечения лежит в плоскости данных трех векторов. Если a, b и c — векторы, то векторное тройное произведение этих векторов будет иметь вид:
Результатом тройного перекрестного произведения является вектор. Равнодействующий вектора тройного пересечения лежит в плоскости данных трех векторов. Если a, b и c — векторы, то векторное тройное произведение этих векторов будет иметь вид:



 Величина результирующего вектора является произведением греха угла между векторами и величиной двух векторов. а × б = | а | |б| грех θ.
Величина результирующего вектора является произведением греха угла между векторами и величиной двух векторов. а × б = | а | |б| грех θ. \overrightarrow{b} = |a| |b| \cos(\theta)\)
\overrightarrow{b} = |a| |b| \cos(\theta)\) Скалярное произведение — это произведение величины векторов и cos угла между ними. а . б = |а| |б| cosθ. Векторное произведение — это произведение величины векторов на синус угла между ними. а × б = | а | |б| грех θ.
Скалярное произведение — это произведение величины векторов и cos угла между ними. а . б = |а| |б| cosθ. Векторное произведение — это произведение величины векторов на синус угла между ними. а × б = | а | |б| грех θ. Например, \(\overrightarrow{a}\)= \(a_1\hat i+a_2 \hat j+a_3 \hat k\) и \(\overrightarrow{b}\) = \(b_1 \hat i+b_2 \hat j+b_3 \hat k\), то мы можем записать результат как \(\overrightarrow{a} \times \overrightarrow{b} = \hat i (a_2b_3-a_3b_2) \\- \hat j (a_1b_3- a_3b_1)\\+ \шляпа k (a_1b_2-a_2b_1)\)
Например, \(\overrightarrow{a}\)= \(a_1\hat i+a_2 \hat j+a_3 \hat k\) и \(\overrightarrow{b}\) = \(b_1 \hat i+b_2 \hat j+b_3 \hat k\), то мы можем записать результат как \(\overrightarrow{a} \times \overrightarrow{b} = \hat i (a_2b_3-a_3b_2) \\- \hat j (a_1b_3- a_3b_1)\\+ \шляпа k (a_1b_2-a_2b_1)\) Если мы направим правую руку в направлении первой стрелки, а пальцы согнем в направлении второй, то наш большой палец окажется в направлении векторного произведения двух векторов. Правило большого пальца правой руки дает формулу векторного произведения для нахождения направления результирующего вектора.
Если мы направим правую руку в направлении первой стрелки, а пальцы согнем в направлении второй, то наш большой палец окажется в направлении векторного произведения двух векторов. Правило большого пальца правой руки дает формулу векторного произведения для нахождения направления результирующего вектора. Это простой расчет с 3 компонентами.
Это простой расчет с 3 компонентами. Или что Север и Северо-Восток похожи на 70% ($\cos(45) = 0,707$, помните, что триггерные функции представляют собой проценты.) Сходство показывает количество одного вектора, которое «проявляется» в другом.
Или что Север и Северо-Восток похожи на 70% ($\cos(45) = 0,707$, помните, что триггерные функции представляют собой проценты.) Сходство показывает количество одного вектора, которое «проявляется» в другом. Само по себе это не отличает $\vec{x} \times \vec{y}$ от $\vec{x} \times \vec{z}$.
Само по себе это не отличает $\vec{x} \times \vec{y}$ от $\vec{x} \times \vec{z}$. Я проверяю правильность ориентации, проводя пальцем от $\vec{a}$ до $\vec{b}$. Когда направление выяснено, величина векторного произведения равна $|a| |б| \sin(\theta)$, который пропорционален величине каждого вектора и «проценту разницы» (синусу).
Я проверяю правильность ориентации, проводя пальцем от $\vec{a}$ до $\vec{b}$. Когда направление выяснено, величина векторного произведения равна $|a| |б| \sin(\theta)$, который пропорционален величине каждого вектора и «проценту разницы» (синусу). Я использовал единичные векторы, но мы могли масштабировать термины:
Я использовал единичные векторы, но мы могли масштабировать термины:
 Это (1)(5) минус (4)(2), или 5 – 8 = -3. Сначала я сделал
Это (1)(5) минус (4)(2), или 5 – 8 = -3. Сначала я сделал 

 Быть «двойным перпендикуляром» означает, что вы вернулись на исходную ось.
Быть «двойным перпендикуляром» означает, что вы вернулись на исходную ось. В результате получается левосторонняя система. (Попробуйте: используя правую руку, вы можете увидеть
В результате получается левосторонняя система. (Попробуйте: используя правую руку, вы можете увидеть  Площадь прямоугольника – это площадь формы и периметра прямоугольника. Вычисление площади в 3 простых шага — это простая процедура, как кусок пирога. Студенты обычно считают, что их очень сложно понять, но это несложно, поскольку с этим вы видите, что вычисление площади и векторного произведения двух векторов можно выполнить всего за три простых шага. Для вычисления площади, с точки зрения формы, прямоугольник считается самым простым.
Площадь прямоугольника – это площадь формы и периметра прямоугольника. Вычисление площади в 3 простых шага — это простая процедура, как кусок пирога. Студенты обычно считают, что их очень сложно понять, но это несложно, поскольку с этим вы видите, что вычисление площади и векторного произведения двух векторов можно выполнить всего за три простых шага. Для вычисления площади, с точки зрения формы, прямоугольник считается самым простым. Используется правило правой руки для получения соответствующей ориентации перекрестного произведения. Направьте указательный палец (правой руки) в направлении первого вектора. Затем выровняйте руку по второму вектору так, чтобы ваш средний палец указывал на него. Разверните большой палец. Направление вашего большого пальца указывает направление перекрестного произведения.
Используется правило правой руки для получения соответствующей ориентации перекрестного произведения. Направьте указательный палец (правой руки) в направлении первого вектора. Затем выровняйте руку по второму вектору так, чтобы ваш средний палец указывал на него. Разверните большой палец. Направление вашего большого пальца указывает направление перекрестного произведения. Таким образом, двухмерный многоугольник представляет собой прямоугольник с четырьмя гранями, четырьмя вершинами и четырьмя прямыми углами. В прямоугольнике две противоположные стороны параллельны. Прямоугольная область – это пространство в форме. Площадь прямоугольника также является периметром прямоугольника. Это отличает площадь прямоугольника от интегрирования, в котором мы вычисляем площадь под кривой.
Таким образом, двухмерный многоугольник представляет собой прямоугольник с четырьмя гранями, четырьмя вершинами и четырьмя прямыми углами. В прямоугольнике две противоположные стороны параллельны. Прямоугольная область – это пространство в форме. Площадь прямоугольника также является периметром прямоугольника. Это отличает площадь прямоугольника от интегрирования, в котором мы вычисляем площадь под кривой. Как известно, площадь прямоугольника равна произведению его ширины на длину. Таким образом, вы наверняка сможете вычислить площадь прямоугольника за три простых шага.
Как известно, площадь прямоугольника равна произведению его ширины на длину. Таким образом, вы наверняка сможете вычислить площадь прямоугольника за три простых шага.

 Требуется найти:
Требуется найти: 3) Объем параллелепипеда, построенного на векторах , и. Контрольная работа по теме «Элементы теории линейных пространств…
3) Объем параллелепипеда, построенного на векторах , и. Контрольная работа по теме «Элементы теории линейных пространств…
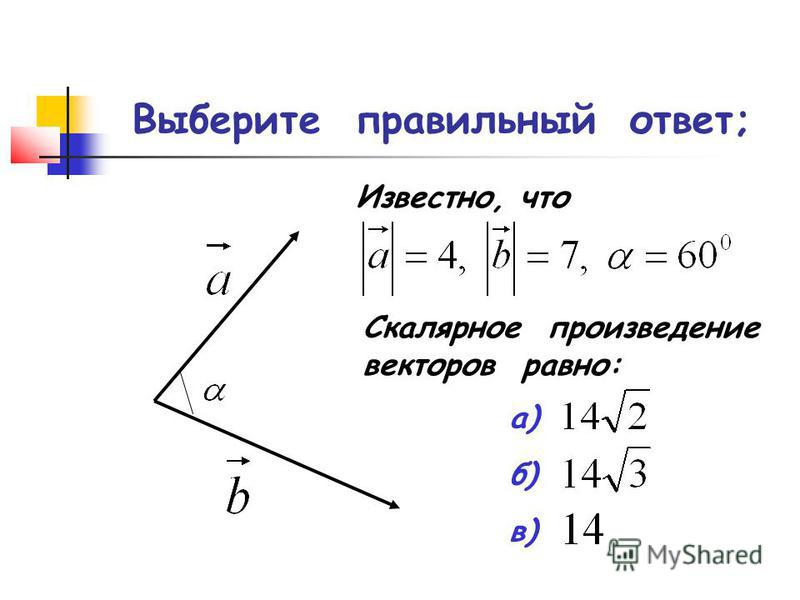

 е. замена $(x_2,y_2)$ на $(x_2+cx_1,y_2+cy_1)$ не меняет ни площадь, ни векторное произведение (дополнительные члены отменить)
е. замена $(x_2,y_2)$ на $(x_2+cx_1,y_2+cy_1)$ не меняет ни площадь, ни векторное произведение (дополнительные члены отменить) 3: Если q угол, образованный u и v , то
3: Если q угол, образованный u и v , то
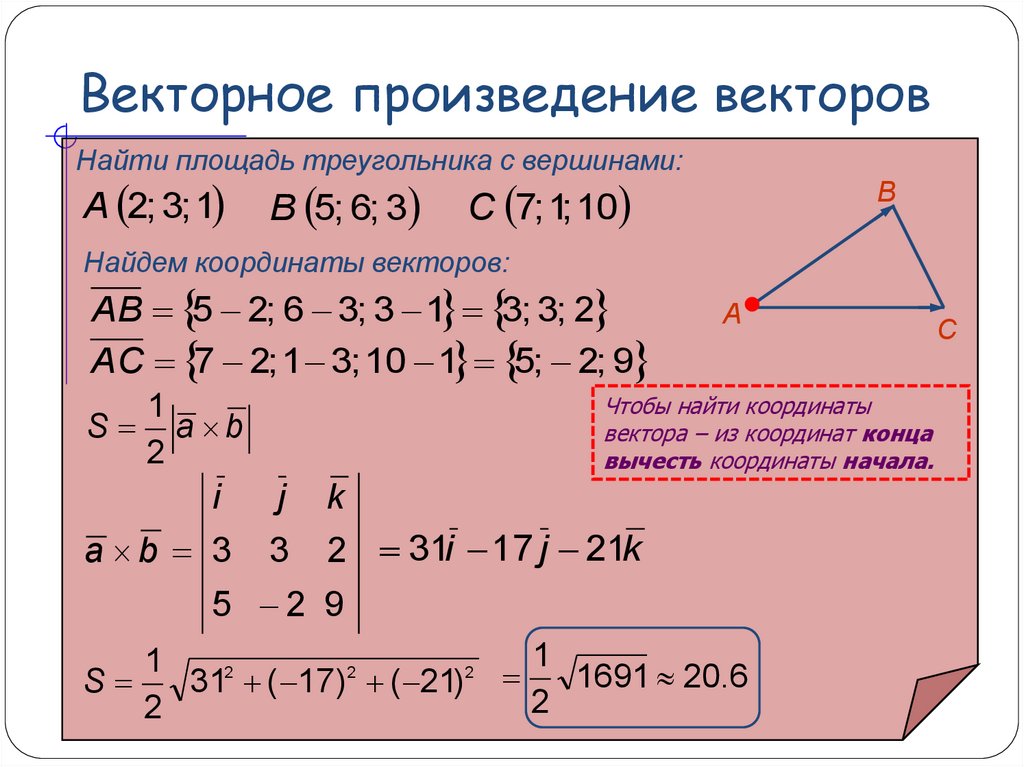 Таким образом, их векторное произведение равно
Таким образом, их векторное произведение равно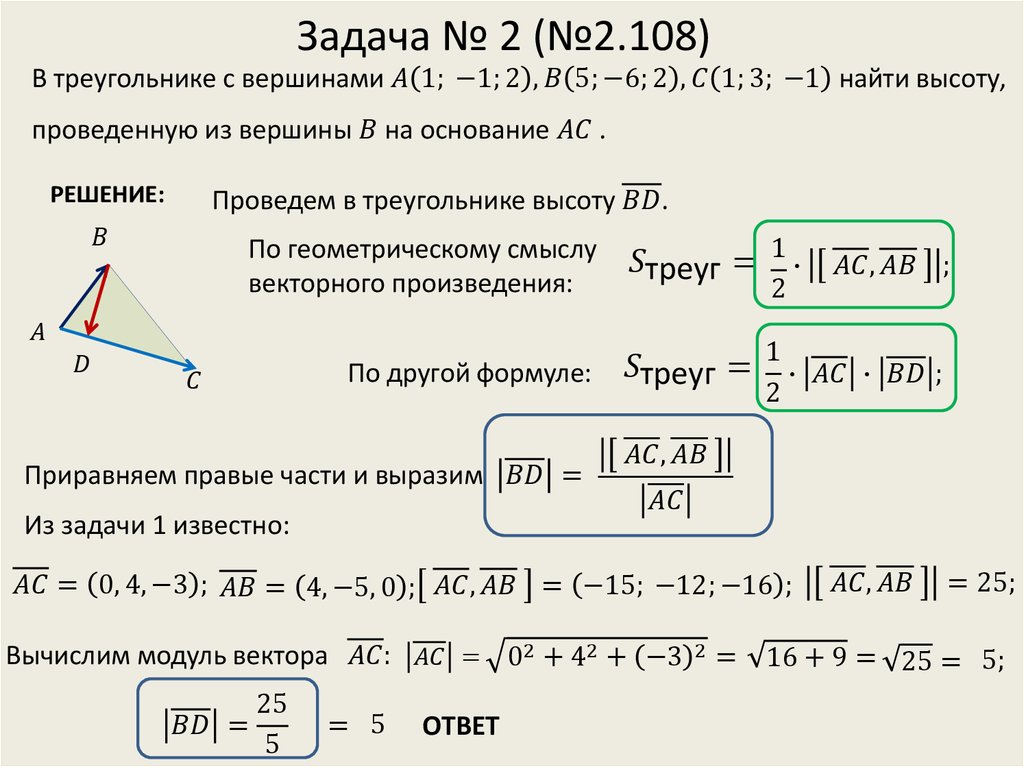



 Дети наиболее восприимчивы, а потому развитие инфекции у них происходит в ускоренном темпе. Сначала отмечается легкое недомогание и озноб, затем возникает сильная боль в горле, повышение температуры и тошнота.
Дети наиболее восприимчивы, а потому развитие инфекции у них происходит в ускоренном темпе. Сначала отмечается легкое недомогание и озноб, затем возникает сильная боль в горле, повышение температуры и тошнота. Чем сильнее гнойные процессы, тем хуже состояние малыша, так как симптоматика дополняется признаками интоксикации организма.
Чем сильнее гнойные процессы, тем хуже состояние малыша, так как симптоматика дополняется признаками интоксикации организма. Однако такие осложнения возникают, когда больной пренебрегает рекомендациями врача и занимается самолечением.
Однако такие осложнения возникают, когда больной пренебрегает рекомендациями врача и занимается самолечением.
 Но чтобы избавиться от нее без последствий, антибактериальная терапия должна дополняться другими лекарственными средствами.
Но чтобы избавиться от нее без последствий, антибактериальная терапия должна дополняться другими лекарственными средствами. При заложенности носа применяются сосудосуживающие средства. А чтобы избежать возникновение аллергической реакции на применяемые препараты, назначаются антигистаминные средства.
При заложенности носа применяются сосудосуживающие средства. А чтобы избежать возникновение аллергической реакции на применяемые препараты, назначаются антигистаминные средства.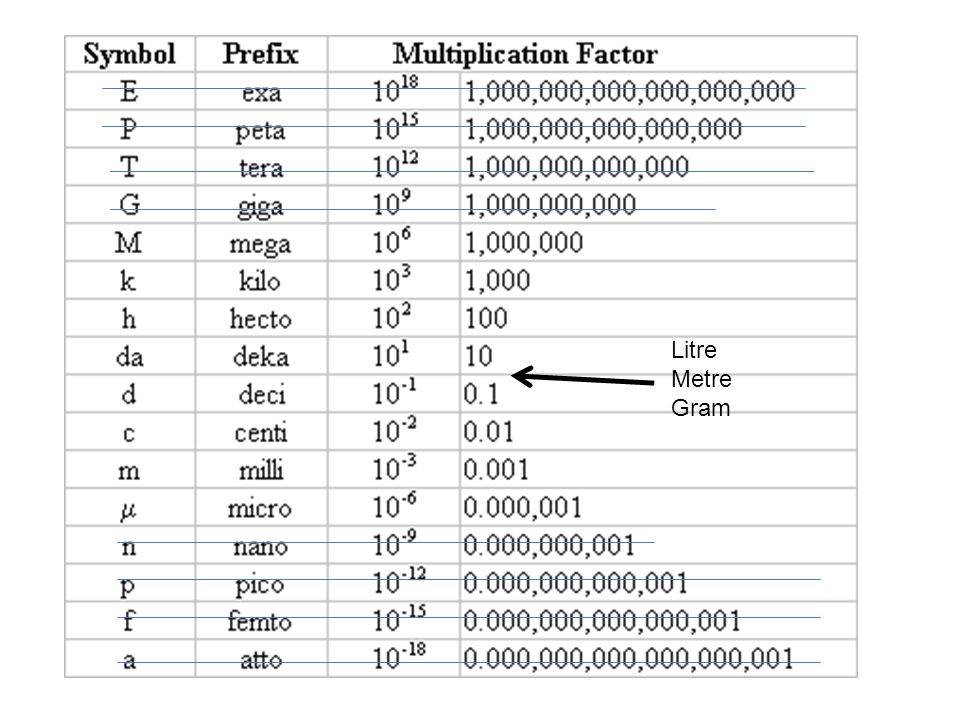 Возьмите ингредиенты в количестве 1 ч. л., измельчите и залейте стаканом крутого кипятка. Оставьте настаиваться на 30 минут, после чего выпийте. Принимайте такой напиток не менее 2 раз в день.
Возьмите ингредиенты в количестве 1 ч. л., измельчите и залейте стаканом крутого кипятка. Оставьте настаиваться на 30 минут, после чего выпийте. Принимайте такой напиток не менее 2 раз в день. Стрептококки опасны тем, что легко проникают в кровь, достигая головного мозга, легких и сердца. А потому медлительность может стоить жизни маленького пациента.
Стрептококки опасны тем, что легко проникают в кровь, достигая головного мозга, легких и сердца. А потому медлительность может стоить жизни маленького пациента. Вернулись отек, дискомфорт и появились выделения ярко желтого цвета. Сдала анализы (прикрепляю свои и мужа) сегодня их получила и очень расстроилась(, лечение было такое сильное антибиотиков в прошлый раз, Цефтриаксон внутривенно, и прочее. И все вернулось и в большей степени. Во время ожидания анализов мне назначили Полижинакс 6 дней (от него был ужасный зуд и отек, кларитин мне в помощь) перестала делать, все прошло. Помимо этого орошать Эпиген спреем, метилурациловая мазь чередовать с Орнионой. Доктор в отпуске, на сообщение с анализами пока ничего мне ответила: (я расстроена, не понимаю по какой причине возвращается это вновь? Надеюсь доктор мне ответит, и мы с вами обсудим назначения?
Вернулись отек, дискомфорт и появились выделения ярко желтого цвета. Сдала анализы (прикрепляю свои и мужа) сегодня их получила и очень расстроилась(, лечение было такое сильное антибиотиков в прошлый раз, Цефтриаксон внутривенно, и прочее. И все вернулось и в большей степени. Во время ожидания анализов мне назначили Полижинакс 6 дней (от него был ужасный зуд и отек, кларитин мне в помощь) перестала делать, все прошло. Помимо этого орошать Эпиген спреем, метилурациловая мазь чередовать с Орнионой. Доктор в отпуске, на сообщение с анализами пока ничего мне ответила: (я расстроена, не понимаю по какой причине возвращается это вновь? Надеюсь доктор мне ответит, и мы с вами обсудим назначения?
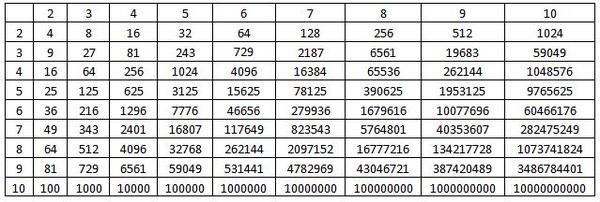
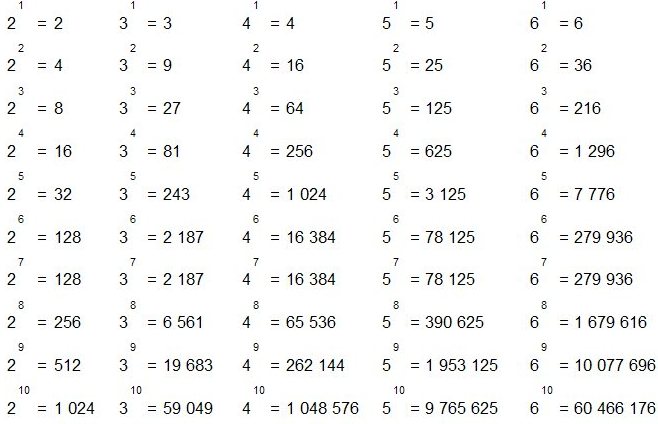 Иными словами, Атман есть «То, посредством чего проявлено все, но который сам в себе не проявлен ни в чем»;[49] и вот этого никогда не следует терять из виду во всем последующем. Напомним еще, что Атман и Пуруша суть один и тот же принцип и что это от Пракрити, а не от Пуруши проистекает всякая манифестация; но если Санкхья рассматривает эту манифестацию преимущественно как развитие или «актуализацию» потенциальных возможностей Пракрити, ибо ее точка зрения, ее «оптика» является прежде всего «космологической», а не собственно метафизической, то Веданта должна видеть здесь иное, потому что она рассматривает Атмана, который пребывает вне изменения и «становления», как истинный принцип, с которым, в конечном счете, должно быть соотносимо все. Мы могли бы сказать, что в данном случае есть две точки зрения, «субстанции» и «эссенции», и что именно первая является «космологической», ибо она есть точка зрения Природы и «становления»; но, с другой стороны, метафизика не ограничивается «эссенцией», понимаемой как коррелят «субстанции»; ни даже Сущим, в котором соединяются эти два термина.
Иными словами, Атман есть «То, посредством чего проявлено все, но который сам в себе не проявлен ни в чем»;[49] и вот этого никогда не следует терять из виду во всем последующем. Напомним еще, что Атман и Пуруша суть один и тот же принцип и что это от Пракрити, а не от Пуруши проистекает всякая манифестация; но если Санкхья рассматривает эту манифестацию преимущественно как развитие или «актуализацию» потенциальных возможностей Пракрити, ибо ее точка зрения, ее «оптика» является прежде всего «космологической», а не собственно метафизической, то Веданта должна видеть здесь иное, потому что она рассматривает Атмана, который пребывает вне изменения и «становления», как истинный принцип, с которым, в конечном счете, должно быть соотносимо все. Мы могли бы сказать, что в данном случае есть две точки зрения, «субстанции» и «эссенции», и что именно первая является «космологической», ибо она есть точка зрения Природы и «становления»; но, с другой стороны, метафизика не ограничивается «эссенцией», понимаемой как коррелят «субстанции»; ни даже Сущим, в котором соединяются эти два термина. Она идет гораздо дальше, потому что она простирается также до Параматмана, или Пурушоттамы, который есть Высший Брахман (Брахма) и потому что, таким образом, его точка зрения (в той мере, в какой это выражение еще применимо здесь), поистине безгранична.
Она идет гораздо дальше, потому что она простирается также до Параматмана, или Пурушоттамы, который есть Высший Брахман (Брахма) и потому что, таким образом, его точка зрения (в той мере, в какой это выражение еще применимо здесь), поистине безгранична.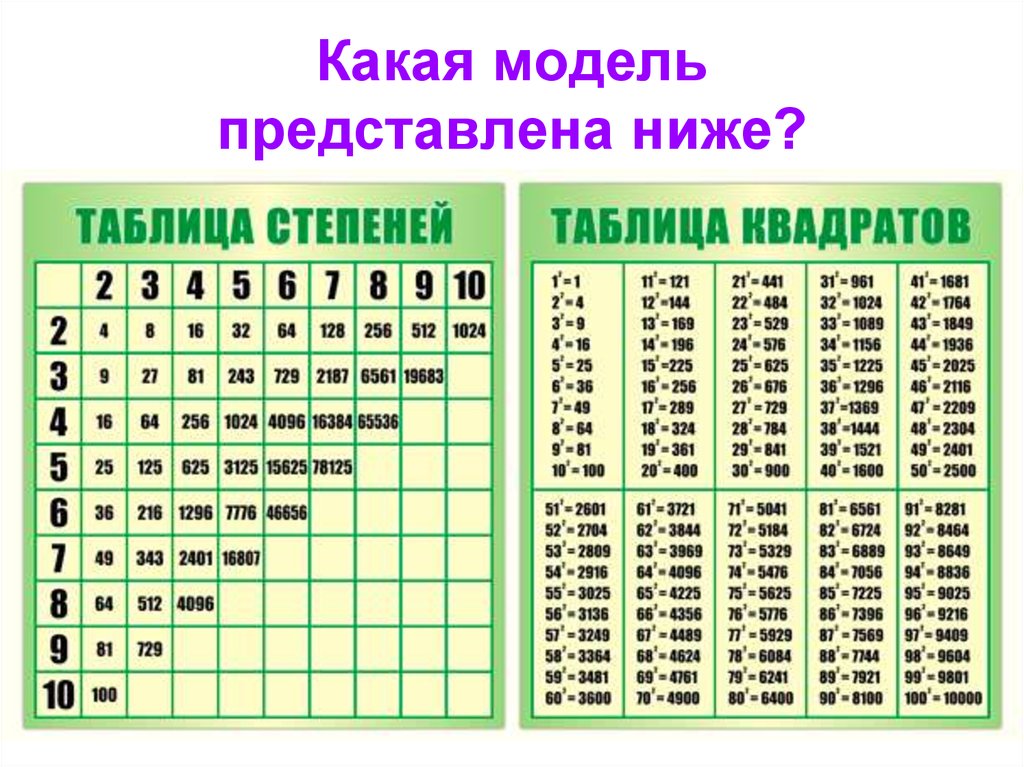 И, таким образом, все предстает как бы взаимосвязанным во многих смыслах — будь то в самой манифестации либо же в той мере, в какой последняя, образуя в своей бесконечной множественности единое целое, связуется со своим принципом, т. е. с Сущим и, через него, с Верховным (Высшим) Принципом. Множественность — поскольку она возможна — существует согласно своему собственному модусу, но этот модус иллюзорен — в том смысле, который мы уже уточняли (в смысле «ничтожно малой реальности», потому что само существование этой множественности основывается на единстве, из которого она возникла и в котором она заключена изначально. Рассматривая таким образом совокупность универсальной манифестации, можно сказать, что в самой множественности своих модусов. «Существование едино», согласно формуле, которую мы заимствуем в исламском эзотеризме. И здесь очень важно отметить тонкое различие между «единством» и «единичностью»: первое охватывает множественность как таковую, вторая же есть его принцип (не «корень», в том смысле, в каком это слово прилагается только к Пракрити, но как заключающее в себе возможности манифестации — «эссенциально» так же, как и «субстанциально»).
И, таким образом, все предстает как бы взаимосвязанным во многих смыслах — будь то в самой манифестации либо же в той мере, в какой последняя, образуя в своей бесконечной множественности единое целое, связуется со своим принципом, т. е. с Сущим и, через него, с Верховным (Высшим) Принципом. Множественность — поскольку она возможна — существует согласно своему собственному модусу, но этот модус иллюзорен — в том смысле, который мы уже уточняли (в смысле «ничтожно малой реальности», потому что само существование этой множественности основывается на единстве, из которого она возникла и в котором она заключена изначально. Рассматривая таким образом совокупность универсальной манифестации, можно сказать, что в самой множественности своих модусов. «Существование едино», согласно формуле, которую мы заимствуем в исламском эзотеризме. И здесь очень важно отметить тонкое различие между «единством» и «единичностью»: первое охватывает множественность как таковую, вторая же есть его принцип (не «корень», в том смысле, в каком это слово прилагается только к Пракрити, но как заключающее в себе возможности манифестации — «эссенциально» так же, как и «субстанциально»).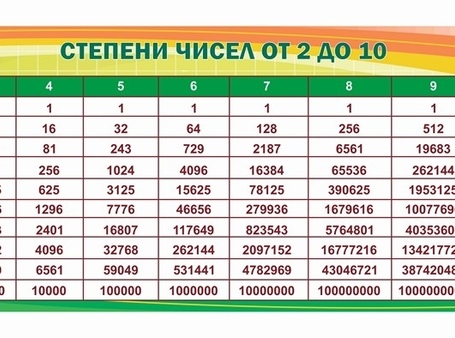 Стало быть, можно сказать, что Сущее едино и что оно есть сама Единичность[50] — однако в метафизическом, а не в математическом смысле, ибо здесь мы обретаемся далеко за пределами количества. Между метафизической Единичностью и единичностью математической существует аналогия, но не тождество. Точно так же, когда говорят о множественности манифестации, речь отнюдь не идет о количественной множественности, ибо количество есть особая характеристика определенных проявленных состояний. Наконец, если Сущее едино, то, как мы увидим далее, «не двойственен» и сам Верховный Принцип; в самом деле, единичность есть первая из всех определенностей, но она уже есть определенность и, как таковая, не может быть приложима к Верховному Принципу.
Стало быть, можно сказать, что Сущее едино и что оно есть сама Единичность[50] — однако в метафизическом, а не в математическом смысле, ибо здесь мы обретаемся далеко за пределами количества. Между метафизической Единичностью и единичностью математической существует аналогия, но не тождество. Точно так же, когда говорят о множественности манифестации, речь отнюдь не идет о количественной множественности, ибо количество есть особая характеристика определенных проявленных состояний. Наконец, если Сущее едино, то, как мы увидим далее, «не двойственен» и сам Верховный Принцип; в самом деле, единичность есть первая из всех определенностей, но она уже есть определенность и, как таковая, не может быть приложима к Верховному Принципу.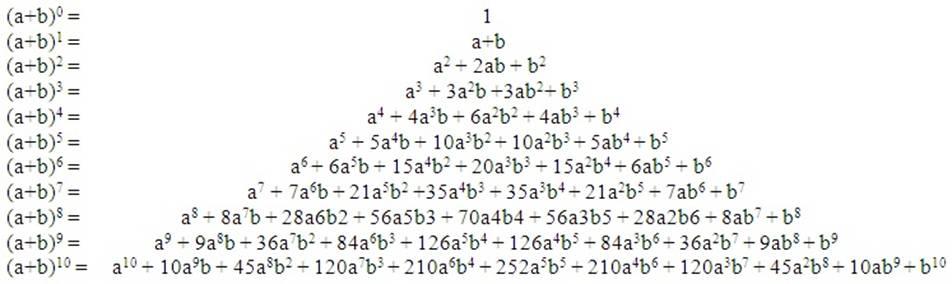 Собственно человеческое состояние так же, как и любое другое индивидуальное состояние, целиком принадлежит к порядку оформленной манифестации, потому что именно наличие формы, в ряду условий определенного модуса существования, характеризует этот модус как индивидуальный. Стало быть, если нам надлежит рассматривать не имеющий формы элемент, то это будет элемент над-индивидуальный, и, что касается его отношений с человеческой индивидуальностью, он никогда не должен рассматриваться как конститутивный для последней или как в каком-либо роде являющийся ее частью, но лишь как связующий индивидуальность с личностью. В самом деле, последняя не проявлена — даже и в той мере, в какой ее более специально рассматривают как принцип проявленных состояний, точно так же, как Самосущее, действительно будучи принципом универсальной манифестации, находится за пределами и выше этой манифестации (и здесь можно вспомнить о «неподвижном двигателе» Аристотеля). Но, с другой стороны, неоформленная манифестация также является изначальной, — конечно, в относительном смысле, по отношению к манифестации оформленной.
Собственно человеческое состояние так же, как и любое другое индивидуальное состояние, целиком принадлежит к порядку оформленной манифестации, потому что именно наличие формы, в ряду условий определенного модуса существования, характеризует этот модус как индивидуальный. Стало быть, если нам надлежит рассматривать не имеющий формы элемент, то это будет элемент над-индивидуальный, и, что касается его отношений с человеческой индивидуальностью, он никогда не должен рассматриваться как конститутивный для последней или как в каком-либо роде являющийся ее частью, но лишь как связующий индивидуальность с личностью. В самом деле, последняя не проявлена — даже и в той мере, в какой ее более специально рассматривают как принцип проявленных состояний, точно так же, как Самосущее, действительно будучи принципом универсальной манифестации, находится за пределами и выше этой манифестации (и здесь можно вспомнить о «неподвижном двигателе» Аристотеля). Но, с другой стороны, неоформленная манифестация также является изначальной, — конечно, в относительном смысле, по отношению к манифестации оформленной. И, таким образом, она устанавливает связь между последней и ее высшим непроявленным принципом, который, уместно сказать, есть общий принцип этих двух порядков манифестации. Точно так же, если вслед затем на уровне оформленной, или индивидуальной манифестации провести различие между тонким и грубым состоянием, то первое является, также относительно, изначальным по отношению ко второму и, следовательно, иерархически оно располагается между этим последним и неоформленной манифестацией. Следовательно, посредством ряда более или менее относительных и определенных принципов, мы получаем одновременно логическую и онтологическую цепочку (впрочем, две точки зрения согласуются таким образом, что разделить их можно только искусственно), простирающуюся от непроявленного к грубой проявленности, через опосредование манифестацией неоформленной, а затем через манифестацию тонкую. И идет ли речь о «макрокосме» или «микрокосме», таков общий порядок, которому должно следовать в разворачивании возможностей манифестации.
И, таким образом, она устанавливает связь между последней и ее высшим непроявленным принципом, который, уместно сказать, есть общий принцип этих двух порядков манифестации. Точно так же, если вслед затем на уровне оформленной, или индивидуальной манифестации провести различие между тонким и грубым состоянием, то первое является, также относительно, изначальным по отношению ко второму и, следовательно, иерархически оно располагается между этим последним и неоформленной манифестацией. Следовательно, посредством ряда более или менее относительных и определенных принципов, мы получаем одновременно логическую и онтологическую цепочку (впрочем, две точки зрения согласуются таким образом, что разделить их можно только искусственно), простирающуюся от непроявленного к грубой проявленности, через опосредование манифестацией неоформленной, а затем через манифестацию тонкую. И идет ли речь о «макрокосме» или «микрокосме», таков общий порядок, которому должно следовать в разворачивании возможностей манифестации.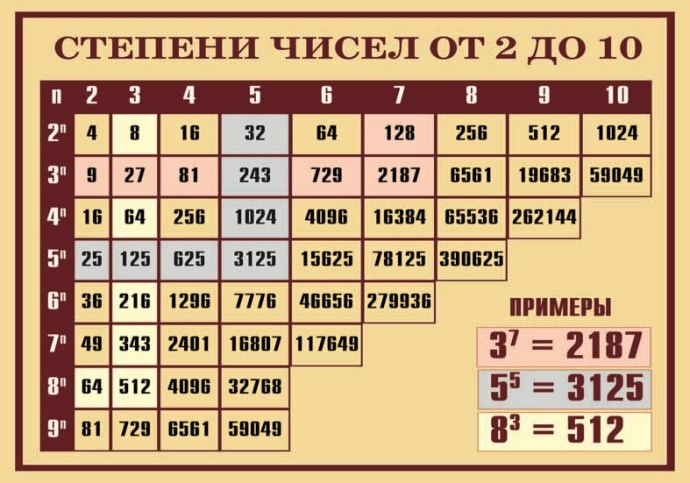
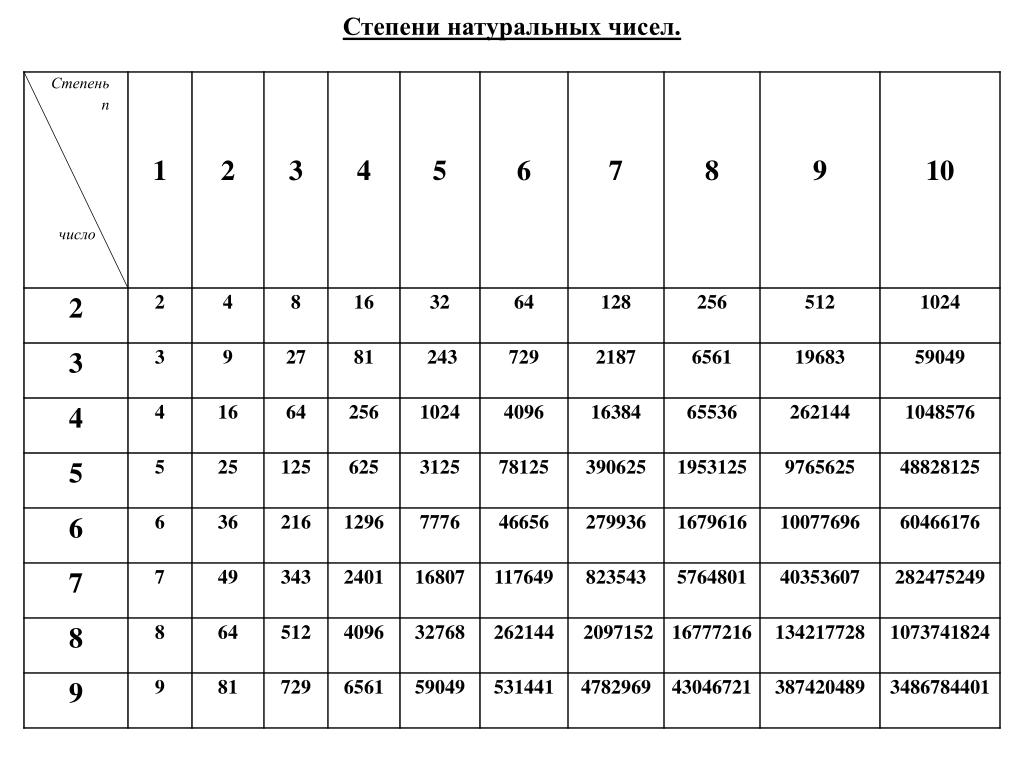
 Это же примечание можно сделать, когда мы говорим, что тонкая манифестация является производящей по отношению к грубой манифестации. Чтобы быть вполне точными, нужно привнести сюда — в том, что касается первой — ограничение, на которое мы только что указали, так как обычное соотношение не может быть установлено для других, равным образом индивидуальных, но не-человеческих состояний, состояний абсолютно иных по их обусловленностям (за исключением наличия формы). Их, однако, также следует понимать в соотношении с манифестацией, коль скоро человеческая индивидуальность принимается за эталон сравнения, как это следует делать неизбежно, вполне отдавая себе отчет в том, что в действительности такое состояние не больше и не меньше любого другого состояния.
Это же примечание можно сделать, когда мы говорим, что тонкая манифестация является производящей по отношению к грубой манифестации. Чтобы быть вполне точными, нужно привнести сюда — в том, что касается первой — ограничение, на которое мы только что указали, так как обычное соотношение не может быть установлено для других, равным образом индивидуальных, но не-человеческих состояний, состояний абсолютно иных по их обусловленностям (за исключением наличия формы). Их, однако, также следует понимать в соотношении с манифестацией, коль скоро человеческая индивидуальность принимается за эталон сравнения, как это следует делать неизбежно, вполне отдавая себе отчет в том, что в действительности такое состояние не больше и не меньше любого другого состояния. В самом деле, разворачивание во времени соответствует лишь одному особому условию существования, одному из тех, что определяют область, в которую помещено человеческое состояние; и существует бесконечное множество других модусов разворачивания, равным образом возможных и равным образом включенных в универсальную манифестацию. Стало быть, человеческая индивидуальность не может быть размещена в каком-то временном порядке по отношению к другим состояниям существа, потому что последние, в общем, являются вневременными. И это так даже и тогда, когда речь идет только о состояниях, сходным образом соотносящихся с той же самой оформленной проявленностью. Мы могли бы еще добавить, что некоторые способы расширения человеческой индивидуальности за пределы ее телесной модальности уже вырываются из-под власти времени, не будучи вследствие этого освобождены от других общих условий состояния, к которому принадлежит эта индивидуальность, так что они в действительности располагаются в простых продолжениях этого же самого состояния.
В самом деле, разворачивание во времени соответствует лишь одному особому условию существования, одному из тех, что определяют область, в которую помещено человеческое состояние; и существует бесконечное множество других модусов разворачивания, равным образом возможных и равным образом включенных в универсальную манифестацию. Стало быть, человеческая индивидуальность не может быть размещена в каком-то временном порядке по отношению к другим состояниям существа, потому что последние, в общем, являются вневременными. И это так даже и тогда, когда речь идет только о состояниях, сходным образом соотносящихся с той же самой оформленной проявленностью. Мы могли бы еще добавить, что некоторые способы расширения человеческой индивидуальности за пределы ее телесной модальности уже вырываются из-под власти времени, не будучи вследствие этого освобождены от других общих условий состояния, к которому принадлежит эта индивидуальность, так что они в действительности располагаются в простых продолжениях этого же самого состояния.
 Актуализация знаний
Актуализация знаний f(х) = х3
f(х) = х3 f(х) =
f(х) =
 к. не выполняются
равенства f(– х) = – f(х), f(–
х) = f(х)
к. не выполняются
равенства f(– х) = – f(х), f(–
х) = f(х) А верно ли
обратное утверждение, если область определения
функции симметричное множество, то она чётна,
либо нечётна?
А верно ли
обратное утверждение, если область определения
функции симметричное множество, то она чётна,
либо нечётна?
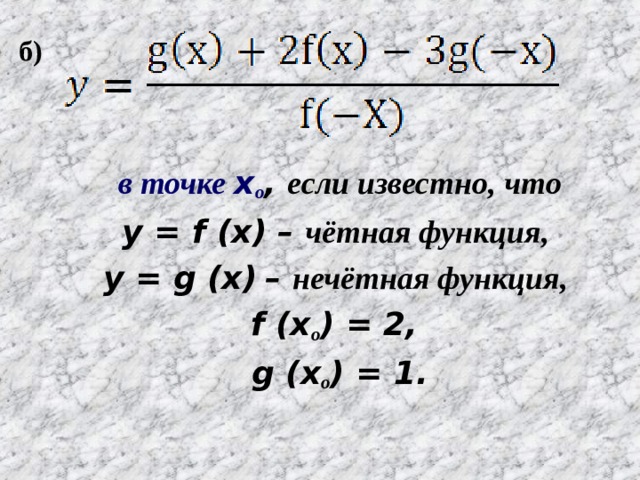 Какие? Можно
ли по графику функции выявить её четность?
Давайте вернёмся к заданию, которое мы выполняли
в начале урока, найдём соответствие между
аналитически заданными функциями и их
графиками (изображёнными на доске), что вы
находите примечательного в расположении
графиков чётных функций? Нечётных?
Какие? Можно
ли по графику функции выявить её четность?
Давайте вернёмся к заданию, которое мы выполняли
в начале урока, найдём соответствие между
аналитически заданными функциями и их
графиками (изображёнными на доске), что вы
находите примечательного в расположении
графиков чётных функций? Нечётных?


 a
a е. функция является четной.
е. функция является четной. Такова, например, функция у = 2х + 3. В самом деле, f(1) = 5, а f (-1) = 1. Как видите, здесь Значит, не может выполняться ни тождество f(-х) = f (х), ни тождество f(-х) = -f(х).
Такова, например, функция у = 2х + 3. В самом деле, f(1) = 5, а f (-1) = 1. Как видите, здесь Значит, не может выполняться ни тождество f(-х) = f (х), ни тождество f(-х) = -f(х). Если же D (f) — несимметричное множество, то функция у = f(х) не является ни четной, ни нечетной.
Если же D (f) — несимметричное множество, то функция у = f(х) не является ни четной, ни нечетной.

 Эти точки симметричны относительно оси у (рис. 73). Таким образом, для каждой точки А графика четной функции у = f(х) существует симметричная ей относительно оси у точка В того же графика. Это означает, что график четной функции симметричен относительно оси у.
Эти точки симметричны относительно оси у (рис. 73). Таким образом, для каждой точки А графика четной функции у = f(х) существует симметричная ей относительно оси у точка В того же графика. Это означает, что график четной функции симметричен относительно оси у. е. у = f(х) — четная функция.
е. у = f(х) — четная функция.
 a
a От свойств и вида также зависит четность. Первое рекомендуется применять в частных случаях, например, произведение двух нечетных тождеств. Результат следует проверять при помощи соответствующего программного обеспечения. Например, онлайн-калькулятор четности и нечетности функций позволяет следить за правильностью решения.
От свойств и вида также зависит четность. Первое рекомендуется применять в частных случаях, например, произведение двух нечетных тождеств. Результат следует проверять при помощи соответствующего программного обеспечения. Например, онлайн-калькулятор четности и нечетности функций позволяет следить за правильностью решения.
 Если функция представлена в виде обыкновенной дроби, то значение аргумента, приводящее к пустому множеству (знаменатель равен нулю), нужно исключить. Когда аргумент находится под знаком радикала (корня), тогда она считается иррациональной. Однако следует проверить, чтобы под корнем четной степени не было отрицательного значения, которое приводит к неопределенности.
Если функция представлена в виде обыкновенной дроби, то значение аргумента, приводящее к пустому множеству (знаменатель равен нулю), нужно исключить. Когда аргумент находится под знаком радикала (корня), тогда она считается иррациональной. Однако следует проверить, чтобы под корнем четной степени не было отрицательного значения, которое приводит к неопределенности. Первая группа характеризуется постоянностью, то есть она либо убывает, либо возрастает. Все остальные могут убывать и возрастать на определенных промежутках. Примером является y = cos (x), поскольку она является убывающей и возрастающей через определенный период.
Первая группа характеризуется постоянностью, то есть она либо убывает, либо возрастает. Все остальные могут убывать и возрастать на определенных промежутках. Примером является y = cos (x), поскольку она является убывающей и возрастающей через определенный период.



 2 — 1 = y 2 — 1.
2 — 1 = y 2 — 1. Если бы было произведение двух нечетных выражений, то результат являлся бы четным. Об этой особенности свидетельствует свойство под номером 4.
Если бы было произведение двух нечетных выражений, то результат являлся бы четным. Об этой особенности свидетельствует свойство под номером 4.



 8).
8). , испр. и доп. — М.: Мнемозина, 2008.
, испр. и доп. — М.: Мнемозина, 2008.
 То, что у неё в скобках — это аргумент. То, чему она равна — её значение.
То, что у неё в скобках — это аргумент. То, чему она равна — её значение.  cos60 = -0,5; cos60 = 0,5
cos60 = -0,5; cos60 = 0,5
 Графики, обладающие симметрией относительно оси Y, называются четными функциями . Графики, обладающие симметрией относительно начала координат, называются нечетными функциями .
Графики, обладающие симметрией относительно оси Y, называются четными функциями . Графики, обладающие симметрией относительно начала координат, называются нечетными функциями .




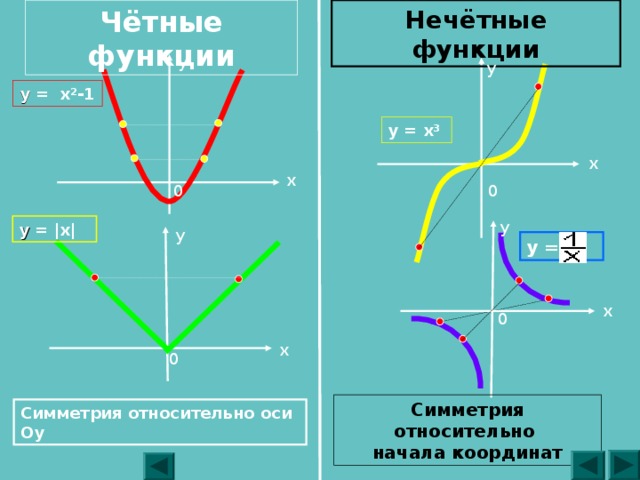 3 + 1 не является ни одной из функций. 92 – 3 $$
3 + 1 не является ни одной из функций. 92 – 3 $$ 
 список.
список.

 {2}+1\) по-прежнему четная. Как видите, четная функция будет иметь четные показатели степени .
{2}+1\) по-прежнему четная. Как видите, четная функция будет иметь четные показатели степени . Эта функция не симметрична относительно оси \(y\), поэтому она не является четной. И хотя он проходит через начало координат, он не является странным, потому что он не выглядел бы таким же, если бы мы повернули изображение на 180°.
Эта функция не симметрична относительно оси \(y\), поэтому она не является четной. И хотя он проходит через начало координат, он не является странным, потому что он не выглядел бы таким же, если бы мы повернули изображение на 180°. И они не должны проходить через источник. Однако нечетные функции должны проходить через начало координат, и они будут выглядеть одинаково при повороте на 180°.
И они не должны проходить через источник. Однако нечетные функции должны проходить через начало координат, и они будут выглядеть одинаково при повороте на 180°.
 График будет таким же, если его повернуть на 180° вокруг начала координат. Это означает, что любая точка \((x,y)\) на графике функции отражает точку \((-x,-y)\), которая также находится на графике функции. Ниже приведен график функции и ее отражение относительно начала координат, показанное красным цветом.
График будет таким же, если его повернуть на 180° вокруг начала координат. Это означает, что любая точка \((x,y)\) на графике функции отражает точку \((-x,-y)\), которая также находится на графике функции. Ниже приведен график функции и ее отражение относительно начала координат, показанное красным цветом.
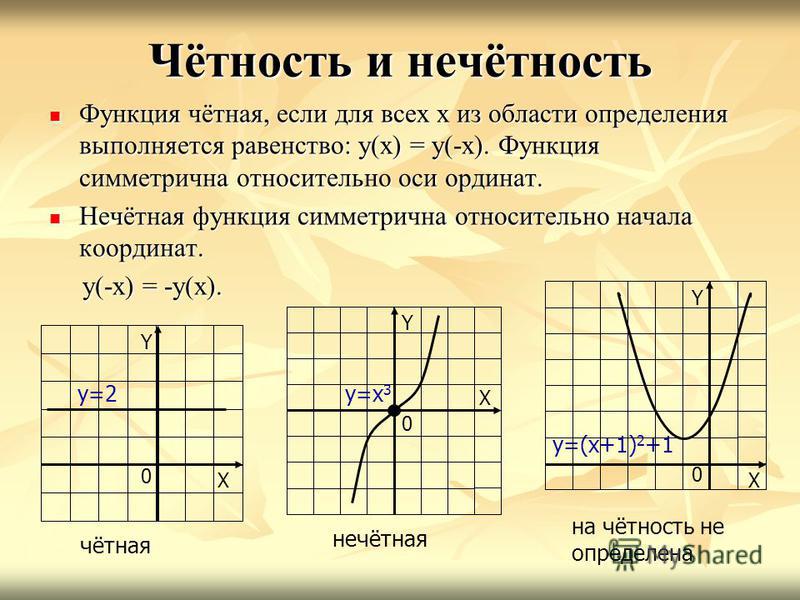
 Пусть поперечное сечение криволинейной формы пандуса есть функция \(y=f(x)\).
Пусть поперечное сечение криволинейной формы пандуса есть функция \(y=f(x)\). Одна такая точка на графике рампы подтверждает это, и это верно для всех точек на графике рампы. Таким образом, график функции \(y=f(x)\), представляющий рампу конька, имеет симметрию относительно оси \(y\), поэтому это четная функция.
Одна такая точка на графике рампы подтверждает это, и это верно для всех точек на графике рампы. Таким образом, график функции \(y=f(x)\), представляющий рампу конька, имеет симметрию относительно оси \(y\), поэтому это четная функция. Существует много типов радиоволн, встречающихся в природе, таких как световые волны, и те, которые искусственно генерируются машинами. Одна такая искусственная волна, называемая радиоволной FM (частотная модуляция), передает несущий сигнал от радиостанции, которая передает информацию на антенну вашего радиоприемника, в которой амплитуда несущего сигнала постоянна, но частота модулируется или изменяется. Ниже приведен пример 2 циклов или периодов модулированной несущей FM.
Существует много типов радиоволн, встречающихся в природе, таких как световые волны, и те, которые искусственно генерируются машинами. Одна такая искусственная волна, называемая радиоволной FM (частотная модуляция), передает несущий сигнал от радиостанции, которая передает информацию на антенну вашего радиоприемника, в которой амплитуда несущего сигнала постоянна, но частота модулируется или изменяется. Ниже приведен пример 2 циклов или периодов модулированной несущей FM. Это означает, что любая точка \((x,y)\) на графике функции отражает точку \((-x,y)\), которая также находится на графике функции. Ниже приведен график радиоволны и ее отражения относительно оси \(y\), показанной красным цветом.
Это означает, что любая точка \((x,y)\) на графике функции отражает точку \((-x,y)\), которая также находится на графике функции. Ниже приведен график радиоволны и ее отражения относительно оси \(y\), показанной красным цветом. Две такие точки на графике радиоволны подтверждают это, и это верно для всех точек на графике радиоволны. Таким образом, график функции, представляющей радиоволну, имеет симметрию относительно начала координат, поэтому это нечетная функция.
Две такие точки на графике радиоволны подтверждают это, и это верно для всех точек на графике радиоволны. Таким образом, график функции, представляющей радиоволну, имеет симметрию относительно начала координат, поэтому это нечетная функция.
 physics.manchester.ac.uk/PDEs/Notes/Notes
physics.manchester.ac.uk/PDEs/Notes/Notes


 Есть примеры, когда емкость не соответствует смыслу четных и нечетных функций. Емкость f(x) = (x + 1)2 является иллюстрацией емкости, которая не является ни нечетной, ни четной.
Есть примеры, когда емкость не соответствует смыслу четных и нечетных функций. Емкость f(x) = (x + 1)2 является иллюстрацией емкости, которая не является ни нечетной, ни четной.

 -t,text(if ) 0 le t lt pi):}`
-t,text(if ) 0 le t lt pi):}`
 Особенно если эти прямые – скрещиваются. Напомним, что так называются прямые, которые не параллельны и не пересекаются. Они лежат в параллельных плоскостях.
Особенно если эти прямые – скрещиваются. Напомним, что так называются прямые, которые не параллельны и не пересекаются. Они лежат в параллельных плоскостях. Найдите косинус угла между прямыми AE и BK.
Найдите косинус угла между прямыми AE и BK.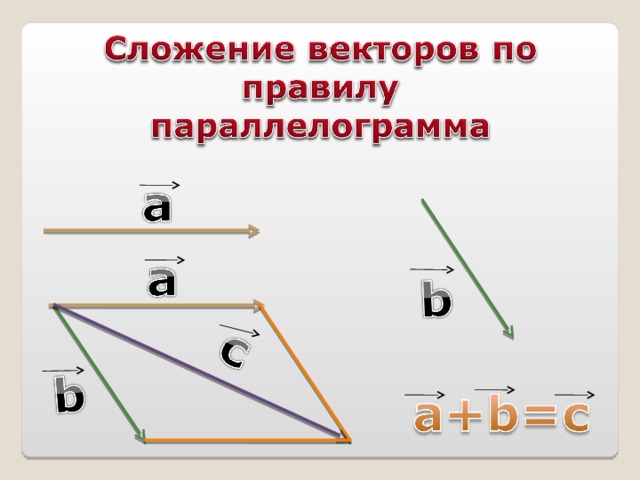 Нарисуем отдельно нижнее основание призмы.
Нарисуем отдельно нижнее основание призмы. Подставляем их по очереди в уравнение плоскости. Решаем полученную систему.
Подставляем их по очереди в уравнение плоскости. Решаем полученную систему.
 Просто отметим координаты нужных нам точек и найдем угол между нормалями к плоскостям AEF и BDD1.
Просто отметим координаты нужных нам точек и найдем угол между нормалями к плоскостям AEF и BDD1. Найдите тангенс угла между плоскостью грани AA1D1D и плоскостью, проходящей через середину ребра CD перпендикулярно прямой B1D, если расстояние между прямыми A1C1 и BD равно √3.
Найдите тангенс угла между плоскостью грани AA1D1D и плоскостью, проходящей через середину ребра CD перпендикулярно прямой B1D, если расстояние между прямыми A1C1 и BD равно √3.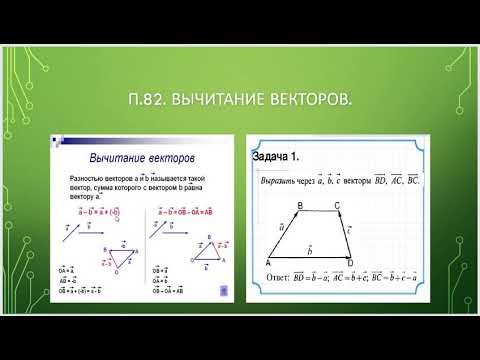 А отрезок OO1 и равен высоте параллелепипеда.
А отрезок OO1 и равен высоте параллелепипеда.
 Высота параллелепипеда AA1 = . Найдите расстояние от точки A до плоскости A1DB.
Высота параллелепипеда AA1 = . Найдите расстояние от точки A до плоскости A1DB.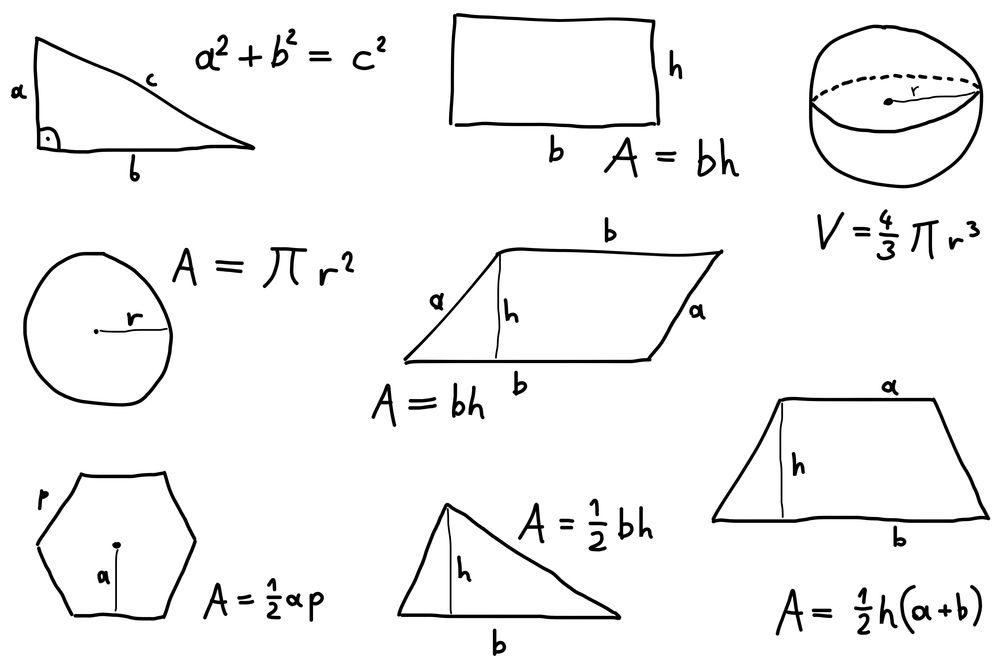

 Координаты вектора. Длина вектора
Координаты вектора. Длина вектора
 По этим данным вы найдёте точку,
проходя 3 метра в направлении, указываемом правой рукой, затем 1 метр в направлении,
указываемом левой рукой, а далее Вас ждёт лестница и, поднимаясь на 5 метров, Вы, наконец,
окажетесь в конечной точке.
По этим данным вы найдёте точку,
проходя 3 метра в направлении, указываемом правой рукой, затем 1 метр в направлении,
указываемом левой рукой, а далее Вас ждёт лестница и, поднимаясь на 5 метров, Вы, наконец,
окажетесь в конечной точке. На рисунке
конец вектора указывается стрелкой (рис. 1)
На рисунке
конец вектора указывается стрелкой (рис. 1)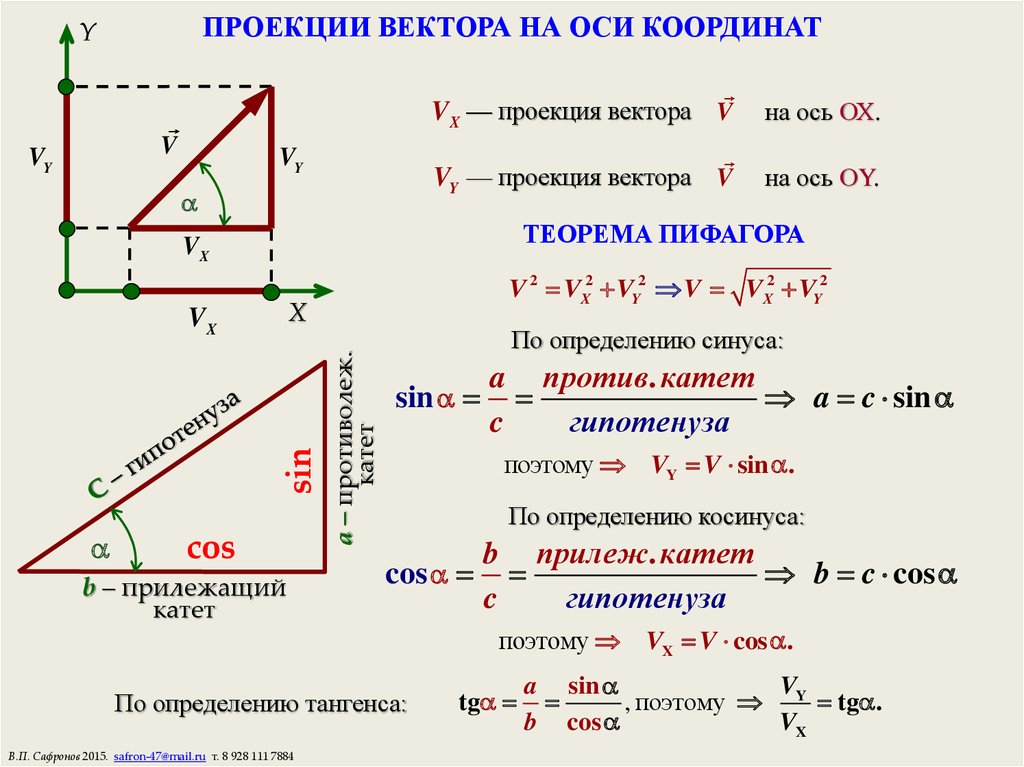
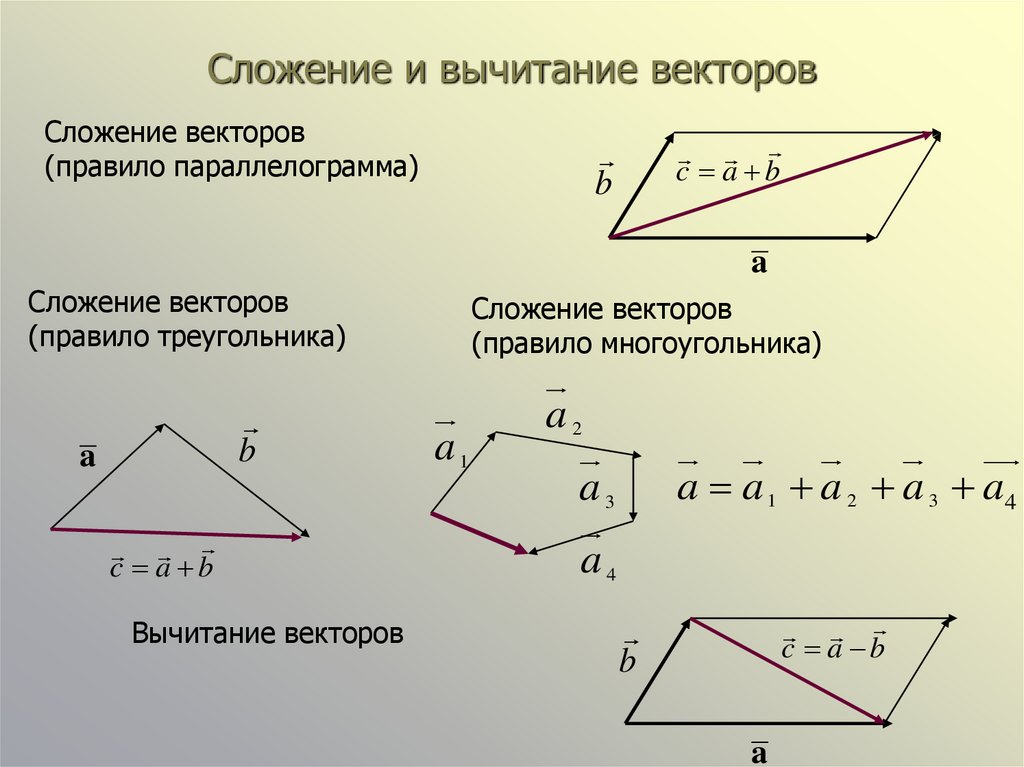 Обозначим через
Обозначим через
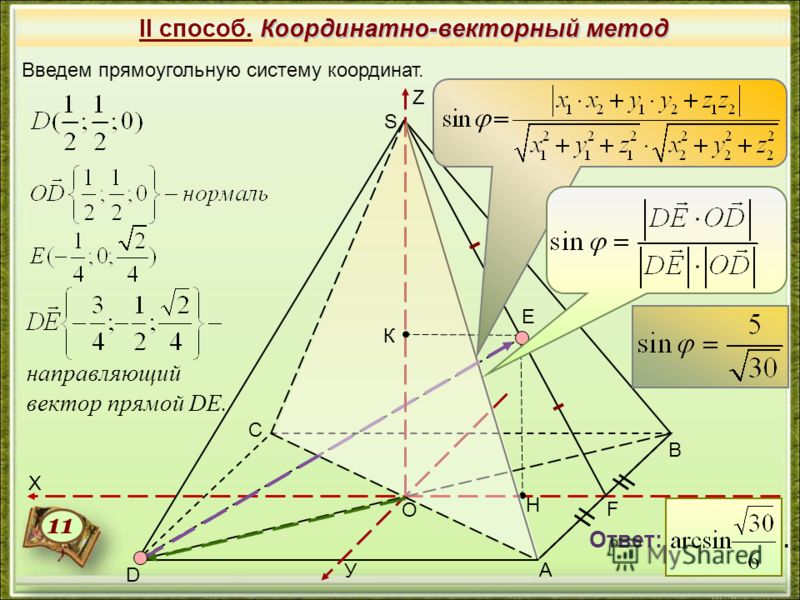
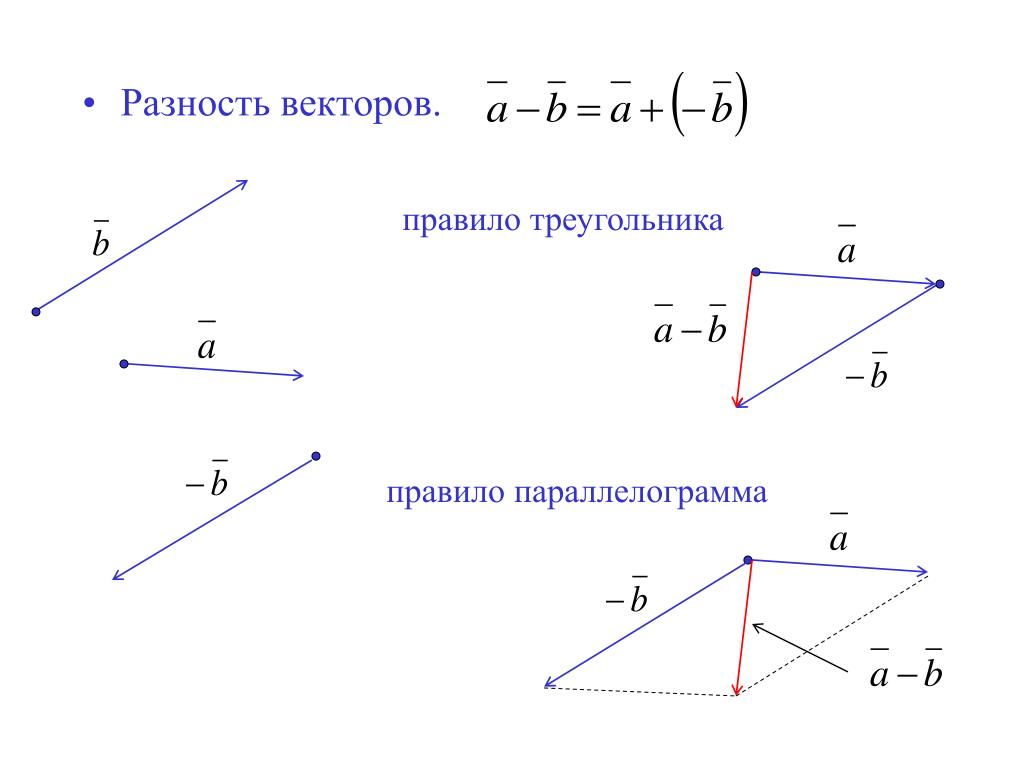
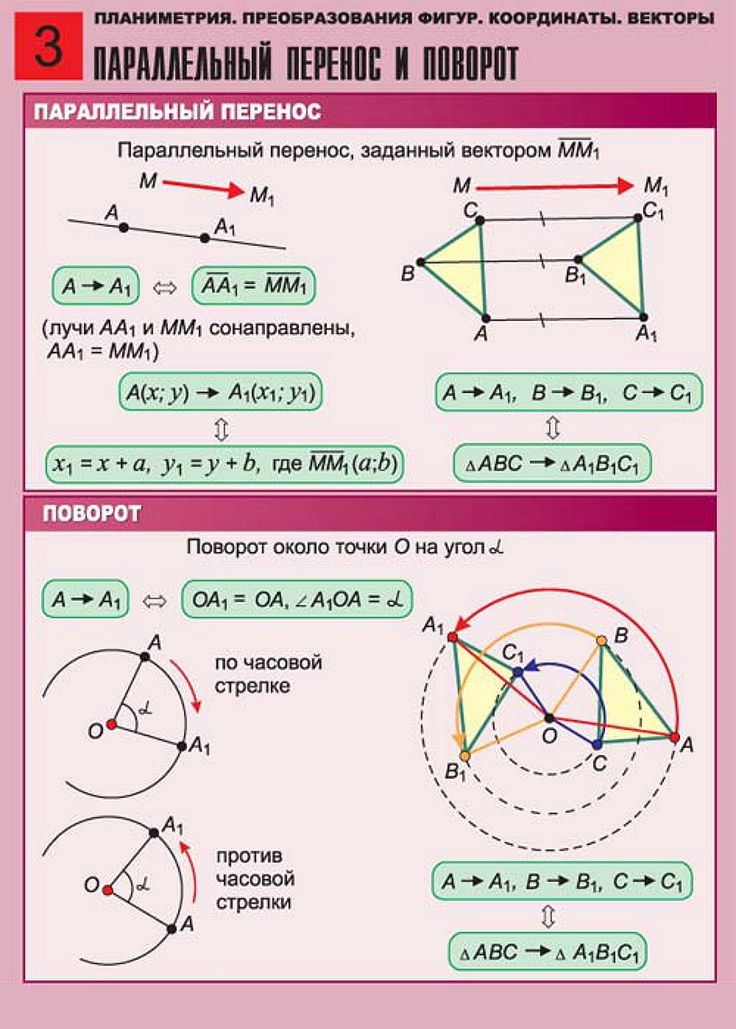
 Аффинные координаты
Аффинные координаты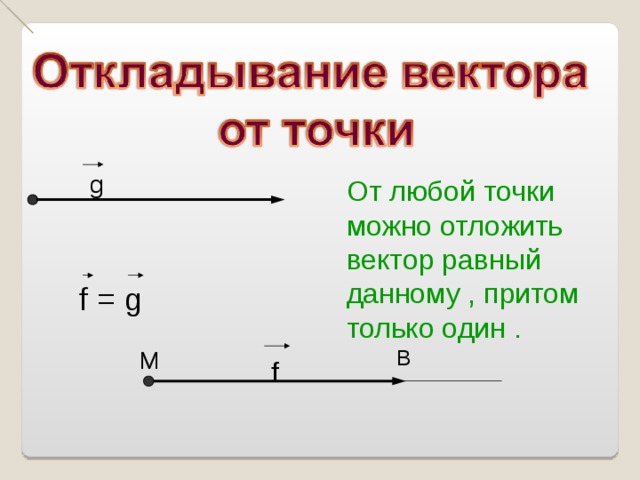
 mccme. Зато теперь я очень рад, что прошел через все испытания и знаю, что же такое задачи вычислительной геометрии.
mccme. Зато теперь я очень рад, что прошел через все испытания и знаю, что же такое задачи вычислительной геометрии. Такой вектор называется нулевым. Начало и конец нулевого вектора совпадают, и он не имеет какого-либо определенного направления.
Такой вектор называется нулевым. Начало и конец нулевого вектора совпадают, и он не имеет какого-либо определенного направления.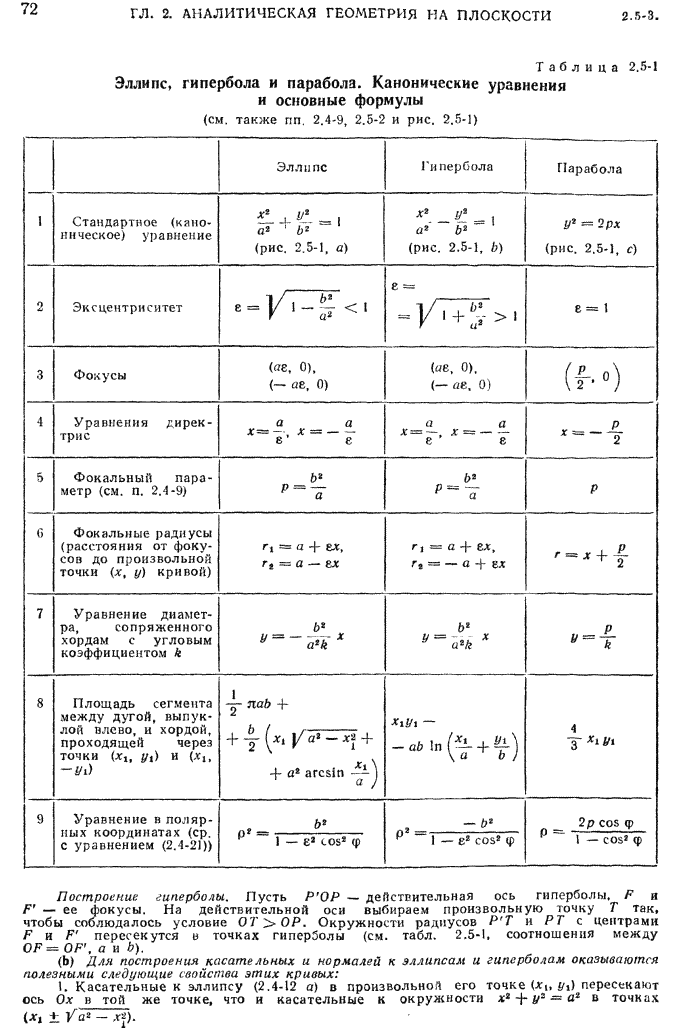

 Оказывается, что если треугольник задан координатами своих вершин, то вычислять длины его сторон и проверять неравенство треугольника не требуется. В этом случае треугольника не существует тогда и только тогда, когда данные три точки лежат на одной прямой. А это легко проверяется через косое произведение векторов. Если оно равно нулю, то векторы коллинеарные, то есть все три точки лежат на одной прямой.
Оказывается, что если треугольник задан координатами своих вершин, то вычислять длины его сторон и проверять неравенство треугольника не требуется. В этом случае треугольника не существует тогда и только тогда, когда данные три точки лежат на одной прямой. А это легко проверяется через косое произведение векторов. Если оно равно нулю, то векторы коллинеарные, то есть все три точки лежат на одной прямой. 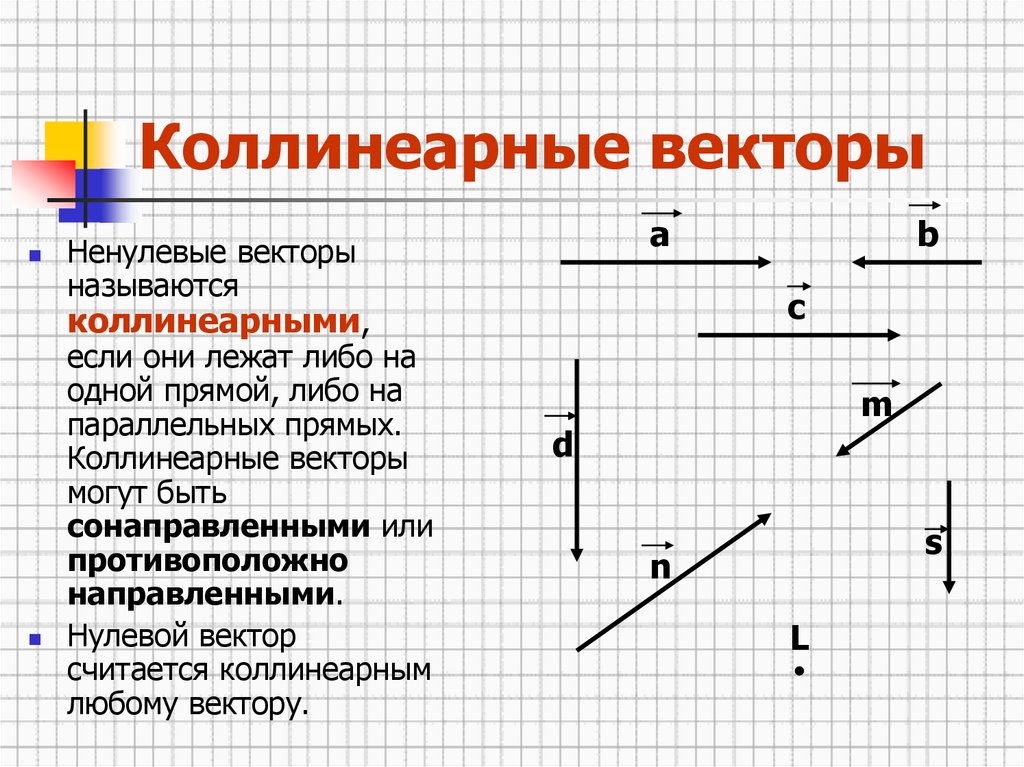 Однако немного поразмыслив можно понять, что вычислять косинус угла не обязательно, необходимо учесть лишь его знак:
Однако немного поразмыслив можно понять, что вычислять косинус угла не обязательно, необходимо учесть лишь его знак: Аналогично предыдущей задаче, необходимо определить каким является наибольший из углов треугольника. Вид угла легко определяется по знаку скалярного произведения образующих его векторов: оно положительно для острого угла, равно нулю для прямого угла и отрицательно для тупого угла. Поэтому необходимо посчитать все три скалярных произведения и перемножить их и по знаку данного числа можно судить о типе треугольника.
Аналогично предыдущей задаче, необходимо определить каким является наибольший из углов треугольника. Вид угла легко определяется по знаку скалярного произведения образующих его векторов: оно положительно для острого угла, равно нулю для прямого угла и отрицательно для тупого угла. Поэтому необходимо посчитать все три скалярных произведения и перемножить их и по знаку данного числа можно судить о типе треугольника. Геометрически косое произведение двух векторов определяет ориентированную площадь параллелограмма натянутого на эти вектора. Поскольку диагональ параллелограмма разбивает его на два равновеликих треугольника, то можем найти площадь нашего треугольника, как половину площади параллелограмма.
Геометрически косое произведение двух векторов определяет ориентированную площадь параллелограмма натянутого на эти вектора. Поскольку диагональ параллелограмма разбивает его на два равновеликих треугольника, то можем найти площадь нашего треугольника, как половину площади параллелограмма. Если же сумма первых трех площадей равна четвертой, то нужно проверить, не равна ли нулю одна из трех площадей. Если равна, то точка лежит на границе треугольника, иначе – внутри.
Если же сумма первых трех площадей равна четвертой, то нужно проверить, не равна ли нулю одна из трех площадей. Если равна, то точка лежит на границе треугольника, иначе – внутри.
 5 * (A1B1 + A2B2) *(B2 — B1)
5 * (A1B1 + A2B2) *(B2 — B1) Тем более, что при втором решении площади треугольников надо вычислять через косое произведение. О формуле Герона надо забыть!!!
Тем более, что при втором решении площади треугольников надо вычислять через косое произведение. О формуле Герона надо забыть!!! Требуется подсчитать количество точек с целочисленными координатами, лежащих внутри него (но не на его границе).
Требуется подсчитать количество точек с целочисленными координатами, лежащих внутри него (но не на его границе).
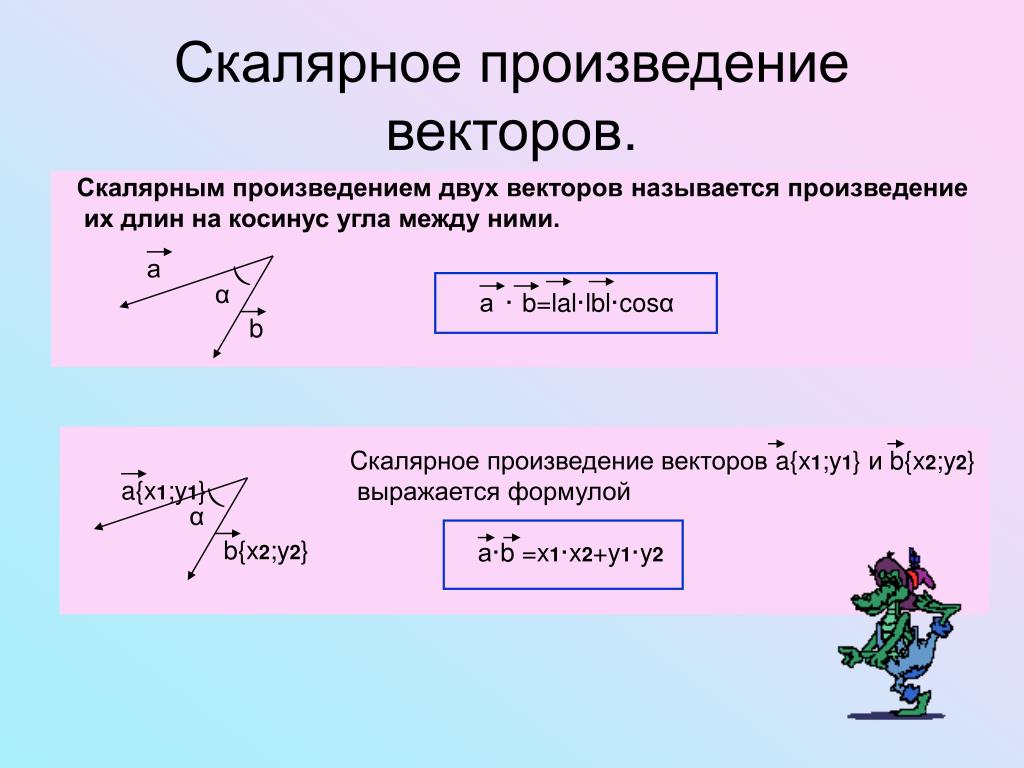
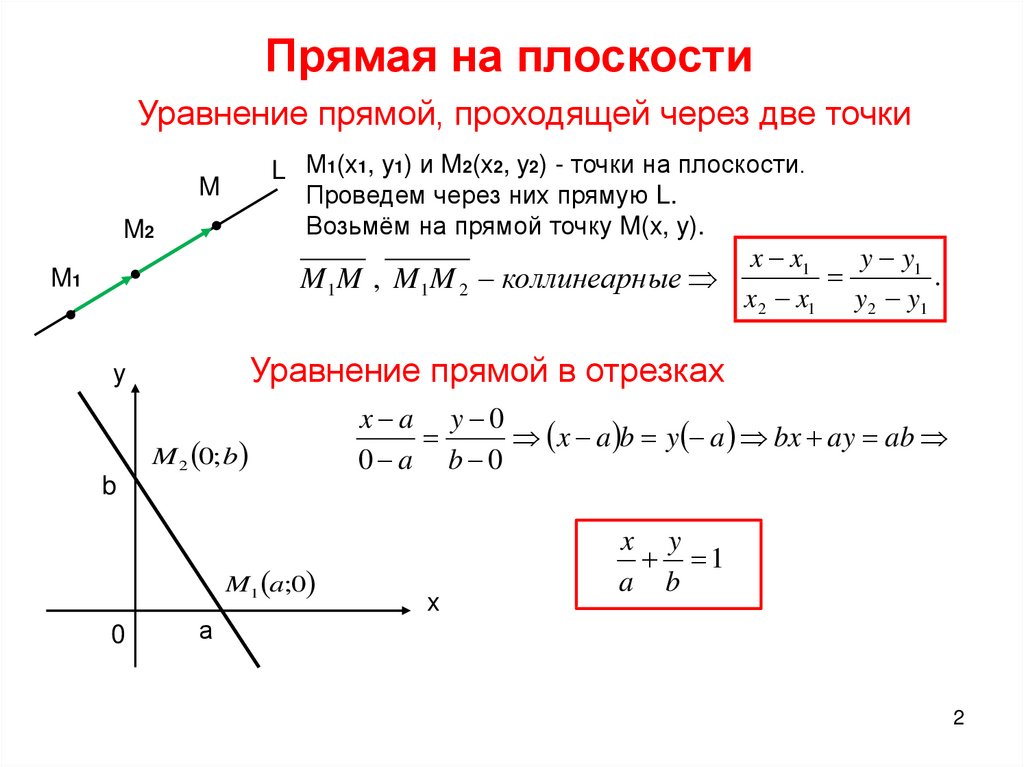
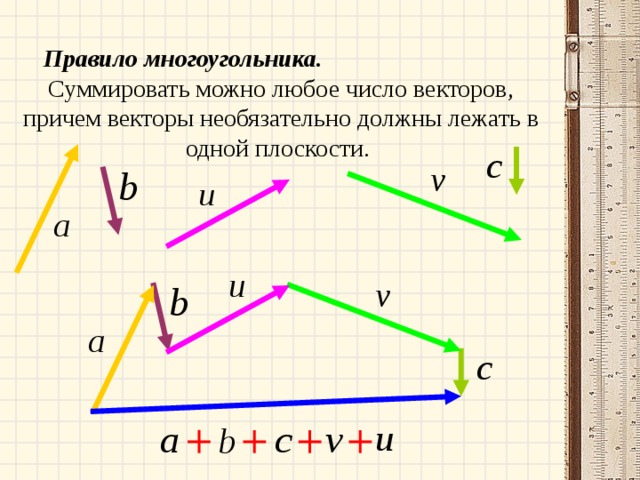
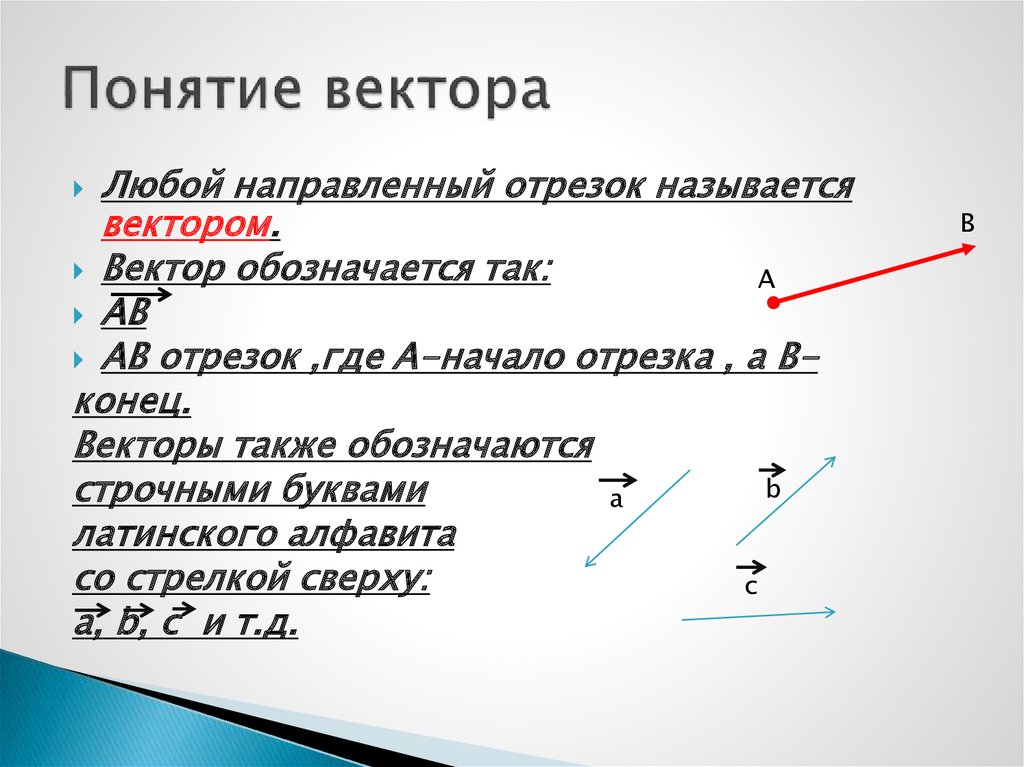

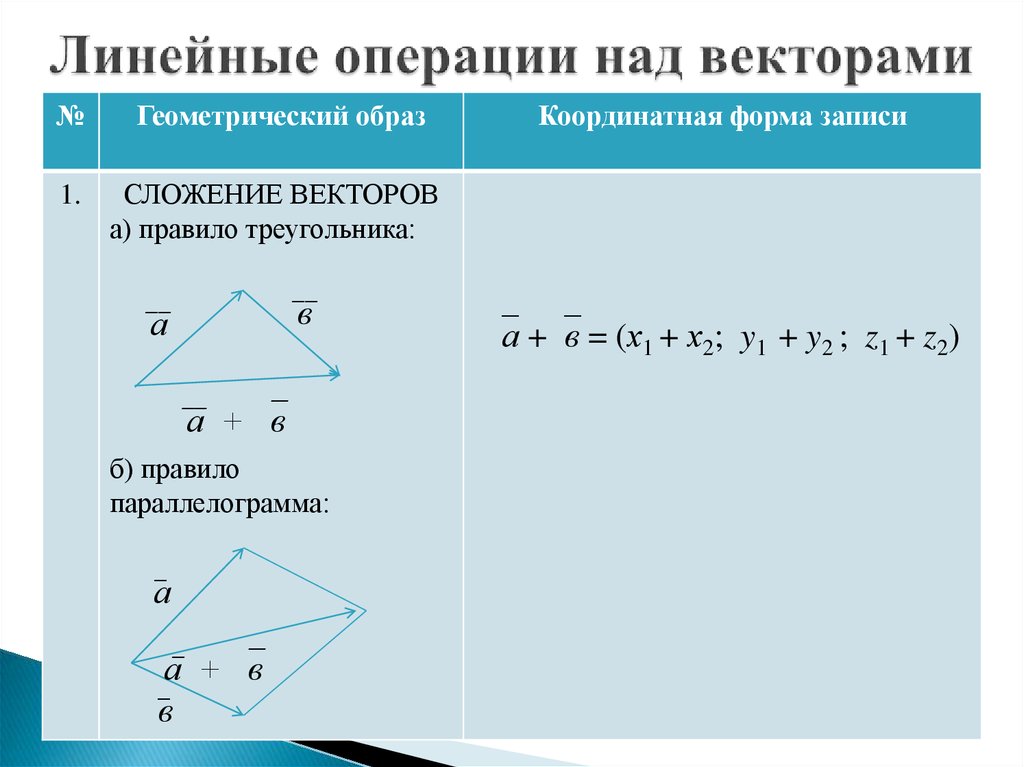

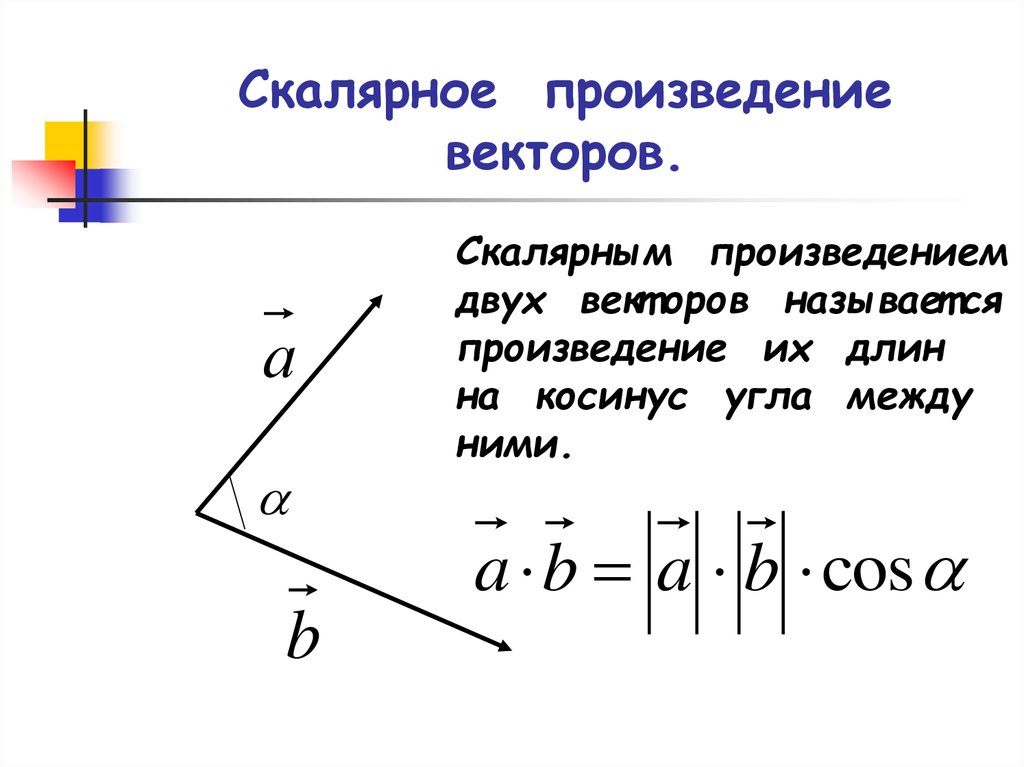
 _________________-это
отображение пространства на себя, при котором любая точка М переходит в
симметричную ей точку М, относительно данного центра.
_________________-это
отображение пространства на себя, при котором любая точка М переходит в
симметричную ей точку М, относительно данного центра.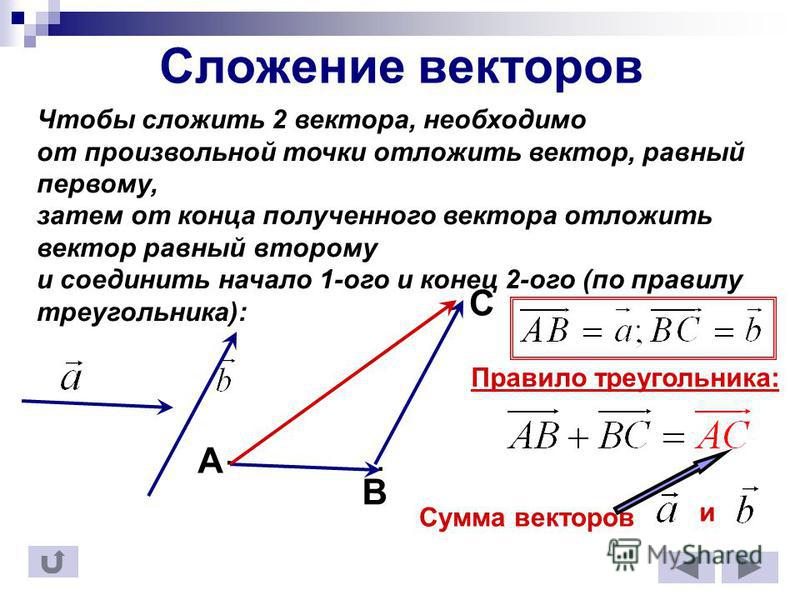
 Отрезок,
для которого указано, какой из его концов считается началом, а какой – концом,
называется ______________
Отрезок,
для которого указано, какой из его концов считается началом, а какой – концом,
называется ______________ Скалярный
квадрат равен __________________________________
Скалярный
квадрат равен __________________________________ Умножение вектора на число
Умножение вектора на число Проекция вектора на вектор
Проекция вектора на вектор
 Этот треугольник равносторонний, значит, угол равен 60°.
Этот треугольник равносторонний, значит, угол равен 60°. Следовательно, ABCD – квадрат, что и требовалось доказать.
Следовательно, ABCD – квадрат, что и требовалось доказать. opredelim.com/docs/index-42169.html
opredelim.com/docs/index-42169.html






 Если векторы сонаправлены, то угол между ними равен 0°.
Если векторы сонаправлены, то угол между ними равен 0°.
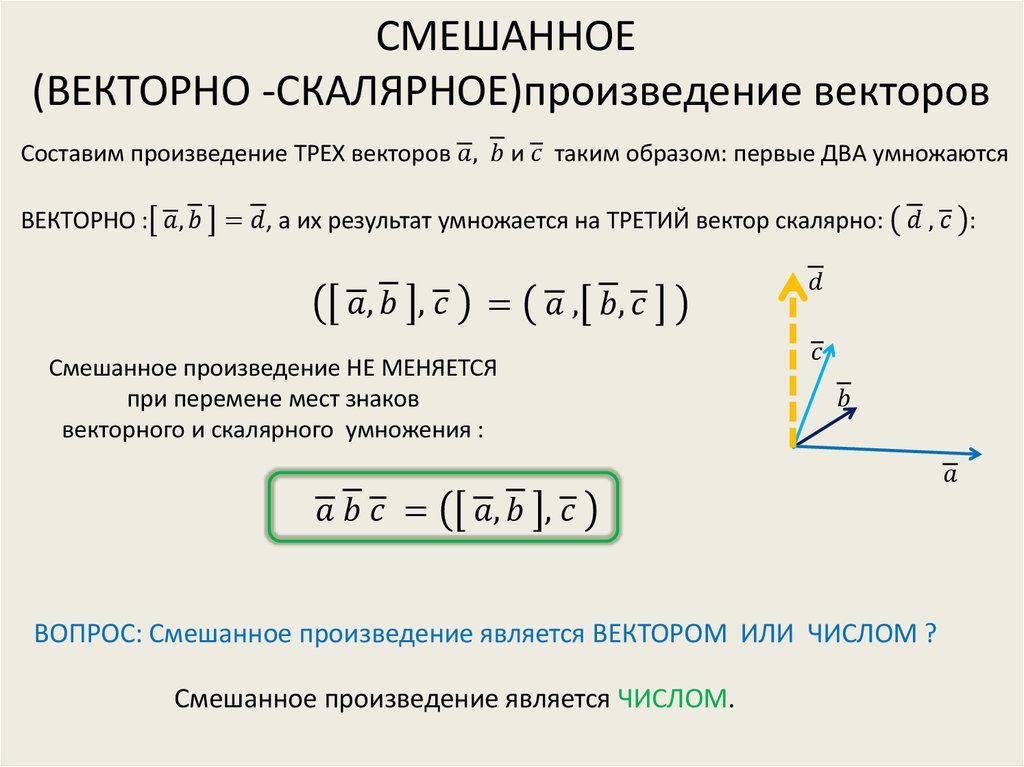

 В результате получается нуль, если вектор равен нулевому вектору.
В результате получается нуль, если вектор равен нулевому вектору. В силу свойства коммутативности операции умножения действительных чисел, справедливо ax*bx = bx*ax b ay*by = by*ay, тогда ax*bx + ay*by = bx*ax + by*ay.
В силу свойства коммутативности операции умножения действительных чисел, справедливо ax*bx = bx*ax b ay*by = by*ay, тогда ax*bx + ay*by = bx*ax + by*ay.

 Найдем их: →KL(-2-3; 0-5) = →KL(-5; -5), →MN(1-8; 4-(-1)) = →MN(-7;5)
Найдем их: →KL(-2-3; 0-5) = →KL(-5; -5), →MN(1-8; 4-(-1)) = →MN(-7;5) Для краткости можно также записать просто ∠B.
Для краткости можно также записать просто ∠B.
 .. ; an} и b = {b1 ; b2 ; … ; bn} можно найти воспользовавшись следующей формулой:
.. ; an} и b = {b1 ; b2 ; … ; bn} можно найти воспользовавшись следующей формулой:
 Найти скалярное произведение векторов a = {1; 2; -5; 2} и b = {4; 8; 1; -2}.
Найти скалярное произведение векторов a = {1; 2; -5; 2} и b = {4; 8; 1; -2}. Коллинеарные векторы. Действия с векторами и их свойства — сложение и
Коллинеарные векторы. Действия с векторами и их свойства — сложение и ru
ru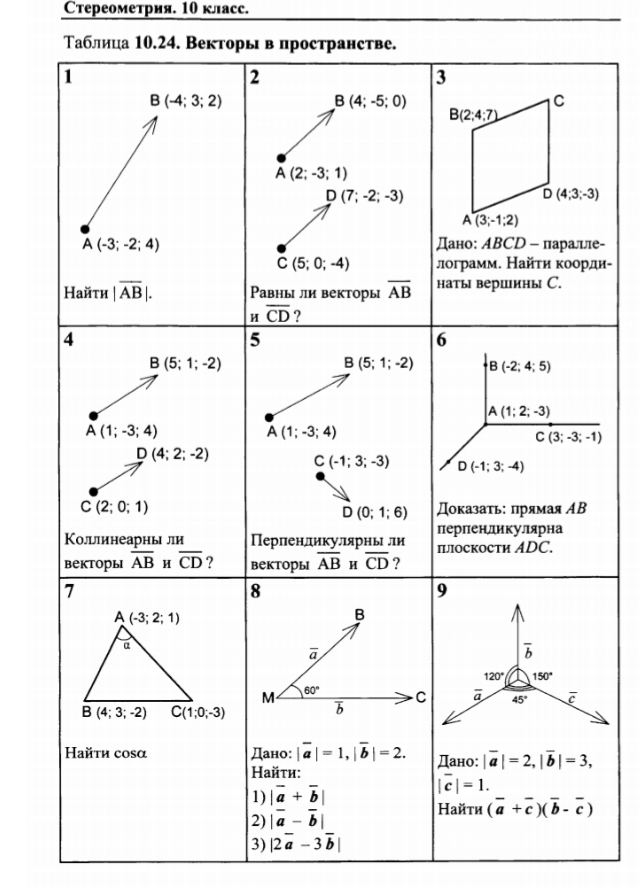
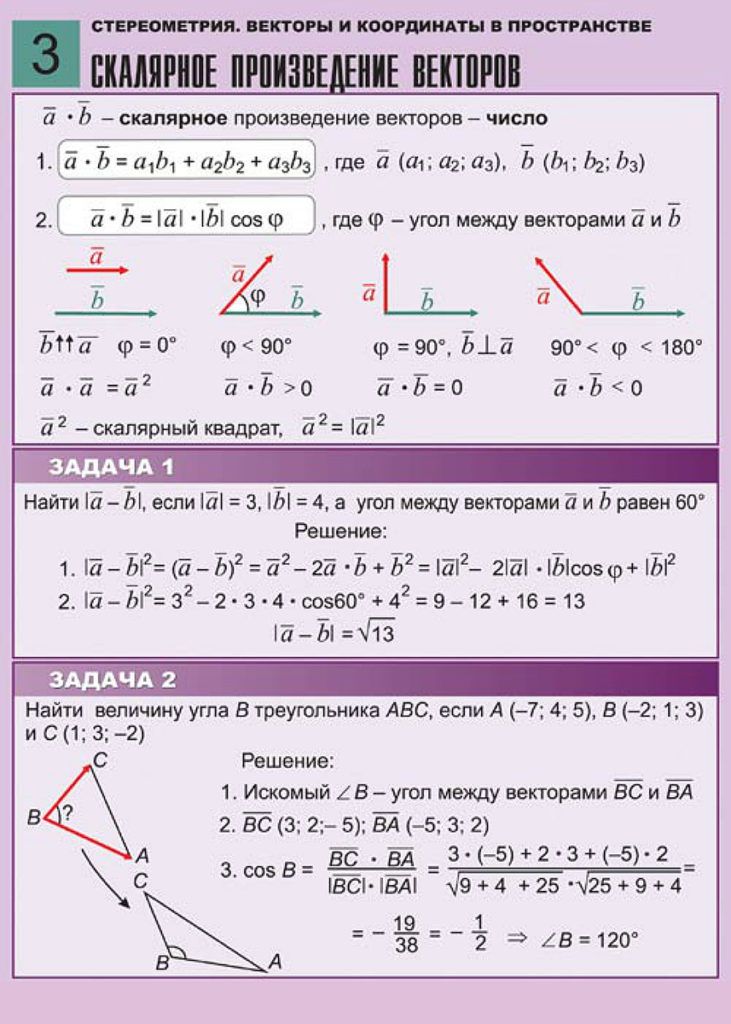
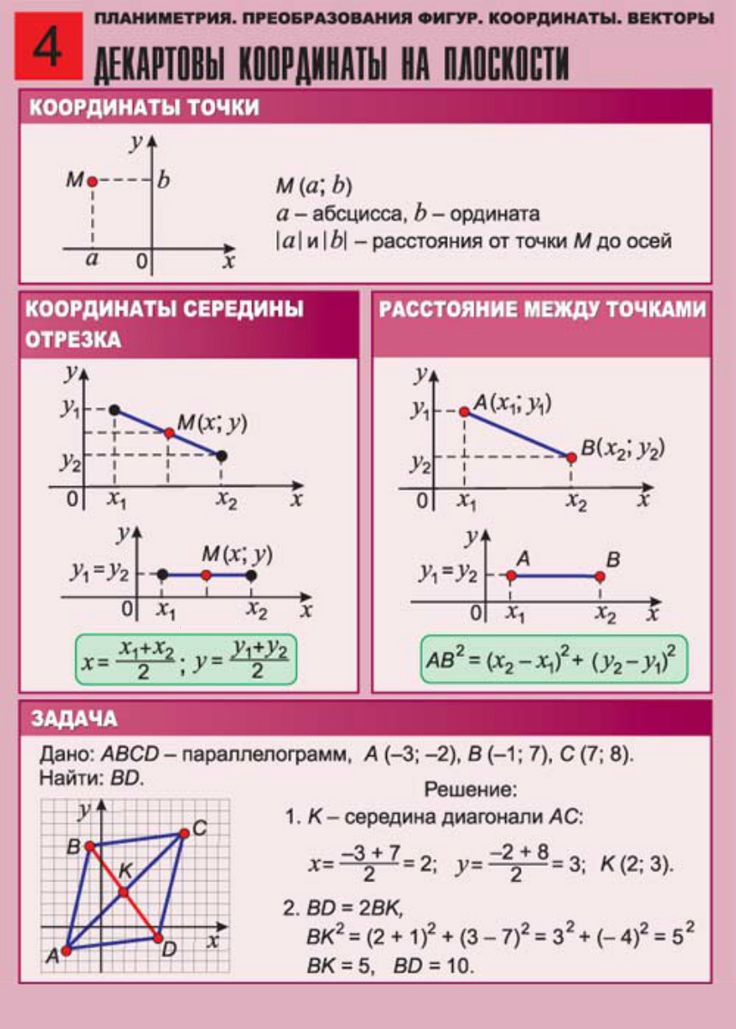 Единичный вектор в направлении оси x равен i , единичный вектор в направлении оси y равен j , а единичный вектор в направлении оси z равен k .
Единичный вектор в направлении оси x равен i , единичный вектор в направлении оси y равен j , а единичный вектор в направлении оси z равен k .
 Итак, умножьте коэффициенты i вместе, коэффициенты j вместе и коэффициенты k вместе и сложите их все.
Итак, умножьте коэффициенты i вместе, коэффициенты j вместе и коэффициенты k вместе и сложите их все.






 Вектор имеет как величину, так и направление, которое показано над направленным отрезком линии, где длина обозначает величину вектора, а стрелка указывает направление от хвоста к голове.
Вектор имеет как величину, так и направление, которое показано над направленным отрезком линии, где длина обозначает величину вектора, а стрелка указывает направление от хвоста к голове. Как правило, один вектор представлен в обеих формах — алфавитах в верхнем и нижнем регистре. Если вектор записан в виде AB, то A — это хвост, а B — голова.
Как правило, один вектор представлен в обеих формах — алфавитах в верхнем и нижнем регистре. Если вектор записан в виде AB, то A — это хвост, а B — голова. Векторы изначально были названы алгеброй отрезков и ориентированы на перемещения. Давайте посмотрим на некоторые преимущества, по которым студенты должны изучать векторы в школе, а также во время учебы в высших учебных заведениях.
Векторы изначально были названы алгеброй отрезков и ориентированы на перемещения. Давайте посмотрим на некоторые преимущества, по которым студенты должны изучать векторы в школе, а также во время учебы в высших учебных заведениях. Вектор любой физической величины представлен в виде прямой линии со стрелкой. В векторном определении длина прямой линии обозначает величину вектора, а острие стрелки указывает его направление. Любые два вектора можно рассматривать как идентичные векторы, если они имеют одинаковую величину и направление. Лучшим примером вектора является сила, приложенная к объекту, потому что и сила, и направление приложенной силы влияют на ее действие на объект. Вращение или перемещение вектора вокруг себя никогда не изменит его величину.Изображение будет скоро загружено.
Вектор любой физической величины представлен в виде прямой линии со стрелкой. В векторном определении длина прямой линии обозначает величину вектора, а острие стрелки указывает его направление. Любые два вектора можно рассматривать как идентичные векторы, если они имеют одинаковую величину и направление. Лучшим примером вектора является сила, приложенная к объекту, потому что и сила, и направление приложенной силы влияют на ее действие на объект. Вращение или перемещение вектора вокруг себя никогда не изменит его величину.Изображение будет скоро загружено.


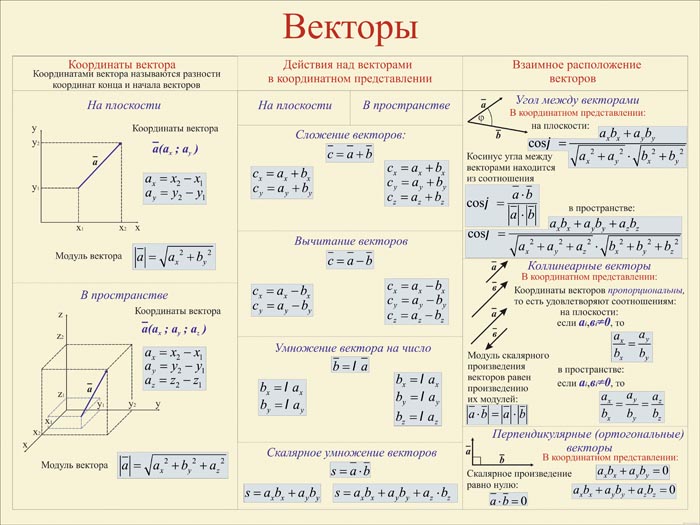 b = | a || b | cos θ
b = | a || b | cos θ
 Некоторые физические и геометрические величины, называемые скалярами, можно полностью определить, указав их величину в подходящих единицах измерения. Таким образом, масса может быть выражена в граммах, температура — в градусах по некоторой шкале, а время — в секундах. Скаляры могут быть представлены графически точками на некоторой числовой шкале, такой как часы или термометр. Также существуют величины, называемые векторами, которые требуют указания направления, а также величины. Скорость, сила и смещение являются примерами векторов.Векторная величина может быть представлена графически направленным линейным сегментом, обозначенным стрелкой, указывающей в направлении векторной величины, при этом длина сегмента представляет величину вектора.
Некоторые физические и геометрические величины, называемые скалярами, можно полностью определить, указав их величину в подходящих единицах измерения. Таким образом, масса может быть выражена в граммах, температура — в градусах по некоторой шкале, а время — в секундах. Скаляры могут быть представлены графически точками на некоторой числовой шкале, такой как часы или термометр. Также существуют величины, называемые векторами, которые требуют указания направления, а также величины. Скорость, сила и смещение являются примерами векторов.Векторная величина может быть представлена графически направленным линейным сегментом, обозначенным стрелкой, указывающей в направлении векторной величины, при этом длина сегмента представляет величину вектора.
 Таким образом, логично записать a + b = c .Это построение суммы c , a и b дает тот же результат, что и закон параллелограмма, в котором результирующее c задается диагональю A C параллелограмма, построенного на векторах. A B и A D как стороны. Поскольку положение начальной точки B вектора B C = b несущественно, отсюда следует, что B C = A D .На рисунке 1 показано, что A D + D C = A C , так что коммутативный закон
Таким образом, логично записать a + b = c .Это построение суммы c , a и b дает тот же результат, что и закон параллелограмма, в котором результирующее c задается диагональю A C параллелограмма, построенного на векторах. A B и A D как стороны. Поскольку положение начальной точки B вектора B C = b несущественно, отсюда следует, что B C = A D .На рисунке 1 показано, что A D + D C = A C , так что коммутативный закон

 Рисунок 2).Если a и b параллельны, a × b = 0. Величина a × b может быть представлена площадью параллелограмма, имеющей соседние a и b . стороны. Кроме того, поскольку вращение от b к a противоположно вращению от a к b ,
Рисунок 2).Если a и b параллельны, a × b = 0. Величина a × b может быть представлена площадью параллелограмма, имеющей соседние a и b . стороны. Кроме того, поскольку вращение от b к a противоположно вращению от a к b , Введение специальной системы отсчета или системы координат устанавливает соответствие между векторами и наборами чисел, представляющими компоненты векторов в этой системе координат, и вводит определенные правила работы с этими наборами чисел, которые следуют из правил операций на линии сегменты.
Введение специальной системы отсчета или системы координат устанавливает соответствие между векторами и наборами чисел, представляющими компоненты векторов в этой системе координат, и вводит определенные правила работы с этими наборами чисел, которые следуют из правил операций на линии сегменты. Когда два вектора A 1 и A 2 представлены как
Когда два вектора A 1 и A 2 представлены как Например, состояние газа обычно зависит от давления p , объема v , температуры T и времени t . Четверка чисел ( p , v , T , t ) не может быть представлена точкой в трехмерной системе отсчета. Но поскольку геометрическая визуализация не играет роли в алгебраических вычислениях, образный язык геометрии все еще можно использовать, введя четырехмерную систему отсчета, определяемую набором базовых векторов a 1 , a 2 , a 3 , a 4 с компонентами, определяемыми строками матрицы
Например, состояние газа обычно зависит от давления p , объема v , температуры T и времени t . Четверка чисел ( p , v , T , t ) не может быть представлена точкой в трехмерной системе отсчета. Но поскольку геометрическая визуализация не играет роли в алгебраических вычислениях, образный язык геометрии все еще можно использовать, введя четырехмерную систему отсчета, определяемую набором базовых векторов a 1 , a 2 , a 3 , a 4 с компонентами, определяемыми строками матрицы Поскольку положение конечной точки r зависит от времени, r является векторной функцией t . Его компоненты в направлениях декартовых осей, представленные в O , являются коэффициентами i , j и k в представлении
Поскольку положение конечной точки r зависит от времени, r является векторной функцией t . Его компоненты в направлениях декартовых осей, представленные в O , являются коэффициентами i , j и k в представлении В составе Windows 7 и 8.1 есть штатный скриншотер – утилита «Ножницы». А в Windows 10 их целых два: утилита «Ножницы» и современное UWP-приложение «Фрагмент и набросок». Последнее можно запустить клавишами Win+Shift+S или в системном центре уведомлений.
В составе Windows 7 и 8.1 есть штатный скриншотер – утилита «Ножницы». А в Windows 10 их целых два: утилита «Ножницы» и современное UWP-приложение «Фрагмент и набросок». Последнее можно запустить клавишами Win+Shift+S или в системном центре уведомлений.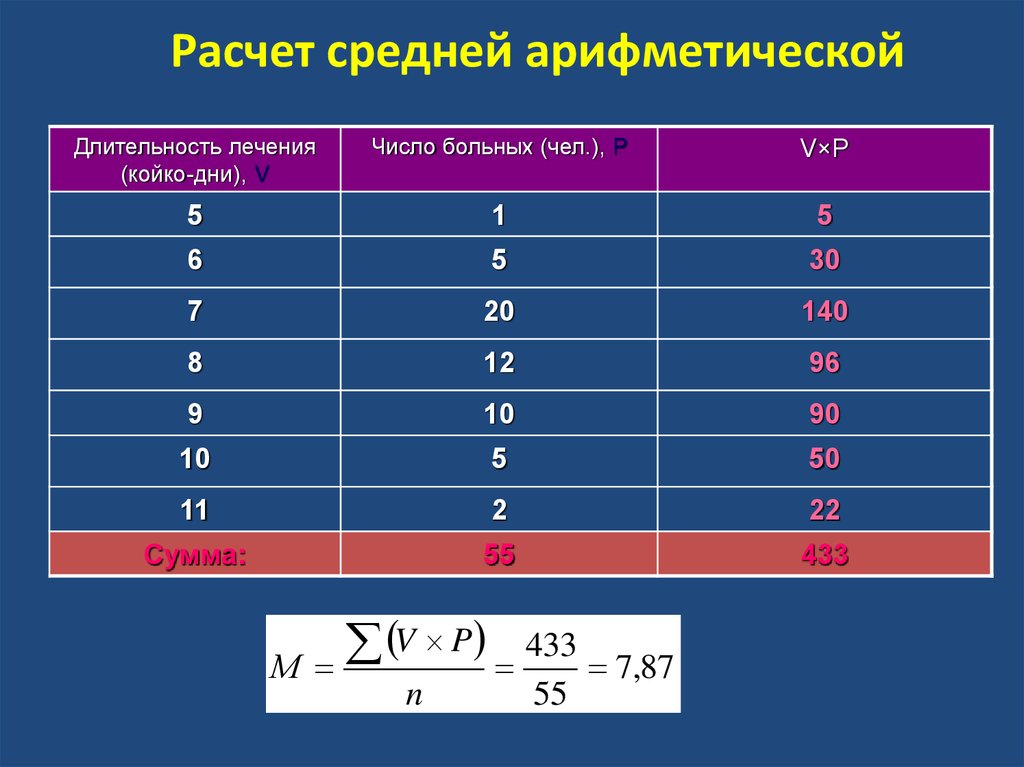 Поскольку в каждом треугольнике имеется три вершины, то в каждом треугольнике можно провести три медианы. … Медиана треугольника делит его на два треугольника равной площади (равновеликих треугольника).
Поскольку в каждом треугольнике имеется три вершины, то в каждом треугольнике можно провести три медианы. … Медиана треугольника делит его на два треугольника равной площади (равновеликих треугольника).

 Если квадрат наибольшей стороны больше суммы квадратов двух других сторон: с² > a²+b² – треугольник тупоугольный.
Если квадрат наибольшей стороны больше суммы квадратов двух других сторон: с² > a²+b² – треугольник тупоугольный. Тупоугольный треугольник — треугольник, все стороны которого есть тупой угол.
Тупоугольный треугольник — треугольник, все стороны которого есть тупой угол.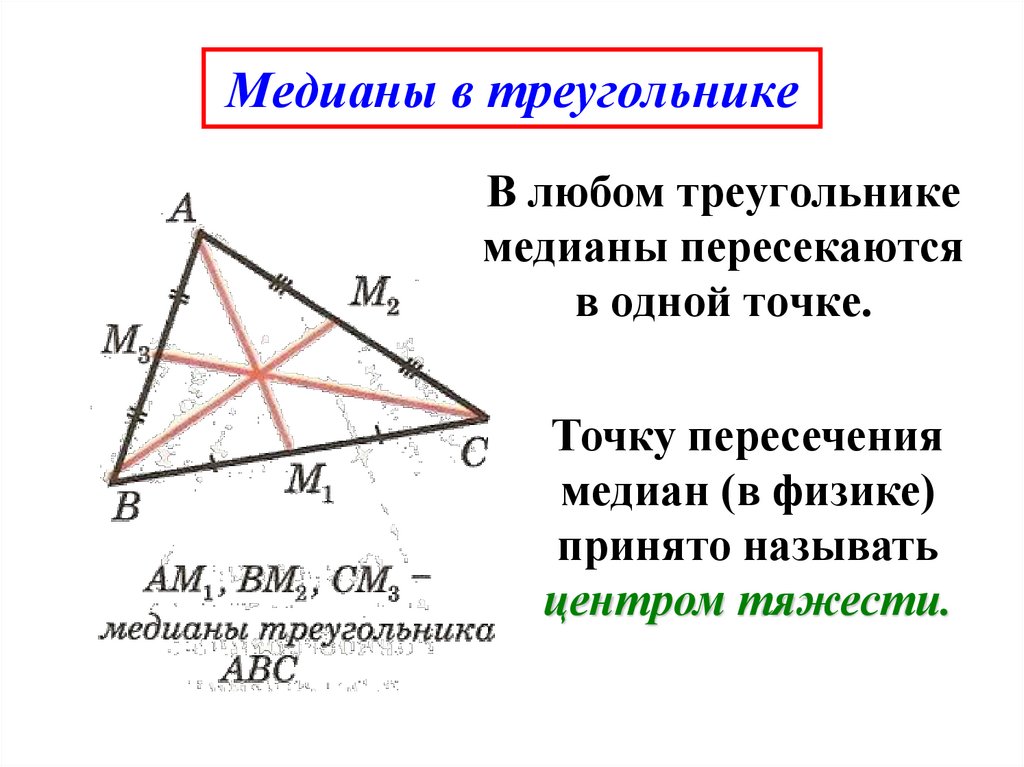 Длина гипотенузы может быть найдена различными способами. Если известна длина обоих катетов, то ее размер вычисляется по теореме Пифагора: сумма квадратов двух катетов равняется квадрату гипотенузы. К примеру: катет a = 3 см, катет b = 4 см.
Длина гипотенузы может быть найдена различными способами. Если известна длина обоих катетов, то ее размер вычисляется по теореме Пифагора: сумма квадратов двух катетов равняется квадрату гипотенузы. К примеру: катет a = 3 см, катет b = 4 см. Длина гипотенузы прямоугольного треугольника может быть найдена с помощью теоремы Пифагора: Квадрат длины гипотенузы равен сумме квадратов длин катетов.
Длина гипотенузы прямоугольного треугольника может быть найдена с помощью теоремы Пифагора: Квадрат длины гипотенузы равен сумме квадратов длин катетов.

 тг) на начало каждого месяца:
тг) на начало каждого месяца:
 В разделе Справка вы найдете обучающие видео.
В разделе Справка вы найдете обучающие видео. Нажимте кнопку «исправить матрицу» чтобы исправить матрицу или кнопку «справка» чтобы открыть справку о формате матрицы
Нажимте кнопку «исправить матрицу» чтобы исправить матрицу или кнопку «справка» чтобы открыть справку о формате матрицы
 ..
..
 Кликните по любой вершине графа
Кликните по любой вершине графа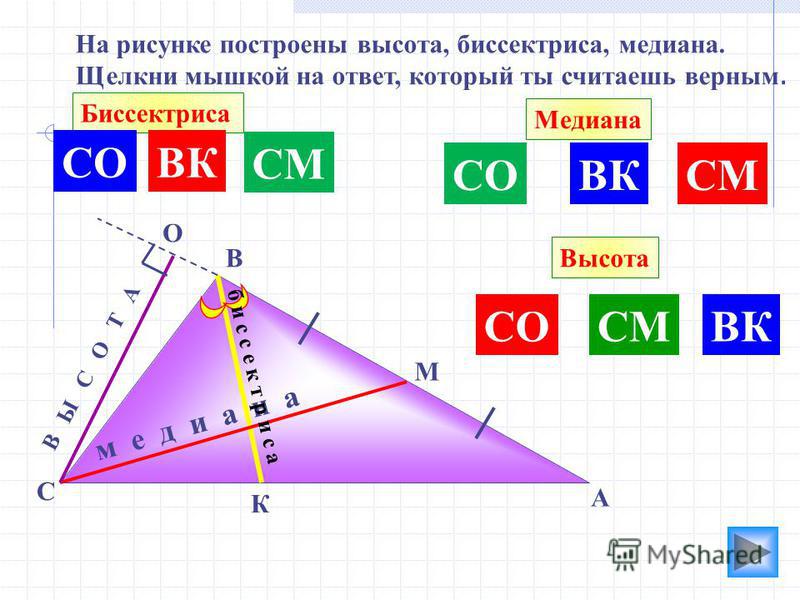 Решение задач и контрольных работ по статистике онлайн
Решение задач и контрольных работ по статистике онлайн
 Самый известный квантиль – медиана, делящая совокупность на две равные части. Кроме медианы часто используются квартили, делящие ранжированный ряд на 4 равные части, децили -10 частей и перцентили — на 100
частей.
Самый известный квантиль – медиана, делящая совокупность на две равные части. Кроме медианы часто используются квартили, делящие ранжированный ряд на 4 равные части, децили -10 частей и перцентили — на 100
частей.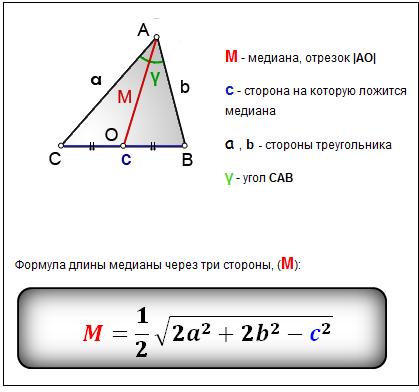 Для определения этого интервала сумму частот
делят пополам и на основании последовательного накопления (суммирования)
частот интервалов, начиная с первого, находят интервал, где расположена
медиана. Значение медианы в интервальном ряду вычисляют по формуле:
Для определения этого интервала сумму частот
делят пополам и на основании последовательного накопления (суммирования)
частот интервалов, начиная с первого, находят интервал, где расположена
медиана. Значение медианы в интервальном ряду вычисляют по формуле: Для интервального ряда:
Для интервального ряда: 5
5


 р.,
другая половина — более 28 тыс.р.
р.,
другая половина — более 28 тыс.р. 2
2
 15
15
 Половина детей имеет возраст менее 7,3 лет, другая половина – более 7,3
лет.
Половина детей имеет возраст менее 7,3 лет, другая половина – более 7,3
лет. Вместо этого во многих регионах страны были выполнены (иногда неоднократно) автономные проекты, включающие исследование КЙМ у школьников (реже – у других групп населения) с расчетом медианной КЙМ (мКЙМ) или, просто говоря, “медианы йодурии”. Несмотря на недостатки такого подхода (отсутствие единых критериев выбора кластеров и целевых групп населения), уже к началу нулевых годов исследования были проведены во всех федеральных округах и большинстве крупных регионов и показали, что практически на всей территории Российской Федерации потребление йода было недостаточным [1]. Снижение мКЙМ выявили даже там, где его меньше всего ожидали, – на берегу Черного моря и у жителей острова Сахалин, за исключением небольшой популяции корейцев, традиционно использующих в питании много морепродуктов и морских водорослей.
Вместо этого во многих регионах страны были выполнены (иногда неоднократно) автономные проекты, включающие исследование КЙМ у школьников (реже – у других групп населения) с расчетом медианной КЙМ (мКЙМ) или, просто говоря, “медианы йодурии”. Несмотря на недостатки такого подхода (отсутствие единых критериев выбора кластеров и целевых групп населения), уже к началу нулевых годов исследования были проведены во всех федеральных округах и большинстве крупных регионов и показали, что практически на всей территории Российской Федерации потребление йода было недостаточным [1]. Снижение мКЙМ выявили даже там, где его меньше всего ожидали, – на берегу Черного моря и у жителей острова Сахалин, за исключением небольшой популяции корейцев, традиционно использующих в питании много морепродуктов и морских водорослей. В отличие от ряда других стран (например, Китая) только в одном населенном пункте России (г. Туринске Свердловской области) был выявлен природный избыток йода в питьевой воде, а мКЙМ у школьников составила 719 мкг/л, что было примерно в 6 раз выше, чем в соседнем городе [2].
В отличие от ряда других стран (например, Китая) только в одном населенном пункте России (г. Туринске Свердловской области) был выявлен природный избыток йода в питьевой воде, а мКЙМ у школьников составила 719 мкг/л, что было примерно в 6 раз выше, чем в соседнем городе [2]. Часто получалось, что мКЙМ у школьников на фоне проводимых профилактических мероприятий возрастала до оптимальных показателей, в то время как частота зоба если и снижалась, то ненамного и оставалась выше эндемического порога в 5%.
Часто получалось, что мКЙМ у школьников на фоне проводимых профилактических мероприятий возрастала до оптимальных показателей, в то время как частота зоба если и снижалась, то ненамного и оставалась выше эндемического порога в 5%. У некоторых исследователей даже возникало впечатление, что для исследования йодного статуса населения необходимо применять всю батарею индикаторов (частоту зоба, экскрецию йода с мочой, уровень тиреоглобулина в крови и частоту повышения более 3% уровней неонатального тиреотропного гормона (ТТГ) свыше 5 мИЕ/л). Только в самой последней редакции руководства ВОЗ, ЮНИСЕФ и ГСЙ [6], выпущенной в 2007 г., приоритетным и наиболее информативным методом оценки текущего статуса йодной обеспеченности населения было названо определение йода в моче.
У некоторых исследователей даже возникало впечатление, что для исследования йодного статуса населения необходимо применять всю батарею индикаторов (частоту зоба, экскрецию йода с мочой, уровень тиреоглобулина в крови и частоту повышения более 3% уровней неонатального тиреотропного гормона (ТТГ) свыше 5 мИЕ/л). Только в самой последней редакции руководства ВОЗ, ЮНИСЕФ и ГСЙ [6], выпущенной в 2007 г., приоритетным и наиболее информативным методом оценки текущего статуса йодной обеспеченности населения было названо определение йода в моче. С любезного согласия д-ра Р. Купки, советника по микронутриентам штаб-квартиры ЮНИСЕФ в Нью-Йорке, наш журнал опубликовал в этом номере перевод данных рекомендаций с небольшой редакторской адаптацией [8].
С любезного согласия д-ра Р. Купки, советника по микронутриентам штаб-квартиры ЮНИСЕФ в Нью-Йорке, наш журнал опубликовал в этом номере перевод данных рекомендаций с небольшой редакторской адаптацией [8]. Все это не новости. Новость в том, что впервые четко сформулирована рекомендация прекратить исследование распространенности зоба при рутинных обследованиях статуса йодной обеспеченности населения, отдавая предпочтение анализу показателей мКЙМ, являющейся наилучшим индикатором потребления йода с питанием.
Все это не новости. Новость в том, что впервые четко сформулирована рекомендация прекратить исследование распространенности зоба при рутинных обследованиях статуса йодной обеспеченности населения, отдавая предпочтение анализу показателей мКЙМ, являющейся наилучшим индикатором потребления йода с питанием.
 И если в уездном городе N мКЙМ у школьников оптимальная, это может не отражать статус йодной обеспеченности у остальных обывателей, не охваченных заботой государства российского.
И если в уездном городе N мКЙМ у школьников оптимальная, это может не отражать статус йодной обеспеченности у остальных обывателей, не охваченных заботой государства российского. По мнению ведущих специалистов4 , диапазоны мКЙМ у детей в целом должны с определенной осторожностью распространяться на взрослых лиц, нормативы для которых пока еще не разработаны.
По мнению ведущих специалистов4 , диапазоны мКЙМ у детей в целом должны с определенной осторожностью распространяться на взрослых лиц, нормативы для которых пока еще не разработаны. Об этом писали уже не раз, но ошибки в интерпретации данных носили массовый характер.
Об этом писали уже не раз, но ошибки в интерпретации данных носили массовый характер.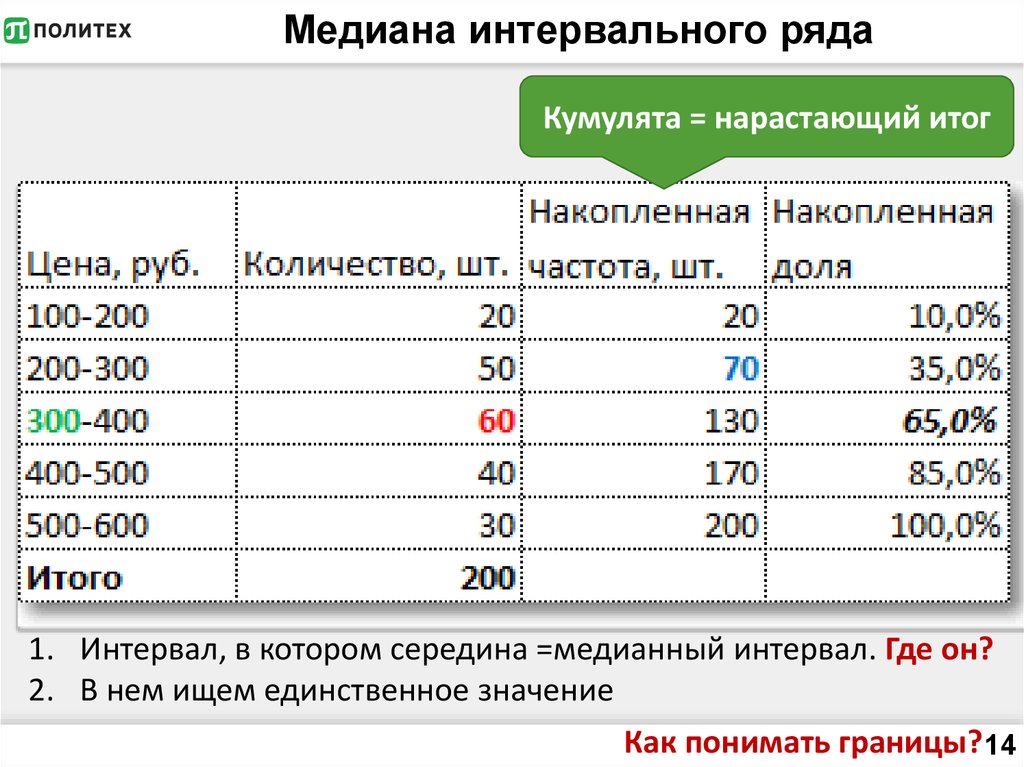


 В 2015 г. такой скрининг проводился в 85 субъектах Федерации, а доля охвата новорожденных скринингом составила 99,1% [14]. Учитывая то, что все лаборатории уже имеют базы данных по уровню ТТГ у новорожденных, на мой взгляд, не должно возникнуть существенных проблем с расчетом процентной доли уровней ТТГ в крови свыше 5 мМЕ/л. По крайней мере, такие наблюдения в течение уже более 20 лет проводят в Тюменской области. И за этот период времени частота неонатального ТТГ снизилась с 44% в 1993 г. до 5,0–5,4% в 2013–2015 гг. [15].
В 2015 г. такой скрининг проводился в 85 субъектах Федерации, а доля охвата новорожденных скринингом составила 99,1% [14]. Учитывая то, что все лаборатории уже имеют базы данных по уровню ТТГ у новорожденных, на мой взгляд, не должно возникнуть существенных проблем с расчетом процентной доли уровней ТТГ в крови свыше 5 мМЕ/л. По крайней мере, такие наблюдения в течение уже более 20 лет проводят в Тюменской области. И за этот период времени частота неонатального ТТГ снизилась с 44% в 1993 г. до 5,0–5,4% в 2013–2015 гг. [15].




 Диффуравнение, для которого определено начальное условие в представленном формате, называется уравнением с заданной задачей Коши.
Диффуравнение, для которого определено начальное условие в представленном формате, называется уравнением с заданной задачей Коши.



 Это уравнения,
связывающие независимые переменные ,
неизвестную функцию этих переменных и её частные производные по тем же переменным. Но мы будем рассматривать только обыкновенные дифференциальные уравнения и поэтому будем для краткости опускать слово «обыкновенные».
Это уравнения,
связывающие независимые переменные ,
неизвестную функцию этих переменных и её частные производные по тем же переменным. Но мы будем рассматривать только обыкновенные дифференциальные уравнения и поэтому будем для краткости опускать слово «обыкновенные». Только в уравнении (3) содержатся явно все производные, функция и независимая переменная.
Только в уравнении (3) содержатся явно все производные, функция и независимая переменная. е.
е.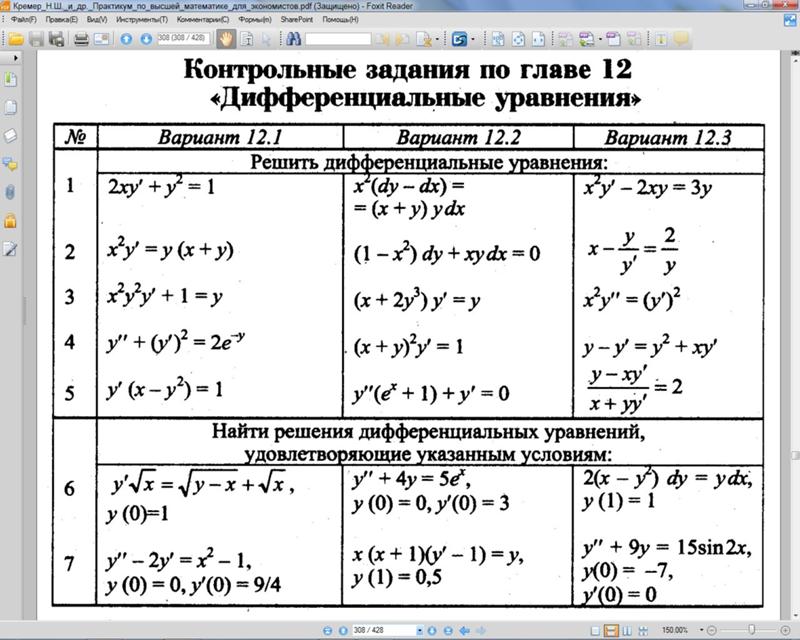 В общее решение уравнения подставляют значения и
и находят значение произвольной постоянной C,
а затем частное решение уравнения при найденном значении C. Это и есть решение задачи Коши.
В общее решение уравнения подставляют значения и
и находят значение произвольной постоянной C,
а затем частное решение уравнения при найденном значении C. Это и есть решение задачи Коши.
 Таков следующий пример.
Таков следующий пример.
 {-3 x}
\)
{-3 x}
\) Решение задач и контрольных работ по высшей математике онлайн
Решение задач и контрольных работ по высшей математике онлайн
 Характеристическое уравнение и дает
возможность найти
. Это уравнение второй степени, поэтому
имеет два корня. Обозначим их через
и
. Возможны три случая:
Характеристическое уравнение и дает
возможность найти
. Это уравнение второй степени, поэтому
имеет два корня. Обозначим их через
и
. Возможны три случая:
 Рассмотрим
некоторые случаи:
Рассмотрим
некоторые случаи:

 Дифференциальное уравнение (ДУ) – это уравнение, которое связывает значение некоторой неизвестной функции в некоторой точке со значением производных этой функции различных порядков в той же точке. В состав ДУ входит неизвестная функция под знаком производной или дифференциала. Обыкновенное дифференциальное уравнение (ОДУ) – имеет неизвестную функцию с одной переменной. Уравнение частными производными (УРЧП) — неизвестная функция зависит от многих переменных. Стохастическое дифференциальное уравнение (СДУ) — включающее случайные процессы. Изучение дифференциальных уравнений по видео урокам будет полезно как для начинающих, так и для более опытных математиков. Видеоуроки из рубрики Дифференциальные уравнения Вы можете смотреть бесплатно в любое удобное время. К некоторым видео урокам по дифференциальным уравнениям приложены дополнительные материалы, которые можно скачать. Приятного Вам обучения!
Дифференциальное уравнение (ДУ) – это уравнение, которое связывает значение некоторой неизвестной функции в некоторой точке со значением производных этой функции различных порядков в той же точке. В состав ДУ входит неизвестная функция под знаком производной или дифференциала. Обыкновенное дифференциальное уравнение (ОДУ) – имеет неизвестную функцию с одной переменной. Уравнение частными производными (УРЧП) — неизвестная функция зависит от многих переменных. Стохастическое дифференциальное уравнение (СДУ) — включающее случайные процессы. Изучение дифференциальных уравнений по видео урокам будет полезно как для начинающих, так и для более опытных математиков. Видеоуроки из рубрики Дифференциальные уравнения Вы можете смотреть бесплатно в любое удобное время. К некоторым видео урокам по дифференциальным уравнениям приложены дополнительные материалы, которые можно скачать. Приятного Вам обучения! Здесь приводится доказательство и формулировка геометрического смысла дифференциального уравнения как уравнения, которое определяет в некоторой области поле направлений, совпадающее с касательными к графикам решений этого уравнения — интегральными кривыми. Это позволяет, не решая дифференциального уравнения, строить графики его решений. На данном занятии также рассматривается пример, в котором требуется приближенно…
Здесь приводится доказательство и формулировка геометрического смысла дифференциального уравнения как уравнения, которое определяет в некоторой области поле направлений, совпадающее с касательными к графикам решений этого уравнения — интегральными кривыми. Это позволяет, не решая дифференциального уравнения, строить графики его решений. На данном занятии также рассматривается пример, в котором требуется приближенно… ..
.. Решить его можно с помощью соответствующей замены переменной, в результате которого происходит преобразование исходного уравнения к уравнению первого порядка. Такое преобразование называется понижение порядка. На этом занятии дана схема последовательная…
Решить его можно с помощью соответствующей замены переменной, в результате которого происходит преобразование исходного уравнения к уравнению первого порядка. Такое преобразование называется понижение порядка. На этом занятии дана схема последовательная… В первой части занятия будет сформулировано определение, какое дифференциальное уравнение первого порядка, выраженное через дифференциалы своих переменных, называется уравнением в полных дифференциалах. Здесь вы также научитесь определять, является ли заданное уравнение, уравнением в полных дифференциалах. В данном видео уроке кроме теоретического материала…
В первой части занятия будет сформулировано определение, какое дифференциальное уравнение первого порядка, выраженное через дифференциалы своих переменных, называется уравнением в полных дифференциалах. Здесь вы также научитесь определять, является ли заданное уравнение, уравнением в полных дифференциалах. В данном видео уроке кроме теоретического материала… В этом видео…
В этом видео… При такой записи говорят, что дифференциальное уравнение представлено в симметричной форме. При этом переменные x и y равноправны, и каждую из них можно рассматривать как функцию другой. На этом занятии рассказывается, как решать такие уравнения. Решение производится путем преобразования исходного…
При такой записи говорят, что дифференциальное уравнение представлено в симметричной форме. При этом переменные x и y равноправны, и каждую из них можно рассматривать как функцию другой. На этом занятии рассказывается, как решать такие уравнения. Решение производится путем преобразования исходного… Для этого Вам необходимо загрузить их на видеохостинг (например, YouTube) и добавить код видео в форму добавления уроков. Возможность добавлять свои материалы доступна только для зарегистрированных пользователей.
Для этого Вам необходимо загрузить их на видеохостинг (например, YouTube) и добавить код видео в форму добавления уроков. Возможность добавлять свои материалы доступна только для зарегистрированных пользователей.
 По II закону Ньютона где – ускорение движущегося тела, – сумма сил, действующих на тело – силы тяжести и силы сопротивления воздуха. Таким образом, имеем уравнение, связывающее искомую функцию v(t) и ее производную
По II закону Ньютона где – ускорение движущегося тела, – сумма сил, действующих на тело – силы тяжести и силы сопротивления воздуха. Таким образом, имеем уравнение, связывающее искомую функцию v(t) и ее производную Переходя к реальным объектам исследования, студенты, инженеры и аспиранты сталкиваются с более сложными моделями и их математической реализацией. Даже в кругах исследователей – «чистых математиков» довольно долго интегрирование уравнений в квадратурах, теоретико-групповой подход к уравнениям считались тупиковой ветвью в науке. Тем не менее, теория обыкновенных дифференциальных уравнений является базой для уравнений математической физики и, кроме того, развитие современной физики показало, что именно те самые редкие и хорошо изученные случаи и представляют наибольший физический интерес. А успехи, достигнутые в ряде разделов математики – в алгебраической топологии, дифференциальной геометрии и коммутативной алгебре, позволяют надеяться на то, что общая теория уравнений с частными производными будет построена.
Переходя к реальным объектам исследования, студенты, инженеры и аспиранты сталкиваются с более сложными моделями и их математической реализацией. Даже в кругах исследователей – «чистых математиков» довольно долго интегрирование уравнений в квадратурах, теоретико-групповой подход к уравнениям считались тупиковой ветвью в науке. Тем не менее, теория обыкновенных дифференциальных уравнений является базой для уравнений математической физики и, кроме того, развитие современной физики показало, что именно те самые редкие и хорошо изученные случаи и представляют наибольший физический интерес. А успехи, достигнутые в ряде разделов математики – в алгебраической топологии, дифференциальной геометрии и коммутативной алгебре, позволяют надеяться на то, что общая теория уравнений с частными производными будет построена.
 График решения (интеграла) дифференциального уравнения называется интегральной кривой.
График решения (интеграла) дифференциального уравнения называется интегральной кривой. Таких уравнений сравнительно немного. В нашем курсе мы рассмотрим основные типы дифференциальных уравнений, интегрируемых в квадратурах.
Таких уравнений сравнительно немного. В нашем курсе мы рассмотрим основные типы дифференциальных уравнений, интегрируемых в квадратурах. 9{ αx } \ [ \ c_{1} \ cos( βx) + c_{2} \ sin( βx) \ ] \]
9{ αx } \ [ \ c_{1} \ cos( βx) + c_{2} \ sin( βx) \ ] \] Решение представляет собой функцию x относительно y .
Решение представляет собой функцию x относительно y . Коэффициенты y´´ , y´ и y равны 1 , 4 и 0 соответственно.
Коэффициенты y´´ , y´ и y равны 1 , 4 и 0 соответственно.
 {2} + br + c = 0\) — вещественные различные корни. 9{2} + br + c = 0\), повторяются, т. е. двойных, корней. Мы будем использовать понижение порядка, чтобы получить второе решение, необходимое для получения общего решения в этом случае.
{2} + br + c = 0\) — вещественные различные корни. 9{2} + br + c = 0\), повторяются, т. е. двойных, корней. Мы будем использовать понижение порядка, чтобы получить второе решение, необходимое для получения общего решения в этом случае. Мы также дадим и альтернативный метод нахождения вронскиана.
Мы также дадим и альтернативный метод нахождения вронскиана. Мы также допускаем введение в систему демпфера и действия общих внешних сил на объект. Также обратите внимание, что, хотя в этом разделе мы приводим примеры механических вибраций, простое изменение обозначений (и соответствующее изменение в том, что представляют величины) может перенести это практически в любую другую область техники.
Мы также допускаем введение в систему демпфера и действия общих внешних сил на объект. Также обратите внимание, что, хотя в этом разделе мы приводим примеры механических вибраций, простое изменение обозначений (и соответствующее изменение в том, что представляют величины) может перенести это практически в любую другую область техники.
 ) = 0
) = 0 Ответ на этот вопрос зависит от констант p и q .
Ответ на этот вопрос зависит от констант p и q . 4)(r − 5) = 0
4)(r − 5) = 0 е. оба действительных корня равны).
е. оба действительных корня равны).