от литературных затей до шахмат»
Сайт «Занимательные и методические материалы из книг Игоря Сухина: от литературных затей до шахмат»
Сайт «Занимательные и методические материалы из книг Игоря Сухина: от литературных затей до шахмат»
Избранные страницы из книги И.Г.Сухина «800 новых логических и математических головоломок» (часть 2)
ЧАСТЬ 1 РАСПОЛОЖЕНА ЗДЕСЬ
И.Г. СУХИН
НАТУРАЛЬНЫЕ, ПРОСТЫЕ, СОСТАВНЫЕ, ЧЁТНЫЕ, НЕЧЁТНЫЕ, КРУГЛЫЕ
Шпаргалка
Цифры: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Однозначные числа: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Натуральные числа: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13…
Простые числа: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41…
Составные числа: 4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 22…
Чётные числа: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26…
Нечётные числа: 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25…
Круглые числа: 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 110, 120…
Примечание: в задачах на вычитание уменьшаемое не должно быть меньше вычитаемого.
И.Г. СУХИН
Задачи из тетради гнома Загадалки
ОТ НУЛЯ ДО ДЕВЯТИ
(однозначные числа)
1. Что больше: наименьшее натуральное число или наименьшее простое?
2. Что меньше: самое маленькое натуральное число или самое маленькое однозначное?
3. Что больше: наименьшее чётное число или наименьшее нечётное?
4. Какое однозначное число не является натуральным?
5. Сумма двух неких однозначных чисел равна их разности. Назови одно из них.
6. Сумма двух слагаемых равна первому слагаемому. Назови второе слагаемое.
7. Сумма трёх одинаковых однозначных чисел равна их произведению. Что это за числа?
8. Какое из натуральных чисел наименьшее?
9. Произведение двух натуральных чисел равно частному от их деления. Назови один из сомножителей и делитель.
10. Произведение двух натуральных чисел меньше их суммы. Назови одно из чисел.
11. Если произведение двух натуральных чисел – простое число, то чему равен меньший сомножитель?
12. Сумма девяти натуральных чисел – однозначное число. Что это за числа?
13. Произведение двух неких натуральных чисел не является ни простым, ни составным числом. Что это за числа?
14. Какое натуральное число в 4 раза меньше самого маленького составного числа?
15. Сумма двух однозначных чисел в 2 раза больше их произведения. Какие это числа?
16. Какое чётное число является простым?
17. Чему равна наименьшая разность неодинаковых нечётных чисел?
18. Назови все чётные простые числа.
19. Сумма двух неких простых чисел есть нечётное число. Назови одно из слагаемых.
20. Произведение трёх простых чисел – однозначное число. Что это за числа?
21. Сумма четырёх чётных чисел – однозначное число. Какие это числа?
22. Произведение двух простых чисел равно их сумме. Что это за числа?
23. Сумма двух чётных чисел – однозначное число. Чему равно меньшее слагаемое?
24. Подсчитай сумму двух простых чётных чисел.
25. Вычти из наибольшего однозначного числа наименьшее простое. Сколько получилось?
26. Какое однозначное простое число больше 5?
27. Вычти из самого большого однозначного числа самое маленькое натуральное. Каков ответ?
28. Сумма двух однозначных чисел равна 1. Назови эти числа.
29. Разность двух однозначных чисел равна 9. Что это за числа?
30. Сумма двух натуральных чисел равна 3. Назови слагаемые.
31. Сумма двух чисел равна 4, а разность – в 2 раза меньше. Что это за числа?
32. Частное от деления двух однозначных чисел равно 5. Назови эти числа.
33. Произведение двух однозначных чисел равно 7. Что это за числа?
34. Сумма двух натуральных чисел равна 9, а произведение есть число однозначное. Найди эти числа.
35. Разность двух неодинаковых однозначных чисел равна 8. Назови эти числа.
36. Разность двух нечётных однозначных чисел равна 8. Какие это числа?
37. Произведение каких различных простых чисел будет числом однозначным?
38. Если сумма двух чётных чисел равна 6, то каковы слагаемые?
39. Если произведение двух неодинаковых чётных однозначных чисел – также число однозначное, то что это за числа?
40. Произведение двух однозначных чисел в 4 раза больше их разности. Вычисли эти числа.
41. Сумма каких двух простых чисел равна наибольшему однозначному простому числу?
42. Разность двух чисел равна 4, а сумма – в 2 раза больше. Что это за числа?
43. Сумма двух простых чисел равна 9. Назови эти числа.
44. Разность двух однозначных чётных чисел равна 6. Что это за числа?
45. Сумма двух простых чисел равна 8. Какие это числа?
46. Какие два соседних числа натурального ряда надо сложить, чтобы получить наибольшее однозначное число?
47. Сумма каких трёх последовательных чисел натурального ряда равна их произведению?
48. Каким натуральным числам не может равняться сумма нескольких простых чисел?
49. Какие три последовательных числа натурального ряда надо сложить, чтобы получить наибольшее однозначное число?
50. Если частное от деления двух неодинаковых однозначных чётных чисел будет числом нечётным, то чему равны частное и эти чётные числа?
И.Г. СУХИН
ОТ НУЛЯ ДО ДВАДЦАТИ
(однозначные и двузначные числа)
51. Если сумма двух неодинаковых однозначных чисел равна 16, то чему равна их разность?
52. Разность двух чётных однозначных чисел равняется 6. Вычисли их сумму.
53. Если разность двух нечётных однозначных чисел равна 8, то чему равна их сумма?
54. Подсчитай сумму самого маленького простого числа и самого большого однозначного.
55. Найди наибольшую сумму двух однозначных чисел.
56. Произведение однозначного и двузначного чисел равно 15. Найди эти числа.
57. Произведение двух неодинаковых однозначных чисел равно 16. Что это за числа?
58. Произведение двух однозначных чисел равняется 15. Каковы сомножители?
59. Сумма двух неодинаковых простых чисел равна 14. Назови слагаемые.
60. Произведение двух однозначных чисел равно 20. Что это за числа?
61. Сумма двух разных чётных однозначных чисел равна 12. Какие это числа?
62. Сумма двух простых чисел равна 12. Каковы слагаемые?
63. Сумма двух разных нечётных однозначных чисел равна 14. Назови их.
64. Сумма двух однозначных чисел равна 15, а разность – 3. Вычисли эти числа.
65. Сумма двух однозначных чисел равна 17. Что это за числа?
66. Разность двузначного и однозначного чисел равна единице. Каковы уменьшаемое и вычитаемое?
67. Даны 4 разных однозначных числа. Первое – 9. Если умножить 9 на второе, то получим столько же, сколько и при умножении третьего на четвёртое. Назови неизвестные числа.
68. Даны 4 неодинаковых однозначных числа. Известно, что первое – 2, а числа 9 среди них нет. Если умножить 2 на второе, то получим столько же, сколько и при перемножении третьего и четвёртого. Каковы неизвестные числа?
69. Какие последовательные числа натурального ряда надо сложить, чтобы получить наименьшее двузначное число?
70. Сумма нескольких разных простых чисел равна 17. Назови эти числа.
71. Что меньше: сумма чётных однозначных чисел или сумма простых однозначных чисел?
И.Г. СУХИН
СЮЖЕТНЫЕ ЗАДАЧИ
156. Какую отметку впервые в жизни получил по математике Фома, если известно, что она является числом не простым, а составным?
157. Таня послала Игорю некоторое чётное число писем, а Игорь Тане – на 2 письма больше. При этом общее число писем есть число однозначное. Какое?
158. Сколько всего мячей оказалось на поле во время матча между командами «Зубило» и «Шайба», когда старик Хоттабыч наколдовал каждому футболисту по одному мячу?
159. Сколько яиц снесла за месяц курочка ряба, если известно, что число их не составное, а простое, больше 19, но меньше 29?
160. Сколько лет сиднем просидел на печи Илья Муромец? Известно, что если бы он просидел ещё 2 раза по столько, то его возраст составил бы наибольшее двузначное число.
161. В какой известной сказке богатырей можно было бы выстроить несколькими равными рядами по 11 в каждом ряду? Каково число богатырей?
162. Барон Мюнхгаузен по секрету сообщил нам, что он пересчитал число волшебных волос в бороде старика Хоттабыча. Оно оказалось равным сумме наименьшего трёхзначного числа и наибольшего двузначного. Что это за число?
163. Если наибольшее двузначное число ты умножишь на 4 и прибавишь 4, то узнаешь, сколько муравьёв послал Артемон, чтобы перегрызть верёвку, на которой разбойники повесили за ноги главного героя сказки А.Толстого «Золотой ключик, или Приключения Буратино».
164. Раздели самое маленькое четырёхзначное число на наименьшее простое и узнаешь, сколько лет не умывалась, не чистила зубы и даже пальцем не прикасалась к воде злая волшебница Гингема из повести-сказки А.Волкова «Волшебник Изумрудного города».
165. В русской народной сказке «Притворная болезнь» у трёх чудищ было разное однозначное число голов, кратное трём. Какое?
166. В русской народной сказке «Хрустальная гора» Иван-царевич сражался по очереди с тремя змеями. У первого из них было в 2 раза меньше голов, чем у второго, а у второго – в 2 раза меньше, чем у третьего. Общее число голов у змеев – 21. Сколько голов было у каждого змея до встречи с Иваном-царевичем?
167. Сколько голов у каждого чуда-юда из русской народной сказки «Иван – коровий сын», если известно, что у второго чуда-юда на три головы больше, чем у первого, а у третьего – на 3 больше, чем у второго, причём всего голов было – 27?
И.Г. СУХИН
ИСПРАВЛЕНИЕ, ЗАЧЁРКИВАНИЕ, ПРЕВРАЩЕНИЕ, ОТГАДЫВАНИЕ ЦИФР И ЧИСЕЛ
Задачи из тетради гнома Загадалки
1. Зачеркни одинаковые цифры. Какое число осталось?
5 3 7 1 8 3 5 8 7
2. Какую цифру надо зачеркнуть в числе 621, чтобы оставшееся число делилось на 3?
3. Это число от 2 до 10, но не 5; кроме того, оно нечётное и не делится на 3. Назови его.
4. Перед тобой однозначные числа. Вычеркни нечётные. Какая цифра осталась?
7 9 3 1 9 5 8 7
5. Зачеркни в следующем числе цифры, которые встречаются только один раз. Остальные цифры соедини. Что за число получилось?
7290342615
6. Угадай число от 1 до 28, если в его написание не входят цифры 1, 5 и 7; кроме того, оно нечётное и не делится на 3.
7. Отгадай число от 1 до 58, если в его написание не входят цифры 1, 2 и 3; кроме того, оно нечётное и не делится на 3, 5 и 7.
8. Угадай число от 1 до 88, если в его написание не входят цифры 1, 2, 3 и 7; кроме того, оно нечётное и не делится на 3, 5 и 7.
9. Отгадай число от 1 до 408, если в его написание не входят цифры 1, 2, 3, 5, 7; кроме того, оно нечётное и не делится на 3 и 7.
10. Перед тобой однозначные числа. Зачеркни чётные. Оставшиеся цифры соедини. Какое число осталось?
4 2 6 4 8 2 9 6 5
11. Преврати в числе 123 одну цифру в пятёрку так, чтобы получившееся число делилось на 9. Каково оно?
12. Исправь в числе 982 одну цифру на четвёрку так, чтобы получившееся число делилось на 3. Назови новое число.
13. Вычти из произвольного двузначного числа сумму его цифр. Всегда ли разность разделится на 3? А на 9?
И.Г. СУХИН
РАЗДЕЛ 4. ИГРЫ И ФОКУСЫ
И.Г. СУХИН
КАК ВСЕГДА ВЫИГРЫВАТЬ В ПОПУЛЯРНЫХ ИГРАХ МАТЕМАТИЧЕСКОГО СОДЕРЖАНИЯ
ИГРА В ДЕСЯТЬ
По очереди играют двое. Начинающий игру называет 1 или 2. Его товарищ прибавляет в уме к исходному числу 1 или 2 и сообщает сумму партнёру. Последний также увеличивает её на 1 или 2 и называет свой результат. Так игра продолжается, и побеждает тот, кто скажет число 10.
Чтобы выиграть, тебе нужно начать игру и независимо от ответов партнёра называть числа 1, 4, 7. Когда произнесено число 7, противнику приходится назвать 8 или 9. Ты говоришь: «Десять!» – и побеждаешь.
В другом варианте этой игры тот, кто скажет: «Десять», – проигрывает. Чтобы всегда выигрывать, здесь предложи товарищу начать игру. Как бы он ни играл, ты должен называть числа 3, 6, 9. Тут товарищу придётся сказать: «Десять». И снова ты победитель.
ИГРА В ПЯТНАДЦАТЬ
Массовики-затейники часто играют с желающими не в «Десять», а в «Пятнадцать», причём прибавляют также не больше двух. В первом варианте игры (сказавший 15 побеждает) предложи товарищу начать и называй числа 3, 6, 9, 12, 15. Во втором варианте игры (сказавший 15 проигрывает) первое число должно быть твоё. Ты называешь числа 2, 5, 8, 11, 14.
ИГРА В СТО
Играют в эту игру и до 100 (сказавший 100 выигрывает). Здесь первое число должно быть от 1 до 10, затем игроки по очереди прибавляют к предыдущему числу от 1 до 10. Чтобы победить, надо начать игру и называть 1, 12, 23, 34, 45, 56, 67, 78, 89, 100.
Конечно, можно запомнить все «выигрышные» числа в этих играх, но лучше установи закономерность, чтобы успешно играть не только в «Десять», «Пятнадцать» и «Сто», но и в другие варианты игры до любого числа, набавляя иные числа. Это пригодится тебе при решении заданий из тетради гнома Загадалки. Играй и побеждай!
И.Г. СУХИН
Задания гнома Загадалки
В следующих играх тот, кто скажет последнее число, выигрывает. Ты начинаешь. Какое первое число ты назовёшь, чтобы победить, если:
1. Вы с приятелем играете в «Десять», набавляете от 1 до 3?
2. Играете в «Десять», набавляете от 1 до 5?
3. Играете в «Десять», набавляете от 1 до 6?
4. Вы с другом играете в «Пятнадцать», набавляете от 1 до 3?
5. Играете в «Пятнадцать», набавляете от 1 до 5?
6. Играете в «Пятнадцать», набавляете от 1 до 6?
7. Играете в «Пятнадцать», набавляете от 1 до 7?
8. Играете в «Пятнадцать», набавляете от 1 до 8?
9. Вы с другом играете в «Сто», набавляете от 1 до 2?
10. Играете в «Сто», набавляете от 1 до 5?
11. Играете в «Сто», набавляете от 1 до 20?
12. Вы с товарищем играете в «Сто», набавляете от 1 до 30?
13. Играете в «Сто», набавляете от 1 до 40?
14. Играете в «Сто», набавляете от 1 до 50?
В следующих играх тот, кто скажет последнее число, проигрывает. Ты начинаешь. Какое первое число ты назовёшь, чтобы победить, если:
15. Вы с приятелем играете в «Десять», набавляете от 1 до 3?
16. Играете в «Десять», набавляете от 1 до 4?
17. Играете в «Десять», набавляете от 1 до 5?
18. Играете в «Десять», набавляете от 1 до 6?
19. Вы с другом играете в «Пятнадцать», набавляете от 1 до 3?
20. Играете в «Пятнадцать», набавляете от 1 до 4?
21. Играете в «Пятнадцать», набавляете от 1 до 5?
22. Играете в «Пятнадцать», набавляете от 1 до 7?
23. Играете в «Пятнадцать», набавляете от 1 до 8?
24. Вы с другом играете в «Сто», набавляете от 1 до 3?
25. Играете в «Сто», набавляете от 1 до 4?
26. Играете в «Сто», набавляете от 1 до 5?
27. Играете в «Сто», набавляете от 1 до 20?
28. Вы с товарищем играете в «Сто», набавляете от 1 до 30?
29. Играете в «Сто», набавляете от 1 до 40?
30. Играете в «Сто», набавляете от 1 до 50?
ИГРА В ШЕСТЬ ФАНТИКОВ
Ты и твой товарищ выкладываете на столе 2 горизонтальных ряда фантиков, по 3 фантика в каждом ряду. Вместо фантиков могут быть камешки, конфеты, копейки, пуговицы, спички или счётные палочки.
I I I
I I I
Пусть начинает партнёр-товарищ. Он должен взять любое число фантиков из первого или из второго ряда. Нельзя брать фантики одновременно из обоих рядов. Затем ты берёшь фантики – тоже из одного ряда (первого или второго). Так по очереди продолжаете игру. Кто возьмёт последний фантик, тот проиграл.
Условия игры просты, но, чтобы победить, нужно проявить смекалку.
Предположим, противник берёт все 3 фантика из любого ряда. Тогда ты возьмёшь 2 из другого ряда. На столе останется последний фантик.
Партнёр проиграет, ведь пропускать очередь хода нельзя.
Если же первым ходом он возьмёт 2 фантика из одного ряда, то ты выберешь все 3 из другого. Опять твоя победа.
Твоему товарищу лучше всего первым ходом взять 1 фантик. Чтобы не проиграть, ты тоже возьмёшь 1, но из другого ряда. Теперь в обоих рядах останется по 2 фантика. Поражение твоего противника неизбежно.
Ведь если он берёт 2 фантика, то ты возьмёшь 1.
А если он выберет 1, ты возьмёшь 2.
В обоих случаях перед товарищем останется лежать 1 фантик. Победа за тобой.
Запомни: в этой игре тот, кто начинает, проигрывает (при точной игре обоих противников).
ИГРА В ДЕВЯТЬ ФАНТИКОВ
Здесь фантики расположены в 3 ряда. В первом ряду – 1 фантик, во втором – 3, в третьем – 5.
I
I I I
I I I I I
Это расположение можно записать так: 1 3 5.
Условия игры такие же, как и в предыдущей игре.
При безошибочной игре партнёров здесь побеждает тот, кто начинает. Договорись с другом, чтобы первый ход был твоим, и возьми 3 фантика из третьего ряда. Оставшиеся фантики будут расположены так: 1 3 2.
Теперь, если твой товарищ заберёт единственный фантик из первого ряда, то ты возьмёшь 1 фантик из следующего ряда и получится расположение: 2 2, которое мы проанализировали в предыдущей игре. Ход за противником, и он проигрывает.
Твой партнёр терпит поражение и при других взятиях.
Если он возьмёт все 3 фантика из второго ряда, то ты заберёшь оба из третьего.
Если соперник выберет 2 фантика из второго ряда, ты возьмёшь 1 из третьего и получится положение: 1 1 1. Победа останется за тобой.
Если он возьмёт 1 фантик из второго ряда, ты заберёшь единственный фантик из первого ряда и снова получится выгодное для тебя положение: 2 2.
Если противник заберёт 2 фантика из третьего ряда, ты возьмёшь все 3 из второго.
Если он заберёт 1 фантик из третьего ряда, ты возьмёшь 2 из второго, и снова получится выигрышное для тебя положение: 1 1 1.
Всё, твоя победа, других вариантов нет.
И.Г. СУХИН
Положения для игры в девять фантиков из тетради гнома Загадалки
Представь, что игру начинает твой товарищ и своим ходом в исходном положении 1 3 5 берёт:
31. Единственный фантик из первого ряда: 3 5. Сколько фантиков и из какого ряда сейчас надо взять, чтобы победить?
32. 3 фантика из второго ряда: 1 5. Как выиграть?
33. 2 фантика из второго ряда: 1 1 5. Как сыграть теперь?
34. 1 фантик из второго ряда: 1 2 5. Сколько фантиков из какого ряда ты возьмёшь?
35. Все 5 фантиков из третьего ряда: 1 3. Как победить?
36. 4 фантика из третьего ряда: 1 3 1. Как сыграть?
37. 3 фантика из третьего ряда: 1 3 2. Можно ли тебе избежать поражения?
38. 2 фантика из третьего ряда: 1 3 3. Что делать?
39. 1 фантик из третьего ряда: 1 3 4. Каков твой ответ?
Итак, проанализировав игры в шесть и девять фантиков, мы установили 4 важных расположения, к которым должны стремиться. В них очередь хода за противником, но он неизбежно проигрывает. Запомни их!
N1: 2 2.
N2: 3 3.
N3: 1 1 1.
N4: 1 2 3.
Чтобы побеждать в этих играх, нельзя забывать: если остался всего один ряд с числом фантиков не менее двух, то своим ходом тебе надо забрать все фантики, кроме одного. А если осталось 2 ряда, в первом из которых находится 1 фантик, а во втором – любое количество фантиков, то нужно взять все фантики из второго ряда.
Всё это пригодится тебе в следующей игре.
ИГРА В ШЕСТНАДЦАТЬ ФАНТИКОВ
Мы постепенно подвели тебя к одной из самых интересных игр на свете, которую иногда называют «Мариенбад».
Здесь фантики расположены в 4 ряда. В первом ряду – 1 фантик, во втором – 3, в третьем – 5, в четвёртом – 7.
I
I I I
I I I I I
I I I I I I I
Это расположение можно записать так: 1 3 5 7.
Условия игры такие же, как и в предыдущих играх.
Проанализировать все варианты игры «Мариенбад» гораздо сложнее, чем для случаев с меньших числом фантиков.
Кроме положений: N1 – N4 своим ходом надо создавать ещё и такие: N5: 4 4, N6: 5 5 (эти 2 положения сводятся к: 2 2), N7: 1 4 5, N8: 2 4 6, N9: 2 5 7, N10: 3 4 7, N11: 3 5 6, N12: 1 1 х х (где х>1), N13: 1 2 4 7, N14: 1 2 5 6, N15: 1 3 4 6.
И наконец N16: 1 3 5 7. То есть в «Мариенбаде»тот, кто начинает, проигрывает!
Итак, если ты хочешь наверняка победить в этой игре, начать её должен твой товарищ. Чтобы быстро не проиграть, ему лучше всего взять один фантик из любого ряда. Теперь у тебя 3 равноценных ответа: надо взять один фантик в любом из трёх остальных рядов, получив расположения N9 – N11 или N13 – N15. Затем партнёр возьмёт фантик в одном из двух рядов, из которых фантики ещё не брали. А ты выберешь фантик из последнего такого ряда, и получится положение N8. Далее в зависимости от хода партнёра ты создашь расположения N1, N4, N5 или N7 и быстро выиграешь.
Всё это не так-то уж и трудно. Приобретя игровой опыт, ты убедишься: достаточно помнить 4 важных положения: N4, N7, N8 и N12, чтобы быстро находить лучший ход.
И.Г. СУХИН
Положения для игры в «Мариенбад» из тетради гнома Загадалки
Представь, что игру начинает твой товарищ и своим ходом в исходном положении 1 3 5 7 берёт:
40. 2 фантика из второго ряда: 1 1 5 7. Сколько фантиков и из какого ряда сейчас надо взять, чтобы победить?
41. 3 фантика из второго ряда: 1 5 7. Как выиграть?
42. 2 фантика из третьего ряда: 1 3 3 7. Как сыграть теперь?
43. 3 фантика из третьего ряда: 1 3 2 7. Сколько фантиков из какого ряда ты возьмёшь?
44. 4 фантика из третьего ряда: 1 3 1 7. Как победить?
45. Все 5 фантиков из третьего ряда: 1 3 7. Как сыграть?
46. 2 фантика из четвёртого ряда: 1 3 5 5. Твой ход?
47. 3 фантика из четвёртого: 1 3 5 4. Что делать?
48. 4 фантика из четвёртого: 1 3 5 3. Каков твой ответ?
49. 5 фантиков из четвёртого: 1 3 5 2. Как сыграть?
50. 6 фантиков из четвёртого: 1 3 5 1. Что делать?
51. Все 7 фантиков из четвёртого: 1 3 5. Каков твой ответ?
ИГРА В ДВАДЦАТЬ ПЯТЬ ФАНТИКОВ
Здесь фантики в пяти рядах. Это расположение можно записать так: 1 3 5 7 9.
Условия игры такие же, как и в предыдущих играх.
Чтобы выиграть, тебе надо начать и первым ходом забрать все 9 фантиков из последнего ряда. Получается игра «Мариенбад», в которой тот, кто начинает, проигрывает.
И.Г. СУХИН
ИГРЫ, ГДЕ ВЗЯВШИЙ ПОСЛЕДНИЙ ФАНТИК ВЫИГРЫВАЕТ
В игры с фантиками можно играть и иначе: тот, кто берёт последний фантик, считается победителем. Самое интересное здесь то, что тебе всё равно нужно стремиться в основном к тем же промежуточным положениям, которые мы уже рассмотрели. Т.е. старайся, чтобы после твоего хода создавались положения: N1 – N2, N4 – N16. Если сможешь сделать это, выиграешь. Стратегическое различие проявляется в самом конце. К примеру, если в положении: 2 2 партнёр возьмёт один фантик, то здесь и ты выберешь не два фантика, как в первом варианте игры, а 1 из другого ряда и получится: 1 1, что обеспечит тебе победу. А если соперник возьмёт 2 фантика, то и ты заберёшь оба оставшихся и выиграешь.
Что теперь? Научи товарища правилам игры в такие фантики и обыгрывай. Можешь провести чемпионат класса, турнир во дворе.
МАТЕМАТИЧЕСКИЕ ФОКУСЫ
Старинные фокусы из тетради гнома Загадалки
1. Напиши такое трёхзначное число, чтобы первая цифра была по крайней мере на 2 больше, чем третья. Например: 311. Запиши его цифрами в обратном порядке: 113. Из первого вычти второе: получится 198. Это число снова напиши наоборот: 891. И два последние числа сложи.
891 + 198 = 1089.
Удивительное дело: какие бы числа мы ни брали, в ответе всегда будет 1089!
Теперь предложи провести все эти действия с числами кому-то из друзей. Представляешь, как он удивится, когда ты, не спрашивая у него, сколько получилось в результате (как это бывает в других математических фокусах), сам назовёшь ответ! Для эффекта можешь сообщить его не сразу, а через несколько секунд, как-бы что-то подсчитывая в уме.
2. Попроси товарища задумать какое-нибудь двузначное число, вычесть из него сумму его цифр, зачеркнуть в полученном результате одну цифру и сообщить, какое число осталось. После этого ты тотчас скажешь, какая цифра зачёркнута! Для этого ты всего навсего из 9 вычтешь оставшееся однозначное число.
Пример: 97 – 16 = 81, 8 зачёркивается и друг говорит, что осталось 1. Ты выполняешь в уме вычитание и получаешь в результате зачёркнутую цифру: 9 – 1 = 8.
Для информации: СОДЕРЖАНИЕ КНИГИ
Предисловие для учителя
РАЗДЕЛ 1. ГНОМЫ ЗАГАДАЛКА, ПУТАЛКА И ЗАБЫВАЛКА
Знакомство с гномами Математические приключения гномов (в шутку и всерьёз) Говорят гномы Зачёркиваем буквы – получаем числа Задачи из тетради гнома Загадалки Переставляем буквы – получаем числа Задачи из тетради гнома Забывалки Числа прячутся в предложениях Задачи из тетради гнома Загадалки Задачи-шутки из тетради гнома Загадалки
РАЗДЕЛ 2. ЧИСЛА В КЛЕТКАХ
Шпаргалка Числовая горизонталь гнома Забывалки (задачи с дополнительными условиями и подсказками) Задачи из тетради гнома Забывалки Задачи на вычитание Задачи на сложение Задачи на умножение Задачи на деление Сочетание арифметических действий Числовая горизонталь гнома Путалки (задачи с дополнительными условиями и подсказками) Задачи из тетради гнома Путалки Математические дорожки Задачи из тетради гнома Забывалки Цифры в буквах Задачи из тетради гнома Забывалки Цифры в цифрах Задачи из тетради гнома Забывалки Волшебные квадраты Задачи из тетради гнома Загадалки
РАЗДЕЛ 3. НЕОБЫЧНЫЕ ЗАДАЧИ И ГОЛОВОЛОМКИ
Подумай и ответь Задачи из тетради гнома Загадалки Натуральные, простые, составные, чётные, нечётные, круглые Шпаргалка Задачи из тетради гнома Загадалки От нуля до девяти (однозначные числа) От нуля до двадцати (однозначные и двузначные числа) От нуля до девяноста девяти (однозначные и двузначные числа) От нуля до тысячи Чётные и нечётные числа Круглые числа Сюжетные задачи Исправление, зачёркивание, превращение, отгадывание цифр и чисел Задачи из тетради гнома Загадалки
РАЗДЕЛ 4. ИГРЫ И ФОКУСЫ
Как всегда выигрывать в популярных играх математического содержания Игра в десять Игра в пятнадцать Игра в сто Задания гнома Загадалки Игра в шесть фантиков Игра в девять фантиков Положения для игры в девять фантиков из тетради гнома Загадалки Игра в шестнадцать фантиков Положения для игры в «Мариенбад» из тетради гнома Загадалки Игра в двадцать пять фантиков Игры, где взявший последний фантик выигрывает Математические фокусы Старинные фокусы из тетради гнома Загадалки
ОТВЕТЫ
ОТВЕТЫ
РАЗДЕЛ 1. ГНОМЫ ЗАГАДАЛКА, ПУТАЛКА И ЗАБЫВАЛКА
МАТЕМАТИЧЕСКИЕ ПРИКЛЮЧЕНИЯ ГНОМОВ
1. Двух. 2. У Забывалки одна, а у Путалки две. 3. У Забывалки две, у Загадалки одна, у Путалки три. 4. По две у Загадалки и Путалки и одна у Забывалки. 5. У Загадалки – 2, у Забывалки – 1, у Путалки – 3 (он 2 носка натянул на одну ногу). 6. За 11 секунд. 7. 12+3+45 = 60. 8. 54+3+2+1 = 60. 9. Одна. 10. Две. 17. Ни одного. 18. Он забил гол в свои ворота. 19. Это был тренер команды соперника. 20. Его товарищи играли за команду «Дырка». 23. Потому что, возвращаясь из магазина, Путалка снова свернул направо. Загадалка и Забывалка пошли по дороге прямо, не сворачивая у перекрёстка. 24. Он перепутал рубашки, надел без колокольчиков. 25. Он забыл надеть рубашку. 26. Забывалка зачитался в доме книгой о Мюнхгаузене и забыл пойти за грибами. 27. Ни от одной. 28. Трое (гномов).
ГОВОРЯТ ГНОМЫ
5. Две и четыре. 6. Нет, 15.
ЗАЧЁРКИВАЕМ БУКВЫ – ПОЛУЧАЕМ ЧИСЛА
1. Нуль. 2. Один. 3. Два. 4. Три. 5. Пять. 13. Тысяча.
ПЕРЕСТАВЛЯЕМ БУКВЫ – ПОЛУЧАЕМ ЧИСЛА
1. Три. 2. Нуль. 3. Сорок. 4. Один. 5. Два. 13-15. Двенадцать. 19. Тридцать. 22. Пятьдесят. 25. Семьдесят. 28. Восемьдесят. 71. Миллиард.
ЗАДАЧИ-ШУТКИ ИЗ ТЕТРАДИ ГНОМА ЗАГАДАЛКИ
1. Один. 2. Двадцать. 3. Нуль, потому что у осла нет рогов. 4. Одна. 5. Ни одного. 6. В норе Кролика. 7. Стон.
НАТУРАЛЬНЫЕ, ПРОСТЫЕ, СОСТАВНЫЕ, ЧЁТНЫЕ, НЕЧЁТНЫЕ, КРУГЛЫЕ
1. Простое. 2. Однозначное. 3. Чётное. 4-7. 0. 8-15. 1. 16-23. 2. 24. 4. 25-26. 7. 27. 8. 28. 1 и 0. 29. 9 и 0. 30. 1 и 2. 31. 3 и 1. 32. 5 и 1. 33. 1 и 7. 34. 8 и 1. 35-36. 9 и 1. 37. 2 и 3. 38-40. 4 и 2. 41. 2 и 5. 42. 6 и 2. 43. 2 и 7. 44. 8 и 2. 45. 3 и 5. 46. 4 и 5. 47-48. 1, 2, 3. 49. 2, 3 и 4. 50. 3, 6 и 2. 51. 2; (9 – 7). 52. 10; (8 + 2). 53. 10; (9 + 1). 54. 11. 55. 18. 56. 1 и 15. 57. 2 и 8. 58. 3 и 5. 59. 3 и 11. 60. 4 и 5. 61. 4 и 8. 62. 5 и 7. 63. 5 и 9. 64. 9 и 6. 65. 8 и 9. 66. 10 и 9. 67. 2, 3 и 6. 68. 6, 3 и 4. 69. 1, 2, 3 и 4. 70. 2, 3, 5, 7. 71. Простых.
156. Четвёрку. 157. 6; (2 + 4). 158. 23 (1 уже был, а 22 упали с неба). 159. 23. 160. 33. 161. А.Пушкин «Сказка о царе Салтане…»; 33. 162. 199. 163. 400. 164. 500. 165. 3, 6, 9. 166. 3, 6, 12. 167. 6, 9, 12.
ИСПРАВЛЕНИЕ, ЗАЧЁРКИВАНИЕ, ПРЕВРАЩЕНИЕ,
ОТГАДЫВАНИЕ ЦИФР И ЧИСЕЛ
1. 1. 2. 6. 3. 7. 4. 8. 5. 22. 6. 23. 7. 47. 8. 59. 9. 89. 10. 95. 11. 153. 12. 942. 13. Да.
РАЗДЕЛ 4. ИГРЫ И ФОКУСЫ
КАК ВСЕГДА ВЫИГРЫВАТЬ В ПОПУЛЯРНЫХ ИГРАХ МАТЕМАТИЧЕСКОГО СОДЕРЖАНИЯ
1. 2. 2. 4. 3-5. 3. 6. 1. 7. 7. 8. 6. 9. 1. 10. 4. 11. 16. 12. 7. 13. 18. 14. 49. 15. 1. 16. 4. 17. 3. 18-19. 2. 20. 4. 21. 2. 22. 6. 23. 5. 24. 3. 25. 4. 26. 3. 27. 15. 28. 6. 29. 17. 30. 48. 31. 2 из последнего ряда. 32. Взять все 5 фантиков из последнего ряда. 33. Забрать 4 из третьего ряда. 34. 2 из третьего. 35. Взять все 3 из второго ряда. 36. Забрать 2 из второго ряда. 37. Нет. 38. Взять 1 фантик из любого ряда. 39. Забрать 2 из третьего ряда. 40. 2 из четвёртого ряда. 41. Взять 3 фантика из последнего ряда. 42. Забрать 6 из четвёртого ряда. 43. Все 7 из четвёртого. 44. Взять 4 из четвёртого ряда. 45. Забрать 5 из последнего ряда. 46. Взять 2 из второго ряда. 47. Взять все 3 фантика из второго ряда. 48. Взять 4 из третьего ряда. 49. Взять все 5 фантиков из третьего ряда. 50. Взять 2 из третьего ряда. 51. Взять 3 из третьего ряда.
О ЛИТЕРАТУРНЫХ ПРИКЛЮЧЕНИЯХ ГНОМОВ МОЖНО ПРОЧИТАТЬ ЗДЕСЬ
ОСНОВНЫЕ РУБРИКИ САЙТА
ЛИТЕРАТУРНЫЕ ЗАТЕИ
Лучшие книги:
«Литературные викторины, тесты и сказки-загадки для дошкольников и младших школьников» (1998) и «Незнайка, Хоттабыч, Карлсон и все-все-все: литературные викторины, кроссворды и чайнворды для детей».
ЗАГАДКИ, ЗАГАДКИ-ШУТКИ, СКАЗКИ-ЗАГАДКИ, ЗАНИМАТЕЛЬНЫЕ ЗАДАНИЯ
Лучшая книга:
«Новые 500 загадок – 70 кроссвордов».
ЛОГОПЕДИЯ И СКОРОГОВОРКИ
Лучшие книги:
«Чистоговорки, наоборотки, запрятки на звук «С» и «Весёлые скороговорки для «непослушных» звуков».
ЗАНИМАТЕЛЬНАЯ МАТЕМАТИКА
Лучшие книги:
«800 новых логических и математических головоломок» и «Весёлая математика: 1500 головоломок для математических олимпиад, уроков, досуга: 1-7 класс».
ШАХМАТЫ ДЛЯ ДЕТЕЙ
Лучшие книги:
«Волшебные фигуры, или Шахматы для детей 2–5 лет» и «Удивительные приключения в Шахматной стране» (для детей 5-–8 лет).
ЗАНИМАТЕЛЬНАЯ БИБЛИОГРАФИЯ
Занимательная библиография
ЧТО УЖЕ РАЗМЕЩЕНО НА САЙТЕ КНИГИ, РУКОПИСИ, СТАТЬИ И.Г.СУХИНА КТО ЗАЩИТИТ АВТОРА, ИЛИ ОХОТА НА ПЛАГИАТОРА ИЗ ПЕРЕПИСКИ С ЧИТАТЕЛЯМИ Калейдоскоп интересных ссылок
НА ГЛАВНУЮ СТРАНИЦУ
mailto:[email protected]
Home Page URL: http://suhin.narod.ru
© 2001-2006 Сухин И.Г. Все права защищены.
Обновление от 13 марта 2006 года.
Сайт управляется системой uCozЧетное или нечетное число
Хотите начать заниматься математикой прямо сейчас
Уже в дошкольном возрасте ребята узнают, что бывают четные и нечетные числа. Определить абстрактно, четное число или нечетное, бывает непросто. Зато каждому понятно, получится ли некоторое количество разделить на двоих без остатка, или нет. Объяснить ребенку четные и нечетные числа помогут занимательные упражнения.
Что такое четные и нечетные числа
Четные числа — те, которые делятся на два без остатка. Но как же объяснить ребенку деление на два, если сложные математические операции осваивать еще рано? Самый простой способ — запомнить наизусть: на два делятся числа 2, 4, 6, 8 и все многозначные числа, которые оканчиваются на них же, а также на 0. Нечетные числа на 2 ровно не делятся , это числа 1, 3, 5, 7, 9 и те многозначные числа, которые оканчиваются на них же.
Таблица четных и нечетных чиселЧтобы быстро определить, четным или нечетным является число, можно воспользоваться таблицей до 100. В ней четные и нечетные числа будут чередоваться. В нашей таблице выделены четные числа.
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 |
41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 |
61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 |
71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 |
81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 |
91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 |
Определяем, четный или нечетный
Сначала расскажите ребенку, что такое четные и нечетные числа.
Проиллюстрируйте это на примерах – раскладывайте перед ребенком разное количество карандашей и попытайтесь разделить на две равные части. Если так получилось сделать, то число карандашей является четным. Если остался лишний карандаш – число нечетное.
Наглядно показать четность или нечетность можно на любых предметах — игрушках, фишках, ложечках. Если получились две равные группы и не осталось лишних предметов, то общее количество является четным. Если остался лишний предмет – число нечетноеЗакрепляем знание о четных и нечетных числах
Запоминание приходит с практикой. Вначале пусть ребенок продолжает ряды четных или нечетных чисел, начиная с указанного вами числа. В этом упражнении пригодится навык счета через один. Следующим этапом предлагайте определить четность или нечетность любого числа. Поиграйте в игру: вы загадываете число в небольшом диапазоне и сообщаете, что оно находится между 4 и 7. А ребенок, используя вопрос: «Это четное или нечетное число?», пытается угадать задуманное число. Если ребенок угадал, то следующий вопрос задает он.
Правила сложения четных и нечетных чисел
Даже если ребенок не умеет складывать числа в уме, он может запомнить несколько простых правил:
при сложении двух четных чисел всегда получится тоже четное число. 24+32=56 — четное
при сложении двух нечетных чисел получается четное число. 13+17=30 — четное
при сложении одного четного и одного нечетного числа всегда получится нечетное число. 43+32=65 — нечетное
Какое число 0 – четное или нечетное?
Ноль – это четное число.
Некоторые взрослые до сих пор затрудняются правильно ответить на этот вопрос. Как же это доступно объяснить детям?
Во-первых, чтобы определить четность или нечетность, нужно вспомнить какие числа называются четными – те, которые делятся на 2 без остатка. Ноль делится на 2 без остатка. Значит, ноль – четное число.
Во-вторых, мы уже знаем, что четные и нечетные числа чередуются. После ноля стоит нечетное число 1. Значит ноль – четное число.
Также поможет запомнить четность ноля тот факт, что все числа, которые заканчиваются на 0 – четные. Значит и ноль тоже четное число.
Игры с четными и нечетными числами
Для того чтобы знания о четных и нечетных числах закрепились у малыша в памяти, регулярно используйте эти понятия в игре.
Например, в игре в магазин вы можете “печатать” для товаров ценники только с нечетными числами, выдумывая двузначные или трёхзначные числа из головы. Остается только вспомнить, на какие цифры должны оканчиваться эти числа.
Поиграйте в подвижную игру: если ты услышишь четное число, хлопни в ладоши. А если нечетное — топни ногой. 37, 18, 24, 53, 22, 95, 38, 14…
Еще можно играть в шпионов, которые передают друг другу информацию четными числами. Если каждое число ассоциировать с каким-то словом, то можно играть в сочинение предложений. Например, один шпион получил радиограмму: 2 8 4 6 10. А у него в ключе написано: 2 — апельсин, 4 — радость, 6 — бежит, 8 — красный, 10 — немедленно. Какое предложение можно составить, если по порядку расположить Апельсин Красный Радость Бежит Немедленно?
Напомнить знания о четных и нечетных поможет обычное русское лото. Когда вы с ребенком заполняете фишками карточки лото, проговаривайте вслух, является ли число четным.
Айкьюша поможет легко и в игровой форме познакомиться с математикой для детей 6-7 лет. Раздел включает задания и игры по арифметике для дошкольников: счет, сложение, вычитание, сравнение, умножение, деление, изучение геометрических фигур. Познавательные уроки и занятия для развития мальчиков и девочек.
Материалы для самостоятельных занятий по математике с дошкольником
| Предложите ребенку раскрасить предметы с четными числами в зеленый цвет, а с нечетными – в красный. | Распечатайте картинку и предложите ребенку продолжить последовательность четных и нечетных чисел, начиная с шеи жирафа. |
Превратите изучение четных и нечетных чисел в увлекательное занятие – и ребенок без труда освоит эту непростую тему!
Хотите начать заниматься математикой прямо сейчас
1 | нечетная | 1 сентября — 6 сентября |
2 | четная | 7 сентября — 13 сентября |
3 | нечетная | 14 сентября — 20 сентября |
4 | четная | 21 сентября — 27 сентября |
5 | нечетная | 28 сентября — 4 октября |
6 | четная | 5 октября — 11 октября |
7 | нечетная | 12 октября — 18 октября |
8 | четная | 19 октября — 25 октября |
9 | нечетная | 26 октября — 1 ноября |
10 | четная | 2 ноября — 8 ноября |
11 | нечетная | 9 ноября — 15 ноября |
12 | четная | 16 ноября — 22 ноября |
13 | нечетная | 23 ноября — 29 ноября |
14 | четная | 30 ноября — 6 декабря |
15 | нечетная | 7 декабря — 13 декабря |
16 | четная | 14 декабря — 20 декабря |
17 | нечетная | 21 декабря — 27 декабря |
18 | четная | 28 декабря — 3 января |
19 | нечетная | 4 января — 10 января |
20 | четная | 11 января — 17 января |
21 | нечетная | 18 января — 24 января |
22 | четная | 25 января — 31 января |
23 | нечетная | 1 февраля — 7 февраля |
24 | четная | 8 февраля — 14 февраля |
25 | нечетная | 15 февраля — 21 февраля |
26 | четная | 22 февраля — 28 февраля |
27 | нечетная | 1 марта — 7 марта |
28 | четная | 8 марта — 14 марта |
29 | нечетная | 15 марта — 21 марта |
30 | четная | 22 марта — 28 марта |
31 | нечетная | 29 марта — 4 апреля |
32 | четная | 5 апреля — 11 апреля |
33 | нечетная | 12 апреля — 18 апреля |
34 | четная | 19 апреля — 25 апреля |
35 | нечетная | 26 апреля — 2 мая |
36 | четная | 3 мая — 9 мая |
37 | нечетная | 10 мая — 16 мая |
38 | четная | 17 мая — 23 мая |
39 | нечетная | 24 мая — 30 мая |
40 | четная | 31 мая — 6 июня |
41 | нечетная | 7 июня — 13 июня |
42 | четная | 14 июня — 20 июня |
43 | нечетная | 21 июня — 27 июня |
44 | четная | 28 июня — 4 июля |
Четные и нечетные числа, 1 класс
Дата публикации: .
Определение четных и нечетных чисел от 1 до 10 с картинками.
1. Сколько собачек на картинке? Это число четное или не четное?
2. Сколько клоунов на картинке? Это число четное или не четное?
3. Сколько стульев на картинке? Это число четное или не четное?
4. Сколько ламп на картинке? Это число четное или не четное?
5. Сколько мужчин на картинке? Это число четное или не четное?
6. Сколько морковок на картинке? Это число четное или не четное?
7. Сколько девочек на картинке? Это число четное или не четное?
Четные и нечетные числа до 10
1. Обведите все нечетные числа.
10, 8, 7, 9, 5, 6, 4, 1, 3
2. Обведи все четные числа.
9, 7, 3, 4, 8, 5, 2, 1, 10,
3. Выбери наибольшее четное число из числового ряда.
2, 3, 6, 5, 1
4. Выбери наименьшее четное число из числового ряда.
1, 7, 9, 6, 5
5. Выбери наибольшее нечетное число из числового ряда.
5, 4, 2, 6, 7
6. Выбери наименьшее нечетное число из числового ряда.
4, 10, 6, 6, 1
7. Выбери наибольшее четное число из заданной числовой последовательности.
8, 4, 1, 8, 6
Сложи или вычти числа от 1 до 10. Определи, является ли результат четным или нечетным. Подчеркни правильный ответ.
2 + 2 = _____ четное/нечетное 4 + 5 = _____ четное/нечетное 3 + 5 = _____ четное/нечетное 4 + 2 = _____ четное/нечетное 3 + 1 = _____ четное/нечетное 8 + 2 = _____ четное/нечетное 7 + 3 = _____ четное/нечетное 8 + 2 = _____ четное/нечетное 3 + 3 = _____ четное/нечетное 8 + 1 = _____ четное/нечетное 7 + 2 = _____ четное/нечетное 1 + 3 = _____ четное/нечетное 6 + 4 = _____ четное/нечетное 4 + 2 = _____ четное/нечетное 4 + 4 = _____ четное/нечетное 3 + 6 = _____ четное/нечетное 1 + 4 = _____ четное/нечетное 2 + 1 = _____ четное/нечетное 9 + 1 = _____ четное/нечетное 2 + 1 = _____ четное/нечетное 3 - 3 = _____ четное/нечетное 8 - 1 = _____ четное/нечетное 7 - 2 = _____ четное/нечетное 1 - 3 = _____ четное/нечетное 6 - 3 = _____ четное/нечетное 4 - 2 = _____ четное/нечетное 4 - 4 = _____ четное/нечетное 3 + 6 = _____ четное/нечетное 1 + 4 = _____ четное/нечетное 2 - 1 = _____ четное/нечетное 9 - 1 = _____ четное/нечетное 2 - 1 = _____ четное/нечетное 4 - 4 = _____ четное/нечетное 3 + 6 = _____ четное/нечетное 1 + 4 = _____ четное/нечетное 2 - 1 = _____ четное/нечетное 9 - 1 = _____ четное/нечетное 2 - 1 = _____ четное/нечетное
Определение четных и нечетных чисел о 1 до 20 с картинками.
1. Количество головок чеснока четное или нечетное? _______
2. Количество очков четное или нечетное? _______
3. Количество зонтов четное или нечетное? _______
4. Количество туфель четное или нечетное? _______
5. Количество мальчиков четное или нечетное? _______
Четные и нечетные числа до 20
1. Обведи все нечетные числа.
7, 10, 11, 14, 1, 1, 2, 12, 11, 10
2. Обведи все четные числа.
12, 4, 8, 7, 14, 7, 20, 17, 15, 8
3. Обведи все нечетные числа.
15, 19, 14, 4, 15, 11, 1, 10, 15, 9
4. Обведи все четные числа.
15, 9, 1, 7, 5, 9, 14, 8, 3, 15
5. Подчеркни все нечетные числа.
9, 18, 20, 13, 12, 10, 6, 20, 10, 2
6. Подчеркни все четные числа.
7, 17, 3, 3, 15, 10, 8, 14, 17, 1
7. Выбери наибольшее четное число из заданной числовой последовательности.
5, 5, 15, 7, 15, 4, 17, 19, 17, 11
8. Выбери наименьшее четное число из заданной числовой последовательности.
11, 16, 8, 8, 19, 10, 15, 15, 15, 9
9. Выбери наибольшее нечетное число из заданной числовой последовательности.
3, 9, 6, 7, 13, 11, 11, 13, 6, 3
10. Выбери наименьшее нечетное число из заданной числовой последовательности.
20, 20, 8, 12, 8, 1, 18, 2, 2, 17
11. Выбери наибольшее четное число из заданной числовой последовательности.
8, 7, 15, 15, 8, 2, 5, 19, 15, 5
12. Выбери наибольшее нечетное число из заданной числовой последовательности.
20, 11, 2, 13, 3, 1, 14, 5, 19, 2
13. Выбери наименьшее четное число из заданной числовой последовательности.
4, 11, 20, 9, 15, 14, 16, 9, 17, 13
14. Выбери наименьшее нечетное число из заданной числовой последовательности.
15, 20, 8, 18, 16, 17, 9, 5, 12, 8
Сложи или вычти числа от 1 до 20. Определи, является ли результат четным или нечетным. Подчеркни правильный ответ.
2 + 4 = _____ четное/нечетное 16 - 5 = _____ четное/нечетное 5 + 13 = _____ четное/нечетное 14 + 4 = _____ четное/нечетное 7 + 9 = _____ четное/нечетное 16 - 16 = _____ четное/нечетное 7 + 10 = _____ четное/нечетное 2 + 18 = _____ четное/нечетное 18 - 6 = _____ четное/нечетное 9 - 6 = _____ четное/нечетное 3 + 7 = _____ четное/нечетное 5 + 11 = _____ четное/нечетное 15 - 2 = _____ четное/нечетное 18 - 6 = _____ четное/нечетное 20 - 18 = _____ четное/нечетное 2 + 5 = _____ четное/нечетное 19 - 5 = _____ четное/нечетное 4 + 9 = _____ четное/нечетное 1 + 3 = _____ четное/нечетное 14 - 11 = _____ четное/нечетное 3 + 7 = _____ четное/нечетное 5 + 8 = _____ четное/нечетное 15 + 2 = _____ четное/нечетное 18 - 6 = _____ четное/нечетное 20 - 18 = _____ четное/нечетное 2 + 5 = _____ четное/нечетное 19 - 5 = _____ четное/нечетное 4 + 9 = _____ четное/нечетное 1 + 3 = _____ четное/нечетное 14 - 11 = _____ четное/нечетное
Четные и нечетные числа до 50
1. Обведи все нечетные числа.
6, 36, 22, 25, 19, 24, 10, 39, 48, 37, 26, 50, 8, 35, 7, 3, 40, 47, 11, 9, 38, 28, 43, 41, 18, 23, 21, 1, 46, 30
2. Обведи все нечетные числа.
18, 31, 12, 28, 29, 35, 10, 4, 40, 39, 20, 6, 45, 30, 14, 36, 16, 48, 25, 24, 47, 37, 34, 11, 46, 32, 42, 2, 27, 41
3. Обведи все нечетные числа.
28, 35, 32, 47, 37, 43, 22, 14, 45, 24, 39, 29, 21, 42, 8, 41, 17, 36, 20, 9, 38, 46, 1, 23, 15, 27, 4, 12, 34, 26
4. Обведи все четные числа.
17, 36, 48, 12, 29, 49, 20, 9, 47, 27, 28, 6, 37, 4, 16, 25, 7, 34, 41, 18, 42, 32, 5, 23, 40, 2, 39, 45, 26, 14
5. Обведи все четные числа.
13, 47, 18, 50, 6, 5, 34, 48, 45, 33, 15, 3, 42, 26, 17, 22, 39, 25, 2, 30, 29, 4, 38, 8, 16, 35, 40, 31, 20, 23
6. Выбери наибольшее четное число из заданной числовой последовательности.
30, 39, 46, 40, 2, 17, 50, 16, 19, 31, 50, 9, 20, 2, 12
7. Выбери наибольшее четное число из заданной числовой последовательности.
15, 37, 38, 45, 46, 26, 49, 25, 35, 22, 33, 42, 13, 8, 31
8. Выбери наибольшее нечетное число из заданной числовой последовательности.
39, 28, 50, 14, 32, 11, 8, 40, 18, 34, 6, 45, 21, 37, 43
9. Выбери наибольшее нечетное число из заданной числовой последовательности.
24, 41, 49, 35, 21, 37, 20, 10, 1, 36, 8, 25, 4, 12, 40
10. Выбери наименьшее четное число из заданной числовой последовательности.
2, 21, 10, 45, 36, 48, 40, 14, 38, 13, 25, 28, 30, 42, 8
11. Выбери наименьшее нечетное число из заданной числовой последовательности.
39, 6, 26, 11, 50, 17, 7, 30, 10, 24, 19, 33, 1, 25, 31
12. Выбери наименьшее четное число из заданной числовой последовательности.
28, 42, 21, 36, 39, 10, 2, 37, 13, 20, 38, 11, 17, 18, 40
Сложи или вычти числа от 1 до 50. Определи, является ли результат четным или нечетным. Подчеркни правильный ответ.
21 + 18 = _____ четное/нечетное 42 + 3 = _____ четное/нечетное 10 + 40 = _____ четное/нечетное 12 + 14 = _____ четное/нечетное 7 + 29 = _____ четное/нечетное 15 - 3 = _____ четное/нечетное 5 + 12 = _____ четное/нечетное 47 - 1 = _____ четное/нечетное 46 - 46 = _____ четное/нечетное 47 - 26 = _____ четное/нечетное 38 - 41 = _____ четное/нечетное 23 + 25 = _____ четное/нечетное 24 + 13 = _____ четное/нечетное 7 + 40 = _____ четное/нечетное 19 + 2 = _____ четное/нечетное 26 + 8 = _____ четное/нечетное 8 + 36 = _____ четное/нечетное 19 + 28 = _____ четное/нечетное 40 + 9 = _____ четное/нечетное 25 + 15 = _____ четное/нечетное 22 + 14 = _____ четное/нечетное 19 + 24 = _____ четное/нечетное 46 - 48 = _____ четное/нечетное 13 + 23 = _____ четное/нечетное 21 + 21 = _____ четное/нечетное 36 + 2 = _____ четное/нечетное 20 - 19 = _____ четное/нечетное 14 + 13 = _____ четное/нечетное 35 - 23 = _____ четное/нечетное 39 - 34 = _____ четное/нечетное 43 + 4 = _____ четное/нечетное 6 + 10 = _____ четное/нечетное 20 + 26 = _____ четное/нечетное 2 + 43 = _____ четное/нечетное 17 + 23 = _____ четное/нечетное 37 + 5 = _____ четное/нечетное 16 + 15 = _____ четное/нечетное 22 + 15 = _____ четное/нечетное 33 + 6 = _____ четное/нечетное
Четные и нечетные числа до 100.
1. Обведи все нечетные числа.
25, 72, 53, 47, 14, 92, 91, 45, 73, 27, 31, 7, 19, 28, 26, 82, 66, 65, 32, 69, 90, 13, 40, 77, 88, 86, 12, 16, 38, 59
2. Обведи все нечетные числа.
8, 16, 42, 62, 36, 64, 45, 35, 51, 98, 99, 81, 83, 65, 77, 82, 43, 4, 10, 33, 68, 27, 13, 34, 48, 21, 49, 90, 11, 25
3. Обведи все нечетные числа.
83, 42, 13, 99, 27, 37, 73, 67, 38, 95, 66, 63, 6, 92, 12, 89, 5, 77, 74, 21, 39, 59, 78, 15, 35, 20, 54, 32, 75, 81
4. Обведи все четные числа.
49, 74, 2, 1, 100, 32, 54, 7, 51, 82, 33, 47, 96, 46, 78, 65, 36, 69, 75, 19, 31, 77, 35, 64, 97, 84, 37, 98, 85, 30
5. Обведи все четные числа.
22, 77, 90, 33, 10, 41, 23, 49, 53, 40, 84, 32, 13, 8, 60, 85, 89, 31, 30, 42, 96, 28, 62, 27, 45, 65, 66, 26, 55, 56
6. Выбери наибольшее четное число из заданной числовой последовательности.
9, 20, 55, 7, 100, 37, 52, 65, 19, 28, 47, 61, 32, 57, 93
7. Выбери наибольшее четное число из заданной числовой последовательности.
62, 90, 12, 34, 74, 37, 75, 91, 97, 53, 33, 60, 45, 16, 61
8. Выбери наибольшее нечетное число из заданной числовой последовательности.
81, 12, 49, 3, 52, 33, 34, 64, 41, 94, 93, 83, 80, 23, 24
9. Выбери наибольшее нечетное число из заданной числовой последовательности.
56, 4, 67, 34, 60, 88, 76, 85, 99, 33, 17, 79, 61, 7, 10
10. Выбери наименьшее четное число из заданной числовой последовательности.
94, 95, 25, 80, 71, 32, 99, 24, 8, 44, 69, 93, 38, 4, 68
11. Выбери наименьшее нечетное число из заданной числовой последовательности.
20, 12, 5, 68, 32, 54, 57, 13, 64, 82, 35, 38, 52, 92, 46
12. Выбери наименьшее четное число из заданной числовой последовательности.
2, 70, 82, 87, 27, 38, 55, 73, 84, 37, 60, 23, 63, 4, 86
Сложи или вычти числа от 1 до 100. Определи, является ли результат четным или нечетным. Подчеркни правильный ответ.
9 + 18 = _____ четное/нечетное 46 + 28 = _____ четное/нечетное 43 + 52 = _____ четное/нечетное 76 - 43 = _____ четное/нечетное 84 - 42 = _____ четное/нечетное 12 + 84 = _____ четное/нечетное 95 - 87 = _____ четное/нечетное 38 + 6 = _____ четное/нечетное 84 - 48 = _____ четное/нечетное 94 - 53 = _____ четное/нечетное 69 - 48 = _____ четное/нечетное 96 - 39 = _____ четное/нечетное 27 + 62 = _____ четное/нечетное 48 - 26 = _____ четное/нечетное 44 + 32 = _____ четное/нечетное 26 + 52 = _____ четное/нечетное 37 + 48 = _____ четное/нечетное 97 - 43 = _____ четное/нечетное 74 - 36 = _____ четное/нечетное 30 + 3 = _____ четное/нечетное 69 + 2 = _____ четное/нечетное 37 + 44 = _____ четное/нечетное 34 + 55 = _____ четное/нечетное 44 + 38 = _____ четное/нечетное 25 + 26 = _____ четное/нечетное 55 + 43 = _____ четное/нечетное 33 + 92 = _____ четное/нечетное 44 + 35 = _____ четное/нечетное 64 + 34 = _____ четное/нечетное 5 + 46 = _____ четное/нечетное 67 + 2 = _____ четное/нечетное 73 + 42 = _____ четное/нечетное 51 - 33 = _____ четное/нечетное 9 + 23 = _____ четное/нечетное 48 - 34 = _____ четное/нечетное 34 + 35 = _____ четное/нечетное 21 - 6 = _____ четное/нечетное 42 - 20 = _____ четное/нечетное 71 - 50 = _____ четное/нечетное 4 + 94 = _____ четное/нечетное 36 + 53 = _____ четное/нечетное 39 + 48 = _____ четное/нечетное 99 - 33 = _____ четное/нечетное 83 - 34 = _____ четное/нечетное 87 - 83 = _____ четное/нечетное 42 + 4 = _____ четное/нечетное 8 + 15 = _____ четное/нечетное 24 + 50 = _____ четное/нечетное 39 + 46 = _____ четное/нечетное 81 - 30 = _____ четное/нечетное
Расписание приема специалистов | СПБ ГБУЗ «Поликлиника № 98»
Расписание приема специалистов
В СВЯЗИ С ОТПУСКАМИ, ПРОСЬБА УТОЧНЯТЬ РАСПИСАНИЕ ПРИЕМА ВРАЧЕЙ
ПО ☏ 417-61-55
| Специалист | ФИО | кабинет | понедельник | вторник | среда | четверг | пятница | суббота |
| Кардиолог | Аюгова Н.Н. | 88 | четные числа 14-20, нечетные числа 8-14 | |||||
| Кардиолог | Криворучко В.А | 80 | четные числа 8-14, нечетные числа 14-20 | |||||
| Гастроэнтеролог | Жигарев А.А. | 88 | отпуск | |||||
| Невролог, зав. отдел. | Сазонов М.И. | 26 | 9-12.30 | 9-12.30 | 9-12.30 | 9-12.30 | 9-12.30 | |
| Невролог | Муравьева Ю.А. | 68 | четные числа 14-20, нечетные числа 8-14 | |||||
| Невролог днев.стационара | Руденко Е.Е. | 28 | отпуск | отпуск | отпуск | отпуск | отпуск | |
| Невролог | Гришина Т.А. | 31 | отпуск | |||||
| Отоларинголог | Муравьева Е.В. | 33 | нет приема | |||||
| Отоларинголог | Мухортова О.Ф. | 33 | четные числа 14-20, нечетные числа 9-15 | |||||
| Отоларинголог | Митрофанова Ю.В. | 33 | нет приема | |||||
| Офтальмолог | 27 | |||||||
| Офтальмолог | Артюшенко А.Ю. | 27 | четные числа 15-20, нечетные числа 8-14.30 | |||||
| Офтальмолог | Кудрявцева Н.Л. | 27 | отпуск | отпуск | отпуск | отпуск | отпуск | |
| Хирург | Гуменников В.Г. | 59 | четные числа 14-20, нечетные числа 9-15 | |||||
| Хирург | Полонская В.Д. | 61 | отпуск | |||||
| Уролог | Ал-Заанейн О.М. | 38 | 15-19 | 9.15-12.30 | 9.15-12.30 | 9.15-12.30 | 15-19 | |
| Уролог | Судник А.А. | 38 | 9 — 15 | 14 — 20 | 14-20 | 14-20 | 9-15 | |
| Эндоскопист | Булатов Л.А. | 51/53 | 9-14 | 9-14 | 9 — 13 | 9-14 | 9-14 | |
| Эндоскопист | Мамедова Ю.А | 51/53 | отпуск | отпуск | отпуск | отпуск | отпуск | |
| Эндокринолог | Ступкина Е.Н. | 79 | отпуск | отпуск | отпуск | отпуск | отпуск | |
| Эндокринолог | Иванова Е.В | 67 | четные числа 14-20, нечетные числа 8-14 | |||||
| Эндокринолог | Рамаев Х.А. | 79 | нет приема | нет приема | нет приема | нет приема | нет приема | |
| Инфекционист | Вагина Г.В. | 47 | отпуск | отпуск | отпуск | отпуск | отпуск | |
| Гинеколог | Милиш В.Г. | 36 | нет приема | нет приема | нет приема | нет приема | нет приема | |
| Гинеколог | Валуева Г.Н. | 36 | 10.15-13 | 10.15-13 | 16-19 | 10.15-13 | 10.15-13 | |
| Гериатр | Горенчук Н.А. | 21 | отпуск | отпуск | отпуск | отпуск | отпуск | |
| Логопед | Зинковская Н.П. | 22 | четные числа 09 — 13, нечетные числа 12-17 | |||||
| Ревматолог | Ходот Д.З. | Прием в субботу: 9-15, в воскресенье: 9-15 | ||||||
| Психотерапевт | Покровская А.В. | 23 | отпуск | отпуск | отпуск | отпуск | отпуск | |
| Психотерапевт | Зорина А.В. | 9-15 | 13-19 | 14-20 | 13-19 | 9-15 | ||
| Заведующая дневного стационара, врач-терап. | Кравец Е.С | 25 | 9-15 | 9-15 | 9-15 | 9-15 | 9-15 | |
| Заведующая физиотер.отд., врач-физиотерапевт | Зарайская О.В. | 31 | отпуск | отпуск | отпуск | отпуск | отпуск | |
1 ТЕРАПЕВТИЧЕСКОЕ ОТДЕЛЕНИЕ
| № кабинета | Ф.И.О. | Адреса | Расписание |
| 39 | Васильева Е.Н. | Заведующая отделением | По четным числам с 9.00 до 16.00, По нечетным числам с 13.00- до 20.00 |
| 57 | Светличная А.В. | Ул. Аэродромная , 7/4, 9/1, 11/1, 13/1 пр. Богатырский, 11, ул. Полевая Сабировская, 47/1, 47/2 Пр.Коломяжский,20 (современная медицина) | По четным числам с 9.00 до 13.00, По нечетным числам с 16.00- до 20.00 |
| 42 | Герасимов А.А. | Ул. Аэродромная , 3, 5/1, 7/1 Пр. Коломяжский, 12, ул. Г.Хрулева, 6 | По четным числам с 9.00 до 13.00, По нечетным числам с 16.00- до 20.00 |
| 50 | Водопьян О.А. | Ул. Байконурская, 5/1, б-р. Серебристый, 6/1
| По четным числам с 9.00 до 13.00, По нечетным числам с 16.00- до 20.00 |
| 41 | Туваева А.А. | Богатырский пр., д. 5/2, 5/3, 7/3 ; б-р. Серебристый, 9/1 | По четным числам с 9.00 до 13.00, По нечетным числам с 16.00- до 20.00 |
| 40 | Валитова Д.А. | Комендантский пр. 8, 8/2, 8/3, 10 ; Коменд.пл. 8А | По четным числам с 9.00 до 13.00, По нечетным числам с 16.00- до 20.00 |
| Богатырский пр., д. 11 ; Полевая Сабировская 47,57 | По четным числам с 9.00 до 13.00, По нечетным числам с 16.00- до 20.00 | ||
| 55 | Вальцев Е.А. | Аэродромная ул.,11/3,15; Богатырский пр, д.6,8 ; Серебристый бул., д.5/1 Пр.Коломяжский,15/1, 15/2 (современная медицина) | По четным числам с 9.00 до 13.00, По нечетным числам с 16.00- до 20.00 |
| 43 | Гаккелевская ул., 25/1, 25/2, 27/2, 31/2, 33/1
| По четным числам с 9.00 до 13.00, По нечетным числам с 16.00- до 20.00
| |
| 55 | Муравьева Е.В. | Богатырский пр, д. 3/2, 5/1, 7/2, 7/8 Аэродромная ул.,7/3; Богатырский пр, д.4 (современная медицина) | По четным числам с 9.00 до 13.00, По нечетным числам с 16.00- до 20.00 |
| 56 | Герасимова И.А. | Байконурская ул, д. 7/1; б-р. Серебристый, 12/1 | По четным числам с 9.00 до 13.00, По нечетным числам с 16.00- до 20.00 |
2 ТЕРАПЕВТИЧЕСКОЕ ОТДЕЛЕНИЕ
| № кабинета | Ф.И.О. | Адреса | Расписание |
| 54 | Ахмедзянова Л.Г. | Заведующая отделением | По четным числам с 13.00 до 20.00, По нечетным числам с 9.00- до 16.00 |
| 57 | Гаврилов В.Ю. | Пр. Испытателей, 10,12,14,15,16, Б-р Серебристый, 17/1 | По четным числам с 16.00 до 20.00, По нечетным числам с 9.00- до 13.00 |
| 50 | Шаурбин Д.Ю. | Сизова 12/1,12/2,14; Ул. Байконурская, 15 | По четным числам с 16.00 до 20.00, По нечетным числам с 9.00- до 13.00 |
| 42 | Б-р Серебристый 22/1, 19; Ул. Байконурская, 19 | По четным числам с 16.00 до 20.00, По нечетным числам с 9.00- до 13.00 | |
| 41 | Б-р Серебристый 16/4,18/1,18/2 Пр. Испытателей, 20 | По четным числам с 16.00 до 20.00, По нечетным числам с 8.00- до 12.00 | |
| 56 | Комендантский пр.7,9,11 | По четным числам с 16.00 до 20.00, По нечетным числам с 9.00- до 13.00 | |
| 40 | Пр. Испытателей, 24; Б-р Серебристый 21,22/3 | По четным числам с 16.00 до 20.00, По нечетным числам с 9.00- до 13.00 | |
| 59 | Тафинцев В.А. | Богатырский пр., 7/5, Б-р Серебристый 11, 16/1 | По четным числам с 16.00 до 20.00, По нечетным числам с 9.00- до 13.00 |
| 43 | Венгеренко Л.П. | Пр. Испытателей, 8/2, Б-р Серебристый 13, 15, | По четным числам с 16.00 до 20.00, По нечетным числам с 9.00- до 13.00 |
| 55 | Роговенко С.Ю. | Пр. Испытателей, 26, 28/2,28/3,28/4 | По четным числам с 16.00 до 20.00, По нечетным числам с 9.00- до 13.00 |
| 42 | Богатырский пр., 3/1, Пр. Испытателей, 6/1, 6/3, 8/1 | По четным числам с 16.00 до 20.00, По нечетным числам с 8.00- до 12.00 |
Дома №4, №9, №10 по Богатырскому пр., ; Дома №7/3, №21 по Аэродромной ул. ; Дома №15/1, №15/2, №20 по Коломяжскому пр.,
обслуживает офис «Современная медицина», расположенный по адресу Коломяжский пр.,д.20
| Лебедева Наталья Эдуардовна | Врач-стоматолог детский 1 категории | с 8-00 до 14-00
|
| Боронина Людмила Викторовна | Врач-стоматолог детский | четные с 15-00 до 21-00 нечетные с 8-00 до 14-00 |
| Живулина Светлана Владимировна | Врач-стоматолог детский высшей категории | четные с 15-00 до 21-00 нечетные с 8-00 до 14-00 |
| Иконникова Татьяна Ивановна | Врач-стоматолог детский | четные с 15-00 до 21-00 нечетные с 8-00 до 14-00 |
| Койванен Марина Валерьевна | Врач-стоматолог детский | четные с 8-00 до 14-00 нечетные с 15-00 до 21-00 |
| Лембер Ольга Викторовна | Врач-стоматолог детский высшей категории | четные с 15-00 до 21-00 нечетные с 8-00 до 14-00 |
| Николаева Анна Игоревна | Врач-стоматолог детский 2 категории | четные с 8-00 до 14-00 нечетные с 15-00 до 21-00 |
| Николаева Светлана Васильевна | Врач-стоматолог детский 1 категории | четные с 8-00 до 14-00 нечетные с 15-00 до 21-00 |
| Федорова Анжелика Викторовна | Врач-стоматолог детский | четные с 8-00 до 14-00 нечетные с 15-00 до 21-00 |
| Иванова Наталия Евсеевна | Врач-стоматолог детский 2 категории | четные с 8-00 до 14-00 нечетные с 15-00 до 21-00 |
| Воротникова Надежда Григорьевна | Врач-стоматолог детский | четные с 15-00 до 21-00 нечетные с 8-00 до 14-00 |
| Пелепягина Светлана Викторовна | Ортодонт | четные с 15-00 до 21-00 нечетные с 8-00 до 14-00 |
| Кошелева Анна Игоревна | Ортодонт | четные с 8-00 до 14-00 нечетные с 15-00 до 21-00 |
| Крень Надежда Александровна | Врач-стоматолог детский | четные с 15-00 до 21-00 нечетные с 8-00 до 14-00 |
График приема специалистов | Санкт-Петербургское государственное бюджетное учреждение здравоохранения «Стоматологическая поликлиника №11»
График приема специалистов
График работы Стоматологической поликлиники № 11 и ее должностных лиц определяется правилами внутреннего трудового распорядка Поликлиники с учетом ограничений, установленных Трудовым кодексом Российской Федерации. График работы специалистов устанавливаются главным врачом в соответствии с типовыми должностными инструкциями персонала и по согласованию с профсоюзными органами. График и режим работы утверждаются главным врачом.
1-е терапевтическое отделение
График работы отделения: четные числа – с 8:00 до 14:00, нечетные числа – с 15:00 до 21:00.
| Врач | Профиль | Время работы |
| Шунтикова Наталья Валентиновна | Зав.отделением | по графику работы отделения |
| Арсеньева Алла Александровна | врач-стом.терапевт | по графику работы отделения |
| Большакова Екатерина Ивановна | врач-стом.терапевт | индивидуальное распиание |
| Бадалян Армине Ервандовна | врач-стом.терапевт | по графику работы отделения |
| Воронинская Светлана Викторовна | врач-стом.терапевт | по графику работы отделения |
| Друзь Татьяна Васильевна | врач-стом.терапевт | по графику работы отделения |
| Иванова Лариса Николаевна | врач-стом.терапевт | по графику работы отделения |
| Ивачева Ирина Алексеевна | врач-стом.терапевт | индивидуальное расписание |
| Мелковский Роман Валерьевич | врач-стом.терапевт | по графику работы отделения |
| Онищук Ольга Михайловна | врач-стом.терапевт | по графику работы отделения |
| Распопова Елена Альбертовна | врач-стом.терапевт | по графику работы отделения |
| Розина Маргарита Геннадьевна | врач-стом.терапевт | отпуск по уходу за ребенком |
| Смирнова Юлия Сергеевна | врач-стом.терапевт | индивидуальное расписание |
| Татаренцева Галина Николаевна | врач-стом.терапевт | по графику работы отделения |
2-е терапевтическое отделение
График работы отделения: четные числа – с 15:00 до 21:00, нечетные числа – с 8:00 до 14:00.
| Врач | Профиль | Время работы |
| Вишневская Елена Александровна | зав.отделением | по графику работы отделения |
| Артемьева Ольга Николаевна | врач-стом.терапевт | по графику работы отделения |
| Бухальцова Татьяна Михайловна | врач стом.терапевт | четные: с 15:00 до 21:00; нечетные: с 8:00 до 14:00 |
| Владимирова Елена Михайловна | врач-стом.терапевт | по графику работы отделения |
| Макарова Марина Владимировна | врач-стом.-терапевт | четные: с 15:00 до 21:00 |
| Лосева Елена Аркадьевна | врач-стом.терапевт | по графику работы отделения |
| Ильенко Наталья Ивановна | врач-стом.терапевт | по графику работы отделения |
| Петрова Надежда Валентиновна | врач-стом.общ. практики | отпуск по уходу за ребенком |
| Самойлова Ксения Сергеевна | врач-стом.общ. практики | отпуск по уходу за ребенком |
| Синицына Татьяна Евгеньевна | врач-стом.терапевт | по графику работы отделения |
| Холодняк Валерия Сергеевна | врач-стом.терапевт | по графику работы отделения |
| Шолохова Екатерина Валерьевна | врач-стом.терапевт | по графику работы отделения |
| Яковлева Елена Владимировна | врач-стом.терапевт | по графику работы отделения |
Кабинет пародонтологии
| Врач | Профиль | Время работы |
| Кихай Надежда Сергеевна | врач-парадонтолог | четные- утро; нечетные вечер; |
| Кузьмина Екатерина Петровна | врач-стоматолог-терапевт | четные- утро; нечетные вечер; |
Кабинет рентгенодианостики
График работы: с понедельника по пятницу с 8:30 до 14:30 и с 15:00 до 20:30, в субботу с 8:30 до 14:30, в воскресенье — выходной.
| Врач | Профиль | Время работы |
| Валькова Надежда Михайловна | рентгенолаборант | по графику работы отделения |
| Ракова Елена Владимировна | рентгенолаборант | по графику работы отделения |
Кабинет хирургический
График работы: с понедельника по пятницу с 8:30 до 14:30 и с 15:00 до 20:30, в субботу с 8:30 до 14:30, в воскресенье — выходной.
| Кабинет хирургии | Профиль | Время работы |
| Артемьев Алексей Олегович | врач-стомат.хирург | четные-утро; нечетные- вечер, кроме среды |
| Кучеев Дмитрий Иванович | врач-стомат.хирург | четные-вечер, нечетные-утро; операционные дни: не четные вторники с 8:00 до 14:30 |
| Лебедев Максим Юрьевич | врач-стомат.хирург | четные-утро; нечетные- вечер. |
| Назаров Максим Игоревич | врач-стомат.хирург | четные-вечер, нечетные-утро; операционные дни: не четные четверги с 8:00 до 14:30 |
Нечетных и четных чисел
Что такое четные и нечетные числа?
Целое число, которое можно разделить на 2, является четным числом, а целое число, которое нельзя разделить на 2, является нечетным числом. Они могут быть как положительными, так и отрицательными. Нечетные числа всегда находятся между четными и наоборот.
Чтобы различать четные и нечетные числа, всегда ищите их конечную цифру. Последняя цифра четного числа всегда равна 0, 2, 4, 6 или 8, а последняя цифра нечетного числа всегда равна 1, 3, 5, 7 или 9.
Примеры
Несколько примеров четных чисел:
-22, -10, 0, 6, 18, 234.
Вышеупомянутые числа четные, потому что они заканчиваются на 0, 2, 4, 6 или 8.
Несколько Примеры нечетных чисел:
-101, -17, 1, 9, 23, 985.
Приведенные выше числа нечетные, потому что они заканчиваются на 1, 3, 5, 7 или 9.
Свойства
нечетные и четные числа обладают особыми свойствами в отношении алгебраических операций (сложение, вычитание и умножение).Когда мы применяем алгебраические операции к двум четным или нечетным числам, мы всегда получаем четное или нечетное число. Мы исключаем деление здесь, потому что деление иногда дает результат в дробях, когда речь идет об особых свойствах.
- Когда мы складываем или вычитаем два четных числа, результатом всегда будет четное число. Например, 6 + 4 = 10
6 — 4 = 2
- Когда мы складываем или вычитаем четное и нечетное число, результат всегда нечетный. Например, 7 + 4 = 11
7 — 4 = 3
- Когда мы складываем или вычитаем два нечетных числа, результатом всегда будет четное число. Например, 7 + 3 = 10
7 — 3 = 4
- Когда мы умножаем два четных числа, результатом всегда будет четное число. Например,
6 × 4 = 24 - Когда мы умножаем четное и нечетное число, результатом всегда будет четное число. Например,
7 × 4 = 28 - Когда мы умножаем два нечетных числа, результатом всегда будет нечетное число. Например,
7 × 3 = 21
Обобщение нечетных и четных чисел
Мы также можем обобщить четные и нечетные числа.Например, если «n» — четное число, то следующее нечетное число будет «n + 1», а следующее четное число — «n + 2» и так далее. Аналогично, если «n» — нечетное число, то следующее четное число — «n + 1», следующее нечетное число — «n + 2» и так далее.
Например, если мы хотим записать серию из пяти нечетных чисел, начиная с 73, мы можем записать это как:
73, 73 + 2, 73 + 4, 73 + 6, 73 + 7
73, 75 , 77, 79, 81
Таблица чисел
Следующая таблица представляет собой таблицу чисел от 1 до 100, где нечетные числа выделены желтым цветом , а четные числа выделены зеленым цветом .
Предыдущий урок | Главная страница | Следующий урокСписок нечетных чисел — ChiliMath
Не стесняйтесь повторить понятие нечетного числа. Щелкните изображение ниже, чтобы перейти к моему уроку о нечетных числах.
Если вы ищете исчерпывающий список нечетных чисел от 1 до 1000 , это место для вас!
Я разделил нечетные числа на десять (10) групп.
Нечетные числа от 1 до 100
1
3
5
7
9
11
13
15
17
19
21
23
25
27
29
31
33
35
37
39
41
43
45
47
49
51
53
55
57
59
61
63
65
67
69
71
73
75
77
79
81
83
85
87
89
91
93
95
97
99
Нечетные числа от 101 до 200
101
103
105
107
109
111
113
115
117
119
121
123
125
127
129
131
133
135
137
139
141
143
145
147
149
151
153
155
157
159
161
163
165
167
169
171
173
175
177
179
181
183
185
187
189
191
193
195
197
199
Нечетные числа от 201 до 300
201
203
205
207
209
211
213
215
217
219
221
223
225
227
229
231
233
235
237
239
241
243
245
247 249
251
253
255
257
259
261
263
265
267
269
271
273
275
277
279
281
283
285
287
289
291
293
297
297 299
Нечетные числа от 301 до 400
301
303
305
307
309
311
313
315
317
319
321
323
325
327
329
331
333
335
337
339
341
343
345
345 349
351
353
355
357
359
361
363
365
367
369
371
373
375
377
379
381
383
385
387
389
391
393
395
397 399
Нечетные числа от 401 до 500
401
403
405
407
409
411
413
415
417
419
421
423
425
427
429
431
433
435
437
439
441
443
445 900 449
451
453
455
457
459
461
463
465
467
469
471
473
475
477
479
481
483
485
487
489
491
493 9007
495
499
Нечетные числа от 501 до 600
501
503
505
507
509
511
513
515
517
519
521
523
525
527
529
531
533
535
537
539
541
543 9007 10 545
539
541
543 9007 10 545 900 549
551
553
555
557
559
561
563
565
567
569
571
573
575
577
579
581
583
585
587
589
591
593 9007 5910 59
599
Нечетные числа от 601 до 700
601
603
605
607
609
611
613
615
617
619
621
623
625
627
629
631
633
635
637
639
641
643 9007 10 641
643 9007
641
643
641 649
651
653
655
657
659
661
663
665
667
669
671
673
675
677
679
681
683
685
687
689
691
693
695
695
695 699
Нечетные числа от 701 до 800
701
703
705
707
709
711
713
715
717
719
721
723
725
727
729
731
733
735
737
739
741
743 710 710 900
739
741
743 710 745 900 749
751
753
755
757
759
761
763
765
767
769
771
773
775
777
779
781
783
785
787
789
791
7930
799
Нечетные числа от 801 до 900
801
803
805
807
809
811
813
815
817
819
821
823
825
827
829
831
833
835
837
839
841
81043
845
839
841
81043
845 849
851
853
855
857
859
861
863
865
867
869
871
873
875
877
879
881
883
885
887
889
891
893
895
899
Нечетные числа от 901 до 1000
901
903
905
907
909
911
913
915
917
919
921
923
925
927
929
931
933
935
937
939
941
943
949
951
953
955
957
959
961
963
965
967
969
971
973
975
977
979
981
983
985
987
989
991
993
995
999
Возможно, вас заинтересует:
Список четных чисел
Что такое нечетное число?
Что такое четное число?
нечетных и четных чисел
Четные и нечетные числа - это только натуральные числа.См. Следующую числовую строку.
Из приведенной выше диаграммы мы видим, что для четных чисел диаграмма полная, а для нечетных чисел на 1 квадрат меньше. Четные числа можно разделить на две группы. Например, четыре можно разделить на две группы по два. ( .... , это 4 точки, можно разделить как .. | .. ) Но нечетные числа не могут быть разделены поровну, как четные числа.
Таким образом, четные числа начинаются с 0, а нечетные - с 1.
Четные числа: 0,2,4,6,8,10, ...
Итак, в целом мы можем сказать, что числа, заканчивающиеся цифрами выше, являются четными числами.
Нечетные числа: 1,3,5,7,9, ...
Число, единица измерения которого отличается от 0,2,4,6,8, является нечетным числом.
Наименьшее четное натуральное число - 2, а наименьшее натуральное нечетное - 1.
_______________________________________________________________
Q.1 Напишите все четные числа от 22 до 60.
22, ___, ___, ___, ___, ___, ___, ___, ___, ___, ___, ___, ___, ___, ___, ___, ___
, ___, ___, 60.
Q.2 Запишите все нечетные числа от 61 до 99.
61, ___, ___, ___, ___, ___, ___, ___, ___, ___, ___, ___, ___, ___, ___, ___, ___ ,
___, ___, 99
Q.3 Напишите следующее четное число.
1) 98, ___ 2) 26, ___ 3) 58, ___ 4) 52, ___ 5) 48, ___ 6) 34, ___
7) 88, ___
8) 66, ___ 9) 78, ___ 10) 66, ___
Q.4 Запишите следующее нечетное число.
1) 53, ___ 2) 81, ___ 3) 17, ___ 4) 63, ___ 5) 27, ___ 6) 87, ___
7) 99, ___
8) 49, ___ 9) 95, ___ 10) 33, ___
Q.5 Обведите четные числа.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28 900 10 29 30 1 32 33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48 49 50 51 52 53
54 55 56 57 58 59 60
61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77
78 79 80
81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100
Нечетные и четные числа
Математика 2-го класса
Домашняя страница
Covid-19 заставил мир пройти через феноменальный переход.
За электронным обучением будущее уже сегодня.
Оставайтесь дома, оставайтесь в безопасности и продолжайте учиться !!!
Covid-19 повлиял на физическое взаимодействие между людьми.
Не позволяйте этому влиять на ваше обучение.
Четные и нечетные числа
Четные числа - это числа, которые можно разделить на 2 поровну. Четные числа могут отображаться в виде набора следующим образом:
{? -4, -2, 0, 2, 4,? }
Нечетные числа - это числа, которые нельзя разделить на 2 без остатка.Нечетные числа могут быть представлены в виде набора следующим образом:
{? -5, -3, -1, 1, 3, 5,? }
Ноль считается четным числом.
Он четный или нечетный?
Чтобы определить, четное или нечетное число, посмотрите на число в разряде единиц. Это единственное число подскажет, четное или нечетное целое число.
- Четное число заканчивается на 0, 2, 4, 6 или 8.
- Нечетное число заканчивается на 1, 3, 5, 7 или 9.
Рассмотрим число 3 842 917 .Он заканчивается на 7, нечетное число. Следовательно, 3 842 917 - нечетное число. Аналогично, 8322 - четное число, потому что оно заканчивается на 2.
Сложение четных и нечетных чисел
- четное + четное = четное
4 + 2 = 6
- четное + нечетное = нечетное
4 + 3 = 7
- нечетный + нечетный = четный
5 + 3 = 8
Вычитание четных и нечетных чисел
- четное - четное = четное
4 - 2 = 2
- четное - нечетное = нечетное
4 - 3 = 1
- нечетное - нечетное = четное
5 - 3 = 2
Умножение четных и нечетных чисел
- четное x четное = четное
4 x 2 = 8
- четное x нечетное = четное
4 x 3 = 12
- нечетный x нечетный = нечетный
5 x 3 = 15
Деление или задача дроби
Как видите, существует правила, которые говорят, что происходит, когда вы складываете, вычитаете или умножаете четное и нечетные числа.В любой из этих операций вы всегда будете получать целое число определенного вида.
Но , когда вы делите числа, может случиться что-то хитрое - у вас может остаться дробь. Дроби не являются четными или нечетными числами, , потому что они не являются целыми числами. Это всего лишь части чисел, и их можно записать по-разному.
Например, нельзя сказать, что дробь 1/3 нечетная, потому что знаменатель - нечетное число. С таким же успехом можно записать ту же дробь, что и 2/6, знаменатель которой - четное число.
Термины ? Четное число? и ? Нечетное число? используются только для целых чисел и их противоположностей (аддитивные обратные).
Что такое нечетные числа - определение, список, типы и свойства нечетных чисел
Числа бывают двух типов: четные и нечетные числа. Нечетные числа - это целые числа, которые не делятся на 2. Кроме того, дроби не могут быть нечетными числами. Веданту дает вам подробное объяснение концепции нечетных чисел на очень простом языке.Учебные материалы легко доступны в формате PDF и могут быть бесплатно загружены с Vedantu.
Итак, что такое нечетные числа?
Нечетные числа - это целые числа, которые всегда оставляют остаток при делении на 2. Эти числа представляют собой целые числа в форме n = 2k + 1, где k - целое число. Примеры нечетных чисел: -5, -3, -1, 1, 3, 5, 7 и так далее. Нечетные числа при делении на 2 всегда оставляют остаток 1, напротив, четные числа при делении на 2 оставляют остаток 0.Наименьшее положительное нечетное число - 1.
Список нечетных чисел:
Всего имеется 50 нечетных чисел от 1 до 100 и 24 нечетных числа от 1 до 50.
Вот список нечетных чисел от -5 на 25:
-5, -3, -1, 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25.
И список четных чисел :
-4, -2, 0,2, 4, 6, 8,10, 12, 14, 16, 18, 20, 22, 24.
Типы нечетных чисел:
Составные нечетные числа: эти составные числа, которые нельзя разделить на 2, являются составными нечетными числами, а все положительные целые числа, имеющие множитель, отличный от 1, называются составными числами.Список составных нечетных чисел от 1 до 50 выглядит следующим образом.
9, 15, 21, 25, 27, 33, 45, 49.
Последовательные нечетные числа: последовательные нечетные числа следуют друг за другом в последовательном порядке. Между ними разница в 2 раза.
Последовательные нечетные числа от 1 до 10:
1, 3, 5, 7, 9.
Свойства нечетных чисел
-
Нечетный + Нечетный = Четный
Когда два нечетных числа складываются, их сумма - четное число.Например,
1 + 3 = 4
Здесь 1 и 3 - нечетные числа, но их сумма равна 4, что является четным числом.
-
Нечетный - Нечетный = Четный
Когда нечетное число вычитается из другого нечетного числа, результатом является четное число. Например,
3-1 = 2
7-3 = 4
Здесь 7, 3 и 1 - нечетные числа, а результат - четное число.
-
Нечетный × Нечетный = Нечетный
Произведение двух нечетных чисел всегда является нечетным числом.Например,
5 × 3 = 15
3 × 3 = 9
Здесь 5 и 3 - нечетные числа, а продукты - тоже нечетные числа.
-
Нечетный / Нечетный = Нечетный
При делении двух нечетных чисел всегда получается нечетное число. Например,
3/3 = 1
15/5 = 3
Здесь 5, 3 и 15 являются нечетными числами, и результат их деления также будет нечетным числом.
Ключевые особенности нечетного числа заключаются в следующем.
-
Когда мы делим нечетные числа на 2, остаток всегда должен быть 1.
-
1 - первое положительное нечетное число в числовой строке.
О Веданту
Веданту - это платформа для онлайн-обучения. В нем представлены учебные материалы по всем предметам, входящим в учебные планы 6–12 классов, в формате PDF. Электронные книги NCERT по каждому предмету также доступны в формате PDF на нашем веб-сайте и в мобильном приложении. Мы, в Vedantu, стремимся предоставить лучшие учебные материалы, чтобы помочь вам с вашей успеваемостью на экзаменах совета директоров и на многих конкурсных экзаменах.
Ключевые особенности Веданту:
-
Он предоставляет решения по главам для всех предметов.
-
Все учебные решения и учебные материалы подготовлены в соответствии с рекомендациями Совета CBSE.
-
Все учебные материалы подготовлены нашими предметными экспертами в простой для понимания форме для всех студентов.
-
Все концепции поясняются иллюстративными диаграммами и графиками.
-
Учебные материалы по Веданту можно найти и загрузить бесплатно.
Следуя решениям NCERT и другим учебным материалам по Веданту, студенты могут получить представление о шаблонах вопросов, тематическом весе, схеме выставления оценок и т. Д. Для своих экзаменов. Наши высококвалифицированные преподаватели предоставляют учащимся наиболее эффективные методы решения проблем с помощью этих решений, чтобы учащиеся могли лучше подготовиться к экзаменам. Студенты также могут записаться на живые занятия и сеансы по устранению сомнений, чтобы лучше понять концепции.
Как умножать нечетные числа
Пояснение:Допустим, у нас есть два числа, и их единицы - цифры и B соответственно. Если мы хотим узнать единичные цифры произведения и, все, что нам нужно сделать, это взглянуть на единичные цифры произведения и. Например, если мы умножим 137 и 219, то цифра единиц будет такой же, как цифра единиц. Поскольку единичная цифра 63 равна 3, единичная цифра 137 x 219 также будет 3. Короче говоря, нам действительно нужно беспокоиться только о единичных цифрах чисел, которые мы умножаем, когда мы пытаемся найти единичную цифру их произведения. .
Мы хотим найти единственную цифру. По сути, экспонента - это всего лишь короткая стрелка для повторного умножения. Давайте посмотрим на разряды первых нескольких показателей 2013 года.
- единица цифры 3.
Чтобы найти единичную цифру 2013 года во второй степени, нам нужно думать об этом как о произведении 2013 и 2013 годов. Как обсуждалось ранее, если мы хотим, чтобы единичные цифры двух чисел умножались вместе, нам просто нужно умножить их единичные цифры. Таким образом, если умножить 2013 год на 2013, то цифра из единиц будет такой же, как.
- единица цифра 9.
Далее мы хотим найти единичную цифру 2013 года в третьей степени. Для этого мы умножим квадрат 2013 года на 2013 год. Не имеет значения, что мы не знаем точно, чему равен 2013 квадрат, потому что нам нужно беспокоиться только о единичной цифре, которая равна 9. Другими словами, В 2013 году в третьей степени будет одна цифра, которая равна единице произведения 9 (которая была единицей в квадрате 2013 года) и 3 (которая является единицей цифры 2013 года).Когда мы умножаем 9 на 3, мы получаем 27, так что единица 2013 года в третьей степени равна 7.
- одна цифра 7.
Чтобы найти единичную цифру 2013 года в четвертой степени, нам нужно только позаботиться о том, чтобы умножить единичную цифру 2013 года в третьей степени (то есть 7) на единичную цифру 2013 года. Когда мы умножаем 7 и 3, мы получаем 21, что означает, что цифра 2013 в четвертой степени равна 1.
- одна цифра 1.
Чтобы найти единственную цифру 2013 года в пятой степени, мы умножим 1 на 3, что даст нам 3.
- единица цифры 3.
Обратите внимание, что мы вернулись к цифре из единиц с 3. Если мы умножим это на 2013, мы получим цифру из единиц 9. Другими словами, цифры из единиц повторяются в каждой четвертой степени.
Значение разряда степеней 2013 года следующее (с 2013 года в первой степени):
3, 9, 7, 1, 3, 9, 7, 1, ....
По сути, мы хотим найти 2013-й член приведенной выше последовательности. Обратите внимание, что каждый четвертый член равен 1, т.е.е. последовательность повторяется каждые четыре члена. Если позиция терминов в последовательности кратна 4, тогда термин будет 1. Короче говоря, 4-й, 8-й, 12-й, 16-й члены и так далее будут равны 1. Поскольку 2012 кратно 4, 2012-й член в последовательности будет равен 1. (Мы можем определить, кратно ли число 4, посмотрев на его последние две цифры.) Это означает, что 2013-й член будет 3. Таким образом, 2013 год в степени 2013 имеет одна цифра 3.
Ответ 3.
Python Упражнение: подсчитайте количество четных и нечетных чисел из ряда чисел
Условие Python: Упражнение 6 с Решением
Напишите программу на Python для подсчета количества четных и нечетных чисел из ряда чисел.
Изображение четных чисел:
Изображение нечетных чисел:
Пример раствора:
Код Python:
numbers = (1, 2, 3, 4, 5, 6, 7, 8, 9) # Объявление кортежа
count_odd = 0
count_even = 0
для x в числах:
если не x% 2:
count_even + = 1
еще:
count_odd + = 1
print ("Количество четных чисел:", count_even)
print ("Количество нечетных чисел:", count_odd)
Пример вывода:
Количество четных чисел: 4 Количество нечетных чисел: 5
Схема:
Четные числа от 1 до 100:
Нечетные числа от 1 до 100:
Визуализировать выполнение кода Python:
Следующий инструмент визуализирует, что делает компьютер, шаг за шагом, когда он выполняет указанную программу:
Редактор кода Python:
Есть другой способ решить эту проблему? Разместите свой код (и комментарии) через Disqus.
Пред .: Напишите программу на Python, которая принимает слово от пользователя и меняет его местами.
Далее: Напишите программу Python, которая печатает каждый элемент и соответствующий ему тип из следующего списка.
Python: советы дня
Несколько присвоений:
>>> # вместо выполнения a = 8; б = 5
>>> а, б = 8, 5
>>> print (f'a - {a}; b - {b} ')
а равно 8; b равно 5
>>> # Поменять местами две переменные
>>> а, Ь = Ь, а
>>> print (f'a - {a}; b - {b} ')
а равно 5; b равно 8
>>> # Поменять местами первый и последний элементы в списке
>>> числа = [1, 2, 3, 4, 5]
>>> числа [0], числа [-1] = числа [-1], числа [0]
>>> числа
[5, 2, 3, 4, 1]
.

 {x} \sin xdx\]
{x} \sin xdx\]
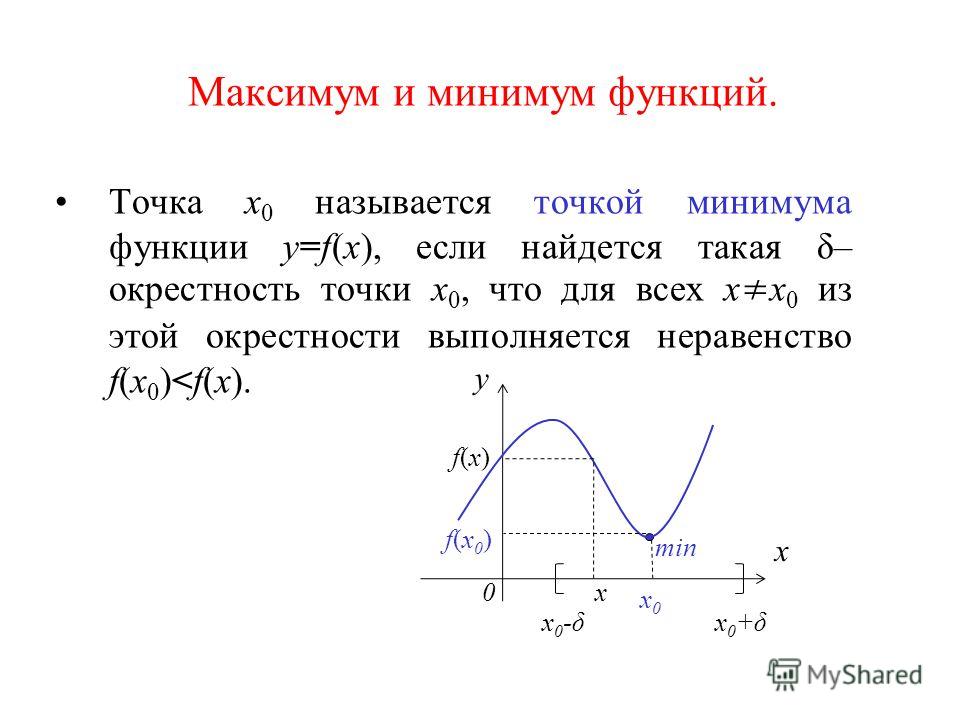 рисунок) к оси Ox, ближе к началу
координат. Поэтому при малых значениях (и при ) приращение функции можно приближенно заменить его главной частью , т.е.
рисунок) к оси Ox, ближе к началу
координат. Поэтому при малых значениях (и при ) приращение функции можно приближенно заменить его главной частью , т.е. Найти дифференциалы функций:
Найти дифференциалы функций:



 Оценить точность полученного результата.
Оценить точность полученного результата.

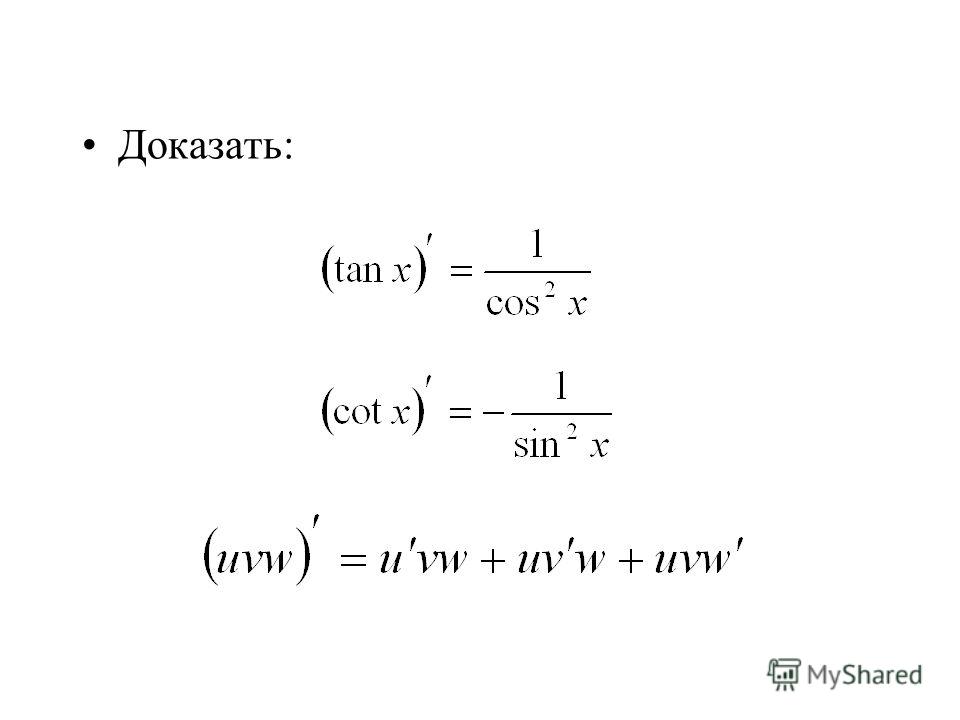 И уравнение, которое представляет отношения между этими переменными, называется дифференциальным уравнением.
И уравнение, которое представляет отношения между этими переменными, называется дифференциальным уравнением. производный
производный Это относится к наклону графика в данной точке.
Это относится к наклону графика в данной точке. В двух словах, дифференциальные уравнения включают производные, которые фактически указывают, как величина изменяется по отношению к другой. Решая дифференциальное уравнение, вы получаете формулу для количества, которое не содержит производных. Метод вычисления производной называется дифференцированием. Проще говоря, производная функции — это скорость изменения выходного значения относительно его входного значения, тогда как дифференциал — это фактическое изменение функции..
В двух словах, дифференциальные уравнения включают производные, которые фактически указывают, как величина изменяется по отношению к другой. Решая дифференциальное уравнение, вы получаете формулу для количества, которое не содержит производных. Метод вычисления производной называется дифференцированием. Проще говоря, производная функции — это скорость изменения выходного значения относительно его входного значения, тогда как дифференциал — это фактическое изменение функции.. Возьмем, к примеру: утверждение «y является функцией x» означает, что что-то, связанное с y, напрямую связано с x по какой-либо формуле. Скажем, если входной сигнал равен 6, а функция — добавить 5 к входу 6. Результат будет 6 + 5 = 11, что является вашим выходом.
Возьмем, к примеру: утверждение «y является функцией x» означает, что что-то, связанное с y, напрямую связано с x по какой-либо формуле. Скажем, если входной сигнал равен 6, а функция — добавить 5 к входу 6. Результат будет 6 + 5 = 11, что является вашим выходом. Другая ветвь называется интегральным исчислением.
Другая ветвь называется интегральным исчислением.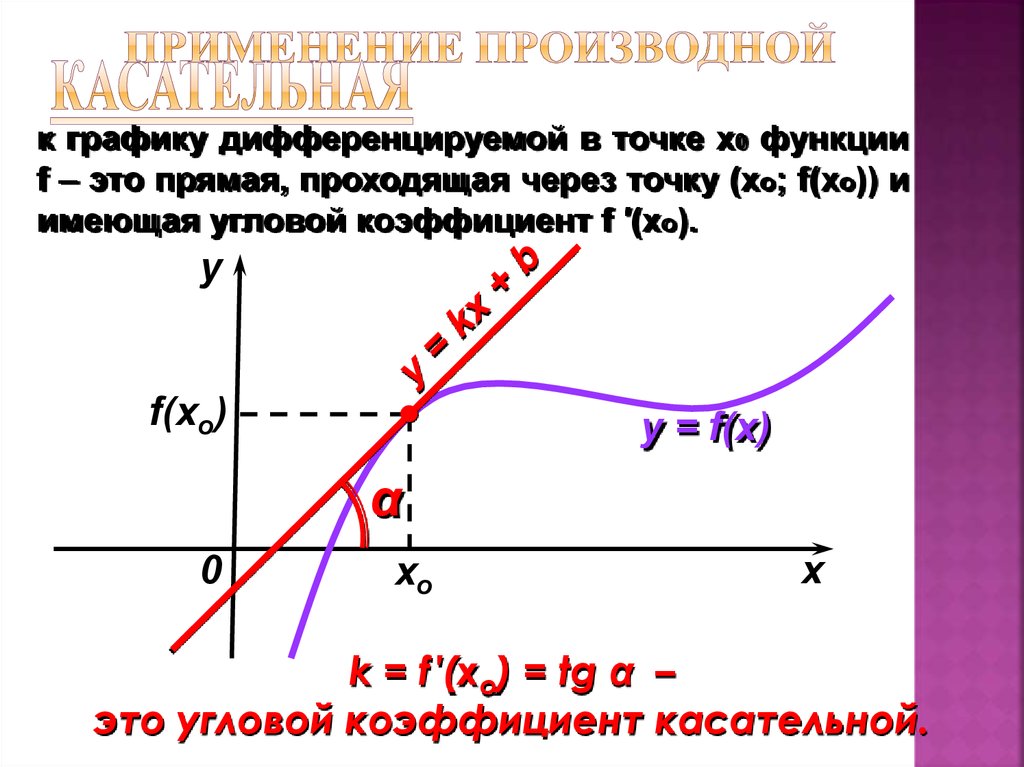 Производной функции обычно является новая функция, которая называется производной функцией или функцией скорости.
Производной функции обычно является новая функция, которая называется производной функцией или функцией скорости. Дифференциация — это процесс нахождения производной. Производной функции является скорость изменения выходного значения по отношению к его входному значению, тогда как дифференциал — это фактическое изменение функции.
Дифференциация — это процесс нахождения производной. Производной функции является скорость изменения выходного значения по отношению к его входному значению, тогда как дифференциал — это фактическое изменение функции.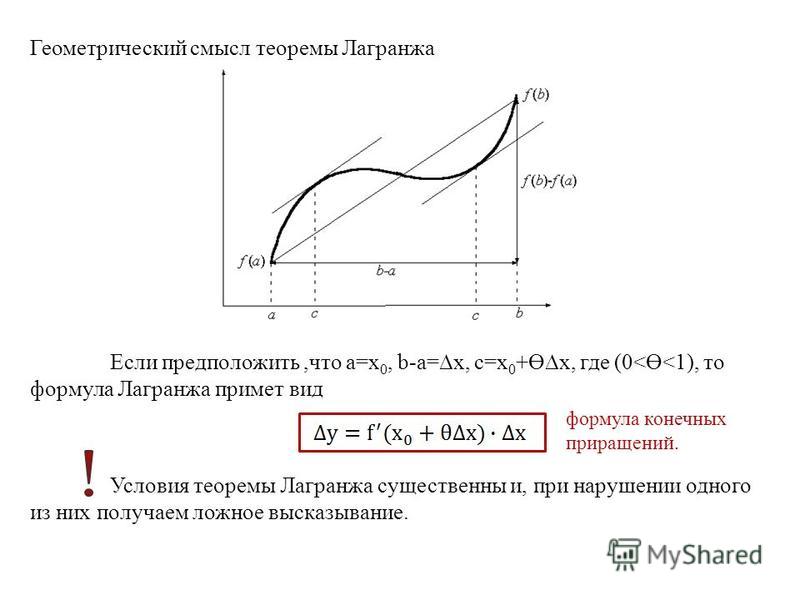 При сравнении изменений связанных величин, где y — функция x, дифференциал dy может быть записана как:
При сравнении изменений связанных величин, где y — функция x, дифференциал dy может быть записана как: Проще говоря, производной функции является скорость изменения выходного значения по отношению к его входному значению, тогда как дифференциал — это фактическое изменение функции.
Проще говоря, производной функции является скорость изменения выходного значения по отношению к его входному значению, тогда как дифференциал — это фактическое изменение функции. Если данный предел существует, то говорят, что функция f(x) дифференцируема в точке x0.
Если данный предел существует, то говорят, что функция f(x) дифференцируема в точке x0.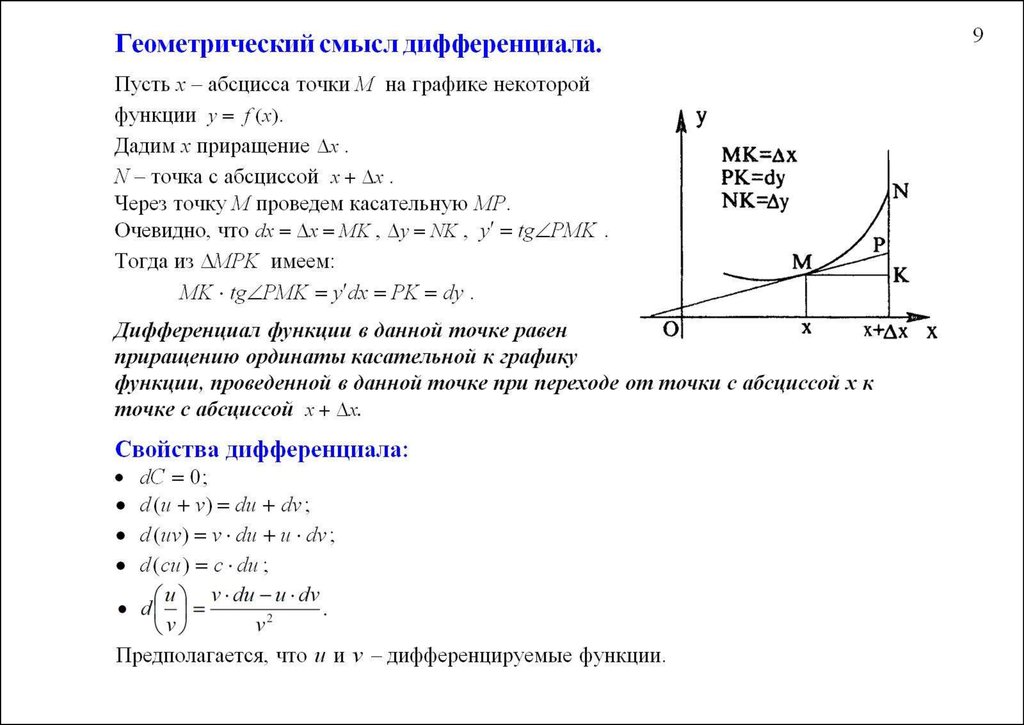 sin xdx]
sin xdx] {-35}\)м.). Несмотря на это вся современная наука (в том числе квантовая механика и теория струн) пропитана дифференциальным исчислением. Даже дискретные результаты типа квантования энергетических уровней атомов получаются из рассмотрения непрерывных функций и дифференциальных уравнений.
{-35}\)м.). Несмотря на это вся современная наука (в том числе квантовая механика и теория струн) пропитана дифференциальным исчислением. Даже дискретные результаты типа квантования энергетических уровней атомов получаются из рассмотрения непрерывных функций и дифференциальных уравнений.
 2}{\Delta x}=\) \( \displaystyle 2x+\Delta x=2x\) при \( \displaystyle \Delta x\rightarrow 0\)
2}{\Delta x}=\) \( \displaystyle 2x+\Delta x=2x\) при \( \displaystyle \Delta x\rightarrow 0\) Это просто произведение квадратной матрицы на вектор-столбец (исходная функция), которое дает другой вектор-столбец (производная функция). То есть получившийся вектор-столбец как раз будет являться аппроксимацией производной исходной функции. Проверьте, что умножая приведенную матрицу по стандартному правилу «строка на столбец» мы получим вектор, состоящий из разниц значений функции в соседних точках, например: \( \displaystyle \Delta y_{12}=y_{2}-y_{1}\) и т.п., что по определению и есть производная (если поделить на \( \displaystyle \Delta t\)). Это еще одна наглядная демонстрация откуда пошло название дифференциал (разность по-русски), достаточно посмотреть на вектор-столбец результата.
Это просто произведение квадратной матрицы на вектор-столбец (исходная функция), которое дает другой вектор-столбец (производная функция). То есть получившийся вектор-столбец как раз будет являться аппроксимацией производной исходной функции. Проверьте, что умножая приведенную матрицу по стандартному правилу «строка на столбец» мы получим вектор, состоящий из разниц значений функции в соседних точках, например: \( \displaystyle \Delta y_{12}=y_{2}-y_{1}\) и т.п., что по определению и есть производная (если поделить на \( \displaystyle \Delta t\)). Это еще одна наглядная демонстрация откуда пошло название дифференциал (разность по-русски), достаточно посмотреть на вектор-столбец результата.
 Действие оператора можно представить графически как изменение сигнала неким преобразователем:
Действие оператора можно представить графически как изменение сигнала неким преобразователем: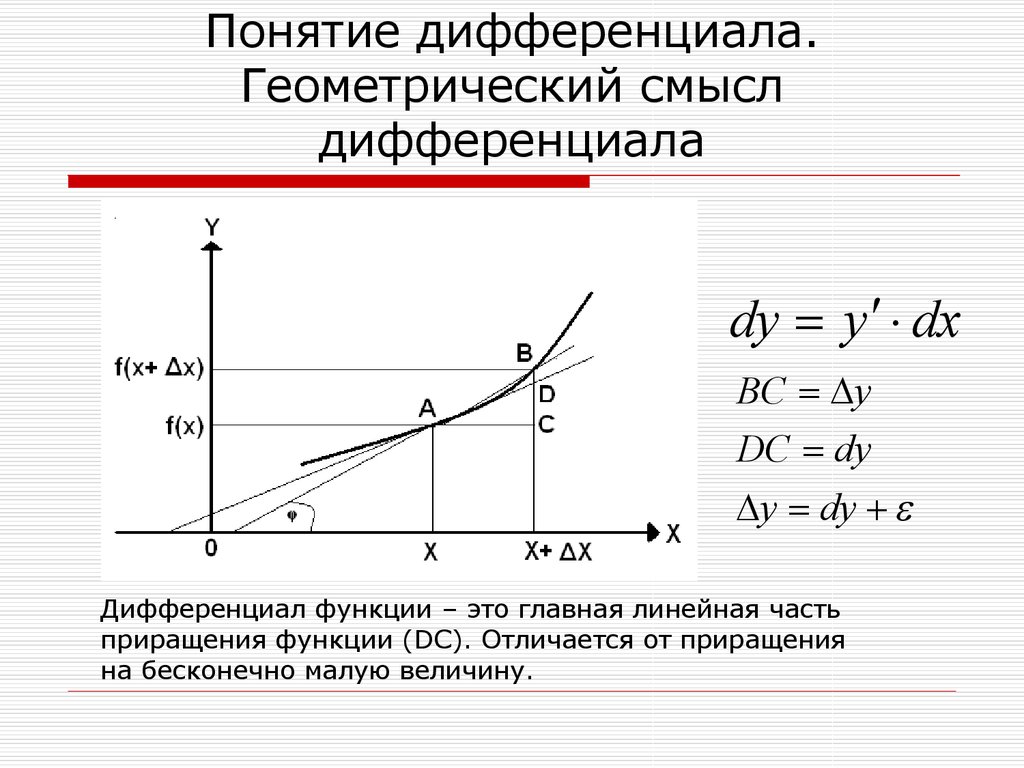 2$. 9{n — 1} f (t_i) (x_ {i + 1} — x_i),
$$
где предел берется по всем размеченным разделам $\mathscr P = (a = x_0 \le t_0 \le x_1 \le t_1 \le \dotsb \le t_{n — 1} \le x_n = b)$ как $\lVert \mathscr P\rVert = \sup \{x_{i + 1} — x_i : 0 \le i < n\}$ сжимается до $0$, если предел существует; и, если прищуриться, можно увидеть $\int$ как обобщенную $\sum$ (действительно, Лейбниц выбрал оператор, чтобы предложить $\int\text{um}$), и $\Delta x_i = x_{i + 1 } - x_i$ как макроскопическое приращение, которое в пределе становится бесконечно малым приращением $\mathrm dx$. 92=27, тогда вы можете провести касательную к этой точке функции.
2$. 9{n — 1} f (t_i) (x_ {i + 1} — x_i),
$$
где предел берется по всем размеченным разделам $\mathscr P = (a = x_0 \le t_0 \le x_1 \le t_1 \le \dotsb \le t_{n — 1} \le x_n = b)$ как $\lVert \mathscr P\rVert = \sup \{x_{i + 1} — x_i : 0 \le i < n\}$ сжимается до $0$, если предел существует; и, если прищуриться, можно увидеть $\int$ как обобщенную $\sum$ (действительно, Лейбниц выбрал оператор, чтобы предложить $\int\text{um}$), и $\Delta x_i = x_{i + 1 } - x_i$ как макроскопическое приращение, которое в пределе становится бесконечно малым приращением $\mathrm dx$. 92=27, тогда вы можете провести касательную к этой точке функции. dx на самом деле является очень небольшим изменением x, и именно это и означает интегрирование. Когда мы берем бесконечно много прямоугольников, наше приближение становится все лучше и лучше.
dx на самом деле является очень небольшим изменением x, и именно это и означает интегрирование. Когда мы берем бесконечно много прямоугольников, наше приближение становится все лучше и лучше.


 Они используются для обозначения наклона касательной. В течение заданного периода времени производные измеряют крутизну наклона функции.
Они используются для обозначения наклона касательной. В течение заданного периода времени производные измеряют крутизну наклона функции.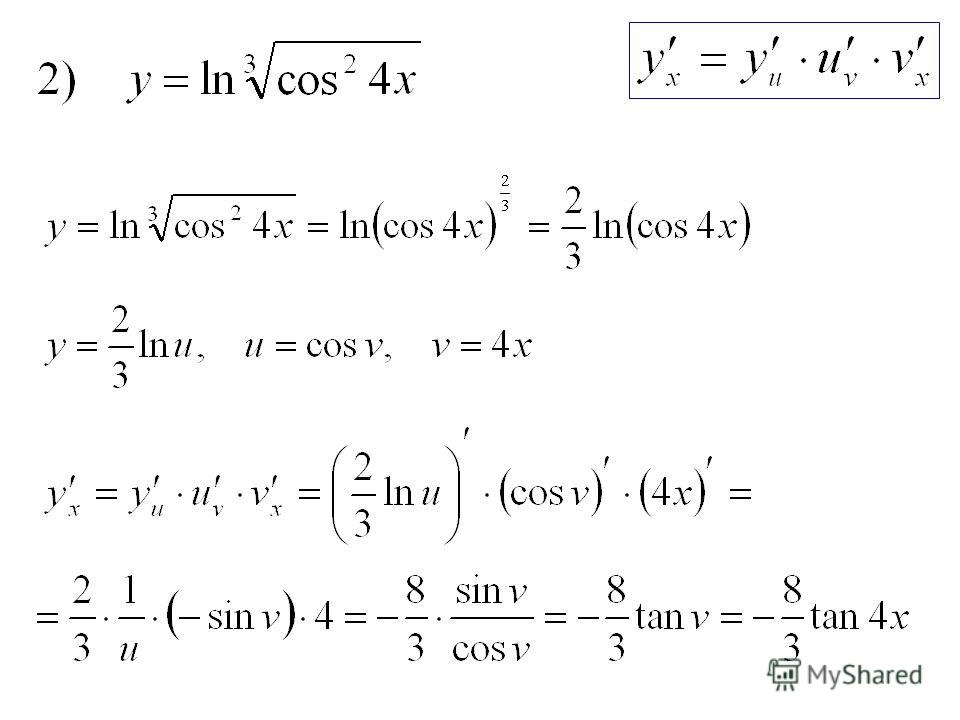 Первый — это подобласть исчисления, которая означает бесконечно малую разницу в некоторой флуктуирующей величине. Производные, с другой стороны, относятся к изменению выходной стоимости из-за соответствующего изменения входной стоимости. Это означает скорость этого изменения.
Первый — это подобласть исчисления, которая означает бесконечно малую разницу в некоторой флуктуирующей величине. Производные, с другой стороны, относятся к изменению выходной стоимости из-за соответствующего изменения входной стоимости. Это означает скорость этого изменения.
 Они используют производные, чтобы четко определить эту связь и измерить бесконечно малые изменения.
Они используют производные, чтобы четко определить эту связь и измерить бесконечно малые изменения.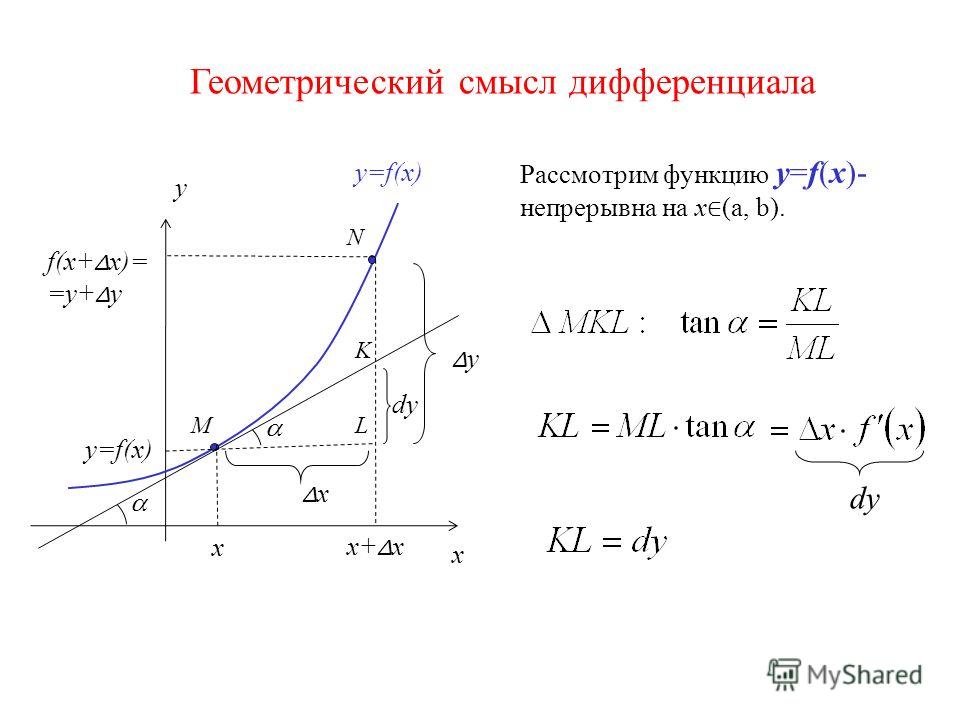 Предположим, что в какой-то момент x 0 ∈ [ a , b ] независимая переменная увеличивается на Δ х . Приращение функции Δ y , соответствующее изменению независимой переменной Δ x , равно
Предположим, что в какой-то момент x 0 ∈ [ a , b ] независимая переменная увеличивается на Δ х . Приращение функции Δ y , соответствующее изменению независимой переменной Δ x , равно \]
\]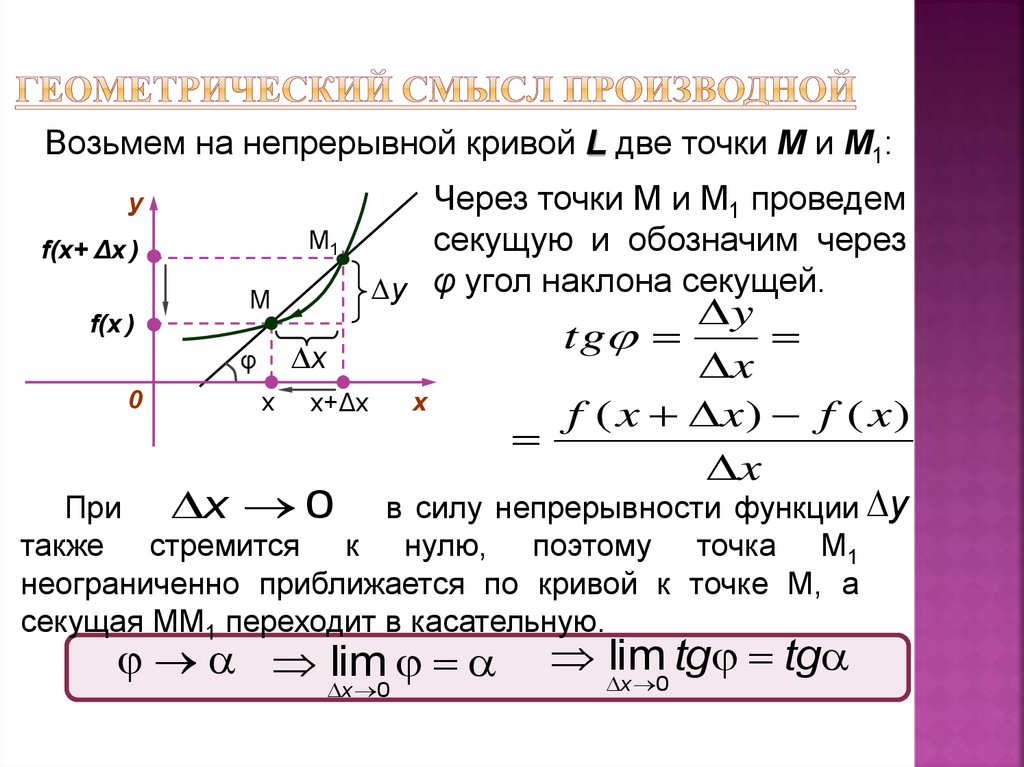 \]
\] Оставшаяся часть полного приращения \(\Delta y\) (отрезок \(N{M_1}\)) соответствует «нелинейной» добавке более высокого порядка малости по \(\Delta x.\)
Оставшаяся часть полного приращения \(\Delta y\) (отрезок \(N{M_1}\)) соответствует «нелинейной» добавке более высокого порядка малости по \(\Delta x.\) \] 9{n — 1}}dx,\;\;\;d\left( {\ln x} \right) = \frac{{dx}}{x},\;\;\;d\left( {\ sin x} \right) = \cos x dx,\]
\] 9{n — 1}}dx,\;\;\;d\left( {\ln x} \right) = \frac{{dx}}{x},\;\;\;d\left( {\ sin x} \right) = \cos x dx,\] Это свойство называется формоинвариантностью дифференциала.
Это свойство называется формоинвариантностью дифференциала. раздел 2, смысл 1) или дифференциал
раздел 2, смысл 1) или дифференциал значение произведения 1) производной функции одной переменной на приращение независимой переменной
значение произведения 1) производной функции одной переменной на приращение независимой переменной 0165 дифференциальных уравнений, как в колебательных контурах, и решения уравнения Шрёдингера в квантовой механике.
Ретт Аллен, Wired , 14 марта 2022 г.
С этой точки зрения дифференциальная конфиденциальность делает данные переписи более точными и прозрачными, а не менее. New York Times , 21 апреля 2022 г.
Меньшая машина активна 9Дифференциал 0165 передает крутящий момент на внешнее колесо во время энергичного прохождения поворотов, создавая забавное ощущение надвигающейся избыточной поворачиваемости даже за пределами точки, в которой задние шины фактически теряют сцепление с дорогой.
Майк Дафф, Автомобиль и водитель , 11 мая 2022 г.
Хотя подкачка является грубым способом маскировки данных, дифференциальные алгоритмы конфиденциальности могут быть настроены для точного удовлетворения требований конфиденциальности.
0165 дифференциальных уравнений, как в колебательных контурах, и решения уравнения Шрёдингера в квантовой механике.
Ретт Аллен, Wired , 14 марта 2022 г.
С этой точки зрения дифференциальная конфиденциальность делает данные переписи более точными и прозрачными, а не менее. New York Times , 21 апреля 2022 г.
Меньшая машина активна 9Дифференциал 0165 передает крутящий момент на внешнее колесо во время энергичного прохождения поворотов, создавая забавное ощущение надвигающейся избыточной поворачиваемости даже за пределами точки, в которой задние шины фактически теряют сцепление с дорогой.
Майк Дафф, Автомобиль и водитель , 11 мая 2022 г.
Хотя подкачка является грубым способом маскировки данных, дифференциальные алгоритмы конфиденциальности могут быть настроены для точного удовлетворения требований конфиденциальности. New York Times , 21 апреля 2022 г.
В программе поощрения говорится, что больницы, которые обязуются постоянно предоставлять отчеты о пропускной способности, будут иметь право на дифференцированную скорректированную выплату, увеличенную на 0,25%.
Стефани Иннес, , Республика Аризона, , 12 апреля 2022 г.
А теперь, когда прибывают первые беженцы из Украины, мало где более ярко иллюстрирует дифференциал 9Получают лечение 0166 беженцев. Washington Post , 11 марта 2022 г.
Уровень избирательности приема также был связан с дифференциальным ростом объема заявлений.
Майкл Т. Нитцель, Forbes , 26 января 2022 г.
Таким образом, цифра 99 процентов не является репрезентативной для реального использования, поскольку минимальное измерение фильтрации маски N95 составляет 9.
New York Times , 21 апреля 2022 г.
В программе поощрения говорится, что больницы, которые обязуются постоянно предоставлять отчеты о пропускной способности, будут иметь право на дифференцированную скорректированную выплату, увеличенную на 0,25%.
Стефани Иннес, , Республика Аризона, , 12 апреля 2022 г.
А теперь, когда прибывают первые беженцы из Украины, мало где более ярко иллюстрирует дифференциал 9Получают лечение 0166 беженцев. Washington Post , 11 марта 2022 г.
Уровень избирательности приема также был связан с дифференциальным ростом объема заявлений.
Майкл Т. Нитцель, Forbes , 26 января 2022 г.
Таким образом, цифра 99 процентов не является репрезентативной для реального использования, поскольку минимальное измерение фильтрации маски N95 составляет 9. 5 процентов (что составляет перепад давления, посадку, утечку и т. д.).
Кори Гаскин, Ars Technica , 18 декабря 2021 г.
5 процентов (что составляет перепад давления, посадку, утечку и т. д.).
Кори Гаскин, Ars Technica , 18 декабря 2021 г. Крис Солари, 9 лет0165 Detroit Free Press , 16 февраля 2022 г.
Эта чудовищная мельница с шестиступенчатой автоматической коробкой передач Ford, соединенной с 9-дюймовым дифференциалом Strange Engineering , встроена в точную копию корпуса фастбэка Dynacorn Classic Bodies от Mustang 1967 года.
Роберт Росс, Robb Report , 20 декабря 2021 г.
Шесть разных бомбардиров привели «Иглз» к доминирующему голу 14:0 дифференциал в трех турнирных играх.
Кэм Керри, BostonGlobe.com , 15 ноября 2021 г.
Не потренировавшись с США, Букеру, Миддлтону и Холидей пришлось преодолевать долгий перелет и приспосабливаться к времени дифференциал для игры.
Дуэйн Рэнкин, , Республика Аризона, , 6 августа 2021 г.
Крис Солари, 9 лет0165 Detroit Free Press , 16 февраля 2022 г.
Эта чудовищная мельница с шестиступенчатой автоматической коробкой передач Ford, соединенной с 9-дюймовым дифференциалом Strange Engineering , встроена в точную копию корпуса фастбэка Dynacorn Classic Bodies от Mustang 1967 года.
Роберт Росс, Robb Report , 20 декабря 2021 г.
Шесть разных бомбардиров привели «Иглз» к доминирующему голу 14:0 дифференциал в трех турнирных играх.
Кэм Керри, BostonGlobe.com , 15 ноября 2021 г.
Не потренировавшись с США, Букеру, Миддлтону и Холидей пришлось преодолевать долгий перелет и приспосабливаться к времени дифференциал для игры.
Дуэйн Рэнкин, , Республика Аризона, , 6 августа 2021 г. Задний двигатель идентичен переднему блоку, но коробка передач добавляет электронный блокирующий механизм к 9.Дифференциал 0165 для обеспечения дополнительного сцепления при движении по бездорожью.
Сэм Абуэльсамид, Forbes , 20 мая 2021 г.
Нотр-Дам должен был закрыться со счетом 41-0, чтобы вернуться к этой точке дифференциал .
Том Нойе, The Indianapolis Star , 11 марта 2021 г.
Сохранение и улучшение этого числа может стать решающим фактором, если конференц-стол или «Щит болельщиков» сведутся к цели 9.0165 дифференциал .
Джулия По, orlandosentinel.com , 5 октября 2020 г.
Узнать больше
Задний двигатель идентичен переднему блоку, но коробка передач добавляет электронный блокирующий механизм к 9.Дифференциал 0165 для обеспечения дополнительного сцепления при движении по бездорожью.
Сэм Абуэльсамид, Forbes , 20 мая 2021 г.
Нотр-Дам должен был закрыться со счетом 41-0, чтобы вернуться к этой точке дифференциал .
Том Нойе, The Indianapolis Star , 11 марта 2021 г.
Сохранение и улучшение этого числа может стать решающим фактором, если конференц-стол или «Щит болельщиков» сведутся к цели 9.0165 дифференциал .
Джулия По, orlandosentinel.com , 5 октября 2020 г.
Узнать больше Мнения, выраженные в примерах, не отражают точку зрения Merriam-Webster или ее редакторов. Отправьте нам отзыв.
Мнения, выраженные в примерах, не отражают точку зрения Merriam-Webster или ее редакторов. Отправьте нам отзыв. Словарь Merriam-Webster.com , Merriam-Webster, https://www.merriam-webster.com/dictionary/дифференциал. По состоянию на 16 сентября 2022 г.
Словарь Merriam-Webster.com , Merriam-Webster, https://www.merriam-webster.com/dictionary/дифференциал. По состоянию на 16 сентября 2022 г. com: Энциклопедическая статья о дифференциал
com: Энциклопедическая статья о дифференциал 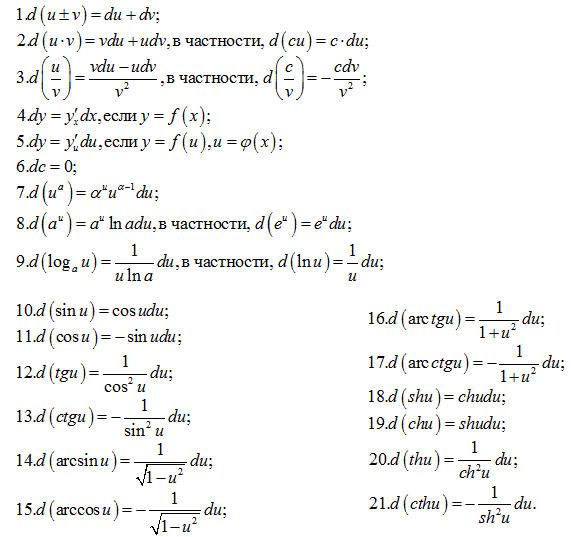
 Например, скорость движущегося объекта можно интерпретировать как скорость изменения расстояния во времени. Если y = f(x) — функция, которая дифференцируется, то, согласно дифференциальному исчислению, используется обозначение f'(x) = dy/dx. Некоторые важные термины, связанные с дифференциальным исчислением, перечислены ниже:
Например, скорость движущегося объекта можно интерпретировать как скорость изменения расстояния во времени. Если y = f(x) — функция, которая дифференцируется, то, согласно дифференциальному исчислению, используется обозначение f'(x) = dy/dx. Некоторые важные термины, связанные с дифференциальным исчислением, перечислены ниже: Другими словами, значение зависимой переменной определяется независимой переменной.
Другими словами, значение зависимой переменной определяется независимой переменной. Производная функции f(x) представляется как f'(x), dy/dx, df/dx.
Производная функции f(x) представляется как f'(x), dy/dx, df/dx. ln .a , где a > 0, a ≠ 1
ln .a , где a > 0, a ≠ 1 Существуют два основных типа дифференциальных уравнений, а именно, обыкновенные дифференциальные уравнения и уравнения в частных производных. Обыкновенное дифференциальное уравнение — это уравнение, в котором есть только одна независимая переменная и уравнение содержит одну или несколько производных по этой переменной. Уравнение в частных производных состоит из одной или нескольких независимых переменных и их частных производных.
Существуют два основных типа дифференциальных уравнений, а именно, обыкновенные дифференциальные уравнения и уравнения в частных производных. Обыкновенное дифференциальное уравнение — это уравнение, в котором есть только одна независимая переменная и уравнение содержит одну или несколько производных по этой переменной. Уравнение в частных производных состоит из одной или нескольких независимых переменных и их частных производных. Правила дифференциального исчисления перечислены в таблице, приведенной ниже.
Правила дифференциального исчисления перечислены в таблице, приведенной ниже.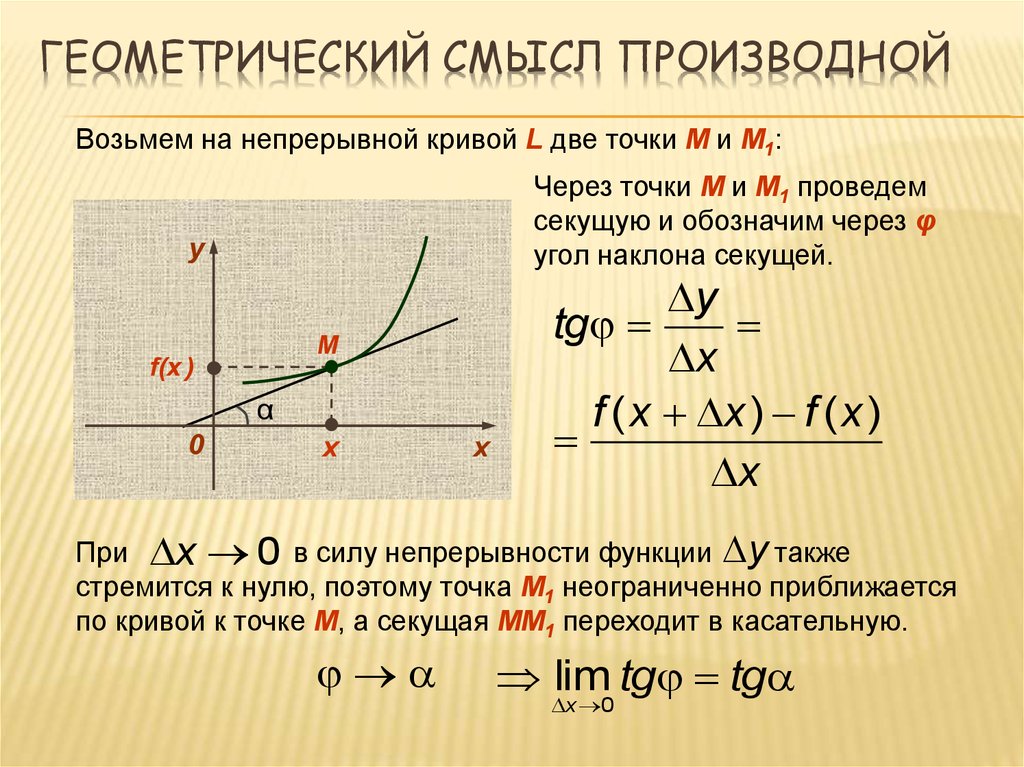 \ frac {\ mathrm {d} u} {\ mathrm {d} x} \) = f'[ г(х)]г'(х)
\ frac {\ mathrm {d} u} {\ mathrm {d} x} \) = f'[ г(х)]г'(х)



 Дифференциальное исчисление связано с нахождением скорости изменения функции, в то время как интегральное исчисление связано с нахождением площади под кривой.
Дифференциальное исчисление связано с нахождением скорости изменения функции, в то время как интегральное исчисление связано с нахождением площади под кривой. Термин «первый порядок» означает, что первый
появляется производная от $y$, но не производные более высокого порядка.
93/3+t+8/3$.
$\квадрат$
Термин «первый порядок» означает, что первый
появляется производная от $y$, но не производные более высокого порядка.
93/3+t+8/3$.
$\квадрат$ 2}$,
позволяя $A$ быть равным нулю.
$\квадрат$
2}$,
позволяя $A$ быть равным нулю.
$\квадрат$ 2-1$ имеет постоянные решения $y(t)=1$ и $y(t)=-1$.
2-1$ имеет постоянные решения $y(t)=1$ и $y(t)=-1$.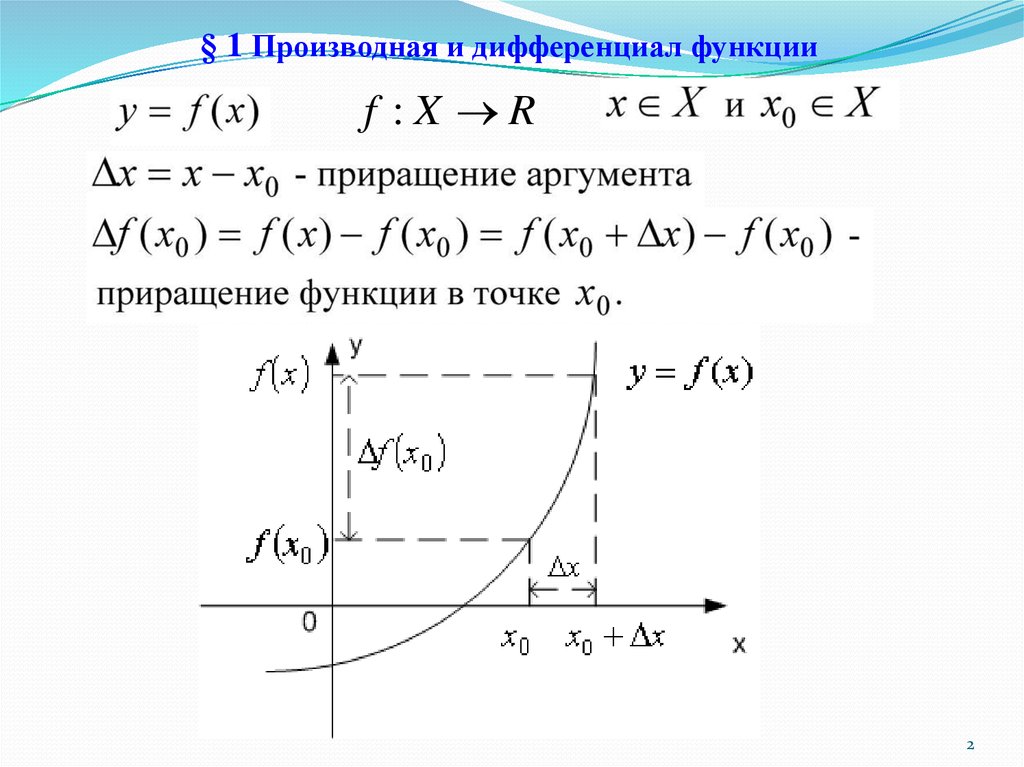 Пока это слишком
просто для моделирования большинства реальных популяций, в некоторых случаях это полезно
ограниченное время. Когда $k 9\circ$?
(отвечать)
Пока это слишком
просто для моделирования большинства реальных популяций, в некоторых случаях это полезно
ограниченное время. Когда $k 9\circ$?
(отвечать)
 9
9 5
5 8
8 4
4 8
8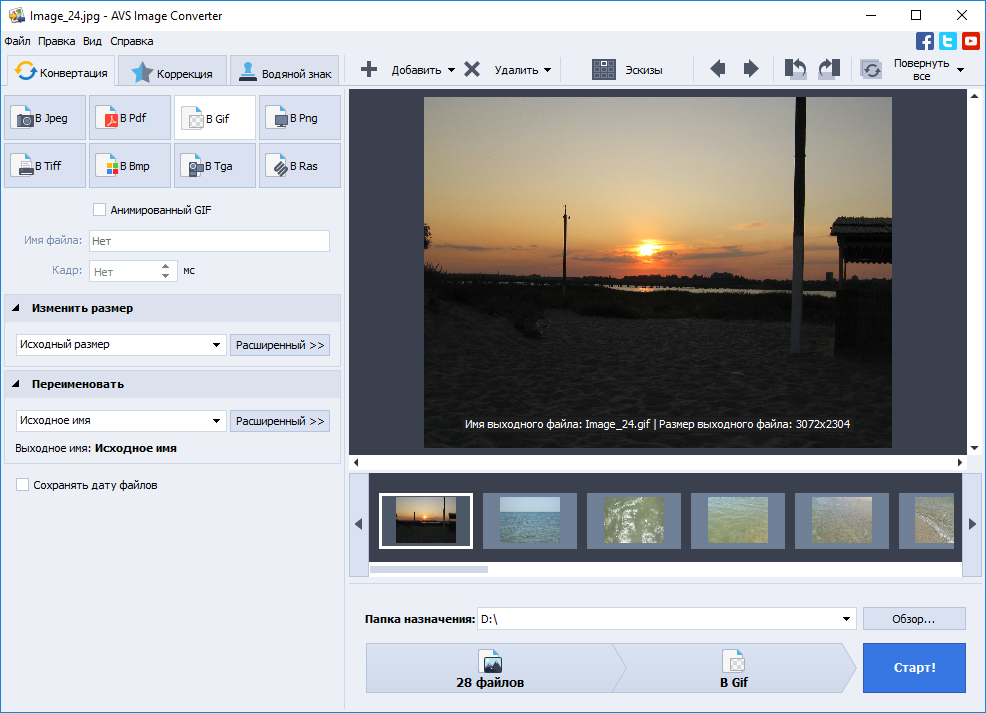 7
7 7
7 7
7 7
7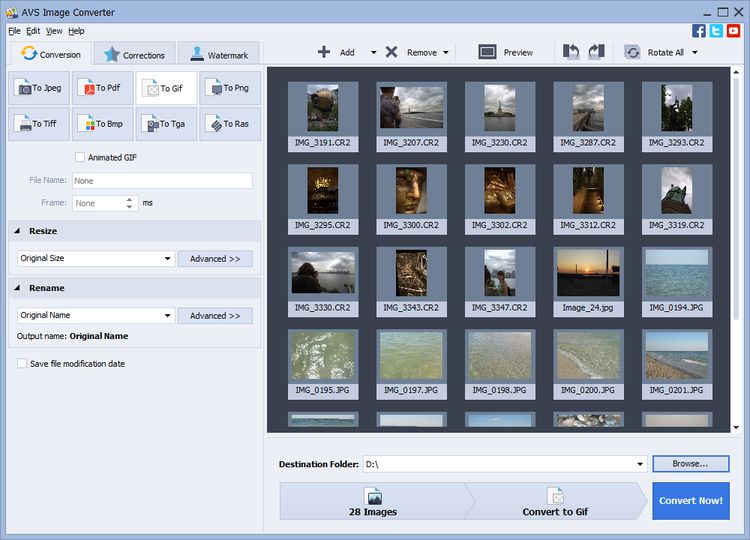 7
7 8
8 5
5 5
5 4
4 5
5 Мощный бесплатный онлайн TIFF конвертер документов легко. Установка программного обеспечения для настольных ПК, таких как Microsoft Word, OpenOffice или Adobe Acrobat, не требуется. Все конверсии вы можете сделать онлайн с любой платформы: Windows, Linux, macOS и Android. Мы не требуем регистрации. Этот инструмент абсолютно бесплатный.
Мощный бесплатный онлайн TIFF конвертер документов легко. Установка программного обеспечения для настольных ПК, таких как Microsoft Word, OpenOffice или Adobe Acrobat, не требуется. Все конверсии вы можете сделать онлайн с любой платформы: Windows, Linux, macOS и Android. Мы не требуем регистрации. Этот инструмент абсолютно бесплатный. 
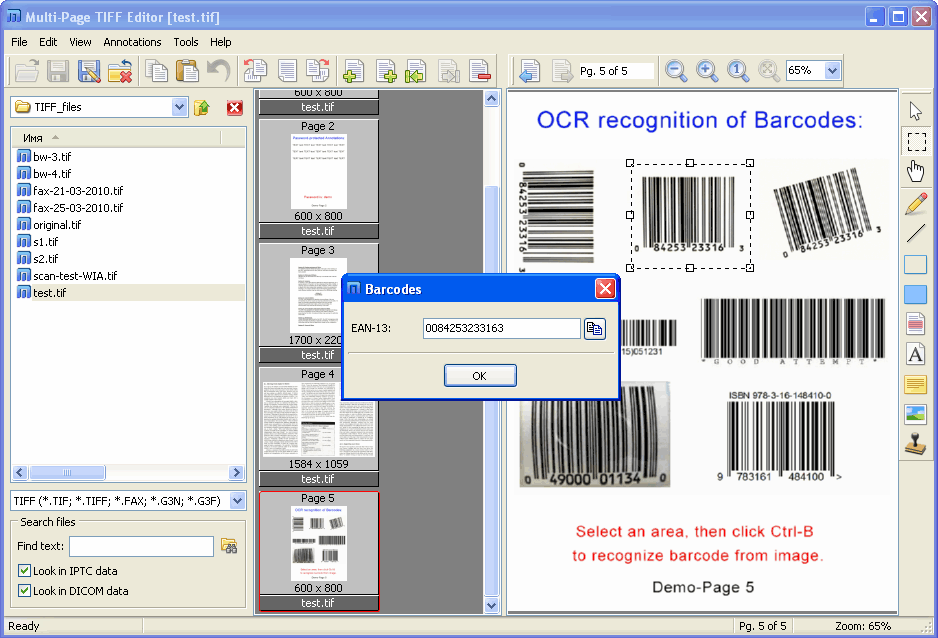 Мы удаляем загруженные файлы через 24 часа, и ссылки для скачивания перестают работать после этого периода времени. Никто не имеет доступа к вашим файлам. Конвертация файлов абсолютно безопасна.
Мы удаляем загруженные файлы через 24 часа, и ссылки для скачивания перестают работать после этого периода времени. Никто не имеет доступа к вашим файлам. Конвертация файлов абсолютно безопасна. Все файлы обрабатываются на наших серверах. Вам не требуется установка плагинов или программного обеспечения.
Все файлы обрабатываются на наших серверах. Вам не требуется установка плагинов или программного обеспечения.
 Мы не требуем регистрации. Этот инструмент абсолютно бесплатный.
Мы не требуем регистрации. Этот инструмент абсолютно бесплатный. 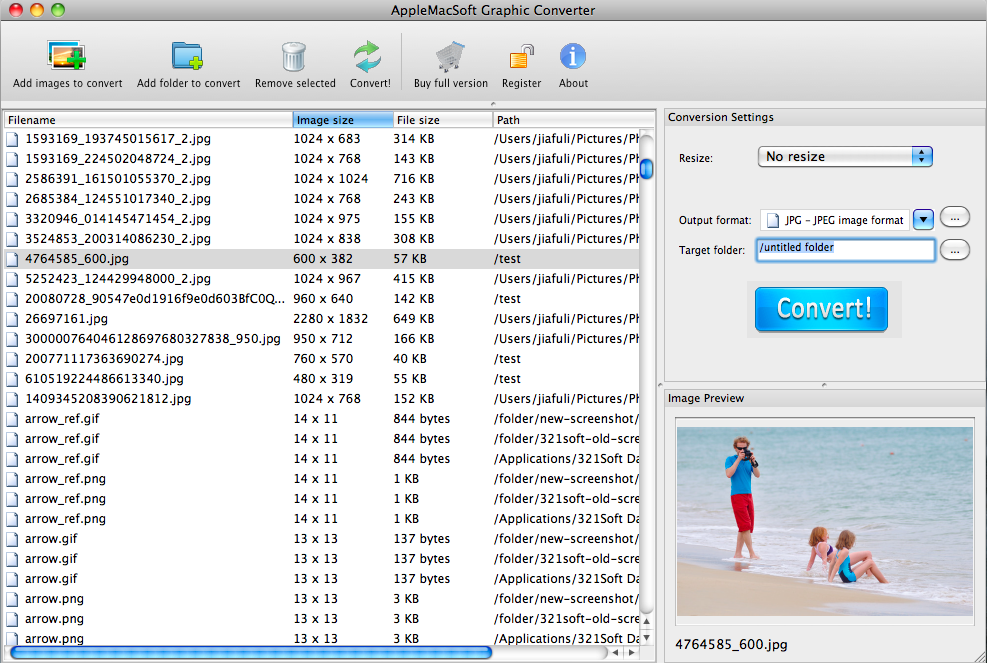 Он способен описывать данные двувея, градаций серого, палитры и полноцветного изображения в нескольких цветовых пространствах. Он поддерживает схемы сжатия с потерями, а также без потерь для выбора между пространством и временем для приложений, использующих формат
Он способен описывать данные двувея, градаций серого, палитры и полноцветного изображения в нескольких цветовых пространствах. Он поддерживает схемы сжатия с потерями, а также без потерь для выбора между пространством и временем для приложений, использующих формат Затем нажмите кнопку «Конвертировать». После завершения TIFF конвертации можно загрузить файл результатов.
Затем нажмите кнопку «Конвертировать». После завершения TIFF конвертации можно загрузить файл результатов. Наш TIFF конвертер работает онлайн и не требует установки программного обеспечения.
Наш TIFF конвертер работает онлайн и не требует установки программного обеспечения.
 g. http://48ers.com/magnacarta.pdf
g. http://48ers.com/magnacarta.pdf Он был создан из-за популярности сканеров и задумывался как стандартный формат файла отсканированного изображения. Это популярный формат для сохранения изображений с большой глубиной цвета и адаптирован для сохранения изображений в оттенках серого.
Он был создан из-за популярности сканеров и задумывался как стандартный формат файла отсканированного изображения. Это популярный формат для сохранения изображений с большой глубиной цвета и адаптирован для сохранения изображений в оттенках серого. Каждый файл TIFF начинаются с заголовка файла изображения, который затем указывает на файл изображения в директории, в которой хранятся данные изображения и информация об изображении.
Каждый файл TIFF начинаются с заголовка файла изображения, который затем указывает на файл изображения в директории, в которой хранятся данные изображения и информация об изображении. doc
doc DOC файлы могут также содержать информацию о слиянии, что позволяет шаблону обработки слов быть использованным в сочетании с таблицей или базой данных.
DOC файлы могут также содержать информацию о слиянии, что позволяет шаблону обработки слов быть использованным в сочетании с таблицей или базой данных. Пожалуйста, смотрите полный список ниже.
Пожалуйста, смотрите полный список ниже. Но при этом неизбежно произойдет некоторая потеря качества. TIFF – это формат хранения растровой графики. Чаще всего он используется для сохранения изображений с наибольшей глубиной цвета. Его применяют в полиграфии, верстке и в профессиональной фотографии, в дизайне и моделировании.
Но при этом неизбежно произойдет некоторая потеря качества. TIFF – это формат хранения растровой графики. Чаще всего он используется для сохранения изображений с наибольшей глубиной цвета. Его применяют в полиграфии, верстке и в профессиональной фотографии, в дизайне и моделировании. Например, перевести документ из PDF в TIFF с разрешением 300 dpi для налоговой службы. Расскажем, как проходит конвертация изображений и их дальнейшее редактирование. Вы можете преобразовывать один или несколько графических файлов – просто следуйте инструкции.
Например, перевести документ из PDF в TIFF с разрешением 300 dpi для налоговой службы. Расскажем, как проходит конвертация изображений и их дальнейшее редактирование. Вы можете преобразовывать один или несколько графических файлов – просто следуйте инструкции. В нашем случае это JPG.
В нашем случае это JPG.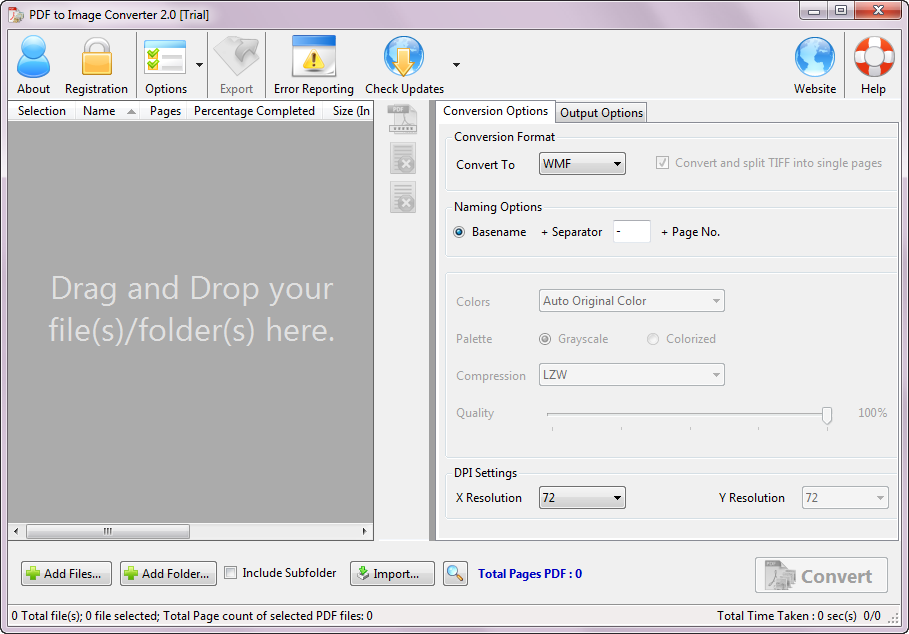 При этом обеспечивается хорошее качество файла на выходе – максимальное в рамках выбранного формата.
При этом обеспечивается хорошее качество файла на выходе – максимальное в рамках выбранного формата. Сильная сторона этого сервиса – возможность добавлять изображения всех популярных форматов. Причем не только напрямую с ПК или мобильного устройства, так и через Dropbox или Google Диск.
Сильная сторона этого сервиса – возможность добавлять изображения всех популярных форматов. Причем не только напрямую с ПК или мобильного устройства, так и через Dropbox или Google Диск. При конвертации можно сразу задать необходимые параметры – например, выбрать сжатие изображений до определенного размера или установить необходимую величину dpi. Также сервис имеет опцию предварительного просмотра конвертируемых изображений.
При конвертации можно сразу задать необходимые параметры – например, выбрать сжатие изображений до определенного размера или установить необходимую величину dpi. Также сервис имеет опцию предварительного просмотра конвертируемых изображений. В первом случае вы получите больше возможностей для редактирования файлов и сэкономите время. Безусловно, установка займет несколько минут, но она выполняется разово. В дальнейшем вы сможете переводить файлы из одного формата в другой без загрузки софта, регистрации и авторизации. При этом работа программного обеспечения не будет зависеть от скорости Интернета.
В первом случае вы получите больше возможностей для редактирования файлов и сэкономите время. Безусловно, установка займет несколько минут, но она выполняется разово. В дальнейшем вы сможете переводить файлы из одного формата в другой без загрузки софта, регистрации и авторизации. При этом работа программного обеспечения не будет зависеть от скорости Интернета. Несмотря на то, что TIFF предназначен для хранения растровой графики, его все же можно перевести в DOC или DOCX. Используйте для этого программы и сервисы, представленные в нашем обзоре. С их помощью можно быстро конвертировать TIFF в Word и задать нужные параметры получаемого файла, также объединить несколько документов в один и совершить дополнительные изменения.
Несмотря на то, что TIFF предназначен для хранения растровой графики, его все же можно перевести в DOC или DOCX. Используйте для этого программы и сервисы, представленные в нашем обзоре. С их помощью можно быстро конвертировать TIFF в Word и задать нужные параметры получаемого файла, также объединить несколько документов в один и совершить дополнительные изменения.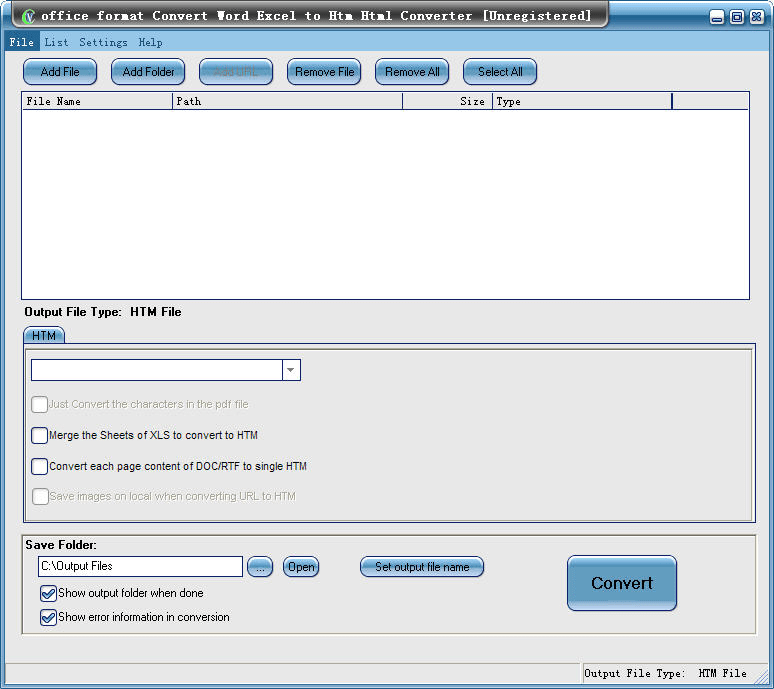 Однако существенно изменить размер без потери качества практически невозможно. В случае со сжатием достаточно использования редактора. А вот для перевода файла TIFF в другой формат потребуется конвертер. Последний, кстати, может иметь встроенный редактор, с помощью которого можно сжать документ, задать нужный размер и даже внести изменения в кодировку.
Однако существенно изменить размер без потери качества практически невозможно. В случае со сжатием достаточно использования редактора. А вот для перевода файла TIFF в другой формат потребуется конвертер. Последний, кстати, может иметь встроенный редактор, с помощью которого можно сжать документ, задать нужный размер и даже внести изменения в кодировку. Максимальный размер файла 100 МБ или регистрация
Максимальный размер файла 100 МБ или регистрация 7
7 4
4 7
7 7
7 7
7 7
7 7
7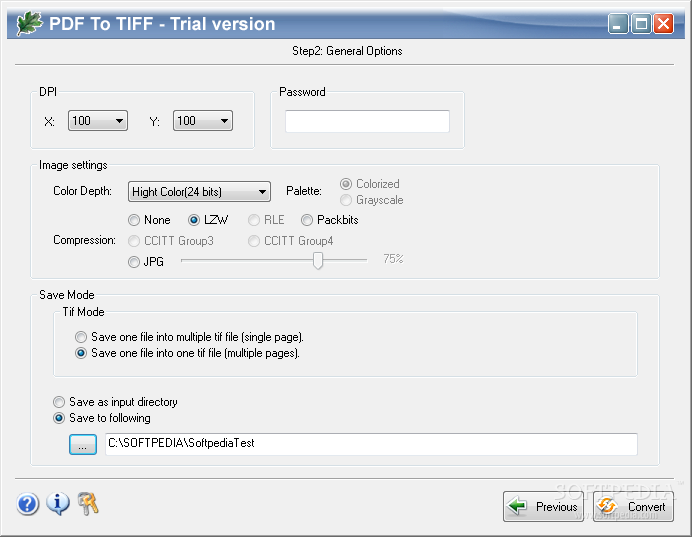 6
6 4
4 7 (94 120 голосов)
7 (94 120 голосов)
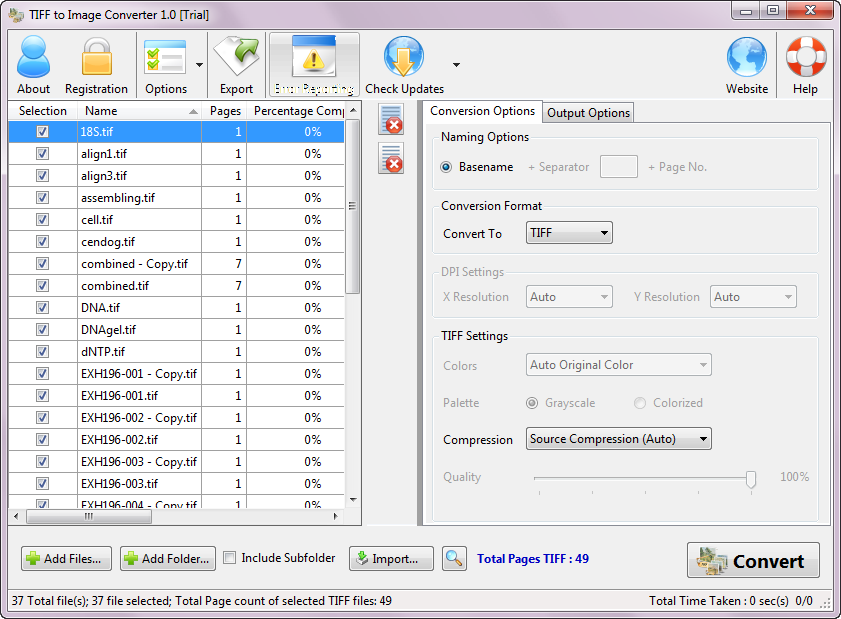 Bravo Free PDF to TIFF Converter
Bravo Free PDF to TIFF Converter Это бесплатное программное обеспечение для преобразования PDF в TIFF также поставляется со встроенным средством чтения PDF-файлов, которое также может получать доступ к защищенным паролем PDF-файлам.
Это бесплатное программное обеспечение для преобразования PDF в TIFF также поставляется со встроенным средством чтения PDF-файлов, которое также может получать доступ к защищенным паролем PDF-файлам.
 Imaging
Imaging

 Imaging Conversion?
Imaging Conversion?
 Создайте точный файл в другом формате с сохраненной структурой данных.
Создайте точный файл в другом формате с сохраненной структурой данных. 8 Mountain Lion и всеми последними версиями.
8 Mountain Lion и всеми последними версиями.
 Получите точные данные изображения в другом расширении даже после преобразования TIFF в JPG для Mac, TIFF в PDF для Mac, TIFF в PNG и т. д.
Получите точные данные изображения в другом расширении даже после преобразования TIFF в JPG для Mac, TIFF в PDF для Mac, TIFF в PNG и т. д. 8 Mountain Lion и все последние версии.
8 Mountain Lion и все последние версии.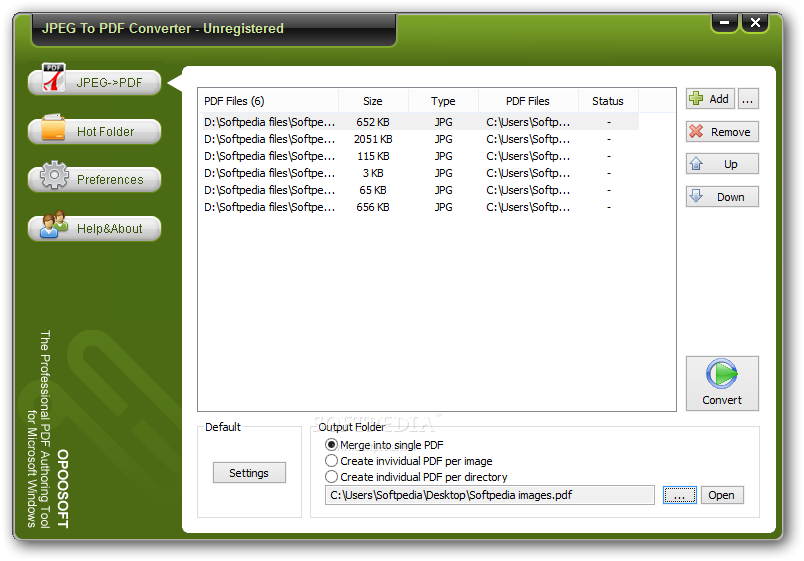 д. и проверки работы инструмента. Чтобы преодолеть ограничение, приобретите обновленную версию инструмента.
д. и проверки работы инструмента. Чтобы преодолеть ограничение, приобретите обновленную версию инструмента. tiff без каких-либо ограничений на количество файлов.
tiff без каких-либо ограничений на количество файлов. 
 Либо оценить и сравнить между собой «квадраты» всех участвующих в оценке чисел, т.е. «квадрат 2», «квадрат корня из 3» и «квадрат корня из 30». Получаем, что:
Либо оценить и сравнить между собой «квадраты» всех участвующих в оценке чисел, т.е. «квадрат 2», «квадрат корня из 3» и «квадрат корня из 30». Получаем, что: Тем самым мы проявляем уважение к языку и сохраняем его для будущих поколений.
Беру в работу как начальные, так и средние классы; осуществляю подготовку детей в ВПР, ОГЭ, олимпиадам, проектам; даю консультации.
Методы преподавания, которые используются в работе с учеником, направлены на определение целей и задач обучения русскому языку как родному и их результативность.
Тем самым мы проявляем уважение к языку и сохраняем его для будущих поколений.
Беру в работу как начальные, так и средние классы; осуществляю подготовку детей в ВПР, ОГЭ, олимпиадам, проектам; даю консультации.
Методы преподавания, которые используются в работе с учеником, направлены на определение целей и задач обучения русскому языку как родному и их результативность. Математика очень интересная и важная наука. Все в нашем мире подчиняется законам математики и знания по этому предмету нужны человеку постоянно.
Математика очень интересная и важная наука. Все в нашем мире подчиняется законам математики и знания по этому предмету нужны человеку постоянно. Я обожаю моменты, когда даже самые трудные задачи решаются! Эмоциональное удовлетворение, духовный подъем — вот что дарит математика
Я обожаю моменты, когда даже самые трудные задачи решаются! Эмоциональное удовлетворение, духовный подъем — вот что дарит математика Благодаря людям, которые заняты этими расчётами, большинство может спокойно забыть о том, что многие важные аспекты нашей жизни зависят от чисел и их свойств. К старту нашего флагманского курса по Data Science напоминаем о математической красоте формата бумаги A4.
Благодаря людям, которые заняты этими расчётами, большинство может спокойно забыть о том, что многие важные аспекты нашей жизни зависят от чисел и их свойств. К старту нашего флагманского курса по Data Science напоминаем о математической красоте формата бумаги A4.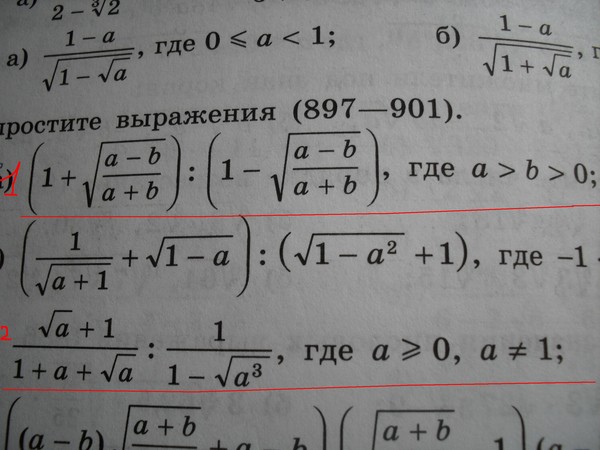 Эти слова до сих пор звучат у меня в ушах с того школьного урока черчения, на котором один из моих товарищей именно в такой форме сетовал об извращённости нашего мира. Не помню, получил ли он ответ, но боюсь, что его боль по этому поводу так никто и не разделил. Давайте потратим остаток статьи на утешение страданий этого мальчика.
Эти слова до сих пор звучат у меня в ушах с того школьного урока черчения, на котором один из моих товарищей именно в такой форме сетовал об извращённости нашего мира. Не помню, получил ли он ответ, но боюсь, что его боль по этому поводу так никто и не разделил. Давайте потратим остаток статьи на утешение страданий этого мальчика.
 Хотите две копии на листе? Запросто — они отлично там уместятся! Но стоит взять любой другой формат (хотя бы, 8,5 х 11 дюймов, который североамериканцы величают «letter size») — и вы увидите, как куча бумаги уйдёт на совершенно ненужный зазор между двумя страницами.
Хотите две копии на листе? Запросто — они отлично там уместятся! Но стоит взять любой другой формат (хотя бы, 8,5 х 11 дюймов, который североамериканцы величают «letter size») — и вы увидите, как куча бумаги уйдёт на совершенно ненужный зазор между двумя страницами.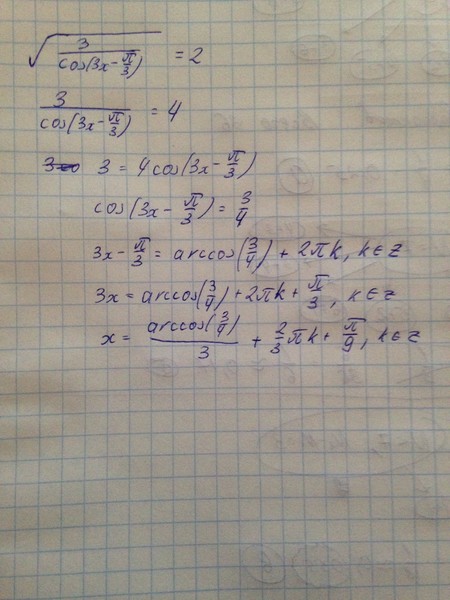 Дальше я напишу, как его рассчитали.
Дальше я напишу, как его рассчитали.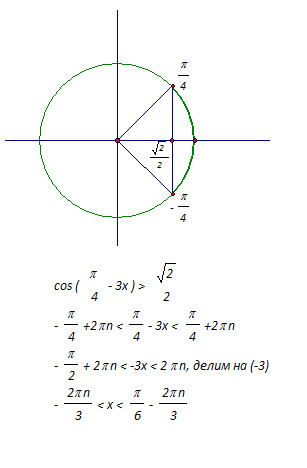 Теперь складывайте этот лист вдвое и режьте его, пока он не уместится в папку и не станет удобным для работы. Вы получите формат A4, отсюда и «4» в названии.
Теперь складывайте этот лист вдвое и режьте его, пока он не уместится в папку и не станет удобным для работы. Вы получите формат A4, отсюда и «4» в названии.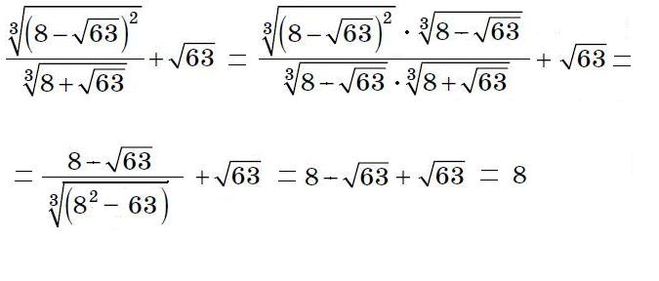 Бумага формата А4 такой плотности весит 5 г, так как её сложили пополам 4 раза [уменьшили в 24, то есть в 16 раз].
Бумага формата А4 такой плотности весит 5 г, так как её сложили пополам 4 раза [уменьшили в 24, то есть в 16 раз].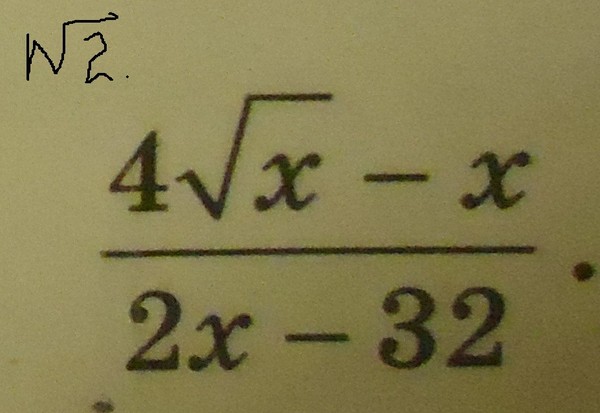 И тот самый Бекман, который ввёл в науку термин «технология». Теперь вы это знаете.
И тот самый Бекман, который ввёл в науку термин «технология». Теперь вы это знаете.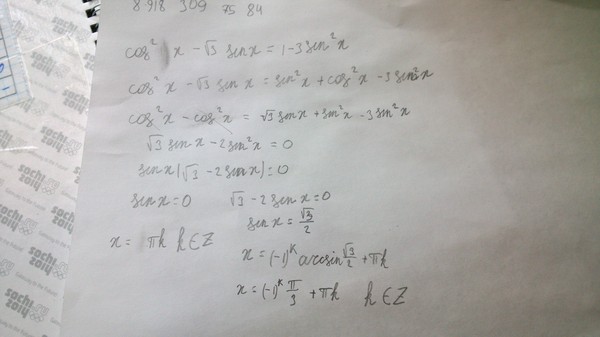 В горах он заблудился, долго плутал по лесу и, наконец, вышел к зеленому озеру. Ему очень хотелось пить, поэтому вода была кстати.
В горах он заблудился, долго плутал по лесу и, наконец, вышел к зеленому озеру. Ему очень хотелось пить, поэтому вода была кстати.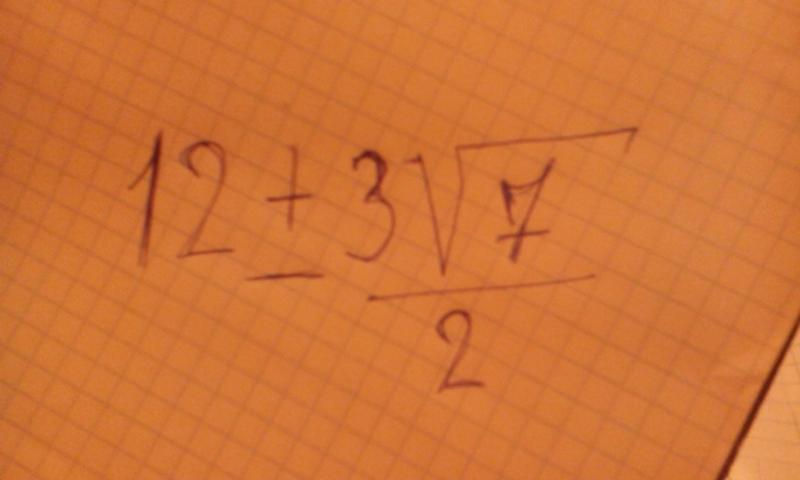 За младшего отпрыска семьи Жань я отдала ему эликсиры четвертого уровня. Также я попросила его организовать ему выезд за границу. Мальчика тайно вывезли в Швецию.
За младшего отпрыска семьи Жань я отдала ему эликсиры четвертого уровня. Также я попросила его организовать ему выезд за границу. Мальчика тайно вывезли в Швецию.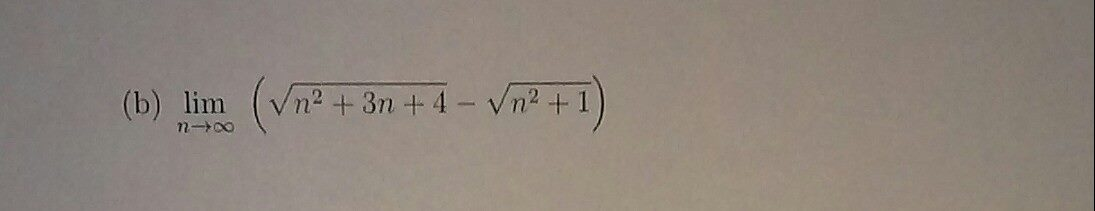 Я решила, что искать корни нужно после того, как база совершенствования станет выше.
Я решила, что искать корни нужно после того, как база совершенствования станет выше.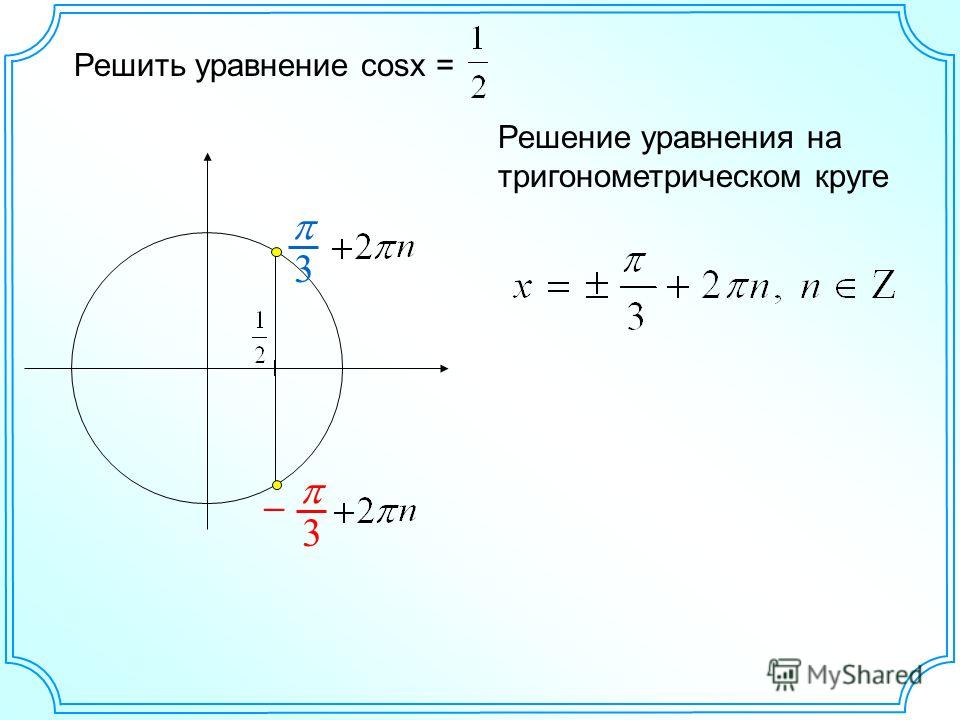
 Действительно ли я хочу, чтобы он забыл меня? Действительно хочу? Я не смела спросить свое сердце, так как боялась получить ужасные ответы.
Действительно ли я хочу, чтобы он забыл меня? Действительно хочу? Я не смела спросить свое сердце, так как боялась получить ужасные ответы.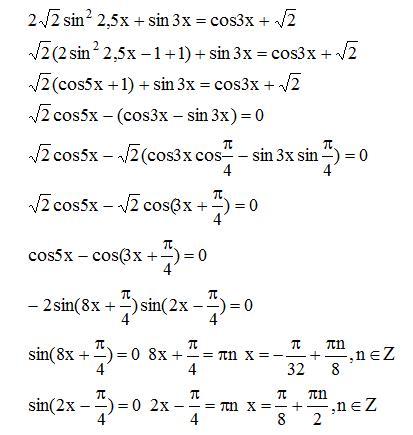


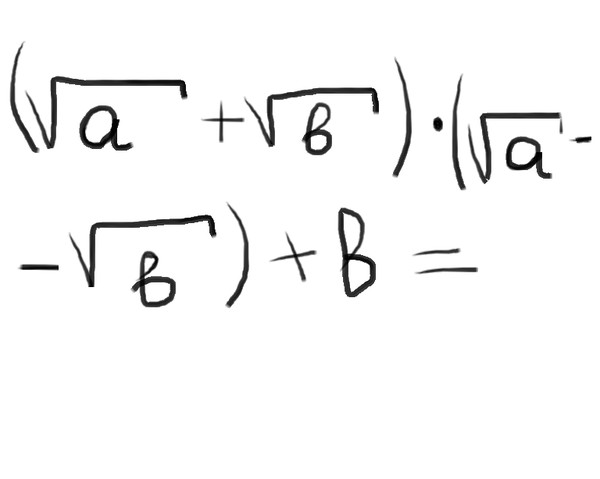 Слезы текли по моим щекам.
Слезы текли по моим щекам. )/3
)/3

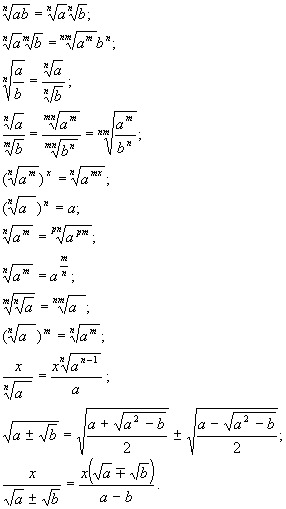
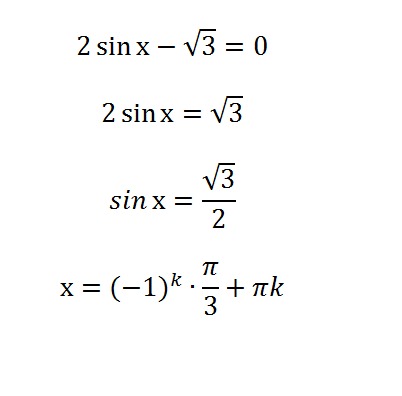

 Это положительное решение уравнения x 2 = 3.
Это положительное решение уравнения x 2 = 3.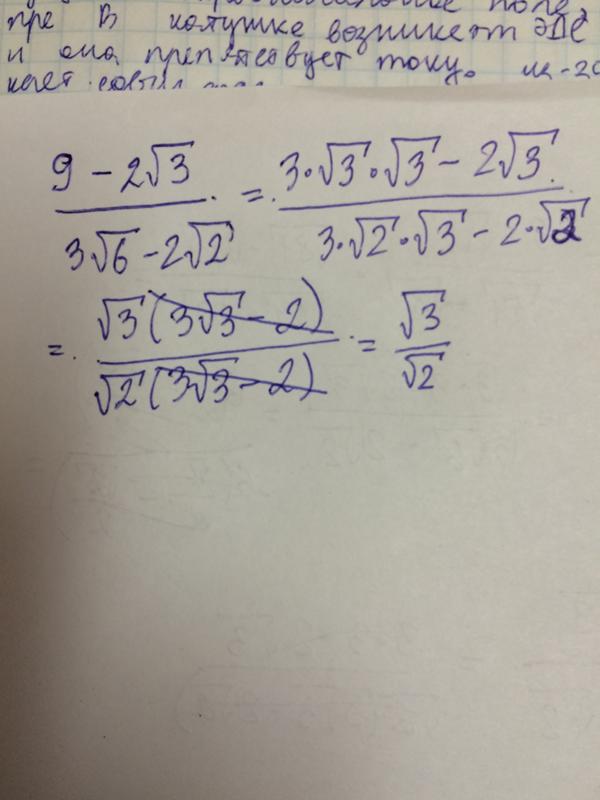 Например, квадратный корень из 25 равен 5, так как 5 умножить на 5 дает 25. Однако у вас также могут быть квадратные корни некоторых чисел, которые не дают целых чисел, например 3. Мы можем выразить квадратный корень из 3 разными способами
Например, квадратный корень из 25 равен 5, так как 5 умножить на 5 дает 25. Однако у вас также могут быть квадратные корни некоторых чисел, которые не дают целых чисел, например 3. Мы можем выразить квадратный корень из 3 разными способами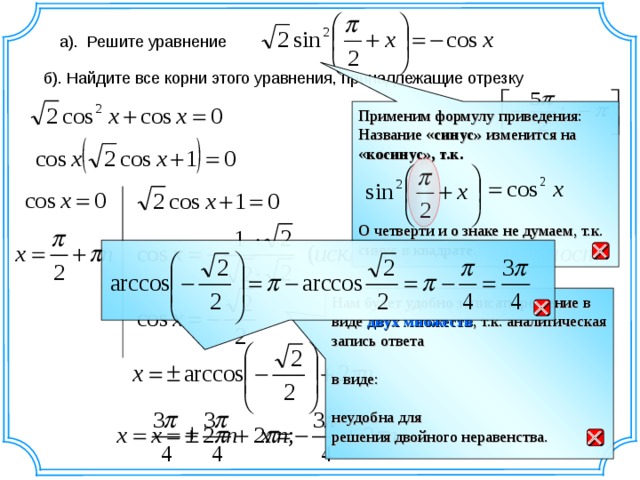

 Что вы думаете?
Что вы думаете?
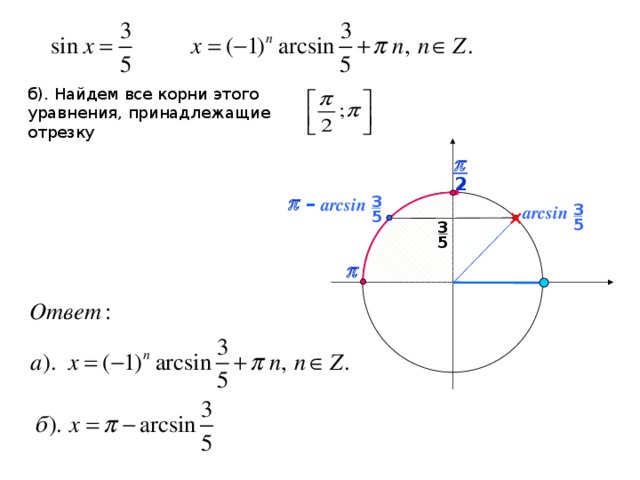 Мы знаем, что квадратный корень из 3 равен 1,732. Следовательно, 14 + 16 √3 = 14 + 16 × 1,732 = 14 + 27,713 = 41,713
Мы знаем, что квадратный корень из 3 равен 1,732. Следовательно, 14 + 16 √3 = 14 + 16 × 1,732 = 14 + 27,713 = 41,713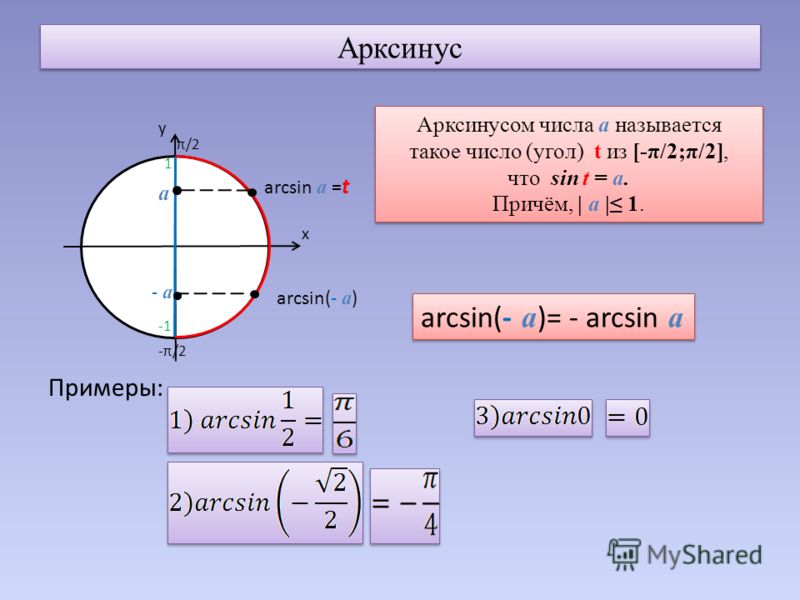 Решайте задачи с двумя, тремя и более дробями и числами в одном выражении.
Решайте задачи с двумя, тремя и более дробями и числами в одном выражении. Наиболее распространенные мнемоники для запоминания этого порядка операций:
Наиболее распространенные мнемоники для запоминания этого порядка операций:  6 детей — девочки. Какую часть детей составляют девочки?
6 детей — девочки. Какую часть детей составляют девочки?
 д., эти числа также используются для измерения и используются для маркировки.
д., эти числа также используются для измерения и используются для маркировки. С помощью этих цифр любой может составить бесконечное число.
С помощью этих цифр любой может составить бесконечное число. Называется подкоренным символом. Чтобы представить число «а» в виде квадратного корня, с помощью этого символа можно записать как: «√a», где a — это число.
Называется подкоренным символом. Чтобы представить число «а» в виде квадратного корня, с помощью этого символа можно записать как: «√a», где a — это число.


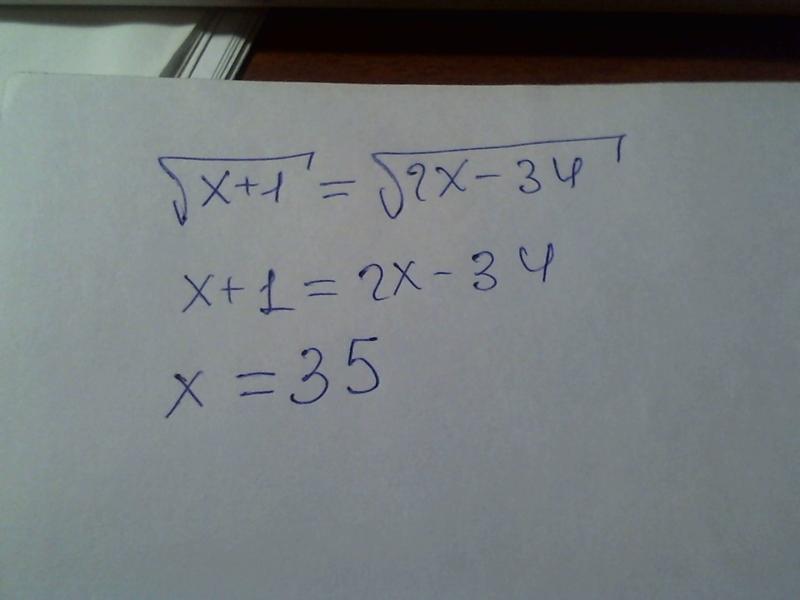
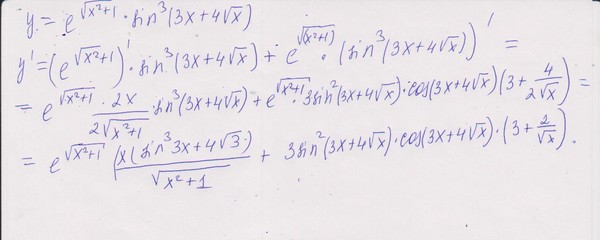
 sqrt()
sqrt() 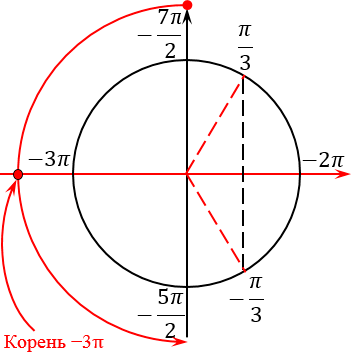 sqrt(49)
7,0
sqrt(49)
7,0

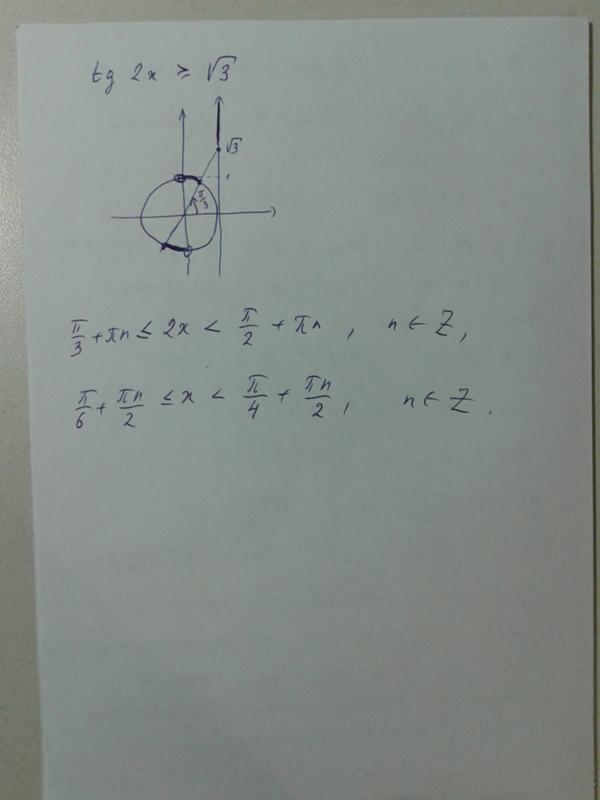



 Приведем пример такого уравнения:
Приведем пример такого уравнения: И чтобы преуспеть в решении ДУ, нужна практика (как и во всем). А если у Вас в данный момент нет времени разбираться с тем, как решаются дифференциальные уравнения или задача Коши встала как кость в горле или вы не знаете, как правильно оформить презентацию, обратитесь к нашим авторам. В сжатые сроки мы предоставим Вам готовое и подробное решение, разобраться в подробностях которого Вы сможете в любое удобное для Вас время. А пока предлагаем посмотреть видео на тему «Как решать дифференциальные уравнения»:
И чтобы преуспеть в решении ДУ, нужна практика (как и во всем). А если у Вас в данный момент нет времени разбираться с тем, как решаются дифференциальные уравнения или задача Коши встала как кость в горле или вы не знаете, как правильно оформить презентацию, обратитесь к нашим авторам. В сжатые сроки мы предоставим Вам готовое и подробное решение, разобраться в подробностях которого Вы сможете в любое удобное для Вас время. А пока предлагаем посмотреть видео на тему «Как решать дифференциальные уравнения»:

 Для получения решения исходного дифференциального уравнения
следует интегрировать обе части уравнения. При этом при разделении переменных не обязательно переносить один его член
в правую часть, можно почленно интегрировать без такого переноса.
Для получения решения исходного дифференциального уравнения
следует интегрировать обе части уравнения. При этом при разделении переменных не обязательно переносить один его член
в правую часть, можно почленно интегрировать без такого переноса. Таков следующий пример.
Таков следующий пример. Найти общее решение диффференциального уравнения
Найти общее решение диффференциального уравнения
 Обычно это следует делать в
тех случаях, когда слева искомая функция под логарифмом находится вместе с каким-нибудь слагаемым. Рассмотрим два
таких примера.
Обычно это следует делать в
тех случаях, когда слева искомая функция под логарифмом находится вместе с каким-нибудь слагаемым. Рассмотрим два
таких примера.
 Если недостаточно уверенно освоен материал по нахождению производной и решению
интегралов, то требуется его повторить. Во многих задачах на путь к решению уравнения наводят знания и приёмы из
элементарной (школьной) математики.
Если недостаточно уверенно освоен материал по нахождению производной и решению
интегралов, то требуется его повторить. Во многих задачах на путь к решению уравнения наводят знания и приёмы из
элементарной (школьной) математики. Обыкновенные дифференциальные
уравнения
Обыкновенные дифференциальные
уравнения Действительно, ,
подставляя y’ в уравнение, получим
– тождество.
Действительно, ,
подставляя y’ в уравнение, получим
– тождество. Значения произвольных постоянных
находится при определённых начальных
значениях аргумента и функции.
Значения произвольных постоянных
находится при определённых начальных
значениях аргумента и функции.




 Согласно условию
Согласно условию
 Этот метод решения называется методом
Бернулли.
Этот метод решения называется методом
Бернулли. Решим его с помощью
подстановки y=uv, .y’ = u’v + uv’
Решим его с помощью
подстановки y=uv, .y’ = u’v + uv’ 1. Основные понятия и определения
1. Основные понятия и определения

 Найти частные решения дифференциальных
уравнений:
Найти частные решения дифференциальных
уравнений: В данной статье постараюсь показать примеры решения некоторых видов таких уравнений.
В данной статье постараюсь показать примеры решения некоторых видов таких уравнений.
 Дифференциальное уравнение I-го порядка имеет, вообще говоря, не одно, а бесконечное множество число решений. Чтобы из этого множества решений выделить определенное решение, задают значение неизвестной функции y = y0 при некотором значении аргумента x = x0.
Дифференциальное уравнение I-го порядка имеет, вообще говоря, не одно, а бесконечное множество число решений. Чтобы из этого множества решений выделить определенное решение, задают значение неизвестной функции y = y0 при некотором значении аргумента x = x0.



 Далее, для увеличения продажи продукции, были сделаны рекламные объявления на радио и телевидении. Далее информация о товаре распространяется между клиентами через общение. После рекламы скорость изменения числа клиентов, которые знают о продукции B, пропорциональная не только числу клиентов, которые знают о товаре, но и числу клиентов, которые еще не знают.
Далее, для увеличения продажи продукции, были сделаны рекламные объявления на радио и телевидении. Далее информация о товаре распространяется между клиентами через общение. После рекламы скорость изменения числа клиентов, которые знают о продукции B, пропорциональная не только числу клиентов, которые знают о товаре, но и числу клиентов, которые еще не знают. 4)
4) 6. Решить “дифур” y’ + 2x2y’ + 2xy– 2x = 0.
6. Решить “дифур” y’ + 2x2y’ + 2xy– 2x = 0. Буду рад Вам помочь. Онлайн репетитор Андрей Зварыч.
Буду рад Вам помочь. Онлайн репетитор Андрей Зварыч. Обычно
производная по переменной t обозначается точкой ˙x(t), а не штрихом.
Таким образом, наш закон роста размера популяции можно записать так:
Обычно
производная по переменной t обозначается точкой ˙x(t), а не штрихом.
Таким образом, наш закон роста размера популяции можно записать так:

 Также отметим, что в уравнении (1.4) фигурирует
только первая производная неизвестной функции — это уравнение первого
порядка. Позже мы обсудим, что делать с уравнениями более высоких порядков
(например, таких как (1.3)). Пока же остановимся на рассмотрении
уравнений вида (1.4).
Также отметим, что в уравнении (1.4) фигурирует
только первая производная неизвестной функции — это уравнение первого
порядка. Позже мы обсудим, что делать с уравнениями более высоких порядков
(например, таких как (1.3)). Пока же остановимся на рассмотрении
уравнений вида (1.4). Заметим, что даже
в таком простейшем случае мы имеем не одно, а сразу целое семейство решений.
Аналогичная ситуация будет и в более сложных примерах.
Заметим, что даже
в таком простейшем случае мы имеем не одно, а сразу целое семейство решений.
Аналогичная ситуация будет и в более сложных примерах. Нетрудно видеть, что это
в точности задача интегрирования (отыскания первообразной). Решение такого
уравнения задаётся таким образом неопределенным интегралом, который можно
записать в виде
Нетрудно видеть, что это
в точности задача интегрирования (отыскания первообразной). Решение такого
уравнения задаётся таким образом неопределенным интегралом, который можно
записать в виде Например, можно рассмотреть такую задачу:
Например, можно рассмотреть такую задачу: Получим следующее уравнение:
Получим следующее уравнение:
 График решения называется интегральной
кривой. Интегральные кривые живут в расширенном фазовом пространстве.
Построим некоторые интегральные кривые для уравнения ˙x=x. Как мы уже
знаем, ими будут графики экспонент.
График решения называется интегральной
кривой. Интегральные кривые живут в расширенном фазовом пространстве.
Построим некоторые интегральные кривые для уравнения ˙x=x. Как мы уже
знаем, ими будут графики экспонент. 2
2
_2-500x500.jpg)

 Вариант 1. Тест 1,
Моро, Волкова, Проверочные работы
Вариант 1. Тест 1,
Моро, Волкова, Проверочные работы
 Урок 39,
Петерсон, Учебник, часть 2
Урок 39,
Петерсон, Учебник, часть 2
 Вариант 2. Тест 1,
Моро, Волкова, Проверочные работы
Вариант 2. Тест 1,
Моро, Волкова, Проверочные работы

 В качестве знака умножения в разных источниках используют разные символы. Выше был показан пример со знаком « x », в этот раз сделаем запись с помощью приподнятой точки ( ∙ ).
В качестве знака умножения в разных источниках используют разные символы. Выше был показан пример со знаком « x », в этот раз сделаем запись с помощью приподнятой точки ( ∙ ). Картинка:
Картинка: 


