Взгляни на своё тело со стороны — интересный сервис с 3D-моделью твоего тела | Loliminti l Арт-фотограф
Привет! Меня зовут Света, я фотограф, ретушер и веду свой креативный инста-блог. Часто путешествую по просторам интернета, и не только русскоязычного. Знаете, если иногда гуглить что-то кроме погоды и одноклассников, можно найти сотни полезных ресурсов. Наткнулась на интересную штуку — визуализатор тела.
Забавно, но я только недавно поняла, какой у меня тип фигуры. Но мне сложно было определить свои проблемные места, над которыми мне нужно работать с помощью физических упражнений и активного спорта.
Согласитесь, что в зеркале мы не можем трезво оценить — устраивает ли нас объем бёдер, грудной мышцы, талии, вес при соотношении с нашим ростом. Этот сайт делает это за нас.
Он на английском, но страницу можно перевести для удобства, если у вас нет, например, знания языка, но есть Яндекс.Браузер. Для начала внизу меняем систему исчислений. Мы же все русские люди, измеряем вес в килограммах, а длину и обхват — в сантиметрах.
Выставляем параметры — рост, вес, далее программа сама предсказывает пропорциональные параметры, но можно скорректировать — грудной обхват, талия, бедра, длина ног, количество спорта часов в неделю. Можно даже поменять цвет модельки, повертеть, вращать.
Построила 2 модельки (гендер меняется в самой верхней строчке) — мою и моего парня. Что-то около того, правда, у меня плечи чуть шире, а голова меньше.
Если у вас более-менее стандартная, естественная фигура, то она с лёгкостью построится. Понятно, что ресурс не идеален — нет длины рук, ширины плеч, параметров головы. Но это уже прикольный способ посмотреть на себя со стороны, не тк ди?
Сразу уточню — построить какую-то необычную фигуру, например, измененную хирургически не получится (мы пробовали). Но от души посмеялись.
Сайт >>> Визуализатор тела
P.S. По какой-то причине сайт на данный момент (11.02.20) недоступен. Возможно, его существование окончено.
Спасибо за прочтение! Подписывайся на мой канал — я пишу о фотографии, макияже, творчестве и просто о своей жизни.
3D моделирование онлайн: 2 рабочих варианта
Существует достаточно много программ для трехмерного моделирования, так как оно активно применяется во многих областях. Кроме этого, для создания 3D-моделей можно прибегнуть к специальным онлайн-сервисам, предоставляющим не менее полезные инструменты.
3D-моделирование онлайн
На просторах сети можно найти немало сайтов, позволяющих создавать 3Д-модели в режиме онлайн с последующим скачиванием готового проекта. В рамках данной статьи мы расскажем о наиболее удобных в использовании сервисах.
Способ 1: Tinkercad
Данный онлайн-сервис, в отличие от большинства аналогов, обладает максимально упрощенным интерфейсом, во время освоения которого у вас вряд ли возникнут вопросы. Более того, прямо на сайте можно пройти полностью бесплатное обучение основам работы в рассматриваемом 3D-редакторе.
Перейти к официальному сайту Tinkercad
Подготовка
- Чтобы использовать возможности редактора, нужно зарегистрироваться на сайте. При этом если у вас уже есть аккаунт Autodesk, можно воспользоваться им.
- После авторизации на главной странице сервиса нажмите кнопку «Создать новый проект».
- Основная зона редактора вмещает в себя рабочую плоскость и непосредственно сами 3Д-модели.
- С помощью инструментов в левой части редактора вы можете масштабировать и вращать камеру.
Примечание: Зажав правую кнопку мыши, камеру можно перемещать свободно.
- Одним из самых полезных инструментов является «Линейка».
Для размещения линейки необходимо выбрать место на рабочей области и кликнуть левой кнопкой мыши. При этом зажав ЛКМ, данный объект можно перемещать.
- Все элементы будут автоматически прилипать к сетке, размеры и вид которой можно настроить на специальной панели в нижней области редактора.
Создание объектов
- Для создания каких-либо 3D-фигур используйте панель, размещенную в правой части страницы.
- После выбора нужного объекта щелкните в подходящем для размещения месте на рабочей плоскости.
- Когда модель отобразится в основном окне редактора, у нее появятся дополнительные инструменты, используя которые фигуру можно перемещать или видоизменять.
В блоке «Форма» вы можете установить основные параметры модели, что касается и ее цветовой гаммы. Допускается ручной выбор любого цвета из палитры, но текстуры использовать невозможно.
Если выбрать тип объекта «Отверстие», модель станет полностью прозрачной.
- Кроме изначально представленных фигур, вы можете прибегнуть к использованию моделей с особыми формами. Для этого откройте раскрывающийся список на панели инструментов и выберите нужную категорию.
- Теперь выберите и разместите модель в зависимости от ваших требований.
При использовании разных фигур вам будут доступны несколько отличающиеся параметры их настройки.
Примечание: При использовании большого количества сложных моделей производительность сервиса может падать.
Стиль просмотра
Завершив процесс моделирования, вы можете изменить представление сцены, переключившись на одну из вкладок на верхней панели инструментов. Не считая основного 3D-редактора, к использованию доступно две разновидности представления:
- Blocks;
- Bricks.
Как-либо воздействовать на 3D-модели в таком виде невозможно.
Редактор кода
Если вы владеете знанием скриптовых языков, переключитесь на вкладку «Shape Generators».
С помощью представленных здесь возможностей можно создавать собственные фигуры, используя JavaScript.
Создаваемые фигуры впоследствии могут быть сохранены и опубликованы в библиотеке Autodesk.
Сохранение
- На вкладке «Design» нажмите кнопку «Общий доступ».
- Кликните по одному из представленных вариантов, чтобы сохранить или опубликовать снимок готового проекта.
- В рамках той же панели нажмите кнопку «Экспорт», чтобы открыть окно сохранения. Можно скачать все или некоторые элементы как в 3D, так и 2D.
На странице «3dprint» вы можете прибегнуть к помощи одного из дополнительных сервисов, чтобы распечатать созданный проект.
- По необходимости сервис позволяет не только экспортировать, но также импортировать различные модели, в том числе ранее созданные в Tinkercad.
Сервис отлично подойдет для реализации несложных проектов с возможностью организации последующей 3D-печати. При возникновении вопросов обращайтесь в комментариях.
Способ 2: Clara.io
Основное предназначение этого онлайн-сервиса заключается в предоставлении практически полнофункционального редактора в интернет-обозревателе. И хотя данный ресурс не имеет стоящих конкурентов, воспользоваться всеми возможностями можно только при покупке одного из тарифных планов.
Перейти к официальному сайту Clara.io
Подготовка
- Чтобы перейти к 3D-моделированию с помощью этого сайта, необходимо пройти процедуру регистрации или авторизации.
Во время создания нового аккаунта предоставляется несколько тарифных планов, включая бесплатный.
- После завершения регистрации вы будете перенаправлены в личный кабинет, откуда можно перейти к загрузке модели с компьютера или созданию новой сцены.
- На следующей странице вы можете воспользоваться одной из работ других пользователей.
- Для создания пустого проекта нажмите кнопку «Create Empty Scene».
- Настройте рендеринг и доступ, дайте вашему проекту название и щелкните по кнопке «Create».
Модели могут быть открыты лишь в ограниченном количестве форматов.
Создание моделей
Начать работу с редактором вы можете путем создания одной из примитивных фигур на верхней панели инструментов.
Полный список создаваемых 3D-моделей вы можете посмотреть, открыв раздел «Create» и выбрав один из пунктов.
Внутри области редактора можно вращать, перемещать и масштабировать модель.
Для настройки объектов используйте параметры, размещенные в правой части окна.
В левой области редактора переключитесь на вкладку «Tools», чтобы открыть дополнительные инструменты.
Возможна работа сразу с несколькими моделями путем их выделения.
Материалы
- Для изменения текстуры созданных 3D-моделей откройте список «Render» и выберите пункт «Material Browser».
- Материалы размещены на двух вкладках в зависимости от сложности текстуры.
- Кроме материалов из указанного списка, вы можете выбрать один из исходников в разделе «Materials».
Сами текстуры также можно настраивать.
Освещение
- Чтобы добиться приемлемого вида сцены, необходимо добавить источники света. Откройте вкладку «Create» и выберите тип освещения из списка «Light».
- Разместите и настройте источник света, используя соответствующую панель.
Рендеринг
- Для просмотра финальной сцены, нажмите кнопку «3D Stream» и выберите подходящий тип рендеринга.
Время обработки будет зависеть от сложности созданной сцены.
Примечание: Во время рендеринга автоматически добавляется камера, но также ее можно создать вручную.
- Результат рендеринга может быть сохранен в виде графического файла.
Сохранение
- В правой части редактора нажмите кнопку «Share», чтобы поделиться моделью.
- Предоставив другому пользователю ссылку из строки «Link to Share», вы позволите ему просматривать модель на специальной странице.
Во время просмотра сцена будет автоматический отрендеренной.
- Откройте меню «File» и выберите из списка один из вариантов экспорта:
- «Export All» — будут включены все объекты сцены;
- «Export Selected» — будут сохранены только выделенные модели.
- Теперь вам нужно определиться с форматом, в котором сцена сохранится на ПК.
На обработку требуется время, которое зависит от количества объектов и сложности рендеринга.
- Нажмите кнопку «Download», чтобы скачать файл с моделью.
Благодаря возможностям этого сервиса можно создавать модели, мало чем уступающие проектам, сделанным в специализированных программах.
Читайте также: Программы для 3D-моделирования
Заключение
Все рассмотренные нами онлайн-сервисы, даже учитывая большое количество дополнительных инструментов для реализации многих проектов, несколько уступают программному обеспечению, созданному специально для трехмерного моделирования. Особенно если сравнивать с таким софтом, как Autodesk 3ds Max или Blender.
Мы рады, что смогли помочь Вам в решении проблемы.Опишите, что у вас не получилось. Наши специалисты постараются ответить максимально быстро.
Помогла ли вам эта статья?
ДА НЕТ3 визуализатора тела по указанным параметрам для мужчин и женщин
Вы когда-нибудь задумывались о том, как будете выглядеть с добавлением пары килограммов мышц? Или если бы вы были более подтянутой или более толстой версией себя? У Bodywhat имеется визуализатор тела, названный Bodywhat Morphing. Вам обязательно следует его попробовать.
А потом посмотрите на себя со стороны и подумайте: хватит ли у вас мотивации, чтобы достичь таких результатов. С помощью приложения Model My Diet для iPhone, которое недавно получило обновление, можно визуализировать этот непростой путь к здоровому телу путём добавления всего одного фото. Они останутся приватными, а вы сможете сравнить, с чего начинали и как изменились.
Body Visualizer
Абсолютно бесплатный сервис Body Visualizer разработан Институтом вычислительных систем Макса Планка в Германии. Он был создан для того, чтобы каждый желающий мог оценить свою физическую форму. Большинство параметров анализатор вычисляет на основе статистических данных, достаточно лишь ввести два ключевых показателя: рост и вес. После этого показывается трёхмерная модель с указанными параметрами, причём конституция тела определяется довольно точно.
Передвигая в нижней части страницы ползунок Exercise, можно увидеть, как преобразится тело после регулярных тренировок в тренажёрном зале: чем больше часов нагрузки, тем более худым и мускулистым оно станет. Эти изменения тоже появятся на макете, расположенном в левой части экрана.
Сервис устроен очень просто, достаточно выставить свои параметры с помощью нескольких ползунков:
- Height — рост;
- Weight — вес;
- Chest — окружность груди;
- Waist — окружность талии;
- Hips — окружность бёдер;
- Inseam — уровень расположения паха.
Inseam — шаговый шов брюк. Измерьте свой внутренний шов от промежности до пола. Ваша промежность — это самая верхняя внутренняя точка ноги. Exercise — интенсивность нагрузок, который измеряется в часах в неделю. По умолчанию стоит значение 2, его можно уменьшить или увеличить.
Важно! Когда будете снимать мерки, расслабьтесь: мышцы не должны быть напряжены. Замеряя талию, максимально выдохните. Измеряя объём бёдер, делайте это в самом широком их месте.
По умолчанию все величины приводятся в дюймах, но можно переключиться на более привычную метрическую систему (в сантиметрах), нажав кнопку Switch Units в нижней части экрана. Регуляторы имеют английские названия, есть возможность переключиться на немецкий язык. Хотя русский язык не поддерживается, можно перевести страницу с помощью встроенной функции в браузер Google Chrome. Для этого кликните правой кнопкой мыши и выберите в контекстном меню пункт «Перевести страницу».
Поскольку телосложение у мужчин и женщин разное, для них есть два отдельных модулятора. Переключение между ними происходит с помощью кнопки Switch to female (с мужчины на женщину и наоборот).
Обнуляется модулятор кнопкой RESET ALL MEASUREMENTS: она сбросит все ранее выставленные значения, и можно начинать процесс заново.
Modelmydiet.com
Model My Diet Inc. — это независимая компания, созданная для того, чтобы помогать своим пользователям контролировать и сбрасывать лишний вес с помощью бесплатного визуализатора Modelmydiet.com. Более 10 миллионов человек из 223 стран уже создали собственные модели.
Узнайте, как может измениться ваш облик! Для этого введите свой рост, вес и выберите форму тела (груша, яблоко, песочные часы). Виртуальная модель появится на экране с указанными габаритами. Ее можно сделать более похожей на оригинал: придав нужный цвет или оттенок коже и волосам, сформировав причёску, форму носа, глаз и рта, вы получите мини-версию самих себя!
Для этого задействуйте кнопку More Options: 12 стилей причёсок с 6 разными оттенками цвета волос станут доступны после покупки лицензии. Эти волосы даже будут расти так же, как настоящие. Персонализируйте свою модель, экспериментируйте с разными опциями, чтобы она выглядела максимально похожей на вас.
У сервиса имеется собственное мобильное приложение, которое показывает ваши персональные тенденции в похудении. Функция графика позволяет прогнозировать, что вас ждёт с таким темпом в будущем и каких целей вы можете добиться в ближайшее время.
Bodywhat.com
Сервис Bodywhat помогает отслеживать состояние тела и достигать поставленных целей. Перед тем как начать, нужно сделать всего одно фото.
Bodywhat начинался как эксперимент в рамках технологии компьютерного зрения, целью которого было узнать, сколько информации о здоровье человека можно получить из одной фотографии. Это детище Чарльза Лэброя, 25-летнего учёного в области больших данных родом из Франции, и Максима Лонна, 23-летнего бизнесмена и фитнес-энтузиаста. Bodywhat собирает информацию, сортирует её и использует технологии, такие как компьютерное зрение и байесовская статистика.
Хотите узнать, как ваше тело выглядит по сравнению с телом чемпиона мира по бодибилдингу? Благодаря искусственному интеллекту Bodywhat может рассказать массу любопытных вещей о вас, сравнивая с тысячами других тел, например:
- процент жира в вашем теле;
- сексуально ли вы выглядите;
- какой у вас тип тела;
- на кого из звёзд вы похожи и многое другое.
Сравнивайте себя с другими и отслеживайте свой прогресс. А захотите проверить свои параметры до и после изменений, Bodywhat сделает и это!
3D-моделирование онлайн (обзор 7 сервисов)
3D-моделирование обычно ассоциируется с покупкой дорогостоящих программ, долгим обучением и повышенными требованиями к компьютеру. А что если мы скажем, что теперь вы можете строить даже очень сложные 3D-модели прямо в браузере?
Что такое 3D-моделирование и где его применяют
3D-моделирование — это создание трёхмерных изображений (моделей) предметов, строений, фигур и всего прочего, что имеет объем. 3D-модели создаются на основе двухмерных чертежей, а иногда просто воображения.
Трехмерное моделирование применяют в следующих сферах:
- печати предметов на 3D-принтере;
- создания персонажей и объектов для видеоигр и спецэффектов в видео;
- создания анимации и иллюстраций;
- проектирования интерьеров, ландшафтов, архитектурных сооружений;
- производства, строительства и многого другого.
Рассмотрим несколько популярных бесплатных сервисов, которые позволят создавать 3D-модели онлайн.
Популярные веб-сервисы для 3Д-моделирования
Tinkercad
Это интернет-приложение называют онлайн-версией 3ds Max — самого известного и популярного трёхмерного редактора. Причина путаницы в том, что оба продукта создал один разработчик — компания Autodesk. И хотя официальной версии 3d Max онлайн не существует, вы вполне сможете обойтись Tinkercad, если ваша задача — построить относительно простую 3D-модель.
Сервис полностью бесплатен и очень дружелюбен к новичкам. Вместо сложных подходов к моделированию, Tinkerpad использует принцип создания комплексных объектов за счёт комбинации простых форм. Полученный результат можно скачать в практически в любом формате файлов для 3D-принтеров и сразу напечатать.
Интерфейс сайта переведен на русский язык, но, к сожалению, не полностью. При желании вы можете создать на нем аккаунт либо просто войти при помощи социальных сетей, нажав эту кнопку:
Чтобы создать модель в редакторе Tinkercad, сделайте следующее:
- Нажмите на иконку своего аккаунта в правом верхнем углу экрана и выберите «Создать».
- Перетащите нужные простые формы с правой стороны экрана на рабочую плоскость слева.
- Настройте размеры, форму и положение объектов в пространстве при помощи управляющих маркеров.
- Цвет и ряд других свойств можно поменять в секции «Форма» в правой части экрана.
- Несколько выделенных объектов можно объединить или выровнять относительно друг друга при помощи специальной панели.
- После завершения создания модели нажмите «Экспорт» и сохраните результат себе на компьютер в удобном формате. Если не знаете, какой формат вам больше подойдет, выбирайте OBJ.
Более подробные инструкции по работе с этим редактором вы найдете на его официальном сайте.
3D Slash
3D Slash — сервис для тех, кому не хватает возможностей Tinkercad. Он тоже очень прост в освоении, но инструментов для работы с моделями здесь больше: есть средства для «гравировки», вырезания, создания фигурных отверстий, окраски и т. д.
Бесплатная версия сервиса имеет ограничения: пользователю доступно лишь 8 цветов, нет поддержки командой работы, готовые файлы сохраняются только в низком разрешении. Цена полнофункционального доступа к 3D Slash начинается с $2 в месяц. Однако русского языка, к сожалению, нет ни в той, ни в другой версии.
Регистрация для работы в 3D Slash обязательна. Для этого нажмите на «Sign In» в правом верхнем углу экрана.
Затем заполните небольшую анкету и подтвердите адрес электронной почты.
Как моделировать в 3D Slash:
- Выберите, будете ли вы создавать объект с нуля, на основании готовой модели или рисунка. Если не знаете, нажмите Classic.
- Чтобы повернуть куб, который появится в рабочей области экрана, захватите его левой кнопкой мыши, а чтобы переместить — правой. Ползунки снизу и справа меняют размеры фигуры. Чтобы начать создавать из куба модель, нажмите на кнопку выбора инструментов справа вверху.
- Одни инструменты «выдалбливают» из фигуры кусочки, другие надстраивают их, третьи красят и так далее.
- Чтобы выгрузить модель на компьютер, нажмите на показанную ниже иконку и выберите подходящий формат.
SketchUp
Этот 3D конструктор несколько отличается от описанных выше по принципу работы. Если предыдущие сервисы брали за основу простые трёхмерные объекты (кубы, шары и так далее) и позволяли их модифицировать и объединять, то здесь вам придется чертить, создавая модели из линий. SketchUp организован сложнее 3D Slash и Tinkercad, но всё равно это простой и интуитивный редактор, в котором сможет разобраться любой желающий. Его чаще всего используют для дизайна мебели и архитектурных сооружений.
У SketchUp есть русская версия, но по умолчанию открывается английская. Для некоммерческого использования он полностью бесплатен, но с ограничениями: в общедоступной версии не поддерживаются некоторые форматы, нельзя с нуля создавать материалы и стили оформления. Платная же подписка обойдется вам от 119 долларов в год.
Как пользоваться SketchUp. Краткое описание интерфейса:
- Регистрация на SketchUp необязательна, войти сюда можно через свой аккаунт Google, нажав на указанную ниже кнопку.
- Набор инструментов для черчения (прямые линии, кривые линии, базовые фигуры и так далее) находится на панели слева. Именно с их помощью вам предстоит создавать трёхмерные модели.
- Справа вы найдете вспомогательные инструменты, включая материалы для ваших чертежей, поиск готовых моделей, настройку слоёв и многое другое.
- Как только вы закончите работу над моделью, нажмите на значок папочки, затем «Export» («Экспорт» в русской версии) и сохраните файл на компьютере в удобном формате.
Clara.io
Clara.io — онлайн-программа, больше подходящая пользователям с опытом работы в профессиональных 3D-редакторах. Зато и модели она позволяет создавать куда более сложные. Особый плюс этого сервиса — возможность запуска даже на слабых компьютерах, так как обработка объектов происходит в облаке.
У Clara.io тоже есть бесплатная и платная версии. В первой ограничено место для хранения моделей в облаке и процессорное время на их обработку. Во второй доступно все, но подписка стоит от 100 долларов в год. К сожалению, ни платная, ни бесплатная версия не поддерживают русский язык.
Порядок использования У Clara.io:
- Зарегистрируйтесь на сайте через форму на главной странице (это обязательно).
- Нажмите на New Scene.
- Создайте новую сцену (так здесь называют отдельные проекты) либо выберите одну из сотен готовых и бесплатно доступных на сайте. Для этого есть форма поиска.
- В центре находятся 4 окна вида 3D-объекта. Слева над ними — кнопки для создания простых геометрических форм, справа — инструменты для работы с освещением и камерой.
- Слева во вкладке Tools находятся инструменты для редактирования трёхмерной модели. С их помощью вы сможете её резать, скручивать и так далее.
- После окончания работы с моделью откройте верхнее меню (File-Export All) и сохраните файл на компьютере.
Plastisketch
Это онлайн-приложение самое шустрое в нашем списке, а кроме того, не требующее регистрации. Принцип его работы отличается от всего вышеперечисленного. В Plastisketch вы просто рисуете слои, которые программа объединяет в одну модель. Представьте, что вы разрезали трёхмерный объект по горизонтали на несколько тонких кусочков. Затем вы сложили эти кусочки стопкой на некотором удалении друг от друга, а пространство меду ними заполнилось само по себе. Примерно так функционирует этот редактор.
К сожалению, Plastisketch имеет только английскую версию. Он полностью бесплатен для всех, но в выгружаемых файлах будет стоять ссылка на официальный сайт.
Как работать с сервисом:
- Нажмите Start PlastiSketch на главной странице.
- В режиме векторного обзора, показанного ниже, редактируйте горизонтальный срез, двигая и добавляя точки, изгибая кривые. Изменения сразу же отображаются справа — в окне трёхмерного обзора.
- Чтобы переключаться между слоями и добавлять новые, используйте инструменты в нижней части окна.
- Через меню слева вы можете управлять различными параметрами проекта.
- Чтобы сохранить модель на компьютер, нажмите Export.
Planoplan
Planoplan – это трёхмерный редактор специфической направленности. Он позволяет строить и визуализировать 3D-интерьеры по чертежам. Работать с ним довольно просто, однако он требователен к ресурсам компьютера. Базовые функции редактирования доступны в Planoplan в режиме онлайн, но для реализации всех возможностей придётся скачать одноименное десктопное приложение.
Сервис позволяет бесплатно хранить не более одного проекта одноэтажного помещения площадью до 350 м2. Платные тарифы начинаются от 10$ в месяц и убирают все ограничения.
К сожалению, Planoplan не имеет полноценной русской версии.
Как пользоваться сервисом:
- Чтобы начать работу, нажмите «Create your project».
- Откроется типовой трёхмерный проект квартиры, который можно редактировать, перемещая предметы с помощью мыши. Для навигации также можно использовать стрелки на клавиатуре.
- Чтобы видоизменить стены, нужно переключиться в двухмерный режим, нажав соответствующую кнопку.
- Чтобы сохранить проект и продолжить его редактировать в десктопной программе, нужно зарегистрироваться, воспользовавшись формой в левом нижнем углу экрана. Кроме того, авторизоваться на сайте можно при помощи соцсетей (FB или ВК).
Roomtodo
В отличие от предыдущего сервиса, Roomtodo позволяет без особых ограничений моделировать интерьеры полностью в браузере без установки дополнительного ПО. Здесь есть возможность импорта моделей из других 3D-редакторов.
Сервис полностью бесплатен для частного применения. Платным он остается только для коммерческих целей (например, компания, желающая внедрить возможность дизайна интерьера на свой сайт, сможет это сделать только за деньги).
Roomtodo полностью на русском и обладает простым и интуитивно понятным интерфейсом.
Как пользоваться:
- Чтобы начать работу над проектом, нажмите «Старт» на главной странице.
- Для включения режима рисования стен (отмечено стрелкой) или переключения обзора между режимами 2D и 3D воспользуйтесь панелью в левой части экрана.
- Панель в правой части поможет вам разместить отдельные элементы на стенах, например, окна. Просто перетащите их на проект.
- Чтобы сохранить результат в файл, воспользуйтесь панелью наверху (предварительно сайт попросит вас авторизоваться).
Все рассмотренные сервисы успешно работают в любом современном браузере (Google Chrome, Firefox, Safari и т. д.) в Windows 10, Mac OS X и любой другой системе. Причем как в современной, так и в устаревшей.
Моделирование фигуры человека в связке программ Makehuman + Blender
Хочу обратить внимание 3Dпечатников на программу MakeHuman для моделирования фигуры человека. Ранее она уже упоминалась товарищем 3d20, но почему то больше здесь не всплывала. Удобна она тем, что позволяет создать любую человеческую фигуру в диапазоне от брутального бойца до соблазнительной нимфы, всего лишь путём регулировки параметров внешности. Грубо говоря двигая ползунок в настройках, выбираем длину рук, ног объем мускулов , груди и многого другого.Черты лица также настраиваются соответствующими параметрами, но абсолютного сходства добиться с заданным персонажем непросто. Скорее это достаточно удобный инструмент для создания качественной заготовки, устраняющий необходимость создавать модель с нуля.
Сама программа на английском, но всё достаточно понятно без изучения какого либо руководства. Программа бесплатная с открытым кодом написанным на Python. Существует целое сообщество, которое продолжает её совершенствовать.
Скачать программу можно здесь.
Там же можно скачать дополнительные элементы одежды, стили причёсок, бород, ногтей, модификаторы формы тела, позы и другое.
Работу в программе я хотел показать на примере создания героя известной фотографии “комбат”.
Я не пытался сделать модель один в один, но хотелось получить человека максимально похожего. Переходя от вкладки к вкладке постепенно без особого напряжения улучшаем сходство.После подбора всех параметров внешности получился такой персонаж:
(Прошу прощения за получившееся выражение лица. Ну уж какой родился…)Так как нам всё-таки нужна модель для печати, то нужно стараться получить максимально замкнутую поверхность модели с минимальными отверстиями. Для этого нужно на вкладке Geometries убрать галочку “Hide faces under clothes”, тогда программа не будет отсекать фрагменты тела, спрятанные под одеждой. При обработке в Blender это сильно облегчит создание замкнутой модели.
И кстати, на мой взгляд лучше избегать распахивающихся элементов одежды таких как рубашки, так как они будут представлены в модели незамкнутой поверхностью, которую потом придётся замыкать. Теперь бы я заменил её футболкой. Потом все равно перерисовывать под гимнастёрку.И в заключении формирования модели нужно установить скелет:
Его наличие позволит придать модели нужную позу при редактировании в Blender.Важный момент: нужно установить плагины для конвертации в формат MHX2 для программ MakeHuman и Blender.
Для этого нужно скопировать плагины в соответствующие папки plugins и addons, и для Blender активировать аддон Import MakeHuman Exchange2. (Чтобы открыть вкладку настроек используйте клавиши Ctrl+Alt+U)
Иначе созданную в MakeHuman модель вы не сможете редактировать как поверхностную.Созданную модель нужно будет сохранить в формате MHX2, а затем уже открыть данный формат в Blender.
Обсуждение проблем конвертации здесь и здесь.
При открытии импортированного файла в Blender мы увидим фигуру со скелетом:
Двигая “косточки” выставим нужную позу. Дальше идёт кропотливая работа по оттачиванию замысла. Я в основном работал в скульптурном режиме.Blender пока мною не совсем освоен, поэтому мне проще и быстрее было сделать некоторые предметы амуниции в SolidWorks и импортировать в blender-модель в виде stl-файлов:
В конце концов получилось так: Полезные ссылки для освоения Blender.В заключение хотел отметить, что обе программы я освоил на начальном уровне, но знаю, что на этот сайт заходит достаточно много людей хорошо владеющих ими. Хотелось, чтобы меня поправили, если где приврал, а ещё лучше подсказали бы какие то более лёгкие приёмы в работе с ними.
Всем пока! Берегите себя и своих близких.
Как создать виртуальную модель тела человека??
Хотите узнать, какой будет ваша виртуальная модель тела? Посмотрите, на каком этапе вы находитесь сейчас, и какой красоткой или красавчиком вы сможете стать в ближайшем будущем!
Идеал красоты
Создать виртуальную модель фигуры онлайн можно с помощью одного полезного сайта. Там всё написано на английском, но интуитивно разобраться тем, кто не понимает язык, вполне возможно. Сейчас мы вам обо всём подробно расскажем.
Здесь всё довольно просто:
- Зайти на сайт моя виртуальная модель тела.
- Кликнуть на блок, который находится справа за центральным. Вы увидите надпись Find Your Body Shape.
- На верхней панели во вкладке Model, где изображено много девушек в полотенцах (или чалме???) можно выбрать ваш оттенок кожи.
- Height – это рост, weight – вес. Рост там измеряется в футах, а вес в фунтах. Ниже в табличках посмотрите ваши значения и введите данные на сайт.
- Далее нужно выбрать тип вашей фигуры: песочные часы, перевернутый или прямой треугольник.
- На вкладке Hairstyle&face можно подобрать идеальную для себя прическу и оттенок волос.
- Age – это возраст: young – молодой, mature – взрослый.
- Nose – нос: small – маленький и аккуратный, large – широкий.
- Lips – губы: thinner – тонкие, fuller – пышные и объемные.
- Eyes – глаза: round – круглые, almond – миндалевидные.
- Waist – талия; defind – выразительная, undefined – невыразительная.
- Dress Size – выбрать размер одежды (наш 44 – это американский 16, 46 – 18, 48 – 20 и тд).
- Bust Size – размер груди в обхвате, Bust Cup – чашечка бюста.
- Frame Size – тип телосложения. Нужно измерить обхват запястья. Small – от 15 до 17,5 см, medium – от 17,5 до 20 см, large – свыше 20 см.
- Ваша виртуальная модель тела готова!
Что дальше
После того, как виртуальная модель человека создана, можно примерять на нее любую одежду. Посмотреть различные варианты можно в самом низу. Там находится огромное количество вкладок со всякими купальниками, платьями, джинсами, повседневной одеждой и многим другим. На все выбранные предметы есть ссылки, где их можно купить на Ebay.
Другие секретики:
Теперь вы знаете, как создается виртуальная модель тела и фигуры человека онлайн! Пользуйтесь этой простой подсказкой, чтобы понять, какая одежда вам больше всего подойдет к лицу. Ну или создайте модельку мечты и стремитесь к совершенству.
Спасибо за ваше потраченное время
Посольство красоты Программы коррекции и моделирования фигуры
Для достижения наибольшего эффекта при работе над телом необходим комплексный подход, сочетающий в себе разные методы воздействия на жировую ткань. Правильно подобранный комплекс процедур — залог успеха!
Специалисты клиники «Посольство Красоты» индивидуально составляютпрограммы коррекции и моделирования фигуры, учитывая пол, возраст, особенности образа жизни, что позволит эффективно убрать не только лишний жир и разгладить кожу, но и поможет смоделировать пропорции тела, близкие к идеалу.
Программы коррекции и моделирования фигуры — это комплекс процедур для устранения неэстетичных жировых отложений (коррекция фигуры и веса), которые нарушают пропорции фигуры.
При всем разнообразии подходов к моделированию фигуры, все сводится к определенной системе воздействия: необходимо разбить жир и вывести лишнюю жидкость. Существуют и дополнительные факторы, которые помогают — это коррекция питания, поддержание минерально-витаминного баланса.
Главное преимущество наших программ для коррекции и моделирования фигуры — их комплексность: Вам не только проведут целую серию процедур, но и дадут рекомендации по правильному образу жизни, подберут индивидуальную диету.
Методы коррекции и моделирования фигуры
Помочь скорректировать линии тела можно разными способами, в нашей клинике для формирования вашего идеального тела мы выбираем только безопасные, но эффективные методики:
- аппаратные (аппаратная коррекция фигуры)
- ручные (массаж, обертывание, пилинг…)
- мезотерапия
Из чего состоит программа коррекции и моделирования фигуры
1. Первое с чего мы начинаем программу коррекции и моделирования фигуры — это уникальная методика компьютерного определения и последующего анализа внутреннего состава тела человека на аппарате InBody 720 — водно-жировом анализаторе. По результатам диагностики преступаем к следующим этапам.
2. Подбор вспомогательных методик, которые улучшают кровообращение в жировой и мышечной тканях, тем самым подготавливая тело к основным процедурам, а также многократно усиливают и удлиняют их действие (Le Skin V6 (дерматония ), Thermo-C (термолифтинг), VIP Complex (миостимуляция), обертывания и пилинги.
3. Основные липолитические методы, (Lipo-X (кавитация), Криолиполиз CoolipoTwin) расщепляют жиры и уменьшают жировые клетки.
4. Процедура формирования контуров тела — Thermo-C радиоволновое омоложение и подтяжка кожи. Позволит Вам бережно, эффективно и в короткие сроки избавиться от локальных жировых отложений, подтянуть кожу и улучшить ее структуру.
5. Криолиполиз на аппарате CoolipoTwin — удаление жира холодом.
6. Дренирующие методы выводят продукты распада и токсины, образующиеся при липолизе (Le Skin V6 (дерматония ), Thermo-C (термолифтинг), обертывания.
7. Поддерживающие методы (любая из выше перечисленных по назначению специалиста) — позволяют сохранять достигнутый результат
Косметика для моделирования и коррекции фигуры
Наряду с профессионализмом специалиста, второй по важности фактор в процессе моделирования и коррекции фигуры — это косметические средства, которые используются для этой цели, как в процедуре, так и для домашнего ухода. В нашей Клинике своим клиентам мы предлагаем лучшие — высокоэффективные французские (BiologiqueRecherche) и испанские (Alqvimia) косметические линии.
Важный фактор для моделирования и коррекции фигуры:
Мы честны перед своими клиентами, поэтому говорим открыто, что диета и разумная физическая активность являются главными факторами, которые запускают разрушение жировой ткани. Нет смысла начинать мероприятия на фоне переедания и неподвижного образа жизни. Конечно, результаты и без усилий с вашей стороны будут заметны. Но результат будет менее заметным, мене стойким. Без изменения наших привычек все вернется на круги своя. Мы же заботимся о своих пациентах и хотим видеть их здоровыми и красивыми на протяжении долгих лет. Поэтому в процессе программы мы разрабатываем для каждого нашего пациента рекомендации по питанию и образу жизни, рекомендуем витаминные добавки и фиточаи.
Поддерживающие факторы коррекции фигуры:
Вы с нашей помощью достигли результатов, теперь наша задача — сохранить их как можно дольше. Поддерживающие факторы должны использоваться как в процессе, так и после выполненной программы. Профилактика — это выполнение рекомендаций по рациональному питанию, уменьшению вредных привычек, физическим нагрузкам, которые будут даны вам нашими специалистами.
В поддерживающий комплекс входит и индивидуальная разрабатываемая программа посещения поддерживающих курсов (1-2 раз в месяц). Поддерживающий курс — это небольшой комплекс процедур, направленный на предотвращение образования новых жиров в организме.
Прайс
С действующими скидками и рекламными акциями
Вы можете ознакомиться на страничке Скидки
Криолиполиз + вакуум + хромотерапия / Coolshaping
| Наименование процедуры | Длительность процедуры, мин. | Стоимость процедуры, руб |
|---|---|---|
| Тело (одна насадка) | 75 | 12 000,00 |
| Тело (две насадки) Акция! Скидка 15% | 75 | 20 000,00 |
Ульфит
| Наименование процедуры | Длительность процедуры, мин. | Стоимость процедуры, руб |
|---|---|---|
| 800 линий | 25 000,00 | |
| 1000 линий | 30 000,00 |
Радиоволновой лифтинг 3-МАХ
| Наименование процедуры | Длительность процедуры, мин. | Стоимость процедуры, руб |
|---|---|---|
| Все тело | 40 | 6 000,00 |
Термаж
| Наименование процедуры | Длительность процедуры, мин. | Стоимость процедуры, руб |
|---|
Endospheres Therapy® / Эндосфера терапия для тела
| Наименование процедуры | Длительность процедуры, мин. | Стоимость процедуры, руб |
|---|---|---|
| Все тело | 60 | 6 000,00 |
Прессотерапия
| Наименование процедуры | Длительность процедуры, мин. | Стоимость процедуры, руб |
|---|---|---|
| Прессотерапия | 1 500,00 |
Эксклюзивные косметологические уходы для тела на линии БИОЛОДЖИК РЕШЕРШ/ BIOLOGIQUE RECHERCHE
| Наименование процедуры | Длительность процедуры, мин. | Стоимость процедуры, руб |
|---|---|---|
| Дренажный массаж всего тела «The Care» | 60 | 6 500,00 |
| Программа «Slimming body» | 60 | 8 500,00 |
| Программа лифтинг всего тела «Love your body» | 60 | 10 500,00 |
| Лёгкие ножки «Flying legs» с обёртыванием | 90 | 4 500,00 |
| Лёгкие ножки «Flying legs» без обёртывания | 60 | 3 500,00 |
| Лифтинг массаж 1 зона | 2 500,00 |
Ручной массаж
| Наименование процедуры | Длительность процедуры, мин. | Стоимость процедуры, руб | |
|---|---|---|---|
| Общий массаж (женский) | |||
| Массаж | 60 | 3 300,00 | |
| Массаж | 90 | 4 000,00 | |
| Массаж | 120 | 5 000,00 | |
| Общий массаж (мужской) | |||
| Массаж | 60 | 4 000,00 | |
| Массаж | 90 | 5 000,00 | |
| Массаж | 120 | 6 000,00 | |
| Массаж | |||
| Антицеллюлитный массаж | 90 | 4 000,00 | |
| Биоэнергетический массаж | 90 | 4 000,00 | |
| Тейпирование: Малая зона/большая зона | 1 000,00/1 800,00 | ||
СПА процедуры
| Наименование процедуры | Длительность процедуры, мин. | Стоимость процедуры, руб |
|---|---|---|
| Хамам-прогрев+пилинг+скраб на spa-table | 60 | 3 000,00 |
| Хамам-прогрев+обёртывание | 60 | 3 000,00 |
| Хамам-прогрев+пилинг+скрабирование+обёртывание | 120 | 6 000,00 |
| Хамам+пилинг+скрабирование+обёртывание+массаж | 180-210 | 9 000,00 |
| Хамам+пилинг+скрабирование+обёртывание+массаж со средствами Biologique Recherche | 180-210 | 12 000,00 |
Пожалуйста, уточняйте стоимость процедур в день обращения!
Процедуру выполняют врачи-физиотерапевты:
-
Коликова Полина Николаевна
-
Сиденко Ирина Семеновна
-
Дыбова Наталья Александровна
Онлайн-визуализатор анатомии тела зиготы 3D
Онлайн-визуализатор анатомии тела зиготы | Анатомия человека 3DZygoteBody ™ и 3D-данные © 2012-2017 Zygote Media Group, Inc.
Краткое руководствоНавигация
- Щелкните и перетащите мышью, чтобы повернуть, прокрутите для увеличения.
- Или воспользуйтесь кнопками вверху слева. Кнопка «Домой» сбрасывает вид.
- Перейдите из режима капсулы в режим орбиты в правом верхнем углу, чтобы включить полную 3D.
- поворот и удерживайте Ctrl, чтобы панорамировать вид. (Только для премиум-пользователей)
- Используйте ползунок непрозрачности слева, чтобы отобразить слои.
- Щелкните переключатель под ползунком, чтобы управлять слоями по отдельности.
- Используйте поле поиска в правом верхнем углу для поиска или щелкните объекты, чтобы выбрать их.
- Щелкните фон или X, чтобы отменить выбор.
- Ctrl + щелчок по объектам, чтобы быстро скрыть объекты. (Cmd + щелкните на Mac.)
- Shift + щелкните объекты или метки (или щелкните значок «булавка» на этикетке), чтобы закрепить объект. Это будет держать его выбранным, пока вы выбираете больше.
- Используйте значок видимости на имени объекта, чтобы скрыть элемент. В отличие от Ctrl + щелчка по объекту, инструмент видимости будет скрывать элементы до тех пор, пока не будет нажата кнопка «Показать все» в правом верхнем углу.
- Используйте инструмент «Увеличить до» на имени элемента, чтобы центрировать изображение на элементе.
- Используйте стрелку вниз на имени элемента, чтобы отобразить информацию об элементе.
- Используйте инструмент «Закрепить» на имени элемента, чтобы закрепить элемент, позволяя выбрать несколько элементов.
- Используйте значок выбора модели над ползунком анатомии слева для загрузки различных моделей.
- Мои сцены позволяет загружать и сохранять созданные вами сцены. Все аннотации, булавки и видимые элементы будут сохранены.
- Zygote Scenes — это набор сцен, созданный Zygote Media Group, с аннотациями, определяющими анатомические ориентиры.
- Иерархия — это список всех сущностей, которые есть в вашей текущей сцене. Вы можете включать и выключать детали, используя галочки у каждого объекта или группы объектов.
- Annotations позволяет вам создавать свои собственные заметки и маркеры, которые будут сохранены при сохранении вашей сцены.
- инструментов:
- Pick возвращает вас к стандартному режиму выбора деталей и поворота камеры.
- Slice позволяет вам разрезать части сцены в плоскости X, Y или Z.
- Explode перемещает все части сцены в сторону от центральной точки, которую вы можете расположить в интерактивном режиме.
- Викторина при включении, когда вы выбираете деталь, а не отображаете ее имя, появляется меню с множественным выбором, позволяющее вам проверить себя.
- Значок снимка в центре вверху делает снимок сцены, который затем можно сохранить в формате jpg или нарисовать с помощью прилагаемых инструментов пера.
| Контент | |||
| мужская анатомия человека с системами | |||
| женская анатомия человека с системами | |||
| доступ к мужским и женским покровным системам | |||
| рассеченное сердце (вид сверху) | |||
| рассеченное сердце (вид сбоку) | |||
| рассеченное сердце (вид спереди) | |||
| шарнирный череп высокого разрешения | |||
| глаз с высоким разрешением и анатомия орбиты | |||
| поддерживается рекламой | |||
| Навигация | |||
| базовая навигация (орбита капсулы) | |||
| увеличение и уменьшение масштаба | |||
| перемещение просмотра вверх и вниз | |||
| фокус на выбранном объекте | |||
| выбор отдельного объекта | |||
| автоматическое наименование выбранного объекта | |||
| поиск анатомического объекта по имени | |||
| слой-раскрытие внутренней анатомии | |||
| слой-раскрытие внутренней анатомии по системе | |||
| Справочник по анатомическим функциям wiki hot-link | |||
| видео справки по инструменту | |||
| скрыть и показать все | |||
| панорамирование камеры | полный поворот камеры 3D | ||
| полная трехмерная орбита вокруг определенного объекта | |||
| показать / скрыть любые комбинации анатомии из списка названий деталей | |||
| Инструменты | |||
| закрепить имя объекта на экране | |||
| пользовательский инструмент аннотации | |||
| сохранить несколько сцен и конфигураций | |||
| срезать / рассекать видимую анатомию в плоскостях x, y и z | |||
| динамическое покомпонентное изображение для выявления анатомических компонентов | |||
| программно сгенерированные тесты (учебная деятельность и оценка) | |||
| снимок экрана / создать и использовать изображение s * | |||
| * Подробную информацию см. в лицензионном соглашении с конечным пользователем | |||
Это приложение для трехмерного моделирования человека может революционизировать онлайн-магазины одежды
Группа ученых из Гонконга разработала приложение для трехмерного моделирования человека, которое может радикально изменить то, как мы делаем покупки в Интернете.Этот инструмент, получивший название 1Measure, «одним щелчком мыши» позволяет пользователям записывать измерения своего тела за считанные секунды, загружая две фотографии всего тела.
После создания снимков с видом спереди и сбоку приложение использует искусственный интеллект для создания трехмерной цифровой модели тела пользователя менее чем за 10 секунд. Рядом с этим изображением отображается более 50 измерений размеров, включая все, от обхвата колена до наклона плеча. Эту информацию можно сохранить и получить к ней доступ позже, и в приложении также указан ваш размер в других странах, что позволяет с легкостью покупать одежду по всему миру.
Эта революционная технология была разработана доцентом Трэйси П.Ю. Мок и доктор философии доктор Чжу Шуайинь из Института текстиля и одежды Гонконгского политехнического университета (PolyU).
Другие современные технологии могут выполнять аналогичные функции моделирования, но команда PolyU заявляет, что эти методы требуют использования дорогостоящих и громоздких сканеров, а их результаты являются приблизительными. По словам разработчиков, погрешность приложения 1Measure составляет 1 сантиметр для пользователей, сфотографированных в облегающей одежде, и 2 сантиметра для тех, кто носит свободную одежду.
Приложение особенно полезно, когда дело касается покупок в Интернете. Доктор Чжу говорит, что эта технология «освобождает нас от ограничений, накладываемых физическими измерениями тела, помогая клиентам выбрать правильный размер при покупке одежды в Интернете».
Приложение также может сохранять несколько измерений одновременно и отслеживать любые изменения, которые претерпевает тело, что делает его подходящим для тех, кто стремится к фитнесу.
1Measure можно загрузить бесплатно и в настоящее время доступно в App Store на английском и китайском языках.
DesignDoll | Terawell
Дом тера 2020-11-25T02: 59: 24 + 00: 00Отличные новости!
Версия Design Doll _CurrentVersion_ уже здесь!
Design Doll Ver_CurrentVersion_ была выпущена _ReleaseDate_! О новых функциях читайте ниже!
Давайте посмотрим, что внутри!
Design Doll — это программа, которая может свободно манипулировать моделями человеческого тела в трехмерном пространстве.
Совершенно новая кукла-эскиз нового поколения
Она поддержит вашу жизнь как художника
Для максимального эффекта
Design Doll может создавать позы и композиции, которые требуются художникам, с помощью простых и интуитивно понятных операций.
Большинство встроенных функций основано на запросах наших клиентов
Воспроизведите ваше любимое соотношение головы и тела
Design Doll использует метод смешивания, при котором формы и размеры различных частей могут быть свободно изменены, что позволяет воспроизводить модели с соотношением головы к телу, которое интуитивно соответствует рисункуВоспроизведение любой перспективы по желанию
Благодаря различным функциям перспективы возможны деформации, напоминающие рисунки от руки или выразительные выражения, которые не могут быть представлены с помощью другого программного обеспечения для 3D.Наряду с параллельной проекцией, ложными перспективами, реальными перспективами и перспективами объектива также доступны такие функции, как отображение уровня глаз и изменение перспективы камеры (угла обзора)Палец-контроллер
Доступен специальный контроллер для мгновенного движения пальцами. Создав грубую форму в простом режиме, а затем перейдя в подробный режим, можно быстро создать формы рукС легкостью создавайте множественные изображения фигур
Design Doll может устанавливать несколько моделей тела в одной сцене, позволяя легко рисовать сложные композиции, в которых эскизы имеют тенденцию к перекосу.Наблюдение со всех сторон увеличивает диапазон возможных выражений лицаСоздайте собственную коллекцию поз
Создаваемые вами данные можно использовать многократно, сокращая время создания, просто перетаскивая значки поз и форм тела на новые модели.Управляйте меньшим количеством контроллеров
В поисках скорости создания позы Design Doll позволяет управлять позами с минимальным количеством контроллеров. Можно даже внести незначительные изменения, просто перетаскивая точки на 3D-моделях.Импорт внешних 3D-моделей
Благодаря функции прикрепления костей Design Doll может связывать предметы, созданные с помощью внешнего программного обеспечения, с конкретными частями. Нет необходимости выполнять утомительные процедуры, такие как прикрепление меча к руке, после принятия решения о выборе позыСинтезировать данные
Design Doll может создавать промежуточные лица и формы тела, синтезируя разницу между двумя существующими моделями в одну новую модель. Посредством многократного синтеза можно легко создать процесс роста персонажаДелитесь позами и моделями
Используется вместе с сайтом для обмена поз и моделями «Doll-Atelier»,Пользователи Design Doll могут обмениваться дизайнами для свободного использования в любых коммерческих или некоммерческих целях
Множество эффектов
Design Doll может применять предустановленные или индивидуальные эффекты одним щелчком мыши.Настраивая эффекты, которые вам подходят, вы можете сосредоточить больше внимания на взаимосвязи между вашими моделями и их средойСвободные от перспективы
Создавая элементы в форме коробки вдоль сеток, Design Doll устраняет утомительную задачу рисования линий перспективыКраска непосредственно на моделях
Теперь стало возможным рисование непосредственно на 3D-моделях. Рисуя вспомогательные линии, такие как расположение глаз или волос на каждом персонаже, вы можете создавать персонализированные эскизные куклы, что сложно сделать с настоящими эскизными кукламиТени и ссылка на оттенки
С Design Doll вы можете свободно устанавливать источники света для создания вашего воображаемого изображения.Поскольку это способствует лучшему пониманию трехмерных объектов, это также оптимальный инструмент для практики иллюстрацииПревратите свои данные в библиотеку
Щелкнув значок позы или значок руки, можно легко применить данные библиотеки к создаваемой позе. Храните ваши любимые данные — и проблемы с поиском или воссозданием 3D-моделей могут быть устранены, что позволяет быстро создавать высококачественные черновикиКросс-совместимые данные
Design Doll может экспортировать, импортировать и синтезировать 2D-данные, а также экспортировать 3D-данные в другие 3D-программыС помощью Design Doll вы можете создать коллекцию поз модели человека и экспортировать 3D-модели на наш веб-сайт для обмена позами «Doll-Atelier.”
СКАЧАТЬ
Попробуйте «Design Doll», бесплатную куклу нового поколения для рисования!
Щелкните ниже, чтобы установить Design Doll и настроить автоматические обновления
СКАЧАТЬ СЕЙЧАСБольше эффекта с функцией ложной перспективы
При использовании регулировки угла обзора для удара ваша степень свободы в композиции ограничена, и результаты часто кажутся неправильными. Используя функцию « ложной перспективы » в Design Doll, вы можете легко и свободно создавать перспективные искажения, чтобы добиться естественного соответствия вашему художественному видению.
- Можно выделить отдельные детали
- Поскольку функция ложной перспективы использует манипуляции с камерой, нет необходимости повторно редактировать соотношение головы и тела модели или позу
Смягчающие средства, которые помогают создать ощущение ручной работы
Перспективные функции камеры в Design Doll идеально подходят для создания « композиций с естественным, нарисованным от руки ощущением » вместо компьютерной графики, как в других 3D-программах.Мы знаем, что вам понравится эта удобная функция, которая приближает ваши композиции к изображениям, видимым невооруженным глазом, при этом сохраняя целостность вашего иллюстративного видения.
- Реальные перспективы, которые можно адаптировать к естественным изгибам
- Перспективы объектива, позволяющие воспроизводить эффекты широкоугольного объектива и объектива «рыбий глаз»
- Функции отображения уровня глаз или высоты камеры
Неограниченное использование огромного количества поз и моделей
Вы можете скачать любые позы и модели, загруженные на сайт пользователя «Кукла-Ателье»
- Импортируйте свои любимые позы с веб-сайта одним щелчком мыши
- Значительно сократить время создания модели за счет синтеза предустановленных данных и создания из них элементов
- Импортированные позы можно использовать бесплатно в коммерческих или некоммерческих целях
-
Отдых на земле
-
Автообновление
-
Библиотека камеры
-
Прозрачный режим
-
Инструмент для переворота и зеркала
-
Пользовательский снимок экрана
-
Обод света
-
Анизотропное отражение
-
Предварительный просмотр Heads-Tall
-
Каркас
-
Расширенный MiniView
-
Режим самого верхнего окна
-
Инструмент для фиксации
-
Сохранить инкрементально
-
Простой свет окружающей среды
-
Окклюзия окружающей среды
-
Система плечевого и запястья
-
Fit Eye Level
-
Удобный интерфейс
-
Инструмент изменения размера
-
Режим предварительного просмотра
-
Карта теней
-
Цвет градиента глубины
-
Edge Shader
3D-визуализация формы тела для покупок в Интернете
Интернет-магазины, не выходя из собственного дома, набирают популярность в течение многих лет, и эта тенденция еще больше усилилась пандемией коронавируса.Но при заказе одежды угадать, какой размер вам нужен, может стать настоящей проблемой. Представляем Shavatar, дочернюю компанию UAntwerp и imec, которая собирается оставить эти догадки в прошлом благодаря инновационным технологиям. Все, что вам нужно сделать, это создать свой собственный аватар для трехмерной визуализации формы тела.
Европейская индустрия моды генерирует 13,2% оборота через электронную торговлю. Некоторое время назад исследование показало, что к 2023 году онлайн-продажи будут расти в среднем на 8,6% в год.И это было до того, как пандемия коронавируса подняла свою голову. Однако розничные торговцы сталкиваются с рядом проблем: например, до 70% товаров, заказанных через Интернет, возвращаются, часто потому, что оказывается, что одежда не подходит.
«Кроме того, наш собственный опрос среди 200 человек показывает, что 73% потребителей, которые хотят покупать одежду в Интернете, в конечном итоге решают не размещать заказ, потому что не уверены, что это правильный размер», — сказал Герт Мертенс, генеральный директор Shavatar. новейшее дочернее предприятие Антверпенского университета и исследовательского института imec.«Из тех, кто размещает заказ, 40% признают, что они, как правило, заказывают один и тот же товар в нескольких разных размерах, чтобы убедиться, что они получат нужный размер. Эти наблюдения, очевидно, имеют серьезное влияние на бизнес-модели в отрасли».
Трехмерная визуализация формы тела
Enter Shavatar, созданный Фемке Данкаерс во время ее докторской диссертации в Vision Lab, исследовательской группе imec на факультете физики Университета Антверпена.
«Я разработал модель для прогнозирования и визуализации формы человеческого тела в 3D, основанную на ограниченном количестве параметров, со средней погрешностью всего семь миллиметров по сравнению с реальной формой тела человека», — объяснил Данкаерс, соавтор. основал спин-офф.«Потребители могут делать это дома, без сканера».
Технология была разработана и усовершенствована в дополнительном проекте Shavatar при поддержке программы ускорения imec.istart. Герт Мертенс сказал: «Мы проконсультировались с 36 заинтересованными сторонами из индустрии моды, чтобы придумать инструмент, который позволил бы потребителям создавать свои собственные аватары. Затем инструмент предлагает правильный размер и соответствие любого предмета. На более позднем этапе мы будем уметь накладывать одежду на фигуру покупателя.Наша конечная цель — таким образом представить себе всю одежду ».
В ближайшее время инструмент будет интегрирован в интернет-магазины различных брендов одежды, но если вас заинтересовали, вы уже можете посетить www.shavatar.me сегодня и создать свой собственный 3D-аватар. Вы сразу получите индивидуальный совет для более чем 50 брендов.
Чем больше людей используют этот инструмент, тем более ценные данные о формах тела потребителей может собрать индустрия моды. Эти идеи позволят брендам одежды еще больше оптимизировать свои коллекции и адаптировать их к своим конкретным целевым группам.С момента своего создания Shavatar уже привлек 200 000 евро финансирования, что позволило компании разработать первую версию продукта.
Imec довольна запуском спин-оффа. Джо Де Бок, директор по безопасности в imec, сказал: «Благодаря нашим дочерним предприятиям мы помогаем формировать предпринимательский ландшафт во Фландрии. Мы гордимся инкубационным процессом, который в конечном итоге привел к созданию Shavatar в сотрудничестве с исследователями и UAntwerp Успех этого сотрудничества также привел к успешному выбору проекта для imec.программа istart »
Профессор Сильвия Ленертс, проректор по оценке и развитию в UAntwerp, добавила: «Шаватар — отличный пример научных исследований, ведущих к приложениям, которые мы можем использовать. В нескольких случаях исследовательской группе Vision Lab удавалось переводить свои обширные воплощение опыта в инновационные практические решения. Инструмент «аватар» приведет к меньшему количеству возвратов и, следовательно, меньшему количеству транспорта, что является важным шагом на пути к большей устойчивости. Как предприимчивый и устойчивый университет, мы можем только приветствовать это.»
Обзор модели моего тела — Melly Sews
Нарисуйте свои идеи одежды на собственном персонализированном кроки
Привет всем, сегодня я делюсь своим обзором приложения My Body Model, которое представляет собой классное приложение, которое вы можете использовать для создания личных кроки на основе ваших личных измерений тела. Все эскизы, которые вы видите на изображении выше, сделаны приложением на моем теле.
Когда я обратился к создателю My Body Model по поводу этой публикации, она была достаточно щедрой, чтобы предоставить мне файлы для просмотра, но все мнения здесь мои собственные.И после того, как я поигрался с моими собственными кроки, я искренне считаю, что они полностью окупаются. Я сделал видео с другими своими мыслями, которое вы можете посмотреть ниже или на YouTube здесь.
Хотя я и умею рисовать, мне сложно создавать искусство от случая к случаю. Для меня это всегда включает в себя зонирование в определенном свободном пространстве, чтобы получить хороший отрезок времени, чтобы иметь возможность перенести на бумагу или холст то, что у меня в голове. В то время как одежда для меня находится на более легком конце шкалы с точки зрения того, что я рисую, иллюстрации тел в одежде — нет.Особенно мое собственное тело!
Мне нравится, что это очень удобный ярлык для меня. Я могу импортировать фигуры на свой iPad и рисовать на них цифровыми набросками, пока я сижу с тренером и смотрю телевизор. На видео выше есть промежуток времени, когда я делаю именно это. Бумажные для печати из загрузки планировщика также удобны для прикрепления образцов ткани и создания заметок по рисунку. Все это означает, что в последнее время я делал НАМНОГО больше идей, генерирующих идеи, и это не что иное, как хорошо для моего собственного творчества.
Еще одна замечательная особенность My Body Model — это то, что вы можете предварительно просмотреть свои кроки перед покупкой. Итак, вы вводите свои измерения, а затем вы видите, как он вас зарисовывает. Моя была очень близка сразу с места в карьер, но я использовал одну из дополнительных регулировок, чтобы немного опустить линию груди (что также является корректировкой рисунка, что для меня не является необычным). Вы можете увидеть на сравнительном изображении выше, как сравниваются сгенерированные приложением Croquis и мое реальное тело.
Как я уже говорил ранее в этом посте, я определенно рекомендую этот инструмент и буду много использовать его для себя!
Как попасть в моделирование
Начало работы в мире моделирования может показаться сложной задачей.У вас, наверное, есть самые разные вопросы, например: «Есть ли у меня то, что нужно?» «Как мне получить агента?» «Каковы плюсы и минусы того, чтобы стать моделью?» Если вам нужна помощь в моделировании, эта статья поможет ответить на некоторые из ваших вопросов о том, как проникнуть в отрасль, и поможет вам стать успешной моделью.
У меня есть то, что нужно?
А у вас есть взгляд? Модель — это не просто «хорошо выглядеть» или «быть красивой».«В мире много красивых людей. Если вы серьезно относитесь к модельному бизнесу, важно «взглянуть». В том, как вы выглядите или в вашем телосложении, должно быть что-то уникальное. Это может быть знак красоты (а-ля Синди Кроуфорд), то, как выглядят ваши ямочки на щеках, когда вы улыбаетесь, что-то в форме вашего подбородка или носа, добавляющее объемности вашему лицу, или другое уникальное качество. Примите это. Это будет то, что отличает вас от других моделей в отрасли.
Что касается общих характеристик, которые важны для любого, кто хочет заняться моделированием, высота, вероятно, является самым важным физическим атрибутом для большинства моделей, при этом 5’7 ’’ обычно считается минимальным.Конечно, из этого правила есть исключения (например, Кейт Мосс), но это хорошее место для начала, чтобы определить, предназначены ли вы для модельной индустрии. Подиумные модели должны быть не менее 5 футов 8 дюймов для женщин и 6 футов для мужчин. Для редакционного моделирования более важен правильный внешний вид, чем высота или тонкая оправа. Для моделей условного продвижения / продвижения важны привлекательная личность и способность выступать в качестве представителя продукта. К разным типам моделирования предъявляются определенные требования, но прежде чем приступить к моделированию, вы должны понять, каким типом моделирования вы будете заниматься.Вы будете на подиуме? Вы хотите сниматься в журналах или участвовать в частных мероприятиях?
В последние годы, например, в бизнесе наблюдается тенденция к увеличению количества моделей больших размеров, наряду с ростом в других нишевых областях, таких как модели с татуировками. Ваш взгляд может помочь определить, в какую область моделирования вы лучше всего впишетесь, поскольку существует множество подразделений под большим зонтом моделирования. Помните, что заниматься модельным бизнесом — это не просто быть высоким и худым с идеальной осанкой.Это означает выявление своих сильных сторон и использование их в поисках работы, которая подходит именно вам.
Какие существуют типы моделирования?
Многие модели, совершенно новые для отрасли, выражают удивление по поводу того, сколько разных жанров доступно для них, чтобы найти работу.
Вот список самых известных жанров:
- Моделирование подиумов (кошачьих прогулок) — модели высокого класса, обычно снимаемые для редакционных статей, дизайнеров высокого класса, подиумов и модных кампаний.У моделей есть особые возраст, рост и стандарты измерения. Типичный возраст — 16-21 год. Модели могут быть моложе этого возраста, но многие агентства требуют, чтобы модели были не менее 16 лет. Точно так же модели могут быть старше, но агентствам и клиентам, как правило, нравится, что их модели выглядят моложе и моложе. Рост обычно составляет от 5’9 ″ -6 ″, бюст от 32 ″ -36 ″, талия от 22 ″ -26 ″, а бедра должны быть от 33 ″ -35 ″. Конечно, большинство женщин не соответствуют этим стандартам, и именно поэтому модели, как правило, больше всего получают зарплату и больше всего работают.Если вы не соответствуете этим требованиям, не волнуйтесь, большинство женщин этого не делают, и это не значит, что агентства не делают исключений, и вы не можете ходить по взлетно-посадочной полосе.
- Печатное (каталог, редакционное) моделирование — еще один прибыльный жанр моделирования, который несколько менее ограничен, чем моделирование моды. Рост обычно составляет от 5’8 до 5’11 дюймов, а типичные размеры следующие: бюст 32-35 дюймов, бедра 33-35 дюймов и талия 22-26 дюймов. Каталог и мода — два самых специфических модельных жанра.Поэтому они самые прибыльные.
- Моделирование нижнего белья / купальников — Модели также имеют особые требования к измерениям. Типичные размеры нижнего белья: рост 5’7 ″ -6 ’, бюст 32 ″ -35 ″ чашка C, талия 22 ″ -26 ″ и бедра 33 ″ -35 ″. Модель в бикини будет похожа на модель в нижнем белье, но с немного большим размером груди.
- Другие типы моделирования включают телевизионную рекламу, прямой эфир продукта / бренда, шоу-рум, Интернет и нишевое моделирование (татуировки, пирсинг, миниатюрные, большие размеры, зрелые, части тела, фитнес / бодибилдинг, без одежды и др.) .Размеры всегда будут различаться в зависимости от типа моделирования и отрасли, в которой вы работаете.
Есть ли перечисленные выше области моделирования, с которыми вы не знакомы? Вы, наверное, не одиноки. Итак, какой жанр вам подходит? Что ж, модели с образом соседской девушки часто отлично подходят для коммерческого и каталожного моделирования, чтобы продавать косметические товары, одежду и аксессуары в журналах и рекламных объявлениях. Если фитнес — ваша страсть, основной растущей областью моделирования является фитнес-моделирование для девушек, которые находятся в отличной форме и могут помочь продвинуть спортивную одежду и фитнес-компании.Знание того, какой тип модели вы лучше всего воплощаете, позволит вам добиться большего успеха, потому что вы сможете сосредоточиться на этой области. В индустрии развлечений есть много возможностей. Это поможет вам избежать разочарования, когда вы попытаетесь приступить к работе в модельном бизнесе, и позволит агентствам и кастинг-директорам увидеть, как вы более четко вписываетесь в их состав или удовлетворяете их потребности для определенной работы. .
Если вы только начинаете заниматься моделированием, возможно, вы захотите узнать, есть ли уроки специально для моделирования.Важно проявлять осторожность, если вы считаете, что нашли уроки моделирования, потому что это может быть мошенничество. Как правило, безопаснее и выгоднее посещать другие типы занятий, например, танцевальный класс, чтобы улучшить качество движений и осознание тела, урок актерского мастерства, чтобы помочь вам чувствовать себя более комфортно, говоря и принимая коммерческую работу, или класс фитнеса, чтобы помочь сохранить ваше тело в форме. Также очень полезно проводить время с профессиональным фотографом, поскольку он может дать вам реальный совет о том, что именно хотят другие фотографы и режиссеры от своих объектов.
С чего начать?
Итак, вы решили испытать модельную жизнь. Первый шаг к успешной карьере — найти квалифицированного, опытного агента. Как и в случае с упомянутыми выше «модельными классами», некоторые модельные агентства на самом деле являются мошенниками. Чрезвычайно важно убедиться, что агентства, с которыми вы собираетесь работать, являются законными. Проведите свое исследование! Просмотр веб-сайтов интересующих вас агентств поможет вам понять, какие типы моделей они ищут, какие вакансии заказали их клиенты и их общий профессионализм.Управление моделями очень важно, лучше всего провести исследование, прежде чем подписываться на компанию.
В Интернете часто есть ссылки или рекомендации, которые могут помочь вам в правильном направлении. Один из самых больших красных флажков — это то, что агентство просит деньги у нового клиента авансом, будь то пакет фотографий / портфолио или по любой другой причине. У агентств с хорошей репутацией никогда не будет затрат. Они зарабатывают деньги, если вы бронируете работу, и только если вы бронируете работу. Если вы видите признаки того, что они пытаются заработать деньги другим способом, бегите — не ходите, бегите — прочь.
Создание портфолио
После того, как вы составили список авторитетных агентств, представляющих тот тип модели, которым вы хотели бы быть, пора отправить им свою «книгу». Это будет включать вашу «статистику» (ваши основные измерения, рост и вес) и портфолио с фотографиями. Самые важные фотографии — это простые цифровые изображения. Попробуйте сфотографироваться с небольшим количеством макияжа или без него, в очень простой одежде с минимальным количеством аксессуаров и при естественном освещении.Агентству важно видеть и ваше лицо, и тело, поэтому обязательно включите широкоугольный снимок, который показывает ваше тело, и более крупный снимок вашего лица. Носите приталенную одежду, чтобы агентство могло видеть основную форму вашего тела. Если вы надеетесь попасть на концерты в купальниках или нижнем белье, вы также должны приложить эти фотографии. Поиграйте с ракурсами и позами, чтобы найти наиболее привлекательный образ для отправки в агентства. Запланируйте аналогичный подход при посещении открытых звонков по моделированию; ваша одежда должна быть хорошо подогнана, а прическа и макияж должны быть минимальными.
Если у вас есть предыдущий опыт моделирования и есть профессиональные фотографии с прошлых работ, их тоже можно включить. Однако, если вы только начинаете, вероятно, стоит потратить деньги на профессионального фотографа с целью получения высококачественных фотографий для отправки в агентства. Таким образом, если вы можете позволить себе инвестировать в качественные и актуальные фотографии каждый год, это будет для вас огромной выгодой.
Плюсы и минусы
Моделирование — это нечто большее, чем просто красивый вид перед камерой.Это, прежде всего, бизнес, поэтому очень важно, чтобы начинающие модели относились к нему как к такому и подходили к нему так же, как и к любой другой работе, с профессионализмом, изяществом и стойкостью. Быть моделью дает много больших преимуществ. У вас есть шанс помочь воплотить в жизнь взгляды других. Это действительно прекрасная возможность заняться любимым делом, познакомиться с действительно замечательными людьми — будь то фотографы, дизайнеры или коллеги-модели — и исследовать города по всему миру.
Тем не менее, индустрия, конечно, не только о блеске и гламуре, как это может показаться с точки зрения стороннего наблюдателя.Если вы не супермодель, проводящая крупные кампании, вы, как правило, не зарабатываете много денег (по крайней мере, не постоянно). Моделирование может быть физически, умственно и эмоционально утомительно. Между моделями может быть сильная конкуренция, поскольку часто есть несколько моделей, каждая из которых соперничает за один и тот же небольшой пул рабочих мест. Это неизбежно означает отказ, который может истощить вас эмоционально.
Важно развить толстую кожу, чтобы защитить себя от отвержения, с которым вы столкнетесь. Постарайтесь не принимать отказы на свой счет.Они произойдут. Компании, нанимающие моделей для съемок и кастинг для шоу, имеют особые потребности, и вы можете не соответствовать тому, что они ищут в этот конкретный день. Если вы сможете принять реалии бизнеса и оставаться настойчивыми, это не только принесет пользу вашей карьере, но и сделает вас более сильным человеком.
Несколько советов для каждой модели
- Будьте вовремя! Коммуникация — ключ к успеху
- Покажите приверженность
- Будьте настойчивы и оставайтесь позитивными
- Вы услышите «нет» больше раз, чем «да».Не позволяйте этому повлиять на вашу уверенность. Не позволяйте этому влиять на вашу жизнь.
- Позаботьтесь о себе, своем теле, своем образе жизни.
- Будьте осторожны с тем, с кем вы работаете и что вы готовы делать.
- Имейте план Б. Возможно, вам не хватит работы, чтобы заработать на жизнь
- Убедитесь, что у вас настоящие отношения со своим агентом. Будьте готовы отдавать и брать. Помогите им, и они помогут вам.
- Всегда расширяйте свои таланты. Если вы хотите заказать новые виды работы, приобретите новые навыки.
Не сдавайся
Человек с толстой кожей и сильным чувством собственного достоинства находится в хорошем психологическом и эмоциональном положении, чтобы вступить в мир моделирования. А как насчет финансов? Работа на ранних этапах вашей карьеры может быть редкой, и вам не будет платить достаточно, чтобы покрыть арендную плату, особенно если вы живете на крупном рынке. Эти крупные города могут предложить больше всего возможностей трудоустройства, но они также могут быть чрезвычайно дорогими для проживания. Когда вы начнете заниматься моделированием, вам следует запланировать поиск другой работы, чтобы оплачивать счета.Например, работа в сфере гостеприимства может быть хорошим вариантом для модели, поскольку она предлагает гибкий график работы и при этом позволяет вам зарабатывать приличные деньги в ограниченное время. Планируйте это заранее.
Важно быть терпеливым и решительным, делая карьеру в модельном бизнесе. Возможности могут появиться не сразу. Потребуется время, чтобы наладить отношения с влиятельными людьми в отрасли. Модельная и модная индустрии постоянно меняются и движутся, поэтому вы никогда не знаете, кого вы можете встретить и как они могут помочь вам в будущем.Будьте гибкими, и вы сможете идти в ногу с постоянно меняющимся бизнесом и продолжать добиваться успеха в качестве профессиональной модели!
Мы можем делать все и вся
Имея офисы в Лас-Вегасе и Майами, мы сформированы нашей дальновидной средой.

 Бюджетное блюдо из минимума продуктов
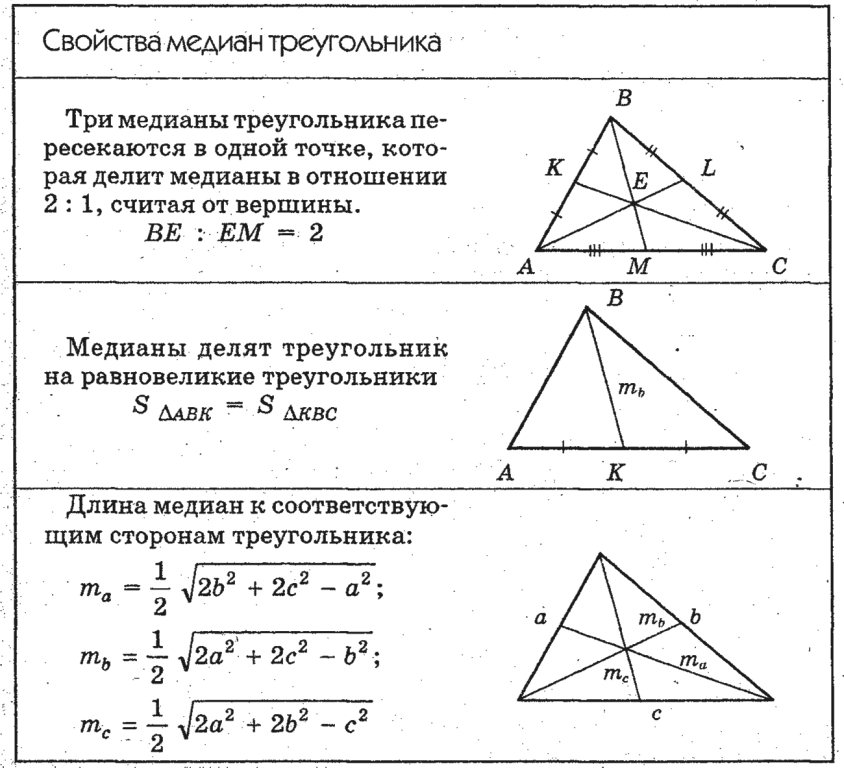
Бюджетное блюдо из минимума продуктов  Формула ее длины выражается через стороны:
Формула ее длины выражается через стороны:

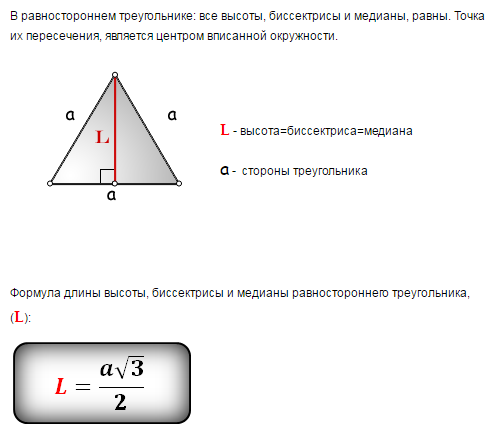
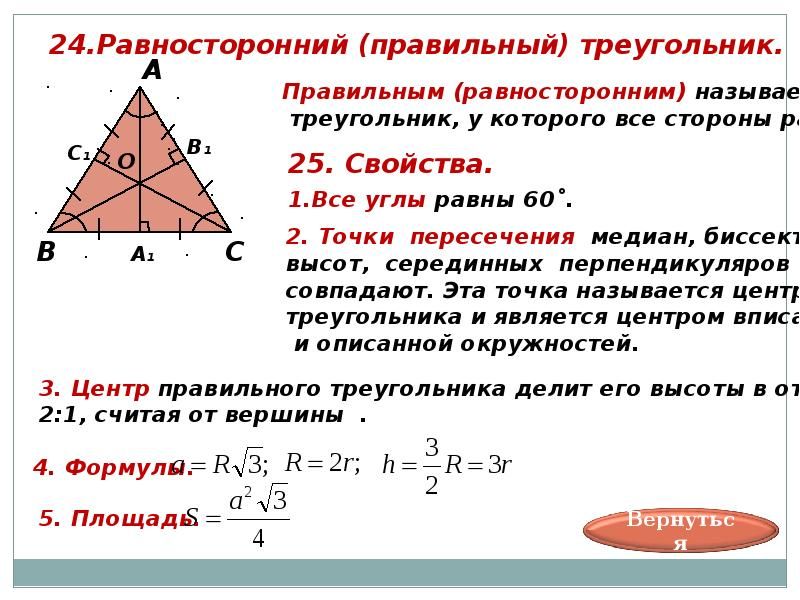 Свойства медианы прямоугольного треугольника
Свойства медианы прямоугольного треугольника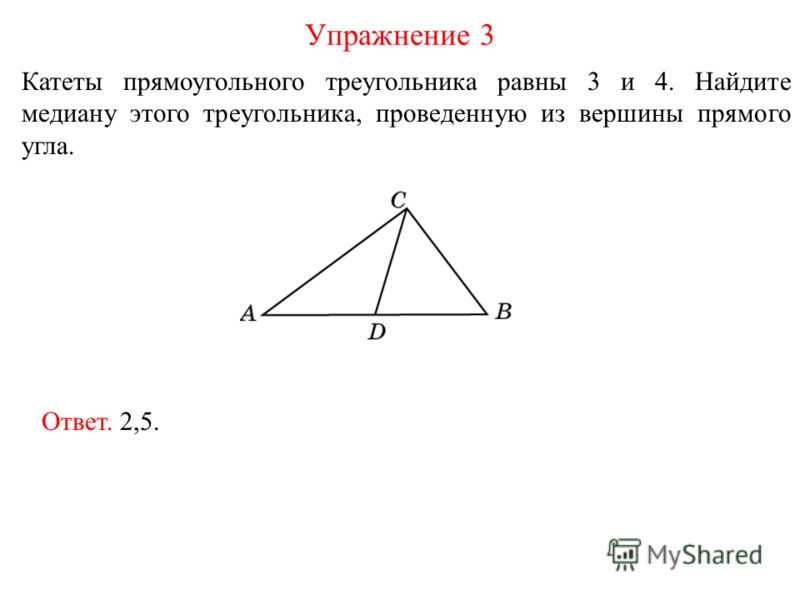
 Найдите гипотенузу треугольника
Найдите гипотенузу треугольника
 У него также угол С прямой по условию задачи, катет BC является общим с катетом BC исходного треугольника ABC, а катет EC по свойству медианы равен половине катета AC исходного треугольника ABC.
У него также угол С прямой по условию задачи, катет BC является общим с катетом BC исходного треугольника ABC, а катет EC по свойству медианы равен половине катета AC исходного треугольника ABC. 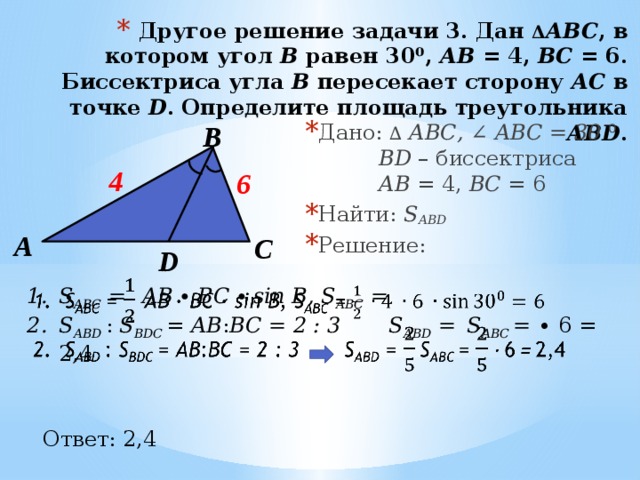 Формула ее длины выражается через стороны:
Формула ее длины выражается через стороны: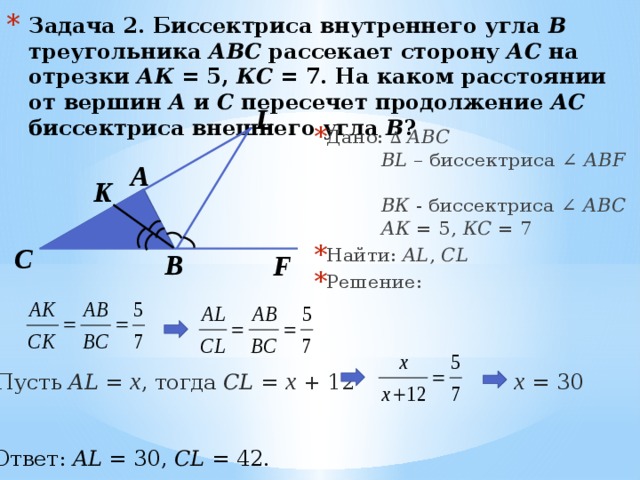




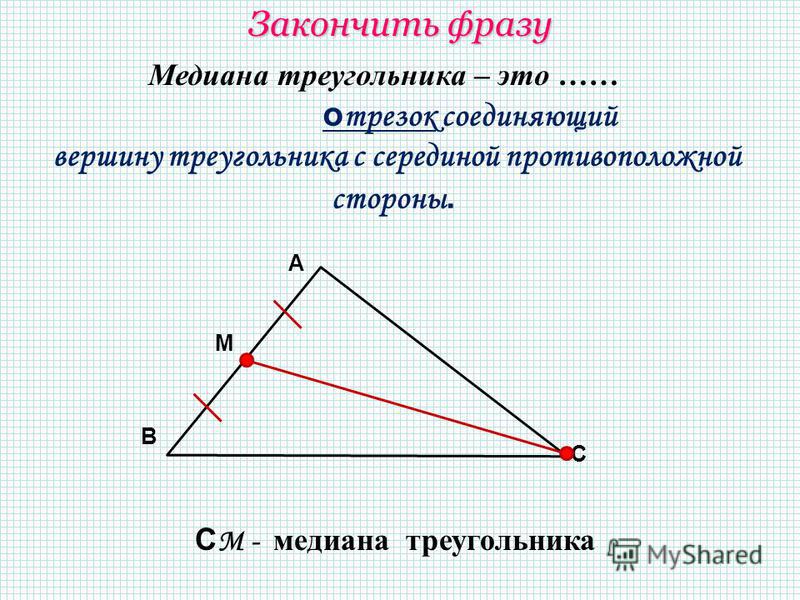 Две его смежные стороны равны.
Две его смежные стороны равны.
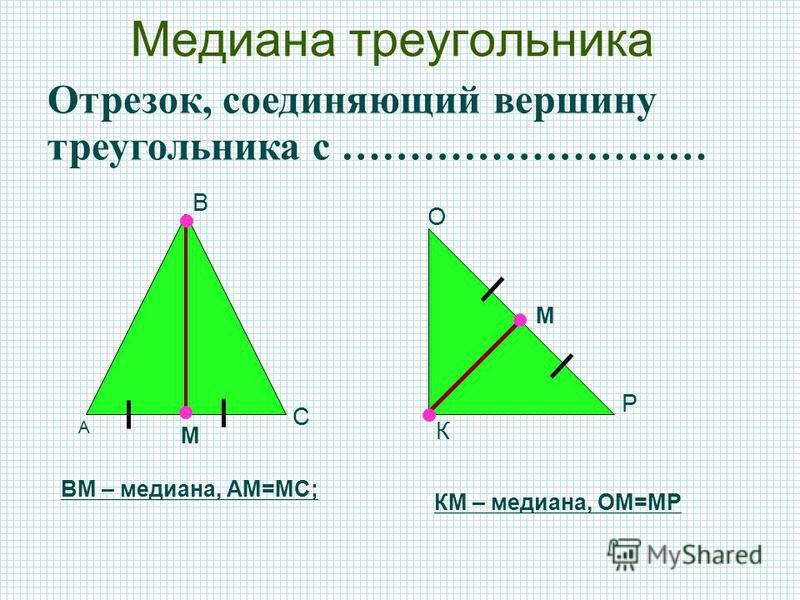
 4
4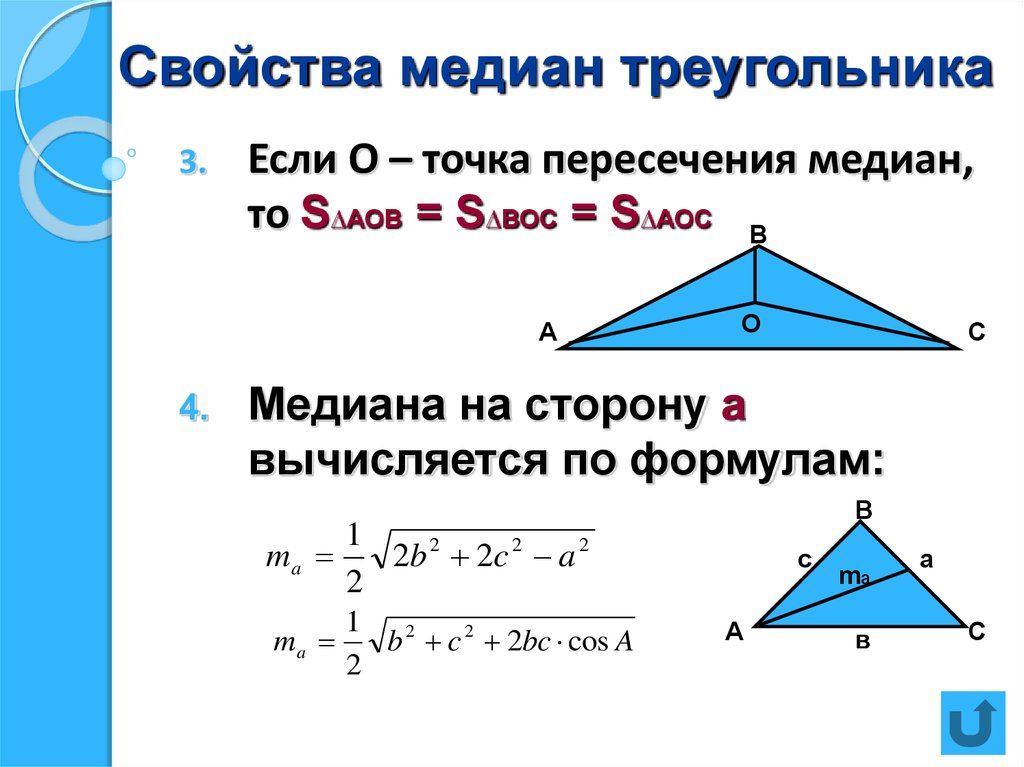
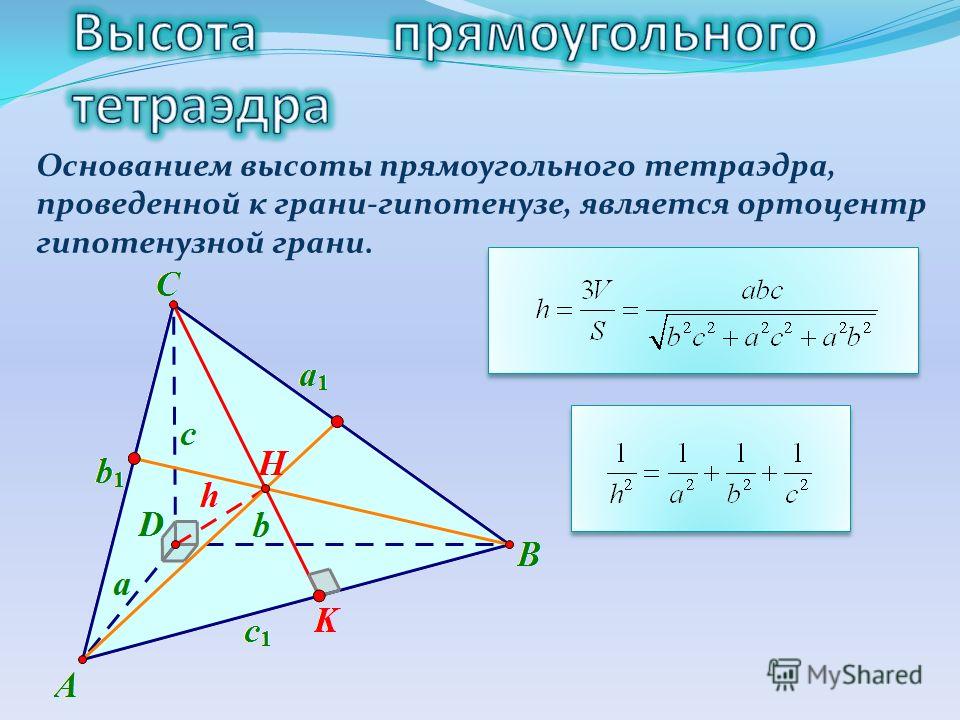
 Длина медианы треугольника (рис. 10) вычисляется по формуле:
Длина медианы треугольника (рис. 10) вычисляется по формуле:
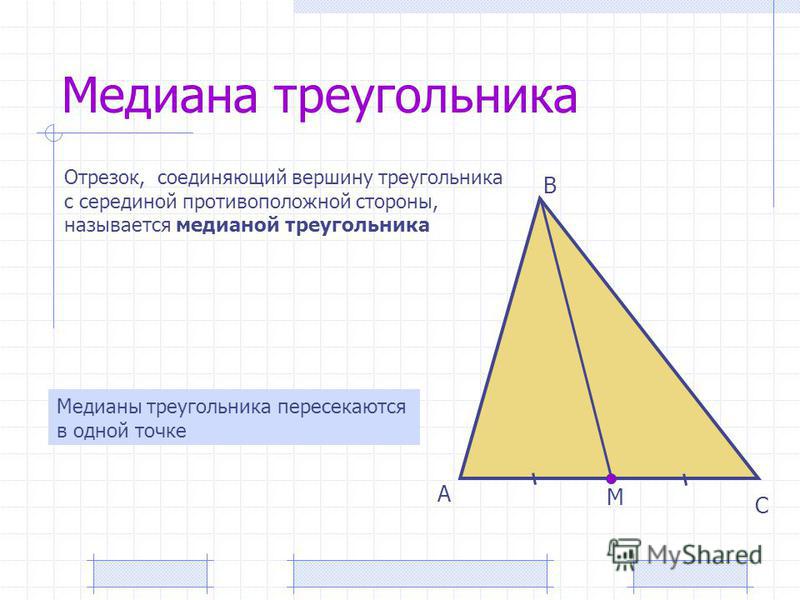

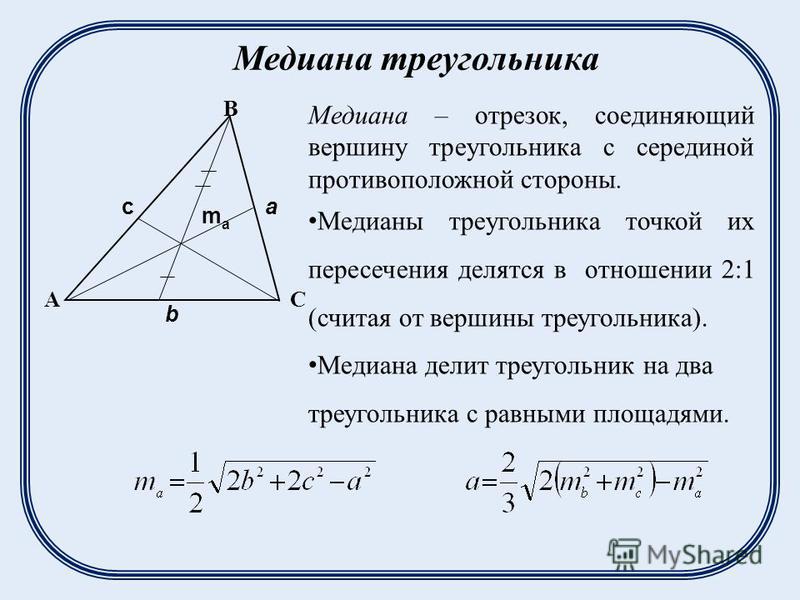 Это означает, что точки А 2
и M
делят медиану АА 2
на три равные части, т. е. AM = 2МА 2 . Аналогично СМ = 2MC 1
. Итак, точка М пересечения двух медиан АА 2
и CC 2
треугольника ABC делит каждую из них в отношении 2:1, считая от вершин треугольника. Совершенно аналогично доказывается, что точка пересечения медиан АА 1 и BB 1 делит каждую из них в отношении 2:1, считая от вершин треугольника.
Это означает, что точки А 2
и M
делят медиану АА 2
на три равные части, т. е. AM = 2МА 2 . Аналогично СМ = 2MC 1
. Итак, точка М пересечения двух медиан АА 2
и CC 2
треугольника ABC делит каждую из них в отношении 2:1, считая от вершин треугольника. Совершенно аналогично доказывается, что точка пересечения медиан АА 1 и BB 1 делит каждую из них в отношении 2:1, считая от вершин треугольника. Таким образом,S AMB = S AMC = S CMB .
n
Таким образом,S AMB = S AMC = S CMB .
n


 Тогда
Тогда Например, проведение операции у пациента с деформацией 50 градусов позволяет добиться полной коррекции, чего сложнее добиться у пациентов с деформацией 80 градусов и более.
Например, проведение операции у пациента с деформацией 50 градусов позволяет добиться полной коррекции, чего сложнее добиться у пациентов с деформацией 80 градусов и более.
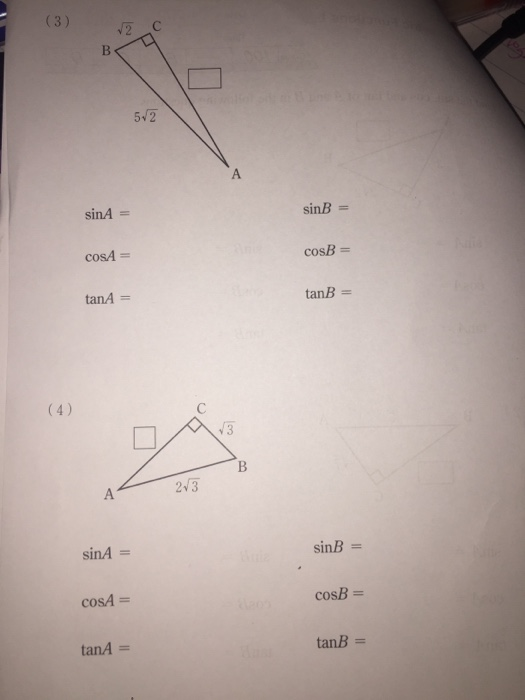
 Вычитание дает соs (А + В) (8), поэтому формула, которая нам нужна:
Вычитание дает соs (А + В) (8), поэтому формула, которая нам нужна:
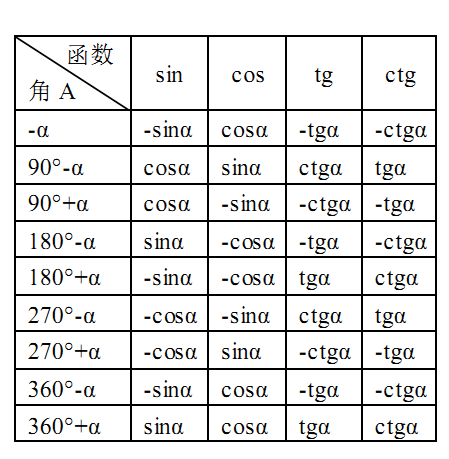


 Проходя через точку в 180 градусов, функция тангенса повторяет то, что она «делала» проходя 0 или 360 градусов. На 270 градусах она повторяет то же, было на 90 градусах.
Проходя через точку в 180 градусов, функция тангенса повторяет то, что она «делала» проходя 0 или 360 градусов. На 270 градусах она повторяет то же, было на 90 градусах.
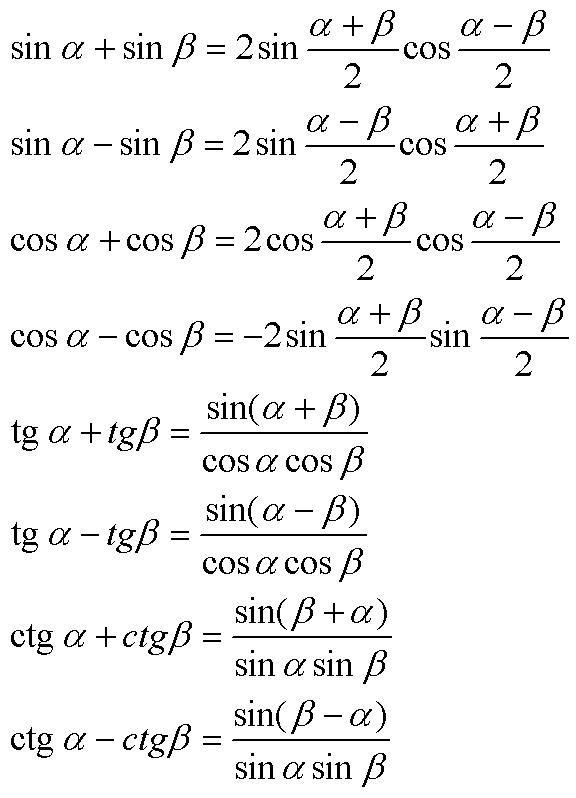 A2 было бы то же самое число, возведенное в квадрат. Его значение зависело бы от использованного числового значения, поэтому это не очень хороший член для использования. Это означает квадрат синуса ли косинуса, не сам угол.
A2 было бы то же самое число, возведенное в квадрат. Его значение зависело бы от использованного числового значения, поэтому это не очень хороший член для использования. Это означает квадрат синуса ли косинуса, не сам угол.
 Используя теорему Пифагора, изменяем это к виду: cos 2A = 2cos2 A — 1. Наконец, tg 2A = 2 tg A/[1 — tg2 A].
Используя теорему Пифагора, изменяем это к виду: cos 2A = 2cos2 A — 1. Наконец, tg 2A = 2 tg A/[1 — tg2 A].
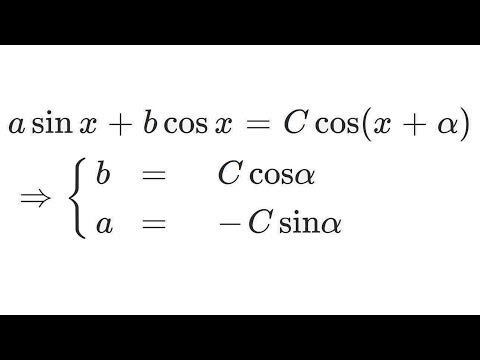 Перпендикуляр из третьего угла на третью сторону делит ее пополам. Таким образом весь треугольник делится на два равных прямоугольных треугольника.
Перпендикуляр из третьего угла на третью сторону делит ее пополам. Таким образом весь треугольник делится на два равных прямоугольных треугольника.

 Вы видите, что для любого сегмента круга, угол в центре всегда в два раза больше угла, опирающегося на окружность.
Вы видите, что для любого сегмента круга, угол в центре всегда в два раза больше угла, опирающегося на окружность.
 Когда два угла образовывают угол 180 градусов (два прямых угла), они называются дополнительными. Если два угла добавить до 90 градусов (один прямой угол), их называют комплементарными
Когда два угла образовывают угол 180 градусов (два прямых угла), они называются дополнительными. Если два угла добавить до 90 градусов (один прямой угол), их называют комплементарными
 Если бы наблюдения были сделаны горизонтально от точки наблюдения в вопросе 2 (к востоку от первой, к западу от второй), под каким углом была бы линия пересечения наблюдений?
Если бы наблюдения были сделаны горизонтально от точки наблюдения в вопросе 2 (к востоку от первой, к западу от второй), под каким углом была бы линия пересечения наблюдений?

 Приведите приближенные значения из таблицы или используя калькулятор.
Приведите приближенные значения из таблицы или используя калькулятор.
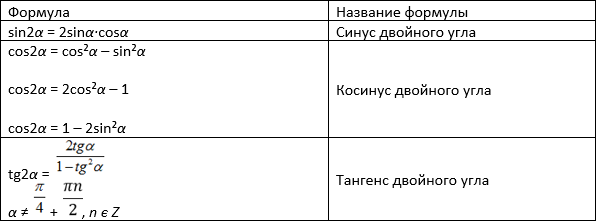 )
) )
) )
)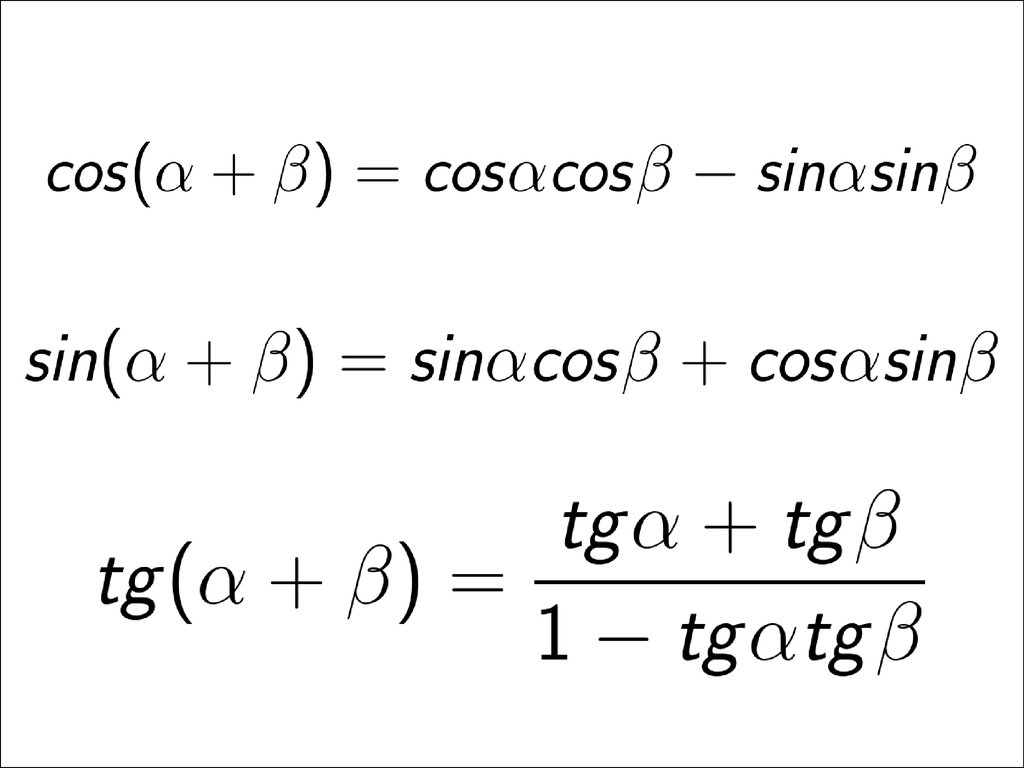 )
)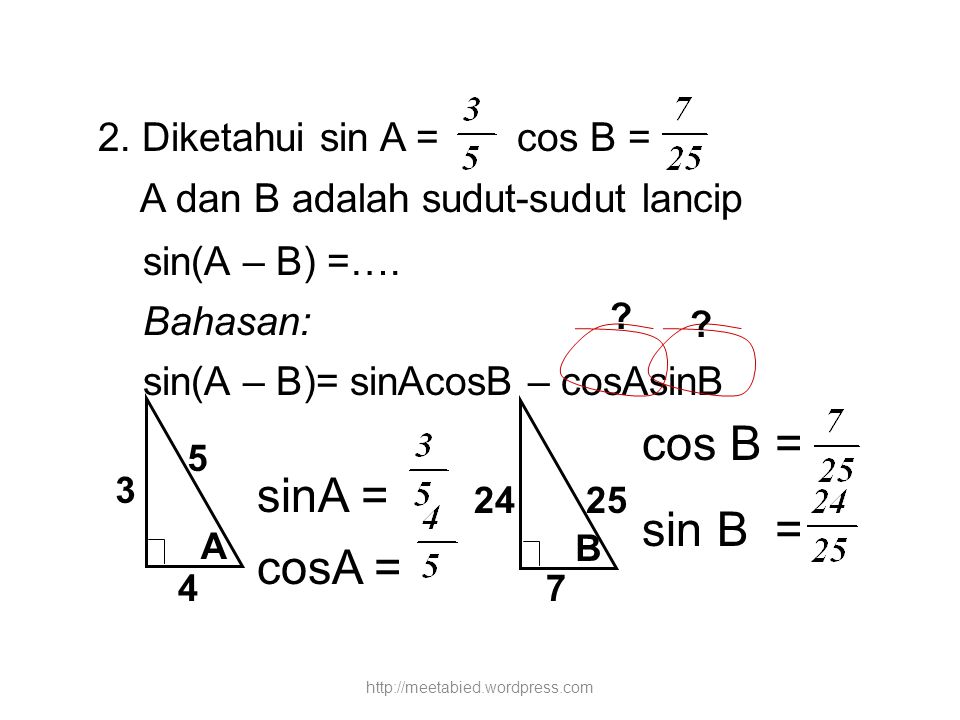 )
) )
)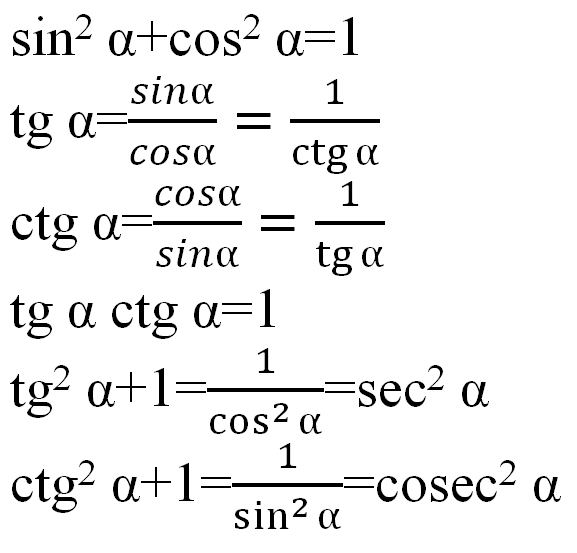 )
)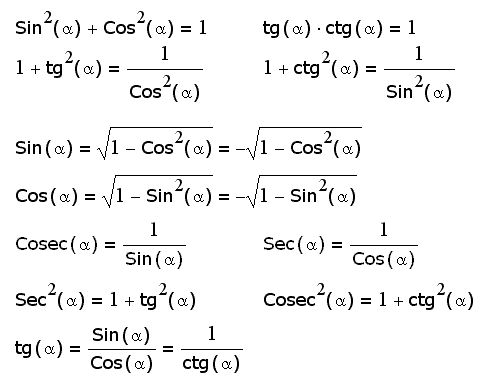 )
) )
)
 Определение реакций опор и моментов защемления
Определение реакций опор и моментов защемления
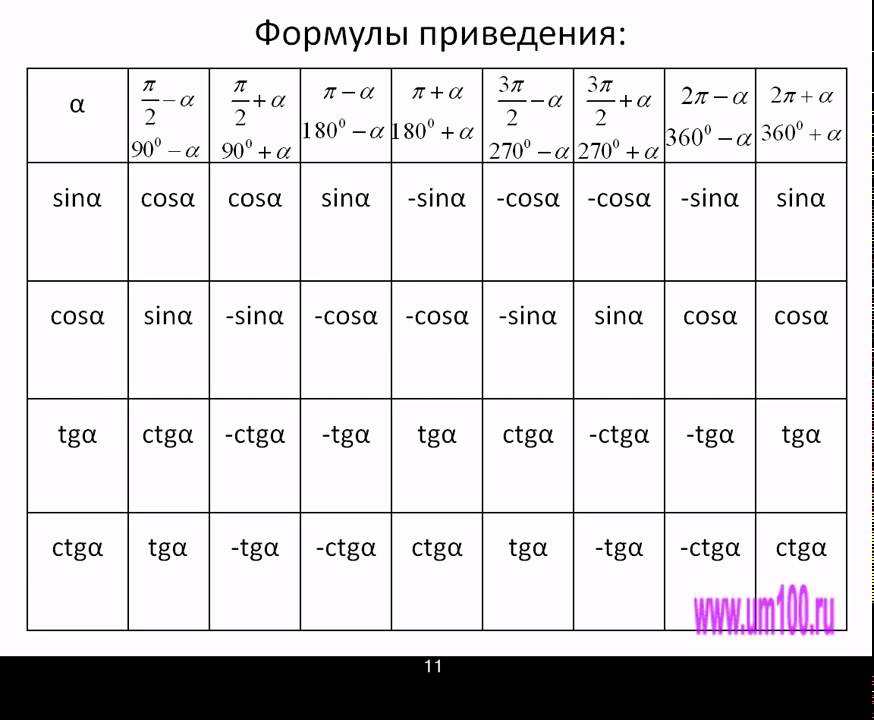

 Перевод градусов в радианы и наоборот. Полный круг содержит 360 градусов, или 2π радиан.
Перевод градусов в радианы и наоборот. Полный круг содержит 360 градусов, или 2π радиан. График функции y = tgx
График функции y = tgx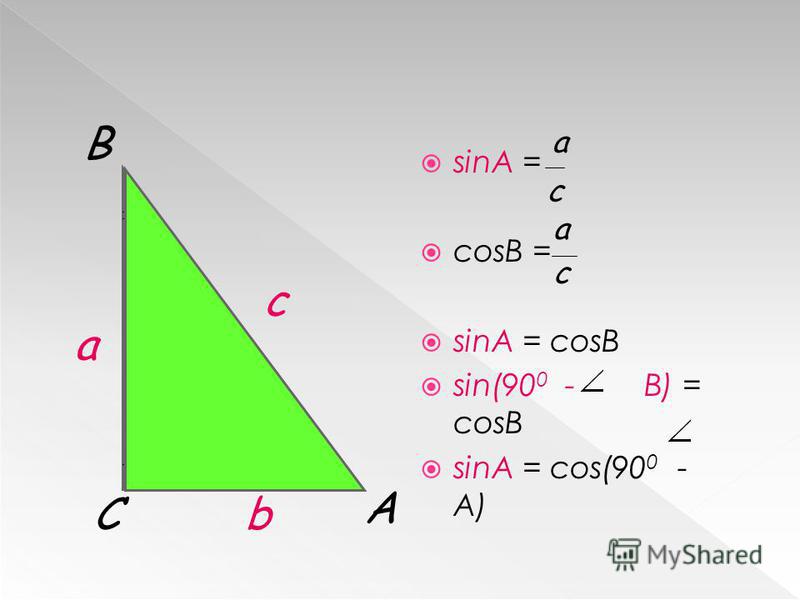
 Есть ли среди пяти основных форму та, в которой мы используем три стороны? Да, это формула Герона. Тогда:
Есть ли среди пяти основных форму та, в которой мы используем три стороны? Да, это формула Герона. Тогда: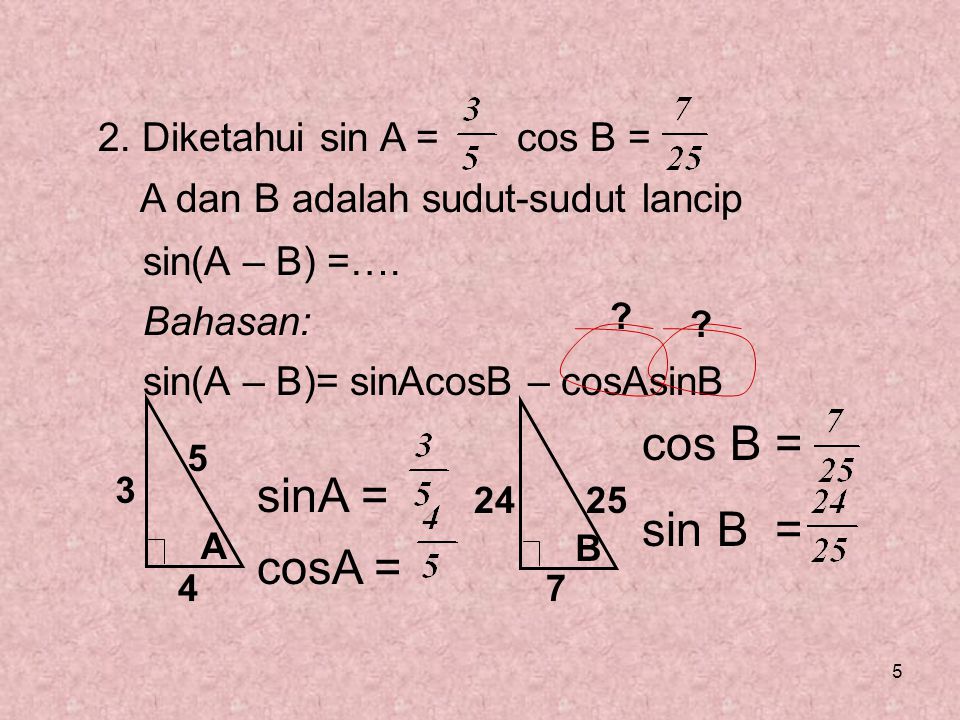 Подходящая формула: S = a∙ b ∙ sinγ. Подставим данные из условия задачи:
Подходящая формула: S = a∙ b ∙ sinγ. Подставим данные из условия задачи: su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 176.9.44.166 (0.017 с.)
su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 176.9.44.166 (0.017 с.) 
 Создание благоприятной атмосферы на уроке. Мотивация учащихся. (5мин)
Создание благоприятной атмосферы на уроке. Мотивация учащихся. (5мин)
 Предлагает ответить на вопрос: «А что бы вы хотели узнать об основных формулах для синуса и косинуса?»
Предлагает ответить на вопрос: «А что бы вы хотели узнать об основных формулах для синуса и косинуса?»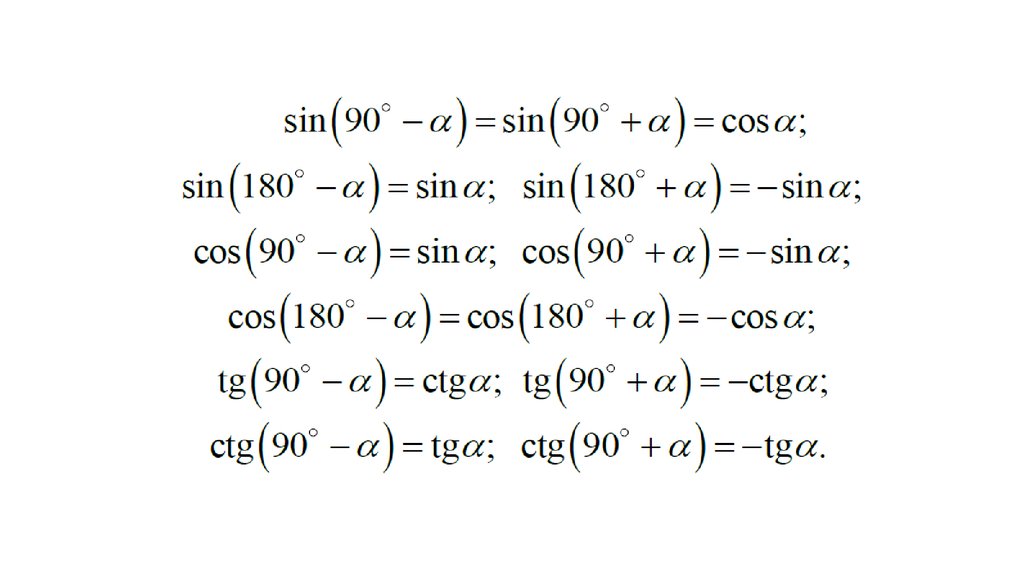
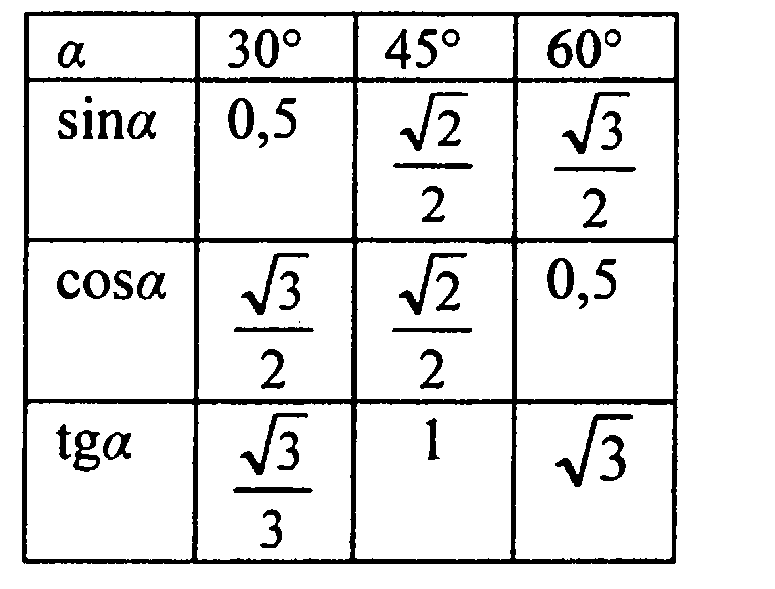
 Предлагает подвести итоги работы в таблице. «Знаю», «Хочу узнать», «Узнал». — Итак, давайте вернёмся к теме и целям нашего занятия. Назовите их. — Достигли ли поставленной цели?
Предлагает подвести итоги работы в таблице. «Знаю», «Хочу узнать», «Узнал». — Итак, давайте вернёмся к теме и целям нашего занятия. Назовите их. — Достигли ли поставленной цели? 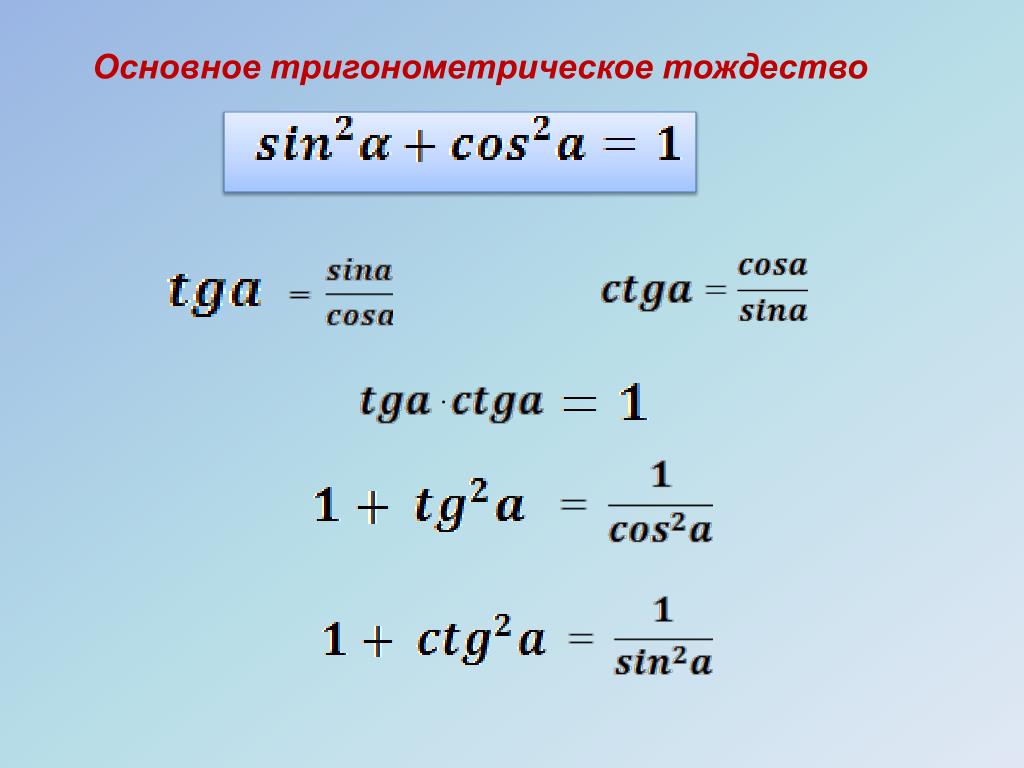
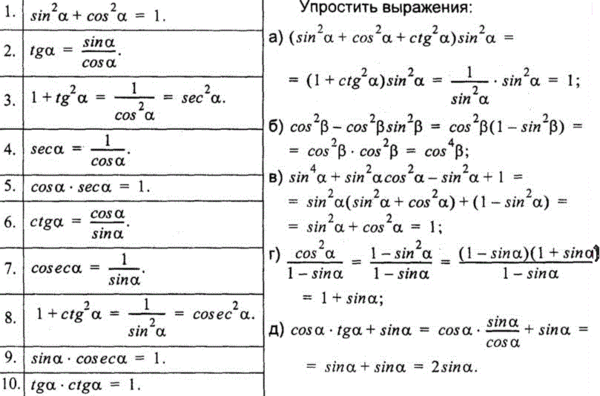
 Оценивание. Рефлексия. Постановка домашнего задания.(10 мин) Приложение 3
Оценивание. Рефлексия. Постановка домашнего задания.(10 мин) Приложение 3 Спасибо за урок, До свидания.
Спасибо за урок, До свидания.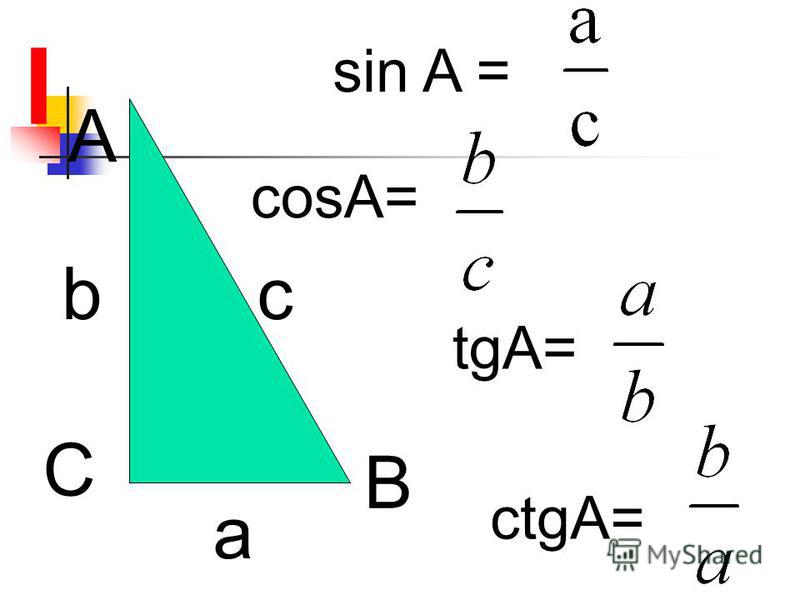 Фазовый угол. Сдвиг по фазе.
Фазовый угол. Сдвиг по фазе.
 Тогда sin Θ2=+/+ = +; cos Θ2=+/- = -; tg Θ2=+/- = -. Пусть ОА вращается дальше таким образом, что Θ3 — любой угол в третьем квадранте, и построим АD так, чтобы образовался прямоугольный треугольник ОАD. Тогда sin Θ3= -/+ = -; cos Θ3= -/+ = -; tg Θ3 = -/- =+ .
Тогда sin Θ2=+/+ = +; cos Θ2=+/- = -; tg Θ2=+/- = -. Пусть ОА вращается дальше таким образом, что Θ3 — любой угол в третьем квадранте, и построим АD так, чтобы образовался прямоугольный треугольник ОАD. Тогда sin Θ3= -/+ = -; cos Θ3= -/+ = -; tg Θ3 = -/- =+ .
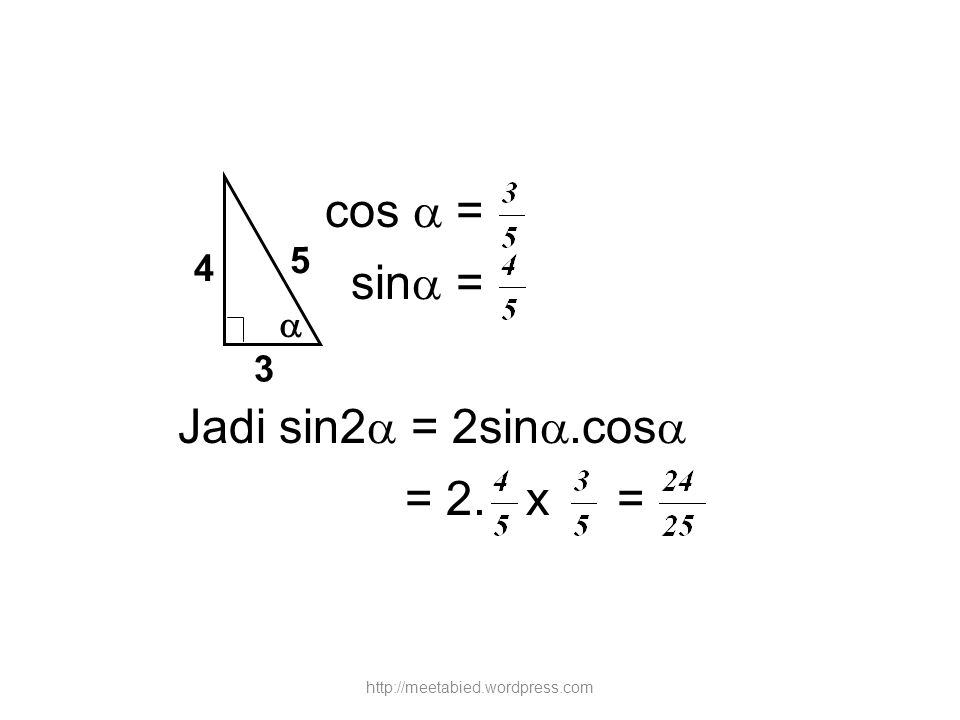

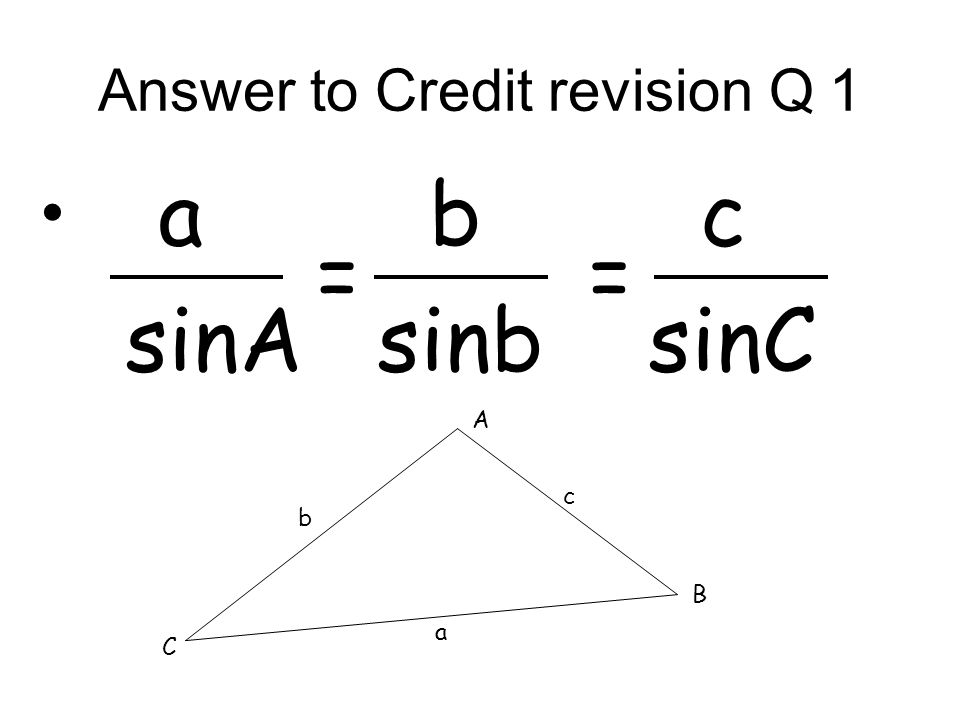 Построение синусоиды.
Построение синусоиды.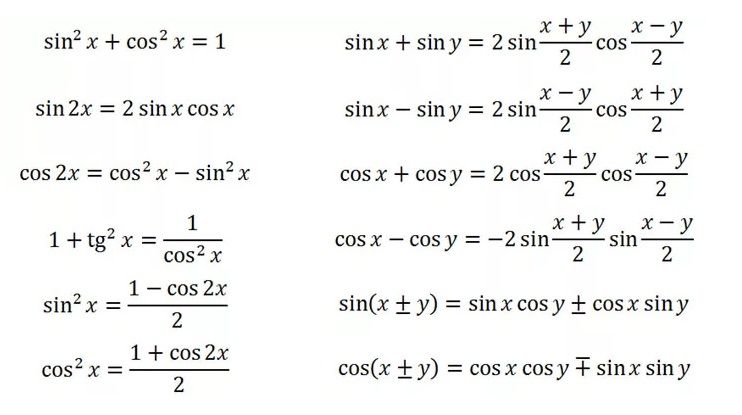


 y=sin(A-60o) (синусоида).
y=sin(A-60o) (синусоида).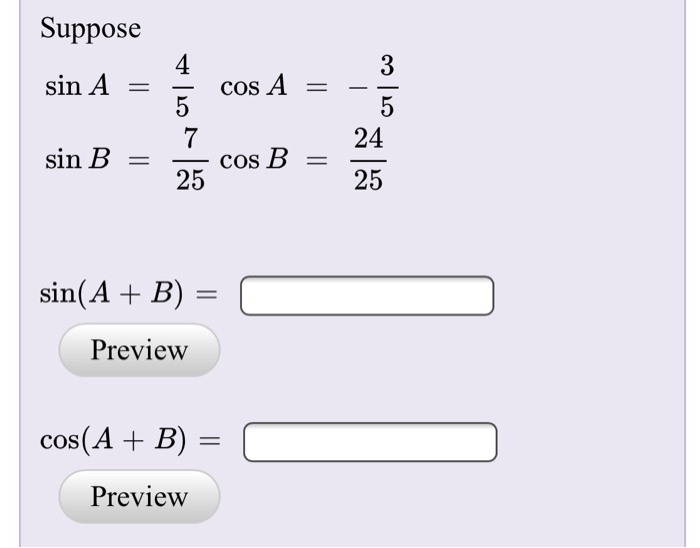
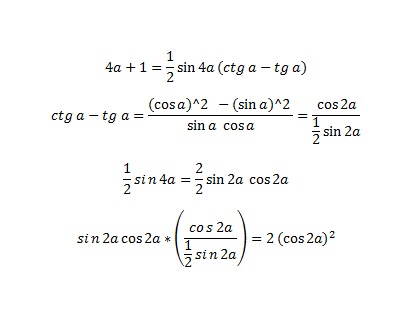 слева это угол TOR). Если перпендикулярно к OR построить ST, то sinωt=ST/OT, т.e. ST=OTsinωt.
слева это угол TOR). Если перпендикулярно к OR построить ST, то sinωt=ST/OT, т.e. ST=OTsinωt.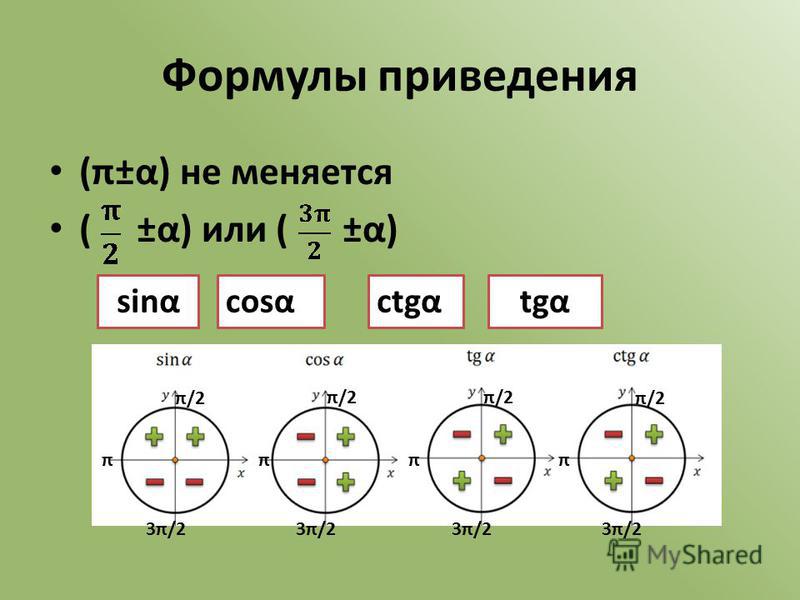

 Колебательный механизм
Колебательный механизм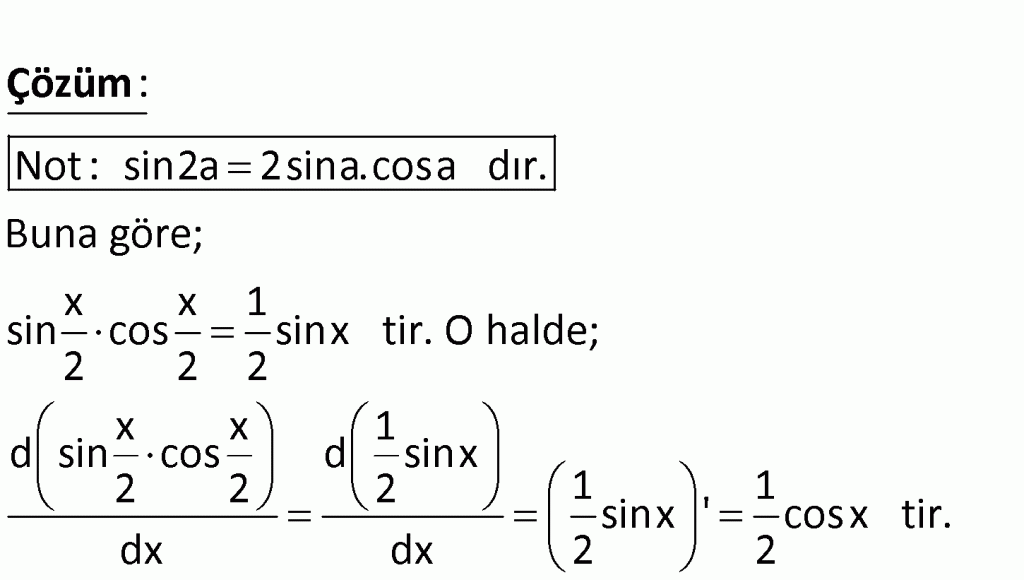 В этой статье давайте изучим различные тригонометрические формулы sin cos и основные тригонометрические отношения.
В этой статье давайте изучим различные тригонометрические формулы sin cos и основные тригонометрические отношения.  Давайте изучим основные формулы sin и cos.
Давайте изучим основные формулы sin и cos. 
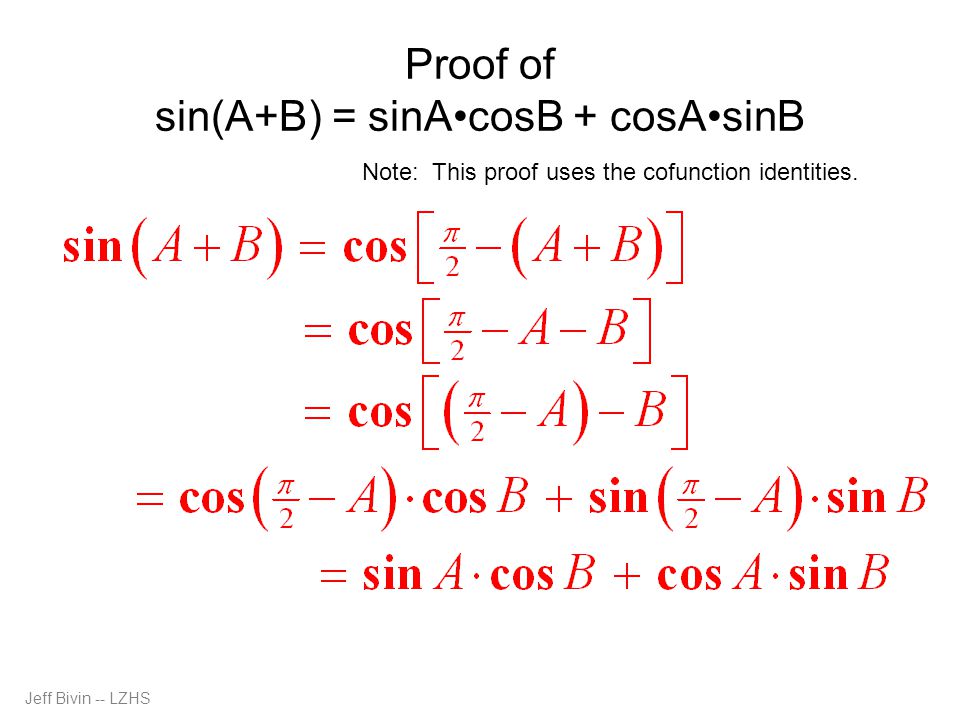 cos(B) + cos(A)sin(B)
cos(B) + cos(A)sin(B) 
 Куда бы вы ни шли за продуктами или покупали какие-либо вещи, вы рассчитываете цену за единицу, взвешиваете продукты, вычисляете процентные скидки и оцениваете окончательную стоимость, вы используете Math, чтобы упростить процесс покупок. Таким образом, эти основные понятия действительно полезно запомнить, чтобы эффективно и легко выполнять повседневную деятельность.
Куда бы вы ни шли за продуктами или покупали какие-либо вещи, вы рассчитываете цену за единицу, взвешиваете продукты, вычисляете процентные скидки и оцениваете окончательную стоимость, вы используете Math, чтобы упростить процесс покупок. Таким образом, эти основные понятия действительно полезно запомнить, чтобы эффективно и легко выполнять повседневную деятельность. 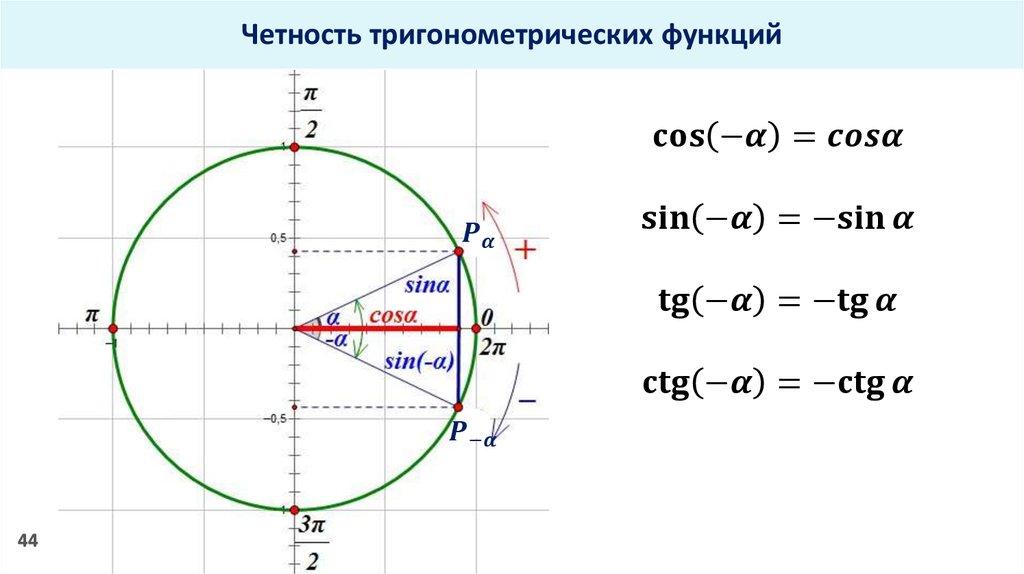
 Последние термины в каждой строке будут отменены:
Последние термины в каждой строке будут отменены: 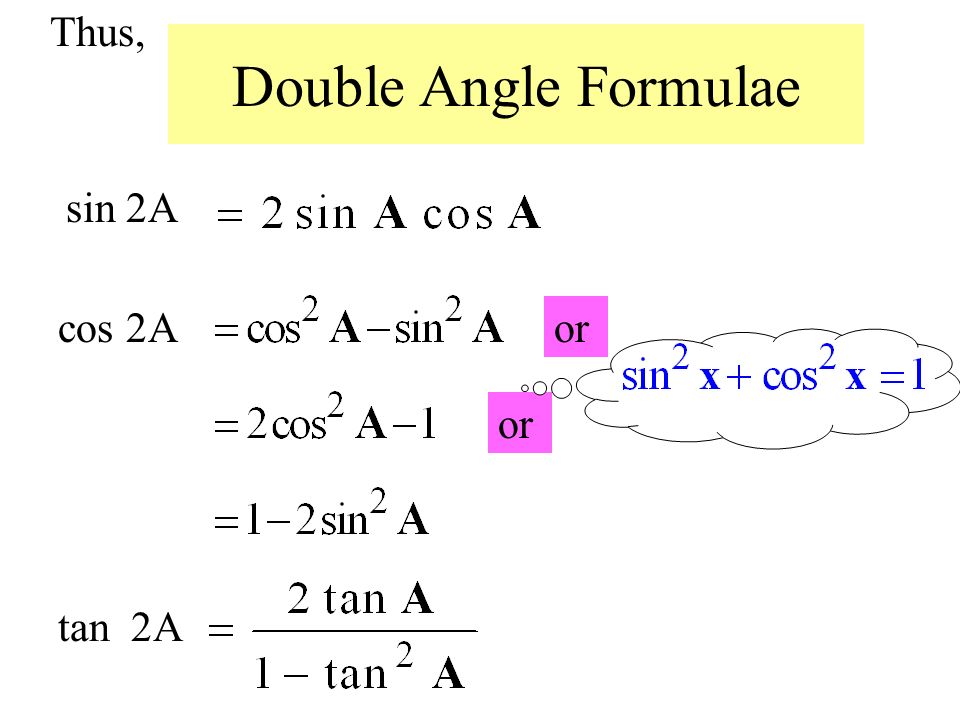


 В этой главе вам нужно усвоить две вещи:
В этой главе вам нужно усвоить две вещи:
 Нижняя часть, разделенная линией между углами (2), есть sin A. Линия между двумя углами, разделенная гипотенузой (3), есть cos B. Умножьте два вместе. Средняя линия находится как в числителе, так и в знаменателе, поэтому каждая из них сокращается и оставляет нижнюю часть противоположной над гипотенузой (4).
Нижняя часть, разделенная линией между углами (2), есть sin A. Линия между двумя углами, разделенная гипотенузой (3), есть cos B. Умножьте два вместе. Средняя линия находится как в числителе, так и в знаменателе, поэтому каждая из них сокращается и оставляет нижнюю часть противоположной над гипотенузой (4).

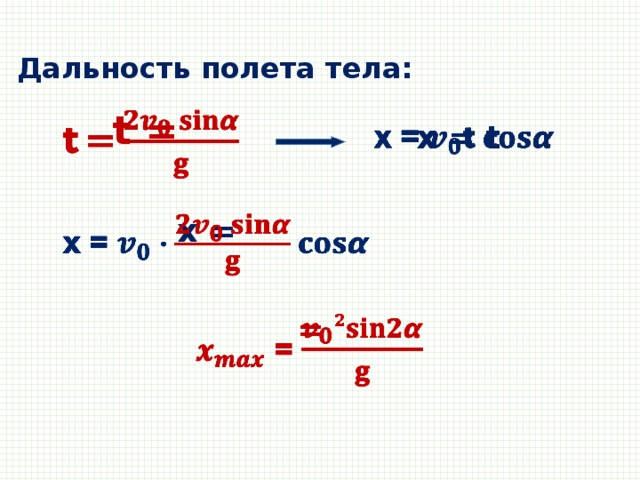 Вычитание дает cos(A + B) (8), так что нужная нам формула:
Вычитание дает cos(A + B) (8), так что нужная нам формула:

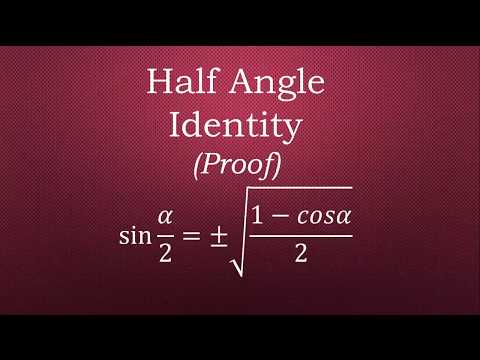

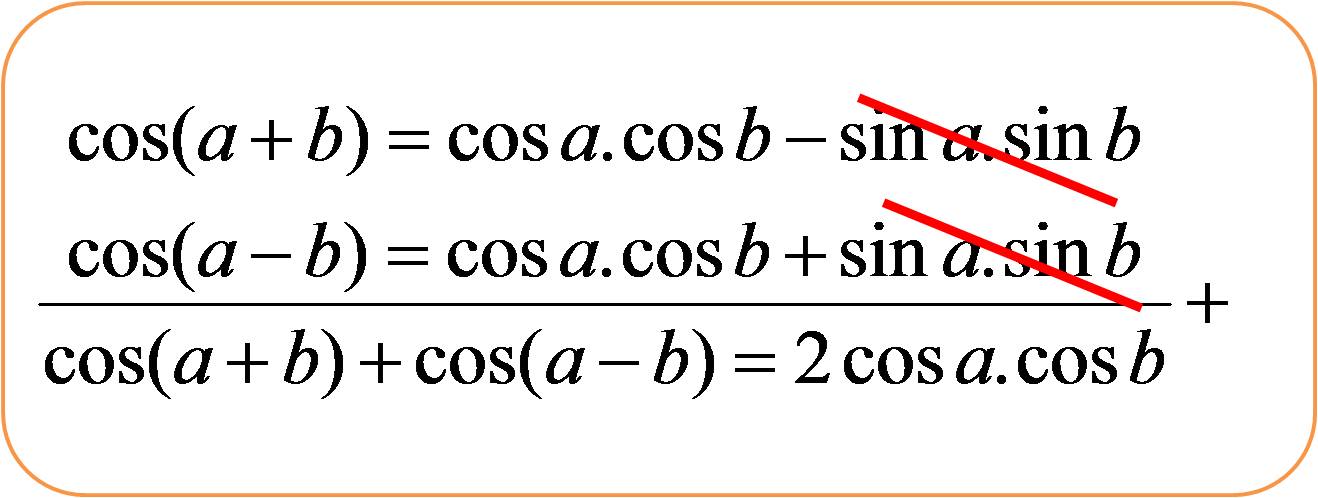
 Зашкаливая в положительную сторону, она «заходит» с отрицательной стороны на другую сторону 90 градусов. Проходя через точку 180 градусов, касательная кривая дублирует то, что она делает, проходя через 0 или 360 (в зависимости от того, как вы это видите). При 270 градусах он повторяет то, что делал при 9.0 градусов.
Зашкаливая в положительную сторону, она «заходит» с отрицательной стороны на другую сторону 90 градусов. Проходя через точку 180 градусов, касательная кривая дублирует то, что она делает, проходя через 0 или 360 (в зависимости от того, как вы это видите). При 270 градусах он повторяет то, что делал при 9.0 градусов.
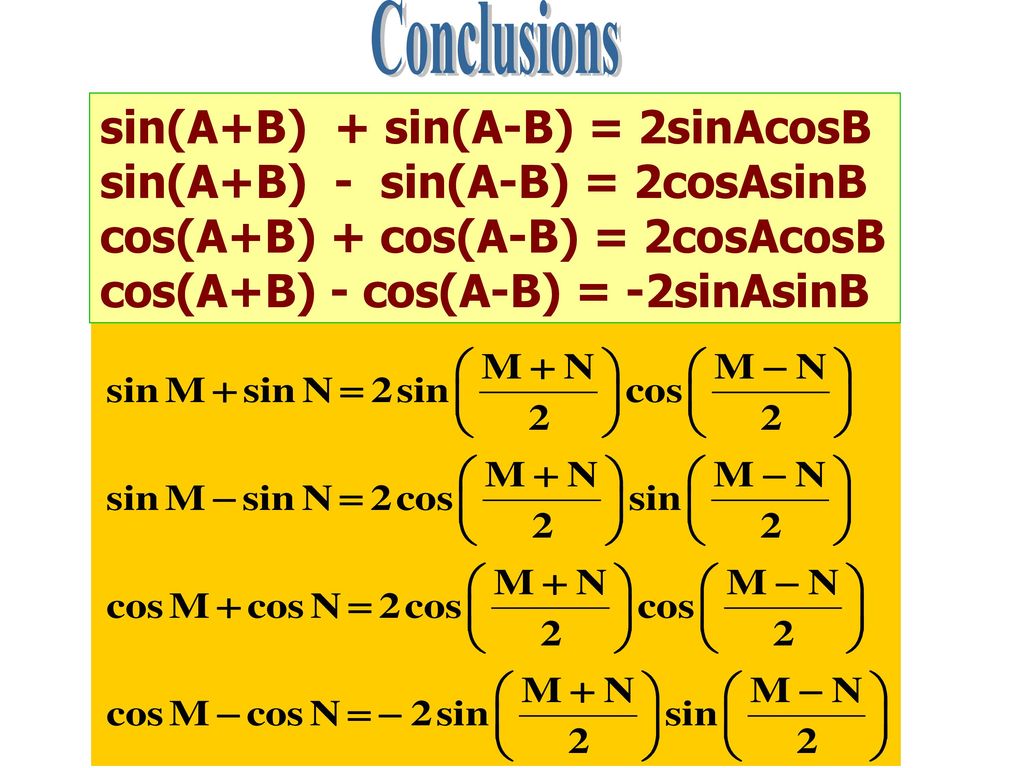 Cos 2 A означает (cos A) 2 . Если бы вы написали это потому, что A 2 , уравнение означало бы что-то другое. A — это число в некотором угловом представлении, представляющее угол. 2 будет тем же числом в квадрате. Его значение будет зависеть от используемой угловой записи, поэтому этот термин не подходит для использования. Имеется в виду квадрат синуса или косинуса угла, а не сам угол.
Cos 2 A означает (cos A) 2 . Если бы вы написали это потому, что A 2 , уравнение означало бы что-то другое. A — это число в некотором угловом представлении, представляющее угол. 2 будет тем же числом в квадрате. Его значение будет зависеть от используемой угловой записи, поэтому этот термин не подходит для использования. Имеется в виду квадрат синуса или косинуса угла, а не сам угол.
 Однако sin(A + A) на самом деле является sin 2A. Итак, sin 2A — это sin A cos A + cos A sin A. Они оба являются одним и тем же произведением в противоположном порядке, поэтому это утверждение можно упростить до sin 2A = 2 sin A cos A.
Однако sin(A + A) на самом деле является sin 2A. Итак, sin 2A — это sin A cos A + cos A sin A. Они оба являются одним и тем же произведением в противоположном порядке, поэтому это утверждение можно упростить до sin 2A = 2 sin A cos A.
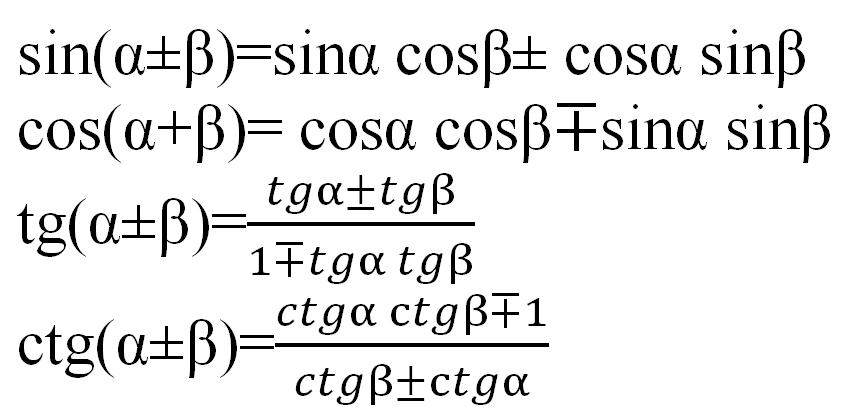 Равнобедренный треугольник имеет несколько иное применение. Но факт, на котором основаны эти употребления, заключается в том, что равнобедренный треугольник имеет две равные стороны и два равных угла, противоположных этим двум сторонам. Перпендикуляр из третьего угла (не из равных) на третью сторону (не из равных) делит эту третью сторону пополам. То есть делит его на две равные части, превращая весь треугольник в зеркальные прямоугольные треугольники.
Равнобедренный треугольник имеет несколько иное применение. Но факт, на котором основаны эти употребления, заключается в том, что равнобедренный треугольник имеет две равные стороны и два равных угла, противоположных этим двум сторонам. Перпендикуляр из третьего угла (не из равных) на третью сторону (не из равных) делит эту третью сторону пополам. То есть делит его на две равные части, превращая весь треугольник в зеркальные прямоугольные треугольники.

 Три угла в сумме составляют 2A + 2B + 2C. Это, знаете ли, в сумме составляет 180 градусов.
Три угла в сумме составляют 2A + 2B + 2C. Это, знаете ли, в сумме составляет 180 градусов.
 Таким образом, все углы в окружности, опирающиеся на одну и ту же хорду, должны быть равны. Предположим, что хорда имеет угол 120 градусов. Углы на окружности будут ровно 60 градусов.
Таким образом, все углы в окружности, опирающиеся на одну и ту же хорду, должны быть равны. Предположим, что хорда имеет угол 120 градусов. Углы на окружности будут ровно 60 градусов.



 Мы используем формулу cos a cos b, чтобы найти значение произведения косинуса двух разных углов.
Мы используем формулу cos a cos b, чтобы найти значение произведения косинуса двух разных углов.

 Эти тождества полезны при интеграции и вычислении преобразований Лапласа.
Эти тождества полезны при интеграции и вычислении преобразований Лапласа.

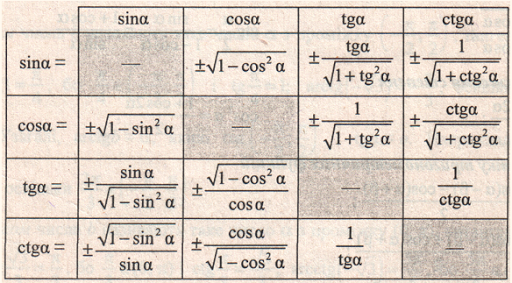 com
com  Это одно из важных тригонометрических тождеств, которое используется для решения различных тригонометрических и интегральных задач.
Это одно из важных тригонометрических тождеств, которое используется для решения различных тригонометрических и интегральных задач.
 Все эти тригонометрические соотношения определяются с использованием сторон прямоугольного треугольника, таких как прилежащая сторона, противоположная сторона и сторона гипотенузы. Все фундаментальные тригонометрические тождества выводятся из шести тригонометрических соотношений.
Все эти тригонометрические соотношения определяются с использованием сторон прямоугольного треугольника, таких как прилежащая сторона, противоположная сторона и сторона гипотенузы. Все фундаментальные тригонометрические тождества выводятся из шести тригонометрических соотношений.
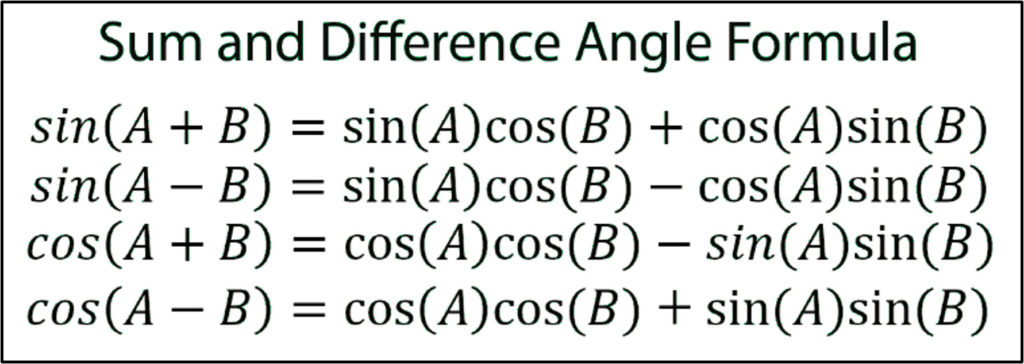 com
com  ( A + B. 2. )
( A + B. 2. )  2 (cos(a − b) − cos(a + b))
2 (cos(a − b) − cos(a + b)) 

 парижская экспозиция?
парижская экспозиция?  )
)
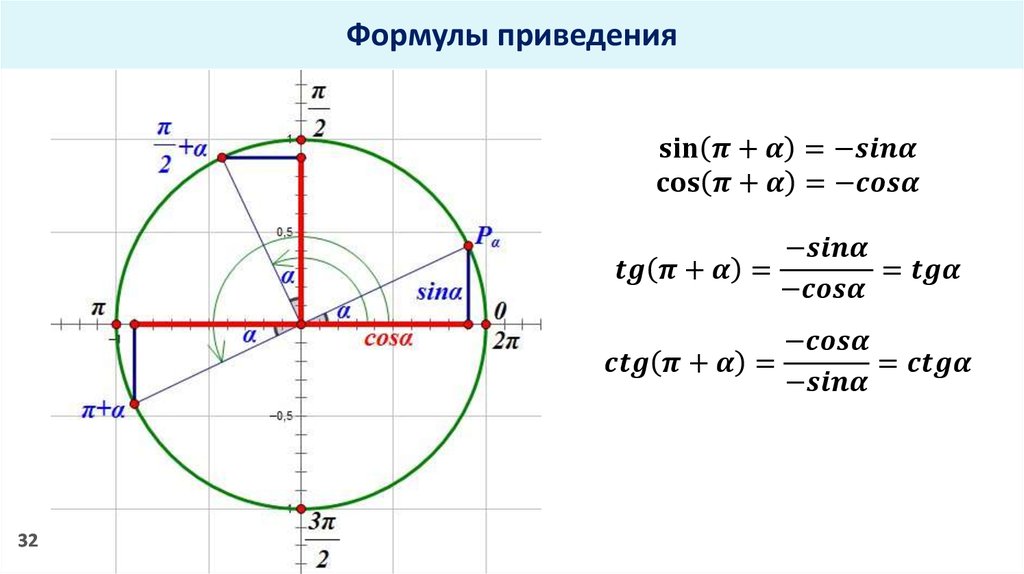 Серия
Серия 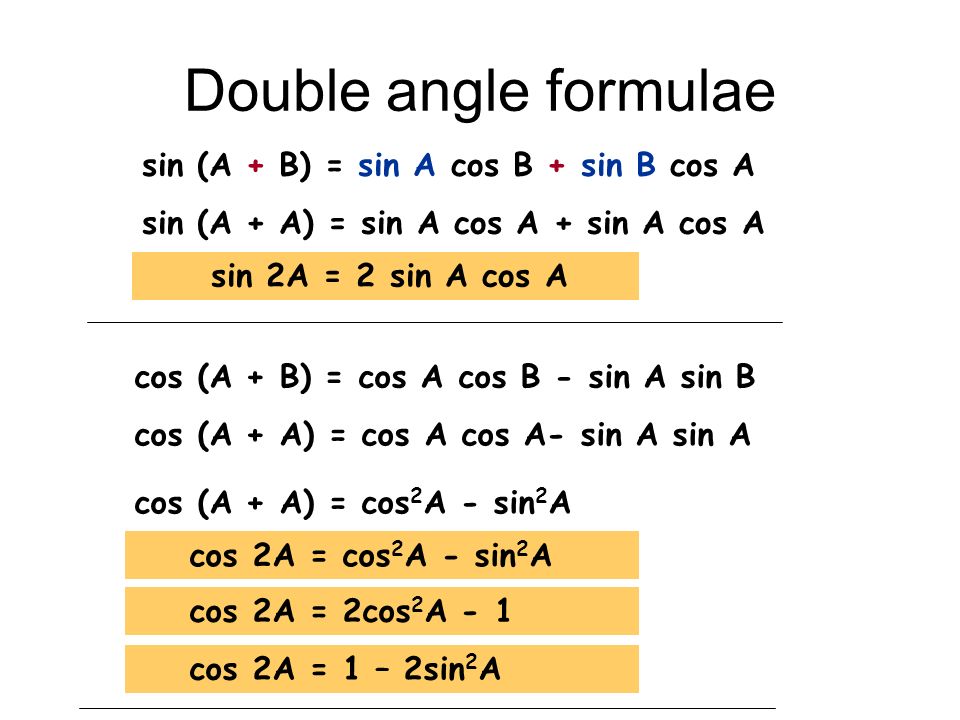 .. для всех х
.. для всех х
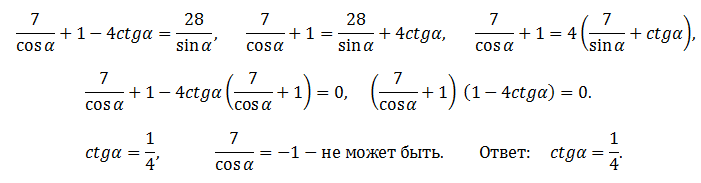 .. для (-1 < x ≤ 1)
.. для (-1 < x ≤ 1)
 .. для (-1 < x < 1)
.. для (-1 < x < 1)
 . , для (-1 < x < 1)
. , для (-1 < x < 1)
 ..+ a r n-1 = a (1 — r n )/(1 — r)
..+ a r n-1 = a (1 — r n )/(1 — r)
 1 3 + 2 3 + 3 3 + … + n 3 = [ (1 / 2) n (n + 1) ] 2
1 3 + 2 3 + 3 3 + … + n 3 = [ (1 / 2) n (n + 1) ] 2 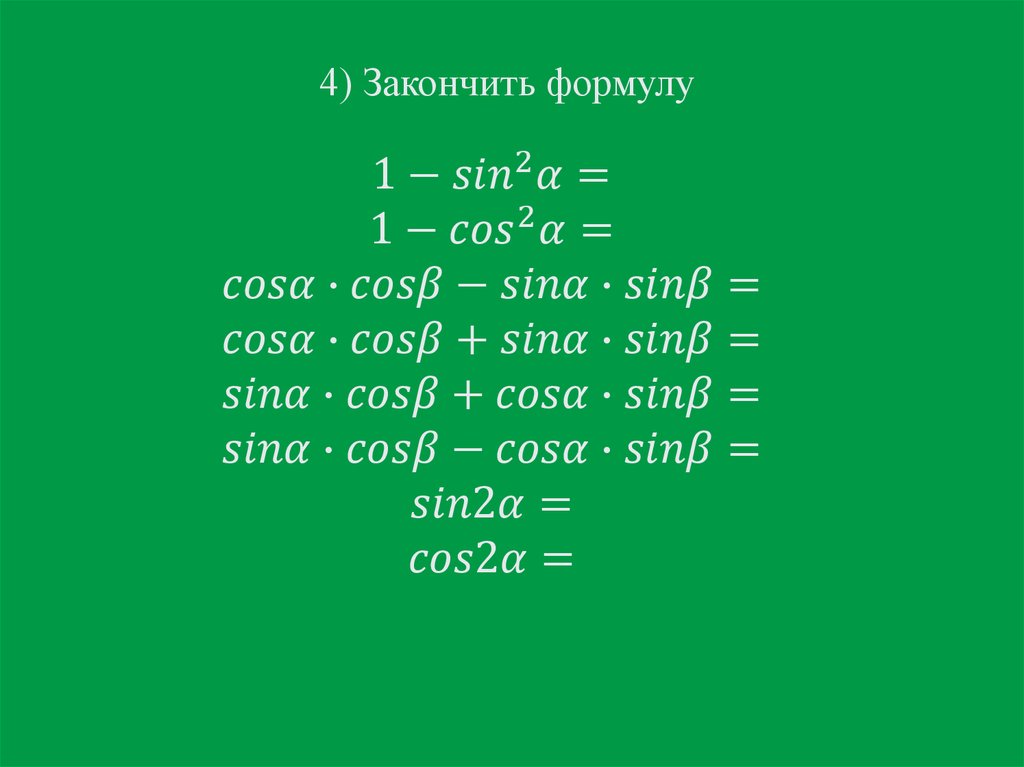 Комбинации n объектов, взятых r в момент времени:
Комбинации n объектов, взятых r в момент времени:
 .. + n C n y n
.. + n C n y n  tan(A — B) = [ tan A — tan B ] / [ 1 + tan A tan B]
tan(A — B) = [ tan A — tan B ] / [ 1 + tan A tan B]


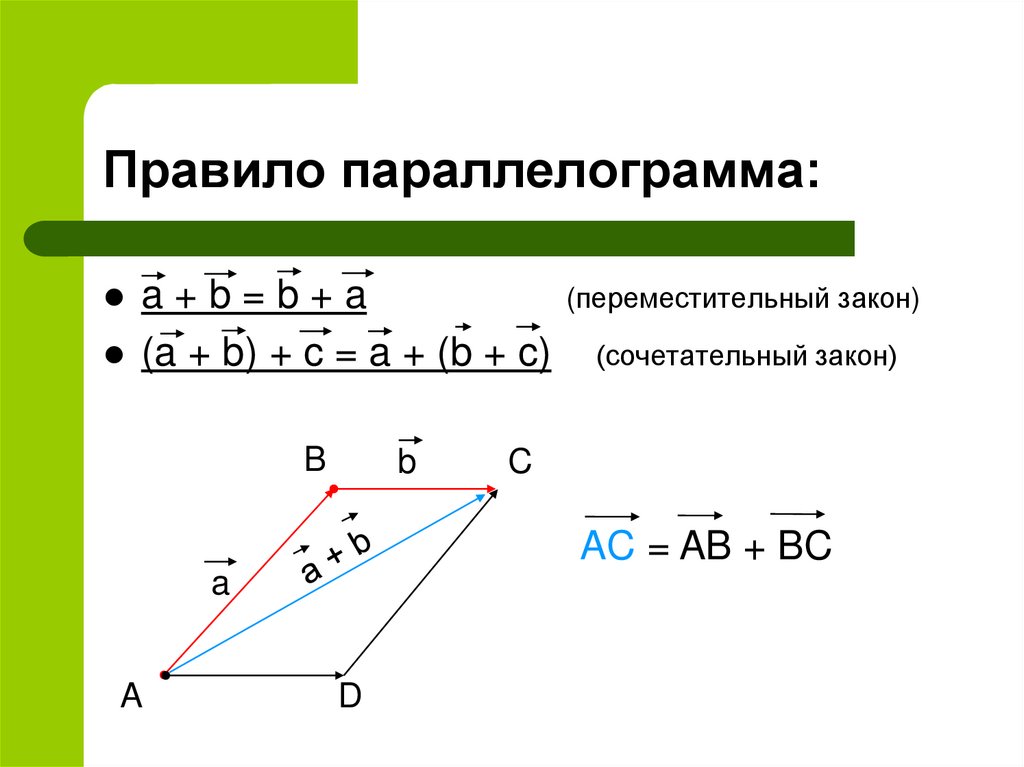 Это значит, что если привести их к общему началу из конца третьего вектора (р), то кратчайший поворот от первого вектора (m) ко второму вектору (n) будет совершаться против часовой стрелки.
Это значит, что если привести их к общему началу из конца третьего вектора (р), то кратчайший поворот от первого вектора (m) ко второму вектору (n) будет совершаться против часовой стрелки. 0=30\times\frac12=15\\\\\\\)
0=30\times\frac12=15\\\\\\\) 2}=\sqrt{676+400+576}=\sqrt{1652}\\\\\\\)
2}=\sqrt{676+400+576}=\sqrt{1652}\\\\\\\)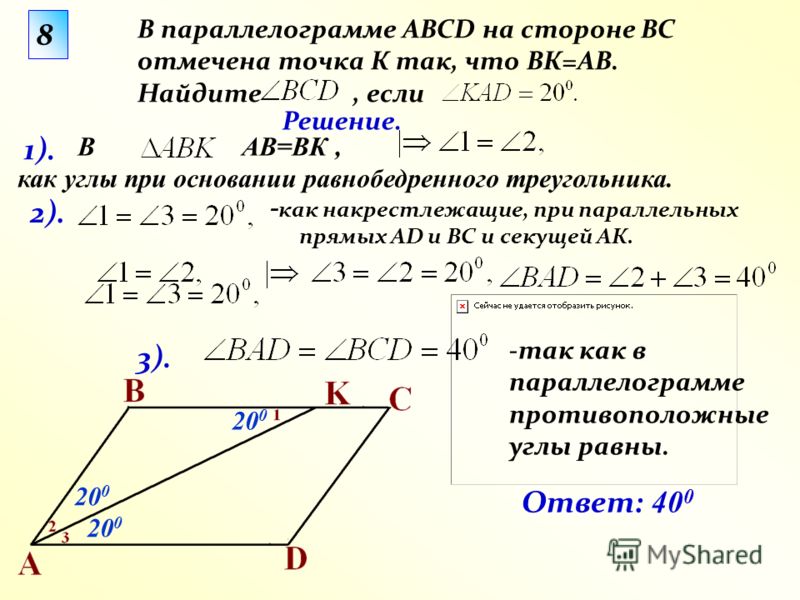 Если известны только координаты векторов, то для вычисления нужно применять координатные методы, в том числе и для определения угла между векторами.
Если известны только координаты векторов, то для вычисления нужно применять координатные методы, в том числе и для определения угла между векторами.
 Пусть координаты вектора а(x1;y1;z1), вектора b(x2;y2;z2).
Пусть координаты вектора а(x1;y1;z1), вектора b(x2;y2;z2).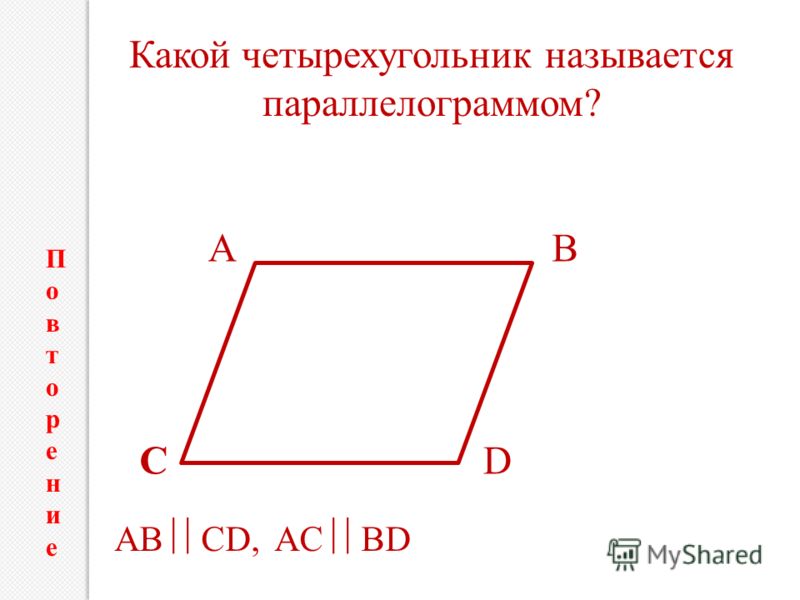 5.
5.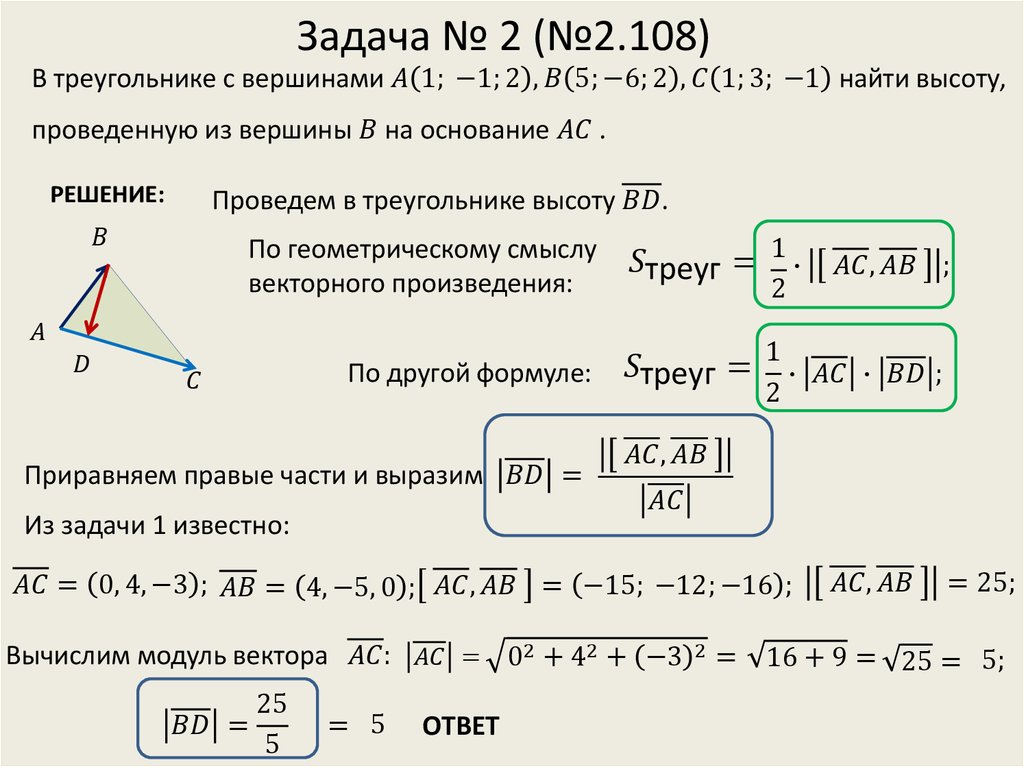 также обратите внимание, что если в результате мы получаем выражение ,то оно будет преобразовано в. Теперь проводим итоговые вычисления:
также обратите внимание, что если в результате мы получаем выражение ,то оно будет преобразовано в. Теперь проводим итоговые вычисления: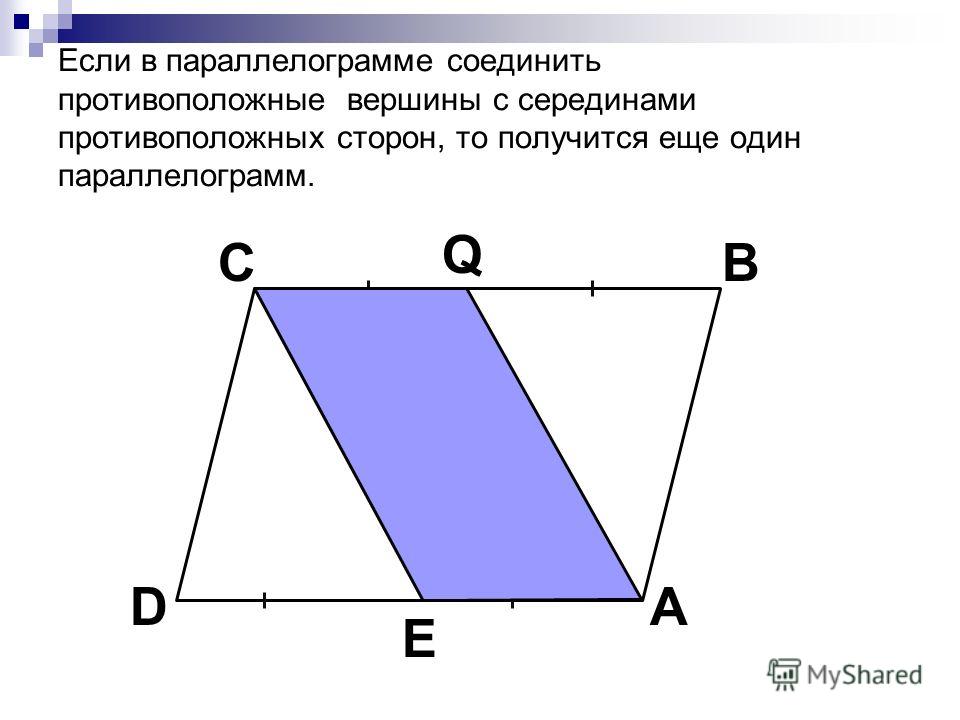
 Более подготовленные читатели могут знакомиться с информацией выборочно, я постарался собрать максимально полную коллекцию примеров, которые часто встречаются в практических работах
Более подготовленные читатели могут знакомиться с информацией выборочно, я постарался собрать максимально полную коллекцию примеров, которые часто встречаются в практических работах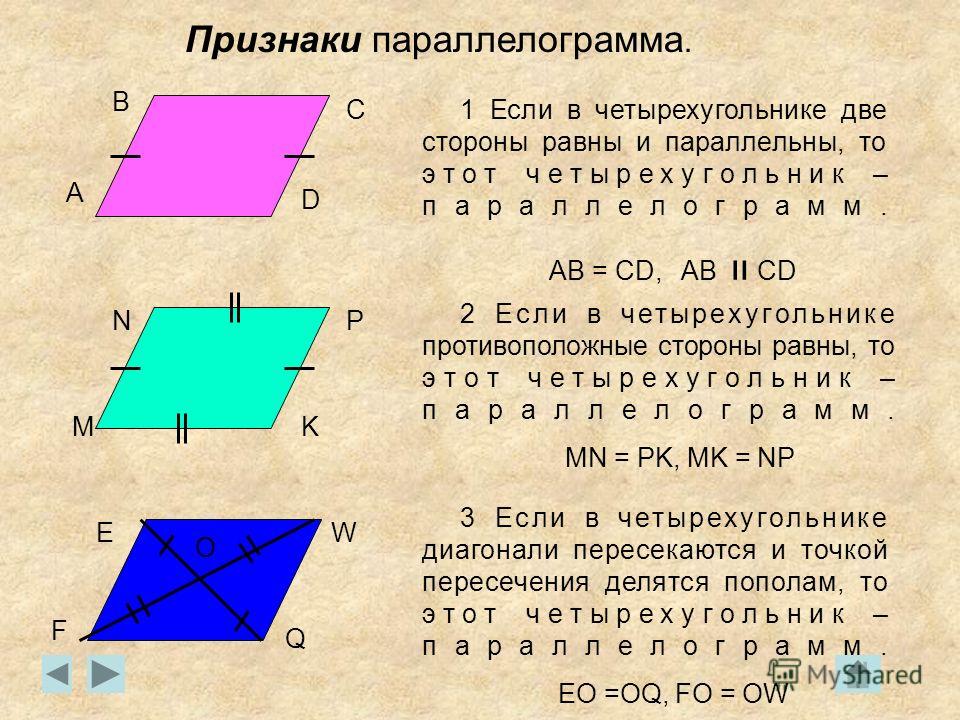 Закрытый клуб. Собственно, отсюда и название операции. В различной учебной литературе обозначения тоже могут варьироваться, я буду использовать букву .
Закрытый клуб. Собственно, отсюда и название операции. В различной учебной литературе обозначения тоже могут варьироваться, я буду использовать букву .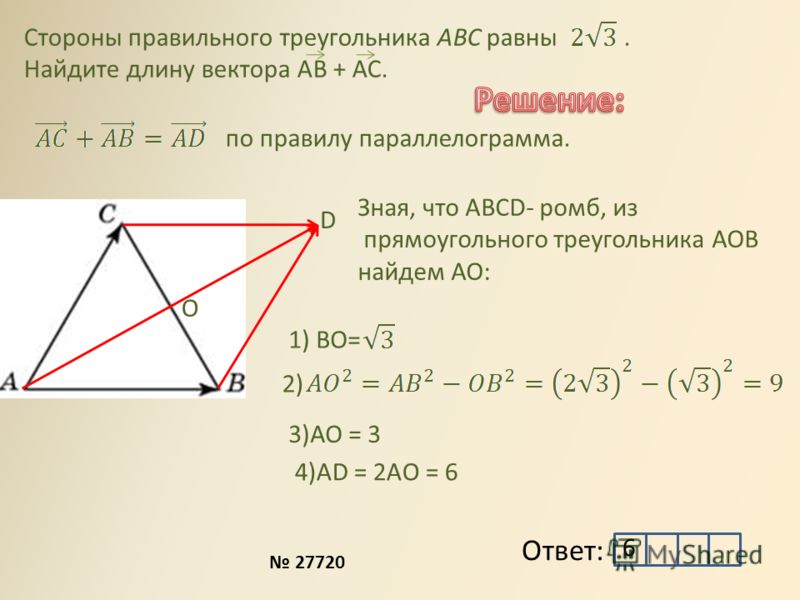 Результатом умножения векторов
является ВЕКТОР , который обозначен синим цветом. Если векторы умножить в обратном порядке, то получим равный по длине и противоположный по направлению вектор (малиновый цвет). То есть, справедливо равенство .
Результатом умножения векторов
является ВЕКТОР , который обозначен синим цветом. Если векторы умножить в обратном порядке, то получим равный по длине и противоположный по направлению вектор (малиновый цвет). То есть, справедливо равенство .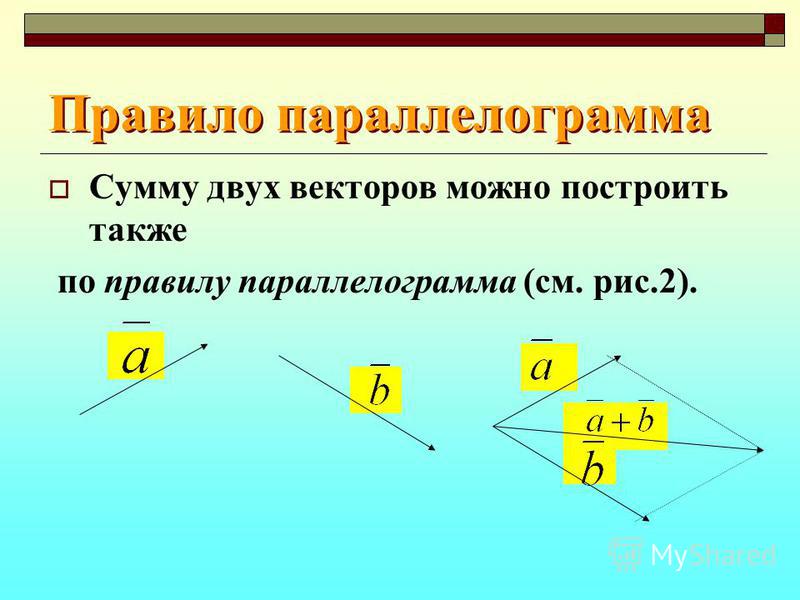 Каков практический смысл? А смысл таков, что в задачах аналитической геометрии площадь параллелограмма часто находят через понятие векторного произведения:
Каков практический смысл? А смысл таков, что в задачах аналитической геометрии площадь параллелограмма часто находят через понятие векторного произведения: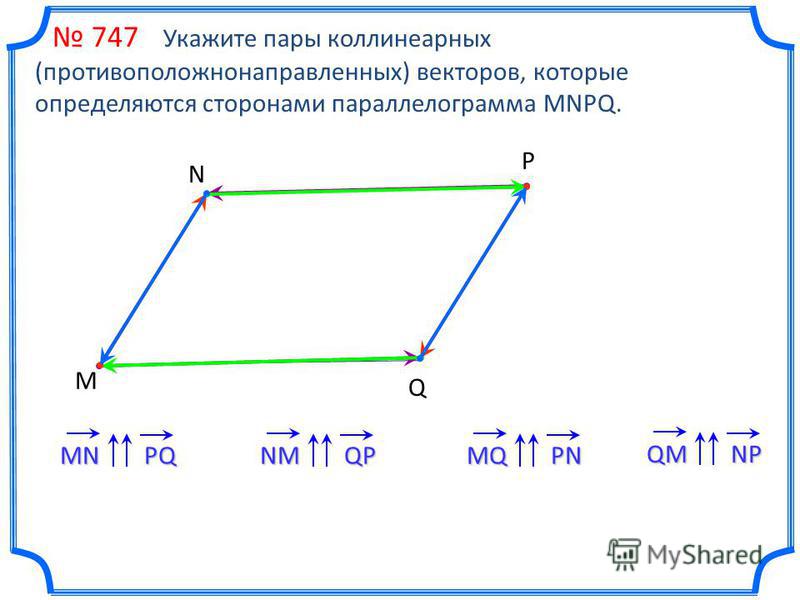 В результате большой палец
– векторное произведение будет смотреть вверх. Это и есть правоориентированный базис (на рисунке именно он). Теперь поменяйте векторы (указательный и средний пальцы
) местами, в результате большой палец развернётся, и векторное произведение уже будет смотреть вниз. Это тоже правоориентированный базис. Возможно, у вас возник вопрос: а какой базис имеет левую ориентацию? «Присвойте» тем же пальцам левой руки
векторы , и полУчите левый базис и левую ориентацию пространства (в этом случае большой палец расположится по направлению нижнего вектора)
. Образно говоря, данные базисы «закручивают» или ориентируют пространство в разные стороны. И это понятие не следует считать чем-то надуманным или абстрактным – так, например, ориентацию пространства меняет самое обычное зеркало, и если «вытащить отражённый объект из зазеркалья», то его в общем случае не удастся совместить с «оригиналом». Кстати, поднесите к зеркалу три пальца и проанализируйте отражение;-)
В результате большой палец
– векторное произведение будет смотреть вверх. Это и есть правоориентированный базис (на рисунке именно он). Теперь поменяйте векторы (указательный и средний пальцы
) местами, в результате большой палец развернётся, и векторное произведение уже будет смотреть вниз. Это тоже правоориентированный базис. Возможно, у вас возник вопрос: а какой базис имеет левую ориентацию? «Присвойте» тем же пальцам левой руки
векторы , и полУчите левый базис и левую ориентацию пространства (в этом случае большой палец расположится по направлению нижнего вектора)
. Образно говоря, данные базисы «закручивают» или ориентируют пространство в разные стороны. И это понятие не следует считать чем-то надуманным или абстрактным – так, например, ориентацию пространства меняет самое обычное зеркало, и если «вытащить отражённый объект из зазеркалья», то его в общем случае не удастся совместить с «оригиналом». Кстати, поднесите к зеркалу три пальца и проанализируйте отражение;-) Если векторы коллинеарны, то их можно расположить на одной прямой и наш параллелограмм тоже «складывается» в одну прямую. Площадь такого, как говорят математики, вырожденного
параллелограмма равна нулю. Это же следует и из формулы – синус нуля или 180-ти градусов равен нулю, а значит, и площадь нулевая
Если векторы коллинеарны, то их можно расположить на одной прямой и наш параллелограмм тоже «складывается» в одну прямую. Площадь такого, как говорят математики, вырожденного
параллелограмма равна нулю. Это же следует и из формулы – синус нуля или 180-ти градусов равен нулю, а значит, и площадь нулевая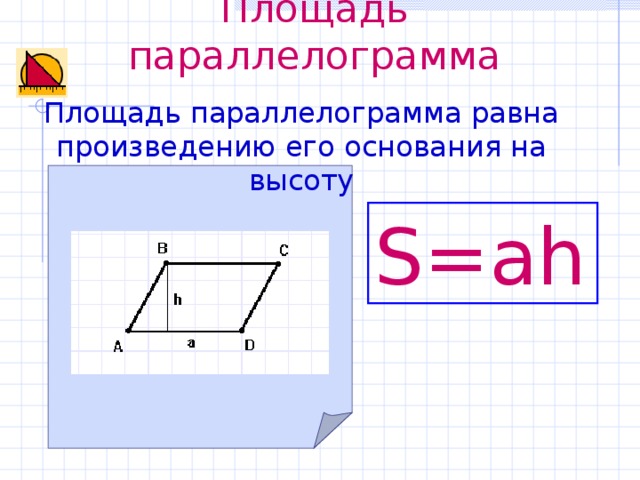 Потому что оформление решений будет отличаться!
Потому что оформление решений будет отличаться!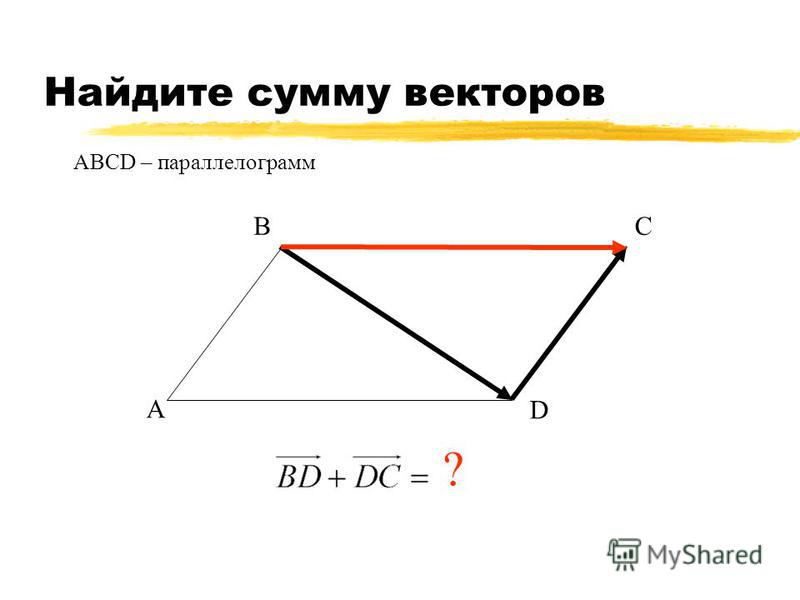 Этот момент всегда нужно держать на контроле, решая любую задачу по высшей математике, да и по другим предметам тоже.
Этот момент всегда нужно держать на контроле, решая любую задачу по высшей математике, да и по другим предметам тоже.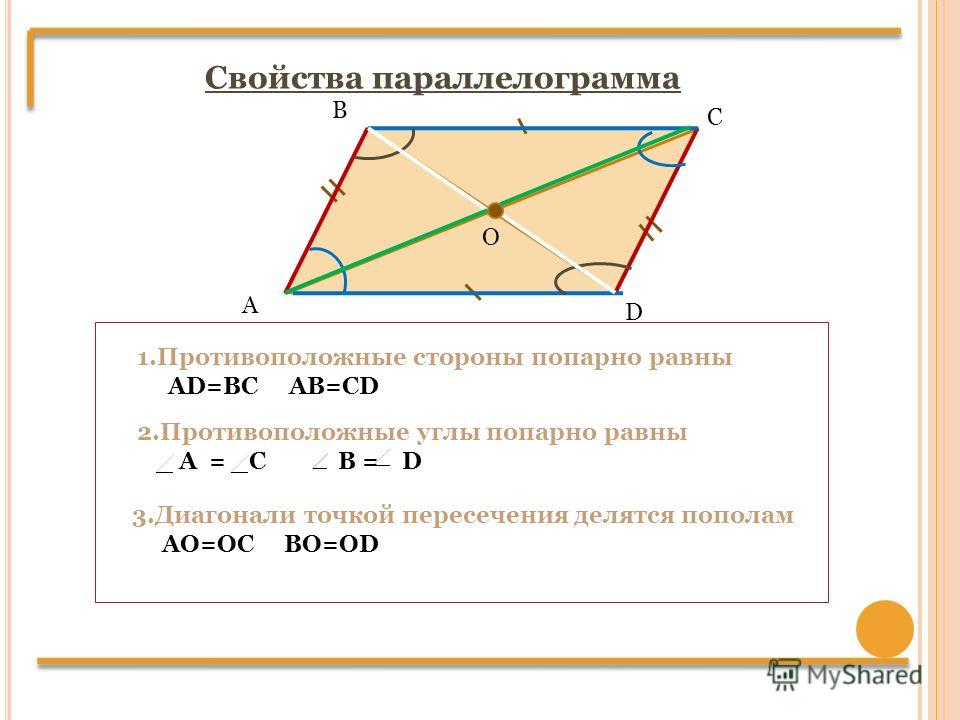 Поэтому пусть будет.
Поэтому пусть будет. Загвоздка состоит в том, что векторы «цэ» и «дэ» сами представлены в виде сумм векторов. Алгоритм здесь стандартен и чем-то напоминает примеры № 3 и 4 урока Скалярное произведение векторов
. Решение для ясности разобьём на три этапа:
Загвоздка состоит в том, что векторы «цэ» и «дэ» сами представлены в виде сумм векторов. Алгоритм здесь стандартен и чем-то напоминает примеры № 3 и 4 урока Скалярное произведение векторов
. Решение для ясности разобьём на три этапа: Данное действие напоминает Пример 3:
Данное действие напоминает Пример 3: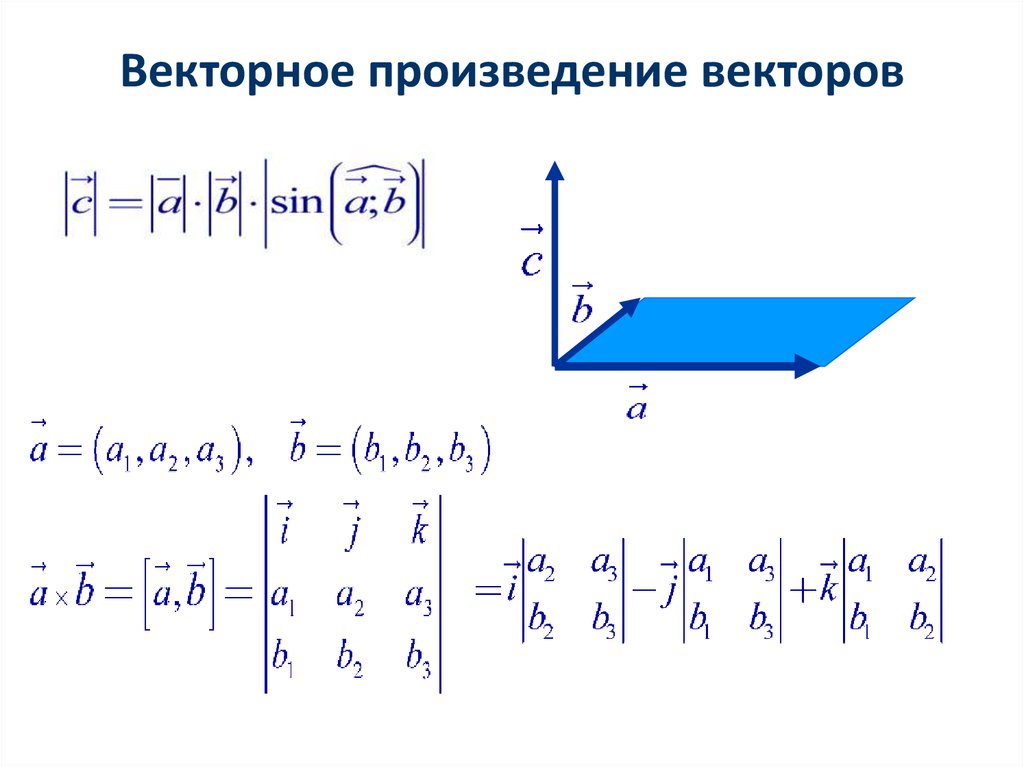
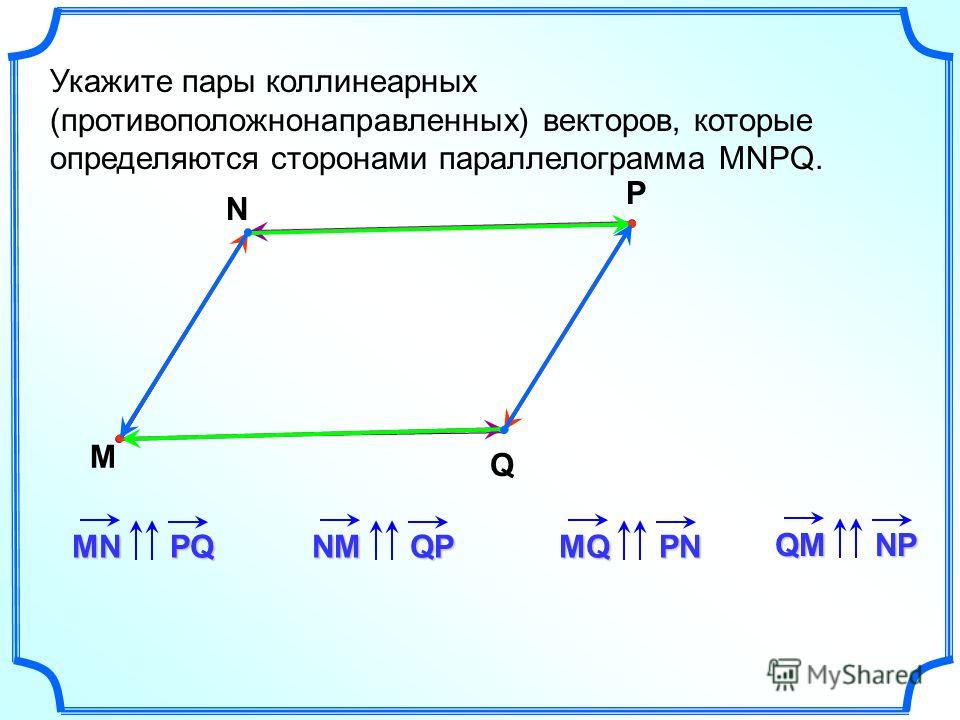
 Смешанное произведение векторов
Смешанное произведение векторов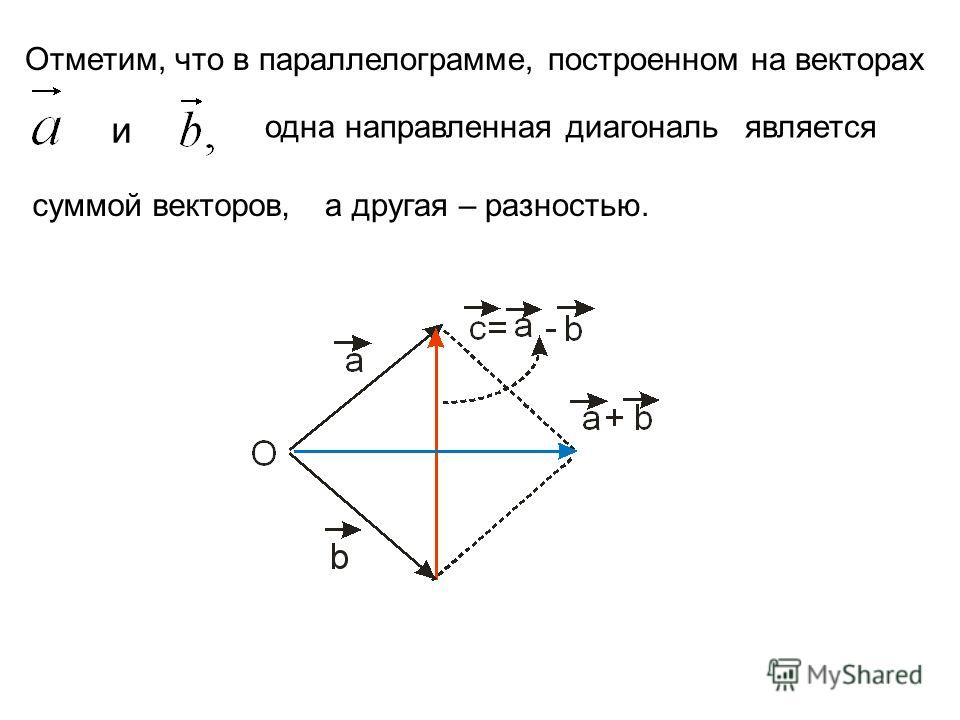 Теперь проводим итоговые вычисления:
Теперь проводим итоговые вычисления: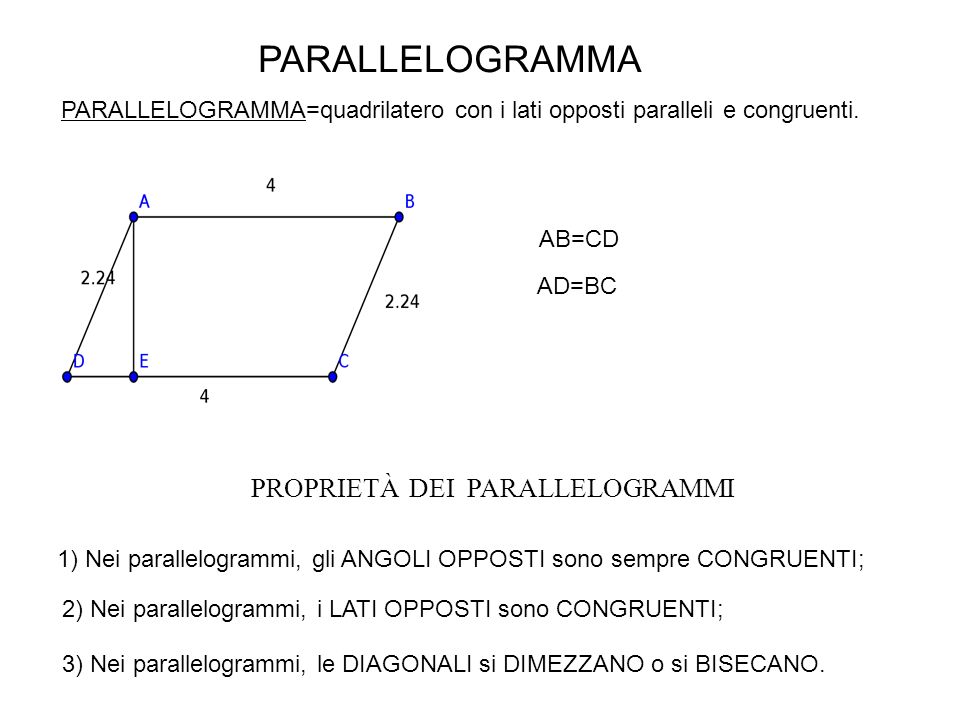
 Более подготовленные читатели могут знакомиться с информацией выборочно, я постарался собрать максимально полную коллекцию примеров, которые часто встречаются в практических работах
Более подготовленные читатели могут знакомиться с информацией выборочно, я постарался собрать максимально полную коллекцию примеров, которые часто встречаются в практических работах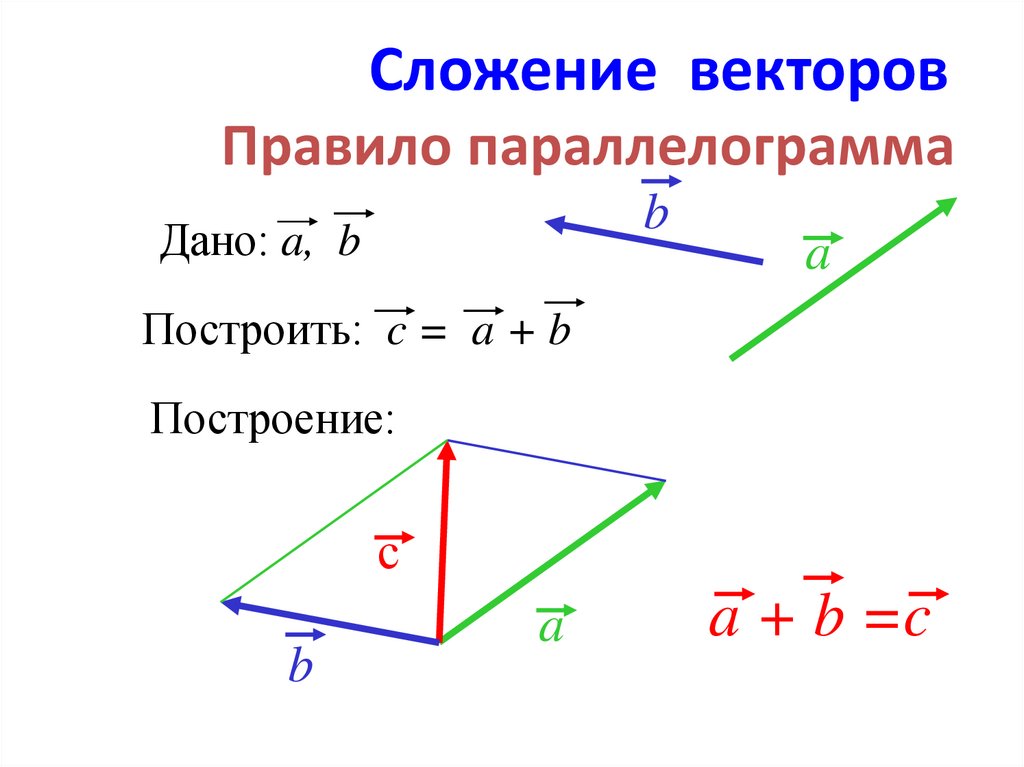 Закрытый клуб. Собственно, отсюда и название операции. В различной учебной литературе обозначения тоже могут варьироваться, я буду использовать букву .
Закрытый клуб. Собственно, отсюда и название операции. В различной учебной литературе обозначения тоже могут варьироваться, я буду использовать букву . Результатом умножения векторов
является ВЕКТОР , который обозначен синим цветом. Если векторы умножить в обратном порядке, то получим равный по длине и противоположный по направлению вектор (малиновый цвет). То есть, справедливо равенство .
Результатом умножения векторов
является ВЕКТОР , который обозначен синим цветом. Если векторы умножить в обратном порядке, то получим равный по длине и противоположный по направлению вектор (малиновый цвет). То есть, справедливо равенство . Каков практический смысл? А смысл таков, что в задачах аналитической геометрии площадь параллелограмма часто находят через понятие векторного произведения:
Каков практический смысл? А смысл таков, что в задачах аналитической геометрии площадь параллелограмма часто находят через понятие векторного произведения: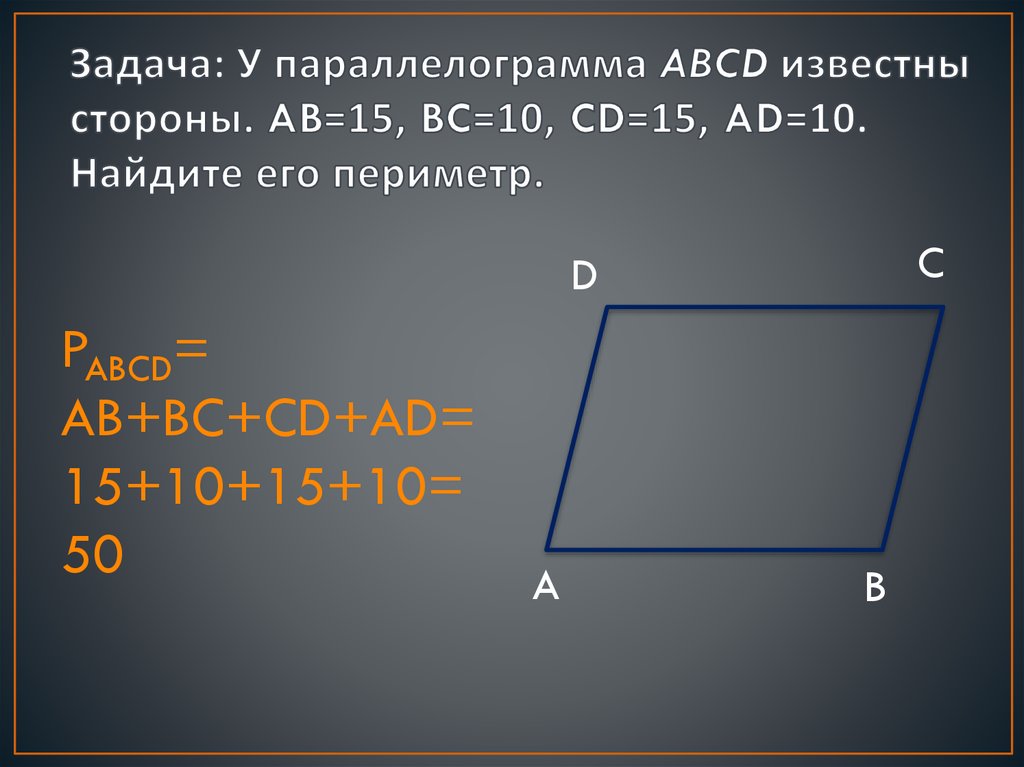 В результате большой палец
– векторное произведение будет смотреть вверх. Это и есть правоориентированный базис (на рисунке именно он). Теперь поменяйте векторы (указательный и средний пальцы
) местами, в результате большой палец развернётся, и векторное произведение уже будет смотреть вниз. Это тоже правоориентированный базис. Возможно, у вас возник вопрос: а какой базис имеет левую ориентацию? «Присвойте» тем же пальцам левой руки
векторы , и полУчите левый базис и левую ориентацию пространства (в этом случае большой палец расположится по направлению нижнего вектора)
. Образно говоря, данные базисы «закручивают» или ориентируют пространство в разные стороны. И это понятие не следует считать чем-то надуманным или абстрактным – так, например, ориентацию пространства меняет самое обычное зеркало, и если «вытащить отражённый объект из зазеркалья», то его в общем случае не удастся совместить с «оригиналом». Кстати, поднесите к зеркалу три пальца и проанализируйте отражение;-)
В результате большой палец
– векторное произведение будет смотреть вверх. Это и есть правоориентированный базис (на рисунке именно он). Теперь поменяйте векторы (указательный и средний пальцы
) местами, в результате большой палец развернётся, и векторное произведение уже будет смотреть вниз. Это тоже правоориентированный базис. Возможно, у вас возник вопрос: а какой базис имеет левую ориентацию? «Присвойте» тем же пальцам левой руки
векторы , и полУчите левый базис и левую ориентацию пространства (в этом случае большой палец расположится по направлению нижнего вектора)
. Образно говоря, данные базисы «закручивают» или ориентируют пространство в разные стороны. И это понятие не следует считать чем-то надуманным или абстрактным – так, например, ориентацию пространства меняет самое обычное зеркало, и если «вытащить отражённый объект из зазеркалья», то его в общем случае не удастся совместить с «оригиналом». Кстати, поднесите к зеркалу три пальца и проанализируйте отражение;-)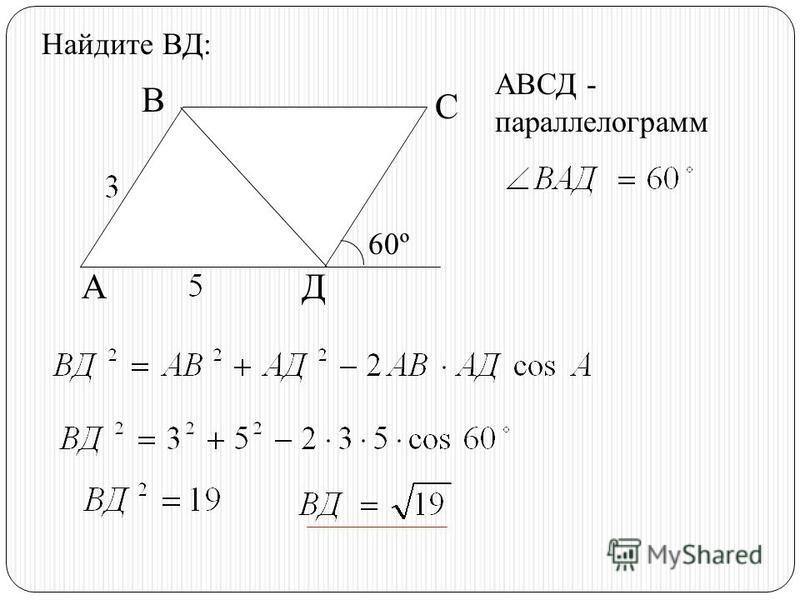 Если векторы коллинеарны, то их можно расположить на одной прямой и наш параллелограмм тоже «складывается» в одну прямую. Площадь такого, как говорят математики, вырожденного
параллелограмма равна нулю. Это же следует и из формулы – синус нуля или 180-ти градусов равен нулю, а значит, и площадь нулевая
Если векторы коллинеарны, то их можно расположить на одной прямой и наш параллелограмм тоже «складывается» в одну прямую. Площадь такого, как говорят математики, вырожденного
параллелограмма равна нулю. Это же следует и из формулы – синус нуля или 180-ти градусов равен нулю, а значит, и площадь нулевая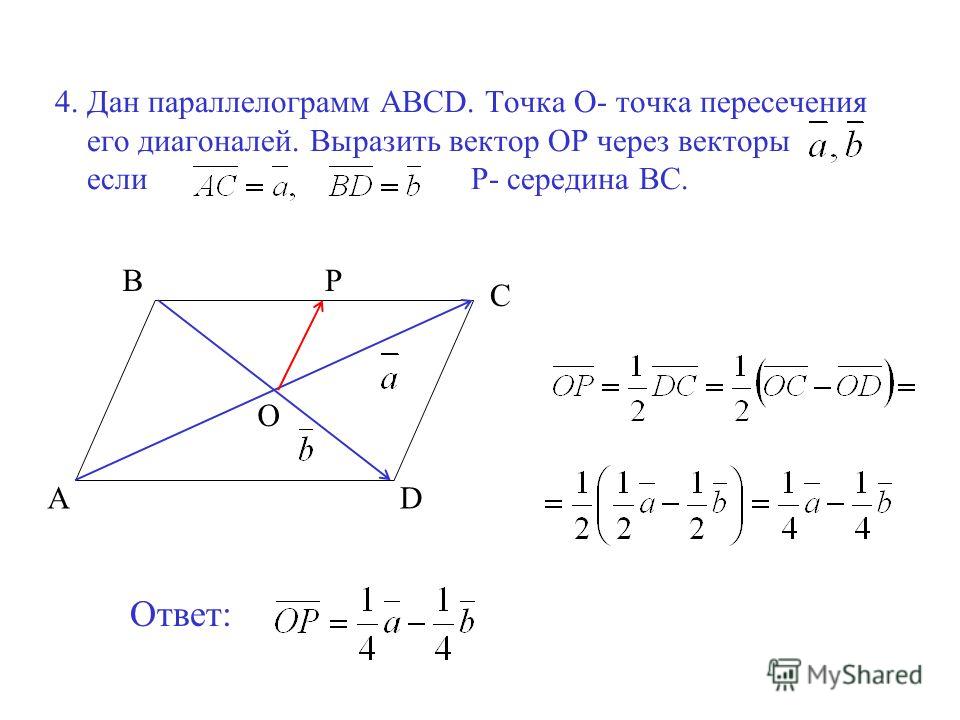 Потому что оформление решений будет отличаться!
Потому что оформление решений будет отличаться!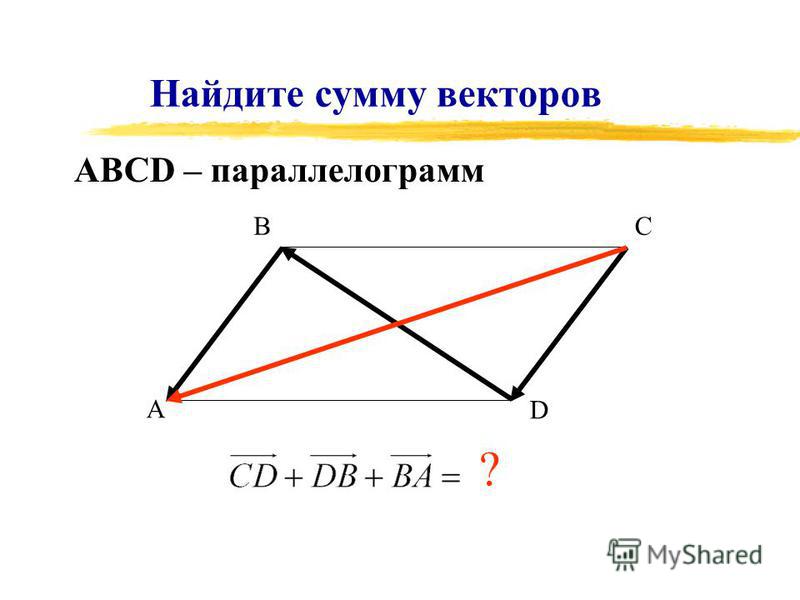 Этот момент всегда нужно держать на контроле, решая любую задачу по высшей математике, да и по другим предметам тоже.
Этот момент всегда нужно держать на контроле, решая любую задачу по высшей математике, да и по другим предметам тоже.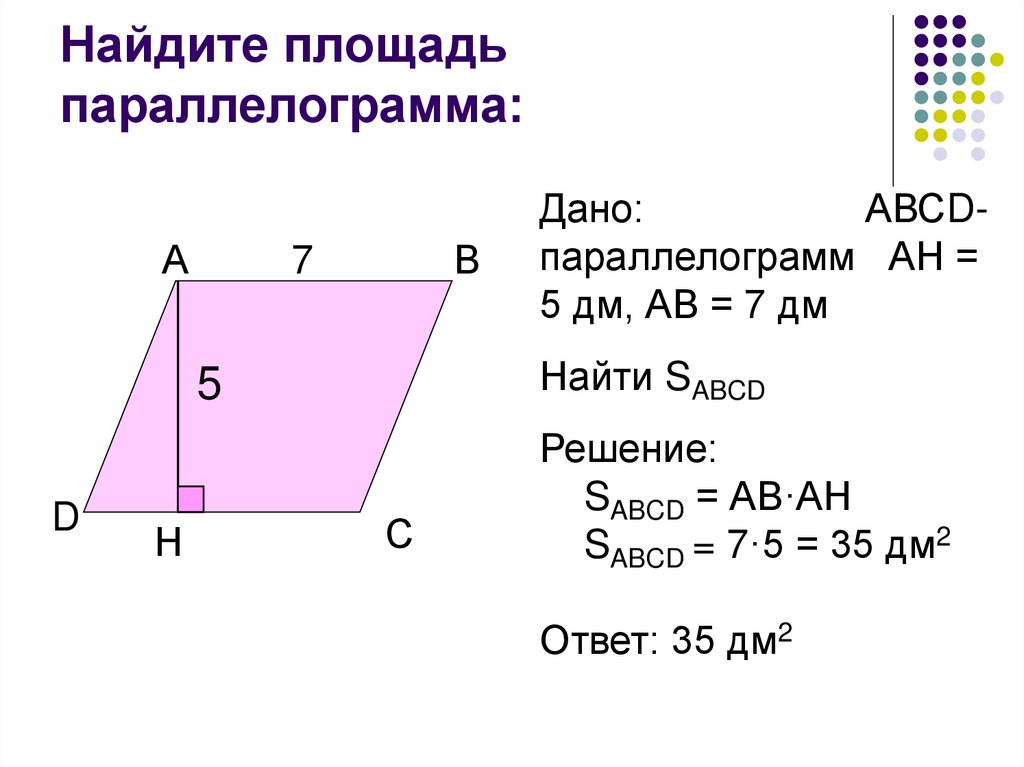 Поэтому пусть будет.
Поэтому пусть будет. Загвоздка состоит в том, что векторы «цэ» и «дэ» сами представлены в виде сумм векторов. Алгоритм здесь стандартен и чем-то напоминает примеры № 3 и 4 урока Скалярное произведение векторов
. Решение для ясности разобьём на три этапа:
Загвоздка состоит в том, что векторы «цэ» и «дэ» сами представлены в виде сумм векторов. Алгоритм здесь стандартен и чем-то напоминает примеры № 3 и 4 урока Скалярное произведение векторов
. Решение для ясности разобьём на три этапа: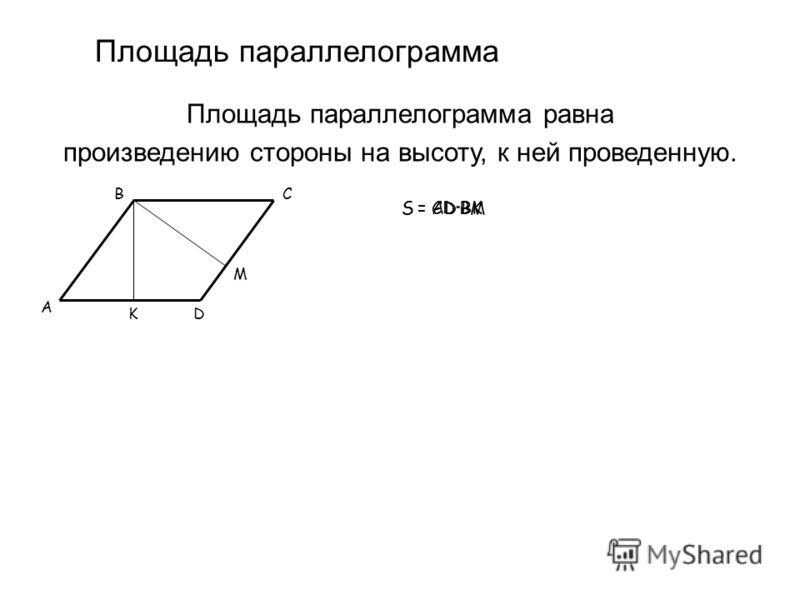 Данное действие напоминает Пример 3:
Данное действие напоминает Пример 3:

 Если известны только координаты векторов, то для вычисления нужно применять координатные методы, в том числе и для определения угла между векторами.
Если известны только координаты векторов, то для вычисления нужно применять координатные методы, в том числе и для определения угла между векторами.
 Пусть координаты вектора а(x1;y1;z1), вектора b(x2;y2;z2).
Пусть координаты вектора а(x1;y1;z1), вектора b(x2;y2;z2). 5.
5. Найдите площадь, если , а угол между ними 30°.
Найдите площадь, если , а угол между ними 30°.
 Так как логарифмическая функция по основанию 2 является возрастающей на множестве всех положительных чисел, то последнее неравенство будет выполняться при условии, что х-4≤8, но в то же время: х-4>0. Из первого условия следует: х≤12, а из второго, что х>4. Общим будет значение х∈(4; 12].
Так как логарифмическая функция по основанию 2 является возрастающей на множестве всех положительных чисел, то последнее неравенство будет выполняться при условии, что х-4≤8, но в то же время: х-4>0. Из первого условия следует: х≤12, а из второго, что х>4. Общим будет значение х∈(4; 12]. Вспахано 35%, следовательно не вспахано 100%-35%=65%. Нам осталось найти 65% от 10800. Обращаем проценты в десятичную дробь: 65%=0,65 и умножаем эту дробь на 10800.
Вспахано 35%, следовательно не вспахано 100%-35%=65%. Нам осталось найти 65% от 10800. Обращаем проценты в десятичную дробь: 65%=0,65 и умножаем эту дробь на 10800. Классическое решение этого задания: 1) найти производную данной функции; 2) найти критические точки и отметить их на числовой прямой; 3) определить знаки производной на промежутках, определенных критическими точками; 4) выяснить, какие из критических точек являются точками минимума и какие точками максимума; 5) найти значения самой функции в этих точках минимума и максимума — это и будут ординаты точек экстремума; 6) сложить эти значения ординат. Но в этом конкретном задании все гораздо проще! Функция нам дана нечетная, т.е. для всех возможных значений х выполняется равенство: f(-x)=f(x). График нечетной функции симметричен относительно начала координат. Что это значит, и чем это нам поможет? Рассуждаем: если эта функция имеет максимум в точке с абсциссой а
, то в симметричной ей точке с абсциссой (-а)
она будет иметь минимум. Опять же значения функции в этих точках а
и -а
также будут являться противоположными числами. А чему равна сумма противоположных чисел? Правильно: нулю.
Классическое решение этого задания: 1) найти производную данной функции; 2) найти критические точки и отметить их на числовой прямой; 3) определить знаки производной на промежутках, определенных критическими точками; 4) выяснить, какие из критических точек являются точками минимума и какие точками максимума; 5) найти значения самой функции в этих точках минимума и максимума — это и будут ординаты точек экстремума; 6) сложить эти значения ординат. Но в этом конкретном задании все гораздо проще! Функция нам дана нечетная, т.е. для всех возможных значений х выполняется равенство: f(-x)=f(x). График нечетной функции симметричен относительно начала координат. Что это значит, и чем это нам поможет? Рассуждаем: если эта функция имеет максимум в точке с абсциссой а
, то в симметричной ей точке с абсциссой (-а)
она будет иметь минимум. Опять же значения функции в этих точках а
и -а
также будут являться противоположными числами. А чему равна сумма противоположных чисел? Правильно: нулю. Помечаем точками поля «Планирование» и «По датам».
Помечаем точками поля «Планирование» и «По датам».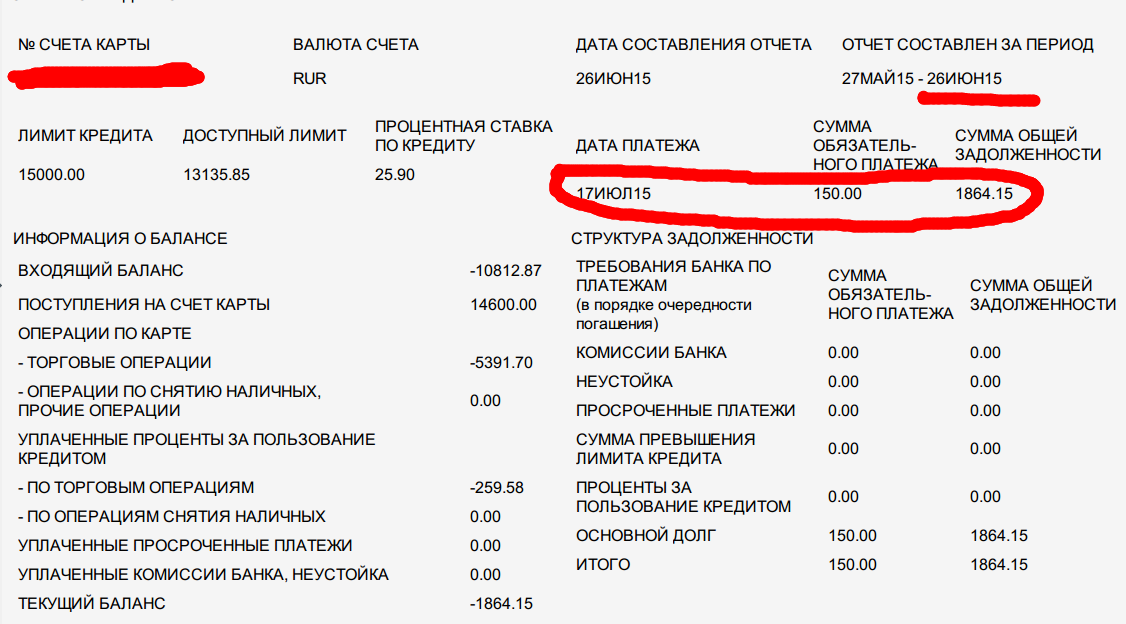 Возможен и другой способ: вручную менять даты в полях поездок. Сверяйтесь с пометками в собственном загранпаспорте, если уверены, что они проставлены корректно. В противном же случае придется руководствоваться собственными записями, а при их отсутствии – надеяться на память.
Возможен и другой способ: вручную менять даты в полях поездок. Сверяйтесь с пометками в собственном загранпаспорте, если уверены, что они проставлены корректно. В противном же случае придется руководствоваться собственными записями, а при их отсутствии – надеяться на память. Для этого помечаем точкой поле «Произвольно» и повторяем все предыдущие действия. Внимание: менять слово «Въезд» на «Выезд» и обратно в правой части калькулятора можно одним «мышиным» кликом.
Для этого помечаем точкой поле «Произвольно» и повторяем все предыдущие действия. Внимание: менять слово «Въезд» на «Выезд» и обратно в правой части калькулятора можно одним «мышиным» кликом. Вычисление разности дат в Microsoft Excel
Вычисление разности дат в Microsoft Excel

 То есть если человек работает с 1 июля по 8 июля, то получается 8 дней. Так как последний день считается рабочим.
То есть если человек работает с 1 июля по 8 июля, то получается 8 дней. Так как последний день считается рабочим.
 Через точку удобнее вводить на сотовых и планшетах, а через слеш удобнее на компьютере на клавиатуре справа (панели цифровой)
Через точку удобнее вводить на сотовых и планшетах, а через слеш удобнее на компьютере на клавиатуре справа (панели цифровой)
 Сборник онлайн-калькуляторов поможет вам легко оперировать таким сложным параметром как время.
Сборник онлайн-калькуляторов поможет вам легко оперировать таким сложным параметром как время. Естественно, что заваленные кучей незначимой работы они не успевают выполнять приоритетные задачи, в результате чего и становятся неэффективными.
Естественно, что заваленные кучей незначимой работы они не успевают выполнять приоритетные задачи, в результате чего и становятся неэффективными.

 Итак, выбираем тип калькулятора, вводим дату и юбилейные 100 дней. Ваша памятная дата – 26 марта 2017, воскресенье. Стоит обвести эту дату в календаре.
Итак, выбираем тип калькулятора, вводим дату и юбилейные 100 дней. Ваша памятная дата – 26 марта 2017, воскресенье. Стоит обвести эту дату в календаре.


 Это бы упростило бы работу определенному кругу лиц.
Это бы упростило бы работу определенному кругу лиц. д.
д.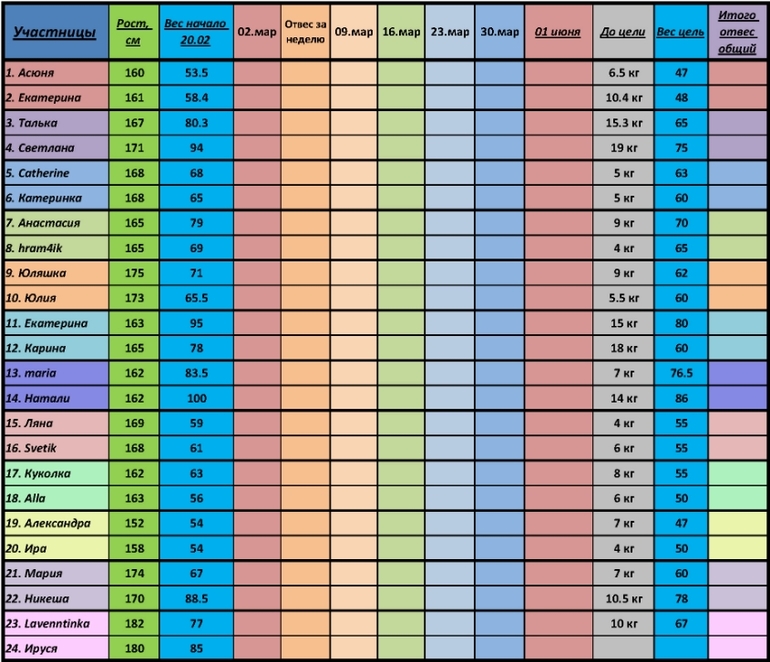 Как вариант использования сменные дежурства, охрана и т.п.
Как вариант использования сменные дежурства, охрана и т.п.
 Свое название техника «Помодоро» получила потому, что ее создатель отмерял промежутки времени при помощи кухонного таймера в виде помидора. С тех пор модернизированные версии тайм-менеджмента легли в основу успеха видных представителей бизнеса.
Свое название техника «Помодоро» получила потому, что ее создатель отмерял промежутки времени при помощи кухонного таймера в виде помидора. С тех пор модернизированные версии тайм-менеджмента легли в основу успеха видных представителей бизнеса. Не слишком информативно при планировании. Программа выражает это время так же в днях, неделях или месяцах. Смотрим. У вас есть ровно 90 дней или 12 рабочих недель. С этим уже можно построить эффективную систему тайм-менеджмента и не допустить дедлайна.
Не слишком информативно при планировании. Программа выражает это время так же в днях, неделях или месяцах. Смотрим. У вас есть ровно 90 дней или 12 рабочих недель. С этим уже можно построить эффективную систему тайм-менеджмента и не допустить дедлайна. Представьте, что вы получили смс-сообщение, в котором ваша пассия поздравляет вас с 100 днем совместной жизни. Это важная дата, которую забывать не стоит, поэтому лучше воспользоваться программой и узнать ее. Вы получили смску 4 июля 2017 года, теперь легко узнать, когда же вы съехались со своей пассией. Итак, выбираем тип калькулятора, вводим дату и юбилейные 100 дней. Ваша памятная дата – 26 марта 2017, воскресенье. Стоит обвести эту дату в календаре.
Представьте, что вы получили смс-сообщение, в котором ваша пассия поздравляет вас с 100 днем совместной жизни. Это важная дата, которую забывать не стоит, поэтому лучше воспользоваться программой и узнать ее. Вы получили смску 4 июля 2017 года, теперь легко узнать, когда же вы съехались со своей пассией. Итак, выбираем тип калькулятора, вводим дату и юбилейные 100 дней. Ваша памятная дата – 26 марта 2017, воскресенье. Стоит обвести эту дату в календаре.
 05
.
1945
01
:
43
05
.
1945
01
:
43
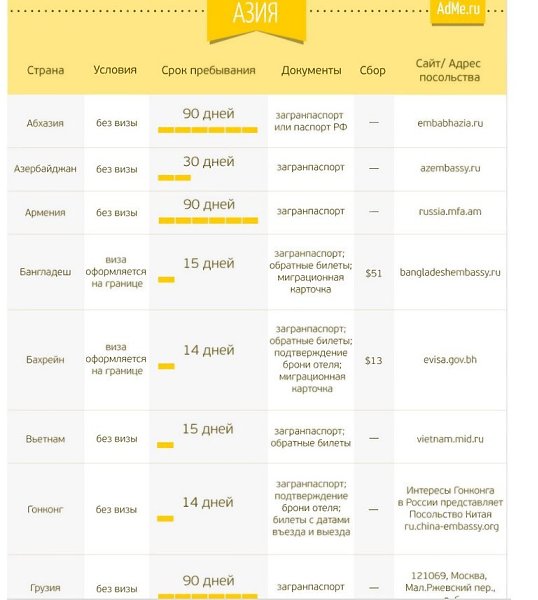
 При больших промежутках времени
между датами, расчеты количества рабочих дней ведутся в предположении пятидневной рабочей недели, праздники не учитываются
.
При больших промежутках времени
между датами, расчеты количества рабочих дней ведутся в предположении пятидневной рабочей недели, праздники не учитываются
.
 Новый год в России встречают 1 января с начиная 1700 года (правда, на самом деле, по современному календарю этот новый год наступил 11 января 1700 года). Страна перешла из 7208 года в 1700! Так что, в новый тогда 18 век, наступивший в 1701 году Россия вошла почти в ногу с Европой. Почти в ногу, потому что летоисчисление, как и прежде велось по юлианскому календарю (изменилась только датировка, теперь она называется старым стилем
)
, в то время как Европа уже частично перешла на григорианский календарь.
Новый год в России встречают 1 января с начиная 1700 года (правда, на самом деле, по современному календарю этот новый год наступил 11 января 1700 года). Страна перешла из 7208 года в 1700! Так что, в новый тогда 18 век, наступивший в 1701 году Россия вошла почти в ногу с Европой. Почти в ногу, потому что летоисчисление, как и прежде велось по юлианскому календарю (изменилась только датировка, теперь она называется старым стилем
)
, в то время как Европа уже частично перешла на григорианский календарь. .
.

 Поставьте в нее «=»
и нажмите сначала позднюю (В1
) дату, потом раннюю (А1
). Чтобы вычислить между ними количество дней, жмите «Enter»
.
Поставьте в нее «=»
и нажмите сначала позднюю (В1
) дату, потом раннюю (А1
). Чтобы вычислить между ними количество дней, жмите «Enter»
.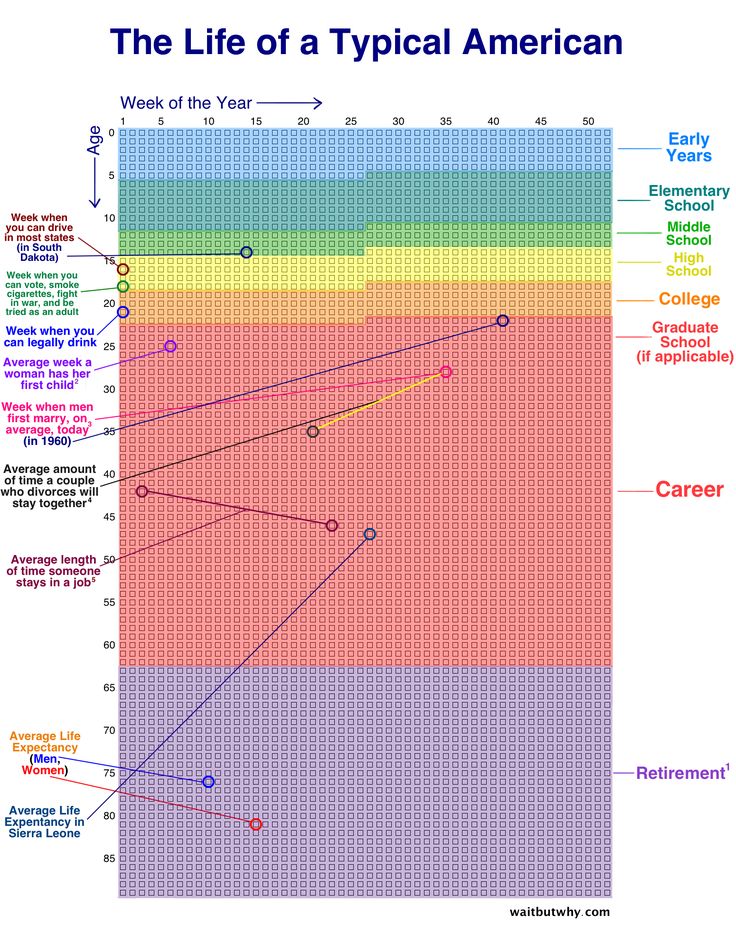

 Вводим функцию и заполняем ее аргументы:
Вводим функцию и заполняем ее аргументы: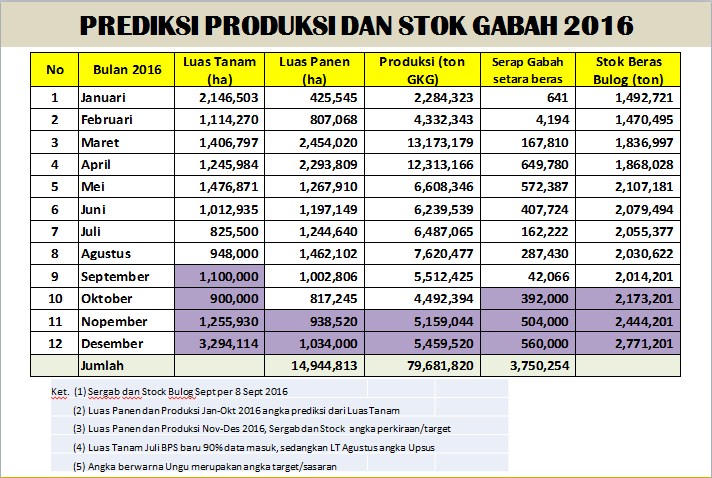








 Установить Фотоконвертер
Установить Фотоконвертер

 11.16
11.16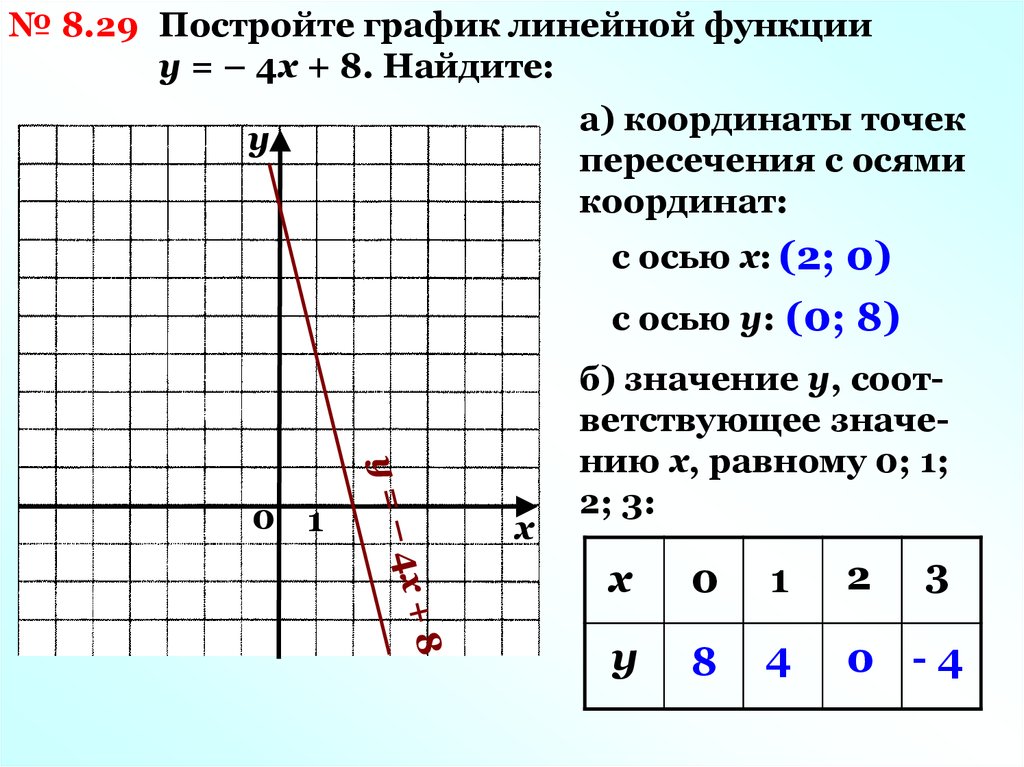 В каком букете больше роз в первом или
В каком букете больше роз в первом или Однако, все не так плохо. Достаточно запомнить несколько алгоритмов решения таких задач, и вы сможете без труда построить график даже самой на вид сложной функции. Давайте разберемся, что же это за алгоритмы.
Однако, все не так плохо. Достаточно запомнить несколько алгоритмов решения таких задач, и вы сможете без труда построить график даже самой на вид сложной функции. Давайте разберемся, что же это за алгоритмы.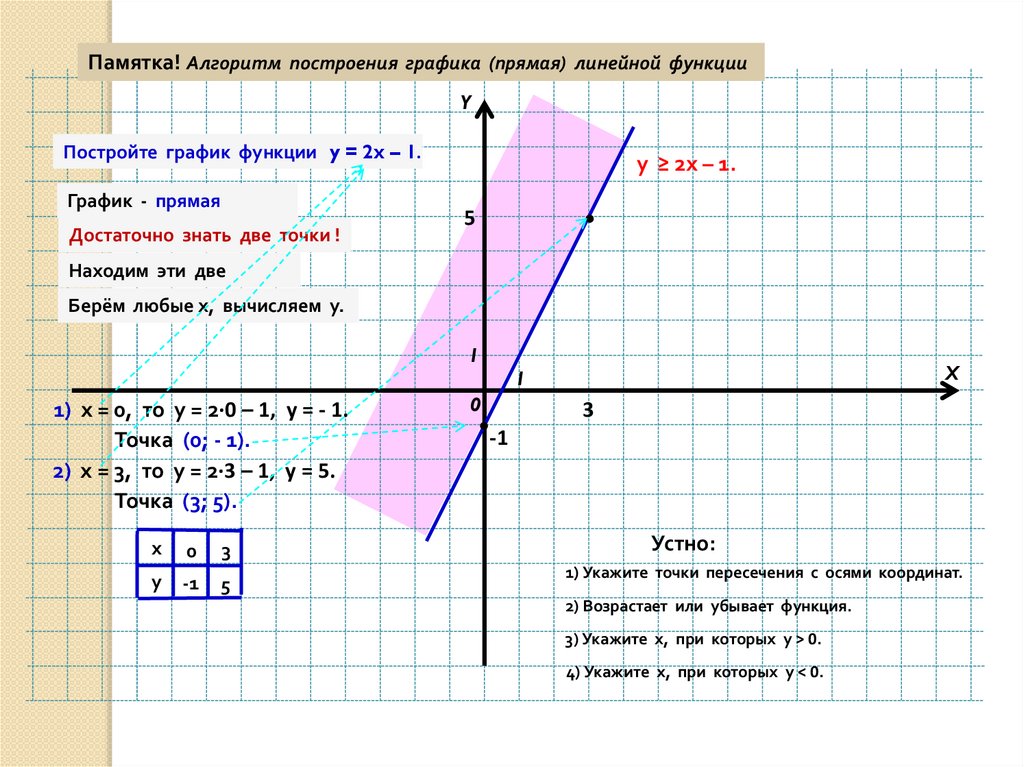
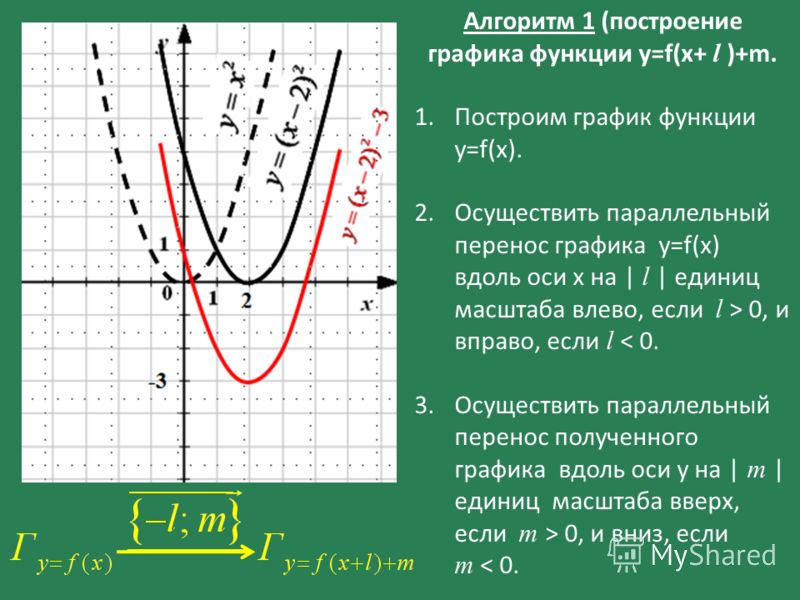
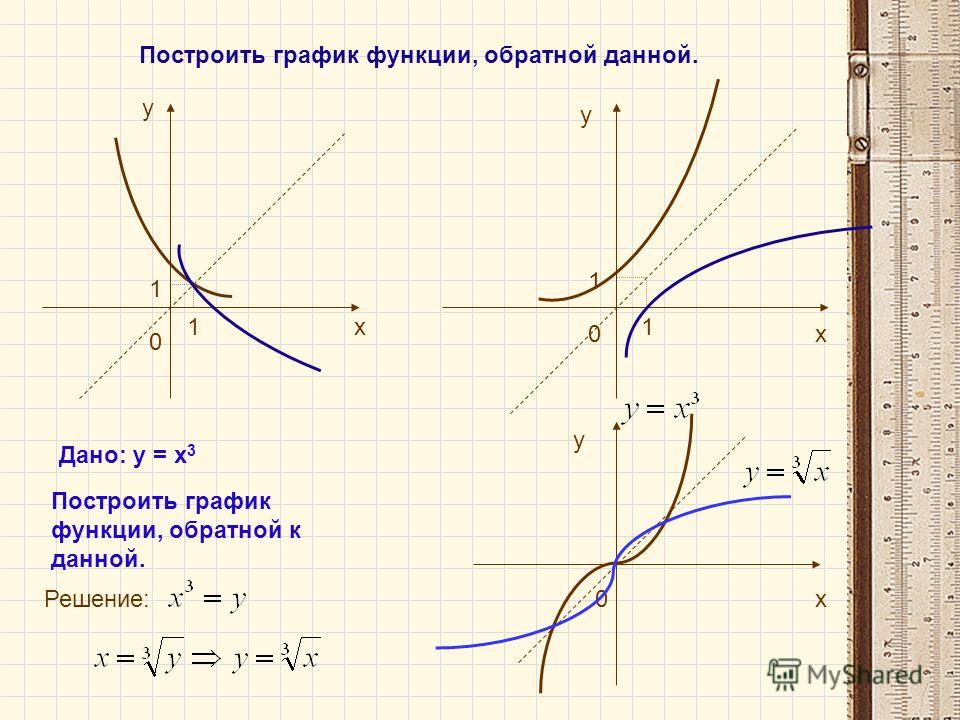 Действительно, y(-x) = y = |f(|-x|)| = y = |f(|x|)| = y(x), и поэтому, их графики симметричны относительно оси 0y. Множество значений таких функций: y ≥
0. Значит, графики таких функций расположены полностью в верхней полуплоскости.
Действительно, y(-x) = y = |f(|-x|)| = y = |f(|x|)| = y(x), и поэтому, их графики симметричны относительно оси 0y. Множество значений таких функций: y ≥
0. Значит, графики таких функций расположены полностью в верхней полуплоскости.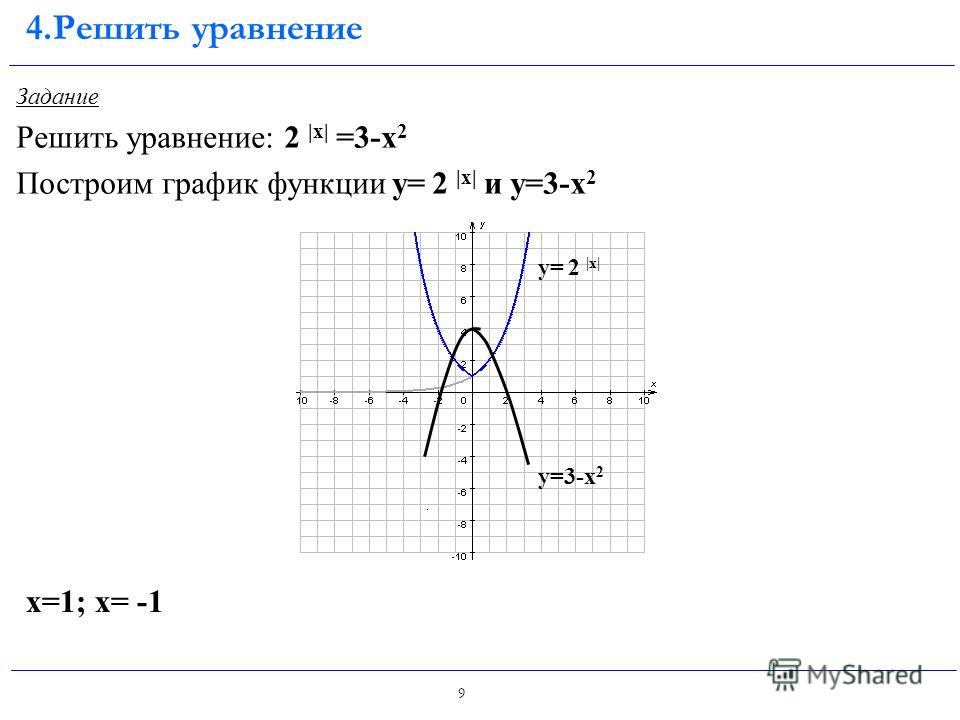 6)
.
6)
.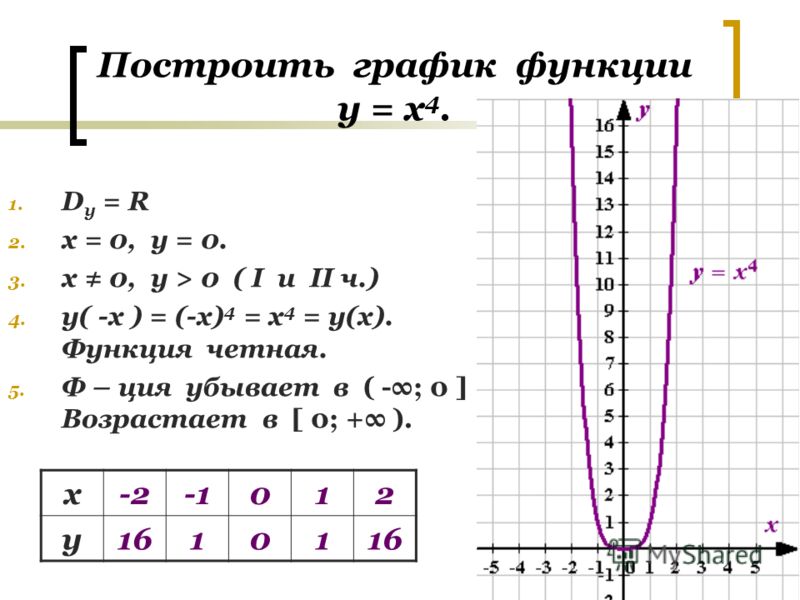
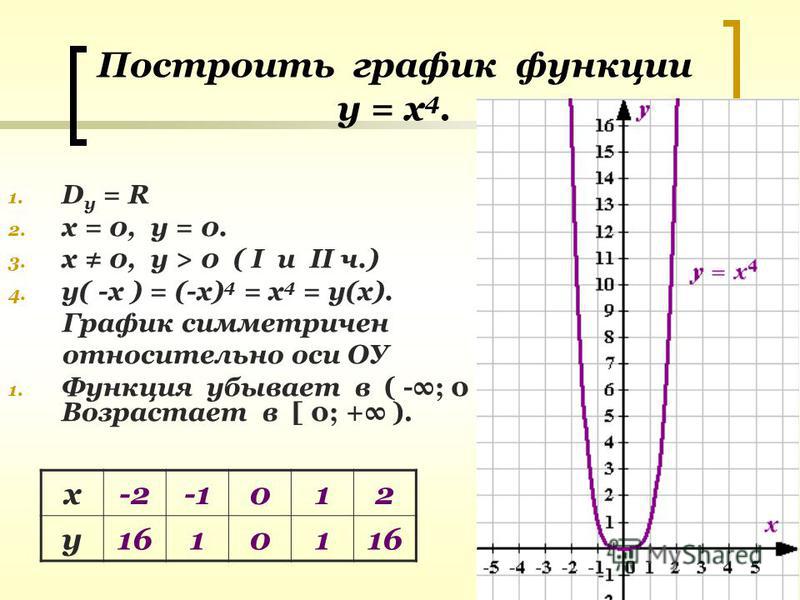
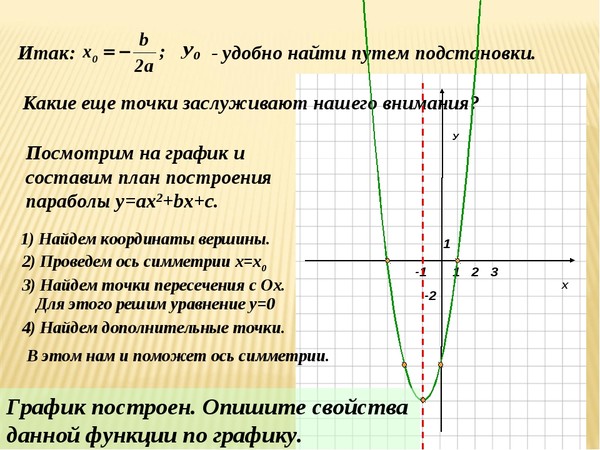

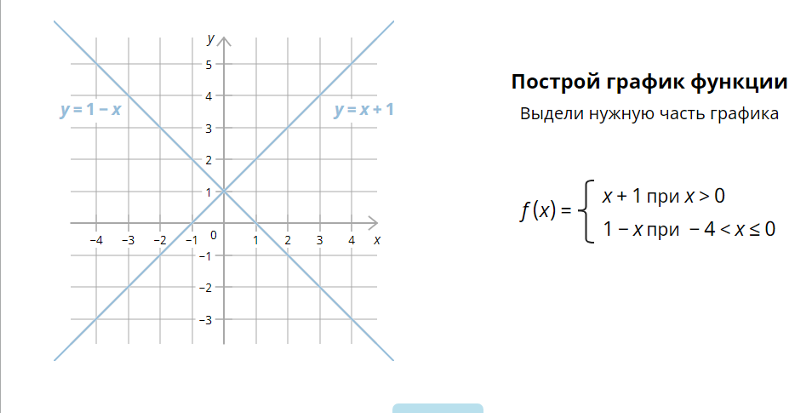
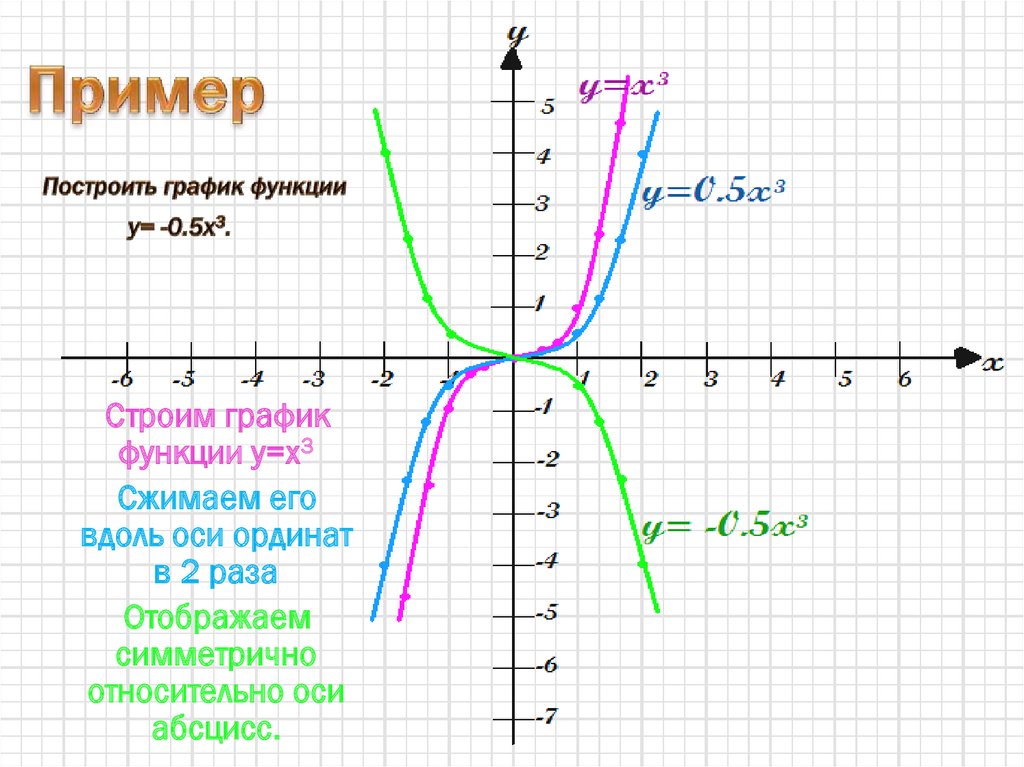

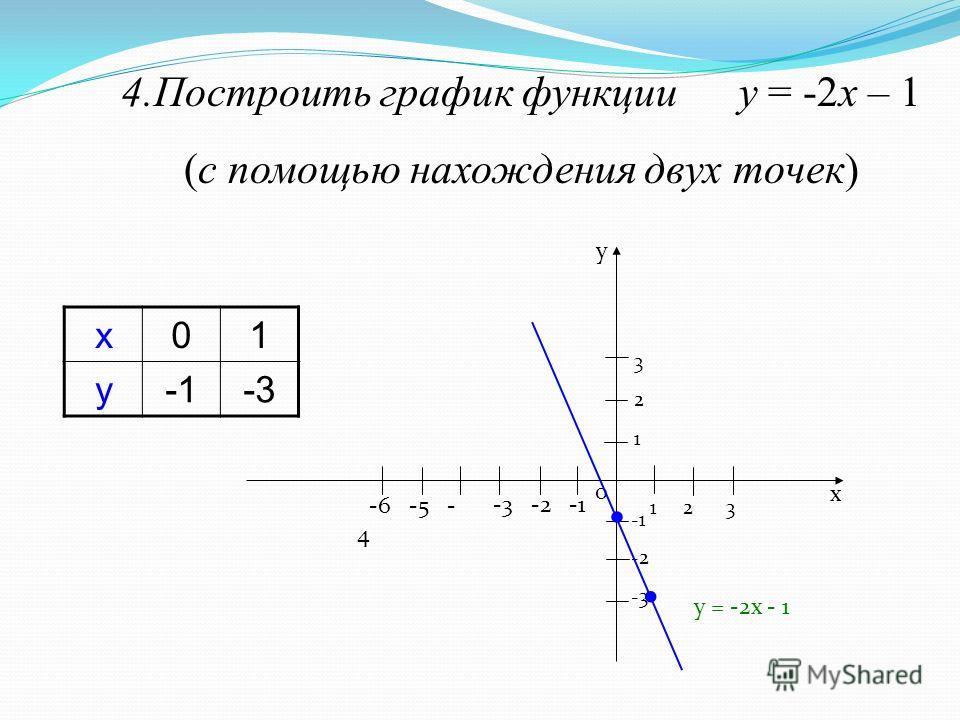
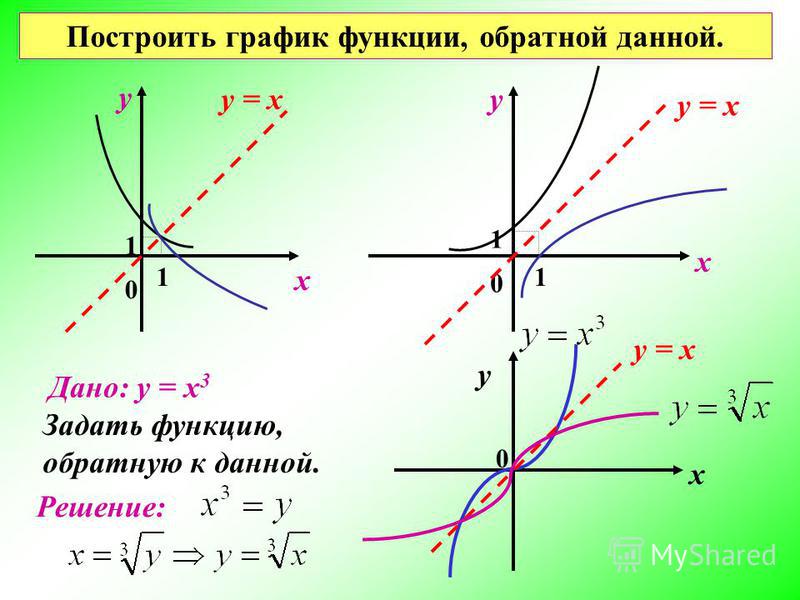 Чем больше основание a (если a>1) показательной функции y = ax, тем ближе расположена кривая к оси Оу.
Чем больше основание a (если a>1) показательной функции y = ax, тем ближе расположена кривая к оси Оу.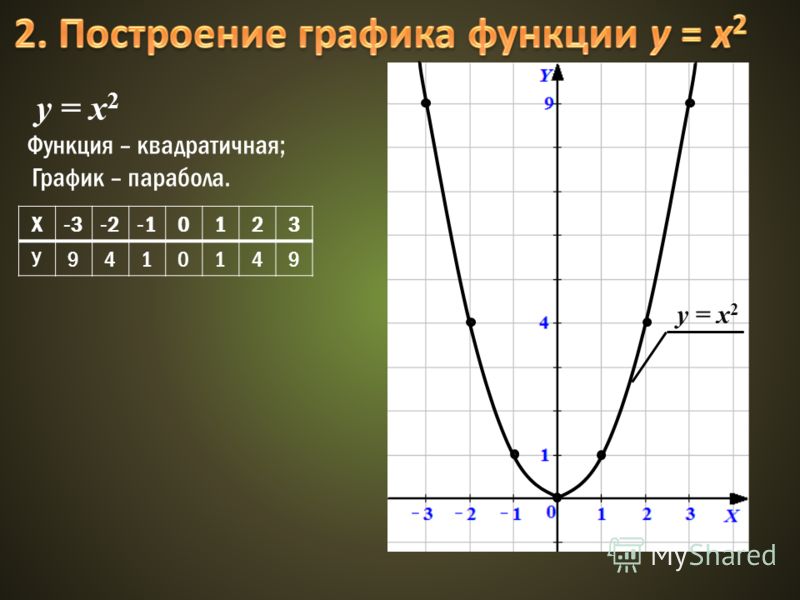 Функция убывает на всей своей области определения: D(y)=R, так как основание функции 0 < < 1.
Функция убывает на всей своей области определения: D(y)=R, так как основание функции 0 < < 1.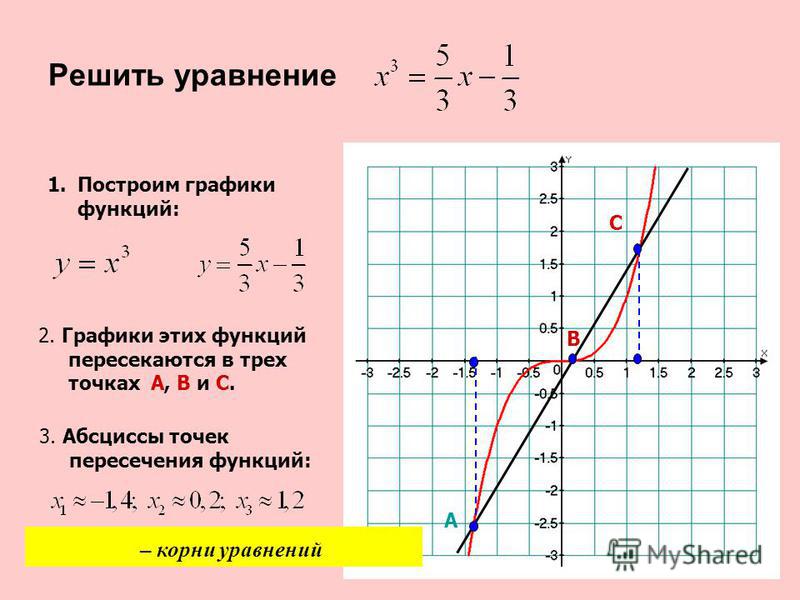 е. 0 < 2x < +∞. Значит, умножая каждую часть двойного неравенства на (-1), получаем: -∞ < 2x < 0.
е. 0 < 2x < +∞. Значит, умножая каждую часть двойного неравенства на (-1), получаем: -∞ < 2x < 0.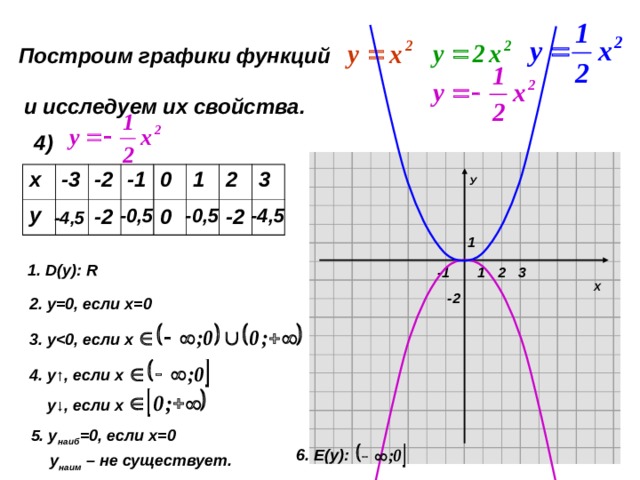
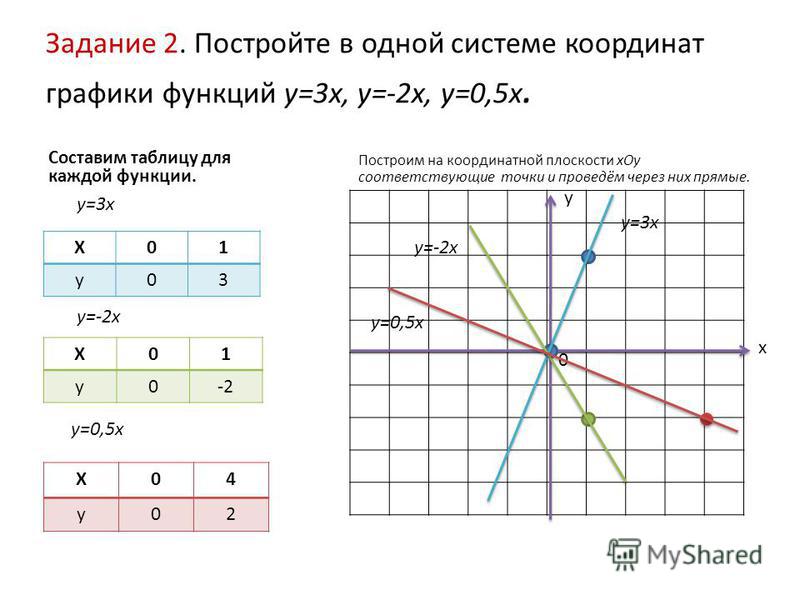 ..)
..)
 ..)
..)
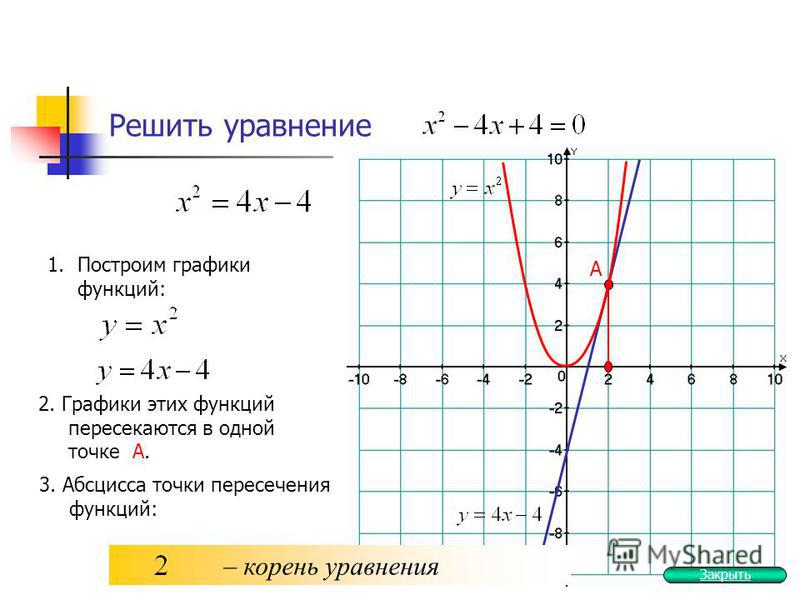 ..)
..)
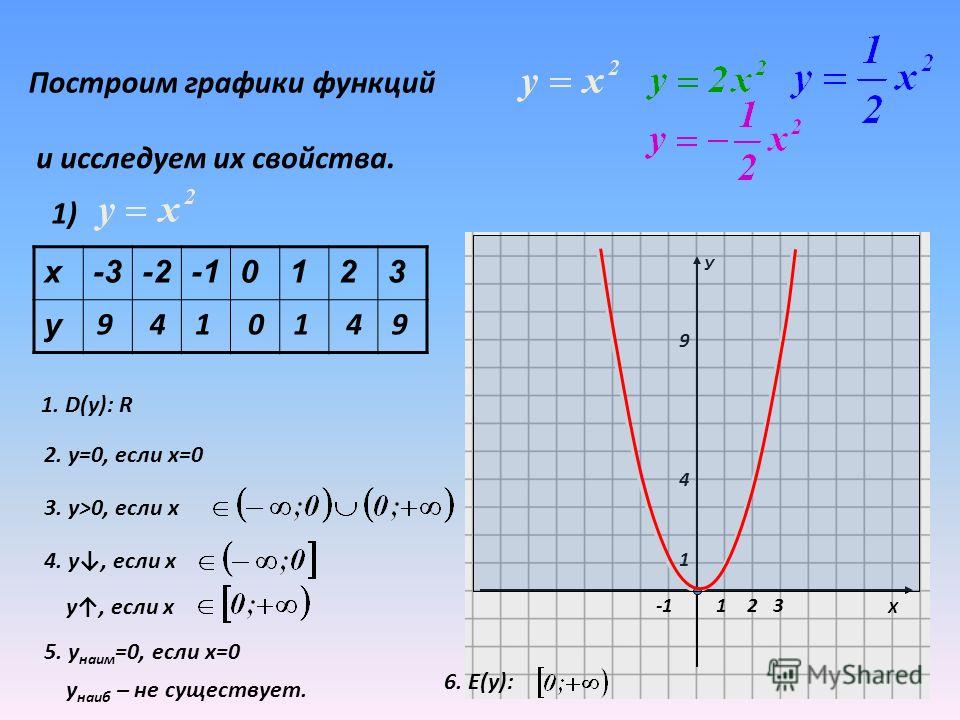
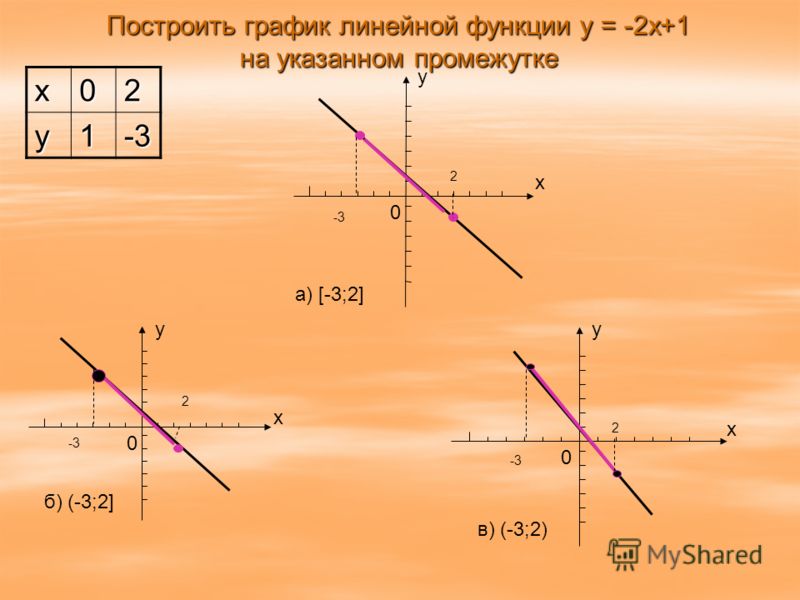 к. установлена абсолютная ссылка.
к. установлена абсолютная ссылка.
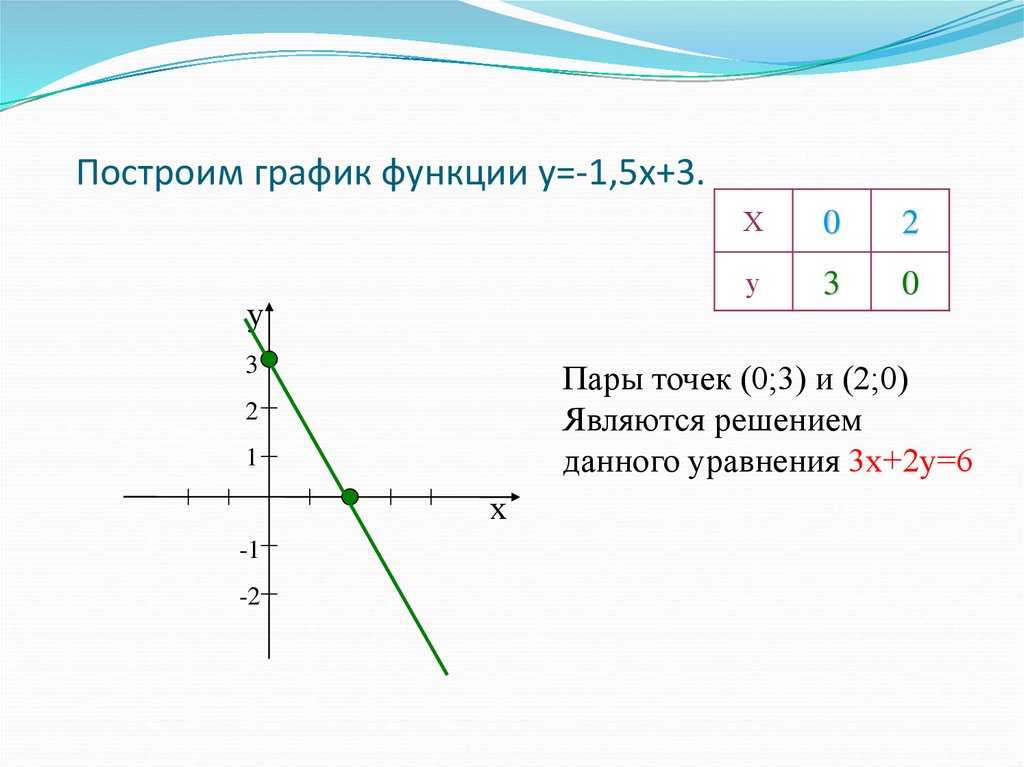
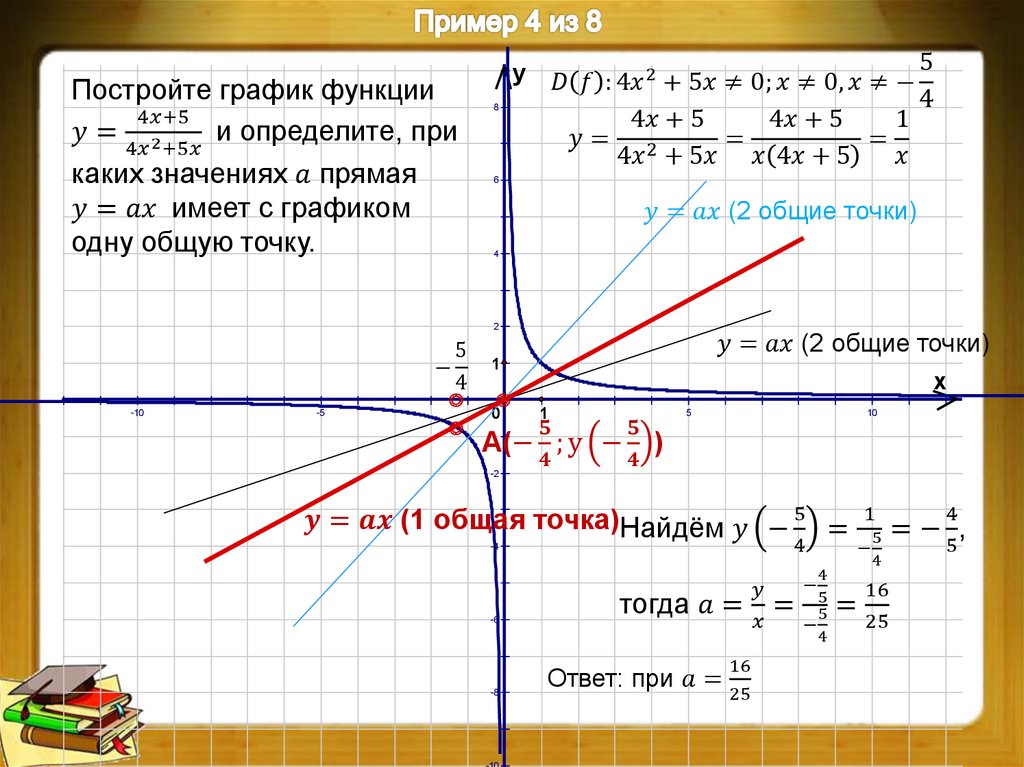 Если же нужно одновременно просматривать диаграмму и данные, на основе которых она была построена, то тогда создаётся внедрённая диаграмма.
Если же нужно одновременно просматривать диаграмму и данные, на основе которых она была построена, то тогда создаётся внедрённая диаграмма.
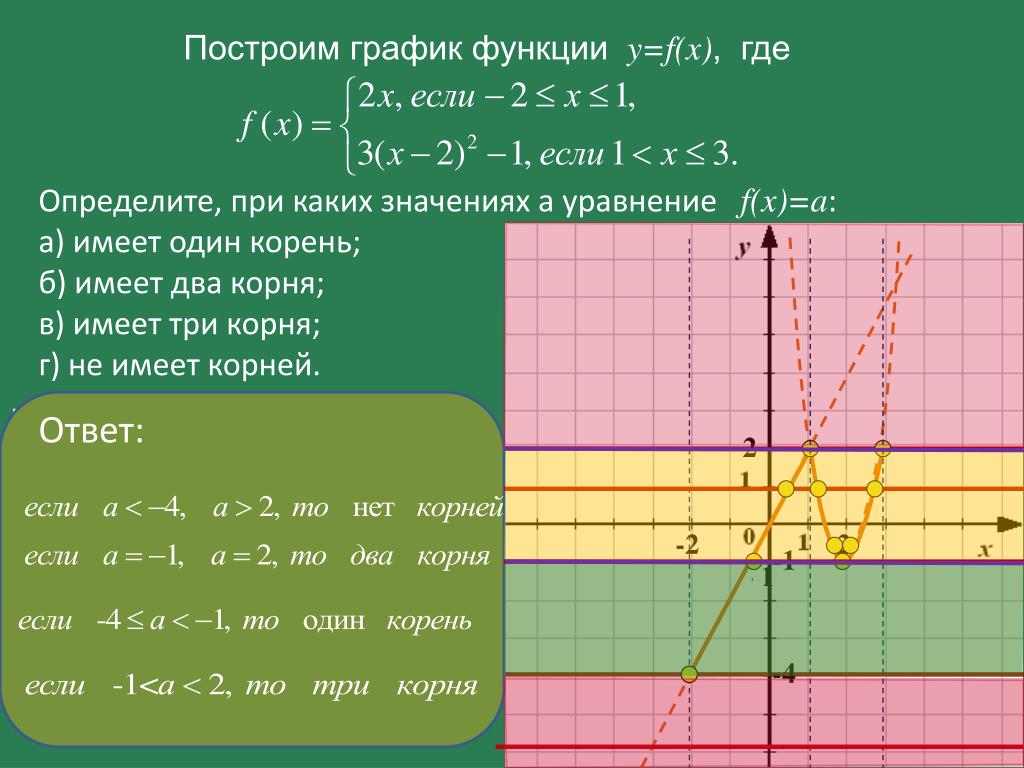 Ниже приведены некоторые примеры линейных уравнений:
Ниже приведены некоторые примеры линейных уравнений: 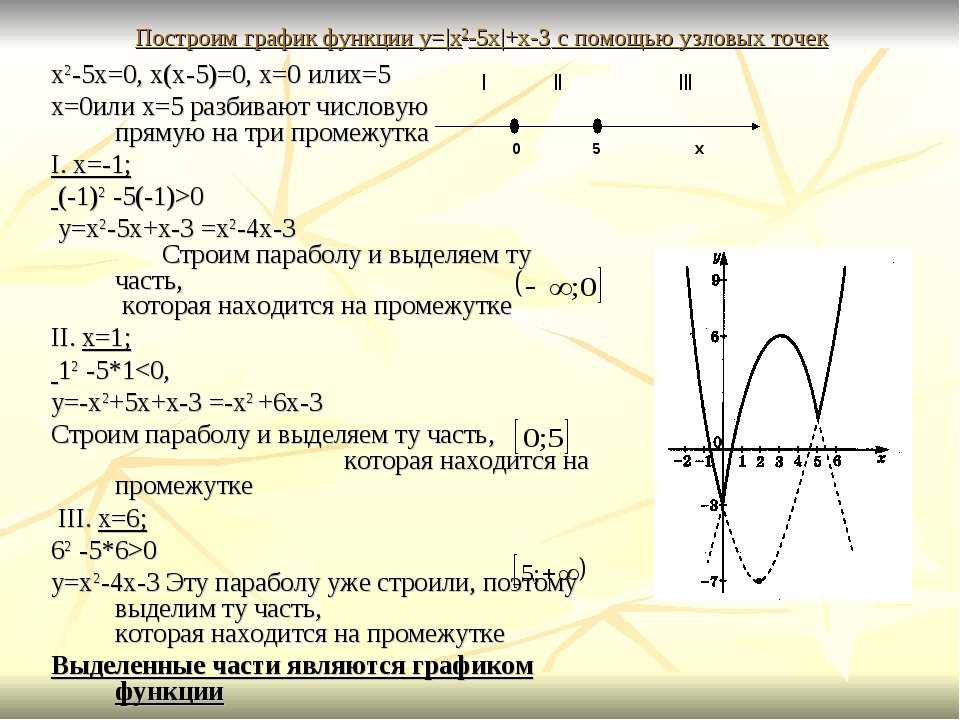
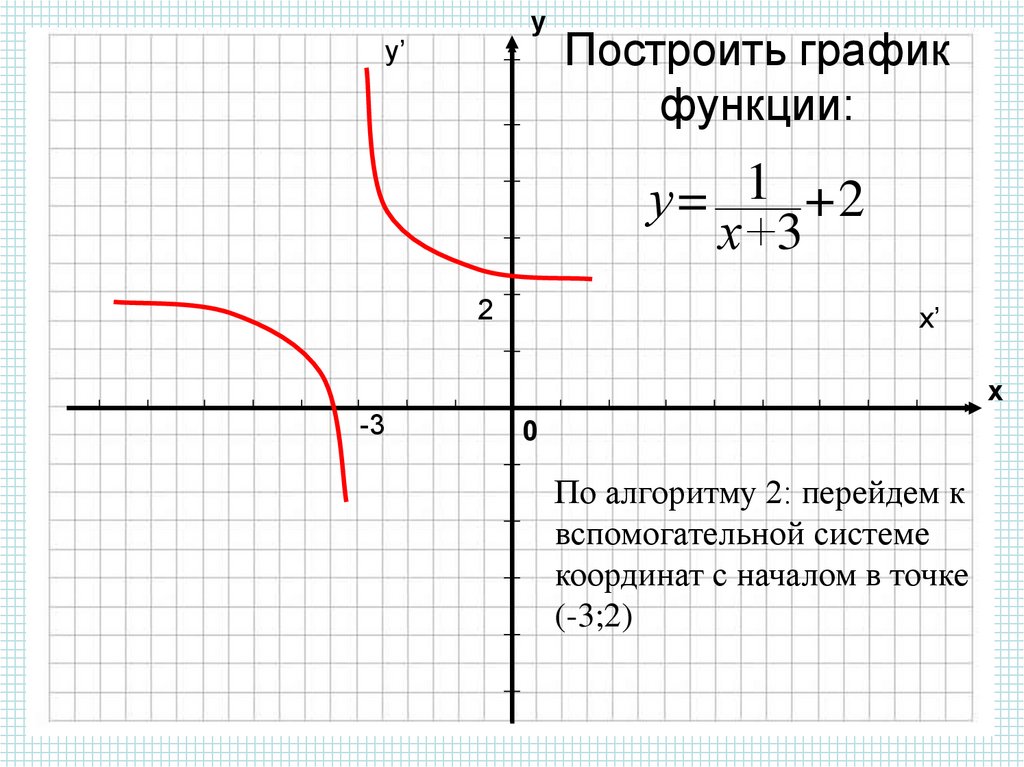
 Например, \(x = 3 + 2t\), \(y = 1 + t\). Буква \(t\) называется параметром или фиктивной переменной.
Например, \(x = 3 + 2t\), \(y = 1 + t\). Буква \(t\) называется параметром или фиктивной переменной. 
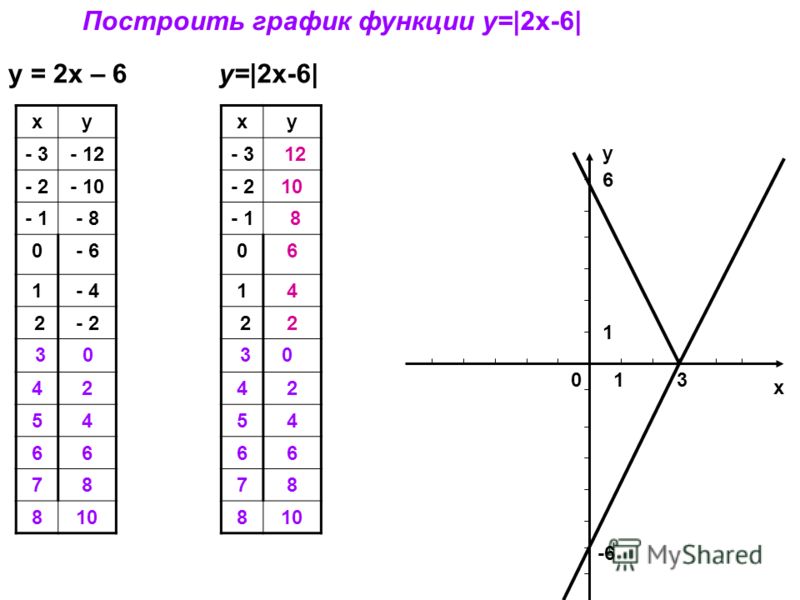
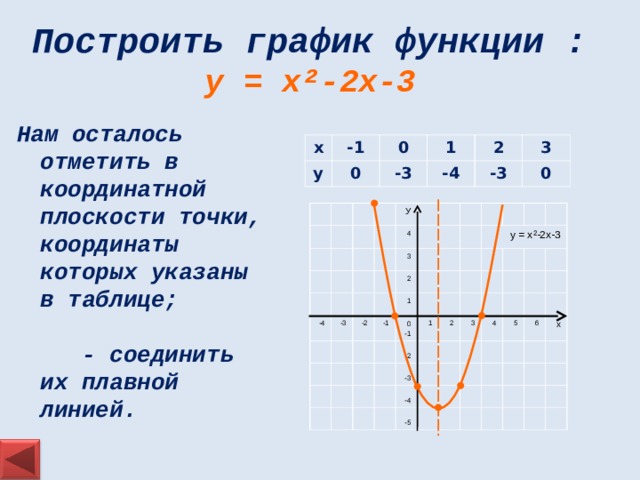 deanza.edu/faculty/bloomroberta/math21/afm3files.html.html
deanza.edu/faculty/bloomroberta/math21/afm3files.html.html 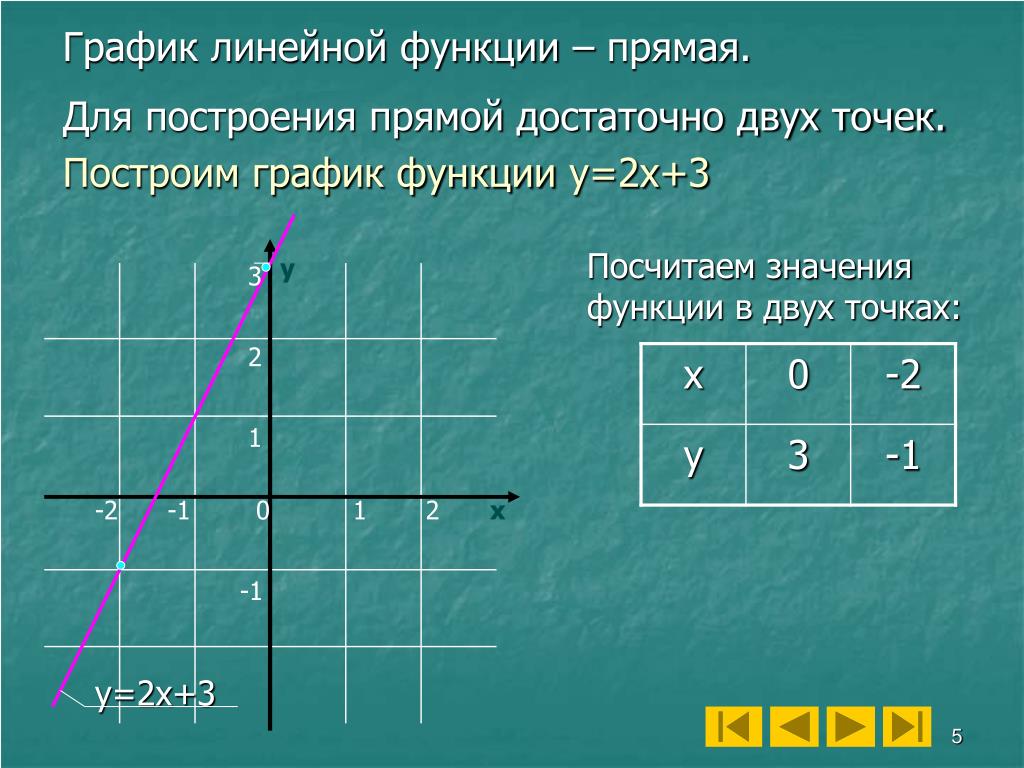 11.
11.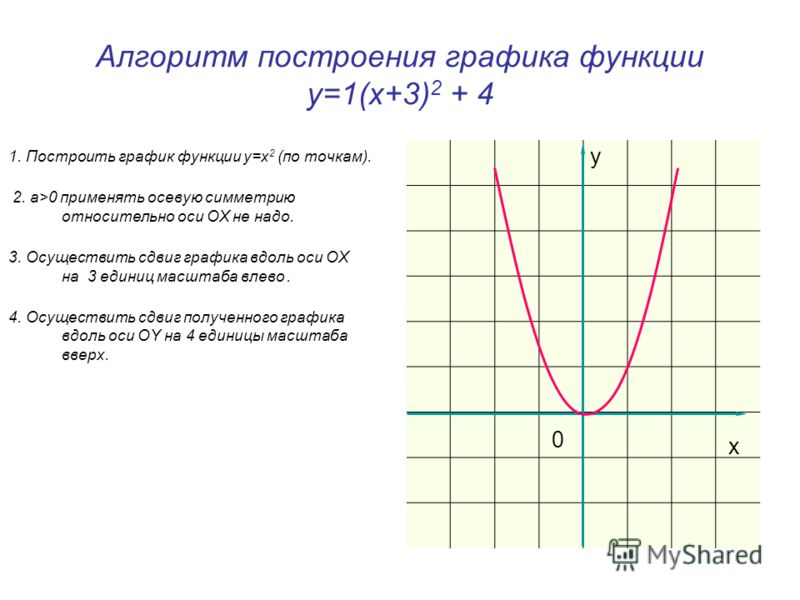 07.
07.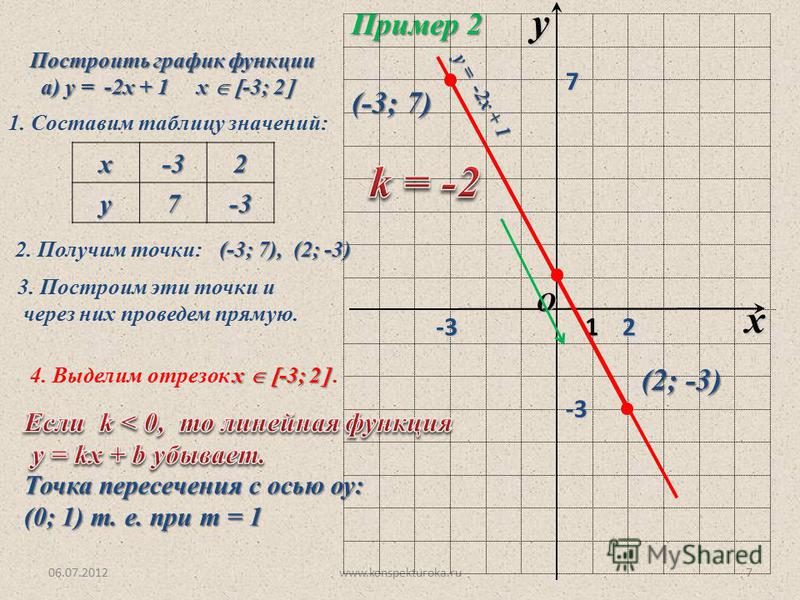 Чтобы найти упорядоченные пары, удовлетворяющие такому уравнению, как y = 2x + 3, мы можем выбрать любое значение для одной переменной, а затем найти соответствующее значение для другой переменной, подставив его в уравнение. Например,
Чтобы найти упорядоченные пары, удовлетворяющие такому уравнению, как y = 2x + 3, мы можем выбрать любое значение для одной переменной, а затем найти соответствующее значение для другой переменной, подставив его в уравнение. Например,  Символ f(x) (читается как «f of x») используется для представления значения зависимой переменной, связанной с x. Например,
Символ f(x) (читается как «f of x») используется для представления значения зависимой переменной, связанной с x. Например, 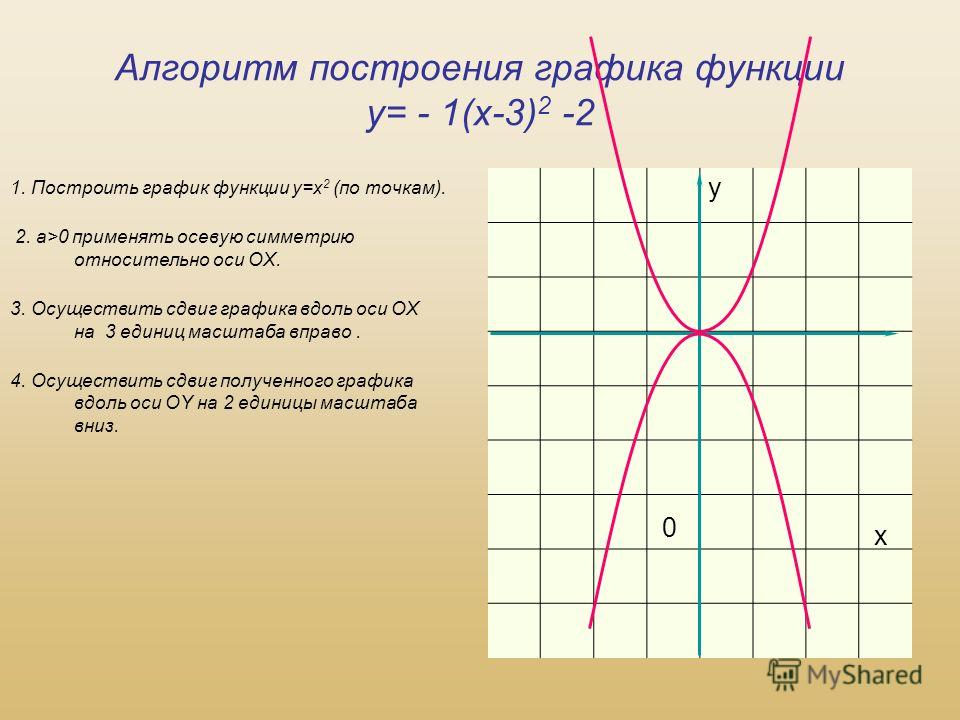 Это важное соотношение является краеугольным камнем декартовой системы координат.
Это важное соотношение является краеугольным камнем декартовой системы координат.  Существует бесконечное число таких точек. точки. Мы построим график пяти, чтобы попытаться найти закономерность (см. рис. 8.3).
Существует бесконечное число таких точек. точки. Мы построим график пяти, чтобы попытаться найти закономерность (см. рис. 8.3).  ) Выбор двух точек зависит от выбора любых двух значений x или любых двух значений y.
) Выбор двух точек зависит от выбора любых двух значений x или любых двух значений y. 
 В только что приведенных примерах 1 и 2 мы будем говорить, что точка пересечения с осью y равна 2, а не давать координаты (0, 2). Точно так же в примере 1 точка пересечения по оси x равна 3, а в примере 2 точка пересечения по оси x равна -3. Если линия проходит через начало координат, то точка пересечения по оси x и по оси y будет равна 0. В этом случае необходимо использовать какую-то другую точку.
В только что приведенных примерах 1 и 2 мы будем говорить, что точка пересечения с осью y равна 2, а не давать координаты (0, 2). Точно так же в примере 1 точка пересечения по оси x равна 3, а в примере 2 точка пересечения по оси x равна -3. Если линия проходит через начало координат, то точка пересечения по оси x и по оси y будет равна 0. В этом случае необходимо использовать какую-то другую точку.  Что это значит для плотника? Это означает, что он должен построить крышу так, чтобы на каждые 5 дюймов подъема (расстояние по вертикали) приходилось 12 дюймов пробега (расстояние по горизонтали). То есть отношение подъема к пробегу составляет 5/12 (см. рис. 8.4.)
Что это значит для плотника? Это означает, что он должен построить крышу так, чтобы на каждые 5 дюймов подъема (расстояние по вертикали) приходилось 12 дюймов пробега (расстояние по горизонтали). То есть отношение подъема к пробегу составляет 5/12 (см. рис. 8.4.)  -1 y=3(-1)-1=-3-1=-4
-1 y=3(-1)-1=-3-1=-4  Рис. 8.8 Пусть P_1(x_1,y_1) и P_2(x_2, y_2) — две точки на прямой. Тогда P_3(x_2, y_1) находится под прямым углом, как показано на рисунке 8.10, и можно вычислить наклон.
Рис. 8.8 Пусть P_1(x_1,y_1) и P_2(x_2, y_2) — две точки на прямой. Тогда P_3(x_2, y_1) находится под прямым углом, как показано на рисунке 8.10, и можно вычислить наклон.  рис. 8.11). Все линии с отрицательным наклоном наклонены вниз вправо, а все линии с положительным наклоном наклонены вверх вправо.
рис. 8.11). Все линии с отрицательным наклоном наклонены вниз вправо, а все линии с положительным наклоном наклонены вверх вправо.  Если линейное уравнение решается относительно y, всегда ли коэффициент при x будет наклоном? Это важный вопрос, и ответ на него можно найти в следующем обсуждении.
Если линейное уравнение решается относительно y, всегда ли коэффициент при x будет наклоном? Это важный вопрос, и ответ на него можно найти в следующем обсуждении.  Затем нарисуйте линию.
Затем нарисуйте линию. 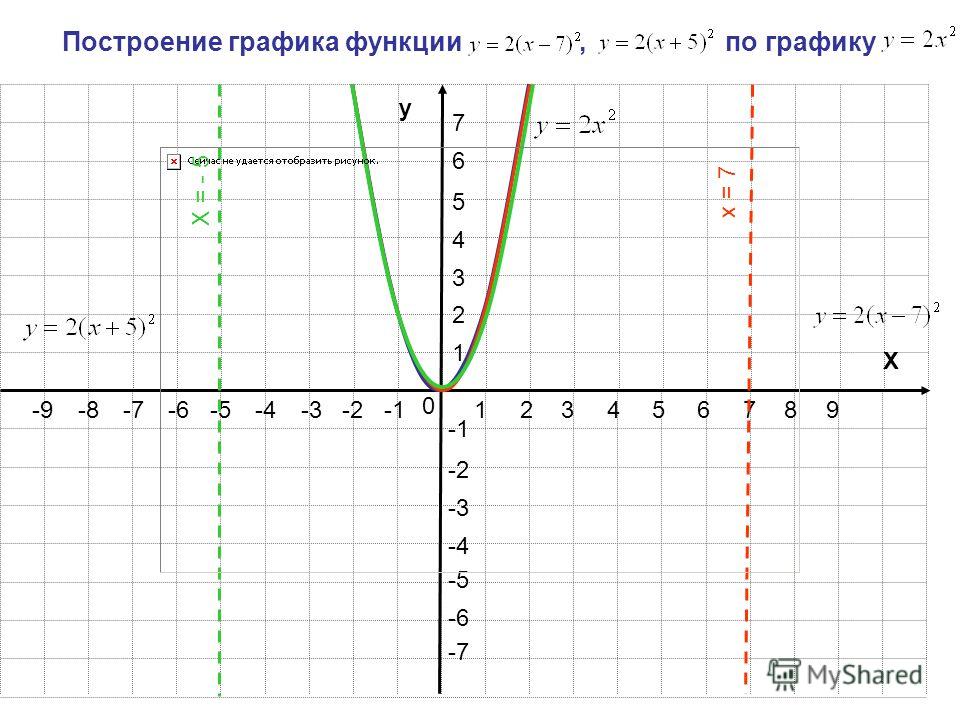
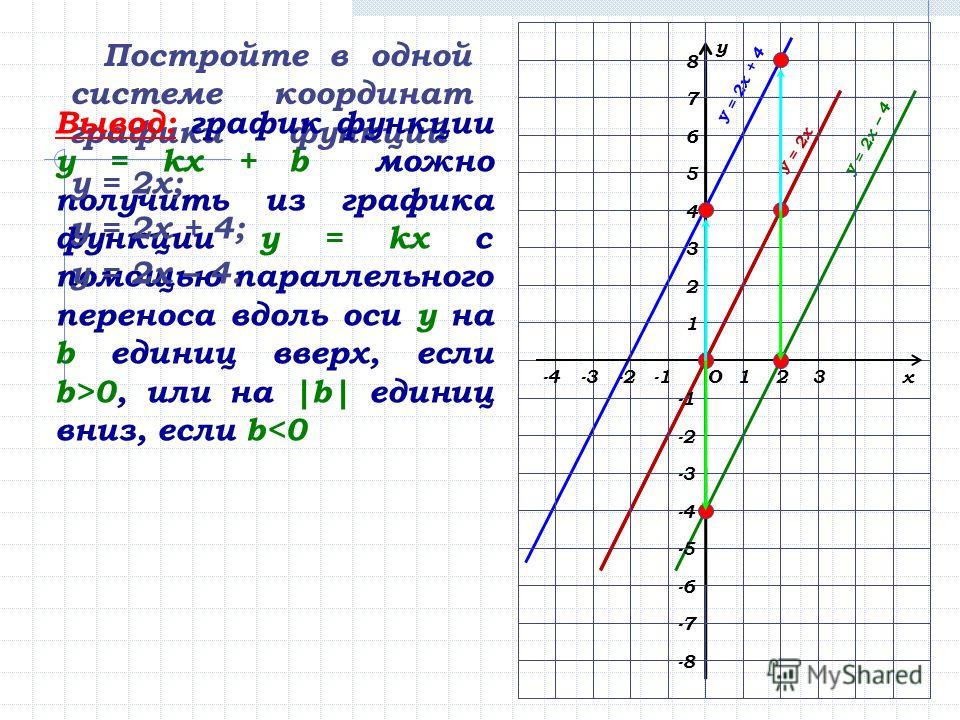 0034
0034 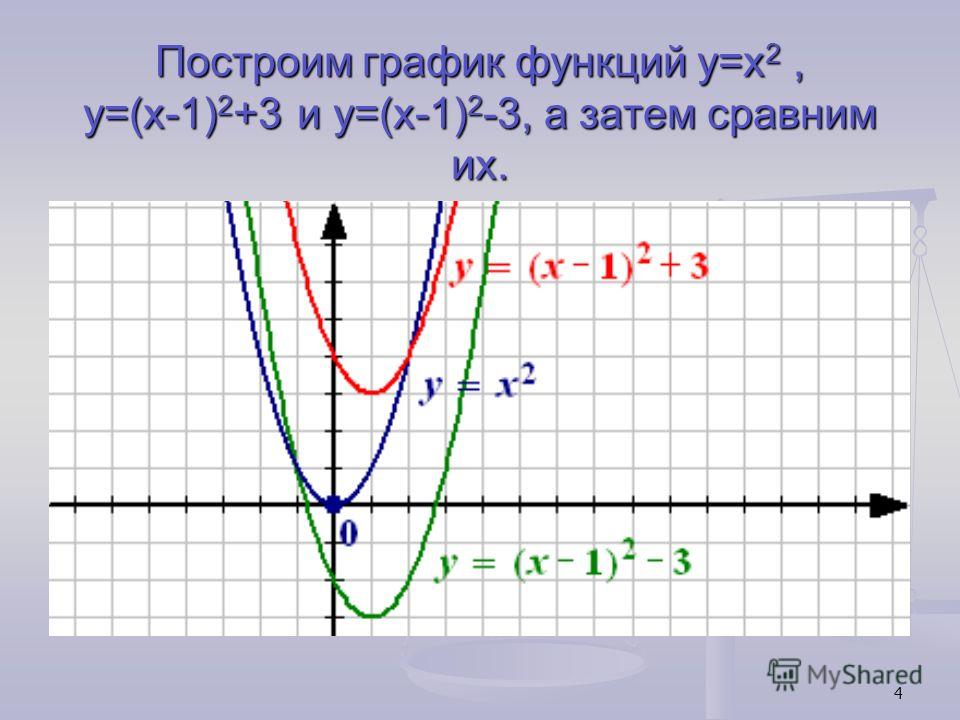 На самом деле любое уравнение вида y = b (или y = 0x + b) является горизонтальной линией с наклоном 0 (см. рис. 8.13). Теперь рассмотрим уравнение x = 2. Если y = 4, чему равно x? Если у = -3, что такое х? Если у = 0, то чему равен х? В каждом случае x = 2. Все точки (2, 4), (2, -3) и (2, 0) удовлетворяют условию x = 2. y может иметь любое значение, но x должно быть равно 2. Мы можно записать x = 2 в виде 0y + x = 2 или x = 0y + 2. График уравнения x = 2 представляет собой вертикальную линию, и каждая координата x равна 2 (см. рис. 8.14).
На самом деле любое уравнение вида y = b (или y = 0x + b) является горизонтальной линией с наклоном 0 (см. рис. 8.13). Теперь рассмотрим уравнение x = 2. Если y = 4, чему равно x? Если у = -3, что такое х? Если у = 0, то чему равен х? В каждом случае x = 2. Все точки (2, 4), (2, -3) и (2, 0) удовлетворяют условию x = 2. y может иметь любое значение, но x должно быть равно 2. Мы можно записать x = 2 в виде 0y + x = 2 или x = 0y + 2. График уравнения x = 2 представляет собой вертикальную линию, и каждая координата x равна 2 (см. рис. 8.14). 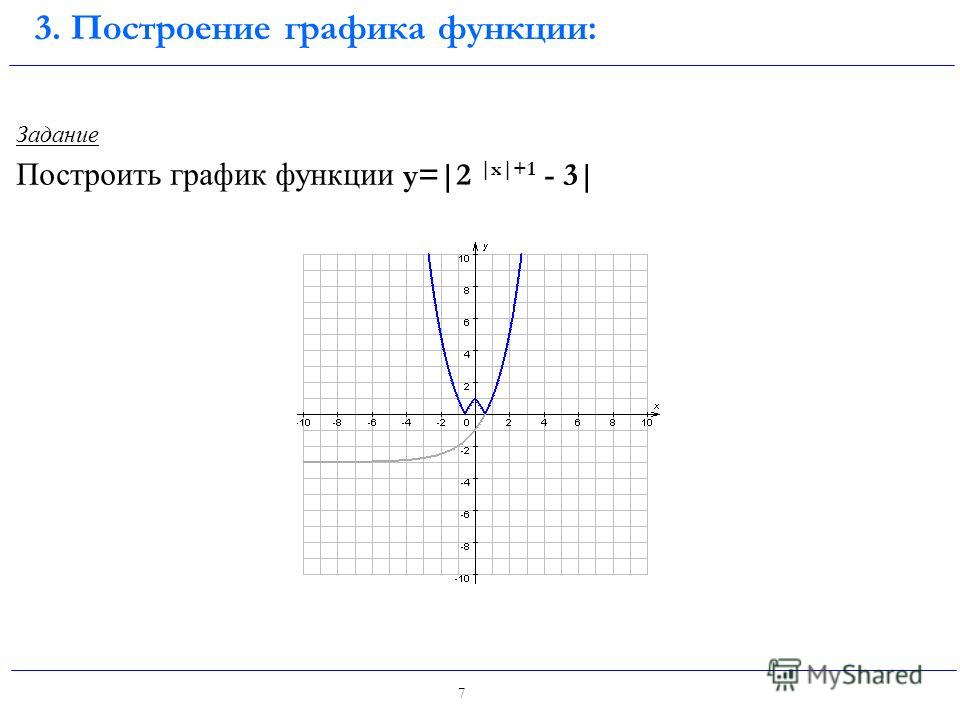 И уравнения для горизонтальных линий ((y = b)) и уравнения для вертикальных линий (x=a)) являются частными случаями общего линейного уравнения в стандартной форме Ax + By = C, обсуждаемого в разделе 8.2.
И уравнения для горизонтальных линий ((y = b)) и уравнения для вертикальных линий (x=a)) являются частными случаями общего линейного уравнения в стандартной форме Ax + By = C, обсуждаемого в разделе 8.2. 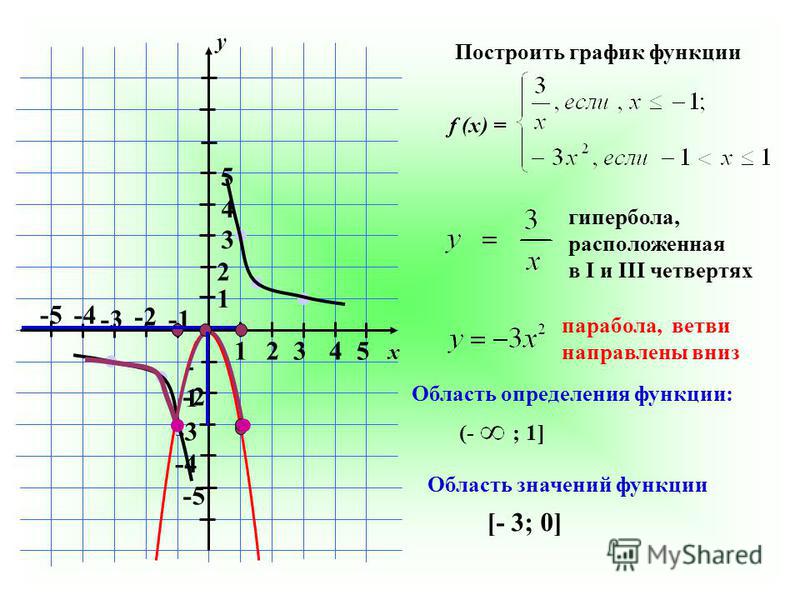 Вы нашли
Вы нашли 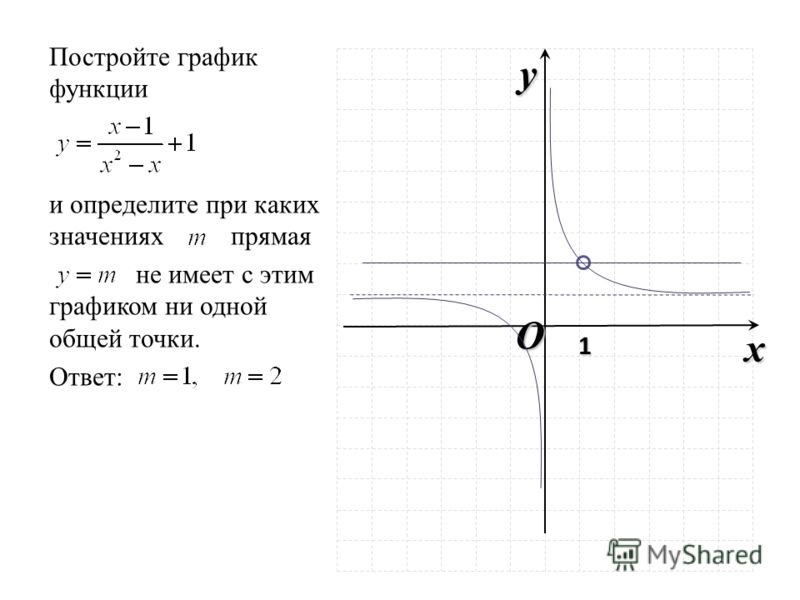 Нам нужна теорема Пифагора. Сформулированная здесь теорема Пифагора будет более подробно обсуждаться в разделе 10.6.
Нам нужна теорема Пифагора. Сформулированная здесь теорема Пифагора будет более подробно обсуждаться в разделе 10.6.  2 Линейные функции и их графики
2 Линейные функции и их графики  Переменная, определяющая значения других переменных. Обычно мы думаем о x -значение упорядоченной пары ( x , y ) как о независимой переменной. а y — зависимая переменная. Переменная, значение которой определяется значением независимой переменной. Обычно мы думаем о у -значение упорядоченной пары ( x , y ) в качестве зависимой переменной. Выберите не менее двух x -значений и найдите соответствующие y -значения. Рекомендуется выбирать ноль, некоторые отрицательные числа, а также некоторые положительные числа. Здесь мы выберем пять значений x , определим соответствующие значения y , а затем сформируем репрезентативный набор упорядоченных парных решений.
Переменная, определяющая значения других переменных. Обычно мы думаем о x -значение упорядоченной пары ( x , y ) как о независимой переменной. а y — зависимая переменная. Переменная, значение которой определяется значением независимой переменной. Обычно мы думаем о у -значение упорядоченной пары ( x , y ) в качестве зависимой переменной. Выберите не менее двух x -значений и найдите соответствующие y -значения. Рекомендуется выбирать ноль, некоторые отрицательные числа, а также некоторые положительные числа. Здесь мы выберем пять значений x , определим соответствующие значения y , а затем сформируем репрезентативный набор упорядоченных парных решений. 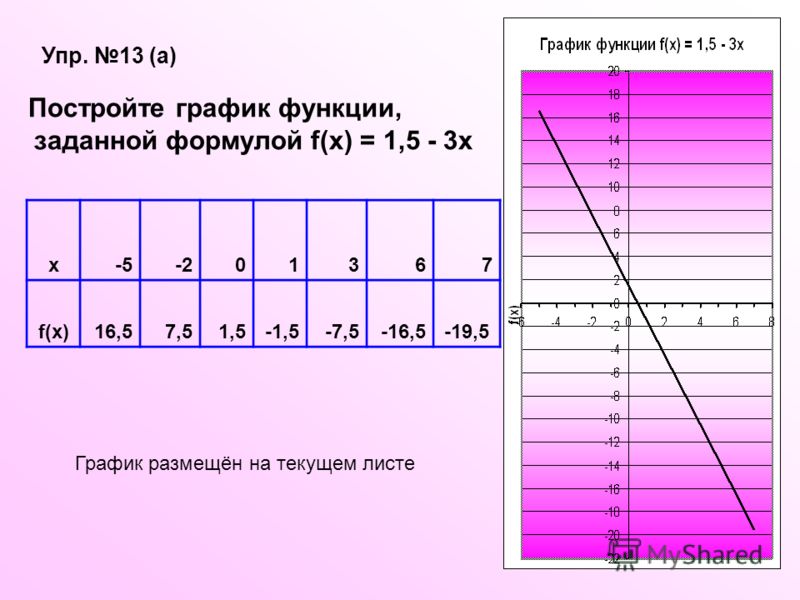 Вышеприведенный процесс описывает метод построения графика, известный как построение точек. Способ построения графика с использованием конечного числа репрезентативных упорядоченных парных решений. Этот метод будет использоваться для построения графиков более сложных функций по мере продвижения в этом курсе.
Вышеприведенный процесс описывает метод построения графика, известный как построение точек. Способ построения графика с использованием конечного числа репрезентативных упорядоченных парных решений. Этот метод будет использоваться для построения графиков более сложных функций по мере продвижения в этом курсе. 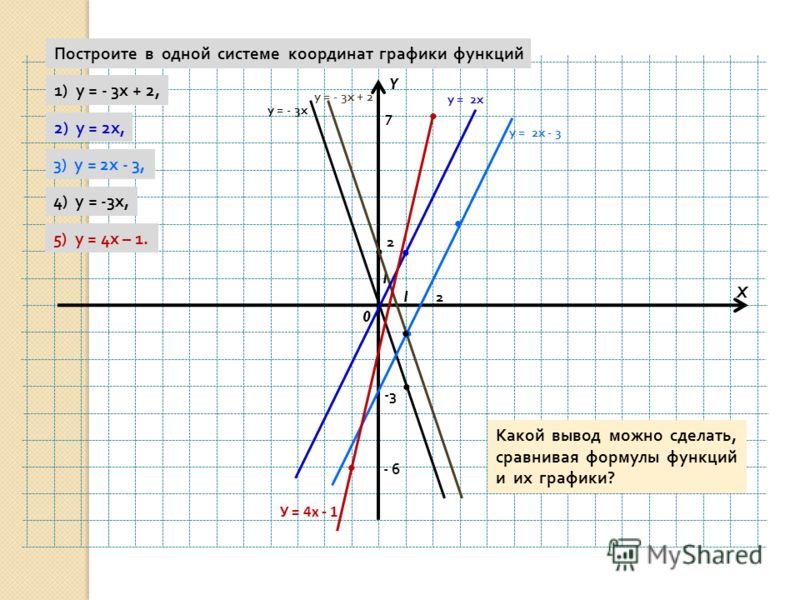
 Например, мы получим тот же результат, если применим формулу наклона с переключением точек:
Например, мы получим тот же результат, если применим формулу наклона с переключением точек: 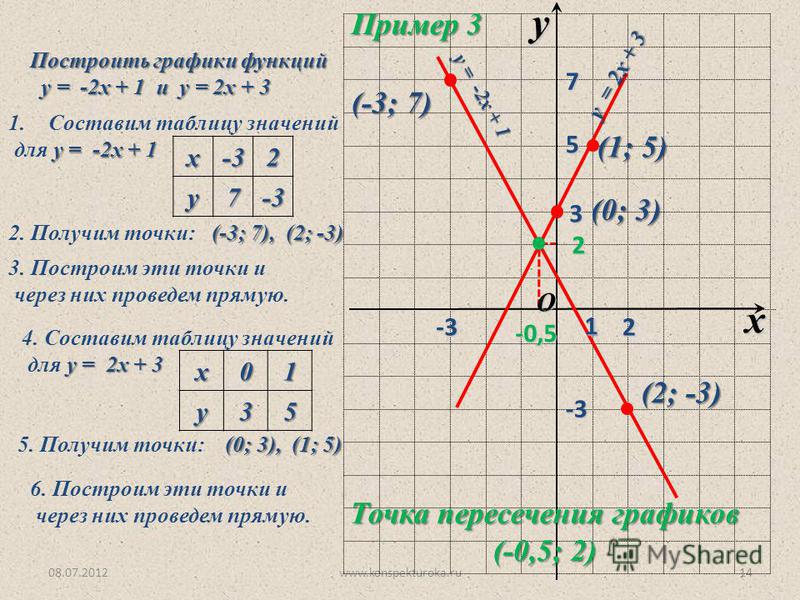
 Например,
Например, 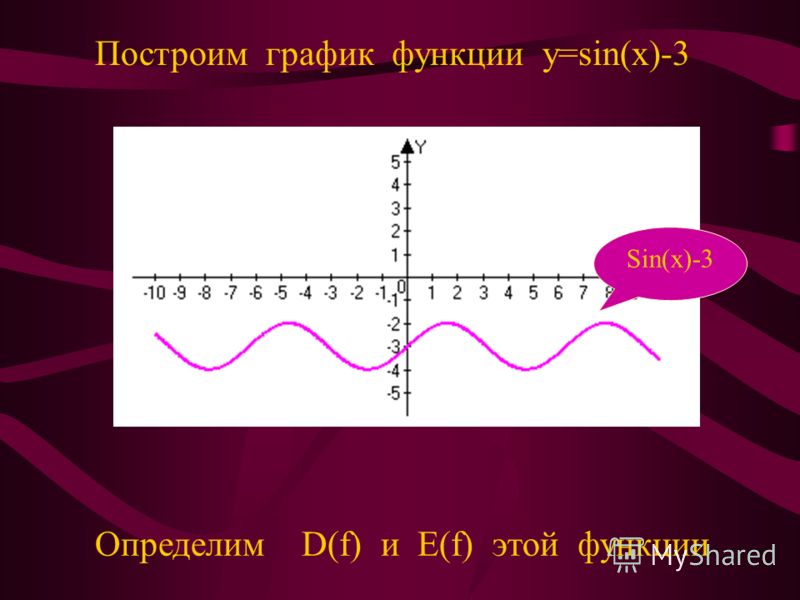 Поскольку y=f(x), мы можем использовать y и f(x) взаимозаменяемо, а упорядоченные парные решения на графе (x,y) можно записать в виде (x,f(x)).
Поскольку y=f(x), мы можем использовать y и f(x) взаимозаменяемо, а упорядоченные парные решения на графе (x,y) можно записать в виде (x,f(x)). 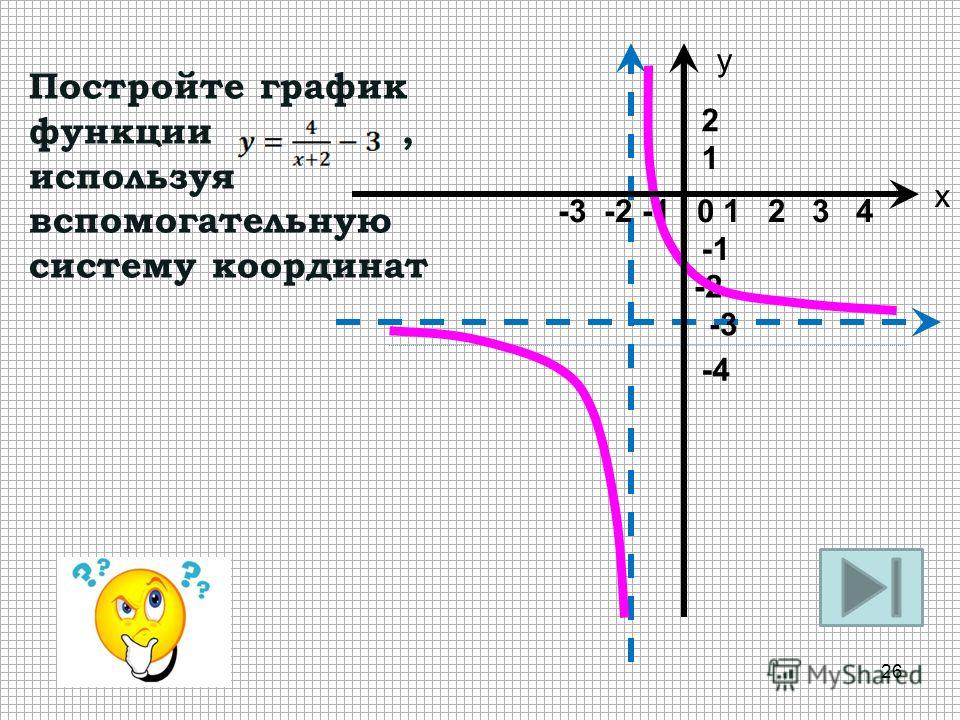 Начиная с точки пересечения и , отметьте вторую точку на 5 единиц вниз и на 3 единицы вправо. Проведите линию, проходящую через эти две точки, с помощью линейки.
Начиная с точки пересечения и , отметьте вторую точку на 5 единиц вниз и на 3 единицы вправо. Проведите линию, проходящую через эти две точки, с помощью линейки. 
 Для любого действительного числа c ,
Для любого действительного числа c , 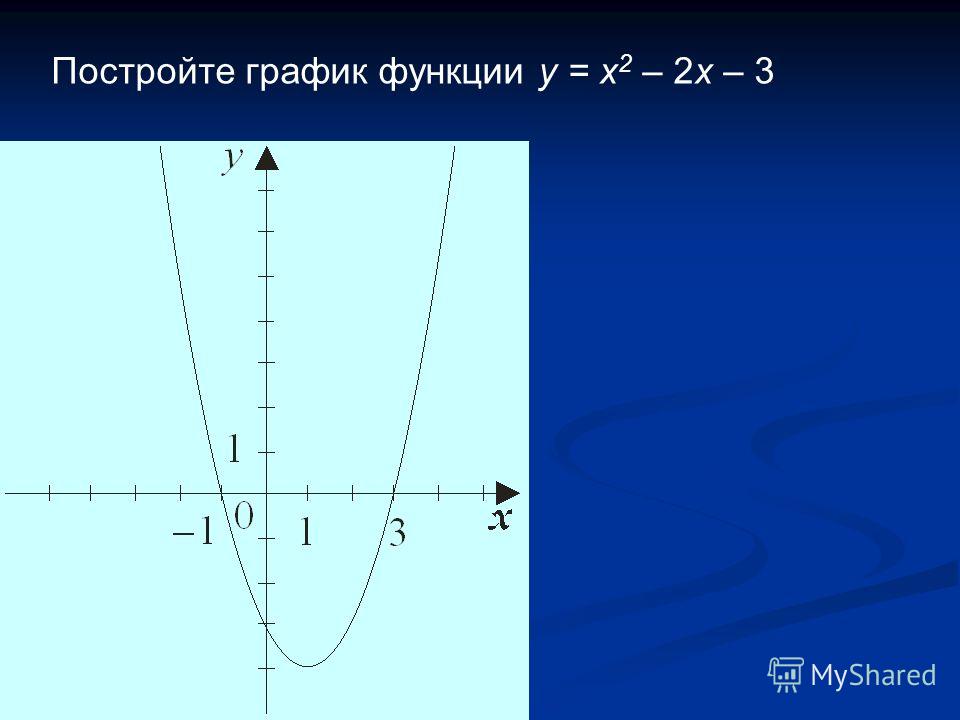 Идея состоит в том, чтобы построить графики линейных функций по обе стороны уравнения и определить, где графики совпадают.
Идея состоит в том, чтобы построить графики линейных функций по обе стороны уравнения и определить, где графики совпадают. 
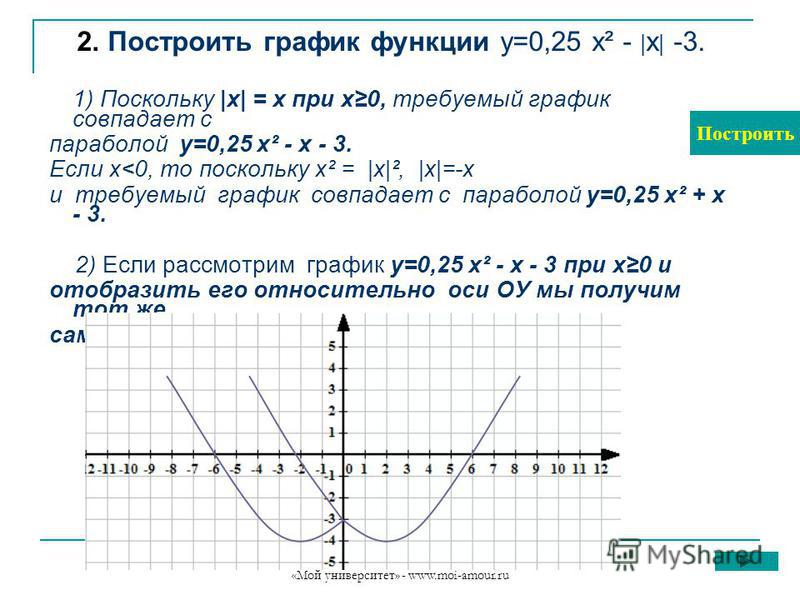

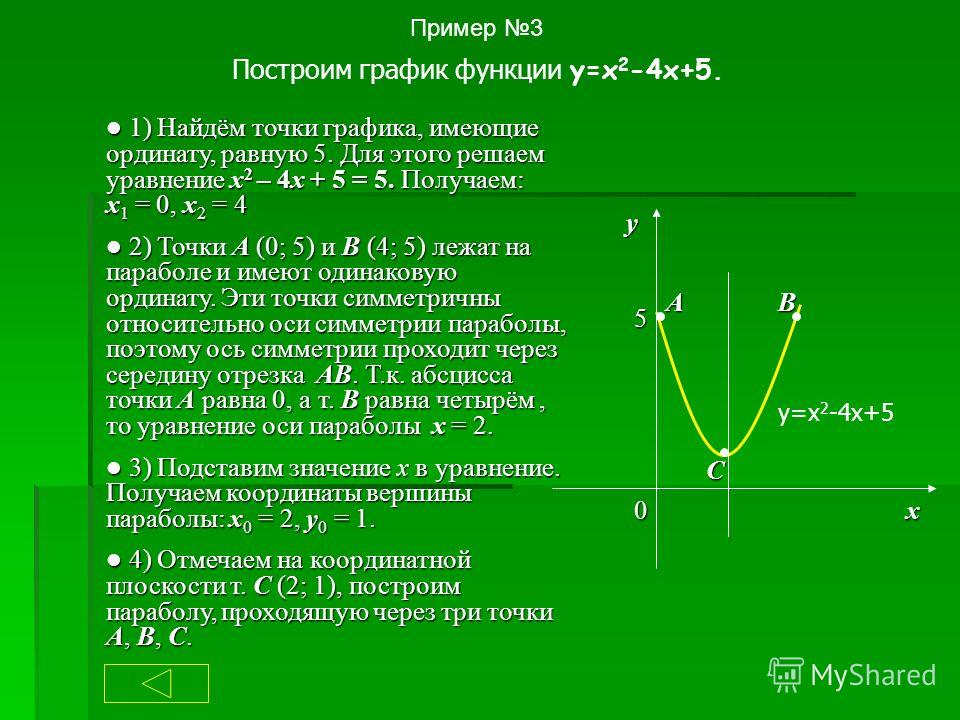

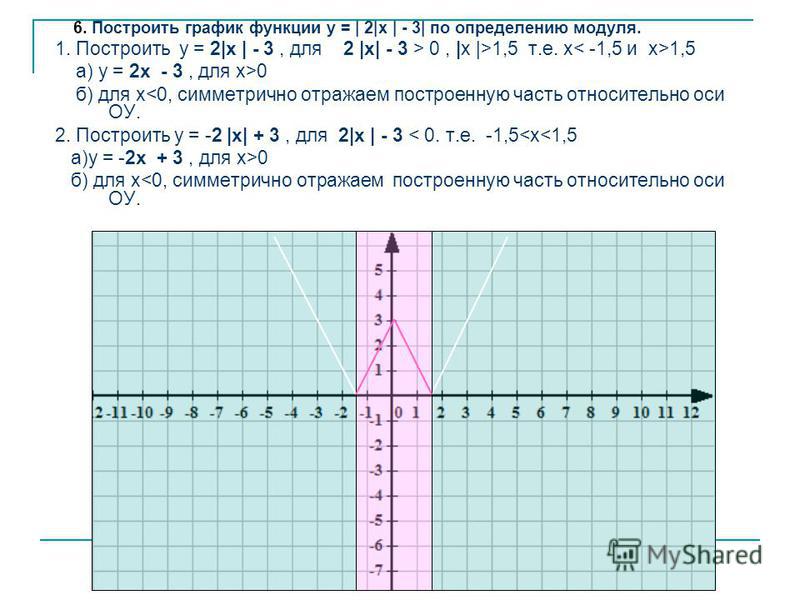
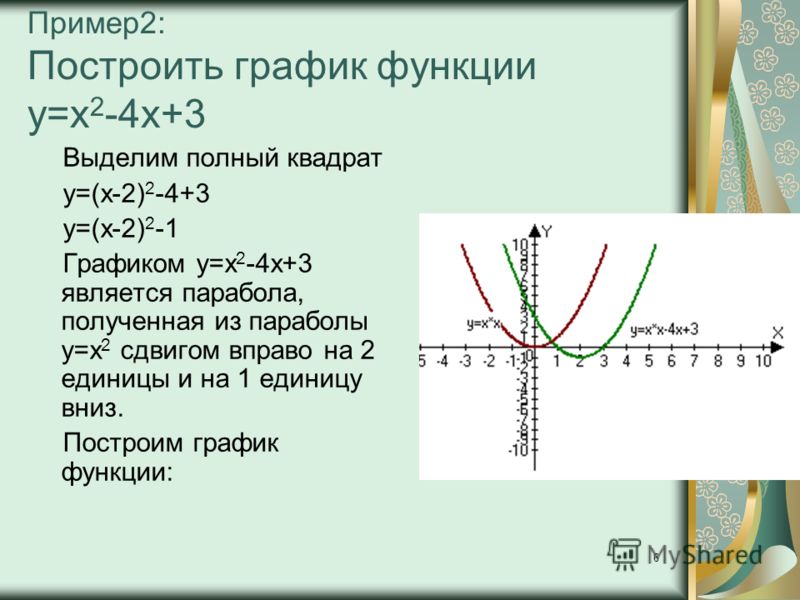 Подтвердите свой ответ алгебраически.
Подтвердите свой ответ алгебраически. 
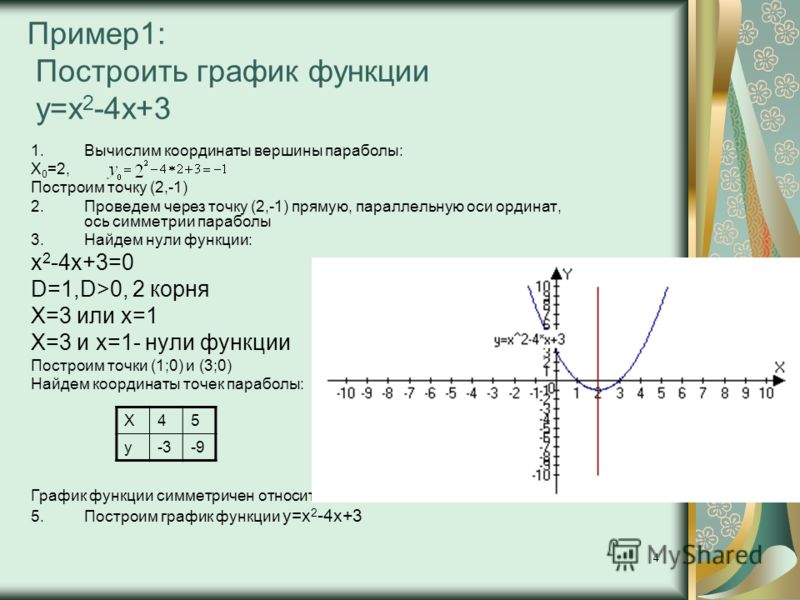 Мы также смогли увидеть точки функции, а также начальное значение на графике.
Мы также смогли увидеть точки функции, а также начальное значение на графике. 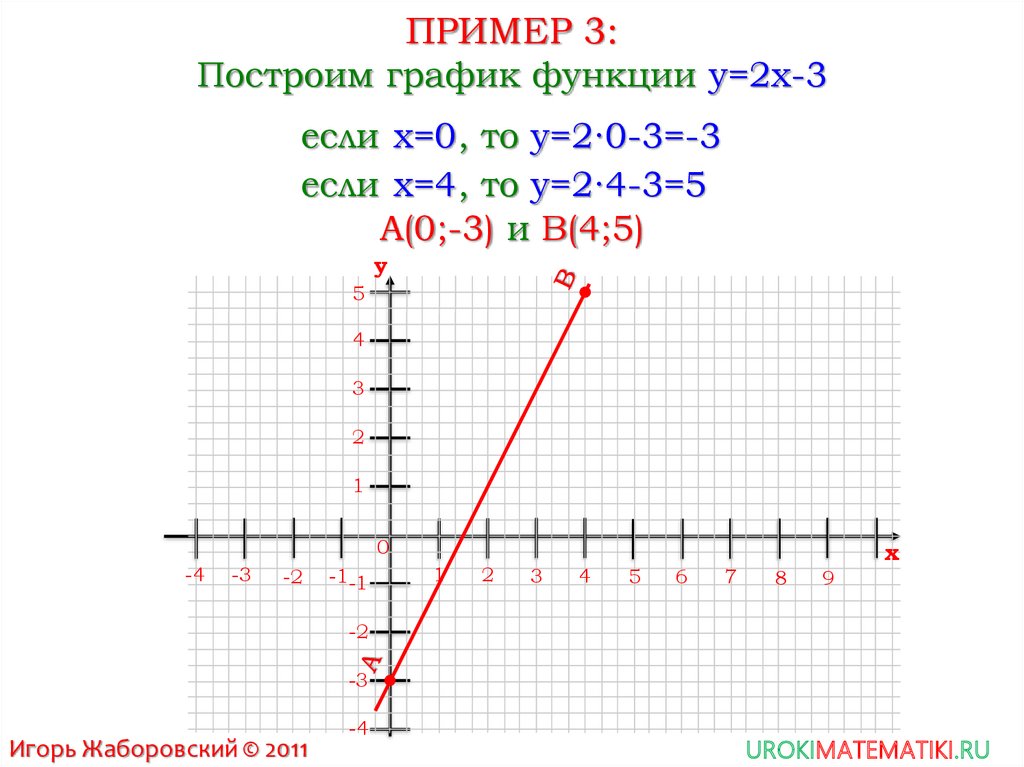 Оценка функции для входного значения 2 дает выходное значение 4, которое представлено точкой (2, 4). Часто рекомендуется выбирать три точки, потому что, если все три точки не лежат на одной линии, мы знаем, что допустили ошибку.
Оценка функции для входного значения 2 дает выходное значение 4, которое представлено точкой (2, 4). Часто рекомендуется выбирать три точки, потому что, если все три точки не лежат на одной линии, мы знаем, что допустили ошибку. 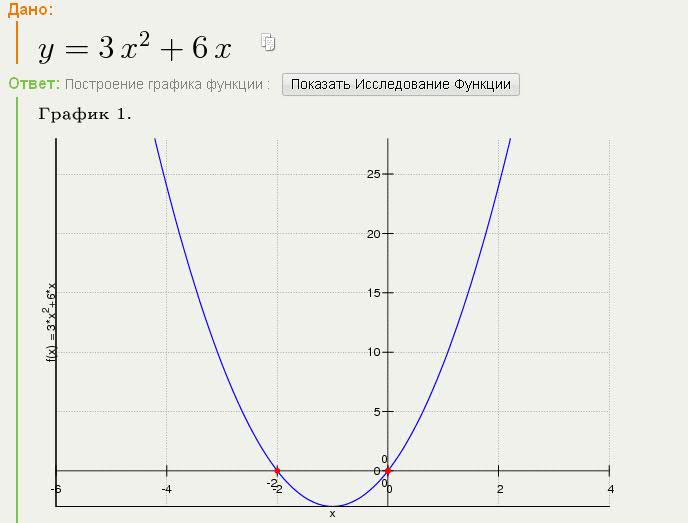 Первой характеристикой является точка пересечения y-, которая является точкой, в которой входное значение равно нулю. Чтобы найти у- перехват , мы можем установить [latex]x=0[/latex] в уравнении.
Первой характеристикой является точка пересечения y-, которая является точкой, в которой входное значение равно нулю. Чтобы найти у- перехват , мы можем установить [latex]x=0[/latex] в уравнении. 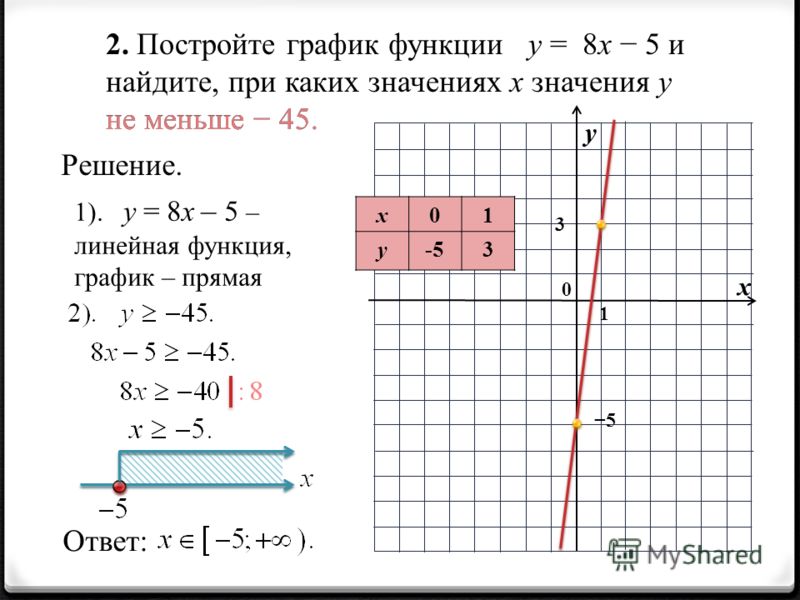 Точка пересечения y- представляет собой точку на графике, когда x = 0. График пересекает ось y в точке (0, 1). Теперь мы знаем наклон и точку пересечения и . Мы можем начать построение графика, нанеся точку (0, 1). Мы знаем, что наклон увеличивается по сравнению с пробегом, [латекс] м = \ гидроразрыва {\ текст {подъем}} {\ текст {прогон}} [/латекс]. В нашем примере у нас есть [latex]m=\frac{1}{2}[/latex], что означает, что подъем равен 1, а пробег равен 2. Начиная с нашего y -intercept (0, 1), мы можем подняться на 1, а затем подняться на 2 или подняться на 2, а затем подняться на 1. Мы повторяем, пока у нас не будет несколько точек, а затем мы проводим линию через точки, как показано ниже.
Точка пересечения y- представляет собой точку на графике, когда x = 0. График пересекает ось y в точке (0, 1). Теперь мы знаем наклон и точку пересечения и . Мы можем начать построение графика, нанеся точку (0, 1). Мы знаем, что наклон увеличивается по сравнению с пробегом, [латекс] м = \ гидроразрыва {\ текст {подъем}} {\ текст {прогон}} [/латекс]. В нашем примере у нас есть [latex]m=\frac{1}{2}[/latex], что означает, что подъем равен 1, а пробег равен 2. Начиная с нашего y -intercept (0, 1), мы можем подняться на 1, а затем подняться на 2 или подняться на 2, а затем подняться на 1. Мы повторяем, пока у нас не будет несколько точек, а затем мы проводим линию через точки, как показано ниже.