Предел (lim), предел последовательности
Мы уже знаем, что арифметическая и геометрическая прогрессии — это последовательность чисел. Давайте возьмем последовательность an = 1/n, если k
и m натуральные числа, тогда для каждого k верно ak > am, поэтому, чем больше становится
n тем меньше становится an и это число всегда позитивно, но никогда не становится равным нулю. В этом случае, мы говорим, что 0 есть
пределом lim an->∞ если n->∞, или, если записать по-другому: limn->∞ an = 0.
Определение предела
Число a называется пределом последовательности, если для каждого ε > 0 может быть найдено число nε, то для всех членов последовательности an with index n > nε верно, что a — ε n .
Основное правило
Если limn->∞ an = a, an -> a an — a -> 0 |an — a| -> 0
Последовательность не всегда имеет предел, а иногда имеет предел бесконечности ( -∞ or +∞ ). Пределы +∞ and -∞ называются соответсвенно пределом плюс бесконечности и минус бесконечности.
Пределы +∞ and -∞ называются соответсвенно пределом плюс бесконечности и минус бесконечности.
Если обе последовательности an and bn имеют действительные пределы, тогда последовательности
an + bn,
an — bn, an.bn и an / bn также имеют действительный предел и:
limn -> ∞(an + bn) = limn -> ∞an + limn -> ∞bn
limn -> ∞(an — bn) = limn -> ∞an — limn -> ∞bn
limn -> ∞(an . bn) = limn -> ∞an . limn -> ∞bn
limn -> ∞(an/ bn) = limn -> ∞an / limn -> ∞bn
если bn ≠ 0 and limn->∞bn ≠ 0
Если ann для каждого натурального n
и limn->∞an = a,
limn->∞bn = b
тогда a ≤ b
Если an ≤ bn ≤ cn или каждое действительное
n и если limn->∞an = limn->∞cn = A
тогда limn->∞bn = A.
Если an ≥ 0 и limn->∞an = a, тогда последовательность bn = √an также имеет предел и limn->∞√an = √an.
Если an = 1/nk и k ≥ 1 тогда limn->∞an = 0.
Если -1 n->∞qn = 0.
limn->∞(1 — 1/n)n = limn->∞(1 + 1/n)n+1 = e
(1+1/n)nn-1
e is the number of Neper.
Если последовательность an имеет предел бесконечность ( -∞ или +∞ ) тогда последовательность 1/an имеет предел и limn->∞1/an = 0
Если последовательности an иbn имеют бесконечные пределы и limn->∞an=+∞, limn->∞bn=+∞ тогда:
limn->∞(an + bn) = +∞
limn->∞(an . bn) = +∞
bn) = +∞
limn->∞ank = +∞ если k > 0
limn->∞ank = 0; если k
limn->∞-an = -∞
Упражнения с пределами
Упражнение 1:
Если an = 5.4n, limn->0an = ?
Ответ:
limn->0an = limn->05 . limn->04n = 5 . 40 = 5.1 = 5
Упражнение 2:
| Если an = | then limn->∞an = ? |
Ответ:
| limn->∞ | = limn->∞ | . | = limn->∞ | = -3 |
Упражнение 3:
Ответ:
| liman->1 = | = | liman->∞ | = |
Больше о пределах на страницах математического форума
Для участия в математическом форуме регистрация не требуется!
Предел последовательности
4.1Примеры и мотивировка
В этой лекции мы введём, пожалуй, главное понятие математического анализа — понятие предела. Это сложное понятие. Человеческий мозг не привык работать с бесконечностями. Думая про какую-то последовательность, мы как правило представляем себе лишь её первые несколько элементов. Сейчас же нам предстоит вглядеться в бесконечный хвост последовательности и понять, как он устроен.Пусть есть последовательность {an}. Можно думать про неё как про последовательность результатов измерения какого-то параметра (скажем, населения некоторой страны) в последовательные моменты времени (например, каждый год). Правда, в отличие от реальных результатов измерения, наша последовательность простирается бесконечно далеко в будущее, и именно это «бесконечное будущее» нас и интересует. Есть ли какое-то значение A, к которому члены последовательности будут становиться всё ближе и ближе — так, что, со временем их будет всё сложнее и сложнее отличить от A?
Давайте рассмотрим несколько примеров.
4.1.1Последовательность 1/2n
Пусть an=12n. Давайте выведем первые двадцать членов этой последовательности. Я написал для этого короткий код на языке Python, который приведён ниже вместе с результатом его выполнения. Код можно скрывать и открывать, нажимая на кнопку-уголок. Если вы не знаете Python, ничего страшного — для понимания он не понадобится. Но если знаете, возможно, вам будет интересно самостоятельно проводить эксперименты, похожие на приведенные.print("n a_n")
for n in range(1, 21):
a_n = 1 / 2 ** n
print(f"{n} {a_n:0.5f}")
# 0.5f означает, что будут выведены 5 знаков после десятичной точкиn a_n
1 0.50000
2 0.25000
3 0.12500
4 0.06250
5 0.03125
6 0.01562
7 0.00781
8 0.00391
9 0.00195
10 0.00098
11 0.00049
12 0.00024
13 0.00012
14 0.00006
15 0.00003
16 0.00002
17 0.00001
18 0.00000
19 0.00000
20 0.00000
Но ведь можно увеличить точность! Давайте отображать шесть цифр после запятой!
print("n a_n")
for n in range(1, 21):
a_n = 1 / 2 ** n
print(f"{n} {a_n:0.6f}")
# 0.6f означает, что будут выведены 6 знаков после десятичной точкиn a_n
1 0.500000
2 0.250000
3 0.125000
4 0.062500
5 0.031250
6 0.015625
7 0.007812
8 0.003906
9 0.001953
10 0.000977
11 0.000488
12 0.000244
13 0.000122
14 0.000061
15 0.000031
16 0.000015
17 0.000008
18 0.000004
19 0.000002
20 0.000001
print("n a_n")
for n in range(20, 25):
a_n = 1 / 2 ** n
print(f"{n} {a_n:0.6f}")
# 0.6f означает, что будут выведены 6 знаков после десятичной точкиn a_n
20 0.000001
21 0.000000
22 0.000000
23 0.000000
24 0.000000
print("n a_n")
for n in range(20, 25):
a_n = 1 / 2 ** n
print(f"{n} {a_n:0.7f}")
# 0.7f означает, что будут выведены 6 знаков после десятичной точкиn a_n
20 0.0000010
21 0.0000005
22 0.0000002
23 0.0000001
24 0.0000001
print("n a_n")
for n in range(24, 30):
a_n = 1 / 2 ** n
print(f"{n} {a_n:0.7f}")
# 0.7f означает, что будут выведены 6 знаков после десятичной точкиn a_n
24 0.0000001
25 0.0000000
26 0.0000000
27 0.0000000
28 0.0000000
29 0.0000000
Это и означает, что она стремится к нулю.
4.1.2Последовательность n+1n
Пусть теперь an=n+1n. Тоже можно вывести первые несколько значений.print("n a_n")
for n in range(1, 10):
a_n = (n + 1) / n
print(f"{n} {a_n:0.5f}") n a_n
1 2.00000
2 1.50000
3 1.33333
4 1.25000
5 1.20000
6 1.16667
7 1.14286
8 1.12500
9 1.11111
import matplotlib.pyplot as plt
import numpy as np
import qqmbr.odebook as ob
# see https://github.com/ischurov/qqmbr/blob/master/qqmbr/odebook.py
nmax = 20
n = np.arange(1, nmax + 1)
plt.plot(n, (n + 1) / n, 'o', markersize=4, label='$y=a_n$')
plt.xticks(range(0, nmax + 1))
plt.legend()
ob.center_spines(grid=False, minor_ticks=False)
ob.settle_axes(xmin=-0.9, xmax=nmax + 1, ymin=-0.4, ymax=2.9,
xlabel="n", ylabel="y") import matplotlib.pyplot as plt
import numpy as np
import qqmbr.odebook as ob
# see https://github.com/ischurov/qqmbr/blob/master/qqmbr/odebook.py
nmax = 20
n = np.arange(1, nmax + 1)
plt.plot(n, (n + 1) / n, 'o', markersize=4, label='$y=a_n$')
n_full = np.linspace(0, nmax + 1)
plt.plot(n_full, np.ones_like(n_full), label='$y=1$')
plt.xticks(range(0, nmax + 1))
plt.legend()
ob.center_spines(grid=False, minor_ticks=False)
ob.settle_axes(xmin=-0.9, xmax=nmax + 1, ymin=-0.4, ymax=2.9,
xlabel="n", ylabel="y") import matplotlib.pyplot as plt
import numpy as np
import qqmbr.odebook as ob
# see https://github.com/ischurov/qqmbr/blob/master/qqmbr/odebook.py
nmax = 75 ##
n = np.arange(1, nmax + 1)
plt.plot(n, (n + 1) / n, 'o', markersize=4, label='$y=a_n$')
n_full = np.linspace(0, nmax + 1)
plt.plot(n_full, np.ones_like(n_full), label='$y=1$')
#plt.xticks(range(0, nmax + 1))
plt.legend()
ob.center_spines(grid=False, minor_ticks=False)
ob.settle_axes(xmin=-0.9, xmax=nmax + 1, ymin=-0.4, ymax=2.9,
xlabel="n", ylabel="y") import matplotlib.pyplot as plt
import numpy as np
import qqmbr.odebook as ob
# see https://github.com/ischurov/qqmbr/blob/master/qqmbr/odebook.py
nmax = 75 ##
n = np.arange(1, nmax + 1)
plt.plot(n, (n + 1) / n, 'o', markersize=2, label='$y=a_n$')
n_full = np.linspace(0, nmax + 1)
plt.plot(n_full, np.ones_like(n_full), label='$y=1$')
#plt.xticks(range(0, nmax + 1))
plt.legend()
ob.center_spines(grid=False, minor_ticks=False)
ob.settle_axes(xmin=-0.9, xmax=nmax + 1, ymin=0, ymax=1.11,
xlabel="n", ylabel="y") import matplotlib.pyplot as plt
import numpy as np
import qqmbr.odebook as ob
# see https://github.com/ischurov/qqmbr/blob/master/qqmbr/odebook.py
nmax = 420
n = np.arange(1, nmax + 1)
plt.plot(n, (n + 1) / n, 'o', markersize=2, label='$y=a_n$')
n_full = np.linspace(0, nmax + 1)
plt.plot(n_full, np.ones_like(n_full), label='$y=1$')
#plt.xticks(range(0, nmax + 1))
plt.legend()
ob.center_spines(grid=False, minor_ticks=False)
ob.settle_axes(xmin=-0.9, xmax=nmax + 1, ymin=0, ymax=1.11,
xlabel="n", ylabel="y") Так можно продолжать до бесконечности. Увеличивать масштаб вертикальной оси (и следовательно нашу способность различать близкие точки) — находить зазор — увеличивать количество точек — делать зазор неразличимым.
В общем, можно предположить, что наша последовательность стремится к числу 1. В принципе, это неудивительно. Можно преобразовать формулу для общего члена последовательности:
an=n+1n=1+1n
Когда n становится очень большим, 1n становится очень маленьким, поэтому вся сумма становится очень близкой к 1. Что мы и видим на графике.4.1.4«Скачущая» последовательность
При рассмотрении предыдущих примеров, у вас могло возникнуть искушение дать такое определение: «последовательность {an} стремится к какому-то числу a, если её члены с ростом n становятся всё ближе и ближе к a: каждый следующий член ближе, чем предыдущий».Более внимательный анализ показывает, что это определение неверно. Например, последовательность n+1n, которую мы только что рассматривали, «становится всё ближе и ближе» не только к 1, но и, например, к 0 — причём каждый следующий член ближе, чем предыдущий. Тем не менее, нельзя сказать, что она стремится к 0.
Более того, требование «каждый следующий член ближе, чем предыдущий», оказывается излишним.
Давайте рассмотрим такую последовательность:
an={n+1n,n — нечётное;n+3n,n — чётное.
Её первые члены выглядят следующим образом:2, 52, 43, 74, 65,…
График этой последовательности изображен на рис. 4.6. Тут видно, что требование «каждый следующий элемент ближе к 1, чем предыдущий», нарушается: элементы с чётными номерами ближе к 1, чем элементы с нечётными номерами.import matplotlib.pyplot as plt
import numpy as np
import qqmbr.odebook as ob
# see https://github.com/ischurov/qqmbr/blob/master/qqmbr/odebook.py
nmax = 20
n = np.arange(1, nmax + 1)
plt.plot(n, 1 + np.where(n % 2 == 1, 1 / n, 3 / n),
'--o', markersize=4, label='$y=a_n$')
plt.xticks(range(0, nmax + 1))
n_full = np.linspace(0, nmax + 1)
plt.plot(n_full, np.ones_like(n_full), label='$y=1$')
plt.legend()
ob.center_spines(grid=False, minor_ticks=False)
ob.settle_axes(xmin=-0.9, xmax=nmax + 1, ymin=0, ymax=3.11,
xlabel="n", ylabel="y") import matplotlib.pyplot as plt
import numpy as np
import qqmbr.odebook as ob
# see https://github.com/ischurov/qqmbr/blob/master/qqmbr/odebook.py
nmax = 90
n = np.arange(1, nmax + 1)
plt.plot(n, 1 + np.where(n % 2 == 1, 1 / n, 3 / n), '--o', markersize=4, label='$y=a_n$')
# plt.xticks(range(0, nmax + 1))
n_full = np.linspace(0, nmax + 1)
plt.plot(n_full, np.ones_like(n_full), label='$y=1$')
plt.legend()
ob.center_spines(grid=False, minor_ticks=False)
ob.settle_axes(xmin=-0.9, xmax=nmax + 1, ymin=0, ymax=3.11,
xlabel="n", ylabel="y") 4.1.5Последовательности без предела
Последовательности, рассмотренные выше, стремились к какому-то числу. Приведём несколько примеров последовательностей, у которых предела нет. Пример 1. Последовательность an=n2:1, 4, 9, 16,…
Эта последовательность неограничена, и выглядит очевидным, что она не стремится ни к какому числу. У неё нет предела. Пример 2. Последовательностьan=(−1)n+1n.(4.1)
В зависимости от чётности n, первое слагаемое оказывается равно 1 или −1. Посмотрим, как выглядит график этой последовательности (рис. 4.8).import matplotlib.pyplot as plt
import numpy as np
import qqmbr.odebook as ob
# see https://github.com/ischurov/qqmbr/blob/master/qqmbr/odebook.py
nmax = 20
n = np.arange(1, nmax + 1)
plt.plot(n, (-1) ** n + 1 / n, '--o', markersize=4, label='$y=a_n$')
plt.xticks(range(0, nmax + 1))
n_full = np.linspace(0, nmax + 1)
plt.plot(n_full, np.ones_like(n_full), label='$y=1$')
plt.plot(n_full, -np.ones_like(n_full), label='$y=-1$')
plt.legend()
ob.center_spines(grid=False, minor_ticks=False)
ob.settle_axes(xmin=-0.9, xmax=nmax + 1, ymin=-1.9, ymax=1.9,
xlabel="n", ylabel="y") an={12,∃k∈N:n=2k;n+1n,∀k∈N:n≠2k.(4.2)
Эта последовательность устроена так. Для тех n, которые являются степенями двойки (1, 2, 4, 8, 16 и т.д.), an равно 12. Для остальных n, an равно n+1n. Посмотрим на график на рис. 4.9.import matplotlib.pyplot as plt
import numpy as np
import qqmbr.odebook as ob
# see https://github.com/ischurov/qqmbr/blob/master/qqmbr/odebook.py
nmax = 20
n = np.arange(1, nmax + 1)
plt.plot(n, np.where(np.isclose(np.log2(n) % 1, 0), 0.5, (n + 1) / n),
'--o', markersize=4, label='$y=a_n$')
plt.xticks(range(0, nmax + 1))
n_full = np.linspace(0, nmax + 1)
plt.plot(n_full, np.ones_like(n_full), label='$y=1$')
plt.legend()
ob.center_spines(grid=False, minor_ticks=False)
ob.settle_axes(xmin=-0.9, xmax=nmax + 1, ymin=-0.4, ymax=1.9,
xlabel="n", ylabel="y") Тем не менее, нельзя сказать, что её предел равен 1. Мы знаем, что с какого бы начального момента времени мы ни стартовали, рано или поздно n окажется степенью двойки, и в этот момент последовательность «скакнёт» в число 1/2, уйдя от 1 на заметное расстояние.
4.2Определение предела
4.2.1Интуитивные соображения
Из обсуждения в предыдущем разделе должно быть понятно — по крайней мере, на интуитивном уровне — чего бы мы хотели потребовать от последовательности, чтобы сказать, что она стремится к некоторому числу A. Подведём промежуточный итог.- Первые сколько-то членов могут быть достаточно далеки от A, это никак не мешает последовательности стремиться к A. Иными словами, «стремление» — это эффект, который зависит только от «хвоста» последовательности.
- Для достаточно больших значениий n члены последовательности должны становиться настолько близкими к A, чтобы их нельзя было отличить от A, скажем, на графике или на компьютерной распечатке, на которой числа выводятся с конечной точностью.
- Этот эффект должен сохраняться для всех достаточно больших n. Если последовательность время от времени «убегает» от A на какое-то заметное расстояние, и это происходит сколь угодно далеко в будущем, последовательность не будет стремиться к A.
- Мы можем увеличить точность измерения — например, выводить больше цифр после запятой или увеличить масштаб на графике — и увидеть зазор между членами последовательности и числом A. Однако, мы можем взять ещё большие значения n, чтобы эффект «неразличимости» вернулся.
4.2.2Вспомогательные понятия
Нам потребуется несколько вспомогательных определений и обозначений. Определение 1. Расстоянием между вещественными числами a и b называется модуль их разности: |a−b|. Это довольно естественное определение, если думать про числа как про точки на числовой прямой, см. рис. 4.10. Рис. 4.10: Модуль разности — это расстояние между числами как точками числовой прямой.Буквой ε (читается «эпсилон» — почему-то со слуха часто кажется, что там в конце есть буква «т» — нет, её нет) мы будем обозначать положительные и как правило маленькие вещественные числа.
Определение 2. Скажем, что два числа ε-близки («эпсилон-близки») друг к другу, если расстояние между ними меньше ε.
Вместо ε здесь можно подставлять другие буквы или конкретные числа — например, δ-близки («дельта-близки») или 0,1-близки. Скажем, утверждение «число π 0,1-близко к числу 3,14» является верным, поскольку расстояние между π и 3,14 (модуль разности) меньше, чем 0,1. Числа a и b будут ε-близки, если модуль их разности меньше ε: |a−b|<ε.
Определение 3. Рассмотрим последовательность {an}. Скажем, что её хвост ε-близок к числу A, если все её члены, начиная с некоторого, ε-близки к A. Иными словами, если все члены, начиная с некоторого, находятся на расстоянии меньше ε от A.Формально это записывается так:
∃N∈N ∀n∈N:(n>N)⇒|an−A|<ε.(4.3)
∃N∈N ∀n∈N:(n>N)⇒⇒|an−A|<ε.(4.3)
Здесь сказано, что найдётся такой номер N, что все члены последовательности с номерами от N+1 и больше находятся на расстоянии меньше ε от A.Импликация в этом определении говорит, что нас интересует выполнение условия |an−A|<ε не для всех n, а только для тех, для которых выполнено n>N, то есть «начиная с некоторого члена»; если оно нарушается для членов с меньшими номерами, это не будет нарушать утверждение, поскольку в этом случае посылка импликации n>N окажется ложной, и значит импликация будет истинной. Более кратко это определение можно записать так:
∃N∈N ∀n>N:|an−A|<ε.
На рис. 4.11 приведена иллюстрация к этому определению. Множество точек, ε-близких к точке A — это интервал (A−ε,A+ε). Если на графике последовательности нарисовать горизонтальные прямые y=A+ε и y=A−ε, они образуют своего рода коридор вокруг A (его можно назвать ε-коридором). Утверждение, что хвост последовательности ε-близок к A, означает, что начиная с некоторого номера n=N+1, все члены последовательности находятся в интервале (A−ε,A+ε), а соответствующие им точки на графике живут в нарисованном нами ε-коридоре. Точки с номерами меньше или равными N, могут как принадлежать коридору, так и выходить из него.
Рис. 4.11: Хвост последовательности ε-близок к числу A.Заметим, что в этом определении не сказано, с какого именно члена начинается «хвост последовательности». Более того, для одной и той же последовательности «хвосты» могут быть разными, в зависимости от ε.
Пример 4. Рассмотрим последовательность an=1n. Её хвост 0,1-близок к 0. Действительно, возьмём N=10. Для всех n>N, an меньше 0,1 (поскольку n больше 10 обратная величина 1/n меньше 1/10).
Вопрос 1. Верно ли, что хвост последовательности an=1n является 0,01-близким к 0? Нет, потому что существуют n>10, при которых расстояние между an и 0 больше, чем 0,01 — например, n=20, an=120=0,05, |an−0|=|an|=0,05>0,01.Неверный ответ. Это рассуждение неверно: совсем не обязательно в качестве N брать именно 10, можно попробовать подобрать другое число, так, чтобы требование выполнялось.
Неизвестно, зависит от N.Неверный ответ. Нет, в формуле (4.3) переменная N является связанной (на неё «навешан» квантор) — мы не спрашиваем, при каких N верно или неверно то-то и то-то — мы спрашиваем, «найдётся ли такое N?»
Да, верно.Верный ответ. Конечно! Чему равняется N?
10Неверный ответ. Не-а.
20Неверный ответ. Нет.
100Верный ответ. Да, например, 100 подойдёт. (Или любое большее число.)
Пример 5. Последовательность из примера 2 (см. (4.1)) имеет хвост, 1,2-близкий к числу 0, однако неверно, что её хвост 0,9-близок к 0. Вопрос 2. Для какого ε хвост этой последовательности ε-близок к числу 1? ε=0,5Неверный ответ. Нет, у последовательности есть члены со сколь угодно большими номерами, лежащие на расстоянии больше 0,5 от 1 — например, все члены с нечётными номерами.
ε=1,5Неверный ответ. Нет, у последовательности есть члены со сколь угодно большими номерами, лежащие на расстоянии больше 0,5 от 1 — например, все члены с нечётными номерами, большими 2 (хотя a1=0 находится на расстоянии 1 от числа 1).
ε=2Верный ответ. Верно!
Ни для какого.Неверный ответ. Нет, неверно.
Теперь мы готовы к Самому Главному Определению.
4.2.3Аккуратное определение предела
Мы хотим дать определение понятию, которое бы формализовало утверждение о том, что члены последовательности an с ростом n становятся очень-очень близки к некоторому фиксированному числу A — так, что, начиная с некоторого момента, мы их практически не можем отличить от A.Понятие ε-близости призвано формализовать идею о том, что два числа близки, если расстояние между ними маленькое. Можно думать, что ε — это точность или разрешающая способность наших измерительных приборов (чем меньше ε, тем точнее приборы). В этом случае если два числа отличаются меньше, чем на ε, у нас нет практической возможности их различить, для нас они совпадают. Например, если мы печатаем все числа лишь с двумя знаками после запятой, мы можем не различить два числа, расстояние между которыми меньше 0,001.
Но какой ε «достаточно маленький»? В отличие от других дисциплин, в математике нет никакого естественного масштаба. С точки зрения географии, расстояние в 1/10 метра — это очень маленькое расстояние — потому что мы сравниваем его с типичными объектами, изучаемыми географией — странами, городами, морями. А с точки зрения микробиологии — фантастически большое — по сравнению с бактериями или ядром клетки. С точки зрения математики, невозможно даже задать вопрос «является ли 1/10 маленьким числом?» — потому что непонятно, с чем его сравнивать. Поэтому мы не можем выбрать какой-то конкретный ε и сказать: «последовательность стремится к A, если её члены, начиная с некоторого, ε-близки к A». Как же быть?
Очень просто. Мы потребуем, чтобы утверждение «хвост последовательности ε-близок к A», выполнялось для любого положительного ε. Какой бы ни была разрешающая способность наших измерительных приборов, если подождать достаточно долго, мы перестанем отличать члены нашей последовательности от A.
Определение 4. Последовательность {an} имеет предел A, если для всякого ε>0 её хвост ε-близок к A.Формально:
∀ε>0 ∃N∈N ∀n>N:|an−A|<ε.(4.4)
∀ε>0 ∃N∈N ∀n>N:|an−A|<ε.(4.4)
Если последовательность {an} имеет предел A, говорят также, что она стремится к A.Коротко пишут так:
limn→∞an=A,
(читается «предел при n стремящемся к бесконечности от an равен A») илиan→A при n→∞,
(читается «an стремится к A при n стремящемся к бесконечности»).Последовательность, имеющая предел, называется также сходящейся, а не имеющая предела — расходящейся.
Заметим, что в определении предела, число N (граница «хвоста последовательности») выбирается в зависимости от ε — для разных ε получаются разные N. Если последовательность {an} стремится к A, гарантируется, что для любого ε найдётся «хорошее» N. Часто бывает удобно это «хорошее» N, подходящее для какого-то ε, обозначать через N(ε). (Вообще говоря, это N определяется не единственным образом — например, если N подходит, то N+1 тоже подходит — но мы выберем какое-нибудь из подходящих значений N и обозначим его через N(ε).) На рис. 4.12 приведена иллюстрация: для ε=ε1 мы могли выбрать N=3, то есть положить N(ε1)=3. Но для ε=ε2 (см. нижний рисунок) это значение N уже «не работает» (например, a4 выходит за границы нового коридора), однако увеличив N до 8 (то есть положив N(ε2)=8) мы снова добились соблюдения условия «все члены, начиная с n=N+1, находятся на расстоянии меньше ε от A».
Мы могли бы ещё сильнее уменьшить ε — и снова должно было найтись своё N, которое бы обеспечивало выполнение этого условия. Это и значит, что последовательность стремится к A.
4.3Пример доказательств утверждений о пределах
4.3.1Существование предела
Самый лучший способ понять определение — доказать какое-нибудь утверждение про него. Доказательство. Нам нужно научиться по любому ε>0 строить такое N=N(ε), что для всех n>N,∣∣∣n+1n−1∣∣∣<ε.(4.5)
Преобразуем это неравенство: ∣∣∣1+1n−1∣∣∣<ε;∣∣∣1n∣∣∣<ε. Заметим, что n — натуральное число, значит положительное, значит 1n — тоже положительное, значит его модуль всегда равен ему самому. Следовательно, знак модуля можно просто снять. Получим неравенство:1n<ε.
Можно умножить обе части этого неравенства на n и поделить на ε (благодаря тому, что n>0 и ε>0, эта операция является эквивалентным преобразованием и не приведёт к изменению знака неравенства). Получим такое неравенство:1ε<n.
Наконец, можно переписать его справа налево:n>1ε.(4.6)
Нам нужно найти такое N, что если n>N, то неравенство (4.5) выполняется. Наши преобразования были эквивалентными, поэтому, в частности, если выполняется неравенство (4.6), то выполняется и неравенство (4.5). Значит, достаточно сделать так, чтобы выполнялось неравенство (4.6). Очевидно, если выбрать какое-нибудь N≥1ε, мы победим: в этом случае любое n, большее N, будет также больше и 1ε, а значит неравенство (4.6) выполнено. В принципе, можно было бы просто положить N=1ε, но мы потребовали в определении 4, чтобы N было натуральным числом. Значит, нужно выбрать какое-нибудь натуральное число, не меньшее 1ε. Это всегда можно сделать. Однако, для определенности, давайте предложим конкретный механизм.Определение 5. Пусть x — вещественное число. Его округлением вверх называется наименьшее целое число, не меньшее x. Например, 2,1 округляется вверх до 3. Число 17 округляется вверх до 17, потому что оно уже целое. Результат округления вверх числа x обозначается через ⌈x⌉. Функция y=⌈x⌉ также называется функцией «потолок» (англ. ceil).
Упражнение 1. Опишите, как действует функция ⌈x⌉, пользуясь представлением числа x в виде бесконечной десятичной дроби.
Итак, для всякого ε>0, положим N(ε):=⌈1ε⌉. По определению функции потолок, N(ε)≥1ε. Значит, для всех натуральных n, если n>N(ε), то n>1ε, а значит выполняется (4.6), а значит и (4.5). Ура!∎
Давайте рассмотрим ещё один пример.
Утверждение 2. Предел последовательности an=1n2+5n+12 равен нулю:limn→∞1n2+5n+12=0.
Доказательство. По аналогии с предыдущим примером, запишем, что мы хотим получить. Мы хотим научиться для всякого ε>0 строить такое N=N(ε), что для всех n>N выполняется неравенство:∣∣∣1n2+5n+12−0∣∣∣<ε.(4.7)
Можно попробовать преобразовать это неравенство. Во-первых, вычитание нуля ничего не меняет. Во-вторых, при натуральных n дробь положительна и знак модуля можно снять. Получаем такое неравенство:1n2+5n+12<ε.(4.8)
Теоретически, дальше его можно мучительно решать относительно n, найдя для каждого фиксированного ε все возможные значения n, которые ему удовлетворяют. Делать это, однако, не нужно. Дело в том, что нам не нужны все без исключения значения n. Нам нужно добиться того, чтобы неравенство (4.8) выполнялось, но нам не нужно находить все значения n, при которых оно выполняется. Поэтому вместо эквивалентных переходов, которые мы должны делать, когда решаем неравенство, нам достаточно переходов к более сильным неравенствам — таким, из которых наше следует. И это существенно упрощает жизнь! Смотрите.Заметим, что для натуральных n,
n2+5n+12>n2.
Действительно, 5n и 12 — положительные числа. Более того: для натуральных n, n2≥n (можно поделить это неравенство на n, поскольку n больше нуля, и получить неравенство n≥1, справедливое для всех натуральных n). Имеем цепочку неравенств:n2+5n+12>n2≥n.
Значитn2+5n+12>n
и следовательно1n2+5n+12<1n.(4.9)
Оценивая знаменатель дроби снизу, мы оцениваем саму дробь сверху.Пусть теперь мы подобрали какое-нибудь такое N, что при всех n>N выполняется неравенство 1n<ε. Тогда в силу неравнства (4.9), для тех же самых n, будет выполняться неравенство
1n2+5n+12<ε.
(Мы опять используем транзитивность неравенства: если A<B и B<C, то A<C.)Таким образом, в качестве N(ε) можно взять то же выражение, что и в предыдущем примере: N(ε):=⌈1ε⌉. И оно сработает! Это гораздо проще, чем решать квадратное неравенство с параметром (можете попробовать — хотя вам вряд ли понравится).
Итак, если отбросить все мотивировки, полное доказательство выглядит так: для всякого ε>0, положим N(ε):=⌈1ε⌉. Тогда для всякого натурального n>N(ε) справедлива цепочка равенств и неравенств:
∣∣∣1n2+5n+12−0∣∣∣=∣∣∣1n2+5n+12∣∣∣==1n2+5n+12<1n<1⌈1/ε⌉≤11/ε=ε.
∣∣∣1n2+5n+12−0∣∣∣==∣∣∣1n2+5n+12∣∣∣==1n2+5n+12<<1n<1⌈1/ε⌉≤11/ε=ε.
Доказательство законечно. (Конечно, в аккуратном тексте нужно обосновать каждое из равенств и неравенств в цепочке, но мы это уже сделали выше.) ∎4.3.2Предел не равен какому-то числу
Утверждение 3. Предел последовательности {an}, an=1n, не равен 1:limn→∞1n≠1.
Доказательство. Нам нужно доказать, что неверно, что предел равен 1. Иными словами, опровергнуть следующее утверждение:∀ε>0 ∃N∈N ∀n>N:∣∣∣1n−1∣∣∣<ε.
Опровергнуть утверждение — это всё равно, что доказать его отрицание. Запишем отрицание, пользуясь разделом 2.3.3 лекции 2:∃ε>0 ∀N∈N ∃n>N:∣∣∣1n−1∣∣∣≥ε.(4.10)
∃ε>0 ∀N∈N ∃n>N:∣∣∣1n−1∣∣∣≥ε.(4.10)
Иными словами, нам нужно доказать, что существует такой ε>0, что какой бы номер N мы ни выбрали, найдётся номер n, больший, чем N, для которого элемент с номером n не является ε-близким к 1. Попросту нам нужно доказать, что для какого-то конкретного ε, время от времени — сколь угодно далеко в будущем — элементы последовательности будут на расстоянии как минимум ε от 1. В этом случае, конечно, ни о каком стремлении к 1 речи уже идти не будет.Давайте посмотрим на картинку (рис. 4.13).
import matplotlib.pyplot as plt
import numpy as np
import qqmbr.odebook as ob
# see https://github.com/ischurov/qqmbr/blob/master/qqmbr/odebook.py
nmax = 20
n = np.arange(1, nmax + 1)
n_full = np.linspace(0, nmax + 1 - 0.5)
plt.plot(n_full, np.ones_like(n_full), color="#cf356b")
plt.plot(n, 1 / n, 'o', markersize=4, label='$y=a_n$')
plt.xticks(range(0, nmax + 1))
plt.legend()
ob.center_spines(grid=False, minor_ticks=False)
ob.settle_axes(xmin=-0.9, xmax=nmax + 1, ymin=-0.25, ymax=2.27,
xlabel="n", ylabel="y") import matplotlib.pyplot as plt
import numpy as np
import qqmbr.odebook as ob
# see https://github.com/ischurov/qqmbr/blob/master/qqmbr/odebook.py
nmax = 20
n = np.arange(1, nmax + 1)
eps = 1.5
n_full = np.linspace(0, nmax + 1 - 0.5)
plt.fill_between(n_full, np.ones_like(n_full) * (1 + eps),
np.ones_like(n_full) * (1 - eps), color='#ee5d306b')
plt.plot(n_full, np.ones_like(n_full), color="#cf356b")
plt.plot(n_full, np.ones_like(n_full) * (1 + eps), color="#ee5e30")
plt.plot(n_full, np.ones_like(n_full) * (1 - eps), color="#ee5e30")
plt.plot(n, 1 / n, 'o', markersize=4, label='$y=a_n$')
plt.xticks(range(0, nmax + 1))
plt.legend()
ob.center_spines(grid=False, minor_ticks=False)
ob.settle_axes(xmin=-0.9, xmax=nmax + 1, ymin=-2.47, ymax=5.47,
xlabel="n", ylabel="y") Однако, уже значение ε=1/3 подходит. Действительно, лишь одна точка лежит внутри коридора с «размахом» 1/3 вокруг прямой y=1, см. рис. 4.15.
import matplotlib.pyplot as plt
import numpy as np
import qqmbr.odebook as ob
# see https://github.com/ischurov/qqmbr/blob/master/qqmbr/odebook.py
nmax = 20
n = np.arange(1, nmax + 1)
eps = 1/3
n_full = np.linspace(0, nmax + 1 - 0.5)
plt.fill_between(n_full, np.ones_like(n_full) * (1 + eps),
np.ones_like(n_full) * (1 - eps), color='#ee5d306b')
plt.plot(n_full, np.ones_like(n_full), color="#ee5e30")
plt.plot(n_full, np.ones_like(n_full), color="#cf356b")
plt.plot(n_full, np.ones_like(n_full) * (1 + eps), color="#ee5e30")
plt.plot(n_full, np.ones_like(n_full) * (1 - eps), color="#ee5e30")
plt.plot(n, 1 / n, 'o', markersize=4, label='$y=a_n$')
plt.xticks(range(0, nmax + 1))
plt.legend()
ob.center_spines(grid=False, minor_ticks=False)
ob.settle_axes(xmin=-0.9, xmax=nmax + 1, ymin=-2.47, ymax=5.47,
xlabel="n", ylabel="y") ∣∣∣1n−1∣∣∣≥1/3.(4.11)
По картинке видно, что нам подойдёт любое n, начиная с n=2. Поскольку минимальное значение для N равно 1, то любое n, удовлетворяющее условию n>N, удовлетворяет и условию n≥2, и значит, нам подходит. Осталось построить натуральное число n, которое гарантированно больше данного натурального числа N. Как это сделать? Можно просто прибавить единицу к N, и всё!Итак, положим: n:=N+1. Осталось доказать, что выполняется неравенство (4.11). Действительно:
∣∣∣1N+1−1∣∣∣=1−1N+1≥1−12=12≥13=ε.(4.12)
∣∣∣1N+1−1∣∣∣=1−1N+1≥≥1−12==12≥13=ε.(4.12)
Первое равенство следует из того факта, что 1N+1 меньше единицы для натуральных N и модуль может быть раскрыт только так, первое неравенство следует из того факта, что 1N+1 ещё и меньше 1/2, т.к. N натуральное и не меньше 1.∎4.3.3Несуществование предела
Не у всякой последовательности существует предел. Доказательство. Нас пожидает некоторая трудность в самом начале. Определение предела требует, чтобы мы назвали конкретное число A, которое является пределом. Здесь никакого A нет.Формально, утверждение «последовательность {an} имеет предел» записывается так: найдётся какое-то число A, которое является пределом {an}. В кванторах:
∃A∈R ∀ε>0 ∃N∈N ∀n>N:|an−A|<ε.
Ух! Четыре квантора.Давайте напишем отрицание к этому утверждению (это как раз то, что нам нужно доказать):
∀A∈R ∃ε>0 ∀N∈N ∃n>N:|an−A|≥ε.
Иными словами, для всякого вещественного числа A, справедливо утверждение: A не является пределом нашей последовательности.Теперь будем его доказывать. Тут нужно разобрать два случая: A≠1 и A=1.
Случай A≠1. Как обычно, начнём с картинки, см. рис. 4.16. Мы отметили точку A между 0 и −1, но на самом деле она может быть какой угодно, кроме 1.
Рис. 4.16: График последовательности {(−1)n}. Теперь нужно выбрать такое ε>0, что последовательность будет время от времени выскакивать из ε-коридора сколько угодно далеко в будущем. Как найти ε? Поскольку мы знаем, что A≠1, и также знаем, что сколь угодно далеко в будущем последовательность посещает точку 1, логично выбрать такой размах коридора, при котором он не будет содержать точки с y=1. Это легко сделать: достаточно в качестве ε взять число, которое было бы меньше, чем расстояние от A до 1. В этом случае, если элемент последовательности равен 1, его расстояние до A будет гарантированно больше, чем ε.Положим
ε=|A−1|2.
Тут важно, что A≠1 и следовательно ε>0.Тогда одна из границ коридора будет проходить в точности посередине между A и 1, см. рис. 4.17. Пусть теперь дано произвольное натуральное N. Из рисунка видно, что каким бы ни было это N, найдутся элементы последовательности, лежащие вне коридора между A+ε и A−ε после n=N (заштрихованная область на рисунке). Собственно, мы именно так и выбирали ε: для любого чётного n, an=1 и следовательно соответстующая точка лежит вне указанного коридора. Для любого N найдётся чётное натуральное число n>N — оно-то нам и нужно.
Рис. 4.17: График последовательности {(−1)n} и коридор для выбранного значения ε. Чтобы сделать рассуждение совсем железобетонным, нужно привести явный способ построения n по N. Тут можно действовать разными методами — например, можно выбирать первое чётное, большее N, но можно проще: положитьn=2N.
Действительно, 2N>N для всех натуральных N и число 2N гарантированно чётное.Наконец, нужно доказать, что для выбранного таким образом n, будет выполняться неравенство |an−A|≥ε. Поскольку n чётно, an=1. Подставляя значение ε, имеем:
|1−A|≥|A−1|2.
Поскольку |1−A|=|A−1| и это положительное число, это неравенство заведомо верно.Таким образом, для любого A≠1 мы предъявили такое значение ε=|A−1|2>0, что для всех натуральных N мы построили такое n=2N, что n>2N и |an−A|≥ε. Значит, A не является пределом нашей последовательности.
Случай A=1. Он доказывается полностью аналогично, и даже проще, потому что теперь значение A известно. Хорошее упражнение — написать это доказательство явно и аккуратно, подобно тому, как выше разборан случай A≠1. Пожалуйста, сделайте это, прежде, чем идти дальше!∎
4.4Единственность предела
Когда мы записываем выражение типаlimn→∞an=A,(4.13)
мы подразумеваем, что левая часть равенства является каким-то однозначно определенным числом. Конечно, мы понимаем, что не всякое выражение обязано иметь числовое значение (например, арифметическое выражение 1/0 не имеет никакого числового значения), но если уж имеет, то мы предполагаем, что это значение определяется однозначно. Тем не менее, в определении предела никаких требований, связанных с единственностью предела, не накладывается. Как видно, это определение отвечает на вопрос «является ли A пределом последовательности {an}», но вдруг для одной и той же последовательности найдутся два разных числа, для которых ответ будет положительным? В этом случае запись вроде (4.13) потеряла бы всякую определенность.К счастью, так не бывает. Давайте это докажем.
Теорема 1. Если предел последовательности существует, то он единственный. Иными словами, пусть есть последовательность {an} и два числа, A1 и A2, удовлетовряющие определению предела для этой последовательности. Тогда обязательно A1=A2. Доказательство. Будем доказывать от противного. Пусть A1 и A2 оба являются пределами последовательности {an}, но при этом A1≠A2. Запишем формально утверждения про пределы:∀ε1>0 ∃N1=N1(ε1) ∀n>N1:|an−A1|<ε1;∀ε2>0 ∃N2=N2(ε2) ∀n>N2:|an−A2|<ε2.(4.14)(4.15)
∀ε1>0 ∃N1=N1(ε1) ∀n>N1:|an−A1|<ε1;∀ε2>0 ∃N2=N2(ε2) ∀n>N2:|an−A2|<ε2.(4.14)(4.15)
Мы обсуждали (см. раздел 3.2.3), что когда есть несколько утверждений с кванторами, в которых участвуют одни и те же буквы, никакой связи между этими буквами за пределами соответствующих утверждений нет. Так что чтобы не путаться, мы добавили немножко индексов — например, ε1 для утверждения про предел A1 и ε2 для утверждения про предел A2. Мы также ввели очень полезное обозначение N1(ε1) и N2(ε2) — таким образом мы сразу понимаем, N из какого определения взято и для какого ε оно найдено.Впрочем, давайте вернёмся с формального уровня на интуитивный. У нас есть два разных числа, A1 и A2, и два утверждения: одно говорит, что весь хвост последовательности, начиная с какого-то элемента, будет близок к A1, а другое утверждение говорит, что хвост той же самый последовательности (начинающийся, впрочем, с какого-нибудь другого элемента) целиком близок к A2. Могут ли эти два утверждения друг другу не противоречить? Зависит от того, что считать «близкими точками». Но это как раз регулируются нашими значениями ε1 и ε2. И они сейчас находятся в нашей власти — мы можем их выбирать какими хотим!
Действительно, до сих пор когда мы доказывали, что предел равен какому-то числу, мы воспринимали ε как нечто данное, что от нас не зависит. Потому что нам нужно было доказать утверждение, взятое из определения предела, а оно начинается квантором «для всякого ε>0». В этот же раз мы находимся в обратной ситуации. Нам дано (по предположению), что предел последовательности равен A1. Значит, нам сказано, что для всякого ε1>0 найдётся такое N1=N1(ε1), что какое-то там неравенство выполняется. Если мы хотим найти N1 для ε1=1/10, мы можем это сделать. И для ε1=1/100. И для любого другого положительного ε1 можем найти. Аналогично и со вторым утверждением.
Как выбрать ε1 и ε2, чтобы имеющиеся у нас утверждения пришли к явному противоречию? Давайте посмотрим на картинку, рис. 4.18.
Известно, что, начиная с некоторого номера n=N1, все элементы последовательности лежат в ε1-коридоре вокруг точки A1. В то же время, начиная с некоторого n=N2, все элементы последовательности лежат в ε2-коридоре вокруг точки A2. Если выбрать эти коридоры непересекающимися, будет явное противоречие — точки не смогут жить в обоих одновременно!Какими выбрать ε1 и ε2, чтобы коридоры не пересекались? Это легко: давайте разделим расстояние между A1 и A2 на три. Тогда верхняя граница нижнего (на картинке) коридора вокруг A2 будет проходить по нижней трети отрезка [A2,A1], а нижняя граница верхнего коридора — по верхней трети этого же отрезка. Конечно, пересечения не будет, и мы победим.
Давайте сделаем железобетонное рассуждение. Итак, пусть
ε1=ε2=|A1−A2|3.
Здесь мы воспользовались предположением, что A1≠A2, и значит наши ε1 и ε2 положительны.Пусть также
N1:=N1(ε1)=N1(|A1−A2|3),N2:=N2(ε1)=N2(|A1−A2|3).(4.16)
N1:=N1(ε1)==N1(|A1−A2|3),N2:=N2(ε1)==N2(|A1−A2|3).(4.16)
Теперь нужно найти элемент (достаточно будет одного), который приведёт нас к противоречию. Его номер должен одновременно удовлетворять условию n>N1 (потому что утверждение про предел A1 (см. (4.14)) даёт нетривиальную оценку именно для таких n, а про меньшие n оно ничего не утверждает) и n>N2 (аналогично с утверждением про A2). Как найти такое n? Очень просто: можно взять максимум из N1 и N2 и прибавить 1. Положим:n=max(N1,N2)+1.
Тогда n>N1 и согласно (4.14) в этом случае обязательно|an−A1|<ε1=|A1−A2|3.
Одновременно n>N2 и согласно (4.15) в этом случае обязательно|an−A2|<ε2=|A1−A2|3.
Чтобы не возиться с раскрытием модулей и рассмотрением разных случаев, применим известное неравенство треугольника: расстояние от A1 до A2 не превосходит сумму расстояний от A1 до an и от an до A2. Имеем:|A1−A2|≤|A1−an|+|an−A2|<|A1−A2|3+|A1−A2|3=23|A1−A2|.(4.17)
|A1−A2|≤≤|A1−an|+|an−A2|<<|A1−A2|3+|A1−A2|3==23|A1−A2|.(4.17)
Но |A1−A2| — положительное число! Положительные числа уменьшаются, если их умножить на 2/3, а не увеличиваются, как следует из нашего неравенства. Противоречие! Теорема доказана.∎4.5Заключение
Уфф, это была длинная лекция, но мы сделали самое главное: ввели аккуратное определение предела последовательности и убедились, что оно корректно — то есть для всякой последовательности, для которой предел существует, он задан однозначно. Мы также рассмотрели несколько примеров доказательств утверждений о существовании и не существовании пределов для конкретных последовательностей. На следующей лекции мы докажем больше общих свойств о пределах, а на семинаре потренируемся пользоваться определениями.← Предыдущая глава Следующая глава →
Магический трехслойный графен преодолел предел Паули и вернул сверхпроводимость
Муаровый узор на трехслойном графене
Condensed Matter Theory Center / Youtube
Физики из США и Японии обнаружили, что сверхпроводимость скрученного под магическим углом трехслойного графена выдерживает магнитные поля, в 2-3 раза превышающие теоретически предсказанный предел Паули для спин-синглетного спаривания, а также зафиксировали эффект возвратной сверхпроводимости на температурах, близких к абсолютному нулю. Эти и другие результаты экспериментов указывают на то, что трехслойный графен не относится к спин-синглетным сверхпроводникам — наиболее распространенным сверхпроводникам, описываемым теорией Бардина — Купера — Шриффера. Статья опубликована в Nature.
Известно множество соединений, проявляющих сверхпроводимость — свойство обладать нулевым сопротивлением ниже критической температуры. Помимо простых элементов и сплавов в этот список входят керамики, пниктиды железа, гидриды и органические соединения. Три года назад группа физиков под руководством Пабло Харильо-Эрреро (Pablo Jarillo-Herrero) из MIT обнаружила сверхпроводимость при температуре 1,7 кельвин в двухслойном графене, листы которого повернуты на магический угол в 1,1 градус. При таком скручивании слоев зависимость энергии от импульса электронов в двухслойном графене становится плоской, что позволяет им локализоваться в долинах максимального совпадения ячеек обеих решеток, которые располагаются в центрах шестиугольников муаровой сверхрешетки. Одним из преимуществ этой конструкции является возможность регулировать плотность носителей заряда в сверхпроводнике не прерывая эксперимента, что позволяет изучать фазовую диаграмму сверхпроводимости во всех подробностях. Примечательно, что своей фазовой диаграммой, а также «страннометаллическими» свойствами повернутый на магический угол двухслойный графен напоминает купраты — высокотемпературные сверхпроводники-рекордсмены при атмосферном давлении. Исследование вызвало большой резонанс в научном сообществе, вышло свыше 30 теоретических исследований первопричин сверхпроводимости в графене, а про фононную гипотезу мы писали в другом нашем материале.
Зависимость энергии электронов от импульса, муаровый узор и узлы муаровой сверхрешетки (желтые пятна) для двухслойного графена, повернутого на магический угол
Stanford Physics / Youtube
В прошлом году те же авторы исследовали сверхпроводимость трехслойного графена, причем максимальная температура сверхпроводимости 2,9 кельвин наблюдалась, когда средний слой был повернут относительно двух других на магический угол в 1,57 градуса. С точки зрения зависимости энергии электронов от импульса такая структура может быть сведена к слою уединенного графена и двухслойному графену, скрученному на магический угол трехслойного графена делить на корень из двух. Регулировка электронной структуры здесь стала шире и теперь позволяет исследовать свойства графена в зависимости от наложенного электрического поля. Более того, с помощью усовершенствованной регулировки физики смогли перевести соединение в состояние сверхсильной связи, что сделало его самым сильносвязанным из известных сверхпроводников и приблизило сверхпроводник к переходу в конденсат Бозе — Эйнштейна.Связь электронной структуры трехслойного графена с одно- и двухслойным графеном
Khalaf et al. / Phys. Rev. B, 2019
Схема экспериментальной установки и зависимость энергии электронов от импульса в трехслойном графене при нулевом и включенном электрическом поле: фиолетовым обозначена дисперсия, соответствующая одиночному графену, оранжевым — двухслойному графену
Stanford Physics / Youtube
В большинстве сверхпроводящих материалов (в том числе тех, что описываются теорией БКШ) преобладает спин-синглетное спаривание — это значит, что спины электронов в куперовской паре направлены противоположно, причем импульсы электронов, входящих в пару, также противоположно направлены и находятся в тонком слое вблизи поверхности ферми. При включении магнитного поля возникает эффект Зеемана: энергии электронов с противоположными спинами и равными энергиями расходятся на величину, пропорциональную величине поля, что уменьшает количество куперовских пар и разрушает сверхпроводимость. Точный подсчет в теории БКШ с критической температурой Tc и множителем Ланде g=2 дает значение BP = 1.86 Tс для критического поля, при котором пропадает сверхпроводящая фаза. Такое поле называют пределом Паули.В новой работе все та же группа ученых продолжила исследование трехслойного магически-повернутого графена и обнаружила у него непредвиденную способность преодолевать предел Паули. Для получения больших сведений о сверхпроводимости образца физики установили два электрода параллельно пластинам графена, и далее, в зависимости от подаваемого напряжения, при фиксированном значении электрической индукции D регулировали параметр заполнения ν, равный числу электронов в муаровой ячейке. Измерение сопротивления образца в зависимости от параллельно приложенного магнитного поля, температуры и параметра заполнения выявило область сверхпроводимости при 10 Тесла, что превышает лимит Паули в 2-3 раза.
Нарушение предела Паули в графене на графике зависимости сопротивления от магнитного поля, параметра заполнения и температуры
Yuan Cao, Pablo Jarillo Herrero et al. / Nature, 2021
Экспериментаторы отмечают, что нарушение предела Паули для сверхпроводников спин-синглетного типа обычно возникает за счет сильного спин-орбитального взаимодействия (взаимодействия спина электрона с его собственным орбитальным движением), которое может значительно влиять на сверхпроводящие свойства вещества, но в графене это взаимодействие в 30 раз слабее необходимого. Другой причиной завышенной резистивности к магнитному полю у спин-синглетных сверхпроводников может выступить образование пар Ларкина — Овчинникова — Фульде — Феррелла (FFLO-пара), которые, в отличие от куперовских пар, имеют ненулевой полный импульс, однако за счет такого эффекта предел Паули не может быть превышен более чем на сорок процентов (ученые наблюдали увеличение критического поля в разы). Третий вариант — превышение предела за счет сильной связи у электронов также разбивается об экспериментальные данные. Неприменимость известных механизмов для описания данного эффекта побудила авторов выдвинуть гипотезу, что в магическом трехслойном графене сверхпроводимость имеет спин-триплетный характер — электроны образуют пары с полным спином равным 1 (мы уже писали о различных механизмах сверхпроводимости в материале «Ниже критической температуры»).Теоретически эта гипотеза может быть подкреплена следующим рассуждением. В триплетном сверхпроводнике спиновая конфигурация параметра порядка описывается комплексным вектором d, а реакция спин-триплетных состояний на внешнее магнитное поле B зависит от угла между d и B. Состояния с параллельно расположенными B и d полностью подавляются, как в случае спин-синглетной сверхпроводимости, тогда как состояния ESP (equal-spin pairing), когда вектор d лежит перпендикулярно B, совершенно не реагируют на поле. Однако и эти состояния в конечном счете разрушаются — в графеновых системах с магическим углом дополнительная спиновая степень свободы может привести к эффекту разрыва пар из-за орбитальных эффектов. Таким образом, состояние триплета ESP может быть жизнеспособным кандидатом на роль состояния, при котором допустимо большое нарушение предела Паули.
Также ученые измерили зависимость сопротивления от магнитного поля выше 5 Тесла при температурах меньше 2 кельвинов и обнаружили возвратную сверхпроводимость — явление, при котором увеличение магнитного поля приводит к разрушению сверхпроводимости, ее повторному появлению и затем к окончательному разрушению при достаточно больших полях. Более детальное исследование зависимости сопротивления от магнитного поля, электрического поля D и параметра заполнения при фиксированной температуре 0,4 кельвина выявило сложную структуру перехода: между большими областями сверхпроводимости (SC-I и SC-II) наблюдаются островки сверхпроводимости меньших размеров.
Возвратная сверхпроводимость графена на графиках зависимости сопротивления от магнитного поля, температуры и тока при фиксированном значении поля D
Yuan Cao, Pablo Jarillo Herrero et al. / Nature, 2021
Возвратная сверхпроводимость графена на графиках зависимости сопротивления от магнитного поля, температуры, поля D и параметра заполнения
Yuan Cao, Pablo Jarillo Herrero et al. / Nature, 2021
Прежде возвратная сверхпроводимость наблюдалась в соединениях урана, таких как UPt3, UGe2, UTe2. Стоит заметить, что сверхпроводимость в этих соединениях предположительно также носит спин-триплетный характер, что убеждает в правильности выдвинутой учеными гипотезы.Сравнивая трехслойный магически-повернутый графен с другими сверхпроводниками, способными выдерживать большие магнитные поля, а также со сверхтекучим гелием-3 физики пришли к выводу, что переход между низкополевой (SC-I) и возвратной фазой (SC-II) может быть фазовым переходом первого рода, причем фазы, по-видимому, спин-триплетные и имеют разные параметры порядка. Авторы надеются, что будущие исследования дадут полную картину парных процессов в различных сверхпроводящих фазах соединения.
Ранее мы рассказывали о других необычных способностях двухслойного графена: он может превращаться в аномальный магнит, приобретать свойства алмаза и становиться полупроводником.
Елизавета Чистякова
Электронный учебник по математическому анализу
3.1 Предел последовательности
3.n$ не имеет предела.
Определение. Говорят, что последовательность $a_n$ имеет пределом $+\infty$, если для любого $A>0$ существует такое $N$, что при всех $n>N$ выполняется неравенство $a_n>A$.
Обозначение. Этот факт обозначают \[ \lim _{n\rightarrow +\infty}a_n=+\infty, \]
или
\[ a_n \xrightarrow[n\to +\infty]{} +\infty. \]
Аналогично определяется ситуация, когда $ \lim _{n\rightarrow +\infty}a_n=-\infty$.
Определение. Если предел последовательности равен $0$, последовательность называют бесконечно малой. Если предел последовательности равен $\infty$, последовательность называют бесконечно большой.
Теорема. Пусть последовательность $a_n$ имеет конечный предел. Тогда $a_n$ — ограниченная последовательность.
Доказательство.
Возьмем какое-нибудь $\varepsilon >0$. Согласно определению предела, существует такое $N$, что при всех $n>N$ выполняется $|a_n-A|
Теорема. Пусть последовательность $a_n$ имеет конечный предел $A$, \[ a_n \xrightarrow[n\to +\infty]{} A. \]
Тогда последовательность $b_n=(a_n-A)$ является бесконечно малой.
Теорема. Последовательность может иметь только один предел.
Доказательство.
Предположим, что последовательность имеет два предела, \[ a_n \xrightarrow[n\to +\infty]{} A, \] \[ a_n \xrightarrow[n\to +\infty]{} B, \]
$A \neq B$. Будем для определенности считать, что числа $A$ и $B$ конечные. Возьмем $\varepsilon = |A-B|/3$.
Согласно определению предела, найдется такое $N_1$, что при $n >N_1$ выполняется $A-\varepsilon
По тем же причинам найдется $N_2$ такое, что при $n>N_2$ выполняется $B-\varepsilon
Тогда при $n>max(N_1,N_2)$ выполняются оба набора неравенств, что невозможно — отрезки $(A-\varepsilon,A+\varepsilon)$, $(B-\varepsilon,B+\varepsilon)$ не пересекаются. ч.т.д.
3.1.2 Арифметика пределов
Здесь приведена серия теорем, описывающая предел суммы, произведения и частного последовательностей, имеющих конечный предел.
Теорема. Пусть \[ \lim _{n\rightarrow +\infty}a_n=A, \, \lim _{n\rightarrow +\infty}b_n=B, \]
причем $A$ и $B$ — конечные числа. Тогда последовательность $(a_n+b_n)$ имеет конечный предел, причем
\[ \lim _{n\rightarrow +\infty}(a_n+b_n)=A+B. \]
Доказательство.
Возьмем произвольное число $\varepsilon >0 $. Согласно определению предела, существует такое $N_1$, что при всех $n>N_1$ выполняется: \begin{equation} |a_n-A|
По тем же причинам существует такое $N_2$, что при всех $n>N_2$ выполняется: \begin{equation} |b_n-B|
Пусть $N=max(N_1,N_2)$. Тогда при всех $n>N$ выполняются неравенства (1) и (2). Используя неравенство треугольника, получаем: при всех $n>N$ выполняется \begin{equation} |(a_n+b_n)-(A+B)| \[ \varepsilon /2+\varepsilon /2=\varepsilon.(3)\]
ч.т.д.
Теорема. Пусть \[ \lim _{n\rightarrow +\infty}a_n=A, \, \lim _{n\rightarrow +\infty}b_n=B, \]
причем $A$ и $B$ — конечные числа. Тогда последовательность $(a_n\cdot b_n)$ имеет конечный предел, причем
\[ \lim _{n\rightarrow +\infty}(a_n\cdot b_n)=A\cdot B. \]
Теорема. Пусть \[ \lim _{n\rightarrow +\infty}a_n=A, \, \lim _{n\rightarrow +\infty}b_n=B, \]
причем $A$ и $B$ — конечные числа, $B \neq 0$. Тогда последовательность $(a_n / b_n)$ имеет конечный предел, причем
\[ \lim _{n\rightarrow +\infty}(a_n / b_n)=A / B. \]
Теорема. Пусть при всех $n$ выполняется $a_n
Тогда $A \leq M$ (переход в неравенствах к пределу).
Замечание. Разумеется, существуют аналоги этих теорем и в том случае, когда один из пределов (или оба предела) бесконечен.
Контрольный вопрос.
Сформулируйте теорему о пределе суммы, если одна из последовательностей имеет конечный предел, вторая — бесконечный.
3.1.3 Арифметика бесконечно малых
Теорема. Пусть $a_n$, $b_n$ — бесконечно малые при $n \rightarrow +\infty$. Тогда $(a_n+b_n)$ — бесконечно малая при $n \rightarrow +\infty$.
Теорема. Пусть $a_n$ — бесконечно малая при $n \rightarrow +\infty$, $b_n$ — ограниченная последовательность. Тогда $a_n\cdot b_n$ — бесконечно малая при $n \rightarrow +\infty$.
Теорема. Пусть $a_n$ — бесконечно малая при $n \rightarrow +\infty$, \[ \lim _{n\rightarrow +\infty}b_n=B, \] причем $B$ — конечное число, $B \neq 0$. Тогда последовательность $(a_n / b_n)$ бесконечно малая при $n \rightarrow +\infty$.
Определение. Бесконечно малые $a_n$, $b_n$ называются эквивалентными, если существует предел \[ \lim _{n\rightarrow +\infty}a_n/b_n=\theta, \] причем $\theta \neq 0$, $\theta \neq \pm \infty$. Этот факт обозначают следующим образом: $a_n \sim b_n$ при $n \rightarrow +\infty$.
3.1.4 Признаки существования пределов
Следующие теоремы указывают условия, при которых последовательность имеет предел.
Теорема. Пусть $a_n$ — монотонно возрастающая последовательность, ограниченная сверху. Тогда она имеет конечный предел.
Следствие. Если $a_n$ — монотонно возрастающая последовательность, она имеет пределом либо $=+\infty$, либо конечное число. Соответственно, для монотонно убывающей последовательности.
Теорема. Пусть $a_n$ — монотонно убывающая последовательность, ограниченная снизу. Тогда она имеет конечный предел.
Теорема. Пусть для всех $n$ выполняются неравенства $a_n\leq b_n \leq c_n$, и \[ \lim _{n\rightarrow +\infty}a_n=A, \, \lim _{n\rightarrow +\infty}c_n=A. \] Тогда $b_n$ также имеет предел, причем \[ \lim _{n\rightarrow +\infty}b_n=A. \]
Критерий Коши. Для того, чтобы последовательность $a_n$ имела конечный предел, необходимо и достаточно, чтобы для любого $ \varepsilon >0$ существовало такое $N$, что при всех $m,n>N$ выполнялось $|a_n-a_m|
3.1.5 Вычисление пределов
Здесь мы приведем несколько примеров вычисления пределов последовательностей. При этом мы используем приведенные выше теоремы об арифметике пределов.{-1}$. ч.т.д.
Внеклассный урок — Предел последовательности. Виды последовательности.
Предел последовательностиПредел последовательности – это число, в окрестности которой содержатся все члены последовательности.
Пример: Пределом последовательности чисел 1/2, 1/3, 1/4, 1/5, 1/6 и т.д. является 0.
Пояснение: ряд чисел стремится к нулю и ниже нуля не опустится.
Не любая последовательность имеет предел. К примеру, последовательность 1, 2, 3, 4, 5, 6 и т.д. бесконечна и не имеет предела.
Свойство последовательности иметь или не иметь предел называется сходимостью. Если у последовательности есть предел, то говорят, что она сходится. Если у последовательности нет предела, то говорят, что она расходится.
Случай, когда последовательность не имеет предела.
Если |q| > 1, то последовательность yn = qn расходится и не имеет предела.
Пример: Пусть q = 3. Тогда мы можем создать следующую последовательность чисел:
32; 33; 34; 35; 36; 37 и т.д. Ряд стремится к бесконечности. Предела нет.
Виды последовательности.
Последовательность (yn) называется ограниченной снизу, если все ее члены не меньше некоторого числа. Для любого n выполняется неравенство yn ≥ m |
Последовательность (yn) называется ограниченной сверху, если все ее члены не больше некоторого числа. Для любого n выполняется неравенство yn ≤ М |
Если каждый член последовательности yn больше предыдущего, то это возрастающая последовательность. Если а > 1, то последовательность yn = an возрастает. Пример: y1 < y2 < y3 < y4 < y5… |
Если каждый член последовательности меньше предыдущего, то это убывающая последовательность. Если 0 < a < 1, то последовательность убывает.
|
Теорема.
Если lim xn = b, lim yn = c, то 1) предел суммы равен сумме пределов: lim (xn + yn) = b + c
lim (xn yn) = bc
lim (xn/yn) = b/c, при c ≠ 0
lim (kxn) = kb |
Пример 1: Найти предел последовательности
dn = 6/n – 4/n2 + 8.
Решение:
lim 6/n – lim 4/n2 + lim 8 = 0 – 0 + 8 = 8.
n→∞ n→∞ n→∞
Пример решен.
Пример 2: Найти предел последовательности
2n2 + 3
lim ————
n→∞ n2 + 4
Решение.
Разделим числитель и знаменатель дроби на n2, произведем сокращения и получим ответ:
2n2/n2 + 3/n2 2 + 3/n2 2 + 0
lim ——————— = lim ————— = ———— = 2.
n→∞ n2/n2 + 4/n2 n→∞ 1 + 4/n2 1 + 0
Пример решен.
Страница не найдена — ПриМат
© 2012-2016: Нохум-Даниэль Блиндер (11), Анастасия Лозинская (10), Юлия Стерлянко (8), Денис Стехун (8), Валентин Малявко (8), Елизавета Савицкая (8), Игорь Любинский (8), Олег Шпинарев (7), Александр Базан (7), Анна Чалапчий (7), Константин Берков (7), Влад Радзивил (6), Максим Швандт (6), Людмила Рыбальченко (6), Кирилл Волков (6), Татьяна Корнилова (6), Мария Корень (5), Анна Семененко (5), Мария Илларионова (5), Сергей Черкес (5), Алиса Ворохта (5), Валерия Заверюха (5), Елизавета Снежинская (5), Вадим Покровский (5), Даниил Радковский (5), Влад Недомовный (5), Александр Онищенко (5), Андрей Метасов (5), Денис Базанов (5), Александр Ковальский (5), Александр Земсков (5), Марина Чайковская (5), Екатерина Шибаева (5), Николай Царев (4), Валентин Цушко (4), Павел Жуков (4), Роман Бронфен-Бова (4), Артём Романча (4), Анна Шохина (4), Иван Киреев (4), Никита Савко (4), Кондрат Воронов (4), Алина Зозуля (4), Иван Чеповский (4), Артем Рогулин (4), Игорь Чернега (4), Даниил Кубаренко (4), Ольга Денисова (4), Татьяна Осипенко (4), Яков Юсипенко (4), Ольга Слободянюк (4), Руслан Авсенин (4), Екатерина Фесенко (4), Дмитрий Заславский (4), Алина Малыхина (4), Андрей Лисовой (4), Полина Сорокина (4), Кирилл Демиденко (4), Дмитрий Стеценко (4), Александр Рапчинский (4), Святослав Волков (4), Иван Мясоедов (4), Владислав Стасюк (4), Алёна Гирняк (4), Илья Черноморец (3), Евгений Фищук (3), Анна Цивинская (3), Михаил Бутник (3), Станислав Чмиленко (3), Катя Писова (3), Дмитрий Дудник (3), Дарья Кваша (3), Игорь Стеблинский (3), Артем Чернобровкин (3), Виктор Булгаков (3), Дмитрий Мороз (3), Богдан Павлов (3), Игорь Вустянюк (3), Андрей Яроцкий (3), Лаура Казарян (3), Екатерина Мальчик (3), Анатолий Осецимский (3), Иван Дуков (3), Дмитрий Робакидзе (3), Вячеслав Зелинский (3), Данила Савчак (3), Дмитрий Воротов (3), Стефания Амамджян (3), Валерия Сиренко (3), Георгий Мартынюк (3), Виктор Иванов (3), Вячеслав Иванов (3), Валерия Ларикова (3), Евгений Радчин (3), Андрей Бойко (3), Милан Карагяур (3), Александр Димитриев (3), Иван Василевский (3), Руслан Масальский (3), Даниил Кулык (3), Стас Коциевский (3), Елизавета Севастьянова (3), Павел Бакалин (3), Антон Локтев (3), Андрей-Святозар Чернецкий (3), Николь Метри (3), Евелина Алексютенко (3), Константин Грешилов (3), Марина Кривошеева (3), Денис Куленюк (3), Константин Мысов (3), Мария Карьева (3), Константин Григорян (3), Колаев Демьян (3), Станислав Бондаренко (3), Ильдар Сабиров (3), Владимир Дроздин (3), Кирилл Сплошнов (3), Карина Миловская (3), Дмитрий Козачков (3), Мария Жаркая (3), Алёна Янишевская (3), Александра Рябова (3), Дмитрий Байков (3), Павел Загинайло (3), Томас Пасенченко (3), Виктория Крачилова (3), Таисия Ткачева (3), Владислав Бебик (3), Илья Бровко (3), Максим Носов (3), Филип Марченко (3), Катя Романцова (3), Гасан Мурадов (2), Богдан Подгорный (2), Алексей Никифоров (2), Настя Филипчук (2), Гук Алина (2), Михаил Абабин (2), Дмитрий Калинин (2), Бриткариу Ирина (2), Никита Шпилевский (2), Алексей Белоченко (2), Юлиана Боурош (2), Никита Семерня (2), Владимир Захаренко (2), Дмитрий Лозинский (2), Яна Колчинская (2), Юрий Олейник (2), Кирилл Бондаренко (2), Елена Шихова (2), Татьяна Таран (2), Наталья Федина (2), Настя Кондратюк (2), Никита Гербали (2), Сергей Запорожченко (2), Николай Козиний (2), Георгий Луценко (2), Владислав Гринькив (2), Александр Дяченко (2), Анна Неделева (2), Никита Строгуш (2), Настя Панько (2), Кирилл Веремьев (2), Даниил Мозгунов (2), Андрей Зиновьев (2), Андрей Данилов (2), Даниил Крутоголов (2), Наталия Писаревская (2), Дэвид Ли (2), Александр Коломеец (2), Александра Филистович (2), Евгений Рудницкий (2), Олег Сторожев (2), Евгения Максимова (2), Алексей Пожиленков (2), Юрий Молоканов (2), Даниил Кадочников (2), Александр Колаев (2), Александр Гутовский (2), Павел Мацалышенко (2), Таня Спичак (2), Радомир Сиденко (2), Владислав Шиманский (2), Илья Балицкий (2), Алина Гончарова (2), Владислав Шеванов (2), Андрей Сидоренко (2), Александр Мога (2), Юлия Стоева (2), Александр Розин (2), Надежда Кибакова (2), Майк Евгеньев (2), Евгений Колодин (2), Денис Карташов (2), Александр Довгань (2), Нина Хоробрых (2), Роман Гайдей (2), Антон Джашимов (2), Никита Репнин (2),
x} = e \]Если предел последовательности равен 0, сходится ли ряд?
Это часть серии о распространенных заблуждениях.
Какое распространенное заблуждение?
Если члены последовательности становятся все меньше и меньше, гарантировано ли, что сумма всей последовательности будет некоторым конечным числом? Например, этот простой ряд, который приближается к 000, имеет сумму, сходящуюся к 2:
.1 + 12 + 14 + 18 + 116 + ⋯ + 12n = ∑n = 0∞12n = 2.{\ infty} a_n <\ infty n → ∞lim an = 0⟹n = 1∑∞ an <∞
Почему некоторые люди говорят, что это правда: Когда члены складываемой последовательности становятся все ближе и ближе к 0, сумма сходится к некоторому определенному конечному значению. Следовательно, пока условия становятся достаточно маленькими, сумма не может расходиться.
Почему некоторые говорят, что это ложь: Сумма не сходится только потому, что ее члены очень малы.
Выявите правильный ответ: \ color {# 20A900} {\ text {Выявите правильный ответ:}} Выявите правильный ответ:111 222 2π2 \ pi2π Не сходитсяУтверждение, что limn → ∞an = 0 ⟹ ∑n = 1∞an <∞ \ lim \ limits_ {n \ rightarrow \ infty} a_n = 0 \, подразумевает \ sum \ limits_ {n = 1} ^ {\ infty } a_n <\ infty n → ∞lim an = 0⟹n = 1∑∞ an <∞ является ложным \ color {# D61F06} {\ textbf {false}} ложным.{N} \ frac {1} {n} n = 1∑N n1 расходится при N → ∞.N \ rightarrow \ infty.N → ∞. (См. Доказательство здесь.)
Контрпример 2:
Мы также можем целенаправленно построить ряд, который совершенно очевидно не будет сходиться к конечной сумме, хотя расширенные члены ряда произвольно близки к 0. Рассмотрим этот ряд:1 + 12 + 12 + 13 + 13 + 13 + 14 + 14 + 14 + 14 + 15 + ⋯ .1 + \ frac {1} {2} + \ frac {1} {2} + \ frac {1} {3} + \ frac {1} {3} + \ frac {1} {3} + \ frac {1} {4} + \ frac {1} {4} + \ frac {1} {4} + \ frac {1} {4} + \ frac {1} {5} + \ cdots.1 + 21 +21 +31 +31 +31 +41 +41 +41 +41 +51 + ⋯.
Просто сгруппировав наборы одинаковых терминов, мы можем сказать, что эта сумма не сходится:
1+ (12 + 12) + (13 + 13 + 13) + (14 + 14 + 14 + 14) + (15 + ⋯) + ⋯ = 1 + 1 + 1 + 1 + 1 + ⋯ = ∞. 1 + \ left (\ frac {1} {2} + \ frac {1} {2} \ right) + \ left (\ frac {1} {3} + \ frac {1} {3} + \ frac {1 } {3} \ right) + \ left (\ frac {1} {4} + \ frac {1} {4} + \ frac {1} {4} + \ frac {1} {4} \ right) + \ left (\ frac {1} {5} + \ cdots \ right) + \ cdots = 1 + 1 + 1 + 1 + 1 + \ cdots = \ infty.1 + (21 +21) + (31 +31 +31) + (41 +41 +41 +41) + (51 + ⋯) + ⋯ = 1 + 1 + 1 + 1 + 1 + ⋯ = ∞.{N} a_n \ text {расходится как} N \ rightarrow \ infty .n → ∞lim an = 0⟹n = 1∑N an расходится при N → ∞. Следовательно, если предел ana_nan равен 0, тогда сумма должна сходиться.
Ответ:
Да, одна из первых вещей, которые вы узнаете о бесконечных рядах, это то, что если члены ряда не приближаются к нулю, то ряды не могут сходиться. Это правда. Однако противоположное утверждение неверно: как доказано выше, даже если члены ряда приближаются к нулю, это не гарантирует, что сумма сходится.Существует также правильный способ «перевернуть» утверждение в вашем заявлении, но это синтаксическое обращение, создание второго утверждения, которое логически эквивалентно первому. Утверждение «если члены ряда не приближаются к нулю, тогда ряд, возможно, не может сходиться» логически эквивалентно утверждению о том, что «если ряд сходится, то гарантируется, что члены ряда приближаются к нулю». Более формально,
∑n = 1Nan сходится при N → ∞ ⟹ limn → ∞an = 0.{N} a_ {n} \ text {сходится как} N \ rightarrow \ infty \ подразумевает \ lim \ limits _ {n \ rightarrow \ infty} a_ {n} = 0.n = 1∑N an сходится как N → ∞⟹n → ∞lim an = 0.
Если ваш учитель сказал, что «обратное» исходное утверждение также верно, то, вероятно, он имел в виду именно такой поворот.
Обратите внимание, что 1n → 0 \ frac {1} {n} \ rightarrow 0n1 → 0 при n → ∞. 2
8.1: Последовательности — математика LibreTexts
В этом разделе мы вводим последовательности и определяем, что это означает для последовательности сходиться или расходиться. Мы показываем, как найти пределы сходящихся последовательностей, часто используя свойства пределов для функций, которые обсуждались ранее. Мы завершаем этот раздел теоремой о монотонной сходимости, инструментом, который мы можем использовать для доказательства сходимости определенных типов последовательностей.
Терминология последовательностей
Чтобы работать с этой новой темой, нам нужны новые термины и определения.∞_n = 1, \]
или просто \ (\ displaystyle {a_n} \) для обозначения этой последовательности. Аналогичное обозначение используется для наборов, но последовательность — это упорядоченный список, а набор — неупорядоченный. Поскольку конкретное число \ (\ displaystyle a_n \) существует для каждого положительного целого числа \ (\ displaystyle n \), мы также можем определить последовательность как функцию, домен которой является набором положительных целых чисел.
Рассмотрим бесконечный упорядоченный список
\ [\ displaystyle 2,4,8,16,32,…. \]
Это последовательность, в которой первый, второй и третий члены задаются как \ (\ displaystyle a_1 = 2, a_2 = 4, \) и \ (\ displaystyle a_3 = 8.n}. \]
В качестве альтернативы, мы можем описать эту последовательность по-другому. Поскольку каждый член в два раза больше предыдущего, эту последовательность можно определить рекурсивно, выразив \ (\ displaystyle nth \) термин \ (\ displaystyle a_n \) через предыдущий термин \ (\ displaystyle a_ {n − 1} \ ). В частности, мы можем определить эту последовательность как последовательность \ (\ displaystyle {a_n} \), где \ (\ displaystyle a_1 = 2 \) и для всех \ (\ displaystyle n≥2 \), каждый термин an определяется повторение отношение
\ [\ Displaystyle a_n = 2a_ {n-1}.\]
Определение: бесконечная последовательность
Бесконечная последовательность \ (\ displaystyle {a_n} \) — это упорядоченный список чисел в форме
\ (\ Displaystyle a_1, a_2,…, a_n,…. \)
Нижний индекс \ (\ displaystyle n \) называется индексной переменной последовательности. Каждое число \ (\ displaystyle a_n \) является членом последовательности. Иногда последовательности определяются явными формулами, в этом случае \ (\ displaystyle a_n = f (n) \) для некоторой функции \ (\ displaystyle f (n) \), определенной над положительными целыми числами.В других случаях последовательности определяются с использованием отношения повторения . В рекуррентном отношении один член (или несколько) последовательности задается явно, а последующие термины определяются в терминах более ранних терминов в последовательности.
Обратите внимание, что индекс не обязательно должен начинаться с \ (\ displaystyle n = 1 \), но может начинаться с других целых чисел. Например, последовательность, заданная явной формулой \ (\ displaystyle a_n = f (n) \), может начинаться с \ (\ displaystyle n = 0 \), и в этом случае последовательность будет
\ [\ displaystyle a_0, a_1, a_2,….\]
Аналогичным образом, для последовательности, определенной рекуррентным соотношением, термин \ (\ displaystyle a_0 \) может быть задан явно, а термины \ (\ displaystyle a_n \) для \ (\ displaystyle n≥1 \) могут быть определены в члены \ (\ Displaystyle a_ {n − 1} \). Поскольку последовательность \ (\ displaystyle {a_n} \) имеет ровно одно значение для каждого положительного целого числа \ (\ displaystyle n \), ее можно описать как функцию, домен которой является набором положительных целых чисел. В результате имеет смысл обсудить график последовательности.п \)}.
Часто встречаются два типа последовательностей, которым даны специальные названия: арифметические последовательности и геометрические последовательности. В арифметической последовательности разница между каждой парой следующих друг за другом членов одинакова. Например, рассмотрим последовательность
\ [\ Displaystyle 3,7,11,15,19, \ ldots \]
Вы можете видеть, что разница между каждой последовательной парой терминов равна \ (\ displaystyle 4 \). Если предположить, что этот шаблон продолжается, эта последовательность является арифметической последовательностью. Его можно описать с помощью рекуррентного соотношения
\ [\ displaystyle \ begin {cases} a_1 = 3 \\ a_n = a_ {n − 1} + 4 & для n≥2 \ end {cases}.\]
Обратите внимание, что
\ [\ Displaystyle a_2 = 3 + 4 \]
\ [\ Displaystyle a_3 = 3 + 4 + 4 = 3 + 2⋅4 \]
\ [\ Displaystyle a_4 = 3 + 4 + 4 + 4 = 3 + 3⋅4. \]
Таким образом, последовательность также может быть описана с помощью явной формулы
\ [\ Displaystyle a_n = 3 + 4 (n − 1) = 4n − 1. \]
В общем, арифметическая последовательность — это любая последовательность вида \ (\ displaystyle a_n = cn + b. \)
В геометрической последовательности , соотношение каждой пары следующих друг за другом членов одинаково.Например, рассмотрим последовательность
\ [\ displaystyle 2, — \ dfrac {2} {3}, \ dfrac {2} {9}, — \ dfrac {2} {27}, \ dfrac {2} {81},…. {n − 1}.п \).
Пример \ (\ displaystyle \ PageIndex {1} \): поиск явных формул
Для каждой из следующих последовательностей найдите явную формулу для члена \ (\ displaystyle nth \) последовательности.
- \ (\ displaystyle — \ dfrac {1} {2}, \ dfrac {2} {3}, — \ dfrac {3} {4}, \ dfrac {4} {5}, — \ dfrac {5} {6},… \)
- \ (\ displaystyle \ dfrac {3} {4}, \ dfrac {9} {7}, \ dfrac {27} {10}, \ dfrac {81} {13}, \ dfrac {243} {16}, … \).
Решение :
а.п} \).
Упражнение \ (\ PageIndex {2} \)
Найдите явную формулу для последовательности, определенной рекурсивно, такой что \ (\ displaystyle a_1 = −4 \) и \ (\ displaystyle a_n = a_ {n − 1} +6 \).
- Подсказка
Это арифметическая последовательность.
- Ответ
\ (\ Displaystyle a_n = 6n − 10 \)
Предел последовательности
Фундаментальный вопрос, который возникает в отношении бесконечных последовательностей, — это поведение членов при увеличении \ (\ displaystyle n \).Поскольку последовательность — это функция, определенная на положительных целых числах, имеет смысл обсудить предел терминов как \ (\ displaystyle n → ∞ \). Например, рассмотрим следующие четыре последовательности и их различное поведение как \ (\ displaystyle n → ∞ \) (Рисунок \ (\ PageIndex {2} \)):
а. \ (\ displaystyle {1 + 3n} = {4,7,10,13,…}. \) Термы \ (\ displaystyle 1 + 3n \) становятся произвольно большими, как \ (\ displaystyle n → ∞ \). В этом случае мы говорим, что \ (\ displaystyle 1 + 3n → ∞ \) как \ (\ displaystyle n → ∞. \)
г.n} {n} → 0 \) как \ (\ displaystyle n → ∞. \)
Рисунок \ (\ PageIndex {2} \): (a) члены в последовательности становятся произвольно большими, как \ (\ displaystyle n → ∞ \). (b) Термины в последовательном подходе \ (\ displaystyle 1 \) как \ (\ displaystyle n → ∞ \). (c) Термины в последовательности чередуются между \ (\ displaystyle 1 \) и \ (\ displaystyle −1 \) как \ (\ displaystyle n → ∞ \). (d) Члены в последовательности чередуются между положительными и отрицательными значениями, но приближаются к \ (\ displaystyle 0 \) как \ (\ displaystyle n → ∞ \).Из этих примеров мы видим несколько возможностей поведения членов последовательности как \ (\ displaystyle n → ∞ \).В двух последовательностях члены приближаются к конечному числу, как \ (\ displaystyle n → ∞. \). В двух других последовательностях члены этого не делают. Если члены последовательности приближаются к конечному числу \ (\ displaystyle L \) как \ (\ displaystyle n → ∞ \), мы говорим, что последовательность является сходящейся последовательностью, а действительное число L является пределом последовательности. Мы можем дать здесь неформальное определение.
Определение: сходящиеся и расходящиеся последовательности
Учитывая последовательность \ (\ displaystyle {a_n}, \), если члены an становятся сколь угодно близкими к конечному числу \ (\ displaystyle L \), когда n становится достаточно большим, мы говорим, что \ (\ displaystyle {a_n} \) равно сходящаяся последовательность и \ (\ displaystyle L \) — это предел последовательности.n} \) — сходящаяся последовательность, и ее предел равен \ (\ displaystyle 1 \). Напротив, из рисунка мы видим, что члены в последовательности \ (\ displaystyle 1 + 3n \) не приближаются к конечному числу, поскольку \ (\ displaystyle n \) становится больше. Мы говорим, что \ (\ displaystyle {1 + 3n} \) — расходящаяся последовательность.
В неформальном определении предела последовательности мы использовали термины «произвольно близкие» и «достаточно большие». Хотя эти фразы помогают проиллюстрировать значение сходящейся последовательности, они несколько расплывчаты.Чтобы быть более точным, мы теперь представляем более формальное определение предела для последовательности и графически показываем эти идеи на рисунке.
Определение: конвергенция
Последовательность \ (\ displaystyle {a_n} \) сходится к действительному числу \ (\ displaystyle L \), если для всех \ (\ displaystyle ε> 0 \) существует целое число \ (\ displaystyle N \) такое, что \ (\ Displaystyle | a_n-L | <ε \), если \ (\ Displaystyle n≥N \). Число \ (\ displaystyle L \) является пределом последовательности, и мы пишем
\ [\ lim_ {n → ∞} a_n = Lora_n → L.\]
В этом случае мы говорим, что последовательность \ (\ displaystyle {a_n} \) является сходящейся последовательностью. Если последовательность не сходится, это расходящаяся последовательность, и мы говорим, что предела не существует.
Мы отмечаем, что сходимость или расхождение последовательности \ (\ displaystyle {a_n} \) зависит только от того, что происходит с членами \ (\ displaystyle a_n \) как \ (\ displaystyle n → ∞ \). Следовательно, если конечное число терминов \ (\ displaystyle b_1, b_2,…, b_N \) помещается перед \ (\ displaystyle a_1 \) для создания новой последовательности
\ [\ displaystyle b_1, b_2,…, b_N, a_1, a_2,…, \]
эта новая последовательность будет сходиться, если \ (\ displaystyle {a_n} \) сходится, и расходиться, если \ (\ displaystyle {a_n} \) расходится.Кроме того, если последовательность \ (\ displaystyle {a_n} \) сходится к \ (\ displaystyle L \), эта новая последовательность также сходится к \ (\ displaystyle L \).
Рисунок \ (\ PageIndex {3} \): по мере увеличения \ (\ displaystyle n \) термины \ (\ displaystyle a_n \) становятся ближе к \ (\ displaystyle L \). Для значений \ (\ displaystyle n≥N \) расстояние между каждой точкой \ (\ displaystyle (n, a_n) \) и линией \ (\ displaystyle y = L \) меньше \ (\ displaystyle ε \ ).Как определено выше, если последовательность не сходится, говорят, что это расходящаяся последовательность.n} \) расходится, потому что термины чередуются между \ (\ displaystyle 1 \) и \ (\ displaystyle −1 \), но не приближаются к одному значению как \ (\ displaystyle n → ∞ \). С другой стороны, последовательность \ (\ displaystyle {1 + 3n} \) расходится, потому что члены \ (\ displaystyle 1 + 3n → ∞ \) как \ (\ displaystyle n → ∞ \). Мы говорим, что последовательность \ (\ displaystyle {1 + 3n} \) расходится до бесконечности, и пишем \ (\ displaystyle \ lim_ {n → ∞} (1 + 3n) = ∞ \). Важно понимать, что это обозначение не означает, что существует предел последовательности \ (\ displaystyle {1 + 3n} \).На самом деле последовательность расходится. Запись о том, что предел равен бесконечности, предназначена только для предоставления дополнительной информации о том, почему последовательность расходится. Последовательность также может расходиться до отрицательной бесконечности. Например, последовательность \ (\ displaystyle {−5n + 2} \) расходится к отрицательной бесконечности, потому что \ (\ displaystyle −5n + 2 → −∞ \) как \ (\ displaystyle n → −∞ \). Мы записываем это как \ (\ displaystyle \ lim_ {n → ∞} (- 5n + 2) = → −∞. \)
Поскольку последовательность — это функция, домен которой является набором положительных целых чисел, мы можем использовать свойства пределов функций, чтобы определить, сходится ли последовательность.Например, рассмотрим последовательность \ (\ displaystyle {a_n} \) и связанную функцию \ (\ displaystyle f \), определенную для всех положительных действительных чисел, такую, что \ (\ displaystyle f (n) = a_n \) для всех целых чисел \ (\ Displaystyle п≥1 \). Поскольку домен последовательности является подмножеством области \ (\ displaystyle f \), если существует \ (\ displaystyle \ lim_ {x → ∞} f (x) \), то последовательность сходится и имеет тот же предел . Например, рассмотрим последовательность \ (\ displaystyle {\ dfrac {1} {n}} \) и связанную функцию \ (\ displaystyle f (x) = \ dfrac {1} {x} \).Поскольку функция \ (\ displaystyle f \), определенная для всех действительных чисел \ (\ displaystyle x> 0 \), удовлетворяет \ (\ displaystyle f (x) = \ dfrac {1} {x} → 0 \) как \ (\ displaystyle x → ∞ \), последовательность \ (\ displaystyle {\ dfrac {1} {n}} \) должна удовлетворять \ (\ displaystyle \ dfrac {1} {n} → 0 \) как \ (\ displaystyle n → ∞. \)
Предел последовательности, определяемой функцией
Рассмотрим последовательность \ (\ displaystyle {a_n} \) такую, что \ (\ displaystyle a_n = f (n) \) для всех \ (\ displaystyle n≥1 \). Если существует такое вещественное число \ (\ displaystyle L \), что
\ [\ Displaystyle \ lim_ {х → ∞} е (х) = L, \]
, тогда \ (\ displaystyle {a_n} \) сходится и
\ [lim_ {n → ∞} a_n = L.n} \) сходится к \ (\ displaystyle 0 + 0 = 0 \). Так же, как мы смогли оценить предел, включающий алгебраическую комбинацию функций \ (\ displaystyle f \) и \ (\ displaystyle g \), посмотрев на пределы \ (\ displaystyle f \) и \ (\ displaystyle g \ ) (см. Введение в пределы), мы можем оценить предел последовательности, члены которой представляют собой алгебраические комбинации \ (\ displaystyle a_n \) и \ (\ displaystyle b_n \), оценивая пределы \ (\ displaystyle {a_n } \) и \ (\ displaystyle {b_n} \).
Алгебраические предельные законы
Данные последовательности \ (\ displaystyle {a_n} \) и \ (\ displaystyle {b_n} \) и любое действительное число \ (\ displaystyle c \), если существуют константы \ (\ displaystyle A \) и \ (\ displaystyle B \) такая, что \ (\ displaystyle \ lim_ {n → ∞} a_n = A \) и \ (\ displaystyle \ lim_ {n → ∞} b_n = B \), то
- \ (\ Displaystyle \ lim_ {п → ∞} с = с \)
- \ (\ Displaystyle \ lim_ {n → ∞} ca_n = с \ lim_ {n → ∞} a_n = cA \)
- \ (\ Displaystyle \ lim_ {n → ∞} (a_n ± b_n) = \ lim_ {n → ∞} a_n ± \ lim_ {n → ∞} b_n = A ± B \)
- \ (\ Displaystyle \ lim_ {n → ∞} (a_n⋅b_n) = (\ lim_ {n → ∞} a_n) ⋅ (\ lim_ {n → ∞} b_n) = A⋅B \)
- \ (\ Displaystyle \ lim_ {n → ∞} (\ dfrac {a_n} {b_n}) = \ dfrac {\ lim_ {n → ∞} a_n} {\ lim_ {n → ∞} b_n} = \ dfrac {A } {B} \) при условии \ (\ displaystyle B ≠ 0 \) и каждый \ (\ displaystyle b_n ≠ 0.\)
Проба
Докажем часть iii.
Пусть \ (\ Displaystyle ϵ> 0 \). Поскольку \ (\ displaystyle \ lim_ {n → ∞} a_n = A \), существует постоянное положительное целое число \ (\ displaystyle N_1 \) такое, что для всех \ (\ displaystyle n≥N_1 \). Поскольку \ (\ displaystyle \ lim_ {n → ∞} b_n = B \), существует константа \ (\ displaystyle N_2 \) такая, что \ (\ displaystyle | b_n − B | <ε / 2 \) для всех \ ( \ Displaystyle п≥N_2 \). Пусть \ (\ displaystyle N \) будет наибольшим из \ (\ displaystyle N_1 \) и \ (\ displaystyle N_2 \).x] = \ lim_ {x → ∞} xln (1+ \ dfrac {4} {x}) \).
Поскольку правая часть этого уравнения имеет неопределенную форму \ (\ displaystyle ∞⋅0 \), перепишите ее как дробь, чтобы применить правило Л’Опиталя. Напишите
\ (\ Displaystyle \ lim_ {x → ∞} xln (1+ \ dfrac {4} {x}) = \ lim_ {x → ∞} \ dfrac {ln (1 + 4 / x)} {1 / x} \).
Поскольку правая часть теперь имеет неопределенную форму 0/0, мы можем применить правило L’Hôpital. Делаем вывод, что
\ (\ Displaystyle \ lim_ {x → ∞} \ dfrac {ln (1 + 4 / x)} {1 / x} = \ lim_ {x → ∞} \ dfrac {4} {1 + 4 / x} = 4.n}. \) Определите, сходится ли последовательность. Если он сходится, найдите его предел.
- Подсказка
Используйте правило L’Hôpital.
- Ответ
Последовательность сходится, и ее предел равен \ (\ displaystyle 0 \)
Напомним, что если \ (\ displaystyle f \) является непрерывной функцией со значением \ (\ displaystyle L \), то \ (\ displaystyle f (x) → f (L) \) как \ (\ displaystyle x → L \).2})} = \ sqrt {5}. \]
Непрерывные функции, определенные на сходящихся последовательностях
Рассмотрим последовательность \ (\ displaystyle {a_n} \) и предположим, что существует действительное число \ (\ displaystyle L \) такое, что последовательность \ (\ displaystyle {a_n} \) сходится к \ (\ displaystyle L \). Предположим, \ (\ displaystyle f \) — непрерывная функция в \ (\ displaystyle L \). Тогда существует целое число \ (\ displaystyle N \) такое, что \ (\ displaystyle f \) определено для всех значений an для \ (\ displaystyle n≥N \), и последовательность \ (\ displaystyle {f (a_n) } \) сходится к \ (\ displaystyle f (L) \) (Рисунок \ (\ PageIndex {4} \)).
Рис. \ (\ PageIndex {4} \): Поскольку \ (\ displaystyle f \) является непрерывной функцией, поскольку входы \ (\ displaystyle a_1, a_2, a_3,… \) подход \ (\ displaystyle L \), выходы \ (\ displaystyle f (a_1), f (a_2), f (a_3),… \) подход \ (\ displaystyle f (L) \).Проба
Пусть \ (\ displaystyle ϵ> 0. \) Поскольку \ (\ displaystyle f \) непрерывен в \ (\ displaystyle L \), существует \ (\ displaystyle δ> 0 \) такое, что \ (\ displaystyle | f (Икс) −f (L) | <ε \), если \ (\ Displaystyle | x − L | <δ \). Поскольку последовательность \ (\ displaystyle {a_n} \) сходится к \ (\ displaystyle L \), существует \ (\ displaystyle N \) такая, что \ (\ displaystyle | a_n − L | <δ \) для всех \ ( \ Displaystyle п≥N \).2}) = cos (0) = 1. \)
Упражнение \ (\ PageIndex {4} \)
Определите, сходится ли последовательность \ (\ displaystyle {\ sqrt {\ dfrac {2n + 1} {3n + 5}}} \). Если он сходится, найдите его предел.
- Подсказка
Рассмотрим последовательность \ (\ displaystyle {\ dfrac {2n + 1} {3n + 5}}. \)
- Ответ
Последовательность сходится, и ее предел равен \ (\ displaystyle \ sqrt {2/3} \).
Другая теорема, касающаяся пределов последовательностей, является расширением теоремы сжатия для пределов, обсуждаемых во введении в пределы.
Теорема сжатия для последовательностей
Рассмотрим последовательности \ (\ displaystyle {a_n}, {b_n}, \) и \ (\ displaystyle {c_n} \). Предположим, существует целое число \ (\ displaystyle N \) такое, что
\ [\ displaystyle a_n≤b_n≤c_n \) для всех \ (\ displaystyle n≥N. \]
Если существует действительное число \ (\ displaystyle L \) такое, что
\ [\ Displaystyle \ lim_ {n → ∞} a_n = L = \ lim_ {n → ∞} c_n, \]
, тогда \ (\ displaystyle {b_n} \) сходится и \ (\ displaystyle \ lim_ {n → ∞} b_n = L \) (рисунок \ (\ PageIndex {5} \)).
Рисунок \ (\ PageIndex {5} \): каждый член bn удовлетворяет \ (\ displaystyle a_n≤b_n≤c_n \), а последовательности \ (\ displaystyle {a_n} \) и \ (\ displaystyle {c_n} \) сходятся к тот же предел, поэтому последовательность \ (\ displaystyle {b_n} \) также должна сходиться к тому же пределу.Проба
Пусть \ (\ displaystyle ε> 0. \) Поскольку последовательность \ (\ displaystyle {a_n} \) сходится к \ (\ displaystyle L \), существует целое число \ (\ displaystyle N_1 \) такое, что \ (\ displaystyle | a_n − L | <ε \) для всех \ (\ displaystyle n≥N_1 \).Точно так же, поскольку \ (\ displaystyle {c_n} \) сходится к \ (\ displaystyle L \), существует целое число \ (\ displaystyle N_2 \) такое, что \ (\ displaystyle | c_n − L | <ε \) для всех \ (\ Displaystyle п≥N_2 \). По предположению существует целое число \ (\ displaystyle N \) такое, что \ (\ displaystyle a_n≤b_n≤c_n \) для всех \ (\ displaystyle n≥N \). Пусть \ (\ displaystyle M \) будет наибольшим из \ (\ displaystyle N_1, N_2 \) и \ (\ displaystyle N \). Мы должны показать, что \ (\ displaystyle | b_n − L | <ε \) для всех \ (\ displaystyle n≥M \). Для всех \ (\ displaystyle n≥M \),
\ [\ displaystyle −ε <- | a_n − L | ≤a_n − L≤b_n − L≤c_n − L≤ | c_n − L | <ε \]
Следовательно, \ (\ displaystyle −ε
Ограниченные последовательности
Теперь обратим наше внимание на одну из наиболее важных теорем, касающихся последовательностей: теорему о монотонной сходимости. Прежде чем сформулировать теорему, нам нужно ввести некоторую терминологию и мотивацию. Начнем с определения того, что означает ограниченность последовательности.
Определение: Связанные последовательности
Последовательность \ (\ displaystyle {a_n} \) имеет значение , ограниченное выше , если существует действительное число \ (\ displaystyle M \) такое, что
\ (\ Displaystyle a_n≤M \)
для всех положительных целых чисел \ (\ displaystyle n \).
Последовательность \ (\ displaystyle {a_n} \) имеет значение , ограниченное ниже , если существует действительное число \ (\ displaystyle M \) такое, что
\ (\ Displaystyle M≤a_n \)
для всех положительных целых чисел \ (\ displaystyle n \).
Последовательность \ (\ displaystyle {a_n} \) — это ограниченная последовательность , если она ограничена сверху и ограничена снизу.
Если последовательность не ограничена, это неограниченная последовательность .
Например, последовательность \ (\ displaystyle {1 / n} \) ограничена выше, потому что \ (\ displaystyle 1 / n≤1 \) для всех положительных целых чисел \ (\ displaystyle n \).n} \) — неограниченная последовательность.
Теперь обсудим связь между ограниченностью и сходимостью. Предположим, что последовательность \ (\ displaystyle {a_n} \) неограничена. Тогда он не ограничен сверху, не ограничен снизу или и тем, и другим. В любом случае есть члены, произвольно большие по величине по мере того, как \ (\ displaystyle n \) становится больше. В результате последовательность \ (\ displaystyle {a_n} \) не может сходиться. Следовательно, ограниченность — необходимое условие сходимости последовательности.
Сходящиеся последовательности ограничены
Если последовательность \ (\ displaystyle {a_n} \) сходится, то она ограничена.n} \) ограничен, но последовательность расходится, потому что последовательность колеблется между \ (\ displaystyle 1 \) и \ (\ displaystyle −1 \) и никогда не приближается к конечному числу. Теперь обсудим достаточное (но не необходимое) условие сходимости ограниченной последовательности.
Рассмотрим ограниченную последовательность \ (\ displaystyle {a_n} \). Предположим, что последовательность \ (\ displaystyle {a_n} \) увеличивается. То есть \ (\ displaystyle a_1≤a_2≤a_3…. \) Поскольку последовательность увеличивается, члены не колеблются. Следовательно, есть две возможности.Последовательность могла расходиться до бесконечности, а могла сходиться. Однако, поскольку последовательность ограничена, она ограничена сверху и последовательность не может расходиться до бесконечности. Мы заключаем, что \ (\ displaystyle {a_n} \) сходится. Например, рассмотрим последовательность
\ [\ displaystyle {\ dfrac {1} {2}, \ dfrac {2} {3}, \ dfrac {3} {4}, \ dfrac {4} {5},…}. \]
Поскольку эта последовательность возрастает и ограничена сверху, она сходится. Далее рассмотрим последовательность
\ [\ displaystyle {2,0,3,0,4,0,1, — \ dfrac {1} {2}, — \ dfrac {1} {3}, — \ dfrac {1} {4}, …}.\]
Несмотря на то, что последовательность не увеличивается для всех значений \ (\ displaystyle n \), мы видим, что \ (\ displaystyle -1/2 <-1/3 <-1/4 <⋯ \). Следовательно, начиная с восьмого члена \ (\ displaystyle a_8 = −1 / 2 \), последовательность увеличивается. В этом случае мы говорим, что последовательность в конечном итоге увеличивается. Поскольку последовательность ограничена сверху, она сходится. Верно также и то, что если последовательность убывает (или со временем убывает) и ограничена снизу, она также сходится.
Определение
Последовательность \ (\ displaystyle {a_n} \) увеличивается для всех \ (\ displaystyle n≥n_0 \), если
\ (\ displaystyle a_n≤a) n + 1 \) для всех \ (\ displaystyle n≥n_0 \).
Последовательность \ (\ displaystyle {a_n} \) уменьшается для всех \ (\ displaystyle n≥n_0 \), если
\ (\ displaystyle a_n≥a_ {n + 1} \) для всех \ (\ displaystyle n≥n_0 \).
Последовательность \ (\ displaystyle {a_n} \) — это монотонная последовательность для всех \ (\ displaystyle n≥n_0 \), если она увеличивается для всех \ (n≥n_0 \) или уменьшается для всех \ (\ Displaystyle п≥n_0 \).
Теперь у нас есть необходимые определения, чтобы сформулировать теорему о монотонной сходимости, которая дает достаточное условие сходимости последовательности.
Определение: теорема о монотонной сходимости
Если \ (\ displaystyle {a_n} \) является ограниченной последовательностью и существует такое положительное целое число n0, что \ (\ displaystyle {a_n} \) является монотонным для всех \ (\ displaystyle n≥n_0 \), то \ ( \ displaystyle {a_n} \) сходится.
Доказательство этой теоремы выходит за рамки этого текста. Вместо этого мы предоставляем график, чтобы интуитивно показать, почему эта теорема имеет смысл (рис. \ (\ PageIndex {6} \)).
Рисунок \ (\ PageIndex {6} \): поскольку последовательность \ (\ displaystyle {a_n} \) возрастает и ограничена сверху, она должна сходиться.n} {n!} = \ dfrac {4} {n + 1} ⋅a_n≤a_n \), если \ (\ displaystyle n≥3. \)Следовательно, последовательность убывает для всех \ (\ displaystyle n≥3 \). Кроме того, последовательность ограничена внизу \ (\ displaystyle 0 \), потому что \ (\ displaystyle 4n / n! ≥0 \) для всех положительных целых чисел \ (\ displaystyle n \). Следовательно, по теореме о монотонной сходимости последовательность сходится.
Чтобы найти предел, мы используем тот факт, что последовательность сходится, и пусть \ (\ displaystyle L = \ lim_ {n → ∞} a_n \). Обратите внимание на это важное наблюдение.Рассмотрим \ (\ displaystyle \ lim_ {n → ∞} a_ {n + 1} \). С
\ (\ Displaystyle {a_ {n + 1}} = {a_2, a_3, a_4,…}, \)
единственное различие между последовательностями \ (\ displaystyle {a_ {n + 1}} \) и \ (\ displaystyle {a_n} \) состоит в том, что \ (\ displaystyle {a_ {n + 1}} \) опускает первую срок. Поскольку конечное число членов не влияет на сходимость последовательности,
\ (\ Displaystyle \ lim_ {n → ∞} a_ {n + 1} = \ lim_ {n → ∞} a_n = L. \)
Объединяя этот факт с уравнением
\ (\ Displaystyle a_ {n + 1} = \ dfrac {4} {n + 1} a_n \)
и взяв предел обеих частей уравнения
\ (\ Displaystyle \ lim_ {п → ∞} a_ {n + 1} = \ lim_ {n → ∞} \ dfrac {4} {n + 1} a_n \),
можно сделать вывод, что
\ (\ Displaystyle L = 0⋅L = 0. 2_n + 1} {2a_n} \).2_н \).
Разделив обе стороны на \ (\ displaystyle 2a_n \), получаем
\ (\ Displaystyle \ dfrac {a_n} {2} + \ dfrac {1} {2a_n} ≤a_n. \)
Используя определение \ (\ displaystyle a_ {n + 1} \), мы заключаем, что
\ (\ displaystyle a_ {n + 1} = \ dfrac {a_n} {2} + \ dfrac {1} {2a_n} ≤a_n \).
Поскольку \ (\ displaystyle {a_n} \) ограничено снизу и убывает по теореме о монотонной сходимости, он сходится.
Чтобы найти предел, пусть \ (\ displaystyle L = \ lim_ {n → ∞} a_n \).2 = 1 \), что означает \ (\ Displaystyle L = ± 1 \). Поскольку все члены положительны, предел \ (\ displaystyle L = 1 \).
Упражнение \ (\ PageIndex {6} \)
Рассмотрим последовательность \ (\ displaystyle {a_n} \), определенную рекурсивно, так что \ (\ displaystyle a_1 = 1 \), \ (\ displaystyle a_n = a_ {n − 1} / 2 \). Используйте теорему о монотонной сходимости, чтобы показать, что эта последовательность сходится, и найдите ее предел.
- Подсказка
Показать, что последовательность убывает и ограничена снизу.
- Ответ
\ (\ Displaystyle 0 \).
Определение: числа Фибоначчи
Число Фибоначчи определяется рекурсивно последовательностью \ (\ displaystyle {F_n} \), где \ (\ displaystyle F_0 = 0, F_1 = 1 \) и для \ (\ displaystyle n≥2, \)
\ (\ Displaystyle F_n = F_ {n − 1} + F_ {n − 2}. \)
Здесь мы рассмотрим свойства чисел Фибоначчи.
1.п \). Используйте начальные условия \ (\ displaystyle F_0 \) и \ (\ displaystyle F_1 \), чтобы определить значения констант \ (\ displaystyle c_1 \) и \ (\ displaystyle c_2 \), и напишите закрытую формулу \ (\ displaystyle Ф_н \).
3. Используйте ответ в 2 c. чтобы показать, что
\ [\ displaystyle \ lim_ {n → ∞} \ dfrac {F_ {n + 1}} {F_n} = \ dfrac {1+ \ sqrt {5}} {2}. \]
Число \ (\ displaystyle ϕ = (1+ \ sqrt {5}) / 2 \) известно как золотое сечение (рисунок и рисунок).
Рисунок \ (\ PageIndex {7} \): Семена подсолнечника имеют спиральные узоры, изгибающиеся влево и вправо.Количество спиралей в каждом направлении всегда является числом Фибоначчи — всегда. (кредит: модификация работы Эсдраса Кальдерана, Wikimedia Commons) Рисунок \ (\ PageIndex {8} \): пропорция золотого сечения встречается во многих известных образцах искусства и архитектуры. Древнегреческий храм, известный как Парфенон, был спроектирован с такими пропорциями, и соотношение снова проявляется во многих мелких деталях. (кредит: модификация работы TravelingOtter, Flickr).Предел, Предел последовательности
Мы уже знаем, что такое арифметическая и геометрическая прогрессия — последовательность значений.Возьмем последовательность a n = 1 / n, если k и м натуральные числа, тогда для каждого k истинно a k > a m , так как чем меньше становится, тем меньше становится n и он всегда положительный, но никогда не достигает нуля. В этом случае мы говорим, что 0 — это
, предел n-> ∞ если n-> ∞, или другой способ записать это lim n-> ∞ a n = 0.Определение предела
Число a называется пределом последовательности, если для любого ε> 0 можно найти число n ε , так что для всех членов последовательности a n с индексом n> n ε верно, что a — ε n.
Основное правило
Если lim n-> ∞ a n = a, a n -> a a n — a -> 0 | a n — a | -> 0
Последовательность не всегда имеет предел, а иногда и нереальный предел (-∞ или + ∞). Пределы + ∞ и -∞ называются нереальными пределами.
Если обе последовательности a n и b n имеют реальные пределы, то последовательности
a n + b n , a n — b n , a n .b n и a n / b n также имеют реальный предел и:lim n -> ∞ (a n + b n ) = lim n -> ∞ a n + lim n -> ∞ b n
lim n -> ∞ (a n — b n ) = lim n -> ∞ a n — lim n -> ∞ b n
lim n -> ∞ (a n . b n ) = lim n -> ∞ a n .lim n -> ∞ b n
lim n -> ∞ (a n / b n ) = lim n -> ∞ a n / lim n -> ∞ b n
если b n ≠ 0 и lim n-> ∞ b n ≠ 0Если a n n для каждого натурального n и lim n-> ∞ a n = a,
lim n-> ∞ b n = b тогда a ≤ bЕсли a n ≤ b n ≤ c n или каждое действительное n и если lim n-> ∞ a n = lim n-> ∞ c n = A
, то lim n-> ∞ b n = A.Если a n ≥ 0 и lim n-> ∞ a n = a, тогда последовательность b n = √a n также имеет предел и lim n-> ∞ √a n = √a n .
Если n = 1 / n k и k ≥ 1, тогда lim n-> ∞ a n = 0.
Если -1 n-> ∞q n = 0.
lim n-> ∞ (1 — 1 / n) n = lim n-> ∞ (1 + 1 / n) n + 1 = e
(1 + 1 / n) n п-1е — число Непер.
Если последовательность a n имеет нереальный предел (-∞ или + ∞) тогда последовательность 1 / a n имеет предел и lim n-> ∞ 1 / a n = 0
Если последовательности a n и b n имеют нереальные пределы и lim n-> ∞ a n = + ∞, lim n-> ∞ b n = + ∞, тогда:
lim n-> ∞ (a n + b n ) = + ∞
lim n-> ∞ (a n .b n ) = + ∞
lim n-> ∞ a n k = + ∞, если k> 0
lim n-> ∞ a n k = 0; если k lim n-> ∞ -a n = -∞Лим проблемы
Упражнение 1:
Если n = 5,4 n , lim n-> 0 a n =?Ответ:
lim n-> 0 a n = lim n-> 0 5.lim n-> 0 4 n = 5. 4 0 = 5,1 = 5Упражнение 2:
Если n = , тогда lim n-> ∞a n =? Ответ:
lim n-> ∞ = lim n-> ∞ . = lim n-> ∞ = -3 Упражнение 3:
Ответ:
= lim a n -> 1 (2a n + 1) = 3
lim a n -> 1 = = lim a n -> ∞ = Предел графопостроителя
Подробнее о lim на математическом форуме
Регистрация на форуме
Конвергенция в распределении
7.2.4 Конвергенция в распределении
Сходимость распределения — это в некотором смысле самый слабый тип сходимости. Все, что он говорит, это то, что CDF $ X_n $ сходится к CDF $ X $, когда $ n $ стремится к бесконечности. Не требует какой-либо зависимости между $ X_n $ и $ X $. Мы видели подобную сходимость раньше, когда обсуждали центральную предельную теорему. Чтобы сказать, что $ X_n $ сходится по распределению к $ X $, мы пишем
\ begin {align}% \ label {eq: union-bound} X_n \ \ xrightarrow {d} \ X.\ end {align}Вот формальное определение сходимости в распределении:
Конвергенция в распределении
Последовательность случайных величин $ X_1 $, $ X_2 $, $ X_3 $, $ \ cdots $ сходится в распределении к случайной величине $ X $, показанной $ X_n \ \ xrightarrow {d} \ X $, если \ begin {align}% \ label {eq: union-bound} \ lim_ {n \ rightarrow \ infty} F_ {X_n} (x) = F_X (x), \ end {align} для всех $ x $, при которых $ F_X (x) $ непрерывно. {nx} & \ quad x> 0 \\ & \ quad \\ 0 & \ quad \ text {в противном случае} \ end {array} \ right.{-Икс}\\ & = F_X (x), \ qquad \ textrm {для всех} x. \ end {align} Таким образом, мы заключаем, что $ X_n \ \ xrightarrow {d} \ X $.
При работе с целочисленными случайными величинами часто бывает полезна следующая теорема.
Теорема Рассмотрим последовательность $ X_1 $, $ X_2 $, $ X_3 $, $ \ cdots $ и случайную величину $ X $. Предположим, что $ X $ и $ X_n $ (для всех $ n $) неотрицательные и целочисленные, т. Е. \ begin {align}% \ label {} & R_X \ subset \ {0,1,2, \ cdots \}, \\ & R_ {X_n} \ subset \ {0,1,2, \ cdots \}, \ qquad \ textrm {for} n = 1,2,3, \ cdots.\ end {align} Тогда $ X_n \ \ xrightarrow {d} \ X $ тогда и только тогда, когда \ begin {align}% \ label {eq: union-bound} \ lim_ {n \ rightarrow \ infty} P_ {X_n} (k) = P_X (k), \ qquad \ textrm {for} k = 0,1,2, \ cdots. \ end {align}
- Проба
- Поскольку $ X $ является целочисленным, его CDF, $ F_X (x) $, непрерывна во всех $ x \ in \ mathbb {R} — \ {0,1,2, … \} $. Если $ X_n \ \ xrightarrow {d} \ X $, то \ begin {align}% \ label {eq: union-bound} \ lim_ {n \ rightarrow \ infty} F_ {X_n} (x) = F_X (x), \ qquad \ textrm {для всех} x \ in \ mathbb {R} — \ {0,1,2 ,… \}. \ end {align} Таким образом, для $ k = 0,1,2, \ cdots $ имеем \ begin {align}% \ label {eq: union-bound} \ lim_ {n \ rightarrow \ infty} P_ {X_n} (k) & = \ lim_ {n \ rightarrow \ infty} \ left [F_ {X_n} \ left (k + \ frac {1} {2} \ right) — F_ {X_n} \ left (k- \ frac {1} {2} \ right) \ right] \ hspace {25pt} \ textrm {($ X_n $ имеют целочисленные значения)} \\ & = \ lim_ {n \ rightarrow \ infty} F_ {X_n} \ left (k + \ frac {1} {2} \ right) — \ lim_ {n \ rightarrow \ infty} F_ {X_n} \ left (k- \ гидроразрыв {1} {2} \ right) \\ & = F_ {X} \ left (k + \ frac {1} {2} \ right) — F_ {X} \ left (k- \ frac {1} {2} \ right) \ hspace {30pt} \ textrm { (поскольку $ X_n \ \ xrightarrow {d} \ X $)} \\ & = P_X (k) \ hspace {30pt} \ textrm {(поскольку $ X $ является целочисленным).{\ lfloor x \ rfloor} P_ {X} (k) \ qquad \ textrm {(по предположению)} \\ & = Р (Х \ leq х) = F_X (х). \ end {align}
Пример
Пусть $ X_1 $, $ X_2 $, $ X_3 $, $ \ cdots $ — последовательность случайных величин, такая что \ begin {align}% \ label {eq: union-bound} X_n \ sim Биномиальный \ left (n, \ frac {\ lambda} {n} \ right), \ qquad \ textrm {for} n \ in \ mathbb {N}, n> \ lambda, \ end {align} где $ \ lambda> 0 $ — постоянная. Покажите, что $ X_n $ сходится по распределению к $ Poisson (\ lambda) $.к} {к!}. \ end {уравнение}В конце этого раздела напомним, что наиболее известным примером сходимости в распределении является центральная предельная теорема (ЦПТ). CLT утверждает, что нормализованное среднее значение i.i.d. случайные величины $ X_1 $, $ X_2 $, $ X_3 $, $ \ cdots $ сходятся по распределению к стандартной нормальной случайной величине.
сравнительных тестов
Тест \ (N \) -го члена, вообще говоря, не гарантирует сходимости ряда.


 Теперь добавим d еще раз, получим: a3 = a2+d. Продолжая эту математическую операцию, можно получить целый ряд чисел, который будет называться прогрессией арифметической.
Теперь добавим d еще раз, получим: a3 = a2+d. Продолжая эту математическую операцию, можно получить целый ряд чисел, который будет называться прогрессией арифметической. В частности, является арифметической прогрессией с разностью .
В частности, является арифметической прогрессией с разностью .

 {infty }}_{=1}
{infty }}_{=1}
 Следует обратить на один важный момент внимание: разности берутся между “старшим” и “младшим” членами, то есть n > m (“старший” – имеется в виду стоящий дальше от начала последовательности, его абсолютное значение может быть как больше, так и меньше более “младшего” элемента).
Следует обратить на один важный момент внимание: разности берутся между “старшим” и “младшим” членами, то есть n > m (“старший” – имеется в виду стоящий дальше от начала последовательности, его абсолютное значение может быть как больше, так и меньше более “младшего” элемента). Тем не менее такой подход к решению задачи является непродуктивным в плане развития школьника и понимания сути поставленной перед ним задачи.
Тем не менее такой подход к решению задачи является непродуктивным в плане развития школьника и понимания сути поставленной перед ним задачи. Заметим, что это выражение обращается в неопределенность (0/0), если n=1. Связано это с тем, что необходимо знание как минимум 2-х элементов ряда, чтобы определить его разность.
Заметим, что это выражение обращается в неопределенность (0/0), если n=1. Связано это с тем, что необходимо знание как минимум 2-х элементов ряда, чтобы определить его разность.
 Он заметил, что такая прогрессия является симметричной, то есть сумма симметрично расположенных с начала и конца членов прогрессии является постоянной для данного ряда.
Он заметил, что такая прогрессия является симметричной, то есть сумма симметрично расположенных с начала и конца членов прогрессии является постоянной для данного ряда. Аналогично происходит, если нужно найти сумму первых шести членов или любого другого количества.
Аналогично происходит, если нужно найти сумму первых шести членов или любого другого количества. ru/node/1002
ru/node/1002 К. Характеристическое свойство показательной прогрессии или новое числовое среднее / Н. К. Гульманов. — Текст : непосредственный // Молодой ученый. — 2018. — № 6 (192). — С. 1-4. — URL: https://moluch.ru/archive/192/48026/ (дата обращения: 16.09.2022).
К. Характеристическое свойство показательной прогрессии или новое числовое среднее / Н. К. Гульманов. — Текст : непосредственный // Молодой ученый. — 2018. — № 6 (192). — С. 1-4. — URL: https://moluch.ru/archive/192/48026/ (дата обращения: 16.09.2022). 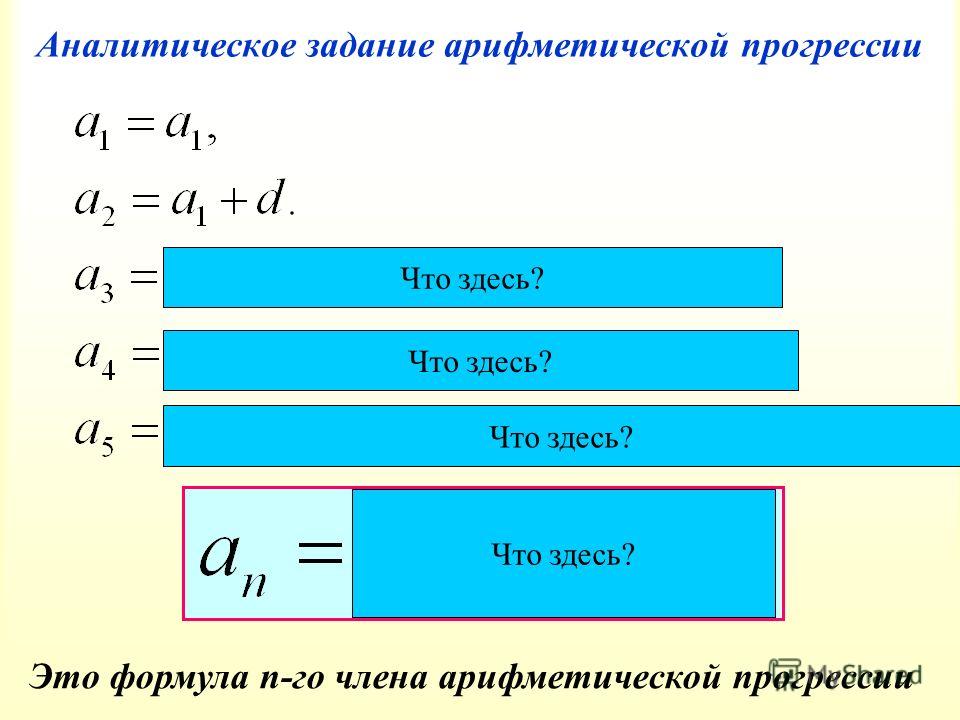
 е.
е.


 С. Соминский / Метод математической индукции / Популярные лекции по математике, выпуск № 3/ — М.: Издательство «Наука», 1972. — С. 63
С. Соминский / Метод математической индукции / Популярные лекции по математике, выпуск № 3/ — М.: Издательство «Наука», 1972. — С. 63 ..
.. ..
.. ..
..
 ..
.. ..
..
 Формула (1) называется формулой общего члена арифметической прогрессии, а формула (2) представляет собой основное свойство арифметической прогрессии: каждый член прогрессии совпадает со средним арифметическим своих соседних членов и .
Формула (1) называется формулой общего члена арифметической прогрессии, а формула (2) представляет собой основное свойство арифметической прогрессии: каждый член прогрессии совпадает со средним арифметическим своих соседних членов и . (6)
(6)
 Найти , если .
Найти , если . Так как по формуле (3) имеем, что , то из условия задачи вытекает система уравнений
Так как по формуле (3) имеем, что , то из условия задачи вытекает система уравнений 
 Найти максимальное значение при условии, что и .
Найти максимальное значение при условии, что и .
 – 216 с.
– 216 с. д.).
д.).

 Надо найти 45-й член этой прогрессии.
Надо найти 45-й член этой прогрессии. д.+100.
д.+100.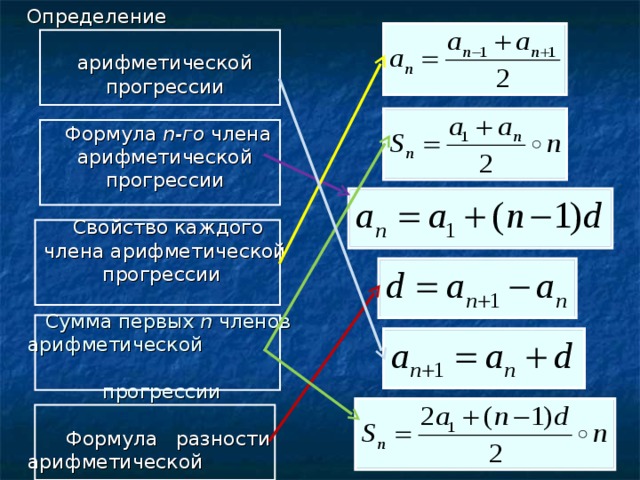

 . .
. .

 Учащиеся
6-го класса еще не проходили и не знают определение корней в математике.
Учащиеся
6-го класса еще не проходили и не знают определение корней в математике. 3\over3}$
3\over3}$
 7
. Всего получено оценок: 105.
7
. Всего получено оценок: 105. Зная определение степени,
можно записать формулу площади сферы следующим образом.
Зная определение степени,
можно записать формулу площади сферы следующим образом.
 Площадь поверхности сферы через радиус или диаметр:
Площадь поверхности сферы через радиус или диаметр:
 Диаметральная плоскость — это секущая плоскость, проходящая через центр сферы или шара, сеченме образует соответственно большую окружность и большой круг . Большая окружность и большой круг имеют центр, который совпадают с центром сферы (шара).
Диаметральная плоскость — это секущая плоскость, проходящая через центр сферы или шара, сеченме образует соответственно большую окружность и большой круг . Большая окружность и большой круг имеют центр, который совпадают с центром сферы (шара).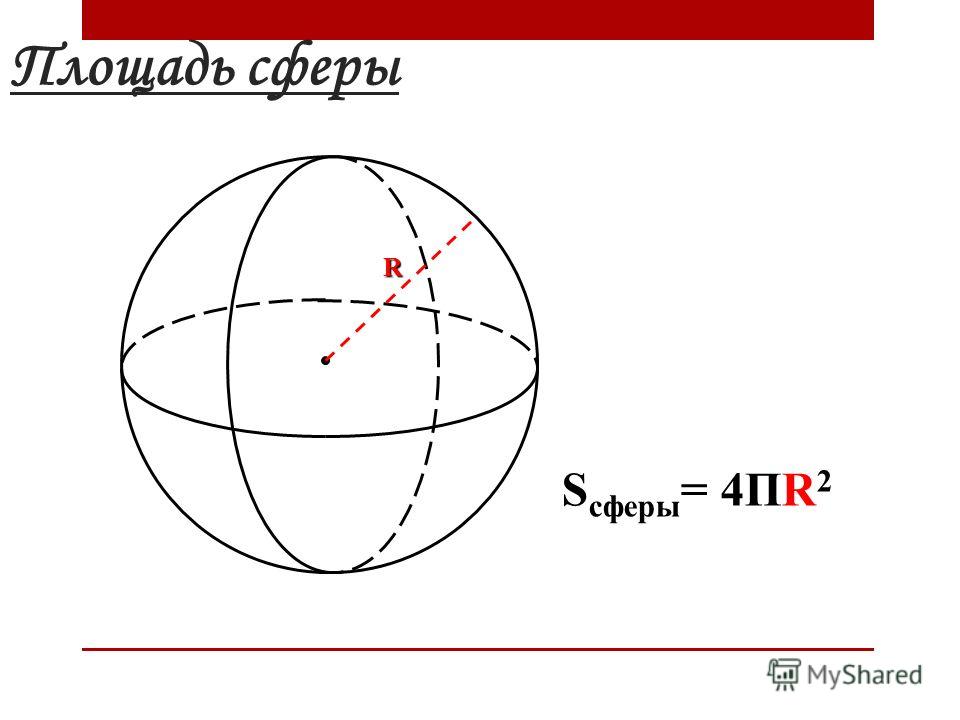
 Площадь ее поверхности, в сравнении с другими трёхмерными телами, имеет наибольший объём. По сути, это шар, имеющий однородную форму, то есть как ни повернуть, он всегда будет выглядеть одинаково.
Площадь ее поверхности, в сравнении с другими трёхмерными телами, имеет наибольший объём. По сути, это шар, имеющий однородную форму, то есть как ни повернуть, он всегда будет выглядеть одинаково. Далее, следует подставить цифры в уравнение:
Далее, следует подставить цифры в уравнение: Такая же формула применяется при нахождении S сегмента (часть между двумя параллельными плоскостями) и зоны сферы (изогнутая поверхность сферического сегмента).
Такая же формула применяется при нахождении S сегмента (часть между двумя параллельными плоскостями) и зоны сферы (изогнутая поверхность сферического сегмента).
 И здесь прослеживается аналогия с окружностями Аполлония, то есть с фигурами в плоскости.
И здесь прослеживается аналогия с окружностями Аполлония, то есть с фигурами в плоскости.
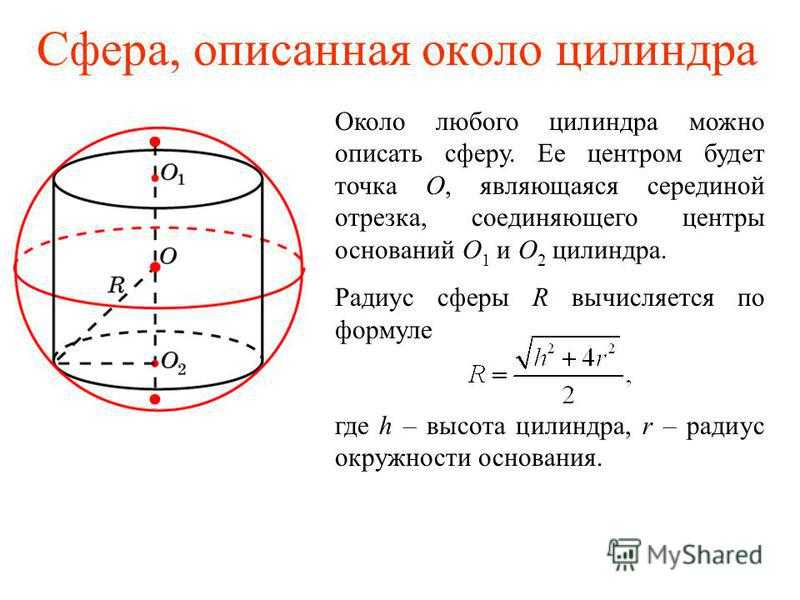
 Он даже попросил сделать чертёж этих предметов на своей надгробной плите. Позже римский философ Цицерон обнаружил такую гробницу, к сожалению, сильно заросшую окружающей растительностью.
Он даже попросил сделать чертёж этих предметов на своей надгробной плите. Позже римский философ Цицерон обнаружил такую гробницу, к сожалению, сильно заросшую окружающей растительностью. Площадь ее поверхности, в сравнении с другими трёхмерными телами, имеет наибольший объём. По сути, это шар, имеющий однородную форму, то есть как ни повернуть, он всегда будет выглядеть одинаково.
Площадь ее поверхности, в сравнении с другими трёхмерными телами, имеет наибольший объём. По сути, это шар, имеющий однородную форму, то есть как ни повернуть, он всегда будет выглядеть одинаково. Известно, что радиус детского мяча 10 см. Остаётся ещё одна неизвестная — число π. Это математическая константа, которая выражает отношение длины окружности к её диаметру и равна примерно 3,14. Далее, следует подставить цифры в уравнение:
Известно, что радиус детского мяча 10 см. Остаётся ещё одна неизвестная — число π. Это математическая константа, которая выражает отношение длины окружности к её диаметру и равна примерно 3,14. Далее, следует подставить цифры в уравнение: Все эти термины используются для приблизительно сфероидальных астрономических тел. Любая плоскость, которая включает в себя центр шара, делит его на два равных полушария (полусферы).
Все эти термины используются для приблизительно сфероидальных астрономических тел. Любая плоскость, которая включает в себя центр шара, делит его на два равных полушария (полусферы). Можно сделать единственный вывод: это обычное определение и оно однозначно. А также отношение расстояний между двумя фиксированными точками является постоянным. И здесь прослеживается аналогия с окружностями Аполлония, то есть с фигурами в плоскости.
Можно сделать единственный вывод: это обычное определение и оно однозначно. А также отношение расстояний между двумя фиксированными точками является постоянным. И здесь прослеживается аналогия с окружностями Аполлония, то есть с фигурами в плоскости. Для сферы кривизны всех нормальных сечений одинаковы, поэтому омбилической будет каждая точка.
Для сферы кривизны всех нормальных сечений одинаковы, поэтому омбилической будет каждая точка.
 Он даже попросил сделать чертёж этих предметов на своей надгробной плите. Позже римский философ Цицерон обнаружил такую гробницу, к сожалению, сильно заросшую окружающей растительностью.
Он даже попросил сделать чертёж этих предметов на своей надгробной плите. Позже римский философ Цицерон обнаружил такую гробницу, к сожалению, сильно заросшую окружающей растительностью. Но на самом деле, после тройки идёт больше тысячи цифр!
Но на самом деле, после тройки идёт больше тысячи цифр!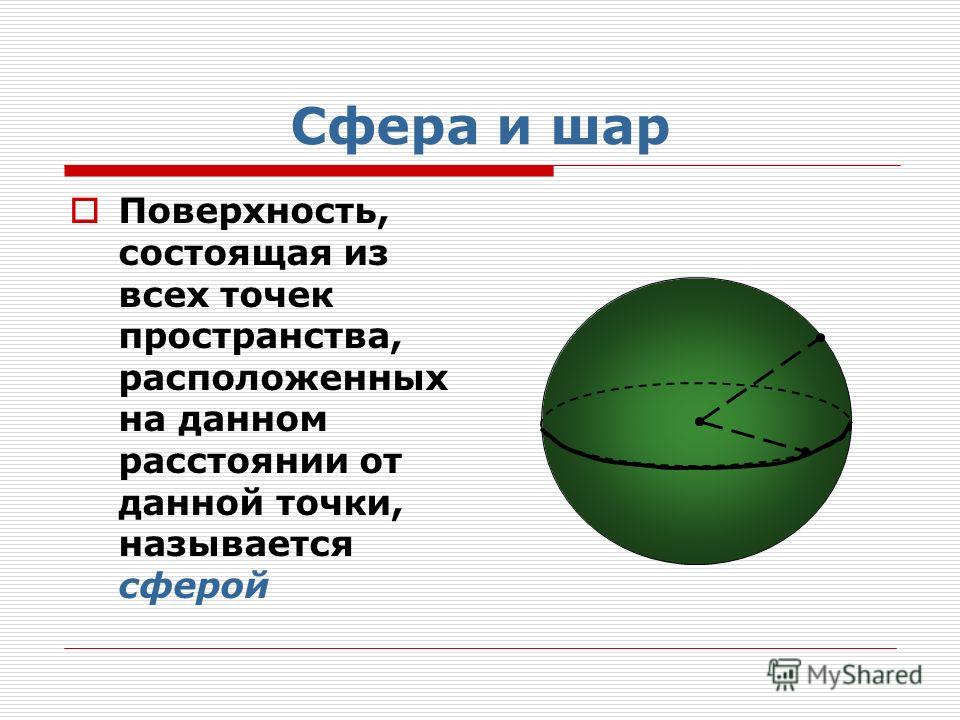
 В итоге получим число в 7 850 квадратных сантиметров.
В итоге получим число в 7 850 квадратных сантиметров.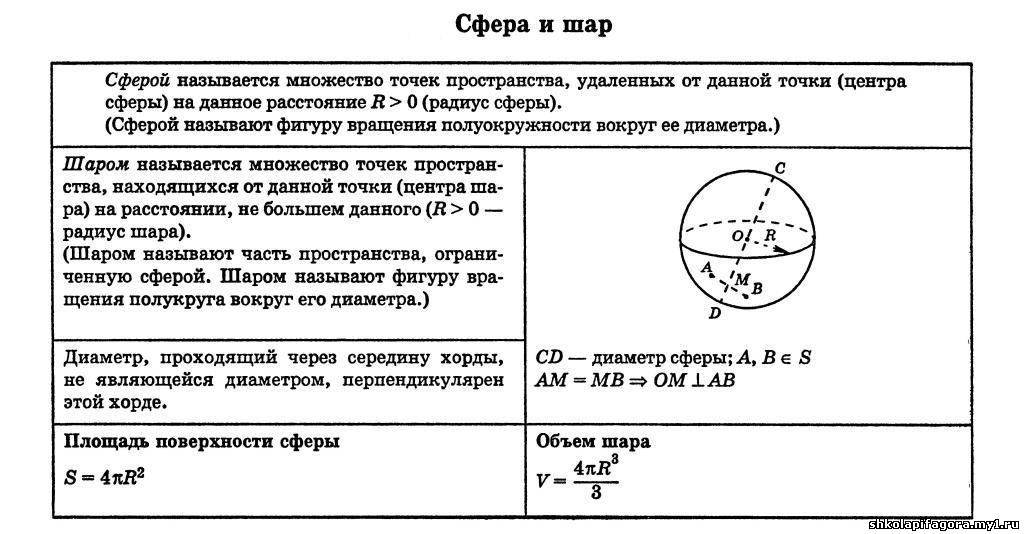 Достаточно иметь подключение к интернету и зайти на любой онлайн-калькулятор.
Достаточно иметь подключение к интернету и зайти на любой онлайн-калькулятор. Итак, пусть дан некоторый шар радиуса R. Выделим на его поверхности какую-либо малую область (рис. 412) и рассмотрим пирамиду или конус с вершиной в центре шара О, имеющие эту область своим основанием; строго говоря, мы лишь условно говорим о конусе или пирамиде, так как основание не плоское, а сферическое. Но при малых размерах основания по сравнению с радиусом шара оно будет весьма мало отличаться от плоского (так, например, при измерении не очень большого земельного участка пренебрегают тем, что он лежит не на плоскости, а на сфере).
Итак, пусть дан некоторый шар радиуса R. Выделим на его поверхности какую-либо малую область (рис. 412) и рассмотрим пирамиду или конус с вершиной в центре шара О, имеющие эту область своим основанием; строго говоря, мы лишь условно говорим о конусе или пирамиде, так как основание не плоское, а сферическое. Но при малых размерах основания по сравнению с радиусом шара оно будет весьма мало отличаться от плоского (так, например, при измерении не очень большого земельного участка пренебрегают тем, что он лежит не на плоскости, а на сфере). Отсюда для площади поверхности имеем формулу
Отсюда для площади поверхности имеем формулу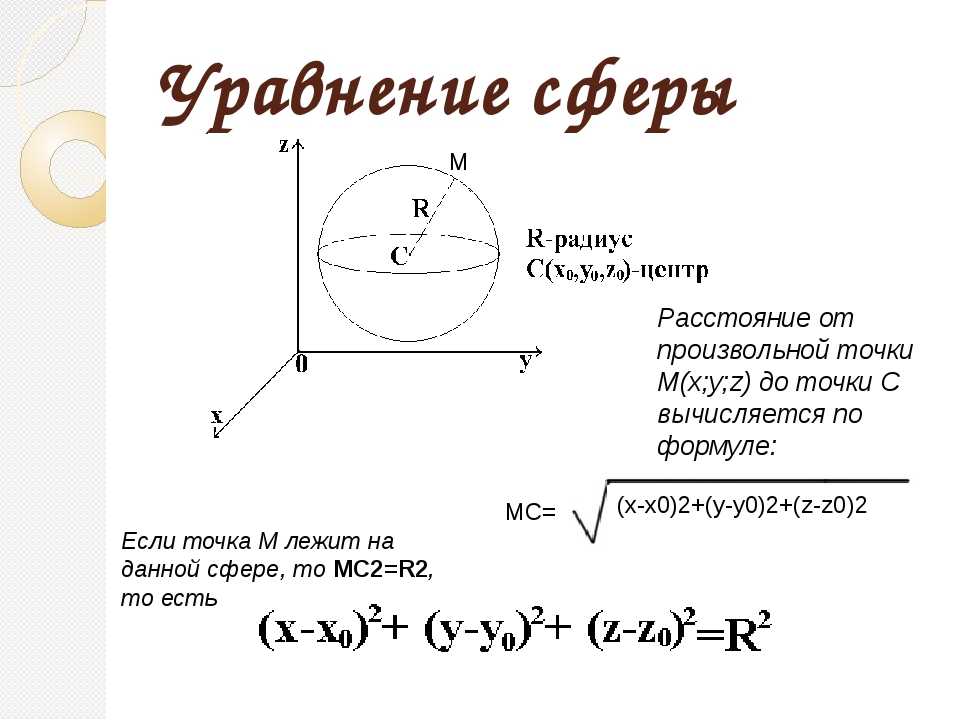 Найти высоту конуса, если радиус шара равен .
Найти высоту конуса, если радиус шара равен .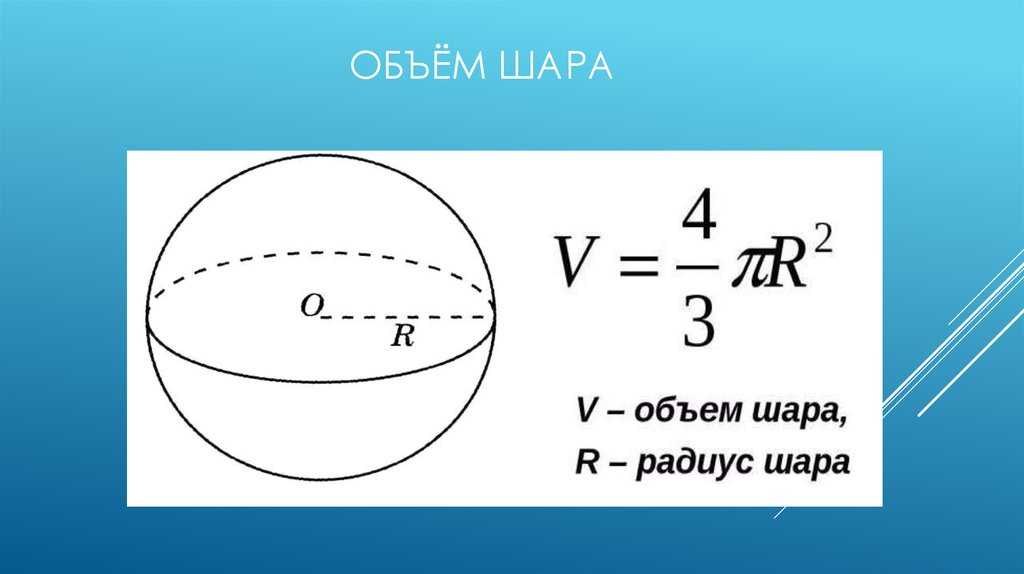 По формулам, которые сегодняшние школьники выводят в 11 классе общеобразовательной школы, вы легко можете рассчитать эти параметры.
По формулам, которые сегодняшние школьники выводят в 11 классе общеобразовательной школы, вы легко можете рассчитать эти параметры. 14 x 11 х 11 х 11.
14 x 11 х 11 х 11.
 Заполните мерный сосуд водой, подметьте ярус, погрузите измеряемое сферическое тело в жидкость и по разнице ярусов определите число вытесненной воды. После этого переведите полученный итог из литров в кубометры так же, как это описано в предыдущем шаге.
Заполните мерный сосуд водой, подметьте ярус, погрузите измеряемое сферическое тело в жидкость и по разнице ярусов определите число вытесненной воды. После этого переведите полученный итог из литров в кубометры так же, как это описано в предыдущем шаге.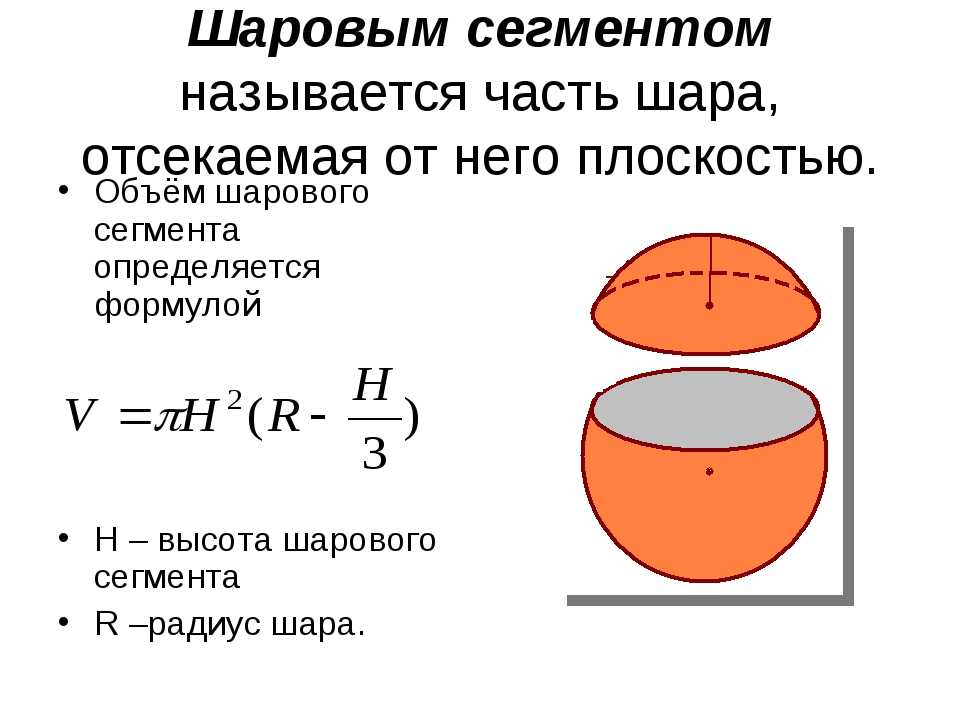 Когда нужно обнаружить площадь произвольной фигуры, то надобно вычислить, сколько квадратов со стороной (которая равняется единице), эта фигура в себя может вместить.
Когда нужно обнаружить площадь произвольной фигуры, то надобно вычислить, сколько квадратов со стороной (которая равняется единице), эта фигура в себя может вместить. Так, формула площади куба: площадь куба равна числу граней умноженное на площадь грани, т.е. 6 * a2
Так, формула площади куба: площадь куба равна числу граней умноженное на площадь грани, т.е. 6 * a2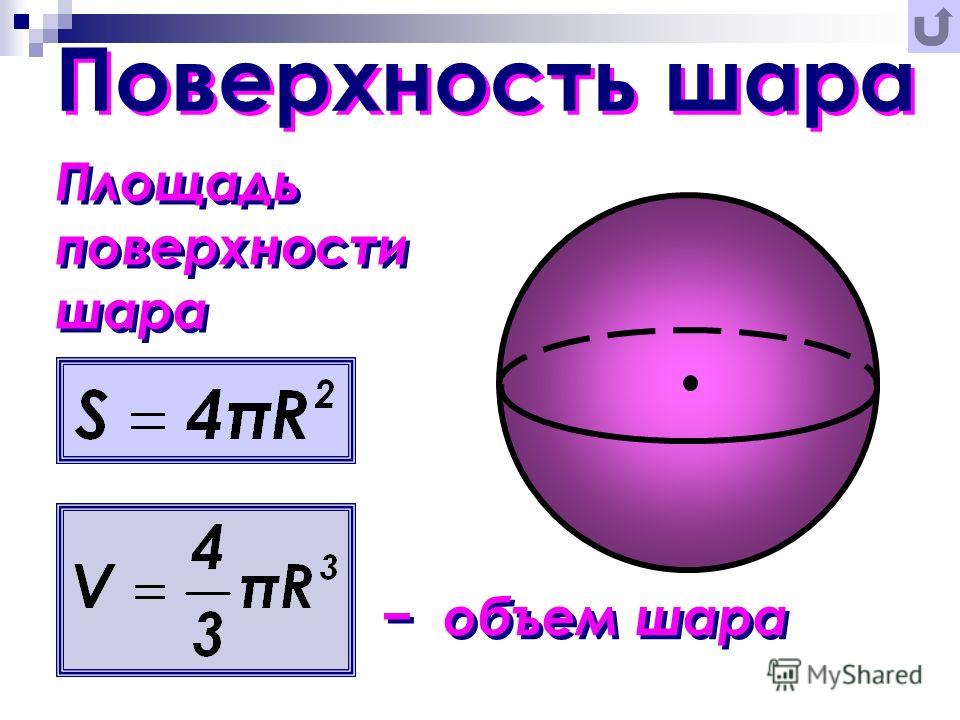 В противоположность сфере, сечения шара представляют собой круги. Форму, близкую к шарообразной, имеет множество планет и небесных тел. В различных точках шара имеются идентичные по форме, но неодинаковые по величине, так называемые сечения – круги различной площади.
В противоположность сфере, сечения шара представляют собой круги. Форму, близкую к шарообразной, имеет множество планет и небесных тел. В различных точках шара имеются идентичные по форме, но неодинаковые по величине, так называемые сечения – круги различной площади. 2
2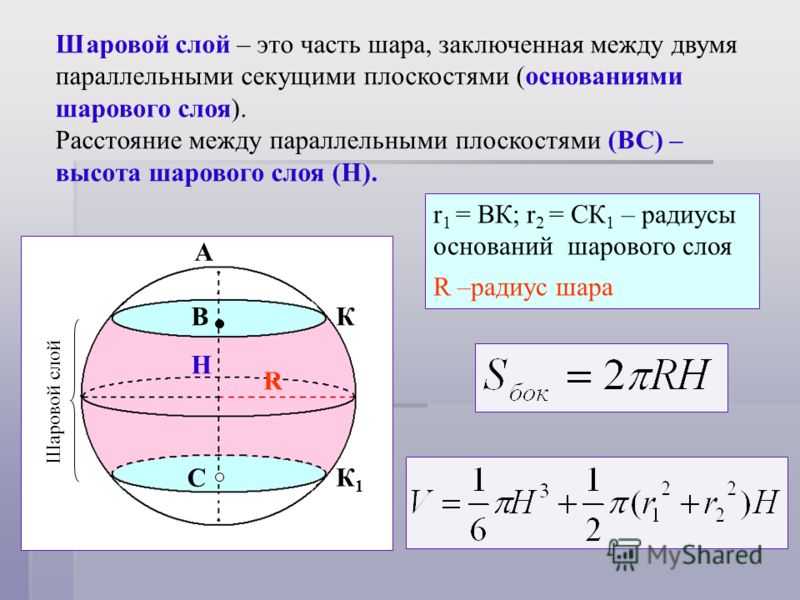 Если требуется измерить объем шара не теоретически, а только подручными средствами, то сделать это дозволено, скажем, определив объем вытесненной им воды. Данный метод применим в том случае, когда есть вероятность разместить шар в какую-нибудь соизмеримую ему емкость – мензурку, стакан, банку, ведро, бочку, бассейн и т.д. В этом случае перед помещением шара подметьте ярус воды, сделайте это вторично позже полного его погружения, а после этого обнаружьте разность между отметками. Традиционно мерная емкость заводского производства имеет деления, показывающие объем в литрах и производных от него единицах – миллилитрах, декалитрах и т.д. Если полученное значение нужно перевести в кубические метры и кратные ему единицы объема, то исходите из того, что один литр соответствует одному кубическому дециметру либо одной тысячной доле кубометра.
Если требуется измерить объем шара не теоретически, а только подручными средствами, то сделать это дозволено, скажем, определив объем вытесненной им воды. Данный метод применим в том случае, когда есть вероятность разместить шар в какую-нибудь соизмеримую ему емкость – мензурку, стакан, банку, ведро, бочку, бассейн и т.д. В этом случае перед помещением шара подметьте ярус воды, сделайте это вторично позже полного его погружения, а после этого обнаружьте разность между отметками. Традиционно мерная емкость заводского производства имеет деления, показывающие объем в литрах и производных от него единицах – миллилитрах, декалитрах и т.д. Если полученное значение нужно перевести в кубические метры и кратные ему единицы объема, то исходите из того, что один литр соответствует одному кубическому дециметру либо одной тысячной доле кубометра. Примитивно поделите итог взвешивания на справочную плотность вещества изготовления: V=m/p.
Примитивно поделите итог взвешивания на справочную плотность вещества изготовления: V=m/p.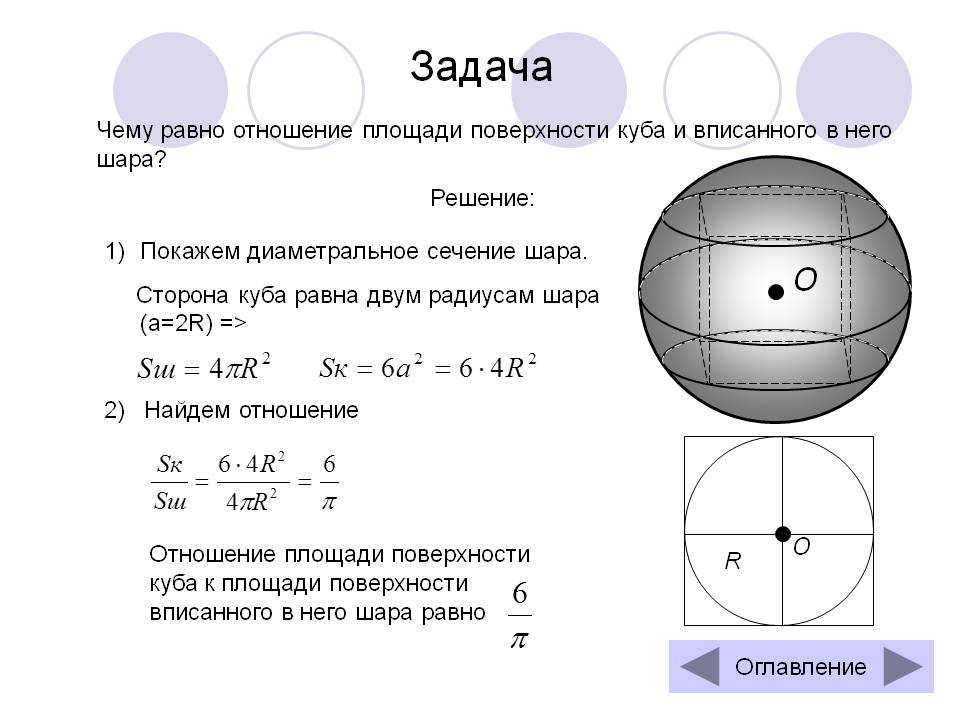 2, где R, r – радиусы внешней и внутренней окружностей кольца соответственно.
2, где R, r – радиусы внешней и внутренней окружностей кольца соответственно.
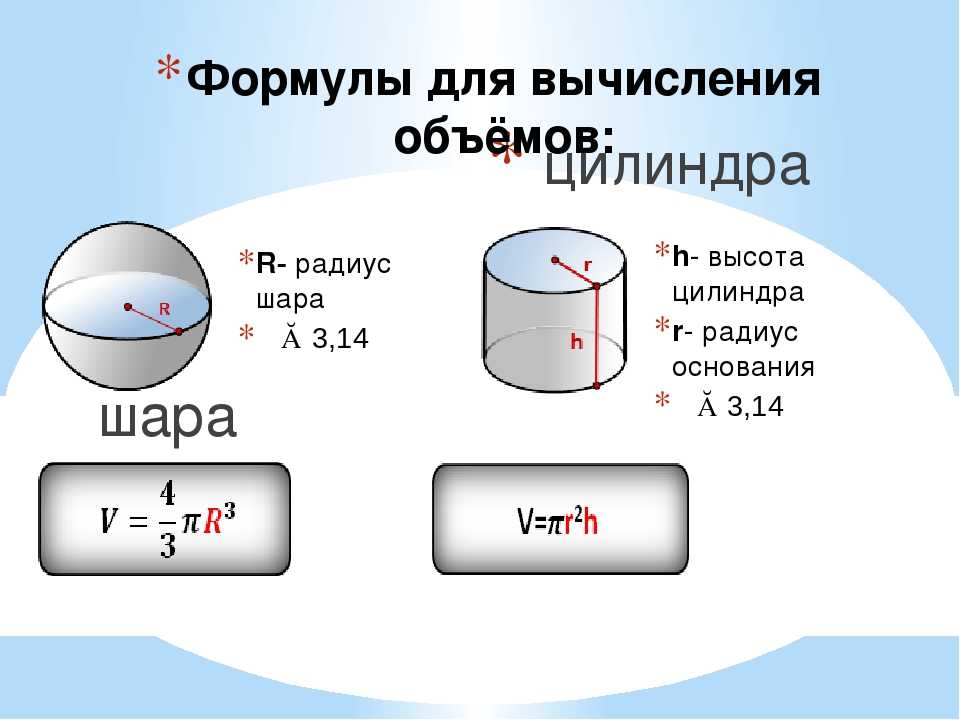 Уравнение сферы с радиусом R и центром в начале декартовой системе координат :
Уравнение сферы с радиусом R и центром в начале декартовой системе координат :
 Большая окружность и большой круг имеют центр, который совпадают с центром сферы (шара).
Большая окружность и большой круг имеют центр, который совпадают с центром сферы (шара). Касательная к сфере — это прямая, которая касается сферы только в одной точке.
Касательная к сфере — это прямая, которая касается сферы только в одной точке. Касательная плоскость к сфере
Касательная плоскость к сфере 3
3 Следовательно, рассчитать площадь фигуры поверхности можно, используя такой вид формулы:
Следовательно, рассчитать площадь фигуры поверхности можно, используя такой вид формулы: При этом уровень жидкости поднялся с отметки 24 см до отметки 26 см.
При этом уровень жидкости поднялся с отметки 24 см до отметки 26 см.
 2, то искомая площадь равна 4cdot 4 = 16.
2, то искомая площадь равна 4cdot 4 = 16. Центр окружности лежит на пересечении диагоналей прямоугольника.
Центр окружности лежит на пересечении диагоналей прямоугольника. ru/ploshad-shara/
ru/ploshad-shara/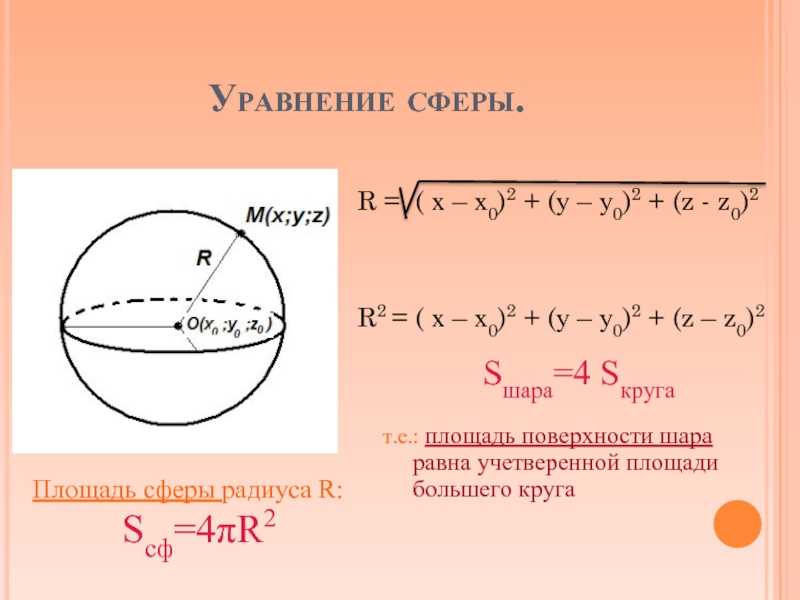
 (Используйте π = 22/7)
(Используйте π = 22/7) Сфера — это полученное трехмерное тело круглой формы, не имеющее ребер или вершин. Общая площадь поверхности сферы такая же, как площадь ее изогнутой поверхности из-за отсутствия ребер или вершин.
Сфера — это полученное трехмерное тело круглой формы, не имеющее ребер или вершин. Общая площадь поверхности сферы такая же, как площадь ее изогнутой поверхности из-за отсутствия ребер или вершин.

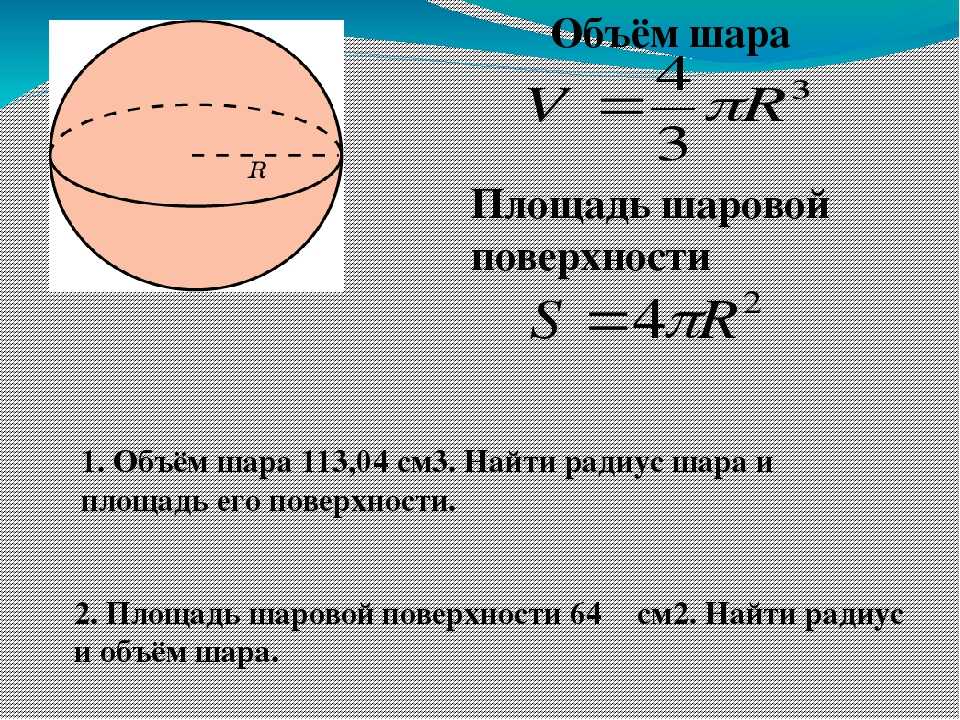
 Используйте 𝜋=227.
Используйте 𝜋=227. Как только мы определили радиус, при необходимости мы можем удвоить это значение, чтобы получить диаметр. В следующем примере показано, как изменить формулу для решения такого типа задач.
Как только мы определили радиус, при необходимости мы можем удвоить это значение, чтобы получить диаметр. В следующем примере показано, как изменить формулу для решения такого типа задач. Хотя мы могли бы сказать, что 𝑟=±3, в этом случае 𝑟 представляет собой длину, и поэтому мы можем игнорировать отрицательное решение.
Хотя мы могли бы сказать, что 𝑟=±3, в этом случае 𝑟 представляет собой длину, и поэтому мы можем игнорировать отрицательное решение.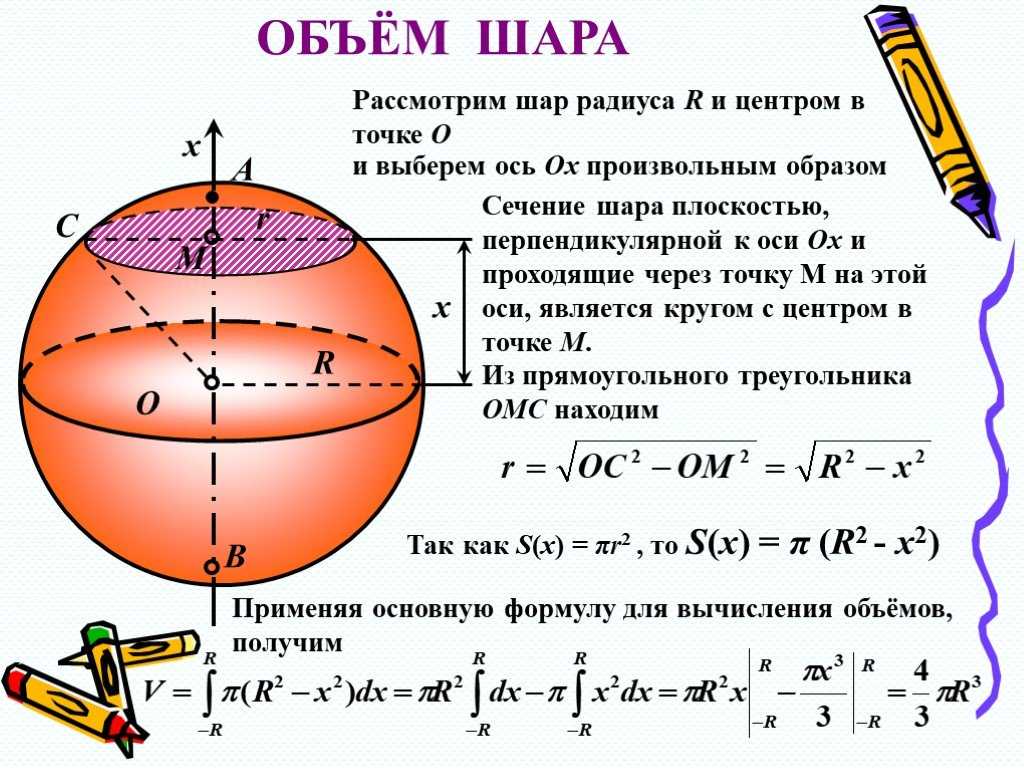 Если бы мы подставили 𝐴=36𝜋 прямо в эту формулу, мы бы получили 𝑟=3. Как и ожидалось, это то же самое значение радиуса, которое мы вычислили в предыдущем примере.
Если бы мы подставили 𝐴=36𝜋 прямо в эту формулу, мы бы получили 𝑟=3. Как и ожидалось, это то же самое значение радиуса, которое мы вычислили в предыдущем примере.


 )
) Сравнить группы предметов известным им способом – путем составления пар, обозначить количество предметов и сравнить.
Сравнить группы предметов известным им способом – путем составления пар, обозначить количество предметов и сравнить. Ведь вы же знаете, как сравнивать группы предметов.
Ведь вы же знаете, как сравнивать группы предметов.




 На сколько сорок больше, чем ворон?(На 3)
На сколько сорок больше, чем ворон?(На 3) У вас есть кружочки.
У вас есть кружочки. – Казань, 2006 г.
– Казань, 2006 г. Что вы заметили? Меняется цифра по середине. Она становится больше на 1.
Что вы заметили? Меняется цифра по середине. Она становится больше на 1.

 Повторение ранее изученного материала. Закрепление навыка счёта в пределах 9.
Повторение ранее изученного материала. Закрепление навыка счёта в пределах 9. Что это значит? (Что к какому-то числу прибавили 4 и получили 7)
Что это значит? (Что к какому-то числу прибавили 4 и получили 7) Число 0.
Число 0.




 Вычислите разность.
Вычислите разность.
 Почему? (решение подходит для ответа на 2 вопроса, так как, чтобы узнать, на сколько одно число больше или меньше другого, надо из большего числа вычесть меньшее)
Почему? (решение подходит для ответа на 2 вопроса, так как, чтобы узнать, на сколько одно число больше или меньше другого, надо из большего числа вычесть меньшее)



 Актуализация знаний и фиксация индивидуального затруднения в пробном учебном действии.
Актуализация знаний и фиксация индивидуального затруднения в пробном учебном действии.  Физминутка
Физминутка  Рефлексия. Подведение итогов.
Рефлексия. Подведение итогов.
 Подготовка к открытию правил:
Подготовка к открытию правил: Практическое (наглядное) сравнение чисел:
Практическое (наглядное) сравнение чисел: ру.
ру.

 Рабочая тетрадь с.58, №2
Рабочая тетрадь с.58, №2 ру: «Необходимо подобрать к рисунку схему».
ру: «Необходимо подобрать к рисунку схему».



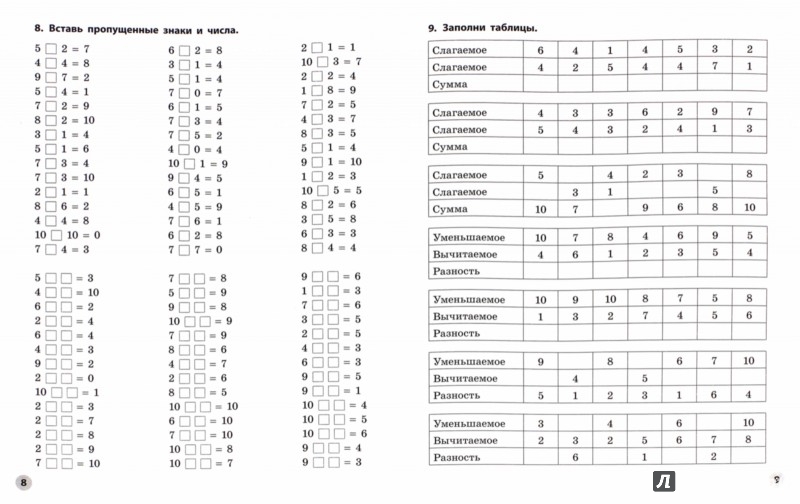

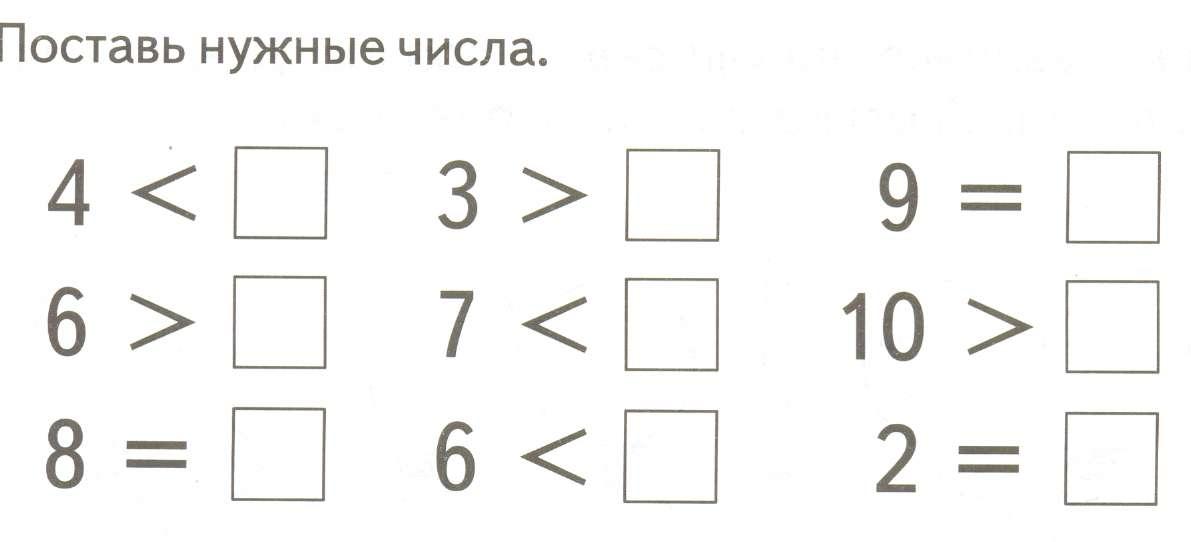

 Присоединяйтесь к нему и Вы – это будет настоящее пиратское приключение!
Присоединяйтесь к нему и Вы – это будет настоящее пиратское приключение!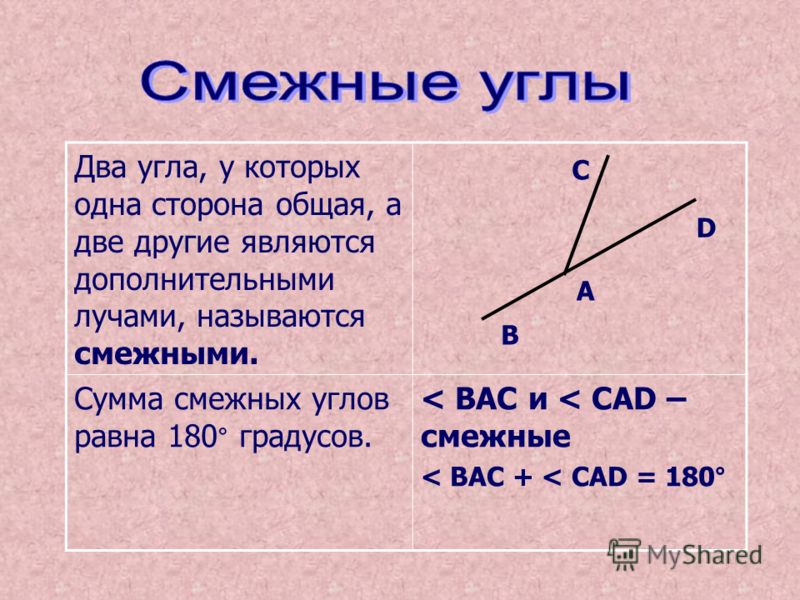 Найти соответствующий положительный угол
Найти соответствующий положительный угол 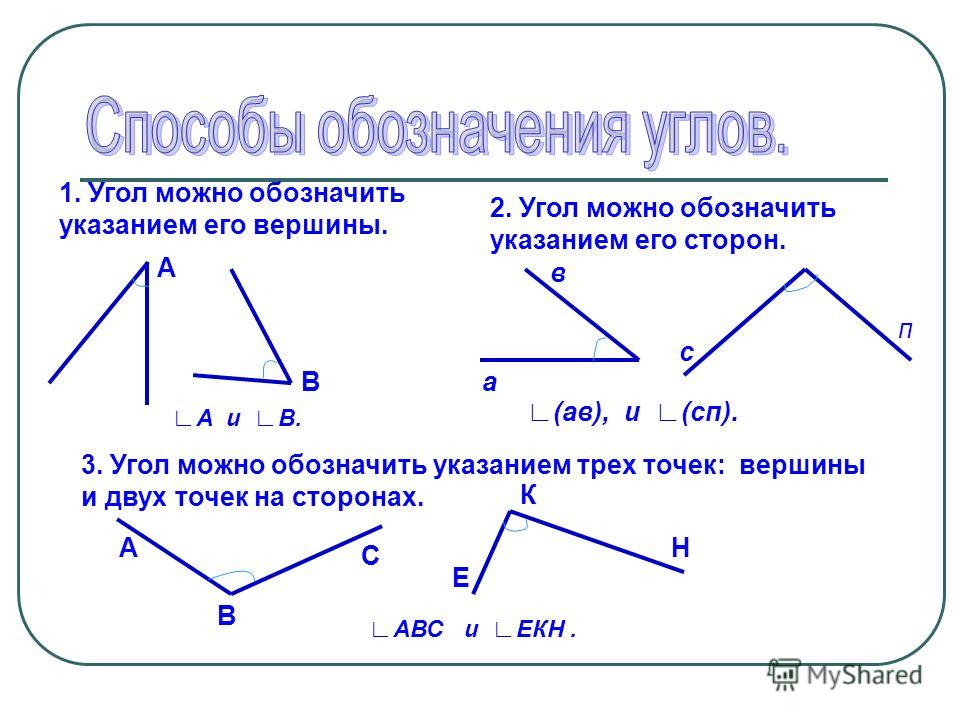 {\circ}$
{\circ}$ 
 В частности, туркменский ученый аль-Маразви ввел такие функции, как тангенс и котангенс, составил первые таблицы значений для синусов, тангенсов и котангенсов. Понятие синуса и косинуса введены индийскими учеными. Тригонометрии посвящено немало внимания в трудах таких великих деятелей древности, как Евклида, Архимеда и Эратосфена.
В частности, туркменский ученый аль-Маразви ввел такие функции, как тангенс и котангенс, составил первые таблицы значений для синусов, тангенсов и котангенсов. Понятие синуса и косинуса введены индийскими учеными. Тригонометрии посвящено немало внимания в трудах таких великих деятелей древности, как Евклида, Архимеда и Эратосфена. Если представить катет a как произведение sin A и гипотенузы с, а катет b в виде cos A * c, то получим следующие формулы для тангенса и котангенса:
Если представить катет a как произведение sin A и гипотенузы с, а катет b в виде cos A * c, то получим следующие формулы для тангенса и котангенса:
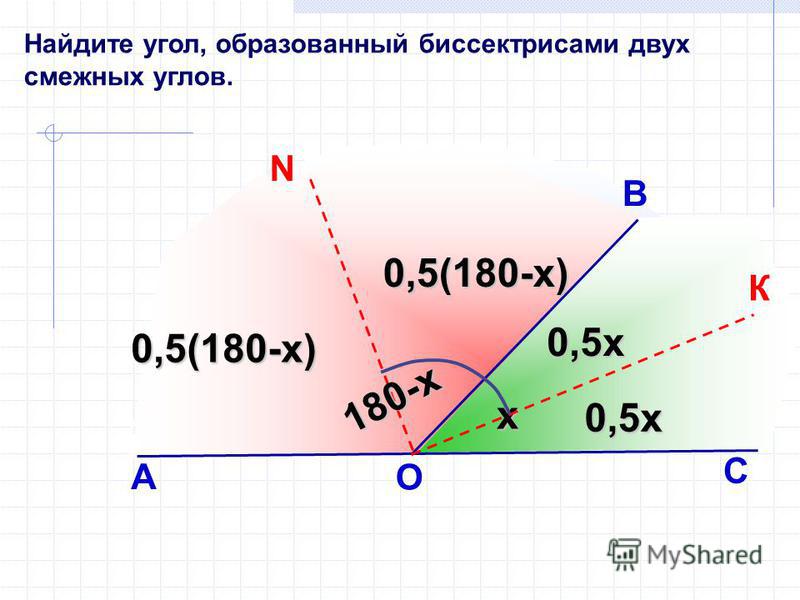 е. функция нечетная
е. функция нечетная Если знаки совпадают, функция четная, в противном случае — нечетная.
Если знаки совпадают, функция четная, в противном случае — нечетная.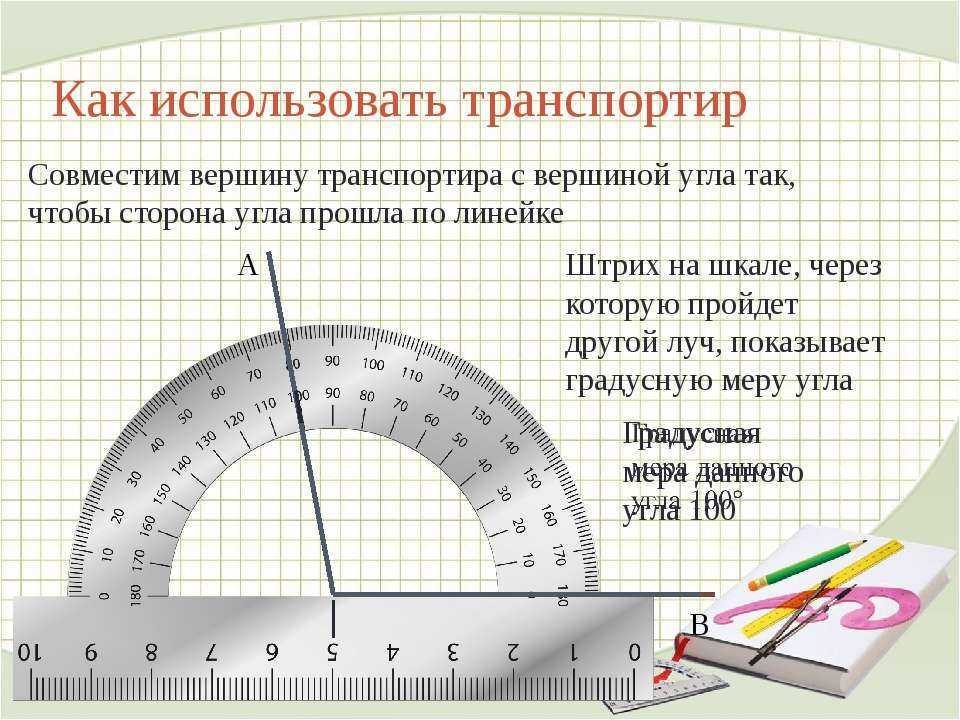
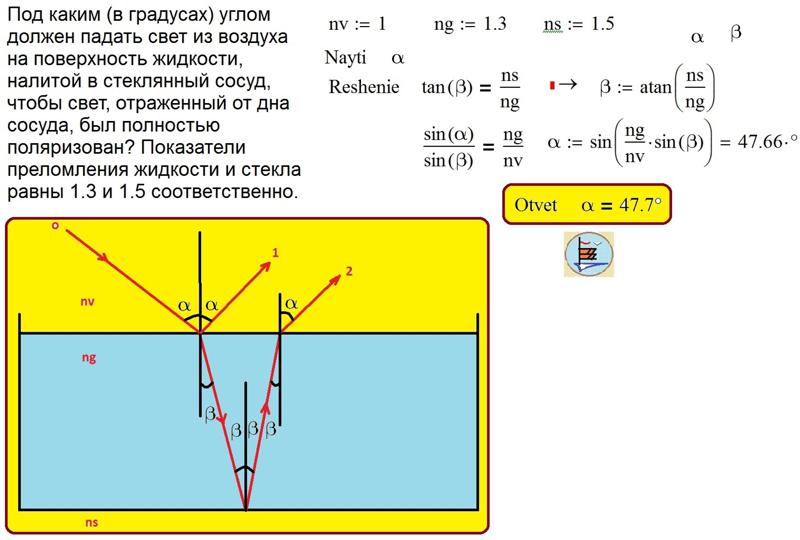 1.1).
1.1). На рис. 1.4 АОВ больше АОС.
На рис. 1.4 АОВ больше АОС.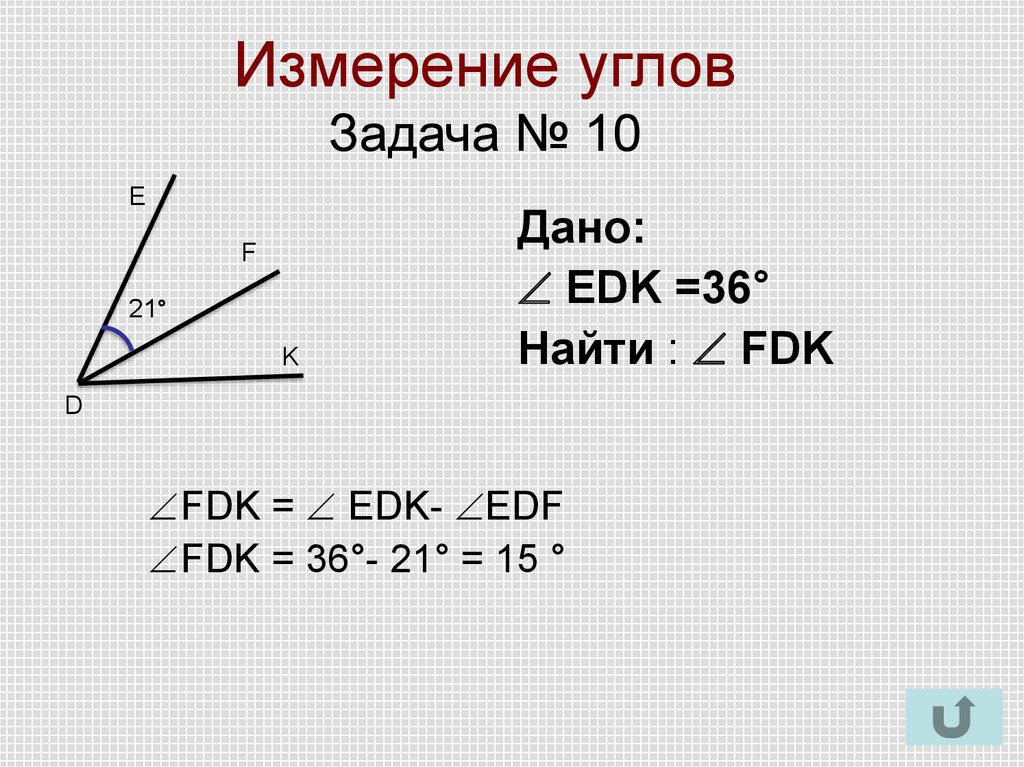 1.7), можно получить в результате вращения подвижного луча вокруг вершины О от начальной стороны угла (ОА) до его конечной стороны (ОВ). Мы будем измерять этот угол, учитывая полное количество оборотов, сделанных при этом вокруг точки О, а также и направление, в котором происходило вращение.
1.7), можно получить в результате вращения подвижного луча вокруг вершины О от начальной стороны угла (ОА) до его конечной стороны (ОВ). Мы будем измерять этот угол, учитывая полное количество оборотов, сделанных при этом вокруг точки О, а также и направление, в котором происходило вращение.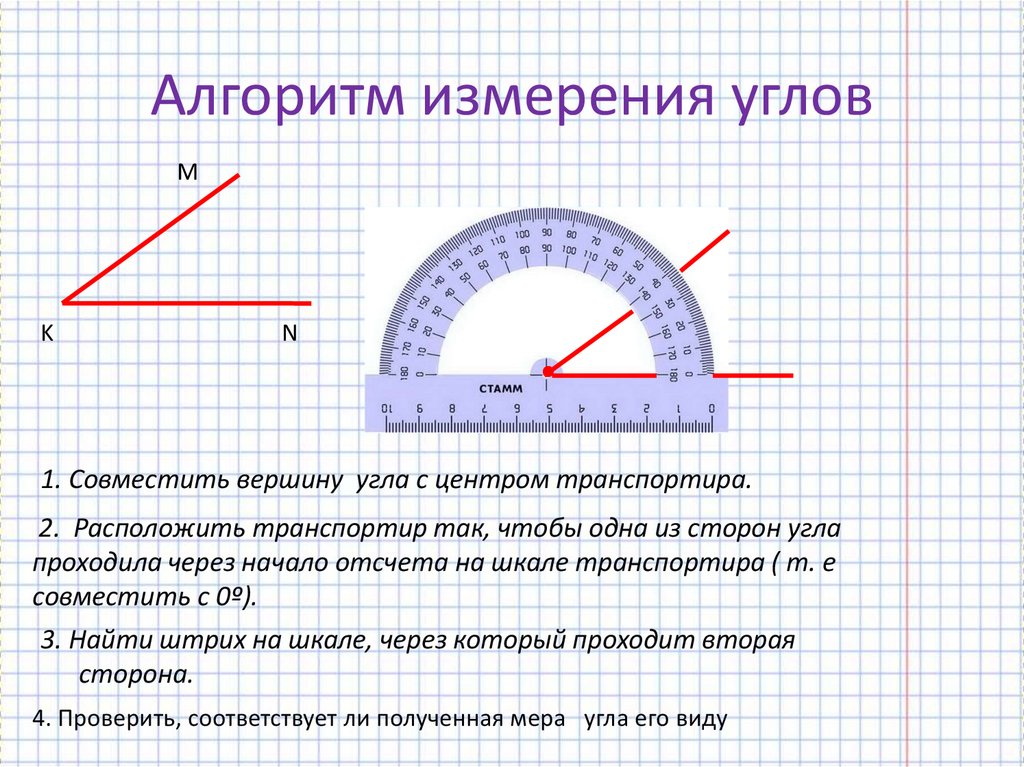
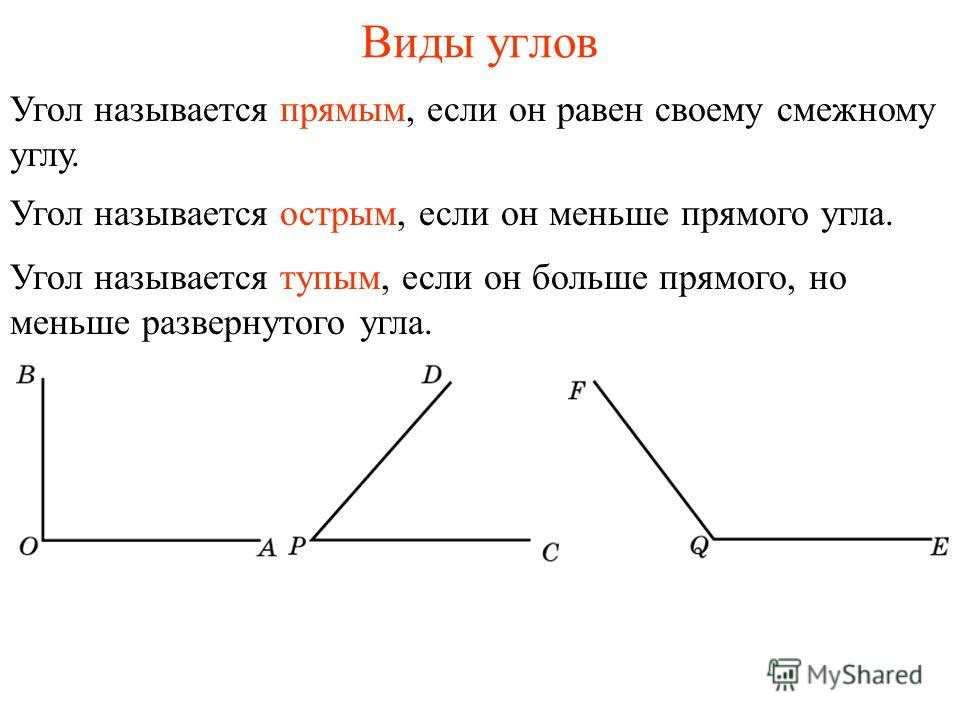 Единицы измерения дуг и углов
Единицы измерения дуг и углов Угол в один градус — это угол, равный 1/180 части развернутого угла. Угол, равный 1/60 части угла в 1°, — это угол в одну минуту (обозначается 1″). Угол, равный 1/60 части угла в одну минуту,— это угол в одну секунду (обозначается 1″).
Угол в один градус — это угол, равный 1/180 части развернутого угла. Угол, равный 1/60 части угла в 1°, — это угол в одну минуту (обозначается 1″). Угол, равный 1/60 части угла в одну минуту,— это угол в одну секунду (обозначается 1″).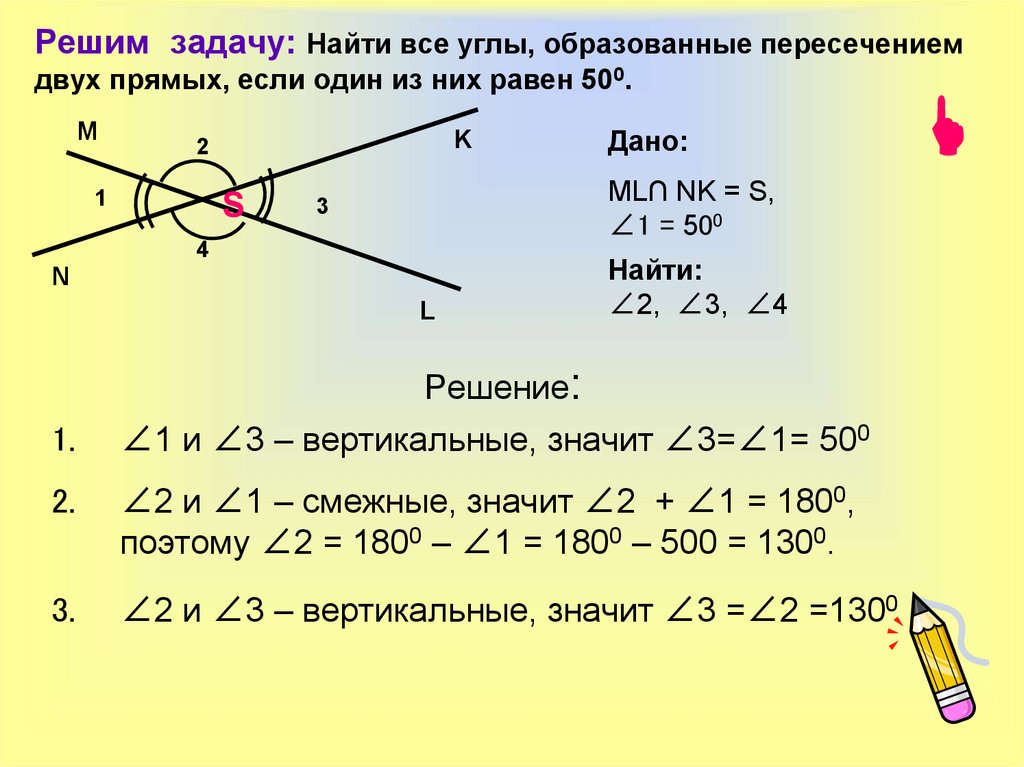
 Добавлены значения угла на осях. Всё понятно, никаких заморочек.
Добавлены значения угла на осях. Всё понятно, никаких заморочек.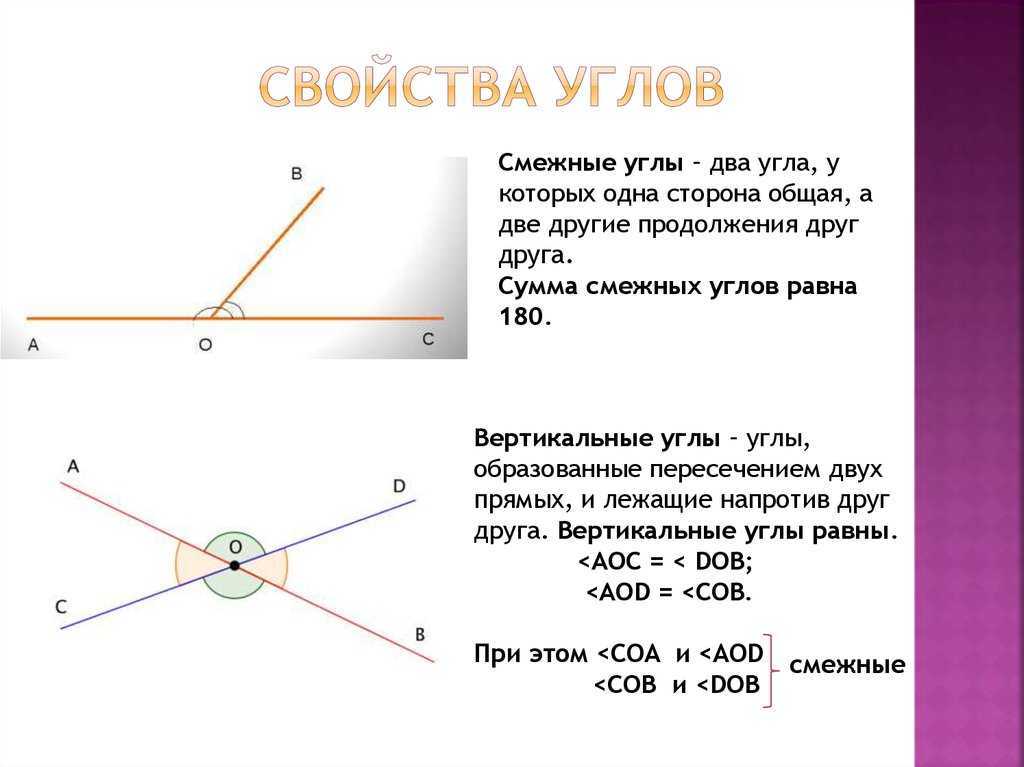 Именно так. Скажем, положительный угол 90 градусов занимает на круге точно такое же положение, что и отрицательный угол в минус 270 градусов. Положительный угол, к примеру, +110° градусов занимает точно такое же положение, что и отрицательный угол -250°.
Именно так. Скажем, положительный угол 90 градусов занимает на круге точно такое же положение, что и отрицательный угол в минус 270 градусов. Положительный угол, к примеру, +110° градусов занимает точно такое же положение, что и отрицательный угол -250°. Останется как раз 250°…
Останется как раз 250°…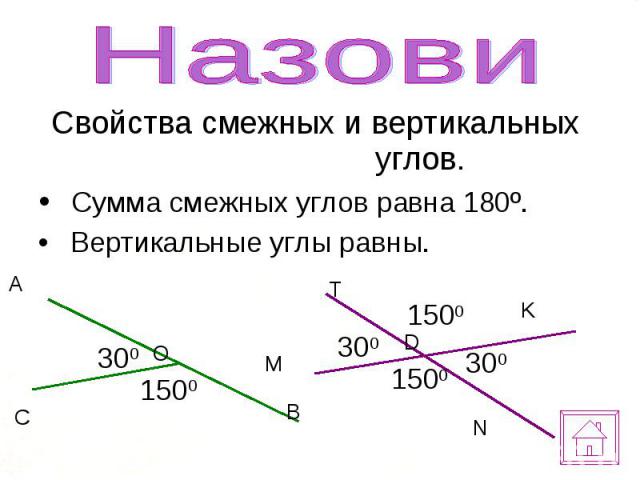 От нашего желания. Ну, и ещё от задания, конечно… Надеюсь, вы поняли и как переходить в тригонометрических функциях от отрицательных углов к положительным и обратно. Нарисовать круг, примерный угол, да посмотреть, сколько недостаёт до полного оборота, т.е. до 360°.
От нашего желания. Ну, и ещё от задания, конечно… Надеюсь, вы поняли и как переходить в тригонометрических функциях от отрицательных углов к положительным и обратно. Нарисовать круг, примерный угол, да посмотреть, сколько недостаёт до полного оборота, т.е. до 360°.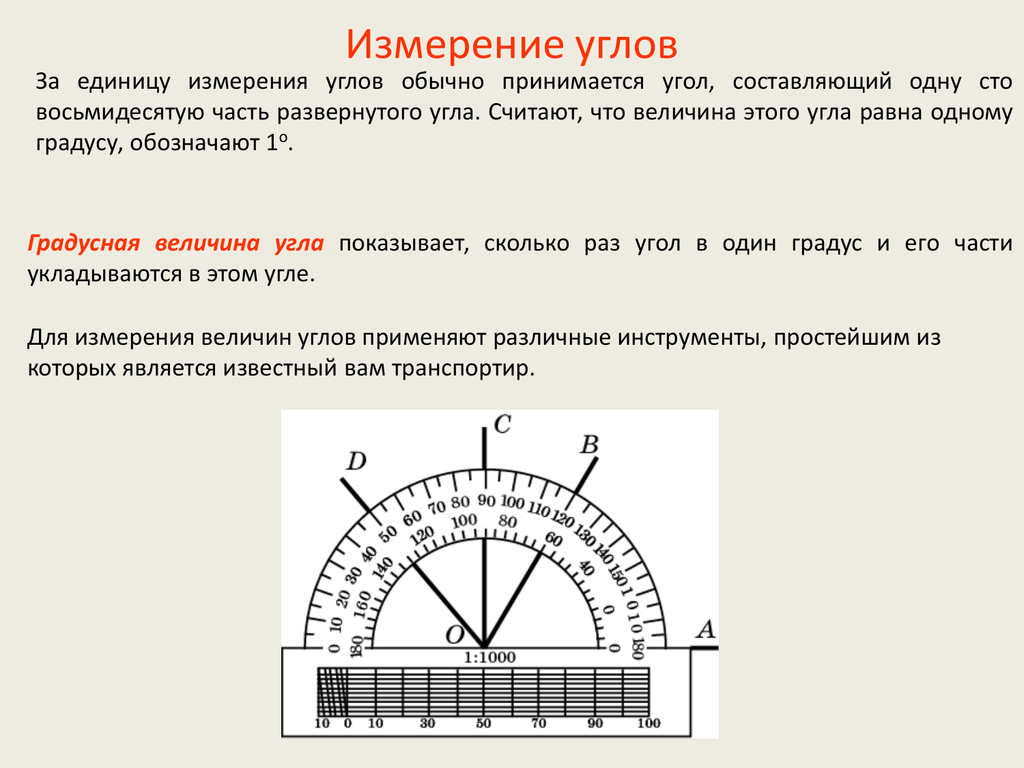 Но тригонометрические функции у этих углов совершенно одинаковые ! Т.е. sin1000° = sin280°, cos1000° = cos280° и т.д. Если бы я был синусом, я бы не заметил разницы между этими двумя углами…
Но тригонометрические функции у этих углов совершенно одинаковые ! Т.е. sin1000° = sin280°, cos1000° = cos280° и т.д. Если бы я был синусом, я бы не заметил разницы между этими двумя углами…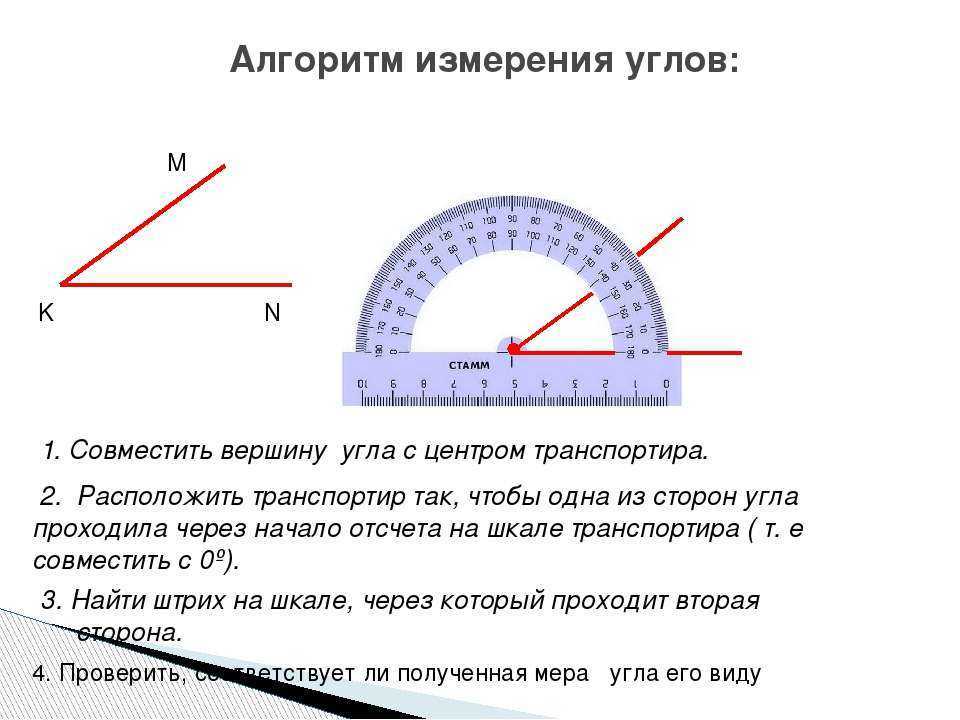 .. Кстати, там научитесь рисовать тангенс и котангенс на тригонометрическом круге. Очень полезная штучка.
.. Кстати, там научитесь рисовать тангенс и котангенс на тригонометрическом круге. Очень полезная штучка. А что делать, знака всего два, а четверти всего четыре… Не разбежишься в вариантах.
А что делать, знака всего два, а четверти всего четыре… Не разбежишься в вариантах.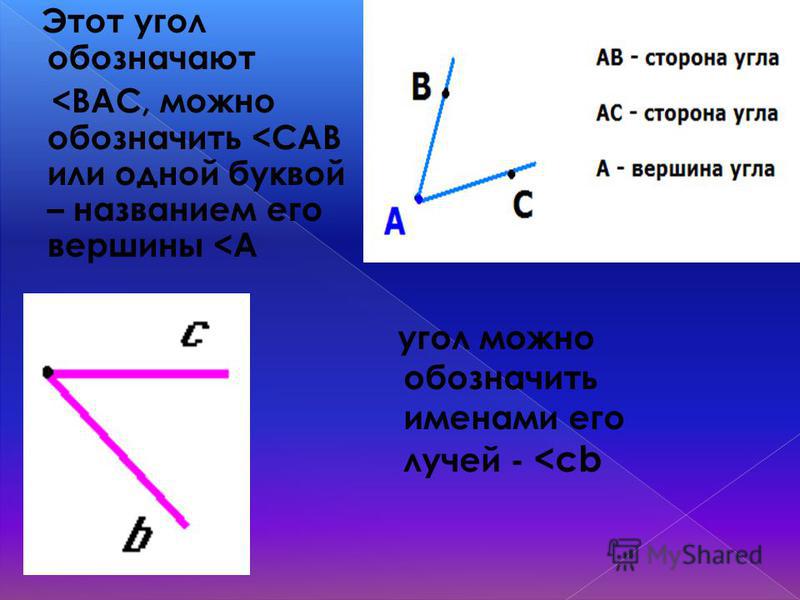 )
) 
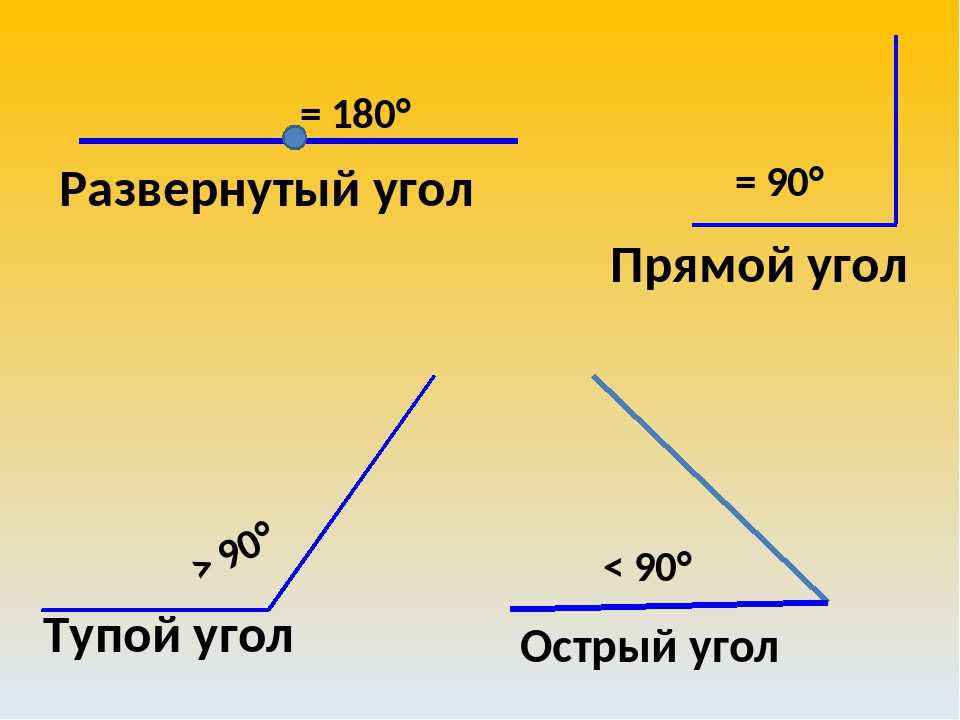
 По направлению поворота судят о том, как осуществляется поворот точки – по часовой стрелке или против часовой стрелки.
По направлению поворота судят о том, как осуществляется поворот точки – по часовой стрелке или против часовой стрелки.