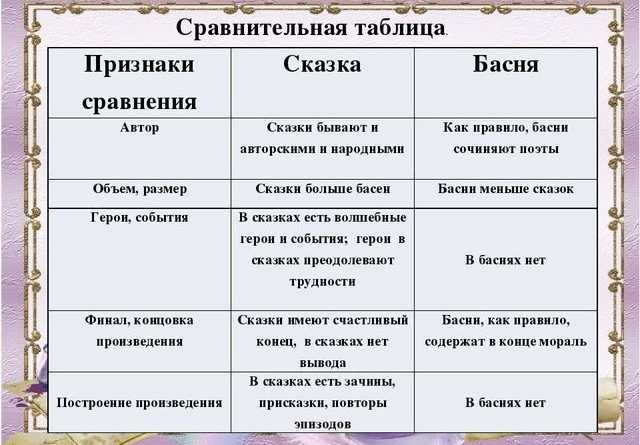
Как компьютер считает синусы — Журнал «Код» программирование без снобизма
Это текст про математику и компьютеры. Если тема интересна, посмотрите также на математический тренажёр Практикума — он бесплатный и интерактивный.
А сейчас — про синусы.
Что такое синус и зачем он нужен?
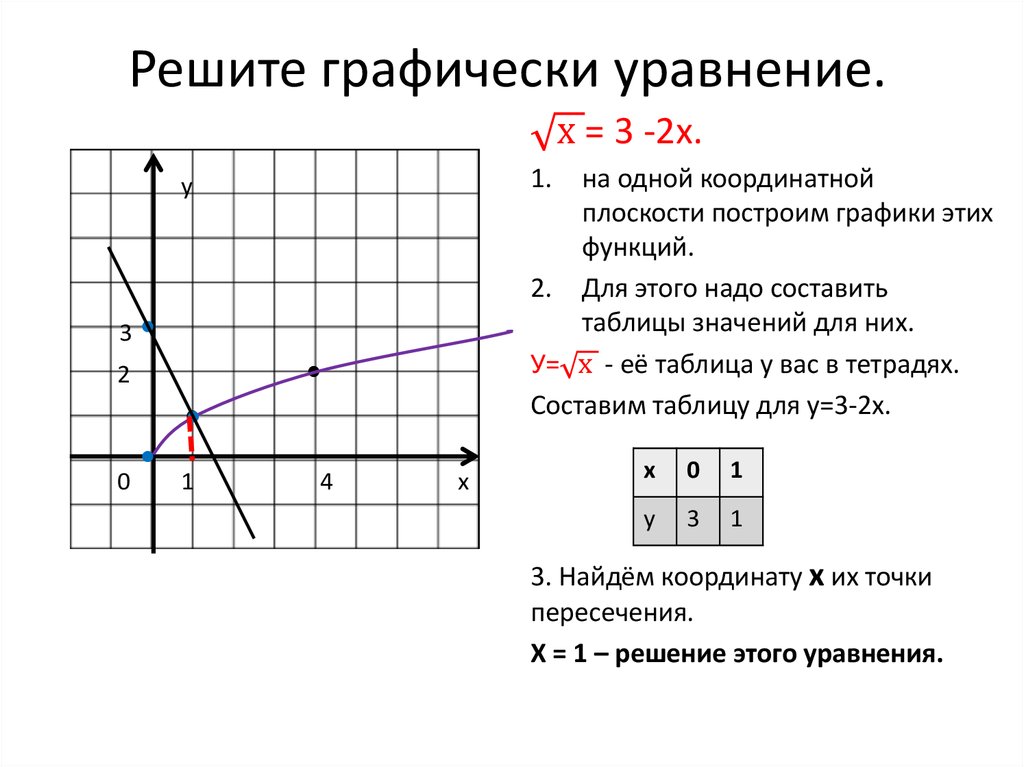
Вульгарное объяснение: синус — это математическая коробка, в которую засовывают любое число, а она в ответ выдаёт числа от −1 до 1. Если эти числа выстроить подряд на некой оси, то получится кривая вот такого вида:
Как читать эту кривую: если затолкать в коробку «sin» число, примерно равное 1,57, то коробка выдаст число, близкое к единице. Если затолкать число 2, на выходе будет примерно 0,909. Если затолкать примерно 3,14 — вернёт примерно 0. Синус от 4,712 даст примерно −0,999. И так дальше: число может быть сколько угодно большим, а синус всегда будет возвращать какие-то дробные значения от −1 до 1.
Это число взято из тригонометрии — то есть из науки, которая занимается углами и сторонами треугольника. В частности, синус описывает отношение сторон прямоугольного треугольника: насколько один из катетов (короткая сторона треугольника) короче, чем гипотенуза (длинная сторона треугольника). Но чаще всего мы знаем не длины сторон, а угол между ними, поэтому в синусы всегда запихивают значения углов.
В частности, синус описывает отношение сторон прямоугольного треугольника: насколько один из катетов (короткая сторона треугольника) короче, чем гипотенуза (длинная сторона треугольника). Но чаще всего мы знаем не длины сторон, а угол между ними, поэтому в синусы всегда запихивают значения углов.
Грубо говоря, вы говорите коробке: «Коробка, у меня тут прямоугольный треугольник. Я смотрю на его острый угол, он равен 30º. Что ты мне на это скажешь»? А коробка отвечает: «Если у тебя угол 30º, то короткая сторона твоего треугольника вдвое короче, чем длинная гипотенуза. Так что sin(30º) = ½».
Это число нужно много где в математике и компьютерах. Например, без синуса невозможно соединить две точки прямой линией на плоскости. Люди это делают без труда с помощью линейки, а компьютеру нужно очень чётко считать, куда поставить пиксель, и для этого нужен синус.
Помимо синуса есть ещё три аналогичные функции — косинус, тангенс и котангенс. Они такие же по принципу работы, но описывают отношения других сторон.
Во многих языках программирования есть встроенная команда нахождения синуса угла — sin(). Внутри этой функции зашита какая-то логика для нахождения этого числа.
Чаще всего, когда не нужна высокая точность, компьютер берёт значения синуса из готовых таблиц — он находит там нужный угол и возвращает значение, ничего не вычисляя. Это быстро и достаточно точно для бытовых вычислений. Вы наверняка использовали его в школе, когда считали синусы по таблице Брадиса.
Но когда нужна высокая точность вычислений (например, 20 знаков после запятой), то синусы и другие тригонометрические функции высчитывают каждый раз с нуля. Для этого используют много разных алгоритмов, и самый простой из них — использование рядов Тейлора.
Таблица Брадиса, по которой компьютер находит значения синусов с точностью 4 знака после запятойЧто такое ряд Тейлора
Брук Тейлор — это английский математик из 17-го века, в честь которого назвали формулу, связывающую значение функции и значение всех её производных в выбранной точке.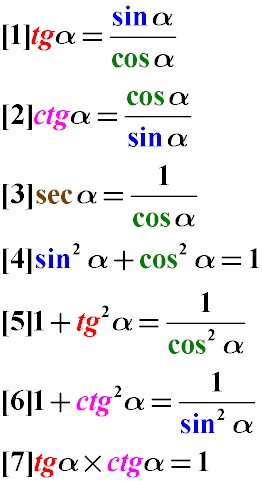 Если сильно упростить и перевести на понятный язык, то формула будет звучать так:
Если сильно упростить и перевести на понятный язык, то формула будет звучать так:
Представим, что значение функции, например, синуса — это круг, заполненный на 100%. Производная функции в этой точке — это часть круга:
Есть производные первого порядка в этой точке, второго, третьего и так до бесконечности. Каждая производная следующего порядка добавляет в круг сектор поменьше:
Если сложить все производные до бесконечности, то получим полный круг — это и будет значение синуса:
В общем виде ряд Тейлора функции выглядит так:
Для каждой функции ряд Тейлора выглядит по-своему. Для синуса он выглядит так:
Выглядит сложно. Но если разложить эту формулу сумму в понятный вид, она будет выглядеть так:
Восклицательный знак — это факториал. Это просто произведение всех целых чисел до этого числа. Например: 5! = 1 × 2 × 3 × 4 × 5 = 120.
Получается, что компьютеру для нахождения синуса достаточно использовать умножение — и для факториала, и для возведения в степень.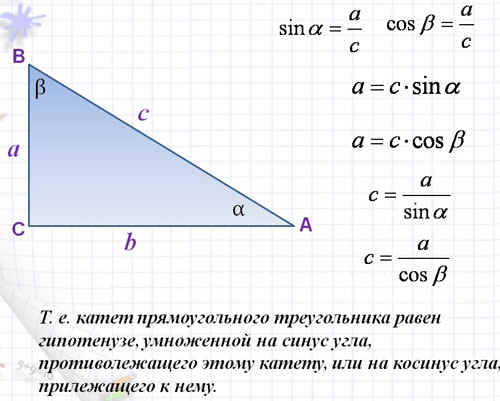 Зная это, можно написать простой алгоритм.
Зная это, можно написать простой алгоритм.
Точность расчётов
Особенность ряда Тейлора в том, что это бесконечный ряд — а значит, и вычисления тоже придётся делать бесконечно. Чтобы обойти это ограничение, используют погрешность — с какой точностью нам нужно посчитать значение формулы. Для этого делают так:
- Определяем точность, например 7 знаков после запятой.
- Минимальное число из 7 знаков после запятой — это 0,0000001. Это и будет наша погрешность.
- Считаем очередное слагаемое ряда Тейлора.
- Если это слагаемое меньше нашей погрешности — прибавляем и останавливаемся, потому что мы достигли нужного результата. Если не меньше — продолжаем.
С таким подходом можно найти синус любого угла с любой точностью, главное, чтобы у компьютера хватило памяти на все эти вычисления.
Радианы
Чтобы использовать ряд Тейлора для вычисления синуса, нам нужно перевести градусы в радианы. Радиан — это мера измерения углов в тригонометрии, которая привязана к числу π.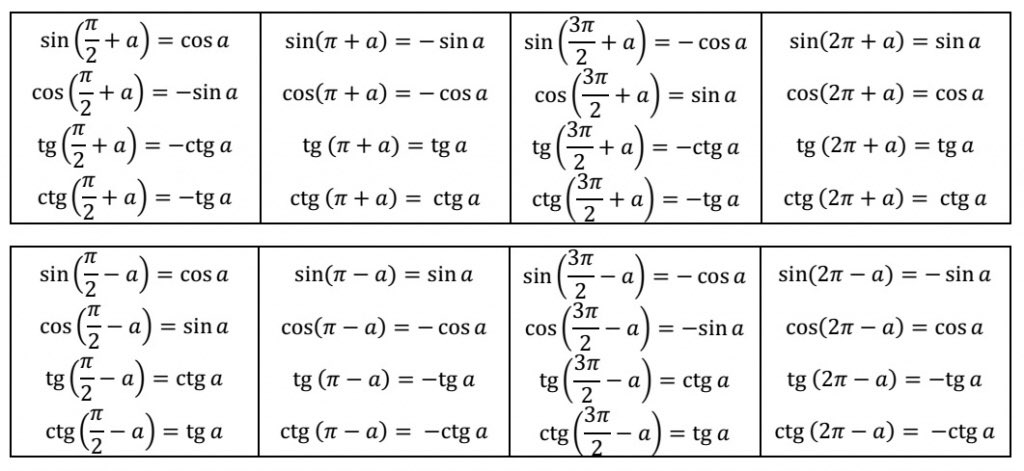
Радианы с углами связаны так:
1 радиан = 180/π градусов
Получается, что для того, чтобы перевести углы в градусах в радианы, нам нужно градусы разделить на 180 и умножить на π.
Теперь мы знаем всё, чтобы написать код вычисления синуса на Python
Пишем код
Логика алгоритма будет такая:
- спрашиваем градусы;
- спрашиваем погрешность, с которой нужно вычислить синус;
- в цикле считаем очередное слагаемое ряда Тейлора и прибавляем его к общей сумме;
- если очередное слагаемое меньше погрешности — останавливаемся и выводим результат.
Читайте комментарии, чтобы разобраться в коде, а потом запустите его у себя, чтобы проверить результаты:
# импортируем математическую библиотеку, чтобы взять оттуда модуль и число пи
import math
# объявляем свою функцию, которая посчитает синус
def computerSinus (x,n):
# переводим градусы в радианы
x = x/180*math.pi
# для проверки выведем результат, который посчитает компьютер
print(str(math. sin(x)) + " — результат вычислений встроенного синуса")
# сразу берём x как первое слагаемое ряда Тейлора
q = x
# сумма ряда на старте равна нулю
s = 0
# порядковый номер слагаемого в ряду Тейлора
i = 1
# пока очередное слагаемое больше погрешности — цикл работает
while abs(q) > n:
# добавляем слагаемое к общей сумме
s = s + q
# вычисляем следующее слагаемое
q = q* (-1) * (x*x) / ((2*i+1) * (2*i))
# увеличиваем порядковый номер слагаемого в ряду Тейлора
i = i+1
# возвращаем сумму как результат работы функции
return s
# запрашиваем стартовые значения
x = float(input("Введите градусы: "))
n = float(input("Введите погрешность: "))
# выводим результат, который мы посчитали сами
print(str(computerSinus(x,n)) + " — синус, который мы посчитали")
sin(x)) + " — результат вычислений встроенного синуса")
# сразу берём x как первое слагаемое ряда Тейлора
q = x
# сумма ряда на старте равна нулю
s = 0
# порядковый номер слагаемого в ряду Тейлора
i = 1
# пока очередное слагаемое больше погрешности — цикл работает
while abs(q) > n:
# добавляем слагаемое к общей сумме
s = s + q
# вычисляем следующее слагаемое
q = q* (-1) * (x*x) / ((2*i+1) * (2*i))
# увеличиваем порядковый номер слагаемого в ряду Тейлора
i = i+1
# возвращаем сумму как результат работы функции
return s
# запрашиваем стартовые значения
x = float(input("Введите градусы: "))
n = float(input("Введите погрешность: "))
# выводим результат, который мы посчитали сами
print(str(computerSinus(x,n)) + " — синус, который мы посчитали")Что дальше
В следующий раз попробуем сделать то же самое с квадратным корнем — посмотрим, как компьютер сможет посчитать его без таблиц.
Текст:
Михаил Полянин
Редактор:
Максим Ильяхов
Художник:
Алексей Сухов
Корректор:
Ирина Михеева
Вёрстка:
Кирилл Климентьев
Соцсети:
Виталий Вебер
Умножение и деление на ноль.
Умножение и деление на ноль.Сегодня принято считать, что любое число, умноженное на ноль, равняется нулю. Это что касается умножения на ноль. Деление на ноль невозможно — так говорят математики, когда им встречается деление на ноль. А как обстоят дела на самом деле?
Вы про такую тригонометрическую функцию, как тангенс, слышали?. Как найти тангенс определенного угла? Правильно, нужно синус этого угла разделить на косинус такого же угла. Элементарная задача для математиков. За исключением случая, когда угол равняется девяносто градусов. Проблема в том, что синус 90 градусов равен единице, а вот косинус 90 градусов равен нулю. Получается, что тангенс 90 градусов равен единице, деленной на ноль. Вот здесь и происходит сбой в мозгах всех математиков на протяжении последних сотен лет. А ведь значение тангенса 90 градусов показывает, что в математике деление на ноль есть и от него никуда не спрятаться. Если мы чего-то не знаем в математике, то это совсем не означает, что этого «чего-то» в математике нет. Для понимания деления на ноль нужно гораздо лучше знать и понимать алгебру, геометрию и физику всех тех разделов математики, которые принято считать «абстрактными» понятиями.
Вот здесь и происходит сбой в мозгах всех математиков на протяжении последних сотен лет. А ведь значение тангенса 90 градусов показывает, что в математике деление на ноль есть и от него никуда не спрятаться. Если мы чего-то не знаем в математике, то это совсем не означает, что этого «чего-то» в математике нет. Для понимания деления на ноль нужно гораздо лучше знать и понимать алгебру, геометрию и физику всех тех разделов математики, которые принято считать «абстрактными» понятиями.
За это время я успел наковырять в математике очень много интересного и результаты шокировали даже меня. «Никогда никому не верь, даже себе — ты тоже можешь ошибаться» — это главная истина, которой меня научила математика. Всё самое интересное вы можете найти на сайте Математика для блондинок? где я под разными углами рассматриваю некоторые математические проблемы, в том числе и проблему деления на ноль.
Чтобы понять умножение и деление на ноль, нужно вообще всю математику переписывать. С самого начала. Во-первых, расставить всё по своим местам и выбросить математический мусор, который на протяжении веков «обобщается и расширяется математиками. Во-вторых, наша математика не с начала начинается, а с истории возникновения чисел. Математической наука должна не с натуральных чисел или аксиом начинаться. На этом я пока прервусь. Ниже написан текст, которому уже много лет.
С самого начала. Во-первых, расставить всё по своим местам и выбросить математический мусор, который на протяжении веков «обобщается и расширяется математиками. Во-вторых, наша математика не с начала начинается, а с истории возникновения чисел. Математической наука должна не с натуральных чисел или аксиом начинаться. На этом я пока прервусь. Ниже написан текст, которому уже много лет.
В позиционной системе счисления все числа записываются в определенном порядке. А вот если какого-то числа нет? Мы пишем вместо него ноль — есть такая цифра. Но ведь отсутствие числа числом быть не может. Ноль не является числом. Нравится это математикам или нет. В письменной речи мы отделяем одно слово от другого пробелами. При чтении слово «пробел» не произносится, ни в одном алфавите пробела нет. Пробел не является буквой точно также, как ноль не является числом.
Если ноль не является числом, тогда и математические действия с ним выполнить невозможно. Математики в своих определениях могут писать всё, что угодно. Ведь никакой ответственности они за это не несут, а все результаты проверяют на соответствие определениям. Получается обычная религия, основанная на Священных Математических Писаниях. Как и любая другая религия, математика соприкасается с действительностью только там, где это выгодно проповедникам. В остальных случаях мы слышим ответ: «Читайте Священное Писание». Как и Библия, математика разделена на «Евангелие От Арифметики», «Евангелие От Алгебры», «Евангелие От Матана» и так далее.
Ведь никакой ответственности они за это не несут, а все результаты проверяют на соответствие определениям. Получается обычная религия, основанная на Священных Математических Писаниях. Как и любая другая религия, математика соприкасается с действительностью только там, где это выгодно проповедникам. В остальных случаях мы слышим ответ: «Читайте Священное Писание». Как и Библия, математика разделена на «Евангелие От Арифметики», «Евангелие От Алгебры», «Евангелие От Матана» и так далее.
Начнем со сложения и вычитания. Если мы берем число и прибавляем к нему или вычитаем из него другое число, то первоначальное число изменяется. Если мы берем число и ничего с ним не делаем, число остается неизменным. Если мы прибавляем или вычитаем ноль, число так же остается неизменным. Не потому, что так в определении написано, а потому, что математическое действие не происходит. Невозможно ноль прибавить или отнять.
Умножение. Если мы умножим одно число на другое, то получим результат умножения. Если мы умножение выполнять не будем, тогда и результата умножения не будет. Что мы в подобных случаях записываем? Правильно, ноль. Если мы умножим число на ноль или ноль умножим на число, результат умножения будет отсутствовать. При умножении на ноль умножение не происходит.
Если мы умножение выполнять не будем, тогда и результата умножения не будет. Что мы в подобных случаях записываем? Правильно, ноль. Если мы умножим число на ноль или ноль умножим на число, результат умножения будет отсутствовать. При умножении на ноль умножение не происходит.
В принятой современной системе аксиом и определений, именуемых «математика», деления на ноль не было, нет и никогда не будет. В Природе деление на ноль было, есть и будет всегда. Как и любой другой закон Природы, деление на ноль не зависит от глубины наших познаний. Например, закон всемирного тяготения исправно работал за долго до того, как появилась Солнечная система и планета Земля. Даже когда люди свято верили в то, что Земля держится на трех китах, падали они всегда, почему-то, вниз. Можно тысячи раз на день повторять, что деление на ноль невозможно, и тысячелетиями пользоваться его плодами:))))
Природа весьма терпима к неведению. Она позволяет пользоваться своими законами, даже если кто-то их не знает или не признает. В то же время, Природа чрезвычайно жестока – никто не может нарушить ее законы, даже Боги.
В то же время, Природа чрезвычайно жестока – никто не может нарушить ее законы, даже Боги.
Понятие деления на ноль является одним из основных понятий Математики и выходит далеко за рамки общепринятого научного мировоззрения. Некоторые математические формулы являются прекрасным математическим доказательством существования деления на ноль. Проблема заключается в том, что математики не в состоянии осмысливать очевидные вещи — их этому никогда не учили. Сегодня математика является не наукой, а религией, тщательно собирающей весь исторический мусор. Осмысливать исторический багаж в математике не принято, ведь, по убеждению математиков, они занимаются абстрактными вещами.
Дабы не вносить сумятицу в пытливые или бестолковые умы, все, что касается деления на ноль и сопутствующие материалы, я убираю с этого сайта. «Математики для блондинок» в рамках школьного курса будет вполне достаточно для посетителей.
Последние добавления материалов на этом сайте:
«Порядок действий.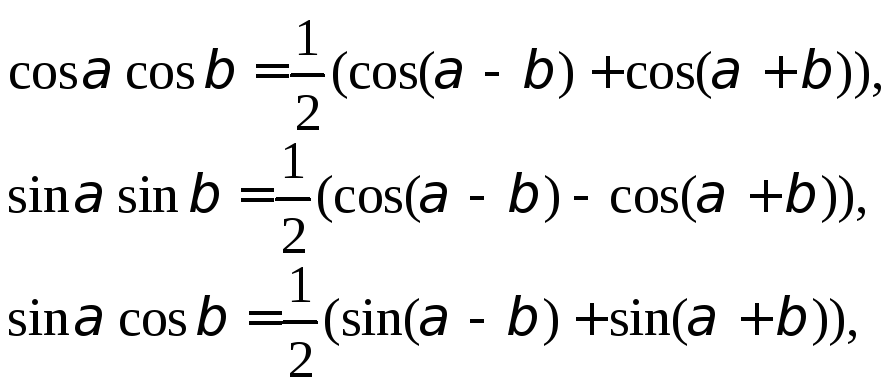 Скобки.» — похоже, я нашел вещь, общую для всех разделов математики не зависимо от того, какие определения исповедуют верующие :)))
Скобки.» — похоже, я нашел вещь, общую для всех разделов математики не зависимо от того, какие определения исповедуют верующие :)))
«Действия над натуральными числами» — страница справочника с моими комментариями, где подробно разобраны правила деления на ноль.
«Таблица Брадиса» — четырехзначные математические таблицы синусов и косинусов, тангенсов и котангенсов в градусах с минутами от 0 до 90 градусов и в радианах от 0 до 3,14 радиан.
«Беседы о математике» — диалог о математике, делении на ноль, законе Бенфорда и о прочих математических премудростях.
Секрет человеческого невежества очень прост: наши учителя, кроме всего прочего, учат нас повторять их же ошибки. Ведь, в свое время, их учили точно так же.
Старые страницы сайта:
МАТЕМАТИКА
ГЕОМЕТРИЯ
НОЛЬ
МИР, В КОТОРОМ Я ЖИВУ
ИНТЕРЕСНЫЕ ССЫЛКИ
ОБМЕН ССЫЛКАМИ
Последняя редакция от 27 марта 2023 года. .
.
© 2006-2023 Николай Хижняк. Все права защищены.
7.4: Формулы суммы к произведению и произведения к сумме
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 1370
- OpenStax
- OpenStax
Цели обучения
- Экспресс-продукты в сумме.
- Выразите суммы как продукты.
Группа марширует по полю, создавая потрясающий звук, который поддерживает толпу. Этот звук распространяется как волна, которую можно интерпретировать с помощью тригонометрических функций.
Рисунок \(\PageIndex{1}\): Оркестр Калифорнийского университета в Лос-Анджелесе (кредит: Эрик Чан, Flickr).
Например, рисунок \(\PageIndex{2}\) представляет звуковую волну для музыкальной ноты A. В этом разделе мы исследуем тригонометрические тождества, лежащие в основе таких повседневных явлений, как звуковые волны. 9
Выражение произведений в виде сумм произведение косинуса и синуса в виде суммы. Мы можем использовать формулы произведения на сумму
, , которые выражают произведения тригонометрических функций в виде сумм. Давайте сначала исследуем тождество косинуса, а затем тождество синуса.Выражение произведений в виде сумм для косинуса
Мы можем вывести формулу произведения на сумму из тождеств суммы и разности для косинуса . Если мы сложим два уравнения, мы получим:
\[\begin{align*} \cos \alpha \cos \beta+\sin \alpha \sin \beta&= \cos(\alpha-\beta)\\[4pt ] \underline{+ \cos \alpha \cos \beta-\sin \alpha \sin \beta}&= \underline{ \cos(\alpha+\beta) }\\[4pt] 2 \cos \alpha \cos \ beta&= \cos(\alpha-\beta)+\cos(\alpha+\beta)\end{align*}\]
Затем мы делим на 2, чтобы выделить произведение косинусов:
\[ \cos \alpha \cos \beta= \dfrac{1}{2}[\cos(\alpha-\beta)+\cos( \alpha+\beta)] \label{eq1}\]
Как: Произведение косинусов выразить в виде суммы
- Запишите формулу произведения косинусов.

- Подставить данные углы в формулу.
- Упростить.
Пример \(\PageIndex{1}\): запись произведения в виде суммы с использованием формулы произведения на сумму для косинуса
Запишите следующее произведение косинусов в виде суммы: \(2\cos\left(\dfrac{7x}{2}\right) \cos\left(\dfrac{3x}{2}\right)\).
Решение
Начнем с записи формулы произведения косинусов (уравнение \ref{eq1}):
\[ \cos \alpha \cos \beta = \dfrac{1}{2}[ \ cos(\alpha-\beta)+\cos(\alpha+\beta) ] \nonumber \]
Затем мы можем подставить заданные углы в формулу и упростить.
\[\begin{align*} 2 \cos\left(\dfrac{7x}{2}\right)\cos\left(\dfrac{3x}{2}\right)&= 2\left(\ dfrac{1}{2}\right)[ \cos\left(\dfrac{7x}{2}-\dfrac{3x}{2}\right)+\cos\left(\dfrac{7x}{2} +\dfrac{3x}{2}\right) ]\\[4pt] &= \cos\left(\dfrac{4x}{2}\right)+\cos\left(\dfrac{10x}{2} \right) \\[4pt] &= \cos 2x+\cos 5x \end{align*}\]
Упражнение \(\PageIndex{1}\)
Используйте формулу произведения на сумму (уравнение \ref{eq1}), чтобы записать произведение в виде суммы или разности: \(\cos(2\theta)\ потому что (4 \ тета) \).
- Ответить
\(\dfrac{1}{2}(\cos 6\theta+\cos 2\theta)\)
Выражение произведения синуса и косинуса в виде суммы
Далее мы выведем формулу произведения на сумму синуса и косинуса из формул суммы и разности для синуса . Если мы добавим тождества суммы и разности, мы получим:
\[\begin{align*} \cos \alpha \cos \beta+\sin \alpha \sin \beta&= \cos(\alpha-\beta)\\ [4pt] \underline{+ \cos \alpha \cos \beta-\sin \alpha \sin \beta}&= \cos(\alpha+\beta)\\[4pt] 2 \cos \alpha \cos \beta&= \cos(\alpha-\beta)+\cos(\alpha+\beta)\\[4pt] \text{Затем делим на 2, чтобы выделить произведение косинусов:}\\[4pt] \cos \alpha \ cos \beta&= \dfrac{1}{2}\left[\cos(\alpha-\beta)+\cos(\alpha+\beta)\right] \end{align*}\]
Пример \(\PageIndex{2}\): Запись произведения в виде суммы, содержащей только синус или косинус
Выразите следующее произведение в виде суммы, содержащей только синус или косинус и не содержащей произведений: \(\sin(4\theta )\cos(2\тета)\).
Решение
Напишите формулу произведения синуса и косинуса. Затем подставьте данные значения в формулу и упростите.
\[\begin{align*} \sin \alpha \cos \beta&= \dfrac{1}{2}[ \sin(\alpha+\beta)+\sin(\alpha-\beta) ]\\[ 4pt] \sin(4\theta)\cos(2\theta)&= \dfrac{1}{2}[\sin(4\theta+2\theta)+\sin(4\theta-2\theta) ]\\[4pt] &= \dfrac{1}{2}[\sin(6\theta)+\sin(2\theta)] \end{align*}\]
Упражнение \(\PageIndex{2}\)
Используйте формулу произведения на сумму, чтобы записать произведение в виде суммы: \(\sin(x+y)\cos(x−y)\).
- Ответить
\(\dfrac{1}{2}(\sin 2x+\sin 2y)\)
Выражение произведения синусов через косинус
Выражение произведения синусов через косинус также получается из тождеств суммы и разности для косинуса. В этом случае мы сначала вычтем две формулы косинуса:
\[\begin{align*} \cos(\alpha-\beta)&= \cos \alpha \cos \beta+\sin \alpha \sin \beta\\[4pt] \underline{-\cos(\ alpha+\beta)}&= -(\cos\alpha\cos\beta-\sin\alpha\sin\beta)\\[4pt] \cos(\alpha-\beta)-\cos(\alpha+\beta) &= 2 \sin \alpha \sin \beta\\[4pt] \text{Затем делим на 2, чтобы выделить произведение синусов:}\\[4pt] \sin \alpha \sin \beta&= \dfrac{ 1}{2}[ \cos(\alpha-\beta)-\cos(\alpha+\beta) ] \end{align*}\]
Аналогичным образом мы могли бы выразить произведение косинусов через синус или вывести другое формулы произведения на сумму.
ФОРМУЛЫ ПРОИЗВЕДЕНИЯ НА СУММУ
Формулы произведения на сумму следующие:
\[\cos \alpha \cos \beta=\dfrac{1}{2}[\cos(\ alpha-\beta)+\cos(\alpha+\beta)]\]
\[\sin \alpha \cos \beta=\dfrac{1}{2}[\sin(\alpha+\beta)+\sin (\alpha-\beta)]\]
\[\sin \alpha \sin \beta=\dfrac{1}{2}[\cos(\alpha-\beta)-\cos(\alpha+\beta) ]\]
\[\cos \alpha \sin \beta=\dfrac{1}{2}[\sin(\alpha+\beta)−\sin(\alpha−\beta)]\]
Пример \ (\PageIndex{3}\): Выразите произведение в виде суммы или разности
Запишите \(\cos(3\theta) \cos(5\theta)\) в виде суммы или разности.
Решение
У нас есть произведение косинусов, поэтому начнем с написания соответствующей формулы. Затем подставляем данные углы и упрощаем.
\[\begin{align*} \cos \alpha \cos \beta&= \dfrac{1}{2}[\cos(\alpha-\beta)+\cos(\alpha+\beta)]\\[ 4pt] \cos(3\theta)\cos(5\theta)&= \dfrac{1}{2}[\cos(3\theta-5\theta)+\cos(3\theta+5\theta) ]\\[4pt] &= \dfrac{1}{2}[\cos(2\theta)+\cos(8\theta)]\qquad \text{Использовать четно-нечетное тождество} \end{align*} \]
Упражнение \(\PageIndex{3}\)
Используйте формулу произведения на сумму для вычисления \(\cos \dfrac{11\pi}{12} \cos \dfrac{\pi}{12}\ ).
- Ответить
\(\dfrac{−2−\sqrt{3}}{4}\)
Выражение сумм в виде произведений
Некоторые задачи требуют обратного процесса, который мы только что использовали. Формулы суммы к произведению позволяют нам выразить суммы синуса или косинуса в виде произведений. Эти формулы могут быть получены из тождеств произведения на сумму. Например, с помощью нескольких замен мы можем получить тождество суммы и произведения для синус . Пусть \(\dfrac{u+v}{2}=\alpha\) и \(\dfrac{u−v}{2}=\beta\).
Затем
\[\begin{align*} \alpha+\beta&= \dfrac{u+v}{2}+\dfrac{u-v}{2}\\[4pt] &= \dfrac{2u} {2}\\[4pt] &= u \end{align*}\]
\[\begin{align*} \alpha-\beta&= \dfrac{u+v}{2}-\dfrac{u-v }{2}\\[4pt] &= \dfrac{2v}{2}\\[4pt] &= v \end{align*}\]
Таким образом, замена \(\alpha\) и \(\ бета\) в формуле произведения на сумму с подстановочными выражениями имеем
\[\begin{align*} \sin \alpha \cos \beta&= \dfrac{1}{2}[\sin(\alpha+\beta)+\sin(\alpha-\beta)]\\[4pt ] \sin \left ( \frac{u+v}{2} \right ) \cos \left ( \frac{u-v}{2} \right )&= \frac{1}{2}[\sin u + \sin v]\qquad \text{Замените} (\alpha+\beta) \text{ и } (\alpha\beta)\\[4pt] 2\sin\left(\dfrac{u+v}{2} \right) \cos\left(\dfrac{u-v}{2}\right)&= \sin u+\sin v \end{align*}\]
Другие тождества суммы-произведения выводятся аналогично.
ФОРМУЛЫ СУММЫ-ПРОИЗВЕДЕНИЕ
Формулы суммы-произведения следующие:
\[\sin \alpha+\sin \beta=2\sin\left(\dfrac{\alpha+\beta}{2}\right)\cos \left(\dfrac{\alpha-\beta}{2}\right)\]
\[\sin\alpha-\sin\beta=2\sin\left(\dfrac{\alpha-\beta}{ 2}\right)\cos\left(\dfrac{\alpha+\beta}{2}\right)\]
\[\cos \alpha-\cos \beta=-2\sin\left(\dfrac{ \alpha+\beta}{2}\right)\sin\left(\dfrac{\alpha-\beta}{2}\right)\]
\[\cos \alpha+\cos \beta=2\sin\ влево(\dfrac{\alpha+\beta}{2}\right)\sin\left(\dfrac{\alpha-\beta}{2}\right)\]
Пример \(\PageIndex{4}\): Запись разности синусов в виде произведения
Запишите следующее выражение разности синусов в виде произведения: \(\sin(4\theta)−\sin(2\theta) \).
Решение
Начнем с написания формулы разности синусов.
\[\begin{align*} \sin \alpha-\sin \beta&= 2\sin\left(\dfrac{\alpha-\beta}{2}\right)\cos\left(\dfrac{\ alpha+\beta}{2}\right)\\[4pt] \text {Подставьте значения в формулу и упростите. }\\[4pt] \sin(4\theta)-\sin(2\theta)& = 2\sin\left(\dfrac{4\theta-2\theta}{2}\right) \cos\left(\dfrac{4\theta+2\theta}{2}\right)\\[4pt ] &= 2\sin\left(\dfrac{2\theta}{2}\right) \cos\left(\dfrac{6\theta}{2}\right)\\[4pt] &= 2 \sin \тета \cos(3\тета) \end{выравнивание*}\]
}\\[4pt] \sin(4\theta)-\sin(2\theta)& = 2\sin\left(\dfrac{4\theta-2\theta}{2}\right) \cos\left(\dfrac{4\theta+2\theta}{2}\right)\\[4pt ] &= 2\sin\left(\dfrac{2\theta}{2}\right) \cos\left(\dfrac{6\theta}{2}\right)\\[4pt] &= 2 \sin \тета \cos(3\тета) \end{выравнивание*}\]
Упражнение \(\PageIndex{4}\)
Используйте формулу приведения суммы к произведению, чтобы записать сумму в виде произведения: \(\sin(3\theta)+\sin(\theta)\).
- Ответить
\(2\sin(2\тета)\cos(\тета)\)
Пример \(\PageIndex{5}\): вычисление с использованием формулы приведения суммы к произведению
Вычисление \(\cos(15°)−\cos(75°)\). Проверьте ответ с помощью графического калькулятора.
Решение
Начнем с написания формулы разности косинусов. 9{\ circ}) \\ [4pt]
& = -2 \ влево (\ dfrac {\ sqrt {2}} {2} \ вправо) \ влево (- \ dfrac {1} {2} \ вправо) \\ [4pt]
&= \dfrac{\sqrt{2}}{2}
\end{align*}\]
Пример \(\PageIndex{6}\): Подтверждение личности
Подтверждение личности:
\[\dfrac{\cos(4t)−\cos(2t)}{\sin(4t)+\sin(2t)}=−\tan t\]
Решение
Начнем с левую часть, более сложную часть уравнения, и переписать выражение, пока оно не совпадет с правой частью.
\[\begin{align*} \dfrac{\cos(4t)-\cos(2t)}{\sin(4t)+\sin(2t)}&= \dfrac{-2 \sin\left( \dfrac{4t+2t}{2}\right) \sin\left(\dfrac{4t-2t}{2}\right)}{2 \sin\left(\dfrac{4t+2t}{2}\ справа) \cos\left(\dfrac{4t-2t}{2}\right)}\\[4pt] &= \dfrac{-2 \sin(3t)\sin t}{2 \sin(3t)\ cos t}\\[4pt] &= -\dfrac{\sin t}{\cos t}\\[4pt] &= -\tan t \end{align*}\]
Анализ
Отзыв что проверка тригонометрических тождеств имеет свой собственный набор правил. Процедуры решения уравнения не совпадают с процедурами проверки личности. Когда мы подтверждаем тождество, мы выбираем одну сторону для работы и делаем замены, пока эта сторона не трансформируется в другую сторону. 92 \ тета \ конец {выравнивание *} \]
Медиа
Получите доступ к этим онлайн-ресурсам для получения дополнительных инструкций и практических занятий с идентификаторами продуктов и сумм.
- Сумма идентификаторов продуктов
- Sum to Product и Product to Sum Identities
Ключевые уравнения
Формулы произведения на сумму
\[\cos \alpha \cos \beta=\dfrac{1}{2}[\cos(\alpha-\beta)+\cos(\ альфа+\бета)] \номер\]
\[\sin \alpha \cos \beta=\dfrac{1}{2}[\sin(\alpha+\beta)+\sin(\alpha-\beta)] \nonumber \]
\[\sin \alpha \sin \beta=\dfrac{1}{2}[\cos(\alpha-\beta)−\cos(\alpha+\beta)] \nonumber \]
\[\cos \alpha \sin \ beta=\dfrac{1}{2}[\sin(\alpha+\beta)−\sin(\alpha−\beta)] \nonumber \]
Формулы суммы к произведению
\[\sin \alpha+\sin \beta=2\sin(\dfrac{\alpha+\beta}{2})\cos(\dfrac{\alpha-\beta}{2}) \nonumber \]
\[\sin \ альфа-\sin\beta=2\sin(\dfrac{\alpha-\beta}{2})\cos(\dfrac{\alpha+\beta}{2}) \nonumber \]
\[\cos \alpha-\cos \beta=-2\sin(\dfrac{\alpha+\beta}{2})\sin(\dfrac{\alpha-\beta}{2}) \nonumber \ ]
\[\cos \alpha+\cos \beta=2\sin(\dfrac{\alpha+\beta}{2})\sin(\dfrac{\alpha-\beta}{2}) \nonumber \]
Ключевые понятия
- Из тождеств суммы и разности мы можем вывести формулы произведения на сумму и формулы произведения суммы на синус и косинус.

- Мы можем использовать формулы произведения на сумму, чтобы переписать произведения синусов, произведения косинусов и произведения синусов и косинусов в виде сумм или разностей синусов и косинусов. См. пример \(\PageIndex{1}\), пример \(\PageIndex{2}\) и пример \(\PageIndex{3}\).
- Мы также можем получить тождества суммы-произведения из тождеств произведения-суммы, используя подстановку.
- Мы можем использовать формулы суммы к произведению, чтобы переписать сумму или разность синусов, косинусов или произведений синуса и косинуса как произведения синусов и косинусов. См. пример \(\PageIndex{4}\).
- Тригонометрические выражения часто проще вычислить с помощью формул. См. пример \(\PageIndex{5}\).
- Тождества можно проверить с помощью других формул или преобразования выражений в синусы и косинусы. Для проверки тождества мы выбираем более сложную сторону знака равенства и переписываем ее до тех пор, пока она не преобразуется в другую сторону.
 См. Пример \(\PageIndex{6}\) и Пример \(\PageIndex{7}\).
См. Пример \(\PageIndex{6}\) и Пример \(\PageIndex{7}\).
Эта страница под заголовком 7.4: Формулы суммы к продукту и продукту к сумме распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами. платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- ОпенСтакс
- Лицензия
- СС BY
- Версия лицензии
- 4,0
- Программа OER или Publisher
- ОпенСтакс
- Показать страницу TOC
- нет
- Включено
- да
- Теги
- Произведение на формулы суммирования
- источник@https://openstax.
 org/details/books/precalculus
org/details/books/precalculus - Суммирование формул произведения
Функции синуса и косинуса
Синус и косинус: свойстваФункция синуса имеет ряд свойств, которые в результате получается периодических и нечетных . Функция косинуса имеет ряд свойств, которые результат периодических и даже . Читателю не следует запоминать большинство следующих уравнений; еще, читатель должен быть в состоянии мгновенно получить их от понимания характеристик функции.
Функции синуса и косинуса являются периодическими с периодом 2р. Отсюда следует, что
sin(q) = sin(q + 2p)
cos(q) = cos(q + 2p)
или, в более общем случае,sin(q) = sin(q + 2pk)
cos(q) = cos(q + 2pk),
где k — целые числа. Функция синуса нечетное ; следовательно,
sin(-q) = -sin(q)
Функция косинуса равна даже ; следовательно,cos(-q) = cos(q)
Формула:
sin(x + y) = sin(x)cos(y) + cos(x)sin(y)
Тогда легко вывести из , чтоsin(x — y) = sin(x)cos(y) — cos(x)sin(y)
Или, в более общем случае,sin(x y) = sin(x)cos(y) cos(x)sin(y)
cos(x + y) = cos(x)cos(y) — sin(x)sin (у)
Тогда легко вывести из , чтоcos(x — y) = cos(x)cos(y) + sin(x)sin(y)
Или, в более общем случае,cos(x y) = cos(x)cos(y) (-/+) sin(x)sin(y)
Из приведенного выше уравнения синусов мы можем вывести, что
sin(2x) = 2sin(x)cos(x)
Из приведенного выше уравнения косинуса мы можем вывести, чтоcos(2x) = cos 2 (x) — sin 2 (x)
(Обозначение sin 2 (x) эквивалентно (sin(x)) 2 .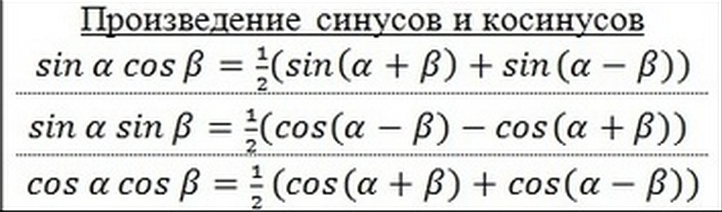 Предупреждение: sin -1 (x) означает arcsin(x), а не обратный мультипликатив.
греха (х).)
Предупреждение: sin -1 (x) означает arcsin(x), а не обратный мультипликатив.
греха (х).) Наблюдая графики синуса и косинуса, мы можем выразить
функция синуса через косинус и наоборот:
sin(x) = cos(90° — x)
и функция косинуса через синус:cos(x) = sin(90° — x)
Такая триггерная функция (f), обладающая свойствомf(q) = g(дополнение(q))
называется кофункцией функции g, отсюда и названия «синус» и « со синус». Пифагорейское тождество,
sin 2 (х) + cos 2 (х) = 1,
дает альтернативное выражение
для синуса через косинус и наоборот
sin 2 (x) = 1 — cos 2 (x)
cos 2 (x) = 1 — sin 2 90 530 (х)
Закон синусов связывает различные стороны и углы произвольного (не обязательно прямоугольного) треугольника:
sin(A)/a = sin(B)/b = sin(C)/c = 2r.
где А, В и С — углы, противоположные сторонам а, b и с соответственно.

 sin(x)) + " — результат вычислений встроенного синуса")
# сразу берём x как первое слагаемое ряда Тейлора
q = x
# сумма ряда на старте равна нулю
s = 0
# порядковый номер слагаемого в ряду Тейлора
i = 1
# пока очередное слагаемое больше погрешности — цикл работает
while abs(q) > n:
# добавляем слагаемое к общей сумме
s = s + q
# вычисляем следующее слагаемое
q = q* (-1) * (x*x) / ((2*i+1) * (2*i))
# увеличиваем порядковый номер слагаемого в ряду Тейлора
i = i+1
# возвращаем сумму как результат работы функции
return s
# запрашиваем стартовые значения
x = float(input("Введите градусы: "))
n = float(input("Введите погрешность: "))
# выводим результат, который мы посчитали сами
print(str(computerSinus(x,n)) + " — синус, который мы посчитали")
sin(x)) + " — результат вычислений встроенного синуса")
# сразу берём x как первое слагаемое ряда Тейлора
q = x
# сумма ряда на старте равна нулю
s = 0
# порядковый номер слагаемого в ряду Тейлора
i = 1
# пока очередное слагаемое больше погрешности — цикл работает
while abs(q) > n:
# добавляем слагаемое к общей сумме
s = s + q
# вычисляем следующее слагаемое
q = q* (-1) * (x*x) / ((2*i+1) * (2*i))
# увеличиваем порядковый номер слагаемого в ряду Тейлора
i = i+1
# возвращаем сумму как результат работы функции
return s
# запрашиваем стартовые значения
x = float(input("Введите градусы: "))
n = float(input("Введите погрешность: "))
# выводим результат, который мы посчитали сами
print(str(computerSinus(x,n)) + " — синус, который мы посчитали")
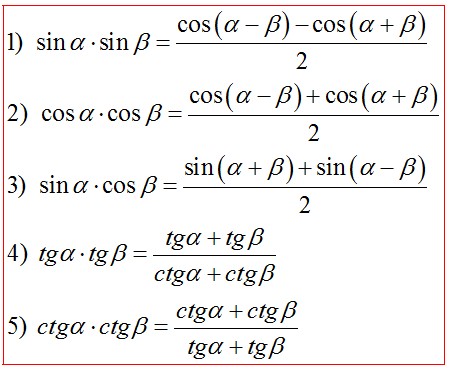
 См. Пример \(\PageIndex{6}\) и Пример \(\PageIndex{7}\).
См. Пример \(\PageIndex{6}\) и Пример \(\PageIndex{7}\). org/details/books/precalculus
org/details/books/precalculus Логика нужна в том числе и для того, чтобы в результате рассуждений не получалась подобная фигня вместо разумных и полезных выводов.
Логика нужна в том числе и для того, чтобы в результате рассуждений не получалась подобная фигня вместо разумных и полезных выводов. com
com html
html Читается относительно легко, затрагиваются несколько подразделов логики. По сути, написана она «для старшего школьного возраста», но, думаю, любому взрослому стоит ее прочесть)
Читается относительно легко, затрагиваются несколько подразделов логики. По сути, написана она «для старшего школьного возраста», но, думаю, любому взрослому стоит ее прочесть)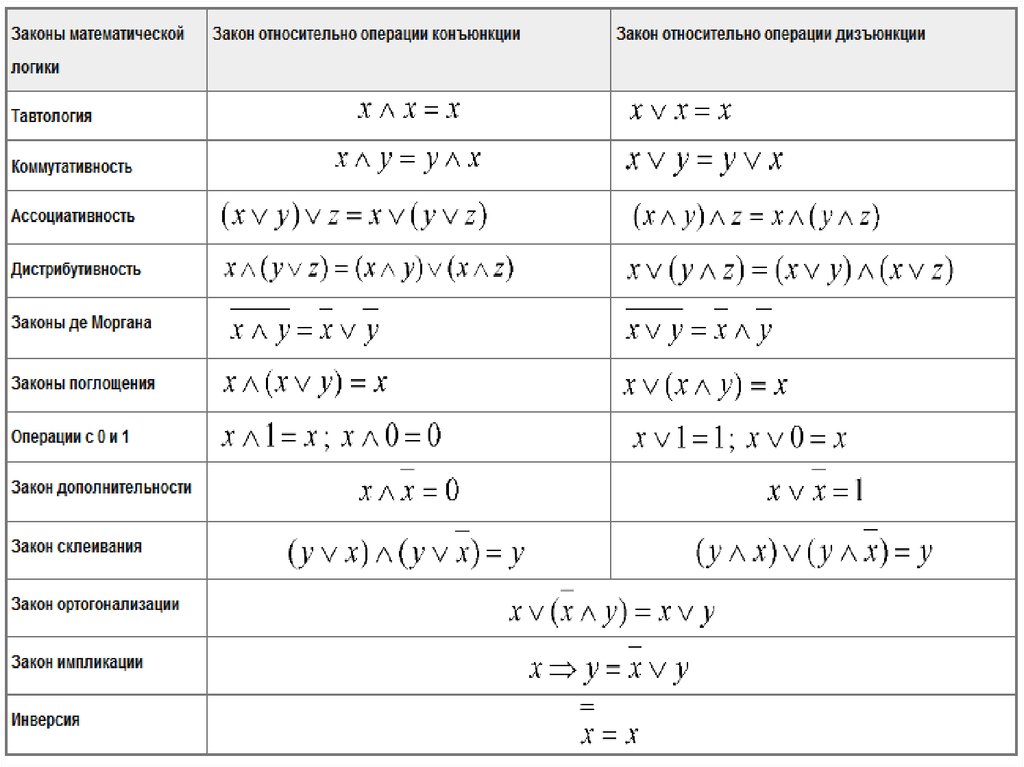 Читала книгу, и там есть все тоже самое, что и в курсе, только еще больше воды.
Читала книгу, и там есть все тоже самое, что и в курсе, только еще больше воды. А.Янковская «Лекции по алгебре логики»; Н.К.Верещагин и А.Шень «Языки и исчисления»; из олдскульной классики — А.Пуанкаре «Математика и логика» и Г.Фреге «Логика и логическая семантика». Думаю, что этого для знакомства с логикой хватит 🙂
А.Янковская «Лекции по алгебре логики»; Н.К.Верещагин и А.Шень «Языки и исчисления»; из олдскульной классики — А.Пуанкаре «Математика и логика» и Г.Фреге «Логика и логическая семантика». Думаю, что этого для знакомства с логикой хватит 🙂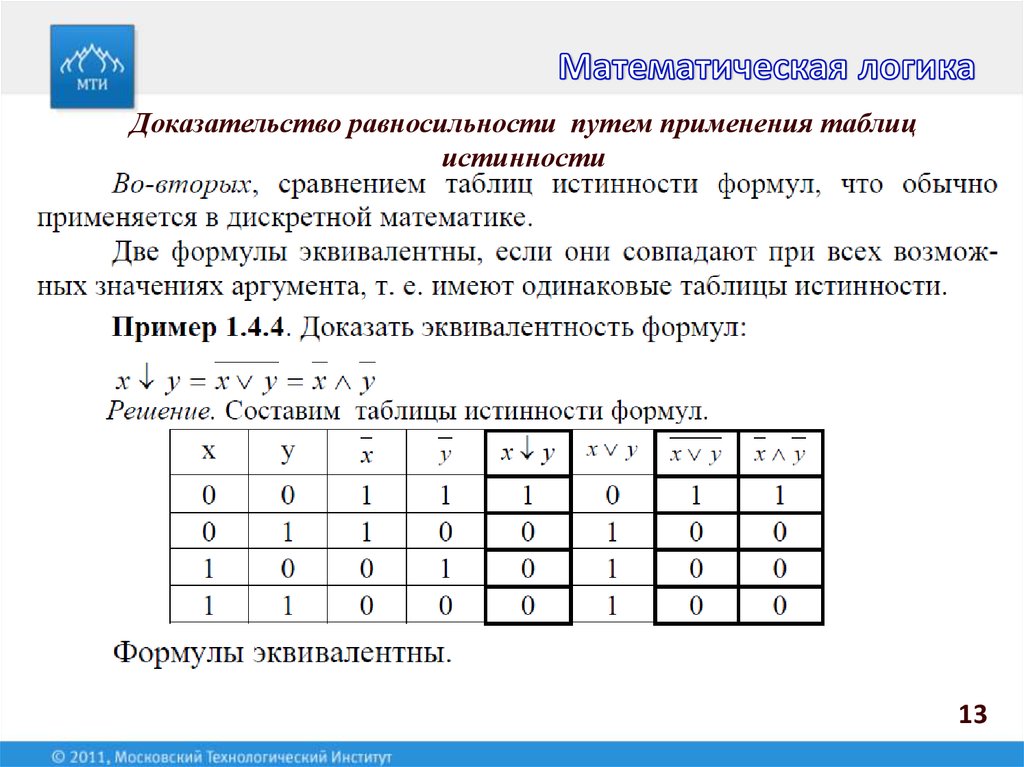 Чтобы использовать этот язык логики, вам нужно знать, какие операторы использовать, таблицы ввода-вывода для этих операторов и правила импликации.
Чтобы использовать этот язык логики, вам нужно знать, какие операторы использовать, таблицы ввода-вывода для этих операторов и правила импликации.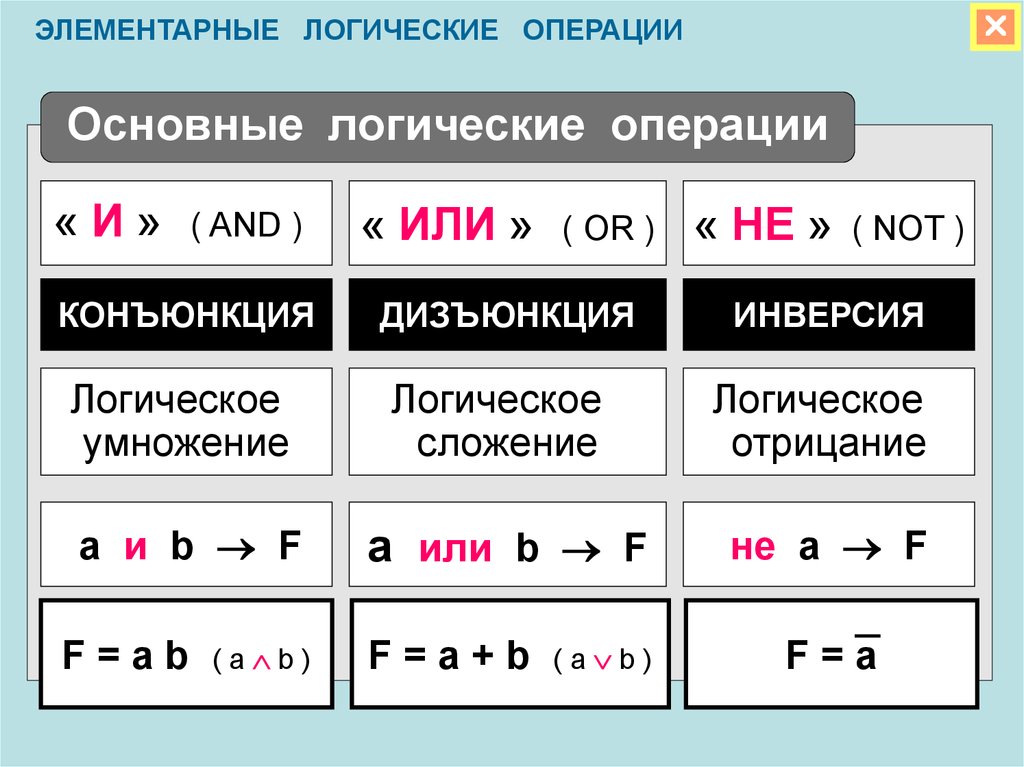 Эти символы вступают в игру, когда вы работаете с тождествами, или взаимозаменяемыми константами. Правила идентификации показаны здесь:
Эти символы вступают в игру, когда вы работаете с тождествами, или взаимозаменяемыми константами. Правила идентификации показаны здесь:
 Для начинающих, для «чайников. Часть I: Основы | Роман Кривцов
Для начинающих, для «чайников. Часть I: Основы | Роман Кривцов Недавно Microsoft даже создала нейронную сеть, которая может сама писать код, используя более неформальные инструкции от людей.
Недавно Microsoft даже создала нейронную сеть, которая может сама писать код, используя более неформальные инструкции от людей.

 Тогда площадь: .
Тогда площадь: . d = C/pi = 20 см/3,14 = 6,36 см = 6,4 см; В итоге получили, что диаметр окружности равty 6.4 см.
d = C/pi = 20 см/3,14 = 6,36 см = 6,4 см; В итоге получили, что диаметр окружности равty 6.4 см.


 Независимо от того, измеряете ли вы размер круглого ковра, который вам нужно купить, или определяете пространство, необходимое для строительства круглого сада или патио, знание того, как рассчитать площадь круга по его диаметру, является ценным навыком. В дальнейшем его можно применить к полукругам или сектору круга.
Независимо от того, измеряете ли вы размер круглого ковра, который вам нужно купить, или определяете пространство, необходимое для строительства круглого сада или патио, знание того, как рассчитать площадь круга по его диаметру, является ценным навыком. В дальнейшем его можно применить к полукругам или сектору круга. Для измерения вам понадобится линейка для маленьких кругов или рулетка для больших кругов. Диаметр круга чрезвычайно полезен при вычислении площади и окружности круга.
Для измерения вам понадобится линейка для маленьких кругов или рулетка для больших кругов. Диаметр круга чрезвычайно полезен при вычислении площади и окружности круга.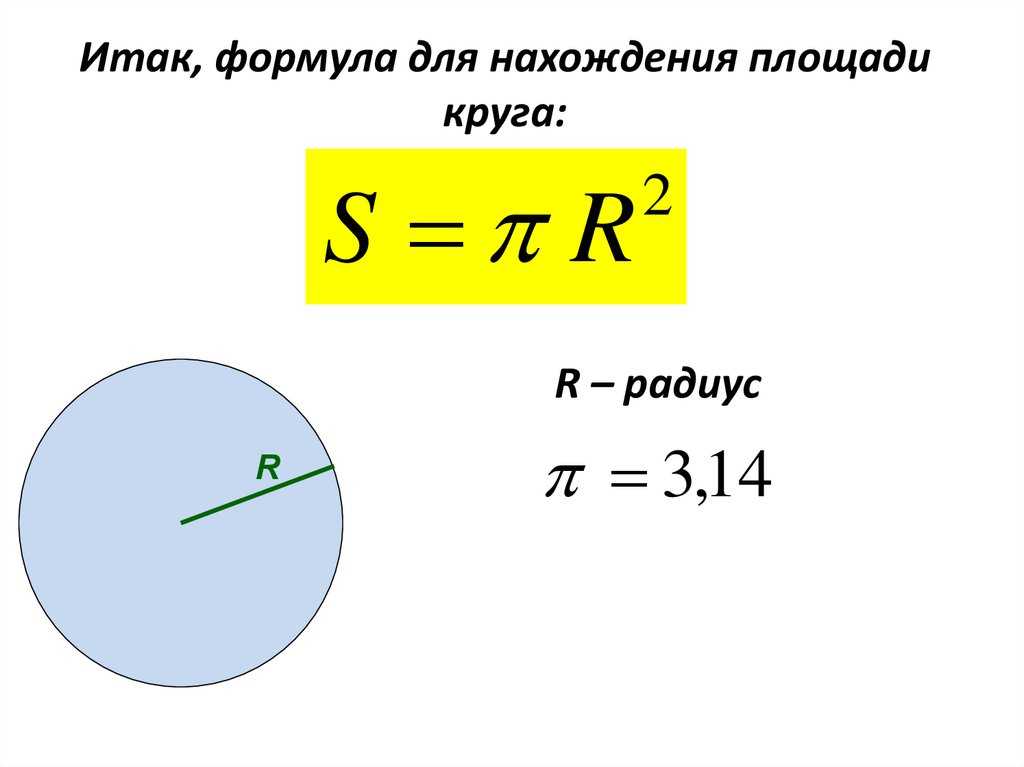
 Пи — это отношение длины окружности к диаметру круга (доли C / d ), поскольку диаметр в два раза больше длины радиуса, оба измерения можно использовать для нахождения длины окружности. круг. В реальной жизни окружность может быть трудно измерить напрямую, но использование диаметра и Пи в формуле окружности может помочь.
Пи — это отношение длины окружности к диаметру круга (доли C / d ), поскольку диаметр в два раза больше длины радиуса, оба измерения можно использовать для нахождения длины окружности. круг. В реальной жизни окружность может быть трудно измерить напрямую, но использование диаметра и Пи в формуле окружности может помочь.
 Вам не придется пройти через хлопоты процесса регистрации, так как это открытая платформа, которая может быть доступна из любого уголка мира.
Вам не придется пройти через хлопоты процесса регистрации, так как это открытая платформа, которая может быть доступна из любого уголка мира.
 Много раз вы, возможно, придется писать на повторяющиеся названия или темы, но оригинальность до сих пор не может быть поставлена под угрозу. Для того, чтобы подтвердить, действительно ли новые и старые тексты являются совершенно уникальными, наше отличие текста проверки приходит играть свою роль. Это становится необходимым, чтобы сравнить тексты для маркетологов и владельцев веб-сайтов, чтобы избежать последствий ожесточенных дублирования.
Много раз вы, возможно, придется писать на повторяющиеся названия или темы, но оригинальность до сих пор не может быть поставлена под угрозу. Для того, чтобы подтвердить, действительно ли новые и старые тексты являются совершенно уникальными, наше отличие текста проверки приходит играть свою роль. Это становится необходимым, чтобы сравнить тексты для маркетологов и владельцев веб-сайтов, чтобы избежать последствий ожесточенных дублирования.

 Вы перепроверяете уник — у каждой статьи он выше 85 % по выбранному вами сервису. По идее, все в порядке и можно размещать. А потом сравниваете эти два текста между собой и выясняете, что разница между ними меньше 70 % — это означает, что после размещения обеих статей только первая будет иметь уник выше 85 %, а вторая окажется уникальной лишь на 10–30 %, что совершенно неудовлетворительно.
Вы перепроверяете уник — у каждой статьи он выше 85 % по выбранному вами сервису. По идее, все в порядке и можно размещать. А потом сравниваете эти два текста между собой и выясняете, что разница между ними меньше 70 % — это означает, что после размещения обеих статей только первая будет иметь уник выше 85 %, а вторая окажется уникальной лишь на 10–30 %, что совершенно неудовлетворительно. Такое сервис проверки уника тоже не найдет. Кстати говоря, это выдает непрофессионала. Здесь мы рассказываем и о других признаках плохого копирайтера по гемблингу.
Такое сервис проверки уника тоже не найдет. Кстати говоря, это выдает непрофессионала. Здесь мы рассказываем и о других признаках плохого копирайтера по гемблингу.
 Помимо процента совпадений и количества одинаковых слов он также показывает куски текста с минимальными изменениями, близким значением и пропущенными словами. Все это отображается разными цветами.
Помимо процента совпадений и количества одинаковых слов он также показывает куски текста с минимальными изменениями, близким значением и пропущенными словами. Все это отображается разными цветами.
 Супер простая процедура включает в себя всего один шаг; вставьте два текста в отдельные поля и нажмите кнопку сравнения, чтобы увидеть различия. Два текста будут отображаться на экране рядом с выделенными различиями. Этот удивительный инструмент не только выделяет слова в кластере строк, которые влекут за собой разницу. Если ваш текст длинный, он также предлагает ссылки, которые помогут вам перейти от одной разницы к другой.
Супер простая процедура включает в себя всего один шаг; вставьте два текста в отдельные поля и нажмите кнопку сравнения, чтобы увидеть различия. Два текста будут отображаться на экране рядом с выделенными различиями. Этот удивительный инструмент не только выделяет слова в кластере строк, которые влекут за собой разницу. Если ваш текст длинный, он также предлагает ссылки, которые помогут вам перейти от одной разницы к другой.
 Пришло время облегчить себе жизнь, попробовав быстрый и быстрый способ изучить различия между двумя текстами, пока не стало слишком поздно!
Пришло время облегчить себе жизнь, попробовав быстрый и быстрый способ изучить различия между двумя текстами, пока не стало слишком поздно!
 Поддерживаются практически все типы файлов, включая Word, PDF, Excel, AI, PPTX и другие.
Поддерживаются практически все типы файлов, включая Word, PDF, Excel, AI, PPTX и другие.
 )
) )
) )
) )
) )
) )
) )
) )
) )/3
)/3 03.2021
03.2021
 Вы также можете использовать функцию распознавания текста для изменения PDF-файла на основе JPG и его преобразования в редактируемый файл, который вы сможете изменять по своему усмотрению. С помощью PDFelement вы можете вносить любые изменения в ваш документ. Благодаря простому интерфейсу, преобразование файлов займет у вас минимум времени.
Вы также можете использовать функцию распознавания текста для изменения PDF-файла на основе JPG и его преобразования в редактируемый файл, который вы сможете изменять по своему усмотрению. С помощью PDFelement вы можете вносить любые изменения в ваш документ. Благодаря простому интерфейсу, преобразование файлов займет у вас минимум времени.
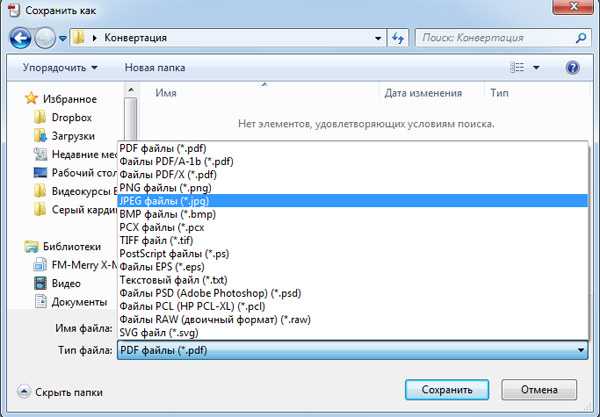
 Ниже приведен порядок действий при сохранении нескольких изображений JPG, а также файлов других типов в одном PDF-документе.
Ниже приведен порядок действий при сохранении нескольких изображений JPG, а также файлов других типов в одном PDF-документе. Однако процесс конвертирования JPG в этом приложении достаточно длительный и может оказаться слишком сложным для новичков.
Однако процесс конвертирования JPG в этом приложении достаточно длительный и может оказаться слишком сложным для новичков.
 jpg nombre.pdf
convert foto.jpg nombre.pdf
jpg nombre.pdf
convert foto.jpg nombre.pdf
 Чтобы сообщить об ошибке, нажмите здесь.
Чтобы сообщить об ошибке, нажмите здесь. Без регистрации и капчи. Здесь вы можете конвертировать документы онлайн и сохранять их в нужном вам формате на свой компьютер или любое другое устройство.
Без регистрации и капчи. Здесь вы можете конвертировать документы онлайн и сохранять их в нужном вам формате на свой компьютер или любое другое устройство. д. Наш инструмент преобразования ZIP в PDF прост в использовании: выберите нужный тип файла, затем определите выходной формат вашего документа, загрузите файл и нажмите ‘Загрузить’.
д. Наш инструмент преобразования ZIP в PDF прост в использовании: выберите нужный тип файла, затем определите выходной формат вашего документа, загрузите файл и нажмите ‘Загрузить’.

 Например, Google Chrome, Firefox, Opera, Safari.
Например, Google Chrome, Firefox, Opera, Safari.
 …
… Умножение на числа 2 и 3.
Умножение на числа 2 и 3. ЗАДАЧИ. УМНОЖЕНИЕ.Стр. 2
ЗАДАЧИ. УМНОЖЕНИЕ.Стр. 2 ЗАДАЧИ. УМНОЖЕНИЕ.Стр. 3
ЗАДАЧИ. УМНОЖЕНИЕ.Стр. 3 ЗАДАЧИ. УМНОЖЕНИЕ.Стр. 4
ЗАДАЧИ. УМНОЖЕНИЕ.Стр. 4 ЗАДАЧИ. УМНОЖЕНИЕ.Стр. 5
ЗАДАЧИ. УМНОЖЕНИЕ.Стр. 5 ЗАДАЧИ. УМНОЖЕНИЕ. ОТВЕТЫ.Стр. 1
ЗАДАЧИ. УМНОЖЕНИЕ. ОТВЕТЫ.Стр. 1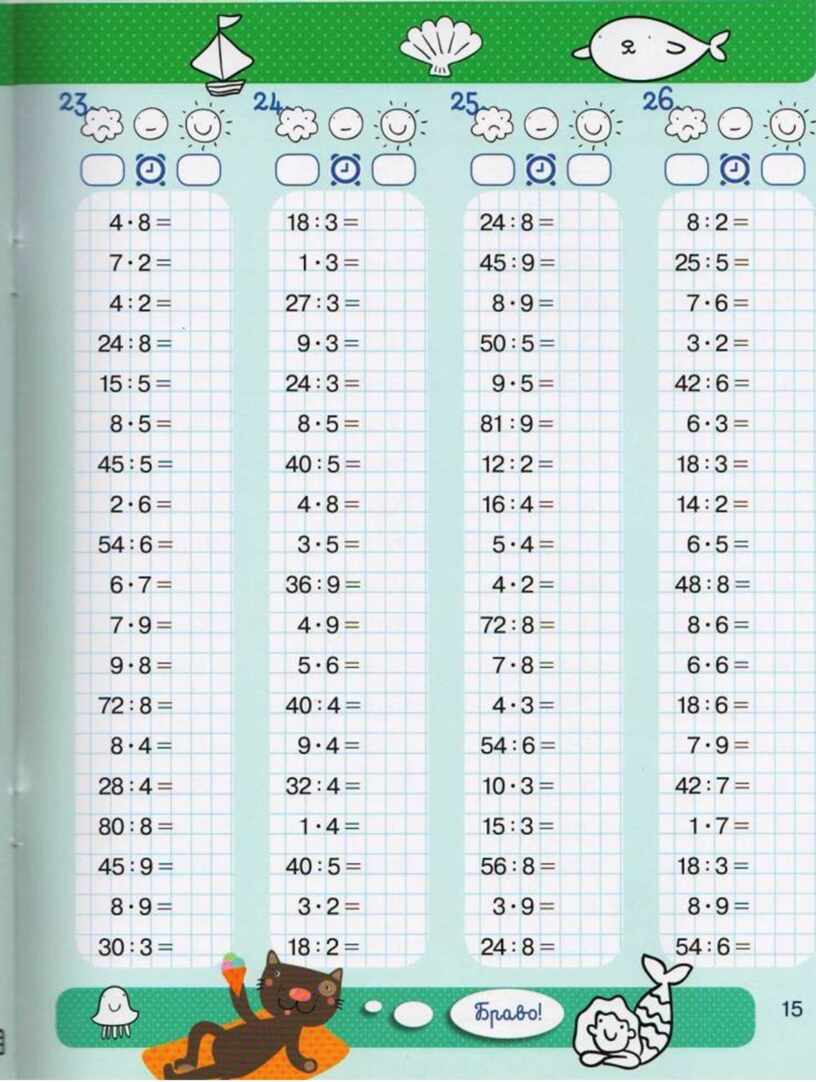 ЗАДАЧИ. УМНОЖЕНИЕ. ОТВЕТЫ.Стр. 2.
ЗАДАЧИ. УМНОЖЕНИЕ. ОТВЕТЫ.Стр. 2. ЗАДАЧИ. УМНОЖЕНИЕ. ОТВЕТЫ.Стр. 3.
ЗАДАЧИ. УМНОЖЕНИЕ. ОТВЕТЫ.Стр. 3. ЗАДАЧИ. УМНОЖЕНИЕ. ОТВЕТЫ.Стр. 4.
ЗАДАЧИ. УМНОЖЕНИЕ. ОТВЕТЫ.Стр. 4. ЗАДАЧИ. УМНОЖЕНИЕ. ОТВЕТЫ.Стр. 5.
ЗАДАЧИ. УМНОЖЕНИЕ. ОТВЕТЫ.Стр. 5. Учебная таблица 2 очень важна для каждого ученика, чтобы хорошо успевать по математике. Таблица 2 — это таблица умножения, в которой записаны числа, кратные двум. Студентов просят выучить таблицы и особенно таблицу 2, чтобы ускорить их вычисления.
Учебная таблица 2 очень важна для каждого ученика, чтобы хорошо успевать по математике. Таблица 2 — это таблица умножения, в которой записаны числа, кратные двум. Студентов просят выучить таблицы и особенно таблицу 2, чтобы ускорить их вычисления. Таблица 2 составляет основу умножения и ускоряет решение задач на умножение. Таблица от 2 до 10 раз приведена ниже,
Таблица 2 составляет основу умножения и ускоряет решение задач на умножение. Таблица от 2 до 10 раз приведена ниже, Таблица чисел 2 от 11 до 20 приведена ниже,
Таблица чисел 2 от 11 до 20 приведена ниже,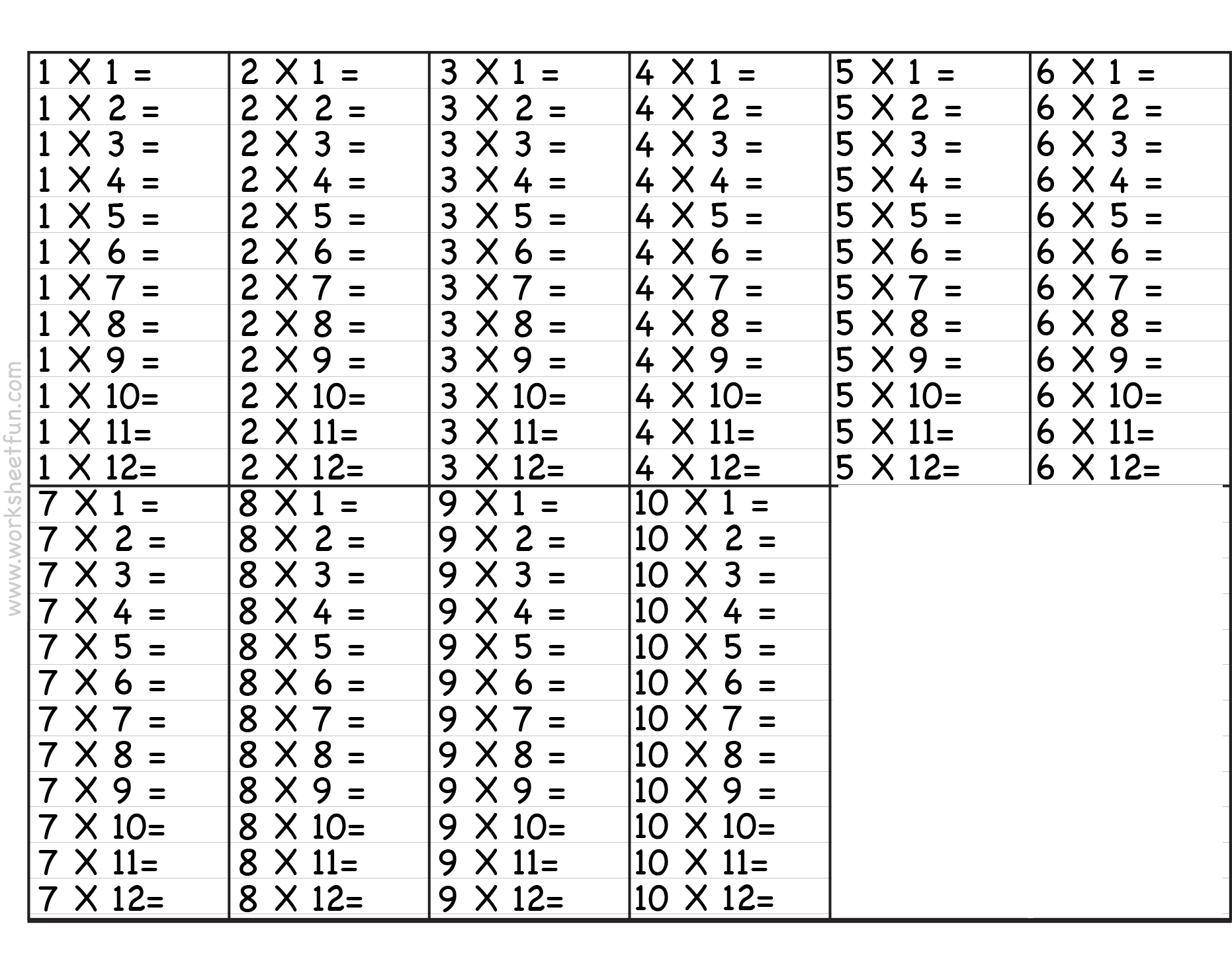 Давайте посмотрим, как читать таблицу 2.
Давайте посмотрим, как читать таблицу 2.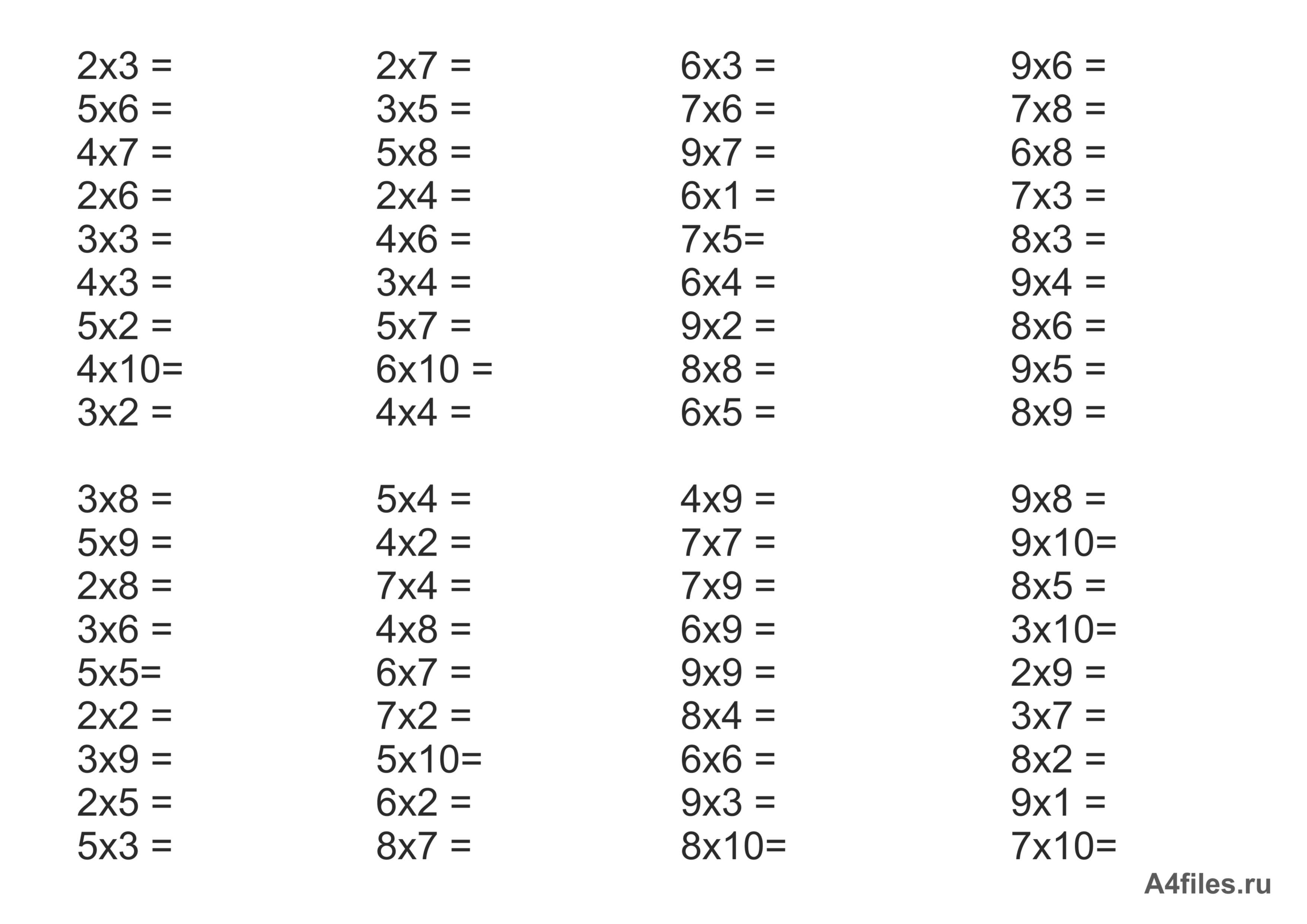


 То есть общее количество бабочек равно 3, умноженному на 4, или 4 + 4 + 4, или 12.
То есть общее количество бабочек равно 3, умноженному на 4, или 4 + 4 + 4, или 12.
 Затем ищем поле, где они пересекаются. Они пересекаются под номером 21.
Затем ищем поле, где они пересекаются. Они пересекаются под номером 21. Значит, в 4 мешках будет 4 раза по 7 шариков.
Значит, в 4 мешках будет 4 раза по 7 шариков. Значит, через 9 лет количество посаженных деревьев будет 9 умножить на 3.
Значит, через 9 лет количество посаженных деревьев будет 9 умножить на 3.


 Обозначается: .
Обозначается: .
 Это упростит вычисление определителя.
Умножим первую строку на (-3) и прибавим ко второй строке, затем умножим
первую строку на (-7) и прибавим к третьей строке: . Заметим, что вторая строка имеет общий множитель (-2), а
третья — (-1). Поэтому, применяя дважды 5-ое свойство, получим: . В первом столбце остался лишь один элемент, отличный от
нуля. Тогда, разложив определитель по элементам первого столбца, получим:
.
Это упростит вычисление определителя.
Умножим первую строку на (-3) и прибавим ко второй строке, затем умножим
первую строку на (-7) и прибавим к третьей строке: . Заметим, что вторая строка имеет общий множитель (-2), а
третья — (-1). Поэтому, применяя дважды 5-ое свойство, получим: . В первом столбце остался лишь один элемент, отличный от
нуля. Тогда, разложив определитель по элементам первого столбца, получим:
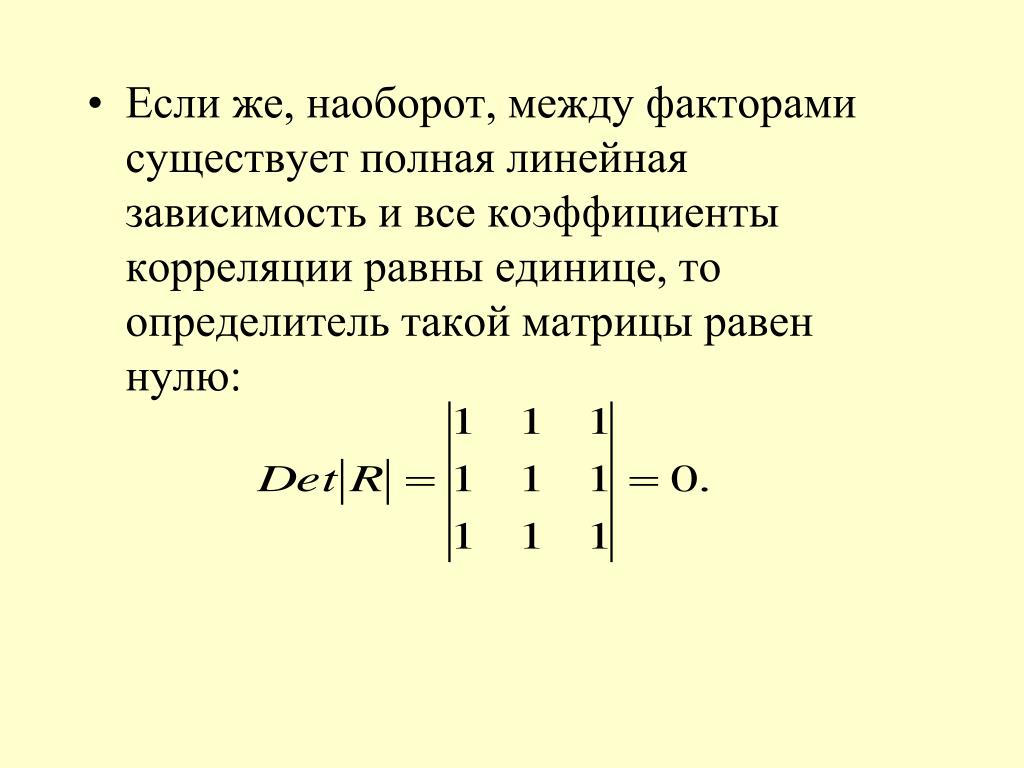
. (обозначается ∆, det a, |a|, d)
(обозначается ∆, det a, |a|, d)



 Находим иксы
по формуле:
Находим иксы
по формуле: Записать в виде матрицы,
отдельно Х, отдельно коэффициенты,
отдельно свободные члены (0-ли) 2. Привести
к ступенчатому виду (элементарные
преобразования).
Записать в виде матрицы,
отдельно Х, отдельно коэффициенты,
отдельно свободные члены (0-ли) 2. Привести
к ступенчатому виду (элементарные
преобразования). Векторы можно: умножать на число,
складывать, перемножать, находить модуль
вектора. При сложении, умножении – можно
менять местами, выносить за скобки.
Векторы можно: умножать на число,
складывать, перемножать, находить модуль
вектора. При сложении, умножении – можно
менять местами, выносить за скобки.
 ..,λn,
при котором линейная комбинация векторов
λ1*A1+λ2*A2+…+λn*An равна нулевому вектору. Условие: все
λ≠0. Если λ=0, то система линейно
независима. Эквивалентные системы
– системы, которые можно выразить друг
через друга. Их ранги равны. Эквивалентные
преобразования – изменение нумерации
вектора, удаление нулевого вектора,
удаление линейной комбинации векторов,
умножение на число, прибавление к одному
вектору линейную комбинацию других
векторов системы.
..,λn,
при котором линейная комбинация векторов
λ1*A1+λ2*A2+…+λn*An равна нулевому вектору. Условие: все
λ≠0. Если λ=0, то система линейно
независима. Эквивалентные системы
– системы, которые можно выразить друг
через друга. Их ранги равны. Эквивалентные
преобразования – изменение нумерации
вектора, удаление нулевого вектора,
удаление линейной комбинации векторов,
умножение на число, прибавление к одному
вектору линейную комбинацию других
векторов системы.
 д.) между всеми векторами. Если один вектор равен нулю или компланарен другим, то он не будет вносить вклад в «высоту» объема, и определитель будет равен нулю.
д.) между всеми векторами. Если один вектор равен нулю или компланарен другим, то он не будет вносить вклад в «высоту» объема, и определитель будет равен нулю.
 Это может дать вам корреляцию с вектором.
Это может дать вам корреляцию с вектором. Для этого вам в основном нужно будет умножить обе части уравнения на транспонированную матрицу, а затем решить как обычно.
Для этого вам в основном нужно будет умножить обе части уравнения на транспонированную матрицу, а затем решить как обычно. В общем, для задач, которые являются «статически неопределенными». То есть количество неизвестных больше, чем количество уравнений.
В общем, для задач, которые являются «статически неопределенными». То есть количество неизвестных больше, чем количество уравнений.

 Что касается того, что это такое, студентов традиционно сначала знакомят с тем, как вычисляется определитель, а затем с практической связью и ее геометрической интерпретацией.
Что касается того, что это такое, студентов традиционно сначала знакомят с тем, как вычисляется определитель, а затем с практической связью и ее геометрической интерпретацией.

 Но прежде чем мы это сделаем, мы объясним, почему элемент в вычислении -детерминанта имел знак минус.
Но прежде чем мы это сделаем, мы объясним, почему элемент в вычислении -детерминанта имел знак минус.
 Например, как в:
Например, как в: Пусть следующая обратимая матрица:
Пусть следующая обратимая матрица:
 Тогда у нас есть:
Тогда у нас есть:
 Найдите угол АМС, если углы ВАС и ВСА равны 45 градусов и 30 градусов соответственно
Найдите угол АМС, если углы ВАС и ВСА равны 45 градусов и 30 градусов соответственно
 (x+1) > 2(2-x) сторона, использующая Распределительное свойство
(x+1) > 2(2-x) сторона, использующая Распределительное свойство
 Это даст другой открытый кружок на числовой прямой.
Это даст другой открытый кружок на числовой прямой.
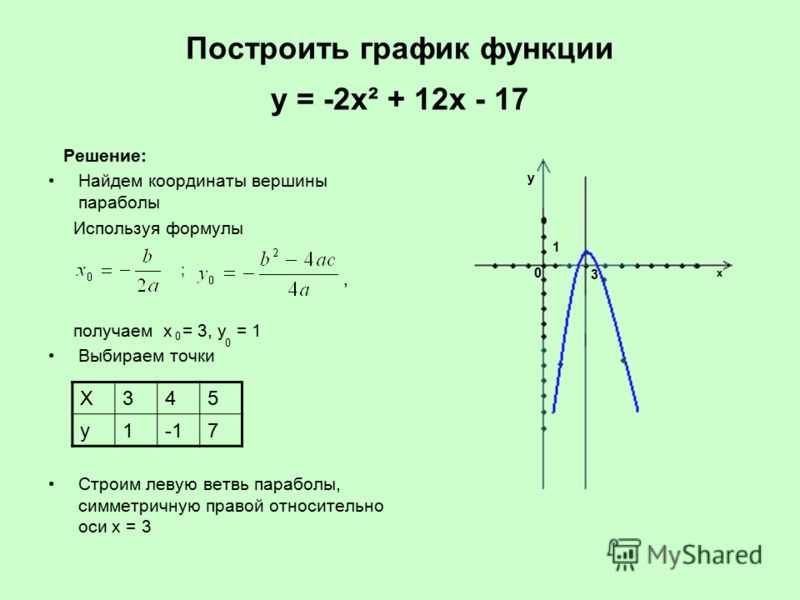
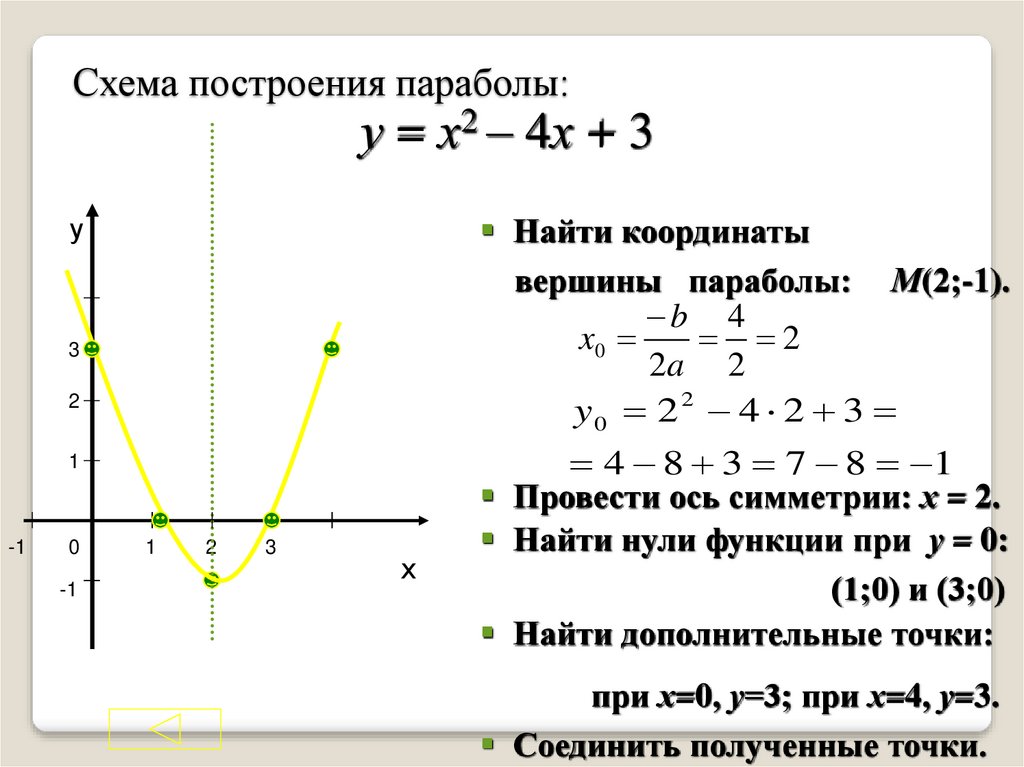
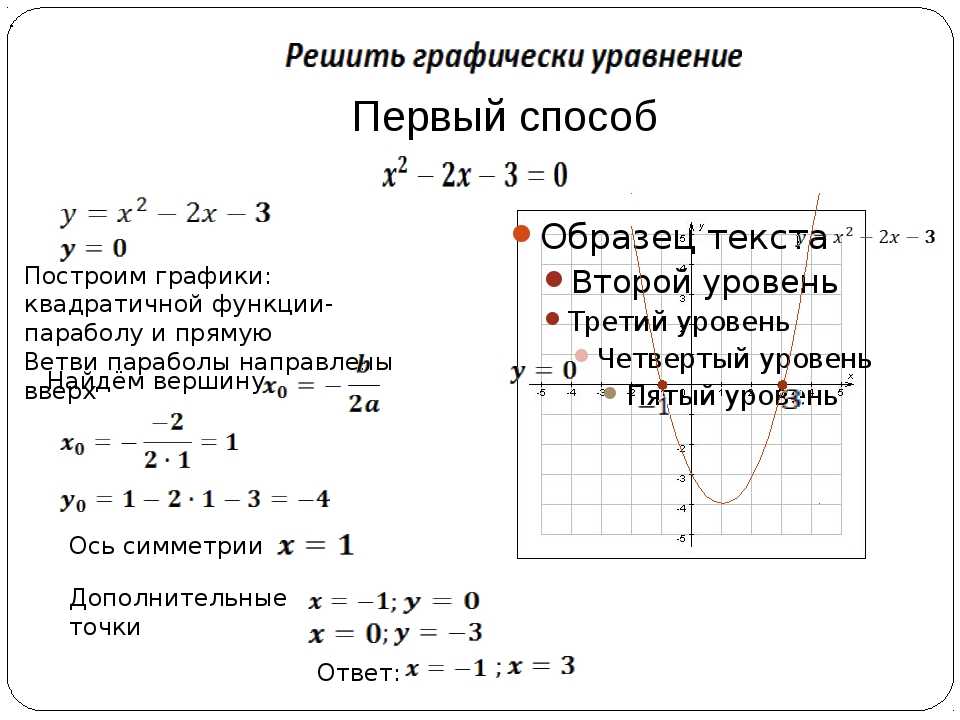
 Найдем координаты всех точек пересечения параболы с осями координат и координаты вершины параболы.
Найдем координаты всех точек пересечения параболы с осями координат и координаты вершины параболы.
 4) .
4) .
 Горизонтальная – y = 2/1 (отношение коэффициентов при x в числителе и знаменателе дроби), вертикальная – x = -3.
Горизонтальная – y = 2/1 (отношение коэффициентов при x в числителе и знаменателе дроби), вертикальная – x = -3. Соответственно, графиком функции будет называться множество точек, координаты которых удовлетворяют заданному выражению.
Соответственно, графиком функции будет называться множество точек, координаты которых удовлетворяют заданному выражению. Также при необходимости можно задать уравнение параметрическим методом или строить графики в полярной системе координат.
Также при необходимости можно задать уравнение параметрическим методом или строить графики в полярной системе координат.
 Список лучших был сформирован так, чтобы удовлетворить требования любого математика от мала до велика. Успехов вам в постижении «царицы наук»!
Список лучших был сформирован так, чтобы удовлетворить требования любого математика от мала до велика. Успехов вам в постижении «царицы наук»! А недостаток — в том, что сервис не полностью переведен на русский язык.
А недостаток — в том, что сервис не полностью переведен на русский язык.
 Us или в личном кабинете Onlinecharts.ru. Первый вариант могут использовать все, второй — только зарегистрированные.
Us или в личном кабинете Onlinecharts.ru. Первый вариант могут использовать все, второй — только зарегистрированные.
 Также при необходимости можно задать уравнение параметрическим методом или строить графики в полярной системе координат.
Также при необходимости можно задать уравнение параметрическим методом или строить графики в полярной системе координат.
 Список лучших был сформирован так, чтобы удовлетворить требования любого математика от мала до велика. Успехов вам в постижении «царицы наук»!
Список лучших был сформирован так, чтобы удовлетворить требования любого математика от мала до велика. Успехов вам в постижении «царицы наук»! 2/16=1)
2/16=1)
 ..)
..) Проанализировав потребность, разработчики React Native предложили решение для удовлетворения своих потребностей, создав приложения для обеих платформ с использованием одного и того же кода. Действительно, он стал самым популярным инструментом для миллионов разработчиков. Но в настоящее время многие фреймворки способны создавать мультиплатформенные приложения. React Native постоянно вызывает различные споры, и один из них касается будущего React Native и того, будет ли он обслуживать обе платформы в будущем. И чтобы ответить на эти аргументы, наша статья о будущем масштабе React Native в 2022 году поможет вам и многим разработчикам понять его траекторию и стоит ли его изучать или нет. Что такое React Native Framework? React Native — это среда JavaScript, которая используется разработчиками для создания многоплатформенных приложений, таких как iOS, macOS, Android, Windows и многих других. Он основан на библиотеке JavaScript Facebook, которая используется для создания интерфейсов для веб-приложений, но вместо веб-приложений React Native выбирает мобильные платформы.
Проанализировав потребность, разработчики React Native предложили решение для удовлетворения своих потребностей, создав приложения для обеих платформ с использованием одного и того же кода. Действительно, он стал самым популярным инструментом для миллионов разработчиков. Но в настоящее время многие фреймворки способны создавать мультиплатформенные приложения. React Native постоянно вызывает различные споры, и один из них касается будущего React Native и того, будет ли он обслуживать обе платформы в будущем. И чтобы ответить на эти аргументы, наша статья о будущем масштабе React Native в 2022 году поможет вам и многим разработчикам понять его траекторию и стоит ли его изучать или нет. Что такое React Native Framework? React Native — это среда JavaScript, которая используется разработчиками для создания многоплатформенных приложений, таких как iOS, macOS, Android, Windows и многих других. Он основан на библиотеке JavaScript Facebook, которая используется для создания интерфейсов для веб-приложений, но вместо веб-приложений React Native выбирает мобильные платформы. Другими словами, это означает, что даже веб-разработчики могут создавать нативные приложения, отражающие эстетику веб-приложений. И это приносит огромную пользу многим компаниям и стартапам, чтобы завоевать популярность среди аудитории мобильных платформ. Почему React Native так популярен? Популярность имеет тенденцию к росту, когда инструмент предоставляет некоторые уникальные функции, в которых отчаянно нуждаются разработчики, и React Native делает то же самое. По этой причине его рассматривают популярные бренды, такие как Facebook, Tesla, Ubereats, Instagram, Airbnb, Discord и многие другие. что еще больше увеличивает его популярность, потому что потребители предпочитают продукты, предлагаемые самыми передовыми технологическими компаниями. Более того, родные функциональные возможности, переносимость и надежность React выделяются среди других фреймворков, что делает его уникальным и эффективным инструментом. Кроме того, его быстрые операции ускоряют процедуры разработки для доставки программных продуктов в установленные сроки.
Другими словами, это означает, что даже веб-разработчики могут создавать нативные приложения, отражающие эстетику веб-приложений. И это приносит огромную пользу многим компаниям и стартапам, чтобы завоевать популярность среди аудитории мобильных платформ. Почему React Native так популярен? Популярность имеет тенденцию к росту, когда инструмент предоставляет некоторые уникальные функции, в которых отчаянно нуждаются разработчики, и React Native делает то же самое. По этой причине его рассматривают популярные бренды, такие как Facebook, Tesla, Ubereats, Instagram, Airbnb, Discord и многие другие. что еще больше увеличивает его популярность, потому что потребители предпочитают продукты, предлагаемые самыми передовыми технологическими компаниями. Более того, родные функциональные возможности, переносимость и надежность React выделяются среди других фреймворков, что делает его уникальным и эффективным инструментом. Кроме того, его быстрые операции ускоряют процедуры разработки для доставки программных продуктов в установленные сроки. И все мы знаем, насколько важны сроки выполнения. Вот почему разработчики предпочитают React Native как лучшее оружие в своем арсенале. Будущее React Native в значительной степени зависит от удовлетворенности разработчиков, и сообщество обещает это сделать. Еще одна фантастическая особенность React Native заключается в том, что он позволяет программистам повторно использовать существующий код из одного приложения для улучшения и реализации его в другом, экономя массу времени и позволяя программистам больше сосредоточиться на добавлении новых функций в приложение. Согласно приведенной выше статистике тенденций Google, популярность React Natives росла в течение последних нескольких лет и по-прежнему возглавляет диаграмму. Это показывает, что будущее React Native по-прежнему многообещающе, и этот инструмент широко используется разработчиками для ускорения процесса разработки React Native. React Native против Flutter 2022 Как React Native, так и Flutter являются идеальными платформами для создания кроссплатформенных мобильных приложений.
И все мы знаем, насколько важны сроки выполнения. Вот почему разработчики предпочитают React Native как лучшее оружие в своем арсенале. Будущее React Native в значительной степени зависит от удовлетворенности разработчиков, и сообщество обещает это сделать. Еще одна фантастическая особенность React Native заключается в том, что он позволяет программистам повторно использовать существующий код из одного приложения для улучшения и реализации его в другом, экономя массу времени и позволяя программистам больше сосредоточиться на добавлении новых функций в приложение. Согласно приведенной выше статистике тенденций Google, популярность React Natives росла в течение последних нескольких лет и по-прежнему возглавляет диаграмму. Это показывает, что будущее React Native по-прежнему многообещающе, и этот инструмент широко используется разработчиками для ускорения процесса разработки React Native. React Native против Flutter 2022 Как React Native, так и Flutter являются идеальными платформами для создания кроссплатформенных мобильных приложений. Хотя они и являются конкурентами, у них схожая цель, то есть предоставить пользователям самое эффективное мобильное приложение. Нелегко понять, какой из них лучше, поскольку оба имеют свои плюсы и минусы, которые делают их уникальными, но тем не менее, чтобы взглянуть на будущее React Native, сравнение между React Native и Flutter прояснит многие аспекты разработки. 1. Технический стек Основное различие между ними заключается в том, что они работают на разных языках программирования. Например, у Flutter есть собственный родной язык программирования Dart, который можно использовать для создания мобильных приложений. тогда как React Native сильно зависит от наиболее широко используемого языка программирования в мире, то есть JavaScript. И многие согласятся с нами, что JavaScript широко используется, и выбор React Native для разработки мобильных приложений будет иметь больше смысла. С другой стороны, Flutter требует знания языка программирования Dart, который следует сначала изучить, чтобы выбрать экосистему Flutter.
Хотя они и являются конкурентами, у них схожая цель, то есть предоставить пользователям самое эффективное мобильное приложение. Нелегко понять, какой из них лучше, поскольку оба имеют свои плюсы и минусы, которые делают их уникальными, но тем не менее, чтобы взглянуть на будущее React Native, сравнение между React Native и Flutter прояснит многие аспекты разработки. 1. Технический стек Основное различие между ними заключается в том, что они работают на разных языках программирования. Например, у Flutter есть собственный родной язык программирования Dart, который можно использовать для создания мобильных приложений. тогда как React Native сильно зависит от наиболее широко используемого языка программирования в мире, то есть JavaScript. И многие согласятся с нами, что JavaScript широко используется, и выбор React Native для разработки мобильных приложений будет иметь больше смысла. С другой стороны, Flutter требует знания языка программирования Dart, который следует сначала изучить, чтобы выбрать экосистему Flutter. 2. Кроссплатформенная разработка Когда дело доходит до кроссплатформенной разработки, и React Native, и Flutter предлагают схожие функции и функции для разработки мобильного приложения (за исключением некоторых встроенных уникальных функций). Изначально React был создан для оптимизации процесса разработки для обеих платформ, и будущее React Native основано на улучшении производительности и простоте разработки. С другой стороны, Flutter был создан, чтобы упростить процесс разработки приложений и сделать его более доступным, используя язык программирования Dart, который легко освоить. Разница между ними заключается в том, что в React компоненты и код пользовательского интерфейса не являются общими для iOS и Android, а объединяются отдельно для пользовательского интерфейса с использованием JavaScript. С другой стороны, пользовательский интерфейс и компоненты кода являются общими для iOS и Android, что делает его намного быстрее. 3. Производительность React Native оснащен улучшенной виртуальной машиной JavaScript, которая обеспечивает быструю компиляцию с помощью JIT-компилятора.
2. Кроссплатформенная разработка Когда дело доходит до кроссплатформенной разработки, и React Native, и Flutter предлагают схожие функции и функции для разработки мобильного приложения (за исключением некоторых встроенных уникальных функций). Изначально React был создан для оптимизации процесса разработки для обеих платформ, и будущее React Native основано на улучшении производительности и простоте разработки. С другой стороны, Flutter был создан, чтобы упростить процесс разработки приложений и сделать его более доступным, используя язык программирования Dart, который легко освоить. Разница между ними заключается в том, что в React компоненты и код пользовательского интерфейса не являются общими для iOS и Android, а объединяются отдельно для пользовательского интерфейса с использованием JavaScript. С другой стороны, пользовательский интерфейс и компоненты кода являются общими для iOS и Android, что делает его намного быстрее. 3. Производительность React Native оснащен улучшенной виртуальной машиной JavaScript, которая обеспечивает быструю компиляцию с помощью JIT-компилятора. Опять же, вы можете отправлять коды всякий раз, когда это необходимо, чтобы они выполнялись в родном коде. Более того, React Native предлагает почти такую же производительность, как и нативное приложение для iOS, что является плюсом для будущих аспектов React Native. Напротив, Flutter поставляется с собственным улучшенным компилятором, который загружает коды как для платформ iOS, так и для Android. Потому что здесь, в отличие от React Native, вам не нужно отправлять коды, и из-за этого вы получаете более высокую нативную производительность после завершения проекта. 4. Кривая обучения Каждый разработчик рассматривает кривую обучения, прежде чем выбирать новые фреймворки и технологические стеки. Потому что легкая кривая обучения экономит время. Будущее React Native привлекательно, поскольку это фреймворк мечты для разработчиков. Он работает на языке программирования JavaScript. А поскольку большинство разработчиков во всем мире знакомы с JavaScript, они могут легко выбрать этот React Native.
Опять же, вы можете отправлять коды всякий раз, когда это необходимо, чтобы они выполнялись в родном коде. Более того, React Native предлагает почти такую же производительность, как и нативное приложение для iOS, что является плюсом для будущих аспектов React Native. Напротив, Flutter поставляется с собственным улучшенным компилятором, который загружает коды как для платформ iOS, так и для Android. Потому что здесь, в отличие от React Native, вам не нужно отправлять коды, и из-за этого вы получаете более высокую нативную производительность после завершения проекта. 4. Кривая обучения Каждый разработчик рассматривает кривую обучения, прежде чем выбирать новые фреймворки и технологические стеки. Потому что легкая кривая обучения экономит время. Будущее React Native привлекательно, поскольку это фреймворк мечты для разработчиков. Он работает на языке программирования JavaScript. А поскольку большинство разработчиков во всем мире знакомы с JavaScript, они могут легко выбрать этот React Native. Flutter, с другой стороны, использует язык программирования Dart, с которым многие разработчики могут быть даже не знакомы. Язык программирования Dart был признан самым удобным для пользователя языком, несмотря на то, что многие люди не знают об экосистеме его разработки. Даже некоторые из новых пользователей Dart утверждают, что на его изучение уходят всего выходные. Поэтому мы настоятельно рекомендуем использовать оба фреймворка хотя бы один раз. Это позволит вам всесторонне оценить их обоих и определить, какой из них лучше всего соответствует вашим требованиям. Потому что как разработчик, от вашего выбора будет зависеть будущее React Native или будущее Flutter. Есть ли у React Native будущее? Теперь мы обсудим будущее React Native. Мы упомянули некоторые факторы ниже, которые помогут нам определить будущее React Native. А в качестве спойлера скажем, что будущее у React Native более чем светлое. Эти факторы смело говорят о том, что React никуда не денется и предоставит разработчикам расширенные возможности для улучшения процесса разработки.
Flutter, с другой стороны, использует язык программирования Dart, с которым многие разработчики могут быть даже не знакомы. Язык программирования Dart был признан самым удобным для пользователя языком, несмотря на то, что многие люди не знают об экосистеме его разработки. Даже некоторые из новых пользователей Dart утверждают, что на его изучение уходят всего выходные. Поэтому мы настоятельно рекомендуем использовать оба фреймворка хотя бы один раз. Это позволит вам всесторонне оценить их обоих и определить, какой из них лучше всего соответствует вашим требованиям. Потому что как разработчик, от вашего выбора будет зависеть будущее React Native или будущее Flutter. Есть ли у React Native будущее? Теперь мы обсудим будущее React Native. Мы упомянули некоторые факторы ниже, которые помогут нам определить будущее React Native. А в качестве спойлера скажем, что будущее у React Native более чем светлое. Эти факторы смело говорят о том, что React никуда не денется и предоставит разработчикам расширенные возможности для улучшения процесса разработки.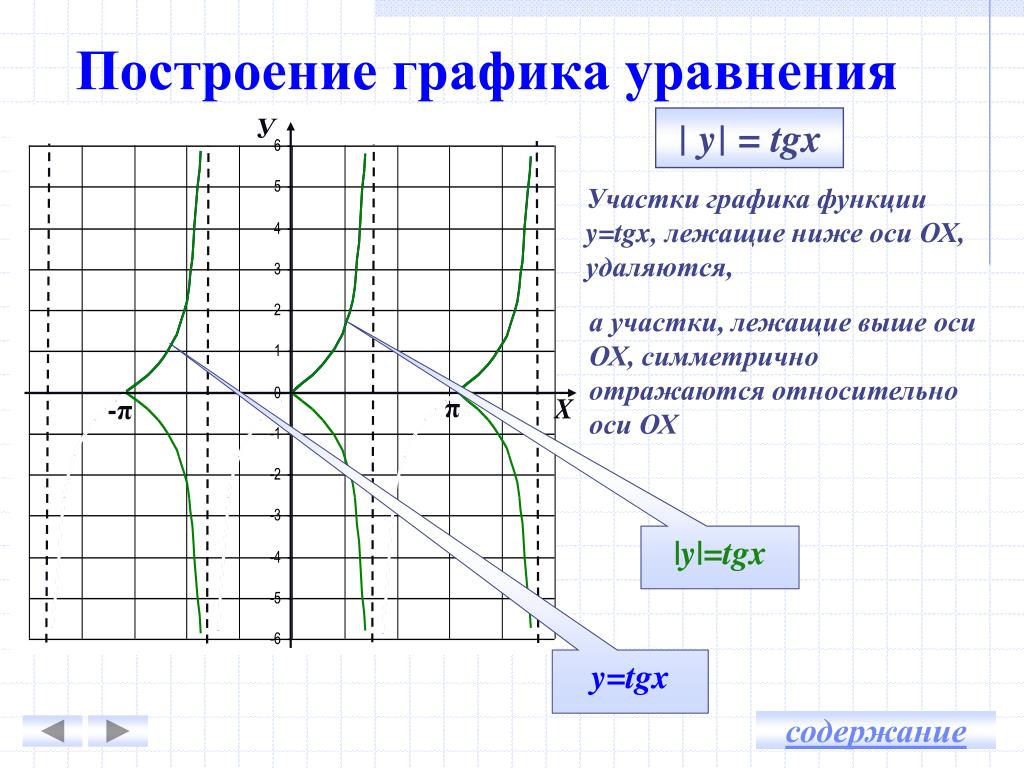 1. Популярность Одним из важных факторов, определяющих будущее React Native, является его популярность. Как обсуждалось ранее, популярность React Native в последние несколько лет росла, потому что он предлагает совершенно новый конвейер для работы над созданием кросс-платформенных приложений. Разработчики всегда ищут решение, которое может выжить в долгосрочной перспективе, и, поскольку оно используется многими популярными технологическими гигантами в их повседневной работе, поэтому можно с уверенностью сказать, что оно будет обслуживать огромную аудиторию в течение более длительного периода. 2. Огромная поддержка сообщества Другим важным фактором для светлого будущего React Native является активное сообщество разработчиков. Он поддержит вас, когда вы столкнетесь с какими-либо трудностями. React Native используется миллионами разработчиков по всему миру, и нет сомнений, что его сообщество уже может быть заполнено экспертами и техническими специалистами, которые могут ответить на ваши вопросы и даже порекомендовать вас на работу.
1. Популярность Одним из важных факторов, определяющих будущее React Native, является его популярность. Как обсуждалось ранее, популярность React Native в последние несколько лет росла, потому что он предлагает совершенно новый конвейер для работы над созданием кросс-платформенных приложений. Разработчики всегда ищут решение, которое может выжить в долгосрочной перспективе, и, поскольку оно используется многими популярными технологическими гигантами в их повседневной работе, поэтому можно с уверенностью сказать, что оно будет обслуживать огромную аудиторию в течение более длительного периода. 2. Огромная поддержка сообщества Другим важным фактором для светлого будущего React Native является активное сообщество разработчиков. Он поддержит вас, когда вы столкнетесь с какими-либо трудностями. React Native используется миллионами разработчиков по всему миру, и нет сомнений, что его сообщество уже может быть заполнено экспертами и техническими специалистами, которые могут ответить на ваши вопросы и даже порекомендовать вас на работу. 3. Регулярные обновления Одним из наиболее многообещающих аспектов будущего React Native является то, что эта структура помогает предоставлять новые обновления для различных приложений, чтобы пользователи могли пользоваться современными функциями приложения. Конечно, вы можете сказать, что в этом нет ничего нового, поскольку приложения часто получают обновления из магазина приложений или магазина игр. Здесь все по-другому. В отличие от любой другой платформы, React Native делает обновления доступными только через приложение, поэтому больше не нужно полагаться на одобрение магазина приложений для публикации последнего обновления. И по мере того, как новые технологические улучшения совершенствуют фреймворк, новые функции React Native еще больше увеличат скорость разработки разработчиков, что снова повысит его популярность, а будущее React Native станет более многообещающим. Стоит ли React Native в 2022 году? Будущее React Native сильно зависит от легкости изучения языка программирования, поддержки сообщества и других технологических гигантов, а также технологических улучшений.
3. Регулярные обновления Одним из наиболее многообещающих аспектов будущего React Native является то, что эта структура помогает предоставлять новые обновления для различных приложений, чтобы пользователи могли пользоваться современными функциями приложения. Конечно, вы можете сказать, что в этом нет ничего нового, поскольку приложения часто получают обновления из магазина приложений или магазина игр. Здесь все по-другому. В отличие от любой другой платформы, React Native делает обновления доступными только через приложение, поэтому больше не нужно полагаться на одобрение магазина приложений для публикации последнего обновления. И по мере того, как новые технологические улучшения совершенствуют фреймворк, новые функции React Native еще больше увеличат скорость разработки разработчиков, что снова повысит его популярность, а будущее React Native станет более многообещающим. Стоит ли React Native в 2022 году? Будущее React Native сильно зависит от легкости изучения языка программирования, поддержки сообщества и других технологических гигантов, а также технологических улучшений. Как мы уже говорили ранее, React Native — один из лучших фреймворков, если вы хотите создать кроссплатформенное мобильное приложение. Учитывая, что он использует самый популярный и известный язык программирования, он позволяет как новичкам, так и опытным разработчикам легко начать свой путь разработки приложений. Кроме того, учитывая популярность React Naive, можно с уверенностью сказать, что вы не пожалеете, если адаптируетесь к его экосистеме, поскольку он активно поддерживается сообществом и Facebook. Не забывайте, что он имеет все необходимые функции и функции, которые вам нужны для разработки мобильного приложения. Более того, поскольку миллионы разработчиков используют JavaScript в своей повседневной жизни, есть вероятность, что они адаптируются к этой среде, что даст огромный импульс будущему React Native. Но если вы новичок и только начинаете свою карьеру в мобильной разработке, то вам может быть немного тяжело. Тем не менее, это того стоит, поскольку вам понравится разрабатывать приложения с использованием React Native.
Как мы уже говорили ранее, React Native — один из лучших фреймворков, если вы хотите создать кроссплатформенное мобильное приложение. Учитывая, что он использует самый популярный и известный язык программирования, он позволяет как новичкам, так и опытным разработчикам легко начать свой путь разработки приложений. Кроме того, учитывая популярность React Naive, можно с уверенностью сказать, что вы не пожалеете, если адаптируетесь к его экосистеме, поскольку он активно поддерживается сообществом и Facebook. Не забывайте, что он имеет все необходимые функции и функции, которые вам нужны для разработки мобильного приложения. Более того, поскольку миллионы разработчиков используют JavaScript в своей повседневной жизни, есть вероятность, что они адаптируются к этой среде, что даст огромный импульс будущему React Native. Но если вы новичок и только начинаете свою карьеру в мобильной разработке, то вам может быть немного тяжело. Тем не менее, это того стоит, поскольку вам понравится разрабатывать приложения с использованием React Native. Каковы будущие возможности React Native? React Native используется разработчиками уже более 6 лет и, безусловно, набирает обороты благодаря высокой оценке среди технологических гигантов. Тем не менее, будущее React Native выглядит многообещающе и рассматривается как фреймворк с опережением времени. В наш цифровой век мы находим каждое приложение, которое обслуживает определенную услугу, такую как доставка еды, покупки, недвижимость и многие другие. Раньше мы полагались на магазины и агентов, чтобы получить нужные нам товары, но технологии изменили все. React Native расширяет всю ИТ-экосистему, делая приложения доступными для пользователей. По этой причине, даже с учетом аргументов React Native Future 2022, это по-прежнему самый надежный инструмент, способный преобразовать всю ИТ-индустрию. Кроме того, React работает над крупномасштабным проектом, известным как Fabric, цель которого — улучшить React Native, сделав его более отзывчивым и гибким. Это также заставит фреймворк адаптироваться к гибридной инфраструктуре на основе JavaScript.
Каковы будущие возможности React Native? React Native используется разработчиками уже более 6 лет и, безусловно, набирает обороты благодаря высокой оценке среди технологических гигантов. Тем не менее, будущее React Native выглядит многообещающе и рассматривается как фреймворк с опережением времени. В наш цифровой век мы находим каждое приложение, которое обслуживает определенную услугу, такую как доставка еды, покупки, недвижимость и многие другие. Раньше мы полагались на магазины и агентов, чтобы получить нужные нам товары, но технологии изменили все. React Native расширяет всю ИТ-экосистему, делая приложения доступными для пользователей. По этой причине, даже с учетом аргументов React Native Future 2022, это по-прежнему самый надежный инструмент, способный преобразовать всю ИТ-индустрию. Кроме того, React работает над крупномасштабным проектом, известным как Fabric, цель которого — улучшить React Native, сделав его более отзывчивым и гибким. Это также заставит фреймворк адаптироваться к гибридной инфраструктуре на основе JavaScript. Проект Fabric уже начал улучшать React Native с помощью новой модели многопоточности, возможностей асинхронного рендеринга и упрощенных мостов. Эти и другие изменения сделают React Native более гибким и производительным в будущем, и, следовательно, будущее React Native будет ярче, чем когда-либо. Заключение Будущее React Native было улучшено за счет создания кроссплатформенных мобильных приложений. Многие технологические гиганты полагаются на эту платформу для создания и поддержания своих мобильных приложений в актуальном состоянии, и это одна из причин ее популярности. Несмотря на то, что React Native предлагает свои предложения, он предоставляет лучшие функции и возможности для повышения эффективности процесса разработки мобильных приложений. Будущее React Native по-прежнему многообещающе и будет многообещающим, поскольку оно претерпевает технологические усовершенствования, такие как проект Fabric. Кроме того, по мере увеличения числа мобильных пользователей потребность в разработке приложений будет набирать обороты, и действительно, React Native воспользуется этой возможностью и предоставит пользователям самые современные приложения.
Проект Fabric уже начал улучшать React Native с помощью новой модели многопоточности, возможностей асинхронного рендеринга и упрощенных мостов. Эти и другие изменения сделают React Native более гибким и производительным в будущем, и, следовательно, будущее React Native будет ярче, чем когда-либо. Заключение Будущее React Native было улучшено за счет создания кроссплатформенных мобильных приложений. Многие технологические гиганты полагаются на эту платформу для создания и поддержания своих мобильных приложений в актуальном состоянии, и это одна из причин ее популярности. Несмотря на то, что React Native предлагает свои предложения, он предоставляет лучшие функции и возможности для повышения эффективности процесса разработки мобильных приложений. Будущее React Native по-прежнему многообещающе и будет многообещающим, поскольку оно претерпевает технологические усовершенствования, такие как проект Fabric. Кроме того, по мере увеличения числа мобильных пользователей потребность в разработке приложений будет набирать обороты, и действительно, React Native воспользуется этой возможностью и предоставит пользователям самые современные приложения.