способы узнать бесплатно и онлайн
Требования к картинкам Процесс работы с определителями шрифтов WhatTheFont Font Identifier Fontspring IdentiFont WhatFontIs Не могу узнать шрифт. Что делать?
Мы в Telegram
В канале «Маркетинговые щи» только самое полезное: подборки, инструкции, кейсы.
Не всегда на серьёзных щах — шуточки тоже шутим =)
Подписаться
Станьте email-рокером 🤘
Пройдите бесплатный курс и запустите свою первую рассылку
Подробнее
Если вам понравился шрифт на сайте или баннере, его можно найти и использовать. Популярные Arial или Times New Roman можно узнать и без специальных сервисов — например, по отсутствию или присутствию засечек. А более редкие и незнакомые надписи можно распознать онлайн: по картинке или скриншоту. Рассказываю, как это сделать.
Популярные Arial или Times New Roman можно узнать и без специальных сервисов — например, по отсутствию или присутствию засечек. А более редкие и незнакомые надписи можно распознать онлайн: по картинке или скриншоту. Рассказываю, как это сделать.
Требования к картинкам
В любом из сервисов, позволяющих определить шрифт по картинке, схожие требования к загружаемым изображениям:
- Буквы чёткие и имеют различимый контур.
- Каждый символ отделён от соседних (не нарушено расстояние между буквами).
- Изображение сохранено в формате jpeg или png.
- Картинка не теряет качество при увеличении. Лучше использовать разрешение не менее 600 точек на дюйм.
Если все условия соблюдены, сервис выдаст похожий шрифт и даже предложит варианты для бесплатного использования.
Процесс работы с определителями шрифтов
Чтобы определить шрифт, подготовьте исходное изображение: сохраните картинку или скриншот на компьютер. Дальше алгоритм работы всех сервисов похожий:
- Вставьте изображение в поисковую строку программы и запустите сравнение.

- По запросу выделите область сканирования, особенно если на картинке несколько разных начертаний.
- Получите результат: обычно программа предлагает несколько вариантов, которые могут быть похожи на нужный.
- Скопируйте название шрифта, максимально похожего на искомый. Часть сервисов предлагают скачать или купить найденный образец.
Теперь разберу несколько онлайн-сервисов, которые распознают шрифт онлайн.
WhatTheFont
Ссылка: https://www.myfonts.com/pages/whatthefont
Стоимость. Бесплатно.
Язык. Английский. (Кириллицу также не распознает.)
База. 230 000+ шрифтов.
Популярная платформа для тех, кто хочет узнать шрифт. Можно загрузить файл и выбрать конкретное место на картинке. Также есть поиск по категориям.
Сервис работает быстро, большая база. Правда, в РФ будет доступен только через VPN.
✅
Не требуется регистрация
Быстрый поиск по базе 230+ тыс. шрифтов.
шрифтов.
Есть приложения (iOS, Android) для распознавания шрифта на смартфонах (можно просканировать с фотографии)
❌
Не распознает кириллицу
Найденные по скриншоту шрифты предлагает купить, даже если есть бесплатный аналог
Не работает в РФ без VPN
Font Identifier
Ссылка: https://www.fontsquirrel.com/matcherator
Стоимость. Бесплатно.
Язык. Английский.
База. У самого сервиса всего несколько тысяч шрифтов, но он ищет и в других коллекциях.
Англоязычный сервис, но работает и с кириллицей. Распознает шрифт по каждой букве, поэтому результаты сканирования глубокие.
✅
Не требуется регистрация
Распознает шрифты на десяти языках, в том числе на русском, украинском, белорусском
В поисковой выдаче есть платные и бесплатные варианты шрифтов
❌
Много рекламы внутри платформы
Не сразу получается правильно настроить matcherator
Fontspring
Ссылка: https://www. fontspring.com/matcherator
fontspring.com/matcherator
Стоимость. Бесплатно.
Язык. Английский.
База. 900 000+ шрифтов.
По сути аналогичен предыдущему сервису. Сразу видно, у самого определителя шрифтов и редактора картинок тот же интерфейс.
✅
Не требуется регистрация
Есть редактор для обрезки и поворота загруженных изображений
Можно сканировать изображение по ссылке
❌
Не очень хорошо работает с кириллицей
В основном только платные шрифты
IdentiFont
Ссылка: http://www.identifont.com/
Стоимость. Бесплатно.
Язык. Английский.
База. 150 000+ шрифтов.
Главное отличие от других сервисов по распознаванию — отсутствие автоматического поиска. Найти шрифт можно по наводящим вопросам, символу, имени дизайнера, части названия или по внешним признакам. Несмотря на устаревший дизайн, новые шрифты появляются регулярно. Ресурс позиционируется как крупнейший независимый каталог.
✅
Не требуется регистрация
Постоянно пополняется база
Можно найти шрифт по названию, дизайнеру или наводящим вопросам
❌
Нельзя определить по картинке
WhatFontIs
Ссылка: https://www.whatfontis.com/
Стоимость. Бесплатно или дополнительные возможности поиска за $40 в год.
Язык. Английский. (Также не работает с кириллицей.)
База. 840 000+ шрифтов.
Напоминает первый сервис из нашей подборки. Помимо стандартных настроек распознавания, встроенный редактор может разделять символы — эта функция пригодится для работы с рукописными шрифтами.
✅
Можно сохранить результат сканирования (понадобится регистрация)
Если изображение не подходит, платформа поможет отредактировать его онлайн. В том числе разделить символы
Можно искать похожие варианты по фильтру «только бесплатные»
❌
Работает только с латиницей
Не более 10 символов на исходной картинке
Не очень удобно пользоваться без регистрации и подписки
За красивыми рассылками — в Unisender
Удобный конструктор писем. В пару кликов вставляйте текст, ссылки, картинки, гифки, видео. 15 минут — и рассылка готова!
В пару кликов вставляйте текст, ссылки, картинки, гифки, видео. 15 минут — и рассылка готова!
Попробовать
Не могу узнать шрифт. Что делать?
Иногда сервис отказывается распознавать шрифт по картинке. Что в этом случае можно сделать:
- Визуально проверьте картинку: возможно, надпись в тексте сделана из разных шрифтов. Если это так, скормите сервису только часть изображения.
- Отредактируйте изображение, чтобы надпись читалась чётче. Некоторые сервисы имеют встроенный редактор. Иногда можно найти картинку в лучшем разрешении.
- Попробуйте скормить картинку другому сервису. Возможно, он распознает образец.
- Вернитесь к распознаванию через некоторое время. Базы регулярно обновляются.
- Если шрифт кириллический, загружайте только символы одинаковые в написании на латинице и кириллице. Это буквы, а, е, с, p, y и некоторые заглавные буквы.
Также можно поискать шрифт вручную на форумах или задать вопрос там же: форум MyFonts, форум Fontmassive, форум Ruldtp.
Кстати, у FontMassive ещё есть инструмент FontDetect для определения шрифта. Это бесплатная программа под Windows, которая распознает кириллицу. Но она ищет только среди вариантов, которые установлены на компьютере.
Поделиться
СВЕЖИЕ СТАТЬИ
Другие материалы из этой рубрики
Не пропускайте новые статьи
Подписывайтесь на соцсети
Делимся новостями и свежими статьями, рассказываем о новинках сервиса
«Честно» — авторская рассылка от редакции Unisender
Искренние письма о работе и жизни. Свежие статьи из блога. Эксклюзивные кейсы и интервью с экспертами диджитала.
Оставляя свой email, я принимаю Политику конфиденциальностиНаш юрист будет ругаться, если вы не примете 🙁
Как запустить email-маркетинг с нуля?
В бесплатном курсе «Rock-email» мы за 15 писем расскажем, как настроить email-маркетинг в компании. В конце каждого письма даем отбитые татуировки об email ⚡️
В конце каждого письма даем отбитые татуировки об email ⚡️
*Вместе с курсом вы будете получать рассылку блога Unisender
Оставляя свой email, я принимаю Политику конфиденциальностиНаш юрист будет ругаться, если вы не примете 🙁
Как распознать шрифт с картинки: лучшие онлайн-сервисы
Определение шрифта на картинке – частая ситуация, с которой сталкивается как профессиональный дизайнер, так и обычный пользователь. Если шрифт был найден на фотографии знакомого, то не составит труда спросить его о том, какое решение было использовано. Но что делать, если яркий и интересный шрифт встретился на просторах интернета?
В таких случаях можно воспользоваться специальными сервисами, речь о которых пойдет в сегодняшней статье.
Определяем шрифт на фото с помощью WhatTheFont
Один из самых простых способов распознать шрифт – зайти в онлайн-сервис, загрузить туда картинку и получить результат. Чаще всего подобные инструменты позволяют идентифицировать практически любой шрифт. Однако все зависит от используемого сервиса, например, WhatTheFont позволяет найти лишь тот шрифт, который есть в его фирменном магазине.
Чаще всего подобные инструменты позволяют идентифицировать практически любой шрифт. Однако все зависит от используемого сервиса, например, WhatTheFont позволяет найти лишь тот шрифт, который есть в его фирменном магазине.
Сейчас все покажу на примере:
- Открываем онлайн-инструмент WhatTheFont и загружаем в него картинку со шрифтом, который мы хотим найти. Выделяем нужную нам область и нажимаем на стрелочку внизу. Рекомендую выбрать одно слово либо использовать предложенный вариант: сервис автоматически выделяет нужное слово после загрузки картинки.
- В результате получаем список похожих шрифтов, которые есть на WhatTheFont.
Я использовал популярный шрифт Lobster и решил проверить, найдет ли сервис его. К сожалению, в результатах отобразилось не то, что ожидалось. Как я уже говорил, WhatTheFont позволяет найти лишь тот шрифт, который есть в базе. Так что вердикт такой: это отличный сервис, если вы ищете шрифт из базы данного сервиса. Во всех других случаях – лучше использовать альтернативные способы.
Во всех других случаях – лучше использовать альтернативные способы.
А для тех, кому понравился данный сервис, я покажу, как пользоваться им на телефоне. Результат будет тот же, но вот функционал у официального приложения чуть-чуть отличается.
Комьюнити теперь в Телеграм
Подпишитесь и будьте в курсе последних IT-новостей
Подписаться
Мобильное приложение WhatTheFont
WhatTheFont позволяет найти шрифт в онлайн-режиме с помощью камеры телефона. Приложение было разработано специально для тех, кому часто приходится иметь дело с разными шрифтами, определять их название или пополнять собственный шрифтовой архив. Приложение доступно как на iOS, так и на Android.
Процесс работы с WhatTheFont довольно прост: достаточно навести устройство на картинку, и сервис автоматически определит шрифт.
Рассмотрим на примере:
- Скачиваем приложение и запускаем его – в результате перед нами сразу же запускается камера. Наводим смартфон на нужную картинку и фотографируем ее.
 После этого будет предложено выделить область (как и в десктопной версии). Выделяем ту область, где находится интересующий нас шрифт, и жмем на стрелку внизу.
После этого будет предложено выделить область (как и в десктопной версии). Выделяем ту область, где находится интересующий нас шрифт, и жмем на стрелку внизу. - Мы получаем список похожих шрифтов. Напомню, что шрифт вы можете не найти, так как отображаются только те, что есть в базе приложения.
Также можно скачать приложение Find My Font, которое включает в себя более 150 000 различных шрифтов. Его главное отличие от вышерассмотренного сервиса состоит в том, что он берет данные не только из своего архива, но и из сторонних источников. Таким образом, Find My Font дает больше шансов найти интересующий шрифт.
Другие сервисы для определения шрифта по изображению онлайн
Поговорим о других сервисах, которые помогут найти шрифт. Работа в них аналогична тем сервисам, что мы рассмотрели выше, поэтому я не буду показывать, как в них работать. Только расскажу об их ключевых особенностях.
WhatFontis
WhatFontis использует тот же принцип, что и WhatTheFont. Однако есть одна особенность: при загрузке можно уточнить, темнее ли фон изображения, чем буквы. Также можно задать фильтры для поиска, например, искать похожие варианты только среди бесплатных шрифтов.
Однако есть одна особенность: при загрузке можно уточнить, темнее ли фон изображения, чем буквы. Также можно задать фильтры для поиска, например, искать похожие варианты только среди бесплатных шрифтов.
Требования к картинке во многом совпадают с WhatTheFont, главное отличие в максимальном количестве букв на картинке – здесь их может быть не более 10. Если изображение не подходит, сайт предлагает отредактировать его онлайн.
Официальная страница: WhatFontis
FontDetect (FontMassive)
FontDetect – это бесплатная программа на Windows, которая ищет подходящие варианты среди уже имеющихся на компьютере шрифтов, поэтому выбор может быть сильно ограничен. Но зато приложение умеет распознавать кириллицу.
Ссылка на скачивание: FontDetect
Identifont
Identifont – интересный сервис с необычным алгоритмом. На него не нужно загружать изображение со шрифтом, ведь сайт предлагает найти подходящие варианты с помощью перебора характерных признаков. Чтобы получить результат, нужно ответить на несколько вопросов.
Чтобы получить результат, нужно ответить на несколько вопросов.
Также Identifont предлагает искать шрифт по названию или какой-нибудь характеристике (компании-издателю или фамилии дизайнера). Кроме того, можно ввести название уже известного шрифта и подобрать похожие на него варианты.
Официальная страница: Identifont
FontSpring
Данный сервис по своему функционалу похож на уже упомянутый ранее WhatTheFont. При этом у него есть несколько специфических особенностей, например, на сайте есть фоторедактор, который позволяет обрабатывать текст для наилучшего распознавания шрифта в режиме онлайн. Кроме того, на FontSpring можно добавлять характеристики для загружаемой картинки, чтобы лучше идентифицировать шрифт.
Официальная страница: FontSpring
FontMatch
FontMatch – это приложение, которое изначально было разработано для ОС Windows, но позже разработчики выпустили программу и для macOS. Поиск по картинке здесь происходит аналогично другим сервисам: загружаем картинку и запускаем анализатор приложения, в результате которого будет отображен список похожих шрифтов. Из минусов: англоязычный интерфейс, но разобраться в нем не составит никакого труда даже тому, кто совсем не знает языка.
Из минусов: англоязычный интерфейс, но разобраться в нем не составит никакого труда даже тому, кто совсем не знает языка.
Ссылка на скачивание: FontMatch
FontSquirrel
Последний сервис, о котором я расскажу – Font Squirrel. Это еще один англоязычный ресурс для поиска шрифта онлайн. Как и в случае со многими сервисами, он позволяет не просто распознать нужный шрифт, но и сразу скачать его из базы: бесплатно или платно.
Официальная страница: Font Squirrel
Что делать, если не получилось найти шрифт
Если у вас не получается определить шрифт автоматически, обратитесь за помощью на специализированный форум или в группы в социальных сетях.
Вот ссылки на некоторые из них:
- форум на ресурсе Whatthefont;
- форум Fontmassive;
- группы «Опознание шрифтов» и «Поиск шрифтов» во ВКонтакте;
- форум Ruldtp.
Выложите изображение с нужным шрифтом и ждите ответа. Лучше оставить запрос на нескольких сайтах. Ответ обычно приходит в течение нескольких часов.
Лучше оставить запрос на нескольких сайтах. Ответ обычно приходит в течение нескольких часов.
Заключение
Поиск шрифта – это несложная задача, которая решается с помощью любых сервисов, рассмотренных выше. Некоторые из них содержат не такую большую базу шрифтов, как остальные, однако на помощь всегда может прийти форум или группа в социальных сетях, где вас проконсультируют уже реальные пользователи.
База данных социальных детерминант здоровья
Загрузить данные
База данных AHRQ по социальным детерминантам здоровья (SDOH) была создана в рамках проекта, финансируемого Целевым фондом исследования результатов, ориентированных на пациента (PCOR). Целью этого проекта является создание простых в использовании, легко связываемых данных, ориентированных на SDOH, для использования в исследованиях PCOR, информирования о подходах к решению возникающих проблем со здоровьем и, в конечном итоге, содействия улучшению результатов в отношении здоровья.
База данных была разработана, чтобы упростить поиск ряда хорошо задокументированных, легко связываемых переменных SDOH в разных доменах без необходимости доступа к нескольким исходным файлам, что облегчает исследования и анализ SDOH.
Переменные в файлах соответствуют пяти ключевым доменам SDOH: социальный контекст (например, возраст, раса/этническая принадлежность, статус ветерана), экономический контекст (например, доход, уровень безработицы), образование, физическая инфраструктура (например, жилье, преступность, транспорт) и контекст здравоохранения (например, медицинское страхование). Файлы могут быть связаны с другими данными по географическому признаку (округ, почтовый индекс и переписной район). База данных включает файлы данных и кодовые книги по годам на трех уровнях географии, а также файл документации.
Данные, содержащиеся в базе данных SDOH, получены из нескольких источников, и переменные могут иметь различную доступность, модели отсутствия и методологические соображения в зависимости от источников, географических регионов и лет. Пользователи должны обращаться к документации по источникам данных и книгам кодов, а также к исходным источникам данных, чтобы помочь идентифицировать эти шаблоны. AHRQ приветствует отзывы о базе данных SDOH. Если у пользователей есть вопросы, предложения или какие-либо проблемы с данными, отправьте отзыв по адресу [email protected].
Пользователи должны обращаться к документации по источникам данных и книгам кодов, а также к исходным источникам данных, чтобы помочь идентифицировать эти шаблоны. AHRQ приветствует отзывы о базе данных SDOH. Если у пользователей есть вопросы, предложения или какие-либо проблемы с данными, отправьте отзыв по адресу [email protected].
Загрузить данные и документацию
Документация по источникам данных (PDF, 6 МБ) содержит информацию для исследователей о структуре и содержании базы данных, а также описание каждого источника данных, используемого для заполнения базы данных.
| Файлы кодовой книги 2009-2020 | Данные округа за 2009–2020 годы | Почтовый индекс Данные 2011-2020 | Данные переписи населения за 2009–2020 годы |
|---|---|---|---|
| 2009 (XLSX, 374 КБ) | 2009 (XLSX, 9 МБ) | 2009 (XLSX, 82 МБ) | |
| 2010 (XLSX, 411 КБ) | 2010 (XLSX, 11 МБ) | 2010 (XLSX, 102 МБ) | |
| 2011 (XLSX, 435 КБ) | 2011 (XLSX, 11 МБ) | 2011 (XLSX, 49 МБ) | 2011 (XLSX, 92 МБ) |
| 2012 (XLSX, 439 КБ) | 2012 (XLSX, 11 МБ) | 2012 г. (XLSX, 51 МБ) (XLSX, 51 МБ) | 2012 (XLSX, 96 МБ) |
| 2013 (XLSX, 459 КБ) | 2013 г. (XLSX, 12 МБ) | 2013 г. (XLSX, 56 МБ) | 2013 (XLSX, 107 МБ) |
| 2014 (XLSX, 466 КБ) | 2014 г. (XLSX, 13 МБ) | 2014 г. (XLSX, 56 МБ) | 2014 (XLSX, 108 МБ) |
| 2015 (XLSX, 496 КБ) | 2015 г. (XLSX, 13 МБ) | 2015 г. (XLSX, 56 МБ) | 2015 (XLSX, 120 МБ) |
| 2016 (XLSX, 482 КБ) | 2016 г. (XLSX, 14 МБ) | 2016 г. (XLSX, 56 МБ) | 2016 (XLSX, 108 МБ) |
| 2017 (XLSX, 482 КБ) | 2017 г. (XLSX, 13 МБ) | 2017 г. (XLSX, 60 МБ) | 2017 (XLSX, 115 МБ) |
| 2018 (XLSX, 498 КБ) | См. примечание для пользователя (в поле справа вверху) | 2018 (XLSX, 62 МБ) | 2018 (XLSX, 120 МБ) |
| 2019 (XLSX, 479 КБ) | 2019 (XLSX, 13 МБ) | 2019 (XLSX, 61 МБ) | 2019 (XLSX, 127 МБ) |
| 2020 (XLSX, 440 КБ) | 2020 (XLSX, 10 МБ) | 2020 (XLSX, 59 МБ) | 2020 (XLSX, 129 МБ) |
Эти файлы заменяют базу данных SDOH (бета-версия). Для обеспечения согласованности в именах переменных и построении анализы не должны объединять данные из бета-версии и обновленной базы данных. Архивная база данных SDOH (бета-версия) доступна для ознакомления.
Для обеспечения согласованности в именах переменных и построении анализы не должны объединять данные из бета-версии и обновленной базы данных. Архивная база данных SDOH (бета-версия) доступна для ознакомления.
Визуализация данных SDOH
Чтобы продемонстрировать возможности файлов данных SDOH, AHRQ создала визуализацию «Бедность и доступ к Интернету по округам», которая показывает процентную долю домохозяйств с компьютерами и смартфонами на уровне округа, а также процентную долю домохозяйств с любым типом широкополосный доступ (включая планы сотовой связи). Поскольку эти показатели увеличиваются с ростом дохода, на карте также показан процент бедных на уровне округов.
Сканирование окружающей среды SDOH
AHRQ провела сканирование окружающей среды (XLSX, 46 КБ) источников данных SDOH, чтобы сообщить о разработке файлов бета-данных AHRQ SDOH, опубликованных в декабре 2020 года. AHRQ публикует сканирование окружающей среды в качестве ресурса для аналитиков, заинтересованных в выявлении связанных с SDOH источники данных. Сканирование направлено на выявление как можно большего количества источников данных SDOH по состоянию на июль 2020 года на уровне почтового индекса, округа и штата для областей социального контекста, экономического контекста, образования, физической инфраструктуры и контекста здравоохранения. Сканирование организовано в виде электронной таблицы Excel для поддержки функции фильтрации каждого столбца в сканировании, чтобы аналитики могли сортировать по переменным, таким как домен SDOH или уровень географии.
Сканирование направлено на выявление как можно большего количества источников данных SDOH по состоянию на июль 2020 года на уровне почтового индекса, округа и штата для областей социального контекста, экономического контекста, образования, физической инфраструктуры и контекста здравоохранения. Сканирование организовано в виде электронной таблицы Excel для поддержки функции фильтрации каждого столбца в сканировании, чтобы аналитики могли сортировать по переменным, таким как домен SDOH или уровень географии.
Эта работа была поддержана Офисом Секретаря Целевого фонда исследований результатов, ориентированных на пациента, в соответствии с межведомственным соглашением 750119PE0K0036.
Интернет-цитирование: База данных социальных детерминант здоровья. Последнее рассмотрение содержания: ноябрь 2022 г. Агентство медицинских исследований и качества, Роквилл, Мэриленд.
https://www.ahrq.gov/sdoh/data-analytics/sdoh-data.html
Вернуться к началу
Социальные детерминанты здоровья — Здоровые люди 2030
Что такое социальные детерминанты здоровья?
Социальные детерминанты здоровья (СДЗ) — это условия в среде, в которой люди рождаются, живут, учатся, работают, играют, поклоняются и стареют, которые влияют на широкий спектр результатов в отношении здоровья, функционирования и качества жизни и риски.
SDOH можно сгруппировать в 5 доменов:
Изображение
Загрузить графику SDOH (141,23 КБ)
Социальные детерминанты здоровья (СДОЗ) оказывают большое влияние на здоровье, благополучие и качество жизни людей. Примеры SDOH включают:
- Безопасное жилье, транспорт и микрорайоны
- Расизм, дискриминация и насилие
- Образование, возможности трудоустройства и доход
- Доступ к питательным продуктам и возможностям физической активности
- Загрязненный воздух и вода
- Языковые навыки и грамотность
SDOH также вносят свой вклад в широкое неравенство и несправедливость в отношении здоровья. Например, люди, у которых нет доступа к продуктовым магазинам со здоровой пищей, с меньшей вероятностью будут правильно питаться. Это повышает риск таких заболеваний, как болезни сердца, диабет и ожирение, и даже снижает продолжительность жизни по сравнению с людьми, которые имеют доступ к здоровой пище.
Простая пропаганда здорового образа жизни не устранит эти и другие различия в состоянии здоровья. Вместо этого организации общественного здравоохранения и их партнеры в таких секторах, как образование, транспорт и жилье, должны принять меры для улучшения условий жизни людей.
Вместо этого организации общественного здравоохранения и их партнеры в таких секторах, как образование, транспорт и жилье, должны принять меры для улучшения условий жизни людей.
Вот почему Healthy People 2030 уделяет повышенное внимание SDOH.
Как Healthy People 2030 решает вопросы SDOH?
Одна из 5 всеобъемлющих целей Healthy People 2030 конкретно связана с SDOH: «Создать социальную, физическую и экономическую среду, способствующую раскрытию всего потенциала здоровья и благополучия для всех».
В соответствии с этой целью Healthy People 2030 включает в себя множество задач, связанных с SDOH. Эти цели подчеркивают важность «предшествующих» факторов — обычно не связанных с оказанием медицинской помощи — в улучшении здоровья и сокращении неравенства в отношении здоровья.


 После этого будет предложено выделить область (как и в десктопной версии). Выделяем ту область, где находится интересующий нас шрифт, и жмем на стрелку внизу.
После этого будет предложено выделить область (как и в десктопной версии). Выделяем ту область, где находится интересующий нас шрифт, и жмем на стрелку внизу. 
 Оно записывается 3 цифрами.
Сумма цифр, из которых состоит число 120, равна 3, а их произведение равно 0.
Число 120 является четным.
Всего число 120 имеет 16 делителей:
1,
2,
3,
4,
5,
6,
8,
10,
12,
15,
20,
24,
30,
40,
60,
120,
. Сумма делителей равна 360. Куб числа 120 равен 14400, а квадрат составляет 1728000.
Квадратный корень рассматриваемого числа равен 10,9544511501033. Кубический корень равен 4,93242414866094.
Число, которое является обратным к числу 120, выглядит как 0,00833333333333333.
Оно записывается 3 цифрами.
Сумма цифр, из которых состоит число 120, равна 3, а их произведение равно 0.
Число 120 является четным.
Всего число 120 имеет 16 делителей:
1,
2,
3,
4,
5,
6,
8,
10,
12,
15,
20,
24,
30,
40,
60,
120,
. Сумма делителей равна 360. Куб числа 120 равен 14400, а квадрат составляет 1728000.
Квадратный корень рассматриваемого числа равен 10,9544511501033. Кубический корень равен 4,93242414866094.
Число, которое является обратным к числу 120, выглядит как 0,00833333333333333.
 Всего существует 8 делителей 54, среди которых 54 — самый большой множитель, а его положительные множители равны 1 , 2, 3, 6, 9, 18, 27 и 54. Парные множители числа 54 равны (1, 54), (2, 27), (3, 18) и (6, 9), а его простые множители равны 1, 2, 3, 6, 9, 18, 27, 54.
Всего существует 8 делителей 54, среди которых 54 — самый большой множитель, а его положительные множители равны 1 , 2, 3, 6, 9, 18, 27 и 54. Парные множители числа 54 равны (1, 54), (2, 27), (3, 18) и (6, 9), а его простые множители равны 1, 2, 3, 6, 9, 18, 27, 54.

 9не является простым числом и может быть диссоциировано как произведение 3 на квадрат 3 на третьем шаге, в соответствии с критериями 54 может быть записано как 54 = 6 × 9 = 2 × 3 × 3 × 3. Оно также может можно записать как 54 = 2 × 3 3 .
9не является простым числом и может быть диссоциировано как произведение 3 на квадрат 3 на третьем шаге, в соответствии с критериями 54 может быть записано как 54 = 6 × 9 = 2 × 3 × 3 × 3. Оно также может можно записать как 54 = 2 × 3 3 . 
 Сколько апельсинов получит каждый из них?
Сколько апельсинов получит каждый из них?




 Тогда система имеет единственное решение, определяемое формулами Крамера: , и
Тогда система имеет единственное решение, определяемое формулами Крамера: , и

 Мат. вычисл.},
год = {2010},
объем = {217},
страницы={2024-2030}
}
Мат. вычисл.},
год = {2010},
объем = {217},
страницы={2024-2030}
}  Мат. вычисл.
Мат. вычисл.
 Ding
Ding Мат. вычисл.
Мат. вычисл.
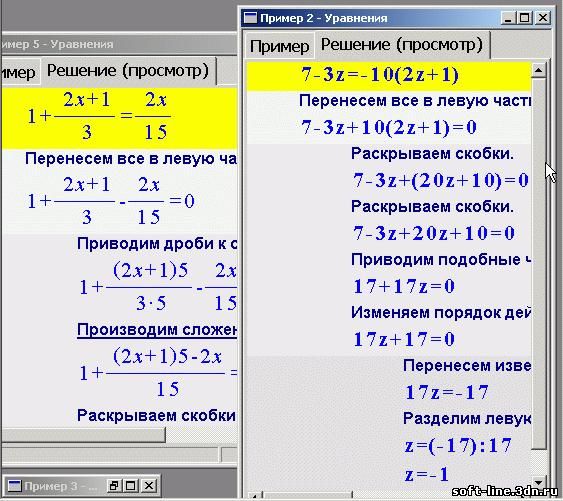

 3-2x+1 приведёт выражение к (x – 1)(x2 +x +1).
3-2x+1 приведёт выражение к (x – 1)(x2 +x +1). 8
8 Если 90 % респондентов ответят да , а 10 % ответят нет , вы, возможно, сможете допустить большее количество ошибок, чем если бы
респонденты делятся 50-50 или 45-55.
Если 90 % респондентов ответят да , а 10 % ответят нет , вы, возможно, сможете допустить большее количество ошибок, чем если бы
респонденты делятся 50-50 или 45-55. 
 Если вы не знаете, используйте 50%, что дает наибольшее значение.
размер образца. См. ниже в разделе Дополнительная информация , если это
сбивает с толку.
Если вы не знаете, используйте 50%, что дает наибольшее значение.
размер образца. См. ниже в разделе Дополнительная информация , если это
сбивает с толку. 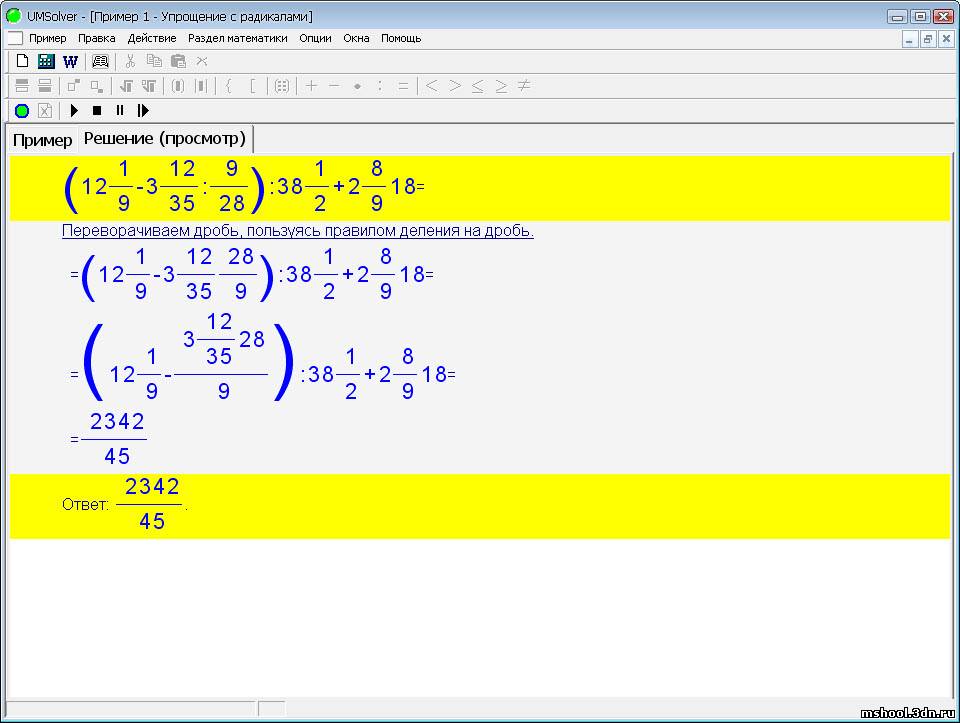 Руководить
ваш опрос онлайн
с Вовичи.
Руководить
ваш опрос онлайн
с Вовичи. В противном случае посмотрите на более продвинутые книги .
В противном случае посмотрите на более продвинутые книги .
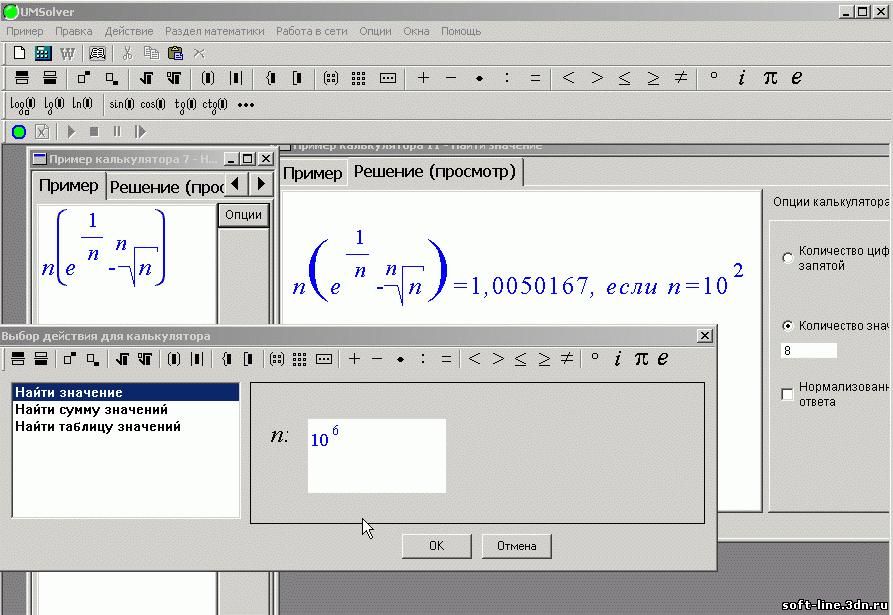



 Разложение вектора по базису происходит автоматически. Zaochnik дает возможность учащимся осуществлять подготовку к занятиям по сложным темам, быстрее осваивать новый и непонятный материал. Сервисом пользуются, потому что:
Разложение вектора по базису происходит автоматически. Zaochnik дает возможность учащимся осуществлять подготовку к занятиям по сложным темам, быстрее осваивать новый и непонятный материал. Сервисом пользуются, потому что: Он оперативно ответит на ваш вопрос, связанный с разложением вектора по базису онлайн, или предложит помощь опытного преподавателя по выгодной цене.
Он оперативно ответит на ваш вопрос, связанный с разложением вектора по базису онлайн, или предложит помощь опытного преподавателя по выгодной цене. Опять же, хотя иллюстрация этих концепций ограничена двумерным пространством, все эти идеи могут быть расширены до n -мерностей.
Опять же, хотя иллюстрация этих концепций ограничена двумерным пространством, все эти идеи могут быть расширены до n -мерностей. Чтобы найти угол (\(\theta\)), мы можем вычислить арккосинус этого отношения. В нашем примере 9{\circ}\). Ниже приведен синтаксис R для вычисления этого угла.
Чтобы найти угол (\(\theta\)), мы можем вычислить арккосинус этого отношения. В нашем примере 9{\circ}\). Ниже приведен синтаксис R для вычисления этого угла.
 Два вектора коллинеарны, если один можно представить в виде линейной комбинации другого. В нашем примере
Два вектора коллинеарны, если один можно представить в виде линейной комбинации другого. В нашем примере Затем
Затем 3: Ортогональная проекция вектора a (выделены красным) на вектор b (синий). Результатом проекции является вектор p (черный цвет).
3: Ортогональная проекция вектора a (выделены красным) на вектор b (синий). Результатом проекции является вектор p (черный цвет). На рис. 5.4 показано разложение вектора a на две аддитивные компоненты, \(\mathbf{p}_1\) и \(\mathbf{p}_2\). то есть
На рис. 5.4 показано разложение вектора a на две аддитивные компоненты, \(\mathbf{p}_1\) и \(\mathbf{p}_2\). то есть
 Так как квадрат гипотенузы прямоугольного треугольника равен сумме квадратов его сторон, то 92
Так как квадрат гипотенузы прямоугольного треугольника равен сумме квадратов его сторон, то 92  Итак, до сих пор мы могли использовать векторную математику для многих наших векторов без использования сеток или квадратов, поэтому мы могли разбить это на треугольник. Мы можем посчитать коробки, чтобы вычислить ножки, например, три и четыре и тому подобное. К сожалению, многих векторов, которые мы увидим, не будет на диаграммах, где нет сетки или квадрата. И нам придется заняться векторной математикой без их использования. Итак, в этом видео я покажу вам, что на самом деле нам нужны четыре уравнения, чтобы описать все, что нам нужно знать о векторе. Эти четыре уравнения составляют математические уравнения треугольника. Они называются уравнениями векторной композиции и декомпозиции. Давайте проверим это. Итак, ребята, есть три вещи, которые нам нужны для описания вектора. Когда у нас есть сетка, которой нет, вы знаете, когда у нас есть ах, диаграмма не имеет сетки квадратов. Таким образом, у векторов есть величина длины этой стрелки прямо здесь. Векторы также имеют направление, и без сетки мы указываем это направление с помощью угла относительно оси X, называемого тета X.
Итак, до сих пор мы могли использовать векторную математику для многих наших векторов без использования сеток или квадратов, поэтому мы могли разбить это на треугольник. Мы можем посчитать коробки, чтобы вычислить ножки, например, три и четыре и тому подобное. К сожалению, многих векторов, которые мы увидим, не будет на диаграммах, где нет сетки или квадрата. И нам придется заняться векторной математикой без их использования. Итак, в этом видео я покажу вам, что на самом деле нам нужны четыре уравнения, чтобы описать все, что нам нужно знать о векторе. Эти четыре уравнения составляют математические уравнения треугольника. Они называются уравнениями векторной композиции и декомпозиции. Давайте проверим это. Итак, ребята, есть три вещи, которые нам нужны для описания вектора. Когда у нас есть сетка, которой нет, вы знаете, когда у нас есть ах, диаграмма не имеет сетки квадратов. Таким образом, у векторов есть величина длины этой стрелки прямо здесь. Векторы также имеют направление, и без сетки мы указываем это направление с помощью угла относительно оси X, называемого тета X. И последнее, что векторы также являются треугольниками, что означает, что у них есть стороны. Эти ноги просто получили причудливое имя. Они называются компонентами. В общем, вот этот вектор, этот треугольник можно разбить на части. Эти ножки просто называются компонентами. Итак, я упомянул, что есть четыре уравнения, и на самом деле они просто разбиваются на две разные ситуации, называемые векторной композицией и декомпозицией. И действительно, разница в том, что вам дано и что вы пытаетесь найти. Векторная композиция — это когда вам даны одномерные компоненты или стороны треугольника, и вы пытаетесь выяснить, какая величина и направление отличается от декомпозиции новостей с большим банком, что противоположно. Это наше, когда тебе уже заданы величина и направление, и теперь ты пытаешься выяснить, каковы стороны вектора. Ребята, давайте проверим это более подробно, когда мы делали векторную композицию, это точно так же, как мы делали, когда добавляли перпендикулярные векторы, такие как три и четыре.
И последнее, что векторы также являются треугольниками, что означает, что у них есть стороны. Эти ноги просто получили причудливое имя. Они называются компонентами. В общем, вот этот вектор, этот треугольник можно разбить на части. Эти ножки просто называются компонентами. Итак, я упомянул, что есть четыре уравнения, и на самом деле они просто разбиваются на две разные ситуации, называемые векторной композицией и декомпозицией. И действительно, разница в том, что вам дано и что вы пытаетесь найти. Векторная композиция — это когда вам даны одномерные компоненты или стороны треугольника, и вы пытаетесь выяснить, какая величина и направление отличается от декомпозиции новостей с большим банком, что противоположно. Это наше, когда тебе уже заданы величина и направление, и теперь ты пытаешься выяснить, каковы стороны вектора. Ребята, давайте проверим это более подробно, когда мы делали векторную композицию, это точно так же, как мы делали, когда добавляли перпендикулярные векторы, такие как три и четыре. Поэтому, когда мы добавили три и четыре, мы просто объединили их. Бен, у нас был результирующий или кратчайший путь от начала до конца, чтобы вычислить этот вектор, который я назову здесь. Мы просто используем теорию Пифагора, потому что получился треугольник. Таким образом, три и четыре, новость о большом банке просто возводится в квадрат три в квадрате на четыре в квадрате, и это m. Итак, вот эти компоненты, эти ноги три и четыре, просто получили причудливое название. Они называются компонентами. И так моя тройка это моя бывшая составляющая. Это то, какая часть этого вектора не является. Буква А находится на оси X, а вот эти четыре — в компонентах «Почему моя жена?». Это то, какая часть вектора лежит в направлении Y. И они объединились, чтобы сформировать вектор величины. А. Итак, я пошел в этом направлении. Это что-то вроде Зиффа. Я прошел три, а потом четыре в этом направлении. Единственное, о чем мы еще не говорили, это то, что этот вектор указывает на некоторое направление, называемое тета X.
Поэтому, когда мы добавили три и четыре, мы просто объединили их. Бен, у нас был результирующий или кратчайший путь от начала до конца, чтобы вычислить этот вектор, который я назову здесь. Мы просто используем теорию Пифагора, потому что получился треугольник. Таким образом, три и четыре, новость о большом банке просто возводится в квадрат три в квадрате на четыре в квадрате, и это m. Итак, вот эти компоненты, эти ноги три и четыре, просто получили причудливое название. Они называются компонентами. И так моя тройка это моя бывшая составляющая. Это то, какая часть этого вектора не является. Буква А находится на оси X, а вот эти четыре — в компонентах «Почему моя жена?». Это то, какая часть вектора лежит в направлении Y. И они объединились, чтобы сформировать вектор величины. А. Итак, я пошел в этом направлении. Это что-то вроде Зиффа. Я прошел три, а потом четыре в этом направлении. Единственное, о чем мы еще не говорили, это то, что этот вектор указывает на некоторое направление, называемое тета X. И способ, которым мы вычисляем эти данные X здесь, — это просто использование другого набора математических уравнений треугольника, называемого Саката. Итак, в основном, чтобы вычислить этот угол здесь, все, что мне нужно использовать, это просто новое уравнение, которое ваши учебники и ваши профессора выведут. Данные X — это арктангенс или арктангенс моих белых компонентов по моим бывшим компонентам. Итак, в этом примере у моей жены компонентов для X три. Это означает, что моя тета X здесь будет просто арктангенсом. Так что вы можете найти это в своих калькуляторах, и это будет 4/3. И эта тета X составляет всего 53 градуса. Убедитесь, что ваш калькулятор находится в режиме градусов. И на самом деле это просто угол, который выше положительной оси X. Так что это угол, который идет вот так. Ладно, ребята, на этом все. Вот только эти два уравнения, и это когда у вас есть стороны треугольника, и вы пытаетесь вычислить величину и направление. Другое дело — векторное разложение. Это в основном обратный процесс.
И способ, которым мы вычисляем эти данные X здесь, — это просто использование другого набора математических уравнений треугольника, называемого Саката. Итак, в основном, чтобы вычислить этот угол здесь, все, что мне нужно использовать, это просто новое уравнение, которое ваши учебники и ваши профессора выведут. Данные X — это арктангенс или арктангенс моих белых компонентов по моим бывшим компонентам. Итак, в этом примере у моей жены компонентов для X три. Это означает, что моя тета X здесь будет просто арктангенсом. Так что вы можете найти это в своих калькуляторах, и это будет 4/3. И эта тета X составляет всего 53 градуса. Убедитесь, что ваш калькулятор находится в режиме градусов. И на самом деле это просто угол, который выше положительной оси X. Так что это угол, который идет вот так. Ладно, ребята, на этом все. Вот только эти два уравнения, и это когда у вас есть стороны треугольника, и вы пытаетесь вычислить величину и направление. Другое дело — векторное разложение. Это в основном обратный процесс. Итак, здесь у меня есть величина угла. Теперь я хочу выяснить ноги, поэтому мы хотим выяснить, что такое мой бывший, и я хочу выяснить, каковы мои компоненты A Y. И действительно, все сводится к этим двум уравнениям, которые мы пришли из Китона. Итак, теперь мы хотим разложить a на его компоненты a X и A y. Так вот в чем дело. Пока этот фатальный угол X обращен к ближайшей оси x, мы будем использовать здесь эти уравнения. Мой бывший будет умножен на косинус угла. Таким образом, это величина, умноженная на знак угла, умноженная на CO, а A Y будет умноженной на знак угла. Так, например, если бы мне дали такой угол, как вот эти данные, это данные, которые относятся к направлению Y. Это плохо. Я не могу использовать это. Ну, я не буду использовать это в своих уравнениях. Это этот угол закончился. С другой стороны, Data X хорош. Так что это то, что я включаю в свои уравнения. Так, например, через X будет величина, умноженная на косинус. Итак, величина равна пяти. Косинус угла равен 53 градусам, поэтому я возьму три.
Итак, здесь у меня есть величина угла. Теперь я хочу выяснить ноги, поэтому мы хотим выяснить, что такое мой бывший, и я хочу выяснить, каковы мои компоненты A Y. И действительно, все сводится к этим двум уравнениям, которые мы пришли из Китона. Итак, теперь мы хотим разложить a на его компоненты a X и A y. Так вот в чем дело. Пока этот фатальный угол X обращен к ближайшей оси x, мы будем использовать здесь эти уравнения. Мой бывший будет умножен на косинус угла. Таким образом, это величина, умноженная на знак угла, умноженная на CO, а A Y будет умноженной на знак угла. Так, например, если бы мне дали такой угол, как вот эти данные, это данные, которые относятся к направлению Y. Это плохо. Я не могу использовать это. Ну, я не буду использовать это в своих уравнениях. Это этот угол закончился. С другой стороны, Data X хорош. Так что это то, что я включаю в свои уравнения. Так, например, через X будет величина, умноженная на косинус. Итак, величина равна пяти. Косинус угла равен 53 градусам, поэтому я возьму три. И затем, если вы подставите y, вы получите звездную величину, которая в пять раз превышает, извините, не береговую линию знака 53. А если вы подставите это, вы получите четыре. Обратите внимание, что мы в основном только что придумали те же числа три и четыре, что и здесь. И это не должно быть сюрпризом, потому что мы в основном только что образовали точно такой же треугольник, как и здесь. Просто мы начали с катетов треугольника вот здесь, а здесь мы начали с величины и направления. Так что неудивительно, что мы получили одинаковые цифры. Ладно, ребята, на этом все. Вы просто будете использовать эти уравнения, основываясь на том, что вы пытаетесь найти, и на том, что вам дано. Итак, давайте продолжим и попрактикуемся в каждом из следующих действий. Вы нарисуете вектор, а затем найдёте недостающие переменные. Итак, мои бывшие съели мои A и шесть, пытаясь определить величину и направление, так что мне дали компоненты. Итак, позвольте мне просто нарисовать вот этот маленький вектор. У меня есть стороны треугольника, так что я знаю, что это восьмерки, а это шесть.
И затем, если вы подставите y, вы получите звездную величину, которая в пять раз превышает, извините, не береговую линию знака 53. А если вы подставите это, вы получите четыре. Обратите внимание, что мы в основном только что придумали те же числа три и четыре, что и здесь. И это не должно быть сюрпризом, потому что мы в основном только что образовали точно такой же треугольник, как и здесь. Просто мы начали с катетов треугольника вот здесь, а здесь мы начали с величины и направления. Так что неудивительно, что мы получили одинаковые цифры. Ладно, ребята, на этом все. Вы просто будете использовать эти уравнения, основываясь на том, что вы пытаетесь найти, и на том, что вам дано. Итак, давайте продолжим и попрактикуемся в каждом из следующих действий. Вы нарисуете вектор, а затем найдёте недостающие переменные. Итак, мои бывшие съели мои A и шесть, пытаясь определить величину и направление, так что мне дали компоненты. Итак, позвольте мне просто нарисовать вот этот маленький вектор. У меня есть стороны треугольника, так что я знаю, что это восьмерки, а это шесть. Это мой бывший. Это мой Ай. И теперь я на самом деле пытаюсь найти величину и направление. Это значит, что я буду использовать свои векторные уравнения композиции. Так что, чтобы вычислить мою А, мне просто нужно использовать теорему Пифагора. Я просто использую восемь в квадрате плюс шесть в квадрате. И если я это сделаю, я получу 10. Так что это моя величина. А теперь про угол. Помните углы, нарисованные относительно оси X? Это мой тха X, и вот этот фатальный X будет арктангенсом, арктангенсом моих белых компонентов, который на шесть больше моего бывшего компонента, который равен восьми. И если вы продолжите и проработаете это, вы должны получить 37 градусов. Вот мой угол теперь 37 градусов. Хорошо, давайте перейдем к части B, которая теперь у меня есть угол, или теперь у меня есть величина 13 и у меня есть угол 67,4, и теперь я хочу вычислить компоненты. Итак, давайте нарисуем этот вектор здесь. Это не компонент. На самом деле это просто вектор. Так что я просто нарисую это вот так.
Это мой бывший. Это мой Ай. И теперь я на самом деле пытаюсь найти величину и направление. Это значит, что я буду использовать свои векторные уравнения композиции. Так что, чтобы вычислить мою А, мне просто нужно использовать теорему Пифагора. Я просто использую восемь в квадрате плюс шесть в квадрате. И если я это сделаю, я получу 10. Так что это моя величина. А теперь про угол. Помните углы, нарисованные относительно оси X? Это мой тха X, и вот этот фатальный X будет арктангенсом, арктангенсом моих белых компонентов, который на шесть больше моего бывшего компонента, который равен восьми. И если вы продолжите и проработаете это, вы должны получить 37 градусов. Вот мой угол теперь 37 градусов. Хорошо, давайте перейдем к части B, которая теперь у меня есть угол, или теперь у меня есть величина 13 и у меня есть угол 67,4, и теперь я хочу вычислить компоненты. Итак, давайте нарисуем этот вектор здесь. Это не компонент. На самом деле это просто вектор. Так что я просто нарисую это вот так.

 В связи с этим Американская Ассоциация клинической химии в 1993 году сформировала подкомитет по стандартизации методов измерения гликозилированного гемоглобина. В результате его работы была разработана Национальная программа по стандартизации исследований гликозилированного гемоглобина (NGSP). Производителей тест-систем для измерения гликозилированного гемоглобина обязали проходить строжайшую проверку на соответствие результатов с данными, полученными референсными методами DCCT. В случае положительного результата проверки производителю выдается «сертификат соответствия DCCT». Американская Диабетическая Ассоциация рекомендует всем лабораториям пользоваться только тестами, сертифицированными NGSP [7].
В связи с этим Американская Ассоциация клинической химии в 1993 году сформировала подкомитет по стандартизации методов измерения гликозилированного гемоглобина. В результате его работы была разработана Национальная программа по стандартизации исследований гликозилированного гемоглобина (NGSP). Производителей тест-систем для измерения гликозилированного гемоглобина обязали проходить строжайшую проверку на соответствие результатов с данными, полученными референсными методами DCCT. В случае положительного результата проверки производителю выдается «сертификат соответствия DCCT». Американская Диабетическая Ассоциация рекомендует всем лабораториям пользоваться только тестами, сертифицированными NGSP [7].

 Это исследование 23-10-002 — Гликозилированный гемоглобин.
Это исследование 23-10-002 — Гликозилированный гемоглобин.
 Концентрация глюкозы в сыворотке крови приблизительно на 15% выше.
Концентрация глюкозы в сыворотке крови приблизительно на 15% выше.
 В Российской Федерации, согласно Целевой Федеральной программе «Сахарный диабет», исследование HbA1c должно проводиться 4 раза в год при любом типе диабета [1].
В Российской Федерации, согласно Целевой Федеральной программе «Сахарный диабет», исследование HbA1c должно проводиться 4 раза в год при любом типе диабета [1].
 Исследования в рамках DCCT показали, что интенсивное лечение предохраняет пациента от развития отдаленных осложнений, таких как ретинопатия, нефропатия и нейропатия, или значительно отодвигает срок их клинического проявления. Если пациенты строго придерживаются режима, направленного на нормализацию углеводного обмена, частота возникновения ретинопатии снижается на 75%, нефропатии — на 35-36%, на 60% уменьшается риск полинейропатий [10].
Исследования в рамках DCCT показали, что интенсивное лечение предохраняет пациента от развития отдаленных осложнений, таких как ретинопатия, нефропатия и нейропатия, или значительно отодвигает срок их клинического проявления. Если пациенты строго придерживаются режима, направленного на нормализацию углеводного обмена, частота возникновения ретинопатии снижается на 75%, нефропатии — на 35-36%, на 60% уменьшается риск полинейропатий [10].



 , Kilo C. et al. Hemoglobin A1c as an Indicator of the Degree of Glucose Intolerance in Diabetes. // Diabetes 1976, 25(3): 230-2.
, Kilo C. et al. Hemoglobin A1c as an Indicator of the Degree of Glucose Intolerance in Diabetes. // Diabetes 1976, 25(3): 230-2. — 1998.
— 1998. Это может показаться фантастическим, но мы объясним это без жаргона! Давай сделаем это.
Это может показаться фантастическим, но мы объясним это без жаргона! Давай сделаем это. Давайте посмотрим на это более наглядно:
Давайте посмотрим на это более наглядно:



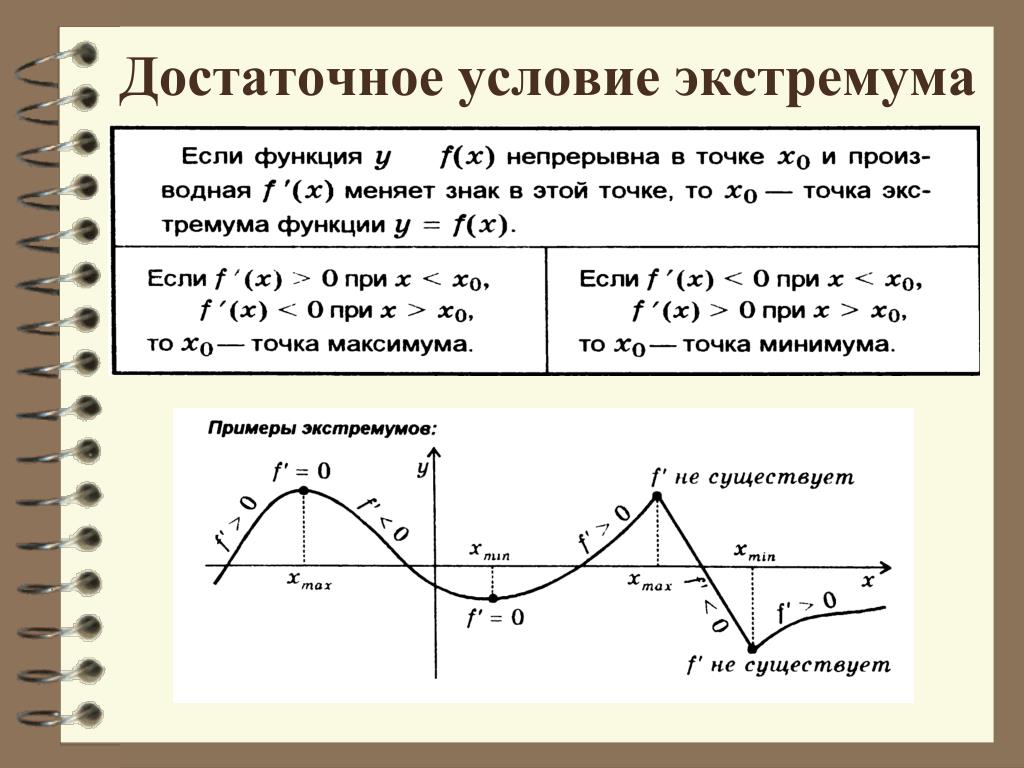 В точке x1 у функции опять перегибается, и после этого
функция опять возрастает.
В точке x1 у функции опять перегибается, и после этого
функция опять возрастает.



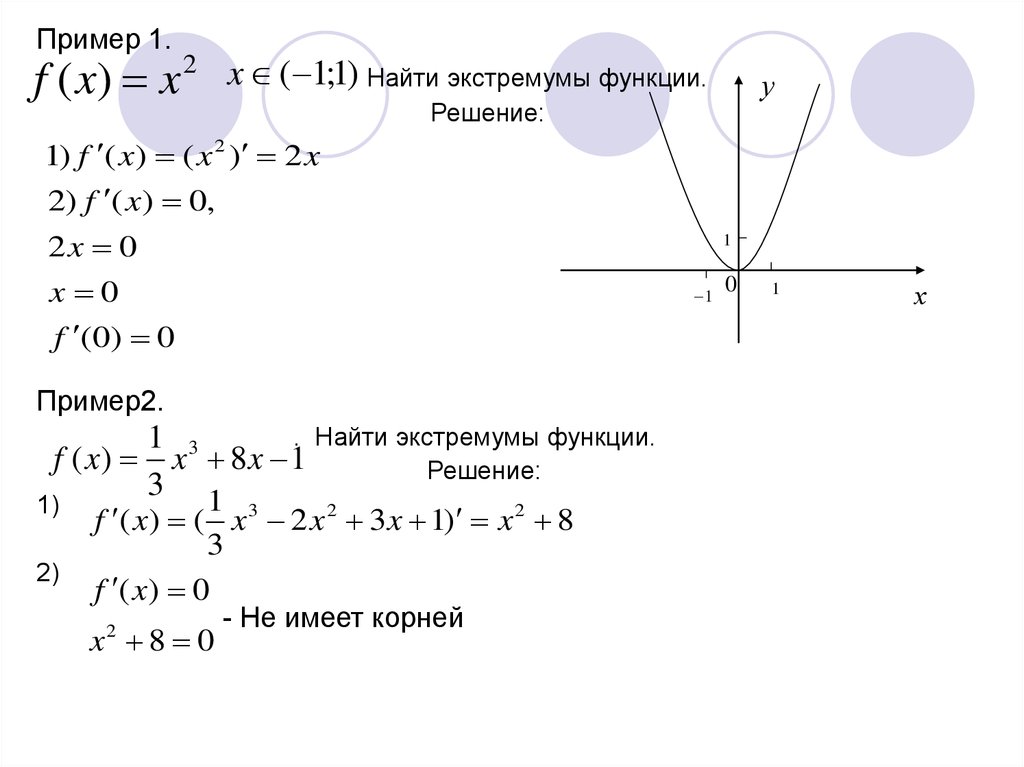 е. если $x=0$ или если $y = -3x/2$. Мы рассматриваем эти два решения как
два отдельных случая. Для каждого случая мы найдем решения для
уравнение \eqref{cond2}.
е. если $x=0$ или если $y = -3x/2$. Мы рассматриваем эти два решения как
два отдельных случая. Для каждого случая мы найдем решения для
уравнение \eqref{cond2}.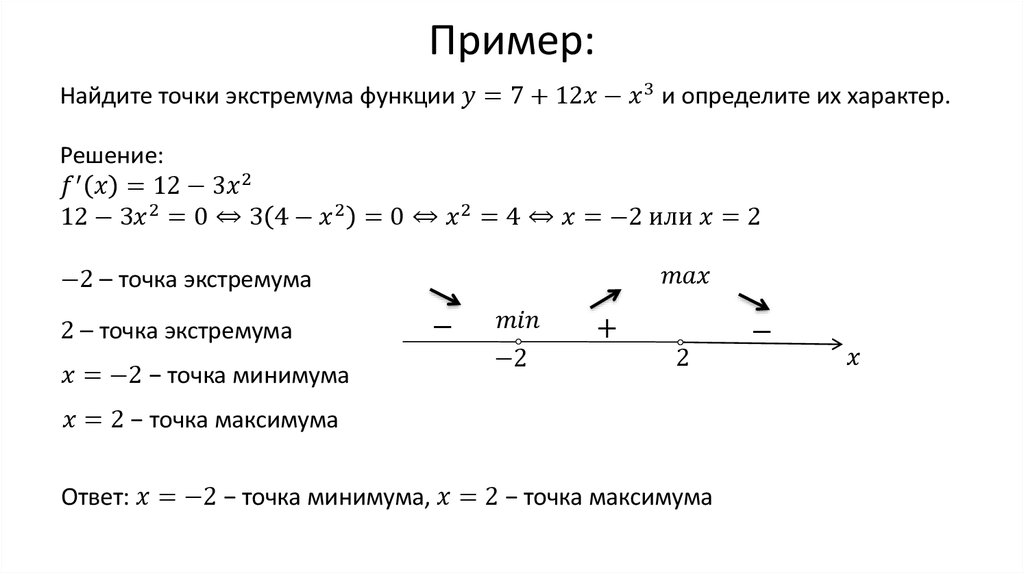

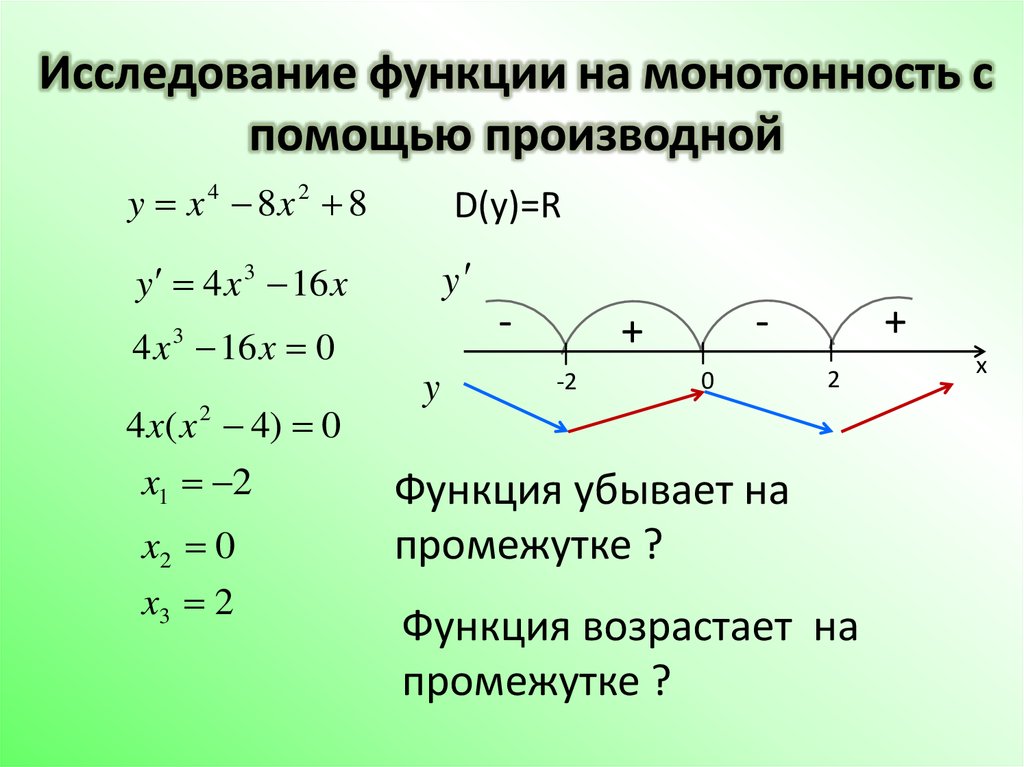
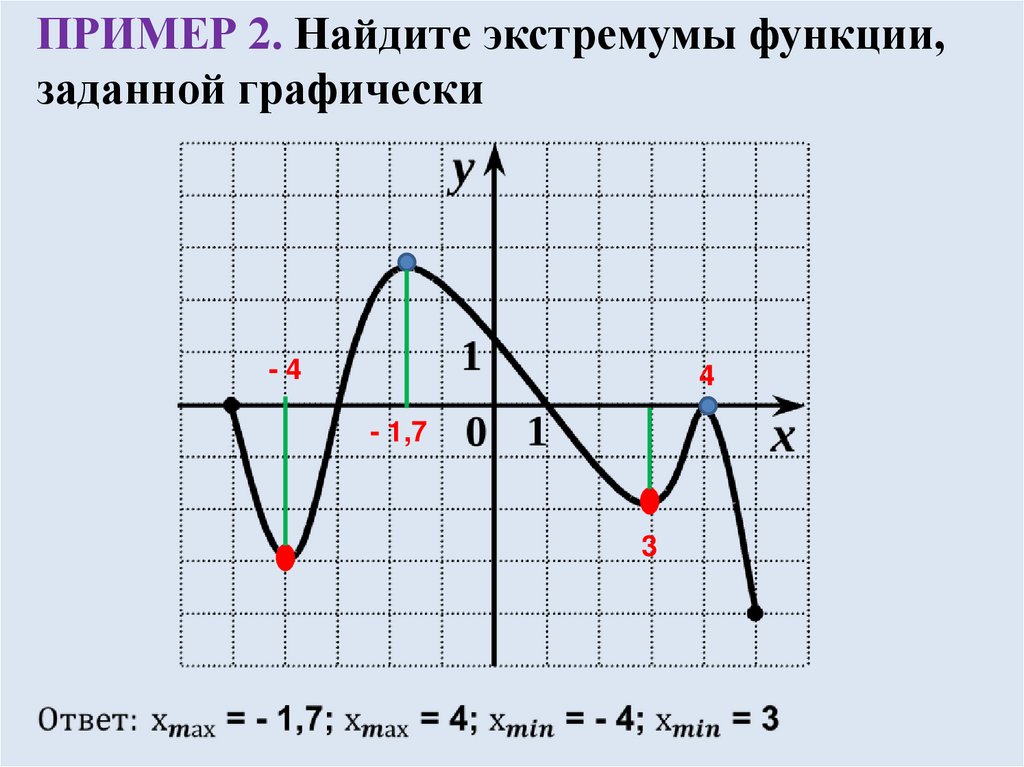
 ), максимальное значение на всем интервале фактически находится в верхней конечной точке, когда . При поиске экстремумов вдоль интервала поиск нулей первой производной не учитывает экстремумы конечных точек.
), максимальное значение на всем интервале фактически находится в верхней конечной точке, когда . При поиске экстремумов вдоль интервала поиск нулей первой производной не учитывает экстремумы конечных точек. На первом интервале первая производная положительна, на втором – отрицательна, на третьем – положительна. Первая производная изменяется с положительной на отрицательную при , поэтому здесь существует относительный максимум.
На первом интервале первая производная положительна, на втором – отрицательна, на третьем – положительна. Первая производная изменяется с положительной на отрицательную при , поэтому здесь существует относительный максимум.




 Это позволило нам сократить множители и упростить решение.
Это позволило нам сократить множители и упростить решение.
 Во втором действии мы также не умножили сразу, а сократили на тройку в числителе и тройку в знаменателе.
Во втором действии мы также не умножили сразу, а сократили на тройку в числителе и тройку в знаменателе. Чтобы выполнить это действие, нужно умножить числитель дроби на это число, а знаменатель оставить без изменений. После подсчета можно выделить целую часть, превратив обыкновенную дробь в смешанную.
Чтобы выполнить это действие, нужно умножить числитель дроби на это число, а знаменатель оставить без изменений. После подсчета можно выделить целую часть, превратив обыкновенную дробь в смешанную.



 Возможно, вам также придется
уменьшить дробь
чтобы получить его в простейшей форме.
Возможно, вам также придется
уменьшить дробь
чтобы получить его в простейшей форме. Изучите этот важный математический навык, а затем проверьте свои знания, пройдя наш тест в конце этого руководства.
Изучите этот важный математический навык, а затем проверьте свои знания, пройдя наш тест в конце этого руководства. д.
д.
 Теперь мы хотим, чтобы знаменатель был равен 1, чтобы избавиться от дроби, поэтому мы делим каждую часть дроби на 10. Это дает нам ,6 /1, что также равно всего 0,6. Объедините это с целым числом (1) из ответа, и ваш окончательный ответ в десятичной форме будет 1,6.
Теперь мы хотим, чтобы знаменатель был равен 1, чтобы избавиться от дроби, поэтому мы делим каждую часть дроби на 10. Это дает нам ,6 /1, что также равно всего 0,6. Объедините это с целым числом (1) из ответа, и ваш окончательный ответ в десятичной форме будет 1,6. 7 входит в число 85 двенадцать раз с остатком 1. Наш окончательный ответ: 12 1 /7, или 12,14 в десятичной форме.
7 входит в число 85 двенадцать раз с остатком 1. Наш окончательный ответ: 12 1 /7, или 12,14 в десятичной форме. 0003
0003 Сократите свои шансы на ошибку, следуя этим трем советам.
Сократите свои шансы на ошибку, следуя этим трем советам. Большинство ошибок совершается, когда люди умножают неправильные числа или помещают ответ числителя в место знаменателя (или наоборот).
Большинство ошибок совершается, когда люди умножают неправильные числа или помещают ответ числителя в место знаменателя (или наоборот).
