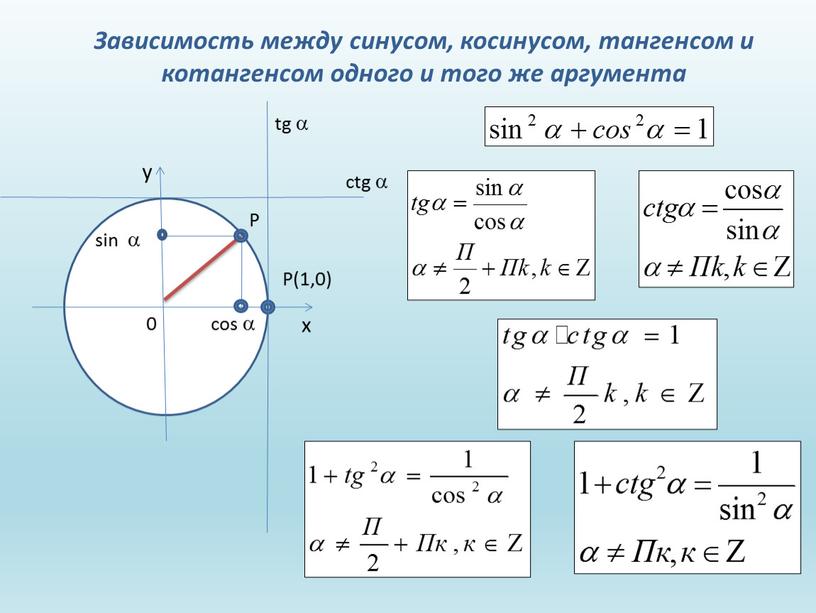
формула, чему равна, как найти
Что такое площадь треугольника
Определение
Треугольник — это многоугольник с тремя сторонами и тремя вершинами.
Определение
Площадь треугольника — это величина плоскости, заключенной между сторонами этой геометрической фигуры.У треугольника она равна произведению половины основания на высоту.
Математически это выглядит так:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
\(S=\frac12a\times h\)
где a — основание треугольника, а h — его высота.
Способы нахождения площади
Но существуют также и другие способы, по которым можно найти S этого многоугольника. Рассмотрим основные из них.
Через две стороны и угол
Источник: lifehacker. ru
ruЕсли вам известны две стороны любого треугольника и угол между ними, найти площадь можно по формуле:
\(S=\frac12a\times b\times\sin\alpha\)
где a и b — стороны фигуры, а α — угол между ними.
Через радиус описанной окружности и три стороны
Источник: lifehacker.ruЕсли вам известен радиус окружности, которая описана вокруг вашего треугольника, а также все его стороны, можно вычислить S следующим образом:
\(S=\frac{a\times b\times c}{4\times R}\)
где a, b и c — стороны фигуры, а R — радиус описанной окружности.
Через радиус вписанной окружности и три стороны
Источник: lifehacker.ruВ случае, если вам известны все три стороны и радиус вписанной в треугольник окружности, можно найти его площадь по формуле:
\(S=r\times\frac{a+b+c}2\)
где r — радиус вписанной окружности, \(\frac{a+b+c}2\) — полупериметр фигуры.
Таким образом, формулу можно выразить всего двумя множителями:
\(S=r\times p\)
где p — полупериметр треугольника. \circ-(\alpha+\beta)\)
\circ-(\alpha+\beta)\)
Для прямоугольного треугольника
В случае треугольника с прямым углом формулы для нахождения площади будут немного отличаться. Найти S можно будет несколькими способами.
По двум сторонам
Источник: lifehacker.ruЕсли вам известны оба катета данной фигуры, рассчитать S можно умножив их друг на друга, а потом разделив на пополам:
\(S=\frac{a\times b}2\)
где a и b — катеты прямоугольного треугольника.
Через гипотенузу и острый угол
Источник: spravochnick.ruЗная длину гипотенузы и величину одного из острых углов, мы можем найти один из его катетов по определению косинуса. И уже потом можем использовать формулу для нахождения площади треугольника через две стороны и синус угла между ними.
Начнем с поиска катета:
\(\cos\left(\alpha\right)=\frac ac\)
\(a=c\times\cos\left(\alpha\right)\)
где c — гипотенуза треугольника, a — его катет, а α — угол между ними. 2\times\tan\left(\alpha\right)\)
2\times\tan\left(\alpha\right)\)
Через радиус вписанной окружности и гипотенузу
Источник: mnogoformul.ruЗная радиус вписанной в данную фигуру окружности и гипотенузу, мы можем использовать следующее уравнение для расчета:
\(S=r\times(r+c)\)
где r — радиус вписанной окружности, c — гипотенуза.
Через вписанную окружность
Источник: mnogoformul.ruРадиус, опущенный в точку касания окружности и гипотенузы прямоугольного треугольника, делит эту гипотенузу на неравные отрезки. Если нам известны величины этих отрезков, мы можем найти площадь фигуры по формуле:
\(S=с_1\times с_2\)
где \(с_1\) и \(с_2\) — неравные отрезки гипотенузы.
По формуле Герона
Источник: mnogoformul.ruЕсли мы знаем длины всех сторон данного многоугольника, мы можем рассчитать S по формуле Герона:
\(S=(p-a)\times(p-b)\)
где \(p=\frac{a+b+c}2\) — полупериметр фигуры.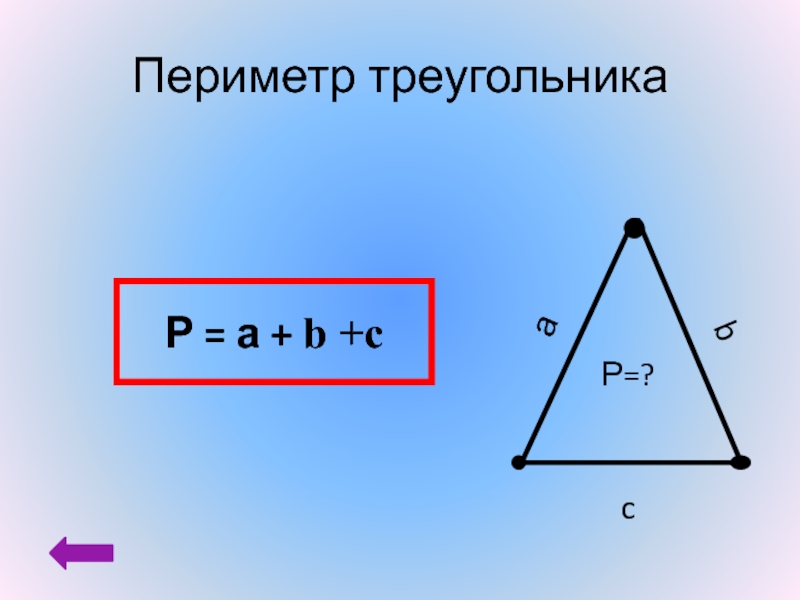 2\).
2\).
Площадь треугольника — все формулы
Теперь вам не нужно тратить время на долгие вычисления, прежде чем вы сможете узнать площадь треугольника. Зная методы расчета, используемые для расчета площади треугольника, вы легко сможете это сделать самостоятельно. Действительно, всегда лучше знать формулы площади треугольника. Треугольники могут быть разными и вы это знаете, но как найти площадь треугольника если вам практически ничего неизвестно о треугольнике? И что нужно знать из размеров треугольника, чтобы найти его площадь. Давайте разбираться. При этом тема не так проста как кажется на первый взгляд, наверное, поэтому задачи нахождения площади треугольника есть и в ОГЭ и в ЕГЭ по математике.
Содержание
Что такое треугольник
Треугольник – это геометрическая фигура. По определению, это многоугольник, имеющий три стороны. Следовательно, треугольник также должен иметь три угла.
Сумма трех углов треугольника должна быть равна 180°.
Чтобы иметь возможность вычислить площадь треугольника, мы должны сначала знать меру его основания, а также высоту.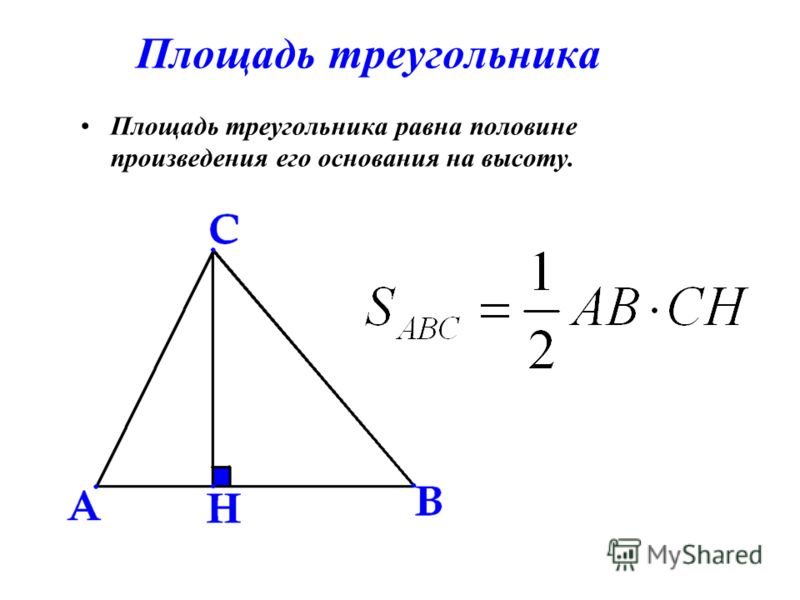 Основание треугольника представляет одну из его сторон. Высота, с другой стороны, представляет собой каждую из трех прямых линий, которые проходят через одну из вершин треугольника и перпендикулярны стороне, лежащей напротив принятой вершины (то есть перпендикулярно основанию).
Основание треугольника представляет одну из его сторон. Высота, с другой стороны, представляет собой каждую из трех прямых линий, которые проходят через одну из вершин треугольника и перпендикулярны стороне, лежащей напротив принятой вершины (то есть перпендикулярно основанию).
Прежде всего, помните, что треугольник состоит из трех сторон и трех углов. Это значит, что у него должно быть три вершины. Треугольник, вершинами которого являются A, B и C, может быть представлен как: ΔABC. Существуют разные виды треугольников. Они могут быть классифицированы двумя различными способами: либо по свойству его сторон, либо по свойству его углов.
Различные типы треугольников в зависимости от длины их сторон
Разносторонний треугольник
Мы узнаем разносторонний треугольник по трем сторонам, которые имеют разную длину. Эта треугольная форма может быть построена только с тремя разными углами. Кроме того, один из них может быть прямым углом (или углом 90 °). В общем, название «произвольный треугольник» используется для разностороннего треугольника.
Равнобедренный треугольник
Мы говорим, что треугольник равнобедренный, если он имеет две стороны одинаковой длины и два равных угла при основании. Равнобедренный треугольник также можно узнать по тому факту, что его высота представляет его ось симметрии, его медиану и биссектрису.
Прямоугольный треугольник
Прямоугольный треугольник обязательно имеет прямой угол. Другими словами, сумма двух других его углов должна быть равна 90°. Прямоугольный треугольник также имеет гипотенузу.
Это противоположная сторона вершине с прямым углом. Прямой треугольник может быть разносторонним (или любым), если его три стороны имеют разную длину.
Кроме того, он может быть равнобедренным в том случае, если он имеет два одинаковых катета.
Равносторонний треугольник
Треугольник называется равносторонним, если он имеет три стороны одинаковой длины. Поэтому все его углы также равны и каждый по 60°. В равностороннем треугольнике любая высота также выступает в качестве медианы и биссектрисы.
Площадь треугольника
Площадь разностороннего треугольника
Вычисляем площадь треугольника без особенностей – все его стороны разные и все углы разные.
Если известны две стороны треугольника и угол между ними, то площадь разностороннего треугольника вычисляется по формуле “площадь треугольника через две стороны и угол между ними”:
Если известны высота в треугольнике и основание, то используется формула площади треугольника через основание и высоту:
Формула Герона определения площади треугольника
Если известны стороны любого треугольника, то его площадь можно определить по формуле Герона.
, где
Площадь равнобедренного треугольника
Площадь треугольника через основание и сторону можно найти, если известны сторона и основания равнобедренного треугольника.
К равнобедренному треугольнику также применима формула площади треугольника через основание, сторону и угол между ними:
Найти площадь равнобедренного треугольника можно также через боковые стороны и угол между ними.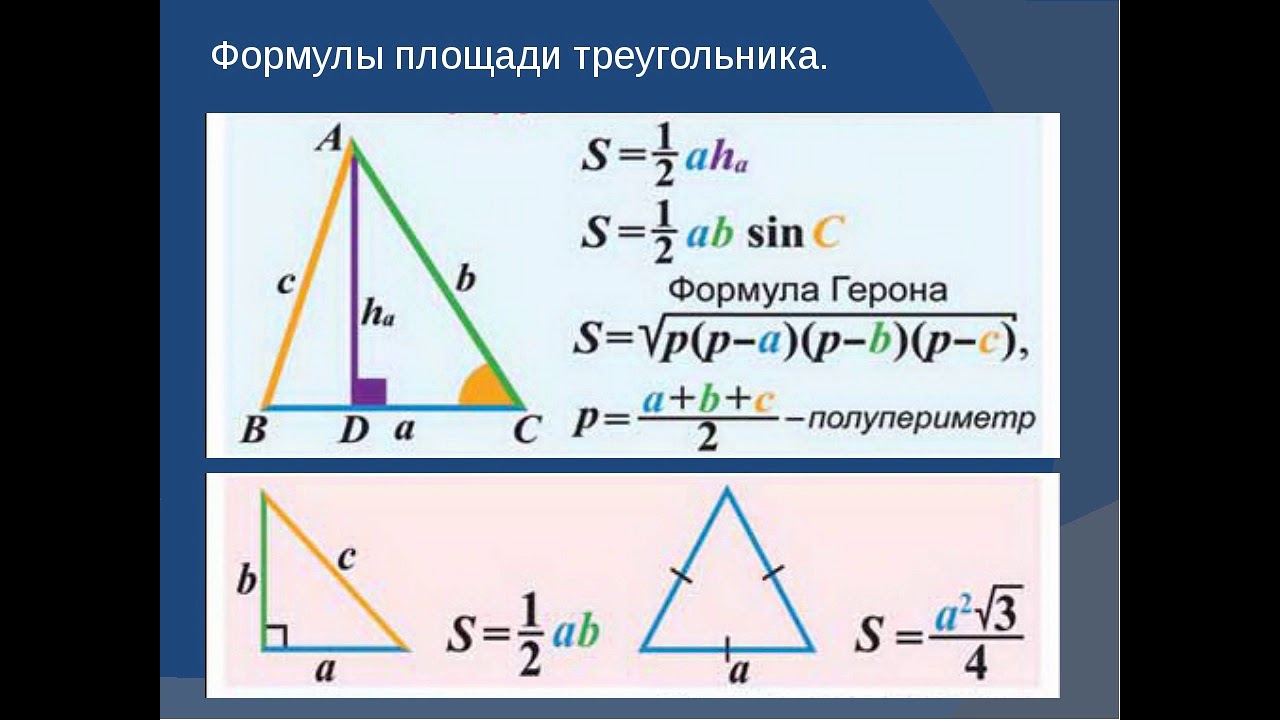
Площадь равнобедренного треугольника через основание и угол между боковыми сторонами:
Площадь прямоугольного треугольника
Приведем формулы площади прямоугольного треугольника. Формула площади прямоугольного треугольника через катет и прилежащий угол:
Площадь прямоугольного треугольника по радиусу вписанной окружности и гипотенузе
Площадь прямоугольного треугольника, если в него вписана окружность:
Площадь равностороннего треугольника
Площадь равностороннего треугольника можно найти через радиус описанной окружности.
Если дан радиус вписанной окружности, то площадь равностороннего треугольника можно найти по формуле:
Площадь равностороннего треугольника, если известна сторона треугольника:
Площадь равностороннего треугольника, если известна высота треугольника:
Площадь треугольника Определения и примеры
Площадь треугольника Определения и примеры
Введение
Определения треугольников и примеры важны для математики. В этом сообщении блога мы рассмотрим три различных определения треугольника площади и примеры. Таким образом вы сможете лучше понять, как работают эти концепции и как они могут помочь вашим математическим навыкам.
В этом сообщении блога мы рассмотрим три различных определения треугольника площади и примеры. Таким образом вы сможете лучше понять, как работают эти концепции и как они могут помочь вашим математическим навыкам.
Какова площадь треугольника?
Площадь треугольника равна половине произведения основания на высоту.
Формула: A = 1/2 × b × h .
Определение треугольника
Треугольник — это трехсторонняя фигура с двумя углами, равными 90 градусам. Угол при вершине — это угол между основанием и вершиной треугольника, а два других угла называются боковыми углами. Прямоугольный треугольник имеет прямой угол при вершине и сумму углов, равных 180 градусам. В случае треугольника с острым углом, например, 90 градусов, один из его углов умножается на 3, чтобы найти его меру.
Площадь треугольника
Треугольник — это трехсторонняя геометрическая фигура с двумя равными сторонами и третьей стороной, которая короче двух других. Треугольник имеет шесть точек пересечения, которые называются вершинами. Три вершины одинакового размера образуют основание треугольника. Точка в середине основания называется вершиной треугольника.
Треугольник имеет шесть точек пересечения, которые называются вершинами. Три вершины одинакового размера образуют основание треугольника. Точка в середине основания называется вершиной треугольника.
Три вершины на одной стороне треугольника называются внутренними углами. Угол, противолежащий любому внутреннему углу с одной стороны, называется внешним углом. Внешний угол с одной стороны также считается внутренним углом, если он имеет общую вершину с другим внешним углом с той же стороны. 93
Если треугольник прямоугольный, то значение «base_a» равно 0, а все остальные значения равны 1. Если треугольник не прямоугольный, то «base_a» может быть любым действительным числом, а «height_a» всегда будет положительный.
Площадь треугольника с двумя сторонами и прилежащим углом (SAS)
Формула: Площадь = (a x b x sin c)/2 , где a, b — две стороны, а c — угол между ними.
Другим определением является сумма длин трех сторон, также известная как мера длины или линейная мера. Другой способ подумать об этом — представить, что каждая сторона отрезается посередине между двумя концами, и подсчитывается, сколько дюймов (или сантиметров) получаются разрезы. Это также называется базовой длиной или иногда просто базой.
Другой способ подумать об этом — представить, что каждая сторона отрезается посередине между двумя концами, и подсчитывается, сколько дюймов (или сантиметров) получаются разрезы. Это также называется базовой длиной или иногда просто базой.
Третье определение называется радиусом описанной окружности, и это как раз то, что вы ожидаете — радиус вокруг одного из углов треугольника. Наконец, есть особый тип треугольника, называемый равносторонним треугольником, у которого все углы равны 90 градусам. Все эти определения важны при работе с Треугольниками в задачах и расчетах, поэтому к ним стоит привыкнуть!
Площадь прямоугольного треугольника
Площадь прямоугольного треугольника равна сумме трех сторон. Основание всегда самая длинная сторона, а высота самая короткая.
Площадь треугольника можно найти, умножив длину основания на высоту. Например, если у вас есть треугольник с основанием 10 дюймов и высотой 12 дюймов, то его площадь составит 120 квадратных дюймов.
Типы треугольников
Существует много типов треугольников, некоторые из них более распространены, чем другие. Вот некоторые из них:
Равнобедренный треугольник
Равнобедренный треугольник имеет две равные стороны, а третья сторона имеет ту же длину, что и две другие.
Треугольник в правой вертикальной плоскости
В геометрии треугольник в правой вертикальной плоскости — это треугольник, вершины которого центрированы на верхнем, нижнем и левом краях листа. Прямоугольный треугольник в этом контексте имеет один угол, равный 90 градусам.
Заключение
В этой статье мы обсудили три наиболее распространенных типа треугольников и их определения. Прочитав это, вы должны лучше понять, что такое треугольник и как его идентифицировать в различных ситуациях. Надеюсь, вам понравится узнавать об этих важных формах!
Результат
Определение
Определяющие неравенства
Свойства пластин
Механические свойства
Свойства расстояния 900 05
Альтернативная форма
Альтернативные формы при условии, что a, b и c положительны
Площадь треугольника: формула Герона, решенные примеры
- Автор Асит Баранкар
- Последнее изменение 25-01-2023
Площадь треугольника: В двумерной плоскости площадь треугольника — это область, заключенная в нем. Треугольник, как мы все знаем, представляет собой замкнутую форму с тремя сторонами и тремя вершинами. В результате площадь треугольника равна общему пространству, занимаемому тремя сторонами треугольника. Половина произведения основания треугольника на высоту — это обычная формула вычисления его площади.
Треугольник, как мы все знаем, представляет собой замкнутую форму с тремя сторонами и тремя вершинами. В результате площадь треугольника равна общему пространству, занимаемому тремя сторонами треугольника. Половина произведения основания треугольника на высоту — это обычная формула вычисления его площади.
Область, занимаемая внутри границы плоского объекта или фигуры, определяется как «площадь» в целом. Измерение производится в квадратных единицах, при этом квадратные метры являются обычной единицей измерения (м2). Существуют предопределенные формулы для вычисления площади квадратов, прямоугольников, кругов, треугольников и других фигур. В этом посте мы изучим формулы площади треугольников для нескольких видов треугольников, а также рассмотрим некоторые примеры задач.
Треугольник — это многоугольник с тремя сторонами. Его также можно определить фигурой, ограниченной или заключенной в трехлинейные отрезки. Ясно, что треугольник будет иметь три стороны и три вершины.
Узнайте о треугольниках здесь
Классификация треугольников
Треугольники классифицируются двумя основными способами:
а) классификация на основе длины сторон треугольника
б) классификация на основе внутренних углов треугольника.
Классификация треугольников по длине сторон
В зависимости от длины сторон треугольники делятся на три типа: разносторонний треугольник, равнобедренный треугольник и равносторонний треугольник.
Разносторонние треугольникиЕсли все три стороны треугольника различны по длине или если ни одна из сторон треугольника не равна, то такой треугольник называется разносторонним. Треугольник, приведенный ниже, является разносторонним треугольником. В этом треугольнике все три угла имеют разную величину.
Равнобедренные треугольникиЕсли любые две из трех сторон треугольника равны, то такой треугольник называется равнобедренным.
В приведенном выше треугольнике указаны две равные стороны. Это равнобедренный треугольник. В равнобедренном треугольнике два угла, противолежащие двум равным сторонам, равны по величине.
Равносторонний треугольник Если все три стороны треугольника имеют одинаковую длину, то такой треугольник называется равносторонним. 9{\rm{o}}}\) называется тупоугольным треугольником.)
9{\rm{o}}}\) называется тупоугольным треугольником.)
Термины, относящиеся к площади треугольника
Высота треугольника
Перпендикуляр, проведенный из любой вершины в сторону, противоположную вершине, называется высотой треугольника из этой вершины.
На приведенном выше рисунке перпендикуляр \(AD\) проведен из вершины \(A\) на сторону \(BC.\). Итак, \(AD\) называется высотой треугольника.
На приведенном выше рисунке перпендикуляры \(AD,\,BE\) и \(CF\) проведены из вершин \(A,\,B\) и \(C\) на противоположных сторонах \(BC ,\,CA\) и \(AB,\) соответственно. В этом случае \(AD\) считается высотой треугольника из вершины \(A\) относительно основания \(BC.\). Аналогично, \(BE\) и \(CF\) считаются высотами треугольника из вершины \(B\) и \(C\) относительно оснований \(CA\) и \(AB,\) соответственно. Три высоты треугольника всегда совпадают. Общая точка называется ортоцентром треугольника.
Иногда перпендикуляр, проведенный из вершины, не достигает противоположной стороны.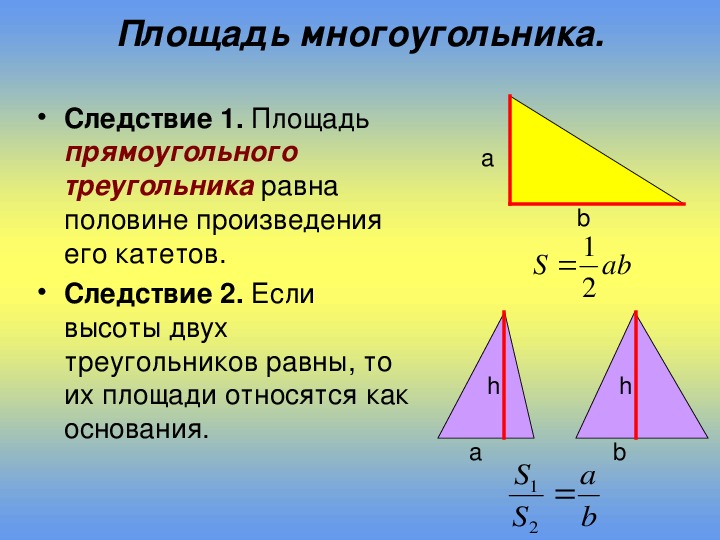 Он лежит на расширенной противоположной стороне.
Он лежит на расширенной противоположной стороне.
На приведенном выше рисунке перпендикуляр \(AD\) проведен к продолжению \(BC.\). В этом случае \(AD\) считается высотой треугольника \(ABC\) относительно основания \(BC .\)
Медиана треугольника
Медиана определяется как отрезок, соединяющий вершину треугольника и среднюю точку противоположной стороны треугольника.
На приведенном выше рисунке, если \(D\) является серединой \(BC,\), то \(AD\) называется медианой, проведенной из вершины \(A\) на противоположной стороне \(BC .\)
В любом треугольнике из каждой вершины на противоположных сторонах можно провести три медианы, как показано на рисунке выше. В любом треугольнике три медианы пересекаются в одной точке. Точка пересечения медиан треугольника называется центром тяжести треугольника.
Какова площадь треугольника?
Площадь треугольника — это область или пространство, ограниченное тремя сторонами треугольника.
Формула площади треугольника Существует несколько формул, используемых для расчета площади треугольника. Они обсуждаются ниже:
Они обсуждаются ниже:
Площадь треугольника при заданных основании и высоте
Площадь треугольника \({\rm{ = }}\frac{{\rm{1}}}{{\rm{2} }}{\rm{ \times base \times height}}\)
Приведенная выше формула используется, когда известны или даны длина любой стороны и соответствующая высота.
Для приведенного выше рисунка площадь треугольника \(= \frac{1}{2} \times {\rm{основание \times height}} = \frac{1}{2} \times BC \times AD = \frac{1}{2} \times b \times h\)
Площадь прямоугольного треугольника
Приведенная выше формула используется непосредственно для прямоугольных треугольников.
Следовательно, формула, используемая для вычисления площади треугольника, выглядит следующим образом: \(\frac{1}{2} \times {\rm{основание \times height}} = \frac{1}{2} \times b \ раз h\), где \(b\) — основание, а \(h\) — высота.
Типы треугольников, для которых используется эта формула
Помимо прямоугольных треугольников, эта формула может использоваться для расчета площади любого типа треугольника, если длина основания и высота заданы или могут быть получены из заданных Информация о треугольнике.
Площадь треугольника с 3 сторонами: формула Герона
Эта формула используется для вычисления площади треугольника, если известны или даны длины всех трех сторон.
Согласно этой формуле площадь треугольника определяется выражением
\({\rm{площадь}} = \sqrt {s(s — a)(s — b)(s — c)} \), где , \(a,\,b\) и \(c\) — длины сторон треугольника, а \(s\) — полупериметр треугольника, определяемый выражением \(s = \frac{{a + b + c}}{2}.\)
Площадь равностороннего треугольника
Формулу Герона можно использовать для получения специальной формулы, применимой для расчета площади равностороннего треугольника.
В равностороннем треугольнике все три стороны равны по длине. Итак, в этом случае \(a = b = c.\)
Итак, \(s = \frac{{a + b + c}}{2} = \frac{{a + a + a}}{2 } = \frac{{3\,a}}{2}\)
Итак, \({\rm{площадь}} = \sqrt {s(s – a)(s – b)(s – c )} = \ sqrt {\ frac {{3a}} {2} \ times \ left ( {\ frac {{3a}} {2} — a} \ right) \ times \ left ( {\ frac {{3a}) {2} – a} \right) \times \left( {\frac {{3a}}{2} – a} \right)} \) 92}}}{4}} \)
Площадь треугольника при заданных координатах его вершин
Площадь треугольника можно вычислить, если известны координаты трех вершин треугольника на декартовой плоскости.
В треугольнике \(ABC\), показанном выше, \(A\left( {{x_1},\,{y_1}} \right),\,B\left( {{x_2},\,{y_2} } \right)\) и \(C\left( {{x_3},\,{y_3}} \right)\) — координаты вершин треугольника.
Площадь этого треугольника можно рассчитать по формуле
\( {{площадь}} = \frac{1}{2}\left| { {x_1}\left({{y_2} – {y_3}} \right) + {x_2}\left({{y_3} – {y_1}} \right) + {x_3}\left({{y_1} – {y_2}} \right)} \right|\)
Связь между площадями двух треугольников, лежащих на одном основании и между одинаковыми параллелями
Существует интересная связь между площадями двух разных треугольников, если они лежат на одном основании и находятся между двумя одинаковыми параллельными прямыми. Можно доказать, что площади двух треугольников с одинаковым основанием, лежащих между двумя одинаковыми параллельными прямыми, равны.
Здесь прямая \(BC\) параллельна прямой \(DQ.\) Отсюда ясно, что \(\Delta ABC\) и \(\Delta PBC\) имеют одно и то же основание \(BC\) и они лежат между одними и теми же параллельными прямыми \(BC\) и \(DQ. \)
\)
Итак, площади \(\Delta ABC\) и \(\Delta PBC\) равны. Следовательно, \({\mathop{\rm area}\nolimits} \Delta ABC = {\rm{area}}\Delta PBC.\)
Связь между площадью треугольника и площадью параллелограмма, лежащего на одном и том же треугольнике. Основание и между одинаковыми параллелями
Интересная связь также существует между площадью треугольника и площадью параллелограмма, если они лежат на одном основании и между одними и теми же двумя параллельными прямыми. Можно доказать, что площадь треугольника равна половине площади параллелограмма, если они имеют одно основание и лежат между одними и теми же двумя параллельными прямыми.
Здесь прямая \(AB\) параллельна прямой \(QD\) Отсюда, очевидно, \(\Delta ABC\) и параллелограмм \(ABDC\) и \(ABPQ\) имеют одно и то же основание \(AB\) и лежат между одними и теми же параллельными прямыми \(AB\) и \(QD\)
Значит, площадь \(\Delta ABC\) равна половине площади параллелограмма \(ABDC\) а также параллелограмм \(ABPQ\)..jpg) 2}.\)
2}.\)
Q.2. Найдите площадь треугольника, длины сторон которого равны \({\rm{3\,см}}\).\({\rm{4\,см}}\) и \({\rm{ 5\,см}}\)
Ответ: Здесь даны длины трех сторон. Итак, воспользуемся формулой Герона для вычисления площади треугольника. Здесь \(a = 3\;{\rm{см}},b = 4\;{\rm{см}}\) и \(c = 5\,{\rm{см}}\) согласно по этой формуле площадь треугольника определяется выражением \({\rm{area}} = \sqrt {s(s — a)(s — b)(s — c)} ,\), где \(a ,\,b\) и \(c\) — длины сторон треугольника, а \(s\) — полупериметр треугольника, определяемый выражением \(s = \frac{{a + b + c }}{2}.\) Итак, \(s = \frac{{a + b + c}}{2} = \frac{{3 + 4 + 5}}{2} = \frac{{12} }{2} = 6\;{\rm{см}}\)Следовательно, площадь данного треугольника\( = \sqrt {s\left( {s – a} \right)\left( {\left( {s – b} \right)\left( {s – c} \right)} \right)} = \sqrt {6\left( {6 – 3} \right)\left( {6 – 4} \right )\left( {6 – 5} \right)} \)\(= \sqrt {6 \times 3 \times 2 \times 1} = \sqrt {36} = 6\;{\rm{c}}{ {\ гт {м}} ^ 2} \) 92}]\)
Резюме
В двумерной плоскости площадь треугольника определяется как общее пространство, занимаемое тремя его сторонами.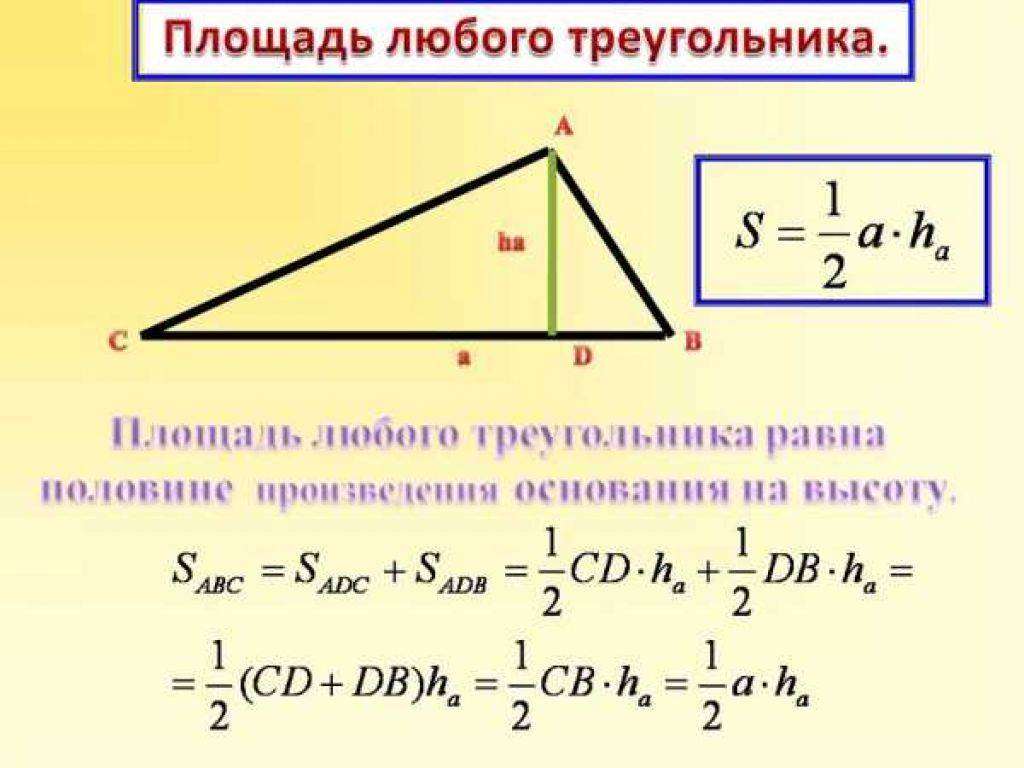 Площадь треугольника равна половине произведения его основания на высоту, поэтому A = 1/2bh — основная формула. Эта формула работает для любого треугольника, будь то разносторонний треугольник, равнобедренный треугольник или равносторонний треугольник. Важно помнить, что основание и высота треугольника перпендикулярны друг другу.
Площадь треугольника равна половине произведения его основания на высоту, поэтому A = 1/2bh — основная формула. Эта формула работает для любого треугольника, будь то разносторонний треугольник, равнобедренный треугольник или равносторонний треугольник. Важно помнить, что основание и высота треугольника перпендикулярны друг другу.
Эта статья поможет всесторонне узнать о том, как вычислить площадь различных видов треугольников в зависимости от того, какая информация доступна о треугольнике. Зная это, можно рассчитать площадь любой земли треугольной формы или любого другого предмета треугольной формы.
Это также помогает в вычислении площади любой земли правильной или неправильной многоугольной формы или любого другого объекта путем деления многоугольника на треугольники по диагоналям, а затем получения площади каждого треугольника и сложения их.
Часто задаваемые вопросы о площади треугольника
Q.1. Сколько высот может быть у треугольника?
Ответ: Треугольник может иметь \(3\) (три) высоты.
Q.2 . Как найти площадь треугольника, если не дана высота, но даны длины трех сторон?
Ответ: Если высота не дана, но даны длины трех сторон, то можно использовать формулу Герона.
Согласно этой формуле площадь треугольника определяется выражением
\({\rm{площадь}} = \sqrt {s(s — a)(s — b)(s — c)} ,\)
где \(a,b\) и \(c\) — длины сторон треугольника, а \(s\) — полупериметр треугольника, определяемый выражением \(s = \frac{{a + b + c}}{2}.\)
Q.3 . Какая формула обычно используется для нахождения площади прямоугольного треугольника, если известны длина и высота?
Ответ: Если длина основания и высота известны, то можно использовать формулу \({\rm{area = }}\frac{{\rm{1}}}{{ \rm{2}}}{\rm{ \times base \times height}}{\rm{.}}\)
Q.4. Для расчета площади треугольника по формуле \(\frac{{\rm{1}}}{{\rm{2}}}{\rm{ \times base \times height}}\) 9{\rm{2}}}\)
Q.

 При нахождении области определения функции y=f(x)= √(n&x) (корень n-ой степени) следует обращать внимание на четность или нечетность n.
При нахождении области определения функции y=f(x)= √(n&x) (корень n-ой степени) следует обращать внимание на четность или нечетность n.  67] =19: integral part of (19.67) — выделяет целую часть числа (integerPart)
67] =19: integral part of (19.67) — выделяет целую часть числа (integerPart) Исследует диапазон, в котором существует область определения определенной математической функции. Не только это, но вы также получите результаты в правильно заданных интервальных обозначениях.
Исследует диапазон, в котором существует область определения определенной математической функции. Не только это, но вы также получите результаты в правильно заданных интервальных обозначениях. В нашем случае это 10, так что;
В нашем случае это 10, так что; Приступая к делу, его областью определения являются все действительные числа, а диапазон — только 7. Для дальнейшей проверки вы можете поместить выражение в онлайн-калькулятор домена и диапазона с шагами, чтобы свести на нет ваши сомнения.
Приступая к делу, его областью определения являются все действительные числа, а диапазон — только 7. Для дальнейшей проверки вы можете поместить выражение в онлайн-калькулятор домена и диапазона с шагами, чтобы свести на нет ваши сомнения. На одном конце воображаемой сборочной линии есть винты и болты, а на другом конце – автомобиль в сборе. Здесь машину посередине можно назвать функцией.
На одном конце воображаемой сборочной линии есть винты и болты, а на другом конце – автомобиль в сборе. Здесь машину посередине можно назвать функцией.

 Откроется новое окно для отображения вывода.
Откроется новое окно для отображения вывода.





 2009 март-апрель; 3 (2 Приложение 1): S33–S35.
2009 март-апрель; 3 (2 Приложение 1): S33–S35. При раке прямой кишки повышенное внимание к адекватным периферическим радиальным краям и использование предоперационной лучевой терапии для опухолей промежуточного и высокого риска может усложнить оценку взаимосвязи между количеством исследованных лимфатических узлов и результатами лечения пациентов; данные свидетельствуют о том, что количество лимфатических узлов (общее и количество положительных) в ректальном образце значительно ниже после проведения предоперационной лучевой терапии. Несмотря на то, что остается мало споров о прогностической важности увеличения числа лимфатических узлов для отдельных пациентов, неясно, является ли количество лимфатических узлов полезным индикатором качества больницы.
При раке прямой кишки повышенное внимание к адекватным периферическим радиальным краям и использование предоперационной лучевой терапии для опухолей промежуточного и высокого риска может усложнить оценку взаимосвязи между количеством исследованных лимфатических узлов и результатами лечения пациентов; данные свидетельствуют о том, что количество лимфатических узлов (общее и количество положительных) в ректальном образце значительно ниже после проведения предоперационной лучевой терапии. Несмотря на то, что остается мало споров о прогностической важности увеличения числа лимфатических узлов для отдельных пациентов, неясно, является ли количество лимфатических узлов полезным индикатором качества больницы. В дополнение к описанию степени поражения лимфатических узлов может быть важно исследовать достаточное общее количество лимфатических узлов. Адекватная хирургическая резекция важна для местного контроля рака. Получение большего количества лимфатических узлов может принести пользу пациентам, поскольку позволяет более точно определить стадию рака и правильно использовать адъювантную химиотерапию для пациентов с положительными лимфатическими узлами (стадия III).
В дополнение к описанию степени поражения лимфатических узлов может быть важно исследовать достаточное общее количество лимфатических узлов. Адекватная хирургическая резекция важна для местного контроля рака. Получение большего количества лимфатических узлов может принести пользу пациентам, поскольку позволяет более точно определить стадию рака и правильно использовать адъювантную химиотерапию для пациентов с положительными лимфатическими узлами (стадия III). В нескольких обсервационных исследованиях была обнаружена связь между оценкой «адекватного» количества лимфатических узлов и улучшением выживаемости. 1 , 2 Во многих исследованиях преимущества наблюдались в группах стадирования узлов, отмечая улучшение выживаемости с увеличением числа удаленных лимфатических узлов среди пациентов с раком толстой кишки с поражением узлов и поражением узлов. 3 , 4 Поскольку увеличение выживаемости наблюдалось у пациентов с известным поражением лимфатических узлов, было предложено терапевтическое преимущество извлечения верхних лимфатических узлов.
В нескольких обсервационных исследованиях была обнаружена связь между оценкой «адекватного» количества лимфатических узлов и улучшением выживаемости. 1 , 2 Во многих исследованиях преимущества наблюдались в группах стадирования узлов, отмечая улучшение выживаемости с увеличением числа удаленных лимфатических узлов среди пациентов с раком толстой кишки с поражением узлов и поражением узлов. 3 , 4 Поскольку увеличение выживаемости наблюдалось у пациентов с известным поражением лимфатических узлов, было предложено терапевтическое преимущество извлечения верхних лимфатических узлов. Данные убедительны, и существует общее согласие относительно прогностического значения этой переменной для долгосрочной выживаемости отдельных пациентов с раком толстой кишки.
Данные убедительны, и существует общее согласие относительно прогностического значения этой переменной для долгосрочной выживаемости отдельных пациентов с раком толстой кишки. 7 – 9 Колледж американских патологоанатомов в течение многих лет рекомендовал патоморфологическое исследование не менее 12 лимфатических узлов, чтобы точно предсказать их отсутствие. 10 Если после тщательного макроскопического исследования обнаружено менее 12 узлов, рекомендуется использовать дополнительные методы улучшения зрения.
7 – 9 Колледж американских патологоанатомов в течение многих лет рекомендовал патоморфологическое исследование не менее 12 лимфатических узлов, чтобы точно предсказать их отсутствие. 10 Если после тщательного макроскопического исследования обнаружено менее 12 узлов, рекомендуется использовать дополнительные методы улучшения зрения. 5 Выводы варьировались от 6 узлов 13 до 40 узлов. 14 Минимум в 12 узлов был одобрен многими группами, потому что было предположение о «убывающей отдаче» после изучения 12–17 узлов. 5 Однако неясно, улучшает ли более высокая скорость извлечения лимфатических узлов определение стадии рака толстой кишки, и причинно-следственный механизм между числом лимфатических узлов и выживаемостью остается неясным.
5 Выводы варьировались от 6 узлов 13 до 40 узлов. 14 Минимум в 12 узлов был одобрен многими группами, потому что было предположение о «убывающей отдаче» после изучения 12–17 узлов. 5 Однако неясно, улучшает ли более высокая скорость извлечения лимфатических узлов определение стадии рака толстой кишки, и причинно-следственный механизм между числом лимфатических узлов и выживаемостью остается неясным. 5 Количество пораженных лимфатических узлов также может отражать улучшенный иммунный ответ пациента; как таковая, взаимосвязь между количеством узлов и выживаемостью может быть искажена реакцией опухоль-хозяин, поскольку более сильный иммунологический ответ приводит к улучшению выживаемости. 16
5 Количество пораженных лимфатических узлов также может отражать улучшенный иммунный ответ пациента; как таковая, взаимосвязь между количеством узлов и выживаемостью может быть искажена реакцией опухоль-хозяин, поскольку более сильный иммунологический ответ приводит к улучшению выживаемости. 16  Кроме того, лапароскопические резекции толстой кишки должны проводиться по тем же стандартам, что и открытые операции. 17
Кроме того, лапароскопические резекции толстой кишки должны проводиться по тем же стандартам, что и открытые операции. 17  Предоперационная лучевая терапия, по-видимому, уменьшает количество исследованных лимфоузлов. 21 Неизвестно, уменьшает ли предоперационная химиолучевая терапия число лимфатических узлов в большей степени, чем только облучение. Из-за более широкого использования предоперационной лучевой терапии у пациентов с раком прямой кишки среднего и высокого риска прогностическое значение количества лимфатических узлов при раке прямой кишки менее ясно.
Предоперационная лучевая терапия, по-видимому, уменьшает количество исследованных лимфоузлов. 21 Неизвестно, уменьшает ли предоперационная химиолучевая терапия число лимфатических узлов в большей степени, чем только облучение. Из-за более широкого использования предоперационной лучевой терапии у пациентов с раком прямой кишки среднего и высокого риска прогностическое значение количества лимфатических узлов при раке прямой кишки менее ясно. 22
22  24 , 25 Количество лимфатических узлов, которые больницы исследуют в резекционных образцах рака толстой кишки, по-видимому, не оказывает существенного влияния на стадирование, использование адъювантной химиотерапии или выживаемость пациентов. 25 Вполне вероятно, что неучтенные факторы, связанные с пациентом или больницей, искажают взаимосвязь. Хотя существует консенсус в отношении того, что качество лечения рака можно улучшить, неясно, является ли обеспечение минимального количества лимфатических узлов правильной мерой качества для использования.
24 , 25 Количество лимфатических узлов, которые больницы исследуют в резекционных образцах рака толстой кишки, по-видимому, не оказывает существенного влияния на стадирование, использование адъювантной химиотерапии или выживаемость пациентов. 25 Вполне вероятно, что неучтенные факторы, связанные с пациентом или больницей, искажают взаимосвязь. Хотя существует консенсус в отношении того, что качество лечения рака можно улучшить, неясно, является ли обеспечение минимального количества лимфатических узлов правильной мерой качества для использования. При резекциях рака важно придерживаться строгих онкологических принципов, включая перевязку сосудов и полную резекцию брыжейки толстой кишки единым блоком, лимфаденэктомию и периферические края (при раке прямой кишки). Кроме того, патологоанатомам важно тщательно исследовать резецированные образцы.
При резекциях рака важно придерживаться строгих онкологических принципов, включая перевязку сосудов и полную резекцию брыжейки толстой кишки единым блоком, лимфаденэктомию и периферические края (при раке прямой кишки). Кроме того, патологоанатомам важно тщательно исследовать резецированные образцы. Энн Сург. 2006; 244: 602–610. [Бесплатная статья PMC] [PubMed] [Google Scholar]
Энн Сург. 2006; 244: 602–610. [Бесплатная статья PMC] [PubMed] [Google Scholar] Нью-Йорк, штат Нью-Йорк: Спрингер; 1997. Ободочная и прямая кишка; стр. 64–67. [Google Scholar]
Нью-Йорк, штат Нью-Йорк: Спрингер; 1997. Ободочная и прямая кишка; стр. 64–67. [Google Scholar] Для пациентов с колоректальной карциномой Dukes B (стадия II по TNM) исследование шести или менее лимфатических узлов связано с плохим прогнозом. Рак. 1998; 83: 666–672. [PubMed] [Академия Google]
Для пациентов с колоректальной карциномой Dukes B (стадия II по TNM) исследование шести или менее лимфатических узлов связано с плохим прогнозом. Рак. 1998; 83: 666–672. [PubMed] [Академия Google] Энн Сург. 2007;246:655–662. [PubMed] [Google Scholar]
Энн Сург. 2007;246:655–662. [PubMed] [Google Scholar] 2005; 61: 426–431. [PubMed] [Академия Google]
2005; 61: 426–431. [PubMed] [Академия Google] дои: 10.1259/0007-1285-68-807-266. PMid:7735765. [PubMed] [Академия Google]
дои: 10.1259/0007-1285-68-807-266. PMid:7735765. [PubMed] [Академия Google] doi:10.1016/j.ejrad.2003.10.020. PMid:15544903. [PubMed] [Google Scholar]
doi:10.1016/j.ejrad.2003.10.020. PMid:15544903. [PubMed] [Google Scholar] Эйнштейн Д.М., Сингер А.А., Чилкот В.А., Десаи Р.К. Абдоминальная лимфаденопатия: спектр данных КТ. Рентгенография. 1991; 11: 457–72. [PubMed] [Google Scholar]
Эйнштейн Д.М., Сингер А.А., Чилкот В.А., Десаи Р.К. Абдоминальная лимфаденопатия: спектр данных КТ. Рентгенография. 1991; 11: 457–72. [PubMed] [Google Scholar] Радиология. 1988;167:367–72. [PubMed] [Google Scholar]
Радиология. 1988;167:367–72. [PubMed] [Google Scholar] AJR Am J Рентгенол. 2000;175:759–66. [PubMed] [Google Scholar]
AJR Am J Рентгенол. 2000;175:759–66. [PubMed] [Google Scholar] , Кастеллино Р.А. Хиллиозные цистерны: потенциальная имитация ретрокруральной лимфаденопатии на КТ. Радиология. 1996; 199: 477–80. [PubMed] [Google Scholar]
, Кастеллино Р.А. Хиллиозные цистерны: потенциальная имитация ретрокруральной лимфаденопатии на КТ. Радиология. 1996; 199: 477–80. [PubMed] [Google Scholar] Спенсер Дж., Голдинг С. КТ-оценка состояния лимфатических узлов при раке предстательной железы. Бр Дж Радиол. 1992; 65: 199–201. дои: 10.1259/0007-1285-65-771-199. PMid:1547445. [PubMed] [Google Scholar]
Спенсер Дж., Голдинг С. КТ-оценка состояния лимфатических узлов при раке предстательной железы. Бр Дж Радиол. 1992; 65: 199–201. дои: 10.1259/0007-1285-65-771-199. PMid:1547445. [PubMed] [Google Scholar] 1016/S0009-9260(99)91158-3. [PubMed] [Google Scholar]
1016/S0009-9260(99)91158-3. [PubMed] [Google Scholar]
 Так называют числа, которые можно встретить в математических формулах, выражающих фундаментальные законы природы, — в физике, статистике, биологии или экономике.
Так называют числа, которые можно встретить в математических формулах, выражающих фундаментальные законы природы, — в физике, статистике, биологии или экономике. Значит, рост вклада зависит от того, сколько он пролежит в банке, то есть сколько раз начисляются проценты. А что будет через сто лет? А если найти такой банк, где процент начисляется не раз в год, а раз в день? И пусть даже каждый день начисляется совсем небольшой процент, но ведь дней-то много! Верно ли, что можно положить в такой банк один доллар под одну сотую процента в день, а через пару десятков лет забрать из банка миллион?
Значит, рост вклада зависит от того, сколько он пролежит в банке, то есть сколько раз начисляются проценты. А что будет через сто лет? А если найти такой банк, где процент начисляется не раз в год, а раз в день? И пусть даже каждый день начисляется совсем небольшой процент, но ведь дней-то много! Верно ли, что можно положить в такой банк один доллар под одну сотую процента в день, а через пару десятков лет забрать из банка миллион? Можно сказать, что будет стремиться к нулю.
Можно сказать, что будет стремиться к нулю. Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
 н. «интеграл Пуассона» или «интеграл Гаусса»
н. «интеграл Пуассона» или «интеграл Гаусса»
 Неправдоподобно предположение, что Эйлер выбрал e как первую букву в своей фамилии (нем. Euler).
Неправдоподобно предположение, что Эйлер выбрал e как первую букву в своей фамилии (нем. Euler). Затем — опять-таки равнобедренный прямоугольный треугольник.
Затем — опять-таки равнобедренный прямоугольный треугольник. В то время, в 60-е и 70-е годы, FORTRAN использовал только заглавные буквы. Возможно, это произошло потому, что большинство старых устройств ввода были телетайпами, работавшими с 5-битовым кодом Бодо, который не поддерживал строчные буквы. Буква E в экспоненциальной записи тоже была заглавной и не смешивалась с основанием натурального логарифма e, которое всегда записывается маленькой буквой. Символ E просто выражал экспоненциальный характер, то есть обозначал основание системы — обычно таким было 10. В те годы программисты широко использовали восьмеричную систему. И хотя я не замечал такого, но если бы я увидел восьмеричное число в экспоненциальной форме, я бы предположил, что имеется в виду основание 8. Первый раз я встретился с использованием маленькой e в экспоненциальной записи в конце 70-х годов, и это было очень неудобно. Проблемы появились потом, когда строчные буквы по инерции перешли в FORTRAN. У нас существовали все нужные функции для действий с натуральными логарифмами, но все они записывались прописными буквами.
В то время, в 60-е и 70-е годы, FORTRAN использовал только заглавные буквы. Возможно, это произошло потому, что большинство старых устройств ввода были телетайпами, работавшими с 5-битовым кодом Бодо, который не поддерживал строчные буквы. Буква E в экспоненциальной записи тоже была заглавной и не смешивалась с основанием натурального логарифма e, которое всегда записывается маленькой буквой. Символ E просто выражал экспоненциальный характер, то есть обозначал основание системы — обычно таким было 10. В те годы программисты широко использовали восьмеричную систему. И хотя я не замечал такого, но если бы я увидел восьмеричное число в экспоненциальной форме, я бы предположил, что имеется в виду основание 8. Первый раз я встретился с использованием маленькой e в экспоненциальной записи в конце 70-х годов, и это было очень неудобно. Проблемы появились потом, когда строчные буквы по инерции перешли в FORTRAN. У нас существовали все нужные функции для действий с натуральными логарифмами, но все они записывались прописными буквами.
 Вы также можете интерпретировать число Эйлера как основу экспоненциальной функции, значение которой всегда равно ее производной. Другими словами, e — единственное возможное число, такое что e x увеличивается со скоростью e x для каждого возможного x.
Вы также можете интерпретировать число Эйлера как основу экспоненциальной функции, значение которой всегда равно ее производной. Другими словами, e — единственное возможное число, такое что e x увеличивается со скоростью e x для каждого возможного x.

 Он обычно используется в широком спектре приложений, включая рост популяции живых организмов и радиоактивный распад тяжелых элементов, таких как уран, учеными-ядерщиками. Его также можно использовать в тригонометрии, вероятности и других областях прикладной математики.
Он обычно используется в широком спектре приложений, включая рост популяции живых организмов и радиоактивный распад тяжелых элементов, таких как уран, учеными-ядерщиками. Его также можно использовать в тригонометрии, вероятности и других областях прикладной математики. 9{rt}\\&\textbf{где:}\\&\text{FV} = \text{Будущая стоимость}\\&\text{PV} =\text{Текущая стоимость баланса или суммы}\\&e = \text{Формула Эйлера}\\&r = \text{Процентная ставка начисляется}\\&t = \text{Время в годах}\end{выровнено}
FV=PVertwhere:FV=Будущее значениеPV=Текущая стоимость баланса или = Формула Эйлера=Процентная ставка начисляется t=Время в годах есть: 9{ 12 \ умножить на 3 } = \ $ 1061,78
$1000(1+12,02)12×3=$1061,78
9{rt}\\&\textbf{где:}\\&\text{FV} = \text{Будущая стоимость}\\&\text{PV} =\text{Текущая стоимость баланса или суммы}\\&e = \text{Формула Эйлера}\\&r = \text{Процентная ставка начисляется}\\&t = \text{Время в годах}\end{выровнено}
FV=PVertwhere:FV=Будущее значениеPV=Текущая стоимость баланса или = Формула Эйлера=Процентная ставка начисляется t=Время в годах есть: 9{ 12 \ умножить на 3 } = \ $ 1061,78
$1000(1+12,02)12×3=$1061,78 Другим случаем является радиометрическое датирование, когда ожидается, что количество радиоактивных атомов уменьшится в течение фиксированного периода полураспада измеряемого элемента.
Другим случаем является радиометрическое датирование, когда ожидается, что количество радиоактивных атомов уменьшится в течение фиксированного периода полураспада измеряемого элемента. Он часто появляется в задачах, связанных с экспоненциальным ростом или спадом, где скорость роста пропорциональна существующему населению. В финансах, e также используется в расчетах сложных процентов, когда богатство растет с заданной скоростью с течением времени.
Он часто появляется в задачах, связанных с экспоненциальным ростом или спадом, где скорость роста пропорциональна существующему населению. В финансах, e также используется в расчетах сложных процентов, когда богатство растет с заданной скоростью с течением времени.  Это число, как и π, является иррациональным числом, потому что оно имеет неповторяющуюся десятичную дробь, простирающуюся до бесконечности. Подобно иррациональному человеку, иррациональное число кажется бессмысленным, но число, которое обозначает e, не обязательно должно иметь смысл, чтобы быть полезным. На самом деле, это одно из самых полезных чисел в математике.
Это число, как и π, является иррациональным числом, потому что оно имеет неповторяющуюся десятичную дробь, простирающуюся до бесконечности. Подобно иррациональному человеку, иррациональное число кажется бессмысленным, но число, которое обозначает e, не обязательно должно иметь смысл, чтобы быть полезным. На самом деле, это одно из самых полезных чисел в математике. Например, число 1 миллион можно записать как 1E6. В обычной научной записи это 1 × 10 6 , или 1 с 6 нулями. Точно так же 5 миллионов будут 5E6, а 42 732 будут 4,27E4. При написании числа в экспоненциальном представлении, независимо от того, используете ли вы E или нет, вы обычно округляете число до двух знаков после запятой.
Например, число 1 миллион можно записать как 1E6. В обычной научной записи это 1 × 10 6 , или 1 с 6 нулями. Точно так же 5 миллионов будут 5E6, а 42 732 будут 4,27E4. При написании числа в экспоненциальном представлении, независимо от того, используете ли вы E или нет, вы обычно округляете число до двух знаков после запятой.
 А конкретно к углам α (альфа) и β (бета), которые наглядно показаны на следующем рисунке.
А конкретно к углам α (альфа) и β (бета), которые наглядно показаны на следующем рисунке.
 Решили мы тут вспомнить, для чего же мы все изучали все эти синусы и косинусы. И в итоге разговор свелся к тому, что «где-то они все-таки нужны, наверное. Зачем-то их изучают».
Решили мы тут вспомнить, для чего же мы все изучали все эти синусы и косинусы. И в итоге разговор свелся к тому, что «где-то они все-таки нужны, наверное. Зачем-то их изучают». Даже их Боги не ездили на машинах, не пользовались мобильной связью, не общались по Интернету. Зато всё это есть у нас и мы постоянно этим пользуемся. Откуда же всё это невиданное богатство взялось? Его создали мы сами. Сперва ученые делали научные открытия. Потом инженеры, на основании сделанных учеными открытий, создавали всякие полезные штуки. Мы сегодня этими штуками пользуемся, не имея ни малейшего понятия о том, что находится внутри этих штук и какие научные законы положены в основу их работы. Так вот, если бы не было синусов и косинусов, не было бы и всех этих клевых штук.
Даже их Боги не ездили на машинах, не пользовались мобильной связью, не общались по Интернету. Зато всё это есть у нас и мы постоянно этим пользуемся. Откуда же всё это невиданное богатство взялось? Его создали мы сами. Сперва ученые делали научные открытия. Потом инженеры, на основании сделанных учеными открытий, создавали всякие полезные штуки. Мы сегодня этими штуками пользуемся, не имея ни малейшего понятия о том, что находится внутри этих штук и какие научные законы положены в основу их работы. Так вот, если бы не было синусов и косинусов, не было бы и всех этих клевых штук. При помощи синусов и косинусов углы можно превратить в длины или координаты точек на земной поверхности.
При помощи синусов и косинусов углы можно превратить в длины или координаты точек на земной поверхности. То, что мы этим инструментом почти никогда не пользуемся, говорит не о том, что изучать их не надо, а о том, что эффективность применения полученных нами знаний практически равна нулю. Но это уже совсем другая тема.
То, что мы этим инструментом почти никогда не пользуемся, говорит не о том, что изучать их не надо, а о том, что эффективность применения полученных нами знаний практически равна нулю. Но это уже совсем другая тема.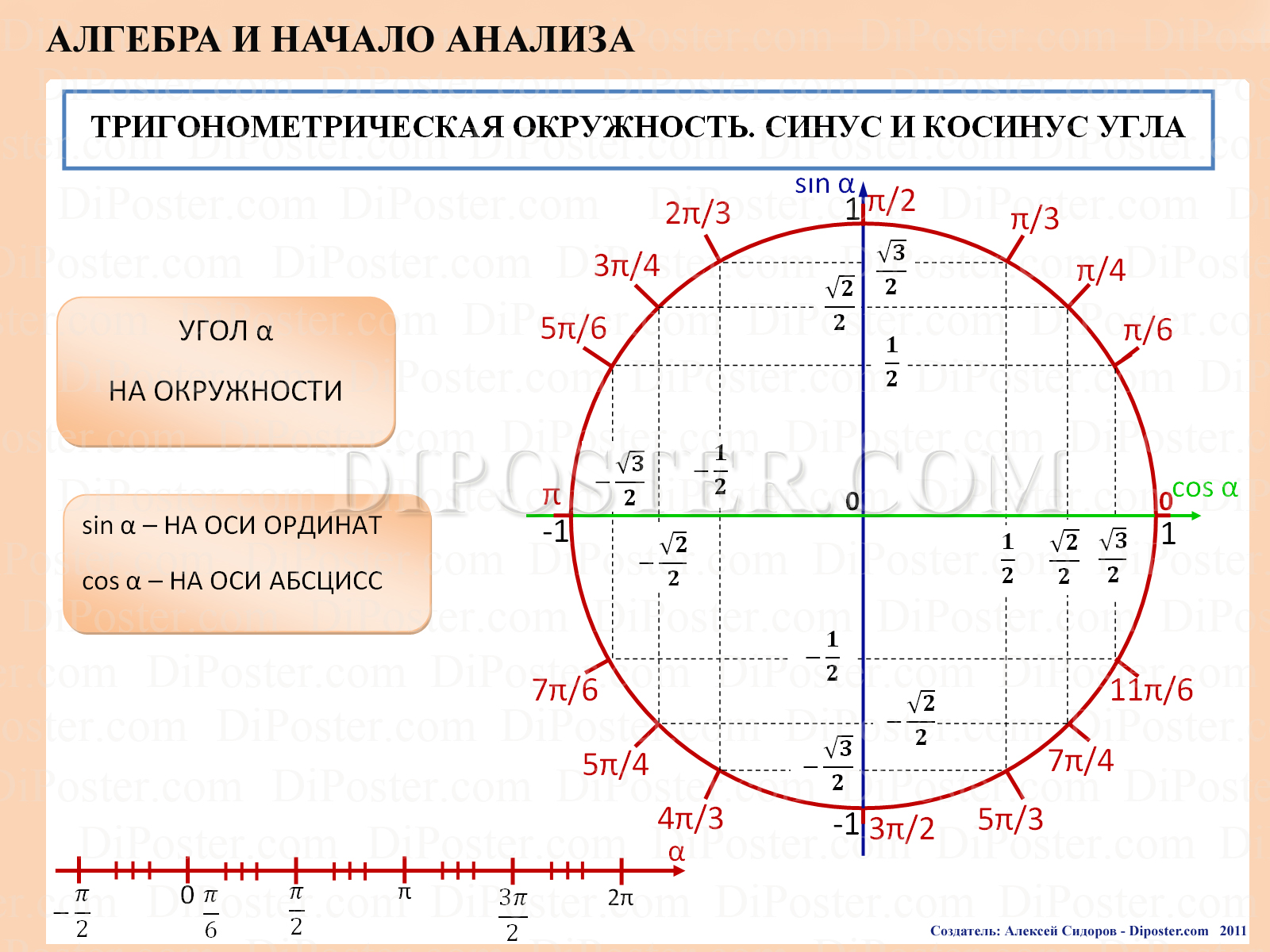 Например, \(\sin 0=0,\) означает, что точка \((0,0)\) является точкой на синусоидальном графике. Если мы нанесем значения функции синуса для большого числа углов \(\theta\), мы увидим, что точки образуют кривую, называемую синусоида :
Например, \(\sin 0=0,\) означает, что точка \((0,0)\) является точкой на синусоидальном графике. Если мы нанесем значения функции синуса для большого числа углов \(\theta\), мы увидим, что точки образуют кривую, называемую синусоида :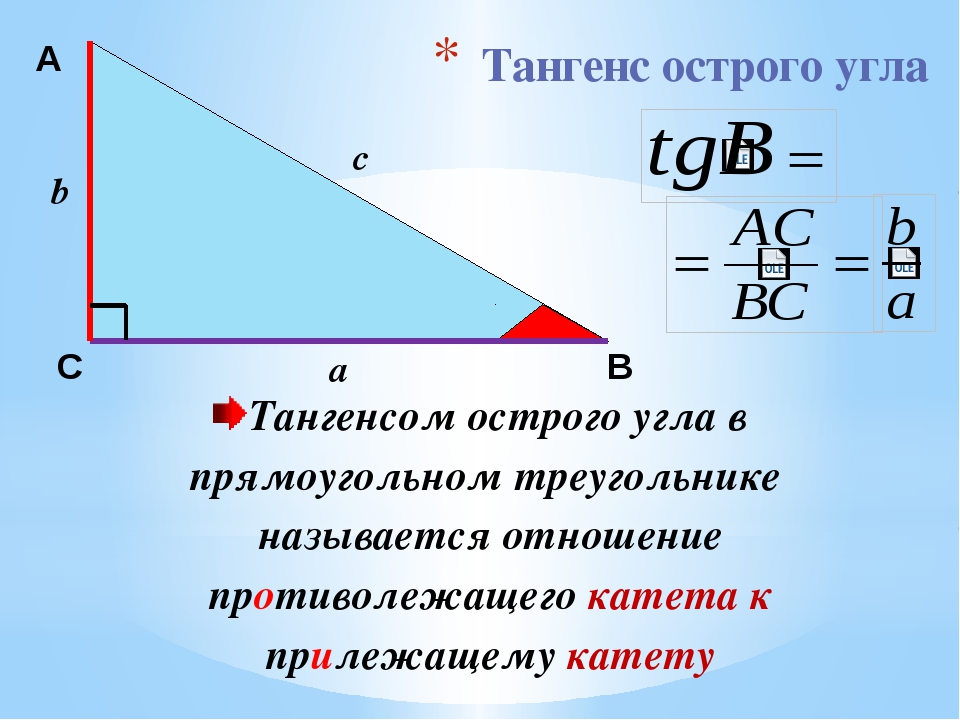 \(_\квадрат\)
\(_\квадрат\)


 \ _\квадрат \]
\ _\квадрат \]

 SRT.6 Геометрия для старших классов
SRT.6 Геометрия для старших классов 
 Вы можете использовать Sin, потому что дано обратное, а гипотенуза отсутствует.
Вы можете использовать Sin, потому что дано обратное, а гипотенуза отсутствует.  Сегодня мы собираемся установить, как найти грех и косинус. Давайте рассмотрим, Sin острого угла равен противоположному по гипотенузе. Косинус острого угла равен прилежащему к гипотенузе. Как мы определяем, какая сторона какая? Сначала давайте посмотрим на угол A из угла a, мы должны посмотреть на наши исходные стороны. Если мы пойдем на нашу противоположную сторону, это будет наша противоположная сторона, и я обозначу ее как противоположную. Гипотенуза (обозначенная h) всегда находится напротив угла схватки, поэтому она примыкает к углу А или находится рядом с ним. (обозначенная а) Теперь давайте добавим некоторые измерения. Предположим, что противоположная сторона равна 6, а гипотенуза равна 10, чтобы найти мой грех, он будет противоположен гипотенузе, поэтому грех угла А будет равен 6/10, что является моей противоположностью гипотенузе. Косинус примыкает к гипотенузе. Длина а неизвестна, поэтому я могу использовать теорему Пифагора, чтобы найти эту сторону. Итак, я возьму в квадрате плюс b в квадрате, что равно 6, плюс с, что равно 10 в квадрате, поэтому, чтобы записать это, я получаю a^2+6^2 = 10^2, что становится a^2+36=100, поэтому a^2 равно 64, поэтому длина A должна быть равна 8 (возьмите квадратный корень из 64).
Сегодня мы собираемся установить, как найти грех и косинус. Давайте рассмотрим, Sin острого угла равен противоположному по гипотенузе. Косинус острого угла равен прилежащему к гипотенузе. Как мы определяем, какая сторона какая? Сначала давайте посмотрим на угол A из угла a, мы должны посмотреть на наши исходные стороны. Если мы пойдем на нашу противоположную сторону, это будет наша противоположная сторона, и я обозначу ее как противоположную. Гипотенуза (обозначенная h) всегда находится напротив угла схватки, поэтому она примыкает к углу А или находится рядом с ним. (обозначенная а) Теперь давайте добавим некоторые измерения. Предположим, что противоположная сторона равна 6, а гипотенуза равна 10, чтобы найти мой грех, он будет противоположен гипотенузе, поэтому грех угла А будет равен 6/10, что является моей противоположностью гипотенузе. Косинус примыкает к гипотенузе. Длина а неизвестна, поэтому я могу использовать теорему Пифагора, чтобы найти эту сторону. Итак, я возьму в квадрате плюс b в квадрате, что равно 6, плюс с, что равно 10 в квадрате, поэтому, чтобы записать это, я получаю a^2+6^2 = 10^2, что становится a^2+36=100, поэтому a^2 равно 64, поэтому длина A должна быть равна 8 (возьмите квадратный корень из 64). Теперь я могу решить для A. Cos of A будет 8 на 10, потому что он смежн по гипотенузе, и именно так я бы решил. Вы также можете посмотреть из угла B, противоположная сторона будет здесь нижним углом, примыкающая здесь, а гипотенуза всегда находится напротив прямого угла. Таким образом, противоположное и соседнее будут переворачиваться в зависимости от того, под каким углом. Надеюсь, это было полезно.
Теперь я могу решить для A. Cos of A будет 8 на 10, потому что он смежн по гипотенузе, и именно так я бы решил. Вы также можете посмотреть из угла B, противоположная сторона будет здесь нижним углом, примыкающая здесь, а гипотенуза всегда находится напротив прямого угла. Таким образом, противоположное и соседнее будут переворачиваться в зависимости от того, под каким углом. Надеюсь, это было полезно. 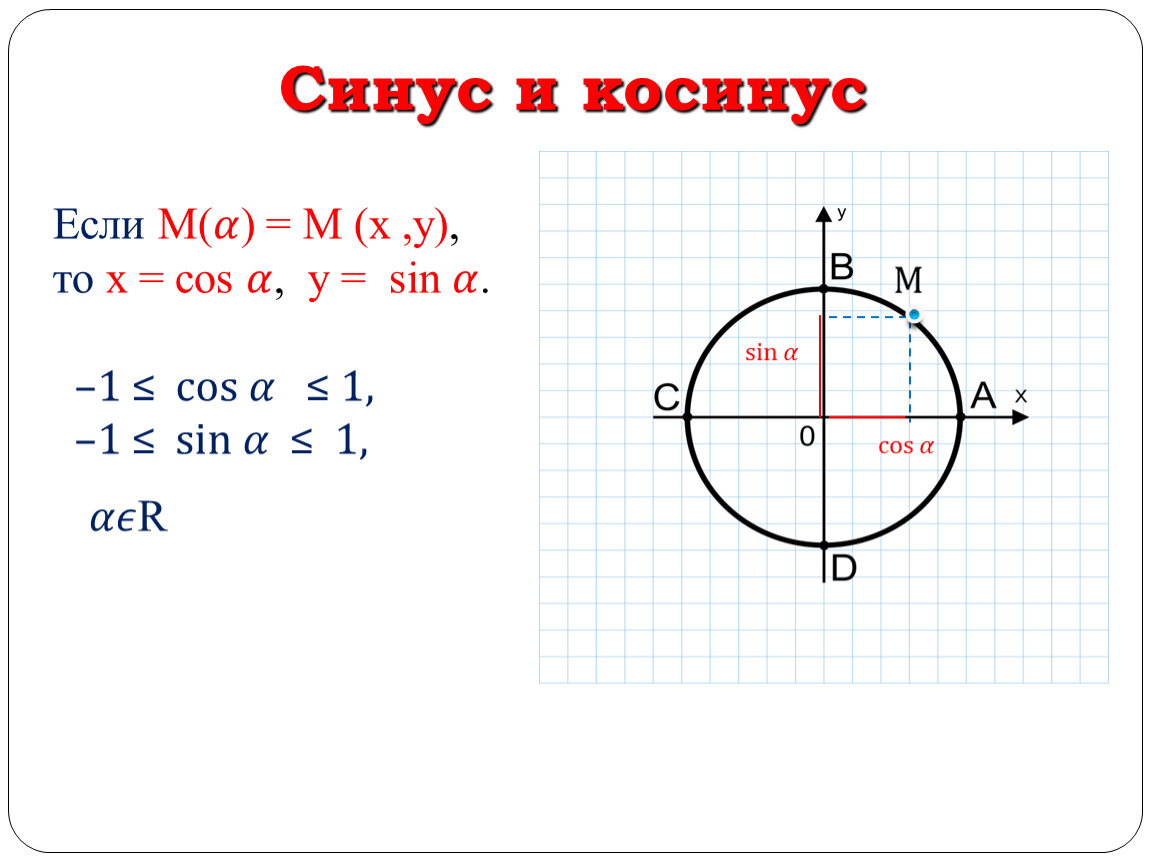
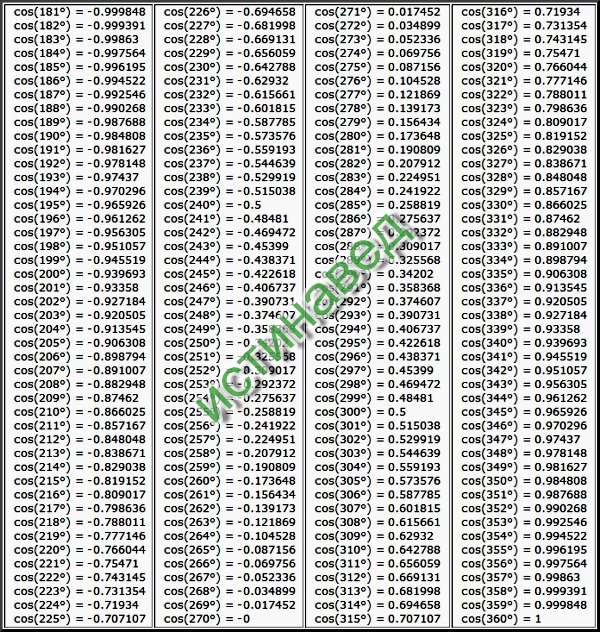 o=\frac{1}{16}(-1+\sqrt{17}+\sqrt{34-2\sqrt{17}}+ 2\sqrt{17+3\sqrt{17}- \sqrt{34-2\sqrt{17}}- 2\sqrt{34+2\sqrt{17}}})$
o=\frac{1}{16}(-1+\sqrt{17}+\sqrt{34-2\sqrt{17}}+ 2\sqrt{17+3\sqrt{17}- \sqrt{34-2\sqrt{17}}- 2\sqrt{34+2\sqrt{17}}})$ д.
д.  Наиболее распространенными углами являются: 0, 30, 45, 60 и 90 , и для этих углов нам обычно приходится запоминать таблицу «Тригонометрических соотношений стандартных углов», которая может быть ошеломляющей и казаться «ракетной наукой». .
Наиболее распространенными углами являются: 0, 30, 45, 60 и 90 , и для этих углов нам обычно приходится запоминать таблицу «Тригонометрических соотношений стандартных углов», которая может быть ошеломляющей и казаться «ракетной наукой». .
 Принцип единства
Принцип единства  Так, темой 2021 года были семейные ценности. А темой 2022 года станут эмоции и чувства.
Так, темой 2021 года были семейные ценности. А темой 2022 года станут эмоции и чувства. 11.2017
4596
11.2017
4596
 Ответив на вопросы этой викторины, вы узнаете, что праздник 1 мая также известен нам и под другими названиями: Праздник весны, Первомай, Праздник Труда, а также День международной солидарности трудящихся. И, что в такой день обычно состоятся парады, проходят празднества. Люди встречаются, в праздник 1 мая, на главной площади страны, где для горожан начинают выступать разные творческие, танцевальные коллективы, а также работают ярмарки. У этого праздника есть своя история и традиции, которые вам, вашим близким и друзьям будет полезно узнать.
Ответив на вопросы этой викторины, вы узнаете, что праздник 1 мая также известен нам и под другими названиями: Праздник весны, Первомай, Праздник Труда, а также День международной солидарности трудящихся. И, что в такой день обычно состоятся парады, проходят празднества. Люди встречаются, в праздник 1 мая, на главной площади страны, где для горожан начинают выступать разные творческие, танцевальные коллективы, а также работают ярмарки. У этого праздника есть своя история и традиции, которые вам, вашим близким и друзьям будет полезно узнать. 11.2017
2252
0
11.2017
2252
0
 12.2022
30
0
12.2022
30
0
 К.А. Тимирязева) по направлению Профессиональное обучение (заочно).
85-100% — отлично; 70-84% — хорошо; 60 — 69 % — удовлетворительно
К.А. Тимирязева) по направлению Профессиональное обучение (заочно).
85-100% — отлично; 70-84% — хорошо; 60 — 69 % — удовлетворительно Проверка своих личных качеств может помочь вам определить степень созависимости в вашей жизни. Пожалуйста, ответьте на все вопросы правдиво. Обычно первый ответ, который пришел вам в голову, является самым правдивым и самым точным.
Заранее благодарим за помощь!
Проверка своих личных качеств может помочь вам определить степень созависимости в вашей жизни. Пожалуйста, ответьте на все вопросы правдиво. Обычно первый ответ, который пришел вам в голову, является самым правдивым и самым точным.
Заранее благодарим за помощь!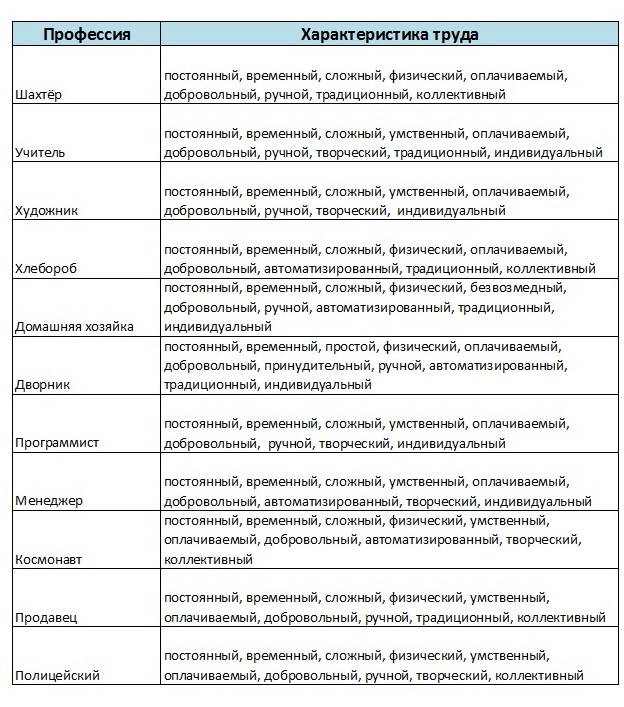 04.2018
199
0
04.2018
199
0
 Внимательно читай условие задание прежде чем его выполнить.
Внимательно читай условие задание прежде чем его выполнить.
 Выберите один и несколько правильных ответов.
Выберите один и несколько правильных ответов. 09.2022
4
0
09.2022
4
0
 Можно стать кем угодно: врачом, экономистом, продавцом, учителем, адвокатом и т. д., всё зависит от вашего желания и способностей. Нельзя сказать, что есть плохие профессии. К выбору своей профессии нужно подойти с большой ответственностью ведь от этого выбора напрямую зависит, с чем вы свяжете своё будущие. Прежде всего, ваш выбор зависит от того, чем бы вы хотели заниматься, но когда задумываемся о том, кем быть, нельзя забывать, что у всякой профессии свои требования к человеку. Бывает так, что тебе нравится профессия, а по состоянию здоровья она противопоказана. Разные виды труда требуют от человека разных качеств характера.
Можно стать кем угодно: врачом, экономистом, продавцом, учителем, адвокатом и т. д., всё зависит от вашего желания и способностей. Нельзя сказать, что есть плохие профессии. К выбору своей профессии нужно подойти с большой ответственностью ведь от этого выбора напрямую зависит, с чем вы свяжете своё будущие. Прежде всего, ваш выбор зависит от того, чем бы вы хотели заниматься, но когда задумываемся о том, кем быть, нельзя забывать, что у всякой профессии свои требования к человеку. Бывает так, что тебе нравится профессия, а по состоянию здоровья она противопоказана. Разные виды труда требуют от человека разных качеств характера.

 Расчетное влияние 17-альфа-гидроксипрогестерона капроата на преждевременные роды в США. Акушерство Гинекол. 2005;105:267-72.
Расчетное влияние 17-альфа-гидроксипрогестерона капроата на преждевременные роды в США. Акушерство Гинекол. 2005;105:267-72. Если тест PreTRM был заказан для пациента, не предназначенного для данного теста, следует проявлять осторожность при интерпретации результатов персонализированного риска.
Если тест PreTRM был заказан для пациента, не предназначенного для данного теста, следует проявлять осторожность при интерпретации результатов персонализированного риска. Однако ваш врач может порекомендовать следующие лекарства:
Однако ваш врач может порекомендовать следующие лекарства:

 Если у вас диагностирована короткая шейка матки до 24-й недели беременности, ваш лечащий врач может также рекомендовать использование прогестерона до 37-й недели беременности.
Если у вас диагностирована короткая шейка матки до 24-й недели беременности, ваш лечащий врач может также рекомендовать использование прогестерона до 37-й недели беременности. Если у вас схватки, которые, по вашему мнению, могут быть симптомом преждевременных родов, попробуйте ходить, отдыхать или менять положение. Это может остановить ложные родовые схватки. Однако, если у вас настоящие преждевременные роды, ваши схватки продолжатся.
Если у вас схватки, которые, по вашему мнению, могут быть симптомом преждевременных родов, попробуйте ходить, отдыхать или менять положение. Это может остановить ложные родовые схватки. Однако, если у вас настоящие преждевременные роды, ваши схватки продолжатся.


