12 лучших шахматных онлайн-сайтов | Советы/Руководства
Узнав немного больше об игре королей, давайте поговорим о лучших шахматных онлайн-сайтах, чтобы вы могли проверить свои знания. Необязательно быть гроссмейстером, как Бобби Фишер, чтобы играть в шахматы. На самом деле, вам даже не нужна шахматная доска (но если она вам нужна, у нас есть отличные предложения в статье, следите за обновлениями). Все, что вам нужно, это приличное подключение к Интернету и один из тех удивительных сайтов для онлайн-шахмат, где вы можете научиться играть или отточить свои навыки против других игроков. Если вы не знаете правил игры, не беда, мы все объясняем здесь!
Вообще говоря, большинство шахматных сайтов предлагают сбалансированный набор ресурсов для игры в шахматы и изучения того, как эта игра работает. Они также предлагают варианты как для обычных рейтинговых матчей, так и для турниров. Сайты также отлично подходят для обзора игр и просмотра прямых трансляций профессионалов, участвующих в глобальных турнирах, и большинство из них поддерживает многоязычие, поскольку шахматы — это игра, любимая во всем мире.
резюме
Быстрый FAQ
Какой самый лучший бесплатный шахматный онлайн-сайт?
Топ-5 бесплатных шахматных сайтов
Chess.com
LICHESS
Chess24
Интернет Шахматный Клуб
playchess.com
На каком шахматном сайте больше всего возможностей?
Chess.com (бесплатно, с дополнительными опциями) — один из лучших сайтов для игры и обучения игре в шахматы. Вы можете получить к нему доступ в Интернете или через приложения для iOS и Android. На сайте есть феноменальные инструменты и ресурсы для начинающих и гроссмейстеров.
Кто играл в шахматы против компьютера?
Гарри Каспаров
В финальной партии матча из шести партий чемпион мира по шахматам Гарри Каспаров одерживает победу над Deep Blue, шахматным компьютером IBM, и выигрывает матч со счетом 4: 2. Однако в следующем году Deep Blue победил Каспарова в широко разрекламированном матче-реванше.
Кто изобрел шахматы?
Шахматы были изобретены в Индии примерно в XNUMX веке. Затем он был известен как чатранг и менялся на протяжении веков арабами, персами и, наконец, средневековыми европейцами, которые изменили названия и внешний вид фигур, чтобы они напоминали английский двор.
Затем он был известен как чатранг и менялся на протяжении веков арабами, персами и, наконец, средневековыми европейцами, которые изменили названия и внешний вид фигур, чтобы они напоминали английский двор.
Шахматные онлайн-сайты, чтобы играть, учиться и многое другое
Новым игрокам или тем, кто хочет улучшить свои навыки, следует выбрать сайт, который предлагает надежные инструменты обучения, от уроков и головоломок до видеоуроков и инструкторов по тактике. Это поможет вам не только знать основы, но и научиться думать, как шахматный мастер. А если вы хотите стать серьезным, на некоторых сайтах даже есть профессиональные тренеры, которых вы можете нанять для регулярных занятий, которые помогут научить вас тактике, анализу и стратегиям.
Chess.com
Chess.comChess.com (бесплатно, с опциями премиум-класса) — один из лучших сайтов, где можно поиграть и научиться играть в шахматы. Вы можете получить к нему доступ в Интернете или через приложения для iOS и Android. На сайте есть феноменальные инструменты и ресурсы для начинающих и гроссмейстеров. (Иногда вы даже можете увидеть, как кто-то играет там, например, Магнус Карлсен или Хикару Накамура.)
На сайте есть феноменальные инструменты и ресурсы для начинающих и гроссмейстеров. (Иногда вы даже можете увидеть, как кто-то играет там, например, Магнус Карлсен или Хикару Накамура.)
На сайте есть множество вариантов игр и головоломок с искусственным интеллектом, турниров и образовательных ресурсов. Вы можете легко найти противника на своем уровне, независимо от того, хотите ли вы играть в игру в реальном времени или «матчем» (вы делаете свой ход, а другой игрок, находясь в сети, делает свой ход). Вы даже можете отслеживать свою позицию в таблице лидеров, в которой хранится статистика для трех миллионов пользователей сайта.
Уроки сайта ранжируются от абсолютного начала игры (обучение тому, как перемещать каждую фигуру) до освоения маневров уровня (таких как продвинутая тактика и шаблоны эндшпиля). Вы также можете смотреть прямые трансляции от опытных игроков, просматривать ключевые партии и просматривать список шахматных экспертов (включая гроссмейстеров), которых можно нанять в качестве вашего тренера по шахматам. Или, если вы эксперт, вы можете присоединиться к PRO Chess League или Chess.com Speed Chess Championship.
Или, если вы эксперт, вы можете присоединиться к PRO Chess League или Chess.com Speed Chess Championship.
Базовое членство является бесплатным и позволяет вам играть в неограниченное количество игр в реальном времени и по почте, а также участвовать в форумах. Три премиальных плана варьируются от 20 до 59 реалов в месяц и предлагают доступ к дополнительным функциям, таким как неограниченное количество головоломок и уроков, игровые отчеты и аналитика, а также неограниченный доступ к видеотеке. Независимо от того, решите вы перейти на платный план или нет, Chess.com предлагает бесценные функции, которые должны понравиться как обычным, так и профессиональным игрокам.
И если вам интересно, да, вот где Фелипе Нето был забанен за обман.
LICHESS
LICHESSЕще один отличный сайт для тактических тренировок — это LICHESS, бесплатный сайт. Сайт является сервером с открытым исходным кодом, поэтому на нем нет рекламы или платного доступа премиум-класса, и вы можете получить доступ к сайту онлайн или через свои приложения для iOS и Android. Вы можете играть против друга или ИИ или участвовать в швейцарских турнирах, ежедневных или ежемесячных турнирах Арены или одновременных выставках. Если вы новичок, вы можете начать работу с функцией Lichess ‘Chess Basics, попробовать свои силы в решении различных головоломок, потренироваться и изучить или даже нанять опытного тренера по шахматам.
Вы можете играть против друга или ИИ или участвовать в швейцарских турнирах, ежедневных или ежемесячных турнирах Арены или одновременных выставках. Если вы новичок, вы можете начать работу с функцией Lichess ‘Chess Basics, попробовать свои силы в решении различных головоломок, потренироваться и изучить или даже нанять опытного тренера по шахматам.
В дополнение к стандартным играм Lichess также поддерживает различные типы игр, такие как Crazy House, Chess Fischer, King of the Hill, 3-Check, Anti-Chess, Atomic Chess, Horde Chess и Race of Kings, и вы можете установить ваши собственные параметры для увеличения количества игр и минут для каждой стороны, чтобы сделать их ходы.
Сайт имеет интеграцию с Twitch, поэтому вы можете смотреть игры в шахматы со всего мира, не покидая сайта. Вы также можете просмотреть исторические игры в библиотеке сайта или просмотреть форум сообщества, чтобы найти информацию о сайте или игре.
Chess24
Chess24Хотя главная страница сайта, похоже, ориентирована на турниры, Chess24 (бесплатно с опциями премиум-класса) также имеет фантастические инструменты для обучения. Есть вкладка для просмотра живых турниров и других событий между играми, или вы можете найти что-нибудь для покупки в магазине товаров на сайте.
Есть вкладка для просмотра живых турниров и других событий между играми, или вы можете найти что-нибудь для покупки в магазине товаров на сайте.
У новых игроков есть множество вариантов обучения, таких как шахматные курсы Chess24, серии видео (с уроками от лучших игроков), электронные книги, тренер по тактике, а также база данных и анализ движений. Playzone Chess24 позволяет легко играть в игру, с возможностью играть против ранжированных противников с различным контролем времени или в турнире. Существует регулярно обновляемое табло игроков и тренер по тактике, доступный в Интернете и в приложении для iOS.
Однако, чтобы получить доступ к некоторым из этих функций, вам необходимо перейти на один из премиальных планов, стоимость которых варьируется от 14,99 долларов в месяц или 12,50 долларов в год (в реалах нет такой возможности). Обновление дает вам полный доступ ко всему на сайте, например к электронным книгам и видео, тактическому обучению, анализу игр, премиальному обучению в режиме реального времени от опытных тренеров и многому другому.
Интернет Шахматный Клуб
ICCДо Chess.com и Lichess существовала Интернет Шахматный Клуб (от 9,95 долларов в месяц). Это один из старейших шахматных серверов, и, хотя другие сайты украли его блеск, ICC по-прежнему остается отличным местом для игры против других крупных игроков, многие из которых имеют титулы. Сайт работает по предоплате и по подписке, но предлагает 30-дневную бесплатную пробную версию.
Интернет-шахматный клуб предлагает множество возможностей для обучения и игры в шахматы. Хотя регистрация бесплатной учетной записи позволяет вам играть в ограниченные бесплатные игры и получать доступ к более чем 3.000 видеоуроков на сайте, вы получите максимальную отдачу от сайта, перейдя на платный план. Оттуда вы можете играть на сайте и в турнирах с рейтингом USCF, проходить шахматные курсы и практиковаться в Учебном центре ICC, следить за элитными глобальными шахматными турнирами и смотреть, как соревнуются гроссмейстеры.
На сайте есть обширный список тренеров, которых можно нанять, если вам нужна помощь в развитии или оттачивании своих шахматных навыков. Точно так же игровые возможности ICC также надежны: еженедельные онлайн-турниры, казуальные игры с друзьями и официальные рейтинговые онлайн-турниры шахматной федерации США.
Точно так же игровые возможности ICC также надежны: еженедельные онлайн-турниры, казуальные игры с друзьями и официальные рейтинговые онлайн-турниры шахматной федерации США.
Вы можете приглашать своих друзей и зарабатывать на них деньги, читать последние шахматные новости и общаться с другими игроками на форумах. Есть даже продуктовый магазин, где вы можете купить всевозможные шахматные угощения, от одежды и DVD до досок и книг. С помощью ICC вы можете загрузить клиент на свои устройства Windows, Mac, Kindle и Chromebook или через приложения для iOS и Android.
Научитесь играть в шахматы у лучших учителей
Бестселлер # 1
Моя система: первый учебник по шахматам
ценаБестселлер # 2
Обучать и изучать шахматы
Бестселлер # 3
Как научиться играть в шахматы
playchess.
 comИграть в шахматы
comИграть в шахматыplaychess.com (бесплатно с дополнительными опциями) управляется ChessBase, которая сделала популярное шахматное программное обеспечение. Он предлагает всевозможные возможности для участия в мире шахмат, от тренировок и игры до учебы и даже наблюдения за игрой гроссмейстеров на турнирах. Вы также можете просматривать профили других игроков, в том числе гроссмейстеров, а также просматривать их ходы и игровую статистику.
В Playchess есть игры для новичков, которые могут дать вам ограниченное количество подсказок, или вы можете играть в обычную игру с элементами управления временем (например, пуля, блиц или медленные игры) и без подсказок. А если вы в основном профессионал, вы можете принять участие в турнире и (надеюсь) выиграть приз. Сайт также предлагает большую базу данных из более чем восьми миллионов игр и даже позволяет хранить ваши собственные игры в облаке для дальнейшего анализа.
Для обучения сайт предлагает множество обучающих видео, тактических тренировок и инструментов для разработки и применения ваших дебютных стратегий. Хотя этот сайт — единственный в нашем сравнении, который не предлагает мобильное приложение, стоит проверить его библиотеку обучающих инструментов и вариантов игрового процесса, независимо от вашего уровня или рейтинга.
Хотя этот сайт — единственный в нашем сравнении, который не предлагает мобильное приложение, стоит проверить его библиотеку обучающих инструментов и вариантов игрового процесса, независимо от вашего уровня или рейтинга.
Шахматный темп
Шахматный темпO ChessTime предлагает место для игры в шахматы онлайн бесплатно, но настоящая ценность этого сайта заключается в его многочисленных ресурсах для анализа и понимания игры. Каждый раз, когда вы играете в рейтинговую игру, ChessTempo проходит через мощный механизм анализа, который предоставляет подробную статистику о том, что произошло в игре. Позволит вам узнать больше о вашем собственном стиле игры.
ChessTempo на самом деле предназначен для людей, которые уже знают основы игры в шахматы, но хотят улучшить свои навыки, пройдя серьезную тренировку по шахматной тактике. Бесплатная версия сайта уже предлагает хардкорную тактическую подготовку, и если у вас закончится то, что есть в вашем распоряжении, вы будете более чем готовы начать платить за услугу, так как к этому моменту вы будете есть и дышать шахматами.
Другие хорошие сайты для игры в шахматы онлайн
Некоторые другие сайты могут помочь вам учиться и тренироваться, прежде чем вы начнете играть на большом сайте с самыми известными шахматистами в мире. Давайте выделим несколько хороших сайтов, на которых вы можете поиграть, если вы ищете варианты, отличные от больших порталов.
FICS: бесплатный шахматный сервер в Интернете
FICSFICS — один из старейших шахматных онлайн-серверов. Первоначально он был создан как бесплатная альтернатива ICC, когда ICC начала взимать с игроков плату за членство. Поскольку официального интерфейса FICS нет, то для игры на этом сервере необходимо загрузить совместимый интерфейс.
GameKnot
узелGameKnot — один из крупнейших шахматных сайтов с доступом только по электронной почте, насчитывающий более миллиона участников, и играть в него можно бесплатно. Интерфейс приятный, есть другие функции, такие как игровая база данных, тактическое обучение и аннотированные игры.
Красная горячая пешка
Красная горячая пешкаЕще один единственный сайт по доставке по почте с большой базой игроков, Красная горячая пешка в нем есть турниры и лестницы, а также команды (называемые на веб-сайте «кланами») и другие игровые режимы. Базовая подписка бесплатна, но поставляется с подпиской премиум-класса для расширенных функций.
Выйдите из сети и воспользуйтесь возможностью взять доску домой и изучить расширенные правила Игры Королей.
Бестселлер # 1
Игра Шахматы Шашка Нарды Деревянная Доска 3 В 1 …
ценаБестселлер # 2
Шахматы школы Ксалинго, Многоцветный
ценаБестселлер # 3
Магнитный шахматный набор 19,5 x 19,5 см
chessworld.net
Шахматный мирchessworld.net — популярный заочный шахматный сайт, основанный популярным влогером по шахматам Трифоном Гавриилом, также известным как Kingscrusher. Базовое членство является бесплатным, но есть ряд дополнительных функций, доступных для платных участников.
Базовое членство является бесплатным, но есть ряд дополнительных функций, доступных для платных участников.
ItYourTurn.com
Твоя очередьГораздо более простой вариант, чем другие, и лучше для обычных игроков, чем для тех, кто ищет серьезную конкуренцию. ItYourTurn.com предлагает простую игру на совпадение. Большим преимуществом этого сайта является большое количество других игр, в которые вы можете играть — Нарды и Морской бой!
Sparkchess
SparkchessSparkchess — один из самых ограниченных вариантов бесплатных шахмат в этом списке. Хотя вы можете играть против компьютера и других людей онлайн, вы лишены доступа к обучающим функциям по шахматам, если не заплатите за премиум-версию. Если все, что вам нужно, это быстрая онлайн-игра, у Sparkchess есть хорошая веб-версия своего шахматного приложения.
А теперь оставьте в комментариях, какой сайт, по вашему мнению, является лучшим для игры. Вы подписаны на какие-либо премиальные сайты? У вас есть какие-нибудь рекомендации? Оставьте это в комментариях и наслаждайтесь прочтением. чаевые на нашем сайте.
чаевые на нашем сайте.
Шахматы онлайн и без регистрации. Пять лучших сайтов
13.07.2018
«Живу Спортом» рассказывает, где можно устроить интеллектуальный шахматный баттл, не выходя из дома.
Предполагается, что более 600 миллионов людей постоянно играют в шахматы. Недавно было проведено исследование, которое доказало, что количество шахматистов увеличивается. Ранее были опасения, что всеми любимая интеллектуальная игра умрёт из-за того, что все участники научатся пользоваться компьютерными программами, но время идёт, а шахматы продолжают развиваться. На сайтах научились бороться с мошенниками, и теперь любой шахматист вне зависимости от уровня подготовки может найти себе оппозицию в онлайн-режиме и не думать, что его обманывают.
«Живу Спортом» рассказывает, где можно играть в шахматы онлайн, лучшие шахматные ресурсы с живыми игроками, в том числе и без регистрации. Пять лучших шахматных сайтов специально для вас.
Lichess. org
org
По мнению большей части игроков, лучший ресурс для игры в шахматы. Сайт предлагает не только классические партии, но и рассчитан на современных шахматистов. Молодёжь не любит ждать, поэтому на Lichess.org активно развиваются быстрые игры. Возможно, проводить партии даже за три и пять минут. Как? Очень просто – побеждает тот, у кого остаётся больше фигур на доске.
Lichess.org – самый популярный шахматный ресурс. Каждый вечер здесь собирается более 30 тысяч игроков разного уровня. Доступно играть не только онлайн, но и с компьютером, выбирая уровень сложности.
Большой плюс ресурса – обучающий раздел. В формате видео здесь показывают примеры из игр профессионалов. Ученикам предлагается сборник шахматных задач, направленный на постепенный прогресс начинающего шахматиста.
Chess.com
Самый известный шахматный ресурс. Количество игроков в онлайне переваливает за 70 тысяч. У сайта практически идеальная репутация за счёт политики честной игры, которая лишает шахматистов беспокойства относительно мошенничества соперников. На Chess.com доступны великолепные инструменты для обучения. Можно не только смотреть видео лучших игроков в мире, но и проходить специально выстроенную программу тренировок.
На Chess.com доступны великолепные инструменты для обучения. Можно не только смотреть видео лучших игроков в мире, но и проходить специально выстроенную программу тренировок.
Chess.com привлекает не только классической игрой за компьютером, но и возможностью заниматься любимым делом в дороге. У Chess.com доступны шахматные приложения для любых устройств.
Ещё один плюс – наличие аккаунтов звёзд на сайте. Например, здесь зарегистрирован легендарный чемпион мира Магнус Карлсен.
Chessgames
Очень простой ресурс, не перегруженный лишней информацией. Рассчитан, скорее, на опытных любителей шахмат, кому не слишком интересна посторонняя мишура, нужна только сама игра. Здесь вы не увидите шахматных звёзд, яркого интерфейса, странных вариаций шахматных баталий. Очень простой ресурс, но имеет существенный минус. Бесплатная игра ограничена по времени. Для тех, кто заинтересовался – годовая подписка обойдётся в 30 евро.
Chess-samara. ru
ru
Очень интересный ресурс от шахматных энтузиастов. Сайт с очень простым интерфейсом, однако постоянно обновляется и выполнен с душой. Можно сказать, что на ресурсе царит домашняя атмосфера, шахматисты годами заходят на этот ресурс. Уровень игры выше среднего, но есть место и для новичков. Портал работает уже 13 лет и продолжает держать высокую планку в своей работе.
Chesswood
Chesswood – ресурс больше ориентированный на новичков. Очень большой раздел с тренировочными материалами. Портал предлагает необычные шахматные задачи, уроки от известных тренеров, а также редкие тренажёры. Разобраться в премудростях шахмат новичкам помогают с помощью видеороликов с реальных турниров под комментарии профессионалов.
Сама игра достаточно необычна. Можно выбирать цвет шахмат, доски и другие параметры. Сайт также является информационным ресурсом. Заходя на Chesswood, вы всегда будете в курсе того, как играют профессионалы.
Автор: Георгий Шаков.
Теги: Лайфхак, Шахматы
лучших сайтов для игры в онлайн-шахматы в 2021 году | Майкл Заги | Знакомство с шахматами
Выбор правильной платформы важен для вашего общего опыта и роста как шахматиста. Я рассматриваю некоторые из наиболее популярных вариантов, доступных сегодня, чтобы вы могли принять обоснованное решение о том, с чего начать.
Фото Харуна Бенли с сайта pexels.com Учитывая приток новых шахматистов, впервые прибывающих в сообщество (и, в конечном итоге, на шахматные веб-сайты), я подумал, что было бы неплохо рассмотреть некоторые из наиболее популярных вариантов. Моя цель здесь не в том, чтобы высказать свое мнение о том, что такое «лучший» шахматный сайт в целом. Вместо этого я хочу сосредоточить этот обзор на том, какая из платформ лучше всего подходит для абсолютного новичка. Это означает, что с учетом таких функций, как; доступ к турнирам мирового уровня и их освещение на самом деле не будут рассматриваться. Наконец, обзор основан только на бесплатных функций, доступных на каждом сайте, использующем их веб-платформу (и не мобильных ).
Просто чтобы уточнить, что я имею в виду под «абсолютным новичком», я имею в виду любого, кто никогда не играл в игру до того, чтобы знать, куда двигаются фигуры ( т.е. они играли, но не имеют глубокого понимания стратегии и тактика). При этом некоторые критерии по-прежнему будут актуальны для любого уровня игрока, поэтому обзор должен по-прежнему иметь определенную ценность для всех.
- Пользовательский интерфейс (UI) и общее взаимодействие с пользователем (UX): Является ли сайт чистым, отзывчивым и простым в навигации?
- Особенности обучения: Предоставляет ли сайт функции и контент, предназначенные для начинающих?
- Сообщество: Существуют ли группы пользователей (клубы), друзья, турниры и связанный с сообществом контент, который будет поддерживать интерес и участие пользователей?
- Уникальные особенности: Любые примечательные особенности, которые отличают сайт от конкурентов.

Каждому критерию будет присвоен весовой коэффициент 5 для наилучшего возможного результата 20/20.
Общий балл: 17,5/20
Описание
Lichess — это шахматный веб-сайт с открытым исходным кодом, которым управляют всего два или три разработчика. У него одна из самых больших баз игроков, и на момент написания этой статьи я вижу около 80 000 пользователей, находящихся в сети. Сайт существует с 2014 года, но, насколько я помню, большую популярность он приобрел только за последние три года или около того. На мой взгляд, Lichess наиболее известен своей простотой, стильным дизайном пользовательского интерфейса и регулярными турнирами, которые очень популярны среди шахматного сообщества. Кроме того, это 100% бесплатно.
Пользовательский интерфейс и общее взаимодействие с пользователем
Оценка: 5/5
У Lichess лучший пользовательский интерфейс и UX со значительным отрывом. Платформа проста и оптимизирована, чтобы вы могли найти игру или другой контент как можно быстрее. Страницы загружаются быстро, а доска отзывчива. Кроме того, сайт не перегружен (какими-либо) надоедливыми дополнениями, которые постоянно перезагружаются, пока вы пытаетесь играть.
Страницы загружаются быстро, а доска отзывчива. Кроме того, сайт не перегружен (какими-либо) надоедливыми дополнениями, которые постоянно перезагружаются, пока вы пытаетесь играть.
Особенности обучения
Оценка: 5/5
Lichess делает его простым, но эффективным с точки зрения обучающих функций и содержания. Он использует интерактивные модули, которые заинтересуют и вовлекут нового пользователя. Самое главное, у Lichess есть бесплатный тренер по тактике, который является таким же всеобъемлющим, как и любой другой. Обратите внимание, что на других сайтах это обычно платная функция. Наконец, вы получаете полную аналитическую доску с Stockfish, работающей на полную глубину.
Сообщество
Оценка: 3,5/5
Lichess имеет довольно стандартные функции сообщества. По сути, вы можете присоединиться к командам, которые могут проводить свои собственные турниры и иметь свои собственные форумы. Существует также глобальный форум для всего сайта. Что касается чата, у вас есть варианты только внутриигрового чата и глобального лобби чата.
Что касается чата, у вас есть варианты только внутриигрового чата и глобального лобби чата.
Уникальные особенности
Счет: 4/5
У Lichess есть несколько очень популярных турнирных сетапов, которые действительно отличают его от конкурентов. В частности, его турниры на аренах включают в себя функцию, с помощью которой вы можете сократить свое время в начале игры, чтобы получить возможность удвоить свои очки на табло. Команда Lichess также организует турниры «24-часовой марафон», в которых участвует множество игроков. Помимо турниров, у вас также есть возможность играть во множество различных вариантов шахмат, таких как Crazyhouse, chess960 и Царь горы, которые стоит изучить.
Заключение
Мой голос за лучший шахматный сайт для начинающих от Lichess. Он придерживается основ и имеет самые важные функции, которые вы ожидаете от шахматного веб-сайта (и реализует их очень хорошо). Как я уже упоминал ранее, это также бесплатно. Хотя я уважаю тот факт, что многие премиальные подписки стоят денег для активного шахматиста, маловероятно, что новый игрок захочет сразу вложить деньги.
Счет: 16/20
Описание
Chess.com — крупнейшая шахматная платформа и самое популярное место для онлайн-шахмат. На момент написания этой статьи я вижу 315 000 игроков онлайн. Он также имеет самое большое количество титулованных игроков по сравнению с любым другим сайтом. Chess.com существует в той или иной форме с конца 90-х годов. Хотя chess.com всегда был популярным местом для новых игроков (вероятно, из-за отличного доменного имени), я помню, что у меня были серьезные проблемы с их платформой, и я предпочитал настольные клиенты ICC (Internet Chess Club) и Playchess (рассмотрено позже). Это было в конце 2000-х и начале 2010-х, когда я играл больше всего. Примерно в 2016 году они переработали свой медленный пользовательский интерфейс и привлекли много титулованных игроков, таких как (Хикару Накамура). Совсем недавно они активно участвовали в потоковом сообществе в twitch.tv и в результате значительно выросли.
Пользовательский интерфейс и общее взаимодействие с пользователем
Оценка: 4/5
Пользовательский интерфейс chess. com выглядит прилично, отзывчив и довольно быстро загружается. Что касается UX для новых игроков, я думаю, что платформа слишком загружена. Компонент живых шахмат хорош, но в целом я бы сказал, что сайт страдает от слишком многих функций (на боковой панели). Было бы интересно посмотреть, сколько из них на самом деле регулярно используется игроками. Я чувствую, что все эти опции могут быть немного сложными или ненужными для новых игроков.
com выглядит прилично, отзывчив и довольно быстро загружается. Что касается UX для новых игроков, я думаю, что платформа слишком загружена. Компонент живых шахмат хорош, но в целом я бы сказал, что сайт страдает от слишком многих функций (на боковой панели). Было бы интересно посмотреть, сколько из них на самом деле регулярно используется игроками. Я чувствую, что все эти опции могут быть немного сложными или ненужными для новых игроков.
Особенности обучения
Счет: 3/5
Chess.com предлагает множество отличных обучающих материалов, но большинство из них оплачивается пользователями. Это включает в себя тренер по тактике (который, я думаю, является самым важным инструментом для новых игроков). Они дают вам своего рода бесплатную пробную версию, но она ограничена тремя головоломками в день. Видеоконтент отличный, но опять же, за членством. Вероятно, наиболее заметными бесплатными учебными материалами являются упражнения 9.0014 (например, эндшпили, маты и т. д.). Я бы сказал, что он сравним с модулями Lichess, о которых я говорил ранее.
д.). Я бы сказал, что он сравним с модулями Lichess, о которых я говорил ранее.
Сообщество
Счет: 5/5
Сообщество является одной из сильных сторон chess.com. Вы получаете полные и настраиваемые профили пользователей, клубы, форумы и блоги. Они также поддерживают сообщество, участвуя в прямых трансляциях, контенте и турнирах. Значительная часть этого контента ориентирована на новичков.
Уникальные особенности
Счет: 4/5
Chess.com предлагает ежедневные шахматы, которые в основном представляют собой шахматы по переписке (играются в течение нескольких дней или месяцев). Если вас это интересует, я думаю, что chess.com — единственный сайт из четырех, который предлагает это. Сайт также предлагает даже больше вариантов шахмат, чем Lichess. Опять же, большинство интересных функций, которые отличают chess.com, находятся за платным доступом.
Заключение
Я придерживаюсь общего мнения, что на данный момент у Chess. com лучшая шахматная платформа. У них больше всего игроков, самое большое сообщество и шахматные личности, а также самый титулованный игрок. Но, ставя себя на место начинающих шахматистов, я должен отдать Lichess преимущество за его доступность. Если вы настолько увлечены шахматами, что хотите начать платить за дополнительный контент, я думаю, что в какой-то момент переход на chess.com будет естественным переходом.
com лучшая шахматная платформа. У них больше всего игроков, самое большое сообщество и шахматные личности, а также самый титулованный игрок. Но, ставя себя на место начинающих шахматистов, я должен отдать Lichess преимущество за его доступность. Если вы настолько увлечены шахматами, что хотите начать платить за дополнительный контент, я думаю, что в какой-то момент переход на chess.com будет естественным переходом.
Счет: 11.5/20
Описание
Chess24 была основана в 2014 году и поддерживается рядом известных и ведущих гроссмейстеров, таких как чемпион мира Магнус Карлсен и экс-чемпион мира Вишванатан Ананд. На момент написания этой статьи в сети было около 3000 пользователей. Честно говоря, раньше я не слишком много играл на Chess24, но провел там несколько дней, играя в игры и изучая их платформу, готовясь к этому обзору. Насколько я понимаю, они наиболее известны своим освещением турниров, экспертным контентом и видео. Они также показывают Магнуса Карлсена и других ведущих гроссмейстеров в своей серии видео «Banter Blitz».
Пользовательский интерфейс и общий пользовательский интерфейс
Оценка: 3/5
На самом деле я не слишком большой поклонник пользовательского интерфейса Chess24. Это кажется немного вялым и устаревшим. Еще одна проблема, с которой я столкнулся, — это размер платы. Я использую 15-дюймовый монитор, и размер по умолчанию практически не воспроизводится. Вы можете переключиться на больший размер, что делает его играбельным (но все еще маленьким). Конечно, вы можете использовать функцию масштабирования в своем браузере, но в этом нет необходимости. Кроме этого, я думаю, что сайт довольно интуитивно понятен для навигации и поиска того, что вы ищете.
Особенности обучения
Оценка: 3/5
Chess24 имеет хороший набор модулей (разделенных на «Правила шахмат», «Фиски» и «Мат»). В целом, я бы сказал, что это самый подробный бесплатный учебник на любом сайте, но я чувствую, что большинство новичков предпочли бы 100% взаимодействие, которое обеспечивают модули Lichess. Chess24 сочетает в себе чтение, видео и некоторое взаимодействие для каждого модуля. Если это больше ваша чашка чая, то, возможно, стоит проверить. Помимо этого, Chess24, кажется, не предлагает много других функций. Тренер по тактике ограничен пятью головоломками в день для бесплатных учетных записей. Даже если вы хотите платить за контент, есть очень мало обучающих видео для игроков менее 1200 эло.
Chess24 сочетает в себе чтение, видео и некоторое взаимодействие для каждого модуля. Если это больше ваша чашка чая, то, возможно, стоит проверить. Помимо этого, Chess24, кажется, не предлагает много других функций. Тренер по тактике ограничен пятью головоломками в день для бесплатных учетных записей. Даже если вы хотите платить за контент, есть очень мало обучающих видео для игроков менее 1200 эло.
Сообщество
Оценка: 2,5/5
Сообщество Chess24 в основном состоит из простого форума и стандартных функций чата. Важно отметить, что здесь нет клубов или команд. Когда я проверял сайт, в турнирах участвовало очень мало людей, примерно 5–10, если их было достаточно, чтобы начать его с самого начала.
Уникальные функции
Оценка: 2/5
Что касается бесплатных вещей, то Chess24 не предлагает ничего уникального или особенного.
Заключение
На мой взгляд, chess.com и Lichess предлагают все то же, что и Chess24, но лучше. При этом я ни в коем случае не считаю, что Chess24 плохи, просто они больше ориентированы на другую аудиторию. Если вам нравится следить за международными турнирами и вы готовы платить за высококачественный контент, я думаю, что Chess24 — хороший вариант.
При этом я ни в коем случае не считаю, что Chess24 плохи, просто они больше ориентированы на другую аудиторию. Если вам нравится следить за международными турнирами и вы готовы платить за высококачественный контент, я думаю, что Chess24 — хороший вариант.
Оценка: 10/20
Описание
Playchess — это шахматный сервер, управляемый ChessBase, который, вероятно, является одной из старейших (до сих пор действующих) шахматных мультимедийных компаний. Я думаю, что они лучше всего известны своим шахматным движком Fritz и их ChessBase (базой данных) игр, которая является одной из крупнейших. Просто предупреждение: их браузерная версия Playchess пригодна для использования, но довольно ужасна. Мне потребовалось немного времени, чтобы найти, но у них все еще есть свой настольный клиент (правда, только для Windows), поэтому вместо этого я буду использовать его для обзора. Это своего рода мошенничество, так как я говорю «веб-сайты» в заголовке, но, насколько я знаю, у них есть лучший бесплатный настольный клиент, поэтому я думаю, что стоит обратить на это внимание людей. На момент написания этой статьи у Playchess было около 1000 пользователей онлайн.
На момент написания этой статьи у Playchess было около 1000 пользователей онлайн.
Пользовательский интерфейс и общее взаимодействие с пользователем
Оценка: 4/5
Пользовательский интерфейс красиво оформлен, а доступ ко всем функциям с помощью интуитивно понятных значков прост и ясен. Сам пользовательский интерфейс, вероятно, не изменился за последние 10 лет, но он не кажется слишком устаревшим.
Функции обучения
Оценка: 2,5/5
В Playchess не так уж много функций обучения. Вы получаете бесплатную тактику через их онлайн-приложение, но она настолько же проста, насколько и функциональна. Насколько я мог судить, он не сохраняет ваш рейтинг, а головоломки кажутся случайными. Есть несколько интересных типов игр (например, та, в которой вам разрешено использовать ограниченное количество различных типов подсказок во время игры — что-то вроде Jeopardy), но я не думаю, что одного этого достаточно, чтобы оправдать использование Playchess. Как и на большинстве других сайтов, за подпиской стоят обучающие видео и (полный) тренер по тактике.
Как и на большинстве других сайтов, за подпиской стоят обучающие видео и (полный) тренер по тактике.
Сообщество
Оценка: 1/5
Единственная приятная особенность Playchess заключается в том, что вы получаете различные каналы чата. К сожалению, не так много людей, с которыми можно пообщаться. Клубы существуют, но в основном они немецкие, так как Chessbase оттуда. Турниры проводятся в определенное время, но не на регулярной основе. Наконец, похоже, что для их платформы не существует какого-либо форума.
Уникальные функции
Оценка: 2,5/5
Я просто скажу, что их настольный клиент позволяет им реализовывать некоторые функции способами, которые вы не сможете реализовать в веб-браузере. Это немного отличает Playchess. В остальном все достаточно стандартно.
Заключение
Похоже, что база пользователей Playchess сильно пострадала из-за таких сайтов, как Chess.com и Lichess. Опять же, я думаю, что платформа заслуживает упоминания, но как новичок я не думаю, что их бесплатный контент будет очень полезен для вашего развития.
- Lichess.org: 17.5/20
- Chess.com: 16/20
- Chess24: 11.5 7 Плей 0
Написание отзыва может показаться излишним. вот так, ведь шахматы есть шахматы. Тем не менее, у новых игроков гораздо больше шансов остаться, если они найдут солидное сообщество игроков своего уровня. Хорошо изложить все варианты, чтобы люди могли получить представление о ландшафте и принять взвешенное решение. Надеюсь, по крайней мере, эта статья сэкономит вам немного времени. Кроме того, дайте мне знать ваше мнение о любом из этих сайтов, и если я упустил какие-либо важные детали.
13 лучших платформ для игры в шахматы онлайн
Шахматы, развлечение с тысячелетней историей, продолжают пользоваться повышенным вниманием. Понятно, что у вас может не быть возможности насладиться настоящей шахматной доской. К счастью, вы можете использовать многие шахматные онлайн-платформы, чтобы получить доступ к полезному шахматному сообществу в несколько кликов.
Веб-сайты и приложения предлагают различные функции и предназначены для разных аудиторий. Здесь мы рассмотрим 13 лучших платформ для игры в шахматы онлайн и то, что каждая из них может предложить.
1. Amphy
Чтобы начать наш список, Amphy — отличная платформа для обучения игре в шахматы. Благодаря множеству классов, предназначенных как для начинающих, так и для продвинутых игроков, каждый найдет урок.
Продолжительность видеороликов на платформе Amphy варьируется от 30 минут до 2 часов, так что вы можете ежедневно смотреть несколько видеороликов, которые научат вас различным вещам, связанным с шахматами. Каждое видео посвящено отдельному навыку, движению или стилю игры, что дает вам всестороннюю возможность обучения.
2. Chess.com
Эта платформа является одной из лучших для обучения и игры в шахматы. Chess.com доступен в Интернете или через приложения для Android и iOS.
Платформа предлагает широкий выбор головоломок и игр с искусственным интеллектом и живыми играми, обучающими ресурсами и турнирами. Кроме того, сайт предоставляет быстрый способ найти противников вне зависимости от вашего уровня.
Кроме того, сайт предоставляет быстрый способ найти противников вне зависимости от вашего уровня.
Он также имеет исчерпывающую таблицу лидеров со статистикой для более чем трех миллионов пользователей платформы; следовательно, вы можете легко отслеживать свое положение.
3. ChessTempo
Хотя это может быть одна из бесплатных платформ для игры в шахматы, ценность ChessTempo заключается в ее многочисленных ресурсах для понимания и анализа игры.
Платформа позволяет вам играть в неограниченное количество онлайн-игр и получать доступ к анализу движка ваших рейтинговых игр. Вы также получите доступ к базе данных записанных игр и будете решать две задачи на эндшпиль ежедневно.
Платформа предназначена не только для людей, которые понимают основы. Вы также можете отточить свои навыки с помощью серьезной тактической подготовки.
4. Lichess
Lichess — это игровая платформа и сервер с открытым исходным кодом. Вы можете играть против ИИ или друга, но у вас также есть возможность участвовать в турнирах Арены, сеансах одновременной игры и швейцарских турнирах.
Эта платформа доступна в Интернете, но вы также можете загрузить ее приложения для Android и iOS, чтобы играть на ходу.
5. Sparkchess
Sparkchess — одна из лучших платформ для онлайн-шахмат, но ее бесплатная версия — одна из самых ограниченных. Хотя вы можете выбирать между противником-человеком или искусственным интеллектом, вы не можете получить доступ к функциям обучения.
Тем не менее, веб-версия платформы отличается полноэкранным режимом игры и трехмерной шахматной доской. Бесплатные пользователи могут тренироваться против трех разных противников ИИ. Тем не менее, вы должны вложить деньги, чтобы насладиться соревнованиями для двух игроков в реальном времени.
6. Playchess
Стоит попробовать еще одну популярную шахматную онлайн-платформу Playchess. Эта платформа является детищем ChessBase и предлагает различные варианты участия в мире шахмат.
Помимо регулярных турниров, вы можете изучить игру, потренироваться и даже посмотреть, как сражаются гроссмейстеры. Кроме того, вы можете просматривать профили других участников, статистику и игровые ходы.
Кроме того, вы можете просматривать профили других участников, статистику и игровые ходы.
7. Listudy
Если вы еще новичок в игре, попробуйте бесплатный Listudy, удобный для начинающих.
Эта шахматная платформа идеально подходит для тех, кто пытается запомнить стратегии, благодаря методу интервального повторения для улучшения памяти.
Платформа позволяет вам периодически изучать и практиковать такие стратегии, как скандинавская защита и ферзевый гамбит. Он также имеет базу данных тактик, которые вы можете использовать, чтобы проверить себя.
Вы можете использовать множество шахматных онлайн-платформ, чтобы получить доступ к полезному шахматному сообществу в несколько кликов.
8. Интернет-шахматный клуб
Также известная как ICC, это была ведущая онлайн-игра в шахматы. Но за последние несколько лет его обогнали конкуренты. Тем не менее, он входит в число лучших и доступен для пользователей iOS и Android.
Платформа предлагает широкие возможности для обучения и игры, а ее бесплатная версия позволяет вам получить доступ к ограниченным бесплатным играм и более 3000 видеоуроков.
Отличные функции доступны в платном плане, где вы можете участвовать в соревнованиях с рейтингом USCF и на сайтах, проходить курсы, смотреть соревнования гроссмейстеров и следить за элитными турнирами мира.
9. MBChess
Если ваша личная информация является приоритетом, MBChess может стать идеальной платформой для вас. Сайт позволяет вам развлекаться, играть и зарабатывать, не беспокоясь о раскрытии ваших данных.
Популярная платформа имеет удобный интерфейс. Вы можете начать играть онлайн бесплатно, развивать свое мастерство и участвовать в соревнованиях, где вы сможете заработать настоящие деньги. Но на вашей учетной записи игрока должны быть реальные очки, прежде чем вы будете соревноваться за наличные.
10. Red Hot Pawn
Red Hot Pawn была разработана, чтобы доставить уникальный опыт игрокам, предпочитающим медленные шахматы. На других сайтах в этом списке есть вариант шахмат по переписке, но эта платформа полностью сосредоточена на этом подходе. Таким образом, легче присоединяться, управлять и разрабатывать игры по переписке.
Таким образом, легче присоединяться, управлять и разрабатывать игры по переписке.
Эта платформа имеет функциональную доску и большое, информативное, поддерживающее онлайн-сообщество. Почти все бесплатно. Единственное преимущество платной подписки в том, что она избавляет от назойливой рекламы.
11. Chessable
Chessable относительно новая и небольшая платформа, но она является одной из лучших платформ для игры в шахматы онлайн. Платформа больше ориентирована на обучение, чем на игру, и может помочь вам изучить стратегии эндшпиля, миттельшпиля и дебюта. В результате это один из самых надежных сайтов для изучения теории и техники шахмат.
Эта платформа позволяет вам практиковать изученную тактику и получать доступ к ценным книгам по шахматам. Подписки на видеоуроки относительно дороже, но они того стоят. К сожалению, вы не можете соревноваться с реальными игроками.
12. Chess2Play
Эта платформа выделяется своим пользовательским интерфейсом. Несмотря на то, что Chess2Play в основном работает через Интернет и доступен только через браузер, он невероятно удобен для мобильных устройств. Это позволяет играть в любимую настольную игру на ходу.
Несмотря на то, что Chess2Play в основном работает через Интернет и доступен только через браузер, он невероятно удобен для мобильных устройств. Это позволяет играть в любимую настольную игру на ходу.
Сайт позволяет делать ставки против других игроков в игре и выигрывать реальные деньги. Он также предлагает официальные турниры трижды в месяц. Однако вы будете платить комиссию, основанную на ваших выигрышах или розыгрышах в официальных соревнованиях.
13. Chesskid
ChessKid, дочерняя компания Chess.com, позволяет юным любителям шахмат развивать свои навыки в безопасной среде. Сайт предлагает все, что нужно вашему ребенку, чтобы овладеть искусством. Он также поставляется с родительским контролем, чтобы ограничить обмен контактами и неразрешенные чаты.
Детям также нравится веселый видеоконтент, который поможет им освоить игру. Это также без рекламы, и вам не нужно ничего платить за доступ к играм. Тем не менее, участники со статусом Gold наслаждаются неограниченным количеством видео и головоломок.



 Принято выделять следующие их виды:
Принято выделять следующие их виды: Причина
Причина
 Он еще и немного меняется в течение года из-за того, что орбита Земли не круговая, а эллиптическая.
Он еще и немного меняется в течение года из-за того, что орбита Земли не круговая, а эллиптическая.

 С 7 по 9 класс. Геометрия — углы и градусы. Объяснение 1. С 7 по 9 класс.
С 7 по 9 класс. Геометрия — углы и градусы. Объяснение 1. С 7 по 9 класс.
 Соответствующие углы в
подобные треугольники равны по размеру. Это правило относится ко всем
многоугольники.
Соответствующие углы в
подобные треугольники равны по размеру. Это правило относится ко всем
многоугольники.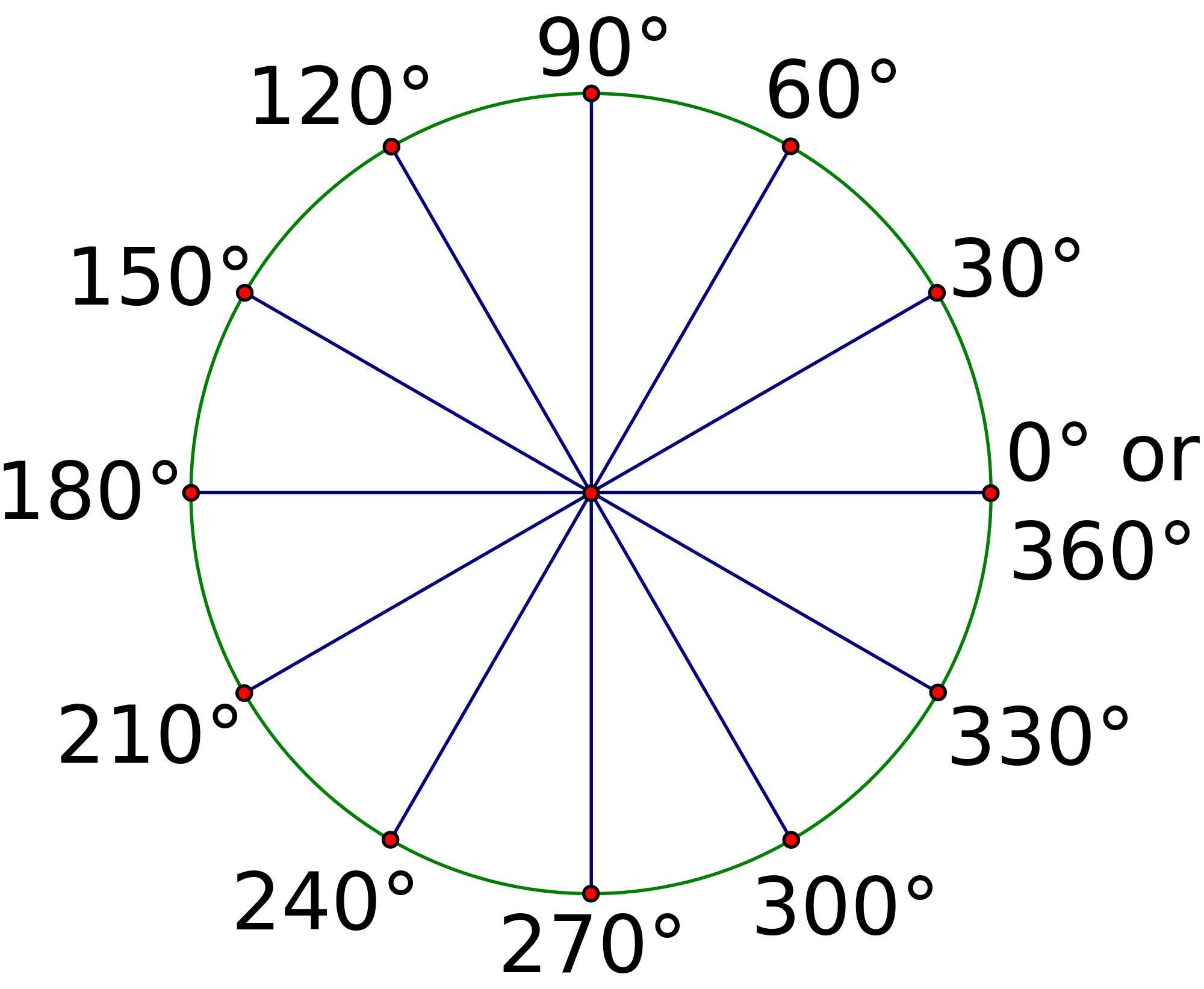
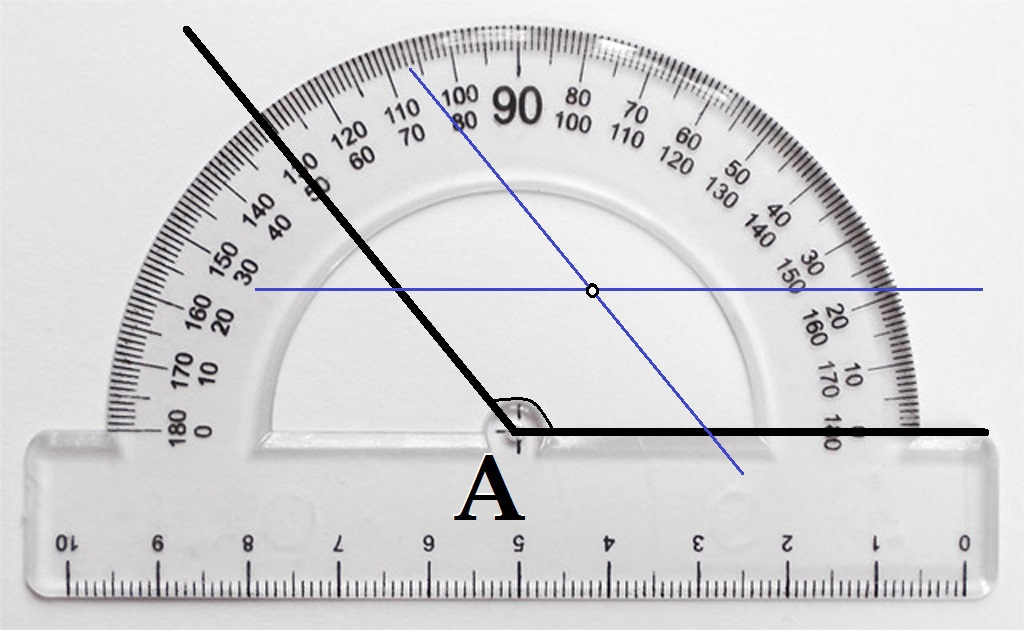 {\circ}\) }\) .
{\circ}\) }\) .
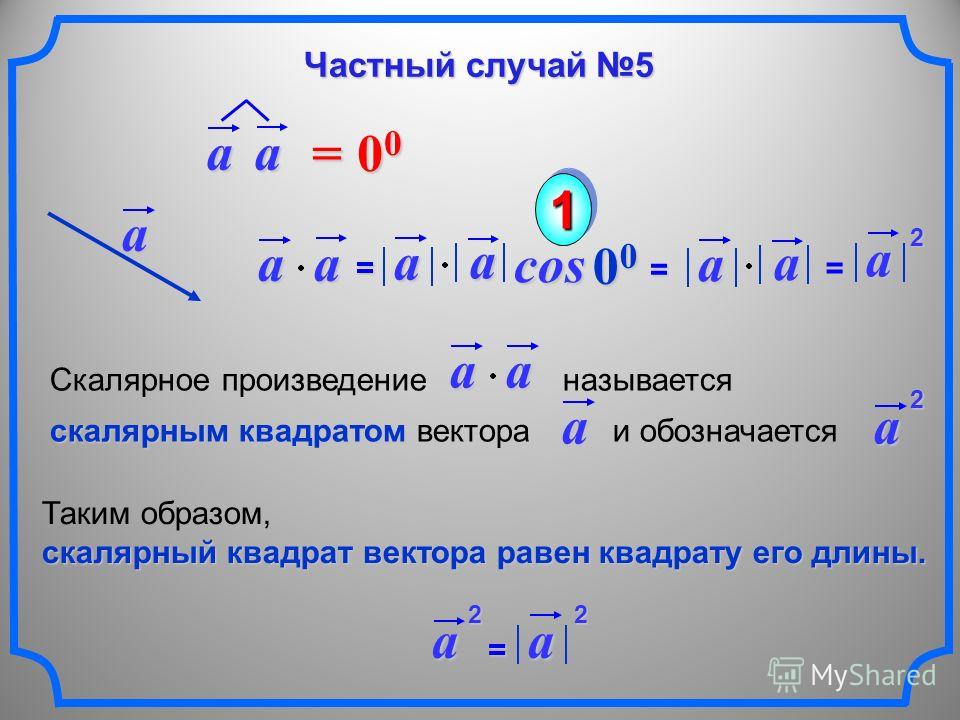 Векторным произведением или двух векторов называется вектор , который отвечает следующим условиям:
Векторным произведением или двух векторов называется вектор , который отвечает следующим условиям:
 Изучайте правила и свойства операций над векторами, они станут Вам полезны при обучении.
Изучайте правила и свойства операций над векторами, они станут Вам полезны при обучении.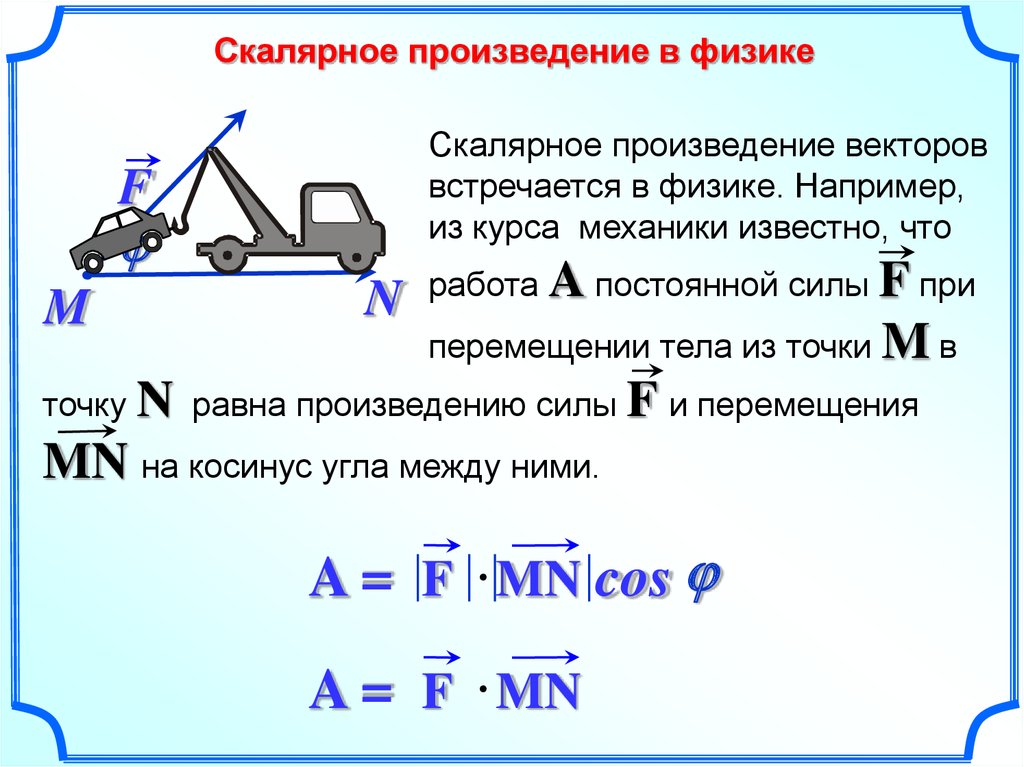 Часть 1″. В первой части рассказывается о том, что такое вектор и о простейших операциях с векторами (сложение и разность векторов, умножении вектора на число).
Часть 1″. В первой части рассказывается о том, что такое вектор и о простейших операциях с векторами (сложение и разность векторов, умножении вектора на число). В этом случае скалярное произведение векторов — это конкретное число — работа силы. Так как работа измеряется в Джоулях и каждый вектор имеет свой физический смысл, то и результат скалярного произведения в данном случае будет измеряться в Джоулях.
В этом случае скалярное произведение векторов — это конкретное число — работа силы. Так как работа измеряется в Джоулях и каждый вектор имеет свой физический смысл, то и результат скалярного произведения в данном случае будет измеряться в Джоулях.
 В результате большой палец – результирующий вектор [ā x b̅] будет смотреть вверх. Это правоориентированный базис.
В результате большой палец – результирующий вектор [ā x b̅] будет смотреть вверх. Это правоориентированный базис.

 \overrightarrow b\) = \(|\overrightarrow a||\ b|\) cos θ.
\overrightarrow b\) = \(|\overrightarrow a||\ b|\) cos θ. Он получается путем умножения величины данных векторов на косинус угла между двумя векторами. Результатом формулы векторной проекции является скалярное значение.
Он получается путем умножения величины данных векторов на косинус угла между двумя векторами. Результатом формулы векторной проекции является скалярное значение. Косинус угла между двумя векторами равен сумме произведений отдельных составляющих двух векторов, деленной на произведение величины двух векторов. Формула для угла между двумя векторами выглядит следующим образом. 92}}\)
Косинус угла между двумя векторами равен сумме произведений отдельных составляющих двух векторов, деленной на произведение величины двух векторов. Формула для угла между двумя векторами выглядит следующим образом. 92}}\) Матрица транспонирования первого вектора получается как матрица-строка. Производится умножение матриц. Матрица-строка и матрица-столбец перемножаются, чтобы получить сумму произведения соответствующих компонентов двух векторов.
Матрица транспонирования первого вектора получается как матрица-строка. Производится умножение матриц. Матрица-строка и матрица-столбец перемножаются, чтобы получить сумму произведения соответствующих компонентов двух векторов. Это свойство можно распространить на любое количество векторов.
Это свойство можно распространить на любое количество векторов. ].
]. \overrightarrow a\) = \(|\overrightarrow a\)| 2 (или) можно записать как 2
\overrightarrow a\) = \(|\overrightarrow a\)| 2 (или) можно записать как 2  Скалярное произведение единичных векторов \(\hat i\), \(\hat j\), \(\hat k\) подчиняется тем же правилам, что и скалярное произведение векторов. Угол между одинаковыми векторами равен 0º, а значит, их скалярное произведение равно 1. А угол между двумя перпендикулярными векторами равен 90º, а их скалярное произведение равно 0,9.0003
Скалярное произведение единичных векторов \(\hat i\), \(\hat j\), \(\hat k\) подчиняется тем же правилам, что и скалярное произведение векторов. Угол между одинаковыми векторами равен 0º, а значит, их скалярное произведение равно 1. А угол между двумя перпендикулярными векторами равен 90º, а их скалярное произведение равно 0,9.0003 \overrightarrow b\) = 0
\overrightarrow b\) = 0 Алгебраически скалярное произведение двух векторов равно сумме произведений отдельных компонентов двух векторов. \(\overrightarrow a. \overrightarrow b\) = \(a_1b_1\) + \(a_2b_2\)+ \(a_3b_3\). Геометрически скалярное произведение двух векторов есть произведение величины векторов и косинуса угла между двумя векторами. ( \(\overrightarrow a. \overrightarrow b\) = \(|\overrightarrow a||\overrightarrow b|\) cos θ). Результат скалярного произведения векторов является скалярным значением.
Алгебраически скалярное произведение двух векторов равно сумме произведений отдельных компонентов двух векторов. \(\overrightarrow a. \overrightarrow b\) = \(a_1b_1\) + \(a_2b_2\)+ \(a_3b_3\). Геометрически скалярное произведение двух векторов есть произведение величины векторов и косинуса угла между двумя векторами. ( \(\overrightarrow a. \overrightarrow b\) = \(|\overrightarrow a||\overrightarrow b|\) cos θ). Результат скалярного произведения векторов является скалярным значением. Скалярное произведение двух векторов равно \(\overrightarrow a. \overrightarrow b\) = \(|\overrightarrow a|.|\overrightarrow b|\)Cosθ, а перекрестное произведение двух векторов равно \(\overrightarrow a \) × \(\overrightarrow b\) = \(|\overrightarrow a|.|\overrightarrow b|\) Sinθ.\(\hat{n}\). Результат скалярного произведения двух векторов лежит в той же плоскости, что и два вектора, тогда как результат перекрестного произведения лежит в плоскости, перпендикулярной плоскости, охватывающей два вектора.
Скалярное произведение двух векторов равно \(\overrightarrow a. \overrightarrow b\) = \(|\overrightarrow a|.|\overrightarrow b|\)Cosθ, а перекрестное произведение двух векторов равно \(\overrightarrow a \) × \(\overrightarrow b\) = \(|\overrightarrow a|.|\overrightarrow b|\) Sinθ.\(\hat{n}\). Результат скалярного произведения двух векторов лежит в той же плоскости, что и два вектора, тогда как результат перекрестного произведения лежит в плоскости, перпендикулярной плоскости, охватывающей два вектора.
 Если скалярное произведение равно 0, то мы можем заключить, что либо длина одного или обоих векторов равна 0, либо угол между ними равен 90 градусов.
Если скалярное произведение равно 0, то мы можем заключить, что либо длина одного или обоих векторов равна 0, либо угол между ними равен 90 градусов. (\(\overrightarrow a. \overrightarrow b\) = \(|\overrightarrow a|.|\overrightarrow b|\).Cosθ. Также проверьте калькулятор скалярного произведения, чтобы легко найти векторное скалярное произведение.
(\(\overrightarrow a. \overrightarrow b\) = \(|\overrightarrow a|.|\overrightarrow b|\).Cosθ. Также проверьте калькулятор скалярного произведения, чтобы легко найти векторное скалярное произведение.
 Для двух ненулевых векторов скалярное произведение равно нулю, если угол между двумя векторами равен 90º, потому что Cos90º = 0.
Для двух ненулевых векторов скалярное произведение равно нулю, если угол между двумя векторами равен 90º, потому что Cos90º = 0.


 Поскольку координаты x и y не влияют друг на друга (как держать ведро боком под водопадом — ничего не падает), полное поглощение энергии равно поглощению (x) + поглощению (y):
Поскольку координаты x и y не влияют друг на друга (как держать ведро боком под водопадом — ничего не падает), полное поглощение энергии равно поглощению (x) + поглощению (y):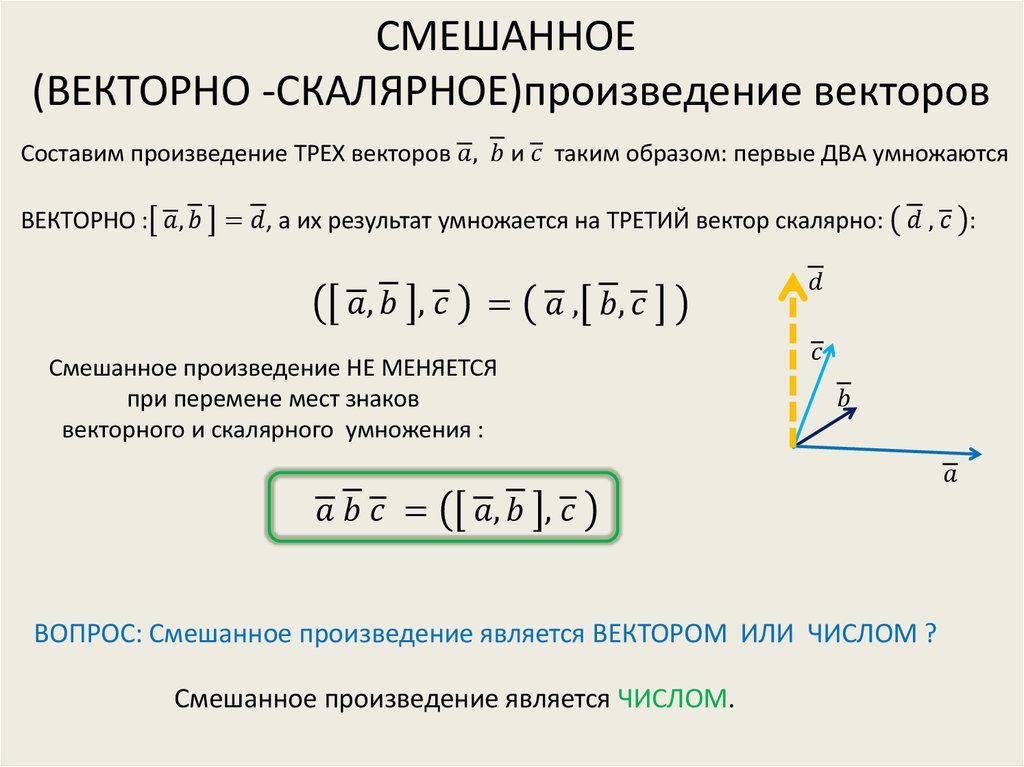 Вот некоторые аналогии, которые меня зацепили:
Вот некоторые аналогии, которые меня зацепили: Чем больше число, тем больше сила.
Чем больше число, тем больше сила.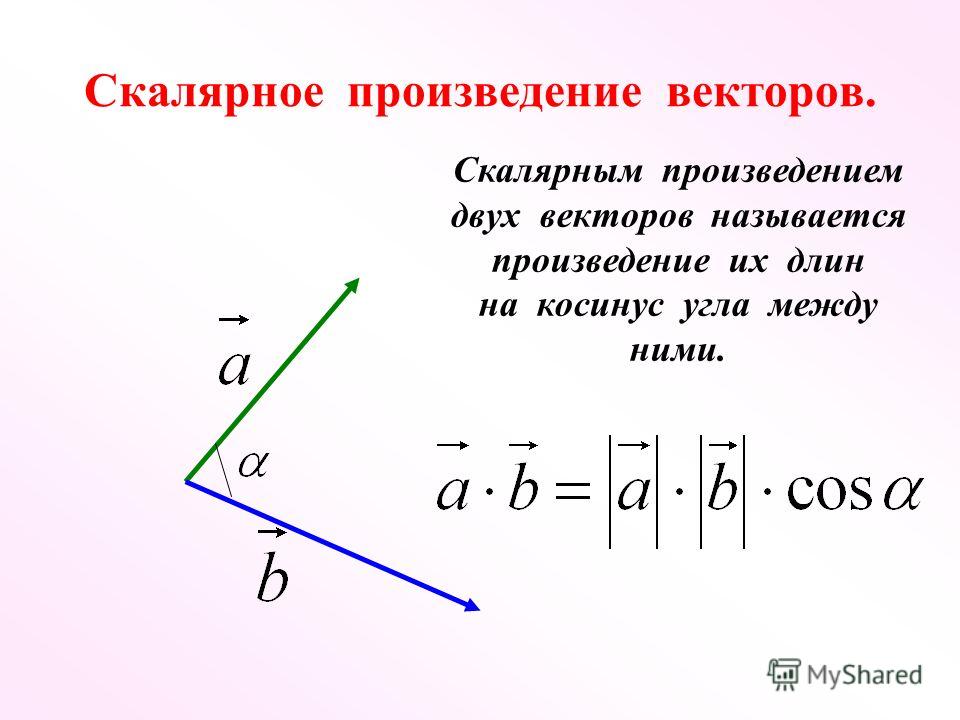 Они стоят \$1, \$2 и \$3 каждый соответственно.
Они стоят \$1, \$2 и \$3 каждый соответственно.
 Цены, отзывы, описание > Каталог оборудования > Санкт-ПетербургWilo NOC 30/8 отопительные однофазные циркуляционные насосы. Цены, отзывы, описание > Каталог оборудования > Санкт-Петербург
Цены, отзывы, описание > Каталог оборудования > Санкт-ПетербургWilo NOC 30/8 отопительные однофазные циркуляционные насосы. Цены, отзывы, описание > Каталог оборудования > Санкт-Петербург
 Подробнее
Подробнее
 Устройство способно перекачивать как воду, так и водогликолевую смесь, необходимую для предотвращения замерзания теплоносителя в системе отопления. Ротор «мокрого типа» смазывается перекачиваемой жидкостью и не требует дополнительного обслуживания.
Устройство способно перекачивать как воду, так и водогликолевую смесь, необходимую для предотвращения замерзания теплоносителя в системе отопления. Ротор «мокрого типа» смазывается перекачиваемой жидкостью и не требует дополнительного обслуживания.

 37
37 PriceOne}}
{{if !ModelPrice.Undefined}}
${ModelPrice.PriceMin}
{{else}}
Стоимость по запросу
{{/if}}
{{else}}
${ModelPrice.PriceMin} — ${ModelPrice.PriceMax}
{{/if}}
{{/if}}
PriceOne}}
{{if !ModelPrice.Undefined}}
${ModelPrice.PriceMin}
{{else}}
Стоимость по запросу
{{/if}}
{{else}}
${ModelPrice.PriceMin} — ${ModelPrice.PriceMax}
{{/if}}
{{/if}}
 6/10
6/10 производство, касса и информация о компании
производство, касса и информация о компании
 (США)
(США)


 Константа, задающая первую неделю года. Если не указано, первой считается неделя, на которую вы хотите 1 января.
Константа, задающая первую неделю года. Если не указано, первой считается неделя, на которую вы хотите 1 января.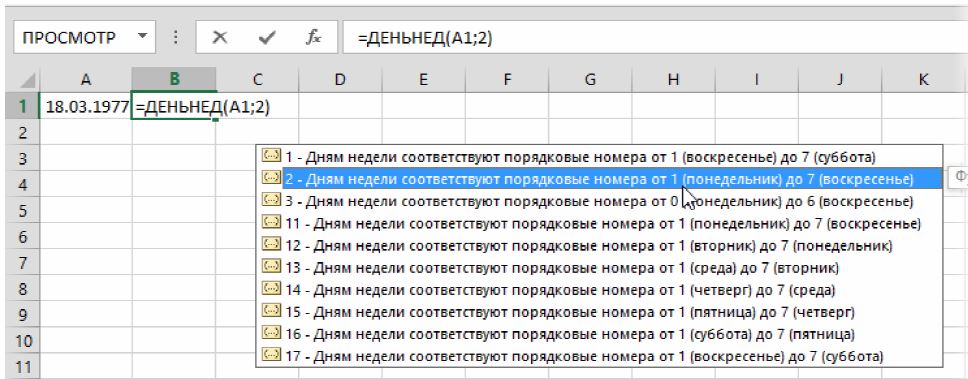

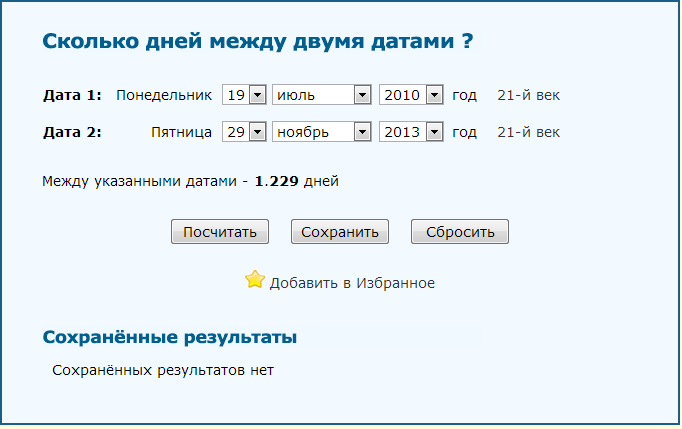
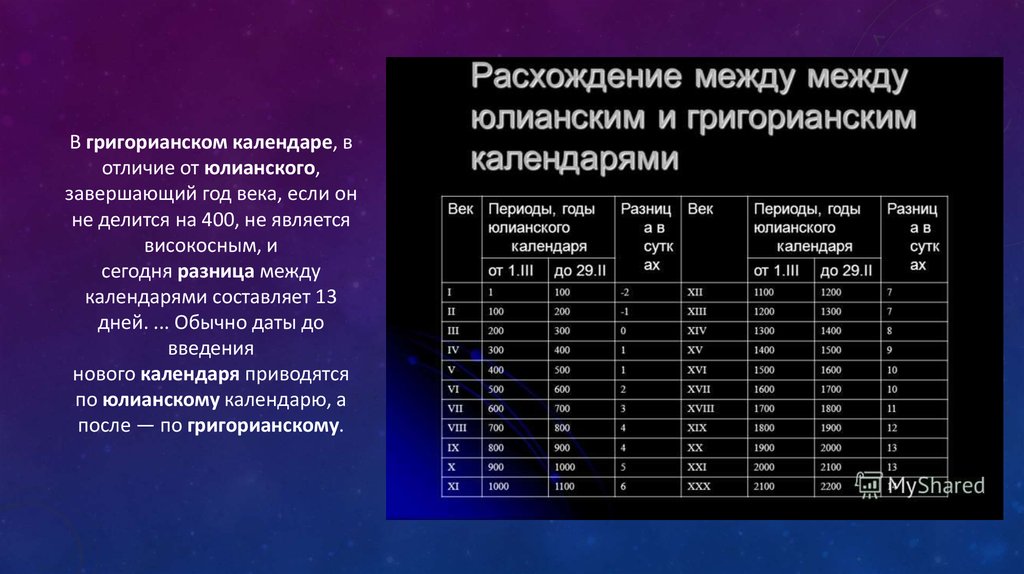 Например, DateDiff можно использовать для вычисления числа дней между двумя датами или числа недель между сегодняшним днем и концом года.
Например, DateDiff можно использовать для вычисления числа дней между двумя датами или числа недель между сегодняшним днем и концом года.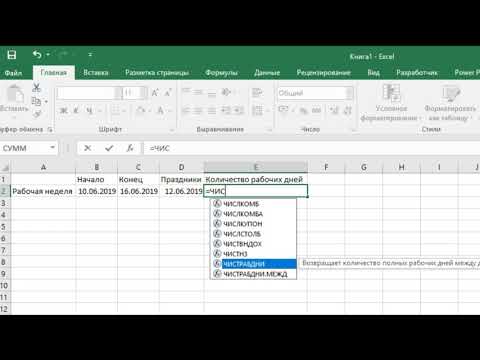
 Если используется календарь Хиджра, дата должна соответствовать ему.
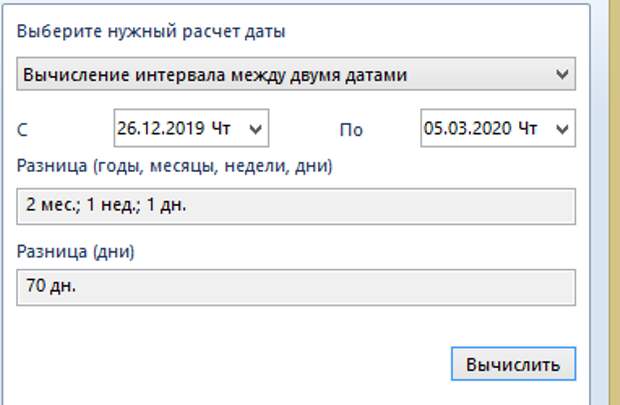
Если используется календарь Хиджра, дата должна соответствовать ему. возвращает разницу между системной датой и значением DateofSale как число месяцев и отображает в столбце «DaysSinceSale».
возвращает разницу между системной датой и значением DateofSale как число месяцев и отображает в столбце «DaysSinceSale».
 Если «DateofSale» приходится на понедельник, DateDiff считает количество понедельников до системной даты. При подсчете учитываются системные даты, но не значение в «DateofSale».
Если «DateofSale» приходится на понедельник, DateDiff считает количество понедельников до системной даты. При подсчете учитываются системные даты, но не значение в «DateofSale».

 Предположим, у вас есть форма, используемая для выполнения заказов клиентов. В таблице «Заказы» есть поле ReceiveBefore, в котором указана дата получения заказа клиентом. Функцию DateDiff можно использовать вместе с текстовым полем в форме, чтобы отобразить количество дней до даты, до того как заказ должен отгрузываться.
Предположим, у вас есть форма, используемая для выполнения заказов клиентов. В таблице «Заказы» есть поле ReceiveBefore, в котором указана дата получения заказа клиентом. Функцию DateDiff можно использовать вместе с текстовым полем в форме, чтобы отобразить количество дней до даты, до того как заказ должен отгрузываться.


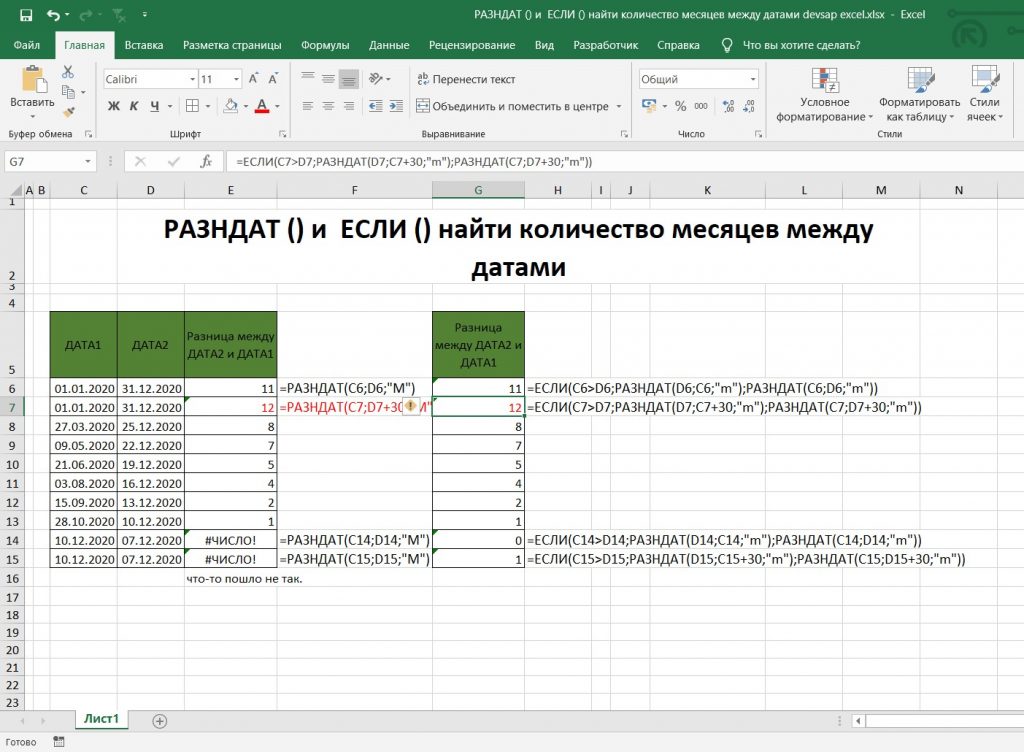 День, соответствующий значению аргумента дата2, учитывается, а дата1 — нет.
День, соответствующий значению аргумента дата2, учитывается, а дата1 — нет.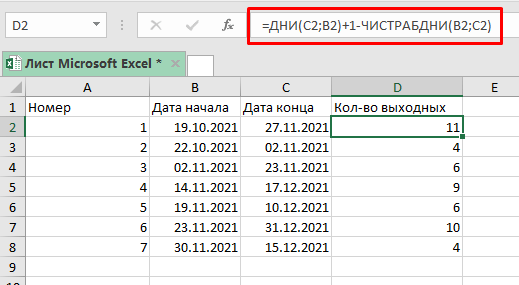 Это позволяет писать код, который можно использовать для разных лет.
Это позволяет писать код, который можно использовать для разных лет. в статье Поддержка Office VBA и обратная связь.
в статье Поддержка Office VBA и обратная связь. Нажмите CTRL + 1. Затем нажмите Число 9.0006 > Десятичных разрядов: 2 .
Нажмите CTRL + 1. Затем нажмите Число 9.0006 > Десятичных разрядов: 2 .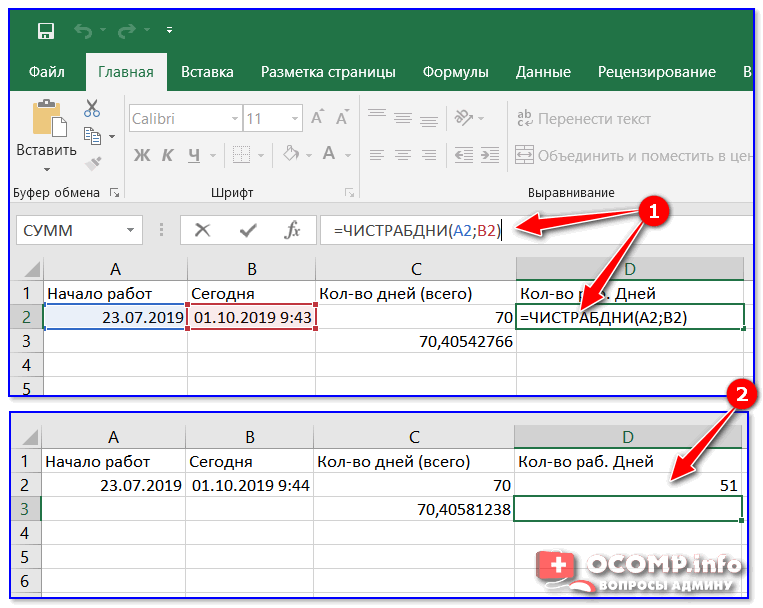
 Имейте в виду, что это изменится, когда файл снова откроется в будущем.
Имейте в виду, что это изменится, когда файл снова откроется в будущем. 1 в формуле устанавливает субботу и воскресенье как выходные дни и исключает их из общего числа.
1 в формуле устанавливает субботу и воскресенье как выходные дни и исключает их из общего числа. Если вы используете Excel 2007, приведенный выше пример будет таким: =ЧИСТРАБДНИ(D53,E53,Моипраздники) .
Если вы используете Excel 2007, приведенный выше пример будет таким: =ЧИСТРАБДНИ(D53,E53,Моипраздники) .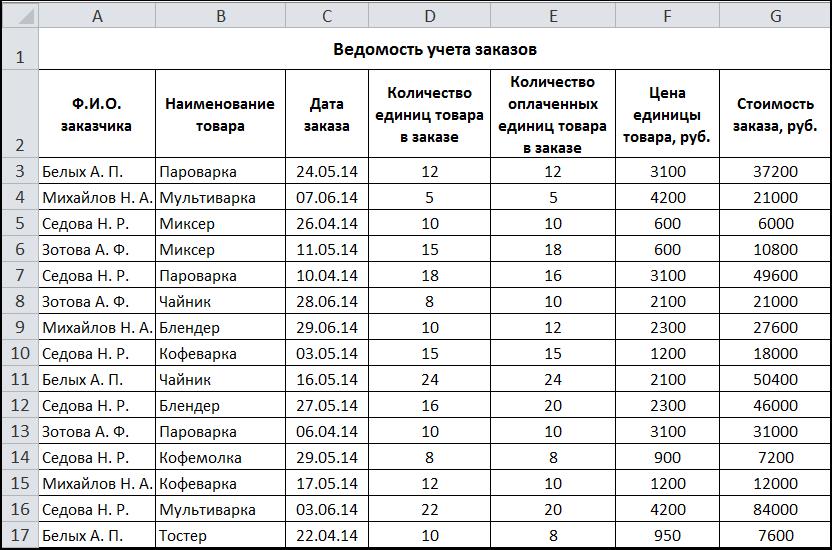 Обязательно введите час, минуту, и пробел перед AM или PM .
Обязательно введите час, минуту, и пробел перед AM или PM .

 Круглые скобки позволяют вам контролировать порядок операций, которые мы хотим вычесть, прежде чем делить.
Круглые скобки позволяют вам контролировать порядок операций, которые мы хотим вычесть, прежде чем делить.
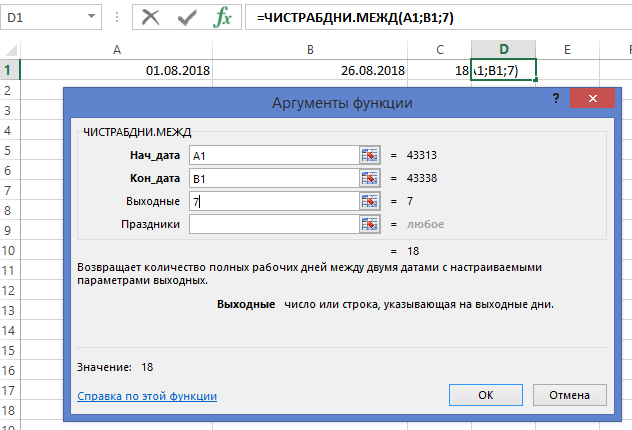 Функция SWITCH предназначена для точного совпадения, однако существует обходной путь, позволяющий использовать символы большего и меньшего размера.
Функция SWITCH предназначена для точного совпадения, однако существует обходной путь, позволяющий использовать символы большего и меньшего размера.
 ..])
..]) На изображении выше показана формула в ячейке […]
На изображении выше показана формула в ячейке […]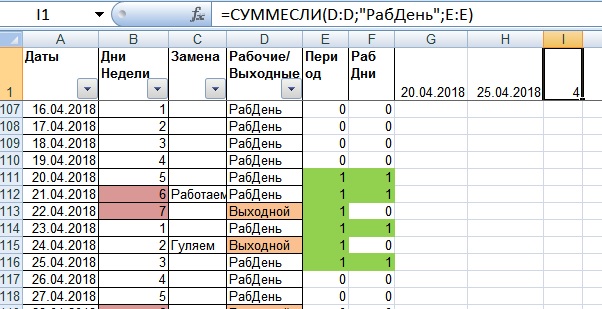

 Очевидно, что φ определяется не однозначно, а
Очевидно, что φ определяется не однозначно, а Действия над комплексными числамиНа основании этого правила получим:
Действия над комплексными числамиНа основании этого правила получим: Действия над комплексными числамиНайти произведение и частное комплексных чисел:
Действия над комплексными числамиНайти произведение и частное комплексных чисел:
 Показательная форма комплексного числаПусть z x i y . Если х и y – действительные переменные, то
Показательная форма комплексного числаПусть z x i y . Если х и y – действительные переменные, то Тогда:
Тогда:







 0, static_cast<double>(d)}
0, static_cast<double>(d)} также: Аргумент комплексного числа
также: Аргумент комплексного числа За исключением явной лицензии с открытым исходным кодом (указано Creative Commons/бесплатно), алгоритма «Комплексный числовой модуль/величина», апплета или фрагмента (преобразователь, решатель, шифрование/дешифрование, кодирование/декодирование, шифрование/дешифрование, дешифратор, транслятор) или функции «Комплексный числовой модуль/величина» (вычисление, преобразование, решение, расшифровка/шифрование, расшифровка/шифрование, декодирование/кодирование, перевод), написанные на любом информационном языке (Python, Java, PHP, C#, Javascript, Matlab и т. д.). ) и все загрузки данных, сценарии или доступ к API для «Комплексного числового модуля/величины» не являются общедоступными, то же самое для автономного использования на ПК, мобильных устройствах, планшетах, iPhone или в приложениях для Android!
За исключением явной лицензии с открытым исходным кодом (указано Creative Commons/бесплатно), алгоритма «Комплексный числовой модуль/величина», апплета или фрагмента (преобразователь, решатель, шифрование/дешифрование, кодирование/декодирование, шифрование/дешифрование, дешифратор, транслятор) или функции «Комплексный числовой модуль/величина» (вычисление, преобразование, решение, расшифровка/шифрование, расшифровка/шифрование, декодирование/кодирование, перевод), написанные на любом информационном языке (Python, Java, PHP, C#, Javascript, Matlab и т. д.). ) и все загрузки данных, сценарии или доступ к API для «Комплексного числового модуля/величины» не являются общедоступными, то же самое для автономного использования на ПК, мобильных устройствах, планшетах, iPhone или в приложениях для Android!  csv или .txt осуществляется нажатием значка export . 06-01, https://www.dcode.fr/complex-number-modulus
csv или .txt осуществляется нажатием значка export . 06-01, https://www.dcode.fr/complex-number-modulus  также: Аргумент комплексного числа
также: Аргумент комплексного числа За исключением явной лицензии с открытым исходным кодом (указано Creative Commons/бесплатно), алгоритма «Комплексный числовой модуль/величина», апплета или фрагмента (преобразователь, решатель, шифрование/дешифрование, кодирование/декодирование, шифрование/дешифрование, дешифратор, транслятор) или функции «Комплексный числовой модуль/величина» (вычисление, преобразование, решение, расшифровка/шифрование, расшифровка/шифрование, декодирование/кодирование, перевод), написанные на любом информационном языке (Python, Java, PHP, C#, Javascript, Matlab и т. д.). ) и все загрузки данных, сценарии или доступ к API для «Комплексного числового модуля/величины» не являются общедоступными, то же самое для автономного использования на ПК, мобильных устройствах, планшетах, iPhone или в приложениях для Android!
За исключением явной лицензии с открытым исходным кодом (указано Creative Commons/бесплатно), алгоритма «Комплексный числовой модуль/величина», апплета или фрагмента (преобразователь, решатель, шифрование/дешифрование, кодирование/декодирование, шифрование/дешифрование, дешифратор, транслятор) или функции «Комплексный числовой модуль/величина» (вычисление, преобразование, решение, расшифровка/шифрование, расшифровка/шифрование, декодирование/кодирование, перевод), написанные на любом информационном языке (Python, Java, PHP, C#, Javascript, Matlab и т. д.). ) и все загрузки данных, сценарии или доступ к API для «Комплексного числового модуля/величины» не являются общедоступными, то же самое для автономного использования на ПК, мобильных устройствах, планшетах, iPhone или в приложениях для Android! 
 Обозначают: .
Обозначают: . Ординату, равную , имеет точка единичной окружности . Эта точка получается из точки поворотом на угол , на угол , на угол и так далее. А также на угол , на угол и так далее.
Ординату, равную , имеет точка единичной окружности . Эта точка получается из точки поворотом на угол , на угол , на угол и так далее. А также на угол , на угол и так далее.
 Итак, ординату, равную нулю,
имеет точка и точка . Эти точки получаются поворотом точки на углы , , , и так далее. А также на углы , , и так далее.
Итак, ординату, равную нулю,
имеет точка и точка . Эти точки получаются поворотом точки на углы , , , и так далее. А также на углы , , и так далее.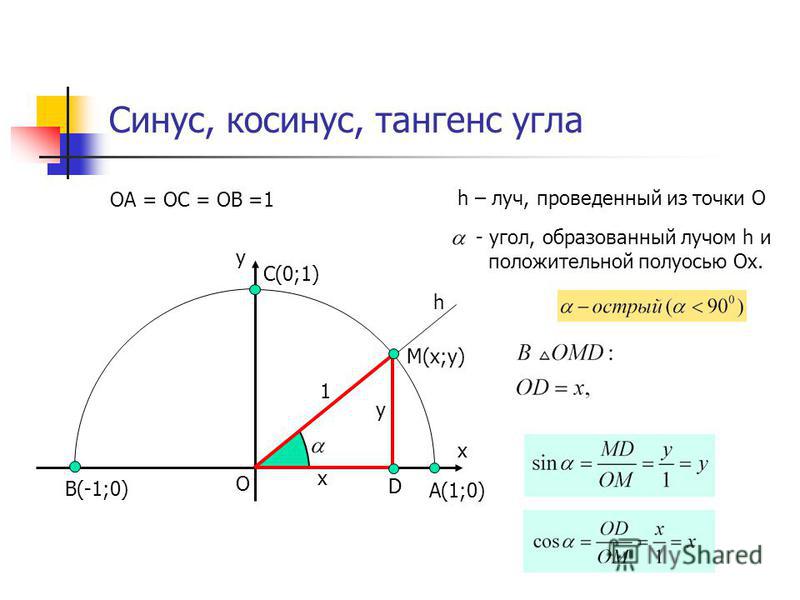 Как определить тригонометрические функции синус и косинус на единичной окружности? Как определить и запомнить значения синуса и косинуса 0°, 90°, 180°, 270°, 360°, -90° и т.д.? Сегодня мы ответим на эти вопросы. Если Вы не видели наш первый урок по теме: «Что такое единичная окружность и зачем она нужна. Тригонометрические функции», то обязательно посмотрите его, тогда этот урок будет Вам очень понятен. Мы объясним Вам, что такое синус и косинус на единичной окружности. Научим Вас видеть синус и косинус на единичной окружности. Дадим Вам шпагалку, которая позволит Вам в любой момент вспомнить значения синуса и косинуса 0°, 90°, 180°, 270°, 360°, -90° и т.д. Обратим Ваше внимание на то, что даёт нам рассмотрение тригонометрических функций на единичной окружности и в треугольнике. Поясним, почему тригонометрические функции называют круговыми. Подробный план урока и ссылки на предыдущие уроки Вы можете найти в описании под видео.
00:00 Начало видео.
00:43 Итак начинаем.
06:14 Что такое sin α на единичной окружности?
08:27 Что такое cos α на единичной окружности?
09:38 Учимся видеть sin α и cos α на рисунке.
Как определить тригонометрические функции синус и косинус на единичной окружности? Как определить и запомнить значения синуса и косинуса 0°, 90°, 180°, 270°, 360°, -90° и т.д.? Сегодня мы ответим на эти вопросы. Если Вы не видели наш первый урок по теме: «Что такое единичная окружность и зачем она нужна. Тригонометрические функции», то обязательно посмотрите его, тогда этот урок будет Вам очень понятен. Мы объясним Вам, что такое синус и косинус на единичной окружности. Научим Вас видеть синус и косинус на единичной окружности. Дадим Вам шпагалку, которая позволит Вам в любой момент вспомнить значения синуса и косинуса 0°, 90°, 180°, 270°, 360°, -90° и т.д. Обратим Ваше внимание на то, что даёт нам рассмотрение тригонометрических функций на единичной окружности и в треугольнике. Поясним, почему тригонометрические функции называют круговыми. Подробный план урока и ссылки на предыдущие уроки Вы можете найти в описании под видео.
00:00 Начало видео.
00:43 Итак начинаем.
06:14 Что такое sin α на единичной окружности?
08:27 Что такое cos α на единичной окружности?
09:38 Учимся видеть sin α и cos α на рисунке. 11:51 Основная шпаргалка по тригонометрии.
12:49 Точки пересечения единичной окружности с осями координат.
14:50 Углы поворота луча OX против часовой стрелки.
16:13 Углы поворота луча OX по часовой стрелке.
18:23 Sin 0°, cos 0°.
19:32 Sin 90°, cos 90°.
20:33 Sin 180°, cos 180°.
20:48 Sin 270°, cos 270°.
21:06 Sin 360°, cos 360°.
22:08 Sin(- 90°), cos(- 90°).
22:43 Как найти значение sin и cos для любого угла поворота?
28:07 Что дало нам рассмотрение тригонометрических функций на единичной окружности?
29:36 Тригонометрические функции — круговые функции.
30:06 Подводим итоги.
Если Вы впервые на нашем канале или не смотрели наши предыдущие уроки, то рекомендуем Вам посмотреть следующие видео:
Что такое единичная окружность и зачем она нужна. Тригонометрические функции. Часть 1. Алгебра 10 класс. https://rutube.ru/video/05ae6855613d46cdf8a66bd222febe99/
Тригонометрические функции в геометрии. Что это такое. Сколько тригонометрических функций и почему. Геометрия 9 класс. Часть 1. https://rutube.
11:51 Основная шпаргалка по тригонометрии.
12:49 Точки пересечения единичной окружности с осями координат.
14:50 Углы поворота луча OX против часовой стрелки.
16:13 Углы поворота луча OX по часовой стрелке.
18:23 Sin 0°, cos 0°.
19:32 Sin 90°, cos 90°.
20:33 Sin 180°, cos 180°.
20:48 Sin 270°, cos 270°.
21:06 Sin 360°, cos 360°.
22:08 Sin(- 90°), cos(- 90°).
22:43 Как найти значение sin и cos для любого угла поворота?
28:07 Что дало нам рассмотрение тригонометрических функций на единичной окружности?
29:36 Тригонометрические функции — круговые функции.
30:06 Подводим итоги.
Если Вы впервые на нашем канале или не смотрели наши предыдущие уроки, то рекомендуем Вам посмотреть следующие видео:
Что такое единичная окружность и зачем она нужна. Тригонометрические функции. Часть 1. Алгебра 10 класс. https://rutube.ru/video/05ae6855613d46cdf8a66bd222febe99/
Тригонометрические функции в геометрии. Что это такое. Сколько тригонометрических функций и почему. Геометрия 9 класс. Часть 1. https://rutube.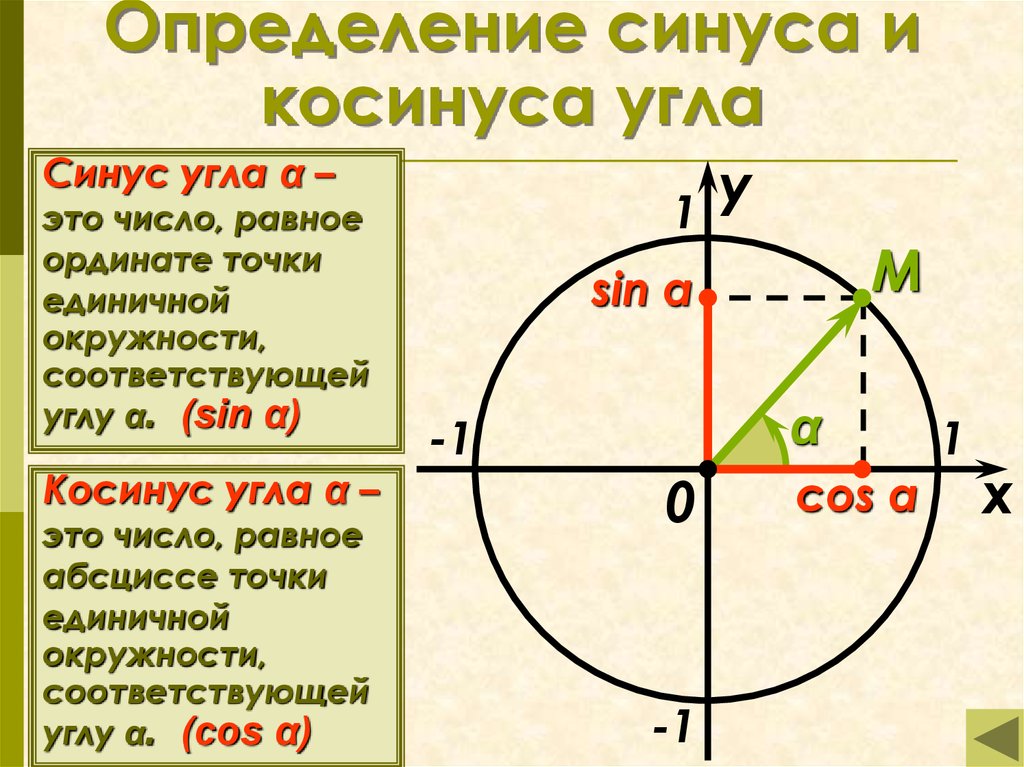 ru/video/b99256c0e2a5f1411c87731142e2a822/
Как запомнить формулы тригонометрических функций. Стандартные обозначения этих функций, треугольника и длин его сторон. Тригонометрические функции в геометрии. Часть 2. Геометрия 9 класс. https://rutube.ru/video/cb235fc7ef53f468f18b151435d18c77/
Как найти sin, cos, tg и ctg угла по двум сторонам треугольника. Как построить угол по sin, cos или tg. Тригонометрические функции в геометрии. Часть 3. Геометрия 9 класс. https://rutube.ru/video/3c8642f0072caa41866cb44fe5cf1eb2/
Как найти значение тригонометрических функций тремя способами. Тригонометрические функции в геометрии. Часть 4. Геометрия 9 класс. https://rutube.ru/video/70f16a0f13b974194b59d3327a03a403/
Функция в математике. Определение. Пример, на котором функцию понимают ВСЕ. https://rutube.ru/video/e39b203540be6b34b1c6728b8a73a8c4/
Компоненты функции: аргумент, значение функции, область определения функции, область значений функции https://rutube.ru/video/b244f058080abfb736bb53076b8ad8cc/
Способы задания функции.
ru/video/b99256c0e2a5f1411c87731142e2a822/
Как запомнить формулы тригонометрических функций. Стандартные обозначения этих функций, треугольника и длин его сторон. Тригонометрические функции в геометрии. Часть 2. Геометрия 9 класс. https://rutube.ru/video/cb235fc7ef53f468f18b151435d18c77/
Как найти sin, cos, tg и ctg угла по двум сторонам треугольника. Как построить угол по sin, cos или tg. Тригонометрические функции в геометрии. Часть 3. Геометрия 9 класс. https://rutube.ru/video/3c8642f0072caa41866cb44fe5cf1eb2/
Как найти значение тригонометрических функций тремя способами. Тригонометрические функции в геометрии. Часть 4. Геометрия 9 класс. https://rutube.ru/video/70f16a0f13b974194b59d3327a03a403/
Функция в математике. Определение. Пример, на котором функцию понимают ВСЕ. https://rutube.ru/video/e39b203540be6b34b1c6728b8a73a8c4/
Компоненты функции: аргумент, значение функции, область определения функции, область значений функции https://rutube.ru/video/b244f058080abfb736bb53076b8ad8cc/
Способы задания функции. Примеры. https://rutube.ru/video/be19beb2a973ffbad226194f7e36e0f8/
#синуснаединичнойокружности #косинуснаединичнойокружности #определениесинусаикосинуса10класс #определениесинуса10класс #определениекосинуса10класс #определениесинусаикосинусаугла10класс #алгебратригонометрическиефункции #тригонометрическиефункцииалгебра10 #уголповоротаединичнойокружности #шпаргалкапотригонометрии #МатематикаОтБаканчиковой
алгебра 10 класс, синус на единичной окружности, косинус на единичной окружности, определение синуса и косинуса 10 класс, определение синуса 10 класс, определение косинуса 10 класс, определение синуса и косинуса угла 10 класс, алгебра тригонометрические функции, тригонометрические функции алгебра 10, угол поворота единичной окружности, шпаргалка по тригонометрии
Примеры. https://rutube.ru/video/be19beb2a973ffbad226194f7e36e0f8/
#синуснаединичнойокружности #косинуснаединичнойокружности #определениесинусаикосинуса10класс #определениесинуса10класс #определениекосинуса10класс #определениесинусаикосинусаугла10класс #алгебратригонометрическиефункции #тригонометрическиефункцииалгебра10 #уголповоротаединичнойокружности #шпаргалкапотригонометрии #МатематикаОтБаканчиковой
алгебра 10 класс, синус на единичной окружности, косинус на единичной окружности, определение синуса и косинуса 10 класс, определение синуса 10 класс, определение косинуса 10 класс, определение синуса и косинуса угла 10 класс, алгебра тригонометрические функции, тригонометрические функции алгебра 10, угол поворота единичной окружности, шпаргалка по тригонометрии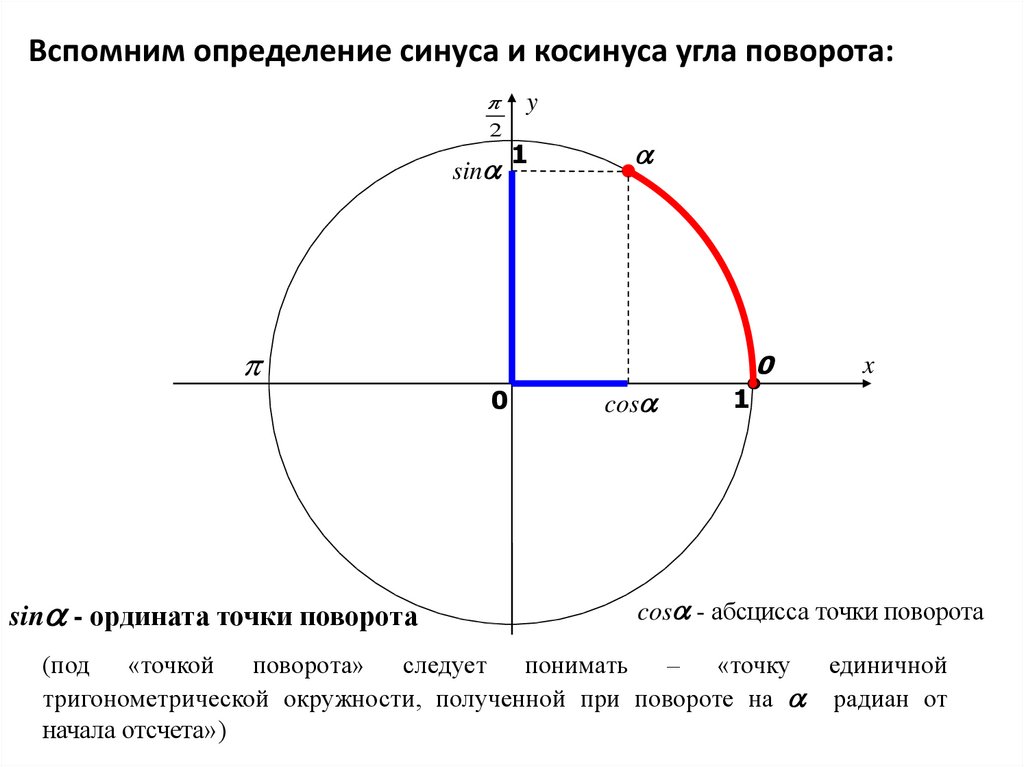 Поскольку радиус (и, следовательно, гипотенуза прямоугольного треугольника) равен 1, знаменатели косинус = соседний / гипотенуза и синус = противоположный / гипотенуза также равны 1. Таким образом, определение синуса — это y = синус и x = косинус.
Поскольку радиус (и, следовательно, гипотенуза прямоугольного треугольника) равен 1, знаменатели косинус = соседний / гипотенуза и синус = противоположный / гипотенуза также равны 1. Таким образом, определение синуса — это y = синус и x = косинус.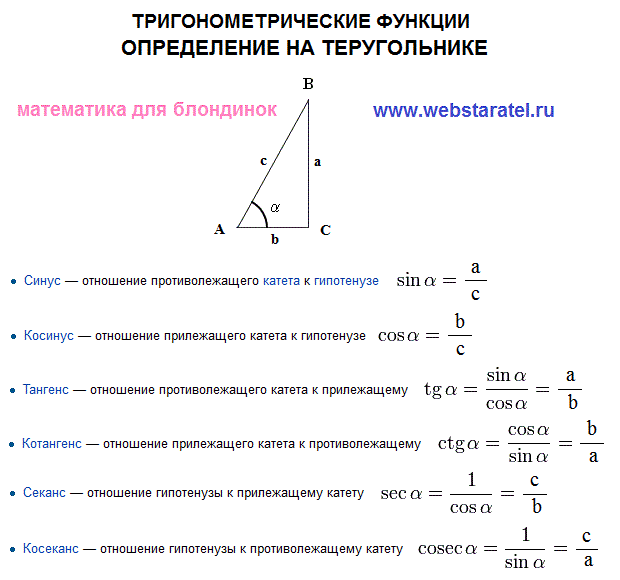 И под соседним мы подразумеваем сторону, которая находится рядом с тета, это гипотенуза, длинная сторона прямоугольного треугольника, и поэтому это означает, что x больше z. Синус определяется как сторона, противоположная тете y относительно гипотенузы, поэтому y больше z.
И под соседним мы подразумеваем сторону, которая находится рядом с тета, это гипотенуза, длинная сторона прямоугольного треугольника, и поэтому это означает, что x больше z. Синус определяется как сторона, противоположная тете y относительно гипотенузы, поэтому y больше z. 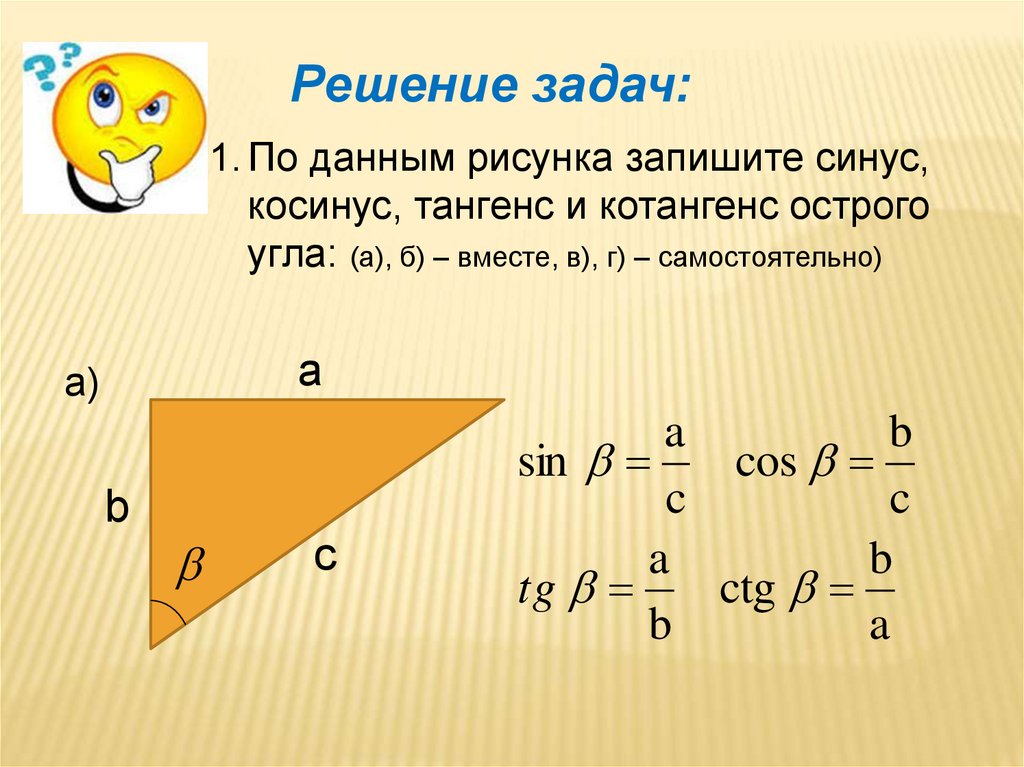 Теперь, чтобы сориентироваться, когда у вас есть радиус окружности 1, он пройдет через точку 1, 0 пройдет через точку 0, 1 минус 1, 0 и 0 минус 1. Тот же угол, который мы хотим отметить точка, в которой крайняя сторона пересекает единичную окружность. Эта точка будет иметь координаты x, y, мы определяем косинус как значение x и синус как значение y. Эта точка, конечно, будет уникальной, она будет однозначно зависеть от тета угла, поэтому для разных тета углов вы получите разные значения синуса и косинуса, но эта идея здесь позволит нам измерить синус и косинус для любого угла вообще. . Это сработает для острых углов, когда тета находится здесь в первом квадранте.
Теперь, чтобы сориентироваться, когда у вас есть радиус окружности 1, он пройдет через точку 1, 0 пройдет через точку 0, 1 минус 1, 0 и 0 минус 1. Тот же угол, который мы хотим отметить точка, в которой крайняя сторона пересекает единичную окружность. Эта точка будет иметь координаты x, y, мы определяем косинус как значение x и синус как значение y. Эта точка, конечно, будет уникальной, она будет однозначно зависеть от тета угла, поэтому для разных тета углов вы получите разные значения синуса и косинуса, но эта идея здесь позволит нам измерить синус и косинус для любого угла вообще. . Это сработает для острых углов, когда тета находится здесь в первом квадранте. 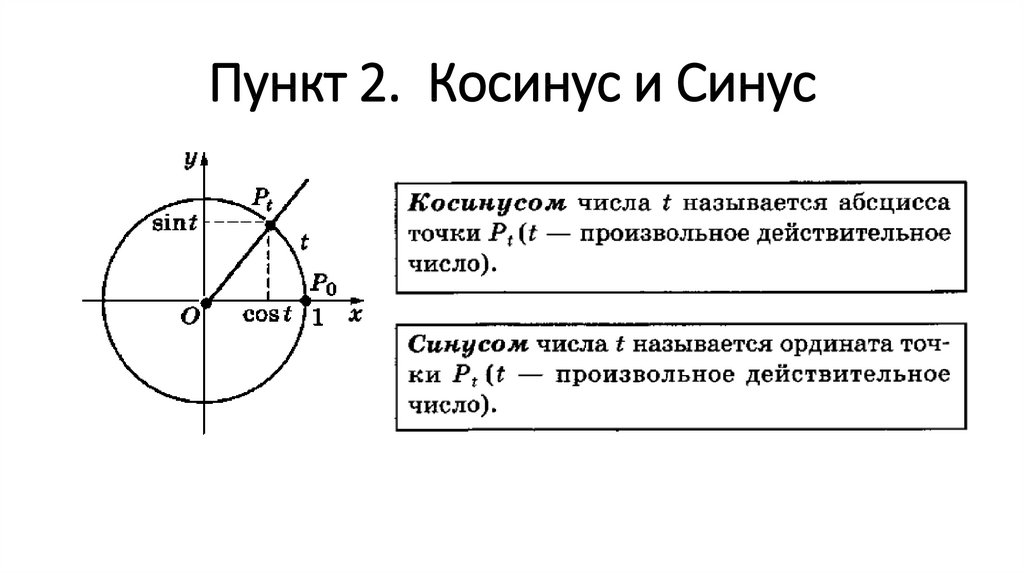 — Лейла Сломан, 9 лет.0033 Scientific American , 10 апреля 2023 г.
Хотя доказательство представляет собой впечатляющую часть математики, другие математики использовали аналогичные подходы раньше, используя синус и косинус , чтобы независимо доказать теорему Пифагора, не полагаясь на sin²α + cos²α = 1.
— Даррен Орф, Popular Mechanics , 31 марта 2023 г.
Иллюстрация: Ретт Аллен Это решение включает тригонометрическую функцию косинус .
— Ретт Аллен, WIRED , 14 марта 2023 г.
Ответ: ничего. Помните, что основные тригонометрические функции (синус, , косинус , тангенс) — это просто отношения сторон прямоугольных треугольников.
— Ретт Аллен, Wired , 14 марта 2022 г.
Среди вещей, которым обычно учат студентов в старшей школе: как найти косинус угла, с чего началась война 1812 года, и химический состав соли.
— Лейла Сломан, 9 лет.0033 Scientific American , 10 апреля 2023 г.
Хотя доказательство представляет собой впечатляющую часть математики, другие математики использовали аналогичные подходы раньше, используя синус и косинус , чтобы независимо доказать теорему Пифагора, не полагаясь на sin²α + cos²α = 1.
— Даррен Орф, Popular Mechanics , 31 марта 2023 г.
Иллюстрация: Ретт Аллен Это решение включает тригонометрическую функцию косинус .
— Ретт Аллен, WIRED , 14 марта 2023 г.
Ответ: ничего. Помните, что основные тригонометрические функции (синус, , косинус , тангенс) — это просто отношения сторон прямоугольных треугольников.
— Ретт Аллен, Wired , 14 марта 2022 г.
Среди вещей, которым обычно учат студентов в старшей школе: как найти косинус угла, с чего началась война 1812 года, и химический состав соли. — BostonGlobe.com , 29 октября 2021 г.
В 1807 году Жозеф Фурье обнаружил, что любая периодическая функция — уравнение, значения которого циклически повторяются, — может быть выражена в виде суммы тригонометрических функций, таких как синус и косинус .
— Журнал Quanta , 13 октября 2021 г.
Рынки движутся как бы по синусоиде, 9Модель 0033 косинус от рынка продавца к рынку покупателя и обратно.
— Дэвид Фридман, Forbes , 24 мая 2021 г.
В качестве примера рассмотрим оператор, преобразующий функцию в ее производную (превращающий синус x в косинус x , например, или x3 в 3×2 и т. д.).
— Журнал Quanta , 19 апреля 2021 г.
Узнать больше
— BostonGlobe.com , 29 октября 2021 г.
В 1807 году Жозеф Фурье обнаружил, что любая периодическая функция — уравнение, значения которого циклически повторяются, — может быть выражена в виде суммы тригонометрических функций, таких как синус и косинус .
— Журнал Quanta , 13 октября 2021 г.
Рынки движутся как бы по синусоиде, 9Модель 0033 косинус от рынка продавца к рынку покупателя и обратно.
— Дэвид Фридман, Forbes , 24 мая 2021 г.
В качестве примера рассмотрим оператор, преобразующий функцию в ее производную (превращающий синус x в косинус x , например, или x3 в 3×2 и т. д.).
— Журнал Quanta , 19 апреля 2021 г.
Узнать больше Любые мнения, выраженные в примерах, не отражают точку зрения Merriam-Webster или ее редакторов. Отправьте нам отзыв об этих примерах.
Любые мнения, выраженные в примерах, не отражают точку зрения Merriam-Webster или ее редакторов. Отправьте нам отзыв об этих примерах.
 Получаем:
Получаем:

 Однако, tgx2 считается сложной функцией, то получаем степенную функцию вида g(x)=x2 и f, являющуюся функцией тангенса. Для этого следует продифференцировать по сумме. Получаем, что
Однако, tgx2 считается сложной функцией, то получаем степенную функцию вида g(x)=x2 и f, являющуюся функцией тангенса. Для этого следует продифференцировать по сумме. Получаем, что Это отношение l(x)=x2+3cos3(2x+1)+7 к m(x)=ex2+33
Это отношение l(x)=x2+3cos3(2x+1)+7 к m(x)=ex2+33 Для ознакомления подобных задач и и для понятия их решения необходимо обратиться к пункту дифференцирования функции, то есть нахождения ее производной.
Для ознакомления подобных задач и и для понятия их решения необходимо обратиться к пункту дифференцирования функции, то есть нахождения ее производной. Например, . Сейчас таким же образом будем находить производные от сложной функции, где вместо линейной функции может быть другая функция.
Например, . Сейчас таким же образом будем находить производные от сложной функции, где вместо линейной функции может быть другая функция.

 -К.: А.С.К., 1997.
-К.: А.С.К., 1997. Задачник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2007.)
Задачник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2007.) \end{eqnarray}
\end{eqnarray}
 Если теперь мы установим
$$z = z_0+ik = x_0 + i(y_0+k), \quad k\in \mathbb R,$$
затем $z\rightarrow 0$ вдоль вертикальной линии как $k\rightarrow 0$. Поэтому у нас также есть
Если теперь мы установим
$$z = z_0+ik = x_0 + i(y_0+k), \quad k\in \mathbb R,$$
затем $z\rightarrow 0$ вдоль вертикальной линии как $k\rightarrow 0$. Поэтому у нас также есть
 Функция
называется аналитическим на $A$, если $f$ дифференцируема в каждом $z_0\in A$.
слово «голоморфный», которое иногда используется, является синонимом слова «аналитический». Фраза «аналитический в $z_0$» означает, что $f$ является аналитическим в окрестности $z_0$
Функция
называется аналитическим на $A$, если $f$ дифференцируема в каждом $z_0\in A$.
слово «голоморфный», которое иногда используется, является синонимом слова «аналитический». Фраза «аналитический в $z_0$» означает, что $f$ является аналитическим в окрестности $z_0$ Это может быть немного неясно, поэтому я приведу пару примеров 92 — 6xy$ и $\frac{\partial v}{\partial x} = 6xy$.
Это может быть немного неясно, поэтому я приведу пару примеров 92 — 6xy$ и $\frac{\partial v}{\partial x} = 6xy$.

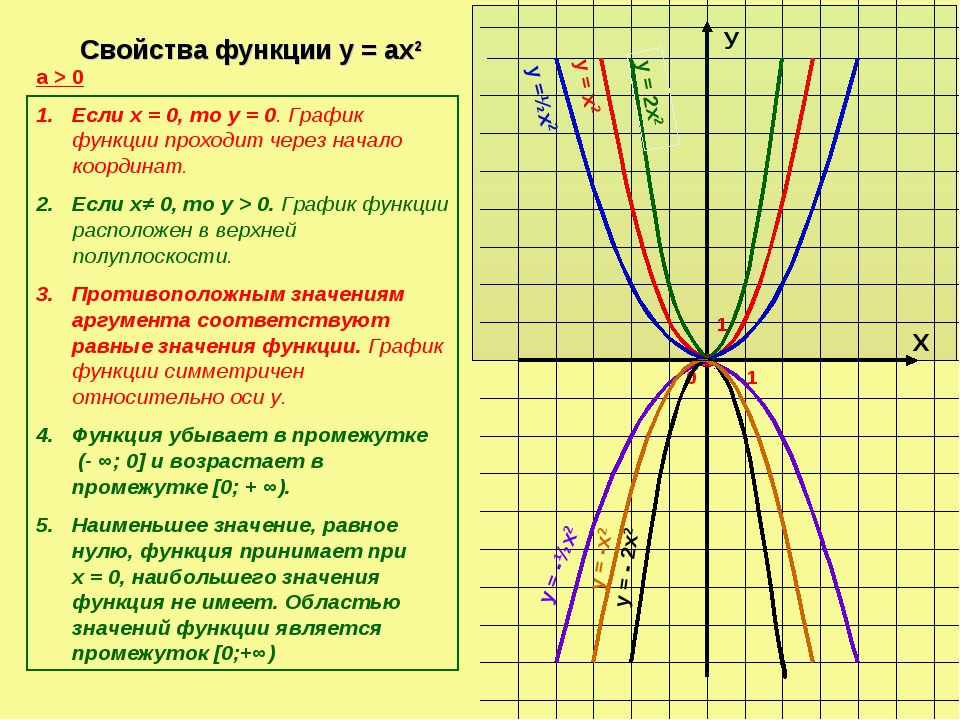 №
№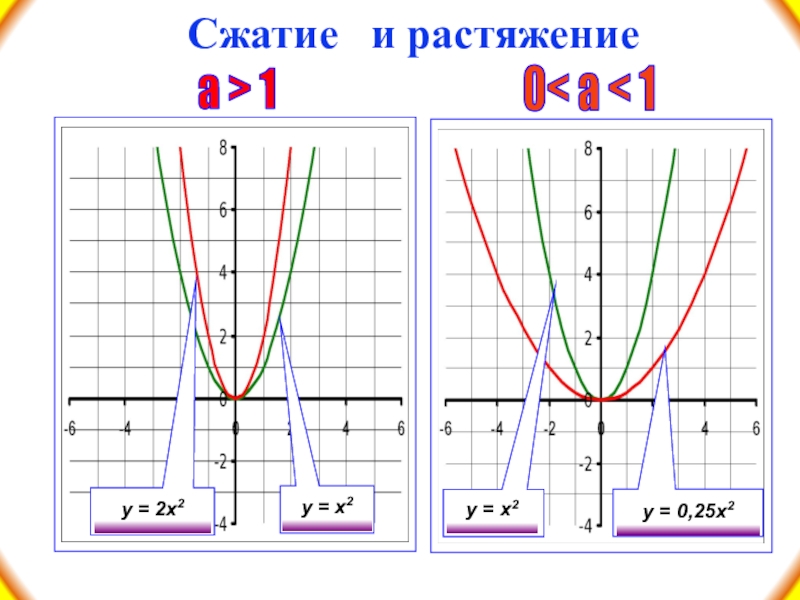
 ) равной длины (2,5м) со светодиодами.
) равной длины (2,5м) со светодиодами.
 4 кг
4 кг Метод Ортеги — очень быстрый способ решения 2×2 (но не самый быстрый). Когда вы полностью уверены во всех алгоритмах, показанных ниже, вы должны быть не ниже 5 (может быть, даже быстрее).
Метод Ортеги — очень быстрый способ решения 2×2 (но не самый быстрый). Когда вы полностью уверены во всех алгоритмах, показанных ниже, вы должны быть не ниже 5 (может быть, даже быстрее).
 Это может занять некоторое время, чтобы изучить, но будьте уверены, как только вы будете уверены в том, что найдете и выполните правильный алгоритм, вы будете на пути к пункту 5.
Это может занять некоторое время, чтобы изучить, но будьте уверены, как только вы будете уверены в том, что найдете и выполните правильный алгоритм, вы будете на пути к пункту 5.  3 (1280 мм), монокамерой ASI294 мм + фильтрами Baader LRGB
3 (1280 мм), монокамерой ASI294 мм + фильтрами Baader LRGB Однако, если я использую CMOS, каждый пиксель все равно будет насыщаться через 10 минут, просто у меня будет больше «сигнала» от этих четырех пикселей.
Однако, если я использую CMOS, каждый пиксель все равно будет насыщаться через 10 минут, просто у меня будет больше «сигнала» от этих четырех пикселей. — 12:14
— 12:14 

 Запишите все двузначные числа, в записи которых используются только цифры 1, 2 и 3 (цифры могут повторяться).
Запишите все двузначные числа, в записи которых используются только цифры 1, 2 и 3 (цифры могут повторяться).


 Какое наибольшее количество вариантов придётся перебрать коту и лисе, чтобы открыть дверь?
Какое наибольшее количество вариантов придётся перебрать коту и лисе, чтобы открыть дверь? Сколько существует различных прямоугольников, периметры которых равны 24 см, а длины сторон выражены целым числом сантиметров?
Сколько существует различных прямоугольников, периметры которых равны 24 см, а длины сторон выражены целым числом сантиметров?




 Расстояние между двумя сёлами равно 28 км. Из этих сёл одновременно в одном направлении выехали мотоциклист и автобус. Автобус ехал впереди со скоростью 42 км/ч, а мотоциклист ехал со скоростью 56 км/ч. Через сколько часов после начала движения мотоциклист догонит автобус?
Расстояние между двумя сёлами равно 28 км. Из этих сёл одновременно в одном направлении выехали мотоциклист и автобус. Автобус ехал впереди со скоростью 42 км/ч, а мотоциклист ехал со скоростью 56 км/ч. Через сколько часов после начала движения мотоциклист догонит автобус?
 Они сидят по двое за 15 партами так, что половина всех девочек сидит с мальчиками. Можно ли учеников класса пересадить так, чтобы половина всех мальчиков сидела с девочками?
Они сидят по двое за 15 партами так, что половина всех девочек сидит с мальчиками. Можно ли учеников класса пересадить так, чтобы половина всех мальчиков сидела с девочками?

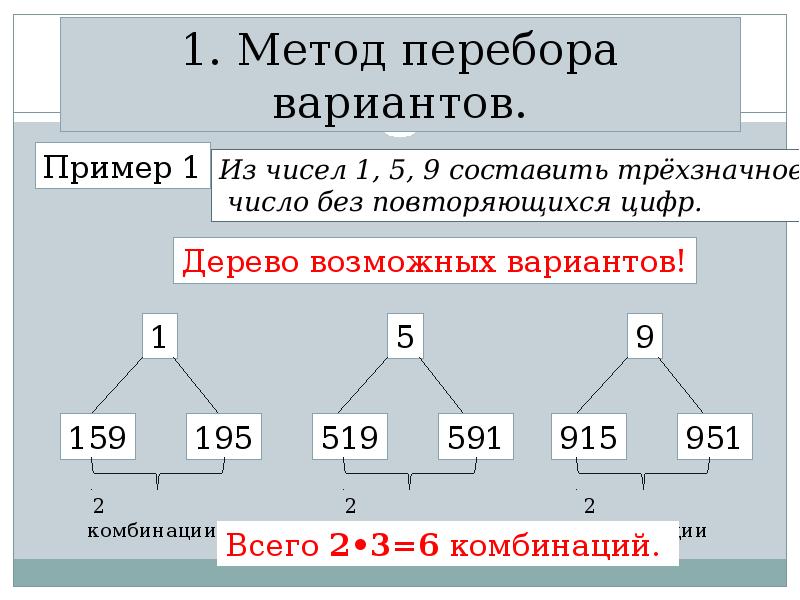 Сколькими способами классный руководитель может расставить девочек по одной на каждом из трёх этажей школы?
Сколькими способами классный руководитель может расставить девочек по одной на каждом из трёх этажей школы? Запишите все двузначные числа, в записи которых используются только цифры 1; 2 и 3 (цифры могут повторятся)
Запишите все двузначные числа, в записи которых используются только цифры 1; 2 и 3 (цифры могут повторятся) У ослика Иа-Иа есть 3 надувных шарика: красный, зелёный и жёлтый. Он хочет подарить по одному шарику своим друзьям: Винни-Пуху, Пятачку и Кролику. Сколько есть вариантов и Иа-Иа?
У ослика Иа-Иа есть 3 надувных шарика: красный, зелёный и жёлтый. Он хочет подарить по одному шарику своим друзьям: Винни-Пуху, Пятачку и Кролику. Сколько есть вариантов и Иа-Иа?
 , перераб. – М.:Вентана-Граф, 2016
, перераб. – М.:Вентана-Граф, 2016 403). .
403). .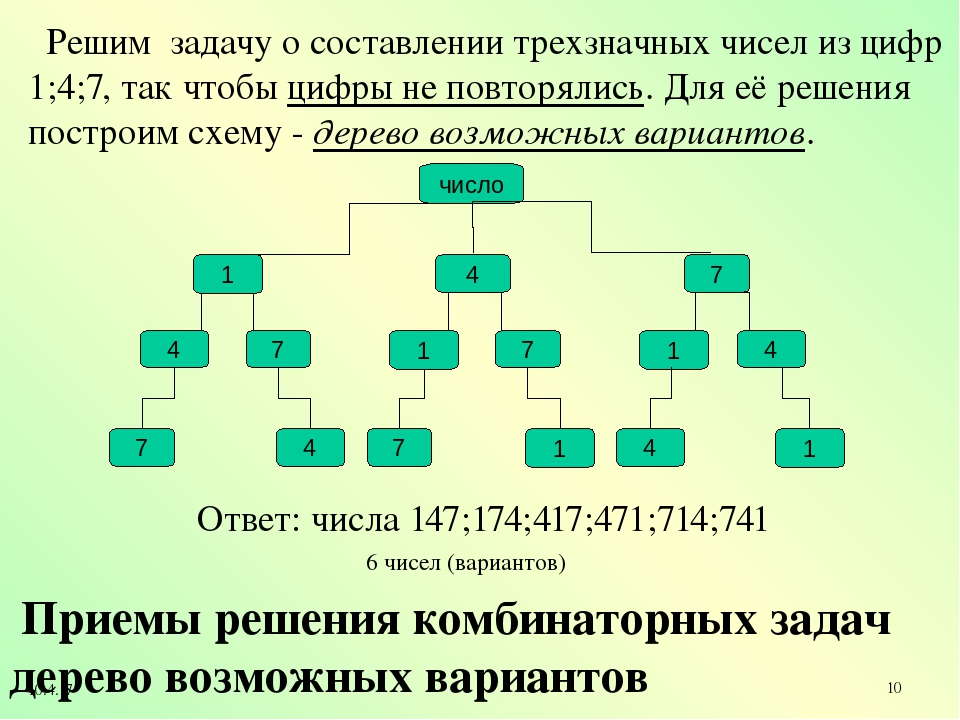 ) состоит из трех компонентов: формул/выражений, процессов подсчета и наборов результатов, а также взаимосвязей между этими компонентами ( см. рис. 1 ниже). 94)\). Процессы подсчета относятся к фактическим пошаговым процедурам, в которых кто-то участвует (мысленно или физически) при решении задачи подсчета. Это может включать в себя применение принципа умножения или внедрение разбивки случаев. Набор из исходов для данной задачи относится к желаемым исходам этой проблемы — элементам, которые фактически подсчитываются. Эти результаты могут быть каким-то образом закодированы (например, в виде строк чисел или букв), и этот компонент может состоять из различных способов кодирования и структурирования результатов.
) состоит из трех компонентов: формул/выражений, процессов подсчета и наборов результатов, а также взаимосвязей между этими компонентами ( см. рис. 1 ниже). 94)\). Процессы подсчета относятся к фактическим пошаговым процедурам, в которых кто-то участвует (мысленно или физически) при решении задачи подсчета. Это может включать в себя применение принципа умножения или внедрение разбивки случаев. Набор из исходов для данной задачи относится к желаемым исходам этой проблемы — элементам, которые фактически подсчитываются. Эти результаты могут быть каким-то образом закодированы (например, в виде строк чисел или букв), и этот компонент может состоять из различных способов кодирования и структурирования результатов.
 Одна организация набора результатов
Одна организация набора результатов
 Затем для каждого размещения и мы можем утверждать, что, поскольку повторение разрешено, теперь мы можем поместить любую из оставшихся 6 букв в оставшиеся две позиции. Этот процесс предлагает формулу/выражение \(3 \cdot 6 \cdot 6\). Этот процесс подсчета, кажется, имеет смысл, и действительно, это очень распространенная реакция среди студентов. Однако это неверный ответ, так как этот процесс слишком много раз подсчитывает некоторые результаты. Чтобы увидеть это, мы должны внимательно рассмотреть результаты и, в частности, то, как результаты генерируются и организуются в процессе подсчета.
Затем для каждого размещения и мы можем утверждать, что, поскольку повторение разрешено, теперь мы можем поместить любую из оставшихся 6 букв в оставшиеся две позиции. Этот процесс предлагает формулу/выражение \(3 \cdot 6 \cdot 6\). Этот процесс подсчета, кажется, имеет смысл, и действительно, это очень распространенная реакция среди студентов. Однако это неверный ответ, так как этот процесс слишком много раз подсчитывает некоторые результаты. Чтобы увидеть это, мы должны внимательно рассмотреть результаты и, в частности, то, как результаты генерируются и организуются в процессе подсчета. Это тоже генерирует пароль eae . Способы завершения процесса не находятся в однозначном соответствии с количеством желаемых результатов, и поэтому этот процесс приводит к пересчету.
Это тоже генерирует пароль eae . Способы завершения процесса не находятся в однозначном соответствии с количеством желаемых результатов, и поэтому этот процесс приводит к пересчету.
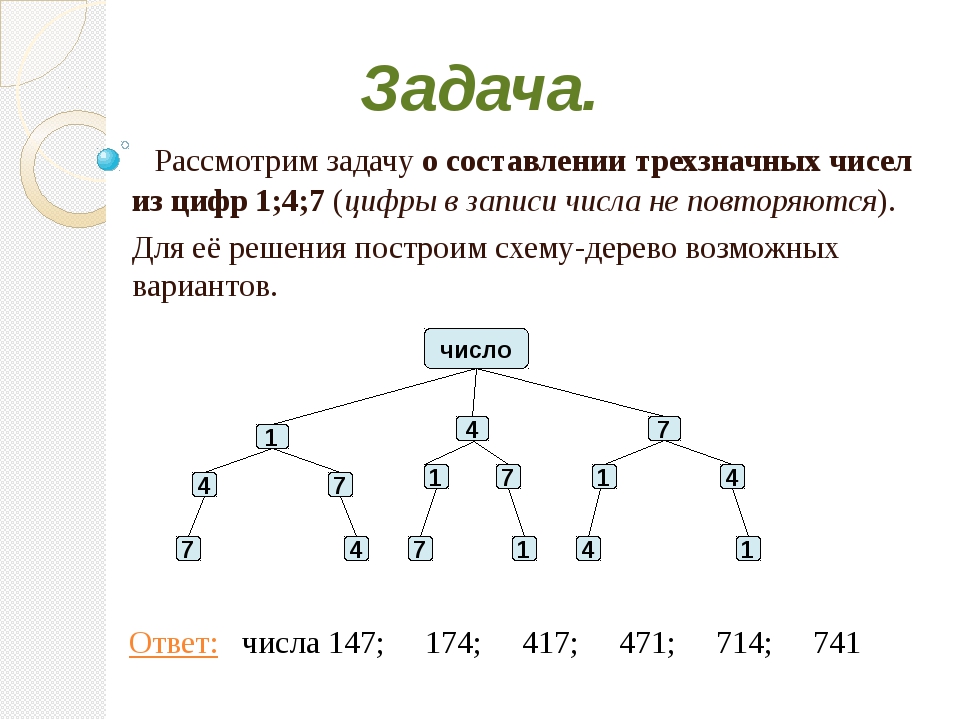 Возможно, если бы мы всегда поощряли учащихся формулировать характер того, что они считают, задавая такие вопросы, как «Что вы пытаетесь считать?». Ваши результаты более уместно моделировать как наборы вещей или их расположение? — учащиеся могут быть более склонны рассматривать счет как деятельность, связанную с результатами. Этот подход к счету, ориентированный на множество, изложен в Lockwood (2014), а также упоминается в Hadar & Hadass (19).81), Мамона Даунс и Даунс (2004 г.) и Батанеро, Наварро-Пелайо и Годино (1997 г.).
Возможно, если бы мы всегда поощряли учащихся формулировать характер того, что они считают, задавая такие вопросы, как «Что вы пытаетесь считать?». Ваши результаты более уместно моделировать как наборы вещей или их расположение? — учащиеся могут быть более склонны рассматривать счет как деятельность, связанную с результатами. Этот подход к счету, ориентированный на множество, изложен в Lockwood (2014), а также упоминается в Hadar & Hadass (19).81), Мамона Даунс и Даунс (2004 г.) и Батанеро, Наварро-Пелайо и Годино (1997 г.).

 Хорошими примерами являются задача домино и задачи с последовательностями из трех букв, а также следующая задача Language Book (также адаптированная из Tucker, 2002): Y У вас есть 5 разных испанских книг, 6 разных французских книг и 4 разных японских книги. Сколькими способами можно выбрать две книги на разных языках?
Хорошими примерами являются задача домино и задачи с последовательностями из трех букв, а также следующая задача Language Book (также адаптированная из Tucker, 2002): Y У вас есть 5 разных испанских книг, 6 разных французских книг и 4 разных японских книги. Сколькими способами можно выбрать две книги на разных языках?  Эти дети не беспокоятся о формулах или получении правильного ответа — они заняты критическим мышлением и решением проблем и, кажется, получают от этого удовольствие!
Эти дети не беспокоятся о формулах или получении правильного ответа — они заняты критическим мышлением и решением проблем и, кажется, получают от этого удовольствие! (1997). Влияние неявной комбинаторной модели на комбинаторное мышление учащихся средней школы. Образовательные исследования по математике, 32, 181–199.
(1997). Влияние неявной комбинаторной модели на комбинаторное мышление учащихся средней школы. Образовательные исследования по математике, 32, 181–199.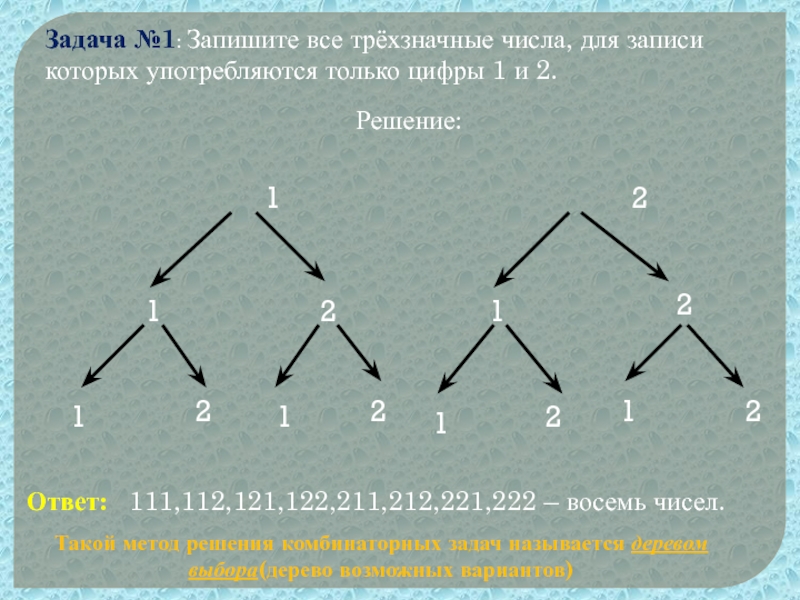 Для изучения математики, 34 (2), 31-37.
Для изучения математики, 34 (2), 31-37. Добавьте постоянную ссылку в закладки.
Добавьте постоянную ссылку в закладки. CombA1 учеников и V.CombA1 стульев, стоящих в ряд. В скольких различных порядках ученики могут сесть на эти стулья?
CombA1 учеников и V.CombA1 стульев, стоящих в ряд. В скольких различных порядках ученики могут сесть на эти стулья? 
 ‘,
4: «На первый стул могут сесть 4 ученика. Тогда есть 3 ученика, которые могут сесть на второй стул. Есть 2 варианта выбора третьего стула и только один вариант выбора последнего стула.’,
3: «На первый стул могут сесть 3 ученика. Затем есть 2 ученика, которые могут сесть на второй стул. Наконец, на третьем стуле остался только один ученик.’,
2: «Есть 2 ученика, которые могут сесть на первый стул. Далее на втором стуле остается только один ученик.’,
1: «Это только один вариант для одного стула».}[V.CombB1] Всего
‘,
4: «На первый стул могут сесть 4 ученика. Тогда есть 3 ученика, которые могут сесть на второй стул. Есть 2 варианта выбора третьего стула и только один вариант выбора последнего стула.’,
3: «На первый стул могут сесть 3 ученика. Затем есть 2 ученика, которые могут сесть на второй стул. Наконец, на третьем стуле остался только один ученик.’,
2: «Есть 2 ученика, которые могут сесть на первый стул. Далее на втором стуле остается только один ученик.’,
1: «Это только один вариант для одного стула».}[V.CombB1] Всего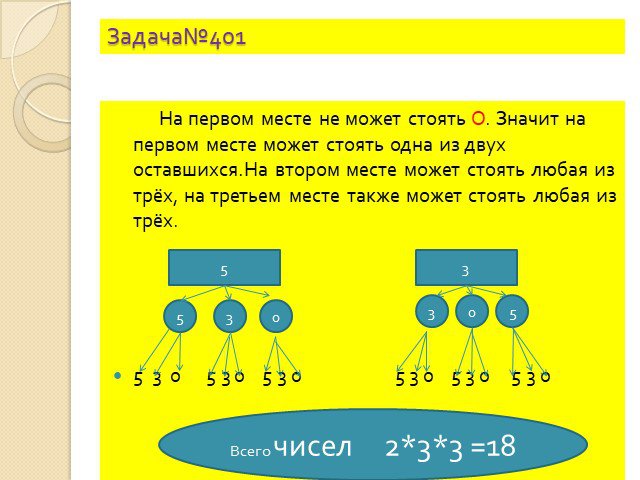
 ‘:»)+
(((Math.min(V.CombC1,V.CombC2))==3||(Math.min(V.CombC1,V.CombC2))==4)?’Тогда есть ‘+(V.CombC1 -2)+’ ученики, которые могли сесть на третий стул. ‘:»)+
(((Math.min(V.CombC1,V.CombC2))==4)?’На последнем стуле остался один ученик. ‘:»)+
((V.CombC1-(Math.min(V.CombC1,V.CombC2))==1||V.CombC1-(Math.min(V.CombC1,V.CombC2))==2||V. CombC1-(Math.min(V.CombC1,V.CombC2))==3)?’Нас не волнуют оставшиеся ‘+(V.CombC1-V.CombC2)+’ дочерние элементы, оставшиеся стоять. ‘:’ ‘) Всего
‘:»)+
(((Math.min(V.CombC1,V.CombC2))==3||(Math.min(V.CombC1,V.CombC2))==4)?’Тогда есть ‘+(V.CombC1 -2)+’ ученики, которые могли сесть на третий стул. ‘:»)+
(((Math.min(V.CombC1,V.CombC2))==4)?’На последнем стуле остался один ученик. ‘:»)+
((V.CombC1-(Math.min(V.CombC1,V.CombC2))==1||V.CombC1-(Math.min(V.CombC1,V.CombC2))==2||V. CombC1-(Math.min(V.CombC1,V.CombC2))==3)?’Нас не волнуют оставшиеся ‘+(V.CombC1-V.CombC2)+’ дочерние элементы, оставшиеся стоять. ‘:’ ‘) Всего Опять же, для этого есть более простое обозначение: 7 Р 3 . Если мы хотим разместить n объектов на m позиций, то есть
Опять же, для этого есть более простое обозначение: 7 Р 3 . Если мы хотим разместить n объектов на m позиций, то есть Сколько разных способов нужно попробовать? Что вы можете сказать о безопасности этих замков?
Сколько разных способов нужно попробовать? Что вы можете сказать о безопасности этих замков? Возможности
Возможности (Чтобы упростить набор текста, мы продолжим использовать первое встроенное обозначение.)
(Чтобы упростить набор текста, мы продолжим использовать первое встроенное обозначение.) Начинаем с 0 C 0. Затем находим 1 C 0 и 1 C 1. Далее 2 C 0, 2 C 1 и 2 C 2. Затем 3 90 007 С 0 , 3 C 1, 3 C 2 и 3 C 3. Запишем все эти результаты в таблицу:
Начинаем с 0 C 0. Затем находим 1 C 0 и 1 C 1. Далее 2 C 0, 2 C 1 и 2 C 2. Затем 3 90 007 С 0 , 3 C 1, 3 C 2 и 3 C 3. Запишем все эти результаты в таблицу: Его можно легко создать, заметив, что любая ячейка является суммой двух ячеек выше. В треугольнике Паскаля скрыты бесчисленные закономерности и числовые последовательности.
Его можно легко создать, заметив, что любая ячейка является суммой двух ячеек выше. В треугольнике Паскаля скрыты бесчисленные закономерности и числовые последовательности.
 Получается r + n – всего 1 место. Любой заказ r звездочек и n – 1 батончиков соответствует ровно одному действительному набору фруктов.
Получается r + n – всего 1 место. Любой заказ r звездочек и n – 1 батончиков соответствует ровно одному действительному набору фруктов. Вот пример:
Вот пример: