Возрастание и убывание функции — как найти?
Поможем понять и полюбить математику
Начать учиться
Сегодня мы поговорим о возрастании и убывании функции. Как вы знаете, эта тема достаточно важна, потому что встречается на ЕГЭ, во вступительных экзаменах. А еще ее подробно разбирают на уроках в школе. Сложная ли она? И да, и нет. Мы бы сказали, что она не трудная, а скорее комплексная — в теме много нюансов и моментов, которые тянутся к ней с начальной школы. Но не беспокойтесь, сегодня мы обязательно во всем разберемся!
Что такое функция
Как обычно, начнем мы с самого начала: с определения слова «функция».
Функция — это взаимосвязь между величинами, то есть зависимость одной переменной величины от другой.
Под функцией понимают правило, формулу, уравнение, которое описывает зависимость одной переменной от другой (например, у от х). Если изучить функцию, мы поймем:
Если изучить функцию, мы поймем:
как изменится одна переменная, если другая увеличится;
что произойдет с аргументом, если мы уменьшим функцию;
что будет, если мы отобразим эту зависимость графически.
Спойлер: если изобразить зависимость в координатной системе, мы получим график! Давайте рассмотрим некоторые виды функций и графики, которые им соответствуют.
Важное напоминание: функция — это зависимая переменная величина (чаще у), аргумент — независимая переменная (чаще х).
Узнай, какие профессии будущего тебе подойдут
Пройди тест — и мы покажем, кем ты можешь стать, а ещё пришлём подробный гайд, как реализовать себя уже сейчас
Возрастание и убывание функции
В исследовании функции особое значение уделяют ее поведению в системе координат — монотонности функции. Функции бывают монотонными, немонотонными и постоянными.
Функции бывают монотонными, немонотонными и постоянными.
Монотонная функция — функция, которая возрастает или убывает на всем промежутке области определения.
Функцию считают немонотонной, если на промежутке области своего определения она чередует возрастание и убывание.
Постоянная функция, как ясно из названия, постоянна на всем промежутке и представляет собой прямую, параллельную оси x.
Теперь к теме раздела: приведем определение возрастающей и убывающей функции.
Функция называется возрастающей, когда при увеличении аргумента увеличивается и сама функция.
Проще говоря, здесь работает правило «чем больше, тем больше»: чем больше значение х, тем больше и значение у.
Функция считается убывающей, когда при увеличении аргумента функция уменьшается: чем больше х, тем меньше у.
Теперь вы знаете, как понять, что функция возрастает или убывает. Давайте решим пару задач, чтобы разобраться во всем наглядно.
Задача 1
Определите, возрастающая или убывающая функция y = 2x + 3.
1) Найдем область определения функции: х ∈ R.
2) Найдем координаты нескольких точек, которые ей принадлежат.
х | 0 | 1 | 2 | 3 |
у | 3 | 6 | 7 | 9 |
Как вы уже заметили, значения х и у одновременно увеличиваются — функция возрастает на всем промежутке.
Задача 2
Определите, возрастающая или убывающая функция y = 1/2х.
1) Найдем область определения функции: х ≠ 0.
2) Найдем координаты нескольких точек, которые ей принадлежат.
х | 1 | 2 | 3 | 4 |
у | ½ | ¼ | ⅙ | ⅛ |
х | -1 | -2 | -3 | -4 |
у | -½ | -¼ | -⅙ | -⅛ |
Мы видим, что функция убывает при любом значении х ≠ 0. Это можно записать так: функция убывает при х∈ (– ∞ ;0) ∪ (0; + ∞). Подытожим эту информацию небольшой схемой.
Это можно записать так: функция убывает при х∈ (– ∞ ;0) ∪ (0; + ∞). Подытожим эту информацию небольшой схемой.
Возрастание и убывание функции на интервале
Мы еще не закончили с возрастающими и убывающими функциями — эх, если бы все было так просто! Дело в том, что нас, математиков, интересуют вот какие вопросы:
Как найти промежутки возрастания и убывания функции по графику?
Что делать, если просят определить характер на числовом промежутке?
Как определить поведение функции без построения?
Давайте разбираться! Сначала узнаем, как определить характер функции на промежутке:
Подставим значение х из промежутка в функцию.
Проанализируем полученные значения у.
Если при увеличении х увеличивается и у — это промежуток возрастания функции.

Если у уменьшается при увеличении х — это промежуток убывания функции.
Достаточно просто, правда? 🙂
Пример
Возьмем функцию y = 4x – 6 и определим ее характер на промежутке [0;2]. Подставим числа из промежутка вместо х в функцию:
Мы видим, что при возрастании х возрастает и значение у, т. е. на этом промежутке функция возрастает.
Точки экстремума, экстремумы функции
Не пугайтесь этих страшных слов! Сейчас разберем их подробнее — это проще, чем кажется.
Экстре́мум (лат. extremum — крайний) в математике — максимальное или минимальное значение функции на заданном множестве.
На графике выше y min — минимальное значение функции, точка минимума.
Точка минимума — это значение переменной х, при которой функция минимальна.
На том же графике y мах — максимальное значение функции, точка максимума.
Точка максимума — это значение переменной х, при которой функция максимальна.
Иначе точки минимума и максимума в математике принято называть точками экстремума, а значения функции, которые соответствуют точкам экстремума — экстремумами функции.
В точках экстремума функция меняет свой характер. Обратите внимание на рисунок ниже: функция стремительно возрастала до точки максимума, но после нее начала также стремительно уменьшаться. И наоборот, после прохождения точки минимума функция снова начинает возрастать.
Здесь вам может стать интересно: наибольшее/наименьшее значение функции на промежутке — это то же самое или нет. Отвечаем: к сожалению, нет. Эти значения иногда могут совпадать, но часто определяются разными точками.
Отвечаем: к сожалению, нет. Эти значения иногда могут совпадать, но часто определяются разными точками.
Достаточные условия возрастания и убывания функции
У нас есть две новости: хорошая и не очень. Начнем с первой: если использовать достаточные условия возрастания/убывания, можно определить промежутки монотонности функции. И для этого даже не придется строить график! Но здесь нам пригодится производная.
Производная функции — это отношение приращения функции к приращению аргумента при бесконечно малом приращении аргумента.
Иначе говоря, производная функции показывает, как быстро увеличивается функция при бесконечно малом увеличении х.
К сожалению, в рамках этой статьи мы не будем долго останавливаться на производных. Как это сделать с помощью таблицы и правил дифференцирования, мы уже разбирали в статье «Таблица производных функций». Советуем почитать!
Достаточные признаки возрастания и убывания функции на интервале:
если производная функции y = f(x) положительна для любого x из интервала, то функция возрастает на этом интервале;
если производная функции y = f(x) отрицательна для любого x из интервала, то функция убывает на этом интервале.

Составим алгоритм действий, который поможет найти интервалы возрастания и убывания функции:
Найдем область определения функции.
Найдем производную функции.
Решим неравенства ƒ`(x) > 0 и ƒ`(x) < 0 на области определения.
К полученным промежуткам добавим граничные точки, в которых функция определена и непрерывна.
Проверим достаточные признаки возрастания и убывания функции, подставив значения из промежутков.
Задача 3
Укажите промежутки возрастания и убывания функции у = х2 + 5х + 6
Решение
Область определения функции: х ∈ R
Найдем производную функции: y’ = 2х + 5
Решим неравенство: 2х + 5 > 0
2х+5 >0 2x>-5 x> –2,5 Исследуем знаки производной с помощью числовой прямой.

Ответ: Функция убывает при х∈ (– ∞; –2,5], возрастает при х∈ [–2,5; +∞)
Задача 4
Определите интервалы возрастания и убывания функции у = х3 – 18х.
Решение
Область определения функции: х ∈ R.
Найдем производную функции: y’ = 3x2 + (–18).
Решим неравенство:
3x2 + (–18) > 0 3 (x2–9) > 0 3(x – 3)(x + 3) > 0 Исследуем знаки производной с помощью числовой прямой. Чтобы определить знак на каждом промежутке, подставим произвольное значение из этого промежутка в выражение для производной.
Ответ: Функция убывает при х∈ [–3;3], возрастает при х∈ (–∞;—3] ∪ [3; +∞).
Первое достаточное условие экстремума
Пусть для функции у = f(x) определены следующие условия:
Функция непрерывна в окрестности точки x0 (нет разрыва).
ƒ′(x0) = 0 или ƒ′(x0) не существует;
Производная ƒ′(x) при переходе через точку x0 меняет свой знак.
Тогда в точке x = x0 функция y = f(x) имеет экстремум, причем это минимум, если при переходе через точку x0 производная меняет свой знак с минуса на плюс; максимум, если при переходе через точку x0 производная меняет свой знак с плюса на минус.
Если производная в точке x0 не меняет свой знак, то в этой точке нет экстремума.
Итак, точки 1 и 4 — точки максимума, точка 3 — точка минимума. В точке 2 экстремума нет.
Алгоритм для нахождения точек экстремума
Теперь разберемся, как найти точки экстремума функции.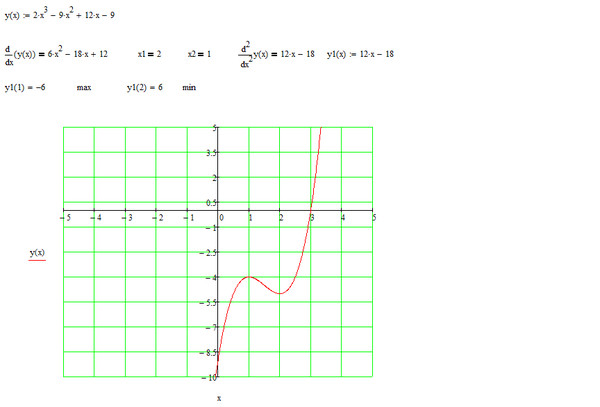 Для этого пройдем по этим шагам:
Для этого пройдем по этим шагам:
Найдем область определения функции.
Найдем производную функции на этой области.
Определим нули и точки, где функция не существует.
Определим знак производной на интервалах.
Выберем точки, где функция меняет знак.
Найдем точки минимума/максимума и экстремумы функции.
Задача 5
Найдите экстремумы функции у = –x2 + 8x – 7.
Решение
Область определения функции: х ∈ R.
Производная функции: y’ = –2x + 8
Решим неравенство:
–2x + 8 > 0 –2x > –8 x < 4 Определим знак производной на числовой прямой.
 Чтобы это сделать, на каждом промежутке подставим произвольное значение из этого промежутка в выражение для производной.
Чтобы это сделать, на каждом промежутке подставим произвольное значение из этого промежутка в выражение для производной.
В точке х = 4 функция меняет свой знак с «+» на «–», значит, точка х = 4 — это точка максимума.
Ответ: у(4) = 9 — экстремум функции.
Задача 6
Найдите экстремумы функции у = ⅓ x3 + 2x2 – 12x + 6.
Решение
Область определения функции: х ∈ R.
Производная функции: y’ = x2 + 4x – 12.
Решим неравенство:
x2 + 4x – 12 > 0 (x – 2)(x + 6) > 0 Определим знак производной на числовой прямой.
 Чтобы это сделать, на каждом промежутке подставим произвольное значение из этого промежутка в выражение для производной.
Чтобы это сделать, на каждом промежутке подставим произвольное значение из этого промежутка в выражение для производной.
Так на интервале (–∞; –6) и (2; +∞) производная положительна — на них функция возрастает. На интервале (–6;2) производная отрицательна — функция убывает.
Ответ: x = 2 — точка минимума, у(2) = –7 ⅓ — экстремум функции; х = –6 — точка максимума, у(–6) = 78 — экстремум функции.
Как можно запомнить переход знаков для точек максимум или минимум:
Когда функция возрастает, а потом убывает, мы будто поднимались на вершину горы — значит, посетили точку максимума.
Когда функция убывает, а потом возрастает, мы будто спускались в овраг и выбрались из него — а значит, были в точке минимума.
Второе достаточное условие экстремума
x0 — это точка экстремума функции f(x), если вторая производная функции в этой точке не равна нулю (f »(x) ≠ 0). Причем, если вторая производная больше нуля (f »(x) > 0), то точкой минимума, а если вторая производная меньше нуля (f »(x) < 0), то точкой максимума.
Причем, если вторая производная больше нуля (f »(x) > 0), то точкой минимума, а если вторая производная меньше нуля (f »(x) < 0), то точкой максимума.
Рассмотрим это условие экстремума на примере из задачи 6 — функции у = ⅓ x3 + 2x2 – 12x + 6:
Ее первая производная равна y’= x2 + 4x – 12.
Определим нули производной — значение х, при котором производная обращается в ноль: x2 + 4x – 12 = 0 при х = 2 и х = –6.
Возьмем вторую производную функции y’’= 2х + 4.
Подставим значения х = 2 и х = –6 во вторую производную и определим, являются ли эти точки максимумом или минимумом:
y’’(2) = 8, y’’ > 0, значит, х = 2 является точкой минимума, y’’(–6) = –8, y’’ < 0, значит, х = –6 является точкой максимум. 
В этом условии есть два важных замечания:
Если в точке x0 и первая, и вторая производные обращаются в ноль, то в этом случае нужно воспользоваться первым достаточным признаком экстремума функции, по второму признаку нельзя судить о наличии или отсутствии экстремумов.
Второй достаточный признак нельзя применять, когда в стационарной точке (нуле производной) первая производная не существует. Ведь тогда не существует и вторая производная.
Третье достаточное условие экстремума
Это условие не используется в школьной программе, так как требует большого количества вычислений и логических размышлений. Мы все равно познакомим вас с ним — возможно, вам захочется изучить это усaловие самостоятельно и блеснуть знаниями перед учителем. Что ж, мы только за!
Пусть функция y=f(x) имеет производные до n-ого порядка в ε-окрестности точки x0 и производные до n+1-го порядка в самой точке x0.




 Чтобы это сделать, на каждом промежутке подставим произвольное значение из этого промежутка в выражение для производной.
Чтобы это сделать, на каждом промежутке подставим произвольное значение из этого промежутка в выражение для производной. Чтобы это сделать, на каждом промежутке подставим произвольное значение из этого промежутка в выражение для производной.
Чтобы это сделать, на каждом промежутке подставим произвольное значение из этого промежутка в выражение для производной.
 3).
3). 7).
7).
 Н. Мишустина и др.; Под ред. А. Г. Мордковича. — 12-е изд., испр. — М.: 2010.-223 с.:ил.
Н. Мишустина и др.; Под ред. А. Г. Мордковича. — 12-е изд., испр. — М.: 2010.-223 с.:ил. Записывается как d(e x )/dx = e x .
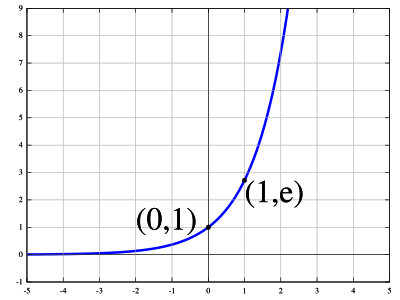
Записывается как d(e x )/dx = e x . Математически это обозначается как d(e x )/dx = e x . e в степени x является экспоненциальной функцией с основанием, равным «e», которое известно как «число Эйлера». Оно записывается как f(x) = e x , где e — число Эйлера, а его значение приблизительно равно 2,718. Дифференцирование e в степени x может быть выполнено с использованием различных методов, таких как первый принцип дифференцирования и производная х .
Математически это обозначается как d(e x )/dx = e x . e в степени x является экспоненциальной функцией с основанием, равным «e», которое известно как «число Эйлера». Оно записывается как f(x) = e x , где e — число Эйлера, а его значение приблизительно равно 2,718. Дифференцирование e в степени x может быть выполнено с использованием различных методов, таких как первый принцип дифференцирования и производная х . Мы знаем, что для двух экспоненциальных функций, если основания одинаковы, мы складываем степени. Для доказательства производной e в степени x воспользуемся следующими формулами показательных функций и производных:
Мы знаем, что для двух экспоненциальных функций, если основания одинаковы, мы складываем степени. Для доказательства производной e в степени x воспользуемся следующими формулами показательных функций и производных: Производная показательной функции f(x) = a x равно f'(x) = (ln a) a x . Используя эту формулу и подставляя значение a = e в f'(x) = (ln a) a x , мы получаем дифференцирование e в степени x, которая определяется выражением f'(x) = (ln e) e x = 1 x e x = e x [Поскольку по правилам журнала, ln e = 1]. Следовательно, производная от e в степени x равна e x .
Производная показательной функции f(x) = a x равно f'(x) = (ln a) a x . Используя эту формулу и подставляя значение a = e в f'(x) = (ln a) a x , мы получаем дифференцирование e в степени x, которая определяется выражением f'(x) = (ln e) e x = 1 x e x = e x [Поскольку по правилам журнала, ln e = 1]. Следовательно, производная от e в степени x равна e x .
 Математически это обозначается как d(e x )/dx = e x .
Математически это обозначается как d(e x )/dx = e x .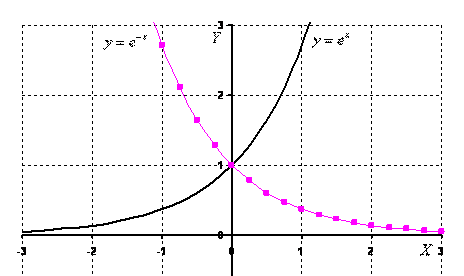 x.$$ 9х$$
является примером экспоненциального распада. Он быстро уменьшается по мере увеличения $x$, как показано на его графике.
x.$$ 9х$$
является примером экспоненциального распада. Он быстро уменьшается по мере увеличения $x$, как показано на его графике.



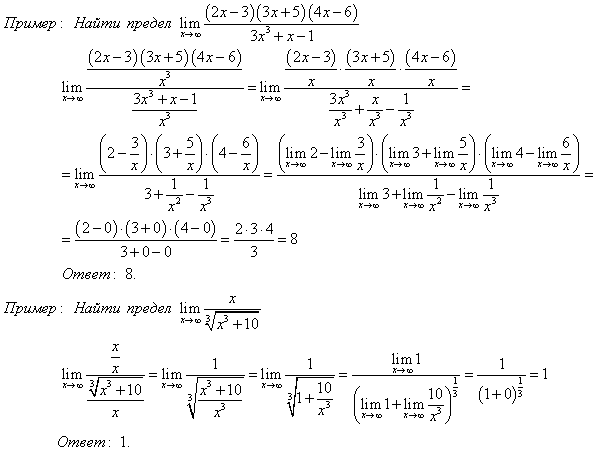 В точке x=1
обнуляется и числитель, и знаменатель. Чтобы найти предел в этой точке,
сократим дробь на (x−1). Получится выражение 1/(x+1). Оно имеет предел,
равный 1/2 при x→1. Значит, вертикальной асимптоты x=1 у функции
нет.
В точке x=1
обнуляется и числитель, и знаменатель. Чтобы найти предел в этой точке,
сократим дробь на (x−1). Получится выражение 1/(x+1). Оно имеет предел,
равный 1/2 при x→1. Значит, вертикальной асимптоты x=1 у функции
нет. Говорят,
что предел функции f(x) при x стремящемся к плюс бесконечности равен
b, если для всякого ε>0 найдётся такое C, что для всех x>C
верно неравенство |f(x)−b|<ε.
Говорят,
что предел функции f(x) при x стремящемся к плюс бесконечности равен
b, если для всякого ε>0 найдётся такое C, что для всех x>C
верно неравенство |f(x)−b|<ε.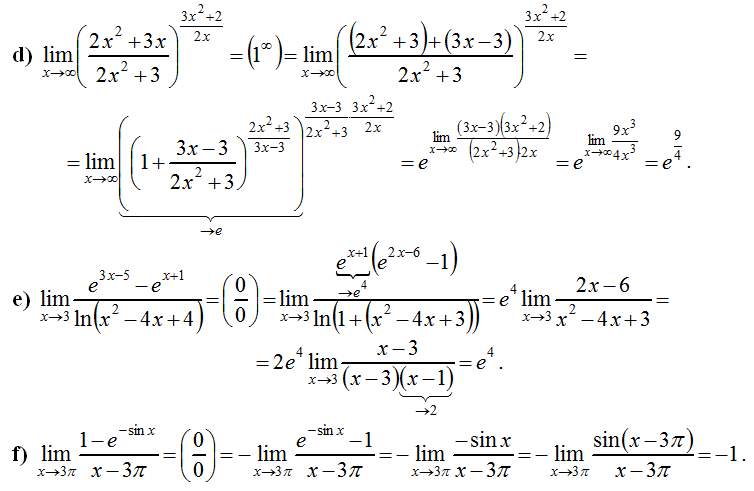 Такая прямая
называется горизонтальной асимптотой.
Такая прямая
называется горизонтальной асимптотой.
 Можно скрестить ужа с ежом и получить бесконечные пределы
при x стремящемся к бесконечности.
Можно скрестить ужа с ежом и получить бесконечные пределы
при x стремящемся к бесконечности.

 (12.1)(12.2)
При этом они обязаны равняться указанным значениям (k и b).
(12.1)(12.2)
При этом они обязаны равняться указанным значениям (k и b). ∎
∎ Для начала, как я могу сделать так, чтобы ограничения начинались с начала символа lim, а не перед ним? Это означает, что символ предела и пределы не должны быть центрированы.
Для начала, как я могу сделать так, чтобы ограничения начинались с начала символа lim, а не перед ним? Это означает, что символ предела и пределы не должны быть центрированы. Выравнивание задается параметром режима (
Выравнивание задается параметром режима ( 



 )
) )
) )
) )
) )
) )
) )
) )
) Темы, содержащиеся в статье, рассматриваются в соответствии с кодификатором, задающим элементы содержания заданий для выпускников образовательных организаций.
Темы, содержащиеся в статье, рассматриваются в соответствии с кодификатором, задающим элементы содержания заданий для выпускников образовательных организаций.
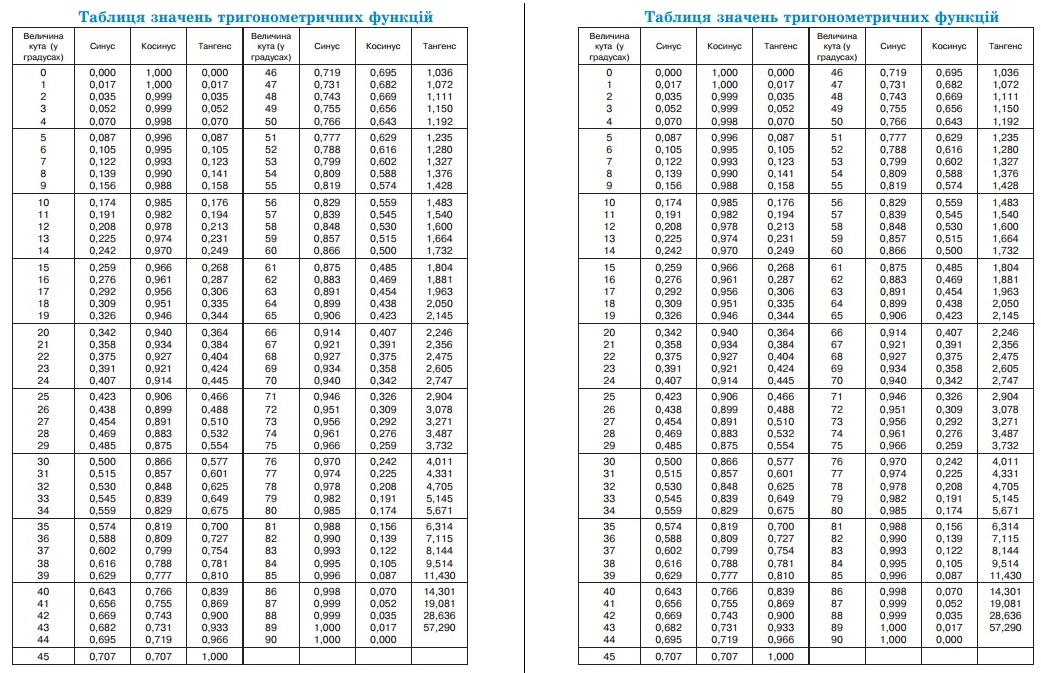
 Отрицательным тангенс является в четвёртой и второй четвертях.
Отрицательным тангенс является в четвёртой и второй четвертях.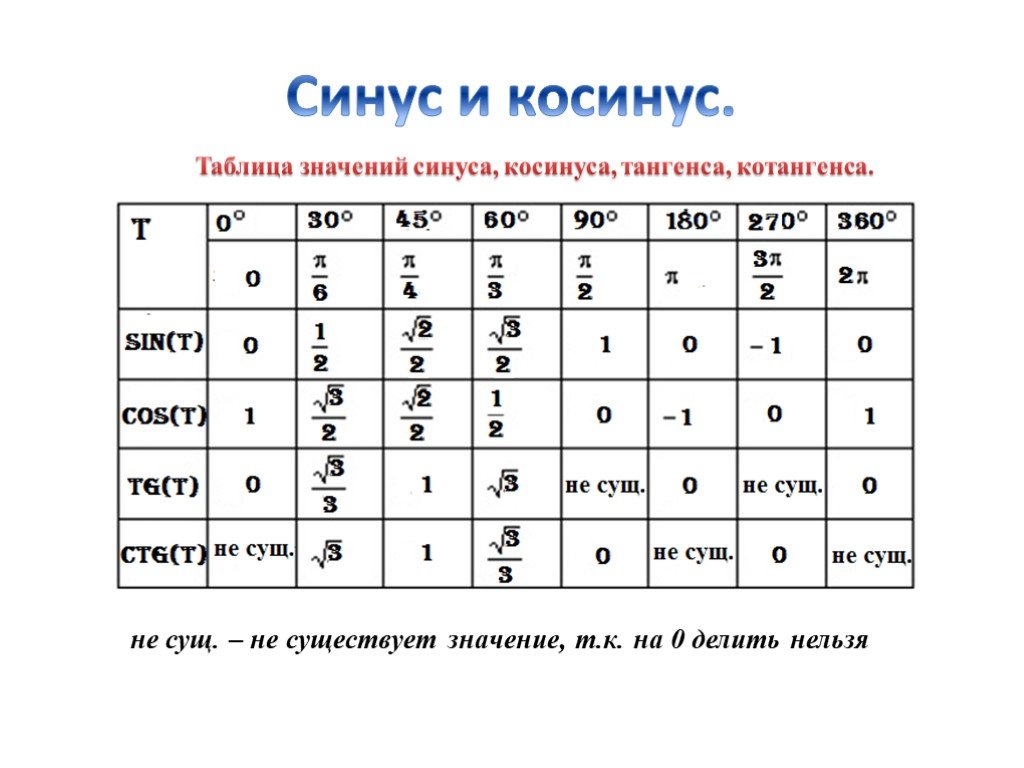 Один градус будет равен п 180 радиан. Один радиан соответственно, будет равен 180п. При этом, окружность будет равняться 2п.
Один градус будет равен п 180 радиан. Один радиан соответственно, будет равен 180п. При этом, окружность будет равняться 2п.

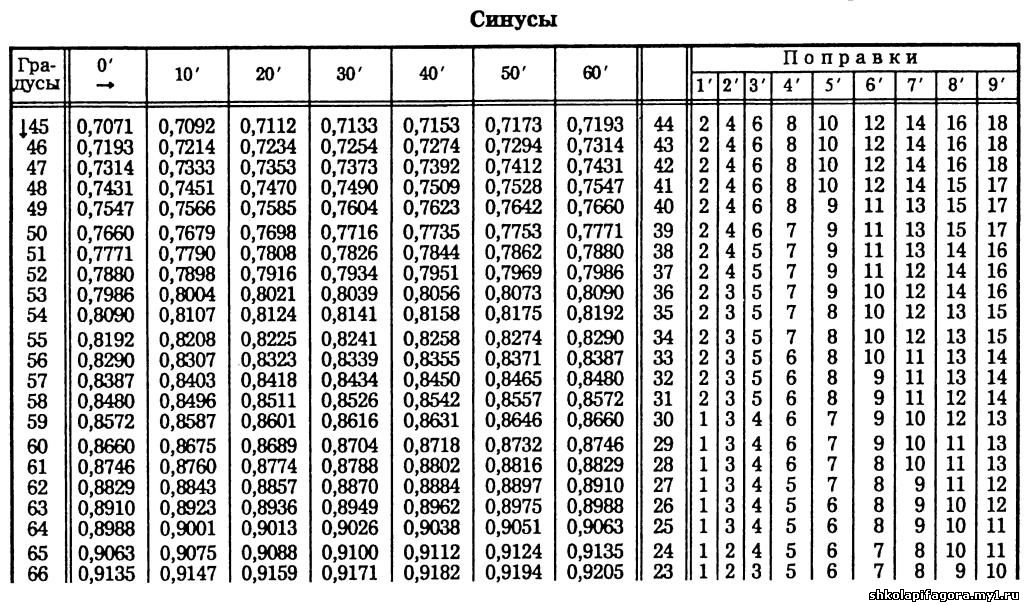
 . . Тангенс 1 градус в радианах записывается как тангенс (1° × π/180°), т. е. тангенс (0,017453…). В этой статье мы обсудим методы определения значения тангенса 1 градуса на примерах.
. . Тангенс 1 градус в радианах записывается как тангенс (1° × π/180°), т. е. тангенс (0,017453…). В этой статье мы обсудим методы определения значения тангенса 1 градуса на примерах.  Поскольку функция тангенса положительна в первом квадранте, значение тангенса 1° = 0,0174550. . .
Поскольку функция тангенса положительна в первом квадранте, значение тангенса 1° = 0,0174550. . .  998) точки пересечения (0,9998, 0,0175) единичной окружности и r.
998) точки пересечения (0,9998, 0,0175) единичной окружности и r. 
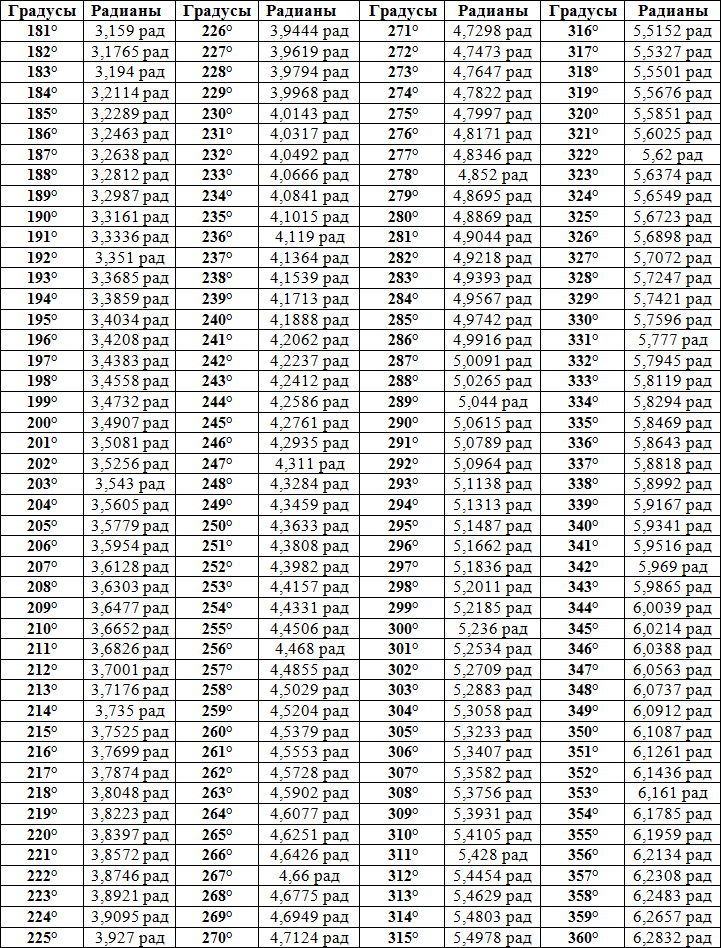
 Здесь значение sin 1° равно 0,0175.
Здесь значение sin 1° равно 0,0175.  Мы здесь, чтобы помочь вам понять, что означают эти уравнения и как их решать.
Мы здесь, чтобы помочь вам понять, что означают эти уравнения и как их решать.  Префикс
Префикс 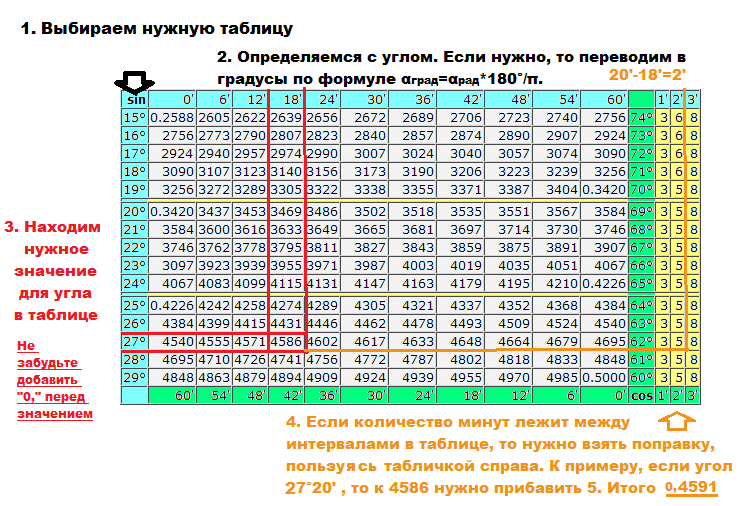 Вот они:
Вот они: 
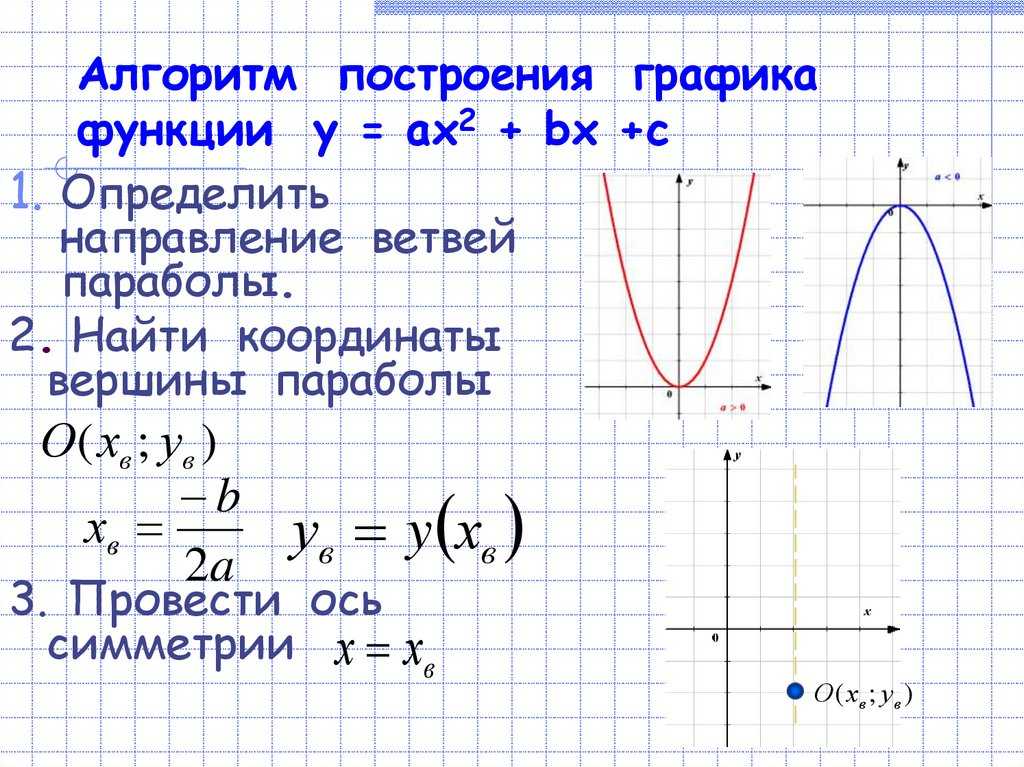 Любая точка на кривой находится на одинаковом расстоянии от фиксированной точки и фиксированной прямой линии. Результат выглядит как половина эллипса или дуги, образованной, когда объект подбрасывается в воздух и падает на небольшое расстояние. Поскольку это не математическая программа, Microsoft Word не может построить график на основе введенных вами данных, но благодаря большому набору инструментов для рисования вы можете нарисовать параболу после того, как рассчитаете ее форму.
Любая точка на кривой находится на одинаковом расстоянии от фиксированной точки и фиксированной прямой линии. Результат выглядит как половина эллипса или дуги, образованной, когда объект подбрасывается в воздух и падает на небольшое расстояние. Поскольку это не математическая программа, Microsoft Word не может построить график на основе введенных вами данных, но благодаря большому набору инструментов для рисования вы можете нарисовать параболу после того, как рассчитаете ее форму. 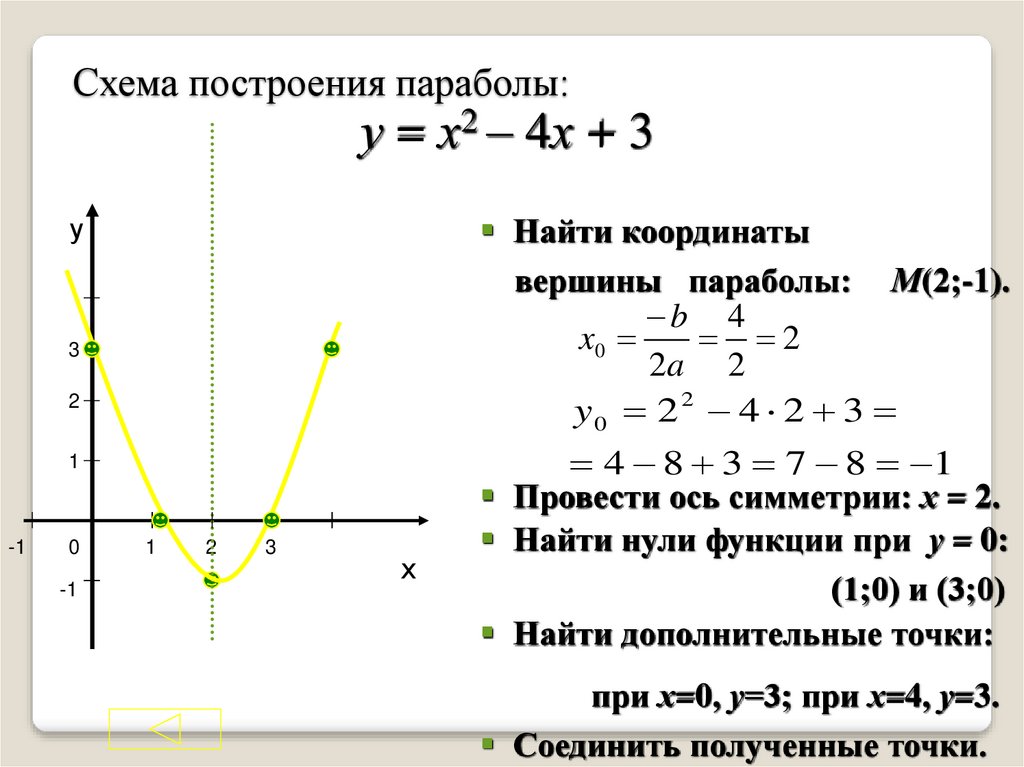 Эта вкладка содержит все команды рисования Word, но появляется только при выборе объекта рисования.
Эта вкладка содержит все команды рисования Word, но появляется только при выборе объекта рисования. 
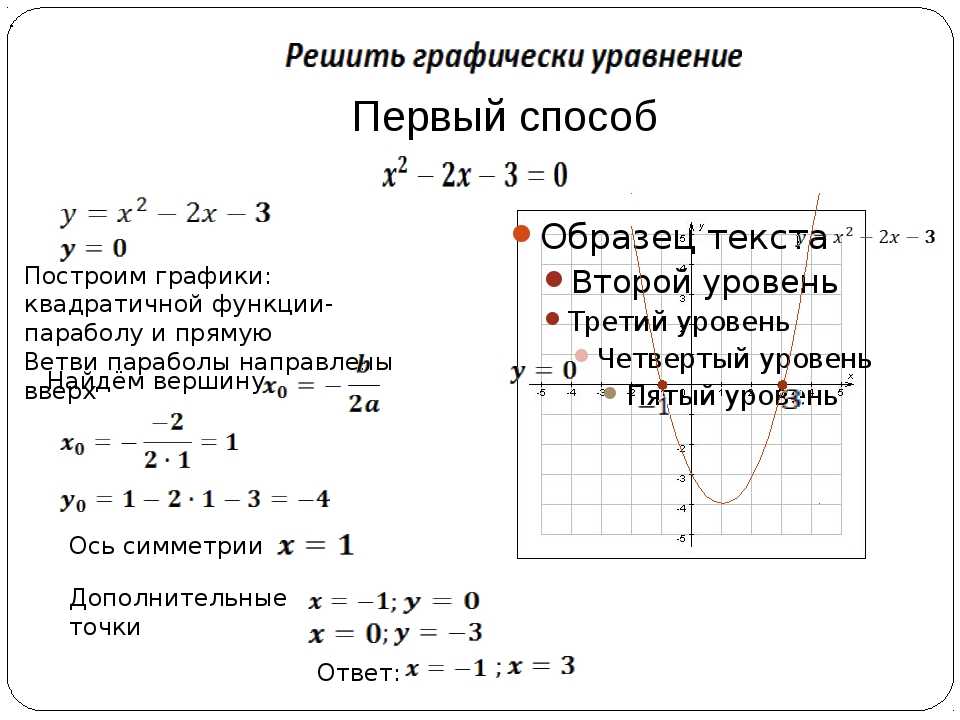


 Этот способ часто применяют в классе на уроке алгебры и при решении домашних заданий.
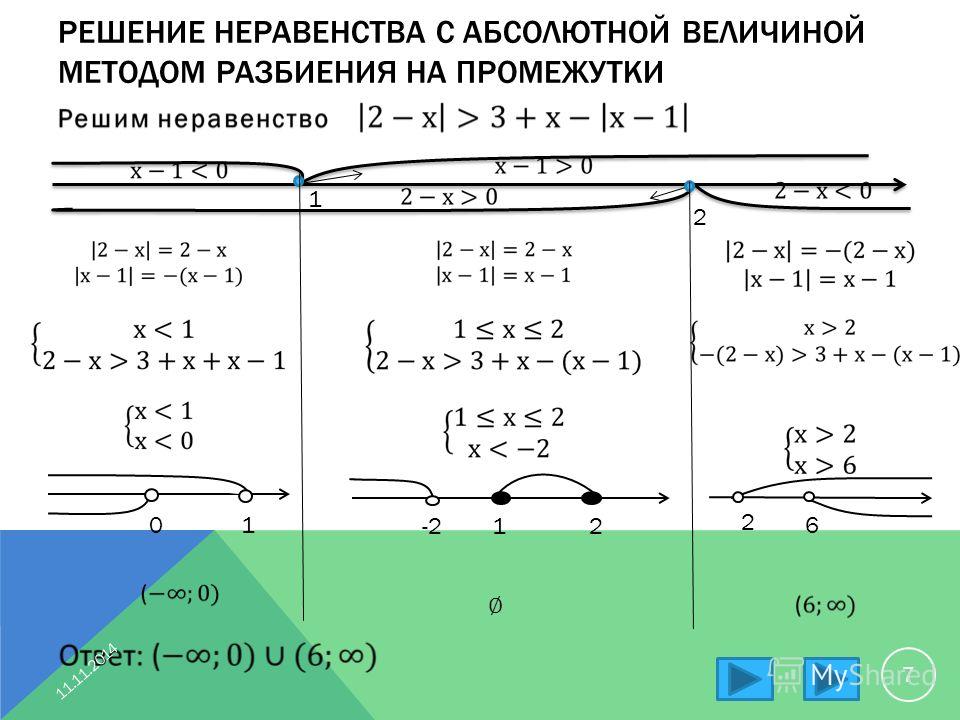
Этот способ часто применяют в классе на уроке алгебры и при решении домашних заданий. Для этого сначала вычислим нули выражений, которые записаны под знаком модуля:
Для этого сначала вычислим нули выражений, которые записаны под знаком модуля:

 Xartli formulasi, kompyuterning ishlashining mantiqiy, 11 A sinf , Noaniq integral haqida ma’ruza va yechish usullari , 1-Test, xosmas integrallarning geometriya va fizikaga tatbiqlari, 2013, 1367254467.0182english-grammar-tests, ielts speaking, art-spok, fizika oqitish metodikasi, Algoritmlash va dasturlash ingliz tili
Xartli formulasi, kompyuterning ishlashining mantiqiy, 11 A sinf , Noaniq integral haqida ma’ruza va yechish usullari , 1-Test, xosmas integrallarning geometriya va fizikaga tatbiqlari, 2013, 1367254467.0182english-grammar-tests, ielts speaking, art-spok, fizika oqitish metodikasi, Algoritmlash va dasturlash ingliz tili Иначе вы рискуете вообще не понять материал сегодняшнего урока.
Иначе вы рискуете вообще не понять материал сегодняшнего урока.

 Исследуйте книгу Купить на Amazon
Исследуйте книгу Купить на Amazon  Абсолютное значение всегда должно быть нулевым или положительным (единственное, что меньше отрицательных чисел, — это другие отрицательные числа). Например, абсолютное неравенство |2 x – 1| < –3 не имеет решения, потому что неравенство меньше отрицательного числа.
Абсолютное значение всегда должно быть нулевым или положительным (единственное, что меньше отрицательных чисел, — это другие отрицательные числа). Например, абсолютное неравенство |2 x – 1| < –3 не имеет решения, потому что неравенство меньше отрицательного числа.  Любое действительное число, которое вы подставите в это уравнение, работает.
Любое действительное число, которое вы подставите в это уравнение, работает. 



 Затем мы решаем каждую отдельно.
Затем мы решаем каждую отдельно.



 Наибольший из них – 15 – является самым большим. Это и есть НОД.
Наибольший из них – 15 – является самым большим. Это и есть НОД. В данном случае – 10.
В данном случае – 10. е. представим каждое число как произведения простых чисел. Множители большего числа запишем сверху:
е. представим каждое число как произведения простых чисел. Множители большего числа запишем сверху:
 У нас также есть несколько вопросов, основанных на наименьшем общем кратном, которое может ответить ваш ребенок, и все, чтобы помочь ему (и вам) быстро освоить математику!
У нас также есть несколько вопросов, основанных на наименьшем общем кратном, которое может ответить ваш ребенок, и все, чтобы помочь ему (и вам) быстро освоить математику!

 Например, чтобы вычислить 3/5 + 1/6, нам нужно найти общий знаменатель, вычислив наименьшее общее кратное 5 и 6 (30). Затем мы можем преобразовать дроби в 18/30 + 5/30 = 23/30.
Например, чтобы вычислить 3/5 + 1/6, нам нужно найти общий знаменатель, вычислив наименьшее общее кратное 5 и 6 (30). Затем мы можем преобразовать дроби в 18/30 + 5/30 = 23/30.
 значения в обоих списках): 12, 24, …
значения в обоих списках): 12, 24, …


 Для других – сделает изучение хотя бы не столь противным (что тоже немаловажно, так как многие дети просто не хотят учить таблицу умножения). Для третьих мало что изменится в ходе заучивания, но зато запомнится все гораздо более устойчиво.
Для других – сделает изучение хотя бы не столь противным (что тоже немаловажно, так как многие дети просто не хотят учить таблицу умножения). Для третьих мало что изменится в ходе заучивания, но зато запомнится все гораздо более устойчиво.
 Все это будет размещаться в разделе КАРП-ВИДЕО.
Все это будет размещаться в разделе КАРП-ВИДЕО. Страницы
Страницы  Например, опишите контекст, в котором общее количество объектов может быть выражено как 5 × 7.
Например, опишите контекст, в котором общее количество объектов может быть выражено как 5 × 7.  Например, определите неизвестное число, которое делает уравнение истинным в каждом из уравнений 8 × ? = 48, 5 = _ ÷ 3, 6 × 6 = ?
Например, определите неизвестное число, которое делает уравнение истинным в каждом из уравнений 8 × ? = 48, 5 = _ ÷ 3, 6 × 6 = ?  Math.Content.3.OA.C. 7 Свободно умножайте и делите в пределах 100, используя такие стратегии, как взаимосвязь между умножением и делением (например, зная, что 8 × 5 = 40, известно, что 40 ÷ 5 = 8) или свойства операций. К концу 3 класса знать наизусть все произведения двух однозначных чисел.
Math.Content.3.OA.C. 7 Свободно умножайте и делите в пределах 100, используя такие стратегии, как взаимосвязь между умножением и делением (например, зная, что 8 × 5 = 40, известно, что 40 ÷ 5 = 8) или свойства операций. К концу 3 класса знать наизусть все произведения двух однозначных чисел. 

 Или нажмите «Файл», затем «Печать». Страницы
Или нажмите «Файл», затем «Печать». Страницы 
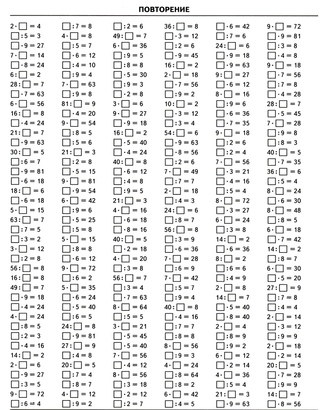
 К концу 3 класса знать наизусть все произведения двух однозначных чисел.
К концу 3 класса знать наизусть все произведения двух однозначных чисел.  Проиллюстрируйте и объясните расчет, используя уравнения, прямоугольные массивы и/или модели площадей.
Проиллюстрируйте и объясните расчет, используя уравнения, прямоугольные массивы и/или модели площадей.  Проиллюстрируйте и объясните расчет, используя уравнения, прямоугольные массивы и/или модели площадей.
Проиллюстрируйте и объясните расчет, используя уравнения, прямоугольные массивы и/или модели площадей.  Наши рабочие листы и печатные формы для разделения на основе навыков помогают учащимся с третьего по пятый класс поднять свои математические навыки на ступеньку выше. Изучите анатомию задач на деление и попрактикуйтесь в многозначном делении и дробях с манипуляциями, используя эти рабочие листы деления и печатные формы!
Наши рабочие листы и печатные формы для разделения на основе навыков помогают учащимся с третьего по пятый класс поднять свои математические навыки на ступеньку выше. Изучите анатомию задач на деление и попрактикуйтесь в многозначном делении и дробях с манипуляциями, используя эти рабочие листы деления и печатные формы!
 Радикальный калькулятор имеет …
Радикальный калькулятор имеет … Du kannst bei Bedarf diesuche unter Einbeziehung der übersprungenen Ergebnisse wiederholen.
Du kannst bei Bedarf diesuche unter Einbeziehung der übersprungenen Ergebnisse wiederholen. ..
.. Введите любую производную функции, чтобы получить решение, шаги и график.
Введите любую производную функции, чтобы получить решение, шаги и график. ..
..
 Общее уравнение прямой и его частные случаи
Общее уравнение прямой и его частные случаи Понятие об определителях высших порядков
Понятие об определителях высших порядков Равенство матриц. Действия над матрицами
Равенство матриц. Действия над матрицами Прямая и плоскость в пространстве
Прямая и плоскость в пространстве Понятие о гиперболических функциях
Понятие о гиперболических функциях Механический смысл второй производной
Механический смысл второй производной Отыскание наибольшего и наименьшего значений функции
Отыскание наибольшего и наименьшего значений функции Метод неопределенных коэффициентов
Метод неопределенных коэффициентов Вычисление объема тела по известным поперечным сечениям
Вычисление объема тела по известным поперечным сечениям Точки разрыва
Точки разрыва Вычисление двойного интеграла в декартовых координатах
Вычисление двойного интеграла в декартовых координатах ФУНКЦИОНАЛЬНЫЕ РЯДЫ
ФУНКЦИОНАЛЬНЫЕ РЯДЫ Особые решения
Особые решения ИНТЕГРИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ПОМОЩЬЮ РЯДОВ
ИНТЕГРИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ПОМОЩЬЮ РЯДОВ






 Группа посетила зона во время охоты.
в районе , окружающем озеро
Шторм нанес ущерб многим районам вдоль побережья.
птица, обитающая только в отдаленных районах США.
во многих район мира
Он является самым популярным политиком столичного региона .
Он жил в немодном районе города.
Она отложила работу площадью на кухню.
Группа посетила зона во время охоты.
в районе , окружающем озеро
Шторм нанес ущерб многим районам вдоль побережья.
птица, обитающая только в отдаленных районах США.
во многих район мира
Он является самым популярным политиком столичного региона .
Он жил в немодном районе города.
Она отложила работу площадью на кухню. Столовая область имеет дополнительные окна.
Узнать больше
Столовая область имеет дополнительные окна.
Узнать больше —Адам Бим, Fortune , 12 мая 2023 г.
Заторы на проезжей части также возникают на популярных началах троп в парке, что приводит к парковке в неустановленных зонах и проблемам безопасности пешеходов из-за ограниченной видимости проезжей части.
— oregonlive , 12 мая 2023 г.
Как закрытие небольших сельских больниц усугубляет кризис материнского здоровья 11 октября 20203:53 Жители района 9По словам Уоррена, 0082 с достаточным уходом за беременными тоже может воспользоваться горячей линией.
— Новости NBC , 12 мая 2023 г.
Наблюдение произошло в Овьедо, в районе метро Орландо-Киссимми-Санфорд, район .
— США СЕГОДНЯ , 12 мая 2023 г.
Советы от представителей общественности, которые видели автомобиль подозреваемых в районе Западного Лос-Анджелеса и Беверли-Хиллз зона привела следователей к жилому комплексу на Уилшире.
—Адам Бим, Fortune , 12 мая 2023 г.
Заторы на проезжей части также возникают на популярных началах троп в парке, что приводит к парковке в неустановленных зонах и проблемам безопасности пешеходов из-за ограниченной видимости проезжей части.
— oregonlive , 12 мая 2023 г.
Как закрытие небольших сельских больниц усугубляет кризис материнского здоровья 11 октября 20203:53 Жители района 9По словам Уоррена, 0082 с достаточным уходом за беременными тоже может воспользоваться горячей линией.
— Новости NBC , 12 мая 2023 г.
Наблюдение произошло в Овьедо, в районе метро Орландо-Киссимми-Санфорд, район .
— США СЕГОДНЯ , 12 мая 2023 г.
Советы от представителей общественности, которые видели автомобиль подозреваемых в районе Западного Лос-Анджелеса и Беверли-Хиллз зона привела следователей к жилому комплексу на Уилшире. — Ричард Уинтон, Los Angeles Times , 12 мая 2023 г.
Это регион, известный мегакатастрофами тропических циклонов — с необычайным штормовым нагоном, обрушившимся на густонаселенный район — и один из них в настоящее время находится в агонии войны.
— Ян Ливингстон, Washington Post , 11 мая 2023 г.
9В районе 0081 также находится Государственный парк Галф, в котором есть пешеходные и велосипедные маршруты, а также возможности для рыбалки и наблюдения за дикой природой.
— Лора Рэтлифф, Country Living , 11 мая 2023 г.
Узнать больше
— Ричард Уинтон, Los Angeles Times , 12 мая 2023 г.
Это регион, известный мегакатастрофами тропических циклонов — с необычайным штормовым нагоном, обрушившимся на густонаселенный район — и один из них в настоящее время находится в агонии войны.
— Ян Ливингстон, Washington Post , 11 мая 2023 г.
9В районе 0081 также находится Государственный парк Галф, в котором есть пешеходные и велосипедные маршруты, а также возможности для рыбалки и наблюдения за дикой природой.
— Лора Рэтлифф, Country Living , 11 мая 2023 г.
Узнать больше Любые мнения, выраженные в примерах, не отражают точку зрения Merriam-Webster или ее редакторов. Отправьте нам отзыв об этих примерах.
Любые мнения, выраженные в примерах, не отражают точку зрения Merriam-Webster или ее редакторов. Отправьте нам отзыв об этих примерах. » Словарь Merriam-Webster.com , Merriam-Webster, https://www.merriam-webster.com/dictionary/area. Доступ 18 мая. 2023. Копия цитирования
» Словарь Merriam-Webster.com , Merriam-Webster, https://www.merriam-webster.com/dictionary/area. Доступ 18 мая. 2023. Копия цитирования м. 4
м. 4 com: Энциклопедическая статья о области
com: Энциклопедическая статья о области 


 Любые мнения в примерах не отражают мнение редакторов Кембриджского словаря, издательства Кембриджского университета или его лицензиаров.
Любые мнения в примерах не отражают мнение редакторов Кембриджского словаря, издательства Кембриджского университета или его лицензиаров. Любые мнения в примерах не отражают мнение редакторов Кембриджского словаря, издательства Кембриджского университета или его лицензиаров.
Любые мнения в примерах не отражают мнение редакторов Кембриджского словаря, издательства Кембриджского университета или его лицензиаров. copyright1}}
copyright1}}