Четность, нечетность, периодичность тригонометрических функций
ЧЕТНОСТЬ, НЕЧЕТНОСТЬ, ПЕРИОДИЧНОСТЬ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
НОВЫЙ МАТЕРИАЛ
Функция
Область определения D(y)
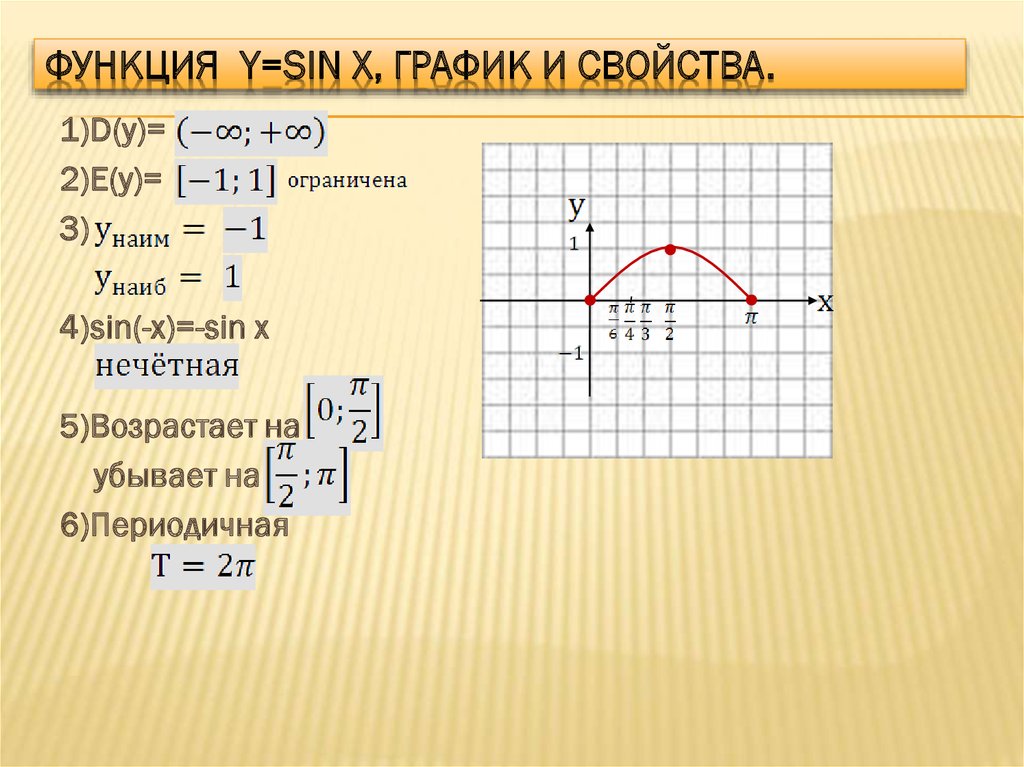
y=sin x
Множество значений E(y)
y=cos x
y=tg x
y=ctg x
R
R
R
R
ДОМАШНЕЕ ЗАДАНИЕ
№ 1 (4,6), № 2 (4,6),
№ 3 (1,2), № 5 (2)
стр.6
РЕШЕНИЕ УПРАЖНЕНИЙ
1. Найдите область определения функции:
РЕШЕНИЕ УПРАЖНЕНИЙ
2. Найти множество значений функции:
РЕШЕНИЕ УПРАЖНЕНИЙ
3. Найдите область определения функции:
Решение
0
0
•
-1
РЕШЕНИЕ УПРАЖНЕНИЙ
3. Найдите область определения функции:
Найдите область определения функции:
ЧЕТНОСТЬ И НЕЧЕТНОСТЬ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
11 класс
ДОМАШНЕЕ ЗАДАНИЕ
П.1.3
№ 18, 32(а.б.в)
Функции
Чётные
Ни чётные,
ни нечётные
Нечётные
СИММЕТРИЯ ОТНОСИТЕЛЬНО ОСИ ОУ И НАЧАЛА КООРДИНАТ
ЧЕТНЫЕ ФУНКЦИИ
- Функция y = f(x) называется четной, если для любого х из области определения функции верно равенство f(-x) = f(x).
- Чтобы узнать является ли функция четной нужно в функцию f(x) вместо переменной х поставить переменную( –x ).
ЧЕТНЫЕ ФУНКЦИИ
- Например: является ли четной функция f(x) = 3x 2 + 2
- f (-x) = 3(-x) 2 + 2 = 3x 2 + 2 = f(x) – функция четная
ЧЕТНЫЕ ФУНКЦИИ
- Проверим являются ли данные функции четными
- f( — x) = 2(-x) 4 – 3(-x) 2 = 2x 4 — 3x 2 — четная
- f ( — x) = (- x ) 3 – 2 (- x ) 2 = – x 3 – 2x 2 Не является четной
- f(x) = 2x 4 — 3x 2
- f (x) = x 3 — 2x 2
ГРАФИК ЧЕТНОЙ ФУНКЦИИ
- График четной функции симметричен относительно оси ординат (ось ОУ).

НЕЧЕТНЫЕ ФУНКЦИИ
- Функция y = f(x) называется нечетной, если для любого х из области определения функции верно равенство
f(-x) = — f(x).
- чтобы узнать является ли функция нечетной нужно в функцию f(x) вместо переменной х поставить переменную ( – x ) и получить первоначальную функцию с противоположными знаками .
НЕЧЕТНЫЕ ФУНКЦИИ
- Например: является ли нечетной функция f(x) = 3x 3 + х
- f (-x) = 3(-x) 3 + (-х) = — 3x 3 — х = -( 3x 3 + х)=
= — f(x) – функция нечетная
НЕЧЕТНЫЕ ФУНКЦИИ
- Проверим являются ли данные функции нечетными
- f ( — x) = 2(-x) 4 + 3(-x) = = 2x 4 — 3x — не является нечетной
- f ( — x) = (- x ) 3 – 2 (- x ) = – x 3 + 2x нечетная
- f(x) = 2x 4 + 3x
- f (x) = x 3 — 2x
ГРАФИК НЕЧЕТНОЙ ФУНКЦИИ
- График нечетной функции симметричен относительно начала координат.

ЧЕТНЫЕ И НЕЧЕТНЫЕ ФУНКЦИИ
- Функции могут быть как четными, нечетными , так и ни четными, ни нечетными.
Пример: y (x) = x 2 + 2x
y(-x) = (-x) 2 + 2(-x) = x 2 — 2x
Для любого значения x верны равенства :
- Sin(-x) = -Sin x Cos(-x) = Cos x
- Sin(-x) = -Sin x Cos(-x) = Cos x
- Sin(-x) = -Sin x
- Cos(-x) = Cos x
Следовательно :
y= Sin x – нечетная функция
y= Cos x – четная функция
Так как для любого значения x из области определения функции
y = tg x верно равенство
tg(-x) = -tg x ,
то y = tg x – нечетная функция.
ПРИМЕР
Выяснить, является ли функция
y = 2 + Sin 2 x четной или нечетной.
Решение :
y(-x) = 2 + Sin 2 (-x) = 2 + (-Sin x) 2 =
=2 + Sin 2 x = y(x)
y = 2 + Sin 2 x – четная функция .
Пример: определите, является ли данная функция четной или нечетной
Решение:
Работа в тетрадях
Определите, являются ли данные функции четными или нечетными:
Разбейте функции на три группы:
- четные
- нечетные
- не являются ни четными, ни нечетными
Проверяем ответы
четные
нечетные
1
ни чет., ни нечет.
2
4
5
3
9
10
7
6
15
8
11
14
12
13
Подведение итогов урока
- y=sinx – нечетная функция,
т.к. sin(-x)=-sinx
График функции симметричен относительно начала координат
2. y=cosx – нечетная функция,
y=cosx – нечетная функция,
т.к. cos(-x)=cosx
График функции симметричен относительно оси Оу
ЧЕТНОСТЬ, НЕЧЕТНОСТЬ, ПЕРИОДИЧНОСТЬ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
11 класс
Для любого значения x верны равенства :
- Sin (x + 2 π ) = Sin x Cos (x + 2 π ) = Cos х
- Sin (x + 2 π ) = Sin x Cos (x + 2 π ) = Cos х
- Sin (x + 2 π ) = Sin x
- Cos (x + 2 π ) = Cos х
Следовательно, значения Sin и Cos периодически повторяются при изменении аргумента на 2 π .
Такие функции называются периодическими с периодом 2 π .
Функция f(x) называется периодической , если существует такое число T ≠ 0 , что для любого x из области определения этой функции выполняется равенство
f(x – T) = f(x) = f(x + T).
Число T называется периодом функции f(x).
Функция y = cos x
y
y=cos x
1
-3 π /2
— π /2
π /2
π
3 π /2
0
— π
x
-1
Графиком функции у = cos x является косинусоида
- D(y) =R
- Периодическая Т=2
- Четная cos(-x)=cos x
- Нули функции:
у=0, cos x=0 при х = 1/2 n, n Z
sin(x+ /2)=cos x
32
32
ПОКАЖЕМ, ЧТО ЧИСЛО 2 Π ЯВЛЯЕТСЯ НАИМЕНЬШИМ ПОЛОЖИТЕЛЬНЫМ ПЕРИОДОМ ФУНКЦИИ Y = COS X.
Пусть Т › 0 – период косинуса, т.е. для любого x выполняется равенство
Cos (x + T) = Cos x. Положив x = 0 , получим Cos T = 1.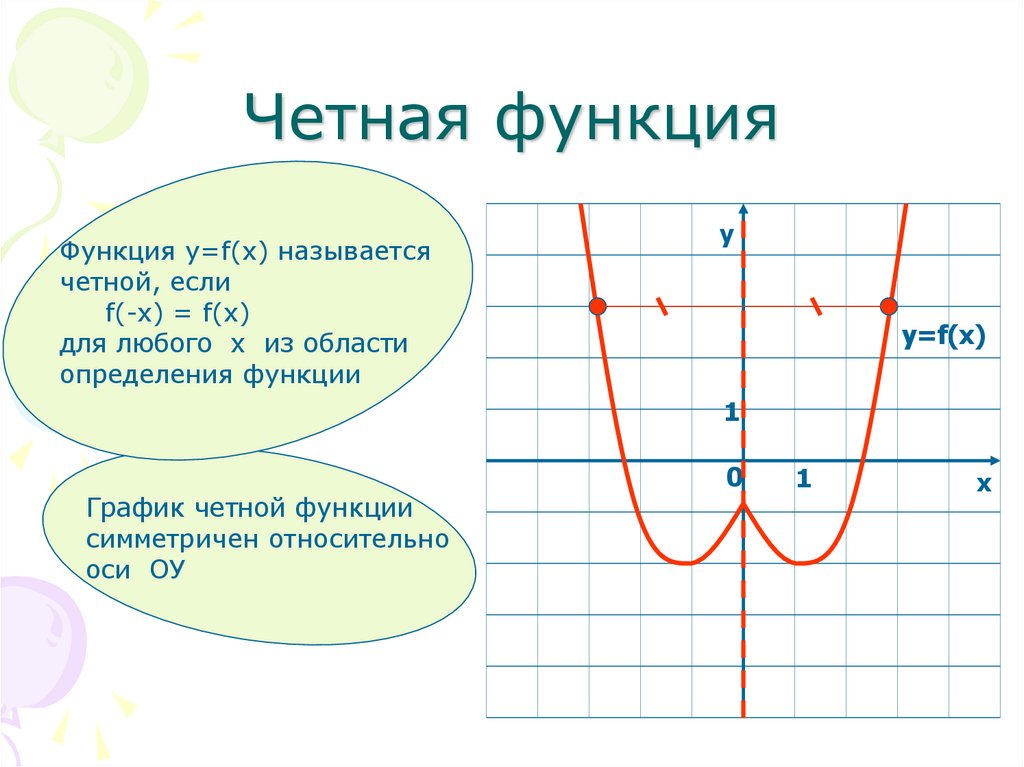 Отсюда T = 2 π k, k є Ζ . Так как Т › 0, то Т может принимать значения 2 π , 4 π , 6 π , …, и поэтому период не может быть меньше 2 π .
Отсюда T = 2 π k, k є Ζ . Так как Т › 0, то Т может принимать значения 2 π , 4 π , 6 π , …, и поэтому период не может быть меньше 2 π .
Функция y=sin x и ее свойства
y
y=sin x
1
0
-3 π /2
3 π /2
π /2
— 2 π
2 π
— π /2
— π
π
x
-1
Графиком функции y=sin x является синусоида
Свойства функции:
- D(y) =R
- Периодическая (Т=2 )
- Нечетная ( sin(-x)=-sin x)
- Нули функции:
у=0, sin x=0 при х = n, n Z
34
АНАЛОГИЧНО МОЖНО ДОКАЗАТЬ, ЧТО НАИМЕНЬШИЙ ПОЛОЖИТЕЛЬНЫЙ ПЕРИОД ФУНКЦИИ Y = SIN X ТАКЖЕ РАВЕН 2 Π
Пример :
Доказать, что f(x) = Sin 3x – периодическая функция с периодом ( 2 π ) /3.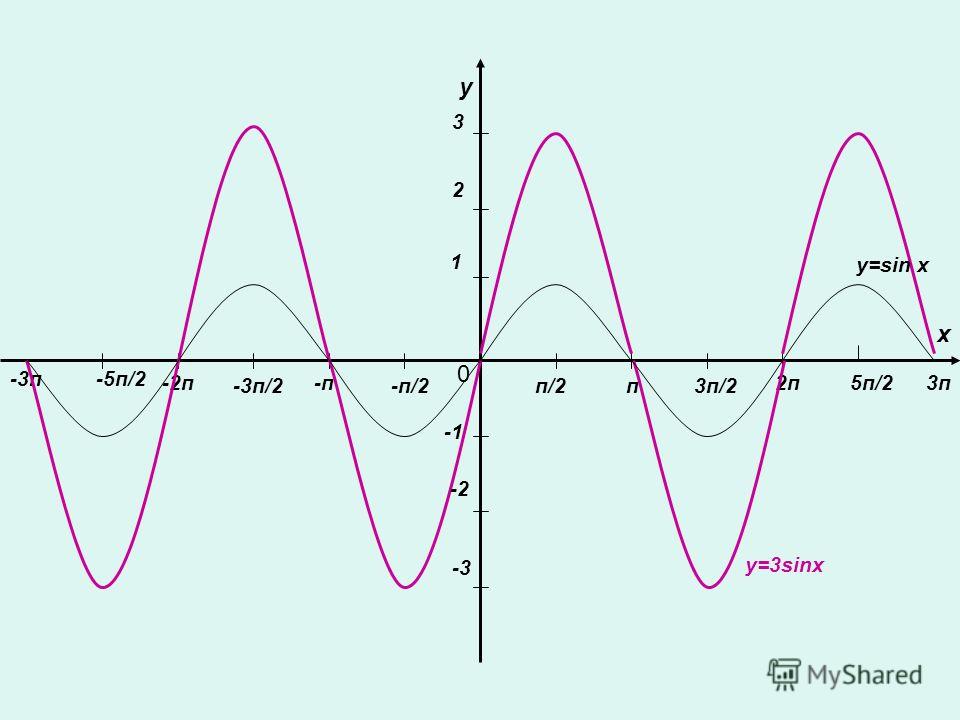
Доказательство :
Данная функция определена для всех x є R , поэтому достаточно показать, что для любого x верно равенство f(x + T) = f(x) .
f(x + (2 π )/3) = Sin 3(x + (2 π )/3) =
= Sin (3x + 2 π ) = Sin 3x = f(x)
Построение графика функции у= tg x на всей бласти определения:
Функция у= tg x периодическая с периодом П, следовательно график этой функции получается на интервале от (-П/2;П/2) сдвигами вдоль оси абсцисс на П k, где
Построить график функции y = — tg (x + /2) .
у
y = ctg x
х
Т.к. — tg (x + /2) = ctg x , то построен график функции
y = ctg x .
ПОКАЖЕМ, ЧТО ФУНКЦИЯ Y= TG X ЯВЛЯЕТСЯ ПЕРИОДИЧЕСКОЙ С ПЕРИОДОМ Π .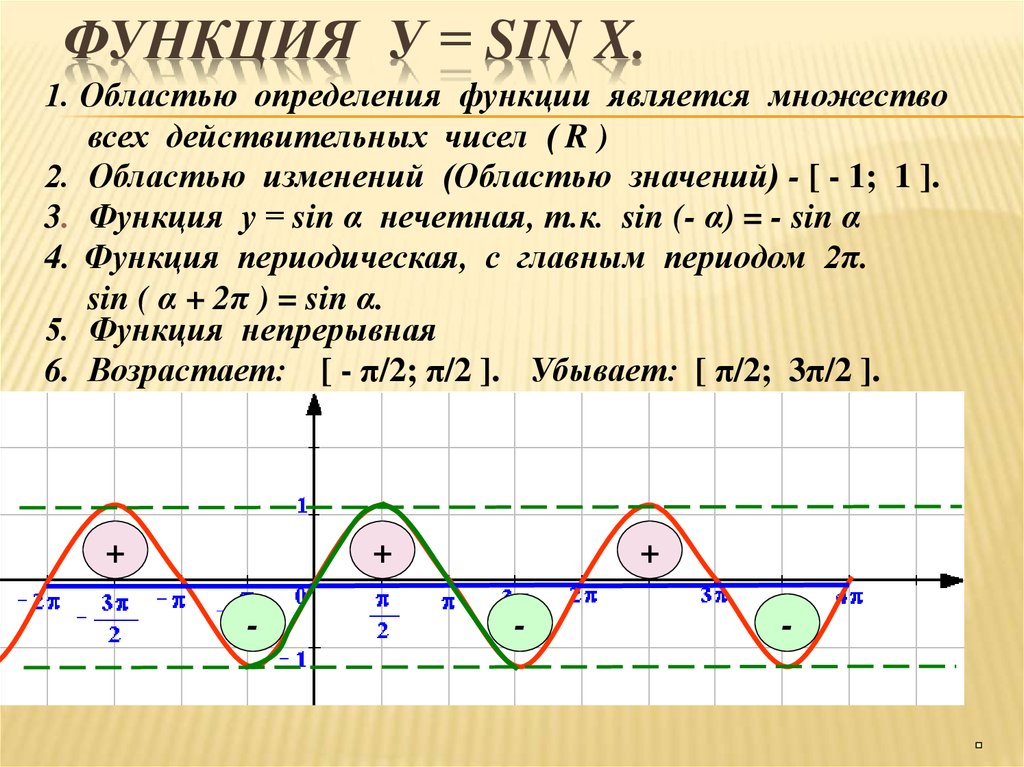
Если x принадлежит области определения этой функции, т.е. x ≠ — π /2 + π n, n є Ζ , то по формулам приведения получаем
tg(x – π ) = -tg( π – x) = -(-tg x) = tg x
tg(x + π ) = tg x
Таким обтазом, tg(x – π ) = tg x = tg(x + π ). Следовательно, π – период функции у = tg x.
ПОКАЖЕМ, ЧТО Π – НАИМЕНЬШИЙ ПОЛОЖИТЕЛЬНЫЙ ПЕРИОД ФУНКЦИИ Y = TG X.
Пусть Т – период тангенса, тогда tg(x + T) = tg x, откуда при x = 0 получаем tg T = 0, T = k π , k є Ζ . Так как наименьшее целое положительное k равно 1, то π – наименьший положительный период функции y = tg x.
ДОКАЗАТЬ, ЧТО У = TG (X/3) – ПЕРИОДИЧЕСКАЯ ФУНКЦИЯ С ПЕРИОДОМ 3 Π .
Доказательство :
Так как tg ((x + 3 π )/3) = tg (x/3 + π ) = tg (x/3)
и
tg((x — 3 π )/3) = tg(x/3 – π ) = tg (x/3), то tg(x/3) – периодическая функция с периодом 3 π .
Чётность и нечётность, периодичность тригонометрических функций с изменениями
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
1. Четность, нечетность, периодичность тригонометрических функций
11 класс2. Новый материал
ФункцияОбласть
определения D(y)
Множество
значений E(y)
y=sin x
R
1 у 1
y=cos x
R
1 у 1
y=tg x
y=ctg x
х n , n Z
2
х n , n Z
R
R
3.
 Решение упражнений1. Найдите область определения функции:
Решение упражнений1. Найдите область определения функции:1
а ) у cos
х
б ) у sin x
D у ;0 0 ;
D у 0 ;
4. Решение упражнений
3. Найдите область определения функции:а ) у sin x 1
б ) у lg sin x
б ) sin x 0 ;
Решение
а ) sin x 1 0 ;
sin x 1 ;
0
0
2 πn х π 2 πn , n Z
Ответ : D у 2πn ; π 2πn , n Z
-1
D y R ;
Ответ : D y R .
5. Решение упражнений
3. Найдите область определения функции:в ) у 1 2 sin x
Решение : 1 2 sin x 0 ;
7π
6
1
sin x ;
2
7π
π
2 πn y 2 πn , n Z
6
6
π
7π
Ответ : D у
2 πn ; 2 πn , n Z
6
6
1
2
π
6
6. Четность и нечетность тригонометрических функций
11 класс7. Симметрия относительно оси Оу и начала координат
8. Четные функции
Функция y = f(x) называется четной, если длялюбого х из области определения функции
верно равенство f(-x) = f(x).
Чтобы узнать является ли функция четной нужно в
функцию f(x) вместо переменной х поставить
переменную(–x).

9. Четные функции
Например: является ли четной функцияf(x) = 3×2 + 2
f(-x) = 3(-x)2 + 2 = 3×2 + 2 = f(x) – функция
четная
10. Четные функции
Проверим являются ли данные функциичетными
f(-x) = 2(-x)4 – 3(-x)2 = 2×4 — 3×2 f(x) = 2×4 — 3×2
четная
f(x) = x3 — 2×2
f(-x) = (-x)3 – 2(-x)2 = – x3 – 2×2
Не является четной
11. График четной функции
График четной функции симметриченотносительно оси ординат (ось ОУ).
12. Нечетные функции
Функция y = f(x) называется нечетной, если длялюбого х из области определения функции верно
равенство
f(-x) = — f(x).
чтобы узнать является ли функция нечетной нужно
в функцию f(x) вместо переменной х поставить
переменную (–x) и получить первоначальную
функцию с противоположными знаками.
13. Нечетные функции
Например: является ли нечетной функцияf(x) = 3×3 + х
f(-x) = 3(-x)3 + (-х) = -3×3 — х = -(3×3 + х)=
= — f(x) – функция нечетная
14.
 Нечетные функцииПроверим являются ли данные
Нечетные функцииПроверим являются ли данныефункции нечетными
f(x) = 2×4 + 3x
f(x) = x3 — 2x
f(-x) = 2(-x)4 + 3(-x) = =2×4
— 3x — не является
нечетной
f(-x) = (-x)3 – 2(-x) = – x3
+ 2x нечетная
15. График нечетной функции
График нечетной функции симметриченотносительно начала координат.
16. Четные и нечетные функции
Функции могут быть как четными,нечетными, так и ни четными, ни нечетными.
Пример: y(x) = x2 + 2x
y(-x) = (-x)2 + 2(-x) = x2 — 2x
Для любого значения x верны равенства:
Sin(-x) = -Sin x
Cos(-x) = Cos x
Следовательно:
y= Sin x – нечетная функция
y= Cos x – четная функция
т.к. sin(-x)=-sinx
1. y=sinx – нечетная функция,
График функции симметричен относительно
начала координат
2. y=cosx – нечетная функция,
т.к. cos(-x)=cosx
График функции симметричен
относительно оси Оу
Так как для любого значения x из
области определения функции
y = tg x верно равенство
tg(-x) = -tg x,
то y = tg x – нечетная функция.

20. Пример
Выяснить, является ли функцияy = 2 + Sin2 x четной или нечетной.
Решение:
y(-x) = 2 + Sin2(-x) = 2 + (-Sin x)2 =
=2 + Sin2x = y(x)
y = 2 + Sin2x – четная функция.
Пример: определите, является ли данная
функция четной или нечетной
Решение:
Работа в тетрадях
Определите, являются ли данные функции
четными или нечетными:
Разбейте функции на три группы:
—
четные
нечетные
не являются ни четными, ни нечетными
Проверяем ответы
четные
нечетные
ни чет., ни
нечет.
1
4
2
3
5
7
9
10
11
6
8
14
15
12
13
Функция f(x) называется периодической,
если существует такое число T ≠ 0, что для
любого x из области определения этой
функции выполняется равенство
f(x – T) = f(x) = f(x + T).
Число T называется периодом функции f(x).
Для любого значения x верны равенства:
Sin (x + 2π) = Sin x
Cos (x + 2π) = Cos х
Следовательно, значения Sin и Cos периодически
повторяются при изменении аргумента на 2π.
Такие функции называются периодическими с
периодом 2π.
28. Покажем, что число 2π является наименьшим положительным периодом функции y = Cos x.
Пусть Т › 0 – период косинуса, т.е. для любого xвыполняется равенство
Cos (x + T) = Cos x. Положив x = 0, получим Cos T
= 1. Отсюда T = 2πk, k є Ζ. Так как Т › 0, то Т
может принимать значения 2π, 4π, 6π, …, и
поэтому период не может быть меньше 2π.
29. Аналогично можно доказать, что наименьший положительный период функции y = Sin x также равен 2π
Пример:Доказать, что f(x) = Sin 3x – периодическая
функция с периодом (2π)/3.
Доказательство:
Данная функция определена для всех x є R,
поэтому достаточно показать, что для любого x
верно равенство f(x + T) = f(x).
f(x + (2π)/3) = Sin 3(x + (2π)/3) =
= Sin (3x + 2π) = Sin 3x = f(x)
30. Покажем, что функция y= tg x является периодической с периодом π.
Если x принадлежит области определения этойфункции, т.
 е. x ≠ -π/2 + πn, n є Ζ, то по формулам
е. x ≠ -π/2 + πn, n є Ζ, то по формуламприведения получаем
tg(x – π) = -tg(π – x) = -(-tg x) = tg x
tg(x + π) = tg x
Таким обтазом, tg(x – π) = tg x = tg(x + π).
Следовательно, π – период функции у = tg x.
31. Покажем, что π – наименьший положительный период функции y = tg x.
Пусть Т – период тангенса, тогда tg(x + T) = tg x,откуда при x = 0 получаем tg T = 0, T = kπ, k є Ζ.
Так как наименьшее целое положительное k
равно 1, то π – наименьший положительный
период функции y = tg x.
32. Доказать, что у = tg (x/3) – периодическая функция с периодом 3π.
Доказательство:Так как tg((x + 3π)/3) = tg (x/3 + π) = tg (x/3)
и
tg((x — 3π)/3) = tg(x/3 – π) = tg (x/3), то tg(x/3)–
периодическая функция с периодом 3π.
English Русский Правила
Какая функция ни четная ни нечетная функция. Как определять четные и нечетные функции
Зависимость переменной y от переменно x, при которой каждому значению х соответствует единственное значение y называется функцией.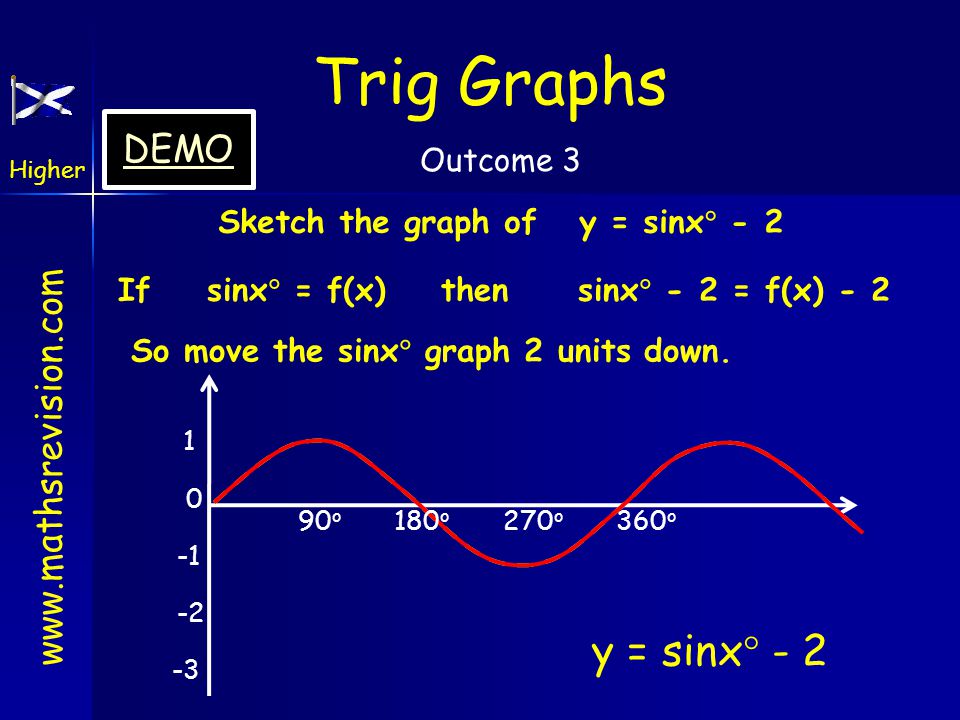 3 симметрична относительно начала координат.
3 симметрична относительно начала координат.
Исследование функции.
1) D(y) – Область опрделения: множество всех тех значений переменной х. при которых алгебраические выражения f(x) и g(x) имеют смысл.
Если функция задана формулой, то область определения состоит из всех значений независимой переменной, при которых формула имеет смысл.
2) Свойства функции: четность/нечетность, периодичность:
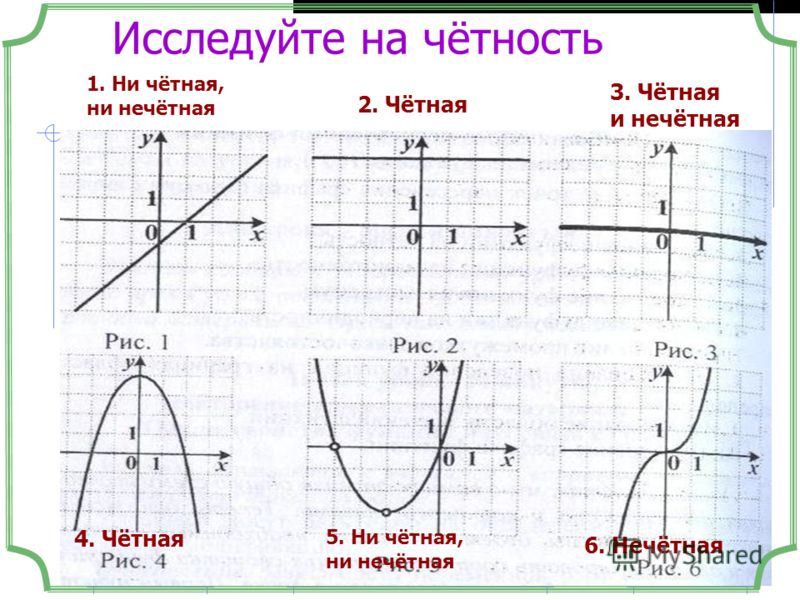
Нечётными и чётными называются функции, графики которых обладают симметрией относительно изменения знака аргумента.
Нечётная функция — функция, меняющая значение на противоположное при изменении знака независимой переменной (симметричная относительно центра координат).
Чётная функция — функция, не изменяющая своего значения при изменении знака независимой переменной (симметричная относительно оси ординат).
Ни
чётная ни нечётная функция (функция
общего вида) —
функция, не обладающая симметрией. В
эту категорию относят функции, не
подпадающие под предыдущие 2 категории.
В
эту категорию относят функции, не
подпадающие под предыдущие 2 категории.
Функции, не принадлежащие ни одной из категорий выше, называются ни чётными ни нечётными (или функциями общего вида).
Нечётные функции
Нечётная степень где — произвольное целое число.
Чётные функции
Чётная степень где — произвольное целое число.
Периоди́ческая фу́нкция ― функция, повторяющая свои значения через некоторый регулярный интервал аргумента, то есть не меняющая своего значения при добавлении к аргументу некоторого фиксированного ненулевого числа (пери́ода функции) на всей области определения.
3) Нули (корни) функции — точки, где она обращается в ноль.
Нахождение
точки пересечения графика с осью Oy . Для
этого нужно вычислить значение f (0).
Найти также точки пересечения графика
с осью Ox ,
для чего найти корни уравнения f (x )
= 0 (или
убедиться в отсутствии корней).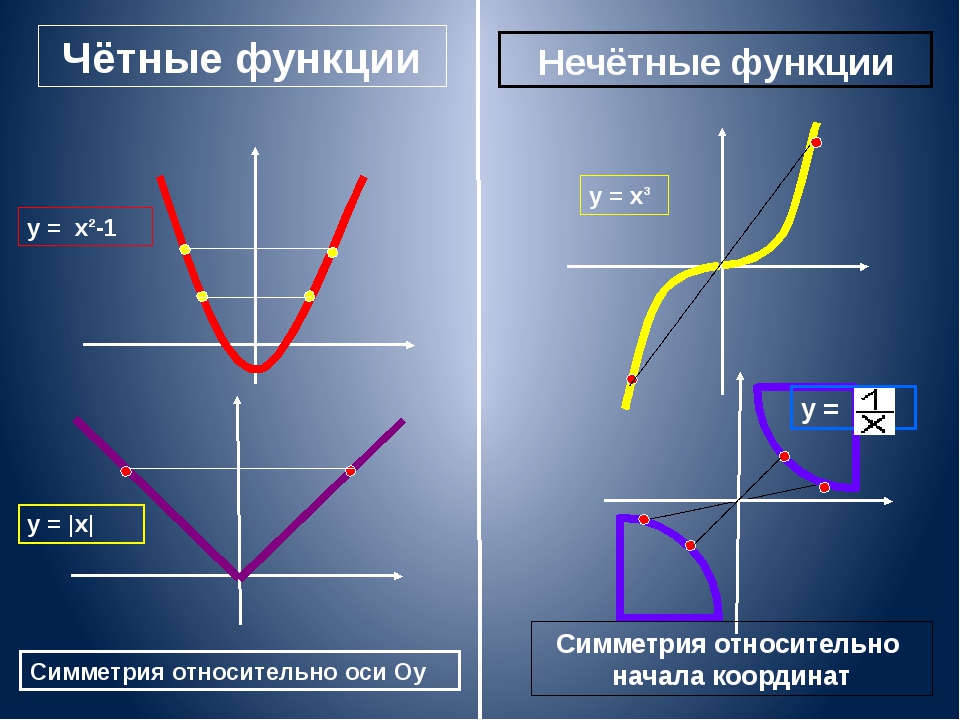
Точки, в которых график пересекает ось , называют нулями функции . Чтобы найти нули функции нужно решить уравнение , то есть найти те значения «икс» , при которых функция обращается в ноль.
4) Промежутки постоянства знаков, знаки в них.
Промежутки, где функция f(x) сохраняет знак.
Интервал знакопостоянства – это интервал, в каждой точке которого функция положительна либо отрицательна.
ВЫШЕ оси абсцисс.
НИЖЕ оси .
5) Непрерывность (точки разрыва, характер разрыва, ассимптоты).
Непрерывная функция — функция без «скачков», то есть такая, у которой малые изменения аргумента приводят к малым изменениям значения функции.
Устранимые точки разрыва
Если предел функции существует , но функция не определена в этой точке, либо предел не совпадает со значением функции в данной точке:
,
то
точка называется точкой
устранимого разрыва функции (в комплексном
анализе -устранимая
особая точка).
Если «поправить» функцию в точке устранимого разрыва и положить , то получится функция, непрерывная в данной точке. Такая операция над функцией называется доопределением функции до непрерывной или доопределением функции по непрерывности , что и обосновывает название точки, как точки устранимого разрыва.
Точки разрыва первого и второго рода
Если функция имеет разрыв в данной точке (то есть предел функции в данной точке отсутствует или не совпадает со значением функции в данной точке), то для числовых функций возникает два возможных варианта, связанных с существованием у числовых функций односторонних пределов :
если оба односторонних предела существуют и конечны, то такую точку называют точкой разрыва первого рода . Точки устранимого разрыва являются точками разрыва первого рода;
если
хотя бы один из односторонних пределов
не существует или не является конечной
величиной, то такую точку называют точкой
разрыва второго рода .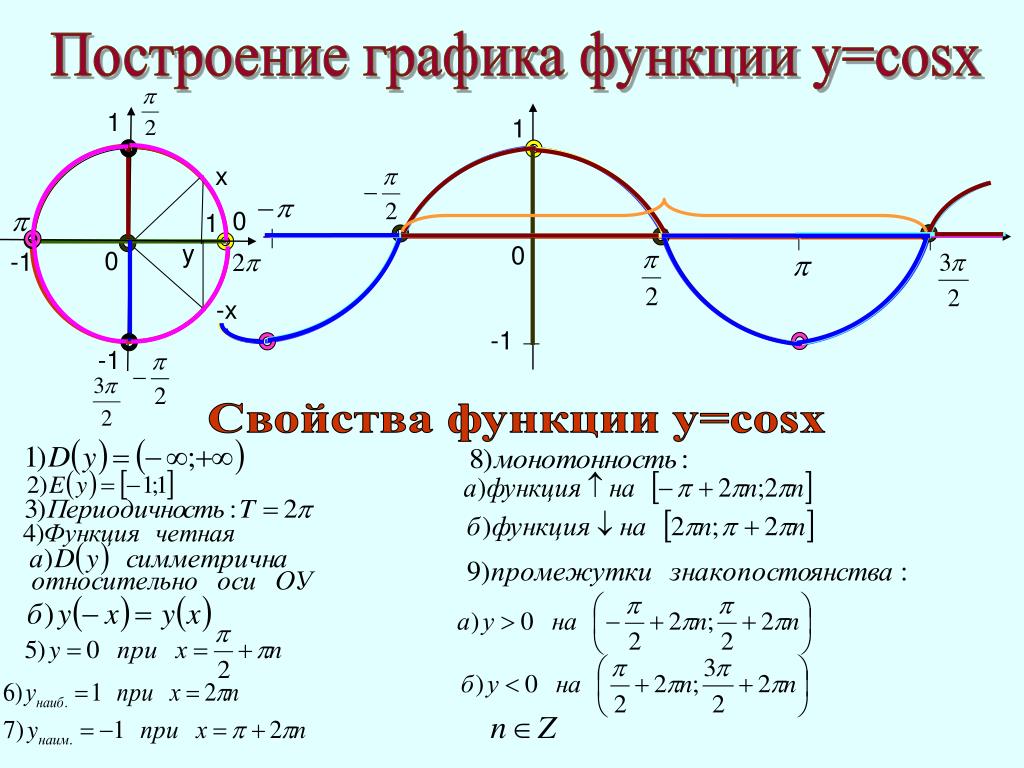
Аси́мпто́та — прямая , обладающая тем свойством, что расстояние от точки кривой до этой прямой стремится к нулю при удалении точки вдоль ветви вбесконечность.
Вертикальная
Вертикальная асимптота — прямая предела .
Как правило, при определении вертикальной асимптоты ищут не один предел, а два односторонних (левый и правый). Это делается с целью определить, как функция ведёт себя по мере приближения к вертикальной асимптоте с разных сторон. Например:
Горизонтальная
Горизонтальная асимптота — прямая вида при условии существования предела
.
Наклонная
Наклонная асимптота — прямая вида при условии существования пределов
Замечание: функция может иметь не более двух наклонных (горизонтальных) асимптот.
Замечание: если хотя бы один из двух упомянутых выше пределов не существует (или равен ), то наклонной асимптоты при (или ) не существует.
если в
п. 2.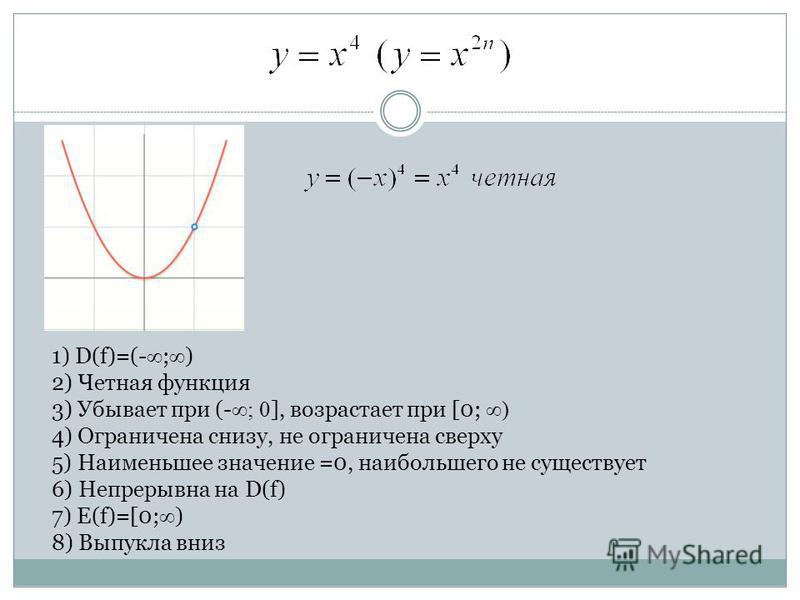 ), то ,
и предел находится
по формуле горизонтальной асимптоты, .
), то ,
и предел находится
по формуле горизонтальной асимптоты, .
6) Нахождение промежутков монотонности. Найти интервалы монотонности функции f (x )(то есть интервалы возрастания и убывания). Это делается с помощью исследования знака производной f (x ). Для этого находят производную f (x ) и решают неравенство f (x )0. На промежутках, где это неравенство выполнено, функция f (x )возрастает. Там, где выполнено обратное неравенство f (x )0, функция f (x )убывает.
Нахождение
локального экстремума. Найдя
интервалы монотонности, мы можем сразу
определить точки локального экстремума
там, где возрастание сменяется убыванием,
располагаются локальные максимумы, а
там, где убывание сменяется возрастанием
— локальные минимумы. Вычислить значение
функции в этих точках. Если функция
имеет критические точки, не являющиеся
точками локального экстремума, то
полезно вычислить значение функции и
в этих точках. {2}-3
, можно вычислить только одно значение функции, которое ему соответствует. Функцию можно представить в виде таблицы:
{2}-3
, можно вычислить только одно значение функции, которое ему соответствует. Функцию можно представить в виде таблицы:
| x | −2 | −1 | 0 | 1 | 2 | 3 |
| y | −4 | −3 | −2 | −1 | 0 | 1 |
Пользуясь данной таблицей, можно разобрать, что для значения аргумента −1 будет соответствовать значение функции −3 ; а значению x=2 будет соответствовать y=0 и т.д. Также важно знать, что каждому значению аргумента в таблице соответствует лишь одно значение функции.
Еще функции возможно задать, используя графики. С помощью графика устанавливается какое значение функции соотносится с определенным значением x . Наиболее часто, это будет приближенное значение функции.
Четная и нечетная функция
Функция является четной функцией , когда f(-x)=f(x)
для любого x
из области определения. Такая функция будет симметрична относительно оси Oy
. {2}} \neq 1
для любого x \in [-1;1]
.
{2}} \neq 1
для любого x \in [-1;1]
.
Ограниченной принято называть функцию y=f(x), x \in X тогда, когда существует такое число K > 0 , для которого выполняется неравенство \left | f(x) \right | \neq K для любого x \in X .
Пример ограниченной функции: y=\sin x ограничена на всей числовой оси, так как \left | \sin x \right | \neq 1 .
Возрастающая и убывающая функция
О функции, что возрастает на рассматриваемом промежутке принято говорить как о возрастающей функции тогда, когда большему значению x будет соответствовать большее значение функции y=f(x) . Отсюда выходит, что взяв из рассматриваемого промежутка два произвольных значения аргумента x_{1} и x_{2} , причем x_{1} > x_{2} , будет y(x_{1}) > y(x_{2}) .
Функция, что убывает на рассматриваемом промежутке, называется убывающей функцией тогда, когда большему значению x будет соответствовать меньшее значение функции y(x) . Отсюда выходит, что взяв из рассматриваемого промежутка два произвольных значений аргумента x_{1} и x_{2} , причем x_{1} > x_{2} , будет y(x_{1})
Корнями функции принято называть точки, в которых функция F=y(x)
пересекает ось абсцисс (они получаются в результате решения уравнения y(x)=0
).
а) Если при x > 0 четная функция возрастает, то убывает она при x
б) Когда при x > 0 четная функция убывает, то возрастает она при x
в) Когда при x > 0 нечетная функция возрастает, то возрастает она и при x
г) Когда нечетная функция будет убывать при x > 0 , то она будет убывать и при x
Экстремумы функции
Точкой минимума функции y=f(x) принято называть такую точку x=x_{0} , у которой ее окрестность будет иметь остальные точки (кроме самой точки x=x_{0} ), и для них тогда будет выполняться неравенство f(x) > f(x_{0}) . y_{min} — обозначение функции в точке min.
Точкой максимума функции y=f(x) принято называть такую точку x=x_{0} , у которой ее окрестность будет иметь остальные точки (кроме самой точки x=x_{0} ), и для них тогда будет выполняется неравенство f(x)
Необходимое условие
Согласно теореме Ферма: f»(x)=0
тогда, когда у функции f(x)
, что дифференцируема в точке x_{0}
, появится экстремум в этой точке.
Достаточное условие
- Когда у производной знак меняется с плюса на минус, то x_{0} будет точкой минимума;
- x_{0} — будет точкой максимума только тогда, когда у производной меняется знак с минуса на плюс при переходе через стационарную точку x_{0} .
Наибольшее и наименьшее значение функции на промежутке
Шаги вычислений:
- Ищется производная f»(x) ;
- Находятся стационарные и критические точки функции и выбирают принадлежащие отрезку ;
- Находятся значения функции f(x) в стационарных и критических точках и концах отрезка. Меньшее из полученных результатов будет являться наименьшим значением функции , а большее — наибольшим .
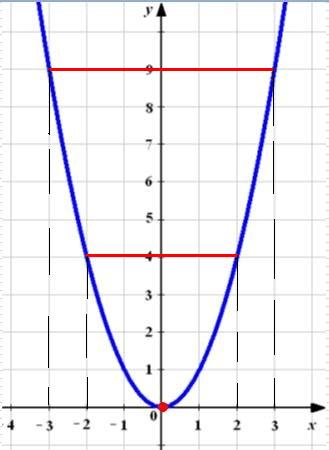
Для этого воспользуйтесь миллиметровкой или графическим калькулятором. Выберите несколько любых числовых значений независимой переменной x {\displaystyle x}
и подставьте их в функцию, чтобы вычислить значения зависимой переменной y {\displaystyle y}
. Найденные координаты точек нанесите на координатную плоскость, а затем соедините эти точки, чтобы построить график функции. {2}+1}
мы получили следующие координаты точек:
{2}+1}
мы получили следующие координаты точек:
- (1,3) и (-1,3)
- (2,9) и (-2,9)
Проверьте, симметричен ли график функции относительно начала координат. Начало координат – это точка с координатами (0,0). Симметрия относительно начала координат означает, что положительному значению y {\displaystyle y} (при положительном значении x {\displaystyle x} ) соответствует отрицательное значение y {\displaystyle y} (при отрицательном значении x {\displaystyle x} ), и наоборот. Нечетные функции обладают симметрией относительно начала координат.
- Если в функцию подставить несколько положительных и соответствующих отрицательных значений x {\displaystyle x}
, значения y {\displaystyle y}
будут различаться по знаку.
 {2}}
. Будучи записанной в такой форме, функция кажется четной, потому что присутствует четный показатель степени. Но этот пример доказывает, что вид функции нельзя быстро определить, если независимая переменная заключена в скобки. В этом случае нужно раскрыть скобки и проанализировать полученные показатели степени.
{2}}
. Будучи записанной в такой форме, функция кажется четной, потому что присутствует четный показатель степени. Но этот пример доказывает, что вид функции нельзя быстро определить, если независимая переменная заключена в скобки. В этом случае нужно раскрыть скобки и проанализировать полученные показатели степени.
Которые в той или иной степени были вам знакомы. Там же было замечено, что запас свойств функций будет постепенно пополняться. О двух новых свойствах и пойдет речь в настоящем параграфе.
Определение 1.
Функцию у = f(x), х є Х, называют четной, если для любого значения х из множества X выполняется равенство f (-х) = f (х).
Определение 2.
Функцию у = f(x), х є X, называют нечетной, если для любого значения х из множества X выполняется равенство f (-х) = -f (х).
Доказать, что у = х 4 — четная функция.
Решение. Имеем: f(х) = х 4 , f(-х) = (-х) 4 . Но (-х) 4 = х 4 . Значит, для любого х выполняется равенство f(-х) = f(х), т.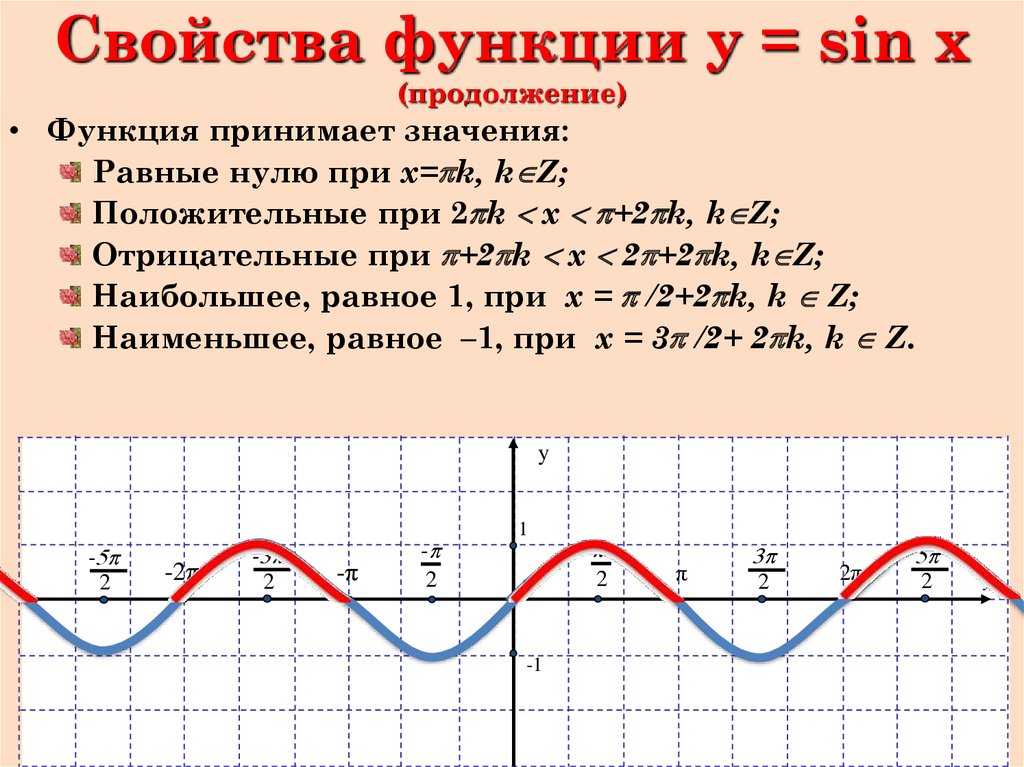 е. функция является четной.
е. функция является четной.
Аналогично можно доказать, что функции у — х 2 ,у = х 6 ,у — х 8 являются четными.
Доказать, что у = х 3 ~ нечетная функция.
Решение. Имеем: f(х) = х 3 , f(-х) = (-х) 3 . Но (-х) 3 = -х 3 . Значит, для любого х выполняется равенство f (-х) = -f (х), т.е. функция является нечетной.
Аналогично можно доказать, что функции у = х, у = х 5 , у = х 7 являются нечетными.
Мы с вами не раз уже убеждались в том, что новые термины в математике чаще всего имеют «земное» происхождение, т.е. их можно каким-то образом объяснить. Так обстоит дело и с четными, и с нечетными функциями. Смотрите: у — х 3 , у = х 5 , у = х 7 — нечетные функции, тогда как у = х 2 , у = х 4 , у = х 6 — четные функции. И вообще для любой функции вида у = х» (ниже мы специально займемся изучением этих функций), где n — натуральное число , можно сделать вывод: если n — нечетное число, то функция у = х» — нечетная; если же n — четное число, то функция у = хn — четная.
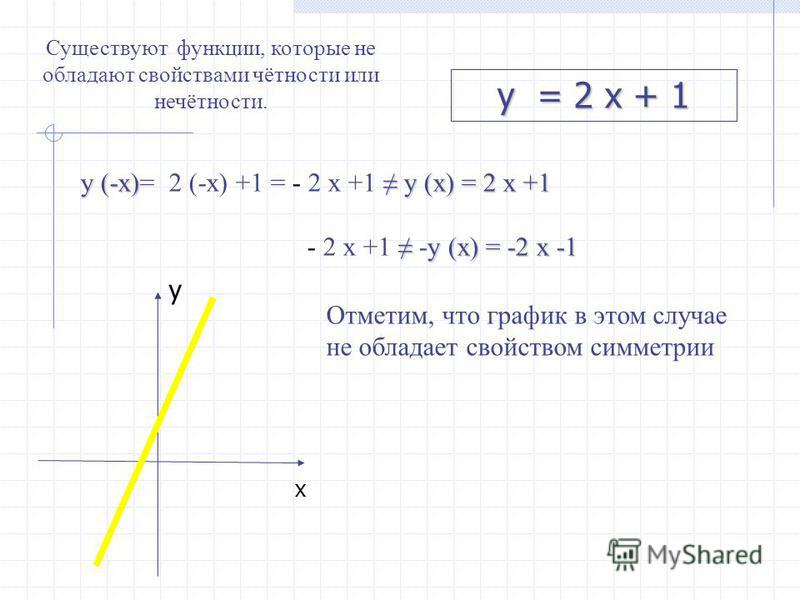
Существуют и функции, не являющиеся ни четными, ни нечетными. Такова, например, функция у = 2х + 3. В самом деле, f(1) = 5, а f (-1) = 1. Как видите, здесь Значит, не может выполняться ни тождество f(-х) = f (х), ни тождество f(-х) = -f(х).
Такова, например, функция у = 2х + 3. В самом деле, f(1) = 5, а f (-1) = 1. Как видите, здесь Значит, не может выполняться ни тождество f(-х) = f (х), ни тождество f(-х) = -f(х).
Итак, функция может быть четной, нечетной, а также ни той ни другой.
Изучение вопроса о том, является ли заданная функция четной или нечетной, обычно называют исследованием функции на четность.
В определениях 1 и 2 речь идет о значениях функции в точках х и -х. Тем самым предполагается, что функция определена и в точке х, и в точке -х. Это значит, что точка -х принадлежит области определения функции одновременно с точкой х. Если числовое множество X вместе с каждым своим элементом х содержит и противоположный элемент -х, то X называют симметричным множеством. Скажем, (-2, 2), [-5, 5], (-оо, +оо) — симметричные множества, в то время как }
Как выяснить четная или нечетная функция. Четность и нечетность функций. Алгоритм исследования функции на чётность
Зависимость переменной y от переменно x, при которой каждому значению х соответствует единственное значение y называется функцией. 3 симметрична относительно начала координат.
3 симметрична относительно начала координат.
Функция
называется четной (нечетной), если для
любогои выполняется равенство
.
График четной
функции симметричен относительно оси
.
График нечетной функции симметричен относительно начала координат.
Пример 6.2. Исследовать на четность или нечетность функции
1)
;
2)
;
3)
.
Решение .
1) Функция определена
при
.
Найдем
.
Т.е.
.
Значит, данная функция является четной.
2) Функция определена
при
Т.е.
.
Таким образом, данная функция нечетная.
3) функция определена для , т.е. для
,
.
Поэтому функция не является ни четной,
ни нечетной. Назовем ее функцией общего
вида.
3. Исследование функции на монотонность.
Функция
называется возрастающей (убывающей) на
некотором интервале, если в этом интервале
каждому большему значению аргумента
соответствует большее (меньшее) значение
функции.
Функции возрастающие
(убывающие) на некотором интервале
называются монотонными.
Если функция
дифференцируема на интервале
и имеет положительную (отрицательную)
производную
,
то функция
возрастает (убывает) на этом интервале.
Пример 6.3 . Найти интервалы монотонности функций
1)
;
3)
.
Решение .
1) Данная функция определена на всей числовой оси. Найдем производную .
Производная равна
нулю, если
и
.
Область определения – числовая ось,
разбивается точками
,
на интервалы. Определим знак производной
в каждом интервале.
В интервале
производная отрицательна, функция на
этом интервале убывает.
В интервале
производная положительна, следовательно,
функция на этом интервале возрастает.
2) Данная функция
определена, если
или
.
Определяем знак квадратного трехчлена в каждом интервале.
Таким образом, область определения функции
Найдем производную
,
,
если
,
т.е.
,
но
.
Определим знак производной в интервалах
.
В интервале
производная отрицательна, следовательно,
функция убывает на интервале
.
В интервале
производная положительна, функция
возрастает на интервале
.
4. Исследование функции на экстремум.
Точка
называется точкой максимума (минимума)
функции
,
если существует такая окрестность точки,
что для всех
из этой окрестности выполняется
неравенство
.
Точки максимума и минимума функции называются точками экстремума.
Если функция
в точкеимеет экстремум, то производная функции
в этой точке равна нулю или не существует
(необходимое условие существования
экстремума).
Точки, в которых производная равна нулю или не существует называются критическими.
5. Достаточные условия существования экстремума.
Правило 1 .
Если при переходе (слева направо) через
критическую точку
производная
меняет знак с «+» на «–», то в точкефункция
имеет максимум; если с «–» на «+», то
минимум; если
не меняет знак, то экстремума нет.
Правило 2 .
Пусть в точке
первая производная функции
равна нулю
,
а вторая производная существует и
отлична от нуля. Если
,
то– точка максимума, если
,
то– точка минимума функции.
Пример 6.4 . Исследовать на максимум и минимум функции:
1)
;
2)
;
3)
;
4)
.
Решение.
1) Функция определена
и непрерывна на интервале
.
Найдем производную
и решим уравнение
,
т.е.
.Отсюда
– критические точки.
Определим знак
производной в интервалах
,
.
При переходе через
точки
и
производная меняет знак с «–» на «+»,
поэтому по правилу 1
– точки минимума.
При переходе через
точку
производная меняет знак с «+» на «–»,
поэтому
– точка максимума.
,
.
2) Функция определена
и непрерывна в интервале
.
Найдем производную
.
Решив уравнение
,
найдем
и
– критические точки. Если знаменатель
,
т.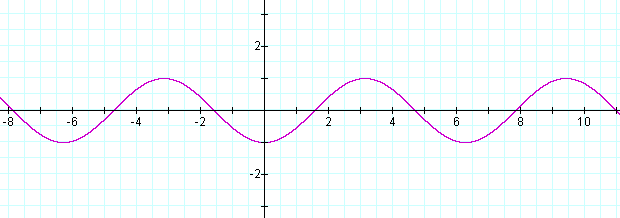 е.
е.
,
то производная не существует. Итак,
– третья критическая точка. Определим
знак производной в интервалах.
Следовательно,
функция имеет минимум в точке
,
максимум в точках
и
.
3) Функция определена
и непрерывна, если
,
т.е. при
.
Найдем производную
.
Найдем критические
точки:
Окрестности точек
не принадлежат области определения,
поэтому они не являются т. экстремума.
Итак, исследуем критические точки
и
.
4) Функция определена
и непрерывна на интервале
.
Используем правило 2. Найдем производную
.
Найдем критические точки:
Найдем вторую
производную
и определим ее знак в точках
В точках
функция имеет минимум.
В точках
функция имеет максимум.
В июле 2020 года NASA запускает экспедицию на Марс. Космический аппарат доставит на Марс электронный носитель с именами всех зарегистрированных участников экспедиции.
Регистрация участников открыта.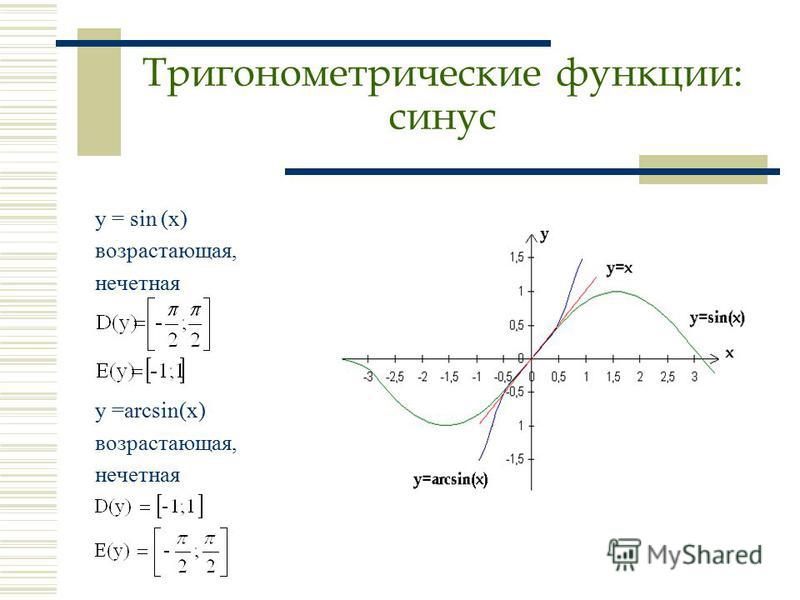 Получите свой билет на Марс по этой ссылке .
Получите свой билет на Марс по этой ссылке .
Если этот пост решил вашу проблему или просто понравился вам, поделитесь ссылкой на него со своими друзьями в социальных сетях.
Один из этих вариантов кода нужно скопировать и вставить в код вашей веб-станицы, желательно между тегами
и или же сразу после тега . По первому варианту MathJax подгружается быстрее и меньше тормозит страницу. Зато второй вариант автоматически отслеживает и подгружает свежие версии MathJax. Если вставить первый код, то его нужно будет периодически обновлять. Если вставить второй код, то страницы будут загружаться медленнее, зато вам не нужно будет постоянно следить за обновлениями MathJax.
Подключить MathJax проще всего в Blogger или WordPress: в панели управления сайтом добавьте виджет, предназначенный для вставки стороннего кода JavaScript, скопируйте в него первый или второй вариант кода загрузки, представленного выше, и разместите виджет поближе к началу шаблона (кстати, это вовсе не обязательно, поскольку скрипт MathJax загружается асинхронно).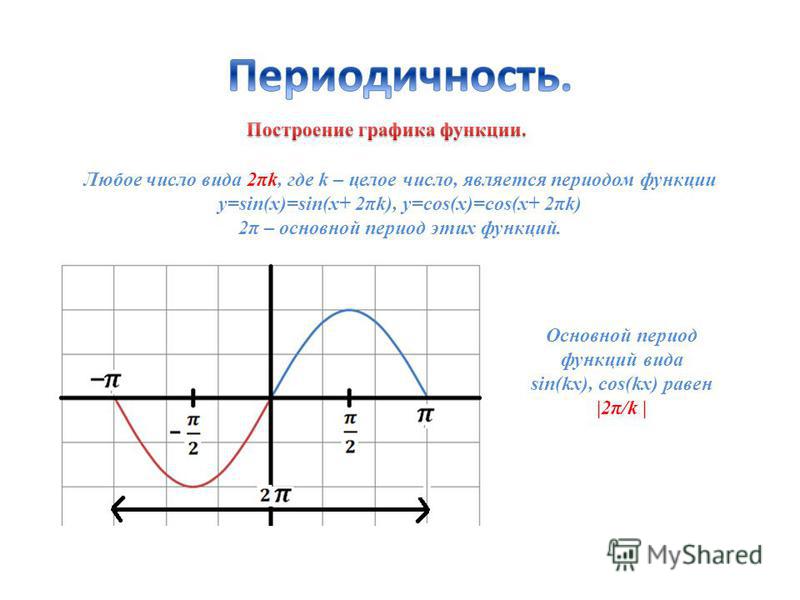 Вот и все. Теперь изучите синтаксис разметки MathML, LaTeX и ASCIIMathML, и вы готовы вставлять математические формулы на веб-страницы своего сайта.
Вот и все. Теперь изучите синтаксис разметки MathML, LaTeX и ASCIIMathML, и вы готовы вставлять математические формулы на веб-страницы своего сайта.
Очередной канун Нового Года… морозная погода и снежинки на оконном стекле… Все это побудило меня вновь написать о… фракталах, и о том, что знает об этом Вольфрам Альфа. По этому поводу есть интересная статья , в которой имеются примеры двумерных фрактальных структур. Здесь же мы рассмотрим более сложные примеры трехмерных фракталов.
Фрактал можно наглядно представить (описать), как геометрическую фигуру или тело (имея ввиду, что и то и другое есть множество, в данном случае, множество точек), детали которой имеют такую же форму, как и сама исходная фигура. То есть, это самоподобная структура, рассматривая детали которой при увеличении, мы будем видеть ту же самую форму, что и без увеличения. Тогда как в случае обычной геометрической фигуры (не фрактала), при увеличении мы увидим детали, которые имеют более простую форму, чем сама исходная фигура.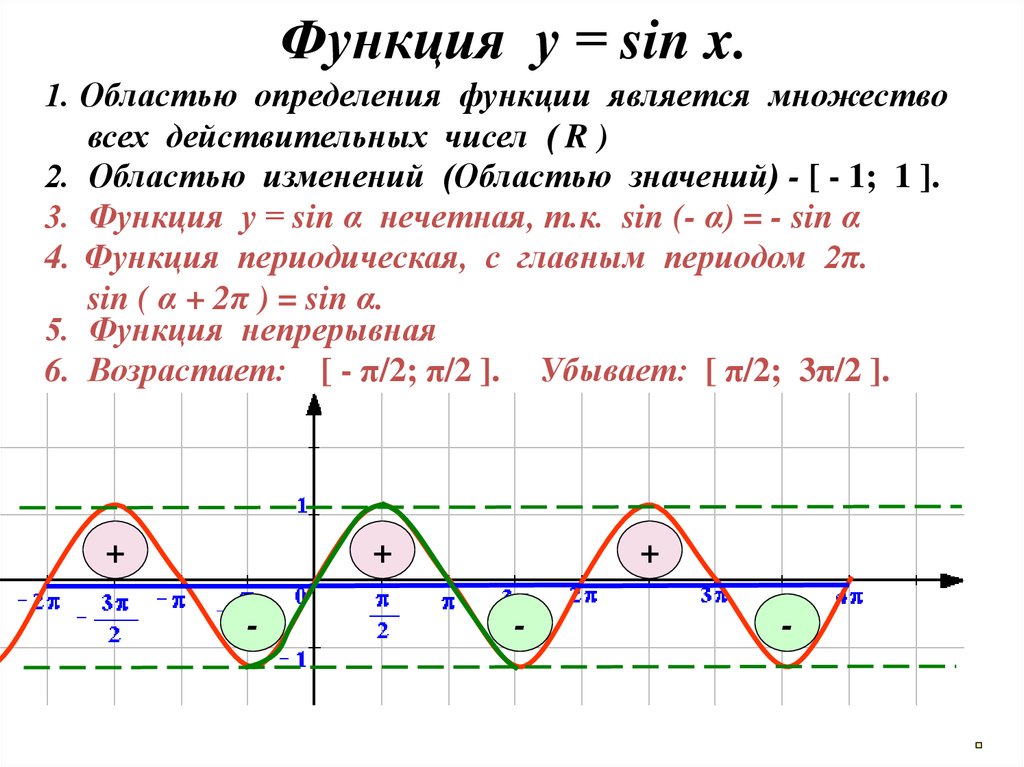 {2}-3
, можно вычислить только одно значение функции, которое ему соответствует. Функцию можно представить в виде таблицы:
{2}-3
, можно вычислить только одно значение функции, которое ему соответствует. Функцию можно представить в виде таблицы:
| x | −2 | −1 | 0 | 1 | 2 | 3 |
| y | −4 | −3 | −2 | −1 | 0 | 1 |
Пользуясь данной таблицей, можно разобрать, что для значения аргумента −1 будет соответствовать значение функции −3 ; а значению x=2 будет соответствовать y=0 и т.д. Также важно знать, что каждому значению аргумента в таблице соответствует лишь одно значение функции.
Еще функции возможно задать, используя графики. С помощью графика устанавливается какое значение функции соотносится с определенным значением x . Наиболее часто, это будет приближенное значение функции.
Четная и нечетная функция
Функция является четной функцией , когда f(-x)=f(x)
для любого x
из области определения. Такая функция будет симметрична относительно оси Oy
. {2}} \neq 1
для любого x \in [-1;1]
.
{2}} \neq 1
для любого x \in [-1;1]
.
Ограниченной принято называть функцию y=f(x), x \in X тогда, когда существует такое число K > 0 , для которого выполняется неравенство \left | f(x) \right | \neq K для любого x \in X .
Пример ограниченной функции: y=\sin x ограничена на всей числовой оси, так как \left | \sin x \right | \neq 1 .
Возрастающая и убывающая функция
О функции, что возрастает на рассматриваемом промежутке принято говорить как о возрастающей функции тогда, когда большему значению x будет соответствовать большее значение функции y=f(x) . Отсюда выходит, что взяв из рассматриваемого промежутка два произвольных значения аргумента x_{1} и x_{2} , причем x_{1} > x_{2} , будет y(x_{1}) > y(x_{2}) .
Функция, что убывает на рассматриваемом промежутке, называется убывающей функцией тогда, когда большему значению x будет соответствовать меньшее значение функции y(x) . Отсюда выходит, что взяв из рассматриваемого промежутка два произвольных значений аргумента x_{1} и x_{2} , причем x_{1} > x_{2} , будет y(x_{1})
Корнями функции принято называть точки, в которых функция F=y(x)
пересекает ось абсцисс (они получаются в результате решения уравнения y(x)=0
).
а) Если при x > 0 четная функция возрастает, то убывает она при x
б) Когда при x > 0 четная функция убывает, то возрастает она при x
в) Когда при x > 0 нечетная функция возрастает, то возрастает она и при x
г) Когда нечетная функция будет убывать при x > 0 , то она будет убывать и при x
Экстремумы функции
Точкой минимума функции y=f(x) принято называть такую точку x=x_{0} , у которой ее окрестность будет иметь остальные точки (кроме самой точки x=x_{0} ), и для них тогда будет выполняться неравенство f(x) > f(x_{0}) . y_{min} — обозначение функции в точке min.
Точкой максимума функции y=f(x) принято называть такую точку x=x_{0} , у которой ее окрестность будет иметь остальные точки (кроме самой точки x=x_{0} ), и для них тогда будет выполняется неравенство f(x)
Необходимое условие
Согласно теореме Ферма: f»(x)=0
тогда, когда у функции f(x)
, что дифференцируема в точке x_{0}
, появится экстремум в этой точке.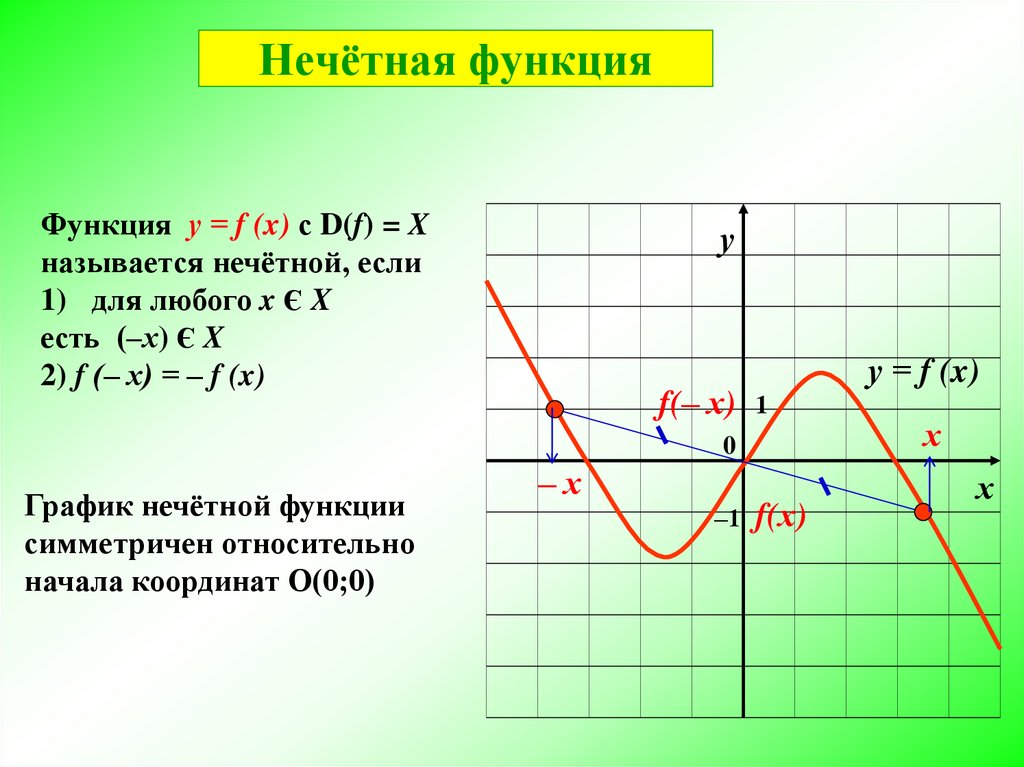
Достаточное условие
- Когда у производной знак меняется с плюса на минус, то x_{0} будет точкой минимума;
- x_{0} — будет точкой максимума только тогда, когда у производной меняется знак с минуса на плюс при переходе через стационарную точку x_{0} .
Наибольшее и наименьшее значение функции на промежутке
Шаги вычислений:
- Ищется производная f»(x) ;
- Находятся стационарные и критические точки функции и выбирают принадлежащие отрезку ;
- Находятся значения функции f(x) в стационарных и критических точках и концах отрезка. Меньшее из полученных результатов будет являться наименьшим значением функции , а большее — наибольшим .
Которые в той или иной степени были вам знакомы. Там же было замечено, что запас свойств функций будет постепенно пополняться. О двух новых свойствах и пойдет речь в настоящем параграфе.
Определение 1.
Функцию у = f(x), х є Х, называют четной, если для любого значения х из множества X выполняется равенство f (-х) = f (х).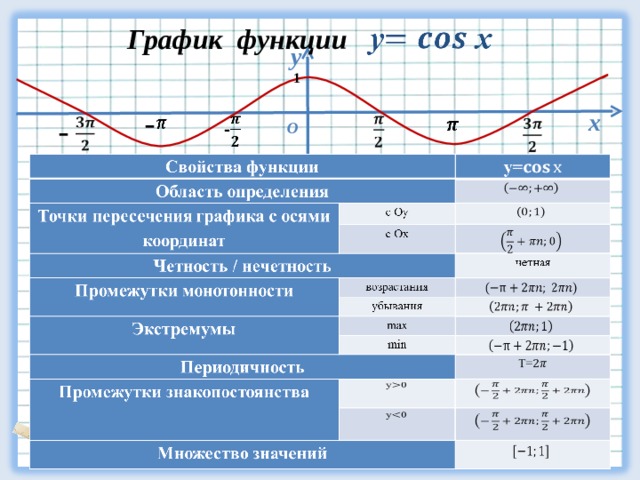
Определение 2.
Функцию у = f(x), х є X, называют нечетной, если для любого значения х из множества X выполняется равенство f (-х) = -f (х).
Доказать, что у = х 4 — четная функция.
Решение. Имеем: f(х) = х 4 , f(-х) = (-х) 4 . Но (-х) 4 = х 4 . Значит, для любого х выполняется равенство f(-х) = f(х), т.е. функция является четной.
Аналогично можно доказать, что функции у — х 2 ,у = х 6 ,у — х 8 являются четными.
Доказать, что у = х 3 ~ нечетная функция.
Решение. Имеем: f(х) = х 3 , f(-х) = (-х) 3 . Но (-х) 3 = -х 3 . Значит, для любого х выполняется равенство f (-х) = -f (х), т.е. функция является нечетной.
Аналогично можно доказать, что функции у = х, у = х 5 , у = х 7 являются нечетными.
Мы с вами не раз уже убеждались в том, что новые термины в математике чаще всего имеют «земное» происхождение, т.е. их можно каким-то образом объяснить. Так обстоит дело и с четными, и с нечетными функциями. Смотрите: у — х 3 , у = х 5 , у = х 7 — нечетные функции, тогда как у = х 2 , у = х 4 , у = х 6 — четные функции.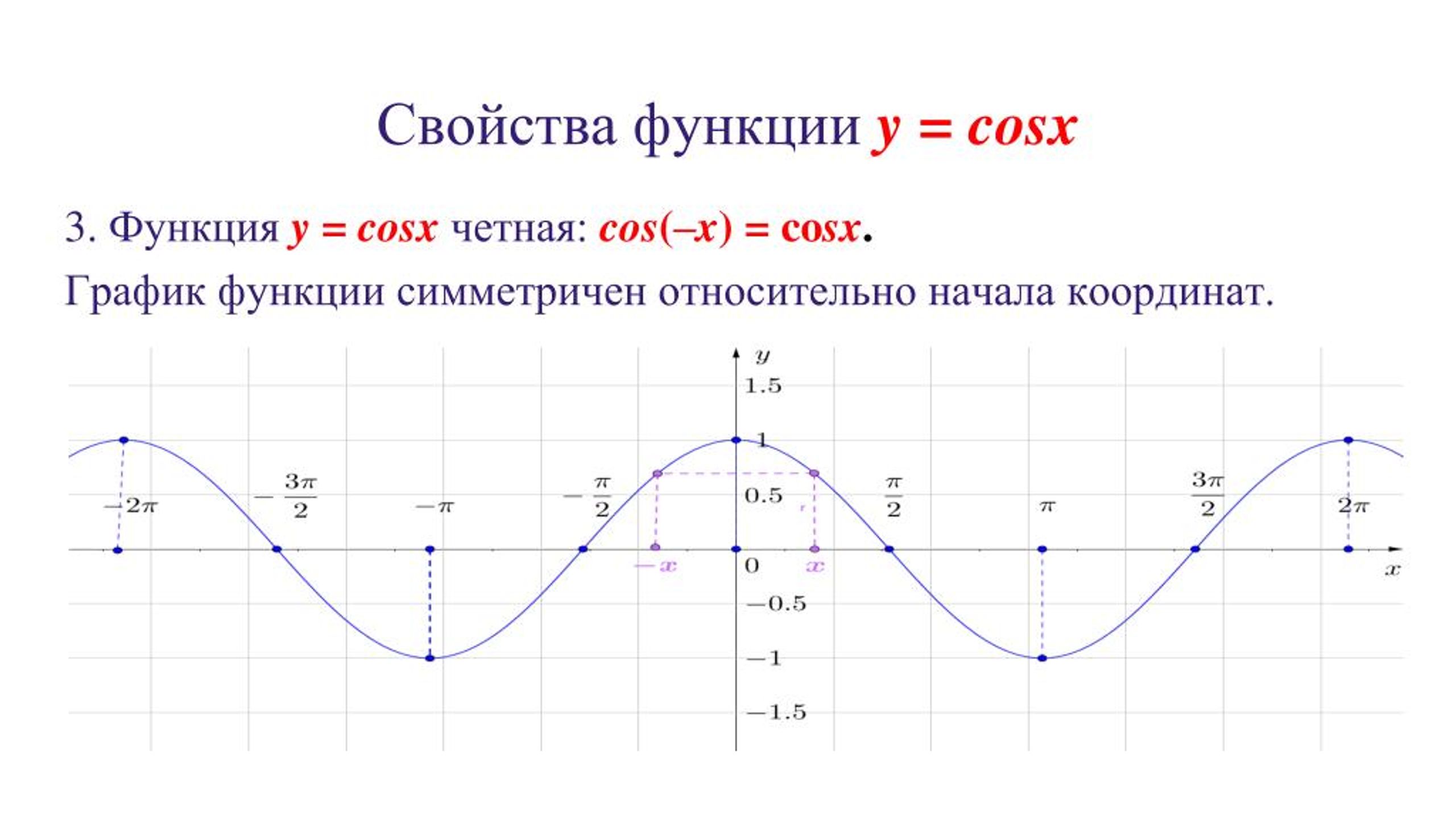 И вообще для любой функции вида у = х» (ниже мы специально займемся изучением этих функций), где n — натуральное число , можно сделать вывод: если n — нечетное число, то функция у = х» — нечетная; если же n — четное число, то функция у = хn — четная.
И вообще для любой функции вида у = х» (ниже мы специально займемся изучением этих функций), где n — натуральное число , можно сделать вывод: если n — нечетное число, то функция у = х» — нечетная; если же n — четное число, то функция у = хn — четная.
Существуют и функции, не являющиеся ни четными, ни нечетными. Такова, например, функция у = 2х + 3. В самом деле, f(1) = 5, а f (-1) = 1. Как видите, здесь Значит, не может выполняться ни тождество f(-х) = f (х), ни тождество f(-х) = -f(х).
Итак, функция может быть четной, нечетной, а также ни той ни другой.
Изучение вопроса о том, является ли заданная функция четной или нечетной, обычно называют исследованием функции на четность.
В определениях 1 и 2 речь идет о значениях функции в точках х и -х. Тем самым предполагается, что функция определена и в точке х, и в точке -х. Это значит, что точка -х принадлежит области определения функции одновременно с точкой х. Если числовое множество X вместе с каждым своим элементом х содержит и противоположный элемент -х, то X называют симметричным множеством. 3 симметрична относительно начала координат.
3 симметрична относительно начала координат.
Графики четной и нечетной функции обладают следующими особенностями:
Если функция является четной, то ее график симметричен относительно оси ординат. Если функция является нечетной, то ее график симметричен относительно начала координат.
Пример. Построить график функции \(y=\left|x \right|\).
Решение. Рассмотрим функцию: \(f\left(x \right)=\left|x \right|\) и подставим вместо \(x \) противоположное \(-x \). В результате не сложных преобразований получим: $$f\left(-x \right)=\left|-x \right|=\left|x \right|=f\left(x \right)$$ Другими словами, если аргумент заменить на противоположный по знаку, функция не изменится.
Значит эта функция — четная, а ее график будет симметричен относительно оси ординат (вертикальной оси). График этой функции приведен на рисунке слева. Это означает что при построении графика, можно строить только половину, а вторую часть (левее вертикальной оси рисовать уже симметрично правой части). Определив симметричность функции перед началом построения ее графика, можно намного упростить процесс построения или исследования функции. Если сложно выполнять проверку в общем виде, можно поступить проще: подставить в уравнение одинаковые значения разных знаков. Например -5 и 5. Если значения функции получатся одинаковыми, то можно надеяться что функция будет четной. С математической точки зрения такой подход не совсем правильный, но с практической — удобный. Чтобы увеличить достоверность результата можно подставить несколько пар таких противоположных значений.
Определив симметричность функции перед началом построения ее графика, можно намного упростить процесс построения или исследования функции. Если сложно выполнять проверку в общем виде, можно поступить проще: подставить в уравнение одинаковые значения разных знаков. Например -5 и 5. Если значения функции получатся одинаковыми, то можно надеяться что функция будет четной. С математической точки зрения такой подход не совсем правильный, но с практической — удобный. Чтобы увеличить достоверность результата можно подставить несколько пар таких противоположных значений.
Пример. Построить график функции \(y=x\left|x \right|\).
Решение. Выполним проверку так же как в предыдущем примере: $$f\left(-x \right)=x\left|-x \right|=-x\left|x \right|=-f\left(x \right)$$ Это означает, что исходная функция является нечетной (знак функции поменялся на противоположный).
Вывод: функция симметрична относительно начала координат. Можно строить только одн половину, а вторую рисовать симметрично. 2$$
В результате получим, что:
$$f\left(-x \right)\not=f\left(x \right),f\left(-x \right)\not=-f\left(x \right)$$
А это означает, что функция не является ни четной, ни нечетной.
2$$
В результате получим, что:
$$f\left(-x \right)\not=f\left(x \right),f\left(-x \right)\not=-f\left(x \right)$$
А это означает, что функция не является ни четной, ни нечетной.
Вывод: функция не симметрична ни относительно начала координат ни относительно центра системы координат. Это произошло потому, что она представляет собой сумму двух функций: четной и не четной. Такая же ситуация будет если вычитать две разные функции. А вот умножение или деление приведет к другому результату. Например, произведение четной и нечетной функций дает нечетную. Или частное двух нечетных приводит к четной функции.
Четность и нечетность функции являются одним из основных ее свойств, и на четность занимает внушительную часть школьного курса по математике. Она во много определяет характер поведения функции и значительно облегчает построение соответствующего графика.
Определим четность функции. Вообще говоря, исследуемую функцию считают четной, если для противоположных значений независимой переменной (x), находящихся в ее области определения, соответствующие значения y (функции) окажутся равными.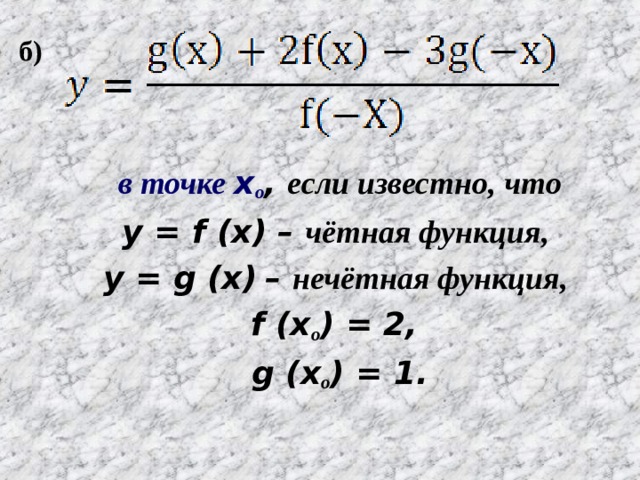 (-x))=- h(x). Следовательно, h(x) — нечетная.
(-x))=- h(x). Следовательно, h(x) — нечетная.
Кстати, следует напомнить, что есть функции, которые невозможно классифицировать по этим признакам, их называют ни четными, ни нечетными.
Четные функции обладают рядом интересных свойств:
- в результате сложения подобных функций получают четную;
- в результате вычитания таких функций получают четную;
- четной, также четная;
- в результате умножения двух таких функций получают четную;
- в результате умножения нечетной и четной функций получают нечетную;
- в результате деления нечетной и четной функций получают нечетную;
- производная такой функции — нечетная;
- если возвести нечетную функцию в квадрат, получим четную.
Четность функции можно использовать при решении уравнений.
Чтобы решить уравнение типа g(x) = 0, где левая часть уравнения представляет из себя четную функцию, будет вполне достаточно найти ее решения для неотрицательных значений переменной. Полученные корни уравнения необходимо объединить с противоположными числами.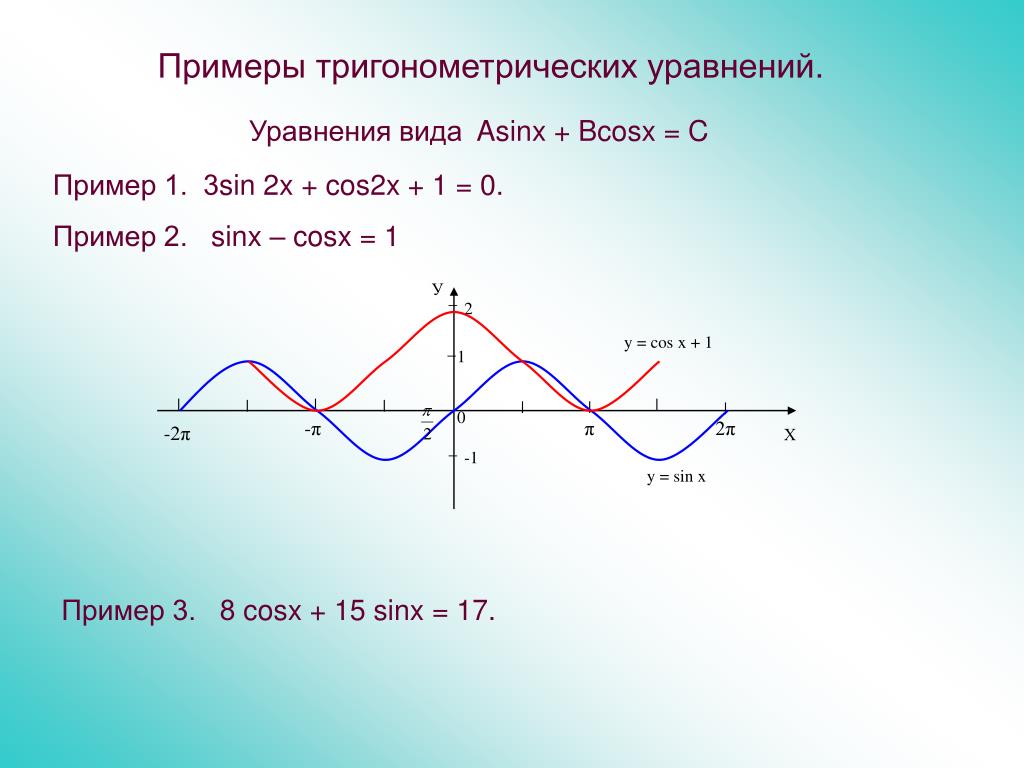 {2}-3
, можно вычислить только одно значение функции, которое ему соответствует. Функцию можно представить в виде таблицы:
{2}-3
, можно вычислить только одно значение функции, которое ему соответствует. Функцию можно представить в виде таблицы:
| x | −2 | −1 | 0 | 1 | 2 | 3 |
| y | −4 | −3 | −2 | −1 | 0 | 1 |
Пользуясь данной таблицей, можно разобрать, что для значения аргумента −1 будет соответствовать значение функции −3 ; а значению x=2 будет соответствовать y=0 и т.д. Также важно знать, что каждому значению аргумента в таблице соответствует лишь одно значение функции.
Еще функции возможно задать, используя графики. С помощью графика устанавливается какое значение функции соотносится с определенным значением x . Наиболее часто, это будет приближенное значение функции.
Четная и нечетная функция
Функция является четной функцией , когда f(-x)=f(x)
для любого x
из области определения. Такая функция будет симметрична относительно оси Oy
.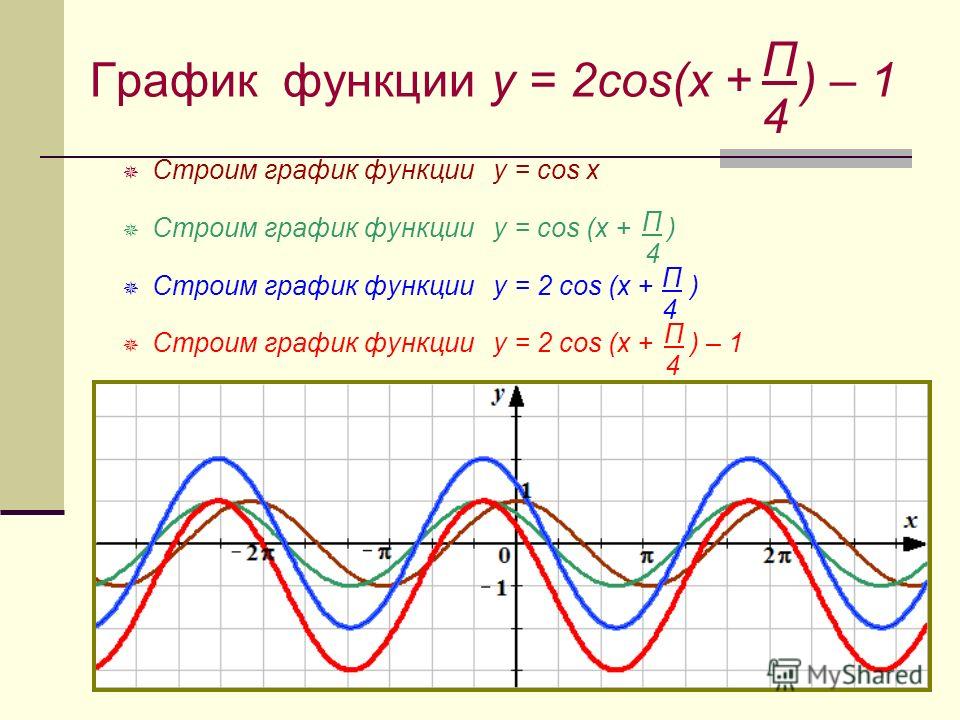 {2}} \neq 1
для любого x \in [-1;1]
.
{2}} \neq 1
для любого x \in [-1;1]
.
Ограниченной принято называть функцию y=f(x), x \in X тогда, когда существует такое число K > 0 , для которого выполняется неравенство \left | f(x) \right | \neq K для любого x \in X .
Пример ограниченной функции: y=\sin x ограничена на всей числовой оси, так как \left | \sin x \right | \neq 1 .
Возрастающая и убывающая функция
О функции, что возрастает на рассматриваемом промежутке принято говорить как о возрастающей функции тогда, когда большему значению x будет соответствовать большее значение функции y=f(x) . Отсюда выходит, что взяв из рассматриваемого промежутка два произвольных значения аргумента x_{1} и x_{2} , причем x_{1} > x_{2} , будет y(x_{1}) > y(x_{2}) .
Функция, что убывает на рассматриваемом промежутке, называется убывающей функцией тогда, когда большему значению x будет соответствовать меньшее значение функции y(x) . Отсюда выходит, что взяв из рассматриваемого промежутка два произвольных значений аргумента x_{1} и x_{2} , причем x_{1} > x_{2} , будет y(x_{1})
Корнями функции принято называть точки, в которых функция F=y(x)
пересекает ось абсцисс (они получаются в результате решения уравнения y(x)=0
).
а) Если при x > 0 четная функция возрастает, то убывает она при x
б) Когда при x > 0 четная функция убывает, то возрастает она при x
в) Когда при x > 0 нечетная функция возрастает, то возрастает она и при x
г) Когда нечетная функция будет убывать при x > 0 , то она будет убывать и при x
Экстремумы функции
Точкой минимума функции y=f(x) принято называть такую точку x=x_{0} , у которой ее окрестность будет иметь остальные точки (кроме самой точки x=x_{0} ), и для них тогда будет выполняться неравенство f(x) > f(x_{0}) . y_{min} — обозначение функции в точке min.
Точкой максимума функции y=f(x) принято называть такую точку x=x_{0} , у которой ее окрестность будет иметь остальные точки (кроме самой точки x=x_{0} ), и для них тогда будет выполняется неравенство f(x)
Необходимое условие
Согласно теореме Ферма: f»(x)=0
тогда, когда у функции f(x)
, что дифференцируема в точке x_{0}
, появится экстремум в этой точке.
Достаточное условие
- Когда у производной знак меняется с плюса на минус, то x_{0} будет точкой минимума;
- x_{0} — будет точкой максимума только тогда, когда у производной меняется знак с минуса на плюс при переходе через стационарную точку x_{0} .
Наибольшее и наименьшее значение функции на промежутке
Шаги вычислений:
- Ищется производная f»(x) ;
- Находятся стационарные и критические точки функции и выбирают принадлежащие отрезку ;
- Находятся значения функции f(x) в стационарных и критических точках и концах отрезка. Меньшее из полученных результатов будет являться наименьшим значением функции , а большее — наибольшим .
| 1 | Найдите количество возможностей | 7 выбрать 3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2 | Найдите количество возможностей | 8 выбрать 3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3 | Найдите количество возможностей | 5 выбрать 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4 | Найдите количество возможностей | 4 выбрать 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5 | Найдите количество возможностей | 8 выбрать 4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6 | Найдите количество возможностей | 10 выбрать 3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7 | Найдите количество возможностей | 7 выбрать 4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 8 | Найдите количество возможностей | 6 выбрать 3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 9 | Найдите количество возможностей | 9 выбрать 3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 10 | Найдите количество возможностей | 3 выбрать 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 11 | Найдите количество возможностей | 6 выбрать 4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 12 | Найдите количество возможностей | 5 выбрать 4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 13 | Найдите количество возможностей | 7 переставить 3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 14 | Найдите количество возможностей | 7 выбрать 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 15 | Найдите количество возможностей | 10 выбрать 5 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16 | Найдите количество возможностей | 10 выбрать 6 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 17 | Найдите количество возможностей | 13 выбрать 5 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 18 | Найдите количество возможностей | 3 выбрать 3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 19 | Найдите количество возможностей | 4 выбрать 1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 20 | Найдите количество возможностей | 4 выбрать 4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 21 | Найдите количество возможностей | 5 выбрать 1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 22 | Найдите количество возможностей | 6 переставить 3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 23 | Найдите количество возможностей | 8 выбрать 5 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 24 | Найдите количество возможностей | 9переставить 4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 25 | Найдите количество возможностей | 13 выбрать 3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 26 | Найдите количество возможностей | 12 выбрать 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 27 | Найдите количество возможностей | 12 выбрать 4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 28 | Найдите количество возможностей | 12 выбрать 3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 29 | Найдите количество возможностей | 9 выбрать 5 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 30 | Найдите количество возможностей | 9 выбрать 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 31 | Найдите количество возможностей | 7 выбрать 5 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 32 | Найдите количество возможностей | 6 переставить 6 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 33 | Найдите количество возможностей | 8 переставить 5 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 34 | Найдите количество возможностей | 8 переставить 3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 35 | Найдите количество возможностей | 7 переставить 5 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 36 | Найдите количество возможностей | 52 выбрать 5 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 37 | Найдите количество возможностей | 5 переставить 3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 38 | Найдите количество возможностей | 12 выбрать 5 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 39 | Найдите количество возможностей | 3 выбрать 1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 40 | Найдите количество возможностей | 11 выбрать 5 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 41 | Найдите количество возможностей | 10 выбрать 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 42 | Найдите количество возможностей | 15 выбрать 3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 43 | Найдите количество возможностей | 52 выбрать 4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 44 | Найдите количество возможностей | 9 выбрать 4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 45 | Найдите количество возможностей | 9 переставить 3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 46 | Найдите количество возможностей | 7 переставить 4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 47 | Найдите количество возможностей | 7 переставить 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 48 | Найдите количество возможностей | 11 выбрать 4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 49 | Найдите количество возможностей | 11 выбрать 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 50 | Найдите количество возможностей | 11 выбрать 3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 51 | Найдите количество возможностей | 10 переставить 5 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 52 | Найдите количество возможностей | 5 выбрать 5 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 53 | Найдите количество возможностей | 6 выбрать 1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 54 | Найдите количество возможностей | 8 переставить 4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 55 | Найдите количество возможностей | 8 выбрать 6 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 56 | Найдите количество возможностей | 13 выбрать 4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 57 | Оценить | и | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 58 | Найти любое уравнение, перпендикулярное прямой | -7x-5y=7 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 59 | Найдите количество возможностей | 13 выбрать 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 60 | Найдите количество возможностей | 10 переставить 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 61 | Найдите количество возможностей | 10 переставить 3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 62 | Найдите количество возможностей | 10 выбрать 7 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 63 | Найдите количество возможностей | 20 выбрать 4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 64 | Найдите количество возможностей | 6 переставить 4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 65 | Найдите количество возможностей | 5 переставить 4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 66 | Найдите количество возможностей | 6 выбрать 5 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 67 | Найдите количество возможностей | 52 выбрать 3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 68 | Найдите количество возможностей | 4 выбрать 0 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 69 | Найдите количество возможностей | 9переставить 7 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 70 | Найдите количество возможностей | 6 выбрать 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 71 | Найдите количество возможностей | 5 переставить 5 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 72 | Найдите количество возможностей | 5 переставить 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 73 | Найдите количество возможностей | 6 выбрать 6 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 74 | Найдите количество возможностей | 7 выбрать 6 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 75 | Найдите количество возможностей | 8 переставить 6 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 76 | Найдите количество возможностей | 7 переставить 7 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 77 | Найдите количество возможностей | 9 переставить 5 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 78 | Найдите количество возможностей | 2 переставить 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 79 | Найдите количество возможностей | 10 выбрать 8 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 80 | Найдите количество возможностей | 12 выбрать 7 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 81 | Найдите количество возможностей | 15 выбрать 5 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 82 | Найдите обратное | [[1,0,1],[2,-2,-1],[3,0,0]] | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 83 | Найти диапазон | 1/4x-7 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 84 | Найдите количество возможностей | 10 переставить 7 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 85 | Найдите количество возможностей | 12 выбрать 6 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 86 | Найдите количество возможностей | 2 выбрать 1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 87 | Найдите количество возможностей | 30 выбрать 3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 88 | Найдите количество возможностей | 9 выбрать 6 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 89 | Найдите количество возможностей | 8 переставить 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 90 | Найдите количество возможностей | 7 выбрать 1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 91 | Найдите количество возможностей | 6 перестановка 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 92 | Найдите количество возможностей | 4 переставить 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 93 | Найдите количество возможностей | 4 переставить 3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 94 | Найдите количество возможностей | 3 переставить 3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 95 | Найдите количество возможностей | 46 выбрать 6 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 96 | Найдите количество возможностей | 5 переставить 1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 97 | Найдите количество возможностей | 52 выбрать 7 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 98 | Найдите количество возможностей | 52 переставить 5 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 99 | Найдите количество возможностей | 93 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6 | Решить для ? | cos(x)=1/2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7 | Найти x | sin(x)=-1/2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 8 | Преобразование градусов в радианы | 225 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 9 | Решить для ? | cos(x)=(квадратный корень из 2)/2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 10 | Найти x | cos(x)=(квадратный корень из 3)/2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 11 | Найти x | sin(x)=(квадратный корень из 3)/2 | 92=9 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 14 | Преобразование градусов в радианы | 120 градусов | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 15 | Преобразование градусов в радианы | 180 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16 | Найти точное значение | желтовато-коричневый(195) | 92-4|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 38 | Найти точное значение | грех(255) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 39 | Оценить | лог база 27 из 36 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 40 | Преобразовать из радианов в градусы | 2 шт.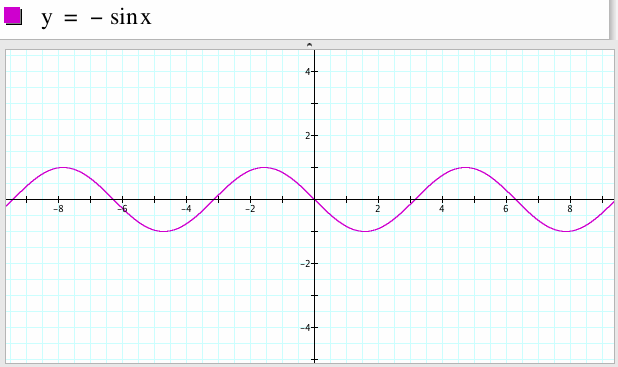 | 92-3sin(x)+1=0|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 43 | Найти x | tan(x)+ квадратный корень из 3=0 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 44 | Найти x | sin(2x)+cos(x)=0 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 45 | Упростить | (1-cos(x))(1+cos(x)) | 92=25|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 59 | График | f(x)=- натуральный логарифм x-1+3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 60 | Найдите значение с помощью единичного круга | угловой синус(-1/2) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 61 | Найти домен | квадратный корень из 36-4x^2 92=0 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 66 | Найти x | cos(2x)=(квадратный корень из 2)/2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 67 | График | у=3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 68 | График | f(x)=- логарифмическая база 3 x-1+3 | 92 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 71 | Найти x | квадратный корень из x+4+ квадратный корень из x-1=5 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 72 | Решить для ? | cos(2x)=-1/2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 73 | Найти x | логарифмическая база x из 16=4 | 9х|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 75 | Упростить | (cos(x))/(1-sin(x))+(1-sin(x))/(cos(x)) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 76 | Упростить | сек(х)sin(х) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 77 | Упростить | кубический корень из 24 кубический корень из 18 | 92=0|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 96 | Найти x | 3x+2=(5x-11)/(8г) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 97 | Решить для ? | sin(2x)=-1/2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 98 | Найти x | (2x-1)/(x+2)=4/5 | 93)=\sin(u)$ |
| 1. | Что такое четные и нечетные функции? |
| 2. | Четные и нечетные функции в тригонометрии |
| 3. | Интегральные свойства четных и нечетных функций |
| 4. | График четных и нечетных функций |
| 5. | Свойства четных и нечетных функций |
| 6. | Часто задаваемые вопросы о четных и нечетных функциях |
Что такое четные и нечетные функции?
г.Обычно мы считаем вещественную функцию четной или нечетной. Чтобы определить, является ли функция четной или нечетной, мы подставляем -x вместо x в функцию f(x), то есть мы проверяем выходное значение f(-x), чтобы определить тип функции. Четные и нечетные функции симметричны. Давайте сначала разберемся с их определениями.
Четные и нечетные функции Определение
- Четная функция — Для функции f(x) с действительным знаком, когда выходное значение f(-x) совпадает с f(x), для всех значений x в области f функция называется четной функцией.
 Четная функция должна содержать следующее уравнение: f(-x) = f(x) для всех значений x в D(f), где D(f) обозначает область определения функции f. Другими словами, мы можем сказать, что уравнение f (-x) — f (x) = 0 выполняется для четной функции для всех x. Рассмотрим пример, f(x) = x 2 .
Четная функция должна содержать следующее уравнение: f(-x) = f(x) для всех значений x в D(f), где D(f) обозначает область определения функции f. Другими словами, мы можем сказать, что уравнение f (-x) — f (x) = 0 выполняется для четной функции для всех x. Рассмотрим пример, f(x) = x 2 .
f(-x) = (-x) 2 = x 2 для всех значений x, поскольку квадрат отрицательного числа равен квадрату положительного значения числа. Отсюда следует f(-x) = f(x) для всех x. Следовательно, f(x) = x 2 — четная функция. Точно так же такие функции, как x 4 , x 6 , x 8 и т. д., являются четными функциями. - Нечетная функция — Для функции f(x) с действительным знаком, когда выходное значение f(-x) совпадает с отрицательным значением f(x), для всех значений x в области определения f, функция называется нечетной. Нечетная функция должна содержать следующее уравнение: f(-x) = -f(x) для всех значений x в D(f), где D(f) обозначает область определения функции f.
 Другими словами, мы можем сказать, что уравнение f (-x) + f (x) = 0 выполняется для нечетной функции для всех x. Рассмотрим пример, f(x) = x 3 .
Другими словами, мы можем сказать, что уравнение f (-x) + f (x) = 0 выполняется для нечетной функции для всех x. Рассмотрим пример, f(x) = x 3 .
f(-x) = (-x) 3 = -(x 3 ) для всех значений x, поскольку куб отрицательного числа совпадает с отрицательным значением куба положительного значения числа . Отсюда следует f(-x) = -f(x) для всех x. Следовательно, f(x) = x 3 — нечетная функция. Точно так же такие функции, как x 5 , x 7 , x 9 и т. д., являются нечетными функциями. - И четные, и нечетные функции — Вещественнозначная функция f(x) называется одновременно четной и нечетной, если она удовлетворяет условию f(-x) = f(x) и f(-x) = -f (x) для всех значений x в области определения функции f(x). Существует только одна функция, которая одновременно является четной и нечетной, и это нулевая функция, f(x) = 0 для всех x. Мы знаем, что для нулевой функции f(-x) = -f(x) = f(x) = 0 для всех значений x.
 Следовательно, f(x) = 0 — четная и нечетная функция. г.
Следовательно, f(x) = 0 — четная и нечетная функция. г. - Ни четная, ни нечетная функция — Говорят, что функция f(x) с действительным знаком не является ни четной, ни нечетной, если она не удовлетворяет f(-x) = f(x) и f(-x) = -f (x) хотя бы для одного значения x в области определения функции f(x). Давайте рассмотрим пример, чтобы лучше понять определение. Рассмотрим f(x) = 2x 5 + 3x 2 + 1, f(-x) = 2(-x) 5 + 3(-x) 2 + 1 = -2x 5 + 3x 2 + 1, что не равно ни f(x), ни -f(x). Следовательно, f(x) = 2x 5 + 3x 2 + 1 не является ни четной, ни нечетной функцией.
Четные и нечетные функции в тригонометрии
В этом разделе мы разделим тригонометрические функции на четные и нечетные. У нас есть шесть тригонометрических отношений (синус, косинус, тангенс, котангенс, косеканс и секанс). Эти тригонометрические отношения дают положительные значения в разных квадрантах для различных мер углов.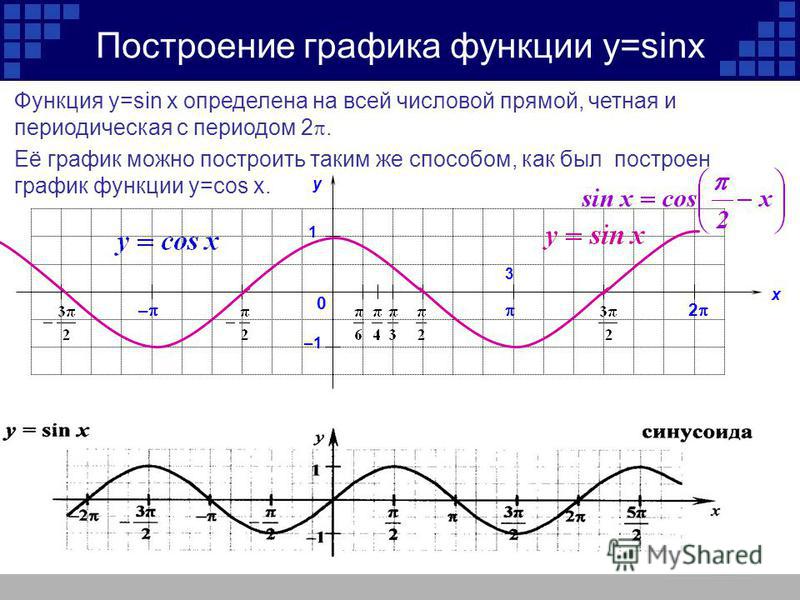
В первом квадранте (где все координаты x и y положительны) все шесть тригонометрических отношений имеют положительные значения. Во втором квадранте положительны только синус и косеканс. В третьем квадранте положительны только тангенс и котангенс. В четвертом квадранте положительны только косинус и секанс. На основании этих признаков мы разделим их на четные и нечетные функции.
Если тригонометрическое соотношение четное или нечетное, можно проверить через единичный круг. Угол, измеренный в направлении против часовой стрелки, является положительным углом, тогда как угол, измеренный в направлении по часовой стрелке, является отрицательным углом.
- sinθ = y, sin(-θ) = -y; Следовательно, sin(-θ) = -sinθ. Следовательно, sinθ — нечетная функция.
- cosθ = y, cos(-θ) = y; Следовательно, cos(-θ) = cosθ. Следовательно, cosθ — четная функция.
- tanθ = y, tan(-θ) = -y; Следовательно, tan(-θ) = -tanθ. Следовательно, tanθ — нечетная функция.
 г.
г. - cosecθ = y, cosec(-θ) = -y; Следовательно, cosec(-θ) = -cosecθ. Следовательно, cosecθ — нечетная функция.
- секθ = у, сек(-θ) = у; Следовательно, sec(-θ) = secθ. Следовательно, secθ — четная функция.
- кроватка θ = у, кроватка (-θ) = -у; Следовательно, cot(-θ) = -cotθ. Следовательно, cotθ — нечетная функция.
Интегральные свойства четных и нечетных функций
Интеграл функции дает площадь под кривой. Мы используем свойства четных и нечетных функций при решении определенных интегралов. Для этого нам нужно знать пределы интеграла и характер функции. Если функция четная или нечетная, а интервал равен [-a, a], мы можем применить следующие два правила: 9{а}\) f(x) dx = 0
График четных и нечетных функций
Теперь посмотрим, как графически ведут себя четные и нечетные функции. График четной функции симметричен относительно оси y . Другими словами, график четной функции остается прежним после отражения относительно оси у. Для любых двух противоположных входных значений x значение функции будет оставаться одинаковым на протяжении всей кривой.
Для любых двух противоположных входных значений x значение функции будет оставаться одинаковым на протяжении всей кривой.
Принимая во внимание, что график нечетной функции симметричен относительно начала координат . Другими словами, график нечетной функции находится на одном и том же расстоянии от начала координат, но в противоположных направлениях. Для любых двух противоположных входных значений x функция имеет противоположные значения y. Вот несколько примеров четных и нечетных функций.
Свойства четных и нечетных функций
- Сумма двух четных функций четна, а сумма двух нечетных функций нечетна.
- Разница между двумя четными функциями четна, а разница между двумя нечетными функциями нечетна. г.
- Сумма четной и нечетной функций не является ни четной, ни нечетной, если только одна из них не является нулевой функцией.
- Произведение двух четных функций является четным, и произведение двух нечетных функций также является четной функцией.

- Произведение четной и нечетной функций нечетно.
- Частное двух четных функций четно, и частное двух нечетных функций также является четной функцией.
- Частное четной и нечетной функций нечетно. г.
- Композиция двух четных функций четна, а композиция двух нечетных функций нечетна.
- Композиция четной и нечетной функций четна.
Важные замечания о четных и нечетных функциях
- Функция f(x) является четной, если f(-x) = f(x), для всех значений x в D(f), и нечетной, если f (-x) = -f(x) для всех значений x.
- В тригонометрии cosθ и secθ — четные функции, а sinθ, cosecθ, tanθ, cotθ — нечетные функции. г.
- График четной функции симметричен относительно оси Y, а график нечетной функции симметричен относительно начала координат.
- f(x) = 0 — единственная функция, которая является четной и нечетной функцией.
Темы, связанные с четными и нечетными функциями
- Функция четности
- Нечетная функция
- Типы функций
Часто задаваемые вопросы о четных и нечетных функциях
Что такое четные и нечетные функции в математике?
Функция f(x) является четной, если f(-x) = f(x), для всех значений x в D(f), и нечетной, если f(-x) = -f(x), для все значения х. График четной функции симметричен относительно оси y, а график нечетной функции симметричен относительно начала координат. Вещественная функция f(x) называется одновременно четной и нечетной, если она удовлетворяет f(-x) = f(x) и f(-x) = -f(x) для всех значений x в области функции f(x).
График четной функции симметричен относительно оси y, а график нечетной функции симметричен относительно начала координат. Вещественная функция f(x) называется одновременно четной и нечетной, если она удовлетворяет f(-x) = f(x) и f(-x) = -f(x) для всех значений x в области функции f(x).
Как определить четные и нечетные функции алгебраически?
Чтобы проверить, является ли функция четной или нечетной алгебраически, мы проверяем, является ли f(-x) = f(x) или f(-x) = -f(x) для всех значений x соответственно. Если мы заменяем x на -x в функции и значение функции становится отрицательным, то функция называется нечетной функцией. Если мы заменим x на -x в функции и значение функции не изменится, то функция будет известна даже как функция.
Если функция f четная, то какой тип симметрии имеет график функции f?
Четные и нечетные функции демонстрируют разные типы симметрии. Даже функции имеют линейную симметрию. Линия симметрии является осью Y. Даже функции — это функции, в которых, когда мы заменяем x на -x, значение функции для этого конкретного x не меняется. График четной функции ведет себя одинаково для всех точек на оси X, которые находятся как слева от начала координат, так и справа от него.
График четной функции ведет себя одинаково для всех точек на оси X, которые находятся как слева от начала координат, так и справа от него.
Какие тригонометрические функции являются четными и нечетными функциями?
В тригонометрии cosθ и secθ — четные функции, а sinθ, cosecθ, tanθ, cotθ — нечетные функции. Различные тригонометрические отношения имеют положительные и отрицательные значения в разных квадрантах. Следовательно, используя единичный круг, мы можем видеть, что cosθ и secθ — четные функции, а остальные четыре тригонометрических отношения — нечетные.
Как определить графически четные и нечетные функции?
График четной функции симметричен относительно оси y. График нечетной функции симметричен относительно начала координат. График четной функции остается прежним после отражения относительно оси у. График нечетной функции находится на одинаковом расстоянии от начала координат, но в противоположных направлениях. Используя те же критерии, мы можем идентифицировать четные и нечетные функции графически.
Если f и g являются четными функциями, является ли f+g четной и нечетной функцией?
Если f и g — четные функции, то f + g — четная функция. Рассмотрим функцию h(x) = f(x) + g(x). Замените x на -x в h(x), h(-x) = f(-x) + g(-x) = f(x) + g(x) = h(x). Поскольку f(x) и g(x) четные, f(-x) = f(x) и g(-x) = g(x). Следовательно, f + g — четная функция. Это не четная и нечетная функция одновременно.
Определенные интегралы четных и нечетных функций — Krista King Math
Что делать, если вы считаете, что функция четная или нечетная
Иногда мы можем упростить определенный интеграл, если узнаем, что интегрируемая функция является четной или нечетной функцией. Если функция не четная и не нечетная, то интегрируем как обычно.
Чтобы узнать, четная функция или нечетная, подставим ???-x??? в функцию для ???x???. Если мы вернем исходную функцию ???f(x)???, функция будет четной. Если мы вернем исходную функцию, умноженную на ???-1???, функция будет нечетной. Другими словами,
Другими словами,
Если ???f(-x)=f(x)???, функция четная
Если ???f(-x)=-f(x)???, функция нечетная
Если мы обнаружим, что функция четная или нечетная, следующим шагом будет проверка пределов интегрирования (интервал, по которому мы интегрируем). Чтобы использовать специальные правила четных или нечетных функций для определенных интегралов, наш интервал должен быть в форме ???[-a,a]???. Другими словами, пределы интегрирования имеют одинаковое числовое значение, но разные знаки, например ???[-1,1]??? или ???[-5,5]???. 9а_{-а}f(x)\dx=0???
Вот два видео. Первый — это обход определенного интеграла четной функции; второй — прохождение определенного интеграла нечетной функции.
Четные функции:
Нечетные функции:
Пройти курс
Хотите узнать больше об исчислении 2? У меня есть пошаговый курс для этого.
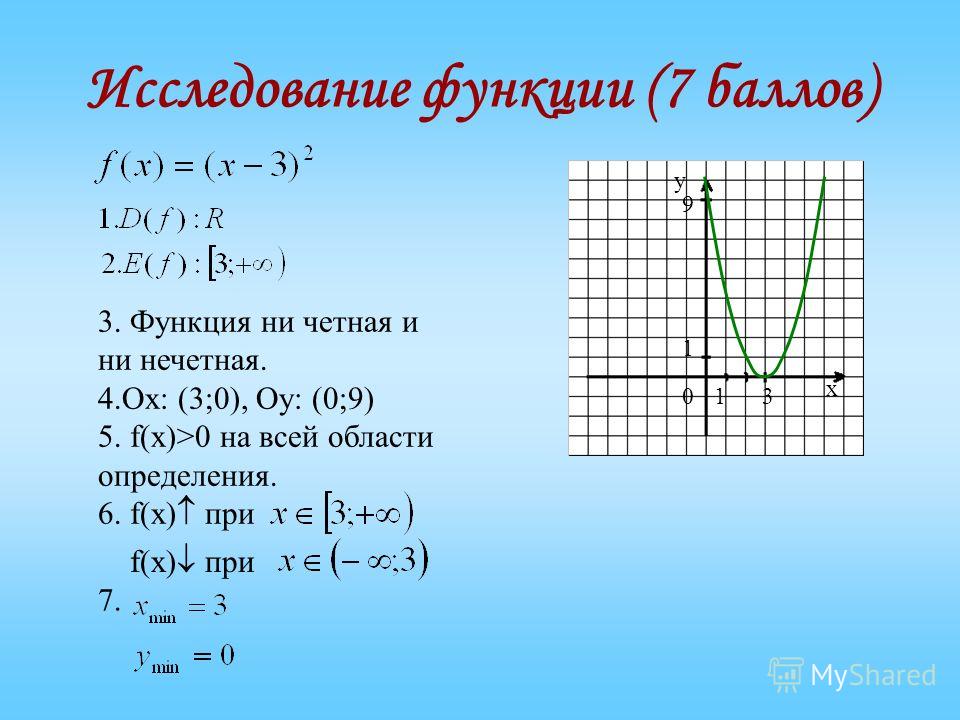 a_0f(x)\dx??? 97+4\sin{x}\dx=0???
a_0f(x)\dx??? 97+4\sin{x}\dx=0???Получите доступ к полному курсу Calculus 2
Начать
Четная функция, нечетная функция, периодическая функция — QuantumStudy
Если f : X → Y — вещественнозначная функция такая, что для всех x ∈ D
⇒ − x ∈ D (где D = область определения f) и :
если f(− x) = f(x) для каждого x ∈ D, то f называется четной функцией
г., и если f(− x) = − f(x), то f называется нечетной функцией.
График четной функции симметричен относительно оси y (т. е. если (x , y) лежит на кривой, то (− x , y) также лежит на кривой), а график нечетной функции симметричен относительно начала координат (т. е. если (x, y) лежит на кривой , то (−x, −y) также лежит на кривой).
Примечания: ⋄ Иногда легко доказать, что f(x) − f(−x) = 0 для четных функций и f(x) + f(−x) = 0 для нечетных функций.
⋄ Функция может быть четной или нечетной или ни четной, ни нечетной.
⋄ Каждая функция, определенная в симметричном интервале D
(т.е. x∈ D ⇒ −x ∈ D), может быть выражена как сумма четной и нечетной функций.
$\large f(x) = (\frac{f(x) + f(-x)}{2}) + (\frac{f(x) — f(-x)}{2})$
Пусть $\large h(x) = (\frac{f(x) + f(-x)}{2}) \; а также \; g(x) = (\frac{f(x) – f(-x)}{2})$
Теперь легко показать, что h(x) четно, а g(x) нечетно.
⋄ Первая производная четной функции является нечетной функцией и наоборот. Это остается вам в качестве упражнения для доказательства.
⋄ Если x = 0 ∈ область определения f, то для нечетной функции f(x), непрерывной в точке x = 0, f(0) = 0, т.е. если для функции f(0) ≠ 0, то эта функция не может быть нечетным.
Отсюда следует, что для дифференцируемой четной функции f ‘(0) = 0, т. е. если для дифференцируемой функции f ‘(0) ≠ 0, то функция f не может быть четной
Иллюстрация : Какая из следующих функций ( являются) четными, нечетными или ни одним из них:
(i) f(x) = x 2 sinx
(ii) $\large f(x) = \sqrt{1 + x + x^2} – \sqrt {1 – х + х^2} $ 9x}{2}$
= f(x)
Следовательно, f(x) четно
Расширение области:
Пусть функция определена в некоторой области, которая полностью неотрицательна (или не положительна).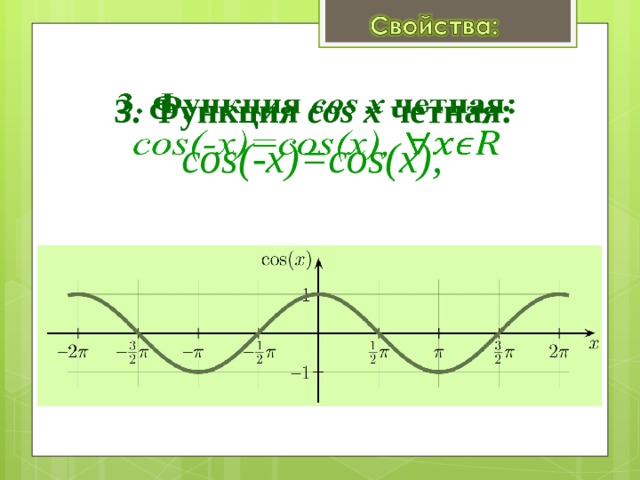 Область определения f(x) может быть расширена до множества
Область определения f(x) может быть расширена до множества
X = {−x : x∈ область определения f(x)} двумя способами:
(i) Четное расширение: Четное расширение равно получается определением новой функции f(−x) для x ∈ X, такой что f(−x) = f(x).
(ii) Нечетное расширение: 92 & \mathrm{,} \; -2 < x \le 0 \end{массив} \right. $
Периодическая функция:
Функция f: X → Y называется периодической функцией, если существует положительное действительное число p такое, что:
f(x + p) = f(x) , для все x ∈ X .
Наименьшее из всех таких положительных чисел p называется главным периодом или просто периодом f.
Все периодические функции могут быть проанализированы на интервале в один период в пределах домена, поскольку один и тот же шаблон должен повторяться во всем домене.
Пример:
sinx, cosx, secx — периодические функции с периодом 2π
tanx, cotx — периодические функции с периодом π (x) периодическая с периодом 1
(вы можете доказать это математически?).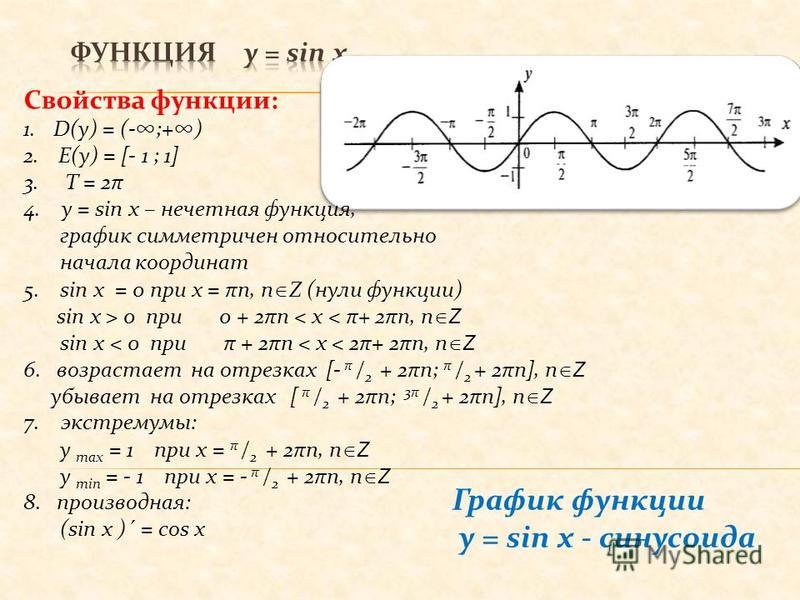
На экзамене задают два типа вопросов. Вас могут попросить проверить периодичность функции или найти период функции.
В первом случае вам просто нужно показать, что f(x + T) = f(x) для одного и того же T ( > 0), не зависящего от x, тогда как во втором вам нужно найти наименьшее положительное число T, не зависящее от x. x, для которого выполняется f(x + T)=f(x).
Следует помнить следующие моменты:Если f(x) периодична с периодом p, то af(x) +b, где a , b ∈ R (a ≠ 0), также периодична с периодом p.
∎ Если f(x) периодична с периодом p , то f(ax + b), где a, b ∈ R ( a ≠0) также периодична с периодом $\large \frac{p}{|a|} $ .
∎ Пусть f(x) имеет период p = m/n (m, n ∈ N и взаимно прост) и g(x) имеет период q = r/s (r, s ∈ N и взаимно прост) и пусть t будет НОК p и q, т.е. $\large t = \frac{LCM \; из (m , r)}{HCF \; из (r , s)}$
Тогда t будет периодом f + g при условии, что не существует положительного числа k (< t), для которого
f(k + x) + g(k + x) = f(x) + g( x), иначе k будет периодом.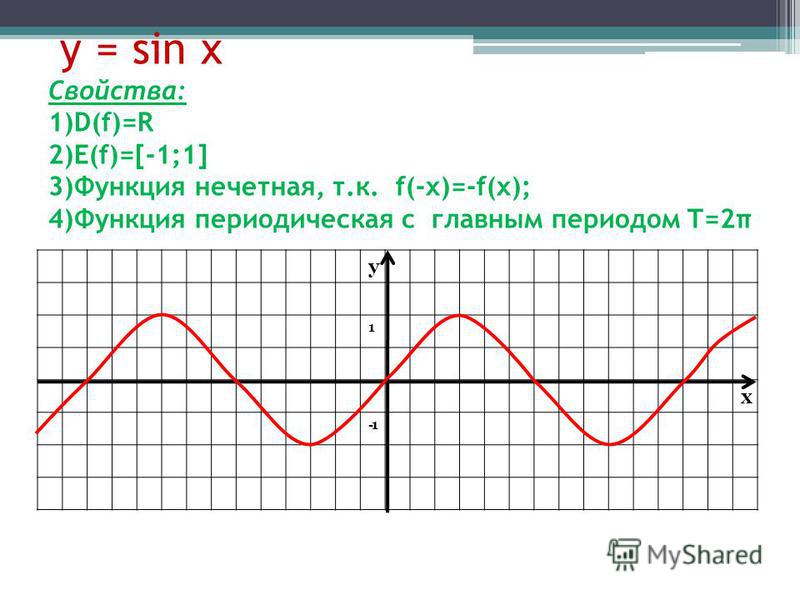
То же правило применимо для любой другой алгебраической комбинации f(x) и g(x)
Примечания:НОК p и q всегда существуют, если p/q — рациональная величина. Если p/q иррационально, то алгебраическая комбинация f и g непериодична.
∎ sin n x, cos n x, cosec n x и sec n x имеют период 2π, если n нечетно, и π, если n четно.
∎ tan n x и cot n x имеют период π независимо от того, является ли n нечетным или четным.
∎ Постоянная функция является периодической, но не имеет четко определенного периода.
∎ Если функция g является периодической, то туман всегда будет периодической функцией. Период тумана может быть, а может и не быть периодом g.
∎ Если f периодическая, а g строго монотонная (отличная от линейной), то туман непериодический. 93 x – cosec(3x-5)$
Период e lnsinx = 2π , tan 3 x = π
cosec(3x-5) = 2π/3 ; период = 2π
(ii) f(x) = x –[x-b] = b+{x –b}
⇒ период = 1
(iii) $\large f(x) = \frac{|sinx + cosx|}{|sinx| + |cosx|} $
Поскольку период |sinx + cox| = π и период |sinx| + | cosx| равно π/2. Векторная величина в физике. Примеры векторных величин Физика и математика не обходятся без понятия «векторная величина». Это необходимо знать и распознавать, а также уметь управлять им. Обязательно стоит научиться, чтобы не запутаться и избежать глупых ошибок. Содержание У первого всегда есть только одна характеристика. Векторная величина, помимо числовой, всегда взятой по модулю, также характеризуется направлением. Поэтому его можно представить графически, то есть в виде стрелки, длина которой равна модулю величины, направленной в определенном направлении. При письме каждая векторная величина обозначается стрелкой на букве. Если мы говорим о числовом значении, то стрелка не пишется или берется по модулю. Сначала противостояние. Они могут быть, а могут и не совпадать. В первом случае их модули совпадают. Но это не единственное условие. Они также должны иметь равные или противоположные направления. В первом случае их следует называть равными векторами. Во втором они оказываются противоположностями. Затем идет добавление. Это можно сделать по двум правилам: треугольник или параллелограмм. Первый предписывает сначала отложить вектор, затем второй — от его конца. Результатом сложения будет то, что нужно нарисовать от начала первого до конца второго. Правило параллелограмма можно использовать, когда вам нужно добавить векторные величины в физике. В отличие от первого правила, здесь их следует отложить на один балл. Затем соберите их до параллелограмма. Результатом действия нужно считать диагональ параллелограмма, проведенную из той же точки. Если одну векторную величину вычесть из другой, они снова откладываются от точки. Только результатом будет вектор, равный вектору, проведенному от конца второго до конца первого. Их столько, сколько скаляров. Вы можете только вспомнить, какие векторные величины существуют в физике. Или узнать признаки, по которым их можно вычислить. Теперь немного подробнее о некоторых из этих ценностей. Начать стоит, чтобы привести примеры векторных величин. Это связано с тем, что он изучается одним из первых. Скорость определяется как характеристика движения тела в пространстве. Задайте числовое значение и направление. Итак, скорость — это векторная величина. Кроме того, его принято делить на виды. Первый — это линейная скорость. Он вводится при рассмотрении равномерного прямолинейного движения. Эту же формулу можно использовать для нерегулярных движений. Только тогда он будет средним. Кроме того, выбираемый временной интервал должен быть как можно короче. Когда временной интервал стремится к нулю, значение скорости уже мгновенное. Если рассматривать произвольное движение, то здесь скорость всегда является векторной величиной. Ведь его нужно разложить на прямые составляющие по каждому вектору, который направляет координатные линии. Кроме того, он определяется как производная по времени от радиус-вектора. Он определяет меру силы воздействия, которое приходит на тело от других тел или полей. Поскольку сила является векторной величиной, она обязательно имеет значение по величине и направлению. Поскольку он действует на тело, то здесь также важна сила. Чтобы получить визуальное представление о векторах силы, вы можете обратиться к следующей таблице. Кроме того, результирующая сила также является векторной величиной. Он определяется как сумма всех механических сил, действующих на тело. Для его определения необходимо провести сложение по принципу правила треугольника. Вам просто нужно отложить векторы по очереди с конца предыдущего. Результатом будет то, что связывает начало первого с концом последнего. Во время движения тело описывает определенную линию. Это называется траектория. Эта строчка может быть совершенно разной. Здесь может возникнуть вопрос: «Является ли путь векторной величиной?» В общем, это утверждение не соответствует действительности. Путь равен длине пути и не имеет определенного направления. Исключением является ситуация, когда рассматривается прямолинейное движение в одном направлении. Следовательно, величина вектора смещения совпадает по величине с траекторией, и их направление оказывается таким же. Следовательно, при рассмотрении движения по прямой без изменения направления движения, путь может быть включен в примеры векторных величин. это характеристика скорости изменения скорости. Кроме того, ускорение может иметь как положительные, так и отрицательные значения. Среднее и мгновенное значения ускорения разделены. Первое следует рассчитывать как отношение изменения скорости за определенный период времени к этому времени. Когда рассматриваемый временной интервал стремится к нулю, мы говорим о мгновенном ускорении. По-другому его еще называют количеством движения. Импульс — это векторная величина, потому что она напрямую связана со скоростью и силой, прилагаемой к телу. У них обоих есть направление и импульс. По определению, последняя равна произведению веса тела и скорости. Используя понятие количества движения тела, вы можете иначе написать известный закон Ньютона. Оказывается, изменение количества движения равно произведению силы на временной интервал. В физике важную роль играет закон сохранения количества движения, который гласит, что в замкнутой системе тел его полный импульс постоянен. Мы очень кратко перечислили, какие (векторные) величины изучаются в курсе физики. Состояние. На путях есть стационарная площадка. К вам приближается карета со скоростью 4 м / с. Вес платформы и вагона — 10 и 40 тонн соответственно. Автомобиль ударяется о платформу, происходит автоматическое сцепление. Необходимо рассчитать скорость системы платформы автомобиля после удара. Решение. Сначала необходимо ввести следующие обозначения: скорость автомобиля до удара — v1, машина с платформой после спаривания — v, масса машины — m1, платформа — m2. В зависимости от состояния задачи необходимо знать значение скорости v. Правила решения таких задач требуют схематического изображения системы до и после взаимодействия. Ось OX целесообразно направить по рельсам в направлении движения каретки. В этих условиях транспортную систему можно считать закрытой. Это определяется тем, что внешними силами можно пренебречь. Сила тяжести и реакция опоры уравновешены, трение о рельсы не учитывается. Согласно закону сохранения количества движения их векторная сумма до взаимодействия между автомобилем и платформой равна общей для сцепления после удара. Сначала платформа не двигалась, поэтому ее импульс был нулевым. Переместилась только машина, ее импульс — произведение m1 и v1. Поскольку удар был неупругим, то есть автомобиль зацепился за платформу, а затем начал катиться вместе в одном направлении, импульс системы не изменил направление. Но его значение изменилось. А именно произведением суммы массы автомобиля с платформой на требуемую скорость. Вы можете записать это равенство: m1 * v1 = (m1 + m2) * v. Это будет верно для проекции векторов момента на выбранную ось. Легко вывести равенство, которое потребуется для вычисления желаемой скорости: v = m1 * v1 / (m1 + m2). Согласно правилам, значения массы следует переводить из тонн в килограммы. Поэтому, когда вы подставляете их в формулу, вы должны сначала умножить известные значения на тысячу. Простые вычисления дают число 0,75 м / с. Отвечать. Скорость вагона-платформы 0,75 м / с. Состояние. Скорость летящей гранаты — 20 м / с. Он разделен на две части. Масса первого 1,8 кг. Продолжайте движение в том направлении, в котором летела граната, со скоростью 50 м / с. Второй осколок имеет массу 1,2 кг. Насколько это быстро? Решение. Обозначьте массы фрагментов буквами m1 и m2. Их скорости будут v1 и v2 соответственно. Начальная скорость гранаты v. В задаче надо вычислить значение v2. Чтобы более крупный осколок продолжал двигаться в том же направлении, что и вся граната, второй должен лететь в противоположном направлении. Если выбрать направление оси, которое было при начальном импульсе, то после разрыва большой фрагмент летит вдоль оси, а маленький — против оси. В этой задаче допустимо использование закона сохранения количества движения в связи с тем, что взрыв гранаты происходит мгновенно. Поэтому, несмотря на то, что на гранату и ее части действует сила тяжести, она не успевает подействовать и изменить направление вектора импульса с его величиной по абсолютной величине. Сумма значений вектора импульса после взрыва гранаты такая же, как и раньше. Если написать закон сохранения количества движения тела в проекции на ось OX, то он будет выглядеть так: (m1 + m2) * v = m1 * v1 — m2 * v2. Легко выразить требуемую скорость. Он будет определяться по формуле: v2 = ((m1 + m2) * v — m1 * v1) / m2. После подстановки числовых значений и расчетов получается 25 м / с. Отвечать. Скорость маленького осколка — 25 м / с. Состояние. Пушка установлена на платформе массой M. Из нее выстреливается снаряд массой m. Он взлетает под углом α к горизонту со скоростью v (заданной относительно земли). Необходимо знать значение скорости платформы после выстрела. Решение. В этой задаче можно использовать закон сохранения количества движения в проекции на ось OX. Но только в том случае, если проекция возникающих внешних сил равна нулю. Для направления оси OX нужно выбрать сторону, по которой будет лететь пуля, и параллельную горизонтальной линии. Проблема будет решена в общем виде, так как конкретных данных для известных значений нет. Ответ — формула. Импульс системы перед выстрелом был равен нулю, так как платформа и пуля были неподвижны. Пусть требуемая скорость платформы обозначается латинской буквой u. Тогда его импульс после выстрела будет определяться как произведение массы и проекции скорости. Поскольку платформа будет втягиваться (против направления оси OX), значение импульса будет со знаком минус. Импульс снаряда является произведением его массы и проекции скорости на ось OX. Из-за того, что скорость направлена под углом к горизонту, ее проекция равна скорости, умноженной на косинус угла. В буквальном равенстве это будет выглядеть так: 0 = — Mu + mv * cos α. Из него путем несложных преобразований получается формула ответа: u = (mv * cos α) / M. Отвечать. Скорость платформы определяется по формуле u = (mv * cos α) / M. Состояние. Ширина реки по всей длине одинакова и равна, берега параллельны. Известны скорость потока воды в реке v1 и собственная скорость лодки v2. 1). При переправе нос лодки направлен строго на противоположный берег. Как далеко он уйдет вниз по течению? 2). Под каким углом α нужно ориентировать нос лодки так, чтобы она доходила до противоположного берега строго перпендикулярно начальной точке? Сколько времени займет такой переход? Решение. 1). Максимальная скорость лодки — это векторная сумма двух значений. Первый из них — течение реки, которая направляется по берегам. Второй — собственная скорость лодки перпендикулярно берегу. На чертеже изображены два одинаковых треугольника. Первый формируется шириной реки и расстоянием, пройденным лодкой. Второй — из векторов скорости. Следующая запись следует: s / l = v1 / v2. После преобразования получается формула искомого значения: s = l * (v1 / v2). 2). В этом варианте задачи вектор полной скорости перпендикулярен берегам. v = (v22 — v12), поэтому t = l / (√ (v22 — v12)). Отвечать. 1) s = l * (v1 / v2), 2) sin α = v1 / v2, t = l / (√ (v22 — v12)). Поделиться: × Рекомендуем посмотреть Adblock Физика и математика не обходятся без понятия «векторная величина». Первая всегда имеет только одну характеристику. Это ее числовое значение. Большинство скалярных величин могут принимать как положительные, так и отрицательные значения. Их примерами может служить электрический заряд, работа или температура. Но есть такие скаляры, которые не могут быть отрицательными, например, длина и масса. Векторная величина, кроме числовой величины, которая всегда берется по модулю, характеризуется еще и направлением. Поэтому она может быть изображена графически, то есть в виде стрелки, длина которой равна модулю величины, направленной в определенную сторону. При письме каждая векторная величина обозначается знаком стрелки на буквой. Если идет речь о числовом значении, то стрелка не пишется или ее берут по модулю. Сначала — сравнение. Потом идет сложение. Его можно сделать по двум правилам: треугольника или параллелограмма. Первое предписывает откладывать сначала один вектор, потом от его конца второй. Результатом сложения будет тот, который нужно провести от начала первого к концу второго. Правило параллелограмма можно использовать, когда нужно сложить векторные величины в физике. В отличие от первого правила, здесь их следует откладывать от одной точки. Потом достроить их до параллелограмма. Результатом действия следует считать диагональ параллелограмма, проведенную из той же точки. Если векторная величина вычитается из другой, то они снова откладываются из одной точки. Их так же много, как скаляров. Можно просто запомнить то, какие векторные величины в физике существуют. Или знать признаки, по которым их можно вычислить. Тем, кто предпочитает первый вариант, пригодится такая таблица. В ней приведены основные векторные физические величины. Теперь немного подробнее о некоторых из этих величин. С нее стоит начать приводить примеры векторных величин. Скорость определяется как характеристика движения тела в пространстве. Ею задается числовое значение и направление. Поэтому скорость является векторной величиной. К тому же ее принято разделять на виды. Первый является линейной скоростью. Ее вводят при рассмотрении прямолинейного равномерного движения. При этом она оказывается равной отношению пути, пройденного телом, ко времени движения. Эту же формулу допустимо использовать при неравномерном движении. Только тогда она будет являться средней. Причем интервал времени, который необходимо выбирать, обязательно должен быть как можно меньше. При стремлении промежутка времени к нулю значение скорости уже является мгновенным. Если рассматривается произвольное движение, то здесь всегда скорость — векторная величина. Ведь ее приходится раскладывать на составляющие, направленные вдоль каждого вектора, направляющего координатные прямые. К тому же определяется он как производная радиус-вектора, взятая по времени. Она определяет меру интенсивности воздействия, которое оказывается на тело со стороны других тел или полей. Поскольку сила — векторная величина, то она обязательно имеет свое значение по модулю и направление. Так как она действует на тело, то важным является еще и точка, к которой приложена сила. Чтобы получить наглядное представление о векторах сил, можно обратиться к следующей таблице. Также еще векторной величиной является равнодействующая сила. Во время движения тело описывает некоторую линию. Она называется траекторией. Эта линия может быть совершенно разной. Важнее оказывается не ее внешний вид, а точки начала и конца движения. Они соединяются отрезком, который называется перемещением. Это тоже векторная величина. Причем оно всегда направлено от начала перемещения к точке, где движение было прекращено. Обозначать его принято латинской буквой r. Здесь может появиться такой вопрос: «Путь — векторная величина?». В общем случае это утверждение не является верным. Путь равен длине траектории и не имеет определенного направления. Исключением считается ситуация, когда рассматривается прямолинейное движение в одном направлении. Оно является характеристикой быстроты изменения скорости. Причем ускорение может иметь как положительное, так и отрицательное значение. При прямолинейном движении оно направлено в сторону большей скорости. Если перемещение происходит по криволинейной траектории, то вектор его ускорения раскладывается на две составляющие, одна из которых направлена к центру кривизны по радиусу. Выделяют среднее и мгновенное значение ускорения. Первое следует рассчитывать как отношение изменения скорости за некоторый промежуток времени к этому времени. При стремлении рассматриваемого интервала времени к нулю говорят о мгновенном ускорении. По-другому его еще называют количеством движения. По определению последний равен произведению массы тела на скорость. Используя понятие импульса тела, можно по-другому записать известный закон Ньютона. Получается, что изменение импульса равно произведению силы на промежуток времени. В физике важную роль имеет закон сохранения импульса, который утверждает, что в замкнутой системе тел ее суммарный импульс является постоянным. Мы очень кратко перечислили, какие величины (векторные) изучаются в курсе физики. Условие. На рельсах стоит неподвижная платформа. К ней приближается вагон со скоростью 4 м/с. Массы платформы и вагона — 10 и 40 тонн соответственно. Вагон ударяется о платформу, происходит автосцеп. Необходимо вычислить скорость системы «вагон-платформа» после удара. Решение. Сначала требуется ввести обозначения: скорость вагона до удара — v1, вагона с платформой после сцепки — v, масса вагона m1, платформы — m2. Правила решения подобных заданий требуют схематичного изображения системы до и после взаимодействия. Ось OX разумно направить вдоль рельсов в ту сторону, куда движется вагон. В данных условиях систему вагонов можно считать замкнутой. Это определяется тем, что внешними силами можно пренебречь. Сила тяжести и реакция опоры уравновешены, а трение о рельсы не учитывается. Согласно закону сохранения импульса, их векторная сумма до взаимодействия вагона и платформы равна общему для сцепки после удара. Сначала платформа не двигалась, поэтому ее импульс был равен нулю. Перемещался только вагон, его импульс — произведение m1 и v1. Так как удар был неупругий, то есть вагон сцепился с платформой, и дальше он стали катиться вместе в ту же сторону, то импульс системы не изменил направления. Но его значение стало другим. А именно произведением суммы массы вагона с платформой и искомой скорости. Можно записать такое равенство: m1 * v1 = (m1 + m2) * v. По правилам следует перевести значения для массы из тонн в килограммы. Поэтому при подстановке их в формулу следует сначала умножить известные величины на тысячу. Простые расчеты дают число 0,75 м/с. Ответ. Скорость вагона с платформой равна 0,75 м/с. Условие. Скорость летящей гранаты 20 м/с. Она разрывается на два осколка. Масса первого 1,8 кг. Он продолжает двигаться в направлении, в котором летела граната, со скоростью 50 м/с. Второй осколок имеет массу 1,2 кг. Какова его скорость? Решение. Пусть массы осколков обозначены буквами m1 и m2. Их скорости соответственно будут v1 и v2. Начальная скорость гранаты — v. В задаче нужно вычислить значение v2. Для того чтобы больший осколок продолжал двигаться в том же направлении, что и вся граната, второй должен полететь в обратную сторону. Если выбрать за направление оси то, которое было у начального импульса, то после разрыва большой осколок летит по оси, а маленький — против оси. В этой задаче разрешено пользоваться законом сохранения импульса из-за того, что разрыв гранаты происходит мгновенно. Поэтому, несмотря на то что на гранату и ее части действует сила тяжести, она не успевает подействовать и изменить направление вектора импульса с его значением по модулю. Сумма векторных величин импульса после разрыва гранаты равна тому, который был до него. Если записать закон сохранения импульса тела в проекции на ось OX, то он будет выглядеть так: (m1 + m2) * v = m1 * v1 — m2 * v2. Из него просто выразить искомую скорость. Она определится по формуле: v2 = ((m1 + m2) * v — m1 * v1) / m2. Ответ. Скорость маленького осколка равна 25 м/с. Условие. На платформе массой M установлено орудие. Из него производится выстрел снарядом массой m. Он вылетает под углом α к горизонту со скоростью v (данной относительно земли). Требуется узнать значение скорости платформы после выстрела. Решение. В этой задаче можно использовать закон сохранения импульса в проекции на ось OX. Но только в том случае, когда проекции внешних равнодействующих сил равна нулю. За направление оси OX нужно выбрать ту сторону, куда полетит снаряд, и параллельно горизонтальной линии. В этом случае проекции сил тяжести и реакции опоры на OX будут равны нулю. Задача будет решена в общем виде, так как нет конкретных данных для известных величин. Ответом в ней является формула. Импульс системы до выстрела был равен нулю, поскольку платформа и снаряд были неподвижны. Импульс снаряда — произведение его массы на проекцию скорости на ось OX. Из-за того, что скорость направлена под углом к горизонту, ее проекция равна скорости, умноженной на косинус угла. В буквенном равенстве это будет выглядеть так: 0 = — Mu + mv * cos α. Из нее путем несложных преобразований получается формула-ответ: u = (mv * cos α) / M. Ответ. Скорость платформы определяется по формуле u = (mv * cos α) / M. Условие. Ширина реки по всей ее длине одинакова и равна l, ее берега параллельны. Известна скорость течения воды в реке v1 и собственная скорость катера v2. 1). При переправе нос катера направлен строго к противоположному берегу. Решение. 1). Полная скорость катера является векторной суммой двух величин. Первая из них течение реки, которое направлено вдоль берегов. Вторая — собственная скорость катера, перпендикулярная берегам. На чертеже получается два подобных треугольника. Первый образован шириной реки и расстоянием, на которое сносит катер. Второй — векторами скоростей. Из них следует такая запись: s / l = v1 / v2. После преобразования получается формула для искомой величины: s = l * (v1 / v2). 2). В этом варианте задачи вектор полной скорости перпендикулярен берегам. Он равен векторной сумме v1 и v2. Синус угла, на который должен отклоняться вектор собственной скорости, равен отношению модулей v1 и v2. v = √(v22 – v12), тогда t = l / (√(v22 – v12)). Ответ. 1). s = l * (v1 / v2), 2). sin α = v1 / v2, t = l / (√(v22 – v12)). Здесь размещена информация по школьной физике: и многое другое. Каждый зарегистрированный пользователь сайта имеет возможность выкладывать свои материалы (см. справку), обсуждать уже созданные. Формулы по физике – 7 класс – 8 класс – 9 класс – 10 класс – 11 класс – Основные понятия кинематики – Прямолинейное движение – Криволинейное движение – Движение в пространстве Законы Ньютона – Силы в механике – Движение под действием нескольких сил Закон сохранения импульса – Закон сохранения энергии Статика твердых тел – Динамика твердых тел – Гидростатика – Гидродинамика Механические колебания – Механические волны Основы МКТ – Газовые законы – МКТ идеального газа Первый закон термодинамики – Второй закон термодинамики – Жидкость-газ – Поверхностное натяжение – Твердые тела – Тепловое расширение Электрическое поле и его параметры – Электроемкость Постоянный электрический ток – Электрический ток в металлах – Электрический ток в жидкостях – Электрический ток в газах – Электрический ток в вакууме – Электрический ток в полупроводниках Магнитное поле – Электромагнитная индукция Электромагнитные колебания – Производство и передача электроэнергии – Электромагнитные волны Прямолинейное распространение света. Отражение света – Преломление света – Линзы Свет как электромагнитная волна – Интерференция света – Дифракция света Фотометрия Квантовая оптика Излучение и спектры СТО Строение атома – Квантовая теория – Излучение атома Атомное ядро – Радиоактивность – Ядерные реакции – Элементарные частицы Измерения – Методы решения – Развитие науки- Статья- Как писать введение в реферате- Подготовка к ЕГЭ — Репетитор по физике Запрос не дал результатов. Векторная величина или вектор — это всякая величина, обладающая направлением. Векторная величина (вектор) – это физическая величина, которая имеет две характеристики – модуль и направление в пространстве. Примеры векторных величин: скорость, сила, ускорение, напряженность и т. д. Геометрически вектор изображается как направленный отрезок прямой линии, длина которого в масштабе – модуль вектора. Ве́кторная величина́ — физическая величина, являющаяся вектором (тензором ранга 1). Противопоставляется с одной стороны скалярным (тензорам ранга 0), с другой — тензорным величинам (строго говоря — тензорам ранга 2 и более). Также может противопоставляться тем или иным объектам совершенно другой математической природы. Вектор — это величина, имеющая численное значение и направление. Векторными величинами, или векторами, называют величины, имеющие и численное значение, и направление. … Примеры — скорость, сила, перемещение (перемещением движущейся точки в данный момент времени называют вектор с началом в точке начала ее движения, и концом в точке ее расположения в этот момент. scalaris «ступенчатый») в физике — величина, каждое значение которой может быть выражено одним (как правило, действительным) числом. … К скалярным величинам относятся длина, площадь, время, температура, электрический заряд, работа, статистический вес и т. д. Скалярная величина также называется скаляром. Не скалярные величины — величины, имеющие направление, векторные. Векторные величины имеют направление (примером может послужит сила «F» или ускорение «a»). … Скалярные же величины имеют лишь значение, например масса «m». Скалярная величина (от лат. То есть скалярная величина определяется только значением, в отличие от вектора, который кроме значения имеет направление. … К скалярным величинам относятся длина, площадь, время, температура и т. Си́ла — физическая векторная величина, являющаяся мерой воздействия на данное тело со стороны других тел или полей. Для того чтобы сложить векторы и , нужно поместить начало вектора в конец вектора . Тогда вектор с началом в начале и концом в конце и будет равен их сумме. Точно так же можно складывать любое число векторов. Перемещение, так же как и путь, обозначается буквой S и измеряется в метрах. Но это две разные величины, которые необходимо различать. Величины, кроме числового значения, имеют направление, называют векторными величинами. Перемещение — это векторная величина. Перемещение s→- перемещение; вектор, соединяющий начальную и конечную точки движения. Проекция вектора перемещения на данную ось: sx = x — x0. Путь (l) — длина траектории. Перемеще́ние (в кинематике) — изменение положения физического тела в пространстве с течением времени относительно выбранной системы отсчёта. Перемещение — векторная величина! … Это вектор, который проведен из начальной точки отправления тела в конечную точку. Имеет численное значение, равное длине вектора. Траектория — воображаемая линия, по которой движется тело. Путь — длина траектории. Перемещение — направленный отрезок, соединяющий начальное и конечное положения тела. Перемещение — направленный отрезок, соединяющий начальную точку и конечную при движении тела, но тело начало движение из той же точки, в которую вернулось, следовательно, перемещение мяча равно нулю: Δr=0. Перемещение — это разница между этими точками, она не зависит от того, каким путём объект попал из первой точки во вторую. Путь всегда больше или равен модулю перемещения. Путь не может быть отрицательным. Двигаясь по окружности радиусом , материальная точка совершила половину полного оборота. Перемещение тела найдем по формуле: S = х — х0. Конечную координату х можно определить, подставляя в уравнение движения время t1: х = 4 — 3t1. В общем виде формула перемещения: S = 4 — 3t1 — х0 = 4 — 3t1 — 4 = — 3t1 = -3 · 2 = — 6 м (Тело движется в отрицательном направлении оси ОХ). Скорость равномерного прямолинейного движения прямо пропорциональна перемещению тела и обратно пропорциональна значению времени этого перемещения. v → = s → t . Можно выразить перемещение из этой формулы, умножив обе части на значение времени: s → = v → ⋅ t . Если начальная скорость тела равна нулю, то формула проекции перемещения тела имеет вид: sx = . Чтобы получить уравнение движения тела, подставим в формулу проекции перемещения ее выражение через разность координат sx = x – x0. x = x0 + v0xt + . равноускоренном движении: Sх = V0x t + ахt2/2. Ускорение тела при его равноускоренном движении — это величина, равная отношению изменения скорости к промежутку времени, за которое это изменение произошло: a → = v → − v 0 → t . 1. Скорость и путь при равноускоренном движении Формулы для равноускоренного движения v=v0+at v = v 0 + a t . Здесь v0 — начальная скорость тела, a=const a = c o n s t — ускорение. Покажем на графике, что при равноускоренном движении зависимость v(t) имеет вид прямой линии. Ускорение можно определить по углу наклона графика скорости. где ˉv0 – начальная скорость движения, ˉa=const . Расчет пути при равномерном движении Чтобы определить путь, который прошло тело при равномерном движении, необходимо скорость движения тела умножить на время которое это тело двигалось. S=V*t. Путь, пройденный телом— это длина траектории. А длина траектории-это линия по которой движется тело. Величиной в физике и математике называют свойства физических тел, измеряемых при помощи выполнения математических операций. Содержание Скалярные величины характеризуются только одним параметром — числовым значением. Они разделяются на 2 вида: В физике в список скалярных величин входят: Если скаляры выражают одно единственное свойство физического тела, то они называются однородными. Величины, описывающие несколько свойств объекта, именуются разнородными. Однородные скаляры сравнимы: они либо равны, либо одна из них больше или меньше другой. Но скалярные величины разного рода не могут сравниваться друг с другом. Понятие положительной скалярной величины и ее измерения позволяет сравнивать между собой однородные скаляры. Чтобы получить скалярную величину, достаточно умножить ее числовое значение на ее единицу измерения. Для структуризации и стандартизации вычислений физических параметров тела была разработана Международная система СИ. Она устанавливает единицы измерения для каждой величины. Во время проведения расчетов скалярных величин применяют алгебраические действия — сложение, вычитание, деление и умножение (отдельный подвид — возведение в степень). Их определение: «В физике векторными величинами называются свойства материи, характеризующиеся несколькими параметрами: модулем и направлением». В физике и математике примерами векторных величин являются: На графиках функции векторные величины изображаются в виде прямой линии, имеющей направление и свои собственные координаты в заданном масштабе. Вектор — математический элемент, представляющий собой прямой отрезок с направлением. Он обозначается либо 2 заглавными латинскими буквами, либо одной прописной. Длиной вектора является его модуль. Если длина вектора равняется 0, то он называется нулевым. Вектор, имеющий длину 1 см, именуется единичным. Длина ненулевого вектора выражается в виде расстояния между началом и концом направленного отрезка. Коллинеарные векторы — отрезки, располагающиеся либо на одной прямой, либо на параллельных прямых. Нулевой вектор коллинеарен всегда. Если коллинеарные векторы направлены в одну сторону, то они называются сонаправленными. Если отрезки направлены в диаметрально противоположные стороны, то они называются противоположно направленными. Коллинеарные векторы являются равными, если они одинаковы по модулю и направлению. Построение отрезков с направлением на плоскости осуществляется при помощи его координат для осей абсцисса и ордината. С векторами также можно производить операции сложения, деления, вычитания и умножения. Чтобы сложить два вектора, необходимо от произвольной точки на плоскости отложить первый направленный отрезок и от него отложить второй вектор. Отрезок, соединяющий начало первого вектора и конец второго, будет считаться их суммой. Этот способ сложения именуется методом треугольника. Вторым способом нахождения суммы векторов является метод параллелограмма. От произвольной точки откладываются оба направленных отрезка. Полученный рисунок нужно достроить до параллелограмма. Диагональ фигуры будет являться суммой векторов. Для осуществления вычитания необходимо отложить от произвольной точки первый вектор. От полученного отрезка откладывается следующий вектор. Второй отрезок нужно направить в противоположную сторону. Линия, соединяющая отрезки, будет являться разностью векторов. С векторами также можно проводить операцию умножения. Произведение длин направленных отрезков на косинус угла между ними называется скалярным. В результате вычислений получается число — скаляр. Скалярное произведение равно 0 в случае, когда отрезки пересекаются под углом 90°. Зная скалярное произведение, человек сможет найти косинус угла между построенными векторами. Полученные в результате выполнения алгебраических операций выражения применяются для исследования перемещения тел вокруг оси вращения и изучения элементов высшей математики. Также направленные отрезки нашли широкое применение в геометрии и астрономии. Предыдущая ФизикаПружинный маятник — формулы и уравнения нахождения величин Следующая ФизикаМатематический маятник — определение, формулы и принцип действия В физике имеются многие величины, для
знания которых недостаточно знать, чему
равна эта величина. Физические величины, характеризуемые
размером величины и ее направлением,
называются векторными. Размер
векторной величины чаще называется ее модулем. В отличие от векторных,
величины, характеризующиеся только
своим значением, называются скалярными. Векторные величины на рисунках принято
изображать в виде стрелок. Причем
направление стрелки указывает направление
векторной величины, а длина стрелки
определяется ее модулем. Обозначаются
векторные величины буквами. Причем на
рисунках над буквой, обозначающей
векторную величину рисуется стрелочка,
а в печатном тексте эти буквы печатаются
жирным шрифтом. Пусть при своем движении тело переместилось
из точки А в точку В. Величину изменения
положения тела можно определить как
расстояние от точки А до точки В. Векторные величины можно складывать.
Так пусть, например, тело сначала
переместилось из точки А в точку В, а
затем еще переместилось в точку С. Вектора можно вычитать. Для того, чтобы
из вектора а вычесть вектор b надо к вектору а прибавить вектор
противоположный вектору b: c = a – b = a + (-b).
Заметим, что –b – это не отрицательный вектор, а вектор
противоположный вектору b,
то есть вектор по модулю равный вектору b, а по направлению
противоположный ему. Вектор можно умножать на скаляр. Если
вектор а умножить на скаляр α,
то получится вектор с = α·а,
направление которого совпадает с
направлением вектора а, а модуль
в α раз больше. Вектора можно скалярно умножать друг
на друга. Скалярным произведением
векторов а и b называется скаляр
,
где и — модули векторов а и b,
а α – угол между ними. Замети, что
результатом скалярного произведения
двух векторов является скаляр. Причем
знак этого произведения может быть как
положительный, так и отрицательный. Это
определяется знаком косинуса. Если угол
между векторами острый, то их скалярное
произведение положительно, а если тупой
– то отрицательно. Пусть есть вектор а и координатная
ось Х. Из начала и конца вектора опустим
перпендикуляры на координатную ось.
Длина отрезка на координатной оси между
основаниями этих перпендикуляров – ах — является проекцией вектора а на ось Х. Проекция вектора на ось –
величина скалярная. При этом она может
быть положительной и отрицательной.
Если вектор и ось направлены преимущественно
в одну сторону, то проекция вектора на
ось положительна, а если вектор и ось
направлены в противоположные стороны,
то отрицательна. Так проекция вектора а на ось Х положительная, а
проекция вектора b на ту же ось отрицательная. Если вектор
и ось взаимно перпендикулярны, то
проекция вектора на ось равна нулю. Если
угол между вектором а и осью Х
равен α, то проекция вектора на ось
равна:
.
На рисунке изображен вектор а и система координат XY.
Если угол между вектором и осью Х равен
α, то угол между вектором и осью Y
равен 90° — α. Если
,
то
.
Аналогично в проекции на ось Y. Скалярное произведение векторов а и b можно выразить
через их проекции:
. Любой вектор можно представить в виде
суммы двух или более векторов. Часто
вектора представляют в виде суммы двух
взаимно перпендикулярных векторов,
направленных вдоль координатных осей
X и Y. На
рисунке представлено разложение вектора а на два взаимно перпендикулярных
вектора ах и аy.
Вектора ах и аy называются составляющими вектора а по направлениям Х и Y. Чтобы лучше понять науку движения
необходимо использовать некоторые математические идеи из векторный анализ . В векторном анализе есть много сложных частей, и мы не будем их рассматривать.
Мы собираемся ограничиться самыми основами.
Векторы позволяют нам смотреть на сложные, многомерные проблемы
как более простая группа одномерных задач.
В основном нас будут интересовать определения
Слова немного странные, но идеи
очень мощный, как вы увидите.
Если вы хотите узнать больше о векторах, вы можете скачать
этот отчет о
векторный анализ. Математика и наука были изобретены людьми для описания и
понимать окружающий мир.
Мы живем в (по крайней мере) четырехмерном мире, управляемом
течение времени и трех пространственных измерений; вверх и вниз,
влево и вправо, и вперед и назад.
Заметим, что существуют некоторые величины и процессы в
наш мир, которые зависят от направления , в котором
они происходят, и есть некоторые величины, которые не зависят
по направлению. Векторные величины имеют две характеристики: величину и направление.
Скалярные величины имеют только величину. Когда
сравнение
две векторные величины одного и того же типа, вы должны сравнить обе
величина и направление. Для скаляров вам нужно только
сравнивать
величина. При выполнении любой математической операции над векторной величиной
(например, сложение, вычитание, умножение . На слайде мы перечисляем некоторые из обсуждаемых физических величин
в
Руководство для начинающих по аэронавтике
и сгруппировать их либо в векторные, либо в скалярные величины. особенно
интерес,
силы
которые работают на летающих самолетах,
масса,
тяга и
аэродинамические силы, все
векторные величины. Результирующий
движение
самолета по водоизмещению, скорости и
ускорения также являются векторными величинами.
Эти величины можно определить, применяя
законы Ньютона
для векторов.
Скалярные величины включают большую часть
термодинамическое состояние
переменные, связанные с двигательной системой, такие как
плотность,
давление и
температура пропеллентов. энергия,
Работа,
а также
энтропия
связанные с двигателями также скалярные величины. Векторы имеют величину и направление, скаляры имеют только величину. В то время как законы Ньютона описывают результирующее движение
тела, существуют специальные уравнения, описывающие движение
жидкостей,
газы и жидкости.
Для любой физической системы
масса,
импульс и
энергия
системы необходимо сохранить. Навигация .. При изучении физики существует множество различных аспектов измерения и множество типов инструментов измерения. Скалярные и векторные величины являются двумя из этих типов инструментов измерения. Продолжайте читать примеры скалярной величины и примеры векторной величины в физике. инфографические скалярные и векторные примеры Advertisement Понимание разницы между скалярными и векторными величинами является важным первым шагом в физике. Основное различие в их определениях: Другими словами, скалярная величина имеет величину, такую как размер или длина, но не имеет определенного направления. Когда у него есть конкретное направление, это векторная величина. Скалярные величины, как указано выше, являются измерениями, строго относящимися к величине среды. В скалярной величине совершенно нет направленных составляющих — только величина среды. Если вы измеряете площадь поверхности участка земли или двумерного объекта, у него нет направления, только величина. Вы можете связать с ним направление, когда рассматриваемый объект является трехмерным, поскольку вы измеряете его в разных направлениях. Но площадь является скалярной, когда измерение простое и двумерное. Плотность объекта можно найти, разделив его массу на объем. Поскольку в этом расчете требуется только две точки, это скалярная величина. Направление не влияет на плотность объекта. Сколько вы прошли? Измеряя расстояние, вы определяете величину пройденного вами пространства. Он не включает водоизмещение или скорость; скалярная величина расстояния обсуждает только то, сколько земли было пройдено. Как и другие скалярные величины, энергия является произведением двух факторов (в данном случае силы и перемещения). Он описывает величину использования энергии без измерения направления. Реклама Многие люди используют слова «вес» и «масса» как синонимы, но это не одно и то же. Масса – это количество материи, присутствующей в объекте. Это не зависит от направления; масса объекта одинакова независимо от того, в каком направлении движется объект. Может быть трудно понять разницу между скоростью и скоростью. Однако знание того, что скорость является скалярной величиной, может оказаться полезным, поскольку при измерении скорости направление не имеет значения. Реклама Когда вы измеряете температуру термометром, вы измеряете свою среднюю тепловую энергию. Поскольку вы уже знаете, что энергия является скалярной величиной, вы, вероятно, можете понять, что температура также скалярна. Скалярные величины часто относятся ко времени, которое включает в себя измерение лет, месяцев, недель, дней, часов, минут, секунд и даже миллисекунд. При измерении времени не учитывается или не измеряется направление, хотя кажется, что время всегда движется вперед. Скалярное количество может относиться к объему среды, например, к ее объему. Все, от тонн и унций до граммов, миллилитров и микрограммов, — все это скалярные величины, если они применяются к измеряемой среде, а не к движению среды. Работа – это энергия, переданная объекту силой. Это скалярная величина, поскольку она является произведением силы и перемещения. Работа — это не то же самое, что сила, которая является векторной величиной, потому что работа — это результат действия силы. Векторные величины относятся как к направлению движения среды, так и к измерению скалярной величины. Вы можете заметить, что скалярные произведения часто являются произведениями двух векторных величин. Ознакомьтесь с этими 10 примерами векторных величин, встречающихся в вашей повседневной жизни. Хотя скорость является скалярной величиной, ускорение отличается. Ускорение измеряет скорость изменения скорости объекта. Реклама Скалярная величина расстояния измеряет землю, пройденную движением, а смещение измеряет, насколько далеко она сдвинулась от своего первоначального местоположения. Вы можете видеть, что направление и величина очень важны при измерении смещения! Сила имеет как величину, так и направление. В отличие от скалярного количества работы, сила заставляет объект изменять свою скорость. Думайте о таких силах, как гравитация, когда решаете, является ли это векторной величиной. Измерение температуры среды является скалярной величиной. Однако измерение повышения или понижения температуры среды является векторной величиной. У него есть направление и величина. Поляризация указывает на то, что два устройства отошли друг от друга. Направление (вдали друг от друга), а также величина (насколько далеко или насколько) являются важными факторами при измерении поляризации. Импульс указывает, что объект находится в движении. Это произведение массы и скорости, и его можно рассчитать только в том случае, если вы знаете, как быстро движется объект (величина) и в каком направлении. Может показаться, что фиксированное положение не имеет ни величины, ни направления. И это правильно — если вы определяете «позицию» таким образом. Вектор положения берется относительно начала системы координат; то есть он существует в конце прямой линии, которая соединяется с серединой оси. С этой точки зрения легко увидеть направление и величину. Реклама Тяга — это тип силы реакции, которая также имеет величину и направление. Подумайте о том, что вас толкают или толкают по воздуху — вы определенно движетесь в направлении, имеющем огромную величину! Чаще всего он используется в механике и аэронавтике. Измерение скорости, с которой объект меняет положение, является векторной величиной. Вес объекта является произведением его массы и действующего на него гравитационного ускорения. Поскольку это связано с силой тяжести, вес имеет направление (вниз), а также величину. Реклама Высокотехнические примеры и пояснения, касающиеся скалярных и векторных величин, можно найти на веб-сайте National Aeronautics and Space. Он содержит полное описание скаляров и векторов, а также примеры и способы их использования. Итак, теперь у вас есть несколько примеров скалярных и векторных величин, и вы понимаете некоторые различия между ними. Для получения дополнительной информации о физике ознакомьтесь с этими примерами контактной силы, которые вы, вероятно, увидите в физическом мире. Штатный писатель В этом объяснителе мы научимся описывать, как векторы используются в механике для решения задач в двух измерениях. При моделировании реального движения с помощью математики необходимо различать векторные и скалярные величины. Скалярная величина может принимать только
положительные (или нулевые) значения, указывающие на величину определенных признаков независимо от направления. Расстояние и скорость являются скалярными величинами
потому что они не задают направление, а соответствующие реальные признаки имеют конкретное направление. Например, если нам говорят, что
самолет летит со скоростью 200 километров в час, это говорит нам о его скорости
путешествует, но не туда, куда он идет. Такие величины, как время и масса, также считаются скалярами, поскольку они по своей сути не касаются
направлений и, следовательно, может принимать только положительные значения. С другой стороны, векторная величина указывает как направление, так и величину. Перемещение и скорость являются векторными аналогами
расстояние и скорость соответственно. Другими словами, расстояние — это величина смещения, а скорость — величина скорости. Поскольку
скорость объекта также указывает его направление, самолет, летящий на север со скоростью
200 километров в час будет отличаться от скорости другого самолета, летящего на юг.
с той же скоростью. Рассмотрим, как задается направление в одномерном (или линейном) движении. В линейном движении есть ровно два разных варианта
для направлений, поэтому направления можно указать, поставив положительный или отрицательный знак перед их скалярными аналогами. Для этого мы можем использовать следующие шаги. Чтобы указать направление движения объекта по прямой линии, нам нужно Рассмотрим скорости самолетов из приведенного выше примера. Здесь один самолет летит на север, а другой летит
на юг с той же скоростью. Мы не можем определить скорости двух плоскостей, не назначив сначала либо север, либо юг положительной стороной.
направление. Если мы говорим, что север является положительным направлением, скорость первой плоскости равна
+200 км/ч или просто
200 км/ч, а второй самолет имеет скорость
−200 км/ч. Заметим, что единица скорости равна
скорости. Заметим, что в первом случае мы опустили положительный знак в скорости, чтобы написать
200 км/ч, что соответствует его скорости. В таких случаях мы должны
будьте осторожны, чтобы отличать векторные величины от скалярных величин. Говоря, что самолет имеет скорость
200 км/ч — это не то же самое, что сказать, что он имеет скорость
200 км/ч, так как последний содержит дополнительную информацию о его направлении. В нашем первом примере мы найдем скорость и смещение объекта относительно их скалярных аналогов, когда их направления
указано. Автомобиль движется по шоссе по указанному маршруту. Расстояние между точками А и В составляет 60 км, а расстояние между точками
B и C составляет 30 км. Автомобиль едет из А в С, проходит через В, затем возвращается в
A, проходящий через B. Внутри каждого сегмента автомобиль движется с постоянной скоростью
90 км/ч. Чему равно перемещение автомобиля из С в В? Кроме того, что такое
скорость этого отрезка? Перемещение и скорость являются векторными величинами, скалярными аналогами которых являются расстояние и скорость соответственно. Сначала рассмотрим смещение. Скалярным аналогом смещения является расстояние. Так как мы хотим найти смещение от C до
B, нам нужно сначала найти расстояние между этими двумя точками. Нам дано, что расстояние между B и C равно
30 км, что равно величине водоизмещения. Направление от С
до B направлен влево, что обозначается знаком минус. Следовательно, смещение от C до B задается путем помещения отрицательного знака в
фронт скалярного аналога, который составляет 30 км. Далее найдем скорость. Скалярным аналогом скорости является скорость, и нам известно, что автомобиль движется с постоянной скоростью.
скорость 90 км/ч; следовательно, это равно величине скорости от
C в B. Направление скорости автомобиля из C в B направлено влево, что противоположно положительному направлению. Следовательно,
скорость от C до B задается путем помещения знака минус перед скалярным аналогом,
90 км/ч. Это дает нам
−90 км/ч. Следовательно, перемещение и скорость автомобиля на участке от C до B определяются выражением
−30,−90/.kmkmh В предыдущем примере мы нашли смещение и скорость объекта, используя их скалярные эквиваленты. Другой важный вектор
движущимися величинами являются ускорение и сила. Подобно смещению и скорости, эти величины имеют определенные направления, связанные с
их в движении, на что указывают их знаки в одномерном движении. Однако их скалярные аналоги не имеют специальных имен,
как расстояние и скорость, поэтому мы называем их величиной ускорения или величиной силы. Мы помним, что ускорение — это скорость изменения скорости, поэтому его интерпретация тесно связана со скоростью объекта. В то время как скорость указывает направление движения, ускорение указывает, как изменяется скорость. Рассмотрим, как интерпретировать
направления скорости и ускорения при прямолинейном движении. Направления скорости и ускорения движущегося объекта связаны следующим образом: Мы можем понять указанные выше свойства, рассмотрев следующую диаграмму. На приведенной выше левой диаграмме скорость и ускорение направлены в одном направлении. Например, мы можем представить парусник, путешествующий
вправо, где ветер, действующий как ускорение, дует в том направлении, в котором уже движется лодка.
парусник двигаться быстрее, а это значит, что скорость лодки увеличится. Точно так же мы можем изобразить сценарий, представленный
по схеме справа. В этом случае ветер дует против парусника, что замедляет движение лодки. Это приводит к
скорость лодки уменьшается. В нашем следующем примере мы рассмотрим взаимосвязь между скоростью объекта и его ускорением при линейном движении. Предположим, что положительное направление движения направлено вправо. Что из следующего правильно описывает движение частицы
скорость которого отрицательна, а ускорение положительно? Напомним, что скорость и ускорение являются векторными величинами, знаки которых в контексте линейного движения указывают направление. Так как мы
учитывая, что положительное направление движения направлено вправо, мы знаем, что положительный знак связан с правильным направлением, в то время как
отрицательный знак означает левое направление. Мы можем начать с определения направления скорости. Скорость частицы отрицательна; следовательно, направление его скорости равно
оставил. Ускорение — это скорость изменения скорости, поэтому его значение всегда связано со скоростью. Чтобы интерпретировать знак ускорения, мы
вспомнить связь между направлением скорости и ускорением: Обратите внимание, что в этом примере скорость и ускорение имеют противоположные знаки. Отсюда скорость частицы, равная величине
скорости, уменьшается. Это приводит к ответу B, в котором говорится, что частица замедляется, когда движется влево. До сих пор мы рассматривали векторные величины в линейном движении. Направление в линейном движении простое, потому что есть только два варианта
направление. Когда мы рассматриваем движение на плоскости, т. Вместо знаков мы указываем направления плоскостного движения с помощью векторов. Кратко остановимся на некоторых свойствах векторов. В двоем
размеры, любой вектор можно записать в терминах стандартных единичных векторов ⃑𝑖 и ⃑𝑗. Эти стандартные единичные векторы представляют собой векторы вдоль горизонтальной и вертикальной осей, величина которых равна 1. Мы можем написать общий двумерный вектор, начинающийся с начала координат и заканчивающийся в точке (𝑎,𝑏), умножая
эти стандартные единичные векторы скалярами и сложением их вместе, что приводит к выражению 𝑎⃑𝑖+𝑏⃑𝑗, как показано ниже. Напомним, что величина вектора определяется длиной стрелки, которая определяется выражением
‖‖𝑎⃑𝑖+𝑏⃑𝑗‖‖=√𝑎+𝑏. Эта формула величины взята из теоремы Пифагора. Мы можем видеть это на рисунке выше, так как векторная стрелка (красная) образует
гипотенуза прямоугольного треугольника в сочетании с горизонтальной и вертикальной компонентами. Следовательно, квадрат величины дается добавлением
квадраты длин горизонтальной и вертикальной стрелок, равные 𝑎 и 𝑏 соответственно. Это приводит
к приведенной выше формуле для величины 𝑎⃑𝑖+𝑏⃑𝑗. Мы можем использовать векторы для представления векторных величин, таких как перемещение, скорость, ускорение и сила. Величины этих векторов соответствуют
их скалярным аналогам, которые аналогичны тому, что мы обсуждали в контексте линейного движения. В следующем примере мы найдем скорость объекта, найдя модуль скорости. Скорость частицы равна 4⃑𝑖−3⃑𝑗 м/с. Найдите скорость частицы. Напомним, что скорость является скалярным эквивалентом скорости, которая является векторной величиной. Скорость имеет ту же единицу, что и скорость, и равна
к величине скорости. В этом примере нам задана скорость частицы в виде вектора. Его скорость равна величине
скорость, поэтому мы можем найти скорость, вычислив величину данного вектора. Напомним, что величина вектора 𝑎⃑𝑖+𝑏⃑𝑗 определяется выражением
‖‖𝑎⃑𝑖+𝑏⃑𝑗‖‖=√𝑎+𝑏. Из нашего заданного вектора мы видим, что 𝑎=4 и 𝑏=−3. Подставляя эти значения в приведенную выше формулу, мы
получить величину заданного вектора:
4+(−3)=√25=5. Используя те же единицы измерения, что и скорость, скорость частицы равна 5 м/с. В предыдущем примере мы рассматривали величину векторной величины, которая приводит к ее скалярному эквиваленту. С другой стороны, направление
векторных величин можно понять, используя угол по отношению к любому стандартному единичному вектору. Мы можем получить такие углы, построив
соответствующий прямоугольный треугольник и используя тригонометрию, как показано ниже. Если мы знаем, что вектор принимает форму 𝑎⃑𝑖+𝑏⃑𝑗, то мы знаем, что зеленые стороны
прямоугольный треугольник выше задается 𝑎 и 𝑏 соответственно. Чтобы найти отмеченный угол между диагональным вектором
и стандартный единичный вектор ⃑𝑖, мы можем использовать отношение тангенсов tan𝑏𝑎. Когда угол между векторами превышает 90∘, этот метод потребует небольшого
модификация. В таких случаях мы можем нарисовать прямоугольный треугольник, содержащий остроугольную часть этого угла, опустив прямой угол в
процесса, как показано на следующей диаграмме. На приведенной выше диаграмме мы по-прежнему получаем прямоугольный треугольник, а отмеченный угол можно найти, используя отношение тангенса
загар|𝑎|𝑏. В нашем следующем примере мы найдем угол между ускорением объекта и стандартным единичным вектором. Ускорение частицы равно 4⃑𝑖−3⃑𝑗 м/с 2 . Найдите угол, округлив до ближайшего
степени, что ускорение этой частицы
делает с единичным вектором ⃑𝑖. Напомним, что ускорение — это векторная величина в движении, которая представляет скорость изменения скорости. В этом примере нам дается
ускорение частицы как вектор. Начнем с рисования этого вектора и единичного вектора ⃑𝑖 на
та самая сетка. Мы ищем угол, который обозначен как 𝜃 на диаграмме выше. Мы видим, что вертикальные и горизонтальные
стрелки вместе с диагональной стрелкой образуют прямоугольный треугольник. Две перпендикулярные стороны имеют длины 4 и 3 соответственно. Сторона длины 4 примыкает к углу 𝜃, а сторона длины 3 противоположна 𝜃. Тогда отношение тангенсов этого угла определяется выражением
таннапротив соседнего𝜃==34. Мы можем найти 𝜃 из этого уравнения, применяя арктангенс:
𝜃=34=36,87….tan∘ Округляя этот ответ до ближайшего градуса, угол между
ускорение объекта, а единичный вектор ⃑𝑖 равен
37∘. Полезность векторных величин в движении становится очевидной, когда мы применяем различные векторные операции. Хотя большинство этих операций зарезервировано
для будущих уроков мы можем рассмотреть геометрическое приложение, включающее сложение векторов. Напомним, что сложение двух векторов
⃑𝑣 и ⃑𝑤 можно представить на декартовой сетке, соединив два вектора так
что начальный конец одного вектора лежит на конце стрелки другого вектора. Это геометрическое свойство сложения векторов полезно при моделировании реального движения. В нашем последнем примере мы будем использовать сложение векторов, чтобы найти
расстояние между двумя точками при заданных перемещениях по трем точкам. Частица движется из точки 𝐴 в точку 𝐵 и затем в точку 𝐶. Водоизмещение
из точки 𝐴 в точку 𝐵 есть
3⃑𝑖+5⃑𝑗 см,
а перемещение из точки 𝐵 в точку 𝐶 равно ⃑𝑖−7⃑𝑗 см. Найдите расстояние между точкой 𝐴 и
точка 𝐶 округляется до ближайшей одной сотой
сантиметр. Напомним, что смещение — это векторная величина, которая указывает и направление, и величину, а расстояние — это скалярная величина, представляющая
только величина. Расстояние, которое мы ищем, находится между точкой 𝐴 и точкой 𝐶, что является величиной
смещение от 𝐴 к 𝐶. Напомним, что сложение двух векторов можно представить на декартовой сетке, соединив два вектора так, чтобы начальный конец одного
вектор лежит на конце стрелки другого вектора. Чтобы визуализировать этот процесс, давайте нарисуем диаграмму, содержащую три точки вместе с
два заданных перемещения. Нижний вектор представляет собой смещение от 𝐴 до 𝐶, которое мы ищем. Использование геометрического
свойство сложения векторов, мы можем видеть, что путешествие из 𝐴 в 𝐵 затем из 𝐵 в
𝐶 эквивалентно перемещению из 𝐴 в 𝐶. Другими словами,
𝐴𝐵+𝐵𝐶=𝐴𝐶. Вычислим это сложение векторов:
3⃑𝑖+5⃑𝑗+⃑𝑖−7⃑𝑗=(3+1)⃑𝑖+(5+(−7))⃑𝑗=4⃑𝑖−2⃑𝑗. Это говорит нам о том, что смещение от точки 𝐴 к точке 𝐶 равно
4⃑𝑖−2⃑𝑗 см. С расстояния
является величиной смещения, мы можем найти расстояние между этими двумя точками, вычислив величину этого вектора. Напомним, что
величина вектора 𝑎⃑𝑖+𝑏⃑𝑗 определяется выражением
‖‖𝑎⃑𝑖+𝑏⃑𝑗‖‖=√𝑎+𝑏. Следовательно, величину 4⃑𝑖−2⃑𝑗 можно найти, подставив 𝑎=4
и 𝑏=−2 в приведенную выше формулу:
4+(−2)=√20=4,4721…. Округлив до ближайшей одной сотой сантиметра,
расстояние между точкой 𝐴 и точкой 𝐶 равно 4,47 см. Давайте закончим повторением нескольких важных понятий из этого объяснения. В повседневной жизни мы взаимозаменяемо используем расстояние, перемещение, скорость, скорость, ускорение и т. д. Для физиков все величины, будь то статические или движущиеся, могут быть дифференцированы путем классификации их как либо скаляры, либо векторы. Величина с величиной (размером) только называется скалярной величиной . Масса, энергия, мощность, расстояние и время — вот некоторые примеры скалярных величин, потому что с ними не связано направление. Величина, имеющая величину и связанное с ней направление , является векторной величиной . Ускорение, сила, сила тяжести и вес являются некоторыми векторными величинами. Все векторные величины связаны с определенным направлением. Как мы уже говорили, величина, имеющая модуль и направление, называется векторной величиной. Вес является примером векторной величины, поскольку он является произведением массы и ускорения свободного падения. ускорение силы тяжести направлено вертикально вниз , что делает вес векторной величиной. Давайте рассмотрим несколько примеров скаляров и векторов. Предположим, у вас есть ящик, и вы перемещаете его на расстояние 5 метров. Рис. 1. Движение объекта из точки A в точку B в заданном направлении представляет собой вектор. Oğulcan Tezcan – StudySmarter Originals Если вы скажете кому-нибудь, что расстояние между точками A и B составляет 5 метров, вы говорите о скалярная величина потому что вы не указываете направление . Однако, если вы скажете кому-нибудь , что переместили ящик на 5 метров вправо (на восток) , как показано на рисунке 1, вы теперь говорите о векторной величине . Почему? Поскольку у вас есть , теперь указано направление, связанное с движением . А в физике это называется смещение . Следовательно, перемещение является векторной величиной. Теперь предположим, что вам потребовалось 2 секунды, чтобы передвинуть коробку вправо. Рис. 2. Диаграмма, показывающая вектор смещения относительно времени. Oğulcan Tezcan – StudySmarter Originals Если бы вам нужно было вычислить, как быстро вы переместили коробку, вы вычислили бы скорость движения . В приведенном выше примере скорость равна: Скорость является скалярной величиной , поскольку она не имеет направления. Однако, если вы скажете, что ящик двигался со скоростью 2,5 м/с вправо , это становится векторной величиной . Скорость с направлением — это скорость, , а изменение скорости, в свою очередь, известно как ускорение (м/с 2 ), которое также является векторной величиной. Масса и вес тела могут казаться одинаковыми, но это не так. Масса: количественная мера инерции тела , которая представляет собой тенденцию тела сопротивляться силе, которая может вызвать изменение его скорости или положения. Масса имеет единицу СИ килограмм. Вес: Гравитационное притяжение , действующее на массу. Единицей измерения СИ являются ньютоны. Масса не имеет никакого направления, и она будет одинаковой, где бы вы ни находились во Вселенной! Таким образом, мы можем классифицировать массу как скалярную величину . Вес, с другой стороны, это сила, действующая на объект, и поскольку сила имеет направление, вес является векторной величиной . Другой способ посмотреть на это, если вы поместите один объект на Землю, а другой объект с той же массой на Луну. Оба объекта будут иметь одинаковую массу, но разный вес из-за гравитационного притяжения Луны (1,62 м/с 2 ), что меньше по сравнению с Землей. Мы можем представить векторы стрелкой, как показано ниже. Рис. 3. Представление вектора. Wikimedia Commons Длина отображает величину, хвост — начальную точку вектора, смысл вектора определяется порядком двух точек на линии, параллельной вектору, а ориентация говорит вам, под каким углом вектор указывает. Давайте рассмотрим несколько примеров выполнения сложения векторов. Допустим, у вас есть два вектора 10 северной широты и 15 северной широты, и оба они указывают на восток. Сумма этих векторов становится 25N на восток. Рисунок 4. Добавление векторов в одном направлении. Усама Адил — StudySmarter Originals. Теперь, если мы изменим направление 15 северной широты на запад (-15 северной широты), результирующий вектор становится -5 N (указывая на запад). Векторная величина может иметь положительные и отрицательные знаки . Знак вектора показывает, что направление вектора противоположно опорному направлению (которое произвольно). Рис. 5. Вычитаются векторы в противоположном направлении. Usama Adeel — StudySmarter Originals Теперь, конечно, все сложения векторов не так просты, как показано выше. С помощью этого правила мы можем вычислить результирующий вектор, соединив конец первого вектора с началом второго вектора . Взгляните на рисунки ниже. Рис. 6. Перпендикулярные векторы соединяются по правилу «голова к хвосту». Usama Adeel – StudySmarter Originals Векторная сила 30 Н действует в восточном направлении, а векторная сила 40 Н действует в северном направлении. Мы можем вычислить результирующий вектор, соединив хвост вектора 30N с головой вектора 40N. Вектора перпендикулярны, поэтому мы можем используйте теорему Пифагора для решения результирующего вектора, как показано на рисунке 7. Рисунок 7. Перпендикулярное сложение вектора. Usama Adeel – StudySmarter Originals Немного тригонометрии и применения теоремы Пифагора результирующий вектор становится равным 50N. Используя тот же пример выше, что, если бы у нас была только векторная сила 50 Н с углом от горизонтали, и нас попросили найти ее горизонтальную и вертикальную составляющие? Разделение одного вектора на два или более векторов, производящих эффект, аналогичный исходному вектору, называется разрешением векторов . Давайте рассмотрим пример, объясняющий эту концепцию. Предположим, что вектор силы F в 150 Н приложен под углом 30 градусов к поверхности. Рис. 8. Вектор под углом. Usama Adeel – StudySmarter Originals Мы можем разделить вектор F на горизонтальную составляющую (Fx) и вертикальную (Fy) составляющую, как показано ниже: Рисунок 9. Вычисление Fx и Fy с помощью тригонометрии дает нам: Как вы, возможно, уже поняли, расчеты в физике никогда не бывают такими простыми ! Не каждая поверхность горизонтальна — иногда поверхности могут быть наклонными, и вам придется рассчитывать и разрешать компоненты вдоль наклонной плоскости. Рисунок 10. Направление веса на наклонной плоскости. Usama Adeel – StudySmarter Originals На рис. 10 показана коробка на поверхности под углом θ к горизонтали. Вес коробки, mg, действует вниз с массой m и гравитационным притяжением g. Если мы разделим вектор mg на горизонтальную и вертикальную составляющие, Рис. Угол θ между mg и mgcosθ будет таким же, как угол наклонной поверхности от горизонтали. Сила, которая разгонит ящик вниз по склону, составит mgsin θ (Fg) , а сила реакции Fn (из третьего закона Ньютона) будет равна mgcos θ . Отсюда Рис. 12. Разрешение векторов и направление движения на наклонной плоскости. Usama Adeel – StudySmarter Originals Если силы действуют на тело, и тело неподвижно или движется с постоянной скоростью (без ускорения), такой случай называется равновесием . Силовые линии должны проходить через одну и ту же точку, чтобы тело находилось в равновесии. На приведенном ниже рисунке однородная лестница прислонена к гладкой стене (трение отсутствует). Рис. 13. Лестница, прислоненная к стене, является примером тела, находящегося в равновесии. Usama Adeel — StudySmarter Originals Если вы расширите эти силы, вы увидите, что они пересекаются в определенной точке. Поскольку объект находится в равновесии, сила от земли также должна проходить через ту же точку, что и другие силы. Рис. 14. Силовые линии пересекаются в одной точке, если тело находится в равновесии. Usama Adeel – StudySmarter Originals При разделении силы от земли на ее вертикальную и горизонтальную составляющие, нормальная сила реакции от земли действует вверх, а сила трения от земли действует вдоль поверхности. Рис. 15. Результирующая векторов трения и грунта. Usama Adeel – StudySmarter Originals В сущности, происходит то, что все силы компенсируют друг друга. Скаляр — это величина, которая полностью определяется своей величиной и не имеет направления. Скалярными величинами можно управлять с помощью законов арифметики, применимых к натуральным числам. Например, если я добавляю 20 граммов сахара в рецепт, а затем добавляю еще 20 граммов, в результате получается 40 граммов сахара в рецепте. Если я куплю литровую (1000 мл) бутылку воды и выпью 250 мл, останется 750 мл. Вектор – это величина, которая определяет как величину, так и направление. Такая величина может быть представлена геометрически стрелкой длины, пропорциональной ее величине, указывающей в заданном направлении. Примеры векторов: перемещение, скорость, ускорение, сила и электрическое поле. Векторы можно складывать простыми способами, как и скаляры. Например: Самолет летит на юг со скоростью 500 миль/час. Ветер дует с востока со скоростью 100 миль в час. Результирующая скорость не 600 миль в час и не 400 миль в час. R = 509,9 миль/ч. Направление плоскости можно вычислить с помощью функции косинуса. тангенс = 100/500 = 11,31 градуса (Примечание: схема выполнена не в масштабе)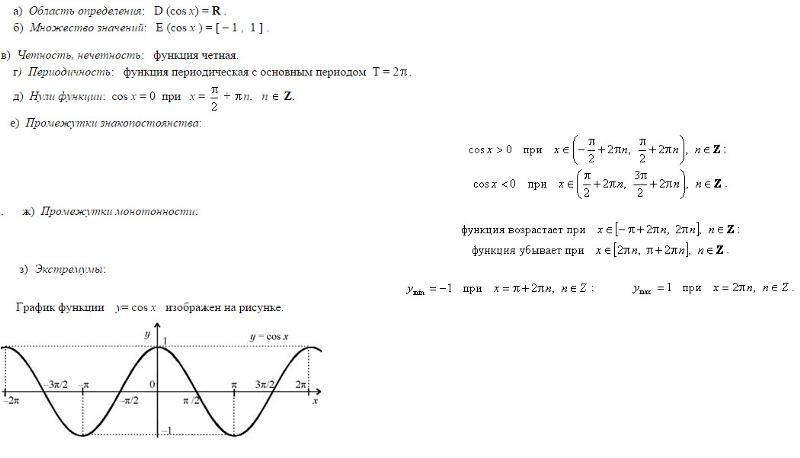
Какие из величин векторные: Какие величины в физике называются векторными и какие скалярными? Какие векторы называются равными? Что можно…
Векторная величина в физике. Примеры векторных величин
Как отличить скалярную величину от векторной?
 Это его числовое значение. Большинство скаляров могут быть как положительными, так и отрицательными. Примеры включают электрический заряд, работу или температуру. Но есть скаляры, которые не могут быть отрицательными, например длина и масса.
Это его числовое значение. Большинство скаляров могут быть как положительными, так и отрицательными. Примеры включают электрический заряд, работу или температуру. Но есть скаляры, которые не могут быть отрицательными, например длина и масса.Какие действия чаще всего выполняются с векторами?
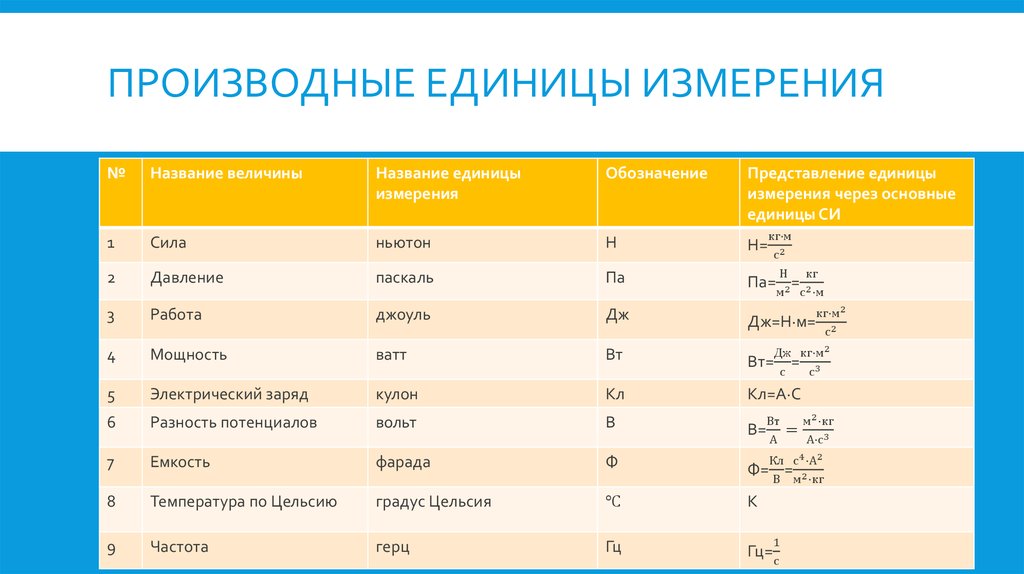 Если хотя бы одно из указанных условий не выполняется, векторы не равны.
Если хотя бы одно из указанных условий не выполняется, векторы не равны.Какие векторы изучают в физике?
 Тем, кто отдает предпочтение первому варианту, такой столик пригодится. Перечисляет основные векторные физические величины.
Тем, кто отдает предпочтение первому варианту, такой столик пригодится. Перечисляет основные векторные физические величины.Обозначение формулы Имя v скорость р в движении а ускорение Ф сила р пульсировать А ТАКЖЕ напряженность электрического поля В магнитная индукция М момент силы Первая величина — скорость
 В этом случае он оказывается равным отношению пути, пройденного телом, и времени движения.
В этом случае он оказывается равным отношению пути, пройденного телом, и времени движения.Вторая величина — сила

Власть Пункт применения Направление строгость центр тела в центре земли вселенская гравитация центр тела в центре другого тела эластичность место контакта взаимодействующих тел от внешних воздействий трение между соприкасающимися поверхностями в обратном направлении движения Третья величина — перемещение
 Важнее не внешний вид, а начальная и конечная точки движения. Они соединены линией, называемой сдвигом. Это тоже векторная величина. Кроме того, он всегда направлен от начала движения к точке, где движение было остановлено. Его принято обозначать латинской буквой r.
Важнее не внешний вид, а начальная и конечная точки движения. Они соединены линией, называемой сдвигом. Это тоже векторная величина. Кроме того, он всегда направлен от начала движения к точке, где движение было остановлено. Его принято обозначать латинской буквой r.Четвертая величина — ускорение
 При движении по прямой он направлен в сторону большей скорости. Если движение происходит по криволинейной траектории, вектор его ускорения раскладывается на две составляющие, одна из которых направлена к центру кривизны по радиусу.
При движении по прямой он направлен в сторону большей скорости. Если движение происходит по криволинейной траектории, вектор его ускорения раскладывается на две составляющие, одна из которых направлена к центру кривизны по радиусу.Пятая величина — импульс

Задача о неупругом ударе

Задача с разделением тела на части
Задача про выстрел под углом
 В этом случае проекции сил тяжести и реакция опоры на OX будут равны нулю.
В этом случае проекции сил тяжести и реакция опоры на OX будут равны нулю.
Задача о переправе через реку
 Он равен векторной сумме v1 и v2. Синус угла, на который должен отклоняться собственный вектор скорости, равен отношению между модулями v1 и v2. Чтобы рассчитать время в пути, вам нужно разделить ширину реки на рассчитанную максимальную скорость. Величина последнего рассчитывается по теореме Пифагора.
Он равен векторной сумме v1 и v2. Синус угла, на который должен отклоняться собственный вектор скорости, равен отношению между модулями v1 и v2. Чтобы рассчитать время в пути, вам нужно разделить ширину реки на рассчитанную максимальную скорость. Величина последнего рассчитывается по теореме Пифагора.
detectorВекторная величина в физике. Примеры векторных величин
 Ее необходимо знать и узнавать, а также уметь с нею оперировать. Этому обязательно стоит научиться, чтобы не путаться и не допускать глупых ошибок.
Ее необходимо знать и узнавать, а также уметь с нею оперировать. Этому обязательно стоит научиться, чтобы не путаться и не допускать глупых ошибок.Как отличить скалярную величину от векторной?
Какие действия чаще всего выполняются с векторами?
 Они могут быть равными или нет. В первом случае их модули одинаковые. Но это не единственное условие. У них должны быть еще одинаковые или противоположные направления. В первом случае их следует называть равными векторами. Во втором они оказываются противоположными. Если не выполняется хотя бы одно из указанных условий, то векторы не равны.
Они могут быть равными или нет. В первом случае их модули одинаковые. Но это не единственное условие. У них должны быть еще одинаковые или противоположные направления. В первом случае их следует называть равными векторами. Во втором они оказываются противоположными. Если не выполняется хотя бы одно из указанных условий, то векторы не равны. Только результатом будет вектор, который совпадает с тем, что отложен от конца второго к концу первого.
Только результатом будет вектор, который совпадает с тем, что отложен от конца второго к концу первого.Какие векторы изучают в физике?
Обозначение в формуле Наименование v скорость r перемещение а ускорение F сила р импульс Е напряженность электрического поля В магнитная индукция М момент силы Первая величина — скорость
 Это обусловлено тем, что ее изучают в числе первых.
Это обусловлено тем, что ее изучают в числе первых.
Вторая величина — сила
Сила Точка приложения Направление тяжести центр тела к центру Земли всемирного тяготения центр тела к центру другого тела упругости место соприкосновения взаимодействующих тел против внешнего воздействия трения между соприкасающимися поверхностями в сторону, противоположную движению  Она определяется как сумма всех действующих на тело механических сил. Для ее определения необходимо выполнить сложение по принципу правила треугольника. Только откладывать векторы нужно по очереди от конца предыдущего. Результатом окажется тот, который соединяет начало первого с концом последнего.
Она определяется как сумма всех действующих на тело механических сил. Для ее определения необходимо выполнить сложение по принципу правила треугольника. Только откладывать векторы нужно по очереди от конца предыдущего. Результатом окажется тот, который соединяет начало первого с концом последнего.Третья величина — перемещение
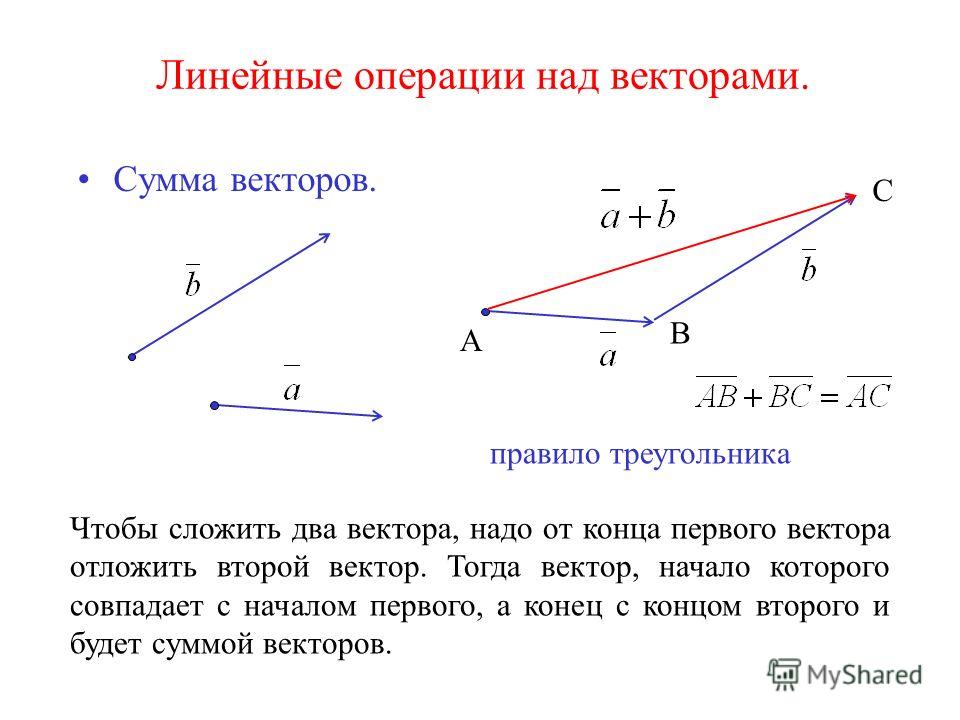 Тогда модуль вектора перемещения совпадает по значению с путем, и направление у них оказывается одинаковым. Поэтому при рассмотрении движения вдоль прямой без изменения направления перемещения путь можно включить в примеры векторных величин.
Тогда модуль вектора перемещения совпадает по значению с путем, и направление у них оказывается одинаковым. Поэтому при рассмотрении движения вдоль прямой без изменения направления перемещения путь можно включить в примеры векторных величин.Четвертая величина — ускорение
Пятая величина — импульс
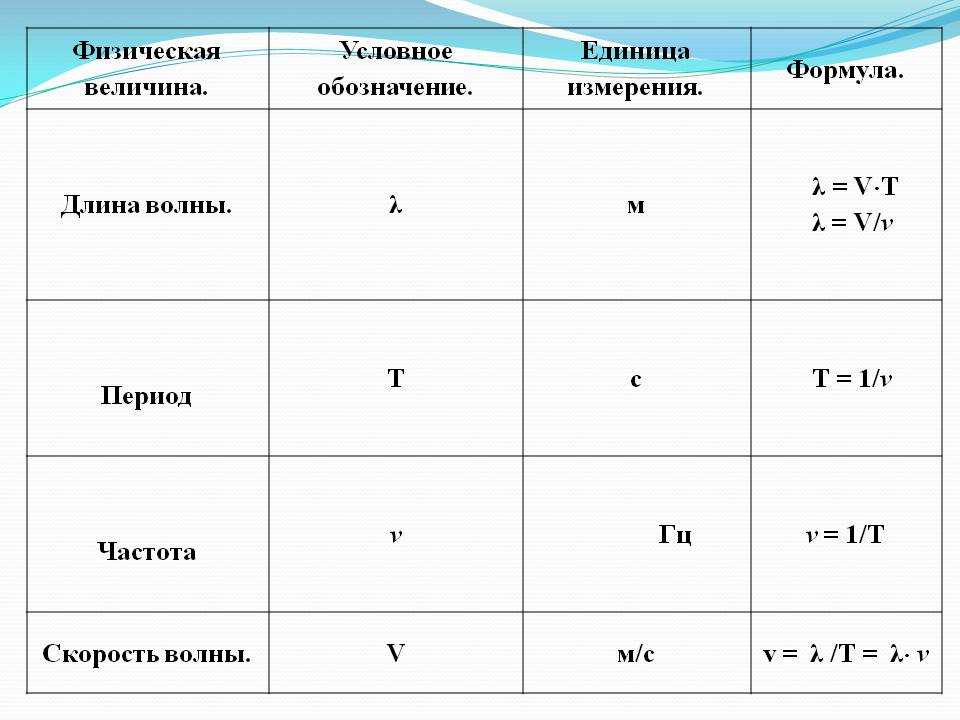 Импульс векторной величиной является из-за того, что напрямую связан со скоростью и силой, приложенной к телу. Обе они имеют направление и задают его импульсу.
Импульс векторной величиной является из-за того, что напрямую связан со скоростью и силой, приложенной к телу. Обе они имеют направление и задают его импульсу.Задача о неупругом ударе
 По условию задачи необходимо узнать значение скорости v.
По условию задачи необходимо узнать значение скорости v. Оно будет верно для проекции векторов импульсов на выбранную ось. Из него легко вывести равенство, которое потребуется для вычисления искомой скорости: v = m1 * v1 / (m1 + m2).
Оно будет верно для проекции векторов импульсов на выбранную ось. Из него легко вывести равенство, которое потребуется для вычисления искомой скорости: v = m1 * v1 / (m1 + m2).Задача с разделением тела на части
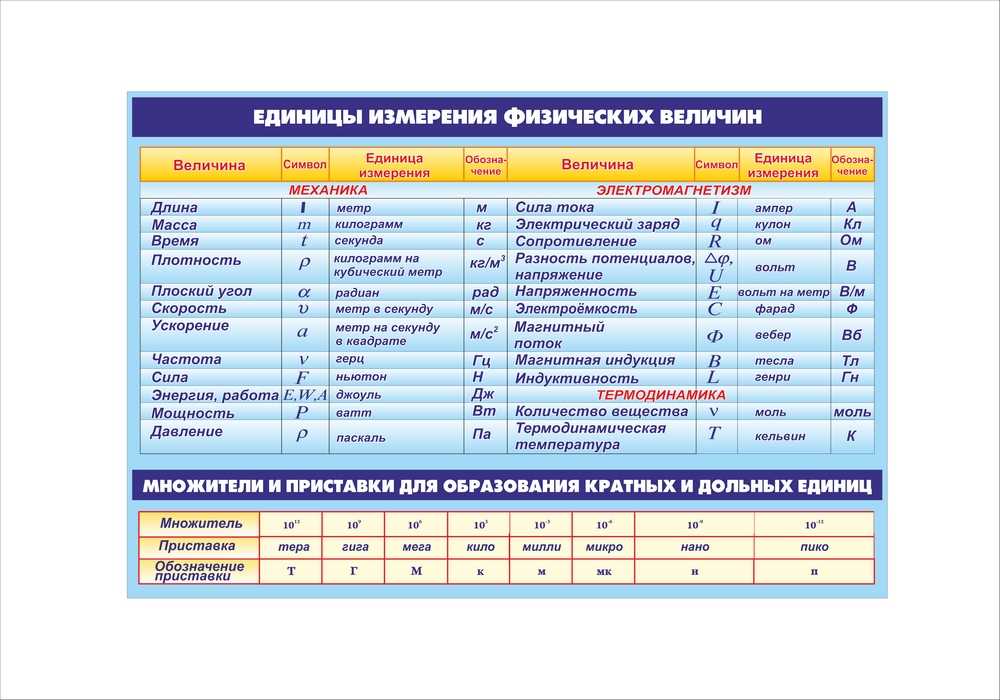 После подстановки числовых значений и расчетов получается 25 м/с.
После подстановки числовых значений и расчетов получается 25 м/с.Задача про выстрел под углом
 Пусть искомая скорость платформы будет обозначена латинской буквой u. Тогда ее импульс после выстрела определится как произведение массы на проекцию скорости. Так как платформа откатится назад (против направления оси OX), то значение импульса будет со знаком минус.
Пусть искомая скорость платформы будет обозначена латинской буквой u. Тогда ее импульс после выстрела определится как произведение массы на проекцию скорости. Так как платформа откатится назад (против направления оси OX), то значение импульса будет со знаком минус.Задача о переправе через реку
 На какое расстояние s его снесет вниз по течению? 2). Под каким углом α нужно направить нос катера, чтобы он достиг противоположного берега строго перпендикулярно к точке отправления? Сколько времени t потребуется на такую переправу?
На какое расстояние s его снесет вниз по течению? 2). Под каким углом α нужно направить нос катера, чтобы он достиг противоположного берега строго перпендикулярно к точке отправления? Сколько времени t потребуется на такую переправу? Для расчета времени движения потребуется разделить ширину реки на сосчитанную полную скорость. Значение последней вычисляется по теореме Пифагора.
Для расчета времени движения потребуется разделить ширину реки на сосчитанную полную скорость. Значение последней вычисляется по теореме Пифагора.PhysBook:Электронный учебник физики — PhysBook
Содержание
 4 Статика
4 Статика СТО
СТО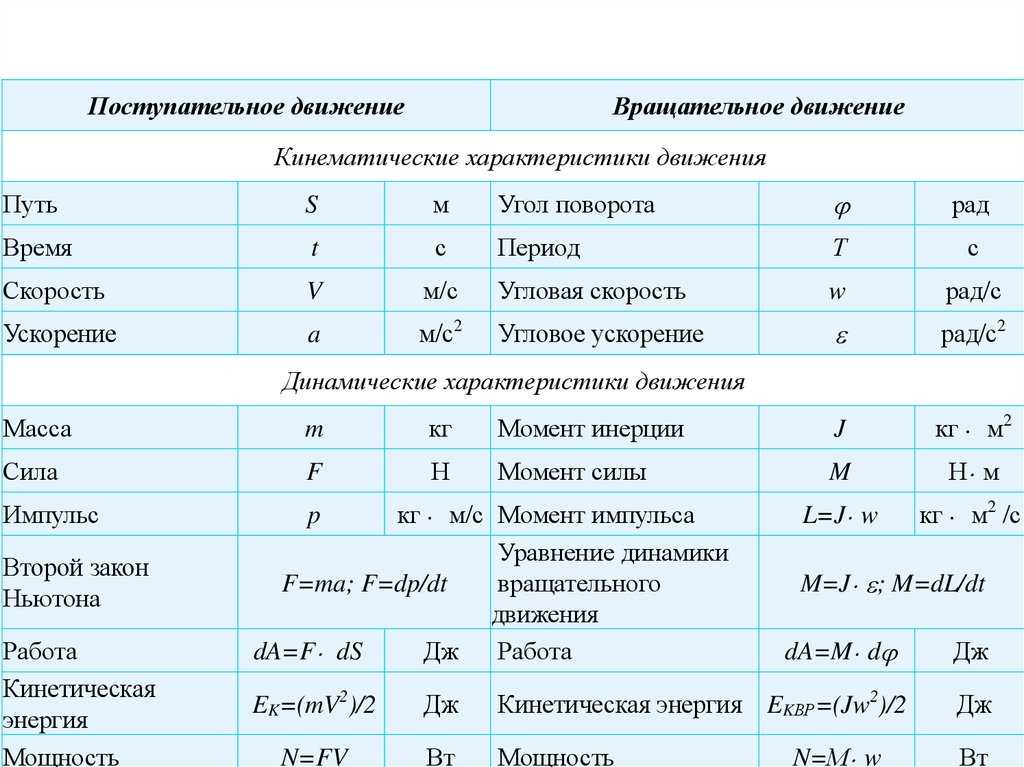
Учебники
Механика
Кинематика
Динамика
Законы сохранения
Статика
Механические колебания и волны
Термодинамика и МКТ
МКТ
Термодинамика
Электродинамика
Электростатика
Электрический ток
Магнетизм
Электромагнитные колебания и волны
Оптика.
 СТО
СТОГеометрическая оптика
Волновая оптика
Фотометрия
Квантовая оптика
Излучение и спектры
СТО
Атомная и ядерная
Атомная физика. Квантовая теория
Ядерная физика
Общие темы
Новые страницы
Что является векторной величиной?
Что является векторной величиной?
 Скалярная величина или скаляр — это всякая величина, не обладающая направлением. Пример 1.
Скалярная величина или скаляр — это всякая величина, не обладающая направлением. Пример 1.Что такое векторная величина в физике?
Что такое векторная величина 7 класс?
Какие из физических величин являются векторными?
 Например скорость, ускорение, сила, перемещение. 3. Скалярная величина, в отличии от векторной, не имеет направления.
Например скорость, ускорение, сила, перемещение. 3. Скалярная величина, в отличии от векторной, не имеет направления.Что называется векторной величиной?
Какую величину называют скаляром приведите примеры?
Что не является скалярной величиной?
 Векторные величины (векторы) — величины, которые кроме численного значения имеют определённое направление в пространстве. Скорость, сила,ускорение, импульс, давление, напряженность электрического поля — векторные величины.
Векторные величины (векторы) — величины, которые кроме численного значения имеют определённое направление в пространстве. Скорость, сила,ускорение, импульс, давление, напряженность электрического поля — векторные величины.Какие величины называют векторными и скалярными приведите примеры?
Какая физическая величина является скалярной а не векторной?
Что такое сила сила векторная величина или скалярная?
 Приложение силы обусловливает изменение скорости тела или появление деформаций и механических напряжений.
Приложение силы обусловливает изменение скорости тела или появление деформаций и механических напряжений.Как складываются векторные величины?
Что такое перемещение Какая это величина?
Какой формулой выражается перемещение?
Что такое перемещение?
 — от итал. spostamento (перемещение). — это модуль перемещения, в Международной системе единиц (СИ) измеряется в метрах; в системе СГС — в сантиметрах.
— от итал. spostamento (перемещение). — это модуль перемещения, в Международной системе единиц (СИ) измеряется в метрах; в системе СГС — в сантиметрах.Что означает фраза перемещение векторная величина?
Что такое траектория перемещения?
Чему равно перемещение в физике?
Что такое перемещение от чего оно зависит?
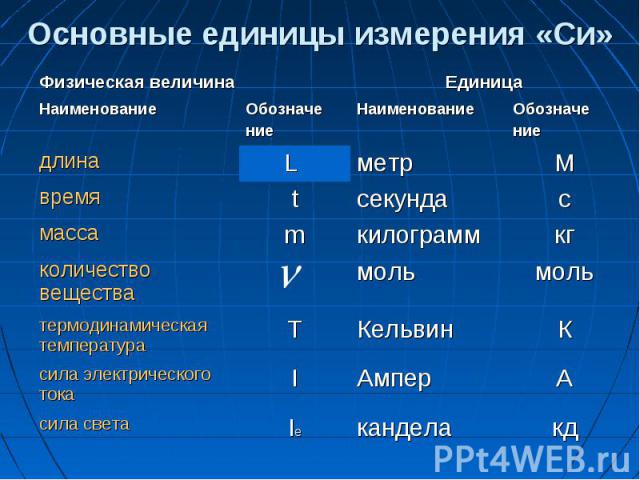 Пройденное же расстояние — это общая длина пути, пройденного объектом, пока он двигался от одной точки в другую.
Пройденное же расстояние — это общая длина пути, пройденного объектом, пока он двигался от одной точки в другую.Что больше Путь или перемещение?
Как найти перемещение по координатам?
Как рассчитать перемещение при равномерном движении?

Как найти перемещение по уравнению?
Как вывести формулу перемещения при равноускоренном движении?
Как найти ускорение при равномерном движении?
Как найти S при равноускоренном движении?
 2/2 выразить начальную скорость, ускорение.
2/2 выразить начальную скорость, ускорение. Как вывести формулу пути равноускоренного движения?
Как в физике обозначается начальная скорость?
Как определить пройденный путь?
Что такое путь пройденный телом?
Скалярные и векторные величины в физике и математике
 Они имеют единицы измерения и зависят от физических законов и аксиом. Выделяют скалярные и векторные величины, обладающие различными характеристиками и параметрами.
Они имеют единицы измерения и зависят от физических законов и аксиом. Выделяют скалярные и векторные величины, обладающие различными характеристиками и параметрами.Особенности скалярных величин
 Измеряется в килограммах и обозначается буквой латинского алфавита m.
Измеряется в килограммах и обозначается буквой латинского алфавита m. Измеряется в м3.
Измеряется в м3.Определение положительного скаляра и его измерения
 Положительная скалярная величина способна принимать значения строго выше 0. Она обозначается знаком «+». Если величина может принимать значения меньше 0, то она называется отрицательной и обозначается символом «-«. Большинство скаляров могут быть только положительными. Для их расчета используют единицы измерения — фиксированного размера объекта.
Положительная скалярная величина способна принимать значения строго выше 0. Она обозначается знаком «+». Если величина может принимать значения меньше 0, то она называется отрицательной и обозначается символом «-«. Большинство скаляров могут быть только положительными. Для их расчета используют единицы измерения — фиксированного размера объекта.Особенности векторных величин
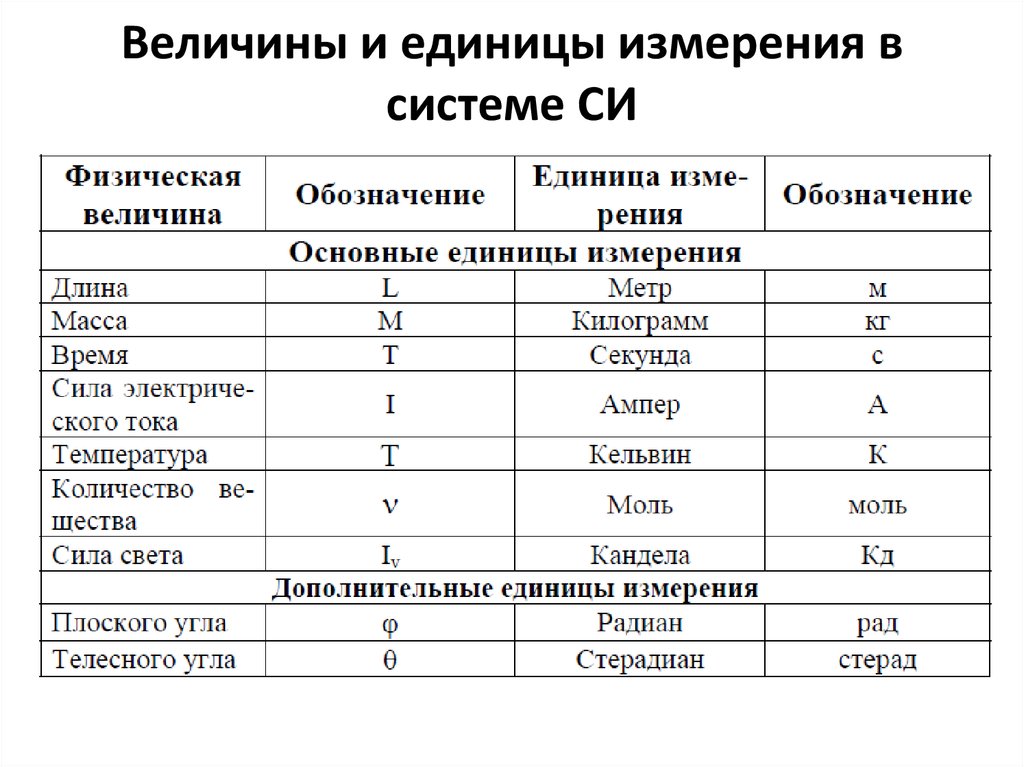 Модулем вектора будет являться числовое значение величины, никогда не принимающее отрицательных значений. Он обозначается символом «||». Для обозначения направления используется стрелка, располагающаяся над символом вектора.
Модулем вектора будет являться числовое значение величины, никогда не принимающее отрицательных значений. Он обозначается символом «||». Для обозначения направления используется стрелка, располагающаяся над символом вектора.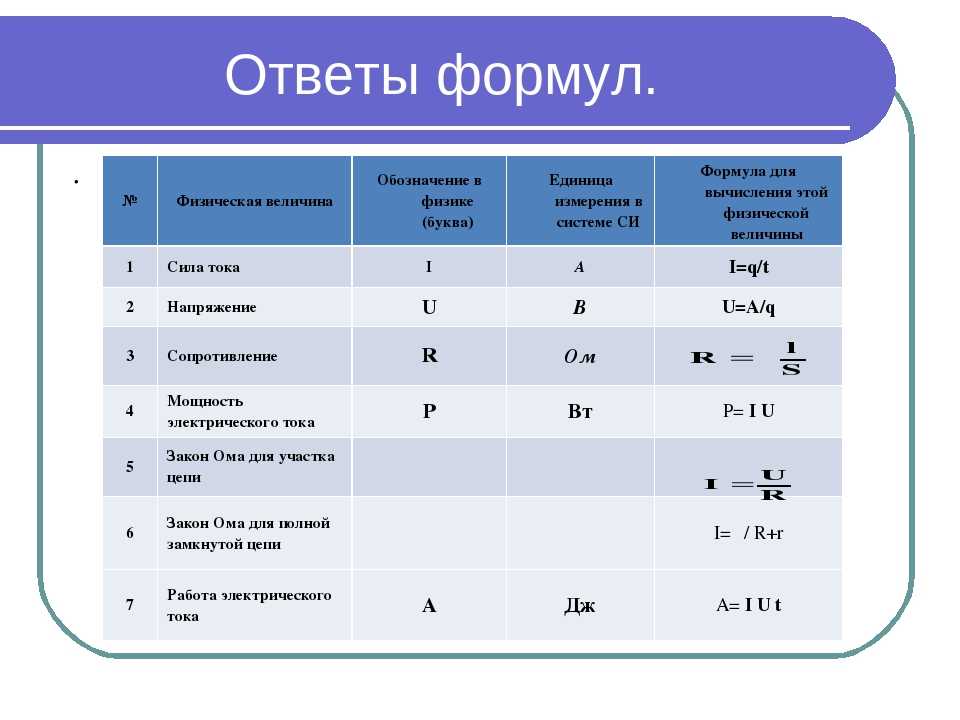 Оно направлено к ядру Земли и равняется 9,8 м/с2
Оно направлено к ядру Земли и равняется 9,8 м/с2 Свойства векторов
 Проекцией вектора на ось является строго положительный отрезок, сонаправленный с исходной осью. Свойства проекции:
Проекцией вектора на ось является строго положительный отрезок, сонаправленный с исходной осью. Свойства проекции: Для изображения направленного отрезка необходимо построить точки, координаты которых соответствуют началу и концу вектора, и соединить их.
Для изображения направленного отрезка необходимо построить точки, координаты которых соответствуют началу и концу вектора, и соединить их.
Векторные величины
 Рассмотрим простую
задачу. Пусть идет пешеход с постоянной
скоростью 5 км/ч. Известно, что в 12 часов
дня он находился в пункте А. Требуется
определить, где будет находиться пешеход
в 14 часов. Зная только величину скорости
пешехода, мы можем только сказать, что
в 14 часов он будет находиться на расстоянии
10 км от пункта А. Но все возможные точки
нахождения пешехода будут находиться
на окружности радиусом 10 км с центром
в точке А. Для определения точного
положения пешехода нам нужно еще знать
в какую сторону он идет. Значит, для
практических целей нам недостаточно
знать величину скорости тела. Требуется
еще знать, куда эта скорость направлена.
Имеется еще очень много физических
величин, для характеристики которых
требуется знание, как размера этой
величины так и ее направления.
Рассмотрим простую
задачу. Пусть идет пешеход с постоянной
скоростью 5 км/ч. Известно, что в 12 часов
дня он находился в пункте А. Требуется
определить, где будет находиться пешеход
в 14 часов. Зная только величину скорости
пешехода, мы можем только сказать, что
в 14 часов он будет находиться на расстоянии
10 км от пункта А. Но все возможные точки
нахождения пешехода будут находиться
на окружности радиусом 10 км с центром
в точке А. Для определения точного
положения пешехода нам нужно еще знать
в какую сторону он идет. Значит, для
практических целей нам недостаточно
знать величину скорости тела. Требуется
еще знать, куда эта скорость направлена.
Имеется еще очень много физических
величин, для характеристики которых
требуется знание, как размера этой
величины так и ее направления. Значение скалярной величины иногда
может иметь знак. При этом говорят, что
скалярная величина характеризуется
своим значением (которое тоже часто
называется модулем) и знаком. При этом
имеются скалярные величины, которые по
своему физическому смыслу не могут
принимать отрицательные значения
(например, масса или пройденный путь).
А некоторые скалярные величины могут
быть как положительными, так и
отрицательными. Заметим, что векторные
величины знаком не характеризуются, то
есть не бывает отрицательных векторов.
Значение скалярной величины иногда
может иметь знак. При этом говорят, что
скалярная величина характеризуется
своим значением (которое тоже часто
называется модулем) и знаком. При этом
имеются скалярные величины, которые по
своему физическому смыслу не могут
принимать отрицательные значения
(например, масса или пройденный путь).
А некоторые скалярные величины могут
быть как положительными, так и
отрицательными. Заметим, что векторные
величины знаком не характеризуются, то
есть не бывает отрицательных векторов. Расстоянием между двумя точками
называется длина отрезка прямой,
соединяющего эти точки. Определяемое
таким образом пройденное расстояние
называется перемещением. Причем,
перемещение – векторная величина.
Перемещением — Δr — называется вектор, начало которого
совпадает с начальным положением тела
(точка А), а конец — с конечным положением
(точка В). Однако, тело из начальной точки
в конечную перемещалось не обязательно
по прямолинейной траектории. Поэтому
существует еще одна величина,
характеризующая величину изменения
положения тела – путь. Пройденным
путем — S — называется длина
траектории перемещения тела. Путь –
скалярная и всегда положительная
величина. Причем путь всегда больше или
равен модуля вектора перемещения. Так
если в результате движения тело вернулось
в исходное положение, то есть точки А и
В совпадают, то перемещение тела равно
нулю, а путь больше нуля.
Расстоянием между двумя точками
называется длина отрезка прямой,
соединяющего эти точки. Определяемое
таким образом пройденное расстояние
называется перемещением. Причем,
перемещение – векторная величина.
Перемещением — Δr — называется вектор, начало которого
совпадает с начальным положением тела
(точка А), а конец — с конечным положением
(точка В). Однако, тело из начальной точки
в конечную перемещалось не обязательно
по прямолинейной траектории. Поэтому
существует еще одна величина,
характеризующая величину изменения
положения тела – путь. Пройденным
путем — S — называется длина
траектории перемещения тела. Путь –
скалярная и всегда положительная
величина. Причем путь всегда больше или
равен модуля вектора перемещения. Так
если в результате движения тело вернулось
в исходное положение, то есть точки А и
В совпадают, то перемещение тела равно
нулю, а путь больше нуля. Суммарное перемещение ΔrAC равно сумме перемещений ΔrAВ и ΔrВC.
На рисунке суммарный вектор ΔrAC является третьей стороной в треугольнике,
образованном векторами ΔrAВ и ΔrВC.
Аналогичным образом складываются все
векторные величины. Для того, чтобы
сложить два вектора а и b,
необходимо нарисовать их друг за другом
так, чтобы начало вектора b совпадало с концом вектора а.
Вектор с, начало которого
совпадает с началом вектора а,
а конец – с концом вектора b и является суммой векторов а и b. (c = a + b).
Этот способ сложения векторов называется
правилом треугольника.
Суммарное перемещение ΔrAC равно сумме перемещений ΔrAВ и ΔrВC.
На рисунке суммарный вектор ΔrAC является третьей стороной в треугольнике,
образованном векторами ΔrAВ и ΔrВC.
Аналогичным образом складываются все
векторные величины. Для того, чтобы
сложить два вектора а и b,
необходимо нарисовать их друг за другом
так, чтобы начало вектора b совпадало с концом вектора а.
Вектор с, начало которого
совпадает с началом вектора а,
а конец – с концом вектора b и является суммой векторов а и b. (c = a + b).
Этот способ сложения векторов называется
правилом треугольника. Можно складывать
вектора по правилу параллелограмма.
Для этого складываемые вектора надо
нарисовать из одной точки, дорисовать
получившуюся фигуру до параллелограмма
и провести в нем из той же точки диагональ.
Она и будет суммой векторов. Для того,
чтобы сложить более чем два вектора,
можно сложить сначала два из них, затем
к их сумме прибавить третий и так далее.
Естественно, для суммы векторов
справедливо правило: a + b = b + a.
Можно складывать
вектора по правилу параллелограмма.
Для этого складываемые вектора надо
нарисовать из одной точки, дорисовать
получившуюся фигуру до параллелограмма
и провести в нем из той же точки диагональ.
Она и будет суммой векторов. Для того,
чтобы сложить более чем два вектора,
можно сложить сначала два из них, затем
к их сумме прибавить третий и так далее.
Естественно, для суммы векторов
справедливо правило: a + b = b + a. Кстати, введенный
выше вектор перемещения равен разности
конечного и начального радиус – векторов,
определяющих положения тела: Δr = r2 – r1.
Кстати, введенный
выше вектор перемещения равен разности
конечного и начального радиус – векторов,
определяющих положения тела: Δr = r2 – r1.
 При этом проекция вектора а на ось Х равна
,
а на ось Y -.
Если известны проекции вектора на оси
прямоугольной декартовой системы
координат, то модуль вектора можно
выразить как
.
При этом проекция вектора а на ось Х равна
,
а на ось Y -.
Если известны проекции вектора на оси
прямоугольной декартовой системы
координат, то модуль вектора можно
выразить как
. Скаляры и векторы
 Большинство людей знакомятся с переносчиками в старшей школе или колледже.
но для учеников начальной и средней школы или математически сложных:
Большинство людей знакомятся с переносчиками в старшей школе или колледже.
но для учеников начальной и средней школы или математически сложных:  Например,
объем
объекта, трехмерное пространство, которое занимает объект,
не зависит от направления.
Если у нас есть блок железа объемом 5 кубических футов, и мы перемещаем его вверх и вниз и
затем влево и вправо, у нас все еще есть 5-кубовый блок железа.
С другой стороны,
расположение,
объекта зависит от направления.
Если мы переместим блок объемом 5 кубических футов на 5 миль в
север, результирующее местоположение сильно отличается от
если мы переместим его на 5 миль на восток.
Математики и ученые называют количество
который зависит от направления a количество векторов . Количество
которая не зависит от направления, называется скалярной величиной .
Например,
объем
объекта, трехмерное пространство, которое занимает объект,
не зависит от направления.
Если у нас есть блок железа объемом 5 кубических футов, и мы перемещаем его вверх и вниз и
затем влево и вправо, у нас все еще есть 5-кубовый блок железа.
С другой стороны,
расположение,
объекта зависит от направления.
Если мы переместим блок объемом 5 кубических футов на 5 миль в
север, результирующее местоположение сильно отличается от
если мы переместим его на 5 миль на восток.
Математики и ученые называют количество
который зависит от направления a количество векторов . Количество
которая не зависит от направления, называется скалярной величиной . .) вы должны
рассмотреть возможность
как по величине, так и по направлению. Это делает работу с вектором
величины немного сложнее, чем скаляры.
.) вы должны
рассмотреть возможность
как по величине, так и по направлению. Это делает работу с вектором
величины немного сложнее, чем скаляры. Тот факт, что величина встречается как для скаляров, так и для векторов, может
привести к некоторой путанице.
Есть некоторые величины, такие как скорость , которые имеют
очень специальные определения для ученых. По определению,
скорость является скалярной величиной вектора скорости . Автомобиль
едет по дороге со скоростью 50 миль в час. Его скорость
составляет 50 миль в час в северо-восточном направлении. Это может стать очень
сбивает с толку, когда термины используются взаимозаменяемо! Другой пример масса и масса . Вес — это сила, которая является вектором
и имеет величину и направление. Масса является скаляром.
Вес и масса
связаны друг с другом, но это не одно и то же количество».
Тот факт, что величина встречается как для скаляров, так и для векторов, может
привести к некоторой путанице.
Есть некоторые величины, такие как скорость , которые имеют
очень специальные определения для ученых. По определению,
скорость является скалярной величиной вектора скорости . Автомобиль
едет по дороге со скоростью 50 миль в час. Его скорость
составляет 50 миль в час в северо-восточном направлении. Это может стать очень
сбивает с толку, когда термины используются взаимозаменяемо! Другой пример масса и масса . Вес — это сила, которая является вектором
и имеет величину и направление. Масса является скаляром.
Вес и масса
связаны друг с другом, но это не одно и то же количество». Масса и энергия
— скалярные величины, а импульс — вектор
количество. В результате получается связанный набор уравнений,
называется
уравнения Навье-Стокса,
которые описывают поведение жидкости под действием внешних сил.
Эти уравнения являются жидким эквивалентом законов движения Ньютона.
и очень трудно решить и понять.
Упрощенная версия уравнений, называемая
уравнения Эйлера
может быть решена для некоторых проблем с жидкостями.
Масса и энергия
— скалярные величины, а импульс — вектор
количество. В результате получается связанный набор уравнений,
называется
уравнения Навье-Стокса,
которые описывают поведение жидкости под действием внешних сил.
Эти уравнения являются жидким эквивалентом законов движения Ньютона.
и очень трудно решить и понять.
Упрощенная версия уравнений, называемая
уравнения Эйлера
может быть решена для некоторых проблем с жидкостями.
Деятельность:
Экскурсии с гидом Примеры векторных и скалярных величин в физике
Определение скалярных и векторных величин
Примеры скалярных величин
 Исследуйте 10 примеров скалярных величин.
Исследуйте 10 примеров скалярных величин. Площадь
Плотность
Расстояние
Энергия
Масса
Скорость
Температура
Время

Объем
Работа
Примеры векторных величин
Ускорение
 Он учитывает период времени, а также направление, что делает его векторной величиной.
Он учитывает период времени, а также направление, что делает его векторной величиной. Смещение
Сила
Повышение/понижение температуры
Магнитная поляризация

Импульс
Положение
Тяга
Скорость
 Чтобы измерить векторную величину среды, необходимо применить направленное измерение к скалярной величине. Другим элементом направления, который может быть применен к векторной величине, является разница между вертикальным и горизонтальным перемещениями.
Чтобы измерить векторную величину среды, необходимо применить направленное измерение к скалярной величине. Другим элементом направления, который может быть применен к векторной величине, является разница между вертикальным и горизонтальным перемещениями. Вес
Источник дополнительной технической информации в Интернете
Физика вокруг нас
 Вы также можете больше углубиться в законы физики с повседневными примерами инерции.
Вы также можете больше углубиться в законы физики с повседневными примерами инерции. Объяснение урока: Векторные величины | Nagwa
Практическое руководство. Определение направлений векторных величин в линейном движении
 скалярный аналог;
скалярный аналог; Даже когда эти две величины принимают одинаковую форму, они имеют разные значения. Следовательно, скалярные и векторные величины не сравнимы напрямую.
Даже когда эти две величины принимают одинаковую форму, они имеют разные значения. Следовательно, скалярные и векторные величины не сравнимы напрямую. Пример 1. Расчет скорости, скорости, расстояния и перемещения по прямым путям
Ответ
 Векторные величины представляют
направление и величина, в то время как скалярные величины указывают только величину. Напомним, что при прямолинейном движении направление векторной величины
можно определить только в терминах положительного или отрицательного знака. Данная цифра указывает на то, что положительное направление направлено вправо,
что означает, что положительный знак означает правое направление, а отрицательный знак означает левое направление.
Векторные величины представляют
направление и величина, в то время как скалярные величины указывают только величину. Напомним, что при прямолинейном движении направление векторной величины
можно определить только в терминах положительного или отрицательного знака. Данная цифра указывает на то, что положительное направление направлено вправо,
что означает, что положительный знак означает правое направление, а отрицательный знак означает левое направление.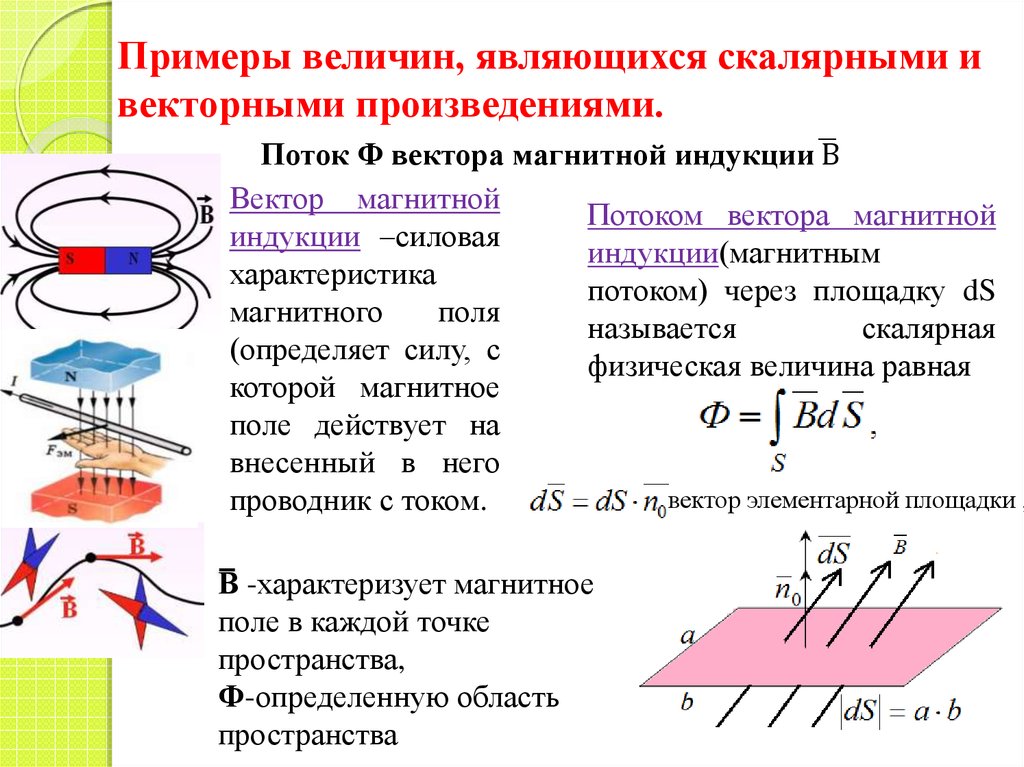 Это дает нам
−30 км.
Это дает нам
−30 км. И векторные, и скалярные аналоги
делят одни и те же единицы. Например, ускорение, как и величина ускорения, может иметь единицу
метры в секунду в квадрате
(м/с 2 ), а условной единицей силы и ее величины является
ньютоны (Н). Мы резюмируем
векторные и скалярные аналоги в таблице ниже.
И векторные, и скалярные аналоги
делят одни и те же единицы. Например, ускорение, как и величина ускорения, может иметь единицу
метры в секунду в квадрате
(м/с 2 ), а условной единицей силы и ее величины является
ньютоны (Н). Мы резюмируем
векторные и скалярные аналоги в таблице ниже. Vector Scalar Unit Displacement Distance m Velocity Speed m/s Acceleration Magnitude of acceleration m/ с 2 Сила Величина силы Н 
Свойства: скорость и ускорение в линейном движении

Пример 2. Интерпретация знаков векторных величин
Ответ
 Направление движения объекта указывается его скоростью, поэтому мы можем видеть, что частица движется влево.
Направление движения объекта указывается его скоростью, поэтому мы можем видеть, что частица движется влево. е. двумерное или плоское движение, мы видим, что существует более двух
возможные направления. Например, автомобиль может двигаться на север, юг, восток или запад, что дает нам четыре направления. Но это не
единственные возможности направления в плоскостном движении. Автомобиль мог двигаться на северо-запад, северо-северо-запад или вообще в любом направлении, заданном
угол, начинающийся с северного направления. Это приводит к бесконечному числу возможных направлений плоскостного движения. Следовательно, мы не можем
надеемся уловить направление в двух измерениях так же, как мы это сделали для одномерного движения.
е. двумерное или плоское движение, мы видим, что существует более двух
возможные направления. Например, автомобиль может двигаться на север, юг, восток или запад, что дает нам четыре направления. Но это не
единственные возможности направления в плоскостном движении. Автомобиль мог двигаться на северо-запад, северо-северо-запад или вообще в любом направлении, заданном
угол, начинающийся с северного направления. Это приводит к бесконечному числу возможных направлений плоскостного движения. Следовательно, мы не можем
надеемся уловить направление в двух измерениях так же, как мы это сделали для одномерного движения.
 Когда мы знаем векторную величину движения, мы
можно использовать теорему Пифагора, чтобы найти ее скалярный аналог.
Когда мы знаем векторную величину движения, мы
можно использовать теорему Пифагора, чтобы найти ее скалярный аналог. Пример 3: Расчет скорости по скорости
Ответ

 Однако нам нужно добавить прямой угол
(90∘) к отмеченному углу, чтобы получить угол между ⃑𝑖
и 𝑎⃑𝑖+𝑏⃑𝑗.
Однако нам нужно добавить прямой угол
(90∘) к отмеченному углу, чтобы получить угол между ⃑𝑖
и 𝑎⃑𝑖+𝑏⃑𝑗. Пример 4. Расчет направления ускорения
Ответ
 Мы должны быть
будьте осторожны, чтобы не ошибиться, что длина вертикальной стороны равна -3, поскольку длина является скалярной величиной, которая не может быть отрицательной.
Мы должны быть
будьте осторожны, чтобы не ошибиться, что длина вертикальной стороны равна -3, поскольку длина является скалярной величиной, которая не может быть отрицательной. Затем полученный вектор можно нарисовать, соединив
два конечных пункта. Это показано на диаграмме ниже.
Затем полученный вектор можно нарисовать, соединив
два конечных пункта. Это показано на диаграмме ниже. Пример 5. Расчет величины смещения с использованием векторов
Ответ
 Сначала найдем это смещение.
Сначала найдем это смещение.
Ключевые точки
Vector Scalar Блок Дистанция VELOCITE 2 Сила Величина силы N 
Скаляр и вектор: определение, количество, примеры

Скаляры и векторы: значение и примеры
 Пять метров — это всего лишь величина (расстояние), а направление может быть любым. Таким образом, расстояние является скалярной величиной.
Пять метров — это всего лишь величина (расстояние), а направление может быть любым. Таким образом, расстояние является скалярной величиной.
Скаляр Вектор Расстояние Перемещение Скорость Скорость и ускорение Масса и вес: что из них скалярная, а какая векторная?

Скаляр
Вектор
Как мы можем представить векторы?
 Комбинация ориентации и смысла определяет направление вектора.
Комбинация ориентации и смысла определяет направление вектора. Примеры векторов: как выполнить сложение векторов?
 Что бы вы сделали, если бы два вектора были перпендикулярны друг другу? Здесь нам нужно немного импровизировать.
Что бы вы сделали, если бы два вектора были перпендикулярны друг другу? Здесь нам нужно немного импровизировать. Правило «голова к хвосту»
 Теперь, как мы обсуждали, векторная величина имеет не только направление, но и величину, поэтому мы можем вычислить угол вектора 50N, используя арктангенс 40/30 (перпендикуляр/основание). Тогда угол составляет 53,1 ° от горизонтали для приведенного выше примера.
Теперь, как мы обсуждали, векторная величина имеет не только направление, но и величину, поэтому мы можем вычислить угол вектора 50N, используя арктангенс 40/30 (перпендикуляр/основание). Тогда угол составляет 53,1 ° от горизонтали для приведенного выше примера. Разложение вектора на его компоненты
 Разрешение векторов. Usama Adeel — StudySmarter Originals
Разрешение векторов. Usama Adeel — StudySmarter Originals Разложение компонентов силы на наклонной плоскости
 11. Разрешение вектора мг на наклонной поверхности. Usama Adeel – StudySmarter Originals
11. Разрешение вектора мг на наклонной поверхности. Usama Adeel – StudySmarter Originals Равновесие компланарных силовых систем
 Вес лестницы действует вниз, а нормальная сила реакции действует под углом 90° к стене.
Вес лестницы действует вниз, а нормальная сила реакции действует под углом 90° к стене.
Скаляр и вектор – ключевые выводы
В чем разница между векторами и скалярами?
 Скаляр может быть описан либо безразмерно, либо в терминах некоторой физической величины. Примеры скаляров: масса, объем, расстояние, энергия и время.
Скаляр может быть описан либо безразмерно, либо в терминах некоторой физической величины. Примеры скаляров: масса, объем, расстояние, энергия и время. 92)
92)
1. ___ _ пример скалярной величины
а) скорость
б) сила
в) том
г) ускорение
2. ___ является примером векторной величины
а) масса
б) сила
в) том
г) плотность
3. Скалярная величина:
а) всегда имеет массу
б) есть величина, полностью определяемая своей величиной
в) показывает направление
г) не имеет единиц
4. Векторная величина
а) может быть безразмерной величиной
б) указывает только величину
в) указывает только направление
г) определяет как величину, так и направление
5. Мальчик давит на стену с силой 50 фунтов. Стена не двигается. Результирующая сила:
Мальчик давит на стену с силой 50 фунтов. Стена не двигается. Результирующая сила:
а) -50 фунтов
б) 100 фунтов
в) 0 фунтов
г) -75 фунтов
6. Человек прошел 3 мили на север, затем повернул направо и прошел 4 мили на восток. Результирующее смещение:
а) 1 миля ЮЗ
б) 7 миль NE
в) 5 миль NE
d) 5 миль E
7. Самолет, летящий со скоростью 500 миль/час строго на север, имеет попутный ветер 45 миль/час, результирующая скорость:
а) 545 миль/час на юг.
б) 455 миль/час на север.
c) 545 миль/ч строго на север.
г) 455 миль/час строго на юг
8. Разница между скоростью и скоростью:
а) скорость не имеет единиц
б) скорость показывает только величину, а скорость представляет и величину (силу), и направление
в) они используют разные единицы для представления своей величины
г) скорость имеет большую величину
9. Результирующая величина двух векторов
Результирующая величина двух векторов
а) всегда положительный
б) никогда не может быть нулевым
в) Никогда не может быть отрицательным
г) Обычно равен нулю
10. Что из следующего неверно.
а) скорость может быть отрицательной
б) скорость есть вектор
б) скорость является скаляром
г) скорость может быть отрицательной
Сила, работа и энергия
Скорость, скорость и ускорение: В чем разница между скоростью и скоростью? Что такое ускорение? График скорости и ускорения. Проверка вашего понимания.
Сила: Что такое сила? Измерение сил. Описание Сил. Что делает сила? Что такое трение? Оценочные вопросы.
Векторы и скаляры: Что такое векторная величина? Примеры векторов. Что такое скалярная величина? Примеры скаляров. Проверьте свое понимание векторов и скаляров.
Проверьте свое понимание векторов и скаляров.
Три закона движения Ньютона: См. «Три закона Ньютона» на латыни и английский перевод. Приведены примеры для каждого закона..
Работа, энергия и мощность: определения работы, энергии и мощности. Виды энергии, расчет работы и мощности.
Разница между массой и весом: Отличная страница для одаренных и талантливых учащихся! Несколько отличных сложных задач.
Гравитация, масса и вес: Гравитация, масса и вес по отношению к Солнечной системе
Основные и производные единицы: Основные и производные единицы, включая физические величины, символы единиц измерения.
Математические отношения в науке: см. лабораторную работу 5, Ускорение.
Связанные виды деятельности
Понимание скалярных и векторных величин
Все ресурсы по физике для старших классов
6 Диагностические тесты 233 практических теста Вопрос дня Карточки Учитесь по концепции
← Предыдущая 1 2 3 4 Следующая →
Школа физики Помощь » Вводные принципы » Понимание скалярных и векторных величин
Что из следующего может быть результатом произведения векторной величины на скалярную величину?
Возможные ответы:
Напряжение
Работа
Вес
Скорость
Все это результат произведения вектора и скаляра
900
Вес
Объяснение:
Скалярные величины определяются величиной без применимого направления. Напротив, векторные величины должны иметь как величину, так и направление действия.
Напротив, векторные величины должны иметь как величину, так и направление действия.
Произведение векторной величины на скалярную величину всегда будет векторной величиной. Сила является результатом произведения массы (скаляр) и ускорения (вектор). Вес — это тип силы, создаваемой ускорением свободного падения.
Напряжение является скалярной величиной и может быть рассчитано как произведение тока (скалярное) на сопротивление (скалярное).
Работа является векторной величиной и может быть рассчитана как произведение силы (вектор) и смещения (вектор).
Скорость является вектором и может быть рассчитана как частное смещения (вектор) в единицу времени (скаляр).
Сообщить об ошибке
Скорость является скалярной величиной. Какая векторная величина представляет скорость в приложенном направлении?
Возможные ответы:
Расстояние
Перемещение
Скорость
Вес
Ускорение
Правильный ответ:
Скорость
Объяснение:
Скалярные величины определяются величиной без применимого направления. Напротив, векторные величины должны иметь как величину, так и направление действия.
Напротив, векторные величины должны иметь как величину, так и направление действия.
Скорость определяется изменением расстояния в единицу времени. Поскольку расстояние и время являются скалярными величинами, результирующая скорость также является скалярной. Напротив, скорость определяется изменением смещения в единицу времени. Поскольку смещение является вектором, результирующая скорость также является вектором. Величина заданной скорости и заданной скорости могут быть равны, но член скорости будет представлять скорость, приложенную в определенном направлении.
Ускорение — векторная величина, определяемая изменением скорости в единицу времени. Вес создается силой тяжести на объекте; все силы являются векторами.
Сообщить об ошибке
Что из следующего является скалярной величиной?
Возможные ответы:
Ускорение
Сила
Расстояние
Смещение
Velocity
Правильный ответ:
Расстояние
Объяснение:
Скалярные величины определяются величиной без применимого направления. Напротив, векторные величины должны иметь как величину, так и направление действия.
Напротив, векторные величины должны иметь как величину, так и направление действия.
Некоторыми распространенными скалярными величинами являются расстояние, скорость, масса и время. Некоторыми распространенными векторными величинами являются сила, скорость, смещение и ускорение.
Сообщить об ошибке
Что из этого является вектором?
Возможные ответы:
Емкость
Время
Скорость
Сила
Расстояние
Правильный ответ:
Сила
Объяснение:
Вектор имеет как величину, так и направление, тогда как скаляр имеет только величину. Спрашивая, является ли что-то вектором или скаляром, спросите, имеет ли смысл направление — в этом случае единственным вектором является сила. Хотя направление помогло бы со скоростью и расстоянием, они оба являются скалярами; векторная версия скорости — это скорость, а векторная версия расстояния — это перемещение.
Сообщить об ошибке
Какая из этих величин является скалярной?
Возможные ответы:
Velocity
Force
Momentum
Смещение
MASS
Правильный ответ:
MASS
Объяснение:
Скалярная величина может быть определена только величиной, тогда как векторная величина должна определяться как величиной, так и направлением действия.
Из предложенных вариантов ответа масса является единственной скалярной величиной. Масса имеет величину, как правило, в килограммах, но не может действовать в направлении. «7kg west», например, бессмысленно.
Напротив, перемещение, скорость, сила и импульс должны быть приложены в заданном направлении. Перемещение — это векторный эквивалент скалярной величины расстояния, а скорость — векторный эквивалент скалярной величины скорости. Силы должны всегда действовать в заданном направлении и не иметь скалярного эквивалента. Точно так же импульс всегда должен быть направленным.
Силы должны всегда действовать в заданном направлении и не иметь скалярного эквивалента. Точно так же импульс всегда должен быть направленным.
Сообщить об ошибке
Ребенок катится по краю катка и финиширует там же, где и начал. Если каток имеет радиус , каково полное перемещение фигуриста?
Возможные ответы:
Правильный ответ:
Объяснение:
Между измерением смещения и измерением расстояния есть четкое и важное различие. Расстояние является скалярной величиной, что означает, что оно зависит от пройденного пути и не зависит от пройденного направления. Расстояние измеряет общую пройденную длину без какой-либо привязки к начальной точке.
Смещение, напротив, является векторной величиной. Это означает, что при расчете необходимо учитывать как величину длины, так и ее направление. Смещение — это, по сути, чистое расстояние, пройденное относительно начальной точки, независимо от пройденного пути.
В этом вопросе фигуристка финиширует точно в том же месте, где и начала. Без какой-либо другой информации мы можем сделать вывод, что ее водоизмещение равно нулю. Неважно, какой путь она выбрала, чтобы вернуться к исходной точке; она могла сделать шаг вперед и шаг назад, проехать весь каток семнадцать раз или просто прыгнуть и приземлиться. Все эти возможности привели бы к нулевому смещению.
Сообщить об ошибке
Какая из следующих величин не является векторной?
Возможные ответы:
Смещение
Ускорение
Вязкость
Velocity
Force
Правильный ответ:
Взысканность
44. Пояснение:
Вязкость – это измерение «густоты» жидкости. Патока, например, является более вязкой жидкостью, чем вода.
Векторные измерения определяются величиной и направлением. Для жидкости иметь измеримую «толщину» логично, но жидкость не может иметь вязкость в направлении. Говорить о том, что жидкость имеет вязкость Восточная, не имеет смысла. Вязкость является скалярной величиной.
Для жидкости иметь измеримую «толщину» логично, но жидкость не может иметь вязкость в направлении. Говорить о том, что жидкость имеет вязкость Восточная, не имеет смысла. Вязкость является скалярной величиной.
Перемещение, сила, скорость и ускорение имеют связанные направления и классифицируются как векторные величины.
Сообщить об ошибке
Какая из следующих величин является векторной?
Возможные ответы:
Расстояние
Масса
Яркость
Время
Сила
Правильный ответ:
2 Сила Объяснение:
Векторные величины определяются как величиной параметра, так и направлением действия. В контракте скалярные величины не зависят от направления и зависят только от величины параметра.
Масса, расстояние, время и яркость — все это скалярные величины. Это означает, что ни один из этих терминов не может быть применен в данном направлении. Было бы нелогично иметь «три грамма на запад» или «восемнадцать секунд налево». Расстояние является скалярным эквивалентом вектора смещения.
Было бы нелогично иметь «три грамма на запад» или «восемнадцать секунд налево». Расстояние является скалярным эквивалентом вектора смещения.
Сила всегда векторная величина, так как направление силы имеет значение при определении параметра. «Четыре ньютона вправо» количественно отличается от «четыре ньютона вниз» или «четыре ньютона влево».
Сообщить об ошибке
Каковы модуль и угол для следующего вектора, измеренного против часовой стрелки от оси x?
Возможные ответы:
Правильный ответ:
Объяснение:
Величина вектора находится по формуле расстояния:
Чтобы вычислить угол, мы должны сначала найти арктангенс:
Это значение угла является главным арктангеном, но оно находится в четвертом квадранте, а наш вектор — во втором.


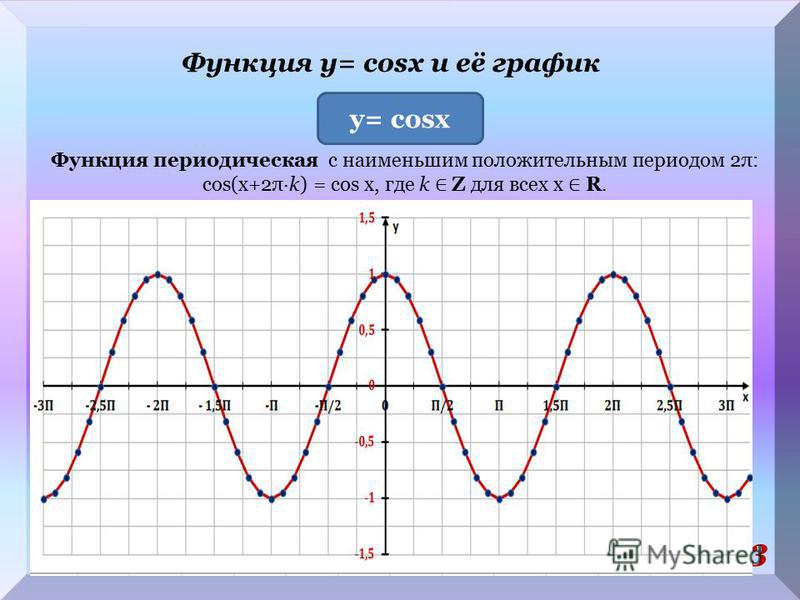
 Если кто-то может объяснить мне, что происходит, это было бы очень полезно. Спасибо.
Если кто-то может объяснить мне, что происходит, это было бы очень полезно. Спасибо.

 Четная функция должна содержать следующее уравнение: f(-x) = f(x) для всех значений x в D(f), где D(f) обозначает область определения функции f. Другими словами, мы можем сказать, что уравнение f (-x) — f (x) = 0 выполняется для четной функции для всех x. Рассмотрим пример, f(x) = x 2 .
Четная функция должна содержать следующее уравнение: f(-x) = f(x) для всех значений x в D(f), где D(f) обозначает область определения функции f. Другими словами, мы можем сказать, что уравнение f (-x) — f (x) = 0 выполняется для четной функции для всех x. Рассмотрим пример, f(x) = x 2 . 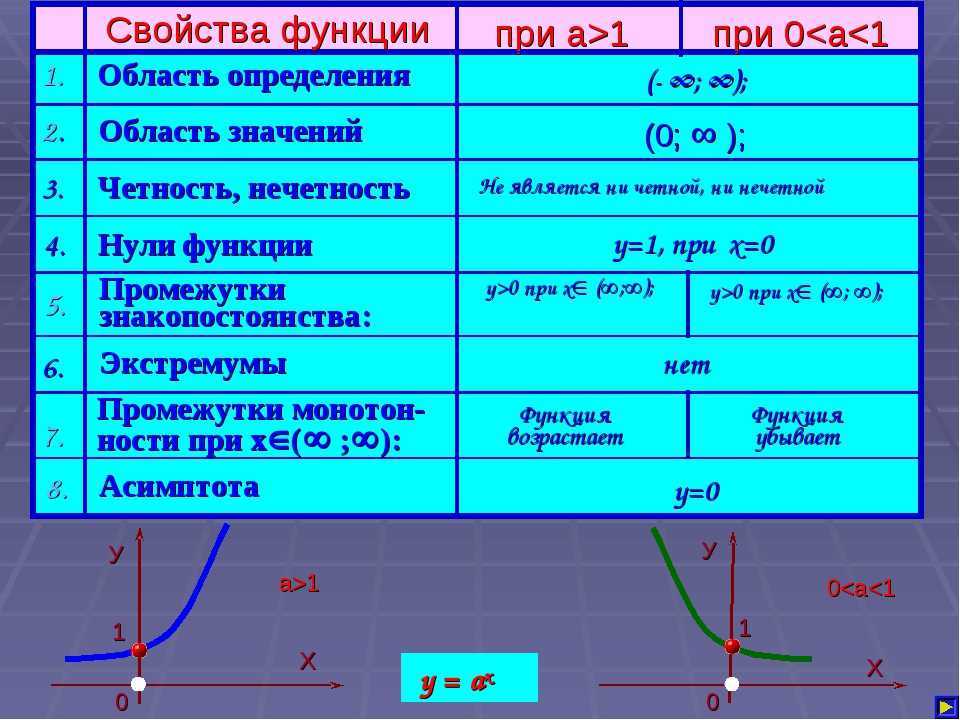 Другими словами, мы можем сказать, что уравнение f (-x) + f (x) = 0 выполняется для нечетной функции для всех x. Рассмотрим пример, f(x) = x 3 .
Другими словами, мы можем сказать, что уравнение f (-x) + f (x) = 0 выполняется для нечетной функции для всех x. Рассмотрим пример, f(x) = x 3 .  Следовательно, f(x) = 0 — четная и нечетная функция.
Следовательно, f(x) = 0 — четная и нечетная функция.
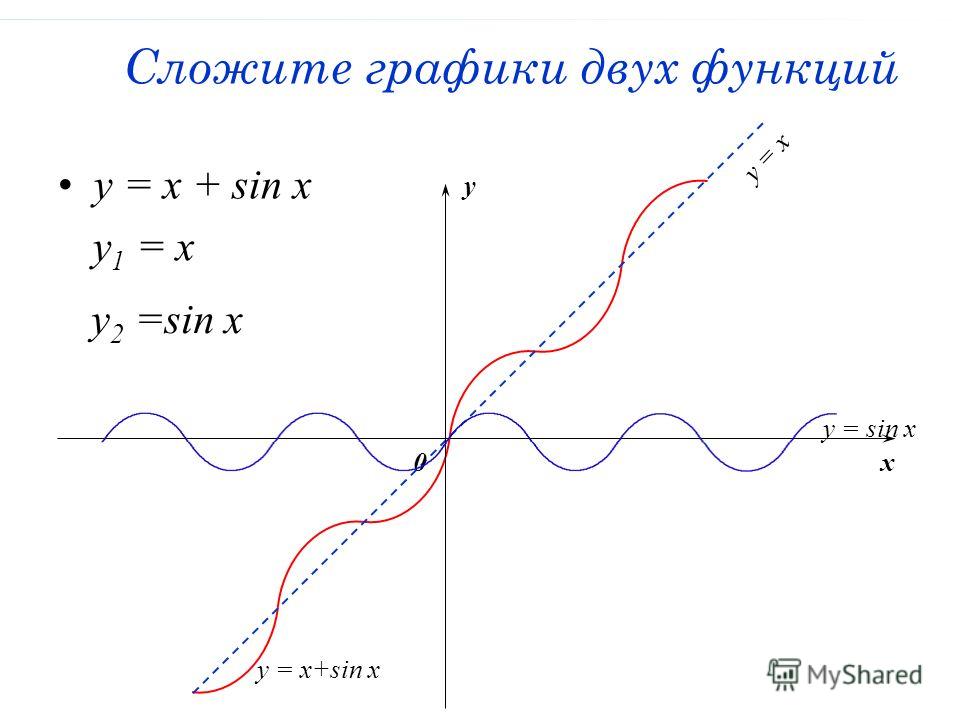




 Онлайн калькулятор расстояния между точками
Онлайн калькулятор расстояния между точками Найди правильный ответ.
Найди правильный ответ. Калькулятор вычисления силы, массы и ускорения.
Калькулятор вычисления силы, массы и ускорения. Для плоского, цилиндрического и сферического конденсаторов
Для плоского, цилиндрического и сферического конденсаторов Например, если вы хотите округлить число до сотых, вы можете использовать этот калькулятор.
Например, если вы хотите округлить число до сотых, вы можете использовать этот калькулятор. Если число меньше 5, к числу слева ничего не добавляется и оно заменяется на 0. Аналогично, если число больше 5, к числу слева добавляется «1».
Если число меньше 5, к числу слева ничего не добавляется и оно заменяется на 0. Аналогично, если число больше 5, к числу слева добавляется «1».
 Если вам нужно округлить его до 3 значащих цифр, 1 в крайнем правом углу будет отброшена, так как оно меньше 5. Следовательно, 0,4521, округленное до трех значащих цифр, будет 0,452.
Если вам нужно округлить его до 3 значащих цифр, 1 в крайнем правом углу будет отброшена, так как оно меньше 5. Следовательно, 0,4521, округленное до трех значащих цифр, будет 0,452.
 ..Меньше
..Меньше

 Они показывают способы округления положительных, отрицательных, целых и дробных чисел, но приведенные примеры охватывают лишь небольшую часть возможных ситуаций.
Они показывают способы округления положительных, отрицательных, целых и дробных чисел, но приведенные примеры охватывают лишь небольшую часть возможных ситуаций. Затем это значение округляется до двух значимых разрядов (880). После этого повторно применяется знак «минус», что дает в результате -880.
Затем это значение округляется до двух значимых разрядов (880). После этого повторно применяется знак «минус», что дает в результате -880.
 В 12-м ящике будет только 6 единиц товара.
В 12-м ящике будет только 6 единиц товара.
 При этом, число может быть округлено до определённого разряда — до разряда десятков, разряда сотен, разряда тысяч.
При этом, число может быть округлено до определённого разряда — до разряда десятков, разряда сотен, разряда тысяч.




 Читают: «Семнадцать целых четыре тысячи тридцать девять десятитысячных приближенно равно семнадцать целых сорок восемь сотых».
Читают: «Семнадцать целых четыре тысячи тридцать девять десятитысячных приближенно равно семнадцать целых сорок восемь сотых».
 Так как первая из отброшенных цифр — 8, к предыдущей прибавляем единицу. Читают: «Шестьдесят девять целых девяносто девять тысяч девятьсот восемьдесят одна стотысячная приближенно равно семьдесят целых нуль тысячных».
Так как первая из отброшенных цифр — 8, к предыдущей прибавляем единицу. Читают: «Шестьдесят девять целых девяносто девять тысяч девятьсот восемьдесят одна стотысячная приближенно равно семьдесят целых нуль тысячных».
 Читают: «Триста пятьдесят две целых семьдесят восемь сотых приближенно равно триста пятьдесят».
Читают: «Триста пятьдесят две целых семьдесят восемь сотых приближенно равно триста пятьдесят».
 Читают: «Семьдесят восемь тысяч пятьсот девять приближенно равно семьдесят восемь тысяч пятьсот».
Читают: «Семьдесят восемь тысяч пятьсот девять приближенно равно семьдесят восемь тысяч пятьсот».
 Первая из замененных нулем цифр равна 7, поэтому к предыдущей цифре прибавляем единицу. Читают: «Сто пятьдесят девять тысяч семьсот тридцать два приближенно равно сто шестьдесят тысяч».
Первая из замененных нулем цифр равна 7, поэтому к предыдущей цифре прибавляем единицу. Читают: «Сто пятьдесят девять тысяч семьсот тридцать два приближенно равно сто шестьдесят тысяч».
 С помощью этого калькулятора вы в один клик сможете округлить любое число.
С помощью этого калькулятора вы в один клик сможете округлить любое число.
 Для этого производят округления чисел, которые участвуют в расчетах а также и конечный результат вычислений. Приближённые значения используют тогда, когда точное значение чего-либо найти невозможно, или же это значение не важно для исследуемого предмета.
Для этого производят округления чисел, которые участвуют в расчетах а также и конечный результат вычислений. Приближённые значения используют тогда, когда точное значение чего-либо найти невозможно, или же это значение не важно для исследуемого предмета.
 Последняя оставляемая цифра 3 усиливается, так как она является нечётной.
Последняя оставляемая цифра 3 усиливается, так как она является нечётной. Читают: «Двести семьдесят четыре целых восемьсот тридцать девять тысячных приближенно равно двести семидесяти пяти целым».
Читают: «Двести семьдесят четыре целых восемьсот тридцать девять тысячных приближенно равно двести семидесяти пяти целым».
 Первая из отброшенных цифр — 6, значит, предыдущую увеличиваем на единицу. Читают: «Сорок девять целых, девятьсот шестьдесят две тысячных приближенно равно пятьдесят целых, нуль десятых».
Первая из отброшенных цифр — 6, значит, предыдущую увеличиваем на единицу. Читают: «Сорок девять целых, девятьсот шестьдесят две тысячных приближенно равно пятьдесят целых, нуль десятых».
 Первая из отброшенных цифр — 3, поэтому предыдущую цифру не изменяем. Читают: «Семнадцать целых четыре тысячи тридцать девять десятитысячных приближенно равно семнадцать целых сорок восемь сотых».
Первая из отброшенных цифр — 3, поэтому предыдущую цифру не изменяем. Читают: «Семнадцать целых четыре тысячи тридцать девять десятитысячных приближенно равно семнадцать целых сорок восемь сотых».
 Так как первая из отброшенных цифр — 8, к предыдущей прибавляем единицу. Читают: «Шестьдесят девять целых девяносто девять тысяч девятьсот восемьдесят одна стотысячная приближенно равно семьдесят целых нуль тысячных».
Так как первая из отброшенных цифр — 8, к предыдущей прибавляем единицу. Читают: «Шестьдесят девять целых девяносто девять тысяч девятьсот восемьдесят одна стотысячная приближенно равно семьдесят целых нуль тысячных».

 Читают: «Семьсот девяносто девять целых, одна десятая приближенно равно восемьсот».
Читают: «Семьсот девяносто девять целых, одна десятая приближенно равно восемьсот». Поскольку первая из замененных нулем цифр равна 8, предыдущую цифру увеличиваем на единицу. Читают: «Четыре тысячи пятьсот восемьдесят один приближенно равно четыре тысячи шестьсот».
Поскольку первая из замененных нулем цифр равна 8, предыдущую цифру увеличиваем на единицу. Читают: «Четыре тысячи пятьсот восемьдесят один приближенно равно четыре тысячи шестьсот». Первая из замененных на нуль цифр равна 7, поэтому к предыдущей цифре прибавляем единицу. Читают: «Тысяча четыреста семьдесят три целых двенадцать сотых приближенно равно тысяча пятьсот».
Первая из замененных на нуль цифр равна 7, поэтому к предыдущей цифре прибавляем единицу. Читают: «Тысяча четыреста семьдесят три целых двенадцать сотых приближенно равно тысяча пятьсот». Читают: «Восемьдесят две тысячи триста семьдесят один приближенно равно восемьдесят две тысячи».
Читают: «Восемьдесят две тысячи триста семьдесят один приближенно равно восемьдесят две тысячи».
 шкалу Чеддока). Например, при анализе тесноты линейной корреляционной связи между двумя переменными получен коэффициент парной линейной корреляции, равный –1. Это означает, что между переменными существует точная обратная линейная зависимость.
шкалу Чеддока). Например, при анализе тесноты линейной корреляционной связи между двумя переменными получен коэффициент парной линейной корреляции, равный –1. Это означает, что между переменными существует точная обратная линейная зависимость.
 Полученное решение сохраняется в файле Word (см. Пример нахождения уравнения регрессии). Также автоматически создается шаблон решения в Excel. Подробнее.
Количество строк
(исходных данных)
Полученное решение сохраняется в файле Word (см. Пример нахождения уравнения регрессии). Также автоматически создается шаблон решения в Excel. Подробнее.
Количество строк
(исходных данных)

 Оценить точность прогноза, рассчитав ошибку прогноза и его доверительный интервал с вероятностью 0,95.
Оценить точность прогноза, рассчитав ошибку прогноза и его доверительный интервал с вероятностью 0,95.
 19
19 26
26 25
25
 62>2.228).
62>2.228).
 94
11
= 30.36
x·y =
∑xi·yi
n
=
19952.07
11
= 1813.82
94
11
= 30.36
x·y =
∑xi·yi
n
=
19952.07
11
= 1813.82
 43
= 4.17
43
= 4.17
 5
5
 5
5
 tнабл = rxy·
√
n-2
√
1-rxy2
= 0.2872·
√
9
√
1-0.28722
= 0.9
tнабл = rxy·
√
n-2
√
1-rxy2
= 0.2872·
√
9
√
1-0.28722
= 0.9
 Другими словами, коэффициент корреляции статистически — не значим
Другими словами, коэффициент корреляции статистически — не значим
 29 + 2.262·
1-0.292
√
11
)
Доверительный интервал для линейного коэффициента корреляции Пирсона: r(-0.9129;0.3386)
29 + 2.262·
1-0.292
√
11
)
Доверительный интервал для линейного коэффициента корреляции Пирсона: r(-0.9129;0.3386)

 Чем меньше разрядное значение, тем точнее будет конечный результат.
Чем меньше разрядное значение, тем точнее будет конечный результат. Это называется округлением.
Это называется округлением.
 Например,
светское общение, которое, предполагает
соблюдение норм этикета и ведение
диалога независимо от субъективного
отношения к личности партнёра.
Например,
светское общение, которое, предполагает
соблюдение норм этикета и ведение
диалога независимо от субъективного
отношения к личности партнёра.
 ).
Поэтому эмоциональный фон делового
общения связан не с интересом к
индивидуальности партнёра, а с вниманием
к информации, которую он
сообщает. Искренний
интерес к обсуждаемой проблеме —
отличительный признак делового уровня
коммуникаций.
).
Поэтому эмоциональный фон делового
общения связан не с интересом к
индивидуальности партнёра, а с вниманием
к информации, которую он
сообщает. Искренний
интерес к обсуждаемой проблеме —
отличительный признак делового уровня
коммуникаций. Выделяют следующие коммуникативные уровни:
Выделяют следующие коммуникативные уровни: Однако коммуникант, использующий манипулятивные техники, как правило, не обладает достаточными ресурсами, для того чтобы открыто принуждать партнёра квыполнению своей цели, в связи с чем вынужден прибегать к обману. Основная цель манипулятивных коммуникаций — оказать на сознание партнёра глубокое устойчивое воздействие и использовать данного партнёра для достижения собственных целей. Широко используется в создании рекламы, в процессе продажи услуг или продукции потребителям.
Однако коммуникант, использующий манипулятивные техники, как правило, не обладает достаточными ресурсами, для того чтобы открыто принуждать партнёра квыполнению своей цели, в связи с чем вынужден прибегать к обману. Основная цель манипулятивных коммуникаций — оказать на сознание партнёра глубокое устойчивое воздействие и использовать данного партнёра для достижения собственных целей. Широко используется в создании рекламы, в процессе продажи услуг или продукции потребителям. К ситуациям гуманистического общения относятся интимное, исповедальное, психотерапевтическое общение, где предполагается удовлетворение такой человеческой потребности, как потребность в сочувствии, понимании, сопереживании. Безоценочное восприятие партнерами друг друга, уважение к личности собеседника — отличительные признаки гуманистического уровня коммуникаций.
К ситуациям гуманистического общения относятся интимное, исповедальное, психотерапевтическое общение, где предполагается удовлетворение такой человеческой потребности, как потребность в сочувствии, понимании, сопереживании. Безоценочное восприятие партнерами друг друга, уважение к личности собеседника — отличительные признаки гуманистического уровня коммуникаций. Существенным отличием игрового уровня коммуникаций от других коммуникативных уровней является готовность к активному эмоциональному взаимодействию с партнером, искренний интерес к своеобразию партнера.
Существенным отличием игрового уровня коммуникаций от других коммуникативных уровней является готовность к активному эмоциональному взаимодействию с партнером, искренний интерес к своеобразию партнера. В основе духовного общения лежит доверие к личности собеседника — человека с богатым внутренним миром и большим жизненным опытом, восприятие его как носителя идеи, духовного начала. Духовное общение обогащает собеседников, выводит их из суеты будней, способствует духовному саморазвитию.
В основе духовного общения лежит доверие к личности собеседника — человека с богатым внутренним миром и большим жизненным опытом, восприятие его как носителя идеи, духовного начала. Духовное общение обогащает собеседников, выводит их из суеты будней, способствует духовному саморазвитию. Расскажите о видах коммуникаций. Каковы основания для их выделения?
Расскажите о видах коммуникаций. Каковы основания для их выделения?

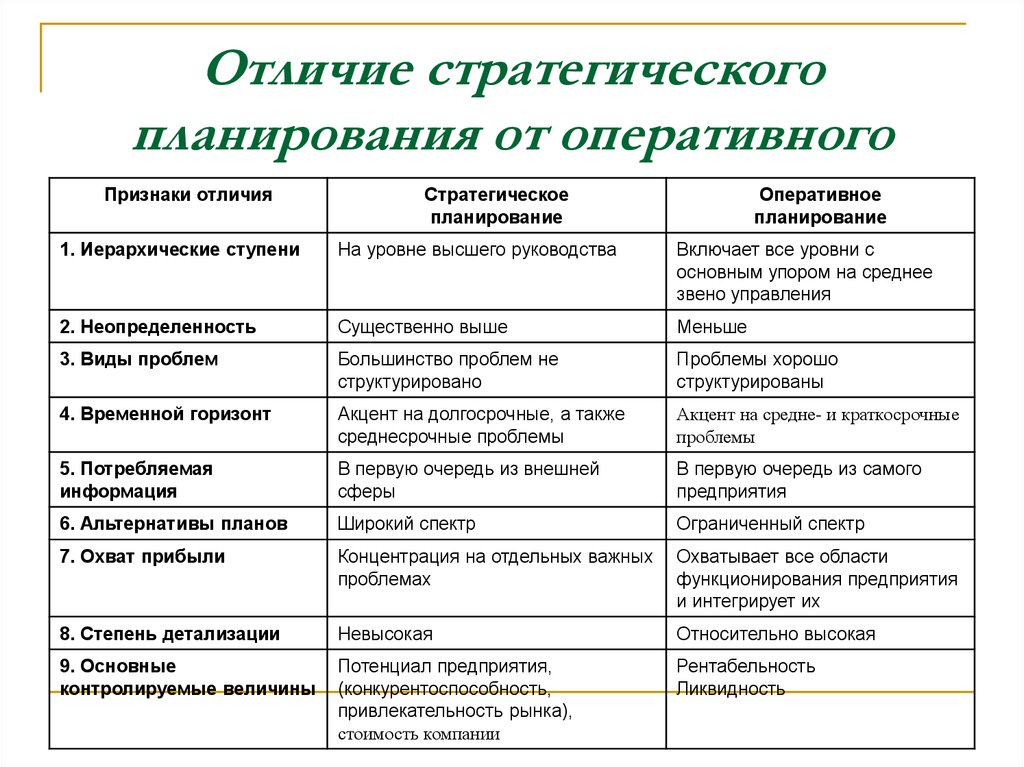
 «Увидев вошедшего, Рюхин побледнел, кашлянул и робко сказал:
–– Здравствуйте, доктор.
Доктор поклонился Рюхину, но, кланяясь, смотрел не на него, а на Ивана Николаевича.
Иван Николаевич сидел совершенно неподвижно, со злым лицом, сдвинув брови, и даже не шевельнулся при входе врача.
–– Вот, доктор,–– почему-то таинственным шёпотом заговорил Рюхин, пугливо оглядываясь на Ивана Николаевича,–– известный поэт Иван Бездомный… вот, видите ли… мы опасаемся, не белая ли горячка…
–– Тараканов, крыс, чёртиков или шмыгающих собак не ловил?
–– Нет,–– вздрогнув, ответил Рюхин,–– я его вчера видел и сегодня утром. Он был совершенно здоров…
–– А почему в кальсонах? С постели взяли?
–– Он, доктор, в ресторан пришёл в таком виде…
–– Так, так, так,–– сказал доктор и, повернувшись к Ивану, добавил: –– Зравствуйте!
–– Здорово, вредитель! –– злобно и громко ответил Иван.
«Увидев вошедшего, Рюхин побледнел, кашлянул и робко сказал:
–– Здравствуйте, доктор.
Доктор поклонился Рюхину, но, кланяясь, смотрел не на него, а на Ивана Николаевича.
Иван Николаевич сидел совершенно неподвижно, со злым лицом, сдвинув брови, и даже не шевельнулся при входе врача.
–– Вот, доктор,–– почему-то таинственным шёпотом заговорил Рюхин, пугливо оглядываясь на Ивана Николаевича,–– известный поэт Иван Бездомный… вот, видите ли… мы опасаемся, не белая ли горячка…
–– Тараканов, крыс, чёртиков или шмыгающих собак не ловил?
–– Нет,–– вздрогнув, ответил Рюхин,–– я его вчера видел и сегодня утром. Он был совершенно здоров…
–– А почему в кальсонах? С постели взяли?
–– Он, доктор, в ресторан пришёл в таком виде…
–– Так, так, так,–– сказал доктор и, повернувшись к Ивану, добавил: –– Зравствуйте!
–– Здорово, вредитель! –– злобно и громко ответил Иван. Рюхин сконфузился до того, что не посмел поднять глаза на вежливого доктора.»
В данной ситуации общения психическое состояние Рюхина можно назвать стрессовым, а сам он, по определениям Булгакова, в данном эпизоде был «крайне взволнованным» и «сконфуженным». Он как бы стыдился того, что оказался втянут в эту историю, стыдился разбуянившегося Ивана Николаевича, который в кальсонах разгуливал по городу, робел перед уважаемым доктором. И все невербальные средства передают эту сконфуженность:
а) двигательные средства:
––– мимика: « Побледнел», «Не смел поднять глаза».
––– движения тела: « Пугливо оглянулся» (пугливо потому,что Рюхин побаивался грубого Ивана).
б) околоречевые средства
––– звуки, сопутствующие речи: « Кашлянул».
––– громкость: « Таинственным шёпотом заговорил».
––– темп речи (медленный, с паузами: «…вот, видите ли… мы опасаемся, не белая ли горячка…)
Таким образом, невербальное коммуникативное поведение Рюхинаможно назвать скорее закрытым, чем открытым (от робости и смущения), а все коммуникативные проявления включающими.
Рюхин сконфузился до того, что не посмел поднять глаза на вежливого доктора.»
В данной ситуации общения психическое состояние Рюхина можно назвать стрессовым, а сам он, по определениям Булгакова, в данном эпизоде был «крайне взволнованным» и «сконфуженным». Он как бы стыдился того, что оказался втянут в эту историю, стыдился разбуянившегося Ивана Николаевича, который в кальсонах разгуливал по городу, робел перед уважаемым доктором. И все невербальные средства передают эту сконфуженность:
а) двигательные средства:
––– мимика: « Побледнел», «Не смел поднять глаза».
––– движения тела: « Пугливо оглянулся» (пугливо потому,что Рюхин побаивался грубого Ивана).
б) околоречевые средства
––– звуки, сопутствующие речи: « Кашлянул».
––– громкость: « Таинственным шёпотом заговорил».
––– темп речи (медленный, с паузами: «…вот, видите ли… мы опасаемся, не белая ли горячка…)
Таким образом, невербальное коммуникативное поведение Рюхинаможно назвать скорее закрытым, чем открытым (от робости и смущения), а все коммуникативные проявления включающими.
 прямой личным контактом непосредственной косвенной
прямой личным контактом непосредственной косвенной Фрейда Д. Келли и К. Роджерса К. Юнга
Фрейда Д. Келли и К. Роджерса К. Юнга Рожерсг Д. Келли 3. Фрейда К. Юнга
Рожерсг Д. Келли 3. Фрейда К. Юнга Давайте лучше обсудим план, чтобы обеспечить согласованность действий» «Перспектива развития данного проекта слишком расплывчата, и я не вижу необходимости его развивать» «Мне тяжело смириться с обострением ситуации, возникшим в нашем коллективе. Сейчас мне так необходима теплота и поддержка»
Давайте лучше обсудим план, чтобы обеспечить согласованность действий» «Перспектива развития данного проекта слишком расплывчата, и я не вижу необходимости его развивать» «Мне тяжело смириться с обострением ситуации, возникшим в нашем коллективе. Сейчас мне так необходима теплота и поддержка» . манипулятивные переговоры спасительные переговоры приспособленческие переговоры эгоистические переговоры
. манипулятивные переговоры спасительные переговоры приспособленческие переговоры эгоистические переговоры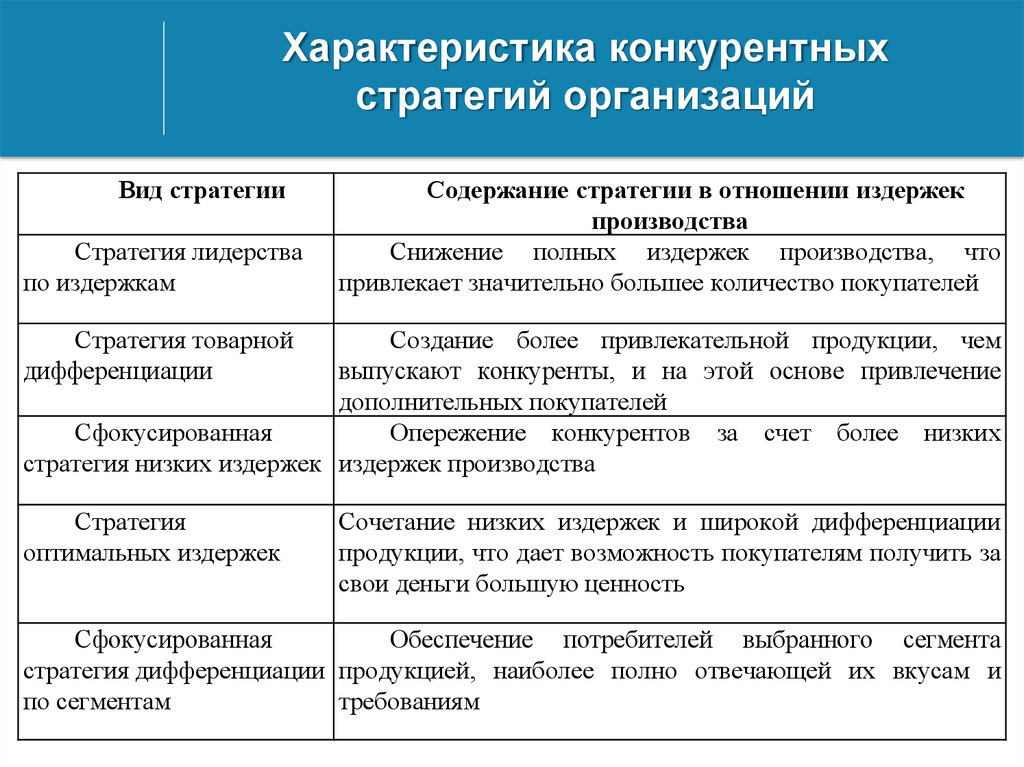 Признаки: выдвижение различных вариантов при изменении условий — упорствование в своем мнении соответствуют критерию оценки поведения участников переговоров … гибкость — отсутствие гибкости аргументированность — голословность высказываний интегративность мышления — консервативность мышления. концентрация на теме – отклонение от темы
Признаки: выдвижение различных вариантов при изменении условий — упорствование в своем мнении соответствуют критерию оценки поведения участников переговоров … гибкость — отсутствие гибкости аргументированность — голословность высказываний интегративность мышления — консервативность мышления. концентрация на теме – отклонение от темы Давайте лучше обсудим план, чтобы обеспечить согласованность действий» «Перспектива развития данного проекта слишком расплывчата, и я не вижу необходимости его развивать» «Мне тяжело смириться с обострением ситуации, возникшим в нашем коллективе. Сейчас мне так необходима теплота и поддержка»
Давайте лучше обсудим план, чтобы обеспечить согласованность действий» «Перспектива развития данного проекта слишком расплывчата, и я не вижу необходимости его развивать» «Мне тяжело смириться с обострением ситуации, возникшим в нашем коллективе. Сейчас мне так необходима теплота и поддержка» Когда отношения работают, акт общения, кажется, протекает относительно легко. Когда отношения ухудшаются, акт общения может быть таким же разочаровывающим, как восхождение на песчаную горку».
Когда отношения работают, акт общения, кажется, протекает относительно легко. Когда отношения ухудшаются, акт общения может быть таким же разочаровывающим, как восхождение на песчаную горку». 
 С другой стороны, мы можем подобрать слова, которые нормализуют вопросы и проблемы и уменьшают сопротивление. Такие фразы, как «в некоторых районах люди могут …», «нередко для …» и «для некоторых людей в подобных ситуациях» являются примерами этого.
С другой стороны, мы можем подобрать слова, которые нормализуют вопросы и проблемы и уменьшают сопротивление. Такие фразы, как «в некоторых районах люди могут …», «нередко для …» и «для некоторых людей в подобных ситуациях» являются примерами этого.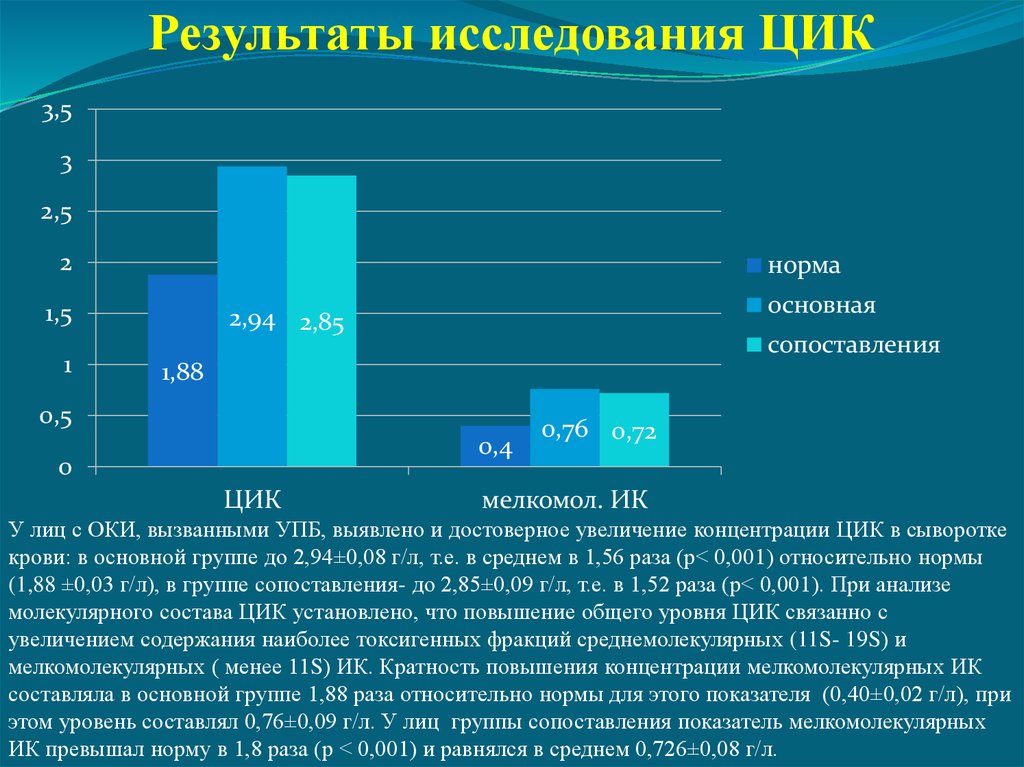 свободны от жаргона
свободны от жаргона 
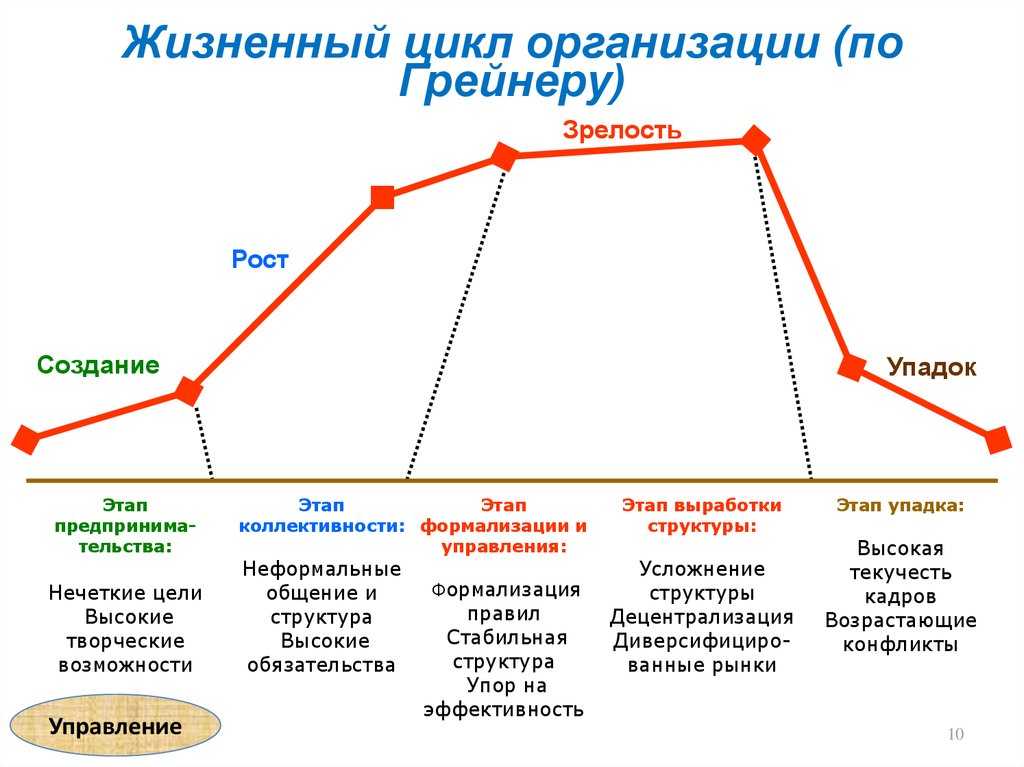 Предложение может передавать совершенно разные значения в зависимости от ударения слов и тона голоса. Например, утверждение «Я не говорил, что ты глупый» имеет шесть разных значений, в зависимости от того, на каком слове делается ударение.
Предложение может передавать совершенно разные значения в зависимости от ударения слов и тона голоса. Например, утверждение «Я не говорил, что ты глупый» имеет шесть разных значений, в зависимости от того, на каком слове делается ударение. Когда наши сообщения непоследовательны, слушатель может запутаться. Непоследовательность может также привести к отсутствию доверия и подорвать возможность построить хорошие рабочие отношения.
Когда наши сообщения непоследовательны, слушатель может запутаться. Непоследовательность может также привести к отсутствию доверия и подорвать возможность построить хорошие рабочие отношения.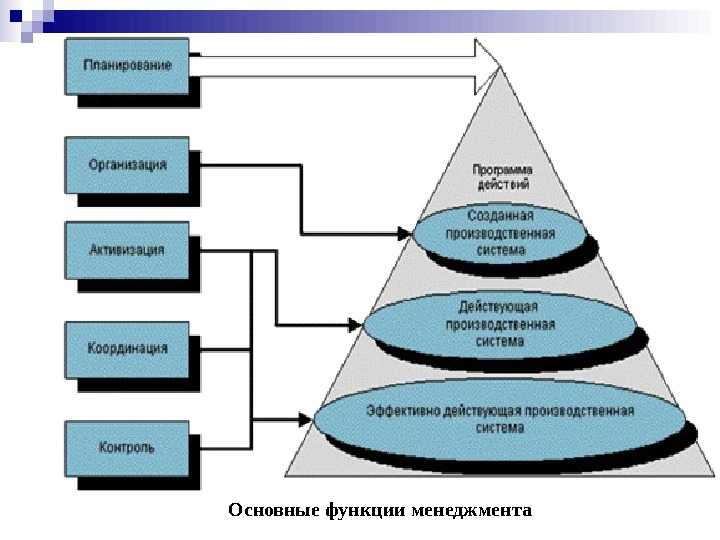
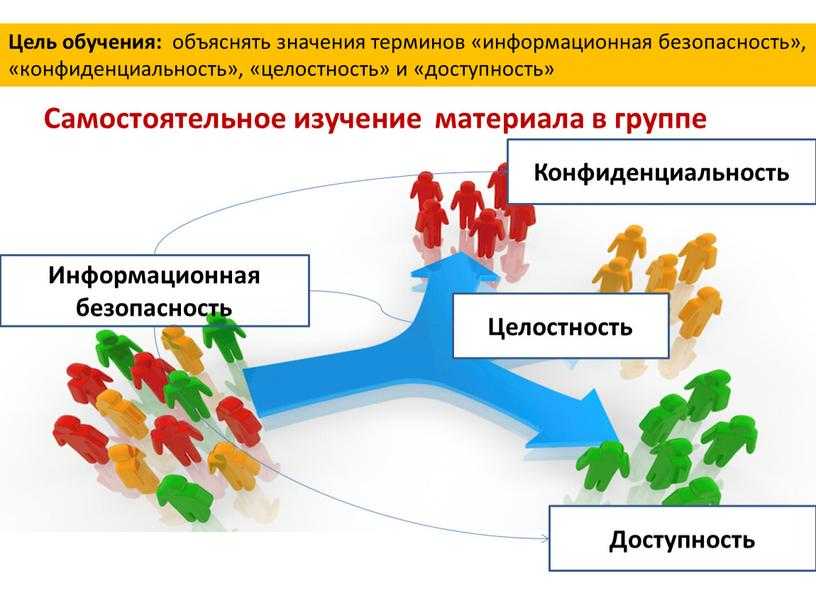 У нас есть более глубокое понимание проблемы и возможных путей достижения согласия.
У нас есть более глубокое понимание проблемы и возможных путей достижения согласия. Тем не менее, конкретные навыки эффективного слушания можно освоить. Наша конечная цель — интегрировать эти навыки в чувствительный и унифицированный способ слушания.
Тем не менее, конкретные навыки эффективного слушания можно освоить. Наша конечная цель — интегрировать эти навыки в чувствительный и унифицированный способ слушания.
 .. Когда другие видимые движения прекратилось, а частота моргания упала до менее чем одного раза за шесть секунд, прослушивание в практических целях прекратилось».
.. Когда другие видимые движения прекратилось, а частота моргания упала до менее чем одного раза за шесть секунд, прослушивание в практических целях прекратилось».  Наша тенденция состоит в том, чтобы попытаться игнорировать эмоциональный аспект сообщения/конфликта и перейти непосредственно к сути проблем. <
Наша тенденция состоит в том, чтобы попытаться игнорировать эмоциональный аспект сообщения/конфликта и перейти непосредственно к сути проблем. <
 В ситуациях публичных выступлений люди чаще всего используют само- или объектно-ориентированные адаптеры. Обычные действия, связанные с прикосновением к себе, такие как почесывание, накручивание волос или ерзание пальцами или руками, считаются самоадаптирующими. Некоторые самоадаптеры проявляются внутренне, как кашель или звуки откашливания. Моя личная слабость — объектные адаптеры. В частности, я подсознательно тяготею к металлическим предметам, таким как канцелярские скрепки или скобы, которые скрепляют мои заметки, и ловлю себя на том, что сгибаю их или ерзаю ими во время разговора. Другие люди играют с маркерами, карточками для заметок, мелочью в карманах или на кафедре во время разговора. Использование адаптеров для предметов также может сигнализировать о скуке, когда люди играют с соломинкой в своем напитке или снимают этикетку с бутылки пива. Смартфоны стали обычными объектными адаптерами, поскольку люди могут возиться со своими телефонами, чтобы уменьшить тревогу. Наконец, как уже отмечалось, другие адаптеры более распространены в социальных ситуациях, чем в ситуациях публичных выступлений, учитывая расстояние говорящего от аудитории.
В ситуациях публичных выступлений люди чаще всего используют само- или объектно-ориентированные адаптеры. Обычные действия, связанные с прикосновением к себе, такие как почесывание, накручивание волос или ерзание пальцами или руками, считаются самоадаптирующими. Некоторые самоадаптеры проявляются внутренне, как кашель или звуки откашливания. Моя личная слабость — объектные адаптеры. В частности, я подсознательно тяготею к металлическим предметам, таким как канцелярские скрепки или скобы, которые скрепляют мои заметки, и ловлю себя на том, что сгибаю их или ерзаю ими во время разговора. Другие люди играют с маркерами, карточками для заметок, мелочью в карманах или на кафедре во время разговора. Использование адаптеров для предметов также может сигнализировать о скуке, когда люди играют с соломинкой в своем напитке или снимают этикетку с бутылки пива. Смартфоны стали обычными объектными адаптерами, поскольку люди могут возиться со своими телефонами, чтобы уменьшить тревогу. Наконец, как уже отмечалось, другие адаптеры более распространены в социальных ситуациях, чем в ситуациях публичных выступлений, учитывая расстояние говорящего от аудитории. Другие адаптеры включают в себя приспособление или уход за другими, подобно тому, как приматы, такие как шимпанзе, отрывают вещи друг от друга. Было бы определенно странно, если бы оратор подошел к слушателю и содрал с его или ее свитера ворсинки, починил кривой галстук, заправил бирку или погладил выбившиеся волосы посреди выступления.
Другие адаптеры включают в себя приспособление или уход за другими, подобно тому, как приматы, такие как шимпанзе, отрывают вещи друг от друга. Было бы определенно странно, если бы оратор подошел к слушателю и содрал с его или ее свитера ворсинки, починил кривой галстук, заправил бирку или погладил выбившиеся волосы посреди выступления.
 В отличие от эмблем, иллюстраторы обычно не имеют значения сами по себе и используются более подсознательно, чем эмблемы. Эти в значительной степени непроизвольные и кажущиеся естественными жесты исходят от нас, когда мы говорим, но различаются по интенсивности и частоте в зависимости от контекста. Хотя нас никогда специально не учат использовать иллюстративные жесты, мы делаем это автоматически. Подумайте о том, как вы все еще жестикулируете во время анимированного разговора по телефону, даже если другой человек вас не видит.
В отличие от эмблем, иллюстраторы обычно не имеют значения сами по себе и используются более подсознательно, чем эмблемы. Эти в значительной степени непроизвольные и кажущиеся естественными жесты исходят от нас, когда мы говорим, но различаются по интенсивности и частоте в зависимости от контекста. Хотя нас никогда специально не учат использовать иллюстративные жесты, мы делаем это автоматически. Подумайте о том, как вы все еще жестикулируете во время анимированного разговора по телефону, даже если другой человек вас не видит. Этот невербальный сигнал начинается с рождения, еще до того, как ребенок узнает, что он имеет соответствующее значение. Младенцы качают головой из стороны в сторону, чтобы отвергнуть материнскую грудь, а затем качают головой, чтобы отвергнуть попытки кормления с ложки (Pease & Pease, 2004). Затем это биологически обоснованное движение остается с нами, чтобы быть узнаваемым сигналом «нет». Мы также двигаем головой, чтобы показать интерес. Например, поднятая голова обычно указывает на заинтересованное или нейтральное отношение, наклон головы указывает на интерес и является врожденным жестом подчинения, который обнажает шею и подсознательно заставляет людей чувствовать к нам больше доверия, а опущенная голова сигнализирует о негативном или агрессивном отношении. Пиз и Пиз, 2004).
Этот невербальный сигнал начинается с рождения, еще до того, как ребенок узнает, что он имеет соответствующее значение. Младенцы качают головой из стороны в сторону, чтобы отвергнуть материнскую грудь, а затем качают головой, чтобы отвергнуть попытки кормления с ложки (Pease & Pease, 2004). Затем это биологически обоснованное движение остается с нами, чтобы быть узнаваемым сигналом «нет». Мы также двигаем головой, чтобы показать интерес. Например, поднятая голова обычно указывает на заинтересованное или нейтральное отношение, наклон головы указывает на интерес и является врожденным жестом подчинения, который обнажает шею и подсознательно заставляет людей чувствовать к нам больше доверия, а опущенная голова сигнализирует о негативном или агрессивном отношении. Пиз и Пиз, 2004). Большая часть нашего общения происходит, когда мы стоим или сидим. Одна интересная поза стоя включает в себя размещение рук на бедрах и является невербальным сигналом, который мы используем подсознательно, чтобы казаться крупнее и проявлять напористость. Когда локти направлены, это мешает другим так же легко пройти мимо нас и является признаком попытки доминирования или жестом, говорящим о том, что мы готовы к действию. С точки зрения сидения, откидывание назад показывает неформальность и безразличие, положение верхом на стуле является признаком доминирования (но также и некоторой неуверенности, поскольку человек защищает уязвимую переднюю часть своего тела), а наклон вперед показывает интерес и внимательность (Pease и Пиз, 2004).
Большая часть нашего общения происходит, когда мы стоим или сидим. Одна интересная поза стоя включает в себя размещение рук на бедрах и является невербальным сигналом, который мы используем подсознательно, чтобы казаться крупнее и проявлять напористость. Когда локти направлены, это мешает другим так же легко пройти мимо нас и является признаком попытки доминирования или жестом, говорящим о том, что мы готовы к действию. С точки зрения сидения, откидывание назад показывает неформальность и безразличие, положение верхом на стуле является признаком доминирования (но также и некоторой неуверенности, поскольку человек защищает уязвимую переднюю часть своего тела), а наклон вперед показывает интерес и внимательность (Pease и Пиз, 2004). Лицо и глаза находятся в центре внимания во время общения, и наряду с нашими ушами наши глаза воспринимают большую часть коммуникативной информации вокруг нас. Высказывание «Глаза — зеркало души» на самом деле верно с точки зрения того, где люди обычно думают, что другие «находятся», то есть прямо за глазами (Андерсен, 19).99). Определенное поведение глаз стало привязываться к личностным чертам или эмоциональным состояниям, о чем свидетельствуют такие фразы, как «голодные глаза», «злые глаза» и «глаза в спальне». Чтобы лучше понять окулесику, мы обсудим характеристики и функции зрительного контакта и расширения зрачка.
Лицо и глаза находятся в центре внимания во время общения, и наряду с нашими ушами наши глаза воспринимают большую часть коммуникативной информации вокруг нас. Высказывание «Глаза — зеркало души» на самом деле верно с точки зрения того, где люди обычно думают, что другие «находятся», то есть прямо за глазами (Андерсен, 19).99). Определенное поведение глаз стало привязываться к личностным чертам или эмоциональным состояниям, о чем свидетельствуют такие фразы, как «голодные глаза», «злые глаза» и «глаза в спальне». Чтобы лучше понять окулесику, мы обсудим характеристики и функции зрительного контакта и расширения зрачка. Я уверен, что все мы были в той неловкой ситуации, когда учитель задает вопрос, никто другой не предлагает ответа, и он или она смотрит прямо на нас, как бы говоря: «Что вы думаете?» В этом случае зрительный контакт учителя используется, чтобы побудить нас ответить. Во время взаимодействия зрительный контакт также меняется, когда мы переключаемся с говорящего на слушателя. Американцы обычно меняют зрительный контакт во время разговора — отводят взгляд от слушателя, а затем каждые несколько секунд оглядываются на его или ее лицо. Ближе к концу нашего выступления мы устанавливаем более прямой зрительный контакт с нашим слушателем, чтобы показать, что мы заканчиваем. Во время прослушивания мы склонны поддерживать более продолжительный зрительный контакт, не отводя взгляда так регулярно, как во время разговора (Martin & Nakayama, 2010).
Я уверен, что все мы были в той неловкой ситуации, когда учитель задает вопрос, никто другой не предлагает ответа, и он или она смотрит прямо на нас, как бы говоря: «Что вы думаете?» В этом случае зрительный контакт учителя используется, чтобы побудить нас ответить. Во время взаимодействия зрительный контакт также меняется, когда мы переключаемся с говорящего на слушателя. Американцы обычно меняют зрительный контакт во время разговора — отводят взгляд от слушателя, а затем каждые несколько секунд оглядываются на его или ее лицо. Ближе к концу нашего выступления мы устанавливаем более прямой зрительный контакт с нашим слушателем, чтобы показать, что мы заканчиваем. Во время прослушивания мы склонны поддерживать более продолжительный зрительный контакт, не отводя взгляда так регулярно, как во время разговора (Martin & Nakayama, 2010). Наши глаза передают визуальную информацию, необходимую нам для интерпретации движений, жестов и зрительного контакта людей. Говорящий может использовать зрительный контакт, чтобы определить, занята ли аудитория, смущена или ей скучно, а затем соответствующим образом адаптировать свое сообщение. Наши глаза также посылают информацию другим. Люди знают, что нельзя перебивать, когда мы глубоко задумались, потому что мы естественным образом отворачиваемся от других, когда обрабатываем информацию. Зрительный контакт с другими также сообщает, что мы обращаем внимание и заинтересованы в том, что говорит другой человек. Как мы узнаем из главы 5 «Слушание», зрительный контакт является ключевой частью активного слушания.
Наши глаза передают визуальную информацию, необходимую нам для интерпретации движений, жестов и зрительного контакта людей. Говорящий может использовать зрительный контакт, чтобы определить, занята ли аудитория, смущена или ей скучно, а затем соответствующим образом адаптировать свое сообщение. Наши глаза также посылают информацию другим. Люди знают, что нельзя перебивать, когда мы глубоко задумались, потому что мы естественным образом отворачиваемся от других, когда обрабатываем информацию. Зрительный контакт с другими также сообщает, что мы обращаем внимание и заинтересованы в том, что говорит другой человек. Как мы узнаем из главы 5 «Слушание», зрительный контакт является ключевой частью активного слушания. Как мы узнали, зрительный контакт — это ключ к непосредственному поведению, и он сигнализирует другим, что мы доступны для общения. Как только общение начинается, зрительный контакт помогает установить взаимопонимание или связь. Мы также можем использовать зрительный контакт, чтобы сигнализировать о том, что мы не хотим устанавливать связь с другими. Например, в общественном месте, таком как аэропорт или спортзал, где люди часто ведут светскую беседу, мы можем избегать зрительного контакта с другими, чтобы показать, что мы не хотим вступать в светскую беседу с незнакомцами. Однако другой человек может использовать зрительный контакт, чтобы попытаться уговорить вас заговорить. Например, когда один человек продолжает смотреть на другого человека, который не отвечает взаимностью на зрительный контакт, человек, избегающий зрительного контакта, может в конце концов сдаться, проявить любопытство или раздражение и сказать: «Могу ли я чем-нибудь вам помочь?» Как видите, зрительный контакт посылает и получает важные коммуникативные сообщения, которые помогают нам интерпретировать поведение других, передавать информацию о наших мыслях и чувствах, а также облегчать или препятствовать установлению взаимопонимания или связи.
Как мы узнали, зрительный контакт — это ключ к непосредственному поведению, и он сигнализирует другим, что мы доступны для общения. Как только общение начинается, зрительный контакт помогает установить взаимопонимание или связь. Мы также можем использовать зрительный контакт, чтобы сигнализировать о том, что мы не хотим устанавливать связь с другими. Например, в общественном месте, таком как аэропорт или спортзал, где люди часто ведут светскую беседу, мы можем избегать зрительного контакта с другими, чтобы показать, что мы не хотим вступать в светскую беседу с незнакомцами. Однако другой человек может использовать зрительный контакт, чтобы попытаться уговорить вас заговорить. Например, когда один человек продолжает смотреть на другого человека, который не отвечает взаимностью на зрительный контакт, человек, избегающий зрительного контакта, может в конце концов сдаться, проявить любопытство или раздражение и сказать: «Могу ли я чем-нибудь вам помочь?» Как видите, зрительный контакт посылает и получает важные коммуникативные сообщения, которые помогают нам интерпретировать поведение других, передавать информацию о наших мыслях и чувствах, а также облегчать или препятствовать установлению взаимопонимания или связи. В этом списке рассматриваются конкретные функции зрительного контакта:
В этом списке рассматриваются конкретные функции зрительного контакта: Боль, сексуальное влечение, общее возбуждение, тревога/стресс и обработка информации (мышление) также влияют на расширение зрачка. Исследователи измеряют расширение зрачка по ряду причин. Например, рекламодатели используют расширение зрачков как индикатор потребительских предпочтений, предполагая, что большее расширение указывает на возбуждение и влечение к продукту. Мы не считываем сознательно расширение зрачков других людей в наших повседневных взаимодействиях, но экспериментальные исследования показали, что мы подсознательно воспринимаем расширение зрачков, что влияет на наши впечатления и общение. В целом расширенные зрачки повышают привлекательность человека. Даже если мы не осознаем этот тонкий невербальный сигнал, у нас есть социальные нормы и практики, которые могут подсознательно основываться на расширении зрачка. Возьмем, к примеру, понятие декоративного освещения и обычную практику создания «романтической» атмосферы при свечах или свете камина. Более мягкий и непрямой свет приводит к расширению зрачков, и хотя мы намеренно манипулируем освещением, чтобы создать романтическую атмосферу, а не расширять зрачки, расширенные зрачки все же воспринимаются подсознательно, что усиливает восприятие привлекательности (Andersen, 19).
Боль, сексуальное влечение, общее возбуждение, тревога/стресс и обработка информации (мышление) также влияют на расширение зрачка. Исследователи измеряют расширение зрачка по ряду причин. Например, рекламодатели используют расширение зрачков как индикатор потребительских предпочтений, предполагая, что большее расширение указывает на возбуждение и влечение к продукту. Мы не считываем сознательно расширение зрачков других людей в наших повседневных взаимодействиях, но экспериментальные исследования показали, что мы подсознательно воспринимаем расширение зрачков, что влияет на наши впечатления и общение. В целом расширенные зрачки повышают привлекательность человека. Даже если мы не осознаем этот тонкий невербальный сигнал, у нас есть социальные нормы и практики, которые могут подсознательно основываться на расширении зрачка. Возьмем, к примеру, понятие декоративного освещения и обычную практику создания «романтической» атмосферы при свечах или свете камина. Более мягкий и непрямой свет приводит к расширению зрачков, и хотя мы намеренно манипулируем освещением, чтобы создать романтическую атмосферу, а не расширять зрачки, расширенные зрачки все же воспринимаются подсознательно, что усиливает восприятие привлекательности (Andersen, 19). 99).
99). По мере того, как мы становимся старше, мы учимся и начинаем следовать правилам отображения мимики и других сигналов эмоций, а также учимся лучше контролировать свое эмоциональное выражение на основе норм нашей культуры.
По мере того, как мы становимся старше, мы учимся и начинаем следовать правилам отображения мимики и других сигналов эмоций, а также учимся лучше контролировать свое эмоциональное выражение на основе норм нашей культуры. Именно непроизвольное и спонтанное сокращение этих мышц приводит в движение кожу вокруг наших щек, глаз и носа, создавая улыбку, которая отличается от фальшивой или вежливой улыбки (Evans, 2001). Люди способны различать эти улыбки, поэтому фотографы часто шутят со взрослыми или используют реквизит с детьми, чтобы вызвать искреннюю улыбку перед тем, как сделать снимок.
Именно непроизвольное и спонтанное сокращение этих мышц приводит в движение кожу вокруг наших щек, глаз и носа, создавая улыбку, которая отличается от фальшивой или вежливой улыбки (Evans, 2001). Люди способны различать эти улыбки, поэтому фотографы часто шутят со взрослыми или используют реквизит с детьми, чтобы вызвать искреннюю улыбку перед тем, как сделать снимок. Выражение лица может сообщить, что говорящий устал, взволнован, зол, сбит с толку, разочарован, грустен, уверен в себе, самодовольен, застенчив или скучает. Например, даже если вам не скучно, вялое лицо с небольшой анимацией может привести аудиторию к мысли, что вам надоела ваша речь, что вряд ли вызовет у них интерес. Поэтому убедитесь, что выражение вашего лица передает эмоции, настроение или личностные черты, которые, по вашему мнению, будут благосклонно восприняты вашей аудиторией и которые помогут вам достичь целей речи. Также убедитесь, что выражение вашего лица соответствует содержанию вашей речи. Когда вы говорите что-то беззаботное или юмористическое, улыбка, яркие глаза и слегка приподнятые брови невербально усиливают ваше вербальное сообщение. Когда вы говорите что-то серьезное или мрачное, нахмуренные брови, сжатый рот и даже легкий кивок головы могут усилить это сообщение. Если ваши выражения лица и содержание речи не совпадают, ваша аудитория может быть сбита с толку смешанными сообщениями, что может привести к тому, что они усомнятся в вашей честности и достоверности.
Выражение лица может сообщить, что говорящий устал, взволнован, зол, сбит с толку, разочарован, грустен, уверен в себе, самодовольен, застенчив или скучает. Например, даже если вам не скучно, вялое лицо с небольшой анимацией может привести аудиторию к мысли, что вам надоела ваша речь, что вряд ли вызовет у них интерес. Поэтому убедитесь, что выражение вашего лица передает эмоции, настроение или личностные черты, которые, по вашему мнению, будут благосклонно восприняты вашей аудиторией и которые помогут вам достичь целей речи. Также убедитесь, что выражение вашего лица соответствует содержанию вашей речи. Когда вы говорите что-то беззаботное или юмористическое, улыбка, яркие глаза и слегка приподнятые брови невербально усиливают ваше вербальное сообщение. Когда вы говорите что-то серьезное или мрачное, нахмуренные брови, сжатый рот и даже легкий кивок головы могут усилить это сообщение. Если ваши выражения лица и содержание речи не совпадают, ваша аудитория может быть сбита с толку смешанными сообщениями, что может привести к тому, что они усомнятся в вашей честности и достоверности.
 Прикосновение необходимо для социального развития человека, и оно может быть приветственным, угрожающим или убеждающим. Исследовательские проекты показали, что студенты более положительно оценивали библиотеку и ее сотрудников, если библиотекарь кратко прикасался к посетителю, возвращая его или ее читательский билет, что официанты-женщины в ресторане получали более крупные чаевые, когда они касались посетителей, и что люди с большей вероятностью подписывали прошение, когда проситель прикасался к ним во время их взаимодействия (Андерсен, 1999).
Прикосновение необходимо для социального развития человека, и оно может быть приветственным, угрожающим или убеждающим. Исследовательские проекты показали, что студенты более положительно оценивали библиотеку и ее сотрудников, если библиотекарь кратко прикасался к посетителю, возвращая его или ее читательский билет, что официанты-женщины в ресторане получали более крупные чаевые, когда они касались посетителей, и что люди с большей вероятностью подписывали прошение, когда проситель прикасался к ним во время их взаимодействия (Андерсен, 1999). На социально-вежливом уровне социально санкционированное прикосновение помогает инициировать взаимодействие и показать, что другие участвуют и уважают. Рукопожатие, похлопывание по руке и по плечу — примеры вежливых прикосновений. На самом деле рукопожатие — это сокращенный жест рукопожатия, но мы знаем, что продолжительное рукопожатие было бы сочтено слишком интимным и, следовательно, неуместным на функционально-профессиональном или социально-вежливом уровне. На функционально-профессиональном и социально-вежливом уровнях прикосновение по-прежнему имеет значение для межличностных отношений. Прикосновения, хотя и профессиональные и не интимные, между парикмахером и клиентом или между медсестрой и пациентом, могут быть терапевтическими и утешительными. Кроме того, социально-вежливый обмен прикосновениями играет роль в формировании первоначального впечатления, которое может иметь важные последствия для развития взаимодействия и отношений.
На социально-вежливом уровне социально санкционированное прикосновение помогает инициировать взаимодействие и показать, что другие участвуют и уважают. Рукопожатие, похлопывание по руке и по плечу — примеры вежливых прикосновений. На самом деле рукопожатие — это сокращенный жест рукопожатия, но мы знаем, что продолжительное рукопожатие было бы сочтено слишком интимным и, следовательно, неуместным на функционально-профессиональном или социально-вежливом уровне. На функционально-профессиональном и социально-вежливом уровнях прикосновение по-прежнему имеет значение для межличностных отношений. Прикосновения, хотя и профессиональные и не интимные, между парикмахером и клиентом или между медсестрой и пациентом, могут быть терапевтическими и утешительными. Кроме того, социально-вежливый обмен прикосновениями играет роль в формировании первоначального впечатления, которое может иметь важные последствия для развития взаимодействия и отношений. На уровне дружбы-теплоты прикосновение важнее и неоднозначнее, чем на уровне социально-вежливого. На этом уровне сенсорные взаимодействия важны, потому что они служат цели поддержания отношений и сообщают о близости, симпатии, заботе и заботе. Типы прикосновений на этом уровне также сильно различаются: от более формальных и ритуализированных до более интимных, что означает, что друзьям иногда приходится договариваться о своем собственном уровне комфорта с различными типами прикосновений, и они могут столкнуться с некоторой двусмысленностью, если их предпочтения не совпадают с их отношениями. партнера. Например, в дружбе слишком много прикосновений может сигнализировать о сексуальном или романтическом интересе, а слишком мало прикосновений может сигнализировать о отдалении или недружелюбии. На уровне любви-близости прикосновения носят более личный характер и обычно обмениваются только между значимыми людьми, такими как лучшие друзья, близкие члены семьи и романтические партнеры. Прикосновения к лицам, рукопожатия и полные объятия — примеры прикосновений на этом уровне.
На уровне дружбы-теплоты прикосновение важнее и неоднозначнее, чем на уровне социально-вежливого. На этом уровне сенсорные взаимодействия важны, потому что они служат цели поддержания отношений и сообщают о близости, симпатии, заботе и заботе. Типы прикосновений на этом уровне также сильно различаются: от более формальных и ритуализированных до более интимных, что означает, что друзьям иногда приходится договариваться о своем собственном уровне комфорта с различными типами прикосновений, и они могут столкнуться с некоторой двусмысленностью, если их предпочтения не совпадают с их отношениями. партнера. Например, в дружбе слишком много прикосновений может сигнализировать о сексуальном или романтическом интересе, а слишком мало прикосновений может сигнализировать о отдалении или недружелюбии. На уровне любви-близости прикосновения носят более личный характер и обычно обмениваются только между значимыми людьми, такими как лучшие друзья, близкие члены семьи и романтические партнеры. Прикосновения к лицам, рукопожатия и полные объятия — примеры прикосновений на этом уровне. Хотя этот уровень прикосновения не является сексуальным, он усиливает чувство близости и близости и может привести к прикосновению сексуального возбуждения, которое является наиболее интимной формой прикосновения, поскольку оно предназначено для физической стимуляции другого человека.
Хотя этот уровень прикосновения не является сексуальным, он усиливает чувство близости и близости и может привести к прикосновению сексуального возбуждения, которое является наиболее интимной формой прикосновения, поскольку оно предназначено для физической стимуляции другого человека. Например, похлопывание по спине — это сокращенное объятие (Andersen, 1999). В общем, наличие или отсутствие прикосновения подсказывает нам эмоции людей. Так как партнеры сидят напротив друг друга, один человек может слегка похлопать другого по руке после того, как он или она сказал что-то смешное. Если партнеры сидят рядом, один человек может скрестить ноги и наклониться к другому человеку так, чтобы колени или ступни каждого человека время от времени соприкасались. Прикосновение как способ выражения чувств часто бывает взаимным. За легким прикосновением одного датера последует легкое прикосновение другого, что указывает на то, что первое прикосновение было в порядке. Хотя вербальное общение также может использоваться для обозначения романтического интереса, многие люди чувствуют себя слишком уязвимыми на этом раннем этапе отношений, чтобы выразить что-то словами. Если ваше свидание немного передвинулось, а вы не заинтересованы, также маловероятно, что вы сразу же выйдете и скажете: «Извините, но мне это не очень интересно».
Например, похлопывание по спине — это сокращенное объятие (Andersen, 1999). В общем, наличие или отсутствие прикосновения подсказывает нам эмоции людей. Так как партнеры сидят напротив друг друга, один человек может слегка похлопать другого по руке после того, как он или она сказал что-то смешное. Если партнеры сидят рядом, один человек может скрестить ноги и наклониться к другому человеку так, чтобы колени или ступни каждого человека время от времени соприкасались. Прикосновение как способ выражения чувств часто бывает взаимным. За легким прикосновением одного датера последует легкое прикосновение другого, что указывает на то, что первое прикосновение было в порядке. Хотя вербальное общение также может использоваться для обозначения романтического интереса, многие люди чувствуют себя слишком уязвимыми на этом раннем этапе отношений, чтобы выразить что-то словами. Если ваше свидание немного передвинулось, а вы не заинтересованы, также маловероятно, что вы сразу же выйдете и скажете: «Извините, но мне это не очень интересно». Вместо этого, из-за распространенных ритуалов вежливости, вы, скорее всего, отреагируете другими формами невербального общения, например, отступите назад, скрестите руки или просто не подтвердите прикосновение.
Вместо этого, из-за распространенных ритуалов вежливости, вы, скорее всего, отреагируете другими формами невербального общения, например, отступите назад, скрестите руки или просто не подтвердите прикосновение. Это объятие распространено среди друзей, романтических партнеров, членов семьи и, возможно, даже коллег. Объятие за шею и талию обычно происходит в более интимных отношениях, поскольку оно включает в себя руки одного человека вокруг шеи другого и руки другого человека вокруг талии другого. Я думаю об этом типе объятий как о «медленных танцевальных объятиях». Поглощающее объятие похоже на медвежье объятие в том смысле, что один человек полностью обнимает другого, в то время как этот человек в основном стоит там. Такое поведение с объятиями обычно происходит, когда кто-то очень взволнован и без предупреждения обнимает другого человека.
Это объятие распространено среди друзей, романтических партнеров, членов семьи и, возможно, даже коллег. Объятие за шею и талию обычно происходит в более интимных отношениях, поскольку оно включает в себя руки одного человека вокруг шеи другого и руки другого человека вокруг талии другого. Я думаю об этом типе объятий как о «медленных танцевальных объятиях». Поглощающее объятие похоже на медвежье объятие в том смысле, что один человек полностью обнимает другого, в то время как этот человек в основном стоит там. Такое поведение с объятиями обычно происходит, когда кто-то очень взволнован и без предупреждения обнимает другого человека. Объятие происходит после того, как рукопожатие было начато, когда одна рука обнимает другого человека, как правило, всего одно касание, затем шаг назад и рукопожатие отпускают. В этом поведении с объятиями рукопожатие, которое поддерживается между сундуками, сводит к минимуму физическую близость и близость, которую можно интерпретировать из перекрестного или поглощающего объятия, когда соприкасается большинство туловищ обнимающих. Этот отход от физической близости, вероятно, связан с американской нормой, которая ограничивает физическое выражение привязанности мужчинами из-за гомофобии или беспокойства о том, что их будут воспринимать как геев. Объятие пощечины также является менее физически интимным объятием и включает в себя объятие, когда один или оба человека неоднократно хлопают другого человека по спине, часто во время разговора друг с другом. Я видел, как этот тип объятий длится много секунд и с разной степенью силы, связанной с пощечиной. Когда пощечина больше похожа на постукивание, это на самом деле признак того, что один человек хочет отпустить.
Объятие происходит после того, как рукопожатие было начато, когда одна рука обнимает другого человека, как правило, всего одно касание, затем шаг назад и рукопожатие отпускают. В этом поведении с объятиями рукопожатие, которое поддерживается между сундуками, сводит к минимуму физическую близость и близость, которую можно интерпретировать из перекрестного или поглощающего объятия, когда соприкасается большинство туловищ обнимающих. Этот отход от физической близости, вероятно, связан с американской нормой, которая ограничивает физическое выражение привязанности мужчинами из-за гомофобии или беспокойства о том, что их будут воспринимать как геев. Объятие пощечины также является менее физически интимным объятием и включает в себя объятие, когда один или оба человека неоднократно хлопают другого человека по спине, часто во время разговора друг с другом. Я видел, как этот тип объятий длится много секунд и с разной степенью силы, связанной с пощечиной. Когда пощечина больше похожа на постукивание, это на самом деле признак того, что один человек хочет отпустить. 1.
Множества на плоскости
1.
Множества на плоскости

 Найти A \ B и B \ A.
Найти A \ B и B \ A. ru
ru Формально это записывается так:
Формально это записывается так: Обозначается:
Обозначается: Операция объединения и другие операции иллюстрируются кругами Эйлера представленными на рис. 1.1—1.5.
Операция объединения и другие операции иллюстрируются кругами Эйлера представленными на рис. 1.1—1.5. Обозначение: . Отметим, что в А могут находиться не все элементы из вычитаемого множества В (см. рис.1.3). Например,
Обозначение: . Отметим, что в А могут находиться не все элементы из вычитаемого множества В (см. рис.1.3). Например,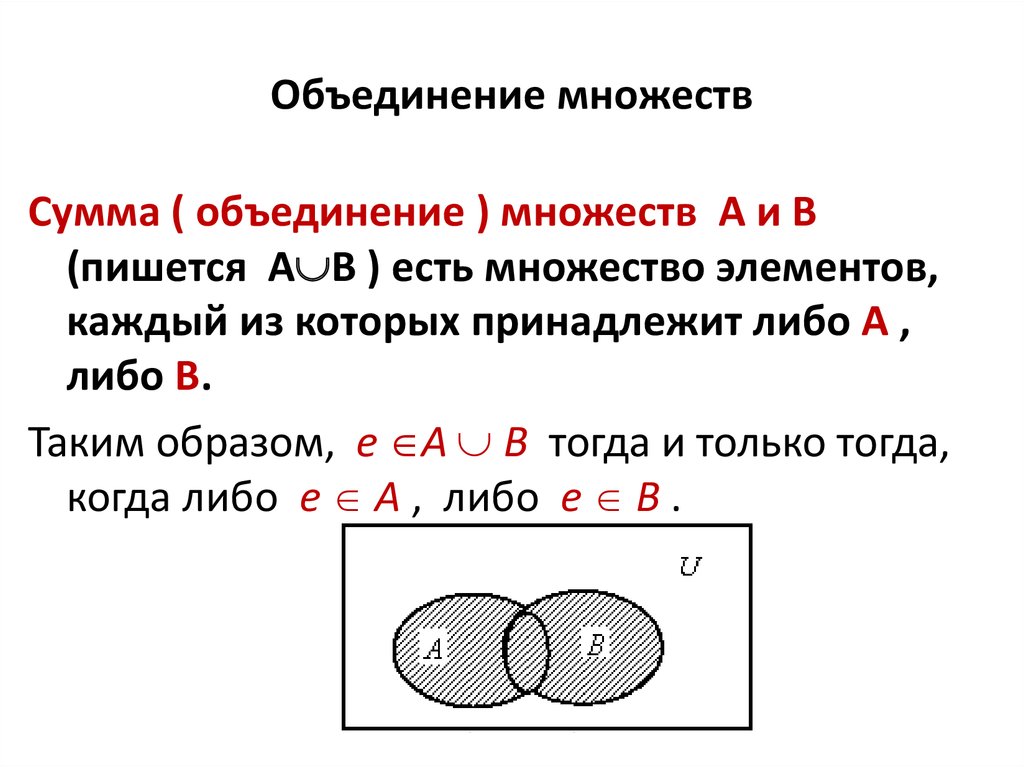 3. Дистрибутивный, или распределительный, закон:
3. Дистрибутивный, или распределительный, закон: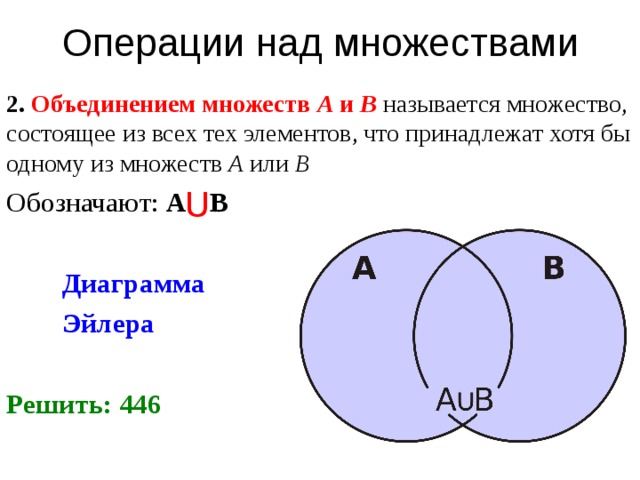 1.2
1.2
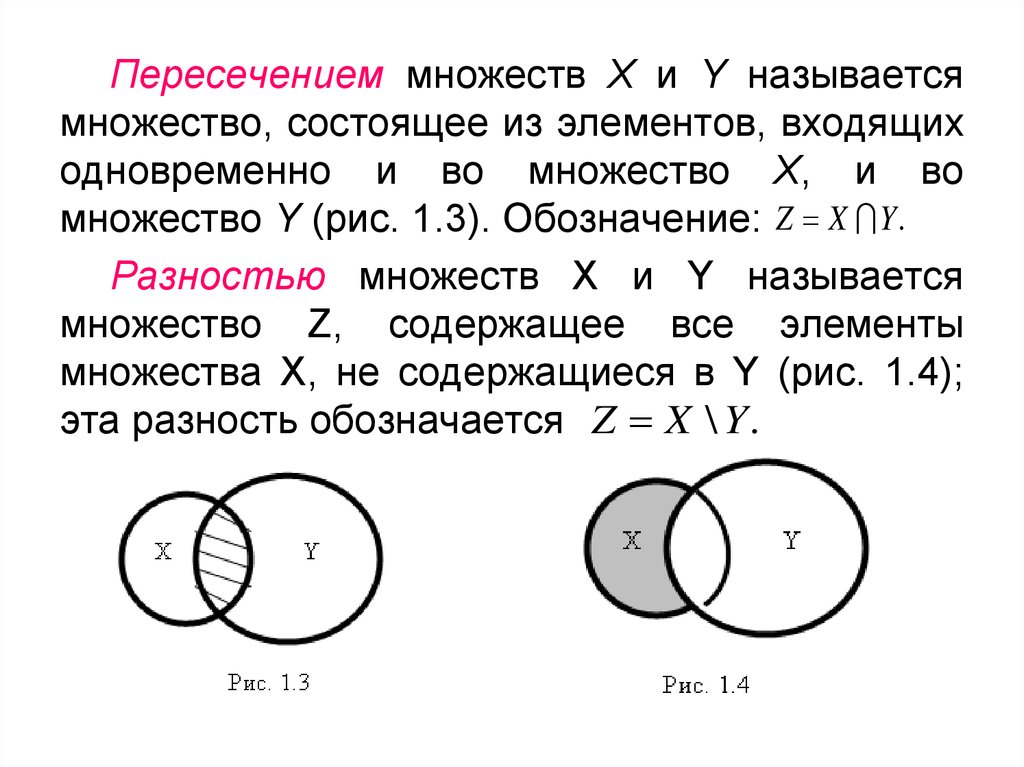 1.6 Рис. 1.7
1.6 Рис. 1.7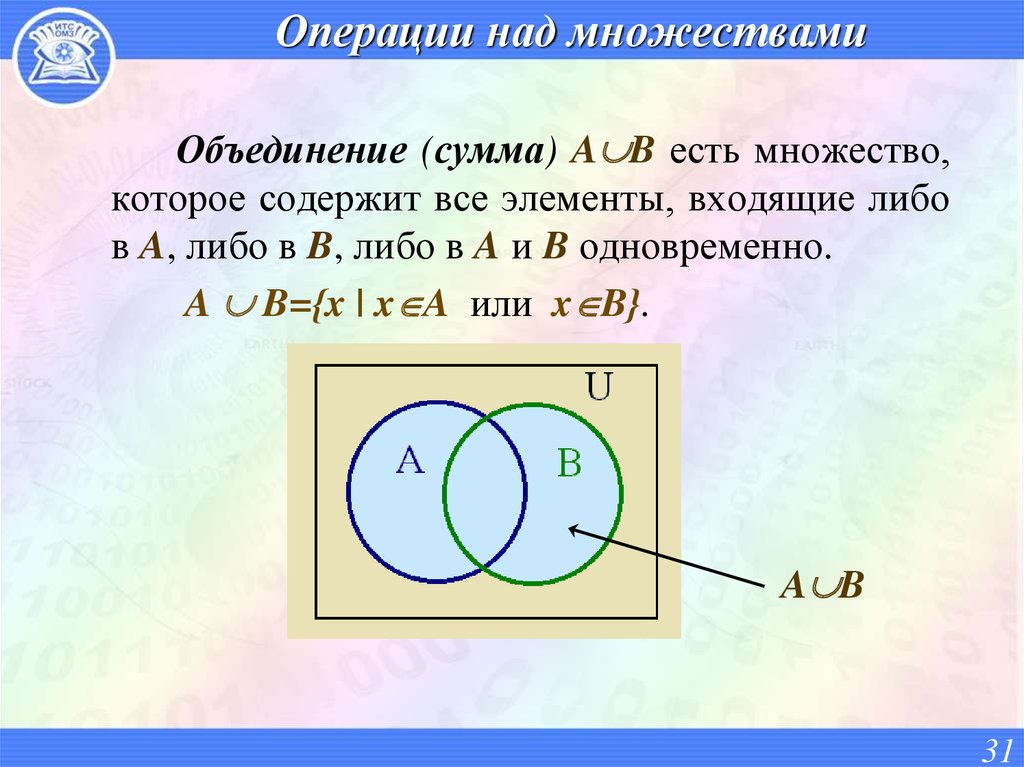
 Пусть Согласно определению разности, получаем и Поскольку выполняются оба эти условия, то это возможно только в случае Получаем, что и т. е. Этим мы доказали, что
Пусть Согласно определению разности, получаем и Поскольку выполняются оба эти условия, то это возможно только в случае Получаем, что и т. е. Этим мы доказали, что 8), из которой выражаем
8), из которой выражаем Обозначение: . Пересечением любого (конечного или счётного) числа множеств называется множество элементов, содержащееся в каждом из множеств .
Обозначение: . Пересечением любого (конечного или счётного) числа множеств называется множество элементов, содержащееся в каждом из множеств .
 Известно, что из них легкой атлетикой занимаются 35 студентов, посещают бассейн 23, играют в настольный теннис 30, занимаются легкой атлетикой и посещают бассейн 10, занимаются легкой атлетикой и играют в настольный теннис 11, посещают бассейн и играют в настольный теннис 7, занимаются во всех трех спортивных секциях 4 студента. Остальные студенты не посещают ни одной спортивной секции. Дайте ответы на следующие вопросы:
Известно, что из них легкой атлетикой занимаются 35 студентов, посещают бассейн 23, играют в настольный теннис 30, занимаются легкой атлетикой и посещают бассейн 10, занимаются легкой атлетикой и играют в настольный теннис 11, посещают бассейн и играют в настольный теннис 7, занимаются во всех трех спортивных секциях 4 студента. Остальные студенты не посещают ни одной спортивной секции. Дайте ответы на следующие вопросы:
 Количество студентов, занимающихся легкой атлетикой, но при этом не играющих в настольный теннис . Количество студентов, которые не посещают ни одной спортивной секции . Количество студентов, которые не занимаются легкой атлетикой и не посещают бассейн , поскольку в это число входят студенты, которые не занимаются ни в одной спортивной секции либо занимаются только настольным теннисом.
Количество студентов, занимающихся легкой атлетикой, но при этом не играющих в настольный теннис . Количество студентов, которые не посещают ни одной спортивной секции . Количество студентов, которые не занимаются легкой атлетикой и не посещают бассейн , поскольку в это число входят студенты, которые не занимаются ни в одной спортивной секции либо занимаются только настольным теннисом.

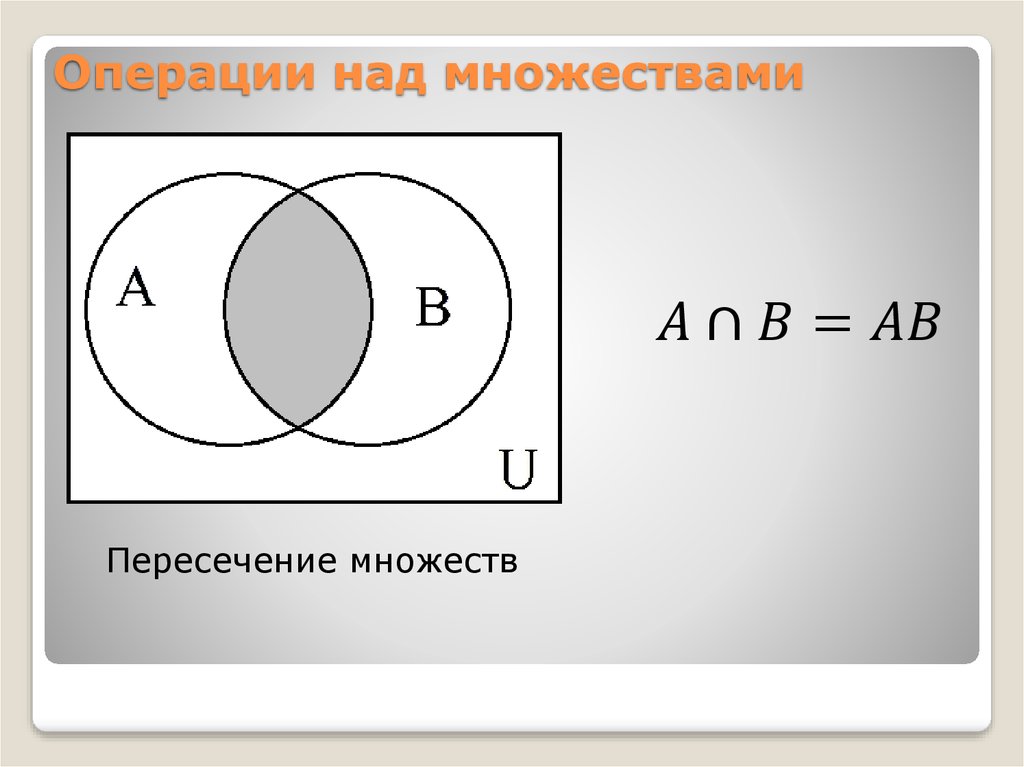 Рассмотрим два множества: множество A, состоящее из чисел 1, 2, 3, 5, 7 и множество B, состоящее из чисел 1, 2, 3, 4, 6, 12, 18
Рассмотрим два множества: множество A, состоящее из чисел 1, 2, 3, 5, 7 и множество B, состоящее из чисел 1, 2, 3, 4, 6, 12, 18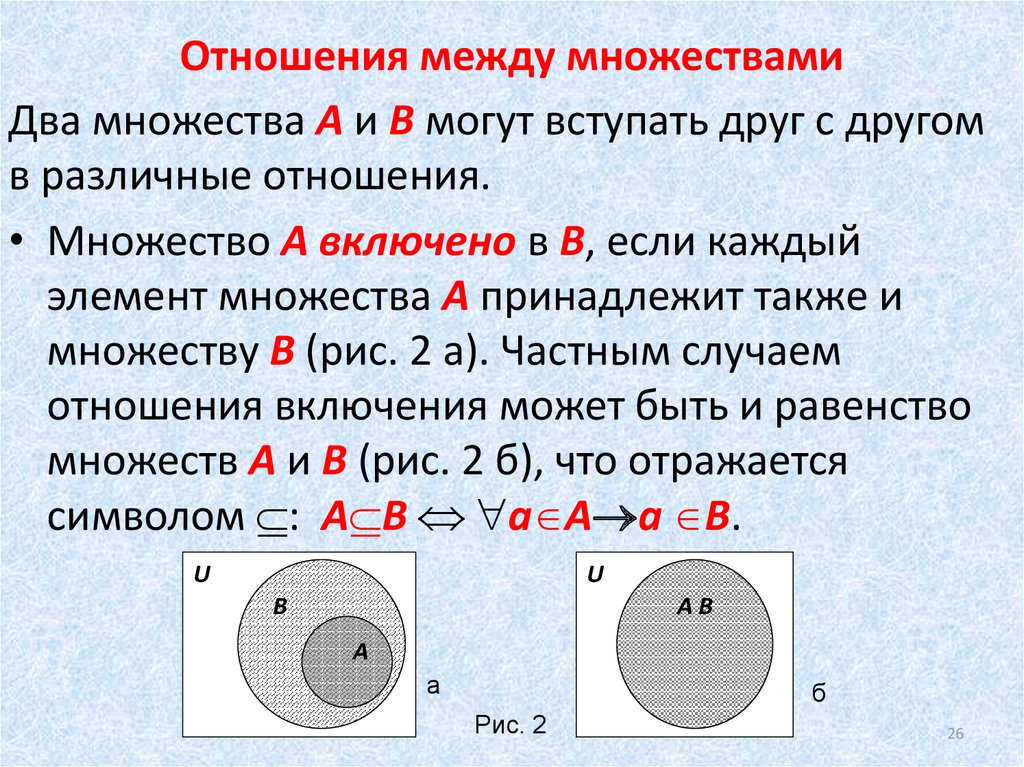
 Чтобы записать пересечение, можно воспользоваться прямым перечислением:
Чтобы записать пересечение, можно воспользоваться прямым перечислением: Рассмотрим несколько примеров.
Рассмотрим несколько примеров.
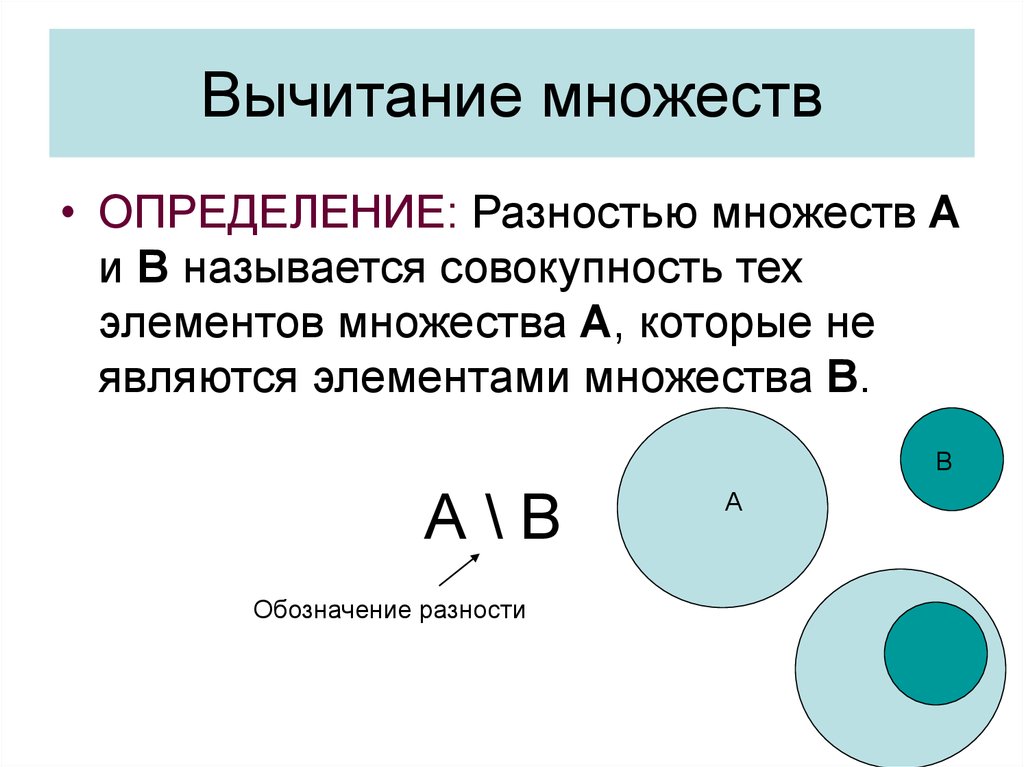 Вспомните, как мы решали их. Сначала находили множество решений первого неравенства, затем множество решений второго. Затем находили множество решений, которые удовлетворяют обоим неравенствам.
Вспомните, как мы решали их. Сначала находили множество решений первого неравенства, затем множество решений второго. Затем находили множество решений, которые удовлетворяют обоим неравенствам.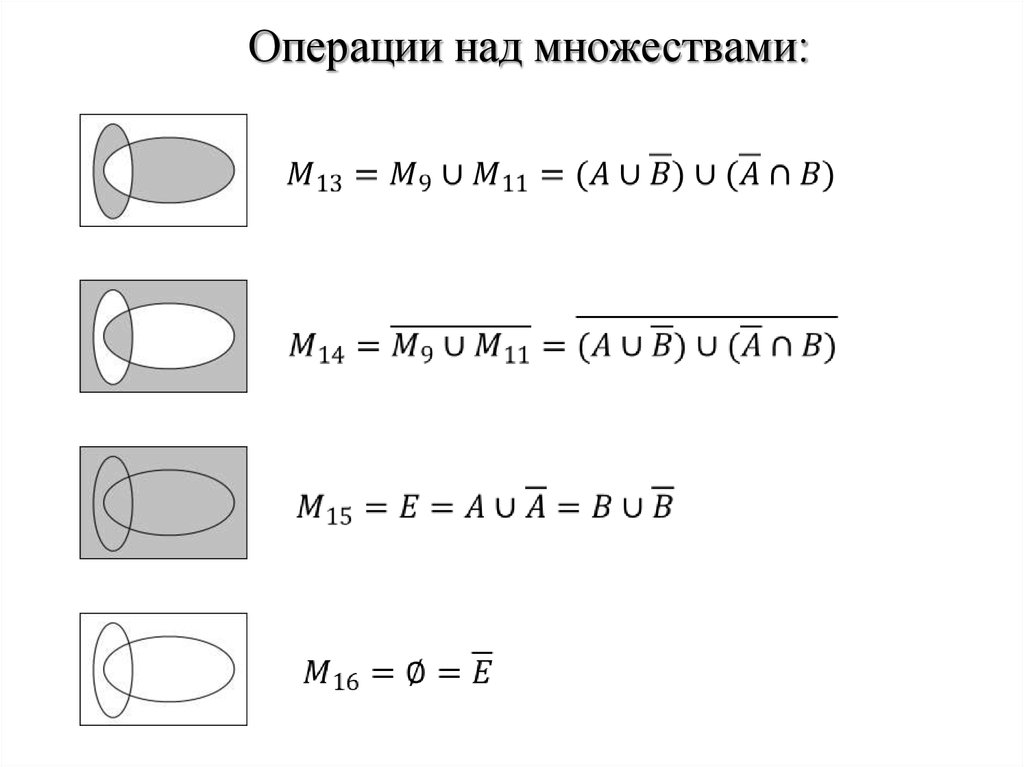 Решить неравенство
Решить неравенство 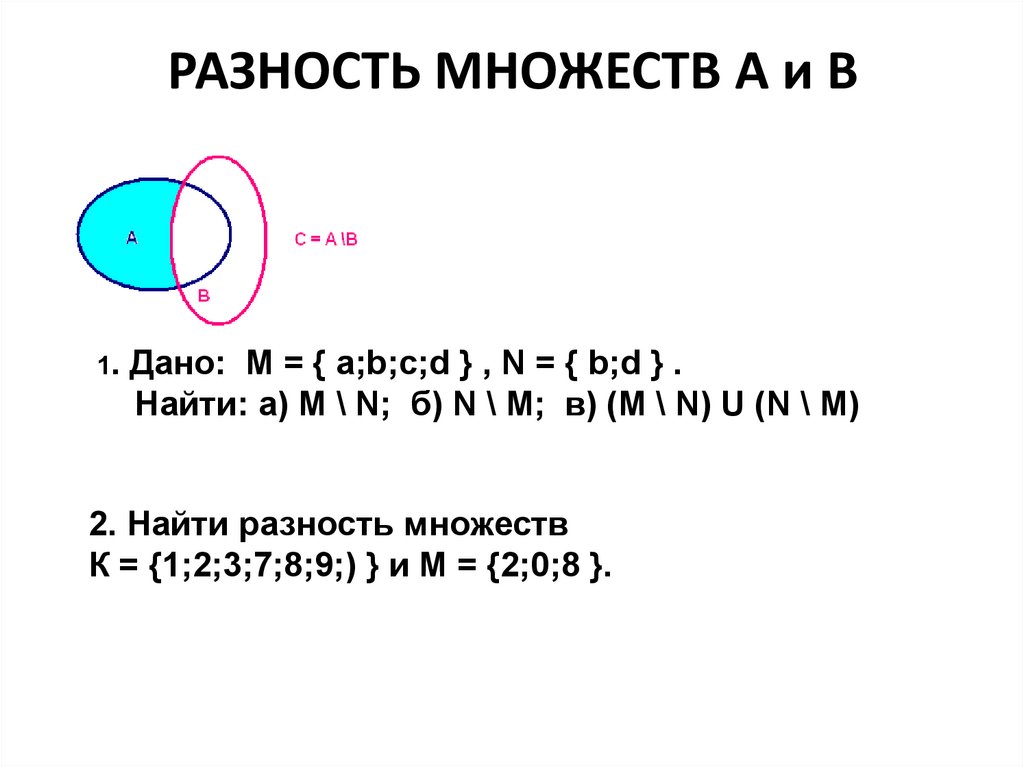
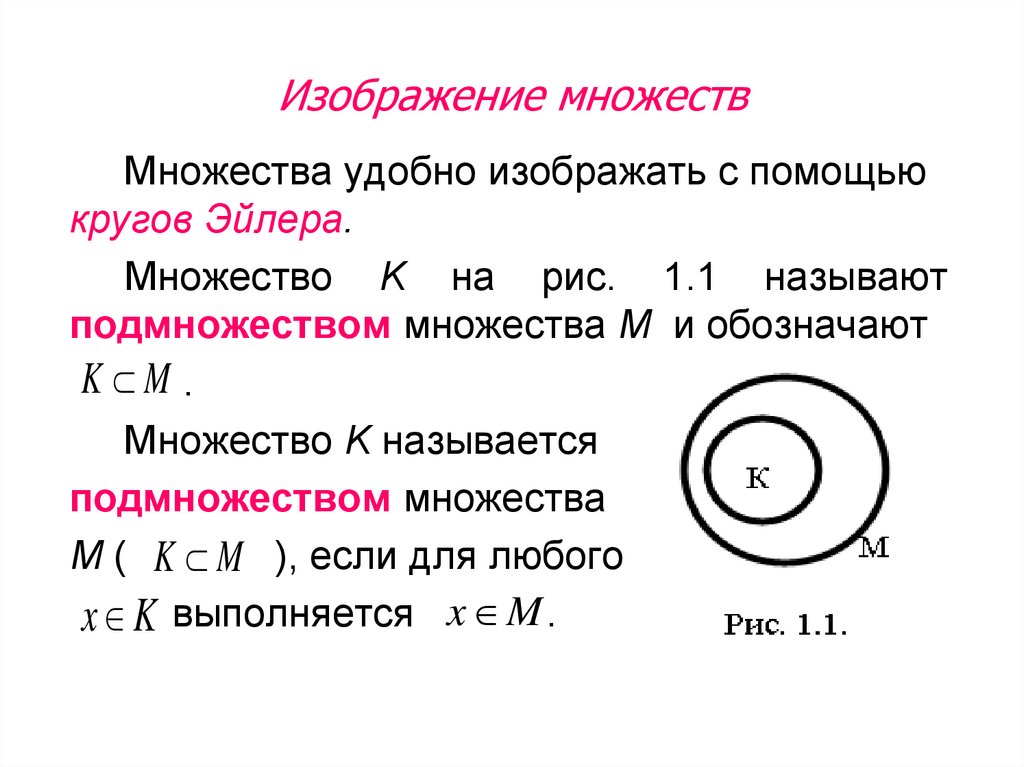
 Что можно про него сказать?
Что можно про него сказать?
 Множеству A не принадлежат элементы 5 и 6. Их и добавим во множество C
Множеству A не принадлежат элементы 5 и 6. Их и добавим во множество C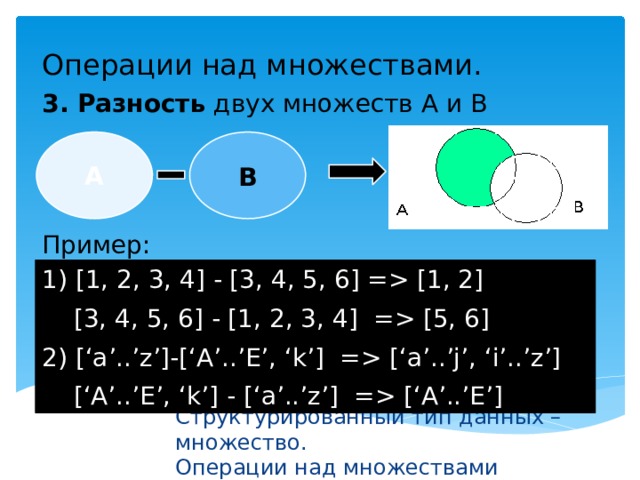
 Но поскольку в объединение допускается включать такие элементы только один раз, мы включили их единоразово.
Но поскольку в объединение допускается включать такие элементы только один раз, мы включили их единоразово.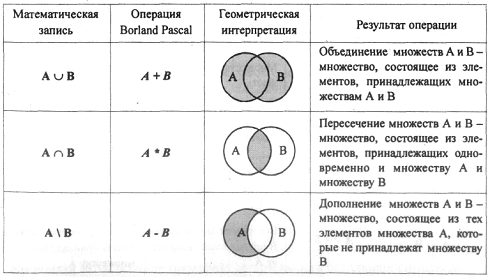 В данном случае число 2 принадлежит промежутку [−3; 5]
В данном случае число 2 принадлежит промежутку [−3; 5]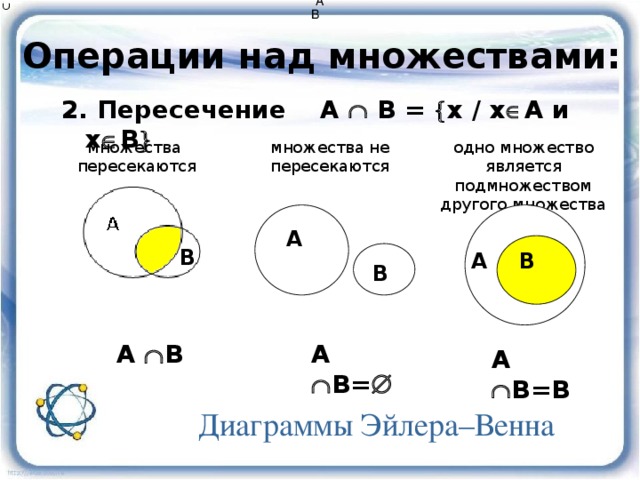 Это множество не является числовым промежутком по причине того, что числа, располагающиеся между −1 и 4, не вошли в полученное множество
Это множество не является числовым промежутком по причине того, что числа, располагающиеся между −1 и 4, не вошли в полученное множество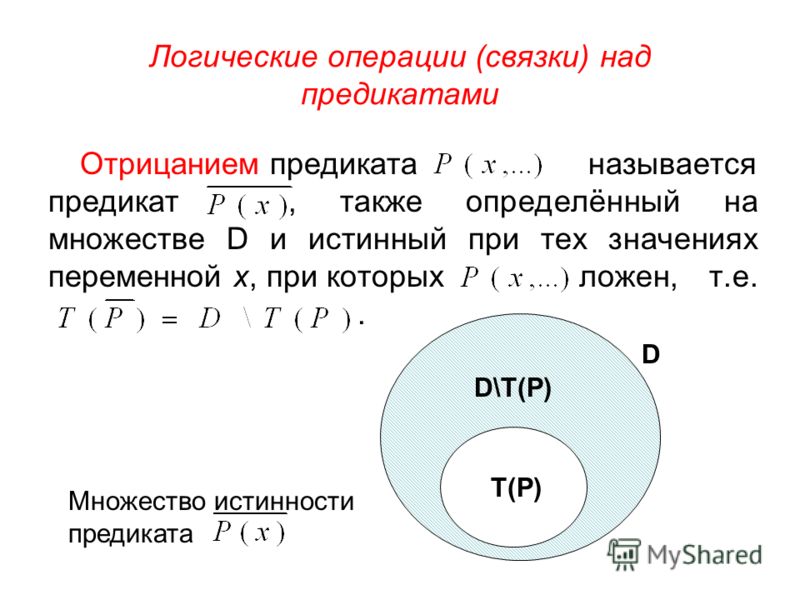
 Для этого воспользуемся объединением множеств. Любое число, являющееся решением неравенства 2x ≠ 8 будет принадлежать либо промежутку (−∞; 4) либо промежутку (4; +∞). Так и записываем, что значения переменной x принадлежат (−∞; 4) или (4; +∞). Напомним, что для слова «или» используется символ ∪
Для этого воспользуемся объединением множеств. Любое число, являющееся решением неравенства 2x ≠ 8 будет принадлежать либо промежутку (−∞; 4) либо промежутку (4; +∞). Так и записываем, что значения переменной x принадлежат (−∞; 4) или (4; +∞). Напомним, что для слова «или» используется символ ∪
 Такой тип неравенств, возможно, вы будете решать редко, но для общего развития полезно изучить и их.
Такой тип неравенств, возможно, вы будете решать редко, но для общего развития полезно изучить и их. Так и записываем:
Так и записываем: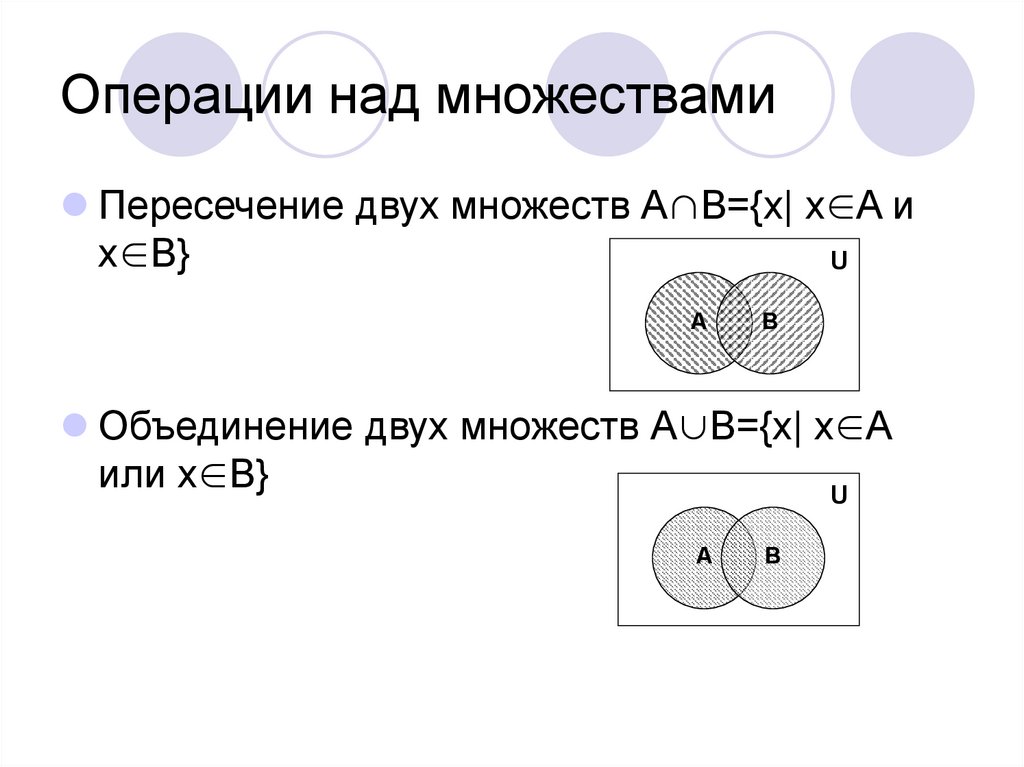
 Решить совокупность неравенств
Решить совокупность неравенств 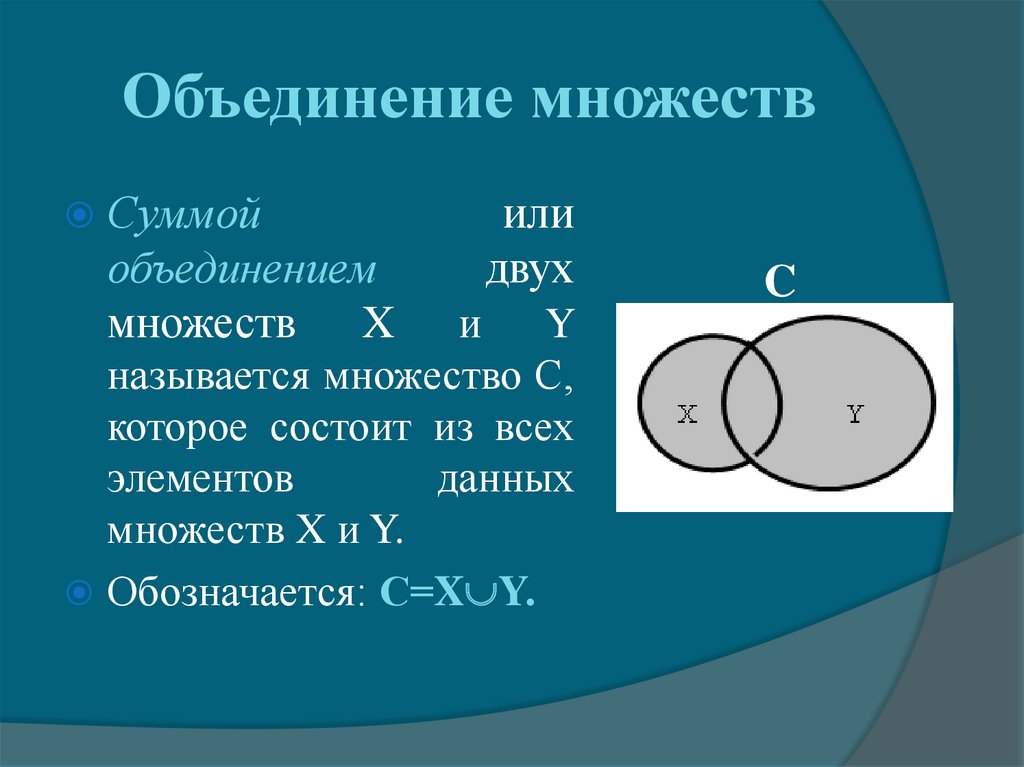 Решить совокупность неравенств
Решить совокупность неравенств 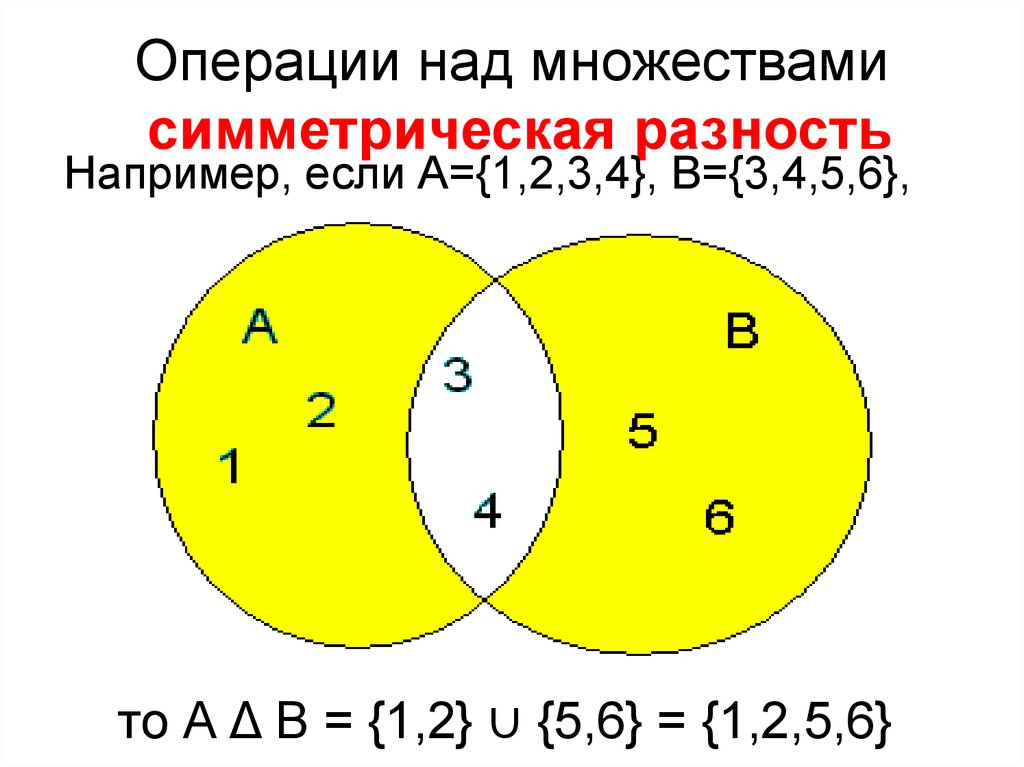 Найдите пересечение и объединение следующих множеств:
Найдите пересечение и объединение следующих множеств: Найдите пересечение и объединение следующих числовых промежутков:
Найдите пересечение и объединение следующих числовых промежутков: На первый взгляд им хочется составить систему уравнений, но в процессе решения остается много неизвестных, что ставит их в тупик. Для того, чтобы уметь решать эти задачи, необходимо предварительно рассмотреть некоторые теоретические разделы теории множеств.
На первый взгляд им хочется составить систему уравнений, но в процессе решения остается много неизвестных, что ставит их в тупик. Для того, чтобы уметь решать эти задачи, необходимо предварительно рассмотреть некоторые теоретические разделы теории множеств.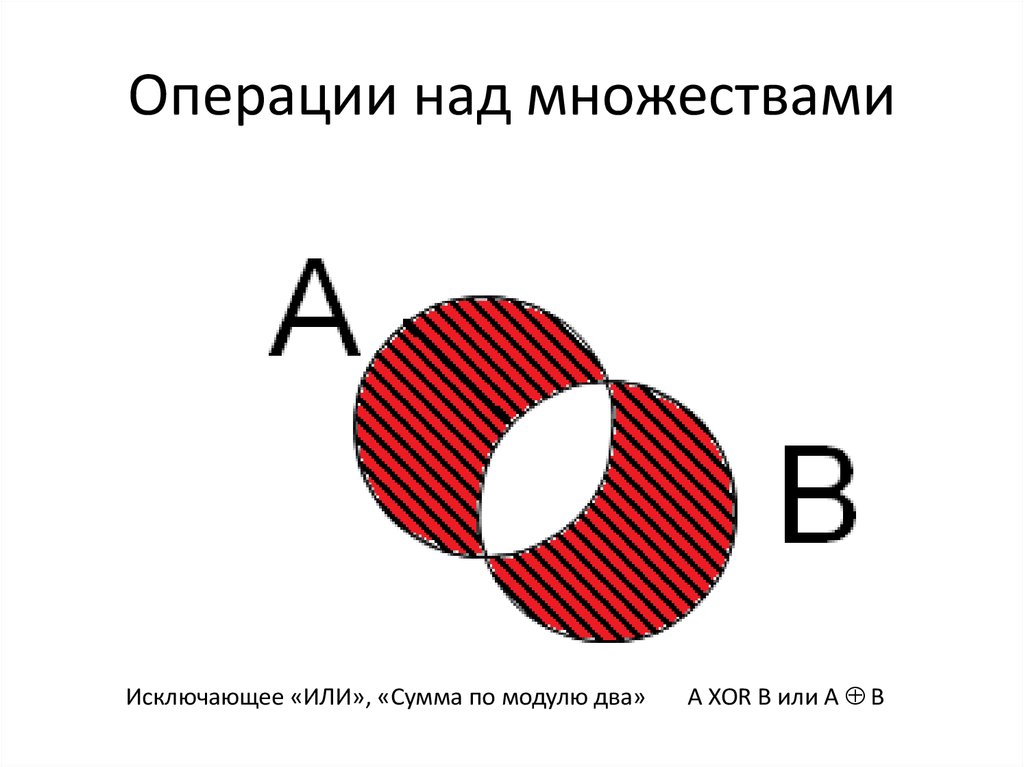 е. если , то , где “С” знак подмножества или включения.
е. если , то , где “С” знак подмножества или включения.
 Здесь уже ключевое слово “и”. Запишем коротко:
Здесь уже ключевое слово “и”. Запишем коротко:
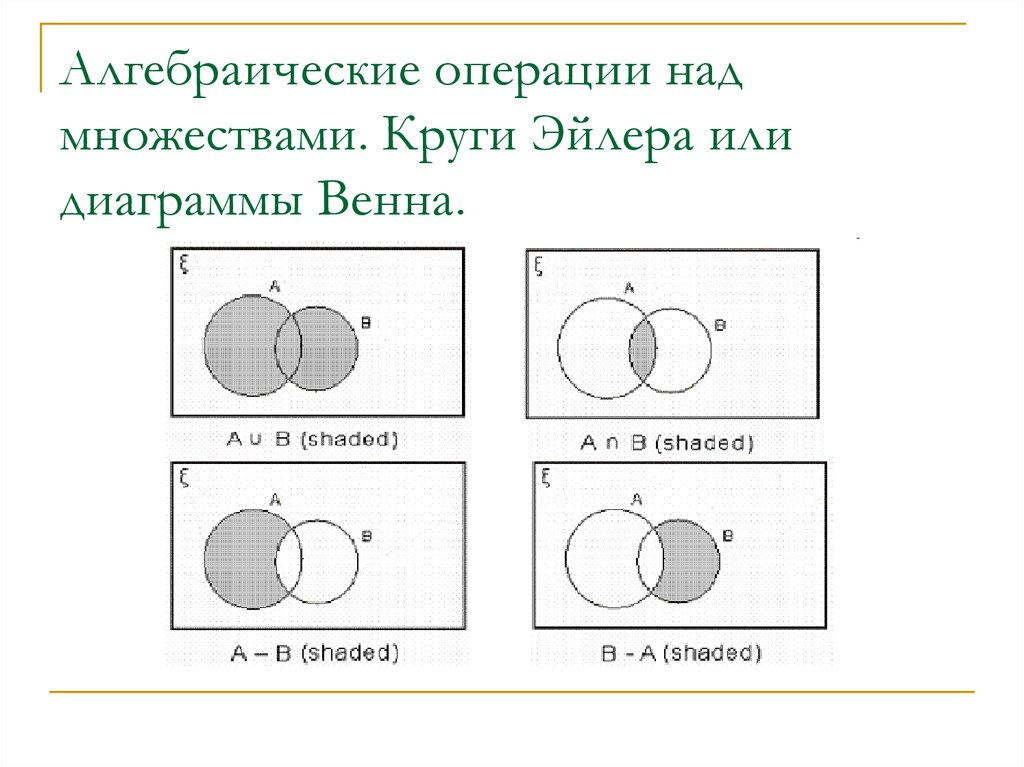 Ни одной задачи не решили 3 человека.
Ни одной задачи не решили 3 человека.
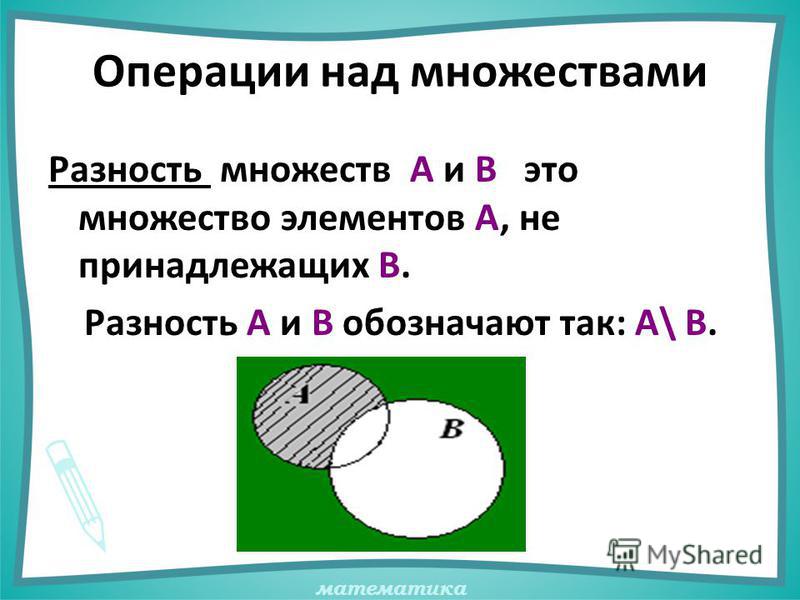 5).
5).

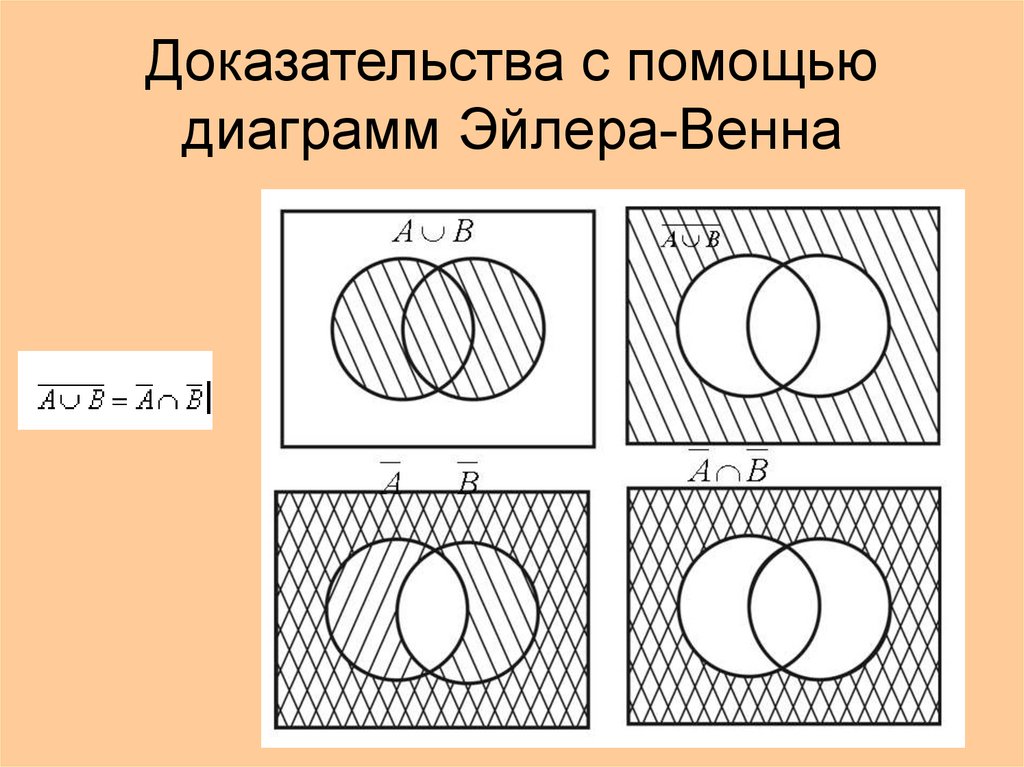
 Например, $\{1,2\}\cup\{2,3\}=\{1,2,3\}$. Таким образом, мы можем написать $x\in(A\cup B)$
тогда и только тогда, когда $(x\in A)$ или $(x\in B)$. Обратите внимание, что $A \cup B=B \cup A$. На рисунке 1.4,
объединение множеств $A$ и $B$ показано заштрихованной областью на диаграмме Венна. 9{n} A_i.$$
Например, если $A_1=\{a,b,c\}, A_2=\{c,h\}, A_3=\{a,d\}$, то $\bigcup_{i} A_i=A_1 \cup А_2
\cup A_3=\{a,b,c,h,d\}$. Аналогичным образом мы можем определить объединение бесконечного числа множеств
$A_1 \чашка A_2 \чашка A_3 \чашка\cdots$.
Например, $\{1,2\}\cup\{2,3\}=\{1,2,3\}$. Таким образом, мы можем написать $x\in(A\cup B)$
тогда и только тогда, когда $(x\in A)$ или $(x\in B)$. Обратите внимание, что $A \cup B=B \cup A$. На рисунке 1.4,
объединение множеств $A$ и $B$ показано заштрихованной областью на диаграмме Венна. 9{n} A_i.$$
Например, если $A_1=\{a,b,c\}, A_2=\{c,h\}, A_3=\{a,d\}$, то $\bigcup_{i} A_i=A_1 \cup А_2
\cup A_3=\{a,b,c,h,d\}$. Аналогичным образом мы можем определить объединение бесконечного числа множеств
$A_1 \чашка A_2 \чашка A_3 \чашка\cdots$. е. их пересечение есть пустое множество $A \cap B=\emptyset$. В общем, несколько наборов
называются непересекающимися, если они попарно не пересекаются, т. е. никакие два из них не имеют общих элементов.
На рис. 1.9 показаны три непересекающихся множества.
е. их пересечение есть пустое множество $A \cap B=\emptyset$. В общем, несколько наборов
называются непересекающимися, если они попарно не пересекаются, т. е. никакие два из них не имеют общих элементов.
На рис. 1.9 показаны три непересекающихся множества.
 $$
Например, если $A=\{1,2,3\}$ и $B=\{H,T\}$, то
$$A \times B=\{(1,H),(1,T),(2,H),(2,T),(3,H),(3,T)\}.$$
Обратите внимание, что здесь пары упорядочены, например, $(1,H)\neq (H,1)$. Таким образом, $A \times B$ равно не то же, что $B \times A$.
$$
Например, если $A=\{1,2,3\}$ и $B=\{H,T\}$, то
$$A \times B=\{(1,H),(1,T),(2,H),(2,T),(3,H),(3,T)\}.$$
Обратите внимание, что здесь пары упорядочены, например, $(1,H)\neq (H,1)$. Таким образом, $A \times B$ равно не то же, что $B \times A$.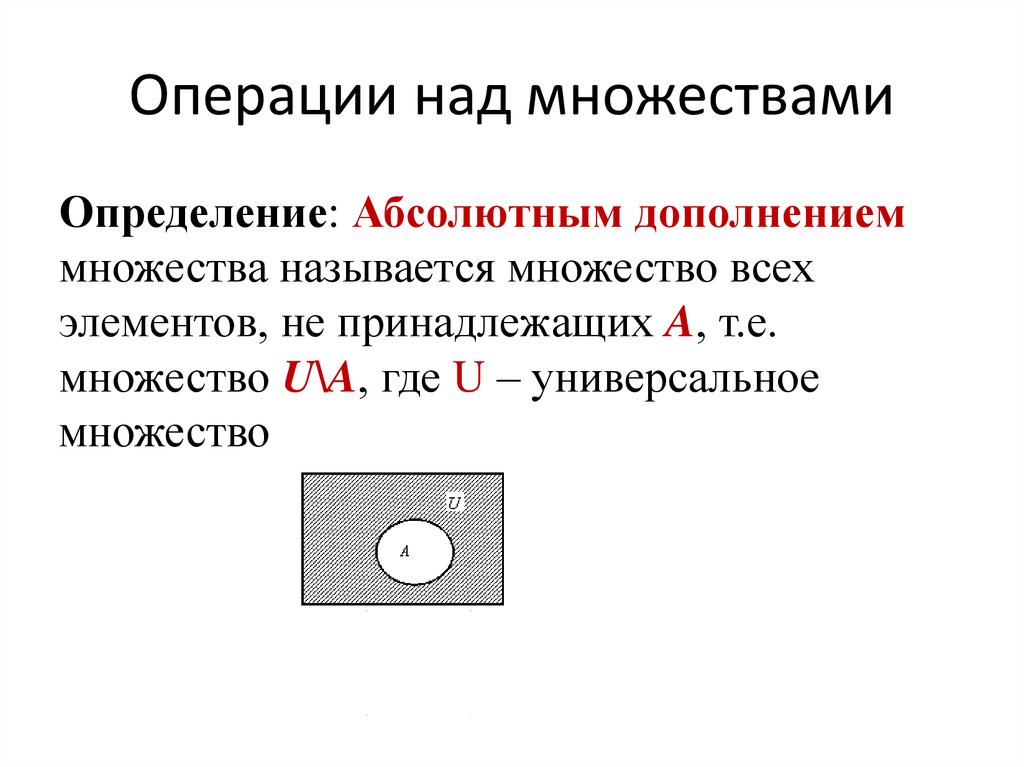 $$ 93=\mathbb{R}\times \mathbb{R} \times \mathbb{R}$ и так далее.
$$ 93=\mathbb{R}\times \mathbb{R} \times \mathbb{R}$ и так далее.
 Диаграмма Венна — это логическая диаграмма, показывающая возможную связь между различными конечными множествами. Диаграмму Венна можно представить следующим образом.
Диаграмма Венна — это логическая диаграмма, показывающая возможную связь между различными конечными множествами. Диаграмму Венна можно представить следующим образом.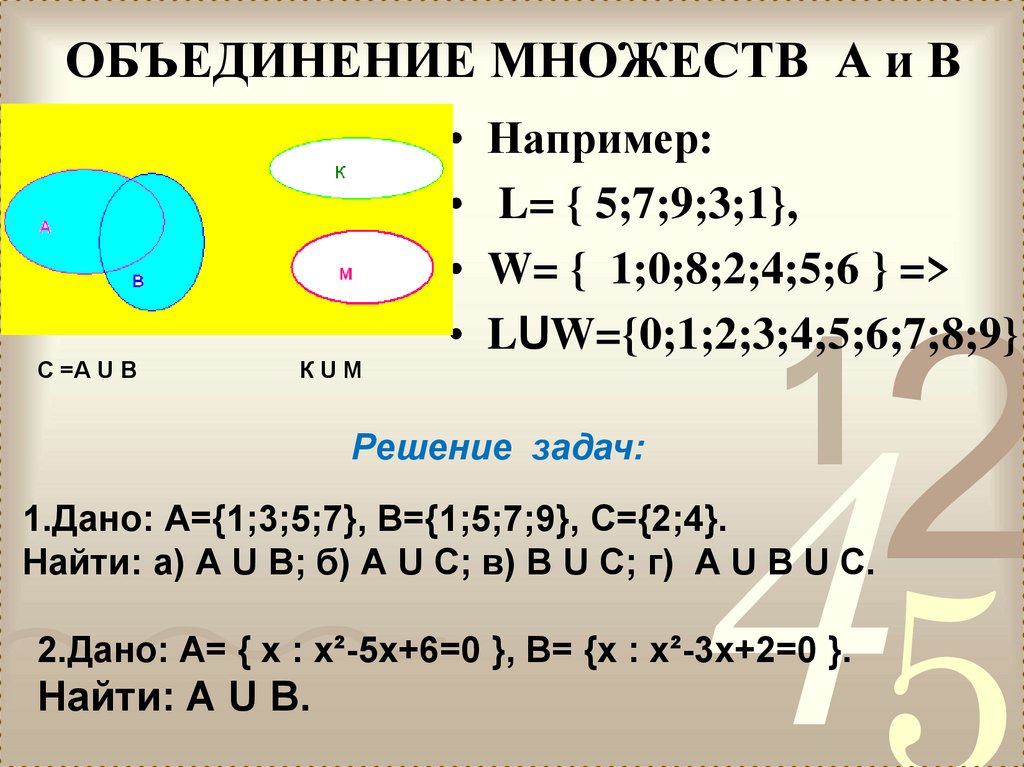 Количество элементов в A ∩ B определяется выражением n(A∩B) = n(A)+n(B)−n(A∪B), где n(X) — количество элементов в множестве X. Чтобы лучше понять эту операцию пересечения множеств, рассмотрим пример: если A = {1, 2, 3, 4} и B = {3, 4, 5, 7}, то пересечение A и B задается A ∩ B = {3, 4} .
Количество элементов в A ∩ B определяется выражением n(A∩B) = n(A)+n(B)−n(A∪B), где n(X) — количество элементов в множестве X. Чтобы лучше понять эту операцию пересечения множеств, рассмотрим пример: если A = {1, 2, 3, 4} и B = {3, 4, 5, 7}, то пересечение A и B задается A ∩ B = {3, 4} .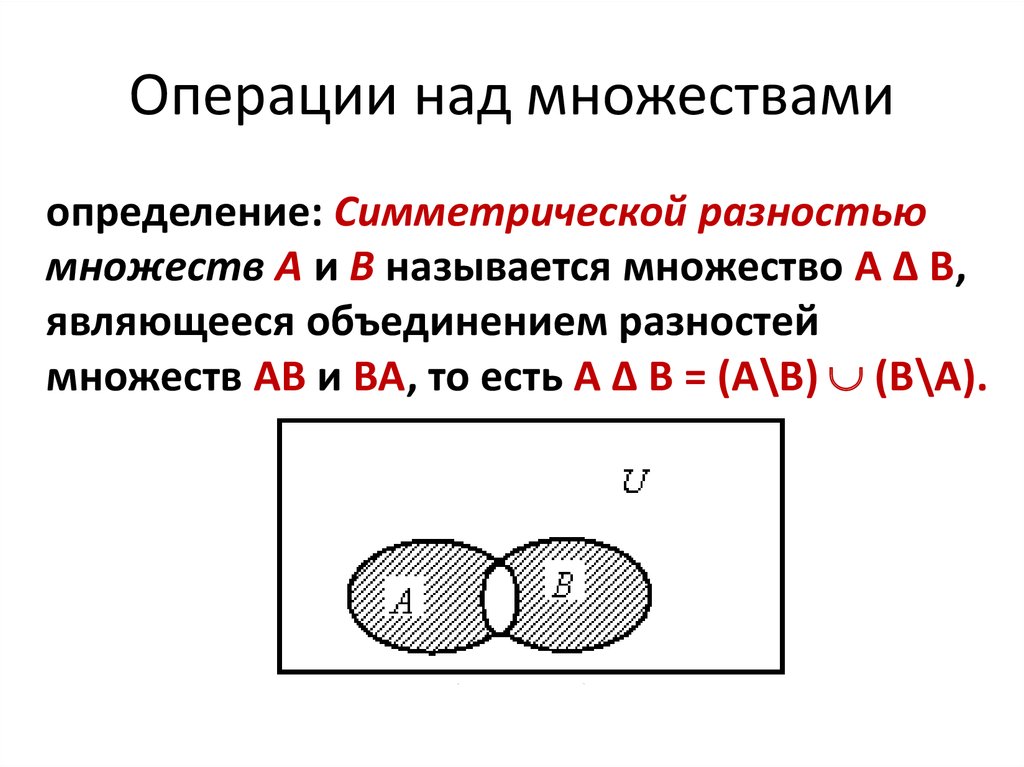 Чтобы понять эту операцию дополнения множеств лучше, рассмотрим пример: если U = {1, 2, 3, 4, 5, 6, 7, 8, 9} и A = {1, 2, 3, 4}, тогда дополнение множества A задается как A’ = {5, 6, 7, 8, 9}.
Чтобы понять эту операцию дополнения множеств лучше, рассмотрим пример: если U = {1, 2, 3, 4, 5, 6, 7, 8, 9} и A = {1, 2, 3, 4}, тогда дополнение множества A задается как A’ = {5, 6, 7, 8, 9}.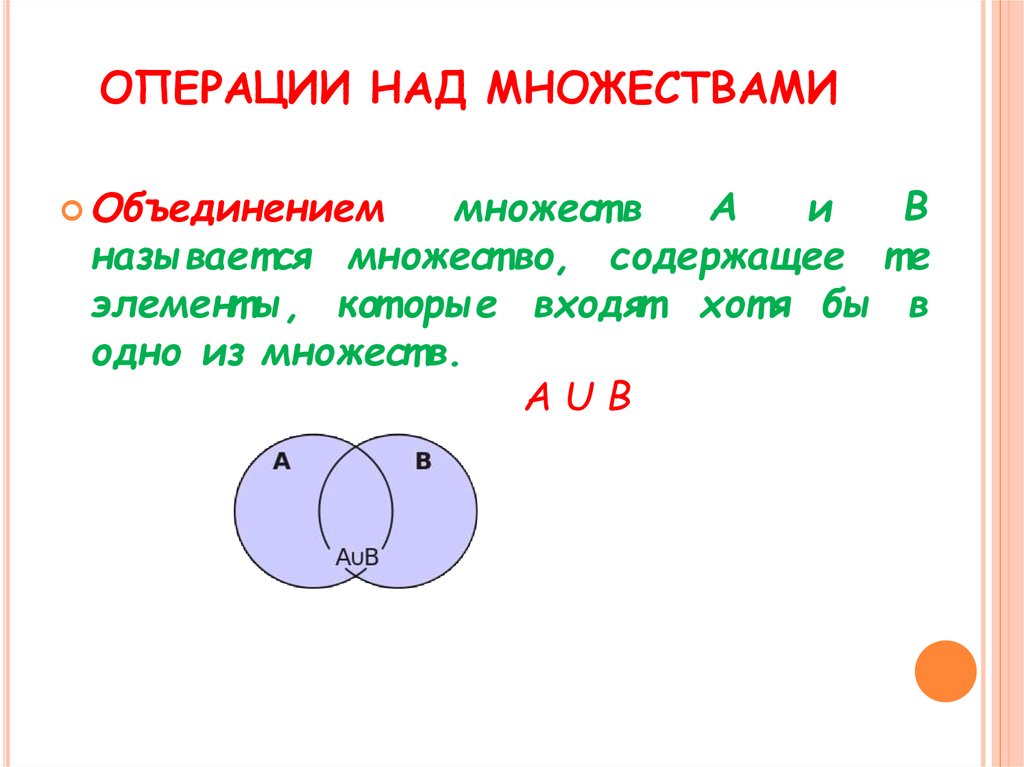

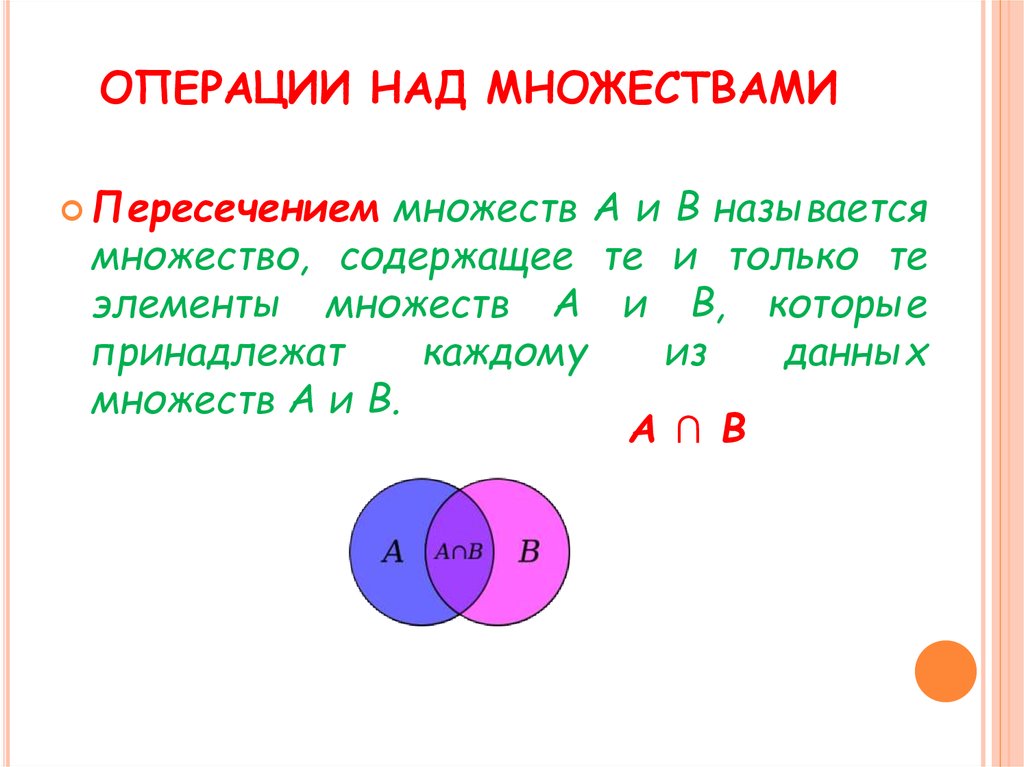 Некоторыми реальными примерами множеств являются список всех штатов в стране, список всех фигур в геометрии, список всех целых чисел от 1 до 100. Мы можем определить общие области, используя операцию пересечения множества.
Некоторыми реальными примерами множеств являются список всех штатов в стране, список всех фигур в геометрии, список всех целых чисел от 1 до 100. Мы можем определить общие области, используя операцию пересечения множества.


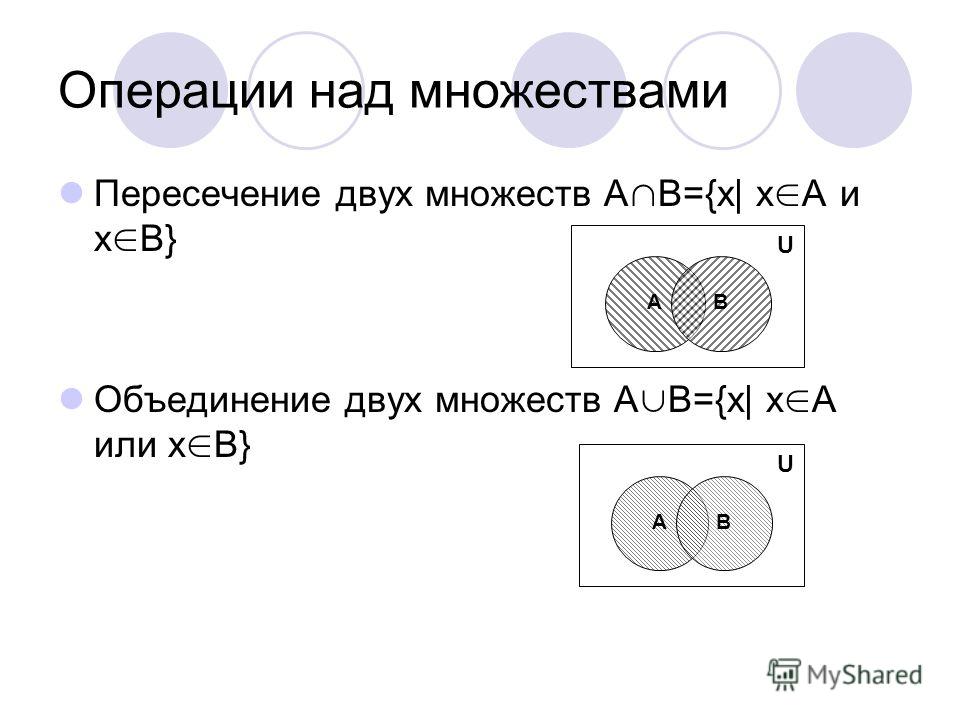 Разность A и B, обозначаемая \(A – B\), представляет собой множество всех элементов A, которые не входят в B .
Разность A и B, обозначаемая \(A – B\), представляет собой множество всех элементов A, которые не входят в B .
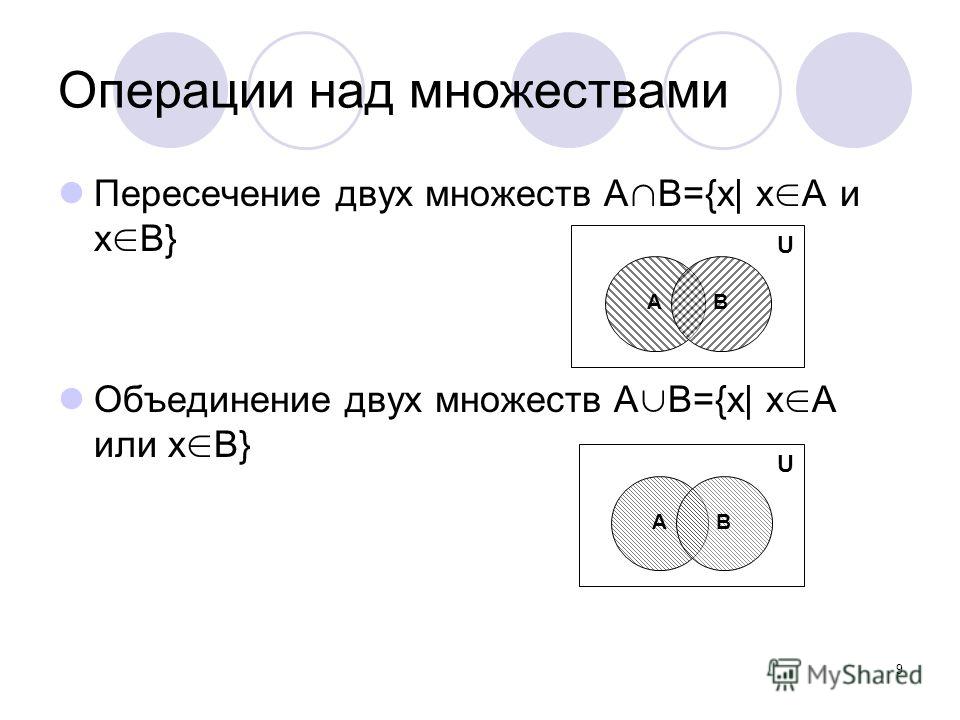 д. Теория множеств в основном используется в Исследование аксиоматической вероятности .
д. Теория множеств в основном используется в Исследование аксиоматической вероятности . Пусть \(U\) обозначает множество опрошенных студентов, \(A\) обозначает множество студентов, пьющих яблочный сок, а \(B\) обозначает множество студентов, пьющих апельсиновый сок. Затем
Пусть \(U\) обозначает множество опрошенных студентов, \(A\) обозначает множество студентов, пьющих яблочный сок, а \(B\) обозначает множество студентов, пьющих апельсиновый сок. Затем

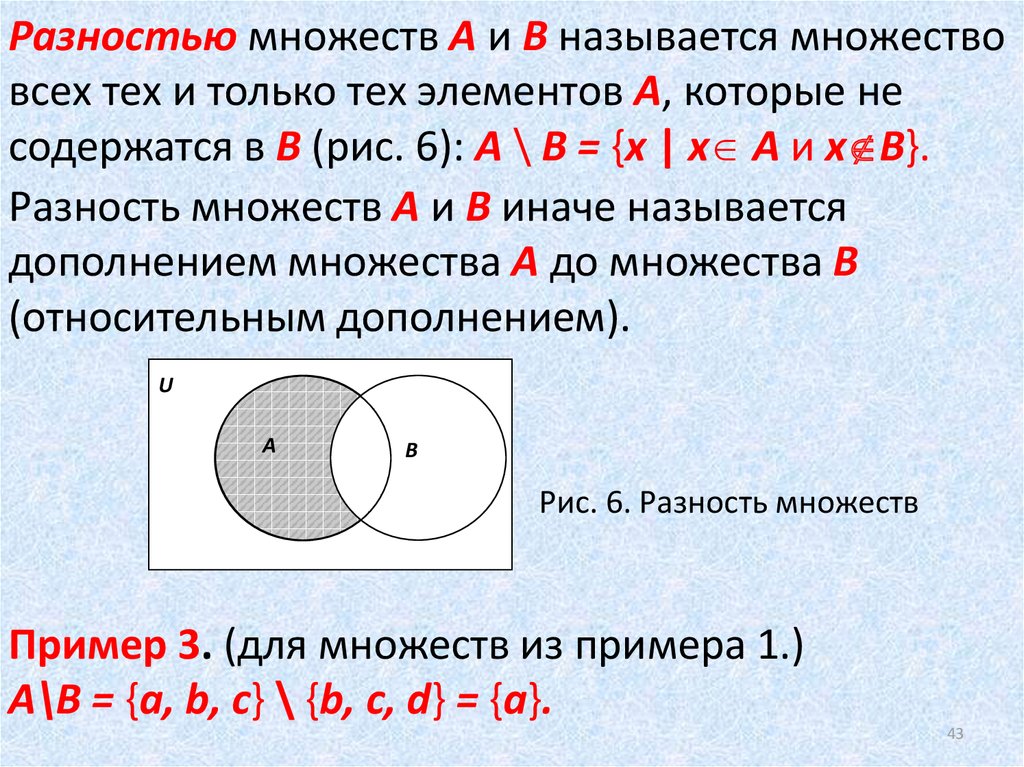 Синтаксис
Синтаксис 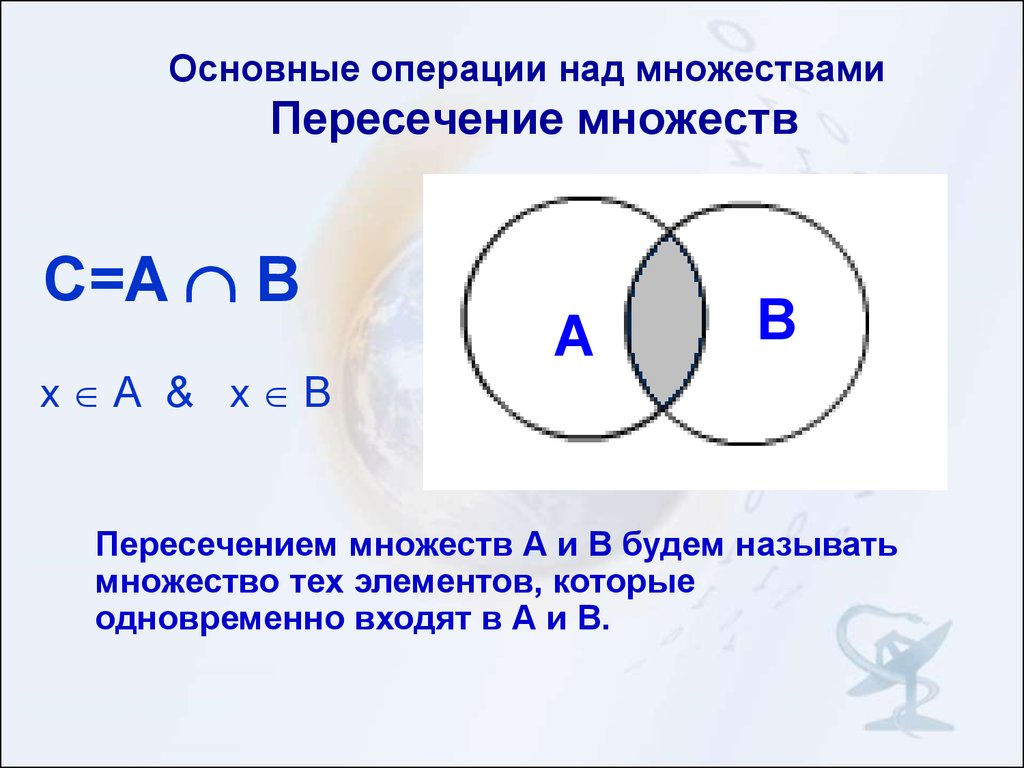 update(("виолончель" ,))
>>> add_Set
{1, 2, 3, 4, "скрипка", "виолончель"}
update(("виолончель" ,))
>>> add_Set
{1, 2, 3, 4, "скрипка", "виолончель"} 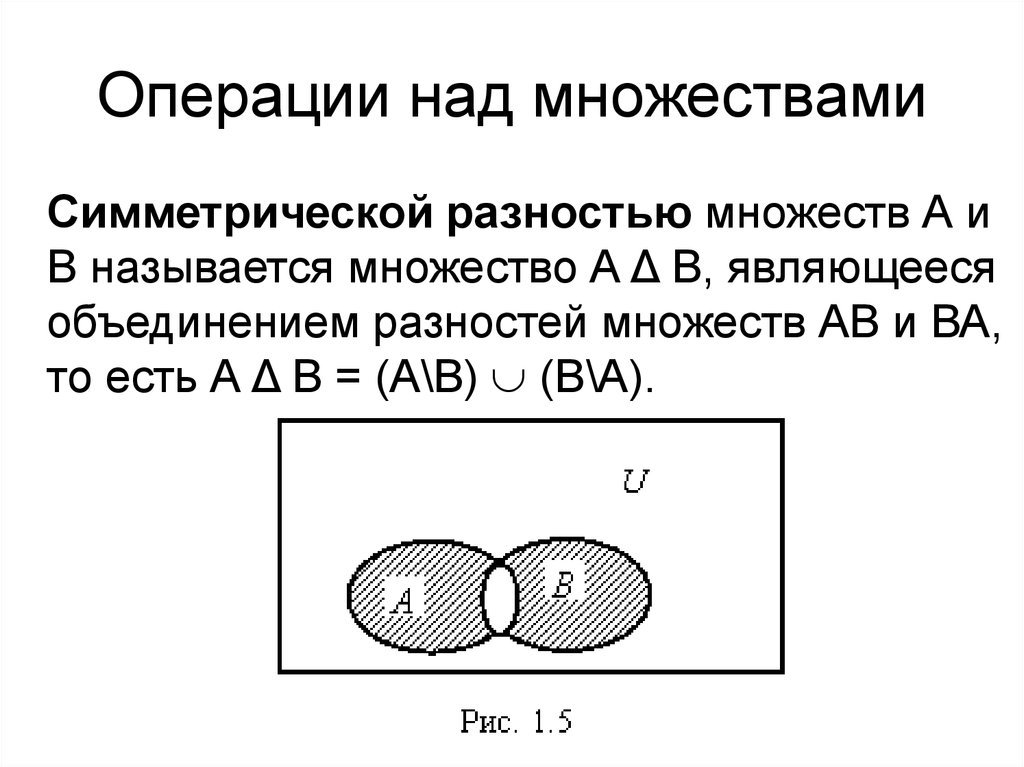
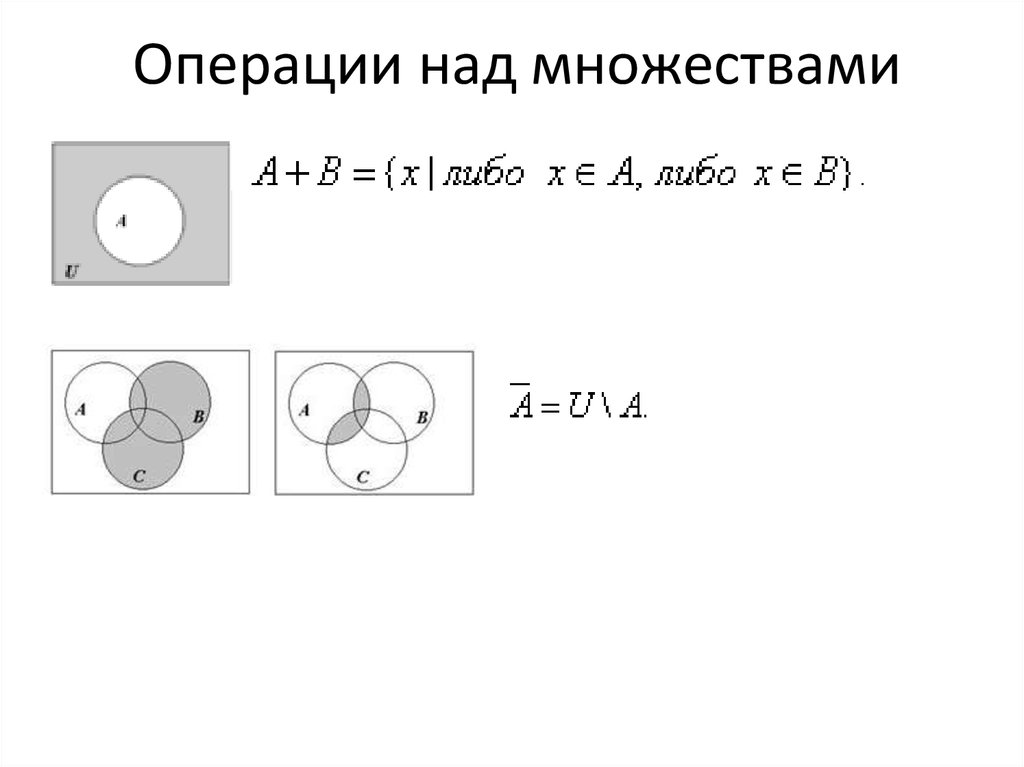
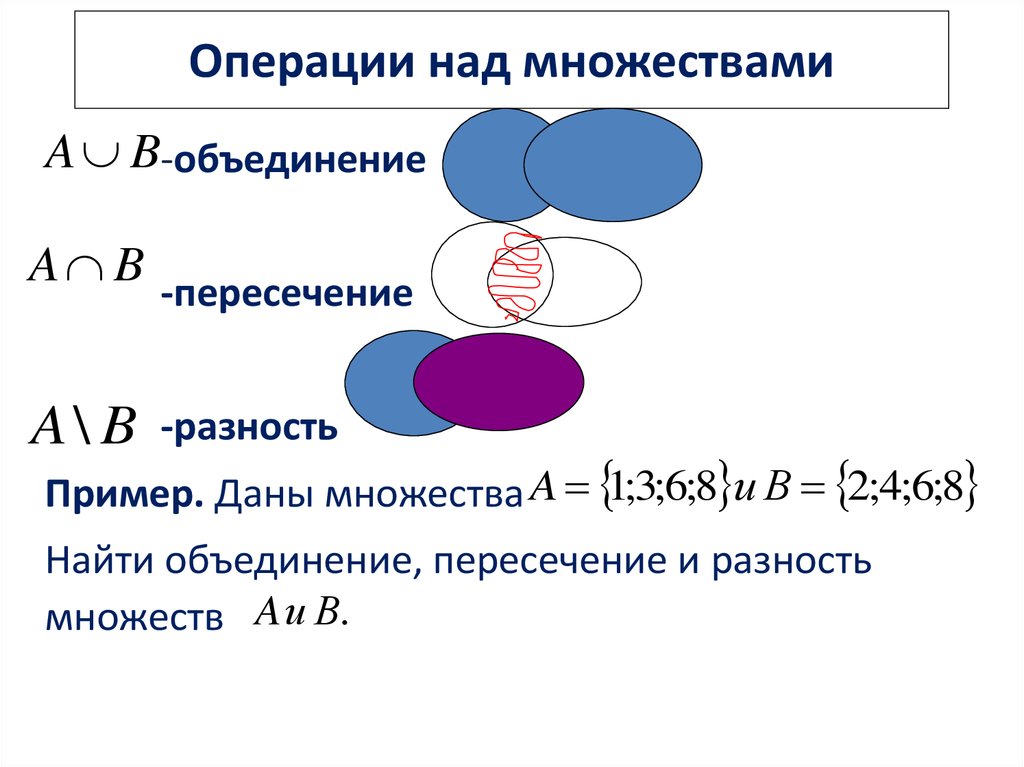 difference(second_set)
{1, 2, 3}
>>>
>>> first_set - second_set # с использованием оператора `-`
{1, 2, 3}
>>>
>>> второй_набор - первый_набор
{8, 9, 7}
difference(second_set)
{1, 2, 3}
>>>
>>> first_set - second_set # с использованием оператора `-`
{1, 2, 3}
>>>
>>> второй_набор - первый_набор
{8, 9, 7} 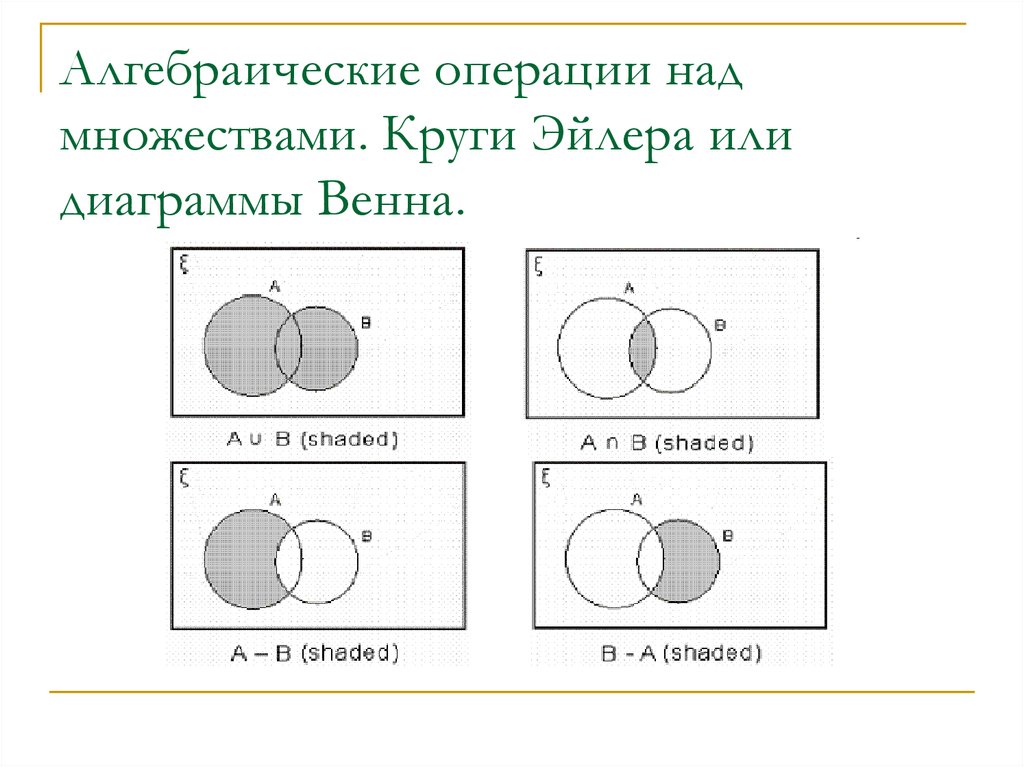 isdisjoint(b)
isdisjoint(b) 

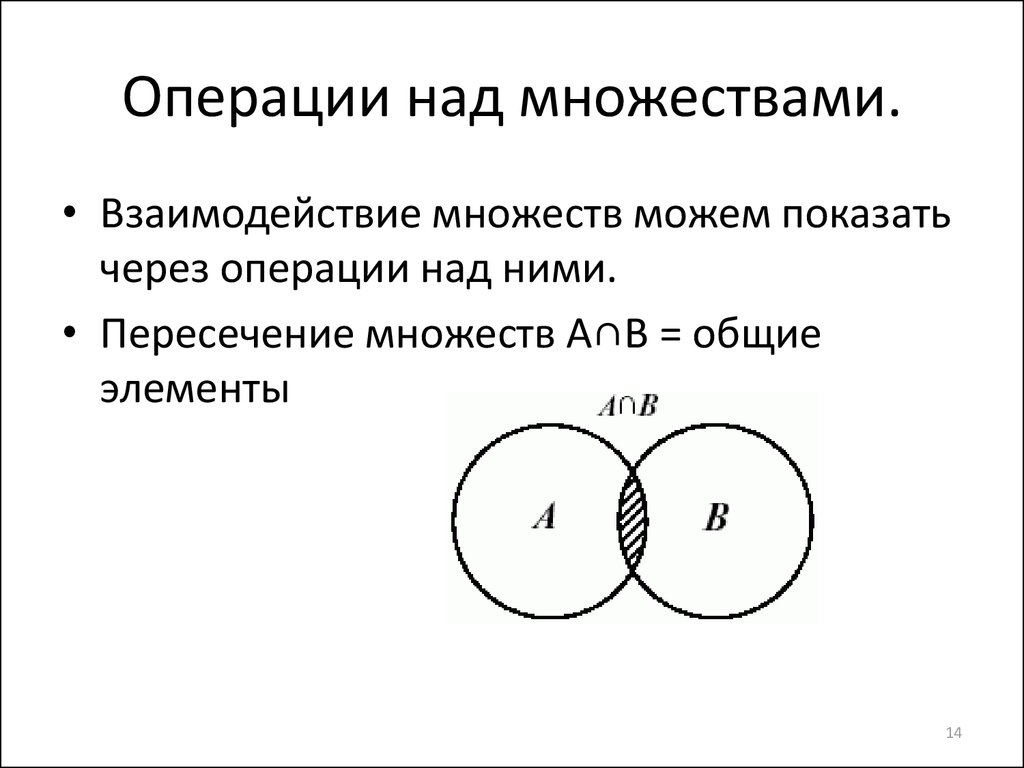

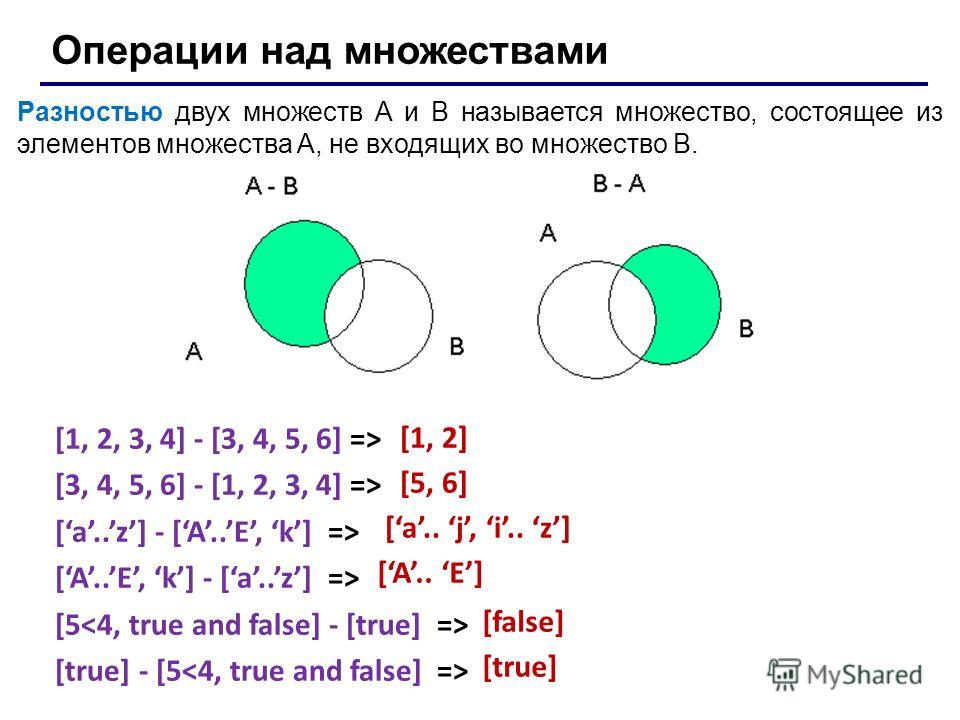 Это может создать проблемы, когда у нас есть клиенты с одним и тем же именем, но в разных странах или городах.
Это может создать проблемы, когда у нас есть клиенты с одним и тем же именем, но в разных странах или городах.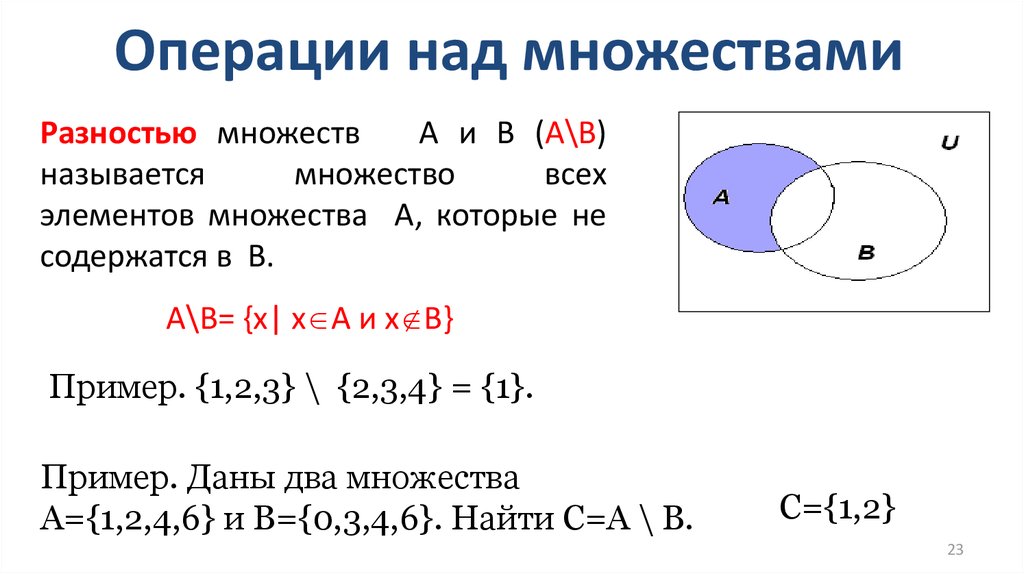 Оператор Union ALL тоже принял во внимание и дважды вернул Акшая Гупту. То же самое и с Аканшей Сингхом.
Оператор Union ALL тоже принял во внимание и дважды вернул Акшая Гупту. То же самое и с Аканшей Сингхом.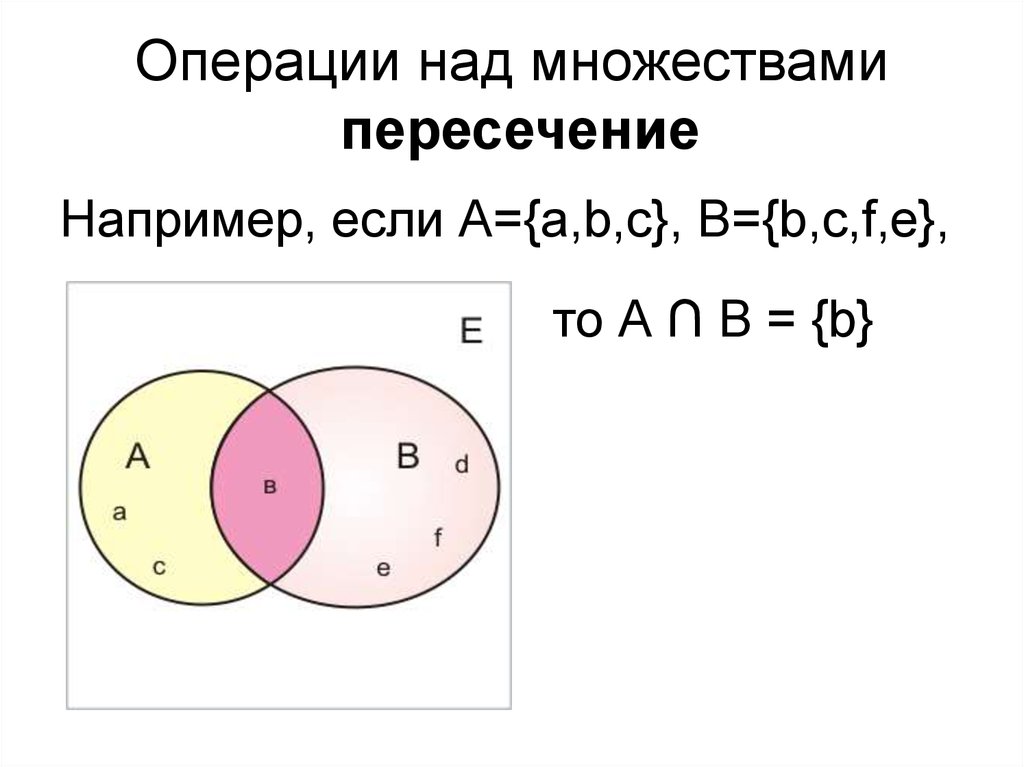
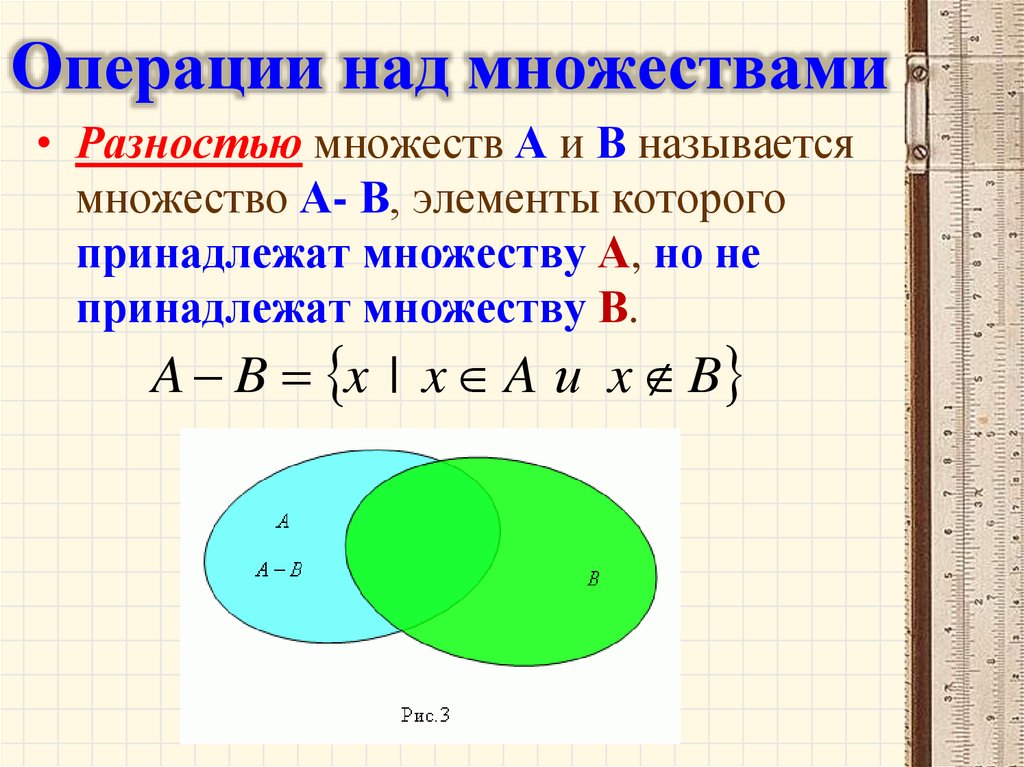 Набор определяется как четко определенный набор объектов, и эти объекты известны как элементы набора. Набор обозначается заглавными буквами.
Набор определяется как четко определенный набор объектов, и эти объекты известны как элементы набора. Набор обозначается заглавными буквами. Там, где требуется установить связь между двумя или более множествами, возникает понятие операций над множествами.
Там, где требуется установить связь между двумя или более множествами, возникает понятие операций над множествами.
 Символически представляется как:
Символически представляется как: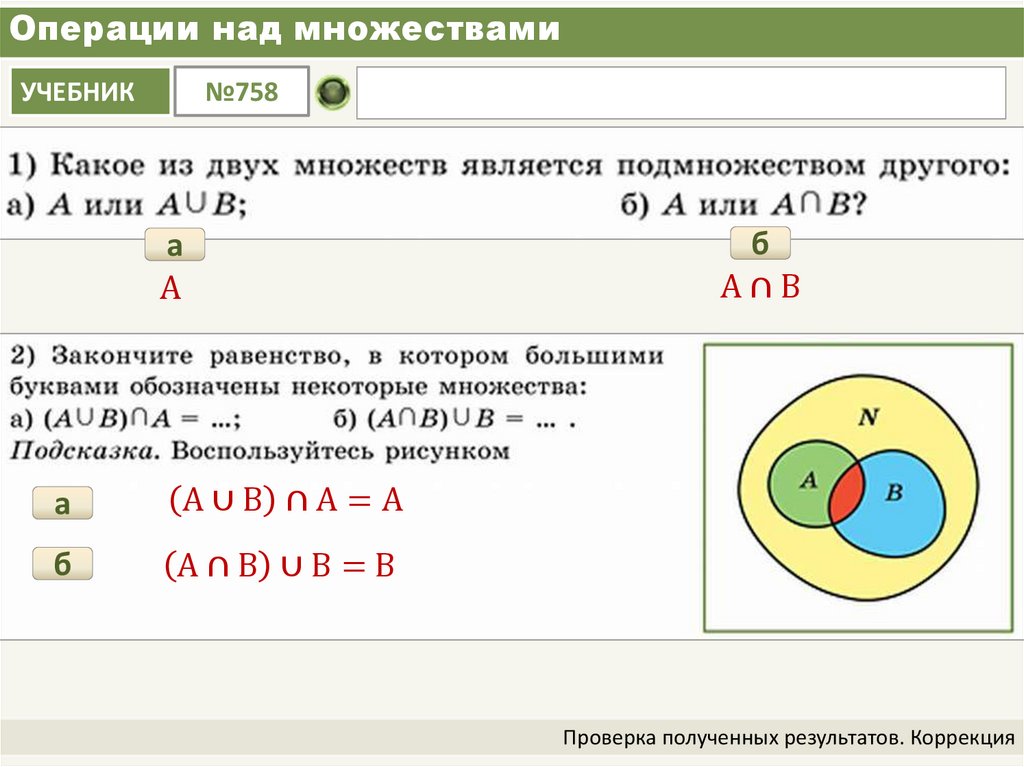 Мы можем составить это пересечение по формуле:
Мы можем составить это пересечение по формуле: т. е. множества не содержат общих элементов.
т. е. множества не содержат общих элементов.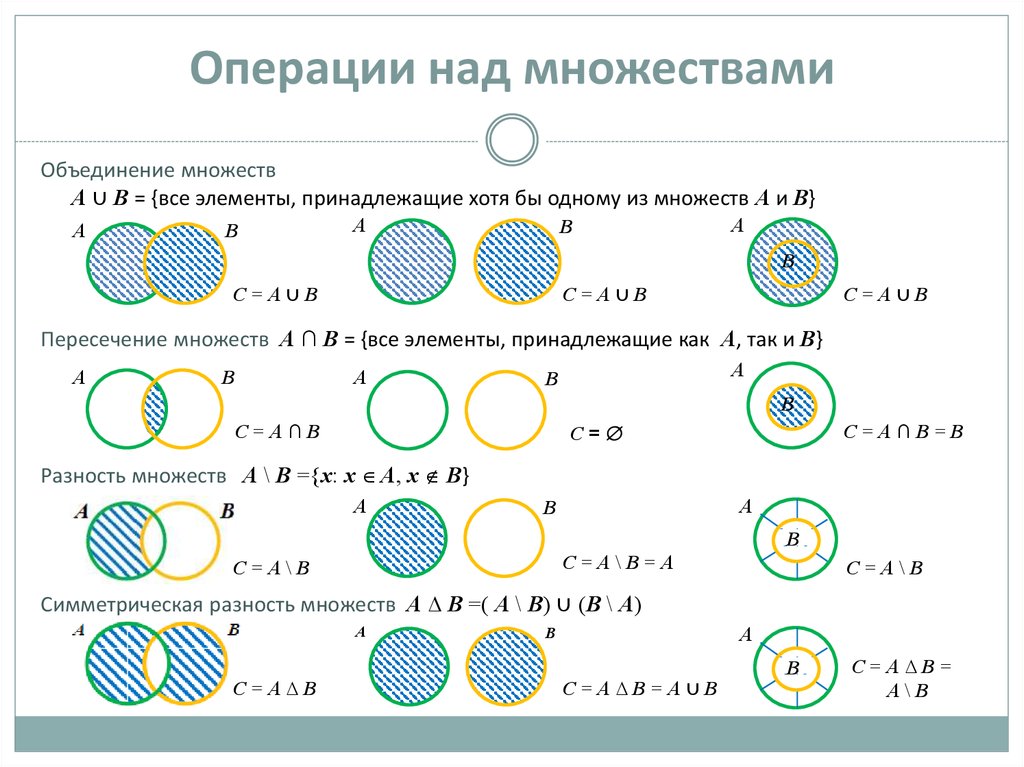

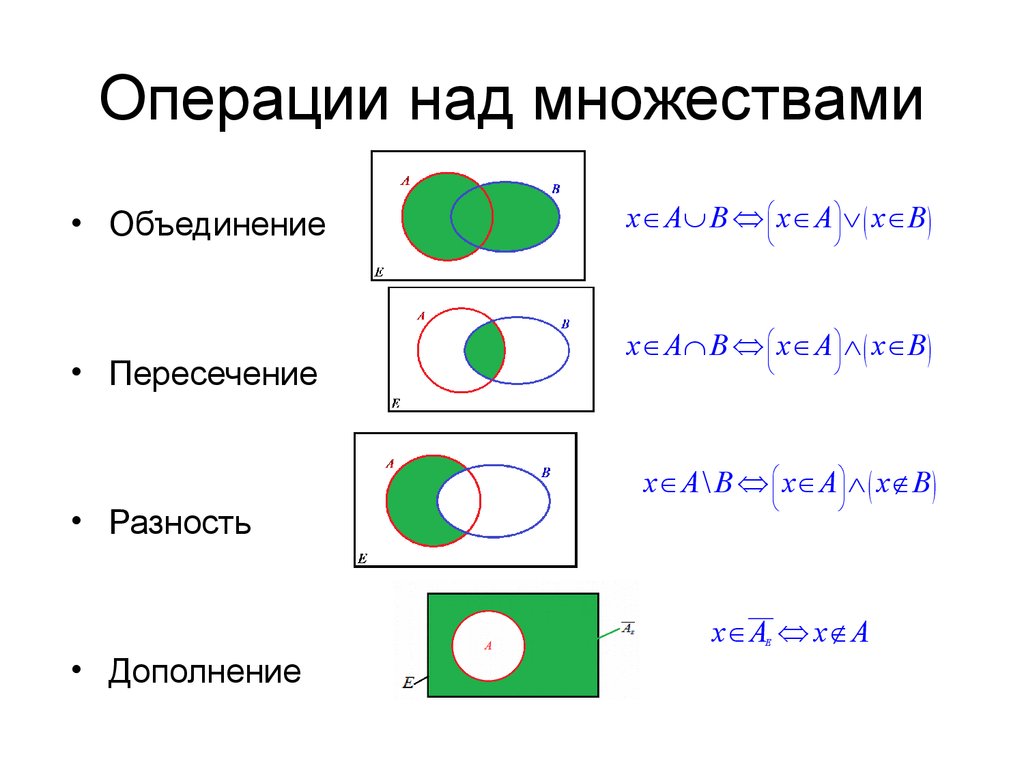 Кроме того, обратитесь к серии тестов, доступных для проверки ваших знаний по нескольким экзаменам.
Кроме того, обратитесь к серии тестов, доступных для проверки ваших знаний по нескольким экзаменам. 4 Приложения теории множеств чаще всего используются в науке, физике и математике, а также в компьютерной и электрической технике. При подготовке логических основ по геометрии, по созданию алгебры топологии и многого другого.
4 Приложения теории множеств чаще всего используются в науке, физике и математике, а также в компьютерной и электрической технике. При подготовке логических основ по геометрии, по созданию алгебры топологии и многого другого.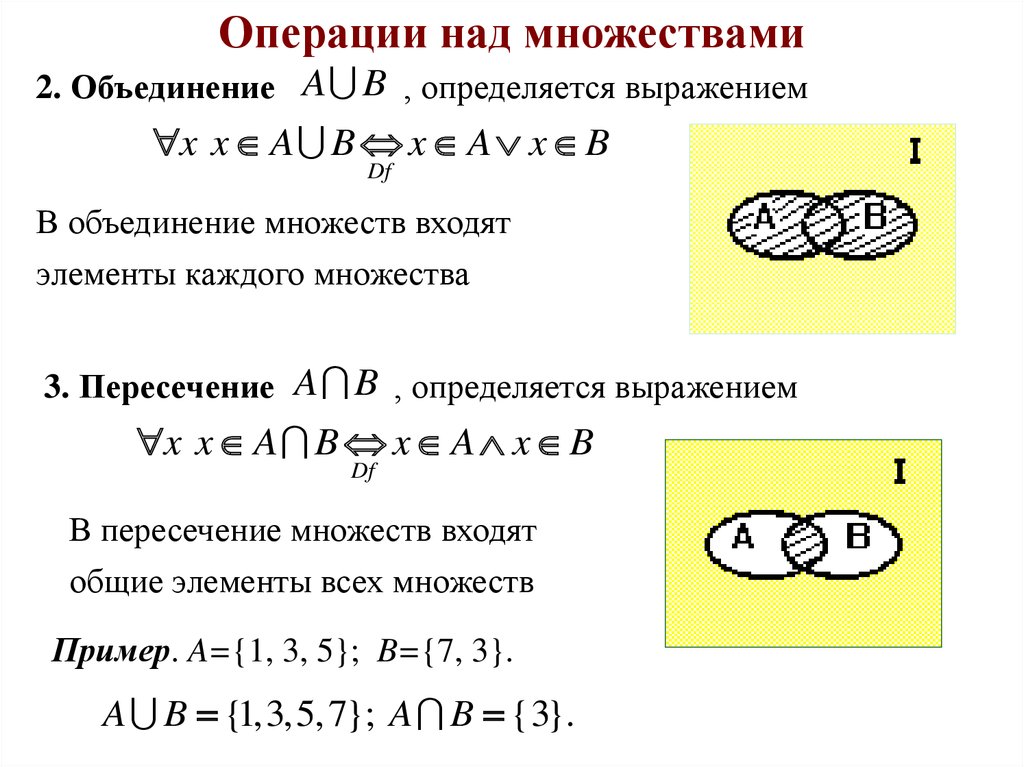



 com
com С. Весьма доволен форумом!!!
С. Весьма доволен форумом!!! .. А ряд функций работают и в демо-режиме…
.. А ряд функций работают и в демо-режиме…  Выбираешь любой векторный объект нажимаешь соответсвующую кнопку и получаешь результат.
Выбираешь любой векторный объект нажимаешь соответсвующую кнопку и получаешь результат. 
 А если про длину всех выбранных веторов — сам писал програмку на дельфи если надо могу скинуть. Выбираешь все вектора делаешь УП Обработка вдоль векторов глубина любая фреза любая и сохраняешь ее в формате выходного файла Cipher (*.plt) (с этим форматом работает моя программа).
А если про длину всех выбранных веторов — сам писал програмку на дельфи если надо могу скинуть. Выбираешь все вектора делаешь УП Обработка вдоль векторов глубина любая фреза любая и сохраняешь ее в формате выходного файла Cipher (*.plt) (с этим форматом работает моя программа).  2 месяца работы с ним меня полностью убедили, что работать с ним невозможно. Это окно постоянно мешается во всех прогах что неизбежно приводит к его закрытию, после чего по закону подлости возникает острая необходимость что-нибудь измерить. Расскидывает объекты коряво на мой взгляд — вручную проще и экономичнее. Метод упрощения чистки пленки у нас как-то не прижился. Меасуре и проще и удобнее. Все ИМХО
2 месяца работы с ним меня полностью убедили, что работать с ним невозможно. Это окно постоянно мешается во всех прогах что неизбежно приводит к его закрытию, после чего по закону подлости возникает острая необходимость что-нибудь измерить. Расскидывает объекты коряво на мой взгляд — вручную проще и экономичнее. Метод упрощения чистки пленки у нас как-то не прижился. Меасуре и проще и удобнее. Все ИМХО  ..
..  Для этого потребуется использовать теорему косинусов. Такую задачу приходится решать, например, когда дорога из
пункта A в пункт С — не прямая, а отклоняется от прямой, чтобы
пройти ещё через какой-то пункт B, а нужно узнать длину предполагаемой прямой дороги.
Кстати, геодезия — одна из тех сфер деятельности, где тригонометрические функции применяются
во всех их полноте.
Для этого потребуется использовать теорему косинусов. Такую задачу приходится решать, например, когда дорога из
пункта A в пункт С — не прямая, а отклоняется от прямой, чтобы
пройти ещё через какой-то пункт B, а нужно узнать длину предполагаемой прямой дороги.
Кстати, геодезия — одна из тех сфер деятельности, где тригонометрические функции применяются
во всех их полноте.
 Из элементарной тригонометрии известно, что .
Из элементарной тригонометрии известно, что . По теореме косинусов составляем уравнение, чтобы найти
косинус угла, смежного с углом между векторами и находим его:
По теореме косинусов составляем уравнение, чтобы найти
косинус угла, смежного с углом между векторами и находим его: Выполняем сложение векторов. Находим длину суммы векторов, подставляя в формулу косинус смежного угла:
Выполняем сложение векторов. Находим длину суммы векторов, подставляя в формулу косинус смежного угла: Какому условию должны удовлетворять векторы
и , чтобы имели место
слелующие соотношения:
Какому условию должны удовлетворять векторы
и , чтобы имели место
слелующие соотношения:
 ..
..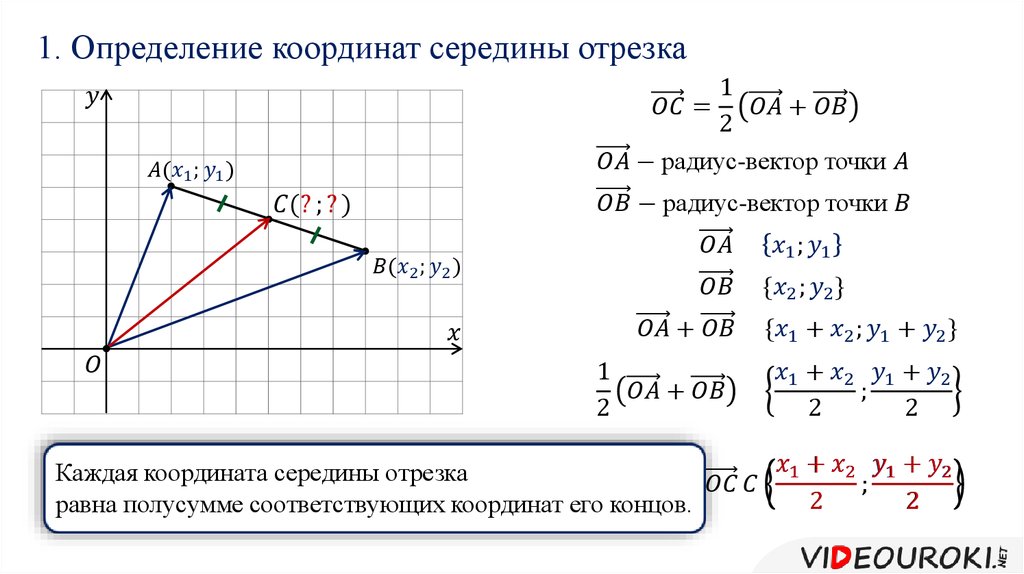 Мне нужно обработать большое количество файлов с похожими названиями, каждый блок файлов относится к отдельному объекту, например:
file_1_1.txt
file_1_2.txt
file_1_3.txt
file_1_4.txt
fil…
Мне нужно обработать большое количество файлов с похожими названиями, каждый блок файлов относится к отдельному объекту, например:
file_1_1.txt
file_1_2.txt
file_1_3.txt
file_1_4.txt
fil… На входе сигнала подала последоватльномть с Генератора Бернули бинарного. Sample time: 1/8000. ПРи выводе сигнала на анализатор спек…
На входе сигнала подала последоватльномть с Генератора Бернули бинарного. Sample time: 1/8000. ПРи выводе сигнала на анализатор спек…

 1.
1. 2)
2) Обозначения для максимальной нормы: || x || inf, где inf — индекс.
Обозначения для максимальной нормы: || x || inf, где inf — индекс.
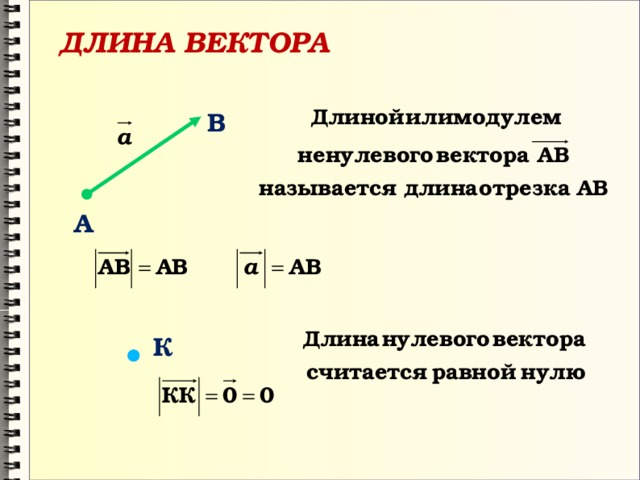
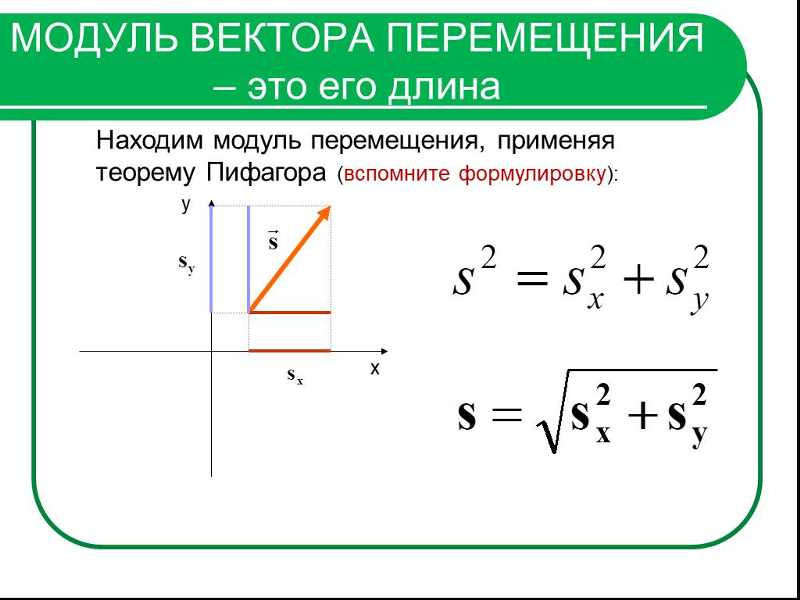
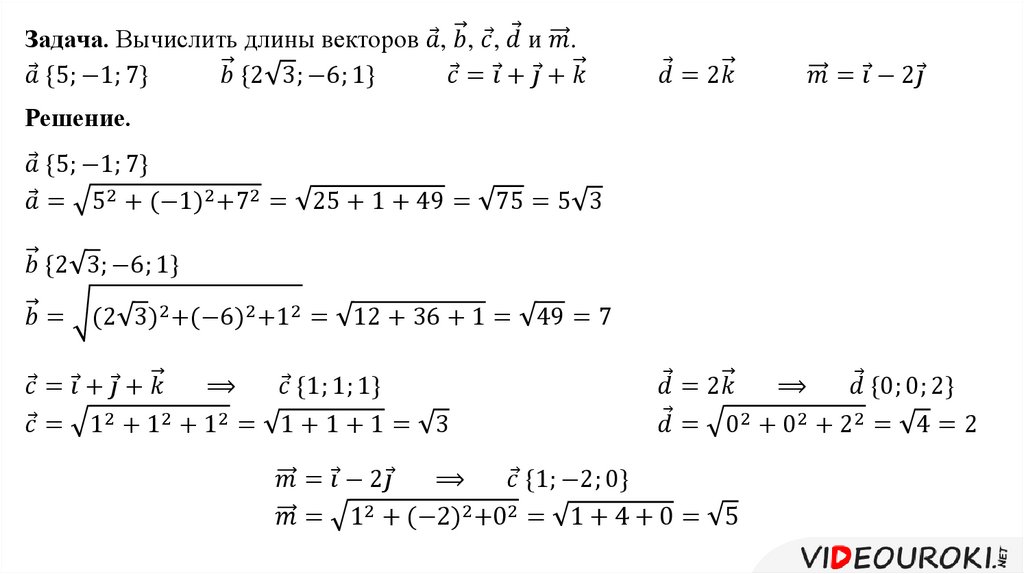 Угол, образованный лучами, на которых лежат вектора, называется углом между векторами:
Угол, образованный лучами, на которых лежат вектора, называется углом между векторами: 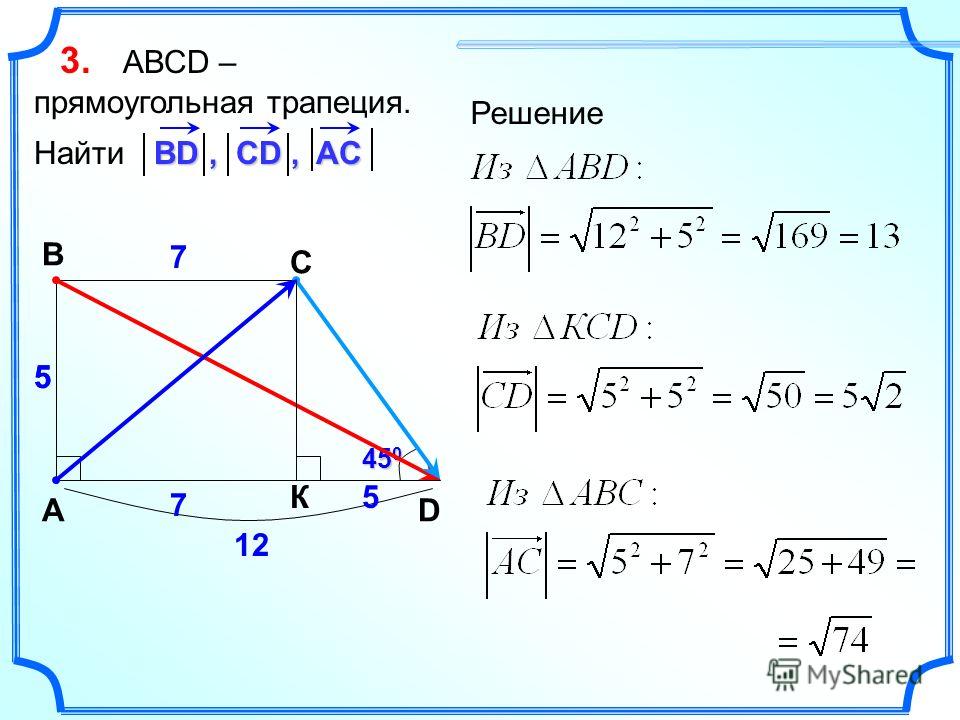 (чертеж из предыдущей задачи).
(чертеж из предыдущей задачи). Найдите скалярное произведение векторов и .(чертеж из предыдущей задачи).
Найдите скалярное произведение векторов и .(чертеж из предыдущей задачи). Это также помогает нам понимать векторные величины, такие как перемещение, скорость, сила и т. д. Понимание формулы для вычисления длины вектора поможет нам установить формулу для длины дуги векторной функции.
Это также помогает нам понимать векторные величины, такие как перемещение, скорость, сила и т. д. Понимание формулы для вычисления длины вектора поможет нам установить формулу для длины дуги векторной функции. 2}\конец{выровнено}
2}\конец{выровнено}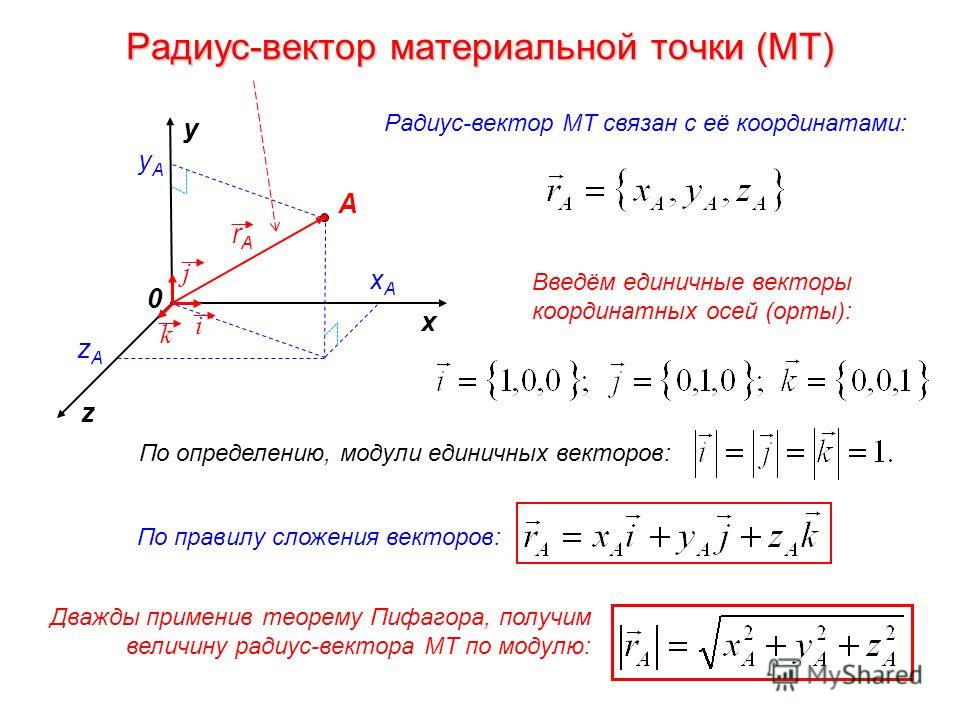 Длину вектор-функции $\textbf{r}(t)$ в интервале $[a, b]$ можно рассчитать по приведенной ниже формуле. 9{b} |\textbf{r}\prime(t)| \phantom{x} dt\end{aligned}
Длину вектор-функции $\textbf{r}(t)$ в интервале $[a, b]$ можно рассчитать по приведенной ниже формуле. 9{b} |\textbf{r}\prime(t)| \phantom{x} dt\end{aligned} 2} \\&= \sqrt{ 20}\end{выровнено} 94\\&= 2\sqrt{5}( 4 -0)\\&= 8\sqrt{5}\end{aligned}
2} \\&= \sqrt{ 20}\end{выровнено} 94\\&= 2\sqrt{5}( 4 -0)\\&= 8\sqrt{5}\end{aligned}
 Запишите квадратный корень из суммы, чтобы выразить величину через $t$. 9{2\pi} \phantom{x}dt\\&= 2\sqrt{5}(2\pi – 0)\\&= 4\sqrt{5}\pi\\&\примерно 28,10\end{выровнено }
Запишите квадратный корень из суммы, чтобы выразить величину через $t$. 9{2\pi} \phantom{x}dt\\&= 2\sqrt{5}(2\pi – 0)\\&= 4\sqrt{5}\pi\\&\примерно 28,10\end{выровнено } Работая только с геометрическим определением величины и направления
векторов, мы смогли определить такие операции, как сложение, вычитание,
и умножение на скаляры.
Мы также обсудили свойства этих операций.
Работая только с геометрическим определением величины и направления
векторов, мы смогли определить такие операции, как сложение, вычитание,
и умножение на скаляры.
Мы также обсудили свойства этих операций. 2$, чтобы обозначить, что его можно описать двумя действительными координатами. 92} = 5$.
2$, чтобы обозначить, что его можно описать двумя действительными координатами. 92} = 5$.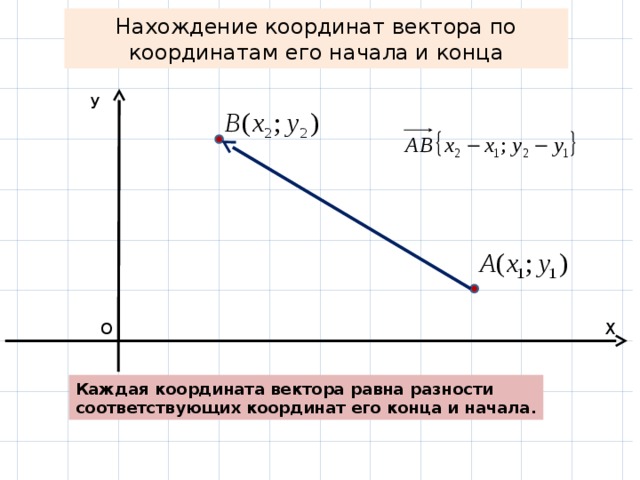
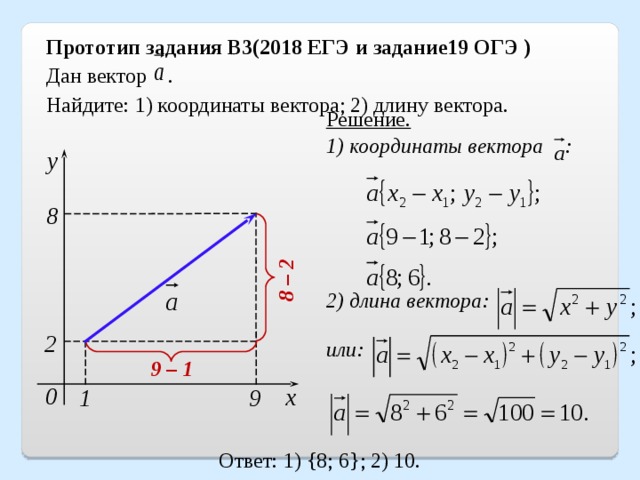 То же самое можно сделать, поместив хвост вектора $\vc{a}$ в начало вектора $\vc{b}$. Обе конструкции вместе образуют параллелограмм, сумма $\vc{a}+\vc{b}$ которого является диагональю. (По этой причине закон перестановки $\vc{a}+\vc{b}=\vc{b}+\vc{a}$ иногда называют законом параллелограмма.) Вы можете изменить $\vc{a} $ и $\vc{b}$, перетаскивая желтые точки.
То же самое можно сделать, поместив хвост вектора $\vc{a}$ в начало вектора $\vc{b}$. Обе конструкции вместе образуют параллелограмм, сумма $\vc{a}+\vc{b}$ которого является диагональю. (По этой причине закон перестановки $\vc{a}+\vc{b}=\vc{b}+\vc{a}$ иногда называют законом параллелограмма.) Вы можете изменить $\vc{a} $ и $\vc{b}$, перетаскивая желтые точки. В координатах мы можем написать $\vc{i}=(1,0)$. Точно так же вектор $\vc{j}$ является единичным вектором в направлении положительной оси $y$: $\vc{j}=(0,1)$.
Мы можем записать любой двумерный вектор в терминах этих единичных векторов как
$\vc{a}=(a_1,a_2) = a_1\vc{i}+a_2\vc{j}$.
В координатах мы можем написать $\vc{i}=(1,0)$. Точно так же вектор $\vc{j}$ является единичным вектором в направлении положительной оси $y$: $\vc{j}=(0,1)$.
Мы можем записать любой двумерный вектор в терминах этих единичных векторов как
$\vc{a}=(a_1,a_2) = a_1\vc{i}+a_2\vc{j}$. Отрицательная часть каждой оси находится на противоположной стороне начала координат, где оси пересекаются.
Отрицательная часть каждой оси находится на противоположной стороне начала координат, где оси пересекаются.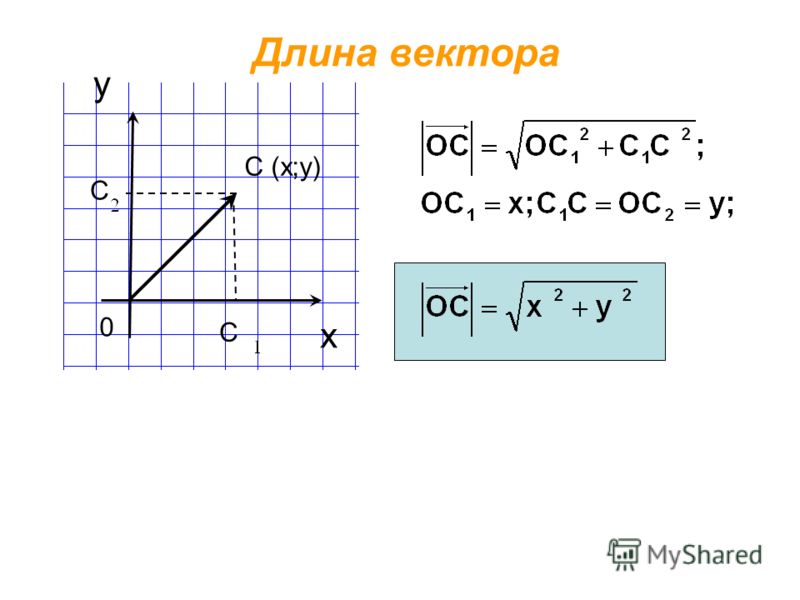 Если вы сделаете это, вы будете жить в математической вселенной, в которой некоторые формулы будут отличаться на знак минус от формулы во вселенной, которую мы здесь используем. Ваша вселенная будет такой же достоверной, как и наша, но будет много путаницы.
Мы предлагаем вам жить в нашей вселенной, изучая эти страницы.
Если вы сделаете это, вы будете жить в математической вселенной, в которой некоторые формулы будут отличаться на знак минус от формулы во вселенной, которую мы здесь используем. Ваша вселенная будет такой же достоверной, как и наша, но будет много путаницы.
Мы предлагаем вам жить в нашей вселенной, изучая эти страницы.
 Эти векторы являются единичными векторами в положительных направлениях $x$, $y$ и $z$ соответственно. В терминах координат мы можем записать их как $\vc{i}=(1,0,0)$, $\vc{j}=(0,1,0)$ и $\vc{k}= (0,0,1)$.
Мы можем выразить любой трехмерный вектор как сумму скалярных кратных этих единичных векторов в форме
$\vc{a}=(a_1,a_2,a_3) = a_1\vc{i}+a_2\vc{j}+a_3\vc{k}$.
Эти векторы являются единичными векторами в положительных направлениях $x$, $y$ и $z$ соответственно. В терминах координат мы можем записать их как $\vc{i}=(1,0,0)$, $\vc{j}=(0,1,0)$ и $\vc{k}= (0,0,1)$.
Мы можем выразить любой трехмерный вектор как сумму скалярных кратных этих единичных векторов в форме
$\vc{a}=(a_1,a_2,a_3) = a_1\vc{i}+a_2\vc{j}+a_3\vc{k}$. 2}.$$ 9n$, где $n$ — некоторое натуральное число.
2}.$$ 9n$, где $n$ — некоторое натуральное число.
 Обратите внимание, что формулы определены для гладких кривых: кривых, где вектор-функция \(\vecs r(t)\) дифференцируема с ненулевой производной. Условие гладкости гарантирует, что кривая не имеет точек возврата (или углов), которые могли бы сделать формулу проблематичной.
Обратите внимание, что формулы определены для гладких кривых: кривых, где вектор-функция \(\vecs r(t)\) дифференцируема с ненулевой производной. Условие гладкости гарантирует, что кривая не имеет точек возврата (или углов), которые могли бы сделать формулу проблематичной.
 \nonumber \]
\nonumber \] Теперь вектор-функция записывается в терминах параметра \(s\) . Поскольку переменная \(s\) представляет длину дуги, мы называем это параметризацией длины дуги исходной функции \(\vecs r(t)\). Одним из преимуществ нахождения параметризации длины дуги является то, что расстояние, пройденное вдоль кривой, начиная с \(s=0\), теперь равно параметру \(s\). Параметризация длины дуги также появляется в контексте кривизны (которую мы рассмотрим позже в этом разделе) и линейных интегралов.
Теперь вектор-функция записывается в терминах параметра \(s\) . Поскольку переменная \(s\) представляет длину дуги, мы называем это параметризацией длины дуги исходной функции \(\vecs r(t)\). Одним из преимуществ нахождения параметризации длины дуги является то, что расстояние, пройденное вдоль кривой, начиная с \(s=0\), теперь равно параметру \(s\). Параметризация длины дуги также появляется в контексте кривизны (которую мы рассмотрим позже в этом разделе) и линейных интегралов.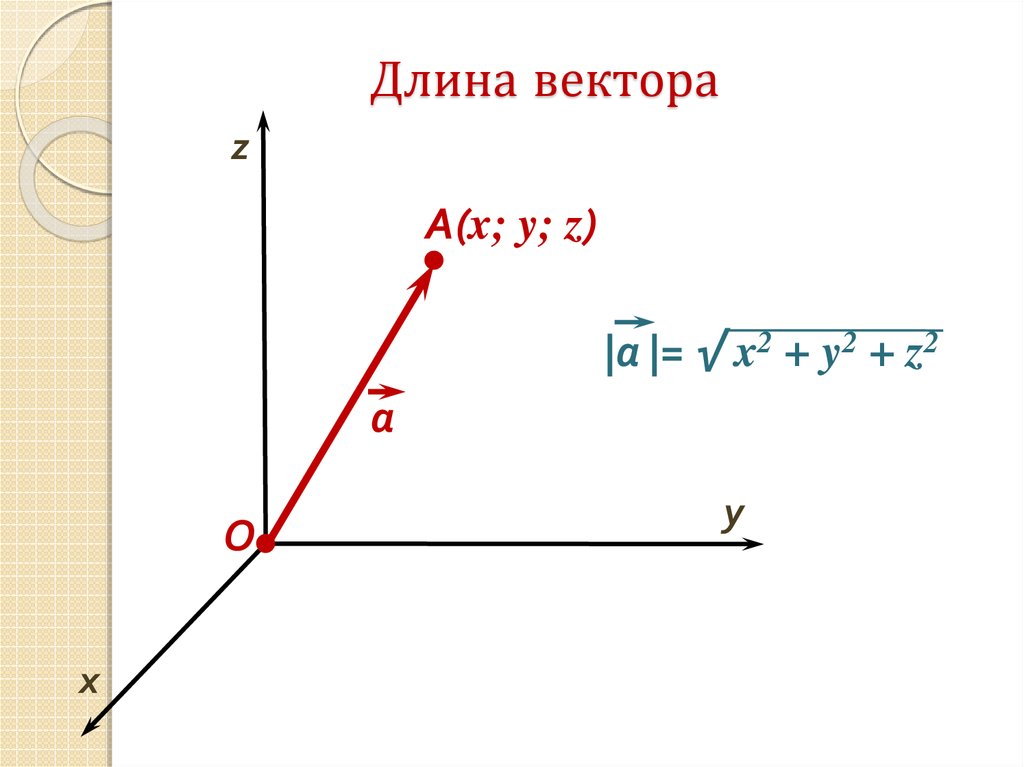 Далее заменяем переменную \(t\) в исходной функции \(\vecs r(t)=4 \cos t \,\hat{\mathbf{i}}+4 \sin t \,\hat{\mathbf {j}}\) с выражением \(s/4\), чтобы получить
Далее заменяем переменную \(t\) в исходной функции \(\vecs r(t)=4 \cos t \,\hat{\mathbf{i}}+4 \sin t \,\hat{\mathbf {j}}\) с выражением \(s/4\), чтобы получить
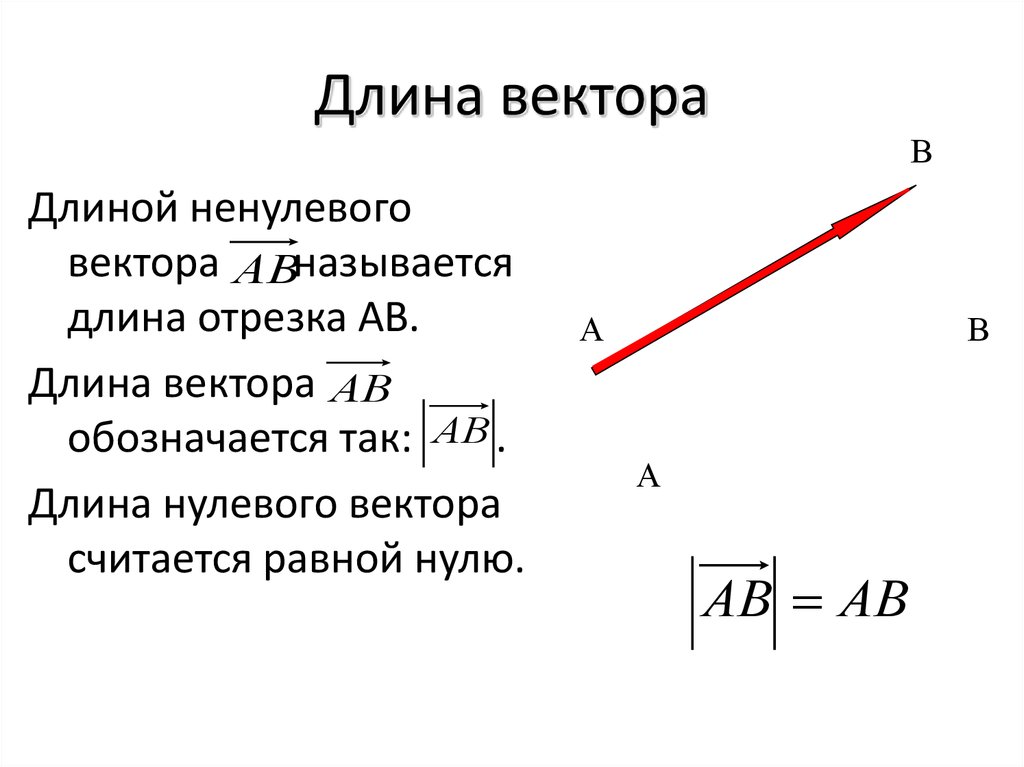
 \nonumber \]
\nonumber \] Разделив обе части на \(ds/dt\) и взяв величину обеих сторон, мы получим
Разделив обе части на \(ds/dt\) и взяв величину обеих сторон, мы получим При изучении движения в трех измерениях для описания движения частицы по траектории в пространстве полезны два других вектора: главный единичный вектор нормали и вектор бинормальный вектор .
При изучении движения в трех измерениях для описания движения частицы по траектории в пространстве полезны два других вектора: главный единичный вектор нормали и вектор бинормальный вектор .

 Единичный вектор нормали и вектор бинормали образуют плоскость, перпендикулярную кривой в любой точке кривой, называемую плоскостью нормали. Кроме того, эти три вектора образуют систему отсчета в трехмерном пространстве, называемую 9.0008 Система координат Френе (также называемая системой координат TNB ) (рис. \(\PageIndex{2}\)). Наконец, плоскость, определяемая векторами \(\vecs T\) и \(\vecs N\), образует соприкасающуюся плоскость \(C\) в любой точке \(P\) на кривой.
Единичный вектор нормали и вектор бинормали образуют плоскость, перпендикулярную кривой в любой точке кривой, называемую плоскостью нормали. Кроме того, эти три вектора образуют систему отсчета в трехмерном пространстве, называемую 9.0008 Система координат Френе (также называемая системой координат TNB ) (рис. \(\PageIndex{2}\)). Наконец, плоскость, определяемая векторами \(\vecs T\) и \(\vecs N\), образует соприкасающуюся плоскость \(C\) в любой точке \(P\) на кривой. Мы называем \(r\) радиусом кривизны кривой, и он равен обратной величине кривизны. Если эта окружность лежит на вогнутой стороне кривой и касается кривой в точке \(P\), то эта окружность называется соприкасающийся круг из \(C\) в точке \(P\), как показано на рисунке \(\PageIndex{3}\).
Мы называем \(r\) радиусом кривизны кривой, и он равен обратной величине кривизны. Если эта окружность лежит на вогнутой стороне кривой и касается кривой в точке \(P\), то эта окружность называется соприкасающийся круг из \(C\) в точке \(P\), как показано на рисунке \(\PageIndex{3}\).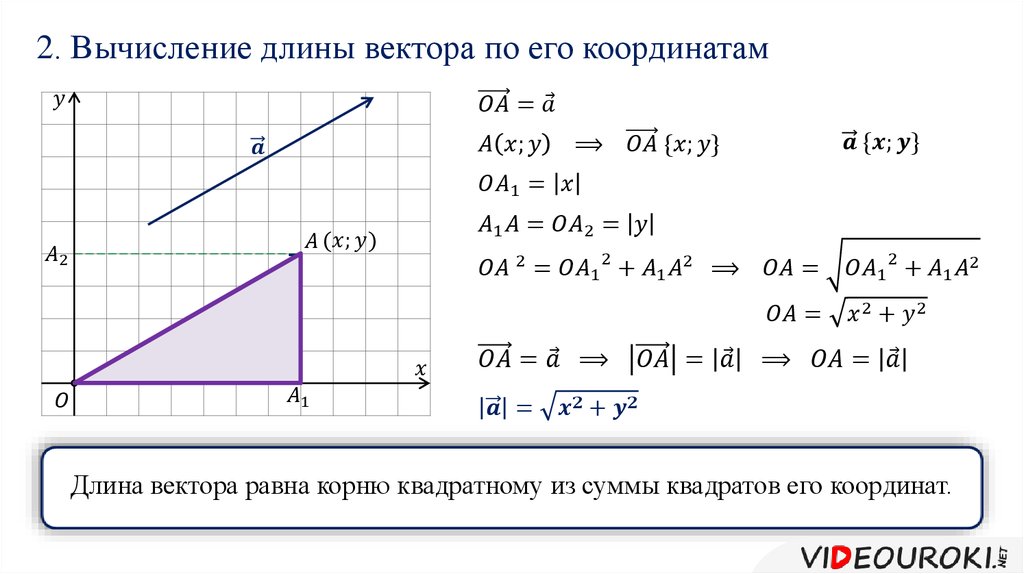 2=\frac{1}{36}\). График и его соприкасающийся круг показаны на следующем графике. 9{3/2}}\)
2=\frac{1}{36}\). График и его соприкасающийся круг показаны на следующем графике. 9{3/2}}\)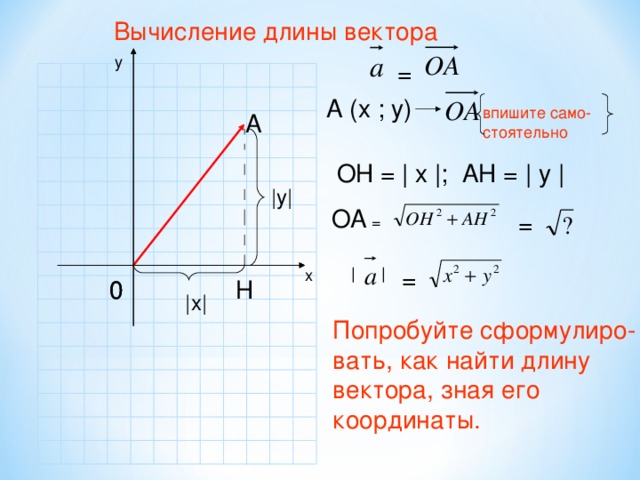 3: Длина дуги и кривизна распространяется под лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована Гилбертом Стрэнгом и Эдвином «Джедом» Херманом (OpenStax) через исходный контент, который был отредактировано в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
3: Длина дуги и кривизна распространяется под лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована Гилбертом Стрэнгом и Эдвином «Джедом» Херманом (OpenStax) через исходный контент, который был отредактировано в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу. org/details/books/calculus-volume-1
org/details/books/calculus-volume-1
 То есть справедлива следующая запись: di = d * d* d *… * dk, где k — число, обозначающее количество перемножаемых чисел, равное n. Например, 112 = 11 * 11 = 121. Степень, присущая числу, может быть отрицательной, рациональной, десятичной, вещественной и даже комплексной. Фактически получается, что для того, чтобы посчитать степень числа, его нужно умножить на себя столько раз, сколько указано в степенном показателе.
То есть справедлива следующая запись: di = d * d* d *… * dk, где k — число, обозначающее количество перемножаемых чисел, равное n. Например, 112 = 11 * 11 = 121. Степень, присущая числу, может быть отрицательной, рациональной, десятичной, вещественной и даже комплексной. Фактически получается, что для того, чтобы посчитать степень числа, его нужно умножить на себя столько раз, сколько указано в степенном показателе. Согласно ему, для решения задачи нужно отдельно возвести сначала числитель выражения, а затем знаменатель, не меняя занимаемые ими позиции. Например, дробь три шестых во второй степени будет равна: (3/6)2 = 9/36. Используя свойства сокращения дробей, числитель и знаменатель можно разделить на девять. В итоге получится равенство: (3/6)2 = 1/4.
Согласно ему, для решения задачи нужно отдельно возвести сначала числитель выражения, а затем знаменатель, не меняя занимаемые ими позиции. Например, дробь три шестых во второй степени будет равна: (3/6)2 = 9/36. Используя свойства сокращения дробей, числитель и знаменатель можно разделить на девять. В итоге получится равенство: (3/6)2 = 1/4. Эту дробь сократить, то есть упростить, нельзя. Если нужно получить численное значение, то следует просто разделить числитель на знаменатель: 1331 : 2744 = 0,485.
Эту дробь сократить, то есть упростить, нельзя. Если нужно получить численное значение, то следует просто разделить числитель на знаменатель: 1331 : 2744 = 0,485.
 Тут нужно отметить, что основание не должно быть равным нулю, иначе получится недопустимое деление на ноль. Если a = b, то равенство можно переписать в виде: ca / cb = ca — a = c0. Так как c другой стороны частное ca / сa = 1, то можно утверждать, что с0 = 1.
Тут нужно отметить, что основание не должно быть равным нулю, иначе получится недопустимое деление на ноль. Если a = b, то равенство можно переписать в виде: ca / cb = ca — a = c0. Так как c другой стороны частное ca / сa = 1, то можно утверждать, что с0 = 1.



 Определить ответ в задании вида: (2 11/12)-1 = ((2 * 12 + 11) / 12)-1 = (35 / 12)-1 = (12 / 35 )1 = 12 1 / 351 =12 / 35.
Определить ответ в задании вида: (2 11/12)-1 = ((2 * 12 + 11) / 12)-1 = (35 / 12)-1 = (12 / 35 )1 = 12 1 / 351 =12 / 35. Так как буквой e обозначают экспоненту, то e—3 = 2,718-3 = 0,049. Отсюда можно сделать вывод, что знак в неравенстве неверный: -2,43 < 0,049
Так как буквой e обозначают экспоненту, то e—3 = 2,718-3 = 0,049. Отсюда можно сделать вывод, что знак в неравенстве неверный: -2,43 < 0,049 Весь процесс вычисления занимает несколько секунд.
Весь процесс вычисления занимает несколько секунд. ru
ru

 Это все имеет вид a b n = a n b n , где а и b являются произвольными многочленами, b является ненулевым, а n натуральным числом.
Это все имеет вид a b n = a n b n , где а и b являются произвольными многочленами, b является ненулевым, а n натуральным числом. Тогда получим выражение вида
Тогда получим выражение вида Это не упрощает ее для дальнейшего решения. Когда заданная дробь может быть сокращена, тогда при возведении в степень получаем, что необходимо выполнение сокращения алгебраической дроби, во избежание выполнения сокращения после того, как возведем в степень.
Это не упрощает ее для дальнейшего решения. Когда заданная дробь может быть сокращена, тогда при возведении в степень получаем, что необходимо выполнение сокращения алгебраической дроби, во избежание выполнения сокращения после того, как возведем в степень.
 k}\]
k}\]

 ….
….
 {4} \]
\[ = 3.4563 \times 10000= 34563 \]
{4} \]
\[ = 3.4563 \times 10000= 34563 \]

 Первые полторы тысяч разложений.
Первые полторы тысяч разложений. Угол между ними.
Угол между ними. Матрица смежности онлайн
Матрица смежности онлайн X)
X) x.
x.
 Чтобы произвести вычисления, заполните поля соответствующие числителям и знаменателям двух дробей. Если дробь имеет вид «смешанной дроби», то также заполните поле, соответствующее целой части дроби. Если у дроби нет целой части, т.е. дробь имеет вид «простой дроби», то оставьте данное поле пустым. Затем нажмите кнопку «Вычислить».
Чтобы произвести вычисления, заполните поля соответствующие числителям и знаменателям двух дробей. Если дробь имеет вид «смешанной дроби», то также заполните поле, соответствующее целой части дроби. Если у дроби нет целой части, т.е. дробь имеет вид «простой дроби», то оставьте данное поле пустым. Затем нажмите кнопку «Вычислить». Смешанной называется дробь, записанная в виде целого числа и правильной дроби, и понимается как сумма этого числа и дробной части. Соответственно, дробь, не имеющая целую часть,называется простой дробью. Любая смешанная дробь может быть преобразована в неправильную простую дробь (см. пример ниже).
Смешанной называется дробь, записанная в виде целого числа и правильной дроби, и понимается как сумма этого числа и дробной части. Соответственно, дробь, не имеющая целую часть,называется простой дробью. Любая смешанная дробь может быть преобразована в неправильную простую дробь (см. пример ниже). (-2) +1.
(-2) +1. Операция вычисления куба числа – это частный случай возведения числа в степень, в данном случае в втретью:
Операция вычисления куба числа – это частный случай возведения числа в степень, в данном случае в втретью: ·a
·a 

 Arenas , опубликовано 22 октября 2019 г.
Arenas , опубликовано 22 октября 2019 г. В раннем английском языке это означает «отломанный кусок или
фрагмент». Английское слово «перелом» также
имеет такое же происхождение слова.
В раннем английском языке это означает «отломанный кусок или
фрагмент». Английское слово «перелом» также
имеет такое же происхождение слова. Вот несколько примеров из Math Through the Ages :
Вот несколько примеров из Math Through the Ages : до н.э.) или знака, функционирующего как десятичная точка для указать доли целого числа. Это затрудняло интерпретацию чисел.
до н.э.) или знака, функционирующего как десятичная точка для указать доли целого числа. Это затрудняло интерпретацию чисел.
 Таким образом, дроби
имеют знаменатели со значениями, делящимися на 12.
Таким образом, дроби
имеют знаменатели со значениями, делящимися на 12. 
 Это в конечном итоге привело к тому, как мы пишем дроби в современную эпоху.
Это в конечном итоге привело к тому, как мы пишем дроби в современную эпоху.

 апельсинового сока.
апельсинового сока.
 Чтобы дать вам представление, посмотрите таблицу ниже.
Чтобы дать вам представление, посмотрите таблицу ниже. Другие ее тематические статьи можно прочитать на Inquirer.net и Manileno.com. Она имеет степень магистра творческого письма Филиппинского университета, одного из ведущих учебных заведений мира, и степень бакалавра коммуникативных искусств Колледжа Мириам.
Другие ее тематические статьи можно прочитать на Inquirer.net и Manileno.com. Она имеет степень магистра творческого письма Филиппинского университета, одного из ведущих учебных заведений мира, и степень бакалавра коммуникативных искусств Колледжа Мириам. Чтобы вычислить смешанные числа, установите флажок «Рассчитать смешанные числа». Входные данные числителя и знаменателя принимают только целые числа. При вычислении смешанных чисел можно использовать десятичные дроби, если числитель и знаменатель пусты. После вычисления десятичные дроби будут преобразованы в дроби.
Чтобы вычислить смешанные числа, установите флажок «Рассчитать смешанные числа». Входные данные числителя и знаменателя принимают только целые числа. При вычислении смешанных чисел можно использовать десятичные дроби, если числитель и знаменатель пусты. После вычисления десятичные дроби будут преобразованы в дроби. Если вы съели 3 куска пиццы, значит, вы съели 3 части всей пиццы или, используя дроби, пиццы. Дроби — это эффективный способ представления частей целого с помощью чисел, вместо того чтобы описывать понятие словами.
Если вы съели 3 куска пиццы, значит, вы съели 3 части всей пиццы или, используя дроби, пиццы. Дроби — это эффективный способ представления частей целого с помощью чисел, вместо того чтобы описывать понятие словами.
 В этом случае имеется 1 целое, или , и 1 часть целого, или . Объединив их, неправильная дробь записывается как смешанное число.
В этом случае имеется 1 целое, или , и 1 часть целого, или . Объединив их, неправильная дробь записывается как смешанное число.
 является наиболее упрощенной формой дроби, представляющей половину целого. Каждая последующая дробь, указанная выше, представляет собой просто первую дробь , умноженную на дробное представление числа 1. Напомним, что любое значение, умноженное на 1, равно тому же самому значению, и что любая дробь, в которой числитель и знаменатель имеют одинаковое значение равно 1. Эти факты позволяют преобразовать любую дробь в дробь, имеющую одно и то же значение, представленное разными числителями и знаменателями; эти дроби называются эквивалентными дробями. Например, отметив, что умножение дробей включает умножение числителя на числитель и знаменателя на знаменатель,
является наиболее упрощенной формой дроби, представляющей половину целого. Каждая последующая дробь, указанная выше, представляет собой просто первую дробь , умноженную на дробное представление числа 1. Напомним, что любое значение, умноженное на 1, равно тому же самому значению, и что любая дробь, в которой числитель и знаменатель имеют одинаковое значение равно 1. Эти факты позволяют преобразовать любую дробь в дробь, имеющую одно и то же значение, представленное разными числителями и знаменателями; эти дроби называются эквивалентными дробями. Например, отметив, что умножение дробей включает умножение числителя на числитель и знаменателя на знаменатель, Для этого примера мы могли бы оставить в покое, если бы знали, что 8 является общим знаменателем для двух дробей:
Для этого примера мы могли бы оставить в покое, если бы знали, что 8 является общим знаменателем для двух дробей: Только представьте, у профессиональных бегунов, которые часто пробегают марафоны, пульс в абсолютно спокойном состоянии находится на уровне около 37 ударов в минуту. Чтобы лучше понять эту величину, достаточно помнить, что среднестатистическая норма у обычного человека – 60-100 ударов, а у спортсменов с хорошей физической подготовкой – около 40-60.
Только представьте, у профессиональных бегунов, которые часто пробегают марафоны, пульс в абсолютно спокойном состоянии находится на уровне около 37 ударов в минуту. Чтобы лучше понять эту величину, достаточно помнить, что среднестатистическая норма у обычного человека – 60-100 ударов, а у спортсменов с хорошей физической подготовкой – около 40-60. Лидьярд, к примеру, утверждает, что этот резерв сохраняется, в том числе, и после нескольких сердечных приступов. Существуют вполне ясные симптомы сердечного перенапряжения – боль в груди и сильная отдышка. Если Вы ощутили нечто подобное, необходимо немного снизить нагрузку.
Лидьярд, к примеру, утверждает, что этот резерв сохраняется, в том числе, и после нескольких сердечных приступов. Существуют вполне ясные симптомы сердечного перенапряжения – боль в груди и сильная отдышка. Если Вы ощутили нечто подобное, необходимо немного снизить нагрузку.
 Повысится количество эритроцитов в крови, они в свою очередь будут активно перемещать по сосудам гемоглобин, а тот начнет активно вырабатывать гликоген. Этот самый гликоген, так сказать, самое качественное горючее для тела. То, как организм может его вырабатывать, напрямую влияет на количество кислорода, которое кровь переносит по телу. Если его недостаточно, то наступает «кислородное голодание», и организм начинает очень быстро истощаться, если физической подготовки человека недостаточно.
Повысится количество эритроцитов в крови, они в свою очередь будут активно перемещать по сосудам гемоглобин, а тот начнет активно вырабатывать гликоген. Этот самый гликоген, так сказать, самое качественное горючее для тела. То, как организм может его вырабатывать, напрямую влияет на количество кислорода, которое кровь переносит по телу. Если его недостаточно, то наступает «кислородное голодание», и организм начинает очень быстро истощаться, если физической подготовки человека недостаточно.
 Занятия в таком режиме активно улучшают вашу форму, но всего лишь 15% калорий организм будет брать из жировых запасов.
Занятия в таком режиме активно улучшают вашу форму, но всего лишь 15% калорий организм будет брать из жировых запасов. Или же необходимо находиться в состоянии полного покоя не менее 10 минут перед тем, как начать замерять. Так же есть очень много приложений для смартофонов, которые могут измерить для Вас этот показатель как на базе iOS, так и на базе Android.
Или же необходимо находиться в состоянии полного покоя не менее 10 минут перед тем, как начать замерять. Так же есть очень много приложений для смартофонов, которые могут измерить для Вас этот показатель как на базе iOS, так и на базе Android. 4K
4K

 Ошибки бывают у всех, мы готовы дорабатывать бесплатно и в сжатые сроки, а если у вас появятся вопросы, готовы на них ответить.
Ошибки бывают у всех, мы готовы дорабатывать бесплатно и в сжатые сроки, а если у вас появятся вопросы, готовы на них ответить. 12.18
12.18

 36 увеличить на 60.
36 увеличить на 60. К какому числу прибавили 40 и получили 92?
К какому числу прибавили 40 и получили 92? Найти сумму.
Найти сумму. Какое число уменьшили на 48 и получили78?
Какое число уменьшили на 48 и получили78?  Найти произведение.
Найти произведение. Вычислить: 21:3х2=
Вычислить: 21:3х2=
 42 увеличить на 34.
42 увеличить на 34. К какому числу прибавили 8 и получили 60?
К какому числу прибавили 8 и получили 60? 78 уменьшить на 50.
78 уменьшить на 50. Первый множитель 2, второй множитель 8. Найти произведение.
Первый множитель 2, второй множитель 8. Найти произведение. Первый множитель 8, второй множитель 4. Найти произведение.
Первый множитель 8, второй множитель 4. Найти произведение. Во сколько раз 6 меньше 24?
Во сколько раз 6 меньше 24? На сколько 43 меньше 96
На сколько 43 меньше 96 Найти разность.
Найти разность. Вычислить: 30+40-50+60-20=
Вычислить: 30+40-50+60-20= Вычислить: 50+40-60+20+50-20=
Вычислить: 50+40-60+20+50-20= Какое число прибавили к 38 и получили 89?
Какое число прибавили к 38 и получили 89?

 Вычислить: 4+8-7+6-9=
Вычислить: 4+8-7+6-9= Найти частное чисел: 48 и 8.
Найти частное чисел: 48 и 8. Какое число уменьшили на 42 и получили 31?
Какое число уменьшили на 42 и получили 31? Найти произведение.
Найти произведение. Какое число разделили на 9 и получили 6?
Какое число разделили на 9 и получили 6? 35 уменьшить в 5 раз.
35 уменьшить в 5 раз. Чему равен делитель, если делимое 54,а частное 9.
Чему равен делитель, если делимое 54,а частное 9. На какое число разделили 42 и получили 6?
На какое число разделили 42 и получили 6? 92 уменьшить на 50.
92 уменьшить на 50. Из какого числа вычли 30 и получили67?
Из какого числа вычли 30 и получили67? Какое число уменьшили в 8 раз и получили 4?
Какое число уменьшили в 8 раз и получили 4?
 Какое число умножили на 4 и получили 24.
Какое число умножили на 4 и получили 24.

 Вычислить: 7+8-9+5-4+7=
Вычислить: 7+8-9+5-4+7= Найти разность чисел: 50 и 43.
Найти разность чисел: 50 и 43. Найти произведение чисел: 6 и 7.
Найти произведение чисел: 6 и 7. Какое число прибавили к 35 и получили 95?
Какое число прибавили к 35 и получили 95? На сколько 19 больше 7?
На сколько 19 больше 7?
 На какое число разделили 81 и получили 9?
На какое число разделили 81 и получили 9?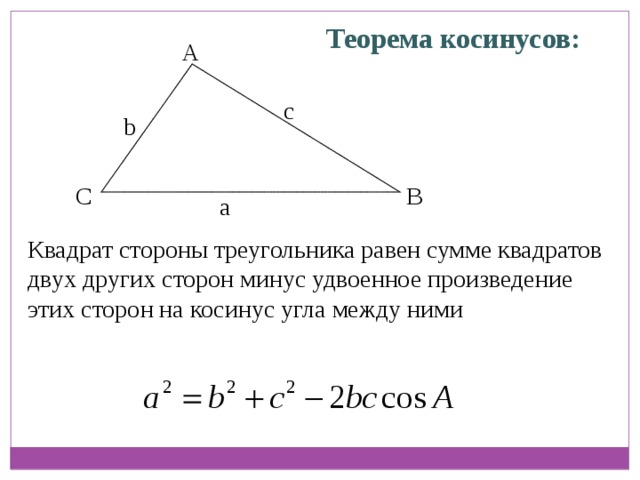 ru
ru ru
ru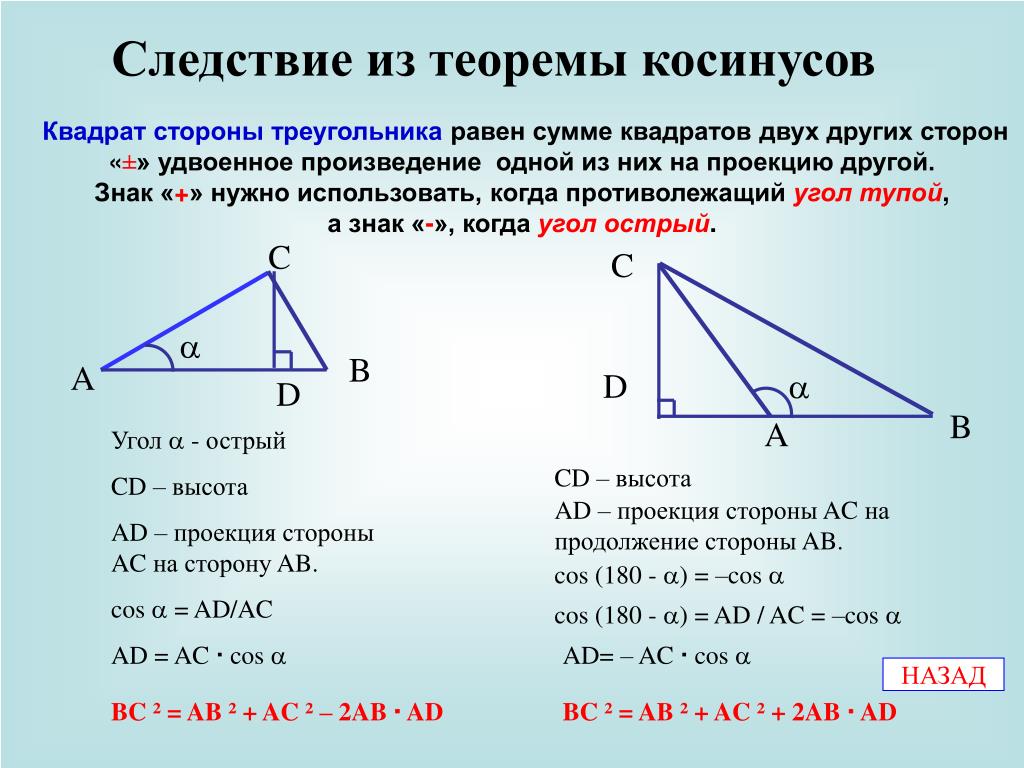

 = 1 2 · a → 2 + b → 2 – b → – a → 2 a → · b →
= 1 2 · a → 2 + b → 2 – b → – a → 2 a → · b → Требуется найти косинус угла между векторами.
Требуется найти косинус угла между векторами.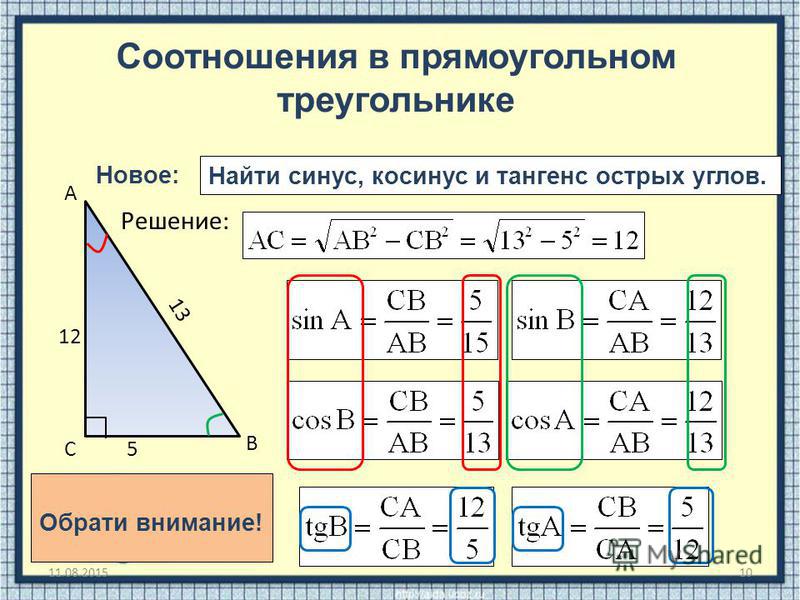 =a→, b→a→·b→
=a→, b→a→·b→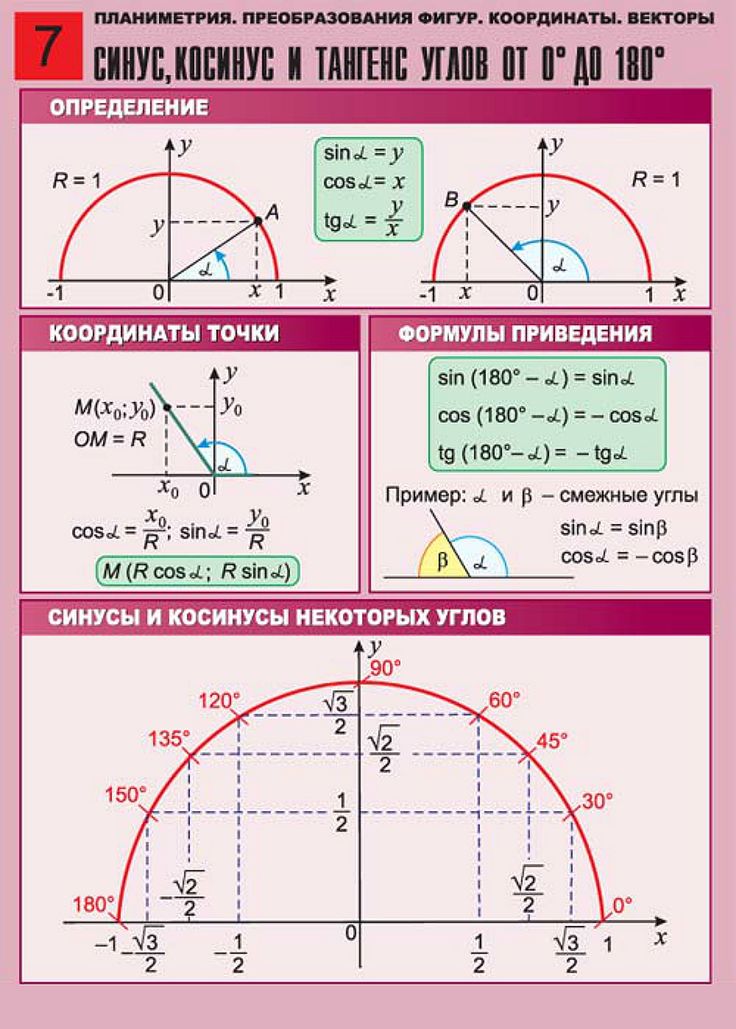

 Для решения задач нам поможет таблица, которая находится чуть ниже. Рассмотрим эти варианты.
Для решения задач нам поможет таблица, которая находится чуть ниже. Рассмотрим эти варианты.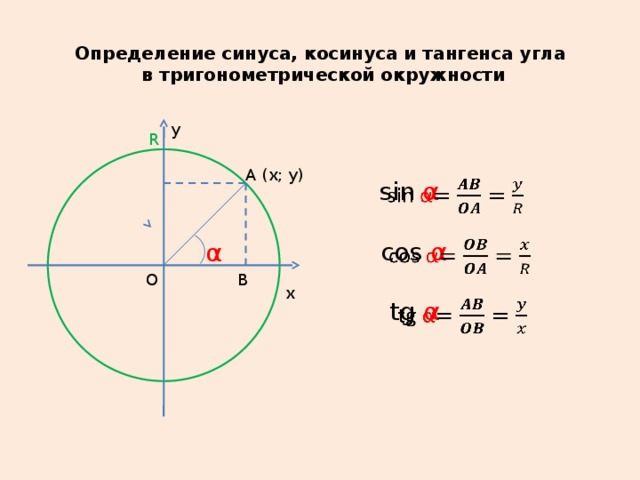 Формула: tg=a/b, где а – противолежащий к углу катет, а b – прилежащий. Преобразуем формулу и получаем: a=tg*b.
Формула: tg=a/b, где а – противолежащий к углу катет, а b – прилежащий. Преобразуем формулу и получаем: a=tg*b. Пусть в нем сторона BC = a, сторона CA = b и S — площадь этого треугольника. Необходимо доказать, что S = (1/2)*a*b*sin(C) .
Пусть в нем сторона BC = a, сторона CA = b и S — площадь этого треугольника. Необходимо доказать, что S = (1/2)*a*b*sin(C) .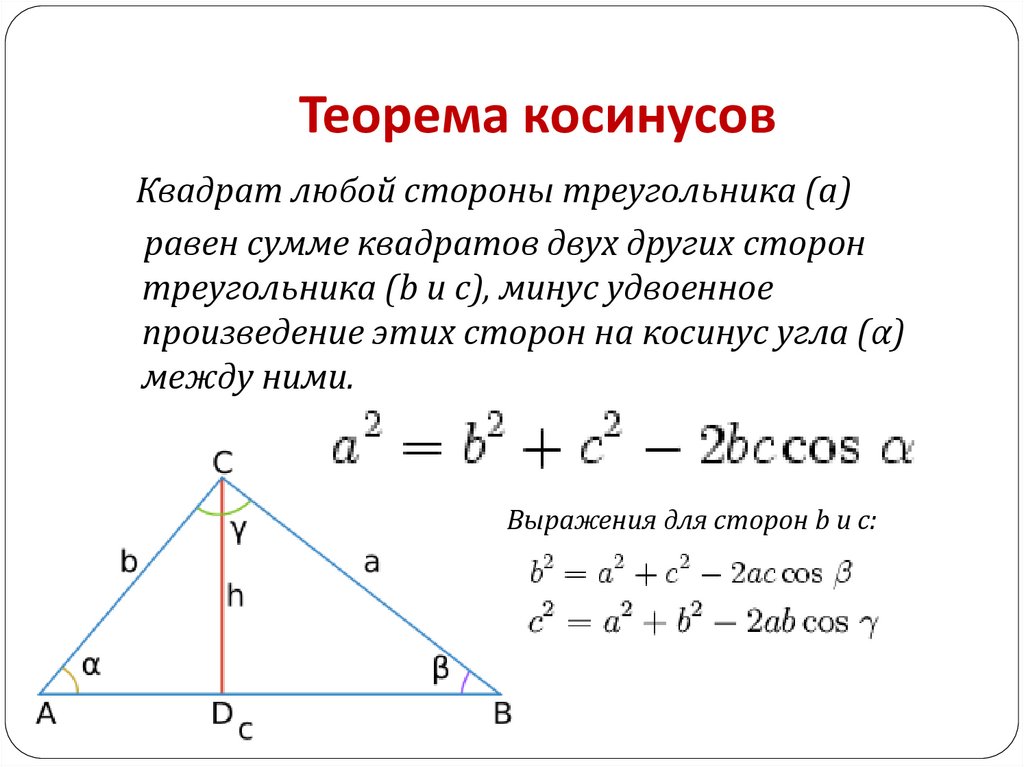 2. Найдите сторону AB, если AC = 15 см, угол А = 30˚.
2. Найдите сторону AB, если AC = 15 см, угол А = 30˚. От того что синус , как знаменито, представляет собой отношение противолежащего катета к гипотенузе, а косинус – отношение прилежащего катета к гипотенузе, для решения поставленной задачи воспользуйтесь дальнейшим соотношением между этими параметрами:sin ?=НB/BCСоответственно, если вы хотите узнать катет прямоугольного треугольника, выразите его через гипотенузу дальнейшим образом:НB=BC*sin ?
От того что синус , как знаменито, представляет собой отношение противолежащего катета к гипотенузе, а косинус – отношение прилежащего катета к гипотенузе, для решения поставленной задачи воспользуйтесь дальнейшим соотношением между этими параметрами:sin ?=НB/BCСоответственно, если вы хотите узнать катет прямоугольного треугольника, выразите его через гипотенузу дальнейшим образом:НB=BC*sin ?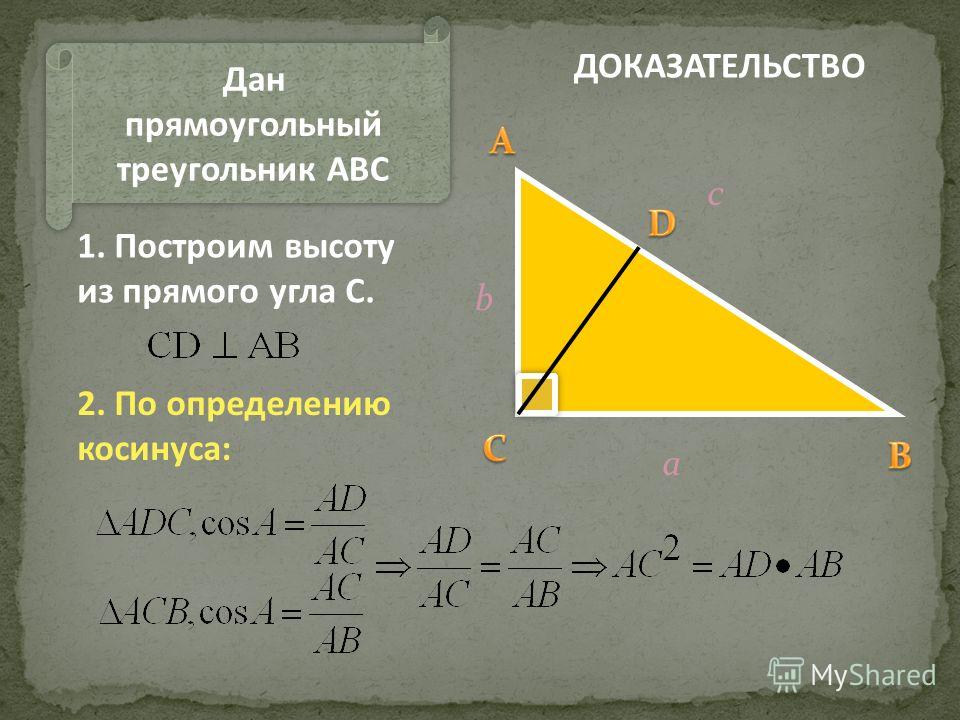 2-2ab*cos ?
2-2ab*cos ?
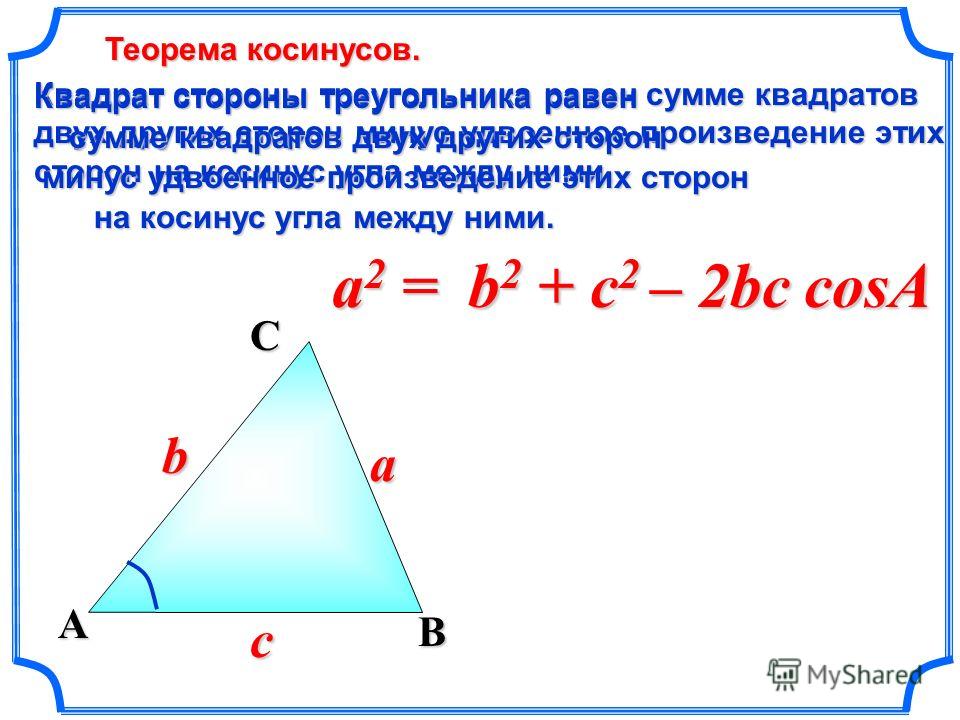 Дабы обнаружить значение тупого либо острого угла, стороны всякого треугольника, довольно применить теорему косинусов и синусов.Теорема косинусов достаточно примитивна: «Квадрат стороны треугольника равен сумме квадратов 2-х других сторон за вычетом удвоенного произведения этих сторон на косинус угла между ними». Существует две трактовки теоремы синусов: малая и расширенная. Согласно малой: «В треугольнике углы пропорциональны противолежащим сторонам». Данную теорему зачастую расширяют за счет свойства описанной около треугольника окружности: «В треугольнике углы пропорциональны противолежащим сторонам, а их отношение равно диаметру описанной окружности».
Дабы обнаружить значение тупого либо острого угла, стороны всякого треугольника, довольно применить теорему косинусов и синусов.Теорема косинусов достаточно примитивна: «Квадрат стороны треугольника равен сумме квадратов 2-х других сторон за вычетом удвоенного произведения этих сторон на косинус угла между ними». Существует две трактовки теоремы синусов: малая и расширенная. Согласно малой: «В треугольнике углы пропорциональны противолежащим сторонам». Данную теорему зачастую расширяют за счет свойства описанной около треугольника окружности: «В треугольнике углы пропорциональны противолежащим сторонам, а их отношение равно диаметру описанной окружности». Производной синуса является косинус, а косинуса – синус, но со знаком «минус».
Производной синуса является косинус, а косинуса – синус, но со знаком «минус». Вообще, вычисление синуса поможет закрепить чертёжные навыки и знание тригонометрических тождеств.
Вообще, вычисление синуса поможет закрепить чертёжные навыки и знание тригонометрических тождеств.
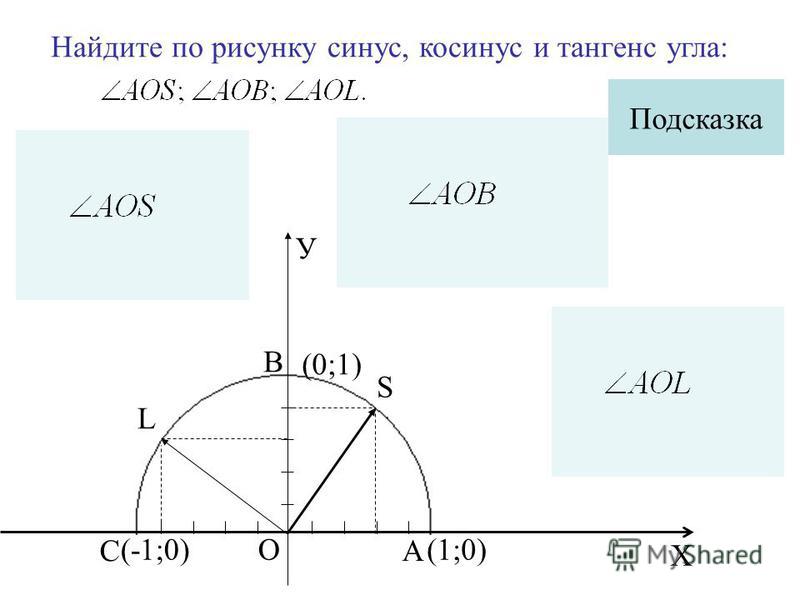

 В ее числителе находится произведение синусов прилегающих углов, а в знаменателе синус противолежащего угла. Теперь рассчитываем площадь по следующим формулам:
В ее числителе находится произведение синусов прилегающих углов, а в знаменателе синус противолежащего угла. Теперь рассчитываем площадь по следующим формулам:
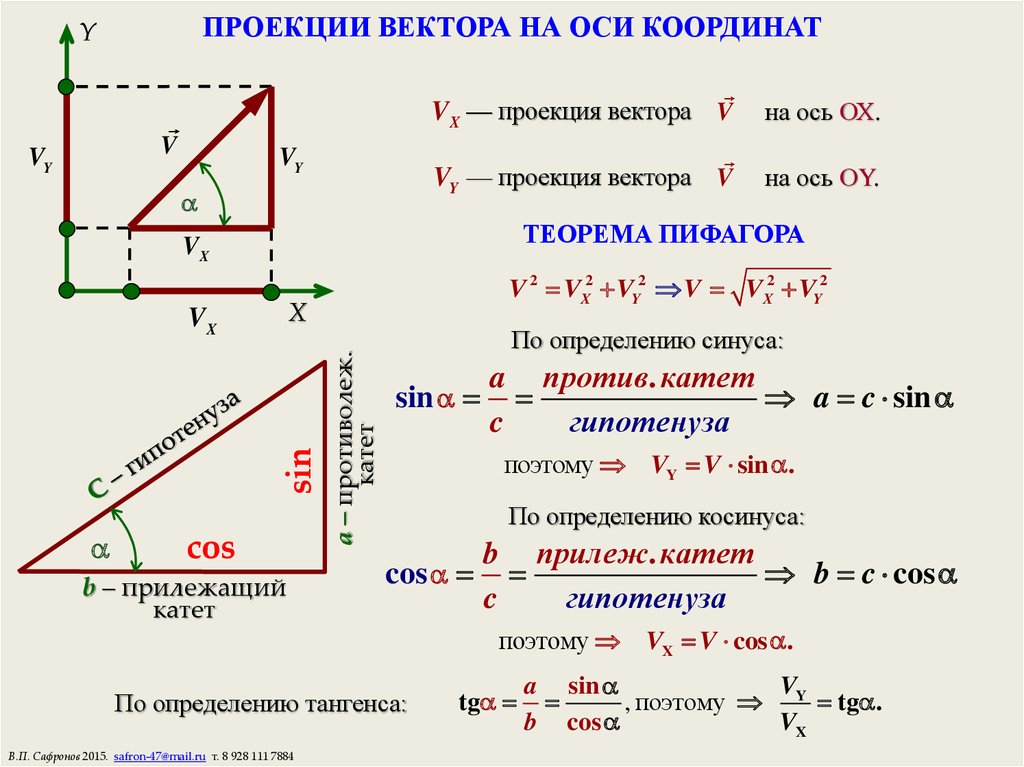 Для любого угла α верно утверждение:
Для любого угла α верно утверждение: А именно:
А именно:
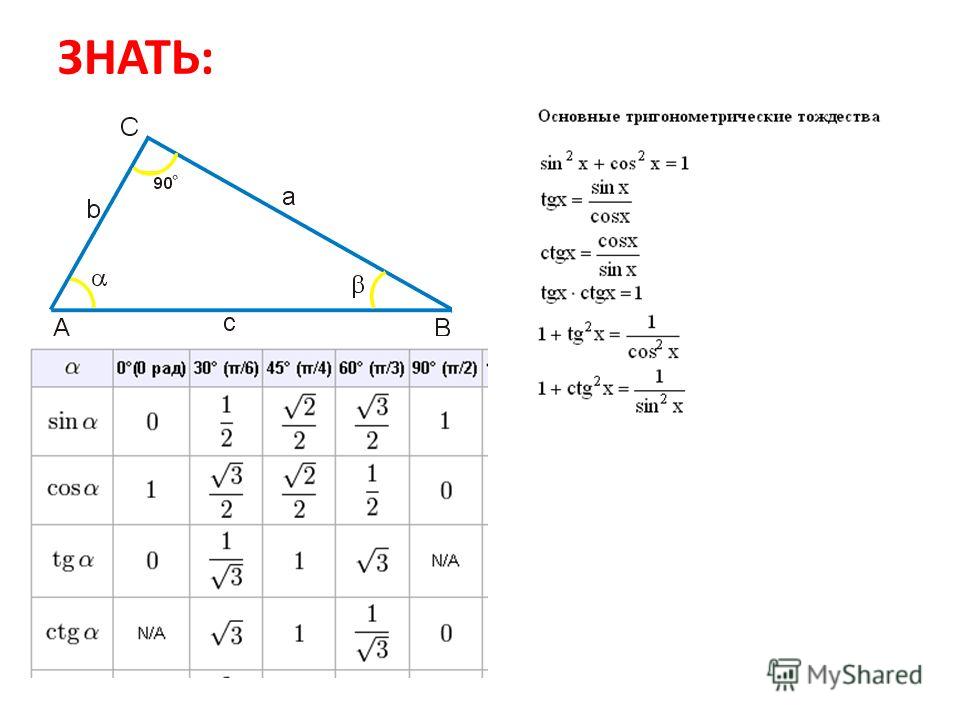 Известно, что α ∈ (3π/2; 2π). Переведем углы из радианной меры в градусную — получим α ∈ (270°; 360°).
Известно, что α ∈ (3π/2; 2π). Переведем углы из радианной меры в градусную — получим α ∈ (270°; 360°). Известно, что угол α ∈ (0; π/2). В градусной мере это записывается так: α ∈ (0°; 90°) — I координатная четверть.
Известно, что угол α ∈ (0; π/2). В градусной мере это записывается так: α ∈ (0°; 90°) — I координатная четверть. А в знаменателе расположено произведение модулей векторов. Каждый модуль равен извлеченному квадратному корню из суммы квадратов координат вектора.
А в знаменателе расположено произведение модулей векторов. Каждый модуль равен извлеченному квадратному корню из суммы квадратов координат вектора. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!
Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!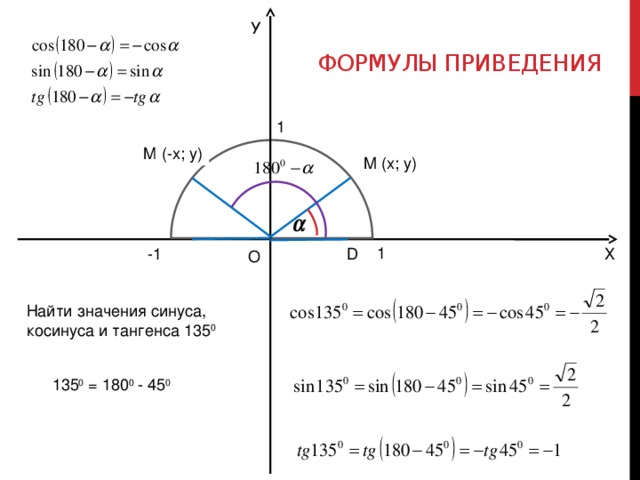

 = 1 2 · a → 2 + b → 2 – b → – a → 2 a → · b →
= 1 2 · a → 2 + b → 2 – b → – a → 2 a → · b → Помимо этой общей формулы, в тригонометрии есть много других формул, которые определяют функцию косинуса, которую вы можете увидеть на следующем изображении.
Помимо этой общей формулы, в тригонометрии есть много других формул, которые определяют функцию косинуса, которую вы можете увидеть на следующем изображении.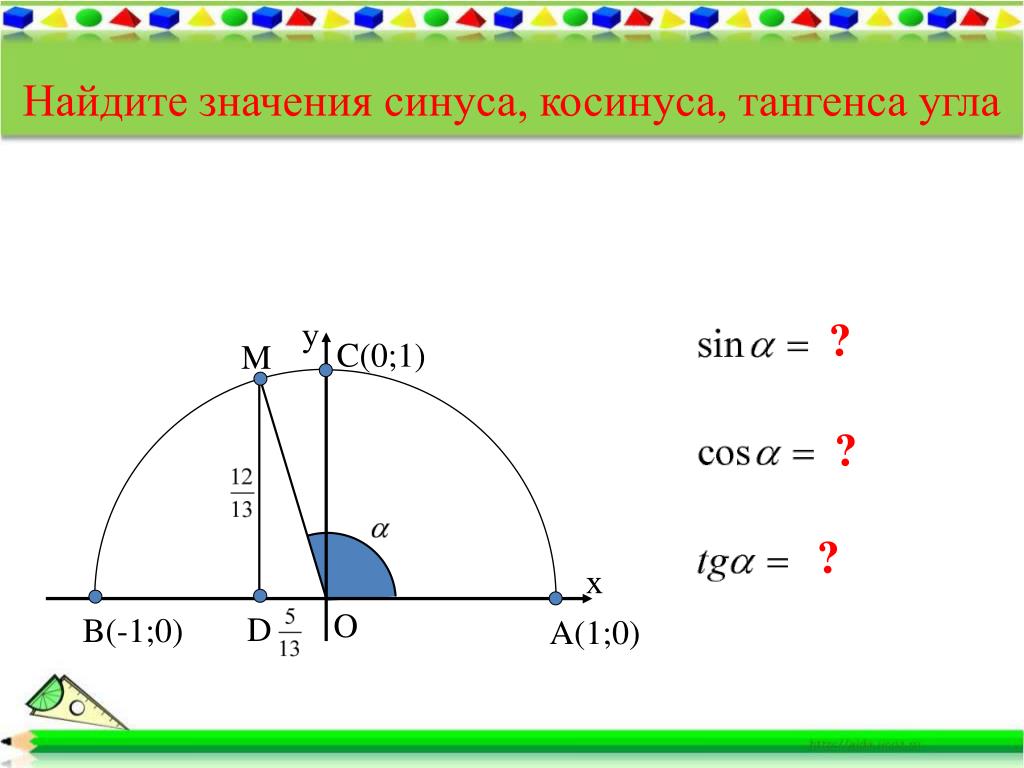 Используя одно из тождеств кофункций,
Используя одно из тождеств кофункций, Среди них формула тройного угла функции косинуса:
Среди них формула тройного угла функции косинуса: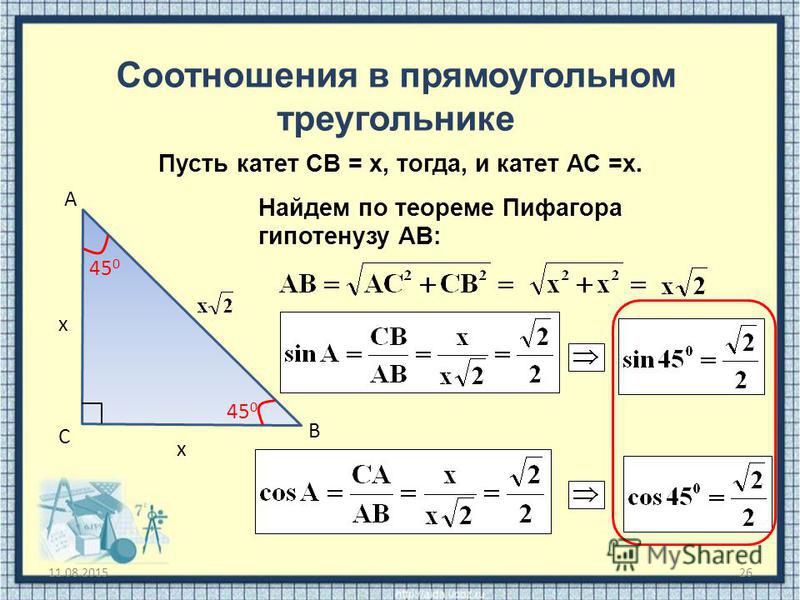 С Cuemath находите решения простыми и легкими шагами.
С Cuemath находите решения простыми и легкими шагами.
 Заменив x на (x/2) с обеих сторон, мы получим cos x = 2 cos 2 (x/2) — 1. . Решая это для cos (x/2), мы получаем cos (x/2) = ± √[ (1 + cos x) / 2 ].
Заменив x на (x/2) с обеих сторон, мы получим cos x = 2 cos 2 (x/2) — 1. . Решая это для cos (x/2), мы получаем cos (x/2) = ± √[ (1 + cos x) / 2 ].
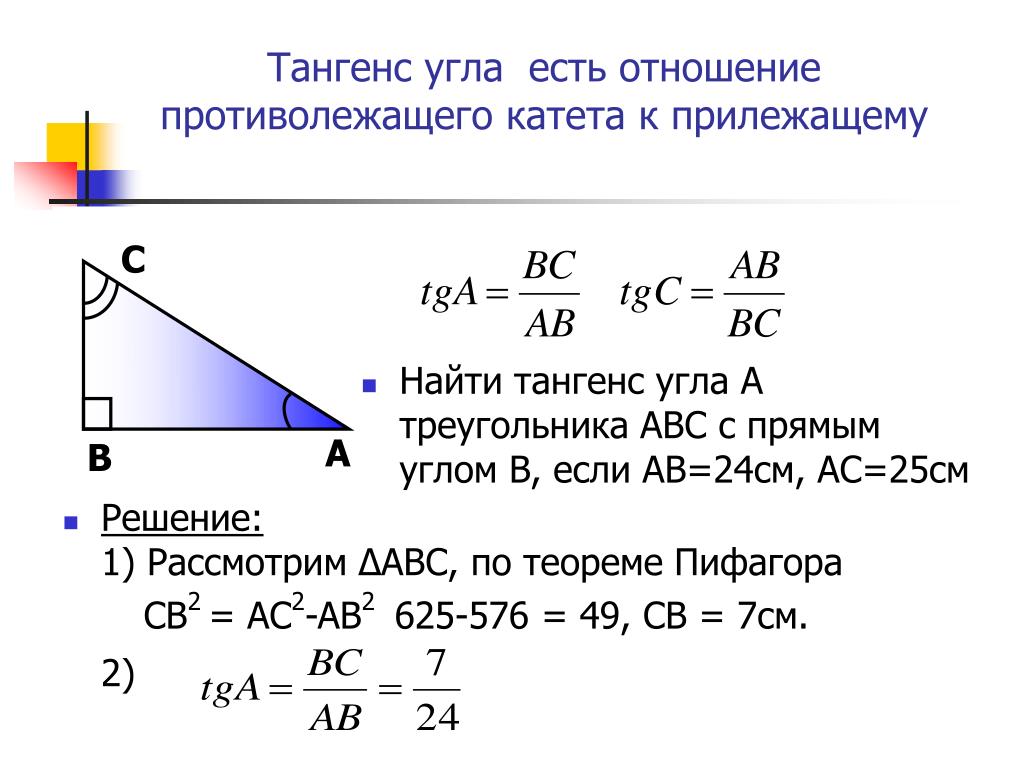 обозначают сторону, противоположную углу B, и мы используем букву c для обозначения стороны, противоположной углу C.
обозначают сторону, противоположную углу B, и мы используем букву c для обозначения стороны, противоположной углу C. Эти и следующие примеры относятся к прямоугольному треугольнику, использованному выше.
Эти и следующие примеры относятся к прямоугольному треугольнику, использованному выше.
 7$°
7$° Таким образом, определение тангенса представляет собой отношение перпендикуляра к основанию и представляется как тангенс θ.
Таким образом, определение тангенса представляет собой отношение перпендикуляра к основанию и представляется как тангенс θ. cot θ = 1
cot θ = 1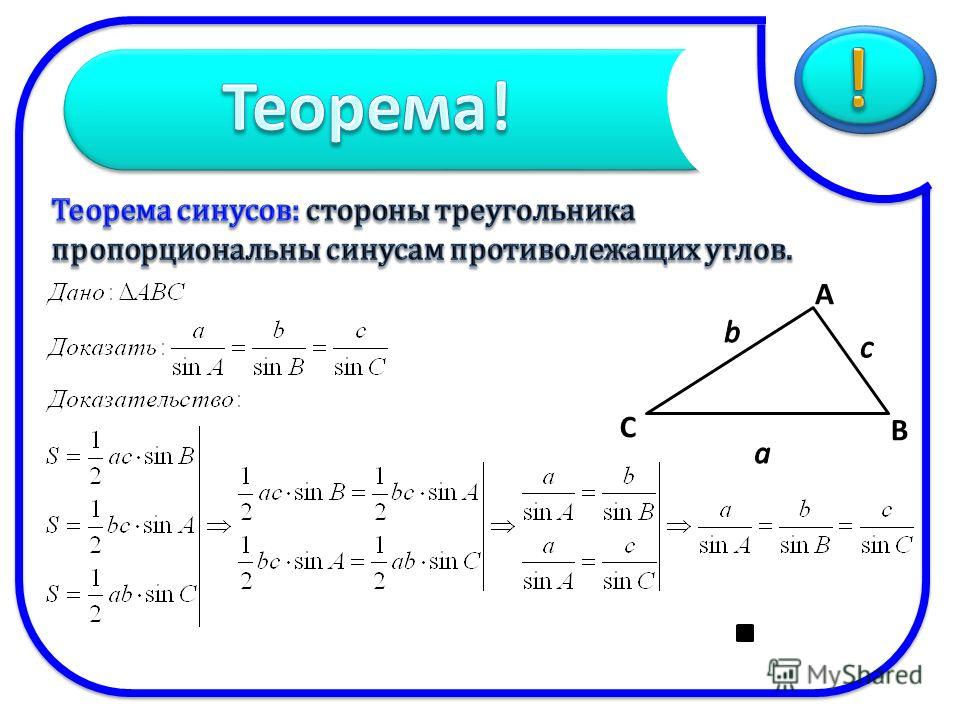
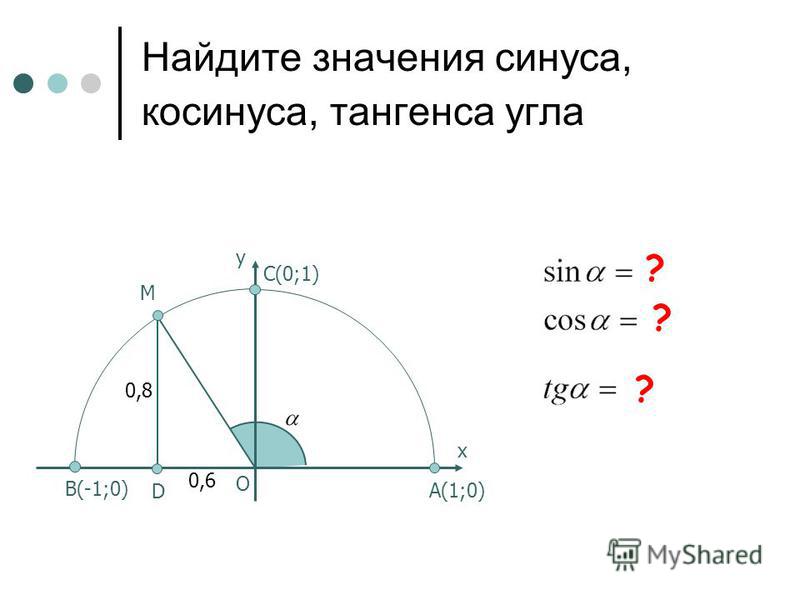



 Теперь еще раз взглянем на те же формулы. Формулы двойного угла являются частным случаем формул суммы, где \(\alpha=\beta\). Вывод формулы двойного угла для синуса начинается с формулы суммы
Теперь еще раз взглянем на те же формулы. Формулы двойного угла являются частным случаем формул суммы, где \(\alpha=\beta\). Вывод формулы двойного угла для синуса начинается с формулы суммы
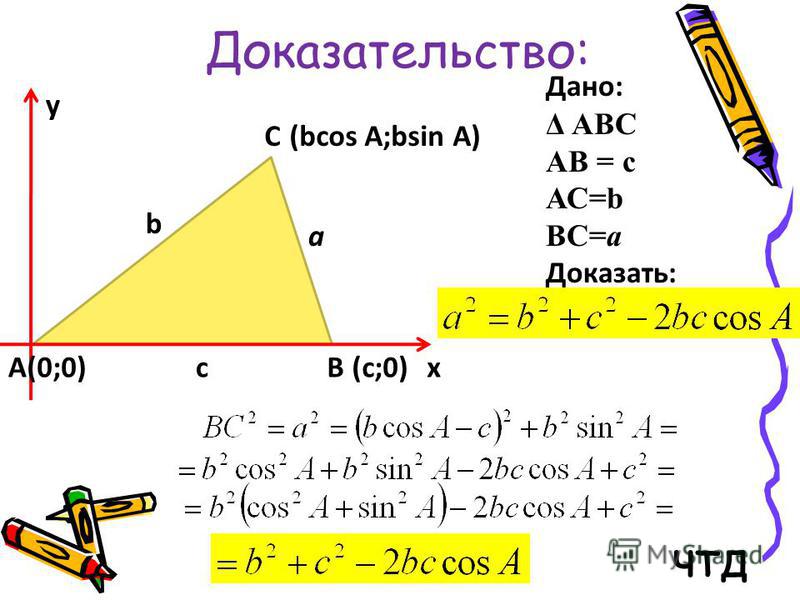
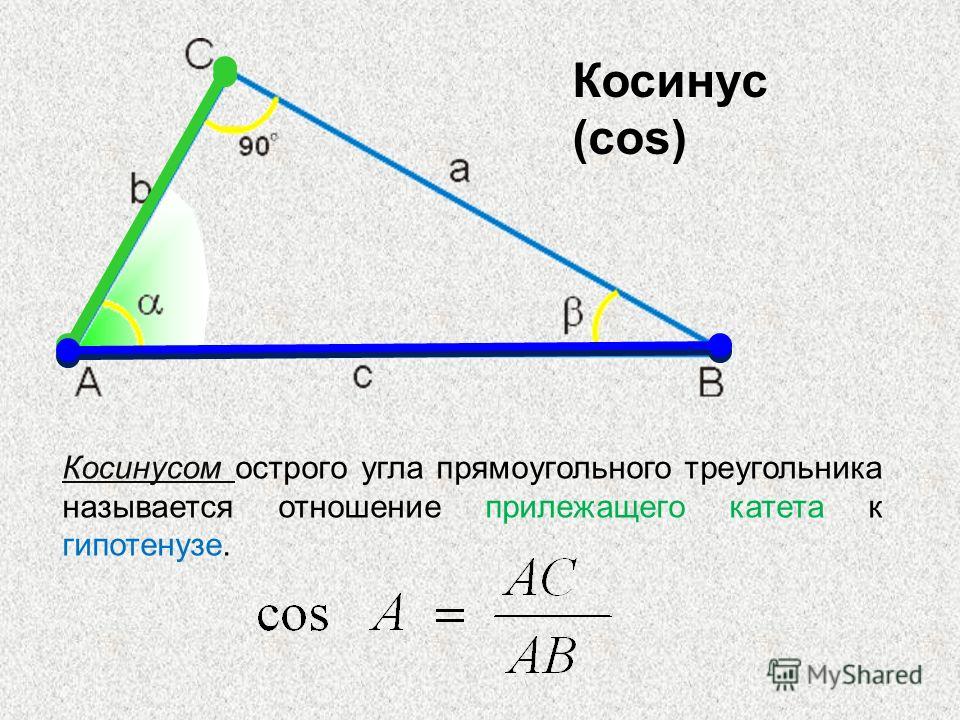 Он подчеркивает, что шаблон — это то, что нам нужно помнить, и что тождества верны для всех значений в области определения тригонометрической функции.
Он подчеркивает, что шаблон — это то, что нам нужно помнить, и что тождества верны для всех значений в области определения тригонометрической функции. 3(2x)=\left[ \dfrac{ 1}{2} \sin(2x) \right] [ 1−\cos(4x) \) 92 x\\[5pt] &= \dfrac{10}{4}+\dfrac{10}{2} \cos(2x)+\dfrac{10}{8}+\dfrac{10}{8}\ cos(4x)\\[5pt] &= \dfrac{30}{8}+5\cos(2x)+\dfrac{10}{8}\cos(4x)\\[5pt] &= \dfrac{ 15}{4}+5\cos(2x)+\dfrac{5}{4}\cos(4x) \end{align*}\]
3(2x)=\left[ \dfrac{ 1}{2} \sin(2x) \right] [ 1−\cos(4x) \) 92 x\\[5pt] &= \dfrac{10}{4}+\dfrac{10}{2} \cos(2x)+\dfrac{10}{8}+\dfrac{10}{8}\ cos(4x)\\[5pt] &= \dfrac{30}{8}+5\cos(2x)+\dfrac{10}{8}\cos(4x)\\[5pt] &= \dfrac{ 15}{4}+5\cos(2x)+\dfrac{5}{4}\cos(4x) \end{align*}\] 92\left(\dfrac{\alpha}{2}\right)&= \dfrac{1-\cos\left(2\cdot \dfrac{\alpha}{2}\right)}{1+\cos\ влево (2 \ cdot \ dfrac {\ alpha} {2} \ right)} \\ \ tan \ left (\ dfrac {\ alpha} {2} \ right) & = \ pm \ sqrt {\ dfrac {1- \ cos \alpha}{1+\cos \alpha}} \end{align*}\]
92\left(\dfrac{\alpha}{2}\right)&= \dfrac{1-\cos\left(2\cdot \dfrac{\alpha}{2}\right)}{1+\cos\ влево (2 \ cdot \ dfrac {\ alpha} {2} \ right)} \\ \ tan \ left (\ dfrac {\ alpha} {2} \ right) & = \ pm \ sqrt {\ dfrac {1- \ cos \alpha}{1+\cos \alpha}} \end{align*}\]
 Используя теорему Пифагора, мы находим, что гипотенуза равна 17. Следовательно, мы можем вычислить {17}\).
Используя теорему Пифагора, мы находим, что гипотенуза равна 17. Следовательно, мы можем вычислить {17}\).

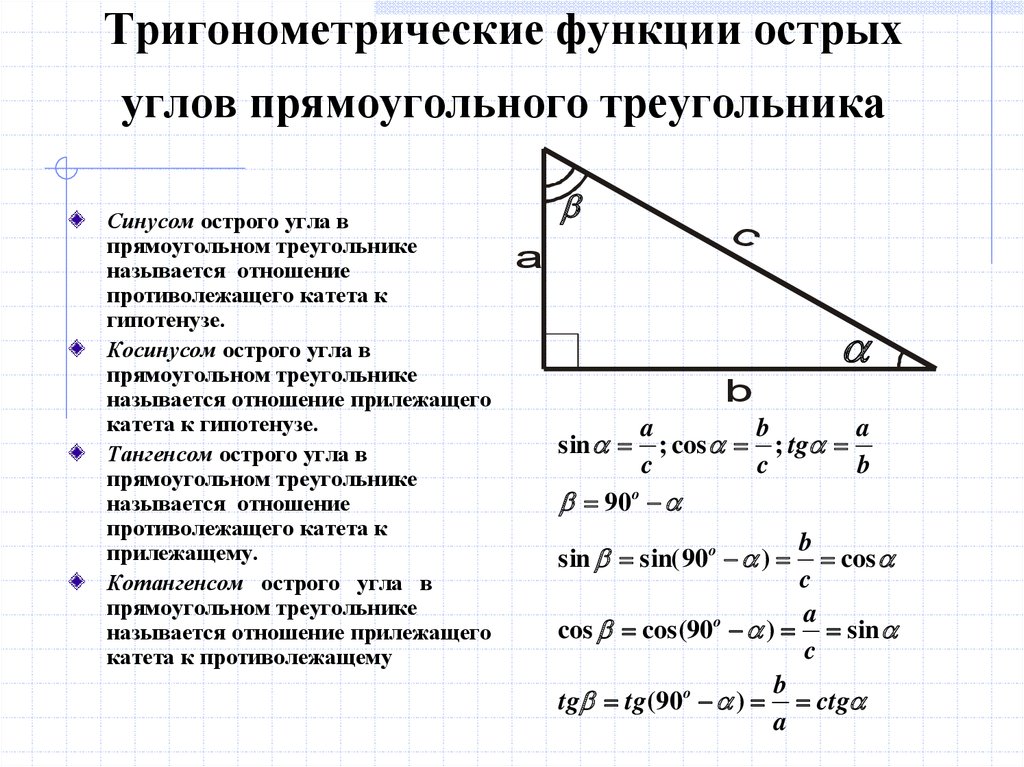
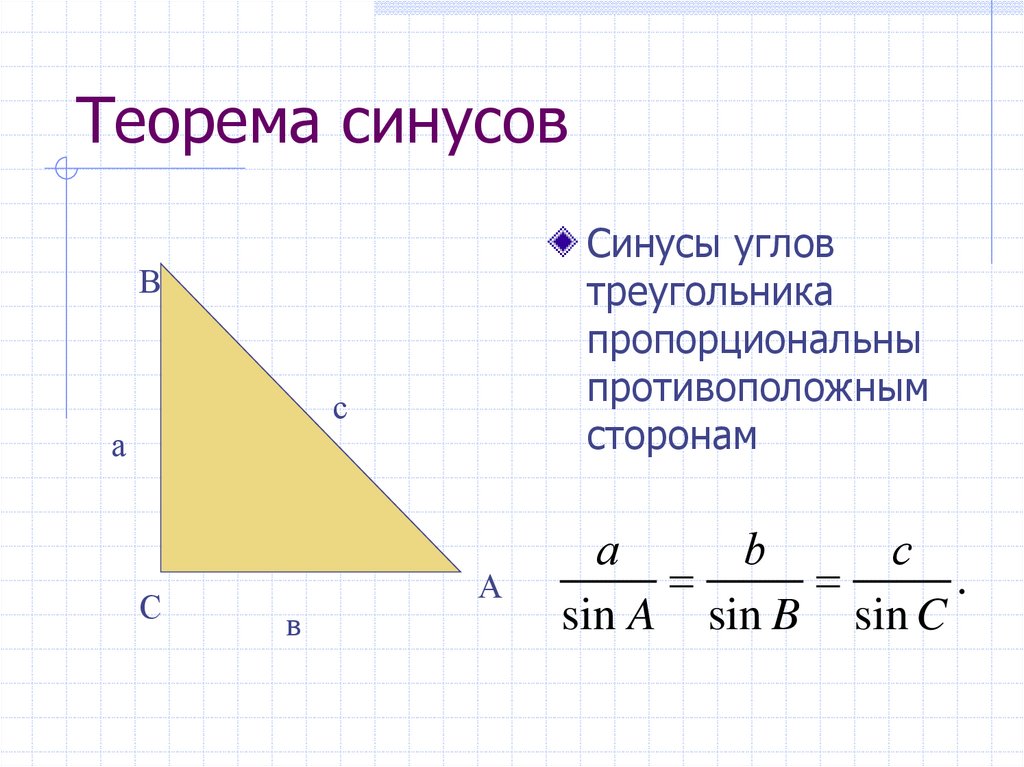 См. Пример \(\PageIndex{1}\), Пример \(\PageIndex{2}\), Пример \(\PageIndex{3}\) и Пример \(\PageIndex{4}\).
См. Пример \(\PageIndex{1}\), Пример \(\PageIndex{2}\), Пример \(\PageIndex{3}\) и Пример \(\PageIndex{4}\).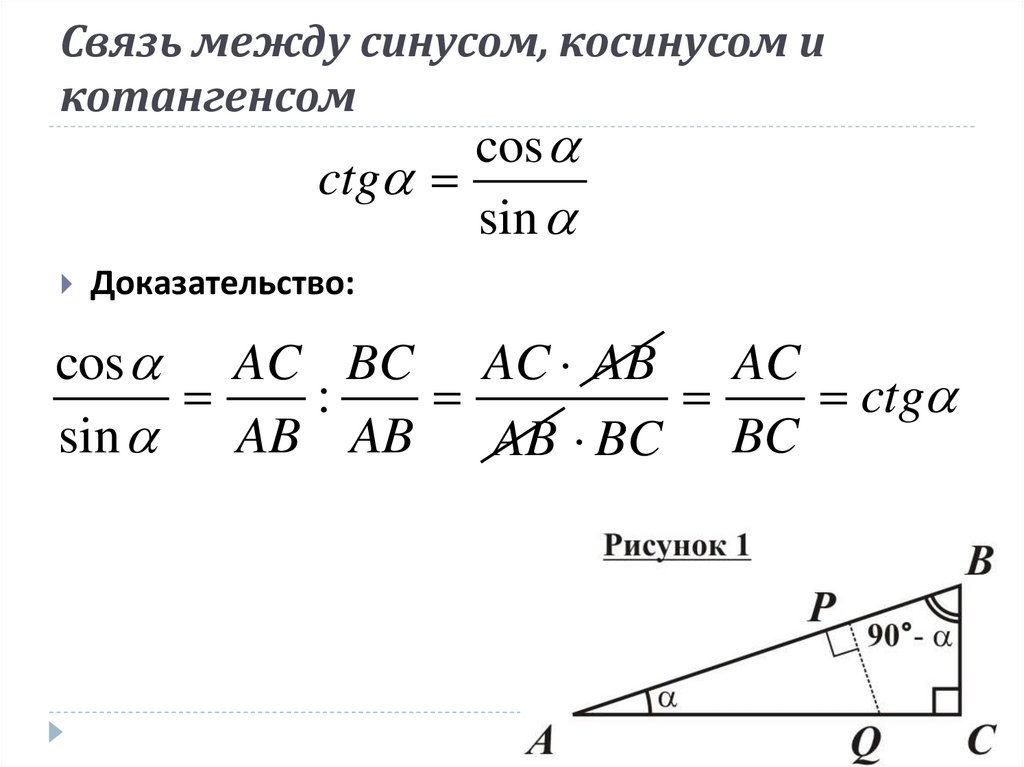 org/details/books/precalculus
org/details/books/precalculus
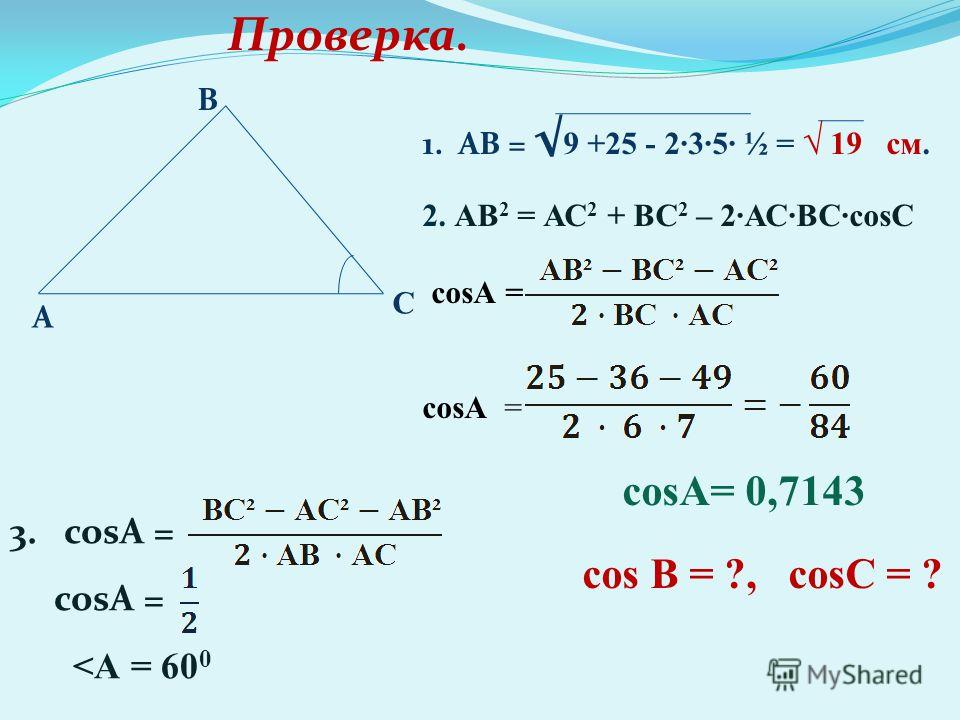
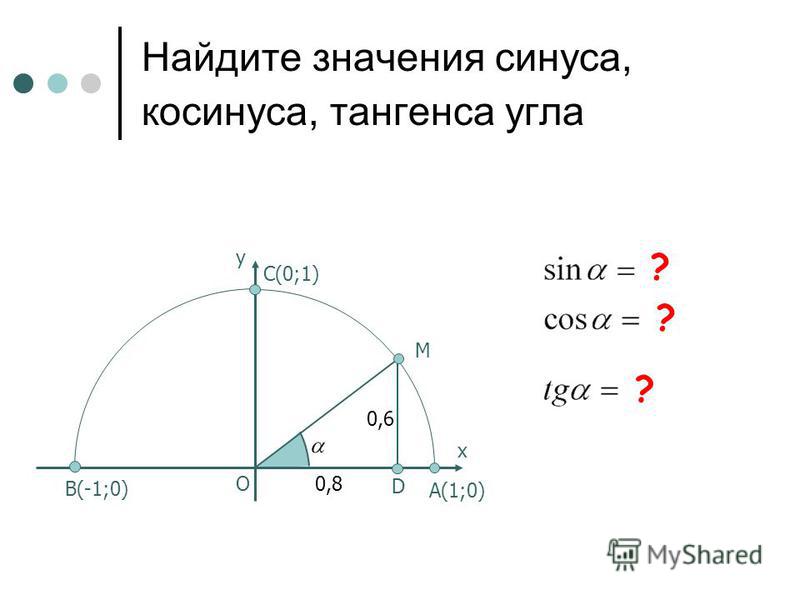
 Включает рассуждения и прикладные вопросы.
Включает рассуждения и прикладные вопросы. Для ответа на этот вопрос нам нужно найти сторону длины x, противоположную углу R. 9{2}&=110619,7432…\\
\\x&=\sqrt{110619.7432…}\\
\\x&=333\mathrm{m}\quad(3sf)\\
\end{aligned}
Для ответа на этот вопрос нам нужно найти сторону длины x, противоположную углу R. 9{2}&=110619,7432…\\
\\x&=\sqrt{110619.7432…}\\
\\x&=333\mathrm{m}\quad(3sf)\\
\end{aligned}

 Обычно вместо угла А используется один из углов треугольника, поэтому расчет будет неверным.
Обычно вместо угла А используется один из углов треугольника, поэтому расчет будет неверным.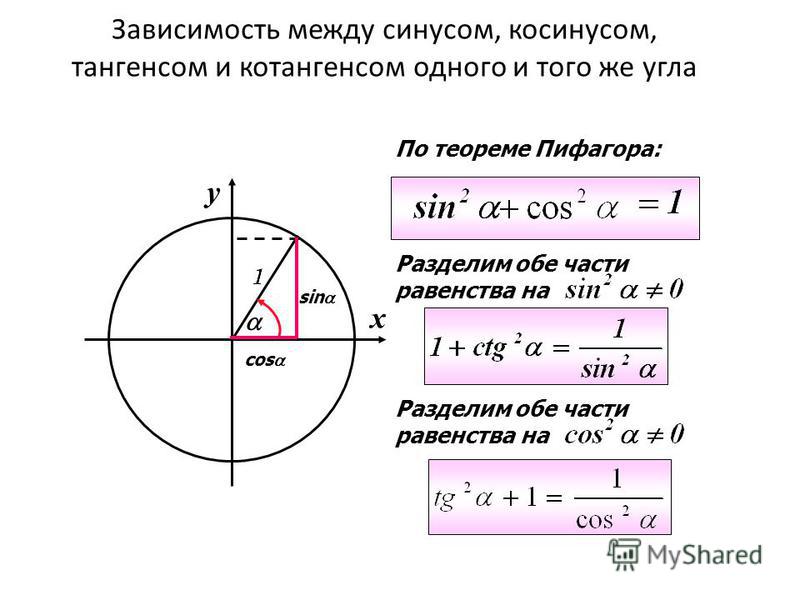 Например.
Например. 


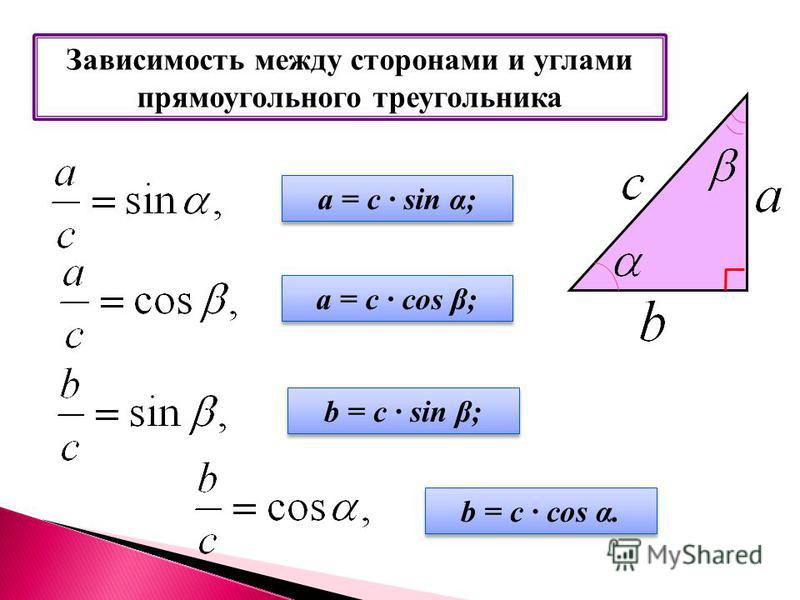 Косинус 90° = 0, поэтому в этом частном случае формула закона косинусов сводится к известному уравнению теоремы Пифагора:
Косинус 90° = 0, поэтому в этом частном случае формула закона косинусов сводится к известному уравнению теоремы Пифагора: В 16 веке закон был популяризирован известным французским математиком Виете, прежде чем он получил свою окончательную форму в 19 веке.
В 16 веке закон был популяризирован известным французским математиком Виете, прежде чем он получил свою окончательную форму в 19 веке.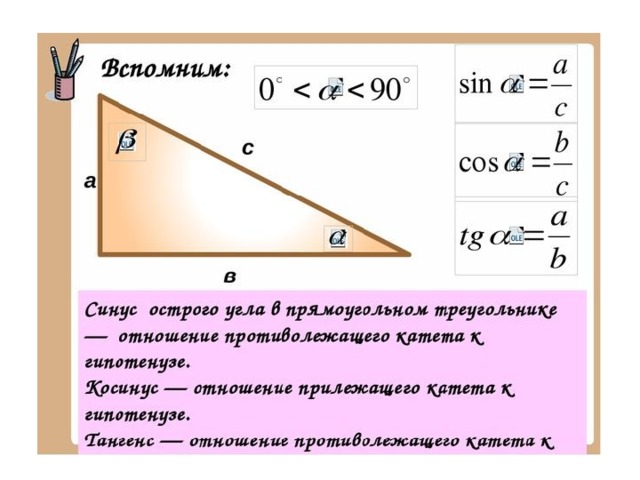 Вот почему мы решили реализовать в этом инструменте SAS и SSS, но не SSA.
Вот почему мы решили реализовать в этом инструменте SAS и SSS, но не SSA. Отсюда:
Отсюда: Теорема Птолемея
Теорема Птолемея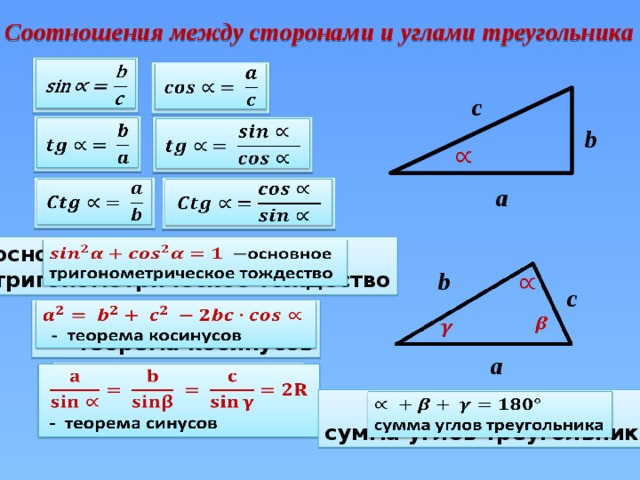
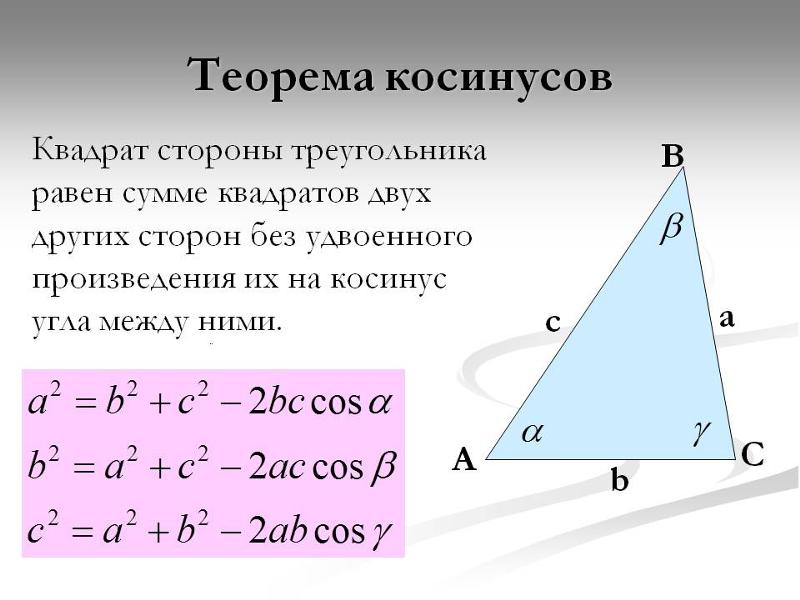 Не забудьте еще раз свериться с рисунком выше, правильно ли вы обозначили стороны и углы правильными символами.
Не забудьте еще раз свериться с рисунком выше, правильно ли вы обозначили стороны и углы правильными символами.


 Тогда дискриминант — это просто число D = b2 − 4ac.
Тогда дискриминант — это просто число D = b2 − 4ac. Аналогично разбираем второе уравнение:
Аналогично разбираем второе уравнение: Наконец, если D < 0, корней нет — ничего считать не надо.
Наконец, если D < 0, корней нет — ничего считать не надо. Например, первую:
Например, первую:
 Если там положительное число — корней будет два. Если отрицательное — корней не будет вообще.
Если там положительное число — корней будет два. Если отрицательное — корней не будет вообще.
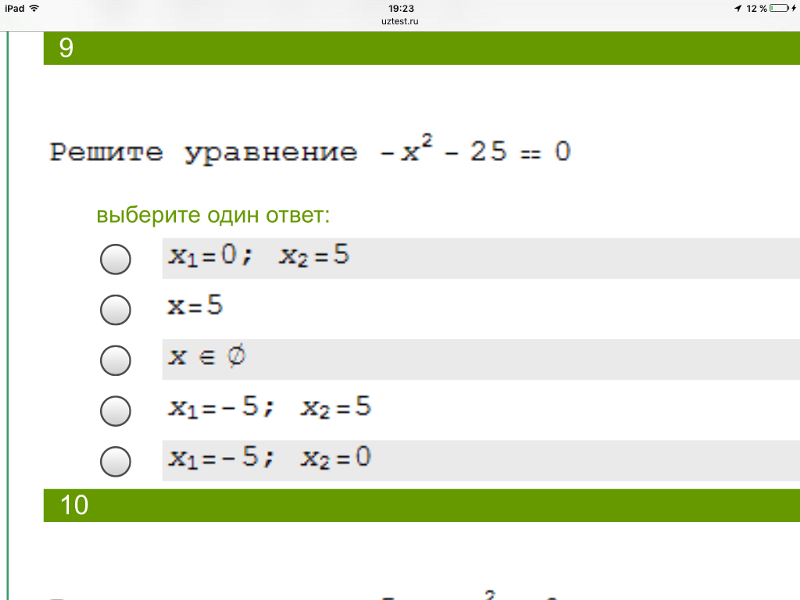 2) 5 ∙ 9 = 45 (кг)
Ответ: 45 кг масса 9 коробок с бананами.
2) 5 ∙ 9 = 45 (кг)
Ответ: 45 кг масса 9 коробок с бананами.
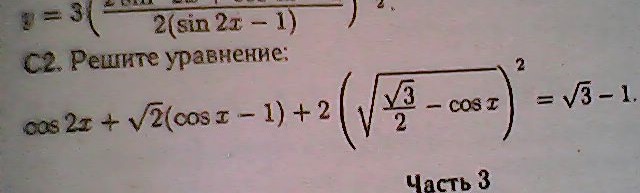 1).
Таня закрасила одну шестую (рис.3).
А Оля закрасила одну двенадцатую (рис. 2).
1).
Таня закрасила одну шестую (рис.3).
А Оля закрасила одну двенадцатую (рис. 2).

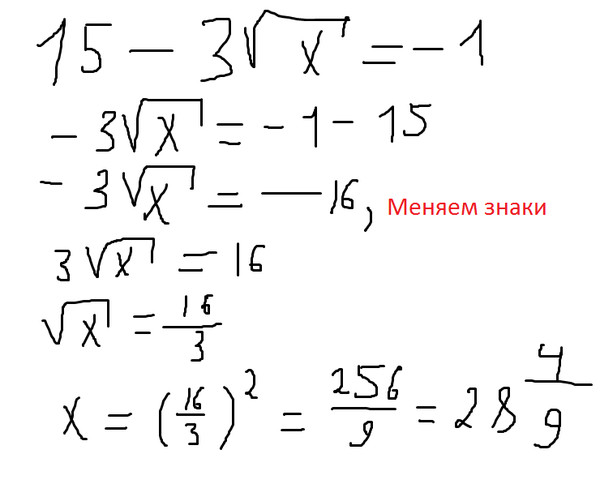 Данные ярче яркого.
Данные ярче яркого. Основание стало плоским. За счёт этого стекло приобрело более надёжную форму с повышенной устойчивостью к трещинам.
Основание стало плоским. За счёт этого стекло приобрело более надёжную форму с повышенной устойчивостью к трещинам. А измерить этот показатель теперь можно с помощью потрясающего датчика и специального приложения на Apple Watch Series 7. Они даже умеют делать это в фоновом режиме днём и ночью.3
А измерить этот показатель теперь можно с помощью потрясающего датчика и специального приложения на Apple Watch Series 7. Они даже умеют делать это в фоновом режиме днём и ночью.3 Или, наоборот, может определить, что у вас синусовый ритм, а значит, сердце бьётся в нормальном режиме.5
Или, наоборот, может определить, что у вас синусовый ритм, а значит, сердце бьётся в нормальном режиме.5 А новая функция «Размышление» в приложении «Осознанность» поможет привести в порядок мысли и обрести баланс. И всё это с невероятно красивой анимацией. Кроме того, в Apple Fitness+ вас ждут медитации с сопровождением — видеосеансы и аудио.9 С их помощью можно улучшить общее самочувствие, фокусируясь на таких темах, как спокойствие, доброта или благодарность.
А новая функция «Размышление» в приложении «Осознанность» поможет привести в порядок мысли и обрести баланс. И всё это с невероятно красивой анимацией. Кроме того, в Apple Fitness+ вас ждут медитации с сопровождением — видеосеансы и аудио.9 С их помощью можно улучшить общее самочувствие, фокусируясь на таких темах, как спокойствие, доброта или благодарность.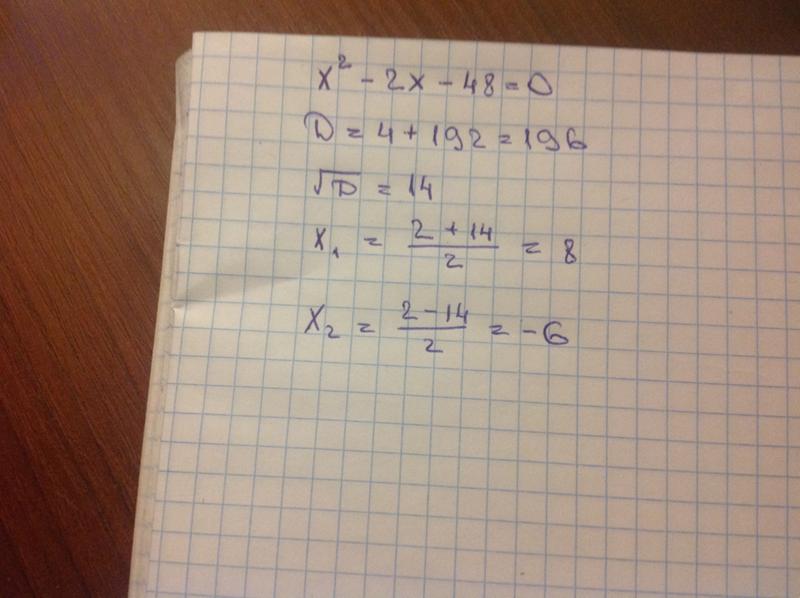 Больше движения, больше эндорфинов. Стартуйте. Прямо с запястья.
Больше движения, больше эндорфинов. Стартуйте. Прямо с запястья.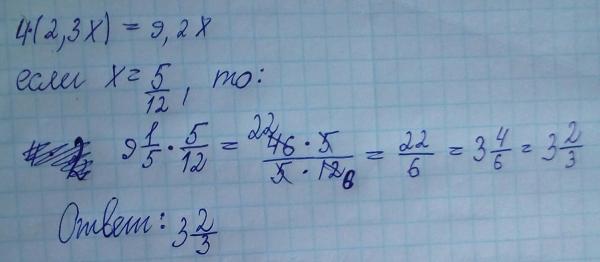
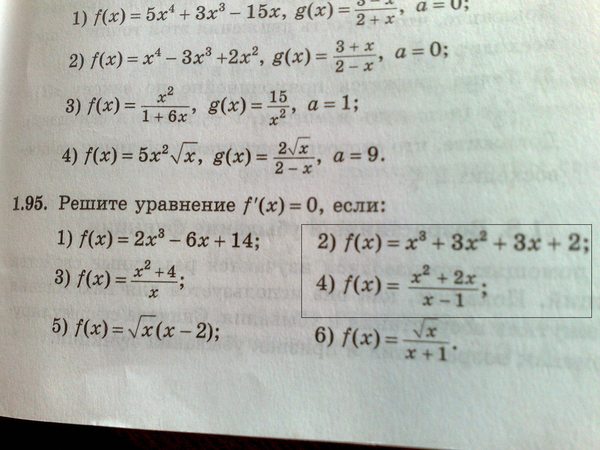 Позвоните в офис, ответьте на срочное письмо, определите верное направление по встроенному компасу, отправьте своим детям сообщение с эмодзи. Когда Apple Watch подключены к iPhone, все важные связи, полезная информация и любимый контент у вас под рукой.
Позвоните в офис, ответьте на срочное письмо, определите верное направление по встроенному компасу, отправьте своим детям сообщение с эмодзи. Когда Apple Watch подключены к iPhone, все важные связи, полезная информация и любимый контент у вас под рукой.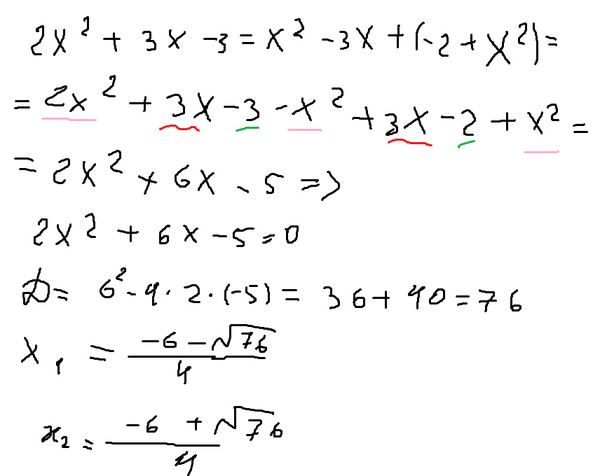
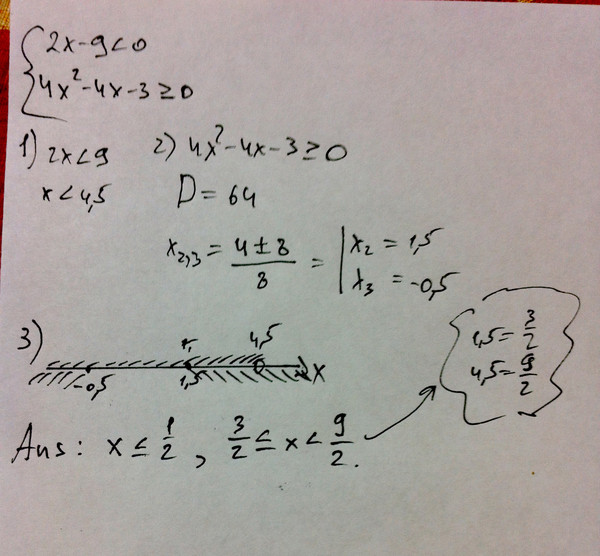
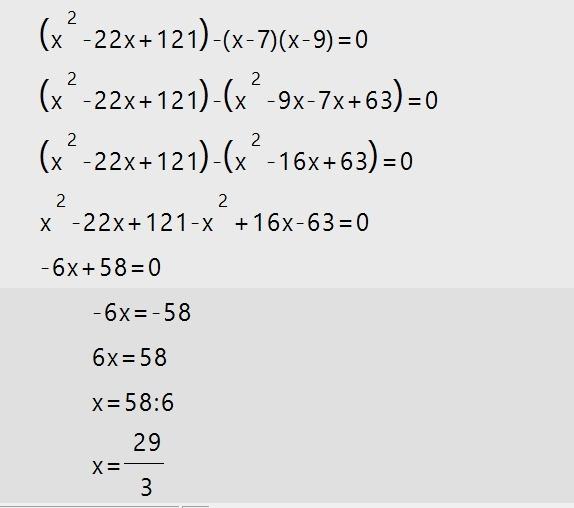
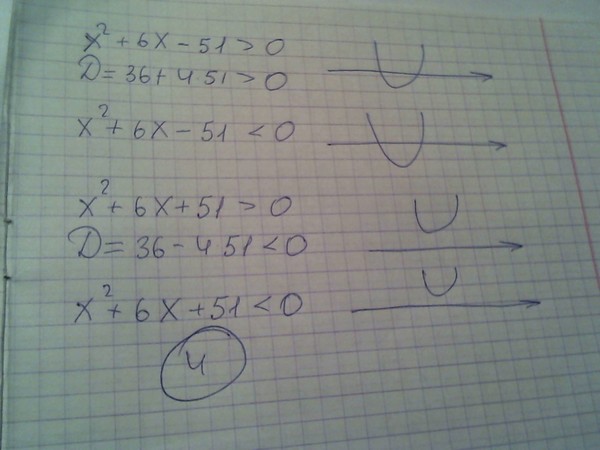 Это изменение сделает сражения более комфортными для всех игроков, особенно для новых.
Это изменение сделает сражения более комфортными для всех игроков, особенно для новых.
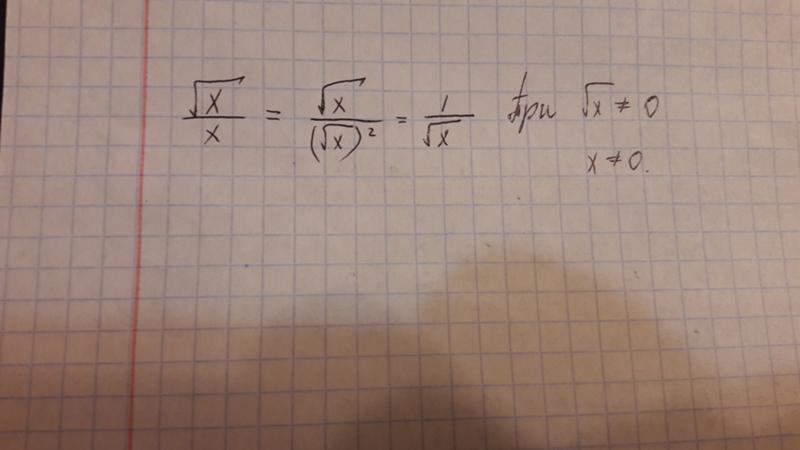

 Квартал зданий в квадрате F9 будет иметь форму, аналогичную кварталу с северной стороны, чтобы обеспечить обеим командам равные возможности для удержания позиций.
Квартал зданий в квадрате F9 будет иметь форму, аналогичную кварталу с северной стороны, чтобы обеспечить обеим командам равные возможности для удержания позиций.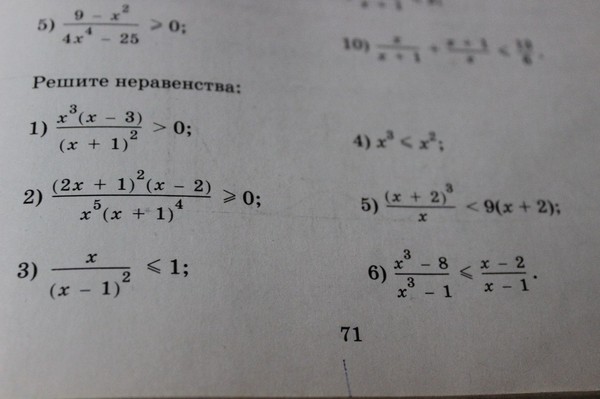 18.1 вместо значений бонусов личного резерва будет отображаться строка текста с надписью «bonus%». Во второй итерации общего теста это будет исправлено. Приносим свои извинения за доставленные неудобства.
18.1 вместо значений бонусов личного резерва будет отображаться строка текста с надписью «bonus%». Во второй итерации общего теста это будет исправлено. Приносим свои извинения за доставленные неудобства.

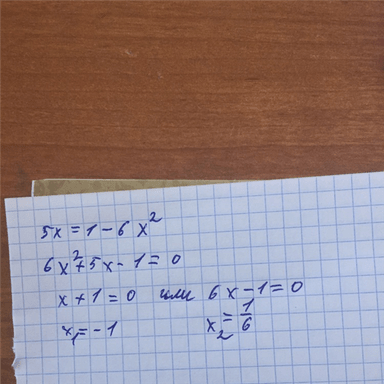
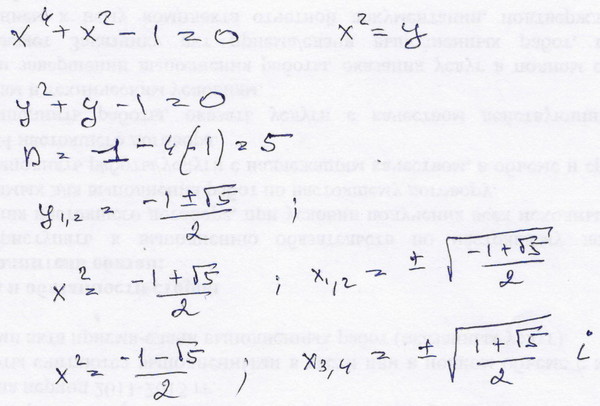 ответил 10.12.14
ответил 10.12.14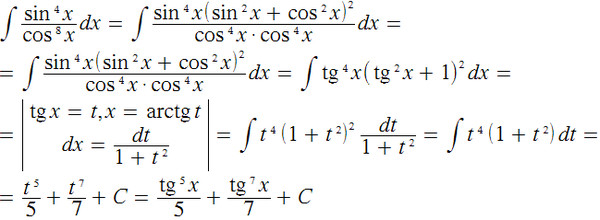 ответил 08.08.13
ответил 08.08.13 7. ac ))/2 a
7. ac ))/2 a 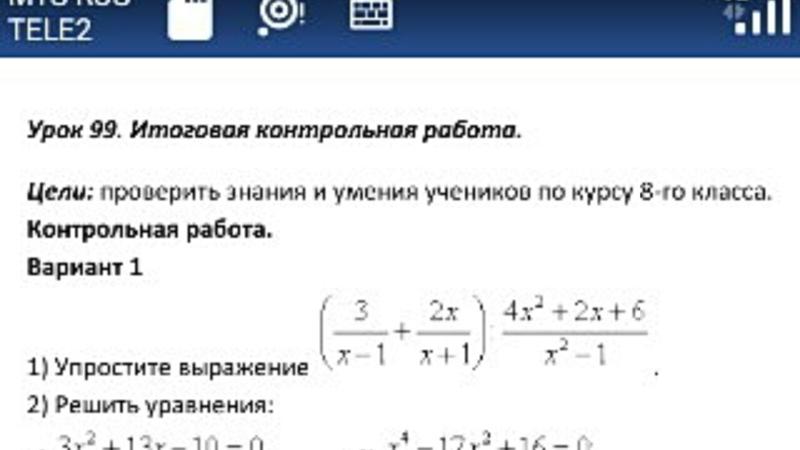
 также график):
также график):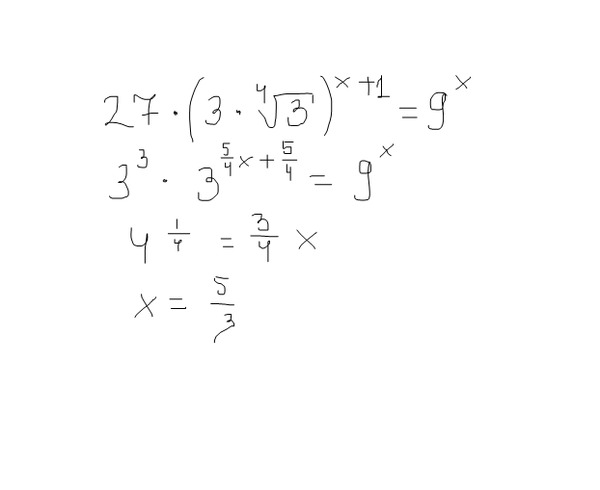 как стандартное квадратное уравнение)
как стандартное квадратное уравнение)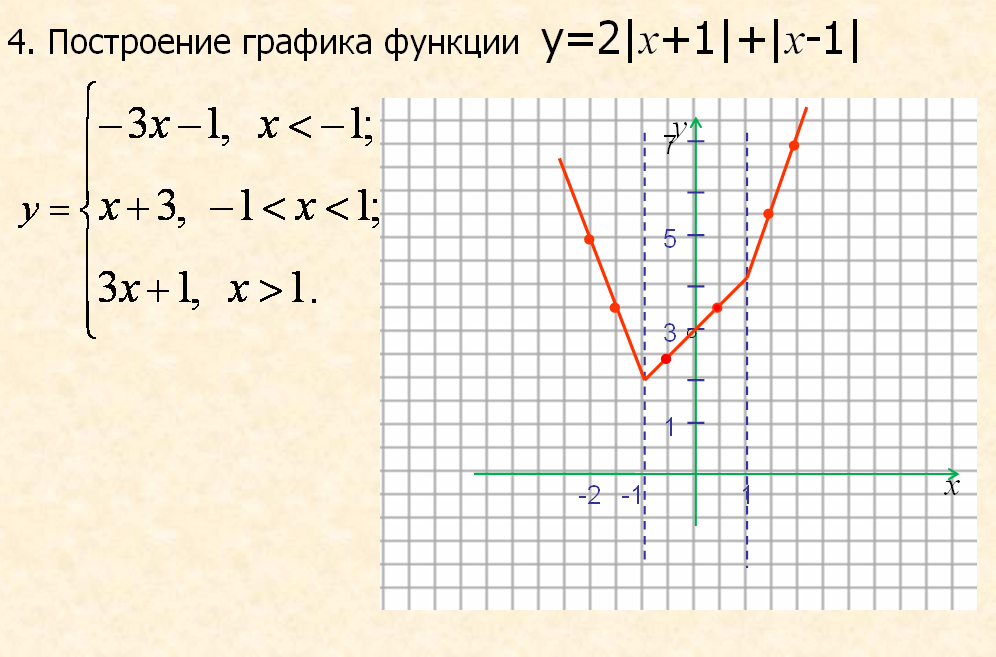
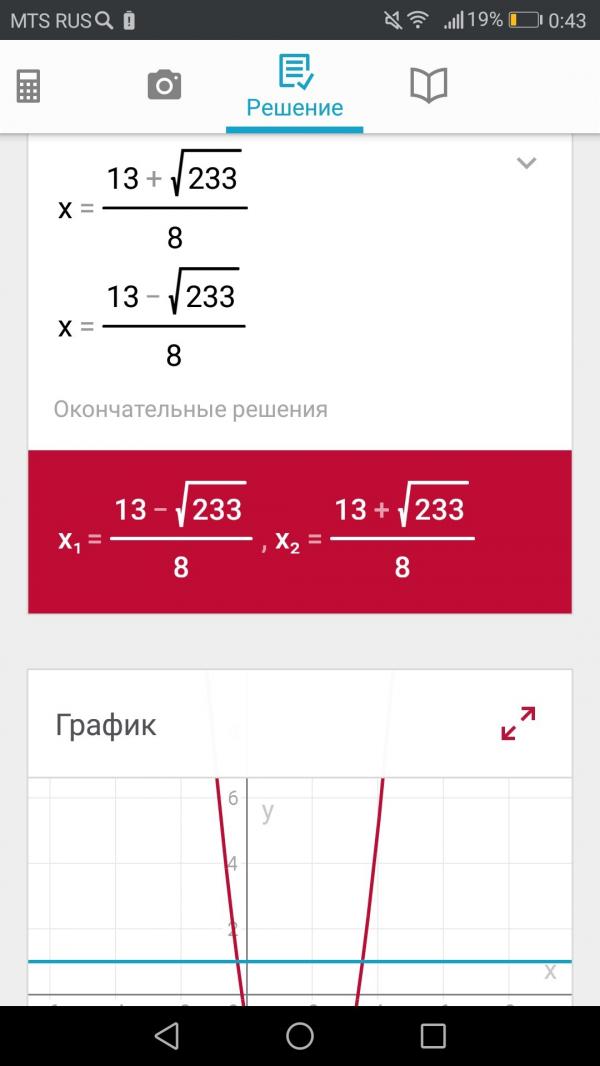 Пожалуйста, включите его, чтобы вы могли испытать все возможности этого сайта.
Пожалуйста, включите его, чтобы вы могли испытать все возможности этого сайта.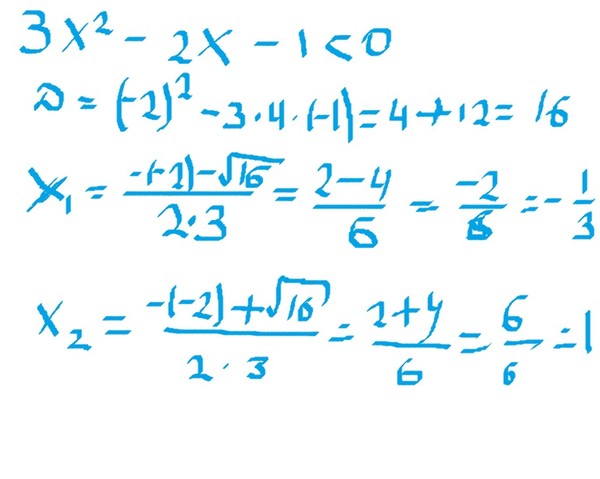
 Вы можете измерить с помощью линейки или просто использовать формулу, включающую координаты каждой конечной точки сегмента. Средняя точка — это просто среднее значение каждой координаты сечения, образующее новую точку координат. Мы проиллюстрируем это ниже.
Вы можете измерить с помощью линейки или просто использовать формулу, включающую координаты каждой конечной точки сегмента. Средняя точка — это просто среднее значение каждой координаты сечения, образующее новую точку координат. Мы проиллюстрируем это ниже.