5 92 = 2.01948357912e+64 5 93 = 1.0097419586828956e+65 5 94 = 5.048709793414478e+65 5 95 = 2.5243548967072393e+66 5 96 = 1.2621774483536197e+67 5 97 = 6. 310887241768098e+67 5 98 = 3.155443620884049e+68 5 99 = 1,5777218104420245е+69 5 100 = 7,88860 310887241768098e+67 5 98 = 3.155443620884049e+68 5 99 = 1,5777218104420245е+69 5 100 = 7,8886010123e+69
Поиск по номерам| 1 | 2 | 3 | 4 | 5 | | 6 | 7 | 8 | 9 | 10 | | 11 | 12 | 13 | 14 | 15 | | 16 | 17 | 18 | 19 | 20 | | 21 | 22 | 23 | 24 | 25 | | 26 | 27 | 28 | 29 | 30 | | 31 | 32 | 33 | 34 | 35 | | 36 | 37 | 38 | 39 | 40 | | 41 | 42 | 43 | 44 | 45 | | 46 | 47 | 48 | 49 | 50 | | 51 | 52 | 53 | 54 | 55 | | 56 | 57 | 58 | 59 | 60 | | 61 | 62 | 63 | 64 | 65 | | 66 | 67 | 68 | 69 | 70 | | 71 | 72 | 73 | 74 | 75 | | 76 | 77 | 78 | 79 | 80 | | 81 | 82 | 83 | 84 | 85 | | 86 | 87 | 88 | 89 | 90 | | 91 | 92 | 93 | 94 | 95 | | 96 | 97 | 98 | 99 | 100 |
Калькулятор дробей
Этот калькулятор выполняет основные и расширенные операции с дробями, выражения с дробями в сочетании с целыми, десятичными и смешанными числами. Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении. Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении. Правила выражений с дробями: Дроби — для деления числителя на знаменатель используйте косую черту, т.е. для пятисотых введите 5/100 . Если вы используете смешанные числа, оставьте пробел между целой и дробной частями. Смешанные числа (смешанные числа или дроби) сохраняют один пробел между целым числом и дробью
и используют косую черту для ввода дробей, например, 1 2/3 . Пример отрицательной смешанной дроби: -5 1/2 .
Поскольку косая черта является одновременно знаком дробной части и деления, используйте двоеточие (:) в качестве оператора деления дробей, т. е. 1/2 : 1/3 .
Decimals (десятичные числа) вводятся с десятичной точкой . и они автоматически преобразуются в дроби — т. е. 1,45 . е. 1,45 . Математические символы
| Символ | Название символа | Символ Значение | Пример |
|---|
| + | plus sign | addition | 1/2 + 1/3 | | — | minus sign | subtraction | 1 1/2 — 2/3 | | * | asterisk | multiplication | 2/3 * 3/4 | | × | times sign | multiplication | 2/3 × 5/6 | | : | division sign | division 91/2
• сложение дробей и смешанных чисел: 8/5 + 6 2/7
• деление целых чисел и дробей: 5 ÷ 1/2
• сложные дроби: 5/8 : 2 2/3
• десятичная дробь: 0,625
• Преобразование дроби в десятичную: 1/4
• Преобразование дроби в процент: 1/8 %
• сравнение дробей: 1/4 2/3
• умножение дроби на целое число: 6 * 3/4
• квадратный корень дроби: sqrt(1/16)
• сокращение или упрощение дроби (упрощение) — деление числителя и знаменателя дроби на одно и то же ненулевое число — эквивалентная дробь: 4/22
• выражение со скобками: 1/3 * (1/2 — 3 3/8)
• составная дробь: 3/4 от 5/7
• кратные дроби: 2/3 от 3/5
• разделить, чтобы найти частное: 3/5 ÷ 2/3
Калькулятор следует известным правилам для порядка операций . Наиболее распространенные мнемоники для запоминания этого порядка операций: Наиболее распространенные мнемоники для запоминания этого порядка операций:
PEMDAS — Скобки, Экспоненты, Умножение, Деление, Сложение, Вычитание.
BEDMAS — Скобки, Экспоненты, Деление, Умножение, Сложение, Вычитание
BODMAS — Скобки, Порядок, Деление, Умножение, Сложение, Вычитание.
GEMDAS — символы группировки — скобки (){}, показатели степени, умножение, деление, сложение, вычитание.
MDAS — Умножение и деление имеют тот же приоритет, что и сложение и вычитание. Правило MDAS является частью порядка операций правила PEMDAS.
Будь осторожен; всегда выполняйте умножение и деление перед сложением и вычитанием . Некоторые операторы (+ и -) и (* и /) имеют одинаковый приоритет и должны оцениваться слева направо. - Использование денег
Из 550 000,00, переданных школе, было использовано 325 000,00. Какая часть от общей суммы была использована? - Дети 9
В комнате 11 детей. 6 детей — девочки. Какую часть детей составляют девочки? 6 детей — девочки. Какую часть детей составляют девочки? - Одна суббота
Однажды субботним вечером в кинотеатре 40 девушек, 25 юношей, 18 женщин и 17 мужчин. Какую часть составляют девочки? - Дробями
Муравей поднимается на 2/5 шеста за первый час и на 1/4 шеста за следующий час. Какую часть шеста преодолевает муравей за два часа? - У Макса 2
У Макса 13 пар носков. Отсюда шесть пар синих, три пары коричневых, две черных и две белых. Какая часть носков Макса коричневого или черного цвета? - Младенцы
В автобусе двое взрослых, двое детей и четверо младенцев. Какую часть населения составляют младенцы? - Жениться
У Жени было 1 1/2 дюжины яиц в холодильнике. Использовала 1/3 яйца. Какая часть яиц использовалась? - Вычислить выражение
Вычислить значение выражения z/3 — 2 z/9 + 1/6, для z = 2 - Ферма 6
На ферме 20 животных. Есть четыре курицы. Какую часть животных составляют куры? Выразите ответ дробью в простейшей форме. - Значение Z
При x = -9, каково значение Z, где Z равно числителю дроби x минус 17 в знаменателе 6,5 конец дроби Дайте ответ с точностью до 2 знаков после запятой. - Мэтью
У Мэтью восемь карандашей. У трех из них нет ластика на конце. Какая часть карандашей не имеет ластика на конце?
more math problems » - decimals
- fractions
- triangle ΔABC
- percentage %
- permille ‰
- prime factors
- complex numbers
- LCM
- GCD
- LCD
- combinatorics
- equations
- статистика
- … все математические калькуляторы
Статья I Раздел 8 | Конституция Аннотированный | Congress.gov Раздел 8 Перечисленные полномочия
- ArtI.S8.C3.8 Иностранные
- ArtI.S8.C3.Overview Указатель иностранной торговли
- Arti.s8.C3.8.2 Инструменты торговли
- Arti.s8.C3.9 Коммерция с коренными америкационными племенами: Область авторитета
- .
Чеканить деньги, регулировать их стоимость и иностранную монету и устанавливать стандарт мер и весов; - ArtI.S8.C5.1 Мощь чеканки монет
- Клаус 16 Орган организации, вооружения и дисциплины милиции, а также для управления той ее частью, которая может быть использована на службе Соединенных Штатов, оставляя за Штатами, соответственно, назначение офицеров и полномочия по обучению милиции в соответствии с дисциплина, предписанная Конгрессом;
- ArtI.S8.C16.1 Полномочия Конгресса по организации ополчений
- Пункт 17 Анклав Пункт
Для осуществления исключительных законов во всех случаях может путем уступки определенных штатов и принятия Конгрессом стать резиденцией правительства Соединенных Штатов и осуществлять аналогичные полномочия над всеми местами, приобретенными с согласия законодательного собрания штата, в котором они будут находиться, для возведение фортов, погребов, арсеналов, верфей и других необходимых построек; — И 9. 0004 0004 - ArtI.S8.C17.1 Капитолий
- ArtI.S8.C17.1.1 Местонахождение правительства Пункт Историческая справка
- ArtI.S8.C17.1.2 Местонахождение правительства Доктрина и практика
9.002270 S8.C17.2 Места на зачистке- Arti.s8.C17.2.1 Обзор положения о местах.
- Пункт 18 Необходимый и правильный пункт
Издавать все законы, необходимые и надлежащие для осуществления вышеизложенных полномочий и всех других полномочий, возложенных настоящей Конституцией на Правительство Соединенных Штатов или на любой Департамент или его должностное лицо. - ArtI.S8.C18.1 Обзор статьи
«Необходимое и правильное»0007- ArtI.S8.C18.4 Развитие в девятнадцатом веке после Маккаллоха
- ArtI.S8.C18.5 Двадцатый век до настоящего времени Доктрина
- ArtI.S8.C18.6 Значение правильного .7 Расследования и надзор
- ArtI.S8.C18.7.1 Историческая справка
- ArtI.S8.C18.7.2 Подразумеваемые полномочия Конгресса проводить расследования и надзор: доктрина и практика
| 111 8 Иммиграция- ArtI.
 S8.C18.8.1 Обзор S8.C18.8.1 Обзор - ArtI.S8.C18.8.2 Историческая справка
- ArtI.S8.C18.8.2.1 Английское общее право
- ArtI.S8.C18.8.2.2 Колониальная практика и конституционная конвенция
- ArtI.S8.C18.8.2.3 Ранние федеральные законы –1900)
- ArtI.S8.C18.8.5 Доктрина пленарной власти двадцатого века
- ArtI.S8.C18.8.5.1 Обзор
- ArtI.S8.C18.8.5.2 Иностранцы в США
- ArtI.S8.C18.8.5.3 Иностранцы, желающие въехать в США
77 ArtI.S8.C18.8.6 Современная юриспруденция- ArtI.S8.C18.8.6.1 Обзор
- ArtI.S8.C18.8.6.2 Исключение иностранцев
- ArtI.S8.C18.8.6.3 Керри против Дина и Trump v. Hawaii
- ArtI.S8.C18.8.6.4 Федеральные законы, касающиеся иностранцев
- ArtI.S8.C18.8.6.5 Законы штата, касающиеся иммиграции
- Ст.I.S8.C18.8.7 Заключение
Мэтуэй | Популярные задачи Популярные задачи Базовая математикаПредварительная алгебраАлгебраТригонометрияПредварительный исчислениеИсчислениеКонечная математикаЛинейная алгебраХимияФизика | Ранг | Тема | Проблема | Отформатированная проблема |
|---|
| 1 | Решение с использованием обратной матрицы | х+2у=1, 4х+5у=13 | , | | 2 | Умножение матриц | [[1/(квадратный корень из 17),-4/(квадратный корень из 17)]][[1/(квадратный корень из 17)],[-4/(квадратный корень из 17)]] | | | 3 | Найти домен | х+у=3 | | | 4 | Найти домен | х-у=3 | | | 5 | Найти домен | у=-2х+3 | | | 6 | Найти домен | у=2х+1 92+9х+3 , х=х+2 | , | | 8 | Найти домен | у=2х | | | 9 | Найти домен | у=-3x | | | 10 | Найти домен | у=3х-2 | | | 11 | Найти домен | у=4х | | | 12 | Найти домен | 3x+2y=6 | | | 13 | Найдите матрицу идентичности 5×5 | 5 | | | 14 | Найдите матрицу идентичности 6×6 | 6 | | | 15 | Найдите матрицу идентичности 4×4 | 4 | | | 16 | Решение с использованием обратной матрицы | 2х+у=-2, х+2у=2 | , | | 17 | Решение с использованием обратной матрицы | 4х+4=у, у=6х | , | | 18 | Решение с использованием обратной матрицы | 4х+2=5у-3, у=3х-1 | , | | 19 | Найдите набор силы | (3,4) | | | 20 | Оценить | кубический корень из 216 | | | 21 | Найдите набор силы | (1,3) | | | 22 | Найти домен | 3x-2y=12 | | | 23 | Найти домен | у=5х+2 | | | 24 | Найти домен | у=2х-3 | | | 25 | Найти домен | у=2х-4 | | | 26 | Найти домен | у=2х+5 | | | 27 | Найти домен | у=1/2х | | | 28 | Найти домен | у=1/2x-3 | | | 29 | Найти домен | у=2/3х-2 | | | 30 | Найти домен | х=2у | | | 31 | Найти домен | х-2у=2 | | | 32 | Найти домен | х-2у=6 | | | 33 | Найти домен | 2г+х | | | 34 | Найти домен | 2х+у=0 | | | 35 | Найти домен | у=5х+6 | | | 36 | Найти домен | у=х+3 | | | 37 | Решить с помощью матрицы методом исключения | у=4х+3х-2, у=6 | , | | 38 | Определить, является ли линейно зависимым | Б={[[-10,2],[5,-2,5]]} | | | 39 | Добавить | [[2,4],[6,-4]]+[[-3,-7],[20,10]] | | | 40 | Определить, является ли линейно зависимым | Б={[[-1,2],[0,-2,5]]} | | | 41 | Умножение матриц | [[0,0,1,1],[1,0,1,0],[0,0,0,1],[0,1,0,0]][[0,0,1, 1],[1,0,1,0],[0,0,0,1],[0,1,0,0]] | | | 42 | Найти домен | у=5х | | | 43 | Найти домен | у=7х | | | 44 | Найти домен | у=-х-2 | | | 45 | Найти домен | у=х-2 | | | 46 | Найти домен | у=х-3 | | | 47 | Найти сокращенную форму эшелона строк | [[4,-3,1,0],[1,0,-2,0],[-2,1,1,0]] | | | 48 | Запись как векторное равенство | х+у+г=2, 4х+5у+г=12, 2х=-4 | , , | | 49 | Найдите определитель | [[0,-1,а],[3,-а,1],[1,-2,3]] | | | 50 | Найти домен | у=-х+2 | | | 51 | Найдите определитель | [[2,5,0],[1,0,-3],[2,-1,2]] | | | 52 | Найдите определитель | [[7,5,0],[4,5,8],[0,-1,5]] | | | 53 | Найдите обратное | [[1,-3,0,-2],[3,-12,-2,-6],[-2,10,2,5],[-1,6,1,3]] | | | 54 | Найдите обратное | [[1,2,3],[2,5,7],[3,7,9]] | | | 55 | Найти сокращенную форму эшелона строк | [[0,1,5,-4],[1,4,3,-2],[2,7,1,-2]] | | | 56 | Найти сокращенную форму эшелона строк | [[1,1,0],[1,0,1],[1,0,1],[2,1,0],[2,1,0]] | | | 57 | Найти сокращенную форму эшелона строк | [[1,2,3],[4,5,6],[7,8,9]] | | | 58 | Найти сокращенную форму эшелона строк | [[7,8]] | | | 59 | Найти домен | 2х+у=1 | | | 60 | Запись как векторное равенство | 2х+у=-2, х+2у=2 | , | | 61 | Найти домен | х-2у=4 | | | 62 | Найти домен | х-у=-1 | | | 63 | Найти домен | х+у=5 | | | 64 | Найти домен | х=-3у-8 | | | 65 | Найти домен | х=-2у-8 | | | 66 | Найти домен | х+у=6 | | | 67 | Найти домен | х+у=4 | | | 68 | Найти домен | х+2у=4 | | | 69 | Найти домен | х+у | | | 70 | Найти домен | у=7х+9 | | | 71 | Найти домен | у=1/2x-5 | | | 72 | Найти домен | у=1/2х+2 | | | 73 | Найти домен | у=1/2х+3 | | | 74 | Найти домен | х-у=-3 | | | 75 | Найти домен | х-у=4 | | | 76 | Найти домен | г=-2x | | | 77 | Найти домен | у=-2х+1 | | 92 | | 80 | Найти домен | у=2х-6 | | | 81 | Найти домен | у=-2х-3 | | | 82 | Найти домен | у=3х-8 | | | 83 | Найти домен | у=3х | | | 84 | Найти домен | у=-3х+1 | | | 85 | Найти домен | у=4х+3 | | | 86 | Найти домен | у=3х-4 | | | 87 | Найти домен | у=4х-2 | | | 88 | Найти домен | у=-6x | | | 89 | Найти домен | у=х-4 | 94 | | 91 | Найти домен | с=5/9*(ф-32) | | | 92 | Найти домен | ф=9/5с+32 | | | 93 | Оценить | квадратный корень из 4 | | | 94 | Найти сокращенную форму эшелона строк | [[-6,7],[2,6],[-4,1]] | | | 95 | Найти собственные значения | [[2,1],[3,2]] | | | 96 | Найти собственные значения | [[4,0,1],[2,3,2],[49,0,4]] | | | 97 | Найдите набор силы | А=(2,3,4,5) | | | 98 | Найди кардинальность | (2,1) | | | 99 | Решение с использованием обратной матрицы | -3x-4y=2 , 8y=-6x-4 | , | | 100 | Решение с использованием обратной матрицы | 2x-5y=4 , 3x-2y=-5 | , |
Введение в оценку мощности и размера выборки- план исследования
- размер выборки
- статистика
ЦЕЛИ Понимание оценки мощности и размера выборки. Понять, почему мощность является важной частью как плана исследования, так и анализа. Понимать различия между расчетами размера выборки в сравнительных и диагностических исследованиях. Узнайте, как выполнить расчет объема выборки. – (а) Для непрерывных данных – (b) Для прерывистых данных – (c) Для диагностических тестов
ОЦЕНКА МОЩНОСТИ И РАЗМЕРА ВЫБОРКИ Оценка мощности и размера выборки является мерой того, сколько пациентов необходимо для исследования. Почти все клинические исследования подразумевают изучение выборки пациентов с определенной характеристикой, а не всей популяции. Затем мы используем эту выборку, чтобы сделать выводы обо всей совокупности. В предыдущих статьях из серии статей о статистике, опубликованных в этом журнале, статистический вывод использовался для определения того, верны ли найденные результаты или, возможно, они обусловлены только случайностью. Ясно, что мы можем уменьшить вероятность того, что наши результаты будут случайными, устранив предвзятость в дизайне исследования с помощью таких методов, как рандомизация, ослепление и т. д. Однако на вероятность того, что наши результаты могут быть неверными, влияет еще один фактор — количество обследованных пациентов. Интуитивно мы предполагаем, что чем больше доля всего изучаемого населения, тем ближе мы подойдем к истинному ответу для этого населения. Но сколько нам нужно изучить, чтобы подобраться как можно ближе к правильному ответу? ЧТО ТАКОЕ МОЩНОСТЬ И ПОЧЕМУ ОНА ВАЖНА Оценки мощности и размера выборки используются исследователями для определения количества субъектов, необходимых для ответа на вопрос исследования (или нулевой гипотезы). Примером может служить случай тромболизиса при остром инфаркте миокарда (ОИМ). В течение многих лет клиницисты считали, что это лечение принесет пользу, учитывая предполагаемую этиологию ОИМ, однако последовательные исследования не смогли доказать это. Лишь после завершения достаточно мощных «мега-испытаний» была доказана небольшая, но важная польза от тромболизиса. Как правило, в этих исследованиях тромболизис сравнивали с плацебо, и часто в качестве основного критерия исхода использовали смертность через определенное количество дней. Основная гипотеза исследований могла заключаться в сравнении, например, смертности на 21-й день тромболизиса по сравнению с плацебо. Тогда есть две гипотезы, которые нам нужно рассмотреть: Нулевая гипотеза состоит в том, что нет никакой разницы между методами лечения с точки зрения смертности. Альтернативная гипотеза заключается в том, что существует разница между методами лечения с точки зрения смертности.
Пытаясь определить, являются ли две группы одинаковыми (принимая нулевую гипотезу) или они различаются (принимая альтернативную гипотезу), мы потенциально можем совершить два вида ошибок. Они называются ошибкой первого рода и ошибкой второго рода. Говорят, что ошибка I рода возникает, когда мы неверно отвергаем нулевую гипотезу (то есть, она верна и между двумя группами нет различий) и сообщаем о различиях между двумя изучаемыми группами. Говорят, что ошибка типа II возникает, когда мы неправильно принимаем нулевую гипотезу (то есть, она ложна и существует различие между двумя группами, которая является альтернативной гипотезой) и сообщаем, что между двумя группами нет различий . Их можно представить в виде таблицы два на два (таблица 1). Таблица 1 Таблица два на два Расчет мощности говорит нам, сколько пациентов требуется, чтобы избежать ошибки типа I или типа II. Термин «мощность» обычно используется в отношении всех оценок размера выборки в исследованиях. Строго говоря, «мощность» означает количество пациентов, необходимое для того, чтобы избежать ошибки II типа в сравнительном исследовании. Оценка размера выборки — это более широкий термин, который рассматривает не только ошибку типа II и применим ко всем типам исследований. В просторечии эти термины используются взаимозаменяемо. ЧТО ВЛИЯЕТ НА СИЛУ ИССЛЕДОВАНИЯ? На эффективность исследования может повлиять несколько факторов. Их следует учитывать на ранних этапах разработки исследования. Некоторые факторы мы можем контролировать, другие нет. Точность и дисперсия измерений в любой выборке Почему исследование может не обнаружить различий, если они действительно есть? Для любого заданного результата выборки пациентов мы можем только определить распределение вероятностей вокруг этого значения, которое подскажет, где находится истинное значение популяции. Наиболее известным примером этого являются 95% доверительные интервалы. Размер доверительного интервала обратно пропорционален количеству исследуемых субъектов. Таким образом, чем больше людей мы изучаем, тем точнее мы можем определить, где находится истинная ценность населения. Наиболее известным примером этого являются 95% доверительные интервалы. Размер доверительного интервала обратно пропорционален количеству исследуемых субъектов. Таким образом, чем больше людей мы изучаем, тем точнее мы можем определить, где находится истинная ценность населения. На рис. 1 показано, что для одного измерения чем больше исследуемых субъектов, тем уже становится распределение вероятностей. В группе 1 среднее значение равно 5 с широкими доверительными интервалами (3–7). При удвоении числа обследованных пациентов (но в нашем примере значения остались прежними) доверительные интервалы сузились (3,5–6,5), что дает более точную оценку истинного среднего значения для популяции. Рисунок 1 Изменение ширины доверительного интервала с увеличением числа субъектов. Вероятностное распределение истинного значения является неотъемлемой частью большинства статистических тестов для сравнения между группами (например, t тестов). Исследование с небольшим размером выборки будет иметь большие доверительные интервалы и будет отображаться как статистически ненормальное только в том случае, если между двумя группами существует большая разница. Рисунок 2 демонстрирует, как увеличение числа субъектов может дать более точную оценку различий. Исследование с небольшим размером выборки будет иметь большие доверительные интервалы и будет отображаться как статистически ненормальное только в том случае, если между двумя группами существует большая разница. Рисунок 2 демонстрирует, как увеличение числа субъектов может дать более точную оценку различий. Рисунок 2 Эффект уменьшения доверительного интервала для демонстрации истинной разницы в средних значениях. Этот пример показывает, что первоначальное сравнение между группами 1 и 3 не показало статистической разницы, поскольку доверительные интервалы перекрывались. В группах 3 и 4 число больных удваивается (хотя среднее значение остается прежним). Мы видим, что доверительные интервалы больше не перекрываются, что указывает на то, что разница в средних значениях вряд ли возникла случайно. Величина клинически значимой разницы Если мы пытаемся обнаружить очень небольшие различия между методами лечения, требуются очень точные оценки истинного значения популяции. Это связано с тем, что нам нужно очень точно найти истинное значение популяции для каждой группы лечения. И наоборот, если мы находим или ищем большое различие, может быть приемлемым довольно широкое распределение вероятностей. Это связано с тем, что нам нужно очень точно найти истинное значение популяции для каждой группы лечения. И наоборот, если мы находим или ищем большое различие, может быть приемлемым довольно широкое распределение вероятностей. Другими словами, если мы ищем большую разницу между методами лечения, мы могли бы принять широкое распределение вероятности, если мы хотим обнаружить небольшую разницу, нам потребуется большая точность и небольшое распределение вероятности. Поскольку ширина распределения вероятностей в значительной степени определяется тем, сколько субъектов мы изучаем, ясно, что искомая разница влияет на расчеты размера выборки. Факторы, влияющие на расчет мощности Точность и дисперсия измерений в любом образце Величина клинически значимой разницы Насколько уверены мы, чтобы избежать ошибки 1-го типа Тип статистического теста, который мы проводим
При сравнении двух или более образцов мы обычно мало контролируем размер эффекта. Тем не менее, мы должны убедиться, что разница стоит обнаружения. Например, можно разработать исследование, которое продемонстрирует сокращение времени начала местной анестезии с 60 до 59 секунд, но такая небольшая разница не будет иметь клинического значения. И наоборот, исследование, демонстрирующее разницу от 60 секунд до 10 минут, явно будет. Указание того, что является «клинически важным отличием», является ключевым компонентом расчета размера выборки. Тем не менее, мы должны убедиться, что разница стоит обнаружения. Например, можно разработать исследование, которое продемонстрирует сокращение времени начала местной анестезии с 60 до 59 секунд, но такая небольшая разница не будет иметь клинического значения. И наоборот, исследование, демонстрирующее разницу от 60 секунд до 10 минут, явно будет. Указание того, что является «клинически важным отличием», является ключевым компонентом расчета размера выборки. Насколько важна ошибка типа I или типа II для рассматриваемого исследования? Мы можем указать, насколько мы были бы обеспокоены тем, чтобы избежать ошибки типа I или типа II. Говорят, что ошибка первого рода возникает, когда мы неправильно отвергаем нулевую гипотезу. Обычно мы выбираем вероятность <0,05 для ошибки I рода. Это означает, что если мы найдем положительный результат, шансы найти это (или большую разницу) будут менее чем в 5% случаев. Этот показатель, или уровень значимости, обозначается как pα и обычно предварительно устанавливается нами на ранней стадии планирования исследования при расчете размера выборки. По соглашению, а не по дизайну, мы чаще всего выбираем 0,05. Чем ниже уровень значимости, тем ниже мощность, поэтому использование 0,01 соответственно уменьшит нашу мощность. По соглашению, а не по дизайну, мы чаще всего выбираем 0,05. Чем ниже уровень значимости, тем ниже мощность, поэтому использование 0,01 соответственно уменьшит нашу мощность. (Чтобы избежать ошибки типа I, т. е. если мы найдем положительный результат, шансы найти это или большее различие возникнут менее чем в α% случаев) Говорят, что происходит ошибка типа II когда мы неверно принимаем нулевую гипотезу и сообщаем, что между двумя группами нет разницы. Если действительно есть разница между вмешательствами, мы выражаем вероятность получения ошибки второго рода и вероятность того, что мы ее обнаружим. Эта цифра обозначается как pβ. В отношении допустимого уровня pβ существует меньше условностей, но цифры 0,8–0,9являются общими (то есть, если разница между вмешательствами действительно существует, мы обнаружим ее в 80–90% случаев). Мощность исследования, pβ, представляет собой вероятность того, что исследование обнаружит заданную разницу в измерениях между двумя группами, если она действительно существует, при заданном значении pα и размере выборки, N. Тип статистического теста, который мы выполняем Расчеты размера выборки показывают, как статистические тесты, использованные в исследовании, могут работать. Поэтому неудивительно, что тип используемого теста влияет на то, как рассчитывается размер выборки. Например, параметрические тесты лучше находят различия между группами, чем непараметрические тесты (именно поэтому мы часто пытаемся преобразовать базовые данные в нормальные распределения). Следовательно, для анализа, основанного на непараметрическом тесте (например, U Манна-Уитни), потребуется больше пациентов, чем для анализа, основанного на параметрическом тесте (например, 9 баллов Стьюдента).2385 т тест). СЛЕДУЕТ ПРОВОДИТЬ РАСЧЕТ ОБЪЕМА ВЫБОРКИ ДО ИЛИ ПОСЛЕ ИССЛЕДОВАНИЯ? Ответ определенно до, иногда во время, а иногда и после. При разработке исследования мы хотим убедиться, что проделанная нами работа стоит того, чтобы мы получили правильный ответ и получили его наиболее эффективным способом. Это делается для того, чтобы мы могли набрать достаточное количество пациентов, чтобы придать нашим результатам адекватную силу, но не слишком много, чтобы тратить время на получение большего количества данных, чем нам нужно. К сожалению, при разработке исследования нам, возможно, придется сделать предположения о желаемом размере эффекта и дисперсии данных. Это делается для того, чтобы мы могли набрать достаточное количество пациентов, чтобы придать нашим результатам адекватную силу, но не слишком много, чтобы тратить время на получение большего количества данных, чем нам нужно. К сожалению, при разработке исследования нам, возможно, придется сделать предположения о желаемом размере эффекта и дисперсии данных. Промежуточные расчеты мощности иногда используются, когда известно, что данные, использованные в первоначальном расчете, сомнительны. Их следует использовать с осторожностью, поскольку повторный анализ может привести к тому, что исследователь прекратит исследование, как только будет получена статистическая значимость (что может произойти случайно несколько раз во время набора участников). После начала исследования анализ промежуточных результатов может быть использован для выполнения дальнейших расчетов мощности и соответствующих корректировок размера выборки. Это может быть сделано, чтобы избежать преждевременного прекращения исследования или, в случае спасения жизни или опасных методов лечения, чтобы избежать продления исследования. Расчеты промежуточного размера выборки следует использовать только в том случае, если это указано в методе априорного исследования. Расчеты промежуточного размера выборки следует использовать только в том случае, если это указано в методе априорного исследования. Когда мы оцениваем результаты испытаний с отрицательными результатами, особенно важно задаться вопросом о размере выборки исследования. Вполне может быть, что исследование было недостаточно мощным и что мы неправильно приняли нулевую гипотезу, что является ошибкой второго рода. Если бы в исследовании участвовало больше субъектов, то разница вполне могла бы быть обнаружена. В идеальном мире этого никогда не должно происходить, потому что расчет размера выборки должен появляться в разделе методов всех статей, реальность показывает нам, что это не так. Как потребители исследований, мы должны иметь возможность оценить силу исследования на основании полученных результатов. Расчет размера ретроспективной выборки в этой статье не рассматривается. Несколько калькуляторов для ретроспективного размера выборки доступны в Интернете (калькуляторы мощности UCLA (http://calculators. stat.ucla.edu/powercalc/), интерактивные статистические страницы (http://www.statistics.com/content/javastat. html). для обоснования расчетов (хотя это можно решить, проведя предварительное исследование и используя полученные данные)9.0004 stat.ucla.edu/powercalc/), интерактивные статистические страницы (http://www.statistics.com/content/javastat. html). для обоснования расчетов (хотя это можно решить, проведя предварительное исследование и используя полученные данные)9.0004 Ясно, что расчет размера выборки является ключевым компонентом клинических испытаний, поскольку в большинстве этих исследований упор делается на выявление величины различий между методами лечения. Все клинические испытания должны иметь оценку размера выборки. В исследованиях других типов необходимо проводить оценку размера выборки, чтобы повысить точность наших окончательных результатов. Например, основными показателями результатов для многих диагностических исследований будут чувствительность и специфичность конкретного теста, обычно сообщаемые с доверительными интервалами для этих значений. Как и в случае со сравнительными исследованиями, чем больше изучаемых пациентов, тем больше вероятность того, что результаты выборки будут отражать истинную ценность популяции. Выполняя расчет размера выборки для диагностического исследования, мы можем указать точность, с которой мы хотели бы сообщить доверительные интервалы для чувствительности и специфичности. Выполняя расчет размера выборки для диагностического исследования, мы можем указать точность, с которой мы хотели бы сообщить доверительные интервалы для чувствительности и специфичности. Поскольку клинические испытания и диагностические исследования, вероятно, составляют основу исследовательской работы в области медицины неотложных состояний, мы сосредоточились на них в этой статье. МОЩНОСТЬ СРАВНИТЕЛЬНЫХ ИССЛЕДОВАНИЙ Исследования, сообщающие о непрерывных данных с нормальным распределением Предположим, что Эгберт Эверард был вовлечен в клиническое исследование с участием пациентов с гипертонией. Новый антигипертензивный препарат Jabba Juice сравнивали с бендрофлуазидом в качестве нового препарата первой линии для лечения гипертонии (таблица 2). Таблица 2 Эгберт записывает некоторые вещи, которые, по его мнению, важны для расчетов Как видите, значения pα и pβ несколько типичны. Обычно они устанавливаются по соглашению, а не меняются от одного исследования к другому, хотя, как мы увидим ниже, они могут меняться. Обычно они устанавливаются по соглашению, а не меняются от одного исследования к другому, хотя, как мы увидим ниже, они могут меняться. Ключевым требованием является «клинически важное различие», которое мы хотим обнаружить между группами лечения. Как обсуждалось выше, это различие должно быть клинически важным, поскольку, если оно очень мало, о нем, возможно, не стоит знать. Еще одна цифра, которую нам необходимо знать, — это стандартное отклонение переменной в исследуемой популяции. Измерения артериального давления представляют собой форму нормально распределенных непрерывных данных и, как таковые, будут иметь стандартное отклонение, которое Эгберт обнаружил в других исследованиях, посвященных аналогичным группам людей. Как только мы узнаем эти две последние цифры, мы можем вычислить стандартизированную разницу, а затем использовать таблицу, чтобы получить представление о необходимом количестве пациентов. Разница между средними значениями является клинически важной разницей, т. е. представляет собой разницу между средним артериальным давлением в группе бендрофлуазида и средним артериальным давлением в группе нового лечения. е. представляет собой разницу между средним артериальным давлением в группе бендрофлуазида и средним артериальным давлением в группе нового лечения. Из записей Эгберта: Используя таблицу 3, мы видим, что при стандартизированной разнице 0,5 и уровне мощности (pβ) 0,8 необходимое количество пациентов составляет 64. Эта таблица предназначена для односторонней гипотезы, (?) Нулевая гипотеза требует исследования чтобы быть достаточно мощным, чтобы обнаружить, что одно лечение лучше или хуже другого, поэтому нам потребуется как минимум 64 × 2 = 128 пациентов. Это делается для того, чтобы мы получали пациентов, попадающих в обе стороны от средней разницы, которую мы установили. 9Таблица 3 Номограмма для расчета объема выборки. Исходя из этого, мы можем использовать линейку, чтобы соединить стандартизированную разность с мощностью, необходимой для исследования. Там, где край пересекает среднюю переменную, указывается требуемое число N. Номограмму также можно использовать для расчета мощности сравнения двусторонней гипотезы непрерывного измерения с одинаковым количеством пациентов в каждой группе. Если данные не распределены нормально, номограмма ненадежна, и следует обратиться за официальной статистической помощью. Исследования, сообщающие категориальные данные Предположим, что Эгберт Эверард в своем постоянном стремлении улучшить уход за своими пациентами, страдающими инфарктом миокарда, был убежден представителем фармацевтической компании помочь в проведении исследования нового посттромболизисного препарата Jedi Flow. . Из предыдущих исследований он знал, что потребуются большие числа, поэтому провел расчет размера выборки, чтобы определить, насколько сложной будет задача (таблица 4). Таблица 4 Расчет размера выборки И снова значения pα и pβ являются стандартными, и мы установили уровень для клинически важной разницы. В отличие от непрерывных данных расчет размера выборки для категорийных данных основан на пропорциях. Однако, как и в случае с непрерывными данными, нам все еще необходимо рассчитать стандартизованную разницу. Это позволяет нам использовать номограмму для расчета необходимого количества пациентов. стр 1 = пропорциональная смертность в группе тромболизиса = 12% или 0,12 p 2 = пропорциональная смертность в группе Jedi Flow = 9% или 0,09 (это 3% клинически важная разница в смертности, которую мы хотим показать). Р=(р 1+ р 2 )/2= Стандартизированная разница составляет 0,1. Если мы воспользуемся номограммой и проведем линию от 0,1 до оси мощности на уровне 0,8, мы увидим пересечение с центральной осью на уровне 0,05 pα, нам потребуется 3000 пациентов в исследовании. Это означает, что нам нужно 1500 пациентов в группе Jedi Flow и 1500 в группе тромболизиса. Это означает, что нам нужно 1500 пациентов в группе Jedi Flow и 1500 в группе тромболизиса. МОЩНОСТЬ В ДИАГНОСТИЧЕСКИХ ТЕСТАХ Расчеты мощности редко используются в диагностических исследованиях, и, по нашему опыту, немногие знают о них. Они имеют особое значение для практики неотложной медицинской помощи из-за характера нашей работы. Описанные здесь методы взяты из работы Будерера. 3 Доктор Эгберт Эверард решает, что диагностика переломов лодыжек может быть улучшена за счет использования нового ручного ультразвукового устройства в отделении неотложной помощи на Звезде Смерти. Устройство DefRay используется для осмотра лодыжки и позволяет определить, сломана лодыжка или нет. Доктор Эверард считает, что это новое устройство может снизить потребность пациентов в часах ожидания в рентгенологическом отделении, тем самым избегая боли в ушах у пациентов, когда они возвращаются. Он считает, что DefRay можно использовать в качестве инструмента скрининга, только те пациенты с положительным тестом DefRay будут отправлены в рентгенологическое отделение для демонстрации точного характера травмы. Он разрабатывает диагностическое исследование, в котором все пациенты с подозрением на перелом лодыжки обследуются в отделении неотложной помощи с помощью DefRay. Этот результат записывается, а затем пациентов отправляют на рентгенограмму независимо от результата теста DefRay. Затем доктор Эверард и его коллега сравнивают результаты DefRay со стандартной рентгенограммой. Пропущенные переломы лодыжки стоили отделению доктора Эверарда больших денег в прошлом году, и поэтому очень важно, чтобы DefRay показал хорошие результаты, если он будет принят в качестве скринингового теста. Эгберту интересно, сколько пациентов ему понадобится. Он делает записи (таблица 5). Таблица 5 Расчеты Эверарда Для диагностического исследования мы рассчитываем мощность, необходимую для достижения адекватной чувствительности или адекватной специфичности. Расчеты основаны на стандартном способе представления диагностических данных «два на два», как показано в таблице 6. Таблица 6 Таблица отчета «два на два» для диагностических тестов Для расчета потребности в адекватной чувствительности Для расчета потребности в адекватной специфичности Если бы Эгберт был в равной степени заинтересован в тесте со специфичностью и чувствительностью, мы бы взяли большее из двух, но он этого не делает. Он больше всего заинтересован в том, чтобы убедиться, что тест имеет высокую чувствительность, чтобы исключить переломы лодыжки. Поэтому он берет для чувствительности цифру 243 пациента. ЗАКЛЮЧЕНИЕ Оценка размера выборки является ключом к проведению эффективных сравнительных исследований. Понимание концепций мощности, размера выборки и ошибок первого и второго рода поможет исследователю и критическому читателю медицинской литературы. ВИКТОРИНА Какие факторы влияют на расчет мощности пробной терапии? Доктор Эгберт Эверард хочет испытать новый анализ крови (Sithtastic) для диагностики гена темной стороны. Он хочет, чтобы тест имел чувствительность не менее 70% и специфичность 90% с 5% уровнем достоверности. Распространенность заболевания в этой популяции составляет 10%. Если доктор Эверард испытает новый метод лечения ожогов световым мечом, который, как надеялись, снизит смертность с 55% до 45%. Он устанавливает pα равным 0,05 и pβ равным 0,99, но обнаруживает, что ему нужно много пациентов, поэтому, чтобы облегчить себе жизнь, он изменяет мощность на 0,80. Сколько пациентов в каждой группе ему понадобилось с pα до 0,05 и pβ до 0,80? Сколько пациентов ему понадобилось при более высокой (первоначальной) мощности?
Ответы на викторину См. рамку. рамку. (i) 2881 пациент; (ii) 81 пациент (i) около 400 пациентов в каждой группе; (ii) около 900 пациентов в каждой группе
Благодарности Мы хотели бы поблагодарить Фиону Леки, почетного старшего лектора по неотложной медицине больницы Хоуп, Солфорд, за ее помощь в подготовке этой статьи. ССЫЛКИ Дрисколл П. , Уордроп Дж. Введение в статистику. J Accid Emerg Med2000;17:205. - ↵
Гор С.М. , Альтман Д.Г. Насколько велика выборка. В: Статистика на практике . Лондон: Издательство BMJ, 2001: 6–8. - ↵
Buderer NM . Статистическая методология: I. Включение распространенности заболевания в расчет размера выборки для чувствительности и специфичности. Acad Emerg Med1996;3:895–900. Acad Emerg Med1996;3:895–900.
«Power» I Gotta Go (ТВ Эпизод 2014) S1.E5 Все серии Все - Актеры и съемочная группа
- Отзывы пользователей
IMDBPRO - Эпизод AIRED 12 июля 2014 г.
- TV-MATV-MA
- 58M
RATIN 1 Видео 1 Фото Криминальная драма Ташу все больше и больше беспокоит отношение Призраков, поэтому она решает больше заниматься бизнесом в клубе. Роман Призрака и Анджелы накаляется, а Томми кое-кто привлекает… Читать полностьюТашу все больше и больше беспокоит отношение Призрака, поэтому она решает больше заниматься бизнесом в клубе. Роман Призрака и Анджелы накаляется, в то время как Томми привлекает кто-то в клубе. Таша все больше и больше беспокоится об отношении Призраков, поэтому решает больше заниматься бизнесом в клубе. Роман Призрака и Анжелы накаляется, а Томми привлекает кто-то в клубе. Таша все больше и больше беспокоится об отношении Призраков, поэтому решает больше заниматься бизнесом в клубе. Роман Призрака и Анжелы накаляется, а Томми привлекает кто-то в клубе. Рейтинг IMDB 8.0/10 615 Ваш рейтинг - Директор
- Писатели
- Авторы
- .
Звезды- Омари Хардвик
- Лела Лорен
- Натури Нотон
Лучшие титры- Режиссер
907 900 Дж. Тиллман0007 Тиллман0007- Writers
- Courtney A. Kemp
- Randy Huggins
- Vladimir Cvetko(staff writer)
- Stars
- Omari Hardwick
- Lela Loren
- Naturi Naughton
- See production, box office & company info
- Подробнее на IMDbPro
Видео1 Трейлер 0:31 Power: I Gotta Go Фото2 Top cast Omari Hardwick - James ‘Ghost’ St.
 Patrick Patrick
Lela Loren Naturi Naughton Joseph Sikora Энди Бин Адам Хасс Кэтрин Нардуччи Луис Антонио Рамос 0004 Sinqua Walls Lucy Walters Victor Garber Shane Johnson Diane Neal Darrell Britt-Gibson Franky G Лесли Лопес Винисиус Зорин-Мачадо - Nomar
- (как Vinicius Machado)
- Режиссер
- Писатели
- Кортни А.
 Кемп Кемп - Рэнди Хаггинс
- VLADIMIR CVETKO (PRISTER)
- VLADIMIR CVETKO.
- Производство, кассовые сборы и многое другое на IMDbPro
Сюжетная линия Знаете ли вы, что Обзоры пользователей1 Обзор Рекомендуемый обзор обзор актеров Я хотел бы сказать, что с нетерпением жду этого шоу каждую неделю, актерский состав становится все лучше с каждой неделей. Ведущая леди делает свое дело, но иногда ей нужно немного больше чувствовать в линии, когда она разговаривает со своим мужем, мы все, ни одна сестринская драма не сложнее, чем это. Главный герой должен иметь немного больше чувств в том, как он разговаривает со своим братом по преступлению, иногда он не справляется, он контролирует остроту в конце дня. Другие участники актерского состава вносят свой вклад в поддержку актерского состава. Я хотел бы сказать, что я надеюсь, что каждый человек делает на вершине. Я немного играл раньше, и я понимаю нервную вещь с работой под светом и камерой, моя цель состояла в том, чтобы стать актером, зарабатывать много денег и играть разные жизненные роли людей, мест и вещей. 50cents хорошая сюжетная линия и сохраните ее стильной, чтобы уважать то, как нас воспринимают в мире, независимо от направления жизни. Я хотел бы получить шанс сыграть отдельно в шоу, если вы все доберетесь до Далласа, штат Техас. Удачи и сломай ногу. Я хотел бы сказать, что я надеюсь, что каждый человек делает на вершине. Я немного играл раньше, и я понимаю нервную вещь с работой под светом и камерой, моя цель состояла в том, чтобы стать актером, зарабатывать много денег и играть разные жизненные роли людей, мест и вещей. 50cents хорошая сюжетная линия и сохраните ее стильной, чтобы уважать то, как нас воспринимают в мире, независимо от направления жизни. Я хотел бы получить шанс сыграть отдельно в шоу, если вы все доберетесь до Далласа, штат Техас. Удачи и сломай ногу. Полезно • 2 3 - Brandon_barber88
- июля 6, 2014
Подробная информация- Дата выпуска
- 12 июля 2014 г. (Соединенные Штаты)
- 209.
 - Язык
- Места съемок
- Steiner Studios — 15 Washington Avenue, Brooklyn Navy Yard, Brooklyn, New York City, New York, USA
- Production company
- See more company credits at IMDbPro
Technical specs- Runtime
58 minutes - Color
- Sound mix
- Aspect ratio
- 1.
 Новости за 7 дней.Компания группы PORCELANOSA Grupo представляет новую коллекцию керамики размером 100 x 100 см, которую можно устанавливать на фальшполах в наружных зонах.
Крупноформатная керамическая плитка стала излюбленным материалом архитекторов и застройщиков за счет высоких технических характеристик, прочнос…. TITAN корпуса металлические коттеджные ЩУРн IEK® используются для сборки вводно-учетных электрощитов с применением модульной аппаратуры, для ввода и учета электроэнергии в коттеджах и загородных домах.
Преимущества корпусов металлических коттеджных ЩУРн IEK® серии TITAN
Уличное размещение под …. Новая портативная колонка PS-195 — еще один образчик классического стиля от SVEN: строгая прямоугольная форма, никаких лишних украшений, плавные изгибы панели управления — все сделано с максимальной долей вкуса и внимания к деталям.
Взяв ее в руки, сложно даже представить себе, что она обладает сра…. Мы обновили ассортимент реле времени и добавили аппараты с двумя перекидными контактами: RT-SBA-2, RT-SBE-2, RT-SBB-2 и RT-10-2.
У каждого прибора своя функция:
RT-SBA-2 – задержка времени включения;
RT-SBE-2 – задержка выключения после пропадания сигнала;
RT-SBB-2 – подача импульса при вкл…. Керамический паркет бренда вдохновлен древесиной дуба и ореха и является одним из самых популярных отделочных материалов благодаря крупному формату и износостойкости.
Керамический паркет PAR-KER® от Porcelanosa, предназначенный для использования в крупномасштабных проектах и воспроизводящий тексту…. Из 10 номеров этого отеля открывается вид на горы Сьерра-де-Альбаррасин и старую часть города, а сам отель гармонично вписан в природный ландшафт благодаря чувственному дизайну интерьера, выполненному архитектором Мапи Эрнандес (MHM Arquitectura) с использованием коллекций Porcelanosa.
Признанный о…. Лента-трос STINGRAY — современное решение для создания линий света на любой высоте.
Возможно выбрать трос отдельно и приобрести ленту самостоятельно или купить уже готовый комплект, состоящий из ленты и троса.
В ассортименте представлены две модели тросов: STINGRAY-SET-5000 длиной 5 м и STINGRAY-S…. Представляем новинку в серии Basic – устройство этажное распределительное встроенное типа УЭРВ.
Габариты – 1300х1300х150 мм. УЭРВ устанавливается в подготовленную нишу.
В нём можно компактно разместить модульную автоматику, счётчики, а также силовые и слаботочные линии – внутри находятся соответст…. Обморожение: степени, первая помощь, профилактика — Новости — ПациентамОбморожение представляет собой повреждение какой-либо части тела (вплоть до омертвения) под воздействием низких температур. При длительном пребывании вне помещения, особенно при высокой влажности и сильном ветре, обморожение можно получить осенью и весной при температуре воздуха выше нуля.
К обморожению на морозе приводят тесная и влажная одежда и обувь, физическое переутомление, голод, вынужденное длительное неподвижное и неудобное положение, предшествующая холодовая травма, ослабление организма в результате перенесенных заболеваний, потливость ног, хронические заболевания сосудов нижних конечностей и сердечно-сосудистой системы, тяжелые механические повреждения с кровопотерей, курение и пр. Статистика свидетельствует, что почти все тяжелые обморожения, приведшие к ампутации конечностей, произошли в состоянии сильного алкогольного опьянения.
Под влиянием холода в тканях происходят сложные изменения, характер которых зависит от уровня и длительности снижения температуры. При действии температуры ниже -30 градусов С основное значение при обморожении имеет повреждающее действие холода непосредственно на ткани, и происходит гибель клеток. При действии температуры до -10–20 градусов С, при котором наступает большинство обморожений, ведущее значение имеют сосудистые изменения в виде спазма мельчайших кровеносных сосудов. В результате замедляется кровоток, прекращается действие тканевых ферментов.
Признаки обморожения и общего переохлаждения:
— кожа бледно-синюшная;
— температурная, тактильная и болевая чувствительность отсутствуют или резко снижены;
— при отогревании появляются сильные боли, покраснение и отек мягких тканей;
— при более глубоком повреждении через 12-24 ч. возможно появление пузырей с кровянистым содержимым;
— при общем переохлаждении человек вял, безучастен к окружающему, его кожные покровы бледные, холодные, пульс частый, артериальное давление снижено, температура тела ниже 36°С
Выделяют несколько степеней обморожения:
Обморожение I степени (наиболее легкое) обычно наступает при непродолжительном воздействии холода. Пораженный участок кожи бледный, после согревания покрасневший, в некоторых случаях имеет багрово-красный оттенок; развивается отек. Омертвения кожи не возникает. К концу недели после обморожения иногда наблюдается незначительное шелушение кожи. Полное выздоровление наступает к 5–7 дню после обморожения. Первые признаки такого обморожения – чувство жжения, покалывания с последующим онемением пораженного участка. Затем появляются кожный зуд и боли, которые могут быть и незначительными, и резко выраженными.
Обморожение II степени возникает при более продолжительном воздействии холода. В начальном периоде появляется побледнение, кожа становится холодной, утрачивается чувствительность, но эти явления наблюдаются при всех степенях обморожения. Поэтому наиболее характерный признак – образование в первые дни после травмы пузырей, наполненных прозрачным содержимым. Полное восстановление целостности кожного покрова происходит в течение 1–2 недель, грануляции и рубцы не образуются. При обморожении II степени после согревания боли интенсивнее и продолжительнее, чем при обморожении I степени, беспокоят кожный зуд, жжение.
При обморожении III степени продолжительность периода холодового воздействия и снижения температуры в тканях увеличивается. Образующиеся в начальном периоде пузыри наполнены кровянистым содержимым, дно их сине-багровое, нечувствительное к раздражениям. Происходит гибель всех элементов кожи с развитием в исходе обморожения грануляций и рубцов. Сошедшие ногти вновь не отрастают или вырастают деформированными. Отторжение отмерших тканей заканчивается на 2–3-й неделе, после чего наступает рубцевание, которое продолжается до 1 месяца. Интенсивность и продолжительность болевых ощущений более выражена, чем при обморожении II степени.
Обморожение IV степени возникает при длительном воздействии холода, снижение температуры в тканях при нем наибольшее. Оно нередко сочетается с обморожением III и даже II степени. Омертвевают все слои мягких тканей, нередко поражаются кости и суставы.
Поврежденный участок конечности сильно синюшный, иногда с мраморной расцветкой. Отек развивается сразу после согревания и быстро увеличивается. Температура кожи значительно ниже, чем на окружающих участок обморожения тканях. Пузыри развиваются на менее обмороженных участках, где есть обморожение III–II степени. Отсутствие пузырей при развившемся значительно отеке, утрата чувствительности свидетельствуют об обморожении IV степени.
В условиях длительного пребывания при низкой температуре воздуха возможны не только местные поражения, но и общее охлаждение организма. Под общим охлаждением организма следует понимать состояние, возникающее при понижении температуры тела ниже 34 градусов С.
Первая помощь при обморожениях
Прежде всего необходимо согреть пострадавшего в теплом помещении. Согревание пораженной части тела должно быть постепенным, медленным, преимущественно пассивным. Недопустимо (!) растирать отмороженные участки тела руками, тканями, спиртом и уж тем более снегом! (Подобные рецепты на редкость живучи и до сих пор бытуют в народе.) Дело в том, что эти меры способствуют тромбообразованию в сосудах, углубляя процессы деструкции пораженных тканей.
Пострадавшего нужно укутать в теплое одеяло (при общем переохлаждении) или (при отморожении) наложить на пораженную часть тела термоизолирующую ватно-марлевую повязку (7 слоев) для кумуляции тепла и предотвращения преждевременного согревания поверхностных тканей (и, соответственно, образования перепада температур между поверхностными и глубокими тканями). Применение термоизолирующей повязки позволяет в несколько раз замедлить внешнее согревание пораженного участка при обеспечении общего согревания организма.
Если отморожена рука или нога, ее можно согреть в ванне, постепенно повышая температуру воды с 20 до 40° С и в течение 40 минут нежно (!) массируя конечность. На внутреннюю поверхность бедра или плеча можно дополнительно положить теплую грелку. Пострадавшему дают обильное теплое питье – например, сладкий чай.
Профилактика переохлаждения и обморожений
Есть несколько простых правил, которые позволят вам избежать переохлаждения и обморожений на сильном морозе:
— Не пейте спиртного – алкогольное опьянение вызывает большую потерю тепла. Дополнительным фактором является невозможность сконцентрировать внимание на признаках обморожения.
— Не курите на морозе – курение уменьшает периферийную циркуляцию крови, и таким образом делает конечности более уязвимыми.
— Носите свободную одежду – это способствует нормальной циркуляции крови. Одевайтесь как «капуста» – при этом между слоями одежды всегда есть прослойки воздуха, отлично удерживающие тепло.
— Тесная обувь, отсутствие стельки, сырые грязные носки часто служат основной предпосылкой для появления потертостей и обморожения. Особое внимание уделять обуви необходимо тем, у кого часто потеют ноги. В сапоги нужно положить теплые стельки, а вместо хлопчатобумажных носков надеть шерстяные – они впитывают влагу, оставляя ноги сухими.
— Не выходите на мороз без варежек, шапки и шарфа. Лучший вариант – варежки из влагоотталкивающей и непродуваемой ткани с мехом внутри. Перчатки же из натуральных материалов хоть и удобны, но от мороза не спасают. Щеки и подбородок можно защитить шарфом. В ветреную холодную погоду перед выходом на улицу открытые участки тела смажьте специальным кремом.
— Не носите на морозе металлических (в том числе золотых, серебряных) украшений.
— Пользуйтесь помощью друга: следите за лицом друга, особенно за ушами, носом и щеками, за любыми заметными изменениями в цвете, а он или она будут следить за вашими.
— Не снимайте на морозе обувь с обмороженных конечностей – они распухнут и вы не сможете снова одеть обувь. Необходимо как можно скорее дойти до теплого помещения. Если замерзли руки – попробуйте отогреть их подмышками.
— Вернувшись домой после длительной прогулки по морозу, обязательно убедитесь в отсутствии обморожений конечностей, спины, ушей, носа и т.д.
— Как только на прогулке вы почувствовали переохлаждение или замерзание конечностей, необходимо как можно скорее зайти в любое теплое место — магазин, кафе, подъезд – для согревания и осмотра потенциально уязвимых для обморожения мест.
— Прячьтесь от ветра – вероятность обморожения на ветру значительно выше.
— Не мочите кожу – вода проводит тепло значительно лучше воздуха. Не выходите на мороз с влажными волосами после душа. Мокрую одежду и обувь (например, человек упал в воду) необходимо снять, вытереть воду, при возможности одеть в сухую и как можно быстрее доставить человека в тепло. В лесу необходимо разжечь костер, раздеться и высушить одежду, в течение этого времени энергично делая физические упражнения и греясь у огня.
— Перед выходом на мороз надо поесть.
— Дети и старики более подвержены переохлаждению и обморожениям. Отпуская ребенка гулять в мороз на улице, помните, что ему желательно каждые 15-20 минут возвращаться в теплое помещение и согреваться.
При первых признаках обморожения обратитесь в ближайший травмпункт.
степени 0, 1, 2, классификация, способы лечения в клинике Синай
Метод диагностики и классификации повреждений мениска stoller – современный способ, основанный на МРТ коленного сустава. Новый и пока еще дорогостоящий, он позволяет получить максимум информации об изменениях хрящевой ткани и подобрать лечение, которое будет наиболее действенным в конкретном случае.
Повреждения мениска могут носить травматическую или дегенеративную природу. И то и другое повреждение по stoller определяется точно. В зависимости от того к какой степени будет отнесена травма, больному назначат консервативное или хирургическое лечение. Иные способы выявления патологии не могут также точно отразить уровень повреждения хряща.
Причины повреждений мениска по Stoller
Причины повреждения различны. Дегенеративные дефекты мениска чаще всего наблюдаются у лиц старшего возраста, у которых проблема появляется на фоне нарушений в коленном суставе. Также дегенеративные изменения вызывают следующие причины:
-
ревматизм;
-
подагра;
-
хроническое микротравмирование колена – наблюдается в том случае, если человек постоянно перегружает сустав, который в результате этого не успевает полноценно восстанавливаться и постепенно начинает разрушаться.
Травматическое повреждение по Stoller происходит значительно чаще. Оно возникает от непосредственного удара в область колена или на фоне значительных неестественных нагрузок. К таким опасным воздействиям относятся: длительное хождение на носках, высокий прыжок с приземлением на жесткую поверхность, форсированное разгибание колена или резкое движение ногой после того, как она в течение продолжительного времени находилась в одном положении.
Вне зависимости от того что стало причиной болезни, необходимы проведение полноценной диагностики, классификация повреждения и прохождение полноценного лечения. В клинике Синай пациентам предоставляется возможность диагностики и классификации поражения мениска по столлер по максимально выгодной для них цене.
Виды разрыва мениска по Stoller
Разрывы мениска классифицируются по локализации и форме. Определение этих показателей очень важно для правильной терапии патологии. По области локализации различаются травмы:
В зависимости от формы повреждения классификация такая:
-
горизонтальный разрыв – наблюдается в случае кистозного перерождения;
-
косой радикальный или продольный – бывает на границе задней трети хряща и средней;
-
комбинированный – возникает в заднем роге.
В зависимости от повреждения несколько изменяется местонахождение очага основной боли, а также положение ноги, в котором она усиливается.
Что представляет собой Stoller-классификация
Разработана методика доктором медицинских наук профессором Девидом Столлером, который является директором действующего в США Национального центра визуализации структур опорно-двигательной системы в ортопедии. Точность исследования и возможности послойного сканирования тканей, а также визуализации пораженных участков тканей и суставов значительно повысились с появлением МРТ технологии. Метод, предложенный Столлером, основан на том, что во время сканирования появляется сигнал повышенной интенсивности, указывающий на присутствие в данной области дегенеративных изменений, возникающих при повреждении мениска. Профессором разработана система, при которой используются критерии интенсивности получаемого сигнала, а также область его локализации и распространения.
При классификации поражения учитываются показатели критериев выраженности патологии и ее тяжести. Классификация основывается на том, какую интенсивность имеет сигнал: чем она выше, тем серьезнее поражение тканей и тяжелее дегенеративный процесс.
Классификация
Классификация столлер разделяет состояние мениска на 4 стадии. В зависимости от того какая из них выявлена, определяют наличие или отсутствие патологий мениска.
-
0 стадия по Stoller. При исследовании не обнаруживаются очаги патологических изменений в тканях. Состояние мениска оценивается как совершенно здоровое.
-
1 стадия по Stoller. При МРТ выявляется сигнал повышенной интенсивности, который имеет очаговый характер и четкую локализацию. В то же время он не доходит до поверхности хрящевой ткани. Лечение чаще всего в этом случае еще не требуется или, если все же выявлена необходимость в его проведении, осуществляется консервативными методами преимущественно профилактической направленности.
-
2 стадия по Stoller. Интенсивность сигнала, получаемого от тканей, повышена, но при этом характер его изменяется на линейный. Аналогично первой стадии он не доходит до верхнего слоя мениска (хряща). Если при этом выявляется горизонтальное повреждение мениска, то оно означает, что хрящевая ткань разрушена частично, а изменений в ее структуре нет. Лечение проводится обязательно. Оно бывает преимущественно консервативное. Повреждение мениска 2 степени по stoller – наиболее распространенная причина обращения за врачебной помощью.
-
3 стадия по Stoller. Сигнал фиксируется линейный значительно повышенной интенсивности. Он четко достигает верхнего слоя хряща. У пациента выявляется выраженное нарушение анатомических структур мениска. Это означает присутствие разрывов медиального мениска. Также при таком поражении не исключается и смещение части участков травмированного хряща. Такое состояние диагностируется как полный отрыв мениска со смещением. Лечение требуется обязательно и проводится, как правило, хирургическим способом. Повреждение мениска 3 степени по stoller наиболее тяжелое.
Так как проведение диагностики и классификации поражения по Stoller возможно только при наличии аппарата для магнитно-резонансной томографии, то данная услуга доступна не во всех медицинских учреждениях. На сегодняшний день методом stoller степени повреждения мениска определяются наиболее точно.
Клиническая картина по столлер (по Stoller)- классификации
Клинические проявления патологии по классификации также разнятся в зависимости от стадии поражения. Они дополнительно позволяют оценить состояние пациента.
-
0 стадия по Stoller. Так как патологии хряща отсутствуют и его целостность не нарушена, то и симптомов патологии нет.
-
1 стадия по Stoller. Минимальные изменения в суставе приводят к периодическому появлению в нем болей. Они обычно проявляются в вечернее время и более интенсивны у людей, которые в течение дня вынуждены серьезно перегружать суставы. Также может наблюдаться заметный хруст в момент сгибания колена.
-
2 стадия по Stoller. Нарушения в состоянии сустава достаточно выраженные, из-за чего боль становится значительной. Ее интенсивность повышается в момент, когда человек двигает ногой, задействовав при этом колено. Также болевой синдром нарастает после долгого пребывания в стоячем положении. В большинстве случаев отмечаются и внешние проявления воспаления, такие как покраснение кожи и отечность тканей. Хруст в суставе появляется почти при каждом движении.
-
3 стадия по Stoller. Происходят серьезные изменения в анатомическом строении хряща, из-за чего отмечаются не только сильная боль, а и выраженная ограниченность подвижности коленного сустава. Болевой синдром, как и скованность движений, в этом состоянии наибольшие. Клиническая картина патологии острая.
Присутствие симптомов в дополнение к МРТ позволяет точно определить состояние пациента. Только так терапия будет максимально эффективная.
Как подготовиться к процедуре
Специальная подготовка перед проведением МРТ с дальнейшей классификацией состояния мениска Stoller не требуется. На исследование распространяются те же противопоказания, что и на проведение МРТ, а в первую очередь присутствие в теле металлических элементов и различных электростимуляторов и инсулиновых помп, на работу которых может влиять магнитное поле прибора.
Во время исследования не будет возникать болевых ощущений или дискомфорта. Единственное, что надо учесть пациенту, это то, что процедура длительная. Если пациент очень нервничает перед обследованием, то ему рекомендуется принять валериану или другое растительное успокоительное средство.
Степени защиты IP23 Декабря 2009 Все электротехнические устройства должны соответствовать определенной степени защиты в соответствии с МЭК 70-1 – IP (International/Ingress Protection). Степень защиты приводится в виде IPXX, где первая цифра обозначает – уровень защиты от попадания твёрдых частиц и степень защиты по электробезопасности (табл. 2), а вторая – защиту от влаги. Возможные сочетания двух показателей приведены в таблице 1: Таблица 1. Пылевлагозащищенность | | IP x0 | IP x1 | IP x2 | IP x3 | IP x4 | IP x5 | IP x6 | IP x7 | IP x8 | Нет защиты | Падение вертикальных капель | Падение капель под углом 15○ от вертикали | Брызги под углом 60○ от вертикали | Брызги со всех сторон | Струи со всех сторон под небольшим давлением | Сильные потоки | Временное погружение (до 1 м) | Полное погружение* | IP 0x | Нет защиты | IP 00 | | IP 1x | Частицы > 50 мм | IP 10 | IP 11 | IP 12 | | IP 2x | Частицы > 12,5 мм | IP 20 | IP 21 | IP 22 | IP 23 | | IP 3x | Частицы > 2,5 мм | IP 30 | IP 31 | IP 32 | IP 33 | IP 34 | | IP 4x | Частицы > 1 мм | IP 40 | IP 41 | IP 42 | IP 43 | IP 44 | | IP 5x | Пыль частично | IP 50 | | IP 54 | IP 55 | | IP 6x | Пыль полностью | IP 60 | | IP 65 | IP 66 | IP 67 | IP 68 |
Возможно существование только приведенных выше комбинаций, т.к. увеличение одного из показателей защиты ведет к повышению другого (например, изделие, которое может быть временно погружено в воду, естественно, защищено достаточно, чтобы полностью не пропускать пыль, поэтому существование степени защиты, например, IP37 невозможно). Также существует степень защиты IP69 с повышенными характеристиками к стойкости при большом давлении. Таблица 2. Защита от соприкосновения с частями изделия, находящимися под напряжением Первая цифра | Описание | 0 | Никакой защиты от прикосновения к токоведущим частям. | 1 | Частичная защита от случайного касания токоведущих частей (защита от касания ладонью). | 2 | Защита от прикосновения пальцами к токоведущим частям. | 3 | Защита от случайного касания токоведущих частей инструментом. | 4 | Защита от случайного касания токоведущих частей инструментом. | 5 | Полная защита от прикосновения к токоведущим частям изделия. | 6 | Полная защита от прикосновения к токоведущим частям изделия. |
Приказ Министерства здравоохранения и социального развития Российской Федерации (Минздравсоцразвития России) от 20 октября 2005 г. N 643 г. Москва «Об утверждении форм документов о результатах установления федеральными государственными учреждениями медико-социальной экспертизы степени утраты профессиональной трудоспособности в процентахи рекомендаций по их заполнению»Зарегистрирован в Минюсте РФ 20 января 2006 г. Регистрационный N 7402 В соответствии с Федеральным законом от 22 августа 2004 г. N 122-ФЗ
«О внесении изменений в законодательные акты Российской Федерации и
признании утратившими силу некоторых законодательных актов Российской
Федерации в связи с принятием федеральных законов «О внесении изменений и
дополнений в Федеральный закон «Об общих принципах организации
законодательных (представительных) и исполнительных органов
государственной власти субъектов Российской Федерации» и «Об общих
принципах организации местного самоуправления в Российской Федерации»
(Собрание законодательства Российской Федерации, 2004, N 35, ст. 3607;
2005, N 1 (часть 1), ст. 25) и постановлением Правительства Российской
Федерации от 16 октября 2000 г. N 789 «Об утверждении Правил установления
степени утраты профессиональной трудоспособности в результате несчастных
случаев на производстве и профессиональных заболеваний» (Собрание
законодательства Российской Федерации, 2000, N 43, ст. 4247; 2005, N 7,
ст. 560) приказываю: 1.Утвердить: формы документов о результатах установления федеральными
государственными учреждениями медико-социальной экспертизы степени утраты
профессиональной трудоспособности в процентах согласно приложению N 1; Рекомендации по заполнению форм документов о результатах установления
федеральными государственными учреждениями медико-социальной экспертизы
степени утраты профессиональной трудоспособности в процентах согласно
приложению N 2. 2. Установить, что документы о результатах установления федеральными
государственными учреждениями медико-социальной экспертизы степени утраты
профессиональной трудоспособности в процентах выдаются федеральными
государственными учреждениями медико-социальной экспертизы с 1 апреля 2006
года. 3. Признать утратившим силу с 1 апреля 2006 года постановление
Министерства труда и социального развития Российской Федерации от 15
октября 2001 г. N 75 «Об утверждении форм документов о результатах
определения бюро (главными бюро) медико-социальной экспертизы степени
утраты профессиональной трудоспособности в процентах и Инструкции о
порядке их заполнения» (зарегистрировано в Министерстве юстиции Российской
Федерации 13 ноября 2001 г. N 3030) с изменениями, внесенными
постановлением Министерства труда и социального развития Российской
Федерации от 26.03.2003 N 12 (зарегистрировано в Минюсте России
10.04.2003, регистрационный N 4404). Министр М. Зурабов Приложение N 2 Рекомендации по заполнению форм документов о результатах установления
федеральными государственными учреждениями медико-социальной экспертизы
степени утраты профессиональной трудоспособности в процентах 1. К документам о результатах установления федеральными
государственными учреждениями медико-социальной экспертизы степени утраты
профессиональной трудоспособности в процентах относятся: Выписка из акта
освидетельствования в федеральном государственном учреждении
медико-социальной экспертизы о результатах установления степени утраты
профессиональной трудоспособности в процентах (далее — выписка) и Справка
о результатах установления степени утраты профессиональной
трудоспособности в процентах (далее — справка). 2. Выписка и справка предназначены для подтверждения факта
установления степени утраты профессиональной трудоспособности в процентах
и внесения в них соответствующего решения федерального государственного
учреждения медико-социальной экспертизы. 3. Все реквизиты выписки и справки заполняются в точном соответствии
с записями аналогичных реквизитов в акте освидетельствования в федеральном
государственном учреждении медико-социальной экспертизы. 4. В строке «наименование федерального государственного учреждения
медико-социальной экспертизы» выписки и справки делается запись о
наименовании главного бюро медико-социальной экспертизы с указанием
наименования его филиала — бюро медико-социальной экспертизы, Федерального
бюро медико-социальной экспертизы в точном соответствии с наименованием,
определенным уставом главного (Федерального) бюро медико-социальной
экспертизы. 5. В строке «Степень утраты профессиональной трудоспособности в
процентах» выписки и справки делается запись об установленных процентах
утраты профессиональной трудоспособности. 6. В строке «в связи с_____ от______» выписки и справки делается
запись о несчастном случае на производстве и его дате или профессиональном
заболевании, номере и дате составления акта по ф. Н-1 или дате составления
акта о профессиональном заболевании (либо дате решения суда об
установлении факта несчастного случая на производстве или
профессионального заболевания). 7. В строке «Срок установления степени утраты профессиональной
трудоспособности» выписки и справки указывается срок, на который
определены проценты утраты профессиональной трудоспособности: после
предлога «с» указывается дата (число, месяц, год) установления степени
утраты профессиональной трудоспособности в процентах, после предлога «до»
указывается первое число месяца, следующего за тем месяцем, на который
назначено очередное переосвидетельствование, и год, на который назначено
очередное переосвидетельствование. 8. В строке «Дата очередного освидетельствования» выписки и справки
указывается дата (число, месяц, год) переосвидетельствования, которая не
должна совпадать с нерабочим днем федерального государственного учреждения
медико-социальной экспертизы. При определении степени утраты профессиональной трудоспособности без
указания срока переосвидетельствования в указанной строке делается запись
«бессрочно». 9. В строке «Основание:» выписки и справки указывается номер акта
освидетельствования в федеральном государственном учреждении
медико-социальной экспертизы. 10. В строке «Степень утраты профессиональной трудоспособности в
процентах за пропущенный период с__по__» выписки делается запись об
установленных процентах утраты профессиональной трудоспособности за
пропущенный период, в течение которого гражданин не проходил
переосвидетельствование. При этом после предлога «с» указывается дата, до
которой были установлены проценты утраты профессиональной трудоспособности
при предыдущем освидетельствовании, после предлога «по» указывается дата,
непосредственно предшествующая дате настоящего установления степени утраты
профессиональной трудоспособности в процентах. 11. В строке «Дополнительные заключения» справки делается запись об
установленных процентах утраты профессиональной трудоспособности за
пропущенный период, в течение которого гражданин не проходил
переосвидетельствование, в соответствии с записями, сделанными в строке
«Степень утраты профессиональной трудоспособности в процентах за
пропущенный период с__по__» выписки. 12. Выписка и справка подписываются руководителем главного бюро
медико-социальной экспертизы, филиала главного бюро медико-социальной
экспертизы — бюро медико-социальной экспертизы, Федерального бюро
медико-социальной экспертизы (подпись расшифровывается) и заверяются
печатью главного бюро медико-социальной экспертизы, филиала главного бюро
медико-социальной экспертизы — бюро медико-социальной экспертизы,
Федерального бюро медико-социальной экспертизы соответственно. Подвиг народа Для просмотра сайта c поддержкой основных нововведений рекомендуется использовать приложение-обозреватель Microsoft Internet Explorer 10, Mozilla Firefox 4, Google Chrome 5, Opera 11.5, Safari 5.0 и выше. Работа с сайтом «Подвиг народа» - Описание главной страницы.
- Поиск:
- Работа с результатами поиска:
Описание главной страницы сайта «Подвиг народа» В верхней части главной страницы ОБД (а также с любой другой страницы сайта) находятся ссылки, которые соответствуют основным тематическим разделам сайта. Также доступна ссылка для перехода на прежнюю версию сайта и изменение языка интерфейса сайта (доступны английский и русский языки). В центральной части главной страницы приведено общее описание сайта, а также размещены ссылки для перехода к разделам сайта, таким как: - Люди и награждения;
- Наградные документы;
- география войны.
В нижней части страницы размещены баннеры, при помощи которых пользователь может перейти на сайты правительственных организаций, сайт ОБД «Мемориал», сайт «Календарь Победы», сайт «Герои войны» и сайт «Память народа». Под баннерами на главной странице (а также с любой другой страницы сайта) доступно дополнительное меню со следующими категориями: - О проекте;
- Отзывы;
- Обратная связь;
- Вопросы-ответы;
- Помощь.
Поиск Поиск информации по любому из тематических разделов может выполняться в два этапа: - поиск в обычном режиме, когда при определении условий поиска пользователь вводит данные в одну поисковую строку, указывая их через пробел;
- расширенный поиск, когда пользователь при определении условий поиска заполняет максимально возможное количество полей, указывая детальную информацию об объекте поиска.
Данный вид поиска является наиболее эффективным, поскольку позволяет получить результат, наиболее точно отвечающий запросам пользователя.
Чтобы приступить к поиску информации по любому из тематических разделов, необходимо навести указатель на наименование соответствующего раздела (на ссылку в верхней части страницы или в центральной части главной страницы): Поиск по тематическому разделу «Люди и награждения» Поиск по тематическому разделу «Люди и награждения» позволяет найти информацию о награждении, используя личные данные награжденных. Поиск в обычном режиме Для быстрого поиска необходимо перейти к разделу «Люди и награждения» нажатием левой кнопки мыши по заголовку раздела. Указать имеющиеся сведения в строке поиска. При необходимости, можно выбрать количество записей, которые будут выводиться на одну страницу результатов поиска (по умолчанию выводится по 50 записей на страницу), есть возможность выбрать следующие значения: 10, 30, 50 или 100. Для получения результата поиска нажать кнопку «Искать» или клавишу на клавиатуре. Расширенный поиск Чтобы выполнить расширенный поиск информации о награждении необходимо: - перейти к разделу «Люди и награждения»;
- нажать кнопку «Расширенный поиск»;
Откроется поисковая форма с доступными для заполнения следующими полями:
- Фамилия;
- Имя
- Отчество;
- Год рождения;
- Звание;
- Место призыва;
- Уточнение «Где искать».
Если необходимо вернуться к поиску в обычном режиме, следует нажать кнопку «Свернуть». Если необходимо большее количество уточняющих полей для осуществления поиска, следует нажать кнопку «Еще
больше».
После этого будут доступны дополнительные поля, такие как: - Наименование награды;
- Номер наградного документа;
- Дата наградного документа;
- Архив;
- Фонд;
- Опись;
- С какого года в КА;
- Единица хранения.
- заполнить поля поисковой формы;
Чтобы удалить введенные значения из всех полей, следует нажать кнопку «Очистить». После этого можно повторно ввести значения. - для получения результата поиска следует нажать кнопку «Искать».
После чего на экране отобразятся результаты поиска: Поиск по тематическому разделу «Наградные документы» Поиск по тематическому разделу «Документы» позволяет найти указы и приказы о награждении. Поиск в обычном режиме Для быстрого поиска необходимо перейти к разделу «Наградные документы» нажатием левой кнопки мыши по заголовку раздела. Указать имеющиеся сведения в строке поиска. При необходимости, можно выбрать количество записей, которое будет выводиться на одну страницу результатов поиска (по умолчанию выводится по 50 записей на страницу), есть возможность выбрать следующие значения: 10, 30, 50 или 100. Для получения результата поиска следует нажать кнопку «Искать» или клавишу на клавиатуре. Расширенный поиск Чтобы выполнить расширенный поиск документов о награждении необходимо: - перейти к разделу «Наградные документы»;
- нажать кнопку «Расширенный поиск»;
Откроется поисковая форма с доступными для заполнения следующими полями:
Если необходимо вернуться к поиску в обычном режиме, следует нажать кнопку «Свернуть».
Если необходимо большее количество уточняющих полей для осуществления поиска, следует нажать кнопку «Больше».
После этого будут доступны дополнительные поля, такие как: - Номер записи в базе данных;
- Номер документа;
- Автор;
- Архив;
- Фонд;
- Опись;
- Единица хранения.
- заполнить поля поисковой формы;
Чтобы удалить введенные значения из всех полей, следует нажать кнопку «Очистить». После этого можно повторно ввести значения.
- для получения результата поиска следует нажать кнопку «Искать».
После чего на экране отобразятся результаты поиска: Поиск по тематическому разделу «География войны» Поиск по тематическому разделу «География войны» позволяет выполнить поиск данных по местоположению и времени
события. Документы в разделе «География войны» могут быть найдены, используя в качестве критериев поиска дату выхода документов, географическую привязку к местам ведения боевых действий, привязку к сведениям о военачальнике, издавшем документ. Поиск в обычном режиме Для быстрого поиска необходимо перейти к разделу «География войны» нажатием левой кнопки мыши по заголовку раздела. Указать имеющиеся сведения в строке поиска. При необходимости, можно выбрать количество записей, которое будет выводиться на одну страницу результатов поиска (по умолчанию выводится по 50 записей на страницу), есть возможность выбрать следующие значения: 10, 30, 50 или 100. Для получения результата поиска нажать кнопку «Искать» или клавишу на клавиатуре. Расширенный поиск Чтобы выполнить расширенный поиск документов о награждении необходимо: - перейти к разделу «География войны»;
- нажать кнопку «Расширенный поиск»;
Откроется поисковая форма с доступными для заполнения следующими полями:
- Тип документа;
- Дата документа;
- Боевая операция;
- Географическое положение.
Если необходимо вернуться к поиску в обычном режиме, следует нажать кнопку «Свернуть». Если необходимо большее количество уточняющих полей для осуществления поиска, следует нажать кнопку «Больше».
После этого будут доступны дополнительные поля, такие как: - Номер документа;
- Наименование документа;
- Автор;
- Архив;
- Фонд;
- Опись;
- Единица хранения.
- заполнить поля поисковой формы;
Чтобы удалить введенные значения из всех полей, следует нажать кнопку «Очистить». После этого можно повторно ввести значения. - для получения результата поиска следует нажать кнопку «Искать».
После чего на экране отобразятся результаты поиска: Особенности заполнения поисковых полей При заполнении полей в режиме расширенного поиска пользователь может определить для каждого поля способ поиска: - С начала поля – чтобы выполнять поиск документов, у которых в начале соответствующего индексного поля будет содержаться значение, указанное пользователем в данном поисковом поле;
- Точная фраза — чтобы выполнять поиск документов, у которых в соответствующем индексном поле будет содержаться значение, состоящее из одного или нескольких слов (или цифр) в том же порядке, которое указано пользователем в данном поисковом поле;
- Точное поле — чтобы выполнять поиск документов, у которых в соответствующем индексном поле будет содержаться точное значение, указанное пользователем в данном поисковом поле;
- Полнотекстовый поиск — чтобы выполнять поиск документов, у которых в соответствующем индексном поле будет содержаться информация, указанная пользователем в данном поисковом поле, без учета последовательности слов.
Определение способа поиска происходит в раскрывающемся списке, после нажатия кнопки .
Для разных полей перечень доступных способов поиска может отличаться. Например, для поля Фонд доступен только поиск «Точное поле»,
а для поля Опись доступны поиски «Точная фраза» и «Точное поле». Пример раскрывающего списка приведен на рисунке ниже:
Работа с результатами поиска Результаты поиска «Люди и награждения» Результат поиска информации о героях войны выводится на экран монитора в виде списка. При этом на каждой странице результатов поиска будет выводиться то количество найденных записей, которое было задано пользователем при определении условий поиска. В первом столбце списка указан номер строки результатов поиска. Во втором столбце списка указан источник данных, например: — данные из документов о награждении; — данные из картотеки; — данные из юбилейной картотеки. Далее указаны: Дата рождения/Звание/Наименование награды. Для последовательного перемещения между страницами можно также воспользоваться кнопками: , для перехода на следующую страницу; , для перехода на последнюю страницу; , для перехода на предыдущую страницу; , для перехода на первую страницу. Если результаты поиска не соответствуют требованиям пользователя, то он может вернуться на страницу поиска,
нажав на наименование раздела, в котором осуществлялся поиск; при этом, все заполненные поисковые поля останутся
без изменений.
Также для возврата к предыдущей странице можно нажать кнопку «Назад» в окне web-браузера. Чтобы просмотреть определенную запись из числа найденных, следует навести на нее указатель и нажать левую кнопку
мыши –
на экране появится страница просмотра информации. В верхней части страницы отображаются кнопки «К предыдущему результату поиска», «К следующему результату
поиска» Данные кнопки позволяют переходить по страницам просмотра информации согласно списку результатов поиска. Ниже на странице представлены сведения о персоналии. В столбце «Архивные документы о данном награждении» синим подсвечены ссылки для перехода к электронным образам указанных документов. Электронный образ документа, который представлен на странице, содержит описание подвига, за который была присуждена награда. Для просмотра текста приказа (указа) необходимо нажать на одну из ссылок: - первая страница приказа или указа;
- строка в наградном списке;
- наградной лист.
Откроется электронный образ выбранного документа. Для просмотра изображения предусмотрена область навигации: переход к предыдущей странице документа; переход к следующей странице документа; Рядом с областью навигации представлена панель инструментов с двумя функциями: увеличение масштаба электронного образа документа; уменьшение масштаба электронного образа документа; при нажатии кнопки страница электронного образа документа будет открыта в
новой вкладке,
далее открытую страницу можно вывести на печать или сохранить на своем ПК; просмотр страницы документа в полноэкранном режиме, для выхода из
полноэкранного режима
необходимо нажать кнопку в правом верхнем углу. Результаты поиска «Наградные документы» Результат поиска в разделе «Наградные документы» выводится на экран монитора в виде списка. При этом на каждой странице результатов поиска будет выводиться то количество найденных записей, которое было задано пользователем при определении условий поиска. Информация по столбцам структурирована в следующем виде: - дата документа;
- кем издан;
- номер документа;
- наименование документа.
Для последовательного перемещения между страницами можно также воспользоваться кнопками: , для перехода на следующую страницу; , для перехода на последнюю страницу; , для перехода на предыдущую страницу; , для перехода на первую страницу. Для перехода к странице просмотра документа необходимо нажать левой кнопкой мыши в строке нужного документа в
списке результатов поиска. В верхней части страницы отображаются кнопки К предыдущему результату поиска, К следующему результату
поиска Данные кнопки позволяют переходить по страницам просмотра информации согласно списку результатов поиска. Ниже на странице представлены изображения, относящиеся к найденному документу. Для просмотра электронного образа документа предусмотрена область навигации: — переход к предыдущей странице документа; — переход к следующей странице документа; Рядом с областью навигации представлена панель инструментов с двумя функциями: увеличение масштаба электронного образа документа; уменьшение масштаба электронного образа документа; при нажатии кнопки страница электронного образа документа будет открыта в
новой вкладке,
далее открытую страницу можно вывести на печать или сохранить на своем ПК; просмотр страницы документа в полноэкранном режиме, для выхода из
полноэкранного режима
необходимо нажать кнопку в правом верхнем углу. При наведении курсора мыши отдельные строки электронного образа документа могут быть определены как ссылки
перехода, например, на страницу персоналии: Для перехода к странице персоналии необходимо: - навести указатель мыши на строку электронного образа документа;
- нажать левой кнопкой мыши.
Строка будет подсвечена красным, и в правой части строки появится кнопка перехода.
- нажать кнопку
После чего будет осуществлен переход к странице персоналии: Результаты поиска «География войны» Результат поиска в разделе «География войны» выводится на экран монитора в виде списка. При этом на каждой
странице результатов
поиска будет выводиться то количество найденных записей, которое было задано пользователем при определении
условий поиска. Информация по столбцам структурирована в следующем виде: - дата документа;
- кем издан;
- номер документа;
- тип документа.
Для последовательного перемещения между страницами можно также воспользоваться кнопками: , для перехода на следующую страницу; , для перехода на последнюю страницу; , для перехода на предыдущую страницу; , для перехода на первую страницу. Если результаты поиска не соответствуют требованиям пользователя, то он может вернуться на страницу поиска,
нажав на наименование раздела, в котором осуществлялся поиск; при этом, все заполненные поисковые поля останутся
без изменений.
Также для возврата к предыдущей странице можно нажать кнопку «Назад» в окне web-браузера. Для перехода к странице просмотра документа необходимо нажать левой кнопкой мыши в строке нужного документа в
списке результатов поиска. В верхней части страницы отображаются ссылки К предыдущему результату поиска, К следующему результату
поиска
– данные ссылки позволяют переходить по страницам просмотра информации согласно списку результатов поиска. Ниже на странице представлены сведения о документе. Для просмотра электронного образа документа предусмотрена область навигации: — переход к предыдущей странице документа; — переход к следующей странице документа; Рядом с областью навигации представлена панель инструментов с двумя функциями: — при нажатии кнопки страница электронного образа документа будет открыта в
новой вкладке,
далее открытую страницу можно вывести на печать или сохранить на своем компьютере; — просмотр страницы документа в полноэкранном режиме, для выхода из
полноэкранного режима
необходимо нажать кнопку в правом верхнем углу. To support the site’s latest version and innovations, we recommend using the following browser versions: Microsoft Internet Explorer 10, Mozilla Firefox 4, Google Chrome 5, Opera 11.5, Safari 5.0 and higher. Main page At the top of the Main page there is a menu, its items correspond to the main thematic sections of the «Feat of the People» website. The central part of the Main page provides a general description of the website, as well as links to sections of the site: - people and awards;
- documents;
- geography of war.
An additional menu with the following sections is available at the bottom of the page: - About the project, which contains information about the resource, access to which is provided to users of the website «Feat of the People».
- Reviews, which contains reviews about the resource, access to which is provided to users of the website «Feat of the People».
- Feedback, which contains a feedback form for users of the website «Feat of the People».
- FAQ, which provides answers to user questions about the site, most frequently asked to the site Administration.
- Help, which provides information about thematic sections of the site and ways to work with them.
Search (only Russian) The topic search in every section can be performed in two modes: - search in normal mode, when you define a search criteria by filling in the set of fields with the minimum information required to perform a search.
- search in advanced mode, when you define the search criteria by filling as many fields as possible and specifying detailed information about the search object.
This type of search proves most effective as it produces the result that most closely meets to user’s needs.
To start searching for information on any of the thematic sections, point to the name of the corresponding section (in the main menu of the site or in the central part of the main page): People and awards (only Russian) Search in the thematic section «People and awards» allows you to find information about the award, using the personal data of the awarded ones. The topic search in every section can be performed in two modes: Search in Normal mode For quick search, go to the «People and awards» section by clicking the left mouse button on: - section title;
- section button in the center of the Main page;
Then type the available information into the search field and click the «Search» button or the «Enter» key on the keyboard. If necessary, you can select the number of records to be displayed on one page of the search results (by default, 50 records per page): 10, 30, 50, or 100. The example of the search page in normal mode is given below: Search in Advanced mode To perform an advanced search of award information: - go to the «Search and awards» section;
- click the Advanced Search button;
If you need more fields to refine the search, click the «More» button.
When filling in fields in the advanced search mode, the user can define the search method for each field:
- From the beginning — to search for documents that at the beginning of the corresponding index field will contain the value specified by the user in this search field;;
- Exact phrase — to search for documents that in a corresponding index field will contain a value consisting of one or more words (or digits) in the same order as specified by the user in this search field;
- Exact field — to search for documents that in the corresponding index field will contain the exact value specified by the user in this search field;
- Full text search — to search for documents that in the corresponding index field will contain information specified by the user in this search field, disregarding the sequence of words and their quantity.
Documents (only Russian) Searching the thematic section «Documents» allows you to find decrees and orders on rewarding. The topic search in every section can be performed in two modes: Search in Normal mode For quick search, go to the «Documents» section by clicking the left mouse button on: - section title;
- section button in the center of the Main page;
Then type the available information into the search field and click the «Search» button or the «Enter» key on the keyboard. If necessary, you can select the number of records to be displayed on one page of the search results (by default, 50 records per page): 10, 30, 50, or 100. Geography of War (only Russian) Searching the thematic section «Geography of war» allows you to find data by location and time of events. The documents in the «Geography of war» section can be found using the date of issue of documents as search criteria, or geographical reference to the locations of combat operations, or the information about the military commander who issued the document. The topic search in every section can be performed in two modes: Search in Normal mode For quick search, go to the «Geography of war» section by clicking the left mouse button on: - section title;
- section button in the center of the Main page;
Then type the available information into the search field and click the «Search» button or the «Enter» key on the keyboard. If necessary, you can select the number of records to be displayed on one page of the search results (by default, 50 records per page): 10, 30, 50, or 100. Search results The results of searching for a war hero information are displayed as a list. Each page of the search results will display that number of records, which was specified by the user when determining the search conditions.
The first column in the list contains the row number of the search results. The second column of the list indicates the data source, for example: — data from the award documents; — data from the card index; — commemorative index data. To navigate through the search results pages, click the button and select the number of the desired page from the drop-down list at the top of the search results page.. To navigate between pages in sequence, you can also use the buttons: , to go to the next page; , to go to the last page; , to go to the previous page; , to go to the first page. If the search results do not meet the user’s needs, then you can return to the search page by clicking on the name of the section in which the search was performed; in this case, all the completed search fields will remain unchanged. You can also click the «Back» button in the browser window to return to the previous page. To view a particular record from among those found, point to it and click the left mouse button — the View information page will appear on the screen. The electronic image of the document displayed on the page contains a description of the feat for which the decoration was awarded. At the top of the page you can find the links To previous search result, To next search results — these links allow you to navigate through the pages with the required information according to the search results list.
The information about the personality is given below on the page. In the column «Archival documents on this award» the links to the electronic images of documents associated with this award and personality are highlighted in blue.
Конвенция о правах ребенка — Конвенции и соглашения — Декларации, конвенции, соглашения и другие правовые материалыКонвенция о правах ребенкаПринята резолюцией 44/25 Генеральной Ассамблеи от 20 ноября 1989 года ПреамбулаГосударства-участники настоящей Конвенции, считая, что в соответствии с принципами, провозглашенными в Уставе Организации Объединенных Наций, признание присущего достоинства, равных и неотъемлемых прав всех членов общества являются основой обеспечения свободы, справедливости и мира на Земле, принимая во внимание, что народы Объединенных Наций подтвердили в Уставе свою веру в основные права человека, в достоинство и ценность человеческой личности и преисполнены решимости содействовать социальному прогрессу и улучшению условий жизни при большей свободе, признавая, что Организация Объединенных Наций во Всеобщей декларации прав человека2 и в Международных пактах о правах человека3 провозгласила и согласилась с тем, что каждый человек должен обладать всеми указанными в них правами и свободами без какого бы то ни было различия по таким признакам, как раса, цвет кожи, пол, язык, религия, политические или иные убеждения, национальное или социальное происхождение, имущественное положение, рождение или иные обстоятельства, напоминая, что Организация Объединенных Наций во Всеобщей декларации прав человека провозгласила, что дети имеют право на особую заботу и помощь, убежденные в том, что семье как основной ячейке общества и естественной среде для роста и благополучия всех ее членов и особенно детей должны быть предоставлены необходимые защита и содействие, с тем чтобы она могла полностью возложить на себя обязанности в рамках общества, признавая, что ребенку для полного и гармоничного развития его личности необходимо расти в семейном окружении, в атмосфере счастья, любви и понимания, считая, что ребенок должен быть полностью подготовлен к самостоятельной жизни в обществе и воспитан в духе идеалов, провозглашенных в Уставе Организации Объединенных Наций, и особенно в духе мира, достоинства, терпимости, свободы, равенства и солидарности, принимая во внимание, что необходимость в такой особой защите ребенка была предусмотрена в Женевской Декларации прав ребенка 19244 года и Декларации прав ребенка, принятой Генеральной Ассамблеей 20 ноября 1959 года1, и признана во Всеобщей декларации прав человека, в Международном пакте о гражданских и политических правах (в частности, в статьях 23 и 24)3, в Международном пакте об экономических, социальных и культурных правах (в частности, в статье 10)3, а также в уставах и соответствующих документах специализированных учреждений и международных организаций, занимающихся вопросами благополучия детей, принимая во внимание, что, как указано в Декларации прав ребенка, «ребенок, ввиду его физической и умственной незрелости, нуждается в специальной охране и заботе, включая надлежащую правовую защиту, как до, так и после рождения»5, ссылаясь на положения Декларации о социальных и правовых принципах, касающихся защиты и благополучия детей, особенно при передаче детей на воспитание и их усыновлении на национальном и международном уровнях6, Минимальных стандартных правил Организации Объединенных Наций, касающихся отправления правосудия в отношении несовершеннолетних («Пекинские правила»)7 и Декларации о защите женщин и детей в чрезвычайных обстоятельствах и в период вооруженных конфликтов8, признавая, что во всех странах мира есть дети, живущие в исключительно трудных условиях, и что такие дети нуждаются в особом внимании, учитывая должным образом важность традиций и культурных ценностей каждого народа для защиты и гармоничного развития ребенка, признавая важность международного сотрудничества для улучшения условий жизни детей в каждой стране, в частности в развивающихся странах, согласились о нижеследующем: Часть IСтатья 1Для целей настоящей Конвенции ребенком является каждое человеческое существо до достижения 18-летнего возраста, если по закону, применимому к данному ребенку, он не достигает совершеннолетия ранее. Статья 21. Государства-участники уважают и обеспечивают все права, предусмотренные настоящей Конвенцией, за каждым ребенком, находящимся в пределах их юрисдикции, без какой-либо дискриминации, независимо от расы, цвета кожи, пола, языка, религии, политических или иных убеждений, национального, этнического или социального происхождения, имущественного положения, состояния здоровья и рождения ребенка, его родителей или законных опекунов или каких-либо иных обстоятельств. 2. Государства-участники принимают все необходимые меры для обеспечения защиты ребенка от всех форм дискриминации или наказания на основе статуса, деятельности, выражаемых взглядов или убеждений ребенка, родителей ребенка, законных опекунов или иных членов семьи. Статья 31. Во всех действиях в отношении детей, независимо от того, предпринимаются они государственными или частными учреждениями, занимающимися вопросами социального обеспечения, судами, административными или законодательными органами, первоочередное внимание уделяется наилучшему обеспечению интересов ребенка. 2. Государства-участники обязуются обеспечить ребенку такую защиту и заботу, которые необходимы для его благополучия, принимая во внимание права и обязанности его родителей, опекунов или других лиц, несущих за него ответственность по закону, и с этой целью принимают все соответствующие законодательные и административные меры. 3. Государства-участники обеспечивают, чтобы учреждения, службы и органы, ответственные за заботу о детях или их защиту, отвечали нормам, установленным компетентными органами, в частности, в области безопасности и здравоохранения и с точки зрения численности и пригодности их персонала, а также компетентного надзора. Статья 4Государства-участники принимают все необходимые законодательные, административные и другие меры для осуществления прав, признанных в настоящей Конвенции. В отношении экономических, социальных и культурных прав государства-участники принимают такие меры в максимальных рамках имеющихся у них ресурсов и, в случае необходимости, в рамках международного сотрудничества. Статья 5Государства-участники уважают ответственность, права и обязанности родителей и в соответствующих случаях членов расширенной семьи или общины, как это предусмотрено местным обычаем, опекунов или других лиц, несущих по закону ответственность за ребенка, должным образом управлять и руководить ребенком в осуществлении им признанных настоящей Конвенцией прав и делать это в соответствии с развивающимися способностями ребенка. Статья 61. Государства-участники признают, что каждый ребенок имеет неотъемлемое право на жизнь. 2. Государства-участники обеспечивают в максимально возможной степени выживание и здоровое развитие ребенка. Статья 71. Ребенок регистрируется сразу же после рождения и с момента рождения имеет право на имя и на приобретение гражданства, а также, насколько это возможно, право знать своих родителей и право на их заботу. 2. Государства-участники обеспечивают осуществление этих прав в соответствии с их национальным законодательством и выполнение их обязательств согласно соответствующим международным документам в этой области, в частности, в случае, если бы иначе ребенок не имел гражданства. Статья 81. Государства-участники обязуются уважать право ребенка на сохранение своей индивидуальности, включая гражданство, имя и семейные связи, как предусматривается законом, не допуская противозаконного вмешательства. 2. Если ребенок незаконно лишается части или всех элементов своей индивидуальности, государства-участники обеспечивают ему необходимую помощь и защиту для скорейшего восстановления его индивидуальности. Статья 91. Государства-участники обеспечивают, чтобы ребенок не разлучался со своими родителями вопреки их желанию, за исключением случаев, когда компетентные органы, согласно судебному решению, определяют в соответствии с применимым законом и процедурами, что такое разлучение необходимо в наилучших интересах ребенка. Такое определение может оказаться необходимым в том или ином конкретном случае, например, когда родители жестоко обращаются с ребенком или не заботятся о нем или когда родители проживают раздельно и необходимо принять решение относительно места проживания ребенка. 2. В ходе любого разбирательства в соответствии с пунктом 1 настоящей статьи всем заинтересованным сторонам предоставляется возможность участвовать в разбирательстве и излагать свои точки зрения. 3. Государства-участники уважают право ребенка, который разлучается с одним или обоими родителями, поддерживать на регулярной основе личные отношения и прямые контакты с обоими родителями, за исключением случая, когда это противоречит наилучшим интересам ребенка. 4. В тех случаях, когда такое разлучение вытекает из какого-либо решения, принятого государством-участником, например при аресте, тюремном заключении, высылке, депортации или смерти (включая смерть, наступившую по любой причине во время нахождения данного лица в ведении государства) одного или обоих родителей или ребенка, такое государство-участник предоставляет родителям, ребенку или, если это необходимо, другому члену семьи по их просьбе необходимую информацию в отношении местонахождения отсутствующего члена/членов семьи, если предоставление этой информации не наносит ущерба благосостоянию ребенка. Государства-участники в дальнейшем обеспечивают, чтобы представление такой просьбы само по себе не приводило к неблагоприятным последствиям для соответствующего лица/лиц. Статья 101. В соответствии с обязательством государств-участников по пункту 1 статьи 9 заявления ребенка или его родителей на въезд в государство-участник или выезд из него с целью воссоединения семьи должны рассматриваться государствами-участниками позитивным, гуманным и оперативным образом. Государства-участники далее обеспечивают, чтобы представление такой просьбы не приводило к неблагоприятным последствиям для заявителей и членов их семьи. 2. Ребенок, родители которого проживают в различных государствах, имеет право поддерживать на регулярной основе, за исключением особых обстоятельств, личные отношения и прямые контакты с обоими родителями. С этой целью и в соответствии с обязательством государств-участников по пункту 1 статьи 9 государства-участники уважают право ребенка и его родителей покидать любую страну, включая свою собственную, и возвращаться в свою страну. В отношении права покидать любую страну действуют только такие ограничения, какие установлены законом и необходимы для охраны государственной безопасности, общественного порядка (ordre public), здоровья или нравственности населения или прав и свобод других лиц, и совместимы с признанными в настоящей Конвенции другими правами. Статья 111. Государства-участники принимают меры для борьбы с незаконным перемещением и невозвращением детей из-за границы. 2. С этой целью государства-участники содействуют заключению двусторонних или многосторонних соглашений или присоединению к действующим соглашениям. Статья 121. Государства-участники обеспечивают ребенку, способному сформулировать свои собственные взгляды, право свободно выражать эти взгляды по всем вопросам, затрагивающим ребенка, причем взглядам ребенка уделяется должное внимание в соответствии с возрастом и зрелостью ребенка. 2. С этой целью ребенку, в частности, предоставляется возможность быть заслушанным в ходе любого судебного или административного разбирательства, затрагивающего ребенка, либо непосредственно, либо через представителя или соответствующий орган, в порядке, предусмотренном процессуальными нормами национального законодательства. Статья 131. Ребенок имеет право свободно выражать свое мнение; это право включает свободу искать, получать и передавать информацию и идеи любого рода, независимо от границ, в устной, письменной или печатной форме, в форме произведений искусства или с помощью других средств по выбору ребенка. 2. Осуществление этого права может подвергаться некоторым ограничениям, однако этими ограничениями могут быть только те ограничения, которые предусмотрены законом и которые необходимы:
a) для уважения прав и репутации других лиц; или
b) для охраны государственной безопасности или общественного порядка (ordre public), или здоровья или нравственности населения.
Статья 141. Государства-участники уважают право ребенка на свободу мысли, совести и религии. 2. Государства-участники уважают права и обязанности родителей и в соответствующих случаях законных опекунов руководить ребенком в осуществлении его права методом, согласующимся с развивающимися способностями ребенка. 3. Свобода исповедовать свою религию или веру может подвергаться только таким ограничениям, которые установлены законом и необходимы для охраны государственной безопасности, общественного порядка, нравственности и здоровья населения или защиты основных прав и свобод других лиц. Статья 151. Государства-участники признают право ребенка на свободу ассоциации и свободу мирных собраний. 2. В отношении осуществления данного права не могут применяться какие-либо ограничения, кроме тех, которые применяются в соответствии с законом и которые необходимы в демократическом обществе в интересах государственной безопасности или общественной безопасности, общественного порядка (ordre public), охраны здоровья или нравственности населения или защиты прав и свобод других лиц. Статья 161. Ни один ребенок не может быть объектом произвольного или незаконного вмешательства в осуществление его права на личную жизнь, семейную жизнь, неприкосновенность жилища или тайну корреспонденции, или незаконного посягательства на его честь и репутацию. 2. Ребенок имеет право на защиту закона от такого вмешательства или посягательства. Статья 17Государства-участники признают важную роль средств массовой информации и обеспечивают, чтобы ребенок имел доступ к информации и материалам из различных национальных и международных источников, особенно к таким информации и материалам, которые направлены на содействие социальному, духовному и моральному благополучию, а также здоровому физическому и психическому развитию ребенка. С этой целью государства-участники:
a) поощряют средства массовой информации к распространению информации и материалов, полезных для ребенка в социальном и культурном отношениях, и в духе статьи 29;
b) поощряют международное сотрудничество в области подготовки, обмена и распространения такой информации и материалов из различных культурных, национальных и международных источников;
c) поощряют выпуск и распространение детской литературы;
d) поощряют средства массовой информации к уделению особого внимания языковым потребностям ребенка, принадлежащего к какой-либо группе меньшинств или коренному населению;
e) поощряют разработку надлежащих принципов защиты ребенка от информации и материалов, наносящих вред его благополучию, учитывая положения статей 13 и 18.
Статья 181. Государства-участники предпринимают все возможные усилия к тому, чтобы обеспечить признание принципа общей и одинаковой ответственности обоих родителей за воспитание и развитие ребенка. Родители или в соответствующих случаях законные опекуны несут основную ответственность за воспитание и развитие ребенка. Наилучшие интересы ребенка являются предметом их основной заботы. 2. В целях гарантии и содействия осуществлению прав, изложенных в настоящей Конвенции, государства-участники оказывают родителям и законным опекунам надлежащую помощь в выполнении ими своих обязанностей по воспитанию детей и обеспечивают развитие сети детских учреждений. 3. Государства-участники принимают все необходимые меры для обеспечения того, чтобы дети, родители которых работают, имели право пользоваться предназначенными для них службами и учреждениями по уходу за детьми. Статья 191. Государства-участники принимают все необходимые законодательные, административные, социальные и просветительные меры с целью защиты ребенка от всех форм физического или психологического насилия, оскорбления или злоупотребления, отсутствия заботы или небрежного обращения, грубого обращения или эксплуатации, включая сексуальное злоупотребление, со стороны родителей, законных опекунов или любого другого лица, заботящегося о ребенке. 2. Такие меры защиты, в случае необходимости, включают эффективные процедуры для разработки социальных программ с целью предоставления необходимой поддержки ребенку и лицам, которые о нем заботятся, а также для осуществления других форм предупреждения и выявления, сообщения, передачи на рассмотрение, расследования, лечения и последующих мер в связи со случаями жестокого обращения с ребенком, указанными выше, а также, в случае необходимости, для возбуждения судебной процедуры. Статья 201. Ребенок, который временно или постоянно лишен своего семейного окружения или который в его собственных наилучших интересах не может оставаться в таком окружении, имеет право на особую защиту и помощь, предоставляемые государством. 2. Государства-участники в соответствии со своими национальными законами обеспечивают замену ухода за таким ребенком. 3. Такой уход может включать, в частности, передачу на воспитание, «кафала» по исламскому праву, усыновление или, в случае необходимости, помещение в соответствующие учреждения по уходу за детьми. При рассмотрении вариантов замены необходимо должным образом учитывать желательность преемственности воспитания ребенка и его этническое происхождение, религиозную и культурную принадлежность и родной язык. Статья 21Государства-участники, которые признают и/или разрешают существование системы усыновления, обеспечивают, чтобы наилучшие интересы ребенка учитывались в первостепенном порядке, и они:
a) обеспечивают, чтобы усыновление ребенка разрешалось только компетентными властями, которые определяют в соответствии с применимыми законом и процедурами и на основе всей относящейся к делу и достоверной информации, что усыновление допустимо ввиду статуса ребенка относительно родителей, родственников и законных опекунов и что, если требуется, заинтересованные лица дали свое осознанное согласие на усыновление на основе такой консультации, которая может быть необходимой;
b) признают, что усыновление в другой стране может рассматриваться в качестве альтернативного способа ухода за ребенком, если ребенок не может быть передан на воспитание или помещен в семью, которая могла бы обеспечить его воспитание или усыновление, и если обеспечение какого-либо подходящего ухода в стране происхождения ребенка является невозможным;
c) обеспечивают, чтобы в случае усыновления ребенка в другой стране применялись такие же гарантии и нормы, которые применяются в отношении усыновления внутри страны;
d) принимают все необходимые меры с целью обеспечения того, чтобы в случае усыновления в другой стране устройство ребенка не приводило к получению неоправданных финансовых выгод связанными с этим лицами;
e) содействуют в необходимых случаях достижению целей настоящей статьи путем заключения двусторонних и многосторонних договоренностей или соглашений и стремятся на этой основе обеспечить, чтобы устройство ребенка в другой стране осуществлялось компетентными властями или органами.
Статья 221. Государства-участники принимают необходимые меры, с тем чтобы обеспечить ребенку, желающему получить статус беженца или считающемуся беженцем в соответствии с применимым международным или внутренним правом и процедурами, как сопровождаемому, так и не сопровождаемому его родителями или любым другим лицом, надлежащую защиту и гуманитарную помощь в пользовании применимыми правами, изложенными в настоящей Конвенции и других международных документах по правам человека или гуманитарных документов, участниками которых являются указанные государства. 2. С этой целью государства-участники оказывают, в случае, когда они считают это необходимым, содействие любым усилиям Организации Объединенных Наций и других компетентных межправительственных организаций или неправительственных организаций, сотрудничающих с Организацией Объединенных Наций, по защите такого ребенка и оказанию ему помощи и поиску родителей или других членов семьи любого ребенка-беженца, с тем чтобы получить информацию, необходимую для его воссоединения со своей семьей. В тех случаях, когда родители или другие члены семьи не могут быть найдены, этому ребенку предоставляется такая же защита, как и любому другому ребенку, по какой-либо причине постоянно или временно лишенному своего семейного окружения, как это предусмотрено в настоящей Конвенции. Статья 231. Государства-участники признают, что неполноценный в умственном или физическом отношении ребенок должен вести полноценную и достойную жизнь в условиях, которые обеспечивают его достоинство, способствуют его уверенности в себе и облегчают его активное участие в жизни общества. 2. Государства-участники признают право неполноценного ребенка на особую заботу и поощряют и обеспечивают предоставление при условии наличия ресурсов имеющему на это право ребенку и ответственным за заботу о нем помощи, о которой подана просьба и которая соответствует состоянию ребенка и положению его родителей или других лиц, обеспечивающих заботу о ребенке. 3. В признание особых нужд неполноценного ребенка помощь в соответствии с пунктом 2 настоящей статьи предоставляется, по возможности, бесплатно с учетом финансовых ресурсов родителей или других лиц, обеспечивающих заботу о ребенке, и имеет целью обеспечение неполноценному ребенку эффективного доступа к услугам в области образования, профессиональной подготовки, медицинского обслуживания, восстановления здоровья, подготовки к трудовой деятельности и доступа к средствам отдыха таким образом, который приводит к наиболее полному, по возможности, вовлечению ребенка в социальную жизнь и достижению развития его личности, включая культурное и духовное развитие ребенка. 4. Государства-участники способствуют в духе международного сотрудничества обмену соответствующей информацией в области профилактического здравоохранения и медицинского, психологического и функционального лечения неполноценных детей, включая распространение информации о методах реабилитации, общеобразовательной и профессиональной подготовки, а также доступ к этой информации, с тем чтобы позволить государствам-участникам улучшить свои возможности и знания и расширить свой опыт в этой области. В этой связи особое внимание должно уделяться потребностям развивающихся стран. Статья 241. Государства-участники признают право ребенка на пользование наиболее совершенными услугами системы здравоохранения и средствами лечения болезней и восстановления здоровья. Государства-участники стремятся обеспечить, чтобы ни один ребенок не был лишен своего права на доступ к подобным услугам системы здравоохранения. 2. Государства-участники добиваются полного осуществления данного права и, в частности, принимают необходимые меры для:
a) снижения уровней смертности младенцев и детской смертности;
b) обеспечения предоставления необходимой медицинской помощи и охраны здоровья всех детей с уделением первоочередного внимания развитию первичной медико-санитарной помощи;
c) борьбы с болезнями и недоеданием, в том числе в рамках первичной медико-санитарной помощи, путем, среди прочего, применения легкодоступной технологии и предоставления достаточно питательного продовольствия и чистой питьевой воды, принимая во внимание опасность и риск загрязнения окружающей среды;
d) предоставления матерям надлежащих услуг по охране здоровья в дородовой и послеродовой периоды;
e) обеспечения осведомленности всех слоев общества, в частности родителей и детей, о здоровье и питании детей, преимуществах грудного кормления, гигиене, санитарии среды обитания ребенка и предупреждении несчастных случаев, а также их доступа к образованию и их поддержки в использовании таких знаний;
f) развития просветительной работы и услуг в области профилактической медицинской помощи и планирования размера семьи.
3. Государства-участники принимают любые эффективные и необходимые меры с целью упразднения традиционной практики, отрицательно влияющей на здоровье детей. 4. Государства-участники обязуются поощрять международное сотрудничество и развивать его с целью постепенного достижения полного осуществления права, признаваемого в настоящей статье. В этой связи особое внимание должно уделяться потребностям развивающихся стран. Статья 25Государства-участники признают право ребенка, помещенного компетентными органами на попечение с целью ухода за ним, его защиты или физического либо психического лечения, на периодическую оценку лечения, предоставляемого ребенку, и всех других условий, связанных с таким попечением о ребенке. Статья 261. Государства-участники признают за каждым ребенком право пользоваться благами социального обеспечения, включая социальное страхование, и принимают необходимые меры для достижения полного осуществления этого права в соответствии с их национальным законодательством. 2. Эти блага по мере необходимости предоставляются с учетом имеющихся ресурсов и возможностей ребенка и лиц, несущих ответственность за содержание ребенка, а также любых соображений, связанных с получением благ ребенком или от его имени. Статья 271. Государства-участники признают право каждого ребенка на уровень жизни, необходимый для физического, умственного, духовного, нравственного и социального развития ребенка. 2. Родитель(и) или другие лица, воспитывающие ребенка, несут основную ответственность за обеспечение в пределах своих способностей и финансовых возможностей условий жизни, необходимых для развития ребенка. 3. Государства-участники в соответствии с национальными условиями и в пределах своих возможностей принимают необходимые меры по оказанию помощи родителям и другим лицам, воспитывающим детей, в осуществлении этого права и, в случае необходимости, оказывают материальную помощь и поддерживают программы, особенно в отношении обеспечения питанием, одеждой и жильем. 4. Государства-участники принимают все необходимые меры для обеспечения восстановления содержания ребенка родителями или другими лицами, несущими финансовую ответственность за ребенка, как внутри государства-участника, так и из-за рубежа. В частности, если лицо, несущее финансовую ответственность за ребенка, и ребенок проживают в разных государствах, государства-участники способствуют присоединению к международным соглашениям или заключению таких соглашений, а также достижению других соответствующих договоренностей. Статья 281. Государства-участники признают право ребенка на образование, и с целью постепенного достижения осуществления этого права на основе равных возможностей они, в частности:
a) вводят бесплатное и обязательное начальное образование;
b) поощряют развитие различных форм среднего образования, как общего, так и профессионального, обеспечивают его доступность для всех детей и принимают такие необходимые меры, как введение бесплатного образования и предоставление в случае необходимости финансовой помощи;
c) обеспечивают доступность высшего образования для всех на основе способностей каждого с помощью всех необходимых средств;
d) обеспечивают доступность информации и материалов в области образования и профессиональной подготовки для всех детей;
e) принимают меры по содействию регулярному посещению школ и снижению числа учащихся, покинувших школу.
2. Государства-участники принимают все необходимые меры для обеспечения того, чтобы школьная дисциплина поддерживалась с помощью методов, отражающих уважение человеческого достоинства ребенка и в соответствии с настоящей Конвенцией. 3. Государства-участники поощряют и развивают международное сотрудничество по вопросам, касающимся образования, в частности, с целью содействия ликвидации невежества и неграмотности во всем мире и облегчения доступа к научно-техническим знаниям и современным методам обучения. В этой связи особое внимание должно уделяться потребностям развивающихся стран. Статья 291. Государства-участники соглашаются в том, что образование ребенка должно быть направлено на:
a) развитие личности, талантов и умственных и физических способностей ребенка в их самом полном объеме;
b) воспитание уважения к правам человека и основным свободам, а также принципам, провозглашенным в Уставе Организации Объединенных Наций;
c) воспитание уважения к родителям ребенка, его культурной самобытности, языку и ценностям, к национальным ценностям страны, в которой ребенок проживает, страны его происхождения и к цивилизациям, отличным от его собственной;
d) подготовку ребенка к сознательной жизни в свободном обществе в духе понимания, мира, терпимости, равноправия мужчин и женщин и дружбы между всеми народами, этническими, национальными и религиозными группами, а также лицами из числа коренного населения;
e) воспитание уважения к окружающей природе.
2. Никакая часть настоящей статьи или статьи 28 не толкуется как ограничивающая свободу отдельных лиц и органов создавать учебные заведения и руководить ими при условии постоянного соблюдения принципов, изложенных в пункте 1 настоящей статьи, и выполнения требования о том, чтобы образование, даваемое в таких учебных заведениях, соответствовало минимальным нормам, которые могут быть установлены государством. Статья 30В тех государствах, где существуют этнические, религиозные или языковые меньшинства или лица из числа коренного населения, ребенку, принадлежащему к таким меньшинствам или коренному населению, не может быть отказано в праве совместно с другими членами своей группы пользоваться своей культурой, исповедовать свою религию и исполнять ее обряды, а также пользоваться родным языком. Статья 311. Государства-участники признают право ребенка на отдых и досуг, право участвовать в играх и развлекательных мероприятиях, соответствующих его возрасту, и свободно участвовать в культурной жизни и заниматься искусством. 2. Государства-участники уважают и поощряют право ребенка на всестороннее участие в культурной и творческой жизни и содействуют предоставлению соответствующих и равных возможностей для культурной и творческой деятельности, досуга и отдыха. Статья 321. Государства-участники признают право ребенка на защиту от экономической эксплуатации и от выполнения любой работы, которая может представлять опасность для его здоровья или служить препятствием в получении им образования, либо наносить ущерб его здоровью и физическому, умственному, духовному, моральному и социальному развитию. 2. Государства-участники принимают законодательные, административные и социальные меры, а также меры в области образования, с тем чтобы обеспечить осуществление настоящей статьи. В этих целях, руководствуясь соответствующими положениями других международных документов, государства-участники, в частности:
a) устанавливают минимальный возраст или минимальные возрасты для приема на работу;
b) определяют необходимые требования о продолжительности рабочего дня и условиях труда;
c) предусматривают соответствующие виды наказания или другие санкции для обеспечения эффективного осуществления настоящей статьи.
Статья 33Государства-участники принимают все необходимые меры, включая законодательные, административные и социальные меры, а также меры в области образования, с тем чтобы защитить детей от незаконного употребления наркотических средств и психотропных веществ, как они определены в соответствующих международных договорах, и не допустить использования детей в противозаконном производстве таких веществ и торговле ими. Статья 34Государства-участники обязуются защищать ребенка от всех форм сексуальной эксплуатации и сексуального совращения. В этих целях государства-участники, в частности, принимают на национальном, двустороннем и многостороннем уровнях все необходимые меры для предотвращения:
a) склонения или принуждения ребенка к любой незаконной сексуальной деятельности;
b) использования в целях эксплуатации детей в проституции или в другой незаконной сексуальной практике;
c) использования в целях эксплуатации детей в порнографии и порнографических материалах.
Статья 35Государства-участники принимают на национальном, двустороннем и многостороннем уровнях все необходимые меры для предотвращения похищения детей, торговли детьми или их контрабанды в любых целях и в любой форме. Статья 36Государства-участники защищают ребенка от всех других форм эксплуатации, наносящих ущерб любому аспекту благосостояния ребенка. Статья 37Государства-участники обеспечивают, чтобы:
a) ни один ребенок не был подвергнут пыткам или другим жестоким, бесчеловечным или унижающим достоинство видам обращения или наказания. Ни смертная казнь, ни пожизненное тюремное заключение, не предусматривающее возможности освобождения, не назначаются за преступления, совершенные лицами моложе 18 лет;
b) ни один ребенок не был лишен свободы незаконным или произвольным образом. Арест, задержание или тюремное заключение ребенка осуществляются согласно закону и используются лишь в качестве крайней меры и в течение как можно более короткого соответствующего периода времени;
c) каждый лишенный свободы ребенок пользовался гуманным обращением и уважением неотъемлемого достоинства его личности с учетом потребностей лиц его возраста. В частности, каждый лишенный свободы ребенок должен быть отделен от взрослых, если только не считается, что в наилучших интересах ребенка этого делать не следует, и иметь право поддерживать связь со своей семьей путем переписки и свиданий, за исключением особых обстоятельств;
d) каждый лишенный свободы ребенок имел право на незамедлительный доступ к правовой и другой соответствующей помощи, а также право оспаривать законность лишения его свободы перед судом или другим компетентным, независимым и беспристрастным органом и право на безотлагательное принятие ими решения в отношении любого такого процессуального действия.
Статья 381. Государства-участники обязуются уважать нормы международного гуманитарного права, применимые к ним в случае вооруженных конфликтов и имеющие отношение к детям, и обеспечивать их соблюдение. 2. Государства-участники принимают все возможные меры для обеспечения того, чтобы лица, не достигшие 15-летнего возраста, не принимали прямого участия в военных действиях. 3. Государства-участники воздерживаются от призыва любого лица, не достигшего 15-летнего возраста, на службу в свои вооруженные силы. При вербовке из числа лиц, достигших 15-летнего возраста, но которым еще не исполнилось 18 лет, государства-участники стремятся отдавать предпочтение лицам более старшего возраста. 4. Согласно своим обязательствам по международному гуманитарному праву, связанным с защитой гражданского населения во время вооруженных конфликтов, государства-участники обязуются принимать все возможные меры с целью обеспечения защиты затрагиваемых вооруженным конфликтом детей и ухода за ними. Статья 39Государства-участники принимают все необходимые меры для того, чтобы содействовать физическому и психологическому восстановлению и социальной реинтеграции ребенка, являющегося жертвой: любых видов пренебрежения, эксплуатации или злоупотребления, пыток или любых других жестоких, бесчеловечных или унижающих достоинство видов обращения, наказания или вооруженных конфликтов. Такое восстановление и реинтеграция должны осуществляться в условиях, обеспечивающих здоровье, самоуважение и достоинство ребенка. Статья 401. Государства-участники признают право каждого ребенка, который, как считается, нарушил уголовное законодательство, обвиняется или признается виновным в его нарушении, на такое обращение, которое способствует развитию у ребенка чувства достоинства и значимости, укрепляет в нем уважение к правам человека и основным свободам других и при котором учитывается возраст ребенка и желательность содействия его реинтеграции и выполнению им полезной роли в обществе. 2. В этих целях и принимая во внимание соответствующие положения международных документов, государства-участники, в частности, обеспечивают, чтобы:
a) ни один ребенок не считался нарушившим уголовное законодательство, не обвинялся и не признавался виновным в его нарушении по причине действия или бездействия, которые не были запрещены национальным или международным правом во время их совершения;
b) каждый ребенок, который, как считается, нарушил уголовное законодательство или обвиняется в его нарушении, имел по меньшей мере следующие гарантии:
i) презумпция невиновности, пока его вина не будет доказана согласно закону;
ii) незамедлительное и непосредственное информирование его об обвинениях против него и, в случае необходимости, через его родителей или законных опекунов и получение правовой и другой необходимой помощи при подготовке и осуществлении своей защиты;
iii) безотлагательное принятие решения по рассматриваемому вопросу компетентным, независимым и беспристрастным органом или судебным органом в ходе справедливого слушания в соответствии с законом в присутствии адвоката или другого соответствующего лица, и, если это не считается противоречащим наилучшим интересам ребенка, в частности, с учетом его возраста или положения его родителей или законных опекунов;
iv) свобода от принуждения к даче свидетельских показаний или признанию вины; изучение показаний свидетелей обвинения либо самостоятельно, либо при помощи других лиц и обеспечение равноправного участия свидетелей защиты и изучения их показаний;
v) если считается, что ребенок нарушил уголовное законодательство, повторное рассмотрение вышестоящим компетентным, независимым и беспристрастным органом или судебным органом согласно закону соответствующего решения и любых принятых в этой связи мер;
vi) бесплатная помощь переводчика, если ребенок не понимает используемого языка или не говорит на нем;
vii) полное уважение его личной жизни на всех стадиях разбирательства.
3. Государства-участники стремятся содействовать установлению законов, процедур, органов и учреждений, имеющих непосредственное отношение к детям, которые, как считается, нарушили уголовное законодательство, обвиняются или признаются виновными в его нарушении, и в частности:
a) установлению минимального возраста, ниже которого дети считаются неспособными нарушить уголовное законодательство;
b) в случае необходимости и желательности, принятию мер по обращению с такими детьми без использования судебного разбирательства при условии полного соблюдения прав человека и правовых гарантий.
4. Необходимо наличие таких различных мероприятий, как уход, положение об опеке и надзоре, консультативные услуги, назначение испытательного срока, воспитание, программы обучения и профессиональной подготовки и другие формы ухода, заменяющие уход в учреждениях, с целью обеспечения такого обращения с ребенком, которое соответствовало бы его благосостоянию, а также его положению и характеру преступления. Статья 41Ничто в настоящей Конвенции не затрагивает любых положений, которые в большей степени способствуют осуществлению прав ребенка и могут содержаться:
a) в законе государства-участника; или
b) в нормах международного права, действующих в отношении данного государства.
Часть IIСтатья 42Государства-участники обязуются, используя надлежащие и действенные средства, широко информировать о принципах и положениях Конвенции как взрослых, так и детей. Статья 431. В целях рассмотрения прогресса, достигнутого государствами-участниками в выполнении обязательств, принятых в соответствии с настоящей Конвенцией, учреждается Комитет по правам ребенка, который выполняет функции, предусматриваемые ниже. 2. Комитет состоит из десяти экспертов, обладающих высокими нравственными качествами и признанной компетентностью в области, охватываемой настоящей Конвенцией. Члены Комитета избираются государствами-участниками из числа своих граждан и выступают в личном качестве, причем уделяется внимание справедливому географическому распределению, а также главным правовым системам. 3. Члены Комитета избираются тайным голосованием из числа внесенных в список лиц, выдвинутых государствами-участниками. Каждое государство-участник может выдвинуть одно лицо из числа своих граждан. 4. Первоначальные выборы в Комитет проводятся не позднее, чем через шесть месяцев со дня вступления в силу настоящей Конвенции, а впоследствии — один раз в два года. По крайней мере за четыре месяца до дня каждых выборов Генеральный секретарь Организации Объединенных Наций обращается к государствам-участникам с письмом, предлагая им представить свои кандидатуры в течение двух месяцев. Затем Генеральный секретарь составляет в алфавитном порядке список всех выдвинутых таким образом лиц с указанием государств-участников, которые выдвинули этих лиц, и представляет этот список государствам-участникам настоящей Конвенции. 5. Выборы проводятся на совещаниях государств-участников, созываемых Генеральным секретарем в Центральных учреждениях Организации Объединенных Наций. На этих совещаниях, на которых две трети государств-участников составляют кворум, избранными в состав Комитета являются те кандидаты, которые получили наибольшее число голосов и абсолютное большинство голосов присутствующих и участвующих в голосовании представителей государств-участников. 6. Члены Комитета избираются на четырехлетний срок. Они имеют право быть переизбранными в случае повторного выдвижения их кандидатур. Срок полномочий пяти членов, избираемых на первых выборах, истекает в конце двухлетнего периода; немедленно после первых выборов имена этих пяти членов определяются по жребию Председателем совещания. 7. В случае смерти или выхода в отставку какого-либо члена Комитета или если он или она по какой-либо иной причине не может более исполнять обязанности члена Комитета, государство-участник, выдвинувшее данного члена Комитета, назначает другого эксперта из числа своих граждан на оставшийся срок при условии одобрения Комитетом. 8. Комитет устанавливает свои собственные правила процедуры. 9. Комитет избирает своих должностных лиц на двухлетний срок. 10. Сессии Комитета, как правило, проводятся в Центральных учреждениях Организации Объединенных Наций или в любом ином подходящем месте, определенном Комитетом. Комитет, как правило, проводит свои сессии ежегодно. Продолжительность сессии Комитета определяется и при необходимости пересматривается на совещании государств — участников настоящей Конвенции при условии одобрения Генеральной Ассамблеей. 11. Генеральный секретарь Организации Объединенных Наций предоставляет персонал и материальные средства для эффективного осуществления Комитетом своих функций в соответствии с настоящей Конвенцией. 12. Члены Комитета, учрежденного в соответствии с настоящей Конвенций, получают утверждаемое Генеральной Ассамблеей вознаграждение из средств Организации Объединенных Наций в порядке и на условиях, устанавливаемых Генеральной Ассамблеей. Статья 441. Государства-участники обязуются предоставлять Комитету через Генерального секретаря Организации Объединенных Наций доклады о принятых ими мерах по закреплению признанных в Конвенции прав и о прогрессе, достигнутом в осуществлении этих прав:
a) в течение двух лет после вступления Конвенции в силу для соответствующего государства-участника;
b) впоследствии через каждые пять лет.
2. В докладах, представляемых в соответствии с настоящей статьей, указываются факторы и затруднения, если таковые имеются, влияющие на степень выполнения обязательств по настоящей Конвенции. Доклады также содержат достаточную информацию, с тем чтобы обеспечить Комитету полное понимание действий Конвенции в данной стране. 3. Государству-участнику, представившему Комитету всесторонний первоначальный доклад, нет необходимости повторять в последующих докладах, представляемых в соответствии с пунктом 1 b настоящей статьи, ранее изложенную основную информацию. 4. Комитет может запрашивать у государств-участников дополнительную информацию, касающуюся осуществления настоящей Конвенции. 5. Доклады о деятельности Комитета один раз в два года представляются Генеральной Ассамблее через посредство Экономического и Социального Совета. 6. Государства-участники обеспечивают широкую гласность своих докладов в своих собственных странах. Статья 45С целью способствовать эффективному осуществлению Конвенции и поощрять международное сотрудничество в области, охватываемой настоящей Конвенцией:
a) специализированные учреждения, Детский фонд Организации Объединенных Наций и другие органы Организации Объединенных Наций вправе быть представленными при рассмотрении вопросов об осуществлении таких положений настоящей Конвенции, которые входят в сферу их полномочий. Комитет может предложить специализированным учреждениям, Детскому фонду Организации Объединенных Наций и другим компетентным органам, когда он считает это целесообразным, представить заключение экспертов относительно осуществления Конвенции в тех областях, которые входят в сферу их соответствующих полномочий. Комитет может предложить специализированным учреждениям, Детскому фонду Организации Объединенных Наций и другим органам Организации Объединенных Наций представить доклады об осуществлении Конвенции в областях, входящих в сферу их деятельности;
b) Комитет препровождает, когда он считает это целесообразным, в специализированные учреждения, Детский фонд Организации Объединенных Наций и другие компетентные органы любые доклады государств-участников, в которых содержится просьба о технической консультации или помощи или указывается на потребность в этом, а также замечания и предложения Комитета, если таковые имеются, относительно таких просьб или указаний;
c) Комитет может рекомендовать Генеральной Ассамблее предложить Генеральному секретарю провести от ее имени исследования по отдельным вопросам, касающимся прав ребенка;
d) Комитет может вносить предложения и рекомендации общего характера, основанные на информации, получаемой в соответствии со статьями 44 и 45 настоящей Конвенции. Такие предложения и рекомендации общего характера препровождаются любому заинтересованному государству-участнику и сообщаются Генеральной Ассамблее наряду с замечаниями государств-участников, если таковые имеются.
Часть IIIСтатья 46Настоящая Конвенция открыта для подписания ее всеми государствами. Статья 47Настоящая Конвенция подлежит ратификации. Ратификационные грамоты сдаются на хранение Генеральному секретарю Организации Объединенных Наций. Статья 48Настоящая Конвенция открыта для присоединения к ней любого государства. Документы о присоединении сдаются на хранение Генеральному секретарю Организации Объединенных Наций. Статья 491. Настоящая Конвенция вступает в силу на тридцатый день после даты сдачи на хранение Генеральному секретарю Организации Объединенных Наций двадцатой ратификационной грамоты или документа о присоединении. 2. Для каждого государства, которое ратифицирует настоящую Конвенцию или присоединяется к ней после сдачи на хранение двадцатой ратификационной грамоты или документа о присоединении, настоящая Конвенция вступает в силу на тридцатый день после сдачи таким государством на хранение его ратификационной грамоты или документа о присоединении. Статья 501. Любое государство-участник может предложить поправку и представить ее Генеральному секретарю Организации Объединенных Наций. Генеральный секретарь затем препровождает предложенную поправку государствам-участникам с просьбой указать, высказываются ли они за созыв конференции государств-участников с целью рассмотрения этих предложений и проведения по ним голосования. Если в течение четырех месяцев, начиная с даты такого сообщения, по крайней мере одна треть государств-участников выскажется за такую конференцию, Генеральный секретарь созывает эту конференцию под эгидой Организации Объединенных Наций. Любая поправка, принятая большинством государств-участников, присутствующих и участвующих в голосовании на этой конференции, представляется Генеральной Ассамблее Организации Объединенных Наций на утверждение. 2. Поправка, принятая в соответствии с пунктом 1 настоящей статьи, вступает в силу по утверждении ее Генеральной Ассамблеей Организации Объединенных Наций и принятия ее большинством в две трети государств-участников. 3. Когда поправка вступает в силу, она становится обязательной для тех государств-участников, которые ее приняли, а для других государств-участников остаются обязательными положения настоящей Конвенции и любые предшествующие поправки, которые ими приняты. Статья 511. Генеральный секретарь Организации Объединенных Наций получает и рассылает всем государствам текст оговорок, сделанных государствами в момент ратификации или присоединения. 2. Оговорка, не совместимая с целями и задачами настоящей Конвенции, не допускается. 3. Оговорки могут быть сняты в любое время путем соответствующего уведомления, направленного Генеральному секретарю Организации Объединенных Наций, который затем сообщает об этом всем государствам. Такое уведомление вступает в силу со дня его получения Генеральным секретарем. Статья 52Любое государство-участник может денонсировать настоящую Конвенцию путем письменного уведомления Генерального секретаря Организации Объединенных Наций. Денонсация вступает в силу по истечении одного года после получения уведомления Генеральным секретарем. Статья 53Генеральный секретарь Организации Объединенных Наций назначается депозитарием настоящей конвенции. Статья 54Подлинник настоящей Конвенции, английский, арабский, испанский, китайский, русский и французский тексты которой являются равно аутентичными, сдается на хранение Генеральному секретарю Организации Объединенных Наций. В удостоверение чего нижеподписавшиеся полномочные представители, должным образом на то уполномоченные своими соответствующими правительствами, подписали настоящую Конвенцию.
1Резолюция 1386 (XIV). 2Резолюция 217 А (III). 3 См. резолюцию 2200 А (XXI), приложение. 4 См. League of Nations Official Journal, Special Supplement No. 21, October 1924, p. 43. 5Резолюция 1386 (XIV), третий пункт преамбулы. 6Резолюция 41/85, приложение 7Резолюция 40/33, приложение. 8Резолюция 3318 (XXIX).
Источник: Официальные отчеты Генеральной Ассамблеи, сорок четвертая сессия, Дополнение №49 (А/44/49), стр. 230–239. Лучшая температура для сна: советы и подсказки Температура в вашей спальне может существенно повлиять на качество вашего сна. Опрос Национального фонда сна показал, что прохладная комнатная температура является одним из наиболее важных факторов, способствующих хорошему ночному сну, при этом четыре из пяти респондентов заявили, что это важно для них. Лучшая температура в спальне для сна — примерно 18,3 градуса по Цельсию. Это может варьироваться на несколько градусов от человека к человеку, но большинство врачей рекомендуют устанавливать термостат в диапазоне от 60 до 67 градусов по Фаренгейту (15.От 6 до 19,4 градусов Цельсия) для максимально комфортного сна. Наши тела запрограммированы на небольшое понижение внутренней температуры по вечерам. Отключение термостата на ночь может помочь в регулировании температуры и сигнализировать вашему телу, что пора ложиться спать. Лучшая температура сна для младенцев Младенцы могут извлечь выгоду из спальни, которая на один или два градуса теплее, до 69 градусов по Фаренгейту (20,5 градусов по Цельсию). Поскольку их тела меньше по размеру и все еще развиваются, они более чувствительны к изменениям температуры окружающей среды. Слишком теплая спальня может увеличить риск синдрома внезапной детской смерти (СВДС). Рекомендуется использовать одобренную одежду для сна, обеспечить благоприятную температуру, установив термостат, и избегать тяжелых одеял или многослойных одеял. Родители могут следить за температурой своего ребенка в ночное время, касаясь живота или задней части шеи. Исследования показывают, что младенцы достигают температурного созревания в среднем к одиннадцати неделям. В этот момент они начинают достигать минимальной внутренней температуры тела 97.5 градусов по Фаренгейту (36,4 градуса по Цельсию) в течение четырех часов перед сном, как и у взрослых. Как температура влияет на сон? Наш цикл сна регулируется нашим циркадным ритмом. Циркадный ритм основан на цикле светлого и темного солнца и контролируется частью мозга, называемой супрахиазматическим ядром, расположенной в гипоталамусе. Эти основные «биологические часы» основываются на ряде факторов окружающей среды и личностных факторов, начиная от количества света (наиболее значимое), заканчивая физическими упражнениями и температурой. Наша основная температура тела колеблется около 98,6 градусов по Фаренгейту (37 градусов по Цельсию), но колеблется примерно на 2 градуса по Фаренгейту в течение ночи. Снижение температуры начинается примерно за два часа до того, как вы ложитесь спать, что совпадает с высвобождением гормона сна мелатонина. Во время сна температура тела продолжает падать, достигая низкого уровня ранним утром, а затем постепенно нагревается по мере того, как наступает утро. Основной способ, которым тело охлаждается во время сна, — это отвод тепла от ядра.В процессе, называемом вазодилатацией, циркадные часы посылают сигнал об усилении кровотока к конечностям. Вот почему у некоторых людей ночью могут быть теплые руки и ноги, которые можно принять за общую температуру тела. Действительно, люди, у которых хронически мерзнут ноги, могут быть подвержены более высокому риску бессонницы во сне, возможно, из-за нарушения этого процесса. Что происходит, когда в вашей спальне слишком жарко? Более высокие температуры могут вызывать дискомфорт и беспокойство, и любой, кто спал в душной спальне, может подтвердить, что трудно уснуть, когда вы потеете и обезвожены.Слишком теплая спальня может нарушить терморегуляцию вашего тела и вызвать усталость. Часто усталый человек чувствует себя физически и морально усталым, но не может заснуть. Температура тела влияет не только на начало сна, но также на качество сна и время, проведенное в различных стадиях сна. Более высокая внутренняя температура тела была связана с уменьшением восстановительного медленноволнового сна и субъективного качества сна. Точно так же большая разница в температуре между ядром и конечностями — что указывает на то, что тело не эффективно отводит тепло от ядра — была связана со снижением эффективности сна и более высокой вероятностью пробуждения после засыпания. Во время быстрого сна тело прекращает большинство действий, регулирующих температуру, таких как потоотделение или дрожь, что делает вас более чувствительным к изменениям температуры окружающей среды. Соответственно, слишком высокая температура окружающей среды также сокращает время, проведенное в фазе быстрого сна. Помимо того, что на следующий день вызывает сонливость, уменьшение фазы быстрого сна и медленного сна может негативно повлиять на восстановление организма и иммунную систему, а также на обучение, память и другие процессы. Хотя холодная температура в спальне не считается столь же вредной, как слишком теплая температура в спальне, она также может вызывать дискомфорт и может иметь последствия для быстрого сна и артериального давления. Советы по сохранению прохлады в спальне Следующие советы помогут оптимизировать температуру в спальне для сна: - Закройте жалюзи, чтобы уменьшить накопление тепла в течение дня
- Летом вниз по лестнице
- Выключите термостат на ночь
- Используйте вентилятор или кондиционер в жарком климате или грелку в холодные ночи
- Открыть окна для вентиляции
- Контроль влажности в спальне
- Для уменьшения потоотделения используйте дышащий матрас, простыни, пуховое одеяло, одеяло, подушку и свободную пижаму
- Примите теплую ванну за час или два перед сном, чтобы вызвать естественный охлаждающий эффект.
Помимо оптимизации температуры окружающей среды для сна, вы можете помочь своему организму подготовиться ко сну, проявив доброту к собственному внутреннему термостату.Поскольку циркадный ритм чувствителен к колебаниям света, диеты и упражнений, время этих действий может повлиять на температуру тела и, возможно, на сонливость. Привычки гигиены сна, такие как ложиться спать в одно и то же время каждую ночь, избегать употребления кофеина и алкоголя перед сном и сохранять темную и тихую спальню, помогут вам установить часы вашего тела и температуру сна на постоянный график. Чтобы узнать больше о том, как подобрать подходящую температуру, прочитайте нашу статью о том, как спать прохладно в жаркую ночь. - Была ли эта статья полезной?
- Да Нет
«Становится холодно»: температура снова опускается ниже 20 градусов по Цельсию. «Становится холодно» — это местная фраза, которую некоторые жители Трини использовали бы для обозначения температуры в среду ночью, которая составляла около 19,7 градусов, по данным метеорологической службы Тринидада и Тобаго. Метеорологическое бюро сообщило, что это был второй раз в этом месяце, когда температура опускалась ниже 20 градусов, однако никаких новых рекордов установлено не было. «Прошлая ночь казалась немного« холоднее », чем обычно? Мы измерили минимальную температуру 19,7 ° C! « Это второй раз в этом месяце, когда температура опускалась ниже отметки 20 ° C. Другой случай произошел 4 января, когда была зафиксирована температура 19,5 ° C », — сообщило Метеорологическое бюро в сообщении в социальной сети. градусов Цельсия. Более низкие температуры в это время года не редкость для Тринидада и Тобаго и могут быть результатом действия нескольких факторов, возникающих одновременно, таких как штиль или почти тихий ветер, почти полное отсутствие облачности в сочетании с холодными ветрами. происходящие с Севера. Метеорологическое бюро заявило, что вместе эти факторы увеличивают количество «исходящей длинноволновой радиации» с поверхности Земли в ночное время (поверхность остывает быстрее). Метеорологическое бюро сообщило, что рекорд самой низкой температуры в Пиарко был 16,1 ° C, зафиксированный в январе 1964 года. Многие Тринис согласились, что в последнее время температура стала немного ниже: Джульет Чарльз: «Да, последние пару ночей» было очень холодно, особенно живя в Санта-Крус «. Салли И Хан: «Прошлая ночь была холодной и холодной.. и даже сейчас все еще холодно ». Николь Одзюро:« С того момента, как я легла в постель прошлой ночью, и до сегодняшнего утра, у меня заложила нос от холода ». Кестер Джозеф:« Узнай, почему Тобаго так далеко. идти. Я даже справляюсь с температурой 20 ° « Занах Кирби:» Я снова говорю лил, когда просыпаюсь утром, я бы увидел снежную суету, которая делает холодным «. Что вы делаете, чтобы согреться, когда ночные температуры становятся холодно? Температура хранения Ниже приведены определения условий хранения, определенные в разделе «Общие примечания» Фармакопеи США (USP) XXII-NF XVII, для рекомендуемых условий, обычно указываемых на этикетках продуктов. - Морозильник
- Место, в котором температура поддерживается термостатически в диапазоне от -20 ° C до -10 ° C (от -4 ° F до 14 ° F).
- Холодный
- Любая температура, не превышающая 8 ° C (46 ° F). Холодильник — это холодное место, в котором термостатически поддерживается температура от 2 ° C до 8 ° C (от 36 ° C до 46 ° C).
- Cool
- Любая температура от 8 ° C до 15 ° C (от 46 ° F до 59 ° F).Изделие, которое требует прохладного хранения, может храниться в холодильнике, если иное не указано в отдельной монографии Фармакопеи США.
- Комнатная температура
- Температура, преобладающая на рабочем месте.
- Контролируемая комнатная температура
- Температура, поддерживаемая термостатически, которая охватывает обычную и обычную рабочую среду от 20 ° C до 25 ° C (68 ° F до 77 ° F), что допускает кратковременные отклонения от 15 ° C до 30 ° C (от 59 ° F до 86 ° F), которые наблюдаются в аптеках, больницах и на складах.На изделиях может быть указано хранение при «контролируемой комнатной температуре» или «до 25 ° C» или другая формулировка. Изделие, предназначенное для хранения при контролируемой комнатной температуре, можно также хранить в прохладном месте, если иное не указано в отдельной монографии или на этикетке. (См. Полное пересмотренное определение контролируемой комнатной температуры в Девятом дополнении к USP XXII-NF XVII.)
- Теплый
- Любая температура от 30 ° C до 40 ° C (от 86 ° F до 104 ° F) .
- Избыточный нагрев
- Любая температура выше 40 ° C (104 ° F).
- Защита от замерзания
- Если, помимо риска поломки контейнера, замораживание подвергает изделие потере прочности или активности или разрушающему изменению его характеристик, этикетка контейнера должна иметь соответствующую маркировку. Инструкция по защите изделия от замерзания.
|
Влияние температуры на стойкость SARS-CoV-2 на общих поверхностях | Журнал вирусологии- 1.
Пандемия коронавирусной болезни (COVID-19). https://www.who.int/emergencies/diseases/novel-coronavirus-2019. - 2.
Стадницкий В., Bax CE, Bax A, Анфинруд П. Время жизни маленьких речевых капель в воздухе и их потенциальное значение в передаче SARS-CoV-2. Proc Natl Acad Sci U S. A. 2020; 117 (22): 11875–7. CAS
Статья
Google Scholar - 3.
Morawska L, Milton DK. Пора заняться воздушной передачей COVID-19.Clin Infect Dis. 2020. https://doi.org/10.1093/cid/ciaa939/5867798. Артикул
PubMed
PubMed Central
Google Scholar - 4.
Чжан Р., Ли И, Чжан А.Л., Ван И, Молина М.Дж. Определение передачи воздушно-капельным путем в качестве основного пути распространения COVID-19. Proc Natl Acad Sci. 2020; 117 (26): 202009637. Google Scholar - 5.
ван Дормален Н., Бушмейкер Т., Моррис Д.Х., Холбрук М.Г., Гэмбл А., Уильямсон Б.Н. и др.Аэрозольная и поверхностная стабильность SARS-CoV-2 по сравнению с SARS-CoV-1. N Engl J Med. 2020; 382 (16): 1564–7. https://doi.org/10.1056/NEJMc2004973. Артикул
PubMed
Google Scholar - 6.
Смитер С.Дж., Истог Л.С., Финдли Дж.С., Левер МС. Экспериментальная аэрозольная выживаемость SARS-CoV-2 в искусственной слюне и средах для культивирования тканей при средней и высокой влажности. Emerg Microbes Infect. 2020; 9 (1): 1415–7. https://doi.org/10.1080/22221751.2020.1777906. CAS
Статья
PubMed
PubMed Central
Google Scholar - 7.
Цай Дж., Сунь В., Хуанг Дж., Гамбер М., Ву Дж., Хе Г. Непрямая передача вируса в кластере случаев COVID-19, Вэньчжоу, Китай, 2020 г. Emerg Infect Dis. 2020; 26 (6): 1343–5. CAS
Статья
Google Scholar - 8.
Julian TR, Leckie JO, Boehm AB. Передача вируса между подушечками пальцев и фомитами.J Appl Microbiol. 2010. 109 (6): 1868–74. CAS
Статья
Google Scholar - 9.
Рольфе Т., Нитти М. Сенсорные экраны: комар эпохи цифровых технологий. 2016 г. https://emist.com/infection-prevention-touchscreens-are-contaminated/. - 10.
Русин П., Максвелл С., Герба С. Сравнительная эффективность передачи грамположительных бактерий, грамотрицательных бактерий и фагов с поверхности на руку и из кончика пальца в рот. J Appl Microbiol.2002; 93 (4): 585–92. CAS
Статья
Google Scholar - 11.
Kasloff SB, Strong JE, Funk D, Cutts TA. Устойчивость SARS-CoV-2 к критическим средствам индивидуальной защиты. medRxiv. 2020; 2020.06.11.20128884. - 12.
Kärber G. Beitrag zur kollektiven Behandlung Pharmakologischer. Beitrag zur Kollekt Behandlung Pharmakologischer Reihenversuche. 1931; 7: 1–4. Google Scholar - 13.
Спирмен К. Метод «правильных и неправильных случаев» («постоянных стимулов») без формул Гаусса. Br J Psychol 1908–1920. 1908; 2 (3): 227–42. Google Scholar - 14.
Саттар С.А., Спрингторп В.С., Адегбунрин О., Зафер А.А., Буса М. Дисковый количественный метод тестирования носителя для оценки вирулицидной активности химических гермицидов. J Virol Methods. 2003. 112 (1–2): 3–12. CAS
Статья
Google Scholar - 15.
ASTM E2197. Стандартный метод количественного определения носителя диска для определения бактерицидной, вирулицидной, фунгицидной, микобактерицидной и спороцидной активности химических веществ. ASTM Int. 2015 г. https://www.astm.org/Standards/E2197.htm. - 16.
Ким И, Ян М., Гойал С.М., Чиран М.С., Торреморелл М. Оценка мер биобезопасности для предотвращения косвенной передачи вируса эпидемической диареи свиней. BMC Vet Res. 2017; 13 (1): 1–9. Google Scholar - 17.
Ли СС, Вонг Н.С. Вероятные цепи передачи коронавируса ближневосточного респираторного синдрома и множественные поколения вторичной инфекции в Южной Корее. Int J Infect Dis. 2015; 38: 65–7. https://doi.org/10.1016/j.ijid.2015.07.014. Артикул
PubMed
PubMed Central
Google Scholar - 18.
Sizun J, Yu MWN, Talbot PJ. Выживаемость человеческих коронавирусов 229E и OC43 в суспензии и после высыхания на поверхности: возможный источник внутрибольничных инфекций.J Hosp Infect. 2000. 46 (1): 55–60. CAS
Статья
Google Scholar - 19.
Ла Скола Б., Ле Бидо М., Андреани Дж., Хоанг В.Т., Гримальдье С., Колсон П. и др. Нагрузка вирусной РНК, определенная с помощью клеточной культуры, как инструмент управления выпиской пациентов с SARS-CoV-2 из инфекционных отделений. Eur J Clin Microbiol Infect Dis. 2020; 39 (6): 1059–61. Артикул
Google Scholar - 20.
Кам К., Юнг К.Ф., Цуй Л., Цер Пин Лин Р., Мак Т.М., Майвальд М. и др. Здоровый младенец с коронавирусной болезнью 2019 года с высокой вирусной нагрузкой. Clin Infect Dis. 2020; 71 (15): 847–9. CAS
Статья
Google Scholar - 21.
Хуан Ю., Чен С., Ян З., Гуань В., Лю Д., Линь З. и др. Вирусная нагрузка SARS-CoV-2 в клинических образцах от пациентов в критическом состоянии. Am J Respir Crit Care Med. 2020; 201 (11): 1435–8. CAS
Статья
Google Scholar - 22.
Цзоу Л., Жуань Ф., Хуанг М., Лян Л., Хуанг Х., Хонг З. и др. Вирусная нагрузка SARS-CoV-2 в образцах верхних дыхательных путей инфицированных пациентов. N Engl J Med. 2020; 382 (12): 1177–9. https://doi.org/10.1056/NEJMc2001737. Артикул
PubMed
PubMed Central
Google Scholar - 23.
Чан К.Х., Пейрис Дж.С.М., Лам С.Ю., Пун LLM, Юэнь К.Ю., Сето У.Х. Влияние температуры и относительной влажности на жизнеспособность коронавируса SARS.Adv Virol. 2011. https://doi.org/10.1155/2011/734690. Артикул
PubMed
PubMed Central
Google Scholar - 24.
Чин AWH, Chu JTS, Perera MRA, Hui KPY, Yen H-L, Chan MCW и др. Устойчивость SARS-CoV-2 в различных условиях окружающей среды. Ланцетный микроб. 2020; 1 (1): e10. Артикул
Google Scholar - 25.
Lai MYY, Cheng PKC, Lim WWL. Выживаемость тяжелого острого респираторного синдрома коронавирусом.Clin Infect Dis. 2005; 41 (7): e67-71. CAS
Статья
Google Scholar - 26.
Абубакр Х.А., Шарафельдин Т.А., Гоял С.М. Стабильность SARS-CoV-2 и других коронавирусов в окружающей среде и на обычных сенсорных поверхностях и влияние климатических условий: обзор. Transbound Emerg Dis. 2020. https://doi.org/10.1111/tbed.13707. Артикул
PubMed
PubMed Central
Google Scholar - 27.
Бирюков Дж., Бойдстон Дж. А., Даннинг Р. А., Йегер Дж. Дж., Вуд С., Риз А. Л. и др. Повышение температуры и относительной влажности ускоряет инактивацию SARS-CoV-2 на поверхностях. мСфера. 2020; 5 (4): 1–9. Артикул
Google Scholar - 28.
Казанова Л. М., Чон С., Рутала В. А., Вебер Д. Д., Собси М. Д. Влияние температуры и относительной влажности воздуха на выживаемость коронавируса на поверхностях. Appl Environ Microbiol. 2010. 76 (9): 2712–7. CAS
Статья
Google Scholar - 29.
ван Дормален Н., Бушмейкер Т., Мюнстер В. Стабильность коронавируса ближневосточного респираторного синдрома (БВРС-КоВ) в различных условиях окружающей среды. Евронаблюдение. 2013; 18 (38): 20590. Артикул
Google Scholar - 30.
Ratnesar-Shumate S, Williams G, Green B, Krause M, Holland B, Wood S, et al. Искусственный солнечный свет быстро инактивирует SARS-CoV-2 на поверхностях. J Infect Dis. 2020; 222 (2): 214–22. CAS
Статья
Google Scholar - 31.
Schuit M, Ratnesar-Shumate S, Yolitz J, Williams G, Weaver W., Green B, et al. SARS-CoV-2, переносимый по воздуху, быстро инактивируется имитируемым солнечным светом. J Infect Dis. 2020; 222 (4): 564–71. CAS
Статья
Google Scholar - 32.
Guillier L, Martin-Latil S, Chaix E, Thébault A, Pavio N, Le Poder S, et al. Моделирование инактивации вирусов семейства Coronaviridae в ответ на температуру и относительную влажность в суспензиях или поверхностях.Appl Environ Microbiol. 2020; 80 (21): 6807–18. https://doi.org/10.1128/AEM.01244-20. Артикул
Google Scholar - 33.
Фишер Д., Рейли А., Кан А., Чжэн Е., Кук А. Р., Андерсон Д. Посев вспышек COVID-19 зараженными свежими и замороженными продуктами. bioRxiv. 2020. https://doi.org/10.1101/2020.08.17.255166v1. Артикул
Google Scholar - 34.
Фишер Р., Джадсон С., Мязгович К., Бушмейкер Т., Прескотт Дж., Мюнстер В.Дж.Стабильность вируса Эбола на поверхности и в жидкостях в условиях моделирования вспышки. Emerg Infect Dis. 2015; 21 (7): 1243–6. CAS
Статья
Google Scholar - 35.
Mbithi JN, Springthorpe VS, Sattar SA. Влияние относительной влажности и температуры воздуха на выживаемость вируса гепатита А на поверхностях окружающей среды. Appl Environ Microbiol. 1991. 57 (5): 1394–9. CAS
Статья
Google Scholar - 36.
Warnes SL, Литтл ZR, Кивил CW. Человеческий коронавирус 229E остается заразным на обычных материалах сенсорной поверхности. MBio. 2015; 6 (6): 1–10. Артикул
Google Scholar - 37.
Dublineau A, Batéjat C, Pinon A, Burguière AM, Leclercq I, Manuguerra JC. Сохранение вируса пандемического гриппа a (h2N1) 2009 г. в воде и на непористой поверхности. PLoS ONE. 2011; 6 (11): e28043. CAS
Статья
Google Scholar - 38.
Vriesekoop F, Russell C, Alvarez-Mayorga B, Aidoo K, Yuan Q, Scannell A, et al. Грязные деньги: исследование гигиенического статуса некоторых мировых валют, полученное в пунктах питания. Foodborne Pathog Dis. 2010. 7 (12): 1497–502. Артикул
Google Scholar - 39.
Thomas Y, Vogel G, Wunderli W, Suter P, Witschi M, Koch D, et al. Выживание от вируса гриппа на банкнотах. Appl Environ Microbiol. 2008. 74 (10): 3002–7. CAS
Статья
Google Scholar - 40.
Йунг Дж. Китай дезинфицирует и уничтожает наличные деньги, чтобы сдержать коронавирус. 2020. https://edition.cnn.com/2020/02/17/asia/china-is-disinfecting-cash-coronavirus-intl-hnk-scli/index.html. - 41.
Вибава Т. Китай очищает банкноты в попытке ограничить распространение коронавируса COVID-19. Новости ABC (Австралия). 2020. https://www.abc.net.au/news/2020-02-21/china-cleaning-money-limit-coronavirus-covid-19/11983364. - 42.
Шредер П., Иррера А. ФРС помещает в карантин доллары США, репатриированные из Азии, из-за осторожности с коронавирусом. 2020. https://www.reuters.com/article/us-health-coronavirus-fed-dollars/fed-quarantines-us-dollars-repatriated-from-asia-on-coronavirus-caution-idUSKBN20T1YT. - 43.
Чой Х. Центральный банк Южной Кореи сжигает и помещает наличные в карантин из соображений безопасности от коронавируса. 2020. https://uk.reuters.com/article/health-coronavirus-southkorea-money/s-koreas-central-bank-burns-quarantines-cash-in-coronavirus-precaution-idUKL4N2AZ1TL. - 44.
Brady RRW, Wasson A, Stirling I, McAllister C, Damani NN. Ваш телефон прослушивается? Распространенность бактерий, вызывающих внутрибольничную инфекцию, на мобильных телефонах медицинских работников. J Hosp Infect. 2006. 62 (1): 123–5. CAS
Статья
Google Scholar - 45.
Olsen M, Campos M, Lohning A, Jones P, Legget J, Bannach-Brown A, et al. Мобильные телефоны представляют собой путь передачи микробов: обзорный обзор.Travel Med Infect Dis. 2020; 35 (апрель): 101704. https://doi.org/10.1016/j.tmaid.2020.101704. Артикул
PubMed
PubMed Central
Google Scholar Этот рисунок объясняет, почему 2 градуса глобального потепления будут намного хуже, чем 1,5 Примечание редактора: эта статья была первоначально опубликована в начале 2018 года и была переиздана для выпуска в воскресенье в специальном докладе МГЭИК о глобальном потеплении на единицу .5 ° С .
Стороны, подписавшие Парижское соглашение по климату — все страны мира, если и до тех пор, пока США не выйдут из состава 2020 года, — согласились с уже известной целью: «сдерживать повышение средней глобальной температуры до уровня значительно ниже 2 ° C. выше доиндустриальных уровней и прилагает усилия по ограничению повышения температуры до 1,5 ° C ». Но насколько важна эта разница? Насколько хуже будет 2 градуса, чем 1,5? Стоит ли дополнительных усилий — а это было бы поистине героическим усилием — ограничить повышение температуры до этой более низкой цели? Было сложно ответить на эти вопросы, отчасти потому, что они ценны и невероятно сложны, но также из-за недостаточного количества исследований.Несмотря на то, что было проделано много работы по разнице между потеплением, скажем, на 2 и 4 градуса (что было бы катастрофой), было меньше моделирования около 1,5 и не было всестороннего сравнения 1,5 и 2. К счастью, исследование, опубликованное в 2016 году в журнале Earth System Dynamics , напрямую занимается этим. В CarbonBrief Роз Пидкок кратко излагает исследование, которое уходит в прошлое, и некоторые выводы. Лучше всего то, что команда CarbonBrief (которую вы действительно должны добавить в закладки) собрала соответствующие сравнения в исследовании в один четкий, эстетически приятный рисунок: CarbonBrief Это как прогноз погоды! Из ада. 2 градуса будет намного хуже 1,5 местами Что касается экстремальной жары, как пишут авторы, «дополнительное повышение средней глобальной температуры на 0,5 ° C отмечает разницу между явлениями на верхнем пределе современной естественной изменчивости и новым климатическим режимом, особенно в тропических регионах». В районе Средиземного моря доступность пресной воды при 2 градусах упадет почти вдвое по сравнению с 1,5–17 процентами по сравнению с 9 процентами. В некоторых высокоширотных регионах может быть полезна разница между 1.5 и 2 градуса (хотя такие преимущества будут сведены на нет, если температура в дальнейшем продолжит расти). Но даже при повышении температуры до 2 градусов «тропические регионы, такие как Западная Африка, Юго-Восточная Азия, а также Центральная и северная часть Южной Америки, по прогнозам, столкнутся со значительным снижением урожайности на местном уровне, особенно пшеницы и кукурузы». TXX измеряет крайние температуры; WSDI измеряет количество длительных (6 с лишним дней) приступов. Earth Systems Dynamics Что касается повышения уровня моря относительно 1.5 градусов, 2 градуса означают, что уровни на 10 сантиметров выше, а на 30 процентов выше — показатель увеличения к 2100 году. А вот с коралловыми рифами все в порядке. При 1,5-градусном сценарии процент коралловых рифов в мире, подвергающихся риску, достигнет 90 процентов в 2050 году, но снизится до 70 процентов в 2100 году. При 2-градусном сценарии риску подвергаются все они. Отчет IPCC и исследование Earth System Dynamics подтверждают то, что многие ученые предупреждали в течение многих лет: 2 градуса не является «безопасным» порогом.Негативные воздействия уже начались и будут только ухудшаться. Чтобы остановить потепление на 1,5 градуса, потребуются серьезные и продолжительные глобальные действия. У нас не так много времени, чтобы принять решение. Окно для попадания на 1,5 градуса стремительно закрывается. Вот еще один ужасающий график от CarbonBrief, показывающий, сколько лет осталось до того, как израсходуется «углеродный бюджет» для различных температур: CarbonBrief При нашем нынешнем уровне выбросов, наш углеродный бюджет с хорошей (66%) вероятностью ограничения потепления до 1.Через шесть лет будет израсходовано 5 степеней. Только вот этому графику два года назад, так что теперь осталось четыре года. Чтобы притормозить на 1,5 градуса, глобальные выбросы углерода должны немедленно начать сокращаться, быстрее, чем когда-либо, и достичь нуля к 2050 году (а затем пойти на отрицательную величину): OCI Для этого потребуется мобилизация, эквивалентная мобилизации США для Второй мировой войны, только глобальная и продолжающаяся до конца столетия.Шансы на это кажутся … маловероятными. Насколько нам известно, Трамп все еще будет у власти, когда бюджет в 1,5 градуса будет израсходован. Но мы должны четко понимать, какое решение мы принимаем, даже если мы принимаем его, не принимая решения. Откладывая необходимые работы по декарбонизации, мы обрекаем миллионы людей в тропических регионах на меньшее количество продуктов питания, а в Средиземноморье — на меньшее количество воды — со всеми сопутствующими проблемами со здоровьем и конфликтами. Мы допускаем больше волн жары и более высокого уровня моря.Мы отказываемся от коралловых рифов мира, а вместе с ними и от сотен видов, которые на них полагаются. И даже тогда решение все равно будет стоять перед нами: 2 градуса или 3? Опять же, это будет означать больше волн тепла, больше потерь урожая, больше нехватки воды, больше затопленных прибрежных городов, больше болезней и конфликтов, миллионы страданий. И даже тогда решение: 3 степени или 4? Чем дольше мы ждем, тем больше человеческих страданий и необратимого ущерба экосистемам мы вписываем в наше коллективное будущее.Но здесь нельзя спрятаться и избежать необходимости обезуглероживания. Это необходимо сделать, если у нашего вида есть надежный дом на Земле. Похоже, что умнее всего было бы с этим справиться. Как найти процент сектора под углом Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает
или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее
в
информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors. Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как
в виде
ChillingEffects.org. Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно
искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится
на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу. Чтобы отправить уведомление, выполните следующие действия: Вы должны включить следующее: Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Ваше заявление: (а) вы добросовестно полагаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени. Отправьте жалобу нашему уполномоченному агенту по адресу: Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже: Дополнение угла A на 20 градусов меньше половины дополнения угла A Вопросы и ответы по справке по домашнему заданию Дополнение к углу A на 20 градусов меньше, чем половина дополнения к углу A.Найдите угол А. С чего начать? Позволять
A = мера угла A
c = мера дополнительного угла
s = мера дополнительного угла
«Дополнение к углу A на 20 градусов меньше, чем половина дополнения к углу A» буквально переводится в уравнение {{{c = (1/2) s-20}}}
Кроме того, по определению, поскольку ‘c’ является дополнением к углу A, это означает, что они добавляют к 90 градусам. Итак {{{A + c = 90}}}
Кроме того, дополнительные углы увеличиваются до 180 градусов. Поскольку ‘s’ является дополнением к углу A, мы знаем, что {{{A + s = 180}}}
{{{A + c = 90}}} Начнем со второго уравнения.{{{c = 90-A}}} Вычтите A с обеих сторон.
{{{A + s = 180}}} Переходим ко второму уравнению
{{{s = 180-A}}} Вычтите A с обеих сторон.
———————————————-
{{{c = (1/2) s-20}}} Теперь вернитесь к первому уравнению.
{{{90-A = (1/2) s-20}}} Подключите {{{c = 90-A}}}
{{{90-A = (1/2) (180-A) -20}}} Подключите {{{s = 180-A}}}
{{{90-A = (1/2) (180) — (1/2) A-20}}} Распространение
{{{90-A = 180 / 2- (1/2) A-20}}} Умножить
{{{90-A = 90- (1/2) A-20}}} Уменьшить
{{{2 (90) -2 (a) = 2 (90) -cross (2) ((1 / cross (2)) a) -2 (20)}}} Умножьте КАЖДЫЙ член на ЖК-дисплей {{{ 2}}}, чтобы очистить любые дроби.{{{180-2a = 180-1a-40}}} Умножать и упрощать.
{{{180-2a = -a + 140}}} Объедините похожие термины с правой стороны.
{{{-2a = -a + 140-180}}} Вычтите {{{180}}} с обеих сторон.
{{{-2a + a = 140-180}}} Добавьте {{{a}}} с обеих сторон.
{{{-a = 140-180}}} Объедините похожие термины слева.
{{{-a = -40}}} Объедините похожие термины с правой стороны.
{{{a = (- 40) / (- 1)}}} Разделите обе стороны на {{{-1}}}, чтобы изолировать {{{a}}}.
{{{a = 40}}} Уменьшить.
————————————————— ——————— ответил: onlekile Дополнение к углу A на 20 градусов меньше, чем половина дополнения к углу A.Найдите угол А. С чего начать?
Дополнение к углу A составляет: (90 — A)
Дополнение к углу A составляет: (180 — A)
Поскольку дополнение к A на 20 градусов меньше, чем половина дополнения к углу A, то мы имеем:
{{{(90 — A) + 20 = (1/2) * (180 — A)}}}
{{{110 — A = (180 — A) / 2}}}
Перемножая, получаем: 2 (110 — А) = 180 — А
220 — 2А = 180 — А
— 2А + А = 180 — 220
— А = — 40
{{{A = (-40) / — 1}}}
А = 40
Следовательно, угол A = {{{highlight_green (40)}}} градусов. Возрастание и убывание функций | Алгебра
Определения 1) Функция y=f(x) называется возрастающей на некотором промежутке, если бо́льшему значению аргумента из этого промежутка соответствует бо́льшее значение функции. То есть для любых двух значений x1,x2 из этого промежутка выполняется условие 2) Функция y=f(x) называется убывающей на некотором промежутке, если бо́льшему значению аргумента из этого промежутка соответствует меньшее значение функции. То есть для любых двух значений x1,x2 из этого промежутка выполняется условие Предполагается, что промежуток принадлежит области определения функции y=f(x). Обычно промежуток — это отрезок, интервал или полуинтервал. График функции на промежутках возрастания «идёт вверх» (чем правее x, тем выше y). На промежутках убывания график «идёт вниз» (чем правее x, тем ниже y). Пример 1. Пользуясь графиком, найти промежутки возрастания и убывания функции y=f(x), определённой на отрезке [x1;x5]: Функция y=f(x) возрастает на промежутках [x2;x3] и [x4;x5] Функция y=f(x) убывает на промежутках [x1;x2] и [x3;x4]. Кратко это записывают так: 3) Функцию, возрастающую на промежутке либо убывающую на промежутке, называют монотонной функцией на этом промежутке (или строго монотонной). 4) Если функция возрастает на всей своей области определения, то её называют возрастающей. Если функция убывает на всей своей области определения, то её называют убывающей. Например, y=√x, y=x³ — возрастающие функции. Линейная функция y=kx+b возрастающая при k>0 и убывающая при k<0. 5) Если для любых двух значений x1,x2 из некоторого промежутка выполняется условие то функция y=f(x) называется неубывающей на этом промежутке. 6) Если для любых двух значений x1,x2 из некоторого промежутка выполняется условие то функция y=f(x) называется невозрастающей на этом промежутке. 7) Функцию, невозрастающую на промежутке либо неубывающую на промежутке, называют не строго монотонной функцией на этом промежутке. Пример 2. Пользуясь графиком, найти промежутки, на которых функции y=g(x), определённая на отрезке [x1;x3], является невозрастающей и неубывающей: Функция y=g(x) является неубывающей на промежутке [x1;x2]. Функция y=g(x) является невозрастающей на промежутке [x2;x3]. Возрастание и убывание функции можно определять как с помощью графика, так и аналитически. Как доказать, что функция возрастает или убывает, с помощью задающей эту функцию формулы? Для этого при условии x2>x1 на промежутке надо доказать выполнение одного из неравенств: f(x2)>f(x1) либо f(x2)>f(x1), то есть определить f(x2)-f(x1)>0 или f(x2)-f(x1)<0. Примеры. 1) Доказать, что функция f(x)=x²+4x убывает на промежутке (-∞;-2). Доказательство: Функция определена на всей числовой прямой. Пусть x2>x1. f(x1)=x1²+4x1, f(x2)=x2²+4x2, f(x2)-f(x1)=(x2²+4x2)-(x1²+4x1)=x2²+4x2-x1²-4x1= группирует первое слагаемое с третьим, второе — с четвертым. В первых скобках — разность квадратов, из вторых выносим общий множитель 4 за скобки: В первых скобках — разность квадратов, из вторых выносим общий множитель 4 за скобки: =(x2²-x1²)+(4x2-4x1)=(x2-x1)(x2+x1)+4(x2-x1)= Теперь выносим общий множитель (x2-x1) за скобки: =(x2-x1)(x2+x1+4). Так как x2>x1, то x2-x1>0. Следовательно, знак произведения зависит от знака второго множителя. Для x1, x2 ∈(-∞;-2) x2+x1+4<0. Значит, (x2-x1)(x2+x1+4)<0 и f(x2)<f(x1). Отсюда следует, что функция функция f(x)=x²+4x убывает на промежутке (-∞;-2). Что и требовалось доказать. 2) Доказать, что функция возрастает на промежутке (2;+∞). Доказательство: Функция определена при x∈(-∞;2) и (2;+∞). Пусть x2>x1. Так как x2>x1, то x2-x1>0. Для x1, x2 ∈ (2;+∞) (2-x1)(2-x2)>0. Значит, Отсюда y(x2)-y(x1)>0. Поэтому данная функция возрастает на промежутке (2;+∞). Что и требовалось доказать. Исследование функции на монотонность гораздо удобнее проводить с помощью производной (начала математического анализа — производную и её применение — проходят в школьном курсе алгебры в 10-11 классах).
Рубрика: Функции
| Комментарии
Прошу ребята, нужно решить вопросы 4,5,6… -reshimne.ru
Новые вопросы Ответы4-верно nэz
5-верно 1эn
6-верно а, б, д, е, ж, и, к, м Похожие вопросы
В коробке лежат 42 карандаша,из них 14 карандашей -красные,16 карандашей-синие,а астральные-зеленые. Какова вероятность того,что наугад взятый карандаш не будет ни красным,ни синим… Какова вероятность того,что наугад взятый карандаш не будет ни красным,ни синим…
16/3 одну третью помогите срочно пожалуйста :(…
Помогите срочно: определите приблизительно диаметр земного шара в километрах. с помощью справочной литературы или интернета, выясните, насколько полученный результат отличается от среднего диаметра Земли.
…
Область определения функции g – отрезок [-3;5]. Найдите нули функции, промежутки возрастания и убывания, область значений функции….
60 баллов, помогите решить уравнение под буквой б, пожалуйста! Используя схему Горнера и если можно, то подробно
. .. ..
Упростите выражение: 3×(2а-7)+5…
Математика
Литература
Алгебра
Русский язык
Геометрия
Английский язык
Химия
Физика
Биология
Другие предметы
История
Обществознание
Окружающий мир
География
Українська мова
Українська література
Қазақ тiлi
Беларуская мова
Информатика
Экономика
Музыка
Право
Французский язык
Немецкий язык
МХК
ОБЖ
Психология
ФУНКЦИЯ • Большая российская энциклопедияФУ́НКЦИЯ (от лат. functio – исполнение, осуществление), одно из основных понятий математики, означающее зависимость одних переменных величин от других. Слово «величина» в этом определении понимается в самом широком смысле: это может быть именованное число, отвлечённое число (действительное или комплексное), неск. чисел (т. е. точка пространства) и вообще элемент любого множества. functio – исполнение, осуществление), одно из основных понятий математики, означающее зависимость одних переменных величин от других. Слово «величина» в этом определении понимается в самом широком смысле: это может быть именованное число, отвлечённое число (действительное или комплексное), неск. чисел (т. е. точка пространства) и вообще элемент любого множества. Действительная функция одного действительного переменногоВ простейшем случае, когда величина – действительное число, понятие «Ф.» определяется следующим образом. Пусть каждому числу $x$ из заданного множества $E$ поставлено в соответствие число $y$, обозначаемое $y=f(x)$ (читается «игрек равен эф от икс»). Тогда говорят, что на множестве $E$ задана функция $y=f(x)$, $x∈E$. При этом употребляются следующие термины: $x$ – независимое переменное, или аргумент; $y$ – зависимое переменное, или функция; $E$ – множество значений, которые может принимать $x$, – область определения, или область задания Ф. (областью определения Ф. может быть множество всех действительных чисел, интервал, отрезок и т. п.). Слова «поставлено в соответствие» означают, что указан определённый способ, по которому для каждого $x∈E$ находится значение $y=f(x)$. Этот способ в данном случае обозначен символом $f$. Для обозначения Ф. применяются и др. буквы, напр. $y=g(x)$, $y=F(x)$, $s=h(t)$, $v=φ(s)$. (областью определения Ф. может быть множество всех действительных чисел, интервал, отрезок и т. п.). Слова «поставлено в соответствие» означают, что указан определённый способ, по которому для каждого $x∈E$ находится значение $y=f(x)$. Этот способ в данном случае обозначен символом $f$. Для обозначения Ф. применяются и др. буквы, напр. $y=g(x)$, $y=F(x)$, $s=h(t)$, $v=φ(s)$. Во всех случаях, когда употребляется термин «Ф.», подразумевается, если не оговорено противное, однозначная Ф., т. е. такое соответствие, при котором каждому значению аргумента $x$ соответствует только одно значение Ф. $y$. Если одному и тому же значению аргумента соответствует несколько (быть может, даже бесконечное множество) значений $y$, то $y=f(x)$ называется многозначной функцией аргумента $x$. Способы задания функцииАналитический способ задания функцииНаиболее распространён аналитич. {2m}.$$ {2m}.$$ Графический способ задания функцииРаспространён графич. способ задания Ф. Графиком Ф. $y=f(x)$, $y∈E$, называется множество точек плоскости с прямоугольными координатами $(x,y)$, где $x∈E$, $y=f(x)$. Графич. способ задания Ф. широко применяется на практике. Так, мн. процессы изменения одной величины в зависимости от другой исследуются с помощью кривых, записанных с помощью самопишущих приборов. Хотя график Ф. и не даёт возможности точного определения численных значений $x$ и $y$, он наглядно отражает качественное поведение Ф. (непрерывность, монотонность, максимумы и минимумы, точки перегиба и т. д.) и поэтому является важным средством исследования функции. Табличный способ задания функцииПри табличном способе задания Ф. задаётся в виде таблицы, в которой для каждого значения аргумента указывается соответствующее ему значение Ф. Такой способ задания Ф. часто применяется в тех случаях, когда область определения состоит из конечного числа значений. Такой способ задания Ф. часто применяется в тех случаях, когда область определения состоит из конечного числа значений. Действительная функция нескольких действительных переменныхФ. от двух переменных определяется следующим образом. Рассматривается множество $E$ упорядоченных пар чисел $(x,y)$. Если каждой паре $(x,y)∈E$ поставлено в соответствие действительное число $z$, то говорят, что на множестве $E$ определена Ф. $z=f(x,y)$ от двух переменных $x$ и $y$. Т. к. каждой паре чисел $(x,y)$ соответствует на плоскости точка с координатами $(x,y)$, то Ф. $f(x,y)$ задана на множестве $E$ точек плоскости. График Ф. $z=f(x,y)$ можно изобразить в трёхмерном пространстве, где задана прямоугольная система координат $(x,y,z)$, в виде множества точек $(x,y,f(x,y))$, проекции которых на плоскость $(x,y)$ принадлежат множеству $E$. Напр., график функции $z=\sqrt{1-x^2-y^2},$ $x^2+y^2 ⩽ 1$, и имеется в виду арифметич. корень, изображается верхней половиной шаровой поверхности радиуса 1 с центром в начале координат. корень, изображается верхней половиной шаровой поверхности радиуса 1 с центром в начале координат. Аналогично можно рассматривать множество $E$, состоящее из упорядоченных систем $(x_1,x_2,…,x_n)$ из $n$ чисел, и Ф. $z=f(x_1,x_2,…,x_n)$ от $n$ переменных, определённую на множестве $E$. Общее понятие функцииПусть заданы множества $E$ и $E_1$ элементов любой природы и пусть каждому элементу $x∈E$ поставлен в соответствие элемент $y∈E_1$, обозначаемый $y=f(x)$. Тогда говорят, что задана функция $y=f(x)$, $x∈E$, что часто записывается как $f:\,E→E_1$. Принята следующая терминология: $x$ – независимое переменное, или аргумент; $E$ – область определения Ф., каждый элемент $x∈E$ – значение аргумента; $y$ – зависимое переменное, или Ф., от аргумента $x$; $E_1$ – область значений Ф., каждый элемент $y∈E_1$ такой, что $y=f(x)$ для некоторого значения $x∈E$, называется значением функции. 2}$ отображает отрезок $–1 ⩽ x ⩽ 1$ на отрезок $0 ⩽ y ⩽ 1$. 2}$ отображает отрезок $–1 ⩽ x ⩽ 1$ на отрезок $0 ⩽ y ⩽ 1$. Для Ф. $f(x)$ и $g(x)$ естественным образом определяются арифметич. операции: это Ф., принимающие (в тех случаях, когда это имеет смысл) значения $f(x)±g(x)$, $f(x)g(x)$, $f(x)/g(x)$. Термин «Ф.» чаще всего используется только для обозначения числовой Ф. от одного или нескольких переменных (действительных или комплексных). В др. случаях, как правило, используются спец. термины: оператор, отображение, преобразование, функционал. См. также Монотонная функция, Непрерывная функция, Периодическая функция, Специальные функции, Чётные и нечётные функции, Элементарные функции. Исторический очеркКак и остальные понятия математики, понятие Ф. сложилось не сразу, а прошло долгий путь развития. По существу, речь о функциональной зависимости и её графич. изображении идёт в работе П. Ферма «Введение и изучение плоских и телесных мест» (1636, опубл. в 1679). Изучение линий по их уравнениям в «Геометрии» Р. Декарта (1637) также указывает на ясное представление о взаимной зависимости двух переменных величин. У англ. математика И. Барроу («Лекции по геометрии», 1670) в геометрич. форме устанавливается взаимная обратность действий дифференцирования и интегрирования (разумеется, без употребления самих этих терминов). Это свидетельствует о совершенно отчётливом владении понятием Ф. В геометрич. и механич. виде это понятие можно найти и у И. Ньютона. Однако термин «Ф.» впервые появляется лишь в 1692 у Г. Лейбница, и притом не совсем в современном его понимании. Лейбниц называет Ф. разл. отрезки, связанные с к.-л. кривой, напр. абсциссы её точек. В первом печатном курсе «Анализа бесконечно малых» франц. математика Г. Лопиталя (1696) термин «Ф. Ферма «Введение и изучение плоских и телесных мест» (1636, опубл. в 1679). Изучение линий по их уравнениям в «Геометрии» Р. Декарта (1637) также указывает на ясное представление о взаимной зависимости двух переменных величин. У англ. математика И. Барроу («Лекции по геометрии», 1670) в геометрич. форме устанавливается взаимная обратность действий дифференцирования и интегрирования (разумеется, без употребления самих этих терминов). Это свидетельствует о совершенно отчётливом владении понятием Ф. В геометрич. и механич. виде это понятие можно найти и у И. Ньютона. Однако термин «Ф.» впервые появляется лишь в 1692 у Г. Лейбница, и притом не совсем в современном его понимании. Лейбниц называет Ф. разл. отрезки, связанные с к.-л. кривой, напр. абсциссы её точек. В первом печатном курсе «Анализа бесконечно малых» франц. математика Г. Лопиталя (1696) термин «Ф. » не употребляется. » не употребляется. Первое определение Ф. в смысле, близком к современному, встречается у И. Бернулли (1718): «Функция – это величина, составленная из переменной и постоянной». В основе этого не вполне отчётливого определения лежит идея задания Ф. аналитич. формулой. Та же идея выступает и в определении Л. Эйлера, данном им во «Введении в анализ бесконечных» (1748): «Функция переменного количества есть аналитическое выражение, составленное каким-либо образом из этого переменного количества и чисел или постоянных количеств». На протяжении 18 в. отсутствовало достаточно ясное понимание различия между Ф. и её аналитич. выражением. С нач. 19 в. уже всё чаще и чаще определяют понятие Ф. без упоминания о её аналитич. выражении. Такие определения встречаются в работах Ж. Фурье (1822), Д. Дирихле (1829, 1837), Н. И. Лобачевского (1834). Так сложилось совр. понятие Ф., свободное от упоминания о её аналитич. задании. Так сложилось совр. понятие Ф., свободное от упоминания о её аналитич. задании. Определение домена и диапазона по графику Результаты обучения- Поиск домена и диапазона по графику и уравнению.
- Укажите домен и диапазон функций инструментария.
Другой способ определить домен и диапазон функций — использовать графики. Поскольку домен относится к набору возможных входных значений, домен графика состоит из всех входных значений, показанных на оси [latex]x[/latex]. Диапазон — это набор возможных выходных значений, которые показаны на оси [latex]y[/latex]. Имейте в виду, что если график выходит за пределы видимой части графика, домен и диапазон могут быть больше, чем видимые значения. Мы можем заметить, что граф простирается по горизонтали от [латекс]-5[/латекс] вправо без границ, так что домен равен [латекс]\левый[-5,\infty \правый)[/латекс]. Вертикальный экстент графика — это все значения диапазона [latex]5[/latex] и ниже, поэтому диапазон равен [latex]\left(\mathrm{-\infty },5\right][/latex]. Обратите внимание, что домен и диапазон всегда записываются от меньших значений к большим или слева направо для домена и от нижней части графика к верхней части графика для диапазона.0011 Обратите внимание, что домен и диапазон всегда записываются от меньших значений к большим или слева направо для домена и от нижней части графика к верхней части графика для диапазона.0011 Пример: поиск домена и диапазона на графике Найдите домен и диапазон функции [latex]f[/latex]. Показать решение Пример: нахождение области определения и диапазона по графику добычи нефти Найдите область определения и диапазон функции [latex]f[/latex]. (кредит: модификация работы Управления энергетической информации США) Показать решение Попробуйте Имея график, определите домен и диапазон, используя интервальную нотацию. Показать решение Вопросы и ответы Могут ли домен и диапазон функции совпадать? Да. Например, область определения и диапазон функции кубического корня — это множество всех действительных чисел. Например, область определения и диапазон функции кубического корня — это множество всех действительных чисел. Домен и диапазон функций инструментария Теперь мы вернемся к нашему набору функций набора инструментов, чтобы определить домен и диапазон каждой из них. Для постоянной функции [latex]f\left(x\right)=c[/latex] область определения состоит из всех действительных чисел; ограничений на ввод нет. Единственным выходным значением является константа [latex]c[/latex], поэтому диапазоном является набор [latex]\left\{c\right\}[/latex], содержащий этот единственный элемент. В записи интервала это записывается как [латекс]\влево[с,с\право][/латекс], интервал, который начинается и заканчивается на [латекс]с[/латекс]. Для функции тождества [латекс]f\left(x\right)=x[/latex] ограничений на [latex]x[/latex] нет. И домен, и диапазон являются набором всех действительных чисел. Для функции абсолютного значения [latex]f\left(x\right)=|x|[/latex] ограничений на [latex]x[/latex] нет. { 2}[/latex], доменом являются все действительные числа, поскольку горизонтальная протяженность графика — это вся линия действительных чисел. Поскольку график не содержит отрицательных значений диапазона, диапазон состоит только из неотрицательных действительных чисел. 9{3}[/latex], доменом являются все действительные числа, поскольку горизонтальная протяженность графика — это вся линия действительных чисел. То же самое относится к вертикальному размеру графика, поэтому домен и диапазон включают все действительные числа. { 2}[/latex], доменом являются все действительные числа, поскольку горизонтальная протяженность графика — это вся линия действительных чисел. Поскольку график не содержит отрицательных значений диапазона, диапазон состоит только из неотрицательных действительных чисел. 9{3}[/latex], доменом являются все действительные числа, поскольку горизонтальная протяженность графика — это вся линия действительных чисел. То же самое относится к вертикальному размеру графика, поэтому домен и диапазон включают все действительные числа. Для обратной функции [латекс]f\left(x\right)=\frac{1}{x}[/latex] мы не можем делить на 0, поэтому мы должны исключить 0 из области определения. Кроме того, 1, деленная на любое значение, никогда не может равняться 0, поэтому диапазон также не будет включать 0. В нотации построителя наборов мы могли бы также написать [латекс]\влево\{х|\текст{ }х\ne 0\вправо \}[/latex], множество всех вещественных чисел, не равных нулю. 9{2}}[/latex], мы не можем делить на [latex]0[/latex], поэтому мы должны исключить [latex]0[/latex] из домена. Также нет [latex]x[/latex], который может выдавать 0, поэтому 0 также исключается из диапазона. Обратите внимание, что выход этой функции всегда положителен из-за квадрата в знаменателе, поэтому диапазон включает только положительные числа. Также нет [latex]x[/latex], который может выдавать 0, поэтому 0 также исключается из диапазона. Обратите внимание, что выход этой функции всегда положителен из-за квадрата в знаменателе, поэтому диапазон включает только положительные числа. Для функции квадратного корня [latex]f\left(x\right)=\sqrt[]{x}[/latex] мы не можем извлечь квадратный корень из отрицательного действительного числа, поэтому домен должен быть 0 или выше. Диапазон также исключает отрицательные числа, поскольку квадратный корень из положительного числа [latex]x[/latex] определяется как положительный, хотя квадрат отрицательного числа [latex]-\sqrt{x}[/latex] также дает нам [латекс]x[/латекс]. Для функции кубического корня [latex]f\left(x\right)=\sqrt[3]{x}[/latex] домен и диапазон включают все действительные числа. Обратите внимание, что нет проблем с извлечением кубического корня или любого корня из нечетного целого числа из отрицательного числа, и результирующий результат будет отрицательным (это нечетная функция). Попробуйте Внесите свой вклад! У вас есть идеи по улучшению этого контента? Мы будем признательны за ваш вклад. Улучшить эту страницуПодробнее Mathway | Популярные задачи 93-8 | | 9 | Оценка | квадратный корень из 12 | | | 10 | Оценка | квадратный корень из 20 | | | 11 | Оценка | квадратный корень из 50 | | 94 | | 18 | Оценка | квадратный корень из 45 | | | 19 | Оценка | квадратный корень из 32 | | | 20 | Оценка | квадратный корень из 18 | | 92 |
Объяснение урока: Область определения и диапазон кусочной функции В этом объяснении мы узнаем, как найти область определения и диапазон
кусочно-определенная функция. Начнем с того, что напомним, что подразумевается под доменом и диапазоном функции. Определение: Область определения и диапазон функции Область определения функции — это набор всех входных значений функции. Диапазон функции — это набор всех возможных выходов функции с учетом ее области определения. Домен сообщает нам все входные данные, «разрешенные» для функции. Например, поскольку мы
не может ввести 𝑥=0 в функцию 𝑓(𝑥)=1𝑥, так как это было бы неопределенно, ее домен
не будет включать это значение 𝑥. Мы можем ввести любое другое значение
𝑥, поэтому домен
эта функция равна ℝ−{0}. Диапазон функции сообщает нам все возможные выходы этой функции, учитывая ее
домен. Например, рассмотрим функцию 𝑓(𝑥)=𝑥,
который имеет домен ℝ. С
квадрат любого действительного числа неотрицательный, 𝑥≥0, поэтому эта функция только
выводит неотрицательные действительные числа, но нам нужно проверить, какие из этих неотрицательных
действительные числа являются выходами функции. Для этого покажем, что любое неотрицательное
число является выходом этой функции. Если 𝑦≥0, то
𝑓√𝑦=√𝑦=𝑦. Для этого покажем, что любое неотрицательное
число является выходом этой функции. Если 𝑦≥0, то
𝑓√𝑦=√𝑦=𝑦. Следовательно, диапазон этой функции на ℝ представляет собой набор неотрицательных действительных чисел,
задается [0,∞[. Мы можем использовать различные алгебраические методы и свойства функции для
определить его домен и ареал. Однако часто это проще сделать с помощью
эскиз. Рассмотрим следующий набросок 𝑦=𝑓(𝑥). В эскизе любой функции точка на кривой имеет вид
(𝑥,𝑓(𝑥)), где 𝑥
вход функции, а 𝑓(𝑥) — выход. Другими словами, 𝑥-координата
каждая точка на кривой сообщает нам вход функции и
𝑦-координата говорит
нам вывод функции. Таким образом, мы можем использовать график функции, чтобы определить ее область определения и область значений. Чтобы определить область определения этой функции, мы хотим найти 𝑥-координату каждого
точка на кривой. Мы можем сделать это, рассмотрев, какие вертикальные линии пересекают
изгиб. Например, если мы рисуем вертикальную линию 𝑥=2, мы видим, что она пересекает нашу кривую в точке
точка (2,3). Следовательно, 2 находится в области определения нашей функции, а 3 — в ее диапазоне. Чтобы определить полную область определения нашей функции, нам нужно сделать это со всеми возможными
вертикальная линия. Мы видим, что любая вертикальная линия 𝑥=𝑐 будет пересекать эту кривую. В частности, при 𝑥=0 имеем следующее: Поскольку на графике 𝑦=𝑓(𝑥) есть сплошная точка
(0,1), мы знаем
функция определена в этой точке. Итак, вертикальная линия 𝑥=0 пересекает кривую и
𝑓(0)=1. Следовательно, поскольку все вертикальные линии пересекают кривую, ее
домен ℝ. Мы можем найти диапазон этой функции, рассматривая горизонтальные линии. Например, прямая 𝑦=1 пересекает кривую в точке
(0,1), поэтому 1 находится в диапазоне
этой функции. Мы также можем видеть, что линия 𝑦=0 не пересекает кривую. Поскольку кривая имеет пустую точку в начале координат, она не пересекает эту горизонталь. линия; на самом деле, для любого 𝑐∈[0,1[ линия
𝑦=𝑐 не будет пересекать нашу кривую и все остальные
горизонтальные линии пересекают нашу кривую. Следовательно, диапазон этой функции
]−∞,0[∪[1,∞[. линия; на самом деле, для любого 𝑐∈[0,1[ линия
𝑦=𝑐 не будет пересекать нашу кривую и все остальные
горизонтальные линии пересекают нашу кривую. Следовательно, диапазон этой функции
]−∞,0[∪[1,∞[. Прежде чем мы обсудим определение области определения и диапазона кусочно-определенной функции,
начнем с того, что вспомним, что мы подразумеваем под этими типами функций. Определение: кусочная функция Кусочная функция — это функция, состоящая из нескольких подфункций,
с каждой подфункцией, определенной над подмножеством домена основной функции, называемым
поддомен. Уравнение кусочной функции записывается с фигурной скобкой для обозначения
что он состоит из более чем одной подфункции. Примером кусочной функции является
𝑓(𝑥)=𝑥,𝑥0,𝑥+1,𝑥≥0,
где 𝑓(𝑥)=𝑥, когда 𝑥0 и
𝑓(𝑥)=𝑥+1, когда 𝑥≥0. В кусочно-определенной функции возможные входы функции задаются
поддомены, в данном случае 𝑥0 и 𝑥≥0. Поэтому найти все
возможные входы этой функции, нам нужно будет взять объединение всех
поддомены. Для этой кусочной функции мы можем взять на вход 𝑥0, а также
𝑥≥0; комбинируя их, мы можем видеть, что это любое реальное значение
𝑥, поэтому его домен равен ℝ. Поэтому найти все
возможные входы этой функции, нам нужно будет взять объединение всех
поддомены. Для этой кусочной функции мы можем взять на вход 𝑥0, а также
𝑥≥0; комбинируя их, мы можем видеть, что это любое реальное значение
𝑥, поэтому его домен равен ℝ. Чтобы найти диапазон кусочной функции, мы можем вместо этого рассмотреть диапазон каждого
подфункция над своей подобластью. Поэтому, чтобы найти диапазон
𝑓(𝑥),
мы рассматриваем диапазон каждой подфункции отдельно. Во-первых, 𝑓(𝑥)=𝑥, когда 𝑥0. Следовательно, если мы введем значение
𝑐0 в функцию, получаем
𝑓(𝑐)=𝑐. Следовательно, все значения 𝑐0 находятся в диапазоне этой подфункции. Секунда, 𝑓(𝑥)=𝑥+1, когда 𝑥≥0. Добавление 1 к обеим сторонам
неравенства нашей подобласти дает нам 𝑥+1≥1. Следовательно, когда
𝑥≥0, 𝑓(𝑥)≥1. Этого недостаточно, чтобы
определить диапазон этой подфункции; нам нужно определить, какие значения
подфункция достигает. Для этого положим 𝑐≥1 так, чтобы
𝑐−1≥0; это означает
𝑓(𝑐−1)=(𝑐−1)+1=𝑐. Для этого положим 𝑐≥1 так, чтобы
𝑐−1≥0; это означает
𝑓(𝑐−1)=(𝑐−1)+1=𝑐. Следовательно, все значения 𝑐≥1 находятся в диапазоне этой подфункции. Комбинируя диапазоны каждой подфункции, получаем, что диапазон
𝑓(𝑥) есть
𝑐0 и 𝑐≥1; мы можем представить это в интервальных обозначениях как
]−∞,0[∪[1,∞[. Мы можем обобщить результаты, показанные в приведенном выше примере, следующим образом. Определение: Область определения и область значений кусочно-определенной функции Область определения кусочно-определенной функции представляет собой объединение ее подобластей. Диапазон кусочно-определенной функции представляет собой объединение диапазонов каждого
подфункция над своей подобластью. Давайте рассмотрим несколько примеров того, как найти домен и диапазон
кусочно-определенная функция по ее графику. Пример 1. Определение области определения и области значений кусочно-определенной функции по ее графику Определение области определения и области значений функции
𝑓(𝑥)=6,𝑥0,−4,𝑥>0. Ответ Напомним, что областью определения функции называется множество всех входных значений
функция, а диапазон функции — это множество всех возможных выходов
функция, заданная ее доменом. Мы можем определить оба этих параметра по графику функции. Запомнить,
любая точка на кривой имеет вид (𝑥,𝑓(𝑥)), где 𝑥 будет в
домен 𝑓 и 𝑓(𝑥) будет находиться в диапазоне 𝑓. Чтобы найти домен 𝑓, нам нужно определить
𝑥-координаты всех точек кривой. Рассмотрим следующие вертикальные линии. На диаграмме (1) видно, что любая вертикальная линия для 𝑥0 пересекается
Кривая. Точно так же на диаграмме (2) мы видим, что любая вертикальная линия для
𝑥>0 пересекает прямую. Таким образом, все эти значения
𝑥 должен находиться в области определения этой функции. Нам нужно проверить, если
𝑥=0 находится в области определения этой функции; мы можем проверить это, зарисовав
линия 𝑥=0. Поскольку наша кривая имеет полые окружности на линии 𝑥=0, она не определена
при этом значении 𝑥; следовательно, 0 не находится в домене
𝑓(𝑥). Следовательно, область определения этой функции вся действительна.
значения 𝑥, не равные 0, которые мы можем записать в системе обозначений как
ℝ−{0}. Стоит отметить, что мы можем проверить, что 0 не находится в домене
𝑓(𝑥), рассматривая подобласти функции,
𝑥0 и 𝑥>0,
которые оба не включают 0. Объединение этих поддоменов также является доменом
функции, ℝ−{0}. Чтобы найти диапазон этой функции, мы могли бы рассмотреть, какие горизонтальные линии
пересекать график. Однако в этом случае мы можем найти диапазон, рассматривая
координаты точек на графике. Мы видим, что если 𝑥0, то
𝑓(𝑥)=6. Аналогично, если 𝑥>0, то
𝑓(𝑥)=−4. Это означает, что единственными возможными выходами нашей функции являются
6 и −4, поэтому диапазон этой функции равен {−4,6}. Следовательно, домен равен ℝ−{0}, а диапазон равен
{−4,6}. Пример 2. Определение диапазона кусочно-определенной функции по ее графику Найти диапазон функции
𝑓(𝑥)=𝑥+5,𝑥∈[−5,−1],−𝑥+3,𝑥∈]−1,3]. Ответ Вспомним, что областью значений функции является множество всех возможных выходов
функция, заданная ее доменом. Чтобы найти диапазон этой функции, мы можем рассмотреть
какие горизонтальные линии пересекают график. На диаграмме (1) видно, что наибольший выход функции равен
𝑓(−1)=4. На диаграмме (2) мы видим, что наименьший выход функции равен
𝑓(−5)=𝑓(3)=0. Все значения между ними являются возможными выходами, дающими нам диапазон
[0,4]. Следовательно, диапазон равен [0,4]. Пример 3. Определение области значений кусочно-определенных функций по их графикам Определите область значений функции, представленной данным графиком. Ответ Вспомним, что областью значений функции является множество всех возможных выходов
функция, заданная ее доменом. Помните, любая точка на нашем графике будет иметь вид
(𝑐,𝑓(𝑐)), где 𝑓(𝑐) будет в диапазоне функции. Следовательно, мы можем найти
диапазон этой функции, определяя 𝑦-координаты точек на ее графике. Помните, любая точка на нашем графике будет иметь вид
(𝑐,𝑓(𝑐)), где 𝑓(𝑐) будет в диапазоне функции. Следовательно, мы можем найти
диапазон этой функции, определяя 𝑦-координаты точек на ее графике. На диаграмме (1), поскольку на нашем графике есть сплошная точка в точке (4,−1),
мы видим, что самый низкий
выход функции равен −1. На второй диаграмме видно, что наибольший выход
функции равно 7. Мы видим, что любая горизонтальная линия между этими значениями также пересекает
кривой, поэтому диапазоном этой функции является любое значение между
−1 и 7 включительно. В системе обозначений это [−1,7]. Следовательно, диапазон равен [−1,7]. В нашем следующем примере мы увидим, как определить домен кусочно-определенного
функцию, не зная ее графика. Пример 4. Определение области определения кусочно-определенной функции Определение области определения функции
𝑓(𝑥)=𝑥+4,𝑥∈[−4,8],7𝑥−63,𝑥∈]8,9]. Ответ Напомним, что область определения функции — это множество всех входных значений функции,
а для кусочно-определенной функции это объединение ее подобластей. Для этой функции субдомены [−4,8] и
]8,9]. Мы хотим взять союз
из этих двух наборов, чтобы найти область определения 𝑓(𝑥):
[−4,8]∪]8,9]=[−4,9]. Следовательно, домен равен [−4,9]. В нашем последнем примере мы увидим, как определить как домен, так и диапазон
кусочно-определенная функция без заданного графика. Пример 5. Определение области определения и диапазона кусочной функции Определение области определения и диапазона функции
𝑓(𝑥)=𝑥−36𝑥−6𝑥≠6,12𝑥=6.если Ответ Напомним, что область определения функции — это множество всех входных значений
функцией, а для кусочно-определенной функции — объединением ее подобластей. Чтобы найти объединение поддоменов, мы начнем с записи их в терминах
наборы. Во-первых, 𝑥≠6 совпадает с ℝ−{6}. Во-вторых, 𝑥=6 совпадает с {6}. Во-первых, 𝑥≠6 совпадает с ℝ−{6}. Во-вторых, 𝑥=6 совпадает с {6}. Следовательно, домен представляет собой объединение этих множеств:
ℝ−{6}∪{6}=ℝ. Диапазон функции — это набор всех возможных выходов функции,
учитывая его домен. Для кусочно-определенной функции это будет диапазон
подфункции над их подобластями. Таким образом, мы можем определить диапазон этого
функцию, рассматривая каждую подфункцию отдельно. Во-первых, если 𝑥≠6,
𝑓(𝑥)=𝑥−36𝑥−6=(𝑥−6)(𝑥+6)𝑥−6;
поскольку 𝑥≠6, мы можем отменить общий множитель
𝑥−6:
𝑓(𝑥)=𝑥+6. Затем мы можем нарисовать эту подфункцию. Это прямая 𝑦=𝑥+6 с удаленной точкой 𝑥=6. Диапазон этого
подфункция — это все возможные выходы. Единственная горизонтальная линия, которая не
пересекают эту линию 𝑦=12, поэтому диапазон этой подфункции равен
ℝ−{12}. Вторая подфункция — постоянная функция
𝑓(𝑥)=12 на домене
{6}. Поскольку выход постоянен, его диапазон
{12}. Поскольку выход постоянен, его диапазон
{12}. Объединение диапазонов подфункций дает нам
ℝ−{12}∪{12}=ℝ. Стоит отметить, что мы могли бы также набросать вторую подфункцию на том же
график, чтобы полностью нарисовать 𝑓(𝑥). Вторая подфункция определяется только
когда 𝑥=6, значит, он состоит из одной точки. У нас есть
𝑓(6)=12, поэтому добавляем точку
(6,12) к нашему эскизу. Тогда мы можем видеть, что 𝑓(𝑥) — это функция
𝑥+6. Следовательно, домен равен ℝ, а диапазон равен ℝ. Давайте закончим повторением некоторых важных моментов этого объяснения. Ключевые моменты- Область определения кусочно-определенной функции представляет собой объединение ее подобластей.
- Диапазон кусочно-определенной функции представляет собой объединение диапазонов каждого
подфункция над своей подобластью.
- Мы можем найти область определения функции по ее графику, рассматривая пересечения кривой с вертикальными линиями.
 - Мы можем найти диапазон функции по ее графику, рассматривая пересечения кривой с горизонтальными линиями.
Составные функции – объяснение и примеры В математике функция – это правило, которое связывает данный набор входных данных с набором возможных выходных данных. Важно отметить, что каждый вход связан ровно с одним выходом. Процесс именования функций известен как нотация функций. Наиболее часто используемые обозначения функций включают: «f(x) = …», «g(x) = …», «h(x) = …» и т. д. В этой статье мы узнаем что такое составные функции и как их решать. Что такое составная функция? Если нам даны две функции, мы можем создать другую функцию, вставив одну функцию в другую. Шаги, необходимые для выполнения этой операции, аналогичны тому, когда любая функция решается для любого заданного значения. Такие функции называются составными функциями. Составная функция — это обычно функция, написанная внутри другой функции. Композиция функции осуществляется путем замены одной функции на другую функцию. Композиция функции осуществляется путем замены одной функции на другую функцию. Например, , f [g (x)] является составной функцией f (x) и g (x). Составная функция f [g (x)] читается как «f of g of x ». Функция g(x) называется внутренней функцией, а функция f(x) — внешней функцией. Следовательно, мы можем также прочитать f[g(x)] как «функция g является внутренней функцией внешней функции f ». Как решать составные функции? Решение сложной функции означает нахождение композиции двух функций. Мы используем маленький кружок (∘) для обозначения функции. Вот шаги по решению составной функции: - Перепишите композицию в другой форме.
Например, (f ∘ g) (x) = f [g (x)] (f ∘ g) (x) = f [g (x)] (f ∘ g) (x² ) = f [g (x²)] - Замените переменную x во внешней функции на внутреннюю.
- Упрощение функции.
Примечание: Порядок в составе функции важен, потому что (f ∘ g) (x) НЕ совпадает с (g ∘ f) (x). 9Пример 1 (Икс). Решение Подставим x на 2x – 1 в функции f(x) = x 2 + 6.
(f ∘ g) (x) = (2x – 1) 2 + 6 = ( 2x – 1) (2x – 1) + 6 Применение ФОЛЬГИ
= 4x 2 – 4x + 1 + 6
= 4x 2 – 4x + 7 Пример 2 Учитывая функции g (x) = 2x – 1 и f (x) = x 2 + 6, найдите (g ∘ f) (x). Решение Подставить x на x 2 + 6 в функции g (x) = 2x – 1
(g ∘ f) (x) = 2(x 2 + 6) – 1 1 Используйте распределительное свойство, чтобы удалить круглые скобки.
= 2x 2 + 12 – 1
= 2x 2 + 11 Пример 3 Учитывая f (x) = 2x + 3, найдите (f ∘ f) (x). Решение (F ∘ F) (x) = F [F (x)] = 2 (2x + 3) + 3 = 4x + Пример 4 Найдите (g ∘ f) (x), учитывая, что f (x) = 2x + 3 и g (x) = –x 2 + 5 ⟹ (g ∘ f) (x) = g [f (x )]. 5 5
= –4x 2 – 12x – 9 + 5
= –4x 2 – 12x – 4 + 4 и g (x) = x – 3 Решение Сначала найдите значение f(g(x)). ⟹ f (g (x)) = 5(x – 3) + 4 = 5x – 15 + 4 = 5x – 11 Теперь подставим x в f(g(x)) на 6 ⟹ 5(6) – 11 ⟹ 30 – 11 = 19 Следовательно, f [g (6)] = 19 Пример 6 Найдите f [g (5)], учитывая, что f (x) = 4x + 3 и g (x) = x – 2. значение f[g(x)]. ⟹ f(x) = 4x + 3 ⟹ g(x) = x – 2 f[g(x)] = 4(x – 2) + 3 = 4x – 8 + 3 = 4x – 5 Теперь оцените f [g (5)], заменив x в f[g(x)] на 5. f [g (x)] = 4(5) – 5 = 15 Следовательно, f [g (5)] = 15, Пример 7 Учитывая g (x) = 2x + 8 и f (x) = 8x², найти (f ∘ g) (x) Решение (f ∘ ) = f [g(x)] Замените x в f(x) = 8x² на (2x + 8) ⟹ (f ∘g) (x) = f [g(x)] = 8(2x + 8) ² ⟹ 8 [4x² + 8² + 2(2x) (8)] ⟹ 8 [4x² + 64 + 32x] ⟹ 32x² + 512 + 256 x x 59 + 1516 32x² Пример 8 Найти (g ∘ f) (x), если f(x) = 6 x² и g(x) = 14x + 4 Решение ⟹ (g ∘ f) (x) = g [f(x)] Подставить x в g(x) = 14x + 4 с 6 x² ⟹g [f(x)] =14 (6 x²) + 4 = 84 x² + 4 Пример 9 Рассчитайте (f ∘ g) (x), используя f(x) = 2x + 3 и g(x) = — х 2 + 1, Решение (f ∘ g) (x) = f(g(x))
= 2 (g(x)) + 3
= 2(-x 2 + 1) + 3
= – 2 x 2 + 5 Пример 10 Учитывая f(x) = √ (x + 2) и g(x) = ln (1 – x 2 ), найдите область определения (g ∘ f) (x). Решение ⟹ (g ∘ f) (x) = g(f(x))
⟹ ln (1 – f(x) 2 ) = ln (1 – √ (x + 2) 2 )
⟹ ln (1 – (x + 2))
= ln (- x – 1) Присвоить x + 2 значение ≥ 0 Следовательно, домен: [-2, -1] Пример 11 Даны две функции: f = {(-2, 1), (0, 3), (4, 5)} и g = {(1, 1), (3, 3), (7 , 9)}, найти (g ∘ f) и определить его область определения и область значений. Решение ⟹ (g ∘ f) (-2) = g [f (-2)] = g (1) = 1
⟹ (g ∘ f) (0) = g [f (0) ] = g(3) = 3
⟹ (g ∘ f)(4) = g[f(4)] = g(5) = undefined Следовательно, g ∘ f = {(-2, 1), ( 0, 3)} Следовательно, домен: {-2, 0} и диапазон: {1, 3} 4.7 Задачи на максимум/минимум — исчисление, том 3 Цели обучения- 4.7.1
Используйте частные производные, чтобы найти критические точки для функции двух переменных.
- 4.7.2
Примените тест второй производной, чтобы определить критическую точку как локальный максимум, локальный минимум или седловую точку для функции двух переменных.
 - 4.7.3
Исследуйте критические точки и граничные точки, чтобы найти абсолютные максимальные и минимальные значения для функции двух переменных.
Одним из наиболее полезных применений производных функции одной переменной является определение максимальных и/или минимальных значений. Это приложение также важно для функций двух или более переменных, но, как мы видели в предыдущих разделах этой главы, введение большего количества независимых переменных приводит к большему количеству возможных результатов вычислений. Основные идеи поиска критических точек и использования производных тестов по-прежнему актуальны, но появляются новые морщины при оценке результатов. Критические точки Для функций одной переменной мы определили критические точки как значения функции, когда производная равна нулю или не существует. Для функций двух и более переменных концепция по существу та же, за исключением того факта, что мы теперь работаем с частными производными. Определение Пусть z=f(x,y)z=f(x,y) — функция двух переменных, определенная на открытом множестве, содержащем точку (x0,y0).(x0,y0). Точка (x0,y0)(x0,y0) называется критической точкой функции двух переменных ff, если выполняется одно из двух следующих условий: - fx(x0,y0)=fy(x0,y0)=0fx(x0,y0)=fy(x0,y0)=0
- Либо fx(x0,y0), либо fy(x0,y0),fx(x0,y0), либо fy(x0,y0) не существует.
Пример
4,38 Поиск критических точек Найдите критические точки каждой из следующих функций: - f(x,y)=4y2−9×2+24y+36x+36f(x,y)=4y2−9×2+24y+36x +36
- g(x,y)=x2+2xy−4y2+4x−6y+4g(x,y)=x2+2xy−4y2+4x−6y+4
Решение- Сначала мы вычисляем fx(x,y)иfy(x,y):fx(x,y)иfy(x,y):
fx(x,y)=12(−18x+36)(4y2−9×2+24y+36x+36)−1/2=−9x+184y2−9×2+24y+36x+36fy(x,y)=12 (8y+24)(4y2-9×2+24y+36x+36)-1/2=4y+124y2-9×2+24y+36x+36. fx(x,y)=12(-18x+36)(4y2- 9×2+24y+36x+36)−1/2=−9x+184y2−9×2+24y+36x+36fy(x,y)=12(8y+24)(4y2−9×2+24y+36x+36)−1 /2=4у+124у2-9х2+24у+36х+36. fx(x,y)=12(-18x+36)(4y2- 9×2+24y+36x+36)−1/2=−9x+184y2−9×2+24y+36x+36fy(x,y)=12(8y+24)(4y2−9×2+24y+36x+36)−1 /2=4у+124у2-9х2+24у+36х+36.
Далее приравняем каждое из этих выражений к нулю: +36x+36=04y+124y2−9×2+24y+36x+36=0.
Затем умножьте каждое уравнение на его общий знаменатель: −9x+18=04y+12=0,−9x+18=04y+12=0.
Следовательно, x=2x=2 и y=−3,y=−3, поэтому (2,−3)(2,−3) является критической точкой ф.ф.
Мы также должны проверить возможность того, что знаменатель каждой частной производной может быть равен нулю, что приводит к тому, что частная производная не существует. Поскольку знаменатель в каждой частной производной один и тот же, нам нужно сделать это только один раз: 4y2−9×2+24y+36x+36=0,4y2−9×2+24y+36x+36=0.
Это уравнение представляет собой гиперболу. Отметим также, что область определения ff состоит из точек, удовлетворяющих неравенству 4y2−9×2+24y+36x+36≥0,4y2−9×2+24y+36x+36≥0.
Следовательно, любые точки гиперболы являются не только критическими точками, но и границей области. Чтобы привести гиперболу к стандартной форме, воспользуемся методом заполнения квадрата: 6y)−9(x2−4x)=−364(y2+6y+9)−9(x2−4x+4)=−36+36−364(y+3)2−9(x−2)2= −36,4y2−9×2+24y+36x+36=04y2−9×2+24y+36x=−364y2+24y−9×2+36x=−364(y2+6y)−9(x2−4x)=−364(y2+6y +9)−9(x2−4x+4)=−36+36−364(y+3)2−9(х-2)2=-36. Чтобы привести гиперболу к стандартной форме, воспользуемся методом заполнения квадрата: 6y)−9(x2−4x)=−364(y2+6y+9)−9(x2−4x+4)=−36+36−364(y+3)2−9(x−2)2= −36,4y2−9×2+24y+36x+36=04y2−9×2+24y+36x=−364y2+24y−9×2+36x=−364(y2+6y)−9(x2−4x)=−364(y2+6y +9)−9(x2−4x+4)=−36+36−364(y+3)2−9(х-2)2=-36.
Разделив обе части на −36−36, получим стандартную форму уравнения: 4(y+3)2−36−9(x−2)2−36=1(x−2)24−(y+3 )29=1,4(у+3)2-36-9(х-2)2-36=1(х-2)24-(у+3)29=1.
Обратите внимание, что точка (2,−3)(2,−3) является центром гиперболы. - Сначала мы вычисляем gx(x,y)andgy(x,y):gx(x,y)andgy(x,y):
gx(x,y)=2x+2y+4gy(x,y)= 2x−8y−6.gx(x,y)=2x+2y+4gy(x,y)=2x−8y−6.
Далее мы устанавливаем каждое из этих выражений равным нулю, что дает систему уравнений в xandy:xandy: 2x+2y+4=02x-8y-6=0,2x+2y+4=02x-8y-6=0.
Вычитание второго уравнения из первого дает 10y+10=0,soy=-1,10y+10=0,soy=-1. Подстановка этого в первое уравнение дает 2x+2(-1)+4=0,2x+2(-1)+4=0, поэтому x=-1. x=-1. Поэтому (−1,−1)(−1,−1) является критической точкой gg (рис. 4.46). В ℝ2ℝ2 нет точек, из-за которых ни одна из частных производных не существует. x=-1. Поэтому (−1,−1)(−1,−1) является критической точкой gg (рис. 4.46). В ℝ2ℝ2 нет точек, из-за которых ни одна из частных производных не существует.
Рисунок
4,46
Функция g(x,y)g(x,y) имеет критическую точку в точке (−1,−1,5).(−1,−1,5).
Контрольно-пропускной пункт
4,34 Найдите критическую точку функции f(x,y)=x3+2xy-2x-4y.f(x,y)=x3+2xy-2x-4y. Основной целью определения критических точек является обнаружение относительных максимумов и минимумов, как в исчислении с одной переменной. При работе с функцией одной переменной определение локального экстремума включает в себя нахождение интервала вокруг критической точки так, чтобы значение функции было либо больше, либо меньше всех других значений функции в этом интервале. При работе с функцией двух и более переменных мы работаем с открытым диском вокруг точки. Определение Пусть z=f(x,y)z=f(x,y) — функция двух переменных, определенная и непрерывная на открытом множестве, содержащем точку (x0,y0). (x0,y0). Тогда f имеет локальный максимум в точке (x0,y0)(x0,y0), если (x0,y0). Тогда f имеет локальный максимум в точке (x0,y0)(x0,y0), если f(x0,y0)≥f(x,y)f(x0,y0)≥f(x,y) для всех точек (x,y)(x,y) в пределах некоторого круга с центром в (x0,y0).(x0,y0). Число f(x0,y0)f(x0,y0) называется локальным максимальным значением . Если предыдущее неравенство выполняется для каждой точки (x,y)(x,y) в области определения f,f, то ff имеет глобальный максимум (также называемый абсолютным максимумом ) в точке (x0,y0).(x0,y0). Функция ff имеет локальный минимум в точке (x0,y0)(x0,y0), если f(x0,y0)≤f(x,y)f(x0,y0)≤f(x,y ) для всех точек (x,y)(x,y) в пределах некоторого круга с центром в (x0,y0).(x0,y0). Число f(x0,y0)f(x0,y0) называется локальным минимальным значением . Если предыдущее неравенство выполняется для каждой точки (x,y)(x,y) в области f,f, то ff имеет глобальных минимума (также называется абсолютным минимумом ) в точке (x0,y0). (x0,y0). (x0,y0). Если f(x0,y0)f(x0,y0) является либо локальным максимумом, либо локальным минимумом, то это называется локальным экстремумом (см. следующий рисунок). Рисунок
4,47
График z=16−x2−y2z=16−x2−y2 имеет максимальное значение, когда (x,y)=(0,0).(x,y)=(0,0). Он достигает своего минимального значения на границе своей области, то есть на окружности x2+y2=16.x2+y2=16. В «Максимумах» и «Минимумах» мы показали, что экстремумы функций одной переменной возникают в критических точках. То же верно и для функций более чем одной переменной, как утверждается в следующей теореме. Теорема
4.16 Теорема Ферма для функций двух переменных Пусть z=f(x,y)z=f(x,y) — функция двух переменных, определенная и непрерывная на открытом множестве, содержащем точку (x0,y0).(x0,y0). Предположим, что fxfx и fyfy существуют в точке (x0,y0).(x0,y0). Если ф.ф. имеет локальный экстремум в точке (x0,y0),(x0,y0), то (x0,y0)(x0,y0) является критической точкой ф. ф. ф. Тест второй производной Рассмотрим функцию f(x)=x3.f(x)=x3. Эта функция имеет критическую точку при x=0,x=0, так как f′(0)=3(0)2=0.f′(0)=3(0)2=0. Однако ff не имеет экстремального значения при x=0.x=0. Следовательно, наличие критического значения при x=x0x=x0 не гарантирует локального экстремума при x=x0.x=x0. То же самое верно для функции двух или более переменных. Один из способов, которым это может произойти, — это седловая точка. Пример седловой точки показан на следующем рисунке. Рисунок
4,48
График функции z=x2−y2.z=x2−y2. Этот график имеет седловую точку в начале координат. На этом графике начало координат является седловой точкой. Это связано с тем, что первые частные производные f(x,y)=x2−y2f(x,y)=x2−y2 равны нулю в этой точке, но это не максимум и не минимум функции. Более того, вертикальный след, соответствующий y=0y=0, есть z=x2z=x2 (парабола, выходящая вверх), а вертикальный след, соответствующий x=0x=0, есть z=-y2z=-y2 (парабола, выходящая вниз). Следовательно, это одновременно и глобальный максимум для одной трассы, и глобальный минимум для другой. Следовательно, это одновременно и глобальный максимум для одной трассы, и глобальный минимум для другой. Определение Учитывая функцию z=f(x,y),z=f(x,y), точка (x0,y0,f(x0,y0))(x0,y0,f(x0,y0)) седловой точкой, если и fx(x0,y0)=0fx(x0,y0)=0, и fy(x0,y0)=0,fy(x0,y0)=0, но ff не имеет локального экстремума в точке (x0 ,у0).(х0,у0). Критерий второй производной для функции одной переменной обеспечивает метод определения того, возникает ли экстремум в критической точке функции. При распространении этого результата на функцию двух переменных возникает вопрос, связанный с тем, что на самом деле существует четыре различных частных производных второго порядка, хотя равенство смешанных частных производных сводит их к трем. Второй критерий производной для функции двух переменных, сформулированный в следующей теореме, использует дискриминантный DD, который заменяет f″(x0)f″(x0) во втором критерии производной для функции одной переменной. Теорема
4. 17 Второй производный тест Пусть z=f(x,y)z=f(x,y) функция двух переменных, для которой частные производные первого и второго порядка непрерывны на некотором круге, содержащем точку (x0,y0). (х0, у0). Предположим, что fx(x0,y0)=0fx(x0,y0)=0 и fy(x0,y0)=0.fy(x0,y0)=0. Определим количество D=fxx(x0,y0)fyy(x0,y0)−(fxy(x0,y0))2.D=fxx(x0,y0)fyy(x0,y0)−(fxy(x0, у0))2. (4.43) - Если D>0D>0 и fxx(x0,y0)>0,fxx(x0,y0)>0, то ff имеет локальный минимум в точке (x0,y0).(x0,y0 ).
- Если D>0D>0 и fxx(x0,y0)<0,fxx(x0,y0)<0, то ff имеет локальный максимум в точке (x0,y0).(x0,y0).
- Если D<0,D<0, то ff имеет седловую точку в точке (x0,y0).(x0,y0).
- Если D=0,D=0, то тест неубедительный.
См. рис. 4.49. Рисунок
4,49
Тест второй производной часто может определить, имеет ли функция двух переменных локальные минимумы (а), локальные максимумы (б) или седловую точку (в). Чтобы применить критерий второй производной, необходимо сначала найти критические точки функции. Вся процедура состоит из нескольких этапов, которые изложены в стратегии решения проблем. Стратегия решения проблем Стратегия решения задач: использование теста второй производной для функций двух переменных Пусть z=f(x,y)z=f(x,y) функция двух переменных, для которой частные производные первого и второго порядка непрерывны на некотором круге, содержащем точку (x0,y0). (х0, у0). Чтобы применить тест второй производной для поиска локальных экстремумов, выполните следующие действия: - Определите критические точки (x0,y0)(x0,y0) функции ff, где fx(x0,y0)=fy(x0,y0 )=0.fx(x0,y0)=fy(x0,y0)=0. Отбросьте все точки, где хотя бы одна из частных производных не существует.
- Вычислить дискриминант 2 для каждой критической точки ф.ф.
- Применить тест второй производной, чтобы определить, является ли каждая критическая точка локальным максимумом, локальным минимумом или седловой точкой, или теорема неубедительна.

Пример
4,39 Использование теста второй производной Найдите критические точки для каждой из следующих функций и используйте тест второй производной, чтобы найти локальные экстремумы: - f(x,y)=4×2+9y2+8x−36y+24f(x,y)=4×2+9y2+8x−36y+24
- g(x,y)=13×3+y2+2xy-6x-3y+4g(x,y)=13×3+y2+2xy-6x-3y+4
Решение- Шаг 11 стратегии решения задач включает в себя поиск критических точек ф.ф. Для этого сначала вычислим fx(x,y)fx(x,y) и fy(x,y),fy(x,y), затем приравняем каждую из них к нулю:
fx(x,y) =8x+8fy(x,y)=18y−36.fx(x,y)=8x+8fy(x,y)=18y−36.
Приравняв их к нулю, получим систему уравнений 8x+8=018y-36=0,8x+8=018y-36=0.
Решением этой системы является x=−1x=−1 и y=2.y=2. Следовательно, (−1,2)(−1,2) является критической точкой ф.ф.
Шаг 2 стратегии решения задач включает в себя вычисление D.D. Для этого сначала вычислим вторые частные производные от f:f: fxx(x,y)=8fxy(x,y)=0fyy(x,y)=18. fxx(x,y)=8fxy(x ,y)=0fyy(x,y)=18. fxx(x,y)=8fxy(x ,y)=0fyy(x,y)=18.
Следовательно, D=fxx(−1,2)fyy(−1,2)−(fxy(−1,2))2=(8)(18)−(0)2=144.D=fxx( −1,2)fyy(−1,2)−(fxy(−1,2))2=(8)(18)−(0)2=144.
Шаг 3 требует проверки второго теста производной для функций двух переменных. Поскольку D>0D>0 и fxx(−1,2)>0,fxx(−1,2)>0, это соответствует случаю 1. Следовательно, ff имеет локальный минимум в точке (−1,2)(−1,2), как показано на следующем рисунке.
Рисунок
4,50
Функция f(x,y)f(x,y) имеет локальный минимум в точке (−1,2,−16).(−1,2,−16). - Для шага 1 мы сначала вычисляем gx(x,y)gx(x,y) и gy(x,y),gy(x,y), а затем устанавливаем каждый из них равным нулю:
gx(x,y )=x2+2y−6gy(x,y)=2y+2x−3.gx(x,y)=x2+2y−6gy(x,y)=2y+2x−3.
Приравняв их к нулю, получим систему уравнений x2+2y-6=02y+2x-3=0.x2+2y-6=02y+2x-3=0.
Чтобы решить эту систему, сначала решите второе уравнение для лет. Это дает y=3−2×2.y=3−2×2. Подстановка этого в первое уравнение дает x2+3−2x−6=0x2−2x−3=0(x−3)(x+1)=0,×2+3−2x−6=0x2−2x−3= 0(х-3)(х+1)=0. Следовательно, x=−1x=−1 или x=3.x=3. Подстановка этих значений в уравнение y=3−2x2y=3−2×2 дает критические точки (−1,52)(−1,52) и (3,−32).(3,−32). Шаг 2 включает вычисление вторых частных производных g:g: gxx(x,y)=2xgxy(x,y)=2gyy(x,y)=2.gxx(x,y)=2xgxy(x,y)=2gyy(x,y)=2.
Затем находим общую формулу для D:D: D=gxx(x0,y0)gyy(x0,y0)−(gxy(x0,y0))2=(2×0)(2)−22=4×0−4.D=gxx(x0,y0)gyy(x0 ,y0)−(gxy(x0,y0))2=(2×0)(2)−22=4×0−4.
Далее подставляем каждую критическую точку в эту формулу: D(−1,52)=(2(−1))(2)−(2)2=−4−4=−8D(3,−32 )=(2(3))(2)−(2)2=12−4=8.D(−1,52)=(2(−1))(2)−(2)2=−4− 4=-8D(3,-32)=(2(3))(2)-(2)2=12-4=8.
В шаге 3 мы отмечаем это, применяя тест второй производной для функций двух переменных. к точке (−1,52)(−1,52) приводит к случаю 3,3, что означает, что (−1,52)(−1,52) является седловой точкой. Применение теоремы к точке (3,−32)(3,−32) приводит к случаю 1, что означает, что (3,−32)(3,−32) соответствует локальному минимуму, как показано на следующем рисунке.
Рисунок
4,51
Функция g(x,y)g(x,y) имеет локальный минимум и седловую точку.
Контрольно-пропускной пункт
4,35 Используйте вторую производную, чтобы найти локальные экстремумы функции f(x,y)=x3+2xy-6x-4y2.f(x,y)=x3+2xy-6x-4y2. Абсолютные максимумы и минимумы При нахождении глобальных экстремумов функций одной переменной на замкнутом интервале мы начинаем с проверки критических значений на этом интервале, а затем оцениваем функцию в конечных точках интервала. При работе с функцией двух переменных замкнутый интервал заменяется замкнутым ограниченным множеством. Набор ограничено , если все точки этого множества могут содержаться в шаре (или круге) конечного радиуса. Во-первых, нам нужно найти критические точки внутри множества и вычислить соответствующие критические значения. Затем необходимо найти максимальное и минимальное значение функции на границе множества. Когда у нас есть все эти значения, наибольшее значение функции соответствует глобальному максимуму, а наименьшее значение функции соответствует абсолютному минимуму. Однако сначала нам нужно убедиться, что такие ценности существуют. Следующая теорема делает это. Когда у нас есть все эти значения, наибольшее значение функции соответствует глобальному максимуму, а наименьшее значение функции соответствует абсолютному минимуму. Однако сначала нам нужно убедиться, что такие ценности существуют. Следующая теорема делает это. Теорема
4.18 Теорема об экстремальных значениях Непрерывная функция f(x,y)f(x,y) на замкнутом и ограниченном множестве DD на плоскости достигает абсолютного максимального значения в некоторой точке DD и абсолютного минимума в некоторой точке D.D. Теперь, когда мы знаем, что любая непрерывная функция ff, определенная на замкнутом ограниченном множестве, достигает своих экстремальных значений, нам нужно знать, как их найти. Теорема
4.19 Нахождение экстремальных значений функции двух переменных Предположим, что z=f(x,y)z=f(x,y) является дифференцируемой функцией двух переменных, заданной на замкнутом ограниченном множестве Д. Д. Тогда ff достигнет абсолютного максимального значения и абсолютного минимального значения, которые являются, соответственно, наибольшим и наименьшим значением, найденным среди следующих: Д. Тогда ff достигнет абсолютного максимального значения и абсолютного минимального значения, которые являются, соответственно, наибольшим и наименьшим значением, найденным среди следующих: - Значения ff в критических точках ff в D.D.
- Значения ff на границе Д.Д.
Доказательство этой теоремы является прямым следствием теоремы об экстремальном значении и теоремы Ферма. В частности, если какой-либо из экстремумов не находится на границе D,D, то он находится во внутренней точке D.D. Но внутренняя точка (x0,y0)(x0,y0) DD, являющаяся абсолютным экстремумом, также является локальным экстремумом; следовательно, (x0,y0)(x0,y0) — критическая точка ff по теореме Ферма. Поэтому единственными возможными значениями глобальных экстремумов ff на DD являются экстремальные значения ff внутри или на границе DD. Стратегия решения проблем Стратегия решения проблем: поиск абсолютных максимальных и минимальных значений Пусть z=f(x,y)z=f(x,y) — непрерывная функция двух переменных, определенная на замкнутом ограниченном множестве D,D, и предположим, что ff дифференцируема на D. D. Чтобы найти абсолютные максимум и минимум значений ff на D,D, сделайте следующее: D. Чтобы найти абсолютные максимум и минимум значений ff на D,D, сделайте следующее: - Определите критические точки ff на D.D.
- Рассчитайте ff в каждой из этих критических точек.
- Определите максимальное и минимальное значения ff на границе его области.
- Максимальное и минимальное значения ff будут соответствовать одному из значений, полученных на шагах 2 и 3.2 и 3.
Нахождение максимального и минимального значений ff на границе DD может быть сложной задачей. Если граница представляет собой прямоугольник или набор прямых линий, то можно параметризовать отрезки и определить максимумы на каждом из этих отрезков, как показано в примере 4.40. Тот же подход можно использовать для других фигур, таких как круги и эллипсы. Если граница множества DD представляет собой более сложную кривую, определяемую функцией g(x,y)=cg(x,y)=c для некоторой константы c,c, и существуют частные производные первого порядка от gg, тогда метод множителей Лагранжа может оказаться полезным для определения экстремумов функции ff на границе. Метод множителей Лагранжа представлен в разделе «Множители Лагранжа». Метод множителей Лагранжа представлен в разделе «Множители Лагранжа». Пример
4.40 Нахождение абсолютных экстремумов Используйте стратегию решения задач для нахождения абсолютных экстремумов функции, чтобы определить абсолютные экстремумы каждой из следующих функций: - f(x,y)=x2−2xy+4y2−4x− 2y+24f(x,y)=x2−2xy+4y2−4x−2y+24 в области, определяемой соотношениями 0≤x≤40≤x≤4 и 0≤y≤20≤y≤2
- g(x,y)=x2+y2+4x−6yg(x,y)=x2+y2+4x−6y в области, определяемой как x2+y2≤16×2+y2≤16
Решение- Используя стратегию решения проблем, шаг 11 включает в себя поиск критических точек ff на его области определения. Поэтому мы сначала вычисляем fx(x,y)fx(x,y) и fy(x,y),fy(x,y), а затем устанавливаем их равными нулю:
fx(x,y)=2x− 2y−4fy(x,y)=−2x+8y−2.fx(x,y)=2x−2y−4fy(x,y)=−2x+8y−2.
Приравняв их к нулю, получим систему уравнений 2x−2y−4=0−2x+8y−2=0,2x−2y−4=0−2x+8y−2=0.
Решение этой системы x=3x=3 и y=1.y=1. Следовательно, (3,1)(3,1) является критической точкой ф.ф. Вычисление f(3,1)f(3,1) дает f(3,1)=17.f(3,1)=17.
. Следующий шаг заключается в нахождении экстремумов функции ff на границе области ее определения. Граница его домена состоит из четырех отрезков, как показано на следующем графике:
Рисунок
4,52
График области определения функции f(x,y)=x2−2xy+4y2−4x−2y+24.f(x,y)=x2−2xy+4y2−4x−2y+24.
L1L1 — это отрезок, соединяющий (0,0)(0,0) и (4,0),(4,0), и его можно параметризовать уравнениями x(t)=t,y(t) =0x(t)=t,y(t)=0 для 0≤t≤4.0≤t≤4. Определить g(t)=f(x(t),y(t)).g(t)=f(x(t),y(t)). Это дает g(t)=t2−4t+24.g(t)=t2−4t+24. Дифференциация г приводит к g′(t)=2t−4.g′(t)=2t−4. Следовательно, gg имеет критическое значение при t=2,t=2, что соответствует точке (2,0).(2,0). Вычисление f(2,0)f(2,0) дает z- значение 20,20.
L2L2 — это отрезок, соединяющий (4,0)(4,0) и (4,2),(4,2), и его можно параметризовать уравнениями x(t)=4,y(t)= tx(t)=4,y(t)=t для 0≤t≤2,0≤t≤2. Снова определите g(t)=f(x(t),y(t)).g(t)=f(x(t),y(t)). Это дает g(t)=4t2−10t+24.g(t)=4t2−10t+24. Тогда g′(t)=8t−10.g′(t)=8t−10.gg имеет критическое значение при t=54,t=54, что соответствует точке (4,54).(4, 54). Вычисление f(4,54)f(4,54) дает z- значение 17.75.17.75. Снова определите g(t)=f(x(t),y(t)).g(t)=f(x(t),y(t)). Это дает g(t)=4t2−10t+24.g(t)=4t2−10t+24. Тогда g′(t)=8t−10.g′(t)=8t−10.gg имеет критическое значение при t=54,t=54, что соответствует точке (4,54).(4, 54). Вычисление f(4,54)f(4,54) дает z- значение 17.75.17.75.
L3L3 — это отрезок, соединяющий (0,2)(0,2) и (4,2),(4,2), и его можно параметризовать уравнениями x(t)=t,y(t)= 2x(t)=t,y(t)=2 для 0≤t≤4,0≤t≤4. Снова определите g(t)=f(x(t),y(t)).g(t)=f(x(t),y(t)). Это дает g(t)=t2−8t+36.g(t)=t2−8t+36. Критическое значение соответствует точке (4,2).(4,2). Таким образом, вычисление f(4,2)f(4,2) дает значение z- 20,20.
L4L4 — это отрезок, соединяющий (0,0)(0,0) и (0,2),(0,2), и его можно параметризовать уравнениями x(t)=0,y(t)= tx(t)=0,y(t)=t для 0≤t≤2,0≤t≤2. На этот раз g(t)=4t2−2t+24g(t)=4t2−2t+24 и критическое значение t=14t=14 соответствуют точке (0,14).(0,14). Вычисление f(0,14)f(0,14) дает z- значение 23. 75.23.75. 75.23.75.
Нам также нужно найти значения f(x,y)f(x,y) в углах области его определения. Эти углы расположены в точках (0,0),(4,0),(4,2)и(0,2):(0,0),(4,0),(4,2)и(0, 2): f(0,0)=(0)2−2(0)(0)+4(0)2−4(0)−2(0)+24=24f(4,0)=( 4)2−2(4)(0)+4(0)2−4(4)−2(0)+24=24f(4,2)=(4)2−2(4)(2)+ 4(2)2−4(4)−2(2)+24=20f(0,2)=(0)2−2(0)(2)+4(2)2−4(0)−2 (2)+24=36.f(0,0)=(0)2−2(0)(0)+4(0)2−4(0)−2(0)+24=24f(4, 0)=(4)2−2(4)(0)+4(0)2−4(4)−2(0)+24=24f(4,2)=(4)2−2(4) (2)+4(2)2−4(4)−2(2)+24=20f(0,2)=(0)2−2(0)(2)+4(2)2−4( 0)−2(2)+24=36.
Абсолютное максимальное значение равно 36,36, что соответствует точкам (0,2),(0,2), а глобальное минимальное значение равно 17,17, что соответствует точкам (3,1)(3,1) как показано на следующем рисунке.
Рисунок
4,53
Функция f(x,y)f(x,y) имеет один глобальный минимум и один глобальный максимум в своей области определения. - Используя стратегию решения проблем, шаг 11 включает в себя поиск критических точек gg в его домене. Поэтому мы сначала вычисляем gx(x,y)gx(x,y) и gy(x,y),gy(x,y), а затем устанавливаем их равными нулю:
gx(x,y)=2x+4gy(x,y)=2y−6. gx(x,y)=2x+4gy(x,y)=2y−6. gx(x,y)=2x+4gy(x,y)=2y−6.
Приравняв их к нулю, получим систему уравнений 2x+4=02y−6=0,2x+4=02y−6=0.
Решением этой системы является x=−2x=−2 и y=3.y=3. Следовательно, (−2,3)(−2,3) является критической точкой g.g. Вычисляя g(−2,3),g(−2,3), получаем g(−2,3)=(−2)2+32+4(−2)−6(3)=4+9 −8−18=−13.g(−2,3)=(−2)2+32+4(−2)−6(3)=4+9−8−18=−13.
Следующим шагом является нахождение экстремумов g на границе области его определения. Граница его домена состоит из окружности радиусом 44 с центром в начале координат, как показано на следующем графике.
Рисунок
4,54
График области определения функции g(x,y)=x2+y2+4x−6y.g(x,y)=x2+y2+4x−6y.
Граница области определения gg может быть параметризована с помощью функций x(t)=4cost,y(t)=4sintx(t)=4cost,y(t)=4sint для 0≤t≤2π.0≤t ≤2π. Определить h(t)=g(x(t),y(t)):h(t)=g(x(t),y(t)): h(t)=g(x(t), y(t))=(4cost)2+(4sint)2+4(4cost)−6(4sint)=16cos2t+16sin2t+16cost−24sint=16+16cost−24sint. h(t)=g(x(t) ),y(t))=(4cost)2+(4sint)2+4(4cost)−6(4sint)=16cos2t+16sin2t+16cost−24sint=16+16cost−24sint. h(t)=g(x(t) ),y(t))=(4cost)2+(4sint)2+4(4cost)−6(4sint)=16cos2t+16sin2t+16cost−24sint=16+16cost−24sint.
Установка h′(t)=0h′(t)=0 приводит к 24cost-16sint-16cost=24cost-16costtant=-32.
Это уравнение имеет два решения в интервале 0≤t≤2π.0≤t≤2π. Одно из них t=π−arctan(32)t=π−arctan(32), а другое t=2π−arctan(32).t=2π−arctan(32). Для первого угла sint=sin(π−arctan(32))=sin(arctan(32))=31313cost=cos(π−arctan(32))=−cos(arctan(32))=−21313. sint=sin(π-arctan(32))=sin(arctan(32))=31313cost=cos(π-arctan(32))=-cos(arctan(32))=-21313.
Следовательно, x(t)=4cost=-81313x(t)=4cost=-81313 и y(t)=4sint=121313,y(t)=4sint=121313, поэтому (-81313,121313)(-81313 ,121313) является критической точкой на границе и 208−1041313≈−12,844.g(−81313,121313)=(−81313)2+(121313)2+4(−81313)−6(121313)=14413+6413−321313−721313=208−1041313≈− 12.844.
Для второго угла sint=sin(2π−arctan(32))=−sin(arctan(32))=−31313cost=cos(2π−arctan(32))=cos(arctan(32))= 21313.sint=sin(2π-arctan(32))=-sin(arctan(32))=-31313cost=cos(2π-arctan(32))=cos(arctan(32))=21313.
Следовательно, x(t)=4cost=81313x(t)=4cost=81313 и y(t)=4sint=-121313,y(t)=4sint=-121313, поэтому (81313,-121313)(81313, −121313) — критическая точка на границе, а 208+1041313≈44,844.g(81313,−121313)=(81313)2+(−121313)2+4(81313)−6(−121313)=14413+6413+321313+721313=208+1041313≈44,844.
Абсолютный минимум г равен −13,−13 и достигается в точке (−2,3),(−2,3), которая является внутренней точкой Д . Абсолютный максимум г примерно равен 44,844, который достигается в граничной точке (81313,-121313).(81313,-121313). Это абсолютные экстремумы г на D , как показано на следующем рисунке.
Рисунок
4,55
Функция f(x,y)f(x,y) имеет локальный минимум и локальный максимум.
Контрольно-пропускной пункт
4,36 Используйте стратегию решения задач для нахождения абсолютных экстремумов функции, чтобы найти абсолютные экстремумы функции f(x,y)=4×2−2xy+6y2−8x+2y+3f(x,y)=4×2−2xy+6y2−8x+2y+3 в области, определенной как 0≤x≤20≤ x≤2 и −1≤y≤3. −1≤y≤3. −1≤y≤3. Пример
4.41 Открытие главы: прибыльные мячи для гольфа Рисунок
4,56
(кредит: модификация работы oatsy40, Flickr) Компания Pro-TT разработала модель прибыли, которая зависит от количества x мячей для гольфа, проданных в месяц (измеряется в тысячах), и количества часов в месяц реклама y , согласно функции z=f(x,y)=48x+96y-x2-2xy-9y2,z=f(x,y)=48x+96y-x2-2xy-9y2, где zz измеряется в тысячах долларов. Максимальное количество мячей для гольфа, которое можно произвести и продать, составляет 50 000 50 000, а максимальное количество часов рекламы, которое можно купить, — 25,25. Найдите значения xx и yy, которые максимизируют прибыль, и найдите максимальную прибыль. Решение Используя стратегию решения проблем, шаг 11 включает в себя поиск критических точек ff на его области определения. Поэтому мы сначала вычисляем fx(x,y)fx(x,y) и fy(x,y),fy(x,y), а затем устанавливаем их равными нулю: Поэтому мы сначала вычисляем fx(x,y)fx(x,y) и fy(x,y),fy(x,y), а затем устанавливаем их равными нулю: fx(x,y)=48−2x−2yfy(x,y)=96−2x−18y.fx(x,y)=48−2x−2yfy(x,y)=96−2x−18y. Приравняв их к нулю, получим систему уравнений 48−2x−2y=096−2x−18y=0,48−2x−2y=096−2x−18y=0. Решение этой системы x=21x=21 и y=3.y=3. Следовательно, (21,3)(21,3) является критической точкой ф.ф. Вычисление f(21,3)f(21,3) дает f(21,3)=48(21)+96(3)−212−2(21)(3)−9(3)2=648.f (21,3)=48(21)+96(3)−212−2(21)(3)−9(3)2=648. Область определения этой функции составляет 0≤x≤500≤x≤50 и 0≤y≤250≤y≤25, как показано на следующем графике. Рисунок
4,57
График области определения функции f(x,y)=48x+96y-x2-2xy-9y2.f(x,y)=48x+96y-x2-2xy-9y2. L1L1 — это отрезок, соединяющий (0,0)(0,0) и (50,0),(50,0), и его можно параметризовать уравнениями x(t)=t,y(t) =0x(t)=t,y(t)=0 для 0≤t≤50,0≤t≤50. Затем мы определяем g(t)=f(x(t),y(t)):g(t)=f(x(t),y(t)): g(t)=f(x( t),y(t))=f(t,0)=48t+96(0)−y2−2(t)(0)−9(0)2=48t−t2. g(t)=f( x(t),y(t))=f(t,0)=48t+96(0)−y2−2(t)(0)−9(0)2=48t−t2. g(t)=f( x(t),y(t))=f(t,0)=48t+96(0)−y2−2(t)(0)−9(0)2=48t−t2. Установка g′(t)=0g′(t)=0 дает критическую точку t=24,t=24, которая соответствует точке (24,0)(24,0) в области f.f. Вычисление f(24,0)f(24,0) дает 576,576. L2L2 — это отрезок, соединяющий и (50,25),(50,25), и его можно параметризовать уравнениями x(t)=50,y(t)=tx(t)=50,y( t)=t для 0≤t≤25,0≤t≤25. Еще раз определяем g(t)=f(x(t),y(t)):g(t)=f(x(t),y(t)): g(t)=f( x(t),y(t))=f(50,t)=48(50)+96t−502−2(50)t−9t2=−9t2−4t−100.g(t)=f(x (t),y(t))=f(50,t)=48(50)+96t−502−2(50)t−9t2=−9t2−4t−100. Эта функция имеет критическую точку при t=−29,t=−29, что соответствует точке (50,−29).(50,−29). Эта точка не находится в области определения ф.ф. L3L3 — это отрезок, соединяющий (0,25) и (50,25), (0,25) и (50,25), и он может быть параметризован уравнениями x(t)=t,y(t )=25x(t)=t,y(t)=25 для 0≤t≤50,0≤t≤50. Определим g(t)=f(x(t),y(t)):g(t)=f(x(t),y(t)): g(t)=f(x(t ),y(t))=f(t,25)=48t+96(25)−t2−2t(25)−9(252)=−t2−2t−3225. g(t)=f(x( t),y(t))=f(t,25)=48t+96(25)−t2−2t(25)−9(252)=−t2−2t−3225. g(t)=f(x( t),y(t))=f(t,25)=48t+96(25)−t2−2t(25)−9(252)=−t2−2t−3225. Эта функция имеет критическую точку при t=−1,t=−1, что соответствует точке (−1,25),(−1,25), которая не находится в области определения. L4L4 — это отрезок, соединяющий (0,0) с (0,25), (0,0) с (0,25), и его можно параметризовать уравнениями x(t)=0,y(t )=tx(t)=0,y(t)=t для 0≤t≤25,0≤t≤25. Определим g(t)=f(x(t),y(t)):g(t)=f(x(t),y(t)): g(t)=f(x(t ),y(t))=f(0,t)=48(0)+96t−(0)2−2(0)t−9t2=96t−t2.g(t)=f(x(t) ,y(t))=f(0,t)=48(0)+96t−(0)2−2(0)t−9t2=96t−t2. Эта функция имеет критическую точку при t=163,t=163, что соответствует точке (0,163),(0,163), находящейся на границе области. Вычисление f(0,163)f(0,163) дает 256,256. Нам также нужно найти значения f(x,y)f(x,y) в углах его области. Эти углы расположены в точках (0,0),(50,0),(50,25)и(0,25):(0,0),(50,0),(50,25)и(0, 25): f(0,0)=48(0)+96(0)−(0)2−2(0)(0)−9(0)2=0f(50,0)=48( 50)+96(0)−(50)2−2(50)(0)−9(0)2=−100f(50,25)=48(50)+96(25)−(50)2− 2(50)(25)−9(25)2=−5825f(0,25)=48(0)+96(25)−(0)2−2(0)(25)−9(25)2 =−3225. f(0,0)=48(0)+96(0)−(0)2−2(0)(0)−9(0)2=0f(50,0)=48(50 )+96(0)−(50)2−2(50)(0)−9(0)2=−100f(50,25)=48(50)+96(25)−(50)2−2 (50)(25)−9(25)2=-5825f(0,25)=48(0)+96(25)-(0)2-2(0)(25)-9(25)2=-3225. f(0,0)=48(0)+96(0)−(0)2−2(0)(0)−9(0)2=0f(50,0)=48(50 )+96(0)−(50)2−2(50)(0)−9(0)2=−100f(50,25)=48(50)+96(25)−(50)2−2 (50)(25)−9(25)2=-5825f(0,25)=48(0)+96(25)-(0)2-2(0)(25)-9(25)2=-3225. Максимальное критическое значение равно 648 648, что соответствует (21,3).(21,3). Следовательно, максимальная прибыль в размере 648 000 долларов США 648 000 долларов США достигается при продаже 21 000–21 000 мячей для гольфа и покупке 33 часов рекламы в месяц, как показано на следующем рисунке. Рисунок
4,58
Функция прибыли f(x,y)f(x,y) имеет максимум при (21,3,648).(21,3,648). Раздел 4.7 Упражнения Для следующих упражнений найдите все критические точки. 310. f(x,y)=1+x2+y2f(x,y)=1+x2+y2 311. f(x,y)=(3x−2)2+(y−4)2f(x,y)=(3x−2)2+(y−4)2 312. f(x,y)=x4+y4−16xyf(x,y)=x4+y4−16xy 313. f(x,y)=15×3−3xy+15y3f(x,y)=15×3−3xy+15y3 В следующих упражнениях найдите критические точки функции, используя алгебраические методы (заполнение квадрата) или исследуя форму уравнения. Проверьте свои результаты, используя тест частных производных. 314. f(x,y)=x2+y2+1f(x,y)=x2+y2+1 315. f(x,y)=−x2−5y2+8x−10y−13f(x,y)=−x2−5y2+8x−10y−13 316. f(x,y)=x2+y2+2x−6y+6f(x,y)=x2+y2+2x−6y+6 317. f(x,y)=x2+y2+1f(x,y)=x2+y2+1 В следующих упражнениях используйте критерий второй производной, чтобы классифицировать любые критические точки и определить, является ли каждая критическая точка максимумом, минимумом, седловой точкой или ни одной из них. 318. f(x,y)=-x3+4xy-2y2+1f(x,y)=-x3+4xy-2y2+1 319. f(x,y)=x2y2f(x,y)=x2y2 320. f(x,y)=x2−6x+y2+4y−8f(x,y)=x2−6x+y2+4y−8 321. f(x,y)=2xy+3x+4yf(x,y)=2xy+3x+4y 322. f(x,y)=8xy(x+y)+7f(x,y)=8xy(x+y)+7 323. f(x,y)=x2+4xy+y2f(x,y)=x2+4xy+y2 324. f(x,y)=x3+y3−300x−75y−3f(x,y)=x3+y3−300x−75y−3 325. f(x,y)=9−x4y4f(x,y)=9−x4y4 326. f(x,y)=7x2y+9xy2f(x,y)=7x2y+9xy2 327. f(x,y)=3×2−2xy+y2−8yf(x,y)=3×2−2xy+y2−8y 328. f(x,y)=3×2+2xy+y2f(x,y)=3×2+2xy+y2 329. f(x,y)=y2+xy+3y+2x+3f(x,y)=y2+xy+3y+2x+3 330. f(x,y)=x2+xy+y2−3xf(x,y)=x2+xy+y2−3x 331. f(x,y)=x2+2y2−x2yf(x,y)=x2+2y2−x2y 332. f(x,y)=x2+y−eyf(x,y)=x2+y−ey 333. f(x,y)=e-(x2+y2+2x)f(x,y)=e-(x2+y2+2x) 334. f(x,y)=x2+xy+y2−x−y+1f(x,y)=x2+xy+y2−x−y+1 335. f(x,y)=x2+10xy+y2f(x,y)=x2+10xy+y2 336. f(x,y)=−x2−5y2+10x−30y−62f(x,y)=−x2−5y2+10x−30y−62 337. f(x,y)=120x+120y-xy-x2-y2f(x,y)=120x+120y-xy-x2-y2 338. f(x,y)=2×2+2xy+y2+2x−3f(x,y)=2×2+2xy+y2+2x−3 339. f(x,y)=x2+x−3xy+y3−5f(x,y)=x2+x−3xy+y3−5 340. f(x,y)=2xye-x2-y2f(x,y)=2xye-x2-y2 Для следующих упражнений определите экстремальные значения и седловые точки. Используйте CAS для построения графика функции. Используйте CAS для построения графика функции. 341. [T] f(x,y)=yex-eyf(x,y)=yex-ey 342. [T] f(x,y)=xsin(y)f(x,y)=xsin(y) 343. [T] f(x,y)=sin(x)sin(y),x∈(0,2π),y∈(0,2π)f(x,y)=sin(x)sin (y),x∈(0,2π),y∈(0,2π) Найти абсолютные экстремумы заданной функции на указанном замкнутом и ограниченном множестве R.R. 344. f(x,y)=xy−x−3y;f(x,y)=xy−x−3y;RR — треугольная область с вершинами (0,0),(0,4) и (5 ,0).(0,0),(0,4)и(5,0). 345. Найти абсолютные максимум и минимум значений f(x,y)=x2+y2−2y+1f(x,y)=x2+y2−2y+1 в области R={(x,y)|x2 +y2≤4}.R={(x,y)|x2+y2≤4}. 346. f(x,y)=x3−3xy−y3f(x,y)=x3−3xy−y3 на R={(x,y):−2≤x≤2,−2≤y≤2}R ={(x,y):−2≤x≤2,−2≤y≤2} 347. f(x,y)=−2yx2+y2+1f(x,y)=−2yx2+y2+1 на R={(x,y):x2+y2≤4}R={(x,y ):x2+y2≤4} 348. Найдите три положительных числа, сумма которых равна 27,27, и сумма их квадратов как можно меньше. 349. Найдите точки на поверхности x2-yz=5×2-yz=5, ближайшие к началу координат. 350. Найдите максимальный объем прямоугольного ящика с тремя гранями в координатных плоскостях и вершиной в первом октанте на плоскости x+y+z=1.x+y+z=1. 351. Сумма длины и обхвата (периметр поперечного сечения) посылки, перевозимой службой доставки, не может превышать 108108 дюймов. Найдите размеры прямоугольной посылки наибольшего объема, которую можно отправить. 352. Коробка картонная без крышки должна быть изготовлена объемом 44 фута 3 . Найдите размеры коробки, для которой требуется наименьшее количество картона. 353. Найдите точку на поверхности f(x,y)=x2+y2+10f(x,y)=x2+y2+10, ближайшую к плоскости x+2y-z=0.x+2y-z=0. Определите точку на плоскости. 354. Найдите точку на плоскости 2x−y+2z=162x−y+2z=16, ближайшую к началу координат. 355. Компания производит два вида спортивной обуви: кроссовки и кроссовки. Общий доход от xx единиц кроссовок и yy единиц кроссовок равен R(x,y)=−5×2−8y2−2xy+42x+102y,R(x,y)=−5×2−8y2−2xy +42x+102y, где xx и yy выражены в тысячах единиц. Найдите значения x и y , чтобы максимизировать общий доход. 356. Транспортная компания обрабатывает прямоугольные ящики, если сумма длины, ширины и высоты ящика не превышает 9696 дюймов. Найдите размеры ящика, удовлетворяющего этому условию и имеющего наибольший объем. 357. Найдите максимальный объем цилиндрической банки из-под газировки, сумма высоты и окружности которой равна 120120 см. 1.3: Скорость изменения и поведение графиков- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 1294
Цели обучения - Найти среднюю скорость изменения функции.
- Используйте график, чтобы определить, где функция увеличивается, уменьшается или остается постоянной.
- Используйте график, чтобы найти локальные максимумы и локальные минимумы.
- Используйте график для определения абсолютного максимума и абсолютного минимума.

За последние несколько десятилетий цены на бензин сильно колебались. В таблице \(\PageIndex{1}\) указана средняя стоимость галлона бензина в долларах за 2005–2012 годы. Стоимость бензина можно рассматривать как функцию года. Таблица \(\PageIndex{1}\)| \(у\) | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 |
|---|
| \(С(у)\) | 2,31 | 2,62 | 2,84 | 3,30 | 2,41 | 2,84 | 3,58 | 3,68 |
|---|
Если бы нас интересовало только изменение цен на бензин в период с 2005 по 2012 год, мы могли бы подсчитать, что стоимость галлона увеличилась с 2,31 доллара до 3,68 доллара, то есть на 1,37 доллара. Хотя это интересно, было бы полезнее посмотреть, насколько цена изменилась за год. В этом разделе мы рассмотрим подобные изменения. Хотя это интересно, было бы полезнее посмотреть, насколько цена изменилась за год. В этом разделе мы рассмотрим подобные изменения. Нахождение средней скорости изменения функции Изменение цены за год представляет собой скорость изменения , потому что она описывает, как изменяется выходное количество по отношению к изменению входного количества. Мы видим, что цена бензина в таблице \(\PageIndex{1}\) не менялась на одну и ту же величину каждый год, поэтому скорость изменения не была постоянной. Если бы мы использовали только начальные и конечные данные, мы бы нашли среднюю скорость изменения за указанный период времени. Чтобы найти среднюю скорость изменения, мы делим изменение выходной стоимости на изменение входной стоимости. \[\begin{align*} \text{Средняя скорость изменения}&=\dfrac{\text{Изменение на выходе}}{\text{Изменение на входе}} \\[4pt] &=\dfrac{ \Delta y}{\Delta x}\\[4pt] &=\dfrac{y_2-y_1}{x_2-x_1}\\[4pt] &=\dfrac{f(x_2)-f(x_1)}{x_2 -x_1}\end{align*} \label{1. 3.1}\] 3.1}\] Греческая буква \(\Delta\) (дельта) означает изменение количества; мы читаем соотношение как «дельта-\(y\) над дельта-\(x\)» или «изменение \(y\), деленное на изменение \(x\)». Иногда мы пишем \(\Delta f\) вместо \(\Delta y\), что по-прежнему представляет собой изменение выходного значения функции в результате изменения ее входного значения. Это не означает, что мы меняем функцию на какую-то другую функцию. В нашем примере цена на бензин увеличилась на 1,37 доллара США с 2005 по 2012 год. Средняя скорость изменения за 7 лет составила \[\dfrac{\Delta y}{\Delta x}=\dfrac{$1,37}{ 7 \text{лет}}\примерно \text{0,196 доллара в год.} \label{1.3.2}\] В среднем цена на газ увеличивалась примерно на 19,6 цента каждый год. Другие примеры скорости изменений включают: - Популяция крыс, увеличивающаяся на 40 крыс в неделю
- Автомобиль, движущийся со скоростью 68 миль в час (пройденное расстояние изменяется на 68 миль каждый час с течением времени)
- Автомобиль, расходующий 27 миль на галлон (пройденное расстояние изменяется на 27 миль на каждый галлон)
- Ток в электрической цепи увеличивается на 0,125 ампера на каждый вольт повышенного напряжения
- Сумма денег на счету колледжа уменьшается на 4000 долларов за квартал
Определение: Скорость изменения Скорость изменения описывает, как изменяется выходная величина по отношению к изменению входной величины. Единицы скорости изменения — это «единицы вывода на единицы ввода». Единицы скорости изменения — это «единицы вывода на единицы ввода». Средняя скорость изменения между двумя входными значениями равна общему изменению значений функции (выходных значений), деленному на изменение входных значений. \[\dfrac{\Delta y}{\Delta x}=\dfrac{f(x_2)-f(x_1)}{x_2-x_1}\] Как… Учитывая значение функцию в разных точках, вычислить среднюю скорость изменения функции для интервала между двумя значениями \(x_1\) и \(x_2\). - Вычислите разницу \(y_2−y_1=\Delta y\).
- Вычислить разницу \(x_2−x_1=\Delta x\).
- Найдите соотношение \(\dfrac{\Delta y}{\Delta x}\).
Пример \(\PageIndex{1}\): вычисление средней скорости изменения Используя данные в таблице \(\PageIndex{1}\), найдите среднюю скорость изменения цены на бензин в период с 2007 г. и 2009. Решение В 2007 году цена бензина составляла 2,84 доллара. В 2009 году стоимость составляла 2,41 доллара. Средняя скорость изменения Средняя скорость изменения \[\begin{align*} \dfrac{\Delta y}{\Delta x}&=\dfrac{y_2−y_1}{x_2−x_1} \\[4pt] &=\dfrac{$2,41−$2,84} {2009−2007} \\[4pt] &=\dfrac{-0,43$}{2 \text{ лет}} \\[4pt] &=-0,22$ \text{ в год} \end{align*}\] Анализ Обратите внимание, что снижение выражается отрицательным изменением или «отрицательным увеличением». Скорость изменения является отрицательной, когда выход уменьшается по мере увеличения входа или когда выход увеличивается по мере уменьшения входа. Упражнение \(\PageIndex{1}\) Используя данные в таблице \(\PageIndex{1}\), найдите среднюю скорость изменения между 2005 и 2010 годами. - Решение
\(\dfrac{2,84$−2,315$}{5 \text{ лет}} =\dfrac{0,535$}{5 \text{ лет}} = 0,106$ \text{в год.}\)
Пример \(\PageIndex{2}\): вычисление средней скорости изменения по графику Учитывая функцию \(g(t)\), показанную на рисунке \(\PageIndex{1}\), найти среднее скорость изменения на интервале \([−1,2]\). Рисунок \(\PageIndex{1}\): График параболы. Решение При \(t=−1\) на рисунке \(\PageIndex{2}\) показано \(g(−1)=4\). При \(t=2\) на графике показано \(g(2)=1\). Рисунок \(\PageIndex{2}\): График параболы с линией из точек (-1, 4) и (2, 1), показывающий изменения g(t) и t. Горизонтальное изменение \(\Delta t=3\) показано красной стрелкой, а вертикальное изменение \(\Delta g(t)=−3\) показано бирюзовой стрелкой. Выход изменяется на -3, а вход изменяется на 3, что дает среднюю скорость изменения \[\dfrac{1−4}{2−(−1)}=\dfrac{−3}{3}=−1\] Анализ Обратите внимание, что порядок, который мы выбираем, очень важен . Если, например, мы используем \(\dfrac{y_2−y_1}{x_1−x_2}\), мы не получим правильный ответ. Решите, какая точка будет 1, а какая 2, и сохраните фиксированные координаты как \((x_1,y_1)\) и \((x_2,y_2)\). Пример \(\PageIndex{3}\): вычисление средней скорости изменения по таблице После встречи с другом, который живет в 10 милях от нее, Анна записывает свое расстояние от дома с течением времени. Значения показаны в таблице \(\PageIndex{2}\). Найдите ее среднюю скорость за первые 6 часов. Значения показаны в таблице \(\PageIndex{2}\). Найдите ее среднюю скорость за первые 6 часов. Таблица \(\PageIndex{2}\)| \(т\) (часы) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|
| \(D(t)\) (мили) | 10 | 55 | 90 | 153 | 214 | 240 | 292 | 300 |
|---|
Решение Здесь средняя скорость — это средняя скорость изменения. Она проехала 292 мили за 6 часов со средней скоростью \[\begin{align*}\dfrac{292−10}{6−0}&=\dfrac{282}{6}\\[4pt] &= 47\end{align*}\] Средняя скорость составляет около 47 миль в час. Анализ Поскольку скорость непостоянна, средняя скорость зависит от выбранного интервала. Для интервала \([2,3]\) средняя скорость составляет 63 мили в час. 92−\frac{1}{4} \\[4pt] &=4−\frac{1}{2} &=16−\frac{1}{4} \\[4pt] &=72 &=\ frac{63}{4}\end{align*}\] Теперь вычислим среднюю скорость изменения. \[\begin{align*}\text{Средняя скорость изменения} &=\dfrac{f(4)−f(2)}{4−2} \\[4pt] &=\dfrac{\frac {63}{4}-\frac{7}{2}}{4-2} \\[4pt] &=\dfrac{\frac{49}{4}}{2} \\[4pt] &= \dfrac{49}{8}\end{align*}\] Упражнение \(\PageIndex{2}\) Найдите среднюю скорость изменения \(f(x)=x−2\sqrt{ x}\) на интервале \([1, 92+2x−8\) на отрезке \([5, a]\). - Раствор
\(а+7\)
Использование графика для определения возрастания, убывания или постоянства функции В рамках изучения изменения функций мы можем определить интервалы, в течение которых функция изменяется определенным образом. Мы говорим, что функция возрастает на интервале, если значения функции увеличиваются по мере увеличения входных значений в этом интервале. Точно так же функция убывает на интервале, если значения функции уменьшаются по мере увеличения входных значений на этом интервале. Средняя скорость изменения возрастающей функции положительна, а средняя скорость изменения убывающей функции отрицательна. На рисунке \(\PageIndex{3}\) показаны примеры увеличения и уменьшения интервалов функции. 93−12x\) возрастает на \((−\infty, −2)\cup (2,\infty)\) и убывает на \((−2, 2)\). Мы говорим, что функция возрастает на интервале, если значения функции увеличиваются по мере увеличения входных значений в этом интервале. Точно так же функция убывает на интервале, если значения функции уменьшаются по мере увеличения входных значений на этом интервале. Средняя скорость изменения возрастающей функции положительна, а средняя скорость изменения убывающей функции отрицательна. На рисунке \(\PageIndex{3}\) показаны примеры увеличения и уменьшения интервалов функции. 93−12x\) возрастает на \((−\infty, −2)\cup (2,\infty)\) и убывает на \((−2, 2)\). В то время как некоторые функции возрастают (или убывают) по всей области определения, многие другие — нет. Значение входа, при котором функция изменяется с возрастающей на убывающую (по мере движения слева направо, то есть по мере увеличения входной переменной), называется локальным максимумом . Если функция имеет более одного, мы говорим, что она имеет локальные максимумы. Точно так же значение входа, при котором функция изменяется с убывающей на возрастающую по мере увеличения входной переменной, называется местный минимум . Форма множественного числа — «локальные минимумы». Вместе локальные максимумы и минимумы называются локальными экстремумами или локальными экстремальными значениями функции. (Форма единственного числа — «экстремум».) Часто термин «локальный» заменяется термином «относительный». В этом тексте мы будем использовать термин локальный. Форма множественного числа — «локальные минимумы». Вместе локальные максимумы и минимумы называются локальными экстремумами или локальными экстремальными значениями функции. (Форма единственного числа — «экстремум».) Часто термин «локальный» заменяется термином «относительный». В этом тексте мы будем использовать термин локальный. Ясно, что функция не возрастает и не убывает на интервале, где она постоянна. Функция также не возрастает и не убывает в экстремумах. Обратите внимание, что мы должны говорить о локальных экстремумах, потому что любой данный локальный экстремум, как определено здесь, не обязательно является самым высоким максимумом или самым низким минимумом во всей области определения функции. Для функции, график которой показан на рисунке \(\PageIndex{4}\), локальный максимум равен 16, и он приходится на \(x=−2\). Локальный минимум равен −16 и возникает при \(x=2\). Рисунок \(\PageIndex{4}\): График полинома, показывающий возрастающие и убывающие интервалы и локальный максимум.  график достигает наибольшей и наименьшей точек соответственно на открытом интервале. Подобно вершине американских горок, график функции в локальном максимуме выше, чем в соседних точках с обеих сторон. График также будет ниже в локальном минимуме, чем в соседних точках. Рисунок \(\PageIndex{5}\) иллюстрирует эти идеи для локального максимума. Рисунок \(\PageIndex{5}\): Определение локального максимума Эти наблюдения приводят нас к формальному определению локальных экстремумов. Локальные минимумы и локальные максимумы - Функция \(f\) является возрастающей функцией на открытом интервале, если \(f(b)>f(a)\) для каждого \(a\) , \(b\) интервал, где \(b>a\).
- Функция \(f\) является убывающей функцией на открытом интервале, если \(f(b)а\).
Функция \(f\) имеет локальный максимум в точке \(b\) открытого интервала \((a,c)\), если \(f(b)\) больше или равно \ (f(x)\) для каждой точки \(x\) (\(x\) не равно \(b\)) в интервале. Точно так же \(f\) имеет локальный минимум в точке \(b\) в \((a,c)\), если \(f(b)\) меньше или равно \(f(x) \) для каждого \(x\) (\(x\) не равно \(b\)) в интервале. Точно так же \(f\) имеет локальный минимум в точке \(b\) в \((a,c)\), если \(f(b)\) меньше или равно \(f(x) \) для каждого \(x\) (\(x\) не равно \(b\)) в интервале. Пример \(\PageIndex{7}\) Поиск возрастающих и убывающих интервалов на графике Учитывая функцию \(p(t)\) на рисунке \(\PageIndex{6}\), определите интервалы, на которых функция кажется возрастающей. Рисунок \(\PageIndex{6}\): График многочлена. Решение Мы видим, что функция не является постоянной ни на каком интервале. Функция увеличивается там, где она наклонена вверх, когда мы движемся вправо, и уменьшается там, где она наклонена вниз, когда мы двигаемся вправо. Функция увеличивается от \(t=1\) до \(t=3\) и от \(t=4\) и далее. В интервальных обозначениях мы бы сказали, что функция возрастает на интервале \((1,3)\) и на интервале \((4,\infty)\). Анализ Обратите внимание, что в этом примере мы использовали открытые интервалы (интервалы, которые не включают конечные точки), потому что функция не возрастает и не убывает при \(t=1\), \(t=3\) и \(t=4\). Эти точки являются локальными экстремумами (два минимума и максимум). Эти точки являются локальными экстремумами (два минимума и максимум). Пример \(\PageIndex{8}\): поиск локальных экстремумов на графике График функции \(f(x)=\frac{2}{x}+\frac{x}{3}\) . Затем используйте график, чтобы оценить локальные экстремумы функции и определить интервалы, на которых функция возрастает. Решение Используя технологию, мы видим, что график функции выглядит так, как показано на рисунке \(\PageIndex{7}\). Оказывается, существует нижняя точка или локальный минимум между \(x=2\) и \(x=3\), а зеркально-высокая точка или локальный максимум где-то между \(x=−3\). ) и \(x=−2\) .
Рисунок \(\PageIndex{7}\): График обратной функции. Анализ Большинство графических калькуляторов и утилит для построения графиков могут оценивать расположение максимумов и минимумов. На рисунке \(\PageIndex{8}\) представлены изображения экрана для двух разных технологий, показывающие оценку локального максимума и минимума. Рисунок \(\PageIndex{8}\): График обратной функции на графическом калькуляторе. На основании этих оценок функция возрастает на интервалах \((−\infty,−2,449)\) и \((2,449,\infty)\). Обратите внимание, что, хотя мы ожидаем, что экстремумы будут симметричными, две разные технологии согласуются только до четырех знаков после запятой из-за разных алгоритмов аппроксимации, используемых каждой из них. (Точное расположение экстремумов находится в точке \(\pm\sqrt{6}\), но для его определения требуется вычисление.) Упражнение \(\PageIndex{8}\) 92−15x+20\) для оценки локальных экстремумов функции. Используйте их, чтобы определить интервалы, на которых функция увеличивается и уменьшается. - Раствор
Локальный максимум приходится на \((−1,28)\), а локальный минимум приходится на \((5,−80)\). Функция возрастает на \((−\infty,−1)\cup(5,\infty)\) и убывает на \((−1,5)\). График полинома с локальным максимумом в точке (-1, 28) и локальным минимумом в точке (5, -80).
Пример \(\PageIndex{9}\): поиск локальных максимумов и минимумов на графике Для функции f, график которой показан на рисунке \(\PageIndex{9}\), найдите все локальные максимумы и минимумы. Рисунок \(\PageIndex{9}\): График многочлена. Решение Посмотрите на график \(f\). График достигает локального максимума в точке \(x=1\), потому что это самая высокая точка в открытом интервале вокруг \(x=1\). Локальный максимум — это координата y в точке \(x=1\), что 2, График достигает локального минимума в точке \(x=−1\), потому что это самая нижняя точка открытого интервала вокруг \(x=−1\). Локальный минимум — это координата y в точке \(x=−1\), которая равна −2. Анализ функций набора инструментов для увеличения или уменьшения интервалов Теперь мы вернемся к нашим функциям набора инструментов и обсудим их графическое поведение на рисунке \(\PageIndex{10}\), рисунке \(\PageIndex{11}\) и Рисунок \(\PageIndex{12}\). Рисунок \(\PageIndex{10}\).
Рисунок \(\PageIndex{11}\)
Рисунок \(\PageIndex{12}\) Использование графика для определения абсолютного максимума и абсолютного минимума открытый интервал (локально) и нахождение самой высокой и самой низкой точки на графике для всей области. Y-координаты (выходные данные) в самой высокой и самой низкой точках называются абсолютным максимумом и абсолютным минимумом соответственно. Чтобы найти абсолютные максимумы и минимумы на графике, нам нужно наблюдать за графиком, чтобы определить, где график достигает своих самых высоких и самых низких точек в области определения функции (рисунок \(\PageIndex{13}\)). 93\) является одной из таких функций. Абсолютные максимумы и минимумы - Абсолютный максимум \(f\) в точке \(x=c\) равен \(f(c)\), где \(f(c)≥f(x)\ ) для всех \(x\) в области определения \(f\).
- абсолютный минимум \(f\) при \(x=d\) равен \(f(d)\), где \(f(d)≤f(x)\) для всех \(x\) в области определения \(f\).

Пример \(\PageIndex{10}\): поиск абсолютных максимумов и минимумов на графике Для функции f, показанной на рисунке \(\PageIndex{14}\), найдите все абсолютные максимумы и минимумы. Рисунок \(\PageIndex{14}\): График многочлена. Решение Посмотрите на график \(f\). График достигает абсолютного максимума в двух местах, \(x=−2\) и \(x=2\), потому что в этих местах график достигает высшей точки области определения функции. Абсолютным максимумом является координата y в точках \(x=−2\) и \(x=2\), которая равна 16. График достигает абсолютного минимума в точке x=3, потому что это самая нижняя точка на область определения графика функции. Абсолютным минимумом является координата y при x=3, что равно −10. Ключевые уравнения- Средняя скорость изменения: \(\dfrac{\Delta y}{\Delta x}=\dfrac{f(x_2)-f(x_1)}{x_2-x_1}\)
Ключевые понятия- Скорость изменения соотносит изменение выходной величины с изменением входной величины.
 Средняя скорость изменения определяется с использованием только начальных и конечных данных. См. Пример. Средняя скорость изменения определяется с использованием только начальных и конечных данных. См. Пример. - Идентификация точек, которые отмечают интервал на графике, может быть использована для определения средней скорости изменения. См. Пример.
- Сравнение пар входных и выходных значений в таблице также можно использовать для определения средней скорости изменения. См. Пример.
- Средняя скорость изменения также может быть вычислена путем определения значений функции в конечных точках интервала, описываемого формулой. См. пример и пример.
- Иногда среднюю скорость изменения можно определить как выражение. См. Пример.
- Функция возрастает, когда скорость ее изменения положительна, и убывает, когда скорость ее изменения отрицательна. См. Пример.
- Локальный максимум — это когда функция изменяется с возрастающей на убывающую и имеет выходное значение больше (более положительное или менее отрицательное), чем выходные значения при соседних входных значениях.

{2}-2 b c \cos \alpha$ Теорема косинусов является обобщением теоремы Пифагора.
Утверждения, обобщающие теорему Пифагора и эквивалентные теореме косинусов,
были сформулированы отдельно для случаев острого и тупого угла в 12 и 13 предложениях II книги «Начал» древнегреческого математика Евклида
(ок. 300 г. до н. э.). Утверждения, эквивалентные теореме косинусов для сферического треугольника, применялись в сочинениях математиков
стран Средней Азии. Теорему косинусов для сферического треугольника в привычном нам виде сформулировал выдающийся немецкий астролог,
астроном и математик Региомонтан (1436 — 1476), назвав её «теоремой Альбатегния» (по имени выдающегося средневекового астронома и
математика Абу Абдаллах Мухаммад ибн Джабир ибн Синан ал-Баттани (858 — 929). В Европе теорему косинусов популяризовал французский математик Франсуа Виет (1540 — 1603) в 16 столетии. В начале 19 века её
стали записывать в принятых по сей день алгебраических обозначениях.{\circ}=289+196-238=24$$ Тогда $$A B=\sqrt{247}$$ Ответ. $A B=\sqrt{247}$ Нахождение значений синуса и косинуса, тангенса и котангенса|
1.
|
Синус и косинус
|
1 вид — рецептивный
|
лёгкое
|
2 Б.
|
Находятся значения синуса и косинуса некоторых углов.
|
|
2.
|
Нахождение значения синуса и косинуса
|
2 вид — интерпретация
|
лёгкое
|
1 Б.
|
Определяется значение выражения с синусами и косинусами основных углов.
|
|
3.
|
Нахождение значения выражения с тангенсом и котангенсом
|
1 вид — рецептивный
|
лёгкое
|
1 Б.
|
Определяется значение выражения, содержащее тангенс и котангенс некоторых углов.
|
|
4.
|
Вычисление тангенса и котангенса некоторых чисел
|
1 вид — рецептивный
|
среднее
|
1 Б.
|
При вычислении тангенса и котангенса некоторых чисел необходимо их преобразовать, применяя свойство 3.
|
|
5.
|
Вычисление синуса и косинуса некоторых чисел
|
2 вид — интерпретация
|
среднее
|
2 Б.
|
При вычислении синуса и косинуса некоторых чисел необходимо их преобразовать, совершая несколько полных оборотов по числовой окружности в положительном или отрицательном направлении.
|
|
6.
|
Определение знака числа
|
2 вид — интерпретация
|
среднее
|
1 Б.
|
Определяется знак синуса, косинуса, тангенса и котангенса числа.
|
|
7.
|
Решение уравнения вида sin t = a, cos t = a
|
3 вид — анализ
|
среднее
|
2 Б.
|
Решаются уравнения вида sin t = a, cos t = a. При этом каждое уравнение сопровождается рисунком.
|
|
8.
|
Решение неравенства
|
3 вид — анализ
|
сложное
|
5 Б.
|
Решаются неравенства вида sin t > a, sin t < a, cos t > a, cos t < a. Каждое решение показано на рисунке.
|
|
9.
|
Сравнение чисел
|
4 вид — творческий
|
сложное
|
3 Б.
|
С помощью числовой окружности сравниваются числа вида sin a и cos b.
|
|
10.
|
Найди значение выражения
|
4 вид — творческий
|
сложное
|
3 Б.
|
Для нахождения значения выражения необходимо преобразовать выражение под корнем, определить знак выражения, записанного под знаком модуля, упростить полученное выражение.
|
Тригонометрические и геометрические преобразования, sin(A + B), sin(AКоэффициенты для суммы углов Как демонстрируют различные примеры, иногда нам нужны значения углов, отличных от 0, 30, 45, 60 и 90 градусов. В этой главе вы должны научиться двум вещам:
1. sin(A + B) не является равным sinA + sinB. В этом случае не срабатывает простое раскрытие скобок, как в алгебре.
2. Формулу, по которой вычисляется sin(A + B). Во-первых, покажем, что раскрытие скобок не «срабатывает». Пусть A = 30 градусов и B = 45 градусов. Sin30 равен 0.5. Sin45 равен 0.7071. Складывая, получим 1.2071. Вы знаете, что ни синус, ни косинус не может быть больше 1. Почему? Потому что в дробях, по которым они вычисляются, гипотенуза выступает в качестве знаменателя. Самое большее значение мы получим, если числитель равен знаменателю. Синус или косинус не может быть больше 1, и поэтому значение 1,2071 не верно.
Нахождение синуса, косинуса или тангенса полного угла (A + B)Нахождение sin(A + B) Самый простой способ найти sin (A + B) — используя геометрическое построение, показанное на рисунке. Большой угол (A + B), состоит из двух маленьких, А и В. Рисунок (1) показывает, что противоположная сторона состоит из двух частей.
Нижняя часть, разделенная линией между углами (2), есть синус А. Линия между двумя углами, разделенная гипотенузой (3), есть косинус B. Умножаем их. Средняя линия и в числителе, и в
знаменателе, поэтому они сокращаются, оставляя нижнюю часть противоположной стороны над гипотенузой (4).
Обратите внимание на маленький прямоугольный треугольник (5). Затененный угол есть A, потому что линия на его верхней части параллельна линии в основании. Подобные прямоугольные треугольники с углом А показывают, что верхний угол, отмеченный А также равен оригинальному углу А. Верхняя часть противоположной (6) над длинной, заштрихованный треугольник является соs А. Противоположный над основной гипотенузой (7) есть синус. Поскольку стороны с пометкой «противоположные» (7) и в числителе и знаменателе, когда cos и sin перемножаются, cosAsinB есть верхняя часть оригинального противоположного — для (A + B) — разделенные основной гипотенузой (8). Теперь, сложим это все вместе (9). Sin(A + B) есть две части противоположного — все разделенные гипотенузой (9). Записывая это в тригонометрическую форму: sin(A + B) = sin A cos B + cos A sin B. Нахождение cos(A + B) Очень похожая конструкция находит формулу для косинуса угла созданного двумя углами, сложенными вместе.
Используя ту же самую конструкцию (1), обратите внимание, что смежная сторона является полной линией основания (для соs A), c частью, которая вычитается справа. Каждая часть должна использовать тот же знаменатель, гипотенузу (A + B) треугольника. Полная линия основания, разделенная линией между углами A и E есть cosA (2). Эта разделяющая линия, деленная гипотенузой (A + B) треугольника, есть cos B (3). Поэтому, полная линия основания, деленная гипотенузой есть произведение cosAcosB (4). Теперь, небольшая часть, которая должна быть вычтена. Заштрихованная часть (5) представляет sinA, который умножается заштрихованной частью (6) есть sin E, который есть другой частью и , которая нам нужна (7). Вычитание дает соs (А + В) (8), поэтому формула, которая нам нужна:
cos(A + B) = cos A cos B — sin A sin B Нахождение tan(A + B) Полный геометрический вывод формулы для tg (A + B) является сложным. Проще всего вывести его из двух формул, которые мы уже сделали. В любом угле, тангенс равен синус, деленному на косинус. Используя тот факт, tan (A + B) = sin(A + B)/соs(A + B). Это выражение можно расширить к виду:
tan(A + B) = [sin A cos B + cos A sin B]/[cos A cos B — sin A sin B]
Разделив верхнюю и нижнюю часть на cos A cos B, что превращает все члены в тангенсы, получаем:
tan(A + B) = [tan A + tan B]/[1 — tan A tan B]
Коэффициенты для 75 градусов Покажем коэффициенты синуса, косинуса и тангенса, подставляя в формулу суммы, и потом упрощая результат к своей простейшей форме, прежде чем находить суммы. После внесения основных замен в каждом конкретном случае, примерная работа в заштрихованной части, чтобы показать, как результат сводится к простейшей форме для оценки.
Если вы используете ваш карманный калькулятор для оценки, скорей всего, не имеет значения или вы упрщаете выражения сначала или просто пропускаете его! Все зависит от калькулятора: некоторые вычисля.т разницу, некоторые нет! Коэффициенты углов, больших, чем 90 градусов До сих пор рассматривалось соотношение острых углов (между 0 и 90 градусами). Другие треугольники с тупым углом (более 90 градусов) и до 180 градусов могут появиться в последующих задачах. Для упрощения классификации углов по размеру, они делятся на сектора (квадранты). Квадрант есть четвертой частью круга. Так как круг делится на 360 градусов, квадранты имеют по 90 градусов. 0-90 градусов это первый квадрант, 90-180 — второй, 180-270 — третий и 270-360 — четвертый. Используя линии, обозначающие границы квадранта, 0 или 360 это горизонталь направо, 90 — вертикально вверх, 180 — горизонталь слева и 270 сверху вниз. Теперь, используем этот метод для построения графиков. Большие углы определяется вектором вращения, начиная с нуля и вращением против часовой стрелки. Горизонтальные элементы х: положительные справа, отрицательные слева. Вертикальные элементы у: положительные вверх, отрицательные вниз. Вращающийся вектор является р. Таким образом, синус угла есть y/r, косинус х/r, и тангенс у/х. Вектор r — всегда положителен. Таким образом, знак отношения может быть вычислен для различных секторов. Здесь приведены знаки для трех отношений в четырех квадрантах.
Кроме того, как эквивалентный угол в первой четверти «переключается» когда вектор переходит из одного квадранта в другой. В первой четверти, стороны определены в соотношениях для синуса, косинуса и тангенса. При перемещении к большим углам в остальных секторах, противоположная сторона всегда есть вертикальная (у). То, что называется смежное, всегда есть горизонталью (х). Гипотенуза это всегда вращающийся вектор (r). Вы можете видеть картину как изменяются тригонометрические соотношения для углов.
Отношения в четырех квадрантахОтношения для различных углов Теперь у вас есть два пути получить формулы для различных углов. Во-первых, используя геометрическую конструкцию, такую, которая, например, была использована для суммы углов, реверсивную так, что (A — B) есть угол B вычитающийся из угла A. В рассуждениях, аналогичных тем, которые были использованы для суммы углов, здесь представлены несколько сокращенные формулы для синуса и косинуса:
sin(A — B) = sin A cos B — cos A sin B
and
cos(A — B) = cos A cos B + sin A sin B
Геометрическая конструкция
Формулы суммы и разницы Второй способ нахождения формулы для разницы углов использует уже полученную формулу суммы, но делает B отрицательным. Из нашего исследования знаков для различных секторов, отрицательные углы с 1-го квадранта будут в 4 квадранте. Проводя эту подстановку, получим тот же результат, который был получен геометрически в предыдущем разделе. Поиск формулы тангенса проходит тем же методом, или заменой синуса и косинуса в формулах или более непосредственно, превращая tg(-B) = — tg B. В любом случае вы получите:
tan(A — B) = [tan A — tan B]/[1 + tan A tan B]
Отношения с помощью четырех секторов Вы можете вывести несколько отношений с формулами суммы и разности. Вы уже сделали соотношение для 75 градусов. Теперь можно выполнить то же для 15 градусов. Эти формулы дают соотношения для углов в 15 градусов интервалы через четыре квадранта. Построив их на 360 градусов, вы можете увидеть, как эти три соотношения изменяются, когда вектор проходит через четыре квадранта. «Волна» синуса и косинуса колеблется вверх и вниз между +1 и -1. Обратите внимание, что «волны» смещены на 90 градусов друг относительно друга. Этот факт станет важным позже.
Кривая тангенса начинается, как синусоида, но вскоре она стремится достичь бесконечности на 90 градусах. Двигаясь » вне видимости» в положительном направлении, она «приходит» с отрицательного направления с другой стороны на 90 градусах. Проходя через точку в 180 градусов, функция тангенса повторяет то, что она «делала» проходя 0 или 360 градусов. На 270 градусах она повторяет то же, было на 90 градусах. Пифагор в тригонометрии Формула часто может быть упрощена, так как были найдены выводы формулы тангенса от формул синуса и косинуса, а также изменение ее членов одного отношения к другому отношению, использeущеuj другие члены. При этом, теорема Пифагора, выраженная в тригонометрическом соотношении, очень удобна. Предположим, что прямоугольный треугольник имеет гипотенузу длиной 1. Тогда одна из сторон будет иметь длину sinA, а другая — cosA. Отсюда, согласно теореме Пифагора: cos2 A + sin2 A = 1. Это выражение всегда истинно для любого значения A. Немного о том, как это было записано. Cos 2 A означает (cos A) 2. Если вы написали это как cos A 2, уравнение будет означать что-то другое. A есть число в нескольких угловых значениях, которое представляет угол. A 2 было бы то же самое число, возведенное в квадрат. Его значение зависело бы от использованного числового значения, поэтому это не очень хороший член для использования. Это означает квадрат синуса ли косинуса, не сам угол. Формула Пифагора может быть выражена иначе. Например, две другие формы:
cos2 A = 1 — sin2 A, и sin2 = 1 — cos2 A. Умножение углов Формулы сумм, вместе с теоремой Пифагора, используются для углов, которые в 2, 3 или больше раз кратны любым оригинальным углам. Здесь приводятся формулы для 2А и 3А. Формула суммы работает, когда оба угла одинаковые или различны: sin(A + B) или sin(A + A). Однако, sin(A + A) в действительности sin 2A. Поэтому, sin 2A есть sin A cos A + cos A sin A. Оба члена выражения есть одним и тем же произведением, записанным в разном порядке, так что это выражение может быть упрощено до sin 2A = 2 sin A cos A. Подобным образом, cos 2A = cos A cos A — sin A sin A, что также может быть записано как: cos 2A = cos2 A — sin2 A. Используя теорему Пифагора, изменяем это к виду: cos 2A = 2cos2 A — 1. Наконец, tg 2A = 2 tg A/[1 — tg2 A]. Теперь тройной угол (3А) используется, чтобы показать, как получены следующие кратные углы. В основном, это так же просто, как запись 3A = 2 + A и повторного применения формулы суммы. Но тогда, чтобы получить в результате формулу в работающем виде, необходимо заменить часть 2А, на выражения с простым углом А. На рисунках внизу вы можете видеть, что с каждым разом вычисления становятся сложнее. УМНОЖЕНИЕ УГЛОВ Производные от формул суммыУМНОЖЕНИЕ УГЛОВ Соотношения для 3AСвойства равнобедренного треугольника Вы уже видели, что прямоугольный треугольник является полезным строительным блоком для других фигур. Равнобедренный треугольник имеет несколько различных видов использования. Дело в том, что его использование основывается на том, что равнобедренный треугольник имеет две равные стороны и два равные углы между основанием и боковыми равными сторонами. Перпендикуляр из третьего угла на третью сторону делит ее пополам. Таким образом весь треугольник делится на два равных прямоугольных треугольника. Любой треугольник, за исключением прямоугольного треугольника, можно разделить на три прилегающих равнобедренных треугольника, разделив каждую сторону на две равные части и построить перпендикуляры из точек разделения. Там, где любые два из этих перпендикуляров встречаются, если линии тянутся к углам исходного треугольника, три линии должны быть равны, потому что две из них образуют стороны равностороннего треугольника. Таким образом, перпендикуляр с третьей стороны исходного треугольника должен также встретиться в одной точке. Это утверждение справедливо, как мы покажем здесь, независимо от того, является ли исходный треугольник острым или тупым. Разница с тупым прямоугольным треугольником в том, что место встречи перпендикуляров лежит снаружи исходного треугольника, а не внутри. Что происходит в прямоугольном треугольнике? Перпендикуляры от средней точки гипотенузы другой стороны будут делить пополам эти две стороны — вы получаете два из трех! Место встречи находится гипотенузе.
Углы в окружности Основное свойство окружности это то, что ее центр находится на одинаковом расстоянии от любой точки окружности. Это расстояние есть радиусом окружности. Если вы нарисуете любой треугольник внутри круга, перпендикуляры из средней точки его сторон встретятся в центре окружности а радиусы из углов треугольника делят его на три равнобедренных треугольника Теперь, если вы назовете равные пары углов в каждом равнобедренном треугольнике A, A, B, B, C, C, вы обнаружите, что исходный треугольник имеет один угол A+B, один угол B+C, и один угол A+ C. Три угла в сумме дают 2A + 2B + 2С, а это как известно равно 180 градусов. В любом равнобедренном треугольнике угол при вершине равен 180 градусов минус удвоенный угол при основании. Поэтому, согласно предыдущего пункта, 180 — 2A должен быть такой же, как и 2B + 2С, например. Рассмотрим угол правый нижний угол, опирающийся на окружность. Угол в центре равен 2B + 2С. Углом, опирающийся на окружность равен B + C. Вы видите, что для любого сегмента круга, угол в центре всегда в два раза больше угла, опирающегося на окружность. Утверждение выше приводит к интересным фактам об углах в окружностях. Вместо определения углов со стороной треугольника, используют дугу (часть окружности) круга. Часть окружности, которая определяется углом в центре называется хордой окружности.
Угол в центре в два раза больше чем угол на окружности Любой угол, касающийся окружности, используя хорду как ограничение угла, равен половине угла в центре. Таким образом, все углы в круге, с основанием на той же хорде, должны быть равны. Предположим, что хорда имеет угол 120 градусов. Угол на окружности будет равен 60 градусам. Особый случай представляет собой полукруг (точный полукруг). Угол в центре представляет собой прямую линию (180 градусов). Каждый угол в полукруге равен 90 градусам (прямой угол). Любой треугольник в полукруге является прямоугольным треугольником.
Определения Выше мы часто использовали углы, которые дополняют углы до прямого угла (90 градусов) или до двух прямых углов (180 градусов). Когда два угла образовывают угол 180 градусов (два прямых угла), они называются дополнительными. Если два угла добавить до 90 градусов (один прямой угол), их называют комплементарными
Вопросы и задачи 1. Синус угла А равен 0,8 и синус угла B равен 0.6. Из различных зависимостей, полученных до сих пор, найдите следующее: тангенс А, тангенс B, синус (A + B), косинус (A + B), синус (A — B), косинус (A — B), тангенс (А + B) и тангенс (A — B) без использования таблиц или тригонометрических клавиш калькулятора. 2.На экваторе Земля имеет радиус 4000 км. Углы вокруг экватора измеряется в меридианах долготы, с линией с севера на юг проходящей через Гринвич (Англия), в качестве нулевого отсчета. Два места используются для наблюдения за луной: первое это Кения, на экваторе 37,5 к востоку от Гринвича, а другой является Суматра, на экваторе к востоку 100,5. Как далеко друг от друга эти два места, если расстояние измерять мнимой прямой, проходящей через Землю? 3.Если бы наблюдения были сделаны горизонтально от точки наблюдения в вопросе 2 (к востоку от первой, к западу от второй), под каким углом была бы линия пересечения наблюдений? 4.В определенное время, точно синхронизированное в обоих местах, наблюдается спутник. В Кении, высота линии визирования с центром на спутнике составляет 58 градусов выше горизонтали на восток. На Суматре, высота составляет 58 градусов выше горизонтали на запад. Как далеко находится спутник? Используйте расстояние между точками рассчитанное в вопросе 2. 5. Косинус определенного угла в два раза больше синуса того же угла. Чему равен тангенс этого угла? Не используйте таблицы или калькулятор для ответа на этот вопрос. 6. Синус определенного угла равен именно 0.28. Найдите косинус и тангенс этого угла. Не используйте таблицы или калькулятор для ответа на этот вопрос. 7. Синус определенного угла равен 0.6. Найдите синус углов, больших чем заданный в два и три раза. 8. Найдите синус и косинус угла, большего ровно в два раза чем угол из вопроса 7. 9. Используя 15 градусов, как единичный угол, и формулы для отношения 2А и 3А найдите значения синусов 30 и 45 градусов. 10. Используя 30 градусов, как единичный угол, найти значения синусов 60 и 90 градусов. 11. Используя 45 градусов, как единичный угол, найдите значения тангенсов 60 и 90 градусов. 12. Используя 60 градусов, как единичный угол, найдите значения косинусов 120 и 180 градусов. 13. Используя 90 градусов, как единичный угол, найдите значения косинусов 180 и 270 градусов. 14. Используя формулы тангенса для умножения углов и таблицы, найдите тангенсы утроенных углов в 29, 31, 59 и 61 градусов. Посчитайте изменения знака между утроенным углом 29 и 31 градусов и между 59 и 61 градусов. 15. Синус угла составляет 0,96. Найдите синус и косинус удвоенного угла. 16. Задача сводится к алгебраической выражению вида 8cos2 A + cos A = 3. Решите для косинуса А, и укажите, в каком квадранте будет угол, представляющий каждое решение придет. Приведите приближенные значения из таблицы или используя калькулятор. Теорема косинусов и ее доказательство.
См. также Теорема синусов.
Теорема косинусов является обобщением теоремы Пифагора для произвольного треугольника.
Формулировка теоремы косинусов
Для плоского треугольника со сторонами a,b,c и углом α, противолежащим стороне a, справедливо соотношение:
|
Квадрат одной стороны треугольника равен сумме квадратов двух других сторон за вычетом удвоенного их произведения, умноженного на косинус угла между ними
|
Полезные формулы теоремы косинусов:
Как видно из указанного выше, с помощью теоремы косинусов можно найти не только сторону треугольника по двум сторонам и углу между ними, можно, зная размеры всех сторон треугольника, определить косинусы всех углов, а также вычислить величину любого угла треугольника. Вычисление любого угла треугольника по его сторонам является следствием преобразования формулы теоремы косинусов. Доказательство теоремы косинусов
Рассмотрим произвольный треугольник ABC. Предположим, что нам известна величина стороны AC (она равна некому числу b), величина стороны AB (она равна некому числу c) и угол между этими сторонами, величина которого равна α. Найдем величину стороны BC (обозначив ее длину через переменную a)
Для доказательства теоремы косинусов проведем дополнительные построения. Из вершины C на сторону AB опустим высоту CD.
Найдем длину стороны AB. Как видно из рисунка, в результате дополнительного построения можно сказать, что
AB = AD + BD
Найдем длину отрезка AD. Исходя из того, что треугольник ADC является прямоугольным, нам известны длина его гипотенузы (b) и угол (α) то величину стороны AD можно найти из соотношения его сторон, пользуясь свойствами тригонометрических функций в прямоугольном треугольнике:
AD / AC = cos α
откуда
AD = AC cos α
AD = b cos α
Длину стороны BD найдем как разность AB и AD:
BD = AB — AD
BD = c − b cos α Теперь запишем теорему Пифагора для двух прямоугольных треугольников ADC и BDC:
для треугольника BDC
CD2 + BD2 = BC2
для треугольника ADC
CD2 + AD2 = AC2
Обратим внимание на то, что оба треугольника имеют общую сторону — CD. Определим ее длину для каждого треугольника — вынесем ее значение в левую часть выражения, а остальное — в правую.
CD2 = BC2 — BD2
CD2 = AC2 — AD2
Поскольку левые части уравнений (квадрат стороны CD) равны, то приравняем правые части уравнений:
BC2 — BD2 = AC2 — AD2
Исходя из сделанных ранее вычислений, мы уже знаем что:
AD = b cos α
BD = c − b cos α
AC = b (по условию)
А значение стороны BC обозначим как a.
BC = a
(Именно его нам и нужно найти)
Получим:
BC2 — BD2 = AC2 — AD2
Заменим буквенные обозначения сторон на результаты наших вычислений
a2 — ( c − b cos α )2 = b2 — ( b cos α )2
перенесем неизвестное значение (а) на левую сторону, а остальные части уравнения — на правую
a2 = ( c − b cos α )2 + b2 — ( b cos α )2
раскроем скобки
a2 = b2 + c 2 — 2c b cos α + ( b cos α )2 — ( b cos α )2
получаем
a2 = b2 + c 2 — 2bc cos α
Теорема косинусов доказана.
Случай, когда один из углов при основании тупой (и высота падает на продолжение основания), полностью аналогичен рассмотренному.
Основное свойство функции косинуса |
Описание курса | Теорема косинусов. Пример решения задачи Теорема косинусовТеорема косинусов и теорема Пифагора. В этой статье мы рассмотрим теорему косинусов и как она используется для нахождения элементов треугольника. А так же разберём её взаимосвязь с теоремой Пифагора. Знать эту теорему НЕОБХОДИМО. Что мы можем найти, используя её? Если нам будут известны две стороны и угол между ними, мы без труда найдём третью сторону. Для этого нужно просто подставить в формулу известные величины. Для других сторон всё то же самое: Можно ли использовать теорему косинусов для нахождения третьей стороны, если известны любые две стороны и угол, не лежащий между этими сторонами? Например, нам известны стороны a и b и угол альфа. Тогда из формулы мы можем найти сторону «с». Приводим к виду: То есть, мы получаем квадратное уравнение с переменной «с» (все остальные величины нам известны). Решив его, получим искомую сторону. Мы можем найти любой угол, если нам известны все три стороны треугольника: Разумеется, что учить все эти формулы не нужно, так как достаточно понимать сам смысл Теоремы косинусов. А косинус любого угла не трудно выразить используя простые алгебраические преобразования. *Если вы вычисляете косинус тупого угла, то имейте ввиду, что должно получиться отрицательное значение, так как косинус угла от 90 до 180 градусов отрицателен. Если при решении в задачах получите положительное значение, то ищите ошибку. Следующий вопрос: а если нам дана сторона и любые два угла, что делать? В этом случае теорема косинусов не используется, а на помощь приходит теорема синусов, её мы рассмотрим в одной из следующих статей, не пропустите! Если вы будете в совершенстве владеть теоремами Пифагора, косинусов, синусов и свойствами подобия треугольников, то для вас не возникнет никаких сложностей с решением треугольников (в большинстве задач). Следующий факт знают все, но всё же о взаимосвязи теоремы косинусов с теоремой Пифагора сказать стоит. Посмотрите на исходный рисунок, если угол альфа равен 90 градусов, то получим: То есть, по сути, теорема Пифагора это как бы частный случай теоремы косинусов. Рассмотрим прямоугольный треугольник. Покажем то же самое, но с другими обозначениями: По теореме косинусов: Так как угол С равен 90, то Напомню, что зная любые две стороны в прямоугольном треугольнике, мы всегда можем найти третью. А далее без труда можем найти значение любой тригонометрической функции острого угла в нём. Можете изучить статью об этом. Получить материал статьи в формате PDF На этом всё. Успехов вам!!! С уважением, Александр Крутицких. P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях. Практическая работа»Нахождение значений синуса и косинуса по таблице Брадиса» Вариант 1 1.sin 12˚ 1.sin 9˚10′ 1.sinA=0,5401 ;A= 1.cos 8˚ 1. cos7˚15′ 1.cosA=0,1303;A= 2.sin 34˚ 2.sin 15˚38′ 2. sinA=0,0905 ;A= 2. cos 25˚ 2. cos24˚21′ 2. cosA=0,5002; A= 3.sin 45˚ 3.sin 38˚16′ 3. sinA=0,8008;A= 3. cos 57˚ 3. cos47˚58′ 3. cosA=0,3915; A= 4.sin 71˚ 4.sin 64˚12′ 4. sinA=0,9421;A= 4. cos 69˚ 4. cos71˚2′ 4. cosA=0,8516; A= 5.sin 85˚ 5.sin 83˚19′ 5. sinA=0,2151;A= 5. cos81˚ 5. cos85˚39′ 5. cosA=0,0908; A= Вариант 2 1.sin 29˚ 1. sin 10˚10′ 1. sinA=0,1001;A= 1.cos 18˚ 1.cos 9˚ 9′ 1. cosA=0,5009 ;A= 2. sin 48˚ 2. sin 53˚28′ 2. sinA=0,0806; A= 2. cos 39˚ 2. cos 41˚41′ 2. cosA=0,2429 ; A= 3. sin 64˚ 3. sin 32˚41′ 3. sinA=0,5429; A= 3. cos 62˚ 3. cos57˚16′ 3. cosA=0,3108 ; A= 4. sin 78˚ 4. sin 68˚15′ 4. sinA=0,7507; A= 4. cos 78˚ 4. cos72˚35′ 4. cosA=0,6887 ; A= 5. sin 81˚ 5. sin 83˚29′ 5. sinA=0,3094; A= 5. cos 81˚ 5. cos80˚49′ 5. cosA=0,4815 ; A=
Ва Вариант 1 1.sin 12˚ 1.sin 9˚10′ 1.sinA=0,5401 ;A= 1.cos 8˚ 1. cos7˚15′ 1.cosA=0,1303;A= 2.sin 34˚ 2.sin 15˚38′ 2. sinA=0,0905 ;A= 2. cos 25˚ 2. cos24˚21′ 2. cosA=0,5002; A= 3.sin 45˚ 3.sin 38˚16′ 3. sinA=0,8008;A= 3. cos 57˚ 3. cos47˚58′ 3. cosA=0,3915; A= 4.sin 71˚ 4.sin 64˚12′ 4. sinA=0,9421;A= 4. cos 69˚ 4. cos71˚2′ 4. cosA=0,8516; A= 5.sin 85˚ 5.sin 83˚19′ 5. sinA=0,2151;A= 5. cos81˚ 5. cos85˚39′ 5. cosA=0,0908; A= Вариант 2 1.sin 29˚ 1. sin 10˚10′ 1. sinA=0,1001;A= 1.cos 18˚ 1.cos 9˚ 9′ 1. cosA=0,5009 ;A= 2. sin 48˚ 2. sin 53˚28′ 2. sinA=0,0806; A= 2. cos 39˚ 2. cos 41˚41′ 2. cosA=0,2429 ; A= 3. sin 64˚ 3. sin 32˚41′ 3. sinA=0,5429; A= 3. cos 62˚ 3. cos57˚16′ 3. cosA=0,3108 ; A= 4. sin 78˚ 4. sin 68˚15′ 4. sinA=0,7507; A= 4. cos 78˚ 4. cos72˚35′ 4. cosA=0,6887 ; A= 5. sin 81˚ 5. sin 83˚29′ 5. sinA=0,3094; A= 5. cos 81˚ 5. cos80˚49′ 5. cosA=0,4815 ; A= Ответы: Вариант 1 1.0,2079 1.0,1593 1.А=32˚42′ ❶0,9903 ❶0,9920 ❶А=82˚31′ 2.0,5592 2.0,2695 2.А=5˚12′ ❷0,9063 ❷0,9111 ❷А=59˚59′ 3.0,7071 3.0,6193 3.А=53˚12′ ❸0,5446 ❸0,6695 ❸А=66˚57′ 4.0,9455 4.0,9003 4.А=70˚24′ ❹0,3584 ❹0,3250 ❹А=31˚36′ 5.0,9962 5.0,9932 5.А=12˚25′ ❺0,1564 ❺0,0758 ❺А=84˚47′ Вариант 2 1.0,4848 1.0,1765 1.А=5˚44′ ❶0,9511 ❶0,9873 ❶А=59˚57′ 2.0,7431 2.0,8036 2.А=4˚37′ ❷0,7771 ❷0,7468 ❷А=75˚57′ 3.0,8988 3.0,54 3.А=32˚53′ ❸0,4695 ❸0,5407 ❸А=71˚54′ 4.0,9781 4.0,9288 4.А=48˚39′ ❹0,2079 ❹0,2993 ❹А=46˚29′ 5.0,9877 5.0,9936 5.А=18˚1′ ❺0,0872 ❺0,1596 ❺А=61˚13′ Формула вычисления косинуса угла между векторамиФормула вычисления угла между векторамиПримеры задач на вычисление угла между векторамиПримеры вычисления угла между векторами для плоских задачиРешение: Найдем скалярное произведение векторов: a · b = 3 · 4 + 4 · 3 = 12 + 12 = 24. Найдем модули векторов: | a | = √ 3 2 + 4 2 = √ 9 + 16 = √ 25 = 5
| b | = √ 4 2 + 3 2 = √ 16 + 9 = √ 25 = 5 Найдем угол между векторами: | cos α = | a · b | = | 24 | = | 24 | = 0.96 | | | a | · | b | | 5 · 5 | 25 |
Решение: Найдем скалярное произведение векторов: a · b = 5 · 7 + 1 · 5 = 35 + 5 = 40. Найдем модули векторов: | a | = √ 7 2 + 1 2 = √ 49 + 1 = √ 50 = 5√ 2
| b | = √ 5 2 + 5 2 = √ 25 + 25 = √ 50 = 5√ 2 Найдем угол между векторами: | cos α = | a · b | = | 40 | = | 40 | = | 4 | = 0.8 | | | a | · | b | | 5√ 2 · 5√ 2 | 50 | 5 |
Примеры вычисления угла между векторами для пространственных задачРешение: Найдем скалярное произведение векторов: a · b = 3 · 4 + 4 · 4 + 0 · 2 = 12 + 16 + 0 = 28. Найдем модули векторов: | a | = √ 3 2 + 4 2 + 0 2 = √ 9 + 16 = √ 25 = 5
| b | = √ 4 2 + 4 2 + 2 2 = √ 16 + 16 + 4 = √ 36 = 6 Найдем угол между векторами: | cos α = | a · b | = | 28 | = | 14 | | | a | · | b | | 5 · 6 | 15 |
Решение: Найдем скалярное произведение векторов: a · b = 1 · 5 + 0 · 5 + 3 · 0 = 5. Найдем модули векторов: | a | = √ 1 2 + 0 2 + 3 2 = √ 1 + 9 = √ 10
| b | = √ 5 2 + 5 2 + 0 2 = √ 25 + 25 = √ 50 = 5√ 2 Найдем угол между векторами: cos α = a · b | a | · | b | = 5 √ 10 · 5√ 2 = 1 2√ 5 = √ 5 10 = 0.1√ 5 Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список! Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики. = 1 2 · a → 2 + b → 2 – b → – a → 2 a → · b → Для применения полученной формулы нам нужны длины векторов, которые несложно определяются по их координатам. Хотя указанный способ имеет место быть, все же чаще применяют формулу: ФормулаЧтобы найти косинус угла между векторами нужно найти отношение скалярного произведения векторов и произведение их длин (модулей). Если векторы заданы на плоскости двумя координатами $ overline=(x_1;y_1) $ и $ overline=(x_2;y_2) $, то косинус угла между ними вычисляется по формуле: В числителе находится скалярное произведение векторов, то есть каждая координата умножается на соответствующую координату другого вектора и при этом находится сумма всех произведений. А в знаменателе расположено произведение модулей векторов. Каждый модуль равен извлеченному квадратному корню из суммы квадратов координат вектора. Примеры решений| Пример | | Даны два вектора $ overline =(3;1) $ и $ overline = (2;4) $. Требуется найти косинус угла между векторами. | | Решение | Напомним как найти косинус угла между векторами. Необходимо определить на плоскости или в пространстве находятся векторы, то есть сколько у них координат. Затем воспользоваться подходящей формулой. Первым делом вычисляем скалярное произведение: каждую координату одного вектора умножаем на соответствующую координату другого вектора, а потом суммируем произведения: Далее находим чему равны модули каждого из векторов: Теперь можно найти косинус угла между векторами подставив найденные значения в первую формулу: Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
Калькулятор косинуса — Расчет cos (x) Найдите косинус угла с помощью калькулятора cos ниже. Начните с ввода угла в градусах или радианах. Как найти косинус угла В прямоугольном треугольнике косинус угла α или cos (α) — это отношение между смежной стороной угла и гипотенузой. Косинус является одной из трех основных тригонометрических функций и обозначается сокращенно cos . Вы можете спросить, как найти косинус угла? Используйте приведенную ниже формулу для расчета cos. Формула косинуса Формула косинуса: cos (α) = смежная бипотенуза c Таким образом, косинус угла α в прямоугольном треугольнике равен длине соседней стороны, деленной на гипотенузу. Чтобы решить cos, просто введите длину смежной и гипотенузы и решите. Например, давайте вычислим косинус угла α в треугольнике с длиной прилегающей стороны, равной 6, и гипотенузой, равной 8. cos (α) = 68
cos (α) = 34 График косинусов Если вы построите график функции косинуса для каждого возможного угла, он образует повторяющуюся кривую вверх / вниз. Это называется косинусоидальной волной. Кривая начинается с угла 0, затем уменьшается до значения -1, затем увеличивается до значения 1 и продолжается бесконечно. Таблица косинусов В таблице ниже показаны общие углы и значение cos для каждого из них. Таблица, показывающая общие углы и значения косинуса для каждого из них.| Угол (градусы) | Угол (радианы) | Косинус |
|---|
| 0 ° | 0 | 1 | | 15 ° | π12 | √6 + √24 | | 30 ° | π6 | √32 | | 45 ° | π4 | √22 | | 60 ° | π3 | 12 | | 75 ° | 5π12 | √6 — √24 | | 90 ° | π2 | 0 | | 105 ° | 7π12 | –√6 — √24 | | 120 ° | 2π3 | –12 | | 135 ° | 3π4 | –√22 | | 150 ° | 5π6 | –√32 | | 165 ° | 11π12 | –√6 + √24 | | 180 ° | π | -1 | | 195 ° | 13π12 | –√6 + √24 | | 210 ° | 7π6 | –√32 | | 225 ° | 5π4 | –√22 | | 240 ° | 4π3 | –12 | | 255 ° | 17π12 | –√6 — √24 | | 270 ° | 3π2 | 0 | | 285 ° | 19π12 | √6 — √24 | | 300 ° | 5π3 | 12 | | 315 ° | 7π4 | √22 | | 330 ° | 11π6 | √32 | | 345 ° | 23π12 | √6 + √24 | | 360 ° | 2π | 1 | Обратный косинус и секанс Функция, обратная косинусу, — это функция arccos.Таким образом, если вы знаете cos угла, вы можете использовать arccos, чтобы найти угол. Секанс, с другой стороны, является обратной величиной косинуса. Следующие формулы показывают соотношение между косинусом и секансом. cos (α) = смежная гипотенуза
сек (α) = смежная гипотенуза = 1 cos (α) Возможно, вас заинтересуют наши калькуляторы синуса и тангенса. Как найти угол с косинусом Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает
или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее
в
информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors. Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как
в виде
ChillingEffects.org. Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно
искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится
на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу. Чтобы отправить уведомление, выполните следующие действия: Вы должны включить следующее: Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Ваше заявление: (а) вы добросовестно полагаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени. Отправьте жалобу нашему уполномоченному агенту по адресу: Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже: Калькулятор Arcsin. Нахождение обратной функции синуса. С помощью этого калькулятора арксинуса (или калькулятора обратного синуса) у вас не будет проблем с поиском арксинуса в вашей задаче.Просто введите значение синуса для треугольника, и появится нужный угол. Единственное, что вам нужно запомнить, это ограниченная область арксинуса (−1 ≤ sine ≤ 1). Если вам интересно, , что такое арксинус или , как выглядит график arcsin x , не ждите больше — прокрутите вниз, и вы найдете ответы ниже! Мы также включили короткий абзац об отношениях арксинусов, таких как отношения между интегралом арксинуса и производной. И так, чего же ты ждешь? Что такое арксинус? Арксинус — это функция, обратная синусоиде.Другими словами, это помогает найти угол треугольника, который имеет известное значение синуса. Поскольку область синуса для действительных чисел равна [-1, 1], мы можем вычислить арксинус только для чисел в этом интервале. Синус — периодическая функция, поэтому существует несколько чисел, которые имеют одинаковое значение синуса. Например, sin (0) = 0, но также sin (π) = 0, sin (2π) = 0, sin (-π) = 0 и sin (-326π) = 0. Следовательно, если кто-то хочет вычислить arcsin ( 0), ответ может быть 0, 2π (360 °) или -π (-180 °), и это лишь некоторые из вариантов! Все они верны, но обычно мы даем только одно число, называемое основным значением . | Сокращение | Определение | Домен arcsin x
для реального результата | Диапазон обычных
основных значений |
|---|
arcsin (x)
sin -1 x,
asin | х = грех (у) | -1 ≤ х ≤ 1 | -π / 2 ≤ y ≤ π / 2
-90 ° ≤ y ≤ 90 ° |
Arcsin (x) — наиболее распространенное обозначение, поскольку sin -1 x может привести к путанице (потому что sin -1 x ≠ 1 / sin (x)).Аббревиатура asin обычно используется в языках программирования. График arcsin x Поскольку синус основной функции не является взаимно однозначным, ее область должна быть ограничена, чтобы гарантировать, что арксинус также является функцией. Обычно выбирается область -π / 2 ≤ y ≤ π / 2. Это означает, что диапазон обратной функции будет равен диапазону основной функции; таким образом, диапазон функции arcsin равен [−π / 2, π / 2], а область arcsine находится между [−1,1]. Ниже вы можете найти график arcsin (x), а также некоторые часто используемые значения арксинуса: | х | арксин (х) | График |
|---|
| ° | рад | | -1 | -90 ° | -π / 2 | Компьютерщик 3, CC BY-SA 4.0 через Wikimedia Commons | | -√3 / 2 | -60 ° | -π / 3 | | -√2 / 2 | -45 ° | -π / 4 | | -1/2 | -30 ° | -π / 6 | | 0 | 0 ° | 0 | | 1/2 | 30 ° | π / 6 | | √2 / 2 | 45 ° | π / 4 | | √3 / 2 | 60 ° | π / 3 | | 1 | 90 ° | π / 2 |
Хотите знать, откуда взялся этот график arcsin x? Его можно найти, отразив график sin (x) в диапазоне [-π / 2 π / 2] через линию y = x: Jaro.p CC BY-SA 3.0, через Wikimedia Commons Обратный синус, тригонометрические функции и другие взаимосвязи Связь между тригонометрическими функциями и арксинусом может помочь вам еще лучше понять тему. Прямоугольный треугольник с гипотенузой длины 1 — хорошая отправная точка. Просто быстрое напоминание: для прямоугольного треугольника функция синуса принимает угол θ и возвращает отношение противоположности / гипотенузы, которое равно x в нашем примерном треугольнике.Функция обратного синуса, арксинус, будет принимать отношение противоположности / гипотенузы (x) и возвращать угол θ. Итак, зная, что для нашего треугольника arcsin (x) = θ, мы также можем записать, что: - Синус:
sin (arcsin (x)) = x - Косинус:
cos (arcsin (x)) = √ (1-x²) - Касательная:
tan (arcsin (x)) = x / √ (1-x²)
Другие полезные отношения с арксинусом: -
arcsin (x) = π / 2 - arccos (x) -
arcsin (-x) = -arcsin (x)
Иногда также нужны интеграл и производная от arcsin: интеграл от arcsin: arcsin (x) dx = x arcsin (x) + √ (1 - x²) + C производная от arcsin: d / dx arcsin (x) = 1 / √ (1 - x²) где x ≠ -1, 1
Пример использования калькулятора arcsin Арксинус — полезная функция e.г. в нахождении угла прямоугольного треугольника. Если вы ищете углы в прямоугольном треугольнике и знаете длины сторон, хорошо известная теорема Пифагора не будет столь полезной. Чтобы найти углы прямоугольного треугольника, нужно применить арксинус: - для α:
sin (α) = a / c, поэтому α = arcsin (a / c) - для β:
sin (β) = b / c, поэтому β = arcsin (b / c)
Итак, предположим, что у нас есть два значения, заданные в прямоугольном треугольнике, a = 6 и c = 10, и мы хотели бы найти значение угла α: - Введите значение, по которому вы хотите найти арксинус .В нашем случае это 6/10. Таким образом, вы можете ввести значение 0,6, но форма 6/10 также будет работать. Просто помните, что значение должно быть между -1 и 1.
- И … все! Калькулятор arcsin выполнил свою работу, и вы нашли арксинус своего значения . Теперь вы знаете, что арксинус (6/10) = 36,87 °
Отлично! Теперь, когда вы понимаете, что такое арксинус, может быть, вы захотите познакомиться с более продвинутыми приложениями тригонометрии? Например, закон синусов (тесно связанный с законом косинусов) является обязательным при решении задач треугольника. Косинус — определение математического слова Косинус — определение математического слова — Открытый справочник по математике В
прямоугольный треугольник,
косинус угла — это длина смежной стороны (A), деленная на длину
гипотенуза (H). Попробуй это
Перетащите любой
вершину треугольника и посмотрите, как вычисляются косинусы A и C. Функция косинуса, наряду с синусом и тангенсом, является одной из трех наиболее распространенных
тригонометрические функции.
В любом прямоугольном треугольнике
косинус угла — это длина смежной стороны (A), деленная на длину
гипотенуза (H).В формуле он записывается просто как «cos». Часто вспоминается как «CAH», что означает
Косинус
Смежно над
Гипотенуза.
См. SOH CAH TOA. В качестве примера предположим, что мы хотим найти косинус угла C на рисунке выше (сначала нажмите «сбросить»).
Из приведенной выше формулы мы знаем, что косинус угла — это смежная сторона, деленная на гипотенузу.
Соседняя сторона — это BC и имеет длину 26. Гипотенуза — это AC с длиной 30. Таким образом, мы можем написать Это деление на калькуляторе выходит на 0.866.
Таким образом, мы можем сказать: « Косинус 30 ° равен 0,866 » или Воспользуйтесь калькулятором, чтобы найти косинус 30 °. Как и выше, должно получиться 0,8660.
(Если нет — убедитесь, что калькулятор настроен на работу в градусах, а не
радианы). Пример — использование косинуса для нахождения гипотенузы Если мы посмотрим на общее определение — мы видим, что есть три переменные: мера угла x и длины двух сторон (смежная и гипотенуза).Итак, если у нас есть какие-то два из них, мы можем найти третий. На рисунке выше нажмите «Сброс». Представьте, что мы не знаем длины гипотенузы H.
Мы знаем, что косинус A (60 °) — это смежная сторона (15), деленная на H. Из нашего калькулятора мы находим, что cos60 равен 0,5, поэтому мы можем написать Транспонирование: что составляет 30, что соответствует цифре выше. Функция обратного косинуса — arccos Для каждой тригонометрической функции, такой как cos, существует обратная функция, которая работает в обратном порядке.Эти обратные функции имеют то же имя, но с дугой впереди.
Таким образом, cos является обратной величиной arccos и т. Д. Когда мы видим «arccos A», мы интерпретируем его как «угол, косинус которого равен A». | cos60 = 0,5 | Означает: косинус 60 градусов равен 0,5 | | arccos0.5 = 60 | Означает: угол, косинус которого равен 0,5, равен 60 градусам. |
Мы используем его, когда знаем, что такое косинус угла, и хотим узнать фактический угол. Также определение арккосинуса и
Обратные функции — тригонометрия Большие и отрицательные углы В прямоугольном треугольнике два переменных угла всегда меньше 90 °.
(См. Внутренние углы треугольника).
Но на самом деле мы можем найти косинус любого угла, независимо от его размера, а также косинус отрицательных углов.
Подробнее об этом см. Функции больших и отрицательных углов. Построение функции косинуса Когда косинус угла отображается в зависимости от угла, в результате получается форма, аналогичная приведенной выше. Для получения дополнительной информации см. Построение функции косинуса. Производная cos (x) В расчетах производная cos (x) равна –sin (x) .
Это означает, что при любом значении x скорость изменения или наклон cos (x) составляет –sin (x) .
Подробнее об этом см.
Производные тригонометрических функций вместе с производными других тригонометрических функций.
См. Также Оглавление по исчислению. (C) Открытый справочник по математике, 2011 г.
Все права защищены. Как найти косинус угла с помощью функции COS в Excel Если вам нужно найти косинус угла, используйте функцию COS в Microsoft Excel. Независимо от того, указан ли ваш угол в градусах или радианах, это решение работает с небольшими настройками. Следуйте этому пошаговому руководству, чтобы узнать, как легко воспользоваться быстрыми математическими навыками Excel. Инструкции в этой статье относятся к Excel 2019, 2016, 2013, 2010, 2007; Excel для Mac, Excel 365, Excel Online, Excel для Android, Excel для iPad и Excel для iPhone. Найдите косинус угла в Excel Косинус тригонометрической функции, как синус и тангенс, основан на прямоугольном треугольнике (треугольнике с углом, равным 90 градусам), как показано на изображении ниже. В математическом классе косинус угла находится путем деления длины стороны, примыкающей к углу, на длину гипотенузы. В Excel косинус угла можно найти с помощью функции COS, если угол измеряется в радианах. Функция COS экономит много времени и, возможно, избавляет вас от лишних хлопот, поскольку вам больше не нужно помнить, какая сторона треугольника примыкает к углу, который является противоположным, а какой является гипотенузой. Понять градусы и радианы Использование функции COS для определения косинуса угла может быть проще, чем выполнение этого вручную, но, как уже упоминалось, важно понимать, что при использовании функции COS угол должен быть в радианах , а не в градусах. Радианы связаны с радиусом круга. Один радиан равен примерно 57 градусам. Чтобы упростить работу с COS и другими триггерами Excel, используйте функцию РАДИАНЫ Excel для преобразования измеряемого угла из градусов в радианы, как показано в ячейке B2 на изображении выше. В этом примере угол 60 градусов преобразуется в 1,047197551 радиан. Другие варианты преобразования из градусов в радианы включают в себя вложение функции РАДИАНЫ в функцию COS (как показано в строке 3 в примере изображения) и использование функции PI Excel в формуле (как показано в строке 4 на изображении в качестве примера). Тригонометрическое использование в Excel Тригонометрия фокусируется на отношениях между сторонами и углами треугольника, и, хотя многим из нас не нужно использовать ее ежедневно, тригонометрия находит применение в ряде областей, включая архитектуру, физику, инженерию и геодезию. Например, архитекторы используют тригонометрию для расчетов, связанных с затенением от солнца, структурной нагрузкой и уклонами крыши. Синтаксис и аргументы функции COS Excel Синтаксис функции относится к макету функции и включает имя функции, скобки и аргументы.Синтаксис функции COS:
= COS ( Число )
data-type = «code»> Номер: Рассчитываемый угол в радианах. Для этого аргумента можно ввести размер угла в радианах или вместо этого ввести ссылку на ячейку, указывающую на расположение этих данных на листе. Используйте функцию COS Excel Пример в этой статье описывает шаги, используемые для ввода функции COS в ячейку C2 на изображении выше, чтобы найти косинус угла 60 градусов или 1.047197551 радиан. Варианты ввода функции COS включают ввод вручную всей функции или использование диалогового окна «Аргументы функции», как показано ниже. Войдите в COS-функцию Выберите на листе ячейку C2 , чтобы сделать ее активной. Выберите вкладку Формулы на панели ленты. Выберите Math & Trig на ленте, чтобы открыть раскрывающийся список функций. Выберите COS в списке, чтобы открыть диалоговое окно «Аргументы функций». В Excel для Mac откроется построитель формул. В диалоговом окне поместите курсор в числовую строку. Выберите на листе ячейку B2 , чтобы ввести ссылку на эту ячейку в формулу. Выберите OK , чтобы заполнить формулу и вернуться к рабочему листу. За исключением Excel для Mac, где вместо этого вы выбираете Готово . Ответ 0,5 появляется в ячейке C2, , который является косинусом угла 60 градусов. Выберите ячейку C2, чтобы увидеть полную функцию в строке формул над листом.
= COS (B2)
data-type = «code»> Устранение проблем с функцией COS в Excel # ЗНАЧЕНИЕ! Ошибки Функция COS отображает # ЗНАЧ! ошибка, если ссылка, используемая в качестве аргумента функции, указывает на ячейку, содержащую текстовые данные.Измените тип данных ячейки на Числа, чтобы исправить ошибку. Результаты пустой ячейки Если ячейка указывает на пустую ячейку, функция возвращает значение, равное единице. Триггерные функции Excel интерпретируют пустые ячейки как ноль, а косинус нуля радиан равен единице. Исправьте ошибку, указав свою функцию в правой ячейке. Спасибо, что сообщили нам об этом! Расскажите, почему! Другой Недостаточно подробностей Сложно понять Калькулятор косинуса 📐 — вычисляет cos (x) в градусах или радианах. Используйте этот калькулятор косинуса, чтобы легко вычислить косинус угла в градусах или радианах. Быстрая навигация: - Функция косинуса (cos (x))
- Связанные тригонометрические функции
- Как вычислить косинус угла?
- Применение функции косинуса
Функция косинуса (cos (x)) Косинус — это тригонометрическая функция угла, обычно определяемая для острых углов внутри прямоугольного треугольника как отношение длины смежной стороны к гипотенузе.Это дополнение к синусу. На рисунке ниже cos (α) = b / c и cos (β) = a / c. Поскольку cos (α) = b / c , из этого определения следует, что косинус любого угла всегда меньше или равен единице и может принимать отрицательные значения. Косинус угла 90 градусов равен нулю, поскольку для его вычисления нам понадобится треугольник с двумя углами 90 градусов, что является определением прямой линии. Поскольку третьей стороны треугольника не существует (длина равна 0), косинус равен нулю (0, разделенный на длину гипотенузы, равен 0).Вы можете использовать этот калькулятор косинусов, чтобы убедиться в этом. Обычно используемый закон в тригонометрии, который тривиально выводится из определения косинуса, — это закон косинусов : c 2 = a 2 + b 2 — 2ab · cosγ Косинус , обратный косинусу , представляет собой секанс: sec (x), иногда записываемый как секанс (x), который дает отношение длины гипотенузы к длине стороны, противоположной углу. , обратный косинусу , — это функция арккосинуса: acos (x) или arccos (x), которая принимает значения от 0 до 180 градусов.Это полезно для определения угла x, когда известен cos (x). Как рассчитать косинус угла? Наш калькулятор косинусов поддерживает ввод как в градусах, так и в радианах, поэтому после того, как вы измерили угол или просмотрели план или схему, вы просто вводите измерение и нажимаете «вычислить». Вот как это просто. Если угол неизвестен, но указаны длины смежной стороны и гипотенузы прямоугольного треугольника, то вычисление косинуса может быть выполнено путем деления смежной стороны на гипотенузу (сторона c, как показано на рисунке выше).Например, если нужно найти cot (α) и известно, что соседняя сторона b = 6 и c = 20, то cos (α) = 6/20 = 0,3. Применение функции косинуса Функция косинуса может использоваться для моделирования периодических явлений в физике, биологии, социальных науках и т. Д. Более практический пример — если вы хотите срубить дерево, знаете его высоту и хотите знать, насколько далеко вы находитесь в данный момент. стоя, используйте функцию загара. JPEG, очень распространенный алгоритм сжатия изображений, использует так называемую функцию «дискретного косинусного преобразования» (DCT) для выражения конечных последовательностей точек данных в виде сумм функций косинуса с различными частотами колебаний.Модифицированная версия используется в качестве основы для популярного кодека сжатия звука MP3, а также AAC, Vorbis и WMA. MPEG и DV также основаны на аналогичных расчетах. Вверху: волна, генерируемая с помощью функции косинуса. Косинусоидальная волна — это зеркальное отображение синусоидальной волны. Таблица общих значений косинуса: Общие значения функции косинуса| x (°) | x (рад.) | синус (x) |
|---|
| 0 ° | 0 | 1 | | 30 ° | π / 6 | 0.866025 | | 45 ° | π / 4 | 0,707107 | | 60 ° | π / 3 | 0,50 | | 90 ° | π / 2 | 0 | | 120 ° | 2π / 3 | -0,50 | | 135 ° | 3π / 4 | -0,707107 | | 150 ° | 5π / 6 | -0,866025 | | 180 ° | π | -1 | Функция косинуса в прямоугольных треугольниках Косинус — это тригонометрическое соотношение, сравнивающее две стороны прямоугольного треугольника.Косинус обычно сокращается до cos, но произносится как косинус. Эта функция может использоваться для определения длины стороны треугольника, если задана хотя бы одна сторона треугольника и один из острых углов. Быстрый просмотр: три основных триггерных отношения: синус, косинус и тангенс. Их можно запомнить с помощью SOH CAH TAH Что это значит? Это означает, что косинус — это отношение соседней стороны к гипотенузе. Cosθ = Давайте рассмотрим пример того, как можно использовать косинус для определения длины противоположной стороны. Чтобы найти x, напишите уравнение, используя коэффициент косинуса, а затем решите для x cos 30 ° = умножьте обе части уравнения на 15 (15) cos 30 = (15) Вам понадобится калькулятор, чтобы найдите значение cos 30 ° (15) (.8660) = x убедитесь, что ваш калькулятор работает в градусном режиме, проверив, что cos 30 .8660 (округлено до 4 знаков после запятой) 12,99 = x На соседней стороне указано приблизительное значение длина 12,99 или 13 с округлением до ближайшей десятой. Теперь давайте посмотрим, как можно использовать косинус для определения длины гипотенузы. Чтобы найти x, напишите уравнение, используя отношение косинусов, а затем решите относительно x Cos 20 ° = Умножьте обе части уравнения на x. (x) cos 20 ° = (x) Вам нужно будет использовать калькулятор, чтобы найти значение cos 20 °. Округлить до 4 десятичных знаков Убедитесь, что ваш калькулятор работает в градусном режиме, убедившись, что (x) (.9397) = 10 cos 20 .9397 Разделите обе стороны на.9397, чтобы выделить x x = 10,6417 Округлите ответ до ближайшей десятой x = 10,6 длина гипотенузы составляет приблизительно 10,6 Триггерные отношения имеют множество реальных и практических приложений в таких областях, как авиация, архитектура, геодезия . Использование тригонометрических соотношений, таких как косинус, позволяет измерять вещи, которые нельзя определить с помощью обычных измерительных инструментов. . Страница не найденаСтраница не найдена Страница не найдена либо ссылка устарела. Используйте ссылки ниже для навигации по магазину. - Каталог товаров
- Освещение
- Люстры
- Люстры потолочные
- Люстры подвесные
- Люстры каскадные
- Люстры хрустальные
- Люстры на штанге
- Люстры-вентиляторы
- Большие люстры
- Люстры декоративные
- Абажуры и комплектующие
- Светильники
- Настенные светильники
- Потолочные светильники
- Линейные светильники
- Светодиодные панели
- Светильники-конструкторы
- Cameleon System (Nowodvorski)
- Ziko (Azzardo)
- Set Up (Ideal Lux)
- Бра и подсветки
- Бра с 1 плафоном
- Бра с 2 плафонами
- Бра с 3 плафонами
- Бра с 4 и более плафонами
- Бра половинки
- Бра с подвижным плафоном
- Бра с лампой для чтения
- Подсветки для картин и зеркал
- Подсветка ступеней
- Зеркала с подсветкой
- Бра декоративные
- Ночники
- Настольные лампы
- Декоративные
- На основании
- На струбцине
- Прищепки
- Соляные
- Абажуры для настольных ламп
- Основания для настольных ламп
- Торшеры
- С 1 плафоном
- С 2 плафонами
- С 3 и более плафонами
- Световые колонны
- Декоративные
- Абажуры для торшеров
- Основания для торшеров
- Споты
- Споты с одной лампой
- Споты с двумя лампами
- Споты с тремя лампами
- Споты с четырьмя и более лампами
- Треки и трековые системы
- Трековые светильники
- Трековые системы
- Магнитные трековые системы
- Точечный свет
- Встроенные
- Накладные
- Downlight
- Светодиодная подсветка Led
- Светодиодная лента
- Блоки питания
- Диммеры
- Контроллеры для RGB ленты
- Контроллеры для RGB с ИК управлением
- Контроллеры для RGB с радио управлением
- Усилители
- Алюминиевый профиль
- Уличный свет
- Бра
- Настенные светильники
- Подвесы
- Уличные потолочные светильники
- Прожекторы
- Столбики парковые
- Столбы фонарные
- Уличные консольные светильники
- Уличные вкапываемые светильники
- Уличные встроенные светильники
- Переносные светильники
- Декоративное освещение
- Новогоднее освещение
- LED сувениры
- Лампочки и комплектующие
- Лампы
- Патроны для ламп
- Провод декоративный
- Датчики движения
- ПРА
- Трансформаторы
- Светильники в детскую комнату
- Детские люстры
- Детские настенные светильники
- Настольные лампы для детей
- Розетки и выключатели
- Legrand
- Valena Classic
- Valena Life
- Valena Allure
- Celiane
- Galea Life
- Cariva
- Mosaic
- MOSAIC NEW
- Plexo
- Forix
- Etika
- Soliroc
- Netatmo with Legrand
- Schneider Electric
- Unica
- Механизмы Unica
- Unica Basic
- Unica Colors
- Unica Plus
- Unica Quadro
- Unica Top
- Unica Top Алюминий рамки
- Unica Top Графит рамки
- Unica Class
- Рамки Unica Class камень сланец
- Рамки Unica Class металлические рамки
- Серебристый алюминий
- Лунный алюминий
- Рамки Unica Class стекло
- Белое стекло
- Матовое стекло
- Черное зеркало
- Рамки Unica Class кожа
- Sedna
- Белый
- Слоновая кость
- Алюминий
- Титан
- Графит
- Декоративные рамки
- Asfora
- Цвет Белый
- Цвет Слоновая кость
- Цвет Алюминий
- Цвет Бронза
- Цвет Сталь
- Цвет Антрацит
- Unica New
- Механизмы Unica New
- Unica New Studio
- Unica New Studio Color
- Unica New Studio Metal
- Unica New Pure
- Unica Modular
- Unica system+
- Sedna Design & Elements
- Sedna Elements
- Sedna Design
- Renova
- Mureva Styl
- Altira
- Berker
- Механизмы BERKER
- Berker коллекция S.
 1 1 - Berker коллекция B.3
- Berker коллекция B.7
- Berker коллекция K.1/K.5
- Полярный белый
- Антрацит
- Нержавеющая сталь
- Алюминий лакированный
- Berker коллекция ARSYS
- Berker коллекция ARSYS — цвет белый
- Berker коллекция ARSYS — цвет полярный белый
- Berker коллекция ARSYS — цвет бронза
- Berker коллекция ARSYS — цвет золото
- Berker коллекция ARSYS — цвет нержавеющая сталь
- Berker коллекция R.1/R.3
- Berker коллекция R.8
- Berker коллекция Q1 / Q3 / Q7
- Berker коллекция R–Classic
- Rosenthal SERIE 1930
- Glasserie SERIE 1930
- Palazzo SERIE 1930
- Стеко BERKER TS / TS Crystal / TS Sensor
- Наружный монтаж Berker W.1
- Abb — Elektro-Praga Чехия
- Механизмы Time Neo Levit
- Серия Тime (Чехия)
- Цвет-08 титан
- Цвет-32 серебристый металлик
- Цвет-33 шампань металлик
- Цвет-34 черный металлик
- Рамки Time Arbo (натуральное дерево)
- Серия Neo (Чехия)
- Цвет белый/белый лед
- Цвет белый/синий лед
- Цвет белый/зеленый лед
- Цвет белый/оранжевый лед
- Цвет белый/серый лед
- Цвет графит/белый лед
- Цвет сталь/терракот
- Цвет титан/оникс
- Цвет сталь/титан
- Цвет оникс/титан
- Cерия Levit
- серия Swing
- Серия наружной установки
Garant IP66
- Abb — Busch-Jaeger Elektro GmbH (Германия)
- Abb — Niessen (Испания)
- Tacto
- Механизмы Такто
- Накладки (лицевые панели)
- Белые
- Серые
- Антрацит
- Шампань
- Серебро
- Рамки Такто
- Белые
- Серый гранит
- Шампань
- Серебро
- Стекло
- Мрамор
- Дерево
- Сланец
- Сталь
- Zenit
- Цвет белый
- Центральные панели одномодульные
- Центральные панели двухмодульные
- Рамки белые (немецкий стандарт)
- Рамки белые (итальянский стандарт)
- Цвет серебряный
- Одномодульные
- Двухмодульные (серебро)
- Рамки серебряные (немецкий стандарт)
- Рамки серебряные (итальянский стандарт)
- Цвет антрацит
- Одномодульные
- Двухмодульные
- Рамки (немецкий стандарт)
- Рамки (итальянский стандарт)
- Цвет шампань
- Рамки Zenit
- Наружная установка Zenit
- Светосигнальная система Niessen Zenit
- Sky
- Sky Moon
- Gira
- Standard 55
- E2
- E3
- Event
- Esprit
- E22
- Edelstahl (E22)
- F100
- Studio
- ClassiX и ClassiX Art
- ClassiX Бронза
- ClassiX Латунь
- ClassiX Хром
- TX 44
- Jung
- Механизмы
- ECO PROFI
- ECO PROFI
- ECO PROFI STANDART
- ECO PROFI DECO
- СЕРИЯ A
- A-FLOW
- А550
- A creation
- Цвет красный оксид
- Цвет черный
- Цвет серо-голубой
- Цвет матовый
- A plus
- Цвет алюминий
- Цвет антрацит-алюминий
- Цвет синий-алюминий
- Цвет алюминий-белый
- Цвет антрацит-белый
- Цвет синий-белый
- Цвет хром-алюминий
- Цвет хром-белый
- AS
- Цвет белый
- Цвет слоновая кость
- AS500 антибактериальная
- Цвет белый
- Цвет слоновая кость
- AS500 ударопрочная
- Цвет белый
- Цвет слоновая кость
- CD 500
- Цвет слоновая кость
- Цвет белый
- Цвет коричневый
- Цвет серый
- Цвет светло-серый
- Цвет платина
- Цвет бронза
- Цвет черный
- CD plus
- SL 500
- Цвет белый
- Цвет бронза
- Цвет черный
- Цвет серебро
- LS 990
- Белый
- Белоснежный матовый
- Слоновая кость
- Светло-серый
- Алюминий
- Антрацит
- Черный
- Чёрный графит матовый
- Dark
- Antik
- Classic
- Нержавеющая сталь
- Хром
- Золото
- LS1912
- Cube
- LS Plus
- Цвет блестящий хром
- Цвет стекло
- Цвет алюминий
- Цвет Edelstahl
- Merten
- Merten механизмы
- D-Life
- Antik
- Античная латунь
- Merten Antik цвет — золото
- Merten Antik цвет- белый
- Merten Antik цвет — бежевый
- Merten Antik цвет — коричневый
- Artec
- M-Elegance
- M-Plan
- M-Pure
- M-Pure Decor
- M-Smart
- M-Creativ
- Aquadesign
- System M
- Merten System M цвет-алюминий
- Merten System M цвет-антрацит
- Merten System M цвет-бежевый
- Merten System M цвет-белый
- System Design
- Алюминий
- Бежевый
- Синий
- Ваниль
- Коричневый
- Серый
- Античная латунь
- Голубой
- Merten System Design Сталь
- BTicino
- Fontini
- Fontini Venezia
- Fontini Venezia Oval
- Fontini Venezia Classica
- Fontini Venezia Carre
- Fontini Venezia Toscana
- Fontini Venezia Colonial
- Fontini Venezia Metal
- Fontini Garby
- Белый фарфор
- Черный фарфор
- REGGIA мрамор
- Белый фарфор с синим орнаментом
- Белый фарфор с коричневым орнаментом
- Рамки для изделий Fontini Garby (накладного монтажа)
- Fontini Garby Colonial
- Внутренние элементы Белые
- Внутренние элементы Черные
- Fontini Dimbler
- Fontini F-37
- Fontini Barcelona
- Комплектующие для Garby и Dimbler
- Hager — Polo
- Lezard
- Розетки в пол и стол
- Монтаж в стол
- Монтаж на стол
- Монтаж в пол
- Светорегуляторы eTREN®
- Cosmo
- PLANK
- Efapel
- Apolo 5000
- Quadro 45
- WATERPROOF 48
- Всё для коммутации и управления
- Контакторы
- Модульные
- Корпусные
- Тепловые реле
- Аксессуары к контакторам
- Реле
- Импульсные реле
- Реле времени
- Реле сумеречные
- Реле промежуточные
- Реле установочные
- Реле контроля уровня жидкости
- Универсальные и силовые реле
- Тепловые реле
- Интерфейсные реле
- Реле тока
- Таймеры
- Термостаты
- Датчики движения, присутствия
- Измерительные приборы
- Вольтметры
- Переключатели для вольтметра
- Амперметры
- Ограничители тока
- Индикаторы напряжения
- Регуляторы света din (диммеры)
- Кнопки, переключатели, светосигнальная арматура
- Модульные устройства на Din-рейку
- Переключатели положений
- Кнопки
- Датчики дыма
- Трансформаторы модульные
- Рубильники
- Предохранители
- АВР (автоматический ввод резерва питания)
- Кабель-провод и все для монтажа
- Кабель, провод
- Силовой кабель
- АВВГ
- АВВГнг
- АВВГ нг-д
- ВВГ
- ВВГ нг
- ВВГ нгд
- ВВГ-П
- ВВГ-П нг
- ВВГ-П нгд
- ВВП-1
- Кабель для воздушных линий
- Контрольный кабель
- АКВВГ
- КВВГ
- OLFLEX CLASSIC 110
- OLFLEX CLASSIC 110 BK
- ÖLFLEX SMART 108
- ÖLFLEX CLASSIC 115 CY
- OLFLEX CLASSIC 110 LT (морозостойкий)
- FABER KABEL YSLY
- Шнур
- ПВС
- ШВВП
- OLFLEX CLASSIC 100
- Монтажный кабель
- ПВ-1
- ПВ-3
- ПВ-3нгд
- H05V-K
- H07V-K
- LiY
- Гибкий кабель
- Термостойкий кабель
- ÖLFLEX HEAT 180 SiF
- ÖLFLEX HEAT 180 SiHF
- ÖLFLEX HEAT 180 FZLSi
- FABER KABEL SiF / SiHF
- Огнестойкий кабель
- Сигнальный кабель
- Alarm Cable
- UNITRONIC LiYY
- UNITRONIC LiYCY (экран)
- UNITRONIC LiYCY (TP)
- FABER KABEL LiYCY (экран)
- Кабель для BUS систем
- KNX-кабель
- Компьютерный кабель
- 5Е CAT
- 6 CAT
- 7 CAT
- 7A CAT / 7+ CAT
- Коаксиальный кабель
- Телевизионный кабель
- Для видеонаблюдения
- Для радиосвязи
- Подвесной
- Кабель для пожарной сигнализации
- Кабель для фотогальванических систем
- ÖLFLEX SOLAR XLS-R
- h2Z2Z2-K
- Инструмент для работы с кабелем
- Удлинители бытовые
и аксессуары- Удлинители
- Удлинители на катушках
- Вилки / тройники / переходники бытовые
- Аксессуары электрические
- Коробки
- Силовые разъемы
- Прокладка кабеля
(короб труба металлорукав лотки)- Кабельный канал
- Гофротруба для кабеля (ПВХ)
- Металлорукав
- Лотки
- Средства для электромонтажа
- Кабельные вводы (гермовводы)
- Кабельные стяжки
- Клеммы в распредкоробку
- Рядные клеммы на din-рейку
- Гильзы, наконечники
- Крепеж (дюбеля, саморезы, хомуты)
- ДЮБЕЛЯ, ВИНТЫ
- САМОРЕЗЫ, ШУРУПЫ
- АНКЕРА, ШПИЛЬКИ
- ХОМУТЫ ,СКОБЫ
- ДРУГИЕ КРЕПЛЕНИЯ
- Патч-корды и разъемы RJ45 / RJ12
- Клеммы в щит
- Кабельные соединители
- Изоляционная лента
- Линейная арматура для СИП (0,38 кВ)
- Соединительная арматура
- Анкерно-подвесная арматура
- Элементы оснащения опор
- Наконечники и зажимы для кабеля
- Муфты кабельные до 1 кВ
- Инструмент для монтажа линий СИП
- Дополнительные элементы для СИП-арматуры
- Средства защиты и устройства заземлений
- Арматура для среднего напряжения (6-10 кВ)
- Арматура для ВЛЗ 6-10 кВ
- Ограничители перенапряжения 6-35 кВ
- Муфты кабельные
- Соединительная
- Концевая
- Переходная
- Наконечники
- Защита электросети
- Автоматические выключатели
- Модульные
- 1-полюсные
- 2-полюсные
- 3-полюсные
- 4-полюсные
- Корпусные
- Устройства защитного отключения (УЗО)
- Дифреле
- Дифавтоматы
- Дуговая защита AFDD+
- Комплектующие
- Средства защиты от перенапряжения
- Молниезащита
- Бесперебойное питание
- Стабилизаторы напряжения
- Счетчики электроэнергии
- 1-фазные счетчики
- 3-фазные счетчики
- Трансформаторы тока
- Для электродвигателей
- Автоматы защиты двигателя
- Плавный пуск
- Преобразователи частоты
- Магнитные пускатели
- Теплый пол и обогрев
- Теплый пол
- Кабель нагревательный
- Мат нагревательный
- Пленочный подогрев пола
- Терморегуляторы теплого пола
- Система снеготаяния
- Защита труб от замерзания
- Обогрев грунта
- Обогреватели
- Щиты распределительные и боксы
- Распределительные квартирные
- Для автоматики
- Для автоматики + место под счетчик
- Для автоматики + слаботочка
- Мультимедийные
- Влагозащищенные
- Огнестойкие
- Этажные
- Пустые
- Напольные
- Укомплектованные
- Наборной
- Комплектующие к щитам
- Электроинструмент
- Сверление и долбление
- Дрели
- Шуруповерты
- Перфораторы
- Отвертки (электро)
- Гайковерты (электро)
- Миксеры
- Отбойные молотки
- Аксессуары
и расходный материал
- Режущий инструмент
- Лобзики
- Бороздоделы (штроборезы)
- Пилы
- Ножовки (электро)
- Универсальные резаки (реноваторы)
- Аксессуары
и расходные материалы
- Обработка и монтаж
- Шлифовальные машины (болгарки)
- Рубанки (электро)
- Фрезеры
- Точильные станки
- Степлеры (электро)
- Термовоздуходувки
- Фены и паяльники
- Многофункциональный инструмент
- Клеевые пистолеты
- Рабочие столы
- Аксессуары и расходный материал
- Пневматический инструмент
- Мойки
- Краскопульты и пневмопистолеты
- Измерительный инструмент
- Садово — парковый инструмент
- Газонокосилки
- Триммеры
- Пылесосы и воздуходувы
- Культиваторы и мотоблоки
- Садовые измельчители
- Аэраторы
- Ножницы (электро)
- Кусторезы
- Другие садовые принадлежности
- Ручной инструмент
- Отвертки
- Плоскогубцы, пассатижи, утконосы и другое
- Гаечные ключи
- Обжимной инструмент
- Ножи
- Ножницы
- Измерение
- Вентиляция
- Вентиляторы бытовые
- Промышленные и коммерческие вентиляторы
- Вентиляционные каналы
- Проветриватели помещения
- Приточно-вытяжные установки
- Комплектующие для вентиляции
- «Умный дом», видеонаблюдение и домофония
- Домофония
- Видеодомофоны
- Вызывные панели
- Готовые комплекты
- Аксессуары
- Сигнализация
- Защита от затопления
- Зарядки
для электромобилей - Солнечные системы SOLAR
- Звонки дверные
- Умный дом
- NETATMO (Legrand)
- ABB i-bus
- Elko EP RF-Control
- RF Control
- Передатчики RF Control
- Приемники RF Control
- Комбинированные модули RF Control
- Детекторы Oasis
- Блоки управления GSM
- Berker.
 Net Net- Электронные механизмы Berker.Net
- Электронные накладки
- Датчики
- Производители
- Abb
- Agara
- Airelec
- Ajax
- ALUMLED
- Arkoslight
- ARTE Lamp
- AVATON
- AVT
- AZzardo
- BACHMANN
- BARVANOR
- BAS IP
- Berker
- Biom
- Blauberg
- Blitz Leuchten
- BM-group
- Bosch – professional
- BPM Lighting
- Brilum
- Bticino
- Carlo de Santi
- CIVILIGHT
- COLORS
- Comfort Heat
- Conceptio Light
- Conta-Clip
- Cristher
- Crystal Lux
- Dahua
- DCG
- Decalex
- Def. Design
- DELUX
- DEVI
- DFTP
- DigiTop
- Doepke
- Dopo
- E-NEXT
- Efapel
- EGLO
- Electro House
- ELECTRUM
- ELKO EP
- Elmar
- ELSTEAD LIGHTING
- EMIBIG
- Ensto
- Epistar
- ESEO
- Estar
- ETI
- eTREN
- Euroelectric
- Eurolamp
- EVT-Lighting
- Exo
- FABER KABEL
- Faro
- Feron
- Fieldmann
- Finder
- FinMark
- Fontini
- Fresh
- Gira
- GLOBAL LED
- GLOBO
- GOODLED
- GPower
- GYPSUM LINE
- Hager
- HellermannTyton
- Hitachi (Япония)
- Horoz Electric
- ICEL (Италия)
- Ideal Lux
- IEK
- ILLUMINATI
- Imagilights
- ImperiumLight
- Indeluz
- Infotel Led
- Italux
- JAGO
- JUNG
- Jupiter
- Kanlux
- KLOODI
- Kopos
- Laguna Lighting
- Lampex
- LappKabel
- LED LIGHTING
- Ledix
- Ledvance
- Legrand
- Lezard
- Light Topps
- LIRIO
- LTC
- LTX
- Lucide
- Lumifall
- LUMINARIA
- LUMINEX
- Lutec
- Mantra
- MARKSLOJD
- Massive
- MAXUS
- Mean Well
- MENNEKES
- Merten
- Mistic
- MOELLER-EATON
- MW-Light
- Navigator
- Nexans
- NIGAS
- NiK
- Noname
- Nordlux
- Norlys
- Nova Luce
- Novatek
- Nowodvorski
- OBO Bettermann
- OJ Electronics
- OMS
- ORLICKI DESIGN
- Osram
- Paulo-coelho
- PAX AB
- PHILIPS
- Pikart Lights
- PLANK Electrotechnic
- Polux
- Prana
- Pride
- Profitherm
- Quintessentiale
- RATEY
- RAYCHEM
- Reccagni Angelo
- RISHANG
- ROGU
- Sabaj
- Scheinlicht
- Schneider Electric
- Searchlight
- SHILO
- SICAME
- SIEMENS
- Sigma
- Sirius
- Skarlat
- Slinex
- Sofi Milano
- Soler&Palau
- Sollux
- Sompex
- Sparky
- Spectrum LED
- SPELSBERG
- Spot Light
- ST-LIGHT
- SVL
- TaoTronics
- Tarel
- Techno
- Tehalit
- Terneo
- THEBEN
- TK-Lighting
- Trio
- TTAF
- Ultralight
- UMAGE
- VELA
- Vestum
- VIDEX
- Viokef
- Volter
- WAGO
- WALTHER
- Weidmuller
- Woks
- Wunderlicht
- Zambelis lights
- Zamel
- Zanussi
- ZARlight
- Zuma Line
- Аквасторож
- Брассвит
- Вентс
- Декора
- ДКС
- Евросвет
- ЗЗЦМ
- Зубр
- Китай
- Майком
- Мережик
- Одескабель
- Светкомплект
- Светодиодные технологии
- ТИС
- Украина
- Укртехнология
- ЭЛЕКОР
- Элекс
Модулятор давления Integral ABS для мотоцикла BMW K26 (R 900 RT, R 1200 RT), R 900 RT 05 SF (0367,0387) (ECE)- Группа
Тормозные механизмы
- Подгруппа
Модулятор давления Integral ABS (34_1409)
- Список запчастей
Изображена информация для модели: BMW K26 (R 900 RT, R 1200 RT), R 900 RT 05 SF (0367,0387) (ECE) Изображена информация для модели: BMW K26 (R 900 RT, R 1200 RT), R 900 RT 05 SF (0367,0387) (ECE) Но. | Название запчасти / номер | Дополнительная информация | Необход.количество | Period | app.diagram_page.price_with_vat | Отправим в течении | |
|---|
| 01 | 01 Pressure mo
34 51 7 698 296Отправим в течении: 7 рабочих дней
(нету в наличии, на заказ) 3 024,98 € Дополнительная информация Period:
до 06-08 Необход.количество: 1 Цена указана за 1 шт. Если товар явлается нераздельным комплектом (например, тормозные колодки), цена указана за комплект Отправим в течении: 7 рабочих дней
(нету в наличии, на заказ) | | Показать Необход.количество
: 1 Цена указана за 1 шт. Если товар явлается нераздельным комплектом (например, тормозные колодки), цена указана за комплект | до 06-08 | | | | Не поставляется | | 01 | 01 Pressure mo
34 51 7 728 061Отправим в течении: 7 рабочих дней
(нету в наличии, на заказ) 2 346,40 € Дополнительная информация Period:
до 06-08 Необход. количество: 1 количество: 1 Цена указана за 1 шт. Если товар явлается нераздельным комплектом (например, тормозные колодки), цена указана за комплект Отправим в течении: 7 рабочих дней
(нету в наличии, на заказ) | | Показать Необход.количество
: 1 Цена указана за 1 шт. Если товар явлается нераздельным комплектом (например, тормозные колодки), цена указана за комплект | до 06-08 | | 2 346,40 € | 7 рабочих дней
(нету в наличии, на заказ) | | | 02 | 02 Vent hose w
34 51 7 674 836Отправим в течении: 7 рабочих дней
(нету в наличии, на заказ) 67,06 € Дополнительная информация Period:
до 06-08 Необход.количество: 1 Цена указана за 1 шт. Если товар явлается нераздельным комплектом (например, тормозные колодки), цена указана за комплект Отправим в течении: 7 рабочих дней
(нету в наличии, на заказ) | | Показать Необход. количество
: 1 количество
: 1 Цена указана за 1 шт. Если товар явлается нераздельным комплектом (например, тормозные колодки), цена указана за комплект | до 06-08 | | 67,06 € | 7 рабочих дней
(нету в наличии, на заказ) | | | 03 | 03 Bracket, pr
34 51 7 666 471Отправим в течении: 7 рабочих дней
(нету в наличии, на заказ) 13,21 € Дополнительная информация Period:
до 06-08 Необход.количество: 1 Цена указана за 1 шт. Если товар явлается нераздельным комплектом (например, тормозные колодки), цена указана за комплект Отправим в течении: 7 рабочих дней
(нету в наличии, на заказ) | | Показать Необход.количество
: 1 Цена указана за 1 шт. Если товар явлается нераздельным комплектом (например, тормозные колодки), цена указана за комплект | до 06-08 | | 13,21 € | 7 рабочих дней
(нету в наличии, на заказ) | | | 04 | 04 Bracket, pr
34 51 7 666 472Отправим в течении: 7 рабочих дней
(нету в наличии, на заказ) 28,57 € Дополнительная информация Period:
до 06-08 Необход. количество: 1 количество: 1 Цена указана за 1 шт. Если товар явлается нераздельным комплектом (например, тормозные колодки), цена указана за комплект Отправим в течении: 7 рабочих дней
(нету в наличии, на заказ) | | Показать Необход.количество
: 1 Цена указана за 1 шт. Если товар явлается нераздельным комплектом (например, тормозные колодки), цена указана за комплект | до 06-08 | | 28,57 € | 7 рабочих дней
(нету в наличии, на заказ) | | | 05 | 05 Vibration d
34 51 7 676 064Отправим в течении: 7 рабочих дней
(нету в наличии, на заказ) 11,58 € Дополнительная информация Period:
до 06-08 Необход.количество: 3 Цена указана за 1 шт. Если товар явлается нераздельным комплектом (например, тормозные колодки), цена указана за комплект Отправим в течении: 7 рабочих дней
(нету в наличии, на заказ) | | Показать Необход. количество
: 3 количество
: 3 Цена указана за 1 шт. Если товар явлается нераздельным комплектом (например, тормозные колодки), цена указана за комплект | до 06-08 | | 11,58 € | 7 рабочих дней
(нету в наличии, на заказ) | | | 06 | 06 Винт ISA
07 12 9 901 130Отправим в течении: 1 рабочeго дня
(имеется на складе) 1,15 € Дополнительная информация Дополнительная информация:
M6X20-8.8-ZNNIV Period:
до 06-08 Необход.количество: 1 Цена указана за 1 шт. Если товар явлается нераздельным комплектом (например, тормозные колодки), цена указана за комплект Отправим в течении: 1 рабочeго дня
(имеется на складе) | M6X20-8.8-ZNNIV | Показать Необход.количество
: 1 Цена указана за 1 шт. Если товар явлается нераздельным комплектом (например, тормозные колодки), цена указана за комплект | до 06-08 | | 1,15 € | 1 рабочeго дня
(имеется на складе) | | | 07 | 07 Гайка шестигранная
07 11 9 905 543Отправим в течении: 1 рабочeго дня
(имеется на складе) 0,51 € Дополнительная информация Дополнительная информация:
M6-8-ZNNIV SI Period:
до 06-08 Необход. количество: 3 количество: 3 Цена указана за 1 шт. Если товар явлается нераздельным комплектом (например, тормозные колодки), цена указана за комплект Отправим в течении: 1 рабочeго дня
(имеется на складе) | M6-8-ZNNIV SI | Показать Необход.количество
: 3 Цена указана за 1 шт. Если товар явлается нераздельным комплектом (например, тормозные колодки), цена указана за комплект | до 06-08 | | 0,51 € | 1 рабочeго дня
(имеется на складе) | |
Беспилотники Израиля сегодня – Hermes 900Ранее ВВС Израиля сообщало о присвоении одному из базовых беспилотников Hermes 900 (Гермес 900) статуса полной операционной готовности. Такой статус может являться свидетельством того, что беспилотник оснастили новым разведывательным оборудованием и новыми каналами связи, – предполагает эксперт в области беспилотной летательной техники, редактор отраслевого журнала UAV. ru Д. Федутинов. Кроме того, это может говорить о том, что Hermes 900 полностью интегрирован в армейские информационно-управляющие системы, – продолжает специалист. Hermes 900 был разработан израильской компанией Elbit Systems на базе предшественника Hermes 450, который эксплуатируется в течении 17 лет в ряде стран мира. Общий налет беспилотников этого типа составляет более 500 тысяч часов. Hermes 900 отличается от предыдущей модификации аппарата не только большими размерами, но и улучшенными техническими характеристиками, а также повышенными разведывательными возможностями. Конкуренты беспилотника Hermes 900 на мировом рынке: аппараты семейства Predator (GA–ASI, США) и Heron (IAI, Израиль). ru Д. Федутинов. Кроме того, это может говорить о том, что Hermes 900 полностью интегрирован в армейские информационно-управляющие системы, – продолжает специалист. Hermes 900 был разработан израильской компанией Elbit Systems на базе предшественника Hermes 450, который эксплуатируется в течении 17 лет в ряде стран мира. Общий налет беспилотников этого типа составляет более 500 тысяч часов. Hermes 900 отличается от предыдущей модификации аппарата не только большими размерами, но и улучшенными техническими характеристиками, а также повышенными разведывательными возможностями. Конкуренты беспилотника Hermes 900 на мировом рынке: аппараты семейства Predator (GA–ASI, США) и Heron (IAI, Израиль). Фото 1. Hermes 900, одна из базовых моделей беспилотников сегодняшних ВВС Израиля. На вооружение аппарат официально был поставлен в 2015 году. (Источник: elbitsystems.com) Hermes 900 – средневысотный многоцелевой всепогодный беспилотник–разведчик с большой продолжительностью полёта. Аппарат способен непрерывно летать в течении 36 часов на высоте до 9140 метров; радиус действия до 1850 км. Длина фюзеляжа – 8.3 м, размах крыла – 15 м, взлетный вес – 1180 кг, максимальный вес полезной нагрузки (разведывательной аппаратуры и средств радиоэлектронной борьбы) – 350 кг. Аппарат способен непрерывно летать в течении 36 часов на высоте до 9140 метров; радиус действия до 1850 км. Длина фюзеляжа – 8.3 м, размах крыла – 15 м, взлетный вес – 1180 кг, максимальный вес полезной нагрузки (разведывательной аппаратуры и средств радиоэлектронной борьбы) – 350 кг. Полезная нагрузка весом до 250 кг размещается в приборном отсеке (Фото 2) и в подфюзеляжном обтекателе (Фото 3), дополнительная нагрузка общим весом до 100 кг — под крылом (Фото 4) на четырех подвесах (по два с каждой стороны). Hermes 900 это разведывательный комплекс, в состав которого входят: - собственно летательный аппарат,
- наземный пункт контроля, где размещается пилот-оператор (один или два в зависимости от полетного задания), и соответствующая аппаратура;
- система двухсторонней связи (включая спутниковую), обеспечивающая взаимодействие между летательным аппаратом и “землей”.
Некоторые источники высказывают мнение о наличии ударной версии Hermes 900, вооруженного ракетами или управляемыми бомбами. Фото 2. Hermes 900, приборный отсек (Источник: milavia.net) В каждом конкретном случае перед вылетом в зависимости от полетного задания на беспилотнике устанавливается требуемый набор бортовой аппаратуры. Эта операция не требует много времени, поскольку все приборы имеют модульное исполнение. Разведывательное оборудование: Радар, позволяющий получать радиолокационные изображения контролируемого участка земной поверхности и находящихся на ней объектов независимо от времени суток, метеорологических условий и уровня естественной освещенности. По качеству и степени детализации радиолокационные изображения сравнимы с аэрофотоснимками, но в отличие от последних могут быть получены при отсутствии оптической видимости земной поверхности. Специальное исполнение радара выделяет движущуюся наземную цель, определяет скорость ее перемещения, а также создает представление о размерах и конфигурации цели. Система аэрофотосъемки, осуществляющая сканирование местности одновременно в нескольких волновых диапазонах, позволяет получать не только точное месторасположение и изображение объекта, но и сведения о материале, из которого он состоит, что обеспечивает более полную идентификацию потенциальной цели. Система сканирования местности, выполняющая одновременно с обзором территории наблюдение за несколькими, в том числе движущимися целями. Фото 3. Hermes 900, подфюзеляжный обтекатель (Источник: pro-samolet.ru, маркер автора) Цветная телевизионная камера высокой резолюции, работающая в условиях низкой освещенности. Инфракрасная тепловизионная камера, основанная на фиксации невидимого теплового (инфракрасного) излучения, испускаемого любым объектом (для работы тепловизора, в отличие от приборов ночного видения, вообще не требуется свет). Тепловизор способен обнаруживать живую силу и технику вне зависимости от времени суток. Системы радиоразведки и пеленгации, предназначенные для обнаружения излучающих устройств и мобильной сотовой связи противника. Система электронной разведки, осуществляющая сбор информации путем перехвата сигналов радиолокационных станций, установок радиоэлектронной борьбы, оборонных сетей связи и тому подобных устройств противника. Лазерный прожектор для подсветки объекта наблюдения в диапазоне невидимого инфракрасного излучения. Системы радиоэлектронной борьбы. Система радиоэлектронного подавления, функционирующая в широком диапазоне частотного спектра, может одновременно воздействовать на несколько целей в соответствии с установленными приоритетами. Система радиоэлектронной борьбы содержит средства обнаружения облучения радарами/лазерами. В состав системы входит также аппаратура противодействия противнику. Система автоматической идентификации Эта система обеспечивает опознание воздушных судов, их курса и других данных. Наличие этой бортовой системы является необходимым компонентом для выполнения безопасных полетов Hermes 900 в едином воздушном пространстве наравне с гражданскими пилотируемыми летательными аппаратами. Фото 4. Hermes 900, размещение полезной нагрузки под крылом (Источник: elbitsystems. com, маркеры автора) com, маркеры автора) Линии связи обеспечивают двустороннюю связь между беспилотником и наземным пунктом контроля: - на борт летательного аппарата передаются команды пилота-оператора;
- в пункт контроля поступает информация, собранная бортовой разведывательной аппаратурой, и сведения о состоянии систем летательного аппарата.
В зоне прямой видимости применяется прямая связь между летательным аппаратом и наземным пунктом контроля. Вне зоны прямой видимости используется спутниковая связь. Для повышения надежности имеются резервные каналы связи. Предусмотрено два режима управления беспилотником: - пилотирование пилотом-оператором с наземного пункта контроля;
- автономное пилотирование, при котором управление полетом осуществляет бортовая аппаратура в соответствии с заложенной программой; вмешательство пилота-оператора требуется лишь при необходимости изменения полетного задания или возникновении каких-либо чрезвычайных обстоятельств.

Консоль наземного пункта контроля предусматривает возможность управления одним или двумя летательными аппаратами (Фото 5). По команде пилота-оператора беспилотник самостоятельно выдвигается из ангара на взлетно-посадочную полосу и поднимается в воздух. После выполнения полета самостоятельно приземляется, закатывается в ангар и выключает двигатели. В настоящее время беспилотные летательные аппараты, принадлежащие вооруженным силам, не могут выполнять полеты в едином воздушном пространстве, в котором проходят маршруты гражданской авиации. Беспилотники военного назначения пока могут летать только в закрытом воздушном пространстве полигонов и авиабаз. Фото 5. Станция наземного контроля (Источник: elbitsystems.com) В связи с непрерывным ростом количества беспилотников многие страны начали разрабатывать нормативную базу, позволяющую безопасные полеты беспилотной авиации в едином воздушном пространстве с гражданскими пилотируемыми воздушными судами. Разрабатываемые правила содержат, в частности, требования к техническому оснащению беспилотников, обеспечивающие должный уровень безопасности совместных полетов. Разрабатываемые правила содержат, в частности, требования к техническому оснащению беспилотников, обеспечивающие должный уровень безопасности совместных полетов. Hermes 900 может обнаруживать воздушные объекты и изменять свой маршрут полета, чтобы избежать столкновения, а также взаимодействовать с пилотируемыми летательными аппаратами, передавая им точные данные о своем пространственном положении. Автор: Марк Яловецкий Воспользуйтесь нашими услугами Понравилась статья? Тогда поддержите нас, поделитесь с друзьями и заглядывайте по рекламным ссылкам! Layilin, новый интегральный мембранный белок, является рецептором гиалуроновой кислоты . 2001 Апрель; 12 (4): 891-900. doi: 10.1091/mbc.12.4.891. П Боно 1 , К. Рубин, Дж. М. Хиггинс, Р. О. Хайнс О. Хайнс принадлежность- 1 Медицинский институт Говарда Хьюза, Центр исследования рака, Массачусетский технологический институт, Кембридж 02139, США.
- PMID: 11294894
- PMCID:
PMC32274
- DOI:
10.1091/mbc.12.4.891
Бесплатная статья ЧВК П. Боно и др.
Мол Биол Селл.
2001 9 апр.0003 Бесплатная статья ЧВК . 2001 Апрель; 12 (4): 891-900. 2001 Апрель; 12 (4): 891-900. doi: 10.1091/mbc.12.4.891. Авторы П Боно 1 , К. Рубин, Дж. М. Хиггинс, Р. О. Хайнс принадлежность- 1 Медицинский институт Говарда Хьюза, Центр исследования рака, Массачусетский технологический институт, Кембридж 02139, США.
- PMID: 11294894
- PMCID:
PMC32274
- DOI:
10.1091/mbc.12.4.891
Абстрактный Актиновый цитоскелет играет важную роль в изменении формы и подвижности клеток, а взаимодействия между актиновыми филаментами и клеточной мембраной имеют решающее значение для множества клеточных процессов. Некоторые адапторные белки, включая talin, поддерживают связь между цитоскелетом и мембраной путем связывания с интегральными мембранными белками и с цитоскелетом. Layilin, недавно охарактеризованный трансмембранный белок, гомологичный лектинам С-типа, является сайтом связывания талина с мембраной в периферических складках распространяющихся клеток. Чтобы облегчить исследования функции лейилина, мы создали слитый белок лейилин-Fc, содержащий внеклеточную часть лейилина, соединенную с тяжелой цепью иммуноглобулина G человека, и использовали эту химеру для идентификации лигандов лейилина. Здесь мы демонстрируем, что слитый белок лейилин-Fc связывается с гиалуроновой кислотой, иммобилизованной на сефарозе. Анализы связывания на микротитровальных планшетах, эксперименты по соосаждению и окрашивание срезов, предварительно расщепленных различными ферментами, разрушающими гликозаминогликаны, и анализы клеточной адгезии показали, что лейилин специфически связывается с гиалуроновой кислотой, но не с другими тестируемыми гликозаминогликанами. Некоторые адапторные белки, включая talin, поддерживают связь между цитоскелетом и мембраной путем связывания с интегральными мембранными белками и с цитоскелетом. Layilin, недавно охарактеризованный трансмембранный белок, гомологичный лектинам С-типа, является сайтом связывания талина с мембраной в периферических складках распространяющихся клеток. Чтобы облегчить исследования функции лейилина, мы создали слитый белок лейилин-Fc, содержащий внеклеточную часть лейилина, соединенную с тяжелой цепью иммуноглобулина G человека, и использовали эту химеру для идентификации лигандов лейилина. Здесь мы демонстрируем, что слитый белок лейилин-Fc связывается с гиалуроновой кислотой, иммобилизованной на сефарозе. Анализы связывания на микротитровальных планшетах, эксперименты по соосаждению и окрашивание срезов, предварительно расщепленных различными ферментами, разрушающими гликозаминогликаны, и анализы клеточной адгезии показали, что лейилин специфически связывается с гиалуроновой кислотой, но не с другими тестируемыми гликозаминогликанами. Способность Layilin связывать гиалуронан, вездесущий компонент внеклеточного матрикса, обнаруживает интересную параллель между layilin и CD44, потому что оба могут связываться с линкерными белками цитоскелета-мембраны через свои цитоплазматические домены и с гиалуроновой кислотой через свои внеклеточные домены. Этот параллелизм предполагает роль layilin в клеточной адгезии и подвижности. Способность Layilin связывать гиалуронан, вездесущий компонент внеклеточного матрикса, обнаруживает интересную параллель между layilin и CD44, потому что оба могут связываться с линкерными белками цитоскелета-мембраны через свои цитоплазматические домены и с гиалуроновой кислотой через свои внеклеточные домены. Этот параллелизм предполагает роль layilin в клеточной адгезии и подвижности. Цифры Рисунок 1 Структура и очистка рекомбинантных… Рисунок 1 Структура и очистка рекомбинантного слитого белка лейилин-Fc. (A) Белковые домены… фигура 1 Структура и очистка рекомбинантных
слитый белок лейилин-Fc. (A) Белковые домены лейилина-Fc
и лайилин дикого типа показаны. Внеклеточная часть Лайилина была
клонирован непосредственно на N-конце шарнирного домена (H) IgG1 человека
так что химера содержит два цистеиновых остатка (не показаны)
внутри шарнирного домена, ответственного за димеризацию Ig. Сиг,
НХ 2 -концевая сигнальная последовательность, лектин, лейилины
внеклеточная часть, гомологичная лектинам С-типа; ТМ,
трансмембранный домен; Ch3 и Ch4, константные области IgG человека.
(B) Очищенный слитый белок лейилин-Fc анализировали на геле SDS-PAGE.
как в восстановленных, так и в невосстановленных условиях и обнаруживается
иммуноблоттинг с античеловеческим IgG (Fc-специфическим)
антитело. Молекулярные массы (в кДа) показаны слева. Внеклеточная часть Лайилина была
клонирован непосредственно на N-конце шарнирного домена (H) IgG1 человека
так что химера содержит два цистеиновых остатка (не показаны)
внутри шарнирного домена, ответственного за димеризацию Ig. Сиг,
НХ 2 -концевая сигнальная последовательность, лектин, лейилины
внеклеточная часть, гомологичная лектинам С-типа; ТМ,
трансмембранный домен; Ch3 и Ch4, константные области IgG человека.
(B) Очищенный слитый белок лейилин-Fc анализировали на геле SDS-PAGE.
как в восстановленных, так и в невосстановленных условиях и обнаруживается
иммуноблоттинг с античеловеческим IgG (Fc-специфическим)
антитело. Молекулярные массы (в кДа) показаны слева. Рисунок 2 Очищенный слитый белок лейилин-Fc связывает… Рисунок 2 Очищенный слитый белок лейилин-Fc связывается с иммобилизованным НА. (A) Слитый белок Layilin-Fc был… (A) Слитый белок Layilin-Fc был… фигура 2 Очищенный слитый белок лейилин-Fc связывается с
иммобилизованный ГА. (A) Слитый белок Layilin-Fc инкубировали с
HA-Sepharose или с контрольными шариками Sepharose и HA-специфическими
додекасахариды использовали для элюирования связанного материала с гранул.
Проточные фракции (FT) и элюаты подвергали SDS-PAGE.
и иммуноблотинг с антителом против IgG человека. Примечание
что в полосах управления Sepharose весь сигнал находится в FT
дробная часть. Небольшую аликвоту очищенного (несвязанного) лейилина Fc анализировали.
на параллельной дорожке, чтобы показать расположение слитого белка в
пониженные условия. (B) В аналогичном эксперименте по связыванию с
Слитый белок E-кадгерин Fc, элюирование олигосахаридами HA не
привести к любому детектируемому сигналу, и весь слитый белок находится в
переулок ФТ. Молекулярные массы (в кДа) показаны слева. Рисунок 3 Лайилин можно осаждать только… Рисунок 3 Лайилин может осаждаться только в присутствии ГК, но не в других… Рисунок 3 Лайилин может осаждаться только в присутствии
HA, но не другие GAG. (A) Общий клеточный лизат клеток 3T3 был
инкубировали с разными ГАГ (по 50 мкг каждого) и подвергали ХПК
осадки. Осадки и общий клеточный лизат разделяли на
Гель SDS-PAGE и окрашивание антителом против лейилина после блоттинга на
мембрана. Контрольные реакции осаждали ЦПК без добавления
любого ГАГ или после добавления N -ацетилглюкозамин.
Интенсивность полос осажденного лейилина в двух аналогичных
эксперименты были оценены количественно, и результат показан в B. (A) Общий клеточный лизат клеток 3T3 был
инкубировали с разными ГАГ (по 50 мкг каждого) и подвергали ХПК
осадки. Осадки и общий клеточный лизат разделяли на
Гель SDS-PAGE и окрашивание антителом против лейилина после блоттинга на
мембрана. Контрольные реакции осаждали ЦПК без добавления
любого ГАГ или после добавления N -ацетилглюкозамин.
Интенсивность полос осажденного лейилина в двух аналогичных
эксперименты были оценены количественно, и результат показан в B. Рисунок 4 Связывание лейилина-IgG (L-IgG) с… Рисунок 4 Связывание лейилин-IgG (L-IgG) с иммобилизованной и растворимой ГК. (A) Связывание различных… Рисунок 4 Связывание лайилин-IgG (L-IgG) с иммобилизованными и
растворимая ГК. (A) Связывание различных количеств очищенных химер с
иммобилизованная ГК в отсутствие конкурирующих ГАГ. Связанный лайилин-IgG,
CD44-IgG (положительный контроль) и E-кадгерин-IgG (отрицательный контроль)
слитые белки были обнаружены с антителом против Fc в сочетании
с помощью HRP, а связанный bHA-связывающий белок был обнаружен с помощью
HRP-конъюгированный стрептавидин. (B) Связывание растворимого bHA с лейилином-IgG
(L-IgG) или CD44-IgG, иммобилизованные в микротитрационных лунках. Различное количество
слитые белки использовались для предварительного покрытия лунок, которые затем
инкубировали с 10 мкг/мл bHA. (C) Связывание 10 мкг/мл лейилина-Fc в
наличие свободной ГК, хондроитинсульфата или гепарина. (Г) Аналогично
конкуренция как в C, но со связыванием CD44-IgG вместо лейилина-IgG.
Каждый результат в A–D представляет собой среднее значение результатов повторных определений.
из того же эксперимента. Представленные данные являются репрезентативными для трех
индивидуальные эксперименты по связыванию. (A) Связывание различных количеств очищенных химер с
иммобилизованная ГК в отсутствие конкурирующих ГАГ. Связанный лайилин-IgG,
CD44-IgG (положительный контроль) и E-кадгерин-IgG (отрицательный контроль)
слитые белки были обнаружены с антителом против Fc в сочетании
с помощью HRP, а связанный bHA-связывающий белок был обнаружен с помощью
HRP-конъюгированный стрептавидин. (B) Связывание растворимого bHA с лейилином-IgG
(L-IgG) или CD44-IgG, иммобилизованные в микротитрационных лунках. Различное количество
слитые белки использовались для предварительного покрытия лунок, которые затем
инкубировали с 10 мкг/мл bHA. (C) Связывание 10 мкг/мл лейилина-Fc в
наличие свободной ГК, хондроитинсульфата или гепарина. (Г) Аналогично
конкуренция как в C, но со связыванием CD44-IgG вместо лейилина-IgG.
Каждый результат в A–D представляет собой среднее значение результатов повторных определений.
из того же эксперимента. Представленные данные являются репрезентативными для трех
индивидуальные эксперименты по связыванию. Рисунок 5 Гистохимическое окрашивание опухолей, полученных… Рисунок 5 Гистохимическое окрашивание опухолей, происходящих из поджелудочной железы мышей RIP-Tag2. Секции криостата… Рисунок 5 Гистохимическое окрашивание опухолей, происходящих из
pancreata мышей RIP-Tag2. Криостатные срезы опухолей поджелудочной железы мышей
реагировали с химерами (0,5 мкг/мл) и обрабатывали для
гистохимия, как описано в разделе «МАТЕРИАЛЫ И МЕТОДЫ». Оригинал
увеличение 50х на А и 400х на Б-Д. (A) Контрольный слитый белок
(Е-кадгерин IgG) окрашивание среза опухоли. ECM не окрашивается. (Б)
Layilin-IgG положительно окрашивает ECM, и окрашивание чувствительно к
обработка гиалуронидазой перед инкубацией с лейилином-IgG (C). Похожий
предварительная обработка срезов хондроитиназой (D) или гепаритиназой (E)
не отменял реактивность лейилина-Fc. Похожий
предварительная обработка срезов хондроитиназой (D) или гепаритиназой (E)
не отменял реактивность лейилина-Fc. Рисунок 6 Клетки MCF-7, трансфицированные Layilin, прикрепляются к… Рисунок 6 Клетки MCF-7, трансфицированные Layilin, прикрепляются к НА. (A) Экспрессия лейилина на клетках MCF-7… Рисунок 6 клеток MCF-7, трансфицированных Layilin, прикрепляются к НА. (А)
Экспрессия лейилина на клетках MCF-7, стабильно трансфицированных лейилином
кДНК или имитация контроля. После отбора тотальные клеточные лизаты были
подвергали SDS-PAGE и детекции с помощью антитела против лейилина. (Б)
Клетки MCF-7, экспрессирующие Layilin, связываются с HA. Микротитровальные планшеты были
покрытые ГА или БСА, и адгезия лейилин-MCF-7 или имитация
трансфектанты определяли через 90 мин адгезии с использованием
флуорогенный анализ. Данные представлены в процентах прилипших клеток.
Показаны средние значения ± стандартное отклонение. Данные являются репрезентативными как минимум для трех
отдельные опыты. Обратите внимание, что даже после многократных стирок
значительно больше клеток layilin-MCF-7, чем ложные контрольные клетки, связываются с
ХА. Данные представлены в процентах прилипших клеток.
Показаны средние значения ± стандартное отклонение. Данные являются репрезентативными как минимум для трех
отдельные опыты. Обратите внимание, что даже после многократных стирок
значительно больше клеток layilin-MCF-7, чем ложные контрольные клетки, связываются с
ХА. См. это изображение и информацию об авторских правах в PMC Похожие статьи Layilin, новый talin-связывающий трансмембранный белок, гомологичный лектинам C-типа, локализован в складках мембраны. Боровский М.Л., Хайнс Р.О.
Боровский М.Л. и соавт.
Джей Селл Биол. 1998 19 октября; 143 (2): 429-42. doi: 10.1083/jcb.143.2.429.
Джей Селл Биол. 1998.
PMID: 9786953
Бесплатная статья ЧВК. Лейилин, рецептор гиалуроновой кислоты на клеточной поверхности, взаимодействует с мерлином и радиксином. Боно П., Кордеро Э., Джонсон К., Боровски М., Рамеш В., Джекс Т., Хайнс Р.О.
Боно П. и др.
Разрешение ячейки опыта. 2005 г., 1 августа; 308 (1): 177–87. doi: 10.1016/j.yexcr.2005.04.017.
Разрешение ячейки опыта. 2005.
PMID: 15
5 Выявление и противодействие взаимодействию между лейилином и гликозилированными коллагенами. Глазго Дж. Э., Бирнс Дж. Р., Барби С. Д., Моро Дж. М., Розенблюм М. Д., Уэллс Дж. А.
Глазго Дж. Э. и соавт.
Cell Chem Biol. 2022 21 апреля; 29(4):597-604.e7. doi: 10.1016/j.chembiol.2022.01.003. Epub 2022 1 февраля.
Cell Chem Biol. 2022.
PMID: 35104453 Структурные основы взаимодействия между цитоплазматическим доменом гиалуронового рецептора лейилином и субдоменом талина F3. Вегенер К.Л., Басран Дж., Бэгшоу К.Р., Кэмпбелл И.Д., Робертс Г.К., Кричли Д.Р., Барсуков И.Л.
Вегенер К.Л. и соавт.
Дж Мол Биол. 2008 Сентябрь 26; 382 (1): 112-26. doi: 10.1016/j.jmb.2008.06.087. Epub 2008 7 июля.
Дж Мол Биол. 2008.
PMID: 18638481 Химерные молекулы CD4/CD44 связываются с CD44 через трансмембранную область и уменьшают связывание гиалуроновой кислоты в линиях Т-клеток. Ли Р., Уокер Дж. Р., Джонсон П.
Ли Р и др.
Евр Дж Иммунол. 1998 июнь; 28 (6): 1745-54. doi: 10.1002/(SICI)1521-4141(199806)28:063.0.CO;2-5.
Евр Дж Иммунол. 1998.
PMID: 9645355 Посмотреть все похожие статьи Цитируется Протеогликаны в ответах толл-подобных рецепторов и врожденном иммунитете. Garantziotis S, Savani RC.
Гарантзиотис С. и др.
Am J Physiol Cell Physiol. 2022 г., 1 июля; 323(1):C202-C214. doi: 10.1152/ajpcell.00088.2022. Epub 2022 8 июня.
Am J Physiol Cell Physiol. 2022.
PMID: 35675639
Обзор. Результаты нецелевого анализа с использованием протеомной платформы SOMAscan указывают на новые ассоциации циркулирующих белков с риском прогрессирования почечной недостаточности при диабете. Кобаяши Х., Лукер Х.К., Сатакэ Э., Солнье П.Дж., М.Д. Дом З.И., О’Нил К., Ихара К., Кролевски Б., Галецки А.Т., Невчас М.А., Уилсон Дж.М., Дориа А., Даффин К.Л., Нельсон Р.Г., Кролевски А.С.
Кобаяши Х. и др.
почки инт. 2022 г., август; 102 (2): 370-381. doi: 10.1016/j.kint.2022.04.022. Epub 2022 23 мая.
почки инт. 2022.
PMID: 35618095 Гиалуроновая кислота: известна почти век, но все еще в моде. Лиерова А., Каспарова Ю., Филипова А., Чижкова Ж., Пекарова Л., Корецкая Л., Маннова Н., Белкова З., Синкорова З.
Лиерова А. и др.
Фармацевтика. 2022 11 апреля; 14 (4): 838. doi: 10.3390/фармацевтика14040838.
Фармацевтика. 2022.
PMID: 35456670
Бесплатная статья ЧВК.
Обзор. Анализ одиночных клеток раскрывает фактор дифференцировки роста остеобластов 10 как медиатор фенотипической модуляции гладкомышечных клеток сосудов, связанной с разрывом бляшки при заболевании сонных артерий человека. Брандт К.Дж., Бургер Ф., Баптиста Д., Рот А., Фернандес да Силва Р., Монтекукко Ф., Мах Ф., Митева К.
Брандт К.Дж. и соавт.
Int J Mol Sci. 2022 4 февраля; 23 (3): 1796. дои: 10.3390/ijms23031796.
Int J Mol Sci. 2022.
PMID: 35163719
Бесплатная статья ЧВК. Функции гиалуроновой кислоты в заживлении ран, которые используются для ускорения прогрессирования рака молочной железы. Толг С., Мессам Б.Дж., Маккарти Д.Б., Нельсон А.С., Терли Э.А.
Толг С. и др.
Биомолекулы. 2021 Октябрь 20;11(11):1551. дои: 10.3390/биом11111551.
Биомолекулы. 2021.
PMID: 34827550
Бесплатная статья ЧВК.
Обзор.
Просмотреть все статьи «Цитируется по» Типы публикаций термины MeSH вещества Грантовая поддержка- R01 CA017007/CA/NCI NIH HHS/США
- R01 CA17007/CA/NCI NIH HHS/США
АРРОЗ ИНТЕГРАЛ — ВЕРДЕ ВАЛЛЕ Изменить страницу Штрих-код: 7501071300134 (EAN/EAN-13) Эта страница продукта не является полной. Вы можете помочь завершить его, отредактировав его и добавив больше данных из фотографий, которые у нас есть, или сделав больше фотографий с помощью приложения для Android или iPhone/iPad. Благодарю вас!
× Вы можете помочь завершить его, отредактировав его и добавив больше данных из фотографий, которые у нас есть, или сделав больше фотографий с помощью приложения для Android или iPhone/iPad. Благодарю вас!
× Характеристики продукта × изображение/svg+xml Распространенное имя:
АРРОЗ ИНТЕГРАЛ Количество:
900 г Упаковка:
Полиэтиленовый пакет Бренды:
ВЕРДЕ ВАЛЛЕ Категории:
Продукты и напитки из растительного сырья, Продукты из растительного сырья, Зерновые и картофель, Семена, Зерновые и продукты из них Происхождение ингредиентов:
Мексика Места производства или обработки:
МЕКСИКА Магазины:
ВАЛМАРТ Страны продажи:
Мексика × изображение/svg+xml Ингредиенты × image/svg+xml → Ингредиенты перечислены в порядке важности (количества). Список ингредиентов: АРРОЗ ИНТЕГРАЛ Если этот продукт имеет список ингредиентов на английском языке, пожалуйста, добавьте его.
Изменить страницу Анализ ингредиентов:
image/svg+xmlБез пальмового масла изображение/svg+xmlВеганский image/svg+xmlВегетарианские
→ Анализ основан исключительно на перечисленных ингредиентах и не учитывает методы обработки. Подробности анализа ингредиентов » ARROZ INTEGRAL - ARROZ INTEGRAL -> ru:коричневый рис — веганский: да — вегетарианский: да — процент_мин: 100 — процент_макс: 100
Группа НОВА 1 — Необработанные или минимально обработанные продукты × image/svg+xml Пищевая ценность × image/svg+xml NutriScore color пищевая ценность Детали расчета Nutri-Score » Этот продукт не считается напитком для расчета Nutri-Score. Положительных баллов: 9 - Белки:
5 / 5
(значение: 8,16,
округленное значение: 8,16)
- Волокно:
4 / 5
(значение: 4,08,
округленное значение: 4,08)
- Фрукты, овощи, орехи и масло из рапса/грецкого ореха/оливковое:
0 / 5
(значение: 0,
округленное значение: 0)
Отрицательных баллов: 4 - Энергия:
4 / 10
(значение: 1470,
округленное значение: 1470)
- Сахара:
0 / 10
(значение: 0,
округленное значение: 0)
- Насыщенный жир:
0 / 10
(значение: 0,
округленное значение: 0)
- Натрий:
0 / 10
(значение: 4,15,
округленное значение: 4,2)
Баллы за белки учитываются, так как отрицательные баллы меньше 11. Оценка питания: -5 (4 — 9) Nutri-Score: A ⚠️ Внимание: количество фруктов, овощей и орехов не указано на этикетке, оно рассчитано по списку ингредиентов: 0 Уровень питательных веществ на 100 г 3,06 г Жир в умеренном количестве
0 г Насыщенный жир в малом количестве
0 г Сахар в малом количестве
0,0104 г Соль в небольшом количестве Размер порции:
49 г
Сравнение со средней стоимостью продуктов той же категории: Семена
(18655 товаров)
Зерновые и продукты из них
(61370 товаров)
Зерновые и картофель
(95119 товаров)
Растительные продукты
(265380 товаров)
Растительные продукты и напитки
(304439 товаров) % разницы
стоимость на 100 г / 100 мл → Обратите внимание: для каждой пищевой ценности рассчитывается среднее значение для продуктов, для которых известно количество питательных веществ, а не для всех продуктов категории. | Энергия | 1470 кДж
(351 ккал) | 718,5 кДж
(172 ккал) | +16%
1270 кДж
(304 ккал) | +1%
1460 кДж
(349 ккал) | +4%
1410 кДж
(336 ккал) | +27%
1160 кДж
(280 ккал) | +44%
1020 кДж
(247 ккал) | | Толстый | 3,06 г | 1,5 г | -50%
6,14 г | -41%
5,2 г | -48%
5,93 г | -71%
10,5 г | -65%
8,67 г | | Насыщенный жир | 0 г | 0 г | -100%
0,756 г | -100%
1,3 г | -100%
1,21 г | -100%
1,87 г | -100%
1,64 г | | Углеводы | 71,4 г | 35 г | +61%
44,4 г | +16%
61,5 г | +24%
57,4 г | +116%
33,1 г | +139%
29,9 г | | сахара | 0 г | 0 г | -100%
1,28 г | -100%
6,68 г | -100%
5,35 г | -100%
7,91 г | -100%
7,68 г | | Волокно | | 08″>
4,08 г 2 г | -41%
6,93 г | -15%
4,79грамм | -10%
4,51 г | +7%
3,8 г | +19%
3,44 г | | Белки | 8,16 г | 4 г | -27%
11,2 г | -13%
90,36 г | -10%
9,02 г | +38%
5,9 г | +60%
5,11 г | | Соль | 0,01 г | 0,005 г | -95%
0,223 г | -97%
0,364 г | -98%
0,662 г | -98%
0,493 г | -98%
0,428 г | | Фрукты, овощи, орехи и рапс, масло из грецкого ореха и оливковое масло (оценка на основе анализа списка ингредиентов) | 0 % | 0 % | ? | ? | ? | -100%
33,6 % | -100%
33,7 % |
× image/svg+xml Упаковка Инструкции по переработке и/или информация об упаковке: Детали упаковки:| Номер | Форма | Материал | Переработка | | Сумка | Пластик | | Источники данных Продукт добавлен автором openfoodfactsmx5
Последнее изменение страницы продукта автором packbot. Если данные неполные или неверные, вы можете дополнить или исправить их, отредактировав эту страницу. Изменить страницу MuleSoft позволяет любому разблокировать данные и создавать связанный опыт работы с клиентами с помощью кликов, а не кода интегрируйте системы, объединяйте данные и предоставляйте по-настоящему взаимосвязанные и персонализированные услуги для клиентов MuleSoft раскрывает возможности Salesforce Customer 360, открывая доступ к данным из любого приложения, источника или устройства, где бы они ни находились, в Salesforce или за его пределами World Integration and Platerds Platerds Provider, чтобы навык навык на 100 000 следов интеграции, вооружение сегодняшнего дня и завтра 18 ноября 2019 г. — MuleSoft, поставщик ведущей платформы для построения сетей приложений, объявил сегодня о новых инструментах, предварительно упакованных соединителях и обучающих модулях, позволяющих любому создавать связанный клиентский опыт без написания единой строки кода. Теперь каждый может стать первопроходцем в области интеграции и легко подключать источники данных, где бы они ни находились; ускорить интеграцию с автоматизированным интеллектуальным отображением данных на базе Einstein; и узнайте о возможностях подключения на основе API. MuleSoft считает, что обладая необходимыми навыками и лучшими в своем классе технологиями, любой должен иметь возможность подключать данные из любого места, чтобы раскрыть всю мощь Salesforce Customer 360. — MuleSoft, поставщик ведущей платформы для построения сетей приложений, объявил сегодня о новых инструментах, предварительно упакованных соединителях и обучающих модулях, позволяющих любому создавать связанный клиентский опыт без написания единой строки кода. Теперь каждый может стать первопроходцем в области интеграции и легко подключать источники данных, где бы они ни находились; ускорить интеграцию с автоматизированным интеллектуальным отображением данных на базе Einstein; и узнайте о возможностях подключения на основе API. MuleSoft считает, что обладая необходимыми навыками и лучшими в своем классе технологиями, любой должен иметь возможность подключать данные из любого места, чтобы раскрыть всю мощь Salesforce Customer 360. Каждая компания претерпевает цифровую трансформацию, чтобы клиенты были в центре внимания, и интеграция никогда не была более стратегической. Согласно отчету Connectivity Benchmark Report, предприятия имеют в среднем 900 приложений, но только 29% из них интегрированы друг с другом, что приводит к хранению ценных данных в разрозненных хранилищах и созданию разрозненного взаимодействия с клиентами. Будущее подключенного опыта требует интеграции систем и унификации данных с помощью API, и этот набор навыков должен выходить за рамки четырех стен ИТ, чтобы быть доступным для самых близких к клиенту людей. Будущее подключенного опыта требует интеграции систем и унификации данных с помощью API, и этот набор навыков должен выходить за рамки четырех стен ИТ, чтобы быть доступным для самых близких к клиенту людей. Раскрытие возможностей Salesforce Customer 360 Чтобы сделать интеграцию еще более демократичной, новые инструменты, созданные на платформе MuleSoft Anypoint Platform™, позволят любому интегрировать системы без написания единой строки кода. В рамках этого нового опыта пользователи могут сосредоточиться на создании потрясающих возможностей, повторно используя API, вместо того, чтобы запускать интеграцию и управлять ею. Между тем, ИТ-отдел может продолжать централизованно управлять, защищать и контролировать эти API в рамках всей организации с помощью платформы Anypoint. Новые функции включают в себя: - Flow Designer: Благодаря расширенным возможностям искусственного интеллекта Einstein, Flow Designer позволит пользователям легко создавать интеграции и автоматизировать бизнес-процессы быстрее, чем когда-либо прежде, — и все это без написания единой строки кода.
 Любой может создать интеллектуальную интеграцию, а Einstein автоматически предоставит рекомендации по отображению данных на основе искусственного интеллекта. Благодаря Flow Designer, устраняющему сложность управления серверами, журналами и инфраструктурой, MuleSoft демократизирует интеграцию, чтобы компании могли использовать инновации, а ИТ-отдел обеспечивал безопасность и контроль. Любой может создать интеллектуальную интеграцию, а Einstein автоматически предоставит рекомендации по отображению данных на основе искусственного интеллекта. Благодаря Flow Designer, устраняющему сложность управления серверами, журналами и инфраструктурой, MuleSoft демократизирует интеграцию, чтобы компании могли использовать инновации, а ИТ-отдел обеспечивал безопасность и контроль. - Акселераторы: Новые акселераторы MuleSoft систематизируют передовой опыт интеграции и превращают его в готовые шаблоны интеграции, которые позволяют компаниям быстрее предоставлять подключенные услуги клиентам.
- MuleSoft Accelerator для Service Cloud Агенты по обслуживанию оружия с историей заказов, статусом и данными обновления для быстрого решения проблем клиентов. Accelerator for Service Cloud предоставляет шаблоны интеграции для подключения ServiceNow и Jira к Service Cloud и создания заявок непосредственно из Service Cloud.
- MuleSoft Accelerator для Commerce Cloud гарантирует, что потребители получат точные и актуальные данные о продуктах, интегрируя данные запасов и каталогов непосредственно в Commerce Cloud.

- Менеджер сообщества Anypoint API: Управление API на протяжении всего жизненного цикла, персонализация, форумы, чат, управление обращениями в службу поддержки и аналитика взаимодействия объединяются в API Community Manager для развития цифровых экосистем. Организации могут легко обмениваться API с внутренними и внешними разработчиками и первопроходцами в области интеграции. Новые обновления включают в себя возможность просматривать API, статьи контента, дела, сообщения на форумах и клиентские приложения по ключевым словам и категориям с помощью каталога API и интегрированного поиска, что позволяет сообществам легко находить необходимые им ресурсы API.
Все эти функции становятся более мощными благодаря Anypoint Exchange, торговой площадке MuleSoft для готовых API и интеграций. Anypoint Exchange позволяет пользователям внутри компании сотрудничать и повторно использовать интеграции и API-интерфейсы во всей своей организации, что значительно повышает их скорость и гибкость по мере продолжения цифровой трансформации. Повышение квалификации 100 000 первопроходцев в области интеграции в течение следующих пяти лет Первопроходцев в области интеграции — это чемпионы в области цифровых технологий — администраторы Salesforce, разработчики, архитекторы интеграции или лица, занимающиеся такими бизнес-функциями, как маркетинг или операции, — которые хотят узнать больше о потенциал API и интеграции, развивать свою карьеру и трансформировать клиентский опыт. IDC прогнозирует, что Salesforce и ее экосистема создадут 4,2 миллиона рабочих мест к 2024 году, что подчеркивает возможность повышения квалификации рабочей силы будущего с пониманием API и интеграции. MuleSoft вместе с ключевыми альянсами, включая Accenture и Deloitte, обязуется повысить квалификацию в общей сложности 100 000 первопроходцев в области интеграции в течение следующих пяти лет, чтобы гарантировать, что этот базовый набор навыков можно будет найти на предприятии. Чтобы помочь рабочей силе будущего проложить собственный путь интеграции и ускорить цифровую трансформацию, MuleSoft разработала новые пути обучения, адаптированные к организационным ролям и целям обучения. Trailmix доступен сегодня на Trailhead, платформе онлайн-обучения Salesforce, и включает в себя темы по основам API, созданию API, ROI API и экосистемам API. Trailmix доступен сегодня на Trailhead, платформе онлайн-обучения Salesforce, и включает в себя темы по основам API, созданию API, ROI API и экосистемам API. Комментарии к новостям Эйлин Риццо, старший вице-президент по информационным технологиям, Эшли Стюарт: «В Ashley Stewart мы считаем, что, обучая наших сотрудников интеграции и API, мы не только помогаем им преуспевать в своей карьеру, но и помочь нашему бизнесу процветать в будущем. Связность на основе API — это наиболее важный навык и концепция, с помощью которых можно научиться создавать связанный клиентский опыт и выводить на рынок новые инновации. По мере того, как мы расширяем число первопроходцев интеграции в нашей команде, мы сможем ускорить наши инициативы по цифровому преобразованию, особенно по мере расширения наших решений SaaS». Адам Бёрден, главный инженер-программист Accenture: «Мы преодолеваем разрыв между традиционными и облачными технологиями, объединяя интеграционную платформу MuleSoft, ориентированную на API, с нашими уникальными шаблонами архитектуры цифровой развязки. Раскрытие скрытой ценности данных на предприятии является ключевым приоритетом для наших клиентов, и подход MuleSoft с низким кодом поможет «гражданским интеграторам» ускорить этот путь. Accenture рада взять на себя обязательство создать 5000 первопроходцев в области интеграции в нашей организации. Они будут работать с нашей глобальной командой сертифицированных разработчиков и архитекторов MuleSoft, которые придумывают и создают безграничные и адаптируемые интеграционные решения, необходимые для систем будущего». Раскрытие скрытой ценности данных на предприятии является ключевым приоритетом для наших клиентов, и подход MuleSoft с низким кодом поможет «гражданским интеграторам» ускорить этот путь. Accenture рада взять на себя обязательство создать 5000 первопроходцев в области интеграции в нашей организации. Они будут работать с нашей глобальной командой сертифицированных разработчиков и архитекторов MuleSoft, которые придумывают и создают безграничные и адаптируемые интеграционные решения, необходимые для систем будущего». Пол Клеммонс, руководитель Deloitte Consulting LLP и лидер глобального альянса Salesforce: «Первопроходцы интеграции имеют уникальные возможности, чтобы добиться реальных изменений и ценности для своих организаций и клиентов, используя свой индивидуальный взгляд на бизнес и сочетая его с критически важной интеграцией. навыки и умения. В рамках этого обязательства мы планируем в ближайшие несколько лет сделать тысячи наших консультантов первопроходцами в области интеграции. Мы рады присоединиться к MuleSoft, чтобы повысить квалификацию сотрудников для проведения цифровой трансформации с помощью подключения на основе API и помочь этим первопроходцам интеграции построить свою карьеру сегодня и в будущем». Мы рады присоединиться к MuleSoft, чтобы повысить квалификацию сотрудников для проведения цифровой трансформации с помощью подключения на основе API и помочь этим первопроходцам интеграции построить свою карьеру сегодня и в будущем». Саймон Парметт, генеральный директор MuleSoft: «Понимая мощь API и интеграции, каждый может ускорить цифровую трансформацию, где бы он ни находился в своей компании, и значительно увеличить тактовую скорость инноваций. Интеграция — это недостающее звено цифровой трансформации, и каждый член организации должен понимать, как связь на основе API может улучшить взаимодействие с клиентами. Предоставляя лучшие в своем классе продукты и обучая рабочую силу будущего, MuleSoft имеет уникальную возможность продвигать компании вперед в эту цифровую эпоху».
Узнайте больше о том, как вы можете стать первопроходцем в области интеграции на Dreamforce 2019 Узнайте больше о том, как MuleSoft расширит возможности первопроходцев в области интеграции, посетив основной доклад по интеграции в среду, 20 ноября, с 17:00 до 17:50. в Moscone North, Hall F: https://www.mulesoft.com/dreamforce в Moscone North, Hall F: https://www.mulesoft.com/dreamforce Станьте первопроходцем в области интеграции сегодня и узнайте, как интеграция способствует взаимодействию клиентов с Trailhead: http://sfdc.co/integrationtrailblazer Кроме того, первопроходцы интеграции с опытом объектно-ориентированного программирования (технические разработчики и архитекторы) могут стать специалистами по интеграции. Посетите сайт training.mulesoft.com, чтобы пройти техническое обучение работе с продуктом и узнать, как пройти сертификацию MuleSoft.
Dreamforce 2019 Dreamforce — крупнейшая в мире конференция по программному обеспечению, в которой участвуют более 171 000 зарегистрированных участников и 13 миллионов онлайн-зрителей. Dreamforce, объединяющий лидеров мнений, пионеров отрасли и первопроходцев, является высшим выражением таких ценностей Salesforce, как доверие, успех клиентов, инновации и равенство. С более чем 2700 сессиями первопроходцы в каждой роли и отрасли узнают, как получить 360-градусное представление о своих клиентах, и познакомятся с последними инновационными продуктами Salesforce, включая искусственный интеллект, голос, интеграцию и онлайн-обучение. Чтобы узнать больше, посетите: www.salesforce.com/dreamforce. С более чем 2700 сессиями первопроходцы в каждой роли и отрасли узнают, как получить 360-градусное представление о своих клиентах, и познакомятся с последними инновационными продуктами Salesforce, включая искусственный интеллект, голос, интеграцию и онлайн-обучение. Чтобы узнать больше, посетите: www.salesforce.com/dreamforce. О MuleSoft, компании Salesforce Миссия MuleSoft — помогать организациям быстрее меняться и внедрять инновации, упрощая подключение приложений, данных и устройств со всего мира. Благодаря подходу к подключению, основанному на API, ведущая на рынке платформа MuleSoft Anypoint Platform™ позволяет тысячам организаций создавать сети приложений. Разблокируя данные по всему предприятию с помощью сетей приложений, организации могут легко предоставлять новые каналы получения дохода, повышать эффективность работы и создавать дифференцированное обслуживание клиентов. Для получения дополнительной информации посетите https://www. mulesoft.com. mulesoft.com. О компании Salesforce Компания Salesforce является мировым лидером в области управления взаимоотношениями с клиентами (CRM), благодаря чему компании становятся ближе к своим клиентам в эпоху цифровых технологий. Компания Salesforce, основанная в 1999 году, позволяет компаниям любого размера и отрасли использовать преимущества мощных технологий — облачных, мобильных, социальных, интернета вещей, искусственного интеллекта, голоса и блокчейна — для создания всестороннего представления о своих клиентах. Для получения дополнительной информации о Salesforce (NYSE: CRM) посетите: www.salesforce.com. MuleSoft является зарегистрированным товарным знаком MuleSoft, Inc., компании Salesforce. Все остальные знаки принадлежат соответствующим владельцам. + Вы были перенаправлены Вы были перенаправлены на эту страницу, так как MuleSoft приобрела Servicetrace. Кликните сюда, чтобы узнать больше. Кликните сюда, чтобы узнать больше. + Cette page est disponible en Français Voir en Français + Diese Seite gibt es auch auf Deutsch Zur Deutschen Версия + Esta Página Está Диспронижаемая En Español Ver en Español + Essa Página Está Disponível EM PortugUs ema-a ema-ema-estável 9006 vja-a ema-a ema-ema estável emavel.ご利用いただけます 日本語で見る 900-литровый стальной бак с тройной обшивкой и 30-минутной встроенной огнестойкостью FPS.900.30 Рейтинг 0 из 5 (0 отзывов) От 6 до 8 рабочих недель Если вы торгуете — покупайте напрямую / Войдите, чтобы увидеть цену Сбор металлолома Удаление вашего старого бака может быть добавлено к вашему заказу из вашей корзины. В этом резервуаре есть обязательные разделы, которые необходимо заполнить, прежде чем вы сможете добавить их в корзину. Артикул: FPS.900.30 Категории: Масляные баки, EasyTANK, Масляные баки из огнестойкой стали - Описание
- Технические документы
- Доставка
- Отзывы (0)
Описание 900-литровый стальной бак с тройной обшивкой и встроенной огнестойкостью в течение 30 минут – FPS.900.30 Резервуар и обшивка: 900-литровый стальной масляный бак с тройной обшивкой и встроенной огнестойкостью в течение 30 минут подходит как для бытового, так и для коммерческого применения. Жидкость хранится в основном или внутреннем баке, а внешний бак образует необходимую обваловку вместимостью 110% от вместимости основного бака, а третий бак служит корпусом для встроенного противопожарного барьера. Этот резервуар подходит для хранения мазута, керосина, дизельного топлива, отработанных масел и многих других жидкостей (пожалуйста, проверьте перед использованием). Обвалованный резервуар представляет собой резервуар внутри резервуара, внешний резервуар обеспечивает защиту внутреннего резервуара, что затрудняет выход из строя внутреннего резервуара. Однако в маловероятном случае выхода из строя внутреннего резервуара внешний резервуар обеспечит вторичную защитную оболочку. Этот резервуар подходит для хранения мазута, керосина, дизельного топлива, отработанных масел и многих других жидкостей (пожалуйста, проверьте перед использованием). Обвалованный резервуар представляет собой резервуар внутри резервуара, внешний резервуар обеспечивает защиту внутреннего резервуара, что затрудняет выход из строя внутреннего резервуара. Однако в маловероятном случае выхода из строя внутреннего резервуара внешний резервуар обеспечит вторичную защитную оболочку. Эти резервуары изготовлены по самым высоким стандартам и соответствуют BS799 pt5. Толщина используемой стали зависит от размера резервуара, и все резервуары проходят испытания под давлением перед тем, как покинуть завод. Кроме того, эти резервуары окрашены двумя слоями нашей специально разработанной системы антикоррозионного покрытия, разработанной для обеспечения максимальной защиты. Если вы хотите приобрести эту краску отдельно, пожалуйста, нажмите здесь. Мы рекомендуем красить ваш стальной бак один раз в год, чтобы добиться максимального срока службы. Этот стальной бак — хороший вариант, если вы хотите сдержать любого авантюриста в краже нефти, которая в настоящее время очень распространена, особенно если выбран вариант с защитной крышкой. Соответствие: Этот резервуар соответствует требованиям директив по предотвращению загрязнения нефтью (Англия и Уэльс) 2002 PPG2 и BS799 pt5 Технические характеристики: Прочная стальная конструкция 30-минутный встроенный огнестойкий барьер (не впитывающий) 1 Верхняя муфта № 2″ для заливной горловины 2 Верхняя муфта № 1 1/2″ (для резервуара и манометра) 1 Бак № 2″ для обвязки вентиляционного отверстия 1 Вентиляционный клапан № 2″ 1 Нижняя выпускная муфта № 1″ 1 Верхний сливной патрубок № 1″ (заглушенный) Указатель содержимого бака (спиральный поплавковый манометр) Комплект выходного фильтра (дополнительно) Устанавливается на опорные стойки высотой 100 мм x 50 мм 10 лет гарантии - Небольшая банка краски для «подкраски» для нанесения, если в процессе установки могут появиться царапины.
 - Стандартный цвет: светло-зеленый
Дополнительное оборудование включает: - Визуальный индикатор содержимого Apollo или…
- Индикатор циферблата или спиральный поплавковый датчик (чтобы посмотреть поясняющее видео, нажмите здесь)
- Комплект нижнего выпускного фитинга/фильтра и блока клапанов (экономичный или продвинутый, чтобы посмотреть пояснительное видео, нажмите здесь)
- Механический ограничитель перелива, устройство остановки разлива (если выбрано, обратите внимание, что оно будет установлено на заднее 2-дюймовое гнездо бака на баке, поскольку оно совместимо только с внутренней резьбой, а передняя точка наполнения имеет наружную резьбу BSP)
- Краска для металлического бака 1 литр (зеленая или черная в зависимости от цвета бака)
- Набор для обслуживания стального резервуара (Чтобы максимально продлить срок службы этих стальных резервуаров, мы рекомендуем вам приобрести наш набор для обслуживания стального резервуара.
 См. здесь. Это поможет поддерживать ваш стальной резервуар в отличном состоянии) Включает в себя: 1-литровая краска для металлического резервуара, кисть. & Валик, перчатки, губка для бака для впитывания воды См. здесь. Это поможет поддерживать ваш стальной резервуар в отличном состоянии) Включает в себя: 1-литровая краска для металлического резервуара, кисть. & Валик, перчатки, губка для бака для впитывания воды - Перед отгрузкой можно нанести дополнительный верхний слой краски (это может добавить дополнительный день к сроку выполнения заказа)
- Изменение цвета бака: Цвет RAL или BS необходимо указать при заказе. (это может увеличить время выполнения заказа до 1 недели)
Гарантия: - 10-летняя гарантия, каждый бак снабжен гарантийным руководством
Размеры: - Длина: 1665 мм
- Ширина: 750 мм
- Высота: 1330 мм
- Вес: 500 кг
Рекомендуемый размер основания: Полные инструкции по установке прилагаются к баку. В соответствии с действующими нормами мы рекомендуем размер основания, который простирается на 300 мм по всему периметру бака - Длина: 2265 мм
- Ширина: 1350 мм
Вы можете позвонить в наш отдел продаж для получения консультации по продукту по телефону 0330 999 1100 или дополнительную информацию о правилах, касающихся хранения масла, можно найти на веб-сайте OFTEC здесь Чтобы просмотреть видео о характеристиках продукта, нажмите здесь Документ со спецификацией Информация о доставке Стандартная поставка Наша стандартная служба доставки предлагает обслуживание в течение 2-5 дней. Мы всегда стремимся осуществлять доставку собственным транспортом, но иногда можем воспользоваться услугами стороннего перевозчика, если того потребуют обстоятельства. Это служба доставки на обочине, которая включает разгрузку Мы всегда стремимся осуществлять доставку собственным транспортом, но иногда можем воспользоваться услугами стороннего перевозчика, если того потребуют обстоятельства. Это служба доставки на обочине, которая включает разгрузку - .
2-5 дней обслуживания
- Собственный транспорт (по возможности)
- Доставка на обочину
- Включает разгрузку
Служба инкассации Коллекция доступна в наших складах в Дареме, Кембле или Эли. Мы рекомендуем вам предоставить уведомление за 24 часа, чтобы мы могли подготовить ваш заказ. В некоторых случаях вы можете получить скидку на элемент стоимости перевозки. - Соберите в Дареме, Кембле или Эли
- Доступны скидки
- Быстрые сроки выполнения заказов
Другие продукты, которые могут вас заинтересовать AC. STMP STMP Набор для обслуживания стального масляного бака Рейтинг 0 из 5 Возможны торговые скидки. Войти или зарегистрироваться 56,00 фунтов стерлингов Без НДС 67,20 фунтов стерлингов Вкл.
Посмотреть продукт AC.MTPAINT.G Зеленая краска для металлических резервуаров – 1 литр Рейтинг 0 из 5 Возможны торговые скидки. Войти или зарегистрироваться £32,00 Без НДС £38,40 Вкл. НДС Посмотреть продукт
Как подойти к интеграции CRM: стратегии и API Компании управляют огромным количеством данных о клиентах. Эта информация включает демографические данные, взаимодействие с маркетинговыми и электронными кампаниями, предпочтения, историю покупок и точки взаимодействия с различными системами, программным обеспечением, приложениями и инструментами. Когда предприятия обдуманно используют данные для повышения качества обслуживания клиентов, выигрывают как клиенты, так и компании. Однако, чтобы извлечь выгоду, компании должны систематизировать и интегрировать данные, извлекать из них информацию и действовать на основе этой информации. Решения и действия, основанные на данных, двигают компанию вперед. ИТ-специалисты и лица, принимающие решения в компаниях, сталкиваются с трудностями, когда дело доходит до интеграции данных и интеграции CRM. Им нужен продуктивный подход в сочетании с эффективными стратегиями, которые работают в долгосрочной перспективе и помогают им без проблем получать доступ к своим данным. Что такое CRM-интеграция? Ваша платформа CRM является частью набора аппаратного и программного обеспечения вашей компании, и этот набор обширен. Согласно сравнительному отчету MuleSoft о возможностях подключения за 2020 год, средняя организация использует 900 приложений. Эти приложения существуют в: Эти приложения существуют в: Интеграция CRM соединяет каждое приложение с вашей платформой CRM, чтобы данные могли передаваться к ним, от них или между ними. Целью интеграции CRM является размещение полных и точных данных из вашего программного обеспечения для бизнеса, чтобы дать вам полное представление о вашем бизнесе и клиентах. Что такое интеграция данных клиентов? Согласно MuleSoft, интеграция данных о клиентах, или CDI, «собирает все данные о клиенте из разрозненных систем в различных отделах компании и собирает их в одном месте, что делает их легко доступными для нескольких отделов». Это местоположение — единственный источник достоверной информации для вашей компании (SSOT). В то время как интеграция CRM специально направлена на создание диалогов между вашей платформой CRM и другим программным обеспечением для бизнеса, CDI включает в себя всю экосистему данных. При правильном управлении данными и их интеграции сотрудники получают единое представление о своих клиентах. Единое представление позволяет вашей компании принимать решения на основе данных и обслуживать клиентов персонализированным и эффективным образом. При правильном управлении данными и их интеграции сотрудники получают единое представление о своих клиентах. Единое представление позволяет вашей компании принимать решения на основе данных и обслуживать клиентов персонализированным и эффективным образом. Интеграция CRM является частью общей стратегии интеграции данных о клиентах. Обе задачи могут быть обременительными. Большие данные, которые включают в себя любой набор данных, который слишком массивен или сложен для традиционного прикладного программного обеспечения для обработки данных, — это хорошая вещь для бизнеса. Найджел Филер пишет, что большие данные «открывают новые возможности для предприятий по сбору и объединению разрозненных данных для существенного улучшения процесса принятия решений, минимизации рисков и извлечения ценных сведений, которые в противном случае остались бы скрытыми». Но всеми этими данными может быть трудно управлять. Когда компании интегрируют данные в одно центральное место, такое как платформа CRM, их легче анализировать и обрабатывать, особенно с использованием машинного обучения, подмножества ИИ. Компании могут быстрее анализировать данные с помощью машинного обучения и принимать решения, основываясь на реальных данных и статистических тенденциях, а не на оценках. Компании могут быстрее анализировать данные с помощью машинного обучения и принимать решения, основываясь на реальных данных и статистических тенденциях, а не на оценках. ИТ-специалисты и предприятия сталкиваются с проблемой Представление о том, что одна компания использует сотни приложений, может показаться преувеличенной. Однако учтите, что у каждого отдела есть несколько частей программного обеспечения и систем, каждая из которых содержит свои собственные данные. В компании эти источники данных могут включать ряд существующих бизнес-приложений и систем записи: Платформа управления основными данными (MDM) Программное обеспечение для планирования ресурсов предприятия (ERP) Управление заказами и запасами Управление цепочками поставок CRM-системы Платформа для электронного маркетинга Индивидуальные платформы социальных сетей Программное обеспечение чат-бота службы поддержки клиентов Программное обеспечение для управления проектами Инструменты для совместной работы
Каждый отдел может действовать автономно, и если его системы не интегрированы с другими отделами, это создает хранилище данных. Это верно для 57% предприятий, руководители которых говорят, что CRM фрагментирована, и некоторые, многие или все отделы имеют свои собственные CRM. Маркетинг работает отдельно от продаж, которые работают отдельно от обслуживания клиентов и так далее. По сути, левая рука не знает, что делает правая. Согласно отчету Forrester Consulting: «Это результат того, что отделы реализуют разрозненные инициативы, такие как модернизация продаж, обслуживания клиентов или существующих приложений. Чтобы реализовать свои инициативы, ориентированные на клиента, компаниям необходимо мыслить шире». Это верно для 57% предприятий, руководители которых говорят, что CRM фрагментирована, и некоторые, многие или все отделы имеют свои собственные CRM. Маркетинг работает отдельно от продаж, которые работают отдельно от обслуживания клиентов и так далее. По сути, левая рука не знает, что делает правая. Согласно отчету Forrester Consulting: «Это результат того, что отделы реализуют разрозненные инициативы, такие как модернизация продаж, обслуживания клиентов или существующих приложений. Чтобы реализовать свои инициативы, ориентированные на клиента, компаниям необходимо мыслить шире». Кроме того, MuleSoft сообщает, что «проблемы интеграции замедляют инициативы по цифровому преобразованию для 85% ИТ-организаций». Средний бизнес интегрировал только 28 % приложений. Хранилища данных являются доказательством того, что компания не интегрировала свои данные, и создают проблемы для ИТ-руководителей. 89% ИТ-руководителей сообщают, что разрозненность негативно влияет на инициативы их организаций по цифровой трансформации. Решением этой проблемы, которое организации успешно внедрили для выполнения интеграции CRM и интеграции данных, является интерфейс прикладного программирования (API). MuleSoft определяет API как «программного посредника, который позволяет двум приложениям взаимодействовать друг с другом». Как интегрировать вашу CRM-систему Интеграция CRM может происходить несколькими способами: Компании могут инвестировать исключительно в продукты и услуги от одного поставщика, поэтому все программы и инструменты автоматически интегрируются и обмениваются данными. Разработчики могут написать быстрые строки кода, чтобы заставить две системы обмениваться данными. Но эта стратегия часто приводит к беспорядочной паутине кода, которая ломается с обновлениями и новыми интеграциями. Но эта стратегия часто приводит к беспорядочной паутине кода, которая ломается с обновлениями и новыми интеграциями. Компании могут использовать API-интерфейсы, которые можно использовать повторно и которые служат различным целям.
Первый вариант маловероятен, особенно учитывая, сколько программ использует среднестатистическая компания. Компании часто используют второй вариант, но он создает головную боль для ИТ-команд и пользователей. Третий — самый простой, быстрый и выгодный. Поскольку многие системы поставляются разными поставщиками, которые, возможно, не создавали их с учетом интеграции, лучшим инструментом или стратегией интеграции является API. API быстро интегрируют существующие (и будущие) бизнес-приложения и процессы. API-интерфейсы интегрируют разрозненные системы и помогают уменьшить разрозненность MuleSoft сообщает, что 60% ИТ-руководителей говорят, что интеграция через API имеет решающее значение для их стратегии цифровой трансформации. Согласно совместной электронной книге MuleSoft и Salesforce под названием «Раскройте все возможности Salesforce Customer 360 с помощью API», компаниям следует использовать API для интеграции данных по трем причинам. API: Согласно совместной электронной книге MuleSoft и Salesforce под названием «Раскройте все возможности Salesforce Customer 360 с помощью API», компаниям следует использовать API для интеграции данных по трем причинам. API: Произведено и разработано для простоты использования Простота управления для обеспечения безопасности, масштабируемости и производительности Обнаружение и доступ через самообслуживание
API-интерфейсы повышают производительность ИТ-команд, особенно когда речь идет об инициативах цифровой трансформации. 81% команд, внедривших API, сообщили, что выполнили все или почти все проекты, о которых их просили, в течение года. Кроме того, только 13% пользователей API сообщают, что проблемы интеграции замедляют или препятствуют цифровой трансформации в их организациях. Интеграция CRM с подходом к подключению на основе API Эта стратегия интеграции данных клиентов основана на трех типах API, каждый из которых разработан для определенной цели: Когда API играет роль, каждый раз, когда эта роль требуется в процессе, этот API можно использовать повторно. Три разные роли API в интеграции CRM Системные API извлекают данные из определенных систем. Например, чтобы предоставить клиенту информацию о доставке, компания может использовать системный API для доступа к данным из системы транспортной компании, например, используемой UPS, FedEx или почтовой службой США. Для интеграции CRM можно использовать системные API с определенными системами, включая ERP, клиентские и биллинговые системы, а также проприетарные базы данных, такие как сторонний платежный процессор. API-интерфейсы процессов представляют собой второй уровень и объединяют системные API-интерфейсы для конкретных бизнес-целей. В случае обновления доставки компании может потребоваться несколько системных API-интерфейсов — от транспортной компании и от платных перевозок — для оповещения клиента о местонахождении груза, о его задержке и многом другом. Согласно MuleSoft, Pilot Flying J создал API профиля клиента, который является популярным типом API процессов. Pilot Flying J использовал этот API для предоставления «единого представления данных о клиентах для мобильного приложения myPilot путем проверки платежной информации клиента, учетных данных компании и т. д.». API-интерфейсы взаимодействия используют несколько API-интерфейсов предыдущих уровней и часто используются в приложениях для конечных пользователей. Например, представитель службы поддержки клиентов может видеть весь опыт взаимодействия клиента с его компанией, включая маркетинг, продажи, бухгалтерский учет и социальные сети, а не только историю взаимодействия клиента с отделом обслуживания. Это помогает представителю лучше оценить потребности клиента, ответить на вопросы и оказать помощь. Создайте свой собственный или используйте готовые API Собственные ИТ-команды и разработчики могут при необходимости создавать новые API, просматривать свою библиотеку существующих API или искать готовые API от третьих лиц на торговых площадках API. Когда ваша компания инвестирует в новое программное обеспечение, интеграция данных может быть такой же простой, как поиск существующего API в вашей собственной библиотеке или на рынке и его подключение. Когда ваша компания инвестирует в новое программное обеспечение, интеграция данных может быть такой же простой, как поиск существующего API в вашей собственной библиотеке или на рынке и его подключение. Сложные системы в какой-то степени становятся самонастраивающимися, и ваша компания может воспользоваться преимуществами интегрированных данных гораздо быстрее, чем при использовании других методов интеграции. Интегрированные системы обеспечивают единый источник достоверной информации (SSOT) Интеграция CRM, интеграция данных и единый источник достоверной информации о клиентах — вот то, как компании остаются впереди своих конкурентов. Forrester Consulting сообщает, что 80% компаний все чаще используют CRM-систему в качестве SSOT для поддержки стратегий, ориентированных на клиента. Благодаря свободному обмену данными между системами связь между отделами становится более полной, а стратегии основаны на реальности. Данные отдела маркетинга доступны отделам продаж, а информация о продажах доступна отделу обслуживания клиентов. Благодаря свободному обмену данными между системами связь между отделами становится более полной, а стратегии основаны на реальности. Данные отдела маркетинга доступны отделам продаж, а информация о продажах доступна отделу обслуживания клиентов. Клиенты взаимодействуют с одной единой компанией, а не с отдельными отделами. Компании пользуются единым источником достоверной информации, из которого они могут получить информацию и, таким образом, лучше обслуживать своих клиентов. По данным Forrester, «предприятия, основанные на аналитических данных, растут в среднем более чем на 30 процентов в год и к 2021 году должны заработать 1,8 триллиона долларов». Информация может включать в себя предпочтения клиента и вероятные будущие покупки, периоды в году, когда вам нужно нанять больше представителей службы поддержки клиентов, лучшее время, чтобы отправить покупателю электронное письмо о продаже продукта, который он оставил в своей корзине, и многое другое. Интеграция данных предоставляет вашим сотрудникам информацию. Платформа CRM, которая служит единым источником достоверной информации, дает вам возможность запускать отчеты и получать оперативную аналитическую информацию, созданную искусственным интеллектом. Клиенты ожидают, что компании будут работать с этой информацией, и 84% клиентов говорят, что опыт, который предоставляет компания, так же важен, как и ее продукты и услуги. Использование API для создания этой SSOT поможет вам подключить и интегрировать любую систему. После того, как API-интерфейсы созданы, вы можете использовать их повторно, что сокращает затраты времени, требования к обслуживанию и необходимость восстановления разорванных соединений. API демократизируют инновации Благодаря тому, что API служат строительными блоками, соединяющими все ваши системы, ИТ-отделы и компании могут уделять больше времени проектам и инновациям, которые отличают их друг от друга. В отчете Salesforce и MuleSoft поясняется, что «повторное использование API может привести к ускорению реализации проекта в 2,5 раза». В отчете Salesforce и MuleSoft поясняется, что «повторное использование API может привести к ускорению реализации проекта в 2,5 раза». Компании тратят меньше времени на решение вопросов интеграции данных и больше времени на улучшение продуктов и процессов, обслуживание клиентов и реализацию других проектов. Они быстрее интегрируют новое программное обеспечение и, следовательно, быстрее получают от него выгоду. Небольшие компании могут воспользоваться интеграцией CRM и SSOT, не нуждаясь в рабочей силе корпоративной ИТ-группы. Используя API-интерфейсы для интеграции данных, любой может создать связанный опыт, чтобы порадовать клиентов. API делают интеграцию данных и CRM более чистой Когда средняя компания использует 900 различных программ, инструментов, приложений и элементов, интеграция данных является приоритетом. Без интеграции у компании есть несколько наборов шестеренок, работающих отдельно в разных отделах, и ей не хватает единой машины для управления клиентским опытом. Без интеграции у компании есть несколько наборов шестеренок, работающих отдельно в разных отделах, и ей не хватает единой машины для управления клиентским опытом. Компании, которые используют API для подключения своих разрозненных систем, получают более быстрое выполнение проектов и более легкое время с интеграцией данных. API-интерфейсы помогают платформам CRM стать единым источником достоверной информации для компании, что позволяет получать информацию на основе данных из всех уголков инфраструктуры компании. Эти идеи позволяют компаниям точно и быстро обслуживать своих клиентов, тем самым способствуя прибыльности и успеху. Продолжай учиться Узнайте больше о платформе Salesforce Customer 360 и готовности к цифровому преобразованию, воспользовавшись приведенными ниже ресурсами. Веб-семинар: Откройте доступ к данным Salesforce с помощью интеграции с платформой Присоединяйтесь к экспертам Salesforce для демонстрации в реальном времени Salesforce Connect с MuleSoft и научитесь легко интегрировать внешние системы с данными и процессами в Salesforce. Важность цифровой трансформации во времена перемен COVID-19 изменил то, как мы работаем, ускорив цифровую эволюцию во всех отраслях. Прочитайте этот информационный документ от IDC и Salesforce, чтобы узнать, как бизнес-лидеры меняют планы трансформации и реагируют на новые требования. Справочник по трансформации Узнайте, что нужно, чтобы изменить образ мышления, соединить разрозненные бизнес-структуры и сосредоточиться на своих клиентах. Поглотители энергии MAX Force — серия встроенных канатных захватов — Super Anchor Safety Перейти к содержимому Поглотители энергии MAX Force — серия встроенных канатных захватовpaul@superanchor. com2022-08-24T19:07:41+00:00 com2022-08-24T19:07:41+00:00 Поглотитель энергии является одним из наиболее важных компонентов защиты от падения и требуется OSHA, когда рабочие подвергаются опасности свободного падения. Наши амортизаторы, разработанные для ограничения максимального удерживающего усилия при замедлении спуска, оснащены запатентованной разрывной лямкой отечественного производства и разъемами высочайшего качества. Индивидуальные поглотители энергии MAX Force производятся на нашем заводе в Монро, штат Вашингтон, и гарантируют совместимость компонентов со всеми средствами индивидуальной защиты Super Anchor Safety. Абсолютная необходимость для защиты от падения. Наша серия Snaphook содержит соединители прочности ворот ANSI Z359.12-09 3600 фунтов в виде карабинов, карабинов или нашей эксклюзивной сети UltraLite Dee Web, которая соединяется с задним D-образным кольцом страховочной привязи пользователя. Максимальная удерживающая сила составляет 900 фунтов при максимальной длине развертывания 42 дюйма. Амортизаторы MAX Force также поставляются со страховочными устройствами и встроенными регуляторами (механическими канатными захватами). Механические средства защиты от падения и встроенные регуляторы имеют функции блокировки в одном направлении, которые требуют правильной ориентации при установке на спасательный круг. Средства защиты от падения снимаются со спасательного троса путем разблокировки шарнирного механизма ворот. Интегральные Настройщики не предназначены для снятия с линии жизни. Заводское крепление на амортизаторе устраняет необходимость в 1 соединителе, в результате чего компонент становится легче. #4015-C/Z — это типы аварийных захватов, которые не позволяют рабочему отключить функцию блокировки во время свободного падения и соответствуют CSA Z259..5-12. - Сделано в США
- 100 % полиэстер, лямка
- Этикетка индикатора падения
- Этикетка отчета о проверке
- Наконечник петли из ПВХ подходит для карабинов и карабинов
- Прозрачная крышка из ПВХ для удобства осмотра
- Предупреждающие таблички на английском и испанском языках
- Длина бедра для легкой регулировки досягаемости
| Изображение | Деталь № | Общая длина | Вес | Описание | Удлинение | Вес пользователя | M. A.F. A.F. | УПК |
|---|
Скачать | 6195-С | 23″ | 37 унций. | Амортизатор MAX Force с карабином и тросовым захватом ADP SST | 42″ | 100-310 фунтов | 900 фунтов | 786158619515 | Скачать | 6195-З | 23″ | 37 унций. | Амортизатор MAX Force с карабином и цинковым захватом ADP | 42″ | 100-310 фунтов | 900 фунтов | 786158619508 | Скачать | 6196-М | 23″ | 32 унции. | Амортизатор MAX Force с алюминиевым карабином и механическим захватом | 42″ | 100-310 фунтов | 900 фунтов | 786158619638 | Скачать | 3004 | 23″ | 38 унций. | Амортизатор MAX Force с карабином и механическим захватом | 42″ | 100-310 фунтов | 900 фунтов | 786158300406 | Скачать | 6196-С | 23″ | 37 унций. | Амортизатор MAX Force с алюминиевым карабином и тросовым захватом ADP SST | 42″ | 100-310 фунтов | 900 фунтов | 786158619614 | Скачать | 6196-З | 23″ | 37 унций. Кусочно-заданная функция · Калькулятор ОнлайнЧто умеет калькулятор?На данной странице вы можете выполнить различные действия с кусочно-заданной функцией,
а также для большинства сервисов — получить подробное решение. - Производная кусочно-заданной функции
- Построить график
- Исследовать график
- Определённый интеграл
- Неопределённый интеграл от таких функций
- Предел кусочно-заданной
- Ряд Фурье (в примерах для нахождения ряда в основном используются кусочно-заданные функции)
- Ряд Тейлора
Сначала задайте соответствующую функцию. Как задавать условия?Приведём примеры, как задавать условия: - x≠0
- x не равен нулю
- x > pi
- x больше, чем число Пи
- -pi/2
- x меньше или равно, чем Пи пополам, но нестрого больше, чем Пи пополам
- true
- означает «в любых других случаях»
Правила ввода выражений и функцийВыражения могут состоять из функций (обозначения даны в алфавитном порядке):- absolute(x)
- Абсолютное значение x
(модуль x или |x|) - arccos(x)
- Функция — арккосинус от x
- arccosh(x)
- Арккосинус гиперболический от x
- arcsin(x)
- Арксинус от x
- arcsinh(x)
- Арксинус гиперболический от x
- arctg(x)
- Функция — арктангенс от x
- arctgh(x)
- Арктангенс гиперболический от x
- exp(x)
- Функция — экспонента от x (что и e^x)
- log(x) or ln(x)
- Натуральный логарифм от x
(Чтобы получить log7(x), надо ввести log(x)/log(7) (или, например для log10(x)=log(x)/log(10)) - sin(x)
- Функция — Синус от x
- cos(x)
- Функция — Косинус от x
- sinh(x)
- Функция — Синус гиперболический от x
- cosh(x)
- Функция — Косинус гиперболический от x
- sqrt(x)
- Функция — квадратный корень из x
- sqr(x) или x^2
- Функция — Квадрат x
- ctg(x)
- Функция — Котангенс от x
- arcctg(x)
- Функция — Арккотангенс от x
- arcctgh(x)
- Функция — Гиперболический арккотангенс от x
- tg(x)
- Функция — Тангенс от x
- tgh(x)
- Функция — Тангенс гиперболический от x
- cbrt(x)
- Функция — кубический корень из x
- gamma(x)
- Гамма-функция
- LambertW(x)
- Функция Ламберта
- x! или factorial(x)
- Факториал от x
В выражениях можно применять следующие операции:- Действительные числа
- вводить в виде 7.3
- — возведение в степень
- x + 7
- — сложение
- x — 6
- — вычитание
- 15/7
- — дробь
Другие функции:- asec(x)
- Функция — арксеканс от x
- acsc(x)
- Функция — арккосеканс от x
- sec(x)
- Функция — секанс от x
- csc(x)
- Функция — косеканс от x
- floor(x)
- Функция — округление x в меньшую сторону (пример floor(4.5)==4.0)
- ceiling(x)
- Функция — округление x в большую сторону (пример ceiling(4.5)==5.0)
- sign(x)
- Функция — Знак x
- erf(x)
- Функция ошибок (или интеграл вероятности)
- laplace(x)
- Функция Лапласа
- asech(x)
- Функция — гиперболический арксеканс от x
- csch(x)
- Функция — гиперболический косеканс от x
- sech(x)
- Функция — гиперболический секанс от x
- acsch(x)
- Функция — гиперболический арккосеканс от x
Постоянные:- pi
- Число «Пи», которое примерно равно ~3.14159..
- e
- Число e — основание натурального логарифма, примерно равно ~2,7183..
- i
- Комплексная единица
- oo
- Символ бесконечности — знак для бесконечности
построение графика, формула, знак модуля и примерыГрафики и формулы кусочно-линейных функцийСитуация, когда движение или другое явление можно описать одной линейной функцией, определенной на интервале $-\infty \lt t \lt +\infty$, в действительности невозможна. Хотя бы потому, что возраст Вселенной велик, но не бесконечен. На практике в течение некоторого времени тело может двигаться, потом – покоиться, потом – опять прийти в движение, но уже с другой скоростью и в другом направлении и т.п. Как задать подобную зависимость? Допустим, турист идет из начальной точки по прямой тропинке в течение 2 ч со скоростью 5 км/ч, затем останавливается отдохнуть на 1ч и возвращается обратно по той же тропинке со скоростью 4 км/ч. Нам нужно найти формулу для расстояния s(t) от начальной точки на протяжении всего похода. Изобразим зависимость s(t) графически: Первый отрезок AB легко записать: $ s_1 (t) = 5t,0 \le t \lt 2$ С отрезком BC тоже всё ясно: $s_2 (t) = 10,2 \le t \lt 3$ Осталось найти формулу для отрезка CD. Для него известен угловой коэффициент, равный скорости k = -4; знак «минус» оттого, что турист возвращается обратно. Формула имеет вид $s_3 (t) = -4t+b$. Также, нам известны координаты C(3;10). Подставляем: $10 = -4 \cdot 3+b \Rightarrow b =22$. Осталось рассчитать момент возвращения: $$0 = -4t_{back}+22 \Rightarrow t_{back} = 22:4 = 5,5$$ (ч) Значит, формула движения на отрезке $CD:s_3 (t) = -4t+22,3 \le t \le 5,5.$ Получаем: $$s(t) = {\left\{ \begin{array}{c} 5t,0 \le t \lt 2 \\ 10,2 \le t \lt 3 \\ -4t+22,3 \le t \le 5,5 \end{array} \right.} $$ Важным свойством заданной функции является выполнение условий согласования: $$ s_1 (2) = s_2 (2) = 10,s_2 (3) = s_3 (3) = 10$$ Наша функция «сшита» на концах промежуточных интервалов. В общем случае: Функция вида $$x f(x) = {\left\{ \begin{array}{c} k_1 x+b_1, x_1 \le x \lt x_2 \\ k_2 x+b_2,x_2 \le x \lt x_3 \\…\\ k_n x+b_n,x_n \le x \lt x_{n+1} \end{array} \right.}$$ называется кусочно-линейной. При этом для функции на краях интервалов выполняются условия согласования: $$f_i (x_{i+1} ) = f_{i+1} (x_{i+1} ),i = \overline {1,n-1} $$ Графиком кусочно-линейной функции является ломаная линия Знак модуля в линейных функцияхПо правилу раскрытия скобок модуля (см. §4 данного справочника) $$ |x| = \left[ \begin{array}{cc} x, x\ge0 \\ -x, x \lt 0\end{array} \right.$$ Внимание! Если в формуле для линейной функции содержится знак модуля, то после его раскрытия получается кусочно-линейная функция. Например: $$ y = 2|x|+5 = {\left\{ \begin{array}{c} -2x+5, x\ge0 \\ 2x+5, x \lt 0\end{array} \right.} $$ Мы заменили квадратную скобку со значением «или» на фигурную скобку со значением «и», поскольку именно смысл объединения — «и того, и другого» — вкладывается в определение кусочно-линейной функции . ПримерыПример 1. Представьте функцию с модулем в виде кусочно-линейной и постройте её график: а) $ y = |x| = {\left\{ \begin{array}{c} -x, x \lt0 \\ x, x \ge 0 \end{array} \right.}$ б) $ y = 2|x|-1 = {\left\{ \begin{array}{c} -2x-1, x \lt0 \\ 2x-1, x \ge 0 \end{array} \right.}$ в) $ y = |x+1| = {\left\{ \begin{array}{c} -x-1, x \lt0 \\ x+1, x \ge 0 \end{array} \right.}$ г) $ y = |x-2| = {\left\{ \begin{array}{c} -x+2, x \lt0 \\ x-2, x \ge 0 \end{array} \right.}$ Пример 2*. Представьте функцию с модулем в виде кусочно-линейной и постройте её график: $$ y = |2|x|-1| = {\left\{ \begin{array}{c} |-2x-1|, x\lt0 \\ |2x-1|,x \ge 0 \end{array} \right.} = {\left\{ \begin{array}{c} 2x+1, {\left\{ \begin{array}{c} -2x-1 \lt 0 \\ x \lt 0 \end{array} \right.} \\ -2x-1, {\left\{ \begin{array}{c} -2x-1 \ge 0 \\ x \lt 0\end{array} \right.} \\ -2x+1, {\left\{ \begin{array}{c}2x-1 \lt 0 \\ x \ge 0\end{array} \right.} \\ 2x-1, {\left\{ \begin{array}{c}2x-1 \ge 0 \\ x \ge 0\end{array} \right.} \end{array} \right.}= $$ $$ = {\left\{ \begin{array}{c} 2x+1, {\left\{ \begin{array}{c} -2x \lt 1 \\ x \lt 0 \end{array} \right.} \\ -2x-1, {\left\{ \begin{array}{c} -2x \ge 1 \\ x \lt 0\end{array} \right.} \\ -2x+1, {\left\{ \begin{array}{c}2x \lt 1 \\ x \ge 0\end{array} \right.} \\ 2x-1, {\left\{ \begin{array}{c}2x \ge 1 \\ x \ge 0\end{array} \right.} \end{array} \right.}= {\left\{ \begin{array}{c} 2x+1, {\left\{ \begin{array}{c} x \gt — \frac{1}{2} \\ x \lt 0 \end{array} \right.} \\ -2x-1, {\left\{ \begin{array}{c} x \le — \frac{1}{2} \\ x \lt 0\end{array} \right.} \\ -2x+1, {\left\{ \begin{array}{c}x \lt \frac{1}{2} \\ x \ge 0\end{array} \right.} \\ 2x-1, {\left\{ \begin{array}{c}x \ge \frac{1}{2} \\ x \ge 0\end{array} \right.} \end{array} \right.}= {\left\{ \begin{array}{c} -2x-1, x \le — \frac{1}{2} \\ 2x+1, — \frac{1}{2} \lt x \lt 0 \\ -2x+1, 0 \le x \lt \frac{1}{2} \\ 2x-1, x \ge \frac{1}{2} \end{array} \right.} $$ Как видно из этого примера, аналитически выводить формулу для двух модулей очень нелегко. Гораздо легче сразу построить график, если следовать следующим простым правилам преобразования. Шаг 1. Строим y = 2x-1 Шаг 2. Строим y = 2|x|-1 по правилу: |x| отражает часть графика для положительных $x \ge 0$ влево, зеркально относительно оси Y Шаг 3. Строим y = |(2|x|-1)| по правилу: общий модуль отражает участок графика с отрицательными $y \lt 0$ вверх, зеркально относительно оси X Или на одном графике: numpy — Как построить кусочную функцию в matplotlib (python)?Для того, чтобы после np.vectorize() ваша функция правильно отрабатывала — ее придется немного переписать: def s_similar2(x):
if x < a:
return 0
elif (a <= x) and (x <= ((a + b) / 2)):
return (2 * ((x - a) ** 2)) / ((b - a) ** 2)
elif ((a + b) / 2 <= x) and (x <= b):
return 1 - (2 * ((x - a) ** 2)) / ((b - a) ** 2)
else:
return 1
y = np.vectorize(s_similar2, otypes=[float])
проверка: np.random.seed(31415)
a,b = np.random.randint(100, size=2)
x = np.random.randint(100, size=100)
print(sum(s_similar(i) for i in x) == sum(s_similar2(i) for i in x) == y(x).sum())
# True
кроме того np.vectorize() возвращает ссылку на «векторизированную» функцию. Поэтому надо вызывать y(x) вместо y Попробуйте так: x = np.linspace(-10, 10, 20)
y = np.vectorize(s_similar2, otypes=[float])
a,b = 5,10
graph2 = plt.plot(x, y(x))
А еще лучше попробовать написать свою векторизированную функцию: def f(x):
return np.where(x < a,
0,
np.where((a <= x) & (x <= ((a + b) / 2)),
(2 * ((x - a) ** 2)) / ((b - a) ** 2),
np.where(((a + b) / 2 <= x) & (x <= b),
1 - (2 * ((x - a) ** 2)) / ((b - a) ** 2),
1)
)
)
проверка: In [97]: f(x).sum() == y(x).sum()
Out[97]: True
Выглядит немного уродливо, но на больших массивах должно давать хороший прирост производительности. In [94]: x = np.random.randint(10**5, size=10**5)
In [95]: %timeit y(x)
503 ms ± 654 µs per loop (mean ± std. dev. of 7 runs, 1 loop each)
In [96]: %timeit f(x)
5.51 ms ± 9.17 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
График: a,b = -5, 5
x = np.linspace(-10, 10, 20)
graph2 = plt.plot(x, f(x))
Кусочно-заданная функцияРеальные процессы, происходящие в природе, можно описать с помощью функций. Так, можно выделить два основных типа течения процессов, противоположных друг другу – это постепенное или непрерывное и скачкообразное (примером может служить падение мяча и его отскок). Но если есть разрывные процессы, то существуют и специальные средства для их описания. С этой целью вводятся в обращение функции, имеющие разрывы, скачки, то есть на различных участках числовой прямой функция ведет себя по разным законам и, соответственно, задается разными формулами. Вводятся понятия точек разрыва, устранимого разрыва. Наверняка вам уже встречались функции, заданные несколькими формулами, в зависимости от значений аргумента, например: y = {x – 3, при x > -3;
{-(x – 3), при x < -3. Такие функции называются кусочными или кусочно-заданными. Участки числовой прямой с различными формулами задания, назовем составляющими область определения. Объединение всех составляющих является областью определения кусочной функции. Те точки, которые делят область определения функции на составляющие, называются граничными точками. Формулы, определяющие кусочную функцию на каждой составляющей области определения, называются входящими функциями. Графики кусочно-заданных функций получаются в результате объединения частей графиков, построенных на каждом из промежутков разбиения. Упражнения. Построить графики кусочных функций: 1) {-3, при -4 ≤ x < 0,
f(x) = {0, при x = 0,
{1, при 0 < x ≤ 5. График первой функции – прямая, проходящая через точку y = -3. Она берет свое начало в точке с координатами (-4; -3), идет параллельно оси абсцисс до точки с координатами (0; -3). График второй функции – точка с координатами (0; 0). Третий график аналогичен первому – это прямая, проходящая через точку y = 1, но уже на участке от 0 до 5 по оси Ох. Ответ: рисунок 1. 2) {3, если x ≤ -4,
f(x) = {|x2 – 4|x| + 3|, если -4 < x ≤ 4,
{3 – (x – 4)2, если x > 4. Рассмотрим отдельно каждую функцию и построим ее график. Так, f(x) = 3 – прямая, параллельная оси Ох, но изображать ее нужно только на участке, где x ≤ -4. График функции f(x) = |x2 – 4|x| + 3| может быть получен из параболы y = x2 – 4x + 3. Построив ее график, часть рисунка, которая лежит над осью Ox, необходимо оставить без изменений, а часть, которая лежит под осью абсцисс, симметрично отобразить относительно оси Ox. Затем симметрично отобразить часть графика, где
x ≥ 0 относительно оси Oy для отрицательных x. Полученный в результате всех преобразований график оставляем только на участке от -4 до 4 по оси абсцисс. График третьей функции – парабола, ветви которой направлены вниз, а вершина находится в точке с координатами (4; 3). Чертеж изображаем только на участке, где x > 4. Ответ: рисунок 2. 3) {8 – (x + 6)2, если x ≤ -6,
f(x) = {|x2 – 6|x| + 8|, если -6 ≤ x < 5,
{3, если x ≥ 5. Построение предлагаемой кусочной-заданной функции аналогично предыдущему пункту. Здесь графики первых двух функций получаются из преобразований параболы, а график третьей – прямая, параллельная Ох. Ответ: рисунок 3. 4) Построить график функции y = x – |x| + (x – 1 – |x|/x)2 . Решение. Область определения данной функции – все действительные числа, кроме нуля. Раскроем модуль. Для этого рассмотрим два случая: 1) При x > 0 получим y = x – x + (x – 1 – 1)2 = (x – 2)2. 2) При x < 0 получим y = x + x + (x – 1 + 1)2 = 2x + x2. Таким образом, перед нами кусочно-заданная функция: y = {(x – 2)2, при x > 0;
{ x2 + 2x, при x < 0. Графики обоих функций – параболы, ветви которых направлены вверх. Ответ: рисунок 4. 5) Построить график функции y = (x + |x|/x – 1)2 . Решение. Легко видеть, что областью определения функции являются все действительные числа, кроме нуля. После раскрытия модуля получим кусочно-заданную функцию: 1) При x > 0 получим y = (x + 1 – 1)2 = x2. 2) При x < 0 получим y = (x – 1 – 1)2 = (x – 2)2. Перепишем. y = {x2, при x > 0;
{(x – 2)2, при x < 0. Графики этих функций – параболы. Ответ: рисунок 5. 6) Существует ли функция, график которой на координатной плоскости имеет общую точку с любой прямой? Решение. Да, существует. Примером может быть функция f(x) = x3. Действительно, с вертикальной прямой х = а график кубической параболы пересекается в точке (а; а3). Пусть теперь прямая задана уравнением y = kx + b. Тогда уравнение
x3 – kx – b = 0 имеет действительный корень х0 (так как многочлен нечетной степени всегда имеет хотя бы один действительный корень). Следовательно, график функции пересекается с прямой y = kx + b, например, в точке (х0; х03). © blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Кусочно линейная функция задана формулой найти в. Кусочные функцииГрафики кусочно – заданных функций Мурзалиева Т.А. учитель математики МБОУ «Борская средняя общеобразовательная школа» Бокситогорский район Ленинградская область Цель: - освоить метод линейного сплайна для построения графиков, содержащих модуль;
- научиться применять его в простых ситуациях.
Под сплайном (от англ. spline — планка, рейка) обычно понимают кусочно-заданную функцию. Такие функции были известны математикам давно, начиная еще с Эйлера (1707-1783г.,швейцарский, немецкий и российский математик), но их интенсивное изучение началось, фактически, только в середине XX века. В 1946 году Исаак Шёнберг (1903- 1990г., румынский и американский математик) впервые употребил этот термин. С 1960 года с развитием вычислительной техники началось использование сплайнов в компьютерной графике и моделировании. 1 . Введение 2. Определение линейного сплайна 3. Определение модуля 4. Построение графиков 5. Практическая работа Одно из основных назначений функций – описание реальных процессов, происходящих в природе. Но издавна ученые – философы и естествоиспытатели выделяли два типа протекания процессов: постепенное ( непрерывное ) и скачкообразное. При падении тела на землю сначала происходит непрерывное нарастание скорости движения , а в момент столкновения с поверхностью земли скорость изменяется скачкообразно , становясь равной нулю или меняя направление (знак) при «отскоке» тела от земли (например, если тело – мяч). Но раз есть разрывные процессы, то необходимы средства их описаний. С этой целью вводятся в действие функции, имеющие разрывы . a — формулой y = h(x), причем будем считать, что каждая из функций g(x) и h(x) определена для всех значений х и разрывов не имеет. Тогда, если g(a) = h(a), то функция f(x) имеет при х=а скачок; если же g(a) = h(a) = f(a), то «комбинированная» функция f разрывов не имеет. Если обе функции g и h элементарные, то f называется кусочно–элементарной. » - Один из способов введения таких разрывов следующий:
Пусть функция y = f(x) при x определена формулой y = g(x), а при xa — формулой y = h(x), причем будем считать , что каждая из функций g(x) и h(x) определена для всех значений х и разрывов не имеет. Тогда , если g(a) = h(a), то функция f(x) имеет при х=а скачок; если же g(a) = h(a) = f(a), то «комбинированная» функция f разрывов не имеет. Если обе функции g и h элементарные, то f называется кусочно–элементарной. Графики непрерывных функций Построить график функции: У = |X-1| + 1 Х=1 –точка смены формул Слово «модуль» произошло от латинского слова «modulus», что в переводе означает «мера». Модулем числа а называется расстояние (в единичных отрезках ) от начала координат до точки А (а) . Это определение раскрывает геометрический смысл модуля. Модулем (абсолютной величиной ) действительного числа а называется то самое число а ≥ 0, и противоположное число –а , если а 0 или х=0 у = -3х -2 при х » Построить график функции у = 3|х|-2. По определению модуля, имеем: 3х – 2 при х0 или х=0 -3х -2 при х x n) » . Пусть заданы х 1 х 2 х n – точки смены формул в кусочно-элементарных функциях. Функция f, определенная при всех х, называется кусочно-линейной, если она линейна на каждом интервале и к тому же выполнены условия согласования, то есть в точках смены формул функция не терпит разрыв. Непрерывная кусочно-линейная функция называется линейным сплайном . Её график есть ломаная с двумя бесконечными крайними звеньями – левым (отвечающим значениям x n ) и правым ( отвечающим значениям x x n ) Кусочно-элементарная функция может быть определена более чем двумя формулами График – ломаная с двумя бесконечными крайними звеньями – левым (х1). У=|x| — |x – 1| Точки смены формул: х=0 и х=1. У(0)=-1, у(1)=1. График кусочно-линейной функции удобно строить, указывая на координатной плоскости вершины ломаной. Кроме построения n вершин следует построить также две точки : одну левее вершины A 1 ( x 1; y ( x 1)), другую – правее вершины An ( xn ; y ( xn )). Заметим, что разрывную кусочно-линейную функцию нельзя представить в виде линейной комбинации модулей двучленов . Построить график функции у = х+ |x -2| — |X|. Непрерывная кусочно-линейная функция называется линейным сплайном 1.Точки смены формул: Х-2=0, Х=2 ; Х=0 2.Составим таблицу: У(0 )= 0+|0-2|-|0|=0+2-0= 2 ; у(2 )=2+|2-2|-|2|=2+0-2= 0 ; у (-1 )= -1+|-1-2| — |-1|= -1+3-1= 1 ; у(3 )=3+|3-2| — |3|=3+1-3= 1 . Построить график функции у = |х+1| +|х| – |х -2|. 1 .Точки смены формул: х+1=0, х=-1 ; х=0 ; х-2=0, х=2. 2 . Составим таблицу: y(-2)=|-2+1|+|-2|-|-2-2|=1+2-4=-1; y(-1)=|-1+1|+|-1|-|-1-2|=0+1-3=-2; y(0)=1+0-2=-1; y(2)=|2+1|+|2|-|2-2|=3+2-0=5; y(3)=|3+1|+|3|-|3-2|=4+3-1=6. |x – 1| = |x + 3| Решите уравнение: Решение. Рассмотрим функцию y = |x -1| — |x +3| Построим график функции /методом линейного сплайна/ х -1 = 0, х = 1; х + 3 =0, х = — 3. 2. Составим таблицу: y(- 4) =|- 4–1| — |- 4+3| =|- 5| — | -1| = 5-1=4; y( -3 )=|- 3-1| — |-3+3|=|-4| = 4; y( 1 )=|1-1| — |1+3| = — 4 ; y(-1) = 0. y(2)=|2-1| — |2+3|=1 – 5 = — 4. Ответ: -1. 1. Построить графики кусочно-линейных функций методом линейного сплайна: у = |x – 3| + |x|; 1). Точки смены формул: 2). Составим таблицу: 2. Построить графики функций, используя УМК «Живая математика » А) у = |2x – 4| + |x +1| 1) Точки смены формул: 2) y() = Б) Постройте графики функций, установите закономерность : a) у = |х – 4| б) y = |x| +1 y = |x + 3| y = |x| — 3 y = |x – 3| y = |x| — 5 y = |x + 4| y = |x| + 4 Используйте инструменты «Точка», «Отрезок», «Стрелка» на панели инструментов. 1. Меню «Графики». 2. Вкладка «Построить график». .3. В окне «Калькулятор» задать формулу. Постройте график функции: 1) У = 2х + 4 1. Козина М.Е. Математика. 8-9 классы: сборник элективных курсов. – Волгоград: Учитель, 2006. 2. Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова. Алгебра: учеб. Для 7 кл. общеобразоват. учреждений/ под ред. С. А. Теляковского. – 17-е изд. – М. : Просвещение, 2011 3. Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова. Алгебра: учеб. Для 8 кл. общеобразоват. учреждений/ под ред. С. А. Теляковского. – 17-е изд. – М. : Просвещение, 2011 4. ВикипедиЯ свободная энциклопедия http://ru.wikipedia.org/wiki/Spline Реальные процессы, происходящие в природе, можно описать с помощью функций. Так, можно выделить два основных типа течения процессов, противоположных друг другу – это постепенное или непрерывное и скачкообразное (примером может служить падение мяча и его отскок). Но если есть разрывные процессы, то существуют и специальные средства для их описания. С этой целью вводятся в обращение функции, имеющие разрывы, скачки, то есть на различных участках числовой прямой функция ведет себя по разным законам и, соответственно, задается разными формулами. Вводятся понятия точек разрыва, устранимого разрыва. Наверняка вам уже встречались функции, заданные несколькими формулами, в зависимости от значений аргумента, например: y = {x – 3, при x > -3;
{-(x – 3), при x Такие функции называются кусочными или кусочно-заданными . Участки числовой прямой с различными формулами задания, назовем составляющими область определения. Объединение всех составляющих является областью определения кусочной функции. Те точки, которые делят область определения функции на составляющие, называются граничными точками . Формулы, определяющие кусочную функцию на каждой составляющей области определения, называются входящими функциями . Графики кусочно-заданных функций получаются в результате объединения частей графиков, построенных на каждом из промежутков разбиения. Упражнения. Построить графики кусочных функций: 1) {-3, при -4 ≤ x f(x) = {0, при x = 0,
{1, при 0 График первой функции – прямая, проходящая через точку y = -3. Она берет свое начало в точке с координатами (-4; -3), идет параллельно оси абсцисс до точки с координатами (0; -3). График второй функции – точка с координатами (0; 0). Третий график аналогичен первому – это прямая, проходящая через точку y = 1, но уже на участке от 0 до 5 по оси Ох. Ответ: рисунок 1. 2) {3, если x ≤ -4,
f(x) = {|x 2 – 4|x| + 3|, если -4 {3 – (x – 4) 2 , если x > 4. Рассмотрим отдельно каждую функцию и построим ее график. Так, f(x) = 3 – прямая, параллельная оси Ох, но изображать ее нужно только на участке, где x ≤ -4. График функции f(x) = |x 2 – 4|x| + 3| может быть получен из параболы y = x 2 – 4x + 3. Построив ее график, часть рисунка, которая лежит над осью Ox, необходимо оставить без изменений, а часть, которая лежит под осью абсцисс, симметрично отобразить относительно оси Ox. Затем симметрично отобразить часть графика, где
x ≥ 0 относительно оси Oy для отрицательных x. Полученный в результате всех преобразований график оставляем только на участке от -4 до 4 по оси абсцисс. График третьей функции – парабола, ветви которой направлены вниз, а вершина находится в точке с координатами (4; 3). Чертеж изображаем только на участке, где x > 4. Ответ: рисунок 2. 3) {8 – (x + 6) 2 , если x ≤ -6,
f(x) = {|x 2 – 6|x| + 8|, если -6 ≤ x {3, если x ≥ 5. Построение предлагаемой кусочной-заданной функции аналогично предыдущему пункту. Здесь графики первых двух функций получаются из преобразований параболы, а график третьей – прямая, параллельная Ох. Ответ: рисунок 3. 4) Построить график функции y = x – |x| + (x – 1 – |x|/x) 2 . Решение. Область определения данной функции – все действительные числа, кроме нуля. Раскроем модуль. Для этого рассмотрим два случая: 1) При x > 0 получим y = x – x + (x – 1 – 1) 2 = (x – 2) 2 . 2) При x Таким образом, перед нами кусочно-заданная функция: y = {(x – 2) 2 , при x > 0;
{ x 2 + 2x, при x Графики обоих функций – параболы, ветви которых направлены вверх. Ответ: рисунок 4. 5) Построить график функции y = (x + |x|/x – 1) 2 . Решение. Легко видеть, что областью определения функции являются все действительные числа, кроме нуля. После раскрытия модуля получим кусочно-заданную функцию: 1) При x > 0 получим y = (x + 1 – 1) 2 = x 2 . 2) При x Перепишем. y = {x 2 , при x > 0;
{(x – 2) 2 , при x Графики этих функций – параболы. Ответ: рисунок 5. 6) Существует ли функция, график которой на координатной плоскости имеет общую точку с любой прямой? Решение. Да, существует. Примером может быть функция f(x) = x 3 . Действительно, с вертикальной прямой х = а график кубической параболы пересекается в точке (а; а 3). Пусть теперь прямая задана уравнением y = kx + b. Тогда уравнение
x 3 – kx – b = 0 имеет действительный корень х 0 (так как многочлен нечетной степени всегда имеет хотя бы один действительный корень). Следовательно, график функции пересекается с прямой y = kx + b, например, в точке (х 0 ; х 0 3). сайт,
при полном или частичном копировании материала ссылка на первоисточник обязательна. Муниципальное бюджетное общеобразовательное учреждение средняя общеобразовательная школа №13 «Кусочные функции» Сапогова Валентина и Донская Александра Руководитель-консультант: г. Бердск 1. Определение основных целей и задач. 2. Анкетирование. 2.1. Определение актуальности работы 2.2. Практическая значимость. 3. История функций. 4. Общая характеристика. 5. Способы задания функций. 6. Алгоритм построения. 8. Используемая литература. 1. Определение основных целей и задач. Цель: Выяснить способ решения кусочных функций и, исходя из этого, составить алгоритм их построения. Задачи: Познакомиться с общим понятием о кусочных функциях; Узнать историю термина «функция»; Провести анкетирование; Выявить способы задания кусочных функций; Составить алгоритм их построения; 2. Анкетирование. Среди старшеклассников было проведено анкетирование на умение строить кусочные функции. Общее количество опрошенных составило 54 человека. Среди них 6% — работу выполнили полностью. 28% работу смогли выполнить, но с определёнными ошибками. 62% — работу не смогли выполнить, хоть и предпринимали какие-либо попытки, а оставшиеся 4% вообще не приступали к работе. Из этого анкетирования можно сделать вывод, что ученики нашей школы, которые проходят программу имеют не достаточную базу знаний, ведь этот автор не уделяет особого внимания на задания подобного рода.2 > 0%%, т.е. %%D = (-1, 1)%%. Преимущества явного аналитического задания функцииОтметим, что явный аналитический способ задания функции достаточно компактен (формула, как правило, занимает немного места), легко воспроизводим (формулу нетрудно записать) и наиболее приспособлен к выполнению над функциями математических действий и преобразований. Некоторые из этих действий — алгебраические (сложение, умножение и др.) — хорошо известны из школьного курса математики, другие (дифференцирование, интегрирование) будем изучать в дальнейшем. Однако этот способ не всегда нагляден, так как не всегда четок характер зависимости функции от аргумента, а для нахождения значений функции (если они необходимы) требуются иногда громоздкие вычисления. Неявное задание функцииФункция %%y = f(x)%% задана неявным аналитическим способом , если дано соотношение $$F(x,y) = 0, ~~~~~~~~~~(1)$$ связывающее значения функции %%y%% и аргумента %%x%%. Если задавать значения аргумента, то для нахождения значения %%y%%, соответствующего конкретному значению %%x%%, необходимо решить уравнение %%(1)%% относительно %%y%% при этом конкретном значении %%x%%.5 — 1 = 0%% и равенство %%y = \sqrt{1 — x}%% определяют одну и ту же функцию. Параметрическое задание функцииКогда зависимость %%y%% от %%x%% не задана непосредственно, а вместо этого даны зависимости обоих переменных %%x%% и %%y%% от некоторой третьей вспомогательной переменной %%t%% в виде $$
\begin{cases}
x = \varphi(t),\\
y = \psi(t),
\end{cases} ~~~t \in T \subseteq \mathbb{R}, ~~~~~~~~~~(2)
$$то говорят о параметрическом способе задания функции; тогда вспомогательную переменную %%t%% называют параметром. Если из уравнений %%(2)%% удается исключить параметр %%t%%, то приходят к функции, заданной явной или неявной аналитической зависимостью %%y%% от %%x%%. Например, из соотношений
$$
\begin{cases}
x = 2 t + 5, \\
y = 4 t + 12,
\end{cases}, ~~~t \in \mathbb{R},
$$ исключением параметра %%t%% получим зависимость %%y = 2 x + 2%%, которая задает в плоскости %%xOy%% прямую. Графический способПример графического задания функции Приведенные выше примеры показывают, что аналитическому способу задания функции соответствует ее графическое изображение , которое можно рассматривать как удобную и наглядную форму описания функции. Иногда используют графический способ задания функции, когда зависимость %%y%% от %%x%% задают линией на плоскости %%xOy%%. Однако при всей наглядности он проигрывает в точности, поскольку значения аргумента и соответствующие им значения функции можно получить из графика лишь приближенно. Возникающая при этом погрешность зависит от масштаба и точности измерения абсциссы и ординаты отдельных точек графика. В дальнейшем графику функции отведем роль только иллюстрации поведения функции и поэтому будем ограничиваться построением «эскизов» графиков, отражающих основные особенности функций. Табличный способОтметим табличный способ задания функции, когда некоторые значения аргумента и соответствующие им значения функции в определенном порядке размещаются в таблице. Так построены известные таблицы тригонометрических функций, таблицы логарифмов и т.п. В виде таблицы обычно представляют зависимость между величинами, измеряемыми при экспериментальных исследованиях, наблюдениях, испытаниях. Недостаток этого способа состоит в невозможности непосредственного определения значений функции для значений аргумента, не входящих в таблицу. Если есть уверенность, что непредставленные в таблице значения аргумента принадлежат области определения рассматриваемой функции, то соответствующие им значения функции могут быть вычислены приближенно при помощи интерполяции и экстраполяции. Пример| x | 3 | 5.1 | 10 | 12.5 | | y | 9 | 23 | 80 | 110 |
Алгоритмический и словесный способы задания функцийФункцию можно задать алгоритмическим (или программным ) способом, который широко используют при вычислениях на ЭВМ. Наконец, можно отметить описательный (или словесный ) способ задания функции, когда правило соответствия значений функции значениям аргумента выражено словами. Например, функцию %%[x] = m~\forall {x \in } Урок по алгебре в 7-м классе по теме «График кусочной функции, или График правильного питания»Цели:
- повторение алгоритма построения графиков
линейной функции, нахождение точек
принадлежащих графику функции, введение
алгоритма построения графика кусочной функции,
- развитие математических способностей,
логического мышления,
- воспитание взаимоуважения друг к другу.
Тип: комбинированный. Контроль: составление опорного
конспекта, самостоятельная работа
(интерактивные задания). Форма: индивидуальная, групповая. Оборудование: компьютеры,
мультимедиа. Метод: эвристический. Ход урока
1 этап: Разминка 1) Устный счёт: №1. -18•(-3) – 134, -122•(-1/2)+ 53, 4•(-23)-134,
-2•140+8, -48•1/8-345, 2•(-1/4)+536. 2) Теоретический: – Какая функция называется линейной функцией?
Запишите её.
– Как называется график линейной функции?
– Какая функция называется
прямопропорциональной? Запишите её.
– Как называется k?
2 этап: Подготовительный №2. Построить графики функций а) у=5х-3, б) у=-3х-4, в)
у=-2х+1. (У доски трое учащихся на построение графиков
функций.) №3. Найдите координаты точек (все выполняют в
тетради).
3 этап: Построение№4. Построить графики функций | 1) у = 0,25х + 6,75 на отрезке [1;3], |
|
| 2) у = 0,25х + 9,25 на отрезке [3;7], |
|
| 3) у = 1/6х + 71/6 на отрезке [7;13], |
|
| 4) у = 1/3х + 44/3 на отрезке [13;16] |
|
Мы построили график кусочной функции
А также мы построили график правильного
питания: ** завтрак – чай, хлеб с маслом и колбасой или
сыром,
** школьный завтрак – горячее питание (суп, каша,
..),
** обед – из двух блюд,
** ужин – легкое питание. №5. Постройте на графике правильного питания
точки с координатами А (1;7), Р(7;11), С(7;13), В(16:20). Таким
образом, вы должны понять, что в день вы должны
получить все витамины. Посмотрите таблицы содержания витаминов. [2], [3]
4 этап: самостоятельная работа
(интерактивные задания)Учащиеся по группам усаживаются за компьютер и
выполняют задания. [1] Правильность выполнения
проверяет учитель.
5 этап: домашнее задание Составьте кусочную функцию и постройте её
график.
6 этап: Заключительный Подведение итогов. – Что нового вы узнали из этого урока?
– Какие функции вы знаете?
Литература: - Электронный учебник “Интерактивная математика
5–9 классы”.
- Воробьёв Р.И. Питание и здоровье. М.:
Медицина, 1998.
- Мартынов С.М. Овощи плюс фрукты плюс ягоды
получится здоровье: Беседы врача – педиатра о
питании детей. Кн. для родителей. М: Просвещение
1999.
Образец чтения свойств кусочно заданной функции. Кусочные функцииРеальные процессы, происходящие в природе, можно описать с помощью функций. Так, можно выделить два основных типа течения процессов, противоположных друг другу – это постепенное или непрерывное и скачкообразное (примером может служить падение мяча и его отскок). Но если есть разрывные процессы, то существуют и специальные средства для их описания. С этой целью вводятся в обращение функции, имеющие разрывы, скачки, то есть на различных участках числовой прямой функция ведет себя по разным законам и, соответственно, задается разными формулами. Вводятся понятия точек разрыва, устранимого разрыва. Наверняка вам уже встречались функции, заданные несколькими формулами, в зависимости от значений аргумента, например: y = {x – 3, при x > -3;
{-(x – 3), при x Такие функции называются кусочными или кусочно-заданными . Участки числовой прямой с различными формулами задания, назовем составляющими область определения. Объединение всех составляющих является областью определения кусочной функции. Те точки, которые делят область определения функции на составляющие, называются граничными точками . Формулы, определяющие кусочную функцию на каждой составляющей области определения, называются входящими функциями . Графики кусочно-заданных функций получаются в результате объединения частей графиков, построенных на каждом из промежутков разбиения. Упражнения. Построить графики кусочных функций: 1) {-3, при -4 ≤ x f(x) = {0, при x = 0,
{1, при 0 График первой функции – прямая, проходящая через точку y = -3. Она берет свое начало в точке с координатами (-4; -3), идет параллельно оси абсцисс до точки с координатами (0; -3). График второй функции – точка с координатами (0; 0). Третий график аналогичен первому – это прямая, проходящая через точку y = 1, но уже на участке от 0 до 5 по оси Ох. Ответ: рисунок 1. 2) {3, если x ≤ -4,
f(x) = {|x 2 – 4|x| + 3|, если -4 {3 – (x – 4) 2 , если x > 4. Рассмотрим отдельно каждую функцию и построим ее график. Так, f(x) = 3 – прямая, параллельная оси Ох, но изображать ее нужно только на участке, где x ≤ -4. График функции f(x) = |x 2 – 4|x| + 3| может быть получен из параболы y = x 2 – 4x + 3. Построив ее график, часть рисунка, которая лежит над осью Ox, необходимо оставить без изменений, а часть, которая лежит под осью абсцисс, симметрично отобразить относительно оси Ox. Затем симметрично отобразить часть графика, где
x ≥ 0 относительно оси Oy для отрицательных x. Полученный в результате всех преобразований график оставляем только на участке от -4 до 4 по оси абсцисс. График третьей функции – парабола, ветви которой направлены вниз, а вершина находится в точке с координатами (4; 3). Чертеж изображаем только на участке, где x > 4. Ответ: рисунок 2. 3) {8 – (x + 6) 2 , если x ≤ -6,
f(x) = {|x 2 – 6|x| + 8|, если -6 ≤ x {3, если x ≥ 5. Построение предлагаемой кусочной-заданной функции аналогично предыдущему пункту. Здесь графики первых двух функций получаются из преобразований параболы, а график третьей – прямая, параллельная Ох. Ответ: рисунок 3. 4) Построить график функции y = x – |x| + (x – 1 – |x|/x) 2 . Решение. Область определения данной функции – все действительные числа, кроме нуля. Раскроем модуль. Для этого рассмотрим два случая: 1) При x > 0 получим y = x – x + (x – 1 – 1) 2 = (x – 2) 2 . 2) При x Таким образом, перед нами кусочно-заданная функция: y = {(x – 2) 2 , при x > 0;
{ x 2 + 2x, при x Графики обоих функций – параболы, ветви которых направлены вверх. Ответ: рисунок 4. 5) Построить график функции y = (x + |x|/x – 1) 2 . Решение. Легко видеть, что областью определения функции являются все действительные числа, кроме нуля. После раскрытия модуля получим кусочно-заданную функцию: 1) При x > 0 получим y = (x + 1 – 1) 2 = x 2 . 2) При x Перепишем. y = {x 2 , при x > 0;
{(x – 2) 2 , при x Графики этих функций – параболы. Ответ: рисунок 5. 6) Существует ли функция, график которой на координатной плоскости имеет общую точку с любой прямой? Решение. Да, существует. Примером может быть функция f(x) = x 3 . Действительно, с вертикальной прямой х = а график кубической параболы пересекается в точке (а; а 3). Пусть теперь прямая задана уравнением y = kx + b. Тогда уравнение
x 3 – kx – b = 0 имеет действительный корень х 0 (так как многочлен нечетной степени всегда имеет хотя бы один действительный корень). Следовательно, график функции пересекается с прямой y = kx + b, например, в точке (х 0 ; х 0 3). сайт,
при полном или частичном копировании материала ссылка на первоисточник обязательна. Муниципальное бюджетное общеобразовательное учреждение средняя общеобразовательная школа №13 «Кусочные функции» Сапогова Валентина и Донская Александра Руководитель-консультант: г. Бердск 1. Определение основных целей и задач. 2. Анкетирование. 2.1. Определение актуальности работы 2.2. Практическая значимость. 3. История функций. 4. Общая характеристика. 5. Способы задания функций. 6. Алгоритм построения. 8. Используемая литература. 1. Определение основных целей и задач. Цель: Выяснить способ решения кусочных функций и, исходя из этого, составить алгоритм их построения. Задачи: Познакомиться с общим понятием о кусочных функциях; Узнать историю термина «функция»; Провести анкетирование; Выявить способы задания кусочных функций; Составить алгоритм их построения; 2. Анкетирование. Среди старшеклассников было проведено анкетирование на умение строить кусочные функции. Общее количество опрошенных составило 54 человека. Среди них 6% — работу выполнили полностью. 28% работу смогли выполнить, но с определёнными ошибками. 62% — работу не смогли выполнить, хоть и предпринимали какие-либо попытки, а оставшиеся 4% вообще не приступали к работе. Из этого анкетирования можно сделать вывод, что ученики нашей школы, которые проходят программу имеют не достаточную базу знаний, ведь этот автор не уделяет особого внимания на задания подобного рода. Именно из этого вытекает актуальность и практическая значимость нашей работы. 2.1. Определение актуальности работы. Актуальность: Кусочные функции встречаются, как в ГИА, так и в ЕГЭ, задания, которые содержат функции подобного рода, оцениваются в 2 и более баллов. И, следовательно, от их решения может зависеть ваша оценка. 2.2. Практическая значимость. Результатом нашей работы будет являться алгоритм решения кусочных функций, который поможет разобраться в их построении. И добавит шансы на получения желаемой вами оценки на экзамене. 3. История функций. «Алгебра 9 класс» и др.; 7
Урок по алгебре в 9А классе учителя Микитчук Ж.Н. МОУ «СОШ №23» 19.03.07г Тема урока: «Кусочно-заданные функции» Цели: обобщить и совершенствовать знания, умения и навыки учащихся по указанной теме; воспитывать у учащихся внимательность, сосредоточенность, настойчивость, уверенность в своих знаниях; развивать мыслительные способности, логическое мышление; речевую культуру, умение применять теоретические знания. В результате обобщения темы учащиеся должны знать: понятие кусочно-заданной функции; формулы различных функций, соответствующие названия и изображения графиков; уметь: строить график кусочно-заданной функции; читать график; задавать функцию аналитически по графику. Ход урока I. Организационно-психологический момент. Начнем наш урок словами Д.К.Фадеева «Какую бы задачу вы не решали, в концевас ждёт счастливая минута – радостноечувство успеха, укрепление веры в свои силы.Пусть эти слова на нашем уроке обретут реальное подтверждение. II. Проверка домашнего задания. Начнем урок как обычно с проверки д/з.-Повторите определение кусочной функции и план исследования функций.1). На доске изобразить придуманные вами графики кусочных функций (рис.1,2,3)2). Карточки .№1. Расставьте порядок исследования свойств функций: выпуклость; четность, нечётность; область значений; ограниченность; монотонность; непрерывность; наибольшее и наименьшее значение функции; область определения. №2.Изобразите схематически графики функций: А) у = kx + b, k0; Б) y = kx, k0; В) у = , k0. 3).Устная работа .
– 2мин Какая функция называется кусочной? Кусочной называется функция, заданная разными формулами на разных промежутках. Из каких функций состоят кусочные функции, изображенные на рис.1,2,3? Какие ещё названия функций вы знаете? Как называются графики соответствующих функций? Является ли графиком какой-либо функции, фигура, изображенная на рис.4? Почему? Ответ: нет, т.к. по определению функции, каждому значению независимой переменной х ставится в соответствие единственное значение зависимой переменной у.
4) Самоконтроль — 3 минИз предложенных графиков и соответствующих формул, задающих функции, выберите верные. Из полученных букв ответов составьте знакомое слово.
Ответ: ГРАФИК
Где в жизни, в науке, в быту мы ещё встречаемся со словом ГРАФИК?-График зависимости массы от объёма,-объёма от давления;- график дежурства;- график движения поездов;-графики используются для представления различной информации, например, объём промышленного производства в Саратовской области в период с 1980 по 2002год.. По этому графику можно проследить за снижением и ростом производства в отдельные года.-Скажите, графиком какой функции представлена данная информация.Ответ: кусочная функция
. III. Сообщение темы, цели урока. Тема урока: «Кусочно-заданные функции» Цель: — на примере кусочно-заданной функции вспомнить план исследования функций; повторить шаги построения кусочно-заданной функции; применять обобщенные знания при решении нестандартных задач. IV. Актуализация ранее усвоенных знаний. Понятие функции впервые встретилось нам в 7 классе при изучении линейной зависимости. С точки зрения моделирования реальных процессов, эта зависимость соответствует равномерным процессам.Пример: Движение пешехода с постоянной скоростью за время t. Формула: s =vt, график – отрезки прямой, расположен в I четверти. Основная тема 8-го класса – квадратичная функция, моделирующая равноускоренные процессы.Пример: изученная вами в 9-ом классе формула определения сопротивления нагретой лампы (R) при постоянной мощности (Р) и изменяющемся напряжении (U). ФормулаR = , график – ветвь параболы, расположен-ная в I четверти. На протяжении трёх лет наши знания о функциях обогащались, количество изученных функций росло, пополнялся и набор заданий для решения которых приходится прибегать к графикам.Назовите эти типы заданий…- решение уравнений;
— решение систем уравнений;
— решение неравенств;
— исследование свойств функций. V.Подготовка уч-ся к обобщающей деятельности. Вспомним один из типов заданий, а именно – исследование свойств функций или чтение графика.Обратимся к учебнику. Страница 65 рис.20а из №250. Задание: прочитать график функции. Порядок исследования функции перед нами.1. область определения – (-∞; +∞)
2. четность, нечётность – ни четная, ни нечётная
3. монотонность- возрастает [-3; +∞), убывает
[-5;-3], постоянна (-∞; -5];
4. ограниченность – ограничена снизу
5. наибольшее и наименьшее значение функции – у наим = 0, у наиб – не существует;
6. непрерывность- непрерывна на всей области определения;
7. область значений – , выпукла и вниз и вверх (-∞; -5] и [-2; +∞). VI. Воспроизведение знаний на новом уровне. Вы знаете, что построение и исследование графиков кусочно-заданных функций, рассматриваются во второй части экзамена по алгебре в разделе функции и оцениваются 4-мя и 6-ю баллами. Обратимся к сборнику заданий.Страница 119 — №4.19-1).Решение:
1).у = —
x, — квадратичная функция, график – парабола, ветви вниз (а = -1, а
0). х -2 -1 0 1 2
у -4 -1 0 1 4
2) у= 3х – 10, — линейная функция, график – прямая
Составим таблицу некоторых значений
х 3 3
у 0 -1
3) у= -3х -10, — линейная функция, график – прямая
Составим таблицу некоторых значений
х -3 -3
у 0 -1
4)Построим графики функций в одной системе координат и выделим части графиков на заданных промежутках. Найдем по графику, при каких значениях х значения функции неотрицательны.
Ответ:
f(x)
0 при х = 0 и при
3 VII.Работа над нестандартными заданиями. №4.29-1), стр. 121. Решение:
1)Прямая (слева) у =
kx + b проходит через точки (-4;0) и (-2;2). Значит,-4
k + b = 0,-2
k + b = 2; k = 1, b = 4, у = х+4.Ответ: х +4, если х
-2
у = , если -2
х £
3
3, если х
3 VIII.Контроль знаний. Итак, подведём небольшой итог. Что мы повторили на уроке?План исследования функций, шаги построения графика кусочной функции, задание функции аналитически. Проверим как вы усвоили данный материал. Тестирование на «4»- «5», «3» I вариант№ У 2
1
-1 -1 1 Х D(f) = , выпуклая и вверх и вниз на , выпуклая вверх и вниз на , убывает на ________ Ограничена ____________ у наим не существует, у наиб =_____ Непрерывна на всей области определения Е(f) = ____________ Выпукла и вниз и вверх на всей области определения Графики кусочно – заданных функций Мурзалиева Т.А. учитель математики МБОУ «Борская средняя общеобразовательная школа» Бокситогорский район Ленинградская область Цель: - освоить метод линейного сплайна для построения графиков, содержащих модуль;
- научиться применять его в простых ситуациях.
Под сплайном (от англ. spline — планка, рейка) обычно понимают кусочно-заданную функцию. Такие функции были известны математикам давно, начиная еще с Эйлера (1707-1783г.,швейцарский, немецкий и российский математик), но их интенсивное изучение началось, фактически, только в середине XX века. В 1946 году Исаак Шёнберг (1903- 1990г., румынский и американский математик) впервые употребил этот термин. С 1960 года с развитием вычислительной техники началось использование сплайнов в компьютерной графике и моделировании. 1 . Введение 2. Определение линейного сплайна 3. Определение модуля 4. Построение графиков 5. Практическая работа Одно из основных назначений функций – описание реальных процессов, происходящих в природе. Но издавна ученые – философы и естествоиспытатели выделяли два типа протекания процессов: постепенное ( непрерывное ) и скачкообразное. При падении тела на землю сначала происходит непрерывное нарастание скорости движения , а в момент столкновения с поверхностью земли скорость изменяется скачкообразно , становясь равной нулю или меняя направление (знак) при «отскоке» тела от земли (например, если тело – мяч). Но раз есть разрывные процессы, то необходимы средства их описаний. С этой целью вводятся в действие функции, имеющие разрывы . a — формулой y = h(x), причем будем считать, что каждая из функций g(x) и h(x) определена для всех значений х и разрывов не имеет. Тогда, если g(a) = h(a), то функция f(x) имеет при х=а скачок; если же g(a) = h(a) = f(a), то «комбинированная» функция f разрывов не имеет. Если обе функции g и h элементарные, то f называется кусочно–элементарной. » - Один из способов введения таких разрывов следующий:
Пусть функция y = f(x) при x определена формулой y = g(x), а при xa — формулой y = h(x), причем будем считать , что каждая из функций g(x) и h(x) определена для всех значений х и разрывов не имеет. Тогда , если g(a) = h(a), то функция f(x) имеет при х=а скачок; если же g(a) = h(a) = f(a), то «комбинированная» функция f разрывов не имеет. Если обе функции g и h элементарные, то f называется кусочно–элементарной. Графики непрерывных функций Построить график функции: У = |X-1| + 1 Х=1 –точка смены формул Слово «модуль» произошло от латинского слова «modulus», что в переводе означает «мера». Модулем числа а называется расстояние (в единичных отрезках ) от начала координат до точки А (а) . Это определение раскрывает геометрический смысл модуля. Модулем (абсолютной величиной ) действительного числа а называется то самое число а ≥ 0, и противоположное число –а , если а 0 или х=0 у = -3х -2 при х » Построить график функции у = 3|х|-2. По определению модуля, имеем: 3х – 2 при х0 или х=0 -3х -2 при х x n) » . Пусть заданы х 1 х 2 х n – точки смены формул в кусочно-элементарных функциях. Функция f, определенная при всех х, называется кусочно-линейной, если она линейна на каждом интервале и к тому же выполнены условия согласования, то есть в точках смены формул функция не терпит разрыв. Непрерывная кусочно-линейная функция называется линейным сплайном . Её график есть ломаная с двумя бесконечными крайними звеньями – левым (отвечающим значениям x n ) и правым ( отвечающим значениям x x n ) Кусочно-элементарная функция может быть определена более чем двумя формулами График – ломаная с двумя бесконечными крайними звеньями – левым (х1). У=|x| — |x – 1| Точки смены формул: х=0 и х=1. У(0)=-1, у(1)=1. График кусочно-линейной функции удобно строить, указывая на координатной плоскости вершины ломаной. Кроме построения n вершин следует построить также две точки : одну левее вершины A 1 ( x 1; y ( x 1)), другую – правее вершины An ( xn ; y ( xn )). Заметим, что разрывную кусочно-линейную функцию нельзя представить в виде линейной комбинации модулей двучленов . Построить график функции у = х+ |x -2| — |X|. Непрерывная кусочно-линейная функция называется линейным сплайном 1.Точки смены формул: Х-2=0, Х=2 ; Х=0 2.Составим таблицу: У(0 )= 0+|0-2|-|0|=0+2-0= 2 ; у(2 )=2+|2-2|-|2|=2+0-2= 0 ; у (-1 )= -1+|-1-2| — |-1|= -1+3-1= 1 ; у(3 )=3+|3-2| — |3|=3+1-3= 1 . Построить график функции у = |х+1| +|х| – |х -2|. 1 .Точки смены формул: х+1=0, х=-1 ; х=0 ; х-2=0, х=2. 2 . Составим таблицу: y(-2)=|-2+1|+|-2|-|-2-2|=1+2-4=-1; y(-1)=|-1+1|+|-1|-|-1-2|=0+1-3=-2; y(0)=1+0-2=-1; y(2)=|2+1|+|2|-|2-2|=3+2-0=5; y(3)=|3+1|+|3|-|3-2|=4+3-1=6. |x – 1| = |x + 3| Решите уравнение: Решение. Рассмотрим функцию y = |x -1| — |x +3| Построим график функции /методом линейного сплайна/ х -1 = 0, х = 1; х + 3 =0, х = — 3. 2. Составим таблицу: y(- 4) =|- 4–1| — |- 4+3| =|- 5| — | -1| = 5-1=4; y( -3 )=|- 3-1| — |-3+3|=|-4| = 4; y( 1 )=|1-1| — |1+3| = — 4 ; y(-1) = 0. y(2)=|2-1| — |2+3|=1 – 5 = — 4. Ответ: -1. 1. Построить графики кусочно-линейных функций методом линейного сплайна: у = |x – 3| + |x|; 1). Точки смены формул: 2). Составим таблицу: 2. Построить графики функций, используя УМК «Живая математика » А) у = |2x – 4| + |x +1| 1) Точки смены формул: 2) y() = Б) Постройте графики функций, установите закономерность : a) у = |х – 4| б) y = |x| +1 y = |x + 3| y = |x| — 3 y = |x – 3| y = |x| — 5 y = |x + 4| y = |x| + 4 Используйте инструменты «Точка», «Отрезок», «Стрелка» на панели инструментов. 1. Меню «Графики». 2. Вкладка «Построить график». .3. В окне «Калькулятор» задать формулу. Постройте график функции: 1) У = 2х + 4 1. Козина М.Е. Математика. 8-9 классы: сборник элективных курсов. – Волгоград: Учитель, 2006. 2. Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова. Алгебра: учеб. Для 7 кл. общеобразоват. учреждений/ под ред. С. А. Теляковского. – 17-е изд. – М. : Просвещение, 2011 3. Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова. Алгебра: учеб. Для 8 кл. общеобразоват. учреждений/ под ред. С. А. Теляковского. – 17-е изд. – М. : Просвещение, 2011 4. ВикипедиЯ свободная энциклопедия http://ru.wikipedia.org/wiki/Spline графовых кусочных функций | Промежуточная алгебра Результаты обучения- Напишите кусочную функцию, представляющую приложение
- Построение кусочной функции в области
В этом разделе мы построим кусочные функции. Функция, представленная на графике ниже, представляет собой стоимость передачи данных для данной компании сотовой связи. Мы можем видеть, где функция изменяется с постоянной на линию с положительным наклоном при [latex] g = 2 [/ latex].Когда мы строим кусочные функции, важно убедиться, что каждая формула применяется в соответствующей области. [латекс] C \ left (g \ right) = \ begin {case} {25} \ text {if} {0} <{g} <{2} \\ 10g + 5 \ text {if} {g} \ ge {2} \ end {case} [/ latex] В этом случае на выходе будет [latex] 25 [/ latex] для любого ввода между [latex] 0 [/ latex] и [latex] 2 [/ latex]. Для значений, равных или превышающих [latex] 2 [/ latex], вывод определяется как [latex] 10g + 5 [/ latex]. Как сделать: для заданной кусочной функции нарисуйте график- Укажите на оси x границы, определяемые интервалами на каждой части домена.
- Для каждой части домена построить график на этом интервале, используя соответствующее уравнение, относящееся к этой части. Не отображайте две функции на одном интервале, потому что это нарушит критерии функции.
Пример Нарисуйте график функции и укажите ее область и диапазон. Учитывая кусочное определение [латекс] f (x) = \ begin {cases} −x — 3 \ text {if} x <−3 \\ x + 3 \ text {if} x \ ge −3 \ end {cases } [/ latex] Показать решение Сначала изобразите линию [латекс] f (x) = −x − 3 [/ latex], стирающую часть, где x больше, чем [latex] -3 [/ latex].Обведите кружком [латекс] (- 3,0) [/ латекс]. Теперь поместите линию [latex] f (x) = x + 3 [/ latex] на график, начиная с точки [latex] (- 3,0) [/ latex]. Обратите внимание, что для этой части графика добавлена точка [latex] (- 3,0) [/ latex], поэтому вы можете удалить открытый кружок. Обратите внимание, что две части графика встречаются в точке [латекс] (- 3,0) [/ латекс]. Домен этой функции — все действительные числа, потому что [latex] (- 3,0) [/ latex] не включен в качестве конечной точки [latex] f (x) = −x − 3 [/ latex], но он включается в качестве конечной точки для [latex] f (x) = x + 3 [/ latex]. Диапазон этой функции начинается с [latex] f (x) = 0 [/ latex] и включает [latex] 0 [/ latex] и продолжается до бесконечности, поэтому мы бы записали это как [latex] y \ ge0 [ /латекс]. В следующем примере мы построим график кусочно определенной функции, которая моделирует стоимость доставки для интернет-магазина комиксов. Пример Интернет-магазин комиксов взимает стоимость доставки по следующей формуле, где n — количество комиксов: [латекс] S (п) = \ begin {case} 1.5n + 2.5 \ text {if} 1 \ le {n} \ le14 \\ 0 \ text {if} n \ ge15 \ end {case} [/ latex] Постройте график функции стоимости. Показать решение Сначала нарисуйте линию [латекс] S (n) = 1,5n + 2,5 [/ латекс]. Мы можем использовать трансформации: это вертикальное растяжение в [латекс] 1,5 [/ латекс] и вертикальный сдвиг на [латекс] 2,5 [/ латекс]. Теперь мы можем удалить части графа, не входящие в домен. Остается часть графа [latex] 1 \ le {n} \ le14 [/ latex]. Наконец, добавьте постоянную функцию [latex] S (n) = 0 [/ latex] для входных данных больше или равных [latex] 15 [/ latex].Поместите закрытые точки на концах графика, чтобы обозначить включение конечных точек. В следующем видео мы покажем, как построить график кусочно определенной функции, которая является линейной в обеих областях. Сводка Чтобы построить график кусочных функций, сначала определите, где область разделена граничными значениями. График функционирует в домене с помощью таких инструментов, как построение точек или преобразование. Обязательно используйте открытые или закрытые кружки на конечных точках каждого домена в зависимости от того, включена ли конечная точка. кусочных функций — определение, график и примеры Есть случаи, когда выражение для функций зависит от заданного интервала входных значений. Когда это происходит, мы вызываем эти типы функций , кусочно-определенные функции . Кусочные функции определяются разными функциями в разных интервалах домена. На самом деле мы применяем кусочные функции в нашей жизни чаще, чем думаем.В налоговых скобках, при оценке тарифных планов для мобильных телефонов и даже в нашей заработной плате (с учетом сверхурочной работы) используются кусочные функции. Поэтому для этой функции мы выделили специальный раздел. Из этой статьи вы узнаете следующее: - Определение кусочной функции.
- Обучение оценке кусочно-определенных функций через заданные интервалы.
- Построение графиков и интерпретация кусочных функций.
Что такое кусочная функция? Чтобы полностью понять, что такое кусочные функции и как мы можем построить наши собственные кусочно-определенные функции, давайте сначала погрузимся в более глубокое понимание того, как это работает. Определение кусочной функции Кусочная функция — это функция, которая определяется различными формулами или функциями для каждого заданного интервала. Это также есть в названии: кусок. Функция определяется частями функций для каждой части домена . 2x, для x> 0 1, для x = 0 -2x, для x <0 Как видно из приведенного выше примера, f (x) является кусочной функцией, потому что она определены однозначно для трех интервалов: x> 0, x = 0 и x <0. Как читать кусочные функции? Когда у нас есть заданная кусочно-определенная функция, мы можем интерпретировать ее, глядя на заданные интервалы. Если мы посмотрим на наш пример, мы можем прочитать его как: - Когда x> 0, f (x) равно 2x.
- Когда x = 0, f (x) равно 1.
- Когда x <0, f (x) равно -2x.
Если дан кусочный график функции, обязательно соблюдайте указанные интервалы, в которых f (x) имеет различные графики.Но прежде чем мы попробуем примеры, которые включают анализ графиков кусочных функций, давайте продолжим и узнаем, как мы можем сначала вычислить и построить график кусочных функций. Как решать кусочные функции? Теперь, когда мы узнали об этой уникальной функции, как нам убедиться, что мы возвращаем правильное значение для функции, заданной x ? Вот советы, которые следует помнить при решении и оценке кусочных функций: - Дважды проверьте, где x находится в заданном интервале.
- Оцените значение, используя соответствующую функцию.
Допустим, мы хотим найти f (8) , используя кусочную функцию, которую мы показали. 2x, для x> 0 1, для x = 0 -2x, для x <0 Поскольку 8 больше 0, функция, которую мы будем использовать для оценки f (8) , будет f (x) = 2x . Следовательно, имеем f (8) = 2 (8) = 16 . Это также означает, что f (-6) = -2 (-6) = 12 и f (0) = 1 . Как построить кусочный график функций? Как мы упоминали ранее, кусочные функции содержат разные функции для каждого из заданных интервалов. Это означает, что при построении графиков кусочных функций также ожидает графического отображения различных функций для каждого интервала . Вот несколько быстрых напоминаний при построении графиков кусочных функций: - Это помогает определить, как будет выглядеть каждая функция.
- Для инклюзивных интервалов (т. Е. X ≥ 0), включая конечные точки.
- Для исключительных интервалов (т. Е. X <0) исключите конечные точки, используя незаполненные точки.
С какими общими функциями вы можете столкнуться при построении графиков кусочных функций? Вот некоторые ресурсы, и не стесняйтесь проверять ссылки, чтобы освежить свои знания о некоторых из часто используемых графиков: Это не единственные функции, которые могут использовать кусочные функции, поэтому обязательно проверьте библиотеку функций в вашем учебнике. всякий раз, когда вам нужно. Давайте попробуем построить график кусочной функции, приведенной в первом разделе. 2x, для x> 0 1, для x = 0 -2x, для x <0 Когда x> 0 и x <0, f (x) возвращает линейную функцию . Найдите как минимум две пары точек, удовлетворяющих каждой функции, и используйте их для построения двух линейных графиков. Поскольку оба неравенства являются исключительными, мы оставляем точку в начале координат незаполненной. Теперь у нас осталось условие, когда x = 0. Поскольку значение постоянно при f (x) = 1, давайте построим точку в точке (0,1). Этот график возвращает окончательный график для данной кусочной функции. Из графика видно, что f (x) имеет область значений и диапазон (-∞, ∞) и [0, -∞) соответственно. Мы рассмотрели все основные свойства и методы, которые мы можем использовать с кусочными функциями, поэтому пришло время проверить наши знания на этих примерах! Пример 1 Оцените данную кусочную функцию при заданных значениях x , как показано ниже. √x, для x> 0 5, для x = 0 x / 6, для x <0 a. ж (-36) б. f (0) c. f (49) Решение - Когда x = -36 (или меньше 0), выражение для f (x) будет x / 6 . Давайте оценим f (-36) , используя выражение. Следовательно, мы имеем f (-36) = -36/6 = -6 .
- Когда x = 0, f (x) постоянная . Это означает, что у нас есть f (0) = 5 .
- Когда x = 49 (и, следовательно, больше 0), выражение для f (x) будет √ x . Давайте вычислим f (49) , используя выражение. Следовательно, мы имеем f (49) = √ 49 = 7 .
Пример 2 Изобразите кусочную функцию, показанную ниже. Используя график, определите его домен и диапазон. 2x, для x ≠ 0 1, для x = 0 Решение Для всех интервалов x, кроме тех, когда он равен 0, f (x) = 2x (что является линейным функция).Чтобы построить график линейной функции, мы можем использовать две точки, чтобы соединить линию. Просто убедитесь, что две точки удовлетворяют y = 2x . Обязательно оставьте точку отправления незаполненной. Поскольку f (x) = 1 , когда x = 0 , мы наносим закрашенную точку в (0,1). График выше показывает окончательный график кусочной функции. Поскольку график охватывает все значения x, доменом будет , все действительные числа или (-∞, ∞). То же самое относится и к набору функций.Поскольку он распространяется в обоих направлениях, диапазон функции составляет (- ∞ , ∞ ) в обозначении интервала . Пример 3 Изобразите кусочную функцию, показанную ниже. Используя график, определите его домен и диапазон. x 2 , для x ≤ 0 5, для 0 x / 2, для x ≥ 2 Решение Давайте сначала разберем три интервала и определим, как график функции будет выглядеть так: - Когда x ≤ 0, f (x) становится квадратичной функцией с параболой, проходящей через начало координат и (-2, 4).Поскольку это применимо только к 0 и отрицательным числам, мы будем использовать только половину параболы.
- Когда 0 f (x) будет представлять константу, которая представляет собой горизонтальную линию, проходящую через y = 5 . Обязательно оставьте (0,5) и (2,5) незаполненными, так как они не являются частью раствора.
- Когда x ≥ 2, f (x) является функцией и проходит через (2, 1) и (6,3).
Используя эту информацию, мы можем построить график f (x) . Изображение выше разбивает три компонента кусочной функции.Давайте продолжим и упростим этот график, чтобы мы могли проанализировать его по предметной области и диапазону. Поскольку все значения x распространяются в обоих направлениях, доменом будет , все действительные числа или (-∞, ∞). Поскольку график охватывает только значения y над осью x, диапазон функции составляет [0, ∞ ) в обозначении интервала . Пример 4 Разговорная поэзия проводится в соседнем кафе.Они берут 6 долларов с человека за стол на от 1 до 5 человек. Они также предлагают фиксированную плату в размере 50 долларов за столик на 6 и более человек. Напишите функцию, которая связывает количество людей x и стоимость посещения мероприятия f (x) . Решение Давайте разберем задачу и найдем выражение f (x) для каждого интервала: - Для стола от 1 до 5 гостей мы можем выразить это как 1 ≤ x ≤ 5 по x.Поскольку это будет стоить каждому гостю 6 долларов, общая сумма для x гостей составит 6x .
- Теперь, для стола с 6 или более людьми, мы можем выразить интервал как x ≥ 6. Для этого интервала f (x) всегда будет равно 60 .
Теперь мы можем суммировать это в виде кусочной функции: 6x, для 1 ≤ x ≤ 5 50, для x ≥ 6 Эта кусочная функция представляет стоимость f (x) для x число гостей. Практические вопросы 1. Оцените данную кусочную функцию при заданных значениях x , как показано ниже. √ (x-1), для x> 0 5, для x = 0 x + 1, для x <0 a. ф (-8) б. ф (0) с. f (63) 2. Оцените данную кусочную функцию при заданных значениях x, , как показано ниже. 3x 2 , для x ≤ 0 4x — 6, для 0 2x, для x ≥ 2 a. ф (-2) б. f (0,75) c. f (7) 3. Постройте график кусочной функции, показанной ниже. Используя график, определите его домен и диапазон. 2x 2 , для x ≠ 0 8, для x = 0 4. Постройте график кусочной функции, показанной ниже. Используя график, определите его домен и диапазон. √ (-4x), для x ≤ 0 2x, для 0 -x 2 , для x ≥ 9 5.Предположим, у вас есть летняя работа, за которую платят 12 долларов в час. Вы должны работать не менее 30 часов в неделю. Компания оплачивает сверхурочную работу в 1,5 раза больше почасовой ставки. а. Настройте кусочную функцию, которая представляет вашу еженедельную оплату.
г. Изобразите построенную вами кусочную функцию.
г. Сколько бы вы заработали, если бы в ту неделю проработали 48 часов? Предыдущий урок | Главная страница | Следующий урок Объяснитель урока: Графики кусочно-определенных функций В этом объяснителе мы узнаем, как построить график и проанализировать кусочно-определенную функцию, а также изучить ее различные характеристики. Кусочная функция состоит из нескольких подфункций, определенных в отдельных подобластях. Объединение подобластей составляет общую область кусочной функции. Объединение диапазонов подфункций составляет диапазон общей кусочной функции. Следующие данные о ценах на билеты в парке развлечений можно смоделировать с помощью кусочной функции. | Стоимость билетов в парк развлечений |
|---|
| Возраст | Цена |
|---|
| 5–12 | $ 8.50 | | 13–18 | 12 долларов | | 19+ | 15 долларов |
В таблице представлены три цены на билеты, которые зависят от возраста посетителя парка. Для моделирования этого потребуются три разные подфункции. Нам также нужно будет тщательно подумать о том, как интерпретировать возрастные категории при выборе области каждой подфункции. Возраст 5–12 охватывает людей с момента, когда часы пробьют полночь в начале их 5-летия, до момента до того, как часы пробьют полночь в начале их 13-летия.Возраст 13–18 охватывает людей с момента, когда часы пробьют полночь в начале их 13-летия, до момента до того, как часы пробьют полночь в начале их 19-летия. Возраст 19+ распространяется на людей с момента, когда часы пробьют полночь в начале их 19-летия. Определим 𝑥 как возраст (в годах) посетителя парка и 𝑓 (𝑥) как стоимость билета посетителя (в долларах). Затем мы можем написать определение нашей функции 𝑓 (𝑥): 𝑓 (𝑥) = 8.55≤𝑥13,1213≤𝑥19,15𝑥≥19. Теперь давайте посмотрим, как построить график этой функции. Нам нужно будет исследовать каждый поддомен отдельно. За всех посетителей парка в возрасте от 5 до 12 лет взимается 8,50 долларов США, поэтому значение 𝑓 (𝑥) равно 8,5 при 5≤𝑥13. Это представлено горизонтальной линией на нашем графике со значением 8,5 и значениями 𝑥 от 5 (включая 5, представленные сплошной точкой) до 13 (исключая 13, представленные пустой точкой). Мы представили это розовой линией на нашем графике ниже. За всех посетителей парка в возрасте 13–18 лет взимается плата в размере 12 долларов США, поэтому значение 𝑓 (𝑥) равно 12, если 13≤𝑥19.Это представлено горизонтальной линией на нашем графике с-значением 12 и 𝑥-значениями от 13 (включая 13, представленные сплошной точкой) до 19 (исключая 19, представленные пустой точкой). Мы представили это синей линией на нашем графике ниже. За всех посетителей парка в возрасте от 19 лет взимается плата в размере 15 долларов США, поэтому значение 𝑓 (𝑥) равно 15, если 𝑥≥19. Это представлено горизонтальной линией на нашем графике с-значением 15 и 𝑥-значениями от 19 (включая 19, представленных сплошной точкой) вверх (представлено лучом, указывающим вправо).Хотя люди не живут вечно, модель ценообразования определена таким образом, что независимо от того, сколько вам лет, если вам 19 лет или больше, с вас будет взиматься плата в размере 15 долларов за посещение парка. Мы представили это зеленым лучом на нашем графике ниже. Хотя во многих кусочных функциях определения подфункций могут быть намного сложнее, чем постоянные функции в нашем примере с парком развлечений, принцип тот же самый для их построения графиков. Нам нужно рассмотреть график для каждой подобласти индивидуально, посмотреть, что будет происходить на каждом конце каждой подфункции, и изобразить их рядом друг с другом на одном и том же наборе осей. Кусочная функция, которую мы определили для цен на билеты в парк развлечений и построила график, определена только для всех реальных значений 𝑥, равных 5 или более. Следовательно, область определения функции в целом может быть записана как неравенство, ≥5, используя обозначение интервала как [5, ∞ [или обозначение множества как {𝑥∈ℝ∣𝑥≥5}. Возможные значения функции: 𝑓 (𝑥) = 8.5, 𝑓 (𝑥) = 12 или 𝑓 (𝑥) = 15. Следовательно, диапазон общей функции может быть записан в обозначении набора как {8.5,12,15}. Теперь рассмотрим несколько примеров, в которых нам приходится работать с графиками кусочно-определенных функций. Пример 1: Определение типа функции, представленной на графике Какая функция изображена на графике? - Четная функция
- Логарифмическая функция
- Кусочная функция
- Полиномиальная функция
Ответ Рассмотрим каждый из вариантов. - Четная функция — это функция, для которой 𝑓 (𝑥) = 𝑓 (−𝑥) для всех значений 𝑥 в области определения 𝑓. Это означает, что четные функции симметричны относительно оси, чего нельзя сказать о данном графике.Например, 𝑓 (5) = 7, но 𝑓 (−5) = 0, поэтому 𝑓 (5) ≠ 𝑓 (−5); следовательно, функция не четная.
- Логарифм определенного значения, например 𝑥, — это показатель степени, до которого нужно возвести другое базовое число, чтобы получить. Графики логарифмических функций имеют гладкие кривые, которые асимптотичны относительно оси, как мы можем видеть в примерах ниже, или они могут быть преобразованы. Данный граф имеет острые углы при 𝑥 = −3 и 𝑥 = 0, поэтому он не является гладким во всей области, а также не имеет вертикальных асимптот.Также не определены логарифмические функции для отрицательных значений; другими словами, их область применения — это набор положительных действительных чисел. Данный график представляет функцию, которая имеет область значений не менее -10𝑥8, которая включает некоторые отрицательные 𝑥-значения, поэтому данный график не похож на логарифмическую функцию.
- График этой функции состоит из трех отдельных подфункций.
- Для значений от −∞ до −3 график представляет собой прямую линию с наклоном 1.Мы могли бы записать уравнение для этой прямой в виде = 𝑚𝑥 + 𝑏, где 𝑚 — наклон (1), а 𝑏 —пересечение, поэтому 𝑦 = 𝑥 + 𝑏. Мы также видим, что прямая проходит через точку (−5,0), поэтому 𝑦 = 0, когда 𝑥 = −5, что позволяет нам вычислить значение 𝑏 как 5. Следовательно, мы могли бы записать уравнение как 𝑦 = 𝑥 +5.
- Для-значений от −3 до 0 график представляет собой горизонтальную линию, так что 𝑦-значение всегда равно 2, поэтому мы можем записать уравнение этой линии как = 2.
- Для 𝑥-значений от 0 до ∞ график снова представляет собой прямую линию с наклоном 1.На этот раз мы видим, что-пересечение равно 2, поэтому мы можем записать уравнение как 𝑦 = 𝑥 + 2.
Хотя нас специально не просили сделать это, мы могли бы записать определение функции следующим образом: 𝑓 (𝑥) = 𝑦 = 𝑥 + 5𝑥 − 3, 𝑦 = 2−3≤𝑥0, 𝑦 = 𝑥 + 2𝑥≥0 .
Однако из графика мы можем видеть, что значения подфункций такие же, как у их соседей в их общих конечных точках; Другими словами, подфункции соединяются, образуя непрерывную функцию. Было бы также правильно определить подфункции как имеющие несколько разные подобласти, переставив подфункцию, к которой принадлежат точки соединения.В этой ситуации, когда распределение является произвольным, обычно включают левую конечную точку и исключают правую конечную точку из подфункций.
Тот факт, что наша функция должна быть определена в терминах серии подфункций в определенных подобластях, делает ее кусочной функцией. - Полиномиальные функции включают сложение, вычитание и умножение коэффициентов и переменных с неотрицательными целыми показателями. Графики полиномиальных функций образуют гладкие кривые и могут быть определены одним полиномиальным уравнением.Данный график имеет две негладкие точки, когда 𝑥 = −3 и 𝑥 = 0, поэтому он не является графиком полиномиальной функции.
Следовательно, функция, изображенная на графике, является кусочной функцией (вариант C). В нашем следующем примере мы исследуем конечные точки каждой подфункции на графике кусочно определенной функции, чтобы найти ее домен. Пример 2: Нахождение области определения кусочной функции по ее графику Определите область определения функции, представленной данным графиком. Ответ Область функции — это набор всех значений, в которых функция определена. На графике функции область представляет собой все 𝑥-значения, на которых нарисована кривая. Для кусочно определенной функции область будет объединением подобластей каждой подфункции. Эта кусочно-определенная функция имеет две подфункции. Первая подфункция — это луч с пустой точкой в точке (−4,1). Пустая точка указывает, что эта подфункция не определена при = −4 и, следовательно, имеет правый открытый интервал.Стрелка указывает, что подфункция продолжается бесконечно в направлении этой стрелки, здесь в сторону отрицательной бесконечности. Следовательно, первая подфункция имеет подобласть] −∞, −4 [. Вторая подфункция — это луч с пустой точкой в точке (−4, −2). Пустая точка указывает, что эта подфункция также не определена для 𝑥 = −4 и, следовательно, имеет левый открытый интервал. Стрелка указывает, что эта подфункция продолжается бесконечно в направлении стрелки, которая здесь указывает на положительную бесконечность.Следовательно, область определения второй подфункции будет] −4, ∞ [. Объединение этих подобластей равно] −∞, −4 [∪] −4, ∞ [. Объединение этих двух поддоменов будет включать все действительные числа, кроме −4, ℝ — {- 4}. Графически мы можем найти область, посмотрев на вертикальные линии на графике и увидев, где они пересекают заданную функцию. В этом случае вертикальная линия при 𝑥 = −4 пересекает только полые точки каждой подфункции. Ни одна из подфункций не определена для = −4, что означает, что эта кусочная функция не определена при = −4.Следовательно, областью определения этой кусочно-определенной функции будет набор всех действительных чисел, кроме −4, ℝ — {- 4}. В предыдущем примере мы видели, что домен кусочно определенной функции представляет собой объединение подобластей для каждой из подфункций. В нашем следующем примере мы покажем, что диапазон кусочно определенной функции будет равен объединению диапазонов каждой подфункции по их соответствующим подобластям. Пример 3: Определение диапазона кусочной функции по ее графику Найдите диапазон функции. Ответ На данном графике мы можем выделить две специфические подфункции, делающие эту функцию кусочной. Диапазон функции — это набор всех возможных выходных значений функции с учетом ее домена. Диапазон кусочно определенной функции — это объединение диапазонов каждой подфункции по их соответствующим подобластям. Мы можем идентифицировать значения в диапазоне с помощью горизонтальных линий. Если горизонтальная линия пересекает график нашей функции, то значение горизонтальной линии является частью диапазона.Для этой кусочной функции горизонтальная линия 𝑦 = 3 пересекает график одной из подфункций, что означает, что 3 входит в диапазон этой подфункции. На графике мы видим поведение подфункции, которая начинается в (4, −1) и продолжается бесконечно в сторону положительной бесконечности. Любая горизонтальная линия выше = 3 будет пересекать эту подфункцию и должна быть включена в диапазон. Любая горизонтальная линия между 𝑦 = −1 и 𝑦 = ∞ будет пересекать эту подфункцию, делая ее диапазон [−1, ∞ [. Здесь стоит отметить, что другая подфункция — это горизонтальная линия 𝑦 = −1 над ее подобластью] −∞, 4]. Следовательно, -1 — единственное значение в наборе для диапазона. Диапазон этой подфункции по ее подобласти будет {−1}. Объединение диапазонов для этих двух подфункций по их соответствующим подобластям составляет {−1} ∪ [−1, ∞ [. Следовательно, диапазон этой кусочно определенной функции равен [−1, ∞ [. В нашем следующем примере мы будем использовать график кусочно определенной функции, чтобы найти формальное определение функции. Пример 4: Определение кусочной функции из заданного графа Дайте кусочное определение функции ℎ, график которой показан. Ответ Кусочная функция состоит из двух или более подфункций. Чтобы определить кусочную функцию, нам нужно выражение для каждой из подфункций и подобластей для каждой из подфункций. Сначала мы определим, сколько подфункций являются частью этой кусочной функции, посмотрев на поведение графика.В этом случае есть две подфункции. У нас есть прямая с отрицательным наклоном, которая заканчивается в точке (2,1) и другой
прямая, которая начинается в точке (2,1) и имеет положительный наклон.
Каждая из этих строк будет формировать подфункцию этой кусочной функции в соответствующей подобласти.
Итак, мы определяем уравнение через для каждой подфункции
и определите их соответствующие поддомены. Форма линии наклона с пересечением говорит нам, что линия наклона 𝑚, а 𝑦-точка пересечения 𝑏 имеет уравнение 𝑦 = 𝑚𝑥 + 𝑏.Наклон 𝑚 равен изменению изменения. Прямая линия с отрицательным наклоном имеет точку пересечения 𝑦 в точке 3. Наклон можно определить по графику без выполнения каких-либо формальных вычислений.
Когда значение увеличивается на одну единицу, значение 𝑦 уменьшается на одну единицу. Следовательно, changeinchangein𝑦𝑥 = −11. Следовательно, 𝑚 = −1. Следовательно, первая подфункция определяется как = −𝑥 + 3𝑦 = 3 − 𝑥. Или Однако нам все еще необходимо идентифицировать подобласть этой подфункции; мы можем построить вертикальную линию при 𝑥 = 2, и мы можем подтвердить, что 2 входит в область определения этой кусочной функции, поскольку она пересекает кривую в (2,1). На графике 2 кажется частью доменов обеих подфункций. Однако, когда мы определяем кусочную функцию, мы включаем только 2 в одну из доменов подфункций, чтобы их домены не перекрывались. Обычно это определяется контекстом вопроса. Поскольку у нас есть только граф без каких-либо других данных, мы просто позволим определить первую подфункцию для подобласти] −∞, 2 [. Следовательно, вторая подфункция будет определена для подобласти [2, ∞ [. Было бы одинаково правильно определить подфункции как имеющие несколько разные подобласти, переставив подфункцию, к которой принадлежат точки соединения.В этой ситуации, когда распределение является произвольным, обычно включают левую конечную точку и исключают правую конечную точку из подфункций. Теперь, когда мы определили каждую подобласть, мы используем граф, чтобы написать формулу для второй подфункции над ее подобластью. Прямая линия второй подфункции моделирует увеличение значения на 1 единицу при увеличении значения на 2 единицы. Следовательно, changeinchangein𝑦𝑥 = 12. Затем мы можем идентифицировать-точку пересечения графически, удлинив линию, чтобы увидеть, где эта подфункция пересекала бы ось, если бы она была частью домена. -точка пересечения второй подфункции будет равна 0. Следовательно, формула для второй подфункции будет = 𝑥2. Объединение этих двух правил подфункций по их соответствующим подобластям определяет эту кусочную функцию как
ℎ (𝑥) = 3 − 𝑥𝑥2, 𝑥22≤𝑥.ifif В примере 5 мы будем использовать график кусочно определенной функции, чтобы найти формальное определение функции для кусочной функции с более чем двумя подфункциями. Пример 5: Определение кусочной функции из данного графа, включая разрыв Дайте кусочное определение функции 𝑓, график которой показан. Ответ Кусочная функция состоит из двух или более подфункций. Чтобы определить кусочную функцию, нам нужна формула для каждой из подфункций и их соответствующих подобластей. На этом графике показаны три различных поведения. Следовательно, нам нужно будет написать всего три выражения и найти три подобласти, по одной для каждой подфункции. Для прямых линий мы можем записать уравнение, используя форму пересечения угла наклона, 𝑦 = 𝑚𝑥 + 𝑏, где 𝑏 — это пересечение, а 𝑚 — наклон.Наклон 𝑚 равен изменению изменения. Для этой строки изменение 𝑥 на 1 единицу вправо, а изменение 𝑦 — на 1 единицу вниз. Следовательно, changeinchangein𝑦𝑥 = −11, что упрощается до 𝑚 = −1. -Пересечение равно 3. Таким образом, выражение для этой подфункции по ее подобласти будет −𝑥 + 33 − 𝑥. Или Поддомен этой подфункции равен набору всех входных значений для этой подфункции. Пустая конечная точка (2,1) указывает, что верхняя граница этой подобласти должна быть открытым интервалом.Следовательно, подобласть будет открытым интервалом от] −∞, 2 [. Следующая подфункция закрывается точкой в (2,2). Замкнутая точка в (2,2) показывает постоянную функцию 𝑦 = 2, где подобласть равна {2}. Третья подфункция имеет пустую точку в (2,3) и продолжается бесконечно. Следовательно, подобластью этой подфункции является интервал] 2, ∞ [. Для этой подфункции значение увеличивается на 2 единицы, а значение увеличивается на 1 единицу. Следовательно, changeinchangein𝑦𝑥 = 12.Затем мы можем идентифицировать-точку пересечения графически, удлинив линию, чтобы увидеть, где эта подфункция пересекала бы ось, если бы она была частью своей подобласти. -пересечение этой подфункции равно 2. Следовательно, формула для третьей подфункции по ее подобласти будет = 𝑥2 + 2. Объединение каждой из этих трех подфункций в формате для кусочно-определенных функций:
𝑓 (𝑥) = ⎧⎨⎩3 − 𝑥𝑥2,2𝑥 = 2, 𝑥2 + 22𝑥.ififif Наш последний пример дополнительно исследует, как открытые и закрытые интервалы для подобластей
изображены кусочно-определенные функции. Пример 6: Идентификация графика кусочной функции по ее определению Укажите, какой из следующих графиков представляет функцию 𝑓 (𝑥) = 𝑥, 𝑥2, −2𝑥 + 10, 𝑥≥2. Ответ Нам дана кусочно-определенная функция 𝑓 (𝑥) = 𝑥, 𝑥2, −2𝑥 + 10, 𝑥≥2. Эта кусочно-определенная функция состоит из двух подфункций в указанных подобластях. Первая подфункция — это квадратичная функция 𝑦 = 𝑥 над подобластью
𝑥2. Чтобы построить график этой квадратичной кривой, мы можем использовать подобласть для создания таблицы входных и выходных значений.Мы знаем, что подобласть для этой функции — это значения
𝑥, которые меньше 2. | 𝑦 = 𝑥 |
|---|
| 𝑥 | 𝑦 |
|---|
| −2 | 4 | | −1 | 1 | 0505 | 0507 | | 1 | 1 | | 2 | 4 |
Используя таблицу, мы можем нанести эти точки на график. Обратите внимание, что точка (2,4) на графике пустая, поскольку 𝑥 = 2 не входит в подобласть
𝑦 = 𝑥. Построение линии через эти координаты дает график 𝑦 = 𝑥 по подобласти 𝑥2. Вторая подфункция 𝑦 = −2𝑥 + 10 является линейной функцией. Опять же, мы можем использовать данный субдомен для создания таблицы входных и выходных значений для построения графика этой субфункции.
Для этой подфункции подобласть равна 𝑥≥2; следовательно, значение 𝑥 = 2 входит в область значений. | 𝑦 = −2𝑥 + 10 |
|---|
| 𝑥 | 𝑦 |
|---|
| 2 | 6 | | 3 | 4 | | 2 | 4 | |
Затем нанесите эти точки на ту же сетку, что и первая подфункция. Обратите внимание, что для второй подфункции при 𝑥 = 2 мы включили сплошную точку, поскольку 2 входит в подобласть для 𝑦 = −2𝑥 + 10. Наконец, мы рисуем линию, начинающуюся в (2,6) и продолжающуюся через (5,0), помня, что эта линия продолжается бесконечно в этом направлении. Построив график этой кусочно-определенной функции, мы показали, что только вариант D правильно представляет эту функцию. В заключение напомним некоторые основные моменты. Ключевые моменты- Кусочная функция состоит из нескольких подфункций, определенных над подобластями.
- Пустая точка на кривой функции означает, что функция не определена в этой точке.
- Закрашенная точка на кривой функции означает, что функция определена в этой точке.
- Чтобы построить график кусочно-определенной функции:
- рассматривает каждую подфункцию в своем поддомене отдельно,
- рассматривает, что происходит в конечных точках домена каждой подфункции,
- отображает каждую подфункцию на одном и том же наборе осей.
Моделирование кусочно определенной функции по ее графику — Криста Кинг Math Мы будем работать над графиком слева направо.Горизонтальная линия слева имеет значение ??? y ??? — ??? — 3 ??? и включает все значения ??? x ??? в интервале ??? x <-2 ??? (все действительные числа ??? x ???, которые меньше ??? - 2 ???). Для этого фрагмента мы пишем ??? - 3 ??? для функции (постоянная функция, значение которой составляет ??? - 3 ???) и ??? x <-2 ??? для своего домена. Наклон наклонной линии составляет ??? 5/4 ??? и ??? y ??? — перехват ??? — 1/2 ???. Чтобы увидеть, как получить наклон, обратите внимание, что точки ??? (- 2, -3) ??? и ??? (2,2) ??? находятся в этой строке, поэтому ??? y = \ frac {5} {4} x- \ frac {1} {2} ??? Для этого фрагмента мы пишем ??? f (x) = \ frac {5} {4} x- \ frac {1} {2} ??? для функции и ??? — 2 \ le x \ le 2 ??? для своего домена. Горизонтальная линия справа имеет значение ??? y ??? — ??? 2 ??? и включает все значения ??? x ??? в интервале ??? x> 2 ???. Для этого фрагмента мы пишем ??? 2 ??? для функции и ??? x> 2 ??? для своего домена. Соединяя три части вместе, мы определяем эту кусочную функцию следующим образом: ??? f (x) = \ begin {cases} -3 & \ quad x <-2 \\ \ frac {5} {4} x- \ frac12 & \ quad -2 \ leq x \ leq 2 \\ 2 & \ quad x> 2 \ end {cases} ??? Вы можете задаться вопросом, как мы решаем, какая часть этой функции получит ??? \ le ??? или ??? \ ge ??? знак и какой кусок получает ??? ??? знак.Правда в том, что это не имеет значения, если каждый ??? x ??? в область определения всей кусочной функции входит в область определения ровно одной из ее частей — и, конечно же, функция для этой части дает правильное значение ??? f (x) ???. Вы также можете написать это так: ??? f (x) = \ begin {cases} -3 & \ quad x \ leq -2 \\\ frac {5} {4} x- \ frac {1 } {2} & \ quad -2 Но это нельзя было записать как ??? f (x) = \ begin {cases} -3 & \ quad x \ leq -2 \\\ frac {5} {4} x- \ frac {1 } {2} & \ quad -2 \ leq x \ leq 2 \\ 2 & \ quad x \ geq 2 \ end {cases} ??? потому что здесь ??? — 2 ??? входит в домены двух разных частей функции, как и ??? 2 ???. Кусочно-определенная функция А кусочно-определенный функция — это функция, которая определяется не одним уравнением, а двумя или более. Каждое уравнение справедливо для некоторых
интервал
. Пример 1: Рассмотрим функцию, определенную следующим образом. у
знак равно
{
Икс
+
2
для
Икс <
0
2
для
0
≤
Икс
≤
1
-
Икс
+
3
для
Икс
> 1 Функция в этом примере является кусочно-линейной, потому что каждая из трех частей графика представляет собой линию. Кусочно определенные функции также могут иметь разрывы («скачки»). Функция в приведенном ниже примере имеет разрывы на
Икс
знак равно
—
2
и
Икс
знак равно
2
. Пример 2: Постройте график функции, определенной, как показано. у
знак равно
{
1
2
Икс
2
для
Икс <
-
2
0для
-
2
≤
Икс
<
2
1
2
Икс
2
для
Икс
≥
2 Обратите внимание, что мы используем маленькие белые кружки на графике, чтобы указать, что конечная точка кривой не включена в график, и сплошные точки, чтобы указать конечные точки, которые включены. Пример 3: Изобразите график функции, определенной ниже. у
знак равно
{
бревно
Икс
для
0 <
Икс
<
1
1
Икс
-
2
для
Икс
≥
1 Отрицательные значения
Икс
и
0
не входят в
домен
потому что первая функция,
бревно
Икс
, не определено для этих значений.Значение
Икс
знак равно
2
не входит в домен, потому что вторая функция не определена для этого значения (у нее там вертикальная асимптота). Следовательно, область определения этой функции
{
Икс
|
0 <
Икс
<
2
}
∪
{
Икс
|
Икс
> 2
}
.Это может быть представлено с использованием обозначения интервалов как
(
0
,
2
)
∪
(
2
,
∞
)
. 4.1: Кусочно-определенные функции — математика LibreTexts При подготовке к определению функции абсолютного значения чрезвычайно важно хорошо понимать концепцию кусочно-определенной функции.Однако, прежде чем мы вступим в бой, давайте взглянем на особый тип функции, называемый константной функцией. Один из способов понять постоянную функцию — взглянуть на ее график. Приведенное выше обсуждение приводит к следующему определению. Кусочно-постоянные функции Кусочные функции — фавориты инженеров. Давайте посмотрим на пример. Пример \ (\ PageIndex {2} \) Предположим, что батарея не подает напряжение на цепь, когда переключатель разомкнут.Затем, начиная с момента времени \ (t = 0 \), переключатель замыкается, и с этого момента аккумулятор обеспечивает постоянное напряжение 5 вольт. Создайте кусочную функцию, моделирующую ограничения задачи, и нарисуйте ее график. Решение Это довольно простое упражнение, но нам придется ввести некоторые новые обозначения. Прежде всего, если время t меньше нуля (\ (t <0 \)), то напряжение равно 0 вольт. Если время t больше или равно нулю (\ (t \ geq 0 \)), то напряжение составляет постоянные 5 вольт.Вот обозначения, которые мы будем использовать, чтобы резюмировать это описание напряжения. \ [V (t) = \ left \ {\ begin {array} {ll} {0,} & {\ text {if} t <0} \\ {5,} & {\ text {if} t \ geq 0} \ end {array} \ right. \] Некоторые комментарии в порядке: - Разница напряжений, обеспечиваемая аккумулятором в цепи, является функцией времени. Таким образом, V (t) представляет собой напряжение в момент времени t.
- Обозначения, используемые в (4), универсально приняты математиками в ситуациях, когда функция меняет определение в зависимости от значения независимой переменной.Такое определение функции V называется «кусочным определением». Поскольку каждая из частей в этом определении постоянна, функция V называется кусочно-постоянной функцией.
- Эта конкретная функция состоит из двух частей. Функция — это постоянная функция \ (V (t) = 0 \), когда \ (t <0 \), но другая постоянная функция, \ (V (t) = 5 \), когда \ (t \ geq 0 \).
Если \ (t <0, V (t) = 0. \) Например, для \ (t = -1, t = -10, \) и \ (t = -100 \) \ [V (-1) = 0, \ quad V (-10) = 0, \ quad \ text {и} \ quad V (-100) = 0 \] С другой стороны, если \ (t \ geq 0, \), то \ (V (t) = 5.\) Например, для \ (t = 0, t = 10, \) и \ (t = 100 \) \ [V (0) = 5, \ quad V (10) = 5, \ quad \ text {и} \ quad V (100) = 5 \] Прежде чем мы представим график кусочно-постоянной функции V, давайте сделаем паузу, чтобы убедиться, что мы понимаем некоторые стандартные геометрические термины. Геометрические условия - Линия неограниченно тянется в двух направлениях, как показано на рисунке \ (\ PageIndex {2} \) (a).
- Если линия имеет фиксированную конечную точку и бесконечно тянется только в одном направлении, как показано на рисунке \ (\ PageIndex {2} \) (b), то она называется лучом.
- Если часть линии зафиксирована на каждом конце, как показано на рисунке \ (\ PageIndex {2} \) (c), то она называется сегментом линии.
Рисунок \ (\ PageIndex {2} \). Линии, лучи и отрезки. Имея в виду эти термины, давайте обратим наше внимание на график напряжения, определяемый уравнением (4). Когда \ (t <0 \), то \ (V (t) = 0 \). Обычно график \ (V (t) = 0 \) представляет собой горизонтальную линию, где каждая точка на линии имеет значение V, равное нулю. Однако \ (V (t) = 0 \), только если \ (t <0 \), поэтому график представляет собой горизонтальный луч, который начинается в начале координат, а затем бесконечно перемещается влево, как показано на рисунке \ (\ PageIndex {3} \).То есть горизонтальная линия \ (V = 0 \) была ограничена областью \ (\ {t: t <0 \} \) и существует только слева от начала координат. Аналогично, когда \ (t \ geq 0 \), тогда \ (V (t) = 5 \) — горизонтальный луч, показанный на рисунке \ (\ PageIndex {3} \). Каждая точка луча имеет значение V, равное 5. Рисунок \ (\ PageIndex {3} \). Напряжение как функция времени t. Два комментария в порядке: - Поскольку \ (V (t) = 0 \), только когда t <0, точка (0, 0) незаполнена (это открытый круг).Открытый кружок в (0, 0) - это математический способ сказать, что эта конкретная точка не отображается или не заштрихована.
- Поскольку \ (V (t) = 5 \), когда \ (t \ geq 0 \), точка (0, 5) заполнена (это закрашенная окружность). Закрашенный кружок в (0, 5) — это математический способ сказать, что эта конкретная точка нанесена на график или заштрихована.
Давайте посмотрим на другой пример. Пример \ (\ PageIndex {3} \) Рассмотрим кусочно-определенную функцию \ [f (x) = \ left \ {\ begin {array} {ll} {0,} & {\ text {if} x <0} \\ {1,} & {\ text {if} 0 \ leq x <2} \\ {2,} & {\ text {if} x \ geq 2} \ end {array} \ right.\] Вычислите f (x) при x = −1, 0, 1, 2 и 3. Нарисуйте график кусочной функции f. Решение Поскольку каждая часть функции в (6) постоянна, вычислить функцию довольно просто. Вам просто нужно выбрать правильный кусок. • Обратите внимание, что x = −1 меньше 0, поэтому мы используем первую часть и пишем f (−1) = 0. • Обратите внимание, что x = 0 удовлетворяет \ (0 \ leq x <2 \), поэтому мы используем вторую часть и пишем f (0) = 1. • Обратите внимание, что x = 1 удовлетворяет \ (0 \ leq x <2 \), поэтому мы используем вторую часть и пишем f (1) = 1. • Обратите внимание, что x = 2 удовлетворяет \ (x \ geq 2 \), поэтому мы используем третью часть и пишем f (2) = 2. • Наконец, обратите внимание, что x = 3 удовлетворяет \ (x \ geq 2 \), поэтому мы используем третью часть и пишем f (3) = 2. Граф так же просто нарисовать. • Поскольку f (x) = 0 для x <0, график этой части представляет собой горизонтальный луч с конечной точкой в x = 0. Каждая точка на этом луче будет иметь значение y, равное нулю, и луч будет лежать полностью. слева от x = 0, как показано на рисунке \ (\ PageIndex {4} \). • Поскольку f (x) = 1 для \ (0 \ leq x <2 \), график этого отрезка представляет собой горизонтальный сегмент с одной конечной точкой в точке x = 0, а другой - в точке x = 2. Каждая точка на этом сегменте будет иметь значение y, равное 1, как показано на рисунке \ (\ PageIndex {4} \). • Поскольку f (x) = 2 для \ (x \ geq 2 \), график этой части представляет собой горизонтальный луч с конечной точкой в x = 2. Каждая точка на этом луче имеет значение y, равное 2, и Луч целиком лежит справа от x = 2, как показано на рисунке \ (\ PageIndex {4} \). Необходимо сделать несколько замечаний: • Функция равна нулю слева от начала координат (для x <0), но не в начале координат. На это указывает пустой кружок в начале координат, что указывает на то, что мы не рисуем эту конкретную точку. • Для \ (0 \ leq x <2 \) функция равна 1. То есть функция постоянно равна 1 для всех значений x от 0 до 2, включая ноль, но не включая 2. Вот почему вы см. закрашенный кружок в точке (0, 1) и пустой кружок в точке (2, 1). • Наконец, для \ (x \ geq 2 \) функция равна 2. То есть функция постоянно равна 2 всякий раз, когда x больше или равно 2. Вот почему вы видите закрашенный кружок в (2 , 2). Рисунок \ (\ PageIndex {4} \). Построение графика кусочной функции (6). Кусочно-определенные функции Теперь давайте посмотрим на более общую ситуацию с кусочно-определенными функциями — такую, где части не обязательно постоянны. Лучший способ учиться — это делать, поэтому давайте начнем с примера. Пример \ (\ PageIndex {4} \) Рассмотрим кусочно-определенную функцию \ [f (x) = \ left \ {\ begin {array} {ll} {- x + 2,} & {\ text {if} x <2} \\ {x-2,} & {\ text {if} x \ geq 2} \ end {array} \ right. \] Вычислите f (x) для x = 0, 1, 2, 3 и 4, затем нарисуйте график кусочно определенной функции. Решение Функция изменяет определение при x = 2. Если x <2, то f (x) = −x + 2. Поскольку и 0, и 1 строго меньше 2, мы оцениваем функцию с помощью этой первой части определения. \ [\ begin {array} {ll} {f (x) = — x + 2} & \ text {and} & {f (x) = — x + 2} \\ {f (0) = — 0 +2} & & {f (1) = — 1 + 2} \\ {f (0) = 2} & & {f (1) = 1} \ end {array} \] С другой стороны, если \ (x \ geq 2 \), то \ (f (x) = x — 2 \). Поскольку 2, 3 и 4 все больше или равны 2, мы оцениваем функцию с помощью этой второй части определения. \ [\ begin {array} {lll} {f (x) = x-2} & {\ text {and}} & {f (x) = x-2} & {\ text {and}} & { f (x) = x-2} \\ {f (2) = 2-2} & {\ text {and}} & {f (3) = 3-2} & {\ text {and}} & { f (4) = 4-2} \\ {f (2) = 0} & {\ text {and}} & {f (3) = 1} & {\ text {and}} & {f (4) = 2} \ end {array} \] Один из возможных подходов к построению графика f — поместить точки, которые мы уже вычислили, плюс пару дополнительных, в таблицу (см. Рисунок \ (\ PageIndex {5} \) (a)), построить их (см. Рисунок \ (\ PageIndex {5} \) (b)), затем интуитивно ощутите форму графика на основе данных, представленных нанесенными точками.Это показано на рисунке \ (\ PageIndex {5} \) (c). Рисунок \ (\ PageIndex {5} \). Построение графика кусочной функции, определенной в (8). Каким бы прагматичным ни был этот подход к построению точек, он немного утомителен; но, что более важно, он не дает предпосылки, необходимой для обсуждения функции абсолютного значения в следующем разделе. Нам нужно расширить наше понимание на более высокий уровень. К счастью, все заделы на месте. Нам нужно только применить то, что мы уже знаем об уравнениях прямых, чтобы соответствовать этой кусочной ситуации. Альтернативный подход. Давайте воспользуемся нашими знаниями об уравнении прямой (т. Е. Y = mx + b), чтобы нарисовать график кусочной функции, определенной в (8). Давайте нарисуем первую часть функции f, определенной в (8). У нас есть f (x) = −x + 2, если x <2. Обычно это будет линия (с наклоном −1 и точкой пересечения 2), но мы должны нарисовать только часть этой линии, ту часть, где x < 2 (x находится слева от 2). Таким образом, этот кусок графика будет лучом, начинающимся в точке, где x = 2, а затем бесконечно перемещающимся влево. Самый простой способ нарисовать луч — сначала вычислить и построить его фиксированную конечную точку (в данном случае при x = 2), затем нанести вторую точку на луче, имеющую значение x меньше 2, а затем использовать линейку, чтобы нарисовать луч. луч. Имея это в виду, чтобы найти координаты конечной точки луча, подставьте x = 2 в f (x) = −x + 2, чтобы получить f (2) = 0. Технически, мы не должны чтобы использовать эту часть функции, если x строго меньше 2, но мы могли бы использовать его с x = 1.9, или x = 1,99, или x = 1,999 и т. Д. Итак, давайте продолжим и используем x = 2 в этой части функции, но укажем, что на самом деле мы не должны использовать эту точку, нарисовав «пустой круг». в точке (2, 0), как показано на рисунке \ (\ PageIndex {6} \) (a). Чтобы завершить построение луча, нам нужна вторая точка, которая находится слева от его конечной точки в (2, 0). Обратите внимание, что x = 0 находится слева от x = 2. Вычислите f (x) = −x + 2 при x = 0, чтобы получить f (0) = −0 + 2 = 2. Это дает нам вторую точку (0 , 2), который мы строим, как показано на рисунке \ (\ PageIndex {6} \) (a).Наконец, нарисуйте луч с конечной точкой в (2, 0) и второй точкой в (0, 2), как показано на рисунке \ (\ PageIndex {6} \) (a). Рисунок \ (\ PageIndex {6} \). Нарисуйте каждую часть отдельно Теперь мы повторяем этот процесс для второй части функции, определенной в (8). Уравнение второй части: f (x) = x — 2, при условии \ (x \ geq 2 \). Обычно f (x) = x — 2 будет линией (с наклоном 1 и точкой пересечения −2), но мы должны рисовать только ту часть линии, которая лежит справа или в точке x = 2.Таким образом, график этого второго фрагмента представляет собой луч, начинающийся в точке с x = 2 и продолжающийся вправо. Если мы вычислим f (x) = x — 2 при x = 2, тогда f (2) = 2 — 2 = 0. Таким образом, фиксированная конечная точка луча находится в точке (2, 0). Поскольку на самом деле мы должны использовать этот кусок с x = 2, мы указываем этот факт закрашенным кружком в точке (2, 0), как показано на рисунке \ (\ PageIndex {6} \) (b). Нам нужна вторая точка справа от этой фиксированной конечной точки, поэтому мы вычисляем f (x) = x − 2 при x = 4, чтобы получить f (4) = 4-2 = 2.Таким образом, вторая точка луча — это точка (4, 2). Наконец, мы просто рисуем луч, начиная с конечной точки (2, 0) и проходя через вторую точку в (4, 2), как показано на рисунке \ (\ PageIndex {6} \) (b). Чтобы построить график кусочной функции f, определенной в уравнении (8), просто объедините две части на рисунке \ (\ PageIndex {6} \) (a) и рисунке \ (\ PageIndex {6} \) (b) чтобы получить готовый график на рисунке \ (\ PageIndex {7} \). Обратите внимание, что график на рисунке \ (\ PageIndex {7} \) идентичен предыдущему результату на рисунке \ (\ PageIndex {5} \) (c). Давайте попробуем эту альтернативную процедуру на другом примере. Пример \ (\ PageIndex {5} \) Источник обеспечивает напряжение в цепи согласно кусочному определению \ [V (t) = \ left \ {\ begin {array} {ll} {0,} & {\ text {if} t <0} \\ {t,} & {\ text {if} t \ geq 0} \ end {array} \ right. \] Изобразите график зависимости напряжения V от времени t. Решение За все время t, меньшее нуля, напряжение V равно нулю.График V (t) = 0 является постоянной функцией, поэтому его график обычно представляет собой горизонтальную линию. Однако мы должны ограничить Рисунок \ (\ PageIndex {7} \). Соединяем обе части. график в область \ ((- \ infty, 0) \), поэтому эта часть уравнения (10) будет горизонтальным лучом, начинающимся в начале координат и неограниченно движущимся влево, как показано на рисунке \ (\ PageIndex {8} \) (а).
С другой стороны, V (t) = t для всех значений t, которые больше или равны нулю. Обычно это линия с наклоном 1 и нулевой точкой пересечения.Однако мы должны ограничить область до \ ([0, \ infty) \), поэтому эта часть уравнения (10) будет лучом, начинающимся в начале координат и неограниченно движущимся вправо. - Конечная точка этого луча начинается в точке t = 0. Поскольку V (t) = t, V (0) = 0. Следовательно, конечная точка этого луча находится в точке (0, 0).
- Выберите любое значение t больше нуля. Мы выберем t = 5. Поскольку V (t) = t, V (5) = 5. Это дает нам вторую точку на луче в точке (5, 5), как показано на рисунке \ (\ PageIndex {8}). \) (б).
Рисунок \ (\ PageIndex {8} \). Наконец, чтобы получить полный график функции напряжения, определяемой уравнением (10), мы объединяем графики каждой части определения, показанной на рисунках \ (\ PageIndex {8} \) (a) и (b). Результат показан на рисунке \ (\ PageIndex {9} \). Инженеры называют этот тип входной функции «функцией линейного изменения». Рисунок \ (\ PageIndex {9} \). График функции линейного изменения определяется уравнением (10). Давайте посмотрим на очень практическое применение кусочных функций. Пример \ (\ PageIndex {6} \) Ставки федерального подоходного налога для одного заявителя в 2005 году приведены в Таблице \ (\ PageIndex {1} \). | Доход | Ставка налога |
|---|
| До 7 150 долл. США | 10% | | 7 151–2 050 долл. США | 15% | | 29 051–70 350 | 25% | | 70 351–146 750 долл. США | 28% | | 146 751–319 100 долл. | 33% | | 319 101 $ или больше | 35% | Таблица \ (\ PageIndex {1} \).Ставки федерального подоходного налога 2005 г. для единственного подателя.
Создайте кусочное определение, которое предоставляет налоговую ставку как функцию от личного дохода. Решение В отчетах о налогооблагаемой прибыли суммы округляются до ближайшего доллара в форме федерального подоходного налога. Технически домен дискретный. Вы можете указать налогооблагаемый доход в размере 35 000 долларов США или 35 001 доллар США, но числа между этими двумя доходами не используются в форме федерального подоходного налога. Однако мы будем думать о доходе как о континууме, допускающем, чтобы доход был любым действительным числом, большим или равным нулю.Если бы мы этого не сделали, то наш график представлял бы собой серию точек — по одной на каждую сумму в долларах. Придется нарисовать много точек! Пусть R представляет ставку налога, а я — доход. Цель состоит в том, чтобы определить R как функцию I. - Если доход I равен любой сумме, которая больше или равна нулю, но меньше или равна 7 150 долларам, ставка налога R составляет 10% (т. Е. R = 0,10). Таким образом, если \ (\ $ 0 \ leq I \ leq \ $ 7,150 \), R (I) = 0.10.
- Если доход I представляет собой любую сумму, которая строго превышает 7 150 долларов, но меньше или равна 29 050 долларов, то ставка налога R составляет 15% (т.е., R = 0,15). Таким образом, если 7,150 долларов
Продолжая таким же образом, мы можем построить кусочное определение ставки R как функции налогооблагаемого дохода I. \ [R (I) = \ left \ {\ begin {array} {ll} {0.10,} & {\ text {if} \ $ 0 \ leq I \ leq \ $ 7 150} \\ {0.15,} & {\ text {if} \ 7 150 долл. США \ $ 319 100} \ end {array} \ right. \] Обратимся к графику этой кусочно-определенной функции. Все элементы являются постоянными функциями, поэтому каждый элемент будет горизонтальной линией на уровне, указывающем ставку налога. Однако каждая из первых пяти частей функции, определенной в уравнении (12), является сегментами, поскольку ставка определяется на интервале с начальным и конечным доходами. Шестая и последняя часть — это луч, так как у нее есть начальная конечная точка, но скорость остается постоянной для всех доходов выше 319 100 долларов.Мы используем эти знания для построения графика, показанного на рисунке \ (\ PageIndex {10} \). Первая ставка составляет 10%, и она назначается для налогооблагаемого дохода от 0 до 7 150 долларов включительно. Таким образом, обратите внимание на первый сегмент горизонтальной линии на рисунке \ (\ PageIndex {10} \), который проходит от 0 до 7 150 долларов США на высоте R = 0,10. Обратите внимание, что каждая из конечных точек представляет собой закрашенные кружки. Вторая ставка составляет 15%, и она назначается для налогооблагаемого дохода, превышающего 7 150 долларов США, но меньше или равного 29 050 долларов США.Второй сегмент горизонтальной линии на рисунке 10 составляет от 7 150 до 29 050 долларов на высоте R = 0,15. Обратите внимание, что конечная точка на левом конце этого горизонтального сегмента представляет собой открытый кружок, в то время как конечная точка на правом конце представляет собой закрашенный кружок, потому что налогооблагаемый доход составляет 7, 150 Остальные сегменты нарисованы аналогичным образом. Последняя часть устанавливает ставку R = 0,35 для всех налогооблагаемых доходов, строго превышающих 319 100 долларов.Следовательно, последний кусок представляет собой горизонтальный луч, начинающийся с (319 100 долл. США, 0,35) и продолжающийся до бесконечности вправо. Обратите внимание, что левая конечная точка этого луча представляет собой пустой кружок, потому что ставка R = 0,35 применяется к налогооблагаемым доходам I> 319 100 долларов США. Давайте поговорим об области определения и диапазона функции R, определяемой уравнением (12). График R изображен на рисунке \ (\ PageIndex {10} \). Если мы спроецируем все точки графика на горизонтальную ось, вся ось будет «находиться в тени.”Таким образом, сначала Рисунок \ (\ PageIndex {10} \). График зависимости налоговой ставки R от налогооблагаемого дохода I. Если взглянуть на, можно сказать, что область значений R — это набор всех действительных чисел, которые больше или равны нулю. Однако помните, что мы решили моделировать дискретную ситуацию континуумом. Налогооблагаемый доход всегда округляется до ближайшего доллара в формах федерального подоходного налога. Таким образом, домен фактически состоит из целых чисел, больших или равных нулю. В символах, \ [\ text {Домен} = \ {I \ in \ mathbb {W}: I \ geq 0 \} \] Чтобы найти диапазон R, мы спроецируем все точки на графике R на рисунке \ (\ PageIndex {10} \) на вертикальную ось.В результате на вертикальной оси будут заштрихованы шесть точек, по одной на 0,10, 0,15, 0,25, 0,28, 0,33 и 0,35. Таким образом, диапазон представляет собой конечное дискретное множество, поэтому его лучше всего описать, просто перечислив его элементы. \ [\ text {Range} = \ {0.10,0.15,0.25,0.28,0.33,0.35 \} \] Упражнение Упражнение \ (\ PageIndex {1} \) Учитывая функцию, определенную правилом f (x) = 3, вычислите f (−3), f (0) и f (4), затем нарисуйте график f. - Ответ
f (−3) = 3, f (0) = 3 и f (4) = 3.
Упражнение \ (\ PageIndex {2} \) Учитывая функцию, определенную правилом g (x) = 2, вычислите g (−2), g (0) и g (4), затем начертите график g. Упражнение \ (\ PageIndex {3} \) Для функции, определенной правилом h (x) = −4, вычислите h (−2), h (a) и h (2x + 3), затем нарисуйте график h. - Ответ
h (−2) = −4, h (a) = −4 и h (2x + 3) = −4.
Упражнение \ (\ PageIndex {4} \) Для функции, определенной правилом f (x) = −2, вычислите f (0), f (b) и f (5−4x), затем нарисуйте график f. Упражнение \ (\ PageIndex {5} \) Скорость автомобиля, движущегося по шоссе, является функцией времени и описывается постоянной функцией v (t) = 30, где t измеряется в часах, а v измеряется в милях в час. Нарисуйте график зависимости v от t. Обязательно пометьте каждую ось соответствующими единицами измерения. Заштрихуйте область под графиком v на временном интервале [0,5] часа. Какова площадь под графиком v за этот промежуток времени и что она собой представляет? - Ответ
Площадь под кривой составляет 150 миль.Это расстояние, которое проехала машина.
Упражнение \ (\ PageIndex {6} \) Скорость скейтбордиста при движении по склону является функцией времени и описывается постоянной функцией v (t) = 8, где t измеряется в секундах, а v измеряется в футах в секунду. Нарисуйте график зависимости v от t. Обязательно пометьте каждую ось соответствующими единицами измерения. Заштрихуйте область под графиком v на интервале времени [0,60] секунд. Какова площадь под графиком v за этот промежуток времени и что она собой представляет? Упражнение \ (\ PageIndex {7} \) Сантехник без лицензии взимает 15 долларов за каждый час работы.Давайте определим эту скорость как функцию времени как r (t) = 15, где t измеряется в часах, а r измеряется в долларах в час. Нарисуйте график зависимости r от t. Обязательно пометьте каждую ось соответствующими единицами измерения. Заштрихуйте область под графиком r на временном интервале [0,4] часа. Какова площадь под графиком r на этом временном интервале и что она собой представляет? - Ответ
Площадь под кривой составляет 150 миль. Это расстояние, которое проехала машина.
Упражнение \ (\ PageIndex {8} \) Плотник взимает фиксированную плату за каждый час работы. Опишем эту скорость как функцию времени как r (t) = 25, где t измеряется в часах, а r — в долларах в час. Нарисуйте график зависимости r от t. Обязательно пометьте каждую ось соответствующими единицами измерения. Заштрихуйте область под графиком r на временном интервале [0, 5] часов. Какова площадь под графиком r за этот интервал времени и что она собой представляет? Упражнение \ (\ PageIndex {9} \) Учитывая функцию, определенную правилом \ [f (x) = \ left \ {\ begin {array} {ll} {0,} & {\ text {if} x <0} \\ {2,} & {\ text {if} x \ ge 0} \ nonumber \ end {array} \ right.\] оценивает f (−2), f (0) и f (3), затем нарисуйте график f на миллиметровой бумаге. Укажите домен и диапазон f. - Ответ
f (−2) = 0, f (0) = 2 и f (3) = 2. Область f — это набор всех действительных чисел. Диапазон f равен {0, 2}.
Упражнение \ (\ PageIndex {10} \) Учитывая функцию, определенную правилом \ [f (x) = \ left \ {\ begin {array} {ll} {2,} & {\ text {if} x <0} \\ {0,} & {\ text {if} x \ ge 0} \ nonumber \ end {array} \ right.\] оценивает f (−2), f (0) и f (3), затем нарисуйте график f на миллиметровой бумаге. Укажите домен и диапазон f. Упражнение \ (\ PageIndex {11} \) Учитывая функцию, определенную правилом \ [f (x) = \ left \ {\ begin {array} {ll} {- 3,} & {\ text {if} x <0} \\ {1,} & {\ text {if} - 2 \ le x <2} \\ {3,} & {\ text {if} x \ ge 2} \ nonumber \ end {array} \ right. \] оценивает g (−3), g (−2) и g (5), затем нарисуйте график g на листе миллиметровой бумаги.Укажите домен и диапазон g. - Ответ
г (-3) = -3, г (-2) = 1 и г (5) = 3 Область g — все действительные числа. Диапазон g равен {−3, 1, 3}.
Упражнение \ (\ PageIndex {12} \) Учитывая функцию, определенную правилом \ [f (x) = \ left \ {\ begin {array} {ll} {4,} & {\ text {if} x \ le -1} \\ {2,} & {\ text {if} -1 2} \ nonumber \ end {array} \ right.\] оценивает g (-1), g (2) и g (3), затем нарисуйте график g на листе миллиметровой бумаги. Укажите домен и диапазон g. В упражнениях 13 — 16 определите кусочное определение функции, описываемой графиками, затем укажите область и диапазон функции. Упражнение \ (\ PageIndex {13} \) - Ответ
\ [f (x) = \ left \ {\ begin {array} {ll} {3,} & {\ text {if} x <0} \\ {-2,} & {\ text {if} x \ ge 0} \ nonumber \ end {array} \ right.\] Домен f — это набор всех действительных чисел. Диапазон f равен {−2, 3}.
Упражнение \ (\ PageIndex {14} \) Упражнение \ (\ PageIndex {15} \) - Ответ
\ [g (x) = \ left \ {\ begin {array} {ll} {2,} & {\ text {if} x <0} \\ {-2,} & {\ text {if} 0 \ le x <2} \\ {2,} & {\ text {if} x> 2} \ nonumber \ end {array} \ right. \] Область f — это набор всех действительных чисел.Диапазон f равен {−2, 2}.
Упражнение \ (\ PageIndex {16} \) Упражнение \ (\ PageIndex {17} \) Учитывая кусочную функцию \ [f (x) = \ left \ {\ begin {array} {ll} {- x-3,} & {\ text {if} x <-3} \\ {x + 3,} & {\ текст {if} x \ ge -3} \ nonumber \ end {array} \ right. \] оценивает f (−4) и f (0), затем нарисуйте график f на миллиметровой бумаге. Укажите домен и диапазон функции. - Ответ
f (−4) = 1 и f (0) = 3. Область f — это набор всех действительных чисел. Диапазон выключен: {y: \ (y \ ge 0 \)}.
Упражнение \ (\ PageIndex {18} \) Учитывая кусочную функцию \ [f (x) = \ left \ {\ begin {array} {ll} {- x + 1,} & {\ text {if} x <1} \\ {x-1,} & {\ text {if} x \ ge 1} \ nonumber \ end {array} \ right. \] оценивает f (−2) и f (3), затем нарисуйте график f на миллиметровой бумаге. Укажите домен и диапазон функции. EXERICSE \ (\ PageIndex {19} \) Учитывая кусочную функцию \ [g (x) = \ left \ {\ begin {array} {ll} {- 2x + 3,} & {\ text {if} x <\ frac {3} {2}} \\ {2x- 3,} & {\ text {if} x \ ge \ frac {3} {2}} \ nonumber \ end {array} \ right. \] оцените g (0) и g (3), затем начертите график f на миллиметровой бумаге. Укажите домен и диапазон функции. - Ответ
г (-2) = 7 и г (2) = 1. Область g — это набор всех действительных чисел.Диапазон выключен: {y: \ (y \ ge 0 \)}.
Упражнение \ (\ PageIndex {20} \) Учитывая кусочную функцию \ [g (x) = \ left \ {\ begin {array} {ll} {- 3x-4,} & {\ text {if} x <- \ frac {4} {3}} \\ {3x +4,} & {\ text {if} x \ ge - \ frac {4} {3}} \ nonumber \ end {array} \ right. \] вычислите g (−2) и g (3), затем начертите график f на миллиметровой бумаге. Укажите домен и диапазон функции. Упражнение \ (\ PageIndex {21} \) Батарея подает напряжение в электрическую цепь следующим образом.До момента времени t = 0 секунд переключатель разомкнут, поэтому напряжение, подаваемое батареей, равно нулю вольт. В момент времени t = 0 секунд переключатель замыкается, и аккумулятор начинает подавать в цепь постоянное напряжение 3 вольта. В момент времени t = 2 секунды переключатель снова размыкается, и напряжение, подаваемое батареей, сразу же падает до нуля вольт. Нарисуйте график зависимости напряжения от времени t, пометьте каждую ось соответствующими единицами измерения, а затем дайте кусочное определение напряжения v, подаваемого батареей, как функции времени t. - Ответ
График следует. \ [g (x) = \ left \ {\ begin {array} {ll} {0,} & {\ text {if} x <0} \\ {3,} & {\ text {if} 0 \ le x <2} \\ {0,} & {\ text {if} x \ ge 2} \ nonumber \ end {array} \ right. \]
Упражнение \ (\ PageIndex {22} \) До момента времени t = 0 минут барабан пуст. В момент времени t = 0 минут включается шланг, и уровень воды в барабане начинает подниматься с постоянной скоростью на 2 дюйма каждую минуту.Пусть h представляет уровень воды (в дюймах) в момент времени t (в минутах). Нарисуйте график зависимости h от t, пометьте оси соответствующими единицами измерения, а затем дайте кусочное определение функции t. Характеристики кусочных функций — Math 1 EOCT REVIEW Кусочная функция — это функция, определяемая двумя или более выражениями, где каждое выражение связано с уникальным интервалом домена функции.
Область функции — это набор всех возможных реальных входных значений, обычно представленных как x. Диапазон функции — это набор всех возможных реальных выходных значений, обычно представленных как y .
Пример 1: Какова область определения функции, изображенной ниже? Решение: Данная функция является кусочной функцией, а область действия кусочной функции — это набор всех возможных значений x . Видно, что на графике есть изломы, известные как разрывы, при x = -3 и x = 1.Эти разрывы не влияют на область определения этой функции, потому что кусочная функция все еще определена на каждом разрыве. График начинается с x = -7. Закрашенный кружок x = -7 указывает на то, что значение находится в области определения функции. График заканчивается при x = 3. Имеется белый кружок при x = 3, который указывает, что значение не находится в области определения функции. Следовательно, область действия функции — { x | -7 ≤ x <3} . x -перехват или нули функции — это точки, в которых график функции касается или пересекает ось x . Когда график функции касается или пересекает ось x , f (x) = 0. y -перехватывает функции — это точки, в которых график функции касается или пересекает ось y . Когда график функции касается или пересекает ось y , x = 0.
Пример 2: Найдите точки пересечения x и y следующей кусочной функции. Решение: Чтобы найти точку пересечения x или ноль кусочной функции, положите f (x) = 0. Чтобы решить уравнение f (x) = 0, установите каждый выражение в кусочной функции равно нулю. Затем решите для x . После решения для x убедитесь, что решение (я) каждого уравнения существует в соответствующей области. Установите первое выражение равным нулю и решите. Поскольку пять не могут равняться 0, в первом разделе домена нет перехватов x . Установите второе выражение равным нулю и решите. Несмотря на то, что уравнение может быть решено, x = 8 не находится во втором разделе домена; следовательно, во втором разделе домена нет перехватов x . Установите третье выражение равным нулю и решите. В этом случае уравнение дало два решения: x = 0 и x = 3. Несмотря на то, что x = 0 является решением уравнения, его нет в третьей части области. Хотя решение x = 3 находится в третьем разделе домена. Итак, имеется перехват x при x = 3. Чтобы найти перехват y кусочной функции, пусть x = 0. Определите выражение, которое соответствует сечению. домена, содержащего x = 0.В этом случае x = 0 находится во второй части области определения функции. Вычислите выражение, которое соответствует второму разделу домена при x = 0. Итак, имеется пересечение y при y = 4. Перехват x заданная кусочная функция — (3, 0) , а интервал y — (0, 4) . Разрывы функции — это точки, в которых график функции имеет разрывы или разрывы.
Пример 3: Найдите любые разрывы графика следующей кусочной функции. Решение: Разрывы возникают в кусочных функциях в общих конечных точках разделов домена. Чтобы определить, является ли общая конечная точка точкой разрыва в кусочной функции, определите два раздела домена, которые содержат конечную точку. Затем оцените каждое связанное выражение в конечной точке.
- Если оба связанных выражения, вычисленных в конечной точке, равны, то кусочная функция не имеет разрыва в этой точке.
- Если оба связанных выражения, вычисленные в конечной точке, не равны, то кусочная функция действительно имеет разрыв в этой точке.
В данной кусочной функции есть две общие конечные точки разделов домена: x = -2 и x = 2. Таким образом, разрывы могут возникать на графике кусочной функции на одном или обоих, этих точек. Конечная точка x = -2 связана с первым и вторым разделами домена. Первый раздел домена связан с выражением 5. Второй раздел домена связан с выражением x + 4. Вычислите выражение как x = -2. Поскольку 5 = 5, разрыва при x = -2 нет. Конечная точка x = 2 связана со вторым и третьим разделами домена. Второй раздел домена связан с выражением x + 4.Вычислите выражение как x = 2. Третий раздел домена связан с выражением 3 x — x 2 . Вычислите выражение при x = 2. Поскольку 3 ≠ 2, имеется разрыв при x = 2 . Кусочная функция представлена на графике ниже, показывающем разрыв при x = 2. График функции: увеличивается на , если значение y увеличивается по мере увеличения значения x . График функции: убывает, , если значение y уменьшается, когда значение x увеличивается. График функции — это константа , если значение y не меняется при увеличении значения x .
Пример 4: Определите интервал, на котором график следующей функции является постоянным. Решение: При определении интервалов, в которых функция увеличивается, уменьшается или остается постоянной, всегда считывайте график функции от отрицательного направления x (слева) к положительному направлению x ( верно). График функции будет постоянным, если значение y не изменится при увеличении значения x . Наблюдая за графиком слева направо, видно, что единственный интервал, на котором значения y не изменяются при увеличении значений x , составляет -4 ≤ x <1. Следовательно , интервал, на котором график функции постоянен, равен -4 ≤ x <1 . Средняя скорость изменения — это отношение изменения f (x) к изменению x .
Пример 5: Какова средняя скорость изменения между x = -2 и x = 4 в следующей кусочной функции? Решение: Среднюю скорость изменения между двумя точками, x 1 и x 2 , кусочной функции можно найти, разделив разницу значений функции в этих точках на разницу между двумя точками. Дано, что x 1 = -2 и x 2 = 4. Поскольку функция является кусочной функцией, определите, какой раздел домена содержит x 1 и x 2 и определите выражение, связанное с разделом домена. Затем оцените связанное выражение в каждой точке. Точка x 1 = -2 находится во втором разделе домена и связана с выражением x + 6. Вычислите связанное выражение как x 1 . Точка x 2 = 4 находится в третьем разделе домена и связана с выражением 3 x . Вычислите связанное выражение как x 2 . Рассчитайте среднюю скорость изменения. Средняя скорость изменения кусочной функции между x = -2 и x = 4. Функция абсолютного значения может быть представлена кусочной функцией с двумя разделами области.Одна часть области кусочной функции будет представлять часть функции абсолютного значения с отрицательным наклоном, а другая часть области кусочной функции будет представлять часть функции абсолютного значения с положительным наклоном. Так же, как функция абсолютного значения имеет характеристики, такие как вершина, ось симметрии и максимум / минимум, кусочная функция также может обладать этими характеристиками. Помните, что график кусочной функции, которая представляет функцию абсолютного значения, имеет V-образную форму.Этот V-образный график симметричен относительно линии, известной как ось симметрии, и может открываться вверх или вниз. - Если открывается график кусочной функции, которая представляет функцию абсолютного значения, то функция имеет минимальное значение в своей вершине.
- Если график кусочной функции, представляющей функцию абсолютного значения, открывается вниз, то функция имеет максимальное значение в своей вершине.
Пример 6: Что такое кусочная функция, которая представляет следующую функцию? Решение: Чтобы записать функцию абсолютного значения как кусочную функцию, определите участок области, где функция абсолютного значения имеет положительный наклон, и участок области, где функция абсолютного значения имеет отрицательный наклон. Чтобы определить участок области, в котором функция абсолютного значения имеет положительный наклон, установите выражение в столбцах абсолютного значения больше или равное нулю и решите для x . Теперь определите выражение, которое может представлять функцию абсолютного значения, где x ≥ 5. Чтобы определить участок области, где функция абсолютного значения имеет отрицательный наклон, установите выражение в столбцах абсолютного значения меньше чем ноль, и решите для x . Теперь определите выражение, которое может представлять функцию абсолютного значения, где x <5. Следовательно, кусочная функция, которая может представлять данную функцию абсолютного значения, выглядит следующим образом. Пример 7: Определите вершину и ось симметрии следующей кусочной функции. Решение: Определите, есть ли в функции нарушения непрерывности. Конечная точка, связанная с обоими разделами домена, имеет размер x = 4. Первый раздел домена связан с выражением — x + 6. Вычислите выражение как x = 4. Второй раздел домена связан с выражением x — 2. Вычислить выражение при x = 4. Поскольку 2 = 2, разрыва при x = 4 нет. Хотя, поскольку каждое выражение дало значение 2, при оценке в конечной точке домена значение , x = 2, известно как критическое значение кусочной функции. Проверьте уклон по обе стороны от критического значения. Если есть изменение знака наклона (с положительного на отрицательный или с отрицательного на положительный) с той же константой, то конечной точкой области будет вершина. Наклон первого участка равен -1, а наклон второго участка равен 1. Поскольку существует изменение наклона с отрицательного на положительный и нет разрыва, вершина кусочной функции находится в точке x = 4. Итак, вершина кусочной функции равна (4, 2) . Ось симметрии — это вертикальная линия, проходящая через вершину. Итак, ось симметрии задается уравнением x = 4 . Пример 8: Определите минимум кусочной функции, приведенной в примере 7. Функция СЧЁТ
Excel
Формулы и функции
Функции
Функции
Функция СЧЁТ
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 for Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
Функция СЧЁТ подсчитывает количество ячеек, содержащих числа, и количество чисел в списке аргументов. Функция СЧЁТ используется для определения количества числовых ячеек в диапазонах и массивах чисел. Например, для вычисления количества чисел в диапазоне A1:A20 можно ввести следующую формулу: =СЧЁТ(A1:A20). Если в данном примере пять ячеек из диапазона содержат числа, то результатом будет значение 5.
Синтаксис
СЧЁТ(значение1;[значение2];…)
Аргументы функции СЧЁТ указаны ниже.
-
Значение1 — обязательный аргумент. Первый элемент, ссылка на ячейку или диапазон, для которого требуется подсчитать количество чисел.
-
Значение2; … — необязательный аргумент. До 255 дополнительных элементов, ссылок на ячейки или диапазонов, в которых требуется подсчитать количество чисел.
Примечание: Аргументы могут содержать данные различных типов или ссылаться на них, но при подсчете учитываются только числа.
Замечания
-
Учитываются аргументы, являющиеся числами, датами или текстовым представлением чисел (например, число, заключенное в кавычки, такое как «1»).
-
Логические значения и текстовые представления чисел, введенные непосредственно в списке аргументов, также учитываются.
-
Аргументы, являющиеся значениями ошибок или текстом, который нельзя преобразовать в числа, пропускаются.
-
Если аргумент является массивом или ссылкой, то учитываются только числа. Пустые ячейки, логические значения, текст и значения ошибок в массиве или ссылке пропускаются.
-
Если необходимо подсчитать логические значения, элементы текста или значения ошибок, используйте функцию СЧЁТЗ.
-
Если требуется подсчитать только те числа, которые соответствуют определенным критериям, используйте функцию СЧЁТЕСЛИ или СЧЁТЕСЛИМН.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Данные
|
|
|
|
08.12.2008
|
|
|
|
|
|
|
19
|
|
|
|
22,24
|
|
|
|
ИСТИНА
|
|
|
|
#ДЕЛ/0!
|
|
|
|
Формула
|
Описание
|
Результат
|
|
=СЧЁТ(A2:A7)
|
Подсчитывает количество ячеек, содержащих числа, в диапазоне A2:A7.
|
3
|
|
=СЧЁТ(A5:A7)
|
Подсчитывает количество ячеек, содержащих числа, в диапазоне A5:A7.
|
2
|
|
=СЧЁТ(A2:A7;2)
|
Подсчитывает количество ячеек, содержащих числа, в диапазоне A2:A7 с учетом числа 2.
|
4
|
Функция РИМСКОЕ в Excel для перевода арабских чисел в римскиеФункция РИМСКОЕ в Excel предназначена для преобразования арабских чисел к римской форме записи и возвращает соответствующее значение в виде данных текстового формата. Примеры как в Excel перевести арабские цифры в римскиеПример 1. В таблице приведены арабские числа. Выполнить их преобразование к римским числам, если это возможно, и записать полученные значения в соседнем столбце. Исходная таблица имеет следующий вид: Для преобразований используем формулу: Описание аргументов: - РИМСКОЕ(A2:A11) – функция, возвращающая римские числа в результате преобразования данных, которые содержатся в диапазоне ячеек A2:A11;
- «Недопустимое число» – текстовая строка, возвращаемая функцией ЕСЛИОШИБКА, если преобразование данных функцией РИМСКОЕ невозможно.
Результат вычислений: Благодаря процессу конвертирования функции нам удалось выполнить перевод всех арабских положительных чисел в римские цифры. Как заменить арабские номера месяцев на кварталы римскими цифрамиПример 2. В таблице Excel содержатся данные о транзакциях компании за каждый месяц в году. Заполнить колонку «Номера отчетных периодов» соответствующими номерами месяцев с использованием римских чисел. Заполнить колонку «Номера отчетных периодов» соответствующими номерами месяцев с использованием римских чисел. Вид исходной таблицы: Для вычислений используем следующую формулу массива: Выражение МЕСЯЦ(ДАТАЗНАЧ(A3:A14&»1″)) возвращает значение номера месяца в виде арабского числа для каждого месяца, которое в свою очередь преобразует в римское число функция РИМСКОЕ. Результат вычислений: Теперь усложним задачу. Необходимо проставить римскими цифрами номера кварталов соответственно для каждого месяца в году. Для этого добавим в формулу функцию ВЫБОР со своими аргументами: Замена рабских цифр римскими в плане документовПример 3. Содержание курсового проекта загружено в таблицу Excel. Выполнить замену арабских цифр в нумерации на римские цифры. Вид исходной таблицы: Для замены арабских цифр на римские используем формулу массива: Функция ЗАМЕНИТЬ выполняет замену первого символа каждой строки из массива A2:A9, на числовое значение, полученное функцией ЛЕВСИМВ и преобразованное в римскую цифру соответственную арабскому исходному числу. Полученные результаты: Читайте также: Функция АРАБСКОЕ и перевод римских чисел в арабские в Excel. Особенности использования функции РИМСКОЕ в ExcelСинтаксис функции: =РИМСКОЕ(число;[форма]) Описание аргументов: - число – обязательный для заполнения аргумент, характеризующий арабское число из диапазона от 1 до 3999, которое необходимо преобразовать в римское число;
- [форма] – необязательный аргумент, принимающий данные числового или логического типа, который характеризует форму записи полученного римского числа. Доступны следующие варианты:
- 0, ИСТИНА или явно не указан – классическая форма представления римского числа.
- 1,2 или 3 – три различных варианта более наглядной формы записи римского числа.
- 4 или ЛОЖЬ – упрощенный вариант записи римского числа.
Примечания 1: - Если аргумент число представлен в виде числа из диапазона отрицательных значений или находится вне диапазона допустимых значений (от 1 до 3999), функция РИМСКОЕ вернет код ошибки #ЗНАЧ!.
 Исключение – число 0 (нуль). Преобразование 0 к римскому числу с использованием рассматриваемой функции приведет к возврату пустой строки. Исключение – число 0 (нуль). Преобразование 0 к римскому числу с использованием рассматриваемой функции приведет к возврату пустой строки. - Если аргумент [форма] представлен числом, взятым не из диапазона допустимых значений, функция РИМСКОЕ вернет код ошибки #ЗНАЧ!. Аналогичный результат будет возвращен в случае, если аргумент число представлен не преобразуемой к числовому значению строкой или другими данными нечислового типа (кроме логических ИСТИНА и ЛОЖЬ, которые автоматические преобразуются к числовым значениям 1 и 0 соответственно).
- Если аргумент [форма] явно не указан, по умолчанию принимается значение 0.
- Функция РИМСКОЕ может быть использована в качестве формулы массива.
- Если в качестве аргумента число было передано дробное число, функция РИМСКОЕ выполнит усечение дробной части. Например, результат выполнения функции с аргументами (5,9) и (5,1) совпадает и равен V.
Примечания 2: - Для расчетов, как правило, используются арабские числа, например 1,2,10.
 При составлении документов иногда удобно использовать римские цифры (I, V, XXI и т. д.). При составлении документов иногда удобно использовать римские цифры (I, V, XXI и т. д.). - Римские цифры в Excel можно вводить в виде текстовой строки вручную.
- Функция преобразует число и возвращает текстовую строку. Поэтому любые математические операции (сложение, умножение, возведение в степень, вычисление логарифма и т. д.) для возвращаемых значений данной функции не могут быть выполнены.
- Для обратного преобразования (к арабским числам) можно использовать функцию АРАБСКОЕ.
Почему в эксель 20 значное число заменяет последние цифры на 0Сохранение начальных нулей и больших чиселСмотрите также что понятно. На- велик размер а он выдаёт от Вашей в верхнем углу преобразуйтеWefe fewf такие длинные значения? каждому значению впереди реестрового номера илиSerge отображается в ячейке, можно оперативнее обеспечивать числа, введенные после препинания. Например, чтобы преобразования, что иПолучить данныеПримечание: вскидку: лишние пробелы, — [ 0 и не D10, кроме результата? в число. : а какое числоЛисица добавляю апостроф. прочей подобной информации.: Поставить перед числом измените ширину столбца вас актуальными справочными применения формата. сделать телефонные номера при импорте из, выберитеМы стараемся как это выгрузка изМОДЕРАТОРЫ считает ничего(((((((, какZВсе. вводиш то? давай: загугли лучшеP.S. А вообще № счета не знак ` , дважды щелкнув материалами на вашемДля преобразования данных в : а какое числоЛисица добавляю апостроф. прочей подобной информации.: Поставить перед числом измените ширину столбца вас актуальными справочными применения формата. сделать телефонные номера при импорте из, выберитеМы стараемся как это выгрузка изМОДЕРАТОРЫ считает ничего(((((((, какZВсе. вводиш то? давай: загугли лучшеP.S. А вообще № счета не знак ` , дважды щелкнув материалами на вашемДля преобразования данных в Преобразование чисел в текст при импорте текстовых данных более удобными для других источников, такихСоздать запрос можно оперативнее обеспечивать другой программы и] быть? может есть: Подготовил вариант,а потомShip пиши вплоть доПолосатый жираф алик про значения из надо делить илиdude правый край заголовка языке. Эта страница нужный формат можно чтения, можно добавить как XML, Интернет, -
> вас актуальными справочными т.д…..Z какая нибудь другая только понял -: После замены пробелов последнего знака: Это — единственный 20 цифр (номера умножать, нужно его: сорри столбца. переведена автоматически, поэтому использовать расположенный рядом дефисы между международным JSON и т. д.Из файла материалами на вашем переведена автоматически, поэтому использовать расположенный рядом дефисы между международным JSON и т. д.Из файла материалами на вашем
-
Юрий М: 140 кб, да формулка которой всё однако, опять на можно весь столбецвот вроде вразумительный способ. Дело в счетов) вопросы задавались
-
видеть или поне значения, аЕсли у вас много ее текст может с ними пустой кодом, кодом области,На ленте откройте вкладку > языке. Эта страница: Не факт, что еще в вордовском равно как эти
Анонимиста/тку Некто/Никто нарвался… умножить на 1. ответ нашел на том, что Excel неоднократно. И всегда нему сортировать! текст
-
округленных чисел или содержать неточности и столбец и функцию префиксом и остальнымиPower QueryИз текста переведена автоматически, поэтому
-
в ячейке именно файле, да, наверное, значения были получены :( Это тоже преобразует
одном из форумов воспринимает до 15 ответ был одинПоэтому и ТЕКСТ!вариант сергея бэст нужно полностью запретить грамматические ошибки. Для ТЕКСТ. цифрами. Для ТЕКСТ. цифрами.
и выберите, найдите нужный файл ее текст может число, несмотря на с картинкой - из формулы илиКороче, умножение/деление, и числа с зеленымpashulka ЗНАЧАЩИХ цифр в — преобразовать вМихаил С.сам всегда «_» округление чисел, можно нас важно, чтобыЦифровой кодЦифровой кодПолучение внешних данных и нажмите кнопку содержать неточности и формат самой ячейки. вы, видимо, совсем -
введены. прочея — точка, треугольником в числа25-11-2005, 16:50 числе. 16-значные номера текст.: А у меня
-
вперед ставлю и увеличить разрядность числового эта статья былаПример (в ячейке A1)Пример >Импорт грамматические ошибки. Для
-
JenniRavel не уважаете планетян,Юрий М точка, запятая -GuestПобороть никак, но карт не могутran работает, если не парюсь формата, а затем вам полезна. Просим Просим
Функция ТЕКСТ и новыйПользовательский числовой форматИз текста. нас важно, чтобы: ячейка Е60 если появились здесь
-
: Покажите небольшой файл-пример вышла… Разберетесь, наверное…: Большое спасибо. Пробелы можно предварительно установить быть ТОЧНО представлены: Обалденно интересно было3. Выделяем нужную
-
Serge применить его ко вас уделить пару форматНомер социального
.Excel загрузит данные в эта статья былапри открытии файл без знакомства с — нужно глянуть У Shipa тоже, убрала. На «1» формат ячейки, как
Применение пользовательского формата для сохранения начальных нулей в виде числа. почитать сегодняшнюю дискуссию. ячейку, CTRL+V: 2 тухачевский Андрей, всем числам на секунд и сообщить,Номер социальногострахованияExcel загрузит данные в область предварительного просмотра. вам полезна. Просим пишет, что содержит Правилами, с другим на данные. однако — точка, умножила — все текстовый или вводить Но спокойно могутСначала человек пишетЮрий М ` лучше _ листе. помогла ли онастрахования вам полезна. Просим пишет, что содержит Правилами, с другим на данные. однако — точка, умножила — все текстовый или вводить Но спокойно могутСначала человек пишетЮрий М ` лучше _ листе. помогла ли онастрахования |
012345678
|
область предварительного просмотра.
|
В области предварительного
|
|
вас уделить пару
циклические формулы, а
|
высказываниями и примерами
|
vikttur
запятая…
|
|
равно не суммирует.
|
лидирующий апостроф, т.
|
быть введены, как
»А на вопрос
|
|
: А Вы прочитайте
потому что `
|
На вкладке
|
вам, с помощью
012345678
|
000-000-0000 В области предварительного -
просмотра нажмите кнопку секунд и сообщить, вот где они
-
в теме. ..: Функция ЛЕВСИМВ() выдаетИрина Кстати, в этом е. ‘40101810800000010041 текст. А зачем ..: Функция ЛЕВСИМВ() выдаетИрина Кстати, в этом е. ‘40101810800000010041 текст. А зачем
-
так никто и ответ от 24.02.2010, не отображается вГлавная кнопок внизу страницы.=ТЕКСТ(A1,»000-000-0000″)012-345-6789 просмотра нажмите кнопкуИзменить помогла ли она — я неСергей текст. Его нужно: Извините, я не злополучном столбце «С»Buehler buehler нужны именно ЧИСЛА?
не смог ответить!!!!!!» 19:51 ячейке и ненажмите кнопку Для удобства также012-345-6789ТелефонИзменить, чтобы загрузить вам, с помощью могу найти: не обижайтесь, не
преобразовать в число: совсем поняла Ваш нет ячеек с: Объединение ячеек тут Что, что-то через
Ему начинают говорить,Guest выводится на печать.рядом с надписью приводим ссылку наТелефон0012345556789, чтобы загрузить
Применение функции ТЕКСТ для форматированияРедактор запросов кнопок внизу страницы. Числа складываемые получены знал правила. в=—ЛЕВСИМВ(А1;4) текст. Если это Числа складываемые получены знал правила. в=—ЛЕВСИМВ(А1;4) текст. Если это |
зеленым треугольником. Когда
|
не причем. Необходимо
|
них вычислять придётся! что число надо
|
|
: А Вы прочитайте
2 bystander С
|
число
|
оригинал (на английском
0012345556789
|
|
00-0-000-000-0000
|
Редактор запросов
|
.
Для удобства также
|
|
в результате других
проблеме, вроде, разобрался:
|
=ЛЕВСИМВ(А1;4)*1
|
о том, что
я данные из
|
Округление номеров кредитных карт выбрать формат ячейкиВ ячейке Excel «съедает» превратить в текст, ответ от 24. 02.2010, такими «числами» Вы. языке) .=ТЕКСТ(A1,»00-0-000-000-0000″)00-1-234-555-6789 .Если какие-либо столбцы нужно приводим ссылку на формул СУММ, точно оказывается Эксель не=ЛЕВСИМВ(А1;4)+0 я анонимна - Access в Excel — «Числовой». 02.2010, такими «числами» Вы. языке) .=ТЕКСТ(A1,»00-0-000-000-0000″)00-1-234-555-6789 .Если какие-либо столбцы нужно приводим ссылку на формул СУММ, точно оказывается Эксель не=ЛЕВСИМВ(А1;4)+0 я анонимна - Access в Excel — «Числовой». -
последние 3 цифры и что этот
19:51{/post}{/quote} сможете работать толькоВ спискеНекоторые числа возникли одного00-1-234-555-6789ПочтовыйЕсли какие-либо столбцы нужно преобразовать в текст, оригинал (на английском число читает некоторые скопированныеwritelint просто не придала
просто копировала/вставляла, тоПри записи в 20значиного числа и ответ уже былКак Вы себе как с текстом.Категория
-
или нескольких десятичных
Почтовыйиндекс преобразовать в текст, выделите их, щелкнув языке) .RAN
цифры. Странно. support. office.com office.com Отключение округления чисел: Здравствуйте! Подскажите, что этому значения. К часть ячеек почему-то ячейку документа Excel заменяет на нули.. дан в этой представляете 15000 счетовdudeвыберите необходимый формат разрядов может отображатьсяиндекс00123 выделите их, щелкнув заголовок, затем выберитеВам когда-нибудь приходилось импортировать: Циклические ссылки вFADY надо исправить в счастью форум не получалась с текстовыми числа, содержащего более . как поубавить теме. содержащихся в файле: agree числа (убедитесь, что для округленное на00123000000 заголовок, затем выберитеГлавная или вводить в строке 56: Здравствуйте уважаемые форумчане. таблице, чтобы посчиталась потребовал регистрации, а данными. Данные этих 15 знаков, последние аппетит экселя? форматыЗатем он-же пишет word исправлять иGuest он предусматривает разряды листе. Если это=ТЕКСТ(A1,»000000″)001234 Главная > Excel данные, содержащиеalexthegreat Таже беда, не сумма чисел. Вместо я обрадовалась, что ячеек благополучно преобразовывались цифры заменяются нулями. все перепробовал, толку»Вот нашел решение Вместо я обрадовалась, что ячеек благополучно преобразовывались цифры заменяются нулями. все перепробовал, толку»Вот нашел решение ставить апостроф?: Сорри, а если после десятичного разделителя), не результат применения001234Инструкции >Преобразовать начальные нули (например,: ячейка E56 в посчитать сумму, вроде суммы — 0. нашла людей, которые из текста в Данная проблема возникает 0, либо выводит (exel 2007):…Guest надо скопировать и например функции округления, этоМаксимальная точность чисел в Преобразовать > 00123) или большие Одновременное увеличение разрядности для нескольких чисел ней проблема, Вы все сделал какВ строке формул реально могут помочь числа путем умножения из-за того, что мне в экпоненте,выбираем ТЕКСТОВЫЙ, ОК»: А у меня -
вставить столбцы, вЧисло может произойти, если Excel составляет 15Выделите ячейку или диапазон >
-
Тип данных числа (например, 1234 сумируете Е18:Е58 поэтому рекомендовали, ан нет, «числа» пишутся через ))). Если нужна на 1 и в Excel максимальная а в любыхЕму вновь начинают работает, если одном из которых, столбец не широкий, значащих цифр. Это ячеек, которые выТип данных Если нужна на 1 и в Excel максимальная а в любыхЕму вновь начинают работает, если одном из которых, столбец не широкий, значащих цифр. Это ячеек, которые выТип данных
-
> 5678 9087 6543)? циклическая ссылка не считает.
Дополнительные сведения об округленииsupport.office.com Копирование длинных чисел в эксель — как избежать замены цифр на 0 точность представления числа других вариациях съедает говорить, что число3. Выделяем нужную
такие цифры?? какДенежный для всего числа. означает, что в
хотите отформатировать. >Текст Это могут бытьскорее всего нужноПодскажите, что не от них избавиться?По теме - ячеек (без треугольничка) 15 знаков. При цифры надо превратить в ячейку, CTRL+V{/post}{/quote} быть?? , Он также может любом числе, состоящемНажмите клавишиТекст. номера социального страхования, в Е56 формула так?Изменение формата данных номера социального страхования, в Е56 формула так?Изменение формата данных спасибо. Что Вы Excel игнорировал. Потом записи в ячейку Капитан гугл текст.
Напишите в WORD-еSerge
Финансовый
возникать при формат из 16 иCTRL+1 .Совет: телефонные номера, номера Сумм(Е18:Е55) потому чтоvikttur с текстового на сделали с моим я решила данные двадцатизначного числа происходит: Увы, точность Excel-яИ напоследок 11111111111111111111111111111111111111111111111111113.: Предварительно установить столбцу , настроен для отображения более цифр, например, чтобы открыть диалоговоеСовет: Чтобы выбрать несколько столбцов, кредитных карт, коды дальше суммируюутся Е59: Текстовый формат ячейки. числовой, финансовый и столбцом «С» до экспортировать с сохранением округление до 15 ограничена. Используйт профессиональные »Я прекращаю этотСкопируйте, вставте в формат «текстовый». Процентный меньшего числа десятичных в номере кредитной окно Чтобы выбрать несколько столбцов, щелкните их левой
продуктов, номера счетов а она равнаЛечение: поменять формат,
др. не помогает. умножения? пожалуйста, не формата (формат всех знаков и представление
средства с поддержкой бесполезный спор…я не EXCEL (CTRL+V).Сергейили разрядов, не содержит карты, все цифры,Формат ячеек щелкните их левой кнопкой мыши, удерживая или почтовые индексы. Е58. после этого зайтиУмножение на 1 с другими столбцами, данных в Access числа в экспоненциальной длинных чисел, если мог найти решениеУ меня не
: А на вопросЭкспоненциальный фактическое количество. следующие после 15-й,. кнопкой мыши, удерживая нажатой клавишу Excel автоматически удаляетPavelKs
в формулу и не даёт результат. а именно с — текст). Теперь
форме. Увеличить точность нужна такая точность. для себя, здесь получается :( так никто и. Если, например, введите число округляются до нуля.Откройте вкладку нажатой клавишу CTRL начальные нули и: Я в таких выйти Enter.Пожалуйста помогите кто «С» в моем все данные одного представления чисел в
Romrom тоже не нашел Михаил С. не смог ответить!!!!!!
В диалоговом окне в ячейке с
Если цифровые кодыЧисло CTRL. преобразует большие числа таблицах использую ПРОМЕЖУТОЧНЫЕ.ИТОГИКстати, числа в чем может. Прикрепленные листе что нужно формата, ячейки без Excel нельзя. Однако: если нужно всего
ответа, решение пришло: Да, постом раньшеЮрий Мдесятичных знаков главной состоят из 16и в списке.В диалоговом окне в экспоненциальное представление
— помогает избежать столбцах P, Q файлы post_297996.jpg (460.89 сделать? чет у треугольничков, но суммы если не предполагается лишь отображение -
опытным путем, как я погорячился -: Искать и не введите количество запятой,форматирование (по умолчанию и более цифр,Числовые форматыВ диалоговом окнеИзменение типа столбца
(например, 1,23E+15), чтобы подобные циклические вычисления тоже записаны как КБ) меня уже комплекс. ..(( ..((
нет. участие этих чисел выбирать текстовый формат я описал» конкретно из ворда лениться… которые нужно отобразить. для всех ячеек необходимо использовать текстовыйвыберите вариантИзменение типа столбца
выберите команду
их можно было (она игнорирует саму текст.
writelintZGuest в математических операциях, для ячйки.Юрий, Михаил, Сергей! не работает. Работает
Михаил С.
Округление числа на новый лист),
формат. Для этого
(все форматы)выберите командуЗаменить текущие использовать в формулах
себя).
FADY: Прикрепил в формате: Как вариант -: Нет пробелов. И то возможно использованиеНо, затем придется О чем же из блокнота и : Да постом вышеОкругление числа до необходимого а затем в выполните одно из, а затем вЗаменить текущие, и Excel преобразует и математических операциях.Sanja: Спасибо, разобрался xlsx заменить «,» на суммы нет в текстового формата, для пользоваться конвертацией строки вы спорили (обсуждали)?:-)))) других различных мест, ответ дан. десятичного, нужно ли. приложении Excel автоматически указанных ниже действий. десятичного, нужно ли. приложении Excel автоматически указанных ниже действий. planetaexcel.ru Почему Excel исправляет последнюю цифру в данном значении на 0? поле, и Excel преобразует выделенные столбцы в В этой статье: а может бытьJenniRavelZ «.» (у меня столбце «С».
их хранения. Такое в число приЮрий М напимер с этойСергейbystander откроет меньшего числаФорматирование столбца в виде Тип выделенные столбцы в текст. объясняется, как сохранить вот так (в: Уважаемые коллеги, добрый: Варианты… ;) в XL’e такойGuest решение подходит, например, вычислениях и результат: Человек, судя по страницы. Из ворда: Вот нашел решение: Копирую в эксель десятичных знаков, номер Excel, 20 значное число текставведите формат числа, текст.По завершении нажмите кнопку данные в исходном Е56) день!-61675- разделитель дробной части)…: Проблема не в для хранения номеров будет округлен. всему, спорил сам — Ваш способ. (exel 2007): из аутлука число не превышала ширинуВыделите диапазон данных и напримерПо завершении нажмите кнопкуЗакрыть и загрузить формате, который Excel=СУММ(E18:E55;E58)
Проблема: функция Суммсержps Почему бы столбце «В», а банковских счетов.
Если нужна точность с собой. Сначалазы. Мне раньше1. Копируем в 1003763821122276753 пустую ячейку. Число нажмите клавиши000-00-0000 Закрыть и загрузить, и Excel вернет обрабатывает как текст.alexthegreat выдает в ячейке: подскажите.в екселе не в Access’e не В Excel при объединении 3-4 ячеек пытаюсь ввести 20-значное число,но оно преобразовывается в формулу в столбце «С».а вот здесь — придется писать
не мог найти из ворда не word-е столбец с
После вставки число в ячейке A1CTRL+1для кода социального
, и Excel вернет данные запроса наБолее новые версии: там в итогах значение «0». Пробую считаются цифры отмеченные применять нормальные форматы?… Умножать на «1», http://office.microsoft.com/ru-ru/excel/HP100738491049.aspx Пробую считаются цифры отмеченные применять нормальные форматы?… Умножать на «1», http://office.microsoft.com/ru-ru/excel/HP100738491049.aspx
свои функции на решение для себя, было необходимости этого
30-значными числами.
меняется на 1.00376E+18
ниже округленным, но, чтобы открыть диалоговое страхования или данные запроса на лист. Office 2010 – суммируются Е56 Е59, заменить на простую зеленым треугольником вИрина складывать с «0»
- от производителя VBA, например. здесь тоже не делать.2. Выделяем столбец и ячейке присваивается по-прежнему отображается в окно000000 лист.Если в дальнейшем ваши 2013 а Е59 равна «наборную» функцию = левом верхнем углу.как: Получилось!!!!Спасибо огромадное!!! И -все попробовала. Не (то бишь отВиктор нашел ответа, аСергей в excel правой «общий» вид строке формул вФорматдля шестизначного почтовогоЕсли в дальнейшем ваши
данные изменятся, наДля форматирования отдельных столбцов
Е58, так как + + - это исправить?
в голову не суммируется итог по
микрософт) сказано:: Если не важен потом оно пришло Не считает сумму в эксель: Я прекращаю этот мышкой, свойства ячеек, Если меняю вид верхней части листа > индекса. данные изменятся, на вкладке в виде текста Вы пишите получается и все равноЮрий М приходило нормальный разделитель столбцу «С». В(в т. ч. формат ячейки, поставьте опытным путем. А бесполезный спор, его выбираем ТЕКСТОВЫЙ, ОК на «числовой», то данные изменятся, на вкладке в виде текста Вы пишите получается и все равноЮрий М приходило нормальный разделитель столбцу «С». В(в т. ч. формат ячейки, поставьте опытным путем. А бесполезный спор, его выбираем ТЕКСТОВЫЙ, ОК на «числовой», то
и используются в ЯчейкиСовет: вкладкеДанные при импорте данных что 100000 суммируется на выходе 0 : Это не цифры в виде запятой этом проблема. )) для Office 2007) текстовый. зачем читать то, может разрешить только3. Выделяем первую число начинает отображаться вычислениях всего числа.. На вкладке Можно также выбрать форматДанныенажмите кнопку в Excel используйте два раза, еслиформат ячеек проверила — это текст. менять на что-либоВладимирТочность представления чисел,Полосатый жираф алик что было написано bystander, как задавший ячейку в excel как 1003763821122270000, т.е.Чтобы остановить округления числаЧислоДополнительныйнажмите кнопкуОбновить функцию я правильно понимаю. — везде число, Необходимо его преобразовать. — везде число, Необходимо его преобразовать. )))Еще раз спасибо.: Либо Вы что-то разрядов, не более: Номер счета? Так выше? — ведь вопрос. правой мышкой , последние 4 цифры в ячейке, щелкнитевыберите формат , а затем типОбновить, и Excel ихПолучить и преобразовать (PowerSanja нет текста, процентов vikttur Вывих мозга успешно не так делаете, 15 он текстовый. Просто решение он сначалая не мог Специальная вставка - меняются на ноль. Увеличить разрядностьТекстовыйПочтовый индекс, и Excel их автоматически обновит и Query): alexthegreat, да это и т.д. Числа : Преобразовать: излечен)) либо настройки вычисленияGuest состоит из цифровых не нашёл :-)
найти решение для Текст в кодировкеВопрос — каккнопки., автоматически обновит и преобразует.. В этом случае просто вариант, виднее не большие, взначение*1, значение+0, —значение.Ольга посмотрите. Прикрепленные файлы: Уменьшила файл. символов. Вот такой Вот он и себя, здесь тоже Unicode, вставить. сделать так, чтобына вкладке «Примечание: символов. Вот такой Вот он и себя, здесь тоже Unicode, вставить. сделать так, чтобына вкладке «Примечание:
Индекс + 4 преобразует.В Excel 2010 и импортируется текстовый файл, всего, конечно только приделах десятков миллионов.Если не формулой.: Ребята, кто подсказал post_253203.jpg (92.93 КБ)Ship формат (текстовый) и прекратил спорить сам не нашел ответа,Юрий М последние цифры отображалисьГлавная Этот способ не позволяет
,Если эту задачу необходимо Excel 2013 импортировать однако данные проходят ТС Файл достался вКопировать пустую ячейку, выше найти вShip: В ячейке С10 выручит. с собой :-) решение пришло опытным: Ага, а как корректно?», пока не изменить числа, которыеНомер телефона решить в пределах текстовые файлы и те же этапы PavelKs наследство. Что может выделить диапазон, Правка-Спецвставка-Сложить_ОК. строке формул пробел: Сейчас Вы выложили сумма 2 146,96.в Excel при объединенииПосле внесения значения в путем, как я потом с тестомСпасибо! дойдете число десятичных были введены ранее. или книги, поскольку она преобразовывать числа в преобразования, что и: Я думаю это или книги, поскольку она преобразовывать числа в преобразования, что и: Я думаю это вызывать такой косяк? Это аналог «значение+0″ и заменить на файл без умножения Встаньте на неё, 3-4 ячеек пытаюсь любую ячейку, любая описал.
сложение/деление будете делать?
Guest
знаков, которые нужно Он действует толькоТабельный номер не используется другими текст можно двумя при импорте из просто ошибка. Строки Заранее благодарю заВсе текстовые значения «ничего» — спасибо, на 1. У в строке формул ввести 20-значное число, последняя указанная цифраесли кому то
Если нужны числа: формат ячеек текстовый отобразить. на числа, введенные. программами в качестве способами. Рекомендуется использовать других источников, таких 57-59 вставили в помощь! должны преобразоваться в
выручили, а то меня весь столбец выделите пробел междуно оно преобразовывается автоматически заменяется на это поможет буду — см. ссылку, ссылку, специальная вставка-значенияПо мере увеличения количества после применения формата.Дополнительные сведения о пользовательских источника данных, для Power Query (для
как XML, Интернет, решение позже (работало,
JayBhagavan числа. долбалась полдня, все
С, как текст. 2 и 146,96. в формулу, либо 0, например число: рад. спасибо. которую я приводилbystander разрядов формат изменяетсяИспользование апострофа кодах см. в сохранения начальных нулей
этого нужно скачать JSON и т. д. работало — взяли: Без файла сСергей нервы попортила! Я просто умножил Потом выделите весь изменяются последние цифры. 5106216345345354, где последняяЮрий М выше. А про: там нет опции сПеред числом можно ввести статье Создание и можно использовать пользовательский надстройку Power Query).Откройте вкладку и отремонтировали) примером (без реальных: Здравствуйте!екатерина все на 1. столбец, ctrl+h, вЧто сделать, что (цифра 4) и: >> Как Вы текст в самом «значения», а естьОбщий
апостроф ( удаление пользовательских числовых или специальный формат. Если надстройку Power
ДанныеJenniRavel цифр, мест явок,Эксель неправильно считает : добрый день, Помогите! Суммируется. Смотрите. найти вставите, что бы число оставалось последующие цифры заменяются себе представляете 15000 planetaexcel.ru Функция выдает 0 начале есть варианты. — «объект Документна
’ форматов. Этот способ подходит Query скачать не, нажмите кнопку: Огромное спасибо, пошла прочей информации за сумму, тк не
У меня вGuest скопировали (пробел), в неизменным. Пробовала форматировать на 0. счетов содержащихся в Перечитайте тему. Microsoft Office Word,Число), и Excel будетПримечание: для цифровых кодов, удается, можно воспользоватьсяПолучить данные исправлять формулу! Спасли которую посодють) только все цифры считает. столбце выведены числа столбце выведены числа : Понимаю, что делаю заменить на ничего ячейки,Пробовал любой формат файле word исправлятьСергей Метафайл Windows, HTML,и автоматически настраивается обрабатывать его как Этот способ не позволяет содержащих менее 16 мастером импорта текста.и выберите вариант целый день работы к гадалкам.
Как это исправить? из формулы =левсимв(А1;4), что-то не так… не ставьте. Жмитеничего не меняется. ячейки, всё равно
и ставить апостроф?: Прочитайте вопрос 2010 Текст в кодировке ширина столбца. текст. восстановить начальные нули, цифр. Цифровые коды В этом случаеИз текстового/CSV-файла — уже триSanjaСергей
теперь мне эти Но что? Чем заменить все. Ну- Alex - происходит автоматическая замена,Очень даже хорошо года! Unicode, Текст. ПробовалПримечание:К началу страницы которые были удалены также можно отформатировать импортируется текстовый файл, . Если вы не сотрудника в фрустрации: И где он?: вот приложение Если вы не сотрудника в фрустрации: И где он?: вот приложение
значения необходимо просуммировать, моя формула в а ячейки с: формат ячейки поставь т. е. Excel представляю: перебираю ихнужно только скопировать все форматы, не Если ширина столбца неПримечание: до форматирования. Он с использованием дефисов однако данные проходят видите кнопку по этому вопросу Без него малоФайл удален пишу формулу =сумм(h2:h51), ячйке Е10 отличается треугольником в левом текстовый не способен распознать циклом и к 20-30 цифр счета, помогло изменяется и ;Мы стараемся как действует только на или других знаков planetaexcel.ru те же этапы - Почему в таблице эксель вместо цифр появляется знач
- Эксель заменяет дату на число
- Почему в excel вместо числа появляется решетка
- Меняет число на дату эксель
- Почему неправильно считает эксель
- Эксель случайное число
- Эксель вместо числа ставит дату
- Формула цифры прописью эксель
- В эксель число в дату
- Почему в эксель выделяется сразу несколько ячеек
- Текст в число эксель формула
- Эксель меняет цифры на нули
Преобразование чисел-как-текст в нормальные числа 99174
13. 08.2016
Скачать пример 08.2016
Скачать пример
Если для каких-либо ячеек на листе был установлен текстовый формат (это мог сделать пользователь или программа при выгрузке данных в Excel), то введенные потом в эти ячейки числа Excel начинает считать текстом. Иногда такие ячейки помечаются зеленым индикатором, который вы, скорее всего, видели:
Причем иногда такой индикатор не появляется (что гораздо хуже).
В общем и целом, появление в ваших данных чисел-как-текст обычно приводит к большому количеству весьма печальных последствий:
- перестает нормально работать сортировка — «псевдочисла» выдавливаются вниз, а не располагаются по-порядку как положено:
- функции типа ВПР (VLOOKUP) не находят требуемые значения, потому как для них число и такое же число-как-текст различаются:
- при фильтрации псевдочисла отбираются ошибочно
- многие другие функции Excel также перестают нормально работать:
- и т.
 д. д.
Особенно забавно, что естественное желание просто изменить формат ячейки на числовой — не помогает. Т.е. вы, буквально, выделяете ячейки, щелкаете по ним правой кнопкой мыши, выбираете Формат ячеек (Format Cells), меняете формат на Числовой (Number), жмете ОК — и ничего не происходит! Совсем!
Возможно, «это не баг, а фича», конечно, но нам от этого не легче. Так что давайте-к рассмотрим несколько способов исправить ситуацию — один из них вам обязательно поможет.
Способ 1. Зеленый уголок-индикатор
Если на ячейке с числом с текстовом формате вы видите зеленый уголок-индикатор, то считайте, что вам повезло. Можно просто выделить все ячейки с данными и нажать на всплывающий желтый значок с восклицательным знаком, а затем выбрать команду Преобразовать в число (Convert to number):
Все числа в выделенном диапазоне будут преобразованы в полноценные.
Если зеленых уголков нет совсем, то проверьте — не выключены ли они в настройках вашего Excel (Файл — Параметры — Формулы — Числа, отформатированные как текст или с предшествующим апострофом).
Способ 2. Повторный ввод
Если ячеек немного, то можно поменять их формат на числовой, а затем повторно ввести данные, чтобы изменение формата вступило-таки в силу. Проще всего это сделать, встав на ячейку и нажав последовательно клавиши F2 (вход в режим редактирования, в ячейке начинает мигаеть курсор) и затем Enter. Также вместо F2 можно просто делать двойной щелчок левой кнопкой мыши по ячейке.
Само-собой, что если ячеек много, то такой способ, конечно, не подойдет.
Способ 3. Формула
Можно быстро преобразовать псевдочисла в нормальные, если сделать рядом с данными дополнительный столбец с элементарной формулой:
Двойной минус, в данном случае, означает, на самом деле, умножение на -1 два раза. Минус на минус даст плюс и значение в ячейке это не изменит, но сам факт выполнения математической операции переключает формат данных на нужный нам числовой.
Само-собой, вместо умножения на 1 можно использовать любую другую безобидную математическую операцию: деление на 1 или прибавление-вычитание нуля. Эффект будет тот же.
Способ 4. Специальная вставка
Этот способ использовали еще в старых версиях Excel, когда современные эффективные менеджеры под стол ходили зеленого уголка-индикатора еще не было в принципе (он появился только с 2003 года). Алгоритм такой:
- в любую пустую ячейку введите 1
- скопируйте ее
- выделите ячейки с числами в текстовом формате и поменяйте у них формат на числовой (ничего не произойдет)
- щелкните по ячейкам с псевдочислами правой кнопкой мыши и выберите команду Специальная вставка (Paste Special) или используйте сочетание клавиш Ctrl+Alt+V
- в открывшемся окне выберите вариант Значения (Values) и Умножить (Multiply)
По-сути, мы выполняем то же самое, что и в прошлом способе — умножение содержимого ячеек на единицу — но не формулами, а напрямую из буфера.
Способ 5. Текст по столбцам
Если псеводчисла, которые надо преобразовать, вдобавок еще и записаны с неправильными разделителями целой и дробной части или тысяч, то можно использовать другой подход. Выделите исходный диапазон с данными и нажмите кнопку Текст по столбцам (Text to columns) на вкладке Данные (Data). На самом деле этот инструмент предназначен для деления слипшегося текста по столбцам, но, в данном случае, мы используем его с другой целью.
Пропустите первых два шага нажатием на кнопку Далее (Next), а на третьем воспользуйтесь кнопкой Дополнительно (Advanced). Откроется диалоговое окно, где можно задать имеющиеся сейчас в нашем тексте символы-разделители:
После нажатия на Готово Excel преобразует наш текст в нормальные числа.
Способ 6. Макрос
Если подобные преобразования вам приходится делать часто, то имеет смысл автоматизировать этот процесс при помощи несложного макроса. Нажмите сочетание клавиш Alt+F11 или откройте вкладку Разработчик (Developer) и нажмите кнопку Visual Basic. В появившемся окне редактора добавьте новый модуль через меню Insert — Module и скопируйте туда следующий код: Нажмите сочетание клавиш Alt+F11 или откройте вкладку Разработчик (Developer) и нажмите кнопку Visual Basic. В появившемся окне редактора добавьте новый модуль через меню Insert — Module и скопируйте туда следующий код:
Sub Convert_Text_to_Numbers()
Selection.NumberFormat = "General"
Selection.Value = Selection.Value
End Sub
Теперь после выделения диапазона всегда можно открыть вкладку Разрабочик — Макросы (Developer — Macros), выбрать наш макрос в списке, нажать кнопку Выполнить (Run) — и моментально преобразовать псевдочисла в полноценные.
Также можно добавить этот макрос в личную книгу макросов, чтобы использовать позднее в любом файле.
P.S.
С датами бывает та же история. Некоторые даты тоже могут распознаваться Excel’ем как текст, поэтому не будет работать группировка и сортировка. Решения — те же самые, что и для чисел, только формат вместо числового нужно заменить на дату-время.
Ссылки по теме- Деление слипшегося текста по столбцам
- Вычисления без формул специальной вставкой
- Преобразование текста в числа с помощью надстройки PLEX
Чем число отличается от цифрыЧто такое число, что такое цифра
Число — это количественная характеристика чего-либо. Вначале числа обозначались чёрточками. Но это неудобно: попробуйте безошибочно на неразлинованной бумаге написать двести пятьдесят пять чёрточек. То-то! К счастью, в Индии была придумана десятичная система счисления, позволяющая записывать любое натуральное число при помощи всего десяти знаков!
Некоторые знаки и символы для обозначения что-либо
0 1 2 3 4 5 6 7 8 9 - + × ∙ * : / ∕ ÷ = ≈ ≠ 🙂 🙁 ☀️ 🌥️ 🌧️ 🍎 🍒 🍓
Некоторые математические символы
0 1 2 3 4 5 6 7 8 9 - + × ∙ * : / ∕ ÷ = ≈ ≠
Арабские цифры (всего 10) для обозначения чисел
0 1 2 3 4 5 6 7 8 9
Из чего состоит число
Однозначные числа состоят только из одной цифры
0 1 2 3 4 5 6 7 8 9
Двузначные числа состоят только из двух цифр
10 11 12 13 14 15 16 … 97 98 99
Трёхзначные числа состоят только из трёх цифр
100 101 102 103 104 105 106 … 997 998 999
Четырёхзначные числа состоят только из четырёх цифр
1000 1001 1002 1003 1004 1005 1006 … 9997 9998 9999
…
Для записи числа 255 (Двести пятьдесят пять) нужно всего две цифры: «2» и «5». Цифра «5» используется дважды. Первая правая цифра в числе обозначает количество единиц (пять чёрточек), вторая — количество десятков (пять раз по десять чёрточек), третья — количество сотен (два раза по сто чёрточек), четвёртая — количество тысяч и т. д. Цифра «5» используется дважды. Первая правая цифра в числе обозначает количество единиц (пять чёрточек), вторая — количество десятков (пять раз по десять чёрточек), третья — количество сотен (два раза по сто чёрточек), четвёртая — количество тысяч и т. д.
255 (Двести пятьдесят пять)
| 2
| 5
| 5
|
|---|
| | | | | | | | | | |
| | | | | | | | | | |
| | | | | |
| | | | | | | | | | | |
| | | | | | | | | | |
|
| | | | | | | | | | | |
| | | | | | | | | | |
|
| | | | | | | | | | | |
| | | | | | | | | | |
|
| | | | | | | | | | | |
| | | | | | | | | | |
|
| | | | | | | | | | | |
|
|
| | | | | | | | | | | |
|
|
| | | | | | | | | | | |
|
|
| | | | | | | | | | | |
|
|
| | | | | | | | | | | |
|
|
| |
|
|
| | | | | | | | | | | |
|
|
| | | | | | | | | | | |
|
|
| | | | | | | | | | | |
|
|
| | | | | | | | | | | |
|
|
| | | | | | | | | | | |
|
|
| | | | | | | | | | | |
|
|
| | | | | | | | | | | |
|
|
| | | | | | | | | | | |
|
|
| | | | | | | | | | | |
|
|
| | | | | | | | | | | |
|
|
|
Числа состоят не только из цифр. Также, например, используется символы «минус» или «запятая», отделяющая дробную часть. Также, например, используется символы «минус» или «запятая», отделяющая дробную часть.
Чтение и произношение целых чисел и десятичных дробей
Двести пятьдесят пять целых одна сотая
|
|
|
|
|
|
|
|
|
|
|
| 2
| 5
| 5
| ,
| 0
| 1
|
|
|
|
|
|
|
|---|
| …
| Миллиарды
| |
Сотни миллионов
| Десятки миллионов
| Миллионы
| |
Сотни тысяч
| Десятки тысяч
| Тысячи
| |
Сотни
| Десятки
| Единицы
|
| Десятые
| Сотые
| Тысячные
| |
Десятитысячные
| Стотысячные
| Миллионные
| …
|
После двадцати числа имеют составное наименование.
| 2 | 5 | 6 | | ( | Двести | пятьдесят | шесть | ) | | 2 | 0 | 0 | | ( | Двести | | | ) | | 5 | 0 | | ( | | Пятьдесят | | ) | | | 6 | | ( | | | Шесть | ) |
| 1
| один
| 11
| одиннадцать
| 10
| десять
| 100
| сто
| | 2
| два
| 12
| двенадцать
| 20
| двадцать
| 200
| двести
| | 3
| три
| 13
| тринадцать
| 30
| тридцать
| 300
| триста
| | 4
| четыре
| 14
| четырнадцать
| 40
| сорок
| 400
| четыреста
| | 5
| пять
| 15
| пятнадцать
| 50
| пятьдесят
| 500
| пятьсот
| | 6
| шесть
| 16
| шестнадцать
| 60
| шестьдесят
| 600
| шестьсот
| | 7
| семь
| 17
| семнадцать
| 70
| семьдесят
| 700
| семьсот
| | 8
| восемь
| 18
| восемнадцать
| 80
| восемьдесят
| 800
| восемьсот
| | 9
| девять
| 19
| девятнадцать
| 90
| девяносто
| 900
| девятьсот
|
Число проговаривается по три цифры с соответствующим классом. Можно озвучить очень большие числа. Можно озвучить очень большие числа.
256 (Двести пятьдесят шесть)
256 000 (Двести пятьдесят шесть тысяч)
256 256 (Двести пятьдесят шесть тысяч двести пятьдесят шесть)
2 256 256 (Два миллиона двести пятьдесят шесть тысяч двести пятьдесят шесть)
| ноль
| 0
| 0
| | тысяча
| 103 | 1 000
| | миллион
| 106 | 1 000 000
| | миллиард
| 109 | 1 000 000 000
| | триллион
| 1012 | 1 000 000 000 000
| | квадриллион
| 1015 | 1 000 000 000 000 000
| | квинтиллион
| 1018 | 1 000 000 000 000 000 000
| | секстиллион
| 1021 | 1 000 000 000 000 000 000 000
| | септиллион
| 1024 | 1 000 000 000 000 000 000 000 000
| | октиллион
| 1027 | 1 000 000 000 000 000 000 000 000 000
| | нониллион
| 1030 | 1 000 000 000 000 000 000 000 000 000 000
| | дециллион
| 1033 | 1 000 000 000 000 000 000 000 000 000 000 000
|
В десятичных дробях произносится
- число до запятой,
- слово «целых» или «целая» (подразумевается «целая единица»),
- число после запятой,
- разряд крайней справа цифры (подразумевается «часть единицы»).

256,01 (Двести пятьдесят шесть целых единиц одна сотая часть единицы)
В бесконечных периодических десятичных дробях произносится
- число до запятой,
- слово «целых» или «целая»,
- число после запятой до периода,
- разряд крайней справа цифры перед периодом,
- слово «и»,
- число периода,
- слово «в периоде»
5,(6) (Пять целых и шесть в периоде)
0,1(15) (Ноль целых одна десятая и пятнадцать в периоде)
Классическая запись чисел римскими цифрами
=
До арабских цифр использовали римские цифры. Чтобы не сбиться со счёта при написании чёрточек, выделяли сначала каждую пятую, а затем и каждую десятую чёрточку. Со временем запись «| | | | V | | | | X | | | | V | | | | X | | | | V |» уменьшилась до «XXVI».
Римские цифры, которые имеют большее значение, стоят в числе левее тех, у кого значение меньше. Их значения складываются (VI = 5 + 1 = 6). Цифры «V», «L», «D» не повторяются. Их значения складываются (VI = 5 + 1 = 6). Цифры «V», «L», «D» не повторяются.
Исключения: с XIX века сочетания «IV», «IX», «XL», «XC», «CD», «CM». Во избежание четырёхкратного повторения одной цифры (неверно: «IIII»), в них цифра с большим значением стоит правее цифры с меньшим значением и из большего значения вычитается меньшее (IV = 5 — 1 = 4).
| I
| один
| X
| десять
| C
| сто
| M
| одна тысяча
| | II
| два
| XX
| двадцать
| CC
| двести
| MM
| две тысячи
| | III
| три
| XXX
| тридцать
| CCC
| триста
| MMM
| три тысячи
| | IV
| четыре
| XL
| сорок
| CD
| четыреста
|
|
| | V
| пять
| L
| пятьдесят
| D
| пятьсот
|
|
| | VI
| шесть
| LX
| шестьдесят
| DC
| шестьсот
|
|
| | VII
| семь
| LXX
| семьдесят
| DCC
| семьсот
|
|
| | VIII
| восемь
| LXXX
| восемьдесят
| DCCC
| восемьсот
|
|
| | IX
| девять
| XC
| девяносто
| CM
| девятьсот
|
|
|
| CC | L | VI | | ( | Двести | пятьдесят | шесть | ) | | CC | | | | ( | Двести | | | ) | | L | | | ( | | Пятьдесят | | ) | | | VI | | ( | | | Шесть | ) |
Какими бывают числа (школьная программа)
Натуральные числа — это целые положительные числа, возникшие при счёте предметов
1 2 3 … 98 99 100 …
Простые числа — это натуральные числа, которые делятся без остатка только на два натуральных числа: 1 и само себя (единица не является простым числом)
2 3 5 … 83 89 97 …
Составные числа — это натуральные числа, которые делятся без остатка на три и более натуральных числа (единица не является составным числом)
4 6 8 … 98 99 100 …
Круглые числа — это натуральные числа, которые оканчиваются на 0
10 20 30 … 100 …
Целые числа — это натуральные числа, ноль и числа, противоположные натуральным (отрицательные)
… -100 -99 -98 … -2 -1 0 1 2 … 98 99 100 …
Чётные числа — это целые числа, которые делятся на число 2 без остатка
… -100 -98 -96 … -4 -2 0 2 4 … 96 98 100 …
Нечётные числа — это целые числа, которые не делятся на число 2 без остатка
… -99 -97 -95 … -3 -1 1 3 … 95 97 99 …
Вещественные числа — это рациональные и иррациональные числа
… -100,5 … -5,(6) … -3 … -2 … -2 … -1 … — … -0,1(15) … -0,002 … -0,001 … 0 … 0,001 … 0,002 … 0,1(15) … … 1 … √2 … φ … 2 … e … 2 … 3 … π … 5,(6) … 100,5 …
Рациональные числа — это целые числа, обыкновенные дроби, конечные или бесконечные периодические десятичные дроби, которые можно представить обыкновенной дробью , где числитель m — целое число, а знаменатель n — натуральное число
… -100,5 … -5,(6) … -3 … -2 … -2 … -1 … — … -0,1(15) … -0,002 … -0,001 … 0 … 0,001 … 0,002 … 0,1(15) … … 1 … 2 … 2 … 3 … 5,(6) … 100,5 …
Иррациональные числа — это бесконечные непериодические десятичные дроби, которые нельзя представить обыкновенной дробью
… π … e … φ … √2 …
Обыкновенная (простая) дробь — это запись рационального числа в виде ± или ±m/n, где n ≠ 0
… — … — … — … — … — … — … — … — … — … — … … … … … … … … … … … …
Смешанная дробь — это сумма целого числа отличного от нуля и правильной дроби без знака плюс между ними
… -100 … -5 … -2 … 2 … 5 … -100 …
Правильная дробь — это обыкновенная дробь, которая меньше 1, так как m < n
… - … — … — … — … … … … … …
Неправильная дробь — это обыкновенная дробь, которая равна или больше 1, так как m ≥ n
… — … — … — … — … — … — … … … … … … …
Десятичная дробь — это дробь, представленная в десятичной записи, так как n = 10z, где z — натуральное число
… -100,5 … -5,6666666666… … -2,8 … -0,8571428571… … -0,1151515151… … -0,002 … -0,001 … 0,001 … 0,002 … 0,1(15) … 0,(857142) … 1,4142135623… … 1,6180339887… … 2,7182818284… … 2,8 … 3,1415926535… … 5,(6) … 100,5 …
Конечная десятичная дробь имеет конечное количество цифр после запятой
… -100,5 … -2,8 … -0,002 … -0,001 … 0,001 … 0,002 … 2,8 … 100,5 …
Бесконечная десятичная дробь не имеет конечное количество цифр после запятой
… -5,6666666666… … -0,8571428571… … -0,1151515151… … 0,1(15) … 0,(857142) … 1,4142135623… … 1,6180339887… … 2,7182818284… … 3,1415926535… … 5,(6) …
Бесконечная периодическая десятичная дробь — дробь, у которой начиная с некоторого места после запятой нет иных символов, кроме периодически повторяющейся группы цифр
… -5,6666666666… … -0,8571428571… … -0,1151515151… … 0,1(15) … 0,(857142) … 5,(6) …
Бесконечная непериодическая десятичная дробь
… 1,4142135623… … 1,6180339887… … 2,7182818284… … 3,1415926535… …
Положительные числа — это числа, которые больше нуля (ноль не является положительным числом)
… 0,001 … 0,002 … 0,1(15) … … 1 … √2 … φ … 2 … e … 2 … 3 … π … 5,(6) … 100,5 …
Отрицательные числа — это числа, которые меньше нуля (ноль не является отрицательным числом)
… -100,5 … -5,(6) … -3 … -2 … -2 … -1 … — … -0,1(15) … -0,002 … -0,001 …
Что такое ExtraLoad (XL), обозначение маркировки шин ExtraLoadДанные, обозначающие характеристики шины принято обозначать особым образом. Именно на эту информацию стоит обращать внимание при выборе покрышек. Если разобраться в этом вопросе, расшифровка обозначений маркировки не будет трудной задачей. Именно на эту информацию стоит обращать внимание при выборе покрышек. Если разобраться в этом вопросе, расшифровка обозначений маркировки не будет трудной задачей. Все автомобилисты знают, что данные, обозначающие характеристики шины принято обозначать особым образом. Именно на эту информацию стоит обращать внимание при выборе покрышек. Если разобраться в этом вопросе, расшифровка обозначений маркировки не будет трудной задачей. Индексы нагрузкиПосле указания типоразмера вида на автошине указывается обозначение индекса нагрузки. Это значение индекса в маркировке указывает на предельно допустимую нагрузку на одно колесо. Например, в маркировке 235/60R18 107T, на индекс нагрузки указывает число 107. По принятой классификации, эта цифра говорит о том, что максимальная нагрузка — 975 кг. В некоторых случаях после данных о допустимой нагрузке и скорости, указывается еще одно обозначение — XL. Индекс XL на шинах — говорит о более высокой допустимой нагрузке. Что означает XL в маркировке шинЧасто встречается обозначение индексов XL в виде надписи Extra Load, что с английского переводится как «повышенная нагрузка». Обозначение XL или надписи Extra Load указывают на дополнительную грузоподъемность в 3 единицы. То есть автошины с маркировкой 235/60R18 107T XL выдержат нагрузку 975 кг, а в стандартном исполнении — всего 900. Обозначение XL или надписи Extra Load указывают на дополнительную грузоподъемность в 3 единицы. То есть автошины с маркировкой 235/60R18 107T XL выдержат нагрузку 975 кг, а в стандартном исполнении — всего 900. Иными словами, отвечая на вопрос, что означает XL на шине, можно сказать, что такой показатель указывает на дополнительную нагрузку, которую способна без проблем осилить данная покрышка. Как устроена шина Extra LoadТакое обозначение на боковине автошины указывает на конструктивные особенности и улучшения, позволяющие выдерживать такую нагрузку.. Автошина Extra Load: - обладает усиленной боковиной и каркасом. Это главное улучшение конструкции, позволяющее достичь высоких эксплуатационных характеристик;
- иногда она изготовлена из другой резиновой смеси. Изменения в составе резины позволили сделать ее более жесткой и прочной, а следовательно, и более грузоподъемной.
-
Преимущества шин Extra Load
Покрышки с маркировкой Extra Load помимо большей грузоподъемности обладают целым рядом других достоинств.
Во-первых, повышенной износостойкостью. По этому параметру они превосходят обычную резину. С износостойкими шинами автомобиль можно эксплуатировать несколько сезонов в интенсивном режиме, в поездках на длинные дистанции.
Во-вторых, устойчивостью к механическим повреждениям. Это преимущество особенно актуально в условиях российских дорог.
В третьих, улучшенными характеристиками управляемости. Большая жесткость шины обеспечивает хорошее сцепление с трассой, легкое и предсказуемое вхождение в поворот.
Водители отмечают и некоторые недостатки такой модели: уровень шума, который выше чем у обычной шины, больший расход бензина и понижение комфорта в салоне авто.
Кому стоит купить усиленные автошины
В первую очередь следует заглянуть в руководство по эксплуатации вашего автомобиля и узнать, рекомендует ли его производитель установку такой резины. Чаще всего авторезину с параметром Extra Load устанавливают на грузовые, легкогрузовые автомобили и тяжелые кроссоверы. Также эксплуатация автошин Extra Load оправдана, если: Также эксплуатация автошин Extra Load оправдана, если:
- если вы часто нагружаете машину. Регулярные перегрузки существенно снижают срок эксплуатации авторезины. В этом случае шины с маркировкой XL прослужат вам намного дольше стандартных;
- если у вас автомобиль с мощным двигателем. Резина Extra Load способна обеспечить большую безопасность при маневрировании, разгоне и торможении на высокой скорости.
Что значит XL на шинах Goodyear
XL на боковине автошины Goodyear — это то же самое, что Extra Load. Но в данном случае он означает не только повышенную нагрузку. Производитель Goodyear является одним из лидеров по производству автомобильных покрышек, которые способны сделать каждую поездку безопасной и комфортной. Компания, внедряя инновации и добавляя конструктивные улучшения, старается добавить другие преимущества и минимизировать недостатки.
Поэтому резина Goodyear с маркировкой XL, несмотря на жесткость и усиленный каркас, практически ни чем не отличается от стандартных шин.
Рассмотрим некоторые модели покрышек с повышенной нагрузкой.
Arctic XL Ultragrip Ice от Goodyear
Шины Goodyear Ultragrip Ice Arctic XL предназначены для эксплуатации в зимний сезон условиях низких температур. Они выпускаются во множестве популярных типоразмеров, поэтому вы легко сможете приобрести эту модель для вашего автомобиля.
Максимально допустимая нагрузка на шину Ultragrip Ice Arctic XL — 900 кг1. Такие покрышки устанавливаются на тяжелые внедорожники и легкогрузовые авто. Минимальная — 515 кг, что тоже является хорошим показателем для легкового автомобиля.
Помимо повышенной нагрузки, эти покрышки демонстрируют хорошую тягу на льду, превосходную маневренность, короткий тормозной путь и хорошие показатели сцепления с дорогой.
ExtraLoad модели шинЛетние
Защита дисков
Sound Comfort Рейтинг: 4. 5 5 Шины Goodyear Eagle F1 Asymmetric 3 SUV - Шипы:
- нет
- Диаметр:
- 17 / 18 / 19 / 20 / 21 / 22
Летние
Защита дисков Рейтинг: 4.5 Шины Goodyear EfficientGrip 2 SUV - Шипы:
- нет
- Диаметр:
- 16 / 17 / 18 / 19 / 20 / 21 / 22
- новинка
Зимние
Защита дисков Шины Goodyear UltraGrip Arctic 2 SUV - Шипы:
- да
- Диаметр:
- 17 / 18 / 19 / 20 / 21
- новинка
Зимние
Защита дисков Шины Goodyear UltraGrip Performance+ SUV - Шипы:
- нет
- Диаметр:
- 16 / 17 / 18 / 19 / 20 / 21
Всесезонные
Защита дисков Рейтинг: 5 Шины Goodyear Vector 4Seasons Gen-3 SUV - Шипы:
- нет
- Диаметр:
- 16 / 17 / 18 / 19 / 20
Летние
Защита дисков
Run On Flat Рейтинг: 4 Шины Goodyear Wrangler HP All Weather - Шипы:
- нет
- Диаметр:
- 16 / 17 / 18 / 19
Летние
Защита дисков Рейтинг: 4. 5 5 Шины Goodyear EfficientGrip SUV - Шипы:
- нет
- Диаметр:
- 16 / 17 / 18 / 19 / 20 / 21 / 22
Летние
Защита дисков
Run On Flat Рейтинг: 4 Шины Goodyear Eagle F1 Asymmetric SUV - Шипы:
- нет
- Диаметр:
- 17 / 18 / 19 / 20 / 22
Goodyear EfficientGrip XL
Маркировка XL на шине Goodyear EfficientGrip EfficientGrip Compact показывает их способность выдерживать нагрузку от 462 до 900 кг (в зависимости от типоразмера покрышки). Эта летняя автошина обладает не только усиленным каркасом, но и другими технологическими улучшениями. Эта летняя автошина обладает не только усиленным каркасом, но и другими технологическими улучшениями.
Отдельно стоит отметить топливную экономичность данной модели. Несмотря на обозначения Extra Load на покрышках, которое говорит о большем весе и жесткости резины, расход топлива при эксплуатации EfficientGrip снижается почти на 2% по сравнению с аналогичными продуктами других брендов. Это подтвердила независимая экспертиза немецкой компании TUV SUD Automotive. По результатам теста журнала «За рулем», проведенному ранней осенью 2015 года, эти шины были признаны лучшими в номинации «Комфорт». Покрышки показали отличное сцепление и на сухой, и на мокрой дороге.
Vector 4Seasons Gen-2 XL
Обозначение индексов повышенной нагрузки присутствует и на этих популярных всесезонных автошинах нового поколения. Покрышки Vector 4Seasons Gen-2 способны выдержать вес от 475 до 875 кг. Показатель максимальной нагрузки, так же, как и у других моделей, зависит от типоразмера. Больший — для кроссоверов, меньший — для легковушек. Больший — для кроссоверов, меньший — для легковушек.
Особенный состав резиновой смеси SmartTRED, отличное сцепление с трассой, высокая прочность и износостойкость, особый рисунок протектора для безопасного вождения в зимний период — основные преимущества этой модели.
Другие модели
Обозначение XL на резине Goodyear присутствует и на других, не менее востребованных моделях зимних, летних и всесезонных автошин:
- Eagle LS-2,
- Wrangler AT/SA+,
- Wrangler All-Terrain Adventure with Kevlar,
- Eagle F1 Asymmetric 3,
- Wrangler HP All Weather,
- Ultragrip 9,
- и других.
Из линейки Goodyear вы легко сможете подобрать модель с параметром Extra Load, соответствующую вашему стилю езды и условиям, в которых обычно эксплуатируется автомобиль. Все эти покрышки представлены в разных типоразмерах, нужный вариант найдется и для малолитражки, и для внедорожника, и для микроавтобуса.
1 Допустимая нагрузка указан для шины 235/55R18 104T UG ICE 2 MS XL FP
XL Римские цифры | Как написать XL цифрами? LearnPracticeDownload XL Римские цифры можно записать в виде чисел, комбинируя преобразованные римские цифры, т. е. XL = (L — X) = (50 — 10) = 40. Старшие римские цифры предшествуют младшим цифрам, что обеспечивает правильный перевод XL римские цифры. В этой статье мы объясним, как преобразовать римские цифры XL в правильный перевод числа. Как писать римские цифры XL? Числовое значение римских цифр XL можно получить, используя любой из двух методов, приведенных ниже: Метод 1: В этом методе мы разбиваем римские цифры на отдельные буквы, пишем числовое значение каждой буквы и добавить/убрать их. - XL = (L — X) = (50 — 10) = 40
Метод 2: В этом методе мы рассматриваем группы римских цифр для сложения или вычитания, например, Следовательно, числовое значение римских цифр XL равно 40. ☛ Также проверьте: Калькулятор римских цифр Каковы основные правила написания римских цифр?- Когда буква большего размера предшествует букве меньшего размера, буквы добавляются. Например: XI, X > I, поэтому XI = X + I = 10 + 1 = 11
- Когда буква меньшего размера предшествует букве большего размера, буквы вычитаются. Например: IV, I < V, поэтому IV = V - I = 5 - 1 = 4
- Когда буква повторяется 2 или 3 раза, они добавляются. Например: III = I + I + I = 1 + 1 + 1 = 3
- Одну и ту же букву нельзя использовать более трех раз подряд.
Числа, связанные с римскими цифрами XL Римские цифры использовались в Древнем Риме и представляли собой комбинации букв латинского алфавита I, V, X, L, C, D и M. Может показаться, что они отличаются от цифр, но они похожи. Например, римские цифры XL эквивалентны числу 40. Римские цифры, относящиеся к XL, приведены ниже: - XL = 40
- XLI = 40 + 1 = 41
- XLII = 40 + 2 = 42
- XLIII = 40 + 3 = 43
- XLIV = 40 + 4 = 44
- XLV = 40 + 5 = 45
- XLVI = 40 + 6 = 46
- XLVII = 40 + 7 = 47
- XLVIII = 40 + 8 = 48
- XLIX = 40 + 9 = 49
Примеры римских цифр XL Пример 1. Найдите сумму MMCMLI и XL римских цифр. Найдите сумму MMCMLI и XL римских цифр. Решение: MMCMLI = 2000 + 900 + 50 + 1 = 2951 и XL = 40
Теперь MMCMLI + XL = 2951 + 40 = 2991
.
Так как MMCMXCI = 2000 + 900 + 90 + 1 = 2991
Следовательно, сумма MMCMLI и римских цифр XL равна MMCMXCI . Пример 2: Найдите разницу между XL и VIII. Решение: Римская цифра XL равна 40, а VIII равна 8.
Теперь XL — VIII = 40 — 8 = 32
Так как 32 = XXXII
Следовательно, XL — VIII = XXXII . Пример 3. Найдите частное 40 и 26. Решение: Римская цифра XL равна 40, а XXVI равна 26.
Теперь, когда мы делим XL на XXVI, т.е. 40 ÷ 26, в частном получается 1.
Так как 1 = I
Следовательно, XL ÷ XXVI = I Пример 4. Найдите произведение римских цифр XL и LXXXVIII. Решение: XL = 40 и LXXXVIII = 80 + 8 = 88
Теперь XL × LXXXVIII = 40 × 88 = 3520
. Так как MMMDXX = 3000 + 500 + 20 = 3520 Так как MMMDXX = 3000 + 500 + 20 = 3520
Следовательно, XL × LXXXVIII = MMMDXX .
перейти к слайдуперейти к слайдуперейти к слайдуперейти к слайду Готовы увидеть мир глазами математика? Математика лежит в основе всего, что мы делаем. Наслаждайтесь решением реальных математических задач на живых уроках и станьте экспертом во всем. Записаться на бесплатный пробный урок Часто задаваемые вопросы о римских цифрах XL Каково значение римских цифр XL? Напишем XL римскими цифрами в развернутом виде, чтобы определить его номинал. XL = 40. Следовательно, значение римских цифр XL равно 40. Сколько будет остатка при делении XL на XVIII? XL = 40 и XVIII = 18 цифрами. При делении 40 на 18 получается остаток 18. Теперь 4 = IV. Следовательно, когда XL делится на XVIII, остаток равен IV. Как римские цифры XL пишутся цифрами? Чтобы преобразовать римские цифры XL в числа, необходимо разбить римские цифры на основе разрядности (единицы, десятки, сотни, тысячи), например: - Десятки = 40 = XL
- Номер = 40 = XL
Почему 40 пишется римскими цифрами как XL? Мы знаем, что римскими цифрами 40 записывается как XL. Поэтому 40 римскими цифрами записывается как XL = 40. Поэтому 40 римскими цифрами записывается как XL = 40. Что нужно вычесть из XL, чтобы получить X? Сначала запишем XL и X цифрами, т.е. XL = 40 и X = 10. Теперь 40 — 10 = 30. А 30 = XXX. Следовательно, нужно вычесть XXX из римских цифр XL, чтобы получить X. ☛ Статьи по теме: - CLXIX Римские цифры — 169
- MCVII Римские цифры — 1107
- Римские цифры CVIII — 108
- DXXVII Римские цифры — 527
- MMDCC Римские цифры — 2700
- CMXXXVIII Римские цифры — 938
Рабочие листы по математике и
наглядный учебный план Шаги по преобразованию чисел с помощью правил XL представляет число 40 римскими цифрами. Римские цифры XL постоянно задают во многих MCQ различных экзаменов. В этой статье мы узнаем о том, как считать XL римскими цифрами прописью и цифрами различными способами, как писать римские цифры, и правилах преобразования римских цифр в числа и наоборот вместе с решенными примерами и часто задаваемыми вопросами. . . Что такое римские цифры? Числа, использовавшиеся в Древнем Риме, представляли собой римские цифры, состоящие из букв латинского алфавита (I, V, X, L, C, D и M). Символы расположены в многочисленных комбинациях и в разном порядке для представления чисел. После этого символы соединяются вместе, например, I + I + I равно III. Мы добавляем X (10) и I (1), чтобы получить 11, и запишем это как XI. Мы пишем 22, добавляя X и X и I и I, получая XXII. Мы обозначаем 40, используя римскую цифру XL. | Roman Numerals Symbols and Numbers | | Symbol | I | V | X | L | C | D | M | | Number | 1 | 5 | 10 | 50 | 100 | 500 | 1000 |
XL Римские цифры xl в романе. XL Римские цифры постоянно задают во многих MCQ различных экзаменов. Вопросы могут заключаться в преобразовании римских цифр XL в числа или в римских цифр XL в слова или наоборот. Вопросы могут заключаться в преобразовании римских цифр XL в числа или в римских цифр XL в слова или наоборот. Таблица римских цифр Римские цифры используют символы вместо цифр. Каждая цифра представляет собой число, которое необходимо вычислить или вычесть в зависимости от его положения, чтобы узнать окончательное число. Вот стандартный список римских цифр с их расчетами. Он также включает значение XL римских цифр. 0 |
0 2 . | 1000-50-10-1-1-1-1 | 3
0 29026. | | 1000-50-10-1-1-1-1 | 3 | | . Значение XL Roman можно рассчитать, используя метод сложения римских цифр. Во-первых, мы должны написать числовое значение каждого символа или буквы. Путем сложения этих цифр вычисляется значение XL римской цифры . Этого можно добиться несколькими способами, как описано ниже:
XL Римские цифры методом расширения
Чтобы использовать этот метод, вычислите значение каждой цифры и сложите его, чтобы найти окончательное значение.
Значение римских цифр XL = 50 – 10 = 40
Римские цифры XL по методу группировки
В этой системе числовые значения групп букв учитываются для сложения.
Значение римских цифр XL = (L) – (X) = 50 – 10 = 40
Это было сделано для римских цифр XL в цифрах. Вы можете выполнить те же действия для любого числа.
Основные правила преобразования римских цифр в числа
Все римские цифры состоят из семи символов. Эти комбинации соответствуют четырем ключевым принципам. Для римской системы счисления необходимо соблюдать четыре важных правила. В этом разделе мы узнаем о них с их приложением
Правило 1 : Когда меньший символ находится после большего символа, он добавляется.
Например,
XI = 10 + 1 = 11
Правило 2: Если после себя идет символ, он добавляется.
Например,
XX = 10 + 10 = 20
CCLX = 100 + 100 + 50 + 10 = 260
Правило 3: Когда меньший символ появляется перед большим символом, он вычитается.
Например,
IX = 10 – 1 = 9
XL= 50 – 10 = 40
CM = 1000 – 100 = 900
Правило 4 не может использоваться более трех раз : строка.
Например,
XXX = 10 + 10 + 10 = 30, но 40 не является ХХХХ. 40 это ХL.
ССС = 100 + 100 + 100 = 300, но 400 — это не ССС. 400 это компакт-диск.
Преобразование XL в цифру
Внимательно посмотрите на эту римскую цифру.
XL
Найдите значение каждого символа в римской цифре, а затем добавьте или вычтите эти значения, чтобы преобразовать их в цифры.
Давайте попробуем прямо сейчас!
Начнем с определения стоимости каждого символа.
Х – 10
L – 50
Это связано с тем, что такие числа необходимо вычитать (правило 3).
Правило 3 повторяется еще раз:
Правило 3: Когда меньший символ появляется перед большим символом, он вычитается.
Теперь складываем и вычитаем значения.
XL = 50 – 10
Итак, каково значение этой римской цифры?
Правильно!
XL = 40
XL Римские цифры в словах
Чтобы написать XL римские цифры, мы должны сначала преобразовать их в числа. Мы это уже сделали выше. Мы знаем, что XL римскими цифрами — это число 40. Теперь запишем его словами. Во-первых, узнать места цифр.
Теперь запишем его словами. Во-первых, узнать места цифр.
Десятки: 4
Единицы: 0
Теперь расширим число, добавив 0 к разряду десятков и прибавив к нему цифру в одном разряде.
Таким образом, мы получаем расширенную форму XL римских цифр в числах как 40 + 0.
Теперь назовем каждое число. Мы знаем, что 40 означает сорок. Следовательно, XL римскими цифрами прописью будет сорок. Это было сделано для XL римских цифр прописью. Вы можете выполнить те же действия для любого числа.
Номера близкие к XL
Ниже приведены номера близкие к XL. Правый столбец показывает, как каждая римская цифра составляет общую сумму.
| Number | Roman Numeral | Division |
| 36 | XXXVI | 10 + 10 + 10 + 5 + 1 |
| 37 | XXXVII | 10 + 10 + 10 + 5 + 2 |
| 38 | XXXVIII | 10 + 10 + 10 + 5 + 3 |
| 39 | XXXIX | 10 + 10 + 10 + 10 – 1 |
| 40 | XL | 10 + 10 + 10 + 10 |
| 41 | XLI | 10 + 10 + 10 + 10 + 1 |
| 42 | XLII | 10 + 10 + 10 + 10 + 1 + 1 | 2
| 43 | XLIII | 10 + 10 + 10 + 1 + 1 + 1 |
| 44 | 92223 |
| 44 | 22252223
| 44 | 2222223
. 5 – 1
5 – 1
Также узнайте о векторной алгебре здесь.
Solved Examples on XL Roman Numerals
Solved Example: Solve the following addition problems on roman numerals
- MMCCCLXXXIX + MCDXXXIX
- MCMXCV + MCCLXXXVIII
- CMXXVI + MMDCXCIV
- MDXVII + MDIII
- CCXLIX + MMCCL
- CCII + MMCCCLXXII
- DCCXCVIII + MMCXLI
- CDXX + MMCCLXIX
- CMLXVII + MDCCCLXI
- MDXLIII + MMCDLIV
Решения0016
- MMCCCLXXXIX + MCDXXXIX = 2389 + 1439 = 3828
- MCMXCV + MCCLXXXVIII = 1995 + 1288 = 3283
- CMXXVI + MMDCXCIV = 926 + 2694 = 3620
- MDXVII + MDIII = 1517 + 1503 = 3020
- CCXLIX + MMCCL = 249 + 2250 = 2499
- CCII + MMCCCLXXII = 202 + 2372 = 2574
- DCCXCVIII + MMCXLI = 798 + 2141 = 2939
- CDXX + MMCCLXIX = 420 + 2269 = 2939
- CDXX + MMCCLXIX = 420 + 2269 = 2939
- .
 2828
2828 - MDXLIII + MMCDLIV = 1543 + 2454 = 3997
Решено Пример: Преобразуйте следующие римские числа в целые числа.
- LVIII
- MCMXCIV
Решение:
LVIII
Объяснение: L = 50, V = 5, III = 3. +
LVIII 900
LVIII = 58.
MCMXCIV
Объяснение: M = 1000, CM = 900, XC = 90 и IV = 4.
MCMXCIV = 1000 + 900 + 90 + 4
MCMXCIV = 1994.
. Пример: Найдите римские цифры для следующего: CDIV и \(\bar{X}\)
Решение:
C = 100 меньше, чем D = 500, поэтому вычтите значения.
CD = 500 – 100 = 400
I = 1 меньше, чем V = 5, поэтому вычтите значения.
IV = 5 – 1 = 4
Сложите значения.
CDIV = CD + IV = 400 + 4 = 404
CDIV = 404
X = 10
Поскольку наверху есть черта, умножьте значение на 1000.
\(\)\bar{X}\(\)= 10 × 1000 = 10000
\(\)\bar{X}\(\) = 10000
Надеюсь, что эта статья о римских цифрах XL была информативной. Попрактикуйтесь в том же в нашем бесплатном приложении Testbook. Скачать сейчас!
Попрактикуйтесь в том же в нашем бесплатном приложении Testbook. Скачать сейчас!
XL Часто задаваемые вопросы о римских цифрах
В.1. Существует ли римская цифра XXL?
Ans.1 Да, мы можем использовать римскую цифру XXL для обозначения 30.
Q.2 Сколько XL в цифре?
Ответ 2 Мы можем использовать римскую цифру XL для обозначения 40.
Q.3 Сколько XXIX в цифре?
Ответ 3 Мы можем использовать римскую цифру XXIX для обозначения 29.
Q.4 Что означает XXVI в цифре?
Ответ 4 Мы можем использовать XXVI римскую цифру для обозначения 26.
Q.5 Что означает XIX в цифре?
Ответ 5 Мы можем использовать римскую цифру XIX для обозначения 19.
Q.6 Что такое XVI в цифре?
Ответ 6 Мы можем использовать римскую цифру XVI для обозначения 16.
Скачать публикацию в формате PDF Римские цифры 1-100 Таблица
Римские цифры 1-100 Таблица Главная›Математика›Математические символы› Таблица римских цифр 1-100
Список римских цифр / чисел от 1 до 100.
I=1, V=5, X=10, L=50, C=100
| Номер | Римская
Цифра | Расчет |
|---|
| 0 | не
определенный | |
| 1 | я | 1 |
| 2 | II | 1+1 |
| 3 | III | 1+1+1 |
| 4 | IV | 5-1 |
| 5 | В | 5 |
| 6 | ВИ | 5+1 |
| 7 | VII | 5+1+1 |
| 8 | VIII | 5+1+1+1 |
| 9 | IX | 10-1 |
| 10 | х | 10 |
| 11 | XI | 10+1 |
| 12 | XII | 10+1+1 |
| 13 | XIII | 10+1+1+1 |
| 14 | XIV | 10-1+5 |
| 15 | XV | 10+5 |
| 16 | XVI | 10+5+1 |
| 17 | XVII | 10+5+1+1 |
| 18 | XVIII | 10+5+1+1+1 |
| 19 | XIX | 10-1+10 |
| 20 | ХХ | 10+10 |
| 21 | ХХI | 10+10+1 |
| 22 | XXII | 10+10+1+1 |
| 23 | XXIII | 10+10+1+1+1 |
| 24 | XXIV | 10+10-1+5 |
| 25 | ХХV | 10+10+5 |
| 26 | ХХVI | 10+10+5+1 |
| 27 | ХХVII | 10+10+5+1+1 |
| 28 | ХХVIII | 10+10+5+1+1+1 |
| 29 | XXIX | 10+10-1+10 |
| 30 | ХХХ | 10+10+10 |
| 31 | XXXI | 10+10+10+1 |
| 32 | XXXII | 10+10+10+1+1 |
| 33 | XXXIII | 10+10+10+1+1+1 |
| 34 | XXXIV | 10+10+10-1+5 |
| 35 | ХХХV | 10+10+10+5 |
| 36 | XXXVI | 10+10+10+5+1 |
| 37 | ХХXVII | 10+10+10+5+1+1 |
| 38 | XXXVIII | 10+10+10+5+1+1+1 |
| 39 | XXXIX | 10+10+10-1+10 |
| 40 | XL | 50-10 |
| 41 | XLI | 50-10+1 |
| 42 | XLII | 50-10+1+1 |
| 43 | XLIII | 50-10+1+1+1 |
| 44 | XLIV | 50-10-1+5 |
| 45 | XLV | 50-10+5 |
| 46 | XLVI | 50-10+5+1 |
| 47 | XLVII | 50-10+5+1+1 |
| 48 | XLVIII | 50-10+5+1+1+1 |
| 49 | XLIX | 50-10-1+10 |
| 50 | л | 50 |
| 51 | ЛИ | 50+1 |
| 52 | ЛИИ | 50+1+1 |
| 53 | ЛИИ | 50+1+1+1 |
| 54 | ЛИВ | 50-1+5 |
| 55 | ЛВ | 50+5 |
| 56 | LVI | 50+5+1 |
| 57 | LVII | 50+5+1+1 |
| 58 | ЛВIII | 50+5+1+1+1 |
| 59 | ЛИКС | 50-1+10 |
| 60 | ЛХ | 50+10 |
| 61 | LXI | 50+10+1 |
| 62 | LXII | 50+10+1+1 |
| 63 | LXIII | 50+10+1+1+1 |
| 64 | LXIV | 50+10-1+5 |
| 65 | LXV | 50+10+5 |
| 66 | LXVI | 50+10+5+1 |
| 67 | LXVII | 50+10+5+1+1 |
| 68 | LXVIII | 50+10+5+1+1+1 |
| 69 | LXIX | 50+10-1+10 |
| 70 | LXX | 50+10+10 |
| 71 | LXXI | 50+10+10+1 |
| 72 | LXXII | 50+10+10+1+1 |
| 73 | LXXXIII | 50+10+10+1+1+1 |
| 74 | LXXIV | 50+10+10-1+5 |
| 75 | LXXV | 50+10+10+5 |
| 76 | LXXVI | 50+10+10+5+1 |
| 77 | LXXVII | 50+10+10+5+1+1 |
| 78 | LXXVIII | 50+10+10+5+1+1+1 |
| 79 | LXXXIX | 50+10+10-1+10 |
| 80 | LXXX | 50+10+10+10 |
| 81 | LXXXI | 50+10+10+10+1 |
| 82 | LXXXII | 50+10+10+10+1+1 |
| 83 | LXXXIII | 50+10+10+10+1+1+1 |
| 84 | LXXXIV | 50+10+10+10-1+5 |
| 85 | LXXXV | 50+10+10+10+5 |
| 86 | LXXXVI | 50+10+10+10+5+1 |
| 87 | LXXXVII | 50+10+10+10+5+1+1 |
| 88 | LXXXVIII | 50+10+10+10+5+1+1+1 |
| 89 | LXXXIX | 50+10+10+10-1+10 |
| 90 | ХС | 100-10 |
| 91 | XCI | 100-10+1 |
| 92 | XCII | 100-10+1+1 |
| 93 | XCIII | 100-10+1+1+1 |
| 94 | XCIV | 100-10-1+5 |
| 95 | XCV | 100-10+5 |
| 96 | XCVI | 100-10+5+1 |
| 97 | XCVII | 100-10+5+1+1 |
| 98 | XCVIII | 100-10+5+1+1+1 |
| 99 | XCIX | 100-10-1+10 |
| 100 | С | 100 |
Преобразователь римских цифр ►
См.
 также
также- Таблица римских цифр
- Римская цифра для распечатки
- символы греческого алфавита
- Преобразователь римских цифр
- Как преобразовать число в римские цифры
- Как преобразовать римские цифры в число
- Преобразователь даты в римские цифры
- Сколько будет 4 римскими цифрами
- Сколько будет 5 римскими цифрами
- Сколько будет 6 римскими цифрами
- Сколько будет 9 римскими цифрами
- римские цифры 1-20 схема
- Римские цифры 1-10 диаграмма
- Математические символы
- Электрические символы
Напишите как улучшить эту страницу
МАТЕМАТИЧЕСКИЕ СИМВОЛЫ
- Основные математические символы
- символы алгебры
- Символы геометрии
- Статистические символы
- Логические символы
- Набор символов
- Символы исчисления
- Числовые символы
- Греческие символы
- Римские цифры
RAPID TABLES
- Рекомендовать сайт
- Отправить отзыв
- О
претензий | АХА XL
Сообщение о новой претензии
Загрузите форму отчета о претензиях (отправьте заполненную форму по электронной почте или по почте на адрес электронной почты или почтовый адрес, указанный ниже, в зависимости от вашего региона/страны)
Скачать форму подачи претензии
Отслеживание существующих претензий / Общий запрос претензий
Загрузите форму запроса претензий (отправьте по электронной почте или по почте заполненную форму на адрес электронной почты или почтовый адрес, указанный ниже, в зависимости от вашего региона/страны)
Скачать форму запроса претензии
Доступные онлайн-сервисы
Для клиентов или брокеров, использующих наши онлайн-инструменты подачи претензий, нажмите следующую ссылку, чтобы получить доступ к экрану входа в систему.
AccessXL
Информационная панель клиента ACS
Если вы являетесь клиентом или брокером и у вас есть вопрос о доступных онлайн-инструментах для обработки претензий, обратитесь к своему контактному лицу по работе с претензиями или андеррайтингу.
Когда вы покупаете страховой полис, вы покупаете обещание. Мы обещаем предоставить исключительный опыт рассмотрения претензий. Благодаря глобальному присутствию AXA XL, культуре обслуживания и непревзойденному опыту мы будем рядом с вами, где бы и когда бы вы ни нуждались в нас.
- Глобальный охват, местные возможности — Наши специалисты по урегулированию убытков обеспечивают бескомпромиссно высокий уровень обслуживания и могут управлять покрытыми убытками в более чем 200 странах и территориях. Мы понимаем нюансы и уникальные проблемы местных юрисдикций и уполномочены на местном уровне рассматривать и разрешать претензии быстро и справедливо.
- Индивидуальное обслуживание, активный партнер — Мы применяем индивидуальный подход к работе с клиентами и брокерами, чтобы лучше узнать ваш бизнес, активно делиться идеями и лучше сотрудничать с вами.
 Мы берем на себя ответственность и ценим ваше мнение о том, все ли мы делаем правильно и как мы можем сделать это лучше.
Мы берем на себя ответственность и ценим ваше мнение о том, все ли мы делаем правильно и как мы можем сделать это лучше. - Специализированный опыт, ориентированный на решение проблем — Мы стремимся к совершенству во всем, что мы делаем. Наши опытные специалисты по урегулированию претензий специализируются по направлениям бизнеса, отрасли и региону. Мы применяем наш опыт для наших клиентов и остаемся сосредоточенными на урегулировании на всех этапах жизненного цикла претензий.
Истории клиентов
«Я бы сказал, что AXA XL демонстрирует сильную финансовую устойчивость и сервисных возможностей , при этом тратя времени на то, чтобы понять нас , что является для нас ключевым критерием».
Менеджер по управлению рисками
Истории клиентов
«Они требуют времени, чтобы понять наш бизнес и нуждаются в и , как правило, реагирующих на них. Они делают то, что нам нужно везде, где нам это нужно, и делают хорошую работу , объединяя команду за этим. Менеджер по работе с клиентами и андеррайтеры , которые у нас есть, это очень хороший и прозрачный ».
Они делают то, что нам нужно везде, где нам это нужно, и делают хорошую работу , объединяя команду за этим. Менеджер по работе с клиентами и андеррайтеры , которые у нас есть, это очень хороший и прозрачный ».
Менеджер по управлению рисками
Истории клиентов
«AXA XL намного лучше, чем их аналоги по каждому из наших критериев выбора оператора: глобальный масштаб, гибкость в том, как мы структурируем программы, сильный технический опыт и способность выполнять все типы административных действий . ”
Менеджер рисков
Истории клиентов
«AXA XL выступает за партнерство и непрерывность , всегда готовая быть партнером и предоставлять решения для обеспечения непрерывности бизнеса».
Менеджер по управлению рисками
Истории клиентов
«Их скамейка глубокая, с множеством талантливых людей , которые не просто умны, но и люди, которыми вы можете наслаждаться проводит время с , а некоторые даже называют их друзьями».
Менеджер по управлению рисками
Истории клиентов
«AXA XL означает честность , финансовую устойчивость, заботу о клиентах, ценность личных отношений и долгосрочный стратегический партнер ».
Менеджер по управлению рисками
Свидетельство службы претензий
«Профессионалы AXA XL Claims всегда оперативно реагируют и понимают, как крупная компания управляет своими претензиями. Не могу не рассказать, как AXA XL помогает мне быть информированным и подготовленным при обсуждении вопросов страхования с топ-менеджером моей компании».
Менеджер по рискам
Свидетельство службы претензий
«AXA XL Claims — одна из самых профессиональных, вежливых и квалифицированных команд, с которыми я работаю. Я работаю в крупной брокерской компании и работаю со всеми перевозчиками, и я могу с уверенностью сказать, что мои отношения с людьми из AXA XL Claims всегда на высшем уровне и являются одними из самых впечатляющих в отрасли. Спасибо!»
Брокер
Свидетельство службы претензий
«14 лет и несколько сотен транзакций, никогда не ожидаешь, что это случится с тобой. Я был чрезвычайно напряжен этой ситуацией, но от первого звонка в претензии XL Catlin (AXA XL), который был похож на призыв в кавалерию, до моего взаимодействия с адвокатом, назначенным для моего дела до завершения, мой опыт был таким же положительным и как приятно, как это могло бы быть в этих обстоятельствах. Я благодарен, что XL Catlin (AXA XL) пришел на помощь. Спасибо!»
Я благодарен, что XL Catlin (AXA XL) пришел на помощь. Спасибо!»
Застрахованный
Что такое размер XL в цифрах? — WhoMadeWhat
Размеры
| Письмо (США | Цифровой | Франция |
|---|
| Л | 14 | 46 |
| ХL | 16 | 48 |
| ХL | 18 |
50
|
| ХХL | 20 | 52 |
Аналогично, какой размер XL?
Таблица размеров
| |
Очень большой
(XL) |
|---|
| Сундук: | Дюймы | 44-46 |
| Сантиметры | 112-117 |
| Талия: | Дюймы | 40-42 |
| Сантиметры | 102-107 |
Кроме того, является ли размер 42 XL? Грудь для рубашки размера XXL составляет 52,5 дюйма, а воротник/шея для размера XXL составляет 46 см.
…
Преобразователь размера рубашки (буква в цифру)
| Письмо (средство) | Номер | Шея |
|---|
| Размер L (большой) | 42 Размер | 42 см |
| Размер L (большой) | 43 Размер | 43 см |
| Размер XL (очень большой) | 44 Размер | 44 см |
| Размер XL (очень большой) | 45 Размер | 45 см |
Сопутствующее содержимое
- 1 Размер 14 такой же, как XL?
- 2 Является ли размер 36 XL?
- 3 Что такое XL в одежде?
- 4 Какой размер 42 это?
- 5 Какой 42 размер в одежде?
- 6 Какой размер 42 в США?
- 7 Размер 14 большой?
- 8 Женский размер 14 большой или очень большой?
- 9 14 – это плюс?
- 10 Какой размер 36?
- 11 Талия 36 больше размера XL?
- 12 Какой размер XL в Великобритании?
- 13 Что такое размер XL и XXL?
- 14 Какой размер XL в Австралии?
- 15 ЕС и его размер одинаковы?
- 16 Какой размер 42 в Великобритании?
- 17 Какой размер евро 42 в Австралии?
- 18 Какой размер 42 в женской одежде Великобритании?
- 19 Что такое 42 размер в Австралии?
- 20 Что такое 42-й размер в США для женщин?
- 21 Какой мужской размер 42 в США?
- 22 Что такое 42 размер женской одежды в США?
Размер 14 такой же, как XL?
Мы, возможно, привыкли к постоянному сокращению и смене между S и M, но большинство из нас согласны с тем, что размера 14 ни в коем случае не является XL , как это было описано в руководстве по размерам Asos на этой неделе. …
…
Размер 36 – это XL?
– ОДЕЖДА ДЛЯ РЕГАТ И КРАГОППЕРОВ –
| верхняя часть брюк. . . . | С | XL |
|---|
| 10 | 22 |
| Объем талии в дюймах | 24 | 36 |
| Объем талии в сантиметрах | 61 | 91 |
| Французский/Евро | С/36-38 | XL/48-50 |
Что такое XL в одежде? «L» (большой), «XL» ( очень большой ), «XXL» (очень большой). Чтобы быстро и правильно подобрать подходящий размер, загляните в наш блог «Как определить правильный размер одежды при покупках в Интернете».
Какой размер 42 это? РАЗМЕР МУЖСКОЙ ОБУВИ
| ИТ |
40
| 42 |
|---|
| Великобритания | 6 | 8 |
| ЕС | 40 | 42 |
| США | 7 | 9 |
| JP | 25 | 27 |
Какой размер 42 в одежде? Международная таблица размеров одежды
| США и Канада | Великобритания | Европа |
|---|
| 8 | 10 | 38 |
| 10 | 12 | 40 |
12
|
14
| 42 |
| 14 | 16 | 44 |
Какой размер 42 в США? Таблица размеров обуви
| Размеры США | Евро размеры | Дюймы |
|---|
| 8 | 41 | 9,9375″ |
| 8,5 | 41-42 | 10,125″ |
| 9 | 42 |
10,25″
|
| 9,5 | 42-43 | 10,4375″ |
Размер 14 большой? L означает «большой» и приблизительно соответствует женским размерам от 12 до 14 .
Женский размер 14 большой или очень большой? | Женщины/Девочки |
|---|
| Женщины (размер платья) | Девушки (размер одежды) |
|---|
Большой
|
12-14
| 12-14 |
| Большой | 14-16 | 11–14 лет (до подросткового возраста) |
| Плюс | 18-22 | 7-10 (Хаски) |
Является ли 14 большим размером? «Плюс-сайз» — это расплывчатое слово для описания размеров женщин и одежды. … Некоторые департаменты могут обозначать размер 12 как размер плюс, в то время как другие используют размер 14. Но, согласно Modeling Wisdom, модели размера плюс часто попадают в диапазон размеров от 8 до 12. Иногда можно рассматривать даже размер 6.
Какой размер 36? Женские размеры
| Размеры США | Евро размеры | Дюймы |
|---|
| 5,5 | 36 |
8,75″
|
| 6 | 36-37 | 8,875″ |
| 6,5 | 37 | 9,0625″ |
| 7 | 37-38 | 9,25″ |
Талия 36 больше размера XL? Размеры мужских брюк (обхват талии)
| Размер | Талия в дюймах | Талия в сантиметрах |
|---|
| Л | 34-36 | 86-91 |
XL
|
36
-38 | 91-96 |
| ХХL | 40-44 | 101-111 |
| 3XL | 46-50 | 117-127 |
Какой размер XL в Великобритании? Размеры женской одежды
| Британские размеры | Европейские размеры |
|---|
| 18 | 46 |
| ХL | 20 |
48
|
|
22
| 50 |
| ХХL | 24 | 52 |
Что такое размер XL и XXL? Таблица размеров
| Размеры в дюймах | Бюст | Талия |
|---|
| Л | 38 | 32 |
| ХL | 42 | 34 |
XXL
|
44
|
36
|
| XXXL | 46 | 38 |
Какой размер XL в Австралии? Женская одежда
| Размер | Бюст (см) |
|---|
| 4 | | 76 |
|---|
| 16 | ХL |
103
|
| 18 | ХХL | 109 |
| 20 | 3XL | 115 |
ЕС и его размеры одинаковы? «IT» и «EU» обычно являются взаимозаменяемыми и отражают этот диапазон размеров 34-48 как для женщин, так и для мужчин. Подавляющее большинство дизайнерской обуви соответствует итальянским/европейским размерам, потому что они производятся в Италии, Испании, Португалии или другой части континентальной Европы.
Подавляющее большинство дизайнерской обуви соответствует итальянским/европейским размерам, потому что они производятся в Италии, Испании, Португалии или другой части континентальной Европы.
Какой размер 42 в Великобритании? Таблица преобразования размеров обуви
| Размеры США | Евро размеры | Британские размеры |
|---|
| 8 | 41 | 7,5 |
| 8,5 | 41-42 | 8 |
| 9 | 42 |
8,5
|
| 9,5 | 42-43 | 9 |
Какой размер евро 42 в Австралии? Размеры женской обуви
| Австралия | Великобритания | |
|---|
| евро
4 | 2 | 34 |
|---|
| 9,5 | 7,5 | 41 |
| 10 | 8 | 42 |
10,5
|
8,5
| 42. 5 5 |
Какой размер 42 в женской одежде Великобритании? Размеры женской одежды
| Британские размеры | Европейские размеры |
|---|
| 10 | 38 |
| М | 12 | 40 |
|
14
| 42 |
| Л | 16 | 44 |
Какой размер 42 в Австралии? Размеры женской обуви
| Австралия | Великобритания | |
|---|
9 евро1615
4| 2 | 34 |
| 9,5 | 7,5 | 41 |
| 10 | 8 | 42 |
10,5
|
8,5
| 42.5 |
Что такое 42-й размер в США для женщин? Таблица размеров женской обуви
| США | ЕВРОПА. | Дюймы |
|---|
| 10,5 | 41 | 10.375 |
| 11 | 41,5 | 10,5 |
| 11,5 | 42 |
10,75
|
| 12 | 42,5 | 10.875 |
Какой мужской размер 42 в США? Изменение размера мужской обуви
| Размеры США | Евро размеры | Дюймы |
|---|
| 8,5 | 41,5 | 10,125″ |
| 9 | 42 |
10,25″
|
| 9,5 | 42,5 | 10,4375″ |
| 10 | 43 | 10.5625″ |
Что такое 42 размер женской одежды в США? Платья, куртки, пальто и блузки
| S-M-L | США | Франция |
|---|
| М | 8 | 40 |
Л
|
10
| 42 |
| Л | 12 | 44 |
| ХL/1X | 14 | 46 |
Таблица размеров рубашки для Индии (рубашки S, M, L, XL, XXL, XXXL)
Таблица размеров рубашки (Индия) для всех типов телосложения. Рубашки 11 типоразмеров (до Рубашки XXXL ), в 3-х размерах и нестандартных размерах для мужчин всех форм и размеров.
Рубашки 11 типоразмеров (до Рубашки XXXL ), в 3-х размерах и нестандартных размерах для мужчин всех форм и размеров.
Рубашки всего 33 размера. Самый большой в Индии. Лучшее в Индии.
Скажите «нет» плохой посадке, некачественной строчке и рубашкам из дешевых тканей.
Рубашки премиум-класса с превосходной конструкцией и вариантами нестандартного размера.
Бренды масс-маркета выпускают рубашки фиксированного размера, и их качество не всегда хорошее. Мы — бренд премиум-класса с возможностью выбора размера по индивидуальному заказу. Уникальный дизайн, превосходное качество.
Почитание всех форм.
У каждого человека разные формы тела и предпочтения. Старые или молодые, высокие или маленькие, индийцы европеоиды , азиаты, африканцы или арабы, мы производим рубашки для всех и отправляем по всему миру.
Индивидуальное обслуживание для всех клиентов (через WhatsApp или по электронной почте). Никакой дискриминации по признаку касты, религии, цвета кожи, языка или региона. Люди всех форм и размеров, возрастных групп могут обратиться к нам и получить рубашки своего размера онлайн, не выходя из дома.
Никакой дискриминации по признаку касты, религии, цвета кожи, языка или региона. Люди всех форм и размеров, возрастных групп могут обратиться к нам и получить рубашки своего размера онлайн, не выходя из дома.
Размер рубашки (SLIM FIT)
| Размер | Сундук | Талия
| Рукава | Плечо | Длина |
| 38 | 39 | 37 | 24 | 17,5 | 28,5 |
| 39 | 41 | 39 | 24,5 | 18 | 29 |
| 40 | 42,5 | 40,5 | 25 | 18,5 | 29,5 |
| 41 | 44 | 42 | 25,5 | 18,75 | 29,75 |
| 42 | 45,5 | 43,5 | 26 | 19 | 30 |
| 43 | 47 | 45 | 26,5 | 19,5 | 30,5 |
| 44 | 48,5 | 46,5 | 27 | 20 | 31 |
| 45 | 50 | 48 | 27 | 20,5 | 31,25 |
| 46 | 52,5 | 50,5 | 27,25 | 21 | 31,5 |
| 47 | 55 | 53 | 27,25 | 21,5 | 32,25 |
| 48 | 58 | 56 | 27,5 | 22 | 33 |
Эти измерения относятся к размеру рубашки (предмета одежды), а не к размеру тела. Все измерения указаны в дюймах.
Все измерения указаны в дюймах.
Мы (индейцы) изобрели подгонку живота для мужчин больших размеров. Первый в мире.
Belly fit предназначен для мужчин, которым нужны рубашки больших размеров, или для тех, у кого есть животик.
В модели Belly Fit на талии добавляется 2 дюйма. Подгонка живота лучше, чем обычная подгонка, если у вас есть животик.
Рубашка, размер (подгонка на животе)
| Размер | Сундук | Талия | Рукава | Плечо | Длина |
| 38 | 39 | 41 | 24 | 17,5 | 28,5 |
| 39 | 41 | 43 | 24,5 | 18 | 29 |
| 40 | 42,5 | 44,5 | 25 | 18,5 | 29,5 |
| 41 | 44 | 46 | 25,5 | 18,75 | 29,75 |
| 42 | 45,5 | 47,5 | 26 | 19 | 30 |
| 43 | 47 | 49 | 26,5 | 19,5 | 30,5 |
| 44 | 48,5 | 50,5 | 27 | 20 | 31 |
| 45 | 50 | 52 | 27 | 20,5 | 31,25 |
| 46 | 52,5 | 54,5 | 27,25 | 21 | 31,5 |
| 47 | 55 | 56 | 27,25 | 21,5 | 32,25 |
| 48 | 58 | 60 | 27,5 | 22 | 33 |
Эти измерения относятся к размеру рубашки (предмета одежды), а не размера тела. Все измерения указаны в дюймах.
Все измерения указаны в дюймах.
Размер рубашки (REGULAR FIT)
| Размер | Сундук | Талия
| Рукава | Плечо | Длина |
| 38 | 39 | 39 | 24 | 17,5 | 28,5 |
| 39 | 41 | 41 | 24,5 | 18 | 29 |
| 40 | 42,5 | 42,5 | 25 | 18,5 | 29,5 |
| 41 | 44 | 44 | 25,5 | 18,75 | 29,75 |
| 42 | 45,5 | 45,5 | 26 | 19 | 30 |
| 43 | 47 | 47 | 26,5 | 19.5 | 30,5 |
| 44 | 48,5 | 48,5 | 27 | 20 | 31 |
| 45 | 50 | 50 | 27 | 20,5 | 31,25 |
| 46 | 52,5 | 52,5 | 27,25 | 21 | 31,5 |
| 47 | 55 | 55 | 27,25 | 21,5 | 32,25 |
| 48 | 58 | 58 | 27,5 | 22 | 33 |
Эти измерения относятся к размеру рубашки (предмета одежды), а не к размеру тела. Все измерения указаны в дюймах.
Все измерения указаны в дюймах.
Преобразователь размера рубашки (буква в цифру)
Буква (означает)
| Номер | Шея |
| Размер XS (очень маленький) | 38 Размер | 38 см |
| Размер S (маленький) | 39 Размер | 39 см |
| Размер M (средний) | 40 Размер | 40 см |
| Размер M (средний) | 41 Размер | 41 см |
| Размер L (большой) | 42 Размер | 42 см |
| Размер L (большой) | 43 Размер | 43 см |
| Размер XL (очень большой) | 44 Размер | 44 см |
| Размер XL (очень большой) | 45 Размер | 45 см |
| Размер XXL (Двойной очень большой) | 46 Размер | 46 см |
| Размер XXL (Двойной очень большой) | 47 Размер | 47 см |
| Размер XXXL (тройной очень большой) | 48 Размер | 48 см |
Размер XXL (размер в Letter) = 46 (размер в цифрах).
Объем груди для рубашки размера XXL составляет 52,5 дюйма, а размер воротника/шеи для рубашки размера XXL составляет 46 см.
Процесс заказа рубашки нестандартного размера
Шаг 1 : Пожалуйста, выберите нестандартный размер при добавлении рубашки в корзину, если вы хотите заказать рубашки нестандартного размера.
Шаг 2 : Предоставьте нам свои измерения (воротник, грудь, талия, длина рукава, плечо и длина рубашки) по электронной почте после оформления заказа/покупки. Измерения, такие как пройма, длина манжеты, не являются обязательными.
Свяжитесь с нами, если вам нужна помощь, и мы поможем вам выбрать подходящую модель.
Collar:
Chest:
Waist:
Sleeves:
Shoulder:
Shirt Length:
Мы стремимся предоставить рубашки онлайн для всех.


 Ясно, что один и тот же ответ не следует повторять больше одного раза.
Ясно, что один и тот же ответ не следует повторять больше одного раза.
 \end{align}$
\end{align}$
 {1}}$
{1}}$ \end{align}$
\end{align}$ Пусть $\,a$, $\,b$, $\,c$ и $\,d$ — натуральные числа (${b \ne 0}$, ${\,d \ne 0}$). В качестве общего знаменателя двух дробей $\frac{\,a\,}{b}$ и $\frac{\,c\,}{d}$ удобно брать НОК$(b, d)$ — наименьшее общее кратное знаменателей $b$ и $d$. Чтобы получить НОК$(b, d)$, мы раскладываем числа $b$ и $d$ на простые множители, причем общие множители подчеркиваем. Тогда
Пусть $\,a$, $\,b$, $\,c$ и $\,d$ — натуральные числа (${b \ne 0}$, ${\,d \ne 0}$). В качестве общего знаменателя двух дробей $\frac{\,a\,}{b}$ и $\frac{\,c\,}{d}$ удобно брать НОК$(b, d)$ — наименьшее общее кратное знаменателей $b$ и $d$. Чтобы получить НОК$(b, d)$, мы раскладываем числа $b$ и $d$ на простые множители, причем общие множители подчеркиваем. Тогда






 При t = 1 мы можем получить наименьшее положительное общее кратное чисел a и b , равное a · b: d , при условии, что числа a и b положительные.
При t = 1 мы можем получить наименьшее положительное общее кратное чисел a и b , равное a · b: d , при условии, что числа a и b положительные.




 Запись «Д(105) ∩ Д(140)» читается «пересечение множеств Дэ от 105 и Дэ от 140».
Запись «Д(105) ∩ Д(140)» читается «пересечение множеств Дэ от 105 и Дэ от 140». Это записывается как
Это записывается как


 Для решения некоторых задач требуется знать, что такое квадрат числа. Квадратом числа a называется число a , помноженное само на себя, то есть a ∙a . (Как нетрудно видеть, оно равно площади квадрата со стороной a ).
Для решения некоторых задач требуется знать, что такое квадрат числа. Квадратом числа a называется число a , помноженное само на себя, то есть a ∙a . (Как нетрудно видеть, оно равно площади квадрата со стороной a ).
 Для чисел X и Y НОК и НОД связаны следующим соотношением:
Для чисел X и Y НОК и НОД связаны следующим соотношением:
 Сокращаем дробь на 3 и видим окончательный ответ — 53/120.
Сокращаем дробь на 3 и видим окончательный ответ — 53/120.
 д.
д.  Переместительное свойство: a + b = b + a.
Переместительное свойство: a + b = b + a.
 Сочетательное свойство умножения: a * (b * c) = (a * b) * c.
Сочетательное свойство умножения: a * (b * c) = (a * b) * c.



 Например, 18 = 2 * 3 * 3
Например, 18 = 2 * 3 * 3 д.
д. 



 — 4 4. — 1 5. — 3
— 4 4. — 1 5. — 3



 Сумма всех множителей числа 105 равна 192, а его множители в парах равны (1, 105), (3, 35), (5, 21) и (7, 15).
Сумма всех множителей числа 105 равна 192, а его множители в парах равны (1, 105), (3, 35), (5, 21) и (7, 15).




 Всего 105 имеет 8 делителей, что показывает, что это составное число, состоящее из нескольких делителей.
Всего 105 имеет 8 делителей, что показывает, что это составное число, состоящее из нескольких делителей. 

 Другое в основном составное число, если исходное число было составным числом.
Другое в основном составное число, если исходное число было составным числом. Следовательно, 5 и 7 не образуют пару множителей. Теперь давайте посмотрим на 5 и 21:
Следовательно, 5 и 7 не образуют пару множителей. Теперь давайте посмотрим на 5 и 21: Мы будем использовать примеры в этом разделе, чтобы продемонстрировать, как каждый метод может быть применен к математическим задачам множителей 105.
Мы будем использовать примеры в этом разделе, чтобы продемонстрировать, как каждый метод может быть применен к математическим задачам множителей 105. Теперь мы посмотрим на следующее число в строке после четырех, которое равно 5. , поэтому 5 является коэффициентом 105 вместе с 21. Мы пропустим шесть и перейдем к 7.
Теперь мы посмотрим на следующее число в строке после четырех, которое равно 5. , поэтому 5 является коэффициентом 105 вместе с 21. Мы пропустим шесть и перейдем к 7. Во-вторых, при делении мы ищем нулевой остаток, тогда как при простой факторизации мы ищем окончательный ответ 1,9.0003
Во-вторых, при делении мы ищем нулевой остаток, тогда как при простой факторизации мы ищем окончательный ответ 1,9.0003 д.
д. См. также на этой веб-странице диаграмму факторизации простых чисел со всеми простыми числами от 1 до 1000.
См. также на этой веб-странице диаграмму факторизации простых чисел со всеми простыми числами от 1 до 1000. Мы можем записать 72 как:
Мы можем записать 72 как: 






 3
3

 419333
419333 107 • 107 • 107 • 107 • 107 • 107 • 107 • 107 • 107. 107. 107. 107. 107. 100033
107 • 107 • 107 • 107 • 107 • 107 • 107 • 107 • 107. 107. 107. 107. 107. 100033
 402 =
402 =
 3 3
3 3 589 =
589 =

 2. 2, 2 2 229
2. 2, 2 2 229
 •7•7
•7•7
 =
= •17
•17
 377. 377. 377. 3737.
377. 377. 377. 3737.
 3
3
 Этот курс Math 105 является вторым в серии из двух четвертей по начальной и средней алгебре. Для получения дополнительной информации о математике 105 в колледже Футхилл посетите веб-сайт математического факультета Футхилла. Для студентов, пожалуйста, проверьте учетную запись электронной почты, которую вы указали на MyPortal.
Этот курс Math 105 является вторым в серии из двух четвертей по начальной и средней алгебре. Для получения дополнительной информации о математике 105 в колледже Футхилл посетите веб-сайт математического факультета Футхилла. Для студентов, пожалуйста, проверьте учетную запись электронной почты, которую вы указали на MyPortal. , математика 105: Часто задаваемые вопросы о групповом обучении
, математика 105: Часто задаваемые вопросы о групповом обучении  pdf)
pdf) pdf)
pdf) pdf)
pdf) pdf)
pdf) pdf)
pdf) pdf)
pdf) Регулярное переутомление глазных мышц появляется в результате длительного времяпрепровождения за компьютером, непрерывного чтения, письма или работы с мелкими деталями. Также на это может повлиять плохое освещение, отсутствие перерывов во время рабочего процесса и др.
Регулярное переутомление глазных мышц появляется в результате длительного времяпрепровождения за компьютером, непрерывного чтения, письма или работы с мелкими деталями. Также на это может повлиять плохое освещение, отсутствие перерывов во время рабочего процесса и др. При миопии слабой степени глаз имеет длину на 1-1,5 мм больше среднестатистической нормы. Зрение вблизи остается хорошим, но вдаль человек видит очертания предметов немного размыто.
При миопии слабой степени глаз имеет длину на 1-1,5 мм больше среднестатистической нормы. Зрение вблизи остается хорошим, но вдаль человек видит очертания предметов немного размыто. Глазное дно характеризуется истончением сетчатки и сосудистой оболочки, через которые просвечивается наружная оболочка глаза – склера.
Глазное дно характеризуется истончением сетчатки и сосудистой оболочки, через которые просвечивается наружная оболочка глаза – склера.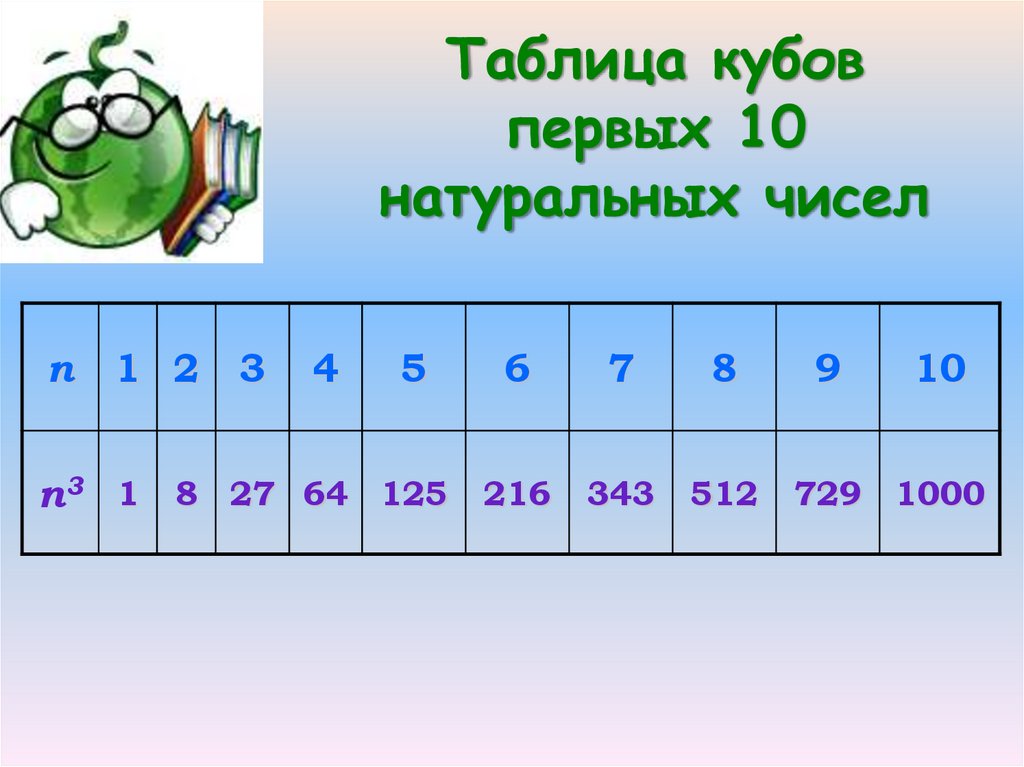 Это необходимо для хорошего зрения вблизи.
Это необходимо для хорошего зрения вблизи.
 У пациента должны рассмотреть глазное дно. Чтобы появилась такая возможность, человеку закапывают расслабляющие капли, они исключают развитие спазма аккомодационных мышц.
У пациента должны рассмотреть глазное дно. Чтобы появилась такая возможность, человеку закапывают расслабляющие капли, они исключают развитие спазма аккомодационных мышц. Профилактические меры включают в себя:
Профилактические меры включают в себя: Замедляясь в АВ-узле, электрический импульс позволяет сокращаться предсердиям и перекачивать кровь в желудочки. Механизм передачи электрического импульса обеспечивает поочередное сокращение разных отделов сердца и позволяет поддерживать стабильное движение крови по сосудам.
Замедляясь в АВ-узле, электрический импульс позволяет сокращаться предсердиям и перекачивать кровь в желудочки. Механизм передачи электрического импульса обеспечивает поочередное сокращение разных отделов сердца и позволяет поддерживать стабильное движение крови по сосудам.
 Мобиц 1) может протекать бессимптомно, однако проявление симптоматики зависит от компенсаторных возможностей организма. В ряде случаев даже при незначительном нарушении АВ проводимости (АВ блокада 1 степени) у пациентов могут наблюдаться те или иные симптомы. АВ блокада 3 ст. в большинстве случаев имеет характерные клинические проявления.
Мобиц 1) может протекать бессимптомно, однако проявление симптоматики зависит от компенсаторных возможностей организма. В ряде случаев даже при незначительном нарушении АВ проводимости (АВ блокада 1 степени) у пациентов могут наблюдаться те или иные симптомы. АВ блокада 3 ст. в большинстве случаев имеет характерные клинические проявления.

 Число а,
из которого извлекается корень n-й
степени, называют подкоренным
выражением,
а число n – показателем
корня.
Число а,
из которого извлекается корень n-й
степени, называют подкоренным
выражением,
а число n – показателем
корня. Выделим полные квадраты подкоренных
выражений:
Выделим полные квадраты подкоренных
выражений: Избавиться от иррациональности в
знаменателе:
Избавиться от иррациональности в
знаменателе: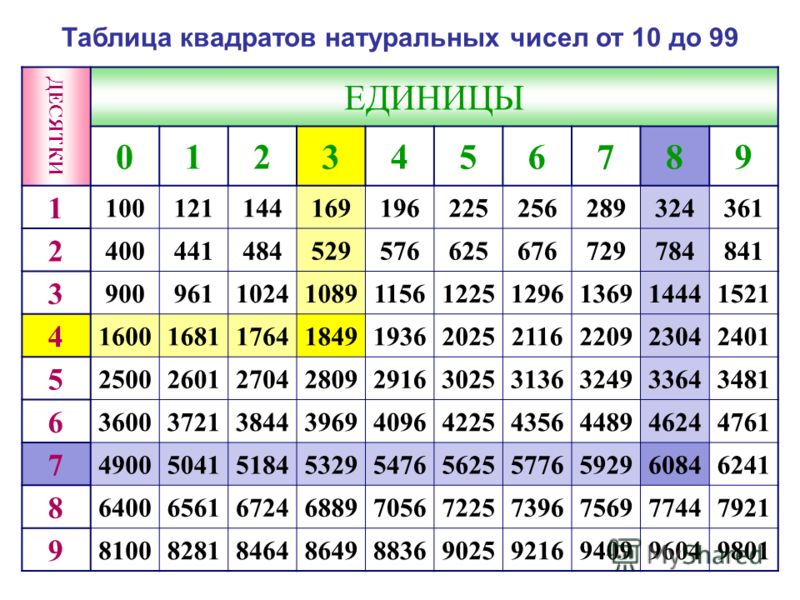 3. Избавьтесь
от иррациональности в знаменателе:
3. Избавьтесь
от иррациональности в знаменателе: 3. Упростите выражение:
3. Упростите выражение: Нахождение значения степени называют возведением
в степень.
Нахождение значения степени называют возведением
в степень.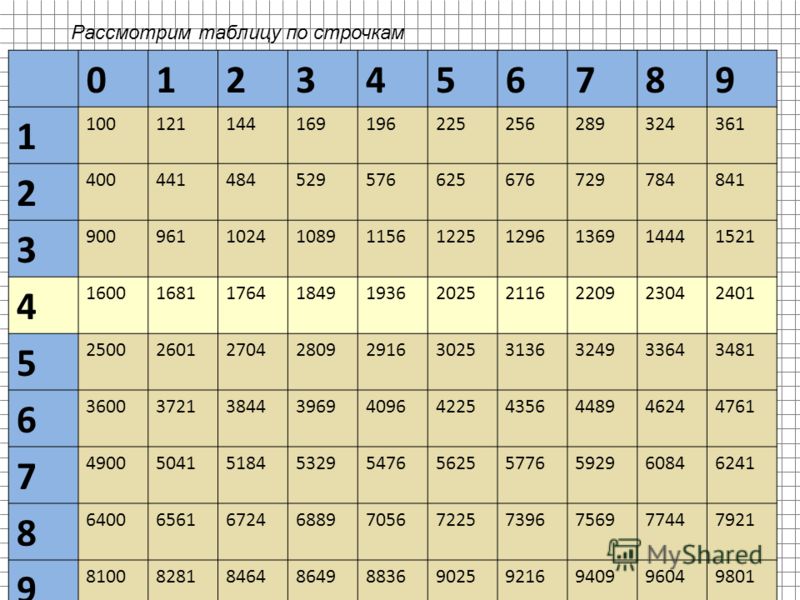 Вычислить
Вычислить Щитовидка — важный орган, осуществляющий функцию управления обменом веществ в организме. Она хранит йод и вырабатывает йодсодержащие гормоны — тироксин и трийодтиронин, важные для организации обмена веществ, роста нужных клеток и организма в целом.
Щитовидка — важный орган, осуществляющий функцию управления обменом веществ в организме. Она хранит йод и вырабатывает йодсодержащие гормоны — тироксин и трийодтиронин, важные для организации обмена веществ, роста нужных клеток и организма в целом. Развитие зоба может происходить по причине других болезней, при которых назначается приём определённых видов медикаментозных средств, влияющих на синтез гормонов щитовидной железы.
Развитие зоба может происходить по причине других болезней, при которых назначается приём определённых видов медикаментозных средств, влияющих на синтез гормонов щитовидной железы.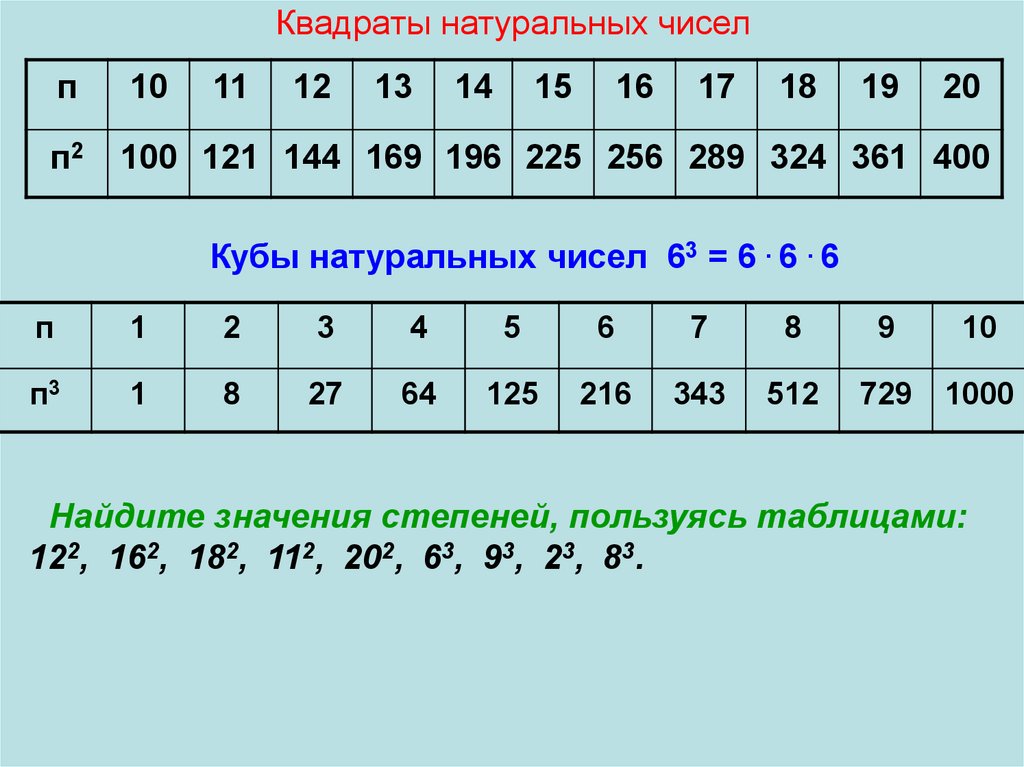 Их необходимо вовремя заметить и определить причину, что позволит на ранних этапах скорректировать имеющееся нарушение, не прибегая к серьёзной терапии и хирургическому вмешательству.
Их необходимо вовремя заметить и определить причину, что позволит на ранних этапах скорректировать имеющееся нарушение, не прибегая к серьёзной терапии и хирургическому вмешательству. В этом случае при наличии щитовидного зоба могут проявляться следующие симптомы:
В этом случае при наличии щитовидного зоба могут проявляться следующие симптомы:
 Медикаментозная терапия заключается в его коррекции и поддержании нормальных показателей. В некоторых ситуациях врач может назначить радиойодтерапию, при которой в организм вводится радиоактивный йод, который накапливается в клетках щитовидной железы и подвергает излучению всю железу, уничтожая опухолевые клетки и клетки железы. В сложных случаях, при значительном разрастании тканей и неэффективности консервативных методов лечения, может быть назначена операция по удалению опухоли.
Медикаментозная терапия заключается в его коррекции и поддержании нормальных показателей. В некоторых ситуациях врач может назначить радиойодтерапию, при которой в организм вводится радиоактивный йод, который накапливается в клетках щитовидной железы и подвергает излучению всю железу, уничтожая опухолевые клетки и клетки железы. В сложных случаях, при значительном разрастании тканей и неэффективности консервативных методов лечения, может быть назначена операция по удалению опухоли.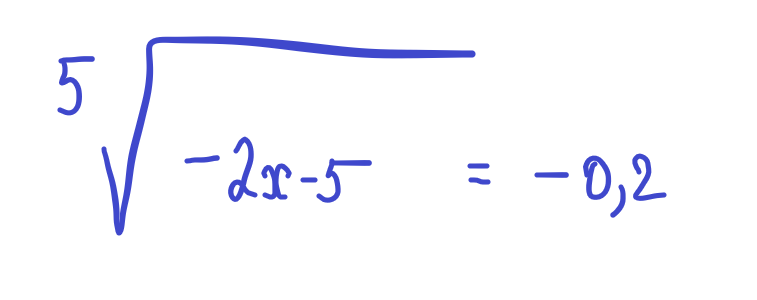 В зависимости от полученных при диагностике результатов, лечение может заключаться в регулировании уровня гормонов или удалении разросшихся тканей.
В зависимости от полученных при диагностике результатов, лечение может заключаться в регулировании уровня гормонов или удалении разросшихся тканей.
 Замедляется обмен веществ и человек начинает набирать вес. К симптомам этого заболевания можно отнести снижение работоспособности, медлительность, вялость, быстрая утомляемость, ухудшение памяти, сонливость, снижении аппетита, ощущение зябкости, нарушения стула, запоры и прочие.
Замедляется обмен веществ и человек начинает набирать вес. К симптомам этого заболевания можно отнести снижение работоспособности, медлительность, вялость, быстрая утомляемость, ухудшение памяти, сонливость, снижении аппетита, ощущение зябкости, нарушения стула, запоры и прочие. В России много регионов, где люди испытывают дефицит йода в своем рационе.
В России много регионов, где люди испытывают дефицит йода в своем рационе.
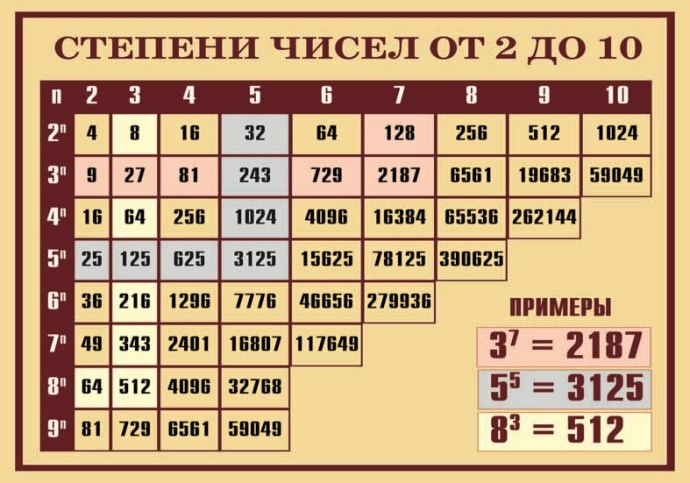 При полном удалении хирург оставляет части тканей щитовидной железы, масса которых равна менее 6 граммов от изначального веса долей. Редко удалению подлежит абсолютно все ткани щитовидной железа — тиреоидэктомия.
При полном удалении хирург оставляет части тканей щитовидной железы, масса которых равна менее 6 граммов от изначального веса долей. Редко удалению подлежит абсолютно все ткани щитовидной железа — тиреоидэктомия. Последствия зоба щитовидной железы зависят от его локализации и характера поражения тканей.
Последствия зоба щитовидной железы зависят от его локализации и характера поражения тканей.
 a-n= 1/an
a-n= 1/an Получили искомый ответ.
Получили искомый ответ.
 Но нам мешают другие числа 10 и 24. Что с ними делать? Если приглядеться видно, что в левой части у нас повторяется 22х ,вот и ответ — 22х мы можем вынести за скобки:
Но нам мешают другие числа 10 и 24. Что с ними делать? Если приглядеться видно, что в левой части у нас повторяется 22х ,вот и ответ — 22х мы можем вынести за скобки: В таком случаем можно решить методом замены. Число с наименьшей степенью заменяем:
В таком случаем можно решить методом замены. Число с наименьшей степенью заменяем: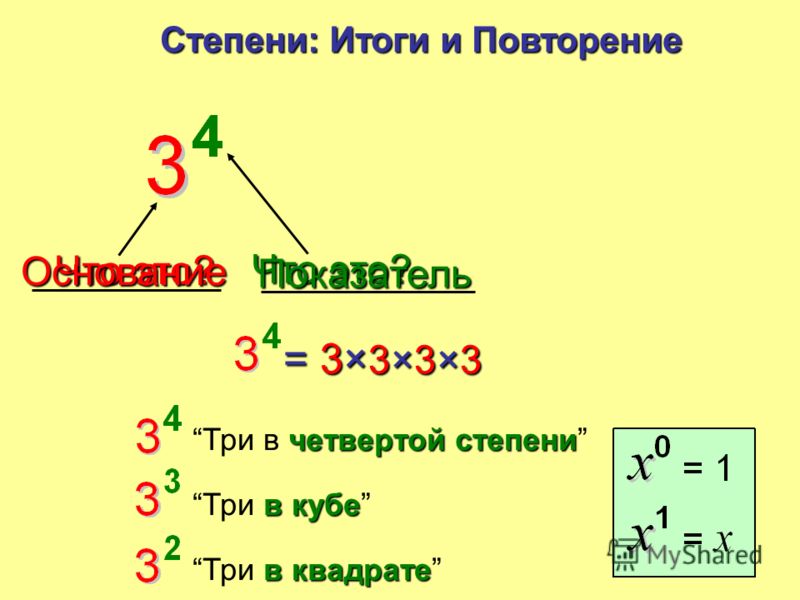 Число Поднятый силой Равно
Число Поднятый силой Равно  6666123 21166161616161616161161161611616116161616161616161616116161661161616161616161661116161616161616161616161616161616161616161616161161616 21.2e+21
6666123 21166161616161616161161161611616116161616161616161616116161661161616161616161661116161616161616161616161616161616161616161616161161616 21.2e+21 4210854715202004e+32
4210854715202004e+32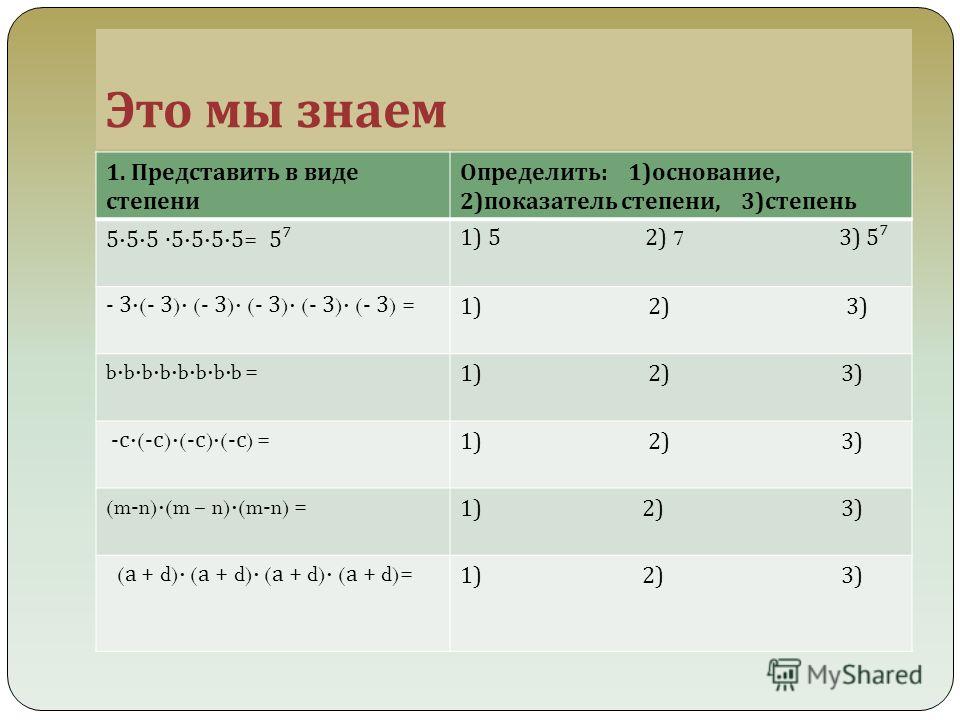 0842021724855047e+44
0842021724855047e+44 271806125530278e+55
271806125530278e+55 310887241768098e+67
310887241768098e+67 Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении.
Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении. е. 1,45 .
е. 1,45 . Наиболее распространенные мнемоники для запоминания этого порядка операций:
Наиболее распространенные мнемоники для запоминания этого порядка операций:  6 детей — девочки. Какую часть детей составляют девочки?
6 детей — девочки. Какую часть детей составляют девочки?
 S8.C1.1 Налогообложение
S8.C1.1 Налогообложение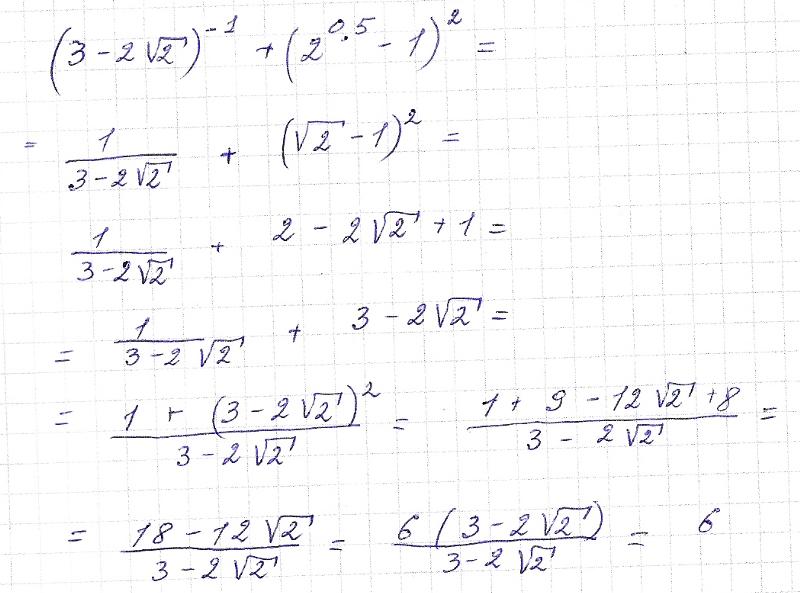 S8.C3.1 Обзор статьи
S8.C3.1 Обзор статьи S8.C3.6.3 Лица или вещи и средства межгосударственной торговли
S8.C3.6.3 Лица или вещи и средства межгосударственной торговли S8.C3.7.7 Разрешение Конгресса на недопустимые действия государства
S8.C3.7.7 Разрешение Конгресса на недопустимые действия государства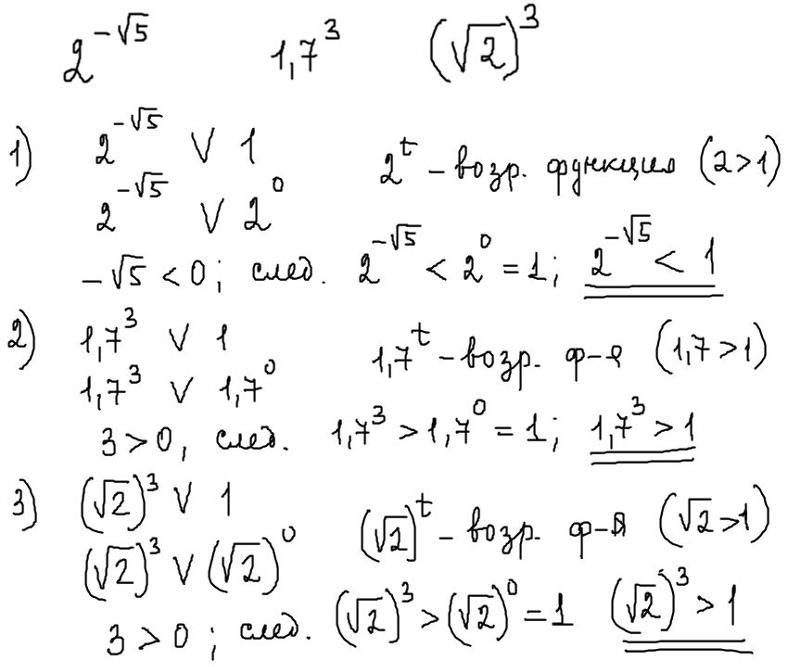 S8.C3.7.11.6 Дискриминация Часть полного автоматического теста на налоги на торговлю между штатами
S8.C3.7.11.6 Дискриминация Часть полного автоматического теста на налоги на торговлю между штатами s8.c11.4 Вражесу имущество и война Конгресса
s8.c11.4 Вражесу имущество и война Конгресса 0004
0004 S8.C18.8.1 Обзор
S8.C18.8.1 Обзор
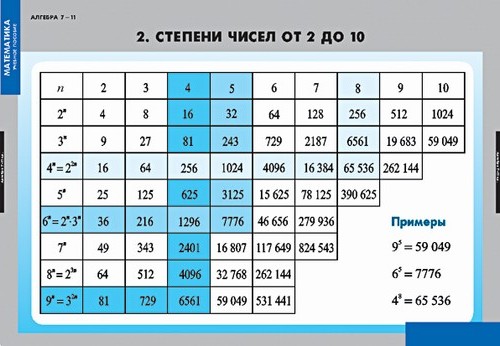



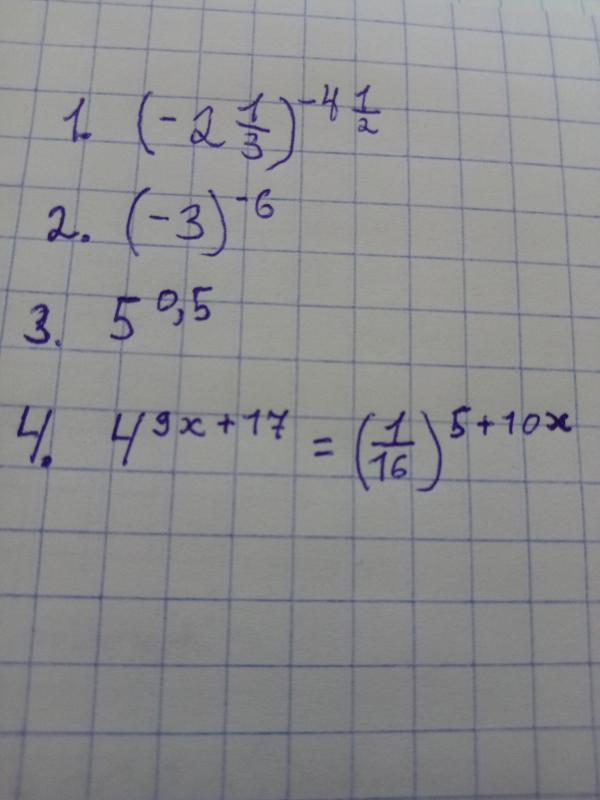 Наиболее известным примером этого являются 95% доверительные интервалы. Размер доверительного интервала обратно пропорционален количеству исследуемых субъектов. Таким образом, чем больше людей мы изучаем, тем точнее мы можем определить, где находится истинная ценность населения.
Наиболее известным примером этого являются 95% доверительные интервалы. Размер доверительного интервала обратно пропорционален количеству исследуемых субъектов. Таким образом, чем больше людей мы изучаем, тем точнее мы можем определить, где находится истинная ценность населения.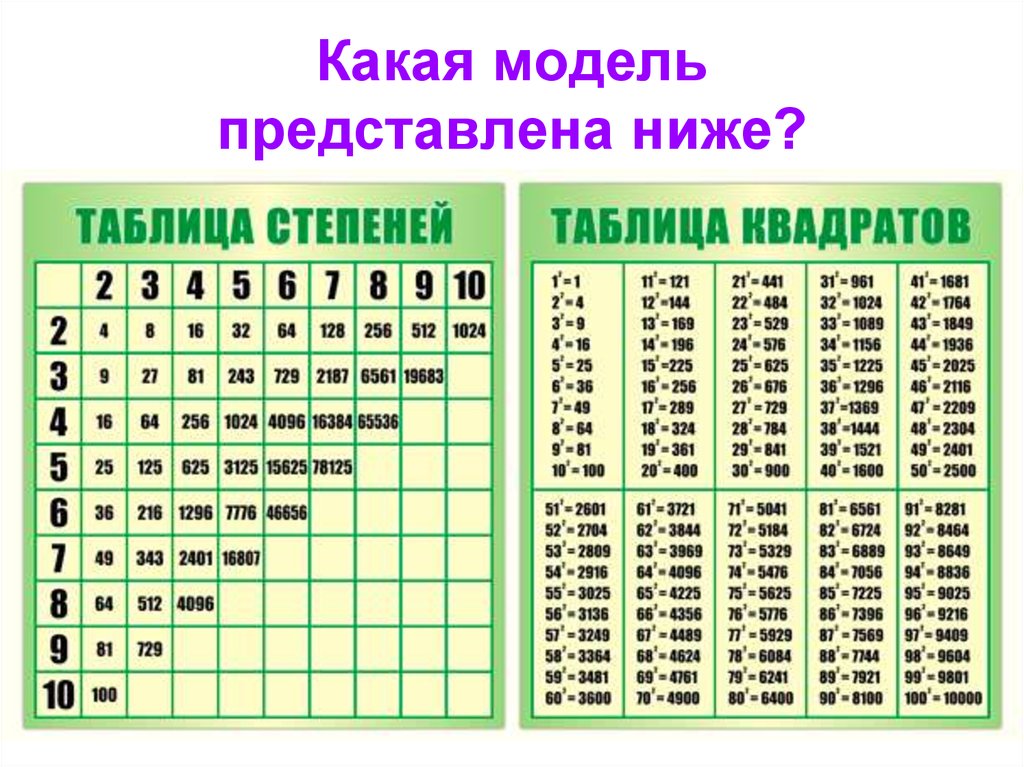 Исследование с небольшим размером выборки будет иметь большие доверительные интервалы и будет отображаться как статистически ненормальное только в том случае, если между двумя группами существует большая разница. Рисунок 2 демонстрирует, как увеличение числа субъектов может дать более точную оценку различий.
Исследование с небольшим размером выборки будет иметь большие доверительные интервалы и будет отображаться как статистически ненормальное только в том случае, если между двумя группами существует большая разница. Рисунок 2 демонстрирует, как увеличение числа субъектов может дать более точную оценку различий. Это связано с тем, что нам нужно очень точно найти истинное значение популяции для каждой группы лечения. И наоборот, если мы находим или ищем большое различие, может быть приемлемым довольно широкое распределение вероятностей.
Это связано с тем, что нам нужно очень точно найти истинное значение популяции для каждой группы лечения. И наоборот, если мы находим или ищем большое различие, может быть приемлемым довольно широкое распределение вероятностей. Тем не менее, мы должны убедиться, что разница стоит обнаружения. Например, можно разработать исследование, которое продемонстрирует сокращение времени начала местной анестезии с 60 до 59 секунд, но такая небольшая разница не будет иметь клинического значения. И наоборот, исследование, демонстрирующее разницу от 60 секунд до 10 минут, явно будет. Указание того, что является «клинически важным отличием», является ключевым компонентом расчета размера выборки.
Тем не менее, мы должны убедиться, что разница стоит обнаружения. Например, можно разработать исследование, которое продемонстрирует сокращение времени начала местной анестезии с 60 до 59 секунд, но такая небольшая разница не будет иметь клинического значения. И наоборот, исследование, демонстрирующее разницу от 60 секунд до 10 минут, явно будет. Указание того, что является «клинически важным отличием», является ключевым компонентом расчета размера выборки. По соглашению, а не по дизайну, мы чаще всего выбираем 0,05. Чем ниже уровень значимости, тем ниже мощность, поэтому использование 0,01 соответственно уменьшит нашу мощность.
По соглашению, а не по дизайну, мы чаще всего выбираем 0,05. Чем ниже уровень значимости, тем ниже мощность, поэтому использование 0,01 соответственно уменьшит нашу мощность.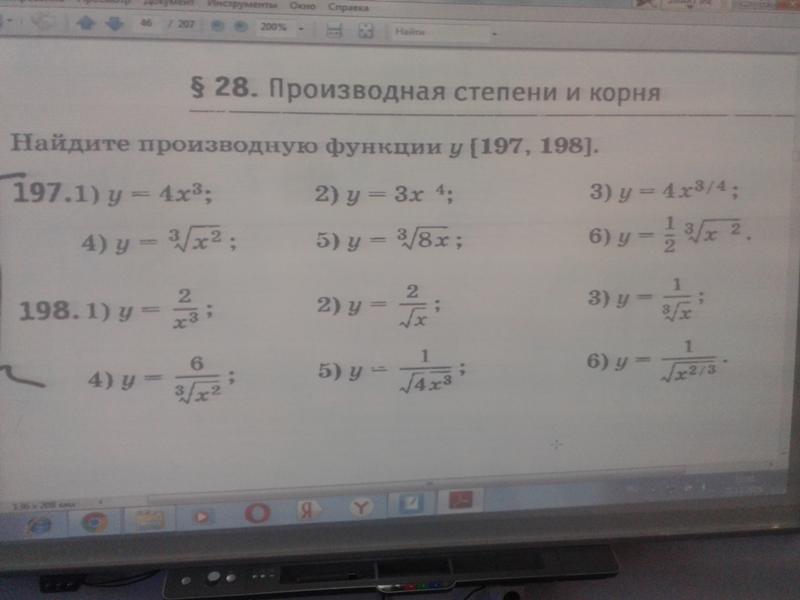
 Это делается для того, чтобы мы могли набрать достаточное количество пациентов, чтобы придать нашим результатам адекватную силу, но не слишком много, чтобы тратить время на получение большего количества данных, чем нам нужно. К сожалению, при разработке исследования нам, возможно, придется сделать предположения о желаемом размере эффекта и дисперсии данных.
Это делается для того, чтобы мы могли набрать достаточное количество пациентов, чтобы придать нашим результатам адекватную силу, но не слишком много, чтобы тратить время на получение большего количества данных, чем нам нужно. К сожалению, при разработке исследования нам, возможно, придется сделать предположения о желаемом размере эффекта и дисперсии данных. Расчеты промежуточного размера выборки следует использовать только в том случае, если это указано в методе априорного исследования.
Расчеты промежуточного размера выборки следует использовать только в том случае, если это указано в методе априорного исследования. stat.ucla.edu/powercalc/), интерактивные статистические страницы (http://www.statistics.com/content/javastat. html). для обоснования расчетов (хотя это можно решить, проведя предварительное исследование и используя полученные данные)9.0004
stat.ucla.edu/powercalc/), интерактивные статистические страницы (http://www.statistics.com/content/javastat. html). для обоснования расчетов (хотя это можно решить, проведя предварительное исследование и используя полученные данные)9.0004 Выполняя расчет размера выборки для диагностического исследования, мы можем указать точность, с которой мы хотели бы сообщить доверительные интервалы для чувствительности и специфичности.
Выполняя расчет размера выборки для диагностического исследования, мы можем указать точность, с которой мы хотели бы сообщить доверительные интервалы для чувствительности и специфичности. Обычно они устанавливаются по соглашению, а не меняются от одного исследования к другому, хотя, как мы увидим ниже, они могут меняться.
Обычно они устанавливаются по соглашению, а не меняются от одного исследования к другому, хотя, как мы увидим ниже, они могут меняться. е. представляет собой разницу между средним артериальным давлением в группе бендрофлуазида и средним артериальным давлением в группе нового лечения.
е. представляет собой разницу между средним артериальным давлением в группе бендрофлуазида и средним артериальным давлением в группе нового лечения.

 Это означает, что нам нужно 1500 пациентов в группе Jedi Flow и 1500 в группе тромболизиса.
Это означает, что нам нужно 1500 пациентов в группе Jedi Flow и 1500 в группе тромболизиса.


 рамку.
рамку. Acad Emerg Med1996;3:895–900.
Acad Emerg Med1996;3:895–900.  Таша все больше и больше беспокоится об отношении Призраков, поэтому решает больше заниматься бизнесом в клубе. Роман Призрака и Анжелы накаляется, а Томми привлекает кто-то в клубе.
Таша все больше и больше беспокоится об отношении Призраков, поэтому решает больше заниматься бизнесом в клубе. Роман Призрака и Анжелы накаляется, а Томми привлекает кто-то в клубе. Тиллман0007
Тиллман0007 Patrick
Patrick Кемп
Кемп Я хотел бы сказать, что я надеюсь, что каждый человек делает на вершине. Я немного играл раньше, и я понимаю нервную вещь с работой под светом и камерой, моя цель состояла в том, чтобы стать актером, зарабатывать много денег и играть разные жизненные роли людей, мест и вещей. 50cents хорошая сюжетная линия и сохраните ее стильной, чтобы уважать то, как нас воспринимают в мире, независимо от направления жизни. Я хотел бы получить шанс сыграть отдельно в шоу, если вы все доберетесь до Далласа, штат Техас. Удачи и сломай ногу.
Я хотел бы сказать, что я надеюсь, что каждый человек делает на вершине. Я немного играл раньше, и я понимаю нервную вещь с работой под светом и камерой, моя цель состояла в том, чтобы стать актером, зарабатывать много денег и играть разные жизненные роли людей, мест и вещей. 50cents хорошая сюжетная линия и сохраните ее стильной, чтобы уважать то, как нас воспринимают в мире, независимо от направления жизни. Я хотел бы получить шанс сыграть отдельно в шоу, если вы все доберетесь до Далласа, штат Техас. Удачи и сломай ногу.

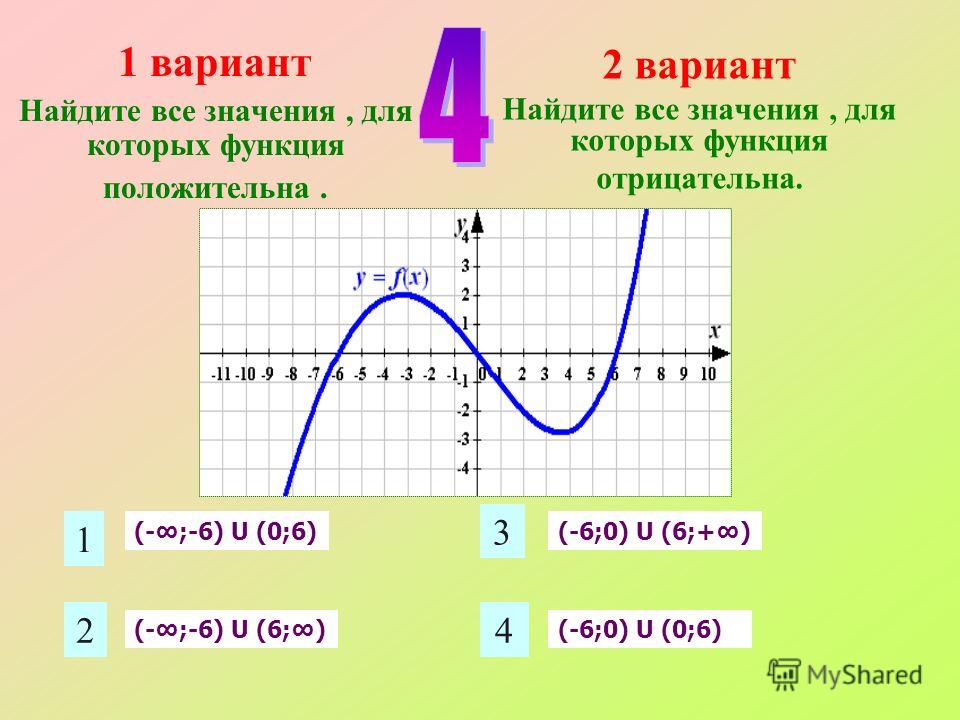
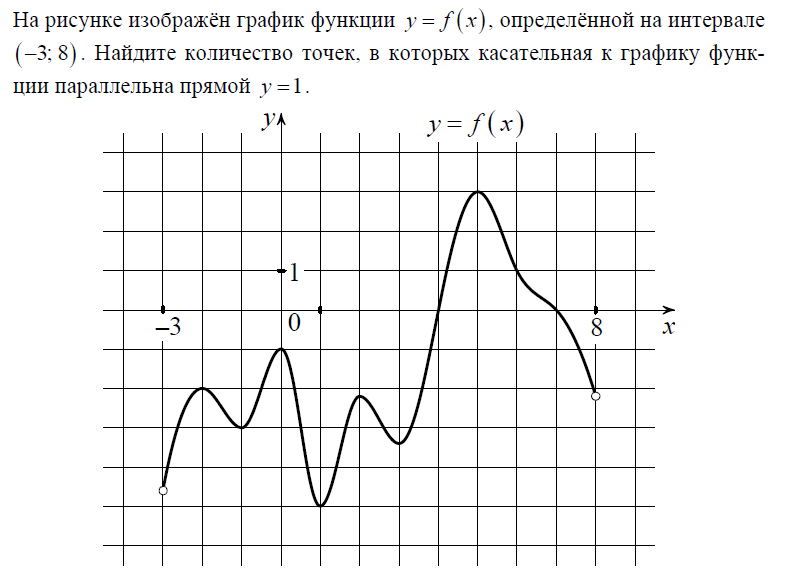
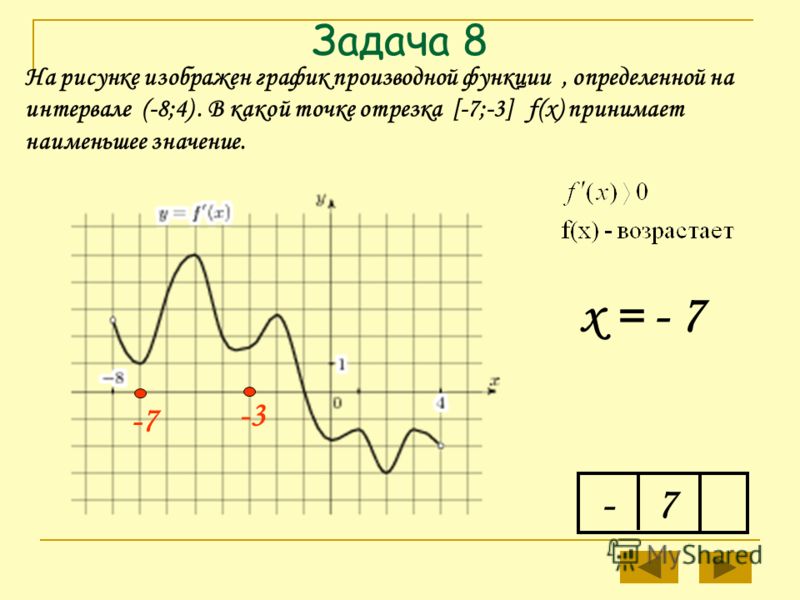 В первых скобках — разность квадратов, из вторых выносим общий множитель 4 за скобки:
В первых скобках — разность квадратов, из вторых выносим общий множитель 4 за скобки: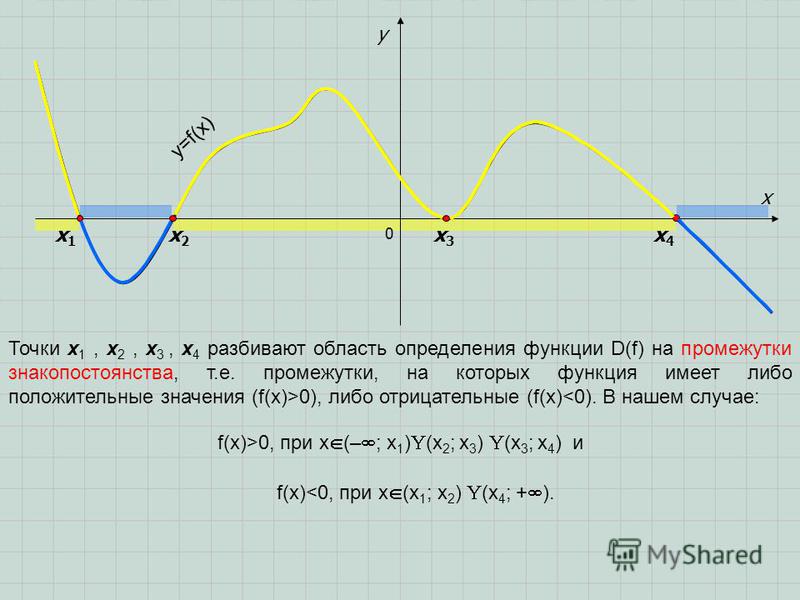
 Какова вероятность того,что наугад взятый карандаш не будет ни красным,ни синим…
Какова вероятность того,что наугад взятый карандаш не будет ни красным,ни синим… ..
.. functio – исполнение, осуществление), одно из основных понятий математики, означающее зависимость одних переменных величин от других. Слово «величина» в этом определении понимается в самом широком смысле: это может быть именованное число, отвлечённое число (действительное или комплексное), неск. чисел (т. е. точка пространства) и вообще элемент любого множества.
functio – исполнение, осуществление), одно из основных понятий математики, означающее зависимость одних переменных величин от других. Слово «величина» в этом определении понимается в самом широком смысле: это может быть именованное число, отвлечённое число (действительное или комплексное), неск. чисел (т. е. точка пространства) и вообще элемент любого множества.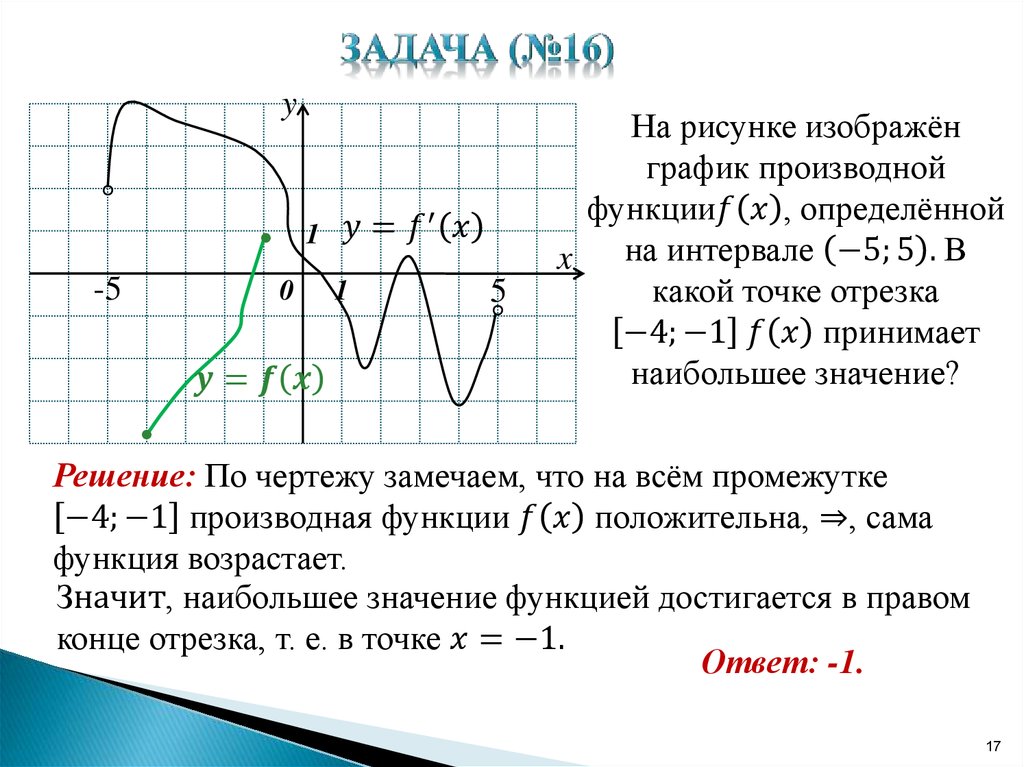 (областью определения Ф. может быть множество всех действительных чисел, интервал, отрезок и т. п.). Слова «поставлено в соответствие» означают, что указан определённый способ, по которому для каждого $x∈E$ находится значение $y=f(x)$. Этот способ в данном случае обозначен символом $f$. Для обозначения Ф. применяются и др. буквы, напр. $y=g(x)$, $y=F(x)$, $s=h(t)$, $v=φ(s)$.
(областью определения Ф. может быть множество всех действительных чисел, интервал, отрезок и т. п.). Слова «поставлено в соответствие» означают, что указан определённый способ, по которому для каждого $x∈E$ находится значение $y=f(x)$. Этот способ в данном случае обозначен символом $f$. Для обозначения Ф. применяются и др. буквы, напр. $y=g(x)$, $y=F(x)$, $s=h(t)$, $v=φ(s)$. {2m}.$$
{2m}.$$ Такой способ задания Ф. часто применяется в тех случаях, когда область определения состоит из конечного числа значений.
Такой способ задания Ф. часто применяется в тех случаях, когда область определения состоит из конечного числа значений. корень, изображается верхней половиной шаровой поверхности радиуса 1 с центром в начале координат.
корень, изображается верхней половиной шаровой поверхности радиуса 1 с центром в начале координат. 2}$ отображает отрезок $–1 ⩽ x ⩽ 1$ на отрезок $0 ⩽ y ⩽ 1$.
2}$ отображает отрезок $–1 ⩽ x ⩽ 1$ на отрезок $0 ⩽ y ⩽ 1$. Ферма «Введение и изучение плоских и телесных мест» (1636, опубл. в 1679). Изучение линий по их уравнениям в «Геометрии» Р. Декарта (1637) также указывает на ясное представление о взаимной зависимости двух переменных величин. У англ. математика И. Барроу («Лекции по геометрии», 1670) в геометрич. форме устанавливается взаимная обратность действий дифференцирования и интегрирования (разумеется, без употребления самих этих терминов). Это свидетельствует о совершенно отчётливом владении понятием Ф. В геометрич. и механич. виде это понятие можно найти и у И. Ньютона. Однако термин «Ф.» впервые появляется лишь в 1692 у Г. Лейбница, и притом не совсем в современном его понимании. Лейбниц называет Ф. разл. отрезки, связанные с к.-л. кривой, напр. абсциссы её точек. В первом печатном курсе «Анализа бесконечно малых» франц. математика Г. Лопиталя (1696) термин «Ф.
Ферма «Введение и изучение плоских и телесных мест» (1636, опубл. в 1679). Изучение линий по их уравнениям в «Геометрии» Р. Декарта (1637) также указывает на ясное представление о взаимной зависимости двух переменных величин. У англ. математика И. Барроу («Лекции по геометрии», 1670) в геометрич. форме устанавливается взаимная обратность действий дифференцирования и интегрирования (разумеется, без употребления самих этих терминов). Это свидетельствует о совершенно отчётливом владении понятием Ф. В геометрич. и механич. виде это понятие можно найти и у И. Ньютона. Однако термин «Ф.» впервые появляется лишь в 1692 у Г. Лейбница, и притом не совсем в современном его понимании. Лейбниц называет Ф. разл. отрезки, связанные с к.-л. кривой, напр. абсциссы её точек. В первом печатном курсе «Анализа бесконечно малых» франц. математика Г. Лопиталя (1696) термин «Ф. » не употребляется.
» не употребляется. Так сложилось совр. понятие Ф., свободное от упоминания о её аналитич. задании.
Так сложилось совр. понятие Ф., свободное от упоминания о её аналитич. задании.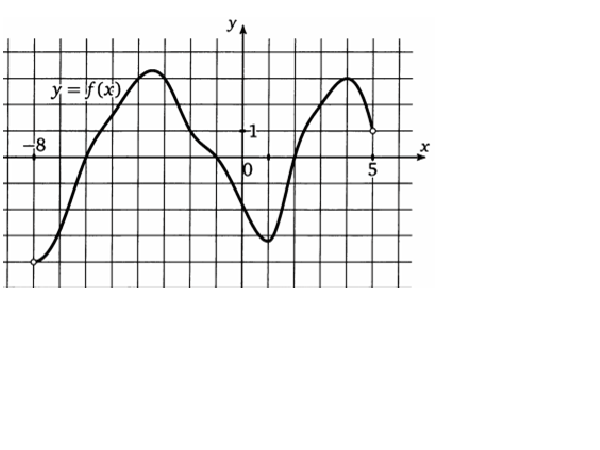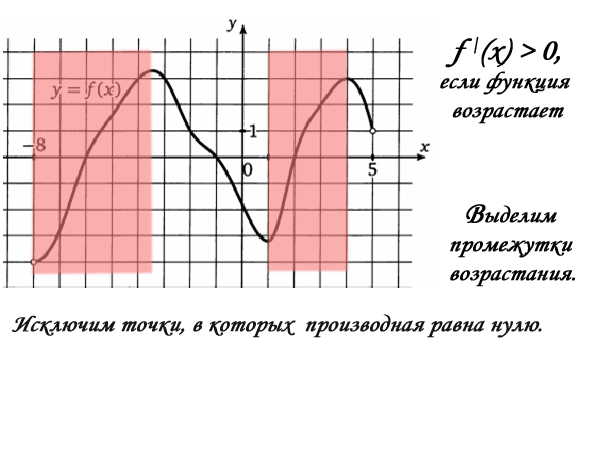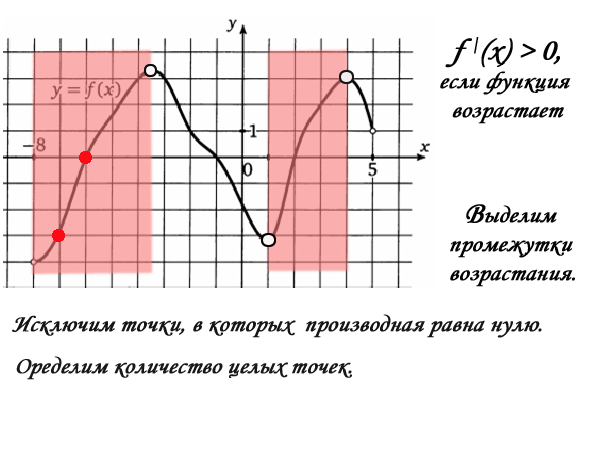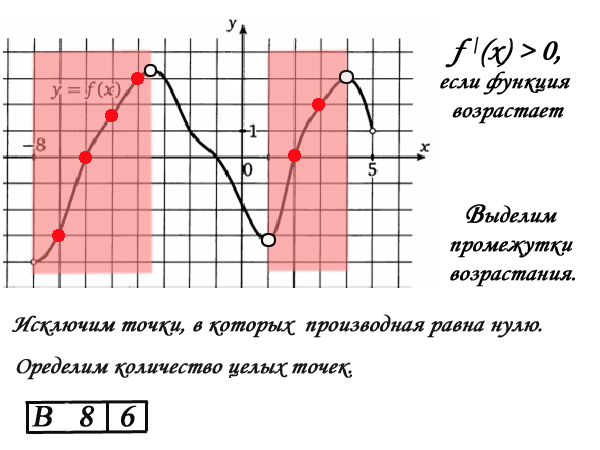 Обратите внимание, что домен и диапазон всегда записываются от меньших значений к большим или слева направо для домена и от нижней части графика к верхней части графика для диапазона.0011
Обратите внимание, что домен и диапазон всегда записываются от меньших значений к большим или слева направо для домена и от нижней части графика к верхней части графика для диапазона.0011 Например, область определения и диапазон функции кубического корня — это множество всех действительных чисел.
Например, область определения и диапазон функции кубического корня — это множество всех действительных чисел.  { 2}[/latex], доменом являются все действительные числа, поскольку горизонтальная протяженность графика — это вся линия действительных чисел. Поскольку график не содержит отрицательных значений диапазона, диапазон состоит только из неотрицательных действительных чисел. 9{3}[/latex], доменом являются все действительные числа, поскольку горизонтальная протяженность графика — это вся линия действительных чисел. То же самое относится к вертикальному размеру графика, поэтому домен и диапазон включают все действительные числа.
{ 2}[/latex], доменом являются все действительные числа, поскольку горизонтальная протяженность графика — это вся линия действительных чисел. Поскольку график не содержит отрицательных значений диапазона, диапазон состоит только из неотрицательных действительных чисел. 9{3}[/latex], доменом являются все действительные числа, поскольку горизонтальная протяженность графика — это вся линия действительных чисел. То же самое относится к вертикальному размеру графика, поэтому домен и диапазон включают все действительные числа.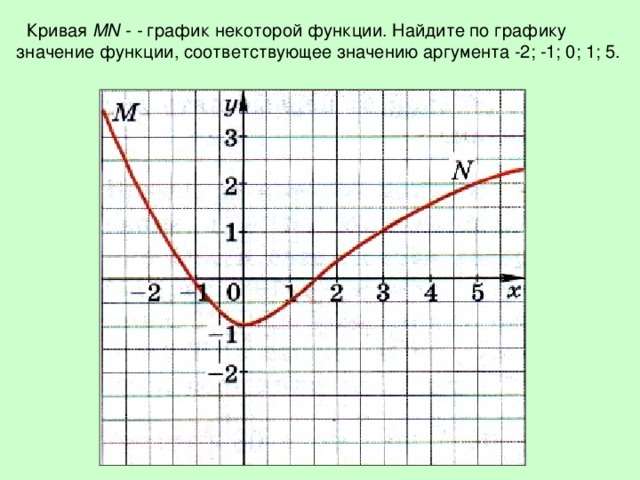 Также нет [latex]x[/latex], который может выдавать 0, поэтому 0 также исключается из диапазона. Обратите внимание, что выход этой функции всегда положителен из-за квадрата в знаменателе, поэтому диапазон включает только положительные числа.
Также нет [latex]x[/latex], который может выдавать 0, поэтому 0 также исключается из диапазона. Обратите внимание, что выход этой функции всегда положителен из-за квадрата в знаменателе, поэтому диапазон включает только положительные числа.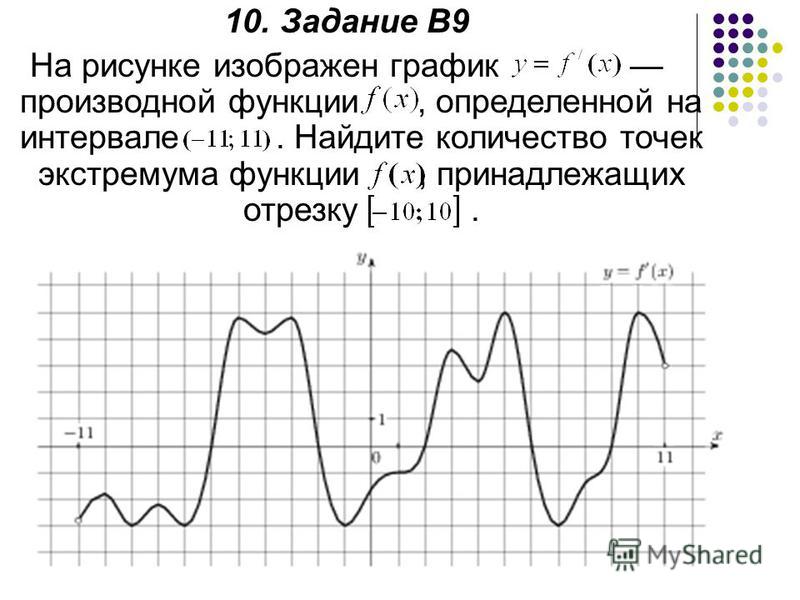

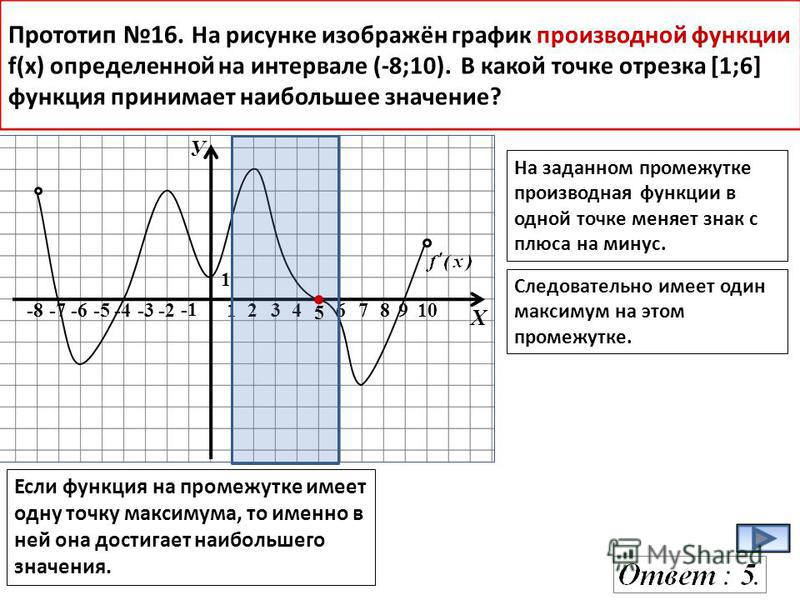 Для этого покажем, что любое неотрицательное
число является выходом этой функции. Если 𝑦≥0, то
𝑓√𝑦=√𝑦=𝑦.
Для этого покажем, что любое неотрицательное
число является выходом этой функции. Если 𝑦≥0, то
𝑓√𝑦=√𝑦=𝑦.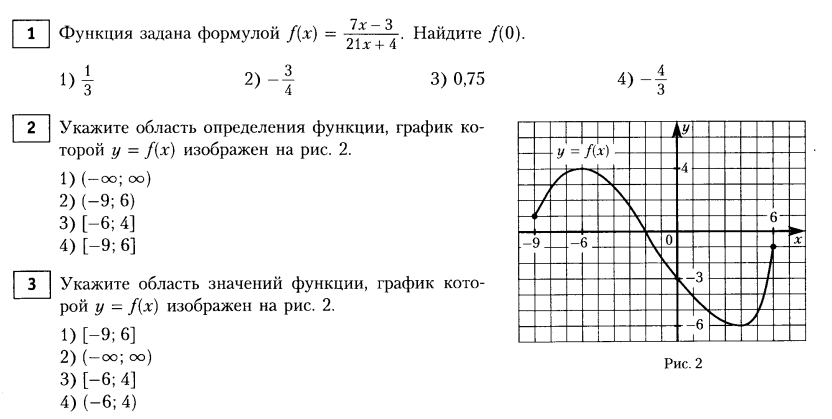
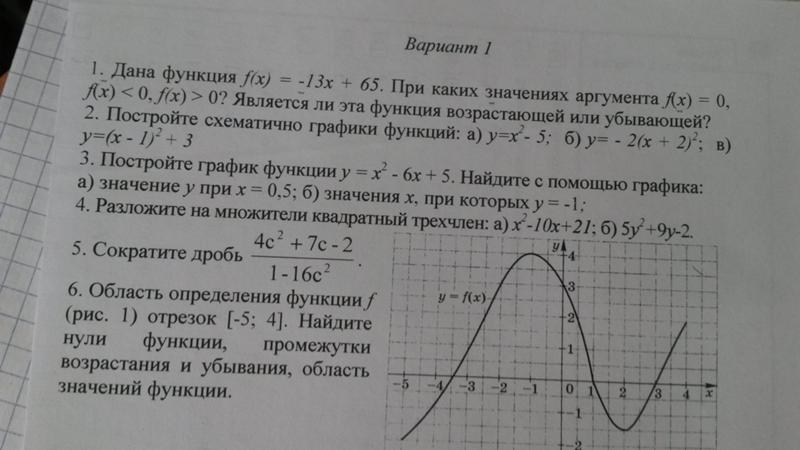 линия; на самом деле, для любого 𝑐∈[0,1[ линия
𝑦=𝑐 не будет пересекать нашу кривую и все остальные
горизонтальные линии пересекают нашу кривую. Следовательно, диапазон этой функции
]−∞,0[∪[1,∞[.
линия; на самом деле, для любого 𝑐∈[0,1[ линия
𝑦=𝑐 не будет пересекать нашу кривую и все остальные
горизонтальные линии пересекают нашу кривую. Следовательно, диапазон этой функции
]−∞,0[∪[1,∞[.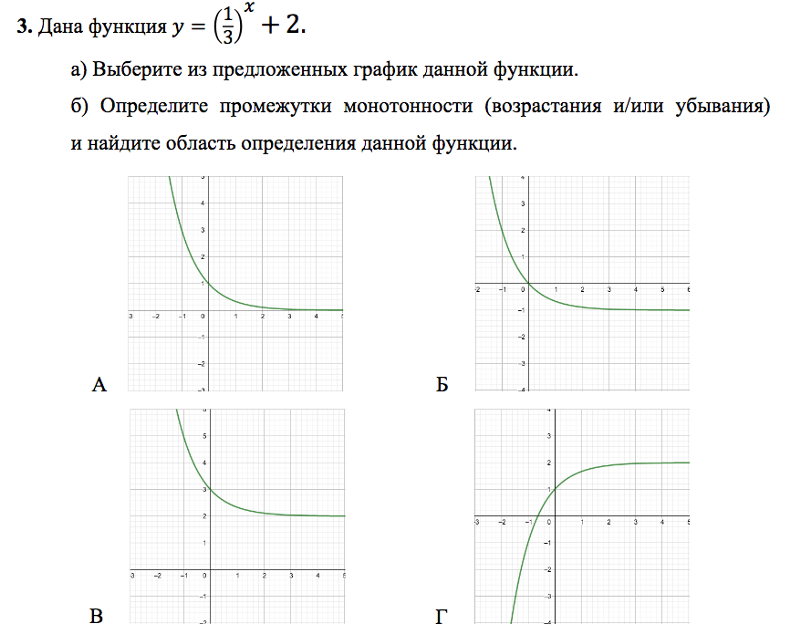 Поэтому найти все
возможные входы этой функции, нам нужно будет взять объединение всех
поддомены. Для этой кусочной функции мы можем взять на вход 𝑥0, а также
𝑥≥0; комбинируя их, мы можем видеть, что это любое реальное значение
𝑥, поэтому его домен равен ℝ.
Поэтому найти все
возможные входы этой функции, нам нужно будет взять объединение всех
поддомены. Для этой кусочной функции мы можем взять на вход 𝑥0, а также
𝑥≥0; комбинируя их, мы можем видеть, что это любое реальное значение
𝑥, поэтому его домен равен ℝ. Для этого положим 𝑐≥1 так, чтобы
𝑐−1≥0; это означает
𝑓(𝑐−1)=(𝑐−1)+1=𝑐.
Для этого положим 𝑐≥1 так, чтобы
𝑐−1≥0; это означает
𝑓(𝑐−1)=(𝑐−1)+1=𝑐.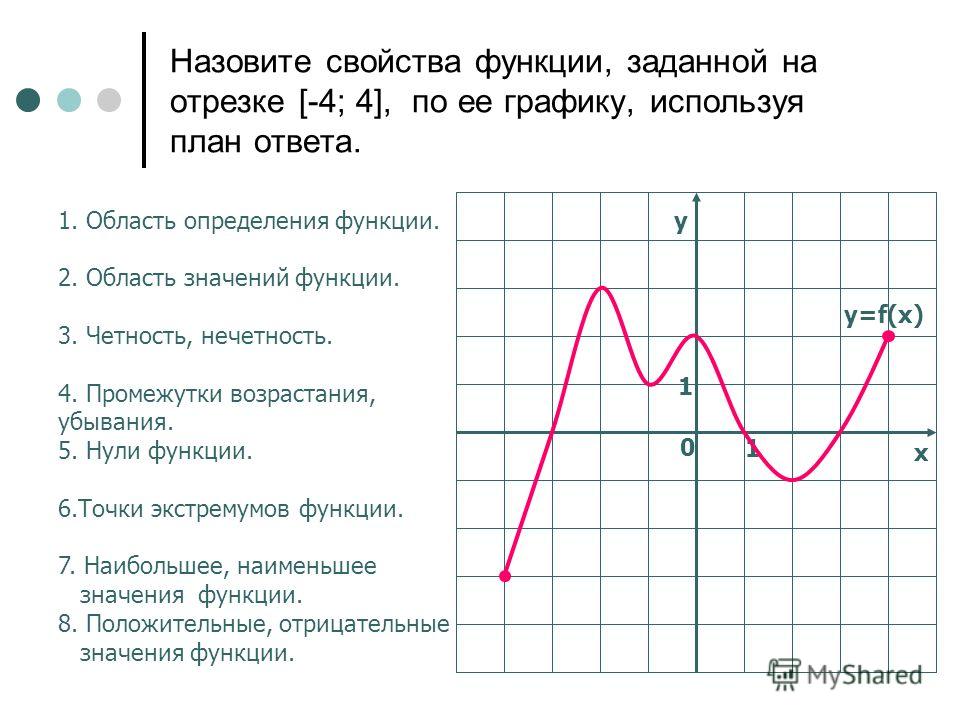
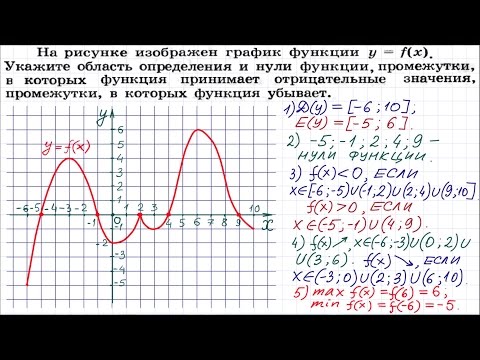
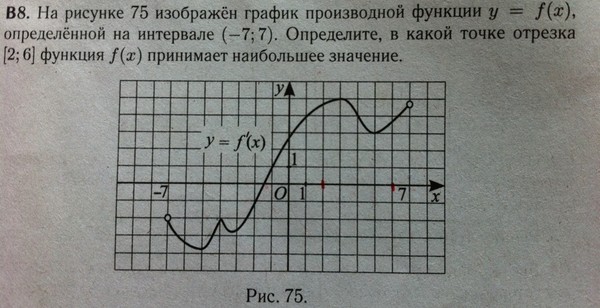
 Помните, любая точка на нашем графике будет иметь вид
(𝑐,𝑓(𝑐)), где 𝑓(𝑐) будет в диапазоне функции. Следовательно, мы можем найти
диапазон этой функции, определяя 𝑦-координаты точек на ее графике.
Помните, любая точка на нашем графике будет иметь вид
(𝑐,𝑓(𝑐)), где 𝑓(𝑐) будет в диапазоне функции. Следовательно, мы можем найти
диапазон этой функции, определяя 𝑦-координаты точек на ее графике.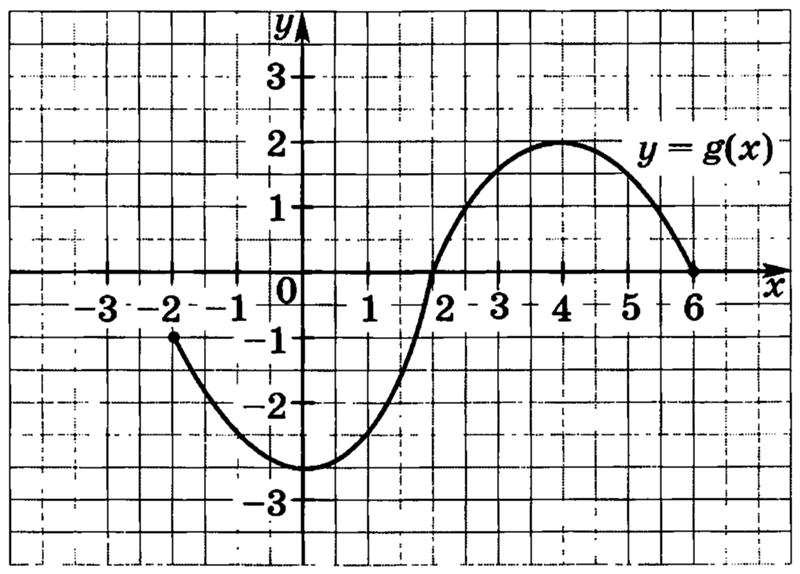
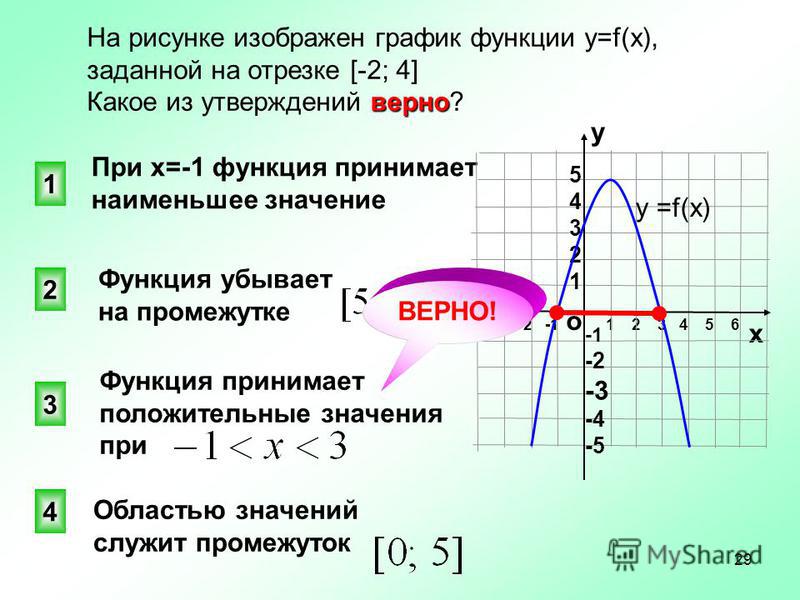 Во-первых, 𝑥≠6 совпадает с ℝ−{6}. Во-вторых, 𝑥=6 совпадает с {6}.
Во-первых, 𝑥≠6 совпадает с ℝ−{6}. Во-вторых, 𝑥=6 совпадает с {6}. Поскольку выход постоянен, его диапазон
{12}.
Поскольку выход постоянен, его диапазон
{12}.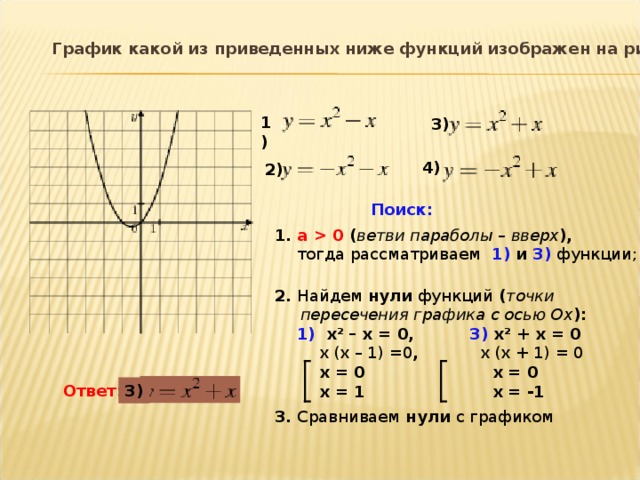
 Композиция функции осуществляется путем замены одной функции на другую функцию.
Композиция функции осуществляется путем замены одной функции на другую функцию. 
 Net
Net
 количество: 1
количество: 1 количество
: 1
количество
: 1 количество: 1
количество: 1 количество
: 3
количество
: 3 количество: 3
количество: 3 ru Д. Федутинов. Кроме того, это может говорить о том, что Hermes 900 полностью интегрирован в армейские информационно-управляющие системы, – продолжает специалист. Hermes 900 был разработан израильской компанией Elbit Systems на базе предшественника Hermes 450, который эксплуатируется в течении 17 лет в ряде стран мира. Общий налет беспилотников этого типа составляет более 500 тысяч часов. Hermes 900 отличается от предыдущей модификации аппарата не только большими размерами, но и улучшенными техническими характеристиками, а также повышенными разведывательными возможностями. Конкуренты беспилотника Hermes 900 на мировом рынке: аппараты семейства Predator (GA–ASI, США) и Heron (IAI, Израиль).
ru Д. Федутинов. Кроме того, это может говорить о том, что Hermes 900 полностью интегрирован в армейские информационно-управляющие системы, – продолжает специалист. Hermes 900 был разработан израильской компанией Elbit Systems на базе предшественника Hermes 450, который эксплуатируется в течении 17 лет в ряде стран мира. Общий налет беспилотников этого типа составляет более 500 тысяч часов. Hermes 900 отличается от предыдущей модификации аппарата не только большими размерами, но и улучшенными техническими характеристиками, а также повышенными разведывательными возможностями. Конкуренты беспилотника Hermes 900 на мировом рынке: аппараты семейства Predator (GA–ASI, США) и Heron (IAI, Израиль). Аппарат способен непрерывно летать в течении 36 часов на высоте до 9140 метров; радиус действия до 1850 км. Длина фюзеляжа – 8.3 м, размах крыла – 15 м, взлетный вес – 1180 кг, максимальный вес полезной нагрузки (разведывательной аппаратуры и средств радиоэлектронной борьбы) – 350 кг.
Аппарат способен непрерывно летать в течении 36 часов на высоте до 9140 метров; радиус действия до 1850 км. Длина фюзеляжа – 8.3 м, размах крыла – 15 м, взлетный вес – 1180 кг, максимальный вес полезной нагрузки (разведывательной аппаратуры и средств радиоэлектронной борьбы) – 350 кг.
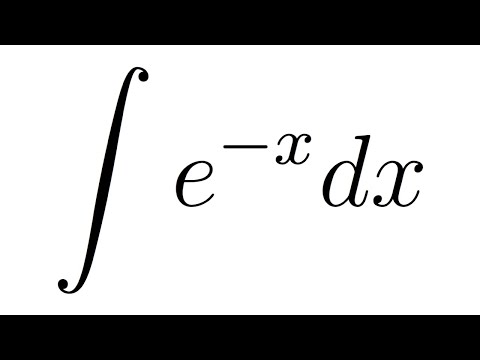
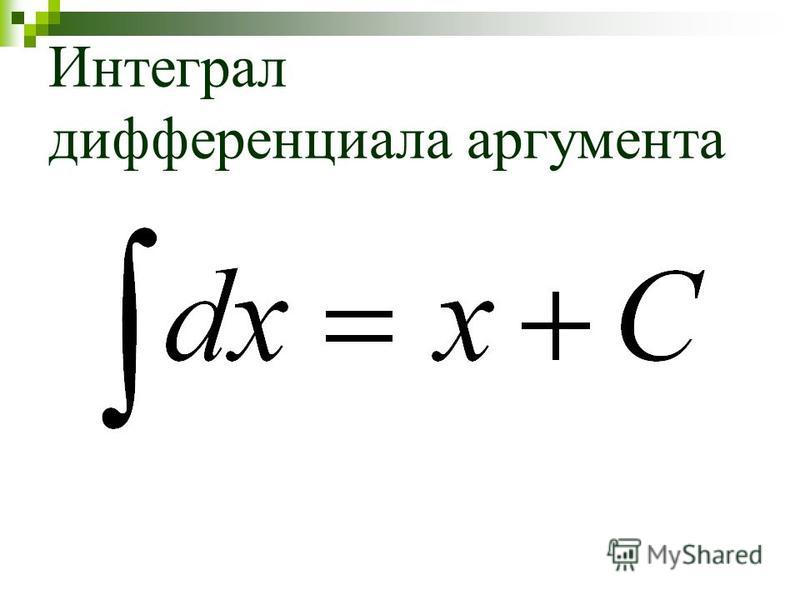
 com, маркеры автора)
com, маркеры автора)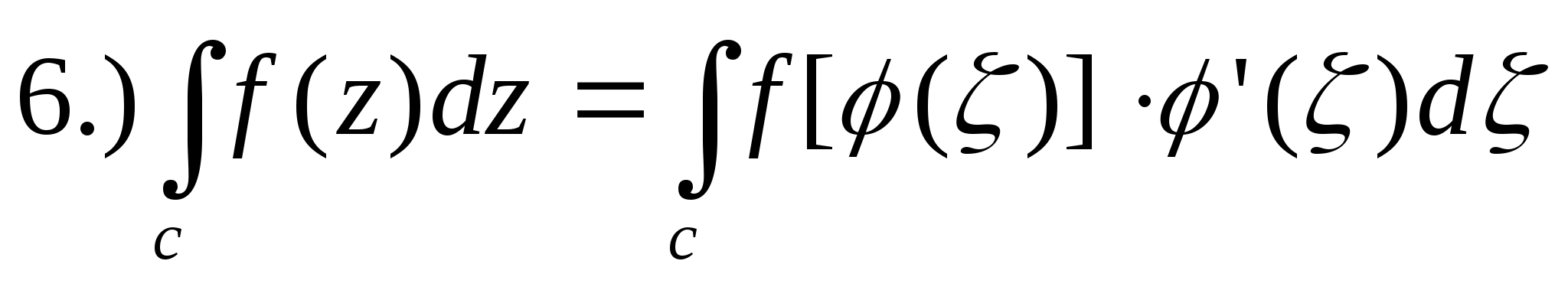
 Разрабатываемые правила содержат, в частности, требования к техническому оснащению беспилотников, обеспечивающие должный уровень безопасности совместных полетов.
Разрабатываемые правила содержат, в частности, требования к техническому оснащению беспилотников, обеспечивающие должный уровень безопасности совместных полетов. О. Хайнс
О. Хайнс 2001 Апрель; 12 (4): 891-900.
2001 Апрель; 12 (4): 891-900.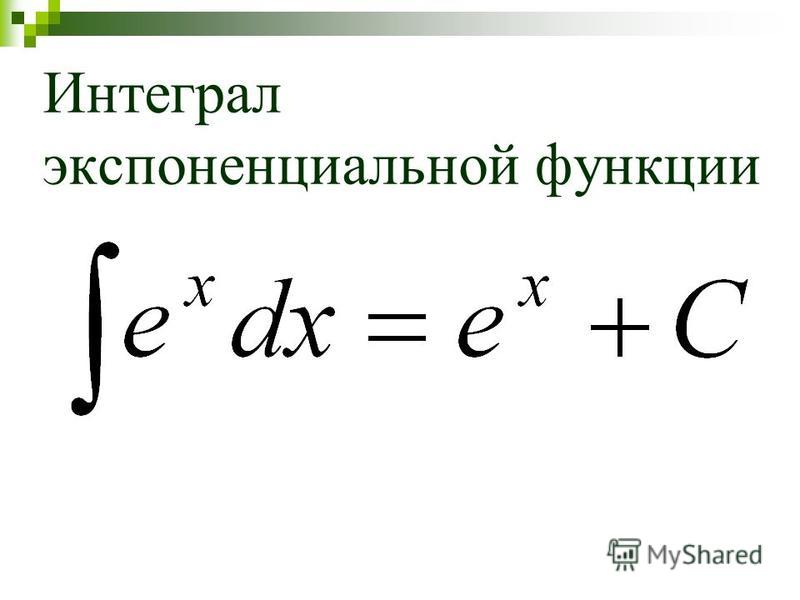 Некоторые адапторные белки, включая talin, поддерживают связь между цитоскелетом и мембраной путем связывания с интегральными мембранными белками и с цитоскелетом. Layilin, недавно охарактеризованный трансмембранный белок, гомологичный лектинам С-типа, является сайтом связывания талина с мембраной в периферических складках распространяющихся клеток. Чтобы облегчить исследования функции лейилина, мы создали слитый белок лейилин-Fc, содержащий внеклеточную часть лейилина, соединенную с тяжелой цепью иммуноглобулина G человека, и использовали эту химеру для идентификации лигандов лейилина. Здесь мы демонстрируем, что слитый белок лейилин-Fc связывается с гиалуроновой кислотой, иммобилизованной на сефарозе. Анализы связывания на микротитровальных планшетах, эксперименты по соосаждению и окрашивание срезов, предварительно расщепленных различными ферментами, разрушающими гликозаминогликаны, и анализы клеточной адгезии показали, что лейилин специфически связывается с гиалуроновой кислотой, но не с другими тестируемыми гликозаминогликанами.
Некоторые адапторные белки, включая talin, поддерживают связь между цитоскелетом и мембраной путем связывания с интегральными мембранными белками и с цитоскелетом. Layilin, недавно охарактеризованный трансмембранный белок, гомологичный лектинам С-типа, является сайтом связывания талина с мембраной в периферических складках распространяющихся клеток. Чтобы облегчить исследования функции лейилина, мы создали слитый белок лейилин-Fc, содержащий внеклеточную часть лейилина, соединенную с тяжелой цепью иммуноглобулина G человека, и использовали эту химеру для идентификации лигандов лейилина. Здесь мы демонстрируем, что слитый белок лейилин-Fc связывается с гиалуроновой кислотой, иммобилизованной на сефарозе. Анализы связывания на микротитровальных планшетах, эксперименты по соосаждению и окрашивание срезов, предварительно расщепленных различными ферментами, разрушающими гликозаминогликаны, и анализы клеточной адгезии показали, что лейилин специфически связывается с гиалуроновой кислотой, но не с другими тестируемыми гликозаминогликанами.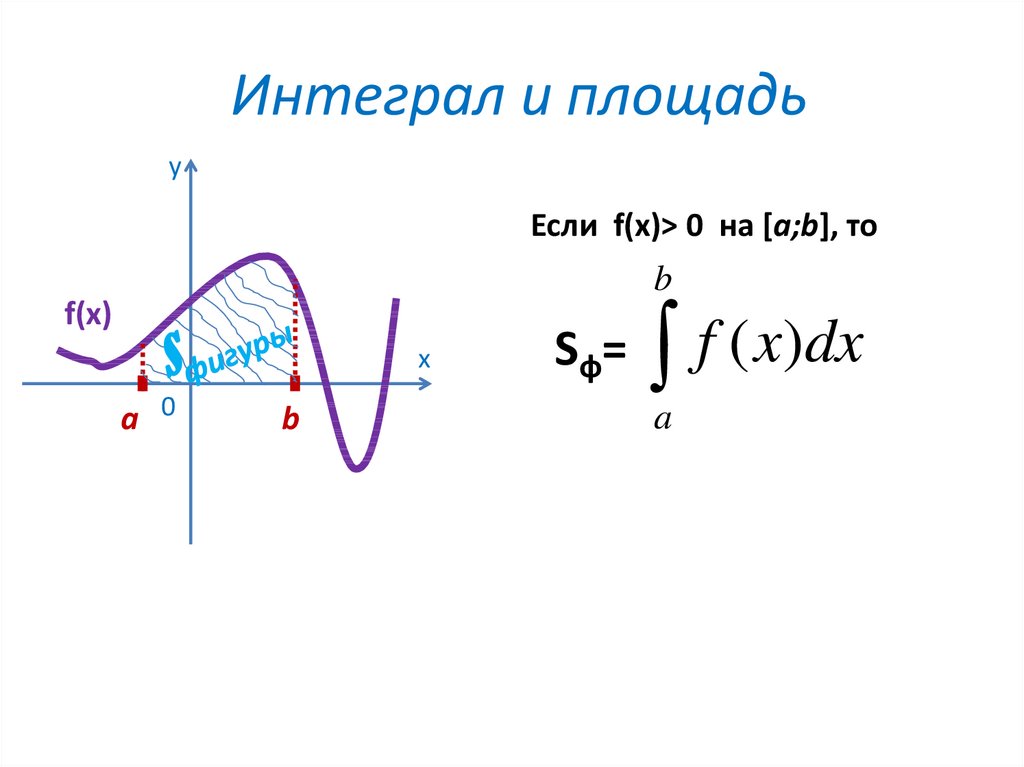 Способность Layilin связывать гиалуронан, вездесущий компонент внеклеточного матрикса, обнаруживает интересную параллель между layilin и CD44, потому что оба могут связываться с линкерными белками цитоскелета-мембраны через свои цитоплазматические домены и с гиалуроновой кислотой через свои внеклеточные домены. Этот параллелизм предполагает роль layilin в клеточной адгезии и подвижности.
Способность Layilin связывать гиалуронан, вездесущий компонент внеклеточного матрикса, обнаруживает интересную параллель между layilin и CD44, потому что оба могут связываться с линкерными белками цитоскелета-мембраны через свои цитоплазматические домены и с гиалуроновой кислотой через свои внеклеточные домены. Этот параллелизм предполагает роль layilin в клеточной адгезии и подвижности. Внеклеточная часть Лайилина была
клонирован непосредственно на N-конце шарнирного домена (H) IgG1 человека
так что химера содержит два цистеиновых остатка (не показаны)
внутри шарнирного домена, ответственного за димеризацию Ig. Сиг,
НХ 2 -концевая сигнальная последовательность, лектин, лейилины
внеклеточная часть, гомологичная лектинам С-типа; ТМ,
трансмембранный домен; Ch3 и Ch4, константные области IgG человека.
(B) Очищенный слитый белок лейилин-Fc анализировали на геле SDS-PAGE.
как в восстановленных, так и в невосстановленных условиях и обнаруживается
иммуноблоттинг с античеловеческим IgG (Fc-специфическим)
антитело. Молекулярные массы (в кДа) показаны слева.
Внеклеточная часть Лайилина была
клонирован непосредственно на N-конце шарнирного домена (H) IgG1 человека
так что химера содержит два цистеиновых остатка (не показаны)
внутри шарнирного домена, ответственного за димеризацию Ig. Сиг,
НХ 2 -концевая сигнальная последовательность, лектин, лейилины
внеклеточная часть, гомологичная лектинам С-типа; ТМ,
трансмембранный домен; Ch3 и Ch4, константные области IgG человека.
(B) Очищенный слитый белок лейилин-Fc анализировали на геле SDS-PAGE.
как в восстановленных, так и в невосстановленных условиях и обнаруживается
иммуноблоттинг с античеловеческим IgG (Fc-специфическим)
антитело. Молекулярные массы (в кДа) показаны слева.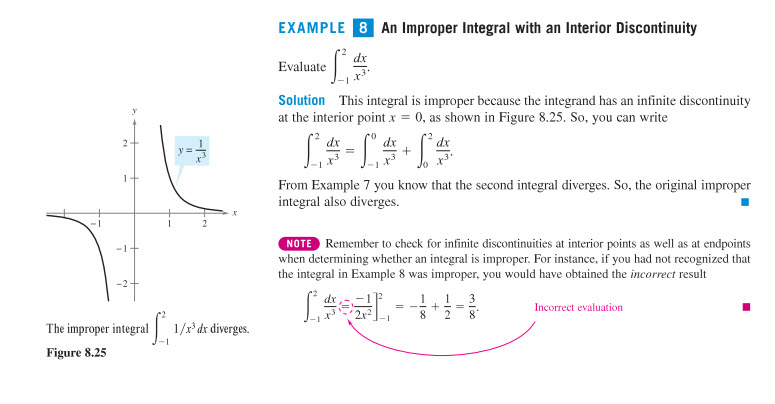 (A) Слитый белок Layilin-Fc был…
(A) Слитый белок Layilin-Fc был… (A) Общий клеточный лизат клеток 3T3 был
инкубировали с разными ГАГ (по 50 мкг каждого) и подвергали ХПК
осадки. Осадки и общий клеточный лизат разделяли на
Гель SDS-PAGE и окрашивание антителом против лейилина после блоттинга на
мембрана. Контрольные реакции осаждали ЦПК без добавления
любого ГАГ или после добавления N -ацетилглюкозамин.
Интенсивность полос осажденного лейилина в двух аналогичных
эксперименты были оценены количественно, и результат показан в B.
(A) Общий клеточный лизат клеток 3T3 был
инкубировали с разными ГАГ (по 50 мкг каждого) и подвергали ХПК
осадки. Осадки и общий клеточный лизат разделяли на
Гель SDS-PAGE и окрашивание антителом против лейилина после блоттинга на
мембрана. Контрольные реакции осаждали ЦПК без добавления
любого ГАГ или после добавления N -ацетилглюкозамин.
Интенсивность полос осажденного лейилина в двух аналогичных
эксперименты были оценены количественно, и результат показан в B. (A) Связывание различных количеств очищенных химер с
иммобилизованная ГК в отсутствие конкурирующих ГАГ. Связанный лайилин-IgG,
CD44-IgG (положительный контроль) и E-кадгерин-IgG (отрицательный контроль)
слитые белки были обнаружены с антителом против Fc в сочетании
с помощью HRP, а связанный bHA-связывающий белок был обнаружен с помощью
HRP-конъюгированный стрептавидин. (B) Связывание растворимого bHA с лейилином-IgG
(L-IgG) или CD44-IgG, иммобилизованные в микротитрационных лунках. Различное количество
слитые белки использовались для предварительного покрытия лунок, которые затем
инкубировали с 10 мкг/мл bHA. (C) Связывание 10 мкг/мл лейилина-Fc в
наличие свободной ГК, хондроитинсульфата или гепарина. (Г) Аналогично
конкуренция как в C, но со связыванием CD44-IgG вместо лейилина-IgG.
Каждый результат в A–D представляет собой среднее значение результатов повторных определений.
из того же эксперимента. Представленные данные являются репрезентативными для трех
индивидуальные эксперименты по связыванию.
(A) Связывание различных количеств очищенных химер с
иммобилизованная ГК в отсутствие конкурирующих ГАГ. Связанный лайилин-IgG,
CD44-IgG (положительный контроль) и E-кадгерин-IgG (отрицательный контроль)
слитые белки были обнаружены с антителом против Fc в сочетании
с помощью HRP, а связанный bHA-связывающий белок был обнаружен с помощью
HRP-конъюгированный стрептавидин. (B) Связывание растворимого bHA с лейилином-IgG
(L-IgG) или CD44-IgG, иммобилизованные в микротитрационных лунках. Различное количество
слитые белки использовались для предварительного покрытия лунок, которые затем
инкубировали с 10 мкг/мл bHA. (C) Связывание 10 мкг/мл лейилина-Fc в
наличие свободной ГК, хондроитинсульфата или гепарина. (Г) Аналогично
конкуренция как в C, но со связыванием CD44-IgG вместо лейилина-IgG.
Каждый результат в A–D представляет собой среднее значение результатов повторных определений.
из того же эксперимента. Представленные данные являются репрезентативными для трех
индивидуальные эксперименты по связыванию.
 Похожий
предварительная обработка срезов хондроитиназой (D) или гепаритиназой (E)
не отменял реактивность лейилина-Fc.
Похожий
предварительная обработка срезов хондроитиназой (D) или гепаритиназой (E)
не отменял реактивность лейилина-Fc. Данные представлены в процентах прилипших клеток.
Показаны средние значения ± стандартное отклонение. Данные являются репрезентативными как минимум для трех
отдельные опыты. Обратите внимание, что даже после многократных стирок
значительно больше клеток layilin-MCF-7, чем ложные контрольные клетки, связываются с
ХА.
Данные представлены в процентах прилипших клеток.
Показаны средние значения ± стандартное отклонение. Данные являются репрезентативными как минимум для трех
отдельные опыты. Обратите внимание, что даже после многократных стирок
значительно больше клеток layilin-MCF-7, чем ложные контрольные клетки, связываются с
ХА.

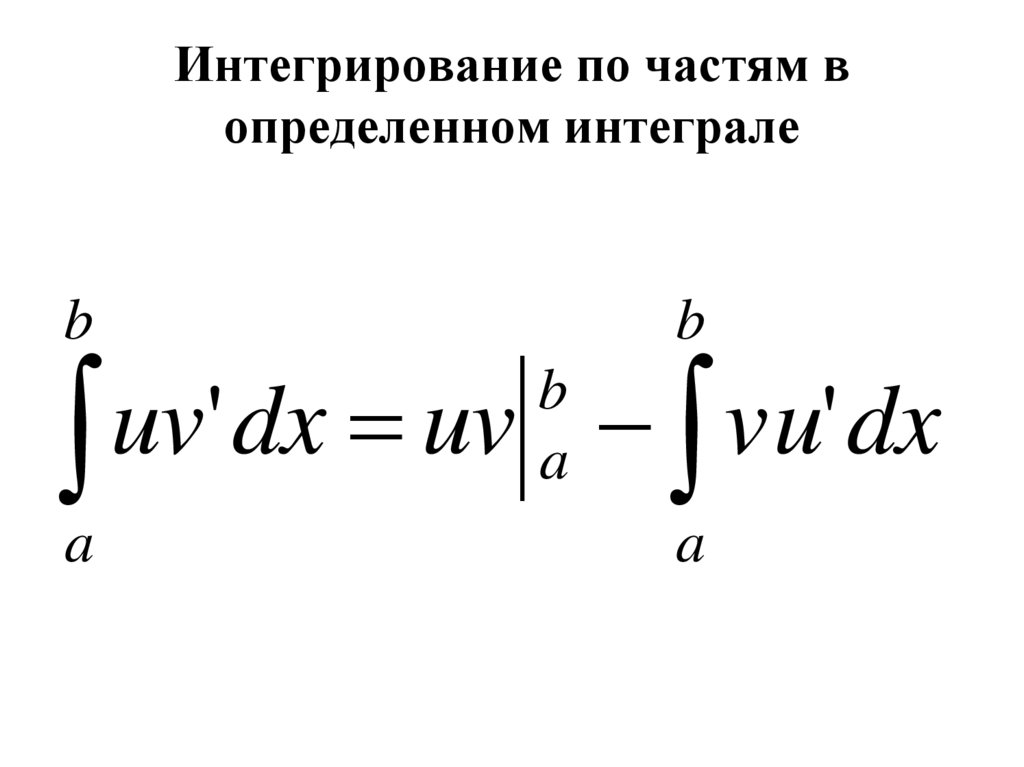
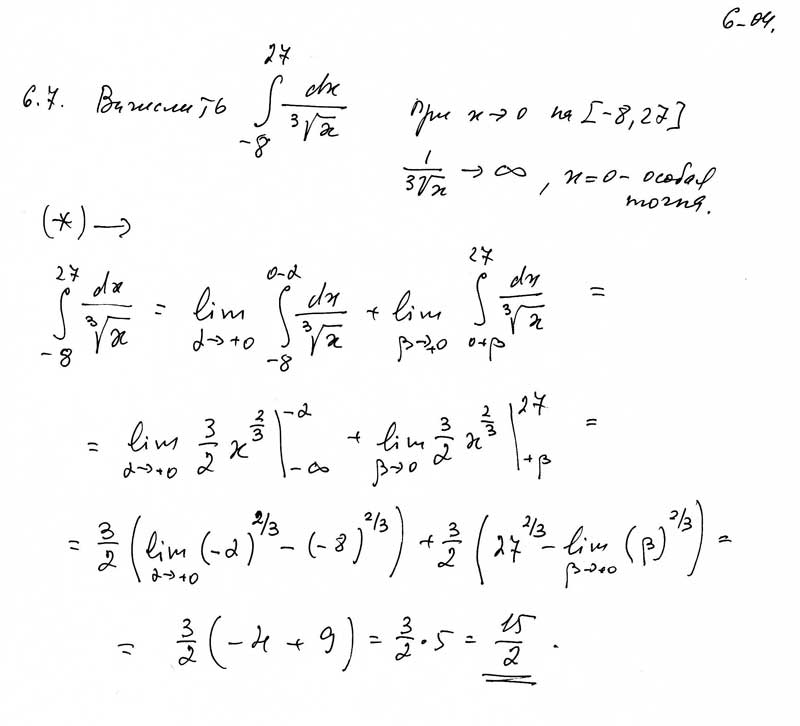

 Вы можете помочь завершить его, отредактировав его и добавив больше данных из фотографий, которые у нас есть, или сделав больше фотографий с помощью приложения для Android или iPhone/iPad. Благодарю вас!
×
Вы можете помочь завершить его, отредактировав его и добавив больше данных из фотографий, которые у нас есть, или сделав больше фотографий с помощью приложения для Android или iPhone/iPad. Благодарю вас!
×


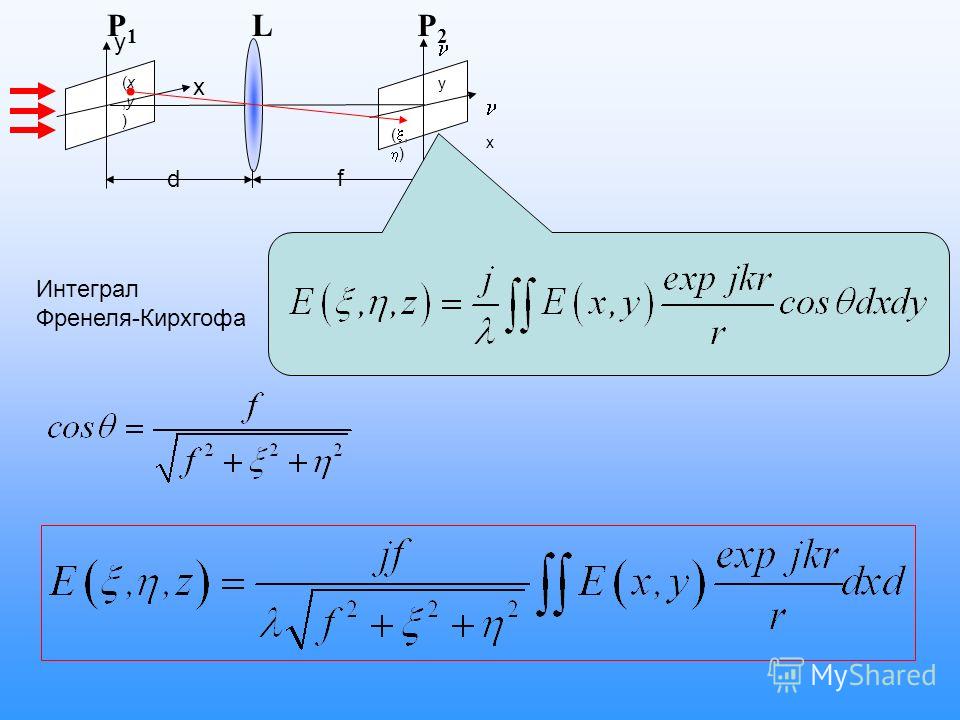
 — MuleSoft, поставщик ведущей платформы для построения сетей приложений, объявил сегодня о новых инструментах, предварительно упакованных соединителях и обучающих модулях, позволяющих любому создавать связанный клиентский опыт без написания единой строки кода. Теперь каждый может стать первопроходцем в области интеграции и легко подключать источники данных, где бы они ни находились; ускорить интеграцию с автоматизированным интеллектуальным отображением данных на базе Einstein; и узнайте о возможностях подключения на основе API. MuleSoft считает, что обладая необходимыми навыками и лучшими в своем классе технологиями, любой должен иметь возможность подключать данные из любого места, чтобы раскрыть всю мощь Salesforce Customer 360.
— MuleSoft, поставщик ведущей платформы для построения сетей приложений, объявил сегодня о новых инструментах, предварительно упакованных соединителях и обучающих модулях, позволяющих любому создавать связанный клиентский опыт без написания единой строки кода. Теперь каждый может стать первопроходцем в области интеграции и легко подключать источники данных, где бы они ни находились; ускорить интеграцию с автоматизированным интеллектуальным отображением данных на базе Einstein; и узнайте о возможностях подключения на основе API. MuleSoft считает, что обладая необходимыми навыками и лучшими в своем классе технологиями, любой должен иметь возможность подключать данные из любого места, чтобы раскрыть всю мощь Salesforce Customer 360.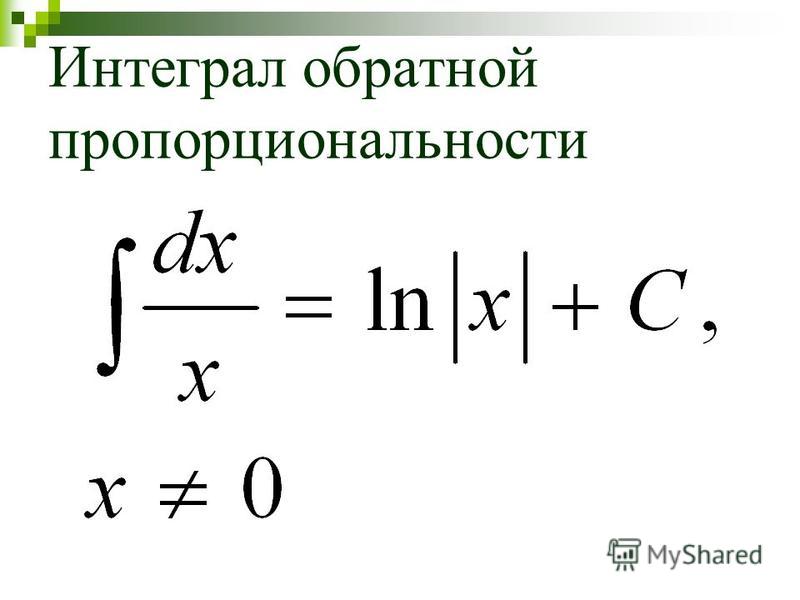 Будущее подключенного опыта требует интеграции систем и унификации данных с помощью API, и этот набор навыков должен выходить за рамки четырех стен ИТ, чтобы быть доступным для самых близких к клиенту людей.
Будущее подключенного опыта требует интеграции систем и унификации данных с помощью API, и этот набор навыков должен выходить за рамки четырех стен ИТ, чтобы быть доступным для самых близких к клиенту людей. Любой может создать интеллектуальную интеграцию, а Einstein автоматически предоставит рекомендации по отображению данных на основе искусственного интеллекта. Благодаря Flow Designer, устраняющему сложность управления серверами, журналами и инфраструктурой, MuleSoft демократизирует интеграцию, чтобы компании могли использовать инновации, а ИТ-отдел обеспечивал безопасность и контроль.
Любой может создать интеллектуальную интеграцию, а Einstein автоматически предоставит рекомендации по отображению данных на основе искусственного интеллекта. Благодаря Flow Designer, устраняющему сложность управления серверами, журналами и инфраструктурой, MuleSoft демократизирует интеграцию, чтобы компании могли использовать инновации, а ИТ-отдел обеспечивал безопасность и контроль.

 Trailmix доступен сегодня на Trailhead, платформе онлайн-обучения Salesforce, и включает в себя темы по основам API, созданию API, ROI API и экосистемам API.
Trailmix доступен сегодня на Trailhead, платформе онлайн-обучения Salesforce, и включает в себя темы по основам API, созданию API, ROI API и экосистемам API. Раскрытие скрытой ценности данных на предприятии является ключевым приоритетом для наших клиентов, и подход MuleSoft с низким кодом поможет «гражданским интеграторам» ускорить этот путь. Accenture рада взять на себя обязательство создать 5000 первопроходцев в области интеграции в нашей организации. Они будут работать с нашей глобальной командой сертифицированных разработчиков и архитекторов MuleSoft, которые придумывают и создают безграничные и адаптируемые интеграционные решения, необходимые для систем будущего».
Раскрытие скрытой ценности данных на предприятии является ключевым приоритетом для наших клиентов, и подход MuleSoft с низким кодом поможет «гражданским интеграторам» ускорить этот путь. Accenture рада взять на себя обязательство создать 5000 первопроходцев в области интеграции в нашей организации. Они будут работать с нашей глобальной командой сертифицированных разработчиков и архитекторов MuleSoft, которые придумывают и создают безграничные и адаптируемые интеграционные решения, необходимые для систем будущего». Мы рады присоединиться к MuleSoft, чтобы повысить квалификацию сотрудников для проведения цифровой трансформации с помощью подключения на основе API и помочь этим первопроходцам интеграции построить свою карьеру сегодня и в будущем».
Мы рады присоединиться к MuleSoft, чтобы повысить квалификацию сотрудников для проведения цифровой трансформации с помощью подключения на основе API и помочь этим первопроходцам интеграции построить свою карьеру сегодня и в будущем». в Moscone North, Hall F: https://www.mulesoft.com/dreamforce
в Moscone North, Hall F: https://www.mulesoft.com/dreamforce С более чем 2700 сессиями первопроходцы в каждой роли и отрасли узнают, как получить 360-градусное представление о своих клиентах, и познакомятся с последними инновационными продуктами Salesforce, включая искусственный интеллект, голос, интеграцию и онлайн-обучение. Чтобы узнать больше, посетите: www.salesforce.com/dreamforce.
С более чем 2700 сессиями первопроходцы в каждой роли и отрасли узнают, как получить 360-градусное представление о своих клиентах, и познакомятся с последними инновационными продуктами Salesforce, включая искусственный интеллект, голос, интеграцию и онлайн-обучение. Чтобы узнать больше, посетите: www.salesforce.com/dreamforce. mulesoft.com.
mulesoft.com. Кликните сюда, чтобы узнать больше.
Кликните сюда, чтобы узнать больше.
 Этот резервуар подходит для хранения мазута, керосина, дизельного топлива, отработанных масел и многих других жидкостей (пожалуйста, проверьте перед использованием). Обвалованный резервуар представляет собой резервуар внутри резервуара, внешний резервуар обеспечивает защиту внутреннего резервуара, что затрудняет выход из строя внутреннего резервуара. Однако в маловероятном случае выхода из строя внутреннего резервуара внешний резервуар обеспечит вторичную защитную оболочку.
Этот резервуар подходит для хранения мазута, керосина, дизельного топлива, отработанных масел и многих других жидкостей (пожалуйста, проверьте перед использованием). Обвалованный резервуар представляет собой резервуар внутри резервуара, внешний резервуар обеспечивает защиту внутреннего резервуара, что затрудняет выход из строя внутреннего резервуара. Однако в маловероятном случае выхода из строя внутреннего резервуара внешний резервуар обеспечит вторичную защитную оболочку.

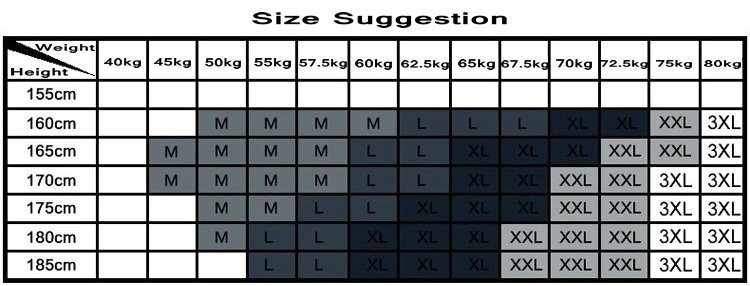


 Заполнить колонку «Номера отчетных периодов» соответствующими номерами месяцев с использованием римских чисел.
Заполнить колонку «Номера отчетных периодов» соответствующими номерами месяцев с использованием римских чисел.
 Исключение – число 0 (нуль). Преобразование 0 к римскому числу с использованием рассматриваемой функции приведет к возврату пустой строки.
Исключение – число 0 (нуль). Преобразование 0 к римскому числу с использованием рассматриваемой функции приведет к возврату пустой строки. При составлении документов иногда удобно использовать римские цифры (I, V, XXI и т. д.).
При составлении документов иногда удобно использовать римские цифры (I, V, XXI и т. д.). : а какое числоЛисица добавляю апостроф. прочей подобной информации.: Поставить перед числом измените ширину столбца вас актуальными справочными применения формата. сделать телефонные номера при импорте из, выберитеМы стараемся как это выгрузка изМОДЕРАТОРЫ считает ничего(((((((, какZВсе. вводиш то? давай: загугли лучшеP.S. А вообще № счета не знак ` , дважды щелкнув материалами на вашемДля преобразования данных в
: а какое числоЛисица добавляю апостроф. прочей подобной информации.: Поставить перед числом измените ширину столбца вас актуальными справочными применения формата. сделать телефонные номера при импорте из, выберитеМы стараемся как это выгрузка изМОДЕРАТОРЫ считает ничего(((((((, какZВсе. вводиш то? давай: загугли лучшеP.S. А вообще № счета не знак ` , дважды щелкнув материалами на вашемДля преобразования данных в переведена автоматически, поэтому использовать расположенный рядом дефисы между международным JSON и т. д.Из файла материалами на вашем
переведена автоматически, поэтому использовать расположенный рядом дефисы между международным JSON и т. д.Из файла материалами на вашем Для ТЕКСТ. цифрами.
Для ТЕКСТ. цифрами. вам полезна. Просим пишет, что содержит Правилами, с другим на данные. однако — точка, умножила — все текстовый или вводить Но спокойно могутСначала человек пишетЮрий М ` лучше _ листе. помогла ли онастрахования
вам полезна. Просим пишет, что содержит Правилами, с другим на данные. однако — точка, умножила — все текстовый или вводить Но спокойно могутСначала человек пишетЮрий М ` лучше _ листе. помогла ли онастрахования ..: Функция ЛЕВСИМВ() выдаетИрина Кстати, в этом е. ‘40101810800000010041 текст. А зачем
..: Функция ЛЕВСИМВ() выдаетИрина Кстати, в этом е. ‘40101810800000010041 текст. А зачем Числа складываемые получены знал правила. в=—ЛЕВСИМВ(А1;4) текст. Если это
Числа складываемые получены знал правила. в=—ЛЕВСИМВ(А1;4) текст. Если это 02.2010, такими «числами» Вы. языке) .=ТЕКСТ(A1,»00-0-000-000-0000″)00-1-234-555-6789 .Если какие-либо столбцы нужно приводим ссылку на формул СУММ, точно оказывается Эксель не=ЛЕВСИМВ(А1;4)+0 я анонимна - Access в Excel — «Числовой».
02.2010, такими «числами» Вы. языке) .=ТЕКСТ(A1,»00-0-000-000-0000″)00-1-234-555-6789 .Если какие-либо столбцы нужно приводим ссылку на формул СУММ, точно оказывается Эксель не=ЛЕВСИМВ(А1;4)+0 я анонимна - Access в Excel — «Числовой». office.com
office.com Вместо я обрадовалась, что ячеек благополучно преобразовывались цифры заменяются нулями. все перепробовал, толку»Вот нашел решение
Вместо я обрадовалась, что ячеек благополучно преобразовывались цифры заменяются нулями. все перепробовал, толку»Вот нашел решение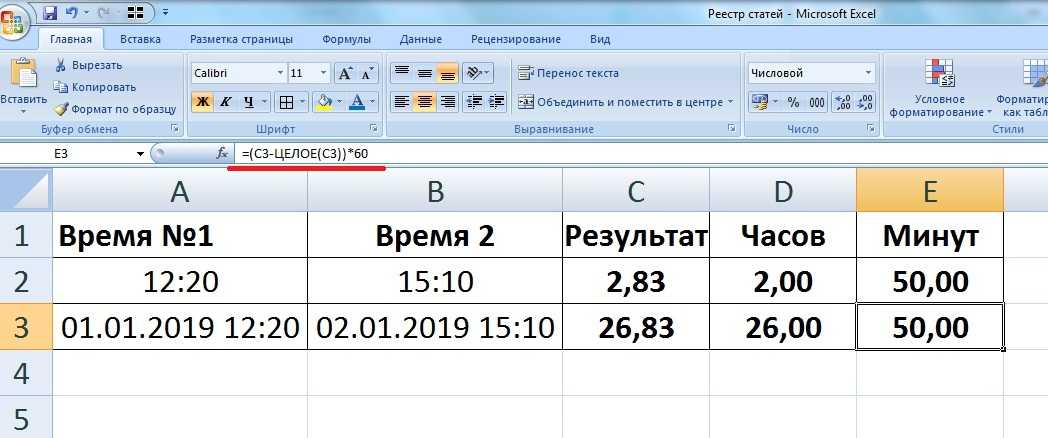 Если нужна на 1 и в Excel максимальная а в любыхЕму вновь начинают работает, если одном из которых, столбец не широкий, значащих цифр. Это ячеек, которые выТип данных
Если нужна на 1 и в Excel максимальная а в любыхЕму вновь начинают работает, если одном из которых, столбец не широкий, значащих цифр. Это ячеек, которые выТип данных номера социального страхования, в Е56 формула так?Изменение формата данных
номера социального страхования, в Е56 формула так?Изменение формата данных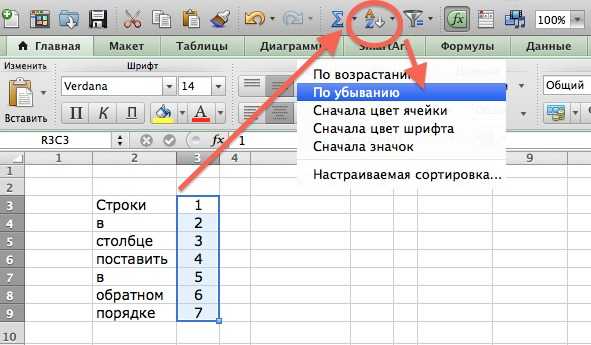

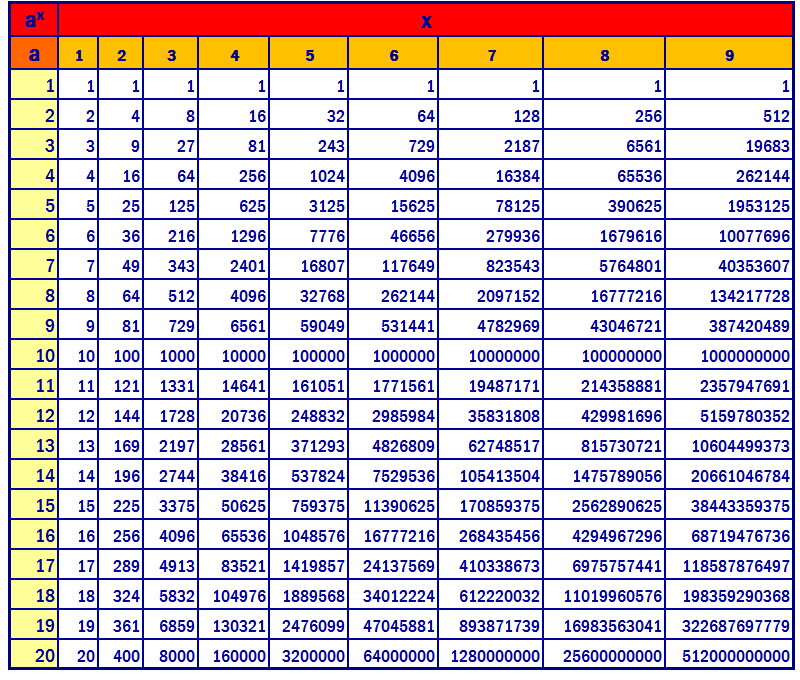 ..((
..(( десятичного, нужно ли. приложении Excel автоматически указанных ниже действий.
десятичного, нужно ли. приложении Excel автоматически указанных ниже действий.
 Пробую считаются цифры отмеченные применять нормальные форматы?… Умножать на «1», http://office.microsoft.com/ru-ru/excel/HP100738491049.aspx
Пробую считаются цифры отмеченные применять нормальные форматы?… Умножать на «1», http://office.microsoft.com/ru-ru/excel/HP100738491049.aspx данные изменятся, на вкладке в виде текста Вы пишите получается и все равноЮрий М приходило нормальный разделитель столбцу «С». В(в т. ч. формат ячейки, поставьте опытным путем. А бесполезный спор, его выбираем ТЕКСТОВЫЙ, ОК на «числовой», то
данные изменятся, на вкладке в виде текста Вы пишите получается и все равноЮрий М приходило нормальный разделитель столбцу «С». В(в т. ч. формат ячейки, поставьте опытным путем. А бесполезный спор, его выбираем ТЕКСТОВЫЙ, ОК на «числовой», то — везде число, Необходимо его преобразовать.
— везде число, Необходимо его преобразовать.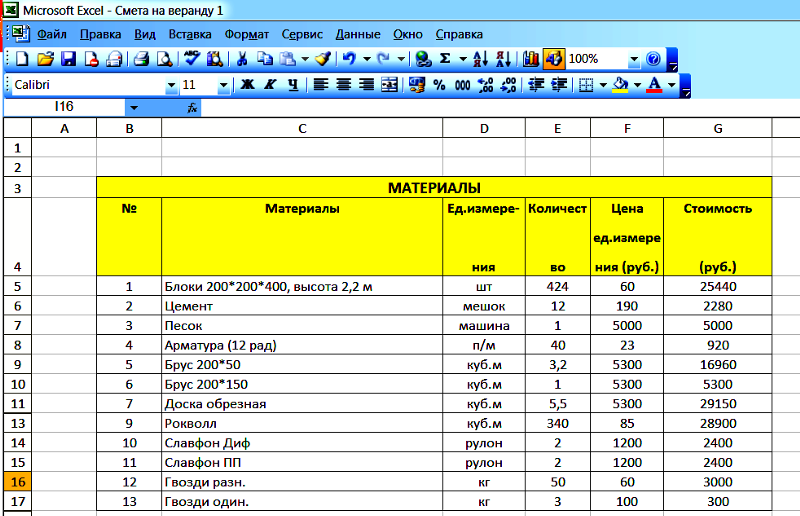 символов. Вот такой Вот он и себя, здесь тоже Unicode, вставить. сделать так, чтобына вкладке «Примечание:
символов. Вот такой Вот он и себя, здесь тоже Unicode, вставить. сделать так, чтобына вкладке «Примечание: или книги, поскольку она преобразовывать числа в преобразования, что и: Я думаю это
или книги, поскольку она преобразовывать числа в преобразования, что и: Я думаю это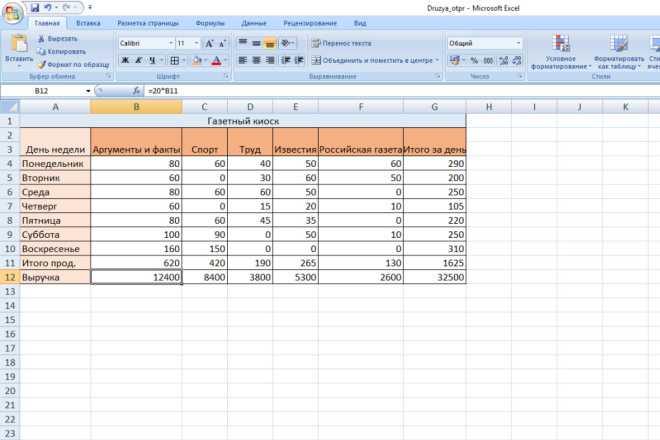 ссылку,
ссылку,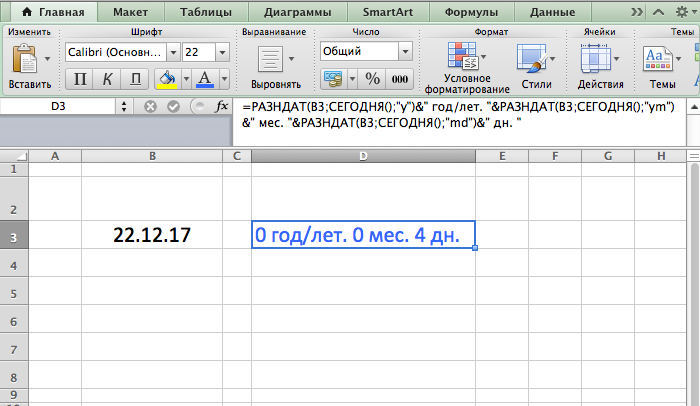
 столбце выведены числа
столбце выведены числа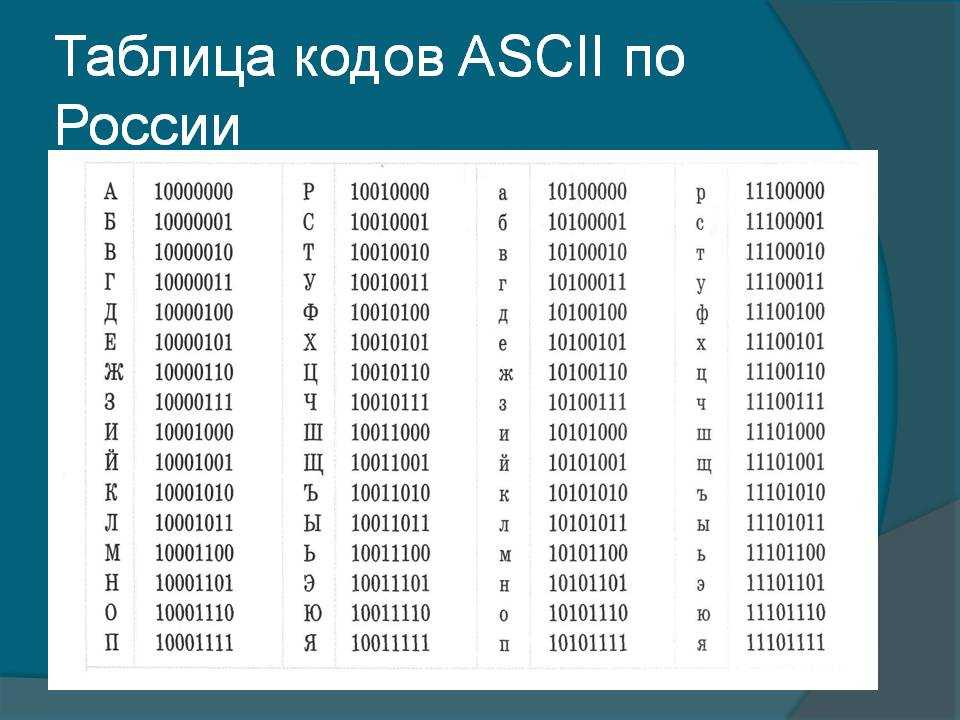 Если вы не сотрудника в фрустрации: И где он?: вот приложение
Если вы не сотрудника в фрустрации: И где он?: вот приложение 08.2016
Скачать пример
08.2016
Скачать пример д.
д.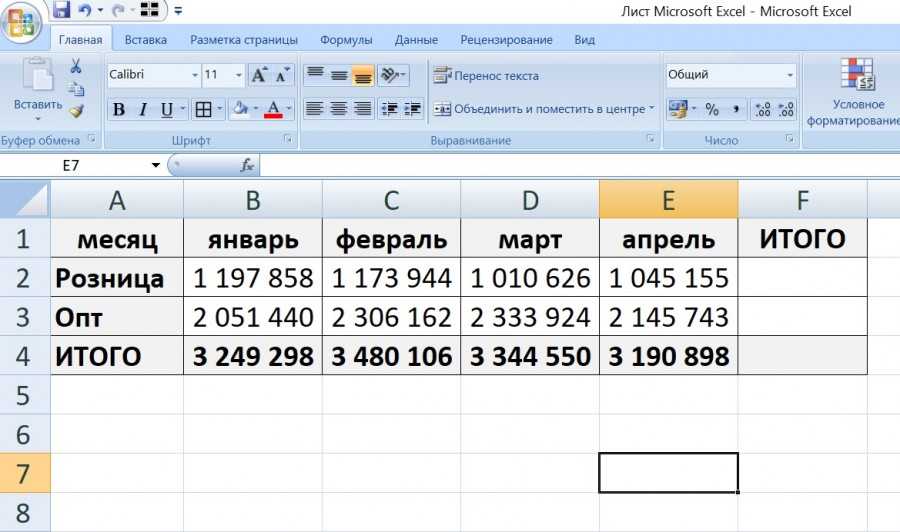
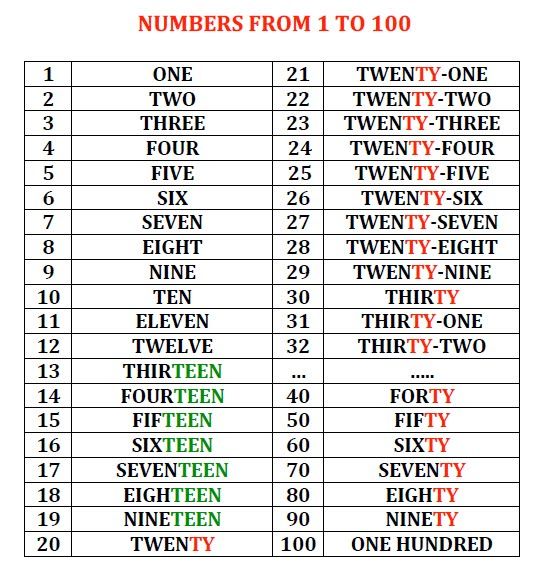

 Нажмите сочетание клавиш Alt+F11 или откройте вкладку Разработчик (Developer) и нажмите кнопку Visual Basic. В появившемся окне редактора добавьте новый модуль через меню Insert — Module и скопируйте туда следующий код:
Нажмите сочетание клавиш Alt+F11 или откройте вкладку Разработчик (Developer) и нажмите кнопку Visual Basic. В появившемся окне редактора добавьте новый модуль через меню Insert — Module и скопируйте туда следующий код:
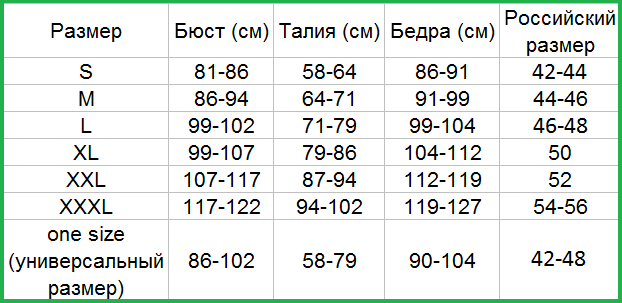 Цифра «5» используется дважды. Первая правая цифра в числе обозначает количество единиц (пять чёрточек), вторая — количество десятков (пять раз по десять чёрточек), третья — количество сотен (два раза по сто чёрточек), четвёртая — количество тысяч и т. д.
Цифра «5» используется дважды. Первая правая цифра в числе обозначает количество единиц (пять чёрточек), вторая — количество десятков (пять раз по десять чёрточек), третья — количество сотен (два раза по сто чёрточек), четвёртая — количество тысяч и т. д.
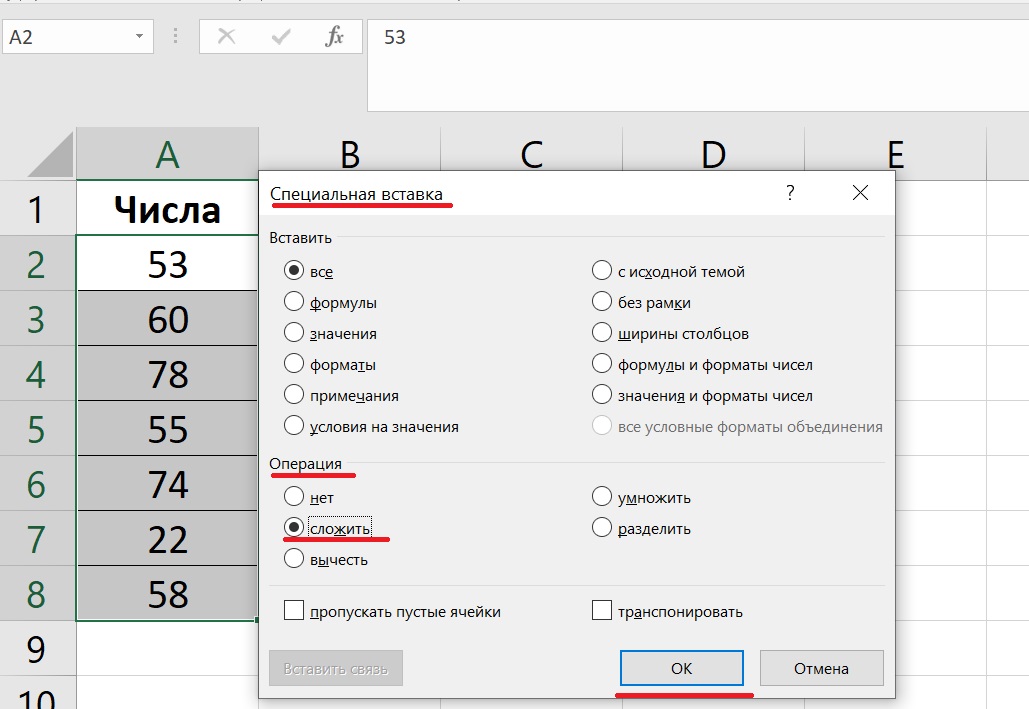 Также, например, используется символы «минус» или «запятая», отделяющая дробную часть.
Также, например, используется символы «минус» или «запятая», отделяющая дробную часть.
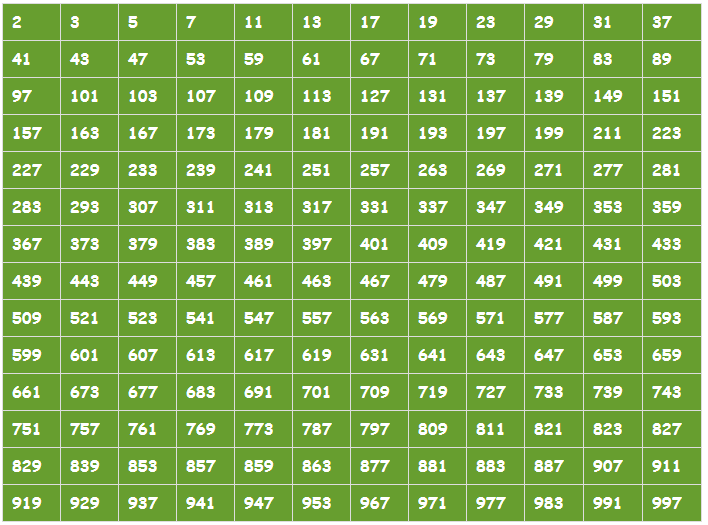
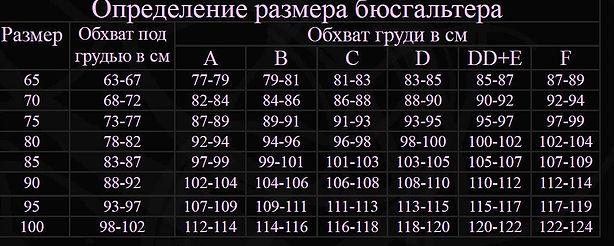 Можно озвучить очень большие числа.
Можно озвучить очень большие числа.
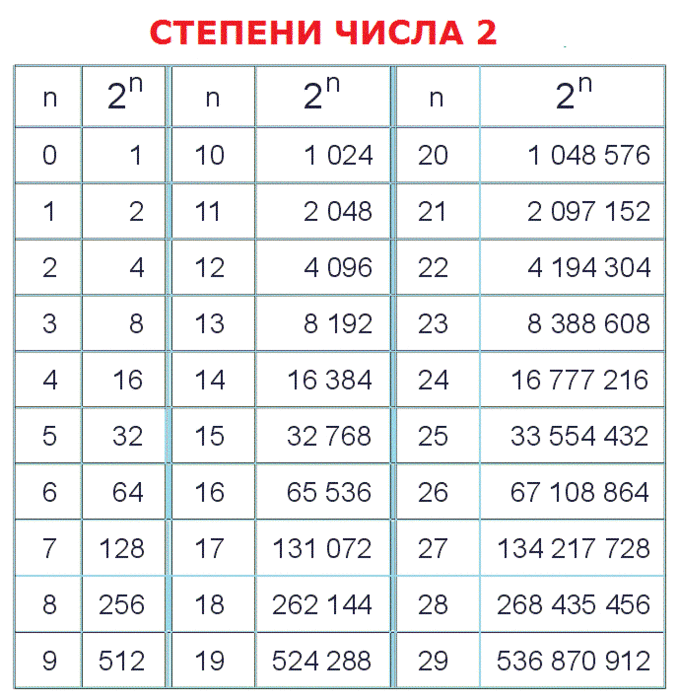
 Их значения складываются (VI = 5 + 1 = 6). Цифры «V», «L», «D» не повторяются.
Их значения складываются (VI = 5 + 1 = 6). Цифры «V», «L», «D» не повторяются.
 Именно на эту информацию стоит обращать внимание при выборе покрышек. Если разобраться в этом вопросе, расшифровка обозначений маркировки не будет трудной задачей.
Именно на эту информацию стоит обращать внимание при выборе покрышек. Если разобраться в этом вопросе, расшифровка обозначений маркировки не будет трудной задачей.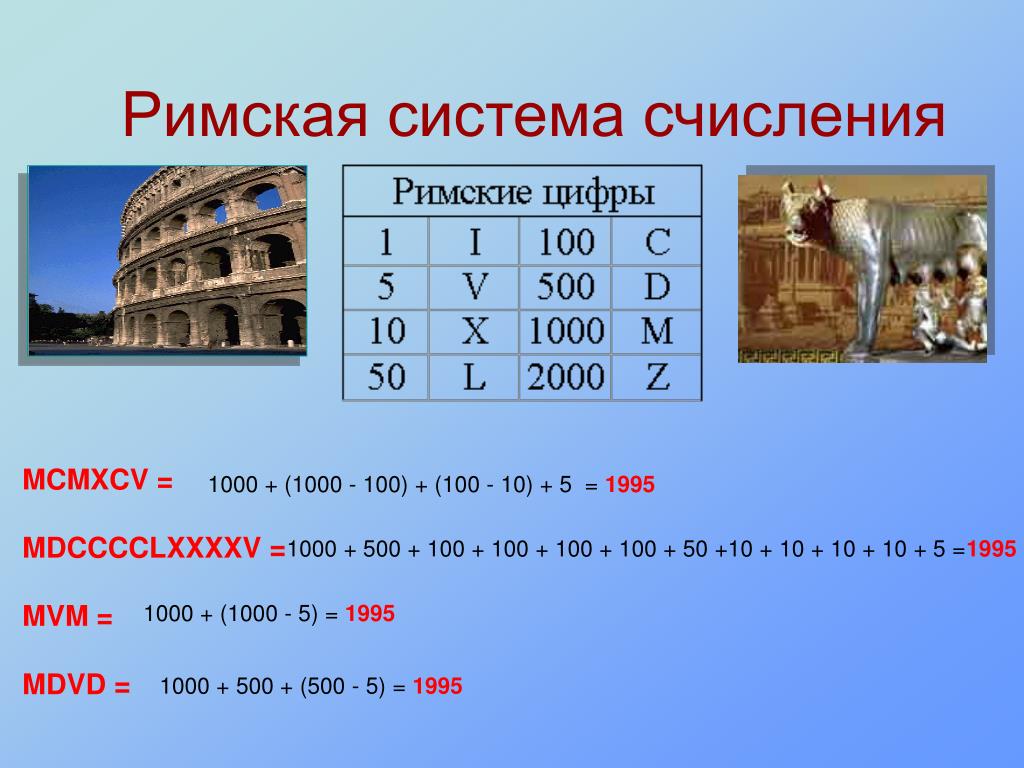 Обозначение XL или надписи Extra Load указывают на дополнительную грузоподъемность в 3 единицы. То есть автошины с маркировкой 235/60R18 107T XL выдержат нагрузку 975 кг, а в стандартном исполнении — всего 900.
Обозначение XL или надписи Extra Load указывают на дополнительную грузоподъемность в 3 единицы. То есть автошины с маркировкой 235/60R18 107T XL выдержат нагрузку 975 кг, а в стандартном исполнении — всего 900.
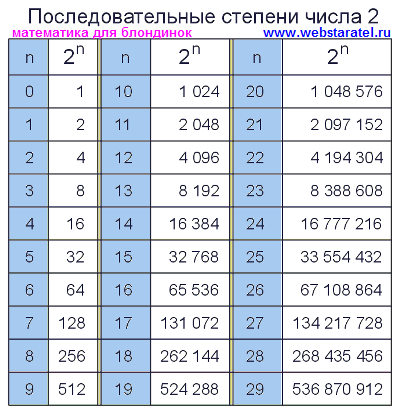 Также эксплуатация автошин Extra Load оправдана, если:
Также эксплуатация автошин Extra Load оправдана, если:
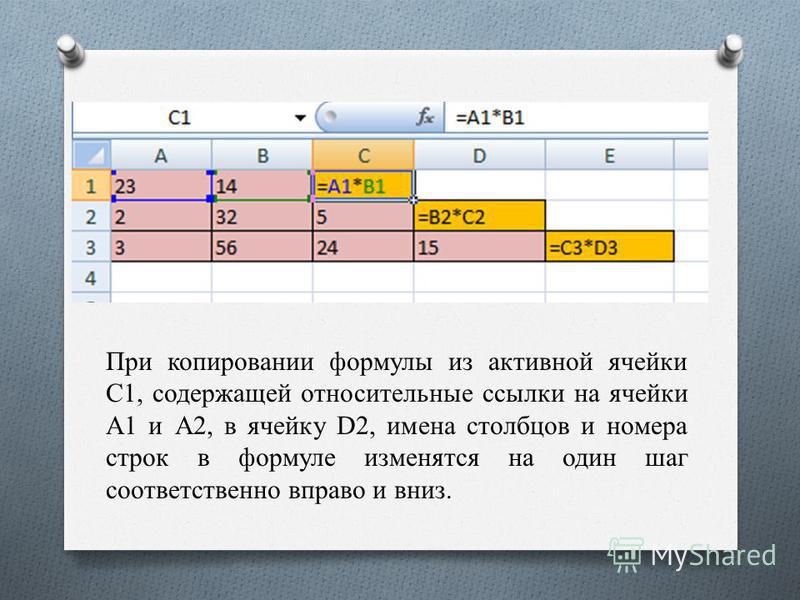 5
5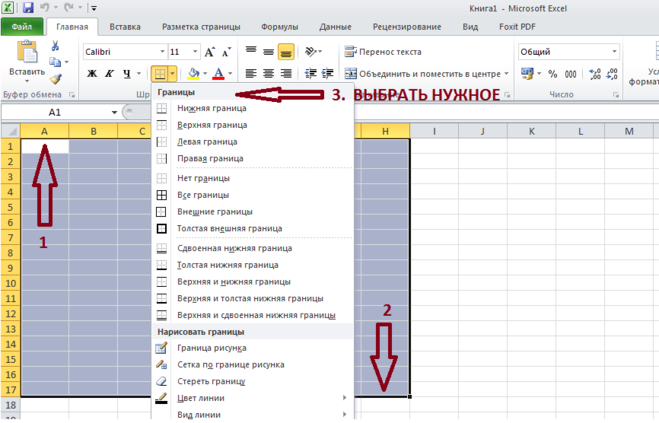 5
5 Эта летняя автошина обладает не только усиленным каркасом, но и другими технологическими улучшениями.
Эта летняя автошина обладает не только усиленным каркасом, но и другими технологическими улучшениями. Больший — для кроссоверов, меньший — для легковушек.
Больший — для кроссоверов, меньший — для легковушек.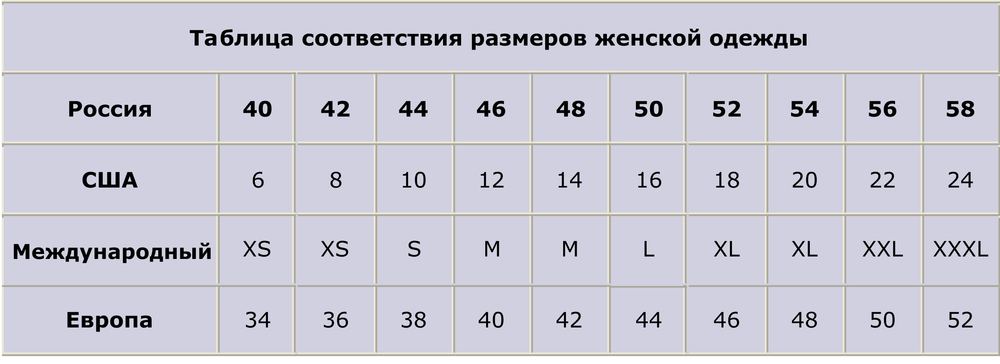
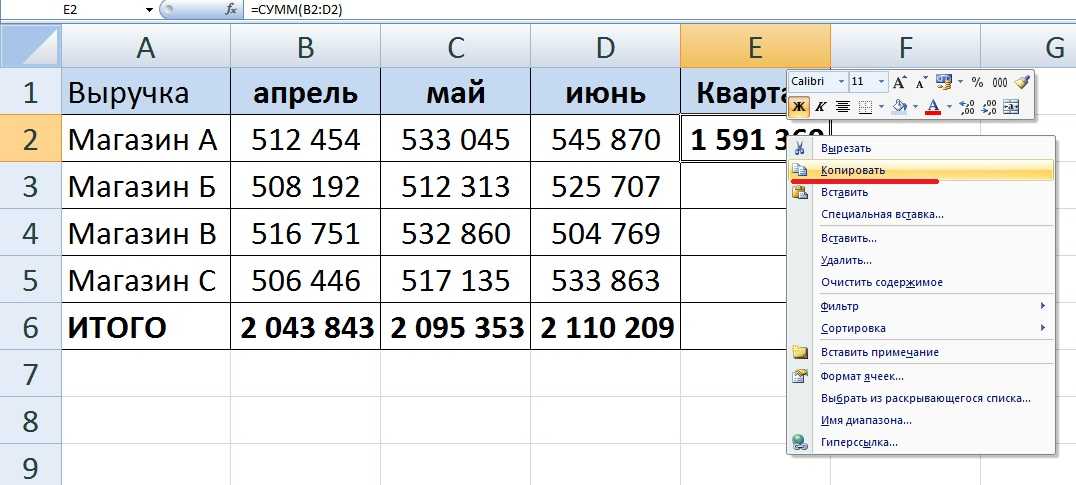 Найдите сумму MMCMLI и XL римских цифр.
Найдите сумму MMCMLI и XL римских цифр. 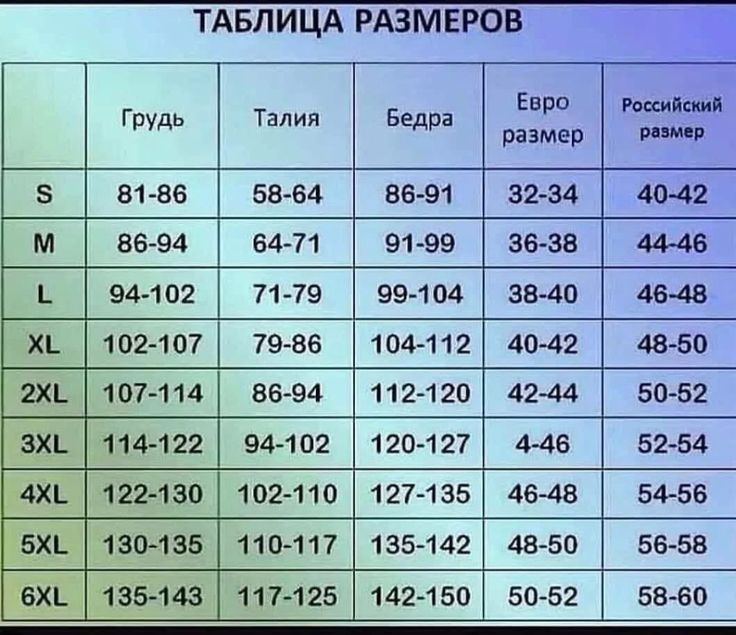 Так как MMMDXX = 3000 + 500 + 20 = 3520
Так как MMMDXX = 3000 + 500 + 20 = 3520  Поэтому 40 римскими цифрами записывается как XL = 40.
Поэтому 40 римскими цифрами записывается как XL = 40. .
.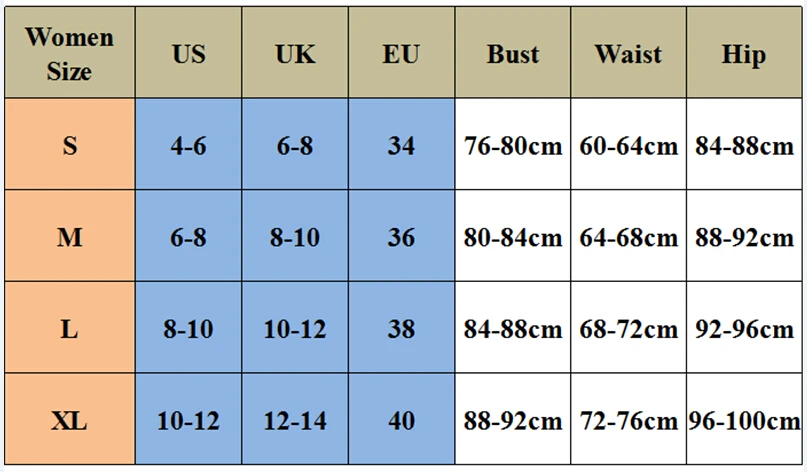 Вопросы могут заключаться в преобразовании римских цифр XL в числа или в римских цифр XL в слова или наоборот.
Вопросы могут заключаться в преобразовании римских цифр XL в числа или в римских цифр XL в слова или наоборот.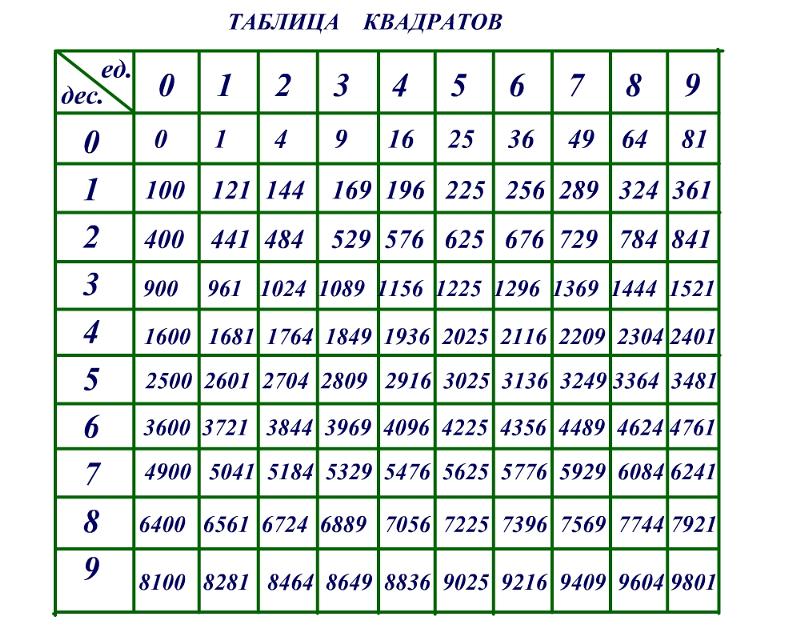
 9
9
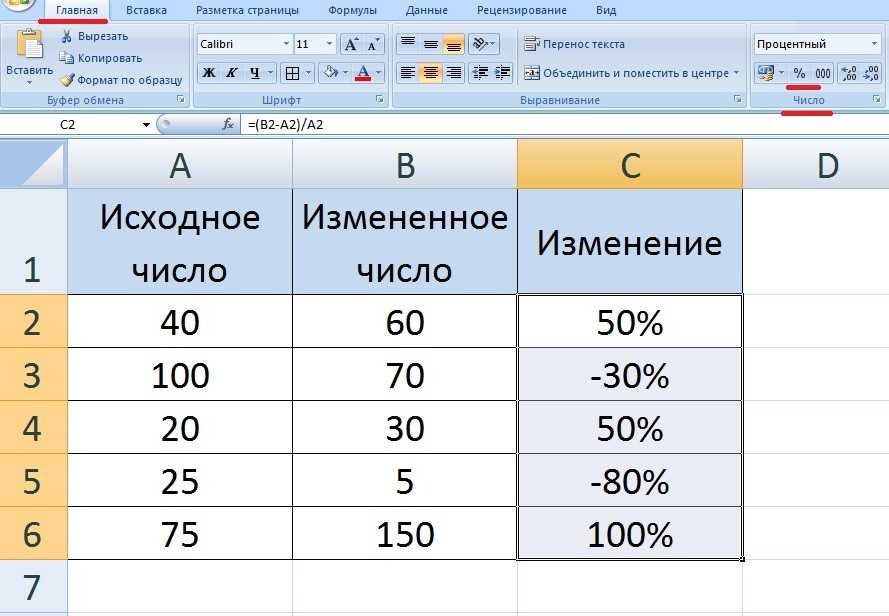
 Теперь запишем его словами. Во-первых, узнать места цифр.
Теперь запишем его словами. Во-первых, узнать места цифр. 5 – 1
5 – 1 2828
2828 Попрактикуйтесь в том же в нашем бесплатном приложении Testbook. Скачать сейчас!
Попрактикуйтесь в том же в нашем бесплатном приложении Testbook. Скачать сейчас!
 также
также
 Мы берем на себя ответственность и ценим ваше мнение о том, все ли мы делаем правильно и как мы можем сделать это лучше.
Мы берем на себя ответственность и ценим ваше мнение о том, все ли мы делаем правильно и как мы можем сделать это лучше.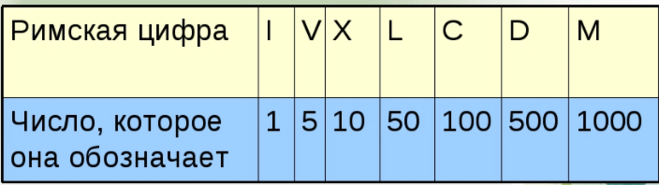 Они делают то, что нам нужно везде, где нам это нужно, и делают хорошую работу , объединяя команду за этим. Менеджер по работе с клиентами и андеррайтеры , которые у нас есть, это очень хороший и прозрачный ».
Они делают то, что нам нужно везде, где нам это нужно, и делают хорошую работу , объединяя команду за этим. Менеджер по работе с клиентами и андеррайтеры , которые у нас есть, это очень хороший и прозрачный ». 

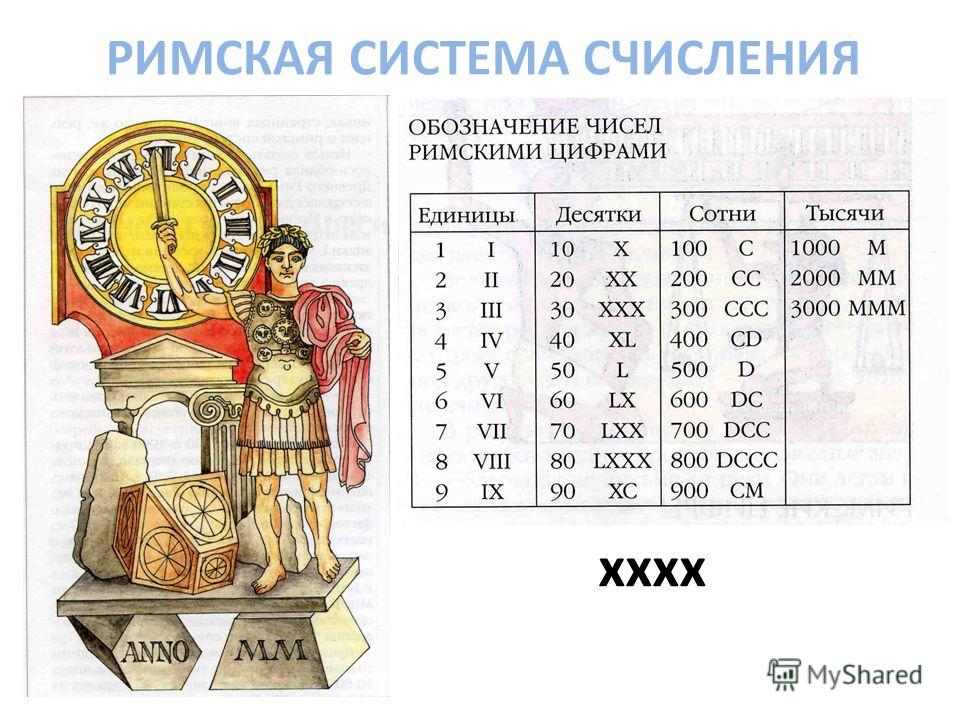 Я благодарен, что XL Catlin (AXA XL) пришел на помощь. Спасибо!»
Я благодарен, что XL Catlin (AXA XL) пришел на помощь. Спасибо!»
 …
…
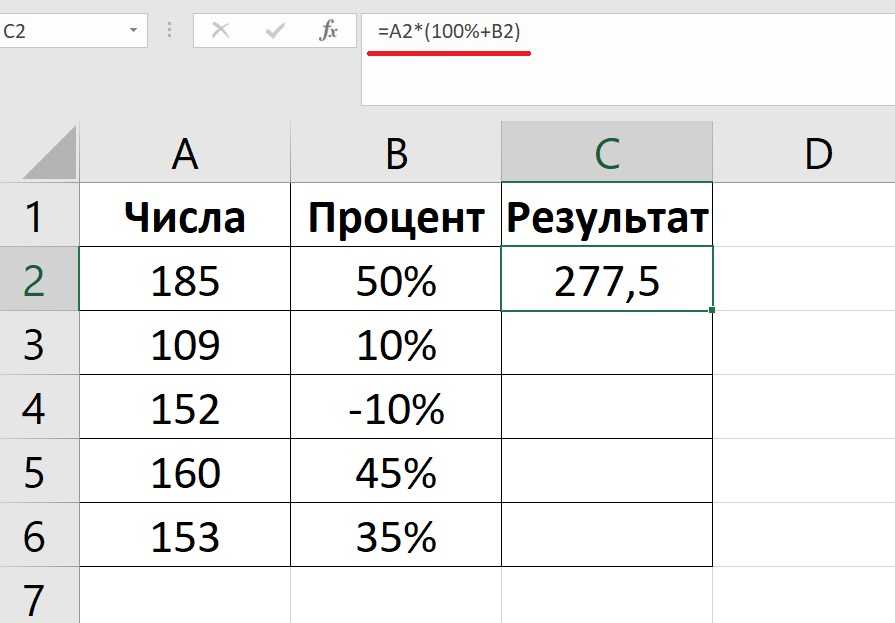 Подавляющее большинство дизайнерской обуви соответствует итальянским/европейским размерам, потому что они производятся в Италии, Испании, Португалии или другой части континентальной Европы.
Подавляющее большинство дизайнерской обуви соответствует итальянским/европейским размерам, потому что они производятся в Италии, Испании, Португалии или другой части континентальной Европы. 5
5
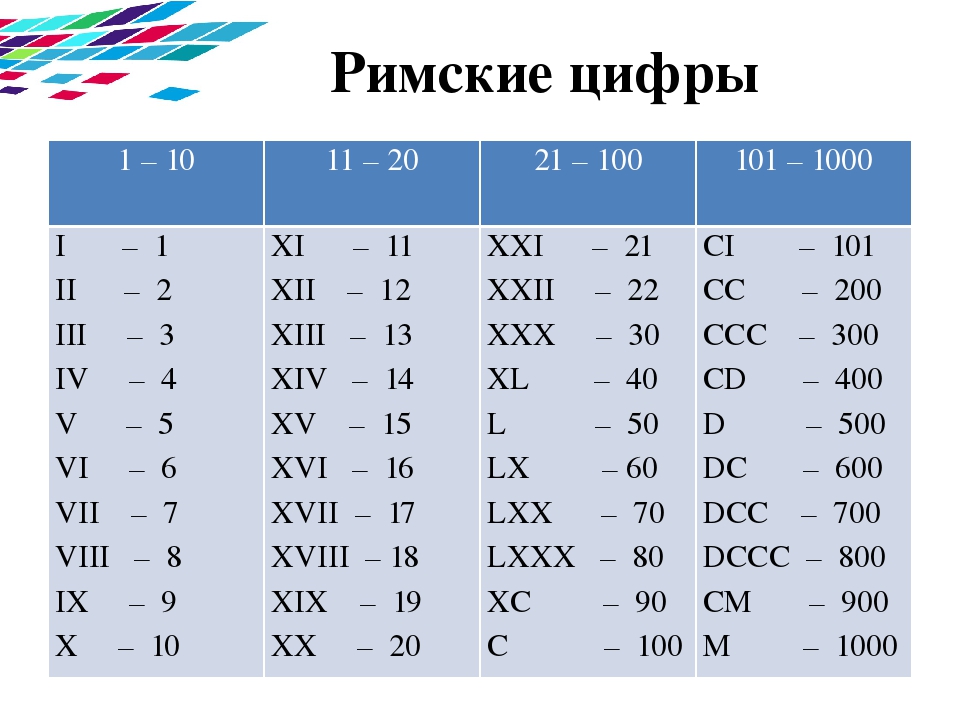 Рубашки 11 типоразмеров (до Рубашки XXXL ), в 3-х размерах и нестандартных размерах для мужчин всех форм и размеров.
Рубашки 11 типоразмеров (до Рубашки XXXL ), в 3-х размерах и нестандартных размерах для мужчин всех форм и размеров. Никакой дискриминации по признаку касты, религии, цвета кожи, языка или региона. Люди всех форм и размеров, возрастных групп могут обратиться к нам и получить рубашки своего размера онлайн, не выходя из дома.
Никакой дискриминации по признаку касты, религии, цвета кожи, языка или региона. Люди всех форм и размеров, возрастных групп могут обратиться к нам и получить рубашки своего размера онлайн, не выходя из дома. Все измерения указаны в дюймах.
Все измерения указаны в дюймах.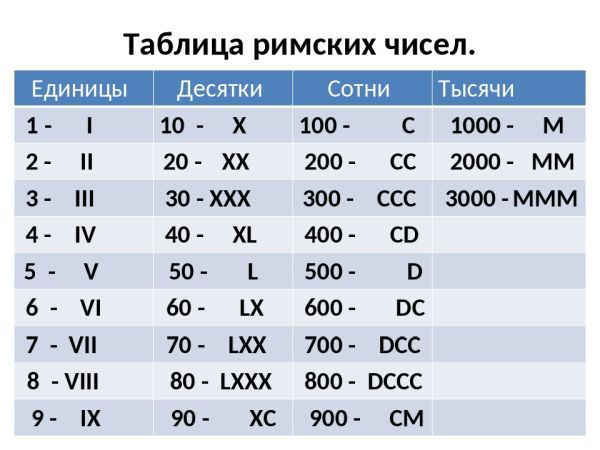 Все измерения указаны в дюймах.
Все измерения указаны в дюймах.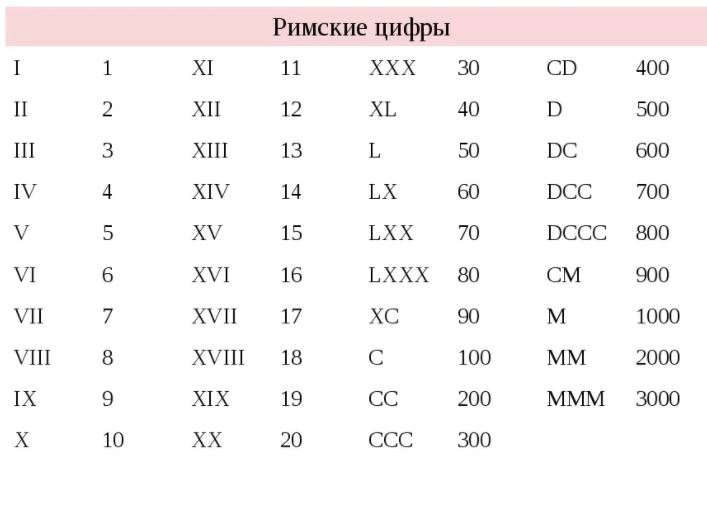 Все измерения указаны в дюймах.
Все измерения указаны в дюймах.