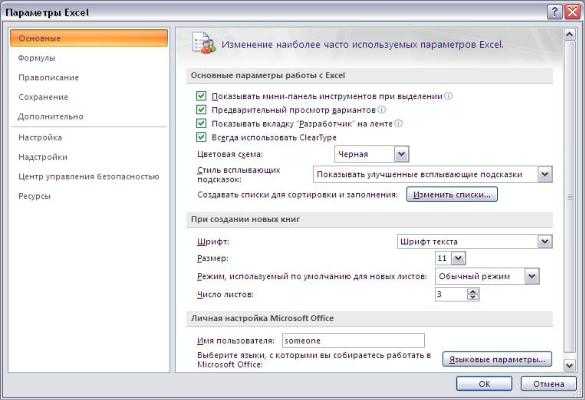
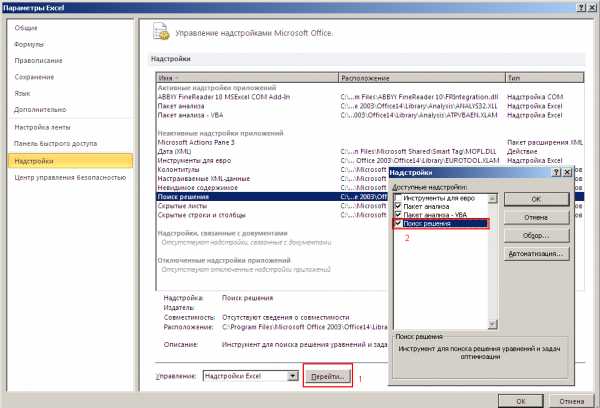
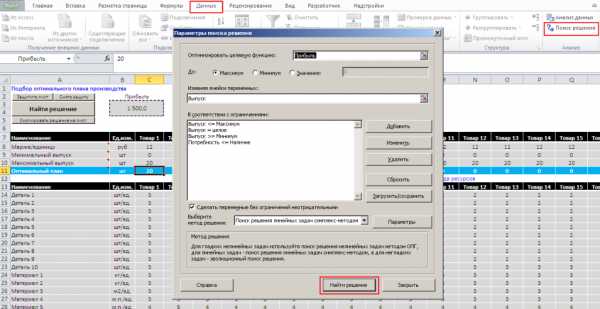
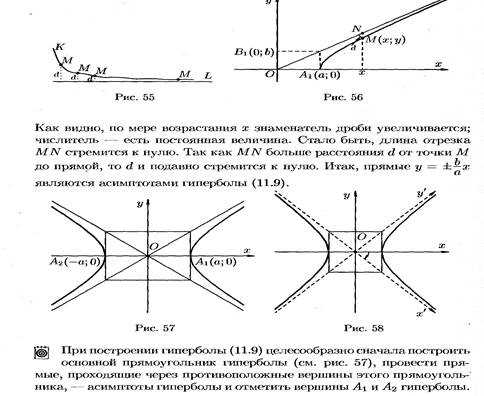
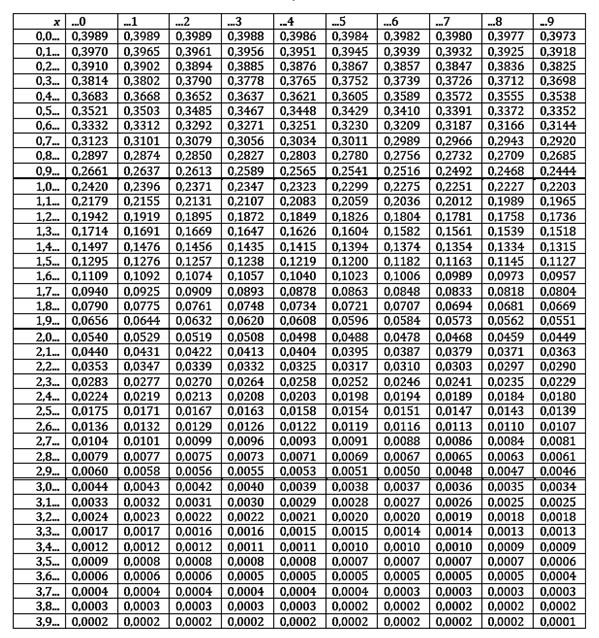
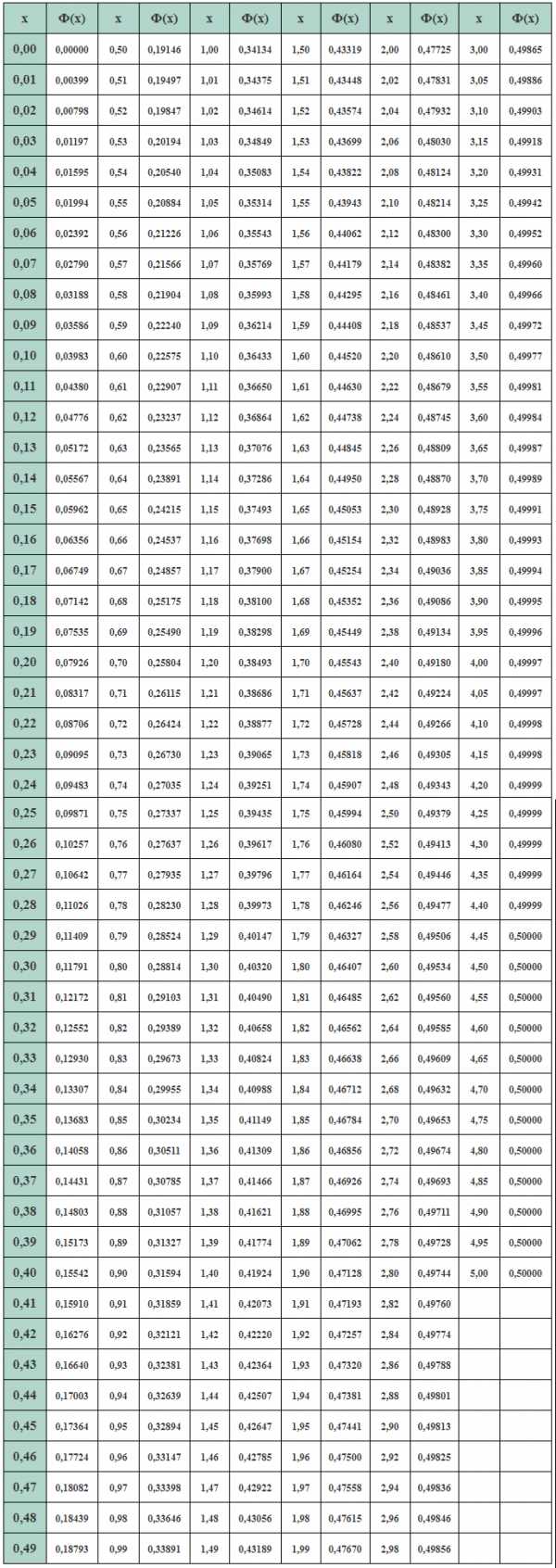
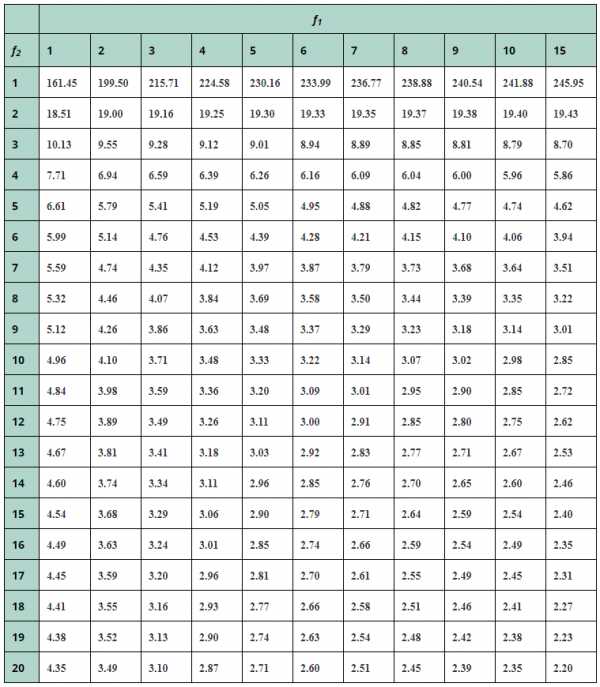
градус — Перевод на английский — примеры русский
На основании Вашего запроса эти примеры могут содержать грубую лексику.
На основании Вашего запроса эти примеры могут содержать разговорную лексику.
Участники саммита в Кочабамбе, Боливия, заявили, что мы должны стабилизировать повышение температуры на 1 градус Цельсия.
The people, at a summit in Cochabamba, Bolivia, said that we must stabilize the temperature increase at 1 degree Celsius.Поэтому я считаю чрезвычайно важным, чтобы мы стабилизировали повышение температуры на 1 градус Цельсия, как заявили представители населения мира.
I therefore find it extremely important that we stabilize the temperature increase at 1 degree Celsius, as the people of the world have said.Лазеры измеряют расстояние, ландшафт, градус наклона и прочее.
Lasers measure distance, terrain, grade of slopes and things.1 градус лево руля, капитан!
1 degree to the left, Captain!При включении этой функции кондиционер будет поддерживать заданную температуру, время от времени поднимая и опуская ее на 1 градус.
When starting this function, the air-conditioner will keep the preset temperature sometimes increasing and decreasing it by 1 degree.Изменение широты Атлантиды с 35 градуса на 45 градус привело к смене циркуляции мирового океана и понижению уровня моря.
Change of breadth Atlantis about 35 degrees on 45 degree has led to change of circulation of World Ocean and downturn of a sea level.Она на один градус ниже чем в прошлый раз, когда мы измеряли.
It just dropped one degree since we last checked.Моз говорил, вся соль в подъеме ЗЗ-й градус, это высшая степень просвещения.
Moz said this was all about ascension — the 33rd degree, the highest level of enlightenment.Температура медленно падает на 1 градус.
Temperature is dropping slowly, one degree —Моя температура поднялась еще на один градус.
My temp has risen another degree.Согласно данным Центра Карибского сообщества по проблемам изменения климата, повышение температуры еще на один градус приведет к массовой гибели запасов тунца и дельфинов.
The Caribbean Community Climate Change Centre has said that a further one degree temperature rise will lead to significant loss of tuna and dolphin stocks.Но, при определённых условиях, один градус может быть очень большим отрезком.
but in certain conditions… one degree can be a very large distanceПохоже, что это — взвесь конденсата водяного пара с температурой примерно 1 градус по Цельсию.
There appears to be a condensed suspension of water vapor approximately one degree Celsius.Изменение климата и истощение природных ресурсов негативно влияют на экономический рост в странах с низким уровнем дохода: на каждое повышение средней глобальной температуры на один градус по Цельсию приходится снижение объема производства в размере от 2 до 3 процентов.
Climate change and natural resource depletion affect growth in low-income countries: for every increase in average global temperatures of one degree Celsius, between 2 and 3 per cent of output will be lost.С повы-шением температуры на 1 градус Цельсия объем поглощаемых атмосферой из почвы осадков увеличивается на 7 процентов, что приводит к серьезному нарушению гидрологического цикла и более экстремальным погодным явлениям, зачастую сопровождаемым стихийными бедстви-ями, такими как сильные наводнения и засухи.
With every temperature increase of 1 degree Celsius, the atmosphere absorbed 7 per cent more precipitation from the ground, resulting in a radical disruption of the water cycle and more extreme weather, with frequent disasters such as severe floods and droughts.Это означает повышение всего на один градус на экваторе, зато больше, чем на 12 на полюсах.
That means an increase of only one degree at the equator, but more than 12 degrees at the pole.Если бы мы смогли отклонить корабль на градус или два, по крайней мере, мы прошли бы мимо Земли.
If we could divert the ship a degree or two, at least we’d miss Earth.Тем не менее, мужайтесь… Один градус изменил мою жизнь.
be of good cheer, however one degree had changed my life it might do so againВ предлагаемых системах Ка-диапазона используется значительное число узких стволов (приблизительно в 1 градус) для обеспечения высокой эффективной мощности изотропного излучения в размере в 50 дБВт со спутника на терминалы потребителей.
The proposed Ka-band systems used a large number of small beams (approximately 1 degree) to deliver a high satellite effective isotropic radiated power (EIRP) of 50 dBW to user terminals.В то время температура (максимум 1 градус по шкале Цельсия в январе и 5 градусов по шкале Цельсия в феврале) была чрезвычайно низкой, чтобы насекомые могли выжить.
At that time, the temperature (1 degree centigrade in January and 5 degrees centigrade in February at the maximum) was extremely low, making it impossible for insects to survive.context.reverso.net
градус — с русского на английский
ГРАДУС — (лат. gradus степень, ступень, мера). 1) одна из равных частей, на которые делится окружность (обыкновенно 1/360 часть). В физике: каждая из равных частей, на которые делится шкала термометра, барометра и др. приборов. 3) в древн. Руси: ученая… … Словарь иностранных слов русского языка
ГРАДУС — ГРАДУС, условная единица, к рой пользуются при измерении самых разнообразных величин, например: температуры, жесткости, кислотности, солености, крепости; градус как единица измерения угловых величин, географический градус и др. Градус… … Большая медицинская энциклопедия
ГРАДУС — (лат. gradus шаг ступень, степень), 1) общее наименование различных единиц температуры, соответствующих разным температурным шкалам. Различают градус шкалы Кельвина, или кельвин (К), градус Цельсия (.С), градусы Реомюра (.R), Фаренгейта (.F). 1К … Большой Энциклопедический словарь
градус — ступень (Даль) См. степень… Словарь русских синонимов и сходных по смыслу выражений. под. ред. Н. Абрамова, М.: Русские словари, 1999. градус высота, степень, ступень; лигрил, десцендент, крепость, мера Словарь русских синоним … Словарь синонимов
ГРАДУС — муж. степень, ступень. Окружность круга делится на 360 градусов, которые и служат мерою для дуги, определяя, какую часть окружности она составляет, и мерою для углов, измеряемых дугою. Градус великого круга земли содержит около 105 верст или 60… … Толковый словарь Даля
ГРАДУС — (от латинского gradus шаг, ступень, степень), 1) общее наименование различных единиц температуры, соответствующих разным температурным шкалам. Различают градусные шкалы Кельвина, или кельвин (К), градус Цельсия (шC), градусы Реомюра (шR),… … Современная энциклопедия
ГРАДУС — ГРАДУС, в математике единица угловой меры, равная одной тристашестидесятой (1/360) части полного круга (360°). Один градус записывается как 1°, он подразделяется на 60 частей, называемых минутами («дуговыми минутами»), которые обозначаются как 1… … Научно-технический энциклопедический словарь
ГРАДУС — ГРАДУС, градуса, муж. (лат. gradus ступень, шаг) (научн.; условно обозначается вверху цифры справа маленьким кружком). 1. Единица измерения дуг и углов, равная 1/360 окружности. Угол в 45 градусов или в 45°. Градус широты. 2. Деление на шкале… … Толковый словарь Ушакова
ГРАДУС — (от лат. gradus шаг, ступень, степень) температурный, общее наименование разл. ед. темп ры, соответствующих разным температурным шкалам. Различают Г. шкалы Кельвина, или кельвин (К), градус Цельсия (°С), Реомюра (°R), Фаренгейта (°F), Ранкина… … Физическая энциклопедия
ГРАДУС — (Degree) 1. Единица измерения угла или дуги, равная 1/90 прямого угла или 1/360 окружности (см. Угол). Применяется для измерения углов, дуг, меридианов, параллелей, широт, долгот, азимутов и т. д. Угол в 1° образуется двумя радиусами,… … Морской словарь
градус — degree Grad 1).Одиниця виміру температури. Розрізняють Г. шкали Кельвіна (К), Цельсія (ОС), Реомюра (ОR), Фаренгейта (ОF). 1 К = 1 ОС = 0,8 ОR = 1,8 ОF. 2). Позасистемна одиниця вимірювання плоского кута, яка допущена міжнародним стандартом для… … Гірничий енциклопедичний словник
translate.academic.ru
кельвин [К] градус Цельсия [°C] • Популярные конвертеры единиц • Конвертер температуры • Компактный калькулятор
Конвертер длины и расстоянияКонвертер массыКонвертер мер объема сыпучих продуктов и продуктов питанияКонвертер площадиКонвертер объема и единиц измерения в кулинарных рецептахКонвертер температурыКонвертер давления, механического напряжения, модуля ЮнгаКонвертер энергии и работыКонвертер мощностиКонвертер силыКонвертер времениКонвертер линейной скоростиПлоский уголКонвертер тепловой эффективности и топливной экономичностиКонвертер чисел в различных системах счисленияКонвертер единиц измерения количества информацииКурсы валютРазмеры женской одежды и обувиРазмеры мужской одежды и обувиКонвертер угловой скорости и частоты вращенияКонвертер ускоренияКонвертер углового ускоренияКонвертер плотностиКонвертер удельного объемаКонвертер момента инерцииКонвертер момента силыКонвертер вращающего моментаКонвертер удельной теплоты сгорания (по массе)Конвертер плотности энергии и удельной теплоты сгорания топлива (по объему)Конвертер разности температурКонвертер коэффициента теплового расширенияКонвертер термического сопротивленияКонвертер удельной теплопроводностиКонвертер удельной теплоёмкостиКонвертер энергетической экспозиции и мощности теплового излученияКонвертер плотности теплового потокаКонвертер коэффициента теплоотдачиКонвертер объёмного расходаКонвертер массового расходаКонвертер молярного расходаКонвертер плотности потока массыКонвертер молярной концентрацииКонвертер массовой концентрации в раствореКонвертер динамической (абсолютной) вязкостиКонвертер кинематической вязкостиКонвертер поверхностного натяженияКонвертер паропроницаемостиКонвертер паропроницаемости и скорости переноса параКонвертер уровня звукаКонвертер чувствительности микрофоновКонвертер уровня звукового давления (SPL)Конвертер уровня звукового давления с возможностью выбора опорного давленияКонвертер яркостиКонвертер силы светаКонвертер освещённостиКонвертер разрешения в компьютерной графикеКонвертер частоты и длины волныОптическая сила в диоптриях и фокусное расстояниеОптическая сила в диоптриях и увеличение линзы (×)Конвертер электрического зарядаКонвертер линейной плотности зарядаКонвертер поверхностной плотности зарядаКонвертер объемной плотности зарядаКонвертер электрического токаКонвертер линейной плотности токаКонвертер поверхностной плотности токаКонвертер напряжённости электрического поляКонвертер электростатического потенциала и напряженияКонвертер электрического сопротивленияКонвертер удельного электрического сопротивленияКонвертер электрической проводимостиКонвертер удельной электрической проводимостиЭлектрическая емкостьКонвертер индуктивностиКонвертер Американского калибра проводовУровни в dBm (дБм или дБмВт), dBV (дБВ), ваттах и др. единицахКонвертер магнитодвижущей силыКонвертер напряженности магнитного поляКонвертер магнитного потокаКонвертер магнитной индукцииРадиация. Конвертер мощности поглощенной дозы ионизирующего излученияРадиоактивность. Конвертер радиоактивного распадаРадиация. Конвертер экспозиционной дозыРадиация. Конвертер поглощённой дозыКонвертер десятичных приставокПередача данныхКонвертер единиц типографики и обработки изображенийКонвертер единиц измерения объема лесоматериаловВычисление молярной массыПериодическая система химических элементов Д. И. Менделеева
Демонстрация «Горячее стекло» в музее стекла в городе Корнинг, штат Нью-Йорк. Стеклодувы работают со стеклом, нагретым до температур 870–1 040 °C или 1 600–1 900 °F.
Общие сведения
Единицы измерения температуры
Температура в физике и химии
Тройная точка воды
Температура в биологии
Анабиоз
Крионика
Температура в кулинарии
Общие сведения
Демонстрация «Горячее стекло» в музее стекла в городе Корнинг, штат Нью-Йорк. Профессиональный стеклодув работает с комком расплавленного стекла на конце стеклодувной трубки. Позже она сделает из него вазу.
Температура — физическая величина, определяющая количество теплоты в теле или материи. Температуру также можно определить как количество кинетической энергии в частицах, составляющих тело или материю. Энергия передается от тел с более высокой температурой к телам более с низкой температурой, пока не будет достигнуто термодинамическое равновесие, то есть, пока температура обоих тел не сравняется. Этот процесс называется теплопередачей. К примеру, если открыть зимой окно, теплый воздух в комнате будет передавать тепло холодному воздуху на улице до тех пор, пока температура воздуха на улице и в комнате не станет одинаковой. В разных материалах тепло передается по-разному, в зависимости от их теплопроводности. Материалы с высокой теплопроводностью нагреваются и охлаждаются быстрее, чем материалы с низкой. Для теплоизоляции, например, в строительстве, используются именно материалы с низкой теплопроводностью.
Температуру измеряют с помощью термометра, и самая низкая температура, которая возможна — это –273,15 °C. Эта температура называется абсолютным нулем.
Единицы измерения температуры
Температуру измеряют в градусах, но существуют несколько температурных шкал: Цельсия (°C, самая распространенная шкала в мире), Фаренгейта (°F, используемая в США и некоторых других странах), и Кельвина (К, используемая в физике и других точных науках). Различие между шкалами Цельсия и Кельвина в том, что за ноль принята разная температура. По Цельсию — это температура замерзания воды, в то время как по Кельвину — это абсолютный ноль, то есть –273,15 °C. Шкала Фаренгейта отличается от шкалы Цельсия не только температурой, принятой за ноль, но еще и разницей между величиной одного градуса. Для перевода градусов Цельсия в градусы Фаренгейта используют формулу:
°C = 5/9 (°F – 32).
Температура замерзания воды равна 32 °F.
В системе СИ используются градусы шкалы Кельвина, называемые кельвинами (К).
Электрический разряд в плазменной лампе
Температура в физике и химии
Агрегатное состояния веществ (плазма, газ, жидкость, или твердое тело) определяется температурой. В любом теле молекулы колеблются, причем при увеличении температуры это движение ускоряется, так же, как и кинетическая энергия этих молекул. Чем больше скорость колебания молекул, тем легче им разойтись на большее расстояние друг от друга. Для каждого агрегатного состояния вещества существует определенный порог расстояния между молекулами. Это расстояние самое маленькое в твердых телах, и самое большое в газах и плазме. Материалы, которые не изменяют агрегатное состояние при высоких температурах, называются огнеупорными материалами. Например, многие керамические смеси огнеупорны, потому что не плавятся при температурах до 1000 °C. Их часто используют на производстве, например в печах с очень высокой температурой. Некоторые материалы плавятся при высокой температуре, в то время как другие материалы, как например, дерево, сгорают. Диапазон температур, при которых вещества могут находиться в состоянии жидкости, невелик. При переходе этого порога, жидкости превращаются в газы. При дальнейшем нагревании, атомы разлагаются на заряженные частицы, ионы и электроны — процесс, называемый ионизацией. Частично или полностью ионизированный газ называется плазмой. Большая часть материи во вселенной находится именно в состоянии плазмы.
Температура влияет на электропроводимость веществ и служит катализатором химических реакций. Изменение температуры замедляет или, наоборот, ускоряет их.
Тройная точка воды
Тройная точка воды — температура и давление, при которых вода может одновременно и равновесно существовать в виде трёх фаз — в твердом (лед), жидком и газообразном (пар) состояниях. Тройная точка воды — температура 0,01°С (273,16 К) и парциальное давление водяного пара 611,73 Па. При таких условиях для превращения всей воды в пар, лед или жидкое состояние достаточно только чуть-чуть изменить давление или температуру.
Тройная точка воды соответствует минимальному давлению, при котором жидкая вода может существовать. При давлении ниже тройной точки (например, в открытом космосе) твердый лед сублимируется в пар, минуя жидкое состояние. При параметрах выше тройной точки лед при нагревании вначале переходит в жидкое состояние и только потом, при более высоких температурах, вода кипит и испаряется.
Тройная точка воды иногда используется как опорная, например, для калибровки измерительной аппаратуры и термометров. Для этого используются ампулы тройной точки воды. Эти ампулы обеспечивают получение температуры точно 0,01°С или 273,16K.
Кривые потока излучения абсолютно чёрных тел с разной температурой. Источник: wikipedia.org. Автор: 4C
Эффективная температура
Эффективной температурой тела называется температура такого абсолютно черного тела, каждый квадратный сантиметр которого излучает во всем спектре такой же поток, как и квадратный сантиметр данного тела.
Абсолютно черное тело – тело, которое поглощает падающее на него излучение во всем диапазоне спектра.
Такую температуру можно вычислить из закона Стефана-Больцмана, который гласит, что мощность излучения абсолютно черного тела пропорциональна четвертой степени температуры. Так, например, для Земли это значение достигает примерно 250 К, что составляет –23 °C, но с другой стороны известно, что у поверхности Земли температура в среднем выше, в районе +15 °C. Данное несоответствие со значением эффективной температуры объясняется тем, что Земля имеет атмосферу, а значит есть воздействие парникового эффекта, который помогает Земле сохранять тепло. Таким образом значение в 250 К, это температура верхних слоев атмосферы нашей планеты. То есть, эффективная температура Земли — это температура, которая видна из космоса.
Зная эффективную температуру звезды, можно узнать к какому спектральному классу она относится, иначе говоря, определить в каком диапазоне длин волн или частот звезда излучает. У Солнца эффективная температура около 6000 К, и максимум энергии излучения приходится на 470 нм, что соответствует зеленой части спектра, а не желтой, как кажется человеческому глазу.
15-метровая рупорно-параболическая антенна, с помощью которой А. Пензиасом и Р. Вильсоном было зарегистрировано реликтовое излучение. За это открытие им была вручена Нобелевская премия. Источник: НАСА
Температура во Вселенной
В астрономии используется очень широкий диапазон значений температур — от невероятно низких до очень высоких.
Например, реликтовое излучение – остаточное электромагнитное излучение, возникшее в следствие Большого взрыва, имеет эффективную температуру всего лишь 2,7 К — значение очень близкое к абсолютному нулю.
Сравнение размеров Солнца и голубого сверхгиганта — звезды Альнитак. Источник: wikipedia.org. Автор: CWitte
Напротив, температуры звезд могут достигать высоких значений более 40000 К. Такие звезды, как правило, имеют большие радиусы, измеряющиеся в десятках радиусов Солнца. Примером такой звезды является Альнитак А – голубой сверхгигант в созвездии Ориона с диаметром в 20 раз больше солнечного.
Еще более высокие температуры можно встретить в ядрах звезд, так как для того, чтобы там протекали термоядерные реакции, требуются колоссальные значения температур. Например, чтобы произошла реакция превращения более легких элементов в более тяжелые, нужно, чтобы ядра имели высокую кинетическую энергию. Следовательно, и высокую температуру. У нашего Солнца в ядре значение температуры достигает 15 000 000 К.
Температура в биологии
Типичная температура тела японского пятнистого оленя Cervus nippon равна 313ºK или 39.8ºC. Парк Нара в городе Нара (Япония) у подножия горы Вакакуса.
Температура влияет на жизненные процессы всех живых существ. Сложные организмы обычно регулируют температуру тела, и стараются поддерживать одинаковую температуру. Температура используется животными как защитный механизм. Например, чтобы избавиться от бактерий и вирусов, у людей поднимается температура выше, чем эти инородные тела могут перенести. А грызуны и некоторые другие млекопитающие, такие как медведи, понижают температуру, тем самым замедляя обмен веществ, дыхание, и сердцебиение, впадая в спячку. Замедленный обмен веществ позволяет животным выжить с меньшими затратами энергии, чем в обычном состоянии. Этот защитный механизм предназначен для того, чтобы пережить время, когда недостаточно или вообще нет еды. Примеры таких замедлений жизнедеятельности — зимняя и летняя спячки. Температура тела у некоторых животных, впадающих в спячку, опускается очень низко, иногда ниже 0°C. Например, у некоторых видов сусликов, проживающих в арктических регионах, температура тела в районе брюшной полости понижается до –2,9°C. Растения также могут находиться в состоянии покоя во время зимних холодов.
Анабиоз
Анабиоз — состояние организма, в котором замедлены жизненные процессы почти до состояния смерти. Организм сам может перейти в такое состояние, но анабиоз также можно инициировать при понижении температуры окружающей среды, и другими способами. Некоторые организмы находятся в естественном состоянии анабиоза во время определенных периодов их жизни. Состояние анабиоза граничит со смертью, но исследования показали, что животных в этом состоянии можно вернуть к жизни без повреждения нервных клеток и тканей. Ученые надеются, что в ближайшем будущем это будет возможно и для людей. Надежда заключается в том, что анабиоз позволит оказывать первую медицинскую помощь и спасать людей с травмами и заболеваниями, опасными для жизни, такими, как инфаркт миoкардa. При травмах обычно происходит большая потеря крови, что вызывает кислородную недостаточность в мозге, так как именно кровь доставляет кислород к органам, которые в нем нуждаются. Недостаток кислорода в жизненно важных органах, особенно в мозге, вызывает отмирание нервных клеток и тканей, что через некоторое время приводит к смерти. Если больной перейдет в состояние анабиоза, то в связи с замедлением всех жизнедеятельных процессов потребность в кислороде также понизится. Это предотвратит повреждение клеток и тканей, и даст врачам дополнительное время и возможность восстановить кровообращение и помочь пациенту. Анабиоз также даст медицинскому персоналу время, чтобы перевезти больного от места аварии в больницу.
Живые организмы в состоянии анабиоза выдерживают очень низкие температуры, и были случаи, когда люди выживали в экстремальных условиях благодаря тому, что впадали в состояние анабиоза. В состоянии гипотермии люди иногда выживали без еды и питья дольше, чем это возможно в нормальном состоянии. В отделениях вспомогательных репродуктивных технологий эмбрионы, предназначенные для использования при лечении бесплодия, хранятся именно в состоянии анабиоза, в котором они могут находиться до десяти лет. В будущем технологии анабиоза будут полезны также и для космонавтов — анабиоз сделает возможным путешествия к отдаленным планетам.
В настоящее врем анабиоз исследуется на животных. В большинстве экспериментов их кровь заменяют раствором солей очень низкой температуры, или подвергают их воздействию газов, в результате чего эти животные переходят в состояние анабиоза. Успех этих экспериментов статистически значим, и с 2008 года начались исследования с участием людей.
Кипящий жидкий азот
Крионика
Ученые надеются, что если сохранить тело или голову человека или животного в условиях очень низкой температуры, то в будущем появятся технологии, позволяющие вернуть этот организм к жизни и даже излечить его от последствий старения. Такое сохранение называется криосохранением, а наука, занимающаяся вопросами сохранения — крионикой. На данный момент технологии по криосохранению позволяют осуществлять замораживание отдельных тканей, органов, и всего тела. Обычно температура замораживания достигает примерно 77 K или –196 °C. Это температура кипения жидкого азота, вещества наиболее часто используемого при замораживании сложных организмов. Эта температура настолько низкая, что предотвращает биохимические реакции, которые вызывают отмирание клеток. Во время замораживания возможны многие осложнения, такие как разрушение клеток льдом. Современные технологии позволяют сохранить ткани в течении тысячи лет, после чего, как предполагают исследователи, имеется вероятность разрушения молекул ДНК. Ученые надеются, что в будущем появятся технологии, которые смогут исправить эти повреждения в ДНК и тканях.
Сейчас существует ряд компаний, предоставляющих услуги по криосохранению умерших людей и домашних животных. Это очень дорогой процесс, и у этих компаний мало клиентов, особенно потому, что в прошлом были проблемы с разморозкой тел. Некоторые клиенты подписывают контракт на полное криосохранение тела, но возможно и сохранение только головы или мозга. Последнее — дешевле, хотя пока неизвестно, как в будущем компании по криосохранению будет покрывать расходы на новое тело.
Кухонный термометр
Температура в кулинарии
Температура часто применяется в кулинарии для того, чтобы сделать пищевые продукты более доступными для пищеварения или изменить их структуру. Например, именно благодаря нагреванию мышечные ткани в мясе изменяют свою структуру и становятся мягкими. Из всех живых существ только люди научились использовать температуру в приготовлении пищи. Ученые антропологи утверждают, что человек готовил еду на огне еще 250 000 лет назад. Замораживание также используется в приготовлении пищи, например для того, чтобы убить паразитов в рыбе, предназначенной для употребления в сыром виде в суши или сашими. В домашних условиях этого добиться невозможно, так как температура должна уменьшиться до –37 °C. Для этого используют промышленные морозильные камеры, в которых достигаются такие температуры.
Литература
Автор статьи: Kateryna Yuri, Tatiana Kondratieva
Вы затрудняетесь в переводе единицы измерения с одного языка на другой? Коллеги готовы вам помочь. Опубликуйте вопрос в TCTerms и в течение нескольких минут вы получите ответ.
www.translatorscafe.com
радиан [рад] градус [°] • Популярные конвертеры единиц • Плоский угол • Компактный калькулятор
Конвертер длины и расстоянияКонвертер массыКонвертер мер объема сыпучих продуктов и продуктов питанияКонвертер площадиКонвертер объема и единиц измерения в кулинарных рецептахКонвертер температурыКонвертер давления, механического напряжения, модуля ЮнгаКонвертер энергии и работыКонвертер мощностиКонвертер силыКонвертер времениКонвертер линейной скоростиПлоский уголКонвертер тепловой эффективности и топливной экономичностиКонвертер чисел в различных системах счисленияКонвертер единиц измерения количества информацииКурсы валютРазмеры женской одежды и обувиРазмеры мужской одежды и обувиКонвертер угловой скорости и частоты вращенияКонвертер ускоренияКонвертер углового ускоренияКонвертер плотностиКонвертер удельного объемаКонвертер момента инерцииКонвертер момента силыКонвертер вращающего моментаКонвертер удельной теплоты сгорания (по массе)Конвертер плотности энергии и удельной теплоты сгорания топлива (по объему)Конвертер разности температурКонвертер коэффициента теплового расширенияКонвертер термического сопротивленияКонвертер удельной теплопроводностиКонвертер удельной теплоёмкостиКонвертер энергетической экспозиции и мощности теплового излученияКонвертер плотности теплового потокаКонвертер коэффициента теплоотдачиКонвертер объёмного расходаКонвертер массового расходаКонвертер молярного расходаКонвертер плотности потока массыКонвертер молярной концентрацииКонвертер массовой концентрации в раствореКонвертер динамической (абсолютной) вязкостиКонвертер кинематической вязкостиКонвертер поверхностного натяженияКонвертер паропроницаемостиКонвертер паропроницаемости и скорости переноса параКонвертер уровня звукаКонвертер чувствительности микрофоновКонвертер уровня звукового давления (SPL)Конвертер уровня звукового давления с возможностью выбора опорного давленияКонвертер яркостиКонвертер силы светаКонвертер освещённостиКонвертер разрешения в компьютерной графикеКонвертер частоты и длины волныОптическая сила в диоптриях и фокусное расстояниеОптическая сила в диоптриях и увеличение линзы (×)Конвертер электрического зарядаКонвертер линейной плотности зарядаКонвертер поверхностной плотности зарядаКонвертер объемной плотности зарядаКонвертер электрического токаКонвертер линейной плотности токаКонвертер поверхностной плотности токаКонвертер напряжённости электрического поляКонвертер электростатического потенциала и напряженияКонвертер электрического сопротивленияКонвертер удельного электрического сопротивленияКонвертер электрической проводимостиКонвертер удельной электрической проводимостиЭлектрическая емкостьКонвертер индуктивностиКонвертер Американского калибра проводовУровни в dBm (дБм или дБмВт), dBV (дБВ), ваттах и др. единицахКонвертер магнитодвижущей силыКонвертер напряженности магнитного поляКонвертер магнитного потокаКонвертер магнитной индукцииРадиация. Конвертер мощности поглощенной дозы ионизирующего излученияРадиоактивность. Конвертер радиоактивного распадаРадиация. Конвертер экспозиционной дозыРадиация. Конвертер поглощённой дозыКонвертер десятичных приставокПередача данныхКонвертер единиц типографики и обработки изображенийКонвертер единиц измерения объема лесоматериаловВычисление молярной массыПериодическая система химических элементов Д. И. Менделеева
Общие сведения
Виды углов
Измерение углов
Транспортир
Использование углов в архитектуре и искусстве
Общие сведения
Плоский угол — геометрическая фигура образованная двумя пересекающимися линиями. Плоский угол состоит из двух лучей с общим началом, и эта точка называется вершиной луча. Лучи называются сторонами угла. У углов много интересных свойств, например, сумма всех углов в параллелограмме — 360°, а в треугольнике — 180°.
Виды углов
Прямые углы равны 90°, острые — меньше 90°, а тупые — наоборот, больше 90°. Углы, равные 180° называются развернутыми, углы в 360° называются полными, а углы больше развернутых но меньше полных называются невыпуклыми. Когда сумма двух углов равна 90°, то есть один угол дополняет другой до 90°, они называются дополнительными. Если они дополняют друг друга до 180°, они называются смежными, а если же до 360° — то сопряженными. В многоугольниках углы внутри многоугольника называются внутренними, а сопряженные с ними — внешними.
Когда сумма двух углов равна 90°, то есть один угол дополняет другой до 90°, они называются дополнительными. Если они дополняют друг друга до 180°, они называются смежными, а если же до 360° — то сопряженными. В многоугольниках углы внутри многоугольника называются внутренними, а сопряженные с ними — внешними.
Два угла, образованные при пересечении двух прямых и не являющихся смежными, называются вертикальными. Они равны.
Измерение углов
Два транспортира: обычный и цифровой
Углы измеряют с помощью транспортира или вычисляют по формуле, измерив стороны угла от вершины и до дуги, и длину дуги, которая эти стороны ограничивает. Углы обычно измеряют в радианах и градусах, хотя существуют и другие единицы.
Можно измерять как углы, образованные между двумя прямыми, так и между кривыми линиями. Для измерения между кривыми используют касательные в точке пересечения кривых, то есть в вершине угла.
Транспортир
Транспортир — инструмент для измерения углов. Большинство транспортиров имеют форму полукруга или окружности и позволяют измерить углы до 180° и до 360° соответственно. В некоторых транспортирах встроена дополнительная вращающаяся линейка для удобства в измерении. Шкалы на транспортирах наносят чаще в градусах, хотя иногда они бывают и в радианах. Транспортиры чаще всего используют в школе на уроках геометрии, но их также применяют в архитектуре и в технике, в частности в инструментальном производстве.
Использование углов в архитектуре и искусстве
Дом с лофтами и квартирами «Pure Spirits» в центре Торонто, Онтарио, Канада
Художники, дизайнеры, мастера и архитекторы издавна используют углы для создания иллюзий, акцентов и других эффектов. Чередование острых и тупых углов или геометрические узоры из острых углов часто используются в архитектуре, мозаике и витражах, например в строении готических соборов и в исламской мозаике.
Музей Турецкого и исламского искусства. Стамбул, Турция. Фотография помещается с разрешения автора.
Одна из известных форм исламского изобразительного искусства — украшение с помощью геометрического орнамента гирих. Этот рисунок применяют в мозаике, резьбе по металлу и дереву, на бумаге и на ткани. Рисунок создается с помощью чередования геометрических фигур. Традиционно используют пять фигур со строго определенными углами из комбинаций в 72°, 108°, 144° и 216°. Все эти углы делятся на 36°. Каждая фигура разделена линиями на несколько более маленьких симметричных фигур, чтобы создать более тонкий рисунок. Изначально гирихом назывались сами эти фигуры или кусочки для мозаики, отсюда и пошло название всего стиля. В Марокко существует похожий геометрический стиль мозаики, зулляйдж или зилидж. Форма терракотовых изразцов, из которых складывают эту мозаику, не соблюдается так строго, как в гирихе, и изразцы часто более причудливой формы, чем строгие геометрические фигуры в гирихе. Несмотря на это, мастера зулляйджа также используют углы для создания контрастных и причудливых узоров.
Руб аль-хизб и звезда аль-кудс
В исламском изобразительном искусстве и архитектуре часто используется руб аль-хизб — символ в форме одного квадрата, наложенного на другой под углом в 45°, как на иллюстрациях. Он может быть изображен как сплошная фигура, или в виде линий — в этом случае этот символ называется звездой Al-Quds (аль кудс). Руб аль-хизб иногда украшают небольшими кругами на пересечении квадратов. Этот символ используют в гербах и на флагах мусульманских стран, например на гербе Узбекистана и на флаге Азербайджана. Основания самых высоких в мире на момент написания (весна 2013) башен близнецов, башен Петро́нас построены в форме руб аль-хизба. Эти башни находятся в Куала-Лумпуре в Малайзии и в их проектировании участвовал премьер-министр страны.
«Флэтайрон-билдинг» или здание «Утюг», Нью-Йорк
Острые углы часто используют в архитектуре как декоративные элементы. Они придают зданию строгую элегантность. Тупые углы, наоборот, придают зданиям уютный вид. Так, например, мы восхищаемся готическими соборами и замками, но они выглядят немного печально и даже устрашающе. А вот дом себе мы скорее всего выберем с крышей с тупыми углами между скатами. Углы в архитектуре также используют для укрепления разных частей здания. Архитекторы проектируют форму, размер и угол наклона в зависимости от нагрузки на стены, нуждающиеся в укреплении. Этот принцип укрепления с помощью наклона использовали еще с древних времен. Например, античные строители научились строить арки без цемента и иных связующих материалов, укладывая камни под определенным углом.
Обычно здания строят вертикально, но иногда бывают исключения. Некоторые здания специально строят с наклоном, а некоторые наклоняются из-за ошибок. Один из примеров наклонных зданий — Тадж-Махал в Индии. Четыре минарета, которые окружают главное строение, построены с наклоном от центра, чтобы в случае землетрясения они упали не вовнутрь, на мавзолей, а в другую сторону, и не повредили основное здание. Иногда здания строят под углом к земле в декоративных целях. Например, Падающая башня Абу-Даби или Capital Gate наклонена на 18° к западу. А одно из зданий в Мире Головоломок Стюарта Лэндсборо в городе Ванка в Новой Зеландии наклоняется к земле на 53°. Это здание так и называется, «Падающая башня».
Иногда наклон здания — результат ошибки в проектировании, как например наклон Пизанской башни. Строители не учли структуру и качество почвы, на которой ее возводили. Башня должна была стоять прямо, но плохой фундамент не смог поддерживать ее вес и здание осело, покосившись на один бок. Башню много раз реставрировали; самая последняя реставрация в 20-м веке остановила ее постепенное оседание и увеличивающийся наклон. Ее удалось выровнять с 5.5°до 4°. Башня церкви СуурХусен в Германии тоже наклонена из-за того, что ее деревянный фундамент прогнил с одной стороны после осушения болотистой почвы, на которой она построена. На данный момент эта башня наклонена больше, чем Пизанская — примерно на 5°.
Литература
Автор статьи: Kateryna Yuri
Вы затрудняетесь в переводе единицы измерения с одного языка на другой? Коллеги готовы вам помочь. Опубликуйте вопрос в TCTerms и в течение нескольких минут вы получите ответ.
www.translatorscafe.com
градус Фаренгейта [°F] градус Цельсия [°C] • Популярные конвертеры единиц • Конвертер температуры • Компактный калькулятор
Конвертер длины и расстоянияКонвертер массыКонвертер мер объема сыпучих продуктов и продуктов питанияКонвертер площадиКонвертер объема и единиц измерения в кулинарных рецептахКонвертер температурыКонвертер давления, механического напряжения, модуля ЮнгаКонвертер энергии и работыКонвертер мощностиКонвертер силыКонвертер времениКонвертер линейной скоростиПлоский уголКонвертер тепловой эффективности и топливной экономичностиКонвертер чисел в различных системах счисленияКонвертер единиц измерения количества информацииКурсы валютРазмеры женской одежды и обувиРазмеры мужской одежды и обувиКонвертер угловой скорости и частоты вращенияКонвертер ускоренияКонвертер углового ускоренияКонвертер плотностиКонвертер удельного объемаКонвертер момента инерцииКонвертер момента силыКонвертер вращающего моментаКонвертер удельной теплоты сгорания (по массе)Конвертер плотности энергии и удельной теплоты сгорания топлива (по объему)Конвертер разности температурКонвертер коэффициента теплового расширенияКонвертер термического сопротивленияКонвертер удельной теплопроводностиКонвертер удельной теплоёмкостиКонвертер энергетической экспозиции и мощности теплового излученияКонвертер плотности теплового потокаКонвертер коэффициента теплоотдачиКонвертер объёмного расходаКонвертер массового расходаКонвертер молярного расходаКонвертер плотности потока массыКонвертер молярной концентрацииКонвертер массовой концентрации в раствореКонвертер динамической (абсолютной) вязкостиКонвертер кинематической вязкостиКонвертер поверхностного натяженияКонвертер паропроницаемостиКонвертер паропроницаемости и скорости переноса параКонвертер уровня звукаКонвертер чувствительности микрофоновКонвертер уровня звукового давления (SPL)Конвертер уровня звукового давления с возможностью выбора опорного давленияКонвертер яркостиКонвертер силы светаКонвертер освещённостиКонвертер разрешения в компьютерной графикеКонвертер частоты и длины волныОптическая сила в диоптриях и фокусное расстояниеОптическая сила в диоптриях и увеличение линзы (×)Конвертер электрического зарядаКонвертер линейной плотности зарядаКонвертер поверхностной плотности зарядаКонвертер объемной плотности зарядаКонвертер электрического токаКонвертер линейной плотности токаКонвертер поверхностной плотности токаКонвертер напряжённости электрического поляКонвертер электростатического потенциала и напряженияКонвертер электрического сопротивленияКонвертер удельного электрического сопротивленияКонвертер электрической проводимостиКонвертер удельной электрической проводимостиЭлектрическая емкостьКонвертер индуктивностиКонвертер Американского калибра проводовУровни в dBm (дБм или дБмВт), dBV (дБВ), ваттах и др. единицахКонвертер магнитодвижущей силыКонвертер напряженности магнитного поляКонвертер магнитного потокаКонвертер магнитной индукцииРадиация. Конвертер мощности поглощенной дозы ионизирующего излученияРадиоактивность. Конвертер радиоактивного распадаРадиация. Конвертер экспозиционной дозыРадиация. Конвертер поглощённой дозыКонвертер десятичных приставокПередача данныхКонвертер единиц типографики и обработки изображенийКонвертер единиц измерения объема лесоматериаловВычисление молярной массыПериодическая система химических элементов Д. И. Менделеева
Демонстрация «Горячее стекло» в музее стекла в городе Корнинг, штат Нью-Йорк. Стеклодувы работают со стеклом, нагретым до температур 870–1 040 °C или 1 600–1 900 °F.
Общие сведения
Единицы измерения температуры
Температура в физике и химии
Тройная точка воды
Температура в биологии
Анабиоз
Крионика
Температура в кулинарии
Общие сведения
Демонстрация «Горячее стекло» в музее стекла в городе Корнинг, штат Нью-Йорк. Профессиональный стеклодув работает с комком расплавленного стекла на конце стеклодувной трубки. Позже она сделает из него вазу.
Температура — физическая величина, определяющая количество теплоты в теле или материи. Температуру также можно определить как количество кинетической энергии в частицах, составляющих тело или материю. Энергия передается от тел с более высокой температурой к телам более с низкой температурой, пока не будет достигнуто термодинамическое равновесие, то есть, пока температура обоих тел не сравняется. Этот процесс называется теплопередачей. К примеру, если открыть зимой окно, теплый воздух в комнате будет передавать тепло холодному воздуху на улице до тех пор, пока температура воздуха на улице и в комнате не станет одинаковой. В разных материалах тепло передается по-разному, в зависимости от их теплопроводности. Материалы с высокой теплопроводностью нагреваются и охлаждаются быстрее, чем материалы с низкой. Для теплоизоляции, например, в строительстве, используются именно материалы с низкой теплопроводностью.
Температуру измеряют с помощью термометра, и самая низкая температура, которая возможна — это –273,15 °C. Эта температура называется абсолютным нулем.
Единицы измерения температуры
Температуру измеряют в градусах, но существуют несколько температурных шкал: Цельсия (°C, самая распространенная шкала в мире), Фаренгейта (°F, используемая в США и некоторых других странах), и Кельвина (К, используемая в физике и других точных науках). Различие между шкалами Цельсия и Кельвина в том, что за ноль принята разная температура. По Цельсию — это температура замерзания воды, в то время как по Кельвину — это абсолютный ноль, то есть –273,15 °C. Шкала Фаренгейта отличается от шкалы Цельсия не только температурой, принятой за ноль, но еще и разницей между величиной одного градуса. Для перевода градусов Цельсия в градусы Фаренгейта используют формулу:
°C = 5/9 (°F – 32).
Температура замерзания воды равна 32 °F.
В системе СИ используются градусы шкалы Кельвина, называемые кельвинами (К).
Электрический разряд в плазменной лампе
Температура в физике и химии
Агрегатное состояния веществ (плазма, газ, жидкость, или твердое тело) определяется температурой. В любом теле молекулы колеблются, причем при увеличении температуры это движение ускоряется, так же, как и кинетическая энергия этих молекул. Чем больше скорость колебания молекул, тем легче им разойтись на большее расстояние друг от друга. Для каждого агрегатного состояния вещества существует определенный порог расстояния между молекулами. Это расстояние самое маленькое в твердых телах, и самое большое в газах и плазме. Материалы, которые не изменяют агрегатное состояние при высоких температурах, называются огнеупорными материалами. Например, многие керамические смеси огнеупорны, потому что не плавятся при температурах до 1000 °C. Их часто используют на производстве, например в печах с очень высокой температурой. Некоторые материалы плавятся при высокой температуре, в то время как другие материалы, как например, дерево, сгорают. Диапазон температур, при которых вещества могут находиться в состоянии жидкости, невелик. При переходе этого порога, жидкости превращаются в газы. При дальнейшем нагревании, атомы разлагаются на заряженные частицы, ионы и электроны — процесс, называемый ионизацией. Частично или полностью ионизированный газ называется плазмой. Большая часть материи во вселенной находится именно в состоянии плазмы.
Температура влияет на электропроводимость веществ и служит катализатором химических реакций. Изменение температуры замедляет или, наоборот, ускоряет их.
Тройная точка воды
Тройная точка воды — температура и давление, при которых вода может одновременно и равновесно существовать в виде трёх фаз — в твердом (лед), жидком и газообразном (пар) состояниях. Тройная точка воды — температура 0,01°С (273,16 К) и парциальное давление водяного пара 611,73 Па. При таких условиях для превращения всей воды в пар, лед или жидкое состояние достаточно только чуть-чуть изменить давление или температуру.
Тройная точка воды соответствует минимальному давлению, при котором жидкая вода может существовать. При давлении ниже тройной точки (например, в открытом космосе) твердый лед сублимируется в пар, минуя жидкое состояние. При параметрах выше тройной точки лед при нагревании вначале переходит в жидкое состояние и только потом, при более высоких температурах, вода кипит и испаряется.
Тройная точка воды иногда используется как опорная, например, для калибровки измерительной аппаратуры и термометров. Для этого используются ампулы тройной точки воды. Эти ампулы обеспечивают получение температуры точно 0,01°С или 273,16K.
Кривые потока излучения абсолютно чёрных тел с разной температурой. Источник: wikipedia.org. Автор: 4C
Эффективная температура
Эффективной температурой тела называется температура такого абсолютно черного тела, каждый квадратный сантиметр которого излучает во всем спектре такой же поток, как и квадратный сантиметр данного тела.
Абсолютно черное тело – тело, которое поглощает падающее на него излучение во всем диапазоне спектра.
Такую температуру можно вычислить из закона Стефана-Больцмана, который гласит, что мощность излучения абсолютно черного тела пропорциональна четвертой степени температуры. Так, например, для Земли это значение достигает примерно 250 К, что составляет –23 °C, но с другой стороны известно, что у поверхности Земли температура в среднем выше, в районе +15 °C. Данное несоответствие со значением эффективной температуры объясняется тем, что Земля имеет атмосферу, а значит есть воздействие парникового эффекта, который помогает Земле сохранять тепло. Таким образом значение в 250 К, это температура верхних слоев атмосферы нашей планеты. То есть, эффективная температура Земли — это температура, которая видна из космоса.
Зная эффективную температуру звезды, можно узнать к какому спектральному классу она относится, иначе говоря, определить в каком диапазоне длин волн или частот звезда излучает. У Солнца эффективная температура около 6000 К, и максимум энергии излучения приходится на 470 нм, что соответствует зеленой части спектра, а не желтой, как кажется человеческому глазу.
15-метровая рупорно-параболическая антенна, с помощью которой А. Пензиасом и Р. Вильсоном было зарегистрировано реликтовое излучение. За это открытие им была вручена Нобелевская премия. Источник: НАСА
Температура во Вселенной
В астрономии используется очень широкий диапазон значений температур — от невероятно низких до очень высоких.
Например, реликтовое излучение – остаточное электромагнитное излучение, возникшее в следствие Большого взрыва, имеет эффективную температуру всего лишь 2,7 К — значение очень близкое к абсолютному нулю.
Сравнение размеров Солнца и голубого сверхгиганта — звезды Альнитак. Источник: wikipedia.org. Автор: CWitte
Напротив, температуры звезд могут достигать высоких значений более 40000 К. Такие звезды, как правило, имеют большие радиусы, измеряющиеся в десятках радиусов Солнца. Примером такой звезды является Альнитак А – голубой сверхгигант в созвездии Ориона с диаметром в 20 раз больше солнечного.
Еще более высокие температуры можно встретить в ядрах звезд, так как для того, чтобы там протекали термоядерные реакции, требуются колоссальные значения температур. Например, чтобы произошла реакция превращения более легких элементов в более тяжелые, нужно, чтобы ядра имели высокую кинетическую энергию. Следовательно, и высокую температуру. У нашего Солнца в ядре значение температуры достигает 15 000 000 К.
Температура в биологии
Типичная температура тела японского пятнистого оленя Cervus nippon равна 313ºK или 39.8ºC. Парк Нара в городе Нара (Япония) у подножия горы Вакакуса.
Температура влияет на жизненные процессы всех живых существ. Сложные организмы обычно регулируют температуру тела, и стараются поддерживать одинаковую температуру. Температура используется животными как защитный механизм. Например, чтобы избавиться от бактерий и вирусов, у людей поднимается температура выше, чем эти инородные тела могут перенести. А грызуны и некоторые другие млекопитающие, такие как медведи, понижают температуру, тем самым замедляя обмен веществ, дыхание, и сердцебиение, впадая в спячку. Замедленный обмен веществ позволяет животным выжить с меньшими затратами энергии, чем в обычном состоянии. Этот защитный механизм предназначен для того, чтобы пережить время, когда недостаточно или вообще нет еды. Примеры таких замедлений жизнедеятельности — зимняя и летняя спячки. Температура тела у некоторых животных, впадающих в спячку, опускается очень низко, иногда ниже 0°C. Например, у некоторых видов сусликов, проживающих в арктических регионах, температура тела в районе брюшной полости понижается до –2,9°C. Растения также могут находиться в состоянии покоя во время зимних холодов.
Анабиоз
Анабиоз — состояние организма, в котором замедлены жизненные процессы почти до состояния смерти. Организм сам может перейти в такое состояние, но анабиоз также можно инициировать при понижении температуры окружающей среды, и другими способами. Некоторые организмы находятся в естественном состоянии анабиоза во время определенных периодов их жизни. Состояние анабиоза граничит со смертью, но исследования показали, что животных в этом состоянии можно вернуть к жизни без повреждения нервных клеток и тканей. Ученые надеются, что в ближайшем будущем это будет возможно и для людей. Надежда заключается в том, что анабиоз позволит оказывать первую медицинскую помощь и спасать людей с травмами и заболеваниями, опасными для жизни, такими, как инфаркт миoкардa. При травмах обычно происходит большая потеря крови, что вызывает кислородную недостаточность в мозге, так как именно кровь доставляет кислород к органам, которые в нем нуждаются. Недостаток кислорода в жизненно важных органах, особенно в мозге, вызывает отмирание нервных клеток и тканей, что через некоторое время приводит к смерти. Если больной перейдет в состояние анабиоза, то в связи с замедлением всех жизнедеятельных процессов потребность в кислороде также понизится. Это предотвратит повреждение клеток и тканей, и даст врачам дополнительное время и возможность восстановить кровообращение и помочь пациенту. Анабиоз также даст медицинскому персоналу время, чтобы перевезти больного от места аварии в больницу.
Живые организмы в состоянии анабиоза выдерживают очень низкие температуры, и были случаи, когда люди выживали в экстремальных условиях благодаря тому, что впадали в состояние анабиоза. В состоянии гипотермии люди иногда выживали без еды и питья дольше, чем это возможно в нормальном состоянии. В отделениях вспомогательных репродуктивных технологий эмбрионы, предназначенные для использования при лечении бесплодия, хранятся именно в состоянии анабиоза, в котором они могут находиться до десяти лет. В будущем технологии анабиоза будут полезны также и для космонавтов — анабиоз сделает возможным путешествия к отдаленным планетам.
В настоящее врем анабиоз исследуется на животных. В большинстве экспериментов их кровь заменяют раствором солей очень низкой температуры, или подвергают их воздействию газов, в результате чего эти животные переходят в состояние анабиоза. Успех этих экспериментов статистически значим, и с 2008 года начались исследования с участием людей.
Кипящий жидкий азот
Крионика
Ученые надеются, что если сохранить тело или голову человека или животного в условиях очень низкой температуры, то в будущем появятся технологии, позволяющие вернуть этот организм к жизни и даже излечить его от последствий старения. Такое сохранение называется криосохранением, а наука, занимающаяся вопросами сохранения — крионикой. На данный момент технологии по криосохранению позволяют осуществлять замораживание отдельных тканей, органов, и всего тела. Обычно температура замораживания достигает примерно 77 K или –196 °C. Это температура кипения жидкого азота, вещества наиболее часто используемого при замораживании сложных организмов. Эта температура настолько низкая, что предотвращает биохимические реакции, которые вызывают отмирание клеток. Во время замораживания возможны многие осложнения, такие как разрушение клеток льдом. Современные технологии позволяют сохранить ткани в течении тысячи лет, после чего, как предполагают исследователи, имеется вероятность разрушения молекул ДНК. Ученые надеются, что в будущем появятся технологии, которые смогут исправить эти повреждения в ДНК и тканях.
Сейчас существует ряд компаний, предоставляющих услуги по криосохранению умерших людей и домашних животных. Это очень дорогой процесс, и у этих компаний мало клиентов, особенно потому, что в прошлом были проблемы с разморозкой тел. Некоторые клиенты подписывают контракт на полное криосохранение тела, но возможно и сохранение только головы или мозга. Последнее — дешевле, хотя пока неизвестно, как в будущем компании по криосохранению будет покрывать расходы на новое тело.
Кухонный термометр
Температура в кулинарии
Температура часто применяется в кулинарии для того, чтобы сделать пищевые продукты более доступными для пищеварения или изменить их структуру. Например, именно благодаря нагреванию мышечные ткани в мясе изменяют свою структуру и становятся мягкими. Из всех живых существ только люди научились использовать температуру в приготовлении пищи. Ученые антропологи утверждают, что человек готовил еду на огне еще 250 000 лет назад. Замораживание также используется в приготовлении пищи, например для того, чтобы убить паразитов в рыбе, предназначенной для употребления в сыром виде в суши или сашими. В домашних условиях этого добиться невозможно, так как температура должна уменьшиться до –37 °C. Для этого используют промышленные морозильные камеры, в которых достигаются такие температуры.
Литература
Автор статьи: Kateryna Yuri, Tatiana Kondratieva
Вы затрудняетесь в переводе единицы измерения с одного языка на другой? Коллеги готовы вам помочь. Опубликуйте вопрос в TCTerms и в течение нескольких минут вы получите ответ.
www.translatorscafe.com
градус Цельсия [°C] кельвин [К] • Популярные конвертеры единиц • Конвертер температуры • Компактный калькулятор
Конвертер длины и расстоянияКонвертер массыКонвертер мер объема сыпучих продуктов и продуктов питанияКонвертер площадиКонвертер объема и единиц измерения в кулинарных рецептахКонвертер температурыКонвертер давления, механического напряжения, модуля ЮнгаКонвертер энергии и работыКонвертер мощностиКонвертер силыКонвертер времениКонвертер линейной скоростиПлоский уголКонвертер тепловой эффективности и топливной экономичностиКонвертер чисел в различных системах счисленияКонвертер единиц измерения количества информацииКурсы валютРазмеры женской одежды и обувиРазмеры мужской одежды и обувиКонвертер угловой скорости и частоты вращенияКонвертер ускоренияКонвертер углового ускоренияКонвертер плотностиКонвертер удельного объемаКонвертер момента инерцииКонвертер момента силыКонвертер вращающего моментаКонвертер удельной теплоты сгорания (по массе)Конвертер плотности энергии и удельной теплоты сгорания топлива (по объему)Конвертер разности температурКонвертер коэффициента теплового расширенияКонвертер термического сопротивленияКонвертер удельной теплопроводностиКонвертер удельной теплоёмкостиКонвертер энергетической экспозиции и мощности теплового излученияКонвертер плотности теплового потокаКонвертер коэффициента теплоотдачиКонвертер объёмного расходаКонвертер массового расходаКонвертер молярного расходаКонвертер плотности потока массыКонвертер молярной концентрацииКонвертер массовой концентрации в раствореКонвертер динамической (абсолютной) вязкостиКонвертер кинематической вязкостиКонвертер поверхностного натяженияКонвертер паропроницаемостиКонвертер паропроницаемости и скорости переноса параКонвертер уровня звукаКонвертер чувствительности микрофоновКонвертер уровня звукового давления (SPL)Конвертер уровня звукового давления с возможностью выбора опорного давленияКонвертер яркостиКонвертер силы светаКонвертер освещённостиКонвертер разрешения в компьютерной графикеКонвертер частоты и длины волныОптическая сила в диоптриях и фокусное расстояниеОптическая сила в диоптриях и увеличение линзы (×)Конвертер электрического зарядаКонвертер линейной плотности зарядаКонвертер поверхностной плотности зарядаКонвертер объемной плотности зарядаКонвертер электрического токаКонвертер линейной плотности токаКонвертер поверхностной плотности токаКонвертер напряжённости электрического поляКонвертер электростатического потенциала и напряженияКонвертер электрического сопротивленияКонвертер удельного электрического сопротивленияКонвертер электрической проводимостиКонвертер удельной электрической проводимостиЭлектрическая емкостьКонвертер индуктивностиКонвертер Американского калибра проводовУровни в dBm (дБм или дБмВт), dBV (дБВ), ваттах и др. единицахКонвертер магнитодвижущей силыКонвертер напряженности магнитного поляКонвертер магнитного потокаКонвертер магнитной индукцииРадиация. Конвертер мощности поглощенной дозы ионизирующего излученияРадиоактивность. Конвертер радиоактивного распадаРадиация. Конвертер экспозиционной дозыРадиация. Конвертер поглощённой дозыКонвертер десятичных приставокПередача данныхКонвертер единиц типографики и обработки изображенийКонвертер единиц измерения объема лесоматериаловВычисление молярной массыПериодическая система химических элементов Д. И. Менделеева
Демонстрация «Горячее стекло» в музее стекла в городе Корнинг, штат Нью-Йорк. Стеклодувы работают со стеклом, нагретым до температур 870–1 040 °C или 1 600–1 900 °F.
Общие сведения
Единицы измерения температуры
Температура в физике и химии
Тройная точка воды
Температура в биологии
Анабиоз
Крионика
Температура в кулинарии
Общие сведения
Демонстрация «Горячее стекло» в музее стекла в городе Корнинг, штат Нью-Йорк. Профессиональный стеклодув работает с комком расплавленного стекла на конце стеклодувной трубки. Позже она сделает из него вазу.
Температура — физическая величина, определяющая количество теплоты в теле или материи. Температуру также можно определить как количество кинетической энергии в частицах, составляющих тело или материю. Энергия передается от тел с более высокой температурой к телам более с низкой температурой, пока не будет достигнуто термодинамическое равновесие, то есть, пока температура обоих тел не сравняется. Этот процесс называется теплопередачей. К примеру, если открыть зимой окно, теплый воздух в комнате будет передавать тепло холодному воздуху на улице до тех пор, пока температура воздуха на улице и в комнате не станет одинаковой. В разных материалах тепло передается по-разному, в зависимости от их теплопроводности. Материалы с высокой теплопроводностью нагреваются и охлаждаются быстрее, чем материалы с низкой. Для теплоизоляции, например, в строительстве, используются именно материалы с низкой теплопроводностью.
Температуру измеряют с помощью термометра, и самая низкая температура, которая возможна — это –273,15 °C. Эта температура называется абсолютным нулем.
Единицы измерения температуры
Температуру измеряют в градусах, но существуют несколько температурных шкал: Цельсия (°C, самая распространенная шкала в мире), Фаренгейта (°F, используемая в США и некоторых других странах), и Кельвина (К, используемая в физике и других точных науках). Различие между шкалами Цельсия и Кельвина в том, что за ноль принята разная температура. По Цельсию — это температура замерзания воды, в то время как по Кельвину — это абсолютный ноль, то есть –273,15 °C. Шкала Фаренгейта отличается от шкалы Цельсия не только температурой, принятой за ноль, но еще и разницей между величиной одного градуса. Для перевода градусов Цельсия в градусы Фаренгейта используют формулу:
°C = 5/9 (°F – 32).
Температура замерзания воды равна 32 °F.
В системе СИ используются градусы шкалы Кельвина, называемые кельвинами (К).
Электрический разряд в плазменной лампе
Температура в физике и химии
Агрегатное состояния веществ (плазма, газ, жидкость, или твердое тело) определяется температурой. В любом теле молекулы колеблются, причем при увеличении температуры это движение ускоряется, так же, как и кинетическая энергия этих молекул. Чем больше скорость колебания молекул, тем легче им разойтись на большее расстояние друг от друга. Для каждого агрегатного состояния вещества существует определенный порог расстояния между молекулами. Это расстояние самое маленькое в твердых телах, и самое большое в газах и плазме. Материалы, которые не изменяют агрегатное состояние при высоких температурах, называются огнеупорными материалами. Например, многие керамические смеси огнеупорны, потому что не плавятся при температурах до 1000 °C. Их часто используют на производстве, например в печах с очень высокой температурой. Некоторые материалы плавятся при высокой температуре, в то время как другие материалы, как например, дерево, сгорают. Диапазон температур, при которых вещества могут находиться в состоянии жидкости, невелик. При переходе этого порога, жидкости превращаются в газы. При дальнейшем нагревании, атомы разлагаются на заряженные частицы, ионы и электроны — процесс, называемый ионизацией. Частично или полностью ионизированный газ называется плазмой. Большая часть материи во вселенной находится именно в состоянии плазмы.
Температура влияет на электропроводимость веществ и служит катализатором химических реакций. Изменение температуры замедляет или, наоборот, ускоряет их.
Тройная точка воды
Тройная точка воды — температура и давление, при которых вода может одновременно и равновесно существовать в виде трёх фаз — в твердом (лед), жидком и газообразном (пар) состояниях. Тройная точка воды — температура 0,01°С (273,16 К) и парциальное давление водяного пара 611,73 Па. При таких условиях для превращения всей воды в пар, лед или жидкое состояние достаточно только чуть-чуть изменить давление или температуру.
Тройная точка воды соответствует минимальному давлению, при котором жидкая вода может существовать. При давлении ниже тройной точки (например, в открытом космосе) твердый лед сублимируется в пар, минуя жидкое состояние. При параметрах выше тройной точки лед при нагревании вначале переходит в жидкое состояние и только потом, при более высоких температурах, вода кипит и испаряется.
Тройная точка воды иногда используется как опорная, например, для калибровки измерительной аппаратуры и термометров. Для этого используются ампулы тройной точки воды. Эти ампулы обеспечивают получение температуры точно 0,01°С или 273,16K.
Кривые потока излучения абсолютно чёрных тел с разной температурой. Источник: wikipedia.org. Автор: 4C
Эффективная температура
Эффективной температурой тела называется температура такого абсолютно черного тела, каждый квадратный сантиметр которого излучает во всем спектре такой же поток, как и квадратный сантиметр данного тела.
Абсолютно черное тело – тело, которое поглощает падающее на него излучение во всем диапазоне спектра.
Такую температуру можно вычислить из закона Стефана-Больцмана, который гласит, что мощность излучения абсолютно черного тела пропорциональна четвертой степени температуры. Так, например, для Земли это значение достигает примерно 250 К, что составляет –23 °C, но с другой стороны известно, что у поверхности Земли температура в среднем выше, в районе +15 °C. Данное несоответствие со значением эффективной температуры объясняется тем, что Земля имеет атмосферу, а значит есть воздействие парникового эффекта, который помогает Земле сохранять тепло. Таким образом значение в 250 К, это температура верхних слоев атмосферы нашей планеты. То есть, эффективная температура Земли — это температура, которая видна из космоса.
Зная эффективную температуру звезды, можно узнать к какому спектральному классу она относится, иначе говоря, определить в каком диапазоне длин волн или частот звезда излучает. У Солнца эффективная температура около 6000 К, и максимум энергии излучения приходится на 470 нм, что соответствует зеленой части спектра, а не желтой, как кажется человеческому глазу.
15-метровая рупорно-параболическая антенна, с помощью которой А. Пензиасом и Р. Вильсоном было зарегистрировано реликтовое излучение. За это открытие им была вручена Нобелевская премия. Источник: НАСА
Температура во Вселенной
В астрономии используется очень широкий диапазон значений температур — от невероятно низких до очень высоких.
Например, реликтовое излучение – остаточное электромагнитное излучение, возникшее в следствие Большого взрыва, имеет эффективную температуру всего лишь 2,7 К — значение очень близкое к абсолютному нулю.
Сравнение размеров Солнца и голубого сверхгиганта — звезды Альнитак. Источник: wikipedia.org. Автор: CWitte
Напротив, температуры звезд могут достигать высоких значений более 40000 К. Такие звезды, как правило, имеют большие радиусы, измеряющиеся в десятках радиусов Солнца. Примером такой звезды является Альнитак А – голубой сверхгигант в созвездии Ориона с диаметром в 20 раз больше солнечного.
Еще более высокие температуры можно встретить в ядрах звезд, так как для того, чтобы там протекали термоядерные реакции, требуются колоссальные значения температур. Например, чтобы произошла реакция превращения более легких элементов в более тяжелые, нужно, чтобы ядра имели высокую кинетическую энергию. Следовательно, и высокую температуру. У нашего Солнца в ядре значение температуры достигает 15 000 000 К.
Температура в биологии
Типичная температура тела японского пятнистого оленя Cervus nippon равна 313ºK или 39.8ºC. Парк Нара в городе Нара (Япония) у подножия горы Вакакуса.
Температура влияет на жизненные процессы всех живых существ. Сложные организмы обычно регулируют температуру тела, и стараются поддерживать одинаковую температуру. Температура используется животными как защитный механизм. Например, чтобы избавиться от бактерий и вирусов, у людей поднимается температура выше, чем эти инородные тела могут перенести. А грызуны и некоторые другие млекопитающие, такие как медведи, понижают температуру, тем самым замедляя обмен веществ, дыхание, и сердцебиение, впадая в спячку. Замедленный обмен веществ позволяет животным выжить с меньшими затратами энергии, чем в обычном состоянии. Этот защитный механизм предназначен для того, чтобы пережить время, когда недостаточно или вообще нет еды. Примеры таких замедлений жизнедеятельности — зимняя и летняя спячки. Температура тела у некоторых животных, впадающих в спячку, опускается очень низко, иногда ниже 0°C. Например, у некоторых видов сусликов, проживающих в арктических регионах, температура тела в районе брюшной полости понижается до –2,9°C. Растения также могут находиться в состоянии покоя во время зимних холодов.
Анабиоз
Анабиоз — состояние организма, в котором замедлены жизненные процессы почти до состояния смерти. Организм сам может перейти в такое состояние, но анабиоз также можно инициировать при понижении температуры окружающей среды, и другими способами. Некоторые организмы находятся в естественном состоянии анабиоза во время определенных периодов их жизни. Состояние анабиоза граничит со смертью, но исследования показали, что животных в этом состоянии можно вернуть к жизни без повреждения нервных клеток и тканей. Ученые надеются, что в ближайшем будущем это будет возможно и для людей. Надежда заключается в том, что анабиоз позволит оказывать первую медицинскую помощь и спасать людей с травмами и заболеваниями, опасными для жизни, такими, как инфаркт миoкардa. При травмах обычно происходит большая потеря крови, что вызывает кислородную недостаточность в мозге, так как именно кровь доставляет кислород к органам, которые в нем нуждаются. Недостаток кислорода в жизненно важных органах, особенно в мозге, вызывает отмирание нервных клеток и тканей, что через некоторое время приводит к смерти. Если больной перейдет в состояние анабиоза, то в связи с замедлением всех жизнедеятельных процессов потребность в кислороде также понизится. Это предотвратит повреждение клеток и тканей, и даст врачам дополнительное время и возможность восстановить кровообращение и помочь пациенту. Анабиоз также даст медицинскому персоналу время, чтобы перевезти больного от места аварии в больницу.
Живые организмы в состоянии анабиоза выдерживают очень низкие температуры, и были случаи, когда люди выживали в экстремальных условиях благодаря тому, что впадали в состояние анабиоза. В состоянии гипотермии люди иногда выживали без еды и питья дольше, чем это возможно в нормальном состоянии. В отделениях вспомогательных репродуктивных технологий эмбрионы, предназначенные для использования при лечении бесплодия, хранятся именно в состоянии анабиоза, в котором они могут находиться до десяти лет. В будущем технологии анабиоза будут полезны также и для космонавтов — анабиоз сделает возможным путешествия к отдаленным планетам.
В настоящее врем анабиоз исследуется на животных. В большинстве экспериментов их кровь заменяют раствором солей очень низкой температуры, или подвергают их воздействию газов, в результате чего эти животные переходят в состояние анабиоза. Успех этих экспериментов статистически значим, и с 2008 года начались исследования с участием людей.
Кипящий жидкий азот
Крионика
Ученые надеются, что если сохранить тело или голову человека или животного в условиях очень низкой температуры, то в будущем появятся технологии, позволяющие вернуть этот организм к жизни и даже излечить его от последствий старения. Такое сохранение называется криосохранением, а наука, занимающаяся вопросами сохранения — крионикой. На данный момент технологии по криосохранению позволяют осуществлять замораживание отдельных тканей, органов, и всего тела. Обычно температура замораживания достигает примерно 77 K или –196 °C. Это температура кипения жидкого азота, вещества наиболее часто используемого при замораживании сложных организмов. Эта температура настолько низкая, что предотвращает биохимические реакции, которые вызывают отмирание клеток. Во время замораживания возможны многие осложнения, такие как разрушение клеток льдом. Современные технологии позволяют сохранить ткани в течении тысячи лет, после чего, как предполагают исследователи, имеется вероятность разрушения молекул ДНК. Ученые надеются, что в будущем появятся технологии, которые смогут исправить эти повреждения в ДНК и тканях.
Сейчас существует ряд компаний, предоставляющих услуги по криосохранению умерших людей и домашних животных. Это очень дорогой процесс, и у этих компаний мало клиентов, особенно потому, что в прошлом были проблемы с разморозкой тел. Некоторые клиенты подписывают контракт на полное криосохранение тела, но возможно и сохранение только головы или мозга. Последнее — дешевле, хотя пока неизвестно, как в будущем компании по криосохранению будет покрывать расходы на новое тело.
Кухонный термометр
Температура в кулинарии
Температура часто применяется в кулинарии для того, чтобы сделать пищевые продукты более доступными для пищеварения или изменить их структуру. Например, именно благодаря нагреванию мышечные ткани в мясе изменяют свою структуру и становятся мягкими. Из всех живых существ только люди научились использовать температуру в приготовлении пищи. Ученые антропологи утверждают, что человек готовил еду на огне еще 250 000 лет назад. Замораживание также используется в приготовлении пищи, например для того, чтобы убить паразитов в рыбе, предназначенной для употребления в сыром виде в суши или сашими. В домашних условиях этого добиться невозможно, так как температура должна уменьшиться до –37 °C. Для этого используют промышленные морозильные камеры, в которых достигаются такие температуры.
Литература
Автор статьи: Kateryna Yuri, Tatiana Kondratieva
Вы затрудняетесь в переводе единицы измерения с одного языка на другой? Коллеги готовы вам помочь. Опубликуйте вопрос в TCTerms и в течение нескольких минут вы получите ответ.
www.translatorscafe.com
Перевод — градус — Большая Энциклопедия Нефти и Газа, статья, страница 1
Перевод — градус
Cтраница 1
Перевод градусов в радианы и наоборот. [1]
Перевод градусов в радианы и обратно. [2]
Перевод градусов Фаренгейта в градусы стоградусной шкалы и обратно. [3]
Перевод градусов условной вязкости ( ВУ) в единицы кинематической ( вязкости выполняется по змипирической формуле Уббелоде. [4]
Таблицу перевода градусов в радианы и обратно см. стр. [5]
Таблицы перевода градусов в радианы и обратно см. стр. [6]
В таблице дается перевод градусов АПИ ( API) в уд. [7]
Примечание: Для перевода градусов Цельсия в кельвины необходимо пользоваться формулой: Т t Т0, где Т — температура в кель-винах, t — температура в градусах Цельсия, Т0 273 15 Кельвина. По размеру градус Цельсия равен Кельвину. [8]
В табл. 26 приведен перевод градусов ФЭ в абсолютную вязкость — пуазы. [9]
Принимая во внимание, что перевод градусов Фаренгейта ( F) в градусы Цельсия ( С) производится не через постоянный коэффициент, в формулах (2.9) — (2.11), а также и в других главах сохранены размерности, принятые в оригинале. [10]
По этим ф-лам составлены таблицы для перевода градусов одной шкалы на другую. [11]
Шкала прибора не строго пропорциональна давлению, поэтому для перевода градусов шкалы в единицы давления пользуются переводной таблицей или номограммой, построенной на основании градуировки прибора по поршневому или ртутному манометру более высокого класса точности. [12]
Мы разработали математическую модель, которая преобразует единицы измерений, используемые внутри программы, в единицы измерений, предпочитаемые инженерами, например перевод градусов Цельсия в градусы Фаренгейта. В этой модели элементы списка EN используются для определения потоков, для которых ответы должны выдаваться в новых единицах измерений. [13]
Кеннингхем [42] вычислил значения давления пара жидкого фенилбензола, повидимому, с помощью уравнения ( 155) Чипмена и Пельтьера ( с переводом градусов стоградусной шкалы в градусы Фаренгейта) без упоминания, однако, этих авторов и без указания источника, откуда взяты данные. По этой причине данные Кеннингхема, перепечатанные также в статье Монтиллона и соавторов [ 100J, не использованы в настоящей работе. [14]
Все обратные тригонометрические функции возвращают результат в радианах. Для перевода градусов в радианы используется функция DTOR ( выр. [15]
Страницы: 1 2
www.ngpedia.ru




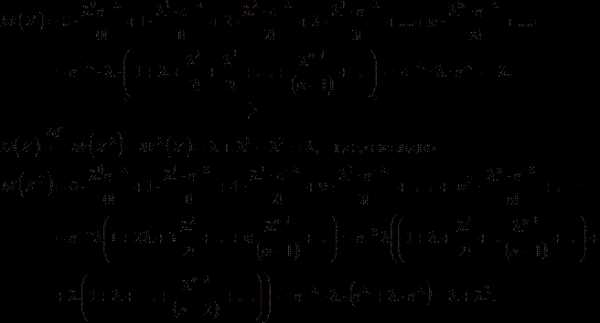
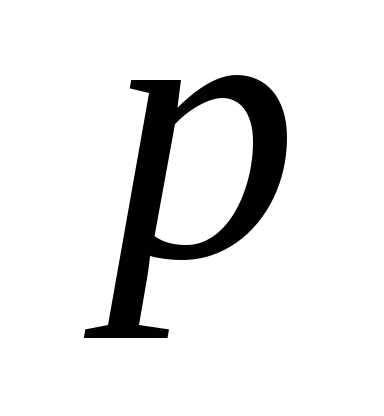 или неудача с вероятностью
или неудача с вероятностью ,
при этом (
,
при этом ( ).
). .
. рассмотрим число успехов в серии из 2
испытаний. Построим ряд распределения
случайной величины
рассмотрим число успехов в серии из 2
испытаний. Построим ряд распределения
случайной величины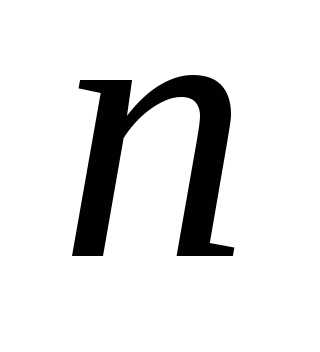 раз.
При каждом опыте событие А (успех)
происходит с вероятностью
раз.
При каждом опыте событие А (успех)
происходит с вероятностью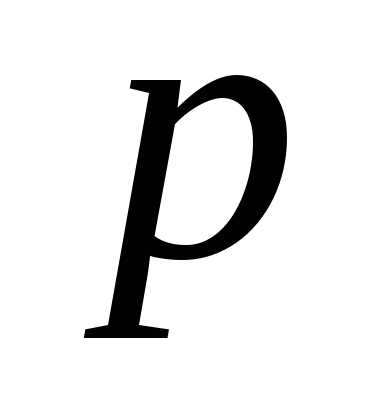 и не происходит с вероятностью
и не происходит с вероятностью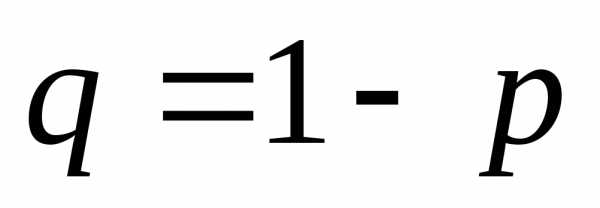 ,
причем эти вероятности от опыта к опыту
не меняются. Случайная
величина
,
причем эти вероятности от опыта к опыту
не меняются. Случайная
величина  – число успехов в серии из
– число успехов в серии из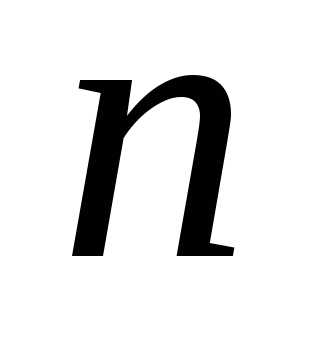 испытаний, Найдем вероятность того, что,
т.е. что событие А (успех) наступит
испытаний, Найдем вероятность того, что,
т.е. что событие А (успех) наступит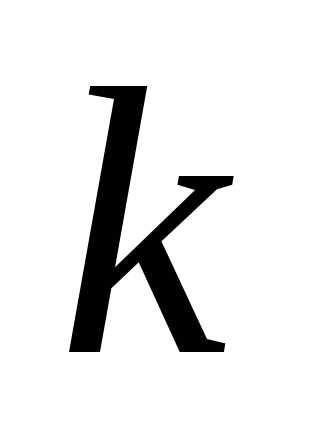 раз (а, следовательно, неуспех наступит
раз (а, следовательно, неуспех наступит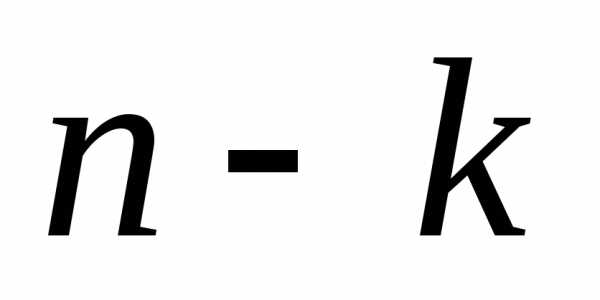 раз).Найдем вначале, что событие А
(успех) произойдет при первых
раз).Найдем вначале, что событие А
(успех) произойдет при первых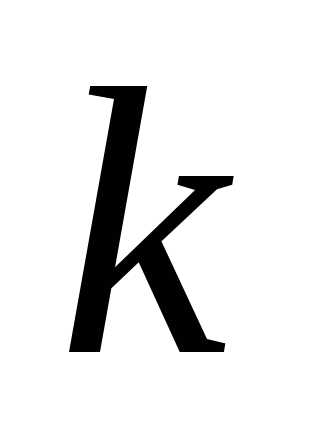 опытах и не произойдет при последних
опытах и не произойдет при последних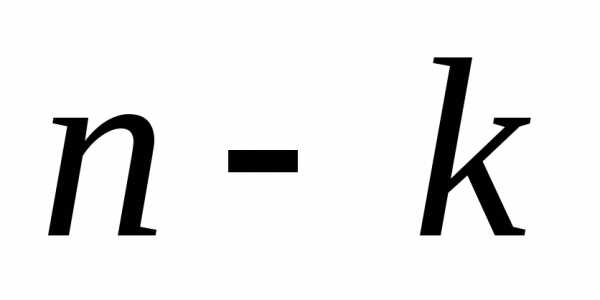 опытах. Применяя теорему умножения
вероятностей, получим.
Но событие А может произойти
опытах. Применяя теорему умножения
вероятностей, получим.
Но событие А может произойти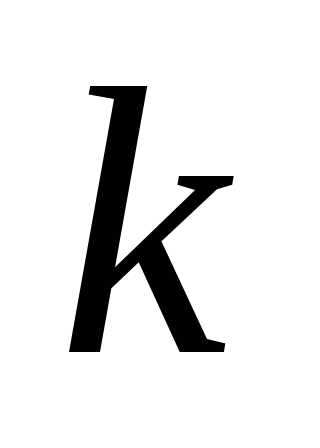 раз и в другой последовательности. Общее
число всех возможных последовательностей
равно
раз и в другой последовательности. Общее
число всех возможных последовательностей
равно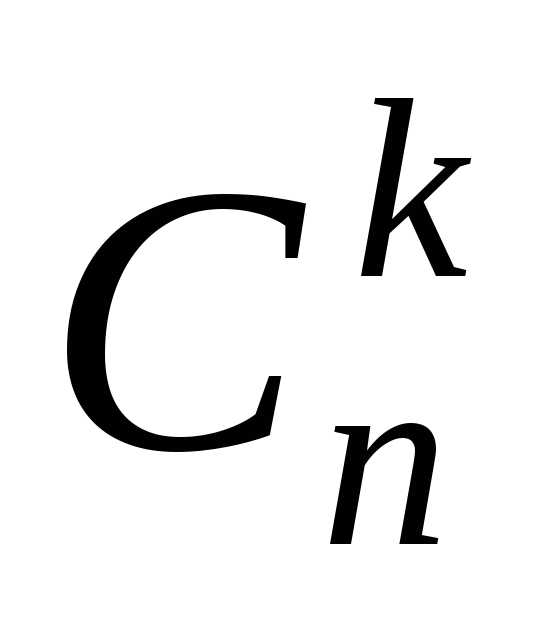 .
Вероятность появления события А для
каждой такой последовательности равна
.
Вероятность появления события А для
каждой такой последовательности равна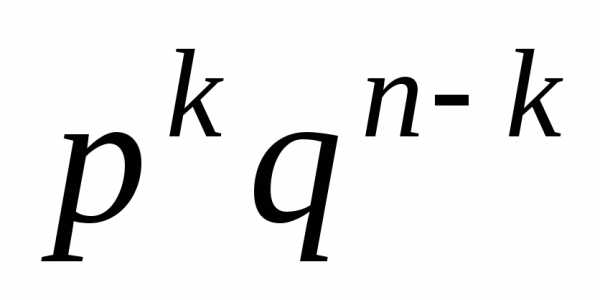 .
Вероятность появления какой либо одной
из этих последовательностей найдем с
помощью теоремы сложения вероятностей
.
Вероятность появления какой либо одной
из этих последовательностей найдем с
помощью теоремы сложения вероятностей –го
члена бинома Ньютона
–го
члена бинома Ньютона .
Поэтому такое распределение вероятностей
называется биномиальным. Впервые это
распределение подробно изучил Бернулли.
Поэтому стохастический эксперимент,
приводящий к биномиальному распределению,
называется схемой Бернулли.
.
Поэтому такое распределение вероятностей
называется биномиальным. Впервые это
распределение подробно изучил Бернулли.
Поэтому стохастический эксперимент,
приводящий к биномиальному распределению,
называется схемой Бернулли. неотрицательное
целое число.
неотрицательное
целое число. .
Найти вероятность отказа 0,1,2,3,4 элементов
во время работы прибора.
.
Найти вероятность отказа 0,1,2,3,4 элементов
во время работы прибора.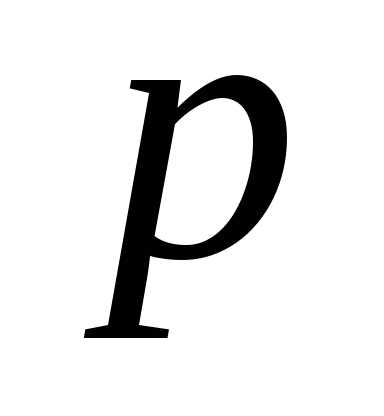 или неудача с вероятностью
или неудача с вероятностью ,
при этом (
,
при этом (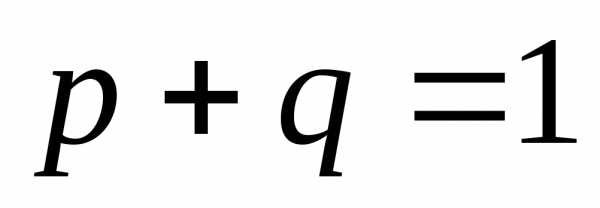 ).
Испытания проводятся до первого успеха.
Случайная величина
).
Испытания проводятся до первого успеха.
Случайная величина – число испытаний до первого успеха.
Найдем распределение случайной величины
– число испытаний до первого успеха.
Найдем распределение случайной величины .
Пространство элементарных событий
.
Пространство элементарных событий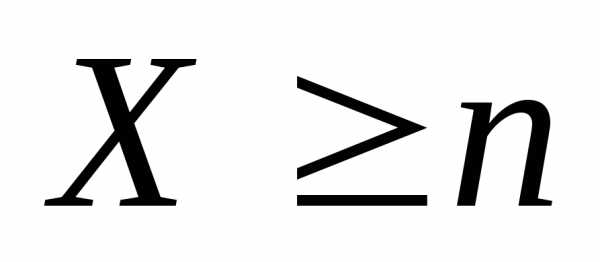 ,
совпадает с безусловной вероятностью
того, что
,
совпадает с безусловной вероятностью
того, что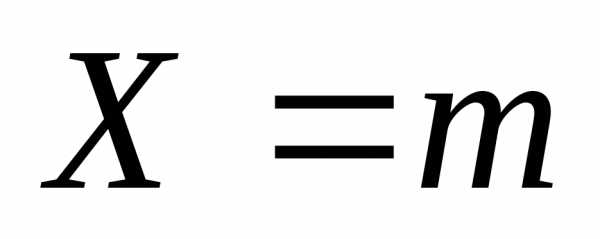 .
.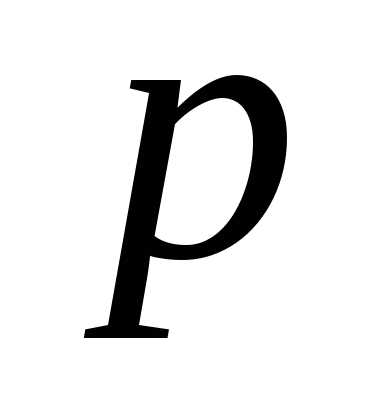 принимается решение закончить разговор
и с вероятностью
принимается решение закончить разговор
и с вероятностью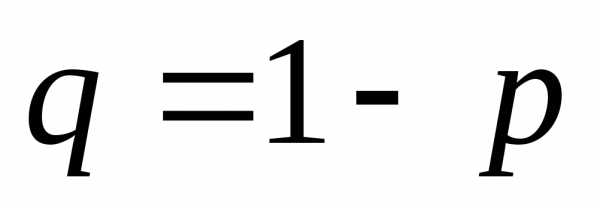 его продолжить. Тогда длительность
телефонного разговора будет случайной
величиной, имеющей геометрическое
распределение. Условная вероятность
того, что телефонный разговор будет
продолжаться ровно
его продолжить. Тогда длительность
телефонного разговора будет случайной
величиной, имеющей геометрическое
распределение. Условная вероятность
того, что телефонный разговор будет
продолжаться ровно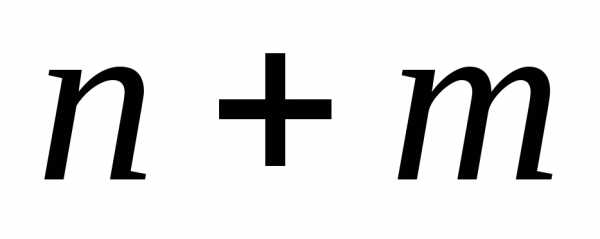 минут, если известно, что он не закончился
за
минут, если известно, что он не закончился
за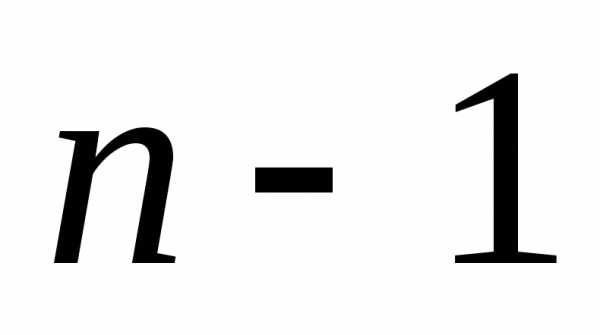 минуту, совпадает с безусловной
вероятностью того, разговор будет
продолжаться ровно
минуту, совпадает с безусловной
вероятностью того, разговор будет
продолжаться ровно минут, т.е. вероятность появления значения
случайной величиныне зависит от того, наступало событие
минут, т.е. вероятность появления значения
случайной величиныне зависит от того, наступало событие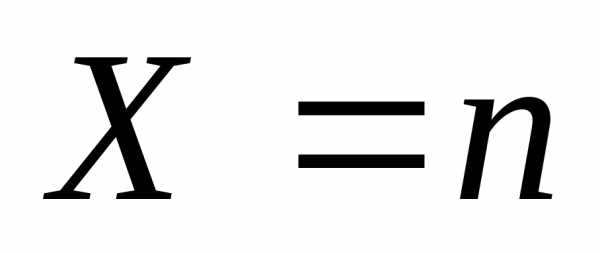 или нет. Это означает, что предыстория
не влияет на вероятность появления
события в ближайшем будущем
или нет. Это означает, что предыстория
не влияет на вероятность появления
события в ближайшем будущем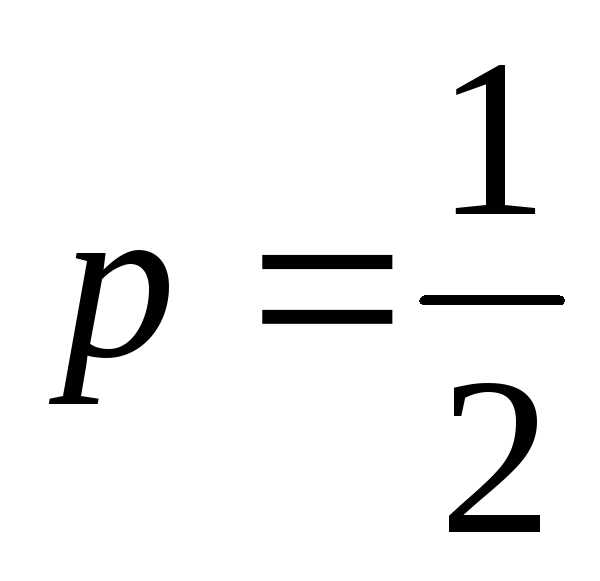 ,
,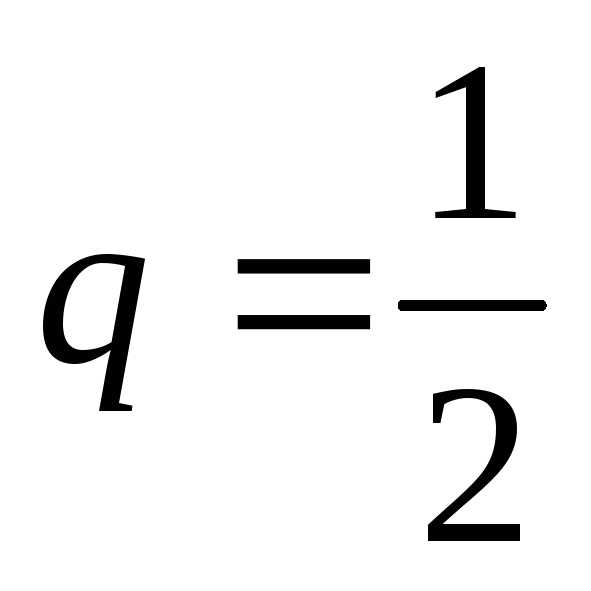 .
Случайная величина – число бросаний
до появления герба имеет геометрическое
распределение. Ряд распределения
.
Случайная величина – число бросаний
до появления герба имеет геометрическое
распределение. Ряд распределения
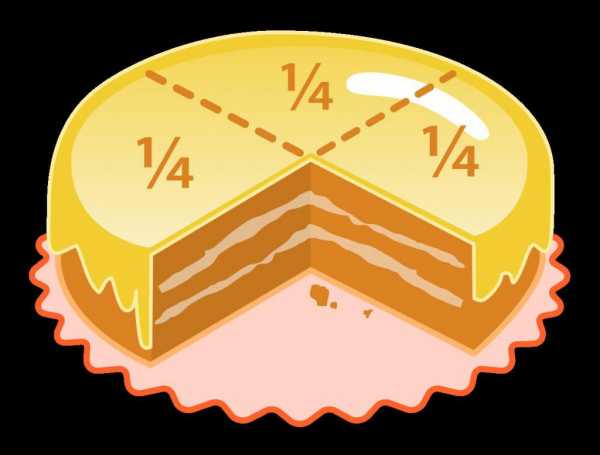
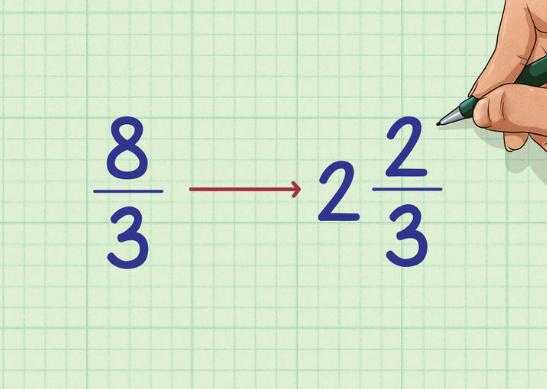
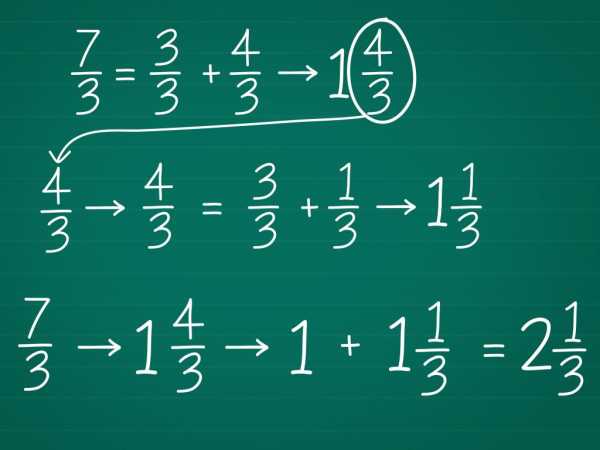
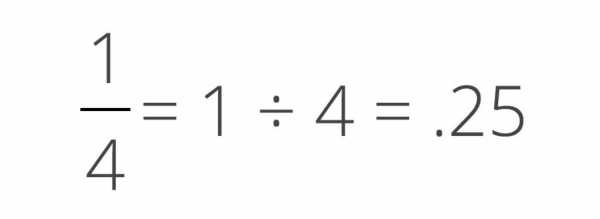
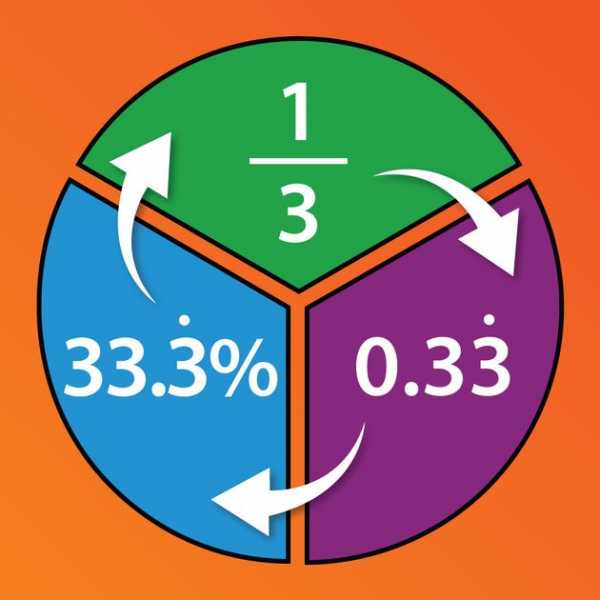
 К слову сказать, нужно заранее определиться, что не любое число можно без проблем записать в десятичном виде. Иногда приходится результат округлять, теряя некоторое количество знаков после запятой, а во многих областях – например, в точных науках – это совершено непозволительная роскошь. В то же время действия с десятичными и обыкновенными дробями в 5 классе позволяют осуществлять такой перевод из одного вида в другой без помех, хотя бы в качестве тренировки.
К слову сказать, нужно заранее определиться, что не любое число можно без проблем записать в десятичном виде. Иногда приходится результат округлять, теряя некоторое количество знаков после запятой, а во многих областях – например, в точных науках – это совершено непозволительная роскошь. В то же время действия с десятичными и обыкновенными дробями в 5 классе позволяют осуществлять такой перевод из одного вида в другой без помех, хотя бы в качестве тренировки. В подготовке чисел к дальнейшим действиям вам поможет правило, известное как основное свойство дроби и используемое как в первые годы изучения предмета, так и в высшей математике, которую изучают в университетах.
В подготовке чисел к дальнейшим действиям вам поможет правило, известное как основное свойство дроби и используемое как в первые годы изучения предмета, так и в высшей математике, которую изучают в университетах. К чему мы это? Да к тому, что обыкновенные дроби при всей своей громоздкости могут сильно упростить жизнь ученику, позволяя при перемножении и делении сокращать целые строки значений, а при расчёте суммы и разности выносить общие аргументы и, опять же, сокращать их.
К чему мы это? Да к тому, что обыкновенные дроби при всей своей громоздкости могут сильно упростить жизнь ученику, позволяя при перемножении и делении сокращать целые строки значений, а при расчёте суммы и разности выносить общие аргументы и, опять же, сокращать их. В старших классах ученики решают квадратные уравнения. Выполнять действия с обыкновенными дробями здесь уже крайне проблематично, поскольку формула для расчёта значений переменной содержит квадратный корень из суммы. При наличии дроби, не сводимой к десятичной, решение усложняется настолько, что рассчитать точный ответ без калькулятора становится практически невозможно.
В старших классах ученики решают квадратные уравнения. Выполнять действия с обыкновенными дробями здесь уже крайне проблематично, поскольку формула для расчёта значений переменной содержит квадратный корень из суммы. При наличии дроби, не сводимой к десятичной, решение усложняется настолько, что рассчитать точный ответ без калькулятора становится практически невозможно.