Тервер Википедия
Тео́рия вероя́тностей — раздел математики, изучающий случайные события, случайные величины, их свойства и операции над ними.
История[ | ]
 Христиан Гюйгенс
Христиан Гюйгенс  Андрей Николаевич Колмогоров
Андрей Николаевич КолмогоровВозникновение теории вероятностей как науки относят к средним векам и первым попыткам математического анализа азартных игр (орлянка, кости, рулетка). Первоначально её основные понятия не имели строго математического вида, к ним можно было относиться как к некоторым эмпирическим фактам, как к свойствам реальных событий, и они формулировались в наглядных представлениях. Самые ранние работы учёных в области теории вероятностей относятся к XVII веку. Исследуя прогнозирование выигрыша в азартных играх, Блез Паскаль и Пьер Ферма открыли первые вероятностные закономерности, возникающие при бросании костей[1]. Под влиянием поднятых и рассматриваемых ими вопросов решением тех же задач занимался и Христиан Гюйгенс. При этом с перепиской Паскаля и Ферма он знаком не был, поэтому методику решения изобрёл самостоятельно. Его работа, в которой вводятся основные понятия теории вероятностей (понятие вероятности как величины шанса; математическое ожидание для дискретных случаев, в виде цены шанса), а также используются теоремы сложения и умножения вероятностей (не сформулированные явно), вышла в печатном виде на двадцать лет раньше (1657 год) издания писем Паскаля и Ферма (1679 год)[2].
Важный вклад в теорию вероятностей внёс Якоб Бернулли: он дал доказательство закона больших чисел в простейшем случае независимых испытаний.
В XVIII веке важное значение для развития теории вероятностей имели работы Томаса Байеса, сформулировавшего и доказавшего Теорему Байеса.
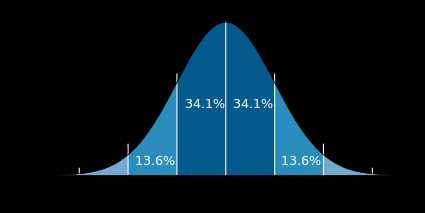
В первой половине XIX века теория вероятностей начинает применяться к анализу ошибок наблюдений; Лаплас и Пуассон доказали первые предельные теоремы. Карл Гаусс детально исследовал нормальное распределение случайной величины (см. график выше), также называемое «распределением Гаусса».
Во второй половине XIX века значительный вклад внес ряд европейских и русских учёных: П. Л. Чебышёв, А.&
ru-wiki.ru
Теория вероятностей — это… Что такое Теория вероятностей?
Тео́рия вероя́тностей — раздел математики, изучающий закономерности случайных явлений: случайные события, случайные величины, их свойства и операции над ними.
История
Возникновение теории вероятностей как науки относят к средним векам и первым попыткам математического анализа азартных игр (орлянка, кости, рулетка). Первоначально её основные понятия не имели строго математического вида, к ним можно было относиться как к некоторым эмпирическим фактам, как к свойствам реальных событий, и они формулировались в наглядных представлениях. Самые ранние работы учёных в области теории вероятностей относятся к XVII веку. Исследуя прогнозирование выигрыша в азартных играх, Блез Паскаль и Пьер Ферма открыли первые вероятностные закономерности, возникающие при бросании костей[1]. Под влиянием поднятых и рассматриваемых ими вопросов решением тех же задач занимался и Христиан Гюйгенс. При этом с перепиской Паскаля и Ферма он знаком не был, поэтому методику решения изобрёл самостоятельно. Его работа, в которой вводятся основные понятия теории вероятностей (понятие вероятности как величины шанса; математическое ожидание для дискретных случаев, в виде цены шанса), а также используются теоремы сложения и умножения вероятностей (не сформулированные явно), вышла в печатном виде на двадцать лет раньше (1657 год) издания писем Паскаля и Ферма (1679 год)[2].
Важный вклад в теорию вероятностей внёс Якоб Бернулли: он дал доказательство закона больших чисел в простейшем случае независимых испытаний. В первой половине XIX века теория вероятностей начинает применяться к анализу ошибок наблюдений; Лаплас и Пуассон доказали первые предельные теоремы. Во второй половине XIX века основной вклад внесли русские учёные П. Л. Чебышев, А. А. Марков и А. М. Ляпунов. В это время были доказаны закон больших чисел, центральная предельная теорема, а также разработана теория цепей Маркова. Современный вид теория вероятностей получила благодаря аксиоматизации, предложенной Андреем Николаевичем Колмогоровым. В результате теория вероятностей приобрела строгий математический вид и окончательно стала восприниматься как один из разделов математики.
Основные понятия теории
См. также
Ссылки
Литература
А
- Ахтямов, А. М. «Экономико-математические методы» : учеб. пособие Башк. гос. ун-т. — Уфа : БГУ, 2007.
- Ахтямов, А. М. «Теория вероятностей». — М.: Физматлит, 2009
Б
- Боровков, А. А. «Математическая статистика», М.: Наука, 1984.
- Боровков, А. А. «Теория вероятностей», М.: Наука, 1986.
- Булдык, Г. М. «Теория вероятностей и математическая статистика», Мн., Высш. шк., 1989.
- Булинский, А. В., Ширяев, А. Н. «Теория случайных процессов», М.: Физматлит, 2003.
- Бекарева, Н. Д. «Теория вероятностей. Конспект лекций», Новосибирск НГТУ
- Баврин, И. И. « Высшая математика» (Часть 2 «Элементы теории вероятностей и математической статистики»), М.: Наука, 2000.
В
Г
- Гихман И. И., Скороход А. В. Введение в теорию случайных процессов. — М.: Наука, 1977.
- Гмурман, В. Е. «Теория вероятностей и математическая статистика»: Учеб. пособие — 12-е изд., перераб.- М.: Высшее образование, 2006.-479 с.:ил (Основы наук).
- Гмурман, В. Е. «Руководство к решению задач по теории вероятностей и математической статистике»: Учеб. пособие — 11-е изд., перераб. — М.: Высшее образование, 2006.-404 с. (Основы наук).
- Гнеденко, Б. В. «Курс теории вероятностей», — М.: Наука, 1988.
- Гнеденко, Б. В. «Курс теории вероятностей», УРСС. М.: 2001.
- Гнеденко Б. В., Хинчин А. Я. «Элементарное введение в теорию вероятностей», 1970.
- Горбань, И. И. «Теория гиперслучайных явлений: физические и математические основы» – К.: Наукова думка, 2011. – 318 с.
- Горбань, И. И. «Справочник по теории случайных функций и математической статистике», Киев: Институт кибернетики им. В. М. Глушкова НАН Украины, 1998.
- Гурский Е. И. «Сборник задач по теории вероятностей и математической статистике», — Минск: Высшая школа, 1975.
Д
- П. Е. Данко, А. Г. Попов, Т. Я. Кожевников. Высшая математика в упражнениях и задачах. (В 2-х частях)- М.: Высш.шк, 1986.
Е
- А. В. Ефимов, А. Е. Поспелов и др. 4 часть // Сборник задач по математике для втузов. — 3-е изд., перераб. и дополн.. — М.: «Физматлит», 2003. — Т. 4. — 432 с. — ISBN 5-94052-037-5
К
- Колемаев, В. А. и др. «Теория вероятностей и математическая статистика», — М.: Высшая школа, 1991. http://www.iqlib.ru/book/preview/b0ce99dc4e1741128564b81841ae6ce0
- Колмогоров, А. Н. «Основные понятия теории вероятностей», М.: Наука, 1974.
- Коршунов, Д. А., Фосс, С. Г. «Сборник задач и упражнений по теории вероятностей», Новосибирск, 1997.
- Коршунов, Д. А., Чернова, Н. И. «Сборник задач и упражнений по математической статистике», Новосибирск. 2001.
- Кремер Н. Ш. Теория вероятностей и математическая статистика: Учебник для ВУЗов. — 2- изд., перераб. и доп.-М:ЮНИТИ-ДАНА, 2004. — 573 с.
- Кузнецов, А. В. «Применение критериев согласия при математическом моделировании экономических процессов», Мн.: БГИНХ, 1991.
Л
- Лихолетов И. И., Мацкевич И. Е. «Руководство к решению задач по высшей математике, теории вероятностей и математической статистике», Мн.: Выш. шк., 1976.
- Лихолетов И. И. «Высшая математика, теория вероятностей и математическая статистика», Мн.: Выш. шк., 1976.
- Лоэв М.В «Теория вероятностей», — М.: Издательство иностранной литературы, 1962.
М
- Маньковский Б. Ю., «Таблица вероятности».
- Мацкевич И. П., Свирид Г. П. «Высшая математика. Теория вероятностей и математическая статистика», Мн.: Выш. шк., 1993.
- Мацкевич И. П., Свирид Г. П., Булдык Г. М. «Сборник задач и упражнений по высшей математике. Теория вероятностей и математическая статистика», Мн.: Выш. шк., 1996.
- Мейер П.-А. Вероятность и потенциалы. Издательство Мир, Москва, 1973.
- Млодинов Л. (Не)совершенная случайность
П
- Прохоров, А. В., В. Г. Ушаков, Н. Г. Ушаков. «Задачи по теории вероятностей», Наука. М.: 1986.
- Прохоров Ю. В., Розанов Ю. А. «Теория вероятностей», — М.: Наука, 1967.
- Пугачев, В. С. «Теория вероятностей и математическая статистика», Наука. М.: 1979.
Р
- Ротарь В. И., «Теория вероятностей», — М.: Высшая школа, 1992.
С
- Свешников А. А. и др., «Сборник задач по теории вероятностей, математической статистике и теории случайных функций», — М.: Наука, 1970.
- Свирид, Г. П., Макаренко, Я. С., Шевченко, Л. И. «Решение задач математической статистики на ПЭВМ», Мн., Выш. шк., 1996.
- Севастьянов Б. А., «Курс теории вероятностей и математической статистики», — М.: Наука, 1982.
- Севастьянов, Б. А., Чистяков, В. П., Зубков, А. М. «Сборник задач по теории вероятностей», М.: Наука, 1986.
- Соколенко А. И., «Высшая математика», учебник. М.: Академия, 2002.
Ф
- Феллер, В. «Введение в теорию вероятностей и её приложения».
Х
- Хамитов, Г. П., Ведерникова, Т. И. «Вероятности и статистики», БГУЭП. Иркутск.: 2006.
Ч
- Чистяков, В. П. «Курс теории вероятностей», М., 1982.
- Чернова, Н. И. «Теория вероятностей», Новосибирск. 2007.
Ш
Примечания
dic.academic.ru
ТерВер
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«КАЗАНСКИЙ ГОСУДАРСТВЕННЫЙ ЭНЕРГЕТИЧЕСКИЙ УНИВЕРСИТЕТ»
ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
ЧАСТЬ I
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
Казань 2012
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«КАЗАНСКИЙ ГОСУДАРСТВЕННЫЙ ЭНЕРГЕТИЧЕСКИЙ УНИВЕРСИТЕТ»
Т.А. ГРИГОРЯН, Е.В. ЛИПАЧЕВА
ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
ЧАСТЬ I
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
Казань 2012
УДК 517.1
ББК 22.1
Т34
Рецензенты:
кандидат физико-математическихнаук, доцент Казанского государственного энергетического университетаР.А. Ишмуратов; кандидат технических наук, доцент Казанского государственного
энергетического университета Т.З. Гимадиева
Т34 Григорян Т.А., Липачева Е.В. Теория вероятностей и математическая статистика. Часть I. Теория вероятностей. – Казань: Казан. гос. энерг. ун-т,2011. – 125 с.
Учебно-методическоепособие охватывает классические разделы теории вероятностей. Каждая глава начинается с подробного изложения теоретического материала, затем приводятся примеры решения задач, и завершается глава набором задач для самостоятельного решения. Все задачи снабжены ответами.
Учебно-методическоепособие предназначено для студентов второго курсаинженерно-экономическихспециальностей и может быть рекомендовано для использования при проведении практических занятий.
УДК 517.1 ББК 22.1
©Григорян Т.А., Липачева Е.В., 2012
©Казанский государственный энергетический университет, 2012
3
ПРЕДИСЛОВИЕ
Книга представляет собой первую часть учебно-методическогопособия по дисциплине «Теория вероятностей и математическая статистика», содержащую классические разделы теории вероятностей.
За последние годы теория вероятностей стала неотъемлемой частью курсов математики большинства вузов. Теоретико-вероятностныеи статистические методы стали необходимы большому числу работников промышленности и планирующих организаций.
Настоящее пособие состоит из шести глав, которые охватывают основные разделы курса лекций, читаемых студентам Казанского государственного энергетического университета инженерно-экономическихспециальностей в четвертом семестре, и может также использоваться при проведении практических занятий, так как содержит большое количество задач по всем разделам дисциплины.
Первая глава содержит описание понятия случайного события и его вероятности, а так же изложение комбинаторного подхода к вычислению вероятностей в наиболее простых примерах. В этой главе приведены также классические примеры, демонстрирующие предмет теории вероятностей, такие как задача о встрече и задача Бюффона.
Во второй главе содержатся основные теоремы теории вероятностей: о сложении, умножении вероятностей, формула полной вероятности и теорема гипотез, а также формулы, связанные с повторением испытаний (Бернулли, Пуассона).
Третья и четвертая главы посвящены описанию случайных величин, одномерных и двумерных, и их числовых характеристик, дается понятие закона распределения случайной величины, функции и плотности распределения.
В пятой главе приводятся известные законы распределения случайных величин с подробным описанием их характеристик и свойств.
Последняя шестая глава посвящена рассмотрению группы теорем, называемых законом больших чисел, а также центральной предельной теореме, доказанной русским математиком Ляпуновым А.М. и имеющей большое практическое значение.
4
Глава 1
ПРЕДМЕТ ТЕОРИИ ВЕРОЯТНОСТЕЙ. АЛГЕБРА СОБЫТИЙ. КЛАССИЧЕСКОЕ, СТАТИСТИЧЕСКОЕ И ГЕОМЕТРИЧЕСКОЕ ОПРЕДЕЛЕНИЯ ВЕРОЯТНОСТИ.
ОСНОВНЫЕ ФОРМУЛЫ КОМБИНАТОРИКИ
В различных разделах науки и техники нередко возникают ситуации, когда результат каждого из многих проводимых опытов заранее предугадать невозможно, однако можно исследовать закономерности, возникающие при проведении серии опытов. Нельзя, например, точно сказать, какая сторона монеты окажется сверху при данном броске: герб или цифра – но при большом количестве бросков число выпадений герба приближается к половине количества бросков; нельзя заранее предсказать результат одного выстрела из данного орудия по данной цели, но при большом числе выстрелов частота попадания приближается к некоторому постоянному числу. Исследование вероятностных закономерностей массовых однородных явлений составляет предмет теории вероятностей.
Основным интуитивным понятием классической теории вероятностей является случайное событие.
События, которые могут произойти в результате опыта, можно подразделить на три вида:
а) достоверное событие – событие, которое всегда происходит при проведении опыта;
б) невозможное событие – событие, которое в результате опыта произойти не может;
в) случайное событие – событие, которое может либо произойти, либо не произойти.
Например, при броске игральной кости достоверным событием является выпадение числа очков, не превышающего 6, невозможным – выпадение 10 очков, а случайным – выпадение 3 очков.
Суммой A B двух событийА иВ называют событие, состоящее в том, что произошло хотя бы одно из событийА иВ.Суммой нескольких событий, соответственно, называется событие, заключающееся в том, что произошло хотя бы одно из этих событий.
Примеры:
1) Два стрелка делают по одному выстрелу по мишени. Если событие А
– попадание первого стрелка, а событие В – второго, то суммаA B – это хотя бы одно попадание при двух выстрелах.
2) Если при броске игральной кости событием Ai назвать выпадениеi очков, то выпадение нечетного числа очков при одном броске является
суммой событий A A | A . | |
1 | 3 | 5 |

5
Назовем все возможные результаты данного опыта его исходами и предположим, что множество этих исходов, при которых происходит событиеА (исходов,благоприятных событиюА), можно представить в виде некоторой области на плоскости. Тогда множество исходов, при которых произойдет событиеA B , является объединением множеств исходов, благоприятных событиямА илиВ (рис. 1.1).
Рис.1.1
Произведением АВ событийА иВ называется событие, состоящее в том, что произошло и событиеА, и событиеВ. Аналогичнопроизведением нескольких событий называется событие, заключающееся в том, что произошли все эти события.
Примеры:
3)В примере 1 событием АВ будет попадание обоих стрелков.
4)Если событие А состоит в том, что из колоды карт извлечена карта пиковой масти, а событиеВ – в том, что из колоды вынута дама, то событиемАВ будет извлечение из колоды дамы пик.
Геометрической иллюстрацией множества исходов опыта, благоприятных появлению произведения событий А иВ, является пересечение областей, соответствующих исходам, благоприятнымА иВ (рис.
1.2).
Разностью событийА иВ называется событиеA \B , состоящее в том, чтоА произошло, аВ – нет (рис. 1.3).
Примеры:
5)Вернемся к примеру 1, где событие A \B – попадание первого стрелка при промахе второго.
6)В примере 4 событие A \B – извлечение из колоды любой карты пиковой масти, кроме дамы. Наоборот, событиеB \A – извлечение дамы любой масти, кроме пик.
6
Введем еще несколько категорий событий.
События А иВ называютсясовместными, если они могут произойти оба в результате одного опыта. В противном случае (то есть если они не могут произойти одновременно) события называютсянесовместными.
Совместными событиями являются, например, попадания двух стрелков в примере 1 и появление карты пиковой масти и дамы в примере 4; несовместными – события A1 A6 в примере 2.
Если изобразить графически области исходов опыта, благоприятных несовместным событиям, то они не будут иметь общих точек.
Из определения несовместных событий следует, что их произведение является невозможным событием.
Пространством элементарных исходов называется множество,
содержащее все возможные результаты данного опыта (эксперимента), из которых в опыте происходит ровно один. Элементы этого множества называют элементарными исходами и обозначают буквой , с индексами или без. Пространство элементарных исходов записывают как
1,2,…,n ,
где 1,…,n элементарные исходы опыта.
Тогда любое случайное событие A , возможное в данном опыте, есть некоторое подмножество пространства элементарных исходов, то есть
A :
A i1 ,i2 ,…,ik , 0ik n,
где k число исходов, благоприятствующих событиюA .
Мы говорим, что в результате опыта произошло событие A , если произошло элементарное событиеj , которое принадлежитA .
Говорят, что события B1,B2,…,Bn образуютполную группу, если в
результате опыта обязательно произойдет хотя бы одно из событий этой группы. В частности, если события, образующие полную группу, попарно несовместны, то в результате опыта произойдет одно и только одно из них.
Такие события называют элементарными событиями полной группы.
Пример.
В примере 2 события A1 A6 (выпадение одного, двух, … , шести
очков при одном броске игральной кости) образуют полную группу элементарных событий.
События называются равновозможными, если нет оснований считать, что одно из них является более возможным, чем другое.
7
Выпадение любого числа очков при броске игральной кости, появление любой карты при случайном извлечении из колоды, выпадение герба или цифры при броске монеты и т.п. – это все равновозможные события.
При изучении случайных событий возникает необходимость количественно сравнивать возможность их появления в результате опыта. Например, при последовательном извлечении из колоды пяти карт более возможна ситуация, когда появились карты разных мастей, чем появление пяти карт одной масти; при десяти бросках монеты более возможно чередование гербов и цифр, нежели выпадение подряд десяти гербов, и т.д. Поэтому с каждым таким событием связывают по определенному правилу некоторое число, которое тем больше, чем более возможно событие. Это число называется вероятностью события и является вторым основным понятием теории вероятностей.
Отметим, что само понятие вероятности, как и понятие случайного события, является аксиоматическим и поэтому не поддается строгому определению. То, что в дальнейшем будет называться различными определениями вероятности, представляет собой способы вычисления этой величины.
Если все события, которые могут произойти в результате данного опыта, попарно несовместны, равновозможны и образуют полную группу, то говорят, что имеет место схема случаев.
Можно считать, что случаи представляют собой все множество исходов опыта. Пусть их число равно п ( число возможных исходов), а прит из них происходит некоторое событиеА (число благоприятных исходов).
Вероятностью события А называется отношение числа исходов опыта, благоприятных этому событию, к числу всех возможных исходов:
P(А) | т |
| (1.1) | |
п | ||||
|
| |||
Это классическое определение вероятности. |
| |||
Из классического определения |
| вытекают следующие | свойства | |
вероятности: |
|
|
| |
1. Вероятность достоверного события равна единице.
Действительно, так как достоверное событие всегда происходит в результате опыта, то все исходы этого опыта являются для него благоприятными, то есть т = п, следовательно,Р(А) = 1.
2. Вероятность невозможного события равна нулю.
Для невозможного события ни один исход опыта не является благоприятным, поэтому т = 0 иР(А) = 0.
3. Вероятность случайного события есть положительное число, заключенное между нулем и единицей.
8
Действительно, случайное событие происходит при некоторых исходах опыта, но не при всех, следовательно, 0 < m < n, и из (1.1) следует, что
0 < Р(A)< 1.
Пример. Из урны, содержащей 6 белых и 4 черных шара, наудачу вынут шар. Найти вероятность того, что он белый.
Решение. Будем считать элементарными событиями, или исходами опыта, извлечение из урны каждого из имеющихся в ней шаров. Очевидно, что эти события удовлетворяют всем условиям, позволяющим считать их схемой случаев. Следовательно, число возможных исходов равно 10, а число исходов, благоприятных событиюА (появлению белого шара) – 6 (таково количество белых шаров в урне). Значит,
P(А)тп 106 0,6.
Классическое определение вероятности применимо только для очень узкого класса задач, где все возможные исходы опыта можно свести к схеме случаев. В большинстве реальных задач эта схема неприменима. В таких ситуациях требуется определять вероятность события иным образом. Для этого введем вначале понятие относительной частоты W(A) событияA как отношения числа опытов, в которых наблюдалось событиеА, к общему количеству проведенных испытаний:
где N – общее число опытов,М – число появлений событияА.
Большое количество экспериментов показало, что если опыты проводятся в одинаковых условиях, то для большого количества испытаний относительная частота изменяется мало, колеблясь около некоторого постоянного числа. Это число можно считать вероятностью рассматриваемого события.
Статистической вероятностью события считают его относительную частоту или число, близкое к ней.
Из формулы (1.2) следует, что свойства вероятности, доказанные для ее классического определения, справедливы и для статистического определения вероятности.
Для существования статистической вероятности события А требуется:
1)возможность производить неограниченное число испытаний;
2)устойчивость относительных частот появления А в различных сериях достаточно большого числа опытов.
Недостатком статистического определения является неоднозначность статистической вероятности.
9
Пример. Если в задаче задается вероятность попадания в мишень для данного стрелка (скажем,р = 0,7), то эта величина получена в результате изучения статистики большого количества серий выстрелов, в которых этот стрелок попадал в мишень около семидесяти раз из каждой сотни выстрелов.
Еще одним из недостатков классического определения вероятности является то, что оно неприменимо к испытаниям с бесконечным количеством исходов. В таких случаях можно воспользоваться понятием геометрической вероятности.
Пусть на отрезок L наудачу брошена точка. Это означает, что точка обязательно попадет на отрезокL и с равной возможностью может совпасть с любой точкой этого отрезка. При этом вероятность попадания точки на любую часть отрезкаL не зависит от расположения этой части на отрезке и пропорциональна его длине. Тогда вероятность того, что брошенная точка попадет на отрезокl, являющийся частью отрезкаL, вычисляется по формуле:
где l – длина отрезкаl, аL – длина отрезкаL.
Можно дать аналогичную постановку задачи для точки, брошенной на плоскую область S и вероятности того, что она попадет на часть этой областиs:
где s – площадь части области, аS – площадь всей области.
В трехмерном случае вероятность того, что точка, случайным образом расположенная в теле V, попадет в его частьv, задается формулой:
где v – объем части тела, аV – объем всего тела.
Пример. Найти вероятность того, что точка, наудачу брошенная в круг, не попадет в правильный шестиугольник, вписанный в него.
Решение. Пусть радиус круга равенR , тогда из курса геометрии следует, что сторона шестиугольника тоже равнаR. При этом площадь круга
S R2, а площадь шестиугольникаs 3 23 R2. Следовательно,
studfiles.net
Тервер Википедия

Тео́рия вероя́тностей — раздел математики, изучающий случайные события, случайные величины, их свойства и операции над ними.
История
 Христиан Гюйгенс
Христиан Гюйгенс  Андрей Николаевич Колмогоров
Андрей Николаевич КолмогоровВозникновение теории вероятностей как науки относят к средним векам и первым попыткам математического анализа азартных игр (орлянка, кости, рулетка). Первоначально её основные понятия не имели строго математического вида, к ним можно было относиться как к некоторым эмпирическим фактам, как к свойствам реальных событий, и они формулировались в наглядных представлениях. Самые ранние работы учёных в области теории вероятностей относятся к XVII веку. Исследуя прогнозирование выигрыша в азартных играх, Блез Паскаль и Пьер Ферма открыли первые вероятностные закономерности, возникающие при бросании костей[1]. Под влиянием поднятых и рассматриваемых ими вопросов решением тех же задач занимался и Христиан Гюйгенс. При этом с перепиской Паскаля и Ферма он знаком не был, поэтому методику решения изобрёл самостоятельно. Его работа, в которой вводятся основные понятия теории вероятностей (понятие вероятности как величины шанса; математическое ожидание для дискретных случаев, в виде цены шанса), а также используются теоремы сложения и умножения вероятностей (не сформулированные явно), вышла в печатном виде на двадцать лет раньше (1657 год) издания писем Паскаля и Ферма (1679 год)[2].
Важный вклад в теорию вероятностей внёс Якоб Бернулли: он дал доказательство закона больших чисел в простейшем случае независимых испытаний.
В XVIII веке важное значение для развития теории вероятностей имели работы Томаса Байеса, сформулировавшего и доказавшего Теорему Байеса.
В первой половине XIX века теория вероятностей начинает применяться к анализу ошибок наблюдений; Лаплас и Пуассон доказали первые предельные теоремы. Карл Гаусс детально исследовал нормальное распределение случайной величины (см. график выше), также называемое «распределением Гаусса».
Во второй половине XIX века значительный вклад внес ряд европейских и русских учёных: П. Л. Чебышёв, А. А. Марков и А. М. Ляпунов. В это время были доказаны закон больших чисел, центральная предельная теорема, а также разработана теория цепей Маркова.
Современный вид теория вероятностей получила благодаря аксиоматизации, предложенной Андреем Николаевичем Колмогоровым. В результате теория вероятностей приобрела строгий математический вид и окончательно стала восприниматься как один из разделов математики.
Основные понятия теории
См. также
Примечания
- ↑ Лейнартас Е. К., Яковлев Е. И. Элементы теории вероятностей: методическое пособие. — 2006.
- ↑ Майстров Л. Е. Развитие понятия вероятности. — М.: Наука, 1980.
Литература
А
- Ахтямов А. М. Экономико-математические методы : учеб. пособие. — Уфа : БГУ, 2007.
- Ахтямов А. М. Теория вероятностей. — М.: Физматлит, 2009.
Б
- Боровков А. А. Математическая статистика. — М.: Наука, 1984.
- Боровков А. А. Теория вероятностей. — М.: Наука, 1986.
- Булдык Г. М. Теория вероятностей и математическая статистика. — Мн.: Высш. шк., 1989.
- Булинский А. В., Ширяев А. Н. Теория случайных процессов. — М.: Физматлит, 2003.
- Бекарева Н. Д. Теория вероятностей. Конспект лекций. — Новосибирск, НГТУ.
- Баврин И. И. Высшая математика (Часть 2 «Элементы теории вероятностей и математической статистики»). — М.: Наука, 2000.
В
Г
- Гихман И. И., Скороход А. В. Введение в теорию случайных процессов. — М.: Наука, 1977.
- Гмурман В. Е. Теория вероятностей и математическая статистика: Учеб. пособие. — 12-е изд., перераб. — М.: Высшее образование, 2006. — 479 с.: ил. (Основы наук).
- Гмурман В. Е. Руководство к решению задач по теории вероятностей и математической статистике: Учеб. пособие. — 11-е изд., перераб. — М.: Высшее образование, 2006. — 404 с. (Основы наук).
- Гнеденко Б. В. Курс теории вероятностей. — М.: Наука, 1988.
- Гнеденко Б. В. Курс теории вероятностей. — М.: УРСС, 2001.
- Гнеденко Б. В., Хинчин А. Я. Элементарное введение в теорию вероятностей. — 1970.
- Гурский Е. И. Сборник задач по теории вероятностей и математической статистике. — Минск: Высшая школа, 1975.
Д
- Данко П. Е., Попов А. Г., Кожевников Т. Я. Высшая математика в упражнениях и задачах. (В 2-х частях)- М.: Высш.шк, 1986.
Е
- Ефимов А. В., Поспелов А. Е. и др. 4 часть // Сборник задач по математике для втузов. — 3-е изд., перераб. и дополн.. — М.: Физматлит, 2003. — Т. 4. — 432 с. — ISBN 5-94052-037-5.
К
- Клейбер И. А. Некоторые приложения теории вероятностей к метеорологии. — СПб., 1887.
- Колемаев В. А. и др. Теория вероятностей и математическая статистика. — М.: Высшая школа, 1991.
- Колмогоров, А. Н. Основные понятия теории вероятностей. — М.: Наука, 1974.
- Коршунов Д. А., Фосс С. Г. Сборник задач и упражнений по теории вероятностей. — Новосибирск, 1997.
- Коршунов Д. А., Чернова Н. И. Сборник задач и упражнений по математической статистике. — Новосибирск, 2001.
- Кремер Н. Ш. Теория вероятностей и математическая статистика: Учебник для ВУЗов. — 2- изд., перераб. и доп.- М.: ЮНИТИ-ДАНА, 2004. — 573 с.
- Кузнецов А. В. Применение критериев согласия при математическом моделировании экономических процессов. — Мн.: БГИНХ, 1991.
Л
- Лихолетов И. И., Мацкевич И. Е. Руководство к решению задач по высшей математике, теории вероятностей и математической статистике. — Мн.: Выш. шк., 1976.
- Лихолетов И. И. Высшая математика, теория вероятностей и математическая статистика. — Мн.: Выш. шк., 1976.
- Лоэв М. В. Теория вероятностей. — М.: Издательство иностранной литературы, 1962.
М
- Маньковский Б. Ю. Таблица вероятности.
- Мацкевич И. П., Свирид Г. П. Высшая математика. Теория вероятностей и математическая статистика. — Мн.: Выш. шк., 1993.
- Мацкевич И. П., Свирид Г. П., Булдык Г. М. Сборник задач и упражнений по высшей математике. Теория вероятностей и математическая статистика. — Мн.: Выш. шк., 1996.
- Мейер П.-А. Вероятность и потенциалы. — М.: Мир, 1973.
- Млодинов Л. (Не)совершенная случайность
Н
П
- Прохоров А. В., Ушаков В. Г., Ушаков Н. Г. Задачи по теории вероятностей. — М.: Наука, 1986.
- Прохоров Ю. В., Розанов Ю. А. Теория вероятностей. — М.: Наука, 1967.
- Пугачев В. С. Теория вероятностей и математическая статистика. — М.: Наука, 1979.
Р
- Ротарь В. И. Теория вероятностей. — М.: Высшая школа, 1992.
С
- Свешников А. А. и др. Сборник задач по теории вероятностей, математической статистике и теории случайных функций. — М.: Наука, 1970.
- Свирид Г. П., Макаренко Я. С., Шевченко Л. И. Решение задач математической статистики на ПЭВМ. — Мн.: Выш. шк., 1996.
- Севастьянов Б. А. Курс теории вероятностей и математической статистики. — М.: Наука, 1982.
- Севастьянов Б. А., Чистяков В. П., Зубков А. М. Сборник задач по теории вероятностей. — М.: Наука, 1986.
- Соколенко А. И. Высшая математика: учебник. — М.: Академия, 2002.
Ф
- Феллер В. Введение в теорию вероятностей и её приложения.
Х
- Хамитов Г. П., Ведерникова Т. И. Вероятности и статистики. — Иркутск: БГУЭП, 2006.
Ч
- Чистяков В. П. Курс теории вероятностей. — М., 1982.
- Чернова Н. И. Теория вероятностей. — Новосибирск, 2007.
Ш
Ссылки
wikiredia.ru
Теорвер Википедия

Тео́рия вероя́тностей — раздел математики, изучающий случайные события, случайные величины, их свойства и операции над ними.
История[ | ]
 Христиан Гюйгенс
Христиан Гюйгенс  Андрей Николаевич Колмогоров
Андрей Николаевич КолмогоровВозникновение теории вероятностей как науки относят к средним векам и первым попыткам математического анализа азартных игр (орлянка, кости, рулетка). Первоначально её основные понятия не имели строго математического вида, к ним можно было относиться как к некоторым эмпирическим фактам, как к свойствам реальных событий, и они формулировались в наглядных представлениях. Самые ранние работы учёных в области теории вероятностей относятся к XVII веку. Исследуя прогнозирование выигрыша в азартных играх, Блез Паскаль и Пьер Ферма открыли первые вероятностные закономерности, возникающие при бросании костей[1]. Под влиянием поднятых и рассматриваемых ими вопросов решением тех же задач занимался и Христиан Гюйгенс. При этом с перепиской Паскаля и Ферма он знаком не был, поэтому методику решения изобрёл самостоятельно. Его работа, в которой вводятся основные понятия теории вероятностей (понятие вероятности как величины шанса; математическое ожидание для дискретных случаев, в виде цены шанса), а также используются теоремы сложения и умножения вероятностей (не сформулированные явно), вышла в печатном виде на двадцать лет раньше (1657 год) издания писем Паскаля и Ферма (1679 год)[2].
Важный вклад в теорию вероятностей внёс Якоб Бернулли: он дал доказательство закона больших чисел в простейшем случае независимых испытаний.
В XVIII веке важное значение для развития теории вероятностей имели работы Томаса Байеса, сформулировавшего и доказавшего Теорему Байеса.
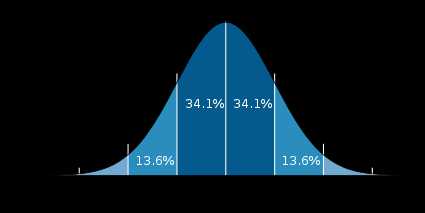
В первой половине XIX века теория вероятностей начинает применяться к анализу ошибок наблюдений; Лаплас и Пуассон доказали первые предельные теоремы. Карл Гаусс детально исследовал нормальное распределение случайной величины (см. график выше), также называемое «распределением Гаусса».
Во второй половине XIX века значительный вклад внес ряд европейских и русских учёных: П. Л. Чебышёв,
ru-wiki.ru
Тервер Вики

Тео́рия вероя́тностей — раздел математики, изучающий случайные события, случайные величины, их свойства и операции над ними.
История[ | код]
 Христиан Гюйгенс
Христиан Гюйгенс  Андрей Николаевич Колмогоров
Андрей Николаевич КолмогоровВозникновение теории вероятностей как науки относят к средним векам и первым попыткам математического анализа азартных игр (орлянка, кости, рулетка). Первоначально её основные понятия не имели строго математического вида, к ним можно было относиться как к некоторым эмпирическим фактам, как к свойствам реальных событий, и они формулировались в наглядных представлениях. Самые ранние работы учёных в области теории вероятностей относятся к XVII веку. Исследуя прогнозирование выигрыша в азартных играх, Блез Паскаль и Пьер Ферма открыли первые вероятностные закономерности, возникающие при бросании костей[1]. Под влиянием поднятых и рассматриваемых ими вопросов решением тех же задач занимался и Христиан Гюйгенс. При этом с перепиской Паскаля и Ферма он знаком не был, поэтому методику решения изобрёл самостоятельно. Его работа, в которой вводятся основные понятия теории вероятностей (понятие вероятности как величины шанса; математическое ожидание для дискретных случаев, в виде цены шанса), а также используются теоремы сложения и умножения вероятностей (не сформулированные явно), вышла в печатном виде на двадцать лет раньше (1657 год) издания писем Паскаля и Ферма (1679 год)[2].
Важный вклад в теорию вероятностей внёс Якоб Бернулли: он дал доказательство закона больших чисел в простейшем случае независимых испытаний.
В XVIII веке важное значение для развития теории вероятностей имели работы Томаса Байеса, сформулировавшего и доказавшего Теорему Байеса.
В первой половине XIX века теория вероятностей начинает применяться к анализу ошибок наблюдений; Лаплас и Пуассон доказали первые предельные теоремы. Карл Гаусс детально исследовал нормальное распределение случайной величины (см. график выше), также называемое «распределением Гаусса».
Во второй половине XIX века значительный вклад внес ряд европейских и русских учёных: П. Л. Чебышёв, А. А. Марков и А. М. Ляпунов. В это время были доказаны закон больших чисел, центральная предельная теорема, а также разработана теория цепей Маркова.
Современный вид теория вероятностей получила благодаря аксиоматизации, предложенной Андреем Николаевичем Колмогоровым. В результате теория вероятностей приобрела строгий математический вид и окончательно стала восприниматься как один из разделов математики.
Основные понятия теории[ | код]
См. также[ | код]
Примечания[ | код]
- ↑ Лейнартас Е. К., Яковлев Е. И. Элементы теории вероятностей: методическое пособие. — 2006.
- ↑ Майстров Л. Е. Развитие понятия вероятности. — М.: Наука, 1980.
Литература[ | код]
А[ | код]
- Ахтямов А. М. Экономико-математические методы : учеб. пособие. — Уфа : БГУ, 2007.
- Ахтямов А. М. Теория вероятностей. — М.: Физматлит, 2009.
Б[ | код]
- Боровков А. А. Математическая статистика. — М.: Наука, 1984.
- Боровков А. А. Теория вероятностей. — М.: Наука, 1986.
- Булдык Г. М. Теория вероятностей и математическая статистика. — Мн.: Высш. шк., 1989.
- Булинский А. В., Ширяев А. Н. Теория случайных процессов. — М.: Физматлит, 2003.
- Бекарева Н. Д. Теория вероятностей. Конспект лекций. — Новосибирск, НГТУ.
- Баврин И. И. Высшая математика (Часть 2 «Элементы теории вероятностей и математической статистики»). — М.: Наука, 2000.
В[ | код]
Г[ | код]
- Гихман И. И., Скороход А. В. Введение в теорию случайных процессов. — М.: Наука, 1977.
- Гмурман В. Е. Теория вероятностей и математическая статистика: Учеб. пособие. — 12-е изд., перераб. — М.: Высшее образование, 2006. — 479 с.: ил. (Основы наук).
- Гмурман В. Е. Руководство к решению задач по теории вероятностей и математической статистике: Учеб. пособие. — 11-е изд., перераб. — М.: Высшее образование, 2006. — 404 с. (Основы наук).
- Гнеденко Б. В. Курс теории вероятностей. — М.: Наука, 1988.
- Гнеденко Б. В. Курс теории вероятностей. — М.: УРСС, 2001.
- Гнеденко Б. В., Хинчин А. Я. Элементарное введение в теорию вероятностей. — 1970.
- Гурский Е. И. Сборник задач по теории вероятностей и математической статистике. — Минск: Высшая школа, 1975.
Д[ | код]
- Данко П. Е., Попов А. Г., Кожевников Т. Я. Высшая математика в упражнениях и задачах. (В 2-х частях)- М.: Высш.шк, 1986.
Е[ | код]
- Ефимов А. В., Поспелов А. Е. и др. 4 часть // Сборник задач по математике для втузов. — 3-е изд., перераб. и дополн.. — М.: Физматлит, 2003. — Т. 4. — 432 с. — ISBN 5-94052-037-5.
К[ | код]
- Клейбер И. А. Некоторые приложения теории вероятностей к метеорологии. — СПб., 1887.
- Колемаев В. А. и др. Теория вероятностей и математическая статистика. — М.: Высшая школа, 1991.
- Колмогоров, А. Н. Основные понятия теории вероятностей. — М.: Наука, 1974.
- Коршунов Д. А., Фосс С. Г. Сборник задач и упражнений по теории вероятностей. — Новосибирск, 1997.
- Коршунов Д. А., Чернова Н. И. Сборник задач и упражнений по математической статистике. — Новосибирск, 2001.
- Кремер Н. Ш. Теория вероятностей и математическая статистика: Учебник для ВУЗов. — 2- изд., перераб. и доп.- М.: ЮНИТИ-ДАНА, 2004. — 573 с.
- Кузнецов А. В. Применение критериев согласия при математическом моделировании экономических процессов. — Мн.: БГИНХ, 1991.
Л[ | код]
- Лихолетов И. И., Мацкевич И. Е. Руководство к решению задач по высшей математике, теории вероятностей и математической статистике. — Мн.: Выш. шк., 1976.
- Лихолетов И. И. Высшая математика, теория вероятностей и математическая статистика. — Мн.: Выш. шк., 1976.
- Лоэв М. В. Теория вероятностей. — М.: Издательство иностранной литературы, 1962.
М[ | код]
- Маньковский Б. Ю. Таблица вероятности.
- Мацкевич И. П., Свирид Г. П. Высшая математика. Теория вероятностей и математическая статистика. — Мн.: Выш. шк., 1993.
- Мацкевич И. П., Свирид Г. П., Булдык Г. М. Сборник задач и упражнений по высшей математике. Теория вероятностей и математическая статистика. — Мн.: Выш. шк., 1996.
- Мейер П.-А. Вероятность и потенциалы. — М.: Мир, 1973.
- Млодинов Л. (Не)совершенная случайность
Н[ | код]
П[ | код]
- Прохоров А. В., Ушаков В. Г., Ушаков Н. Г. Задачи по теории вероятностей. — М.: Наука, 1986.
- Прохоров Ю. В., Розанов Ю. А. Теория вероятностей. — М.: Наука, 1967.
- Пугачев В. С. Теория вероятностей и математическая статистика. — М.: Наука, 1979.
Р[ | код]
- Ротарь В. И. Теория вероятностей. — М.: Высшая школа, 1992.
С[ | код]
- Свешников А. А. и др. Сборник задач по теории вероятностей, математической статистике и теории случайных функций. — М.: Наука, 1970.
- Свирид Г. П., Макаренко Я. С., Шевченко Л. И. Решение задач математической статистики на ПЭВМ. — Мн.: Выш. шк., 1996.
- Севастьянов Б. А. Курс теории вероятностей и математической статистики. — М.: Наука, 1982.
- Севастьянов Б. А., Чистяков В. П., Зубков А. М. Сборник задач по теории вероятностей. — М.: Наука, 1986.
- Соколенко А. И. Высшая математика: учебник. — М.: Академия, 2002.
Ф[ | код]
- Феллер В. Введение в теорию вероятностей и её приложения.
Х[ | код]
- Хамитов Г. П., Ведерникова Т. И. Вероятности и статистики. — Иркутск: БГУЭП, 2006.
Ч[ | код]
- Чистяков В. П. Курс теории вероятностей. — М., 1982.
- Чернова Н. И. Теория вероятностей. — Новосибирск, 2007.
Ш[ | код]
Ссылки[ | код]
ru.wikibedia.ru