Задействованы лица не находящиеся в подчинении друг с другом — Студопедия.Нет
2) оппоненты не выходят за рамки этических норм
3) задействованы лица находящиеся в подчинение друг с другом
4) оппоненты выходят за рамки этических норм
118. Условием возникновения, реализации, видоизменения деятельности выступает…
1) характер
2) ответственность
3) темперамент
Активность
119. Социализация — это процесс и результат включения индивидов в ….
1) воспитание
2) деятельность
3) группу
Социальные отношения
121. В выборе друга старшеклассник руководствуется:
1) успеваемостью
2) деловыми качествами
3) личностными качествами
Нравственными чертами личности
122. Умственная активность в юношеском возрасте приобретает характерную черту:
1) интерес к реальным явлениям
2) интерес не столько к фактам,сколько к их анализу,обсуждению,рассуждению и размышлению над ними
3) повышенное внимание к наклядному материалу
4) внутренний план дейтсвий
123. Ведущая деятельность в юношеском возрасте:
1) интимно-личностное общение
2) учебная деятельность
3) предметно-манипулятивная
Учебно-профессиональная
124. Границы юношеского возраста:
1) 13-18 лет
2) 14-17 лет
3) 15-18 лет
Нет однозначного подхода к выделению границ
125. Я согласен(а) с утверждением,что кризис подросткового возраста-это:
1) следствие несоответствия старой системы воспитания и новых стремлений ребенка
Неизбежный и необходимый момент развития психики
126. Кризис подросткового возраста обусловлен:
1) новым уровнем самосознания ребенка
2) появлением способности и потребности познать себя как личность
3) стремление к самоутверждению
Всем перечисленным
127. Для эмоциональной сферы подростка характерно:
Резкая смена настроения и переживаний
2) бурное развитие «эмоционального языка»
3) эмоционнальная впечатлительность
4) осознание своего состояния
128. Характерная черта подростка:
1) эмоциональная устойчивость
2) покладистость
3) доверчивость
Реакция эмансипации
129. Ведущий мотив в учебной деятельности подростков:
1) значимость самого процесса учения как социально-ценной деятельности
Стремление завоевать определенное положение в классе, добиться признания сверстников
3) получение хорошей оценки
4) стремление к превосходству
130. Ведущая деятельность подросткового возраста:
1) интимно-личностное общение
Учебно-профессиональная
3) учебная
4) общественно-полезная
131. Подростковый возраст называют пубертатным периодом.Это означает:
1) эмоциональная реактивность
2) возмужание, половая зрелость
3) эмансипация от взрослых
4) индивидуализация
132. Общепринятые границы подросткового возраста в отечественной психологии:
1) 9-13 лет
2) 11-14 лет
Лет
4) 12-14 лет
133. Первый объект, который ребенок выделяет из окружающей среды:
1) он сам
2) игрушка
Человеческое лицо
4) окружающие его предметы
134.Анатомо-физиологические особенности младенческого возраста состоят в том, что:
1) заканчивается миелинизация нервных клеток
2) замедляется бурный рост организма
Нервная система недостаточсно развита и ограничивает физическую и умственную активность малыша
4) поведение ребенка обусловлено наличием большого количества безусловных рефлексов
135. Ведущая деятельность в младенческом возрасте:
1) кормление
2) игровая
3) непосредственно-эмоциональное общение
4) сон
136. Границы раннего возраста опредеяются в пределах:
1) 3-6 лет
Лет
3) 2-5 лет
4) 3-5 лет
137. В раннем возрасте реализуется общение:
1) ситуативно-личностное
Внеситуативно-личностное
3) внеситуативно-деловое
4) ситуативно-деловое
138. Главная черта социальной ситуации развития в раннем детстве:
1) рост влияния сверстников
2) ситуация слитности с матерью,ситуация «Мы»
Связанность ребенка с конкретной ситуацией, она определяет поведение ребенка
4) пассивное отношение к окружающему миру
140. В усвоении предметных действий особая роль принадлежит:
1) речи как основному средству общения взрослых с ребенком
2) повтору действий
3) специальному обучению
4) предметному восприятию
141. Ведущей функцией в раннем возрасте выступает:
1) память
2) мышление
Восприятие
4) внимание
142. Словарный запас ребенка к концу третьего года жизни составляет:
1) 100-300 слов
2) 3000-4500 слов
Слов
4) 2000-3000 слов
143. Границы дошкольного возраста определяются в пределах:
1) 3-6 лет
2) 4-6 лет
3) 3-7 лет
4) 3-6\7 лет
144. Отрицательная реакция ребенка, когда ребенок отказывается подчиняться определенным требованиям взрослых:
1) упрямство
Негативизм
3) строптивость
4) своеволие
145 В каком возрасте социальная ситуация развития представлена следующей схемой: «ребенок-предмет-взрослый»:
1) Младенческий возраст.
2) Средний дошкольный возраст.
3) Ранний возраст.
4) Старший дошкольный возраст.
146 Для какого кризиса характерна следующая симптоматика: 1. потеря непосредственности; 2. манерничание; 3. симптом «горькой конфеты»:
1) Кризис новорожденности.
2) Кризис трех лет.
3) Кризис одного года.
4) Кризис семи лет.
147. Кто из психологов является автором закона развития высших психических функции:
Л. С. Выготский.
2) А. Н. Леонтьев.
3) С. Л. Рубинштейн.
4) А. Р. Лурия.
148. Для исследования того, как ребенок в ходе развития усваивает орудия и средства культуры, был разработан метод, позволяющий раскрыть происхождение психического процесса:
1) Формирующий эксперимент.
2) Лонгитюдный метод.
3) Экспериментально — генетический метод.
4) Комплексный метод.
149Система отношений, в которую ребенок вступает в обществе:
1) Кризис.
2) Ведущая деятельность.
3) Новообразования возраста.
studopedia.net
Возмужание, половая зрелость — МегаЛекции
2. Выберите 1 правильный ответ
Социальная ситуация развития в подростковом возрасте заключается в том, что
Характерно господство детского сообщества над взрослым
3. Выберите 1 правильный ответ
Ведущая деятельность подросткового возраста
Интимно-личностное общение
4. Дополните выражение. Одно многоточие — одно слово Подростковый возраст — возраст «бури и натиска», с точки зрения ученого …Халла
5. Выберите 1 правильный ответ
Ведущий мотив в учебной деятельности подростков
Стремление завоевать определенное положение в классе, добиться признания сверстников
6. Дополните выражение. Одно многоточие — одно слово В выборе друга подросток ориентируется на … качества личностные
7. Выберите 1 правильный ответ
Универсальная психологическая цель в подростковом возрасте
Избавление от родительской опеки
8. Дополните выражение. Одно многоточие — одно слово
Ведущий мотив в учебной деятельности … — это стремление завоевать определенное положение в классе, добиться признания сверстников подростка
9. Выберите 1 правильный ответ Термин «пубертат» означает
Возмужание, половая зрелость
10. Выберите 1 правильный ответ
Для интеллектуальной сферы подростка НЕ характерно
Обратимость мышления
11. Выберите 1 правильный ответ
С точки зрения Ж. Пиаже, в подростковом возрасте интеллект развивается до стадии
Формальных операций
12. Дополните выражение. Одно многоточие — одно слово Ведущая деятельность подросткового возраста интимно-… общение личностное
13. Выберите 1 правильный ответ
Главная характеристика социальной ситуации развития в юношеском возрасте
Необходимость профессионального самоопределения
14. Выберите 1 правильный ответ
Умственная активность в юношеском возрасте приобретает характерную черту
Интерес не столько к фактам, сколько к их анализу, обсуждению и размышлению над ними
15. Выберите 1 правильный ответ
Факторы, способствующие формированию гибкого, творческого стиля мышления в юношеском возрасте
Более сложная и более самостоятельная учебная работа
16. Дополните выражение. Одно многоточие — одно слово Ведущая деятельность в юношеском возрасте — это учебно-…профессиональная
Деятельность
17. Выберите 1 правильный ответ
Одно из важнейших новообразований интеллектуальной сферы в юношеском возрасте
Прогрессирующее развитие теоретического мышления
18. Выберите 1 правильный ответ
В выборе друга старшеклассник руководствуется
Нравственными чертами личности
19. Выберите 1 правильный ответ
Споры в юношеском возрасте об отвлеченных предметах, например о философских проблемах, об устройстве мироздания, связаны с развитием
Абстрактно-логического мышления
20. Дополните выражение. Одно многоточие — одно слово
В основе … дружбы лежит потребность в понимании другого и себя другим, в самораскрытии юношеской
21. Выберите 1 правильный ответ
Одно из проявлений кризиса идентичности
Различные страхи
22. Выберите 1 правильный ответ Аффективный центр жизни в юношеском возрасте
2) Обращенность в будущее, построение жизненных планов и перспектив
23. Выберите 1 правильный ответ
Для мотивационной структуры процесса общения в юношеском возрасте характерно
-f 3) Усиление контактов с лицами противоположного пола
24. Дополните выражение. Одно многоточие — одно слово Один из признаков кризиса … — это желание как можно позднее обрести статус взрослого ,. Идентичности
1. Выберите 1 правильный ответ Чувство взрослости НЕ проявляется в
Персонификации
2. Установите правильное соответствие между видами увлечений в подростковом возрасте и их характеристиками
1) Телесно-мануальные увлечения Б) Связаны с намерением укрепить свою силу, выносливость
2) Накопительские увлечения A) Прежде всего коллекционирование во всех его видах
3) Информативно-коммуникативные увлечения B) Проявляется жажда получения новой, не слишком содержательной информации, не требующей никакой критической переработки
3. Выберите 1 правильный ответ
Основное следствие открытия внутреннего мира в юношеском возрасте НЕ является
Трудности в общении
4. Дополните выражение. Одно многоточие — одно слово «Ключевой проблемой подросткового возраста является проблема интересов», — писал отечественный ученый ….Выготский
5. Выберите 1 правильный ответ
В сфере самосознания подростка происходят следующие изменения
Осознание своих недостатков, повышенный интерес к ним
6. Установите правильное соответствие между видами чувства взрослости в подростковом возрасте и их характеристиками
1) Подражание внешним признакам B) Облику и манерам поведения взрослых, некоторым взрослым привилегиям
2) Равнение на психосексуальные образцы своего пола Б) Связано с активной ориентацией подростков на определенное содержание мужского или женского идеала
3) Интеллектуальная взрослость A) Выражается в стремлении подростка что-то знать и уметь по-настоящему
7. Выберите 1 правильный ответ
Самооценка в юношеском возрасте складывается на основе
Собственного анализа
8. Дополните выражение. Одно многоточие — одно слово Важным фактором «Я-концепции» в … возрасте является повышенная чувствительность к особенностям своего тела и внешности Юношеском
9. Выберите 1 правильный ответ
Становление самооценки подростка происходит под влиянием
Сверстников
10. Установите правильное соответствие между особенностями самосознания в период юности и их характеристиками
1) Самоуважение B) Целостное представление о себе
2) Фактор времени A) Юноша начинает жить будущим
3) Устойчивый образ «Я» Б) Самостоятельность, контактность, открытость, развит мотив достижения и соревновательности
11. Выберите 1 правильный ответ
В сфере самосознания главным достижением юношеского возраста выступает
Открытие своего внутреннего мира
12. Дополните выражение. Одно многоточие — одно слово Стремление к самовоспитанию вызвано у подростков процессом развития …самосознания
13. Выберите 1 правильный ответ
Острота подросткового кризиса зависит
От стратегии поведения взрослого
14. Выберите 1 правильный ответ Дисморфофобия — это
Убежденность в мнимом уродстве
15. Выберите 1 правильный ответ Акцентуации личности подростка — это
1) Крайний вариант нормы
16. Дополните выражение. Одно многоточие — одно слово Кризис … возраста — это неизбежный и необходимый момент развития психики подросткового
17. Выберите 1 правильный ответ
Кризис подросткового возраста можно описать формулой
Я-есть»
18. Выберите 1 правильный ответ Замечание подростку рекомендуется делать
В форме совета наедине
19. Выберите 1 правильный ответ Кризис 17 лет связан с
Рекомендуемые страницы:
Воспользуйтесь поиском по сайту:
megalektsii.ru
Подросток
148. Общепринятые границы подросткового возраста в отечественной психологии:
а)9-13 лет
б) 11-14 лет
в) 10—15 лет
г) 12-14 лет
149. Исследователь, назвавший подростковый возраст возрастом «бури и натиска»:
а) Л. С. Выготский
б) Ж. Пиаже
в) 3. Фрейд
г) С. Холл
150. «Пубертатный период» означает:
а) эмоциональная реактивность
б) возмужание, половая зрелость
в) эмансипация от взрослых
г) индивидуализация
151. Фактор, обусловливающий резкие изменения в психике в начальной стадии подросткового возраста:
а) половое созревание
б) посткризисные проявления предыдущего возраста
в) разрушение старой социальной ситуации развития
г) конфликтные отношения с взрослыми
152. Ученые различают три точки созревания: органического, полового и социального. В подростковом возрасте эти линии развития существуют в следующем соотношении:
а) все линии развития совпадают во времени
б) социальное созревание опережает органическое и половое
в) половое развитие опережает органическое и социальное
г) органическое развитие опережает половое и социальное
153. Для подросткового возраста не характерно:
а) повышенная возбудимость
б) относительная неустойчивость нервной системы
в) быстро протекающие изменения в организме
г) завершение физического развития
154. Характерная черта подросткового возраста:
а) повышенная реактивность
б) повышенная обидчивость
в) покладистость
г) эмоциональная устойчивость
155. Специфика социальной ситуации развития в подростковом возрасте заключается в том, что:
а) подросток стоит на пороге вступления в самостоятельную жизнь
б) возникает необходимость определить свое место в жизни
в) характерно господство детского сообщества над взрослым
г) налаживаются отношения со взрослыми
156. Ведущая деятельность подросткового возраста:
а) интимно-личностное общение
б) учебно-профессиональная
в) учебная
г) общественно-полезная
157. Центральным новообразованием подросткового возраста выступает:
а) готовность к профессиональному и личностному самоопределению
б) эго-идентичность
в) произвольность
г) чувство взрослости
158. Уменьшенная поглощенность учением у подростков вызвана:
а) осложнением отношений с учителями
б) усложнением учебного материала
в) удовлетворением прежних мотивов к учению, и отсутствием новых
г) несформированностью навыков учебной деятельности
159. Основной критерий оценки подростками деятельности педагога:
а) отношение учителя к своей работе
б) личностные качества учителя
в) особенности внешности учителя
г) профессионализм учителя
160. Ведущий мотив в учебной деятельности подростков:
а) значимость самого процесса учения как социальноценной деятельности
б) стремление завоевать положение в классе, добиться признания сверстников
в) получение хорошей оценки
г) стремление к превосходству
161. С точки зрения Ж. Пиаже, в подростковом возрасте интеллект развивается до стадии:
а) сенсорно-моторной
б) конкретных операций
в) формальных операций
г) дооперациональной
162. Существенное влияние на широту и содержание мыслей подростка, как и на его способность к моральным рассуждениям, оказывает развитие:
а) конкретных операций
б) абстрактного мышления
в) наглядного мышления
г) образного мышления
163. Я согласен(а) с утверждением, что:
а) память подростка все больше обогащается и замещается мышлением
б) у подростка развита установка привычка заучивать материал путем повторения
в) у подростков развивается произвольная память
г) подростки начинают осваивать приемы запоминания материала
164. Подростки используют преимущественно:
а) логическую память
б) механическую память
в) непроизвольное запоминание
г) непосредственное запоминание
165. Для восприятия подростка характерно:
а) выраженная эмоциональность
б) развитие логического восприятия
в) малая дифференцированность
г) развитие предметного восприятия
166. В мотивационной структуре общения подростков появляется:
а) ярко выраженная познавательная потребность
б) потребность в принадлежности какой-либо группе
в) потребность в самореализации
г) телесные потребности
167. В выборе друга подросток ориентируется:
а) на успеваемость
б) внешний облик
в) личностные качества
г) поведение
168. Для межличностных отношений в подростковом возрасте не характерно:
а) реакция эмансипации от взрослых
б) реакция группирования со сверстниками
в) снижение конфликтности в общении с взрослыми
г) притупление остроты восприятия сверстников
169. Характерная черта межличностных отношений в подростковом возрасте:
а) сужение круга межличностного взаимодействия
б) исповедальный характер межличностного взаимодействия
в) усиление контактов с лицами противоположного пола
г) реакция группирования со сверстниками
170. Характерная черта подростка:
а) эмоциональная устойчивость
б) покладистость
в) доверчивость
г) реакция эмансипации
171. Чувство взрослости проявляется:
а) в подражании внешним признакам взрослости
б) равнении на психосоциальные образцы своего пола
в) социально-моральном и интеллектуальном взрослении
г) во всем перечисленном
172. В сфере самосознания подростка происходят следующие изменения:
а) открытие внутреннего мира и осознание его уникальности
б) повышенный интерес к своей личности
в) осознание временной перспективы
г) осознание своих недостатков, повышенный интерес к ним
173. Потребность, характерная для подросткового возраста:
а) быть принятым и признанным сверстниками
б) в самовоспитание
в) в заботе о другом
г) в оценочной деятельности
174. Становление самооценки подростка происходит под влиянием:
а) самого подростка
б) родителей
в) учителей
г) сверстников
175. Я согласен с утверждением, что:
а) самооценка подростков — воспроизведение, как правило, оценки взрослыми
б) уровень успеваемости подростка существенно влияет на его самооценку
в) самооценка переориентируется на взаимоотношения и на физические качества
г) подросток в состоянии осознать свою особенность и неповторимость
176. Для эмоциональной сферы подростка характерно:
а) резкая смена настроения и переживаний
б) бурное развитие «эмоционального языка»
в) эмоциональная впечатлительность
г) осознание своего состояния
ЮНОСТЬ
177. Границы юношеского возраста:
а) 13-18 лет
б) 14-17 лет
в) 15-18 лет
г) нет однозначного подхода к выделению границ
178. В анатомо-физиологическом плане юноша характеризуется:
а) в основном завершением физического развития
б) бурным половым созреванием
в) активным физическим ростом организма
г) активным созреванием коры головного мозга
179. Главная характеристика социальной ситуации развития в юношеском возрасте:
а) зрелое отношение к жизни
return false»>ссылка скрыта
б) две системы отношений: с взрослыми и сверстниками
в) необходимость профессионального самоопределения
г) реакция группирования со сверстниками
180. Ведущая деятельность в юношеском возрасте:
а) интимно-личностное общение
б) учебная деятельность
в) предметно-манипулятивная
г) учебно-профессиональная
181. Центральное новообразование юношеского возраста:
а) чувство взрослости
б) профессиональное и жизненное самоопределение
в) становление устойчивого самосознания и стабильного образа Я
г) чувство компетентности
182. Аффективный центр жизни в юношеском возрасте:
а) первая влюбленность
б) обращенность в будущее, построение жизненных планов и перспектив
в) отношения с товарищами
г) отношения с родителями
183. В целом познавательные возможности старших школьников характеризуются (выберите лишнее):
а) активизация умственной деятельности
б) развитие способности к постижению отвлеченного, абстрактного
в) рост произвольности интеллектуальной деятельности
г) осознание собственных интеллектуальных операций и управление ими
184. Умственная активность в юношеском возрасте приобретает характерную черту:
а) интерес к реальным явлениям
б) интерес к анализу фактов, обсуждению и размышлению над ними
в) повышенное внимание к наглядному материалу
г) внутренний план действий
185. В старших классах ведущими мотивами учения становятся:
а) значимость самого процесса учения как социально ценной деятельности
б) стремление старшеклассника добиться признания сверстников
в) осознание своей жизненной перспективы и профессиональных намерений
г) стремление к превосходству
186. Одно из важнейших новообразований интеллектуальной сферы в юношеском возрасте:
а) развитие произвольного внимания
б) развитие синтезирующего восприятия
в) развитие произвольной памяти
г) прогрессирующее развитие теоретического мышления
187. Споры в юношеском возрасте об отвлеченных предметах, например о философских проблемах, об устройстве мироздания, связаны с развитием:
а) общих и специальных способностей
б) абстрактно-логического мышления
в) наглядно-действенного мышления
г) наглядно-образного мышления
188. Я согласен, что в юношеском возрасте:
а) развитие интеллектуальной сферы заканчивается
б) развитие интеллектуальной сферы совпадает с развитием личностной сферы
в) развитие интеллектуальной сферы юношей и девушек не имеет различий
г) развитие интеллекта связано с развитием творческих способностей
189. Факторы, способствующие формированию гибкого, творческого стиля мышления:
а) общение с взрослыми
б) более сложная и более самостоятельная учебная работа
в) непосредственное выполнение заданий учителя
г) дискуссии, споры
190. В выборе друга старшеклассник руководствуется:
а) успеваемостью
б) деловыми качествами
в) личностными качествами
г) нравственными чертами личности
191. В основе юношеской дружбы лежит:
а) потребность в понимании другого и себя другим, в самораскрытии
б) потребность быть в коллективе
в) познавательные потребности
г) потребность в признании
192. Половая роль» — это…
а) это проявление врожденных свойств организма
б) форма поведения, приобретаемая в результате освоения социальных эталонов
в) такого понятия в науке нет, это житейская характеристика различных полов
г) форма поведения, обусловленная принадлежностью к физическому полу
193. Для мотивационной структуры процесса общения в юношеском возрасте характерно:
а) неактуальность отношений с родителями
б) приоритетность отношений со сверстниками
в) потребность в принадлежности какой-либо группе
г) усиление контактов с лицами противоположного пола
194. В сфере самосознания главным достижением юношеского возраста выступает:
а) открытие своего внутреннего мира
б) чувство взрослости
в) осознание своих недостатков
г) чувство одиночества
195. В эмоциональной сфере юношей и девушек формируются:
а) мировоззренческие чувства (прекрасного, трагического, юмора и т.д.)
б) предметные чувства
в) эстетические чувства
г) чувство взрослости
196. Эмоциональные сдвиги, неустойчивость в юношеском возрасте вызваны чаще всего:
а) гормональными процессами
б) физиологическими процессами
в) социальными факторами
г) индивидуально-типологическими особенностями
197. Старшеклассникам свойственно:
а) эмоциональная неустойчивость
б) покладистость
в) доверчивость
г) юношеский максимализм
198. Утверждение, с которым можно согласиться:
а) самооценка юношей воспроизводит оценку, которую они получают от взрослых
б) в юношеском возрасте ребенок переориентируется с оценки на самооценку
в) в юношеском возрасте человек не в состоянии осознать свою неповторимость
г) в юношеском возрасте человек смотрит на себя глазами окружающих
199. Особенность мотивационной сферы в юношеском возрасте:
а) сочетание широких социальных и познавательных мотивов
б) мотив превосходства
в) оценочная мотивация
г) социально-ролевой мотив
200. Термин «эго-идентичность» означает:
а) субъективное чувство принадлежности к группе
б) субъективное чувство непрерывной самотождественности
в) субъективное отношение к миру
г) субъективное отношение к своему «Я»
201. Одно из проявлений кризиса идентичности:
а) прояснение образа «Я»
б) развитие самоуважения
в) открытие внутреннего мира
г) ни одно из них
3-net.ru
Ответ:3
Психология
Ответ:3
Количество просмотров публикации Ответ:3 — 31
| Наименование параметра | Значение |
| Тема статьи: | Ответ:3 |
| Рубрика (тематическая категория) | Психология |
|
117. (60c.) Горизонтальный вид конфликта характеризуется как….. (один ответ)
1) задействованы лица не находящиеся в подчинении друг с другом
2) оппоненты не выходят за рамки этических норм
3) задействованы лица находящиеся в подчинение друг с другом
4) оппоненты выходят за рамки этических норм
Ответ˸1
118. (60c.) Условием возникновения, реализации, видоизменения деятельности выступает…(один ответ)
1) характер
2) ответственность
3) темперамент
4) активность
Ответ˸4
119. (60c.) Социализация — это процесс и результат включения индивидов в …. (один ответ)
1) воспитание
2) деятельность
3) группу
4) социальные отношения
Ответ˸4
121. (61c.) В выборе друга старшеклассник руководствуется˸(один ответ)
1) успеваемостью
2) деловыми качествами
3) личностными качествами
4) нравственными чертами личности
Ответ˸4
122. (61c.) Умственная активность в юношеском возрасте приобретает характерную черту˸(один ответ)
1) интнрес к реальным явлениям
2) интерес не столько к фактам,сколько к их анализу,обсуждению,рассуждению и размышлению над ними
3) повышенное внимание к наклядному материалу
4) внутренний план дейтсвий
Ответ˸2
123. (61c.) Ведущая деятельность в юношеском возрасте˸
(один ответ)
1) интимно-личностное общение
2) учебная деятельность
3) предметно-манипулятивная
4) учебно-профессиональная
Читайте также
— Специфический иммунный ответСпецифический иммунный ответ (приобретенный иммунитет) – это второй этап защитной реакции организма. Его отличительной особенностью является распознавание чужеродного антигена и выработка факторов защиты, направленных специально против него. В реализации… [читать подробнее].
— Реобаза (R)– величина порогового тока, соответствующая импульсам максимальной длительности.Хронаксия (&… [читать подробнее].
— Ответ: 1-нервные узлы,2- нервы,3-легкое,4-сердце,5-кр.сосуды,6-кишка,7-желудок,8-терка.На початку практичного заняття викладач визначає рівень підготовки студентів до заняття за допомогою тестових завдань. Основний етап заняття – самостійна робота студента. Під час самостійної роботи студенти здійснюють курацію вагітних, під час якої мають самостійно… [читать подробнее].
— ВСЛЕДСТВИЕ ОТСУТСТВИЯ СООТВЕТСТВУЮЩЕГО ГРАММАТИЧЕСКОГО ЯВЛЕНИЯ В РУССКОМ ЯЗЫКЕЭтот случай не требует особых объяснений. Если в английском предложении имеется какое-либо грамматическое явление, которое не имеет формального соответствия в русском языке, то, само собой разумеется, в переводе будут использованы какие-то иные средства, т. е. будет иметь… [читать подробнее].
— Получение ответа на вопрос о применении правовой нормыРешение задачи рассмотрим на примере выяснения следующего вопроса: Надо ли вносить записи о работе в трудовую книжку дистанционного работника?
Для решения этой задачи необходимо выполнить следующие операции:
1) Перейти к ст. 312.2 Трудового кодекса РФ.
2) Изучить статью. В… [читать подробнее].
— Нахождение ответа на вопрос с использованием перечня возможных ситуацийРешение задачи рассмотрим на примере выяснения следующего вопроса: Какой порядок подтверждения страхового стажа для назначения пенсии?
Для решения этой задачи необходимо выполнить следующие операции:
1) Перейти к правовому навигатору путём нажатия кнопки Правовой… [читать подробнее].
— И изучить вид соответствующих режимов эволюции.Вариант 10
Для модели (7.31) в фазовой плоскости (Ь, Я) найти границы зон, разделяющих режимы монотонного и колебательного установления стационарной численности популяции изучаемой системы.
Для модели (7.31) в фазовой плоскости (Ь, Я) найти границы зон, разделяющих режим… [читать подробнее].
— Ответ СталинаВ то же время и у Сталина собралось совещание по такому же вопросу и даже в еще более расширенном составе. Конструктор В.Г. Грабин вспоминает: «Кроме членов Государственного Комитета Обороны на совещании присутствовали нарком оборонной промышленности Д. Ф. Устинов и его… [читать подробнее].
— Задание 1. Установите соответствие между понятием и определением.1. В.Ф. Дунаев, В.Л. Шпаков. Н.П. Епифанова, В.Н. Лындин. Экономика предприятий нефтяной и газовой промышленности. Учебник., изд-во «Нефть и газ», 2010, 352с.
2.Андреев А.Ф., Лопатина С.Г., Маккавеев М.В., Победоносцева Н.Н. Основы менеджмента (нефтяная и газовая промышленность ) – Учеб. -… [читать подробнее].
— Эксперимент (II). Серьезность и безответственностьНеобходимость идти на риск актуализируется в идее экспериментирования, которая в то же время переносит принцип сознательного использования имеющихся в распоряжении материалов, противостоящий представлению о бессознательно-органичной обработке их, из сферы науки на… [читать подробнее].
referatwork.ru
§ 2.Условия развития
Как протекает
процесс развития в ранней юности? Часто
юность считают бурной, объединяя ее в
один период с подростковым возрастом.
Поиски смысла жизни, своего места в этом
мире могут стать особенно напряженными.
Возникают новые потребности
интеллектуального и социального порядка,
удовлетворение которых станет возможным
только в будущем, иногда –
внутренние конфликты и трудности в
отношениях с окружающими.
Но не у всех детей
этот период оказывается напряженным.
Наоборот, некоторые старшеклассники
плавно и постепенно продвигаются к
переломному моменту в своей жизни, а
затем относительно легко включаются в
новую систему отношений. Им не свойственны
романтические порывы, обычно ассоциирующиеся
с юностью, их радует спокойный,
упорядоченный уклад жизни. Они больше
интересуются общепринятыми ценностями,
в большей степени ориентируются на
оценку окружающих, опираются на авторитет.
У них, как правило, хорошие отношения с
родителями, а учителям они практически
не доставляют хлопот.
Тем не менее, при
таком благополучном протекании ранней
юности существуют и некоторые минусы
в личностном развитии. Дети менее
самостоятельны, более пассивны, иногда
более поверхностны в своих привязанностях
и увлечениях. Вообще считается, что к
полноценному становлению личности
приводят поиски и сомнения, характерные
для юношеского возраста. Те, кто прошел
через них, обычно в большей мере
независимы, творчески относятся к делу,
обладают более гибким мышлением,
позволяющим принимать самостоятельные
решения в сложных ситуациях,
– по сравнению с теми, у кого процесс
формирования личности проходил в это
время легко.
Встречаются еще
два варианта развития. Это, во-первых,
быстрые, скачкообразные изменения,
которые, благодаря высокому уровню
саморегуляции, хорошо контролируются,
не вызывая резких эмоциональных срывов.
Дети рано определяют свои жизненные
цели и настойчиво стремятся к их
достижению. Однако при высокой
произвольности, самодисциплине у них
слабее развиты рефлексия и эмоциональная
сфера. Еще один вариант связан с особенно
мучительными поисками своего пути.
Такие дети не уверены в себе и себя плохо
понимают. Недостаточное развитие
рефлексии,
164
отсутствие глубокого
самопознания здесь не компенсируется
высокой произвольностью. Дети импульсивны,
непоследовательны в поступках и
отношениях, недостаточно ответственны.
Часто они отвергают ценности родителей,
но вместо этого не в состоянии предложить
ничего своего. Влившись во взрослую
жизнь, они продолжают метаться и долго
остаются неприкаянными.
Динамика развития
в ранней юности зависит от ряда условий.
Прежде всего, это особенности общения
со значимыми людьми, существенно влияющие
на процесс самоопределения. Уже в
переходный от подросткового к юношескому
возрасту период у детей возникает особый
интерес к общению со взрослыми. В старших
классах эта тенденция усиливается.
При благоприятном
стиле отношений в семье после подросткового
возраста – этапа эмансипации
от взрослых – обычно
восстанавливаются эмоциональные
контакты с родителями, причем на более
высоком, сознательном уровне. По данным
многочисленных опросов, проводившихся
в России, старшеклассники больше всего
хотели бы видеть в родителях друзей и
советчиков. Отвечая на вопрос: «Чье
понимание для вас важнее всего, независимо
от того, как фактически понимает вас
этот человек?» – большинство
мальчиков на первое место поставили
родителей. Ответы девочек более
противоречивы, но и для них родительское
понимание крайне важно. При ответе на
вопрос: «С кем бы ты стал советоваться
в сложной житейской ситуации?»
– и мальчики, и девочки поставили
на первое место мать, на втором месте у
мальчиков оказался отец, а у девочек
– друг (подруга). При всем своем
стремлении к самостоятельности дети
нуждаются в жизненном опыте и помощи
старших; семья остается тем местом, где
они чувствуют себя наиболее спокойно
и уверенно.
С родителями
обсуждаются в это время жизненные
перспективы, главным образом,
профессиональные. С отцом уточняются
важнейшие планы на будущее, намечаются
способы достижения поставленных целей
и, кроме того, анализируются трудности,
связанные с учебой. Диапазон вопросов,
обсуждаемых с матерью, шире: он включает,
помимо планов на будущее, удовлетворенность
ситуацией в школе и особенности жизни
в семье. Жизненные планы дети могут
обсуждать и с учителями, и со своими
взрослыми знакомыми, чье мнение для них
важно.
Старшеклассник
относится к близкому взрослому как к
идеалу. В разных людях он ценит разные
их качества, они выступают для него как
эталоны в разных сферах –
в области человеческих отношений,
моральных норм, в разных видах деятельности.
К ним
165
он как бы примеривает
свое идеальное «Я» –
каким он хочет стать и будет во взрослой
жизни. Как показал один из опросов,70%старшеклассников «хотели бы быть такими
людьми, как родители», 10%хотели бы походить на родителей «кое в
чем».
Отношения со
взрослыми, хотя и становятся доверительными,
сохраняют определенную дистанцию.
Содержание такого общения личностно
значимо для детей, но это не интимная
информация. Кроме того, в общении со
взрослыми им не обязательно достигать
глубокого самораскрытия, чувствовать
реальную психологическую близость. Те
мнения и ценности, которые они получают
от взрослых, затем фильтруются, могут
отбираться и проверяться в общении со
сверстниками – общении
«на равных».
Общение со
сверстниками тоже необходимо для
становления самоопределения в ранней
юности, но оно имеет другие функции.
Если к доверительному общению со взрослым
старшеклассник прибегает, в основном,
в проблемных ситуациях, когда он сам
затрудняется принять решение, связанное
с его планами на будущее, то общение с
друзьями остается интимно-личностным,
исповедальным. Он так же, как и в
подростковом возрасте, приобщает другого
к своему внутреннему миру –
к своим чувствам, мыслям, интересам,
увлечениям. С лучшим другом или подругой
обсуждаются случаи наибольших
разочарований, переживаемых в настоящее
время, отношения со сверстниками
– представителями противоположного
пола (помимо вопросов проведения
свободного времени, о чем говорят и с
менее близкими друзьями). Содержание
такого общения – реальная
жизнь, а не жизненные перспективы;
передаваемая другу информация достаточно
секретна. Общение требует взаимопонимания,
внутренней близости, откровенности.
Оно основано на отношении к другому как
к самому себе, в нем раскрывается
собственное реальное «Я». Оно поддерживает
самопринятие, самоуважение.
Юношеская дружба
уникальна, она занимает исключительное
положение в ряду других привязанностей.
Однако потребность в интимности в это
время практически ненасыщаема,
удовлетворить ее крайне трудно. Повышаются
требования к дружбе, усложняются ее
критерии. Юность считается привилегированным
возрастом дружбы, но сами старшеклассники
считают настоящую дружбу редкой. Как
выяснилось при опросе, только
33%мальчиков из выпускных классов
находят, что «настоящая дружба среди
сверстников встречается часто».
Эмоциональная
напряженность дружбы снижается при
появлении любви. Юношеская любовь
предполагает большую степень интимности,
чем дружба, и она как бы включает в себя
дружбу.
166
После наигранных,
как правило, увлечений в подростковом
возрасте (хотя и тогда могут быть очень
серьезные исключения), может появиться
первая настоящая влюбленность.
Старшеклассники,
представляя себе, какими они будут в
близкой уже взрослой жизни, ожидают
прихода глубокого, яркого чувства.
Юношеские мечты о любви отражают, прежде
всего, потребность в эмоциональном
тепле, понимании, душевной близости. В
это время часто не совпадают потребность
в самораскрытии, человеческой близости
и чувственность, связанная с физическим
взрослением. Как пишет И.С. Кон, мальчик
не любит женщину, к которой его влечет,
и его не влечет к женщине, которую он
любит.
Противопоставление
любви как высокого чувства и биологической
сексуальной потребности особенно резко
выражено у мальчиков. Влюбляясь, они в
общем-то верно называют дружбой
зарождающуюся привязанность, и в то же
время испытывают сильный, лишенный
тонкого психологического содержания,
эротизм. Мальчики часто преувеличивают
физические аспекты сексуальности, но
некоторые пытаются от этого отгородиться.
Обычно в таких случаях психологической
защитой служат аскетизм или интеллектуализм.
Вместо того, чтобы научиться контролировать
проявления своей чувственности, они
стремятся их полностью подавить: аскеты
– потому, что чувственность «грязна»,
а интеллектуалы – потому,
что она «неинтересна».
Старшеклассники
так же, как и подростки, бывают склонны
подражать друг другу и самоутверждаться
в глазах сверстников с помощью
действительных или мнимых «побед». Не
только в средних, но и в старших классах
легкие влюбленности напоминают эпидемии:
как только появляется одна пара, тут же
влюбляются все остальные. Причем многие
увлекаются одновременно одной и той же
наиболее популярной в классе девочкой
(или мальчиком).
Способность к
интимной юношеской дружбе и романтической
любви, возникающая в этот период, скажется
в будущей взрослой жизни. Эти наиболее
глубокие отношения определят важные
стороны развития личности, моральное
самоопределение и то, кого и как будет
любить уже взрослый человек.
studfiles.net
КРИТЕРИИ ПРОЯВЛЕНИЯ ФЕНОМЕНА ДРУЖБЫ В ПОДРОСТКОВОМ ВОЗРАСТЕ
В статье рассматривается подростковая дружба, подростки понимают феномен дружбы, а также каким критериям они руководствуются при выборе друзей.
Ключевые слова: подросток, симпатия, дружба.
В статье рассматривается подростковая дружба, как подростки понимают феномен дружбы, а также какими критериями они руководствуются при выборе друзей.
Ключевые слова: подросток, симпатия, дружба.
Постановка проблемы. Подростковый возраст похож на мост между детством и юностью, между незрелостью и зрелостью, по которому каждый должен пройти, прежде чем стать ответственным и творческим взрослым человеком. Эта особенность проявляется в физическом, умственном, нравственном, социальном и духовном развитии личности
Как пишет исследователь психологических проблем подросткового возраста Т. Драгунова, что у подростка, в этом возрасте, возникают новые потребности, интересы, стремления, переживания, требования к взрослым и товарищам, а также формируются ценности, которые больше понятны и близки сверстникам, чем взрослому. Поэтому общение со взрослыми уже не может полностью удовлетворить потребность в общении с товарищами [2].
Ведь под воздействием на личность подростка друзей, товарищей, сверстников и социальной среды происходит его идентификация. Осознанный выбор друзей из многочисленного числа знакомых и становится возможным для подростка благодаря новой форме интеллектуальной деятельности — мышления в понятиях.
Появление обобщенных понятий приводит к формированию в сознании ребенка идеалов и, прежде всего, идеалов дружбы и друга. Согласно этих идеалов подростки пытаются найти себе друзей. Следовательно, для понимания развития личности современного подростка важно исследовать не только особенности развития дружеских отношений детей, но и прояснить особенности проявления подростками феномена дружбы и критерии, по которым они выбирают себе друзей.
Анализ последних исследований и публикаций. С конца 19 века и до сих пор к феномену подростковой дружбы проявляют интерес представители различных психологических отраслей и течений, а именно такие, как:
Г. Андреева, Т. Драгунова, Д. Эльконин, I. Кон, В. Казанская, I. Каирова, А.Мудрик JI. Петровская, В. Роменец, Г. Селиванова, В. Семченко, Н. скотный, I. Страхов, I. Стрелкова, Я. Украинский, В.Фомичоватаинши.
Основная цель работы состоит в выяснении критериев проявления подростками феномена дружбы.
Основной материал и результаты исследования. Для подросткового возраста характерно заметное развитие чувства личной дружбы, настоящей потребности в дружеском общении. «Не представляю себе жизни без дружбы», «Дружба — это лучшее, что может быть у человека», — считают подростки. Мотивы дружбы становятся более глубокими. Дружат уже не только потому, что сидят за одной партой или живут в одном доме, как это часто бывает у младших школьников, а на основе общих интересов, увлечений, совместной деятельности, взаимного уважения и симпатии, доверия и понимания, родственных взглядов и вкусов. Если детям младшего возраста присуща одиночество, то подросток не склонен пассивно ждать, когда придет дружба. Он активно стремится найти близкого товарища, друга, среди своих сверстников, испытывает их в качестве друга. Эльконин и Т. Драгунова говорят о наличии специальной деятельности по поиску друга, носит, по их терминологии, «ориентировочно-потребительский» характер [1]. Дружеские отношения в подростковом возрасте более глубокими, содержательными и устойчивыми, носят эмоционально-напряженный характер. Прекращение дружеских отношений часто воспринимается очень болезненно. «Был хороший друг. Его родителей перевели в другой город, он уехал, и всякий интерес к жизни пропал «,» Моя любимая подруга уехала, и мне ничто не мило «.
Подробно исследовал общительны и дружеские отношения подростков
И. Страхов. Он различает три основные формы взаимоотношений подростков — общительность, общество и дружбу, которые являются важным фактором развития их личности. Общительность предполагает выполнение вместе общих дел, контакты в учебной работе, в трудовой деятельности, в проведении досуга, взаимопомощь различных видов. Все это сопровождается специфической эмоциональной атмосферой общения.
Общество — более сложное явление. Его психологической основой является чувство коллективизма, единство мнений по различным вопросам, атмосфера товарищеского сотрудничества, интеллектуальное общение более широкий и свободный обмен мнениями, суждениями, а также такой эмоциональный фактор как привязанность друг к другу, чувство взаимной симпатии.
По отношению к дружбе общество будет генетически ранней формой взаимоотношений. Дружба более избирательна, более интимно, предусматривает тесное сближение подростков, тесный психологический контакт, доверительность отношений. Дружба подростков основывается на единстве потребностей и интересов, целей и стремлений, общности в понимании различных вопросов. Настоящая дружба подростков носит активно-действенный характер, что проявляется в готовности помочь другу, доброжелательной критике его недостатков.
Общество и дружба широко распространены среди детей разного возраста, но, как отмечает И. Страхов, на стадии подросткового возраста дружба по своей структуре и функциям представляет новый уровень развития этой формы взаимоотношений, служит взаимодополнению и обогащением личности друзей, осознание качеств своей личности , самовоспитания и в результате — нравственному развитию подростков [5].
Потребность подростка реализовать себя в общении со сверстниками возникает потому, что они становятся своеобразным зеркалом, каке отражает сходство и отличие подростка с ними. Сверстники становятся эталоном для подражания, по ним подросток сверяет свои ценности, поскольку последние могут быть такими же, как и в других личностей. Потребность быть принятым средой значимых людей, страх быть отвергнутым являются главными в общении подростка. Чтобы понять сущность подростковой дружбы, обратимся к исследованиям А. Петровского, начатые еще в середине 60-х pp .. XX в. Речь идет о сплоченности людей в процессе выполнения совместной деятельности. Ученый пишет: «В сообществах, объединяющих людей на основе общей, общественно значимой деятельности, взаимоотношения людей опосредуются ее содержанием и ценностями» [4, с. 31]. Внимание привлекает в такой позиции указание на то, что отношения в процессе общения зависят от деятельности, которую выполняют люди.
Для подростков отношения с товарищами-сверстниками — это отношение принципиального равенства, позволяет детям быть равноправными участниками всевозможных дел. Отношение ребенка к сверстникам (особенно к друзьям) строится согласно определенным нормам взрослой «морали равенства», а в основе отношений со взрослыми все же есть «детская мораль» послушания. В результате чего возможны следующие последствия: из-за отношений со сверстниками в подростковом возрасте более полно проявляется так называемое общение-сотрудничество. Отношения со взрослыми становятся менее значимыми для формирования личности подростка и его взрослости; общения со сверстниками приносит подросткам больше духовного удовлетворения, чем со взрослыми. Еще Сухомлинский писал, что уже в 13-14-летних подростков основой дружбы, чаще становятся духовные интересы и потребности, чем увлечение каким-то другим видом труда [6, с. 219] Общение становится субъективно более необходимым и значимым.
В дружбе подросток начинает определять ориентиры, жизненно важные для его поведения, постоянно сравнивая то, что он делает, с тем, что от него ждут другие. Дружба с определенной группой сверстников возникает по разным причинам. Если в значимой группе, с которой общается подросток, ценится сила, выносливость, ловкость и т.д., то он объединяется со сверстниками, у которых эти физические качества. Такая дружба способствует тому, что подросток будет заниматься физическими упражнениями или спортом. Он будет чувствовать себя защищенным. В основе такой дружбы лежит внушение, подросток хочет быть таким же, как другие, поэтому следует манеру поведения и общения. Еще один вариант: подросток тянется к сверстникам, которые ценят его за какое-то качество (разум, коммуникабельность, умение хорошо играть в шахматы или шашки и т. п.). Его лицо становится важной для других, и он чувствует себя нужным. Такая дружба развивает навыки управления, командования. Подросток становится более уверенным и чувствует себя лидером и общения подростков при этом происходит в форме доминирования. Третий вариант подростковой дружбы: оба (или несколько) имеют одинаковый потенциал и становятся лидерами. В такой дружбе взаимодействие подростков принимает форму соревнования или борьбы. Такая дружба становится значимой на долгие годы. Бывает и так, что подростки взаимодействуют, то доминируя над другом, то подчиняясь другому. Очевидно, такая дружба скорее всего может быть убыточной и нести в себе заряд неконструктивности (хулиганства, асоциальности, жестокости и др.). [С, с. 75-79].
Исходя из вышесказанного было проведено анкетирование, под названием «Дружба», в котором приняли участие 350 учащихся 13-15 лет общеобразовательных школ I-III ступеней г. Бердянска, школ Бердянского района и школ Токмакского района Запорожской области. Учеников восьмых классов в анкетировании приняло участие 174 девятых — 186.
Целью данного анкетирования было выяснить как понимают подростки феномен дружбы, а также каким критериям они руководствуются при выборе друзей.
Первым шагом в исследовании проявления аттракции в подростковом возрасте, было выяснение степени понимания детьми феномена дружба. Для этого учащимся 8-х и 9-х классов было предложено ответить на ряд вопросов.
Полнота понимания подростками феномена дружба определялась по ответам на вопрос «Что такое дружба?». Ответы были разделены на три группы по уровню понимания этого понятия.
В первую группу вошли ответы, выражающие полное понимание феномена дружба. Это ответы, которые наиболее верно истолковывают данный феномен, путем раскрытия его характерных признаков, как бескорыстие взаимоотношений между людьми, отношения основаны на доверии, взаимоуважении, искренности, взаимных симпатиях, общих интересах и увлечениях.
Вторая группа включает в себя ответы, неполно раскрывают исследуемый феномен. В данных ответах феномен дружбы рассматривается как одна из ее характерных признаков.
Ответы, в которых не было, по крайней мере, приблизительного определения данного феномена, нами были отнесены к третьей группе с низким уровнем понимания такого психологического явления, как дружба.
Данные об уровнях понимания детьми 13-15 лет феномена дружба приведены в табл. 1.
Из таблицы. 1 четко видно, что показатели групп понимания феномена дружба подростками с возрастом растут. Это объясняется тем, что подростки проходят общепсихологическую развитие, которое проявляется в стремительном взросления подростков и получают те знания, которые помогают им глубже познать феномен дружбы в целом.
Таблица 1
Понимание подростками феномена дружба (в%)
|
Группы понимание подростками феномена дружба
|
Количество учащихся%
|
|
8 класс
|
9 класс
|
|
Полное
|
17,4
|
25,9
|
|
Неполное
|
45,2
|
56,8
|
|
Низкое
|
37,4
|
17,3
|
Кроме этого, полученные результаты ответов подростков указывают на то, что разница между 8-й и 9-классников в группе полного понимания составляет 8,5%, это свидетельствует о том, что, ни восьмиклассники, ни девятиклассники не имеют полного багажа знаний, которые позволили детям полностью разобраться в феномене дружбы и для того чтобы, без труда строить дружеские отношения со сверстниками. Однако следует заметить, что показатели девятиклассников выше, чем у восьмиклассников, это можно объяснить большим опытом в межличностных отношениях подростков со сверстниками.
Хотя результаты ответов группы полного понимания исследуемого феномена, имеют более низкие показатели, относительно других групп. Ответы данной группы дали более точные определения исследуемого явления. Например: «Дружба — это взаимоотношения между людьми, которые понимают и доверяют друг другу» (Александр Б., 8 кл.), «Дружба — это когда два человека общаются между собой, доверяют свои тайны, имеют общие жизненные интересы» (Яна ПИ .
кл.), «Дружба — это когда два человека доверяют друг другу, поддерживают в трудную минуту, имеют общие интересы» (Дмитрий 3.
кл.), «Дружба — это когда человек общается с другим человеком бескорыстно и воспринимает ее такой, какая она есть» (Дарья С., 9 кл.).
Ответы большинства детей отнесены к группе неполного понимания феномена дружба, в 8-х классах это 45,2%, а в 9-х классах — 56,8%. В своих ответах они дружбу ассоциируют с отдельными ее характерными признаками, или вообще с понятием «Друг», например: «Дружба — это взаимоуважение» (Аня В., 8 кл.), «Дружба — это общие интересы» (Сергей К., 9 кл.), «Дружба-это человек, которому ты доверяешь» (Никол a JL, 8 кл.).
Анализ полученных результатов показал, что определение феномена дружбы у определенного процента подростков вызывает трудности. Среди учащихся 8-х классов этот процент составляет 37,4%, что значительно выше чем у 9-х классов — 17,3%. Ответы данных учащихся характеризуются отсутствием, хотя бы элементарного определения этого явления. Например: «Дружба — это дружба» (Алексей P., 8 кл.). Проведя индивидуальные беседы с таким детьми, становится понятным то, что в большинстве они не знают какими словами охарактеризовать этот феномен, но и не большой процент 6,7% опрошенных подростков, еще не имели настоящих дружеских отношений, и именно поэтому не знают, что это такое.
Опираясь на результаты полученных ответов, следующих двух вопросов: «Что тебе нравится в отношениях со сверстниками?», «Что тебе не нравится в отношениях со сверстниками?», нами были определены особенности межличностных отношений подростков. Факторы, влияющие на их формирование мы разделили на две группы.
Первую группу составляют положительные факторы, включающие в себя черты характера, типа поведения, вызывают симпатию. В нашем случае к таким факторам мы отнесли следующие компоненты: общие интересы, общение, понимание, искренность, отзывчивость.
Процентные показатели каждого из компонентов, в зависимости от возрастных особенностей, можно проследить, обратившись к табл. 2.
В подростковом возрасте большое разнообразие общих интересов, они могут быть познавательными, общественными, трудовыми, спортивными, эстетическими, читательскими т.п.. Именно поэтому, из полученных данных видно, что общие интересы занимают ведущее место, среди выделенных нами компонентов группы положительных факторов, вызывающих симпатию.
Относительно большие процентные показатели имеют факторы общения и понимания. Это объясняется тем, что общение является одной из ведущих деятельностей подросткового возраста, а потребность в понимании является одной из важнейших потребностей данного возраста. Кроме этого, данные феномены тесно связаны между собой. А. Леонтьев, Г. Андреева считают, что общение — это сложный многоплановый процесс установления и развития контактов между людьми, который формируется потребностями в совместной деятельности и включающий в себя обмен информацией, выработку единой стратегии взаимодействия, восприятие и понимание другого человека.
Таблица 2
|
Компоненты группы положительных факторов
|
Количество учащихся%
|
|
8 класс
|
9 класс
|
|
Общие интересы
|
36,8
|
37
|
|
Общение
|
27,7
|
28,4
|
|
Понимание
|
20,8
|
21
|
|
Искренность
|
10,9
|
11,1
|
|
Отзывчивость
|
4,7
|
2,5
|
Соотношение группы положительных факторов, вызывающих симпатию (в%)
Значительно ниже показатели получили такие положительные факторы, как искренность и отзывчивость. Искренность является необходимым фактором при формировании симпатии подростков друг к другу. Ведь искренность — один из аспектов честности, правдивости и для детей данного возраста. А отсутствие противоречий между реальными чувствами и намерениями в отношении другого человека и тем, как эти чувства и намерения выражаются словами, является одним из важных факторов искренности в подростковом возрасте. Процентные показатели компонента искренности, относительно небольшие, но как в восьмом (10,9%), так и девяти?? М (11,1%) классах почти одинаковы.
Хотя чуткость и не очень распространенный, по сравнению с другими компонентами, но мы его также учитываем в анализ компонентов, вызывающих симпатию между подростками. Однако следует заметить, что компонент чуткости в девятом классе имеет значительно более низкий процент (2,5%), чем процент (4,7%) в восьмом классе. Это объясняется тем, что с возрастом данная черта характера становится менее важной по сравнению с другими чертами, при возникновении симпатии, ибо ведущей деятельностью в этом возрасте является общение, как способ обмена информацией, а чувства занимают второстепенное место в межличностных отношениях подростков.
Если проанализировать все, указанные выше, показатели, то можно сделать вывод, что для подросткового возраста важным для возникновения симпатия есть общие интересы, общение и понимание, более второстепенное место в них занимают искренность и отзывчивость. Это говорит о том, что в этом возрасте дети еще руководствуются когнитивными стилем поведения. Для этого возраста характерно когнитивный диссонанс, потому что в данном возрасте уже складываются определенные представления и знания по правильному поведения при общении со сверстниками, но вместе с тем еще не достаточно знаний как распознать чьи-то и проявить свои эмоции.
соответствии вторая группа включает в себя негативные факторы — это также определенные черты характера, типы поведения и общения, которые,
наоборот, вызывают антипатию. К данной группе факторов входят следующие компоненты: скрытность, эгоизм, зависть, ложь, сварливость.
Процентные соотношения показателей данных компонентов можно сравнить с помощью табл. С
Таблица С
Соотношение группы негативных факторов, вызывающих антипатию (в%)
|
Компоненты группы негативных факторов
|
Количество учащихся%
|
|
8 класс
|
9 класс
|
|
Скрытность
|
32,3
|
33,8
|
|
Эгоизм
|
25,9
|
26,2
|
|
Зависть
|
19,1
|
19,7
|
|
Ложь
|
13,2
|
13,5
|
|
Конфликтность
|
9,5
|
6,8
|
Из таблицы четко видно, что в группе негативных факторов, первые три места занимают: скрытность, эгоизм и зависть. Все эти факторы характерны для детей подросткового возраста. Скрытность — склонность и желание скрывать информацию о себе. Она бывает личным проявлением замкнутости, интроверсии или может быть связана с корыстными мотивами. В подростковом возрасте, как мы уже это заметили, скрытность не одобряется, потому что скрытные сверстники менее предсказуемы, по сравнению с откровенными. Кроме этого, подростки, строя отношения со сверстниками, раскрываются перед нами, открывают свои тайны и этого они требуют от своих друзей. И именно наличие у ребенка такой черты характера, как скрытность, и является основной причиной появления антипатии к ней. Эгоизм занимает второе место, это объясняется возрастными изменениями, ведь с процессом по взросления появляется подростковый максимализм, одной из составляющих, он является эгоизм.
Зависть — еще один компонент, группы негативных факторов, вызывающих антипатию среди подростков. В подростковом возрасте существует много поводов для зависти, среди которых: умение другого сверстника легко общаться с окружающими и завоевывать симпатию, зависть вызывает и неограниченные возможности проводить свободное время по своему благоволению и т.д.. Причину появления зависти среди подростков можно объяснить словами Д. Ролз, который отмечает, что главным психологическим источником склонности к зависти является отсутствие уверенности в собственной значимости, соединенное с чувством бессилия [7].
Последние два фактора, ложь и конфликтность, имеют несколько более низкие показатели, чем предыдущие факторы. Ко лжи подростки прибегают в общении со сверстниками, чтобы украсить свои качества
возможности и способности, то есть привлечь этим к себе еще больше внимания. Конфликтность также негативным фактором, влияющим на возникновение антипатии. Ведь для этого возраста конфликтность является характерным, ибо с помощью нее они, во-первых, что защищают себя от окружающих, а во-вторых, она является одним из способов проявления подростковой поведения.
Итак, подытоживая, следует отметить, что среди факторов, которые не вызывают у подростков симпатию, первые места занимают те качества, которые не удовлетворяют определенные подростковые потребности. А последние места — те качества, которые также не соответствуют подростковым требованиям в отношении их симпатий, однако они являются очень распространенными в поведении самих подростков.
Выводы из данного исследования. Как вывод, отметим, что результаты анкетирования подтверждают тот факт, что дети в подростковом возрасте, еще недостаточно понимают феномен дружбы. И те критерии, по которым они выбирают друзей, вполне соответствуют их возрастным потребностям.
Перспективы дальнейшей нашей работы заключаются в исследовании мотивов развития симпатий и дружбы в подростковом возрасте; факторов, вызывающих абстракцию среди подростков и понимание подростками отношение к самому себе и к своему другу.
Список литературы
Возрастные и индивидуальные особенности младших подростков /Под ред. Д.Б. Эльконина, Т.В. Драгуновой. — М., 1967. — 360 с.
Драгунова Т.В. Подросток. — М.: Знание, 1976. — 96 с.
Казанская В.??. Подросток. Трудности взросления. — СПб.: Питер, 2006. — С. 75-79.
Петровский А.В. Личность, деятельность, коллектив. — М.гПолитиздат, 1982. — С. 31.
Страхов И. В. Психологические типы дружбы подростков //Вопросы психологической типологии. — Саратовский государственный педагогический институт, 1971. -22 С.
Сухомлинский В.А. Рождение гражданина. — М.: Молодая гвардия, 1971. — 219 с.
Ролз Дж. Теория справедливости. — Новосибирск: Издательство Новосибирского университета, 1995. — 535 с.
The article deals with teenage friends, as teenagers understand the phenomenon of friendship, as well as what criteria they are guided in choosing friends.
Key words: adolescent, sympathy, friendship.
Пошук по ключовим словам схожих робіт: |
www.info-library.com.ua
Психологические особенности общения у старшеклассников
Ранняя юность — это время дальнейшего укрепления воли, развития таких черт волевой активности, как целеустремленность, настойчивость, инициативность. В этом возрасте укрепляется выдержка и самообладание, усиливается контроль за движением и жестами, в силу чего старшеклассники и внешне становятся более подтянутыми, чем подростки.
Таким образом, к достижению данного возраста школьник достигает физической зрелости, должен приобретать духовную зрелость, быть готовым к самостоятельной жизни. Ведущим видом деятельности является учебно-профессиональная. Выбор профессии становится центром социальной ситуации развития старшеклассника. Выбор профессии формируется под влиянием родителей, сверстников, запросов общества, престижа. В 10-11 классе стоит проблема профессионального самоопределения, подготовки к экзаменам. Происходят изменения в развитии личности, изменение положения ученика в школе, в системе общественных отношений. Старшеклассник старается воспитать в себе качества личности. «Чувство взрослости» переходит в чувство самоуверенности и самоуважения, проявляющееся в своей самоиндивидуальности.
В этот период жизни складывается «образ Я», который включает 3 основных компонента: познавательный, эмоциональный, поведенческий. Образ я складывается в процессе общения, и в первую очередь общения со сверстниками. Из основных новообразований старшего школьного возраста можно выделить – мировоззрение, самостоятельность суждений, формирование собственной самооценки, стремление к самовоспитанию, индивидуальный стиль учебно-профессиональной деятельности, профессиональное и личностное самоопределение.
С возрастом неуклонно усиливается потребность в общении со сверстниками.
Общение – это канал информации, по которому юноша узнает многие необходимые вещи, вырабатываются необходимые навыки социального взаимодействия, умение подчиняться коллективной дисциплине и в то же время отстаивать свои права. Формируются коммуникативные качества. И, наконец, общение – это специфический вид эмоциональных контактов. Осознание групповой принадлежности формирует у молодежи чувство эмоционального благополучия и устойчивости[4]
.
Для старшеклассников характерно эмоционально-личностное отношение к коллективу. Особенно большое значение придается его сплоченности, причем требование это бывает максималистским.
С возрастом межличностные отношения дифференцируются. С одной стороны, быстро расширяется круг общения, растет число внеклассных и внешкольных друзей, с другой – происходит заметное разделение общения в самом классном коллективе.
В юношеском возрасте очень велика потребность в свободном общении. Свободное общение не просто способ проведения досуга, но средство самовыражения личности, установления новых контактов, новых знакомств.
Структура групп общения и степень их сплоченности во многом зависит от уровня развития взаимоотношений между юношами и девушками. Первичными ячейками общения являются однополые группы мальчиков и девочек. Две такие группы, не теряя своей внутренней общности постепенно могут образовывать смешанную компанию. Позже внутри этой компании складываются пары из юношей и девушек.
В жизни мужчин однополая группа занимает гораздо больше, чем в жизни женщины. Привязанность к ней сохраняется и поддерживается даже после возникновения смешанной компании. Оценку мужских качеств личности юноши дает коллектив сверстников.
Разные виды общения могут сосуществовать, выполняя разные функции. Однако их удельный вес и значимость с возрастом меняются. Разные формы и места общения, сменяя друг друга, сосуществуют в зависимости от психологических потребностей.
Юноша всегда ждет новых знакомств, приключений, переживаний – «ожидаемые общения». Неосознаваемое, внутреннее беспокойство иногда гонит его из дома. Он стремится туда, где люди, ожидает чего-то нового, неожиданного. Но часто эти ожидания не сбываются. И тем не менее он опять стремится к людям.
Наряду с возрастающей значимостью групповой жизни, в ранней юности резко усиливается потребность в индивидуальной интимной дружбе. Самое важное в юношеской дружбе – ее глубина, устойчивость и интимность. Психологическая ценность юношеской дружбы в том, что она является школой самораскрытия и понимания другого человека.
От друга старшеклассник ждет оценок, не только близких к своим, но и превышающих их, более критических. Это значит, что дружба выполняет специальную функцию поддержания самоуважения личности.
Однако в дружбе старшеклассников отчетливо проявляются и противоречия этого возраста. Юность одновременно самая искренняя и самая неискренняя пора. В юности сильна потребность быть в согласии с самим собой, бескомпромиссность, полное самораскрытие. Но собственное «Я» — неустойчивое и расплывчатое, что порождает желание проверить себя путем разыгрывания ролей, самоотрицания.
Прежде всего, дружба является эмоциональной привязанностью. Личная близость в этот период важнее, чем общность предметных интересов. Дружба важна для старшеклассников, потому что в общении с друзьями они встречают поощрение самостоятельности и взрослости[5]
.
Подлинная интимность наблюдается при совмещении жизненных целей двух индивидов и сохранении индивидуальности. Если этого нет, то в отношениях с друзьями существует напряженность. Юноша мечется между желанием активно общаться с другом и боится потерять себя в этом общении.
Юношеский эгоцентризм сужает общение, когда друзья, находясь рядом, не слышат друг друга. Потребность в самовыражении часто перевешивает интерес к собеседнику.
Психология юношеской дружбы тесно связана с особенностями личности. Ранее созревание девушек способствует раннему появлению сложных форм самосознания, а следовательно, и потребности в интимной дружбе. Потребность в глубокой интимной дружбе возникает у девушек на 1,5 – 2 года раньше, чем у юношей. Девушки чаще испытывают дефицит интимности, их дружба более эмоциональна. Для юношей важнейшей референтной группой еще остаются сверстники своего пола. Разнополая дружба в юности существенно отличается от однополой. В слове «друг», как правило, завуалирована зарождающаяся любовь. Глубокая индивидуальная привязанность не только предвосхищает любовь, но отчасти включает ее[6]
.
Юношеская мечта о любви выражает, прежде всего, жажду эмоционального контакта, понимания, душевной близости и много позже сексуальной близости.
Одна из главных особенностей раннего юношеского возраста – смена значимых лиц и перестройка отношений со взрослыми.
Важность для юноши его общения со сверстниками нередко скрывает, отодвигает на дальний план проблемы его взаимоотношений с взрослыми, прежде всего с родителями и педагогами. Что же в сегодняшней социальной ситуации развития старшеклассника порождает те проблемы, с которыми приходится сталкиваться родителям и учителям?
Один из источников этих проблем – непонимание взрослыми внутреннего мира старшего школьника, их ложные или примитивные представления об их переживаниях, мотивах тех или иных поступков, стремлениях, ценностях и т.п. Взрослые явно недооценивают значение сферы общения со сверстниками для ребят этого возраста. Чем старше становится подросток, тем меньше понимания он находит у взрослых. Представления родителей и учителей о субъективном мире подростка и старшего школьника становятся все более непохожими на реальности этого мира[7]
.
В то время как для ребят переживания по поводу общения со сверстниками оказывается наиболее значимыми, наиболее типичными, родители и учителя полагают, что в центре переживаний подростков и старшеклассников оказываются переживания по поводу общения с родителями.
Неудовлетворенность потребностей юношей и девушек в общении с близкими при высокой выраженности этой потребности заставляет задуматься над тем, что же практически означает «доверительность» в реальном взаимодействии взрослых и старшеклассников. Тут приходится признать, что роль взрослых рассматривается в возрастной психологии преимущественно в одном ракурсе – как проводник знаний – и в этом своем значении почти не меняется со сменой возрастов ребенка. Между тем, при первой попытке взглянуть на нее, не отрываясь от почвы совместной жизнедеятельности взрослого и ребенка, их событие становится очевидным, что по мере того как в ходе роста школьника меняются формы и самая мера его активности, должна меняться и роль взрослого. Для старших школьников невыносимо принуждение, вмешательство в их дела извне, но это не значит, что они не будут благодарны за тактичную помощь. Доверие взрослых к развитию личности школьников, вера в его потенциальное «я» – лучшее условие доверительности в общении с ним.
Невнимание к новым особенностям и стремлениям старшего школьника опасно. Нельзя упускать время. Взаимное непонимание может превратиться в явление необратимое. Благополучие в личных отношениях родителей и детей, контакт и понимание между ними совершенно необходимо.
Наилучшие взаимоотношения старшеклассников с родителями складываются обычно тогда, когда родители придерживаются демократического стиля воспитания. Этот стиль наиболее способствует воспитанию самостоятельности, активности, инициативы и социальной ответственности. Поведение ребенка направляется в этом случае последовательно и вместе с тем гибко и рационально:
— родитель всегда объясняет мотивы своих требований и поощряет их обсуждение:
— власть используется лишь в меру необходимости;
mirznanii.com

 Адрес для вставки QR-кода числа 1, размер 500×500:
Адрес для вставки QR-кода числа 1, размер 500×500:







































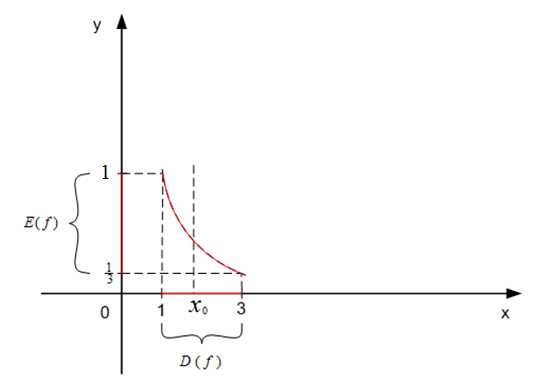
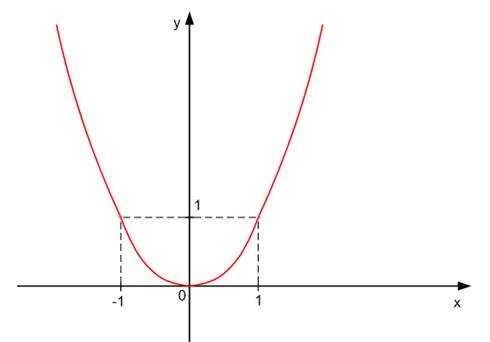
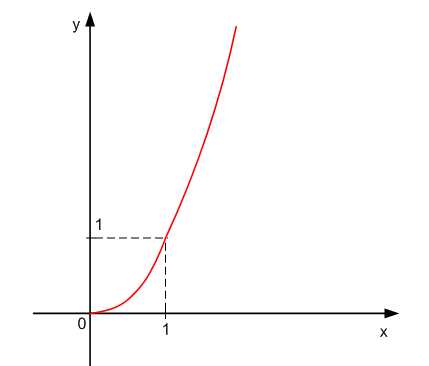
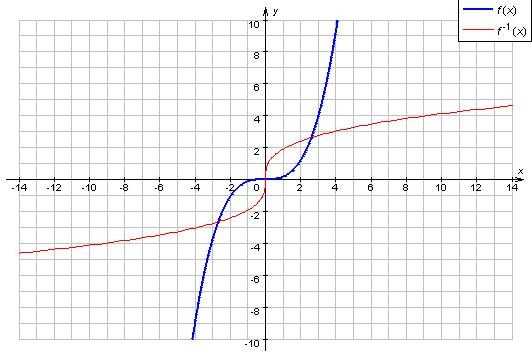
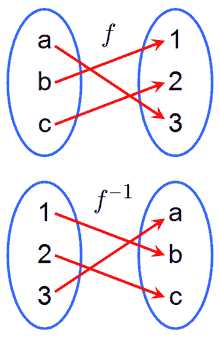 Функция f {\displaystyle f} и обратная ей функция f − 1 {\displaystyle f^{-1}} . Если f ( a ) = 3 {\displaystyle f(a)=3} , то f − 1 ( 3 ) = a {\displaystyle f^{-1}(3)=a}
Функция f {\displaystyle f} и обратная ей функция f − 1 {\displaystyle f^{-1}} . Если f ( a ) = 3 {\displaystyle f(a)=3} , то f − 1 ( 3 ) = a {\displaystyle f^{-1}(3)=a}