Автор: 
Способы нахождения обратной матрицы
Пусть дана квадратная матрица . Требуется найти обратную матрицу.
Первый способ. В теореме 4.1 существования и единственности обратной матрицы указан один из способов ее нахождения.
1. Вычислить определитель данной матрицы. Если, то обратной матрицы не существует (матрицавырожденная).
2. Составить матрицу из алгебраических дополненийэлементов матрицы.
3. Транспонируя матрицу , получить присоединенную матрицу.
4. Найти обратную матрицу (4.1), разделив все элементы присоединенной матрицы на определитель
Второй способ. Для нахождения обратной матрицы можно использовать элементарные преобразования.
1. Составить блочную матрицу , приписав к данной матрицеединичную матрицу того же порядка.
2. При
помощи элементарных преобразований,
выполняемых над строками матрицы ,
привести ее левый блокк
простейшему виду.
При этом блочная матрица приводится к
виду,
где—
квадратная матрица, полученная в
результате преобразований из единичной
матрицы.
3. Если , то блокравен обратной матрице, т.е.. Если, то матрицане имеет обратной.
В самом деле, при помощи элементарных преобразований строк матрицы можно привести ее левый блокк упрощенному виду(см. рис. 1.5). При этом блочная матрицапреобразуется к виду, где— элементарная матрица, удовлетворяющая равенству. Если матрицаневырожденная, то согласно п.2 замечаний 3.3 ее упрощенный вид совпадает с единичной матрицей. Тогда из равенстваследует, что. Если же матрицавырожденная, то ее упрощенный видотличается от единичной матрицы, а матрицане имеет обратной.
11.Матричные уравнения и их решение. Матричная форма записи СЛАУ. Матричный способ (метод обратной матрицы) решения СЛАУ и условия его применимости.
Матричными
уравнениями называются уравнения вида
:
A*X=C;
X*A=C;
A*X*B=C
где матрица А,В,С известны ,матрица Х
не известна, если матрицы А и В не
вырождены, то решения исходных матриц
запишется в соответственном виде :
Х=А-1 *С; Х=С*А-1;
Х=А-1*С*В-1Матричная
форма записи систем линейных алгебраических
уравнений.
С
каждой СЛАУ можно связать несколько
матриц; более того – саму СЛАУ можно
записать в виде матричного уравнения.
Для СЛАУ (1) рассмотрим такие матрицы:
Матрица A называется матрицей системы. Элементы данной матрицы представляют собой коэффициенты заданной СЛАУ.
Матрица A˜ называется расширенной матрицей системы. Её получают добавлением к матрице системы столбца, содержащего свободные члены b1,b2,…,bm. Обычно этот столбец отделяют вертикальной чертой, – для наглядности.
Матрица-столбец B называется матрицей свободных членов, а матрица-столбец X – матрицей неизвестных.
Используя введённые выше обозначения, СЛАУ (1) можно записать в форме матричного уравнения: A⋅X=B.
Примечание
Матрицы,
связанные с системой, можно записать
различными способами: всё зависит от
порядка следования переменных и уравнений
рассматриваемой СЛАУ.
Но в любом случае
порядок следования неизвестных в каждом
уравнении заданной СЛАУ должен быть
одинаков .
Матричный метод подходит для решения СЛАУ, в которых количество уравнений совпадает с числом неизвестных переменных и определитель основной матрицы системы отличен от нуля. Если система содержит больше трех уравнений, то нахождение обратной матрицы требует значительных вычислительных усилий, поэтому, в этом случае целесообразно использовать для решения метод Гаусса.
12.Однородные СЛАУ, условия существования их ненулевых решений. Свойства частных решений однородных СЛАУ.
Линейное уравнение называется однородным, если его свободный член равен нулю, и неоднородным в противном случае. Система, состоящая из однородных уравнений, называется однородной и имеет общий вид:
13.Понятие
линейной независимости и зависимости
частных решений однородной СЛАУ.
Фундаментальная система решений (ФСР)
и её нахождение. Представление общего
решения однородной СЛАУ через ФСР.
Система
функций y1(x), y2(x),
…, yn(x) называется линейно
зависимой на
интервале (a, b), если
существует набор постоянных коэффициентов ,
не равных нулю одновременно, таких, что
линейная комбинация этих функций
тождественно равна нулю
на (a, b): для .
Если
равенство для возможно
только при ,
система функций y1(x), y2(x),
…, yn(x) называется линейно
независимой на
интервале (a, b).
Другими
словами, функции y1(x), y2(x),
…, yn(x) линейно
зависимы на
интервале (a, b),
если существует равная нулю на (a, b) их
нетривиальная линейная комбинация.
Функции y1(x),y2(x),
…, yn(x) линейно
независимы на
интервале (a, b),
если только тривиальная их линейная
комбинация тождественно равна нулю
на (a, b).
Фундаментальной системой решений (ФСР) однородной СЛАУ называется базис этой системы столбцов.
Количество элементов в ФСР равно количеству неизвестных системы минус ранг матрицы системы. Любое решение исходной системы есть линейная комбинация решений ФСР.
Теорема
Общее решение неоднородной СЛАУ равно сумме частного решения неоднородной СЛАУ и общего решения соответствующей однородной СЛАУ.
1. Если столбцы — решения однородной системы уравнений, то любая их линейная комбинациятакже является решением однородной системы.
В самом деле, из равенств следует, что
т.
е.
линейная комбинация решений является
решением однородной системы.
2. Если ранг матрицы однородной системы равен , то система имеетлинейно независимых решений.
Действительно, по формулам (5.13) общего решения однородной системы найдем частных решений, придавая свободным переменным следующиестандартные наборы значений (всякий раз полагая, что одна из свободных переменных равна единице, а остальные — равны нулю):
которые линейно независимы. В самом деле, если из этих столбцов составить матрицу, то последние ее строк образуют единичную матрицу. Следовательно, минор, расположенный в последнихстроках не равен нулю (он равен единице), т.е. является базисным. Поэтому ранг матрицы будет равен. Значит, все столбцы этой матрицы линейно независимы (см. теорему 3.4).
Любая совокупность линейно независимых решенийоднородной системы называетсяфундаментальной системой (совокупностью) решений.
14 Минор
-ого
порядка, базисный минор, ранг матрицы.
Вычисление ранга матрицы.
Минором порядка k матрицы А называется детерминант некоторой ее квадратной подматрицы порядка k.
В матрице А размеров m x n минор порядка r называется базисным, если он отличен от нуля, а все миноры большего порядка, если они существуют, равны нулю.
Столбцы и строки матрицы А, на пересечении которых стоит базисный минор, называются базисными столбцами и строками А.
Теорема 1. (О ранге матрицы). У любой матрицы минорный ранг равен строчному рангу и равен столбцовому рангу.
Теорема 2.(О базисном миноре). Каждый столбец матрицы раскладывается в линейную комбинацию ее базисных столбцов.
Рангом матрицы (или минорным рангом) называется порядок базисного минора или, иначе, самый большой порядок, для которого существуют отличные от нуля миноры. Ранг нулевой матрицы по определению считают 0.
Отметим два очевидных свойства минорного ранга.
1)
Ранг матрицы не меняется при
транспонировании, так как при
транспонировании матрицы все ее
подматрицы транспонируются и миноры
не меняются.
2) Если А’-подматрица матрицы А, то ранг А’ не превосходит ранга А, так как ненулевой минор, входящий в А’, входит и в А.
15.Понятие -мерного арифметического вектора. Равенство векторов. Действия над векторами (сложение, вычитание, умножение на число, умножение на матрицу). Линейная комбинация векторов.
Упорядоченная совокупность n действительных или комплексных чисел называется n-мерным вектором. Числа называются координатами вектора.
Два (ненулевых) вектора a и b равны, если они равнонаправлены и имеют один и тот же модуль. Все нулевые векторы считаются равными. Во всех остальных случаях векторы не равны.
Сложение векторов. Для сложения векторов есть два способа.1. Правило параллелограмма. Чтобы сложить векторы и, помещаем начала обоих в одну точку. Достраиваем до параллелограмма и из той же точки проводим диагональ параллелограмма. Это и будет сумма векторови.
2.
Второй способ сложения векторов —
правило треугольника.
Возьмем те же
векторы и .
К концу первого вектора пристроим
начало второго. Теперь соединим начало
первого и конец второго. Это и есть
сумма векторов и .
По тому же
правилу можно сложить и несколько
векторов. Пристраиваем их один
за другим, а затем соединяем начало
первого с концом последнего.
Вычитание векторов. Вектор направлен противоположно вектору. Длины векторовиравны. Теперь понятно, что такое вычитание векторов. Разность векторов и — это сумма вектора и вектора .
Умножение вектора на число
При умножении вектора на число k получается вектор, длина которого в k раз отличается от длины. Он сонаправлен с вектором, если k больше нуля, и направлен противоположно, если k меньше нуля.
Скалярным произведением векторов называется произведение длин векторов на косинус угла между ними. Если векторы перпендикулярны, их скалярное произведение равно нулю. А вот так скалярное произведение выражается через координаты векторов и .
Линейная комбинация векторов
Линейной комбинацией векторов называют вектор
где —
коэффициенты линейной комбинации.
Если комбинация
называется тривиальной, если —
нетривиальной.
16.Скалярное произведение арифметических векторов. Длина вектора и угол между векторами. Понятие ортогональности векторов.
Скалярным произведением векторов а и в называется число,
Скалярное произведение используется для вычисления:1)нахождения угла между ними;2)нахождение проекции векторов;3)вычисление длины вектора;4)условия перпендикулярности векторов.
Длиной отрезка АВ называют расстоянием между точками А иВ. Угол между векторами А и В называют угол α=(а,в) ,0≤ α ≤П. На который необходимо повернуть 1 вектор,чтоб его направления совпало с другим вектором. При условии,что их начала совпадут.
Ортом а называется вектор а имеющий единичную длину и направления а.
17.Система
векторов и её линейная комбинация.
Понятие линейной зависимости и
независимости системы векторов. Теорема
о необходимом и достаточном условиях
линейной зависимости системы векторов.
Система векторов a1,a2,…,an называется линейно зависимой, если существуют числа λ1,λ2,…,λnтакие, что хотя бы одно из них отлично от нуля и λ1a1+λ2a2+…+λnan=0. В противном случае система называется линейно независимой.
Два вектора a1 и a2 называются коллинеарными если их направления совпадают или противоположны.
Три вектора a1,a2 и a3 называются компланарными если они параллельны некоторой плоскости.
Геометрические критерии линейной зависимости:
а) система {a1,a2} линейно зависима в том и только том случае, когда векторы a1 и a2 коллинеарны.
б) система {a1,a2,a3} линейно зависима в том и только том случае, когда векторы a1,a2 и a3компланарны.
теорема. (Необходимое и достаточное условие линейной зависимости системы векторов.)
Система
векторов векторного пространства является линейно зависимой
тогда и только тогда, когда один из
векторов системы линейно выражается
через другие вектора этой
системы.
Следствие.1. Система векторов векторного пространства является линейно независимой тогда и только тогда, когда ни один из векторов системы линейно не выражается через другие вектора этой системы.2. Система векторов, содержащая нулевой вектор или два равных вектора, является линейно зависимой.
Домашнее задание по теме «Матрица»
ФИНАНСЫЛекция 1
Раздел 1. Основы линейной алгебры
Тема 1.1. Матрицы и операции над матрицами. Определители и их свойства
Цель:приобретение базовых знаний в области фундаментального раздела математики – линейной алгебры. Изучить понятие матрицы, её видов, операции над матрицами, определителей и их свойств.
Задачи:
• развитие творческого профессионального мышления;
• познавательная мотивация;
• овладение языком науки, навыки оперирования понятиями;
• овладение умениями и навыками постановки и решения задач;
• углубление теоретической и практической подготовки;
• развитие инициативы и самостоятельности студентов.
Вид занятия: Комбинированное занятие, включающее в себя ознакомление с новым материалом, применение знаний и умений на практике, закрепление изученного.
Ход занятия.
1.Формулирование темы занятия, пояснение связи темы с другими темами учебной дисциплины;
2.Проверка готовности студентов к занятию;
3.Проведение непосредственно занятия согласно тематике и в соответствии с рабочей программой дисциплины:
Изучить теоретический материал по теме «Матрицы. Выполнение операций над матрицами. Определители и их свойства».
Рассмотреть примеры решения типовых заданий.
Ответить на контрольные вопросы.
Организационный момент.
Приветствует обучающихся. Проверяет подготовленность к учебному занятию, организует внимание обучающихся. Обеспечивает благоприятный настрой.
Создание проблемной ситуации при постановке темы, цели и задач лекции.
В школьном курсе алгебры 7 – 9 классов рассматриваются различные способы решения систем линейных уравнений: метод подстановки, метод сложения, метод двойного сложения, графический метод, метод сравнения.
Возникает вопрос, а существуют ли какие-либо другие способы решения данных систем. Действительно, кроме методов, изучаемых в школе, существуют и другие, доступные для учащихся старших классов методы решения систем линейных уравнений: метод Крамера, метод Гаусса, матричный метод. Эти методы способствуют развитию внимания, памяти. При применении этих методов встречаются новые понятия: «матрица», «определитель», «минор», «дополнение». Возникает необходимость уметь вычислять определители, миноры, дополнения.
При решении систем линейных уравнений методом Гаусса также нужно уметь выполнять преобразования над строками матриц.
Что же такое матрица, какие действия с ними можно выполнять?
Изучение нового материала.
Определение матрицы.
Совокупность чисел, расположенных в виде прямоугольной таблицы, состоящей из строк и столбцов, называют матрицей порядка ( на ) и обозначают символом . В общем виде матрица выглядит так
.
Числа называют элементами матрицы.
Каждый элемент имеет два индекса: первый показывает номер строки, в которой стоит этот элемент, а второй – номер столбца. Размерность матрицы указывать не обязательно. При матрицу называют матрицей-строкой, а при — матрицей-столбцом.
Матрицу, все элементы которой, равны нулю, называют нулевой матрицей и обычно обозначают .
Таким образом, .
Если число строк матрицы совпадает с числом ее столбцов, т.е. , то матрицу называют квадратной порядка и обозначают символом . В квадратной матрице элементы с одинаковыми индексами называют элементами главной диагонали, а элементы, сумма индексов которых равна , элементами побочной диагонали. Во множестве квадратных матриц особую роль играет матрица
.
Ее называют единичной матрицей. Все элементы ее главной диагонали равны единице, а все остальные элементы – нули.
Квадратную матрицу называют треугольной, если все ее элементы, стоящие ниже или выше элементов главной диагонали, равны нулю.
Например, матрицы и треугольные, причем матрицу называют верхнетреугольной, а матрицу – нижнетреугольной.
Определение. Две матрицы одинакового порядка и называют
равными и пишут = , если все элементы с одинаковыми
индексами обеих матриц совпадают.
Матрицей размером тп называется прямоугольная таблица, составленная из тп чисел и имеющая т строк и п столбцов. Числа ij, составляющие матрицу, называютсяэлементами матрицы. Каждый элемент матрицы снабжен двумя индексами: первый индекс указывает номер строки, второй – номер столбца, в котором расположен этот элемент.
Для изображения матрицы употребляют круглые скобки и часто обозначают ее одной буквой, например,
А=(ij)= (1)
Первый индекс i (i = 1, 2, …m) обозначает номер строки, второй j(j = 1, 2, …n) – столбец матрицы.
Матрицу принято обозначать заглавными буквами, напримерА, В, С и т.д.
Горизонтальный ряд чисел называетсястрокой, а вертикальный –столбцом.
Определение. Если т = п, то матрица называется квадратной матрицей порядка n. Число ее строк или столбцов называетсяпорядком матрицы.
Определение. Если же m n, то матрица называется прямоугольной матрицей.
Определение. Две матрицы считаютсяравными, если они имеют одинаковые размеры и их соответствующие элементы равны. Пусть А = (ij) размером т п, В = (ij)размером pq.A = B, если m = p, n = q и ij = ijдляi = 1, 2, …,m, j = 1, 2, …, n.
Определение. Последовательность элементов квадратной матрицы с одинаковыми индексами (i = j)называется главной диагональю матрицы (11,22, 33,…,nn)/
Определение.
Если в квадратной матрице все недиагональные элементы равны нулю (ij= 0, при i = j), то матрица называется диагональной.
А =
Определение. Квадратная диагональная матрица, у которой элементы главной диагонали равны единице, называетсяединичной матрицей Е.
А =
Определение. Матрица, все элементы которой равны нулю, называетсянуль-матрицей.
Определение. Матрица, состоящая только из одной строки, называетсяматрицей-строкой.
Определение. Матрица, состоящая только из одного столбца, называетсяматрицей-столбцом.
Определение. Матрицу Аt называют транспонированнойпо отношению к матрице А ,если она получена из матрицы А заменой строк этой матрицы её столбцами, и, наоборот, столбцов строками.
Например, пусть А — матрица размеровт п:
транспонированная ей матрица:
Можно сказать, что транспонированная матрица получается переворачиванием матрицы вокруг главной диагонали.
Переход от матрицы А к матрице Аt называют операцией транспонирования.
Перечислим свойства операции транспонирования:
(At)t = A,
(A + B)t = At + Bt,
(A)t = At,
(AB)t = BtAt.
2. Операции над матрицами.
Определение. Суммой двух матрицА = (ij) и В = (ij) одинаковых размеров т п называется матрица С того же размера, элементы которых равны сумме соответствующих элементов матриц А и В. С=А + В = (ij + ij) дляi = 1, 2, …, m,j = 1, 2, …, n.
Ясно, что сложение матриц сводится к сложению всех пар соответствующих элементов. Для матриц разных размеров сумма не определена.
Сложение матриц подчиняется законам:
А + В = В + А (переместительный закон)
(А + В) + С = А + (В + С) (сочетательный закон)
А + О = О + А = А.
Для любой матрицы А размеров т п существует матрица В тех же размеров такая, что А + В = В + А = О. При этом если А = (ij) и В = (ij), то ij = — ij. Матрица В называется матрицей,противоположной матрице А и обозначается – А.
Определение. Произведением матрицы А = (ij) размером т п на число называется матрица (ij) тех же размеров, которая обозначаетсяА.
Свойства умножения матрицы на число:
1. (А) = ()А.
( + )А = А + А.
(А + В) = А + В.
1А = А.
Разность двух матриц А иВодинаковых размеров определяется равенствами:
А – В = А + (- В) = А + (-1)В.
Определение. Произведением матрицы А = (ij) размеров т п на матрицу В = (ij) размеров nk называется матрица С = (сij) размеров mk, каждый элемент сij которой вычисляется по формуле
сij = i11j + i22j + … + innj, i = 1,2,…,m; j = 1,2,…,n.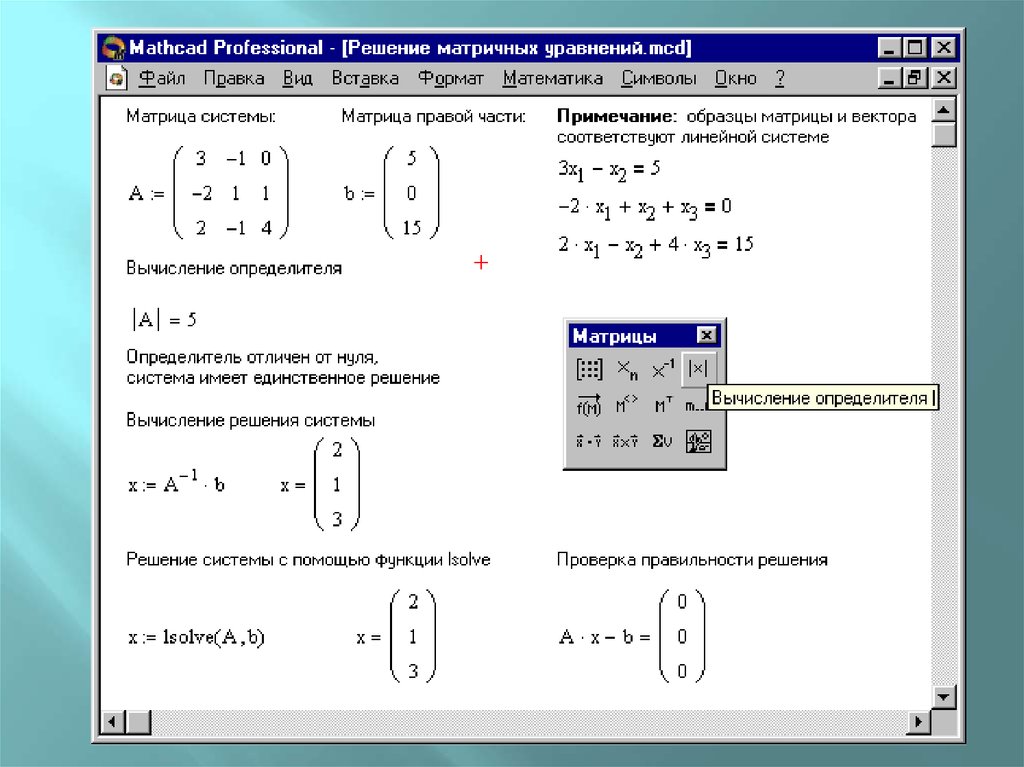
(2)
Другими словами, элемент сij равняется сумме произведений элементов строки с номером i матрицы А на соответствующие элементы столбца с номером j матрицы В. Произведение матрицы А на матрицу В обозначается АВ.
Замечание: Операция умножения двух матриц выполнима лишь в том случае, когда число столбцов первой матрицы – сомножителя А должно равняться числу строк второй матрицы сомножителяВ. Если это условие не выполнено, произведение не существует.
Для запоминания формулы (2) пользуются мнемоническим правилом: «умножениеi-той строки матрицы А наj-тый столбец матрицы В».
Приведем примеры умножения матриц.
Вычислить произведение АВ, где
Число столбцов в первой матрице совпадает с числом строк во второй матрице, поэтому произведение АВ существует. ПоложимС = АВ. В матрице С столько же строк, сколько в матрице А, и столько же столбцов, сколько в матрицеВ, т.
е. матрица С размеров 23. Пусть С = (сij), тогда по формуле (2) получаем
с11 = 2(-1) + 32 = 4, с12 = 22 + 31 = 7, с13 = 20 + 3(-1) = — 3,
с21 =(-1)(-1) + 42 = 9, с22 =(-1)2 + 41 = 2,с23 = (-1)0 + 4(-1) =-4.
Записав эти числа в матрицу, получим
Заметим, что произведение ВА не существует, поскольку число столбцов в матрице В не равно числу строк в матрице А.
2.
3.
4.
5.
Определители и их свойства.
Рассмотрим квадратную матрицу второго порядка .Определителем этой матрицы называют число, обозначаемое , или , или , полученное из элементов матрицы по следующему правилу: . Например, если , то .
Рассмотрим теперь квадратную матрицу третьего порядка . Определителем этой матрицы назовем число .
= , или
(1)
Равенство (1) называют разложением определителя по элементам первой строки.
Выражения ; и называют алгебраическими дополнениями элементов , и соответственно. Таким образом, разложение определителя третьего порядка по элементам первой строки может быть записано в виде: .
Нетрудно заметить, что аналогичным образом определитель третьего порядка может быть разложен по элементам второй и третьей строк, а также по элементам первого, второго или третьего столбца.
Закрепление нового материала.
Пример 1: Найти сумму матриц: А = и В = .
Решение: С = А + В С =
Чтобы вычесть из матрицы А матрицу В, надо к матрице А прибавить матрицу, противоположную матрице В.
А – В = А + (-В)
Пример 2: Найти разность матриц А – В: А = и В = .
Решение: С = А – В -В = С =
Пример 3: Дана матрица А =. Найти матрицу С = 2А.
Решение: С = 2А =
Пример 4: Даны матрицы: А = и В = .
Найти произведение матриц А и В.
Решение: С = АВ С = С =
Задания для решения:
1.Вычислить произведение матриц:
.
Решение. Первая матрица имеет размеры 2´3, а вторая размеры 3´3, поэтому произведение существует. В результате умножения получится матрица С = (cij) размеров 2´3. Вычислим ее элементы.
с11 = (-2)×3 + 3×1 + 1×4 = 1, с12 = (-2)×(-1) + 3×1 + 1×6 = 11,
с13 = (-2)×2+3×0+1×8 = 4, с21 = 0×3 + 5×1 + 6×4 = 29,
с22 = 0×(-1) + 5×1 + 6×6 = 41, с23 = 0×2+5×0+6×8 = 48.
Ответ: .
2.Вычислить произведение матриц:
.
Решение. Первая матрица имеет размеры 3´3, а вторая размеры 2´3. Число столбцов в первой матрице (3) не совпадает с числом строк во второй матрице (2), поэтому произведение не существует,
Ответ: произведение не существует.
3.Вычислить произведение матриц:
.
Ответ: .
4.Вычислить произведение матриц:
.
5.Вычислить произведение матриц:
.
6.Вычислить произведение матриц:
.
7.Вычислить произведение матриц:
.
9.Вычислить степень матрицы:
.
10. Вычислить степень матрицы:
.
Итоги занятия.
Вопросы и задания для самооценки:
ЧТО НАЗЫВАЕТСЯ:
— матрицей, квадратной, единичной, диагональной, транспонированной матрицей;
— обратной матрицей, рангом матрицы, базисным минором;
— определителем, минором, алгебраическим дополнением;
ПЕРЕЧИСЛИТЬ СВОЙСТВА:
— суммы матриц, произведения матрицы на скаляр, произведения матриц;
— определителей.
ЗАПИСАТЬ ФОРМУЛЫ:
— для вычисления определителей второго и n-го порядка, для нахождения обратной матрицы.
СФОРМУЛИРОВАТЬ
— существования и единственности обратной матрицы; теорему о базисном миноре.
Домашнее задание. Учить определения, составить опорную схему конспекта. Выполнить упражнения:
1.Найти , если .
2.Даны матрицы .
Найти: а) б)
9
Как решать линейные уравнения с помощью матриц
Содержание
В математике матрица представляет собой массив чисел, расположенных в виде прямоугольника и разделенных на строки и столбцы. Одним из применений матриц является решение линейных уравнений. Понятие, обратное матрице, наряду с другими операциями над матрицей используется для решения системы $n$ линейных уравнений с $n$ переменными.
Давайте разберемся, как решать линейные уравнения с матрицами с помощью методов и примеров.
Как решать линейные уравнения с матрицами
В этом методе значения переменных в системе уравнений рассчитываются путем умножения обратной матрицы на матрицу значений в правой части.
Если у нас есть система уравнений с $n$ переменными $x_1$, $x_2$, $x_3$, …, $x_n$, представленная как
$a_{11} x_1 + a_{12} x_2 + a_{13} x_3 + … + a_{1n} x_n = c_1$
$a_{21} x_1 + a_{22} x_2 + a_{23} x_3 + … + a_{2n} x_n = c_2$
$a_{31} x_1 + a_{32} x_2 + a_{33} x_3 + … + a_{3n} x_n = c_3$
…………………………………………………………………………
$a_{n1} x_1 + a_{n2} x_2 + a_{n3} x_3 + … + a_{nn} x_n = c_n$
Шаги, необходимые для решения приведенной выше системы линейных уравнений, равны
.
- Все переменные в уравнениях должны быть записаны в соответствующем порядке.
- Переменные, их коэффициенты и константы должны быть написаны на соответствующих сторонах.
Решение системы линейных уравнений методом нахождения обратной состоит из двух новых матриц а именно
- Матрица A: представляет переменные
- Матрица B: представляет константы
После этого решается система уравнений с использованием матричного умножения путем записи приведенных выше уравнений в матричной форме, как показано ниже:
$\begin{bmatrix} a_{11} x_1 + a_{12} x_2 + a_{13} x_3 + … + a_{1n} x_n \\ a_{21} x_1 + a_{22} x_2 + a_{23} x_3 + … + a_{2n} x_n \\ a_{31} x_1 + a_{32} x_2 + a_{33} x_3 + … + a_{3n} x_n \\ ………………………………… . \\ a_{n1} x_1 + a_{n2} x_2 + a_{n3} x_3 + … + a_{nn} x_n \end{bmatrix} = \begin{bmatrix} c_1 \\ c_2 \\ c_3 \\ … \\ c_n \end{bmatrix}$
$=> \begin{bmatrix} a_{11} & a_{12} & a_{13} & … & a_{1n} \\ a_{21} & a_{22} & a_{23} & … & a_ {2n} \\ a_{31} & a_{32} & a_{33} & … & a_{3n} \\ … & … & … & … & … \\ a_{n1} & a_{n2} & a_ {n3} & … & a_{nn} \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ … \\ x_n \end{bmatrix} = \begin{bmatrix} c_1 \\ c_2 \\ c_3 \\ … \\ c_n \end{bmatrix} $
$=> \text{AX} = \text{B}$ —————————— (1)
, где $\text{A} = \begin{bmatrix} a_{11} & a_{12} & a_{13} & … & a_{1n} \\ a_{21} & a_{22} & a_{ 23} & … & a_{2n} \\ a_{31} & a_{32} & a_{33} & … & a_{3n} \\ … & … & … & … & … \\ a_{n1} & a_{n2} & a_{n3} & … & a_{nn} \end{bmatrix}$
$\text{X} = \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ … \\ x_n \end{bmatrix}$
$\text{B} = \begin{bmatrix} c_1 \\ c_2 \\ c_3 \\ … \\ c_n \end{bmatrix}$ 9{-1} \text{B}$
Примечание:
- $\text{AX} = 0$ известна как однородная система линейных уравнений, здесь $\text{B} = 0$. Система однородных уравнений всегда совместна.
- Система имеет нетривиальное решение (ненулевое решение), если $| \текст{А} | = 0$
Примеры решения линейных уравнений с помощью матриц
Пример 1: Решить пару линейных уравнений $3x – 4y = 6$ и $2x – 3y = 6$
Данная пара уравнений равна
$3x – 4y = 6$ ———————————— (1)
$2x – 3y = 6$ ———————————— (2)
Переписав уравнения в виде матриц, получим
$\begin{bmatrix} 3 & -4\\ 2 & -3 \end{bmatrix} \begin{bmatrix} x\\ y \end{bmatrix} = \begin{bmatrix} 6\\ 6 \end{bmatrix }$, который имеет вид $\text{AX} = \text{B}$, где 9{-1} = \frac{\text{Adj}(\text{A})}{|\text{A}|} = \frac{1}{-1} \begin{bmatrix} -3 & 4\ \ -2 & 3 \end{bmatrix} = \begin{bmatrix} 3 & -4\\ 2 & -3 \end{bmatrix}$
Следовательно, $\begin{bmatrix} x\\ y \end{bmatrix} = \begin{bmatrix} 3 & -4\\ 2 & -3 \end{bmatrix} \begin{bmatrix} 6\\ 6 \end {bmatrix}$
$=> \begin{bmatrix} x\\ y \end{bmatrix} = \begin{bmatrix} 3 \times 6 – 4 \times 6\\ 2 \times 6 – 3 \times 6 \end{bmatrix} = \begin{bmatrix} -6 \\ -6 \end{bmatrix}$
Решение пары линейных уравнений $3x – 4y = 6$ и $2x – 3y = 6$ равно $x = -6$ и $y = -6$
Пример 2: Решить пару линейных уравнений $2x – 5y = 9$ и $-6x + 15y = 11$
Данная пара уравнений равна
$2x – 5y = 9$ ———————————— (1)
$-6x + 15y = 11$ ———————————— (2)
Переписав уравнения в виде матриц, получим
$\begin{bmatrix} 2 & -5\\ -6 & 15 \end{bmatrix} \begin{bmatrix} x\\ y \end{bmatrix} = \begin{bmatrix} 9{-1} = \frac{\text{Adj}(\text{A})}{|\text{A}|}$
$|\текст{А}| = \begin{vmatrix} 2 & -5\\ -6 & 15 \end{vmatrix} = 2 \times 15 – (-5) \times (-6) = 30 – 30 = 0$
Поскольку $|\text{A}| = 0$, поэтому данная система уравнений не имеет решений, т.
е. система уравнений несовместна.
Пример 3: Решение системы линейных уравнений
Данная система уравнений равна
$x – y + z = 2$ ———————————— (1)
$-2x + y + z = 6$ ———————————— (2)
$2x + 2y + z = -3$ ———————————— (3)
Переписав уравнения в виде матриц, получим
$\begin{bmatrix} 1 & -1 & 1 \\ -2 & 1 & 1 \\ 2 & 2 & 1 \end{bmatrix} \begin{bmatrix} x\\ y \\ z\end{bmatrix} = \begin{bmatrix} 2\\ 6 \\ -3 \end{bmatrix}$, который имеет вид $\text{AX} = \text{B}$, где
- $\text{A} = \begin{bmatrix} 1 & -1 & 1 \\ -2 & 1 & 1 \\ 2 & 2 & 1 \end{bmatrix}$ 9{-1} = \frac{\text{Adj}(\text{A})}{|\text{A}|}$
$|\текст{А}| = \begin{vmatrix} 1 & -1 & 1\\ -2 & 1 & 1 \\ 2 & 2 & 1\end{vmatrix} = 1 \times (1 \times 1 – 1 \times 2) – (- 1) \times (-2 \times 1 – 1 \times 2) + 1 \times (-2 \times 2 – 1 \times 2)$
$ = 1 \раз (1 – 2) + 1 \раз (-2 – 2) + 1 \раз (-4 – 2) = 1 \раз (-1) + 1 \раз (-4) + 1 \ раз (-6)$
$ = -1 – 4 – 6 = -11$
Поскольку $|\text{A}| \ne 0$, поэтому данная система уравнений имеет единственное решение.
9{-1}$, найдем сопряженную, которая вычисляется транспонированием матрицы кофакторов, а матрица кофакторов получается из миноров матрицы $\text{A}$.Миноры $\text{A} = \begin{bmatrix} 1 & -1 & 1\\ -2 & 1 & 1 \\ 2 & 2 & 1\end{bmatrix}$ равны
$\text{M}_{1, 1} = \begin{bmatrix} 1 & 1\\ 2 & 1 \end{bmatrix} = 1 \times 1 – 1 \times 2 = 1 – 2 = -1 $
$\text{M}_{1, 2} = \begin{bmatrix} -2 & 1\\ 2 & 1 \end{bmatrix} = -2 \times 1 – 1 \times 2 = -2 – 2 = -4$
$\text{M}_{1, 3} = \begin{bmatrix} -2 & 1\\ 2 & 2 \end{bmatrix} = -2 \times 2 – 1 \times 2 = -4 – 2 = -6$
$\text{M}_{2, 1} = \begin{bmatrix} -1 & 1\\ 2 & 1 \end{bmatrix} = -1 \times 1 – 1 \times 2 = -1 – 2 = -3$
$\text{M}_{2, 2} = \begin{bmatrix} 1 & 1\\ 2 & 1 \end{bmatrix} = 1 \times 1 – 1 \times 2 = 1 – 2 = -1$
$\text{M}_{2, 3} = \begin{bmatrix} 1 & -1\\ 2 & 2 \end{bmatrix} = 1 \times 2 – (-1) \times 2 = 2 + 2 = 4$ 9{-1} = \frac{\text{Adj}(\text{A})}{|\text{A}|} = \frac{1}{-11} \begin{bmatrix} -1 & 3 & -2\\ 4 & -1 & -3 \\ -6 & -4 & -1 \end{bmatrix} = \frac{1}{11} \begin{bmatrix} 1 & -3 & 2\\ -4 & 1 & 3 \\ 6 & 4 & 1 \end{bmatrix}$
Следовательно, $\begin{bmatrix} x\\ y \\ z \end{bmatrix} = \frac{1}{11} \begin{bmatrix} 1 & -3 & 2\\ -4 & 1 & 3 \ \ 6 & 4 & 1 \end{bmatrix} \begin{bmatrix} 2\\ 6 \\ -3\end{bmatrix}$
$= \frac{1}{11} \begin{bmatrix} 1 \times 2 – 3 \times 6 + 2 \times (-3) \\ -4 \times 2 + 1 \times 6 + 3 \times ( -3) \\ 6 \times 2 + 4 \times 6 + 1 \times (-3) \end{bmatrix} = \frac{1}{11} \begin{bmatrix} 2 – 18 – 6 \\ -8 + 6 – 9\\ 12 + 24 – 3 \end{bmatrix} = \frac{1}{11} \begin{bmatrix} -22 \\ -11 \\ 33 \end{bmatrix} = \begin{bmatrix} -2 \\ -1\3\end{bmatrix}$
Следовательно, решение системы уравнений $x – y + z = 2$, $-2x + y + z = 6$ и $2x + 2y + z = -3$ равно $x = -2$, $y = -1$ и $z = 3$
Практические задачи
Решите следующую систему уравнений, используя матричный метод.
- $3x + 2y = 8$, $6x – 4y = 9$
- $x + 3y = 6$, $2x – 3y = 12$
- 141 долл. США x + 93 г = 189 долл. США, 93 долл. США x + 141 г. = 45 долл. США 90 028
- $x – y + z = 2$, $2x – y – z = -6$, $2x + 2y + z = -3$
- $3x + y + z = 2$, $x + 2y + z = -3$, $3x + y + 2z = 4$
- $x – 3y + z = -5$, $-3x – y – z = 1$, $2x – 2y + 3z = 1$
Часто задаваемые вопросы
Что вы подразумеваете под линейным уравнением?
Линейное уравнение — это уравнение первой степени, которое имеет одну или несколько переменных.
Что вы подразумеваете под непротиворечивыми уравнениями?
Непротиворечивая система уравнений — это система уравнений, имеющая одно или несколько решений.
Приведите формулу, используемую в методе умножения матриц для решения линейных уравнений.
Формула, используемая в методе умножения матриц для решения линейных уравнений: $\text{AX} = \text{B}$, где $\text{A}$ — матрица коэффициентов, $\text{X}$ — переменная матрица, а $\text{B}$ — постоянная матрица.
{-1} \text{B}$, где $\text{X}$ — матрица переменных , $\text{A}$ — матрица коэффициентов, а $\text{B}$ — матрица констант в правой части уравнений.Рекомендуемое чтение
- Правило Крамера – определение, формулы и примеры
- Что такое обратная матрица – определение, формула и примеры
- Транспонирование матрицы – значение, свойства и примеры
- Свойства определителя (с формулами и примерами)
- Что такое определитель матрицы – значение, определение и примеры
- Операции с матрицами — сложение, вычитание и умножение
- типов матриц (со свойствами и примерами)
- Что такое матрица в математике – значение, определение и примеры
Вам также может понравиться
Правило Крамера – определение, формулы и примеры
Содержание Что такое правило Крамера?Формула правила КрамераПравило Крамера 2 x
Читать далее
Математические карточки для бесплатной печати – скачать PDF
Карточки по математике являются ценным пособием для учащихся всех возрастов и 9 лет.
0003Читать далее
Загружаемые флэш-карты PDF
CodingHero-Maths-Flash-CardsDownload
Читать далее
numpy — Как решить уравнение с двумя матрицами в python?
Во-первых,
linalgне поможет, так как это нелинейная задача: неизвестное A умножается само на себя. Вы хотите решить систему из 18 квадратных уравнений с 9 неизвестными. Для универсальной системы мы не ожидаем никаких решений, но здесь много структуры.В моей версии SymPy (1.1.1) прямые попытки решить даже одно из матричных уравнений
A*B*A=B*A*BилиA*A=Iне завершаются за разумное время. Так что давайте последуем совету Saintsfan342000 и подойдем к задаче численно, как к задаче минимизации. Вот как я это сделал:импортировать numpy как np из scipy.optimize импорт свернуть B = np.массив([[1,0,0], [0,-1,0], [0,0,1]]) функция определения (A, B): A = A. reshape((3, 3))
вернуть np.linalg.norm(A.dot(B).dot(A)-B.dot(A).dot(B))**2 + np.linalg.norm(A.dot(A)-np. глаз(3))**2
пока верно:
предположение = np.random.uniform (-2, 2, размер = (9,))
res = минимизировать (функция, предположение, аргументы = (B,))
если res.fun < 1e-15:
A = res.x.reshape ((3, 3))
печать(А)
Минимизируемая функция представляет собой сумму квадратов норм Фробениуса
A*B*A-B*A*BиA*A-I. Я помещаю минимизацию в цикл, потому что есть некоторые локальные минимумы, гдеминимизациязастревает; поэтому, когда минимальное найденное значение недостаточно близко к нулю, я игнорирую результат и начинаю заново. Через некоторое время скрипт напечатает кучу матриц вроде 9.0003[[ 0,70386835 0,86117949 -1,40305355] [0,17193376 0,49999999 0,81461157] [-0,25409118 0,73892171 -0,20386834]]
, которые имеют две важные особенности:
- центральный элемент A[1,1] равен 1/2
- след матрицы (сумма диагональных элементов) равен 1.
9{-1}$, найдем сопряженную, которая вычисляется транспонированием матрицы кофакторов, а матрица кофакторов получается из миноров матрицы $\text{A}$.
{-1} \text{B}$, где $\text{X}$ — матрица переменных , $\text{A}$ — матрица коэффициентов, а $\text{B}$ — матрица констант в правой части уравнений.
0003
reshape((3, 3))
вернуть np.linalg.norm(A.dot(B).dot(A)-B.dot(A).dot(B))**2 + np.linalg.norm(A.dot(A)-np. глаз(3))**2
пока верно:
предположение = np.random.uniform (-2, 2, размер = (9,))
res = минимизировать (функция, предположение, аргументы = (B,))
если res.fun < 1e-15:
A = res.x.reshape ((3, 3))
печать(А)
)
)
)
)
)
)
)
)
. . вплоть до 100.
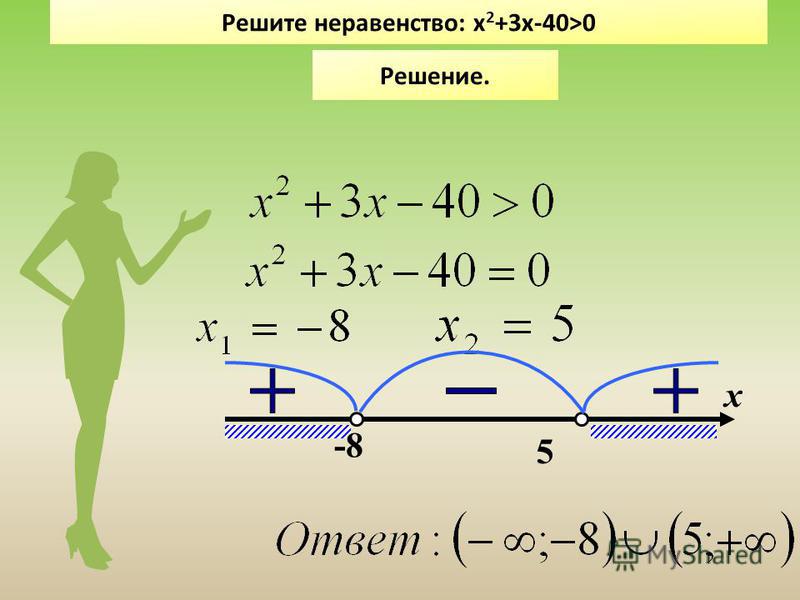
Это означает, что существует почти бесконечное количество значений x, подстановка которых дает истинные утверждения.
Теперь вы понимаете, почему все числа больше 3 являются решениями?
Хотя не имеет значения, где мы храним переменную, слева или справа, имеет смысл все время быть последовательным , изолируя ее с левой стороны. Это просто «стандартный» способ, я думаю.
Решение неравенства x \ge 5 включает 5 и все, что находится справа от него.
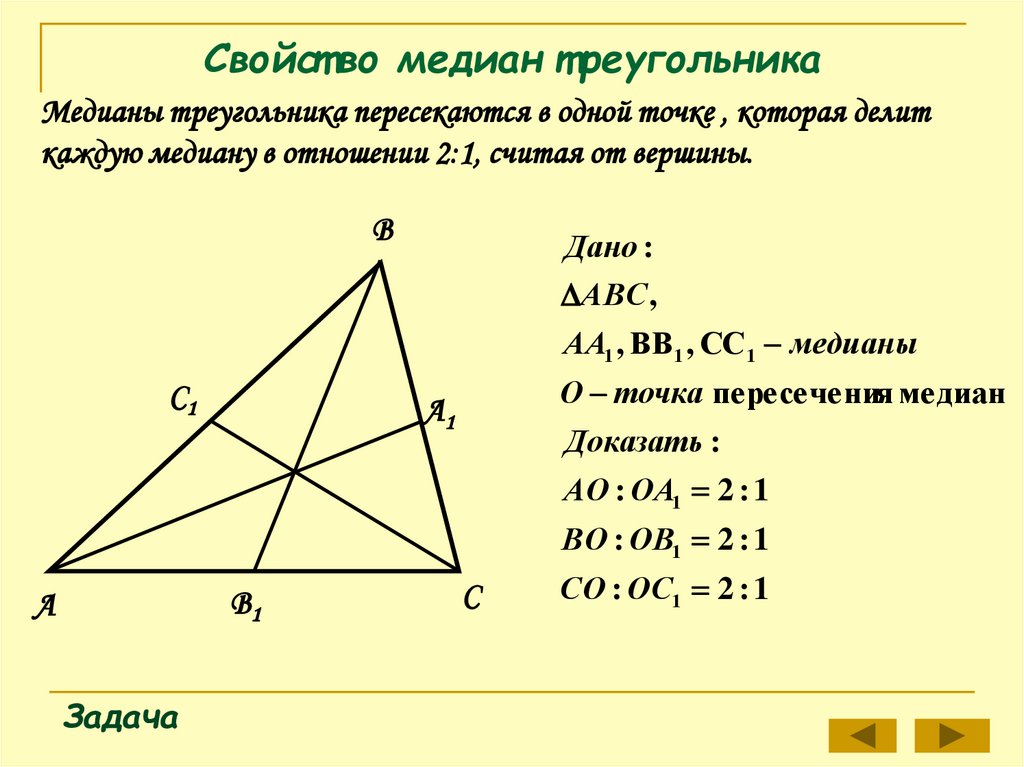
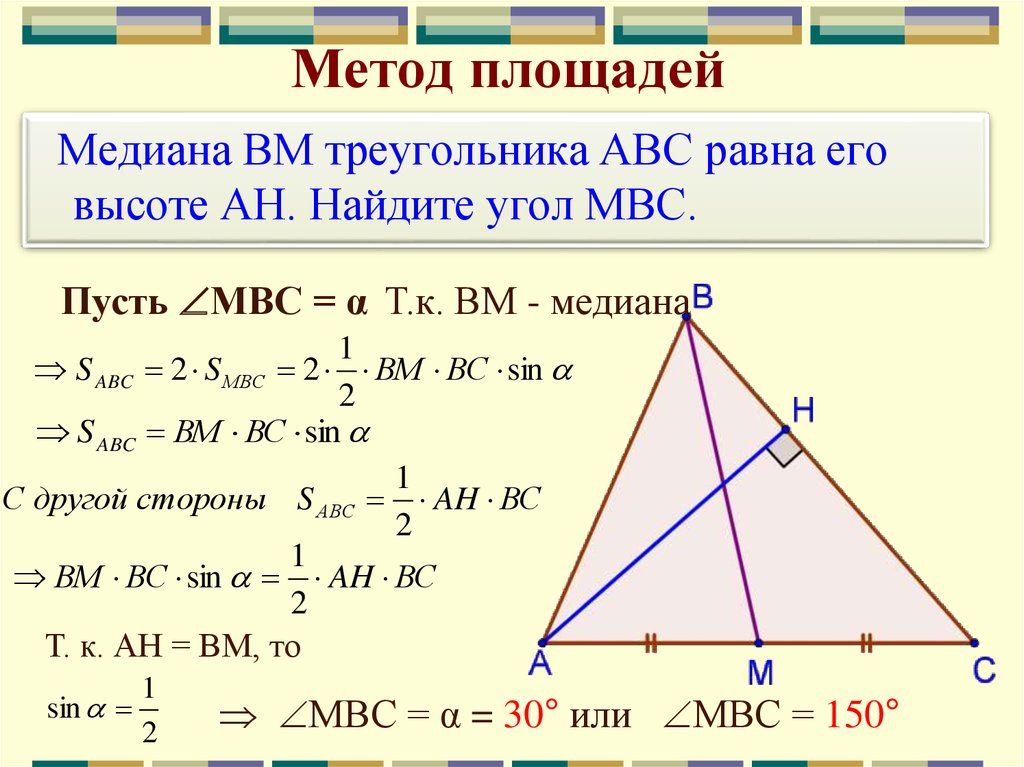Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.
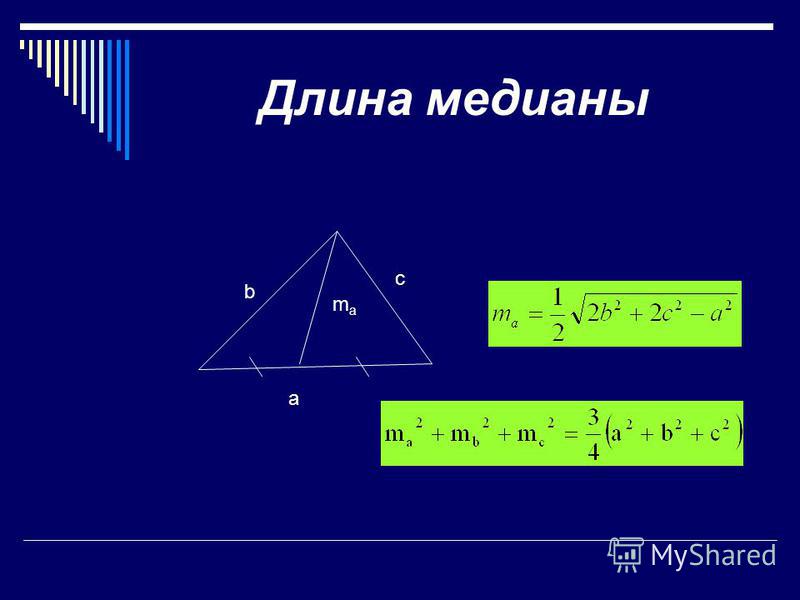В равнобедренном треугольнике углы при основании равны.
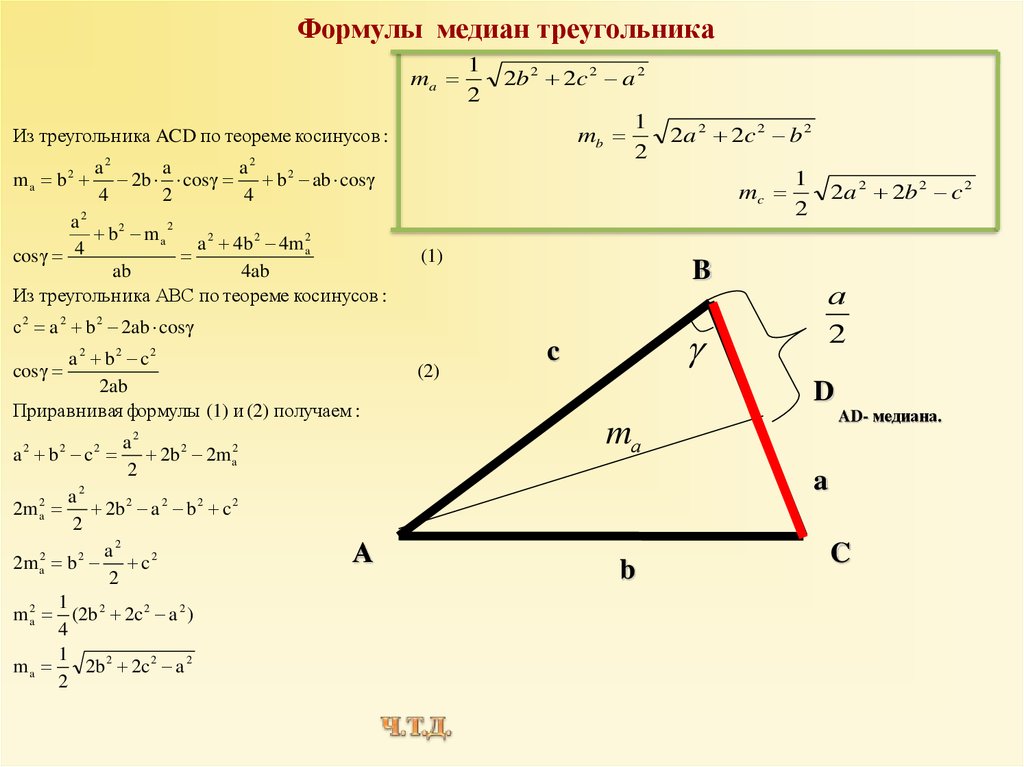Точка пересечения высот, биссектрис и медиан правильного треугольника делит каждую из них в отношении 2:1, считая от вершин
Расстояние от точки пересечения высот, биссектрис и медиан до любой вершины треугольника равно радиусу описанной окружности: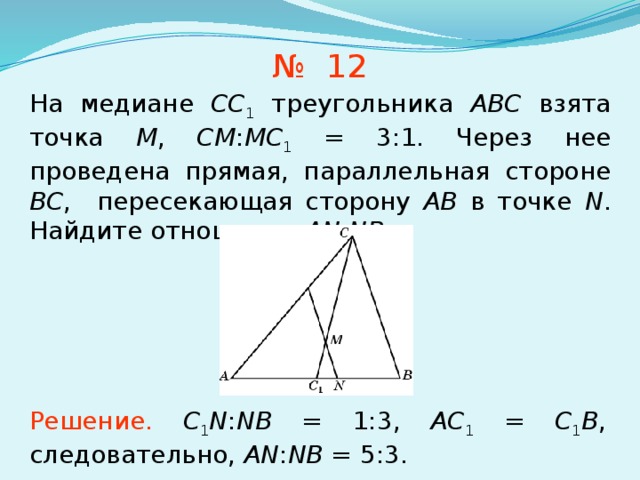
S=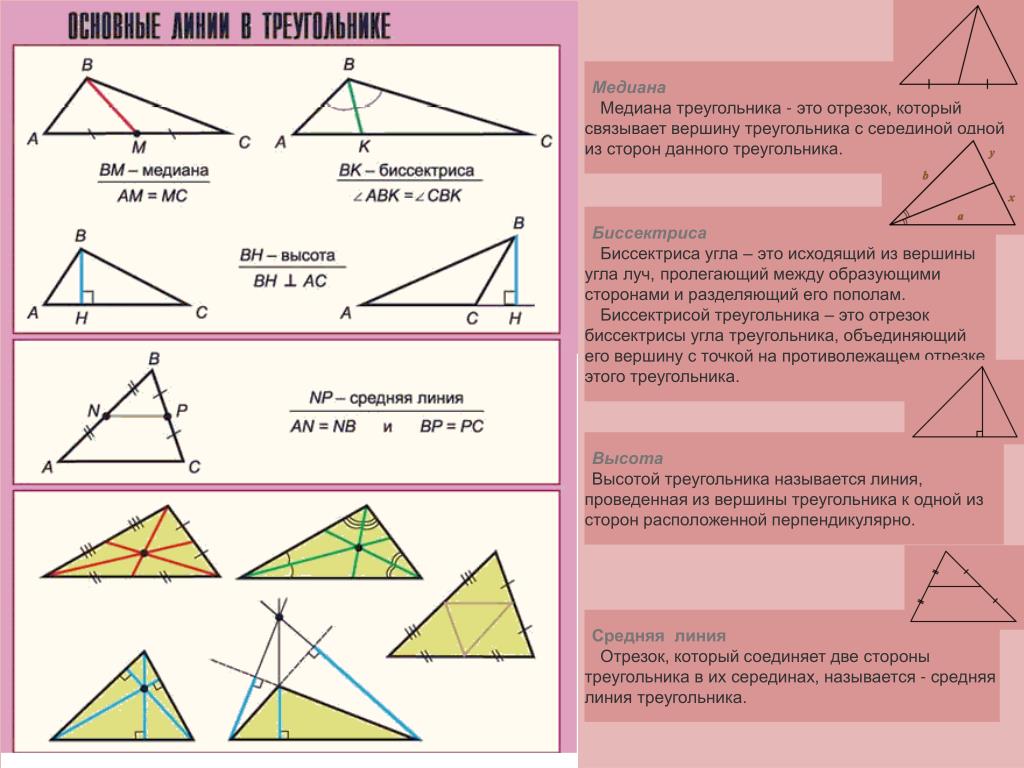
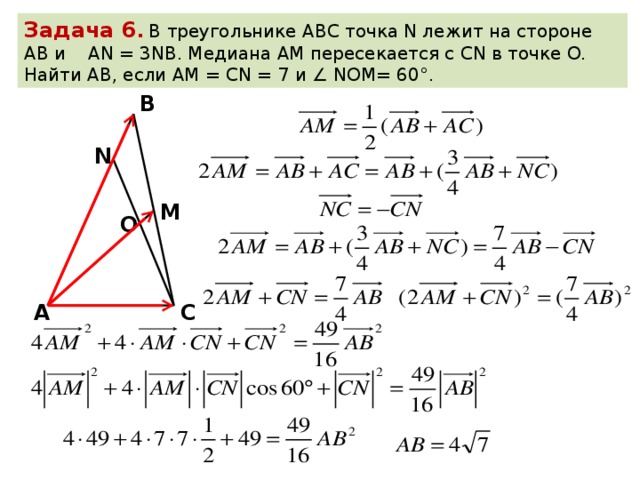е. AC=AD ч.т.д
5NB.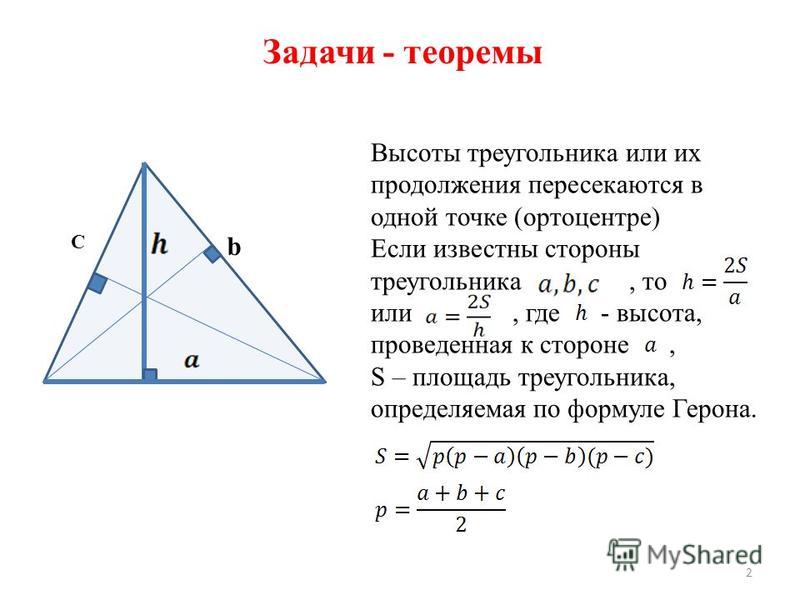
)
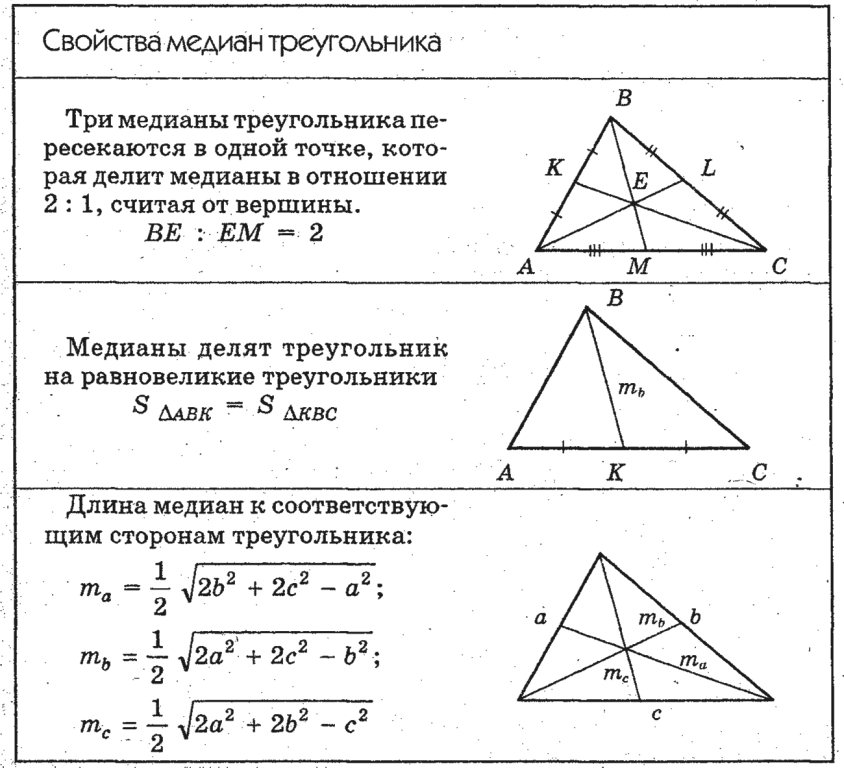
Значит,А 2 С 2 || АС
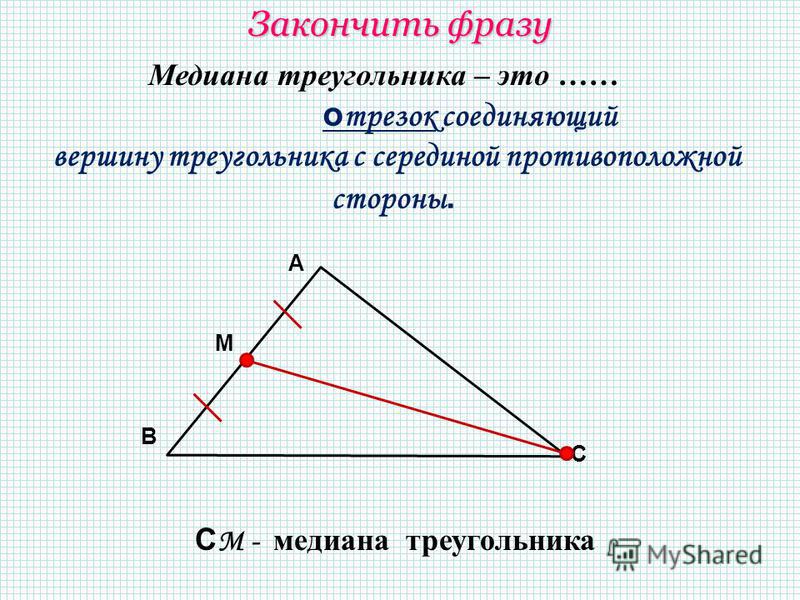Докажите, что отрезки, которые соединяют центроид с вершинами треугольника, делят его на три равновеликие части. Дано: ∆ABC , — его медианы.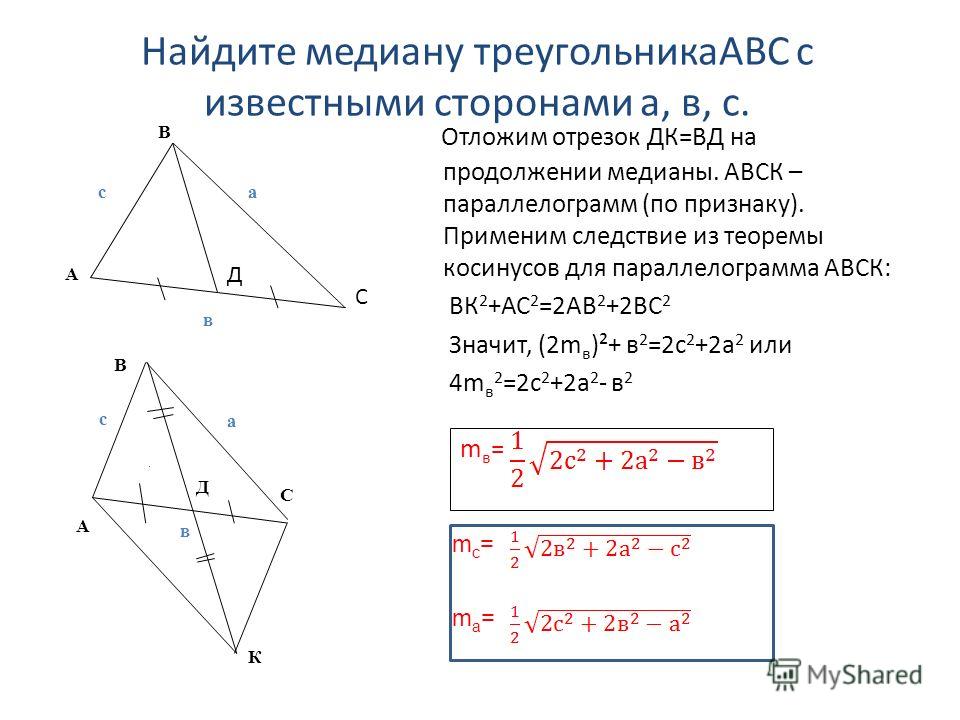
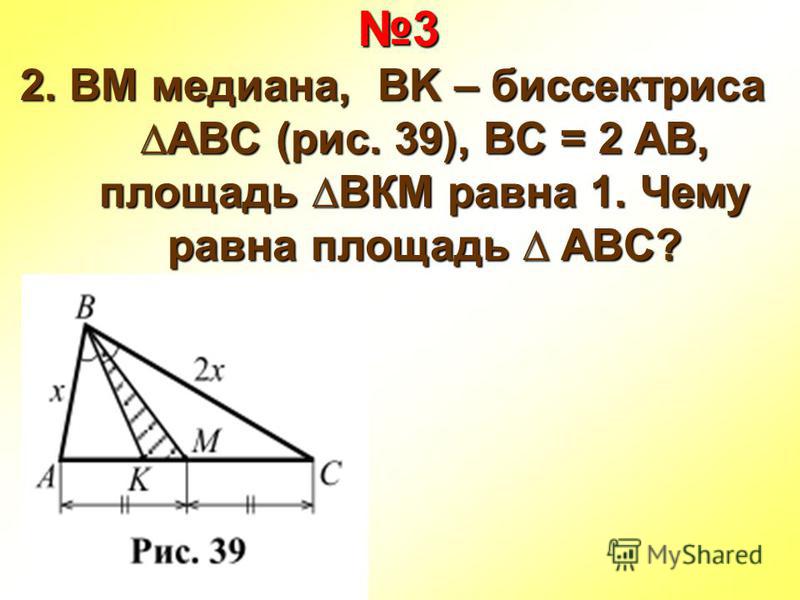
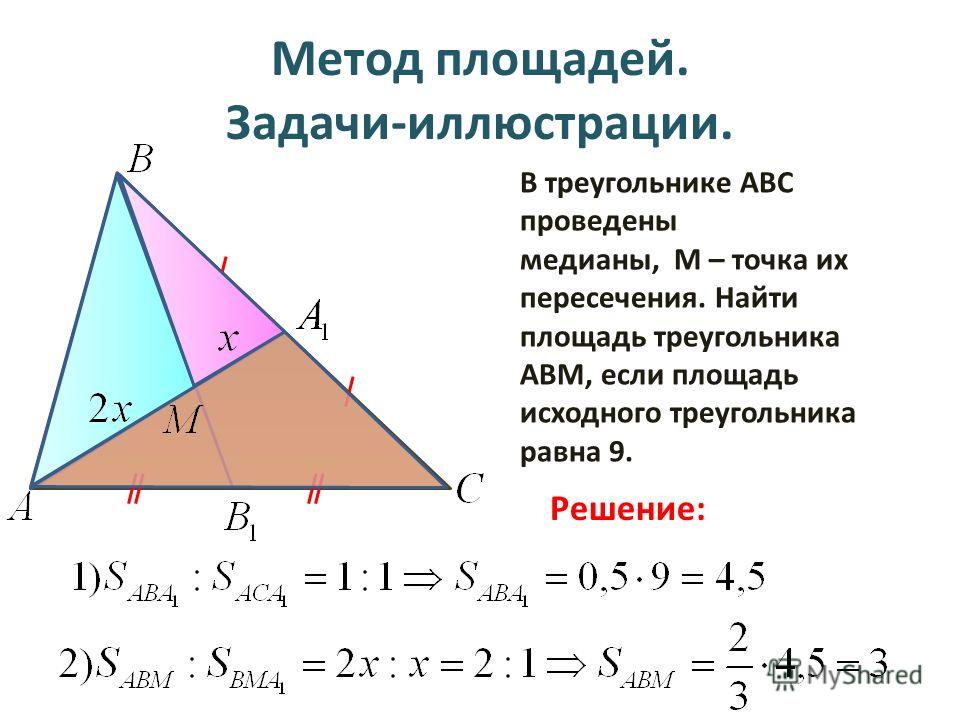
Здесь и проявляется основная особенность метода площадей – из геометрической задачи он «делает» алгебраическую, сводя все к решению уравнения (а иногда системы уравнений).
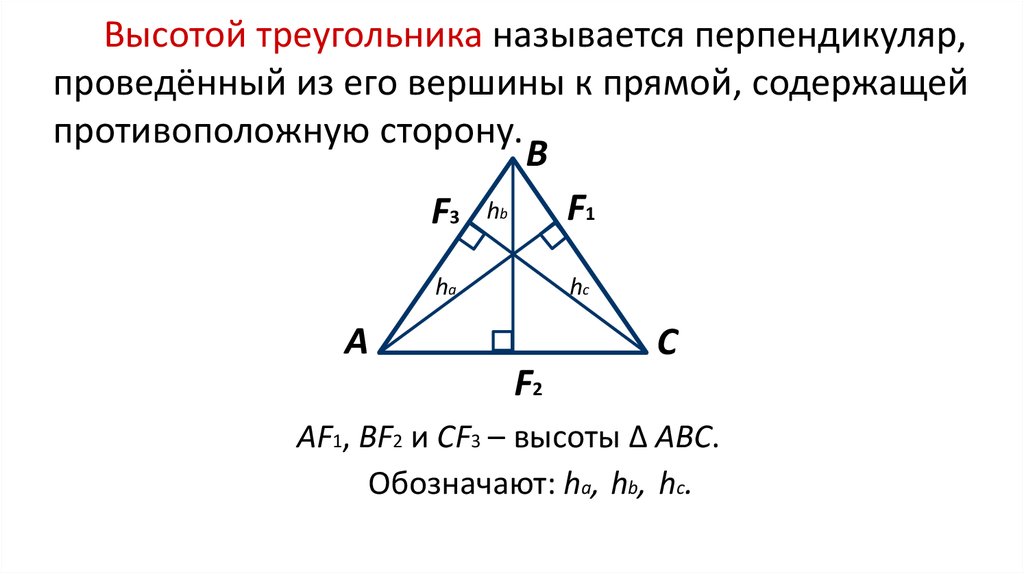По построению, BF — половина BD, следовательно,
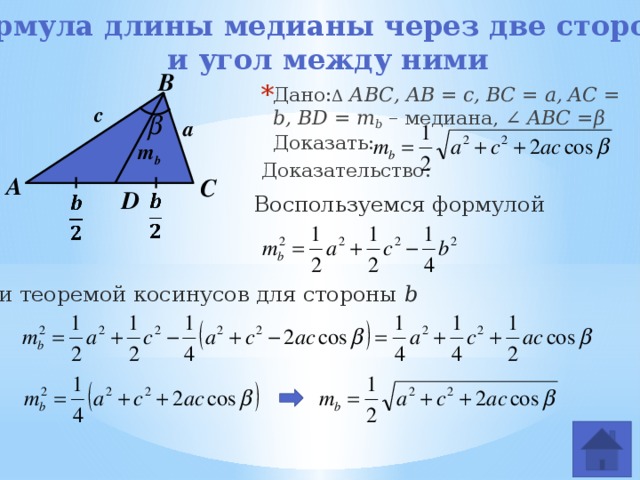
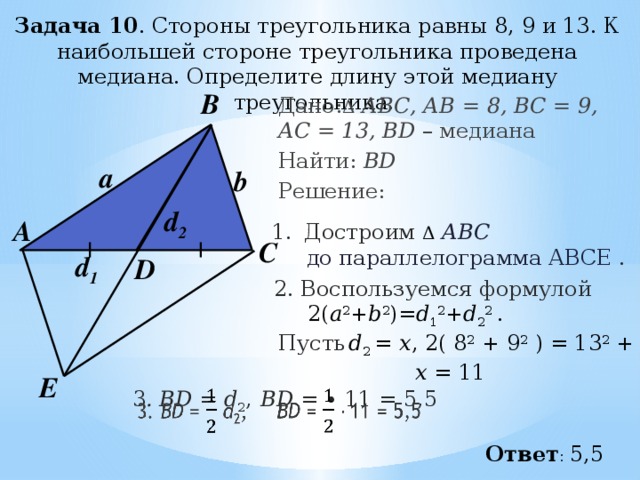
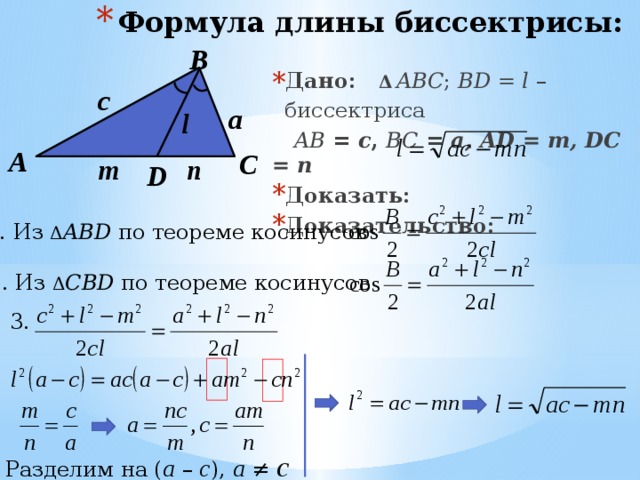
Таким образом выглядит самая простая формула. Медианы треугольника иногда требуется проводить для вспомогательных расчетов. Есть и другие формулы.
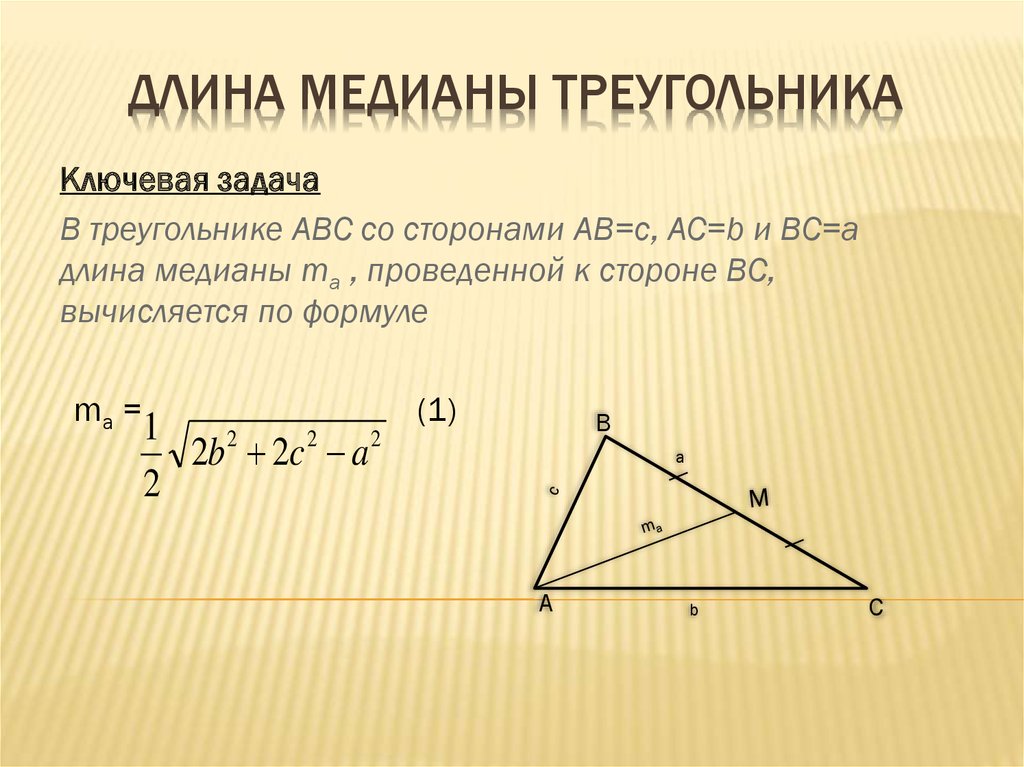5 Медиана (трасса) средняя линия трассы, проведённая между правым и левым … Википедия
Три М. треугольника пересекаются в одной точке, к рая называется центром тяжести треугольника, центроидом, или… … Математическая энциклопедия
2$$
где $$a=8$$ тогда неизвестные $x,h_a,m_a$ можете закончить?
92$
Какова длина медианы до стороны длиной 61 единица от противоположной ей вершины? Я решил это с помощью теоремы Стюарда и получил значение 61/2. Мой вопрос в том, можно ли его рассчитать каким-то другим способом.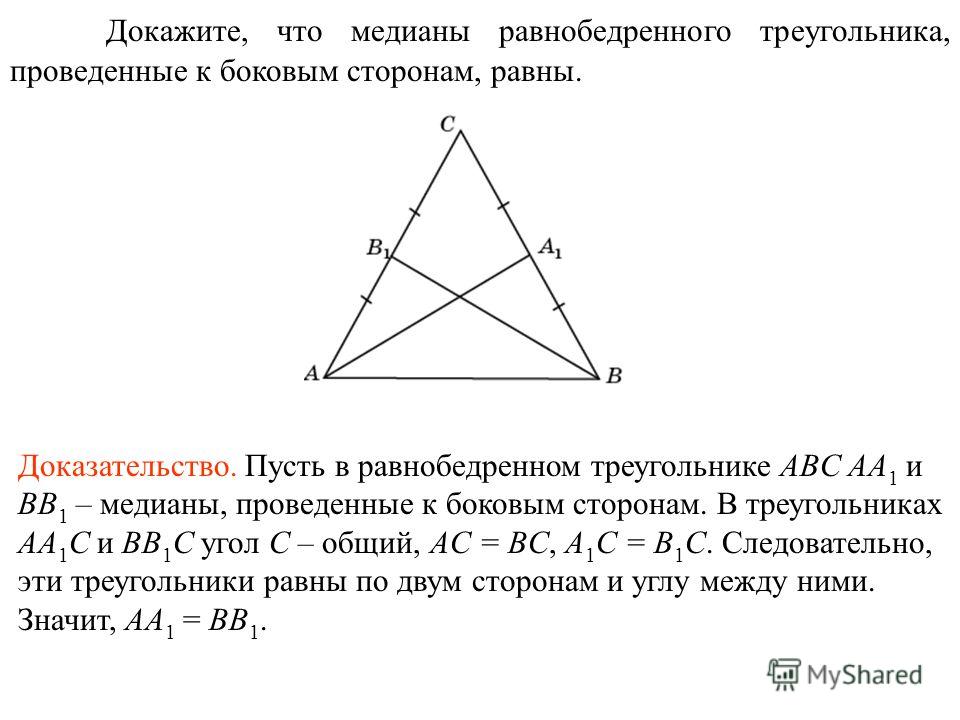
Статусы заказа можете отслеживать в личном кабинете.
Трудоустройство выпускников ПГФА почти 100 %. ПГФА обеспечивает половину кадровой потребности отрасли. Провизоры — аналитики, технологи, организаторы. Обеспечивается полный цикл обучения от создания молекулы до разработки лекарственной формы. Эфир 26 февраля 2019 года
Педагогический (научно-педагогический) состав
Отличительной чертой химической реакции является создание нового материала или материалов вместе с исчезновением массы, которая изменилась, чтобы создать новый. это не означает , что были изготовлены новые элементы. Чтобы образовались новые элементы, необходимо изменить состав ядра. Существуют значительные различия в количестве энергии в обычных химических реакциях по сравнению с ядерными реакциями. Энергия перестройки ядер атомов для превращения в новые элементы огромна по сравнению с меньшими энергиями химических превращений. Алхимики, пытавшиеся заменить менее дорогие металлы золотом, не имели фундаментального понимания того, что они пытались сделать, чтобы оценить разницу.
Материалы слева от стрелки — это реагентов , или материалов, которые будут реагировать. Материалы справа от стрелки — это продукты или материалы, полученные в результате реакции. Закон сохранения массы гласит, что в химической реакции масса не теряется и не увеличивается. Закон сохранения массы применим к отдельным типам атомов. Можно сказать, что для любого элемента нет потери или увеличения этого элемента в химической реакции. Есть такие вещи, как обратимые реакции, реакции, в которых продукты собираются заново, чтобы стать исходными продуктами. Обратимые реакции обозначаются в химических уравнениях двунаправленной стрелкой, но остается стандартом называть материалы слева реагентами, а материалы справа — продуктами.
Серебро реагирует с серой в воздухе, образуя сульфид серебра, черный материал, который мы называем тусклым.
Являются ли эти изменения химическими или физическими? Почему? (Нажимайте * ссылку на обсуждение после каждого, чтобы обсудить, почему этот пример является серой областью.)
Как только материалы, участвующие в реакции, написаны правильно, НЕ ПРИКАСАЙТЕСЬ К НИМ. Если вам нужно обвести каждого участника реакции рамкой, чтобы ваши грязные лапы не касались материалов, сделайте это.
Реакция. Начнем с реакции процесса Габера:
Уравнение реакции:
) _ K + 2(SO4) 2+ (водн.)+ _ h3O(ж)
Умножьте все уравнение (кроме кислорода) на два.
Оставьте коэффициент магнетита и поставьте «4» перед окисью углерода и двуокисью углерода.
Некоторые примеры реакций синтеза: Газообразный водород и газообразный кислород сгорают с образованием воды.
Возможна также анионная одинарная замена. В раствор иодида калия барботируют газообразный хлор. Хлор израсходован, и раствор становится пурпурно-коричневым от йода. Это пример анионной реакции одинарного замещения.
На другой стороне диаграммы мы могли бы рассмотреть ряд активности анионов. Взяв только галогены, самый маленький галоген, фтор является наиболее активным. По мере того, как размер галогена увеличивается вниз по диаграмме, активность уменьшается. Если элемент более активен, чем элемент того же знака в ионном растворе, то более активный элемент заменит его.
Растворенный нитрат серебра становится раствором ионов серебра и нитрат-ионов. Хлористый калий ионизируется таким же образом. Когда два раствора сливаются вместе, ионы серебра и ионы хлора находят друг друга и образуют твердый осадок. (Они «дождятся» или выпадают из раствора, на этот раз в твердом виде.) Поскольку хлорид серебра нерастворим в воде, ионы поглощают друг друга из раствора.
Не все ионы действительно участвуют в реакции. Те ионы, которые остаются в растворе после завершения реакции, называются ионами-спектаторами, т. е. не участвуют в реакции. Есть некоторый вопрос, могут ли они видеть действие других ионов, но это то, как они называются.
SO3 + h3O h3SO4 
H3SO4 + Zn ZnSO4 + H3 
com в качестве источника. В соответствии с тем же исключением, предоставленным классным руководителям, должно быть дано полное признание Chemtutor, когда все или любая часть включена в любое другое электронное представление, такое как веб-сайт, путем прямого включения или гиперссылки. 
Fe(NO3)3 + NaOH Fe(OH)3 + NaNO3
30. Na + h3O h3 + NaOH
31. Na2SO3 + HCl·h3O + SO2 + NaCl
32. Zn + Cu(NO3)2 Cu + Zn(NO3)2
33. С2х3 + О2 СО2 + Н3О
34. h3SO4 + KNO2 HNO2 + K2SO4
35. Cu + HNO3 Cu(NO3)2 + NO2 + h3O
36.I2 + NaOH NaI + NaIO3 + h3O
____ Na2S + ____ Fe(NO3)3 ____ Fe2S3 + ____ NaNO3
19.____ Pb(OH)2 + ____ HCl ____ h3O + ____ PbCl2
20.____ AlBr3 + ____ K2SO4 ____ KBr + ____ Al2(SO4)3
21.____ Na3PO4 + ____ CaCl2 ____ NaCl + ____ Ca3(PO4)2
22.____ Al + ____ HCl ____ h3 + ____ AlCl3
23.____ Кh4 + ____ h3SO4 ____ (Кh5)2SO4
24.____ C8h28 + ____ O2 ____ CO2 + ____ h3O
25.____ CaCO3 + ____ HCl ____ h3O + ______CO2 + ____ CaCl2
26.______Na2O + ____h3O ____NaOH
27.____ NaHCO3 ____ h3O + ____ CO2 + _____Na2CO3
28._____ Р4 + ____ О2 ____ Р2О3
29.____ Fe(NO3)3 + ____ NaOH ____ Fe(OH)3 + ____ NaNO3
30.____Na + ____h3O ____h3 + ____NaOH
31.____ Na2SO3 + ____ HCl ____ h3O + ______SO2 + ____ NaCl
32. ____ Zn + ____ Cu(NO3)2 ____ Cu + _____ Zn(NO3)2
33.____ C2h3 + ____ O2 ____ CO2 + ____ h3O
34.____ h3SO4 + ____ KNO2 ____ HNO2 + ____ K2SO4
35. ________Cu + _____HNO3 _____Cu(NO3)2 + _____NO2 + ______h3O
36.________I2 + _______NaOH _____NaI + _____NaIO3 + ______h3O
N2 + h3 _____ Nh4
____ Na2S + ____ Fe(NO3)3 ____ Fe2S3 + ____ NaNO3
19.____ Pb(OH)2 + ____ HCl ____ h3O + ____ PbCl2
20.____ AlBr3 + ____ K2SO4 ____ KBr + ____ Al2(SO4)3
21.____ Na3PO4 + ____ CaCl2 ____ NaCl + ____ Ca3(PO4)2
22.____ Al + ____ HCl ____ h3 + ____ AlCl3
23.____ Кh4 + ____ h3SO4 ____ (Кh5)2SO4
24.____ C8h28 + ____ O2 ____ CO2 + ____ h3O
25.____ CaCO3 + ____ HCl ____ h3O + ______CO2 + ____ CaCl2
26.______Na2O + ____h3O ____NaOH
27.____ NaHCO3 ____ h3O + ____ CO2 + _____Na2CO3
28._____ Р4 + ____ О2 ____ Р2О3
29.____ Fe(NO3)3 + ____ NaOH ____ Fe(OH)3 + ____ NaNO3
30.____Na + ____h3O ____h3 + ____NaOH
31.____ Na2SO3 + ____ HCl ____ h3O + ______SO2 + ____ NaCl
32. ____ Zn + ____ Cu(NO3)2 ____ Cu + _____ Zn(NO3)2
33.____ C2h3 + ____ O2 ____ CO2 + ____ h3O
34.____ h3SO4 + ____ KNO2 ____ HNO2 + ____ K2SO4
35. ________Cu + _____HNO3 _____Cu(NO3)2 + _____NO2 + ______h3O
36.________I2 + _______NaOH _____NaI + _____NaIO3 + ______h3O
Нам нужно сбалансировать 36 уравнений, и я не буду переписывать все 36. Поэтому, если вы видите число, например, эти двойки и тройки в первом 1, пожалуйста, предположите, что это снова нижние индексы. Есть 36 уравнений, я не переписываю все 36, поэтому просто предположим, что это какие-то обрывки, поэтому первое 1 у нас есть газообразный азот с газообразным водородом, образуя аммиак, так что сразу мы видим, что есть 2 конца или 2 точки азота. . Итак, мы собираемся поставить 2 здесь, так что есть баланс азота, а затем наш h 3. Итак, у нас есть 2 умножить на 3 равно 6. Итак, мы собираемся поставить 3 здесь метан и кислород, образующие воду и углекислый газ. Итак, у нас есть 1 углерод 1 углерод. У нас есть 4 водорода и 2 здесь, поэтому мы собираемся поставить 2 перед этой водой. Это означает, что у нас теперь 4 кислорода справа, поэтому мы просто поставим 2 здесь, чтобы иметь 4 слева. У нас есть фосфор и кислород, поэтому, поскольку у нас слева 4 фосфора, мы собираемся поставить 2 здесь, чтобы сбалансировать тот фосфор, который дает нам 6 кислорода.
Итак, мы собираемся поставить 3 на левый вопрос 4. У нас есть водород и закись азота вместе, поэтому у нас есть 2 азота справа. Итак, мы собираемся поместить 2 слева, и у нас есть 2 водорода справа, у нас есть 2 слева, и у нас есть 1 кислород. Но теперь мы умножили его на 2, поэтому мы поставим здесь 2. Это означает, что мы должны поставить 2 в вопросе 5. У нас есть натрий, смешанный с газообразным хлором, с образованием хлорида натрия или поваренной соли, поэтому нам нужно будет поставить 2 перед хлоридом натрия и 2 перед натрием, который заботится о 2 для хлора номер 6. У нас есть хлорид натрия справа, сбоку, но есть только 1 хлор, поэтому нам придется умножить это на 4, чтобы сбалансировать хлор здесь . Это означает, что мы должны поставить 4 перед этим числом натрия 7. У нас есть сера и кислород, образующие сульфит или триоксид серы, поэтому, поскольку у нас есть 8 серы, это должно быть записано как s 8. У нас есть 8 серы, поэтому это означает, что мы должны поставить 8 перед серой.
Итак, теперь у нас есть 8 умножить на 3 для нашего кислорода, что равняется 24 очкам. Таким образом, мы должны поставить 12 здесь, чтобы сбалансировать кислород номер 8. У нас есть хлорат калия, распадающийся на хлорид калия и кислород. Ключ с кислородом, если у вас когда-нибудь будет 3 и 2. Все, что вам нужно сделать, это поменять местами эти значения. Кислород станет баллонным. Нам просто нужно поставить 2 перед k c l, потому что, если вы заметите, что kcl остается вместе, мы можем просто сбалансировать. Это 1 вещь. Вот еще одно место, где мы можем просто взглянуть на многоатомные ионы. Если мы видим здесь, у нас есть фосфаты, которые остаются вместе, а также наши нитраты, которые остаются вместе. Таким образом, мы можем относиться к ним так, как если бы они были всего лишь одним соединением. Итак, давайте посмотрим на наш натрий. У нас 3 слева. У нас есть 1 справа, поэтому давайте сбалансируем их, поставив 3 сейчас, так как наши нитраты остаются вместе, и 3 из них слева и 3 справа — нитраты сбалансированы.
Теперь, если мы посмотрим на наши фосфаты и наше железо, они уже сбалансированы. Итак, давайте взглянем на пункт номер 10: у нас есть гидроксид кальция с фосфорной кислотой и посмотрите, как получается фосфат кальция в воде. Опять же, наши фосфаты остаются вместе. Таким образом, мы можем просто рассматривать их как 1 объект, но давайте посмотрим на этот bosatif, если вы видите, что слева их 2, или, извините, 2 справа и только 1 слева. Итак, давайте умножим это на 2 пункта, далее идут кальции. У нас есть 3 справа, поэтому нам понадобится 3 слева. Теперь, если это поможет, мы можем написать нашу воду как h, oh h, обратите внимание. Что значит его и их о, есть, разделены и похожи. Они, с левой стороны, сбоку, так что у нас для нашего. О, у нас есть 2 умножить на 3, что равняется 6 для нашего его. У нас есть 2 умножить на 3, что равно 6, так что нам просто нужно поставить 6 перед нашими водами. Смешивание азотной кислоты с бикарбонатом натрия. Итак, давайте посмотрим на наш co 2 или у нас есть 1 углерод и у нас есть 3 кислорода или 2 кислорода.
Скорее, наши натрии сбалансированы. Нитраты держатся вместе, каждого по 1, значит, они сбалансированы. Итак, у нас есть 2, водорода 1212 и у нас есть 3 кислорода 123. Так что это сбалансировано, так как перекись распадается на воду и кислород. Если вы заметили, наш водород уже сбалансирован, у нас есть 2 кислорода, а затем у нас есть 3 справа. Итак, наш кислород не уравновешен, поэтому нам нужно будет поставить 2 перед здесь и 2 перед и здесь, чтобы сбалансировать наш кислород. Это дает нам 4 кислорода слева, на руке, сбоку и 2 плюс 2, что равняется 4 справа, и наш водород все еще сбалансирован. Давайте посмотрим на пункт номер 13. Если мы посмотрим на наши атомы углерода, то увидим, что слева их 3, а справа 1. Итак, давайте сбалансируем их прямо сейчас. Теперь у нас 8. Водород слева и 2 справа, так что мы поместим туда 4. Теперь давайте посчитаем наш кислород, у нас есть 3 умножить на 2, что равняется 6 плюс 4, что равняется 10 баллам. Так что мы собираемся поставить 5 перед этим тоже.
Хитрость в том, что когда у вас есть углеводород, сгорающий в кислороде, всегда двигайтесь в таком порядке, сначала уравновешивайте углероды, затем водород, а затем ваш кислород, третий, всегда двигайтесь в этом порядке, и это станет намного проще. Вопрос 14: у нас есть вода и углекислый газ образуют кислород и вот это прекрасное соединение, так что у нас есть 6 атомов углерода с правой стороны. Итак, давайте сбалансируем их прямо сейчас. Ну, у нас есть 6 там. Теперь давайте сбалансируем наш водород: у нас 12 справа и 2 слева, поэтому нам нужно поставить 6 перед ними. Итак, теперь давайте посмотрим на наш кислород, 6 плюс 6 умножить на 2, что в сумме дает 18 баллов. У нас уже учтено 6, так что у нас есть 18 минус 6. Значит, нам нужно еще 12. Так что мы просто поставим 6 перед кислородом. Итак, нитраты и медь снова объединяются, заметьте. Наши копы остаются вместе. Если у нас есть 2 справа, нам нужно 2 слева, поэтому давайте поместим 2 перед этими серебряными, и теперь все сбалансировано.
Давайте посмотрим на пункт номер 16: начнем с наших бромов, у нас 4 слева и 2 справа. Итак, давайте сбалансируем их прямо сейчас. Теперь наш бром сбалансирован. Наши хлорки — нет. Нам просто нужно поставить 2 перед газообразным хлором, чтобы сбалансировать хлор, и наши углероды все еще сбалансированы. Число. 17. У нас есть медь и серная кислота. Итак, если мы сразу же начнем с наших медей, мы заметим, что они сбалансированы, и мы заметим, что наш водород сбалансирован. Однако наш сульфат, хотя и остается вместе, он 1, все же распадается и образует двуокись серы. Итак, нам нужно сбалансировать их, все, что нам нужно сделать, это поставить 2, чтобы сбалансировать эту дополнительную серу, которая выходит, а затем 2 перед нашими водами. Давайте взглянем на число 18. Если мы сразу заметим, что наши нитраты остаются вместе, давайте поставим 3 перед этим нитратом натрия, чтобы сбалансировать эти нитраты железа. Теперь у нас есть 2 утюга справа, поэтому нам нужно поставить 2 здесь слева, чтобы сбалансировать наш водород.
Но сейчас наши сульфаты не сбалансированы. Итак, давайте заменим это 3 на 6. Итак, теперь у нас здесь 6 натрия, а слева только 2, поэтому мы поместим туда 3, и это сбалансирует нашу серу. Так что теперь мы позволили нашему оксиду свинца и соляной кислоте заметить, что они вместе. Наши проводники сбалансированы, а хлор не такой, давайте поставим 2 перед h cl, и у нас будет 2 кислорода и 2 водорода слева. Таким образом, мы должны сбалансировать тех, кто находится справа. Итак, если мы поставим 2 перед водой, это означает, что у нас будет 2 умножить на 2 плюс 2 для нашего водорода, что равно 4 с обеих сторон. Так что наш водород сбалансирован. Пункт номер 20. Если мы сразу посмотрим на наши брови и наш калий, у нас будет 3 броина и 2 калия слева, но у нас есть только 1 каждого из них справа. Итак, бром, давайте поставим 3 перед tr, а затем нам придется поставить 3 перед нашим калием. Так что теперь это не сбалансировано. Но тогда, если мы посмотрим на наш алюминий, у нас будет 2 справа и только 1 слева.
Итак, давайте поставим 2 перед этим алюминием, и теперь наши бромы равны 6. Таким образом, мы можем поставить 6 перед k. R, и теперь наш калий, бром и алюминий сбалансированы, и наш сульфат остается вместе, и они также сбалансированы. Итак, давайте посмотрим на 21, если мы заметим, что наши фосфаты остаются вместе, как и наш хлор. Итак, давайте начнем балансировать наши фосфаты. Есть 2 справа, сбоку, но только 1 слева. Итак, давайте поставим 2 или натрий в 2 раза. 3 равно 6. Итак, давайте поставим 6 перед хлоридом натрия, чтобы сбалансировать их, и, если вы заметили, у нас есть 3 кальция, поэтому нам понадобится 3. Итак, теперь наши хлоры сбалансированы и поглощают наш кальций. У нас есть алюминий и соляная кислота, образующие хлорид алюминия и газообразный водород, так что сразу. Давайте взглянем на наш хлор. Справа 3, поэтому нам нужно поместить 3 слева, но теперь наш водород не сбалансирован. У нас есть 3 водорода слева, но только 2 справа, отбросьте эти значения, и вы получите 6 водорода справа.
Итак, давайте поставим 6, они поставят 2 перед хлоридами алюминия, чтобы сбалансировать наш хлор. Это означает, что нам понадобится 2 перед нашим алюминием. Теперь у нас есть аммоний и серная кислота, которые вместе образуют сульфат аммония. Теперь наш сульфат остается вместе? Так что мы не беспокоимся об этом, но у нас есть 2, азот, а затем 2 раза по 4 или 8 водорода. Итак, поскольку у нас есть 2 азота, нам нужно поставить 2 перед нашим nh 3. Итак, теперь у нас есть 2 умножить на 3, что равно 6 плюс 2, больше водорода, что равно 8 пунктам. Так что все сбалансировано. 24 пункт снова: давайте сначала проследим за углеродом, у нас есть 8 на левой стороне, поэтому мы поместим 8 на правой руке. Сбоку теперь наш водород, там 18 точка, значит, поставим 9перед нашими водами. Теперь давайте посчитаем наш кислород, у нас есть 8 умножить на 2 плюс 9 баллов? Теперь у нас есть 16 плюс 9, что равно 25 очкам. Это может быть пугающим числом, потому что оно не делится на 2 без остатка, но вот. Что мы можем сделать здесь, так это аккуратный маленький трек.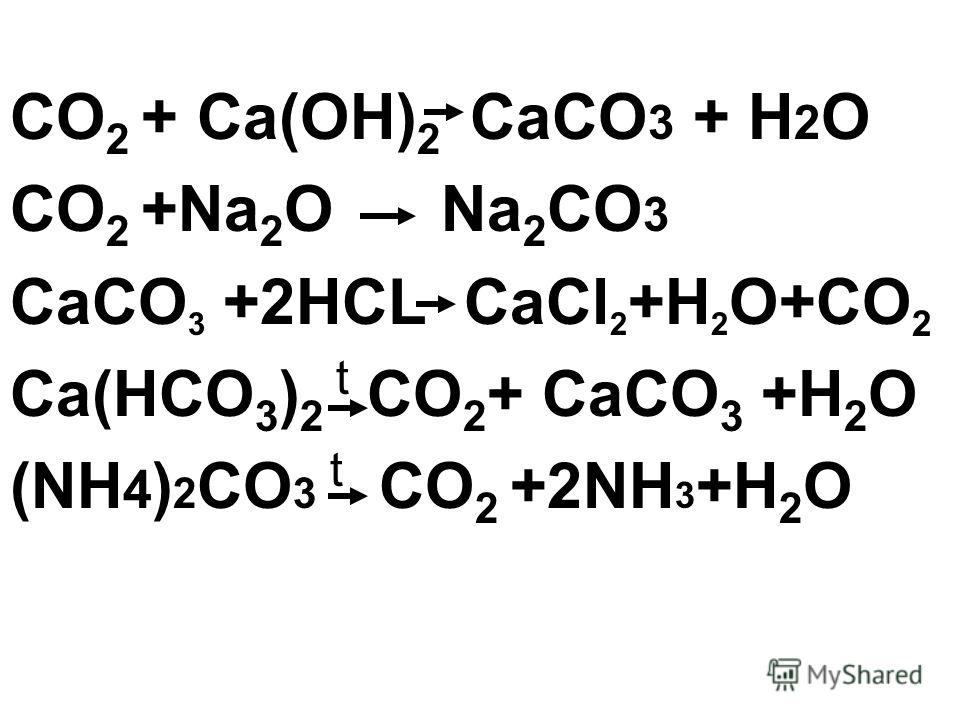
Брать. Это число поместите здесь перед этим кислородом, а затем умножьте все на 2. По сути, удвоив его, и теперь все будет сбалансировано. Давайте взглянем на число: 25, кальций, хлор и h c l. Итак, если мы посмотрим на наши 8 арочных хлоров, мы сразу заметим, что 2 справа и 1 слева. Итак, давайте перейдем к 2 перед этим h, cl кальций сбалансирован, углероды сбалансированы, наш водород сбалансирован. Давайте проверим наш кислород. У нас 3 слева и 1 плюс 2 справа, что равно 3 — это кислород, уравновешиваются 26 точками. Мы замечаем, что у нас есть 2 натрия, слева, сбоку и только 1 справа, так что их нужно сбалансировать сразу. Итак, теперь у нас есть 2 кислорода и 2 водорода справа и столько же слева. Все сбалансировано. 27 пункт. Если мы посмотрим сразу, мы увидим, что наш натрий не сбалансирован. Итак, давайте начнем с этого, и мы сбалансируем наш натрий. Итак, теперь мы должны удвоить все здесь, так что теперь у нас есть 2 и 2 Hes, а затем 2 углерода и 6 кислорода. Вот и все, с левой стороны.
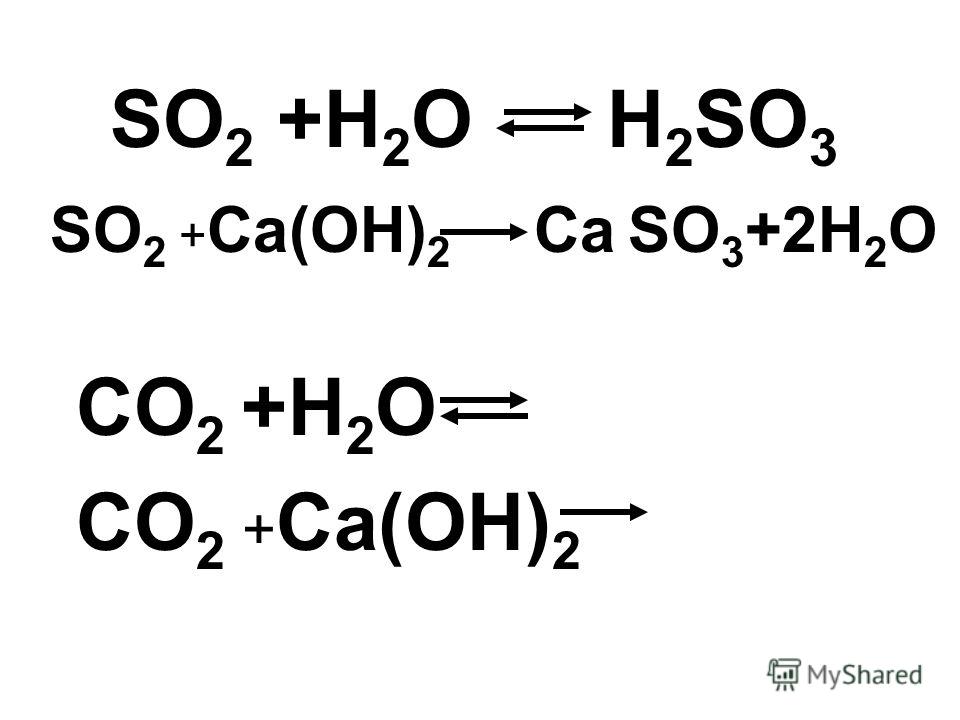Если мы посмотрим на правую сторону, у нас есть 2 водорода, у нас есть 1 плюс 2, что равняется 3 кислорода, а затем у нас есть 2 разных натрия и у нас есть 2 углерода и плюс дополнительные 3 кислорода, всего 6 имеют любые вещи сбалансированы. Итак, теперь у нас есть фосфор и кислород, поэтому у нас есть 2 фосфора справа и сбоку слева. Итак, давайте поместим 2 там, и тогда у нас будет 6 кислорода справа. Итак, давайте поставим 3 перед этим двухатомным слева 29Пункт: если мы посмотрим сразу, наши нитраты не сбалансированы, все еще ругательство 3 перед натрием, чтобы сбалансировать наши нитраты и наш натрий одновременно. Итак, теперь давайте удостоверимся, что наши утюги сбалансированы. Они сбалансированы, давайте проверим наш гидроксид, если заметим, что они остаются вместе, и их по 3 с обеих сторон. Итак, теперь все уравновешено: число 30. У нас есть натрий и вода, образующие натрий или оксид натрия и газообразный водород. Итак, давайте посчитаем наш водород, у нас есть 2 плюс 1, что равно 3, и наш кислород? У нас есть только или 1 очко, поэтому, поскольку здесь у нас 20 часов, нам нужно будет поставить 3 перед этим, чтобы мы получили 6 часов и 30.
Итак, теперь мы должны сбалансировать наш кислород, поэтому мы Поставлю 3 перед натрием, и теперь у нас есть 3 и 3 кислорода, а затем мы просто добавили еще 3 к общему количеству водорода, что равно 6. Все сбалансировано. 31 пункт: давайте посмотрим или натрия: 2 слева, сбоку и 1 справа. Итак, давайте сбалансируем те хлоры, которые сейчас не сбалансированы. Итак, поставим 2. Наша сера сбалансирована. Итак, давайте проверим наш водород. Наш водород сбалансирован, и у нас есть 3 кислорода и 1 плюс 2, что равняется 3 точкам кислорода. Так что теперь все уравновешено. Давайте вместе проверим 32 нитрата, те сбалансированы, цинкки, тоже сбалансированы, и наши котлы сбалансированы. Все проверяется 33 пункт: у нас есть еще одна проблема с углеводородами, так что давайте по порядку. Чоуэлл должен поставить 2 перед нашими углеродами, чтобы сбалансировать их. Итак, теперь у нас есть 2 и 2 точка. Водород был запущен с 2. Слева сбоку у нас есть 2 справа, сбоку кислород. У нас 2? С левой стороны у нас есть 2 умножить на 2 плюс 1, что равно 5.
Так что мы собираемся использовать этот трюк. Мы поставим здесь 5, а все остальное удвоим, и теперь все сбалансировано. У нас есть серная кислота и нитрит калия, и они объединяются в вопросе 34, обратите внимание, наши нитриты остаются вместе, а наши сульфаты остаются вместе, они просто обмениваются партнерами, поэтому мы просто поставим 2 перед нитратом калия и 2 перед нитрат водорода. И теперь все уравновешено: число 35. У нас есть медь и азотная кислота, соединяясь вместе, чтобы сразу образовать медь, нитрат, азот, закись азота и воду. Мы замечаем, что наши нитраты не сбалансированы. Итак, давайте начнем с этого, поэтому нам нужно, чтобы у нас было 2 справа. Так что нам нужно 2 слева, они выглядят, наши нитраты сбалансированы и наш водород. Однако в итоге у нитрата выскочил лишний конец. Так что в конечном итоге мы просто удвоим количество азотной кислоты до 4, а затем удвоим количество нитратов и удвоим количество воды. А сейчас все уравновешено. Давайте проверим это. У нас есть углерод, у нас есть водород, у нас есть и.
.. и я собираюсь переместить сюда кислород, так как у меня кончается счетчик е, все в порядке, чтобы убедиться, что все сбалансировано. 1, медь с обеих сторон. У нас есть 4 водорода 4 водорода с обеих сторон. У нас 4 нитрата и, извините, 4. Азот с обеих сторон, и теперь у нас 4 умножить на 3, что равняется 12 кислорода, а затем, на правой стороне, у нас 2 раза 3 плюс 2 раза 2 плюс 2 раза 1. Для нашего кислорода. Не поэтому ли вы всегда оставляете кислород напоследок и, надеюсь, вместе, если возможно, так что у нас есть 6 плюс 4 плюс 2, что равняется 12 очкам. Все сбалансировано и, наконец, последнее 1 по 36 очко. Я собираюсь пойти дальше и написать все, что у нас есть, слева, сбоку и справа, сбоку, и я собираюсь расположить их в том же порядке, чтобы мы могли сравнить значения, как они идут, так и есть. начальные значения йода. У нас 2 натрия по 1 и кислорода, а водород по 1 слева, сбоку справа, сбоку. У нас есть 2 йода, у нас есть 2 натрия 3 кислорода плюс 1 больше, чем равно 4, и тогда я на самом деле собираюсь стереть ту маленькую силу, чтобы мы не запутались, и тогда наш водород.
У нас их 2, и на самом деле я собираюсь разделить наш натрий и наш йод, потому что нам придется сбалансировать их по отдельности, что внесет небольшую положительную черту. Итак, сразу же, наши йоды сбалансированы или натрии не так, давайте поставим 2 перед нашим оксидом натрия гидроксидом натрия с левой стороны. Итак, теперь все умножается на 2, и у нас есть 2 натрия, 2 кислорода и 2 водорода. Итак, теперь наш натрий сбалансирован, а кислород — нет. Мы должны умножить это. Гидроксид натрия нужно было умножить на 2 или изменить на 4. Итак, теперь все будет умножено на 4, так что все это. Так что теперь у нас есть 4 всего, кроме нашего йода. Итак, теперь наш кислород сбалансирован, а натрий и водород — нет. Итак, давайте начнем с нашего водорода: давайте поставим 2 перед этой водой, и это означает, что 1 кислород будет умножен на 2 балла. Так что теперь мы должны сбалансировать наши натрия. Что я собираюсь сделать, так это просто поработать с этим йодом натрия, чтобы не возиться с кислородом.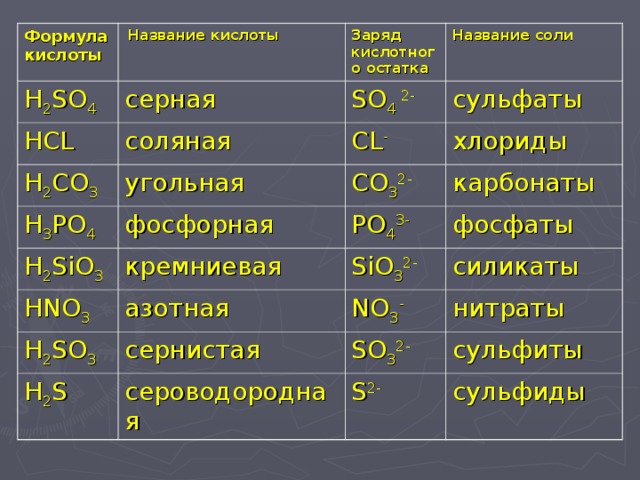
Итак, я поставлю четвертую перед этим йодом натрия, что означает, что этот йод будет умножен на 4, а этот 1 натрий будет умножен на 4, все еще было сделано, потому что теперь у нас есть 5 йода и на правая рука, сторона, и у нас есть только 2 слева, поэтому давайте просто сбалансируем это, поставив 3 перед йодом, так что это означает, что у нас есть 6 йодов. Значит, поставим другой. Давайте добавим это 4, теперь это будет 1 в точке 5. Наши йодиды сбалансированы. Наши натрии теперь не сбалансированы. Теперь это 5 плюс 1, что равняется 6, поэтому мы просто поставим 6 здесь, мы просто избавимся от всего этого. Итак, теперь у нас есть 66 и 6 для нашего натрия или кислорода, и наш водород почти готов. Давайте проверим наш водород, теперь наш йод слева, сторона равна 6 или натрий равен 6. Наш кислород равен 3 плюс 3, что равно 6. Водород. Они не сбалансированы, они все еще на уровне 4. Итак, давайте поместим это в 3, извините, что должно быть боб 5 для нашего кислорода, и теперь это становится 3 плюс 3, что равняется 6.
Ее можно распечатать в хорошем качестве и использовать при подготовке домашнего задания
Придется составлять свою, но это даже хорошо: так ребенок быстрее запомнит вычисления.
На обложках тетрадей, учебниках печатают только таблицу умножения. Бывает, новенькие ученики спрашивают меня: «Почему есть таблица умножения, а таблицы деления нет?» Деление — это действие, обратное умножению. Поэтому результаты не нужно запоминать механически, их нужно выводить из умножения. Следовательно, для того чтобы отлично делить, нужно твердо знать таблицу умножения.
«У нас с тобой 6 яблок, как их поделить между нами поровну? Тебе яблоко, мне яблоко, тебе, мне…»
Чтобы учащиеся были внимательны, сформулируйте факторы и попросите учащихся ответить на вопрос о продукте, прежде чем выбрать учащегося, который расскажет о соответствующем факте. Чтобы поддерживать темп, вы можете случайным образом выбирать учеников, используя колоду именных карточек.
Когда дети хотят большего, попробуйте Часть 2. 
Ваш ребенок разработает стратегии умножения и деления целых чисел. Они будут использовать таблицы умножения, счетчики и калькуляторы. Цели этого подразделения следующие;
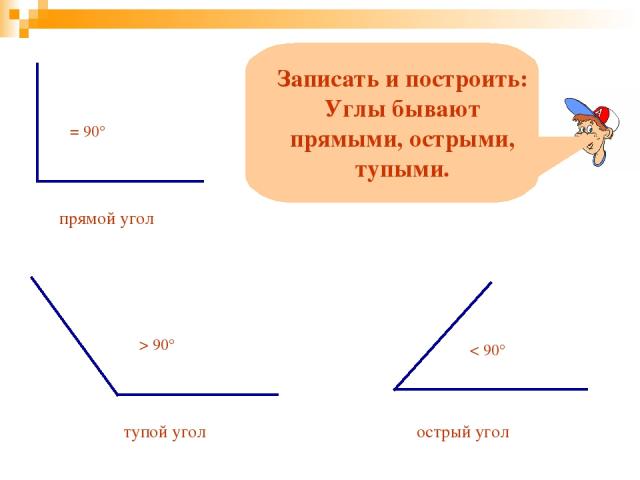Требуется выяснить, какой из представленных углов является острым. 
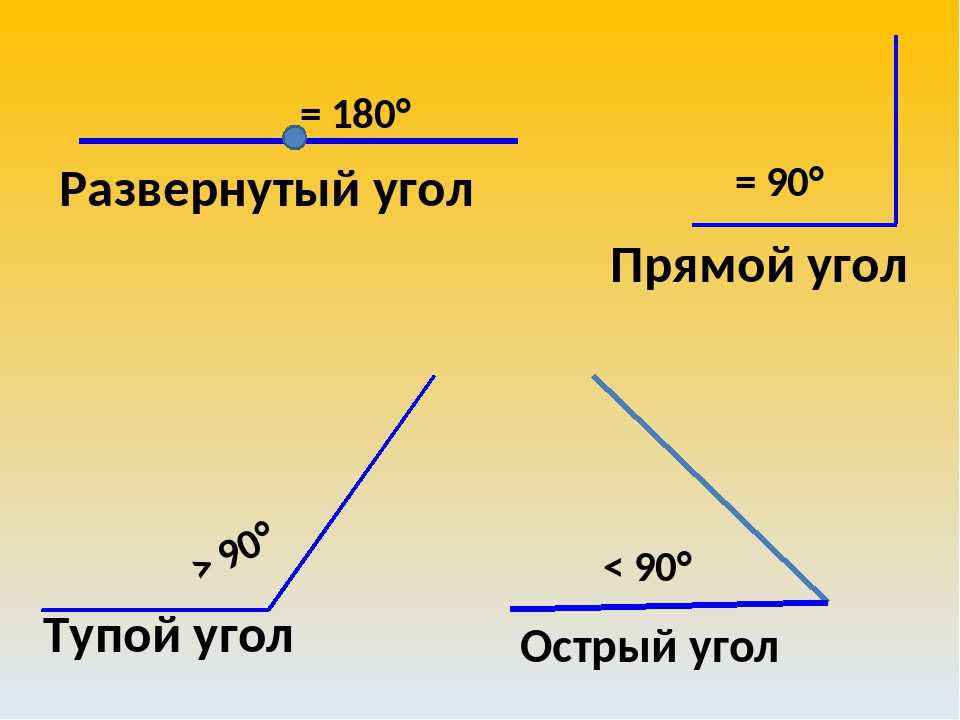Данный угол можно идентифицировать как тупой. Он не является острым.
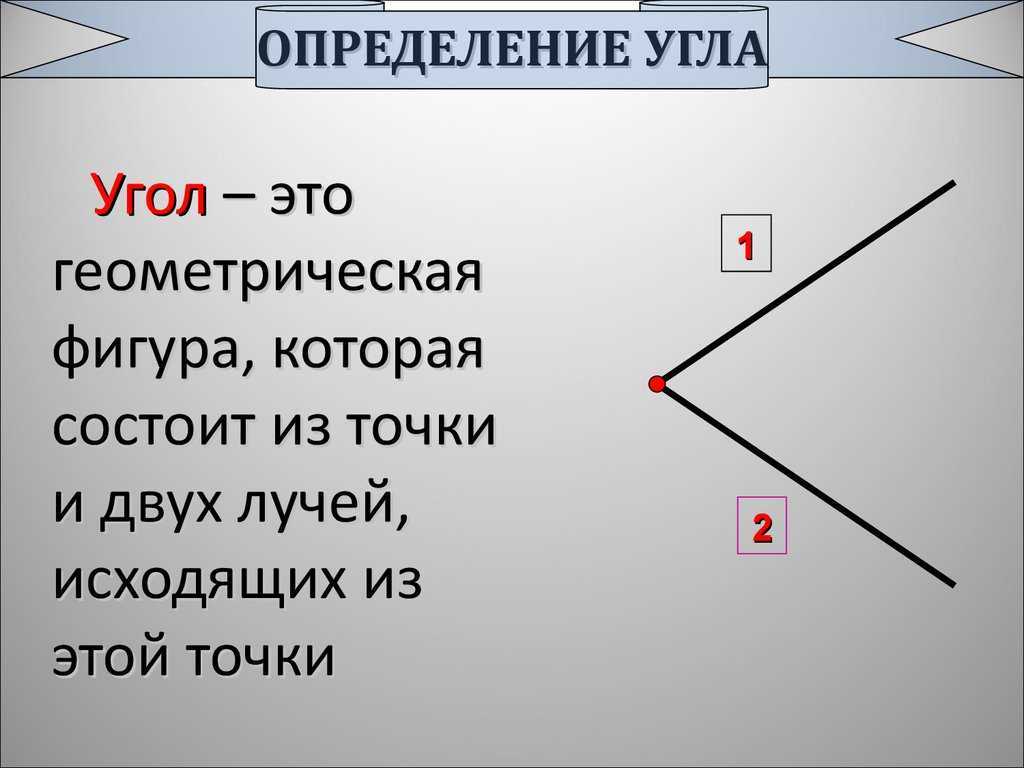На основании этого факта острый угол равен 75°.
Необходимо вычислить, чему равен угол АОЕ при условии, что ОЕ является биссектрисой угла АОС. Аналогично, ОD играет роль биссектрисы угла СОВ. Градусная мера угла ВОD составляет 25°. Необходимо вычислить угол АОЕ.
Узоры и орнаменты на посуде»
..
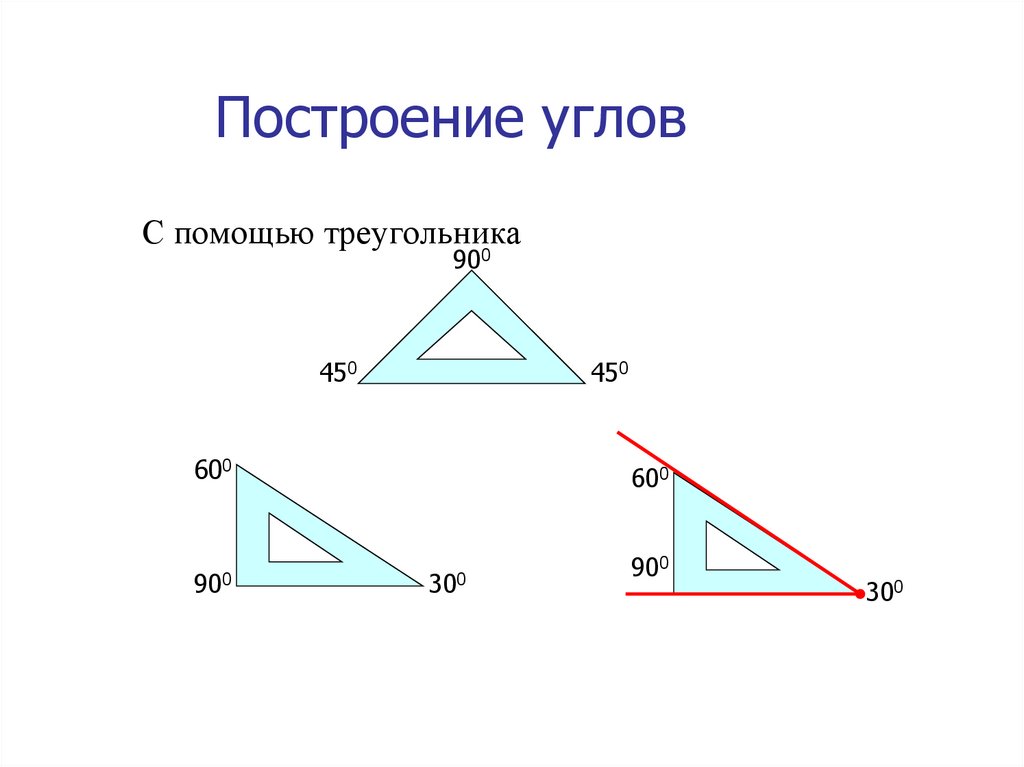
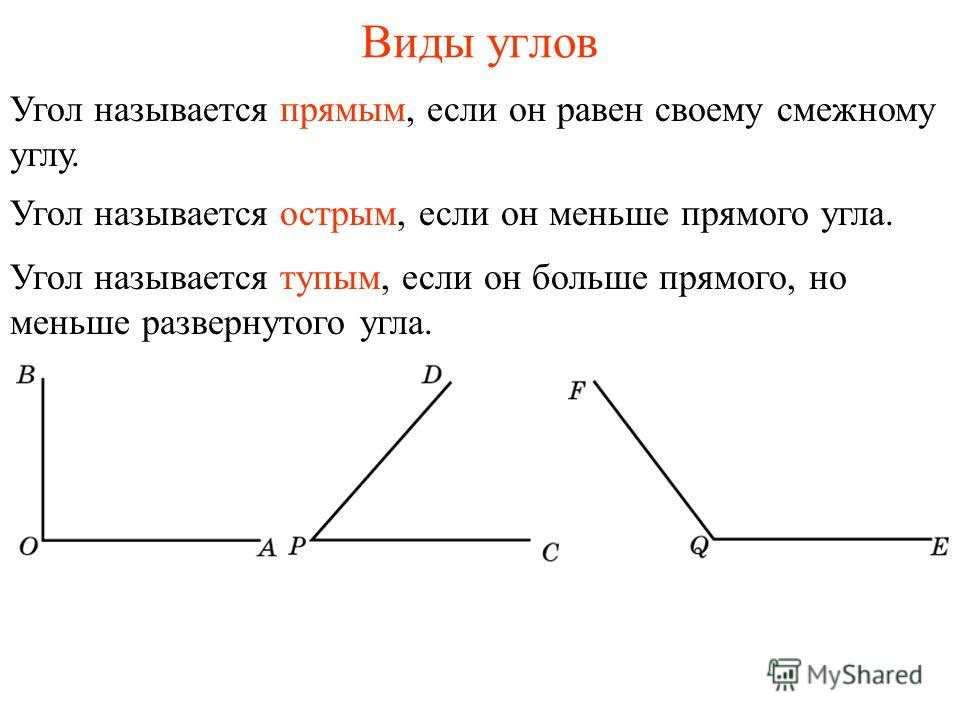Упражнение 11.2.
>
Вопрос 11
В каком направлении вы смотрите после того, как сделаете акварели?
a Постройте ∠FGH, конгруэнтную ∠WXY.
b Постройте дополнение к ∠ABC.
c Построить дополнение к ∠WXY. г Постройте угол, градусом которого является разность ∠WXY и ∠ABC.
e Постройте угол, градусная мера которого в два раза больше угла ∠ABC.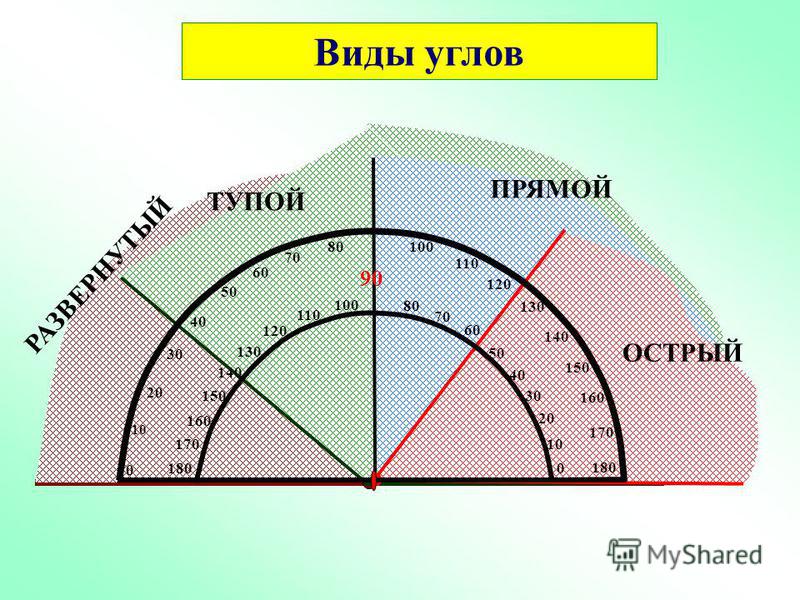
\circ$. Другими словами, это угол, образующий прямую с $\angle WXY$. Вот как его построить:
— Нарисуйте луч $WX$.
— Поместите компас в точку $W$ и начертите дугу, пересекающую $WX$.
— Не меняя ширины компаса, поместите циркуль в точку $X$ и начертите дугу, пересекающую предыдущую дугу.
— Нарисуйте луч $YZ$, проходящий через пересечение двух дуг.
— $\angle WXY$ и $\angle XYZ$ являются дополнительными.
Вычислите периметр треугольника. 22. Сторона ромба 13 см, а одна из его диагоналей 10 см. Найдите другую диагональ.
Найдите длину отрезка АС, если ВД=8 см. 32. Найдите катеты прямоугольного треугольника, если его гипотенуза равна 5 см, а один из углов 60°. 33. Периметр параллелограмма равен 122 см. Одна из его сторон больше другой на 25 см. Найдите стороны параллелограмма. 34. Диагональ квадрата 2 2 . Вычислить площадь квадрата. 35. Меньшее основание ВС трапеции АВСД равно 12 см. АВ=СД, Д=45°. Её высота равна 8 см. Найдите площадь трапеции. 36. Гипотенуза и катет прямоугольного треугольника равны соответственно 9 и 4 2 м. Найдите другой катет треугольника. 37. Периметр параллелограмма равен 122 см. Одна из его сторон больше другой на 25 см. Найдите стороны параллелограмма. 38. Основания равнобедренной трапеции равны 10 см и 20 см, а высота 5 см. Вычислите площадь трапеции. 39. Как изменится длина окружности, если радиус увеличить в 3 раза. 40. Найти площадь ромба, если его периметр равен 40 см, а одна из диагоналей имеет длину 12 см.
6в)
——————————————•————————
((8•(с 2 ))-24с) (12с+36) 
1 Вытягивание одинаковых факторов :
на обоих стороны линии дроби. 
- AB + AB равно нулю и поэтому исключается из выражения. 
2 Факторизация c 2 + 2c - 3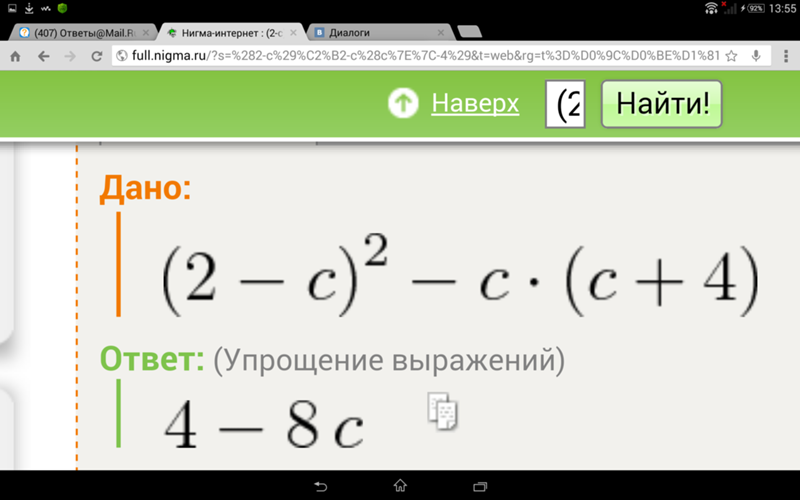 
3 Факторизация 4c 2 -7c+3 
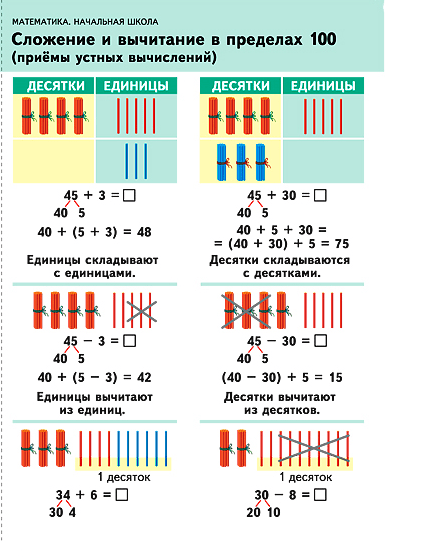Возьмите простой карандаш и проверьте работу соседа, если решено правильно
поставьте +, если нет -.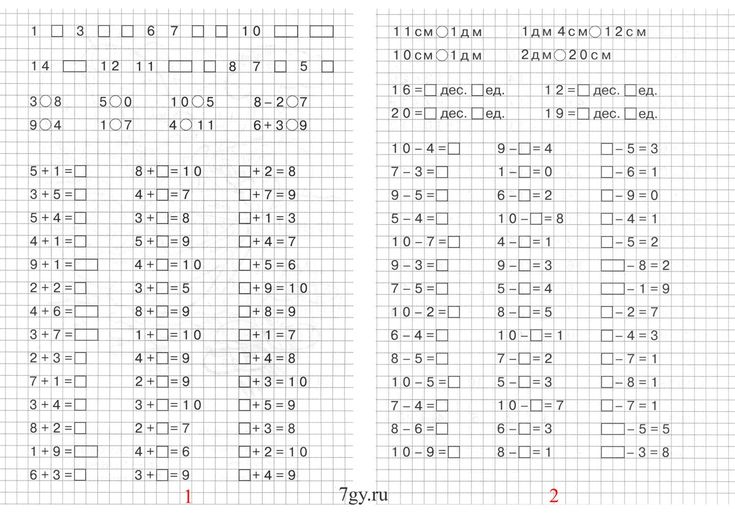
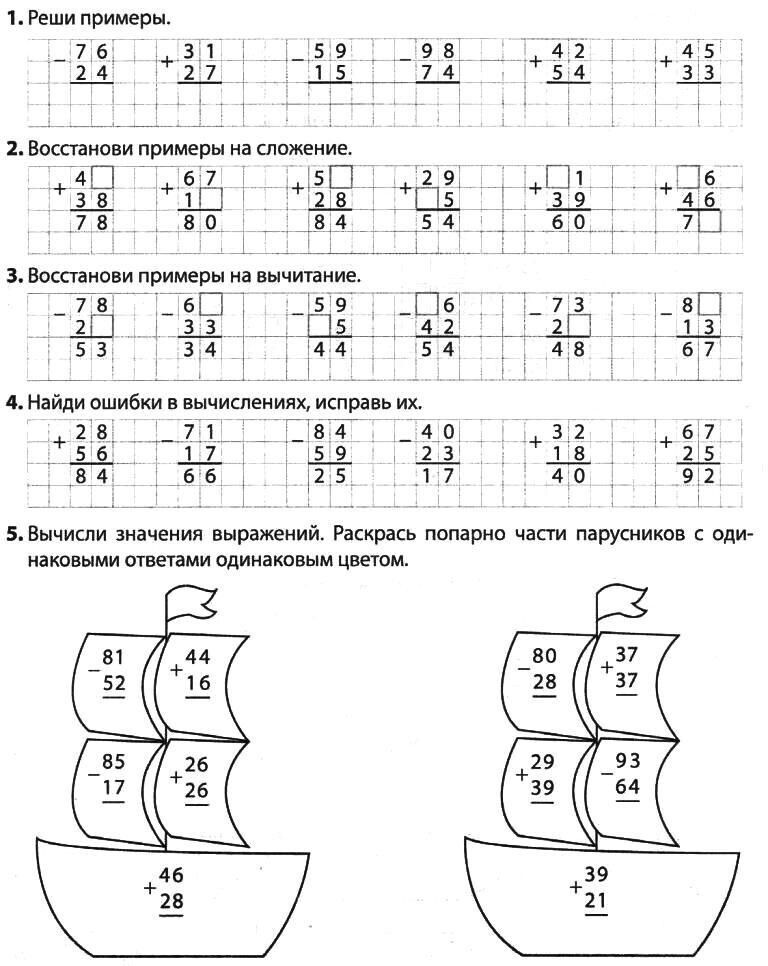читаю выражение
Выслушай ответ учеников. Правильно ответили ребята?
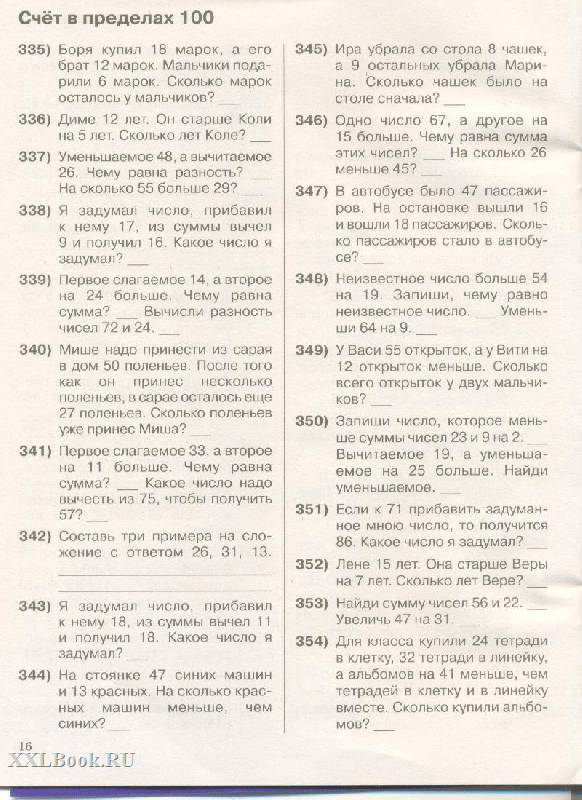Сколько получилось треугольников? Раскрась их разным цветом).
Ответ: 17 треугольников.
Заключение.
ОА.Б. Сложите и вычтите в пределах 20.
МД.А.3. Оцените длину, используя единицы измерения: дюймы, футы, сантиметры и метры.
Покажите измерения, построив линейный график, где горизонтальная шкала отмечена в целых числах.
Сложение и вычитание до 100. . Овладение базовыми навыками сложения и вычитания до 20 является основой для обучения сложению и вычитанию до 100. Кроме того, усвоение фактов вверх до 20 с помощью игр, практических стратегий и большого количества практики помогает учащимся обрести уверенность и мастерство. Затем учащиеся работают над более сложными математическими вычислениями сложения и вычитания до 100 с помощью различных стратегий, моделей и рассуждений.
Модуль 3: Сложение и вычитание Беглость в пределах 100
4. Мини-урок . Обучите, смоделируйте и обсудите новый навык на сегодняшнем уроке.
5. Практика- В каждом разделе практики перечислены три типа занятий, которые хорошо сочетаются с конкретным уроком. Центр(ы)- Новый центр(ы) будет представлен на уроке. Страницы заданий — Для этих страниц требуются некоторые основные материалы, такие как ножницы, клей или игральные кости. Практические страницы- Для этого нужны только карандаш и мелки! Они отлично подходят для работы за столом, домашних заданий или работы в дороге!
Напишите суммы, используя маркер для сухого стирания. Проверьте свои ответы по ключу.
Запишите уравнение на листе для записей.
Раскрашивайте звезду каждый раз, когда решаете задачи.
Выигрывает тот, кто первым наберет три подряд.
Запишите уравнение на листе для записей.
Решать проблему. Покажите свою работу на коврике.
Прочитай задачу. Решите, какие сегменты числовой прямой вам нужны, чтобы решить задачу. Запишите свой ответ в регистрационном листе.
Расставь их по клеточкам так, чтобы уравнение было верным.
Используйте стратегии, основанные на разрядности и свойствах операций для решения.