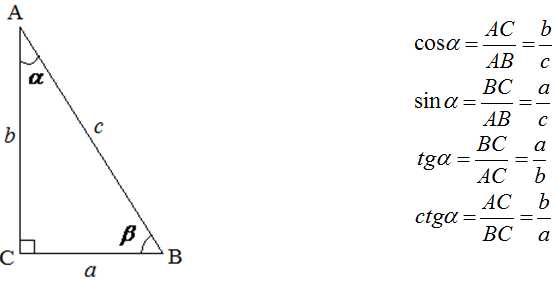От действий над матрицами к пониманию их сути… / Habr
Очень уважаю людей, которые имеют смелость заявить, что они что-то не понимают. Сам такой. То, что не понимаю, — обязательно должен изучить, осмыслить, понять. Статья «Математика на пальцах», и особенно матричная запись формул, заставили меня поделиться своим небольшим, но, кажется, немаловажным опытом работы с матрицами.Лет эдак 20 назад довелось мне изучать высшую математику в вузе, и начинали мы с матриц (пожалуй, как и все студенты того времени). Почему-то считается, что матрицы — самая лёгкая тема в курсе высшей математики. Возможно — потому, что все действия с матрицами сводятся к знанию способов расчёта определителя и нескольких формул, построенных — опять же, на определителе. Казалось бы, всё просто. Но… Попробуйте ответить на элементарный вопрос — что такое определитель, что означает число, которое вы получаете при его расчёте? (подсказка: вариант типа «определитель — это число, которое находится по определённым правилам» не является правильным ответом, поскольку говорит о методе получения, а не о самой сути определителя). Сдаётесь? — тогда читаем дальше…
Сразу хочу сказать, что я не математик ни по образованию, ни по должности. Разве что мне интересна суть вещей, и я порой пытаюсь до них «докопаться». Так же было и с определителем: нужно было разобраться со множественной регрессией, а в этом разделе эконометрики практически всё делается через… матрицы, будь они неладны. Вот и пришлось мне самому провести небольшое исследование, поскольку ни один из знакомых математиков не дал внятного ответа на поставленный вопрос, изначально звучавший как «что такое определитель». Все утверждали, что определитель — это такое число, которое особым образом посчитано, и если оно равно нулю, то… В общем, как в любом учебнике по линейной алгебре. Спасибо, проходили.
Если какую-то идею придумал один человек, то другой человек должен быть в состоянии её понять (правда, для этого порой приходится вооружаться дополнительными знаниями). Обращение к «великому и могучему» поисковику показало, что «площадь параллелограмма равна модулю определителя матрицы, образованной векторами — сторонами параллелограмма». Говоря простым языком, если матрица — это способ записи системы уравнений, то каждое уравнение в отдельности описывает вектор. Построив из точки начала координат векторы, заданные в матрице, мы таким образом зададим в пространстве некоторую фигуру. Если наше пространство одномерное, то фигура — это отрезок; если двумерное — то фигура — параллелограмм, и так далее.
Получается, что для одномерного пространства определитель — это длина отрезка, для плоскости — площадь фигуры, для трёхмерной фигуры — её объём… дальше идут n-мерные пространства, вообразить которые нам не дано. Если объём фигуры (то есть определитель для матрицы 3*3) равен нулю, то это означает, что сама фигура не является трёхмерной (она может быть при этом двухмерной, одномерной или вообще представлять собой точку). Ранг матрицы — это истинная (максимальная) размерность пространства, для которого определитель не равен нулю.
Так, с определителем почти всё понятно: он определяет «объёмность» фигуры, образованной описанными системой уравнений векторами (хотя непонятно, почему его значение не зависит от того, имеем мы дело с исходной матрицей, или с транспонированной — возможно, транспонирование — это вид аффинного преобразования?). Теперь нужно разобраться с действиями над матрицами…
Если матрица — это система уравнений (а иначе зачем нам таблица каких-то цифр, не имеющих к реальности никакого отношения?), то мы можем с ней делать разные вещи. Например, можем сложить две строки одной и той же матрицы, или умножить строку на число (то есть каждый коэффициент строки умножаем на одно и то же число). Если у нас есть две матрицы с одинаковыми размерностями, то мы их можем сложить (главное, чтобы при этом мы не сложили бульдога с носорогом — но разве математики, разрабатывая теорию матриц, думали о таком варианте развития событий?). Интуитивно понятно, тем более что в линейной алгебре иллюстрациями подобных операций являются системы уравнений.
Однако в чём смысл умножения матриц? Как я могу умножить одну систему уравнений на другую? Какой смысл будет иметь то, что я получу в этом случае? Почему для умножения матриц неприменимо переместительное правило (то есть произведение матриц В*А не то что не равно произведению А*В, но и не всегда осуществимо)? Почему, если мы перемножим матрицу на вектор-столбец, то получим вектор-столбец, а если перемножим вектор-строку на матрицу, то получим вектор-строку?
Ну, тут уж не то что Википедия, — тут даже современные учебники по линейной алгебре бессильны дать какое-либо внятное объяснение. Поскольку изучение чего-либо по принципу «вы сначала поверьте — а поймёте потом» — не для меня, копаю в глубь веков (точнее — читаю учебники первой половины XX века) и нахожу интересную фразу…
Если совокупность обычных векторов, т.е. направленных геометрических отрезков, является трёхмерным пространством, то часть этого пространства, состоящая из векторов, параллельных некоторой плоскости, является двумерным пространством, а все векторы, параллельные некоторой прямой, образуют одномерное векторное пространство.
В книгах об этом напрямую не говорится, но получается, что векторам, параллельным некоторой плоскости, необязательно лежать на этой плоскости. То есть они могут находиться в трёхмерном пространстве где угодно, но если они параллельны именно этой плоскости, то они образуют двумерное пространство… Из приходящих мне на ум аналогий — фотография: трёхмерный мир представлен на плоскости, при этом вектору, параллельному матрице (или плёнке) фотоаппарата, будет соответствовать такой же вектор на картинке (при условии соблюдении масштаба 1:1). Отображение трёхмерного мира на плоскости «убирает» одно измерение («глубину» картинки). Если я правильно понял сложные математические концепции, перемножение двух матриц как раз и представляет собой подобное отражение одного пространства в другом. Поэтому, если отражение пространства А в пространстве В возможно, то допустимость отражения пространства В в пространстве А — не гарантируется.
Любая статья заканчивается в тот момент, когда автору надоедает её писать. Поскольку я не ставил перед собой цели объять необъятное, а исключительно хотел понять суть описанных операций над матрицами и то, как именно матрицы связаны с решаемыми мной системами уравнений, я не полез в дальнейшие дебри линейной алгебры, а вернулся к эконометрике и множественной регрессии, но сделал это уже более осознанно. Понимая, что и зачем я делаю и почему только так, а не иначе. То, что у меня получилось в этом материале, можно озаглавить как «глава о сути основных операций линейной алгебры, которую почему-то забыли напечатать в учебниках». Но ведь мы же не читаем учебников, правда? Если честно, когда я учился в университете, мне очень не хватало именно понимания затронутых здесь вопросов, поэтому я надеюсь, что, изложив этот непростой материал по возможности простыми словами, я делаю доброе дело и помогаю кому-то вникнуть в саму суть матричной алгебры, переведя операции над матрицами из раздела «камлание с бубном» в раздел «практические инструменты, применяемые осознанно».
habr.com
Матрицы, определители, системы линейных уравнений (Лекция №12)
ОПРЕДЕЛЕНИЕ МАТРИЦЫ. ВИДЫ МАТРИЦ
Матрицей размером m×n называется совокупность m·n чисел, расположенных в виде прямоугольной таблицы из m строк и n столбцов. Эту таблицу обычно заключают в круглые скобки. Например, матрица может иметь вид:
Для краткости матрицу можно обозначать одной заглавной буквой, например, А или В.
В общем виде матрицу размером m×n записывают так
.
Числа, составляющие матрицу, называются элементами матрицы. Элементы матрицы удобно снабжать двумя индексами aij: первый указывает номер строки, а второй – номер столбца. Например, a23 – элемент стоит во 2-ой строке, 3-м столбце.
Если в матрице число строк равно числу столбцов, то матрица называется квадратной, причём число ее строк или столбцов называется порядком матрицы. В приведённых выше примерах квадратными являются вторая матрица – её порядок равен 3, и четвёртая матрица – её порядок 1.
Матрица, в которой число строк не равно числу столбцов, называется прямоугольной. В примерах это первая матрица и третья.
Различаются также матрицы, имеющие только одну строку или один столбец.
Матрица, у которой всего одна строка , называется матрицей – строкой (или строковой), а матрица, у которой всего один столбец, матрицей – столбцом.
Матрица, все элементы которой равны нулю, называется нулевой и обозначается (0), или просто 0. Например,
.
Главной диагональю квадратной матрицы назовём диагональ, идущую из левого верхнего в правый нижний угол.
Квадратная матрица, у которой все элементы, лежащие ниже главной диагонали, равны нулю, называется треугольной матрицей.
.
Квадратная матрица, у которой все элементы, кроме, быть может, стоящих на главной диагонали, равны нулю, называется диагональной матрицей. Например, или .
Диагональная матрица, у которой все диагональные элементы равны единице, называется единичной матрицей и обозначается буквой E. Например, единичная матрица 3-го порядка имеет вид .
ДЕЙСТВИЯ НАД МАТРИЦАМИ
Равенство матриц. Две матрицы A и B называются равными, если они имеют одинаковое число строк и столбцов и их соответствующие элементы равны aij = bij. Так если и , то A=B, если a11 = b11, a12 = b12, a21 = b21 и a22 = b22.
Транспонирование. Рассмотрим произвольную матрицу A из m строк и n столбцов. Ей можно сопоставить такую матрицу B из n строк и m столбцов, у которой каждая строка является столбцом матрицы A с тем же номером (следовательно, каждый столбец является строкой матрицы A с тем же номером). Итак, если , то .
Эту матрицу B называют транспонированной матрицей A, а переход от A к B транспонированием.
Таким образом, транспонирование – это перемена ролями строк и столбцов матрицы. Матрицу, транспонированную к матрице A, обычно обозначают AT.
Связь между матрицей A и её транспонированной можно записать в виде .
Например. Найти матрицу транспонированную данной.
Сложение матриц. Пусть матрицы A и B состоят из одинакового числа строк и одинакового числа столбцов, т.е. имеют одинаковые размеры. Тогда для того, чтобы сложить матрицы A и B нужно к элементам матрицы A прибавить элементы матрицы B, стоящие на тех же местах. Таким образом, суммой двух матриц A и B называется матрица C, которая определяется по правилу, например,
или
Примеры. Найти сумму матриц:
- .
- — нельзя, т.к. размеры матриц различны.
- .
Легко проверить, что сложение матриц подчиняется следующим законам: коммутативному A+B=B+A и ассоциативному (A+B)+C=A+(B+C).
Умножение матрицы на число. Для того чтобы умножить матрицу A на число k нужно каждый элемент матрицы A умножить на это число. Таким образом, произведение матрицы A на число k есть новая матрица, которая определяется по правилу или .
Для любых чисел a и b и матриц A и B выполняются равенства:
- .
Примеры.
- .
- Найти 2A-B, если , .
.
- Найти C=–3A+4B.
Матрицу C найти нельзя, т.к. матрицы A и B имеют разные размеры.
Умножение матриц. Эта операция осуществляется по своеобразному закону. Прежде всего, заметим, что размеры матриц–сомножителей должны быть согласованы. Перемножать можно только те матрицы, у которых число столбцов первой матрицы совпадает с числом строк второй матрицы (т.е. длина строки первой равна высоте столбца второй). Произведением матрицы A не матрицу B называется новая матрица C=AB, элементы которой составляются следующим образом:
.
Таким образом, например, чтобы получить у произведения (т.е. в матрице C) элемент, стоящий в 1-ой строке и 3-м столбце c13, нужно в 1-ой матрице взять 1-ую строку, во 2-ой – 3-й столбец, и затем элементы строки умножить на соответствующие элементы столбца и полученные произведения сложить. И другие элементы матрицы-произведения получаются с помощью аналогичного произведения строк первой матрицы на столбцы второй матрицы.
В общем случае, если мы умножаем матрицу A = (aij) размера m×n на матрицу B = (bij) размера n×p, то получим матрицу C размера m×p, элементы которой вычисляются следующим образом: элемент cij получается в результате произведения элементов i-ой строки матрицы A на соответствующие элементы j-го столбца матрицы B и их сложения.
Из этого правила следует, что всегда можно перемножать две квадратные матрицы одного порядка, в результате получим квадратную матрицу того же порядка. В частности, квадратную матрицу всегда можно умножить саму на себя, т.е. возвести в квадрат.
Другим важным случаем является умножение матрицы–строки на матрицу–столбец, причём ширина первой должна быть равна высоте второй, в результате получим матрицу первого порядка (т.е. один элемент). Действительно,
.
Примеры.
- Пусть
Найти элементы c12, c23 и c21 матрицы C.
- Найти произведение матриц.
.
- .
- — нельзя, т.к. ширина первой матрицы равна 2-м элементам, а высота второй – 3-м.
- Пусть
Найти АВ и ВА.
Найти АВ и ВА.
, B·A – не имеет смысла.
Таким образом, эти простые примеры показывают, что матрицы, вообще говоря, не перестановочны друг с другом, т.е. A∙B ≠ B∙A. Поэтому при умножении матриц нужно тщательно следить за порядком множителей.
Можно проверить, что умножение матриц подчиняется ассоциативному и дистрибутивному законам, т.е. (AB)C=A(BC) и (A+B)C=AC+BC.
Легко также проверить, что при умножении квадратной матрицы A на единичную матрицу E того же порядка вновь получим матрицу A, причём AE=EA=A.
Можно отметить следующий любопытный факт. Как известно произведение 2-х отличных от нуля чисел не равно 0. Для матриц это может не иметь места, т.е. произведение 2-х не нулевых матриц может оказаться равным нулевой матрице.
Например, если , то
.
ПОНЯТИЕ ОПРЕДЕЛИТЕЛЕЙ
Пусть дана матрица второго порядка – квадратная матрица, состоящая из двух строк и двух столбцов .
Определителем второго порядка, соответствующим данной матрице, называется число, получаемое следующим образом: a11a22 – a12a21.
Определитель обозначается символом .
Итак, для того чтобы найти определитель второго порядка нужно из произведения элементов главной диагонали вычесть произведение элементов по второй диагонали.
Примеры. Вычислить определители второго порядка.
- .
- Вычислить определитель матрицы D, если D= -А+2В и
Аналогично можно рассмотреть матрицу третьего порядка и соответствующий ей определитель.
Определителем третьего порядка, соответствующим данной квадратной матрице третьего порядка, называется число, обозначаемое и получаемое следующим образом:
.
Таким образом, эта формула даёт разложение определителя третьего порядка по элементам первой строки a11, a12, a13 и сводит вычисление определителя третьего порядка к вычислению определителей второго порядка.
Примеры. Вычислить определитель третьего порядка.
- .
- .
- Решите уравнение..
.
(x+3)(4x-4-3x)+4(3x-4x+4)=0.
(x+3)(x-4)+4(-x+4)=0.
(x-4)(x-1)=0.
x1 = 4, x2 = 1.
Аналогично можно ввести понятия определителей четвёртого, пятого и т.д. порядков, понижая их порядок разложением по элементам 1-ой строки, при этом знаки «+» и «–» у слагаемых чередуются.
Итак, в отличие от матрицы, которая представляют собой таблицу чисел, определитель это число, которое определённым образом ставится в соответствие матрице.
toehelp.ru
Нахождение фундаментальной матрицы «для чайников»
Доброго времени суток!
Этот пост для тех, кто хочет научиться строить Фундаментальную Матрицу решений Системы Линейных Дифференциальных Уравнений, но боится.
Предыстория
Если немного погуглить на эту тему, то можно найти достаточное количество статей, большинство из которых описывают построение Фундаментальной матрицы через Жордановы формы.
Мне кажется, что это достаточно сложно понять вот так вот сразу, а тем более воплотить в жизнь.
История
Когда-то мне хотелось открыть браузер, вбить в поисковик «Построить фундаментальную матрицу легко/быстро/понятно/НЕ через Жордановы формы» и получить готовый алгоритм, и чтобы он был, как говорится, на блюдечке с голубой каёмочкой.
Алгоритм
Здесь я привожу один занятный и простой для понимания способ построения Фундаментальной матрицы, который мне когда-то рассказал один замечательный преподаватель. Этот способ наречен «полиномиальным». Быть может, когда-нибудь он пригодится Вам. Я рассчитываю на то, что читатель знаком со всеми сопутствующими определениями, такими как «собственное число», «определитель», и т.д.
Немножко теории

Закрепим на практике
Одной теорией сыт не будешь, поэтому рассмотрим этот способ в действии:
Заключение
Надеюсь, что изложил свои мысли достаточно понятно. И прошу прощения за возможную свою неосведомленность по поводу названия этого метода. Если изложенный метод известен под другими названиями, мне хотелось бы их узнать. Всем спасибо за внимание!
Автор: Tsin
Источник
www.pvsm.ru
размер матрицы, что такое «кроп»
Мне в почте приходит немало вопросов начинающих любителей фотографии, и я решил, что уже пора сделать небольшую серию статей из серии «Фотографии для чайников», в которых предполагается дать объяснения различным фотографическим терминам, рассказать о том, как подбирать себе фотоаппарат под любительские задачи, ну и обязательно будет несколько статей о работе с программой Adobe Lightroom, ибо обработка сделанных снимков не менее важна, чем сам процесс фотографирования.
В данной статье мы поговорим о таком важном параметре, как размер матрицы фотоаппарата, и раскроем завесу тайны над загадочным термином «кроп-фактор».
Продавцы в магазинах и маркетологи обычно любят оперировать количеством мегапикселов у камеры, и их послушать — так какая-нибудь «цифромыльница» с 20 мегапикселами значительно круче зеркалки с 16 мегапикселами. А это вовсе не так. Потому что, кроме всего прочего, в камерах очень важен физический размер матрицы (сенсора), а не только мегапикселы.
Вот в разговорах о фотокамерах продвинутых фотолюбителей и профессионалов часто приходится слышать фразы из серии: «Да у нее же матрица маленькая», «Да там же пятый кроп», «Что можно снять на такую матрицу?», «Full frame — наше все».
Что за матрица такая?
Матрица (светочувствительная матрица, сенсор, фотодатчик) — это микросхема, состоящая из фотодиодов, являющаяся важнейшей частью цифровой фотокамеры.
Проще говоря, матрица — это аналог фотопленки. В пленочных фотоаппаратах изображение через объектив попадало на фотопленку и хранилось на ней, а в цифровых фотоаппаратах изображение через объектив попадает на матрицу, формируется там, но хранится уже на карте памяти или во встроенной памяти камеры.
Так называемая полная матрица (Full Frame) имеет размер, приблизительно равный размеру кадра 35-миллиметровой пленки, на которую производилась съемка в пленочных аппаратах.
Полная матрица дорога в производстве (там высок процент брака), фотоаппараты с ней, как правило, имеют немаленькие размеры, солидный вес и в любом случае стоят дорого, в результате чего камеры с полной матрицей используют в основном только профессионалы. Ну или продвинутые любители с хорошими заработками, для которых термин Full Frame является сакральным.
Чтобы уменьшить стоимость, размер и вес камер, производители додумались делать матрицу меньших размеров — обрезать ее. Английское слово crop и означает — «обрезать». Кроп-фактор — число, показывающее, во сколько раз данную матрицу обрезали по отношению к полной матрице (Full Frame).
Кроп-фактор 1,5 или 1,6 (самый популярный вариант в любительских зеркалках) означает, что матрица тут уменьшена в 1,5 или 1,6 раза по сравнению с полноформатной.
Вот, например, визуальное сравнение размеров матрицы фотокамеры с Full Frame и матрицы любительской зеркалки (с сайта Cameraimagesensor.com).

В продвинутых беззеркальных камерах, которые сейчас активно теснят любительские зеркалки, нередко устанавливается матрица с кроп-фактором 2 — то есть она в два раза меньше полноформатной матрицы. Вот она в сравнении с предыдущими двумя.
В дешевых цифровых «мыльницах» вроде Canon Powershot A1300 устанавливается матрица с кропом что-то вроде 5,62 — вот так это выглядит в сравнении.
Ну и в современных смартфонах сейчас ставят матрицы с кроп-фактором в районе 7,1 — например, в iPhone 5S именно такая установлена. Вот она в масштабе сравнений.
Теперь вопрос: какую все-таки матрицу предпочесть? Нужно ли сразу стремиться к Full Frame, чтобы на нее ежедневно молиться?
С одной стороны, чем больше сенсор, тем лучше качество получаемой фотографии. Конечно, тут играют и многие другие факторы, прежде всего объектив, но просто чисто физически: чем больше матрица, тем лучше качество.
(Кстати, существуют так называемые среднеформатные камеры с сенсорами от 40 мм по ширине и больше, но они уже только для профессионалов и стоят, как хорошие автомобили.)
В чем проявляется это «лучше качество»? В детализации, резкости, четкости, в качестве получаемого отпечатка: если снимок нужно будет использовать в полиграфии, то там полный формат матрицы практически обязателен, чтобы как можно меньше проиграть в качестве при заметном увеличении во время печати.
Кроме того, чем больше исходное изображение, тем проще его кадрировать: то есть вырезать из него кусок кадра и при этом получать приемлемое качество.
Также чем больше матрица, тем лучше камера снимает в плохих условиях освещения: у большой матрицы при высоких значениях светочувствительности значительно меньше проявляется так называемый «шум» (это точки на изображении — как зерно на старых черно-белых фотографиях, снятых на высокочувствительную пленку).
С другой стороны, полный формат, как мы уже говорили, ведет к повышение размеров камеры, увеличению веса и всегда — к высокой цене. И если вы - фотолюбитель, то зачем вам тратить большие деньги и таскать с собой тяжеленную камеру, если вы не очень представляете, что вам это вообще дает?
В результате камеру (и сенсор) нужно подбирать под свои задачи и свой кошелек. Для начинающих вполне подойдет недорогая «мыльница» с кропом 5,7. Продвинутым любителям, которые уже что-то понимают в фотографии и знают, какие возможности им предоставляют те или иные камеры, лучше ориентироваться или на хорошие беззеркалки с кропом 2 — 1,5, или на любительские зеркальные камеры с кропом 1,5 — 1,6, тем более что такие зеркалки сейчас выпускаются компактные и легкие.
www.exler.ru
Умножение матриц, формулы и примеры
ОПРЕДЕЛЕНИЕ Произведением матрицы размером на матрицу размером называется матрица () размером элементы которой определяются формулой:
Иначе говоря, элемент матрицы стоящий в -той строке и -том столбце, равен сумме произведений элементов -той строки матрицы на соответствующие элементы -го столбца матрицы Таким образом, умножение осуществляется по правилу умножения строки на столбец.
Не всякие две матрицы можно перемножить. Произведение двух матриц возможно только в том случае, если число столбцов матрицы совпадает с числом строк в матрице . Для того чтобы перемножить две квадратные матрицы необходимо, чтобы они были одного порядка. При этом в результате получится матрица того же порядка, что и перемножаемые матрицы.
Как умножать матрицы, примеры
ПРИМЕР 1| Задание | Найти произведение матрицы и вектора-столбца .
|
| Решение | Матрица имеет размерность матрица имеет размерность значит размерность произведения будет Действительно,
Заметим, что произведение этих матриц в обратном порядке невозможно. |
| Ответ |
Произведение двух матриц в общем случае зависит от порядка сомножителей, то есть оно не коммутативно:
ПРИМЕР 2
| Задание | Заданы матрицы и . Найти их произведения и
|
| Решение | Матрица имеет размерность а матрица – размерность тогда размерность произведения будет . Действительно, умножая по принципу, строка первой матрицы на столбец второй, получим
Произведение так же будет существовать и его размерность будет .
|
| Ответ |
Но бывают матрицы, для которых выполняется равенство
такие матрицы называются перестановочными или коммутирующими. Такие матрицы будут обязательно квадратными.
ПРИМЕР 3| Задание | Проверить являются ли перестановочными матрицы и , если
|
| Решение | Найдем произведения этих матриц и .
Таким образом, для заданных матриц выполняется равенство поэтому они являются перестановочными. |
| Ответ | Матрицы и перестановочные. |
Определитель матрицы и способы вычисления
Обратная матрица и способы вычисления
Ранг матрицы
Транспонирование матрицы
Сложение матриц
Единичная матрица
ru.solverbook.com
Матрицы. Действия над матрицами. Свойства операций над матрицами. Виды матриц.
Матрицы. Действия над матрицами. Свойства операций над матрицами. Виды матриц.
Матрицы (и соответственно математический раздел — матричная алгебра) имеют важное значение в прикладной математике, так как позволяют записать в достаточно простой форме значительную часть математических моделей объектов и процессов. Термин «матрица» появился в 1850 году. Впервые упоминались матрицы еще в древнем Китае, позднее у арабских математиков.
Матрицей A=Amn порядка m*n называется прямоугольная таблица чисел, содержащая m — строк и n — столбцов.

Элементы матрицы aij, у которых i=j, называются диагональными и образуют главную диагональ.
Для квадратной матрицы (m=n) главную диагональ образуют элементы a11, a22,…, ann .
Равенство матриц.
A=B, если порядки матриц A и B одинаковы и aij=bij (i=1,2,…,m; j=1,2,…,n)
Действия над матрицами.
1. Сложение матриц — поэлементная операция
2. Вычитание матриц — поэлементная операция
3. Произведение матрицы на число — поэлементная операция
4. Умножение A*B матриц по правилу строка на столбец (число столбцов матрицы А должно быть равно числу строк матрицы B)
Amk*Bkn=Cmn причем каждый элемент сijматрицы Cmn равен сумме произведений элементов i-ой строки матрицы А на соответствующие элемеенты j-го столбца матрицы B , т.е.
Покажем операцию умножения матриц на примере
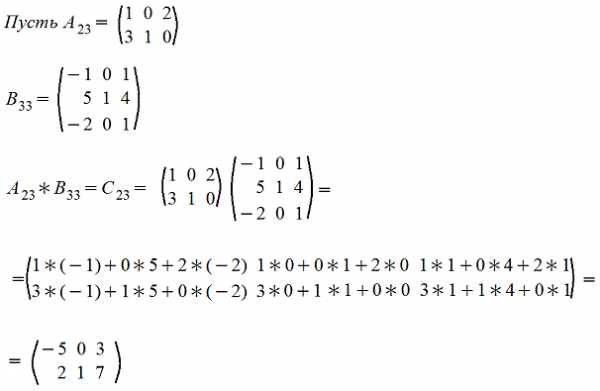
5. Возведение в степень
m>1 целое положительное число. А — квадратная матрица (m=n) т.е. актуально только для квадратных матриц
6. Транспонирование матрицы А. Транспонированную матрицу обозначают AT или A’
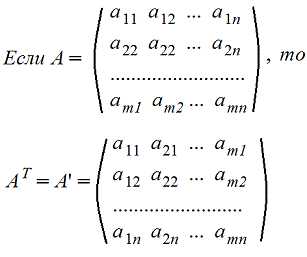
Строки и столбцы поменялись местами
Пример
Свойства опрераций над матрицами
A+B=B+A
(A+B)+C=A+(B+C)
λ(A+B)=λA+λB
A(B+C)=AB+AC
(A+B)C=AC+BC
λ(AB)=(λA)B=A(λB)
A(BC)=(AB)C
(A’)’=A
(λA)’=λ(A)’
(A+B)’=A’+B’
(AB)’=B’A’
Виды матриц
1. Прямоугольные: m и n — произвольные положительные целые числа
2. Квадратные: m=n
3. Матрица строка: m=1. Например, (1 3 5 7 ) — во многих практических задачах такая матрица называется вектором
4. Матрица столбец: n=1. Например
5. Диагональная матрица: m=n и aij=0, если i≠j. Например
6. Единичная матрица: m=n и
7. Нулевая матрица: aij=0, i=1,2,…,m
j=1,2,…,n
8. Треугольная матрица: все элементы ниже главной диагонали равны 0.
Пример.
9. Симметрическая матрица: m=n и aij=aji(т.е. на симметричных относительно главной диагонали местах стоят равные элементы), а следовательно A’=A
Например,
10. Кососимметрическая матрица: m=n и aij=-aji (т.е. на симметричных относительно главной диагонали местах стоят противоположные элементы). Следовательно, на главной диагонали стоят нули (т.к. при i=j имеем aii=-aii)
Пример.
Ясно, A’=-A
11. Эрмитова матрица: m=n и aii=-ãii (ãji— комплексно — сопряженное к aji, т.е. если A=3+2i, то комплексно — сопряженное Ã=3-2i)
Пример
tehtab.ru
Матрицы: определение и основные понятия.
Навигация по странице:
Определение матрицы
Определение.
Матрицей размера n×m называется прямоугольная таблица специального вида, состоящая из n строк и m столбцов, заполненная числами.Количество строк и столбцов задают размеры матрицы.
Обозначение
Матрица — это таблица данных, которая берется в круглые скобки:
| A = | 4 | 1 | -7 | ||
| -1 | 0 | 2 |
Матрица обычно обозначаются заглавными буквами латинского алфавитв. Матрица содержащая n строк и m столбцов, называется матрицей размера n×m. При необходимости размер матрицы записывается следующим образом: An×m.
Элементы матрицы
Элементы матрицы A обозначаются aij, где i — номер строки, в которой находится элемент, j — номер столбца.
Пример.
Элементы матрицы A4×4:| A = | 4 | 1 | -7 | 2 | ||
| -1 | 0 | 2 | 44 | |||
| 4 | 6 | 7 | 9 | |||
| 11 | 3 | 1 | 5 |
a11 = 4
Определение.
Строка матрицы называется нулевой, если все ее элементы равны нулю.Определение.
Если хотя бы один из элементов строки матрицы не равен нулю, то строка называется ненулевой.Пример.
Демонстрация нулевых и ненулевых строк матрицы:| 4 | 1 | -7 | < не нулевая строка | ||
| 0 | 0 | 0 | < нулевая строка | ||
| 0 | 1 | 0 | < не нулевая строка |
Определение.
Столбец матрицы называется нулевым, если все его элементы равны нулю.Определение.
Если хотя бы один из элементов столбца матрицы не равен нулю, то столбец называется ненулевым.Пример.
Демонстрация нулевых и ненулевых столбцов матрицы:| 0 | 1 | -7 | ||
| 0 | 0 | 2 | ||
^ | ^ | ^ |
не не нулевой столбец
Диагонали матрицы
Определение.
Главной диагональю матрицы называется диагональ, проведённая из левого верхнего угла матрицы в правый нижний угол.Определение.
Побочной диагональю матрицы называется диагональ, проведённая из левого нижнего угла матрицы в правый верхний угол.Пример.
Демонстрация главной и побочной диагонали матрицы:| 0 | 1 | -7 | — главнаяпобочная диагональ | ||
| 0 | 0 | 2 |
| 0 | 1 | -7 | — главнаяпобочная диагональ | ||
| 0 | 0 | 2 | |||
| 8 | 2 | 9 |
Определение.
Следом матрицы называется сумма диагональных элементов матрицы.Обозначение.
След матрицы обозначается trA = a11 + a22 + … + ann.ru.onlinemschool.com

 называетсяпределом функциипри
называетсяпределом функциипри и
и (или, что то же самое, при
(или, что то же самое, при ),
если для любого
),
если для любого существует
существует такое, что для всех
такое, что для всех и
и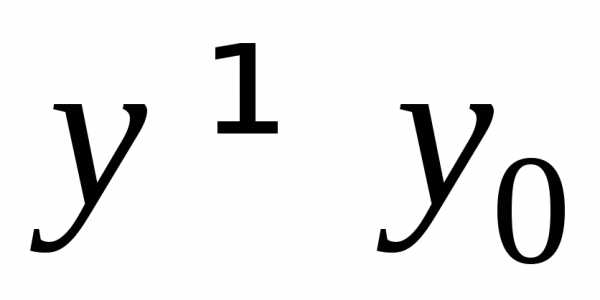 ,
и удовлетворяющих неравенствувыполняется неравенство.
Записывают:
,
и удовлетворяющих неравенствувыполняется неравенство.
Записывают: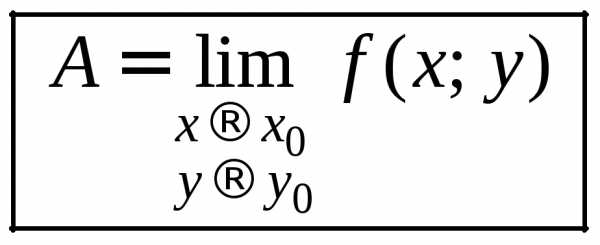
 стремится к
стремится к (число таких направлений бесконечно).
Определения бесконечно малых и бесконечно
больших величин являющихся функциями
двух переменных, аналогичны соответствующим
определениям для функций одной переменной.
(число таких направлений бесконечно).
Определения бесконечно малых и бесконечно
больших величин являющихся функциями
двух переменных, аналогичны соответствующим
определениям для функций одной переменной.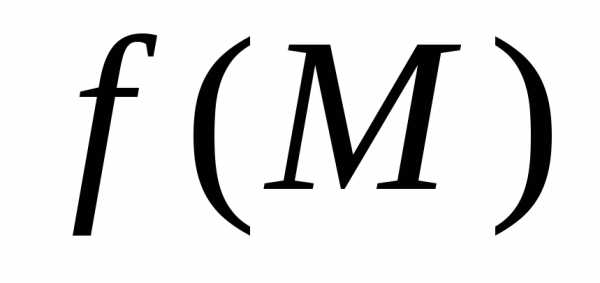 )
называетсянепрерывной в точке ,
если она:
)
называетсянепрерывной в точке ,
если она: в точке
в точке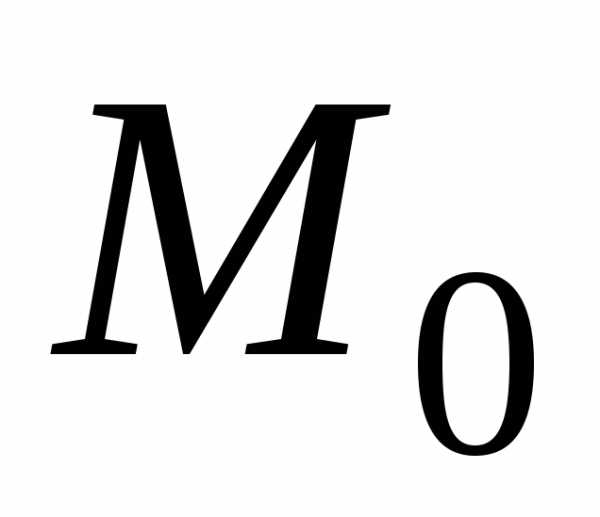 ,
т.е.
,
т.е.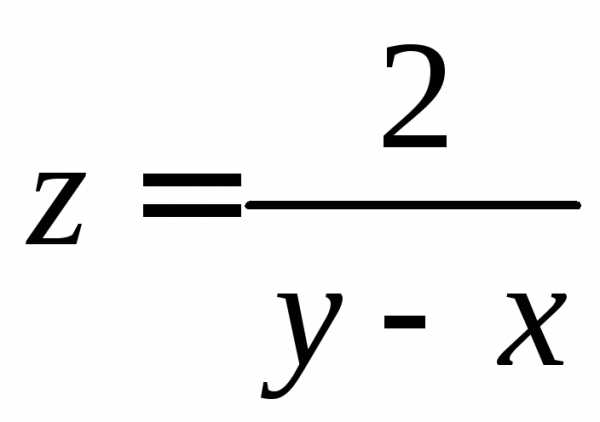 имеет линю разрыва
имеет линю разрыва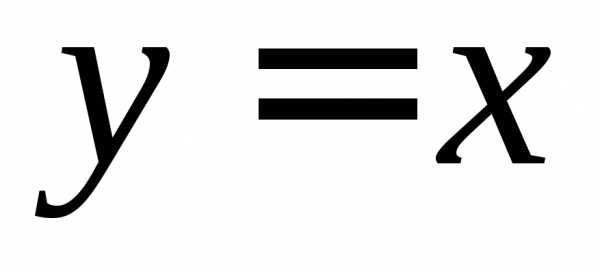 .
. и
и называютсяприращениями аргументов
называютсяприращениями аргументов и
и .
Тогда.
Величина
.
Тогда.
Величина называетсяполным приращением
функциив точке.
называетсяполным приращением
функциив точке. и
и стремится к нулю, т.е.
стремится к нулю, т.е.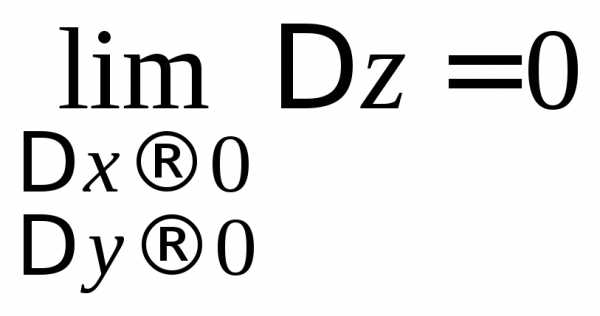 .
. пересечения поверхностис плоскостью,
параллельной плоскости
пересечения поверхностис плоскостью,
параллельной плоскости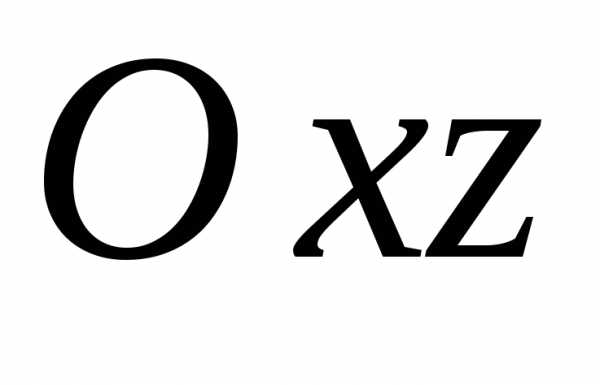 .
Так как в этой плоскости
.
Так как в этой плоскости сохраняет постоянное значение, то
сохраняет постоянное значение, то вдоль кривой
вдоль кривой будет меняться только в зависимости от
изменения
будет меняться только в зависимости от
изменения .
Дадим независимой переменной
.
Дадим независимой переменной приращение
приращение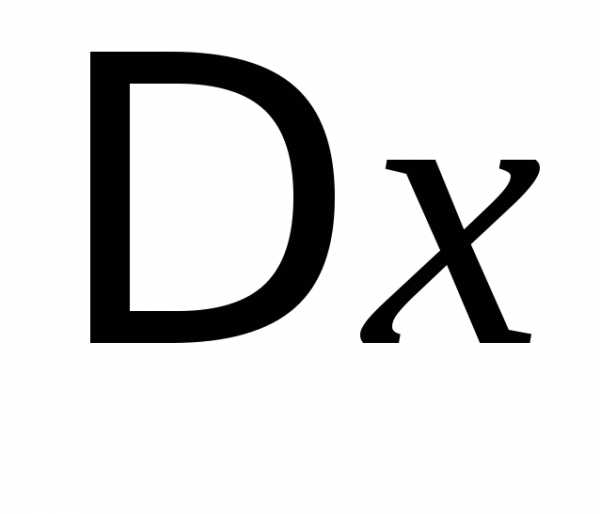 ,
тогда
,
тогда получит приращение, которое называетсячастным приращением
получит приращение, которое называетсячастным приращением по
по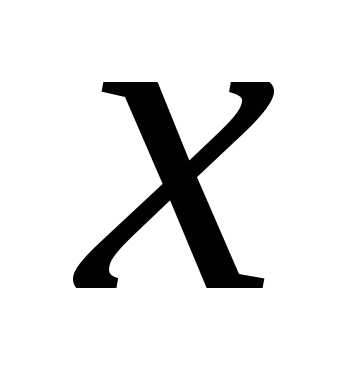 и обозначают через
и обозначают через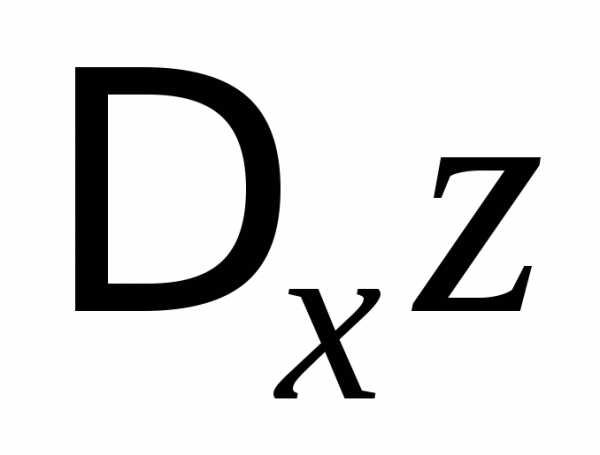 (на рисунке отрезок
(на рисунке отрезок ),
так что
),
так что сохраняет постоянное значение, а
сохраняет постоянное значение, а получает приращение
получает приращение .
. приращение
приращение ,
а аргументу
,
а аргументу приращение
приращение ,
получим для
,
получим для новое приращение
новое приращение ,
которое называетсяполным приращениемфункции
,
которое называетсяполным приращениемфункции и определяется формулой
и определяется формулой изображено отрезком
изображено отрезком .
. от функцииназывается предел отношения частного
приращения
от функцииназывается предел отношения частного
приращения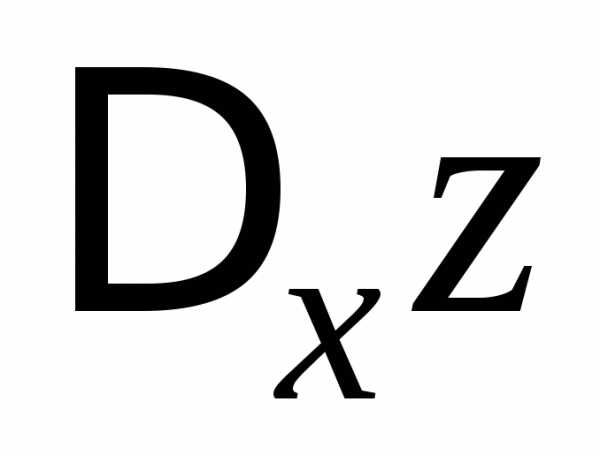 по
по 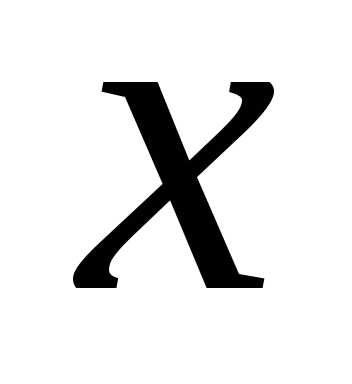 к
приращению
к
приращению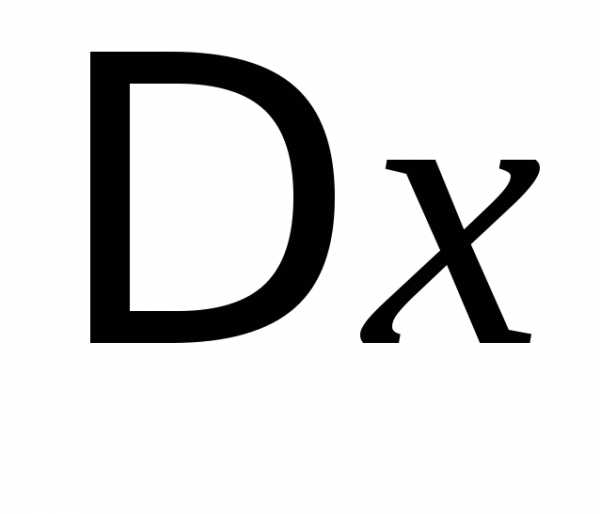 при стремлении
при стремлении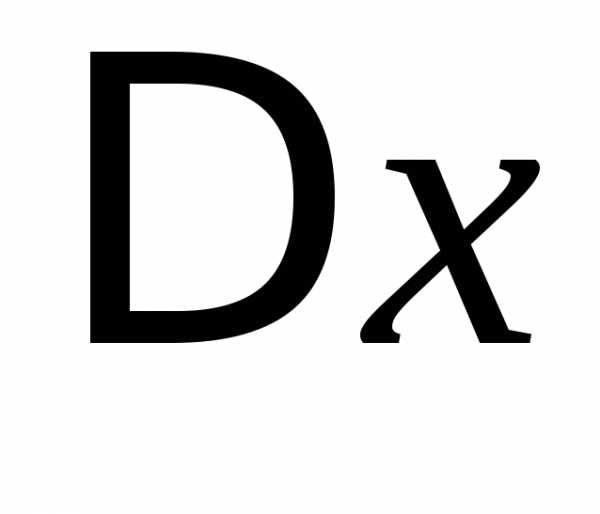 к нулю. Обозначается:.
Тогда
к нулю. Обозначается:.
Тогда от функцииназывается предел отношения частного
приращения
от функцииназывается предел отношения частного
приращения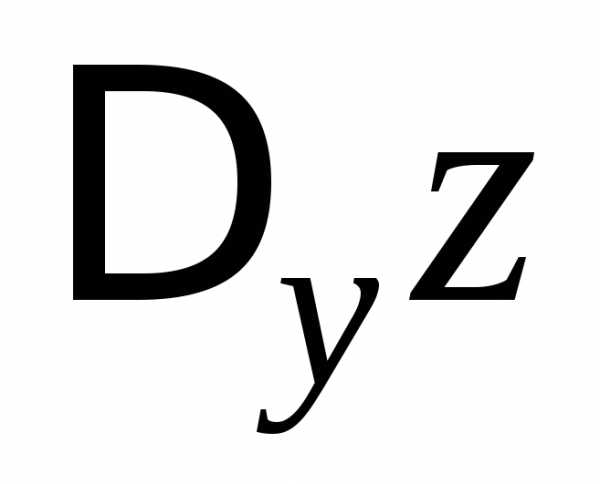 по
по  к
приращению
к
приращению при стремлении
при стремлении к нулю. Обозначается:.
Тогда
к нулю. Обозначается:.
Тогда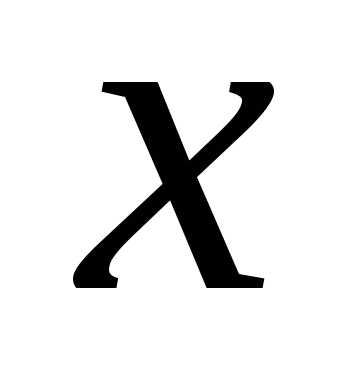 или
или считаются постоянной величиной).
считаются постоянной величиной).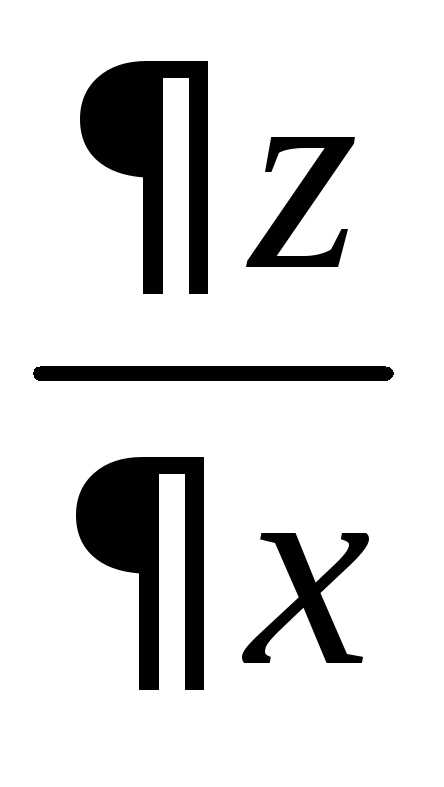 и
и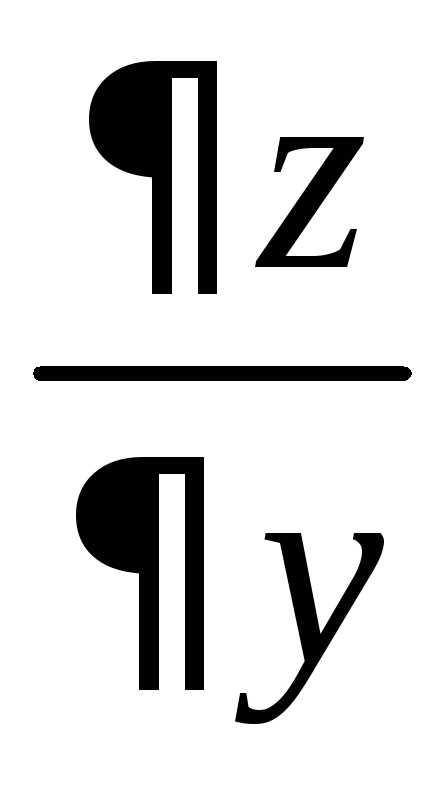 .
Найти значения частных производных в
точке
.
Найти значения частных производных в
точке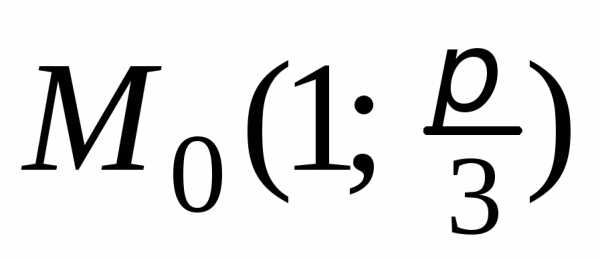 :
: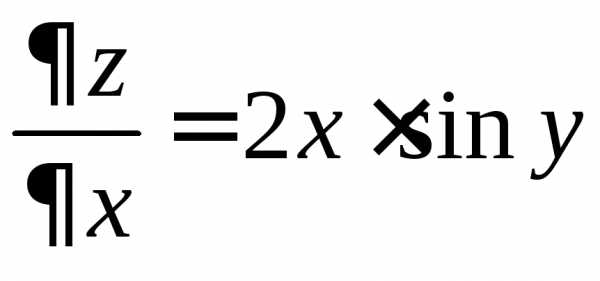 ,
,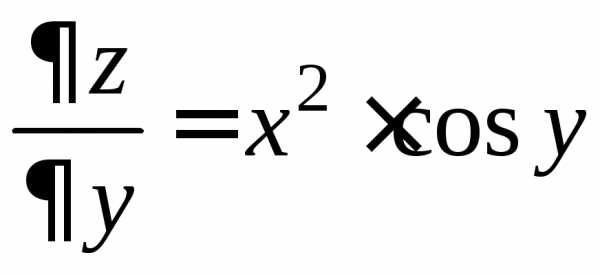 .
.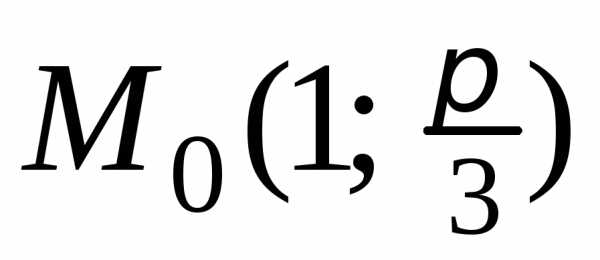 :
: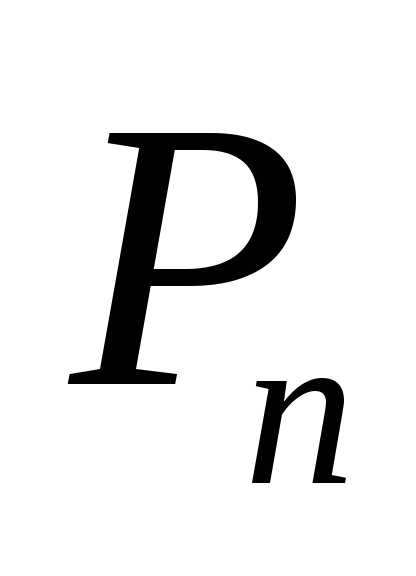 с координатами
с координатами 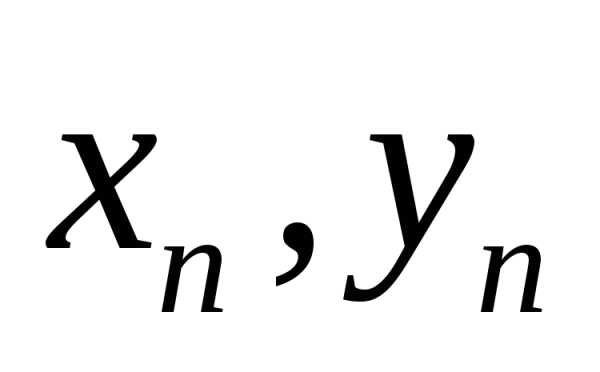 стремится к точке
стремится к точке 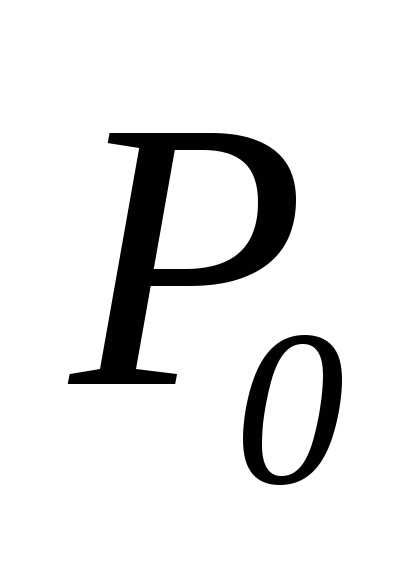 с координатами
с координатами 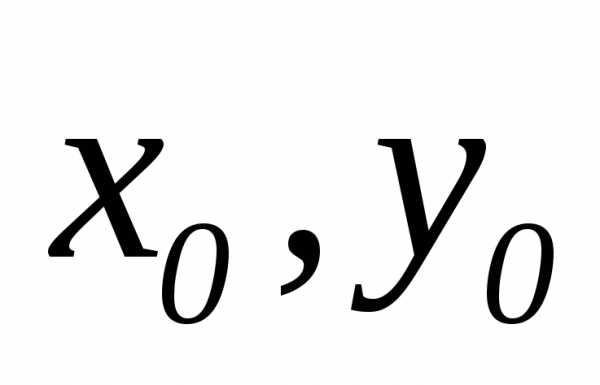 ,
если последовательность расстояний
,
если последовательность расстояний 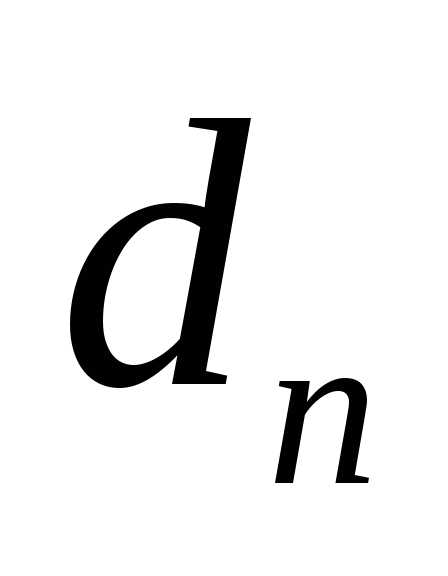 точек
точек 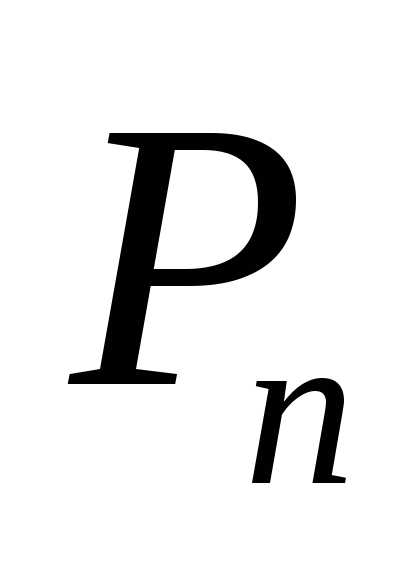 от точки
от точки 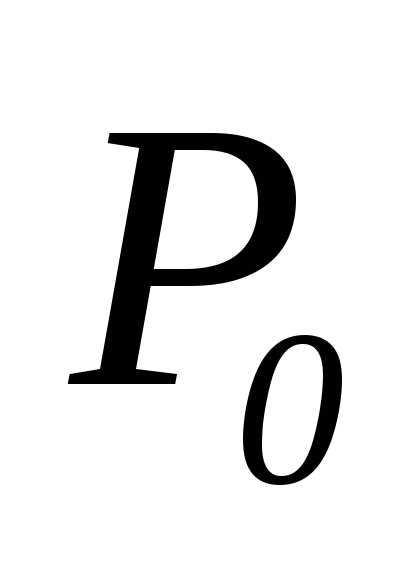 стремится к нулю при
.
Таким образом,
последовательность точек
стремится к нулю при
.
Таким образом,
последовательность точек 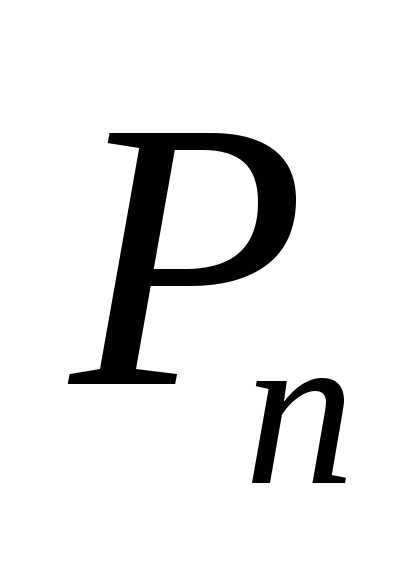 стремится к
стремится к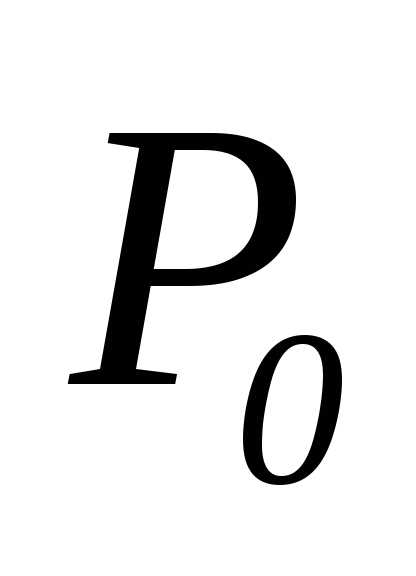 ,
если
,
если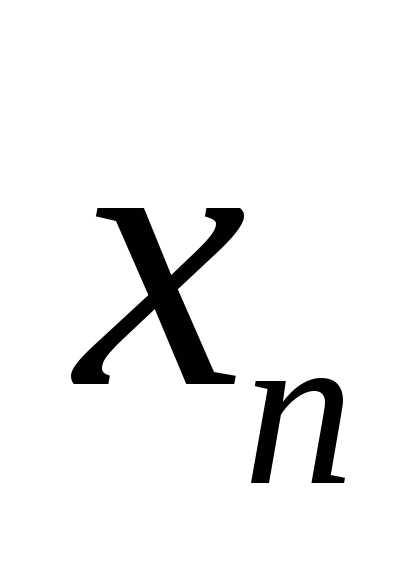 стремится к
стремится к 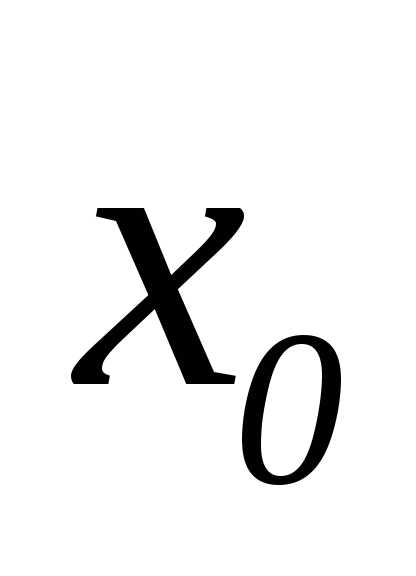 ,
а
,
а 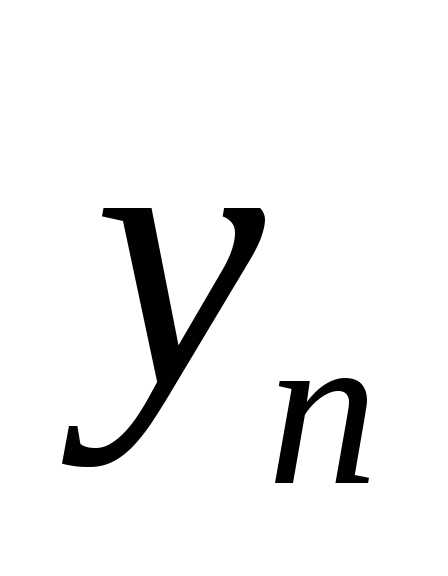 —
к
—
к 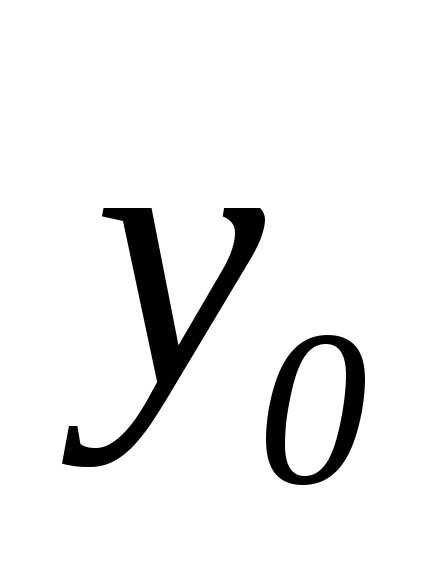 .
.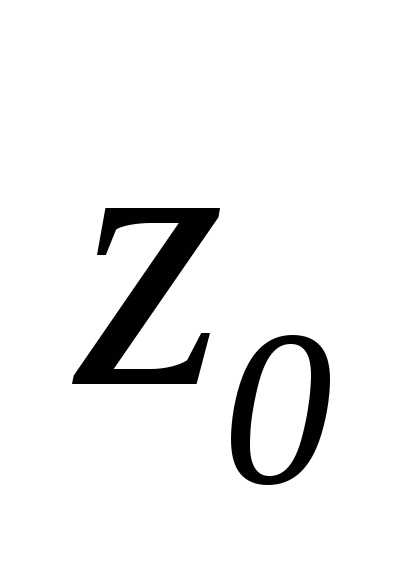 есть предел функции
есть предел функции 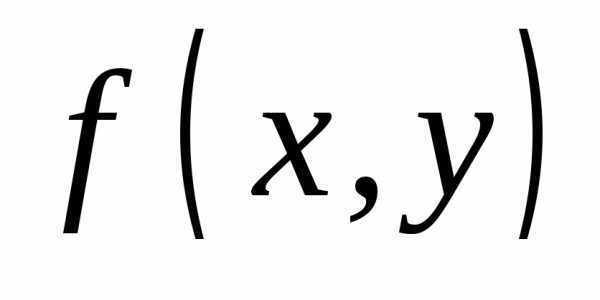 ,
где (х,
у) стремится к
,
где (х,
у) стремится к 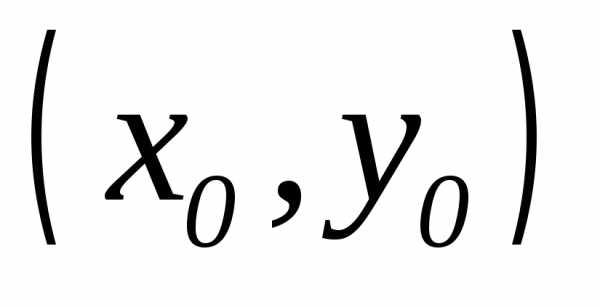 ,
если для каждой последовательности
точек
,
если для каждой последовательности
точек 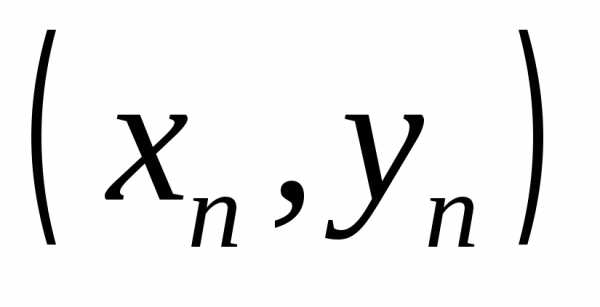 ,
отличных от
,
отличных от 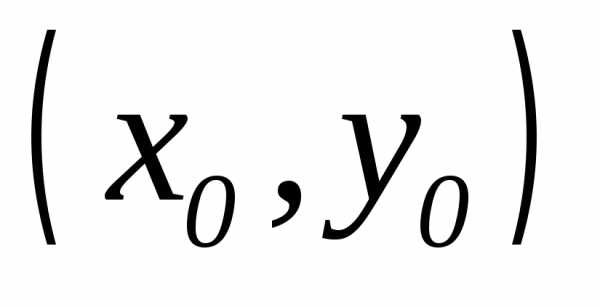 и стремящихся к
и стремящихся к 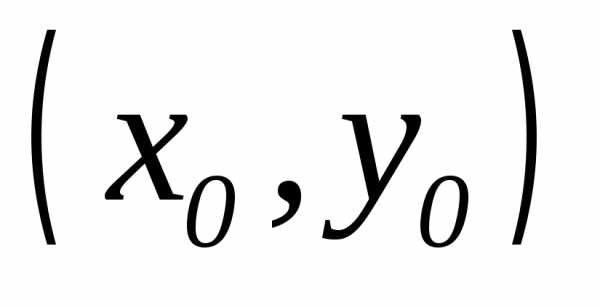 ,
последовательность
,
последовательность 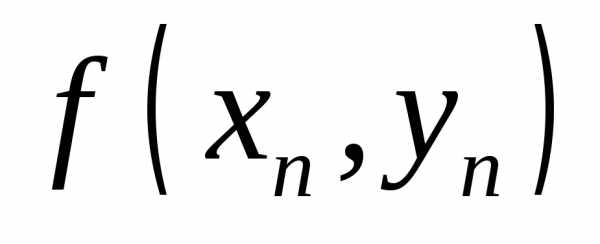 стремится к
стремится к 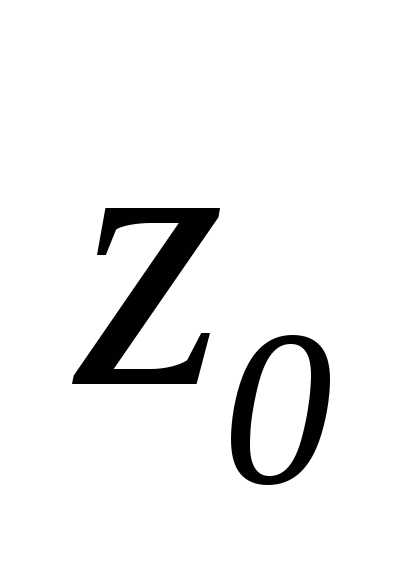 при
.
Это записывается
следующим образом:
при
.
Это записывается
следующим образом: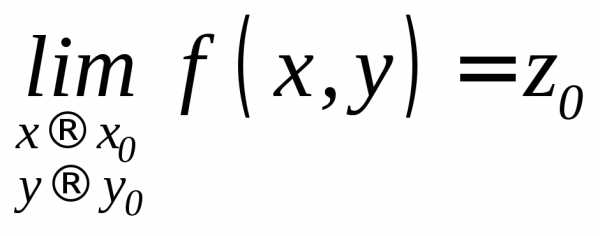
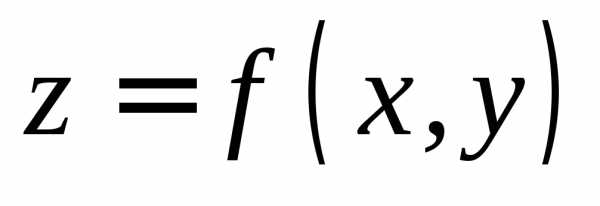 .
Пусть независимая переменная у приняла постоянное значение
.
Пусть независимая переменная у приняла постоянное значение 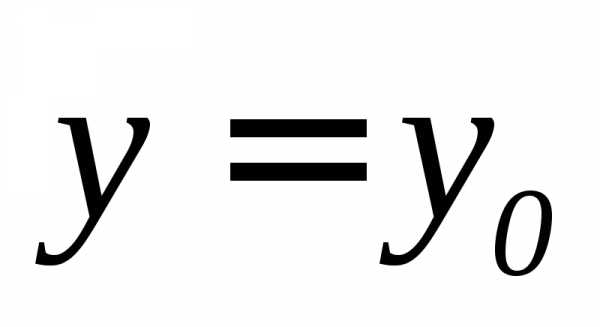 ,
а переменная
,
а переменная 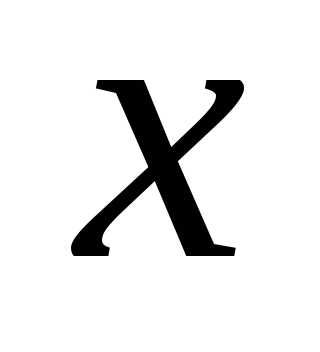 изменяется. Тогда из функции двух
переменных получим функцию одной
независимой переменной .
изменяется. Тогда из функции двух
переменных получим функцию одной
независимой переменной .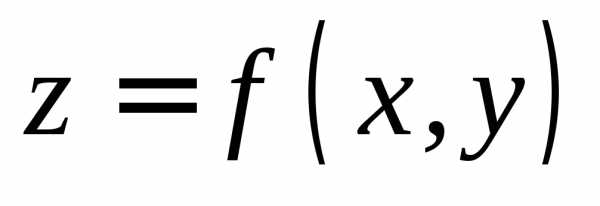 и плоскости
и плоскости 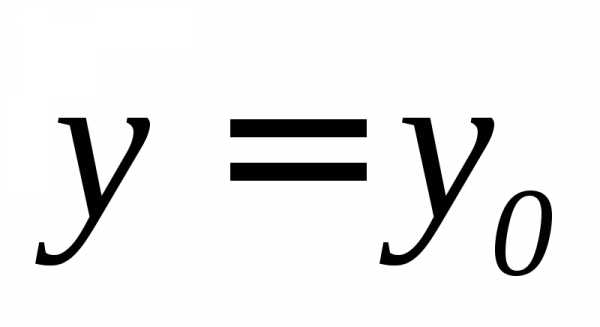 (рис 10).
(рис 10).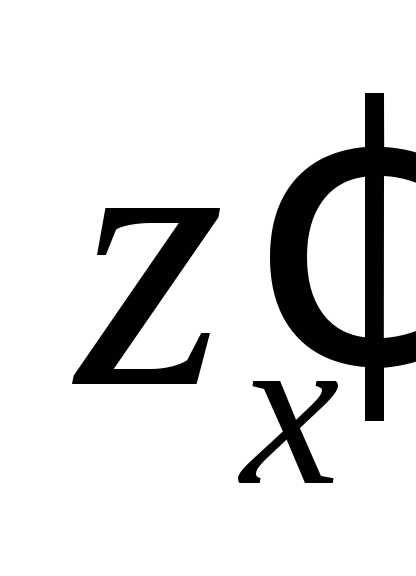 в точке
в точке 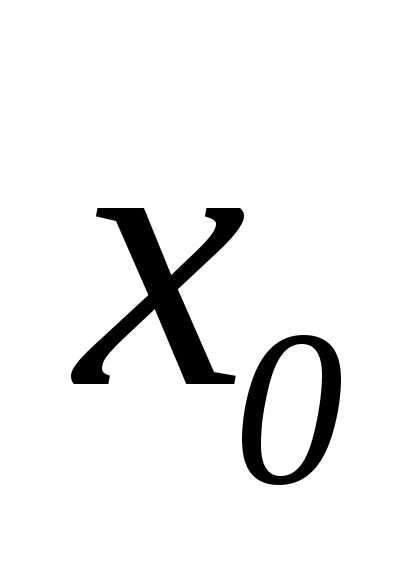 вычисляется по формуле
вычисляется по формуле
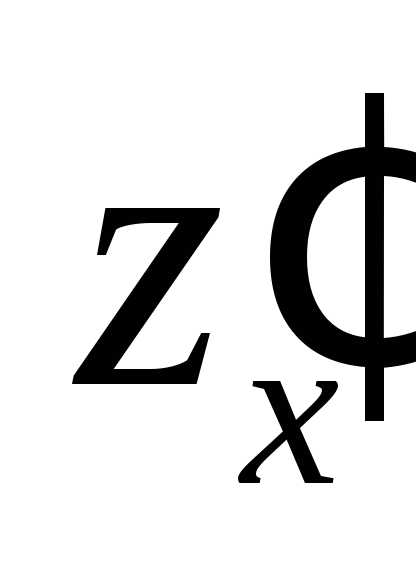 от функции двух переменных
от функции двух переменных 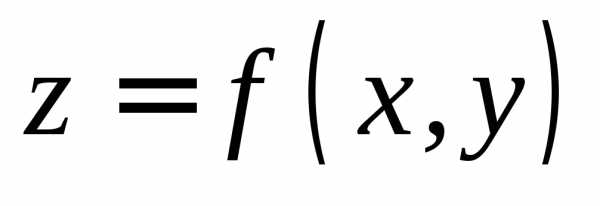 в точке
в точке 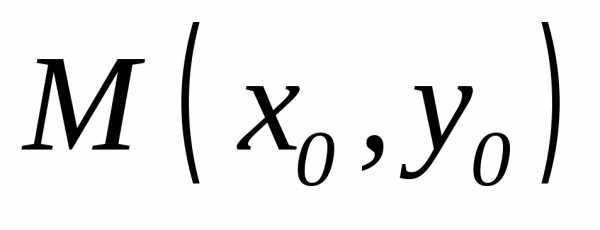 .
. приращение переменной х;
введем также обозначение
приращение переменной х;
введем также обозначение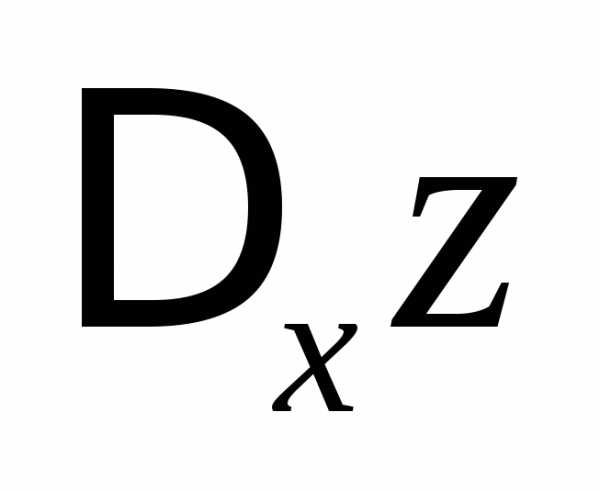 называют частным
приращением функции z по переменной х.
называют частным
приращением функции z по переменной х. ,
а х остается постоянной, то частное приращение
функции z по переменной у имеет следующий вид:
,
а х остается постоянной, то частное приращение
функции z по переменной у имеет следующий вид: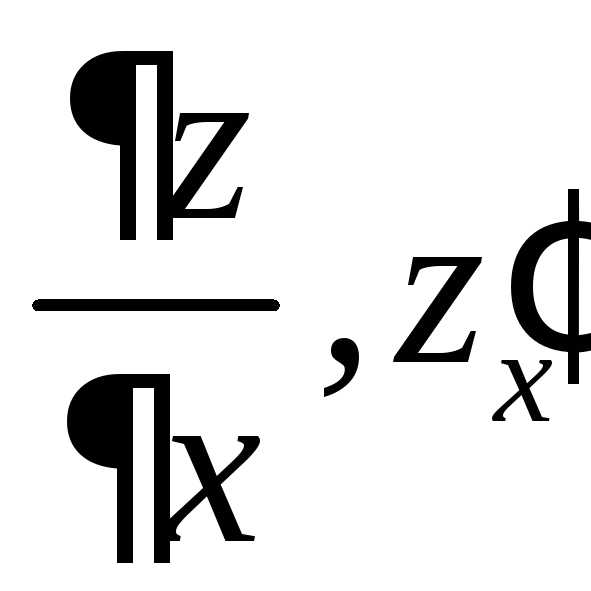 .
.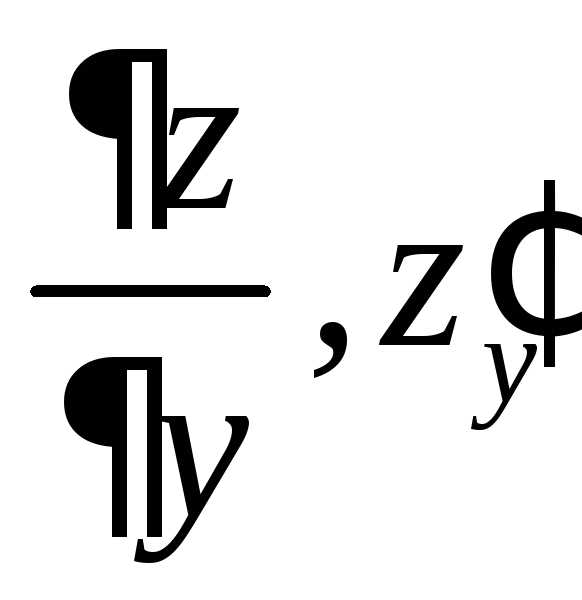
 ,
принимаем у за постоянную и находим
производную по х:
,
принимаем у за постоянную и находим
производную по х: приняли равной нулю, поскольку у считаем
постоянным числом. В первом слагаемом
постоянную
приняли равной нулю, поскольку у считаем
постоянным числом. В первом слагаемом
постоянную  вынесли за знак производной.)
вынесли за знак производной.)  ,
принимаем у за постоянную и находим
производную по х:
,
принимаем у за постоянную и находим
производную по х: за постоянную и находим производную по
у:
за постоянную и находим производную по
у: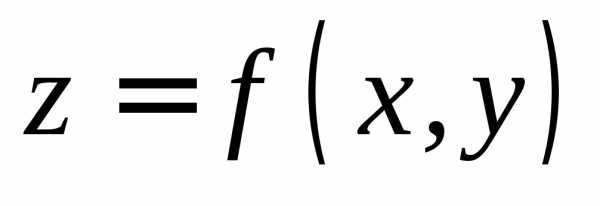 называется вектор, проекциями которого
на оси координат являются частные
производные данной функции:
называется вектор, проекциями которого
на оси координат являются частные
производные данной функции: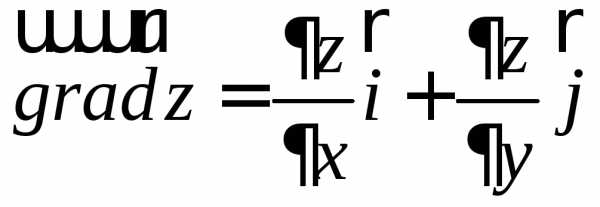 .
.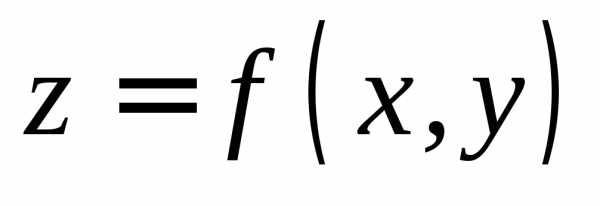 в данном направлении
в данном направлении  называется
называется дифференцируемая, то производную
в данном направлению можно найти по формуле
дифференцируемая, то производную
в данном направлению можно найти по формуле .
. и вектор
и вектор  .
Найти: 1)
.
Найти: 1)  в точке
в точке  ;
2) производную в точке по направлению
вектора
;
2) производную в точке по направлению
вектора  .
.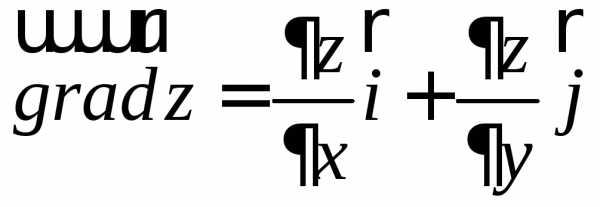
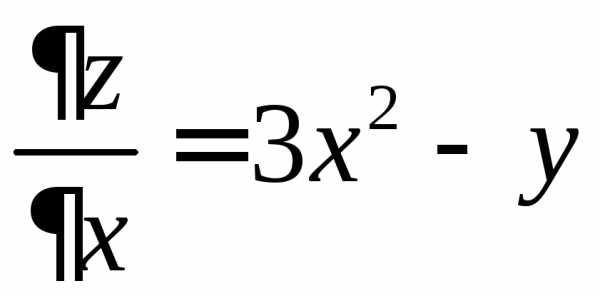 ;
; 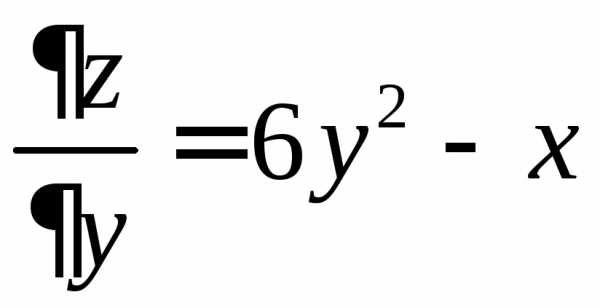 .
. равен
равен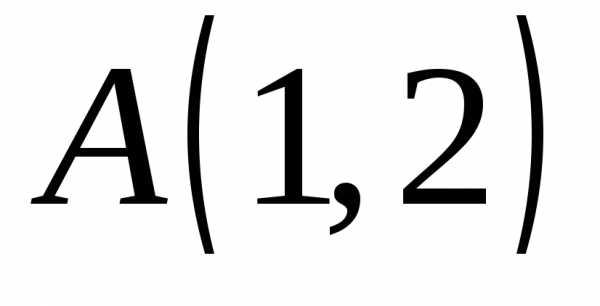
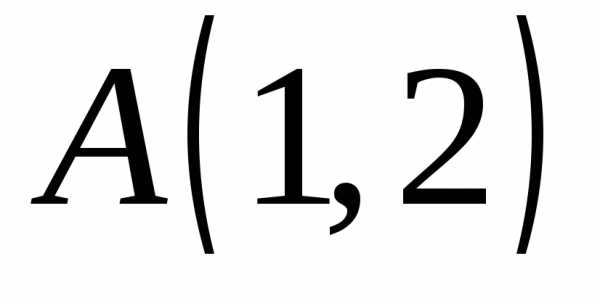 по направлению вектора
по направлению вектора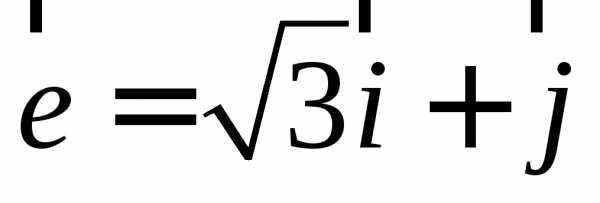 .
. ;
;  .
.
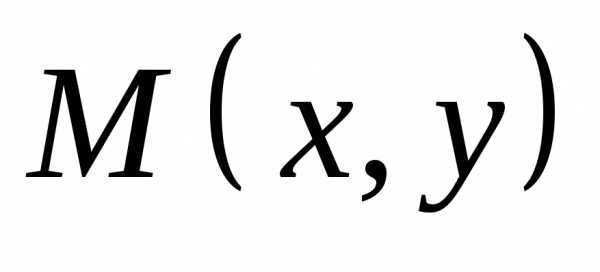 плоскости, координаты которых удовлетворяют
неравенству,
называется-окрестностью
точки
плоскости, координаты которых удовлетворяют
неравенству,
называется-окрестностью
точки 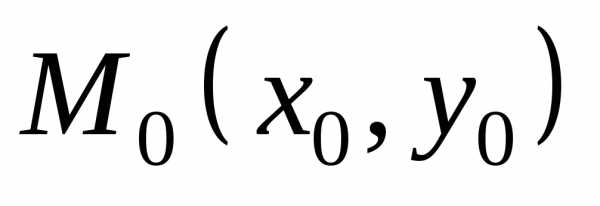 .
Другими словами,-окрестность
точки
.
Другими словами,-окрестность
точки  – это все внутренние точки круга с
центром
– это все внутренние точки круга с
центром и радиусом
(рис. 2).
и радиусом
(рис. 2). ,
кроме, быть может, самой этой точки.
Число А называетсяпределом
функции при(или, что то же самое, при
,
кроме, быть может, самой этой точки.
Число А называетсяпределом
функции при(или, что то же самое, при
 ),
если для любого
),
если для любого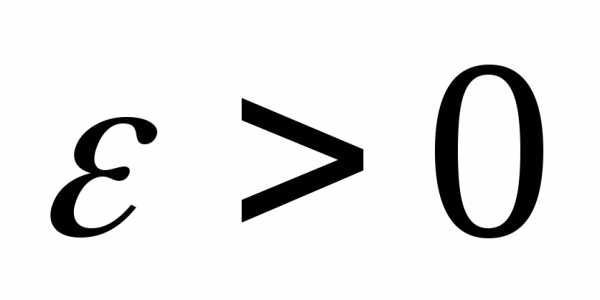 существует
существует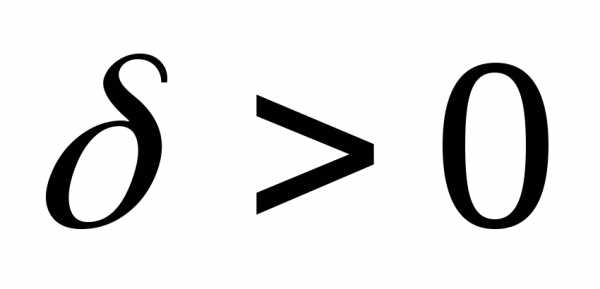 такое, что для всехи удовлетворяющих неравенствувыполняется неравенствоЗаписывают:
такое, что для всехи удовлетворяющих неравенствувыполняется неравенствоЗаписывают: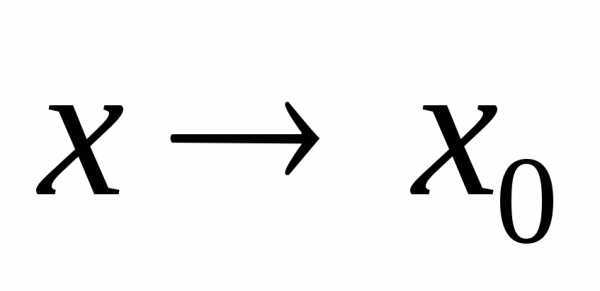 по
двум направлениям: справа и слева).
по
двум направлениям: справа и слева).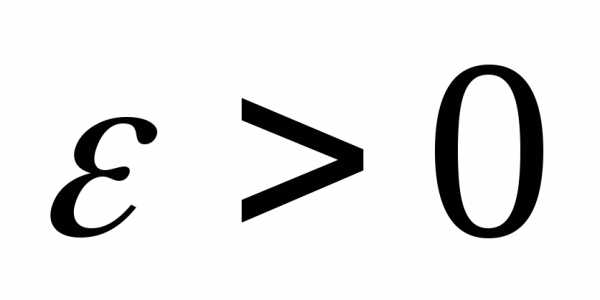 ,
найдется-окрестность
точки
,
найдется-окрестность
точки 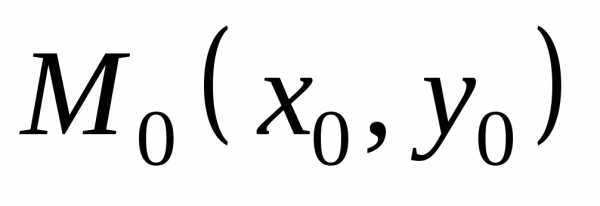 ,
что во всех её точках
,
что во всех её точках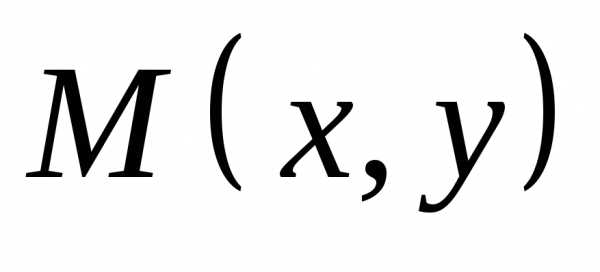 ,
отличных от
,
отличных от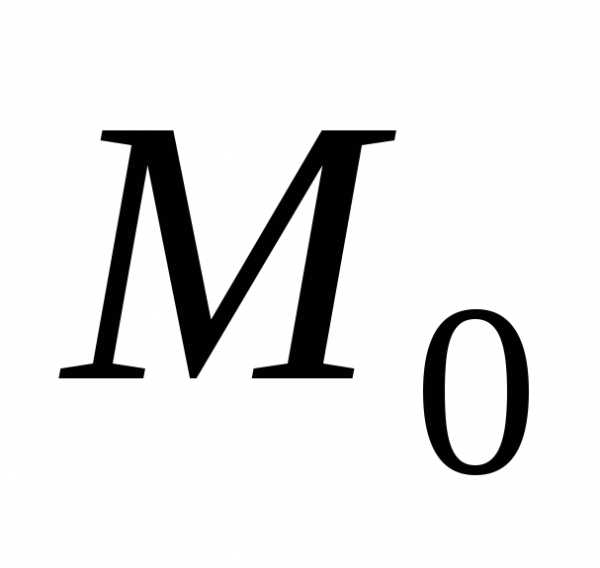 ,
аппликаты соответствующих точек
поверхностиотличаются от числа А по модулю меньше,
чем на.
,
аппликаты соответствующих точек
поверхностиотличаются от числа А по модулю меньше,
чем на.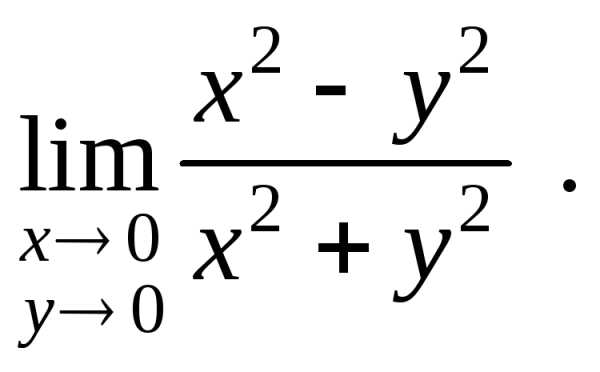
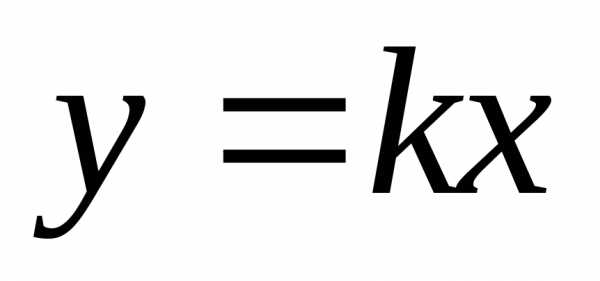 ,
гдеk – некоторое
число. Тогда
,
гдеk – некоторое
число. Тогда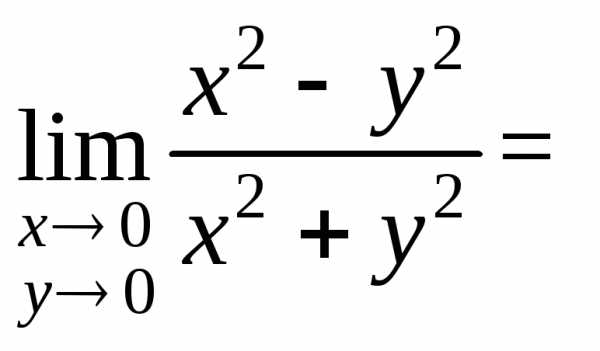
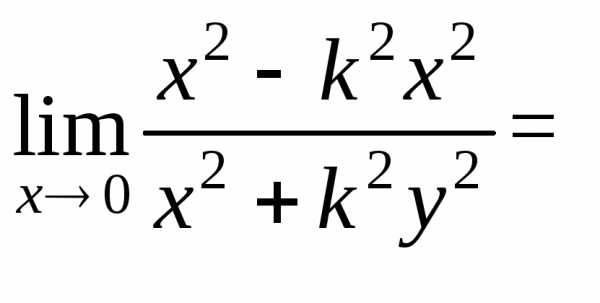
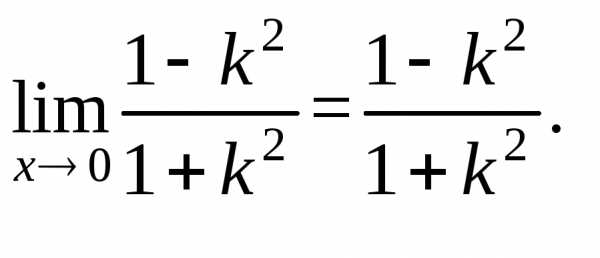
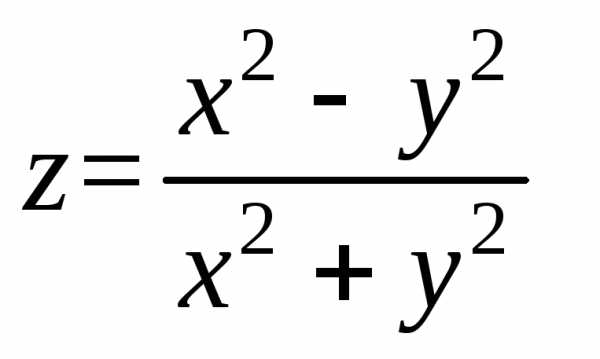 в
точке 0(0;0) предела не имеет, т. к. при
разных значенияхk предел функции не одинаков (функция
имеет различные предельные значения).
в
точке 0(0;0) предела не имеет, т. к. при
разных значенияхk предел функции не одинаков (функция
имеет различные предельные значения).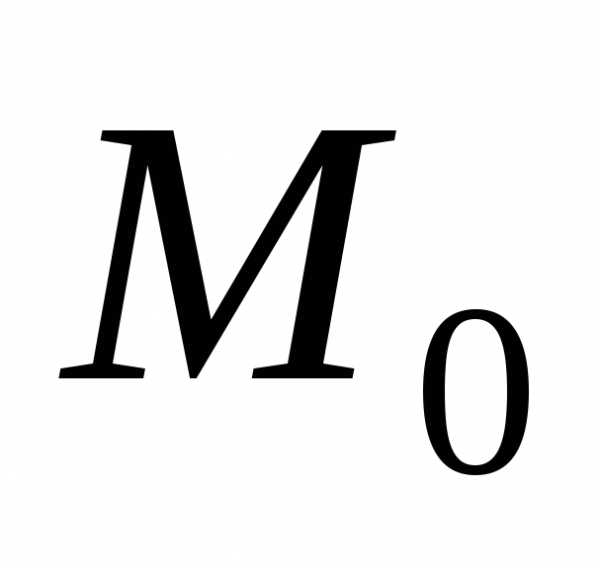 этого множества пределы А и В соответственно,
то и функции
этого множества пределы А и В соответственно,
то и функции имеют
в точке М0 пределы, которые соответственно равны
имеют
в точке М0 пределы, которые соответственно равны 
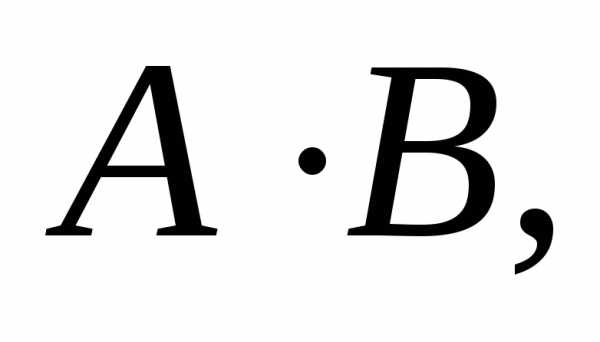
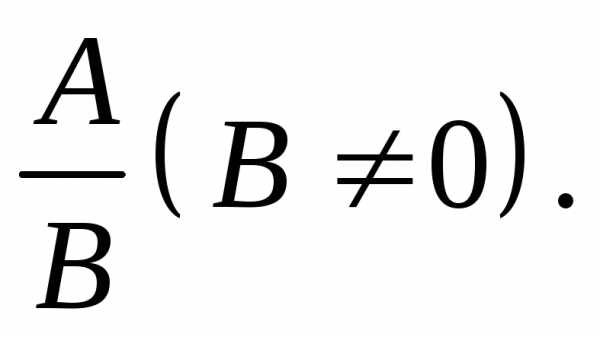
 ,
если она: а) определена в этой точке
и некоторой её окрестности;
,
если она: а) определена в этой точке
и некоторой её окрестности;
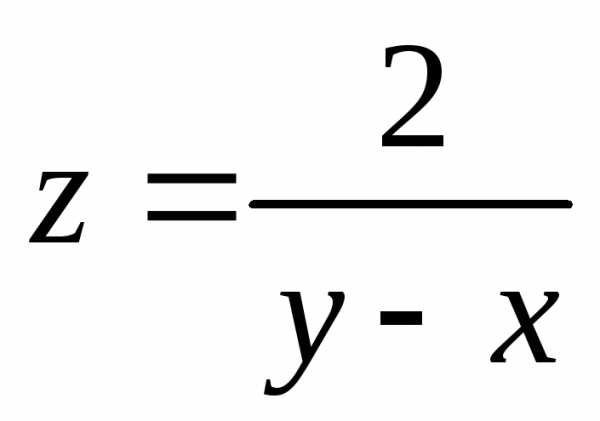 имеет линию разрыва
имеет линию разрыва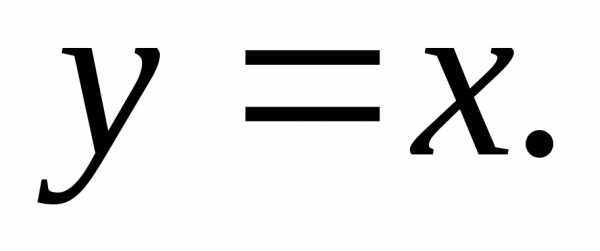
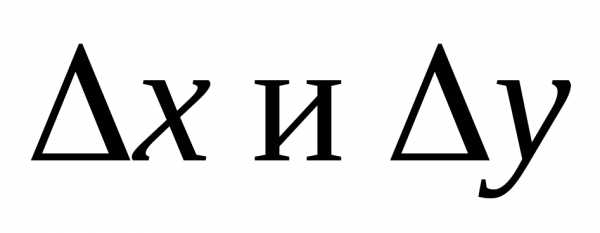 называютсяприращениями
аргументов х и у, а
называютсяприращениями
аргументов х и у, а  –полным
приращением функции
–полным
приращением функции 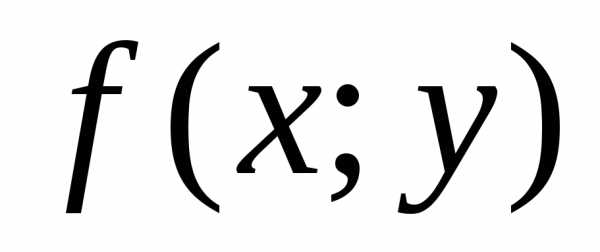 в точке
в точке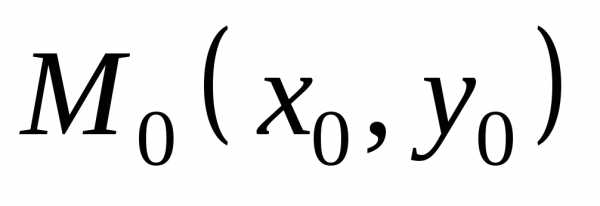 .
.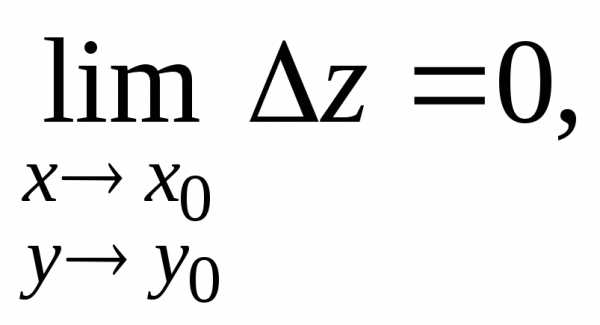 т.
е. полное приращение функции в этой очке
стремится к нулю, когда приращения её
аргументовх и у стремятся к нулю.
т.
е. полное приращение функции в этой очке
стремится к нулю, когда приращения её
аргументовх и у стремятся к нулю. .
Область называетсяограниченной, если все её
точки принадлежат некоторому кругу
радиуса R.
В противном случае область называется неограниченной. Примером неограниченной области может
служить множество точек первого
координатного угла, а примером ограниченной
–
.
Область называетсяограниченной, если все её
точки принадлежат некоторому кругу
радиуса R.
В противном случае область называется неограниченной. Примером неограниченной области может
служить множество точек первого
координатного угла, а примером ограниченной
–  -окрестность
точки
-окрестность
точки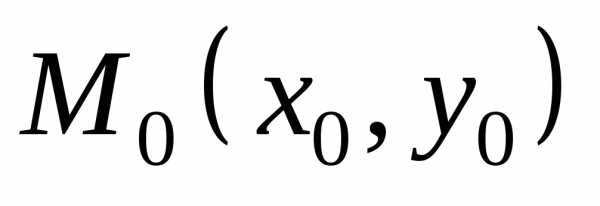 .
. б)
имеет точки, в которых принимает
наименьшееm
и наибольшее M
значения; в) принимает хотя бы в одной
точке области любое численное значение,
заключенной между m
и M
(дается без доказательства).
б)
имеет точки, в которых принимает
наименьшееm
и наибольшее M
значения; в) принимает хотя бы в одной
точке области любое численное значение,
заключенной между m
и M
(дается без доказательства).


 .
. (при условии,
что
(при условии,
что 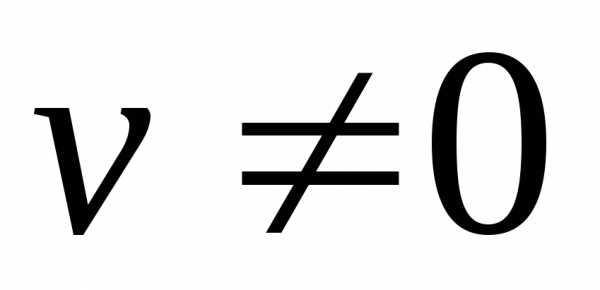 ).
).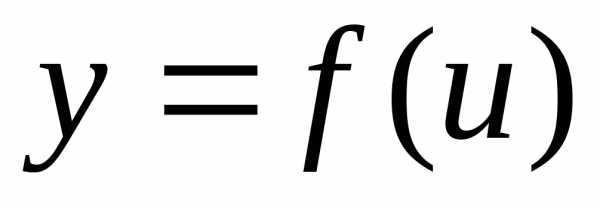 и
и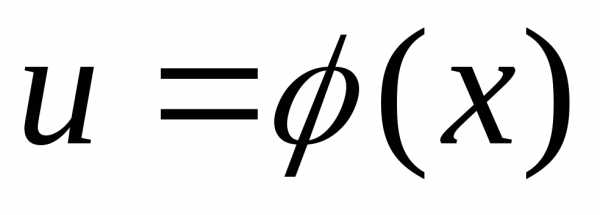
дифференцируемые функции от своих
аргументов, то производная сложной
функции существует и равна производной
данной функции по промежуточному
аргументу и умноженной на производную
промежуточного аргумента по независимой
переменной
дифференцируемые функции от своих
аргументов, то производная сложной
функции существует и равна производной
данной функции по промежуточному
аргументу и умноженной на производную
промежуточного аргумента по независимой
переменной 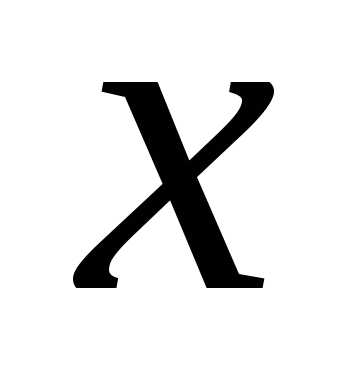 ,
т.е..
,
т.е.. и
и ,
где
,
где
некоторая функция зависящая от
некоторая функция зависящая от  .
. и.
и.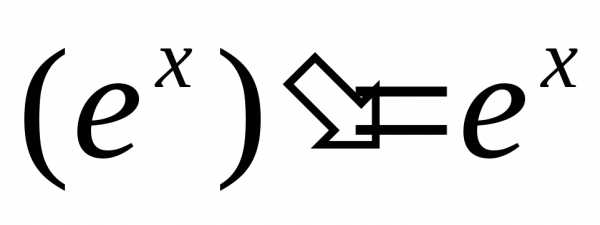 и.
и.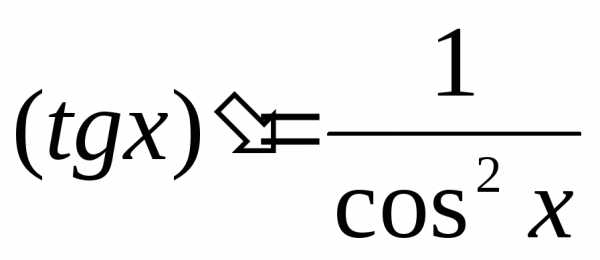 и
и 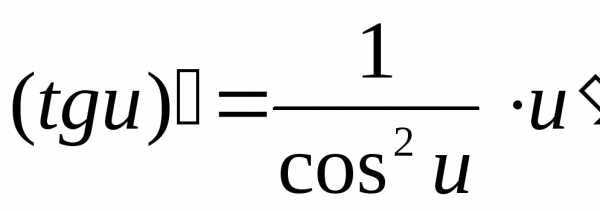 ;
;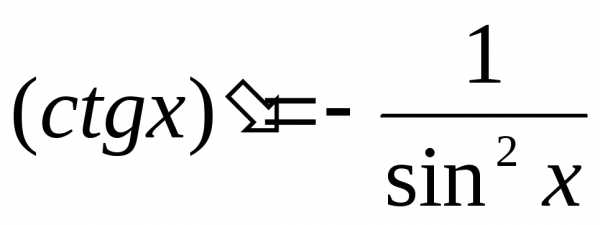 и
.
и
.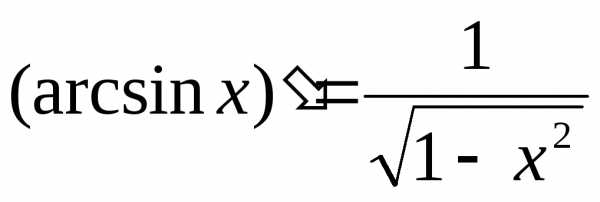 и ;
и ;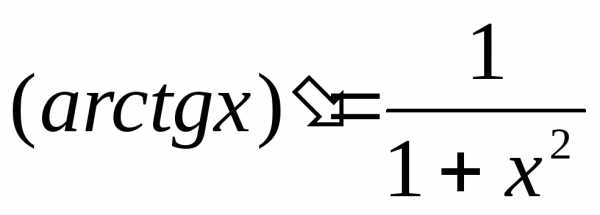 и ;
и ; называется производная от ее первой
производной, т.е.
называется производная от ее первой
производной, т.е. ,
и обозначается
,
и обозначается или
или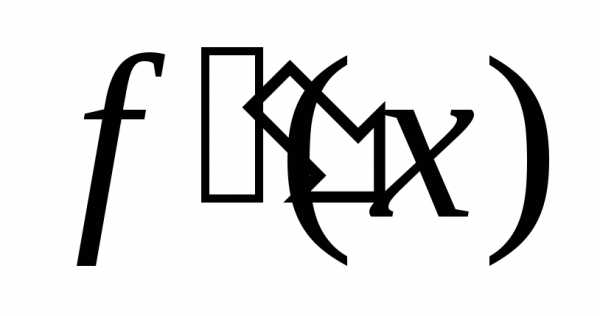 или
или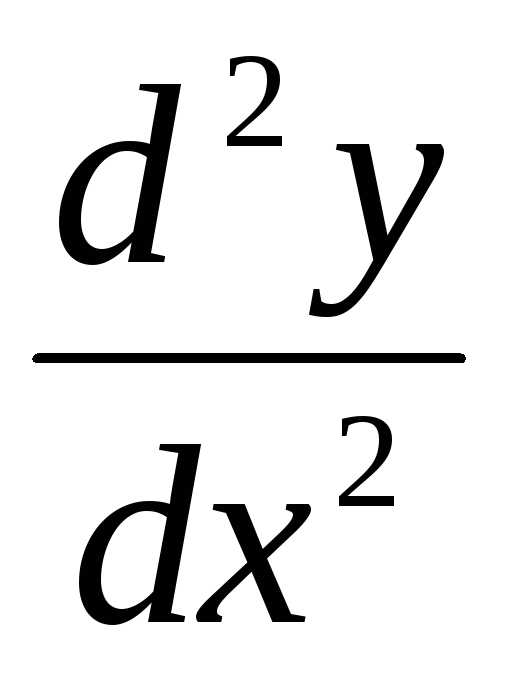 .
.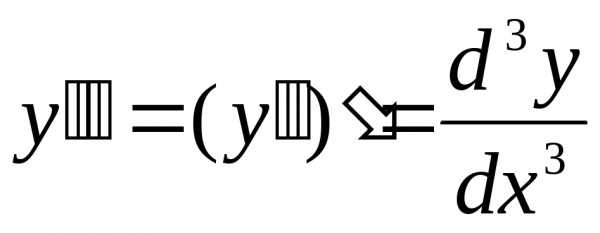 ;
производная 4-го порядка
;
производная 4-го порядка ;
………… производная
;
………… производная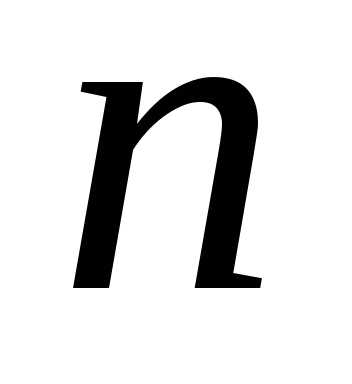 -го
порядка.
-го
порядка.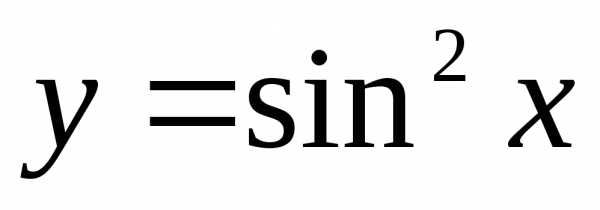
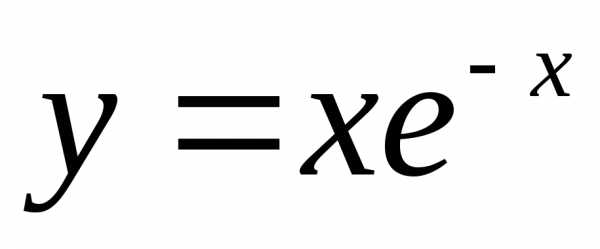
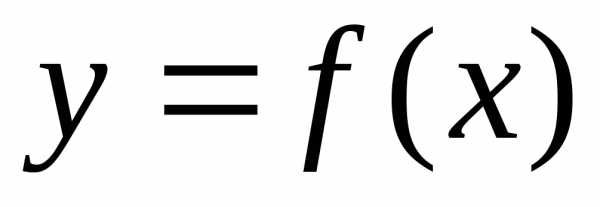 определена на промежутке
определена на промежутке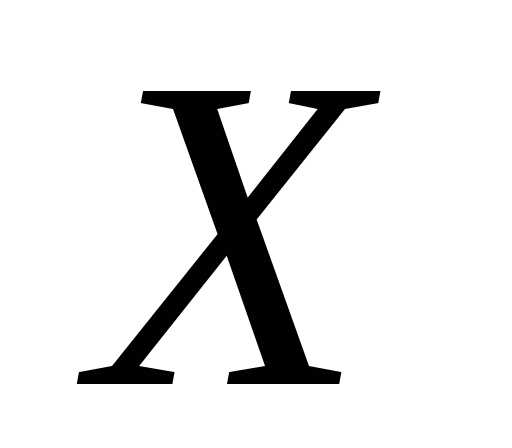 и дифференцируема в окрестности точки
и дифференцируема в окрестности точки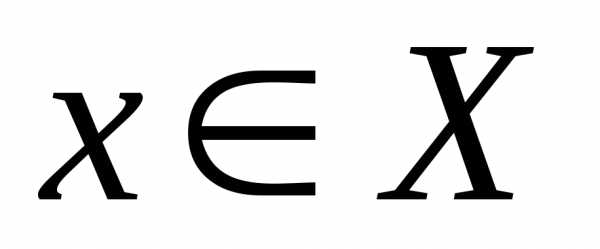 ,тогда
,тогда или по теореме о связи бесконечно малых
с пределами функций имеем,
где
или по теореме о связи бесконечно малых
с пределами функций имеем,
где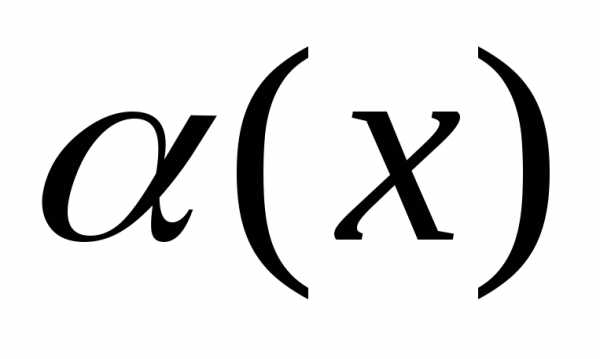
бесконечно малая величина при
.
Отсюда:.
Таким образом, приращение функции
бесконечно малая величина при
.
Отсюда:.
Таким образом, приращение функции состоит из двух слагаемых: 1.
состоит из двух слагаемых: 1.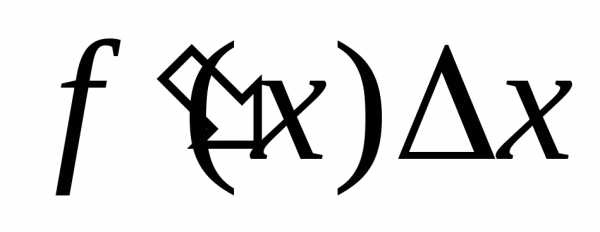
линейного относительно
линейного относительно 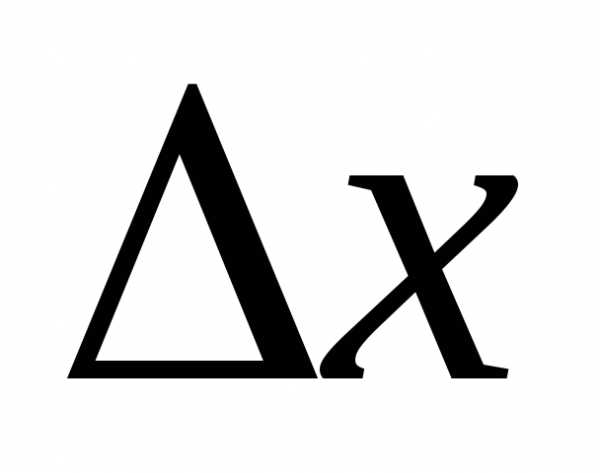 ,
т.к.;
2.
,
т.к.;
2.
нелинейного относительно
нелинейного относительно 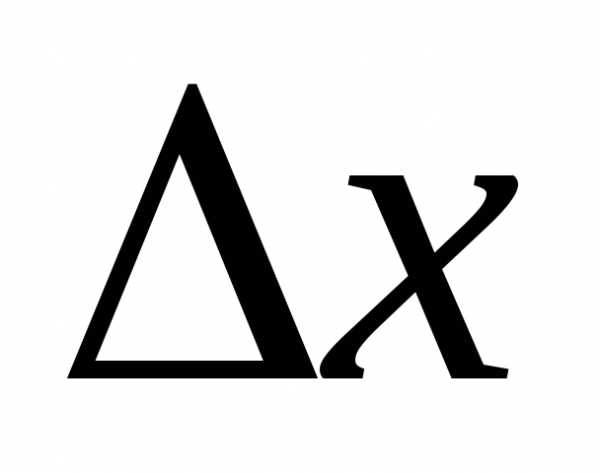 ,
т.к..
,
т.к..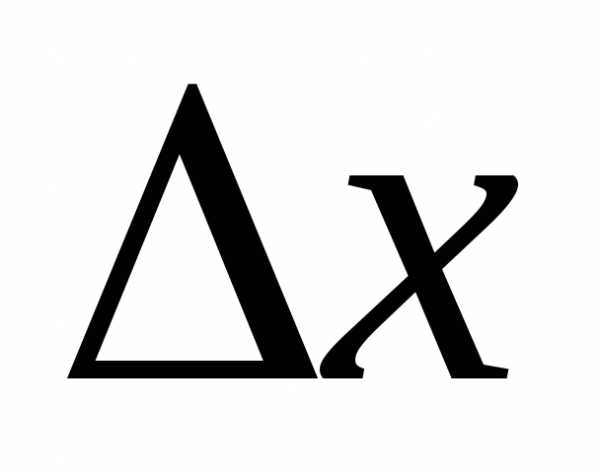 часть приращения функции, равная
произведению производной на приращение
независимой переменной:.
часть приращения функции, равная
произведению производной на приращение
независимой переменной:. и
и
 .
.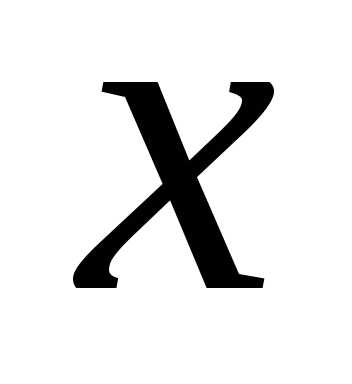 равен приращению этой переменной:.
равен приращению этой переменной:.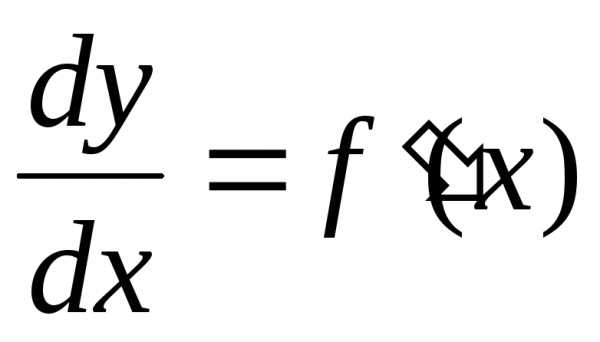 ,
поэтому
,
поэтому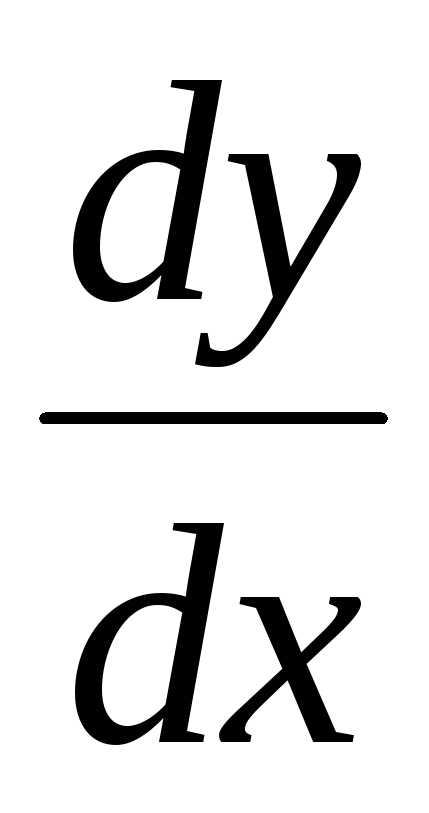 можно рассматривать не только как
символическое обозначение производной,
но и как обычную дробь с числителем
можно рассматривать не только как
символическое обозначение производной,
но и как обычную дробь с числителем и знаменателем
и знаменателем .
.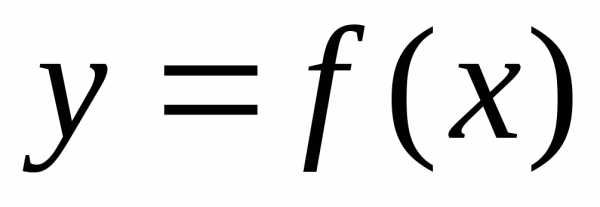 (рис.
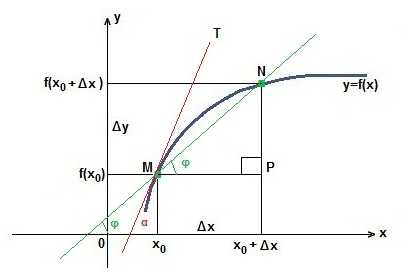
5.) возьмем
произвольную точку
(рис.
5.) возьмем
произвольную точку 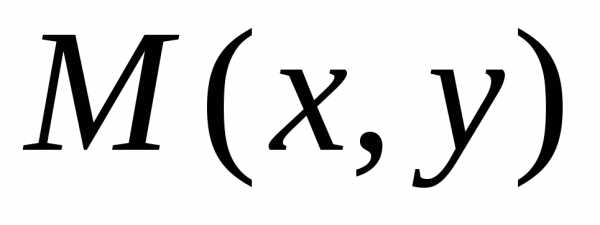 .
Дадим аргументу
.
Дадим аргументу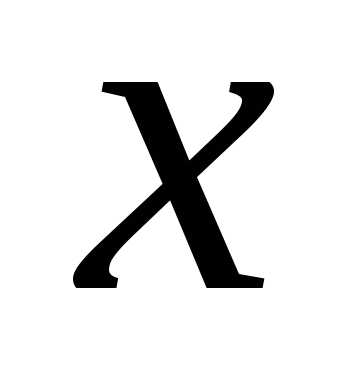 приращение
приращение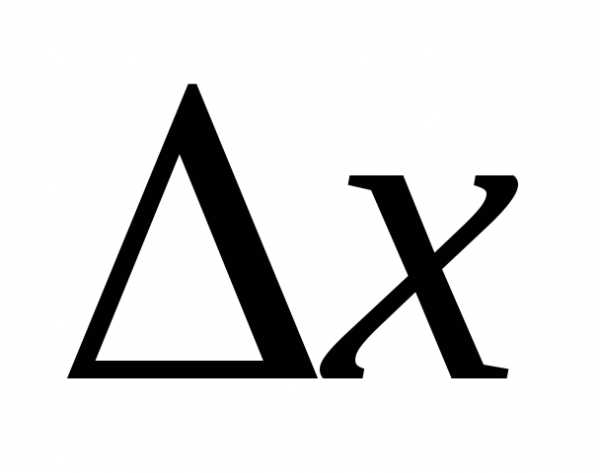 ,
тогда функция получает приращение.
В точке
,
тогда функция получает приращение.
В точке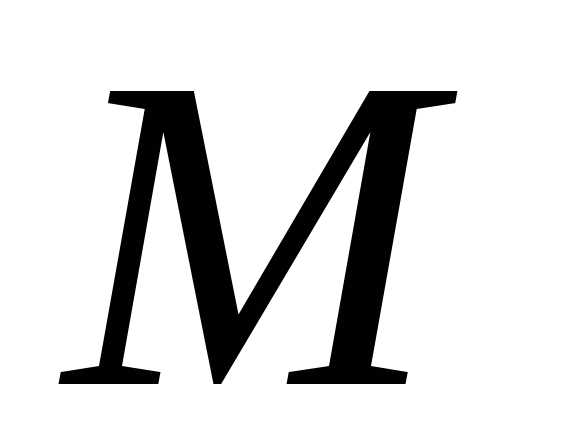 проведем касательную, образующую угол
проведем касательную, образующую угол с осью
с осью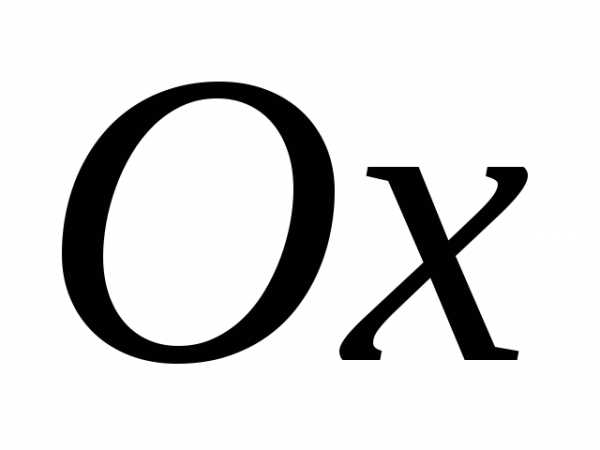 .
Из
.
Из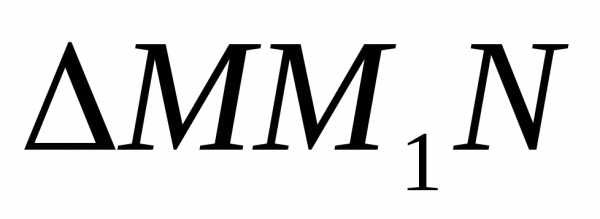 видно,
что.
Из
видно,
что.
Из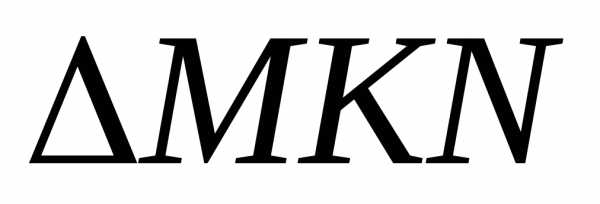 имеем:.
Таким образом,и соответствует формуле.
имеем:.
Таким образом,и соответствует формуле.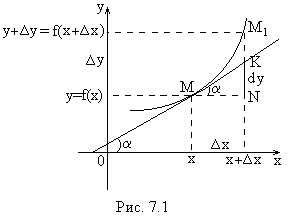
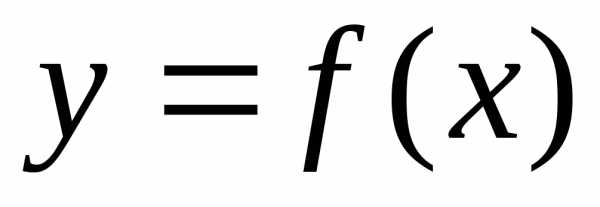 в данной точке, когда
в данной точке, когда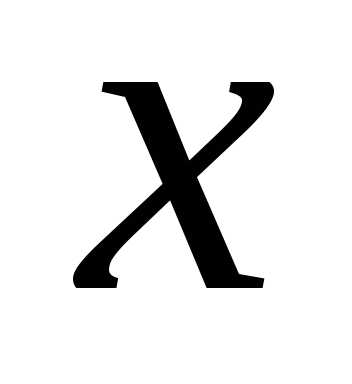 получает приращение
получает приращение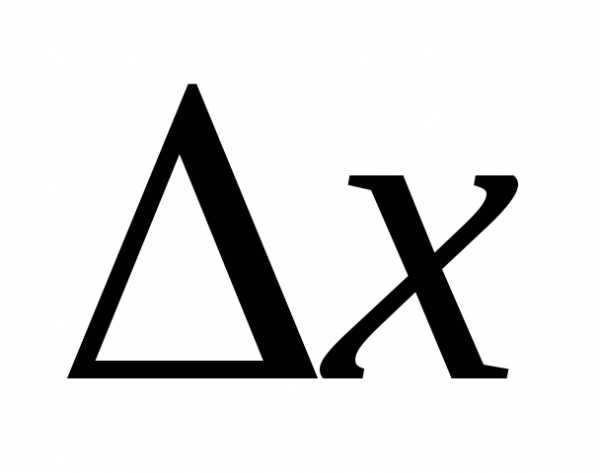 .
. рассматривать функцию от зависимой
переменной
рассматривать функцию от зависимой
переменной .
Это свойство дифференциала получило
названиеинвариантности (т.е. неизменности) формы дифференциала,
т.е.
.
.
Это свойство дифференциала получило
названиеинвариантности (т.е. неизменности) формы дифференциала,
т.е.
.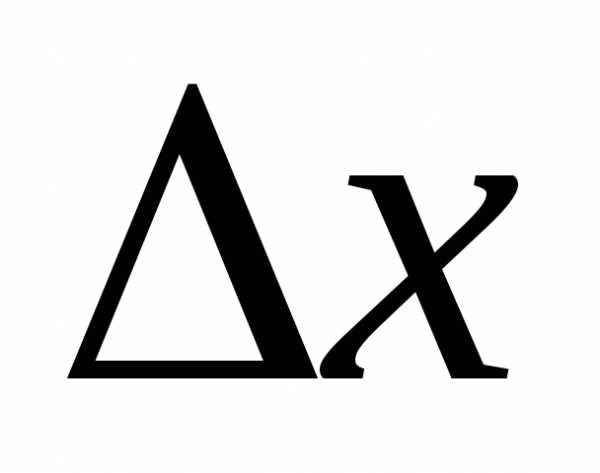 приращение функции
приращение функции приблизительно равно ее дифференциалу
приблизительно равно ее дифференциалу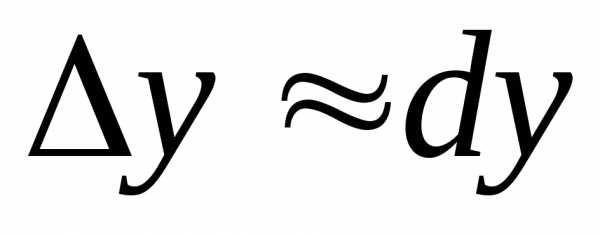 ,.
Эту формулу часто используется в
приближенных вычислениях.
,.
Эту формулу часто используется в
приближенных вычислениях. .
.
 .
.
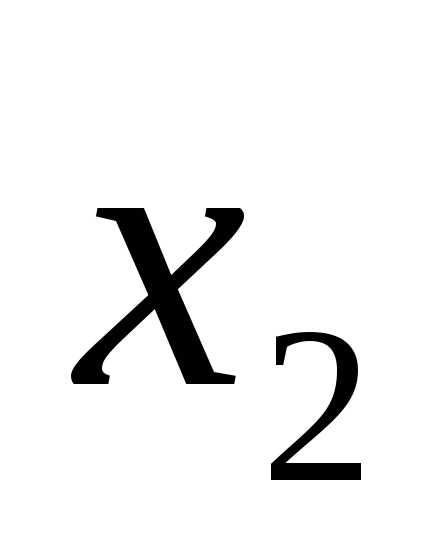 ;F=
;F=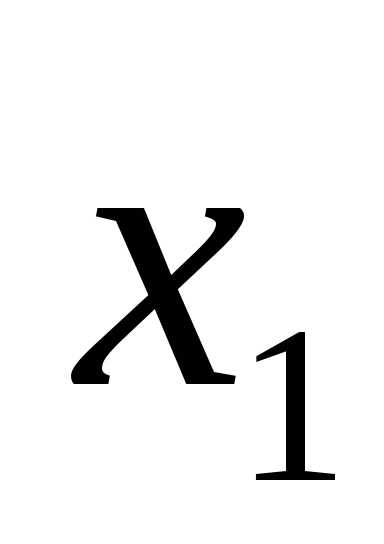 •
•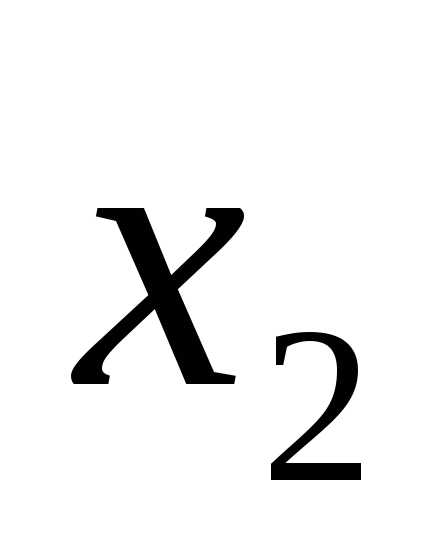 ;F=
;F=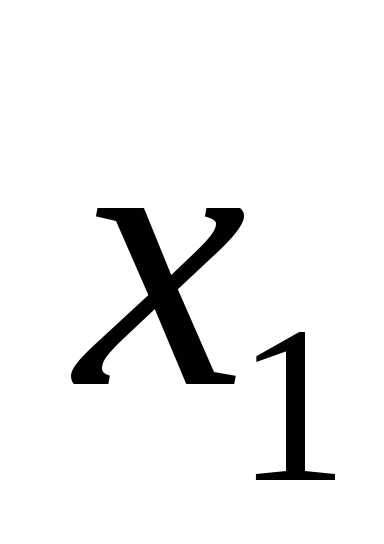
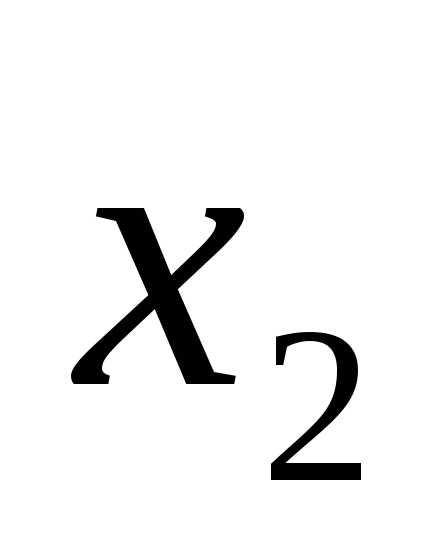 ;F=
;F=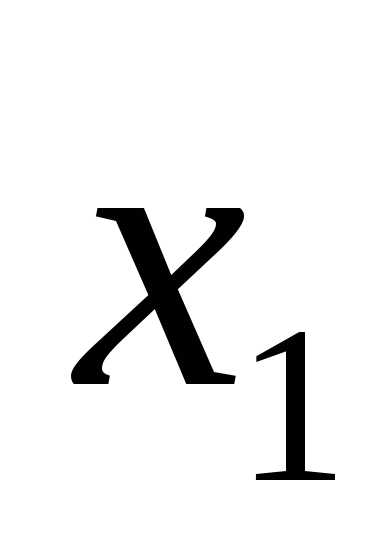 &
&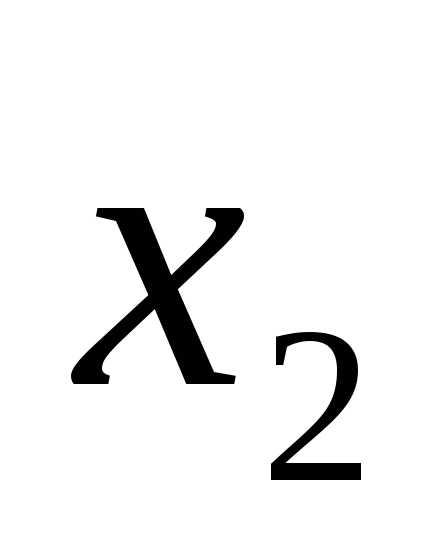 .
.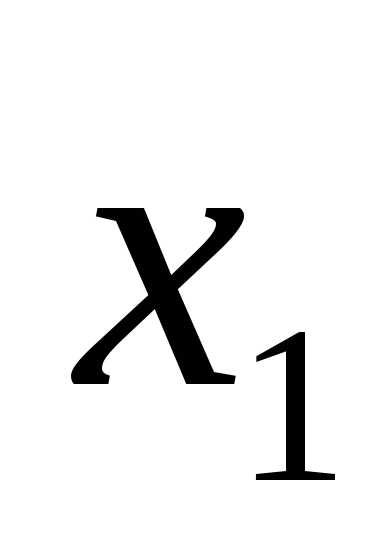
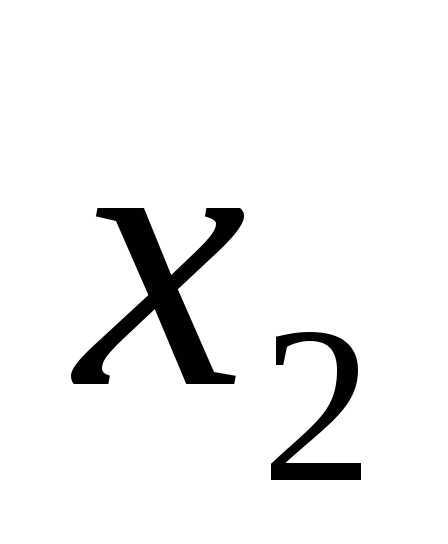
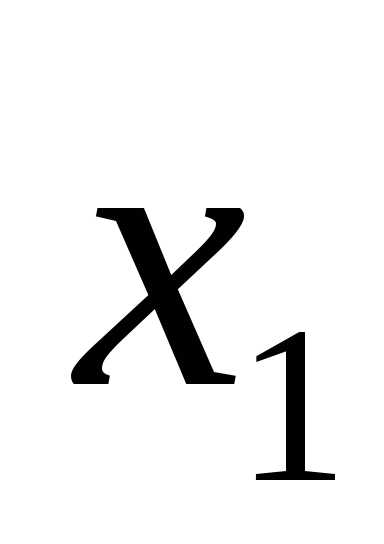 •
•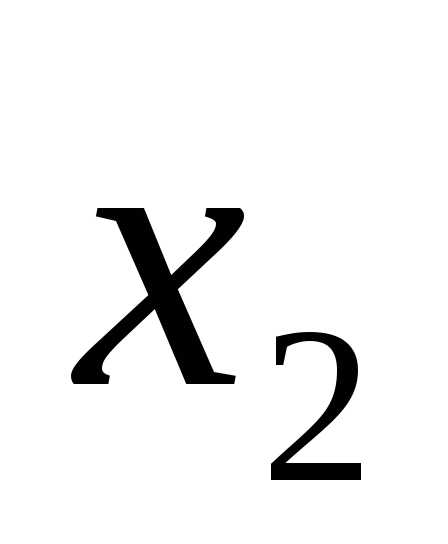 •
•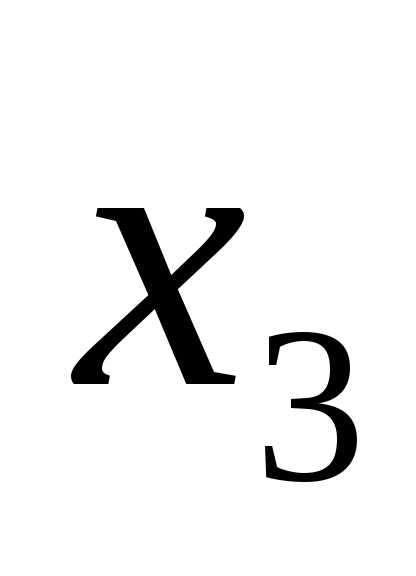 •…•
•…•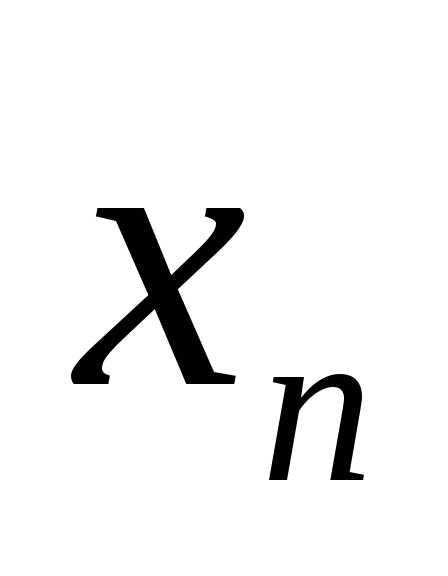 .
.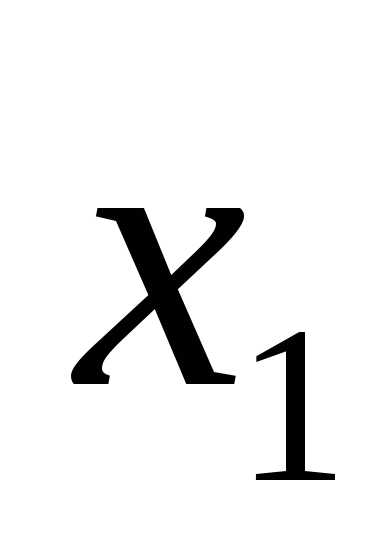
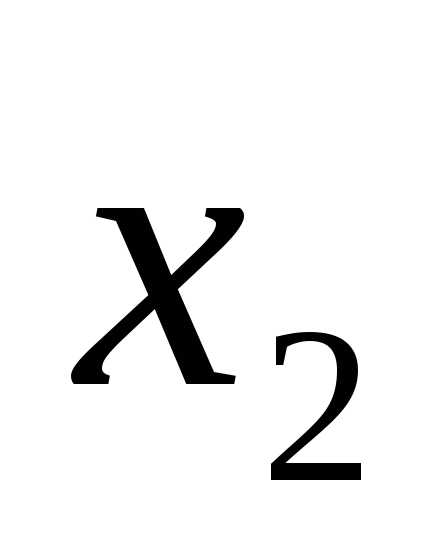 илиF=
илиF=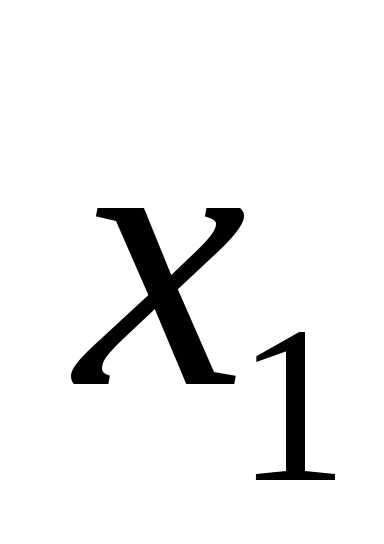 +
+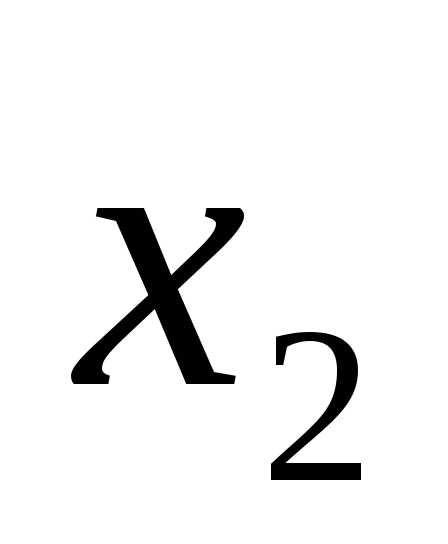 .
.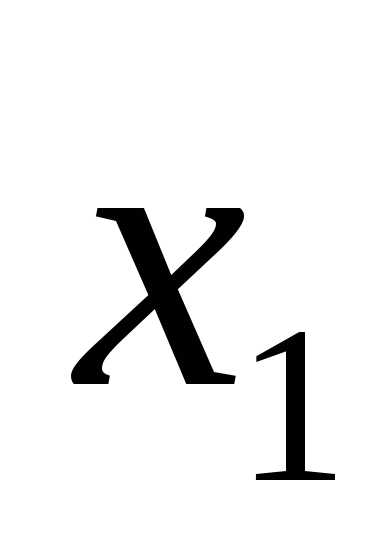 =1,
=1, 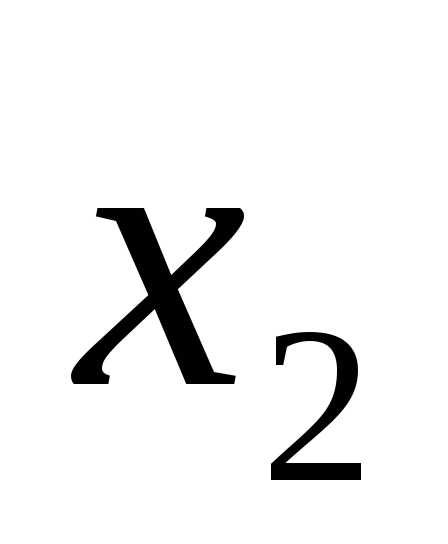 =1
дизъюнкцияF=
=1
дизъюнкцияF=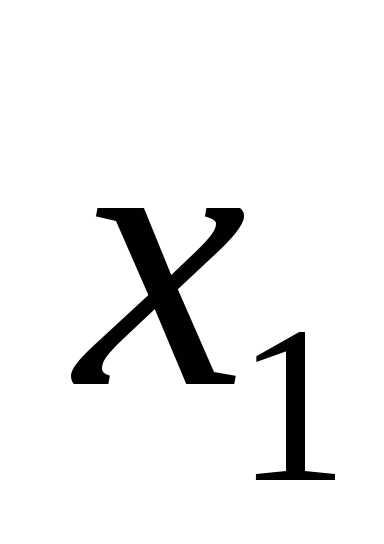 +
+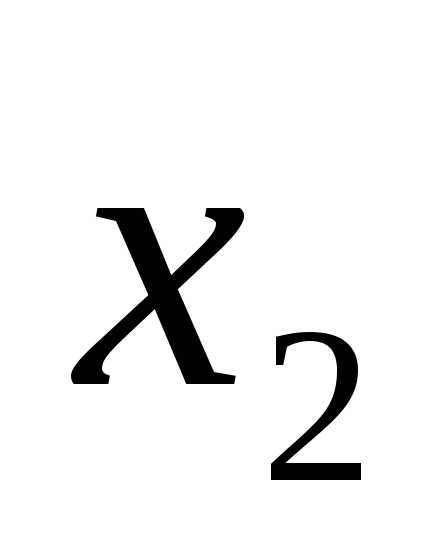 =1
=1 ,
or, или.
,
or, или.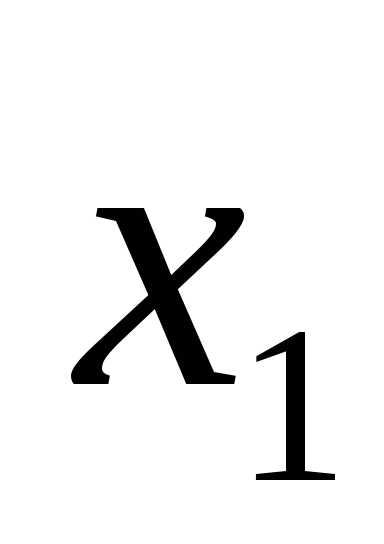
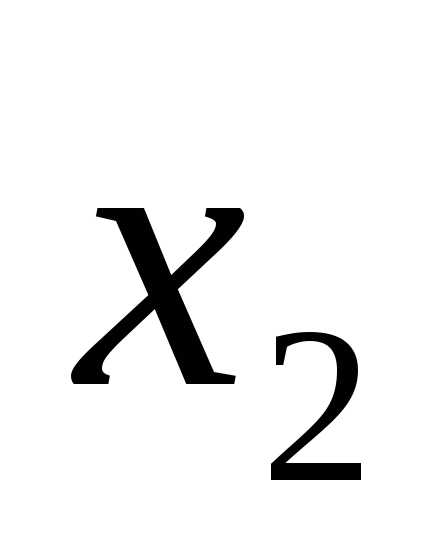
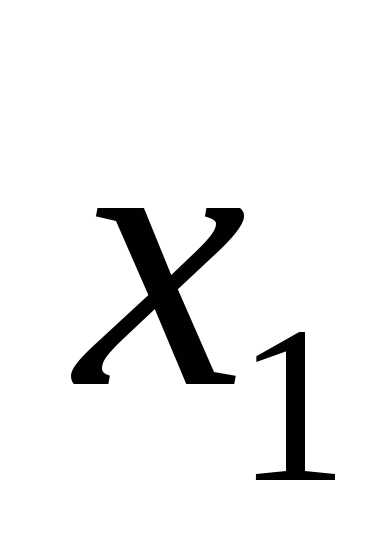
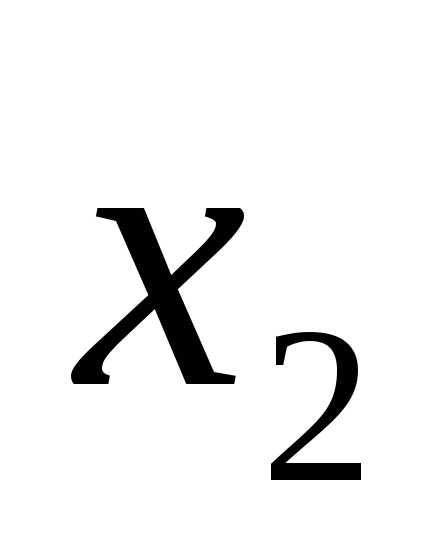 +
+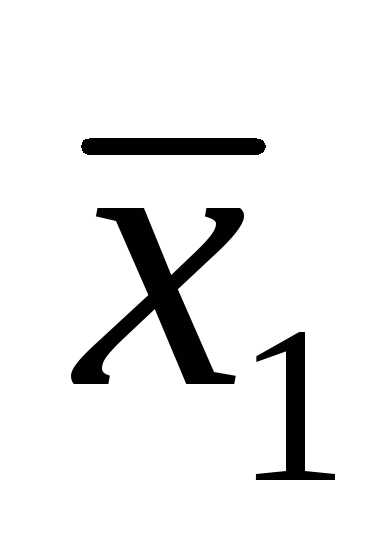
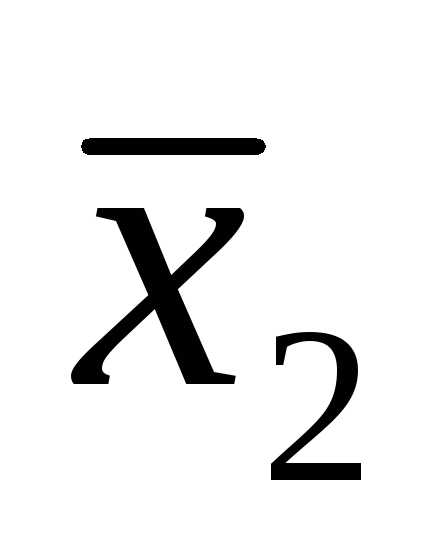 .
. ,
, .
.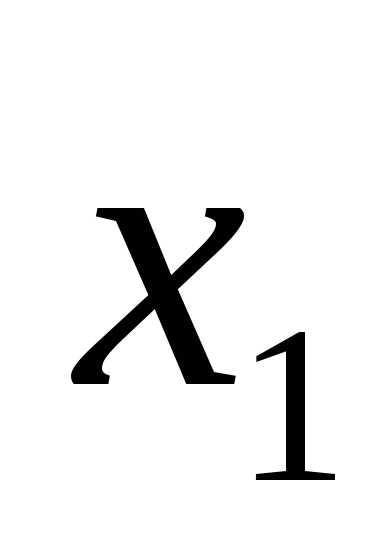
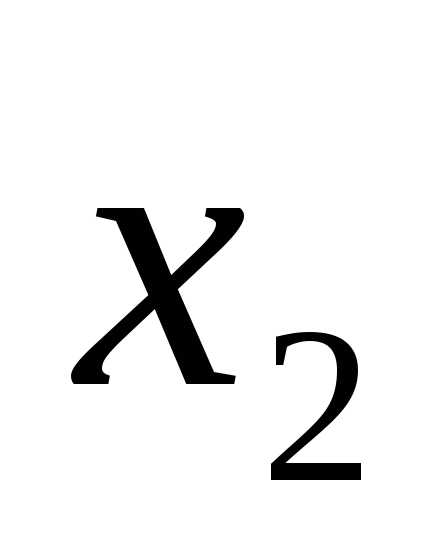
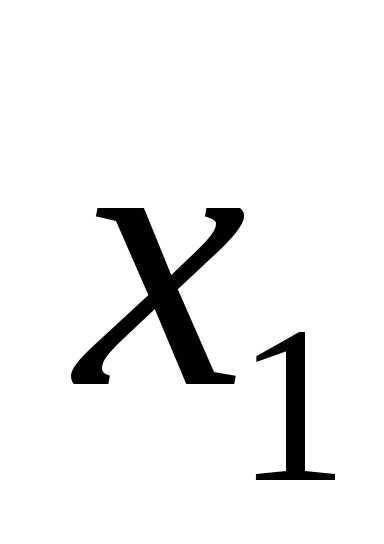 →
→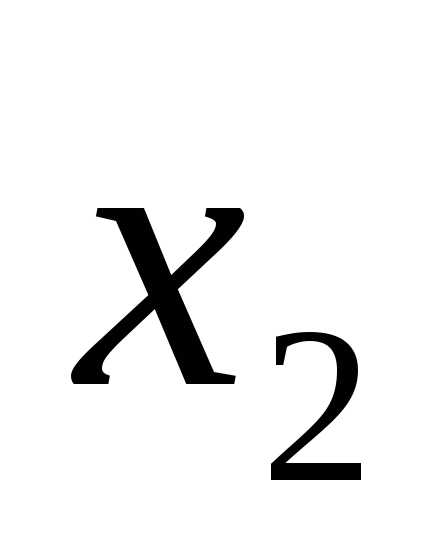 .
. →
→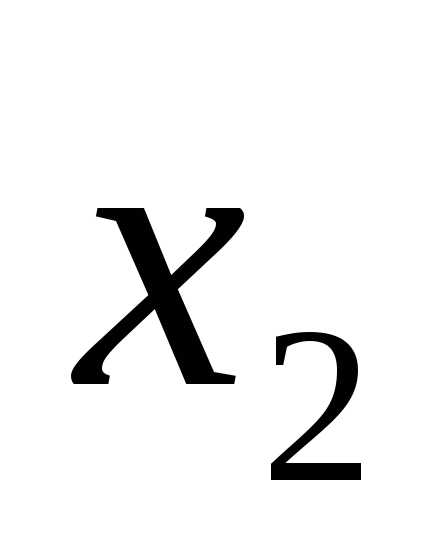 будем
считать истинным во всех случаях, кроме
случая, когда
будем
считать истинным во всех случаях, кроме
случая, когда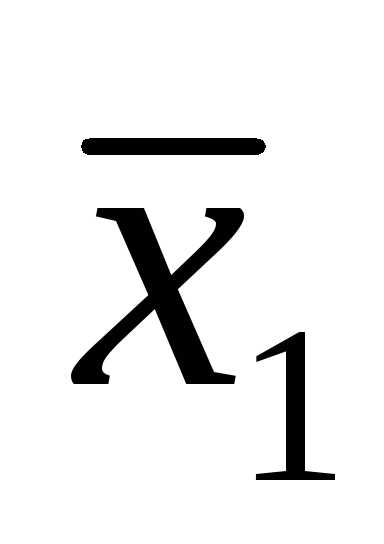 истинно, а
истинно, а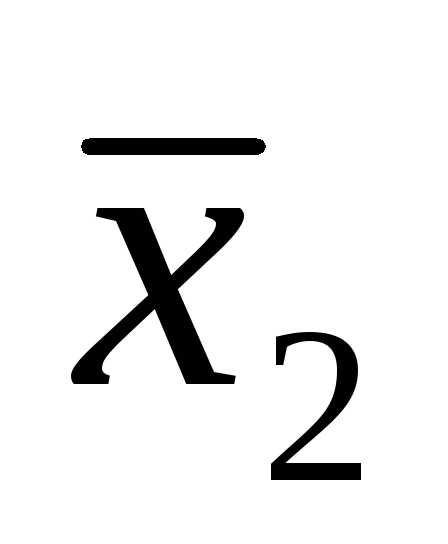 ложно. Таблица истинности представлена
на рис. 8.
ложно. Таблица истинности представлена
на рис. 8.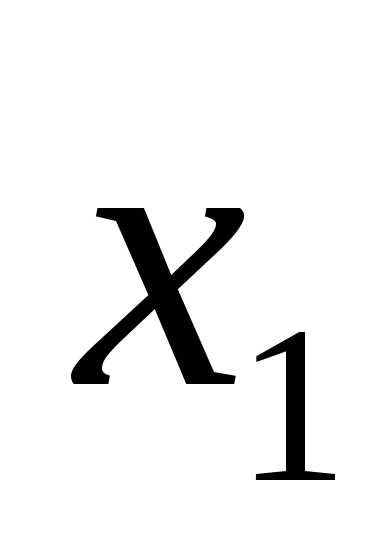
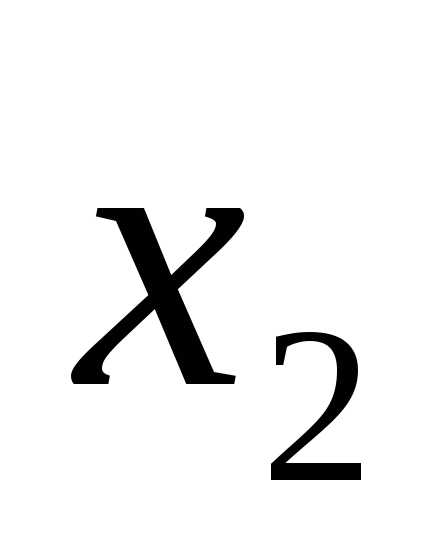
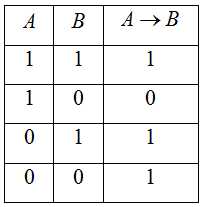
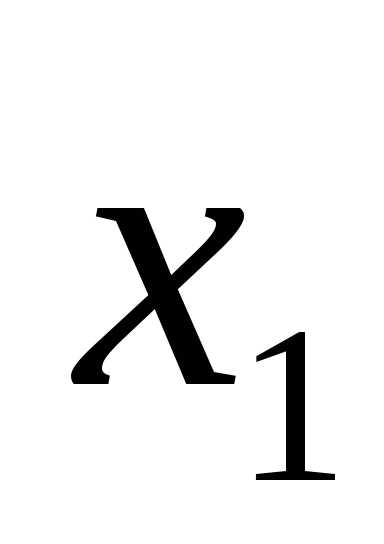 →
→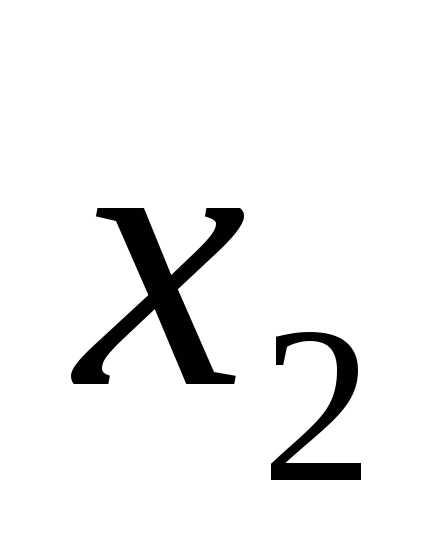
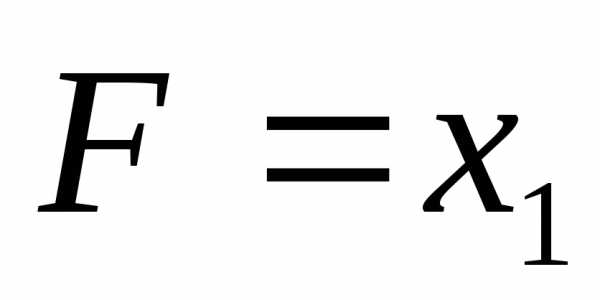
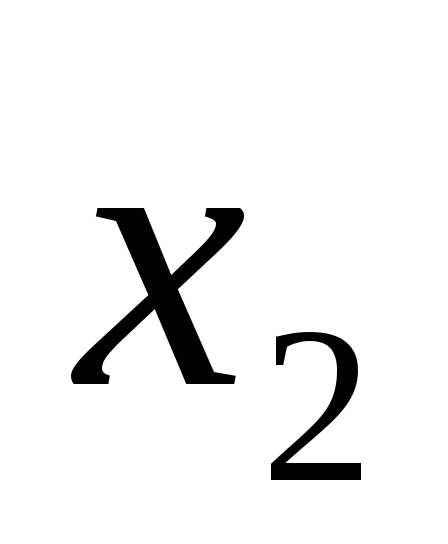 ;.
;.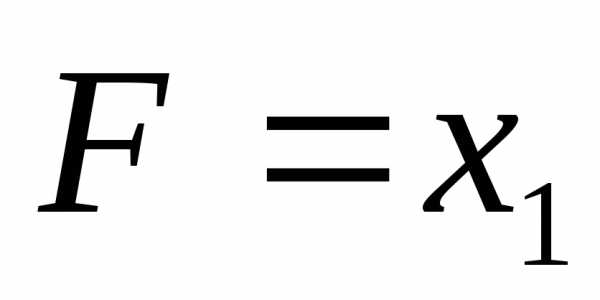
 будем считать ложным, когда
будем считать ложным, когда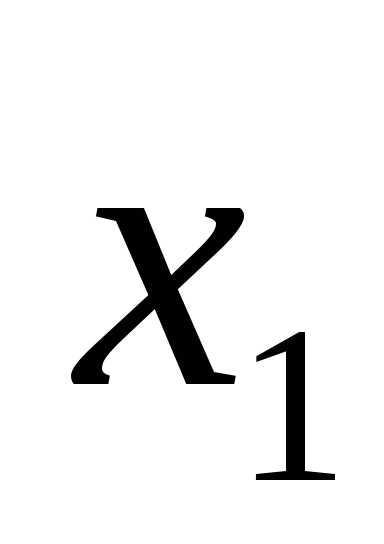 и
и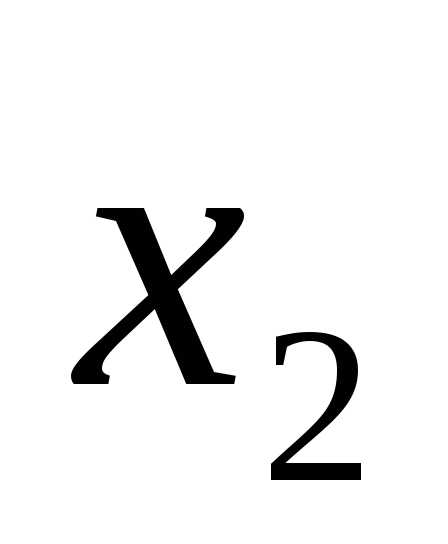 равны единице. Таблица истинности
представлена на рис. 9.
равны единице. Таблица истинности
представлена на рис. 9.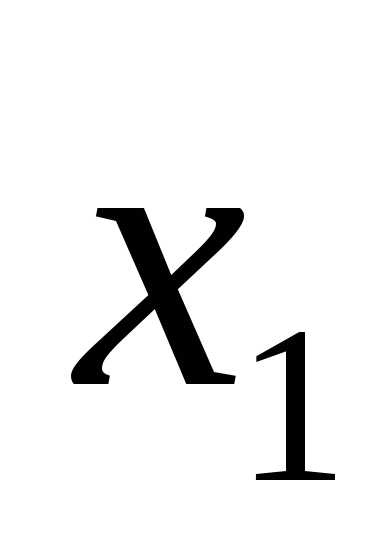
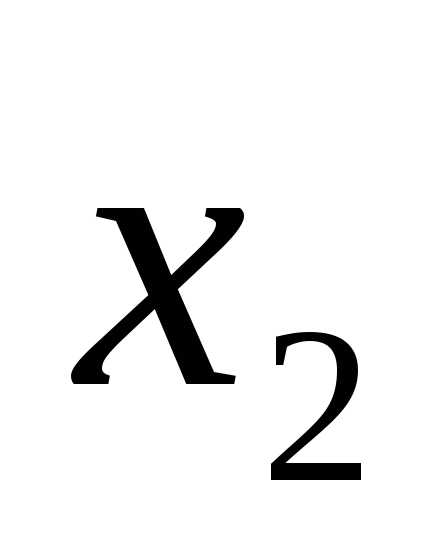
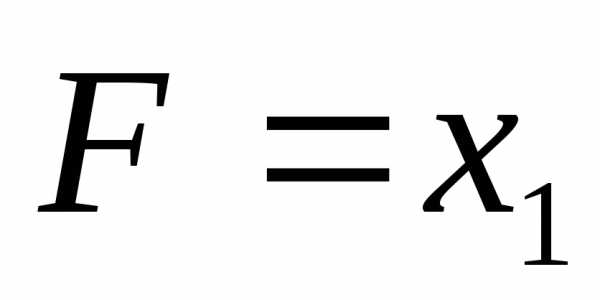
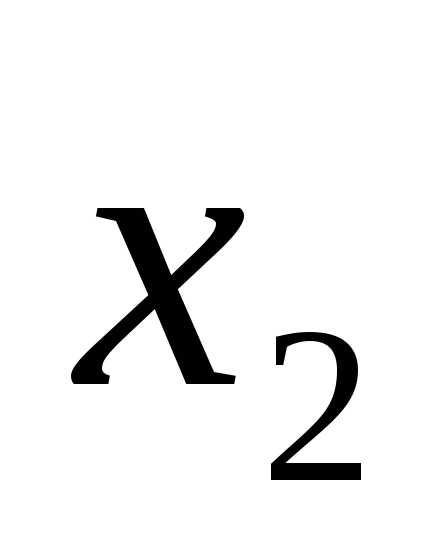
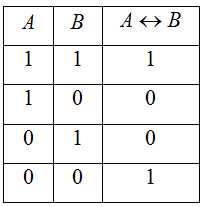
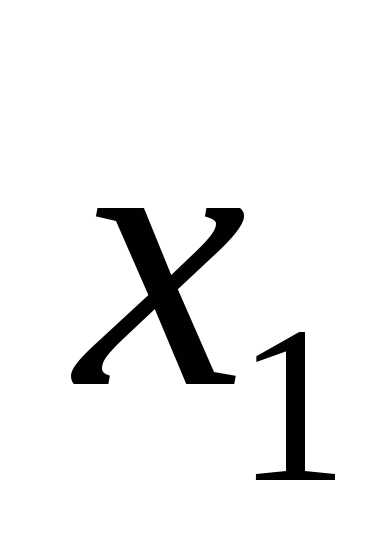 и
и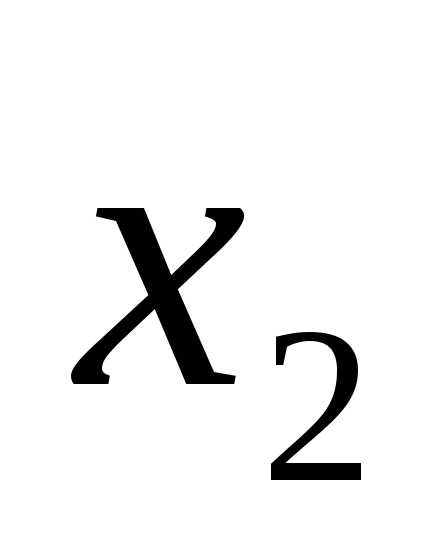 равны нулю. Таблица истинности представлена
на рис.10.
равны нулю. Таблица истинности представлена
на рис.10.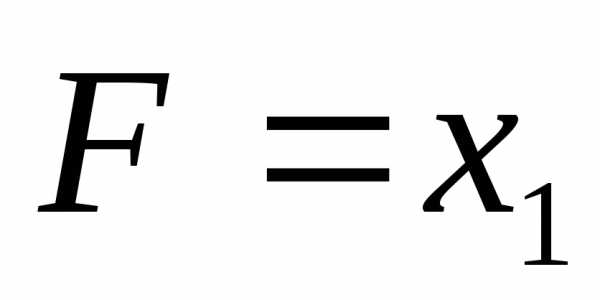 XOR
XOR 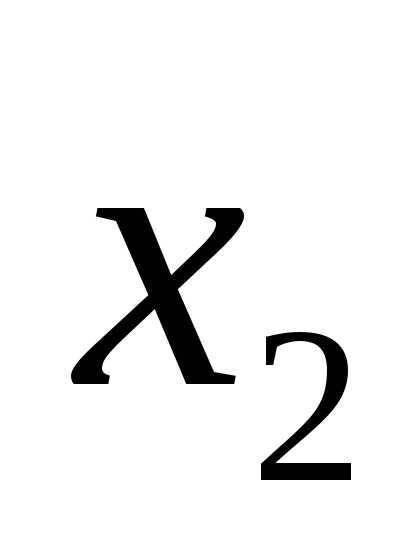 .
. не равен второму операнду
не равен второму операнду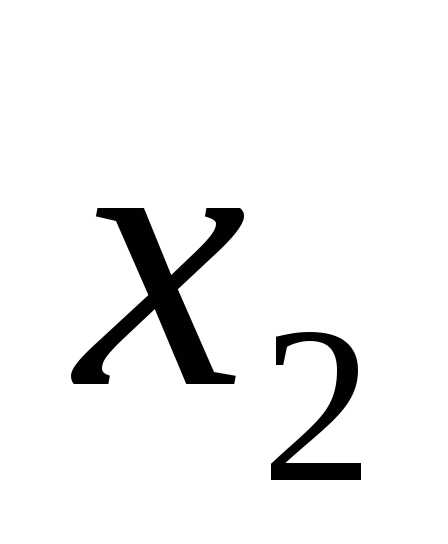 .
Таблица истинности представлена на
рис. 11.
.
Таблица истинности представлена на
рис. 11. .
.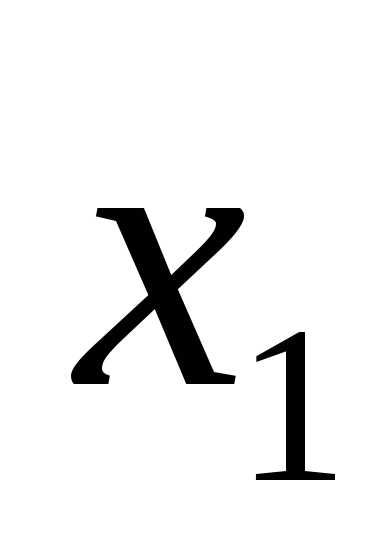 равен 1, а второй операнд
равен 1, а второй операнд 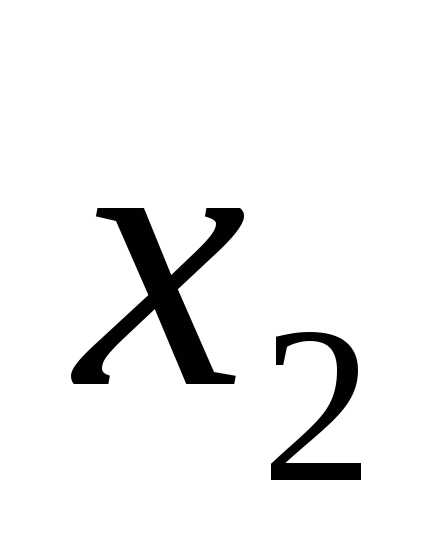 равен 0. Таблица истинности представлена
на рис. 12.
равен 0. Таблица истинности представлена
на рис. 12. .
.

 Ответ: функция
возрастает при ,
убывает на интервале (0;
2]. К
началу страницы
Ответ: функция
возрастает при ,
убывает на интервале (0;
2]. К
началу страницы 







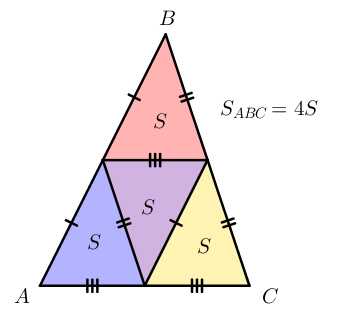
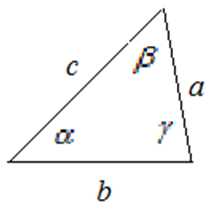
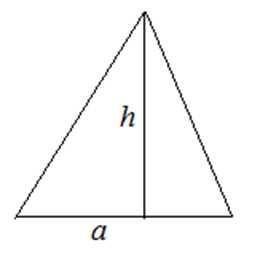
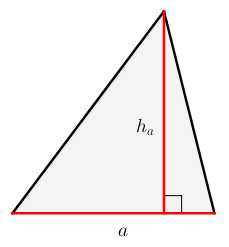 S=12a⋅ha
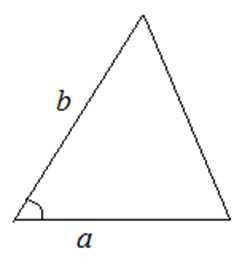
S=12a⋅ha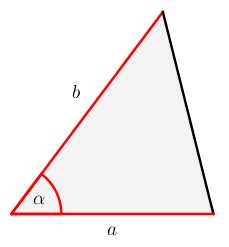 S=12a⋅b⋅sinα
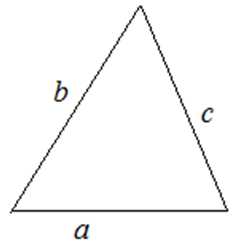
S=12a⋅b⋅sinα S=p(p−a)(p−b)(p−c)p=a+b+c2
S=p(p−a)(p−b)(p−c)p=a+b+c2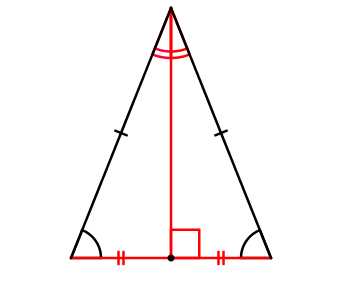
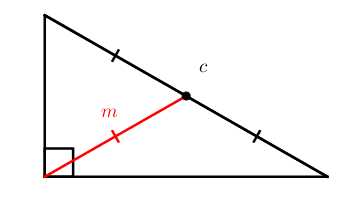 m=c2
m=c2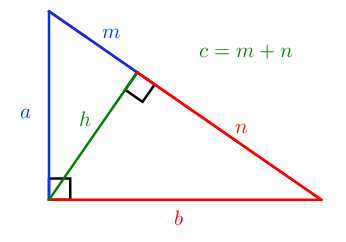 a=m⋅cb=n⋅ch=m⋅n
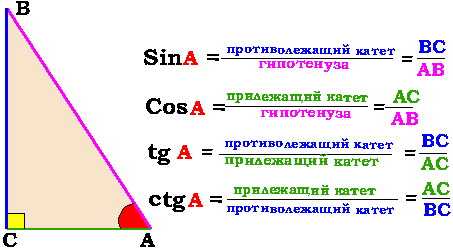
a=m⋅cb=n⋅ch=m⋅n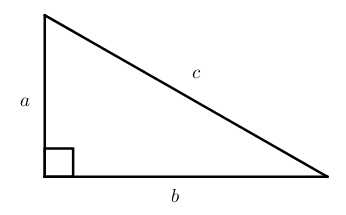
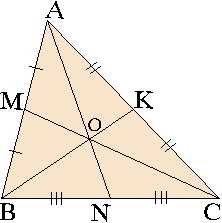
 Теорема 2: Каждая медиана, проведенная в треугольнике делит этот треугольник на две равновеликие части (на два треугольника с равными площадями),
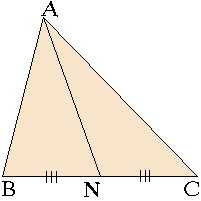
Теорема 2: Каждая медиана, проведенная в треугольнике делит этот треугольник на две равновеликие части (на два треугольника с равными площадями),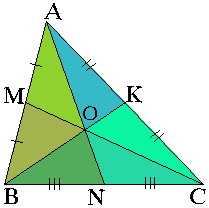
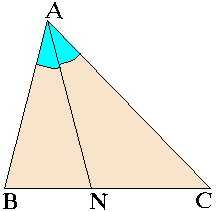 Теорема 1: Каждая биссектриса угла в треугольнике делит его противолежащую сторону на отрезки, пропорциональные к двум другим сторонам треугольника.
Теорема 1: Каждая биссектриса угла в треугольнике делит его противолежащую сторону на отрезки, пропорциональные к двум другим сторонам треугольника.